id
stringlengths 3
12
| title
stringlengths 3
66
| title_slug
stringlengths 3
66
| description
stringlengths 39
25.4k
| description_md
stringlengths 39
4.82k
| difficulty
stringclasses 113
values | tags
listlengths 0
9
| source
stringclasses 5
values | url
stringlengths 37
96
| type
stringclasses 2
values | release_timestamp
int64 1.7B
1.73B
⌀ | release_date
stringlengths 19
19
⌀ | time_limit_nanos
int64 1B
9B
⌀ | memory_limit_bytes
int64 256M
2.1B
⌀ | starter_code
dict | solutions
dict | test_case_generator
stringlengths 521
16.9k
| evaluator
stringlengths 200
5.31k
| generated_tests
stringlengths 3.2k
359M
| test_runners
dict |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
3691
|
Minimum Operations to Make Columns Strictly Increasing
|
minimum-operations-to-make-columns-strictly-increasing
|
<p>You are given a <code>m x n</code> matrix <code>grid</code> consisting of <b>non-negative</b> integers.</p>
<p>In one operation, you can increment the value of any <code>grid[i][j]</code> by 1.</p>
<p>Return the <strong>minimum</strong> number of operations needed to make all columns of <code>grid</code> <strong>strictly increasing</strong>.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">grid = [[3,2],[1,3],[3,4],[0,1]]</span></p>
<p><strong>Output:</strong> <span class="example-io">15</span></p>
<p><strong>Explanation:</strong></p>
<ul>
<li>To make the <code>0<sup>th</sup></code> column strictly increasing, we can apply 3 operations on <code>grid[1][0]</code>, 2 operations on <code>grid[2][0]</code>, and 6 operations on <code>grid[3][0]</code>.</li>
<li>To make the <code>1<sup>st</sup></code> column strictly increasing, we can apply 4 operations on <code>grid[3][1]</code>.</li>
</ul>
<img alt="" src="https://assets.leetcode.com/uploads/2024/11/10/firstexample.png" style="width: 200px; height: 347px;" /></div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">grid = [[3,2,1],[2,1,0],[1,2,3]]</span></p>
<p><strong>Output:</strong> <span class="example-io">12</span></p>
<p><strong>Explanation:</strong></p>
<ul>
<li>To make the <code>0<sup>th</sup></code> column strictly increasing, we can apply 2 operations on <code>grid[1][0]</code>, and 4 operations on <code>grid[2][0]</code>.</li>
<li>To make the <code>1<sup>st</sup></code> column strictly increasing, we can apply 2 operations on <code>grid[1][1]</code>, and 2 operations on <code>grid[2][1]</code>.</li>
<li>To make the <code>2<sup>nd</sup></code> column strictly increasing, we can apply 2 operations on <code>grid[1][2]</code>.</li>
</ul>
<img alt="" src="https://assets.leetcode.com/uploads/2024/11/10/secondexample.png" style="width: 300px; height: 257px;" /></div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>m == grid.length</code></li>
<li><code>n == grid[i].length</code></li>
<li><code>1 <= m, n <= 50</code></li>
<li><code>0 <= grid[i][j] < 2500</code></li>
</ul>
<p> </p>
<div class="spoiler">
<div>
<pre>
</pre>
</div>
</div>
|
You are given a `m x n` matrix `grid` consisting of **non\-negative** integers.
In one operation, you can increment the value of any `grid[i][j]` by 1\.
Return the **minimum** number of operations needed to make all columns of `grid` **strictly increasing**.
**Example 1:**
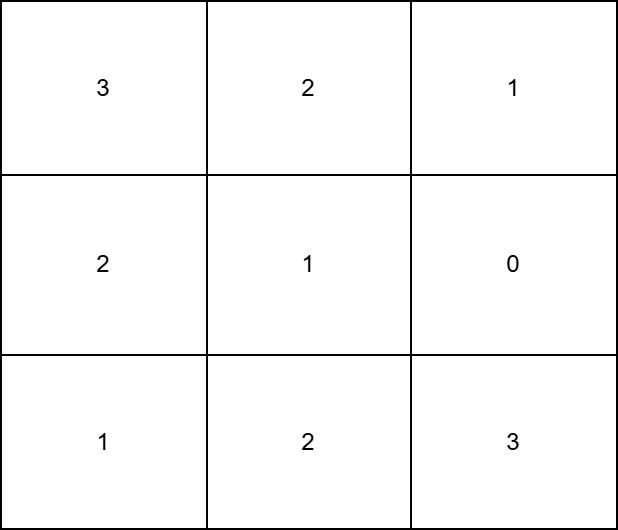
**Input:** grid \= \[\[3,2],\[1,3],\[3,4],\[0,1]]
**Output:** 15
**Explanation:**
- To make the `0th` column strictly increasing, we can apply 3 operations on `grid[1][0]`, 2 operations on `grid[2][0]`, and 6 operations on `grid[3][0]`.
- To make the `1st` column strictly increasing, we can apply 4 operations on `grid[3][1]`.

**Example 2:**
**Input:** grid \= \[\[3,2,1],\[2,1,0],\[1,2,3]]
**Output:** 12
**Explanation:**
- To make the `0th` column strictly increasing, we can apply 2 operations on `grid[1][0]`, and 4 operations on `grid[2][0]`.
- To make the `1st` column strictly increasing, we can apply 2 operations on `grid[1][1]`, and 2 operations on `grid[2][1]`.
- To make the `2nd` column strictly increasing, we can apply 2 operations on `grid[1][2]`.
**Constraints:**
- `m == grid.length`
- `n == grid[i].length`
- `1 <= m, n <= 50`
- `0 <= grid[i][j] < 2500`
```
```
|
Easy
|
[
"array",
"greedy",
"matrix"
] |
leetcode
|
https://leetcode.com/problems/minimum-operations-to-make-columns-strictly-increasing
|
functional
| null | null | null | null |
{
"c": "int minimumOperations(int** grid, int gridSize, int* gridColSize) {\n \n}",
"cpp": "class Solution {\npublic:\n int minimumOperations(vector<vector<int>>& grid) {\n \n }\n};",
"csharp": "public class Solution {\n public int MinimumOperations(int[][] grid) {\n \n }\n}",
"dart": "class Solution {\n int minimumOperations(List<List<int>> grid) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec minimum_operations(grid :: [[integer]]) :: integer\n def minimum_operations(grid) do\n \n end\nend",
"erlang": "-spec minimum_operations(Grid :: [[integer()]]) -> integer().\nminimum_operations(Grid) ->\n .",
"golang": "func minimumOperations(grid [][]int) int {\n \n}",
"java": "class Solution {\n public int minimumOperations(int[][] grid) {\n \n }\n}",
"javascript": "/**\n * @param {number[][]} grid\n * @return {number}\n */\nvar minimumOperations = function(grid) {\n \n};",
"kotlin": "class Solution {\n fun minimumOperations(grid: Array<IntArray>): Int {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param Integer[][] $grid\n * @return Integer\n */\n function minimumOperations($grid) {\n \n }\n}",
"python": "class Solution(object):\n def minimumOperations(self, grid):\n \"\"\"\n :type grid: List[List[int]]\n :rtype: int\n \"\"\"\n ",
"python3": "class Solution:\n def minimumOperations(self, grid: List[List[int]]) -> int:\n ",
"racket": "(define/contract (minimum-operations grid)\n (-> (listof (listof exact-integer?)) exact-integer?)\n )",
"ruby": "# @param {Integer[][]} grid\n# @return {Integer}\ndef minimum_operations(grid)\n \nend",
"rust": "impl Solution {\n pub fn minimum_operations(grid: Vec<Vec<i32>>) -> i32 {\n \n }\n}",
"scala": "object Solution {\n def minimumOperations(grid: Array[Array[Int]]): Int = {\n \n }\n}",
"swift": "class Solution {\n func minimumOperations(_ grid: [[Int]]) -> Int {\n \n }\n}",
"typescript": "function minimumOperations(grid: number[][]): number {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n int minimumOperations(vector<vector<int>>& grid) {\n int m = grid.size();\n int n = grid[0].size();\n long long total = 0;\n for (int j = 0; j < n; j++) {\n int cur = grid[0][j];\n for (int i = 1; i < m; i++) {\n int req = cur + 1;\n if (grid[i][j] < req) {\n total += req - grid[i][j];\n cur = req;\n } else {\n cur = grid[i][j];\n }\n }\n }\n return (int)total;\n }\n};",
"memory": 2800,
"memoryDistribution": "[[2800, 57.0786, \"class Solution {\\npublic:\\n int minimumOperations(vector<vector<int>>& grid) {\\n int m = grid.size();\\n int n = grid[0].size();\\n long long total = 0;\\n for (int j = 0; j < n; j++) {\\n int cur = grid[0][j];\\n for (int i = 1; i < m; i++) {\\n int req = cur + 1;\\n if (grid[i][j] < req) {\\n total += req - grid[i][j];\\n cur = req;\\n } else {\\n cur = grid[i][j];\\n }\\n }\\n }\\n return (int)total;\\n }\\n};\"], [27900, 0.8989, \"class Solution {\\npublic:\\n int minimumOperations(vector<vector<int>>& grid) {\\n const auto n{int(size(grid))};\\n const auto m{int(size(grid.front()))};\\n int res{};\\n for(int j{};j<m;++j){\\n for(int i{1};i<n;++i){\\n auto d=grid[i][j]-grid[i-1][j];\\n if(d<=0){\\n res+=-d+1;\\n grid[i][j]-=(d-1);\\n }\\n }\\n }\\n return res;\\n }\\n};\"], [28000, 14.1573, \"class Solution {\\npublic:\\n int minimumOperations(vector<vector<int>>& grid) {\\n int m = grid.size();\\n int n = grid[0].size();\\n int totalOperations = 0;\\n \\n // Iterate through each column\\n for (int j = 0; j < n; ++j) {\\n // For each column, compare consecutive rows\\n for (int i = 0; i < m - 1; ++i) {\\n // If grid[i][j] >= grid[i+1][j], increment grid[i+1][j]\\n if (grid[i][j] >= grid[i+1][j]) {\\n totalOperations += (grid[i][j] - grid[i+1][j] + 1);\\n grid[i+1][j] = grid[i][j] + 1; // Increment to make the next element strictly larger\\n }\\n }\\n }\\n \\n return totalOperations;\\n }\\n};\\n\"], [28100, 27.8652, null], [28200, 38.6517, \"class Solution {\\npublic:\\n int minimumOperations(vector<vector<int>>& grid) {\\n const auto n{int(size(grid))};\\n const auto m{int(size(grid.front()))};\\n int res{};\\n for(int j{};j<m;++j){\\n for(int i{1};i<n;++i){\\n auto d=grid[i][j]-grid[i-1][j];\\n if(d<=0){\\n res+=-d+1;\\n grid[i][j]-=(d-1);\\n }\\n }\\n }\\n return res;\\n }\\n};\"], [28300, 14.8315, \"class Solution {\\npublic:\\n int minimumOperations(vector<vector<int>>& grid) {\\n const auto n{int(size(grid))};\\n const auto m{int(size(grid.front()))};\\n int res{};\\n for(int j{};j<m;++j){\\n for(int i{1};i<n;++i){\\n auto d=grid[i][j]-grid[i-1][j];\\n if(d<=0){\\n res+=-d+1;\\n grid[i][j]-=(d-1);\\n }\\n }\\n }\\n return res;\\n }\\n};\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 80.2247, \"class Solution {\\npublic:\\n int minimumOperations(vector<vector<int>>& grid) {\\n const auto n{int(size(grid))};\\n const auto m{int(size(grid.front()))};\\n int res{};\\n for(int j{};j<m;++j){\\n for(int i{1};i<n;++i){\\n auto d=grid[i][j]-grid[i-1][j];\\n if(d<=0){\\n res+=-d+1;\\n grid[i][j]-=(d-1);\\n }\\n }\\n }\\n return res;\\n }\\n};\"], [1, 3.1461, \"#include <bits/stdc++.h>\\nusing namespace std;\\n\\nclass Solution {\\npublic:\\n int minimumOperations(vector<vector<int>>& grid){\\n int m = grid.size(), n = grid[0].size();\\n\\n int tot = 0;\\n for(int c = 0; c < n; c++){\\n for(int r = 1; r < m; r++){\\n int del = grid[r][c] - grid[r - 1][c];\\n if(del <= 0){\\n tot += abs(del) + 1;\\n grid[r][c] += abs(del) + 1;\\n }\\n }\\n }\\n\\n return tot;\\n }\\n};\\n\\n\"], [2, 1.7978, null], [3, 7.6404, \"class Solution {\\npublic:\\n int minimumOperations(vector<vector<int>>& grid) {\\n int m=grid.size();\\n int n=grid[0].size();\\n int cnt=0;\\n for(int j=0;j<n;j++){\\n for(int i=1;i<m;i++){\\n if(grid[i][j]<=grid[i-1][j]){ \\n cnt+=(grid[i-1][j]-grid[i][j]+1);\\n grid[i][j]=(grid[i-1][j]+1);;\\n }\\n }\\n }\\n return cnt;\\n }\\n};\"], [4, 3.5955, \"class Solution {\\n public:\\n int minimumOperations(vector<vector<int>>& grid) {\\n int ans = 0;\\n\\n for (int j = 0; j < grid[0].size(); ++j)\\n for (int i = 1; i < grid.size(); ++i)\\n if (grid[i][j] <= grid[i - 1][j]) {\\n ans += grid[i - 1][j] - grid[i][j] + 1;\\n grid[i][j] = grid[i - 1][j] + 1;\\n }\\n\\n return ans;\\n }\\n};\"]]"
},
"golang": {
"code": "func minimumOperations(grid [][]int) int {\n\tm := len(grid)\n\tif m == 0 {\n\t\treturn 0\n\t}\n\tn := len(grid[0])\n\tops := 0\n\tfor j := 0; j < n; j++ {\n\t\tprev := grid[0][j]\n\t\tfor i := 1; i < m; i++ {\n\t\t\trequired := prev + 1\n\t\t\tif grid[i][j] < required {\n\t\t\t\tops += required - grid[i][j]\n\t\t\t\tprev = required\n\t\t\t} else {\n\t\t\t\tprev = grid[i][j]\n\t\t\t}\n\t\t}\n\t}\n\treturn ops\n}",
"memory": 700,
"memoryDistribution": "[[700, 61.2903, \"func minimumOperations(grid [][]int) int {\\n\\tm := len(grid)\\n\\tif m == 0 {\\n\\t\\treturn 0\\n\\t}\\n\\tn := len(grid[0])\\n\\tops := 0\\n\\tfor j := 0; j < n; j++ {\\n\\t\\tprev := grid[0][j]\\n\\t\\tfor i := 1; i < m; i++ {\\n\\t\\t\\trequired := prev + 1\\n\\t\\t\\tif grid[i][j] < required {\\n\\t\\t\\t\\tops += required - grid[i][j]\\n\\t\\t\\t\\tprev = required\\n\\t\\t\\t} else {\\n\\t\\t\\t\\tprev = grid[i][j]\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\treturn ops\\n}\"], [6800, 12.9032, \"func minimumOperations(grid [][]int) int {\\n m, n := len(grid), len(grid[0])\\n operations := 0\\n for j := 0; j < n; j++ {\\n prev := grid[0][j]\\n for i := 1; i < m; i++ {\\n if grid[i][j] <= prev {\\n operations += (prev + 1 - grid[i][j])\\n grid[i][j] = prev + 1\\n }\\n prev = grid[i][j]\\n }\\n }\\n return operations\\n}\"], [6900, 25.8065, \"func minimumOperations(grid [][]int) int {\\n m, n := len(grid), len(grid[0])\\n\\n res := 0\\n for i := range n {\\n for j := range m {\\n if j >= 1 {\\n prev, curr := grid[j - 1][i], grid[j][i]\\n if curr <= prev {\\n diff := prev - curr + 1\\n res += diff\\n grid[j][i] += diff\\n }\\n }\\n }\\n }\\n\\n return res\\n}\"], [7000, 32.2581, null], [7100, 19.3548, \"func minimumOperations(grid [][]int) int {\\n m, n := len(grid), len(grid[0])\\n out := 0\\n for c := range n {\\n for r := 1; r < m; r++ {\\n if grid[r][c] <= grid[r-1][c] {\\n diff := grid[r-1][c] + 1 - grid[r][c]\\n out += diff\\n grid[r][c] += diff\\n }\\n }\\n }\\n return out\\n}\"], [7200, 3.2258, \"func minimumOperations(grid [][]int) int {\\n var res int\\n for i:=0; i<len(grid[0]);i++ {\\n for j:=1;j<len(grid); j++ {\\n if grid[j][i] <= grid[j-1][i] {\\n res, grid[j][i] = res+grid[j-1][i]+1-grid[j][i], grid[j-1][i]+1\\n }\\n }\\n }\\n\\n return res\\n}\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 83.871, \"func minimumOperations(grid [][]int) int {\\n m, n := len(grid), len(grid[0])\\n operations := 0\\n for j := 0; j < n; j++ {\\n prev := grid[0][j]\\n for i := 1; i < m; i++ {\\n if grid[i][j] <= prev {\\n operations += (prev + 1 - grid[i][j])\\n grid[i][j] = prev + 1\\n }\\n prev = grid[i][j]\\n }\\n }\\n return operations\\n}\"], [2, 6.4516, \"func minimumOperations(grid [][]int) int {\\n operations := 0\\n for j := 0; j < len(grid[0]); j++ {\\n prev := grid[0][j]\\n for i := 1; i < len(grid); i++ {\\n if grid[i][j] <= prev {\\n diff := prev - grid[i][j] + 1\\n operations += diff\\n grid[i][j] += diff\\n }\\n prev = grid[i][j]\\n }\\n }\\n return operations\\n}\"], [3, 6.4516, \"func minimumOperations(grid [][]int) int {\\n ans := 0\\n\\n for i := 0; i < len(grid[0]); i++{\\n for j := 1; j < len(grid); j++{\\n if grid[j][i] <= grid[j-1][i]{\\n diff := grid[j-1][i] - grid[j][i] + 1\\n ans += diff\\n grid[j][i] += diff\\n }\\n }\\n }\\n return ans\\n}\"], [5, 3.2258, \"func minimumOperations(grid [][]int) int {\\n cols := make([][]int, len(grid[0]))\\n for _, row := range grid {\\n for j, el := range row {\\n cols[j] = append(cols[j], el)\\n }\\n }\\n if len(cols[0]) < 2 {\\n return 0\\n }\\n ops := 0\\n for _, col := range cols {\\n for i:=1;i<len(col);i++ {\\n for col[i] <= col[i-1] {\\n col[i]++\\n ops++\\n }\\n }\\n }\\n return ops\\n}\"]]"
},
"java": {
"code": "class Solution {\n public int minimumOperations(int[][] grid) {\n int m = grid.length, n = grid[0].length;\n int operations = 0;\n for (int col = 0; col < n; col++) {\n int current = grid[0][col];\n for (int row = 1; row < m; row++) {\n int needed = current + 1;\n if (grid[row][col] < needed) {\n operations += (needed - grid[row][col]);\n current = needed;\n } else {\n current = grid[row][col];\n }\n }\n }\n return operations;\n }\n}",
"memory": 4600,
"memoryDistribution": "[[4600, 8.0429, \"class Solution {\\n public int minimumOperations(int[][] grid) {\\n int m = grid.length, n = grid[0].length;\\n int operations = 0;\\n for (int col = 0; col < n; col++) {\\n int current = grid[0][col];\\n for (int row = 1; row < m; row++) {\\n int needed = current + 1;\\n if (grid[row][col] < needed) {\\n operations += (needed - grid[row][col]);\\n current = needed;\\n } else {\\n current = grid[row][col];\\n }\\n }\\n }\\n return operations;\\n }\\n}\"], [44700, 0.8043, \"class Solution {\\n\\n public int minimumOperations(int[][] grid) {\\n\\n int count = 0;\\n\\n for(int c = 0; c < grid[0].length; c++) {\\n\\n for(int r = 1; r < grid.length; r++) {\\n\\n if(grid[r][c] > grid[r-1][c]) continue;\\n\\n count += grid[r-1][c] - grid[r][c] + 1;\\n\\n grid[r][c] = grid[r-1][c] + 1;\\n\\n }\\n\\n }\\n\\n return count;\\n \\n }\\n\\n}\"], [44800, 1.6086, \"class Solution {\\n public int minimumOperations(int[][] grid) {\\n int ans = 0;\\n for(int i = 0; i < grid[0].length; i++){\\n for(int j = 1; j < grid.length; j++){\\n if(grid[j-1][i] >= grid[j][i]){\\n ans += grid[j-1][i] - grid[j][i]+1;\\n grid[j][i] = 1 + grid[j-1][i]; \\n }\\n }\\n }\\n return ans;\\n }\\n}\"], [44900, 5.63, null], [45000, 12.6005, null], [45100, 14.7453, null], [45200, 16.8901, null], [45300, 13.941, null], [45400, 8.0429, null], [45500, 10.4558, \"class Solution {\\n public int minimumOperations(int[][] grid) {\\n int res = 0;\\n for(int j = 0; j < grid[0].length; ++j) {\\n int currVal = grid[0][j];\\n for(int i = 1; i < grid.length; ++i) {\\n if(grid[i][j] <= currVal) {\\n res += currVal + 1 - grid[i][j];\\n currVal++;\\n } else {\\n currVal = grid[i][j];\\n }\\n }\\n }\\n return res;\\n }\\n}\"], [45600, 7.2386, \"class Solution {\\n public int minimumOperations(int[][] grid) {\\n\\n int m = grid.length;\\n int n = grid[0].length;\\n int o = 0;\\n for(int i = 0 ; i<n ; i++)\\n {\\n for(int j = 0 ;j<m-1 ; j++)\\n {\\n if(grid[j][i]>=grid[j+1][i])\\n {\\n int temp = grid[j+1][i];\\n grid[j+1][i] = grid[j][i] + 1;\\n o = o + (grid[j+1][i] - temp);\\n }\\n }\\n }\\n\\n\\n return o;\\n \\n }\\n}\"]]",
"runtime": 1,
"runtimeDistribution": "[[1, 91.9571, \"class Solution {\\n public int minimumOperations(int[][] grid) {\\n int rows = grid.length, cols = grid[0].length;\\n int totalOps = 0;\\n int j = 0;\\n while(true){\\n if(j >= cols){\\n break;\\n }\\n for(int i=1; i < rows; i++){\\n int prevCellNum = grid[i-1][j];\\n int currCellNum = grid[i][j];\\n if(currCellNum > prevCellNum) continue;\\n grid[i][j] = prevCellNum + 1;\\n totalOps += grid[i][j] - currCellNum;\\n }\\n j++;\\n }\\n return totalOps;\\n }\\n}\"], [2, 0.5362, \"class Solution {\\n public int minimumOperations(int[][] grid) {\\n int result = 0;\\n\\t\\t\\n\\t\\tfor(int i = 1; i < grid.length; i++){\\n\\t\\t\\tfor(int j = 0; j < grid[i].length; j++){\\n\\t\\t\\t\\twhile (grid[i][j] <= grid[i-1][j]){\\n\\t\\t\\t\\t\\tgrid[i][j]++;\\n\\t\\t\\t\\t\\tresult++;\\n\\t\\t\\t\\t}\\n\\t\\t\\t}\\n\\t\\t}\\n\\t\\t\\n\\t\\treturn result;\\n }\\n}\"], [3, 2.681, null], [4, 0.2681, \"class Solution {\\n public int minimumOperations(int[][] grid) {\\n int count = 0;\\n for(int i = 0;i<grid[0].length;i++) {\\n for(int j=0;j<grid.length-1;j++) {\\n // System.out.println(grid[j-1][i] + \\\" \\\" + grid[j][i]);\\n while(grid[j][i] >= grid[j+1][i]) {\\n grid[j+1][i]++;\\n count++;\\n }\\n // System.out.println(\\\"af \\\" + grid[j-1][i] + \\\" \\\" + grid[j][i]);\\n }\\n }\\n return count;\\n }\\n}\"], [5, 0.2681, \"class Solution {\\n public int minimumOperations(int[][] grid) {\\n int count=0;\\n\\t\\tfor (int j=0;j<grid[0].length ;j++ )\\n\\t\\t{\\n\\t\\t\\tfor (int i=0;i<grid.length ;i++ )\\n\\t\\t\\t{\\n\\t\\t\\t\\tfor (int k=i+1;k<grid.length ;k++ )\\n\\t\\t\\t\\t{\\n\\t\\t\\t\\t\\twhile(grid[i][j]>=grid[k][j])\\n\\t\\t\\t\\t\\t{\\n\\t\\t\\t\\t\\t\\tgrid[k][j]++;\\n\\t\\t\\t\\t\\t\\tcount++;\\n\\t\\t\\t\\t\\t}\\n\\t\\t\\t\\t}\\n\\t\\t\\t}\\n\\t\\t}\\n\\t\\treturn count;\\n }\\n}\"]]"
},
"javascript": {
"code": "/**\n * @param {number[][]} grid\n * @return {number}\n */\nvar minimumOperations = function(grid) {\n let m = grid.length, n = grid[0].length, totalOps = 0;\n for (let j = 0; j < n; j++) {\n let prev = grid[0][j];\n for (let i = 1; i < m; i++) {\n let required = prev + 1;\n if (grid[i][j] < required) {\n totalOps += required - grid[i][j];\n prev = required;\n } else {\n prev = grid[i][j];\n }\n }\n }\n return totalOps;\n};",
"memory": 5600,
"memoryDistribution": "[[5600, 55.3846, \"/**\\n * @param {number[][]} grid\\n * @return {number}\\n */\\nvar minimumOperations = function(grid) {\\n let m = grid.length, n = grid[0].length, totalOps = 0;\\n for (let j = 0; j < n; j++) {\\n let prev = grid[0][j];\\n for (let i = 1; i < m; i++) {\\n let required = prev + 1;\\n if (grid[i][j] < required) {\\n totalOps += required - grid[i][j];\\n prev = required;\\n } else {\\n prev = grid[i][j];\\n }\\n }\\n }\\n return totalOps;\\n};\"], [54500, 1.5385, \"/**\\n * @param {number[][]} grid\\n * @return {number}\\n */\\nfunction minimumOperations(grid) {\\n const m = grid.length;\\n const n = grid[0].length;\\n let operations = 0;\\n \\n // Iterate over each column\\n for (let j = 0; j < n; j++) {\\n // Traverse through rows from bottom to top\\n for (let i = 1; i < m; i++) {\\n if (grid[i][j] <= grid[i - 1][j]) {\\n // Calculate how many operations are needed\\n const diff = grid[i - 1][j] - grid[i][j] + 1;\\n operations += diff;\\n // Update the current value to reflect the operation\\n grid[i][j] = grid[i - 1][j] + 1;\\n }\\n }\\n }\\n \\n return operations;\\n}\\n\"], [54900, 1.5385, \"/**\\n * @param {number[][]} grid\\n * @return {number}\\n */\\nvar minimumOperations = function (grid) {\\n let operations = 0;\\n const rows = grid.length;\\n const cols = grid[0].length;\\n\\n for (let col = 0; col < cols; col++) {\\n for (let row = 0; row < rows - 1; row++) {\\n if (grid[row][col] >= grid[row + 1][col]) {\\n const diff = grid[row][col] - grid[row + 1][col] + 1;\\n grid[row + 1][col] += diff;\\n operations += diff;\\n }\\n }\\n }\\n\\n return operations;\\n};\"], [55200, 1.5385, null], [55400, 3.0769, null], [55500, 4.6154, null], [55600, 1.5385, null], [55700, 6.1538, null], [55800, 6.1538, null], [55900, 10.7692, null], [56000, 7.6923, null], [56100, 3.0769, null], [56200, 6.1538, null], [56300, 6.1538, null], [56500, 4.6154, null], [56700, 1.5385, null], [56800, 1.5385, null], [56900, 3.0769, null], [57000, 3.0769, null], [57100, 3.0769, null], [57200, 1.5385, null], [57300, 6.1538, null], [57400, 1.5385, null], [57500, 4.6154, null], [57600, 1.5385, \"/**\\n * @param {number[][]} grid\\n * @return {number}\\n */\\nvar minimumOperations = function(grid) {\\n let result = 0;\\n for(let j=0; j<grid[0].length; j++) {\\n for(let i=1; i<grid.length; i++) {\\n let prev = grid[i-1][j];\\n let curr = grid[i][j];\\n if(prev >= curr) {\\n grid[i][j] = grid[i][j]+prev-curr+1;\\n result += (prev-curr+1);\\n }\\n }\\n }\\n return result;\\n};\"], [57700, 1.5385, \"/**\\n * @param {number[][]} grid\\n * @return {number}\\n */\\nvar minimumOperations = function (grid) {\\n let operations = 0;\\n const rows = grid.length;\\n const cols = grid[0].length;\\n\\n for (let col = 0; col < cols; col++) {\\n for (let row = 0; row < rows - 1; row++) {\\n if (grid[row][col] < grid[row + 1][col]) continue;\\n const diff = grid[row][col] - grid[row + 1][col] + 1;\\n grid[row + 1][col] += diff;\\n operations += diff;\\n }\\n }\\n\\n return operations;\\n};\"]]",
"runtime": 1,
"runtimeDistribution": "[[0, 26.1538, \"/**\\n * @param {number[][]} grid\\n * @return {number}\\n */\\nvar minimumOperations = function(grid) {\\n let count = 0;\\n\\n for(let i=1; i<grid.length; i++){\\n for(let j=0; j<grid[0].length; j++){\\n if(grid[i][j] <= grid[i-1][j]){\\n count+= (grid[i-1][j] + 1) - grid[i][j];\\n grid[i][j] = grid[i-1][j] + 1;\\n }\\n }\\n }\\n\\n return count;\\n};\"], [1, 46.1538, \"/**\\n * @param {number[][]} grid\\n * @return {number}\\n */\\nvar minimumOperations = function(grid) {\\n let cnt = 0;\\n let i = 0;\\n while(i < grid[0].length){\\n let j = 1;\\n let prev = grid[0][i]\\n while(j < grid.length){\\n if(grid[j][i] <= prev){\\n const delta = prev - grid[j][i] +1;\\n cnt += delta;\\n prev += 1;\\n }else{\\n prev = grid[j][i];\\n }\\n j++;\\n }\\n i++;\\n }\\n return cnt;\\n};\"], [2, 16.9231, null], [4, 1.5385, null], [6, 1.5385, \"/**\\n * @param {number[][]} grid\\n * @return {number}\\n */\\nvar minimumOperations = function(grid) {\\n var n = grid[0].length;\\n var res = 0;\\n var m = grid.length;\\n\\n var countIncreaseInArray = (arr) => {\\n for (var i = 0; i < arr.length - 1; i++) {\\n var next = arr[i + 1];\\n var current = arr[i];\\n \\n if (current >= next) {\\n var inc = current - next + 1;\\n var needNext = inc + next;\\n arr[i + 1] = needNext;\\n\\n res += inc;\\n } \\n }\\n \\n return res\\n }\\n\\n for (var j = 0; j < n; j++) {\\n var temp = Array.from({ length: m }, () => 0);\\n\\n for (var i = 0; i < m; i++) {\\n temp[i] = grid[i][j];\\n }\\n\\n countIncreaseInArray(temp);\\n }\\n\\n return res\\n};\"], [7, 1.5385, \"/**\\n * @param {number[][]} grid\\n * @return {number}\\n */\\nvar minimumOperations = function(grid) {\\n let sum = 0;\\n let n = grid[0].length;\\n\\n for (let i = 0; i < n; i++) {\\n let temp = grid.map((row) => row[i]);\\n // return temp;\\n for (let j = 1; j < temp.length; j++) {\\n if (temp[j] <= temp[j - 1]) {\\n // return temp[i];\\n let xx = temp[j];\\n let diff = Math.abs(temp[j] - temp[j - 1]);\\n neww = diff + 1;\\n sum += neww;\\n temp[j] = neww + xx;\\n }\\n }\\n // return temp;\\n }\\n return sum;\\n};\"]]"
},
"python3": {
"code": "class Solution:\n def minimumOperations(self, grid: list[list[int]]) -> int:\n m = len(grid)\n n = len(grid[0])\n operations = 0\n for j in range(n):\n prev = grid[0][j]\n for i in range(1, m):\n expected = prev + 1\n if grid[i][j] < expected:\n operations += expected - grid[i][j]\n prev = expected\n else:\n prev = grid[i][j]\n return operations",
"memory": 1800,
"memoryDistribution": "[[1800, 12.7099, \"class Solution:\\n def minimumOperations(self, grid: list[list[int]]) -> int:\\n m = len(grid)\\n n = len(grid[0])\\n operations = 0\\n for j in range(n):\\n prev = grid[0][j]\\n for i in range(1, m):\\n expected = prev + 1\\n if grid[i][j] < expected:\\n operations += expected - grid[i][j]\\n prev = expected\\n else:\\n prev = grid[i][j]\\n return operations\"], [17600, 0.2398, \"class Solution:\\n def minimumOperations(self, grid: List[List[int]]) -> int:\\n m, n = len(grid), len(grid[0])\\n res = 0\\n\\n for c in range(n):\\n for i in range(1, m):\\n if grid[i][c]<=grid[i-1][c]:\\n res += 1+grid[i-1][c]-grid[i][c]\\n grid[i][c] += 1+grid[i-1][c]-grid[i][c]\\n return res\"], [17700, 0.4796, \"class Solution:\\n def minimumOperations(self, grid: List[List[int]]) -> int:\\n M = len(grid)\\n N = len(grid[0])\\n min_operations = 0\\n for n in range(N):\\n for m in range(1, M):\\n diff = grid[m-1][n] - grid[m][n]\\n if diff >= 0:\\n min_operations += diff + 1\\n grid[m][n] += diff + 1\\n return min_operations\"], [17800, 4.7962, null], [17900, 15.5875, null], [18000, 26.6187, null], [18100, 18.705, \"class Solution:\\n def minimumOperations(self, grid: List[List[int]]) -> int:\\n ans = 0\\n row = len(grid)\\n col = len(grid[0])\\n\\n for j in range(col):\\n cur_num = grid[0][j]\\n for i in range(1, row):\\n if cur_num < grid[i][j]:\\n cur_num = grid[i][j]\\n else:\\n cur_num += 1\\n ans += cur_num - grid[i][j]\\n\\n return ans\"], [18200, 20.8633, \"class Solution:\\n def minimumOperations(self, grid):\\n m = len(grid)\\n n = len(grid[0])\\n total_operations = 0\\n for j in range(n):\\n prev_val_in_col = grid[0][j]\\n for i in range(1, m):\\n current_val = grid[i][j]\\n required_val = prev_val_in_col + 1\\n if current_val < required_val:\\n ops_needed = required_val - current_val\\n total_operations += ops_needed\\n prev_val_in_col = required_val\\n else:\\n prev_val_in_col = current_val\\n return total_operations\"]]",
"runtime": 8,
"runtimeDistribution": "[[0, 1.9185, \"class Solution:\\n def minimumOperations(self, grid: List[List[int]]) -> int:\\n ans = 0\\n for j in range(len(grid[0])):\\n p = grid[0][j]\\n for i in range(1, len(grid)):\\n if grid[i][j] <= p: ans += (p + 1) - grid[i][j]; p = p + 1\\n else: p = grid[i][j]\\n return ans\"], [1, 0.9592, \"class Solution:\\n def minimumOperations(self, grid: List[List[int]]) -> int:\\n res = 0\\n for c in range(len(grid[0])):\\n prev = grid[0][c]\\n for r in range(1, len(grid)):\\n if grid[r][c] <= prev:\\n res += prev - grid[r][c] + 1\\n prev += 1\\n else:\\n prev = grid[r][c]\\n\\n return res\\n \"], [2, 0.9592, null], [3, 9.3525, null], [4, 4.7962, null], [5, 4.3165, null], [6, 1.6787, null], [7, 17.0264, null], [8, 6.7146, null], [9, 4.0767, null], [10, 4.5564, null], [11, 17.506, null], [12, 3.8369, null], [13, 2.1583, null], [14, 0.7194, null], [15, 4.5564, null], [16, 0.9592, null], [17, 1.199, null], [18, 0.4796, null], [19, 2.3981, null], [20, 0.4796, null], [21, 0.2398, null], [22, 0.2398, null], [23, 0.4796, null], [24, 0.4796, null], [27, 0.4796, null], [28, 0.4796, null], [31, 0.4796, null], [32, 0.2398, null], [34, 0.2398, null], [35, 0.4796, null], [38, 0.2398, \"class Solution:\\n def minimumOperations(self, grid: List[List[int]]) -> int:\\n cnt = 0\\n for j in range(0, len(grid[0])):\\n for i in range(1, len(grid)):\\n if grid[i][j] - grid[i-1][j] <= 0:\\n cnt += (grid[i-1][j] - grid[i][j]) + 1\\n grid[i][j] += ((grid[i-1][j] - grid[i][j]) + 1)\\n print(cnt, grid[i][j])\\n \\n return cnt\\n\"], [41, 0.2398, \"class Solution:\\n def minimumOperations(self, grid: List[List[int]]) -> int:\\n\\n ops = 0\\n\\n for i in range(len(grid[0])):\\n for j in range(1,len(grid)):\\n print(grid[j][i],grid[j-1][i])\\n if grid[j][i] <= grid[j-1][i]:\\n diff = (grid[j-1][i] - grid[j][i]) + 1\\n grid[j][i] += diff\\n ops += diff\\n \\n\\n return ops\"]]"
},
"ruby": {
"code": "def minimum_operations(grid)\n m = grid.size\n n = grid[0].size\n total_ops = 0\n (0...n).each do |col|\n current = grid[0][col]\n (1...m).each do |row|\n if grid[row][col] <= current\n diff = current + 1 - grid[row][col]\n total_ops += diff\n current += 1\n else\n current = grid[row][col]\n end\n end\n end\n total_ops\nend",
"memory": 21200,
"memoryDistribution": "[[21200, 71.4286, \"def minimum_operations(grid)\\n m = grid.size\\n n = grid[0].size\\n total_ops = 0\\n (0...n).each do |col|\\n current = grid[0][col]\\n (1...m).each do |row|\\n if grid[row][col] <= current\\n diff = current + 1 - grid[row][col]\\n total_ops += diff\\n current += 1\\n else\\n current = grid[row][col]\\n end\\n end\\n end\\n total_ops\\nend\"], [212000, 14.2857, \"# @param {Integer[][]} grid\\n# @return {Integer}\\ndef minimum_operations(grid)\\n operation = 0\\n \\n for i in 0..(grid[0].length - 1)\\n for j in 1..(grid.length - 1)\\n if grid[j-1][i] >= grid[j][i]\\n diff = grid[j-1][i] - grid[j][i]\\n operation += diff + 1\\n grid[j][i] = diff + grid[j][i] + 1\\n end\\n end\\n end\\n print(grid)\\n operation\\nend\"], [212300, 14.2857, \"# @param {Integer[][]} grid\\n# @return {Integer}\\ndef minimum_operations(grid)\\n cols = grid[0].length\\n changes = 0\\n\\n (0...cols).each do |col|\\n (1...grid.length).each do |row|\\n diff = grid[row][col] - grid[row-1][col]\\n if diff <= 0\\n diff = (diff*-1)+1\\n grid[row][col]+=diff\\n changes+=diff\\n end\\n end\\n end\\n\\n changes\\nend\"], [212400, 28.5714, null], [213000, 14.2857, \"# @param {Integer[][]} grid\\n# @return {Integer}\\ndef minimum_operations(grid)\\n operation = 0\\n \\n for i in 0..(grid[0].length - 1)\\n for j in 1..(grid.length - 1)\\n if grid[j-1][i] >= grid[j][i]\\n diff = grid[j-1][i] - grid[j][i]\\n operation += diff + 1\\n grid[j][i] = diff + grid[j][i] + 1\\n end\\n end\\n end\\n operation\\nend\"], [213100, 14.2857, \"# @param {Integer[][]} grid\\n# @return {Integer}\\n\\nclass Integer\\n\\n def self.gcd(x, y)\\n \\n return x if y == 0\\n\\n Integer.gcd(y, x % y)\\n end\\n\\n\\n def self.lcm(x, y)\\n\\n x / Integer.gcd(x, y) * y\\n\\n end\\n\\n def self.max(x, y)\\n \\n return x if x > y\\n\\n y\\n end\\n\\n def self.min(x, y)\\n return y if y < x\\n\\n x\\n end\\n\\nend\\n\\ndef minimum_operations(grid)\\n n = grid.size\\n m = grid[0].size\\n result = 0\\n for y in 0...m do \\n p = grid[0][y]\\n for x in 1...n do\\n p += 1\\n if p <= grid[x][y] then\\n p = grid[x][y]\\n else\\n result += p - grid[x][y]\\n end\\n end\\n end\\n result\\nend\"]]",
"runtime": 6,
"runtimeDistribution": "[[0, 14.2857, \"# @param {Integer[][]} grid\\n# @return {Integer}\\n\\nclass Integer\\n\\n def self.gcd(x, y)\\n \\n return x if y == 0\\n\\n Integer.gcd(y, x % y)\\n end\\n\\n\\n def self.lcm(x, y)\\n\\n x / Integer.gcd(x, y) * y\\n\\n end\\n\\n def self.max(x, y)\\n \\n return x if x > y\\n\\n y\\n end\\n\\n def self.min(x, y)\\n return y if y < x\\n\\n x\\n end\\n\\nend\\n\\ndef minimum_operations(grid)\\n n = grid.size\\n m = grid[0].size\\n result = 0\\n for y in 0...m do \\n p = grid[0][y]\\n for x in 1...n do\\n p += 1\\n if p <= grid[x][y] then\\n p = grid[x][y]\\n else\\n result += p - grid[x][y]\\n end\\n end\\n end\\n result\\nend\"], [6, 14.2857, \"def minimum_operations(grid)\\n m = grid.size\\n n = grid[0].size\\n total_ops = 0\\n (0...n).each do |col|\\n current = grid[0][col]\\n (1...m).each do |row|\\n if grid[row][col] <= current\\n diff = current + 1 - grid[row][col]\\n total_ops += diff\\n current += 1\\n else\\n current = grid[row][col]\\n end\\n end\\n end\\n total_ops\\nend\"], [7, 14.2857, null], [10, 14.2857, null], [11, 14.2857, \"# @param {Integer[][]} grid\\n# @return {Integer}\\ndef minimum_operations(grid)\\n cols = grid[0].length\\n changes = 0\\n\\n (0...cols).each do |col|\\n (1...grid.length).each do |row|\\n diff = grid[row][col] - grid[row-1][col]\\n if diff <= 0\\n diff = (diff*-1)+1\\n grid[row][col]+=diff\\n changes+=diff\\n end\\n end\\n end\\n\\n changes\\nend\"], [14, 14.2857, \"# @param {Integer[][]} grid\\n# @return {Integer}\\ndef minimum_operations(grid)\\n operation = 0\\n \\n for i in 0..(grid[0].length - 1)\\n for j in 1..(grid.length - 1)\\n if grid[j-1][i] >= grid[j][i]\\n diff = grid[j-1][i] - grid[j][i]\\n operation += diff + 1\\n grid[j][i] = diff + grid[j][i] + 1\\n end\\n end\\n end\\n operation\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list[dict]:
import random
random.seed(seed)
def sample_solution(grid: list[list[int]]) -> int:
m = len(grid)
n = len(grid[0])
operations = 0
for j in range(n):
prev = grid[0][j]
for i in range(1, m):
expected = prev + 1
if grid[i][j] < expected:
operations += expected - grid[i][j]
prev = expected
else:
prev = grid[i][j]
return operations
def serialize_grid(grid: list[list[int]]) -> str:
# Serialization format: first line "m n" (number of rows and columns)
# followed by m lines, each with comma-separated integers.
m = len(grid)
n = len(grid[0])
lines = [f"{m} {n}"]
for row in grid:
lines.append(",".join(str(x) for x in row))
return "\n".join(lines)
test_cases = []
# Predefined test cases covering several categories:
predefined = []
# Boundary: single element
predefined.append([[0]])
# Boundary: single row (m=1): already valid, no operations needed.
predefined.append([[1, 5, 3, 2, 8]])
# Boundary: single column with repeated values; adjustments needed.
predefined.append([[1], [1], [1], [1], [1]])
# Core functionality: already strictly increasing per column.
predefined.append([[0, 0], [1, 1], [2, 2]])
# Example 1 from problem description.
predefined.append([[3, 2], [1, 3], [3, 4], [0, 1]])
# Example 2 from problem description.
predefined.append([[3, 2, 1], [2, 1, 0], [1, 2, 3]])
for grid in predefined:
if len(test_cases) >= num_cases:
break
serialized_input = serialize_grid(grid)
expected_output = str(sample_solution(grid))
test_cases.append({"input": serialized_input, "output": expected_output})
# If more cases are needed, generate random test cases covering general and stress cases.
while len(test_cases) < num_cases:
# Occasionally generate a near-stress test with larger dimensions.
if random.random() < 0.3:
m = random.randint(40, 50)
n = random.randint(40, 50)
else:
m = random.randint(1, 10)
n = random.randint(1, 10)
grid = [[random.randint(0, 2499) for _ in range(n)] for _ in range(m)]
serialized_input = serialize_grid(grid)
expected_output = str(sample_solution(grid))
test_cases.append({"input": serialized_input, "output": expected_output})
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
try:
# Deserialization: Our output is a single integer represented as a string.
expected = int(expected_output.strip())
program = int(program_output.strip())
return expected == program
except Exception:
return False
|
[{"input": "1 1\n0", "output": "0"}, {"input": "1 5\n1,5,3,2,8", "output": "0"}, {"input": "5 1\n1\n1\n1\n1\n1", "output": "10"}, {"input": "3 2\n0,0\n1,1\n2,2", "output": "0"}, {"input": "4 2\n3,2\n1,3\n3,4\n0,1", "output": "15"}, {"input": "3 3\n3,2,1\n2,1,0\n1,2,3", "output": "12"}, {"input": "1 5\n1003,914,571,419,2233", "output": "0"}, {"input": "46 40\n122,383,895,952,2069,2465,108,2298,814,2232,1718,902,1839,2413,1139,26,653,1731,1393,1138,636,881,1378,418,379,1556,396,1470,1408,2472,1083,177,1881,2196,511,1550,322,2261,1200,1481\n2364,787,284,187,933,1185,326,953,413,1556,1138,1857,1494,666,1516,1455,858,1093,292,2495,700,2187,1002,669,1893,1554,1105,2281,899,1328,229,938,131,1292,1643,1096,271,864,2323,1288\n870,2044,1620,1879,585,1084,571,1010,2299,2207,1076,2394,1754,2390,1635,1482,898,566,2087,2021,372,192,449,626,655,1729,2442,260,1576,1563,2440,1917,2167,1029,2266,47,469,2199,1092,1393\n456,1202,1780,647,1858,13,1078,2050,731,2079,435,1222,2079,2494,814,626,1531,661,2209,2172,2,2453,1327,2001,79,458,1486,1259,980,237,986,2323,322,350,1990,283,2181,515,525,1946\n2251,676,1085,2161,2484,1733,867,2208,823,1276,1634,1529,1794,2119,1849,495,1015,920,262,1384,86,2409,2268,942,2410,902,29,290,241,937,276,128,1353,290,2105,974,1140,1988,877,2208\n541,2338,2360,1936,995,1937,1667,779,386,397,1765,1451,1734,1683,1912,221,403,248,1649,1389,447,1018,784,779,2196,1837,574,1728,751,1140,1894,1023,308,1815,2254,401,207,2214,60,382\n968,681,1664,1989,1971,875,1642,240,674,1552,8,1599,1086,1863,1168,1732,2276,1993,634,777,1215,891,239,2372,2220,249,1284,234,205,2392,1952,2059,2175,644,232,2080,328,761,280,2437\n278,963,1653,491,2333,1008,2371,2435,162,335,1717,2390,2315,2141,1295,1068,836,1286,977,1087,1621,536,1228,1872,1295,297,38,1877,2306,409,300,2202,873,2072,1086,542,1429,281,1000,1513\n1167,646,1794,2225,1239,2166,32,2271,1226,424,550,1083,472,438,2266,636,1115,1154,2477,862,1404,833,1081,2070,2001,1028,208,378,1734,1133,180,14,1366,535,1072,661,1809,2259,1751,2297\n39,458,308,610,2234,147,1512,2385,2263,606,1760,522,171,1262,1493,163,1465,860,1022,421,1448,2293,1664,633,969,665,725,1688,101,734,1360,1686,1016,1092,652,442,1566,158,1927,911\n817,1885,1432,1250,932,913,96,791,1632,1344,1141,284,1143,1438,2086,1637,2196,1356,113,472,1069,731,2378,1087,156,444,2443,1779,1415,1284,1787,2483,2094,473,1577,2361,778,1043,181,1786\n6,2129,2205,807,1491,1766,286,1352,1285,510,1230,2077,1266,1672,1336,1648,1211,2270,521,785,1722,1552,712,2331,1232,1663,2244,1,1244,1175,860,1760,2375,2484,1319,1904,1809,1811,875,2093\n1938,695,347,1162,2111,1372,382,962,1271,920,815,603,100,189,1002,1946,298,1865,1697,2357,796,1572,2024,1636,999,604,22,436,1741,896,720,2121,1902,205,2283,1020,497,1869,546,1903\n2175,2289,2438,1299,1812,2067,1747,2244,1826,651,1944,1843,1061,1012,1135,2135,1984,979,1124,1801,317,1170,960,1112,1375,1309,2212,330,566,617,947,1568,625,876,263,1699,1669,1355,2222,1908\n1703,255,847,1720,1595,2392,80,2358,1558,1953,24,1440,1223,1597,1716,2204,2236,2470,903,1999,898,1117,1785,1989,118,1592,1376,1656,676,1914,522,2187,110,1613,2424,2311,111,343,1755,555\n1891,744,205,1065,1552,1340,866,1862,1338,1382,1552,1139,1726,1033,335,1926,79,2209,213,1433,918,281,164,127,1012,816,83,624,977,517,1939,468,2310,892,1904,1049,1510,687,2481,2487\n469,670,1274,442,2370,105,1277,2358,1537,1624,812,311,2425,994,417,1235,2459,495,2318,168,1422,2182,1754,1517,282,2072,1397,51,1720,2007,432,1775,1483,1883,626,1783,721,2137,1106,2204\n1980,1904,1784,2426,1099,1320,1005,354,1142,1846,998,1903,2334,2499,1552,1377,117,2024,1331,744,1997,868,1453,1058,1394,1145,2441,1131,2276,41,2116,782,350,988,1664,2001,2274,984,1950,2010\n1835,70,381,1205,907,1656,996,1254,2382,1511,1938,2267,2174,1408,1742,2254,1354,1441,1858,1109,1255,1029,944,494,788,1292,489,2194,758,784,886,1983,1132,2414,2148,2444,1159,411,795,1213\n931,1478,734,1238,57,2187,518,1123,186,223,2266,1196,517,2010,420,50,2351,1164,1922,1960,1804,1395,755,210,1034,1956,467,267,1641,2014,303,2363,219,621,611,2305,1244,348,1016,485\n2285,1704,2483,2441,924,2140,1558,1845,1813,1217,2410,1756,1250,2329,246,2497,406,851,864,1083,332,643,982,711,2260,307,641,10,1673,1845,2432,1924,1192,133,948,1180,1158,1859,291,956\n1083,2415,810,1741,470,2230,920,610,1088,582,292,244,679,1259,2437,2331,1182,1798,509,1919,1245,1648,1115,2049,2211,2022,1793,329,2449,163,1769,1320,2472,1025,105,374,937,2356,2404,84\n1103,2360,164,717,1927,2125,1811,1139,743,2397,1785,2014,373,1925,1425,1672,1365,1315,428,658,1350,1686,2029,1180,1640,2253,150,1862,360,1288,1033,1324,474,1655,2107,4,2222,1892,1692,222\n768,2123,1481,2041,1810,211,833,1093,2249,536,1179,1794,1985,497,118,2493,980,648,1272,2256,56,2262,1671,381,920,464,1890,481,630,2041,1195,2084,1119,1701,1976,1934,998,1870,2257,592\n1571,780,2455,2081,559,285,1131,1699,1392,2079,1094,10,1158,1222,2404,2375,2005,608,1829,2206,1983,1413,1361,2260,2225,1545,1865,1318,772,978,2342,1568,956,1682,178,1303,1937,1561,1581,623\n2028,151,517,2057,2417,1359,411,1803,408,2154,1871,62,590,1679,632,306,1923,1085,1386,1628,328,1345,2185,1556,1297,1998,2216,147,280,961,1177,931,370,1777,403,411,1817,681,1226,118\n188,1328,229,1201,1468,1535,1764,596,1000,2175,1687,2318,737,696,717,323,2496,1566,986,2038,2388,586,951,1888,1040,1882,1045,38,1905,1178,2238,647,302,1809,1415,2406,1225,1737,1024,1871\n1237,815,1575,1979,436,971,1562,2342,1470,2354,1211,1209,89,1621,1124,33,2318,200,2483,2034,1172,942,2486,1443,897,778,1026,560,397,161,1265,1805,136,2373,1494,538,369,1208,1338,1701\n719,822,541,2209,1498,2174,2055,1116,673,1052,1973,1208,1387,471,1918,308,576,924,1627,2282,1498,369,1616,57,1083,2197,506,1862,1509,1073,2394,1560,1521,443,957,1931,102,2299,1343,2498\n906,258,1901,1237,1672,477,572,185,152,1246,2017,475,398,961,2201,555,1591,1858,1519,2212,1716,2405,632,1699,405,2004,1671,1145,134,1517,889,1816,1821,967,1485,406,1504,2230,1469,248\n1630,1130,777,500,1862,375,868,2445,87,207,1366,997,515,2312,840,281,2270,848,2401,884,954,1345,604,2441,11,1135,592,532,2212,1026,714,450,105,539,60,1467,974,2411,1326,64\n713,1086,214,519,1724,2154,465,260,1950,1836,1482,2102,2431,446,1851,2063,907,177,2135,1235,1876,127,249,1961,1645,1746,442,2008,1816,301,330,1319,2491,607,269,516,1126,2397,2246,1331\n1560,2446,2173,1207,1858,2070,2479,1762,406,468,2258,880,1761,1849,935,1694,1388,1857,1633,1703,389,1280,1748,1280,1044,1533,625,1942,274,373,349,381,1768,395,1526,532,2278,245,2402,2300\n2300,1350,500,1682,1448,1732,210,1178,2459,1279,1440,424,2367,2078,871,633,1975,918,443,1434,2278,1505,470,1141,2351,926,1757,2297,2280,107,2494,1095,118,738,1119,1265,1391,1437,25,743\n586,2319,1641,285,581,125,375,2172,881,1540,1719,1858,1396,644,1515,1276,1328,2324,2442,347,215,637,644,203,334,1114,1814,1736,1989,2486,1810,1696,1118,882,2098,466,1413,1760,454,1160\n2429,1993,2158,1263,186,903,1618,2454,224,31,837,1234,865,562,1046,1185,1343,491,31,2037,1763,719,529,1557,2181,942,2049,2288,1450,295,1626,173,1786,76,1883,318,1282,2358,1758,2348\n1656,1710,1185,471,1659,85,1330,703,1884,1482,360,1788,433,996,1784,2412,1640,2146,322,1621,1270,1390,907,1364,688,312,2090,467,2173,2088,794,1431,1438,604,967,421,599,1048,808,710\n2467,626,308,725,2023,1900,2309,2373,1838,2312,1323,1294,618,1801,279,1920,1811,1240,1125,2422,230,1441,2078,303,1271,1891,1851,154,233,1510,1175,314,369,2433,2076,1574,1895,2377,2270,168\n1842,2341,771,1316,2478,1948,2053,617,253,1845,423,1406,345,2066,706,160,1014,1793,1799,2146,2141,2497,650,1490,1527,1158,1586,1674,1385,2448,214,1370,269,1350,387,2285,1583,1163,1032,2468\n615,1365,333,2386,579,1432,1270,1605,528,2437,347,1268,2289,1542,1345,523,2156,382,1734,2082,1482,74,1485,1265,738,877,1399,1991,786,927,563,634,316,1211,414,2079,2210,2156,154,1379\n536,2446,1543,631,664,740,678,1792,178,1682,1492,972,1819,1167,1838,958,2187,979,1267,1921,794,1506,2336,1804,1891,1154,1564,2059,2160,1714,663,817,2476,566,1024,213,1968,1520,2271,420\n2113,510,1167,343,656,1117,1840,2102,603,1791,375,909,1847,1431,109,1699,218,1623,2056,1531,965,1581,334,1535,919,115,1305,405,1373,598,563,156,1175,1935,568,1921,1837,21,324,77\n1048,883,612,2247,2493,2161,1733,455,1180,973,1233,499,195,976,1719,1872,257,454,2047,2444,2195,67,2110,2355,990,588,1193,1758,6,1445,985,2337,1706,767,350,2144,1477,277,2154,2228\n2078,2079,2269,83,1599,1925,178,1584,1529,1038,66,1462,276,1412,987,424,2383,1361,546,181,1443,2236,1386,717,1903,1960,746,552,258,1874,151,1201,825,179,817,171,1292,1270,2111,1631\n2224,1939,1037,149,782,1171,1462,195,1359,1119,509,1507,1789,1638,1801,1583,1388,765,2032,2037,1504,2126,1092,338,1738,323,1763,2467,739,2234,1203,1315,420,327,1343,1210,1255,1826,2468,1745\n682,1818,1439,1831,173,1444,1781,1124,234,307,1663,1488,2101,655,127,584,2488,1794,142,517,275,966,1500,1483,1568,2323,132,2478,628,1842,1519,1523,1818,314,2350,563,2168,1503,1630,1287", "output": "1955704"}, {"input": "4 2\n106,762\n2044,2120\n1585,2300\n482,1072", "output": "3253"}, {"input": "8 4\n1169,2011,819,502\n555,303,1851,707\n1823,359,1309,1423\n265,2252,2220,1189\n1228,645,713,1480\n2083,918,497,823\n568,969,2023,107\n1478,2269,2344,1511", "output": "18731"}, {"input": "9 3\n353,269,1266\n1630,1960,2153\n1682,1677,2354\n302,513,1298\n303,1843,1908\n2119,1411,525\n2258,2407,745\n528,1772,2059\n226,508,2122", "output": "16958"}, {"input": "42 42\n1321,923,1417,2125,1163,323,1026,804,2256,1124,512,1240,2185,382,2058,690,2424,2378,631,701,2478,1382,2308,168,116,332,186,2362,1084,863,2343,1706,124,2039,2234,1186,1237,1978,1003,1663,1218,1857\n298,245,647,1800,1702,1983,1902,835,1393,2484,588,1280,1307,1414,1633,535,1517,2109,2300,434,1307,990,1910,501,1095,1841,1015,577,396,207,1188,1573,1712,1016,654,1341,2366,1280,777,652,2040,2108\n1912,2042,1263,2037,94,368,1610,2070,1872,986,881,2389,1445,199,207,1152,2027,2447,1927,1170,2198,33,440,1765,548,1083,1498,1651,1498,185,1640,209,2335,2301,797,1484,2266,1182,301,1582,2065,1844\n2252,1145,486,527,396,1613,1528,1388,2284,1497,590,815,2467,2085,1644,2048,164,185,159,561,1364,1940,2127,1871,610,2483,2111,572,1343,1304,665,1609,1225,2431,1377,2077,2087,2180,2006,2305,1227,1945\n68,1508,1356,448,1706,2390,1260,109,2444,1943,1087,2369,2365,932,210,2390,1967,698,2147,1557,605,992,129,2345,450,781,77,1806,1284,1715,620,1691,835,1680,2055,1931,255,565,2124,849,2297,1331\n1959,2152,1543,1285,709,1882,2183,1402,2237,1451,1082,2498,1983,787,1009,1142,2285,1222,921,1219,1183,849,2002,1298,1965,1428,2295,1120,1178,499,2348,2224,1555,1616,1413,599,1189,172,1178,323,1418,1811\n1050,1962,876,827,2206,1110,2302,1112,562,447,2403,980,993,207,2175,924,953,215,410,1692,1352,1934,411,563,21,2254,646,1666,1948,1955,816,1176,1315,1169,242,366,2351,951,2191,152,717,1711\n720,148,1626,2029,763,1185,153,37,1222,2326,2468,439,1372,1165,1861,2225,2147,2023,549,2065,1917,1117,789,461,1354,665,1879,1053,762,57,1380,1208,2325,791,718,1660,1751,2110,1343,355,1641,390\n756,575,1955,1325,1016,27,1068,1571,964,1829,1093,1350,1236,2385,2346,46,1071,1472,967,254,484,1906,1256,654,1660,2058,1273,480,1208,1505,904,897,547,1958,627,1863,2481,1530,1703,2249,1928,2201\n894,1013,2440,335,2152,1829,2163,1481,319,2310,459,252,2243,2070,828,2345,2198,613,673,1343,2131,1809,476,841,2388,2002,372,2090,1824,227,1857,540,2102,1701,1871,2309,236,2288,1893,1262,89,1621\n1042,12,892,2368,299,185,1735,1411,261,2216,246,282,1933,129,1175,1674,737,554,1721,1533,1566,1837,1546,1538,328,2208,544,1424,485,731,2200,1609,2166,521,912,14,93,1222,1896,2230,1737,2178\n1553,940,1013,1886,1417,635,1129,772,462,131,1717,64,985,844,275,413,2432,137,1828,2448,199,1002,181,1647,1797,959,2210,889,231,573,2063,1184,959,2359,1306,2365,2449,1313,970,1236,586,2135\n905,1693,1230,1127,249,2280,2423,717,1749,2276,2030,192,1410,1561,2148,1305,1705,1672,611,1228,1541,753,2203,1939,987,923,1231,591,1896,236,2303,1690,1706,2282,2170,549,1590,994,1044,832,1352,323\n1842,1519,378,2193,780,211,1099,1544,2477,2469,161,298,770,2406,2289,888,1963,855,1363,1241,62,867,778,480,1961,993,2475,837,1624,980,2261,1317,1159,1559,1909,2185,1471,1263,1071,1473,2100,2036\n1908,403,1923,1311,832,1518,1281,1695,187,2304,906,597,66,1068,2266,2392,2372,1710,1209,624,803,1351,942,1555,2333,1006,2045,2255,1382,1054,2001,2009,1887,689,1442,693,573,2238,2000,753,2220,240\n2146,138,304,198,26,1689,563,947,278,618,37,895,2071,1867,1528,247,1979,1998,64,27,2179,2259,1684,48,68,2168,1125,2194,1174,70,2057,1763,734,438,394,2147,609,987,786,2156,1033,1451\n1094,1625,323,1528,1663,1880,2314,996,925,1228,330,129,382,1660,1553,1544,2263,1949,229,38,701,338,2047,1777,1356,2317,390,2163,174,941,865,2321,1947,1110,190,304,1148,2224,2308,134,734,1288\n64,848,2404,590,1631,315,1225,665,2309,984,2321,1593,2214,1358,1572,573,321,2051,1416,219,400,1790,950,311,1395,2478,2439,1624,1336,121,1119,1845,2009,934,1457,2265,1537,1768,760,2399,1556,351\n1209,1009,301,336,1097,631,1556,631,1595,1297,1477,436,374,21,1262,1821,1474,1104,418,542,357,767,1765,1838,2281,2272,2098,1671,423,107,367,1449,2270,381,2445,2449,1328,1577,50,1195,1694,1588\n346,2291,994,2342,2134,694,1559,694,568,1101,1233,1099,2019,597,259,684,1780,1130,1724,1227,1983,315,1479,1030,1010,2030,2432,800,1875,438,554,1247,27,1620,1360,1556,1349,1803,1371,1763,2434,557\n1230,1313,2470,822,1962,1286,727,1631,1307,1193,2011,2358,992,1334,1540,1148,1609,1495,466,2309,818,2425,2234,736,2253,110,1890,858,1795,1193,283,1675,2045,570,1240,991,1034,631,1733,1544,302,1839\n2449,1962,2384,1641,2188,2075,1713,2226,150,1472,2199,2432,348,447,1016,1454,681,181,2306,1636,1358,1763,433,43,403,1059,909,2091,2124,2285,2377,2356,905,1825,1532,1602,1896,2410,2049,617,1412,100\n1977,428,1210,1703,351,475,580,1426,1277,1405,1865,847,2134,1978,1426,1950,399,1794,1853,1306,275,1229,183,471,92,1405,447,673,999,2113,714,2260,655,1355,2293,1746,1892,949,1659,755,763,1770\n1620,119,808,1841,2425,1759,1592,18,879,842,1140,256,2364,416,2199,765,1498,1335,807,1874,466,1074,2004,2161,1283,2445,1591,1607,2404,467,1425,1441,1875,706,1218,2417,347,548,1282,482,977,1250\n479,749,1529,579,2092,1591,1713,2442,564,2354,1571,1732,760,1993,2201,709,2272,683,2005,1183,574,766,1288,1847,219,1470,39,1984,559,799,1572,2300,2070,2027,1675,2014,1702,1818,2001,685,338,2315\n126,903,1196,133,1125,920,2202,1182,688,1873,2316,2028,2251,2092,463,2345,467,1097,2224,1502,2220,170,1807,2237,895,1741,419,1013,1219,132,1842,1076,1427,356,1798,480,970,859,2408,1436,2499,1753\n679,570,846,847,243,2335,1436,2180,1151,2444,2206,689,1325,1198,1185,2345,1095,2107,390,555,1685,242,1135,519,543,1022,599,1319,1013,1608,2004,582,2365,1100,1696,1536,1851,309,381,1650,2111,1139\n1511,1862,1999,1340,2383,10,381,1877,1467,259,2189,1629,892,1759,867,2026,1099,1322,1161,1383,2241,2367,534,2318,1987,1407,198,188,407,1882,66,508,647,1807,1869,2,1752,828,540,1236,651,1122\n382,1476,1025,337,1523,677,212,1623,1251,959,1758,373,389,4,874,1953,319,543,2431,926,2127,1822,38,33,1407,493,1729,541,1956,290,937,1569,365,419,422,1283,1505,1225,561,1567,545,585\n280,2172,2307,34,2499,672,1802,1438,872,620,1686,1812,889,355,411,573,504,2414,1572,1439,1758,1288,572,1014,1134,345,1016,2266,2461,2457,2488,1167,109,1235,841,2120,2485,2087,772,1604,1210,223\n980,2027,1580,461,987,2046,2432,290,2163,49,1479,1296,540,1584,2328,1723,1496,2237,707,1929,298,68,2405,276,56,1073,883,163,247,1630,2075,1173,2052,1701,1734,1647,337,2197,2202,625,1136,342\n1269,323,2094,832,636,2197,1338,1600,2402,270,1270,1791,977,237,1001,353,1779,475,1857,2493,225,1266,719,489,51,562,46,671,2033,1420,2142,2118,1061,683,1523,519,1100,483,120,1372,1758,1114\n2145,261,1077,2361,315,2032,1864,2092,1475,227,2046,2321,683,1506,644,1044,421,2350,472,935,2084,10,180,50,1001,188,1932,1490,1568,614,733,144,2264,1717,919,1318,1016,1704,1310,1111,319,2341\n1527,489,2056,215,734,914,2112,188,1642,282,1905,1156,1272,1340,353,2265,1870,32,1511,821,1194,2309,1244,993,1900,1508,2423,2020,800,2238,1004,616,26,1679,97,954,2218,1418,39,1372,5,1541\n1259,425,840,2170,975,1719,2015,245,583,1146,381,179,948,2128,1691,1525,1877,347,2378,391,2070,546,1615,306,2424,2325,255,1781,535,969,1194,1069,1290,1609,1336,1302,1854,1113,956,305,830,557\n2394,446,636,432,673,1841,1908,1286,1665,494,2195,1467,850,1851,1262,1897,1085,491,370,645,1246,2471,165,880,1342,607,373,1016,1457,1623,2103,200,1224,1065,712,127,1656,1852,2277,2253,1023,387\n1892,417,572,497,48,252,910,535,811,1640,1524,344,2385,2400,1060,307,89,264,809,1816,527,376,1358,501,174,1888,207,688,2350,1774,1617,2032,120,1567,1747,707,1449,879,766,1126,1146,1826\n608,141,1006,1208,2043,1687,2255,1962,249,359,1145,1568,562,1717,816,2153,1020,2226,79,1566,1470,1964,2230,1985,1409,2316,2057,1317,1590,1107,736,106,1306,2445,897,120,1150,239,1932,2168,1464,2392\n953,653,410,1015,987,1091,2185,229,898,2358,1590,1453,711,721,968,2426,1302,1469,2423,115,1440,2325,2308,582,2306,771,2016,2220,1265,719,2008,155,369,230,952,2464,896,81,2156,1957,2,1358\n825,534,1395,726,1325,243,89,605,2402,580,454,2155,1494,297,1530,1620,2400,413,1378,1236,1321,558,645,1789,1995,1299,713,2301,1461,914,2412,718,1549,1256,1206,521,727,7,2346,1603,2324,132\n745,2467,1303,904,2316,426,2032,576,1356,318,974,1420,1308,687,363,1375,1829,46,1086,858,1022,277,1435,1051,442,5,197,1580,1794,1718,681,1695,2019,1551,1438,2236,1537,415,1963,2367,923,666\n1848,301,136,1207,82,1305,1069,428,303,1400,696,1537,659,307,2240,381,1384,2433,1977,126,1766,675,2487,1778,643,219,414,1356,841,778,1676,2269,2212,1086,1153,1218,972,392,203,1609,2341,2251", "output": "1863571"}, {"input": "3 1\n1477\n15\n1751", "output": "1463"}, {"input": "50 50\n2458,1967,817,397,105,847,699,1195,335,1939,473,1263,1628,1928,2003,1085,373,2228,1587,757,1519,1562,1513,764,1825,182,1078,1801,1904,1078,926,1100,2311,252,619,396,351,1408,2217,1695,2415,931,2267,249,1585,2140,1714,2193,1944,2345\n965,1950,1224,323,1617,142,2056,2339,2116,2340,603,492,1839,708,684,867,789,516,174,1734,320,1783,827,605,2437,1056,1309,274,356,1589,2278,1627,2261,1335,1131,2128,1876,50,2406,2140,1718,460,1697,612,607,2320,2408,2386,410,432\n2304,413,1171,2193,1408,1683,1081,1568,1988,2343,2494,1937,153,705,1128,1650,589,2493,1645,158,1621,1357,973,201,1946,1100,1525,82,1383,1241,1273,1148,2013,402,933,550,1230,1814,1314,1103,1707,2477,365,769,1809,865,1667,1984,2115,1531\n230,2110,651,268,1274,2075,1652,555,2147,2329,118,711,789,822,236,1021,135,1869,207,1476,815,1122,1508,1901,2068,1625,507,125,990,1525,2002,2433,1827,727,1943,2403,2258,1432,1410,669,1059,370,1167,112,1583,203,667,2343,877,906\n922,846,1102,1677,2102,82,36,1941,541,709,2462,34,916,1033,2491,1251,1127,1735,1542,1428,1880,1032,893,1911,1237,2132,1626,2394,419,30,2095,1532,2299,2432,2494,1157,1222,442,1973,261,1377,1132,1331,1134,1069,1223,771,614,2118,984\n232,2457,1655,1309,573,104,2037,1210,1062,1714,1657,1590,144,2388,2343,777,1405,910,2189,1948,1468,2077,1229,696,2286,741,1203,399,1928,524,1059,2289,749,1374,365,910,1455,914,1257,1722,1357,1522,1067,2398,1204,1899,482,1927,219,2390\n2376,291,1934,796,2049,490,1563,2170,1222,1692,221,617,562,820,1403,1676,2332,1874,586,1295,738,331,1997,1362,724,1283,237,19,1851,1120,857,690,2360,648,2005,360,530,1776,1758,1652,1757,1955,1570,19,154,2186,816,1528,57,1319\n2175,780,73,16,1019,926,1410,1278,528,420,1571,2061,2411,1253,684,267,187,1221,1191,1867,2131,2442,2146,1383,1776,548,1403,2007,1471,771,675,1652,78,935,918,537,865,89,2415,2066,692,504,1501,153,1536,1047,2190,199,2432,196\n442,80,197,474,1707,1819,1557,506,2241,1035,1943,627,841,38,1233,1723,413,2131,1105,2480,561,1715,429,2095,482,1157,466,435,2038,813,2494,818,1077,2142,826,1466,1678,1209,656,161,2245,2033,850,1968,1354,960,11,52,364,452\n2351,2023,610,368,2095,307,414,1048,946,1870,1212,1081,1901,205,408,715,161,1190,1475,1280,1744,474,389,187,39,566,698,1346,1464,1792,1098,380,1526,1403,749,466,1641,1639,1869,1113,1579,1958,1727,683,463,542,240,652,424,1704\n2419,1977,2330,1794,742,1555,1468,118,535,1978,1999,462,1684,1805,188,259,1071,1287,50,2149,2361,2314,917,1385,2126,2142,390,1772,1018,1973,1416,1576,608,2286,223,47,642,2070,1922,2030,677,306,2013,1313,986,1355,1139,206,2076,912\n2254,1550,1651,962,322,1880,1819,2347,1835,360,2041,1831,1294,486,2037,72,420,1652,1688,146,2282,2249,0,372,2474,1247,2082,2303,847,1868,1396,1488,222,913,1861,1359,2294,2457,1937,1488,1853,467,399,908,8,1398,1454,1195,2243,2138\n1531,435,187,672,2016,575,1676,438,1041,802,768,494,1609,883,1872,780,1384,441,1697,190,2411,504,1845,1873,2413,2065,551,2043,17,2172,198,2266,1772,2396,1978,2082,725,2369,711,525,424,1586,2459,2482,1318,2064,1575,1714,2494,1016\n1120,1629,1404,1204,1854,546,565,1690,2467,2098,1224,2243,1285,2267,890,822,858,1190,1414,543,728,2063,2222,1320,472,1442,2303,1967,2387,2337,1709,2186,1171,1730,52,2141,436,103,1560,595,217,231,818,1093,659,1173,1026,599,254,1208\n835,2216,132,1469,1853,419,2301,918,2298,1592,973,2092,1178,192,1562,1587,1706,1280,2261,220,53,1029,831,1814,923,1506,2410,2238,2471,804,792,1204,1838,726,305,765,711,2104,488,1545,166,1755,1143,2279,1082,532,659,2392,1044,23\n1353,1910,634,163,629,1321,2444,208,1233,2009,2345,2253,1466,298,1301,2152,900,753,2132,279,2069,652,1703,2224,2199,1652,376,1431,906,873,1359,1356,1477,1202,894,2172,1945,2299,36,469,1417,1825,984,998,163,1314,1562,464,1580,1050\n2212,1158,101,2117,1535,2106,2083,1825,1993,179,1214,788,1312,2104,337,393,685,2203,2184,30,268,863,873,1737,425,842,2202,1782,295,629,97,1880,1358,155,358,300,222,729,1031,2285,288,2355,932,1059,1669,1589,1847,1656,1773,1295\n69,1595,484,2190,24,259,2398,186,297,1465,2059,434,1187,1234,2484,354,1153,1792,1562,1618,126,1941,640,2185,900,558,1601,2235,1208,590,1220,1528,45,2267,2273,579,504,171,20,2345,2443,1614,2200,2242,348,1248,860,1408,867,1690\n2099,583,659,753,904,1035,795,469,742,2323,222,2248,1889,2251,299,1190,275,1026,402,808,2378,1995,1355,1462,525,960,409,1167,285,792,1301,1990,1845,1344,1252,2392,624,2316,2321,1492,1295,1754,690,19,1282,1008,907,1786,1133,1472\n550,1358,1965,1895,1824,1469,1251,1994,2259,445,719,2484,335,1149,573,2206,804,1078,313,308,76,2077,127,2383,2371,1659,2416,871,150,2259,1067,2226,2210,1933,608,1498,1607,914,2415,1191,548,1903,2052,2090,370,1625,1490,2056,43,978\n679,2105,574,1827,652,733,2319,2317,598,1980,1469,165,896,1997,949,257,1082,1513,958,175,846,2121,1479,1589,1923,1862,190,163,1327,422,2135,1120,1078,2370,2229,2335,712,1542,1550,1496,2407,318,2116,1030,1541,912,2115,1662,1445,1413\n1994,1974,2474,27,2055,569,1801,678,942,315,2107,1150,866,615,765,644,1483,2465,484,943,1698,1352,464,1972,1961,1962,863,2419,660,1683,91,998,176,523,2349,2426,659,551,2099,160,2344,601,229,681,1057,737,2116,1660,2454,2308\n76,1161,351,887,1839,2484,1930,1972,698,898,1682,2461,584,2386,744,2092,1083,686,1403,1857,2443,2419,281,941,1549,1578,541,444,67,828,2141,2065,1719,612,2480,394,726,1949,2456,159,2176,2061,481,381,1975,533,2471,2208,4,1767\n2138,1723,1517,177,2170,1757,939,1974,1561,1435,2412,2359,400,1742,548,1042,1954,952,343,1160,2450,2227,1673,1055,774,22,29,2367,2140,482,2128,29,1536,841,1293,1674,1483,436,633,1745,2397,1038,1070,2195,1734,2312,1497,1128,1627,834\n1692,2261,2283,1976,732,1516,2290,2272,1981,1039,1256,2366,1410,1630,565,487,941,1829,662,410,878,2082,1640,1386,2255,213,658,1593,21,373,595,1931,2458,1783,361,262,1077,908,1518,327,2494,154,1574,1641,2134,1173,2447,235,717,2024\n1798,43,826,2122,1171,797,137,2455,2091,2112,948,694,147,1473,979,1,644,355,1130,1636,1446,1618,1660,2400,820,2120,62,281,369,2251,1165,2290,2387,1425,1423,1132,926,2483,796,1862,1654,2354,19,1069,716,1667,2073,436,2288,296\n2060,1205,1392,479,2102,1055,2203,2354,1024,1813,1544,2306,1980,996,1391,1879,1887,2403,112,1974,476,1056,276,1567,902,941,1293,1689,1446,2115,2194,39,1078,1016,1176,380,1634,1400,311,2271,731,1951,1285,1448,895,2349,1102,748,778,2043\n817,961,991,1087,846,938,830,1022,1458,638,436,491,321,2017,27,2217,173,1975,1520,1291,2016,2353,1125,2010,749,2093,1147,1629,909,2362,525,221,2153,1733,1959,2214,133,2058,1422,1612,715,1872,493,2122,1884,1292,34,48,863,1554\n2379,412,1332,1481,1063,766,2246,1076,971,1103,1930,1405,1498,753,2042,1736,862,1716,1524,1495,1640,1145,1846,736,2340,537,2358,936,409,1105,965,2274,1770,1560,803,597,612,1937,39,723,1726,2046,550,2117,2187,1293,1993,1228,1027,2302\n2325,195,1631,405,669,245,882,1041,1951,394,1842,1370,1064,1478,1475,2295,2283,1055,1409,81,1686,496,1438,2480,814,2362,2358,2205,714,1165,1454,1331,2090,1996,1830,321,1560,1173,1899,593,686,1381,1727,2341,1657,292,324,663,1407,934\n1284,1297,1193,1095,2479,1619,1111,1822,1487,2404,2133,1844,1695,685,753,94,512,961,1030,327,862,683,1626,421,391,261,1938,2246,220,107,1626,2146,340,425,1075,636,345,1596,1267,939,1013,1163,1815,517,537,2157,698,117,143,1461\n1332,1950,1913,2214,1115,2246,1822,553,2208,725,2420,2447,1870,2310,1781,2144,2186,1268,1422,1972,2210,930,366,1809,1261,1498,1688,1064,637,1243,43,0,2143,558,1408,1174,1921,2191,34,2014,1954,1227,37,1763,1199,2445,947,29,2245,1530\n772,1686,2296,1790,1616,1023,668,1596,1549,903,1077,324,1729,981,2116,1113,1166,2178,1101,1691,770,280,747,559,1186,452,1865,1854,1114,2015,769,1313,79,623,203,2191,90,761,418,1155,1102,512,1795,33,953,369,617,60,2021,889\n1400,1721,1276,2041,1521,1899,129,1352,328,598,229,1091,1607,292,2224,1925,743,787,1024,1562,51,499,1019,1576,1814,1012,137,815,1887,384,2134,853,1936,1593,1278,1323,649,172,2251,2133,500,1037,1971,1223,813,1476,213,892,462,966\n1778,1329,61,685,1130,2394,490,1621,995,36,172,2380,1946,2442,634,1521,366,1018,645,2047,374,1386,245,244,1456,630,2196,439,515,1998,953,1297,2287,1422,1796,790,87,1547,1467,551,1026,161,1987,1792,2289,1207,2223,2007,777,2321\n764,2226,1424,1325,1918,1127,2452,2271,656,282,2175,634,1840,1211,1078,2218,1503,1859,2,2072,1552,759,76,1491,978,1313,259,2207,1587,777,2146,2037,2258,631,1159,1321,1678,1319,452,394,2143,273,179,531,731,128,827,438,1988,784\n404,130,2338,1591,2006,2153,2417,1048,201,1500,904,2481,290,53,854,2012,327,1917,248,1478,2285,1703,1511,238,1088,2166,166,288,1244,319,884,2127,397,414,946,2177,1578,776,791,2155,1018,2334,732,2287,2286,1700,432,2361,1466,1878\n1749,426,683,738,2252,1644,2067,1382,647,2186,2457,1814,1443,1290,2253,1329,1522,1688,1763,1324,2492,985,2306,2234,876,1536,2253,1040,1474,1853,1832,1626,0,141,1165,2440,66,2120,553,1236,26,1230,908,879,1289,88,1130,2267,2094,2278\n2337,2341,633,386,154,1885,1456,639,566,1085,1503,2384,1023,954,1049,1230,376,2336,1637,2330,890,316,1329,1976,708,1999,2360,390,2438,1230,153,2360,1562,321,229,1369,1425,1778,1706,493,928,2467,46,1566,221,1248,2147,168,1307,2211\n2313,612,1338,2057,904,627,206,1609,1825,2437,2356,2067,368,909,1769,1186,1615,606,541,1376,338,1949,2340,201,2245,1635,1075,348,1632,2055,1779,534,552,1969,2290,811,1998,1619,2340,803,2298,2147,1008,992,293,1090,1761,1324,2359,366\n460,1694,1734,1496,1426,780,1313,1411,2432,99,1248,693,1432,1811,597,1804,183,956,817,1531,638,351,460,223,995,604,1178,56,1406,455,1249,1843,1929,93,1359,856,2203,867,834,2238,2143,1059,2247,1978,578,75,1542,2387,2157,178\n1046,697,246,1163,822,1111,217,1904,34,272,1591,1111,1475,441,78,1198,1583,946,1559,2082,407,1292,1985,2445,2177,360,763,814,2050,1875,2296,88,162,1013,2168,1248,1366,2006,1611,643,75,1420,1441,1455,1238,967,2053,1129,253,1055\n1585,120,2273,1147,923,621,1399,1609,562,359,1565,2132,931,1709,984,2346,625,1746,1279,2479,1348,1839,2220,539,846,567,2379,2217,828,565,1265,2145,553,1761,594,2313,647,1300,277,2282,2183,484,754,1300,596,120,1305,1695,1684,1242\n1814,1121,622,769,437,538,756,107,1093,2480,2322,945,2442,951,945,106,1471,325,1952,549,2057,2476,1920,1531,753,1587,2012,1940,563,670,791,926,132,1673,61,1105,1691,911,830,837,270,725,1799,2006,1330,1874,1010,1751,1658,171\n2490,1558,1281,1614,2342,2432,2196,2151,157,2132,447,1849,1871,173,1006,2124,2203,1620,160,2284,1586,2114,201,777,1192,1800,1630,1247,1171,1889,681,1730,1205,223,2117,582,1898,1850,370,2050,463,736,2397,2238,554,1610,1693,1324,1846,102\n732,1858,2417,827,1862,369,1024,1327,671,506,373,467,1840,1486,349,2145,1573,2095,654,1551,2254,1558,179,699,1372,2316,614,664,592,732,210,1718,1261,1267,1827,1182,740,481,538,830,14,1036,50,1878,2038,2042,2226,23,2490,2021\n974,888,2411,1948,1858,1679,1809,325,2462,2458,26,1002,2241,1139,2283,850,200,757,607,225,1429,150,595,132,2367,2471,1222,1356,359,200,446,1707,730,660,1164,2436,2344,2302,726,1865,2371,1475,146,381,1225,1322,1509,1552,277,1750\n2254,265,1199,1928,551,499,1124,1348,2158,1694,2148,859,856,238,447,2340,2166,359,1981,2477,1176,1749,2493,1296,1063,2152,2355,1449,531,2304,2033,2128,2038,2017,736,2496,953,1189,792,6,484,98,1904,483,849,1698,1695,186,1367,1432\n2295,869,46,824,1153,1042,277,1260,1229,2075,2252,1326,25,466,1365,1398,1622,2330,119,719,794,1353,1384,1962,1943,145,556,1972,636,1886,2199,1372,1894,1695,229,2134,1226,2314,1292,2274,2194,76,853,2365,1358,1448,271,611,1148,127\n1389,1536,2188,679,2338,2480,1595,767,2437,478,1262,1288,129,1112,1695,355,2035,973,1522,1851,1239,885,2150,1238,716,459,1532,153,827,379,1817,2072,102,1976,2048,631,779,1393,1980,2144,1271,1340,586,402,2114,543,840,149,1881,1587", "output": "2666604"}, {"input": "46 41\n435,534,2465,492,168,2402,780,790,1825,404,306,2238,1404,1234,1942,827,2185,629,179,523,785,1712,2254,1034,2295,1422,1499,1836,480,1786,277,1977,1716,2145,2063,89,683,2454,1122,528,1186\n186,2319,249,779,1628,2027,2180,2103,307,677,1793,2086,1573,2303,1598,1641,2487,1112,847,753,14,655,2342,892,2425,36,2100,1865,2063,2150,1060,1242,902,1213,1099,2261,487,700,917,186,2185\n975,1195,160,606,1137,544,1107,211,1019,860,2189,475,5,1423,2478,1511,1329,340,2249,1081,547,1672,1207,1329,234,42,1456,898,1145,723,1048,64,2201,2389,435,1564,1054,2475,2256,844,1811\n903,1328,1100,835,2382,1619,637,1827,949,1777,1509,607,1962,383,2031,743,1881,757,721,773,2333,2009,738,1155,86,1270,667,727,1614,2489,769,284,587,295,1746,1004,1863,1648,410,2157,562\n48,2471,408,1547,1572,84,450,55,179,541,1017,342,1096,584,2456,55,38,435,2221,1386,348,828,570,1967,2305,1819,668,1259,1358,1961,632,998,228,2226,1095,2226,504,86,182,421,2230\n1215,420,2095,1701,580,4,918,98,928,1749,1578,603,1447,1174,925,1575,460,2014,694,451,919,416,1154,1463,312,1366,484,1476,347,177,2476,618,729,1755,2172,1371,2456,742,1741,615,1235\n1175,1426,425,1110,2044,1511,1087,312,8,608,600,1311,605,1599,1829,1959,275,463,2366,1750,1140,592,370,1323,522,744,1577,1444,1307,2024,1736,1971,1695,2464,1365,566,1007,1569,1714,2250,2036\n2206,2186,2017,2181,2196,942,1575,342,2379,1727,2158,2366,898,357,963,1481,11,832,70,1484,2287,1941,547,451,244,1430,1478,570,1207,1885,590,2258,1724,993,863,919,228,564,480,586,1546\n107,1739,1522,221,434,2382,302,1953,2432,647,123,601,1496,578,323,1003,315,51,2331,1705,613,747,1924,573,2160,1226,1925,1685,1381,1818,54,1174,455,638,245,131,2474,710,2061,656,44\n1623,1735,1860,2269,1056,2343,2055,1253,931,1735,642,1113,376,2136,1546,512,867,1640,229,896,1606,752,2290,2478,316,1918,1955,1282,1659,1558,675,223,1521,1737,797,1105,444,427,318,1485,2470\n1374,114,981,1155,666,2218,436,267,867,2445,44,1266,768,2259,826,132,984,1102,348,2335,2313,183,2309,1981,187,196,1288,381,1264,34,1460,1156,1630,2048,798,1288,1600,1457,530,398,1357\n1668,2062,413,2056,615,97,2405,1565,1953,2401,153,1188,660,620,1896,322,382,948,883,576,659,2054,2114,2493,2143,1398,1832,537,1388,1191,1475,1764,163,1587,979,855,2485,307,624,2322,2037\n398,61,584,1267,2241,357,2043,385,1862,1284,695,1210,661,279,1147,2361,1488,1447,365,291,733,1887,1056,1938,1048,1810,575,507,2329,1999,162,1488,1174,1642,1675,528,1805,1502,2099,1284,1530\n341,1692,2072,1843,1076,174,233,1002,2297,32,633,431,1190,1539,648,2335,1635,298,913,1590,1893,382,1429,1908,1918,2191,1904,446,351,738,443,1625,1774,817,1644,1346,264,1299,1402,2475,1991\n870,1950,468,1140,1861,156,2232,637,1924,596,874,1311,2327,128,2462,1557,255,1480,1761,1939,874,221,866,93,1732,1105,1032,721,342,580,283,1121,1659,334,1221,1849,1719,2149,876,1062,753\n220,378,1755,1400,1216,673,813,1430,1716,1972,1947,2193,658,1789,1452,2336,1593,40,2297,2445,813,318,2369,592,1326,1296,58,616,1878,604,2045,1296,465,1664,1076,2132,15,1845,514,1840,2369\n399,149,895,768,1721,2236,680,2461,1546,885,1425,859,782,2362,58,1516,1490,66,1236,1257,2056,510,2044,1867,1695,1680,1440,1442,2221,1744,2142,1375,464,720,1879,1754,1528,724,2264,2436,666\n2223,1785,1562,1167,1791,1160,406,358,425,367,67,1684,424,2033,2231,408,1819,2061,2380,133,1187,1722,867,912,1862,2259,1560,468,801,1923,509,1436,1900,1691,1621,31,1534,917,2078,1161,1096\n1083,1259,1698,989,17,1698,133,63,107,628,1533,2125,2457,1300,1372,698,2343,1761,990,2276,1603,789,1611,211,2366,1757,527,1599,711,1651,1303,2118,648,1791,946,407,517,2065,484,2363,1605\n1065,2264,651,1320,834,381,382,105,1791,47,2430,626,113,2226,322,2342,1566,103,534,1858,1466,764,981,908,1216,793,2193,1004,1548,1066,211,1126,339,588,94,2373,423,454,1880,2440,502\n438,580,1156,1073,739,380,316,2024,1480,851,1600,412,2011,89,1694,301,1992,312,861,1719,1537,1284,1846,659,736,1223,41,731,2323,2484,128,480,1404,1420,1982,2457,2238,20,648,2137,1042\n498,789,2482,121,2195,94,2121,2096,624,885,1494,470,888,120,1341,567,900,341,518,1096,1120,1972,816,376,1427,2258,1205,1913,2030,1786,2099,1638,790,1024,708,810,1151,1609,421,2390,2406\n1276,678,843,1998,1775,1827,1735,2442,1112,1305,440,2487,1568,1758,818,2323,1445,1531,263,1840,685,138,2094,1036,2403,1678,1202,2473,2172,1442,1631,122,469,736,1321,1758,761,1465,1004,297,881\n1522,1523,594,1287,500,39,1304,44,1347,875,1906,2324,1317,952,2300,271,1579,1161,2464,869,2159,890,421,2297,1138,2489,306,2350,1727,1782,1301,1311,811,807,203,2023,2042,191,1124,1725,488\n508,1854,700,2463,1338,2421,1568,968,2360,87,1167,73,2358,19,1891,1164,536,1649,151,2185,2160,160,1381,66,284,1924,389,1700,1232,1125,1299,1416,1639,326,2279,1282,2022,192,1611,1222,1861\n2020,497,1531,420,119,917,195,42,568,430,1322,1784,927,697,360,782,1510,2201,20,215,1063,176,453,196,1246,307,1080,1348,1554,1105,697,564,2389,1887,491,517,1307,606,2392,1692,1830\n501,2137,2161,985,2367,1957,2007,1149,1318,1977,925,376,1080,1213,339,1445,2287,992,843,319,307,2025,246,870,53,885,1917,1577,769,1997,428,1394,854,2418,2161,2105,1283,1277,1859,630,2066\n432,532,896,1489,1579,1853,2103,831,1639,769,281,1138,1732,672,1258,2364,418,603,1888,438,451,985,67,1887,766,1092,117,1950,2174,1854,1441,1087,484,2254,344,1451,1767,868,616,1625,2056\n1764,2080,1366,217,1807,1116,1514,400,201,1566,1730,794,1204,775,1649,723,2433,1130,2169,2488,2021,2124,1775,447,204,1019,454,899,471,217,146,2356,1090,977,269,2179,413,1128,927,1657,1605\n1609,414,900,1098,2028,842,700,833,1423,1179,2442,1179,12,386,758,2061,1952,1250,977,697,1290,284,682,767,1360,1864,580,52,1943,1752,1368,85,727,1080,315,699,39,2433,1442,1940,2388\n4,2000,1013,1935,448,185,71,2323,1190,935,2151,2060,685,600,384,409,1247,1374,1853,2009,1436,2235,1054,1992,1038,1492,1879,55,1444,1233,1366,2121,2440,1983,461,1105,2127,84,605,1680,902\n580,1463,2039,126,1000,2365,1764,1472,845,365,793,1547,442,1121,2231,1840,2158,716,1086,1428,1356,1601,2413,1709,1131,1266,780,168,2373,2130,1406,503,1775,1863,2321,1421,1181,451,34,2043,602\n1910,615,2142,1186,2286,666,1243,1994,1180,264,1207,63,1859,167,890,1159,2429,505,217,2000,1252,20,1762,1442,2,204,1029,564,1434,1160,2056,2296,635,352,1108,584,805,1769,2397,330,1191\n896,131,1938,1452,1018,1582,1730,1634,401,1070,1237,2445,1272,709,2309,1785,1320,2368,570,817,1024,555,1705,2270,817,1233,1249,350,1217,2321,1888,2235,751,1539,1789,393,567,2156,1810,1283,2063\n1464,1918,1450,1751,1910,1722,1680,1889,113,2289,108,1724,362,575,1238,993,2377,2097,1528,521,2225,2316,1201,219,1608,515,1650,24,1895,2121,1885,222,346,224,1106,438,1365,2434,398,1190,2316\n1972,1357,249,497,2394,2092,217,839,2114,590,2302,2028,558,915,633,1232,1273,26,1986,822,469,275,0,626,2473,495,2129,396,1012,836,424,1940,100,2071,1817,1600,227,498,1228,1657,1981\n753,962,2239,1066,1798,504,1770,599,88,756,580,985,699,2095,2239,820,1950,1967,1187,1185,409,2411,2019,1504,1127,1602,1580,439,1900,1707,1740,606,114,1160,1872,492,2311,1595,45,2377,1240\n139,1820,174,1452,570,1916,1877,1134,37,648,1465,2050,2061,863,1428,2150,1599,2101,257,714,620,1441,2306,1389,1882,573,1140,1240,1613,279,1981,1542,1932,2481,738,2359,2076,2152,1061,530,1327\n2411,2378,1425,2394,1653,276,184,120,651,949,395,435,2045,1951,1325,948,969,431,712,1573,1720,263,253,1025,468,153,298,1808,1533,2484,120,712,1315,440,1841,1546,545,2350,2279,818,801\n1034,2011,1792,1171,923,824,663,1777,2164,787,352,2384,99,394,833,136,575,21,1472,1671,2327,2238,294,1395,759,2163,2032,778,849,2336,1940,2051,1442,1460,2288,564,275,1797,1751,1540,290\n2331,320,520,2118,1221,413,483,2042,944,210,2463,2214,1355,92,917,1187,1029,1599,1465,278,646,1179,306,2188,2356,988,2120,2048,1278,1635,232,2236,454,2387,1929,1077,122,132,1384,1726,1068\n821,1370,243,570,836,2240,1350,255,965,2021,298,2309,2498,144,1416,289,1704,2450,330,2258,1961,530,1108,170,426,145,2034,2079,922,1434,1767,1956,1242,932,87,226,107,803,2188,2490,1553\n74,2263,1974,213,1585,1545,512,1760,1748,2250,564,473,1793,483,1506,1440,793,1405,1788,237,975,950,376,2410,41,930,1691,2196,2326,187,61,1023,232,313,232,519,1796,739,1157,179,1286\n1432,2467,1000,1197,531,2482,1629,1960,501,314,312,1024,2226,843,2027,1462,902,1816,1239,1502,2258,1198,1000,2157,1095,1306,2217,2062,427,221,1419,1682,1991,1145,321,833,561,2133,944,1249,2264\n863,502,1525,581,146,962,1803,1858,467,87,2043,138,1107,1138,2409,1573,1230,346,244,1143,2497,1572,2028,77,1567,1575,1818,181,919,842,1553,755,1765,2181,214,1249,128,2218,1424,106,2493\n1377,1075,2420,886,112,1396,1777,1751,233,447,2266,1589,1177,2190,1898,1736,2345,2327,2125,1065,665,1561,1914,975,540,62,1149,1123,350,1023,2223,1211,1382,2339,1616,158,1123,1481,1100,1026,2490", "output": "2072759"}, {"input": "44 49\n1314,1083,732,1817,1895,70,1801,36,1910,151,1469,1966,2279,892,1673,239,2373,325,1132,2499,2258,1286,262,1804,736,1056,1131,1063,2027,521,931,714,601,203,953,468,157,754,2075,1803,2375,1299,171,2266,933,249,1061,1054,66\n1447,2213,183,2459,961,1432,447,317,2076,1817,463,2093,317,970,835,1334,2336,1521,1703,292,1746,1159,586,101,1337,2486,1475,1372,1671,1534,1927,1204,127,656,1508,182,1191,614,2421,104,435,2494,866,1282,2092,2081,2381,1409,880\n1551,2386,133,614,1560,321,316,919,2315,2062,2352,2245,1712,2207,496,2161,210,2486,1934,2148,2131,1806,1298,1102,798,2356,1200,999,1346,995,1482,945,1867,1289,472,987,1822,1679,1482,326,1441,2295,2071,313,1483,1983,2478,943,1838\n1715,941,2332,513,2202,1003,1669,2395,565,2480,1066,1175,1399,1285,483,333,1673,1724,2068,607,2359,2024,811,736,1859,63,683,494,1714,1078,2271,1924,413,517,139,1767,98,683,299,542,2109,2168,1589,1729,1451,522,1647,2281,988\n1201,487,1379,1378,2422,2493,441,185,302,1453,1838,1674,1842,1784,1184,1954,551,751,2414,2086,343,623,31,2431,2429,1515,1857,1553,1312,1796,723,2083,2408,1144,396,951,1217,2020,1397,197,2310,2120,2151,2374,2081,1747,1168,1322,1573\n1304,730,586,171,862,1763,2126,1139,2355,1287,407,1422,1166,678,485,1179,1121,1993,1797,916,693,1181,1062,2482,434,948,1141,577,393,847,2261,2083,691,112,2451,162,2211,2203,799,27,2000,105,1513,832,1154,2339,1746,1822,2133\n516,1858,1208,448,491,1820,1770,2020,1077,355,560,1140,477,1448,323,911,304,1339,641,2076,1373,1130,1857,2100,303,1289,157,1775,411,2135,1300,779,2286,145,32,1007,560,2401,1540,901,801,1086,1925,620,1984,766,2034,1157,539\n813,363,2114,877,13,1778,275,2009,2284,854,729,158,1712,1077,1557,2391,961,1428,1983,2172,737,1229,949,1196,1986,2007,1606,2448,1462,2225,1970,1210,395,896,460,1176,1718,1831,1332,1013,1740,474,721,1903,1306,465,1423,1630,524\n1981,2003,2461,1687,961,118,1191,1097,2078,881,1675,249,2303,1323,1071,1300,1684,1603,1810,1741,1632,1067,223,1099,1988,896,1391,186,1263,1833,1678,906,2344,682,2195,844,451,1350,529,2477,2210,81,86,1553,369,1365,1444,2264,259\n201,2124,862,1483,2193,812,643,2194,1620,939,1188,661,1531,1357,1693,883,2264,1018,55,147,82,2156,419,2054,1629,1986,173,642,1159,1234,99,942,1012,138,1115,506,1547,1641,537,1105,347,313,302,2066,1701,82,60,2218,2477\n621,391,2409,1602,795,2480,1278,1325,1741,2098,95,1237,1122,1879,830,408,1082,2360,1930,1542,1192,1759,381,910,1664,2297,1140,1979,1164,2184,2075,1001,1566,70,2035,1612,1526,2238,443,1852,917,2366,101,1627,950,1831,1514,1952,2306\n446,1272,1361,588,342,390,2297,693,850,2006,2430,1023,343,578,1651,1939,2143,2320,952,241,2021,1032,1686,1275,1383,616,149,1316,2315,2452,1665,22,1098,856,2303,2001,2234,2047,1282,965,1318,1889,1978,2107,2272,333,430,1743,317\n1538,521,55,663,2129,497,680,808,1792,465,159,1737,2028,699,2148,1995,572,2240,1712,1635,37,1215,481,1783,1205,1110,2140,1320,1522,2309,679,579,1188,2143,837,1520,2127,2476,1029,1933,1895,862,1352,554,672,2147,1940,40,1301\n1705,734,615,1927,274,22,1277,768,816,384,2202,1878,1355,387,250,1919,2434,640,273,1435,2290,925,1412,57,789,1124,1164,1745,2393,1252,1504,1651,1043,2298,2216,829,317,2427,624,421,886,1146,730,1076,2308,419,518,2139,2405\n1568,1352,2357,2425,2477,1135,1939,857,688,10,949,886,374,600,587,675,1947,1,1324,318,213,561,2095,1800,1742,1932,1339,1239,2049,480,986,2294,1610,1545,1579,1943,1454,1276,2138,1298,2173,320,2479,876,680,1137,585,1790,2295\n1808,2007,1026,492,2285,1783,1426,729,103,1497,1909,1417,1737,875,2292,782,1566,1532,733,43,802,1810,1478,2154,798,22,2401,1271,1345,385,1510,1039,2059,53,2485,1118,137,1126,1960,1631,179,1036,1123,234,2343,124,1928,2488,1861\n2008,711,1939,2234,425,156,1513,118,627,724,539,339,1718,489,229,1816,255,1287,399,2228,1136,795,68,1362,1296,693,2403,1500,2114,58,1651,1705,251,266,790,2054,604,1092,343,706,1816,182,1128,2492,813,2070,1676,708,13\n1274,1121,2296,1436,482,1398,1909,2327,352,2319,1896,361,476,370,747,353,760,1300,2421,82,693,42,890,1534,1885,332,1010,1260,782,543,1271,218,1553,1175,729,1142,575,2314,1292,1695,925,771,1117,816,725,1208,1062,1800,1083\n378,2006,1454,2370,1489,1428,2142,1841,698,150,2397,1579,637,2203,2329,862,1777,1420,1182,849,1401,2063,2259,1101,371,2102,863,1057,893,1915,1068,128,472,2117,763,1946,572,1913,2403,1322,1524,2309,1547,2410,138,1320,428,1469,32\n650,1726,1947,1370,1379,410,766,1466,1254,666,1912,2239,762,89,1798,1869,2431,2359,1781,1635,1939,997,1034,1528,2461,1383,1976,1643,1229,164,959,2076,441,1724,1744,1103,2365,1641,2429,116,671,2097,681,1231,2444,2146,812,2326,571\n532,1364,220,370,1266,579,1417,1878,1621,677,1886,3,604,820,704,1234,1259,329,756,967,832,1788,369,1002,631,2274,1532,20,1955,652,1411,409,1928,2252,1614,870,1934,1541,1898,994,392,1587,526,1303,546,1637,1339,1159,1739\n2445,1613,2187,293,1420,2000,2402,110,908,2492,729,963,1511,1483,1392,2053,6,2454,1630,316,942,565,2047,769,181,865,1236,1783,380,1390,1573,736,1743,617,1167,1274,1584,1968,142,1069,1727,735,669,1631,2119,435,1904,338,1418\n415,1656,50,658,1306,527,2353,2076,1572,1862,47,1991,1645,1730,223,1240,1740,1059,474,2472,1844,2056,1527,1939,1372,2191,1494,457,732,1736,2177,1570,327,615,28,1380,2417,1056,809,2109,1863,1781,198,1903,1153,163,497,2005,1885\n1503,205,2454,1512,1033,1743,1382,1213,96,2223,1094,732,1201,1461,1708,71,1829,1329,1219,145,2440,457,1463,149,2176,1622,1018,717,344,2191,387,516,592,2021,1765,1125,1414,1876,999,2144,2330,1877,166,313,1337,1526,156,601,2495\n414,1564,2099,322,1383,1236,1730,1641,91,753,1052,324,1775,476,784,2338,1068,1241,2105,2208,998,200,1532,2348,1937,881,1789,1125,760,1133,2054,187,2476,1632,742,1167,1116,20,1667,848,76,1697,531,1125,1093,1894,2453,1303,397\n906,920,74,1329,905,261,1178,2495,1886,2408,1723,2438,1346,2217,1593,1948,2284,51,1404,1395,1309,1418,1820,621,1892,2043,862,2180,696,1597,1047,1650,132,2340,321,1992,2299,1414,340,850,2169,1512,1245,1195,1291,1849,1914,121,638\n2395,682,1440,2313,1767,1701,95,1162,2279,2010,961,1537,2201,539,1550,2486,505,397,1620,894,865,453,2337,1185,731,651,1642,2253,1673,1441,891,1712,2454,1142,1308,1487,432,1301,2057,2193,2181,1606,922,1654,2026,1900,1172,1840,642\n727,1638,1181,13,2181,1368,1900,705,402,1570,2376,1712,1713,1680,773,118,918,567,2497,2061,329,2455,2337,1674,93,1331,2497,1023,681,2331,1932,372,1516,93,2463,1594,2261,2094,790,661,1875,1511,980,717,1934,818,1321,543,1200\n265,126,847,2365,1888,1880,1003,2470,1817,990,724,1889,2048,455,2474,1356,652,1002,1893,286,28,132,1664,2128,1925,1578,288,1708,1065,2200,1708,487,1655,2229,135,296,2466,162,1009,1195,591,499,821,1056,2055,1348,1238,2267,1069\n638,245,858,1307,808,305,1742,251,1958,2316,393,1989,2423,408,841,2226,1565,240,327,1326,1968,405,353,2029,475,832,553,400,2387,1267,66,554,1242,1900,17,661,2133,2275,361,1185,376,488,542,2185,1881,1225,1298,559,1984\n307,2488,872,1786,1951,2089,1509,2010,1558,1206,1755,768,2478,293,978,2269,326,153,2045,1235,455,1552,500,2365,1172,693,1021,621,487,1426,1163,196,311,972,337,1374,892,1357,210,1683,2444,1774,759,1591,272,1665,2244,1037,1410\n1380,684,1323,718,2035,1277,307,8,569,1488,1159,1992,266,1910,2391,2223,2446,1130,2132,2153,1470,1744,1599,2476,1156,2075,2335,2448,904,239,125,1512,434,2420,1395,1772,1849,1424,1646,852,1497,1491,2067,1213,596,754,1836,353,1866\n639,1596,1655,545,1481,1659,1503,106,1060,1567,32,1951,92,175,339,1204,1124,455,911,20,1548,2085,1724,737,1067,165,2096,1823,420,21,14,1686,1675,2217,2455,241,1113,410,1990,555,2196,576,31,1932,1669,690,787,2054,455\n498,1438,660,573,939,585,2261,606,741,716,2277,634,1162,53,2195,1137,1929,1338,637,2154,788,1466,2482,2420,2439,1217,130,5,1117,377,159,2270,1097,1852,2479,474,934,1527,416,472,1008,1421,121,1287,795,1305,1814,596,674\n2173,2425,537,31,1788,1184,481,1472,2004,2279,167,2452,1902,2147,984,119,522,2213,70,298,97,1229,419,1178,1349,993,1234,316,1363,517,2091,391,1075,1179,1923,2276,1679,1860,1178,527,2255,149,717,348,2088,2275,2499,914,92\n1579,909,1410,2038,2290,102,931,1903,2286,2396,472,597,398,908,1821,1026,981,1648,2442,2358,56,1306,1359,2263,1323,1410,2019,1524,2426,2343,1253,85,2231,1139,764,2358,2,1716,2468,1760,2320,200,1220,1471,627,2129,2489,2225,1757\n60,1545,273,198,1591,1358,1721,1882,985,956,1852,1119,1520,1818,177,339,1634,1303,589,1819,1697,381,912,1713,2294,283,1224,2407,2260,239,573,1465,900,83,2097,1148,796,1961,1632,658,1629,1211,1103,1234,1883,2043,738,1323,37\n2177,1155,754,984,576,1026,713,870,1234,2098,19,130,1121,327,1861,516,1260,453,1355,1400,1010,1631,2459,442,1341,2189,1384,1291,1878,1154,2395,117,1573,713,2043,2306,1551,61,664,1136,673,1511,1852,251,979,872,907,591,1384\n2456,1192,1469,742,910,338,1319,2202,570,2151,1584,927,188,1144,82,572,2478,1782,1606,752,2457,371,1812,646,406,1988,1210,642,2458,568,536,108,1237,356,1668,1900,2218,724,488,1471,986,2418,721,1663,1566,2474,859,1944,20\n1622,906,516,1453,135,882,496,944,2401,642,2048,184,1237,2177,1467,31,757,619,184,1712,390,2396,199,435,2361,980,997,866,1530,924,2004,2474,1995,347,2472,253,8,238,88,752,2382,1399,1762,407,1543,598,754,1394,1542\n1150,2016,262,2105,1509,1449,2456,1266,10,1841,2373,584,929,1,1170,1409,889,559,959,339,1577,1919,1906,2189,309,1166,1357,1543,1186,1806,1179,1003,1818,52,484,1211,1444,802,427,328,1848,2043,1752,1723,1753,1392,239,1411,724\n1928,1712,274,512,108,2357,655,2268,354,1315,1952,2242,225,1666,303,245,638,540,1007,283,466,1600,1959,2240,1809,98,1582,1957,1751,837,1373,1007,554,619,812,1991,504,2208,1457,2399,636,293,565,1550,2116,1165,2099,1505,1696\n903,2039,343,340,1171,623,2483,1276,788,88,164,118,1002,1857,1378,1006,2333,2203,2312,608,996,299,848,586,1063,1791,1411,2455,2057,1556,1556,854,519,1960,2192,1056,423,2010,2268,826,2035,1690,1402,2335,293,1396,861,2145,571\n168,386,402,1125,124,1588,1446,670,1752,1609,1199,753,1765,1823,902,1510,260,591,1998,749,1145,1294,1414,903,1019,2002,1496,1606,1286,1580,1922,1682,1065,2166,1807,2094,1202,2411,1744,654,674,1141,2366,1179,1505,492,88,1256,1666", "output": "2315101"}, {"input": "6 1\n1692\n2369\n530\n2324\n1715\n1339", "output": "3578"}, {"input": "6 2\n585,222\n1727,517\n1832,1711\n2016,734\n2446,947\n1308,89", "output": "4508"}, {"input": "10 4\n1054,1103,567,298\n536,2357,451,1233\n1790,1520,17,762\n603,802,1198,2021\n1890,2253,25,1175\n1412,2018,2323,1899\n560,1530,476,2128\n1193,212,1879,99\n833,942,2169,548\n383,1198,1854,2275", "output": "25030"}, {"input": "3 4\n790,1821,639,229\n2324,1104,1297,262\n1616,1999,1639,1823", "output": "1427"}, {"input": "43 46\n899,575,2130,1746,821,17,462,275,566,620,110,200,2121,1196,2061,1099,518,1588,1036,2224,833,838,870,1732,1848,2360,1560,93,2086,681,2212,2479,1660,2042,351,847,1561,35,1374,1037,2484,1171,1781,2455,545,98\n2303,1517,1717,1146,2327,212,465,769,596,1071,1513,383,2309,881,1532,204,3,317,443,1359,1195,1603,449,1946,1413,2173,245,2215,199,887,2145,2087,2363,146,1170,1045,279,250,1154,251,1113,991,261,1427,1661,1576\n2084,1392,310,874,1352,782,2139,422,1124,2109,889,1955,1270,1876,1309,1442,2071,204,807,172,49,422,1651,2114,1301,1562,1154,1832,450,1994,1846,2248,1074,147,373,2491,152,633,1894,420,1658,2483,2159,2288,836,1981\n421,1785,382,437,1498,2113,1594,1737,2119,1730,462,348,2329,2339,1925,1578,1796,1459,2372,2135,827,815,654,1695,268,1951,170,1314,115,1363,2196,849,1535,776,1046,1460,2208,274,2408,1424,1728,1340,1801,614,2234,1513\n1011,1493,980,1013,2369,2430,2085,668,1156,652,1588,1639,581,386,1917,1974,1372,2291,177,272,1352,2209,1096,1742,1752,2244,1986,2477,852,17,829,26,621,2111,1396,837,645,1892,732,1961,1573,1761,2426,2294,909,1044\n1297,285,1519,250,674,1310,515,2121,1518,1228,1746,436,977,18,2229,1913,780,31,2192,2311,1932,512,32,1870,916,2275,683,1981,1946,1921,1867,474,495,2053,1198,574,1306,525,1969,2064,1597,812,4,2468,251,35\n1812,339,599,299,196,579,1141,576,792,1209,1188,2002,887,212,1428,1980,1831,1923,384,1749,492,2374,2386,1944,443,1540,1494,2498,1779,1433,1633,1649,1864,1665,1212,166,2487,2496,1546,2146,960,797,1177,1089,65,71\n1501,623,661,1153,566,1555,1493,803,1879,820,746,520,361,2373,311,1058,998,54,1878,87,1482,1165,1958,996,1725,205,467,1370,2018,2403,468,338,1346,152,393,179,283,1625,620,1716,36,125,2064,133,551,1643\n1428,2295,2342,855,1071,1919,1377,2448,1866,2278,832,903,1305,1183,2079,2049,847,1467,2015,365,2458,765,441,1161,2336,1650,1933,2335,373,1032,1574,993,2069,1692,1586,1161,983,638,93,850,375,2026,568,1669,1733,1494\n599,2123,581,1271,1609,2206,1364,1080,2425,681,2040,526,1188,10,161,140,578,85,2236,1602,203,353,1245,1544,71,1309,352,2413,98,2291,1384,1146,853,586,2029,469,1641,831,233,811,960,1311,1723,889,1562,2450\n822,52,366,238,232,154,2413,214,2155,2437,2411,961,270,2265,1816,2134,466,14,1268,2177,183,710,2157,944,1375,1141,264,1372,2227,2458,736,207,942,202,1075,903,1816,1708,1739,362,993,1710,1613,697,2186,101\n2096,337,574,561,1757,2129,273,1428,2343,1241,1879,1050,1875,15,1423,902,301,361,148,1428,2246,868,1001,34,1772,2036,830,2476,1834,2063,1188,571,387,2284,2394,511,1263,573,1729,2483,953,1943,1671,1458,117,425\n1661,1989,1749,1961,402,2085,2028,1960,1630,513,2174,2222,887,1675,967,1771,2231,2154,1464,100,359,1624,661,1883,1644,704,2425,650,753,1741,1770,1781,1818,2108,2108,45,2334,797,1833,1626,350,1618,1330,692,767,2254\n2466,2202,2495,2,1899,1193,2378,2390,990,1302,2316,2193,434,555,1324,1398,1952,1967,1904,623,1776,1321,2470,2031,1557,1213,102,2248,769,2281,1512,2179,100,1298,120,296,1191,511,1805,447,1587,1350,1977,2258,2386,771\n2341,286,569,2417,1443,1623,1437,380,2188,2182,1807,328,467,1263,2152,1755,161,229,1478,178,17,2471,752,1072,1104,2434,741,2141,1831,2298,2012,1431,1896,203,954,68,578,2415,803,73,505,416,614,1392,54,261\n2077,1603,147,2020,1127,700,2341,94,1644,2460,1411,611,742,663,930,774,1671,2476,863,487,2297,64,1574,688,171,55,2041,801,81,557,1071,707,1576,1734,568,1063,2351,1848,1488,979,1923,1180,101,1337,2026,376\n1134,1249,1601,2447,1505,1671,2031,1047,203,1558,2223,2019,853,1482,1244,1036,1526,896,1041,1352,268,1149,1559,1757,2248,2197,1715,1449,2105,813,1096,2075,812,1215,2300,936,1446,2240,1757,655,1705,2025,884,1778,1604,1227\n2120,1282,984,631,120,1887,1936,1494,2148,1929,18,2080,2494,1190,998,651,1673,2498,2297,894,1031,1231,998,1763,2445,1381,2193,129,1458,97,1251,1307,244,1479,130,2440,716,2179,1102,1642,1898,676,33,209,1875,807\n1148,705,2471,803,2323,187,1914,1830,930,2007,581,2417,1289,1104,1414,19,989,2302,117,259,1727,564,1372,2290,1438,450,1451,157,543,19,1228,1406,94,757,2303,385,1276,859,1406,929,265,570,1900,2443,1084,952\n916,2013,1354,770,322,411,457,582,978,1444,2359,119,1125,683,1642,1466,756,1887,1082,610,2258,1778,1557,750,1408,454,209,2144,1488,2031,915,2164,788,2269,1433,1427,1198,1401,328,1063,1766,167,2472,331,2394,950\n1327,384,321,1952,1246,1409,1464,1280,900,1858,128,1711,555,1941,763,2227,440,1702,1866,818,1013,1811,1024,1578,391,575,355,1300,1948,1534,1733,683,1742,1054,415,711,1737,117,2104,1054,2153,485,2093,1810,1606,654\n57,2413,242,1736,2338,958,343,2471,1767,985,82,962,2448,1376,302,1785,2023,242,1272,1374,133,1351,2417,2211,585,512,1715,1805,932,409,709,881,1148,938,2175,2277,2173,157,1263,2056,1409,370,1195,623,234,594\n1512,2489,992,1641,1219,1500,189,592,2264,719,972,438,1008,1045,542,1930,1481,1519,1808,1550,1911,756,2483,2497,261,451,1356,1199,2418,99,1168,1059,794,348,2135,831,1225,1018,1785,1525,921,346,156,642,2397,1981\n1981,486,439,1313,64,1671,602,2394,469,1915,2477,518,1596,1391,263,1851,875,662,2085,456,1750,578,341,219,2062,2003,936,637,641,401,2431,2252,1008,1626,2323,309,1319,1813,892,1886,1782,1982,466,110,1470,560\n2313,2104,1848,1996,4,1810,1196,1418,2436,331,1528,804,231,1041,1122,1301,209,42,727,24,536,1545,2132,999,2295,2024,2273,140,872,1268,1418,226,696,2434,1295,2060,1637,1853,1624,193,973,194,1114,34,2476,842\n1118,1671,1881,1425,1218,281,2197,598,983,1736,2218,2068,394,182,309,997,2250,541,1828,706,293,198,1284,410,998,1001,1150,1537,246,411,2234,1271,654,609,11,403,962,2193,2240,692,1481,966,711,129,2253,806\n314,1584,2142,497,1683,910,1701,37,973,2201,2315,352,1961,1005,1558,2458,51,1908,2090,2426,1254,1991,1754,1974,754,189,175,94,1448,530,330,1052,408,206,1941,36,1870,467,1776,988,1101,2296,1495,112,2183,2484\n1313,426,738,887,1879,26,2167,1520,331,451,2392,329,1084,1244,1481,1063,1488,1721,2480,1935,580,1619,1409,1386,1595,470,2457,762,1857,1752,2041,320,967,1798,1827,476,2052,2049,1700,579,1743,985,2394,1451,1641,436\n550,1645,1563,1804,2227,896,103,1524,1488,2025,849,1879,403,801,2230,2149,1957,1173,190,679,572,890,1182,1559,281,1236,1217,1601,1561,720,2024,1737,838,894,3,1215,452,293,1872,1704,396,1221,713,418,1534,760\n1210,2094,928,461,2461,1625,2178,1726,848,1702,1072,1962,111,1025,1590,1282,1544,2206,2315,1587,2429,2091,1978,89,886,1545,2257,2288,947,12,115,1139,2217,900,1992,2471,933,1644,929,322,1411,2361,741,593,2432,465\n686,1976,236,1570,1350,2450,913,1147,263,178,1082,204,1544,594,2371,385,335,2225,1850,697,525,2103,642,1150,1965,508,2124,788,83,358,2197,467,1828,2389,1640,218,1967,1370,1835,2153,2132,1032,2361,1954,1166,2382\n1838,2458,232,1293,660,552,436,2008,508,452,1143,2237,1676,1375,1710,1457,2116,388,2264,2189,417,38,1772,315,2017,865,1283,1664,996,387,1670,819,385,688,2442,1888,1501,1443,1837,729,1697,423,1714,2444,1249,2493\n1681,892,1998,2296,2077,290,363,2350,865,2152,2416,2378,2397,219,1605,2172,682,193,466,848,53,2046,314,1744,2022,1425,772,703,470,1593,908,796,1726,493,991,314,1925,2158,1349,1096,2369,150,185,1271,2466,230\n993,1950,669,2463,1463,1211,1521,2113,1363,2062,921,1399,1724,960,2448,2400,2245,506,627,1973,1140,892,2472,631,595,1319,1400,433,1793,1115,285,2458,754,1321,2284,273,1040,2021,1724,735,435,746,769,1662,152,497\n2220,1618,955,2340,2450,1069,1466,1057,400,851,2272,1030,1303,957,384,1285,1595,891,215,2470,992,35,1926,2448,1638,2135,1383,188,2404,1755,1252,1484,2372,2205,1903,555,1136,131,2303,2479,720,440,1887,1980,770,1346\n380,1714,1640,2081,263,272,844,883,1927,786,1756,1854,117,1958,557,495,1961,927,1203,45,738,1251,543,703,699,1107,385,2151,940,251,1686,1006,757,961,1777,1280,1263,59,385,2229,409,1269,1188,1099,688,1214\n2264,1108,636,126,644,1144,1002,1506,29,2461,1260,1799,1684,1437,372,483,2108,1744,266,1377,1706,1122,33,2359,1167,422,1265,2027,1439,788,2208,266,788,1914,159,1310,1274,549,1229,1330,382,228,2083,733,1579,311\n289,111,817,1303,1570,1308,1094,742,2367,2431,718,144,714,990,1967,1565,1563,1772,2388,1734,2457,709,687,2334,1421,957,949,2200,1571,382,2329,1024,380,267,2219,785,2493,66,944,1251,519,1148,609,1204,9,1550\n1739,727,2098,769,1106,1679,783,825,1228,2119,2206,2476,942,975,1054,854,1935,1519,419,2157,1561,1786,1042,152,2079,1780,1482,1179,719,1164,1020,2302,723,1571,547,2271,1350,1407,85,1842,1101,836,1392,88,2365,1422\n668,2291,2142,1528,2493,1114,1964,33,1018,2331,1748,2478,1728,1160,1338,858,1321,2461,393,1926,1658,1344,183,1059,1875,510,2250,2142,824,18,154,2424,2411,1393,1122,558,2254,2083,1865,869,1125,1166,1646,1545,2114,1776\n1760,1843,2412,2207,2373,1057,1871,67,1673,436,1874,91,1774,2393,210,348,1068,1803,336,330,107,880,2144,1067,1835,420,1379,1606,1967,1468,1715,1770,1334,0,1387,313,2223,2069,1730,81,392,1574,2012,1198,1068,2305\n740,837,1163,849,1507,1781,2357,2118,1342,76,1139,1327,68,1372,1675,1673,2361,939,1984,1405,1273,186,555,1082,728,2297,1780,295,1931,2199,2407,687,1356,1825,509,1231,136,532,1353,228,985,2207,1325,2009,1752,706\n1541,1232,2106,292,1684,1021,2118,1177,2346,1001,1667,2290,212,1578,802,1323,2097,1436,904,77,346,89,325,578,1799,2249,2367,1545,2462,1365,344,853,6,1204,2063,1510,603,2005,1882,1434,2147,1540,1944,199,885,1586", "output": "2129961"}, {"input": "3 1\n795\n1730\n883", "output": "848"}, {"input": "50 44\n865,2437,1057,1650,2083,2448,1546,1001,952,429,2200,294,616,803,910,1518,1801,1727,363,1952,195,1837,900,508,1828,1234,1146,1463,1888,1890,1753,708,1693,556,1589,1003,1607,1820,2204,1282,168,2086,2270,2479\n2000,2031,1085,2030,1533,1116,1174,980,1168,2057,1369,566,2406,1450,779,1827,1882,1039,112,983,1950,1594,1907,1719,2283,1946,1152,102,1086,615,92,1966,1725,1913,1452,329,1262,2444,1823,1436,818,1220,361,311\n1298,1929,850,851,243,2409,238,132,190,2338,1137,137,1675,1526,1631,1462,2073,614,991,1189,1078,1406,1000,2151,1366,1731,1496,1007,1400,738,820,533,1685,1760,130,55,150,1065,1910,118,2337,322,287,245\n1005,1260,2395,1481,1726,318,322,2457,2448,2055,2325,2423,1634,1287,329,355,2243,416,1303,2057,880,1834,1133,1645,1746,313,1277,1255,1926,1837,1741,380,2091,1672,2093,1994,0,1149,1890,2390,1685,1637,1570,2242\n603,64,1527,545,1510,1655,1405,2459,2400,1535,68,2157,277,1131,672,953,948,14,739,2352,761,2033,1731,1170,71,1292,1139,1970,991,2191,1729,715,637,274,1037,224,1452,275,885,361,2178,1591,1540,132\n1262,1984,1259,1847,997,873,2260,2419,369,1037,1858,2049,1390,686,1069,1864,1225,1238,525,10,769,1340,2480,1075,1155,422,68,681,925,2066,1969,924,1463,336,2200,1664,1694,1270,2035,1962,1238,391,834,369\n833,1501,312,2070,769,35,578,1455,2105,1531,801,1095,1713,1303,2189,321,1430,860,2159,2203,1493,687,487,2002,2254,2467,1342,1407,237,2364,2140,1243,311,699,2269,1536,1352,1478,2125,453,1543,1887,1413,728\n881,2203,841,397,2406,902,1274,2181,2342,375,2243,168,227,803,2182,266,1057,1577,774,1061,520,2485,708,1276,643,421,2491,1515,2352,1897,991,213,2406,416,710,259,2109,1287,633,1934,791,1209,371,356\n1211,1644,360,805,1021,343,1361,1459,1484,801,221,257,1313,915,159,777,241,1258,1215,42,1842,1806,2182,360,408,194,1668,1476,2248,1241,1281,1309,1870,1666,1770,972,1251,1333,1243,490,2287,752,2447,2420\n402,579,1665,2449,1093,1397,625,225,1707,1256,336,421,93,1717,428,1566,1558,382,70,241,2156,542,655,1024,548,505,1656,2193,579,1709,2062,515,622,342,2044,1457,1647,698,1560,2328,1562,598,124,2167\n792,1109,2033,2346,353,15,45,1414,2329,943,569,1440,2016,530,543,2257,1867,201,824,646,597,124,190,1897,1094,2289,1391,2020,527,1040,783,2279,1896,500,592,2498,1432,361,1209,1370,762,183,1356,2096\n94,603,2113,1636,65,1556,179,1179,2262,117,710,745,1073,52,1714,1468,1230,1954,1079,1847,1634,2486,1397,170,2373,95,1053,341,2058,2393,2068,1353,1784,1606,1063,836,144,384,1593,1348,1451,1767,551,903\n2108,2289,2015,2174,2083,2090,1813,1560,1423,1743,973,303,843,1594,214,1706,524,565,2423,94,361,400,792,2277,1565,37,1144,1974,2413,1134,1831,326,2365,63,877,2084,68,849,1348,496,1050,2134,2403,1321\n1007,2294,690,2332,1187,1261,300,2413,499,1063,1882,2307,195,1481,955,1260,1804,524,2297,980,2410,1468,380,1674,1942,880,230,2311,1357,905,516,1613,2021,32,2279,1047,2091,2117,1654,2165,1695,1358,1556,611\n2428,683,1505,2190,760,650,2152,674,2197,6,453,2158,894,631,1005,1529,858,170,1789,2088,2106,1404,1749,2192,1220,1730,1986,1677,2028,2057,75,1635,1140,1326,2259,896,1964,1101,1149,2353,1333,2354,1945,1371\n600,325,946,1463,821,332,1956,1320,1411,1350,2456,649,2060,2001,1124,2201,1873,1132,356,263,1192,2156,1580,640,1755,1817,1323,492,482,2019,1738,1053,1370,917,1098,1664,1456,1303,294,1467,1785,1272,457,1651\n1804,2168,2452,1748,973,32,204,2317,846,1437,2065,752,249,451,1622,785,154,351,1340,2357,1947,635,706,1150,592,517,2147,1150,2217,880,1250,2458,685,1964,1562,1680,2266,199,2325,2129,1040,1785,201,339\n2073,137,1124,33,835,805,1228,2267,20,294,1366,897,1796,991,1534,2158,1634,1639,1990,427,1416,1336,1069,1116,1707,64,1413,1003,2399,631,1609,167,1791,1984,1094,1650,564,2030,557,196,1362,844,1618,1224\n2348,257,438,2454,627,2173,1429,1674,1820,628,2053,1492,174,699,350,1463,1314,890,2281,1007,80,2036,1859,1393,1310,2248,568,365,650,1582,747,1707,1064,891,2487,1518,1628,1956,2097,1093,1181,1619,10,1826\n2298,2496,91,1968,1406,336,2304,2332,409,2486,2067,264,1868,1979,1534,1516,280,627,2345,1135,1224,393,1256,2474,676,1388,843,410,1759,1128,2217,728,2129,1001,2119,1377,2336,1949,1114,1802,1822,1779,1435,1553\n1307,2385,150,1971,76,1481,1335,1241,1078,861,1253,911,1769,2199,1928,2017,417,1377,1681,2308,715,576,10,2384,1088,220,1994,1658,987,1222,461,1416,862,1474,2431,1899,1911,511,208,195,449,504,1364,1033\n1893,1863,936,1178,1076,984,293,1074,2197,1981,546,708,1443,1496,1918,2049,1379,1643,1042,425,914,1403,1107,1998,1265,390,1611,2187,1346,1532,1915,876,1286,621,973,592,2197,1502,1527,1431,2263,72,2384,1409\n1990,2448,1234,1998,1483,2054,400,1674,1648,181,636,2174,1075,481,792,1681,686,976,874,1236,1818,7,1231,74,1904,416,1030,1640,2428,1821,393,1042,2018,2416,2003,1005,1191,509,2277,1430,1308,2342,1392,170\n2122,887,2045,1160,1527,1648,151,502,1890,104,782,2492,1590,412,79,318,1884,1425,127,161,429,1795,144,1569,1884,2346,1104,2353,136,2002,2224,1771,2446,729,2166,1280,1285,400,1629,639,449,1495,2368,968\n2251,2397,1737,1823,1645,1023,1445,810,1754,1993,983,1507,1458,2159,2434,1669,186,2003,236,1861,524,544,2187,2205,878,1106,349,875,944,1414,436,794,29,304,1114,776,193,2472,1917,1269,675,2017,1268,928\n1770,1659,921,1284,1965,2325,1695,1808,256,1097,2130,91,802,45,211,1868,935,1491,1789,1494,2296,628,1596,103,2103,713,1403,743,1700,971,1928,2421,1083,279,579,2074,2142,1598,1757,2389,424,362,517,526\n803,680,309,1080,681,1320,651,1546,338,443,2398,2003,2238,2324,601,1364,1253,1615,1304,1849,1081,1117,1546,1524,879,740,1535,1298,1147,1173,312,448,2133,399,2180,1403,349,875,1564,1843,768,2093,74,1384\n591,237,844,2263,2211,410,2429,886,1820,1756,2101,1232,408,2199,1144,2034,328,1065,1564,551,679,114,305,1069,2139,998,812,995,1325,1093,244,399,455,756,1814,692,2218,848,1594,46,801,6,2081,1972\n1617,1192,1919,1977,189,2347,43,1727,1979,1783,444,2226,971,1904,1545,591,2472,1528,10,1979,1724,1977,269,1704,759,384,2043,603,171,1154,2234,2144,2114,1616,2297,202,1227,421,2052,1597,2352,910,183,926\n662,1585,1218,1345,1640,1051,1758,1913,1222,447,2411,341,1643,151,1322,944,2495,83,1584,1024,2331,135,2312,1992,63,939,1222,535,1377,468,2441,1845,217,505,2262,283,1530,2288,2350,408,769,1626,2231,582\n2373,1602,1902,44,1893,1135,717,482,1360,1010,274,2450,1019,1630,567,1396,703,1644,14,575,713,463,1734,2340,102,2254,2089,1865,1502,1131,2106,42,579,2471,949,815,1507,2233,945,2062,1220,786,338,17\n1672,1483,1837,980,1336,345,1966,1275,1384,1039,1545,2350,891,1413,500,106,667,333,1246,192,362,616,2224,1001,775,355,2340,1353,1505,2102,2387,1975,2319,2368,48,903,1388,2469,1858,409,2018,2019,333,1990\n109,787,133,1414,1682,2049,1850,233,2347,1242,301,530,1038,1564,19,1351,381,1606,1037,2215,949,2274,2419,1313,855,979,1835,1577,2288,1060,472,2282,1857,1653,1873,1903,1784,248,38,1588,1146,919,1270,1329\n2404,1863,955,327,1935,968,182,932,924,725,1082,2376,1721,1848,1365,2047,1081,1393,476,1,1237,2223,1150,2184,176,2402,1243,1797,889,479,2217,379,1410,1585,80,1396,1185,664,1981,210,1863,2434,2390,1474\n2374,1224,1955,1693,480,430,440,209,1982,2359,1936,1606,1256,1841,1482,1187,1438,1713,1398,1889,613,2096,2315,1867,621,681,1586,2361,860,1212,2076,1383,1099,101,832,2375,42,2493,2078,1056,1557,2164,1428,1707\n46,1777,1552,2417,2447,745,1670,277,894,2127,541,1678,2244,1951,138,1813,1805,1868,1798,2441,1534,1918,167,840,2332,2314,1664,591,1541,912,2035,1918,2413,752,1818,285,349,225,1793,976,1464,504,532,2268\n2445,1718,706,767,133,1666,2210,687,1177,826,671,949,788,990,212,586,883,2414,941,1033,1146,1552,92,1643,112,1547,2318,1059,928,9,1633,1408,534,781,1396,1792,2202,1604,1323,575,2452,1251,370,559\n2071,1407,993,1975,198,135,1566,1085,1039,2175,2276,1377,1176,2177,1961,1395,1005,436,476,2370,2131,40,1048,682,1483,1433,1273,586,2168,26,1327,1014,1818,1680,1239,540,1495,1364,122,1964,2282,1737,2255,2171\n1829,2229,1625,112,739,172,936,2417,532,691,501,1020,307,1968,140,381,1335,2294,1643,1698,855,2424,2362,539,2211,1933,2317,2148,1982,653,2127,2035,831,312,1030,645,1268,2324,1483,1674,711,2360,463,1941\n2365,1606,1268,1230,470,1749,34,960,797,748,2219,2280,2074,27,1929,18,79,1327,321,169,732,2158,1997,1278,1386,324,614,86,602,652,14,336,2003,1478,1218,1501,1112,273,1631,1128,2170,2040,563,279\n227,1102,1662,1700,539,1910,1308,73,400,1456,700,1661,2339,1832,1035,1129,699,208,941,1631,226,1971,2189,1399,1197,2223,772,826,54,2346,1525,2079,2021,580,974,2274,885,1629,2190,42,1745,200,360,1063\n1374,1824,2434,628,938,551,1643,1988,309,1097,2177,1401,2048,408,1885,28,391,1494,181,437,2316,1770,2033,2495,1979,541,113,528,1435,301,2340,535,189,488,2303,633,2251,1445,517,975,929,611,2314,1843\n15,1100,2356,809,1952,2398,1394,2070,661,2430,422,1407,2193,1523,1321,511,316,1758,864,2475,1817,341,1156,2463,675,79,1911,1369,1882,1239,453,1268,751,1224,2299,1915,975,2387,1687,649,1578,533,1416,2462\n326,2118,2234,973,287,728,1230,2355,1924,1841,965,1778,1888,1966,703,1056,1216,783,1252,809,1403,1246,1894,2125,2029,674,2472,1541,1482,1951,451,1382,1663,1259,912,2123,176,641,2340,192,927,1106,2187,76\n1215,513,1200,1928,2380,1715,207,125,204,2324,1175,38,2463,269,1716,1451,1978,934,1957,1700,522,1179,687,1660,1564,566,515,1499,1071,2432,629,135,904,1689,2455,945,217,2438,346,1099,240,410,1360,607\n1911,990,445,465,1884,755,746,1622,1272,269,1059,2012,1344,1724,2341,52,47,269,2136,1089,515,912,890,1351,2160,1117,1836,1254,670,646,2356,2206,992,1323,1709,1701,1971,1952,337,1445,1020,2437,81,691\n680,1766,669,1233,1904,967,1649,1328,43,174,830,586,2478,2305,65,2353,155,227,1770,1231,1856,1665,276,1276,1233,596,1849,2061,2002,1021,1330,1302,1064,215,1163,721,1018,511,1640,2018,2452,588,250,1773\n1814,1489,1096,2338,920,804,1252,946,2353,1639,2406,78,1135,1308,868,2416,750,1420,714,2102,1920,2285,911,1369,1870,811,1016,2092,403,906,1008,80,1971,952,1135,1394,1018,852,206,740,942,1733,1270,415\n732,624,1200,1948,1038,88,2334,2206,1533,781,1878,644,225,990,942,1420,183,1327,297,1637,197,514,1018,540,1337,392,116,1996,367,1497,1460,1328,2188,2042,221,2407,1092,214,1119,622,623,1225,1396,1610\n1251,291,322,2431,640,1520,1524,358,539,1313,952,2091,145,1991,2117,308,2401,373,1021,1414,87,1430,914,1270,1040,280,1926,450,1364,2036,1286,1466,2032,496,1606,1770,944,711,2109,538,1137,1677,1007,71", "output": "2362242"}, {"input": "7 2\n1681,549\n304,2197\n1493,1771\n972,1294\n538,37\n3,1876\n1785,299", "output": "10833"}, {"input": "5 3\n224,1287,2486\n2303,1578,2051\n1468,1720,2439\n1824,1886,316\n1253,777,883", "output": "7745"}, {"input": "7 1\n2069\n172\n2428\n155\n447\n180\n322", "output": "10516"}, {"input": "7 2\n205,886\n2457,609\n1988,2103\n2148,2051\n2282,402\n2203,2432\n848,156", "output": "7142"}, {"input": "46 50\n469,1580,995,2272,2142,466,1669,2081,1937,2194,1443,362,2160,1446,1722,2440,187,1435,144,2421,1563,1368,1639,2280,2196,656,1557,1960,721,2146,140,49,1962,639,1999,641,7,2269,459,1189,1832,632,791,1876,863,1440,1720,1158,72,1909\n2112,914,117,2185,909,203,1639,2472,1816,2131,2451,2392,2333,1520,422,1045,1419,1163,2488,2247,837,1686,1890,325,1065,1587,1969,1079,2311,144,1780,1552,2157,2109,1711,1840,1526,280,2298,1382,2012,413,344,1740,1246,1451,1765,186,1438,2488\n1496,1647,848,1243,1019,366,2063,199,1797,858,2410,600,66,132,551,1431,2167,1417,1755,1356,876,983,1923,1953,1974,991,75,819,407,1550,2028,2282,1970,443,2424,658,1702,441,1520,1159,2242,1968,629,51,423,588,1075,235,567,1535\n1188,1380,1315,97,236,1401,1211,2416,128,2077,149,2308,2400,2255,855,2326,2031,1644,1876,970,2131,2088,1959,553,1269,1546,398,1604,878,54,828,1155,1018,2155,900,243,112,122,2376,325,1192,915,1281,644,1258,925,72,2014,1138,435\n1792,2327,2319,1690,1286,1111,1692,1587,625,2097,2033,797,1471,408,2137,2480,1546,642,595,1379,635,1852,1340,1655,228,17,679,521,1023,153,531,919,1175,159,1524,1565,1917,1849,418,755,1472,322,1511,2124,2309,178,1074,418,2115,679\n2076,49,1379,284,1690,1648,1766,177,2221,470,736,890,2372,520,1998,2159,2266,1203,1128,1990,137,2390,2280,1563,793,1705,339,1336,575,1940,1601,1322,2259,1154,1240,1240,636,60,592,655,1063,2274,611,1028,2198,2229,1609,783,288,1000\n1890,961,1892,314,1229,1503,170,927,301,450,2183,129,624,1557,1559,2405,498,1079,497,2475,1018,2350,1674,26,1569,349,100,1080,1860,378,2053,2325,508,417,2376,512,1291,1549,2454,585,1244,1991,1676,2294,2261,865,1185,259,185,902\n1072,321,1150,381,811,285,2112,424,454,2303,424,1278,39,1400,351,948,641,1289,474,1822,2405,9,1268,1277,1844,157,2057,1479,1696,5,2345,1125,195,1582,1856,409,1212,2061,1879,2156,871,283,89,810,428,1075,1448,1596,1113,1289\n1940,512,624,1874,1343,1934,2456,1100,223,1863,1096,111,911,879,1842,1087,1057,2378,2151,1842,15,2475,940,1011,2492,436,936,1610,1183,364,761,1656,1230,290,17,1578,69,918,687,1747,1846,1436,957,267,2279,186,1424,2002,1624,988\n358,148,332,109,2186,2468,1663,1361,1209,1667,387,678,1319,925,1622,153,1591,1182,87,251,1150,1805,1190,2134,1638,1900,2455,1230,2299,1550,2391,2125,2420,1112,2083,1033,2116,284,1914,49,1009,1660,436,103,219,1867,1919,16,294,1820\n1991,908,1968,1282,2351,1269,2439,808,827,151,1819,2161,422,453,302,1811,436,2350,1733,213,149,1138,96,697,380,1097,1173,1203,352,1460,1368,2424,1732,1833,1144,931,951,955,2125,1241,2312,1667,1402,1532,662,937,2324,446,1966,108\n864,959,1475,998,5,226,1274,2398,2390,737,1575,1655,1425,878,1580,457,1956,1869,964,425,1861,886,2326,1242,1751,633,1118,2074,2028,623,803,2294,1429,2154,1540,1349,997,628,1962,1589,2266,1856,378,1068,320,988,1120,2361,822,509\n1972,2494,1599,1803,136,1763,24,1496,1490,2290,414,1956,937,1308,1894,2488,513,485,497,1591,558,1388,100,1610,2406,2282,769,1519,1077,1610,1238,1641,854,2427,2191,2441,1834,63,416,1212,1342,1477,1990,20,945,2454,972,1026,541,1947\n405,2215,1618,1628,2388,618,1483,1319,516,2475,224,1348,97,711,1595,219,29,196,328,455,226,340,1338,1737,302,1700,288,2397,1882,788,2301,1056,1033,2106,335,570,359,946,4,192,2277,2097,573,791,2174,1240,1537,2346,209,2296\n1658,1958,523,805,893,301,251,1080,1074,2167,511,2022,1909,1003,1690,1486,1298,1716,287,2481,567,517,294,2172,2240,557,572,85,1682,873,334,2155,1628,1177,497,1968,1574,258,914,119,637,776,1693,1072,476,1787,2488,977,1734,2075\n775,1297,2496,2420,270,1695,1894,1779,1121,61,998,603,922,2365,277,2341,934,735,1406,573,2185,611,1647,1860,416,716,1558,2467,984,1888,2388,1065,2478,2325,1314,677,763,1282,757,1697,1053,1057,1234,2130,1140,1017,1758,2220,1781,2077\n462,475,304,1266,911,904,189,1745,1054,99,2478,2128,100,1312,2301,2046,1961,348,1367,1299,1424,2432,228,1591,683,1972,2173,1961,2497,213,703,1459,2363,401,622,64,1091,1598,964,1916,689,476,1689,731,1625,1619,92,886,597,779\n1327,2083,1216,296,2192,27,717,1308,1411,2414,2325,2005,1918,931,1865,2339,801,2464,1470,2002,2371,1293,1418,276,2311,598,1043,1849,1103,349,301,263,1963,887,1603,1867,48,894,2161,1743,607,1454,1609,1896,1765,426,423,656,1494,2275\n1194,656,840,851,125,59,2224,175,1480,1629,1020,131,2081,598,2367,680,1035,2288,570,2094,1910,914,701,453,161,1932,2136,2149,830,340,703,1807,940,1748,1446,1190,2231,1429,611,753,10,1933,547,26,262,1839,92,2254,1208,564\n2231,1924,1037,284,1789,656,2007,1760,857,1620,1336,271,643,1340,1447,1359,374,79,75,1488,330,132,2102,470,1243,2202,1048,527,527,1758,708,851,195,52,859,1713,43,1850,551,528,985,1319,156,628,2166,945,11,779,1112,583\n1124,808,1871,1355,838,2352,469,1780,2347,579,2294,123,2482,458,1702,1623,905,507,1728,1746,1579,2286,1930,1251,37,1018,845,5,1041,1531,1140,1035,263,77,1595,407,1785,1601,1080,2376,1901,17,125,2238,1177,1188,1356,2262,112,408\n1348,389,2006,1667,1226,584,2376,1691,696,2112,14,2401,530,1211,392,487,1469,24,1301,74,2497,1670,2347,1702,404,799,500,1351,665,1357,1525,654,1001,666,545,2263,196,1328,2061,2245,790,1867,1822,1245,962,1432,1110,234,1253,2035\n1657,714,1392,812,2440,1491,191,436,356,474,1350,651,1329,1308,2074,1783,743,1896,1824,2225,2261,2204,725,1646,165,905,337,1823,1131,2177,2406,76,974,81,1043,1469,2185,2078,28,2428,1928,482,2226,1768,276,1267,537,729,2495,901\n1507,1345,1208,1492,2442,741,185,1335,1444,2308,1666,1814,1315,1822,2031,2455,2487,361,438,771,1839,2426,2245,915,75,1251,1357,1915,1686,584,1811,1024,1331,426,359,1593,2,2250,2334,1460,2173,2336,1903,159,446,1427,687,743,476,840\n825,1552,2136,2437,1539,248,31,2105,801,1115,1878,1772,288,532,2079,2366,2114,2403,930,28,2030,1150,1599,433,478,1009,2343,2475,1962,2364,1121,2304,1753,1342,663,856,1627,2033,1043,2395,2309,216,582,246,917,2117,1390,1102,155,1792\n3,241,2294,1074,367,1402,2336,336,527,1158,587,1699,2311,1310,1924,1311,906,2225,1395,283,826,2491,1974,1536,1014,1366,659,1164,1708,288,1279,535,1779,686,89,1110,243,2093,1450,576,91,1629,1007,837,1079,1669,312,282,2159,2452\n2040,2152,2031,773,1838,589,2135,735,1566,1430,2470,772,895,2079,168,1174,419,270,1970,348,1575,197,1004,828,947,250,2066,1530,1195,1152,355,2167,1234,1023,1718,1760,222,740,65,2477,815,357,911,1930,2266,2213,197,648,273,128\n2377,984,1701,1988,1692,2042,1874,1899,1863,983,1704,1401,1868,1546,1274,1462,1427,1223,1355,238,852,1024,2065,453,1355,1024,827,1467,454,441,206,572,1563,836,2351,1290,1521,841,962,201,2201,554,787,1021,772,336,842,1495,286,1275\n2130,1289,1377,116,1902,93,586,1542,1025,71,1770,567,1730,58,1579,1802,1152,434,1310,505,1216,1252,2076,1955,1789,643,439,1720,1170,2303,1002,1044,556,1856,2371,1857,1020,223,713,2388,1154,219,1789,2321,1340,1957,691,1412,687,137\n645,937,1479,2077,844,1859,1892,457,658,1532,2237,740,2199,1083,2173,2291,2468,346,2423,2414,1229,2471,1467,338,1573,1367,2385,275,2391,1131,1284,1612,1200,1222,1771,1029,1316,591,975,2392,24,123,1056,297,1517,695,1241,639,2155,1538\n2029,2205,1496,1352,1047,2022,38,283,2056,2408,1924,1999,2453,1419,184,511,1233,1539,1849,178,935,1734,2007,586,1407,182,525,2062,114,234,1268,314,1890,1980,132,2028,988,1105,1734,175,1016,433,1694,400,907,1220,51,1996,2406,522\n359,1578,1098,1433,1971,1325,726,1998,1414,1182,733,2059,824,514,2300,1636,2006,2056,1386,369,1454,213,1732,1602,2134,2081,287,1423,1468,1917,449,1331,1494,1703,1705,331,1725,1698,2292,2384,1235,176,2316,981,1722,978,1589,1027,1668,57\n1399,2329,1517,1284,489,1692,477,293,897,848,2404,1368,1701,769,767,539,1068,1521,305,2092,608,1528,1617,2486,1655,275,2430,526,333,595,1759,2324,1847,1277,2285,1588,2374,1991,2266,1245,2152,1973,2339,2078,2484,1672,811,349,2341,1740\n919,239,1423,663,2026,208,1064,839,1592,2337,750,739,1423,2307,321,1728,1025,545,962,17,493,549,1977,1153,1660,2401,40,453,1998,1599,834,442,2481,370,2337,2057,1741,998,1911,69,2146,1486,1416,926,1590,18,1720,614,711,789\n49,1692,772,1426,1708,1926,844,1445,2008,1862,1530,1603,1185,680,2490,2133,1267,265,7,1220,34,144,889,652,1920,832,75,892,522,1263,2145,713,1820,1247,1560,847,1330,521,939,1398,1692,331,474,2280,2108,619,52,994,2212,13\n1758,2386,1349,2070,1691,568,274,2302,1371,818,262,421,384,670,2058,321,1911,1984,2469,122,856,1602,1736,1576,1610,936,1606,1244,1966,717,2077,301,1008,648,1696,1336,2381,2111,1146,1377,41,788,823,2012,201,708,2462,1139,126,921\n2009,1479,895,1413,810,440,822,636,1027,1404,516,1835,1351,1698,1849,401,2384,1402,194,1022,223,1512,1649,2053,1862,2275,252,1868,274,515,1630,1350,621,1163,1196,2219,2472,295,2050,1456,655,2455,2069,974,2079,2059,693,16,302,1343\n494,1132,2404,1912,1809,2034,1694,1098,2352,365,1007,1638,347,1672,1441,1804,1695,1418,563,2081,682,548,1584,444,2324,1342,1101,2308,97,536,2304,1248,2301,1079,2377,1214,777,1048,1310,1876,1967,1676,1618,314,973,2221,2195,1789,1405,1392\n67,139,2386,370,1505,2434,1419,1639,1816,2111,768,580,853,2311,1493,2421,771,1571,62,479,2372,1166,356,631,1882,125,1700,1568,434,2301,1340,941,1678,140,2175,2018,2190,170,1795,556,2,572,119,915,879,2255,2249,410,273,646\n46,2366,1748,1622,1952,1755,900,1814,671,71,816,1817,915,1209,1024,2061,916,1537,1481,1722,1978,3,1884,412,2372,10,1423,1661,1335,2008,1175,793,2412,1671,2003,1959,139,1301,1067,1601,1845,824,2461,999,310,1607,1029,2445,23,2418\n1399,1108,1743,2251,2181,2028,987,205,1449,2119,2058,1756,2186,510,238,658,1353,869,387,559,2415,721,1730,1718,523,1295,1114,2028,2082,199,133,2308,1342,2112,211,1252,57,371,1203,1581,500,1292,2491,1912,53,167,104,288,2375,227\n143,1846,858,2126,2074,1311,1055,1607,1806,949,1265,2032,1159,999,1646,2344,950,2350,132,2271,2475,1131,428,862,439,2352,2175,1302,2356,1548,2039,277,2144,897,587,447,823,54,1434,1203,515,2218,1036,717,1468,277,424,354,2387,171\n804,1447,2462,1229,58,2366,1203,680,2365,1157,258,743,1284,2313,1836,2415,148,934,571,1011,2284,2221,1833,1715,1917,1594,1762,148,1586,677,2144,2364,1311,290,827,1268,68,870,2310,1926,2253,892,2186,1888,1174,1188,796,87,2162,409\n2091,805,1668,978,659,2328,837,1833,34,738,1576,1564,992,2088,683,18,1932,501,1426,1265,2290,327,2256,1334,480,911,914,431,318,1924,2086,1699,231,1397,1792,1839,1662,1852,2020,292,2428,559,2288,2263,2485,552,136,932,241,639\n2173,1818,1309,1793,1105,137,1464,2062,760,975,52,856,1710,53,1548,1793,2002,2170,1974,453,2435,695,1090,2445,1933,716,1548,1325,1399,1906,262,775,1658,1154,2360,1696,1952,1059,1488,388,1266,1295,937,1853,1459,727,1455,1816,1230,1217\n2122,2178,598,1323,571,1717,2472,2348,198,460,2132,1496,426,421,459,1288,1772,1951,1022,951,2225,1410,305,1309,1883,1752,1174,1722,2025,151,1508,246,1694,2179,37,2492,2230,828,2064,858,277,2387,914,1061,1777,1325,247,726,1986,1310", "output": "2490850"}, {"input": "7 1\n1018\n1225\n1409\n1543\n830\n987\n846", "output": "1972"}, {"input": "10 3\n1000,1231,1472\n566,1142,1314\n1851,219,1388\n315,1297,1381\n1927,2172,546\n1648,787,2193\n2227,30,829\n680,1103,595\n1900,363,1546\n450,2151,1596", "output": "18939"}, {"input": "9 7\n2375,1895,1027,1971,1711,736,883\n1922,100,856,2279,1411,1143,1923\n2294,1818,759,1692,2156,393,2337\n775,503,634,732,2342,1149,369\n719,913,571,2090,3,1604,759\n1427,985,2374,1026,388,2055,1476\n1124,1399,1507,1139,263,2208,672\n1303,2206,2170,979,350,1070,14\n209,951,1421,1647,920,114,831", "output": "50206"}, {"input": "3 9\n617,1765,1944,781,1336,1240,37,1263,1829\n2373,2239,1557,1475,1814,410,1747,2063,2392\n1788,570,378,797,605,1501,244,2148,1711", "output": "9118"}, {"input": "48 46\n2196,1285,1580,1196,861,1220,1795,1583,207,2145,2204,716,863,83,2361,696,1480,2229,1799,725,2132,2449,1185,1618,1912,874,1609,857,319,1624,828,999,67,2269,1202,1586,171,422,1921,645,1614,623,2105,58,965,849\n1659,1276,2493,201,2111,1163,2046,1152,2338,330,369,1774,981,1040,911,141,936,389,250,401,1590,1687,962,1537,1767,732,588,2146,1122,1486,1303,1253,296,1188,10,2184,1356,1858,1549,623,666,2354,1441,311,426,7\n2094,1278,2158,1748,326,149,1567,1698,179,246,748,1595,25,1213,1715,2421,72,425,1811,1072,1374,816,2093,433,1555,549,1279,1136,297,97,1705,1592,2013,2235,2229,1179,1308,1927,904,604,311,1763,1430,229,727,1121\n626,866,2149,2343,798,1419,1089,1041,57,1887,312,277,62,1900,702,2112,1535,98,691,998,104,1417,124,1743,1776,1820,386,1034,2215,1391,958,910,815,499,2046,330,1043,1864,2354,1297,1461,1046,270,699,2305,2262\n679,1198,2371,728,641,23,736,2079,2248,295,1460,741,194,2084,2402,1450,568,453,1804,1607,2242,14,492,646,1708,2487,1761,680,1368,186,1341,233,1954,933,556,1140,2458,259,948,2460,1209,977,221,1011,691,1496\n187,689,1992,1026,2459,1627,622,981,2298,943,2071,1153,1211,193,950,1973,1609,1453,1052,862,2441,2392,2424,1089,632,2302,1459,2148,78,782,920,107,2141,1682,1043,393,1177,2279,1685,1006,524,2419,191,2110,1307,83\n1362,234,1115,2093,2029,433,1370,2394,113,1290,482,2281,513,865,1911,1999,697,429,243,212,1979,1036,1183,1053,1927,2344,948,2326,439,293,1931,511,1984,1029,40,121,820,1049,1460,1615,2162,2064,1134,2170,1622,1349\n1993,852,1961,1203,1139,2452,1549,1658,1544,20,1812,553,897,1612,1550,237,1196,1924,1078,424,606,27,2286,432,2225,6,790,1787,2116,2433,863,2052,630,1456,543,2185,2398,1155,19,1253,884,2379,1011,1495,479,1647\n74,560,1621,2489,1345,1978,1806,1529,542,1763,1715,2296,1186,2289,210,888,404,1750,804,1639,1924,2143,284,1883,1290,612,1071,2267,274,1017,1385,999,1996,1578,1096,641,2497,2110,942,901,46,856,1465,984,2455,1501\n555,1626,171,2137,2200,1416,770,740,2457,2289,1916,969,1188,123,380,344,1040,2467,2002,1247,1864,1347,1115,2004,826,1841,1897,151,1128,2410,163,2358,1708,1879,2187,277,2470,1269,1493,1594,1377,2355,1963,1846,954,2496\n1576,385,128,821,1027,86,1405,1925,842,1644,2217,2377,395,209,2125,82,1201,448,2035,1285,1758,1138,878,129,1940,661,426,2059,2073,1869,1859,279,1738,2360,2409,413,1585,1311,2073,1894,741,948,1680,1012,1262,287\n486,131,1080,2203,1359,1800,2277,1718,1840,452,595,1577,1342,1954,654,2249,273,2266,588,2403,481,680,2009,2302,2187,2084,1503,674,1057,2365,2385,262,1656,105,2170,1196,409,1424,2294,1371,1506,791,1905,929,252,1139\n878,1866,1705,832,507,2169,1314,1509,2316,1652,2023,89,2019,504,1782,1046,1045,2242,391,1109,1251,9,19,242,1113,148,1820,1513,1680,184,610,976,503,208,1731,1279,165,1820,2487,1991,650,2393,1683,2146,660,722\n2301,2061,1352,1251,630,1857,844,1095,1059,2411,1988,2358,2454,611,1535,470,2443,1967,798,1683,1670,1317,1129,1824,1500,2083,1890,2294,996,1983,274,245,1321,768,2404,585,1452,2417,225,1761,2029,1882,493,2286,1326,798\n1643,8,437,1947,1185,919,82,1053,250,646,1434,1544,241,191,1202,495,823,407,1675,1625,2024,1904,1442,604,1967,2,1793,452,637,1834,2357,1919,420,1798,1761,872,1334,37,1681,1210,730,1878,644,2332,2488,96\n1204,862,2096,2243,412,1995,1667,1891,1628,554,687,1795,141,589,1424,1277,1009,294,1623,950,2353,273,1304,2090,1265,1724,1117,1976,516,1374,1714,221,1158,1572,1914,2098,645,183,836,1785,87,1600,440,1311,1437,134\n756,1609,264,973,1054,120,1930,927,383,553,633,227,1769,1572,1798,1783,1662,1322,1173,17,1328,959,732,1137,642,466,1687,2315,1136,906,1371,916,682,2050,1779,300,1910,2253,49,1497,2269,277,982,2127,131,1363\n1855,918,765,474,915,1548,1816,2285,2294,1576,1214,1461,1360,1524,546,1674,451,1291,488,123,1804,45,1424,1496,2038,34,1491,640,1529,147,2302,1632,2177,2018,1093,1184,379,518,782,1407,2403,2386,2237,2413,1777,709\n1302,2299,1626,2444,616,1634,1009,1284,1764,102,143,1568,766,1371,1416,257,1499,357,1976,2405,1829,1487,309,2396,822,1944,2133,1025,2408,1370,892,274,707,1860,810,1094,1028,1369,2170,81,270,2017,1733,653,458,808\n1101,1707,365,1624,1135,1542,315,1310,609,1767,1373,1016,619,578,522,1071,1841,160,2089,388,9,439,1104,2162,442,687,2387,1813,296,2287,2192,1116,178,2275,2462,1028,1008,1832,1237,2268,489,556,1645,2110,450,1996\n2463,1022,33,58,2134,74,1325,2109,2219,2427,2490,48,1350,2080,171,2238,494,1096,65,788,887,1157,103,1392,136,2264,460,197,1388,1542,906,1397,2122,1769,2422,2417,155,755,432,966,280,398,1683,1699,2328,1242\n1712,90,561,307,658,1190,1761,1835,1728,1057,590,2071,470,610,1420,2318,2145,778,1624,650,211,1872,1095,2085,2293,1079,2395,1314,2452,306,705,1592,18,2370,608,1,1002,917,323,1063,1772,1513,1709,1449,2029,491\n1718,1600,1451,2011,2098,395,864,92,1169,2353,1414,234,1241,963,2053,2333,1622,1190,411,1629,1108,1440,161,2164,1579,590,2308,1322,778,533,520,926,94,1932,605,1110,2263,2003,1579,1043,385,763,1692,404,891,2328\n1491,1487,2007,1029,1313,2228,1625,485,2064,54,1322,2064,819,2361,1005,1279,148,2122,898,1511,1111,1143,576,1940,2109,2172,1445,2312,2235,2088,511,2414,704,62,1775,1569,1527,1560,803,728,1517,2449,1698,581,1877,1784\n668,568,983,1697,2207,966,339,712,1925,1394,944,1041,502,2180,843,2487,1410,1389,1926,2297,134,659,549,2105,72,360,1861,2036,330,109,1722,532,2310,1213,1486,72,546,1583,2340,1172,1095,1862,914,1494,874,1136\n391,1154,1010,299,125,888,762,976,506,2165,1766,1748,1919,2347,204,1738,1728,1992,1052,1927,1974,556,211,399,325,251,1209,6,2258,943,2086,1025,1011,1918,2284,710,1614,73,347,2237,1830,1920,1948,1416,908,771\n1157,583,545,1329,867,2422,925,531,548,1080,524,1474,2017,1953,1847,743,1867,1868,1033,1483,1826,1388,196,675,436,2134,2152,1410,764,381,408,1154,2155,1265,1769,142,930,1550,776,2175,943,2385,1622,2188,2003,2220\n2070,1219,722,64,1168,1892,1356,2407,2295,1010,1509,2060,2433,1274,1831,1944,229,1570,2360,1001,2415,727,2155,1394,988,535,223,615,1299,1271,1668,332,1719,1942,2425,1187,1685,1823,1852,2151,279,2129,2332,2116,1779,881\n1696,321,920,2351,1333,1190,1343,2399,553,264,470,2294,1373,1794,708,940,1360,211,357,1150,1886,875,2024,1996,2338,1730,563,1642,805,2069,2389,1552,1446,1196,2304,2021,1903,2335,351,1960,2269,629,553,83,180,2253\n505,95,123,399,1046,728,2066,1670,1704,2441,236,1618,746,1309,351,1318,2000,1324,2400,1393,441,1037,2386,175,2314,1628,1823,402,57,2094,32,6,1086,1446,2108,1981,751,1117,641,714,1981,1200,2413,1614,1734,1431\n526,1218,2114,812,183,1414,470,1870,509,2401,1903,636,1359,261,737,889,1048,842,962,1341,950,1769,1897,1528,1832,1982,2038,1819,871,1026,532,1589,1371,2179,1974,1321,196,847,285,37,1226,2417,1792,2454,377,1051\n4,1926,1955,307,746,2088,122,1691,349,2361,2442,144,1971,1082,1615,1609,1688,2474,2037,1118,1943,620,369,1881,490,697,1187,943,1508,1597,1733,2049,1003,206,893,629,1426,807,1584,2346,1522,591,1484,1334,2179,1824\n1555,2005,847,1311,43,1943,2294,383,226,2044,720,2140,917,2438,1218,1889,1581,1097,1700,294,751,1551,361,1066,2496,2488,838,1658,968,439,2347,1617,721,1807,1367,1615,1221,1047,913,2376,156,2388,1304,260,2478,1379\n1610,1642,891,67,252,1613,822,1597,594,483,220,1469,316,1592,1060,231,1824,2090,1893,227,1230,2053,442,370,837,1490,800,1951,1009,2475,1702,1494,655,1977,668,2439,1298,2378,2228,1607,1804,1887,1920,250,1370,1476\n1221,2116,2427,2395,151,1942,365,746,2407,2478,1573,2494,2463,393,1333,1197,2249,749,1958,38,203,521,2350,1012,888,429,868,527,1601,2086,2342,798,1929,1072,1723,80,641,263,1022,1779,2232,2194,1176,310,1473,2046\n1974,342,554,2488,276,2155,1089,707,1533,258,2418,1446,1694,348,1937,1784,1493,1376,2285,2457,641,635,901,1509,1480,531,2239,1323,2278,2008,105,1790,798,23,619,605,2240,726,2491,912,964,1461,588,2224,1797,2159\n2039,425,1534,794,1436,2451,1679,1230,1984,641,1681,2155,1268,2043,1089,1689,1134,1474,1314,138,1863,618,2129,1005,420,40,503,2255,1447,201,2155,2237,201,2211,1966,1294,1651,1271,1436,104,1386,2223,455,49,1310,2169\n43,445,6,2302,2277,1722,1992,2435,2014,1064,1038,2046,1782,325,2409,868,1829,2176,2244,1748,1543,794,1573,1211,1591,1353,992,898,958,1230,1819,1813,1132,2351,1672,937,813,1964,2364,605,639,1762,697,2056,468,304\n1412,2,742,895,1986,1188,846,2250,2042,1003,1180,1282,205,1323,674,472,2458,1186,35,1308,15,1034,1938,534,1706,108,1958,2308,1749,671,2437,311,1104,1455,2406,1993,1846,967,1678,1546,65,2343,2181,1298,2378,470\n2484,2280,381,1798,1220,1985,949,1592,1785,1494,839,1807,2165,2159,1433,2146,1844,1226,2072,2439,1418,1483,1854,477,1002,463,2192,1036,1074,1081,2461,1598,264,1782,995,2312,1311,741,1388,1961,1027,1955,1952,1979,1137,970\n1796,646,325,580,910,2079,1122,2110,1864,1820,1512,1570,297,333,2245,2305,2126,1921,1360,1529,2018,2427,2203,904,519,767,2435,165,116,244,1325,2413,50,1309,1174,1436,464,1794,942,1555,1319,2254,1492,1164,132,1321\n2323,275,2341,917,1135,1240,757,1189,1674,514,1922,422,551,771,2498,959,1011,226,1664,1377,969,828,1523,797,1509,1934,1285,2397,2218,82,2336,1621,640,2063,761,491,2434,1652,0,2151,2007,2294,2002,1332,1927,2065\n2261,599,1950,779,1904,1740,1013,194,2408,1920,1866,899,2379,2111,1012,1791,1576,1687,111,2331,2046,2332,2042,2061,1334,1372,45,226,1197,1136,1490,189,1817,575,2460,1637,643,2497,111,334,70,1808,947,745,604,1657\n1456,605,1837,2116,648,1415,1186,1580,973,64,1362,1246,321,1438,1742,2047,495,277,1879,1810,1308,832,2392,2257,1811,674,1138,1293,2267,370,2417,2265,1885,140,2072,2051,1245,29,2026,1348,1291,821,2255,9,1493,801\n1605,1387,1954,581,1791,2136,888,1519,136,1857,98,1430,336,777,186,1674,2482,1701,1836,744,265,526,2190,437,1300,1589,2242,992,2264,1842,115,750,1980,2132,1366,919,1842,2331,2280,637,457,1182,2349,698,1270,345\n912,1937,423,1963,988,10,1745,787,2319,144,2167,1523,2173,883,136,1671,2290,1068,2055,836,1741,2113,506,1734,1814,663,814,2194,1616,1743,1376,1694,188,1634,1944,1969,1521,1433,2310,1457,1838,997,1339,1190,411,12\n1304,1810,1971,535,1449,48,1202,160,732,1344,2183,2056,2245,264,105,2214,1311,1332,2165,1833,619,865,1403,1984,2063,1195,1473,1935,610,190,2156,87,626,1180,467,67,1172,350,1514,242,1912,1240,2375,1002,478,1663\n1552,56,2142,486,1753,469,352,1406,1502,1566,1788,365,946,1165,68,1128,1804,1459,184,172,169,1277,1375,2260,1232,138,2268,2405,564,532,1956,94,1663,2337,152,1574,1270,2486,1260,991,1360,1790,1426,2073,166,922", "output": "2287381"}, {"input": "41 44\n914,1702,2348,1111,1926,1035,2475,841,1252,1965,1599,2116,2184,2385,869,2071,1711,333,1601,371,2156,1968,1881,1569,1257,1295,2144,228,2210,1199,774,332,1696,1302,665,275,1831,2311,148,113,1315,793,265,549\n1719,81,1517,1304,2007,1225,254,573,2177,1236,1376,1504,2202,1809,1734,2347,1314,1533,2315,385,698,1702,2112,370,930,142,2031,2123,990,1847,858,447,2130,990,1427,2381,1257,446,700,966,1071,1342,2387,706\n826,722,1514,2114,228,741,1183,1423,1307,2047,317,416,1569,733,1905,1105,850,1363,420,1159,2445,514,2106,1686,823,548,2030,224,630,841,408,1903,1050,136,531,2149,304,182,1557,11,1984,1588,951,1215\n1121,851,850,1146,1700,8,743,1537,852,1006,1501,1630,1137,302,1652,734,2426,2241,2028,154,700,1354,617,387,1474,361,1101,932,1437,390,1944,535,810,1561,2078,1498,178,1078,1277,2195,1489,694,1591,210\n580,1006,1367,1176,1927,629,690,1050,145,1308,1475,971,186,1661,314,474,924,69,17,1090,1497,2174,2475,553,1938,1490,676,804,1097,210,2074,2014,146,1532,1715,2303,923,896,1369,1499,1465,1645,982,2085\n1518,2416,2272,259,2153,630,2279,1067,859,2309,1797,1216,2170,1595,2375,2295,173,179,1414,1472,2000,854,829,2148,13,1887,515,1663,1590,3,2367,1183,41,1245,1031,1867,1516,107,420,1863,1288,63,1364,1689\n1604,1421,1323,2112,2438,159,1629,1323,2190,1625,2419,2035,545,670,827,693,1185,744,172,1032,983,74,250,1635,979,262,2351,430,152,1759,2308,1922,412,1008,1563,991,1392,2423,321,372,1233,602,202,630\n2242,1629,445,547,591,885,646,2268,1684,494,1104,8,539,1177,1351,1220,558,596,1070,2435,639,699,1176,982,91,608,947,538,228,61,111,395,781,530,1833,2156,2472,701,2230,659,1084,965,1363,251\n2400,2000,2323,392,955,1374,943,662,2474,1321,1559,477,1985,1682,752,2410,1149,2127,1125,1670,1999,1539,1170,229,2201,2441,1860,1877,2375,1486,882,1539,283,1126,14,2260,775,1,1904,162,2447,220,1606,1007\n972,1543,224,527,1987,768,499,1369,1732,1924,671,1726,282,2006,810,1758,766,2407,596,1193,1315,2450,2233,2343,1927,1845,1863,800,2227,746,1231,795,2058,639,262,1144,1770,680,2433,655,678,762,657,2171\n913,806,2138,338,806,2048,1332,723,669,890,1383,2463,114,1576,592,1987,112,2379,1193,173,392,1138,1225,304,703,1275,1386,657,759,2417,634,1030,1514,1588,1813,107,2139,2323,903,2356,928,1427,141,1145\n1699,640,774,805,1880,1140,462,1443,805,1400,2264,959,848,2139,1830,2082,2385,1495,326,2496,88,1394,992,132,2372,1097,1393,2299,1975,1480,2336,1415,242,2083,758,1414,1953,528,921,745,782,57,23,1974\n18,2291,1725,286,2283,1784,2469,1243,2060,1220,1613,1869,1167,1910,1433,688,401,1101,2243,1022,1502,1559,1487,169,2277,1560,2340,558,570,1876,2,707,1363,533,1511,1082,423,452,254,1507,1454,1681,728,1242\n293,585,1731,1671,1825,1723,2078,107,2333,1086,202,1282,2328,1647,1237,1981,145,1017,820,1737,1092,698,1183,1330,813,638,96,1761,1311,1108,921,574,1671,275,1208,903,1222,240,850,1959,291,1414,611,1091\n778,490,176,2493,266,1372,1684,2185,1013,123,1495,986,319,763,669,1488,669,1645,1129,2402,1819,1153,1794,2248,1898,252,1781,1795,1561,1189,1154,668,2073,1694,953,151,1911,122,1884,2147,324,162,283,150\n447,553,1205,1187,2145,37,1523,1604,2482,1217,527,429,460,2085,1975,1259,2401,80,104,1144,1049,2392,284,223,252,1799,694,787,292,1201,2334,708,126,1160,2328,2461,851,66,1696,1184,231,1085,350,532\n300,241,1877,164,1124,847,307,119,1425,1517,38,888,361,1492,2138,2103,1866,2251,1296,159,1585,1700,63,1763,1822,1465,474,1094,475,1084,2139,933,1415,294,1360,1651,86,2321,1438,493,1088,538,1875,1942\n211,639,266,1403,943,2211,1590,470,428,1371,500,481,324,1779,713,1928,394,1048,851,1514,789,1078,458,146,1609,430,1727,1333,42,1043,2043,765,1300,1424,882,497,147,2034,819,2044,304,765,596,28\n1796,594,1318,130,2235,1254,1314,724,1231,81,2247,2119,1789,141,2497,1755,2428,525,1300,943,961,1669,159,406,61,2385,2355,973,304,2419,402,1101,241,105,2437,2068,468,674,1850,453,2405,555,756,2114\n2133,1832,1252,314,1373,2421,1052,614,1457,1084,785,1220,1354,180,608,1659,1746,1067,711,1962,994,2181,1775,2438,1612,1791,1140,2247,256,340,153,1369,287,700,2316,555,1918,607,1110,774,78,1745,2018,1928\n2038,2116,956,1578,1865,1879,2079,272,47,2020,12,2091,551,1029,220,2061,2497,913,1468,340,896,782,397,1455,1861,2360,730,224,2301,738,1019,1770,1578,343,1586,671,66,337,1827,618,2415,1332,479,575\n1562,1643,237,2302,1714,2402,1733,452,358,81,2271,1109,6,980,110,2326,739,1955,1601,1980,886,1687,84,2165,1709,936,846,895,2388,2439,1419,180,1602,1601,1656,2020,1753,35,1394,1450,81,2155,108,151\n1391,199,2492,218,2246,893,176,1704,765,1477,196,2418,2068,146,1439,1518,1765,1208,1276,318,2396,2350,1179,276,519,1070,865,1711,269,1607,197,1522,52,737,2442,2393,2498,173,1803,1634,377,2380,481,2067\n448,1271,2197,862,1691,2020,2137,1079,2498,58,970,548,383,1842,1812,1143,2308,383,487,1958,1783,1797,1363,1521,95,166,1143,771,2022,1388,815,430,1361,1825,1451,541,726,1319,214,2205,1014,2289,1612,146\n810,2388,241,872,1738,2030,1192,2274,1758,1810,1474,1620,1933,1504,833,1331,307,1292,1017,1059,2022,1165,827,2451,559,2033,4,2122,428,699,232,1876,2235,183,105,849,2017,2210,364,8,473,12,1020,586\n22,2059,623,980,1053,396,1658,39,2446,100,2362,1900,1423,2003,2130,2190,1448,466,1640,1632,345,2304,75,2042,1623,1067,1279,1088,2454,196,1149,914,2416,1183,1632,306,1778,578,512,691,1909,1818,541,1767\n428,76,1394,1100,154,693,1562,79,737,2143,1238,1688,1456,1356,2395,582,372,2172,2407,1298,1569,2215,2077,1641,1024,2359,889,786,2396,1842,1124,1442,779,2484,259,2180,174,721,955,2216,1204,2279,1805,1681\n345,1244,1243,1044,916,919,1807,949,1547,151,253,2097,1348,1795,1390,912,1916,2469,1253,1813,1607,885,428,2165,892,1044,736,2344,65,53,649,1169,2431,679,1995,2200,1400,643,830,1209,1636,321,1299,284\n653,456,1746,2014,1651,18,2142,2492,1674,181,363,80,1548,1749,1299,2071,1825,2056,655,1271,530,1513,1726,1476,2262,535,2361,895,2280,1350,1026,170,1231,1206,1379,72,952,2352,2254,1635,793,2158,813,1039\n1544,1597,2468,92,2142,490,1054,1205,2486,2175,1602,178,562,2478,1656,1354,922,750,2276,913,314,1411,824,90,1963,68,1909,2461,427,173,1193,2158,2032,2115,1740,93,310,1470,254,2111,925,977,1135,1305\n288,734,2482,2161,610,2469,1030,1421,1119,356,2080,854,816,2032,2294,2133,442,1246,2012,1259,592,1433,96,1875,1263,910,2155,544,187,819,2436,1456,243,227,1815,2082,1752,1831,1828,1363,1368,2,141,1314\n778,1305,1983,1571,244,900,1607,1852,855,889,1593,278,1102,740,1037,1932,1150,346,1459,381,1779,917,613,1294,1788,1702,263,1127,2082,640,1083,991,1706,1235,2235,1400,307,1817,2160,663,1841,1481,2029,1941\n831,246,1584,279,1066,1601,120,327,2017,1044,352,2439,1547,1255,105,246,251,2409,635,1341,1688,2092,828,1351,2459,1747,517,1827,2131,1021,2280,1940,1956,1960,1566,1345,1067,0,549,919,1219,1929,497,1159\n1411,468,791,1850,1116,26,523,2177,669,1712,1458,1767,1400,740,2335,912,1541,1960,1482,1591,732,1860,1514,1031,1396,1058,56,959,1249,2392,2089,2344,1010,2478,1838,1479,1466,1348,970,1635,1222,694,742,201\n2369,1073,1794,137,1358,1052,1064,2027,1629,1466,2065,822,2499,45,278,2302,1918,1577,2484,673,1827,255,1116,983,2094,2212,1356,601,2127,1846,257,1446,2120,955,1111,1091,920,100,538,2387,1909,983,2249,1302\n1272,1107,723,1148,248,638,1063,2193,30,1235,1737,2111,2151,1577,2285,191,2208,1848,1640,816,1044,713,1997,678,1258,1798,1906,424,456,1437,1824,2252,1868,792,1967,2199,348,1398,1665,502,1653,642,266,2002\n866,1548,1940,351,960,2160,2028,808,258,1195,82,882,308,2331,480,1629,1741,1701,492,1737,694,1272,1626,2234,2141,2364,1767,1964,1610,705,311,2057,567,737,1278,1902,2332,742,515,1055,2023,1658,2261,1735\n1802,173,1867,419,1607,1815,376,1096,2125,2337,1471,1885,2497,577,1367,1868,2198,1517,706,787,1292,619,2447,2059,225,106,774,1197,287,912,1808,979,1028,1397,1103,526,1171,1959,392,268,1416,1288,2121,760\n740,271,2282,463,2317,1364,345,1821,377,2472,7,1847,106,1780,1868,1933,1750,2481,808,479,858,398,1602,1219,1280,998,2267,804,791,1639,1212,660,1428,1320,33,913,1477,1002,995,716,362,135,410,657\n1381,1228,1652,1847,1341,2440,282,1196,2372,2411,2479,1467,2338,1839,1930,173,952,390,1966,7,1476,1755,2182,515,1514,2260,803,764,168,274,1088,886,1350,1255,1519,1590,790,1622,1928,2090,2111,943,1789,2050\n1775,963,1717,1230,1277,1267,2373,2079,479,124,1653,794,541,1689,1836,790,2312,571,111,1544,94,1125,575,2377,1206,601,2497,574,312,366,716,1090,1830,1075,870,1397,205,1764,2466,1979,2217,694,244,2358", "output": "1941989"}, {"input": "4 9\n1966,550,486,386,566,75,882,2095,618\n2425,2069,786,2406,2440,167,429,1511,10\n1505,1431,1220,2007,1744,322,1780,2288,249\n1590,2100,141,972,156,1271,126,25,1338", "output": "14234"}, {"input": "5 7\n2133,69,324,821,485,1123,865\n984,1705,3,1465,2021,1073,802\n760,419,441,490,1409,1089,2352\n1361,532,2367,335,1941,2438,441\n2442,1552,193,2466,272,962,1553", "output": "17311"}, {"input": "47 50\n1705,1298,2330,527,74,1509,2350,1239,2220,835,1629,102,2334,111,305,1722,2129,55,439,336,1393,887,1705,73,1576,1195,861,2492,1226,1490,801,1092,2489,2018,850,516,240,12,2389,1695,136,477,1522,804,1371,825,118,1469,902,733\n1408,1769,707,1262,2296,2239,2300,2209,71,1230,2440,2029,176,1084,1686,1131,2258,1353,1321,1459,398,1656,2335,861,667,1158,129,1363,1845,1184,408,329,2317,839,1513,815,2321,402,6,960,2101,2372,301,1623,1639,2038,1804,108,1475,635\n296,2078,1360,2065,1551,2173,175,1069,774,2482,1066,591,2416,57,133,2108,2175,2404,585,1337,2211,1328,1982,2105,818,2493,2229,184,785,1958,97,877,1852,1931,844,338,628,211,1508,2260,2273,1677,2321,1252,2127,1453,840,252,1871,1032\n2131,1879,2257,318,773,1049,91,2426,1429,481,1121,58,1308,234,294,2267,413,994,1582,307,2024,137,9,152,1131,2108,1465,1246,447,553,787,1027,2073,424,34,2386,1164,1332,677,1303,1338,1019,2343,1577,598,1323,1479,1766,320,1112\n1101,414,636,2310,2220,1824,250,256,239,781,529,496,1365,596,2411,1047,441,2032,1766,448,453,394,1261,2109,959,645,1026,154,2453,1663,1404,555,1684,312,539,505,1589,1691,2308,1222,2114,360,247,7,315,263,674,848,898,93\n502,1719,1862,2374,1562,1381,1510,1598,1903,1006,764,906,2246,787,1590,2068,1259,407,1201,986,1258,1153,1610,695,717,2069,92,1993,1080,2468,228,1285,818,2098,2340,55,1403,1504,30,1107,662,2149,281,1785,2225,947,1627,624,1357,1825\n2014,733,351,107,2055,2008,757,1912,1174,500,206,1526,2387,325,1432,1886,2345,2084,344,1528,1390,1376,373,2260,1277,2428,1463,1507,685,1737,1048,1010,1300,575,564,393,1982,812,525,2259,1251,579,1083,2148,1964,702,2320,2190,244,663\n92,634,311,1879,705,1572,1287,435,999,1076,596,134,1279,1374,2009,2112,455,1000,437,1191,1486,1555,561,1527,930,248,895,247,567,1149,267,899,64,62,473,463,863,269,1153,1737,1238,1259,757,342,1155,1017,1904,1958,2056,113\n1520,1375,565,545,1959,1942,96,519,1750,217,1252,2307,1910,1636,1937,2390,2122,1842,752,1439,1650,2423,1786,1252,318,260,867,1424,63,1834,1779,1187,1557,1850,687,1831,1650,778,891,2313,1682,2072,107,164,1814,463,434,1157,2044,1286\n195,1458,753,524,186,389,270,589,1980,33,1154,583,526,1512,2334,915,964,566,861,2260,351,1247,951,869,457,1664,304,1766,1663,1931,1259,1259,1692,2384,1992,162,1997,468,458,2472,2158,2375,1353,278,450,482,1515,2023,2232,1858\n525,982,2387,245,807,2026,481,1318,1511,2112,1641,42,744,1647,1234,533,861,1651,728,1238,1388,2086,2202,1169,1541,2378,845,1826,283,1151,1891,2258,2035,1418,105,2126,94,1462,1882,268,276,2038,2165,1057,1256,1143,201,247,639,1996\n1066,2084,2467,1046,696,1131,1256,946,1808,2488,839,1663,1596,1752,213,1173,1267,2206,1627,1878,478,489,2205,2146,311,1667,277,2154,691,2006,1804,902,1211,1824,1899,1180,2408,1710,1794,2121,1194,1535,513,1895,962,992,419,2115,2129,428\n1301,1701,2029,1339,1166,495,874,1372,1135,1441,1407,1794,2446,1870,122,1885,2462,249,1950,1810,226,1264,1528,1381,862,109,80,291,1986,802,425,1073,427,619,1928,704,1439,2407,718,444,751,2353,2270,1463,1564,1834,520,1058,214,1502\n1499,1400,665,1337,428,2040,1921,1182,2178,1454,1765,1313,639,1652,1261,637,1104,884,1793,1260,632,2069,553,630,96,757,520,210,1127,298,14,1713,1198,2338,1662,171,1874,663,1540,1394,640,252,437,1141,2103,1889,1717,192,1684,1848\n949,1798,697,1531,137,225,2349,977,658,480,2346,1402,1596,799,734,242,1533,4,1730,1422,170,1625,2327,1590,464,1375,2215,2129,1038,1116,1438,518,890,1625,1024,2377,1082,295,423,111,136,698,135,2202,2333,1537,2013,1654,139,1218\n239,1687,588,1003,763,395,1485,490,1909,1290,510,2467,1541,1936,2417,732,2361,1670,112,1381,2142,1762,1448,959,330,1108,867,1107,729,735,134,2028,696,1532,592,448,1724,1430,1008,2259,1870,889,2384,197,1873,1653,1598,1647,1990,1460\n621,1051,1218,744,57,985,425,1313,1969,2413,2431,2022,37,1656,1421,2283,269,419,536,1136,1510,239,1936,1792,2255,957,1784,916,1340,174,1726,2095,199,421,2329,569,599,1882,490,1713,1700,701,845,2487,937,1466,738,1718,5,347\n1888,1832,710,1706,1406,1375,2068,275,835,520,1780,403,777,1374,1064,559,1853,22,336,2256,524,875,828,543,235,211,680,1328,912,176,1128,1634,1929,1265,69,1856,384,2230,1524,901,952,463,317,1393,1653,1208,2077,900,1326,1698\n727,2275,1887,1390,791,436,2085,1059,2223,969,973,1551,1178,2304,617,453,1411,614,2404,1699,1037,1490,2133,1912,258,1549,1572,795,857,193,849,543,659,393,1777,2261,2103,189,1910,12,391,2096,638,342,1369,1377,2004,1076,358,548\n1506,411,730,425,2231,2237,780,798,1189,62,319,1921,2355,296,2428,1245,1090,1400,1497,1939,1789,1590,2383,1543,616,1408,825,1683,1848,422,419,1988,503,558,176,934,1249,1502,1964,1099,500,1820,1395,1559,1411,707,852,23,193,534\n757,1198,730,528,946,1843,375,1648,1577,1274,933,889,788,1456,346,2454,1849,654,268,270,281,1297,546,662,1810,35,2369,869,227,1727,1929,1757,1051,514,194,477,382,2042,1005,307,164,318,164,469,126,1074,1607,146,196,1358\n761,191,1275,2397,1394,1585,1710,2190,1640,1418,364,85,820,2245,2446,1467,862,1934,743,554,1881,2168,942,2349,748,2459,33,682,1394,878,742,1259,1097,2165,2227,2229,91,2014,1676,2451,1784,1461,1895,1937,1633,1288,1277,873,2342,1443\n2441,672,2269,2321,409,1049,1735,966,298,680,1210,1402,968,1061,1857,1071,2383,269,312,1663,139,2086,1086,1906,2228,493,2285,647,593,669,874,1091,1110,2346,1186,1140,1859,1237,2194,1244,2151,1454,1618,1271,1233,1345,329,1075,725,483\n1507,1898,575,2401,381,1051,542,1554,227,1964,263,898,831,2372,349,1105,959,2191,531,1805,1651,1153,1624,472,541,866,2462,1440,1321,1081,1502,603,1372,2339,457,851,1808,707,42,1692,1919,1807,891,246,1887,2300,108,987,875,1045\n1639,2290,1618,659,208,1961,1407,868,2306,474,2455,357,2384,779,2248,647,2117,2311,343,2089,863,1312,53,1812,967,2049,1242,2179,1318,1391,44,1487,150,1602,2086,487,1416,384,354,1085,1697,545,1886,2057,1366,1619,1666,659,292,1922\n1608,663,1892,725,1268,942,2070,504,1249,1102,1485,1677,1437,341,1099,2427,2467,1852,1404,833,143,285,1212,1063,1576,870,999,2228,1071,1316,1328,1162,1366,13,365,512,582,572,300,2134,2059,1216,2293,410,837,323,524,219,1465,2484\n1003,229,2267,2350,2131,959,97,2317,622,759,620,162,675,1264,282,2047,1747,1669,2425,1796,186,1654,2172,824,2242,650,2263,674,1548,1674,1836,1185,247,75,29,2450,1969,1997,906,1342,1202,2377,1677,758,1496,2448,1433,2421,74,472\n578,371,890,1491,1361,773,212,484,662,1384,908,1034,813,1768,1058,1592,1759,2381,911,1904,252,1745,1947,1344,1780,1222,1189,93,862,353,1097,2109,718,751,489,303,1066,1353,2022,739,77,1421,1535,1311,930,666,412,1624,2259,1328\n1440,1299,3,631,1587,2440,1167,1504,56,1444,2141,854,1604,220,1894,651,609,2295,2059,1154,2368,2361,816,2375,613,2179,2289,1664,1589,2070,2369,2164,59,401,127,1638,1394,737,2171,1411,1167,1276,801,131,1286,715,865,1741,422,1042\n391,1770,956,1823,73,1886,663,2034,1067,570,119,184,1431,216,750,1203,19,1812,2335,928,2466,1813,1940,2297,2099,341,193,1075,2080,1513,2399,410,1425,2447,101,1469,1086,699,1212,2277,1831,2141,1157,180,1262,429,1258,2045,427,1066\n25,2098,2122,1896,1998,2360,1430,317,1324,1640,2498,2411,657,548,2422,469,817,1868,2385,138,258,1630,2271,2144,1154,56,1262,1956,1653,965,941,46,2383,1269,1928,2442,409,1248,419,1287,2361,761,2053,1236,567,1913,1556,2008,1870,1139\n419,1775,1376,991,1821,1146,1671,1536,1805,2276,1407,1716,843,1815,415,1547,1214,968,1626,278,465,386,1658,2121,1511,2407,1521,566,1272,290,2024,481,1762,2138,2023,1232,2009,2243,671,1288,1666,1015,1117,835,709,1329,359,41,502,335\n110,678,2280,2143,831,480,1097,2341,276,1105,313,218,347,367,529,186,334,1856,1251,1914,1057,2294,381,1283,1945,2329,1786,395,2408,1122,530,773,2050,231,762,277,707,1054,1319,2207,631,1075,1957,35,2084,102,2040,176,2394,739\n1889,2119,1486,1837,1102,790,1678,1180,670,1351,1124,730,1268,1891,248,705,1581,442,1304,1196,1632,1661,1787,2484,539,6,1981,713,2341,1880,610,538,964,475,2143,1792,104,2083,1680,986,852,1239,1133,1435,944,2384,1800,1474,191,2248\n706,2332,83,823,2103,1319,1594,2437,2054,188,566,2281,1241,1140,7,629,1846,2119,819,1719,540,1550,2261,1130,1212,445,1201,1875,2455,226,1081,1172,1866,1336,335,1418,960,2009,2480,682,1641,73,1766,86,2211,529,1020,2119,600,46\n66,56,705,2433,1935,2196,35,1725,1973,2262,569,1098,1728,1286,1284,829,19,2496,603,611,741,696,495,523,2105,2242,423,1633,85,838,1311,2197,889,714,612,932,681,2027,588,923,1249,1061,566,1097,292,1605,237,2112,877,2278\n2150,333,1041,2225,2392,2436,1110,2219,683,672,879,784,519,722,2056,1233,1740,1618,489,2464,2390,2322,1821,332,185,2082,384,2084,1638,806,600,454,982,928,1827,1302,731,330,1064,1412,1463,1236,1054,1829,537,632,1958,114,210,1081\n2113,2016,1078,1041,677,717,1405,1853,821,130,894,2013,1036,2109,1493,213,2149,868,1793,1101,910,594,206,213,1639,18,2255,1009,8,1862,1996,996,1780,1563,1978,1488,2079,1457,2382,2125,1809,1992,383,1299,1916,959,926,952,1361,910\n2054,867,2043,2415,152,755,1010,2187,2425,1192,229,1337,1789,2433,1185,1878,1555,429,691,1897,2148,490,628,179,1889,2480,1641,633,1146,2215,147,2352,1446,648,654,1073,544,1861,1342,1747,474,1842,1005,1829,619,222,323,1949,93,260\n460,1827,1315,1352,1363,1603,1862,1882,1205,1965,1014,1508,458,176,1714,1856,1243,1216,1066,2477,2480,2081,2308,173,2010,509,1632,1999,2013,2127,2110,214,962,74,678,1172,2357,555,897,7,39,2294,878,918,1239,494,2184,1965,493,1311\n1281,74,802,795,224,941,2087,40,779,1512,1103,842,431,1021,1806,901,447,618,2339,1512,118,1108,2256,2108,2234,443,2216,2042,1494,2314,2318,1894,935,565,726,2389,545,1970,2151,159,2418,586,2137,963,2355,2209,1622,862,2367,385\n159,1718,731,127,1132,1756,1884,2301,1698,804,165,911,2223,260,1587,2370,276,2340,1054,2233,1609,1964,160,1915,1555,2202,1666,1050,1116,1122,2402,263,491,2235,1437,335,173,433,1405,1076,681,1803,717,1322,1369,1881,936,60,419,2064\n190,2152,2024,555,1382,2060,1234,718,918,67,537,660,1947,736,1985,1525,648,469,1408,688,1995,602,988,282,493,1091,907,1176,277,1581,1571,957,2220,649,1711,1892,1798,1496,2386,1798,540,1905,1805,1909,448,2342,2084,1126,1668,108\n1443,772,1233,1614,1357,1803,1173,249,1560,2204,951,1063,2187,1788,2439,2064,2005,384,1749,1189,1640,648,515,2313,382,2037,1967,790,1595,79,1333,988,2445,8,2227,263,349,52,95,130,1974,1928,2213,968,478,2123,640,1673,832,1952\n1024,289,2403,2211,1985,195,851,751,761,1301,231,2110,362,814,945,614,659,1944,1057,1192,1512,1085,1433,1161,1159,1975,656,1817,2124,2024,2456,715,1188,1157,1793,1882,310,1866,1277,97,1671,1605,2285,1587,1840,2328,2366,1068,514,23\n1539,494,895,1934,1757,2495,2178,677,782,1854,1539,349,2297,536,1299,2478,836,121,2230,2016,2120,2022,2309,119,2458,286,724,2049,314,721,337,660,1662,889,1294,2274,457,1496,1779,1958,307,137,708,1592,701,698,1329,418,2489,818\n786,1298,1717,534,2078,1180,1190,941,1995,750,2216,752,2048,1040,114,406,687,1453,543,239,176,1086,1005,762,190,2304,284,2215,641,2049,482,628,1194,1972,1627,1715,1765,1910,2101,844,106,789,399,2007,694,2444,1091,205,2496,884", "output": "2541047"}, {"input": "8 6\n329,872,1994,1703,2191,1056\n2172,460,1241,416,2439,1559\n2026,2307,408,2279,1190,1336\n279,628,11,2083,1113,1747\n1434,1022,2100,1376,373,2334\n1074,160,1528,1651,2210,1187\n1421,2383,876,1032,223,406\n192,1891,1489,715,2247,1854", "output": "36316"}, {"input": "10 10\n1940,674,570,1391,1935,1314,193,527,715,1377\n1017,481,641,756,1945,691,1527,1102,1169,2335\n1498,1289,48,1012,54,1855,2361,1299,2235,542\n1352,1029,1752,1922,1803,608,973,1536,1809,1986\n2130,783,2308,44,1817,1308,329,1667,825,2226\n18,1641,1745,741,1656,1977,1224,53,2493,2368\n157,1880,854,1911,557,695,456,2046,1598,1123\n2182,61,890,1638,282,1170,1457,1243,1027,103\n746,2437,327,1483,1566,1363,79,1330,2140,1150\n2295,1231,290,1111,2337,735,519,2202,917,1343", "output": "66257"}, {"input": "1 3\n552,2430,958", "output": "0"}, {"input": "2 2\n1997,1229\n2093,1663", "output": "0"}, {"input": "49 43\n2213,189,1434,2207,1037,1604,136,1943,24,1076,937,1381,429,1994,1534,2483,784,329,1792,657,1728,268,136,2216,1076,1337,1626,823,312,1027,1830,2423,1626,425,735,1727,1375,205,2160,2193,2493,2479,1992\n1475,1372,2071,1310,796,1936,2418,2462,1953,2207,2095,333,1744,1717,2109,176,1657,1351,319,429,2352,2249,2078,2267,1824,1170,1240,1944,795,740,342,1944,1853,2084,1322,1201,1302,1889,1168,1953,1892,95,1625\n162,2133,1400,1389,2261,2078,781,1278,2213,1528,1696,1161,948,682,1910,1495,1262,337,290,1317,1744,1490,615,1936,1859,209,345,1410,1568,662,1596,1642,2312,2202,332,2211,232,1505,515,1845,2407,612,108\n184,2286,1334,1043,1630,975,417,1730,1136,1675,160,1637,1645,1265,2310,823,658,977,1985,1371,1347,2206,862,2110,2132,825,921,928,364,1078,2381,1019,633,1464,1169,2093,1329,2367,674,2054,712,32,1613\n1759,1780,1318,850,1059,2047,1836,359,143,2324,87,87,621,2199,337,0,160,80,840,687,1712,1635,1676,368,1910,2296,53,2081,2094,1663,1051,1263,2377,284,1603,588,2024,1991,1695,1415,14,605,2494\n1208,662,1451,255,348,631,545,2350,476,1480,824,1509,830,1869,1342,2398,640,1970,299,2426,1900,1618,1615,476,1539,684,1182,558,2482,777,870,2173,101,448,198,1943,182,473,1796,1888,1202,1263,1623\n80,2208,905,1212,2290,1537,1086,2353,479,1996,1324,39,1866,2242,828,389,540,839,911,472,1306,926,1117,2451,2042,1545,708,422,2007,1174,292,122,906,1853,1427,428,1221,436,1555,1147,2298,1672,1574\n2163,2366,2292,765,776,2496,1859,789,535,1823,2167,1610,131,652,2153,1187,1692,882,1473,1500,1457,68,278,578,271,2458,2321,331,1075,2425,2415,1425,529,1317,783,1379,2362,1496,969,30,343,2344,1587\n1494,1112,2331,1998,237,1379,1187,1049,1477,2406,2324,410,1064,1282,605,288,18,560,153,838,2065,2233,1951,6,1851,298,1011,1759,90,1179,538,273,578,406,25,138,1172,1668,2217,1987,2493,1931,1448\n590,331,165,247,2155,1164,2257,1767,1284,1227,718,1421,1356,1775,2118,1571,582,748,677,225,1319,1090,1160,387,1884,362,72,1422,1567,2039,879,2459,588,886,1685,2348,134,1907,37,1556,1028,2114,2017\n580,984,1369,2148,769,2300,2358,1367,338,1892,1492,568,222,1245,1903,1978,95,163,1254,2134,800,29,1829,1600,531,1892,1018,696,1482,1404,873,2237,645,1884,1257,884,2287,959,638,1616,660,522,1381\n239,1743,852,1245,2168,863,1865,965,560,949,11,292,1065,1682,1051,1736,1977,1488,122,1019,2171,230,2466,1338,1208,348,2217,1291,677,252,868,2395,2027,430,178,495,80,1131,1107,886,892,146,1489\n177,2391,2209,218,2379,2406,988,1041,168,2375,1674,80,224,2166,1969,1655,2063,1194,2157,1606,1530,1340,2135,1241,636,666,1439,758,1902,1801,1598,2140,1440,1915,1374,1500,1780,1201,1276,579,2381,718,2024\n2022,1397,94,354,2469,860,599,1472,534,1670,1807,1278,2497,1144,563,766,708,369,1738,1578,237,1455,715,781,2085,419,1124,2494,2242,1843,310,1178,743,89,910,1303,1869,2042,1840,902,492,724,1038\n207,1187,2414,1005,2119,1569,873,1536,600,938,278,2008,1384,1438,835,893,1912,819,1218,1978,1916,1768,891,255,1779,1311,2196,1458,2086,585,1859,1765,1458,1228,1590,2403,277,1414,2270,2334,2004,897,116\n1002,2013,2089,1313,2160,421,1099,1277,519,2321,2146,816,1672,2179,1914,1678,468,86,1884,1283,96,1297,1621,321,406,1421,1446,1490,396,177,2022,1224,2437,2232,502,2303,2134,1644,2481,1561,427,353,1524\n2272,2161,2491,112,262,1998,294,2059,1795,516,2427,1868,32,324,762,1698,2076,875,478,1458,1662,690,1068,762,246,1598,198,1533,283,395,1653,1972,1709,2498,43,1406,1088,1010,1366,623,1660,2259,513\n275,2476,1218,1832,342,2383,5,536,1012,709,2034,431,131,1940,1009,516,1393,1850,1496,573,493,741,983,146,830,1225,2083,2308,251,1329,1678,1029,837,334,1813,563,322,235,1146,1618,858,273,291\n2150,1582,1863,66,272,2319,2201,2027,2189,857,1432,81,1308,1232,1209,1481,776,447,2241,436,910,389,608,1470,1197,1815,14,2364,2376,2046,790,1048,423,966,1465,87,1400,1139,25,1841,1686,1041,1977\n448,2279,1575,532,2405,1105,785,1675,2245,453,776,361,1210,1364,958,1152,2264,34,1919,547,92,1804,2178,1024,1420,2121,1134,1348,2194,1234,221,724,541,661,1816,1980,1551,23,530,392,2269,222,1734\n1776,1986,518,1375,724,1837,2419,786,1162,1042,1110,1437,503,2411,156,1661,1802,2002,1217,588,267,31,2280,787,60,1703,854,1133,1209,818,2006,421,79,2125,1049,684,1358,1820,1416,1104,758,938,1884\n976,1382,863,1057,2316,1868,514,1275,2136,1717,2130,2087,793,679,660,1361,905,1378,107,754,745,1832,1826,1071,1620,2372,30,788,942,2121,1043,2015,453,899,1953,38,1390,2162,2023,2011,1372,575,666\n747,337,656,184,137,1250,50,615,879,1151,544,193,768,926,2232,1960,863,2265,1235,1527,860,1470,134,222,513,397,1285,1684,982,2224,812,1650,1546,1701,2317,1146,773,1667,1387,2079,1537,1245,290\n2481,2363,1964,2220,1315,467,900,1268,1203,1291,1313,1014,661,2443,1596,2039,2037,777,2013,1291,2381,1276,639,2218,856,363,2062,2226,2151,1613,445,1628,1715,1638,940,998,1226,756,2097,142,2470,334,398\n1389,1063,460,1552,2091,705,1209,2480,1902,1869,23,1459,1061,2350,466,289,1067,129,1755,1520,1107,2023,1625,1447,391,743,1736,1976,1120,2445,71,1876,1460,924,1427,415,820,2103,1016,1067,1497,1692,672\n2315,885,905,1236,2460,1332,1728,1354,444,1370,2178,628,634,875,215,2432,1226,1994,1642,148,1401,2324,1748,1832,1672,1491,1772,343,687,1118,2312,2245,894,942,1222,1057,399,1279,1564,1989,2375,1574,2381\n838,2085,2404,613,1522,675,413,1172,2438,916,1939,873,1387,653,195,2126,920,344,328,1600,2108,1727,1833,1081,1079,1835,2147,1789,2153,1844,816,537,13,1873,259,2178,354,397,1654,1037,1028,469,2246\n586,1613,2469,2040,336,2065,1912,232,466,1404,935,2340,2277,1893,1098,85,1436,1113,316,2366,264,2387,2399,2388,1225,2464,2188,1304,497,500,1970,1182,690,1599,327,1275,536,581,1818,1270,116,1215,1465\n335,687,681,2145,1347,2053,2317,895,1884,122,2292,472,202,966,1415,1855,1130,916,357,2279,2320,477,151,121,1275,2385,734,1045,1646,149,493,617,2220,1469,1063,2332,2354,1874,731,1639,933,410,1371\n215,2097,292,32,2267,1781,1791,1811,216,1099,529,2368,1470,1838,2452,75,872,1319,1141,188,1586,1109,613,2163,650,910,1474,2328,2051,1146,2182,2059,1987,1631,322,2202,1714,1157,2123,1156,310,719,329\n608,974,1153,2332,1554,143,1434,2466,836,2046,173,1605,598,1899,586,924,1368,570,1602,1107,859,1562,365,454,1006,2122,2186,1942,236,1312,1922,420,1771,662,2076,1147,2037,1530,1238,2063,2018,183,215\n2329,1763,1044,1686,482,1093,1537,2348,2498,1145,2107,1002,2099,1443,1658,180,501,1780,1731,2060,1386,2268,1694,1861,1800,2157,2471,1363,945,561,1257,1845,1376,882,856,168,929,1600,310,2337,2306,854,515\n1548,88,1015,2219,1626,457,1520,1795,1168,542,775,1609,2191,817,1840,2148,35,895,1851,325,1914,298,2252,1774,1318,2204,2230,87,1868,1166,1651,476,600,161,1029,1694,1383,1238,1337,1547,1300,1778,1596\n905,1578,859,1600,798,2260,464,855,585,575,720,863,238,1163,749,396,232,945,2015,2434,2337,2248,761,125,1237,2200,1826,2305,880,2041,188,378,714,949,822,1372,1832,2330,891,2024,1929,1421,2445\n28,330,732,2459,531,2415,531,633,98,278,959,856,1818,59,1170,1315,1942,1094,28,2262,1318,202,1935,1215,2465,320,331,925,2473,636,2205,550,804,1685,2374,1730,1278,981,2236,605,1772,2297,918\n358,977,2247,56,78,893,1022,2302,809,963,1776,1867,813,1657,287,1225,255,1162,2043,1695,313,2481,1181,1494,1722,357,1308,2195,441,2068,455,306,47,1630,2496,2467,1181,619,2369,755,672,966,260\n2008,2066,2373,1404,2140,2379,861,602,171,263,158,2291,2454,2121,307,29,1969,648,940,605,580,2038,1228,1801,2125,970,141,371,1265,1095,506,24,2084,2195,833,1257,1103,1025,620,1389,1016,1989,1194\n567,1092,2449,1229,377,2031,2052,1358,2248,1076,1947,2045,177,636,881,2391,534,2076,777,334,226,2469,269,1532,1798,280,2446,383,43,1196,983,2427,1821,2367,716,982,1270,371,115,624,1232,591,1426\n188,1319,2485,1597,832,435,229,1542,645,1735,2295,1201,1153,271,2245,1919,1917,1769,2211,1699,358,1921,1751,2184,1793,765,2306,1708,513,81,1234,696,2403,2016,1503,2236,360,237,382,1264,259,192,119\n2159,614,1409,2426,733,866,193,1584,1411,396,474,1960,1693,2283,659,1331,486,1310,622,2068,2104,107,172,1269,2493,1706,100,1493,1123,1715,2309,98,1529,176,2072,1231,2403,1368,356,1944,58,1061,515\n203,1158,1963,862,89,2145,1802,2289,2224,1807,1357,519,1583,918,659,677,2138,1041,1210,473,954,945,786,1317,2260,223,716,302,244,883,1967,1952,61,115,581,977,878,1301,212,1276,1465,558,2135\n2195,1932,1664,1188,1768,2076,2092,87,103,1033,1312,639,1559,113,1373,447,2055,1511,1201,1574,1132,384,827,1991,595,2290,439,432,522,685,855,318,1240,1073,2287,2184,1663,937,1701,1733,2065,135,717\n2491,1300,1505,1097,2230,1406,2308,2442,1831,1348,754,1687,1419,2003,155,232,1418,1681,571,2145,1186,1162,789,598,133,2216,360,381,1745,177,2438,1683,729,1008,2315,1337,1776,374,797,1565,381,1328,418\n34,29,833,2030,1056,2342,607,508,615,36,1717,2099,1582,149,201,2032,1911,1343,1831,381,1482,1483,1353,1579,566,771,2356,1163,2034,1704,1264,1673,257,1155,1381,1870,2089,1532,28,2373,1377,491,2467\n2255,118,2402,1281,2443,250,1467,1540,72,881,524,1596,1662,548,1393,398,224,953,397,1491,1016,103,2085,1917,137,978,929,3,664,1131,1680,1982,1967,1715,1720,2267,2273,1825,21,1740,1203,367,231\n2080,218,271,31,1924,639,2307,1777,2029,700,720,1162,2159,1387,1438,472,1397,1835,147,830,1057,831,1159,2348,379,1798,314,204,216,955,1403,2016,167,1370,2187,929,898,1261,2427,1150,1000,1997,1164\n2009,1535,241,1759,852,1647,2287,1380,854,2309,753,2077,1634,839,1539,2385,952,1031,327,261,1490,560,1458,1714,1101,415,1635,1448,201,1767,1215,866,931,105,1414,1208,249,1655,2334,1743,1514,409,1130\n2094,576,1577,2285,722,1868,578,1388,1664,1009,1014,151,255,2380,605,635,1140,297,374,1942,1940,484,1505,1441,786,1757,2009,991,461,1980,1191,642,270,426,1401,541,418,2376,651,1775,2463,972,1719\n29,2366,2406,2028,161,1925,778,1519,1490,410,952,383,96,985,2328,2205,1754,2216,2131,1759,796,1363,2437,1208,411,576,922,39,1934,1457,1551,1840,1235,1280,1020,1906,2004,147,2488,1619,1038,637,559", "output": "2303504"}, {"input": "4 9\n1490,278,1780,116,812,448,632,260,332\n1228,1084,542,785,2216,322,1276,1357,1129\n232,1002,565,1953,1113,420,1403,1043,1774\n1028,749,635,1490,1514,2327,570,558,2045", "output": "10391"}, {"input": "49 42\n38,1926,1239,1125,320,432,1202,2121,1576,670,2491,1994,2081,774,537,2064,1170,1323,788,2133,472,677,2343,511,1777,1777,234,1103,48,112,2373,2282,2393,922,1732,2220,1839,171,271,1925,593,311\n1505,355,2183,1082,1909,1159,1060,170,254,247,1301,1038,1023,369,662,520,669,1709,1225,2388,760,907,637,1811,676,1216,1262,1470,140,908,2062,2367,855,1247,1971,1738,1146,2394,1313,750,768,619\n1307,816,1937,1947,1212,739,645,1684,1810,258,1557,1179,2246,1046,988,1408,499,1174,1471,1173,1657,550,1596,163,1322,1404,937,2061,1487,1454,1432,2217,2048,1385,2341,2414,402,2168,2319,255,900,1096\n1932,1880,1032,1120,2364,1431,2272,1369,866,2489,429,506,287,913,223,2182,850,593,335,763,428,1748,414,1853,1718,570,1460,374,2353,1866,847,409,123,606,2462,2118,1017,894,385,587,1790,1334\n578,2050,391,6,226,1820,1160,2238,2247,2205,1962,309,39,1459,1047,2141,1194,151,1122,1007,2277,217,234,2219,1558,1675,1681,1354,2126,316,1288,855,1016,1548,637,598,989,986,863,1576,1130,1758\n2347,1431,1095,2324,1273,1765,1473,2306,587,61,1485,1231,2142,2283,2146,1483,210,1914,869,615,1508,1897,2462,358,1674,756,233,1969,1952,678,1700,2482,526,1492,763,860,529,162,2465,1658,1711,599\n1851,546,1392,137,1994,46,284,554,152,51,2252,1164,187,1948,1496,2125,2096,658,533,596,1961,520,1279,2099,1314,2427,916,259,2027,2105,1369,2068,1928,2068,1980,840,1118,217,1438,953,2212,1621\n1963,1655,1799,1866,49,771,1969,777,1811,2316,1658,1947,579,2275,160,831,1674,1815,501,2355,2362,2361,1027,1655,1512,135,361,763,791,1378,1978,2155,596,714,806,1113,1888,149,2220,901,1253,199\n1780,621,1540,576,1509,948,1623,1279,1265,299,1110,2206,1940,2007,1802,1201,1387,2335,2319,1128,497,2053,2196,931,1552,2111,21,2218,2376,2153,2146,253,2400,790,680,80,1797,2451,1597,1167,1197,2157\n266,1948,1455,1453,530,1374,942,2460,271,747,1438,1317,567,1314,115,112,788,208,2228,2358,1908,820,1948,1677,207,714,1926,2123,1941,229,814,1023,545,465,1387,2051,857,1655,852,162,807,514\n2092,1412,2149,1757,1906,1111,916,1575,92,1195,2063,2174,2132,961,988,1606,562,2246,467,1797,1296,26,1775,162,2418,1202,1903,266,2188,2093,2117,52,1596,1414,294,952,345,2397,498,1128,669,2313\n1664,1835,821,63,1829,1035,1601,2245,1593,836,2206,1546,1214,1592,313,249,1866,2246,405,703,1849,1871,2463,1052,501,1929,1738,1332,1310,2098,2263,2084,534,902,2455,266,1676,593,1976,140,1203,412\n1166,487,2137,1487,1704,523,973,970,845,2178,969,450,1644,2042,735,2379,192,142,961,1852,575,1256,2012,241,2394,1041,487,1465,353,801,214,2000,1218,1340,1503,602,2455,141,32,811,1436,692\n82,1501,1958,139,2267,804,2381,538,635,1702,991,8,842,221,2034,2067,958,2035,271,1677,1065,604,2484,1128,1649,413,600,1445,2000,2498,2193,503,679,773,777,480,1727,118,815,210,2209,2460\n757,1522,1649,985,326,357,1195,88,696,386,1432,859,204,2084,60,1158,226,657,1880,1690,295,1911,2002,2235,415,691,2100,2414,1023,1005,540,897,1129,1528,1050,563,597,841,349,1955,2045,2117\n449,1590,727,457,1123,655,1946,1700,1487,1768,1386,1793,88,1956,1737,617,276,1042,494,1673,895,1282,225,569,262,1162,767,337,93,1545,492,499,1079,283,191,1596,1159,1317,1382,2061,762,26\n101,2345,1043,263,520,1107,1038,1471,509,1537,396,2443,1258,1669,1362,1013,1903,10,623,892,2095,1929,2490,2122,960,749,913,694,998,1558,1806,1800,100,2447,2257,2327,1518,834,1221,600,1450,271\n2032,245,498,787,1297,2050,2185,373,643,494,1529,1532,1434,551,1081,2290,2360,1022,5,2068,1935,504,835,53,418,1655,375,2276,2141,109,1264,281,424,742,268,534,1577,502,204,2417,18,1741\n484,198,560,2340,1596,1931,1095,1713,2433,1923,1797,2094,103,793,1164,2340,796,429,1784,953,2432,881,1244,2227,964,1500,1487,1809,1277,2360,120,2219,1399,1801,1227,1997,341,2011,1812,439,1309,1369\n1679,1195,2136,2356,1541,1035,965,624,618,1072,1606,2405,1582,953,437,2187,412,1332,2183,2438,1722,7,2402,806,653,1589,828,1030,803,213,2453,613,1764,645,79,1158,2098,553,1030,81,456,1422\n595,287,1845,849,2210,451,207,276,2137,1821,976,842,748,1166,1954,403,1401,665,1399,2281,2397,2487,1632,1947,958,247,777,422,1588,2330,1825,722,2130,418,2209,2089,1514,2187,1025,152,1872,990\n1184,937,339,2341,83,2248,1452,1834,869,1131,1615,2112,1783,1889,1391,2252,2435,1940,248,381,1350,1174,622,545,2019,162,1506,1532,1948,1864,641,142,192,1315,959,1699,2248,2149,2440,213,2269,2360\n1770,1119,903,1283,1007,2231,721,130,419,2209,1920,2003,1691,1850,324,670,2341,1101,1033,315,284,1516,904,8,441,613,2022,230,1821,792,1579,1638,731,211,1677,619,2034,512,1058,1140,1860,48\n2321,2381,1756,1927,1064,1493,55,1857,265,1768,594,953,2420,635,1460,545,1781,1422,1493,1362,1819,1387,1818,1670,2104,502,454,666,31,148,1465,1717,1313,1296,1416,998,199,1032,83,1974,1139,815\n2439,835,2174,1878,646,1840,39,1947,1480,2482,879,930,1441,721,1171,684,798,2287,1227,1026,2269,530,1011,616,2231,2415,51,397,1931,256,150,1624,824,1993,2150,309,500,2234,1766,2138,2407,994\n2226,864,2392,1407,1066,782,1134,1364,2044,318,547,2288,1166,226,893,2077,1076,254,1507,2263,2170,1900,26,1030,379,2324,813,466,2240,1889,897,531,954,786,1338,417,2322,1346,212,1696,575,774\n1009,1248,1119,105,1490,2320,1000,2264,2228,960,995,805,860,1825,2135,1993,837,941,1337,2147,241,1336,2250,661,2399,2174,2466,1390,2328,2063,277,1159,2119,2196,49,1324,1369,273,1433,1401,1681,1999\n1123,1652,1232,546,749,1894,814,214,152,1700,981,1603,1200,1897,156,1138,2146,1961,245,1203,575,2172,183,1110,2215,2496,445,2473,577,1194,1106,1814,1728,878,801,1865,2001,2467,2344,981,2090,77\n1041,1836,166,464,998,36,815,1858,1760,44,1107,2425,444,2401,401,2019,2436,2314,1916,87,1358,1864,2373,1834,886,408,83,2065,213,709,1998,285,934,1729,680,745,1300,1505,1991,2131,1156,294\n2309,37,1020,608,525,548,303,478,902,2076,2081,1747,278,2272,1658,1775,123,1934,59,1263,326,2382,1318,2031,653,1035,363,1683,2283,1395,2079,1048,1434,854,1597,2320,2083,303,158,1430,817,1266\n38,1489,909,1203,2035,1171,2334,748,868,170,2210,270,205,1929,2388,951,1107,1450,1663,1464,292,919,2415,108,1922,690,1590,1862,1230,1320,1020,922,1537,539,1298,2350,2430,2314,320,1805,2253,120\n746,1969,403,1299,761,569,1853,961,1973,660,570,1694,817,2162,1729,457,1916,451,1557,2302,259,789,2246,776,1389,2152,424,2016,2076,388,119,1470,628,1220,1313,50,769,1286,1858,2192,866,1500\n1272,728,292,477,819,1384,1939,1617,375,1269,1072,1215,94,247,1346,1874,2393,2330,1997,2476,2247,1240,903,339,1396,702,666,1987,345,451,53,1909,1249,1781,1437,1396,165,1662,1513,969,39,735\n27,104,1734,2200,1659,1421,666,772,640,206,1242,556,90,1183,654,606,1140,1904,39,1071,641,2137,1212,2052,1295,198,308,823,1652,1976,564,1211,1377,81,2296,970,576,218,90,2162,1299,2253\n1813,1323,593,265,2332,926,655,1569,2482,1219,1133,1536,1255,899,405,80,515,2410,475,551,110,2310,2004,1784,1398,2128,876,1470,2019,467,1925,2134,1734,557,52,2133,2436,704,1872,2370,2362,2026\n786,1027,2278,872,713,2335,1033,2128,67,2016,1086,576,1646,2059,36,488,1832,1442,249,390,1909,1957,1426,1137,1849,1424,132,902,311,1712,2109,501,1465,1874,783,1750,1754,1274,57,2494,1709,2294\n27,474,719,106,77,861,2319,84,2171,499,2439,1886,235,1258,1814,1662,1387,1360,1215,1183,154,2288,2213,2278,2050,1373,44,807,2009,665,276,2348,839,110,1257,376,2274,69,2129,1222,2283,542\n2400,1670,70,1167,1719,642,228,2254,2045,950,2254,1248,903,568,687,408,1500,1602,944,1214,815,2477,1991,1723,2063,584,1435,525,999,2076,391,1404,1153,1938,1257,858,700,2485,2455,1459,1332,1833\n1449,1281,974,2167,938,1484,127,1784,1410,1034,294,773,2354,123,1931,1122,1029,1017,522,2339,1986,2329,541,10,760,560,760,505,591,962,1854,33,940,639,565,2151,2054,2186,2488,1941,242,741\n1776,124,237,1442,569,250,1734,469,124,2147,1176,447,99,1580,2389,2030,1941,1892,1381,770,571,992,2250,1609,785,1983,1927,841,1651,1210,595,476,1811,2238,1370,1930,657,693,2108,79,1093,915\n1622,2465,367,1798,1207,766,868,2270,217,2192,1785,2468,363,2381,338,2140,219,2348,2207,425,1943,1226,1307,1348,536,1841,1310,814,2030,39,98,1029,454,138,709,821,897,1583,655,2299,1549,1173\n322,281,1606,2473,515,2010,1931,202,999,2260,2435,953,290,917,1750,1057,2383,84,998,1768,1340,1845,308,1734,2161,2127,2446,2004,604,2416,907,295,2460,123,308,159,341,2220,1428,1444,1112,46\n1535,1986,1062,1173,2113,1990,93,903,2274,351,2035,399,1981,1096,1980,1191,2461,91,1942,747,998,583,2154,1515,830,961,1980,1017,1624,599,814,101,1354,1821,1643,618,205,1892,682,1580,1664,2471\n993,500,2183,1497,2050,1390,709,414,2134,1783,581,1513,908,2463,1466,1597,875,2379,1080,2201,2015,1154,761,547,1041,834,1196,2398,234,2416,822,1040,583,1581,2395,640,1676,907,1257,1043,1226,2297\n861,26,1028,456,74,1517,1262,1381,2170,1596,44,287,2439,923,1857,2008,692,2257,1595,2044,1298,1777,1655,2200,96,2012,797,1268,1386,1881,509,95,1901,428,1876,2100,90,1672,1440,1325,153,704\n1750,1242,1951,549,546,826,314,1070,1688,1201,631,188,621,52,1826,1616,1467,1996,2349,1763,1616,1864,1429,2138,330,846,1226,934,1213,1110,1898,1809,1557,689,949,1625,2330,1576,1670,1014,1828,2251\n1750,490,744,21,1068,1447,2021,2035,1679,1973,1034,233,1034,1427,124,1621,2450,682,1429,348,2473,509,355,1421,1528,1756,1406,726,576,1864,2273,509,776,1659,588,1058,2248,44,1090,1775,1971,1923\n2492,896,815,2277,969,2388,1391,220,618,1899,2295,1582,642,1578,826,443,1082,367,935,1298,139,790,2480,1846,2145,1283,333,1227,290,723,64,273,303,2383,99,1576,2022,1992,942,1711,2230,1307\n716,964,1862,1270,1901,1702,499,473,1369,1401,2176,1159,2392,1956,781,2077,1242,39,13,2127,455,307,254,1460,578,373,687,1083,85,1960,1733,1689,1973,2141,1549,415,2177,1592,1561,1186,1447,825", "output": "2214876"}, {"input": "43 47\n929,835,503,187,1797,1235,1793,1638,102,790,353,163,1923,1816,1875,780,1505,1009,965,2367,1677,1080,324,1106,1264,370,674,1969,1512,1965,2329,2195,2261,56,718,1874,572,233,2495,807,1356,671,1492,294,632,3,2172\n1858,1467,1395,1278,1639,2042,230,42,1172,1944,1449,2243,1882,177,406,543,2125,79,2301,1879,133,784,1123,408,493,1605,803,2207,1715,302,144,372,36,2170,819,219,423,1521,794,1405,565,1838,2279,89,185,1338,1673\n153,2084,2182,1670,789,2284,1181,350,2462,1575,574,2230,1277,433,2452,1071,1076,1796,1153,1593,118,1473,2029,2372,681,1018,688,258,2221,810,2340,1321,1969,1701,2208,1410,804,2166,2482,950,776,1340,1536,516,1095,461,2491\n1420,338,1908,2273,1645,961,406,2227,2385,735,1896,2123,1556,2290,1498,1689,2099,1920,2329,1574,1860,828,1905,2443,1484,1568,2189,2132,133,2120,1320,2449,1671,1787,1428,585,485,1560,894,1245,2153,1949,2262,1550,1101,2135,97\n511,210,1350,476,380,2071,1165,568,1536,1246,506,19,642,599,997,454,1162,1814,1656,2146,1147,1653,928,2224,2225,940,1192,2237,1726,855,115,294,2147,2262,1213,1276,1362,7,660,1498,631,2302,1098,907,460,622,2314\n1520,1115,943,494,929,155,981,1529,733,2428,1272,1845,704,814,2357,76,40,1536,1825,756,2099,647,1328,692,1178,1052,746,844,981,372,353,850,767,1854,1979,860,1135,570,494,1799,1780,2368,1864,2313,1954,209,2469\n2276,1093,1493,678,572,122,1344,2347,1967,2454,2161,2178,1136,1503,1280,1244,663,1949,898,15,1421,2119,451,1683,953,36,2072,309,2132,935,729,2143,482,1459,2344,1332,1877,728,1768,1830,1756,2116,1966,2328,2249,1903,1648\n145,1397,2475,372,553,1849,2319,2025,564,2050,2252,591,1039,1756,816,1421,2276,1413,2483,895,593,293,241,2278,1356,1437,1586,1321,1968,1591,2235,45,473,2036,2181,573,2449,702,1730,2075,2226,2132,1508,336,1450,1415,413\n2406,1606,1360,1796,2287,314,1676,2497,456,1913,617,797,475,1024,104,1084,503,1353,1009,1432,1245,2126,408,769,1924,178,741,1755,2105,2382,732,231,70,1391,2252,682,206,991,1412,1845,1195,1167,267,2163,431,1168,1692\n2424,1404,186,1949,264,1230,288,1528,2057,223,1046,1711,1439,1864,537,317,399,2261,1830,607,2062,2188,1064,838,1358,1913,193,793,1535,1564,1412,448,286,1718,2449,2466,2052,1729,15,2019,2025,2134,1225,117,928,448,124\n1531,2475,1369,997,731,1483,50,2076,1474,2137,111,1077,573,1546,1849,577,1767,2401,1701,1588,2296,554,1223,2425,1128,1871,1102,1543,753,1337,1792,1705,2320,525,1024,1690,1333,2166,1123,240,858,1358,583,1674,574,297,698\n232,1182,49,1936,2254,1255,1092,985,1930,457,192,115,945,383,1311,935,369,619,235,1067,137,2245,177,1657,818,1838,1609,905,289,1379,2064,1702,2445,91,1252,1483,336,978,656,867,486,356,1001,1862,429,2286,994\n1167,2260,968,146,2093,1557,988,1955,248,434,628,1762,2036,1993,75,1804,2464,1097,256,1132,526,2136,735,1060,2191,2190,988,358,1263,1123,1749,2181,752,241,1096,79,333,2234,49,2012,1146,2440,2087,38,58,1692,1435\n1533,918,1035,1921,2330,1429,1979,1580,1338,293,880,2495,1791,209,392,883,386,923,525,368,119,1991,51,922,698,1156,1887,547,1862,476,601,524,1231,1647,938,2418,1270,2160,1074,348,2292,1203,2315,2064,1786,925,1288\n20,596,2185,1503,16,418,1071,1785,2151,1869,1794,888,1439,832,1705,2111,1738,1557,1765,2462,1701,260,1816,162,744,1939,1915,1431,2339,316,356,82,1848,682,1051,2153,877,1292,435,1703,1958,21,430,107,975,2021,1919\n1361,1715,1508,2174,1764,1310,2411,1122,1641,1964,856,2276,1396,760,710,434,2373,1855,1736,1640,1127,1475,2283,219,1914,354,2458,251,1672,1147,1369,1895,220,162,636,1138,1624,627,2389,1501,1563,1553,2073,101,1473,296,280\n2370,1243,1867,613,1300,2429,1184,2110,1816,1978,1578,487,684,1775,2102,1398,919,297,1158,14,12,129,738,952,1933,1752,1952,872,1777,117,1509,348,1820,278,959,1591,1161,1133,1381,2494,728,996,1739,1055,2318,2470,1998\n2412,2209,1475,331,513,1218,1649,280,674,1403,1419,2467,1296,1701,2441,760,1009,276,2133,928,461,1099,716,1531,1568,152,784,1473,397,2301,887,1933,834,995,424,2055,1053,2159,1697,88,1767,279,1345,71,1128,2145,1479\n1259,2101,1963,1278,853,2414,161,124,663,241,2069,2476,436,1060,235,2425,1708,1140,1650,1542,1133,741,1250,2305,1160,292,2223,695,1951,1323,1210,889,173,1908,455,1233,337,1833,1248,2046,434,1497,1888,1125,2402,2428,1635\n1084,1883,674,890,1778,1605,339,309,1883,1645,294,1112,2022,61,687,1826,2496,1063,254,1043,2410,2148,1589,293,402,425,1832,689,1093,1843,2257,496,1047,1709,1435,982,1123,1554,333,704,1025,141,10,374,572,202,633\n2369,2059,2398,1435,1466,1262,2151,497,1885,719,1659,1952,928,289,587,2343,845,1162,175,1037,1864,675,381,297,1921,1034,1519,1738,246,593,1696,1934,273,1271,143,1642,612,100,1577,830,258,1809,2271,1559,1038,2261,2462\n1844,395,1033,1023,2456,1783,1688,159,9,2363,2105,1598,1847,2198,1,81,120,271,993,824,160,783,1188,57,729,1464,1968,1377,358,242,2290,328,2396,864,2490,210,504,1414,1255,94,1298,1631,695,1675,2312,1341,2419\n1530,415,2332,2002,1341,840,2470,2217,2320,1429,1203,1843,1713,2459,37,2365,1095,379,1380,2126,1573,914,428,2364,1508,2340,201,1005,1398,2035,2385,242,1665,739,647,1094,2241,319,975,2357,545,2400,1064,761,2124,1969,522\n2013,1710,1316,283,485,1230,142,658,172,73,2040,770,480,97,1567,1493,672,1547,1968,2002,1655,1879,1753,981,2352,473,1897,296,116,1184,1009,1035,266,137,1631,537,2068,1632,1029,2043,2475,731,821,351,1960,1575,331\n403,1085,1804,2123,2107,528,1249,1053,2216,412,1338,1776,1141,541,1633,1210,811,1747,1111,1449,2455,444,1424,464,301,1558,352,1003,416,1191,2107,1801,300,2341,1350,1366,457,1083,1562,736,1011,75,472,891,2019,464,2271\n2436,785,606,1913,1626,1742,1514,545,1685,2061,1472,1014,56,1822,1210,1262,188,390,1120,778,1643,1732,1039,1045,1758,2333,49,663,1122,1755,1639,1717,1143,1454,190,515,2353,2306,1876,309,2073,2348,930,1022,511,2462,1066\n1799,514,986,1361,675,1052,2150,2165,190,1957,391,1648,931,380,1244,586,2326,258,2170,1368,307,1595,2096,1577,634,457,612,1236,936,2330,216,2138,474,1448,2483,1915,768,619,1098,2289,769,458,2496,343,1315,2423,1060\n762,2345,1607,2236,2438,1162,1463,2028,522,2406,2098,1812,690,1658,68,2002,443,2121,2017,85,2441,1812,1407,554,2260,1328,265,805,527,71,2306,1901,465,976,1807,867,2260,2229,1146,2473,1304,2114,778,1053,979,1315,2288\n1215,2480,2019,718,1983,1907,2365,374,868,1279,1459,204,2367,1156,2291,1005,589,1583,312,1616,1957,1552,1085,1377,1674,2190,1962,1251,1630,2251,1533,1809,1593,1904,2091,1619,1004,1089,142,1444,2177,589,144,2499,1917,200,1235\n1731,2131,853,740,622,1895,866,1473,2388,1166,2028,346,1257,1467,1381,980,1254,129,449,194,2354,2358,2283,1614,1702,1061,1817,2340,2486,51,1860,784,1922,76,1816,1112,818,1119,2055,1814,1418,161,86,732,2313,2096,212\n2460,1686,1343,1385,2328,136,1172,723,265,1570,2100,1337,340,1775,807,1429,2014,2035,636,27,2142,2376,1895,429,2076,2212,994,1676,327,1771,1241,1534,1606,2451,919,2479,2239,541,291,1617,347,500,2451,2363,1390,2128,2119\n661,1134,553,1805,2180,274,139,2198,1008,225,225,122,1958,1472,987,1979,358,1162,684,667,1933,1641,2434,188,992,1789,685,1601,1123,1123,908,940,529,1866,2226,2137,1407,1462,1982,1045,2403,527,1562,591,1989,1876,1834\n844,73,549,826,1753,184,983,420,1733,1473,152,2104,1843,1522,1413,315,2035,899,2363,2476,544,147,1285,293,1986,1913,350,2088,2257,2254,1870,1030,2435,1047,1063,724,885,493,2113,497,273,1145,230,1983,992,397,409\n2415,1810,1434,1700,2154,902,718,1646,1967,66,1096,1411,1780,2416,2295,1839,1720,868,1211,2119,1618,1367,1028,1895,539,541,852,219,787,116,2134,1354,916,2247,2269,2040,149,1471,1745,1988,1764,2106,236,640,77,828,1055\n1816,716,997,1000,362,555,667,1796,2247,234,2098,334,42,2294,2302,2069,1888,251,818,1258,1129,1273,2133,161,1901,1940,797,2052,926,1188,1429,773,1604,1329,908,1292,2424,1658,2259,1299,1631,2054,789,2225,2353,59,1425\n179,1308,641,1632,2083,1686,1680,1993,1560,1505,1679,1103,96,1635,28,45,2322,861,113,1006,1916,1267,179,120,1777,915,566,1098,2456,1122,2254,1093,226,957,409,939,1008,2133,773,1940,1915,1112,683,2258,1096,700,2163\n1328,356,1798,2026,1487,1755,1346,1631,1357,2202,2118,1034,1679,2407,511,2234,338,1590,1348,1064,1777,963,1544,2100,247,1461,672,1049,1340,1844,2492,1387,372,1796,186,1538,1178,2362,1484,618,2032,1550,348,1577,1432,1434,1007\n570,742,1654,1788,1039,716,1743,1357,288,2376,1919,1765,568,386,534,1611,1700,980,1284,6,1308,1959,9,1356,2367,428,1946,2063,1998,1673,1668,873,1225,740,2242,920,829,572,851,2091,981,1461,1788,663,1994,865,1922\n384,357,2330,338,2082,628,21,1643,11,1215,1446,1223,121,2473,1775,2083,720,838,252,266,323,850,1161,2227,701,1726,1508,1360,345,556,2195,1804,2267,789,1136,2082,289,2354,1385,1954,410,1276,1636,959,2491,1950,113\n2491,53,800,1356,1427,684,2329,1857,218,2440,1649,1353,118,342,1900,1928,616,1990,979,870,2160,837,693,2384,1947,1712,386,452,996,384,2147,2207,1009,932,1562,1438,2268,2477,1134,630,1842,2085,963,2284,320,1726,1239\n1457,929,1923,1635,1782,448,1048,444,2285,224,363,977,2004,1239,756,1478,2192,2045,325,404,1689,2034,388,1250,532,695,1834,1501,1226,394,204,2398,1300,1849,1283,1677,2064,1370,1217,599,100,1676,1540,1811,443,743,1098\n1108,1094,959,1245,2083,1321,1082,602,112,2315,2252,1743,69,2341,2002,2066,1053,2081,788,2149,2311,800,2353,757,1244,642,2110,277,356,555,768,1706,648,2388,887,2234,622,2073,2173,1856,1830,1999,2212,2032,827,507,923\n1291,54,944,1424,1953,1056,1014,999,2368,1402,109,778,2400,1807,2167,2091,1661,927,8,1072,111,1894,1189,428,2434,2062,2050,2068,2147,1623,1656,977,413,2163,836,1603,1946,1196,1680,825,993,212,1009,1199,2431,1109,1586", "output": "2098584"}, {"input": "1 3\n2000,1547,2277", "output": "0"}, {"input": "46 47\n140,1077,2290,197,803,2191,850,1194,774,55,1777,124,1014,1297,1453,1548,1093,315,1581,1843,758,210,32,1776,2307,487,605,695,421,2294,2149,78,872,590,1787,891,260,59,345,1020,2085,2287,201,2295,1672,658,2467\n1544,1675,702,2484,609,796,480,2339,428,672,730,1644,1721,1810,1447,1531,1409,908,2217,799,1934,850,1316,1952,2444,2079,2021,970,1225,1631,2184,978,400,2260,1399,564,465,1045,1863,2318,1286,2484,2367,808,2240,1720,2410\n868,2270,843,146,1002,2277,1511,1069,1862,633,2118,2353,1533,1031,566,482,508,1107,1407,2105,1417,1546,491,2309,1984,2091,108,1203,2288,404,2058,2413,42,637,2416,160,396,2154,329,2183,344,1041,146,1878,558,2325,1099\n2265,2187,839,270,2147,264,17,147,2002,103,1475,2004,1014,2029,1966,1021,824,2344,2057,1825,407,1146,164,2429,1616,294,2415,2155,1176,1000,736,717,117,812,657,1493,1216,1158,156,2222,495,1023,2019,678,1987,1933,1790\n1009,406,393,1297,256,1018,1668,1612,1493,426,968,92,1773,1936,2452,331,854,931,2283,1052,932,1162,1619,924,290,2137,1170,1814,1593,453,677,1269,135,1598,601,2452,833,1828,2070,2402,1348,1206,213,1106,1990,2012,1971\n2402,1015,697,229,2068,540,2224,1247,427,2129,2286,2341,1135,1693,2372,1326,2241,1097,2020,502,840,1653,2118,1725,1054,780,1688,2295,466,603,2112,275,333,1979,889,311,10,1302,671,327,1348,1693,747,2040,2284,850,289\n514,929,1129,599,2492,675,1572,1043,1961,1574,2486,1697,1312,209,1004,51,264,2154,1381,74,1845,1989,772,124,1528,1396,2499,2017,1838,469,1083,872,1773,2312,392,1821,274,1315,2492,350,533,232,1155,1552,1255,1207,1205\n1659,527,1924,1078,277,869,2483,1989,1246,1712,1662,2324,944,1244,1775,1230,2440,240,1457,1891,1287,667,10,1858,705,1269,2273,1701,818,437,278,977,1119,827,907,2297,382,772,625,45,436,1762,93,1950,1566,600,1576\n1390,122,1747,1279,115,878,1666,2215,1219,0,1657,2415,1843,658,645,1458,1894,765,1005,277,516,443,151,1845,752,1548,1253,617,2006,763,1322,260,1634,156,2436,1722,1070,1888,2000,344,1653,1341,856,1429,1134,980,1029\n1791,2439,2479,1256,2140,63,1335,1990,256,2107,355,2287,2042,2139,333,1981,1878,143,2476,1979,1608,788,763,609,855,1823,785,545,841,1431,473,1178,638,936,1314,1225,1207,1000,751,1176,45,2136,1631,998,561,2114,820\n406,1779,2240,637,1567,2246,2172,719,1939,8,2102,1674,1497,170,666,276,898,1728,198,2054,168,1588,185,2300,912,320,1947,1110,560,1985,1061,1167,2171,2431,2435,2253,2212,487,1561,2290,2258,965,1249,2051,1199,691,1707\n745,1525,83,1198,314,510,2295,1327,1484,1640,1425,1956,1752,414,94,2264,665,2132,2118,964,1061,1755,2331,205,2477,2,1541,2477,1413,1336,1028,1458,1575,818,794,1310,626,1334,746,1723,308,1298,2364,2245,763,1560,2104\n392,214,1299,1745,548,1395,183,1754,1540,2244,168,794,1583,211,689,1676,1297,509,1565,937,1299,846,1962,787,541,862,1199,744,2488,226,73,10,1043,2019,1719,1637,1044,1294,2466,641,1774,2062,107,2225,1902,939,168\n2337,191,2348,1336,674,882,899,1564,775,473,1043,1374,1108,1690,349,1484,739,744,1419,1531,1321,418,2382,1605,2036,1288,2006,2021,1759,333,1788,1092,2049,243,1126,667,475,43,76,35,1753,513,506,2247,705,862,1510\n2158,1743,835,1620,978,2231,1820,2263,2350,834,353,1097,2133,2461,247,1237,1143,2320,1391,745,1682,1551,1597,1132,1502,1914,235,620,1674,2469,488,1273,2087,43,1053,178,1523,1077,418,622,1985,910,850,1175,1502,193,1484\n1567,771,1477,889,2171,1210,1953,1701,706,872,1603,578,628,2134,2100,620,1542,234,1901,502,944,1303,1932,2449,1566,1674,2459,1215,1007,1331,1607,2476,1464,415,938,2396,1220,1907,1316,2434,1251,942,1113,1583,1848,1882,2300\n1935,930,1869,275,1490,751,2047,807,911,231,210,1753,567,1957,1802,583,1887,359,260,1007,1333,1637,2428,1134,1990,275,691,1774,1987,916,1725,1368,225,1926,851,993,486,1035,113,1947,1052,2479,32,26,1745,2068,1022\n665,1786,592,178,724,443,686,905,92,2385,50,2166,1746,453,648,67,2063,2232,1407,2298,865,252,1568,1348,1613,970,943,1499,823,1561,2162,1497,815,172,556,1063,314,2206,1769,1291,2014,568,896,1767,1200,13,811\n97,1572,2014,1315,245,2453,392,2307,1852,1359,1304,1300,1268,60,1199,2002,1571,1769,896,2418,178,1471,1781,1430,573,2377,1363,728,1610,799,1518,2435,211,1138,822,1121,542,118,1901,1429,1823,1931,1612,1594,298,1007,6\n922,70,1666,23,434,2424,1303,1577,1800,2015,792,376,2182,2255,1141,588,585,1090,2022,2202,2455,809,254,1572,2304,592,95,1404,1534,1203,828,2117,289,642,2297,1463,2220,758,2427,1104,865,2208,154,56,752,1269,392\n694,1657,135,855,1364,1262,741,1319,2289,1469,1284,2095,159,290,772,514,1596,1117,1222,1987,883,2397,2250,1050,1969,127,1925,1168,2166,1682,1472,867,394,713,2260,1511,1531,701,1841,2456,2465,815,1565,1615,740,1412,1238\n2063,20,473,224,931,345,1870,1030,2059,2006,118,1164,383,2158,1903,1800,2233,1561,1007,74,1865,2048,265,2145,110,1566,1407,2401,1867,942,893,2169,372,1233,978,1297,2438,1846,823,836,1417,334,328,1401,1499,606,1040\n361,1426,1975,1824,2445,691,1346,2220,1296,885,103,2349,582,667,1786,1553,1494,2122,533,965,2062,463,1098,1167,2440,781,755,2264,2472,1420,1389,1844,2467,466,2113,231,1351,774,838,1934,2298,1288,470,687,625,705,2343\n1496,888,1371,1765,1112,1691,250,54,1472,1773,464,1197,363,191,1093,2288,2065,1558,2074,2374,1636,1405,1793,262,1079,1717,2062,1126,2013,743,2063,2424,1623,914,4,2230,509,526,335,2412,1773,1844,994,2484,1977,501,594\n1556,866,1967,1796,753,1966,825,47,420,1197,127,2132,1491,116,2032,164,2103,1404,338,1867,1655,1817,1392,325,1636,318,126,522,1984,1806,2371,2292,2080,1394,990,900,2419,1773,371,820,2105,348,178,1968,2250,585,2098\n995,1690,1860,2477,1710,457,569,36,2012,2350,1480,2331,2012,67,792,650,429,1107,462,2252,344,2218,1209,937,2473,1926,208,384,2022,1162,91,1000,1815,754,761,1009,1138,708,374,1307,1233,888,2223,136,74,1869,528\n2330,575,858,1725,1432,1820,2466,2155,2410,424,1160,1772,2293,1382,1773,1048,2461,757,631,1748,251,1030,713,446,1974,625,1480,1132,148,387,1043,2289,1774,407,606,1800,385,962,2439,102,1358,795,1691,529,1764,289,1794\n2040,337,948,1340,843,2127,2385,2481,230,2325,1593,2403,1440,2348,1193,1600,2450,1596,618,2325,637,1233,32,1326,2288,208,1814,986,1729,1453,1608,326,339,2104,1853,1058,207,1961,1063,2403,296,487,1480,1469,811,117,509\n1453,2363,1799,785,1638,1190,934,1337,114,1922,191,465,647,2381,1534,11,1449,166,2125,1725,1597,322,29,2489,437,1770,1479,155,1163,802,2348,2153,211,1422,26,1238,1259,683,357,2147,1311,477,514,223,1020,1583,597\n1742,1372,899,846,1542,1361,1734,1192,995,1764,2320,1027,730,11,1831,1515,1153,591,1318,1420,679,1001,1218,2320,998,543,1148,336,1328,1603,2063,2259,163,1856,588,2261,1366,1774,30,116,1998,897,2233,2177,1325,70,484\n2243,24,1359,324,37,1517,478,327,2338,835,346,1164,1296,60,1275,462,379,1498,2068,522,563,2158,602,1282,2066,1468,1909,1834,35,687,2304,2281,159,1848,478,2494,1507,1724,115,1408,541,2089,1478,1540,602,1395,1334\n2121,319,992,1707,1554,1673,345,2182,2272,135,211,1874,635,1126,1511,2472,1525,1330,595,386,563,554,428,1347,1513,1659,785,436,1136,1070,115,1099,1325,1787,2057,1074,1986,1866,1332,1790,661,1559,479,1179,716,663,2383\n595,1869,434,17,1575,2429,1974,1662,1829,1295,1377,2122,1014,394,327,230,2180,429,679,787,1097,2197,2466,1014,762,879,1596,1193,1369,373,478,2233,1771,1333,2143,352,1912,1765,20,2266,194,1940,2462,1161,1654,1682,448\n924,248,825,96,970,1421,1568,597,723,351,776,1389,55,1637,1079,1927,545,100,2426,1532,2183,1920,1655,49,282,656,371,969,911,205,1388,1913,356,1475,436,2456,1480,2499,910,820,1963,575,1507,331,852,926,2186\n1775,876,2358,1846,1426,1183,1778,2238,626,787,2074,1388,1941,809,495,528,1511,1833,880,913,1112,153,1284,787,1021,2307,2371,33,699,1724,1390,2484,617,1781,1645,1359,87,2318,966,1977,822,183,231,405,1690,804,2262\n2227,288,1942,2002,536,623,59,357,43,772,709,2111,902,351,337,271,22,769,1892,1199,1943,628,2448,1525,1782,1182,1734,2350,1213,2004,300,1010,175,1869,587,77,1724,435,27,742,2067,989,1129,2344,1757,6,1655\n441,1590,1133,2267,874,471,762,824,128,1627,2080,304,708,1307,2077,1941,2159,462,346,249,535,1406,724,2002,168,1747,403,572,575,1599,147,1714,389,1177,709,1025,1280,2254,1774,1115,335,1214,1378,2094,750,927,256\n821,2200,1234,675,2294,1909,813,940,820,88,1803,1825,832,1910,1512,873,1269,2045,1111,1907,1137,1553,1217,47,616,790,61,1450,1453,1258,331,524,468,642,1263,595,2131,868,1364,2445,1041,1612,275,243,1688,52,486\n1150,202,990,947,1578,2030,1749,2426,458,558,908,1436,1831,2348,431,117,41,768,803,398,1627,1853,1520,2498,36,1617,728,138,2011,32,2338,2149,1598,1841,2355,1360,351,1215,825,256,1647,1529,2061,1479,1297,2020,1814\n1436,1247,1127,2302,498,1543,172,1792,356,2011,677,327,1452,1670,1675,791,2410,1752,733,1865,2436,1478,1111,816,238,1200,220,1757,1171,2290,1832,313,45,585,1933,0,1102,848,2341,1564,1117,417,411,1930,1950,1057,1188\n1148,145,502,984,1558,348,1680,167,1885,1299,2309,479,410,116,231,95,269,589,2206,878,1801,159,614,1430,1671,716,131,584,2195,949,1490,1656,527,222,1221,896,2068,2383,1418,216,233,1368,1125,280,896,277,1592\n1300,2155,1900,486,619,191,1449,219,449,533,601,836,555,1978,329,929,620,92,2454,250,1268,1571,1577,486,568,1641,994,305,293,1497,1613,2356,1944,413,1929,289,1701,531,1710,2044,2284,533,321,1110,1452,1577,1910\n1152,1848,1343,145,691,1661,501,1467,2134,1708,442,2263,1546,292,976,1250,1838,280,2037,1645,382,798,1854,2356,2242,2220,1696,1903,1207,1029,2396,1462,2454,1960,891,1809,2276,1744,688,1660,1441,2425,494,502,1960,2475,1598\n798,2327,336,282,1990,2445,706,892,2215,2051,2082,957,1122,72,747,1524,2067,1581,671,1674,865,2176,118,2114,1557,2493,672,1869,971,523,466,58,2153,1867,975,1943,1846,1220,708,1203,1267,1001,1305,1744,1224,2111,9\n1972,2059,2340,1043,232,1613,541,1793,2352,898,183,1376,1905,2444,1596,1267,952,2249,2259,1837,785,850,1166,1537,658,670,1166,1647,1144,1110,514,2199,1863,672,699,909,408,770,31,1129,7,24,1370,265,667,1056,2165\n1702,775,1348,82,1219,2488,1469,803,1783,1170,203,962,1441,652,1798,153,875,690,24,818,1719,313,920,1560,574,1636,909,2356,2217,962,2058,1126,762,1206,2230,339,613,246,7,2303,2479,1435,1106,360,919,1523,576", "output": "2399317"}, {"input": "3 9\n2361,2092,378,71,2245,1447,174,142,130\n2456,400,2458,1999,1601,1374,1918,2437,1215\n481,211,1491,153,770,414,2405,2021,339", "output": "12892"}, {"input": "2 8\n26,2194,1999,2296,579,627,958,2104\n1361,1366,1215,2029,1684,2072,1067,1900", "output": "2087"}, {"input": "8 6\n134,1590,813,1146,1035,1913\n33,2392,1113,1178,1222,730\n2025,1074,213,1960,1663,1727\n1148,1219,1178,479,200,1545\n498,2348,680,189,2100,1278\n280,567,580,605,149,971\n2214,2022,1772,1849,850,2189\n1238,562,2394,269,2084,1258", "output": "29187"}, {"input": "2 3\n566,993,2369\n444,2062,554", "output": "1939"}, {"input": "45 50\n396,1169,138,1684,1509,960,1211,171,677,741,1608,1580,2032,891,432,1732,1853,2181,1419,114,1257,772,2026,1082,1168,978,281,2449,1825,1490,1060,556,918,2378,1858,638,2102,35,431,2291,2023,93,1391,704,2095,1043,1448,958,379,477\n1459,2167,1860,174,1865,2456,323,1074,2261,432,772,2468,2122,668,2378,2104,305,26,2108,1615,167,1241,1100,407,1417,2414,916,2161,1345,217,2422,2202,289,2142,276,1148,2395,1544,2322,1700,1109,1488,867,985,1865,391,1300,2408,1924,1074\n941,939,779,1221,851,1116,290,508,2069,728,1486,420,1145,2186,1636,1025,112,584,684,2400,1073,2055,980,242,614,583,35,1239,2123,1793,695,2155,1834,1262,920,1155,777,1434,2284,1598,552,482,977,497,2184,1107,326,2295,163,1957\n479,1823,2301,206,2310,2274,2191,1609,1533,2362,2127,1442,1233,288,2019,845,728,793,1208,647,1365,510,809,2066,1788,480,1798,1307,1298,1712,1337,265,1885,836,1057,691,1642,621,130,1732,417,2337,1201,900,1078,2123,1534,673,111,1460\n2145,1081,1865,0,2210,1405,1176,298,528,1174,1116,1998,2138,2274,1183,864,221,74,1380,66,1902,786,1334,786,1343,782,733,1047,1264,1031,616,2390,1392,1923,2432,1882,2243,1579,465,546,2288,1660,31,227,879,1043,564,685,683,1510\n1580,532,1126,1646,2027,1941,1320,319,1620,1609,1669,931,7,995,312,2029,612,472,412,1742,670,1242,1141,697,273,1700,2344,1567,274,1814,1775,164,10,31,1224,233,2184,768,2327,784,1773,1618,1666,1578,1621,545,1604,128,2079,1382\n1351,2250,2071,815,1937,485,187,848,1353,1345,2295,1113,1465,853,2046,2032,2330,1966,966,1170,486,1907,1268,40,1033,2033,341,1436,2436,566,2329,460,571,492,1013,1419,2062,2191,2018,112,1036,843,580,147,2219,76,1086,1723,2119,2328\n254,211,2373,2054,2186,1769,1333,1766,1961,805,803,1111,1519,2402,2052,1027,174,1976,440,1895,1342,703,1210,1828,1747,2447,955,2260,2491,1350,66,618,29,32,1324,757,2419,1394,1630,1135,642,1603,656,1209,1387,2237,1780,479,769,1141\n1879,1558,305,1287,1204,27,4,441,766,2051,2101,10,377,1190,981,1243,498,2189,710,1156,1466,769,2264,2123,3,1653,1895,1964,625,647,1223,826,954,2354,50,1621,2318,1293,1248,648,678,918,385,80,352,712,1285,260,513,2255\n899,901,1946,71,1803,242,140,858,250,644,735,1138,678,1892,2318,873,396,1616,1614,967,580,1138,348,2057,78,2105,363,1126,1977,2295,1267,262,1459,564,961,1466,2075,2245,633,2053,20,810,300,531,1055,845,2167,1931,224,326\n1827,1625,2484,841,449,1168,127,611,1903,2196,1026,2494,331,2484,600,2426,778,873,1977,690,2385,1828,1230,1455,2437,938,1431,1417,67,1760,603,2422,1218,543,145,1095,2009,1687,848,957,32,365,303,691,100,1297,504,1141,1084,2366\n2128,1140,538,1904,2026,2252,2303,1531,1817,292,121,482,522,1847,884,2339,1967,2186,1687,1076,1348,495,1638,1988,2255,2134,1505,77,1513,472,2143,0,1811,197,351,896,326,1522,118,2216,142,1742,663,1841,697,2350,1941,1230,298,657\n1971,2149,621,761,688,790,1174,742,940,679,584,841,144,2399,1886,229,373,746,1581,2249,548,416,962,822,1096,524,791,1851,1034,916,1700,607,556,802,2401,2151,764,1979,230,73,1580,1742,587,1128,770,2343,1973,690,1087,556\n749,1796,2339,775,1209,1743,644,160,1944,1407,627,687,1803,1965,1401,2167,2083,2172,1848,497,1158,956,1629,1380,1022,2374,812,1074,1896,2465,1923,218,822,512,2136,2209,1207,199,1099,1185,1760,1474,1773,1398,2332,1278,2216,990,1596,1960\n2396,536,254,2230,1205,1470,1649,437,622,494,88,1943,1369,1962,2339,262,2277,2213,634,1736,1744,493,1945,254,364,917,1720,961,1423,917,123,7,1056,1769,1458,641,647,2486,1824,2119,705,2285,92,1890,1288,945,1453,2454,1110,2089\n689,2044,302,1558,2272,518,259,943,936,2244,1452,390,1562,1775,810,454,2102,1080,2367,2272,941,1170,499,792,1219,1517,1971,206,2303,416,2024,1938,1294,893,1193,856,901,1938,1161,1945,2369,1141,1304,1485,915,108,2390,1514,587,1944\n1706,418,985,2258,8,253,1529,1674,974,1056,1853,1128,972,2194,628,2283,2050,563,1364,2330,2486,1934,2207,1498,1244,1440,1419,1299,73,1269,446,1289,2243,1991,2461,115,1146,2068,213,1558,162,1638,1917,2439,733,1147,1069,2475,928,2496\n526,791,356,2273,549,29,1349,2461,212,1227,1631,2233,1213,181,2072,2363,1204,8,1056,808,1084,2023,1094,2001,1986,2318,1984,2112,616,1722,2089,1740,637,1211,1325,2125,795,295,1213,143,2365,479,1811,451,1105,1978,716,1803,141,966\n811,2413,1473,1088,2413,2278,994,1313,826,940,1672,574,610,1761,2006,1910,1328,221,1788,809,1963,886,712,1405,1508,1077,2354,189,1051,448,2230,1259,1474,2076,1634,654,818,2322,315,805,1592,2021,1814,1258,994,1049,430,1096,1541,1805\n292,2039,42,279,1789,1222,1323,694,1977,860,1430,581,2472,61,275,920,848,1200,929,1576,2402,1220,1575,1182,1410,2327,1171,1053,1491,211,19,1233,122,441,1833,1851,1700,1878,1531,568,131,21,956,1259,2365,2468,1084,269,456,1288\n523,2489,2343,656,1650,1198,1256,206,2280,1025,391,74,2209,1536,1935,632,1175,119,895,72,1364,1032,1750,1479,2246,2032,2153,1808,1206,1809,1768,2048,1280,350,2313,987,603,2430,2254,1783,778,763,1877,895,319,456,642,2468,2286,653\n2349,2252,2127,961,2085,22,1126,450,1666,2472,834,1871,1695,1810,18,2069,1767,949,672,2362,1458,1609,2033,1350,2275,1089,2383,896,505,2392,2015,1157,1014,1571,628,2040,401,1052,495,2010,712,599,612,2244,991,79,1234,2106,1719,1881\n2168,592,2145,2057,1372,855,1982,2271,1015,2165,435,1221,2383,1640,720,978,1208,38,646,309,1554,1051,1711,1738,1846,415,1022,1131,613,2475,2179,1705,516,1236,2180,541,740,752,2326,1051,927,540,664,1890,445,317,1305,526,849,1421\n2008,2125,289,1166,2262,463,2246,250,736,151,1507,1152,50,1374,2110,533,2027,272,1149,55,1069,465,2270,1695,2402,236,1426,1655,978,2054,66,1214,126,73,1250,1489,1495,742,1533,610,1677,1282,1139,1598,229,1652,2005,2475,730,1672\n2060,2242,2081,948,1019,1211,1531,2156,37,2346,1773,1682,984,0,2351,1293,1641,1939,1482,1315,212,823,1813,1642,1240,1985,2103,2377,466,934,953,60,30,1962,1230,1783,664,2119,1648,2339,430,500,225,1356,17,1705,2197,879,1498,2051\n1952,2025,1575,1621,792,434,1787,302,2493,2260,1791,1030,209,1525,1018,2004,1726,1810,137,1043,338,1310,469,41,1632,365,724,1372,586,253,1654,252,1281,1838,2441,2457,915,1108,510,724,261,1200,2059,2215,1304,358,1107,1390,2000,2331\n1331,1646,185,1412,1722,133,1964,989,1911,1799,342,490,2075,2209,739,1032,665,114,1304,501,738,1533,964,664,563,35,1641,463,2364,1033,435,1830,950,1950,427,1173,1047,757,465,1182,92,640,170,2434,695,262,239,530,2053,1008\n1064,2101,1722,770,1525,1301,1808,2019,1287,1064,771,1858,735,2441,1305,1184,262,677,1324,719,397,329,487,1620,2387,1802,777,1620,1641,1516,1115,14,2151,136,175,1140,807,2096,1616,1352,751,1668,2140,1171,347,2256,1760,112,1297,824\n163,185,7,1476,2303,1133,2147,378,1000,1688,2426,1415,1712,1298,1695,1406,1677,1623,1620,980,812,184,2263,38,671,1359,1045,879,1918,851,417,1603,1837,1718,2498,2052,1891,1284,511,1269,1628,1074,1621,94,1617,759,1291,291,128,1100\n2239,716,2065,217,303,1868,1174,1424,1246,1772,2466,1641,1651,730,1739,1202,2196,2340,1964,817,22,429,756,851,260,2323,1488,1618,1589,661,1628,2342,1947,2436,1403,1467,844,1597,84,1677,1148,2345,1610,566,490,2315,1977,1761,1424,2065\n2153,1635,109,2244,463,690,1439,495,338,894,933,2130,2402,2045,1951,708,2028,206,2350,1087,277,1556,2271,1262,253,1630,289,1492,1979,782,1737,973,1470,1691,322,2468,169,1765,586,2214,775,1583,56,139,1614,1301,460,445,1752,2066\n44,904,387,1062,361,966,1911,1506,2401,603,1755,503,635,1744,1076,246,1081,169,1799,2385,2243,687,102,1738,785,1008,390,1345,243,1682,1977,697,1711,1113,693,47,1834,335,715,304,404,803,2120,1889,485,654,1845,104,2139,956\n2384,1876,453,1361,804,1232,2055,1849,391,824,1262,146,2181,797,2324,1912,1455,1870,351,862,1178,1532,1419,579,625,1523,2038,1778,1336,21,167,1903,1138,1138,2494,400,1168,643,759,930,1144,1891,347,2385,227,1398,1893,1036,492,1826\n851,726,348,1417,1173,1232,170,2422,2275,1958,1058,461,2108,566,1668,468,2487,2495,2084,2444,22,1379,593,1669,2349,2301,392,1174,2247,2112,1886,311,45,1686,2407,1393,1598,762,1329,314,1220,1617,1423,2170,2390,759,1611,1608,973,308\n1793,1956,1906,500,2137,354,953,115,1540,504,656,368,722,1681,2071,978,1033,657,881,450,2356,1785,1743,175,189,1412,2087,1989,1233,2397,2469,1258,1458,993,402,437,117,633,2398,21,845,1646,1612,2057,1129,24,1968,1270,500,2296\n979,2090,1804,1850,1002,504,2174,1974,2305,2227,1797,2202,281,308,430,885,758,1796,2264,1443,2258,760,305,133,1736,653,1669,334,524,1575,603,1156,83,2050,692,1553,120,607,1647,665,1205,2228,2039,574,1252,2412,1299,2063,227,1761\n2490,1480,871,45,578,194,884,853,265,1385,1238,482,949,2319,822,2100,1453,127,877,1880,2326,2024,43,780,1318,1237,2394,435,1481,2033,1319,461,1071,54,1119,1040,1243,1367,844,2013,1617,248,248,1683,1940,1873,981,873,24,1588\n1649,1496,1409,1722,745,379,577,1558,392,770,1909,342,1619,1238,75,1013,638,1099,2303,1860,810,1420,1890,104,168,150,1903,285,385,1761,2367,343,1848,1141,409,2297,1797,2087,1735,374,1147,2260,1792,832,383,1161,1747,22,482,202\n1040,1819,1493,1996,1493,795,306,1279,967,44,323,1923,261,445,163,1606,1361,2062,769,2165,1436,570,1837,1874,585,2236,753,2111,2324,2000,1393,2054,1504,1359,390,548,671,1091,1157,2493,1139,2142,2071,2009,238,2418,874,1151,1655,1853\n1206,1103,2076,1158,1785,2436,27,2439,813,1548,998,1584,1646,706,254,1490,1844,70,1092,683,1850,2236,1851,1818,481,262,766,1893,2090,285,1556,478,811,421,1578,2057,2203,2285,427,879,2440,2309,191,471,1815,2095,1530,1330,1734,1570\n1355,1866,640,149,85,1845,357,648,189,2062,286,938,1008,714,1160,466,619,1311,1167,2318,1740,18,391,846,983,1262,2195,1498,777,1600,2151,408,2322,235,2389,2197,2009,1874,1747,1937,1180,2324,1691,1851,339,2322,1065,2034,372,593\n1499,170,2345,995,1934,246,156,2472,435,335,471,1668,1293,809,1949,1958,1347,1161,1716,709,2286,1232,161,1619,431,1579,841,753,2060,845,2355,1694,2009,1822,1506,2034,760,2490,2207,1468,1041,64,1902,452,1221,2348,2406,325,2274,2484\n411,1778,649,382,1491,628,2463,968,2148,608,922,411,1276,262,16,1180,1594,2217,1832,440,1434,1701,368,587,763,25,1741,1758,1837,304,1314,1505,1522,1628,1392,58,1067,1568,1810,1571,1493,1391,149,1412,1790,214,1406,1894,547,890\n1546,1160,1958,1252,2273,992,5,519,2310,44,1968,1728,1970,330,1226,1791,647,817,1326,435,470,2099,647,687,699,1106,2238,2255,1270,1400,2189,484,2435,1307,738,1817,1884,459,310,962,308,1422,499,1839,1777,1975,2050,2240,608,974\n1463,1475,318,900,1456,814,726,1879,1441,2417,570,910,1437,325,2427,1165,180,913,2063,254,1943,2283,1896,2090,1284,257,1227,1486,1011,2052,2283,1280,733,2105,883,2166,1557,1552,1027,1893,86,2396,2082,1693,985,1726,1889,2360,1041,893", "output": "2370516"}, {"input": "45 50\n2320,1402,1560,1126,608,576,933,304,1235,1197,2378,169,2183,266,1897,733,562,1483,2112,241,776,2375,2008,542,1960,2055,451,2498,1665,745,874,1673,1208,2338,1380,1591,2458,369,1910,1297,1982,2066,1059,144,338,838,1582,1753,547,613\n229,1746,867,816,1647,117,1648,1660,151,750,1941,1395,2463,1151,1413,1084,576,1438,950,1009,2044,2376,2296,104,1308,1009,148,2244,352,1783,2452,1282,1952,2242,1835,612,861,95,1877,1179,1274,1402,2486,2055,818,194,1437,396,556,740\n2191,2330,1469,721,999,1351,819,1990,14,1537,2334,1248,1307,939,1500,466,216,1912,982,426,445,747,1346,506,878,611,106,1953,135,105,524,317,229,1665,690,1476,2464,1037,1707,1943,853,1662,2462,563,1550,697,2099,1963,1908,1211\n514,1815,1497,867,1962,37,1244,732,254,812,1868,830,2427,2079,1603,2213,2475,500,1091,2144,292,2326,157,949,669,407,2030,2033,2197,673,1730,2167,2493,1507,291,845,1288,2429,1656,1818,1967,1519,535,2056,1964,1052,2371,548,69,1707\n2116,2154,1004,333,654,1294,1575,2270,242,167,287,402,686,2425,1307,584,902,1423,1285,1342,1844,1907,1604,1631,202,1913,2066,1693,2165,1597,1893,2158,1518,85,1276,2343,871,2344,1512,1924,271,1899,188,198,244,1023,236,2076,584,1075\n1249,974,2238,2196,2413,2072,1906,1888,2074,305,1125,82,18,1456,37,802,2063,25,2299,1118,1607,613,2354,964,1589,1480,546,1046,1232,531,399,2478,1617,426,1834,1628,1333,2219,2497,610,1111,2137,888,1598,968,1815,1369,1979,1233,1259\n335,1242,2133,374,1562,1444,2386,1904,1546,50,339,1439,86,653,300,951,1246,496,333,1590,572,1489,659,683,2413,1258,723,1282,1490,2045,505,1023,868,2437,616,499,760,985,922,184,2474,520,2180,2090,2325,252,1671,1050,279,1231\n1759,1316,1068,2495,894,1896,727,1212,1849,145,748,928,1,2056,403,86,708,1930,0,580,1890,376,1856,2294,1759,1875,59,1832,355,553,1416,288,2041,1502,604,1439,648,181,2340,648,384,892,989,757,384,167,2353,2417,2116,646\n178,1107,621,515,2045,1422,514,197,687,377,1544,2035,1597,753,392,1594,822,575,2498,1408,55,201,1801,1562,2166,580,1269,1067,37,2161,16,1924,1396,1941,2448,1376,613,815,2123,1087,1628,617,215,784,786,2397,1540,1832,265,1422\n796,1515,1432,1604,422,595,556,645,2383,1089,1184,473,2328,702,2050,569,652,2473,435,2466,25,68,2418,2459,659,909,730,515,552,1276,2306,920,55,1834,1762,2485,222,2342,2408,1075,1443,1309,193,2335,905,2005,2417,1232,383,1562\n2055,1184,2162,1235,838,1309,2350,761,815,1275,897,477,918,1398,719,174,2358,1748,709,1636,1381,365,329,417,1170,663,570,161,416,1844,2126,2424,936,293,1691,1004,189,2199,494,936,1241,1612,1217,1016,1453,302,108,654,2096,482\n318,1585,1110,908,439,2279,1401,2437,573,577,171,2283,509,2142,1757,1536,1917,1958,1618,39,995,394,1583,2260,740,458,70,1752,2185,2485,777,2430,783,1762,1689,821,1398,334,528,179,2031,2354,351,1678,482,2132,39,974,2229,1255\n1050,740,1468,1035,340,1050,1701,388,1768,287,182,799,606,811,1960,891,226,1062,645,2393,1715,1161,1002,1607,2358,1265,427,2271,415,822,683,1412,1594,991,1216,2484,409,618,993,2274,1253,1930,594,1785,1674,113,2198,1480,1567,2254\n1633,1750,1235,757,2124,177,1474,624,327,1718,2205,1838,1443,758,836,2239,1643,1620,2081,255,992,2215,487,527,310,1591,1740,607,1320,1320,186,273,1748,394,1649,2056,226,190,1150,2477,851,1287,2219,2348,835,237,757,980,1879,1045\n1559,2106,131,392,764,2473,1815,949,1221,1375,1585,2337,2430,90,33,1768,2094,2126,2375,1575,921,515,1874,1000,1540,1105,877,57,755,2320,275,1194,2292,2184,2383,1925,11,1747,2226,1724,72,2161,1633,1239,2367,2191,906,1946,1409,1772\n822,822,1701,1494,447,2261,836,475,1965,1852,2490,310,1118,638,1444,1796,463,1077,373,45,1076,1074,232,632,88,685,315,971,2379,1931,1549,1094,2126,94,1456,1102,381,1875,1146,2027,364,1389,231,140,2160,842,1585,1150,1412,458\n1021,757,2401,814,1701,1299,555,2362,547,2496,1501,2070,575,2489,1149,1622,2322,1214,72,1041,396,112,2071,834,2436,2070,1176,2048,1741,1848,1345,1576,2243,921,1233,445,802,584,1716,483,2124,141,850,1432,33,1074,300,1416,1253,1395\n38,12,765,380,544,1397,735,1088,1782,799,1957,1856,809,778,1074,1082,1188,92,1650,1165,1125,1282,1798,2158,2297,100,847,564,1304,595,412,699,894,1750,1124,1629,1959,229,636,653,2437,755,2237,820,735,72,74,1561,1106,1163\n309,1613,1874,1276,844,1224,421,227,222,57,255,2230,377,2472,1176,2439,1233,1073,1092,243,1728,401,1524,354,1105,2260,2093,1724,823,469,1231,301,1837,1040,1621,1184,682,1304,255,743,464,745,1910,1947,1479,616,1511,1789,967,1689\n1996,2032,1174,1195,120,728,2022,2017,5,407,1003,1169,312,2202,417,951,591,2375,1521,908,14,2044,1063,1506,652,1324,1342,234,1145,1479,2026,96,1841,163,314,2257,1323,773,659,378,127,2294,1367,1876,1181,578,1620,1691,955,1278\n1999,350,2081,215,293,2121,551,2435,207,2360,2267,1823,989,1523,2455,2117,52,1639,2268,35,2496,1,1696,1639,1015,1456,1085,1694,535,718,1687,1753,1350,523,448,1031,2446,1487,2487,94,517,58,1443,2306,1741,1413,944,692,2464,2464\n118,1752,478,1503,87,2447,1242,1905,667,152,418,705,2408,941,1640,43,552,1379,2370,2287,967,234,20,2058,1265,1695,234,1503,512,724,907,233,414,1736,338,1954,695,1598,2152,133,1020,1507,2040,727,2054,191,345,1215,2456,473\n1581,1211,574,792,816,1589,198,2376,2448,2475,806,2366,2324,1360,822,1449,1050,528,1302,734,2182,877,964,2416,1306,1233,1215,1572,993,521,1496,694,2460,1023,1553,2492,1092,1436,1419,453,1628,1905,1513,1569,659,2282,700,538,203,954\n738,2067,671,1619,1873,2318,2017,2250,158,443,205,1466,972,1451,2178,211,739,402,1993,304,2147,1202,1557,1365,2196,413,1454,987,2493,1419,114,231,362,2279,277,2258,531,1855,1756,730,1669,1147,1113,420,152,2001,1368,245,424,530\n1657,1656,454,1433,655,628,617,849,1313,2409,435,1314,650,2241,832,765,1323,841,2176,1303,1530,2321,1236,1353,1410,2083,89,137,552,5,1204,1999,394,1478,2312,366,856,1778,616,1971,2120,1827,1461,201,122,2223,1934,1866,895,2188\n1393,617,1951,472,1234,1682,1729,769,1970,2454,1358,1452,230,603,933,1747,182,2022,2179,1015,1288,1345,26,627,2436,1337,1307,1842,398,769,2393,734,1822,281,25,1955,1504,2393,2293,1790,106,1136,2218,1668,640,2214,1142,1401,2475,2370\n2220,196,873,1059,2168,2298,1247,2166,2487,2184,836,1952,2162,2103,1538,339,1434,814,1005,963,2062,2341,977,161,2475,738,1108,2096,906,1643,2111,765,238,2125,1230,1578,925,97,61,1350,302,760,696,516,653,1085,2373,576,1295,404\n1417,464,1878,144,936,1539,382,69,1582,682,1192,752,205,1061,1451,916,441,540,99,2490,1706,1824,525,1658,666,1582,1632,1605,1925,2320,1958,246,1805,1267,475,1553,1378,326,640,1169,2425,1187,2459,389,478,191,1357,948,1992,1588\n2154,1488,199,1254,169,1186,1620,423,1353,1773,2079,1031,2003,456,1338,1373,249,2233,1445,1550,1233,957,2345,471,354,8,15,1763,1973,273,96,554,2244,2192,1879,2379,1647,2256,1968,1905,2439,303,2422,2151,1417,550,1264,374,1403,1017\n1791,378,2457,1625,2145,857,2392,585,1581,84,413,1834,1949,1618,133,71,1424,1537,90,54,2419,1648,292,2474,638,994,1870,738,1719,2206,2398,486,219,747,1354,1391,1121,1490,2123,1729,1204,1446,2321,676,1580,705,2190,1769,2070,2387\n1853,1014,2106,1985,447,1977,2314,887,341,468,1437,1441,625,1336,1978,353,1189,1726,1517,976,1864,224,2199,848,1743,1763,933,1638,1743,840,579,533,1726,1208,141,653,1915,2272,1360,986,889,1631,1011,1814,1193,849,1136,126,1570,1297\n1673,1137,2370,1485,2037,2345,1886,426,579,495,415,330,1652,100,2163,1084,2339,1442,1305,556,1496,1578,1012,1018,1220,276,961,2278,1833,854,463,1953,704,1276,389,1733,229,1775,804,1753,942,1233,769,290,920,1697,765,1002,557,2477\n1150,1482,810,122,596,1600,1147,670,1373,1570,754,2208,865,2335,2433,1029,992,2388,1519,2495,277,977,1963,1948,664,1770,1563,466,976,77,1086,2244,1816,1529,1760,1521,59,179,1986,2043,1731,177,1425,1607,205,1676,914,2125,474,730\n547,1394,1963,1742,266,2021,1800,1684,958,2234,2133,573,396,1671,1404,10,1591,291,398,1995,921,2312,1600,1113,2437,164,1215,1507,1515,193,158,699,2418,991,2090,1415,448,570,1850,2150,2079,664,2257,388,922,236,704,1492,838,1575\n2202,382,1022,1176,492,2472,1090,1962,829,1812,2419,2047,672,1751,619,1596,1718,1924,1620,1105,518,750,844,114,2076,1120,872,542,674,1071,1907,1858,1929,1324,2336,938,837,1417,1672,1374,1451,2101,267,343,1661,1090,959,272,1599,14\n1859,2252,197,656,2026,681,2154,1334,23,752,1395,569,711,2008,551,1666,1616,439,455,2389,1467,2441,193,2209,1343,1466,2430,1164,1184,1265,487,443,1170,1516,1861,354,1148,1267,522,622,2377,267,258,584,1398,277,735,1497,864,1215\n2010,737,990,1083,1700,1221,1195,1064,689,2039,1113,65,968,233,1830,778,2418,466,577,2012,1216,2265,849,1757,879,382,38,536,2090,931,1571,735,2345,800,942,112,1967,87,295,80,189,2375,1286,1935,1211,462,438,919,1950,1391\n1799,961,2250,230,209,1878,1386,299,2196,1812,877,553,1241,701,1181,2401,1738,613,1295,205,1191,1157,1177,1459,1321,650,2280,1924,1735,1477,1675,375,1198,1599,1632,256,2168,1757,1541,203,2077,2138,1253,1277,290,1953,2016,2358,701,280\n1654,1970,2191,1815,1919,1455,103,1357,365,675,1832,1626,605,1130,161,1717,1109,1040,580,677,1023,1839,2100,950,1619,1292,345,1401,2130,1454,2053,4,1089,674,2222,1898,2272,404,1038,315,1262,2088,506,732,134,493,483,1126,1006,1695\n1710,2346,1688,488,2461,288,2023,226,1182,290,1428,274,1683,2183,37,404,146,2338,2064,1667,2017,1609,1588,329,1037,1572,373,2172,2181,2292,1735,1046,1309,1705,1159,752,1569,723,499,1990,1793,2385,2023,974,2159,475,491,1169,1134,1216\n540,603,2457,1913,1610,348,119,2194,917,637,628,1415,2185,1171,1265,941,182,2417,1501,1377,799,494,517,280,1451,1476,1808,625,2301,439,719,445,1068,692,362,152,224,2033,159,1496,973,1023,447,171,2030,1131,121,374,765,2354\n2025,625,1022,901,810,130,1972,758,161,916,1295,2123,2194,1933,1294,2146,2480,1354,252,309,238,620,2441,1661,1677,939,823,441,2255,959,681,225,689,1119,1089,2115,1583,1154,289,2342,1787,140,1296,499,1004,614,1805,583,1708,89\n1213,882,2096,1700,1422,1775,25,2277,165,1335,1657,421,2179,2371,2209,1464,299,1260,613,1127,794,747,577,368,742,1047,1448,300,71,541,624,1665,553,2108,1721,2010,1503,790,2251,2496,1053,560,2056,262,1906,1902,2404,979,1471,919\n2437,669,2143,562,212,32,782,402,983,684,551,2085,1608,1909,1858,2268,1327,0,2274,920,1164,264,1383,1784,628,589,2157,206,157,2407,1973,358,1989,1160,1698,1895,1665,1052,345,1820,1107,101,1868,2025,1411,618,1869,2420,249,502\n1415,1886,829,1293,928,1212,2128,1818,562,52,190,1704,376,2345,1188,1376,1731,1504,2367,204,1492,2056,734,331,1230,1340,536,1293,1,1353,2026,200,1400,2440,751,665,1481,1938,1152,656,428,514,2176,2410,1173,1123,1335,1803,701,277", "output": "2508750"}, {"input": "2 5\n920,76,1297,1047,254\n607,2427,430,482,140", "output": "1863"}, {"input": "8 7\n537,553,1901,310,1986,394,433\n713,2337,2171,2383,511,1004,125\n851,591,1713,1024,1730,1228,812\n1217,1283,1262,1043,972,1030,1496\n682,1162,1517,2483,1009,689,855\n964,925,1379,1825,2019,2466,516\n823,109,1688,516,843,738,1109\n2330,2263,468,2012,1395,2413,1709", "output": "30104"}, {"input": "4 4\n455,684,2357,1160\n1787,575,2173,26\n594,51,1649,322\n1579,171,1302,2121", "output": "6593"}, {"input": "7 5\n294,2180,1526,2422,744\n2013,696,1651,497,973\n2054,1154,993,2313,1418\n317,2251,57,2495,1709\n357,493,116,373,2366\n1819,1932,1452,587,1663\n2267,1533,1668,867,1012", "output": "22746"}, {"input": "3 4\n2037,2261,404,115\n2371,524,2255,1174\n12,707,147,1192", "output": "7763"}, {"input": "42 50\n1772,1416,2163,20,2157,1553,1567,2418,226,1588,528,41,2453,543,1681,2129,2297,1572,1975,508,968,2366,952,622,1221,1677,1119,1703,788,836,2168,120,600,1364,1123,2394,1913,1010,1757,1235,1208,1133,1842,2328,773,1043,1680,425,760,77\n823,1561,1328,55,2000,982,2302,1426,1793,1202,1064,2144,766,688,2391,1133,137,796,1906,2274,456,2190,871,1877,920,471,647,332,1053,896,1651,1506,1109,960,561,408,701,2150,528,1895,1382,2457,1518,2446,536,1040,696,1572,1425,24\n2269,764,1700,1494,211,1605,650,614,726,778,1529,379,96,1420,963,1230,493,1624,2254,1172,1857,1874,1005,1880,1374,1839,1745,91,370,229,1685,1887,1430,1408,1255,44,1790,1154,514,2060,297,23,426,782,145,809,1356,2088,1833,1371\n712,630,1003,677,2496,1681,2265,314,1408,712,215,1142,1159,2054,475,2197,2028,22,1338,2408,854,609,1684,1861,2186,1084,2138,340,2009,1903,382,1344,1526,1366,627,2357,2076,39,1886,410,307,780,2072,1023,1197,2239,9,1576,1982,1655\n1437,719,191,1507,972,1158,1010,640,2446,125,210,242,1008,211,711,2275,2015,2248,1739,783,2189,1416,495,1257,1307,2078,245,387,1875,698,300,849,2026,892,2496,2325,2471,1846,203,1366,1375,976,64,507,1901,1971,204,174,343,1361\n335,211,2174,2018,1089,1416,2493,1138,2471,352,2323,2226,2377,277,819,501,1908,1334,2151,1023,1324,2310,2459,581,2142,966,2197,6,969,1923,1119,445,2111,590,1142,284,1998,39,535,1743,1997,886,1069,1369,331,2459,710,2075,302,135\n761,2030,1610,169,2137,1081,1712,1010,663,1192,72,776,1549,1121,1684,168,329,369,2201,2253,1719,2490,964,840,1017,704,1364,2103,249,518,197,2127,1632,1809,1929,2445,69,1002,1998,1061,261,1697,2075,1004,74,790,1645,1911,1466,518\n479,108,500,1869,38,713,2147,1466,1419,2258,949,516,2054,2302,1638,2246,2364,309,1167,2032,307,1905,563,2274,2132,2440,2096,1397,1675,481,1551,1927,2307,2027,1008,2174,552,1590,1693,1828,1737,1211,1981,2187,1499,2303,928,307,235,295\n528,1165,1587,290,260,2185,278,312,2213,1991,1563,2222,1420,2336,14,230,2483,1104,77,636,2062,1875,1208,1282,1802,23,2432,166,1171,2033,2440,1203,1641,353,2335,1207,2453,112,2396,1639,1333,1627,2227,1573,896,119,372,2453,854,2379\n2037,2184,1559,1794,1922,0,1762,128,1343,1247,723,1344,151,162,1839,2171,269,1434,1588,617,616,885,1795,924,372,1956,1704,146,953,1164,1229,1393,1612,1809,1772,654,449,757,2466,841,313,2201,997,324,2382,2295,936,466,474,301\n1566,2239,2442,385,579,821,2045,1280,465,2253,2449,1859,1663,591,1473,1801,786,1654,2356,1140,1455,1103,2024,1315,2099,926,252,1135,704,1392,2447,1640,482,2013,1455,882,328,1117,574,113,2346,1487,645,2222,2367,1130,893,433,2399,1740\n390,1053,1140,1082,1979,1135,132,2458,660,1903,1748,532,1420,538,58,2447,1051,739,1924,36,2145,2408,416,1966,1863,2288,1833,472,1760,1713,1945,1247,297,1944,261,812,722,595,925,444,1409,2349,1252,776,202,713,20,2104,1010,57\n547,1073,538,42,999,1481,1879,1976,278,1953,1447,82,47,1626,1769,519,1201,1054,1538,1564,2065,1917,719,1435,1514,1021,1723,2101,477,2476,1557,990,976,2347,2077,1813,819,932,880,1037,233,479,171,1317,316,609,1939,430,885,705\n1924,1978,1974,1350,1260,1722,1917,990,35,249,1264,1057,111,1903,2480,422,769,2363,532,1862,493,268,1766,859,2407,913,1646,789,686,2005,2046,2098,922,1409,1510,1901,623,696,956,1251,106,446,1088,158,2085,696,514,2131,380,1490\n1989,2004,1507,2253,1270,1109,679,2207,321,615,1348,2182,2226,2318,1406,2002,1997,1140,1922,2001,367,757,1146,869,932,319,459,1240,594,1221,953,370,1713,1962,1313,2071,1240,751,1466,755,1770,1926,1656,1793,2484,1809,131,2416,1180,345\n2339,1173,906,2172,995,2405,1075,517,1629,1516,2301,2244,487,1608,2225,238,1588,1056,892,636,2267,148,1186,326,714,167,453,900,1391,257,1345,1912,125,326,399,840,256,1083,406,1787,739,233,996,1012,654,1401,1581,318,2349,716\n1016,1789,482,1154,1471,76,778,2460,1492,1977,1166,187,1245,1581,943,544,2209,2163,1101,1678,567,378,2300,1171,377,641,619,698,2448,594,1995,1559,1280,1119,1854,1938,748,1813,1670,828,2173,970,1597,1294,615,1284,2235,1948,1743,693\n2199,891,775,1522,137,1350,1622,407,347,53,1972,39,1839,2455,866,1120,458,219,1806,675,805,1236,2462,217,2085,1680,1803,373,1458,504,716,1515,179,868,883,2330,403,2353,12,620,390,589,2293,1935,2164,245,2340,764,2228,198\n1044,285,1025,1138,655,2099,2015,2163,1068,2318,61,1082,1265,163,1887,1822,1148,1003,893,1045,819,1613,2383,597,1055,529,2272,21,1553,1309,2082,437,1890,1531,757,1645,230,324,778,1863,610,2482,1057,1801,1186,1764,96,2360,2130,113\n1963,2473,2017,1410,1489,171,404,326,352,1451,1393,1671,51,978,1168,1601,118,1792,1817,2387,293,1534,1885,11,2279,416,1033,2241,1065,1018,1927,684,986,675,2097,1852,1242,2372,1343,1184,996,163,907,168,1225,1752,1129,1299,1814,1027\n1815,118,1478,1127,2494,1347,268,2459,628,1924,2369,2057,208,2108,290,1744,1772,2161,1566,1639,1591,1027,1148,2218,1100,970,2105,1384,478,1453,28,2017,278,2173,2462,860,1061,2266,1120,830,351,2104,416,1834,1982,2325,622,1443,910,1982\n1531,1722,344,933,137,63,384,1348,2463,1889,1390,1675,1219,1618,165,164,2050,439,1788,1663,1644,2086,1520,1474,1400,1247,2320,433,1511,2114,963,1514,1206,2445,1914,142,1645,1118,560,2128,1585,1517,635,848,1797,1235,1700,1317,1288,2126\n548,1550,455,2035,1657,777,2184,933,1856,601,1914,949,600,1868,374,1693,1108,522,1007,1980,71,51,709,666,2124,1497,308,881,2147,1707,2473,290,2319,2154,1054,1968,1913,604,1624,1828,104,1877,418,69,2245,7,1399,1499,795,2441\n1416,1724,1752,2042,1223,1142,616,2099,392,915,2191,158,1222,19,398,1824,1442,507,2077,411,465,1676,2339,2267,435,1940,948,1871,1209,2257,736,1062,1666,252,299,1696,1079,1497,1875,113,1937,1214,976,1705,297,1305,1903,1077,2283,2073\n9,1988,2450,1249,1991,1334,2484,562,284,1981,1949,2071,1578,2133,540,97,1489,855,2011,2381,1986,1607,1129,2112,1513,2398,1049,82,1735,1402,2308,918,2009,2155,1424,583,1973,418,2291,1711,1147,23,143,1198,1810,2138,1850,503,2087,1447\n158,279,1827,1218,993,1804,639,1635,1167,1123,562,1387,266,86,920,1015,1009,531,870,104,1669,297,657,1100,523,245,1556,2333,1034,1628,2197,719,1073,1494,1245,1774,1549,1367,772,950,900,1372,62,988,2073,834,1784,1001,937,1354\n2268,282,1318,1078,928,2154,20,2372,2100,401,1052,1009,1760,1824,631,8,924,2254,1086,2433,431,1686,1258,1235,434,1734,2006,2261,1559,2397,1539,1865,1130,2350,933,196,2447,451,750,1209,2494,243,794,1242,1045,1296,973,1024,1549,115\n238,509,163,1386,1045,809,993,903,4,1729,1643,1749,229,2276,2247,38,2003,1240,292,1769,123,295,2024,1618,1582,1975,913,1155,1975,1858,1674,1027,948,623,2322,694,2300,1906,2374,166,924,2157,577,1930,796,1981,1850,750,2225,1892\n1208,1564,2184,1190,71,24,1416,1104,1050,1828,1936,929,810,2444,776,2012,731,110,1397,1682,1381,523,1880,2161,140,12,652,1606,1136,773,959,1835,731,1278,198,1322,761,2260,1726,2329,1348,465,1898,145,298,2122,1091,622,583,1895\n2350,2421,1551,2442,417,595,425,1486,1706,1062,2084,741,152,68,177,2050,908,1365,1734,1673,1232,1474,235,671,996,754,952,340,2336,15,2232,1819,671,1911,450,2226,375,2042,486,1896,2386,490,106,2041,1256,1838,1387,1539,1005,1085\n409,860,1346,1293,1920,2407,1758,1285,1458,533,2460,523,1078,751,2333,207,1027,1120,192,1705,1938,1994,1493,1154,1375,560,2272,476,128,1817,561,133,1662,1132,813,2266,1900,2148,2091,158,1296,952,956,2256,2143,1695,683,2260,1695,1994\n689,1187,565,2007,1525,1141,29,1517,762,2292,1232,1523,2429,447,1171,1907,2028,1759,40,2070,2122,625,2484,455,1010,2069,1308,1739,1847,1742,326,450,1601,126,2174,497,1025,920,574,883,61,573,1698,352,303,1032,1395,1159,1437,209\n2322,1966,860,1796,1033,2198,1245,770,1022,1970,803,1804,599,523,1725,1151,1322,1609,808,1288,824,794,1398,45,2179,367,2371,1987,1779,1526,1621,2359,1564,2088,1205,1472,481,1704,1299,808,1494,2361,865,2022,1071,1910,2055,2218,224,680\n1118,2186,342,711,2490,2089,2121,586,2215,1183,2478,957,1720,1224,424,2035,2397,2401,1307,1820,1220,1307,618,1678,1400,584,2488,170,1747,1169,35,949,682,1739,290,1321,1032,96,189,2146,218,128,1376,2348,942,2299,1298,811,1398,1601\n2448,1720,848,4,1119,1543,1906,1659,2256,2138,1918,371,1362,567,438,82,1010,1416,870,790,1808,1041,1060,705,152,889,405,2432,321,2418,259,1296,1713,990,1715,2072,1912,1781,684,1201,219,733,1147,1118,1233,788,2393,1769,1454,1114\n1035,672,1713,2040,457,1191,1246,1364,2310,896,1154,696,333,2119,1828,688,931,2051,977,1720,1473,204,1808,2170,498,2105,1595,2461,2397,2283,253,804,1223,1687,2210,1258,263,1591,1822,39,2025,2169,938,990,1549,1248,1403,394,527,1999\n1939,1830,335,1245,1245,222,461,2280,1626,2420,1504,26,1403,2367,318,774,1019,998,2019,1216,1396,1227,632,1746,844,2100,287,2125,623,657,1287,356,600,1472,1261,2376,133,1037,1518,1527,1521,1937,1670,683,1824,1071,984,951,1800,2029\n2387,727,1017,1676,2113,2455,1058,426,2171,679,1357,103,534,1176,139,2086,2463,1314,527,658,1528,2039,578,2100,478,2147,1756,1385,1388,2420,1041,1649,2274,2397,144,1134,2022,726,1927,1034,1670,1929,1127,1214,931,989,1104,2128,597,65\n2487,1748,1362,278,955,504,68,1441,496,2198,182,1069,920,2325,1020,515,652,1359,887,718,2005,297,89,248,1487,1819,1311,575,1387,884,1022,206,1062,104,31,647,2254,339,1748,1289,1701,221,910,804,592,1964,1832,908,32,1629\n1459,1664,407,2422,2150,459,542,1504,30,196,650,1909,1441,681,556,1241,2117,553,1233,1888,233,637,2089,1140,265,637,2375,2497,2153,1911,1341,2376,2384,1617,228,2018,1563,1581,1716,2345,783,54,2472,656,1186,250,1357,176,1433,312\n1728,2088,580,1241,2207,2350,166,1395,1093,1214,1173,804,247,1991,1180,1045,26,1156,2290,1882,916,1099,1110,1600,1248,769,2020,300,171,2406,645,1194,1380,1571,919,2053,2197,2428,1948,715,555,1447,2388,1188,882,167,857,580,77,2167\n1219,188,7,1314,1554,2034,1541,2074,1877,2160,1542,2259,1500,2144,862,1479,1899,1639,2411,1057,1955,140,1399,530,828,2002,198,1367,1658,354,1331,409,692,1940,1022,566,195,2088,1985,477,1010,1101,1181,820,429,494,835,2435,2470,2468", "output": "2221905"}, {"input": "40 48\n141,85,1225,1000,1292,1261,386,248,2065,357,1498,1029,263,1308,2273,978,432,219,341,1062,734,1868,580,1286,394,1663,15,1608,2120,2007,2278,116,721,2317,861,1405,1359,1897,914,1388,435,1349,108,759,1646,597,653,542\n922,1317,537,210,403,1095,1478,1340,1223,523,1571,554,2078,1721,168,1163,429,460,709,2318,350,1335,971,2225,777,1035,1873,1083,1873,708,1416,2270,685,102,200,51,1708,1081,415,135,779,1991,2342,2225,184,2066,10,926\n1390,193,752,1230,299,69,249,2159,1044,26,1862,366,1910,1922,823,1337,1526,2085,1197,1555,1537,1431,2023,1535,961,1714,931,575,807,2197,2050,302,1336,1887,879,1597,1874,2300,901,1917,305,1960,2454,1553,1537,2488,1828,104\n999,391,47,921,1705,925,1212,1802,2387,338,2043,599,527,1856,2244,458,2082,532,1865,1443,1909,2119,2168,175,237,2302,500,394,2085,2114,2250,411,665,1183,2274,1429,2229,705,2443,1997,507,1816,571,1683,1404,1824,871,1103\n81,469,2253,853,1708,162,2345,749,1866,857,1421,631,323,1215,2369,1514,477,2241,831,1945,1363,1060,844,1325,922,1654,697,117,1930,1143,2024,2234,1038,725,2165,2145,2454,724,1230,1108,1686,215,1622,1244,1173,785,1694,2383\n2024,1004,99,2116,1356,1809,812,2092,800,1855,806,2494,2203,1029,771,2221,260,2162,1026,1135,194,2150,1385,1753,1790,2325,2449,775,1807,2036,765,64,2246,2330,770,958,2233,11,517,2112,1956,1488,882,1863,2135,188,1650,1150\n571,630,1899,1957,540,2123,1698,2384,1744,2355,1353,172,2068,2041,1748,1215,2392,2473,1332,173,2038,866,305,2396,1915,2024,577,1399,2328,565,311,1100,1132,1265,113,2284,1336,2033,1423,2024,1262,31,907,941,1976,516,581,1085\n2146,1006,779,1531,2193,1946,1050,2032,1363,1172,1179,2462,129,588,302,2382,7,800,763,1010,414,639,1402,1476,2408,304,533,612,1030,343,2473,732,1475,1059,586,1245,777,2403,2265,1090,270,1005,1339,383,1037,71,2146,201\n2104,434,2273,2248,120,1621,115,1147,2271,1032,890,2389,922,926,1171,1735,1683,1999,563,781,2070,918,2494,732,1830,1331,1282,2360,1093,640,361,669,1622,277,1839,1480,985,1011,1152,672,962,2045,1704,2455,577,1410,1752,835\n2246,860,2473,653,1480,1424,413,1883,2228,810,2390,1004,2273,767,1736,1622,1742,2087,1323,1024,1922,1648,509,1305,991,1368,328,506,2297,1461,776,404,2309,751,2191,658,72,144,1147,1475,1065,1797,2038,1388,383,1196,1279,1348\n1342,2376,1464,2170,678,2212,159,2490,284,909,873,1673,829,743,1144,897,250,1068,332,1897,2260,1353,1392,221,531,247,2308,513,556,328,1537,1364,716,1426,1903,1786,1918,2343,1125,839,61,491,1585,450,1242,1455,1478,2232\n1636,1859,1467,814,2334,1601,954,1956,2122,1712,1337,2157,119,1210,1953,922,2468,1966,1946,1489,1225,492,1116,1868,706,1924,859,2202,119,1943,210,134,114,2263,288,1143,2348,1638,267,1613,1843,2255,2261,1938,627,1802,233,1957\n663,1780,1742,2151,43,369,1694,35,2485,1420,323,1853,1717,418,315,2358,1418,188,1388,1365,1756,1565,869,2301,188,419,1675,1746,89,414,2144,2221,1426,1036,629,1258,1607,1702,316,1446,2123,285,591,136,402,2002,439,135\n907,548,1202,1182,2426,2442,701,2217,2489,1035,1653,1210,1224,2059,2168,1846,2135,964,838,1676,424,1360,2043,734,1074,195,673,1461,366,96,876,1181,877,2145,1372,409,1802,2061,1097,2210,1669,1322,1673,2113,1052,309,1503,1686\n889,2089,1322,2112,598,1633,1767,40,308,1176,2359,2455,1141,2072,970,1225,813,725,480,1418,18,387,1898,564,1717,1911,1700,1794,2370,256,1005,268,2310,162,1489,468,1178,1415,2321,2427,2104,490,273,879,626,2460,1159,359\n135,1338,239,2005,1205,691,182,1880,343,245,1603,982,1239,1100,1558,833,2358,1258,2426,2312,2087,2180,552,1480,1635,1515,1030,1872,1784,1352,1506,224,507,1546,2142,735,1948,655,1970,1968,1569,981,1782,1917,2399,2122,416,1182\n2371,1085,2307,1756,1500,123,2120,155,1491,732,1963,330,1349,615,1912,462,909,2360,316,160,1866,585,1765,306,1956,1301,1187,332,471,1312,1246,2418,809,1064,2019,2397,1645,1457,1489,1517,2361,1818,253,2430,988,422,1029,2327\n676,1425,1807,429,1670,745,253,897,2378,616,848,910,999,766,513,2236,1591,1446,172,89,1917,2049,430,564,146,460,338,1384,66,1177,990,651,159,864,2286,480,1329,609,1806,723,2472,193,1360,670,929,2410,1764,1166\n2251,511,1354,256,972,1085,1932,1850,136,655,572,134,1068,530,328,760,1442,741,2253,1511,1521,251,1561,148,667,766,1583,1537,812,191,1209,1540,288,1142,727,1693,755,1177,190,2178,1532,2316,2345,890,1865,894,1809,2081\n424,85,491,431,709,830,411,71,1844,2249,1531,1502,2012,692,352,2194,2285,1680,2341,2481,219,1882,770,218,270,2156,415,61,2109,142,2025,992,824,2038,24,1888,1941,2467,759,1089,324,1968,1428,1239,910,1222,2454,2449\n458,494,2258,1829,2471,2017,2456,1468,1954,854,2420,731,2301,1582,1160,331,2124,2210,973,780,148,33,773,742,2216,395,1035,1808,1905,206,1218,2325,958,930,1313,1705,612,385,1355,1724,1618,2007,488,1846,68,454,2349,523\n763,739,793,1534,1473,475,2434,2396,2492,1213,1096,301,1476,24,1012,847,1936,2241,1795,377,315,1230,1602,1352,514,2050,1128,1252,392,1104,1643,1598,1128,1581,1143,1466,723,1248,582,1059,1445,66,1239,144,1505,848,777,1412\n594,2361,1573,729,1886,2164,2100,186,459,1069,1091,1829,224,2109,1290,323,2206,38,1054,2178,960,517,574,2307,1739,2425,89,1362,1764,2088,883,447,1315,931,714,2200,437,422,2004,2210,531,1808,681,1268,2089,561,1724,1162\n1464,2189,193,460,1080,2172,1697,2404,1361,2226,1437,193,1810,2122,253,477,1555,93,1358,1656,1177,1225,201,48,553,1402,2079,1883,1123,844,1163,2099,1752,335,2300,1148,2214,804,855,2439,1832,2371,228,1576,1300,1416,162,1689\n1255,2163,1092,1376,1749,1913,1326,2223,792,994,578,2111,1927,157,747,1274,1127,1955,2383,43,1286,2483,1584,1343,2082,952,295,108,824,1215,963,361,926,1747,1910,1908,971,1866,1301,652,579,2490,2479,2483,2277,764,1775,2463\n2235,1453,2344,1134,1700,259,1714,573,353,1306,188,640,1886,1762,229,155,1818,405,1403,467,330,1564,1388,1300,2203,55,1118,1882,1984,271,672,1774,1170,373,1171,1834,870,1981,799,722,975,656,2344,900,438,1932,1146,1601\n1161,454,2288,790,1740,1759,1292,172,220,565,292,2004,1917,237,1729,2351,1899,2078,1598,43,113,1794,2096,2107,2046,107,479,390,2103,808,1310,2271,2284,820,2254,1192,246,527,20,2360,595,488,967,1204,1588,1990,2029,2005\n2313,253,2360,954,1464,667,554,811,2281,1926,1646,2179,490,688,621,43,1209,1296,354,178,1804,515,8,2358,97,355,1244,889,650,1901,1785,2211,2064,2380,311,570,1874,327,668,2463,1937,2066,1474,1208,2283,1629,1096,1173\n1063,1523,1495,936,245,1978,1716,895,2133,1962,2403,778,2181,1717,1297,339,248,606,1460,2226,139,1078,1306,299,244,119,1504,547,37,2316,329,1655,474,2005,1662,603,55,1035,1025,597,821,680,1119,231,2478,872,1125,2416\n1587,1042,2313,2446,258,549,178,1485,1105,1771,978,579,2445,2031,679,2095,1448,2384,1628,829,1672,1006,1581,371,2127,712,2002,425,2323,1719,525,2024,1927,2098,1836,482,1600,1586,637,2050,1937,952,1873,509,2168,2017,1785,1046\n1010,2499,1936,303,1186,599,1339,2024,1609,1642,441,1958,647,363,736,2201,2294,1345,491,648,2269,215,2268,236,1020,1163,569,485,1922,275,1746,619,1184,2445,1690,224,1299,1201,2290,1456,137,1319,2357,1822,864,175,2482,179\n953,1960,995,1798,1992,972,1048,1791,87,1431,1507,494,605,537,101,563,522,1215,1858,1956,2317,1759,82,1607,676,1942,1899,506,2198,2351,2044,1549,1500,2172,243,2165,497,1963,330,2386,112,595,946,629,1595,1102,1648,266\n1245,457,1397,570,433,342,2220,125,679,942,2077,2181,2144,1873,2387,1183,548,521,436,2186,1353,353,657,333,627,497,1568,959,1320,1764,2459,1042,2308,718,2091,1087,754,2424,831,477,537,308,128,716,672,77,2192,597\n1783,27,2167,93,2131,243,1364,1955,125,1391,637,37,614,2416,24,2276,1257,1244,28,551,509,606,319,1929,2296,1022,22,520,291,2325,107,182,1645,2406,389,989,766,803,437,1887,2367,2228,398,231,2405,390,1586,642\n2209,2139,832,399,1758,2202,1541,2446,1909,1674,889,1856,1213,459,1703,1389,2342,930,1457,2242,1685,946,1480,1525,1529,1983,1672,1154,712,1410,2299,774,1664,1028,1224,1852,594,2414,1041,2071,948,2172,1101,1868,1523,233,2292,1460\n1746,673,1933,2335,1380,61,2305,1682,2443,1042,1718,9,2174,2267,1335,2085,2143,772,300,150,2098,1118,1078,1064,222,268,882,1255,811,2283,1722,355,805,449,859,1323,1107,493,2261,1416,1853,991,60,2096,378,309,1247,2445\n76,995,719,754,1252,2370,1739,2336,1603,2066,2429,1099,2380,191,1337,1873,2291,346,467,1958,1553,736,1485,249,2117,2138,485,42,1676,975,1681,910,1861,1483,646,106,1878,1809,531,2216,2073,331,132,506,2235,52,2436,1457\n2284,56,1569,2048,418,1890,2335,87,14,1273,1714,89,2350,1233,247,1690,2266,2463,1036,1008,931,1518,2136,184,100,823,2189,1773,482,1419,1059,1629,1253,231,85,1483,752,553,1501,1633,294,1858,1906,2001,54,1469,615,1759\n1137,664,2049,1841,1998,290,1071,2149,49,1948,1903,77,63,1558,2055,1168,913,1689,2353,263,1827,2465,2157,727,1066,1302,1145,40,1884,1197,2230,1430,2169,565,178,2085,1059,1923,764,2349,1644,1835,1505,2402,940,13,459,669\n1429,71,2249,2336,1338,1357,899,2013,1996,1765,1897,2120,105,88,1108,1017,2011,2031,2021,1938,646,286,669,1192,1193,1153,1757,665,357,2023,913,41,1878,2222,26,1189,1697,1732,2015,1485,151,999,2474,184,859,1843,1660,848", "output": "1987326"}, {"input": "7 4\n488,2470,34,1902\n2470,276,868,1576\n824,1733,1909,1969\n1898,1521,308,1133\n751,2485,759,1608\n102,1450,1245,906\n395,1250,1929,1662", "output": "20879"}, {"input": "5 2\n439,458\n75,1831\n309,409\n33,134\n1781,2261", "output": "4028"}, {"input": "1 2\n1852,1791", "output": "0"}, {"input": "6 6\n2404,1496,2310,1201,1458,516\n1431,15,2300,828,2417,1593\n661,1657,1389,2285,353,978\n1735,1547,560,1043,1046,24\n515,1546,106,1722,2349,1879\n1255,1163,277,2218,1178,1945", "output": "24765"}, {"input": "4 6\n335,923,857,939,1126,2384\n1629,368,1638,1837,34,854\n1983,709,1268,1280,1761,431\n2319,1159,2438,811,1134,1538", "output": "8785"}, {"input": "4 6\n199,557,2274,1335,450,666\n2257,1304,742,1274,24,2495\n570,1205,1769,2328,178,943\n436,2025,736,676,920,1186", "output": "12472"}, {"input": "9 8\n1780,3,720,1974,883,1163,643,1751\n90,2382,1724,2337,1698,1131,2241,2375\n335,1123,2313,1809,1503,1471,516,1216\n2303,105,2170,137,1534,1529,2259,2233\n614,929,181,723,2359,2104,1569,1340\n2204,1769,1321,2360,1006,246,1231,840\n702,1728,2440,1288,1616,2255,897,1090\n2082,454,1556,2442,131,2402,2327,803\n298,41,1588,987,478,980,261,1082", "output": "56030"}, {"input": "40 50\n486,714,1229,2111,671,194,1099,386,2281,264,990,528,1389,360,1060,418,1390,529,1884,869,1329,1606,1601,1592,1416,475,2203,660,437,454,1101,439,1773,1317,87,874,2012,52,2068,2170,1892,714,1534,1372,1203,2112,554,661,2380,2123\n422,279,33,2494,2175,551,261,47,778,602,1518,378,792,1346,2107,2268,2370,2144,1729,1786,1081,1134,382,1662,1539,2257,1200,99,1347,1621,1097,158,391,2296,1532,578,1831,2208,1154,1938,2004,2326,1976,2032,737,2095,600,2378,1325,1670\n1593,2079,191,2322,2485,605,548,1712,2210,1336,2430,766,313,124,1983,1370,10,1062,2455,742,447,1609,234,1626,1696,1795,1807,1456,78,430,1688,1633,1226,2335,334,857,1509,2265,353,1128,1858,852,523,1018,403,1701,564,356,2123,1426\n2490,446,1015,1129,1266,2495,2427,1794,1559,2285,244,1900,152,512,1305,356,405,1552,1267,1418,2027,134,1536,1740,262,1845,1699,2345,915,1065,746,1251,1163,1355,1528,1526,1946,447,190,2006,2484,743,1258,207,271,1915,1327,1974,1618,44\n278,660,2175,933,1330,20,2059,401,639,828,2023,983,1913,297,1271,809,255,2364,133,1138,1452,514,69,602,2249,1783,2249,550,256,1103,1991,742,175,828,2257,2471,1273,1394,1834,703,2458,2119,2258,1624,2290,1800,17,690,1848,2133\n1245,1214,1902,1299,924,1105,2068,2380,2179,1407,238,1994,1181,640,2128,1933,536,1943,2169,1629,1786,2292,2106,1586,954,796,891,1196,766,269,2483,2040,757,2369,2180,1529,341,720,750,1346,1171,2242,777,1765,2347,1928,1120,842,1608,1373\n1639,1436,1838,2401,2479,1176,1266,1815,473,973,822,1386,1066,1910,618,273,611,2325,1017,1722,820,2238,151,409,762,1891,2056,2320,102,64,1608,1039,665,2342,835,1836,422,591,349,56,2395,2410,62,61,563,2351,1652,570,787,1591\n371,1445,2240,2260,726,681,1579,207,1269,2323,561,2163,897,2132,706,640,2350,2348,2328,2306,922,643,2343,475,121,1629,2417,644,858,1774,301,2304,1468,840,31,1400,1674,430,2088,1373,2020,2208,1525,85,999,1476,1895,1503,282,2151\n2098,2267,933,2441,1731,1211,425,2274,1082,2427,19,769,1443,2044,1292,343,1246,2407,492,340,2078,2124,1783,1803,473,2192,537,1599,180,577,1290,1520,1244,312,740,451,1495,1305,475,1469,1427,2484,4,144,1554,1035,1698,625,140,1191\n534,1912,1848,24,542,384,990,1993,837,638,1868,1285,1670,1533,562,2171,856,116,3,1267,2295,2364,363,1238,1296,630,1107,2000,1115,25,2288,1481,2306,1447,38,1337,394,830,199,2402,740,1260,596,303,3,2466,1928,357,2355,1463\n2449,836,1093,5,123,1824,361,51,501,882,467,1299,2388,1079,1195,294,2061,856,1564,1852,1308,1547,1765,1779,1847,387,222,707,573,1235,1936,1248,1871,1453,2387,2200,1399,2256,222,739,1887,1836,649,92,1003,2236,1796,2131,693,2004\n2088,1466,1610,1020,1774,1904,892,1474,517,1358,1274,2475,2439,895,1405,1890,2485,1974,1610,973,290,1934,1515,1356,1230,317,1049,1526,2453,34,1019,1347,1869,2170,1372,1316,2156,1461,1121,1256,1869,1866,2302,808,2059,1408,1463,815,1086,1075\n1897,107,1562,500,1268,1638,424,1521,2093,1537,1383,643,1090,1114,637,1872,543,1267,1306,968,185,1125,1518,1114,1884,2375,1299,1073,229,1611,1172,477,1142,1887,1008,943,1065,1717,1268,654,1815,140,2370,1922,138,2399,2351,1274,2338,1116\n794,2367,1519,272,1356,155,2302,176,31,804,1319,1883,274,335,413,2181,518,1190,740,1928,876,1069,259,1349,405,1922,436,1356,2381,2482,1271,1536,1119,741,970,2231,1967,64,889,704,1081,1335,1446,88,2143,707,2314,1910,1706,2173\n2346,2266,1798,1084,977,352,657,363,2475,634,1860,1535,1990,382,709,2097,96,2008,1846,2478,756,1898,690,200,433,1432,234,2226,1129,2327,1074,1217,287,1055,144,1076,973,746,323,957,1921,1542,1963,2306,1845,257,438,1490,1496,988\n282,712,1563,993,676,1809,942,1480,2080,2453,361,1943,2375,1741,1834,1750,688,376,1569,384,770,2160,836,1129,2253,163,692,904,1728,319,1773,226,1507,161,746,2297,936,2307,1001,1382,447,2331,1276,500,927,547,2474,652,560,1785\n660,318,1031,2228,1402,174,1988,55,2029,398,783,1517,2087,506,1763,1418,2487,236,1572,1942,1457,2051,2284,1914,1357,1177,383,2277,339,1139,1622,1716,1474,68,1670,489,1886,255,1675,2444,2071,121,2423,1505,1699,1545,2017,2345,483,1299\n1334,1759,1049,903,67,838,385,1692,2242,1810,872,775,1108,1829,138,576,358,462,513,2345,1975,105,2065,2171,1034,1367,138,840,2454,2247,787,1253,54,763,1017,1521,1692,1716,835,1547,1477,774,1278,2279,1371,1789,848,795,1999,1028\n2231,2089,1165,2097,1667,2229,231,2390,1788,1329,1076,2286,70,1837,246,1198,206,844,2146,1795,1651,2034,936,1866,876,1970,340,2496,1195,297,782,987,623,1362,1933,1232,931,35,702,720,17,1700,2098,54,424,104,1258,2322,755,1043\n748,378,652,1258,963,1540,391,1719,452,2151,2120,550,2434,32,687,1343,1546,2294,1457,1229,1470,2393,1891,2285,640,2214,2328,808,788,2364,68,970,2097,754,2017,1709,545,891,2130,830,1851,277,1680,744,82,966,1544,1919,1259,570\n1549,443,1718,2301,2209,2467,1504,2212,1059,1132,2376,645,1735,534,2098,2167,2062,858,776,1134,796,245,2430,2330,1697,650,532,19,1304,629,1503,1801,1758,1631,1801,470,418,1637,1024,986,1064,2430,1325,88,944,984,1180,1123,1006,411\n2242,754,2116,696,1619,924,142,1313,201,126,905,1494,1082,1416,341,498,564,752,791,1991,2066,1480,1492,253,553,1749,1290,122,1848,2348,579,424,2264,2433,1424,1201,1440,674,1150,592,1056,2167,408,1330,443,918,190,821,674,1876\n1459,1144,994,1677,330,900,121,154,903,2004,98,807,1662,1635,764,1549,750,288,1644,1914,668,625,227,1307,105,199,275,146,1790,2136,1116,1183,2296,664,1374,1185,1316,69,231,958,929,1532,1015,1648,649,78,1232,1879,252,351\n1682,515,989,804,368,2330,1049,1868,1355,2307,1447,1126,1264,1427,1924,400,2198,1046,411,1463,508,2418,1909,2209,2266,1611,886,1720,1036,2333,2289,2064,729,2187,2226,1923,711,1127,690,1030,2078,2451,218,328,794,2378,1666,1144,2369,1480\n852,106,67,1480,456,1785,2107,1016,1426,1897,2400,2265,1934,2321,1517,23,2124,1557,359,907,1924,46,310,463,2159,1226,580,108,1538,843,1215,592,926,1101,1989,1329,741,960,1287,447,204,229,384,1991,1866,1456,2055,60,443,2441\n1075,2244,2250,170,1065,612,1512,482,2151,1306,1781,1171,368,1289,237,1510,1196,1169,1741,1191,1156,1220,2191,1047,490,1420,366,1508,1268,84,1038,2054,461,1472,2490,769,18,791,410,1211,1026,770,2255,1025,1247,446,2007,2337,681,1870\n724,1620,1082,1963,2130,242,742,1413,1054,756,2044,1649,2087,1454,1690,2436,320,898,351,2131,2382,2254,725,1526,227,2082,1850,1507,1377,1759,2378,876,356,1293,1767,396,585,2230,2471,2370,874,621,531,2388,1796,1637,541,194,1996,613\n484,589,1191,2077,1244,1456,2291,1874,183,221,1162,1879,1310,118,1939,2439,2374,1017,1535,345,605,1408,2314,134,74,2272,1531,1213,160,1536,1231,1639,1613,977,2471,1910,371,1990,1710,2352,1906,704,163,491,1990,1269,388,1831,1169,1712\n2317,69,550,1666,520,291,1465,122,546,586,996,1031,86,573,1521,169,175,2340,2159,2172,1930,1514,478,1443,459,81,2044,1321,332,1863,151,233,588,1580,1419,1987,1425,1780,1976,496,917,844,122,927,267,455,1332,2491,1575,509\n2342,360,2472,1452,342,2458,1225,2241,2348,362,558,722,1698,1301,745,560,2070,1081,2009,2030,912,2459,2293,561,2036,41,887,481,332,1309,1729,2211,655,1516,2282,1101,382,2303,1534,2170,1876,590,620,81,564,433,1845,1351,643,1363\n1898,1822,1735,1160,1720,1250,2441,1970,1304,2266,2343,172,1661,60,2243,569,1731,2204,2438,107,241,2141,1069,1238,370,1210,1350,1329,791,709,1473,2214,445,1333,156,407,1649,270,105,2356,2457,805,866,359,1090,1967,1723,1830,2067,1993\n935,492,1840,473,2254,1554,1627,878,1050,2259,1493,2176,259,1847,1255,884,34,2399,1532,984,732,2094,1322,2462,1416,251,199,1055,1289,2211,1606,206,1110,346,1236,1399,74,583,533,1056,845,1524,343,916,872,276,1541,1913,1208,1780\n1904,1226,397,1092,27,781,1632,436,1575,1309,706,138,1985,531,163,463,2365,1612,1998,2388,2472,74,2057,1965,500,668,478,1325,925,326,416,1242,1064,2479,1382,907,2082,654,1546,514,1851,332,1918,968,1180,1332,967,776,2340,1090\n738,1808,266,389,1320,290,1025,340,856,139,926,1454,1584,1932,2174,1237,715,1168,2255,1079,2358,366,1976,813,1521,837,325,1699,923,1911,252,483,124,1544,1735,799,468,366,40,1983,1826,1462,614,232,2393,1172,2054,2267,1413,1931\n2284,2113,1952,2149,382,2183,1279,306,1850,656,1162,356,1317,1740,737,1700,1072,731,1314,2455,1563,24,248,2458,2168,1451,489,1087,2492,1824,1469,1870,2373,625,777,296,2020,781,1415,449,429,2470,2143,1732,681,2243,1562,2137,1839,388\n497,1200,1591,1490,1115,168,2128,550,335,1125,93,2077,2440,2197,2002,469,367,1395,1443,1158,1872,909,1830,1376,1659,2488,1992,81,1841,2459,904,92,1717,686,1247,2245,1922,1464,1350,159,1907,872,2024,372,857,2195,2054,991,1331,254\n1449,1829,1056,1663,1999,655,734,2244,437,380,2266,1336,713,1526,50,600,1814,1907,274,1864,1655,1498,1101,585,368,358,1100,1980,2462,1288,1974,264,388,272,2152,2329,845,1656,2289,654,134,965,675,2378,560,2073,217,362,794,2018\n2488,2060,1746,1834,1031,1387,1331,533,602,333,861,839,1709,964,1885,709,685,1667,1763,637,190,1381,1018,2435,2443,1239,413,2011,1197,737,2071,2415,773,415,879,1645,1480,224,933,979,117,2043,119,467,2123,1892,510,2478,1836,467\n1719,1225,1545,2458,2329,721,786,1614,1649,694,1942,1872,1580,1368,1980,1625,1265,1305,458,1525,82,1999,223,251,137,372,1124,1253,66,1969,2212,2130,1140,1050,1921,991,1920,346,2053,1345,1820,2234,351,1005,1177,1777,442,2376,974,313\n147,1153,1641,434,1226,2369,1229,978,2473,2423,1519,2028,1410,523,2311,1886,963,1992,31,745,796,56,410,2244,1164,210,1546,153,792,2442,1918,1938,1646,1131,2130,1525,1377,1779,441,488,1145,1389,899,4,1370,2353,2270,499,1217,537", "output": "2102018"}, {"input": "6 4\n1968,1194,1025,1405\n1777,1455,44,1941\n1540,1787,1479,1215\n900,418,1740,1311\n2021,2358,670,464\n2445,1757,1151,2283", "output": "9148"}, {"input": "43 46\n1704,648,1936,236,2277,1561,188,1043,2438,1016,1074,675,563,958,2264,15,62,1153,1919,2364,659,2208,1947,1178,631,1668,1260,1522,1399,870,1507,902,1180,616,2025,953,2237,210,869,1800,1142,149,2001,2480,11,1072\n960,622,1989,1699,628,2405,1858,1631,1288,1921,990,1729,1971,47,861,195,1807,1960,1691,1,696,642,1002,1375,472,1275,891,2183,1383,263,2434,1485,571,1353,493,1398,1287,1631,1475,1723,1993,1829,727,144,1560,983\n1930,1982,2213,1801,1725,2452,2213,214,56,2095,2492,2083,11,1923,1366,1362,1317,545,1159,1701,548,2343,1465,425,2450,2124,2107,1631,351,852,2451,441,1855,1168,632,1331,502,1118,1177,1704,281,1129,2381,2031,1382,1673\n948,1825,1552,726,1263,1444,1890,1506,1492,1921,2211,1425,1976,133,2321,418,1519,712,484,175,1155,1645,1522,923,342,649,1384,100,1759,1739,176,1495,286,538,1266,2327,2109,517,808,1164,1982,2416,2393,2356,2175,516\n82,100,1065,1508,2182,976,2379,697,294,2041,1366,299,578,2465,2116,1525,1027,295,2252,2206,1410,176,1790,736,52,349,1027,1842,1029,2317,2450,483,301,1619,770,2124,2373,1183,820,1983,1999,1447,627,928,2212,534\n810,1620,2474,760,2070,309,1882,1504,2430,670,1017,1681,65,2364,1871,919,1914,999,1722,1936,468,241,1362,1766,720,383,118,411,402,2099,1644,1356,1428,998,1935,1724,1214,1459,1645,1643,2140,783,2486,386,2076,225\n1742,2446,88,1720,695,1480,1372,518,1488,666,611,2357,1216,1069,590,350,15,2381,2426,388,425,15,940,1647,1898,118,1182,489,1019,753,348,1123,191,472,2323,660,2479,985,307,1273,1806,234,2121,446,815,973\n142,561,1003,260,544,1713,2202,2165,697,1403,30,512,2388,1444,2020,526,267,1499,1561,728,2164,1205,1161,960,808,1870,235,2089,1427,381,2257,1629,1105,276,1109,1412,2245,1622,317,1280,1547,2306,1083,2428,1257,1216\n1731,1154,962,666,1603,1667,1590,1049,716,2484,422,2412,421,2323,2138,1910,389,453,146,98,1292,2386,1676,679,1740,2261,2253,1666,899,414,1281,1466,1962,1588,293,62,2320,1634,789,1804,258,1313,1966,1245,2479,401\n1618,795,1419,2039,710,852,2036,703,1449,1828,2247,1650,1472,2017,902,862,2354,1705,2466,662,1739,321,2247,2084,746,879,680,2008,1574,351,781,1387,1843,830,1289,2159,1687,1514,479,751,444,1127,1148,1805,1779,1431\n292,376,20,15,1424,274,329,1059,161,842,1794,1018,1669,1573,1193,1536,1801,714,10,733,2483,1612,1189,2043,1822,1761,1392,488,774,664,1092,2090,1010,1500,369,1442,577,2466,97,800,2201,907,1205,1848,661,1855\n364,639,1161,1699,250,1121,1341,975,1800,2399,1563,1424,2480,1375,2463,1839,457,1441,140,925,1400,2451,1306,1819,768,303,2111,1537,466,633,1252,1786,1123,2,2014,112,13,0,1,13,115,1174,2371,865,1990,2243\n253,2492,899,1304,1402,1774,636,875,781,319,2137,1851,669,1437,1232,19,422,37,1397,1209,1932,674,1987,589,1471,1920,2152,2305,834,1054,1986,1071,432,1057,2252,1176,617,1147,1145,1636,1625,311,2498,508,1926,314\n1737,212,319,336,1635,1819,77,533,1491,643,1588,1804,1056,1870,1556,71,678,1466,566,906,274,2195,417,84,1742,171,1410,1163,2465,560,1447,2132,1527,1800,764,1765,785,1546,2437,1031,1605,1680,1754,2208,33,280\n1043,2013,2338,1259,2228,804,2056,719,1273,1236,2380,1008,1152,757,2173,1780,1245,1803,338,2458,363,744,1106,2196,2424,247,602,1320,707,904,68,19,1723,1625,25,2276,2243,2465,2122,2316,1814,917,1273,849,3,833\n1189,8,1885,15,2199,1863,322,572,1944,2168,235,1294,1805,784,2050,1134,2391,1687,1545,1225,2364,1123,494,1961,1031,1027,2009,1832,1616,72,1217,281,2263,127,2465,470,440,251,1934,1085,1823,25,2361,403,235,889\n1080,476,1683,1818,1620,624,1104,1944,200,791,1327,1617,570,752,521,1395,539,2200,873,1927,1038,429,818,1413,1495,2389,1445,558,973,1714,1075,1961,1753,335,1167,1216,530,1139,765,20,2448,609,1748,872,2298,1035\n1568,10,2383,1350,196,1032,263,752,2198,825,1040,1470,772,1637,601,943,2234,1770,450,674,1642,2177,70,295,2113,1451,685,1222,1877,1659,1081,997,2161,697,1981,502,1845,1395,525,1419,1221,1157,709,1948,195,1925\n461,1062,819,1838,1317,668,1759,647,585,562,1723,1337,855,417,1050,1209,624,1393,1633,2054,516,805,704,1321,297,2023,1291,1488,1030,399,1517,2273,2371,131,2392,196,187,1587,337,1533,820,94,553,322,471,1766\n2273,1696,100,1340,876,102,867,2437,2375,1907,2173,184,693,267,2144,2230,2291,379,2429,1158,1196,2165,2152,211,744,1574,246,1560,1271,594,1415,184,146,675,1615,906,1431,1471,1358,2137,32,305,2293,130,831,355\n2207,2083,855,1038,2124,164,2015,149,1616,1659,1440,785,346,343,198,1038,217,1865,1209,388,1649,1191,731,1189,1079,459,578,359,1603,360,2045,607,2008,449,1237,1438,1479,2446,2192,1773,731,1493,1595,95,1996,660\n861,1990,484,174,2234,1136,2318,2385,1336,674,1081,2498,1433,499,374,1389,1178,620,2171,101,104,1219,440,1164,1663,2306,2028,1050,614,803,1805,143,2351,1653,1482,1517,1445,2256,1903,1019,2460,1148,397,1245,1666,1886\n1615,2444,1338,1228,290,774,976,2086,1355,911,1678,415,1610,1807,1560,1261,778,367,2441,2246,1857,1223,296,1052,2012,573,2100,144,2348,1167,579,2109,16,547,1427,2337,2422,1156,1353,2431,1490,1310,722,293,1156,2179\n2201,1778,2193,874,290,2397,1718,2050,974,1406,1902,1891,840,492,2404,1221,912,341,2142,1825,2092,1381,1778,660,1440,604,1330,2222,895,1047,861,467,1892,1447,466,153,1090,809,557,418,527,1634,1457,1020,2206,1732\n1504,2113,2325,655,150,1393,2189,1529,2170,1333,2070,2180,2032,1640,3,1042,26,2312,23,888,1237,1315,2233,1840,950,900,1984,460,1090,1051,1926,305,1211,914,118,2438,962,1775,1010,80,1936,212,1699,2277,1297,1702\n128,1574,2040,279,743,503,1616,1839,768,1863,117,407,1086,1206,2267,1750,141,517,421,1009,1321,1571,2264,2020,807,2258,2459,2038,455,2154,765,1502,1562,563,2026,1033,471,1228,551,1201,1417,2231,34,663,299,1533\n664,749,65,276,448,564,681,2298,1072,476,550,1412,1609,1294,1676,1216,2367,2160,1799,1573,843,1346,2499,516,224,2330,918,1139,933,2297,1946,1598,1081,565,1389,1095,514,998,2190,26,2206,2240,289,2287,566,1652\n1472,1767,811,2121,2195,448,1281,1452,873,391,1011,1989,1040,1863,2276,1556,1870,315,1664,2384,498,809,359,324,1246,2426,165,40,1792,31,339,2303,462,1845,2496,134,931,820,1137,1263,1759,2106,1464,101,1241,874\n1417,1768,1267,2495,647,2244,628,1136,1798,1199,2465,1915,587,927,842,878,1793,2457,1254,1900,2444,1940,1958,1160,1116,2110,1921,574,1162,1239,109,497,2022,660,1931,1179,2460,1828,836,319,738,826,1590,2267,2294,1056\n1596,63,1261,761,709,329,2381,1301,1380,2223,1058,1251,2318,2397,2272,1729,2261,1582,111,1901,1080,1532,1646,2183,575,1163,2048,716,1952,1850,902,338,864,879,1903,12,2030,400,1212,1628,438,1429,557,1241,1090,1599\n1749,1543,206,595,1938,428,2156,1783,1510,452,1793,1396,61,86,2390,721,1616,414,2378,2219,1443,449,2247,429,1792,2266,1805,1240,220,2028,2276,99,2091,1959,953,458,1031,1965,74,1429,2477,176,249,1954,394,2162\n165,2277,692,1248,2317,2325,993,2021,2248,851,1051,1270,1869,661,2263,402,207,734,1150,914,484,65,2217,1699,2093,1181,372,1176,1348,2468,309,1791,945,1440,927,455,773,1307,2113,63,148,1119,902,1727,2269,2410\n64,572,726,2273,1250,1339,1529,2371,1316,607,55,926,1817,172,2394,703,1352,20,2012,1424,994,1748,1441,1236,454,1652,2266,1934,2049,1625,1956,1558,177,714,1615,1599,951,1526,577,2076,669,2360,1063,3,966,1319\n1323,1995,133,1809,151,1063,158,880,2260,1873,2088,2101,1939,922,1627,688,509,753,1290,1062,740,1400,431,2451,1912,1775,1998,375,2457,1246,987,2345,1814,1949,991,1051,206,712,177,1072,173,1540,1220,1936,792,2060\n1109,302,1234,266,1814,1248,1740,1096,2351,1219,1956,2216,391,1921,2054,80,807,1061,836,658,870,76,1699,2373,1175,2292,1587,1222,1944,2368,1932,2198,964,929,2235,207,732,1602,34,292,849,1295,316,750,1510,2446\n2023,672,350,1099,178,708,1809,232,991,807,1512,146,2430,1949,163,1940,239,524,2294,721,243,1500,1137,476,701,1750,1722,1197,1988,1694,1816,238,1910,725,1544,2117,2208,684,49,1683,217,2363,893,1434,397,744\n1029,1816,147,286,1697,1111,2211,1716,918,833,517,1420,1188,618,1011,909,1831,903,2392,445,1071,1998,2245,1298,1400,1350,0,1137,1597,1837,4,1201,2081,271,51,518,1664,308,1021,1679,355,447,161,915,2321,1739\n717,802,2042,1351,583,383,144,314,1413,770,1347,279,2382,1946,550,2435,2338,700,1938,2337,2338,1246,1228,25,1231,1570,171,1418,595,1933,1674,2121,1815,720,1534,445,382,235,1516,1294,620,2310,1763,706,755,716\n82,1160,678,671,553,214,2012,1755,1695,1630,107,1448,327,660,1765,1057,710,783,2047,1541,699,1865,621,1075,1525,2269,1956,193,2148,450,1260,2247,1547,2133,2092,2487,321,244,1334,1135,420,2404,1740,782,1945,1401\n1068,804,2269,454,791,365,149,1832,1847,1529,835,1683,1528,1278,336,1800,1674,1566,2243,1846,1941,939,2387,876,1092,1876,1321,1113,1385,1897,943,2245,1419,2467,778,384,465,406,1,358,1953,642,2079,273,1800,661\n1329,1216,695,1434,777,951,413,1253,147,1796,253,2174,516,984,1280,29,1952,1852,361,830,1098,418,275,178,719,753,1139,206,577,1451,1412,1476,2382,172,1425,327,1179,1145,1851,2442,1610,2161,1450,1530,2118,465\n2236,2449,1398,631,516,478,1875,284,493,1774,13,2044,2094,1598,587,552,1631,79,1854,995,1840,2493,1090,2492,101,320,82,920,2118,925,1554,1363,1936,922,928,1345,2035,305,169,1708,2273,1805,1127,2356,793,1907\n1108,828,2377,499,2145,1664,1025,2107,932,2083,1222,2345,2115,2450,2423,450,459,1075,974,1760,2493,225,639,940,2239,623,1475,584,73,1894,81,66,1379,1426,2189,1551,416,365,1776,1705,1964,448,1157,40,2125,1653", "output": "2102681"}, {"input": "10 3\n159,23,335\n1480,1931,2005\n683,1626,1268\n493,1788,1392\n2078,528,938\n1272,420,2110\n2136,1328,276\n393,1592,796\n6,74,1590\n1001,1149,2374", "output": "20684"}, {"input": "1 2\n1845,766", "output": "0"}, {"input": "43 41\n756,159,1048,1123,1081,1469,425,779,145,166,2146,2016,607,1239,2341,1964,958,70,1186,199,735,913,2255,543,2496,880,2482,2327,2062,1194,1500,673,1750,1602,2353,445,937,2348,485,1891,41\n1718,1488,397,1734,2258,941,173,207,1016,822,1286,239,282,478,104,895,2246,1006,1171,1199,2040,1444,1205,1292,2290,1820,1650,306,124,1829,2406,1055,2043,1558,1132,640,2294,2391,1849,659,1570\n103,505,1987,413,780,700,95,2350,1539,318,1258,280,328,2153,2256,1832,988,647,1692,768,162,1949,1763,991,2466,1347,2189,2312,2415,2261,99,1663,2281,1599,707,1958,747,439,158,2477,1115\n350,126,64,643,700,497,616,2455,2329,1199,178,1779,2124,1780,1545,2154,1904,409,400,1526,550,1103,1538,1598,485,82,2179,262,2245,1128,1132,1822,2368,961,751,434,1886,1497,692,1969,185\n1961,1211,1058,1523,1170,1444,2216,2248,734,1007,2028,1321,2150,426,486,2431,25,1964,635,180,32,2062,13,950,1099,460,1598,1046,1976,778,1926,1217,2432,1491,243,1243,1577,857,1507,1935,2126\n1718,345,1600,191,1399,2495,1638,2359,2003,1654,2261,829,1684,2107,1175,1474,504,574,120,1597,1955,440,1482,224,1511,348,248,475,303,2096,1433,1522,234,259,862,1429,990,251,2130,2385,1974\n149,2422,50,1733,696,1288,1848,1641,1582,1743,2466,577,2332,199,1147,1169,531,911,1799,1294,1296,2230,1204,761,2350,2310,1669,2288,1207,2186,130,1011,691,520,464,2252,511,1264,2021,2255,2170\n66,1079,1661,1008,1162,2150,1606,2426,1372,2065,2367,776,1019,2100,1033,1300,1943,1330,130,1708,191,1734,1759,20,760,1277,526,81,2347,592,248,691,2120,990,2037,1752,1719,2173,2397,1467,2341\n1848,497,17,681,1886,2131,2113,536,2082,73,2397,719,2370,1451,2384,1281,2443,725,2318,1446,88,1066,447,2151,2187,1522,1177,2470,2017,1088,2239,1539,1710,862,343,2429,1739,137,745,128,864\n327,424,1100,1338,605,457,2094,986,2323,2365,551,968,1717,1909,1753,390,298,1360,1501,1730,2218,2045,634,555,827,1123,1229,535,2035,1260,1042,744,2161,1553,440,2071,1605,442,671,1359,1016\n2471,2098,380,985,1355,376,193,2349,266,600,2394,1388,231,668,1240,655,858,283,50,80,1969,1857,271,1793,1569,1271,1076,2001,520,1373,1841,674,829,1233,1234,1399,1745,327,993,1939,381\n1415,2233,1014,2484,103,2472,2040,2131,2341,165,1828,48,2173,565,2300,1117,733,1626,290,1682,716,173,2365,2109,1813,2471,1655,1953,1371,1679,423,540,1566,238,2242,1874,96,662,94,2392,602\n2273,2468,806,124,2217,1143,1950,327,1617,617,1875,2177,499,781,1075,624,2150,1588,1568,332,726,2143,1432,1639,1380,1315,1673,1825,2433,650,319,1274,1202,1598,616,88,853,1213,236,1878,1658\n2252,1385,832,745,454,1972,1062,1606,1614,151,1487,2181,1412,2004,313,931,1300,117,1324,1556,1225,2438,70,2160,408,2054,361,1378,1842,552,2133,2154,1837,603,1065,2309,1349,496,280,25,2075\n1557,1237,2377,918,1266,2098,1538,465,2102,934,300,2360,28,2263,2254,1932,766,1107,731,1863,1381,2104,146,2268,800,1693,1823,1084,1764,2239,315,1349,560,1825,1142,2093,163,1735,2150,737,2243\n758,810,61,62,2037,965,1324,325,1156,473,999,1162,1936,1316,2499,1069,1631,489,661,2109,2015,2390,1816,739,93,2102,758,868,1758,310,1132,131,2121,2217,2160,1614,1684,769,2253,279,1422\n2489,1987,1784,64,2430,269,1187,1078,837,1451,377,681,1999,1795,1012,1507,1251,2321,1704,1694,2097,1921,2468,1487,222,2452,563,1597,1079,1697,1580,714,1658,1084,1560,922,1704,93,1492,669,1494\n572,2405,478,1979,774,1417,2448,1469,2494,1668,637,1704,2078,2429,570,1762,457,496,794,2317,2047,1580,1319,688,282,81,2090,1267,2383,1150,505,866,151,662,592,2201,1619,1694,1373,1835,2018\n2343,1068,1223,1463,352,1197,1633,2177,1819,217,697,940,2038,1447,546,171,1164,1131,569,458,1631,1419,1785,732,2337,1440,1095,484,1166,995,891,118,157,275,840,666,28,969,1941,2121,121\n1423,1495,812,2343,1549,1934,1919,734,161,288,796,298,363,2445,339,712,375,680,900,162,1905,1275,399,2254,476,447,1427,1891,468,337,1885,240,2375,1198,1389,2125,2178,988,1492,1324,2087\n544,2055,1213,918,1801,781,1923,2269,1629,904,1971,1049,2410,414,2487,247,1069,763,2069,1459,1266,1754,659,1845,2093,1602,1095,726,1386,179,423,1134,1733,47,1525,2165,1238,1192,105,1948,977\n110,1643,2444,306,899,1560,1853,145,1726,1648,1255,884,44,665,1620,1242,2129,2220,1171,1898,1508,54,1197,1875,2277,1675,627,800,2177,1451,1293,497,866,256,1697,1224,478,1861,1503,2080,1272\n1623,1610,1204,521,2439,1611,1312,1203,904,2219,2109,2062,2374,1389,1844,393,168,1549,235,341,1682,190,1804,1280,878,1359,1132,1948,2223,1559,1582,87,2029,2310,785,230,422,1558,2425,575,1092\n1329,375,1232,2453,1289,3,1392,1682,878,1874,515,1205,1533,1336,1796,405,1880,1037,1454,507,372,254,128,837,1808,942,1339,1051,137,2371,661,437,2056,1210,847,2355,757,1425,1279,1835,1673\n1738,789,453,2278,2008,213,1146,1806,170,436,656,2335,842,1535,1552,1739,2089,1039,1065,1227,2189,1486,193,751,2398,490,33,1601,770,932,1828,665,1943,878,2022,2268,1554,1936,505,975,2282\n445,506,1992,1322,2324,2280,107,2281,1159,1800,306,808,1976,1970,234,1533,1610,165,2319,331,328,2431,1343,1205,1445,196,1586,657,1220,2340,1743,47,661,842,1885,1256,1076,2172,473,2142,176\n1095,1540,1189,1479,2338,2259,689,1022,1858,542,986,1991,973,433,150,523,910,1578,1994,615,1774,325,2451,1752,2015,1892,1763,1332,1870,699,1373,2293,1110,1426,1348,2415,1467,1537,427,1733,2041\n2275,782,2472,1101,737,2296,626,758,595,1304,1284,2209,2488,563,698,1786,2024,1896,2138,1459,1674,1932,1668,1206,676,697,28,1337,1435,2462,1622,1660,1129,2383,1109,2440,272,2379,1494,373,1715\n1039,2412,2261,1831,1800,425,55,2352,2049,2440,1882,1291,467,1637,1845,496,1317,249,1996,404,1952,287,1728,2336,2015,1571,1765,2217,2065,1798,2364,791,1952,1899,1040,1545,2141,2459,91,105,2151\n384,959,1728,1885,289,1146,747,1620,1384,2196,852,1321,2289,1243,1735,407,674,910,1010,1163,906,1092,2001,1399,1846,1881,535,620,810,246,1022,435,1305,369,592,1686,1137,1396,2055,939,1248\n1049,1039,1450,2228,2021,1348,422,2295,651,1102,774,225,1697,470,1563,1697,2314,2146,2096,106,757,1797,1294,461,667,1405,1023,1324,2001,433,483,1509,2223,1315,1819,1264,2282,2272,451,2323,1113\n1950,1193,2435,408,2243,8,2052,1562,387,1970,2097,1354,85,2257,1700,1025,639,152,68,1792,1187,1571,518,418,193,2090,1847,2213,1376,2061,477,163,2199,1017,971,1076,1103,176,1635,2377,2239\n889,2067,1951,218,1351,2459,512,1388,2420,1485,998,316,2147,383,1409,1004,1322,2451,325,441,2445,1231,2205,330,537,1516,1666,971,1165,2425,2005,1179,2342,1788,167,243,2026,452,2284,762,2286\n842,1483,535,1509,925,1529,1042,2101,529,2226,1923,430,1245,2257,1760,983,2029,1443,372,1775,542,784,1789,277,285,2452,1264,1950,196,1566,2327,1859,568,508,1911,1303,333,616,1938,2004,1619\n686,597,1343,2327,586,1498,2110,634,1474,2062,2169,515,2042,715,627,1553,1096,570,2070,556,1558,1346,590,1355,265,268,1879,2151,1240,1496,1895,119,937,1668,2463,520,2050,1239,1427,2405,427\n1750,2291,1165,199,2402,43,68,104,1078,2094,233,678,1387,798,2287,969,235,1462,946,767,2082,2096,1371,1152,1207,781,168,2494,1281,1146,307,1071,360,1198,247,1221,1900,1140,56,226,2438\n312,12,376,82,1566,2390,1815,221,1647,564,2116,1087,2358,147,2428,1276,2129,1313,1035,2499,1132,657,2281,1458,457,2301,2214,1478,2436,1981,2080,2323,2416,1957,2142,1055,771,1405,939,781,2032\n680,1571,709,571,277,2076,1382,1077,789,2381,2249,280,91,1840,717,2286,2317,610,1884,2303,438,2177,1388,721,622,1403,2017,177,1182,2460,1548,934,377,2319,542,2432,312,9,142,1216,2068\n1151,1638,2261,2093,271,493,475,2193,2293,703,1621,892,1717,2312,1732,746,2233,2205,1498,911,1122,1768,715,1362,2094,1888,592,663,1809,642,1343,1634,1945,2056,1797,1300,480,1375,1052,445,1118\n349,1544,250,1597,1726,1643,2090,2351,413,652,2333,386,251,1146,43,324,1692,2384,1879,1856,1730,852,479,612,612,116,234,2306,705,2068,655,564,149,1911,1749,2266,1953,1061,1108,1032,739\n1539,535,1323,497,719,1400,722,2281,123,1807,1254,613,1166,71,1290,2335,1497,261,738,803,319,2090,1864,1159,1103,769,648,237,1378,1125,2094,241,1040,1934,259,1743,2374,122,1540,1087,186\n294,1657,1038,1004,1731,1506,1715,944,1778,1152,1406,2020,603,1826,1266,1257,1078,1504,267,1094,961,1945,237,1001,1454,1338,2095,1388,915,1872,2385,1837,108,2300,372,254,2176,513,1683,987,327\n2408,765,1948,1633,1022,1732,1608,264,1094,156,1585,1503,1130,2362,197,2074,547,269,1033,2047,503,2386,352,1955,1955,1679,1281,296,2134,1133,720,2054,1488,2207,310,2038,519,1904,601,294,1555", "output": "1833258"}, {"input": "3 4\n211,1852,1176,910\n2189,651,714,1533\n1392,1707,2220,1252", "output": "2892"}, {"input": "9 7\n553,1705,166,1127,593,639,2219\n2393,1519,318,1884,92,992,774\n2217,1008,2258,223,2092,303,1312\n2487,420,377,426,1552,2426,1277\n774,1253,1147,2201,103,1854,1586\n782,685,2444,642,972,2302,734\n2182,464,1121,482,451,2275,874\n1412,1204,2330,1352,1940,1602,691\n327,303,1400,2350,817,661,1251", "output": "47377"}, {"input": "45 42\n2141,1218,415,2209,1279,425,1226,893,2267,963,683,512,698,1349,2066,61,1750,1508,673,44,1196,2325,4,261,1614,277,2453,1692,479,142,302,66,142,323,563,181,1156,2472,2119,1342,234,1423\n771,490,931,1354,1571,2142,1421,2186,580,324,434,784,2399,141,547,704,1167,1997,2163,512,764,1995,2121,798,1056,1243,696,471,449,1918,1406,443,366,1512,484,2295,1232,1201,2312,704,1166,2476\n2188,107,1259,225,2452,2453,1395,373,298,2035,1922,1192,1106,810,481,1751,2159,1060,455,2153,1930,108,408,2220,1325,710,954,2149,1238,1434,1670,1037,391,747,1288,1549,1620,670,2207,1185,1381,2359\n1322,1791,1625,210,1306,2107,744,610,228,1647,84,192,962,2348,2234,1575,2159,1670,1229,844,364,579,2292,2086,1770,102,2019,2276,1648,1316,1847,1620,94,494,2357,2210,1424,1694,2314,1170,86,1860\n2079,849,475,715,189,243,813,11,464,726,459,1501,2343,287,658,274,1300,1722,784,205,1428,158,671,1646,1272,36,2023,2217,1063,1048,1440,2121,681,100,1818,2389,25,718,98,567,972,1241\n2303,740,1333,1306,1371,1761,278,857,548,2358,636,421,1681,862,2418,1542,312,2227,882,543,1876,1926,1259,485,2096,720,671,1395,1421,1921,2271,1210,641,780,1182,1262,2231,2236,8,1319,151,2379\n977,2334,2258,1501,441,656,1700,82,2151,652,1799,184,983,1686,2436,1184,125,1331,1875,600,2410,2495,1454,1130,370,1981,295,1446,2213,1384,1144,654,2484,70,674,560,1399,1947,366,2147,844,2479\n62,668,1818,1547,627,2082,960,2208,1981,2472,29,1130,1642,390,2420,1404,1809,1718,1733,1542,2180,2226,1004,677,764,811,1759,445,71,1836,1341,2040,466,913,1784,2004,2396,852,1010,2322,2113,1324\n2042,1765,2463,3,1370,1348,612,2055,520,596,1251,1954,464,2349,1568,2369,2186,1713,2350,1407,374,537,2493,1997,1608,178,832,265,1736,1551,313,1466,2372,1583,1130,339,1823,2218,130,1078,2084,190\n1765,1558,1347,599,2118,1603,170,1114,112,1133,2379,172,1364,1148,1407,2415,59,1167,2363,2308,1014,1571,1918,1575,5,1038,1542,2041,1369,1582,2227,1533,1186,626,178,2394,1638,2220,2466,923,1444,192\n95,852,2259,2310,762,2488,981,2166,96,657,312,1306,205,947,296,1539,1850,1028,251,1994,2162,1837,640,1484,677,842,2048,1127,1435,737,747,516,287,733,731,648,1788,2437,128,549,1065,2472\n2037,2018,1995,1862,951,465,818,1013,1619,551,1582,1556,1763,482,1177,1804,1972,1571,866,2128,1301,2486,2463,705,921,990,2111,1696,897,951,916,405,2186,204,39,284,1384,965,878,1934,887,569\n1195,789,1370,2237,868,506,1824,347,1814,1967,2247,2248,1057,2298,72,776,2139,1023,122,2097,2479,1083,1197,826,1933,1335,1280,1342,268,2280,1399,296,1113,1201,261,178,1164,16,1295,1462,844,1876\n579,123,1042,1530,177,1414,1629,403,750,1883,1938,1358,1104,184,1712,1177,1198,1754,2211,1690,755,1139,720,1853,493,1870,2456,676,432,925,1635,112,100,874,1687,325,934,1056,360,1387,1937,881\n2492,1766,1350,773,1174,1736,306,962,978,560,482,71,183,1258,297,595,186,1006,790,1245,1106,2119,1113,2184,1813,1689,2197,949,1439,818,1282,1560,567,1938,1436,153,2034,1292,2269,1372,1527,710\n2291,858,1276,375,1595,148,115,644,2038,450,464,1577,281,549,523,1338,1857,433,1189,886,2066,1413,280,1194,306,1277,241,375,1025,1566,1619,2479,1211,1961,2356,213,794,745,722,931,649,1720\n2211,792,2415,549,2029,2495,1504,857,290,1913,1391,673,1633,788,1780,876,2224,1066,905,2323,1650,1915,1422,2178,2039,2462,2256,519,1881,716,2157,1606,1014,2250,684,1155,185,1866,349,537,1449,2272\n825,1660,830,2058,1452,799,1449,1964,1512,1214,1479,44,479,51,975,123,1479,1777,484,2242,2278,1252,777,479,1790,1690,338,948,304,356,2390,2101,596,837,2384,2151,894,173,1208,1727,1414,545\n1989,947,1221,1292,428,2128,162,192,1202,2074,2292,1304,1180,51,332,932,2303,1488,1160,110,30,1200,949,1465,2466,57,2296,124,807,1569,99,2054,598,1613,335,2058,1792,708,1125,1721,947,321\n406,2348,1097,2325,1648,1226,368,603,1853,889,2484,2217,2085,2256,1079,1569,2120,119,1748,1604,1466,1886,2499,2011,410,1240,1151,1377,190,2189,22,2188,1697,2088,1459,1401,1435,1611,1836,2225,965,2269\n1196,1001,2376,1769,2372,1977,2219,792,785,1749,1738,1026,2172,1970,1035,1156,322,2430,1647,602,536,1157,1046,2095,1588,1103,2442,190,1084,548,2481,1012,1218,434,2367,1194,785,1148,541,2273,1463,2350\n47,276,1640,1090,728,2430,1581,544,1754,1865,2246,2386,64,1670,1083,1612,758,986,156,1439,2000,1270,782,2484,765,1118,912,1555,458,1801,1569,1215,1292,2410,748,1743,179,590,1349,2121,2193,434\n1763,1496,731,220,920,752,871,2342,1357,1323,2049,1904,1288,2072,1549,1373,2336,1903,1587,1879,820,2479,885,1899,1671,1497,2408,1837,642,2216,234,1978,19,102,1696,513,2160,611,1131,2214,1593,1059\n677,2103,1362,511,540,1813,1612,1917,1182,1123,1514,2369,1300,1694,2342,2029,1284,526,1895,1159,551,456,1492,1679,1710,1748,282,2407,467,1859,404,1333,1648,1304,1318,2310,445,2479,2379,1029,1019,1732\n2002,991,862,1509,1930,615,559,1195,1690,1732,96,608,426,2039,1643,344,1569,737,2216,2207,890,1560,465,109,132,110,2397,663,1014,609,1754,2012,1968,2112,1498,1244,879,1049,1537,669,2118,1674\n215,2240,115,623,1461,365,2053,626,1394,2129,1461,1978,1162,913,237,874,2210,1960,2456,1712,1979,964,393,1217,1033,110,295,1530,2482,681,1733,1167,45,2165,1756,1325,2372,1979,1796,24,1448,222\n0,184,2271,1527,926,561,2477,1347,126,2215,2019,1393,942,2158,1473,690,1246,1196,317,2483,1332,2423,820,2087,1628,2405,763,1596,2378,1936,2437,2413,2015,2272,1435,1845,1463,1230,313,185,1128,926\n2285,1517,349,210,640,571,1550,2454,337,1247,397,1823,202,1337,1030,867,2386,1136,1740,391,2419,1140,1638,725,1109,1728,1638,734,2135,1527,417,538,1013,2204,519,1787,470,1319,1105,1261,993,1790\n364,294,630,108,1193,1695,203,1888,1627,1954,2337,1257,2002,1386,555,2167,256,1316,1337,879,2385,740,306,83,1584,337,2108,739,1074,704,1115,833,40,198,37,493,1447,1645,976,321,872,1765\n401,620,1812,1935,1001,1992,1840,724,1581,1871,584,680,781,1642,2257,2297,139,1783,307,1403,1328,1988,2116,1050,763,1757,1547,2477,1311,1631,1369,2273,213,135,70,964,972,2363,1104,1464,805,303\n746,1517,2001,1861,1620,1975,211,546,1025,1967,1554,732,1148,2266,1453,1401,1862,1591,1404,2410,1278,1490,383,789,1367,2102,2329,1989,1109,1875,2461,1623,1786,801,1773,1159,204,93,596,241,1578,1763\n1452,1829,1441,924,1992,286,2222,2310,990,2394,120,992,727,138,12,758,1555,967,2346,846,305,630,1490,2471,2162,885,484,2406,2287,2151,985,1241,2176,653,713,1161,1244,2194,918,2136,96,2209\n1884,582,802,738,2454,722,1915,232,344,1049,1275,334,2348,428,2082,1140,1859,1855,904,282,2001,551,868,1896,2383,989,2240,1342,1161,2335,1074,1425,2057,1497,1471,2042,1587,2075,2183,383,1644,1981\n341,1985,402,1091,1510,1619,1317,85,283,1413,1939,1859,157,1012,1279,366,2132,1281,297,1307,1392,223,2374,1763,1474,1603,2049,1530,1694,541,1143,1938,2483,624,1972,1272,2279,1640,263,2471,1454,1324\n724,748,967,57,175,268,1510,480,2049,1513,1054,1082,1940,2025,177,585,2384,1126,125,422,597,558,2171,797,1064,2498,1,1586,495,1767,1239,1723,477,2394,830,89,764,1632,2342,1437,2000,908\n36,1737,1244,187,413,2294,1200,2069,421,2494,1943,1892,777,1879,853,449,974,2498,105,489,541,442,1417,1238,2233,387,607,2224,1795,2098,2237,1246,1936,2459,1580,1499,1453,1681,1599,2417,656,1038\n2058,2399,1198,1676,2459,931,1984,1665,1634,955,1751,1527,264,2130,1303,1890,1928,1926,306,1328,1907,1540,403,306,779,2156,2290,566,535,1045,2345,1759,1655,743,301,378,1727,230,1162,1769,2413,2337\n277,865,553,564,1133,2327,529,848,1971,1742,330,2297,1169,1989,1018,2311,2115,1445,1765,2177,822,58,1579,727,187,79,983,125,921,147,2071,2151,1353,420,515,958,107,130,193,1442,1065,193\n385,396,719,1712,1973,243,279,1450,611,429,1626,937,1295,2109,2160,554,1547,567,979,1686,153,2122,1250,592,1607,345,1301,1406,628,2413,1127,669,2294,1090,1089,2133,1730,265,134,415,2,930\n2065,216,880,570,1685,2236,1941,1437,1231,2433,1738,160,1731,868,1642,941,1289,55,1232,1638,2415,689,51,1185,2433,1443,200,610,210,723,1200,536,1175,1762,2073,1206,119,2378,482,2099,2021,2109\n1796,617,304,2110,1110,213,1296,1821,2363,1526,646,1501,2226,1233,1655,904,183,2428,1407,1186,2019,1342,2311,1157,585,2162,171,1988,1136,1359,118,728,821,2065,1676,2228,937,2474,564,1510,1634,280\n1696,2258,1461,1828,1792,450,1436,357,1514,1068,343,397,2324,633,2200,206,2420,1687,544,286,2322,1252,1185,1632,419,705,641,1329,2055,918,2413,901,657,929,492,1149,1089,1817,63,1904,705,1412\n683,42,2001,448,2242,709,368,1809,1011,2164,2194,1288,2232,1380,1359,1975,2431,1659,897,1860,446,1541,2193,1402,2440,666,1406,2435,1861,1109,2319,490,252,2099,498,257,2029,251,768,483,2242,2095\n1980,2107,1300,363,847,1596,2446,727,2253,1166,834,2025,1033,149,2012,66,1635,100,1330,323,344,1716,24,411,1296,2449,215,1925,1670,955,1366,2007,1511,1780,311,2451,497,1123,363,277,2466,1721\n2188,160,107,765,740,1211,122,947,1981,2450,181,48,2374,1097,1425,1495,1694,893,1718,996,984,711,646,2277,1347,1406,961,1475,200,2346,2256,1375,1518,74,885,2134,1307,251,1951,490,526,1674", "output": "1983429"}, {"input": "8 7\n127,1264,2012,2407,685,455,1716\n1572,553,2412,1455,72,2479,551\n1295,1967,2278,802,929,1941,2232\n1740,1785,1346,1650,105,977,1829\n2150,288,477,2436,589,1487,1763\n537,1313,1348,29,1127,2220,576\n918,1634,412,241,2440,129,1528\n1775,1543,1317,958,534,1173,2242", "output": "39288"}, {"input": "4 9\n969,1189,1057,540,2105,69,1353,1892,1936\n577,566,1211,2115,1829,2169,2480,1755,186\n726,92,307,434,873,1842,1085,831,834\n1510,1525,2176,2253,997,2014,1654,2318,1790", "output": "14484"}, {"input": "10 2\n2139,2396\n1023,857\n738,344\n1535,969\n1339,1720\n304,2416\n2138,1840\n708,389\n1632,2313\n1193,260", "output": "19262"}, {"input": "1 8\n3,1639,1118,1373,813,2399,2338,1679", "output": "0"}, {"input": "50 44\n2377,2386,1222,246,2080,1681,135,1724,1133,2110,214,2385,20,1758,568,935,2056,2005,2292,55,546,2498,881,1822,1058,562,2082,1413,2280,2374,553,958,1302,208,1391,2478,1311,1553,1829,472,1995,2261,915,1863\n848,1463,1872,1279,1615,1954,1857,268,322,1553,269,2400,388,2254,580,2088,1344,641,1956,2093,2231,182,2422,167,915,2035,2355,1373,2242,2153,336,1272,2171,1584,226,1445,1229,1965,891,1238,829,1535,1237,1486\n2434,1369,54,782,1182,2475,2492,1040,2395,522,1933,51,1707,1170,1538,2425,337,1923,1161,1060,53,1495,2144,2061,825,1138,807,1359,1548,996,108,1942,137,26,2463,1076,261,385,858,781,1726,1049,1795,1230\n252,457,2470,2367,2363,2435,1183,1073,991,1127,1267,582,1827,2088,305,80,151,538,1607,1451,357,1402,1315,2475,272,1144,1774,1534,591,426,2383,1347,1556,878,121,1650,2248,377,1879,1136,877,1292,1700,1556\n33,2481,198,600,1943,1402,1314,2187,346,404,2085,923,1211,1847,2381,925,2054,2193,1176,2235,1627,1148,513,2417,2424,276,1038,952,837,28,963,567,317,985,1134,2347,1893,6,2113,1807,2122,628,1684,1209\n2429,2461,2213,1467,460,1247,692,1860,2263,117,968,975,851,2195,1317,530,1294,2457,2126,1296,1150,336,1202,1214,749,1614,1060,487,2036,1240,1654,1420,551,2008,1748,1076,1115,1657,2272,1811,2467,721,2224,126\n1935,802,1377,1699,1837,888,2216,1592,694,985,2258,823,1216,719,2069,2209,75,289,293,1792,201,2291,2174,1564,2208,2382,1642,1073,1893,1686,1132,698,1494,770,982,732,345,1414,1683,1969,1475,1074,1164,915\n485,212,442,1264,1102,1754,827,389,159,768,1415,1202,2446,311,2203,1195,1059,1202,2006,177,332,1977,1155,1517,1635,739,1793,1532,2004,2365,1507,2409,895,181,1669,1185,2081,675,2271,1498,1055,1232,1731,1214\n136,438,1430,2256,2291,338,107,960,988,57,1170,466,924,1534,767,2452,1700,885,2497,351,2449,1033,1091,1247,1316,487,599,1153,2140,1533,2042,2,2255,660,2181,906,1710,2037,1291,2372,775,2164,1902,1133\n1269,2129,1373,2335,1440,2134,1485,1544,1615,127,841,1117,2005,2387,1272,415,288,385,2311,157,670,1491,2162,1542,1080,2215,1154,487,1907,2224,1483,1284,1422,23,668,386,2422,2016,924,1038,2275,317,2437,720\n2194,355,1973,1619,655,666,445,490,2020,2152,840,2357,137,1589,2316,2457,1511,1196,819,2369,1064,1882,1975,1319,19,2459,1257,678,680,1296,1825,163,1759,698,282,1525,764,1610,1853,936,183,255,1900,2381\n374,419,2428,758,4,1996,1970,1195,818,1579,1907,1485,2429,413,167,188,2151,1801,1871,1970,345,2326,1624,1252,1748,587,2143,1370,974,2013,196,2059,281,1943,2153,1043,1696,628,2455,146,2102,2105,2086,310\n493,2291,1373,314,941,606,263,1682,2163,2190,2291,1685,1144,1809,2111,188,2017,1579,492,345,199,581,1467,1951,1299,1030,311,1051,1057,246,2252,321,1818,676,1268,455,957,1370,782,1194,524,1351,1303,593\n863,2371,1786,875,2491,700,2090,2001,1735,1198,1508,1534,1430,433,1664,1657,2449,997,1623,2362,941,425,570,1037,1728,1950,755,2261,1918,213,1285,27,2199,1929,708,617,1978,1041,1517,935,845,2221,1362,466\n133,2146,206,1536,433,1771,508,1662,1484,1560,2421,49,648,287,1134,2432,2286,1110,1301,205,971,488,1664,1628,119,1865,1578,674,679,643,2466,673,516,198,721,819,1693,899,1649,581,654,1852,1698,1547\n15,2224,1218,1903,938,857,1414,47,481,1403,66,2236,1994,6,1312,100,1275,1036,469,1087,1366,1072,864,1061,594,1168,421,1131,2123,1850,2465,37,1298,88,1016,1142,956,2335,1105,2177,608,1310,514,2084\n1933,2009,2308,12,1593,287,863,1638,1496,22,740,1357,2049,1615,135,2306,1895,1008,579,805,1142,2155,1434,1885,2206,1664,2062,1049,882,469,69,1299,18,2434,1279,2449,1893,127,715,232,263,1883,1614,906\n1041,1182,1982,806,1787,533,2332,566,1875,1260,1631,652,322,1788,723,416,798,189,2445,173,1343,1755,60,63,845,1909,305,1855,367,382,2439,923,1552,944,2108,2007,2013,1247,2446,1878,1658,2443,1397,260\n1553,783,299,2226,1161,2110,1996,2494,1431,2485,869,35,133,96,1003,1809,86,1703,1909,729,308,1365,1004,603,4,1115,1164,57,1449,1177,1456,733,106,800,557,2190,490,1480,1292,211,390,364,1103,268\n1942,1776,1893,2242,543,233,1766,1484,1944,620,1940,164,907,1998,818,457,12,196,819,840,2094,637,2385,831,481,151,2359,1752,1168,1967,769,2265,713,520,2435,1478,46,1246,2046,97,1726,1613,639,333\n1695,1317,475,2066,905,1310,1680,755,576,1716,1450,1812,1413,2462,381,1728,1478,1781,1562,614,699,1838,2233,532,220,2360,717,1237,1527,1736,649,870,8,2153,2283,248,701,82,2074,1405,1300,636,845,581\n1384,1365,283,119,212,1270,223,781,518,2359,1212,1971,1919,1157,1851,2059,294,659,565,1647,1349,599,208,1223,485,751,1648,1996,2425,924,2406,1016,1045,2464,1396,1435,1769,1300,339,1796,809,1396,2224,2419\n620,2464,52,2090,1871,469,467,1559,1823,1451,1608,1876,2175,1693,2366,1258,2452,2356,2069,884,873,1326,1050,2111,1396,2499,2060,1266,1765,835,1439,2169,1521,2215,2410,1324,616,2417,660,659,2270,848,1200,749\n2088,523,1763,1984,1299,998,1715,802,1911,2333,2208,341,664,1561,784,1715,2313,698,1482,1421,207,581,2240,694,1365,340,211,1315,314,1325,428,1393,869,0,1381,693,688,1469,2281,817,208,1409,1561,861\n928,1901,766,914,1550,1159,1263,1586,2469,1893,418,995,1693,1104,2073,572,1954,202,1031,333,216,100,662,623,589,1834,1394,138,2415,342,1407,2243,2028,26,1011,2043,109,1501,1272,2082,2284,952,1775,416\n2178,1906,1287,1810,1424,19,921,964,2117,1158,2348,1749,993,1885,2484,240,289,2465,870,2154,458,576,194,500,875,434,348,1459,1304,1009,1999,707,155,1430,5,1817,1448,29,967,1269,1167,743,659,1140\n2346,1969,2219,986,1924,2258,1346,1146,789,719,612,351,1122,642,475,665,1866,522,2278,1240,1700,6,995,1194,1390,2173,673,1908,795,1609,744,588,1639,1771,1044,103,1860,2016,2383,842,1803,1224,337,2390\n1232,1751,2389,1793,1325,233,998,1936,82,74,1427,2068,263,1825,1731,1950,220,200,1310,12,1514,2146,1567,2268,722,1964,1924,1221,2412,2464,529,969,1627,1816,604,475,1671,1373,1655,1882,365,35,789,1285\n1737,2372,2396,300,1361,1257,16,859,1971,2260,421,2440,1459,1116,80,1667,1138,2314,1672,2322,459,407,2069,2149,1045,2263,2178,642,1188,304,1087,1700,1716,2307,569,172,1153,2211,2436,866,1654,589,2459,1056\n718,1898,2015,964,277,2314,1040,880,427,517,320,538,2202,1341,1092,73,172,389,1812,382,1900,956,1952,758,881,598,343,366,2330,407,1018,893,535,1965,1711,2086,868,1924,2294,2015,1599,1549,1307,434\n1591,2247,1948,1037,168,237,2200,1265,2214,1310,2414,253,2107,903,788,1539,1792,13,1114,1851,1983,2139,1986,495,2260,544,1449,15,731,2211,721,1473,1574,429,1719,2447,1147,93,1388,2078,1040,504,2174,860\n265,1109,2424,482,632,1336,1502,775,1654,596,1189,1517,832,1226,371,1528,485,1559,1580,2421,620,1566,1129,831,1909,1407,1270,1487,1975,194,790,1275,752,1178,1490,643,483,972,99,1726,1766,1820,994,154\n221,2193,447,393,1727,43,1233,1786,2147,2029,1352,1225,1917,1663,43,8,1743,813,716,2117,732,1583,121,1718,154,1653,2210,1458,107,1306,464,1110,126,2014,2261,1430,2235,1676,2317,1038,933,2008,66,1186\n2182,123,2374,1349,1802,689,893,1229,2188,248,105,500,1720,1177,1999,2489,1375,607,2409,1097,348,1573,654,304,1803,1954,733,452,1107,2263,1462,539,1127,2489,1453,2102,815,297,998,0,704,259,44,1092\n707,1576,812,1482,1471,396,74,691,2380,652,929,1334,1473,2056,803,733,578,1049,1278,2228,1244,409,2307,832,2433,113,929,377,2173,2144,1038,158,1520,1311,1488,570,2232,1200,1685,1299,28,1866,497,159\n335,2154,601,912,555,331,602,2112,423,2394,723,1923,1413,1697,2471,1256,520,230,2148,2191,32,222,1395,1465,2334,1170,1837,1487,784,1353,261,1669,152,1556,2432,2143,2393,1898,900,1862,2147,1554,2065,585\n607,1132,873,2125,1927,1875,268,1037,1808,503,2033,1260,2053,2226,2203,266,1395,598,1545,1745,1929,209,1181,2355,185,1189,68,2072,2418,414,1595,1353,712,110,1582,1883,1391,1909,851,26,754,973,643,2486\n468,2113,564,1264,2359,1272,1527,1320,686,1214,290,158,1804,613,1072,217,1578,241,1586,382,485,595,1378,319,1594,945,1468,124,1316,216,977,397,2035,2329,2271,1549,550,151,28,1026,396,473,865,155\n290,2235,1555,725,1939,1233,1420,564,667,1571,79,1420,1970,13,2240,2225,710,864,2275,2376,2319,81,1956,2014,21,1733,2063,152,2268,294,1015,1904,2096,2224,619,220,1659,937,2288,813,1020,2303,150,525\n2345,2369,1282,1767,2040,1390,336,2052,1374,2000,892,2015,1933,1394,1180,2449,317,1,783,2059,1486,1145,2193,1403,976,491,1250,625,545,2453,2396,617,1678,1275,413,1141,606,2096,414,1750,341,23,1219,1160\n1657,2145,2026,2034,1890,785,2090,1702,864,74,1229,334,2302,67,1387,1775,1281,2014,1296,1617,714,2392,493,253,1097,2174,739,105,95,295,2042,1621,1553,2168,707,1276,261,1722,1854,1964,658,2092,729,165\n1133,848,1805,919,1344,1599,1075,1599,424,1103,1304,546,487,686,789,354,2188,163,2102,1347,1086,284,1938,2255,1825,401,245,1548,112,1230,2235,1945,1628,491,767,373,174,2454,1406,700,535,2422,1756,294\n953,1918,642,1166,1351,2465,851,294,220,2373,140,1243,2130,1957,1324,2247,1230,108,1898,99,764,2165,2263,2491,799,31,1974,2152,141,1094,684,1632,1501,364,6,1824,50,1436,1026,2027,738,2079,307,1952\n1631,415,2300,1431,2056,968,1453,401,2079,238,661,1879,2446,1915,1813,699,1639,1745,835,2169,1088,403,1809,35,753,925,1965,1612,2378,2331,1306,2074,2209,2248,1786,1836,1766,6,431,1975,935,713,102,2216\n674,1511,2384,2382,695,1976,1762,1982,2015,1809,1093,210,939,1777,780,2358,188,2464,1381,922,765,1697,441,864,555,2178,938,523,602,72,29,1204,2475,622,1700,2384,2391,2350,954,2207,1126,2200,948,2206\n1193,410,1571,6,582,1332,1322,806,2237,2079,2255,1429,932,1238,1538,1644,1428,1837,2004,170,1866,2034,1015,2291,1263,828,973,1603,631,95,884,944,631,2405,2449,934,597,899,1478,1347,2158,2193,1059,2005\n2487,2461,1866,1083,1656,616,2341,835,864,218,574,1589,1841,1136,2233,1006,1000,1642,2258,530,1542,283,1473,1405,679,931,1817,2160,2202,612,2423,620,647,1688,1665,201,482,2179,492,1238,983,1098,64,863\n1726,2406,2418,619,2091,201,1969,1640,953,1427,2256,571,941,986,1408,1898,928,757,913,294,2353,1486,833,313,1923,1339,2408,698,2021,1071,2299,751,2420,1771,292,2071,1474,1221,570,848,1816,281,2318,1876\n895,943,346,399,2467,1421,862,2049,2438,2369,757,1131,693,1445,1691,630,1075,1298,2206,500,2289,1709,1285,2388,1789,817,679,47,1139,674,960,2095,1873,365,1360,1529,1579,2138,1942,1919,2201,1887,867,2049\n1402,1271,2168,2039,2192,826,501,792,1778,1277,2086,2306,34,1317,2012,728,2072,198,59,1893,1379,2246,1878,1450,2372,904,1239,2203,1080,1820,1051,1961,114,198,382,2260,2181,550,2041,1855,1987,862,1809,509", "output": "2454597"}, {"input": "6 7\n2059,2166,1896,1380,1575,159,748\n949,1395,2309,2100,584,1616,1071\n355,1826,683,1244,324,243,1319\n2075,2352,1656,1845,1452,371,603\n1420,105,313,525,547,191,552\n1530,1283,10,1968,2345,1800,2360", "output": "26803"}, {"input": "2 5\n2294,503,1115,412,984\n167,541,1245,1596,25", "output": "3088"}, {"input": "4 9\n1995,328,1586,1543,1225,1454,1257,1267,1479\n2310,1668,399,1598,1931,1678,108,1660,490\n1540,196,869,243,1957,1116,2260,2279,385\n904,2137,778,2234,2225,1244,737,1616,1850", "output": "14149"}, {"input": "3 8\n2109,1960,1466,1375,1491,2199,593,142\n838,2196,2366,384,1638,1989,2428,384\n884,1779,1225,1805,1097,2439,835,1470", "output": "7398"}, {"input": "2 2\n965,361\n164,1625", "output": "802"}, {"input": "45 43\n1375,1409,1090,1591,2065,1190,1261,2195,9,164,1741,445,1659,279,1599,1813,1891,1602,965,2485,545,1095,1279,1974,1128,542,860,934,2010,2123,1204,746,1299,1894,566,134,856,1401,752,1161,456,86,679\n1070,309,1597,1166,221,2353,1660,226,1713,1156,218,51,1660,2199,2265,470,1954,171,2027,449,2417,2154,2165,2187,2226,1278,326,1662,1574,1743,1725,884,837,2109,912,599,322,2228,746,1443,2074,2277,312\n565,956,295,1270,1632,1440,461,687,1791,510,1974,633,1447,256,969,643,1882,1253,217,2031,1245,2335,637,22,202,1712,2082,1927,1356,821,17,286,13,1356,1908,459,378,86,1835,862,1612,1614,1805\n1776,952,1979,1722,2233,969,12,180,733,102,1074,2205,106,2484,2159,540,1231,1034,293,727,811,441,1361,2296,799,380,1177,1254,1495,1396,495,1438,1559,2074,1039,1551,1348,1,2236,988,447,737,1796\n1588,1968,90,1259,2432,596,2476,1245,370,1652,1287,357,616,412,781,1472,509,1059,1623,2444,825,2134,1,1794,1235,1124,682,1288,1867,224,760,2366,1258,2436,1604,1515,1176,983,565,1098,841,1037,1583\n16,1851,1741,1207,1463,2060,1796,565,822,2136,317,253,1069,1335,1888,996,2040,599,2437,1124,598,2024,300,893,1061,478,868,1820,1755,500,2039,1726,2456,1554,373,1235,1351,1868,2324,2469,21,2493,757\n1189,1061,494,1041,35,1531,723,2351,940,1387,869,1566,1286,2150,648,1575,1330,1420,510,102,474,636,498,986,2052,253,856,506,314,1953,2212,2249,1586,461,449,1192,2273,2417,31,1912,954,2487,2006\n80,2459,2217,169,1745,1458,1558,1346,647,2197,198,1280,1932,1538,2017,5,1192,1506,1258,1766,2463,1792,724,549,2030,441,15,1294,1133,1055,388,472,439,1073,1455,2450,435,248,1636,1860,780,1596,1826\n302,598,647,1730,1480,1963,1382,1728,1351,123,2253,2274,172,687,874,1706,622,1117,1134,1633,1471,2300,1250,216,705,2110,461,747,691,256,1734,1006,1209,151,2370,2425,696,1629,553,1870,2357,1743,2145\n850,1605,2106,1918,2020,1582,2068,648,34,158,2156,1556,943,2310,1441,989,102,148,291,165,2013,2228,1335,1734,695,1155,1107,946,1334,353,1986,307,2472,1033,1242,3,367,606,1809,245,221,1594,329\n679,1190,605,269,253,1468,1295,488,2326,814,763,1504,1021,2035,2111,2428,1165,1862,2219,1206,1355,569,1496,441,1477,1928,1843,452,1302,1644,259,1905,521,1791,1742,1196,480,2484,1072,2035,494,1408,41\n1145,1057,2279,428,1557,463,1953,275,44,1096,62,799,1944,2311,1419,516,744,1553,601,2484,1934,1383,742,1654,1673,202,1916,910,1473,1914,2063,2163,407,116,1445,1486,723,1542,1663,117,1863,469,381\n976,1855,303,1063,667,22,1607,1110,182,1747,727,630,309,542,1154,2154,811,230,1385,1578,2312,2469,1389,1821,1628,594,2059,360,2494,1380,1439,887,122,2372,1466,2456,394,769,1227,1064,835,1750,1946\n2372,1280,961,387,162,432,2055,352,739,7,2117,1124,2401,1990,652,2432,1912,2120,1521,2225,1992,1925,2141,1351,124,1901,505,1468,201,2032,62,1643,1772,700,148,331,1432,2447,895,1644,1577,1794,1314\n1949,915,1759,1285,950,1516,303,2260,1325,1448,2310,1262,1538,1598,1345,1477,1370,2259,1504,166,1051,1065,1508,1438,652,663,687,1514,239,568,1472,19,1055,103,899,1394,2466,2486,1941,1629,87,959,1717\n1863,1807,1168,1370,241,1374,47,283,1207,1464,1900,1428,228,1459,2014,1093,1377,2282,1286,921,983,1300,2086,2239,174,905,991,1846,1094,1339,682,545,1644,1965,1159,1745,2159,1614,1170,2464,688,1022,1967\n445,1506,764,326,1907,1130,717,687,2404,677,1455,678,1455,821,1621,795,803,2198,1581,1897,758,803,791,2308,1257,2069,1044,1005,1791,1385,2372,1612,1762,670,843,1101,651,264,182,150,484,1209,2091\n1192,1597,1526,2156,2145,174,1296,1133,433,990,1055,2059,98,2218,1702,863,2046,1161,1875,2116,1350,94,1176,2122,1290,747,752,1259,514,1605,582,1997,1093,1492,1908,809,1028,2154,1951,1583,762,2124,2384\n966,1376,1301,1376,527,479,1248,1553,653,862,285,2034,555,566,1304,2476,175,994,565,1076,949,207,2410,995,2150,438,1740,1043,2246,2388,1360,1701,1325,704,2190,396,536,583,1932,2174,1864,1522,2393\n1551,882,785,1842,812,250,2281,2202,557,1707,547,993,209,259,391,324,2090,304,2235,1133,1160,156,148,2016,1509,712,1204,718,1890,382,1085,1908,2319,1807,623,1392,1339,351,1441,2240,2404,2129,2272\n1438,1150,1832,526,947,150,1484,318,1298,721,825,1381,268,1292,2224,8,2097,1196,1779,2463,436,1817,672,732,2414,1075,1995,1700,396,337,1542,457,1440,1545,2241,2199,1502,946,564,635,2077,92,920\n878,2151,1771,1429,1536,1916,365,1282,1900,647,1496,997,1101,1854,2146,1300,590,2108,1758,1719,2444,1542,941,863,1814,436,1430,481,926,2211,1825,1979,1489,958,533,2310,2189,1736,217,590,2355,2144,1279\n1319,1079,2403,646,1971,1359,1883,1919,2019,2017,1856,978,2117,1642,1040,177,2360,2177,1777,2454,273,1614,1727,653,1952,460,1567,2131,1601,135,1307,181,1891,2241,1817,2302,2193,1063,480,652,190,668,1215\n923,2199,1529,38,2150,593,891,468,1963,1506,1375,550,1109,2461,1832,1514,680,2346,1157,2315,68,559,1865,1257,1363,2279,567,116,1362,1901,1419,2010,145,1579,1101,555,1597,1797,2233,1364,2457,2160,933\n2452,1525,2018,2049,288,1957,1966,1978,2037,225,1511,240,1577,778,1654,1616,1043,390,462,727,1437,1992,491,1850,2492,416,1941,1947,214,2020,515,1532,2003,990,2325,2331,574,1820,321,192,1114,1708,1343\n2124,1940,1326,42,640,2411,1982,2297,1244,1574,2242,1232,840,1468,1913,840,2404,2364,1877,885,2386,1902,2401,839,2415,1369,39,1315,978,1165,1333,2162,403,146,1326,1077,152,1977,1753,429,843,573,2143\n1586,1070,1476,1397,1803,1074,1214,2282,1611,1460,773,56,624,1799,288,2187,198,814,1896,1847,1966,1709,809,1601,875,1534,737,1934,2039,609,455,2429,1296,33,576,258,1387,1326,7,2045,313,2064,1214\n961,958,839,1700,1695,281,416,2329,1225,138,446,1682,889,552,1896,1290,664,628,1155,520,164,1402,2301,2292,549,86,907,1381,2360,2176,441,1967,2016,931,569,863,2437,677,768,341,2343,209,2328\n257,570,994,599,1369,1002,2316,584,1643,564,1856,1274,2338,7,573,803,1082,1858,242,1842,1469,2482,5,1928,2495,2463,1647,1469,1291,968,777,2176,1038,2121,296,1863,302,2216,2287,283,978,949,97\n1769,601,1497,1430,1908,1580,500,521,1700,1371,797,1694,1683,291,1772,447,504,612,1697,1819,991,2276,376,75,2410,2079,281,747,903,2052,916,2098,364,1222,230,2080,716,2444,88,2216,1880,747,2378\n254,2399,1461,2306,2347,2016,1613,476,687,2011,712,284,936,932,388,2474,1724,1740,534,503,1011,1557,778,1210,351,822,88,1704,399,530,2001,2372,1156,821,1038,1813,835,1542,1984,694,1184,2087,164\n2471,2016,1463,1061,855,2156,2236,2025,1832,1167,1399,566,572,1349,2305,892,1727,690,469,704,2010,482,147,2326,2389,132,786,2140,1039,2101,123,1997,1258,200,605,1374,2154,187,1560,2106,231,1789,1092\n205,1045,185,594,434,1740,2312,1166,1138,734,206,103,602,915,1052,829,1472,433,749,877,316,1236,471,2291,1642,1420,260,2382,1973,165,271,1505,1799,1662,1331,662,776,2243,626,793,1861,840,1213\n2326,2110,829,562,1972,1246,1582,1515,2357,753,1999,358,662,1560,2334,100,757,734,684,3,118,2254,2463,2392,2121,1215,1510,1927,454,371,825,1108,1914,1316,897,1393,2046,428,1129,604,2402,2111,853\n1798,1213,404,1775,1248,478,1662,1274,1700,1285,2015,2486,42,1135,403,744,2022,1929,545,2367,941,1048,1161,966,1402,382,459,796,975,1510,2417,1299,425,1649,2473,921,2378,1155,161,792,385,809,877\n671,2123,1163,79,773,1579,160,198,1229,102,2483,1979,1291,1157,411,1908,1057,293,1760,2051,2082,1499,371,1392,804,685,1111,2008,1846,2292,667,387,2473,1893,997,2357,1964,2032,1192,660,1667,598,2489\n403,1111,586,2471,243,2220,1166,1656,378,285,391,1448,380,899,1227,2366,2130,2291,2334,1679,941,1556,1850,167,228,1427,1905,950,1368,538,1585,2472,1633,1846,287,1488,1662,2044,290,1422,2315,1450,325\n644,1200,2452,388,2118,799,1157,524,548,1079,99,488,1294,1284,550,778,1991,191,1902,2440,363,1604,545,743,314,2394,1296,2141,1118,1606,1136,257,2227,1476,2473,1173,2231,1034,1885,2161,2191,1382,1331\n1320,1923,1820,1042,1068,382,1492,1974,463,2335,660,1000,2056,1273,450,671,829,557,2085,1336,779,590,455,2332,1468,1923,1502,363,2375,845,2384,1241,1773,2494,1130,591,752,2346,817,2084,190,1279,488\n770,641,1153,961,271,1743,456,2182,1473,1671,1855,1766,907,1441,849,638,1321,97,591,2147,347,1023,1604,1730,41,1739,2132,1190,377,192,435,699,1642,2330,2267,1223,550,1010,884,285,707,1013,1144\n179,2493,1472,374,2061,420,2483,1079,941,656,806,591,451,53,1479,2046,1172,1121,1324,2065,2104,500,241,129,1947,241,1846,2239,996,1423,1685,1515,1826,1857,244,1108,1310,1166,916,1099,1065,1490,1010\n753,1844,419,429,1535,2372,1250,614,2426,1100,96,1286,811,70,2379,1432,201,923,1254,719,2054,134,1031,986,1908,222,2315,1892,437,230,9,1940,2296,1878,1245,1694,99,1539,1756,817,2215,1208,856\n596,1049,1733,390,185,1760,598,870,1163,1559,1707,1151,1028,308,2040,1732,1863,2356,147,2490,441,2104,1252,855,187,125,2392,1608,134,1147,1728,680,204,799,759,2124,1211,1532,1962,2032,170,2212,228\n914,932,2446,505,1597,1049,298,562,1339,422,1856,2309,2240,2131,294,49,1789,1570,1586,128,553,1363,2484,889,690,223,227,1859,1863,2407,297,495,2478,661,1572,1494,1776,2226,1260,447,1014,2381,707\n1306,940,1232,29,510,2118,44,896,1115,1226,1673,1878,2174,1732,158,666,2143,586,1142,818,1694,2316,787,385,2396,2135,785,1895,1169,2357,960,1886,363,418,1339,564,1514,1264,957,717,664,263,1672", "output": "2043075"}, {"input": "44 47\n1611,176,841,187,660,2075,1871,1097,1965,868,544,1031,518,1108,1525,220,1669,1886,1420,1315,509,466,2386,316,1886,2476,434,2242,257,1084,2291,2283,2377,2309,325,971,1427,1060,217,2003,2352,343,1074,678,1119,1443,2171\n2200,1222,2350,138,2115,2445,552,430,583,1287,714,673,324,617,2386,1767,1412,2332,936,892,1725,2323,891,1521,1460,665,2394,787,1171,698,1958,1251,142,448,2308,1071,750,29,740,737,1543,1424,1746,2110,2250,2117,768\n2110,1407,1649,1156,134,2337,313,791,1541,1056,757,1783,1807,1408,1248,115,1082,1549,1573,613,319,2403,32,1344,2298,636,2172,372,759,2220,2284,1666,2397,135,34,1192,467,715,1550,1720,569,2117,1091,829,1814,1848,1679\n2073,2149,374,989,1935,499,281,2395,827,2011,153,1551,305,275,790,1259,476,354,831,668,1168,90,1729,1096,1191,1394,1019,1019,2452,1627,978,1942,1628,540,317,226,1805,70,1984,722,2420,1740,224,1182,1687,737,549\n910,987,1684,1638,1309,1964,1204,2239,1262,1277,2353,721,2178,107,1518,2338,2298,1072,1391,418,1230,1376,125,779,1104,1783,1937,759,1264,1021,614,2098,737,2435,950,2016,835,390,521,1637,565,2408,495,1422,214,210,1397\n944,858,2074,1381,729,335,1841,2018,1228,1556,2163,1524,1874,2298,2437,810,166,1770,798,1308,262,2047,367,1271,1154,1133,1884,1440,1614,2303,315,1992,716,1859,136,507,1235,2182,1387,234,373,2143,2010,1621,1975,572,1872\n376,467,2359,1334,1402,2298,259,492,932,835,2462,1713,1783,193,2322,371,1387,1881,405,1535,2420,856,606,2018,1435,104,2327,2153,2380,91,518,2319,1262,2220,899,1926,2351,1146,444,2079,1754,927,115,2039,877,143,477\n817,1366,1009,725,1783,1176,1665,572,2321,586,1354,2458,2295,1844,973,524,665,2316,1934,116,1789,1662,15,835,1368,2366,2496,1404,2201,62,1815,28,2313,729,2276,2207,1718,1766,1854,17,1069,2030,37,805,772,2043,716\n1617,1978,1259,886,2233,478,332,1512,955,616,2285,1263,2454,1240,548,269,1000,309,1363,637,2201,2360,1852,1736,1727,2005,1241,2266,37,1316,1530,992,2170,110,182,1005,1300,1670,1128,2208,777,635,2064,2133,368,435,1507\n1633,376,1889,173,651,2474,278,981,2274,423,287,2117,1959,1072,2154,1808,1285,2371,1047,1535,2333,266,1602,390,0,2168,238,1697,1117,1309,1957,1119,1633,1099,1864,1312,981,747,1110,1704,1306,1251,1095,2432,2201,618,587\n279,1280,2035,1785,1244,1451,2217,1392,912,1002,137,946,280,1882,2223,1604,198,384,1984,1629,2429,179,1033,1730,1931,1694,688,2220,1439,1789,528,2130,674,384,1374,1854,1320,4,1631,2040,191,1625,182,693,562,1119,987\n1384,801,1696,1005,1403,115,986,1966,1744,983,1266,1459,545,629,1607,1539,2346,953,1432,156,2047,971,641,970,903,1885,708,1824,1455,223,738,2000,1977,2195,309,808,256,2056,1057,1416,2398,1227,746,831,498,151,1492\n1224,664,1226,71,69,2342,319,94,547,1527,1,1283,953,945,1959,1383,2360,250,902,1449,1432,1737,1066,320,1270,1256,1584,2018,528,680,1942,1266,1940,1019,2479,680,2408,377,1333,1343,1547,1721,2239,2434,1154,1154,1839\n1761,1776,443,1290,1894,2431,1458,1564,1548,1821,1727,2212,930,1965,793,1711,2322,840,36,1441,0,372,1984,1800,5,621,1070,1893,72,670,1888,706,525,2057,193,82,1999,2298,1043,1633,2433,513,433,493,1669,1891,1528\n1639,954,2065,318,1740,1958,832,1938,1073,293,1333,2052,1707,2106,1131,1430,2286,1371,1354,2089,321,1717,1534,1670,2392,574,2084,1995,772,287,147,2253,2445,833,1398,2068,2256,1485,427,45,1450,197,2018,1745,1252,370,869\n247,1920,2134,326,2,2399,719,1898,43,846,184,1641,1606,1616,1721,768,1534,1257,1228,1904,1293,117,1432,969,826,771,803,1054,1773,184,1119,2354,1702,772,754,359,1999,1099,1751,188,1368,260,1982,1080,1187,1503,1677\n444,567,2129,2319,2201,512,439,884,1215,74,1670,1289,936,1066,1680,1563,1237,855,1279,741,983,1790,1375,2312,2450,2164,1053,1018,2450,1855,753,1889,1020,1600,2430,217,1231,1798,2482,1126,1942,1802,1364,1028,2124,1637,1284\n1728,1934,2169,2456,25,571,2488,632,249,170,1165,2273,1185,2123,1926,0,1404,1854,2429,291,1242,1926,1866,833,1916,708,1626,1816,1125,2038,1537,218,2346,1804,1956,1803,828,1832,922,19,2453,1906,1033,674,2140,198,1759\n337,2058,1466,1658,1838,892,1235,88,1905,300,156,1898,778,697,774,1063,618,440,2135,1789,1936,1750,1201,2441,573,1139,957,2055,396,1727,573,489,1419,11,392,1864,1696,956,1114,1678,1337,1075,560,1389,191,787,1321\n573,0,1192,292,953,2250,1690,648,1908,165,1064,2497,2092,2335,538,2349,879,2041,281,2007,1042,872,2318,1205,1929,337,1179,1114,469,780,470,2461,487,2284,1827,895,77,991,842,529,1024,864,363,458,2314,2052,1995\n1833,594,1060,2172,752,405,20,1614,687,1880,1020,1980,719,228,700,1784,931,1682,2307,1092,896,556,445,1200,954,1189,1798,622,607,50,1379,694,428,2315,1872,1941,191,738,231,1346,2133,0,235,915,2251,2147,1488\n426,1336,1691,2248,1406,55,360,1352,606,1523,2275,59,870,181,1023,827,410,480,1195,2110,587,1961,1164,2204,134,2364,1209,2407,1928,1025,603,2434,1056,925,283,697,1441,961,387,767,41,1331,1583,2342,85,2454,1310\n2139,1266,2472,1279,1358,380,1513,35,2024,1615,1552,2477,1749,1083,1790,2157,1910,1340,579,2252,115,1075,2456,1974,2298,1289,298,887,2453,1418,1984,909,1468,2178,2118,761,2435,2246,727,1663,2166,482,1190,1793,929,841,2362\n1659,481,2011,652,1035,1033,2119,2115,1555,1569,687,1586,76,1854,1551,2017,352,1741,616,1319,1593,2085,382,2103,2233,701,53,2393,198,346,2155,542,1099,1471,946,2263,101,2356,1871,2137,1011,549,1441,2269,405,309,625\n297,1851,1254,1746,438,1411,2041,1111,1832,424,2089,1622,1534,1958,1452,1776,945,831,2026,1701,308,6,382,2454,1920,2047,2102,499,1333,2118,1124,1316,490,125,69,788,2200,2054,2032,1441,446,570,1127,1794,1211,102,1520\n217,563,2273,2314,535,1188,401,661,2081,123,2451,2282,954,13,2463,2392,1140,2480,1216,2325,1092,2408,1959,626,235,1971,1545,2195,7,1737,1998,2180,950,35,444,1978,1163,450,1140,699,742,354,512,810,988,1080,1354\n369,2425,2266,833,1370,1047,2000,342,1433,1746,1652,1129,2193,2367,1968,416,93,669,1958,2261,2024,2369,2428,1553,1044,661,1221,947,34,2224,2186,170,2189,796,376,1335,1396,963,1257,1980,1971,1942,218,1390,1468,2173,1159\n1993,2494,2229,2227,745,2094,787,147,910,256,1897,2206,1151,975,850,2202,2449,499,347,409,829,1412,1958,1171,1589,2000,1633,1060,2155,2108,1601,346,826,2068,1164,1281,1084,2291,552,1647,88,1520,1513,2122,1705,1447,479\n1578,192,499,373,880,292,340,990,2246,475,258,7,2322,104,1468,1292,1367,605,1122,2394,1186,593,274,1572,1522,1586,888,716,367,2218,1319,287,906,2100,2041,1274,1646,2289,389,682,824,2212,36,90,1135,1211,347\n90,146,741,1732,678,467,72,346,2437,1840,518,1756,1182,620,2447,1703,893,1479,328,264,2329,2422,592,1663,1085,915,452,1199,1727,852,1685,976,2043,2482,1409,330,713,406,221,291,619,975,780,2042,1282,1161,1932\n2296,1169,2492,448,416,1794,354,403,620,1960,2061,1291,2494,1303,2059,1912,355,1490,1028,1371,130,1349,709,2475,1574,1363,274,1215,158,1421,1615,1463,823,367,634,1035,1336,2255,1177,693,672,292,192,2280,780,1753,1263\n1572,596,1778,838,1970,801,598,337,1342,1714,1068,521,1957,48,2285,1756,816,210,176,1254,1319,2131,1915,652,269,1927,240,1639,1259,1135,2356,383,138,2003,2440,483,2043,2044,1562,1783,173,2188,1271,737,66,693,1284\n1453,270,1872,99,1373,1984,205,774,2377,1316,2257,1765,1053,1638,1221,1502,966,1562,422,1768,1216,1255,2000,510,1708,833,1990,2194,1878,303,2166,1304,442,1759,329,1521,159,2452,1033,1824,1383,1134,2178,1430,889,1247,1454\n1914,1929,1717,1442,50,2191,2326,1936,2134,811,1929,406,583,2083,2374,2451,447,2334,2150,2154,260,2217,1005,938,1279,1705,1506,89,1815,1129,584,631,1016,1505,2145,2230,1647,967,2223,2146,929,1698,1861,114,717,1134,706\n1613,1413,1574,481,1879,1052,1323,968,1983,967,1414,1902,1890,1085,58,2314,1541,91,636,501,1074,886,299,1652,45,2387,1096,722,2246,774,220,1391,580,466,1073,2308,1138,1542,817,1672,2221,1383,2300,2469,1326,1145,2007\n2200,84,2058,732,852,1411,572,575,693,735,1975,543,1688,1540,250,751,654,1184,1788,527,794,1956,1498,636,1039,785,655,1149,2024,1948,2389,2159,36,2036,1268,293,1986,807,672,2485,938,1166,36,2289,1764,218,1577\n1431,1244,829,507,2433,180,1688,2200,2027,2493,1685,1946,13,777,538,624,1915,558,594,972,966,818,2415,2212,2084,243,1883,2249,1992,2258,1546,586,431,2396,1017,637,1377,2181,131,1018,430,902,1121,553,184,776,1895\n742,2271,1847,2350,1623,2244,2324,1968,846,661,2430,1859,328,638,993,1037,2328,183,2355,662,821,641,1572,568,1162,999,2069,248,1786,2370,247,303,1327,1343,469,376,1604,1567,1343,1212,1419,198,663,1211,335,308,1261\n2383,2039,711,666,1904,1053,721,1777,1675,2123,1208,1952,1540,2362,1003,1146,207,110,305,53,1912,2290,226,1271,790,2199,1243,2372,18,2061,554,2287,1320,2150,2310,997,430,587,1021,374,1031,2259,1570,690,1553,630,891\n1629,2224,1363,220,2074,727,1731,932,958,2381,2301,2419,604,2131,1273,1758,104,511,26,507,2398,1136,2392,1770,2163,642,192,2208,1701,792,1771,1388,1765,261,397,445,2063,208,579,2080,2385,1360,1908,1955,2250,1874,1976\n2315,114,2153,773,2375,2494,257,1443,768,660,1198,369,1924,349,252,1758,1329,1743,251,239,552,477,243,1597,1132,1334,2182,1982,396,621,1566,2202,1251,94,250,714,661,639,780,1286,763,1339,1946,1554,1667,285,1208\n1366,802,2317,2371,1798,2085,2057,1478,1746,2046,1469,66,1158,1643,1616,1850,520,902,1782,1782,1255,64,1757,2139,501,2049,373,908,1619,1914,950,844,625,567,2346,485,2498,741,633,1293,2195,2297,1486,1135,1272,1302,1052\n286,2164,2183,488,1010,458,2417,26,109,1114,1914,1745,1184,913,705,2343,2071,1069,1139,1468,1379,996,1440,177,455,2333,1308,1162,1717,961,1390,2217,161,1068,1517,118,1175,1355,1859,1682,739,1247,2425,2009,1311,1577,1361\n184,1622,1310,2120,63,1996,2118,1728,169,86,2274,645,1015,1314,823,2465,643,2159,1450,464,515,542,709,526,2222,779,401,1726,710,1174,2311,1971,2265,842,1209,1300,1344,1577,2482,1143,1512,1625,896,1497,515,189,2020", "output": "2161396"}, {"input": "7 6\n1233,1235,408,838,2154,1805\n828,743,204,1857,1362,670\n2319,727,2058,1860,1830,322\n142,1553,386,1268,1014,1574\n1919,922,38,58,639,169\n782,1809,1577,1180,2272,2215\n1332,320,480,281,618,1275", "output": "30143"}, {"input": "7 6\n2164,2233,985,244,2128,1487\n261,30,1112,1821,1087,243\n1486,465,589,1507,1948,1622\n535,2470,895,2495,288,1221\n1468,1361,138,1168,89,1509\n1658,2487,979,2275,43,1096\n1551,1127,1764,2214,2355,2211", "output": "25988"}, {"input": "1 1\n2305", "output": "0"}, {"input": "3 6\n741,1361,1386,920,563,836\n545,560,213,540,707,924\n1721,210,1256,1811,866,2080", "output": "3839"}, {"input": "6 4\n653,984,245,1999\n2383,1613,1915,1694\n1200,1136,2436,177\n205,529,1789,1657\n1444,880,1433,164\n43,1847,1516,1629", "output": "16215"}, {"input": "7 5\n145,2228,142,19,1883\n2030,809,1693,1163,465\n1768,2421,1977,286,1029\n1757,248,1723,666,492\n1671,247,2229,1791,2191\n387,1556,2200,1182,1887\n1294,117,2379,345,469", "output": "21652"}, {"input": "5 4\n1296,73,2093,1286\n2130,1777,773,1028\n1181,2177,1023,979\n1894,347,1200,1510\n2275,1644,475,375", "output": "10169"}, {"input": "4 9\n1143,1,1876,715,2242,1413,1092,702,2327\n11,295,1424,800,1058,1775,1731,2003,2225\n525,1829,741,1571,723,2205,2046,1792,1565\n111,106,491,1296,12,760,1315,404,776", "output": "19117"}, {"input": "8 8\n2382,2029,90,1334,1087,980,1695,2355\n1761,135,933,1300,1288,376,705,1132\n2416,1297,1274,1963,1907,2230,591,1799\n1043,1917,423,1179,0,333,860,1952\n1133,1974,1060,2016,576,1357,180,2468\n706,1779,1345,1076,665,821,1743,289\n2105,724,321,735,235,1140,585,1892\n644,1008,1728,1208,1518,427,1753,1156", "output": "44553"}, {"input": "45 42\n660,1063,275,1721,678,1439,1560,1533,666,662,1009,1455,1860,1084,1032,12,1631,841,557,1690,1781,421,23,1322,929,2113,1954,523,1042,2429,549,372,2276,2163,1353,1853,1391,2125,1487,1735,2036,363\n1717,296,1863,63,1841,1259,2065,2086,210,1020,1439,1179,507,2311,63,1845,42,1757,424,739,1426,552,268,1420,1322,1233,2140,1155,1433,469,901,692,2302,779,2239,1842,1784,18,1113,2156,637,1939\n1442,1474,4,1414,1611,1140,1504,1856,2049,753,1479,1589,1470,2485,1065,1247,1541,1230,2153,1084,472,2366,1313,1986,822,1756,828,448,2357,497,96,712,302,868,807,1840,357,1750,2117,146,1838,2467\n663,2046,260,1300,293,1493,164,2389,1216,853,2184,2093,1317,1289,949,2068,1121,203,2169,1206,1949,1206,168,1112,2337,924,973,1631,150,1216,1081,629,1522,226,1017,2410,1398,2219,1848,383,1356,2049\n1763,1877,2109,1727,1748,1986,771,1027,275,1188,1874,502,575,201,1971,1799,1390,121,120,2438,2425,1891,927,2297,2350,1699,1379,1321,397,698,844,1258,2221,898,1448,610,2025,2410,1798,553,1927,687\n443,112,488,267,1222,394,1267,538,1132,828,71,1646,1017,1776,830,89,2034,618,1917,1751,1030,1141,239,860,1962,228,581,1535,1479,2081,892,96,2310,793,657,2261,1294,1151,1585,890,497,574\n1628,1400,960,282,631,127,460,2426,2104,278,1997,824,1313,1129,1088,709,306,2496,2165,1167,625,1481,1498,1291,1346,2363,1785,1336,2398,464,1640,1161,1672,341,427,2295,1723,1056,1624,314,1505,1296\n1075,2023,895,1550,2312,1289,1952,872,1628,868,690,1778,137,640,2149,610,1517,412,1890,2307,49,267,2102,30,1823,783,2459,259,608,560,657,2019,1318,1667,107,842,20,303,124,825,904,1767\n1203,2373,2254,174,503,2163,525,1573,1229,1970,1790,2085,358,2276,701,2444,141,2206,1713,2186,917,1231,69,692,1248,884,496,238,610,1386,803,889,561,937,811,2246,906,607,2461,418,1903,2330\n110,1658,857,1852,1131,467,1923,2142,2422,649,1905,426,2084,150,813,1688,909,2389,1250,1553,1929,1263,1068,515,956,2334,1315,1038,952,2452,860,1628,1797,36,972,932,1378,1704,2451,545,2219,1651\n2476,2207,1619,2471,2196,1916,2426,1013,1467,1451,1705,780,758,1920,1737,188,1322,1520,2087,381,1155,1514,1470,860,1924,1240,2032,740,1116,1471,2402,1157,421,836,2152,68,835,1555,950,2306,1738,1457\n353,2222,471,1209,2477,2067,849,1472,2101,311,216,345,269,83,1091,376,418,2244,1637,861,977,540,1251,2064,977,1911,1214,318,432,593,1292,153,707,2180,1788,1458,2171,1979,1031,350,1414,1239\n1216,539,2085,306,1517,2061,1328,1659,465,1103,404,804,993,981,1446,523,202,234,2488,856,309,450,1110,37,393,1640,10,1175,971,2368,867,2194,2497,1767,2334,708,1979,2010,2237,546,2138,391\n834,2152,1728,941,1724,1436,2028,40,658,1467,675,382,934,1205,500,1569,1460,847,2311,1387,752,243,2338,1098,1299,1917,1228,504,15,2101,934,2434,2032,137,1557,1726,2098,1755,1771,1499,2206,2416\n2387,1089,1106,1616,1666,387,791,2136,48,483,1388,1254,2052,2249,266,1084,84,324,2472,266,2189,1235,1762,1217,2420,1256,2110,1222,1571,1578,1357,966,899,1730,2352,903,140,773,684,1915,320,2250\n333,1925,1025,132,1688,1659,596,2342,520,1457,1279,1830,850,1269,325,2172,693,934,2483,522,202,284,924,200,694,1829,1443,199,811,881,654,2080,1471,277,182,1214,48,2392,902,1141,2208,1404\n481,1040,531,1916,1553,2037,2429,2449,1522,2134,2392,503,1214,2268,776,407,1533,1570,1561,1589,1910,1544,1187,768,1217,2458,500,1188,684,832,691,20,1276,267,1355,1394,273,1360,855,1635,274,120\n525,1772,1383,592,1633,1348,717,2209,958,1493,363,2309,1088,2467,1939,2241,1100,2427,636,832,572,1084,559,7,1015,1532,412,159,517,1551,2178,2163,2419,280,306,1358,2184,1542,120,1791,1248,400\n75,1519,1724,930,2267,13,45,1110,2142,305,2304,1070,311,1791,2373,2137,816,598,1616,1536,199,73,1861,1780,1712,228,711,876,687,430,1761,1430,839,182,892,736,163,1803,978,1659,1406,405\n406,1388,1778,2338,328,1628,1045,2369,445,330,515,1859,1930,1213,502,1506,119,849,742,1319,2472,2295,2402,2359,1249,367,65,1744,1163,1952,1132,1410,2079,645,1125,1817,24,1154,783,2439,1652,919\n819,2266,682,194,1560,1466,895,1513,1759,246,1366,57,2408,443,274,1503,2281,2284,479,1736,327,2061,500,271,87,439,246,267,889,2272,741,1535,777,2496,684,2282,2044,604,1136,2096,2107,133\n1362,33,1364,536,868,1702,1422,2018,1577,1831,1389,2185,1059,1162,445,168,720,1128,1967,62,2126,801,977,2194,1895,622,965,1682,1847,1019,498,263,1898,1932,1912,678,1595,63,2001,515,1850,1413\n74,1407,715,481,1063,1767,2319,2085,402,2213,1429,1293,2375,637,909,758,350,1499,459,2051,760,99,1808,1475,959,1329,783,1128,45,24,474,1174,1259,2210,667,2133,1293,1015,2152,1529,1875,1079\n1004,1757,2283,351,254,2456,1613,966,150,478,1303,1226,2433,813,2292,499,836,1856,2008,582,1786,1637,587,401,1272,608,894,501,259,2189,309,179,1223,1956,798,421,396,907,2336,1504,2096,841\n1751,1217,1185,1936,1790,791,2362,1368,2148,381,591,1283,2083,1962,2055,609,253,1178,1097,1936,2233,2339,1852,831,441,2375,1032,53,543,1940,1814,313,542,1589,474,1553,1789,1026,1971,1034,543,1925\n2036,2037,474,921,2326,2065,92,1259,1982,758,2015,649,1026,983,1677,1457,447,1049,504,464,153,1408,828,772,494,1922,899,303,424,1396,2268,1653,1903,1498,1970,2032,2103,1856,148,2407,2091,293\n56,2311,2032,997,2309,10,2317,913,1056,2482,1712,1526,1180,1929,795,1154,1855,1459,351,2427,48,1783,2466,2278,972,1177,824,509,238,1493,111,1875,1853,1134,1630,940,2115,99,949,2202,2289,700\n1235,134,1023,1060,2210,1521,1264,1416,658,1013,1851,2293,632,1705,719,2192,494,193,1578,1921,1604,656,1424,1589,2190,746,441,2277,739,1167,220,2287,209,475,1302,617,1417,602,605,1585,425,144\n1616,1461,1097,2390,1551,1621,64,267,1760,680,48,360,2074,1998,2354,1598,908,282,1886,2062,751,137,976,520,1808,1517,1905,2409,1315,842,2170,1326,813,2057,1900,1343,1631,248,994,569,989,2246\n1003,1637,2498,2031,2480,1387,1562,405,611,615,1614,332,816,114,1596,197,1906,115,2336,1860,2167,31,2318,175,610,1060,1867,346,959,352,1347,791,161,1191,66,538,1820,1684,1363,1181,729,1408\n500,1182,728,829,2049,509,1415,679,2342,1355,942,1430,325,1903,429,1193,1295,1318,1093,580,1236,2426,616,2352,2077,1702,1430,496,1687,2271,1865,1508,13,511,1026,225,201,2117,769,697,1653,2179\n145,1243,1307,772,1185,114,1863,1998,1785,241,89,2198,866,627,2131,1481,362,207,1547,2152,1869,1458,1391,2439,1956,1165,570,2405,2118,2345,1947,369,1884,600,1839,66,2397,1455,228,1991,1197,902\n1679,2353,236,889,1641,2031,458,792,2085,1027,2475,612,1089,30,793,544,1641,1171,1174,1623,1879,1541,470,363,488,1261,1771,1310,2267,2416,2251,2299,1903,1261,2169,181,74,1737,658,253,2173,2342\n321,324,2052,643,1443,1049,2325,1603,756,846,332,2336,495,876,2434,2219,874,2321,2384,554,24,2022,756,1793,2066,1466,2490,2325,1917,2168,1362,1278,1688,2308,238,903,2409,2207,267,1422,1655,835\n1371,1937,2200,2426,1063,3,1382,371,755,2257,1343,486,388,185,1366,795,1793,1238,819,2,274,1963,1055,58,2237,1262,1876,2113,1187,482,2087,1146,1589,2193,672,1914,1608,332,115,457,2285,206\n1892,870,2493,1738,2354,2166,716,1710,1488,1027,2440,1227,2141,2400,1908,408,2020,2176,2354,2303,2280,2053,1071,397,2135,507,1737,2246,1953,1565,2137,1832,1356,1508,1653,1017,1720,2031,702,712,2367,1714\n1095,2426,848,2333,2381,1148,1551,1466,683,808,658,141,865,1069,1822,841,2095,1134,358,1128,1853,1791,2440,1754,1735,136,2433,1473,1610,1266,1722,109,35,1207,2085,243,2480,1522,731,337,810,1107\n1346,246,444,2278,38,1531,1336,48,392,806,215,1447,1692,1559,484,804,1401,917,1506,1062,549,2437,1523,2289,2223,1036,452,1258,2045,1581,1071,1159,986,2252,1487,919,1396,1446,852,1541,2377,195\n48,992,251,187,150,2059,2432,2170,1999,520,1587,312,1322,944,643,794,1049,446,1717,1472,2464,346,999,1485,1946,132,2461,833,854,1176,894,570,205,2470,2324,9,289,1758,419,1383,1540,1183\n2433,658,1627,2342,1887,2153,280,436,107,137,1759,110,1256,1403,2468,173,2284,9,270,1104,1825,1553,1420,1871,450,2089,879,1090,2383,690,2066,548,1030,1993,1505,1786,343,2172,313,150,447,1988\n1837,2342,1801,604,288,1919,1130,708,2074,760,1674,1854,1212,1100,59,671,497,164,736,1373,1591,16,1660,1076,1135,707,1410,1949,536,1636,1343,2064,719,1097,1783,72,198,358,1541,74,485,195\n481,1774,1217,497,1381,2010,1670,152,276,1057,2429,1922,1618,103,1596,739,138,1082,1745,1300,262,1934,2006,613,836,539,1861,23,1134,946,1375,1831,1599,1796,2036,140,2277,388,1260,1294,1564,721\n2361,1926,755,1153,1159,2322,1328,438,757,437,2062,407,1870,585,2294,1747,1406,1065,1961,2312,950,1815,615,2440,124,2004,1365,1180,555,2334,2053,1786,55,1709,2137,795,1486,1271,2049,1140,2418,55\n249,719,158,370,2498,917,1882,2146,1603,812,1824,1487,996,902,2195,322,277,683,83,1786,398,1293,672,1463,2483,1658,1100,1642,1573,173,777,520,502,145,1951,228,930,0,393,745,507,2265\n682,611,724,1192,1518,2113,812,295,674,1697,1780,992,1173,252,2048,1028,1855,962,1950,1557,954,2130,2132,800,2209,1356,735,2118,1791,1394,2352,836,1341,972,2456,1821,1920,1718,1786,882,1391,120", "output": "2013195"}, {"input": "10 6\n739,753,366,534,1607,1928\n1762,276,212,2394,2000,1625\n1429,519,2046,436,2283,1848\n1333,1449,1449,1753,886,1824\n279,685,1479,1807,2044,510\n676,433,1197,308,1796,2210\n429,762,47,1424,2044,712\n646,1615,441,1889,678,1109\n1719,2086,426,1353,294,2425\n1638,2141,2318,1613,442,1766", "output": "38190"}, {"input": "5 1\n102\n360\n1737\n1335\n1130", "output": "1012"}]
|
{
"cpp": "==Code Submission==\n\nvector<vector<int>> deserialize_stdin(const string& input) {\n vector<vector<int>> grid;\n istringstream iss(input);\n string firstLine;\n getline(iss, firstLine);\n int m, n;\n {\n istringstream fl(firstLine);\n fl >> m >> n;\n }\n for (int i = 0; i < m; i++) {\n string line;\n getline(iss, line);\n vector<int> row;\n istringstream ss(line);\n string token;\n while(getline(ss, token, ',')) {\n if(!token.empty())\n row.push_back(stoi(token));\n }\n grid.push_back(row);\n }\n return grid;\n}\n\nstring serialize_stdout(int result) {\n return to_string(result);\n}\n\nint main() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n string input, line;\n while(getline(cin, line)) {\n input += line + \"\\n\";\n }\n vector<vector<int>> grid = deserialize_stdin(input);\n Solution sol;\n int ans = sol.minimumOperations(grid);\n cout << serialize_stdout(ans);\n return 0;\n}",
"golang": "==Code Submission==\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n firstLine, _ := reader.ReadString('\\n')\n firstLine = strings.TrimSpace(firstLine)\n dims := strings.Split(firstLine, \" \")\n m, _ := strconv.Atoi(dims[0])\n n, _ := strconv.Atoi(dims[1])\n grid := make([][]int, m)\n for i := 0; i < m; i++ {\n line, _ := reader.ReadString('\\n')\n line = strings.TrimSpace(line)\n parts := strings.Split(line, \",\")\n row := make([]int, n)\n for j, s := range parts {\n row[j], _ = strconv.Atoi(s)\n }\n grid[i] = row\n }\n ans := minimumOperations(grid)\n fmt.Print(serialize_stdout(ans))\n}\n\nfunc serialize_stdout(result int) string {\n return strconv.Itoa(result)\n}",
"java": "public class Main {\n private static int[][] deserializeGrid(String[] lines) {\n String[] dims = lines[0].trim().split(\" \");\n int m = Integer.parseInt(dims[0]);\n int n = Integer.parseInt(dims[1]);\n int[][] grid = new int[m][n];\n for (int i = 0; i < m; i++) {\n String[] tokens = lines[i+1].trim().split(\",\");\n for (int j = 0; j < n; j++) {\n grid[i][j] = Integer.parseInt(tokens[j]);\n }\n }\n return grid;\n }\n \n private static String serializeOutput(int result) {\n return String.valueOf(result);\n }\n \n public static void main(String[] args) throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n ArrayList<String> linesList = new ArrayList<>();\n String line;\n while ((line = br.readLine()) != null && !line.isEmpty()) {\n linesList.add(line);\n }\n String[] lines = linesList.toArray(new String[0]);\n int[][] grid = deserializeGrid(lines);\n Solution sol = new Solution();\n int ans = sol.minimumOperations(grid);\n System.out.println(serializeOutput(ans));\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\n\nfunction deserialize_stdin(input) {\n const lines = input.trim().split(\"\\n\");\n const dims = lines[0].trim().split(\" \");\n const m = parseInt(dims[0], 10);\n const n = parseInt(dims[1], 10);\n const grid = [];\n for (let i = 1; i <= m; i++) {\n const row = lines[i].split(\",\").map(Number);\n grid.push(row);\n }\n return grid;\n}\n\nfunction serialize_stdout(result) {\n return result.toString();\n}\n\nlet input = '';\nprocess.stdin.setEncoding('utf8');\nprocess.stdin.on('data', chunk => input += chunk);\nprocess.stdin.on('end', () => {\n const grid = deserialize_stdin(input);\n const ans = minimumOperations(grid);\n console.log(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str: str):\n lines = input_str.strip().splitlines()\n dims = lines[0].split()\n m = int(dims[0])\n n = int(dims[1])\n grid = []\n for i in range(1, m+1):\n row = list(map(int, lines[i].split(',')))\n grid.append(row)\n return grid\n\ndef serialize_stdout(result: int) -> str:\n return str(result)\n\ninput_str = sys.stdin.read()\ngrid = deserialize_stdin(input_str)\nsol = Solution()\nans = sol.minimumOperations(grid)\nsys.stdout.write(serialize_stdout(ans))",
"ruby": "==Code Submission==\ninput = STDIN.read.strip.split(\"\\n\")\ndims = input[0].strip.split(\" \")\nm = dims[0].to_i\nn = dims[1].to_i\ngrid = []\n(1..m).each do |i|\n row = input[i].strip.split(\",\").map(&:to_i)\n grid << row\nend\nans = minimum_operations(grid)\nputs ans.to_s"
}
|
3696
|
Count Substrings Divisible By Last Digit
|
count-substrings-divisible-by-last-digit
|
<p>You are given a string <code>s</code> consisting of digits.</p>
<p>Return the <strong>number</strong> of <span data-keyword="substring-nonempty">substrings</span> of <code>s</code> <strong>divisible</strong> by their <strong>non-zero</strong> last digit.</p>
<p><strong>Note</strong>: A substring may contain leading zeros.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">s = "12936"</span></p>
<p><strong>Output:</strong> <span class="example-io">11</span></p>
<p><strong>Explanation:</strong></p>
<p>Substrings <code>"29"</code>, <code>"129"</code>, <code>"293"</code> and <code>"2936"</code> are not divisible by their last digit. There are 15 substrings in total, so the answer is <code>15 - 4 = 11</code>.</p>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">s = "5701283"</span></p>
<p><strong>Output:</strong> <span class="example-io">18</span></p>
<p><strong>Explanation:</strong></p>
<p>Substrings <code>"01"</code>, <code>"12"</code>, <code>"701"</code>, <code>"012"</code>, <code>"128"</code>, <code>"5701"</code>, <code>"7012"</code>, <code>"0128"</code>, <code>"57012"</code>, <code>"70128"</code>, <code>"570128"</code>, and <code>"701283"</code> are all divisible by their last digit. Additionally, all substrings that are just 1 non-zero digit are divisible by themselves. Since there are 6 such digits, the answer is <code>12 + 6 = 18</code>.</p>
</div>
<p><strong class="example">Example 3:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">s = "1010101010"</span></p>
<p><strong>Output:</strong> <span class="example-io">25</span></p>
<p><strong>Explanation:</strong></p>
<p>Only substrings that end with digit <code>'1'</code> are divisible by their last digit. There are 25 such substrings.</p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>1 <= s.length <= 10<sup>5</sup></code></li>
<li><code>s</code> consists of digits only.</li>
</ul>
|
You are given a string `s` consisting of digits.
Return the **number** of substrings of `s` **divisible** by their **non\-zero** last digit.
**Note**: A substring may contain leading zeros.
**Example 1:**
**Input:** s \= "12936"
**Output:** 11
**Explanation:**
Substrings `"29"`, `"129"`, `"293"` and `"2936"` are not divisible by their last digit. There are 15 substrings in total, so the answer is `15 - 4 = 11`.
**Example 2:**
**Input:** s \= "5701283"
**Output:** 18
**Explanation:**
Substrings `"01"`, `"12"`, `"701"`, `"012"`, `"128"`, `"5701"`, `"7012"`, `"0128"`, `"57012"`, `"70128"`, `"570128"`, and `"701283"` are all divisible by their last digit. Additionally, all substrings that are just 1 non\-zero digit are divisible by themselves. Since there are 6 such digits, the answer is `12 + 6 = 18`.
**Example 3:**
**Input:** s \= "1010101010"
**Output:** 25
**Explanation:**
Only substrings that end with digit `'1'` are divisible by their last digit. There are 25 such substrings.
**Constraints:**
- `1 <= s.length <= 105`
- `s` consists of digits only.
|
Hard
|
[
"string",
"dynamic-programming"
] |
leetcode
|
https://leetcode.com/problems/count-substrings-divisible-by-last-digit
|
functional
| null | null | null | null |
{
"c": "long long countSubstrings(char* s) {\n \n}",
"cpp": "class Solution {\npublic:\n long long countSubstrings(string s) {\n \n }\n};",
"csharp": "public class Solution {\n public long CountSubstrings(string s) {\n \n }\n}",
"dart": "class Solution {\n int countSubstrings(String s) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec count_substrings(s :: String.t) :: integer\n def count_substrings(s) do\n \n end\nend",
"erlang": "-spec count_substrings(S :: unicode:unicode_binary()) -> integer().\ncount_substrings(S) ->\n .",
"golang": "func countSubstrings(s string) int64 {\n \n}",
"java": "class Solution {\n public long countSubstrings(String s) {\n \n }\n}",
"javascript": "/**\n * @param {string} s\n * @return {number}\n */\nvar countSubstrings = function(s) {\n \n};",
"kotlin": "class Solution {\n fun countSubstrings(s: String): Long {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param String $s\n * @return Integer\n */\n function countSubstrings($s) {\n \n }\n}",
"python": "class Solution(object):\n def countSubstrings(self, s):\n \"\"\"\n :type s: str\n :rtype: int\n \"\"\"\n ",
"python3": "class Solution:\n def countSubstrings(self, s: str) -> int:\n ",
"racket": "(define/contract (count-substrings s)\n (-> string? exact-integer?)\n )",
"ruby": "# @param {String} s\n# @return {Integer}\ndef count_substrings(s)\n \nend",
"rust": "impl Solution {\n pub fn count_substrings(s: String) -> i64 {\n \n }\n}",
"scala": "object Solution {\n def countSubstrings(s: String): Long = {\n \n }\n}",
"swift": "class Solution {\n func countSubstrings(_ s: String) -> Int {\n \n }\n}",
"typescript": "function countSubstrings(s: string): number {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n long long countSubstrings(string s) {\n int n = s.size();\n long long ans = 0;\n vector<long long> freq3(3,0), freq9(9,0), freq7(7,0);\n freq3[0] = 1;\n freq9[0] = 1;\n freq7[0] = 1;\n int cur3 = 0, cur9 = 0;\n int P7 = 0;\n vector<int> power7(n+1, 0);\n power7[0] = 1;\n for (int i = 1; i <= n; i++){\n power7[i] = (power7[i-1] * 10) % 7;\n }\n int inv7[7];\n inv7[1] = 1;\n inv7[2] = 4;\n inv7[3] = 5;\n inv7[4] = 2;\n inv7[5] = 3;\n inv7[6] = 6;\n for (int j = 0; j < n; j++){\n int d = s[j] - '0';\n cur3 = (cur3 + d) % 3;\n cur9 = (cur9 + d) % 9;\n P7 = (P7 * 10 + d) % 7;\n int q = (int)((long long)P7 * inv7[ power7[j+1] ] % 7);\n if(d == 0){\n } else if(d == 1 || d == 2 || d == 5){\n ans += (j + 1);\n } else if(d == 3 || d == 6){\n ans += freq3[cur3];\n } else if(d == 9){\n ans += freq9[cur9];\n } else if(d == 4){\n int contrib = 1;\n if(j >= 1){\n int two_digit = ((s[j-1]-'0') * 10 + 4);\n if(two_digit % 4 == 0)\n contrib += j;\n }\n ans += contrib;\n } else if(d == 8){\n int contrib = 1;\n if(j >= 1){\n int two_digit = ((s[j-1]-'0') * 10 + 8);\n if(two_digit % 8 == 0)\n contrib += 1;\n }\n if(j >= 2){\n int three_digit = ((s[j-2]-'0') * 100 + (s[j-1]-'0') * 10 + 8);\n if(three_digit % 8 == 0)\n contrib += (j - 1);\n }\n ans += contrib;\n } else if(d == 7){\n ans += freq7[q];\n }\n freq3[cur3]++;\n freq9[cur9]++;\n freq7[q]++;\n }\n return ans;\n }\n};",
"memory": 2100,
"memoryDistribution": "[[2100, 83.6481, \"class Solution {\\npublic:\\n long long countSubstrings(string s) {\\n int n = s.size();\\n long long ans = 0;\\n vector<long long> freq3(3,0), freq9(9,0), freq7(7,0);\\n freq3[0] = 1;\\n freq9[0] = 1;\\n freq7[0] = 1;\\n int cur3 = 0, cur9 = 0;\\n int P7 = 0;\\n vector<int> power7(n+1, 0);\\n power7[0] = 1;\\n for (int i = 1; i <= n; i++){\\n power7[i] = (power7[i-1] * 10) % 7;\\n }\\n int inv7[7];\\n inv7[1] = 1;\\n inv7[2] = 4;\\n inv7[3] = 5;\\n inv7[4] = 2;\\n inv7[5] = 3;\\n inv7[6] = 6;\\n for (int j = 0; j < n; j++){\\n int d = s[j] - '0';\\n cur3 = (cur3 + d) % 3;\\n cur9 = (cur9 + d) % 9;\\n P7 = (P7 * 10 + d) % 7;\\n int q = (int)((long long)P7 * inv7[ power7[j+1] ] % 7);\\n if(d == 0){\\n } else if(d == 1 || d == 2 || d == 5){\\n ans += (j + 1);\\n } else if(d == 3 || d == 6){\\n ans += freq3[cur3];\\n } else if(d == 9){\\n ans += freq9[cur9];\\n } else if(d == 4){\\n int contrib = 1;\\n if(j >= 1){\\n int two_digit = ((s[j-1]-'0') * 10 + 4);\\n if(two_digit % 4 == 0)\\n contrib += j;\\n }\\n ans += contrib;\\n } else if(d == 8){\\n int contrib = 1;\\n if(j >= 1){\\n int two_digit = ((s[j-1]-'0') * 10 + 8);\\n if(two_digit % 8 == 0)\\n contrib += 1;\\n }\\n if(j >= 2){\\n int three_digit = ((s[j-2]-'0') * 100 + (s[j-1]-'0') * 10 + 8);\\n if(three_digit % 8 == 0)\\n contrib += (j - 1);\\n }\\n ans += contrib;\\n } else if(d == 7){\\n ans += freq7[q];\\n }\\n freq3[cur3]++;\\n freq9[cur9]++;\\n freq7[q]++;\\n }\\n return ans;\\n }\\n};\"], [17900, 16.9808, \"class Solution {\\npublic:\\n long long countSubstrings(const string &s) {\\n int n = s.size();\\n long long ans = 0;\\n\\n long long count3[3] = {1,0,0}, count9[9] = {1};\\n int pref3 = 0, pref9 = 0;\\n\\n int inv10_7 = 5; // 10\\u207b\\u00b9 mod7\\n int prefix7 = 0, invPow7 = 1;\\n long long count7[7] = {};\\n count7[0] = 1;\\n\\n for (int i = 0; i < n; ++i) {\\n int d = s[i] - '0';\\n\\n // update digit\\u2010sum prefixes\\n pref3 = (pref3 + d) % 3;\\n pref9 = (pref9 + d) % 9;\\n\\n // update mod-7 prefix & inverse power\\n prefix7 = (prefix7 * 10 + d) % 7;\\n invPow7 = (int)((long long)invPow7 * inv10_7 % 7);\\n int F7 = (int)((long long)prefix7 * invPow7 % 7);\\n\\n if (d == 0) {\\n // skip zero\\n }\\n else if (d == 1 || d == 2 || d == 5) {\\n ans += (i + 1);\\n }\\n else if (d == 3) {\\n ans += count3[pref3];\\n }\\n else if (d == 4) {\\n if (d % 4 == 0) \\n ++ans;\\n if (i >= 1) {\\n int x = (s[i-1]-'0')*10 + d;\\n if (x % 4 == 0) \\n ans += i;\\n }\\n }\\n else if (d == 6) {\\n // 6=2*3 and last digit even \\u21d2 just mod-3 test\\n ans += count3[pref3];\\n }\\n else if (d == 7) {\\n ans += count7[F7];\\n }\\n else if (d == 8) {\\n // length 1\\n if (d % 8 == 0) \\n ++ans;\\n // length 2\\n if (i >= 1) {\\n int x = (s[i-1]-'0')*10 + d;\\n if (x % 8 == 0) \\n ++ans;\\n }\\n // length 3 and all longer\\n if (i >= 2) {\\n int last3 = (s[i-2]-'0')*100 + (s[i-1]-'0')*10 + d;\\n if (last3 % 8 == 0) {\\n ++ans; // the 3-digit substring\\n ans += (i + 1 - 3); // (i-2) substrings of length \\u22654\\n }\\n }\\n }\\n else if (d == 9) {\\n ans += count9[pref9];\\n }\\n\\n // record prefixes\\n count3[pref3]++;\\n count9[pref9]++;\\n count7[F7]++;\\n }\\n\\n return ans;\\n }\\n};\\n\"], [24900, 2.5156, \"class Solution {\\npublic:\\n long long countSubstrings(string s) {\\n // ends with 1, 2, 5: count it\\n // ends with 3, 6: count it if sum of digits is divisible by 3\\n // ends with 9: count it if sum of digits is divisible by 9\\n // ends with 4: count it if last two digits, taken together, are divisible by 4\\n // ends with 8: as above, but last three digits divisible by 8\\n // ends with 7: ugh. Only if number up to that point is divis by 7, I guess. Is there a fast way to track this?\\n // there is, but it'll be a bitch. Alternating block sums...\\n // can we just track the number of substrings congruent to each option mod 7?\\n\\n // keep track of digit sums up to a given point for 3, 6, 9\\n // 1, 2, 4, 8, and 5 are easy\\n // for 7...ugh\\n\\n\\n long long retVal = 0;\\n vector<int> mod9;\\n vector<int> mod7;\\n vector<int> foo, bar;\\n int cur;\\n int n = s.length();\\n mod9.resize(n, 0);\\n mod7.resize(7, 0);\\n for (int i = 0; i < n; i++) {\\n cur = s[i]-'0';\\n foo.clear();\\n foo.resize(7,0);\\n if (i > 0)\\n bar = mod7;\\n else\\n bar = foo;\\n for (int j = 0; j < 7; j++) {\\n foo[(10*j+cur)%7] = bar[j];\\n }\\n foo[(cur%7)]++;\\n mod7 = foo;\\n\\n foo.clear();\\n foo.resize(9,0);\\n if (i > 0)\\n bar = mod9;\\n else\\n bar = foo;\\n for (int j = 0; j < 9; j++) {\\n foo[(10*j+cur)%9] = bar[j];\\n }\\n foo[(cur%9)]++;\\n mod9 = foo;\\n\\n if (s[i] == '1' || s[i] == '2' || s[i] == '5') {\\n retVal += i+1;\\n } else if (s[i] == '3' || s[i] == '6') {\\n retVal += mod9[0] + mod9[3] + mod9[6];\\n } else if (s[i] == '9') {\\n retVal += mod9[0];\\n } else if (s[i] == '4') {\\n int prev = (i > 0) ? (s[i-1]-'0') : 0;\\n retVal++;\\n if (i > 0 && (prev*10+cur)%4 == 0)\\n retVal += i;\\n } else if (s[i] == '8') {\\n int prev = (i > 0) ? (s[i-1]-'0') : 0;\\n int prev2 = (i > 1) ? (s[i-2]-'0') : 0;\\n \\n retVal++; // the digit itself\\n \\n if (i >= 1 && (10*prev+cur)%8 == 0) {\\n retVal++;\\n } \\n if (i > 1 && (prev2*100+prev*10+cur)%8 == 0)\\n retVal += i-1;\\n } else if (s[i] == '7') {\\n retVal += mod7[0];\\n }\\n\\n //cout << i << \\\": \\\" << retVal << endl;\\n }\\n\\n return retVal;\\n }\\n};\"], [31900, 5.660299999999999, null], [38900, 3.7734999999999994, null], [45900, 0.6289, null], [52900, 3.1445999999999996, null], [59900, 2.5156, null], [66900, 1.2579, null], [73900, 0.6289, null], [80900, 0.6289, null], [87900, 2.5157, null], [94900, 0.6289, null], [101900, 0.6289, null], [108900, 0.6289, null], [115900, 0.6289, null], [122900, 0.6289, null], [129900, 0.6289, null], [136900, 0.6289, null], [143900, 0.6289, null], [150900, 0.6289, null], [157900, 0.6289, null], [164900, 0.6289, null], [171900, 0.6289, null], [178900, 0.6289, null], [185900, 0.6289, null], [192900, 0.6289, null], [199900, 1.8868, null], [206900, 0.6289, null], [213900, 0.6289, null], [220900, 0.6289, null], [227900, 0.6289, null], [234900, 0.6289, null], [241900, 0.6289, null], [248900, 1.2579, null], [255900, 0.6289, null], [262900, 0.6289, null], [269900, 4.4025, null], [276900, 10.0629, null], [283900, 7.5472, null], [290900, 1.2579, null], [297900, 0.6289, null], [304900, 0.6289, null], [311900, 0.6289, null], [318900, 0.6289, null], [325900, 0.6289, null], [332900, 0.6289, null], [339900, 0.6289, null], [346900, 3.1447, null], [353900, 4.4025, \"typedef long long ll;\\nclass Solution {\\npublic:\\n long long countSubstrings(string s) {\\n int n = s.length();\\n vector<vector<vector<ll>>> dp(\\n n, vector<vector<ll>>(10, vector<ll>(10, 0)));\\n for (int i = 1; i <= 9; i++) {\\n int r = ((s[0] - '0') % i);\\n dp[0][i][r] = 1;\\n }\\n for (int i = 0; i < n - 1; i++) {\\n int cur = (s[i + 1] - '0');\\n for (int j = 1; j <= 9; j++) {\\n dp[i + 1][j][cur % j]++;\\n for (int k = 0; k < j; k++) {\\n dp[i + 1][j][(k * 10 + cur) % j] += dp[i][j][k];\\n }\\n }\\n }\\n ll ans = 0;\\n for (int i = 0; i < n; i++) {\\n int cur = (s[i] - '0');\\n if (cur == 0)\\n continue;\\n ans += dp[i][cur][0];\\n }\\n return ans;\\n }\\n};\"], [360900, 0.6289, \"#define ll long long\\nclass Solution {\\npublic:\\n long long countSubstrings(string s) {\\n int n=s.size();\\n vector<vector<vector<ll>>>dp(n,vector<vector<ll>>(10,vector<ll>(10, 0)));\\n int digi=s[0]-'0';\\n for(int i=1;i<10;i++){\\n dp[0][i][digi%i]=1;\\n }\\n for(int idx=1;idx<n;idx++){\\n int digi=s[idx]-'0';\\n for(int i=1;i<10;i++){\\n for(int j=0;j<i;j++){\\n int modu=(10*j+digi)%i;\\n dp[idx][i][modu]+=dp[idx-1][i][j];\\n }\\n dp[idx][i][digi%i]+=1;\\n }\\n }\\n ll ans=0;\\n for(int i=0;i<n;i++){\\n int digi=s[i]-'0';\\n ans+=dp[i][digi][0];\\n }\\n return ans;\\n }\\n};\"]]",
"runtime": 30,
"runtimeDistribution": "[[30, 9.4338, \"// class Solution {\\n// public:\\n// long long countSubstrings(string s) {\\n \\n// }\\n// };\\n#include <string>\\n#include <vector>\\n#include <map> // Can be used, but vector is slightly more efficient for small fixed range keys\\n\\nusing namespace std;\\n\\nclass Solution {\\npublic:\\n /**\\n * @brief Counts the number of substrings divisible by their non-zero last digit.\\n * @param s The input string consisting of digits.\\n * @return The total count of such substrings.\\n *\\n * The approach iterates through the string using index j as the end position of potential substrings.\\n * For each j, if the digit s[j] is non-zero, it determines the divisor k = value(s[j]).\\n * Then, it checks all substrings s[i..j] (for 0 <= i <= j) for divisibility by k.\\n * To do this efficiently in O(N) time, we use prefix properties and frequency maps/arrays.\\n *\\n * For k = 1, 2, 5: The divisibility condition is always met. Add j+1 to the count.\\n * For k = 3, 6, 9: Divisibility depends on the sum of digits modulo 3 or 9. We use prefix sums S[j] = sum(s[0..j]) and frequency maps.\\n * Condition Sum[i..j] % m == 0 is equivalent to S[j] % m == S[i-1] % m (where m=3 or 9).\\n * The count of valid i's is the frequency of S[j] % m among previous prefix sums S[-1]..S[j-1].\\n * For k = 4, 8: Divisibility depends on the last few digits. Specific rules are applied based on s[j], s[j-1], s[j-2].\\n * For k = 7: Divisibility rule is complex. We use a transformation: N(i, j) % 7 == 0 is equivalent to R[j] % 7 == R[i-1] % 7,\\n * where R[x] = P[x] * (10^{-1})^{x+1} mod 7. P[x] is the value of prefix s[0..x]. 10^{-1} mod 7 is 5.\\n * We maintain frequencies of R values modulo 7.\\n *\\n * All checks and updates are done in O(1) time per index j, leading to O(N) total time complexity.\\n * Space complexity is O(1) because the frequency arrays have constant sizes (3, 9, 7).\\n */\\n long long countSubstrings(string s) {\\n long long ans = 0; // Use long long for the answer as it can exceed 32-bit integer limit.\\n int n = s.length();\\n\\n // Frequency arrays to store counts of prefix properties modulo 3, 9, and 7 (for R value).\\n // The index represents the remainder/value, and the value at that index is the count of prefixes having that property.\\n vector<long long> freq3(3, 0); \\n vector<long long> freq9(9, 0); \\n vector<long long> freq7(7, 0); \\n\\n // Initialize counts for the empty prefix (considered index -1).\\n // Empty prefix sum is 0. Its corresponding R value R[-1] is also 0.\\n freq3[0] = 1;\\n freq9[0] = 1;\\n freq7[0] = 1; \\n\\n int S3 = 0; // Current prefix sum modulo 3, S[j] = Sum(s[0..j]) mod 3\\n int S9 = 0; // Current prefix sum modulo 9, S[j] = Sum(s[0..j]) mod 9\\n int P7 = 0; // Current prefix value P[j] = Value(s[0..j]) mod 7\\n \\n // current_pow5 stores 5^(idx+1) mod 7. It's needed for calculating R[idx].\\n // Starts at 5^0=1 (for state before index 0). Updated inside loop before use for index j.\\n long long current_pow5 = 1; \\n\\n // Iterate through the string using index j as the end position of substrings.\\n for (int j = 0; j < n; ++j) {\\n int v_j = s[j] - '0'; // Get the numeric value of the current digit s[j].\\n\\n // Update prefix properties based on the current digit v_j.\\n S3 = (S3 + v_j) % 3;\\n S9 = (S9 + v_j) % 9;\\n P7 = (P7 * 10 + v_j) % 7; // Update prefix value P[j] modulo 7\\n \\n // Update the power of 5: needed for R[j]. We need 5^(j+1) mod 7.\\n // current_pow5 was 5^j before this update, now becomes 5^(j+1).\\n current_pow5 = (current_pow5 * 5) % 7; \\n \\n // Calculate R[j] = P[j] * 5^(j+1) mod 7. Use 1LL for intermediate multiplication to avoid overflow.\\n int R7 = (1LL * P7 * current_pow5) % 7;\\n\\n // Only consider substrings ending with a non-zero digit.\\n if (v_j != 0) {\\n int k = v_j; // The divisor k is the value of the last digit.\\n \\n // Apply divisibility rules based on k.\\n if (k == 1 || k == 2 || k == 5) {\\n // For k=1, any integer is divisible by 1.\\n // For k=2, N(i, j) = N(i, j-1)*10 + 2 is always even.\\n // For k=5, N(i, j) = N(i, j-1)*10 + 5 is always divisible by 5.\\n // In these cases, all j+1 substrings ending at j (i=0..j) are valid.\\n ans += (long long)(j + 1); \\n } else if (k == 3 || k == 6) {\\n // For k=3, need N(i,j) % 3 == 0 <=> Sum[i..j] % 3 == 0.\\n // For k=6, need N(i,j) % 6 == 0. Since v_j=6, N(i,j) is always even.\\n // So we only need N(i,j) % 3 == 0 <=> Sum[i..j] % 3 == 0.\\n // Condition Sum[i..j] % 3 == 0 is equivalent to S[j] % 3 == S[i-1] % 3.\\n // The number of valid starting indices i is the count of previous prefixes p=i-1\\n // (including empty prefix p=-1) such that S[p] % 3 == S[j] % 3. This count is freq3[S3].\\n ans += freq3[S3];\\n } else if (k == 4) {\\n // N(j, j) = 4 is divisible by 4.\\n ans += 1; \\n // For i < j, N(i, j) % 4 depends on last two digits. N(i, j) % 4 = (v_{j-1}*10 + 4) % 4 = (v_{j-1}*2) % 4.\\n // This is 0 iff v_{j-1} is even (0, 2, 4, 6, 8).\\n if (j >= 1) {\\n int v_j_1 = s[j-1] - '0';\\n if (v_j_1 % 2 == 0) {\\n // Substrings s[0..j] to s[j-1..j] are valid. There are j such substrings.\\n ans += (long long)j; \\n }\\n }\\n } else if (k == 7) {\\n // Need N(i, j) % 7 == 0. Using the transformation, this is equivalent to R[j] % 7 == R[i-1] % 7.\\n // The number of valid starting indices i is the count of previous prefixes p=i-1\\n // such that R[p] % 7 == R[j] % 7. This count is freq7[R7].\\n ans += freq7[R7];\\n } else if (k == 8) {\\n // N(j, j) = 8 is divisible by 8.\\n ans += 1; \\n // Check N(j-1, j) % 8 = (v_{j-1}*10 + 8) % 8 = (v_{j-1}*2) % 8. This is 0 iff v_{j-1} is 0, 4, 8.\\n if (j >= 1) {\\n int v_j_1 = s[j-1] - '0';\\n if ((v_j_1 * 2) % 8 == 0) { \\n ans += 1; // Substring s[j-1..j]\\n }\\n }\\n // Check N(i, j) % 8 for i <= j-2. This depends on N(j-2, j) % 8.\\n // N(j-2, j) % 8 = (v_{j-2}*100 + v_{j-1}*10 + 8) % 8 = (v_{j-2}*4 + v_{j-1}*2) % 8.\\n if (j >= 2) {\\n int v_j_1 = s[j-1] - '0';\\n int v_j_2 = s[j-2] - '0';\\n if ((v_j_2 * 4 + v_j_1 * 2) % 8 == 0) {\\n // If N(j-2, j) is divisible by 8, then all N(i, j) for i <= j-2 are also divisible by 8.\\n // Substrings s[0..j] to s[j-2..j] are valid. There are j-1 such substrings (i=0 to j-2).\\n ans += (long long)(j - 1); \\n }\\n }\\n } else if (k == 9) {\\n // Need N(i,j) % 9 == 0 <=> Sum[i..j] % 9 == 0.\\n // Equivalent to S[j] % 9 == S[i-1] % 9. The count is freq9[S9].\\n ans += freq9[S9];\\n }\\n }\\n\\n // After processing index j and potentially adding to ans, update frequency counts\\n // based on the properties of the prefix ending at j. These updated counts will be used for future indices > j.\\n freq3[S3]++;\\n freq9[S9]++;\\n freq7[R7]++; // R7 calculated corresponds to index j.\\n }\\n\\n return ans;\\n }\\n};\"], [68, 4.4024, \"/*\\nU: Understand & Clarify\\n\\n substring: continuous non-empty (size of >= 1) sequence\\n property: divisible by non-zero last digit\\n\\n Example: 12936\\n\\n 1, 2, 9, 3, 6\\n 12, 93, 36\\n 936\\n 1293\\n 12936\\n\\nD: Devise\\n Recurrence Relation: \\n Suppose u already have the solution to s0 (size = k), and we are trying to solve for c (s0).\\n We need to consider new substrings that involves c, where we will have k new substrings. \\n if c == 0: \\n c (s0) = s0 + k\\n else:\\n We iterate through the k possible substrings \\n Since we are only considering non-zero last digit (ld):\\n if ld == 1 || ld == 2: \\n the property holds\\n else: \\n check if c % ld holds && s0 at ld holds \\n \\n \\n \\n*/\\nclass Solution {\\nprivate:\\n // Helper to calculate modular exponentiation (base^exp % mod)\\n long long power(long long base, long long exp, long long mod) {\\n long long res = 1;\\n base %= mod;\\n while (exp > 0) {\\n if (exp % 2 == 1) res = (res * base) % mod;\\n base = (base * base) % mod;\\n exp /= 2;\\n }\\n return res;\\n }\\n\\n // Helper to calculate modular inverse using Fermat's Little Theorem (for prime modulus)\\n long long modInverse(long long n, long long mod) {\\n // Assumes mod is prime (like 7)\\n return power(n, mod - 2, mod);\\n }\\n\\npublic:\\n long long countSubstrings(std::string s) {\\n long long count = 0;\\n int n = s.length();\\n\\n // For d=3, 6, 9 (Prefix Sum Modulo)\\n std::map<int, int> counts3 = {{0, 1}}; // {remainder: frequency}\\n std::map<int, int> counts9 = {{0, 1}};\\n int current_pref_sum3 = 0;\\n int current_pref_sum9 = 0;\\n\\n // For d=7 (Transformed Prefix Value Modulo)\\n std::vector<long long> pow10_mod7(n + 1);\\n std::vector<long long> inv_pow10_mod7(n + 1);\\n pow10_mod7[0] = 1;\\n inv_pow10_mod7[0] = modInverse(1, 7); // inv(1) = 1\\n for(int k = 1; k <= n; ++k) {\\n pow10_mod7[k] = (pow10_mod7[k-1] * 10) % 7;\\n inv_pow10_mod7[k] = modInverse(pow10_mod7[k], 7);\\n }\\n\\n std::map<int, int> counts7 = {{0, 1}}; // {transformed_remainder: frequency}\\n int current_pref_val7 = 0;\\n\\n\\n for (int j = 0; j < n; ++j) {\\n int digit = s[j] - '0';\\n\\n // Update prefix sums/values\\n current_pref_sum3 = (current_pref_sum3 + digit) % 3;\\n current_pref_sum9 = (current_pref_sum9 + digit) % 9;\\n current_pref_val7 = (current_pref_val7 * 10LL + digit) % 7; // Use LL for intermediate product\\n\\n // Calculate transformed prefix for d=7\\n // transformed_pref[j] = (pref_val[j] * inv7(10^(j+1))) % 7\\n int current_transformed7 = (current_pref_val7 * inv_pow10_mod7[j + 1]) % 7;\\n\\n\\n if (digit != 0) {\\n // --- Check Divisibility Conditions ---\\n\\n // Case d=1, 2, 5\\n if (digit == 1 || digit == 2 || digit == 5) {\\n count += (j + 1);\\n }\\n // Case d=3\\n else if (digit == 3) {\\n count += counts3[current_pref_sum3];\\n }\\n // Case d=6\\n else if (digit == 6) {\\n count += counts3[current_pref_sum3];\\n }\\n // Case d=9\\n else if (digit == 9) {\\n count += counts9[current_pref_sum9];\\n }\\n // Case d=4\\n else if (digit == 4) {\\n count++; // Single digit \\\"4\\\"\\n if (j > 0) {\\n int prev_digit = s[j-1] - '0';\\n int num2 = prev_digit * 10 + digit;\\n if (num2 % 4 == 0) {\\n count += j; // Substrings s[0..j], s[1..j] ... s[j-1..j]\\n }\\n }\\n }\\n // Case d=8\\n else if (digit == 8) {\\n count++; // Single digit \\\"8\\\"\\n if (j > 0) {\\n int prev1_digit = s[j-1] - '0';\\n int num2 = prev1_digit * 10 + digit;\\n if (num2 % 8 == 0) {\\n count++; // Substring s[j-1..j]\\n }\\n }\\n if (j > 1) {\\n int prev2_digit = s[j-2] - '0';\\n int prev1_digit = s[j-1] - '0';\\n int num3 = prev2_digit * 100 + prev1_digit * 10 + digit;\\n if (num3 % 8 == 0) {\\n count += (j - 1); // Substrings s[0..j] ... s[j-2..j]\\n }\\n }\\n }\\n // Case d=7\\n else if (digit == 7) {\\n count += counts7[current_transformed7];\\n }\\n }\\n\\n // --- Update Counts Maps ---\\n counts3[current_pref_sum3]++;\\n counts9[current_pref_sum9]++;\\n counts7[current_transformed7]++;\\n }\\n\\n return count;\\n }\\n};\"], [106, 0.6289, null], [145, 0.6289, null], [183, 3.1445999999999996, null], [222, 2.5156, null], [260, 1.8867, null], [298, 2.5157, null], [337, 0.6289, null], [375, 1.8867, null], [413, 0.6289, null], [452, 0.6289, null], [490, 0.6289, null], [529, 0.6289, null], [567, 0.6289, null], [605, 0.6289, null], [644, 0.6289, null], [682, 0.6289, null], [720, 0.6289, null], [759, 0.6289, null], [797, 0.6289, null], [836, 0.6289, null], [874, 0.6289, null], [912, 0.6289, null], [951, 0.6289, null], [989, 0.6289, null], [1027, 0.6289, null], [1066, 0.6289, null], [1104, 0.6289, null], [1143, 0.6289, null], [1181, 0.6289, null], [1219, 0.6289, null], [1258, 0.6289, null], [1296, 0.6289, null], [1334, 0.6289, null], [1373, 0.6289, null], [1411, 0.6289, null], [1450, 0.6289, null], [1488, 0.6289, null], [1526, 0.6289, null], [1565, 0.6289, null], [1603, 0.6289, null], [1641, 0.6289, null], [1680, 0.6289, null], [1718, 0.6289, null], [1757, 0.6289, null], [1795, 0.6289, null], [1833, 0.6289, null], [1872, 0.6289, null], [1910, 0.6289, null], [1948, 0.6289, null], [1987, 1.2579, null], [2025, 0.6289, null], [2064, 0.6289, null], [2102, 0.6289, null], [2140, 0.6289, null], [2179, 0.6289, null], [2217, 0.6289, null], [2255, 0.6289, null], [2294, 0.6289, null], [2332, 1.2579, null], [2371, 0.6289, null], [2409, 0.6289, null], [2447, 0.6289, null], [2486, 0.6289, null], [2524, 0.6289, null], [2562, 0.6289, null], [2601, 0.6289, null], [2639, 3.1445, null], [2678, 1.8868, null], [2716, 3.7733999999999996, null], [2754, 3.1445, null], [2793, 1.2578, null], [2831, 4.402399999999999, null], [2869, 3.7733999999999996, null], [2908, 4.4024, null], [2946, 1.2578, null], [2985, 1.2578, \"#define ll long long\\nclass Solution {\\npublic:\\n long long countSubstrings(string s) {\\n int n=s.size();\\n vector<vector<vector<ll>>>dp(n,vector<vector<ll>>(10,vector<ll>(10, 0)));\\n \\n int digi=s[0]-'0';\\n for(int i=1;i<10;i++){\\n dp[0][i][digi%i]=1;\\n }\\n for(int idx=1;idx<n;idx++)\\n {\\n int digi=s[idx]-'0';\\n for(int i=1;i<10;i++){\\n for(int j=0;j<i;j++){\\n int modu=(10*j+digi)%i;\\n dp[idx][i][modu]+=dp[idx-1][i][j];\\n }\\n dp[idx][i][digi%i]+=1;\\n }\\n\\n }\\n ll ans=0;\\n for(int i=0;i<n;i++){\\n int digi=s[i]-'0';\\n ans+=dp[i][digi][0];\\n }\\n return ans;\\n \\n }\\n};\"], [3023, 1.2578, \"class Solution {\\npublic:\\n long long countSubstrings(string s) {\\n vector<vector<int>> dp(10, vector<int>(10, 0));\\n int n = s.size();\\n long long ans = 0;\\n for (int i=0; i<n; i++) {\\n int d = s[i]-'0';\\n vector<vector<int>> dp2(10, vector<int>(10, 0));\\n for (int num=1; num<=9; num++) {\\n for (int rem=0; rem<=9; rem++) {\\n dp2[num][(rem*10+d)%num] += dp[num][rem];\\n }\\n dp2[num][d%num]++;\\n }\\n ans += dp2[d][0];\\n dp = dp2;\\n }\\n return ans;\\n }\\n};\"]]"
},
"golang": {
"code": "func countSubstrings(s string) int64 {\n\tn := len(s)\n\tvar ans int64\n\tvar freq3 [3]int\n\tvar freq9 [9]int\n\tvar freq7 [7]int\n\t// initial prefix values for mod3, mod9 and mod7\n\tp3, p9, p7 := 0, 0, 0\n\tfreq3[0] = 1\n\tfreq9[0] = 1\n\tfreq7[0] = 1\n\t// Precomputed modular inverses for 10^i mod 7 (period 6):\n\t// 10^0 mod7=1 (inv 1), 10^1 mod7=3 (inv 5), 10^2=2 (inv 4),\n\t// 10^3=6 (inv 6), 10^4=4 (inv 2), 10^5=5 (inv 3)\n\tinv7 := [6]int{1, 5, 4, 6, 2, 3}\n\t\n\tfor j := 0; j < n; j++ {\n\t\tdigit := int(s[j] - '0')\n\t\t// Update prefix sums.\n\t\tnewP3 := (p3 + digit) % 3\n\t\tnewP9 := (p9 + digit) % 9\n\t\tnewP7 := (p7*10 + digit) % 7\n\t\t// Compute transformed value for mod7: F7(x)= prefix7(x)*inv(10^x mod7) mod7.\n\t\tr7 := (newP7 * inv7[(j+1)%6]) % 7\n\t\t\n\t\tswitch digit {\n\t\tcase 0:\n\t\t\t// Last digit 0: skip.\n\t\tcase 1:\n\t\t\t// Divisible by 1 always.\n\t\t\tans += int64(j + 1)\n\t\tcase 2:\n\t\t\t// Any number ending in 2 is even.\n\t\t\tans += int64(j + 1)\n\t\tcase 3:\n\t\t\t// Number divisible by 3 if prefix3[j+1]==prefix3[i] for some i.\n\t\t\tans += int64(freq3[newP3])\n\t\tcase 4:\n\t\t\t// Divisibility by 4: one-digit substring always qualifies (4 mod4=0).\n\t\t\t// For substrings of length>=2, last two digits decide.\n\t\t\tcnt := 1\n\t\t\tif j >= 1 {\n\t\t\t\ttwoDigit := (int(s[j-1]-'0') * 10) + digit\n\t\t\t\tif twoDigit%4 == 0 {\n\t\t\t\t\tcnt += j\n\t\t\t\t}\n\t\t\t}\n\t\t\tans += int64(cnt)\n\t\tcase 5:\n\t\t\t// Any number ending in 5 is divisible by 5.\n\t\t\tans += int64(j + 1)\n\t\tcase 6:\n\t\t\t// Ending in 6: even automatically, so check divisibility by 3.\n\t\t\tans += int64(freq3[newP3])\n\t\tcase 7:\n\t\t\t// Use mod7 transformation.\n\t\t\tans += int64(freq7[r7])\n\t\tcase 8:\n\t\t\t// Divisible by 8: check one-digit, two-digit and length>=3 (last three digits).\n\t\t\tcnt := 1\n\t\t\tif j >= 1 {\n\t\t\t\ttwoDigit := (int(s[j-1]-'0') * 10) + digit\n\t\t\t\tif twoDigit%8 == 0 {\n\t\t\t\t\tcnt += 1\n\t\t\t\t}\n\t\t\t}\n\t\t\tif j >= 2 {\n\t\t\t\tthreeDigit := (int(s[j-2]-'0')*100 + int(s[j-1]-'0')*10 + digit)\n\t\t\t\tif threeDigit%8 == 0 {\n\t\t\t\t\tcnt += j - 1\n\t\t\t\t}\n\t\t\t}\n\t\t\tans += int64(cnt)\n\t\tcase 9:\n\t\t\t// Divisible by 9 if prefix9[j+1]==prefix9[i] for some i.\n\t\t\tans += int64(freq9[newP9])\n\t\t}\n\t\t// Update frequency arrays for prefixes.\n\t\tfreq3[newP3]++\n\t\tfreq9[newP9]++\n\t\tfreq7[r7]++\n\t\tp3, p9, p7 = newP3, newP9, newP7\n\t}\n\treturn ans\n}",
"memory": null,
"memoryDistribution": "[[8100, 50.0, \"func countSubstrings(s string) (ans int64) {\\n\\tf := [10][9]int{}\\n\\tfor _, c := range s {\\n\\t\\td := int(c - '0')\\n\\t\\tfor m := 1; m < 10; m++ {\\n\\t\\t\\tnf := [9]int{}\\n\\t\\t\\tnf[d%m] = 1\\n\\t\\t\\tfor r := range m {\\n\\t\\t\\t\\tnf[(r*10+d)%m] += f[m][r]\\n\\t\\t\\t}\\n\\t\\t\\tf[m] = nf\\n\\t\\t}\\n\\t\\tans += int64(f[d][0])\\n\\t}\\n\\treturn\\n}\"], [8400, 50.0, \"func countSubstrings(s string) int64 {\\n\\tn := len(s)\\n\\tvar ans int64\\n\\tvar freq3 [3]int\\n\\tvar freq9 [9]int\\n\\tvar freq7 [7]int\\n\\t// initial prefix values for mod3, mod9 and mod7\\n\\tp3, p9, p7 := 0, 0, 0\\n\\tfreq3[0] = 1\\n\\tfreq9[0] = 1\\n\\tfreq7[0] = 1\\n\\t// Precomputed modular inverses for 10^i mod 7 (period 6):\\n\\t// 10^0 mod7=1 (inv 1), 10^1 mod7=3 (inv 5), 10^2=2 (inv 4),\\n\\t// 10^3=6 (inv 6), 10^4=4 (inv 2), 10^5=5 (inv 3)\\n\\tinv7 := [6]int{1, 5, 4, 6, 2, 3}\\n\\t\\n\\tfor j := 0; j < n; j++ {\\n\\t\\tdigit := int(s[j] - '0')\\n\\t\\t// Update prefix sums.\\n\\t\\tnewP3 := (p3 + digit) % 3\\n\\t\\tnewP9 := (p9 + digit) % 9\\n\\t\\tnewP7 := (p7*10 + digit) % 7\\n\\t\\t// Compute transformed value for mod7: F7(x)= prefix7(x)*inv(10^x mod7) mod7.\\n\\t\\tr7 := (newP7 * inv7[(j+1)%6]) % 7\\n\\t\\t\\n\\t\\tswitch digit {\\n\\t\\tcase 0:\\n\\t\\t\\t// Last digit 0: skip.\\n\\t\\tcase 1:\\n\\t\\t\\t// Divisible by 1 always.\\n\\t\\t\\tans += int64(j + 1)\\n\\t\\tcase 2:\\n\\t\\t\\t// Any number ending in 2 is even.\\n\\t\\t\\tans += int64(j + 1)\\n\\t\\tcase 3:\\n\\t\\t\\t// Number divisible by 3 if prefix3[j+1]==prefix3[i] for some i.\\n\\t\\t\\tans += int64(freq3[newP3])\\n\\t\\tcase 4:\\n\\t\\t\\t// Divisibility by 4: one-digit substring always qualifies (4 mod4=0).\\n\\t\\t\\t// For substrings of length>=2, last two digits decide.\\n\\t\\t\\tcnt := 1\\n\\t\\t\\tif j >= 1 {\\n\\t\\t\\t\\ttwoDigit := (int(s[j-1]-'0') * 10) + digit\\n\\t\\t\\t\\tif twoDigit%4 == 0 {\\n\\t\\t\\t\\t\\tcnt += j\\n\\t\\t\\t\\t}\\n\\t\\t\\t}\\n\\t\\t\\tans += int64(cnt)\\n\\t\\tcase 5:\\n\\t\\t\\t// Any number ending in 5 is divisible by 5.\\n\\t\\t\\tans += int64(j + 1)\\n\\t\\tcase 6:\\n\\t\\t\\t// Ending in 6: even automatically, so check divisibility by 3.\\n\\t\\t\\tans += int64(freq3[newP3])\\n\\t\\tcase 7:\\n\\t\\t\\t// Use mod7 transformation.\\n\\t\\t\\tans += int64(freq7[r7])\\n\\t\\tcase 8:\\n\\t\\t\\t// Divisible by 8: check one-digit, two-digit and length>=3 (last three digits).\\n\\t\\t\\tcnt := 1\\n\\t\\t\\tif j >= 1 {\\n\\t\\t\\t\\ttwoDigit := (int(s[j-1]-'0') * 10) + digit\\n\\t\\t\\t\\tif twoDigit%8 == 0 {\\n\\t\\t\\t\\t\\tcnt += 1\\n\\t\\t\\t\\t}\\n\\t\\t\\t}\\n\\t\\t\\tif j >= 2 {\\n\\t\\t\\t\\tthreeDigit := (int(s[j-2]-'0')*100 + int(s[j-1]-'0')*10 + digit)\\n\\t\\t\\t\\tif threeDigit%8 == 0 {\\n\\t\\t\\t\\t\\tcnt += j - 1\\n\\t\\t\\t\\t}\\n\\t\\t\\t}\\n\\t\\t\\tans += int64(cnt)\\n\\t\\tcase 9:\\n\\t\\t\\t// Divisible by 9 if prefix9[j+1]==prefix9[i] for some i.\\n\\t\\t\\tans += int64(freq9[newP9])\\n\\t\\t}\\n\\t\\t// Update frequency arrays for prefixes.\\n\\t\\tfreq3[newP3]++\\n\\t\\tfreq9[newP9]++\\n\\t\\tfreq7[r7]++\\n\\t\\tp3, p9, p7 = newP3, newP9, newP7\\n\\t}\\n\\treturn ans\\n}\"]]",
"runtime": 6,
"runtimeDistribution": "[[6, 50.0, \"func countSubstrings(s string) int64 {\\n\\tn := len(s)\\n\\tvar ans int64\\n\\tvar freq3 [3]int\\n\\tvar freq9 [9]int\\n\\tvar freq7 [7]int\\n\\t// initial prefix values for mod3, mod9 and mod7\\n\\tp3, p9, p7 := 0, 0, 0\\n\\tfreq3[0] = 1\\n\\tfreq9[0] = 1\\n\\tfreq7[0] = 1\\n\\t// Precomputed modular inverses for 10^i mod 7 (period 6):\\n\\t// 10^0 mod7=1 (inv 1), 10^1 mod7=3 (inv 5), 10^2=2 (inv 4),\\n\\t// 10^3=6 (inv 6), 10^4=4 (inv 2), 10^5=5 (inv 3)\\n\\tinv7 := [6]int{1, 5, 4, 6, 2, 3}\\n\\t\\n\\tfor j := 0; j < n; j++ {\\n\\t\\tdigit := int(s[j] - '0')\\n\\t\\t// Update prefix sums.\\n\\t\\tnewP3 := (p3 + digit) % 3\\n\\t\\tnewP9 := (p9 + digit) % 9\\n\\t\\tnewP7 := (p7*10 + digit) % 7\\n\\t\\t// Compute transformed value for mod7: F7(x)= prefix7(x)*inv(10^x mod7) mod7.\\n\\t\\tr7 := (newP7 * inv7[(j+1)%6]) % 7\\n\\t\\t\\n\\t\\tswitch digit {\\n\\t\\tcase 0:\\n\\t\\t\\t// Last digit 0: skip.\\n\\t\\tcase 1:\\n\\t\\t\\t// Divisible by 1 always.\\n\\t\\t\\tans += int64(j + 1)\\n\\t\\tcase 2:\\n\\t\\t\\t// Any number ending in 2 is even.\\n\\t\\t\\tans += int64(j + 1)\\n\\t\\tcase 3:\\n\\t\\t\\t// Number divisible by 3 if prefix3[j+1]==prefix3[i] for some i.\\n\\t\\t\\tans += int64(freq3[newP3])\\n\\t\\tcase 4:\\n\\t\\t\\t// Divisibility by 4: one-digit substring always qualifies (4 mod4=0).\\n\\t\\t\\t// For substrings of length>=2, last two digits decide.\\n\\t\\t\\tcnt := 1\\n\\t\\t\\tif j >= 1 {\\n\\t\\t\\t\\ttwoDigit := (int(s[j-1]-'0') * 10) + digit\\n\\t\\t\\t\\tif twoDigit%4 == 0 {\\n\\t\\t\\t\\t\\tcnt += j\\n\\t\\t\\t\\t}\\n\\t\\t\\t}\\n\\t\\t\\tans += int64(cnt)\\n\\t\\tcase 5:\\n\\t\\t\\t// Any number ending in 5 is divisible by 5.\\n\\t\\t\\tans += int64(j + 1)\\n\\t\\tcase 6:\\n\\t\\t\\t// Ending in 6: even automatically, so check divisibility by 3.\\n\\t\\t\\tans += int64(freq3[newP3])\\n\\t\\tcase 7:\\n\\t\\t\\t// Use mod7 transformation.\\n\\t\\t\\tans += int64(freq7[r7])\\n\\t\\tcase 8:\\n\\t\\t\\t// Divisible by 8: check one-digit, two-digit and length>=3 (last three digits).\\n\\t\\t\\tcnt := 1\\n\\t\\t\\tif j >= 1 {\\n\\t\\t\\t\\ttwoDigit := (int(s[j-1]-'0') * 10) + digit\\n\\t\\t\\t\\tif twoDigit%8 == 0 {\\n\\t\\t\\t\\t\\tcnt += 1\\n\\t\\t\\t\\t}\\n\\t\\t\\t}\\n\\t\\t\\tif j >= 2 {\\n\\t\\t\\t\\tthreeDigit := (int(s[j-2]-'0')*100 + int(s[j-1]-'0')*10 + digit)\\n\\t\\t\\t\\tif threeDigit%8 == 0 {\\n\\t\\t\\t\\t\\tcnt += j - 1\\n\\t\\t\\t\\t}\\n\\t\\t\\t}\\n\\t\\t\\tans += int64(cnt)\\n\\t\\tcase 9:\\n\\t\\t\\t// Divisible by 9 if prefix9[j+1]==prefix9[i] for some i.\\n\\t\\t\\tans += int64(freq9[newP9])\\n\\t\\t}\\n\\t\\t// Update frequency arrays for prefixes.\\n\\t\\tfreq3[newP3]++\\n\\t\\tfreq9[newP9]++\\n\\t\\tfreq7[r7]++\\n\\t\\tp3, p9, p7 = newP3, newP9, newP7\\n\\t}\\n\\treturn ans\\n}\"], [117, 50.0, \"func countSubstrings(s string) (ans int64) {\\n\\tf := [10][9]int{}\\n\\tfor _, c := range s {\\n\\t\\td := int(c - '0')\\n\\t\\tfor m := 1; m < 10; m++ {\\n\\t\\t\\tnf := [9]int{}\\n\\t\\t\\tnf[d%m] = 1\\n\\t\\t\\tfor r := range m {\\n\\t\\t\\t\\tnf[(r*10+d)%m] += f[m][r]\\n\\t\\t\\t}\\n\\t\\t\\tf[m] = nf\\n\\t\\t}\\n\\t\\tans += int64(f[d][0])\\n\\t}\\n\\treturn\\n}\"]]"
},
"java": {
"code": "class Solution {\n public long countSubstrings(String s) {\n int n = s.length();\n long ans = 0;\n long[] freq3 = new long[3];\n freq3[0] = 1;\n long[] freq9 = new long[9];\n freq9[0] = 1;\n long[][] freq7 = new long[6][7];\n freq7[0][0] = 1;\n int mod3 = 0, mod9 = 0, mod7 = 0;\n int[] inv7 = {1, 5, 4, 6, 2, 3};\n for (int j = 0; j < n; j++) {\n int d = s.charAt(j) - '0';\n mod3 = (mod3 + d) % 3;\n mod9 = (mod9 + d) % 9;\n mod7 = (mod7 * 10 + d) % 7;\n int k = j + 1, kMod = k % 6;\n char c = s.charAt(j);\n if (c == '0') {\n } else if (c == '1') {\n ans += (j + 1);\n } else if (c == '2') {\n ans += (j + 1);\n } else if (c == '5') {\n ans += (j + 1);\n } else if (c == '3') {\n ans += freq3[mod3];\n } else if (c == '6') {\n ans += freq3[mod3];\n } else if (c == '9') {\n ans += freq9[mod9];\n } else if (c == '4') {\n long add = 1;\n if (j >= 1) {\n int prev = s.charAt(j - 1) - '0';\n int two = prev * 10 + 4;\n if (two % 4 == 0)\n add += j;\n }\n ans += add;\n } else if (c == '8') {\n long add = 1;\n if (j >= 1) {\n int prev = s.charAt(j - 1) - '0';\n int two = prev * 10 + 8;\n if (two % 8 == 0)\n add += 1;\n }\n if (j >= 2) {\n int d1 = s.charAt(j - 2) - '0';\n int d2 = s.charAt(j - 1) - '0';\n int three = d1 * 100 + d2 * 10 + 8;\n if (three % 8 == 0)\n add += (j - 1);\n }\n ans += add;\n } else if (c == '7') {\n for (int r = 0; r < 6; r++) {\n int L0 = (kMod - r + 6) % 6;\n int target = (mod7 * inv7[L0]) % 7;\n ans += freq7[r][target];\n }\n }\n freq3[mod3]++;\n freq9[mod9]++;\n freq7[kMod][mod7]++;\n }\n return ans;\n }\n}",
"memory": 4600,
"memoryDistribution": "[[4600, 98.1132, \"class Solution {\\n public long countSubstrings(String s) {\\n int n = s.length();\\n long ans = 0;\\n long[] freq3 = new long[3];\\n freq3[0] = 1;\\n long[] freq9 = new long[9];\\n freq9[0] = 1;\\n long[][] freq7 = new long[6][7];\\n freq7[0][0] = 1;\\n int mod3 = 0, mod9 = 0, mod7 = 0;\\n int[] inv7 = {1, 5, 4, 6, 2, 3};\\n for (int j = 0; j < n; j++) {\\n int d = s.charAt(j) - '0';\\n mod3 = (mod3 + d) % 3;\\n mod9 = (mod9 + d) % 9;\\n mod7 = (mod7 * 10 + d) % 7;\\n int k = j + 1, kMod = k % 6;\\n char c = s.charAt(j);\\n if (c == '0') {\\n } else if (c == '1') {\\n ans += (j + 1);\\n } else if (c == '2') {\\n ans += (j + 1);\\n } else if (c == '5') {\\n ans += (j + 1);\\n } else if (c == '3') {\\n ans += freq3[mod3];\\n } else if (c == '6') {\\n ans += freq3[mod3];\\n } else if (c == '9') {\\n ans += freq9[mod9];\\n } else if (c == '4') {\\n long add = 1;\\n if (j >= 1) {\\n int prev = s.charAt(j - 1) - '0';\\n int two = prev * 10 + 4;\\n if (two % 4 == 0)\\n add += j;\\n }\\n ans += add;\\n } else if (c == '8') {\\n long add = 1;\\n if (j >= 1) {\\n int prev = s.charAt(j - 1) - '0';\\n int two = prev * 10 + 8;\\n if (two % 8 == 0)\\n add += 1;\\n }\\n if (j >= 2) {\\n int d1 = s.charAt(j - 2) - '0';\\n int d2 = s.charAt(j - 1) - '0';\\n int three = d1 * 100 + d2 * 10 + 8;\\n if (three % 8 == 0)\\n add += (j - 1);\\n }\\n ans += add;\\n } else if (c == '7') {\\n for (int r = 0; r < 6; r++) {\\n int L0 = (kMod - r + 6) % 6;\\n int target = (mod7 * inv7[L0]) % 7;\\n ans += freq7[r][target];\\n }\\n }\\n freq3[mod3]++;\\n freq9[mod9]++;\\n freq7[kMod][mod7]++;\\n }\\n return ans;\\n }\\n}\"], [45500, 1.8868, \"class Solution {\\n public long countSubstrings(String s) {\\n int n = s.length();\\n long ans = 0;\\n long[] freq3 = new long[3];\\n freq3[0] = 1;\\n long[] freq9 = new long[9];\\n freq9[0] = 1;\\n long[][] freq7 = new long[6][7];\\n freq7[0][0] = 1;\\n int mod3 = 0, mod9 = 0, mod7 = 0;\\n int[] inv7 = {1, 5, 4, 6, 2, 3};\\n for (int j = 0; j < n; j++) {\\n int d = s.charAt(j) - '0';\\n mod3 = (mod3 + d) % 3;\\n mod9 = (mod9 + d) % 9;\\n mod7 = (mod7 * 10 + d) % 7;\\n int k = j + 1, kMod = k % 6;\\n char c = s.charAt(j);\\n if (c == '0') {\\n } else if (c == '1') {\\n ans += (j + 1);\\n } else if (c == '2') {\\n ans += (j + 1);\\n } else if (c == '5') {\\n ans += (j + 1);\\n } else if (c == '3') {\\n ans += freq3[mod3];\\n } else if (c == '6') {\\n ans += freq3[mod3];\\n } else if (c == '9') {\\n ans += freq9[mod9];\\n } else if (c == '4') {\\n long add = 1;\\n if (j >= 1) {\\n int prev = s.charAt(j - 1) - '0';\\n int two = prev * 10 + 4;\\n if (two % 4 == 0)\\n add += j;\\n }\\n ans += add;\\n } else if (c == '8') {\\n long add = 1;\\n if (j >= 1) {\\n int prev = s.charAt(j - 1) - '0';\\n int two = prev * 10 + 8;\\n if (two % 8 == 0)\\n add += 1;\\n }\\n if (j >= 2) {\\n int d1 = s.charAt(j - 2) - '0';\\n int d2 = s.charAt(j - 1) - '0';\\n int three = d1 * 100 + d2 * 10 + 8;\\n if (three % 8 == 0)\\n add += (j - 1);\\n }\\n ans += add;\\n } else if (c == '7') {\\n for (int r = 0; r < 6; r++) {\\n int L0 = (kMod - r + 6) % 6;\\n int target = (mod7 * inv7[L0]) % 7;\\n ans += freq7[r][target];\\n }\\n }\\n freq3[mod3]++;\\n freq9[mod9]++;\\n freq7[kMod][mod7]++;\\n }\\n return ans;\\n }\\n}\"], [45600, 5.6604, \"public class Solution {\\n public long countSubstrings(String s) {\\n int n = s.length();\\n long ans = 0;\\n \\n int[] f3 = new int[3];\\n int[] f6 = new int[6];\\n int[] f9 = new int[9];\\n int[][] f7 = new int[6][7];\\n \\n int pref3 = 0, pref6 = 0, pref9 = 0, pref7Val = 0;\\n f3[0] = 1;\\n f6[0] = 1;\\n f9[0] = 1;\\n f7[0][0] = 1;\\n \\n int[] f = {1, 5, 4, 6, 2, 3};\\n \\n for (int j = 0; j < n; j++) {\\n int d = s.charAt(j) - '0';\\n pref3 = (pref3 + d) % 3;\\n pref6 = (pref6 * 4 + d) % 6;\\n pref9 = (pref9 + d) % 9;\\n pref7Val = (pref7Val * 10 + d) % 7;\\n \\n if (d == 0) {\\n } else if (d == 1 || d == 2 || d == 5) {\\n ans += (j + 1);\\n } else if (d == 3) {\\n ans += f3[pref3];\\n } else if (d == 6) {\\n int needed = pref6;\\n for (int r = 0; r < 6; r++) {\\n if ((4 * r) % 6 == needed) {\\n ans += f6[r];\\n }\\n }\\n } else if (d == 9) {\\n ans += f9[pref9];\\n } else if (d == 7) {\\n for (int r = 0; r < 6; r++) {\\n int t = ((j + 1 - r) % 6 + 6) % 6; \\n int needed = (pref7Val * f[t]) % 7;\\n ans += f7[r][needed];\\n }\\n } else if (d == 4) {\\n int contrib = 1;\\n if (j >= 1) {\\n int num = (s.charAt(j - 1) - '0') * 10 + d;\\n if (num % 4 == 0) {\\n contrib += j;\\n }\\n }\\n ans += contrib;\\n } else if (d == 8) {\\n int contrib = 1;\\n if (j >= 1) {\\n int num = (s.charAt(j - 1) - '0') * 10 + d;\\n if (num % 8 == 0) {\\n contrib += 1;\\n }\\n }\\n if (j >= 2) {\\n int num = (s.charAt(j - 2) - '0') * 100 \\n + (s.charAt(j - 1) - '0') * 10 + d;\\n if (num % 8 == 0) {\\n contrib += (j - 1);\\n }\\n }\\n ans += contrib;\\n }\\n \\n f3[pref3]++;\\n f6[pref6]++;\\n f9[pref9]++;\\n f7[(j + 1) % 6][pref7Val]++;\\n }\\n \\n return ans;\\n }\\n}\"], [45900, 3.7736, null], [46100, 3.7736, null], [46700, 3.7736, null], [46800, 1.8868, null], [46900, 3.7736, null], [47000, 3.7736, null], [47200, 3.7736, null], [47300, 1.8868, null], [47400, 5.6604, null], [47500, 1.8868, null], [47700, 1.8868, null], [49000, 1.8868, null], [49100, 1.8868, null], [49300, 1.8868, null], [49500, 1.8868, null], [49700, 1.8868, null], [51400, 1.8868, null], [69700, 1.8868, null], [90200, 1.8868, null], [127700, 1.8868, null], [128400, 1.8868, null], [200000, 1.8868, null], [212900, 1.8868, null], [213000, 3.7736, null], [213200, 1.8868, null], [213600, 1.8868, null], [214100, 1.8868, null], [215400, 1.8868, null], [224800, 1.8868, null], [256500, 1.8868, null], [265500, 1.8868, null], [268600, 1.8868, null], [268800, 1.8868, null], [269000, 1.8868, null], [269500, 1.8868, null], [277900, 1.8868, \"class Solution {\\n public long countSubstrings(String s) {\\n \\n long total=0;\\n int n=s.length();\\n long dp[][][]=new long[n+1][10][10];\\n for(int i=0;i<n;i++){\\n for(int mod=1;mod<10;mod++){\\n for(int rem=0;rem<10;rem++){\\n dp[i+1][(rem*10+s.charAt(i)-'0')%mod][mod]+=dp[i][rem][mod]; \\n }\\n dp[i+1][(s.charAt(i)-'0')%mod][mod]+=1;\\n }\\n total+=dp[i+1][0][s.charAt(i)-'0'];\\n }\\n return total;\\n }\\n}\"], [289000, 1.8868, \"import java.util.Arrays;\\n\\nclass Solution {\\n private static final int MAX_LAST = 9; // last digit we ever test\\n private static final int SENTINEL = 10; // \\u201cno product yet\\u201d\\n private static final long UNSEEN = -1; // memo sentinel\\n\\n private String s;\\n private int n;\\n private int[] digit; // s.charAt(i) \\u2192 int, cached once\\n private long[][][] dp; // primitive: n+1 \\u00d7 10 \\u00d7 11\\n\\n public long countSubstrings(String s) {\\n this.s = s;\\n this.n = s.length();\\n\\n /* 1\\u00a0. cache char\\u2192int conversion */\\n digit = new int[n];\\n for (int i = 0; i < n; i++) digit[i] = s.charAt(i) - '0';\\n\\n /* 2\\u00a0. primitive 3\\u2011D table with a single sentinel value */\\n dp = new long[n + 1][MAX_LAST + 1][SENTINEL + 1];\\n for (long[][] layer : dp)\\n for (long[] row : layer)\\n Arrays.fill(row, UNSEEN);\\n\\n long total = 0;\\n for (int last = 1; last <= MAX_LAST; last++) {\\n for (int start = 0; start < n; start++) {\\n total += solve(start, last, SENTINEL);\\n }\\n }\\n return total;\\n }\\n\\n private long solve(int idx, int last, int prod) {\\n if (idx == n) return 0;\\n\\n long memo = dp[idx][last][prod];\\n if (memo != UNSEEN) return memo;\\n\\n /* 3\\u00a0. one modular reduction instead of two */\\n int d = digit[idx];\\n int newProd = (prod == SENTINEL)\\n ? d % last\\n : (int) (((long) prod * 10 + d) % last);\\n\\n long cnt = (d == last && newProd == 0) ? 1 : 0; // no mod here\\n cnt += solve(idx + 1, last, newProd);\\n\\n dp[idx][last][prod] = cnt;\\n return cnt;\\n }\\n}\\n\"]]",
"runtime": 15,
"runtimeDistribution": "[[14, 1.8868, \"class Solution {\\n public long countSubstrings(String s) {\\n int n = s.length();\\n long ans = 0;\\n int[] freq3 = new int[3], freq9 = new int[9], freqQ = new int[7];\\n freq3[0] = 1; freq9[0] = 1; freqQ[0] = 1;\\n int p3 = 0, p9 = 0, p7 = 0;\\n int[] inv = {1,5,4,6,2,3};\\n for(int j = 0; j < n; j++){\\n int d = s.charAt(j) - '0';\\n p3 = (p3 + d) % 3;\\n p9 = (p9 + d) % 9;\\n p7 = (p7 * 10 + d) % 7;\\n int idx = (j + 1) % 6;\\n int q = (p7 * inv[idx]) % 7;\\n if(d == 0){\\n } else if(d == 1){\\n ans += j + 1;\\n } else if(d == 2){\\n ans += j + 1;\\n } else if(d == 3){\\n ans += freq3[p3];\\n } else if(d == 4){\\n ans += 1;\\n if(j >= 1){\\n int lt = ( (s.charAt(j - 1) - '0') * 10 + 4 );\\n if(lt % 4 == 0) ans += j;\\n }\\n } else if(d == 5){\\n ans += j + 1;\\n } else if(d == 6){\\n ans += freq3[p3];\\n } else if(d == 7){\\n ans += freqQ[q];\\n } else if(d == 8){\\n ans += 1;\\n if(j >= 1){\\n int lt = ((s.charAt(j - 1) - '0') * 10 + 8);\\n if(lt % 8 == 0) ans += 1;\\n }\\n if(j >= 2){\\n int l3 = ((s.charAt(j - 2) - '0') * 100 + (s.charAt(j - 1) - '0') * 10 + 8);\\n if(l3 % 8 == 0) ans += j - 1;\\n }\\n } else if(d == 9){\\n ans += freq9[p9];\\n }\\n freq3[p3]++;\\n freq9[p9]++;\\n freqQ[q]++;\\n }\\n return ans;\\n }\\n}\"], [15, 3.7736, \"class Solution {\\n public long countSubstrings(String s) {\\n int n = s.length();\\n long ans = 0;\\n int[] freq3 = new int[3], freq9 = new int[9], freqQ = new int[7];\\n freq3[0] = 1; freq9[0] = 1; freqQ[0] = 1;\\n int p3 = 0, p9 = 0, p7 = 0;\\n int[] inv = {1,5,4,6,2,3};\\n for(int j = 0; j < n; j++){\\n int d = s.charAt(j) - '0';\\n p3 = (p3 + d) % 3;\\n p9 = (p9 + d) % 9;\\n p7 = (p7 * 10 + d) % 7;\\n int idx = (j + 1) % 6;\\n int q = (p7 * inv[idx]) % 7;\\n if(d == 0){\\n } else if(d == 1){\\n ans += j + 1;\\n } else if(d == 2){\\n ans += j + 1;\\n } else if(d == 3){\\n ans += freq3[p3];\\n } else if(d == 4){\\n ans += 1;\\n if(j >= 1){\\n int lt = ( (s.charAt(j - 1) - '0') * 10 + 4 );\\n if(lt % 4 == 0) ans += j;\\n }\\n } else if(d == 5){\\n ans += j + 1;\\n } else if(d == 6){\\n ans += freq3[p3];\\n } else if(d == 7){\\n ans += freqQ[q];\\n } else if(d == 8){\\n ans += 1;\\n if(j >= 1){\\n int lt = ((s.charAt(j - 1) - '0') * 10 + 8);\\n if(lt % 8 == 0) ans += 1;\\n }\\n if(j >= 2){\\n int l3 = ((s.charAt(j - 2) - '0') * 100 + (s.charAt(j - 1) - '0') * 10 + 8);\\n if(l3 % 8 == 0) ans += j - 1;\\n }\\n } else if(d == 9){\\n ans += freq9[p9];\\n }\\n freq3[p3]++;\\n freq9[p9]++;\\n freqQ[q]++;\\n }\\n return ans;\\n }\\n}\"], [16, 3.7736, null], [17, 1.8868, null], [19, 3.7736, null], [20, 16.9811, null], [49, 1.8868, null], [53, 1.8868, null], [132, 1.8868, null], [136, 1.8868, null], [139, 1.8868, null], [174, 1.8868, null], [177, 1.8868, null], [241, 1.8868, null], [345, 1.8868, null], [381, 1.8868, null], [382, 1.8868, null], [386, 1.8868, null], [389, 1.8868, null], [392, 3.7736, null], [393, 1.8868, null], [394, 1.8868, null], [395, 5.6604, null], [398, 1.8868, null], [399, 1.8868, null], [402, 1.8868, null], [410, 1.8868, null], [450, 1.8868, null], [461, 1.8868, null], [579, 1.8868, null], [628, 1.8868, null], [827, 1.8868, null], [1064, 1.8868, null], [1394, 1.8868, null], [1440, 1.8868, \"class Solution {\\n String s;\\n int n;\\n int[] digit; \\n long[][][] dp; \\n\\n public long countSubstrings(String s) {\\n this.s = s;\\n this.n = s.length();\\n digit = new int[n];\\n for (int i = 0; i < n; i++){digit[i] = s.charAt(i) - '0';}\\n dp = new long[n + 1][10][11];\\n for (long[][] layer : dp){\\n for (long[] row : layer){\\n Arrays.fill(row, -1);\\n }\\n }\\n long total = 0;\\n for (int j = 1; j <= 9; j++) {\\n for (int i = 0; i < n; i++) {\\n total += DP(i, j, 10);\\n }\\n }\\n return total;\\n }\\n\\n public long DP(int i, int j, int k) {\\n if (i == n) return 0;\\n long memo = dp[i][j][k];\\n if (memo != -1){return memo;}\\n int d = digit[i];\\n int newProd = (k == 10) ? d % j : ((k * 10 + d) % j);\\n long cnt = (d == j && newProd == 0) ? 1 : 0;\\n cnt += DP(i + 1, j, newProd);\\n dp[i][j][k] = cnt;\\n return cnt;\\n }\\n}\\n\"], [1464, 1.8868, \"class Solution {\\n String s;\\n int n;\\n int[] digit; \\n long[][][] dp; \\n\\n public long countSubstrings(String s) {\\n this.s = s;\\n this.n = s.length();\\n digit = new int[n];\\n for (int i = 0; i < n; i++) digit[i] = s.charAt(i) - '0';\\n dp = new long[n + 1][10][11];\\n for (long[][] layer : dp)\\n for (long[] row : layer)\\n Arrays.fill(row, -1);\\n long total = 0;\\n for (int last = 1; last <= 9; last++) {\\n for (int start = 0; start < n; start++) {\\n total += solve(start, last, 10);\\n }\\n }\\n return total;\\n }\\n\\n private long solve(int idx, int last, int prod) {\\n if (idx == n) return 0;\\n long memo = dp[idx][last][prod];\\n if (memo != -1) return memo;\\n int d = digit[idx];\\n int newProd = (prod == 10)\\n ? d % last\\n : (int) ((prod * 10 + d) % last);\\n\\n long cnt = (d == last && newProd == 0) ? 1 : 0;\\n cnt += solve(idx + 1, last, newProd);\\n dp[idx][last][prod] = cnt;\\n return cnt;\\n }\\n}\\n\"]]"
},
"javascript": {
"code": "\"use strict\";\nvar countSubstrings = function(s) {\n const n = s.length;\n const toDigit = ch => ch.charCodeAt(0) - 48;\n let total = 0;\n // d = 1,2,5: every substring ending in these digits qualifies.\n for (let d of [1, 2, 5]) {\n for (let j = 0; j < n; j++) {\n if (toDigit(s[j]) === d) total += (j + 1);\n }\n }\n // d = 3 (10 mod3 = 1): condition: (prefix[j+1] - prefix[i]*1)==0 <=> prefix[j+1]==prefix[i]\n {\n const mod = 3;\n let freq = new Array(mod).fill(0);\n let prefix = 0;\n freq[prefix]++;\n for (let j = 0; j < n; j++) {\n let dgt = toDigit(s[j]);\n prefix = (prefix * 10 + dgt) % mod;\n if (dgt === 3) total += freq[prefix];\n freq[prefix]++;\n }\n }\n // d = 9 (10 mod9 = 1): similar to d=3.\n {\n const mod = 9;\n let freq = new Array(mod).fill(0);\n let prefix = 0;\n freq[prefix]++;\n for (let j = 0; j < n; j++) {\n let dgt = toDigit(s[j]);\n prefix = (prefix * 10 + dgt) % mod;\n if (dgt === 9) total += freq[prefix];\n freq[prefix]++;\n }\n }\n // d = 7 (coprime with 10): use Q = prefix * inv(10^k) mod7.\n {\n const mod = 7;\n // Precomputed inverses modulo7 for 1..6.\n const inv = [0, 1, 4, 5, 2, 3, 6];\n let freq = new Array(mod).fill(0);\n let prefix = 0, p = 1;\n let Q = 0; // for k=0: prefix=0, so Q=0.\n freq[Q]++;\n for (let j = 0; j < n; j++) {\n let dgt = toDigit(s[j]);\n prefix = (prefix * 10 + dgt) % mod;\n p = (p * 10) % mod;\n let invP = inv[p];\n Q = (prefix * invP) % mod;\n if (Q < 0) Q += mod;\n if (dgt === 7) total += freq[Q];\n freq[Q]++;\n }\n }\n // d = 6 (10^e mod6 = 4 for any positive exponent)\n {\n const mod = 6;\n let freq = new Array(mod).fill(0);\n let cur = 0; // f(0)\n freq[cur]++;\n for (let j = 0; j < n; j++) {\n let dgt = toDigit(s[j]);\n let newVal = (cur * 10 + dgt) % mod;\n if (dgt === 6) {\n let qsum = 0;\n for (let r = 0; r < mod; r++) {\n if ((4 * r) % mod === newVal) qsum += freq[r];\n }\n // Exclude the case i == j; f(j) is stored as 'cur'\n if ((4 * cur) % mod === newVal) qsum -= 1;\n total += (qsum + 1);\n }\n freq[newVal]++;\n cur = newVal;\n }\n }\n // d = 4: 10^0=1, 10^1 mod4=2, and 10^k mod4=0 for k>=2.\n {\n const mod = 4;\n let prefixArr = new Array(n + 1);\n prefixArr[0] = 0;\n for (let i = 0; i < n; i++) {\n let dgt = toDigit(s[i]);\n prefixArr[i + 1] = (prefixArr[i] * 10 + dgt) % mod;\n }\n for (let j = 0; j < n; j++) {\n if (toDigit(s[j]) === 4) {\n let cnt = 0;\n cnt++; // L = 0: single digit.\n if (j >= 1) {\n let twoDig = parseInt(s.substring(j - 1, j + 1), 10);\n if (twoDig % 4 === 0) cnt++;\n }\n if (j >= 2 && prefixArr[j + 1] % mod === 0) {\n cnt += (j - 1);\n }\n total += cnt;\n }\n }\n }\n // d = 8: 10^0=1, 10^1 mod8=2, 10^2 mod8=4, and 10^k mod8=0 for k>=3.\n {\n const mod = 8;\n let prefixArr = new Array(n + 1);\n prefixArr[0] = 0;\n for (let i = 0; i < n; i++) {\n let dgt = toDigit(s[i]);\n prefixArr[i + 1] = (prefixArr[i] * 10 + dgt) % mod;\n }\n for (let j = 0; j < n; j++) {\n if (toDigit(s[j]) === 8) {\n let cnt = 0;\n cnt++; // L = 0.\n if (j >= 1) {\n let twoDig = parseInt(s.substring(j - 1, j + 1), 10);\n if (twoDig % 8 === 0) cnt++;\n }\n if (j >= 2) {\n let threeDig = parseInt(s.substring(j - 2, j + 1), 10);\n if (threeDig % 8 === 0) cnt++;\n }\n if (j >= 3 && prefixArr[j + 1] % mod === 0) {\n cnt += (j - 2);\n }\n total += cnt;\n }\n }\n }\n return total;\n};",
"memory": 8300,
"memoryDistribution": "[[8300, 100.0, \"\\\"use strict\\\";\\nvar countSubstrings = function(s) {\\n const n = s.length;\\n const toDigit = ch => ch.charCodeAt(0) - 48;\\n let total = 0;\\n // d = 1,2,5: every substring ending in these digits qualifies.\\n for (let d of [1, 2, 5]) {\\n for (let j = 0; j < n; j++) {\\n if (toDigit(s[j]) === d) total += (j + 1);\\n }\\n }\\n // d = 3 (10 mod3 = 1): condition: (prefix[j+1] - prefix[i]*1)==0 <=> prefix[j+1]==prefix[i]\\n {\\n const mod = 3;\\n let freq = new Array(mod).fill(0);\\n let prefix = 0;\\n freq[prefix]++;\\n for (let j = 0; j < n; j++) {\\n let dgt = toDigit(s[j]);\\n prefix = (prefix * 10 + dgt) % mod;\\n if (dgt === 3) total += freq[prefix];\\n freq[prefix]++;\\n }\\n }\\n // d = 9 (10 mod9 = 1): similar to d=3.\\n {\\n const mod = 9;\\n let freq = new Array(mod).fill(0);\\n let prefix = 0;\\n freq[prefix]++;\\n for (let j = 0; j < n; j++) {\\n let dgt = toDigit(s[j]);\\n prefix = (prefix * 10 + dgt) % mod;\\n if (dgt === 9) total += freq[prefix];\\n freq[prefix]++;\\n }\\n }\\n // d = 7 (coprime with 10): use Q = prefix * inv(10^k) mod7.\\n {\\n const mod = 7;\\n // Precomputed inverses modulo7 for 1..6.\\n const inv = [0, 1, 4, 5, 2, 3, 6];\\n let freq = new Array(mod).fill(0);\\n let prefix = 0, p = 1;\\n let Q = 0; // for k=0: prefix=0, so Q=0.\\n freq[Q]++;\\n for (let j = 0; j < n; j++) {\\n let dgt = toDigit(s[j]);\\n prefix = (prefix * 10 + dgt) % mod;\\n p = (p * 10) % mod;\\n let invP = inv[p];\\n Q = (prefix * invP) % mod;\\n if (Q < 0) Q += mod;\\n if (dgt === 7) total += freq[Q];\\n freq[Q]++;\\n }\\n }\\n // d = 6 (10^e mod6 = 4 for any positive exponent)\\n {\\n const mod = 6;\\n let freq = new Array(mod).fill(0);\\n let cur = 0; // f(0)\\n freq[cur]++;\\n for (let j = 0; j < n; j++) {\\n let dgt = toDigit(s[j]);\\n let newVal = (cur * 10 + dgt) % mod;\\n if (dgt === 6) {\\n let qsum = 0;\\n for (let r = 0; r < mod; r++) {\\n if ((4 * r) % mod === newVal) qsum += freq[r];\\n }\\n // Exclude the case i == j; f(j) is stored as 'cur'\\n if ((4 * cur) % mod === newVal) qsum -= 1;\\n total += (qsum + 1);\\n }\\n freq[newVal]++;\\n cur = newVal;\\n }\\n }\\n // d = 4: 10^0=1, 10^1 mod4=2, and 10^k mod4=0 for k>=2.\\n {\\n const mod = 4;\\n let prefixArr = new Array(n + 1);\\n prefixArr[0] = 0;\\n for (let i = 0; i < n; i++) {\\n let dgt = toDigit(s[i]);\\n prefixArr[i + 1] = (prefixArr[i] * 10 + dgt) % mod;\\n }\\n for (let j = 0; j < n; j++) {\\n if (toDigit(s[j]) === 4) {\\n let cnt = 0;\\n cnt++; // L = 0: single digit.\\n if (j >= 1) {\\n let twoDig = parseInt(s.substring(j - 1, j + 1), 10);\\n if (twoDig % 4 === 0) cnt++;\\n }\\n if (j >= 2 && prefixArr[j + 1] % mod === 0) {\\n cnt += (j - 1);\\n }\\n total += cnt;\\n }\\n }\\n }\\n // d = 8: 10^0=1, 10^1 mod8=2, 10^2 mod8=4, and 10^k mod8=0 for k>=3.\\n {\\n const mod = 8;\\n let prefixArr = new Array(n + 1);\\n prefixArr[0] = 0;\\n for (let i = 0; i < n; i++) {\\n let dgt = toDigit(s[i]);\\n prefixArr[i + 1] = (prefixArr[i] * 10 + dgt) % mod;\\n }\\n for (let j = 0; j < n; j++) {\\n if (toDigit(s[j]) === 8) {\\n let cnt = 0;\\n cnt++; // L = 0.\\n if (j >= 1) {\\n let twoDig = parseInt(s.substring(j - 1, j + 1), 10);\\n if (twoDig % 8 === 0) cnt++;\\n }\\n if (j >= 2) {\\n let threeDig = parseInt(s.substring(j - 2, j + 1), 10);\\n if (threeDig % 8 === 0) cnt++;\\n }\\n if (j >= 3 && prefixArr[j + 1] % mod === 0) {\\n cnt += (j - 2);\\n }\\n total += cnt;\\n }\\n }\\n }\\n return total;\\n};\"], [83300, 100.0, \"\\\"use strict\\\";\\nvar countSubstrings = function(s) {\\n const n = s.length;\\n const toDigit = ch => ch.charCodeAt(0) - 48;\\n let total = 0;\\n // d = 1,2,5: every substring ending in these digits qualifies.\\n for (let d of [1, 2, 5]) {\\n for (let j = 0; j < n; j++) {\\n if (toDigit(s[j]) === d) total += (j + 1);\\n }\\n }\\n // d = 3 (10 mod3 = 1): condition: (prefix[j+1] - prefix[i]*1)==0 <=> prefix[j+1]==prefix[i]\\n {\\n const mod = 3;\\n let freq = new Array(mod).fill(0);\\n let prefix = 0;\\n freq[prefix]++;\\n for (let j = 0; j < n; j++) {\\n let dgt = toDigit(s[j]);\\n prefix = (prefix * 10 + dgt) % mod;\\n if (dgt === 3) total += freq[prefix];\\n freq[prefix]++;\\n }\\n }\\n // d = 9 (10 mod9 = 1): similar to d=3.\\n {\\n const mod = 9;\\n let freq = new Array(mod).fill(0);\\n let prefix = 0;\\n freq[prefix]++;\\n for (let j = 0; j < n; j++) {\\n let dgt = toDigit(s[j]);\\n prefix = (prefix * 10 + dgt) % mod;\\n if (dgt === 9) total += freq[prefix];\\n freq[prefix]++;\\n }\\n }\\n // d = 7 (coprime with 10): use Q = prefix * inv(10^k) mod7.\\n {\\n const mod = 7;\\n // Precomputed inverses modulo7 for 1..6.\\n const inv = [0, 1, 4, 5, 2, 3, 6];\\n let freq = new Array(mod).fill(0);\\n let prefix = 0, p = 1;\\n let Q = 0; // for k=0: prefix=0, so Q=0.\\n freq[Q]++;\\n for (let j = 0; j < n; j++) {\\n let dgt = toDigit(s[j]);\\n prefix = (prefix * 10 + dgt) % mod;\\n p = (p * 10) % mod;\\n let invP = inv[p];\\n Q = (prefix * invP) % mod;\\n if (Q < 0) Q += mod;\\n if (dgt === 7) total += freq[Q];\\n freq[Q]++;\\n }\\n }\\n // d = 6 (10^e mod6 = 4 for any positive exponent)\\n {\\n const mod = 6;\\n let freq = new Array(mod).fill(0);\\n let cur = 0; // f(0)\\n freq[cur]++;\\n for (let j = 0; j < n; j++) {\\n let dgt = toDigit(s[j]);\\n let newVal = (cur * 10 + dgt) % mod;\\n if (dgt === 6) {\\n let qsum = 0;\\n for (let r = 0; r < mod; r++) {\\n if ((4 * r) % mod === newVal) qsum += freq[r];\\n }\\n // Exclude the case i == j; f(j) is stored as 'cur'\\n if ((4 * cur) % mod === newVal) qsum -= 1;\\n total += (qsum + 1);\\n }\\n freq[newVal]++;\\n cur = newVal;\\n }\\n }\\n // d = 4: 10^0=1, 10^1 mod4=2, and 10^k mod4=0 for k>=2.\\n {\\n const mod = 4;\\n let prefixArr = new Array(n + 1);\\n prefixArr[0] = 0;\\n for (let i = 0; i < n; i++) {\\n let dgt = toDigit(s[i]);\\n prefixArr[i + 1] = (prefixArr[i] * 10 + dgt) % mod;\\n }\\n for (let j = 0; j < n; j++) {\\n if (toDigit(s[j]) === 4) {\\n let cnt = 0;\\n cnt++; // L = 0: single digit.\\n if (j >= 1) {\\n let twoDig = parseInt(s.substring(j - 1, j + 1), 10);\\n if (twoDig % 4 === 0) cnt++;\\n }\\n if (j >= 2 && prefixArr[j + 1] % mod === 0) {\\n cnt += (j - 1);\\n }\\n total += cnt;\\n }\\n }\\n }\\n // d = 8: 10^0=1, 10^1 mod8=2, 10^2 mod8=4, and 10^k mod8=0 for k>=3.\\n {\\n const mod = 8;\\n let prefixArr = new Array(n + 1);\\n prefixArr[0] = 0;\\n for (let i = 0; i < n; i++) {\\n let dgt = toDigit(s[i]);\\n prefixArr[i + 1] = (prefixArr[i] * 10 + dgt) % mod;\\n }\\n for (let j = 0; j < n; j++) {\\n if (toDigit(s[j]) === 8) {\\n let cnt = 0;\\n cnt++; // L = 0.\\n if (j >= 1) {\\n let twoDig = parseInt(s.substring(j - 1, j + 1), 10);\\n if (twoDig % 8 === 0) cnt++;\\n }\\n if (j >= 2) {\\n let threeDig = parseInt(s.substring(j - 2, j + 1), 10);\\n if (threeDig % 8 === 0) cnt++;\\n }\\n if (j >= 3 && prefixArr[j + 1] % mod === 0) {\\n cnt += (j - 2);\\n }\\n total += cnt;\\n }\\n }\\n }\\n return total;\\n};\"]]",
"runtime": 276,
"runtimeDistribution": "[[276, 100.0, \"\\\"use strict\\\";\\nvar countSubstrings = function(s) {\\n const n = s.length;\\n const toDigit = ch => ch.charCodeAt(0) - 48;\\n let total = 0;\\n // d = 1,2,5: every substring ending in these digits qualifies.\\n for (let d of [1, 2, 5]) {\\n for (let j = 0; j < n; j++) {\\n if (toDigit(s[j]) === d) total += (j + 1);\\n }\\n }\\n // d = 3 (10 mod3 = 1): condition: (prefix[j+1] - prefix[i]*1)==0 <=> prefix[j+1]==prefix[i]\\n {\\n const mod = 3;\\n let freq = new Array(mod).fill(0);\\n let prefix = 0;\\n freq[prefix]++;\\n for (let j = 0; j < n; j++) {\\n let dgt = toDigit(s[j]);\\n prefix = (prefix * 10 + dgt) % mod;\\n if (dgt === 3) total += freq[prefix];\\n freq[prefix]++;\\n }\\n }\\n // d = 9 (10 mod9 = 1): similar to d=3.\\n {\\n const mod = 9;\\n let freq = new Array(mod).fill(0);\\n let prefix = 0;\\n freq[prefix]++;\\n for (let j = 0; j < n; j++) {\\n let dgt = toDigit(s[j]);\\n prefix = (prefix * 10 + dgt) % mod;\\n if (dgt === 9) total += freq[prefix];\\n freq[prefix]++;\\n }\\n }\\n // d = 7 (coprime with 10): use Q = prefix * inv(10^k) mod7.\\n {\\n const mod = 7;\\n // Precomputed inverses modulo7 for 1..6.\\n const inv = [0, 1, 4, 5, 2, 3, 6];\\n let freq = new Array(mod).fill(0);\\n let prefix = 0, p = 1;\\n let Q = 0; // for k=0: prefix=0, so Q=0.\\n freq[Q]++;\\n for (let j = 0; j < n; j++) {\\n let dgt = toDigit(s[j]);\\n prefix = (prefix * 10 + dgt) % mod;\\n p = (p * 10) % mod;\\n let invP = inv[p];\\n Q = (prefix * invP) % mod;\\n if (Q < 0) Q += mod;\\n if (dgt === 7) total += freq[Q];\\n freq[Q]++;\\n }\\n }\\n // d = 6 (10^e mod6 = 4 for any positive exponent)\\n {\\n const mod = 6;\\n let freq = new Array(mod).fill(0);\\n let cur = 0; // f(0)\\n freq[cur]++;\\n for (let j = 0; j < n; j++) {\\n let dgt = toDigit(s[j]);\\n let newVal = (cur * 10 + dgt) % mod;\\n if (dgt === 6) {\\n let qsum = 0;\\n for (let r = 0; r < mod; r++) {\\n if ((4 * r) % mod === newVal) qsum += freq[r];\\n }\\n // Exclude the case i == j; f(j) is stored as 'cur'\\n if ((4 * cur) % mod === newVal) qsum -= 1;\\n total += (qsum + 1);\\n }\\n freq[newVal]++;\\n cur = newVal;\\n }\\n }\\n // d = 4: 10^0=1, 10^1 mod4=2, and 10^k mod4=0 for k>=2.\\n {\\n const mod = 4;\\n let prefixArr = new Array(n + 1);\\n prefixArr[0] = 0;\\n for (let i = 0; i < n; i++) {\\n let dgt = toDigit(s[i]);\\n prefixArr[i + 1] = (prefixArr[i] * 10 + dgt) % mod;\\n }\\n for (let j = 0; j < n; j++) {\\n if (toDigit(s[j]) === 4) {\\n let cnt = 0;\\n cnt++; // L = 0: single digit.\\n if (j >= 1) {\\n let twoDig = parseInt(s.substring(j - 1, j + 1), 10);\\n if (twoDig % 4 === 0) cnt++;\\n }\\n if (j >= 2 && prefixArr[j + 1] % mod === 0) {\\n cnt += (j - 1);\\n }\\n total += cnt;\\n }\\n }\\n }\\n // d = 8: 10^0=1, 10^1 mod8=2, 10^2 mod8=4, and 10^k mod8=0 for k>=3.\\n {\\n const mod = 8;\\n let prefixArr = new Array(n + 1);\\n prefixArr[0] = 0;\\n for (let i = 0; i < n; i++) {\\n let dgt = toDigit(s[i]);\\n prefixArr[i + 1] = (prefixArr[i] * 10 + dgt) % mod;\\n }\\n for (let j = 0; j < n; j++) {\\n if (toDigit(s[j]) === 8) {\\n let cnt = 0;\\n cnt++; // L = 0.\\n if (j >= 1) {\\n let twoDig = parseInt(s.substring(j - 1, j + 1), 10);\\n if (twoDig % 8 === 0) cnt++;\\n }\\n if (j >= 2) {\\n let threeDig = parseInt(s.substring(j - 2, j + 1), 10);\\n if (threeDig % 8 === 0) cnt++;\\n }\\n if (j >= 3 && prefixArr[j + 1] % mod === 0) {\\n cnt += (j - 2);\\n }\\n total += cnt;\\n }\\n }\\n }\\n return total;\\n};\"]]"
},
"python3": {
"code": "class Solution:\n def countSubstrings(self, s: str) -> int:\n n = len(s)\n ans = 0\n freq3 = {0: 1}\n p3 = 0\n freq9 = {0: 1}\n p9 = 0\n freq7 = {0: 1}\n p7 = 0\n power7 = 1\n for j in range(n):\n d = ord(s[j]) - 48\n p3 = (p3 + d) % 3\n p9 = (p9 + d) % 9\n p7 = (p7 * 10 + d) % 7\n power7 = (power7 * 10) % 7\n inv_power7 = pow(power7, -1, 7)\n q7 = (p7 * inv_power7) % 7\n ch = s[j]\n if ch == '0':\n pass\n elif ch in \"125\":\n ans += (j + 1)\n elif ch in \"36\":\n ans += freq3.get(p3, 0)\n elif ch == '9':\n ans += freq9.get(p9, 0)\n elif ch == '4':\n if j == 0:\n ans += 1\n else:\n two = ((ord(s[j - 1]) - 48) * 10 + 4)\n if two % 4 == 0:\n ans += 1 + j\n else:\n ans += 1\n elif ch == '8':\n if j == 0:\n ans += 1\n elif j == 1:\n two = ((ord(s[j - 1]) - 48) * 10 + 8)\n if two % 8 == 0:\n ans += 2\n else:\n ans += 1\n else:\n two = ((ord(s[j - 1]) - 48) * 10 + 8)\n three = ((ord(s[j - 2]) - 48) * 100 + (ord(s[j - 1]) - 48) * 10 + 8)\n tmp = 1\n if two % 8 == 0:\n tmp += 1\n if three % 8 == 0:\n tmp += (j - 1)\n ans += tmp\n elif ch == '7':\n ans += freq7.get(q7, 0)\n freq3[p3] = freq3.get(p3, 0) + 1\n freq9[p9] = freq9.get(p9, 0) + 1\n freq7[q7] = freq7.get(q7, 0) + 1\n return ans",
"memory": 1800,
"memoryDistribution": "[[1800, 22.5352, \"class Solution:\\n def countSubstrings(self, s: str) -> int:\\n n = len(s)\\n ans = 0\\n freq3 = {0: 1}\\n p3 = 0\\n freq9 = {0: 1}\\n p9 = 0\\n freq7 = {0: 1}\\n p7 = 0\\n power7 = 1\\n for j in range(n):\\n d = ord(s[j]) - 48\\n p3 = (p3 + d) % 3\\n p9 = (p9 + d) % 9\\n p7 = (p7 * 10 + d) % 7\\n power7 = (power7 * 10) % 7\\n inv_power7 = pow(power7, -1, 7)\\n q7 = (p7 * inv_power7) % 7\\n ch = s[j]\\n if ch == '0':\\n pass\\n elif ch in \\\"125\\\":\\n ans += (j + 1)\\n elif ch in \\\"36\\\":\\n ans += freq3.get(p3, 0)\\n elif ch == '9':\\n ans += freq9.get(p9, 0)\\n elif ch == '4':\\n if j == 0:\\n ans += 1\\n else:\\n two = ((ord(s[j - 1]) - 48) * 10 + 4)\\n if two % 4 == 0:\\n ans += 1 + j\\n else:\\n ans += 1\\n elif ch == '8':\\n if j == 0:\\n ans += 1\\n elif j == 1:\\n two = ((ord(s[j - 1]) - 48) * 10 + 8)\\n if two % 8 == 0:\\n ans += 2\\n else:\\n ans += 1\\n else:\\n two = ((ord(s[j - 1]) - 48) * 10 + 8)\\n three = ((ord(s[j - 2]) - 48) * 100 + (ord(s[j - 1]) - 48) * 10 + 8)\\n tmp = 1\\n if two % 8 == 0:\\n tmp += 1\\n if three % 8 == 0:\\n tmp += (j - 1)\\n ans += tmp\\n elif ch == '7':\\n ans += freq7.get(q7, 0)\\n freq3[p3] = freq3.get(p3, 0) + 1\\n freq9[p9] = freq9.get(p9, 0) + 1\\n freq7[q7] = freq7.get(q7, 0) + 1\\n return ans\"], [17900, 2.8169, \"class Solution:\\n def countSubstrings(self, s: str) -> int:\\n n = len(s)\\n def solve(d):\\n rem_cnt = defaultdict(int)\\n rem_cnt[0] = 1\\n pref_rem = 0\\n res = 0\\n for i, c in enumerate(s):\\n nrc = defaultdict(int)\\n for rem, cnt in rem_cnt.items():\\n nrc[rem*10 % d] += cnt\\n pref_rem = (pref_rem * 10 + int(c)) % d\\n \\n if int(c) == d:\\n res += nrc[pref_rem]\\n \\n rem_cnt = nrc\\n rem_cnt[pref_rem] += 1\\n \\n return res\\n res = 0\\n for d in range(1, 10):\\n res += solve(d)\\n \\n return res\"], [18000, 15.493, \"class Solution:\\n def countSubstrings(self, s: str) -> int:\\n dp = [[1] + [0] * i for i in range(10)]\\n res = 0\\n\\n for ind, i in enumerate(s):\\n if i != \\\"0\\\":\\n if int(i) in {1, 2, 5}:\\n res += ind + 1\\n else:\\n res += dp[int(i)][0]\\n\\n for x in range(1, 10):\\n if x in {1, 2, 5}:\\n continue\\n\\n new_dp = [1] + [0] * x\\n\\n for n in range(x):\\n new_dp[(10 * (n + int(i))) % x] = dp[x][n] + new_dp[(10 * (n + int(i))) % x]\\n\\n dp[x] = new_dp\\n\\n return res\"], [18100, 22.5352, null], [18200, 19.7183, null], [18300, 16.9014, null], [18400, 5.6338, null], [19100, 1.4085, null], [19400, 1.4085, null], [19600, 2.8169, null], [19900, 1.4085, null], [20600, 1.4085, null], [20700, 1.4085, \"class Solution:\\n def countSubstrings(self, s):\\n n=len(s)\\n res=0\\n P3=[0]*n\\n P7=[0]*n\\n P9=[0]*n\\n P3[0]=int(s[0])%3\\n P7[0]=int(s[0])%7\\n P9[0]=int(s[0])%9\\n for i in range(1,n):\\n P3[i]=(P3[i-1]*10+int(s[i]))%3\\n P7[i]=(P7[i-1]*10+int(s[i]))%7\\n P9[i]=(P9[i-1]*10+int(s[i]))%9\\n f3=[0]*3\\n f9=[0]*9\\n f7=[[0]*7 for _ in range(6)]\\n inv7=[1,5,4,6,2,3]\\n for j in range(n):\\n d = ord(s[j]) - ord('0')\\n if d == 0:\\n pass\\n elif d in (1, 2, 5):\\n res += (j + 1)\\n elif d == 4:\\n if j == 0:\\n res += 1\\n else:\\n num = (ord(s[j-1]) - ord('0')) * 10 + d\\n res += (j + 1) if num % 4 == 0 else 1\\n elif d == 8:\\n if j == 0:\\n res += 1\\n elif j == 1:\\n num = (ord(s[0]) - ord('0')) * 10 + 8\\n res += 2 if num % 8 == 0 else 1\\n else:\\n num3 = (ord(s[j-2]) - ord('0')) * 100 + (ord(s[j-1]) - ord('0')) * 10 + 8\\n num2 = (ord(s[j-1]) - ord('0')) * 10 + 8\\n res += ((j - 1) if num3 % 8 == 0 else 0) + (1 if num2 % 8 == 0 else 0) + 1\\n elif d in (3, 6):\\n res += (1 if P3[j] == 0 else 0) + f3[P3[j]]\\n elif d == 7:\\n res += (1 if P7[j] == 0 else 0)\\n for m in range(6):\\n idx = ((j % 6) - m + 6) % 6\\n req = (P7[j] * inv7[m]) % 7\\n res += f7[idx][req]\\n elif d == 9:\\n res += (1 if P9[j] == 0 else 0) + f9[P9[j]]\\n f3[P3[j]] += 1\\n f7[j % 6][P7[j]] += 1\\n f9[P9[j]] += 1\\n return res\"], [22000, 1.4085, \"class Solution:\\n def countSubstrings(self, s: str) -> int:\\n length = len(s)\\n p3, p7, p9 = [], [], []\\n \\n for index, num in enumerate(s):\\n num = int(num)\\n p3.append(num % 3 if index == 0 else ((p3[-1] * 10) + num ) % 3 )\\n p7.append(num % 7 if index == 0 else ((p7[-1] * 10) + num ) % 7 )\\n p9.append(num % 9 if index == 0 else ((p9[-1] * 10) + num ) % 9 )\\n ans = 0\\n inv7 = [1, 5, 4, 6, 2, 3]\\n modFreq7 = [[0 for _ in range(7)] for _ in range(6)]\\n freq3,freq9 = [0 for _ in range(3)] , [0 for _ in range(9)]\\n for index, num in enumerate(s):\\n num = int(num)\\n if num in (1,2,5):\\n ans += (index + 1)\\n elif num in (3 , 6):\\n ans += 1 if p3[index] == 0 else 0\\n ans += freq3[p3[index]]\\n elif num == 9:\\n ans += 1 if p9[index] == 0 else 0\\n ans += freq9[p9[index]]\\n elif num == 4:\\n ans += 1\\n if index > 0:\\n twoDigitNum = int(s[index - 1]) * 10 + num\\n if twoDigitNum % 4 == 0:\\n ans += (index)\\n elif num == 8:\\n ans += 1\\n twoDigitNum = int(s[index - 1]) * 10 + num\\n if index > 0:\\n if twoDigitNum % 8 == 0:\\n ans += 1\\n if index > 1:\\n threeDigitNum = int(s[index - 2]) * 100 + twoDigitNum\\n if threeDigitNum % 8 == 0:\\n ans += (index - 1)\\n elif num == 7:\\n ans += 1 if p7[index] == 0 else 0\\n for m in range(6):\\n idx = ((index % 6) - m + 6) % 6\\n reqRem = (p7[index] *inv7[m]) % 7\\n ans += modFreq7[idx][reqRem]\\n \\n\\n modFreq7[index % 6][p7[index]] += 1\\n freq3[p3[index]] += 1\\n freq9[p9[index]] += 1\\n \\n return ans\"]]",
"runtime": 614,
"runtimeDistribution": "[[0, 1.4085, \"\\n__import__(\\\"atexit\\\").register(lambda: open(\\\"display_runtime.txt\\\", \\\"w\\\").write(\\\"0\\\"))\\nclass Solution:\\n def countSubstrings(self, s: str) -> int:\\n n = len(s)\\n def solve(d):\\n rem_cnt = defaultdict(int)\\n rem_cnt[0] = 1\\n pref_rem = 0\\n res = 0\\n for i, c in enumerate(s):\\n nrc = defaultdict(int)\\n for rem, cnt in rem_cnt.items():\\n nrc[rem*10 % d] += cnt\\n pref_rem = (pref_rem * 10 + int(c)) % d\\n \\n if int(c) == d:\\n res += nrc[pref_rem]\\n \\n rem_cnt = nrc\\n rem_cnt[pref_rem] += 1\\n \\n return res\\n res = 0\\n for d in range(1, 10):\\n res += solve(d)\\n \\n return res\"], [404, 1.4085, \"def megarun(ds):\\n # pre-evaluations\\n tens7 = [(10**j) % 7 for j in range(6)]\\n qjs7 = [[(q,j) for q in range(7) for j in range(6) if q*(10**j) % 7 == r] for r in range(7)]\\n \\n counters3 = [0]*3\\n counters7 = [[0]*6 for _ in range(7)]\\n counters9 = [0]*9\\n \\n indices3 = [[] for _ in range(3)]\\n indices9 = [[] for _ in range(9)]\\n indices7 = [[[] for _ in range(6)] for _ in range(7)]\\n\\n r3, r3next = 0, 0\\n r7, r7next = 0, 0\\n r9, r9next = 0, 0\\n \\n TOTAL = 0\\n \\n DEBUG = False\\n\\n if DEBUG:\\n print(f'megarun {\\\"\\\".join(map(str,ds))}')\\n print()\\n \\n def tailmod(k, i):\\n r = 0\\n m = ds[i]\\n for d in ds[k:i+1]:\\n r = (r * 10 + d) % m\\n return (f' @ {k:2} : {\\\"\\\".join(map(str,ds[k:i+1]))} {\\\"ok\\\" if r == 0 else f\\\"bad {r} mod {m}\\\"}')\\n\\n else:\\n def tailmpd(k, i):\\n pass\\n \\n for i, d in enumerate(ds):\\n r3, r3next = r3next, (r3next * 10 + d) % 3\\n r7, r7next = r7next, (r7next * 10 + d) % 7\\n r9, r9next = r9next, (r9next * 10 + d) % 9\\n \\n counters3[r3] += 1\\n counters7[r7][i%6] += 1\\n counters9[r9] += 1\\n \\n if DEBUG:\\n indices3[r3].append(i)\\n indices7[r7][i%6].append(i)\\n indices9[r9].append(i)\\n \\n if DEBUG: print(f'{i:2} :: {d} -> ', end='')\\n\\n if d == 0:\\n if DEBUG: print(f'skip')\\n elif d == 1 or d == 2 or d == 5:\\n TOTAL += i+1\\n if DEBUG:\\n print(f'all {i+1}')\\n elif d == 4:\\n d1 = ds[i-1]*10 if i>=1 else 0\\n if d1 % d == 0:\\n TOTAL += i+1\\n if DEBUG:\\n print(f'all {i+1}')\\n else:\\n TOTAL += 1\\n if DEBUG:\\n print(f'only 1')\\n elif d == 8:\\n d2 = ds[i-2]*100 if i>=2 else 0\\n d1 = ds[i-1]*10 if i>=1 else 0\\n if (d2+d1) % d == 0 and d1 % d == 0:\\n TOTAL += i+1\\n if DEBUG:\\n print(f'all {i+1}')\\n elif (d2+d1) % d == 0:\\n TOTAL += i\\n if DEBUG:\\n print(f'all-but-one {i}')\\n elif d1 % d == 0:\\n TOTAL += 2\\n if DEBUG:\\n print(f'just 2')\\n print(tailmod(i-2,i))\\n print(tailmod(i-1,i))\\n else:\\n print(f'only 1')\\n TOTAL += 1\\n elif d == 9:\\n TOTAL += counters9[r9]\\n if DEBUG:\\n print(f'c9[{r9}] = {counters9[r9]}')\\n for k in indices9[r9]:\\n print(tailmod(k,i))\\n elif d == 3 or d == 6:\\n TOTAL += counters3[r3]\\n if DEBUG:\\n print(f'c3[{r3}] = {counters3[r3]}')\\n for k in indices3[r3]:\\n print(tailmod(k,i))\\n elif d == 7:\\n qj = [(q,(i-j)%6) for q,j in qjs7[r7]]\\n c7 = sum((counters7[q][j] for q,j in qj))\\n TOTAL += c7\\n if DEBUG:\\n print(f'{c7} = c7{qj} = {[counters7[q][j] for q,j in qj]}')\\n for k in sorted(kk for q,j in qj for kk in indices7[q][j]):\\n print(tailmod(k,i))\\n else:\\n if DEBUG:\\n print('wtf')\\n assert False, (i,d)\\n \\n if DEBUG:\\n print(f'TOTAL = {TOTAL}')\\n\\n return TOTAL\\n\\nclass Solution:\\n def countSubstrings(self, s: str) -> int:\\n return megarun(list(map(int,s)))\"], [450, 1.4085, null], [453, 1.4085, null], [455, 1.4085, null], [458, 1.4085, null], [464, 1.4085, null], [477, 1.4085, null], [482, 1.4085, null], [571, 1.4085, null], [614, 1.4085, null], [615, 1.4085, null], [620, 1.4085, null], [808, 1.4085, null], [812, 1.4085, null], [926, 1.4085, null], [936, 1.4085, null], [1338, 1.4085, null], [1924, 1.4085, null], [2169, 1.4085, null], [3255, 1.4085, null], [3324, 1.4085, null], [3714, 1.4085, null], [3735, 1.4085, null], [3736, 1.4085, null], [4362, 1.4085, null], [4444, 1.4085, null], [4868, 1.4085, null], [5162, 1.4085, null], [5209, 1.4085, null], [5243, 1.4085, null], [5288, 1.4085, null], [5421, 1.4085, null], [5439, 1.4085, null], [5447, 1.4085, null], [5531, 1.4085, null], [5544, 1.4085, null], [5625, 1.4085, null], [5627, 1.4085, null], [5645, 1.4085, null], [5674, 1.4085, null], [5835, 1.4085, null], [6037, 1.4085, null], [6310, 1.4085, null], [6506, 1.4085, null], [6507, 1.4085, null], [6547, 1.4085, null], [7638, 1.4085, null], [8018, 1.4085, null], [8119, 1.4085, null], [8160, 1.4085, null], [8180, 1.4085, null], [8217, 1.4085, null], [8273, 1.4085, null], [8286, 1.4085, null], [8314, 1.4085, null], [8334, 1.4085, null], [8347, 1.4085, null], [8391, 1.4085, null], [8440, 1.4085, null], [8504, 1.4085, null], [8547, 1.4085, null], [9027, 1.4085, null], [9213, 1.4085, null], [9223, 1.4085, null], [9544, 1.4085, \"class Solution:\\n def countSubstrings(self, s: str) -> int:\\n dp = [[1] + [0] * i for i in range(10)]\\n res = 0\\n\\n for ind, i in enumerate(s):\\n if i != \\\"0\\\":\\n if int(i) in {1, 2, 5}:\\n res += ind + 1\\n else:\\n res += dp[int(i)][0]\\n\\n for x in range(1, 10):\\n if x in {1, 2, 5}:\\n continue\\n\\n new_dp = [1] + [0] * x\\n\\n for n in range(x):\\n new_dp[(10 * (n + int(i))) % x] = dp[x][n] + new_dp[(10 * (n + int(i))) % x]\\n\\n dp[x] = new_dp\\n\\n return res\"], [9703, 1.4085, \"class Solution:\\n def countSubstrings(self, s: str) -> int:\\n dp = [[1] + [0] * i for i in range(10)]\\n res = 0\\n\\n for ind, i in enumerate(s):\\n if i != \\\"0\\\":\\n if int(i) in {1, 2, 5}:\\n res += ind + 1\\n else:\\n res += dp[int(i)][0]\\n\\n for x in range(1, 10):\\n if x in {1, 2, 5}:\\n continue\\n\\n new_dp = [1] + [0] * x\\n\\n for n in range(x):\\n new_dp[(10 * (n + int(i))) % x] = dp[x][n] + new_dp[(10 * (n + int(i))) % x]\\n\\n dp[x] = new_dp\\n\\n return res\"]]"
},
"ruby": {
"code": "# @param {String} s\n# @return {Integer}\ndef count_substrings(s)\n n = s.length\n ans = 0\n\n # Frequencies for prefix sums modulo 3, 9\n # freq[k] stores the count of indices i (including 0) such that PrefixSum(i) % mod == k\n # PrefixSum(i) is sum of digits s[0...i]. PrefixSum(0) = 0.\n # A substring s[i..j] is divisible by 3 (or 9) iff PrefixSum(j+1) % mod == PrefixSum(i) % mod.\n freq3 = { 0 => 1 } # Base case: PrefixSum(0) = 0, count is 1 for index i=0.\n cur3 = 0 # Current PrefixSum(j+1) % 3\n \n freq9 = { 0 => 1 } # Base case: PrefixSum(0) = 0\n cur9 = 0 # Current PrefixSum(j+1) % 9\n\n # Frequencies for transformed prefix values modulo 7\n # freq7[q] stores the count of indices i (including 0) such that Q[i] == q\n # Q[k] = (PrefixValue(k) * (10^k)^(-1)) % 7\n # PrefixValue(k) is the numerical value of s[0...k]. PrefixValue(0) = 0.\n # A substring s[i..j] is divisible by 7 iff Q[j+1] == Q[i].\n freq7 = { 0 => 1 } # Base case: Q[0] = (PrefixValue(0) * (10^0)^-1) % 7 = (0 * 1) % 7 = 0\n cur_p7 = 0 # Current PrefixValue(j+1) % 7\n current_power10_mod7 = 1 # Represents 10^k % 7, starts with k=0 for PrefixValue(0)\n\n (0...n).each do |j|\n d = s[j].to_i\n\n # Update prefix sums/values modulo 3, 9, 7 for index j+1\n cur3 = (cur3 + d) % 3\n cur9 = (cur9 + d) % 9\n cur_p7 = (cur_p7 * 10 + d) % 7\n\n # Update power of 10 mod 7 for the current index j+1\n # This is 10^(j+1) % 7\n current_power10_mod7 = (current_power10_mod7 * 10) % 7\n \n # Compute Q[j+1] for mod 7 logic\n # Q[j+1] = (cur_p7 * (current_power10_mod7)^(-1)) % 7\n # Modular inverse using Fermat's Little Theorem: a^(p-2) mod p since 7 is prime.\n # The inverse is a^5 mod 7.\n inv_power10 = current_power10_mod7.pow(5, 7)\n q7 = (cur_p7 * inv_power10) % 7\n\n # Check divisibility based on last digit d\n if d != 0\n if d == 1 || d == 2 || d == 5\n # Any number ending in d is divisible by d.\n # All substrings s[i..j] for 0 <= i <= j count. There are j+1 such substrings.\n ans += (j + 1)\n elsif d == 3 || d == 6\n # Divisible by 3 (and 2 if d=6, which is guaranteed as it ends in 6).\n # Count indices i <= j such that PrefixSum(j+1)%3 == PrefixSum(i)%3.\n ans += freq3.fetch(cur3, 0)\n elsif d == 9\n # Divisible by 9.\n # Count indices i <= j such that PrefixSum(j+1)%9 == PrefixSum(i)%9.\n ans += freq9.fetch(cur9, 0)\n elsif d == 4\n # Divisible by 4 depends on last 1 or 2 digits.\n contrib = 1 # Substring s[j..j] = \"4\" always counts (4 % 4 == 0).\n if j >= 1\n prev_d = s[j-1].to_i\n two_digit = prev_d * 10 + 4\n # If last two digits form a number divisible by 4, all substrings s[i..j] with i < j count.\n # These are substrings of length >= 2 ending at j. There are j such substrings (i from 0 to j-1).\n contrib += j if two_digit % 4 == 0 \n end\n ans += contrib\n elsif d == 8\n # Divisible by 8 depends on last 1, 2 or 3 digits.\n contrib = 1 # Substring s[j..j] = \"8\" always counts (8 % 8 == 0).\n if j >= 1\n prev_d = s[j-1].to_i\n two_digit = prev_d * 10 + 8\n # Substring s[j-1..j] counts if divisible by 8.\n contrib += 1 if two_digit % 8 == 0 \n end\n if j >= 2\n prev2_d = s[j-2].to_i\n prev_d = s[j-1].to_i\n three_digit = prev2_d * 100 + prev_d * 10 + 8\n # If last three digits form a number divisible by 8, all substrings s[i..j] with i <= j-2 count.\n # These are substrings of length >= 3 ending at j. There are j-1 such substrings (i from 0 to j-2).\n contrib += (j - 1) if three_digit % 8 == 0 \n end\n ans += contrib\n elsif d == 7\n # Divisible by 7.\n # Count indices i <= j such that Q[j+1] == Q[i].\n ans += freq7.fetch(q7, 0)\n end\n end\n\n # Update frequency maps. The current properties (cur3, cur9, q7) correspond to index j+1.\n # We store the frequency of properties associated with indices 0 up to j+1.\n freq3[cur3] = freq3.fetch(cur3, 0) + 1\n freq9[cur9] = freq9.fetch(cur9, 0) + 1\n freq7[q7] = freq7.fetch(q7, 0) + 1\n end\n\n ans\nend",
"memory": 21500,
"memoryDistribution": "[[21500, 100.0, \"# @param {String} s\\n# @return {Integer}\\ndef count_substrings(s)\\n n = s.length\\n ans = 0\\n\\n # Frequencies for prefix sums modulo 3, 9\\n # freq[k] stores the count of indices i (including 0) such that PrefixSum(i) % mod == k\\n # PrefixSum(i) is sum of digits s[0...i]. PrefixSum(0) = 0.\\n # A substring s[i..j] is divisible by 3 (or 9) iff PrefixSum(j+1) % mod == PrefixSum(i) % mod.\\n freq3 = { 0 => 1 } # Base case: PrefixSum(0) = 0, count is 1 for index i=0.\\n cur3 = 0 # Current PrefixSum(j+1) % 3\\n \\n freq9 = { 0 => 1 } # Base case: PrefixSum(0) = 0\\n cur9 = 0 # Current PrefixSum(j+1) % 9\\n\\n # Frequencies for transformed prefix values modulo 7\\n # freq7[q] stores the count of indices i (including 0) such that Q[i] == q\\n # Q[k] = (PrefixValue(k) * (10^k)^(-1)) % 7\\n # PrefixValue(k) is the numerical value of s[0...k]. PrefixValue(0) = 0.\\n # A substring s[i..j] is divisible by 7 iff Q[j+1] == Q[i].\\n freq7 = { 0 => 1 } # Base case: Q[0] = (PrefixValue(0) * (10^0)^-1) % 7 = (0 * 1) % 7 = 0\\n cur_p7 = 0 # Current PrefixValue(j+1) % 7\\n current_power10_mod7 = 1 # Represents 10^k % 7, starts with k=0 for PrefixValue(0)\\n\\n (0...n).each do |j|\\n d = s[j].to_i\\n\\n # Update prefix sums/values modulo 3, 9, 7 for index j+1\\n cur3 = (cur3 + d) % 3\\n cur9 = (cur9 + d) % 9\\n cur_p7 = (cur_p7 * 10 + d) % 7\\n\\n # Update power of 10 mod 7 for the current index j+1\\n # This is 10^(j+1) % 7\\n current_power10_mod7 = (current_power10_mod7 * 10) % 7\\n \\n # Compute Q[j+1] for mod 7 logic\\n # Q[j+1] = (cur_p7 * (current_power10_mod7)^(-1)) % 7\\n # Modular inverse using Fermat's Little Theorem: a^(p-2) mod p since 7 is prime.\\n # The inverse is a^5 mod 7.\\n inv_power10 = current_power10_mod7.pow(5, 7)\\n q7 = (cur_p7 * inv_power10) % 7\\n\\n # Check divisibility based on last digit d\\n if d != 0\\n if d == 1 || d == 2 || d == 5\\n # Any number ending in d is divisible by d.\\n # All substrings s[i..j] for 0 <= i <= j count. There are j+1 such substrings.\\n ans += (j + 1)\\n elsif d == 3 || d == 6\\n # Divisible by 3 (and 2 if d=6, which is guaranteed as it ends in 6).\\n # Count indices i <= j such that PrefixSum(j+1)%3 == PrefixSum(i)%3.\\n ans += freq3.fetch(cur3, 0)\\n elsif d == 9\\n # Divisible by 9.\\n # Count indices i <= j such that PrefixSum(j+1)%9 == PrefixSum(i)%9.\\n ans += freq9.fetch(cur9, 0)\\n elsif d == 4\\n # Divisible by 4 depends on last 1 or 2 digits.\\n contrib = 1 # Substring s[j..j] = \\\"4\\\" always counts (4 % 4 == 0).\\n if j >= 1\\n prev_d = s[j-1].to_i\\n two_digit = prev_d * 10 + 4\\n # If last two digits form a number divisible by 4, all substrings s[i..j] with i < j count.\\n # These are substrings of length >= 2 ending at j. There are j such substrings (i from 0 to j-1).\\n contrib += j if two_digit % 4 == 0 \\n end\\n ans += contrib\\n elsif d == 8\\n # Divisible by 8 depends on last 1, 2 or 3 digits.\\n contrib = 1 # Substring s[j..j] = \\\"8\\\" always counts (8 % 8 == 0).\\n if j >= 1\\n prev_d = s[j-1].to_i\\n two_digit = prev_d * 10 + 8\\n # Substring s[j-1..j] counts if divisible by 8.\\n contrib += 1 if two_digit % 8 == 0 \\n end\\n if j >= 2\\n prev2_d = s[j-2].to_i\\n prev_d = s[j-1].to_i\\n three_digit = prev2_d * 100 + prev_d * 10 + 8\\n # If last three digits form a number divisible by 8, all substrings s[i..j] with i <= j-2 count.\\n # These are substrings of length >= 3 ending at j. There are j-1 such substrings (i from 0 to j-2).\\n contrib += (j - 1) if three_digit % 8 == 0 \\n end\\n ans += contrib\\n elsif d == 7\\n # Divisible by 7.\\n # Count indices i <= j such that Q[j+1] == Q[i].\\n ans += freq7.fetch(q7, 0)\\n end\\n end\\n\\n # Update frequency maps. The current properties (cur3, cur9, q7) correspond to index j+1.\\n # We store the frequency of properties associated with indices 0 up to j+1.\\n freq3[cur3] = freq3.fetch(cur3, 0) + 1\\n freq9[cur9] = freq9.fetch(cur9, 0) + 1\\n freq7[q7] = freq7.fetch(q7, 0) + 1\\n end\\n\\n ans\\nend\"], [214700, 100.0, \"# @param {String} s\\n# @return {Integer}\\ndef count_substrings(s)\\n n = s.length\\n ans = 0\\n\\n # Frequencies for prefix sums modulo 3, 9\\n # freq[k] stores the count of indices i (including 0) such that PrefixSum(i) % mod == k\\n # PrefixSum(i) is sum of digits s[0...i]. PrefixSum(0) = 0.\\n # A substring s[i..j] is divisible by 3 (or 9) iff PrefixSum(j+1) % mod == PrefixSum(i) % mod.\\n freq3 = { 0 => 1 } # Base case: PrefixSum(0) = 0, count is 1 for index i=0.\\n cur3 = 0 # Current PrefixSum(j+1) % 3\\n \\n freq9 = { 0 => 1 } # Base case: PrefixSum(0) = 0\\n cur9 = 0 # Current PrefixSum(j+1) % 9\\n\\n # Frequencies for transformed prefix values modulo 7\\n # freq7[q] stores the count of indices i (including 0) such that Q[i] == q\\n # Q[k] = (PrefixValue(k) * (10^k)^(-1)) % 7\\n # PrefixValue(k) is the numerical value of s[0...k]. PrefixValue(0) = 0.\\n # A substring s[i..j] is divisible by 7 iff Q[j+1] == Q[i].\\n freq7 = { 0 => 1 } # Base case: Q[0] = (PrefixValue(0) * (10^0)^-1) % 7 = (0 * 1) % 7 = 0\\n cur_p7 = 0 # Current PrefixValue(j+1) % 7\\n current_power10_mod7 = 1 # Represents 10^k % 7, starts with k=0 for PrefixValue(0)\\n\\n (0...n).each do |j|\\n d = s[j].to_i\\n\\n # Update prefix sums/values modulo 3, 9, 7 for index j+1\\n cur3 = (cur3 + d) % 3\\n cur9 = (cur9 + d) % 9\\n cur_p7 = (cur_p7 * 10 + d) % 7\\n\\n # Update power of 10 mod 7 for the current index j+1\\n # This is 10^(j+1) % 7\\n current_power10_mod7 = (current_power10_mod7 * 10) % 7\\n \\n # Compute Q[j+1] for mod 7 logic\\n # Q[j+1] = (cur_p7 * (current_power10_mod7)^(-1)) % 7\\n # Modular inverse using Fermat's Little Theorem: a^(p-2) mod p since 7 is prime.\\n # The inverse is a^5 mod 7.\\n inv_power10 = current_power10_mod7.pow(5, 7)\\n q7 = (cur_p7 * inv_power10) % 7\\n\\n # Check divisibility based on last digit d\\n if d != 0\\n if d == 1 || d == 2 || d == 5\\n # Any number ending in d is divisible by d.\\n # All substrings s[i..j] for 0 <= i <= j count. There are j+1 such substrings.\\n ans += (j + 1)\\n elsif d == 3 || d == 6\\n # Divisible by 3 (and 2 if d=6, which is guaranteed as it ends in 6).\\n # Count indices i <= j such that PrefixSum(j+1)%3 == PrefixSum(i)%3.\\n ans += freq3.fetch(cur3, 0)\\n elsif d == 9\\n # Divisible by 9.\\n # Count indices i <= j such that PrefixSum(j+1)%9 == PrefixSum(i)%9.\\n ans += freq9.fetch(cur9, 0)\\n elsif d == 4\\n # Divisible by 4 depends on last 1 or 2 digits.\\n contrib = 1 # Substring s[j..j] = \\\"4\\\" always counts (4 % 4 == 0).\\n if j >= 1\\n prev_d = s[j-1].to_i\\n two_digit = prev_d * 10 + 4\\n # If last two digits form a number divisible by 4, all substrings s[i..j] with i < j count.\\n # These are substrings of length >= 2 ending at j. There are j such substrings (i from 0 to j-1).\\n contrib += j if two_digit % 4 == 0 \\n end\\n ans += contrib\\n elsif d == 8\\n # Divisible by 8 depends on last 1, 2 or 3 digits.\\n contrib = 1 # Substring s[j..j] = \\\"8\\\" always counts (8 % 8 == 0).\\n if j >= 1\\n prev_d = s[j-1].to_i\\n two_digit = prev_d * 10 + 8\\n # Substring s[j-1..j] counts if divisible by 8.\\n contrib += 1 if two_digit % 8 == 0 \\n end\\n if j >= 2\\n prev2_d = s[j-2].to_i\\n prev_d = s[j-1].to_i\\n three_digit = prev2_d * 100 + prev_d * 10 + 8\\n # If last three digits form a number divisible by 8, all substrings s[i..j] with i <= j-2 count.\\n # These are substrings of length >= 3 ending at j. There are j-1 such substrings (i from 0 to j-2).\\n contrib += (j - 1) if three_digit % 8 == 0 \\n end\\n ans += contrib\\n elsif d == 7\\n # Divisible by 7.\\n # Count indices i <= j such that Q[j+1] == Q[i].\\n ans += freq7.fetch(q7, 0)\\n end\\n end\\n\\n # Update frequency maps. The current properties (cur3, cur9, q7) correspond to index j+1.\\n # We store the frequency of properties associated with indices 0 up to j+1.\\n freq3[cur3] = freq3.fetch(cur3, 0) + 1\\n freq9[cur9] = freq9.fetch(cur9, 0) + 1\\n freq7[q7] = freq7.fetch(q7, 0) + 1\\n end\\n\\n ans\\nend\"]]",
"runtime": 573,
"runtimeDistribution": "[[573, 100.0, \"# @param {String} s\\n# @return {Integer}\\ndef count_substrings(s)\\n n = s.length\\n ans = 0\\n\\n # Frequencies for prefix sums modulo 3, 9\\n # freq[k] stores the count of indices i (including 0) such that PrefixSum(i) % mod == k\\n # PrefixSum(i) is sum of digits s[0...i]. PrefixSum(0) = 0.\\n # A substring s[i..j] is divisible by 3 (or 9) iff PrefixSum(j+1) % mod == PrefixSum(i) % mod.\\n freq3 = { 0 => 1 } # Base case: PrefixSum(0) = 0, count is 1 for index i=0.\\n cur3 = 0 # Current PrefixSum(j+1) % 3\\n \\n freq9 = { 0 => 1 } # Base case: PrefixSum(0) = 0\\n cur9 = 0 # Current PrefixSum(j+1) % 9\\n\\n # Frequencies for transformed prefix values modulo 7\\n # freq7[q] stores the count of indices i (including 0) such that Q[i] == q\\n # Q[k] = (PrefixValue(k) * (10^k)^(-1)) % 7\\n # PrefixValue(k) is the numerical value of s[0...k]. PrefixValue(0) = 0.\\n # A substring s[i..j] is divisible by 7 iff Q[j+1] == Q[i].\\n freq7 = { 0 => 1 } # Base case: Q[0] = (PrefixValue(0) * (10^0)^-1) % 7 = (0 * 1) % 7 = 0\\n cur_p7 = 0 # Current PrefixValue(j+1) % 7\\n current_power10_mod7 = 1 # Represents 10^k % 7, starts with k=0 for PrefixValue(0)\\n\\n (0...n).each do |j|\\n d = s[j].to_i\\n\\n # Update prefix sums/values modulo 3, 9, 7 for index j+1\\n cur3 = (cur3 + d) % 3\\n cur9 = (cur9 + d) % 9\\n cur_p7 = (cur_p7 * 10 + d) % 7\\n\\n # Update power of 10 mod 7 for the current index j+1\\n # This is 10^(j+1) % 7\\n current_power10_mod7 = (current_power10_mod7 * 10) % 7\\n \\n # Compute Q[j+1] for mod 7 logic\\n # Q[j+1] = (cur_p7 * (current_power10_mod7)^(-1)) % 7\\n # Modular inverse using Fermat's Little Theorem: a^(p-2) mod p since 7 is prime.\\n # The inverse is a^5 mod 7.\\n inv_power10 = current_power10_mod7.pow(5, 7)\\n q7 = (cur_p7 * inv_power10) % 7\\n\\n # Check divisibility based on last digit d\\n if d != 0\\n if d == 1 || d == 2 || d == 5\\n # Any number ending in d is divisible by d.\\n # All substrings s[i..j] for 0 <= i <= j count. There are j+1 such substrings.\\n ans += (j + 1)\\n elsif d == 3 || d == 6\\n # Divisible by 3 (and 2 if d=6, which is guaranteed as it ends in 6).\\n # Count indices i <= j such that PrefixSum(j+1)%3 == PrefixSum(i)%3.\\n ans += freq3.fetch(cur3, 0)\\n elsif d == 9\\n # Divisible by 9.\\n # Count indices i <= j such that PrefixSum(j+1)%9 == PrefixSum(i)%9.\\n ans += freq9.fetch(cur9, 0)\\n elsif d == 4\\n # Divisible by 4 depends on last 1 or 2 digits.\\n contrib = 1 # Substring s[j..j] = \\\"4\\\" always counts (4 % 4 == 0).\\n if j >= 1\\n prev_d = s[j-1].to_i\\n two_digit = prev_d * 10 + 4\\n # If last two digits form a number divisible by 4, all substrings s[i..j] with i < j count.\\n # These are substrings of length >= 2 ending at j. There are j such substrings (i from 0 to j-1).\\n contrib += j if two_digit % 4 == 0 \\n end\\n ans += contrib\\n elsif d == 8\\n # Divisible by 8 depends on last 1, 2 or 3 digits.\\n contrib = 1 # Substring s[j..j] = \\\"8\\\" always counts (8 % 8 == 0).\\n if j >= 1\\n prev_d = s[j-1].to_i\\n two_digit = prev_d * 10 + 8\\n # Substring s[j-1..j] counts if divisible by 8.\\n contrib += 1 if two_digit % 8 == 0 \\n end\\n if j >= 2\\n prev2_d = s[j-2].to_i\\n prev_d = s[j-1].to_i\\n three_digit = prev2_d * 100 + prev_d * 10 + 8\\n # If last three digits form a number divisible by 8, all substrings s[i..j] with i <= j-2 count.\\n # These are substrings of length >= 3 ending at j. There are j-1 such substrings (i from 0 to j-2).\\n contrib += (j - 1) if three_digit % 8 == 0 \\n end\\n ans += contrib\\n elsif d == 7\\n # Divisible by 7.\\n # Count indices i <= j such that Q[j+1] == Q[i].\\n ans += freq7.fetch(q7, 0)\\n end\\n end\\n\\n # Update frequency maps. The current properties (cur3, cur9, q7) correspond to index j+1.\\n # We store the frequency of properties associated with indices 0 up to j+1.\\n freq3[cur3] = freq3.fetch(cur3, 0) + 1\\n freq9[cur9] = freq9.fetch(cur9, 0) + 1\\n freq7[q7] = freq7.fetch(q7, 0) + 1\\n end\\n\\n ans\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list:
import random
random.seed(seed)
# Sample solution based on the provided implementation.
def sample_solution(s: str) -> int:
n = len(s)
ans = 0
freq3 = {0: 1}
p3 = 0
freq9 = {0: 1}
p9 = 0
freq7 = {0: 1}
p7 = 0
power7 = 1
for j in range(n):
d = ord(s[j]) - 48
p3 = (p3 + d) % 3
p9 = (p9 + d) % 9
p7 = (p7 * 10 + d) % 7
power7 = (power7 * 10) % 7
inv_power7 = pow(power7, -1, 7)
q7 = (p7 * inv_power7) % 7
ch = s[j]
if ch == '0':
pass
elif ch in "125":
ans += (j + 1)
elif ch in "36":
ans += freq3.get(p3, 0)
elif ch == '9':
ans += freq9.get(p9, 0)
elif ch == '4':
if j == 0:
ans += 1
else:
two = ((ord(s[j - 1]) - 48) * 10 + 4)
if two % 4 == 0:
ans += 1 + j
else:
ans += 1
elif ch == '8':
if j == 0:
ans += 1
elif j == 1:
two = ((ord(s[j - 1]) - 48) * 10 + 8)
if two % 8 == 0:
ans += 2
else:
ans += 1
else:
two = ((ord(s[j - 1]) - 48) * 10 + 8)
three = ((ord(s[j - 2]) - 48) * 100 + (ord(s[j - 1]) - 48) * 10 + 8)
tmp = 1
if two % 8 == 0:
tmp += 1
if three % 8 == 0:
tmp += (j - 1)
ans += tmp
elif ch == '7':
ans += freq7.get(q7, 0)
freq3[p3] = freq3.get(p3, 0) + 1
freq9[p9] = freq9.get(p9, 0) + 1
freq7[q7] = freq7.get(q7, 0) + 1
return ans
test_cases = []
fixed_cases = [
"12936",
"5701283",
"1010101010",
"1",
"0",
"11111",
"99999",
"404",
"248",
"0128"
]
for s in fixed_cases:
expected = str(sample_solution(s))
test_cases.append({"input": s, "output": expected})
while len(test_cases) < num_cases:
length = random.randint(1, 20)
s = ''.join(random.choice("0123456789") for _ in range(length))
expected = str(sample_solution(s))
test_cases.append({"input": s, "output": expected})
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
# Use the same deserialization: strip whitespace and treat outputs as integers.
try:
expected = int(expected_output.strip())
result = int(program_output.strip())
return expected == result
except Exception:
return expected_output.strip() == program_output.strip()
|
[{"input": "12936", "output": "11"}, {"input": "5701283", "output": "18"}, {"input": "1010101010", "output": "25"}, {"input": "1", "output": "1"}, {"input": "0", "output": "0"}, {"input": "11111", "output": "15"}, {"input": "99999", "output": "15"}, {"input": "404", "output": "4"}, {"input": "248", "output": "6"}, {"input": "0128", "output": "8"}, {"input": "0433", "output": "5"}, {"input": "18196", "output": "10"}, {"input": "01", "output": "2"}, {"input": "3890838", "output": "7"}, {"input": "37940265423511", "output": "75"}, {"input": "1559407816184", "output": "48"}, {"input": "59310341316475255341", "output": "140"}, {"input": "28327648350305641395", "output": "124"}, {"input": "7672423", "output": "22"}, {"input": "849696532871012269", "output": "106"}, {"input": "669", "output": "4"}, {"input": "848018451462704", "output": "69"}, {"input": "28148932528809570", "output": "85"}, {"input": "5430", "output": "4"}, {"input": "91171822", "output": "28"}, {"input": "8248963834657871", "output": "63"}, {"input": "31509839", "output": "12"}, {"input": "01031051", "output": "24"}, {"input": "34738299737631165", "output": "82"}, {"input": "67010651333872", "output": "55"}, {"input": "24731781080132", "output": "55"}, {"input": "77360260647468", "output": "37"}, {"input": "2343098050097882", "output": "41"}, {"input": "81", "output": "3"}, {"input": "191361", "output": "14"}, {"input": "3990916998543534624", "output": "103"}, {"input": "510799118384251", "output": "82"}, {"input": "54278498", "output": "16"}, {"input": "8", "output": "1"}, {"input": "1241182449", "output": "43"}, {"input": "5348740", "output": "8"}, {"input": "640", "output": "3"}, {"input": "5", "output": "1"}, {"input": "42786", "output": "9"}, {"input": "011280598262045053", "output": "99"}, {"input": "15869232", "output": "22"}, {"input": "602563", "output": "11"}, {"input": "216073375", "output": "20"}, {"input": "3303654145", "output": "38"}, {"input": "68501429401965569", "output": "73"}, {"input": "16934060883561595", "output": "96"}, {"input": "4846", "output": "8"}, {"input": "64823662994", "output": "30"}, {"input": "8044369957773", "output": "38"}, {"input": "72148951343320037", "output": "60"}, {"input": "17693676320163287083", "output": "88"}, {"input": "7278", "output": "5"}, {"input": "957986872774348734", "output": "40"}, {"input": "143455812236231", "output": "84"}, {"input": "65876036690967", "output": "40"}, {"input": "5", "output": "1"}, {"input": "6688937346", "output": "19"}, {"input": "0656272980699016", "output": "51"}, {"input": "72046", "output": "9"}, {"input": "37556464170", "output": "40"}, {"input": "053100330923271937", "output": "81"}, {"input": "529912419", "output": "33"}, {"input": "4", "output": "1"}, {"input": "6631931491905865185", "output": "106"}, {"input": "6", "output": "1"}, {"input": "1657262849877694", "output": "47"}, {"input": "31473799650", "output": "27"}, {"input": "5273545494808313", "output": "67"}, {"input": "78377701436349", "output": "31"}, {"input": "788568557444", "output": "57"}, {"input": "13518233", "output": "19"}, {"input": "4989413435240824", "output": "95"}, {"input": "08", "output": "2"}, {"input": "2710947775", "output": "24"}, {"input": "047116", "output": "14"}, {"input": "1902294131869993", "output": "70"}, {"input": "67749649909133412", "output": "76"}, {"input": "28120679", "output": "14"}, {"input": "4034471349361832", "output": "67"}, {"input": "210249947", "output": "20"}, {"input": "7464", "output": "7"}, {"input": "87719065940139904", "output": "60"}, {"input": "0278742967175655125", "output": "137"}, {"input": "74680715451680", "output": "59"}, {"input": "760385977034824771", "output": "79"}, {"input": "9", "output": "1"}, {"input": "24808613", "output": "23"}, {"input": "7127", "output": "7"}, {"input": "8467737826", "output": "23"}, {"input": "9821465", "output": "20"}, {"input": "40449972787558867", "output": "62"}, {"input": "33963605766", "output": "48"}, {"input": "70289", "output": "6"}, {"input": "17187026217", "output": "40"}, {"input": "596158657", "output": "25"}]
|
{
"cpp": "==Code Submission==\n\nstring deserialize_stdin() {\n string input;\n getline(cin, input);\n return input;\n}\n\nstring serialize_stdout(long long result) {\n return to_string(result);\n}\n\nint main() {\n string s = deserialize_stdin();\n Solution sol; // Submitted solution will be injected here.\n long long ans = sol.countSubstrings(s);\n cout << serialize_stdout(ans);\n return 0;\n}",
"golang": "==Code Submission==\n\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n line, _ := reader.ReadString('\\n')\n s := strings.TrimSpace(line)\n ans := countSubstrings(s) // Submitted solution will be injected here.\n fmt.Printf(\"%d\", ans)\n}",
"java": "public class Main {\n private static String deserializeStdin() throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n return br.readLine().trim();\n }\n \n private static String serializeStdout(long result) {\n return Long.toString(result);\n }\n \n public static void main(String[] args) throws Exception {\n String s = deserializeStdin();\n Solution sol = new Solution(); // Submitted solution will be injected here.\n long ans = sol.countSubstrings(s);\n System.out.println(serializeStdout(ans));\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\n\nconst deserialize_stdin = (input) => {\n return input.trim();\n};\n\nconst serialize_stdout = (result) => {\n return result.toString();\n};\n\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\nlet input = '';\nprocess.stdin.on('data', chunk => input += chunk);\nprocess.stdin.on('end', () => {\n const s = deserialize_stdin(input);\n const ans = countSubstrings(s); // Submitted solution will be injected here.\n process.stdout.write(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str):\n return input_str.strip()\n\ndef serialize_stdout(result):\n return str(result)\n\ndata = sys.stdin.read()\ns = deserialize_stdin(data)\nsol = Solution() # Submitted solution will be injected here.\nans = sol.countSubstrings(s)\nsys.stdout.write(serialize_stdout(ans))",
"ruby": "==Code Submission==\n\ns = gets.strip\nans = count_substrings(s) # Submitted solution will be injected here.\nputs ans.to_s"
}
|
3702
|
Maximum Subarray With Equal Products
|
maximum-subarray-with-equal-products
|
<p>You are given an array of <strong>positive</strong> integers <code>nums</code>.</p>
<p>An array <code>arr</code> is called <strong>product equivalent</strong> if <code>prod(arr) == lcm(arr) * gcd(arr)</code>, where:</p>
<ul>
<li><code>prod(arr)</code> is the product of all elements of <code>arr</code>.</li>
<li><code>gcd(arr)</code> is the <span data-keyword="gcd-function">GCD</span> of all elements of <code>arr</code>.</li>
<li><code>lcm(arr)</code> is the <span data-keyword="lcm-function">LCM</span> of all elements of <code>arr</code>.</li>
</ul>
<p>Return the length of the <strong>longest</strong> <strong>product equivalent</strong> <span data-keyword="subarray-nonempty">subarray</span> of <code>nums</code>.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">nums = [1,2,1,2,1,1,1]</span></p>
<p><strong>Output:</strong> <span class="example-io">5</span></p>
<p><strong>Explanation:</strong> </p>
<p>The longest product equivalent subarray is <code>[1, 2, 1, 1, 1]</code>, where <code>prod([1, 2, 1, 1, 1]) = 2</code>, <code>gcd([1, 2, 1, 1, 1]) = 1</code>, and <code>lcm([1, 2, 1, 1, 1]) = 2</code>.</p>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">nums = [2,3,4,5,6]</span></p>
<p><strong>Output:</strong> <span class="example-io">3</span></p>
<p><strong>Explanation:</strong> </p>
<p>The longest product equivalent subarray is <code>[3, 4, 5].</code></p>
</div>
<p><strong class="example">Example 3:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">nums = [1,2,3,1,4,5,1]</span></p>
<p><strong>Output:</strong> <span class="example-io">5</span></p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>2 <= nums.length <= 100</code></li>
<li><code>1 <= nums[i] <= 10</code></li>
</ul>
|
You are given an array of **positive** integers `nums`.
An array `arr` is called **product equivalent** if `prod(arr) == lcm(arr) * gcd(arr)`, where:
- `prod(arr)` is the product of all elements of `arr`.
- `gcd(arr)` is the GCD of all elements of `arr`.
- `lcm(arr)` is the LCM of all elements of `arr`.
Return the length of the **longest** **product equivalent** subarray of `nums`.
**Example 1:**
**Input:** nums \= \[1,2,1,2,1,1,1]
**Output:** 5
**Explanation:**
The longest product equivalent subarray is `[1, 2, 1, 1, 1]`, where `prod([1, 2, 1, 1, 1]) = 2`, `gcd([1, 2, 1, 1, 1]) = 1`, and `lcm([1, 2, 1, 1, 1]) = 2`.
**Example 2:**
**Input:** nums \= \[2,3,4,5,6]
**Output:** 3
**Explanation:**
The longest product equivalent subarray is `[3, 4, 5].`
**Example 3:**
**Input:** nums \= \[1,2,3,1,4,5,1]
**Output:** 5
**Constraints:**
- `2 <= nums.length <= 100`
- `1 <= nums[i] <= 10`
|
Easy
|
[
"array",
"math",
"sliding-window",
"enumeration",
"number-theory"
] |
leetcode
|
https://leetcode.com/problems/maximum-subarray-with-equal-products
|
functional
| null | null | null | null |
{
"c": "int maxLength(int* nums, int numsSize) {\n \n}",
"cpp": "class Solution {\npublic:\n int maxLength(vector<int>& nums) {\n \n }\n};",
"csharp": "public class Solution {\n public int MaxLength(int[] nums) {\n \n }\n}",
"dart": "class Solution {\n int maxLength(List<int> nums) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec max_length(nums :: [integer]) :: integer\n def max_length(nums) do\n \n end\nend",
"erlang": "-spec max_length(Nums :: [integer()]) -> integer().\nmax_length(Nums) ->\n .",
"golang": "func maxLength(nums []int) int {\n \n}",
"java": "class Solution {\n public int maxLength(int[] nums) {\n \n }\n}",
"javascript": "/**\n * @param {number[]} nums\n * @return {number}\n */\nvar maxLength = function(nums) {\n \n};",
"kotlin": "class Solution {\n fun maxLength(nums: IntArray): Int {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param Integer[] $nums\n * @return Integer\n */\n function maxLength($nums) {\n \n }\n}",
"python": "class Solution(object):\n def maxLength(self, nums):\n \"\"\"\n :type nums: List[int]\n :rtype: int\n \"\"\"\n ",
"python3": "class Solution:\n def maxLength(self, nums: List[int]) -> int:\n ",
"racket": "(define/contract (max-length nums)\n (-> (listof exact-integer?) exact-integer?)\n )",
"ruby": "# @param {Integer[]} nums\n# @return {Integer}\ndef max_length(nums)\n \nend",
"rust": "impl Solution {\n pub fn max_length(nums: Vec<i32>) -> i32 {\n \n }\n}",
"scala": "object Solution {\n def maxLength(nums: Array[Int]): Int = {\n \n }\n}",
"swift": "class Solution {\n func maxLength(_ nums: [Int]) -> Int {\n \n }\n}",
"typescript": "function maxLength(nums: number[]): number {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n int maxLength(vector<int>& nums) {\n int n = nums.size(), ans = 0;\n auto gcdFun = [&](int a, int b) {\n while(b) { int t = a % b; a = b; b = t; }\n return a;\n };\n vector<vector<int>> pe(11, vector<int>(4,0));\n for(int i=1;i<=10;i++){\n int t = i, cnt = 0;\n while(t % 2 == 0 && t){ cnt++; t /= 2; }\n pe[i][0] = cnt;\n cnt = 0; t = i;\n while(t % 3 == 0 && t){ cnt++; t /= 3; }\n pe[i][1] = cnt;\n cnt = 0; t = i;\n while(t % 5 == 0 && t){ cnt++; t /= 5; }\n pe[i][2] = cnt;\n cnt = 0; t = i;\n while(t % 7 == 0 && t){ cnt++; t /= 7; }\n pe[i][3] = cnt;\n }\n for (int i = 0; i < n; i++){\n int curG = nums[i];\n if(nums[i] == 1) ans = max(ans, 1);\n vector<int> cntP(4,0);\n for(int p = 0; p < 4; p++){\n if(pe[nums[i]][p] > 0) cntP[p] = 1;\n }\n for (int j = i + 1; j < n; j++){\n curG = gcdFun(curG, nums[j]);\n for (int p = 0; p < 4; p++){\n if(pe[nums[j]][p] > 0) cntP[p]++;\n }\n int len = j - i + 1;\n bool valid = false;\n if(len == 2)\n valid = true;\n else if(len == 1)\n valid = (nums[i] == 1);\n else {\n if(curG != 1)\n valid = false;\n else {\n valid = true;\n for (int p = 0; p < 4; p++){\n if(cntP[p] > 1) { valid = false; break; }\n }\n }\n }\n if(valid) ans = max(ans, len);\n }\n }\n return ans;\n }\n};",
"memory": 2900,
"memoryDistribution": "[[2900, 6.4726, \"class Solution {\\npublic:\\n int maxLength(vector<int>& nums) {\\n int n = nums.size(), ans = 0;\\n auto gcdFun = [&](int a, int b) {\\n while(b) { int t = a % b; a = b; b = t; }\\n return a;\\n };\\n vector<vector<int>> pe(11, vector<int>(4,0));\\n for(int i=1;i<=10;i++){\\n int t = i, cnt = 0;\\n while(t % 2 == 0 && t){ cnt++; t /= 2; }\\n pe[i][0] = cnt;\\n cnt = 0; t = i;\\n while(t % 3 == 0 && t){ cnt++; t /= 3; }\\n pe[i][1] = cnt;\\n cnt = 0; t = i;\\n while(t % 5 == 0 && t){ cnt++; t /= 5; }\\n pe[i][2] = cnt;\\n cnt = 0; t = i;\\n while(t % 7 == 0 && t){ cnt++; t /= 7; }\\n pe[i][3] = cnt;\\n }\\n for (int i = 0; i < n; i++){\\n int curG = nums[i];\\n if(nums[i] == 1) ans = max(ans, 1);\\n vector<int> cntP(4,0);\\n for(int p = 0; p < 4; p++){\\n if(pe[nums[i]][p] > 0) cntP[p] = 1;\\n }\\n for (int j = i + 1; j < n; j++){\\n curG = gcdFun(curG, nums[j]);\\n for (int p = 0; p < 4; p++){\\n if(pe[nums[j]][p] > 0) cntP[p]++;\\n }\\n int len = j - i + 1;\\n bool valid = false;\\n if(len == 2)\\n valid = true;\\n else if(len == 1)\\n valid = (nums[i] == 1);\\n else {\\n if(curG != 1)\\n valid = false;\\n else {\\n valid = true;\\n for (int p = 0; p < 4; p++){\\n if(cntP[p] > 1) { valid = false; break; }\\n }\\n }\\n }\\n if(valid) ans = max(ans, len);\\n }\\n }\\n return ans;\\n }\\n};\"], [27800, 2.2654, \"class Solution {\\npublic:\\n int maxLength(vector<int>& nums) {\\n int n = nums.size();\\n int maxLen = 0;\\n // iterate over all possible subarrays\\n for (int i = 0; i < n; ++i) \\n {\\n int currentGCD = nums[i];\\n int currentLCM = nums[i];\\n \\n // we store reciprocal product to prevent overflow\\n double reciprocal = 1.0/nums[i];\\n \\n for (int j = i; j < n; ++j) \\n {\\n if (j > i) \\n {\\n currentGCD = gcd(currentGCD, nums[j]);\\n currentLCM = lcm(currentLCM,nums[j]); \\n reciprocal /= nums[j];\\n }\\n // due to decimal precision issues we just check if its accurate enough\\n if (currentGCD * currentLCM * reciprocal>0.99999999) \\n maxLen = max(maxLen, j - i + 1);\\n \\n }\\n }\\n return maxLen;\\n }\\n};\"], [27900, 13.5922, \"class Solution {\\npublic:\\n long long lcm(int a, int b) {\\n return (1LL * a / __gcd(a, b)) * b;\\n }\\n\\n int maxLength(vector<int>& nums) {\\n int n = nums.size();\\n int maxLen = 0;\\n for(int i = 0 ; i < n; i++){\\n long long prod = 1, gcdVal = nums[i], lcmVal = nums[i];\\n for(int j = i ; j < n; j++){\\n prod = prod*(long long)nums[j];\\n if(prod > 1e9) break;\\n gcdVal = gcd(gcdVal, (long long)nums[j]);\\n lcmVal = lcm(lcmVal, (long long)nums[j]);\\n if(prod == gcdVal * lcmVal){\\n maxLen = max(maxLen, j - i + 1);\\n }\\n }\\n }\\n return maxLen;\\n }\\n};\\n\"], [28000, 27.8317, null], [28100, 37.2168, null], [28200, 8.4142, null], [28300, 0.9709, null], [28400, 0.9709, null], [28600, 0.6472, null], [28700, 0.9709, \"class Solution {\\npublic:\\n vector<int> prime_divisors(int x) {\\n vector<int> primes;\\n for (int d = 2; d * d <= x; ++d) {\\n if (x % d == 0) {\\n primes.push_back(d);\\n while (x % d == 0) x /= d; \\n }\\n }\\n if (x > 1) primes.push_back(x); \\n return primes;\\n }\\n int maxLength(vector<int>& nums) {\\n int n=nums.size();\\n int ans=2,i=0;\\n unordered_map<int,int> last;\\n for (int j = 0; j < n; ++j) {\\n vector<int> primes = prime_divisors(nums[j]);\\n for (int p : primes) {\\n i = max(i, last.count(p) ? last[p] + 1 : 0);\\n last[p] = j;\\n }\\n ans = max(ans, j - i + 1);\\n }\\n return ans;\\n }\\n};\"], [28800, 0.6472, \"class Solution {\\npublic:\\n vector<int> prime_divisors(int x) {\\n vector<int> primes;\\n for (int d = 2; d * d <= x; ++d) {\\n if (x % d == 0) {\\n primes.push_back(d);\\n while (x % d == 0) x /= d; \\n }\\n }\\n if (x > 1) primes.push_back(x); \\n return primes;\\n }\\n int maxLength(vector<int>& nums) {\\n int n=nums.size();\\n int ans=2,i=0;\\n unordered_map<int,int> last;\\n for (int j = 0; j < n; ++j) {\\n vector<int> primes = prime_divisors(nums[j]);\\n for (int p : primes) {\\n i = max(i, last.count(p) ? last[p] + 1 : 0);\\n last[p] = j;\\n }\\n ans = max(ans, j - i + 1);\\n }\\n return ans;\\n }\\n};\"]]",
"runtime": 3,
"runtimeDistribution": "[[0, 40.4531, \"class Solution {\\npublic:\\nint gcd(int a, int b){\\n if(b==0) return a;\\n return gcd(b,a%b);\\n}\\n int maxLength(vector<int>& nums) {\\n int n = nums.size(), maxlen = 0;\\n\\n for(int i = 0; i < n; ++i){\\n int prod = 1, hcf = nums[i], lcm = nums[i];\\n\\n for(int j = i; j < n; ++j){\\n prod = (int)(((long long)prod * nums[j]) % (1000000007));\\n hcf = gcd(hcf, nums[j]);\\n lcm = (lcm / gcd(lcm, nums[j])) * nums[j];\\n\\n if(prod == hcf * lcm){\\n maxlen = max(maxlen, j - i + 1);\\n }\\n }\\n }\\n\\n return maxlen;\\n }\\n};\"], [1, 7.1197, \"class Solution {\\npublic:\\n int maxLength(vector<int>& nums) {\\n int n = (int)nums.size(), b = 0, ans = 2;\\n int p[4] = {2, 3, 5, 7};\\n vector<int> C(4, 0);\\n for(int i = 0; i < n; i++)\\n {\\n for(int j = 0; j < 4; j++)\\n if(nums[i] % p[j] == 0) C[j]++;\\n while(1)\\n {\\n bool flag = false;\\n for(int j = 0; j < 4; j++) flag |= C[j] > 1;\\n if(!flag) break;\\n for(int j = 0; j < 4; j++)\\n if(nums[b] % p[j] == 0) C[j]--;\\n b++;\\n }\\n ans = max(ans, i - b + 1);\\n }\\n return ans;\\n }\\n};\"], [2, 4.2071, null], [3, 16.8285, null], [4, 10.356, null], [5, 0.9709, null], [6, 1.2945, null], [7, 3.2362, null], [8, 1.9417, null], [10, 0.3236, null], [11, 1.2945, null], [12, 0.6472, null], [16, 0.3236, null], [17, 0.3236, null], [19, 0.3236, null], [23, 0.3236, null], [39, 0.3236, null], [57, 0.3236, null], [59, 0.6472, null], [62, 0.3236, null], [63, 0.3236, null], [75, 0.3236, null], [77, 0.3236, null], [79, 0.6472, null], [84, 0.3236, null], [89, 0.3236, \"class Solution {\\npublic:\\n int maxLength(vector<int>& nums) {\\n for (int n = nums.size(), s = n; s > 0; s--) {\\n for (int i = 0; i + s <= n; i++) {\\n unsigned long long p = 1;\\n int l = nums[i], g = nums[i];\\n for (int j = i; j < i + s; j++) {\\n p *= nums[j];\\n l = lcm(l, nums[j]);\\n g = gcd(g, nums[j]); \\n }\\n if (p == l * g) return s;\\n }\\n }\\n return 0;\\n }\\n};\"], [96, 0.3236, \"class Solution {\\npublic:\\n int maxLength(vector<int>& nums) {\\n long long m=0;\\n for(int i=0;i<nums.size()-1;i++){\\n long long prod=nums[i],g=nums[i],l=nums[i],count=0;\\n for(int j=i+1;j<nums.size();j++){\\n prod*=nums[j];\\n g=gcd(g,nums[j]);\\n l=lcm(l,nums[j]);\\n if(prod>(g*l)){\\n break;\\n }\\n if(prod==(g*l)){\\n count++;\\n }\\n m=max(m,count);\\n cout << g << l << prod << endl;\\n }\\n }\\n return m+1;\\n }\\n};\"]]"
},
"golang": {
"code": "func maxLength(nums []int) int {\n\tn := len(nums)\n\tmaxLen := 0\n\tprimes := []int{2, 3, 5, 7}\n\tfor i := 0; i < n; i++ {\n\t\tfor j := i; j < n; j++ {\n\t\t\tlength := j - i + 1\n\t\t\tif length == 1 {\n\t\t\t\tif nums[i] == 1 && length > maxLen {\n\t\t\t\t\tmaxLen = length\n\t\t\t\t}\n\t\t\t\tcontinue\n\t\t\t}\n\t\t\tif length == 2 {\n\t\t\t\tif length > maxLen {\n\t\t\t\t\tmaxLen = length\n\t\t\t\t}\n\t\t\t\tcontinue\n\t\t\t}\n\t\t\tvalid := true\n\t\t\tfor _, p := range primes {\n\t\t\t\tcount := 0\n\t\t\t\tfor k := i; k <= j; k++ {\n\t\t\t\t\tif nums[k]%p == 0 {\n\t\t\t\t\t\tcount++\n\t\t\t\t\t\tif count >= 2 {\n\t\t\t\t\t\t\tvalid = false\n\t\t\t\t\t\t\tbreak\n\t\t\t\t\t\t}\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t\tif !valid {\n\t\t\t\t\tbreak\n\t\t\t\t}\n\t\t\t}\n\t\t\tif valid && length > maxLen {\n\t\t\t\tmaxLen = length\n\t\t\t}\n\t\t}\n\t}\n\treturn maxLen\n}",
"memory": 400,
"memoryDistribution": "[[400, 64.0, \"func maxLength(nums []int) int {\\n\\tn := len(nums)\\n\\tmaxLen := 0\\n\\tprimes := []int{2, 3, 5, 7}\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tfor j := i; j < n; j++ {\\n\\t\\t\\tlength := j - i + 1\\n\\t\\t\\tif length == 1 {\\n\\t\\t\\t\\tif nums[i] == 1 && length > maxLen {\\n\\t\\t\\t\\t\\tmaxLen = length\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\tcontinue\\n\\t\\t\\t}\\n\\t\\t\\tif length == 2 {\\n\\t\\t\\t\\tif length > maxLen {\\n\\t\\t\\t\\t\\tmaxLen = length\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\tcontinue\\n\\t\\t\\t}\\n\\t\\t\\tvalid := true\\n\\t\\t\\tfor _, p := range primes {\\n\\t\\t\\t\\tcount := 0\\n\\t\\t\\t\\tfor k := i; k <= j; k++ {\\n\\t\\t\\t\\t\\tif nums[k]%p == 0 {\\n\\t\\t\\t\\t\\t\\tcount++\\n\\t\\t\\t\\t\\t\\tif count >= 2 {\\n\\t\\t\\t\\t\\t\\t\\tvalid = false\\n\\t\\t\\t\\t\\t\\t\\tbreak\\n\\t\\t\\t\\t\\t\\t}\\n\\t\\t\\t\\t\\t}\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\tif !valid {\\n\\t\\t\\t\\t\\tbreak\\n\\t\\t\\t\\t}\\n\\t\\t\\t}\\n\\t\\t\\tif valid && length > maxLen {\\n\\t\\t\\t\\tmaxLen = length\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\treturn maxLen\\n}\"], [4200, 4.0, \"func maxLength(nums []int) int {\\n\\tlength := len(nums)\\n\\tsubArray := 1\\n\\n\\tfor i := 0; i < length; i++ {\\n\\t\\tproduct := nums[i]\\n\\t\\tgcdNum := product\\n\\t\\tlcmNum := product\\n\\t\\t\\n\\t\\tfor j := i + 1; j < length; j++ {\\n\\t\\t\\tproduct *= nums[j]\\n\\t\\t\\tgcdNum = gcd(gcdNum, nums[j])\\n\\t\\t\\tlcmNum = lcm(lcmNum, nums[j])\\n\\t\\t\\tif product == gcdNum*lcmNum {\\n\\t\\t\\t\\tsubArray = max(subArray, j-i+1)\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\n\\treturn subArray\\n}\\n\\nfunc lcm(former int, latter int) int {\\n\\treturn former * latter / gcd(former, latter)\\n}\\n\\nfunc gcd(former int, latter int) int {\\n\\tif latter == 0 {\\n\\t\\treturn former\\n\\t}\\n\\n\\treturn gcd(latter, former%latter)\\n}\\n\"], [4300, 32.0, \"func maxLength(nums []int) int {\\n res := 0\\n for i := 0; i < len(nums)-1; i++ {\\n am := nums[i]\\n for j := i+1; j < len(nums); j++ {\\n am *= nums[j]\\n if gcd(nums[i:j+1]) * lcm(nums[i:j+1]) == am {\\n res = max(res, j - i + 1)\\n }\\n }\\n }\\n return res\\n}\\n\\n\\n\\nfunc gcd2(a, b int) int {\\n if a == 0 { return b}\\n return gcd2(b % a, a)\\n}\\nfunc gcd(a []int) int {\\n res := a[0]\\n for _, num := range a[1:] {\\n res = gcd2(num, res)\\n if res == 1 { return 1 }\\n }\\n return res\\n}\\nfunc lcm2(a, b int) int {\\n return a * b / gcd2(a, b)\\n}\\nfunc lcm(a []int) int {\\n res := a[0]\\n\\tfor _, num := range a[1:] {\\n res = lcm2(res, num)\\n }\\n return res\\n}\"], [4400, 32.0, null], [4500, 12.0, null], [4600, 8.0, \"func maxLength(nums []int) int {\\n if len(nums) == 0 {\\n return 0\\n }\\n \\n size := len(nums)\\n res := 0\\n\\n for i := 0; i < size; i++ {\\n for j := i; j < size; j++ {\\n arr := nums[i:j+1]\\n\\n p, l, g := arr[0], arr[0], arr[0]\\n for k := 1; k < len(arr); k++ {\\n p = p * arr[k]\\n l = lcm(l, arr[k])\\n g = gcd(g, arr[k])\\n }\\n\\n if p == l * g {\\n res = max(len(arr), res)\\n }\\n }\\n }\\n\\n return res\\n}\\n\\nfunc gcd(a, b int) int {\\n\\tfor b != 0 {\\n\\t\\ta, b = b, a%b\\n\\t}\\n\\treturn a\\n}\\n\\nfunc lcm(a, b int) int {\\n\\tif a == 0 || b == 0 {\\n\\t\\treturn 0\\n\\t}\\n\\treturn (a * b) / gcd(a, b)\\n}\"], [4700, 4.0, \"\\nfunc fgcd(a, b int) int {\\n\\tif a < b {\\n\\t\\treturn fgcd(b, a)\\n\\t}\\n\\tif b == 0 {\\n\\t\\treturn a\\n\\t}\\n\\treturn fgcd(b, a%b)\\n}\\n\\nfunc flcm(a, b int) int {\\n\\tgcd := fgcd(a, b)\\n\\treturn a * b / gcd\\n}\\n\\nfunc isValid(nums []int) bool {\\n\\tvar prod, gcd, lcm = nums[0], nums[0], nums[0]\\n\\tfor i := 1; i < len(nums); i++ {\\n\\t\\tprod *= nums[i]\\n\\t\\tgcd = fgcd(gcd, nums[i])\\n\\t\\tlcm = flcm(lcm, nums[i])\\n\\t}\\n\\treturn prod == gcd*lcm\\n}\\n\\nfunc maxLength(nums []int) int {\\n\\tfor length := len(nums); length > 1; length-- {\\n\\t\\tfor i := 0; i+length <= len(nums); i++ {\\n\\t\\t\\tif isValid(nums[i : i+length]) {\\n\\t\\t\\t\\treturn length\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\treturn 0\\n}\"]]",
"runtime": 4,
"runtimeDistribution": "[[0, 32.0, \"func maxLength(num []int) int {\\n res:=1\\n for i, n := range num {\\n currGcd,currLcm,currProd := n,n,n\\n for j:=i+1;j<len(num);j++{\\n currGcd,currLcm,currProd = gcd(currGcd, num[j]), lcm(currLcm, num[j]), currProd*num[j]\\n if currProd == currGcd*currLcm{\\n res = max(res, j-i+1)\\n } else {\\n break\\n }\\n }\\n }\\n return res\\n}\\nfunc gcd(a,b int)int{\\n for b != 0 {\\n a, b = b, a%b\\n }\\n return a\\n}\\nfunc lcm(a, b int)int{\\n return a*b/gcd(a,b)\\n}\\n\"], [1, 8.0, \"func gcd(a,b int)int{\\n for b != 0 {\\n a, b = b, a%b\\n }\\n return a\\n}\\n\\nfunc lcm(a, b int)int{\\n return (a/gcd(a,b))*b\\n}\\nfunc max(a,b int)int{\\n if a>b{\\n return a\\n }\\n return b\\n}\\nfunc maxLength(num []int) int {\\n n := len(num)\\n res:=0\\n for i:=0;i<n;i++{\\n currGcd := num[i]\\n currLcm := num[i]\\n currProd := num[i]\\n\\n for j:=i+1;j<n;j++{\\n currGcd=gcd(currGcd, num[j])\\n currLcm= lcm(currLcm, num[j])\\n currProd=currProd*num[j]\\n if currProd == currGcd*currLcm{\\n res = max(res, j-i+1)\\n }\\n }\\n\\n\\n }\\n return res\\n}\"], [3, 8.0, null], [4, 12.0, null], [13, 4.0, null], [48, 4.0, null], [49, 4.0, null], [52, 4.0, null], [53, 4.0, null], [56, 4.0, null], [64, 4.0, \"\\nfunc fgcd(a, b int) int {\\n\\tif a < b {\\n\\t\\treturn fgcd(b, a)\\n\\t}\\n\\tif b == 0 {\\n\\t\\treturn a\\n\\t}\\n\\treturn fgcd(b, a%b)\\n}\\n\\nfunc flcm(a, b int) int {\\n\\tgcd := fgcd(a, b)\\n\\treturn a * b / gcd\\n}\\n\\nfunc isValid(nums []int) bool {\\n\\tvar prod, gcd, lcm = nums[0], nums[0], nums[0]\\n\\tfor i := 1; i < len(nums); i++ {\\n\\t\\tprod *= nums[i]\\n\\t\\tgcd = fgcd(gcd, nums[i])\\n\\t\\tlcm = flcm(lcm, nums[i])\\n\\t}\\n\\treturn prod == gcd*lcm\\n}\\n\\nfunc maxLength(nums []int) int {\\n\\tfor length := len(nums); length > 1; length-- {\\n\\t\\tfor i := 0; i+length <= len(nums); i++ {\\n\\t\\t\\tif isValid(nums[i : i+length]) {\\n\\t\\t\\t\\treturn length\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\treturn 0\\n}\"], [73, 4.0, \"func maxLength(n []int) int {\\n\\tl := len(n)\\n\\tfor k := range l {\\n\\t\\tall := subArraysWithLen(n, l-k)\\n\\t\\tfor _, v := range all {\\n\\t\\t\\tif arrayMultiply(v) == lcm(v)*gcd(v) {\\n\\t\\t\\t\\treturn len(v)\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\treturn len(n)\\n}\\n\\nfunc lcm(n []int) int {\\n\\tl := len(n)\\n\\tres := LCM(n[0], n[1])\\n\\tfor k := range l - 2 {\\n\\t\\tres = LCM(res, n[k+2])\\n\\t}\\n\\treturn res\\n}\\n\\nfunc gcd(n []int) int {\\n\\tl := len(n)\\n\\tres := GCD(n[0], n[1])\\n\\tfor k := range l - 2 {\\n\\t\\tres = GCD(res, n[k+2])\\n\\t}\\n\\treturn res\\n}\\n\\nfunc arrayMultiply(n []int) int {\\n\\tres := n[0]\\n\\tl := len(n)\\n\\tfor k := 1; k < l; k++ {\\n\\t\\tres *= n[k]\\n\\t}\\n\\treturn res\\n}\\n\\nfunc subArraysWithLen(n []int, length int) [][]int {\\n\\tl := len(n)\\n\\tres := [][]int{}\\n\\ti := 0\\n\\tfor i <= l-length {\\n\\t\\tres = append(res, n[i:i+length])\\n\\t\\ti++\\n\\t}\\n\\treturn res\\n}\\n\\nfunc LCM(a, b int, integers ...int) int {\\n\\tresult := a * b / GCD(a, b)\\n\\n\\tfor i := 0; i < len(integers); i++ {\\n\\t\\tresult = LCM(result, integers[i])\\n\\t}\\n\\n\\treturn result\\n}\\n\\nfunc GCD(a, b int) int {\\n\\tfor b != 0 {\\n\\t\\tt := b\\n\\t\\tb = a % b\\n\\t\\ta = t\\n\\t}\\n\\treturn a\\n}\\n\"]]"
},
"java": {
"code": "class Solution {\n public int maxLength(int[] nums) {\n int n = nums.length;\n int ans = 0;\n for (int i = 0; i < n; i++) {\n java.math.BigInteger prod = java.math.BigInteger.ONE;\n int currGcd = 0;\n int currLcm = 1;\n for (int j = i; j < n; j++) {\n prod = prod.multiply(java.math.BigInteger.valueOf(nums[j]));\n if (j == i) {\n currGcd = nums[j];\n currLcm = nums[j];\n } else {\n currGcd = gcd(currGcd, nums[j]);\n currLcm = lcm(currLcm, nums[j]);\n }\n if (prod.equals(java.math.BigInteger.valueOf((long) currGcd * currLcm))) {\n ans = Math.max(ans, j - i + 1);\n }\n }\n }\n return ans;\n }\n private int gcd(int a, int b) {\n while (b != 0) {\n int tmp = a % b;\n a = b;\n b = tmp;\n }\n return a;\n }\n private int lcm(int a, int b) {\n return (a / gcd(a, b)) * b;\n }\n}",
"memory": 4500,
"memoryDistribution": "[[4500, 5.802, \"class Solution {\\n public int maxLength(int[] nums) {\\n int n = nums.length;\\n int ans = 0;\\n for (int i = 0; i < n; i++) {\\n java.math.BigInteger prod = java.math.BigInteger.ONE;\\n int currGcd = 0;\\n int currLcm = 1;\\n for (int j = i; j < n; j++) {\\n prod = prod.multiply(java.math.BigInteger.valueOf(nums[j]));\\n if (j == i) {\\n currGcd = nums[j];\\n currLcm = nums[j];\\n } else {\\n currGcd = gcd(currGcd, nums[j]);\\n currLcm = lcm(currLcm, nums[j]);\\n }\\n if (prod.equals(java.math.BigInteger.valueOf((long) currGcd * currLcm))) {\\n ans = Math.max(ans, j - i + 1);\\n }\\n }\\n }\\n return ans;\\n }\\n private int gcd(int a, int b) {\\n while (b != 0) {\\n int tmp = a % b;\\n a = b;\\n b = tmp;\\n }\\n return a;\\n }\\n private int lcm(int a, int b) {\\n return (a / gcd(a, b)) * b;\\n }\\n}\"], [41700, 0.6826, \"class Solution {\\n public int maxLength(int[] nums) {\\n int maxLen = 0;\\n int n = nums.length;\\n\\n for (int i = 0; i < n; i++) {\\n int l = i;\\n int r = i;\\n int prod = 1;\\n\\n while (r < n) {\\n prod *= nums[r];\\n\\n int gcd = gcdArray(nums, l, r);\\n int lcm = lcmArray(nums, l, r);\\n\\n if (prod == gcd * lcm) {\\n maxLen = Math.max(maxLen, r - l + 1);\\n }\\n r++;\\n }\\n }\\n\\n return maxLen;\\n }\\n\\n private int gcdArray(int[] arr, int start, int end) {\\n int result = arr[start];\\n for (int i = start + 1; i <= end; i++) {\\n result = gcd(result, arr[i]);\\n }\\n return result;\\n }\\n\\n private int lcmArray(int[] arr, int start, int end) {\\n int result = arr[start];\\n for (int i = start + 1; i <= end; i++) {\\n result = lcm(result, arr[i]);\\n }\\n return result;\\n }\\n\\n private int gcd(int a, int b) {\\n while (b != 0) {\\n int temp = b;\\n b = a % b;\\n a = temp;\\n }\\n return Math.abs(a);\\n }\\n\\n private int lcm(int a, int b) {\\n if (a == 0 || b == 0) return 0;\\n return Math.abs(a * b) / gcd(a, b);\\n }\\n}\"], [41900, 0.6826, \"import java.util.*;\\n\\nclass Solution {\\n\\n public int maxLength(int[] nums) {\\n int n = nums.length;\\n int maxLen = -1;\\n\\n for(int i = 0; i < n; i++) {\\n long product = 1;\\n int gcd = nums[i];\\n long lcm = nums[i];\\n\\n for(int j = i; j < n; j++) {\\n product *= nums[j];\\n gcd = computeGCD(gcd, nums[j]);\\n lcm = lcm(lcm, nums[j]);\\n\\n if(product == (long)gcd * lcm) {\\n maxLen = Math.max(maxLen, j - i + 1);\\n }\\n }\\n }\\n\\n return maxLen;\\n }\\n\\n private int computeGCD(int a, int b) {\\n if(b == 0) return a;\\n return computeGCD(b, a % b);\\n }\\n\\n private long lcm(long a, long b) {\\n return (a * b) / computeGCD((int)a, (int)b);\\n }\\n}\\n\"], [42000, 0.6826, null], [42100, 2.0478, null], [42200, 5.802, null], [42300, 15.3584, null], [42400, 10.9215, null], [42500, 11.6041, null], [42600, 11.9454, null], [42700, 8.5324, null], [42800, 7.1672, null], [42900, 8.8737, null], [43000, 4.0956, null], [43100, 2.7304, null], [43200, 1.0239, null], [44200, 0.3413, null], [44400, 0.3413, null], [44500, 0.6826, \"import java.util.*;\\n\\nclass Solution {\\n public int maxLength(int[] nums) {\\n int n = nums.length;\\n int ans = 2; // minimum subarray length is 2\\n Map<Integer, Integer> last = new HashMap<>(); // prime factor -> last seen index\\n int i = 0;\\n\\n for (int j = 0; j < n; j++) {\\n for (int p : primeDivisors(nums[j])) {\\n if (last.containsKey(p)) {\\n i = Math.max(i, last.get(p) + 1);\\n }\\n last.put(p, j);\\n }\\n ans = Math.max(ans, j - i + 1);\\n }\\n\\n return ans;\\n }\\n\\n private List<Integer> primeDivisors(int x) {\\n List<Integer> primes = new ArrayList<>();\\n int d = 2;\\n while (d * d <= x) {\\n if (x % d == 0) {\\n primes.add(d);\\n while (x % d == 0) {\\n x /= d;\\n }\\n }\\n d += (d == 2) ? 1 : 2; // after 2, try only odd numbers\\n }\\n if (x > 1) {\\n primes.add(x);\\n }\\n return primes;\\n }\\n}\\n\"], [44600, 0.6826, \"class Solution {\\n public int gcd(int a, int b) {\\n return b == 0 ? a : gcd(b, a % b);\\n }\\n\\n public int lcm(int a, int b) {\\n return (a / gcd(a, b)) * b;\\n }\\n\\n public int maxLength(int[] nums) {\\n int n = nums.length;\\n System.out.println(n);\\n for(int i =0;i<nums.length;i++){\\n \\n System.out.println(nums[i]+\\\" \\\");\\n }\\n if(n>2&&nums[2]>20){\\n return 0;\\n }\\n int maxL = 0;\\n \\n for (int i = 0; i < n; i++) {\\n int currGCD = nums[i];\\n int currLCM = nums[i];\\n int currPro = nums[i];\\n \\n for (int j = i + 1; j < n; j++) {\\n currPro *= nums[j];\\n currGCD = gcd(currGCD, nums[j]);\\n currLCM = lcm(currLCM, nums[j]);\\n \\n if (currPro == currLCM * currGCD) {\\n maxL = Math.max(maxL, j - i + 1);\\n }\\n }\\n }\\n return maxL;\\n }\\n}\\n\"]]",
"runtime": 15,
"runtimeDistribution": "[[1, 8.1911, \"class Solution {\\n public int gcd(int a, int b) {\\n return b == 0 ? a : gcd(b, a % b);\\n }\\n\\n public int lcm(int a, int b) {\\n return (a / gcd(a, b)) * b;\\n }\\n\\n public int maxLength(int[] nums) {\\n int n = nums.length;\\n int maxL = 0;\\n \\n for (int i = 0; i < n; i++) {\\n int currGCD = nums[i];\\n int currLCM = nums[i];\\n int currPro = nums[i];\\n \\n for (int j = i + 1; j < n; j++) {\\n currPro *= nums[j];\\n currGCD = gcd(currGCD, nums[j]);\\n currLCM = lcm(currLCM, nums[j]);\\n \\n if (currPro == currLCM * currGCD) {\\n maxL = Math.max(maxL, j - i + 1);\\n }else{\\n break;\\n }\\n }\\n }\\n return maxL;\\n }\\n}\"], [2, 14.3345, \"class Solution {\\n public int maxLength(int[] nums) {\\n int longest = 0;\\n for(int i = 0; i < nums.length-1; i++){\\n int multiple = nums[i];\\n int gcd = nums[i];\\n int lcm = nums[i];\\n for(int j = i+1; j < nums.length; j++){\\n multiple*=nums[j];\\n gcd = getGCD(nums[j], gcd);\\n lcm = getLCM(lcm, nums[j]);\\n if(lcm * gcd == multiple){\\n longest = Math.max(longest, j+1-i);\\n }\\n else break;\\n }\\n }\\n return longest;\\n }\\n public int getGCD(int a, int b){\\n return b == 0 ? a : getGCD(b, a%b);\\n }\\n public int getLCM(int a, int b){\\n return a*b / getGCD(a, b);\\n }\\n}\"], [3, 60.4096, null], [4, 4.7782, null], [5, 0.3413, null], [7, 0.3413, null], [10, 0.3413, null], [15, 0.3413, null], [17, 0.3413, null], [24, 0.3413, null], [30, 0.6826, null], [31, 0.3413, null], [32, 0.3413, null], [35, 0.3413, null], [50, 0.3413, null], [55, 0.6826, null], [61, 0.6826, null], [71, 0.3413, null], [74, 0.3413, null], [75, 0.3413, \"class Solution {\\n public static int gcd(int a, int b) {\\n while (b != 0) {\\n int temp = b;\\n b = a % b;\\n a = temp;\\n }\\n return a;\\n }\\n\\n public static int lcm(int a, int b) {\\n return (a / gcd(a, b)) * b;\\n }\\n\\n public static int proArr(int[] nums) {\\n int pro = 1;\\n for (int i = 0; i < nums.length; i++) {\\n pro *= nums[i];\\n }\\n return pro;\\n }\\n\\n public static int findGcd(int[] nums) {\\n int gcdVal = nums[0];\\n for (int i = 1; i < nums.length; i++) {\\n gcdVal = gcd(gcdVal, nums[i]);\\n }\\n return gcdVal;\\n }\\n\\n public static int findLcm(int[] nums) {\\n int lcmVal = nums[0];\\n for (int i = 1; i < nums.length; i++) {\\n lcmVal = lcm(lcmVal, nums[i]);\\n }\\n return lcmVal;\\n }\\n\\n public int maxLength(int[] nums) {\\n int maxLen = 0;\\n int n = nums.length;\\n\\n for (int l = 0; l < n; l++) {\\n for (int r = l; r < n; r++) {\\n int[] subArray = new int[r - l + 1];\\n for (int k = l; k <= r; k++) {\\n subArray[k - l] = nums[k];\\n }\\n\\n int product = proArr(subArray);\\n int gcdVal = findGcd(subArray);\\n int lcmVal = findLcm(subArray);\\n\\n if (product == gcdVal * lcmVal) {\\n maxLen = Math.max(maxLen, r - l + 1);\\n }\\n }\\n }\\n return maxLen;\\n }\\n}\\n\"], [83, 0.6826, \"class Solution {\\n public int maxLength(int[] nums) {\\n int maxLength = 0;\\n for (int i = 0; i < nums.length; i++) {\\n for (int j = i; j < nums.length; j++) {\\n int[] subarray = new int[j - i + 1];\\n for (int k = i; k <= j; k++) {\\n subarray[k - i] = nums[k];\\n }\\n if (isProductEquivalent(subarray)) {\\n maxLength = Math.max(maxLength, subarray.length);\\n }\\n }\\n }\\n return maxLength;\\n }\\n\\n private boolean isProductEquivalent(int[] arr) {\\n if (arr.length == 0) {\\n return false;\\n }\\n long product = 1;\\n for (int num : arr) {\\n product *= num;\\n }\\n long gcd = arr[0];\\n for (int i = 1; i < arr.length; i++) {\\n gcd = gcd(gcd, arr[i]);\\n }\\n long lcm = arr[0];\\n for (int i = 1; i < arr.length; i++) {\\n lcm = lcm(lcm, arr[i]);\\n }\\n return product == lcm * gcd;\\n }\\n\\n private long gcd(long a, long b) {\\n while (b != 0) {\\n long temp = b;\\n b = a % b;\\n a = temp;\\n }\\n return a;\\n }\\n\\n private long lcm(long a, long b) {\\n return (a * b) / gcd(a, b);\\n }\\n}\"]]"
},
"javascript": {
"code": "/**\n * @param {number[]} nums\n * @return {number}\n */\nvar maxLength = function(nums) {\n const fac = {\n 1: [0,0,0,0],\n 2: [1,0,0,0],\n 3: [0,1,0,0],\n 4: [1,0,0,0],\n 5: [0,0,1,0],\n 6: [1,1,0,0],\n 7: [0,0,0,1],\n 8: [1,0,0,0],\n 9: [0,1,0,0],\n 10: [1,0,1,0]\n };\n let n = nums.length, ans = 0;\n for (let i = 0; i < n; i++) {\n let counts = [0,0,0,0];\n for (let j = i; j < n; j++) {\n let num = nums[j];\n let f = fac[num];\n for (let p = 0; p < 4; p++) {\n if (f[p] > 0) counts[p]++;\n }\n let len = j - i + 1;\n if (len === 1) {\n if (num === 1) ans = Math.max(ans, 1);\n } else if (len === 2) {\n ans = Math.max(ans, 2);\n } else {\n let valid = true;\n for (let p = 0; p < 4; p++) {\n if (counts[p] > 1) { valid = false; break; }\n }\n if (valid) ans = Math.max(ans, len);\n else break;\n }\n }\n }\n return ans;\n};",
"memory": 5700,
"memoryDistribution": "[[5700, 65.3333, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar maxLength = function(nums) {\\n const fac = {\\n 1: [0,0,0,0],\\n 2: [1,0,0,0],\\n 3: [0,1,0,0],\\n 4: [1,0,0,0],\\n 5: [0,0,1,0],\\n 6: [1,1,0,0],\\n 7: [0,0,0,1],\\n 8: [1,0,0,0],\\n 9: [0,1,0,0],\\n 10: [1,0,1,0]\\n };\\n let n = nums.length, ans = 0;\\n for (let i = 0; i < n; i++) {\\n let counts = [0,0,0,0];\\n for (let j = i; j < n; j++) {\\n let num = nums[j];\\n let f = fac[num];\\n for (let p = 0; p < 4; p++) {\\n if (f[p] > 0) counts[p]++;\\n }\\n let len = j - i + 1;\\n if (len === 1) {\\n if (num === 1) ans = Math.max(ans, 1);\\n } else if (len === 2) {\\n ans = Math.max(ans, 2);\\n } else {\\n let valid = true;\\n for (let p = 0; p < 4; p++) {\\n if (counts[p] > 1) { valid = false; break; }\\n }\\n if (valid) ans = Math.max(ans, len);\\n else break;\\n }\\n }\\n }\\n return ans;\\n};\"], [54300, 1.3333, \"function getUniquePrimeFactors(x) {\\n const factors = new Set();\\n let f = 2;\\n if (x % f === 0) {\\n factors.add(f);\\n while (x % f === 0) x /= f;\\n }\\n\\n f += 1\\n while (f * f <= x) {\\n if (x % f === 0) {\\n factors.add(f);\\n while (x % f === 0) x /= f;\\n }\\n if (f & 1) f += 2;\\n else f += 1;\\n }\\n if (x > 1) {\\n factors.add(x);\\n }\\n return Array.from(factors);\\n}\\n\\nfunction maxLength(a) {\\n const n = a.length;\\n let maxLengthFound = Math.min(2, n); // Initial max length (length 2 is always product-equivalent)\\n const lastSeenPrimeFactorIndex = new Map();\\n let windowStart = 0;\\n\\n for (let windowEnd = 0; windowEnd < n; windowEnd++) {\\n const currentNumber = a[windowEnd];\\n const primeFactors = getUniquePrimeFactors(currentNumber);\\n\\n for (const factor of primeFactors) {\\n if (lastSeenPrimeFactorIndex.has(factor) && lastSeenPrimeFactorIndex.get(factor) >= windowStart) {\\n windowStart = lastSeenPrimeFactorIndex.get(factor) + 1;\\n }\\n lastSeenPrimeFactorIndex.set(factor, windowEnd);\\n }\\n maxLengthFound = Math.max(maxLengthFound, windowEnd - windowStart + 1);\\n }\\n\\n return maxLengthFound;\\n}\\n\"], [55300, 1.3333, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar maxLength = function (nums) {\\n function gcd(a, b) {\\n while (b !== 0) {\\n [a, b] = [b, a % b];\\n }\\n return a;\\n }\\n\\n let l = r = 0, max = 2, prod = 1;\\n while(r < nums.length) {\\n let nr = nums[r]\\n r++\\n while(gcd(prod, nr) !== 1 ) {\\n prod /= nums[l]\\n l++\\n }\\n prod *= nr\\n max = Math.max(max, r - l);\\n }\\n return max\\n};\"], [55600, 1.3333, null], [55700, 4.0, null], [55800, 2.6667, null], [55900, 1.3333, null], [56100, 2.6667, null], [56200, 2.6667, null], [56300, 2.6667, null], [56400, 6.6667, null], [56500, 4.0, null], [56800, 2.6667, null], [57000, 1.3333, null], [57100, 1.3333, null], [57200, 1.3333, null], [57400, 2.6667, null], [57500, 1.3333, null], [57600, 4.0, null], [57700, 2.6667, null], [58000, 4.0, null], [58100, 4.0, null], [58200, 5.3333, null], [58300, 1.3333, null], [58400, 2.6667, null], [58600, 1.3333, null], [59000, 1.3333, null], [59300, 1.3333, null], [59400, 1.3333, null], [59500, 1.3333, null], [60600, 2.6667, null], [60900, 1.3333, null], [61200, 1.3333, null], [61500, 2.6667, null], [61600, 1.3333, null], [62000, 1.3333, null], [62300, 1.3333, null], [62500, 1.3333, null], [62700, 1.3333, null], [62800, 1.3333, null], [63100, 1.3333, null], [63300, 1.3333, null], [63500, 1.3333, null], [63700, 1.3333, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar maxLength = function(nums) {\\n\\tconst n = nums.length;\\n\\tlet maxLen = 0;\\n\\tfor (let i = 0; i < n; i++) {\\n\\t\\tlet prod = 1;\\n\\t\\tlet g = nums[i];\\n\\t\\tlet l = nums[i];\\n\\t\\tfor (let j = i; j < n; j++) {\\n\\t\\t\\tprod *= nums[j];\\n\\t\\t\\tg = gcd([g, nums[j]]);\\n\\t\\t\\tl = lcm([l, nums[j]]);\\n\\n\\t\\t\\tif (prod === g * l) {\\n\\t\\t\\t\\tmaxLen = Math.max(maxLen, j - i + 1);\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\n\\treturn maxLen;\\n};\\n\\nconst gcd = arr => Math.abs(arr.reduce(\\n (a, n) => {\\n while (n)\\n [a, n] = [n, a % n];\\n return a;\\n }));\\n\\nconst lcm = arr => arr.reduce((acc, num) => Math.abs(acc * num) / gcd([acc, num]), 1)\"], [64000, 1.3333, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar maxLength = function(nums) {\\n const gcd = (nums, b) => {\\n while(b){\\n [nums, b] = [b, nums%b];\\n }\\n return nums;\\n }\\n const lcm = (nums, b) => {\\n return (nums*b) / gcd(nums, b);\\n }\\n\\n let maxLen = 0;\\n for(let i=0; i<nums.length; i++){\\n let prod = 1;\\n let g = nums[i], l = nums[i];\\n for(let j=i; j<nums.length; j++){\\n prod *= nums[j];\\n g = gcd(g, nums[j]);\\n l = lcm(l, nums[j]);\\n if(prod === g*l) maxLen = Math.max(maxLen, j-i+1);\\n }\\n }\\n return maxLen;\\n};\"]]",
"runtime": 1,
"runtimeDistribution": "[[0, 4.0, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar maxLength = function (nums) {\\n function gcd(a,b) {\\n if(b === 0) {\\n return a\\n } else {\\n return gcd(b, a % b)\\n }\\n }\\n\\n let l = 0\\n let r = 0\\n let max = 2\\n let prod = 1 \\n while(r < nums.length) {\\n let nr = nums[r]\\n r++\\n\\n while(gcd(prod, nr) !== 1 ) {\\n let nl = nums[l]\\n prod = prod / nl\\n l++\\n }\\n\\n prod = prod * nr\\n let len = r - l\\n if(len > max) {\\n max = len\\n }\\n }\\n return max\\n\\n\\n};\"], [1, 12.0, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar maxLength = function (nums) {\\n function gcd(a, b) {\\n while (b !== 0) {\\n [a, b] = [b, a % b];\\n }\\n return a;\\n }\\n\\n let l = r = 0, max = 2, prod = 1;\\n while(r < nums.length) {\\n let nr = nums[r]\\n r++\\n while(gcd(prod, nr) !== 1 ) {\\n prod /= nums[l]\\n l++\\n }\\n prod *= nr\\n max = Math.max(max, r - l);\\n }\\n return max\\n};\"], [2, 12.0, null], [3, 6.6667, null], [4, 9.3333, null], [5, 6.6667, null], [6, 4.0, null], [7, 5.3333, null], [8, 4.0, null], [9, 1.3333, null], [10, 2.6667, null], [11, 1.3333, null], [12, 1.3333, null], [13, 4.0, null], [14, 1.3333, null], [15, 1.3333, null], [17, 1.3333, null], [21, 2.6667, null], [27, 1.3333, null], [41, 1.3333, null], [64, 1.3333, null], [66, 1.3333, null], [96, 1.3333, null], [103, 1.3333, null], [106, 1.3333, null], [113, 1.3333, null], [114, 1.3333, \"const isProductsEqual = str =>\\n str.split(/[24680]/).length <= 2 && \\n str.split(/[369]/).length <= 2 &&\\n str.split(/[50]/).length <= 2 &&\\n str.split(/[7]/).length <= 2;\\n\\nconst maxLength = (nums, toString = nums.join('').replaceAll('10', '0')) => {\\n for (let size = nums.length; size > 2; size--) {\\n for (let j = 0; j <= nums.length - size; j++) {\\n if (isProductsEqual(toString.slice(j, j + size))) {\\n return size;\\n }\\n }\\n }\\n return 2;\\n};\"], [119, 1.3333, \"const isProductsEqual = str =>\\n str.split(/[24680]/).length <= 2 && \\n str.split(/[369]/).length <= 2 &&\\n str.split(/[50]/).length <= 2 &&\\n str.split(/[7]/).length <= 2;\\n\\nconst maxLength = (nums, toString = nums.join('').replaceAll('10', '0')) => {\\n for (let size = nums.length; size > 2; size--) {\\n for (let j = 0; j <= nums.length - size; j++) {\\n if (isProductsEqual(toString.slice(j, j + size))) {\\n return size;\\n }\\n }\\n }\\n return 2;\\n};\"]]"
},
"python3": {
"code": "def gcd(a, b):\n while b:\n a, b = b, a % b\n return a\n\nclass Solution:\n def maxLength(self, nums: list[int]) -> int:\n n = len(nums)\n ans = 0\n for i in range(n):\n prod = 1\n cur_g = 0\n cur_l = 1\n for j in range(i, n):\n prod *= nums[j]\n if j == i:\n cur_g = nums[j]\n cur_l = nums[j]\n else:\n cur_g = gcd(cur_g, nums[j])\n d = gcd(cur_l, nums[j])\n cur_l = (cur_l * nums[j]) // d\n if prod == cur_g * cur_l:\n ans = max(ans, j - i + 1)\n return ans",
"memory": 1800,
"memoryDistribution": "[[1800, 77.1739, \"def gcd(a, b):\\n while b:\\n a, b = b, a % b\\n return a\\n\\nclass Solution:\\n def maxLength(self, nums: list[int]) -> int:\\n n = len(nums)\\n ans = 0\\n for i in range(n):\\n prod = 1\\n cur_g = 0\\n cur_l = 1\\n for j in range(i, n):\\n prod *= nums[j]\\n if j == i:\\n cur_g = nums[j]\\n cur_l = nums[j]\\n else:\\n cur_g = gcd(cur_g, nums[j])\\n d = gcd(cur_l, nums[j])\\n cur_l = (cur_l * nums[j]) // d\\n if prod == cur_g * cur_l:\\n ans = max(ans, j - i + 1)\\n return ans\"], [17400, 0.2717, \"class Solution:\\n def maxLength(self, nums: List[int]) -> int:\\n def lcm(a, b):\\n return (a * b) // gcd(a, b)\\n\\n ans = 0\\n for i in range(len(nums)):\\n lcm_v = gcd_v = prod_v = nums[i]\\n\\n for j in range(i + 1, len(nums)):\\n prod_v *= nums[j]\\n gcd_v = gcd(gcd_v, nums[j]) #Inbuilt in Python \\n lcm_v = lcm(lcm_v, nums[j]) # Defined Above\\n if prod_v == (gcd_v * lcm_v):\\n ans = max(ans, j - i + 1)\\n return ans\"], [17500, 1.3587, \"class Solution:\\n def maxLength(self, nums: List[int]) -> int:\\n result=0\\n for i in range(len(nums)):\\n acumulador_prod=nums[i]\\n acumulador_gcd=nums[i]\\n acumulador_lcm=nums[i] \\n contador_size=1\\n for j in range(i+1, len(nums)):\\n acumulador_prod*=nums[j]\\n acumulador_gcd=gcd(acumulador_gcd,nums[j])\\n acumulador_lcm=lcm(acumulador_lcm,nums[j])\\n contador_size+=1\\n if acumulador_prod < acumulador_gcd*acumulador_lcm:\\n break\\n elif acumulador_prod != acumulador_gcd*acumulador_lcm:\\n continue \\n elif acumulador_prod == acumulador_gcd*acumulador_lcm: \\n result=max(result,contador_size) \\n return result\\n\"], [17600, 6.25, null], [17700, 14.9457, null], [17800, 22.8261, null], [17900, 19.5652, null], [18000, 17.3913, null], [18100, 9.2391, \"import math\\nclass Solution:\\n def maxLength(self, nums) -> int:\\n l = res = 0\\n product = 1\\n\\n for r in range(0, len(nums)):\\n product *= nums[r]\\n\\n temp = math.gcd(*nums[l:r + 1]) * math.lcm(*nums[l:r+1])\\n\\n #print(nums[l:r+1], product, math.gcd(*nums[l:r + 1]), math.lcm(*nums[l:r+1]) )\\n if product == temp:\\n res = max(r - l + 1, res)\\n\\n while product> temp:\\n product /= nums[l]\\n l += 1\\n temp = math.gcd(*nums[l:r + 1]) * math.lcm(*nums[l:r+1])\\n #print(nums[l:r+1], product, math.gcd(*nums[l:r + 1]), math.lcm(*nums[l:r+1]), 'w')\\n\\n\\n return res \\n\\n\"], [18200, 2.9891, \"from functools import reduce\\nfrom math import gcd, inf, lcm\\n\\nclass Solution:\\n def maxLength(self, nums: List[int]) -> int:\\n lo = inf\\n for w in range(len(nums), 1, -1):\\n for i in range(len(nums) - w + 1):\\n x = nums[i:i + w]\\n if reduce(operator.mul, x) == gcd(*x) * lcm(*x):\\n lo = min(lo, len(x))\\n break\\n if lo != inf:\\n break\\n \\n return lo\"]]",
"runtime": 52,
"runtimeDistribution": "[[7, 25.8153, \"class Solution:\\n def gcd(self, a: int, b: int) -> int:\\n if a < b:\\n a, b = b, a\\n while b > 0:\\n r = a % b\\n a = b\\n b = r\\n return a\\n\\n def maxLength(self, nums: List[int]) -> int:\\n n = len(nums)\\n \\n left = 0\\n right = 1\\n max_len = 2\\n while right < n:\\n right_num = nums[right]\\n for i in range(right - 1, left - 1, -1):\\n if self.gcd(right_num, nums[i]) != 1:\\n new_len = right - left \\n if max_len < new_len:\\n max_len = new_len\\n #max_len = max(max_len, right - left)\\n left = i + 1\\n break\\n right += 1\\n new_len = right - left \\n if max_len < new_len:\\n max_len = new_len\\n return max_len\\n\\n\\n\\n # Need to return the length of the largest subarray where every to elements are coprime, if there is such of length 3 or more. Any subarray of length 2 has the property. Subarrays of length 1 do not have it.\\n\\n\\n \"], [21, 9.510900000000001, \"class Solution:\\n def maxLength(self, nums: List[int]) -> int:\\n result=0\\n for i in range(len(nums)):\\n acumulador_prod=nums[i]\\n acumulador_gcd=nums[i]\\n acumulador_lcm=nums[i] \\n for j in range(i+1,len(nums)):\\n acumulador_prod*=nums[j]\\n acumulador_gcd=gcd(acumulador_gcd,nums[j])\\n acumulador_lcm=lcm(acumulador_lcm,nums[j])\\n a=acumulador_gcd*acumulador_lcm\\n if acumulador_prod < a or acumulador_prod>10**10:\\n break\\n elif acumulador_prod == a: \\n result=max(result,j-i+1) \\n return result\\n\"], [35, 23.6412, null], [49, 3.8041, null], [52, 38.3153, \"def gcd(a, b):\\n while b:\\n a, b = b, a % b\\n return a\\n\\nclass Solution:\\n def maxLength(self, nums: list[int]) -> int:\\n n = len(nums)\\n ans = 0\\n for i in range(n):\\n prod = 1\\n cur_g = 0\\n cur_l = 1\\n for j in range(i, n):\\n prod *= nums[j]\\n if j == i:\\n cur_g = nums[j]\\n cur_l = nums[j]\\n else:\\n cur_g = gcd(cur_g, nums[j])\\n d = gcd(cur_l, nums[j])\\n cur_l = (cur_l * nums[j]) // d\\n if prod == cur_g * cur_l:\\n ans = max(ans, j - i + 1)\\n return ans\"], [63, 1.0868, null], [77, 0.2717, null], [91, 0.8150999999999999, null], [105, 0.2717, null], [119, 0.2717, null], [133, 0.2717, null], [148, 0.2717, null], [162, 0.2717, null], [176, 0.2717, null], [190, 0.2717, null], [204, 0.2717, null], [218, 0.2717, null], [232, 0.2717, null], [246, 0.2717, null], [260, 0.2717, null], [274, 0.2717, null], [289, 0.2717, null], [303, 0.2717, null], [317, 0.2717, null], [331, 0.8152, null], [345, 0.2717, null], [359, 0.5435, null], [373, 1.0869, null], [387, 1.3585, null], [401, 0.5435, null], [415, 1.087, null], [430, 1.0868, null], [444, 0.5434, null], [458, 0.8150999999999999, null], [472, 0.2717, null], [486, 0.2717, null], [500, 0.8151999999999999, null], [514, 3.2607, null], [528, 1.6302, null], [542, 0.2717, null], [556, 0.2717, null], [571, 0.2717, null], [585, 0.2717, null], [599, 0.2717, null], [613, 0.2717, null], [627, 0.2717, null], [641, 0.2717, null], [655, 0.2717, null], [669, 0.2717, null], [683, 0.2717, null], [697, 0.2717, null], [712, 0.2717, null], [726, 0.2717, null], [740, 0.2717, null], [754, 0.2717, null], [768, 0.2717, null], [782, 0.2717, null], [796, 0.2717, null], [810, 0.5434, null], [824, 0.2717, null], [838, 0.2717, null], [853, 1.6303, null], [867, 0.5434, null], [881, 0.2717, null], [895, 0.5434, null], [909, 0.5434, null], [923, 0.2717, null], [937, 0.2717, null], [951, 0.5434, \"import math\\nfrom functools import reduce\\nimport operator\\n\\nclass Solution:\\n def maxLength(self, nums: List[int]) -> int:\\n def gcd_mul(arr):\\n return reduce(math.gcd, arr)\\n\\n def lcm_mul(arr):\\n return reduce(lambda x, y: abs(x * y) // math.gcd(x, y), arr)\\n\\n subarray = []\\n for a in range(len(nums)):\\n for b in range(1, len(nums) + 1):\\n subarray.append(nums[a:b])\\n\\n ret = 0\\n for a in subarray:\\n if len(a) < 2:\\n continue\\n\\n if reduce(operator.mul, a) == lcm_mul(a) * gcd_mul(a):\\n ret = max(ret, len(a))\\n\\n return ret\"], [965, 0.2717, \"class Solution:\\n def maxLength(self, nums: List[int]) -> int:\\n\\n length = 0\\n\\n for i in range(len(nums)):\\n for j in range(i+1, len(nums)+1):\\n\\n subarr = nums[i:j]\\n\\n prod = reduce(lambda x,y:x*y, subarr)\\n gcd_ = reduce(lambda x,y:gcd(x,y), subarr)\\n lcm_ = reduce(lambda x,y:lcm(x,y), subarr)\\n\\n if prod == gcd_*lcm_:\\n length = max(length, j-i)\\n \\n return length\\n\\n\\n \"]]"
},
"ruby": {
"code": "def max_length(nums)\n n = nums.size\n max_len = 0\n (0...n).each do |i|\n prod = 1\n cur_g = nil\n cur_l = nil\n (i...n).each do |j|\n a = nums[j]\n prod *= a\n if cur_g.nil?\n cur_g = a\n cur_l = a\n else\n cur_g = cur_g.gcd(a)\n cur_l = cur_l.lcm(a)\n end\n max_len = (j - i + 1) if prod == cur_g * cur_l && (j - i + 1) > max_len\n end\n end\n max_len\nend",
"memory": 21200,
"memoryDistribution": "[[21200, 100.0, \"def max_length(nums)\\n n = nums.size\\n max_len = 0\\n (0...n).each do |i|\\n prod = 1\\n cur_g = nil\\n cur_l = nil\\n (i...n).each do |j|\\n a = nums[j]\\n prod *= a\\n if cur_g.nil?\\n cur_g = a\\n cur_l = a\\n else\\n cur_g = cur_g.gcd(a)\\n cur_l = cur_l.lcm(a)\\n end\\n max_len = (j - i + 1) if prod == cur_g * cur_l && (j - i + 1) > max_len\\n end\\n end\\n max_len\\nend\"], [212200, 100.0, \"# @param {Integer[]} nums\\n# @return {Integer}\\n\\nclass Integer\\n\\n def self.gcd(x, y)\\n \\n return x if y == 0\\n\\n Integer.gcd(y, x % y)\\n end\\n\\n\\n def self.lcm(x, y)\\n\\n x / Integer.gcd(x, y) * y\\n\\n end\\n\\n def self.max(x, y)\\n \\n return x if x > y\\n\\n y\\n end\\n\\n def self.min(x, y)\\n return y if y < x\\n\\n x\\n end\\n\\nend\\n\\nclass Array\\n\\n def gcd\\n result = 0\\n\\n n = self.size\\n\\n for i in 0...n do\\n result = Integer.gcd(result, self[i])\\n end\\n\\n result\\n end\\n\\n def lcm\\n result = 1\\n\\n n = self.size\\n\\n for i in 0...n do\\n result = Integer.lcm(result, self[i])\\n end\\n\\n result\\n end\\n\\n def product\\n result = 1\\n\\n n = self.size\\n\\n for i in 0...n do\\n result *= self[i]\\n end\\n\\n result\\n end\\n\\n def product_equivalent?\\n product == lcm * gcd\\n end\\n\\n def subarray(l, r)\\n result = []\\n\\n for i in Integer.max(l, 0)...Integer.min(r, self.size) do\\n result << self[i]\\n end\\n\\n result\\n end\\n\\n def length_of_longest_product_equivalent_subarray\\n n = self.size\\n length = n\\n\\n while length >= 1 do\\n l = 0\\n r = length\\n while r <= n do\\n\\n return length if subarray(l, r).product_equivalent?\\n\\n l += 1\\n r += 1\\n end\\n \\n length -= 1\\n end\\n\\n length\\n end\\nend\\n\\ndef max_length(nums)\\n nums.length_of_longest_product_equivalent_subarray\\nend\"]]",
"runtime": 40,
"runtimeDistribution": "[[40, 50.0, \"def max_length(nums)\\n n = nums.size\\n max_len = 0\\n (0...n).each do |i|\\n prod = 1\\n cur_g = nil\\n cur_l = nil\\n (i...n).each do |j|\\n a = nums[j]\\n prod *= a\\n if cur_g.nil?\\n cur_g = a\\n cur_l = a\\n else\\n cur_g = cur_g.gcd(a)\\n cur_l = cur_l.lcm(a)\\n end\\n max_len = (j - i + 1) if prod == cur_g * cur_l && (j - i + 1) > max_len\\n end\\n end\\n max_len\\nend\"], [2619, 50.0, \"# @param {Integer[]} nums\\n# @return {Integer}\\n\\nclass Integer\\n\\n def self.gcd(x, y)\\n \\n return x if y == 0\\n\\n Integer.gcd(y, x % y)\\n end\\n\\n\\n def self.lcm(x, y)\\n\\n x / Integer.gcd(x, y) * y\\n\\n end\\n\\n def self.max(x, y)\\n \\n return x if x > y\\n\\n y\\n end\\n\\n def self.min(x, y)\\n return y if y < x\\n\\n x\\n end\\n\\nend\\n\\nclass Array\\n\\n def gcd\\n result = 0\\n\\n n = self.size\\n\\n for i in 0...n do\\n result = Integer.gcd(result, self[i])\\n end\\n\\n result\\n end\\n\\n def lcm\\n result = 1\\n\\n n = self.size\\n\\n for i in 0...n do\\n result = Integer.lcm(result, self[i])\\n end\\n\\n result\\n end\\n\\n def product\\n result = 1\\n\\n n = self.size\\n\\n for i in 0...n do\\n result *= self[i]\\n end\\n\\n result\\n end\\n\\n def product_equivalent?\\n product == lcm * gcd\\n end\\n\\n def subarray(l, r)\\n result = []\\n\\n for i in Integer.max(l, 0)...Integer.min(r, self.size) do\\n result << self[i]\\n end\\n\\n result\\n end\\n\\n def length_of_longest_product_equivalent_subarray\\n n = self.size\\n length = n\\n\\n while length >= 1 do\\n l = 0\\n r = length\\n while r <= n do\\n\\n return length if subarray(l, r).product_equivalent?\\n\\n l += 1\\n r += 1\\n end\\n \\n length -= 1\\n end\\n\\n length\\n end\\nend\\n\\ndef max_length(nums)\\n nums.length_of_longest_product_equivalent_subarray\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list:
import random
random.seed(seed)
# Helper function for computing gcd
def gcd(a, b):
while b:
a, b = b, a % b
return a
# Sample solution function adapted from the provided sample solution.
# It computes the maximum length of a product equivalent subarray.
def sample_maxLength(nums: list) -> int:
n = len(nums)
ans = 0
for i in range(n):
prod = 1
cur_g = 0
cur_l = 1
for j in range(i, n):
prod *= nums[j]
if j == i:
cur_g = nums[j]
cur_l = nums[j]
else:
cur_g = gcd(cur_g, nums[j])
d = gcd(cur_l, nums[j])
cur_l = (cur_l * nums[j]) // d
if prod == cur_g * cur_l:
ans = max(ans, j - i + 1)
return ans
# Serialization helpers (using a simple comma-separated format)
def serialize_input(nums: list) -> str:
return ",".join(map(str, nums))
def serialize_output(result: int) -> str:
return str(result)
test_cases = []
# Include several fixed cases to cover boundary and core functionality.
fixed_cases = [
[1, 1],
[1, 2, 1, 2, 1, 1, 1],
[2, 3, 4, 5, 6],
[1, 2, 3, 1, 4, 5, 1],
[10, 10, 10]
]
for case in fixed_cases:
if len(test_cases) < num_cases:
expected = sample_maxLength(case)
test_cases.append({
"input": serialize_input(case),
"output": serialize_output(expected)
})
# Generate additional random test cases if necessary.
while len(test_cases) < num_cases:
n = random.randint(2, 100) # ensuring length constraint 2 <= n <= 100
case = [random.randint(1, 10) for _ in range(n)]
expected = sample_maxLength(case)
test_cases.append({
"input": serialize_input(case),
"output": serialize_output(expected)
})
return test_cases
# Example usage:
if __name__ == "__main__":
cases = generate_test_cases(10)
for case in cases:
print("Input:", case["input"], "Expected Output:", case["output"])
|
def evaluate(expected_output: str, program_output: str) -> bool:
"""
Compares the expected output with the program output.
Both outputs are deserialized using simple whitespace trimming and then converted to integers.
"""
try:
exp_val = int(expected_output.strip())
prog_val = int(program_output.strip())
return exp_val == prog_val
except Exception:
return False
# Example usage:
if __name__ == "__main__":
# Should return True
print(evaluate("5", "5\n"))
# Should return False
print(evaluate("3", " 4 "))
|
[{"input": "1,1", "output": "2"}, {"input": "1,2,1,2,1,1,1", "output": "5"}, {"input": "2,3,4,5,6", "output": "3"}, {"input": "1,2,3,1,4,5,1", "output": "5"}, {"input": "10,10,10", "output": "2"}, {"input": "2,1,5,4,4,3,2,9,2,10,7,1,1,2,4,4,9,10,1,9,4,9,7,4,8,10,5,1,3,7,6,5,3,4,6,2,2,7,2,6,6,10,5,1,8,9,2,7,2,9,5,10,6,10,4,2,1,4,5,2,4,2,7,5,8,6,3,6,6,4,5,2,10,3,9,4,3,8,7,5,9,4,6", "output": "4"}, {"input": "1,4,1,6,7,5,2,4,10,6,4,8,7,8,3,5,3,4,9,9,5,10,7,10,7,6,4,3,9,8,2,1,2,3,3,7,10,2,7,7,10,8,9,5,9,1,2,9,5,6,2,5,7,3,8,1,5,9,3,9,2,5,9,10,4,3,6,3,9,9,1,10,6,8,1,2,6,5,4,1,4,10,2,2,8,2,9,3,3,8,9,3,5,9,10,7,4,9,4,5", "output": "5"}, {"input": "6,8,9,8,2,4,4,2,6,1,10,9,4,10,4,1,2,1,4,2,1,6,2,9,4,5,8,4,9,3,10,10,8,4,8,7,4,2,2,7,6,7,7,8,1,2,1,7,6,2,4,4,4", "output": "4"}, {"input": "5,1,7,9,5,1,1,1,7,8,10,5,8,2", "output": "7"}, {"input": "10,2,3,1,2,2,2,7,3,9,3,1,6,6,7,5,2,10,10,1,4,10,8,1,10,8,1,5,10,3,3,2,1,6,7,2,3,2,10,10,10,8,6,3,6,5,8,1,8,9,9,4,6,10,10,5,5,8,3,6,2,3,2,3,1,9,7,6,6,1,10,10,1,8,1", "output": "3"}, {"input": "10,5,4,1,6,9,5,8,2,7,4,5,5,2,6", "output": "3"}, {"input": "4,7,2,3,5,1,4,7,1,2,3,8,9,3,8", "output": "6"}, {"input": "10,2", "output": "2"}, {"input": "7,1,3,5,1,3,7,4,6,7,9,9,8,10,6,6,3,10,10,2,1,1,7,3,10,2,7,10,7,8,1,9,4,3,4,9,8,9,3,6,1,9,4,5,1,1,2,8,1,5,8,7,5,1,1,4,9,2,7,1,7,1,4,3", "output": "6"}, {"input": "2,3,5,5,4,4,8,5,10,6,7,9,9,10,7,9,3,8,4,5,8,1,8,3,5,7,3,6,10,10,10,8,10,9,10,7,9,7,3,1,6,6,1,7,8,3,9,3,4,7,1,9,4,6", "output": "5"}, {"input": "4,4,10,2,10,10,9,7,3,8,8,1,3,9,8,5,9,10,3,9,3,4,2", "output": "3"}, {"input": "2,10,8,10,10,2,3,4,1,7,6,6,4,4,6,2,8,5,10,7,5,7,9,5,7,8", "output": "4"}, {"input": "10,5,8,2,5,4,10,6,2,7,2,8,3,5,1", "output": "4"}, {"input": "4,10,5,8,8,3,4,2,4,4,4,7,2,5,4,5,6,7,5,9,7,8,2,2,6,4,10,6,8,4,1,4,4,5,2,7,1,5,7,3,10,1", "output": "4"}, {"input": "8,1,10,6,1,2,5,3,8,6,6,3,7,4,6,5,1,6,8,1,2,4,7,4,3,5,10,4,9,5,6,8,2,6,10,7,7,10,10,2,5,10,9,3,6,1,5,7,2,7,2,8,2,4,3,8,2,5,8,2,2,9,6,7,4,1,7,10,1,7,7,2,4,2,3,2,3,10,9,9,8,5", "output": "4"}, {"input": "7,9,4,6,2,7,2,3,4,5,7,2,2,10,3,7,4,4,10,4,1,10,1,7,6,9,3,3,9,4,1,1,10,5,7,4,5,9,2,9,7,10,6,6,10,7,2,7,9,10,2,5,10,1,9", "output": "4"}, {"input": "10,10,3,2,3,1,4,1,9,3,8,4,7,4,7,6,7,8,6,7,10,7,6,5,3,1,10,6,9,3,3,8,6,1,5,5,7,6,7,8,1,2,7,3,10,10,9,9,6,9,5,10,2,7,6,9,5,10,2,5,5,2,7,9,7,1,6,3,6,8,4,5", "output": "4"}, {"input": "10,9,6,1,4,1,9,4,9,10,3,5,5,10,1,1,10,2,6,5,3,3,2,9,5,4,3,4,1,8,5,9,8,5,6,4,5,1,2,1,8,5,10,1,3,6,8,4,6,10,8,3,9,1,5,7,7,8,5,7,5,10,4,3,6,2,7,5,10,10,9,8,5,3,8,1,2,9,10", "output": "4"}, {"input": "3,4,10,9,6,9,8,10,9,1,7,7,7,6,6,3,5,9,9,6,4,1,4,5,7,9,7,8,4,1,5,1,1,1,10,6,4,7,6,7,8,4,8,3,10,3,7,9,8,7,2,3,9,9,5,5,2,5,3,6,4", "output": "6"}, {"input": "4,7,1,3,9,7,10,1,9,9,8,8,6,8,9,8,4,6,10,5,5,7,4,5,3,9,6,4,6,8,5,7,3,1,7,7,6,3,8,4,6,10,7,6,6,3,9,10,9,1,1,2,8,7,10,7,7,7,8,2,6,7,4,1,8,6,10,3,6,8,10,8,8,7,7,9,1,1,1,3,8,4,2,4,8", "output": "5"}, {"input": "5,3,4,8,9,5,10,10,7,1,4,9,8,6,1,10,9,3,8,3,4,3,10,7,3,6,3,9,6,9,10,5,2,4,1,8,8,10,5,4,8,2,2,4,5,10,5,10,4,4,6,2,9,5,3,3,8,9,6,1,1,7,5,5,8,9,3", "output": "5"}, {"input": "10,6,5,7,6,5,9,3,4,7,10,3,10,1,9,5,9,1,1,3,4,10,6,6,7,10,9,5,3,3,9,10,6,10,9,4,8,9,5,8,3,10,10,9,6,4,8,5,1,10,6,8,7,5,5,4,8,5,3,9,1,7,1,2,3,9,3,6", "output": "5"}, {"input": "9,7,3,7,3,2,9,2,7,8,9,10,9,6,10,1,5,1,4,2,4,3,9,3,3,3,1,1,1,8,7,4,9,3,6,5,5,9,7,6,10,5,5,9,7,8,6,10,8,1,2,6,1,3,5,8,2,8,4,6,8,6,8", "output": "6"}, {"input": "4,7,4,5,6,10,4,7,1,6,6,2,5,7,9,1,1,4,4,10,1,3,4,9,4,5,1,9,9,6,6,10,6,5,10,5,10,1,7,1,5,5,3,2,5,10,2,4,6,7,7,7,2,4,5,7,8,6,7,4,6,2,1,5,2,8,2,3,1,2,5,2,2,7,4,7,6,4,1,10,3,10,6,5,10,4,5,1,5,2,4,9,6,3,5,6,10,4,3,10", "output": "6"}, {"input": "9,1,9,7,3,3,8,10,4,6,5,10,2,2,10,9,9,5,5,2,10,9,7,3,8,2,1,7,10,10,10,3,5,8,9,8,2,6,6,10,7,3,1,6,5,3,10,4,4,9,3,10,9,7,8,2,7,2,7,10,1,2,10,7,6,7,4,5,7,8,5,7,7,8,3,9,4,7,7,1,3,6,5,8,7,7,3,1,8,5,3", "output": "5"}, {"input": "9,8,2,9,3,8,3,9,5", "output": "2"}, {"input": "6,3,9,9,6,6", "output": "2"}, {"input": "3,3,4,1,9,2,5,9,10,10,8,8,3,8,3,9,5,10,9,2,7,5,3,10,6,2,5,5,9,7,8,9,10,9,9,8,5,3,4,10,10,3,9,6,10,4,3,10,10,9,2,5,9,7,5,6,1,1,8,7,1,3,1,4,9,4,5,4,6,2,4,6,10,10,10,10,4,6,10,5,8,7,5,10,2,3,9", "output": "7"}, {"input": "5,6,5,7,7,7,3,9,10,5,8,10,2", "output": "3"}, {"input": "3,6,5,2,3,6,3,3,2,10,3,5,9,5,5,7,8,7,2,1,3,4,5", "output": "4"}, {"input": "1,4,2,8,4,1,8,5,10,7,8,2,5,8,8,5,10,6,1,7,3,3,8,8,1,3,2,5,5,5,6,5,7,8,8,10,7,6,6,1,2,9,7,8,10,3,2,1,10,4,2,6,1,5,3,5,8,2,3,5,10,6,7,1,5,6,5,2,10,10,10,3,6", "output": "4"}, {"input": "5,7,2,2,10,10,1,6,5,1,2,1,5,3,7,1", "output": "7"}, {"input": "1,10,1,2,9,4,5,5,8,7,5,10,4,8,7,9,10,9,10,4,7,6,1,3,10,6,5,9,10,7,2,4,3,5,9,5,8,1,5,10,9,3", "output": "4"}, {"input": "7,5,3,8,10,4,2,8,4,3,3,1,10,7,9,5,4,6,10,4,2,6,10,1,6,8,5,5,2,8,9,10,9,4,7,10,8,9,9,1,6,2,2,9,2,10,3,3,6,1", "output": "4"}, {"input": "8,2,1,5,8,4,5,4,1,5,8,9,9,7,3,7,4,6,3,8,4,8,6,2,1,8,10,10,9,3,8,6,2,2,4,5,8,8,3,5,10,10,10,2,9,7,6,4,2", "output": "4"}, {"input": "9,9,9,6,2,7,6,3,3,7,3,8,8,7,8,5,4,8,3,7,10,10,10,8,6,4,9,5,5,9,5,10,2,1,2,9,6,4,5,10,5,2,5,4,4,10,3,1,9,5,1,7,5,1,7,8,5,9,8,8,6,7,7,8,2,4,8,7,10,8,1,8,4,1,7,3", "output": "5"}, {"input": "2,5,7,6,4,4,3,10,4,9,3,4,10,2,6,10,4,2,6,2,7,10,10,3,6,2,4,10,8,2,6,9,4,9,5,7,10,9,1,7,2,5,3,10,1,6,7,1,10,6,2,2,5,10,5,4,7,6,3,7,7,2,6,8,8", "output": "5"}, {"input": "6,2,7,10,10,6,1,9,4,5,4,7,3,5,10,8,8,10,7,8,1,7,10,1,2,8,8,3,6,4,1,2,7,3,5,5,3,1", "output": "5"}, {"input": "2,1,5", "output": "3"}, {"input": "8,1,7,2,9,2,10,2,9,6,4,1,4,3,9,4,4,10,2,4", "output": "4"}, {"input": "10,7,3,6,10,4,8,1,3,3,6,3,7,6,4,8,7,9,6,5,1,1,3,6,1,4,2,2,9,9,5,1,10,5,4,1,6,8,6,8,10,6,6,8,5,5,7,7,4,5,5,10,9,4,8,5,10,4,8,8,2,2,2,2,8,5,2,6,10,7,10,9,9,4,10,2,2,10,7,2,8,7,2,2,8,2,5,8,8,7,7", "output": "4"}, {"input": "8,1,6,10,5,5,6,1,3,9,10,6,10,7,7,9,9,1,4,10,4,10,9,7,10,7,1,9,9,5,4,6,4,6,2,2,9,5,4,1,9,8,5,1,10,6,10,8,5,1,9,5,8,9,2,3,4,6,5,7,4,4,9,6,7,1,7,10,2,10,7,1,9,9,4,6,5,3,6,7,10,10,6,8,7,3,4,10,2,4,5,8,4,10,5,5,5,6,2", "output": "5"}, {"input": "10,1,2,7,7,10,1,8,6,6,3,4,5,7,8,2,9,7,1,5,4,2,7,7,5,8,6,1,10,7,1", "output": "5"}, {"input": "8,9,8,7,8,5,8,8,10,5,3,8,2,3,8,7,7,4,5,1,3,1,1,1,10,6,7,10,2,4,9,8,4,8,8,7,8,8,8,9,4,1,2,6,6,7,8,9,5,5,6,8,2,6,4,3,8,9,6,6,4,5,1,4,2,4,4,8,7,2,9,2,4,2,1,10,3,4,7,2,3,8,3,1,3,1,1,7,5,8,7", "output": "8"}, {"input": "10,6,2,6,3,1,4,4,1,10,10,8,1,6,9,5,1,9,3,8,7,7,8,4,8,2,7,3,10,9,5,3,2,4,9,3,5,2,3,6,1,3,2,5,9,8,5,7,8,5,3,5,3,9,2,6,1,2,5,2,5,8,8,5,7,5,6,9,10", "output": "4"}, {"input": "10,2,4,3,8,7,7,6,9,8,9,4,9,1,3,1,7,2,7,4,7,5,6,6,1,9,8,7,4,8,2,2,9,2,9,7,4,8,1,5,6,1,5,6,7,1,4,9,7,1,9,8,8,4,8,4,4,8,3,4,6,2,2,7,3,7,10,8,3,10,4,6,3", "output": "5"}, {"input": "8,1,1,3,6,2,8,5,4,10,2,7,4,6,4,3,7,4,2,9,9,1,3,1,6,5,1,8,6", "output": "4"}, {"input": "7,8,4", "output": "2"}, {"input": "2,6,3,6,5,10,3,5,6,3,7,3,7,10,2,9,5,8,1,8,4,9,9,7,5,3,9,5,10,1", "output": "4"}, {"input": "8,3,9,8,7,8,1,8", "output": "3"}, {"input": "4,6,7,4,9,6,6,10,8,7,8,5,9,7,5,5,8,6,7,3,10,7,3,3,8,6,1,9,4,1,3,7,4,8,5,9,5,2,8,6,5,3,6,6,3,6,2,7,2,3,6,2,9,10,5,8,1,4,8,7,4,4,8,2,2,10,5,5,10,7,5,3,8,2,6,7,3,8,4,10,10,6,9,4,8,4,3,9,5", "output": "4"}, {"input": "10,9,10,6,1,10,5,2,3,3,4,8,10,5,5,4,7,8,8,9,2,10,8,7,8,6,9,10,10,8,1,3,10,5,6,9,9,9,9,7,4,3,1,3,3,7,4,5,5,6,1,7,6", "output": "4"}, {"input": "6,2,8,3,1,7,10,6,7,5,7,9", "output": "4"}, {"input": "3,10,6,3,2,7,6,4,6,8,6,10,8,5,1,8,9,2,6,4,5,5,10,7,3,8,1,1,2,7,9,3,10,3,6,2,4,4,8,8,2,6,2,4,9,8,5,7,2,3,2,2,7,5,6,5,9,6,4,3,1,1,8,3,5,9,8,7,4,9,5,3,10,7,10,1,10,4,4,3,2,7,5,1,5,10,5,10,9,7,1,8,2,6,6,6,4,1,8,10", "output": "5"}, {"input": "5,3,5,8,3,7,1,3,1,3,1,4,1,1,8,8,3", "output": "6"}, {"input": "3,3,8,5,3,2,5,3,8,8,10,6,5,2,7,1,5,2,9,8,5,4,4,3,3,1,8,6,9,6,8,8,6,10,5,5,6,5,8,1,4,5,9,4,9,5,9,6,4,4,4,2,3,5,1,8,5,4,5,10,4,6,1,9,6,4,1,4,6,9,3,3,7", "output": "5"}, {"input": "6,2,4,9,1,9,9,10,3,10,10", "output": "3"}, {"input": "2,4,3,5,3,10,10,5,2,6,9,7,9,2,7,9,7,10,4,8,10,3,6,9,1,8,2,1,7,4,8,3,9,5,5,7,6,2,7,6,6,9,6,3,6,2,10,4,9,10,1,6,2,5,5,3,3,5,7,9,6,2,9,10,10,7", "output": "3"}, {"input": "6,2,9,5,9,8,2,10,2,8,8,8,4,8,7,10,6,10,5,2,1,2", "output": "3"}, {"input": "1,1,5,1,3,6,8,6,10,3,5,3,4,9,8", "output": "5"}, {"input": "7,5,7,7,4", "output": "2"}, {"input": "3,5,4,8,3,4,7,9,2,5,1,10,9,2,1,4,7,5,2", "output": "5"}, {"input": "4,9,10,5,10,9,6,10,3,3,3,5,2,4,6,1,2,7,5,1,8,3,8,9,3,8,8,5,9,2,4,6,6,10,3,3,2,5,3,6,6,4,4,8,8,2,8,2,2,4,5,5,9,3,1,1,6,1,3,10,3,5,5,7", "output": "5"}, {"input": "7,9,5,8,2,5,5,7,9,1,7,2,1,9,7,1,5,4,5,7,2,8,6,3,10,10,7,7,9,10,7,4,5,6,2,6,2,10,4,8,2,6,10,4,10,4,1,5,6,6,5,10,9,1,1,7,9,9,1", "output": "6"}, {"input": "4,9,7,3,4,9,8,10,5,8,5,4,8,8,10,1,1,8,5,5,2,3,8,10,6,5,5,4,7,4,10,3,9,8,9,4,8,7,9,6,7,8,5,10,2,5,1,2,6,2,4,4,3,10,8,9,8,9,9,5,5,10,3,8,7,6,2,8,9,8", "output": "4"}, {"input": "6,5,5,10,6,7,7,9,7,8,1,5,6,3,10,5,4,2,8,2,10,9,8,10,1,1,5,7,10,8,3,9,1,9,4,1,10,7,5,1,5,7,8,5,8,7,8,8,6,9,3,6,7,10,2,9,3,10,8,3,5,7,9,6,4,1,7,10,7,4,9,4,5,2,3,1,10,7,8,10,3,7,1,8,10,7,1", "output": "5"}, {"input": "4,2,9,6,3,5,6,7,2,1,10,1,7,7,5,6,6,10,10,10,3,1,2,10,1,4,7,8,6,5,3,1,8,10,8,10,8,10,5,5,6,6,10,4,3,6,6,1,2,9,9,5,4,10,8,10,6,8,6,6,2,4,6,4,1,6,6,3,5,2,4,8,4,7,8,4", "output": "4"}, {"input": "6,10,6,7,6,6,3,8,3,3,2,10,6,1,6,1,10,5,8,4,5,3,2,10,9,10,10,3,5,4,8,2,6,2,6,6,3,9,8,2,6,3,9,3,4,3,6,2,1,1,1,6,9,6,9,10,10,6,10,5,6,1,4,5,2,6,7,6,4,9,6,4,10,7,3,2,1,8,1,3,3,2", "output": "4"}, {"input": "1,7,9,9,10,5,5,8,8,1,2,3,10,10,9,10,10,5,10,7,2,4,1,3,4,9,9,6,2", "output": "3"}, {"input": "1,9,7,3,8,1,3,1,4,6", "output": "4"}, {"input": "6,6,2,4,9,3,5,3,3,4,8,6,2,1,1,4,6,2,10,3,8,6,2,7,10,2,9,2,1,5,3,5,9,4,3,6,4,8,2,10,6,6,1,5,10,5,9,4,7,8,9,7,2,1,10", "output": "4"}, {"input": "6,4,5,8,2,4,1,2,7,7,2,8,1,5,10,3,3,2,1,10,4,5,3,5,3,1,5,8,5,9,8,3,9,2,8,8,9,4,4,1,9,7,10,1,3,2,3,7,10,3,8,7,4,1,9,6,10,6,9,5,1,8,5,5,5,3,6,6,4,2", "output": "5"}, {"input": "3,7,5,1,8,8,10,1,3,9,7,8,2,10,7,2,1,6,3,9,2,3,10,7,9,7,10,8,8,10,5,9,2,8,5,4,4,2,8,9,9,8,1,7,9,8,1,9,1,9,10,8,7,8,4,10,1,2,10,4,9,2,1,5,6,10,5,10,7,8,4,2,7,9,10,1,4,8,7,4,3,3,10,2", "output": "5"}, {"input": "1,9,5,9,9,8,10,8,1,10,1,1,10,6,2,5,1,6,7,7,5,8,2,2,5,1,3,5,9,4,2,2,6,7,6,8,8,5,6,9,3,2,7,10,2,4,2,1,10,9,10,6,10,10,3,7,7,2,5,9,9,4,8,1,5,4,1,1,3,6,7,1,10,5,1,5,7", "output": "6"}, {"input": "9,2,4,1,7,7,3,3,5,2,9,9,2,6,7,4,10,6,1,3,3,7,9,1,1,5,8,8,10,4,6,6,10,4,2,2,5,4,2,6,1,1,6,2,3,1", "output": "6"}, {"input": "8,2,7,8,2,7,5,9,5,7,7,6", "output": "4"}, {"input": "9,6,1,7,2,3,9,7,4,1,1,4,4,6,6,7,6,1,5,4,4,5,7,1,1", "output": "5"}, {"input": "2,9,5,6,6,9,2,3,4,9,2,1,5,6,3,2,10,1,3,2,1,10,8,7,8,10,3,2,7,3,10,10,9,8,1,3,6,5,9,6,3", "output": "4"}, {"input": "1,8,8,3,3,3,1,2,3,9,7,6,4,3,10,9,5,8,5,2,9,2,7,7,8,6,9,1,10,1,10,8,6,3,8,9,9,3,4,6,10,8,4,3,9,10,7,2,2,7,7,7,8,8,3,3,4,3,3,2,5,9,5,8,8,4,6", "output": "4"}, {"input": "3,10,2,5,1,2,8,2,6,8,5,3,5,3,5,5,9,3,2,3,1,4,6,1,6,7,1,1,7,1,8,10,2,8,1,1,8,9,4,10,10,7,3,1,4,4,5,2,2,1", "output": "5"}, {"input": "5,2,4,2,10,1,7,10,6,8,9,2,10,3,3,4,8,5,6,7,5,7,3,8,2,10,2,7,7,8,8,2,6,9,4,7,8,4,2,9,7,3,1,1,3,6,7,9,5,9,8,3,7,7,4,6,7,7,1,3,2,5,1,3,2,10,6,6,3", "output": "6"}, {"input": "3,8,2,4,7,6,6,6,3,6,2,9,9,3,10,9,1,1,5,10,10,5,6,9,1,4,9,9,8,4,7,1,5,10,2,7,6,9,9,6,9,9,7,4", "output": "4"}, {"input": "6,5,9,2,6,7,7", "output": "3"}, {"input": "2,9,7,2,2,2,3,10,7,1,10,10,8,6,7,7,4,1,10,9,8,4,8,7,4,3,5,4,10,2,3,8,4,1,8,6,3,2,3,6,10,7,4,3,3,9,5,3,9,8,4,9,3,10,9,6,9", "output": "4"}, {"input": "4,4,8,2,3,5,3,9,8,4,1,2,2,2,9,10,2,2,7,5,2,7,7,3,5,1,8,4,9,8,2,1,4,3,7,8,4,3,1,9,4,4,9,3,4,4", "output": "5"}, {"input": "1,2,2,3,7,8,7,8,8,2,8,1,7,8,5,9,8,4,1,8,10", "output": "5"}, {"input": "2,7,6,1,3,9,4,6,10,10,8,7,7,1,10,10,9,9,3,6,6,4,2,4,10,7,3,8,2,6,3,8,6,10,1,9,7,5,5,5,7,5,4,4", "output": "4"}, {"input": "7,3,6,3,7,8,5,5,3,4,4,1,8,3,8,5,5,3,9,6,3,2,4,1,1,4,2,2,9,8,6,2,8,5,3,2,7,7,4,10,4,9,9,7,9,10,1,8,10,7,1,7,7,10,10,4,6,2,7,7", "output": "4"}, {"input": "6,3,10,2,4,9,6,8,5,3,5,10,5,1,9,3,6,1", "output": "3"}, {"input": "2,4,9,9", "output": "2"}, {"input": "7,6,3,6,2,9,3,9,1,3,1,5,10,9,10,10,1,7", "output": "4"}, {"input": "6,10,1,6,6,9,1,4,5,7,9,1,10,7,8,7,9,1,2,1,1,1,2,1,7,4,9,10,1,8,6,7,6,1,4,10,8,3,2,10,4,3,6,8,10", "output": "7"}, {"input": "4,1,2,10,9,4,3,7,5,8,8,9,3,5,4,1,4,8,9,9,4,5,2,8,4,3,1,3,9,3,4,6,5,8,7,3,3,6,5,8,10,8,8,2,6,7,9,2,5,1,6,9,1,3,3,1,9,6,10,9,6,7,9,7,3", "output": "5"}, {"input": "5,2,8,6,1,2,4,5,3,10,10,1,2,2,10,4,6,1,7,6,3,7,3,3,4,4,1,5,1,4,6,2,3,4,4,4,4,10,6,5,9,8,6,8,6,7,1,9,3,10,7,2,5,10,8,10,1,1,9,2,8,4,8,8,3,2,10,4,2,10,2,4,9,3,2,6,1,2,4,2,2,7,3,1,5", "output": "5"}, {"input": "10,8,6,4,5,5,3,1,1,5,1,2,8,10,1,4,6", "output": "6"}]
|
{
"cpp": "==Code Submission==\n\nvector<int> deserialize_stdin(const string &input) {\n vector<int> nums;\n stringstream ss(input);\n string token;\n while(getline(ss, token, ',')) {\n if (!token.empty())\n nums.push_back(stoi(token));\n }\n return nums;\n}\n\nstring serialize_stdout(int result) {\n return to_string(result);\n}\n\nint main() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n string line;\n getline(cin, line);\n vector<int> nums = deserialize_stdin(line);\n Solution sol;\n int ans = sol.maxLength(nums);\n cout << serialize_stdout(ans) << \"\\n\";\n return 0;\n}",
"golang": "==Code Submission==\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n line, _ := reader.ReadString('\\n')\n line = strings.TrimSpace(line)\n tokens := strings.Split(line, \",\")\n nums := make([]int, len(tokens))\n for i, s := range tokens {\n nums[i], _ = strconv.Atoi(s)\n }\n ans := maxLength(nums)\n fmt.Printf(\"%d\", ans)\n}",
"java": "public class Main {\n private static int[] deserialize(String input) {\n String[] tokens = input.split(\",\");\n int[] nums = new int[tokens.length];\n for (int i = 0; i < tokens.length; i++) {\n nums[i] = Integer.parseInt(tokens[i].trim());\n }\n return nums;\n }\n \n private static String serializeOutput(int result) {\n return Integer.toString(result);\n }\n \n public static void main(String[] args) throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n String line = br.readLine().trim();\n int[] nums = deserialize(line);\n Solution sol = new Solution();\n int ans = sol.maxLength(nums);\n System.out.println(serializeOutput(ans));\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\n\nconst deserialize_stdin = (input) => {\n const tokens = input.trim().split(',');\n return tokens.map(Number);\n};\n\nconst serialize_stdout = (result) => {\n return result.toString();\n};\n\nlet inputData = \"\";\nprocess.stdin.on(\"data\", chunk => inputData += chunk);\nprocess.stdin.on(\"end\", () => {\n const nums = deserialize_stdin(inputData);\n const ans = maxLength(nums);\n console.log(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\ndef deserialize_stdin(input_str):\n # Deserialize a comma-separated string into a list of integers.\n return list(map(int, input_str.strip().split(',')))\n\ndef serialize_stdout(result):\n # Serialize the integer result as a string.\n return str(result)\n\ndata = sys.stdin.read().strip()\nnums = deserialize_stdin(data)\nsol = Solution()\nans = sol.maxLength(nums)\nsys.stdout.write(serialize_stdout(ans))",
"ruby": "==Code Submission==\ninput = gets.strip\nnums = input.split(',').map(&:to_i)\nans = max_length(nums)\nputs ans"
}
|
3704
|
Count Partitions with Even Sum Difference
|
count-partitions-with-even-sum-difference
|
<p>You are given an integer array <code>nums</code> of length <code>n</code>.</p>
<p>A <strong>partition</strong> is defined as an index <code>i</code> where <code>0 <= i < n - 1</code>, splitting the array into two <strong>non-empty</strong> subarrays such that:</p>
<ul>
<li>Left subarray contains indices <code>[0, i]</code>.</li>
<li>Right subarray contains indices <code>[i + 1, n - 1]</code>.</li>
</ul>
<p>Return the number of <strong>partitions</strong> where the <strong>difference</strong> between the <strong>sum</strong> of the left and right subarrays is <strong>even</strong>.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">nums = [10,10,3,7,6]</span></p>
<p><strong>Output:</strong> <span class="example-io">4</span></p>
<p><strong>Explanation:</strong></p>
<p>The 4 partitions are:</p>
<ul>
<li><code>[10]</code>, <code>[10, 3, 7, 6]</code> with a sum difference of <code>10 - 26 = -16</code>, which is even.</li>
<li><code>[10, 10]</code>, <code>[3, 7, 6]</code> with a sum difference of <code>20 - 16 = 4</code>, which is even.</li>
<li><code>[10, 10, 3]</code>, <code>[7, 6]</code> with a sum difference of <code>23 - 13 = 10</code>, which is even.</li>
<li><code>[10, 10, 3, 7]</code>, <code>[6]</code> with a sum difference of <code>30 - 6 = 24</code>, which is even.</li>
</ul>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">nums = [1,2,2]</span></p>
<p><strong>Output:</strong> <span class="example-io">0</span></p>
<p><strong>Explanation:</strong></p>
<p>No partition results in an even sum difference.</p>
</div>
<p><strong class="example">Example 3:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">nums = [2,4,6,8]</span></p>
<p><strong>Output:</strong> <span class="example-io">3</span></p>
<p><strong>Explanation:</strong></p>
<p>All partitions result in an even sum difference.</p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>2 <= n == nums.length <= 100</code></li>
<li><code>1 <= nums[i] <= 100</code></li>
</ul>
|
You are given an integer array `nums` of length `n`.
A **partition** is defined as an index `i` where `0 <= i < n - 1`, splitting the array into two **non\-empty** subarrays such that:
- Left subarray contains indices `[0, i]`.
- Right subarray contains indices `[i + 1, n - 1]`.
Return the number of **partitions** where the **difference** between the **sum** of the left and right subarrays is **even**.
**Example 1:**
**Input:** nums \= \[10,10,3,7,6]
**Output:** 4
**Explanation:**
The 4 partitions are:
- `[10]`, `[10, 3, 7, 6]` with a sum difference of `10 - 26 = -16`, which is even.
- `[10, 10]`, `[3, 7, 6]` with a sum difference of `20 - 16 = 4`, which is even.
- `[10, 10, 3]`, `[7, 6]` with a sum difference of `23 - 13 = 10`, which is even.
- `[10, 10, 3, 7]`, `[6]` with a sum difference of `30 - 6 = 24`, which is even.
**Example 2:**
**Input:** nums \= \[1,2,2]
**Output:** 0
**Explanation:**
No partition results in an even sum difference.
**Example 3:**
**Input:** nums \= \[2,4,6,8]
**Output:** 3
**Explanation:**
All partitions result in an even sum difference.
**Constraints:**
- `2 <= n == nums.length <= 100`
- `1 <= nums[i] <= 100`
|
Easy
|
[
"array",
"math",
"prefix-sum"
] |
leetcode
|
https://leetcode.com/problems/count-partitions-with-even-sum-difference
|
functional
| null | null | null | null |
{
"c": "int countPartitions(int* nums, int numsSize) {\n \n}",
"cpp": "class Solution {\npublic:\n int countPartitions(vector<int>& nums) {\n \n }\n};",
"csharp": "public class Solution {\n public int CountPartitions(int[] nums) {\n \n }\n}",
"dart": "class Solution {\n int countPartitions(List<int> nums) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec count_partitions(nums :: [integer]) :: integer\n def count_partitions(nums) do\n \n end\nend",
"erlang": "-spec count_partitions(Nums :: [integer()]) -> integer().\ncount_partitions(Nums) ->\n .",
"golang": "func countPartitions(nums []int) int {\n \n}",
"java": "class Solution {\n public int countPartitions(int[] nums) {\n \n }\n}",
"javascript": "/**\n * @param {number[]} nums\n * @return {number}\n */\nvar countPartitions = function(nums) {\n \n};",
"kotlin": "class Solution {\n fun countPartitions(nums: IntArray): Int {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param Integer[] $nums\n * @return Integer\n */\n function countPartitions($nums) {\n \n }\n}",
"python": "class Solution(object):\n def countPartitions(self, nums):\n \"\"\"\n :type nums: List[int]\n :rtype: int\n \"\"\"\n ",
"python3": "class Solution:\n def countPartitions(self, nums: List[int]) -> int:\n ",
"racket": "(define/contract (count-partitions nums)\n (-> (listof exact-integer?) exact-integer?)\n )",
"ruby": "# @param {Integer[]} nums\n# @return {Integer}\ndef count_partitions(nums)\n \nend",
"rust": "impl Solution {\n pub fn count_partitions(nums: Vec<i32>) -> i32 {\n \n }\n}",
"scala": "object Solution {\n def countPartitions(nums: Array[Int]): Int = {\n \n }\n}",
"swift": "class Solution {\n func countPartitions(_ nums: [Int]) -> Int {\n \n }\n}",
"typescript": "function countPartitions(nums: number[]): number {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n int countPartitions(vector<int>& nums) {\n int total = 0;\n for (int num : nums) {\n total += num;\n }\n if (total % 2 != 0) {\n return 0;\n }\n return nums.size() - 1;\n }\n};",
"memory": 2200,
"memoryDistribution": "[[2200, 55.2632, \"class Solution {\\npublic:\\n int countPartitions(vector<int>& nums) {\\n int total = 0;\\n for (int num : nums) {\\n total += num;\\n }\\n if (total % 2 != 0) {\\n return 0;\\n }\\n return nums.size() - 1;\\n }\\n};\"], [22200, 2.2417, \"class Solution {\\npublic:\\n int countPartitions(vector<int>& nums) {\\n int n=nums.size();\\n int count=0;\\n \\n for(int i=0;i<n-1;i++){\\n int N=0;\\n int M=0;\\n for(int j=0;j<=i;j++){ \\n N+=nums[j];\\n }\\n for(int j=i+1;j<n;j++){ \\n M+=nums[j];\\n }\\n if((N-M)%2 ==0) count+=1;\\n\\n }\\n return count;\\n }\\n};\"], [22300, 17.154, \"class Solution {\\npublic:\\n int countPartitions(vector<int>& nums) {\\n int n = nums.size();\\n int sum = 0;\\n for(int i=0;i<n;i++){\\n sum += nums[i];\\n }\\n\\n return (sum%2 == 0) ? (n-1) : 0;\\n }\\n};\"], [22400, 25.3411, null], [22500, 30.3119, null], [22600, 8.577, null], [22700, 0.5848, null], [22800, 0.2924, null], [22900, 0.1949, null], [23000, 1.5595, null], [23100, 2.5341, \"class Solution {\\npublic:\\n int countPartitions(vector<int>& nums) {\\n int n = nums.size();\\n vector<int> pre(n+1,0);\\n for(int i=0; i<n; i++){\\n pre[i+1] = pre[i] + nums[i];\\n }\\n int total = pre[n];\\n int count = 0;\\n for (int i = 1; i < n; i++) {\\n int left = pre[i];\\n int right = total - left;\\n if(abs(left-right)%2==0){\\n count++;\\n }\\n }\\n return count;\\n }\\n};\\n\"], [23200, 5.4581, \"class Solution {\\npublic:\\n int countPartitions(vector<int>& nums) {\\n\\n int count = 0;\\n int n = nums.size();\\n\\n vector<int> prefix(n + 1, 0);\\n for (int i = 0; i < n; ++i) {\\n prefix[i + 1] = prefix[i] + nums[i];\\n }\\n\\n for(int i = 1; i < n; i++)\\n {\\n int left = prefix[i];\\n int right = prefix[n] - prefix[i];\\n\\n int ans = left - right;\\n\\n if(ans%2 == 0)\\n {\\n count++;\\n }\\n\\n }\\n\\n return count;\\n \\n }\\n};\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 87.7193, \"class Solution {\\npublic:\\n int countPartitions(vector<int>& nums) {\\n\\n int count = 0;\\n int n = nums.size();\\n\\n vector<int> prefix(n + 1, 0);\\n for (int i = 0; i < n; ++i) {\\n prefix[i + 1] = prefix[i] + nums[i];\\n }\\n\\n for(int i = 1; i < n; i++)\\n {\\n int left = prefix[i];\\n int right = prefix[n] - prefix[i];\\n\\n int ans = left - right;\\n\\n if(ans%2 == 0)\\n {\\n count++;\\n }\\n\\n }\\n\\n return count;\\n \\n }\\n};\"], [1, 2.4366, \"class Solution {\\npublic:\\n int countPartitions(vector<int>& nums) {\\n int n = nums.size();\\n int sum = 0;\\n for(int i=0;i<n;i++){\\n sum += nums[i];\\n }\\n\\n return (sum%2 == 0) ? (n-1) : 0;\\n }\\n};\"], [2, 1.3645, null], [3, 2.8265, \"class Solution {\\npublic:\\n int countPartitions(vector<int>& nums) {\\n int n=nums.size();\\n vector<int> preSum;\\n for(int i=0;i<n;i++)\\n {\\n if(i==0) preSum.push_back(nums[i]);\\n else{\\n preSum.push_back(preSum[i-1]+nums[i]);\\n }\\n }\\n if(preSum[n-1]%2!=0)return 0;\\n else{\\n return n-1;\\n }\\n\\n }\\n};\"], [4, 1.462, \"class Solution {\\npublic:\\n int countPartitions(vector<int>& nums) {\\n vector<int> prefixsum(nums.size(), 0);\\n int x = nums.size();\\n prefixsum[0] = nums[0];\\n for(int i = 1; i < x; i++){\\n prefixsum[i] = nums[i] + prefixsum[i-1];\\n }\\n int count= 0;\\n for(int i= 0; i < x-1; i++){\\n int leftsum = prefixsum[i];\\n int rightsum = prefixsum[x-1]- prefixsum[i];\\n\\n if(abs(leftsum - rightsum) % 2==0){\\n count++;\\n }\\n }\\n return count;\\n }\\n};\"]]"
},
"golang": {
"code": "func countPartitions(nums []int) int {\n total := 0\n for _, num := range nums {\n total += num\n }\n if total % 2 != 0 {\n return 0\n }\n return len(nums) - 1\n}",
"memory": 400,
"memoryDistribution": "[[400, 58.9285, \"func countPartitions(nums []int) int {\\n total := 0\\n for _, num := range nums {\\n total += num\\n }\\n if total % 2 != 0 {\\n return 0\\n }\\n return len(nums) - 1\\n}\"], [4100, 7.1429, \"func countPartitions(nums []int) int {\\n \\n rs := 0\\n\\n totalSum := 0\\n for i := 0; i < len(nums); i++ {\\n totalSum += nums[i]\\n }\\n\\n leftSum := 0\\n for i := 0; i < len(nums) - 1; i++ {\\n leftSum += nums[i]\\n totalSum -= nums[i]\\n\\n if (totalSum - leftSum) % 2 == 0 {\\n rs++\\n }\\n }\\n\\n return rs\\n}\"], [4200, 33.9286, \"func countPartitions(nums []int) int {\\n var count int\\n var diff int\\n\\n for i:=1; i<=len(nums)-1; i++{\\n diff=0\\n for j:=0; j<len(nums); j++{\\n if j<=i{\\n diff+=nums[j]\\n }else{\\n diff-=nums[j] \\n }\\n }\\n if diff%2==0{\\n count++\\n }\\n }\\n\\n return count\\n}\"], [4300, 39.2857, null], [4400, 14.2857, \"func countPartitions(nums []int) int {\\n l:=make([]int,len(nums)-1)\\n r:=make([]int,len(nums)-1)\\n\\n lt:=nums[0]\\n for i:=1;i<len(nums);i++{\\n l[i-1]=lt\\n lt+=nums[i]\\n }\\n rt:=nums[len(nums)-1]\\n for i:=1;i<len(nums);i++{\\n r[len(r)-i]=rt\\n rt+=nums[len(nums)-i-1]\\n }\\n count:=0\\n for i:=0;i<len(r);i++{\\n if (l[i]-r[i])%2==0{\\n count++\\n }\\n }\\n return count\\n}\"], [4500, 1.7857, \"func countPartitions(nums []int) int {\\n count := 0\\n n := len(nums)\\n leftSum := make([]int, n)\\n rightSum := make([]int, n)\\n prefixSum := 0\\n\\n for i := 0; i < n; i++ {\\n prefixSum += nums[i]\\n leftSum[i] = prefixSum\\n }\\n\\n prefixSum = 0\\n\\n for i := n-1; i >= 0; i-- {\\n rightSum[i] = prefixSum\\n prefixSum += nums[i]\\n }\\n\\n for i := 0; i < n-1; i++ {\\n if (leftSum[i] - rightSum[i]) % 2 == 0 {\\n count++\\n }\\n }\\n\\n return count\\n\\n}\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 98.2143, \"func countPartitions(nums []int) int {\\n \\n rs := 0\\n\\n totalSum := 0\\n for i := 0; i < len(nums); i++ {\\n totalSum += nums[i]\\n }\\n\\n leftSum := 0\\n for i := 0; i < len(nums) - 1; i++ {\\n leftSum += nums[i]\\n totalSum -= nums[i]\\n\\n if (totalSum - leftSum) % 2 == 0 {\\n rs++\\n }\\n }\\n\\n return rs\\n}\"], [24, 1.7857, \"func countPartitions(nums []int) int {\\n count :=0\\n for i:=1;i<len(nums);i++{\\n arr1 := nums[:i]\\n arr2 := nums[i:]\\n fmt.Println(arr1)\\n fmt.Println(arr2)\\n nArr1 := countArr(arr1)\\n nArr2 := countArr(arr2)\\n res := absolute(nArr1, nArr2)\\n if res%2 == 0{\\n count++\\n }\\n }\\n return count\\n}\\n\\nfunc absolute(n,m int) int {\\n if n>m {\\n return n-m\\n }\\n return m-n\\n}\\n\\nfunc countArr(arr []int)int{\\n n := 0\\n for _,val := range arr {\\n n += val\\n }\\n return n\\n}\"]]"
},
"java": {
"code": "class Solution {\n public int countPartitions(int[] nums) {\n int total = 0;\n for (int num : nums) {\n total += num;\n }\n return total % 2 == 0 ? nums.length - 1 : 0;\n }\n}",
"memory": 4200,
"memoryDistribution": "[[4200, 72.8014, \"class Solution {\\n public int countPartitions(int[] nums) {\\n int total = 0;\\n for (int num : nums) {\\n total += num;\\n }\\n return total % 2 == 0 ? nums.length - 1 : 0;\\n }\\n}\"], [41100, 0.272, \"class Solution {\\n public int countPartitions(int[] nums) {\\n int totalSum = 0;\\n for (int i=0;i<nums.length;i++) {\\n totalSum += nums[i]; \\n }\\n\\n int leftSum = 0;\\n int count = 0;\\n\\n for (int i = 0; i < nums.length - 1; i++) { \\n leftSum += nums[i]; \\n int rightSum = totalSum - leftSum; \\n \\n if ((leftSum % 2) == (rightSum % 2)) {\\n count++; \\n }\\n }\\n return count; \\n }\\n }\"], [41200, 0.0907, \"class Solution {\\n public int countPartitions(int[] nums) {\\n int r = 0, len = nums.length;\\n for(int i = 0; i < len-1; ++i){\\n int sumR = 0, sumL = 0, ri = len-1, le = 0;\\n while(le <= i || ri > i){\\n if(le <= i){\\n sumL += nums[le];\\n le++;\\n }\\n if(ri > i){\\n sumR += nums[ri];\\n ri--;\\n }\\n }\\n if((sumL - sumR)%2 == 0) r++;\\n }\\n return r;\\n }\\n}\"], [41300, 0.272, null], [41400, 0.4533, null], [41500, 1.3599, null], [41600, 3.1732, null], [41700, 8.9755, null], [41800, 12.602, null], [41900, 15.1405, null], [42000, 13.8713, null], [42100, 12.2393, null], [42200, 9.0662, null], [42300, 7.6156, null], [42400, 5.7117, \"class Solution {\\n public int countPartitions(int[] nums) {\\n \\n int count=0,sum1=0,sum2=0;\\n \\n for(int i=0;i<nums.length-1;i++)\\n {\\n sum1+=nums[i];\\n for(int j=i+1;j<nums.length;j++)\\n {\\n sum2+=nums[j];\\n }\\n \\n if((sum1-sum2)%2==0)\\n {\\n count++;\\n }\\n sum2=0;\\n }\\n return count;\\n }\\n}\"], [42500, 2.9918, \"class Solution {\\n public int countPartitions(int[] nums) {\\n int count = 0;\\n int sum1 = 0;\\n for(int i = 0; i < nums.length-1; i++){\\n sum1 += nums[i];\\n int sum2 = 0;\\n for(int j = i+1; j < nums.length;j++){\\n sum2 += nums[j];\\n }\\n if( (sum1 - sum2) %2 == 0) count++;\\n }\\n return count;\\n }\\n}\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 54.2158, \"class Solution {\\n public int countPartitions(int[] nums) {\\n int prefix = 0;\\n for(int val : nums){\\n prefix += val;\\n }\\n int count = 0;\\n int sum = 0;\\n for(int i=0;i<nums.length - 1;i++){\\n sum += nums[i];\\n prefix -= nums[i];\\n\\n if(Math.abs(sum - prefix) % 2 == 0 )count++;\\n }\\n return count;\\n }\\n}\"], [1, 38.8939, \"class Solution {\\n public int countPartitions(int[] nums) {\\n int n = nums.length;\\n int diff = 1, count = 0;\\n\\n for (int i = 1; i < n; i++) {\\n nums[i] = nums[i] + nums[i - 1];\\n }\\n int totalsum=nums[n-1];\\n for (int j = 0; j < n - 1; j++) {\\n diff = 2 * nums[j] - totalsum;\\n if (diff % 2 == 0) {\\n count++;\\n }\\n }\\n return count;\\n }\\n}\"], [2, 0.0907, null], [3, 2.4479, \"class Solution {\\n public int countPartitions(int[] nums) {\\n int n = nums.length, res = 0;\\n int sum = Arrays.stream(nums).sum();\\n int currSum = nums[0], remSum = sum - currSum;\\n for(int i = 1; i < n - 1; ++i) {\\n if((remSum - currSum) % 2 == 0)\\n res++;\\n currSum += nums[i];\\n remSum -= nums[i];\\n }\\n if((remSum - currSum) % 2 == 0) res++;\\n return res;\\n }\\n}\"], [4, 0.6346, \"class Solution {\\n public int countPartitions(int[] nums) {\\n int n = nums.length;;\\n int[] prefixSums = new int[n];\\n prefixSums[0] = nums[0];\\n for(int i = 1; i < n; i++) {\\n prefixSums[i] = prefixSums[i-1] + nums[i];\\n }\\n System.out.println(Arrays.toString(prefixSums));\\n int count = 0;\\n for(int i = 0; i < n - 1; i++) {\\n int sumDiff = 2 * prefixSums[i] - prefixSums[n-1];\\n if(sumDiff % 2 == 0) count++;\\n }\\n return count;\\n }\\n}\"]]"
},
"javascript": {
"code": "var countPartitions = function(nums) {\n let total = 0;\n for (let num of nums) {\n total += num;\n }\n return total % 2 === 0 ? nums.length - 1 : 0;\n};",
"memory": 5600,
"memoryDistribution": "[[5600, 24.4903, \"var countPartitions = function(nums) {\\n let total = 0;\\n for (let num of nums) {\\n total += num;\\n }\\n return total % 2 === 0 ? nums.length - 1 : 0;\\n};\"], [52800, 0.5102, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nconst countPartitions = n => n.reduce((a, b) => a ^ b) & 1 ? 0 : n.length - 1\"], [53300, 1.0204, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar countPartitions = function(nums) {\\n let output = 0\\n\\n let letSubArraySum = 0\\n let rightSubArraySum = nums.reduce((a, b) => a + b, 0)\\n\\n for(let i = 0; i < nums.length - 1; i++) {\\n letSubArraySum += nums[i]\\n rightSubArraySum -= nums[i]\\n\\n let diff = letSubArraySum - rightSubArraySum\\n\\n if(Math.abs(diff) % 2 === 0) output++\\n }\\n\\n return output\\n};\"], [53400, 1.0204, null], [53500, 2.551, null], [53600, 1.0204, null], [53700, 1.5306, null], [53800, 1.5306, null], [53900, 3.0612, null], [54000, 3.5714, null], [54100, 5.102, null], [54200, 6.6327, null], [54300, 5.102, null], [54400, 5.102, null], [54500, 5.102, null], [54600, 4.5918, null], [54700, 2.551, null], [54800, 2.551, null], [54900, 2.0408, null], [55000, 1.0204, null], [55100, 1.0204, null], [55200, 2.0408, null], [55300, 0.5102, null], [55400, 3.0612, null], [55500, 2.551, null], [55600, 2.0408, null], [55700, 1.0204, null], [55800, 0.5102, null], [55900, 2.0408, null], [56000, 0.5102, null], [56100, 2.0408, null], [56200, 0.5102, null], [56300, 2.0408, null], [56400, 1.5306, null], [56500, 1.0204, null], [56700, 0.5102, null], [56800, 1.5306, null], [57000, 0.5102, null], [57100, 1.5306, null], [57200, 1.5306, null], [57300, 3.5714, null], [57500, 3.5714, null], [57600, 1.5306, null], [57700, 0.5102, null], [57900, 0.5102, null], [59000, 0.5102, null], [60200, 0.5102, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar countPartitions = function(nums) {\\n let left=[];\\n let right=[];\\n left[0]=nums[0];\\n for(let i=1;i<nums.length;i++){\\n left[i]=nums[i]+left[i-1];\\n }\\n right[nums.length-1]=0;\\n for(let i=nums.length-2;i>=0;i--){\\n right[i]=nums[i+1]+right[i+1];\\n }\\n let count=0;\\n console.log(left,right)\\n for(let i=0;i<nums.length-1;i++){\\n if(Math.abs(left[i]-right[i])%2==0){\\n count++;\\n }\\n }\\n return count;\\n};\"], [60600, 0.5102, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar countPartitions = function(nums) {\\n const length = nums.length;\\n let sum = nums.reduce((a, b) => a + b, 0), count = 0;\\n for(let i = 0; i < length - 1; i++){\\n sum = sum - nums[i] * 2;\\n console.log(sum);\\n if(sum % 2 === 0) count++;\\n }\\n\\n\\n // for(let i = 0; i < length - 1; i++){\\n // arr.push(nums.shift());\\n // const sum = arr.reduce((a, b) => a + b, 0) - nums.reduce((a, b) => a + b, 0);\\n // if(sum % 2 === 0) count++;\\n // }\\n return count;\\n};\"]]",
"runtime": 1,
"runtimeDistribution": "[[0, 42.3469, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar countPartitions = function(nums) {\\n let count = 0;\\n let right = nums.reduce((a, c) => a + c, 0);\\n let left = 0;\\n for (let i=0; i<nums.length-1; ++i) {\\n right -= nums[i];\\n left += nums[i];\\n if ((left - right) % 2 == 0) {\\n ++count;\\n }\\n }\\n return count;\\n};\"], [1, 27.0408, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar countPartitions = function(nums) {\\n let sum = 0, res = 0, subSum=0;\\n for(let n of nums){\\n sum+=n\\n }\\n for(let i=0; i<nums.length-1; i++){\\n subSum+=nums[i]\\n if((subSum-(sum-subSum))%2 == 0) res++\\n }\\n return res\\n};\"], [2, 11.7347, null], [3, 6.6327, null], [4, 3.0612, null], [5, 2.0408, null], [11, 0.5102, null], [26, 0.5102, null], [27, 0.5102, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar countPartitions = function(nums) {\\n let left=[];\\n let right=[];\\n left[0]=nums[0];\\n for(let i=1;i<nums.length;i++){\\n left[i]=nums[i]+left[i-1];\\n }\\n right[nums.length-1]=0;\\n for(let i=nums.length-2;i>=0;i--){\\n right[i]=nums[i+1]+right[i+1];\\n }\\n let count=0;\\n console.log(left,right)\\n for(let i=0;i<nums.length-1;i++){\\n if(Math.abs(left[i]-right[i])%2==0){\\n count++;\\n }\\n }\\n return count;\\n};\"], [43, 0.5102, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar countPartitions = function(nums) {\\n let count=0\\n for(i=0;i<nums.length-1;i++){\\n let s1=0\\n let s2=0\\n for(j=0;j<nums.length;j++){\\n if(j<=i){\\n s1+=nums[j]\\n }else{\\n s2+=nums[j]\\n }\\n }\\n console.log(s1,s2)\\n if((Math.abs(s1-s2))%2==0){\\n count++\\n }\\n }\\n return count\\n};\"]]"
},
"python3": {
"code": "class Solution:\n def countPartitions(self, nums: list) -> int:\n if sum(nums) % 2 != 0:\n return 0\n return len(nums) - 1",
"memory": 1800,
"memoryDistribution": "[[1800, 99.0643, \"class Solution:\\n def countPartitions(self, nums: list) -> int:\\n if sum(nums) % 2 != 0:\\n return 0\\n return len(nums) - 1\"], [17000, 0.117, \"class Solution:\\n def countPartitions(self, nums: List[int]) -> int:\\n n = len(nums)\\n total = sum(nums)\\n count = 0\\n left_sum = 0\\n\\n for i in range(n - 1):\\n left_sum += nums[i]\\n right_sum = total - left_sum\\n diff = abs(left_sum - right_sum)\\n if diff % 2 == 0:\\n count += 1\\n\\n return count\"], [17500, 0.8187, \"class Solution:\\n def countPartitions(self, nums: List[int]) -> int:\\n count = 0\\n for i in range(0, len(nums) - 1):\\n if (sum(nums[:i]) - sum(nums[i:])) % 2 == 0:\\n count += 1\\n return count\\n\"], [17600, 7.3684, null], [17700, 22.3392, null], [17800, 24.6784, null], [17900, 19.5322, \"class Solution:\\n def countPartitions(self, nums: List[int]) -> int:\\n postfix_sum = [nums[-1]]\\n for i in range(2, len(nums), 1):\\n postfix_sum.append(nums[-i] + postfix_sum[i - 2])\\n # print(postfix_sum)\\n counter = 0\\n total = 0\\n for i in range(len(nums) - 1):\\n total += nums[i]\\n if (total - postfix_sum[-(i + 1)])%2==0:\\n counter += 1\\n return counter\"], [18000, 18.9474, \"class Solution:\\n def countPartitions(self, nums: List[int]) -> int:\\n n = len(nums)\\n total = sum(nums)\\n if total % 2 == 0:\\n return n - 1\\n return 0\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 59.0643, \"class Solution:\\n def countPartitions(self, nums: List[int]) -> int:\\n n = len(nums)\\n total = sum(nums)\\n if total % 2 == 0:\\n return n - 1\\n return 0\"], [1, 6.0819, \"class Solution:\\n def countPartitions(self, nums: List[int]) -> int:\\n c = 0\\n s = 0\\n for i in range(len(nums)-1):\\n s = s +nums[i]\\n d =0\\n for j in range(i+1, len(nums)):\\n d +=nums[j]\\n if abs(s-d)%2==0:\\n c+=1\\n return c\\n \"], [2, 5.1462, null], [3, 18.2456, \"class Solution:\\n def countPartitions(self, nums: List[int]) -> int:\\n postfix_sum = [nums[-1]]\\n for i in range(2, len(nums), 1):\\n postfix_sum.append(nums[-i] + postfix_sum[i - 2])\\n # print(postfix_sum)\\n counter = 0\\n total = 0\\n for i in range(len(nums) - 1):\\n total += nums[i]\\n if (total - postfix_sum[-(i + 1)])%2==0:\\n counter += 1\\n return counter\"], [4, 6.9006, \"class Solution:\\n def countPartitions(self, nums: List[int]) -> int:\\n full_summ = sum(nums)\\n cont = 0\\n res = 0\\n\\n pref = []\\n suf = []\\n\\n for i in range(len(nums)-1):\\n cont += nums[i]\\n suf.append(full_summ-cont)\\n pref.append(cont)\\n if ((cont - full_summ + cont) % 2 == 0):\\n res += 1\\n\\n return res\"]]"
},
"ruby": {
"code": "def count_partitions(nums)\n total = nums.sum\n total.even? ? nums.length - 1 : 0\nend",
"memory": null,
"memoryDistribution": "[[211800, 25.0, \"# @param {Integer[]} nums\\n# @return {Integer}\\ndef count_partitions(nums)\\n length_of_array = nums.length\\n count = 0 \\n for i in (1..(length_of_array -1))\\n left_sum = nums[0..i].sum\\n right_sum = nums[(i+1)..(length_of_array-1)].sum\\n if (left_sum - right_sum).abs % 2 == 0\\n count += 1\\n end \\n end\\n count\\n \\nend\"], [212200, 25.0, \"# @param {Integer[]} nums\\n# @return {Integer}\\n\\ndef find_abs(x)\\n if x > 0\\n return x\\n end\\n -x\\nend\\n\\ndef count_partitions(nums)\\n n = nums.size\\n result = 0\\n right = 0\\n left = 0\\n for i in 0 ... n do\\n right += nums[i]\\n end\\n for i in 0 ... (n - 1) do\\n left += nums[i]\\n right -= nums[i]\\n result += 1 if find_abs(right - left) % 2 == 0\\n end\\n result\\nend\"], [212300, 50.0, \"# @param {Integer[]} nums\\n# @return {Integer}\\ndef count_partitions(nums)\\n nums.sum.even? ? nums.length - 1 : 0\\nend\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 75.0, \"# @param {Integer[]} nums\\n# @return {Integer}\\ndef count_partitions(nums)\\n nums.sum.even? ? nums.length - 1 : 0\\nend\"], [4, 25.0, \"# @param {Integer[]} nums\\n# @return {Integer}\\ndef count_partitions(nums)\\n length_of_array = nums.length\\n count = 0 \\n for i in (1..(length_of_array -1))\\n left_sum = nums[0..i].sum\\n right_sum = nums[(i+1)..(length_of_array-1)].sum\\n if (left_sum - right_sum).abs % 2 == 0\\n count += 1\\n end \\n end\\n count\\n \\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list:
import random
random.seed(seed)
# Sample solution based on the provided sample:
def sample_solution(nums):
if sum(nums) % 2 != 0:
return 0
return len(nums) - 1
test_cases = []
categories = []
# Boundary cases (minimum length arrays)
categories.append([1, 1]) # Sum=2 (even) → answer = 1 partition.
categories.append([1, 2]) # Sum=3 (odd) → answer = 0.
categories.append([2, 4]) # Sum=6 (even) → answer = 1.
# Special patterns and core examples
categories.append([2, 4, 6, 8]) # All evens → answer = 3.
categories.append([1, 3, 5, 7]) # All odds → sum=16 (even) → answer = 3.
categories.append([10, 10, 3, 7, 6]) # Provided example → answer = 4.
categories.append([1, 2, 2]) # Provided example → answer = 0.
# Structured and patterned arrays
categories.append(sorted([random.choice(range(2, 101, 2)) for _ in range(10)]))
categories.append(sorted([random.choice(range(1, 100, 2)) for _ in range(10)], reverse=True))
# Fill remaining cases with random arrays (ensure length is at least 2)
while len(categories) < num_cases:
n = random.randint(2, 100)
arr = [random.randint(1, 100) for _ in range(n)]
categories.append(arr)
for arr in categories[:num_cases]:
# Serialize input as comma-separated integers.
input_str = ",".join(map(str, arr))
# Expected output computed using the sample solution.
output_str = str(sample_solution(arr))
test_cases.append({"input": input_str, "output": output_str})
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
try:
# The serialization format is a simple integer in string form.
expected = int(expected_output.strip())
program = int(program_output.strip())
return expected == program
except Exception:
return False
|
[{"input": "1,1", "output": "1"}, {"input": "1,2", "output": "0"}, {"input": "2,4", "output": "1"}, {"input": "2,4,6,8", "output": "3"}, {"input": "1,3,5,7", "output": "3"}, {"input": "10,10,3,7,6", "output": "4"}, {"input": "1,2,2", "output": "0"}, {"input": "4,14,16,18,30,32,36,82,96,96", "output": "9"}, {"input": "95,87,75,69,55,27,11,11,5,3", "output": "9"}, {"input": "65,78,4,72,26,92,84,90,70,54,29,58,76,36,1,98,21,90,55,44,36,20,28,98,44,14,12,49,13,46,45", "output": "30"}, {"input": "34,6,94,59,69,16,49,11,71,38,81,80,47,74,25,91,9,6,85,30,99,38,11,30,13,49,36,59,82,47,21,48,46,27,86,35,90,88,83,10,78,82,22,69,94,32,21,60,49,35,82,89,72,29,88,42,99,100,8,30,5,41,52,35,9,28,73,92,41,28,84,64,51,83,59,19,34,18,32", "output": "78"}, {"input": "72,69,34,96,75,55,75,52,47,29,18,66,64,12,97,7,15,20,81,21,88,55,77,9,50,49,77,60,68,33,71,2,88,93,15,88,69,97,35,99,83,44,15,38,56,21,59,1,93,93,34,65,98,23,65,14,81,39,82,65,78,26,20,48,98,21,70,100,68,1,77,42,63,3,15,47,40,31,8,31,73,11,11,94,63,9,98,69,99,17,17,85,61,71,22,34,68", "output": "96"}, {"input": "55,28,70,97,94,89,26,92,40,52,86,84,48,57,67,58,16,32,29,9,44,3,76,71,30,76,29,1,10,91,81,8,30,9,5,43,10,66,31,36,86,63,28,70,17,93,74,74,61,32,61,53,25,13,13,85,56,46,55,53,60,94,7,87,84,83,13,8,52,94,44,14,32,25,25,69,58,18,55", "output": "0"}, {"input": "36,60,32,10,57,71,13,7,84,70,2,12,97,31,22,53,63,62,28,52,8,22,49,1,50", "output": "24"}, {"input": "59,37,55,90,94,72,85,92,63,20,25,38,28,8,75,95,70,8,96,41,8,7,75,62,65,68,21,8,66,11,24,9,77,9,87", "output": "34"}, {"input": "52,16,73,32,75,77,6,80,11,54,85,75,73,67,41,34,27,86,92,41,31,34,51,17,86,83,39,59,41,97,10,2", "output": "0"}, {"input": "80,73,13,10,69,28,65,34,17,45,9,32,48,37,21,57,70,91,39,79,84,68,2,86,71,39,85,14,18,34,15,14,96,71,20,35,37,78,27,92,44,27,88,82,34,65,63,33,7,12,82,55,36,6,1,43,99,17,82,34", "output": "0"}, {"input": "95,57,71,91,55,72,2,15,10,89,20,70,5,48,75,71,19,56,17,6,40,47", "output": "0"}, {"input": "46,27,88,32,86,14,46", "output": "0"}, {"input": "53,80,96,20,31,21,23,53,4,23,95,43,53,86,95,32,35,21,90,14,49,5,61,29,26,59,45,40,30,29,4,85,25,52,43,36,9,99,36,45,83,66,52,87,69,43,4,15,34,23,75,34,5,14,77,56,45,94,41,56,78,66,15,50,74,25,33,6,91,56,1,67,69", "output": "0"}, {"input": "93,95,95,86,26,47,56,9,86,43,80,41,85,16,93,39,65,40,86,53,42,52,90,38,71,17,25,54,86,49,87,96,23,79,73,39,52,71,1,39,37,27,56,75,78,84,42,60,57,57,87,28,66,61,95,22,85,11,37,66,85,82,80,43,12,97,31,87,40,29,26,19,4,6,32,61,79,99,10,59,54,81,74,25,92,90,50,64,52", "output": "88"}, {"input": "19,84,89,1,97,99,14,100,55,29,23,90,67,60,7,72,32,16,59,18,60,86,68,72,77,41,97,57,79,93,65,55,71", "output": "32"}, {"input": "21,96,61,58,34,97,32,82,36,99,100,67,63,81,31,36,57,10,92,37,31,35,43,41,70,11,18,20,30,50,89,20,91,28,9,54,53,43,70,60,54,8,27,54,50,99,75,90,3,98,74,49,62,1,46,39,97,50,54", "output": "58"}, {"input": "96,95,70,78,29,63,29,35,56,63,4,50,44,86,87,52,93,22,60,17,80,69,4,51,76,73,85,4,11,83,55,18,60,24,7,34,49,42,28,59,42,44,98,49,36,97,54,33,11,61,3,96,70,7,45,29,84,9,100,84,6,97,4,32,26,3,80,20,31,17", "output": "0"}, {"input": "86,15,73,28,60,90,33,99,48,22,78,78,96,92,15,100,21,40,14,75,4,40,74,87,49,51,92,26,10,76,89,81,32,14,90,99,39,88,77,16,73,6,45,69,55,85,48,9,65,83,44,2,54,63,14,56,47,82,59,91,20,56", "output": "0"}, {"input": "94,67,84,35,79,69,100,62,60,56,94,76,35,42,32,12,36,58,32,97,60,73,79,86", "output": "23"}, {"input": "44,4,64,42,24,63,28,46,34,44,36,77,90,36,72,2,67,25,11,31,93,53,63,72,98,31,89,61,83,92,63,58,3,12,38,29,52,89,32,40,85,75,48,61,71,68,45,55,96,71", "output": "49"}, {"input": "46,90,59,35,40,33,30,16,93,25,41,16,96,69,98,89,24,25,28,95,62,36,93,76,98,68,77,37,13,25,38,30,47,23,39,2,91,69,17,36,6,7,71,38", "output": "0"}, {"input": "17,82,97,63,14,2,74,37,61,62,57,44,24,7,33,62,15,9,52,63,10,74,81,88,7,20,20,73,39,11,32,16,72,98,54,78,77,80,29,100,67,49,58,57,39,76,55,40,73,80,8,79,95,13,98,27,81,28,34,85,11,21,31,23,71,10,21,1,53,58,89,77,61,38,5,30,37,91,37,90,59,10,88,30,34,81,76,85,26,55,15", "output": "90"}, {"input": "29,83,20,35,19,10,8,22,40,77,96,73,37,57,16,60,89,39,90,52,35,65,70,64,57,11,77,6,56,95,42,78,33,4,12,30,87,74,76,3,98,87,35,74,6,98,97,23,61,67,84,57,36,24,75,56,82,63,12,61,45,53,43,42,86,14,21,43,53,89,64", "output": "70"}, {"input": "85,52,98,71,5,59,12,41,33,42,15,99,52,66,1,85,70,60,53,7,25,67,47,80,97,64,81,57,98,7,27,35,71,17,37,57,90,63", "output": "37"}, {"input": "4,81,78,31,91,21,40,71,2,71,53,12,29,15,60,16,83", "output": "16"}, {"input": "64,92,38,66,91,35,54,62,61,32,59,71,19,50,25,77,66,96,18,9,36", "output": "0"}, {"input": "54,44,65,35,1,37,93,39,76,75,85,63,20,58,69,62,45,43,71,98,70,49,59,42,25,90,31,74,50,30,100,53,6,41,96,61,91,49,50,85,84,20,64,5,17,65,76,43,13,57,13,68,59,2,93,19,53,84,20,10,61,34,44,80,89,51,84,11,43,87,69,49,41,81,92,98,63,70,5,80,9,31,81,88,37,30,96,12,56,13,98,82,91,13,57,22,89,39,4,6", "output": "99"}, {"input": "8,38,46,48,56,19,32,68,53,73,88,24,22,23,11,79,49,80,88,31,64,75,19,30,60,82,33,59,33,86,2,60,37,87,70,21,10,57,45,76,39,82,55", "output": "42"}, {"input": "33,59,39,26,50,62,14,31,49,74,46,74,38,90,38,3,85,51,36,2,73,88,100,96,7,78,96,64,37,100,30,78,46,29,82,25,80,33,87,97,93,99,85,88,18,81,13,81,83,6,40,57,5,75,47,94,17,12,38,42,96,54,23,26,17,70,47,68,65,35,22,33,62,38,96,44,15,60,10,19,97,29,87,93,87,51,72,47,12,51", "output": "89"}, {"input": "34,69,16", "output": "0"}, {"input": "48,87,96,87,34,75,49,82,48,14,87,30,61,4,80,72,42,79,29,83,9,82,60,90,39,84,53,15,18,6,5,39,64,15,13,31,69,18,50,59,48,86,96,90,70,54,76,96,94,20,54,84,13,63,79,53,36,5,89,48", "output": "59"}, {"input": "57,57,31,47,13,88,48,70,83,46,8,51,36,25,16,59,12,85,28,83,82,77,3,7,43,32,17,73,27", "output": "28"}, {"input": "98,71,27,76,28,30,43,100,19,77", "output": "0"}, {"input": "36,19", "output": "0"}, {"input": "70,33,23,15,85,4,17,2,46,31,76,42,3,23,34,7,17,95", "output": "0"}, {"input": "68,15,96,9,61,58,100,47,66,76,14,58,65,29,79,6,94,85,67,39,59,83,4,8,62,52,55,88,14,63,92,57,10,11,42,78,19,9,17,36,80,82,75,71,92,42,49,77,68,38,59,65,78,56,13", "output": "54"}, {"input": "15,84,84,99,71,93,28,56,58,30,53,44,59,52,54,94,13,41,55,41,86,33,48,20,88,61,9,12,11,12,56,13,96,95,48,17,72,8,76,72,72,43,86,16,53,46,86,97,55,93,7,37,77,40,46,14,74,65,28,20,85,62,29,14,45,72,48,15,98,36,74,29,55,72,99,80,79,87,83,72,4,78,85,89,35,4,24,35,90,98,40", "output": "90"}, {"input": "45,1,24,19,73,85,52,9,19,95,82,4,12,96,68,28,49,54,59,44,21,48,40,93,42,100,73,77,11,7,20,21,97,80,7,87,11,35,57,85,55,63,78,57,54", "output": "0"}, {"input": "28,97,66,15,45,56,15,37,87,87,76,63,68,86,40,6,29,51,77,8,1,27,39,28,99,18,98,33,38,42,16,1,64,96,56,23", "output": "35"}, {"input": "49,69,91,30,65,72,86,46,10,51,95,6,56,3,59,10,41,74", "output": "0"}, {"input": "74,52,91,82,54,38,15,52,3,42,22,80,59,89,47,12,56,14,32,56,76,52,68,11,51,40,96,44,29,43,100,22,10,66,82,15,68,66,25,100,45,45,94,83,19,31,14,19,33,26,23,78,20,98,98,84", "output": "55"}, {"input": "23,99,81,64,60,97,73,98,75,58,88", "output": "10"}, {"input": "83,82,80,42,81,41,20,57,9,61,57,81,39,36,76,8,46,65,10,40,60,58,5,8,48,37,10,83,12,79,77,65,50,60,75,71,95,6,58,74,84,25,42,78,61,65,20,8,58,14,44,92,11,65,83,23,6,32,91,57,57,68,67,79,21,47,48,37,50,53,100,44,87,77", "output": "0"}, {"input": "81,83,43,9,43,13,72,87", "output": "0"}, {"input": "37,33,93,85,78,20,43,11,75,85,19,45,40,84,90,85,51,17,77,91,11,40,72,49,83,43,17,86,90,95,88,68,12,83,86,55,66,47,3,47,40,24,28,44,99,63,25,29,18,20,10", "output": "50"}, {"input": "13,65,99,70,95,68,5,85,44,99,80,17,77,49,20,21,24,89,99,80,22,93,57,6,53,47,87,93,31,57,79,37,97,96,58,30,69,31,40", "output": "38"}, {"input": "25,48,87,74,57,60,99,37,100,49,65,68,54,21,26,78,18,33,7,83,62,48,71,14,92,67,16,37,11,98,21,35,58,66,19,56,12,29,58,45,4,54,7,51,65,48,31,50,11,48,29,4,41,13,92,84,43,19,18,5,37,61", "output": "0"}, {"input": "18,98,91,61,58,79,1,11,3,33,28,20,71,94,78,68,55,15,100,37,31,39,16,7,31,54,82,80,59,9,15,64,77,69,3,81,66,74,31,92,19,38,55,1,79,46,31,74,54,24,86,86,11,68,47,9,68,70,65,65,71,3,50,61,6,82,50,48,33,96,3,46,9,45,31,94,85,81,14,99,75,95,97,43,18,6,46,70,44,83,23", "output": "90"}, {"input": "60,90,62,81,24,18,9,92,100,59,5,38,26,6,26,6,41,40,66,51,70,61,33,5,97,83,25,37,46,100,7,84,43,35,16,48,56,52,96,57,50,44,24,64,89,64,48,67,35,11,94,55,11,56,78,24,70,38,42,14,11,42,85,38,40,58,78,92,55,22,89,57,45,58,6,94,46,79,56,36,82,8,10,86,82,52,47,66,96", "output": "0"}, {"input": "21,4,19,78,87,57,5,17,9,31,100,83,47,47,50,73,5,78,20,87,58,48,48,57,98,10,74,18,68,47,51,41,84,36,32,15,4,95,24,64,67,50,72,16,34,100,34,91,58,28,79,37,89,63,26,16,18,10,58,23,92,57,12,88,41,86,45,91,9,71,70,38,39,21,92,91,90,82,23,47,66,29,16,26,18,31,64,4", "output": "87"}, {"input": "71,74,48,60,71,17,79,12,9,40,51,92,93,62,68,53,99,53,74,10,17,41,83,10,58,60,88,67,45,17,100,71,82,76,24,99,17,56,65,8,16,67,20,39,22,21,42,91", "output": "47"}, {"input": "45,67,37,11,33,26,82,71,36,17,81,39,79,69,12,65,83,22,76,75,20,22,85,80,93,78,44,73,6,4", "output": "0"}, {"input": "6,83,99,74,34,84,27,99,74,54,80,82", "output": "11"}, {"input": "64,81,70,38,83", "output": "4"}, {"input": "62,32,88,52,39,59,10,89,8,21,57,54,62,60,27,44,78,19,41,92,41,94,45,52,17,98,48,66,72,14,41,31,60,16,35,58,32,19,13,7", "output": "0"}, {"input": "50,79,54,32,21,42,74,93,41,25,98,21,64,66,60,64,40,64,3,12,51,65,59,31,28,75,46,7,7,37,64,77,84,87,61,37,69,2,14", "output": "38"}, {"input": "18,34,94,47,98,52,47,6,52,7,73,72,25,47,71,37,10,50,65,58,98,71,36,80,88,79,16,17,13,51,48,44,72,47,97,19,26,78,66,52,65,6,6,5,18,92,43,61,67,59,20,78,66,18,42,79,41", "output": "0"}, {"input": "51,79,95,39,76,44,65,66,69,63,91,73,39,61,3,48,43,87,15,54,75,40", "output": "21"}, {"input": "89,81,4,77,61,34,84,100,75,74,30,93,7,75,62,22,68,81,93,80,100,49,19,88,32,5,74,90,15,25,3,57,41,54,20,53,89,27,53,65,100,79,61,95,94,8,91,18,67,27,72,42,85,62,68,49,41,23,59,69,44,70,46,87,99,93,88,83,89,34,79,62,25,32,36,72,39,29,39,99,37,91,27,89,91,63,41,62,45,72,93,36,37,16", "output": "93"}, {"input": "87,70,49,51,45,99,19,38,6,37,92,11,45,57,84,33,96,62,28,26,69,35,72,90,35,18,14,79,95,76,31,32,7,86,68,29,82,30,7,13,53,43,92,61,13,88,99,18,1,71,21,53,84,61,62,84,26,97,37,42,37,83,8,99,12,84,74,30,69,95,93,5,23,54,23", "output": "74"}, {"input": "51,64,24,96,38,5", "output": "5"}, {"input": "39,73,78", "output": "2"}, {"input": "43,37,59,83,70,68,64,18,65,60,35,25,15,43,21", "output": "14"}, {"input": "59,83,33,92,24,2,95,44,38,73,87,97,25,23,79,82,52,55,66,42,12,52,86,13,24,18,62,42,32,1,34,50,31,58,97,35,43,39,75,93,74,2,34,84,47,89,31,8,86,16,60,40,21,52,88,65,91,99,40,89,16,82,38,48,79,29,29,18,62,20,59,96,78,48,54,90,71,61,97,69,86,28,98,32,88,97,77,11,68,58,68,91,47,10,73", "output": "94"}, {"input": "8,71,65,26,74,69,20,22,42,67,57,15,88,27,92,75", "output": "15"}, {"input": "12,66,58,8,59,17,66,54,59,73,8,72,60,87,40,93,3,51,33,1,96,28,75,10,6,55,45,90,9,70,8,9,61,5,37,53,24,99,18,99,83,94,83,54,48,49,58,49,49,11,88,85,70,18,84,45,16,23,69,51,68,17,94,29", "output": "63"}, {"input": "97,3", "output": "1"}, {"input": "60,87,93,70,55,69,49,30,32,59,45,20,36,25,93,98,15,5,85,54,79,99,3,31,27,9,13,77,5,58,77,87,91,7,32,95,6,52,57,30", "output": "0"}, {"input": "28,97,100,8,18,65,38,30,94,74,41,74,77,99,87,42,31,39,19,85,67,29,53,39,36,8,72,76,95,23,81,87,55,72,64,7,45,83,86,49,68,41,90,54,53,20,39,49,24,97,69,61,31,29,39,91,19,60,8,72,53,54,72,68,18,50,32,33,27,43,83", "output": "70"}, {"input": "58,48,12,69,93,25,7,35,49,87,78,78", "output": "0"}, {"input": "10,25,98,76,93,86,72", "output": "6"}, {"input": "62,27,43,39,2,28,25,95,16,96,97,62,32,90,78,91,27,51,31,71,42,100,37,49,60,69,84,46,40", "output": "28"}, {"input": "47,66,64,60,13,93,61,98,41,27,48,41,53,6,73,29,95,19,3,34,71,75,75,93,54,38,20,26,43,30,49,73,32,64,71", "output": "0"}, {"input": "88,44,33,98,63,93,83,95,63,59,22,94,46,22,18,93,70,63,24,70,83,8,68,5,10,86,7,98,1,53,18,81,30,9,91,20,2,28,65,59,48,8,80,82,86,79,62,85,63,3,1,69,71,53,2,3,68,93,36,69,37,3,65,90,87,56,23,14,13,68,20,31,25,80,68,33,46,35,51,11,48,52,59,73,32", "output": "84"}, {"input": "29,39,88,11,84,84,98,5,12,52,49,49,71,61,8,82,2,90,22,11,64,56,83,43,73,13,68,6,30,28,89,73,61,35,6,10,88,36,70,73,85,5,23,41,3,27,76,19,97,92,51,10,39,21,73,31,73,50,87,70,43,50,97,95,18,89,93,11,65,96,45,7,13,56,30,10,44,78,99,79,77,51,100,42,4,82,35,58,63,30,46", "output": "0"}, {"input": "49,56,24,88,75,85,49,11,99,80,38,32,92,10,11,35,20,49,92,82,20,95,50,41,47,14,12,1,40,57,47,98,35,14,17,12,24,56,58,72,72,66,53,14,4,12,46,71,12,77,77,42,50,2,38,53,50,100,11,93,72,32,74,67,22,88,49,22,18,35,39,35", "output": "0"}, {"input": "19,9,22,56,36,54,39,62,10,47,33,32,93,81,64,77,79,26,59,14,18,39,1,51,43,80,49,43,57,43,56,84,77,18,39,42,78,89,26,62,41,23,51,41,38,95,89,82,63,74,32,42,49,36,51,47,15,73,26,76,70,24,88,99,71", "output": "0"}, {"input": "94,60,91,27,57", "output": "0"}, {"input": "89,9,53,87,64,18,82,39,31,33,85,20,92,55,49,10,58,77,62,75,52,69,65,89,54,70,5,47,90,69,77,82,11,14,99,32,85,86,46", "output": "38"}, {"input": "83,79,6,73,83,87,83,52,97,43,56,14,2,13,34,29,66,96,67,72,75,89,74", "output": "0"}, {"input": "58,48,51,60,99,87,76,89,65,20,45,4,62,14,38,54,11,15,94,19,45,40,44,59,27,67,62,45,61,13", "output": "29"}, {"input": "93,90,58,41,9,39,6,91,15,3,44,83,14,87,22,95,32,67,23,71,21,43,72,55,60,30,52,81,24,24,82,85,56,51,4,95,79,26,58,76,55,50,1,91,28,27,36,97,91,9,74,14,69,24,47,42,26,59", "output": "0"}, {"input": "34,86,63,68,82,41,77,50,79,51,76,15,45,46,59,80", "output": "15"}, {"input": "87,91,39,79,76,11,87,18,41,16,31,40,15,24,48,89,19,66,50,54,77,18,74,50", "output": "23"}, {"input": "24,63,82,69,89,83,23,72,22,63,37,18,24,41,58,80,7,46,2,63,18,25,50,72,65,84,64,53,88,63,54,91,57,63,22,11,73,4,98,29,38,5,36,29,69,37,22,100,59,73,96,99,99,64,71,66", "output": "0"}, {"input": "74,15,35,100,70,47,70,97,6,98,93,57,70,28,55,14", "output": "0"}, {"input": "84,97,32,39,5,58,34,45,12,57,16,100,31,27,95,76,89,45,91,79,81,55,22,79,18,27,27,8,73,45,69,36,77,69,22,42,91,38,38,74,35,66,87,13,18,97,53,8,36,84,17,90,17,32,19,92,42,32,98,87,51,63,19,74,81,35,81,54,49,58,10,82,99,12,52,66,96,36,89,48,59,63,42,75,1,100,94,12,94,59,82,86,90,46,9,69", "output": "95"}, {"input": "28,55,28,64,35,42,37,44,71,74,17,73,63,44,88,98,7,6,13,81,59,3,16,21,57,59,1,55,26,89,17,84,39,21,36,12,84,47,33,11,48,86,84,22,7,51,81,40,93,90,97,30", "output": "0"}, {"input": "84,12,91,13,1,28,62,10,17,76,29,67,88,57,2,2,90,44,16,55,89,17,62,10,30,50,12,94,14,14,41,48,39,18,49,100,97,18,83,87,19,9,68,73,2,79,84,22,57,45,93,28,81,96,20,53", "output": "0"}, {"input": "88,57,28,12,13,18,97,16,76,94,50,45,55,41,18,32,36,83,11,32,71,77,77,93,78,37,100,89,4,85,39,27,67,78,66,25,96,51,38,83,7,31,64,50,15,31,64,82,77,10,68,2,47,41,17,50,73,54,47,70,88,23,98,61,99,10,3,76,9,2,34,28,6,8,51,65,37,81,92,65", "output": "0"}, {"input": "54,55,90,52,11,82,69,69,79,20,36,11,40,11,66,27,20,69,42,51,76,82,98,84,88,83,9,40,90,56,94,31,8,32,12,56,15,59,79,78,8,40,86,95,85,95,23,16,2,91,18,90,2,21,64,45,67,67,93,34,22,48,17,96,100,35,94,16,99,4,43,55,35,68,9,34,92,74,81,10,64,59,66,47,8,64,73,22,48,21,33,99,14,74,87,93,15,30,95,66", "output": "99"}, {"input": "6,2", "output": "1"}, {"input": "6,61,47,50,20,23,5,71,92,95,84,54,29,42,32,54,93,41,35,10,74,48,16,65,87,7,23,29,67,6,52,9,60", "output": "0"}]
|
{
"cpp": "==Code Submission==\nvector<int> deserialize_stdin(const string &input) {\n vector<int> nums;\n string token;\n stringstream ss(input);\n while(getline(ss, token, ',')) {\n if (!token.empty())\n nums.push_back(stoi(token));\n }\n return nums;\n}\n\nstring serialize_stdout(int result) {\n return to_string(result);\n}\n\nint main() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n string line;\n getline(cin, line);\n vector<int> nums = deserialize_stdin(line);\n Solution sol;\n int ans = sol.countPartitions(nums);\n cout << serialize_stdout(ans);\n return 0;\n}",
"golang": "==Code Submission==\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n line, _ := reader.ReadString('\\n')\n line = strings.TrimSpace(line)\n parts := strings.Split(line, \",\")\n nums := make([]int, len(parts))\n for i, v := range parts {\n nums[i], _ = strconv.Atoi(v)\n }\n ans := countPartitions(nums)\n fmt.Printf(\"%d\\n\", ans)\n}",
"java": "public class Main {\n private static int[] deserializeIntArray(String input) {\n String[] parts = input.split(\",\");\n int[] nums = new int[parts.length];\n for (int i = 0; i < parts.length; i++) {\n nums[i] = Integer.parseInt(parts[i].trim());\n }\n return nums;\n }\n \n private static String serializeOutput(int result) {\n return Integer.toString(result);\n }\n \n public static void main(String[] args) throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n String line = br.readLine().trim();\n int[] nums = deserializeIntArray(line);\n Solution sol = new Solution();\n int ans = sol.countPartitions(nums);\n System.out.println(serializeOutput(ans));\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\nconst deserialize_stdin = (input) => {\n input = input.trim();\n if (input === \"\") return [];\n return input.split(',').map(Number);\n};\n\nconst serialize_stdout = (result) => {\n return result.toString();\n};\n\nlet input = '';\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\nprocess.stdin.on('data', chunk => input += chunk);\nprocess.stdin.on('end', () => {\n const nums = deserialize_stdin(input);\n const ans = countPartitions(nums);\n process.stdout.write(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\ndef deserialize_stdin(input_str):\n input_str = input_str.strip()\n if input_str == \"\":\n return []\n return list(map(int, input_str.split(',')))\n\ndef serialize_stdout(result):\n return str(result)\n\nline = sys.stdin.read().strip()\nnums = deserialize_stdin(line)\nsol = Solution()\nans = sol.countPartitions(nums)\nsys.stdout.write(serialize_stdout(ans))",
"ruby": "==Code Submission==\ninput = gets.strip\nnums = input.split(',').map(&:to_i)\nans = count_partitions(nums)\nputs ans.to_s"
}
|
3708
|
Zigzag Grid Traversal With Skip
|
zigzag-grid-traversal-with-skip
|
<p>You are given an <code>m x n</code> 2D array <code>grid</code> of <strong>positive</strong> integers.</p>
<p>Your task is to traverse <code>grid</code> in a <strong>zigzag</strong> pattern while skipping every <strong>alternate</strong> cell.</p>
<p>Zigzag pattern traversal is defined as following the below actions:</p>
<ul>
<li>Start at the top-left cell <code>(0, 0)</code>.</li>
<li>Move <em>right</em> within a row until the end of the row is reached.</li>
<li>Drop down to the next row, then traverse <em>left</em> until the beginning of the row is reached.</li>
<li>Continue <strong>alternating</strong> between right and left traversal until every row has been traversed.</li>
</ul>
<p><strong>Note </strong>that you <strong>must skip</strong> every <em>alternate</em> cell during the traversal.</p>
<p>Return an array of integers <code>result</code> containing, <strong>in order</strong>, the value of the cells visited during the zigzag traversal with skips.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">grid = [[1,2],[3,4]]</span></p>
<p><strong>Output:</strong> <span class="example-io">[1,4]</span></p>
<p><strong>Explanation:</strong></p>
<p><strong><img alt="" src="https://assets.leetcode.com/uploads/2024/11/23/4012_example0.png" style="width: 200px; height: 200px;" /></strong></p>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">grid = [[2,1],[2,1],[2,1]]</span></p>
<p><strong>Output:</strong> <span class="example-io">[2,1,2]</span></p>
<p><strong>Explanation:</strong></p>
<p><img alt="" src="https://assets.leetcode.com/uploads/2024/11/23/4012_example1.png" style="width: 200px; height: 240px;" /></p>
</div>
<p><strong class="example">Example 3:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">grid = [[1,2,3],[4,5,6],[7,8,9]]</span></p>
<p><strong>Output:</strong> <span class="example-io">[1,3,5,7,9]</span></p>
<p><strong>Explanation:</strong></p>
<p><img alt="" src="https://assets.leetcode.com/uploads/2024/11/23/4012_example2.png" style="width: 260px; height: 250px;" /></p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>2 <= n == grid.length <= 50</code></li>
<li><code>2 <= m == grid[i].length <= 50</code></li>
<li><code>1 <= grid[i][j] <= 2500</code></li>
</ul>
|
You are given an `m x n` 2D array `grid` of **positive** integers.
Your task is to traverse `grid` in a **zigzag** pattern while skipping every **alternate** cell.
Zigzag pattern traversal is defined as following the below actions:
- Start at the top\-left cell `(0, 0)`.
- Move *right* within a row until the end of the row is reached.
- Drop down to the next row, then traverse *left* until the beginning of the row is reached.
- Continue **alternating** between right and left traversal until every row has been traversed.
**Note** that you **must skip** every *alternate* cell during the traversal.
Return an array of integers `result` containing, **in order**, the value of the cells visited during the zigzag traversal with skips.
**Example 1:**
**Input:** grid \= \[\[1,2],\[3,4]]
**Output:** \[1,4]
**Explanation:**
****
**Example 2:**
**Input:** grid \= \[\[2,1],\[2,1],\[2,1]]
**Output:** \[2,1,2]
**Explanation:**
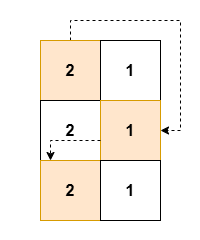
**Example 3:**
**Input:** grid \= \[\[1,2,3],\[4,5,6],\[7,8,9]]
**Output:** \[1,3,5,7,9]
**Explanation:**
**Constraints:**
- `2 <= n == grid.length <= 50`
- `2 <= m == grid[i].length <= 50`
- `1 <= grid[i][j] <= 2500`
|
Easy
|
[
"array",
"matrix",
"simulation"
] |
leetcode
|
https://leetcode.com/problems/zigzag-grid-traversal-with-skip
|
functional
| null | null | null | null |
{
"c": "/**\n * Note: The returned array must be malloced, assume caller calls free().\n */\nint* zigzagTraversal(int** grid, int gridSize, int* gridColSize, int* returnSize) {\n \n}",
"cpp": "class Solution {\npublic:\n vector<int> zigzagTraversal(vector<vector<int>>& grid) {\n \n }\n};",
"csharp": "public class Solution {\n public IList<int> ZigzagTraversal(int[][] grid) {\n \n }\n}",
"dart": "class Solution {\n List<int> zigzagTraversal(List<List<int>> grid) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec zigzag_traversal(grid :: [[integer]]) :: [integer]\n def zigzag_traversal(grid) do\n \n end\nend",
"erlang": "-spec zigzag_traversal(Grid :: [[integer()]]) -> [integer()].\nzigzag_traversal(Grid) ->\n .",
"golang": "func zigzagTraversal(grid [][]int) []int {\n \n}",
"java": "class Solution {\n public List<Integer> zigzagTraversal(int[][] grid) {\n \n }\n}",
"javascript": "/**\n * @param {number[][]} grid\n * @return {number[]}\n */\nvar zigzagTraversal = function(grid) {\n \n};",
"kotlin": "class Solution {\n fun zigzagTraversal(grid: Array<IntArray>): List<Int> {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param Integer[][] $grid\n * @return Integer[]\n */\n function zigzagTraversal($grid) {\n \n }\n}",
"python": "class Solution(object):\n def zigzagTraversal(self, grid):\n \"\"\"\n :type grid: List[List[int]]\n :rtype: List[int]\n \"\"\"\n ",
"python3": "class Solution:\n def zigzagTraversal(self, grid: List[List[int]]) -> List[int]:\n ",
"racket": "(define/contract (zigzag-traversal grid)\n (-> (listof (listof exact-integer?)) (listof exact-integer?))\n )",
"ruby": "# @param {Integer[][]} grid\n# @return {Integer[]}\ndef zigzag_traversal(grid)\n \nend",
"rust": "impl Solution {\n pub fn zigzag_traversal(grid: Vec<Vec<i32>>) -> Vec<i32> {\n \n }\n}",
"scala": "object Solution {\n def zigzagTraversal(grid: Array[Array[Int]]): List[Int] = {\n \n }\n}",
"swift": "class Solution {\n func zigzagTraversal(_ grid: [[Int]]) -> [Int] {\n \n }\n}",
"typescript": "function zigzagTraversal(grid: number[][]): number[] {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n vector<int> zigzagTraversal(vector<vector<int>>& grid) {\n vector<int> result;\n bool take = true;\n for (int i = 0; i < grid.size(); i++) {\n if (i % 2 == 0) {\n for (int j = 0; j < grid[i].size(); j++) {\n if (take) result.push_back(grid[i][j]);\n take = !take;\n }\n } else {\n for (int j = grid[i].size() - 1; j >= 0; j--) {\n if (take) result.push_back(grid[i][j]);\n take = !take;\n }\n }\n }\n return result;\n }\n};",
"memory": 3200,
"memoryDistribution": "[[3200, 23.2183, \"class Solution {\\npublic:\\n vector<int> zigzagTraversal(vector<vector<int>>& grid) {\\n vector<int> result;\\n bool take = true;\\n for (int i = 0; i < grid.size(); i++) {\\n if (i % 2 == 0) {\\n for (int j = 0; j < grid[i].size(); j++) {\\n if (take) result.push_back(grid[i][j]);\\n take = !take;\\n }\\n } else {\\n for (int j = grid[i].size() - 1; j >= 0; j--) {\\n if (take) result.push_back(grid[i][j]);\\n take = !take;\\n }\\n }\\n }\\n return result;\\n }\\n};\"], [31400, 0.4598, \"class Solution {\\npublic:\\n vector<int> zigzagTraversal(vector<vector<int>>& grid) {\\n int m = grid[0].size(), n = grid.size() * m;\\n vector<int> ans(n + 1 >> 1);\\n for (int i = 0, val; i < n; i += 2) {\\n if (i / m & 0b1) val = grid[i / m][m - 1 - i % m];\\n else val = grid[i / m][i % m];\\n ans[i >> 1] = val;\\n }\\n return ans;\\n }\\n};\"], [31600, 2.2989, \"class Solution {\\npublic:\\n vector<int> zigzagTraversal(vector<vector<int>>& grid) {\\n vector<int>vec;\\n int row = grid.size();\\n int col = grid[0].size();\\n int count1 = 0;\\n int count2 = 0;\\n for(int i = 0;i<row;i++){\\n if(count1 == 0){\\n for(int j = 0;j<col;j++){\\n if(count2%2 == 0){\\n cout<<grid[i][j]<<endl;\\n vec.push_back(grid[i][j]);\\n count2++;\\n }\\n else{\\n count2++;\\n }\\n }\\n count1++;\\n }\\n else if(count1 == 1){\\n for(int j = col-1;j>=0;j--){\\n if(count2%2 == 0){\\n cout<<grid[i][j]<<endl;\\n vec.push_back(grid[i][j]);\\n count2++;\\n }\\n else {\\n count2++;\\n }\\n }\\n count1 = 0;\\n }\\n }\\n return vec;\\n }\\n};\"], [31700, 13.5632, null], [31800, 24.8276, null], [31900, 35.6322, null], [32000, 12.8736, null], [32100, 1.1494, null], [32200, 0.4598, null], [32400, 0.2299, null], [32500, 0.9195, \"class Solution {\\npublic:\\n vector<int> zigzagTraversal(vector<vector<int>>& grid) {\\n int n = grid.size(), m = grid[0].size();\\n int r = 0, c = 0;\\n vector<int> ans;\\n int p = 0;\\n for (int i = 0; i < n; i++) {\\n vector<int> res;\\n for (int j = p; j < m; j++) {\\n res.push_back(grid[i][j]);\\n j++;\\n }\\n p ^= 1;\\n if (p == 0) {\\n reverse(res.begin(), res.end());\\n }\\n ans.insert(ans.end(), res.begin(), res.end());\\n }\\n return ans;\\n }\\n};\\n/// 1 2 1 3\\n/// 5 15 7 3 10\\n/// 4 14 12\"], [32600, 0.9195, \"class Solution {\\npublic:\\n vector<int> zigzagTraversal(vector<vector<int>>& grid) {\\n vector<int> zigzag, alternateVec;\\n int rows = grid.size();\\n if (rows == 0) return alternateVec;\\n int cols = grid[0].size();\\n\\n // Zigzag traversal of the grid\\n for (int i = 0; i < rows; i++) {\\n if (i % 2 == 0) { \\n // Even row: Traverse left to right\\n for (int j = 0; j < cols; j++) {\\n zigzag.push_back(grid[i][j]);\\n }\\n } else { \\n // Odd row: Traverse right to left\\n for (int j = cols - 1; j >= 0; j--) {\\n zigzag.push_back(grid[i][j]);\\n }\\n }\\n }\\n\\n // Extract alternate elements\\n for (size_t i = 0; i < zigzag.size(); i += 2) {\\n alternateVec.push_back(zigzag[i]);\\n }\\n\\n return alternateVec;\\n }\\n};\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 67.3563, \"class Solution\\n{\\npublic:\\n vector<int> zigzagTraversal(vector<vector<int>> &grid)\\n {\\n int col = 0;\\n int dim = grid.size() * grid[0].size();\\n\\n vector<int> ansArr;\\n for (int row = 0; row < grid.size(); row++)\\n {\\n if (row % 2 == 0)\\n {\\n while (col < grid[row].size())\\n {\\n ansArr.push_back(grid[row][col]);\\n col += 2;\\n }\\n col -= 2;\\n if (col == grid[row].size() - 1)\\n {\\n col = col - 1;\\n }\\n else if (col == grid[row].size() - 2)\\n col = col + 1;\\n }\\n else if (row % 2 == 1)\\n {\\n while (col >= 0)\\n {\\n ansArr.push_back(grid[row][col]);\\n col -= 2;\\n }\\n col += 2;\\n if (col == 1)\\n col = col - 1;\\n else if (col == 0)\\n col = col + 1;\\n }\\n }\\n return ansArr;\\n }\\n};\"], [1, 6.2069, \"class Solution\\n{\\npublic:\\n vector<int> zigzagTraversal(vector<vector<int>> &grid)\\n {\\n vector<int> ret;\\n int C = grid[0].size();\\n bool pick = true;\\n for (int i = 0; i < grid.size(); i++) {\\n if (i % 2 == 0) {\\n for (int j = 0; j < C; j++) {\\n if (pick) {\\n ret.push_back(grid[i][j]);\\n }\\n pick = !pick;\\n }\\n } else {\\n for (int j = C - 1; j >= 0; j--) {\\n if (pick) {\\n ret.push_back(grid[i][j]);\\n }\\n pick = !pick;\\n }\\n }\\n }\\n return ret;\\n }\\n};\"], [2, 4.1379, null], [3, 10.3448, \"class Solution {\\npublic:\\n vector<int> zigzagTraversal(vector<vector<int>>& grid) {\\n vector<int> ans; // Final result vector to store the zigzag traversal\\n int dir = 1; // Direction flag: 1 = left to right, 0 = right to left\\n int skip = 1; // Skip flag to alternate skipping every other element\\n\\n // Traverse each row in the grid\\n for (int i = 0; i < grid.size(); i++) {\\n if (dir == 1) {\\n // Traverse left to right\\n for (int j = 0; j < grid[i].size(); j++) {\\n skip = 1 - skip; // Toggle skip flag\\n if (skip == 1) continue; // Skip this element\\n ans.push_back(grid[i][j]); // Add element to result\\n }\\n } else {\\n // Traverse right to left\\n for (int j = grid[i].size() - 1; j >= 0; j--) {\\n skip = 1 - skip; // Toggle skip flag\\n if (skip == 1) continue; // Skip this element\\n ans.push_back(grid[i][j]); // Add element to result\\n }\\n }\\n\\n dir = 1 - dir; // Flip direction for the next row\\n }\\n\\n return ans; // Return the final zigzag traversal\\n }\\n};\"], [4, 5.7471, \"class Solution {\\npublic:\\n vector<int> zigzagTraversal(vector<vector<int>>& grid) {\\n vector<int> result;\\n if(grid.size() < 1 || grid.at(0).size() < 1)\\n {\\n return result; \\n }\\n int rowSize = grid.at(0).size();\\n int totalSize = grid.size() * rowSize;\\n int row=0, col=0;\\n bool toRight = true;\\n while(totalSize > 0)\\n {\\n result.emplace_back(grid.at(row).at(col));\\n totalSize -=2;\\n col = (toRight) ? col+2: col-2;\\n if(col >= rowSize || col < 0)\\n //reach the end of the col, move to the next row\\n {\\n row++;\\n col = (col<0)? 0 : (rowSize%2)? rowSize - 2: rowSize -1; \\n toRight = !toRight; //flip the order\\n }\\n }\\n return result;\\n }\\n};\"]]"
},
"golang": {
"code": "func zigzagTraversal(grid [][]int) []int {\n\tres := []int{}\n\tcount := 0\n\tn := len(grid)\n\tm := len(grid[0])\n\tfor i := 0; i < n; i++ {\n\t\tif i%2 == 0 {\n\t\t\tfor j := 0; j < m; j++ {\n\t\t\t\tif count%2 == 0 {\n\t\t\t\t\tres = append(res, grid[i][j])\n\t\t\t\t}\n\t\t\t\tcount++\n\t\t\t}\n\t\t} else {\n\t\t\tfor j := m - 1; j >= 0; j-- {\n\t\t\t\tif count%2 == 0 {\n\t\t\t\t\tres = append(res, grid[i][j])\n\t\t\t\t}\n\t\t\t\tcount++\n\t\t\t}\n\t\t}\n\t}\n\treturn res\n}",
"memory": 700,
"memoryDistribution": "[[700, 21.6217, \"func zigzagTraversal(grid [][]int) []int {\\n\\tres := []int{}\\n\\tcount := 0\\n\\tn := len(grid)\\n\\tm := len(grid[0])\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tif i%2 == 0 {\\n\\t\\t\\tfor j := 0; j < m; j++ {\\n\\t\\t\\t\\tif count%2 == 0 {\\n\\t\\t\\t\\t\\tres = append(res, grid[i][j])\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\tcount++\\n\\t\\t\\t}\\n\\t\\t} else {\\n\\t\\t\\tfor j := m - 1; j >= 0; j-- {\\n\\t\\t\\t\\tif count%2 == 0 {\\n\\t\\t\\t\\t\\tres = append(res, grid[i][j])\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\tcount++\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\treturn res\\n}\"], [6900, 2.7027, \"func zigzagTraversal(grid [][]int) []int {\\n\\tl := len(grid) * len(grid[0])\\n\\tif l&1 == 1 {\\n\\t\\tl /= 2\\n\\t\\tl++\\n\\t} else {\\n\\t\\tl /= 2\\n\\t}\\n\\n\\tres := make([]int, l)\\n\\ti := 0\\n\\tvar alt, skip bool\\n\\n\\tfor _, row := range grid {\\n\\t\\tif alt {\\n\\t\\t\\tfor j := len(row) - 1; j >= 0; j-- {\\n\\t\\t\\t\\tif !skip {\\n\\t\\t\\t\\t\\tres[i] = row[j]\\n\\t\\t\\t\\t\\ti++\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\tskip = !skip\\n\\t\\t\\t}\\n\\t\\t} else {\\n\\t\\t\\tfor j := 0; j < len(row); j++ {\\n\\t\\t\\t\\tif !skip {\\n\\t\\t\\t\\t\\tres[i] = row[j]\\n\\t\\t\\t\\t\\ti++\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\tskip = !skip\\n\\t\\t\\t}\\n\\t\\t}\\n\\n\\t\\talt = !alt\\n\\t}\\n\\n\\treturn res\\n}\"], [7000, 2.7027, \"func zigzagTraversal(grid [][]int) []int {\\n\\tres := make([]int, 0, len(grid)*len(grid[0])/2)\\n\\tskip := false\\n\\tleft := true\\n\\tf := func(a int, skip bool) bool {\\n\\t\\tif !skip {\\n\\t\\t\\tres = append(res, a)\\n\\t\\t}\\n\\t\\treturn !skip\\n\\t}\\n\\tfor i := range grid {\\n\\t\\tif left {\\n\\t\\t\\tfor j := range grid[i] {\\n\\t\\t\\t\\tskip = f(grid[i][j], skip)\\n\\t\\t\\t}\\n\\t\\t} else {\\n\\t\\t\\tfor j := len(grid[i]) - 1; j >= 0; j-- {\\n\\t\\t\\t\\tskip = f(grid[i][j], skip)\\n\\t\\t\\t}\\n\\t\\t}\\n\\t\\tleft = !left\\n\\t}\\n\\treturn res\\n}\\n\"], [7100, 10.8108, null], [7200, 32.4324, null], [7300, 29.7297, null], [7400, 2.7027, null], [7500, 2.7027, null], [7700, 2.7027, null], [7800, 2.7027, \"func zigzagTraversal(grid [][]int) []int {\\n var res = make([]int, 0, (len(grid) + len(grid[0]) + 1) / 2);\\n var row = make([]int, 0, (len(grid[0]) + 1) / 2)\\n\\n for i := 0; i < len(grid); i++ {\\n var start = 0\\n\\n if (i & 1) == 1 {\\n start = 1\\n }\\n\\n row = row[:0]\\n\\n for j := start; j < len(grid[i]); j += 2 {\\n row = append(row, grid[i][j])\\n }\\n\\n if (i & 1) == 1 {\\n slices.Reverse(row)\\n }\\n\\n res = append(res, row...)\\n }\\n\\n return res\\n}\"], [8600, 5.4054, \"package main\\n\\nfunc zigzagTraversal(grid [][]int) []int {\\n\\tfull := []int{}\\n\\tfor i, row := range grid {\\n\\t\\tif i%2 == 0 {\\n\\t\\t\\tfor j := 0; j < len(row); j++ {\\n\\t\\t\\t\\tfull = append(full, row[j])\\n\\t\\t\\t}\\n\\t\\t} else {\\n\\t\\t\\tfor j := len(row) - 1; j >= 0; j-- {\\n\\t\\t\\t\\tfull = append(full, row[j])\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\tres := []int{}\\n\\tfor i := 0; i < len(full); i += 2 {\\n\\t\\tres = append(res, full[i])\\n\\t}\\n\\treturn res\\n}\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 81.0811, \"func zigzagTraversal(grid [][]int) []int {\\n m, n := len(grid), len(grid[0])\\n\\n var res []int\\n\\n for i := 0; i < m; i++ {\\n if i%2 == 0 {\\n for j := 0; j < n; j+= 2 {\\n res = append(res, grid[i][j])\\n }\\n } else {\\n for j := n-1-(n%2); j >= 0; j -= 2 {\\n res = append(res, grid[i][j])\\n }\\n }\\n }\\n return res\\n}\"], [1, 8.1081, \"package main\\n\\nfunc zigzagTraversal(grid [][]int) []int {\\n\\tfull := []int{}\\n\\tfor i, row := range grid {\\n\\t\\tif i%2 == 0 {\\n\\t\\t\\tfor j := 0; j < len(row); j++ {\\n\\t\\t\\t\\tfull = append(full, row[j])\\n\\t\\t\\t}\\n\\t\\t} else {\\n\\t\\t\\tfor j := len(row) - 1; j >= 0; j-- {\\n\\t\\t\\t\\tfull = append(full, row[j])\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\tres := []int{}\\n\\tfor i := 0; i < len(full); i += 2 {\\n\\t\\tres = append(res, full[i])\\n\\t}\\n\\treturn res\\n}\"], [2, 5.4054, \"func zigzagTraversal(grid [][]int) []int {\\n var res = make([]int, 0, (len(grid) + len(grid[0]) + 1) / 2);\\n var row = make([]int, 0, (len(grid[0]) + 1) / 2)\\n\\n for i := 0; i < len(grid); i++ {\\n var start = 0\\n\\n if (i & 1) == 1 {\\n start = 1\\n }\\n\\n row = row[:0]\\n\\n for j := start; j < len(grid[i]); j += 2 {\\n row = append(row, grid[i][j])\\n }\\n\\n if (i & 1) == 1 {\\n slices.Reverse(row)\\n }\\n\\n res = append(res, row...)\\n }\\n\\n return res\\n}\"], [3, 5.4054, \"func zigzagTraversal(grid [][]int) []int {\\n\\n if len(grid) == 0 || len(grid[0]) == 0 {\\n return []int{}\\n }\\n\\n r := len(grid)\\n c := len(grid[0])\\n result := make([]int, 0)\\n shouldNotSkip := true\\n\\n for i:=0; i<r; i++ {\\n if i%2 == 0 {\\n for j:=0; j<c; j++ {\\n if shouldNotSkip {\\n result = append(result, grid[i][j])\\n }\\n shouldNotSkip = !shouldNotSkip\\n }\\n } else {\\n for j:=c-1; j>=0; j-- {\\n if shouldNotSkip {\\n result = append(result, grid[i][j])\\n }\\n shouldNotSkip = !shouldNotSkip\\n }\\n }\\n }\\n \\n return result\\n}\"]]"
},
"java": {
"code": "class Solution {\n public List<Integer> zigzagTraversal(int[][] grid) {\n List<Integer> res = new ArrayList<>();\n int index = 0;\n for (int i = 0; i < grid.length; i++) {\n if (i % 2 == 0) {\n for (int j = 0; j < grid[i].length; j++) {\n if (index % 2 == 0)\n res.add(grid[i][j]);\n index++;\n }\n } else {\n for (int j = grid[i].length - 1; j >= 0; j--) {\n if (index % 2 == 0)\n res.add(grid[i][j]);\n index++;\n }\n }\n }\n return res;\n }\n}",
"memory": 4500,
"memoryDistribution": "[[4500, 64.2104, \"class Solution {\\n public List<Integer> zigzagTraversal(int[][] grid) {\\n List<Integer> res = new ArrayList<>();\\n int index = 0;\\n for (int i = 0; i < grid.length; i++) {\\n if (i % 2 == 0) {\\n for (int j = 0; j < grid[i].length; j++) {\\n if (index % 2 == 0)\\n res.add(grid[i][j]);\\n index++;\\n }\\n } else {\\n for (int j = grid[i].length - 1; j >= 0; j--) {\\n if (index % 2 == 0)\\n res.add(grid[i][j]);\\n index++;\\n }\\n }\\n }\\n return res;\\n }\\n}\"], [44900, 0.2632, \"class Solution {\\n public List<Integer> zigzagTraversal(int[][] grid) {\\n List<Integer> result = new ArrayList<>();\\n int row = grid.length;\\n int col = grid[0].length;\\n\\n for (int i = 0; i < row; i++) {\\n if (i % 2 == 0) {\\n for (int j = 0; j < col; j++) {\\n if (j % 2 == 0) {\\n result.add(grid[i][j]);\\n }\\n }\\n } else {\\n for (int j = col - 1; j >= 0; j--) {\\n if (j % 2 == 1) {\\n result.add(grid[i][j]);\\n }\\n }\\n }\\n }\\n return result;\\n }\\n}\"], [45000, 0.2632, \"class Solution {\\n public List<Integer> zigzagTraversal(int[][] grid) {\\n int m=grid.length,n=grid[0].length;\\n List<Integer>res=new ArrayList<>();\\n \\n for(int i=0;i<m;++i){\\n if((i&1)==0){\\n for(int j=0;j<n;j++)if((j&1)==0)\\n res.add(grid[i][j]);\\n }\\n else{\\n for(int j=n-1;j>=0;j--)if((j&1)>0)\\n res.add(grid[i][j]);\\n }\\n }\\n \\n return res;\\n }\\n}\"], [45100, 0.7895, null], [45200, 2.6316, null], [45300, 4.2105, null], [45400, 8.9474, null], [45500, 18.6842, null], [45600, 16.5789, null], [45700, 13.6842, null], [45800, 12.6316, null], [45900, 10.0, \"class Solution {\\n public List<Integer> zigzagTraversal(int[][] grid) {\\n int n=grid.length;\\n int m=grid[0].length;\\n List<Integer>ans=new ArrayList<>();\\n int [][]dirs={{0,1},{-1,0},{1,0},{0,-1},};\\n boolean vis[][]=new boolean[n][m];\\n for(int i=0;i<n;i++){\\n if(i%2==0){\\n for(int j=0;j<m;j++){\\n boolean flag=true;\\n for(int []dir:dirs){\\n int row=i+dir[0];\\n int col=j+dir[1];\\n if(row<0 || col<0 || row>=n || col>=m) continue;\\n if(vis[row][col]) {\\n flag=false;\\n break;\\n }\\n }\\n if(flag){\\n vis[i][j]=true;\\n ans.add(grid[i][j]);\\n }\\n }\\n }else{\\n for(int j=m-1;j>=0;j--){\\n boolean flag=true;\\n for(int []dir:dirs){\\n int row=i+dir[0];\\n int col=j+dir[1];\\n if(row<0 || col<0 || row>=n || col>=m) continue;\\n if(vis[row][col]) {\\n flag=false;\\n break;\\n }\\n }\\n if(flag){\\n vis[i][j]=true;\\n ans.add(grid[i][j]);\\n }\\n }\\n \\n }\\n \\n }\\n return ans;\\n }\\n}\"], [46000, 6.0526, \"class Solution {\\n public List<Integer> zigzagTraversal(int[][] grid) {\\n List<Integer> list = new ArrayList<>();\\n\\n boolean leftToRight = true;\\n\\n for (int i = 0; i < grid.length; i++) {\\n\\n for (int j = 0; j < grid[i].length; j++) {\\n\\n int rowTotake = leftToRight ? j : grid[i].length - 1 - j;\\n\\n if (leftToRight == (rowTotake %2==0)) {\\n list.add(grid[i][rowTotake]);\\n }\\n\\n }\\n leftToRight = !leftToRight;\\n\\n }\\n\\n return list;\\n }\\n}\"]]",
"runtime": 1,
"runtimeDistribution": "[[1, 84.4737, \"class Solution {\\n public List<Integer> zigzagTraversal(int[][] grid) {\\n boolean flag = true , skip = false;\\n int n = grid.length , m = grid[0].length;\\n List<Integer> ans = new ArrayList<>();\\n for(int i=0;i<n;i++)\\n {\\n if(flag)\\n {\\n for(int j=0;j<m;j++)\\n {\\n if(!skip)\\n { ans.add(grid[i][j]); }\\n skip = !skip;\\n }\\n }\\n else\\n {\\n for(int j=m-1;j>=0;j--)\\n {\\n if(!skip)\\n { ans.add(grid[i][j]); }\\n skip = !skip;\\n }\\n\\n }\\n flag = !flag;\\n }\\n\\n return ans;\\n }\\n}\"], [2, 12.3684, \"class Solution {\\n public List<Integer> zigzagTraversal(int[][] grid) {\\n List<Integer> result = new ArrayList<>();\\n int row = 0;\\n int col = 0;\\n int m = grid.length;\\n int n = grid[0].length;\\n boolean isGngLeft = true;\\n int skip = 1;\\n for(int i=0;i<grid.length;i++){\\n if(isGngLeft){\\n for(int j=0;j<grid[0].length;j++){\\n skip = 1 - skip;\\n if (skip == 1) continue;\\n result.add(grid[i][j]);\\n }\\n } else {\\n for(int j=grid[0].length-1;j>=0;j--){\\n skip = 1 - skip;\\n if (skip == 1) continue;\\n result.add(grid[i][j]);\\n }\\n }\\n isGngLeft = !isGngLeft;\\n }\\n return result;\\n }\\n}\"], [3, 0.7895, null], [5, 0.5263, \"class Solution {\\n public List<Integer> zigzagTraversal(int[][] grid) {\\n ArrayList<Integer> list=new ArrayList<>();\\n \\n int i=0;\\n int j=0;\\n int row=grid.length;\\n int column=grid[0].length;\\n System.out.println(row);\\n \\n while(j<row){\\n if(i==-1){\\n i++;\\n }else if(i==-2){\\n i+=3;\\n }\\n while(i<column){\\n list.add(grid[j][i]);\\n i+=2;\\n }\\n j++;\\n \\n if(i-1==column){\\n i-=3;\\n }else if(i==column){\\n i--;\\n }\\n \\n while(i>=0 && j<row){\\n list.add(grid[j][i]);\\n i-=2;\\n }\\n j++;\\n }\\n return list;\\n }\\n}\"], [6, 0.5263, \"class Solution {\\n public List<Integer> zigzagTraversal(int[][] grid) {\\n //define input variables\\n int cols = grid[0].length;\\n int rows = grid.length;\\n int inp_len = cols*rows;\\n //define output variables\\n int out_len = (inp_len-1)/2 + 1;\\n int[] output = new int[out_len];\\n\\n for(int i = 0; i < out_len; i++){\\n int r = (i*2)/cols;\\n //int c = ((r%2)*(cols-1)) + (1-(r%2)*2)*((i*2)%cols);\\n int c = (i*2)%cols;\\n if(r%2==1){c=cols-1-c;}\\n output[i] = grid[r][c]; \\n }\\n List<Integer> list = Arrays.stream(output).boxed().toList();\\n return list;\\n }\\n}\"]]"
},
"javascript": {
"code": "var zigzagTraversal = function(grid) {\n let result = [];\n let count = 0;\n for (let i = 0; i < grid.length; i++) {\n if (i % 2 === 0) {\n for (let j = 0; j < grid[i].length; j++) {\n if (count % 2 === 0) result.push(grid[i][j]);\n count++;\n }\n } else {\n for (let j = grid[i].length - 1; j >= 0; j--) {\n if (count % 2 === 0) result.push(grid[i][j]);\n count++;\n }\n }\n }\n return result;\n};",
"memory": 5700,
"memoryDistribution": "[[5700, 85.1063, \"var zigzagTraversal = function(grid) {\\n let result = [];\\n let count = 0;\\n for (let i = 0; i < grid.length; i++) {\\n if (i % 2 === 0) {\\n for (let j = 0; j < grid[i].length; j++) {\\n if (count % 2 === 0) result.push(grid[i][j]);\\n count++;\\n }\\n } else {\\n for (let j = grid[i].length - 1; j >= 0; j--) {\\n if (count % 2 === 0) result.push(grid[i][j]);\\n count++;\\n }\\n }\\n }\\n return result;\\n};\"], [55800, 2.1277, \"/**\\n * @param {number[][]} grid\\n * @return {number[]}\\n */\\nvar zigzagTraversal = function(grid) {\\n let res = []\\n let m = grid.length, n = grid[0].length\\n for (let i = 0; i<m; i++) {\\n if (i%2 == 0) {\\n for (let j =0; j<n; j++) {\\n if (j%2 == 0) res.push(grid[i][j])\\n }\\n } else {\\n for (let k = n - 1; k > 0; k--) {\\n if (k % 2 !== 0) res.push(grid[i][k]);\\n }\\n }\\n\\n }\\n return res\\n \\n};\"], [56500, 2.1277, \"/**\\n * @param {number[][]} grid\\n * @return {number[]}\\n */\\nvar zigzagTraversal = function(grid) {\\n let res = [],\\n even = true,\\n evenJ = grid[0].length % 2 === 0;\\n\\n for(let i = 0; i < grid.length; i++){\\n if(i % 2 !== 0) even = false;\\n else even = true;\\n\\n if(even){\\n for(let j = 0; j < grid[0].length; j+= 2){\\n res.push(grid[i][j]);\\n }\\n } else {\\n for(let j = evenJ ? grid[0].length -1 : grid[0].length -2; j >= 0 ; j-= 2){\\n res.push(grid[i][j]);\\n }\\n }\\n }\\n return res;\\n};\"], [56700, 6.383, null], [56900, 4.2553, null], [57100, 6.383, null], [57400, 6.383, null], [57700, 2.1277, null], [57900, 2.1277, null], [58000, 4.2553, null], [58200, 6.383, null], [58300, 4.2553, null], [58400, 2.1277, null], [58500, 8.5106, null], [58600, 2.1277, null], [58700, 6.383, null], [58800, 4.2553, null], [58900, 2.1277, null], [59000, 4.2553, null], [59100, 4.2553, null], [59200, 2.1277, null], [59300, 4.2553, null], [59800, 2.1277, null], [59900, 2.1277, \"/**\\n * @param {number[][]} grid\\n * @return {number[]}\\n */\\nvar zigzagTraversal = function(grid) {\\n let arr = [];\\n let n = grid.length;\\n\\n for (let i = 0; i < n; i++) {\\n let temp = grid[i];\\n if (i % 2 === 0) {\\n for (let j = 0; j < temp.length; j++) {\\n arr.push(temp[j]);\\n }\\n } else if (i % 2 !== 0) {\\n for (let j = temp.length - 1; j >= 0; j--) {\\n arr.push(temp[j]);\\n }\\n }\\n }\\n let resultt = [];\\n for (let i = 0; i < arr.length; i += 2) {\\n resultt.push(arr[i]);\\n }\\n return resultt;\\n};\"], [60000, 2.1277, \"/**\\n * @param {number[][]} grid\\n * @return {number[]}\\n */\\nvar zigzagTraversal = function(grid) {\\n const rows = grid.length;\\n const cols = grid[0].length;\\n const traversal = [];\\n\\n // Step 1: Traverse the grid in zigzag order\\n for (let i = 0; i < rows; i++) {\\n if (i % 2 === 0) {\\n // left to right\\n for (let j = 0; j < cols; j++) {\\n traversal.push(grid[i][j]);\\n }\\n } else {\\n // right to left\\n for (let j = cols - 1; j >= 0; j--) {\\n traversal.push(grid[i][j]);\\n }\\n }\\n }\\n\\n // Step 2: Skip every alternate cell\\n const result = [];\\n for (let i = 0; i < traversal.length; i += 2) {\\n result.push(traversal[i]);\\n }\\n\\n return result;\\n};\"]]",
"runtime": 3,
"runtimeDistribution": "[[0, 14.8936, \"/**\\n * @param {number[][]} grid\\n * @return {number[]}\\n */\\nvar zigzagTraversal = function(grid) {\\n let m = grid.length;\\n let n = grid[0].length;\\n let output = [];\\n\\n for(let r = 0; r < m; r++) {\\n\\n if(r % 2 == 0) {\\n for(let c = 0; c < n; c++) {\\n if((r + c) % 2 == 0) output.push(grid[r][c]);\\n }\\n } else {\\n for(let c = n - 1; c >= 0; c--) {\\n if((r + c) % 2 == 0) output.push(grid[r][c]);\\n }\\n }\\n }\\n\\n return output;\\n};\\n\\n\"], [1, 38.2979, \"/**\\n * @param {number[][]} grid\\n * @return {number[]}\\n */\\nvar zigzagTraversal = function(grid) {\\n let res = [],\\n even = true,\\n evenJ = grid[0].length % 2 === 0;\\n\\n for(let i = 0; i < grid.length; i++){\\n if(i % 2 !== 0) even = false;\\n else even = true;\\n\\n if(even){\\n for(let j = 0; j < grid[0].length; j+= 2){\\n res.push(grid[i][j]);\\n }\\n } else {\\n for(let j = evenJ ? grid[0].length -1 : grid[0].length -2; j >= 0 ; j-= 2){\\n res.push(grid[i][j]);\\n }\\n }\\n }\\n return res;\\n};\"], [2, 14.8936, null], [3, 23.4043, \"/**\\n * @param {number[][]} grid\\n * @return {number[]}\\n */\\nvar zigzagTraversal = function(grid) {\\n let res = []\\n let m = grid.length, n = grid[0].length\\n let forward = true\\n for (let i = 0; i<m; i++) {\\n if (i%2==0) {\\n for (let j =0; j<n; j++) {\\n if (j%2==0) res.push(grid[i][j])\\n }\\n } else {\\n let k = n-1\\n while (k>0) {\\n if (k%2) res.push(grid[i][k])\\n k--\\n }\\n }\\n\\n }\\n return res\\n \\n};\"], [4, 2.1277, \"/**\\n * @param {number[][]} grid\\n * @return {number[]}\\n */\\nvar zigzagTraversal = function(grid) {\\n const res = [];\\n\\n const canMove = (i, j) => {\\n if (grid[i][j-1] === -1 || grid[i][j+1] === -1 || grid[i-1]?.[j] === -1) {\\n return false;\\n }\\n return true;\\n }\\n\\n for (let i = 0; i < grid.length; i++) {\\n for (let k = i % 2 ? -1 : 1, j = i % 2 ? grid[i].length - 1 : 0; i % 2 ? j >= 0 : j < grid[i].length; i % 2 ? j-- : j += k) {\\n if (canMove(i, j)) {\\n res.push(grid[i][j]);\\n grid[i][j] = -1;\\n }\\n }\\n }\\n\\n return res;\\n};\"]]"
},
"python3": {
"code": "class Solution:\n def zigzagTraversal(self, grid: List[List[int]]) -> List[int]:\n res = []\n pick = True\n for i, row in enumerate(grid):\n if i % 2 == 0:\n for val in row:\n if pick:\n res.append(val)\n pick = not pick\n else:\n for val in row[::-1]:\n if pick:\n res.append(val)\n pick = not pick\n return res",
"memory": 1800,
"memoryDistribution": "[[1800, 58.4527, \"class Solution:\\n def zigzagTraversal(self, grid: List[List[int]]) -> List[int]:\\n res = []\\n pick = True\\n for i, row in enumerate(grid):\\n if i % 2 == 0:\\n for val in row:\\n if pick:\\n res.append(val)\\n pick = not pick\\n else:\\n for val in row[::-1]:\\n if pick:\\n res.append(val)\\n pick = not pick\\n return res\"], [17900, 2.0057, \"class Solution:\\n def zigzagTraversal(self, grid: List[List[int]]) -> List[int]:\\n\\n take = 1\\n RtoL = False\\n\\n res = []\\n M, N = len(grid), len(grid[0])\\n for r in range(M):\\n for c in range(N):\\n if take & 1:\\n res.append(grid[r][c] if not(RtoL) else grid[r][N-1-c])\\n take ^= 1\\n RtoL = not(RtoL)\\n return res\"], [18000, 16.3324, \"class Solution:\\n def zigzagTraversal(self, grid: List[List[int]]) -> List[int]:\\n \\n res = []\\n for i in range(len(grid)):\\n g = grid[i]\\n section = g[::-1] if i % 2 else g\\n print(section)\\n res += section\\n return res[::2]\"], [18100, 23.2092, null], [18200, 20.9169, \"class Solution:\\n def zigzagTraversal(self, grid: List[List[int]]) -> List[int]:\\n cols = len(grid[0])\\n rows = len(grid)\\n result = []\\n\\n for i in range(rows):\\n if i % 2 == 0:\\n row = grid[i][::2]\\n else :\\n row = grid[i][::-1][cols%2::2]\\n result.extend(row)\\n return result\\n\\n \"], [18300, 22.9226, \"class Solution:\\n def zigzagTraversal(self, grid: List[List[int]]) -> List[int]:\\n m = len(grid)\\n n = len(grid[0])\\n result = []\\n visit_count = 0\\n for r in range(m):\\n if r % 2 == 0:\\n for c in range(n):\\n if visit_count % 2 == 0:\\n result.append(grid[r][c])\\n visit_count += 1\\n else:\\n for c in range(n - 1, -1, -1):\\n if visit_count % 2 == 0:\\n result.append(grid[r][c])\\n visit_count += 1\\n return result\"]]",
"runtime": 4,
"runtimeDistribution": "[[0, 38.6819, \"class Solution:\\n def zigzagTraversal(self, grid: List[List[int]]) -> List[int]:\\n newGrid = []\\n for i in range(len(grid)):\\n if i%2 == 0:\\n for j in range(0, len(grid[0]), 2):\\n newGrid.append(grid[i][j])\\n else:\\n start = len(grid[0])-1 if len(grid[0])%2==0 else len(grid[0])-2\\n for j in range(start, 0, -2):\\n newGrid.append(grid[i][j])\\n return newGrid\"], [1, 5.1576, \"class Solution:\\n def zigzagTraversal(self, grid: List[List[int]]) -> List[int]:\\n if not grid or not grid[0]:\\n return []\\n \\n m, n = len(grid), len(grid[0])\\n result = []\\n count = 0\\n\\n for i in range(m):\\n if i % 2 == 0:\\n for j in range(n):\\n count += 1\\n if count % 2 == 1:\\n result.append(grid[i][j])\\n else:\\n for j in range(n - 1, -1, -1):\\n count += 1\\n if count % 2 == 1:\\n result.append(grid[i][j])\\n\\n return result\"], [2, 5.4441, null], [3, 23.2092, null], [4, 10.6017, null], [5, 3.1519, null], [6, 3.1519, \"class Solution:\\n def zigzagTraversal(self, grid: List[List[int]]) -> List[int]:\\n m, n = len(grid), len(grid[0])\\n result = []\\n temp_row = []\\n\\n for row in range(m):\\n for col in range(n):\\n if row % 2 == 0 and col % 2 == 0:\\n result.append(grid[row][col])\\n elif row % 2 == 1 and col % 2 == 1:\\n temp_row.append(grid[row][col])\\n if temp_row:\\n temp_row.reverse()\\n for i in range(len(temp_row)):\\n result.append(temp_row[i])\\n temp_row = []\\n return result\\n\\n\"], [7, 5.4441, \"class Solution:\\n def zigzagTraversal(self, grid: List[List[int]]) -> List[int]:\\n\\n take = 1\\n RtoL = False\\n\\n res = []\\n M, N = len(grid), len(grid[0])\\n for r in range(M):\\n for c in range(N):\\n if take & 1:\\n res.append(grid[r][c] if not(RtoL) else grid[r][N-1-c])\\n take ^= 1\\n RtoL = not(RtoL)\\n return res\"]]"
},
"ruby": {
"code": "def zigzag_traversal(grid)\n cells = []\n grid.each_with_index do |row, i|\n if i.even?\n row.each { |val| cells << val }\n else\n row.reverse.each { |val| cells << val }\n end\n end\n result = []\n cells.each_with_index { |val, i| result << val if i.even? }\n result\nend",
"memory": 21300,
"memoryDistribution": "[[21300, 20.0, \"def zigzag_traversal(grid)\\n cells = []\\n grid.each_with_index do |row, i|\\n if i.even?\\n row.each { |val| cells << val }\\n else\\n row.reverse.each { |val| cells << val }\\n end\\n end\\n result = []\\n cells.each_with_index { |val, i| result << val if i.even? }\\n result\\nend\"], [212000, 40.0, \"# @param {Integer[][]} grid\\n# @return {Integer[]}\\ndef zigzag_traversal(grid)\\n output = []\\n grid.each_with_index do |row, i|\\n if i % 2 == 0\\n row.each_with_index do |num, j|\\n if j % 2 == 0\\n output << num\\n end\\n end\\n else\\n (row.length - 1).downto(0) do |k|\\n if k % 2 != 0\\n output << row[k]\\n end\\n end\\n end\\n end\\n output\\nend\"], [212200, 20.0, \"# @param {Integer[][]} grid\\n# @return {Integer[]}\\ndef zigzag_traversal(grid)\\n m, n = grid.length, grid[0].length\\n result = []\\n row, col = 0, 0\\n direction = 1 # 1 for right, -1 for left\\n skip = false\\n\\n while row < m\\n if !skip\\n result << grid[row][col]\\n end\\n skip = !skip\\n\\n if direction == 1 # Moving right\\n if col + 1 < n\\n col += 1\\n else\\n row += 1\\n direction = -1\\n end\\n elsif direction == -1 # Moving left\\n if col - 1 >= 0\\n col -= 1\\n else\\n row += 1\\n direction = 1\\n end\\n end\\n end\\n\\n result\\nend\"], [212300, 20.0, \"# @param {Integer[][]} grid\\n# @return {Integer[]}\\n\\ndef zigzag_traversal(grid)\\n pass = false\\n grid.each_with_index.with_object([]) {|(row, i), res| \\n (i.odd? ? row.reverse_each : row).each {|v| res << v if (pass = !pass) }\\n }\\nend\\n\"], [212700, 20.0, \"def zigzag_traversal(grid)\\n cells = []\\n grid.each_with_index do |row, i|\\n if i.even?\\n row.each { |val| cells << val }\\n else\\n row.reverse.each { |val| cells << val }\\n end\\n end\\n result = []\\n cells.each_with_index { |val, i| result << val if i.even? }\\n result\\nend\"]]",
"runtime": 12,
"runtimeDistribution": "[[3, 40.0, \"# @param {Integer[][]} grid\\n# @return {Integer[]}\\ndef zigzag_traversal(grid)\\n output = []\\n grid.each_with_index do |row, i|\\n if i % 2 == 0\\n row.each_with_index do |num, j|\\n if j % 2 == 0\\n output << num\\n end\\n end\\n else\\n (row.length - 1).downto(0) do |k|\\n if k % 2 != 0\\n output << row[k]\\n end\\n end\\n end\\n end\\n output\\nend\"], [4, 20.0, \"# @param {Integer[][]} grid\\n# @return {Integer[]}\\ndef zigzag_traversal(grid)\\n m, n = grid.length, grid[0].length\\n result = []\\n row, col = 0, 0\\n direction = 1 # 1 for right, -1 for left\\n skip = false\\n\\n while row < m\\n if !skip\\n result << grid[row][col]\\n end\\n skip = !skip\\n\\n if direction == 1 # Moving right\\n if col + 1 < n\\n col += 1\\n else\\n row += 1\\n direction = -1\\n end\\n elsif direction == -1 # Moving left\\n if col - 1 >= 0\\n col -= 1\\n else\\n row += 1\\n direction = 1\\n end\\n end\\n end\\n\\n result\\nend\"], [9, 20.0, \"# @param {Integer[][]} grid\\n# @return {Integer[]}\\n\\ndef zigzag_traversal(grid) = grid.each_with_index.collect_concat {|row, i| (i.odd? ? row.reverse : row) }.each_slice(2).collect(&:first)\\n\"], [12, 20.0, \"def zigzag_traversal(grid)\\n cells = []\\n grid.each_with_index do |row, i|\\n if i.even?\\n row.each { |val| cells << val }\\n else\\n row.reverse.each { |val| cells << val }\\n end\\n end\\n result = []\\n cells.each_with_index { |val, i| result << val if i.even? }\\n result\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list:
import random
random.seed(seed)
# Helper: serialize a 2D grid into a string.
# Rows are separated by ";" and numbers within a row by ","
def serialize_grid(grid):
return ";".join(",".join(str(num) for num in row) for row in grid)
# Helper: serialize a list of integers into a string (comma separated).
def serialize_result(result):
return ",".join(str(num) for num in result)
# Sample solution function based on the provided sample solution.
def sample_solution(grid):
res = []
pick = True
for i, row in enumerate(grid):
if i % 2 == 0:
for val in row:
if pick:
res.append(val)
pick = not pick
else:
for val in row[::-1]:
if pick:
res.append(val)
pick = not pick
return res
# Predefined test cases covering boundary and typical scenarios.
predefined = [
[[1,2],[3,4]], # Example 1: 2x2 grid.
[[2,1],[2,1],[2,1]], # Example 2: 3x2 grid.
[[1,2,3],[4,5,6],[7,8,9]], # Example 3: 3x3 grid.
[[1,1],[1,1]], # 2x2 grid with duplicate values.
[[1,2,3,4],[5,6,7,8]], # 2x4 grid.
[[10,20,30],[40,50,60],[70,80,90],[100,110,120]] # 4x3 grid.
]
test_cases = []
# Add predefined cases first.
for grid in predefined:
if len(test_cases) >= num_cases:
break
inp = serialize_grid(grid)
out = serialize_result(sample_solution(grid))
test_cases.append({"input": inp, "output": out})
# Generate additional random cases if needed.
while len(test_cases) < num_cases:
rows = random.randint(2, 50)
cols = random.randint(2, 50)
grid = [[random.randint(1, 2500) for _ in range(cols)] for _ in range(rows)]
inp = serialize_grid(grid)
out = serialize_result(sample_solution(grid))
test_cases.append({"input": inp, "output": out})
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
# Helper to deserialize output: comma-separated integers.
def deserialize_output(s):
s = s.strip()
if s == "":
return []
return list(map(int, s.split(",")))
expected = deserialize_output(expected_output)
program = deserialize_output(program_output)
return expected == program
|
[{"input": "1,2;3,4", "output": "1,4"}, {"input": "2,1;2,1;2,1", "output": "2,1,2"}, {"input": "1,2,3;4,5,6;7,8,9", "output": "1,3,5,7,9"}, {"input": "1,1;1,1", "output": "1,1"}, {"input": "1,2,3,4;5,6,7,8", "output": "1,3,8,6"}, {"input": "10,20,30;40,50,60;70,80,90;100,110,120", "output": "10,30,50,70,90,110"}, {"input": "103,1127,1004,915,572,420,2234,357,2419;1729,131,123,384,896,953,2070,2466,109;2299,815,2233,1719,903,1840,2414,1140,27;654,1732,1394,1139,637,882,1379,419,380;1557,397,1471,1409,2473,1084,178,1882,2197;512,1551,323,2262,1201,1482,2365,788,285;188,934,1186,327,954,414,1557,1139,1858;1495,667,1517,1456,859,1094,293,2496,701;2188,1003,670,1894,1555,1106,2282,900,1329;230,939,132,1293,1644,1097,272,865,2324;1289,871,2045,1621,1880,586,1085,572,1011;2300,2208,1077,2395,1755,2391,1636,1483,899;567,2088,2022,373,193,450,627,656,1730;2443,261,1577,1564,2441,1918,2168,1030,2267;48,470,2200,1093,1394,457,1203,1781,648;1859,14,1079,2051,732,2080,436,1223,2080;2495,815,627,1532,662,2210,2173,3,2454;1328,2002,80,459,1487,1260,981,238,987;2324,323,351,1991,284,2182,516,526,1947;2252,677,1086,2162,2485,1734,868,2209,824;1277,1635,1530,1795,2120,1850,496,1016,921;263,1385,87,2410,2269,943,2411,903,30;291,242,938,277,129,1354,291,2106,975;1141,1989,878,2209,542,2339,2361,1937,996;1938,1668,780,387,398,1766,1452,1735,1684;1913,222,404,249,1650,1390,448,1019,785;780,2197,1838,575,1729,752,1141,1895,1024;309,1816,2255,402,208,2215,61,383,969;682,1665,1990,1972,876,1643,241,675,1553;9,1600,1087,1864,1169,1733,2277,1994,635;778,1216,892,240,2373,2221,250,1285,235;206,2393,1953,2060,2176,645,233,2081,329;762,281,2438,279,964,1654,492,2334,1009;2372,2436,163,336,1718,2391,2316,2142,1296;1069,837,1287,978,1088,1622,537,1229,1873;1296,298,39,1878,2307,410,301,2203,874;2073,1087,543,1430,282,1001,1514,1168,647;1795,2226,1240,2167,33,2272,1227,425,551;1084,473,439,2267,637,1116,1155,2478,863;1405,834,1082,2071,2002,1029,209,379,1735;1134,181,15,1367,536,1073,662,1810,2260;1752,2298,40,459,309,611,2235,148,1513", "output": "103,1004,572,2234,2419,2466,953,384,131,2299,2233,903,2414,27,419,882,1139,1732,1557,1471,2473,178,2197,788,1482,2262,1551,188,1186,954,1557,1858,2496,1094,1456,667,2188,670,1555,2282,1329,865,1097,1293,939,1289,2045,1880,1085,1011,1483,2391,2395,2208,567,2022,193,627,1730,1030,1918,1564,261,48,2200,1394,1203,648,1223,2080,2051,14,2495,627,662,2173,2454,238,1260,459,2002,2324,351,284,516,1947,2209,1734,2162,677,1277,1530,2120,496,921,903,943,2410,1385,291,938,129,291,975,1937,2339,2209,1989,1938,780,398,1452,1684,1019,1390,249,222,780,1838,1729,1141,1024,383,2215,402,1816,682,1990,876,241,1553,1994,1733,1864,1600,778,892,2373,250,235,2081,645,2060,2393,762,2438,964,492,1009,2142,2391,336,2436,1069,1287,1088,537,1873,2203,410,1878,298,2073,543,282,1514,647,425,2272,2167,2226,1084,439,637,1155,863,379,1029,2071,834,1134,15,536,662,2260,148,611,459,2298"}, {"input": "607,1761,523,172,1263,1494,164,1466,861,1023,422,1449,2294,1665,634,970,666,726,1689,102,735,1361,1687,1017,1093,653,443,1567,159,1928,912,818,1886,1433,1251,933,914;97,792,1633,1345,1142,285,1144,1439,2087,1638,2197,1357,114,473,1070,732,2379,1088,157,445,2444,1780,1416,1285,1788,2484,2095,474,1578,2362,779,1044,182,1787,7,2130,2206;808,1492,1767,287,1353,1286,511,1231,2078,1267,1673,1337,1649,1212,2271,522,786,1723,1553,713,2332,1233,1664,2245,2,1245,1176,861,1761,2376,2485,1320,1905,1810,1812,876,2094;1939,696,348,1163,2112,1373,383,963,1272,921,816,604,101,190,1003,1947,299,1866,1698,2358,797,1573,2025,1637,1000,605,23,437,1742,897,721,2122,1903,206,2284,1021,498;1870,547,1904,2176,2290,2439,1300,1813,2068,1748,2245,1827,652,1945,1844,1062,1013,1136,2136,1985,980,1125,1802,318,1171,961,1113,1376,1310,2213,331,567,618,948,1569,626,877;264,1700,1670,1356,2223,1909,1704,256,848,1721,1596,2393,81,2359,1559,1954,25,1441,1224,1598,1717,2205,2237,2471,904,2000,899,1118,1786,1990,119,1593,1377,1657,677,1915,523;2188,111,1614,2425,2312,112,344,1756,556,1892,745,206,1066,1553,1341,867,1863,1339,1383,1553,1140,1727,1034,336,1927,80,2210,214,1434,919,282,165,128,1013,817,84,625;978,518,1940,469,2311,893,1905,1050,1511,688,2482,2488,470,671,1275,443,2371,106,1278,2359,1538,1625,813,312,2426,995,418,1236,2460,496,2319,169,1423,2183,1755,1518,283;2073,1398,52,1721,2008,433,1776,1484,1884,627,1784,722,2138,1107,2205,1981,1905,1785,2427,1100,1321,1006,355,1143,1847,999,1904,2335,2500,1553,1378,118,2025,1332,745,1998,869;1454,1059,1395,1146,2442,1132,2277,42,2117,783,351,989,1665,2002,2275,985,1951,2011,1836,71,382,1206,908,1657,997,1255,2383,1512,1939,2268,2175,1409,1743,2255,1355,1442,1859;1110,1256,1030,945,495,789,1293,490,2195,759,785,887,1984,1133,2415,2149,2445,1160,412,796,1214,932,1479,735,1239,58,2188,519,1124,187,224,2267,1197,518,2011,421,51;2352,1165,1923,1961,1805,1396,756,211,1035,1957,468,268,1642,2015,304,2364,220,622,612,2306,1245,349,1017,486,2286,1705,2484,2442,925,2141,1559,1846,1814,1218,2411,1757,1251;2330,247,2498,407,852,865,1084,333,644,983,712,2261,308,642,11,1674,1846,2433,1925,1193,134,949,1181,1159,1860,292,957,1084,2416,811,1742,471,2231,921,611,1089,583;293,245,680,1260,2438,2332,1183,1799,510,1920,1246,1649,1116,2050,2212,2023,1794,330,2450,164,1770,1321,2473,1026,106,375,938,2357,2405,85,1104,2361,165,718,1928,2126,1812;1140,744,2398,1786,2015,374,1926,1426,1673,1366,1316,429,659,1351,1687,2030,1181,1641,2254,151,1863,361,1289,1034,1325,475,1656,2108,5,2223,1893,1693,223,769,2124,1482,2042;1811,212,834,1094,2250,537,1180,1795,1986,498,119,2494,981,649,1273,2257,57,2263,1672,382,921,465,1891,482,631,2042,1196,2085,1120,1702,1977,1935,999,1871,2258,593,1572;781,2456,2082,560,286,1132,1700,1393,2080,1095,11,1159,1223,2405,2376,2006,609,1830,2207,1984,1414,1362,2261,2226,1546,1866,1319,773,979,2343,1569,957,1683,179,1304,1938,1562;1582,624,2029,152,518,2058,2418,1360,412,1804,409,2155,1872,63,591,1680,633,307,1924,1086,1387,1629,329,1346,2186,1557,1298,1999,2217,148,281,962,1178,932,371,1778,404;412,1818,682,1227,119,189,1329,230,1202,1469,1536,1765,597,1001,2176,1688,2319,738,697,718,324,2497,1567,987,2039,2389,587,952,1889,1041,1883,1046,39,1906,1179,2239,648;303,1810,1416,2407,1226,1738,1025,1872,1238,816,1576,1980,437,972,1563,2343,1471,2355,1212,1210,90,1622,1125,34,2319,201,2484,2035,1173,943,2487,1444,898,779,1027,561,398;162,1266,1806,137,2374,1495,539,370,1209,1339,1702,720,823,542,2210,1499,2175,2056,1117,674,1053,1974,1209,1388,472,1919,309,577,925,1628,2283,1499,370,1617,58,1084,2198;507,1863,1510,1074,2395,1561,1522,444,958,1932,103,2300,1344,2499,907,259,1902,1238,1673,478,573,186,153,1247,2018,476,399,962,2202,556,1592,1859,1520,2213,1717,2406,633;1700,406,2005,1672,1146,135,1518,890,1817,1822,968,1486,407,1505,2231,1470,249,1631,1131,778,501,1863,376,869,2446,88,208,1367,998,516,2313,841,282,2271,849,2402,885;955,1346,605,2442,12,1136,593,533,2213,1027,715,451,106,540,61,1468,975,2412,1327,65,714,1087,215,520,1725,2155,466,261,1951,1837,1483,2103,2432,447,1852,2064,908;178,2136,1236,1877,128,250,1962,1646,1747,443,2009,1817,302,331,1320,2492,608,270,517,1127,2398,2247,1332,1561,2447,2174,1208,1859,2071,2480,1763,407,469,2259,881,1762,1850;936,1695,1389,1858,1634,1704,390,1281,1749,1281,1045,1534,626,1943,275,374,350,382,1769,396,1527,533,2279,246,2403,2301,2301,1351,501,1683,1449,1733,211,1179,2460,1280,1441;425,2368,2079,872,634,1976,919,444,1435,2279,1506,471,1142,2352,927,1758,2298,2281,108,2495,1096,119,739,1120,1266,1392,1438,26,744,587,2320,1642,286,582,126,376,2173;882,1541,1720,1859,1397,645,1516,1277,1329,2325,2443,348,216,638,645,204,335,1115,1815,1737,1990,2487,1811,1697,1119,883,2099,467,1414,1761,455,1161,2430,1994,2159,1264,187;904,1619,2455,225,32,838,1235,866,563,1047,1186,1344,492,32,2038,1764,720,530,1558,2182,943,2050,2289,1451,296,1627,174,1787,77,1884,319,1283,2359,1759,2349,1657,1711;1186,472,1660,86,1331,704,1885,1483,361,1789,434,997,1785,2413,1641,2147,323,1622,1271,1391,908,1365,689,313,2091,468,2174,2089,795,1432,1439,605,968,422,600,1049,809;711,2468,627,309,726,2024,1901,2310,2374,1839,2313,1324,1295,619,1802,280,1921,1812,1241,1126,2423,231,1442,2079,304,1272,1892,1852,155,234,1511,1176,315,370,2434,2077,1575;1896,2378,2271,169,1843,2342,772,1317,2479,1949,2054,618,254,1846,424,1407,346,2067,707,161,1015,1794,1800,2147,2142,2498,651,1491,1528,1159,1587,1675,1386,2449,215,1371,270;1351,388,2286,1584,1164,1033,2469,616,1366,334,2387,580,1433,1271,1606,529,2438,348,1269,2290,1543,1346,524,2157,383,1735,2083,1483,75,1486,1266,739,878,1400,1992,787,928;564,635,317,1212,415,2080,2211,2157,155,1380,537,2447,1544,632,665,741,679,1793,179,1683,1493,973,1820,1168,1839,959,2188,980,1268,1922,795,1507,2337,1805,1892,1155,1565;2060,2161,1715,664,818,2477,567,1025,214,1969,1521,2272,421,2114,511,1168,344,657,1118,1841,2103,604,1792,376,910,1848,1432,110,1700,219,1624,2057,1532,966,1582,335,1536;920,116,1306,406,1374,599,564,157,1176,1936,569,1922,1838,22,325,78,1049,884,613,2248,2494,2162,1734,456,1181,974,1234,500,196,977,1720,1873,258,455,2048,2445,2196;68,2111,2356,991,589,1194,1759,7,1446,986,2338,1707,768,351,2145,1478,278,2155,2229,2079,2080,2270,84,1600,1926,179,1585,1530,1039,67,1463,277,1413,988,425,2384,1362;547,182,1444,2237,1387,718,1904,1961,747,553,259,1875,152,1202,826,180,818,172,1293,1271,2112,1632,2225,1940,1038,150,783,1172,1463,196,1360,1120,510,1508,1790,1639,1802;1584,1389,766,2033,2038,1505,2127,1093,339,1739,324,1764,2468,740,2235,1204,1316,421,328,1344,1211,1256,1827,2469,1746,683,1819,1440,1832,174,1445,1782,1125,235,308,1664,1489", "output": "607,523,1263,164,861,422,2294,634,666,1689,735,1687,1093,443,159,912,1886,1251,914,2130,1787,1044,2362,474,2484,1285,1780,445,1088,732,473,1357,1638,1439,285,1345,792,808,1767,1353,511,2078,1673,1649,2271,786,1553,2332,1664,2,1176,1761,2485,1905,1812,2094,1021,206,2122,897,437,605,1637,1573,2358,1866,1947,190,604,921,963,1373,1163,696,1870,1904,2290,1300,2068,2245,652,1844,1013,2136,980,1802,1171,1113,1310,331,618,1569,877,1915,1657,1593,1990,1118,2000,2471,2205,1598,1441,1954,2359,2393,1721,256,1909,1356,1700,2188,1614,2312,344,556,745,1066,1341,1863,1383,1140,1034,1927,2210,1434,282,128,817,625,1518,2183,169,496,1236,995,312,1625,2359,106,443,671,2488,688,1050,893,469,518,2073,52,2008,1776,1884,1784,2138,2205,1905,2427,1321,355,1847,1904,2500,1378,2025,745,869,1442,2255,1409,2268,1512,1255,1657,1206,71,2011,985,2002,989,783,42,1132,1146,1059,1110,1030,495,1293,2195,785,1984,2415,2445,412,1214,1479,1239,2188,1124,224,1197,2011,51,1757,1218,1846,2141,2442,1705,486,349,2306,622,2364,2015,268,1957,211,1396,1961,1165,2330,2498,852,1084,644,712,308,11,1846,1925,134,1181,1860,957,2416,1742,2231,611,583,2126,718,2361,85,2357,375,1026,1321,164,330,2023,2050,1649,1920,1799,2332,1260,245,1140,2398,2015,1926,1673,1316,659,1687,1181,2254,1863,1289,1325,1656,5,1893,223,2124,2042,593,1871,1935,1702,2085,2042,482,465,382,2263,2257,649,2494,498,1795,537,1094,212,781,2082,286,1700,2080,11,1223,2376,609,2207,1414,2261,1546,1319,979,1569,1683,1304,1562,1778,932,962,148,1999,1557,1346,1629,1086,307,1680,63,2155,1804,1360,2058,152,624,412,682,119,1329,1202,1536,597,2176,2319,697,324,1567,2039,587,1889,1883,39,1179,648,561,779,1444,943,2035,201,34,1622,1210,2355,2343,972,1980,816,1872,1738,2407,1810,162,1806,2374,539,1209,1702,823,2210,2175,1117,1053,1209,472,309,925,2283,370,58,2198,2406,2213,1859,556,962,476,1247,186,478,1238,259,2499,2300,1932,444,1561,1074,1863,1700,2005,1146,1518,1817,968,407,2231,249,1131,501,376,2446,208,998,2313,282,849,885,2064,447,2103,1837,261,2155,520,1087,65,2412,1468,540,451,1027,533,1136,2442,1346,178,1236,128,1962,1747,2009,302,1320,608,517,2398,1332,2447,1208,2071,1763,469,881,1850,1280,1179,1733,1683,1351,2301,246,533,396,382,374,1943,1534,1281,1281,1704,1858,1695,425,2079,634,919,1435,1506,1142,927,2298,108,1096,739,1266,1438,744,2320,286,126,2173,1264,1994,1161,1761,467,883,1697,2487,1737,1115,204,638,348,2325,1277,645,1859,1541,904,2455,32,1235,563,1186,492,2038,720,1558,943,2289,296,174,77,319,2359,2349,1711,1049,422,605,1432,2089,468,313,1365,1391,1622,2147,2413,997,1789,1483,704,86,472,711,627,726,1901,2374,2313,1295,1802,1921,1241,2423,1442,304,1892,155,1511,315,2434,1575,1371,2449,1675,1159,1491,2498,2147,1794,161,2067,1407,1846,618,1949,1317,2342,169,2378,1351,2286,1164,2469,1366,2387,1433,1606,2438,1269,1543,524,383,2083,75,1266,878,1992,928,1155,1805,1507,1922,980,959,1168,973,1683,1793,741,632,2447,1380,2157,2080,1212,635,2060,1715,818,567,214,1521,421,511,344,1118,2103,1792,910,1432,1700,1624,1532,1582,1536,2445,455,1873,977,500,974,456,2162,2248,884,78,22,1922,1936,157,599,406,116,68,2356,589,1759,1446,2338,768,2145,278,2229,2080,84,1926,1585,1039,1463,1413,425,1362,1639,1508,1120,196,1172,150,1940,1632,1271,172,180,1202,1875,553,1961,718,2237,182,1584,766,2038,2127,339,324,2468,2235,1316,328,1211,1827,1746,1819,1832,1445,1125,308,1489"}, {"input": "656,128,585,2489,1795,143,518,276,967,1501,1484,1569,2324,133,2479,629,1843,1520,1524,1819,315,2351,564,2169,1504,1631,1288,1142,1023,465,107,763,2045,2121,1586,2301,483,1073,1067,1828,879,1170,2012,820,503,556,304,1852,708;1824,360,1310,1424,266,2253,2221,1190,1229,646,714,1481,2084,919,498,824,569,970,2024,108,1479,2270,2345,1512,1915,2260,532,354,270,1267,1631,1961,2154,1683,1678,2355,303,514,1299,304,1844,1909,2120,1412,526,2259,2408,746,529;1773,2060,227,509,2123,627,1246,675,664,1322,924,1418,2126,1164,324,1027,805,2257,1125,513,1241,2186,383,2059,691,2425,2379,632,702,2479,1383,2309,169,117,333,187,2363,1085,864,2344,1707,125,2040,2235,1187,1238,1979,1004,1664;1219,1858,299,246,648,1801,1703,1984,1903,836,1394,2485,589,1281,1308,1415,1634,536,1518,2110,2301,435,1308,991,1911,502,1096,1842,1016,578,397,208,1189,1574,1713,1017,655,1342,2367,1281,778,653,2041,2109,1913,2043,1264,2038,95;369,1611,2071,1873,987,882,2390,1446,200,208,1153,2028,2448,1928,1171,2199,34,441,1766,549,1084,1499,1652,1499,186,1641,210,2336,2302,798,1485,2267,1183,302,1583,2066,1845,2253,1146,487,528,397,1614,1529,1389,2285,1498,591,816;2468,2086,1645,2049,165,186,160,562,1365,1941,2128,1872,611,2484,2112,573,1344,1305,666,1610,1226,2432,1378,2078,2088,2181,2007,2306,1228,1946,69,1509,1357,449,1707,2391,1261,110,2445,1944,1088,2370,2366,933,211,2391,1968,699,2148;1558,606,993,130,2346,451,782,78,1807,1285,1716,621,1692,836,1681,2056,1932,256,566,2125,850,2298,1332,1960,2153,1544,1286,710,1883,2184,1403,2238,1452,1083,2499,1984,788,1010,1143,2286,1223,922,1220,1184,850,2003,1299,1966,1429;2296,1121,1179,500,2349,2225,1556,1617,1414,600,1190,173,1179,324,1419,1812,1051,1963,877,828,2207,1111,2303,1113,563,448,2404,981,994,208,2176,925,954,216,411,1693,1353,1935,412,564,22,2255,647,1667,1949,1956,817,1177,1316;1170,243,367,2352,952,2192,153,718,1712,721,149,1627,2030,764,1186,154,38,1223,2327,2469,440,1373,1166,1862,2226,2148,2024,550,2066,1918,1118,790,462,1355,666,1880,1054,763,58,1381,1209,2326,792,719,1661,1752,2111,1344,356;1642,391,757,576,1956,1326,1017,28,1069,1572,965,1830,1094,1351,1237,2386,2347,47,1072,1473,968,255,485,1907,1257,655,1661,2059,1274,481,1209,1506,905,898,548,1959,628,1864,2482,1531,1704,2250,1929,2202,895,1014,2441,336,2153;1830,2164,1482,320,2311,460,253,2244,2071,829,2346,2199,614,674,1344,2132,1810,477,842,2389,2003,373,2091,1825,228,1858,541,2103,1702,1872,2310,237,2289,1894,1263,90,1622,1043,13,893,2369,300,186,1736,1412,262,2217,247,283;1934,130,1176,1675,738,555,1722,1534,1567,1838,1547,1539,329,2209,545,1425,486,732,2201,1610,2167,522,913,15,94,1223,1897,2231,1738,2179,1554,941,1014,1887,1418,636,1130,773,463,132,1718,65,986,845,276,414,2433,138,1829;2449,200,1003,182,1648,1798,960,2211,890,232,574,2064,1185,960,2360,1307,2366,2450,1314,971,1237,587,2136,906,1694,1231,1128,250,2281,2424,718,1750,2277,2031,193,1411,1562,2149,1306,1706,1673,612,1229,1542,754,2204,1940,988,924;1232,592,1897,237,2304,1691,1707,2283,2171,550,1591,995,1045,833,1353,324,1843,1520,379,2194,781,212,1100,1545,2478,2470,162,299,771,2407,2290,889,1964,856,1364,1242,63,868,779,481,1962,994,2476,838,1625,981,2262,1318,1160;1560,1910,2186,1472,1264,1072,1474,2101,2037,1909,404,1924,1312,833,1519,1282,1696,188,2305,907,598,67,1069,2267,2393,2373,1711,1210,625,804,1352,943,1556,2334,1007,2046,2256,1383,1055,2002,2010,1888,690,1443,694,574,2239,2001,754;2221,241,2147,139,305,199,27,1690,564,948,279,619,38,896,2072,1868,1529,248,1980,1999,65,28,2180,2260,1685,49,69,2169,1126,2195,1175,71,2058,1764,735,439,395,2148,610,988,787,2157,1034,1452,1095,1626,324,1529,1664;1881,2315,997,926,1229,331,130,383,1661,1554,1545,2264,1950,230,39,702,339,2048,1778,1357,2318,391,2164,175,942,866,2322,1948,1111,191,305,1149,2225,2309,135,735,1289,65,849,2405,591,1632,316,1226,666,2310,985,2322,1594;2215,1359,1573,574,322,2052,1417,220,401,1791,951,312,1396,2479,2440,1625,1337,122,1120,1846,2010,935,1458,2266,1538,1769,761,2400,1557,352,1210,1010,302,337,1098,632,1557,632,1596,1298,1478,437,375,22,1263,1822,1475,1105,419;543,358,768,1766,1839,2282,2273,2099,1672,424,108,368,1450,2271,382,2446,2450,1329,1578,51,1196,1695,1589,347,2292,995,2343,2135,695,1560,695,569,1102,1234,1100,2020,598,260,685,1781,1131,1725,1228,1984,316,1480,1031,1011,2031;2433,801,1876,439,555,1248,28,1621,1361,1557,1350,1804,1372,1764,2435,558,1231,1314,2471,823,1963,1287,728,1632,1308,1194,2012,2359,993,1335,1541,1149,1610,1496,467,2310,819,2426,2235,737,2254,111,1891,859,1796,1194,284,1676,2046;571,1241,992,1035,632,1734,1545,303,1840,2450,1963,2385,1642,2189,2076,1714,2227,151,1473,2200,2433,349,448,1017,1455,682,182,2307,1637,1359,1764,434,44,404,1060,910,2092,2125,2286,2378,2357,906,1826,1533,1603,1897,2411,2050,618;1413,101,1978,429,1211,1704,352,476,581,1427,1278,1406,1866,848,2135,1979,1427,1951,400,1795,1854,1307,276,1230,184,472,93,1406,448,674,1000,2114,715,2261,656,1356,2294,1747,1893,950,1660,756,764,1771,1621,120,809,1842,2426;1760,1593,19,880,843,1141,257,2365,417,2200,766,1499,1336,808,1875,467,1075,2005,2162,1284,2446,1592,1608,2405,468,1426,1442,1876,707,1219,2418,348,549,1283,483,978,1251,480,750,1530,580,2093,1592,1714,2443,565,2355,1572,1733;761,1994,2202,710,2273,684,2006,1184,575,767,1289,1848,220,1471,40,1985,560,800,1573,2301,2071,2028,1676,2015,1703,1819,2002,686,339,2316,127,904,1197,134,1126,921,2203,1183,689,1874,2317,2029,2252,2093,464,2346,468,1098,2225;1503,2221,171,1808,2238,896,1742,420,1014,1220,133,1843,1077,1428,357,1799,481,971,860,2409,1437,2500,1754,680,571,847,848,244,2336,1437,2181,1152,2445,2207,690,1326,1199,1186,2346,1096,2108,391,556,1686,243,1136,520,544,1023;600,1320,1014,1609,2005,583,2366,1101,1697,1537,1852,310,382,1651,2112,1140,1512,1863,2000,1341,2384,11,382,1878,1468,260,2190,1630,893,1760,868,2027,1100,1323,1162,1384,2242,2368,535,2319,1988,1408,199,189,408,1883,67,509,648;1808,1870,3,1753,829,541,1237,652,1123,383,1477,1026,338,1524,678,213,1624,1252,960,1759,374,390,5,875,1954,320,544,2432,927,2128,1823,39,34,1408,494,1730,542,1957,291,938,1570,366,420,423,1284,1506,1226,562,1568;546,586,281,2173,2308,35,2500,673,1803,1439,873,621,1687,1813,890,356,412,574,505,2415,1573,1440,1759,1289,573,1015,1135,346,1017,2267,2462,2458,2489,1168,110,1236,842,2121,2486,2088,773,1605,1211,224,981,2028,1581,462,988;2047,2433,291,2164,50,1480,1297,541,1585,2329,1724,1497,2238,708,1930,299,69,2406,277,57,1074,884,164,248,1631,2076,1174,2053,1702,1735,1648,338,2198,2203,626,1137,343,1270,324,2095,833,637,2198,1339,1601,2403,271,1271,1792;978,238,1002,354,1780,476,1858,2494,226,1267,720,490,52,563,47,672,2034,1421,2143,2119,1062,684,1524,520,1101,484,121,1373,1759,1115,2146,262,1078,2362,316,2033,1865,2093,1476,228,2047,2322,684,1507,645,1045,422,2351,473;936,2085,11,181,51,1002,189,1933,1491,1569,615,734,145,2265,1718,920,1319,1017,1705,1311,1112,320,2342,1528,490,2057,216,735,915,2113,189,1643,283,1906,1157,1273,1341,354,2266,1871,33,1512,822,1195,2310,1245,994,1901,1509;2424,2021,801,2239,1005,617,27,1680,98,955,2219,1419,40,1373,6,1542,1260,426,841,2171,976,1720,2016,246,584,1147,382,180,949,2129,1692,1526,1878,348,2379,392,2071,547,1616,307,2425,2326,256,1782,536,970,1195,1070,1291;1610,1337,1303,1855,1114,957,306,831,558,2395,447,637,433,674,1842,1909,1287,1666,495,2196,1468,851,1852,1263,1898,1086,492,371,646,1247,2472,166,881,1343,608,374,1017,1458,1624,2104,201,1225,1066,713,128,1657,1853,2278,2254;1024,388,1893,418,573,498,49,253,911,536,812,1641,1525,345,2386,2401,1061,308,90,265,810,1817,528,377,1359,502,175,1889,208,689,2351,1775,1618,2033,121,1568,1748,708,1450,880,767,1127,1147,1827,609,142,1007,1209,2044", "output": "656,585,1795,518,967,1484,2324,2479,1843,1524,315,564,1504,1288,1023,107,2045,1586,483,1067,879,2012,503,304,708,746,2259,1412,1909,304,514,2355,1683,1961,1267,354,2260,1512,2270,108,970,824,919,1481,646,1190,2253,1424,360,1773,227,2123,1246,664,924,2126,324,805,1125,1241,383,691,2379,702,1383,169,333,2363,864,1707,2040,1187,1979,1664,2038,2043,2109,653,1281,1342,1017,1574,208,578,1842,502,991,435,2110,536,1415,1281,2485,836,1984,1801,246,1858,369,2071,987,2390,200,1153,2448,1171,34,1766,1084,1652,186,210,2302,1485,1183,1583,1845,1146,528,1614,1389,1498,816,699,2391,933,2370,1944,110,2391,449,1509,1946,2306,2181,2078,2432,1610,1305,573,2484,1872,1941,562,186,2049,2086,1558,993,2346,782,1807,1716,1692,1681,1932,566,850,1332,2153,1286,1883,1403,1452,2499,788,1143,1223,1220,850,1299,1429,1177,1956,1667,2255,564,1935,1693,216,925,208,981,448,1113,1111,828,1963,1812,324,173,600,1617,2225,500,1121,1170,367,952,153,1712,149,2030,1186,38,2327,440,1166,2226,2024,2066,1118,462,666,1054,58,1209,792,1661,2111,356,336,1014,2202,2250,1531,1864,1959,898,1506,481,2059,655,1907,255,1473,47,2386,1351,1830,1572,28,1326,576,391,1830,1482,2311,253,2071,2346,614,1344,1810,842,2003,2091,228,541,1702,2310,2289,1263,1622,13,2369,186,1412,2217,283,138,414,845,65,132,773,636,1887,941,2179,2231,1223,15,522,1610,732,1425,2209,1539,1838,1534,555,1675,130,2449,1003,1648,960,890,574,1185,2360,2366,1314,1237,2136,1694,1128,2281,718,2277,193,1562,1306,1673,1229,754,1940,924,1318,981,838,994,481,868,1242,856,889,2407,299,2470,1545,212,2194,1520,324,833,995,550,2283,1691,237,592,1560,2186,1264,1474,2037,404,1312,1519,1696,2305,598,1069,2393,1711,625,1352,1556,1007,2256,1055,2010,690,694,2239,754,1529,1626,1452,2157,988,2148,439,1764,71,2195,2169,49,2260,28,1999,248,1868,896,619,948,1690,199,139,241,1881,997,1229,130,1661,1545,1950,39,339,1778,2318,2164,942,2322,1111,305,2225,135,1289,849,591,316,666,985,1594,1105,1822,22,437,1298,632,632,337,1010,352,2400,1769,2266,935,1846,122,1625,2479,312,1791,220,2052,574,1359,543,768,1839,2273,1672,108,1450,382,2450,1578,1196,1589,2292,2343,695,695,1102,1100,598,685,1131,1228,316,1031,2031,1676,1194,859,111,737,2426,2310,1496,1149,1335,2359,1194,1632,1287,823,1314,558,1764,1804,1557,1621,1248,439,801,571,992,632,1545,1840,1963,1642,2076,2227,1473,2433,448,1455,182,1637,1764,44,1060,2092,2286,2357,1826,1603,2411,618,1842,120,1771,756,950,1747,1356,2261,2114,674,1406,472,1230,1307,1795,1951,1979,848,1406,1427,476,1704,429,101,1760,19,843,257,417,766,1336,1875,1075,2162,2446,1608,468,1442,707,2418,549,483,1251,750,580,1592,2443,2355,1733,1098,2346,2093,2029,1874,1183,921,134,904,2316,686,1819,2015,2028,2301,800,1985,1471,1848,767,1184,684,710,1994,1503,171,2238,1742,1014,133,1077,357,481,860,1437,1754,571,848,2336,2181,2445,690,1199,2346,2108,556,243,520,1023,509,1883,189,1408,2319,2368,1384,1323,2027,1760,1630,260,1878,11,1341,1863,1140,1651,310,1537,1101,583,1609,1320,1808,3,829,1237,1123,1477,338,678,1624,960,374,5,1954,544,927,1823,34,494,542,291,1570,420,1284,1226,1568,462,2028,224,1605,2088,2121,1236,1168,2458,2267,346,1015,1289,1440,2415,574,356,1813,621,1439,673,35,2173,586,2047,291,50,1297,1585,1724,2238,1930,69,277,1074,164,1631,1174,1702,1648,2198,626,343,324,833,2198,1601,271,1792,2351,1045,1507,2322,228,2093,2033,2362,262,1115,1373,484,520,684,2119,1421,672,563,490,1267,2494,476,354,238,936,11,51,189,1491,615,145,1718,1319,1705,1112,2342,490,216,915,189,283,1157,1341,2266,33,822,2310,994,1509,1070,970,1782,2326,307,547,392,348,1526,2129,180,1147,246,1720,2171,426,1542,1373,1419,955,1680,617,2239,2021,1610,1303,1114,306,558,447,433,1842,1287,495,1468,1852,1898,492,646,2472,881,608,1017,1624,201,1066,128,1853,2254,1209,142,1827,1127,880,708,1568,2033,1775,689,1889,502,377,1817,265,308,2401,345,1641,536,253,498,418,388"}, {"input": "1963,250,360,1146,1569,563,1718,817,2154,1021,2227,80,1567,1471,1965,2231,1986,1410,2317,2058,1318,1591,1108,737,107,1307,2446,898,121,1151,240,1933,2169,1465,2393,954,654;411,1016,988,1092,2186,230,899,2359,1591,1454,712,722,969,2427,1303,1470,2424,116,1441,2326,2309,583,2307,772,2017,2221,1266,720,2009,156,370,231,953,2465,897,82,2157;1958,3,1359,826,535,1396,727,1326,244,90,606,2403,581,455,2156,1495,298,1531,1621,2401,414,1379,1237,1322,559,646,1790,1996,1300,714,2302,1462,915,2413,719,1550,1257;1207,522,728,8,2347,1604,2325,133,746,2468,1304,905,2317,427,2033,577,1357,319,975,1421,1309,688,364,1376,1830,47,1087,859,1023,278,1436,1052,443,6,198,1581,1795;1719,682,1696,2020,1552,1439,2237,1538,416,1964,2368,924,667,1849,302,137,1208,83,1306,1070,429,304,1401,697,1538,660,308,2241,382,1385,2434,1978,127,1767,676,2488,1779;644,220,415,1357,842,779,1677,2270,2213,1087,1154,1219,973,393,204,1610,2342,2252,2011,630,224,1478,16,1752,359,1207,2459,1968,818,398,106,848,700,1196,336,1940,474;1264,1629,1929,2004,1086,374,2229,1588,758,1520,1563,1514,765,1826,183,1079,1802,1905,1079,927,1101,2312,253,620,397,352,1409,2218,1696,2416,932,2268,250,1586,2141,1715,2194;1945,2346,966,1951,1225,324,1618,143,2057,2340,2117,2341,604,493,1840,709,685,868,790,517,175,1735,321,1784,828,606,2438,1057,1310,275,357,1590,2279,1628,2262,1336,1132;2129,1877,51,2407,2141,1719,461,1698,613,608,2321,2409,2387,411,433,2305,414,1172,2194,1409,1684,1082,1569,1989,2344,2495,1938,154,706,1129,1651,590,2494,1646,159,1622,1358;974,202,1947,1101,1526,83,1384,1242,1274,1149,2014,403,934,551,1231,1815,1315,1104,1708,2478,366,770,1810,866,1668,1985,2116,1532,231,2111,652,269,1275,2076,1653,556,2148;2330,119,712,790,823,237,1022,136,1870,208,1477,816,1123,1509,1902,2069,1626,508,126,991,1526,2003,2434,1828,728,1944,2404,2259,1433,1411,670,1060,371,1168,113,1584,204;668,2344,878,907,923,847,1103,1678,2103,83,37,1942,542,710,2463,35,917,1034,2492,1252,1128,1736,1543,1429,1881,1033,894,1912,1238,2133,1627,2395,420,31,2096,1533,2300;2433,2495,1158,1223,443,1974,262,1378,1133,1332,1135,1070,1224,772,615,2119,985,233,2458,1656,1310,574,105,2038,1211,1063,1715,1658,1591,145,2389,2344,778,1406,911,2190,1949;1469,2078,1230,697,2287,742,1204,400,1929,525,1060,2290,750,1375,366,911,1456,915,1258,1723,1358,1523,1068,2399,1205,1900,483,1928,220,2391,2377,292,1935,797,2050,491,1564;2171,1223,1693,222,618,563,821,1404,1677,2333,1875,587,1296,739,332,1998,1363,725,1284,238,20,1852,1121,858,691,2361,649,2006,361,531,1777,1759,1653,1758,1956,1571,20;155,2187,817,1529,58,1320,2176,781,74,17,1020,927,1411,1279,529,421,1572,2062,2412,1254,685,268,188,1222,1192,1868,2132,2443,2147,1384,1777,549,1404,2008,1472,772,676;1653,79,936,919,538,866,90,2416,2067,693,505,1502,154,1537,1048,2191,200,2433,197,443,81,198,475,1708,1820,1558,507,2242,1036,1944,628,842,39,1234,1724,414,2132;1106,2481,562,1716,430,2096,483,1158,467,436,2039,814,2495,819,1078,2143,827,1467,1679,1210,657,162,2246,2034,851,1969,1355,961,12,53,365,453,2352,2024,611,369,2096;308,415,1049,947,1871,1213,1082,1902,206,409,716,162,1191,1476,1281,1745,475,390,188,40,567,699,1347,1465,1793,1099,381,1527,1404,750,467,1642,1640,1870,1114,1580,1959;1728,684,464,543,241,653,425,1705,2420,1978,2331,1795,743,1556,1469,119,536,1979,2000,463,1685,1806,189,260,1072,1288,51,2150,2362,2315,918,1386,2127,2143,391,1773,1019;1974,1417,1577,609,2287,224,48,643,2071,1923,2031,678,307,2014,1314,987,1356,1140,207,2077,913,2255,1551,1652,963,323,1881,1820,2348,1836,361,2042,1832,1295,487,2038,73;421,1653,1689,147,2283,2250,1,373,2475,1248,2083,2304,848,1869,1397,1489,223,914,1862,1360,2295,2458,1938,1489,1854,468,400,909,9,1399,1455,1196,2244,2139,1532,436,188;673,2017,576,1677,439,1042,803,769,495,1610,884,1873,781,1385,442,1698,191,2412,505,1846,1874,2414,2066,552,2044,18,2173,199,2267,1773,2397,1979,2083,726,2370,712,526;425,1587,2460,2483,1319,2065,1576,1715,2495,1017,1121,1630,1405,1205,1855,547,566,1691,2468,2099,1225,2244,1286,2268,891,823,859,1191,1415,544,729,2064,2223,1321,473,1443,2304;1968,2388,2338,1710,2187,1172,1731,53,2142,437,104,1561,596,218,232,819,1094,660,1174,1027,600,255,1209,836,2217,133,1470,1854,420,2302,919,2299,1593,974,2093,1179,193;1563,1588,1707,1281,2262,221,54,1030,832,1815,924,1507,2411,2239,2472,805,793,1205,1839,727,306,766,712,2105,489,1546,167,1756,1144,2280,1083,533,660,2393,1045,24,1354;1911,635,164,630,1322,2445,209,1234,2010,2346,2254,1467,299,1302,2153,901,754,2133,280,2070,653,1704,2225,2200,1653,377,1432,907,874,1360,1357,1478,1203,895,2173,1946,2300;37,470,1418,1826,985,999,164,1315,1563,465,1581,1051,2213,1159,102,2118,1536,2107,2084,1826,1994,180,1215,789,1313,2105,338,394,686,2204,2185,31,269,864,874,1738,426", "output": "1963,360,1569,1718,2154,2227,1567,1965,1986,2317,1318,1108,107,2446,121,240,2169,2393,654,82,2465,231,156,720,2221,772,583,2326,116,1470,2427,722,1454,2359,230,1092,1016,1958,1359,535,727,244,606,581,2156,298,1621,414,1237,559,1790,1300,2302,915,719,1257,1581,6,1052,278,859,47,1376,688,1421,319,577,427,905,2468,133,1604,8,522,1719,1696,1552,2237,416,2368,667,302,1208,1306,429,1401,1538,308,382,2434,127,676,1779,1940,1196,848,398,1968,1207,1752,1478,630,2252,1610,393,1219,1087,2270,779,1357,220,1264,1929,1086,2229,758,1563,765,183,1802,1079,1101,253,397,1409,1696,932,250,2141,2194,1336,1628,1590,275,1057,606,1784,1735,517,868,709,493,2341,2340,143,324,1951,2346,2129,51,2141,461,613,2321,2387,433,414,2194,1684,1569,2344,1938,706,1651,2494,159,1358,556,2076,269,2111,1532,1985,866,770,2478,1104,1815,551,403,1149,1242,83,1101,202,2330,712,823,1022,1870,1477,1123,1902,1626,126,1526,2434,728,2404,1433,670,371,113,204,1533,31,2395,2133,1912,1033,1429,1736,1252,1034,35,710,1942,83,1678,847,907,2344,2433,1158,443,262,1133,1135,1224,615,985,2458,1310,105,1211,1715,1591,2389,778,911,1949,491,797,292,2391,1928,1900,2399,1523,1723,915,911,1375,2290,525,400,742,697,2078,2171,1693,618,821,1677,1875,1296,332,1363,1284,20,1121,691,649,361,1777,1653,1956,20,772,2008,549,1384,2443,1868,1222,268,1254,2062,421,1279,927,17,781,1320,1529,2187,1653,936,538,90,2067,505,154,1048,200,197,81,475,1820,507,1036,628,39,1724,2132,369,2024,453,53,961,1969,2034,162,1210,1467,2143,819,814,436,1158,2096,1716,2481,308,1049,1871,1082,206,716,1191,1281,475,188,567,1347,1793,381,1404,467,1640,1114,1959,1773,2143,1386,2315,2150,1288,260,1806,463,1979,119,1556,1795,1978,1705,653,543,684,1974,1577,2287,48,2071,2031,307,1314,1356,207,913,1551,963,1881,2348,361,1832,487,73,436,2139,1196,1399,909,468,1489,2458,1360,914,1489,1869,2304,1248,373,2250,147,1653,673,576,439,803,495,884,781,442,191,505,1874,2066,2044,2173,2267,2397,2083,2370,526,1443,1321,2064,544,1191,823,2268,2244,2099,1691,547,1205,1630,1017,1715,2065,2483,1587,1968,2338,2187,1731,2142,104,596,232,1094,1174,600,1209,2217,1470,420,919,1593,2093,193,24,2393,533,2280,1756,1546,2105,766,727,1205,805,2239,1507,1815,1030,221,1281,1588,1911,164,1322,209,2010,2254,299,2153,754,280,653,2225,1653,1432,874,1357,1203,2173,2300,1738,864,31,2204,394,2105,789,180,1826,2107,2118,1159,1051,465,1315,999,1826,470"}, {"input": "1652,1675,2067,1068,2473,19,1354,942,1657,1732,1799,2054,858,765,131,784,310,1626,506,846,440,1982,1844,2445,61,1399,997,1239,169,850,2272,2188,908,776,818,418,1307,393,2098,65,432,1631,1650,1146,2215,47,646,1023,1735,554;2203,239,489,2446,910,2052,2165,1497,795,295,452,1449,1131,988,2308,1983,2229,387,1473,1986,1008,1066,355,1301,2375,346,89,1547,1747,51,2049,1722,752,966,1557,1447,245,1187,1627,156,579,1681,716,588,1274,2026,2262,2479,540,593;1380,430,2254,600,1746,407,1003,1382,177,1704,514,267,248,2169,1185,136,317,1324,1967,2384,2034,73,1617,557,2145,264,153,2312,1957,1450,754,1732,2175,1621,1714,1533,204,2185,879,1716,2263,381,1603,2283,672,466,1192,172,1813,926;1930,803,221,2153,1858,339,1150,810,2370,74,799,42,2469,636,108,214,1398,1603,726,1630,163,1976,30,727,1166,2018,1170,2104,1337,1839,2144,2189,2170,704,259,947,690,1892,936,2183,481,1353,714,626,2442,849,709,554,2355,1858;716,1344,1049,153,460,1216,2428,1020,2256,1212,2005,1507,1195,962,350,2073,2200,1646,1276,1479,2459,1099,1862,2237,214,236,1948,2352,712,1105,1756,888,1638,1684,2453,2144,992,1959,1436,1473,1498,70,1148,1378,2229,1000,2211,2019,1479,159;56,2048,1904,129,2381,223,772,474,1818,594,390,319,930,1486,2407,2050,10,1159,791,859,969,451,1536,1723,2379,1723,1084,76,474,200,342,1280,1662,127,372,819,856,1339,761,30,1781,682,714,1570,224,2323,849,317,1589,1132;535,1583,1633,929,947,480,1553,388,1200,215,2252,640,780,432,32,262,1948,352,1839,496,2467,2385,1209,1297,1906,1025,190,1370,452,2473,2346,1483,119,2270,302,2450,48,24,1363,1692,1807,954,1467,645,1709,926,1495,2450,1512,357;1933,1771,978,1481,746,1081,449,983,116,615,761,2160,1542,1962,401,223,1626,1697,1338,1735,89,691,1208,2381,687,792,1501,1826,1804,1818,1178,333,1233,2376,180,1505,1929,351,2042,1381,785,620,527,2032,2021,1425,669,1613,500,1294;2159,1903,2141,2147,2437,473,1643,2269,1022,405,1956,434,1300,465,384,274,1058,666,1078,476,644,1200,2052,1277,1493,1251,1706,1801,889,305,836,1818,305,1925,1081,379,2349,3,1679,1648,2446,1316,1271,1301,220,2224,1442,1949,21,787;1042,31,501,372,2020,1652,366,1891,119,1585,428,845,151,465,425,515,1852,874,2181,908,371,2140,360,1864,665,122,1002,1303,1926,2405,1560,1465,1729,1064,51,126,261,2334,262,1300,1191,532,1634,235,1793,2265,609,1192,308,504;1726,1148,843,1111,707,1241,286,501,1039,1938,1299,1195,1622,1788,592,1126,2164,598,520,938,256,1743,1204,518,301,325,1732,2094,1072,1640,225,919,2124,2448,1425,401,1385,610,976,1144,1731,1602,1305,602,265,2029,1175,1740,1054,1331;772,957,404,1775,1108,2378,1289,40,1762,139,1326,1180,424,394,874,1949,427,917,1191,1742,992,431,49,2034,2226,2452,187,1981,2194,1755,2362,1316,1855,1540,220,457,2284,2159,932,57,1124,437,1322,1140,1162,2001,1256,2042,985,976;1096,913,1521,2494,1921,1019,1770,2470,1958,142,385,1748,2057,1476,640,1487,989,314,1982,1310,200,1041,17,2309,878,1941,76,339,474,2124,1342,1630,2282,2345,1834,1101,74,1469,693,2313,88,1342,1452,134,2454,1435,1979,2337,628,2057;277,2174,1094,1831,628,1600,1632,2070,204,1625,842,2484,2481,705,1180,316,1745,389,371,2445,1419,1104,145,1562,728,1999,2101,107,2092,2183,221,1613,2058,825,365,503,615,483,1886,2387,1361,2469,572,2271,609,657,859,989,334,760;1349,1599,1991,2042,562,1419,10,878,2127,1410,1757,505,1740,717,1887,476,1070,377,777,1144,715,2035,2026,773,590,826,1293,2015,953,2008,1042,737,415,1268,619,49,2496,1035,759,143,1800,2433,977,1971,1069,459,1514,2082,1866,269;1178,588,1403,207,1349,2321,557,1352,927,9,2354,1492,1471,2243,2014,2025,2490,2486,917,1620,1210,747,2002,864,1886,2397,1427,1859,611,912,2133,408,1730,293,523,2388,609,349,981,1314,425,418,302,981,850,208,438,121,1948,1345;769,1528,182,730,1066,1659,2363,1143,2152,1182,425,699,865,572,517,743,935,697,137,2285,1983,1022,2146,1318,1944,243,2358,1247,849,2396,430,1019,1967,49,2158,1447,2302,1801,2127,841,1965,695,508,923,458,1738,2269,762,576,1540;222,2113,27,2442,857,1829,277,1526,438,950,306,1840,2226,1236,1106,2452,2231,2291,1010,2214,13,809,1820,1140,1793,948,2228,506,393,915,856,1825,251,1025,2355,1092,1621,693,1255,1501,1283,1264,128,1801,2000,63,64,1315,953,1459;1319,2080,2125,534,838,1081,2261,415,510,2094,113,2275,734,2313,952,2120,1319,238,559,2192,1149,2016,1972,2424,2267,680,1396,2112,1992,1451,898,1903,288,1521,1746,1208,411,1316,962,887,137,1828,67,1562,1684,1705,2022,250,1645,874;955,372,410,2348,283,1765,383,428,2418,1362,1381,903,105,2437,1004,2008,842,468,780,1048,234,944,1998,2019,317,1911,35,881,1990,2344,866,113,1697,400,2206,2379,562,209,60,1175,1520,2120,531,185,1954,590,396,1603,748,1108;1839,1223,521,1223,1768,2290,1106,1959,999,604,1476,1316,249,1740,1346,551,2358,2482,99,1374,897,1576,1807,491,530,100,1845,651,141,1416,1953,2248,2480,93,960,1286,1315,46,2201,405,2329,2476,1698,2211,1078,1138,1319,1784,1338,1830;2207,326,1832,1080,1206,760,138,1289,1067,228,1481,348,1516,1335,1720,1984,1150,40,2311,714,199,480,1613,2042,1295,2464,2445,995,146,99,294,918,1055,322,1242,137,1430,2208,214,1588,1961,79,2339,296,1044,1114,1776,1472,1268,2127;1055,23,201,56,165,1204,154,93,1200,1689,1044,1470,1032,1893,1578,2165,865,1212,2194,1806,1438,698,1480,1665,78,1156,2260,2380,2479,582,1156,1624,1741,552,1296,1817,1729,248,341,789,2173,162,1928,2468,1358,325,366,2078,460,699;438,1574,1446,725,1528,246,2281,482,1508,2319,1352,2465,93,1263,985,446,1386,89,1799,290,2037,1052,292,1773,1125,1971,1984,1587,773,416,164,937,641,1014,499,2392,1879,1647,1933,238,665,1484,1259,1540,409,1693,2089,1041,1199,1139;1556,2432,1718,1159,1497,2069,2487,738,1030,1263,345,2222,934,759,2083,276,361,992,1819,521,1114,1143,2020,2440,644,2369,1875,1330,2354,379,1091,1227,2172,2357,1253,82,21,2353,1268,1575,1392,2230,1045,1660,962,2376,634,1185,2296,2061;2025,2295,75,1953,1000,1960,1628,1956,1713,1044,2344,1926,843,1855,2176,186,1318,1017,1124,607,1437,457,2306,409,2204,1862,503,1735,520,2205,2342,1829,1256,1809,1783,1875,1772,1742,1640,235,335,2410,494,2464,778,1495,671,1559,1037,517;1403,2363,863,464,1837,1783,2374,2033,64,2175,1455,1723,1833,1305,2356,479,108,1536,1787,871,2422,1703,1987,191,1242,1137,1825,1956,1972,455,1113,140,1456,1845,1918,227,553,1496,75,351,1475,1510,1156,1049,1156,147,2205,1314,1878,1327;542,1517,1596,887,2010,1059,1095,2252,1103,1463,1379,1380,1940,1599,1680,863,992,1386,1113,753,14,1368,109,2316,1399,884,41,1841,658,1927,1926,536,2163,586,1945,1594,2343,1340,2079,2279,2040,247,2275,2381,1117,646,1747,1652,94,962;1679,1736,2500,2214,128,768,1904,1783,1255,1083,2216,707,2458,1170,806,1477,190,232,1975,2471,1631,421,1771,1454,918,1959,2031,1913,2153,1049,572,1140,2012,435,1721,1180,2312,265,2402,458,1596,791,1755,2384,1367,89,1929,712,1406,2488;721,1411,148,406,1591,2484,303,1429,1750,1952,2172,254,1968,2088,582,853,220,1959,189,87,2146,260,806,884,1262,2374,76,580,855,1968,1228,950,729,1771,2352,720,1142,1153,401,2262,16,370,1554,2365,1444,483,484,715,2345,1231;1723,1077,162,1013,280,439,2222,638,2267,1893,2456,387,1078,1781,1464,2418,1430,393,337,595,113,773,945,2306,244,1506,2469,1577,1771,1773,2375,1040,632,889,2351,1189,774,2285,852,1973,1464,1176,652,2171,2052,1229,1577,993,1942,1964;989,1256,2253,1330,220,998,40,735,1838,1946,560,325,1860,2358,838,306,1643,649,1466,191,1352,1444,811,647,1739,1817,2484,597,1139,1251,2094,1008,1909,589,1617,2288,1890,1997,2414,986,2090,2157,2333,1100,2436,325,703,2157,1787,1813;679,2075,1998,1967,1054,2040,2206,1572,342,214,1207,74,1815,1555,678,2445,1545,1561,1285,749,1154,411,1298,1991,903,305,2105,206,577,75,1171,83,1081,318,33,1885,419,2322,283,552,2438,1147,1022,1018,1870,231,738,1730,1493,1794;2168,409,1193,1621,910,1465,1302,123,324,2386,859,1516,857,259,326,125,467,1325,2094,1238,1513,1621,1815,923,376,897,1955,236,190,269,1889,1128,2324,781,378,1848,1473,1700,114,2047,956,28,758,425,1824,873,1857,873,967,2440;1971,182,342,24,401,1186,2318,704,1695,641,315,2260,648,653,1070,64,1,1704,317,855,2148,1562,1371,1106,2432,1747,1651,218,701,1283,349,1110,1023,1399,2223,170,1134,1930,342,263,2282,127,134,1241,1389,216,340,1294,993,287;461,2344,1344,1665,239,619,1974,1664,2460,781,1123,2026,1986,2487,1791,1709,204,1341,1052,2058,1362,1541,614,1298,1935,1434,34,1120,693,736,1269,1642,1069,234,1585,2420,1080,2049,1700,450,2016,1383,1057,434,2123,653,2043,2044,448,475;1230,2301,2286,398,1568,228,1512,2279,87,310,2325,2045,1353,1451,2008,173,2281,698,1645,2015,2247,1563,1336,192,1076,1110,1187,375,1225,1143,563,1068,594,1657,2023,77,2172,2207,249,1420,179,266,1346,508,932,1796,2097,1701,725,1683;2089,1033,1820,177,1202,586,1044,258,1684,2308,2069,477,1208,614,23,1824,1566,2208,322,1799,44,181,1758,2191,319,1085,901,1745,1475,2363,1935,632,925,2442,1915,1604,1684,430,195,1282,1031,498,1881,343,1321,155,120,2025,1772,57;330,1873,1425,455,2200,25,23,1839,1939,2268,1026,734,2077,1164,1507,1486,1871,1790,421,2169,1753,1980,1976,188,1776,1753,2000,538,379,2475,653,725,2267,953,1227,2402,481,1061,841,44,2425,619,454,1485,649,1854,724,1490,1988,2191;910,804,1732,1900,1149,223,2146,2361,419,699,185,1415,2429,2393,1097,1174,1906,1602,2421,2185,2210,120,372,723,677,1402,1659,529,250,2180,886,1700,394,60,2292,2211,157,610,1466,2011,158,287,1653,690,194,1632,987,1875,256,928;1523,1381,1441,433,1303,505,1604,1795,1552,315,1785,1694,622,2346,1663,1423,2219,1625,790,1581,223,544,1474,998,1539,2104,2000,771,592,249,607,729,1337,1131,1473,189,2252,81,1587,1099,76,1799,2291,1897,837,2290,2040,397,2195,820;1178,481,230,209,19,1791,1596,1322,2212,1200,2111,1177,987,2309,948,112,24,1134,1764,254,923,1283,1697,6,2186,2496,2034,157,1573,1131,2316,1004,1927,1528,22,1166,1158,1915,209,1290,2272,994,237,1077,1925,61,519,2002,2170,2364;97,655,1866,1743,1077,1509,466,771,18,196,1314,205,485,2235,1343,2011,1346,1224,1976,860,2221,2081,1,2220,1159,738,1986,1260,100,1568,656,2092,675,2054,1334,11,1821,671,1411,1290,917,753,54,1518,574,2197,1478,299,1310,1515;230,480,773,1350,644,1036,1918,331,377,1793,2265,2090,1942,1416,56,1481,501,854,494,2174,1095,360,2101,101,1470,380,1186,418,521,91,14,2018,1058,171,1126,1531,278,1357,1753,2378,2473,872,886,631,1937,1668,596,1568,2301,2342;2392,1087,1836,927,2093,1907,832,173,2324,618,1515,730,835,2469,199,1538,210,1504,1691,814,1686,186,1798,332,610,1236,505,834,1955,841,2498,1217,355,561,1282,2193,285,2325,909,1763,1595,2370,1177,777,1765,1219,851,1752,1434,799;345,1255,1291,2442,1147,1528,1724,2261,481,1508,130,2225,2391,1310,446,1203,1563,954,442,2188,1834,2256,2372,1962,1683,935,983,190,528,813,33,1152,638,861,986,910,2123,2152,981,425,2335,1584,17,595,1329,111,629,2031,67,1059;24,100,1272,1005,2238,1784,1555,1757,2110,1242,1915,165,2047,626,1593,176,657,1901,1289,1953,2074,2483,1715,1748,830,1693,2063,119,1462,841,1989,793,2171,238,2273,2154,604,825,778,177,2312,1886,122,383,2494,2379,2221,696,1207,1902;2048,207,1912,1483,407,2145,1623,568,428,14,2308,2077,1696,771,1654,1886,2161,713,2071,279,1736,2231,2352,1587,47,57,1550,1635,2066,2145,260,654,1993,2409,193,1277,670,1514,704,2230,1091,1546,1322,2063,96,1730,2237,308,1842,2445", "output": "1652,2067,2473,1354,1657,1799,858,131,310,506,440,1844,61,997,169,2272,908,818,1307,2098,432,1650,2215,646,1735,593,2479,2026,588,1681,156,1187,1447,966,1722,51,1547,346,1301,1066,1986,387,1983,988,1449,295,1497,2052,2446,239,1380,2254,1746,1003,177,514,248,1185,317,1967,2034,1617,2145,153,1957,754,2175,1714,204,879,2263,1603,672,1192,1813,1858,554,849,626,1353,2183,1892,947,704,2189,1839,2104,2018,727,1976,1630,1603,214,636,42,74,810,339,2153,803,716,1049,460,2428,2256,2005,1195,350,2200,1276,2459,1862,214,1948,712,1756,1638,2453,992,1436,1498,1148,2229,2211,1479,1132,317,2323,1570,682,30,1339,819,127,1280,200,76,1723,1723,451,859,1159,2050,1486,319,594,474,223,129,2048,535,1633,947,1553,1200,2252,780,32,1948,1839,2467,1209,1906,190,452,2346,119,302,48,1363,1807,1467,1709,1495,1512,1294,1613,1425,2032,620,1381,351,1505,2376,333,1818,1826,792,2381,691,1735,1697,223,1962,2160,615,983,1081,1481,1771,2159,2141,2437,1643,1022,1956,1300,384,1058,1078,644,2052,1493,1706,889,836,305,1081,2349,1679,2446,1271,220,1442,21,504,1192,2265,235,532,1300,2334,126,1064,1465,2405,1303,122,1864,2140,908,874,515,465,845,1585,1891,1652,372,31,1726,843,707,286,1039,1299,1622,592,2164,520,256,1204,301,1732,1072,225,2124,1425,1385,976,1731,1305,265,1175,1054,976,2042,2001,1140,437,57,2159,457,1540,1316,1755,1981,2452,2034,431,1742,917,1949,394,1180,139,40,2378,1775,957,1096,1521,1921,1770,1958,385,2057,640,989,1982,200,17,878,76,474,1342,2282,1834,74,693,88,1452,2454,1979,628,760,989,657,2271,2469,2387,483,503,825,1613,2183,107,1999,1562,1104,2445,389,316,705,2484,1625,2070,1600,1831,2174,1349,1991,562,10,2127,1757,1740,1887,1070,777,715,2026,590,1293,953,1042,415,619,2496,759,1800,977,1069,1514,1866,1345,121,208,981,418,1314,349,2388,293,408,912,1859,2397,864,747,1620,2486,2025,2243,1492,9,1352,2321,207,588,769,182,1066,2363,2152,425,865,517,935,137,1983,2146,1944,2358,849,430,1967,2158,2302,2127,1965,508,458,2269,576,1459,1315,63,1801,1264,1501,693,1092,1025,1825,915,506,948,1140,809,2214,2291,2452,1236,1840,950,1526,1829,2442,2113,1319,2125,838,2261,510,113,734,952,1319,559,1149,1972,2267,1396,1992,898,288,1746,411,962,137,67,1684,2022,1645,1108,1603,590,185,2120,1175,209,2379,400,113,2344,881,1911,2019,944,1048,468,2008,2437,903,1362,428,1765,2348,372,1839,521,1768,1106,999,1476,249,1346,2358,99,897,1807,530,1845,141,1953,2480,960,1315,2201,2329,1698,1078,1319,1338,2127,1472,1114,296,79,1588,2208,137,322,918,99,995,2464,2042,480,714,40,1984,1335,348,228,1289,760,1080,326,1055,201,165,154,1200,1044,1032,1578,865,2194,1438,1480,78,2260,2479,1156,1741,1296,1729,341,2173,1928,1358,366,460,1139,1041,1693,1540,1484,238,1647,2392,1014,937,416,1587,1971,1773,1052,290,89,446,1263,2465,2319,482,246,725,1574,1556,1718,1497,2487,1030,345,934,2083,361,1819,1114,2020,644,1875,2354,1091,2172,1253,21,1268,1392,1045,962,634,2296,517,1559,1495,2464,2410,235,1742,1875,1809,1829,2205,1735,1862,409,457,607,1017,186,1855,1926,1044,1956,1960,1953,2295,1403,863,1837,2374,64,1455,1833,2356,108,1787,2422,1987,1242,1825,1972,1113,1456,1918,553,75,1475,1156,1156,2205,1878,962,1652,646,2381,247,2279,1340,1594,586,536,1927,1841,884,2316,1368,753,1386,863,1599,1380,1463,2252,1059,887,1517,1679,2500,128,1904,1255,2216,2458,806,190,1975,1631,1771,918,2031,2153,572,2012,1721,2312,2402,1596,1755,1367,1929,1406,1231,715,483,2365,370,2262,1153,720,1771,950,1968,580,2374,884,260,87,1959,853,2088,254,1952,1429,2484,406,1411,1723,162,280,2222,2267,2456,1078,1464,1430,337,113,945,244,2469,1771,2375,632,2351,774,852,1464,652,2052,1577,1942,1813,2157,325,1100,2157,986,1997,2288,589,1008,1251,597,1817,647,1444,191,649,306,2358,325,1946,735,998,1330,1256,679,1998,1054,2206,342,1207,1815,678,1545,1285,1154,1298,903,2105,577,1171,1081,33,419,283,2438,1022,1870,738,1493,2440,873,873,425,28,2047,1700,1848,781,1128,269,236,897,923,1621,1238,1325,125,259,1516,2386,123,1465,1621,409,1971,342,401,2318,1695,315,648,1070,1,317,2148,1371,2432,1651,701,349,1023,2223,1134,342,2282,134,1389,340,993,475,2044,653,434,1383,450,2049,2420,234,1642,736,1120,1434,1298,1541,2058,1341,1709,2487,2026,781,1664,619,1665,2344,1230,2286,1568,1512,87,2325,1353,2008,2281,1645,2247,1336,1076,1187,1225,563,594,2023,2172,249,179,1346,932,2097,725,57,2025,155,343,498,1282,430,1604,2442,632,2363,1745,1085,2191,181,1799,2208,1824,614,477,2308,258,586,177,1033,330,1425,2200,23,1939,1026,2077,1507,1871,421,1753,1976,1776,2000,379,653,2267,1227,481,841,2425,454,649,724,1988,928,1875,1632,690,287,2011,610,2211,60,1700,2180,529,1402,723,120,2185,1602,1174,2393,1415,699,2361,223,1900,804,1523,1441,1303,1604,1552,1785,622,1663,2219,790,223,1474,1539,2000,592,607,1337,1473,2252,1587,76,2291,837,2040,2195,2364,2002,61,1077,994,1290,1915,1166,1528,1004,1131,157,2496,6,1283,254,1134,112,2309,1177,1200,1322,1791,209,481,97,1866,1077,466,18,1314,485,1343,1346,1976,2221,1,1159,1986,100,656,675,1334,1821,1411,917,54,574,1478,1310,2342,1568,1668,631,872,2378,1357,1531,171,2018,91,418,380,101,360,2174,854,1481,1416,2090,1793,331,1036,1350,480,2392,1836,2093,832,2324,1515,835,199,210,1691,1686,1798,610,505,1955,2498,355,1282,285,909,1595,1177,1765,851,1434,1059,2031,111,595,1584,425,2152,910,861,1152,813,190,935,1962,2256,2188,954,1203,1310,2225,1508,2261,1528,2442,1255,24,1272,2238,1555,2110,1915,2047,1593,657,1289,2074,1715,830,2063,1462,1989,2171,2273,604,778,2312,122,2494,2221,1207,2445,308,1730,2063,1546,2230,1514,1277,2409,654,2145,1635,57,1587,2231,279,713,1886,771,2077,14,568,2145,1483,207"}, {"input": "1170,414,2498,1870,2477,1814,35,889,506,170,2284,256;2176,869,1083,2289,18,2237,1417,1059,1055,2174,1868,2257;2350,183,1113,2188,1011,789,1045,1706,1304,2209,1545,1876;555,1585,246,749,410,887,288,2066,122,1730,1731,1700;1220,230,1312,2482,2368,1952,1244,912,100,2176,2043,2277;36,867,1824,2147,709,1370,988,1798,438,520,1714,2155;2161,2034,95,1177,329,1367,1311,1994,2214,404,963,1801;821,319,1163,685,490,1958,1386,1589,564,1107,1969,2434;2467,1129,1033,1009,805,456,2035,2231,652,1842,926,160;1442,1957,1674,1781,553,132,2163,1266,58,1805,2134,1124", "output": "1170,2498,2477,35,506,2284,2257,2174,1059,2237,2289,869,2350,1113,1011,1045,1304,1545,1700,1730,2066,887,749,1585,1220,1312,2368,1244,100,2043,2155,520,1798,1370,2147,867,2161,95,329,1311,2214,963,2434,1107,1589,1958,685,319,2467,1033,805,2035,652,926,1124,1805,1266,132,1781,1957"}, {"input": "1037,56,471,1361,1812,1840,1206,1665,1582,569,479,2458,1990,2094,1297,1751,1405,513,1295,1408,1232,614,1078,1369,2303,1729,1647;1862,715,2500,732,2346,2487,225,1898,664,555,1721,1935,1112,179,1776,97,406,1288,1065,427,933,2117,671,1796,956,2282,1668;2202,2153,896,970,553,832,2198,2482,2150,1599,565,636,1467,1036,1734,2053,1726,765,2307,1689,1765,356,248,929,1477,1645,1528;2037,1101,2272,213,2292,1279,823,2010,325,1251,2375,660,1682,597,1971,950,1498,17,1634,129,215,317,609,1753,1690,1169,1599;149,2399,1778,310,1167,2478,149,2321,343,27,193,2447,436,1761,1607,1457,2429,1324,1266,1392,1274,1019,159,224,394,1944,2126;1101,1639,534,2011,1222,641,18,1290,741,535,1393,2253,2338,2075,1875,809,232,2045,813,647,447,1687,1626,1530,1638,2333,435;188,1833,243,2180,1655,270,484,2027,382,875,1036,4,602,1465,138,92,1668,1105,722,605,1878,1723,1054,1005,1271,2357,1256;1696,1387,575,1766,1459,250,1311,789,1166,2045,2009,1079,326,335,1685,61,643,2083,1532,2348,1444,788,2251,2202,2042,1407,1472;2456,2298,2022,1297,2310,768,244,1067,286,1411,1324,671,2169,675,936,204,406,1636,1122,947,84,1009,549,2471,2028,1876,1144;1208,1177,931,934,596,2430,1267,1414,1871,2152,1756,2044,1157,221,1209,1936,1862,531,1073,1612,1123,1970,616,2089,865,1212,421;2306,42,1680,1846,306,90,132,2444,2345,1812,2290,1195,1195,712,2081,677,2372,2335,1015,271,1554,1064,538,497,528,2060,519;1736,1457,2073,1429,2476,1925,207,738,1165,2113,2426,293,8,1403,1490,1924,2310,2347,2327,363,1482,2166,1070,937,1084,1437,1552;1435,480,604,914,1175,838,1087,1128,229,1915,110,2106,83,1698,887,292,981,2421,1347,2500,1198,978,1322,1843,2212,1104,1336;85,1936,858,506,640,2143,670,301,413,293,748,1612,1264,624,388,2093,323,1309,1049,1076,2031,2268,2070,2391,891,1903,1867;213,1998,239,1516,116,1819,103,1520,82,1648,534,1577,891,760,1818,1658,735,1046,829,533,1751,1371,1856,627,14,2032,2484;2152,216,1046,2012,165,1972,2103,990,1807,2476,2119,2043,2027,1347,668,782,2413,1781,800,1593,2318,446,2127,1232,1483,1136,1097;441,2402,2234,920,2077,1485,1853,2330,630,2160,679,1638,602,2477,74,413,1718,1442,429,1294,2472,2365,1285,680,1973,1164,1829;2226,2024,405,1480,1358,918,791,839,290,1827,2352,933,292,874,1224,2028,1350,1569,261,1733,389,1904,1555,1478,208,584,462;84,84,178,703,2043,2165,1738,1261,2307,1462,2138,1901,232,21,1438,495,513,1334,932,2101,219,1728,792,392,12,1356,884;2032,1570,2450,853,699,2279,1916,2358,688,2040,1176,1577,768,734,1619,2112,1949,1300,797,364,315,1426,670,1066,846,2208,2016;549,108,1821,1332,1828,2469,790,398,1272,1228,1029,2494,1097,472,2432,2313,1539,1107,1293,2354,1575,721,1077,830,2265,1139,26;2354,578,2020,1830,305,1454,1846,937,1696,2163,1358,23,1822,241,1313,450,2219,640,1432,364,486,126,785,368,2177,1780,1856;535,78,1954,1455,2372,432,1122,1138,1529,1697,1760,317,1672,1649,1881,1542,40,378,1364,224,1108,961,1115,7,333,5,760;1607,1524,1402,1858,1551,1246,1891,1517,1718,1618,1486,1876,789,571,2409,1953,1965,1233,343,241,1383,12,1775,2129,1329,87,623;989,999,224,1217,1746,762,481,1273,1988,96,1713,401,1537,1370,903,1896,901,52,1319,835,1214,676,2225,2443,1,2011,2164;288,1712,611,2371,830,256,2358,1548,457,1441,231,1962,457,207,1769,1631,499,1628,2474,224,903,1776,1883,237,1359,2361,241;1103,486,490,1885,2352,1923,1815,2494,1765,831,426,2435,2357,1168,1690,1816,133,2326,1587,200,2251,1890,1111,1722,284,610,613;2479,2095,897,76,2102,2008,2217,2118,1274,1922,1853,2307,2209,2083,2068,628,1049,888,1865,1427,1652,2176,1605,2204,1765,725,1831;1039,2058,768,960,51,147,2335,1804,266,1329,1055,2000,1364,2419,1454,66,474,797,886,1576,1853,621,360,269,1342,1565,1828;2138,271,1135,73,2195,653,2191,748,1204,1662,1264,2495,488,983,1841,327,1721,1336,230,2327,1141,687,888,434,1531,2335,1673;966,1922,2207,352,913,484,257,1494,436,2100,306,989,1562,2377,96,108,1130,1803,2434,198,1245,1771,1251,1153,2452,1073,246;1422,2238,266,1346,403,2478,913,1045,638,2026,2293,2313,382,298,658,1778,2191,2444,223,87,2051,1745,205,1732,2141,298,1194;1263,331,1757,1748,1593,394,422,1954,1912,624,2496,1140,669,9,1677,1921,206,2282,123,1403,2126,1412,2271,630,1148,48,1045;1965,1985,2415,1321,1984,724,1167,28,138,945,241,809,343,1498,265,2130,1695,379,1833,1424,2415,2288,2494,1783,730,624,1271;1245,1918,1718,1082,412,2499,1108,2416,1419,2073,868,742,1487,309,2454,2346,156,339,42,559,1653,952,870,1075,549,594,1815;1992,1940,225,2178,1341,2365,1254,678,1732,2074,706,962,1477,1519,1082,814,1140,1049,2205,745,375,988,2141,18,481,495,1284;1389,1955,1661,2466,1133,409,1519,421,864,2236,1485,1510,1018,644,839,1928,1482,58,2066,884,2498,2028,993,481,1896,1310,684;1310,613,903,603,1142,962,1029,593,394,838,2331,1432,1977,2360,1772,1335,1791,680,2260,27,2011,809,913,1532,78,51,1722;1061,1335,1336,2144,182,1249,2124,700,1199,171,1950,2217,653,2128,1553,767,1497,1423,2137,1806,737,2362,776,1851,96,1753,645;1480,2076,1897,892,1559,80,2145,248,1505,1443,2206,545,557,1713,589,831,339,1675,1885,1529,83,261,346,1516,811,556,1841;101,881,1232,391,1170,1818,1953,1383,1556,2232,2087,1727,867,1998,368,969,1801,2418,2408,2201,1936,33,2151,128,1364,1017,2073;755,2211,2390,2256,309,721,615,914,1599,1353,1856,1490,800,1994,1594,1106,1181,1361,467,650,1343,1571,634,693,628,50,2219;842,1150,1671,1051,1102,539,2409,2318,1584,500,859,2121,233,1834,308,2290,1541,182,1772,2336,2428,830,2479,2453,1078,1393,305;152,1575,2168,818,2125,623,578,290,1562,597,2385,2115,1548,61,1254,760,1986,2077,1529,2030,434,235,1006,1727,781,52,1506;528,350,1368,624,1714,1983,828,1850,470,298,52,1852,27,1618,2188,1682,2155,1775,1123,1717,1259,414,1192,1937,964,1434,2486;1274,1752,2250,2332,1375,785,1912,1196,761,1405,707,1301,1882,1820,1556,2206,2388,2334,2013,1976,906,2346,1532,363,1590,1581,140;920,660,1021,1968,124,409,1086,70,1446,254,1802,315,1439,400,2499,1557,912,577,916,238,1258,1998,2013,619,1380,2421,1715", "output": "1037,471,1812,1206,1582,479,1990,1297,1405,1295,1232,1078,2303,1647,2282,1796,2117,427,1288,97,179,1935,555,1898,2487,732,715,2202,896,553,2198,2150,565,1467,1734,1726,2307,1765,248,1477,1528,1169,1753,317,129,17,950,597,660,1251,2010,1279,213,1101,149,1778,1167,149,343,193,436,1607,2429,1266,1274,159,394,2126,2333,1530,1687,647,2045,809,2075,2253,535,1290,641,2011,1639,188,243,1655,484,382,1036,602,138,1668,722,1878,1054,1271,1256,1407,2202,788,2348,2083,61,335,1079,2045,789,250,1766,1387,2456,2022,2310,244,286,1324,2169,936,406,1122,84,549,2028,1144,1212,2089,1970,1612,531,1936,221,2044,2152,1414,2430,934,1177,2306,1680,306,132,2345,2290,1195,2081,2372,1015,1554,538,528,519,1437,937,2166,363,2347,1924,1403,293,2113,738,1925,1429,1457,1435,604,1175,1087,229,110,83,887,981,1347,1198,1322,2212,1336,1903,2391,2268,1076,1309,2093,624,1612,293,301,2143,506,1936,213,239,116,103,82,534,891,1818,735,829,1751,1856,14,2484,1136,1232,446,1593,1781,782,1347,2043,2476,990,1972,2012,216,441,2234,2077,1853,630,679,602,74,1718,429,2472,1285,1973,1829,584,1478,1904,1733,1569,2028,874,933,1827,839,918,1480,2024,84,178,2043,1738,2307,2138,232,1438,513,932,219,792,12,884,2208,1066,1426,364,1300,2112,734,1577,2040,2358,2279,853,1570,549,1821,1828,790,1272,1029,1097,2432,1539,1293,1575,1077,2265,26,1780,368,126,364,640,450,241,23,2163,937,1454,1830,578,535,1954,2372,1122,1529,1760,1672,1881,40,1364,1108,1115,333,760,87,2129,12,241,1233,1953,571,1876,1618,1517,1246,1858,1524,989,224,1746,481,1988,1713,1537,903,901,1319,1214,2225,1,2164,2361,237,1776,224,1628,1631,207,1962,1441,1548,256,2371,1712,1103,490,2352,1815,1765,426,2357,1690,133,1587,2251,1111,284,613,725,2204,2176,1427,888,628,2083,2307,1922,2118,2008,76,2095,1039,768,51,2335,266,1055,1364,1454,474,886,1853,360,1342,1828,2335,434,687,2327,1336,327,983,2495,1662,748,653,73,271,966,2207,913,257,436,306,1562,96,1130,2434,1245,1251,2452,246,298,1732,1745,87,2444,1778,298,2313,2026,1045,2478,1346,2238,1263,1757,1593,422,1912,2496,669,1677,206,123,2126,2271,1148,1045,624,1783,2288,1424,379,2130,1498,809,945,28,724,1321,1985,1245,1718,412,1108,1419,868,1487,2454,156,42,1653,870,549,1815,495,18,988,745,1049,814,1519,962,2074,678,2365,2178,1940,1389,1661,1133,1519,864,1485,1018,839,1482,2066,2498,993,1896,684,51,1532,809,27,680,1335,2360,1432,838,593,962,603,613,1061,1336,182,2124,1199,1950,653,1553,1497,2137,737,776,96,645,556,1516,261,1529,1675,831,1713,545,1443,248,80,892,2076,101,1232,1170,1953,1556,2087,867,368,1801,2408,1936,2151,1364,2073,50,693,1571,650,1361,1106,1994,1490,1353,914,721,2256,2211,842,1671,1102,2409,1584,859,233,308,1541,1772,2428,2479,1078,305,52,1727,235,2030,2077,760,61,2115,597,290,623,818,1575,528,1368,1714,828,470,52,27,2188,2155,1123,1259,1192,964,2486,1581,363,2346,1976,2334,2206,1820,1301,1405,1196,785,2332,1752,920,1021,124,1086,1446,1802,1439,2499,912,916,1258,2013,1380,1715"}, {"input": "375,1481,2493,1412,942,943,2069,1193,376,1612,515,2375,71,1780,759,2243,2085,357,1315,1674,1629,220,791,110,2359,2192,238,1440,344,2139,883,1078,820,1123,2325,839,1669,1023,1318,1783,2161,251,2140,2043,1815,1020;1165,1996,594,1208,1068,386,1739,1900,1588,591,387,2199,2011,1189,989,85,1668,1172,2048,1235,535,2469,824,574,1601,2164,968,1237,2141,1979,100,2475,706,2391,1375,427,1723,692,2295,2414,166,2280,1279,1428,1085,2156;633,1547,573,1795,1953,843,915,419,767,1383,2135,394,536,2296,1905,1612,1649,914,1090,29,1050,428,1812,1034,1071,1916,1743,1398,746,529,1243,1643,1643,2114,1357,471,1689,2428,730,273,1953,1519,296,1890,428,1014;1522,589,2267,1217,1343,1068,1861,120,1340,30,95,1452,1801,1065,1363,2157,179,1986,1704,1719,1280,2191,1883,2121,1222,472,926,2235,1023,488,733,1869,1785,191,2030,2195,963,805,1435,2485,1173,2215,723,523,1050,1485;520,1176,2217,2199,487,1585,64,775,1494,1018,1267,442,1996,1737,1446,1276,1669,437,1074,405,423,2371,448,134,409,1200,1895,911,2328,326,694,2364,2075,964,1284,2130,1026,1154,2294,34,406,552,1879,1945,301,555;1813,2007,431,1318,1578,2056,1385,798,2465,19,2420,394,1847,1155,1112,1997,2335,1034,58,2156,9,788,118,2204,2438,656,683,2320,184,1649,1071,397,2479,1594,1335,2277,1211,135,634,2315,1004,1903,1724,1032,1319,520", "output": "375,2493,942,2069,376,515,71,759,2085,1315,1629,791,2359,238,344,883,820,2325,1669,1318,2161,2140,1815,2156,1428,2280,2414,692,427,2391,2475,1979,1237,2164,574,2469,1235,1172,85,1189,2199,591,1900,386,1208,1996,633,573,1953,915,767,2135,536,1905,1649,1090,1050,1812,1071,1743,746,1243,1643,1357,1689,730,1953,296,428,1485,523,2215,2485,805,2195,191,1869,488,2235,472,2121,2191,1719,1986,2157,1065,1452,30,120,1068,1217,589,520,2217,487,64,1494,1267,1996,1446,1669,1074,423,448,409,1895,2328,694,2075,1284,1026,2294,406,1879,301,520,1032,1903,2315,135,2277,1594,397,1649,2320,656,2204,788,2156,1034,1997,1155,394,19,798,2056,1318,2007"}, {"input": "1307,2274,1855,531,2150,59,691,975,2254,1577,1312,1720,731,1696,180,55,2271,34,1496,2375,2228,106,493,2154,2260,2095,56,29,1014,1,2,1361,800,1869,2204,630,2238,1628,2146,1963,657,634;210,781,42,1861,289,252,2222,257,1738,2340,697,682,840,2418,1915,1551,1604,686,463,1501,1103,284,1428,278,2370,2300,244,1825,11,520,1861,550,683,2435,1263,634,2289,1675,888,1361,2204,974;1255,2392,687,1600,821,2292,2387,2215,1997,1104,1327,1439,2495,363,218,2497,577,941,983,1473,1488,2149,2066,1428,1866,609,2112,906,1076,1639,883,2113,2495,400,1781,335,2458,110,1435,1316,2274,2000;1498,852,76,613,2405,1677,354,1114,2397,2464,234,2498,1220,265,1756,1917,2320,1343,643,173,767,1902,2441,2081,393,1126,1345,1079,2218,332,291,2304,496,1939,663,2103,1146,1382,2114,1233,2196,1982;1108,2404,1055,176,181,2361,714,1724,754,2264,2117,1630,1420,2213,91,2021,760,88,229,2284,93,1457,1872,85,330,2335,2039,1169,862,1319,1829,1317,602,528,1353,1409,1531,1728,2049,101,2242,1100;1739,2457,55,6,426,1391,2303,456,524,865,1558,625,1120,767,1202,1170,1981,153,20,555,1413,476,2344,163,1611,1837,570,1263,1104,1741,208,1473,1938,1985,653,1177,2182,1963,1985,1184,1877,1583;995,223,2177,871,1366,1801,541,2198,2471,122,388,233,152,1711,1024,1094,1885,1260,330,2069,59,1082,552,187,631,643,798,64,1295,2309,1953,1411,1871,1021,880,1773,2275,767,2054,1967,1549,1410;1841,1475,1464,1422,569,1360,2085,1695,2284,1327,1574,2215,1475,101,1746,1575,1096,2052,1954,2151,688,1642,1270,2090,1938,457,919,185,211,221,720,1407,1444,1070,1660,1086,1395,1022,978,1171,1822,2088;1431,559,2397,1088,2084,1173,1179,1865,25,1175,485,1276,1524,145,1348,1580,869,803,1976,166,1751,2472,1372,434,269,2141,428,2419,1614,495,811,2191,1806,1491,1427,1335,2310,1145,670,730,2355,2149;423,783,1009,622,1183,314,1886,1893,357,332,2130,24,443,1546,1809,1888,1207,794,1553,212,1082,2235,11,2430,2129,1360,2473,636,1797,407,1058,915,1703,2349,1112,1927,1036,2476,842,1253,1966,1600;2117,2185,2386,870,2072,1712,334,1602,372,2157,1969,1882,1570,1258,1296,2145,229,2211,1200,775,333,1697,1303,666,276,1832,2312,149,114,1316,794,266,550,1720,82,1518,1305,2008,1226,255,574,2178;1237,1377,1505,2203,1810,1735,2348,1315,1534,2316,386,699,1703,2113,371,931,143,2032,2124,991,1848,859,448,2131,991,1428,2382,1258,447,701,967,1072,1343,2388,707,827,723,1515,2115,229,742,1184;1424,1308,2048,318,417,1570,734,1906,1106,851,1364,421,1160,2446,515,2107,1687,824,549,2031,225,631,842,409,1904,1051,137,532,2150,305,183,1558,12,1985,1589,952,1216,1122,852,851,1147,1701;9,744,1538,853,1007,1502,1631,1138,303,1653,735,2427,2242,2029,155,701,1355,618,388,1475,362,1102,933,1438,391,1945,536,811,1562,2079,1499,179,1079,1278,2196,1490,695,1592,211,581,1007,1368;1177,1928,630,691,1051,146,1309,1476,972,187,1662,315,475,925,70,18,1091,1498,2175,2476,554,1939,1491,677,805,1098,211,2075,2015,147,1533,1716,2304,924,897,1370,1500,1466,1646,983,2086,1519;2417,2273,260,2154,631,2280,1068,860,2310,1798,1217,2171,1596,2376,2296,174,180,1415,1473,2001,855,830,2149,14,1888,516,1664,1591,4,2368,1184,42,1246,1032,1868,1517,108,421,1864,1289,64,1365;1690,1605,1422,1324,2113,2439,160,1630,1324,2191,1626,2420,2036,546,671,828,694,1186,745,173,1033,984,75,251,1636,980,263,2352,431,153,1760,2309,1923,413,1009,1564,992,1393,2424,322,373,1234;603,203,631,2243,1630,446,548,592,886,647,2269,1685,495,1105,9,540,1178,1352,1221,559,597,1071,2436,640,700,1177,983,92,609,948,539,229,62,112,396,782,531,1834,2157,2473,702,2231;660,1085,966,1364,252,2401,2001,2324,393,956,1375,944,663,2475,1322,1560,478,1986,1683,753,2411,1150,2128,1126,1671,2000,1540,1171,230,2202,2442,1861,1878,2376,1487,883,1540,284,1127,15,2261,776;2,1905,163,2448,221,1607,1008,973,1544,225,528,1988,769,500,1370,1733,1925,672,1727,283,2007,811,1759,767,2408,597,1194,1316,2451,2234,2344,1928,1846,1864,801,2228,747,1232,796,2059,640,263;1145,1771,681,2434,656,679,763,658,2172,914,807,2139,339,807,2049,1333,724,670,891,1384,2464,115,1577,593,1988,113,2380,1194,174,393,1139,1226,305,704,1276,1387,658,760,2418,635,1031,1515;1589,1814,108,2140,2324,904,2357,929,1428,142,1146,1700,641,775,806,1881,1141,463,1444,806,1401,2265,960,849,2140,1831,2083,2386,1496,327,2497,89,1395,993,133,2373,1098,1394,2300,1976,1481,2337;1416,243,2084,759,1415,1954,529,922,746,783,58,24,1975,19,2292,1726,287,2284,1785,2470,1244,2061,1221,1614,1870,1168,1911,1434,689,402,1102,2244,1023,1503,1560,1488,170,2278,1561,2341,559,571;1877,3,708,1364,534,1512,1083,424,453,255,1508,1455,1682,729,1243,294,586,1732,1672,1826,1724,2079,108,2334,1087,203,1283,2329,1648,1238,1982,146,1018,821,1738,1093,699,1184,1331,814,639,97;1762,1312,1109,922,575,1672,276,1209,904,1223,241,851,1960,292,1415,612,1092,779,491,177,2494,267,1373,1685,2186,1014,124,1496,987,320,764,670,1489,670,1646,1130,2403,1820,1154,1795,2249,1899;253,1782,1796,1562,1190,1155,669,2074,1695,954,152,1912,123,1885,2148,325,163,284,151,448,554,1206,1188,2146,38,1524,1605,2483,1218,528,430,461,2086,1976,1260,2402,81,105,1145,1050,2393,285;224,253,1800,695,788,293,1202,2335,709,127,1161,2329,2462,852,67,1697,1185,232,1086,351,533,301,242,1878,165,1125,848,308,120,1426,1518,39,889,362,1493,2139,2104,1867,2252,1297,160,1586;1701,64,1764,1823,1466,475,1095,476,1085,2140,934,1416,295,1361,1652,87,2322,1439,494,1089,539,1876,1943,212,640,267,1404,944,2212,1591,471,429,1372,501,482,325,1780,714,1929,395,1049,852", "output": "1307,1855,2150,691,2254,1312,731,180,2271,1496,2228,493,2260,56,1014,2,800,2204,2238,2146,657,974,1361,1675,634,2435,550,520,1825,2300,278,284,1501,686,1551,2418,682,2340,257,252,1861,781,1255,687,821,2387,1997,1327,2495,218,577,983,1488,2066,1866,2112,1076,883,2495,1781,2458,1435,2274,1982,1233,1382,2103,1939,2304,332,1079,1126,2081,1902,173,1343,1917,265,2498,2464,1114,1677,613,852,1108,1055,181,714,754,2117,1420,91,760,229,93,1872,330,2039,862,1829,602,1353,1531,2049,2242,1583,1184,1963,1177,1985,1473,1741,1263,1837,163,476,555,153,1170,767,625,865,456,1391,6,2457,995,2177,1366,541,2471,388,152,1024,1885,330,59,552,631,798,1295,1953,1871,880,2275,2054,1549,2088,1171,1022,1086,1070,1407,221,185,457,2090,1642,2151,2052,1575,101,2215,1327,1695,1360,1422,1475,1431,2397,2084,1179,25,485,1524,1348,869,1976,1751,1372,269,428,1614,811,1806,1427,2310,670,2355,1600,1253,2476,1927,2349,915,407,636,1360,2430,2235,212,794,1888,1546,24,332,1893,314,622,783,2117,2386,2072,334,372,1969,1570,1296,229,1200,333,1303,276,2312,114,794,550,82,1305,1226,574,1184,229,1515,827,2388,1072,701,1258,1428,2131,859,991,2032,931,2113,699,2316,1315,1735,2203,1377,1424,2048,417,734,1106,1364,1160,515,1687,549,225,842,1904,137,2150,183,12,1589,1216,852,1147,1368,581,1592,1490,1278,179,2079,811,1945,1438,1102,1475,618,701,2029,2427,1653,1138,1502,853,744,1177,630,1051,1309,972,1662,475,70,1091,2175,554,1491,805,211,2015,1533,2304,897,1500,1646,2086,1365,1289,421,1517,1032,42,2368,1591,516,14,830,2001,1415,174,2376,2171,1798,860,2280,2154,2273,1690,1422,2113,160,1324,1626,2036,671,694,745,1033,75,1636,263,431,1760,1923,1009,992,2424,373,2231,2473,1834,782,112,229,948,92,1177,640,1071,559,1352,540,1105,1685,647,592,446,2243,203,660,966,252,2001,393,1375,663,1322,478,1683,2411,2128,1671,1540,230,2442,1878,1487,1540,1127,2261,263,2059,1232,2228,1864,1928,2234,1316,597,767,811,283,672,1733,500,1988,225,973,1607,2448,1905,1145,681,656,763,2172,807,339,2049,724,891,2464,1577,1988,2380,174,1139,305,1276,658,2418,1031,2337,1976,1394,2373,993,89,327,2386,1831,849,2265,806,463,1881,775,1700,142,929,904,2140,1814,1416,2084,1415,529,746,58,1975,2292,287,1785,1244,1221,1870,1911,689,1102,1023,1560,170,1561,559,97,814,1184,1093,821,146,1238,2329,203,2334,2079,1826,1732,294,729,1455,255,424,1512,1364,3,1762,1109,575,276,904,241,1960,1415,1092,491,2494,1373,2186,124,987,764,1489,1646,2403,1154,2249,285,1050,105,2402,1976,461,528,2483,1524,2146,1206,448,284,325,1885,1912,954,2074,1155,1562,1782,224,1800,788,1202,709,1161,2462,67,1185,1086,533,242,165,848,120,1518,889,1493,2104,2252,160,852,395,714,325,501,429,1591,944,267,212,1876,1089,1439,87,1361,1416,2140,476,475,1823,64"}, {"input": "2211,420,1640,597,394,129,1006,1909,2094,1812,1269,603,1255,2145,994,2478,1809,53,1133,788,2073,1501,2354,1250,49,1654,975,2482,745,2110,1127,67,1723,587,1317,464;1418,2211,1157,2027,1540,1678,1735,1650,1321,1323,1197,1206,421,975,176,163,2207,1362,1626,137,1223,1375,1152,1171,2031,1929,2182,550,930,1999,1101,365,309,775,1387,2009;2483,1783,1996,829,1711,990,1942,779,2444,2324,901,1358,1413,1284,1090,1077,1658,193,787,533,204,1262,1264,1003,227,1163,931,857,238,1319,786,1725,2381,593,739,42;70,764,1372,2279,588,671,316,1297,692,1892,238,300,74,2142,330,1519,1494,2264,1771,1714,302,1232,236,343,1279,2002,1180,166,1221,665,1725,482,153,882,1091,462;2382,664,2222,1362,49,1311,397,16,970,2215,285,915,866,1595,2249,1328,430,916,386,2217,1074,708,2395,1324,1630,643,2280,2390,410,418,1740,1077,724,1568,14,1780;554,1425,268,1992,2006,1669,2103,2409,1968,243,2275,991,1677,2321,1577,157,1166,670,1711,1143,1078,1646,228,2185,2352,2125,2070,1940,1274,1923,1658,762,1815,1975,1180,616;1409,1166,124,1664,335,915,2254,1226,828,45,254,595,1956,983,491,498,1975,2188,1794,10,249,2358,508,103,1656,229,756,2099,766,1371,456,1169,147,1019,1553,1253;2215,266,2038,2112,1408,1465,1395,928,1795,2001,81,1234,947,352,1334,684,373,35,62,376,755,2423,154,2022,2413,319,1004,2326,1252,1523,146,134,1985,1599,878,315;2062,2280,616,2173,752,1203,1751,453,1858,961,1102,2464,26,2375,1081,167,2396,1396,1211,413,1846,169,615,2399,2429,1890,886,1605,2406,550,1589,1971,1257,2223,2437,858;2007,2071,453,471,544,699,267,2288,1302,26,862,1448,23,1154,1453,720,2158,1492,878,1441,2261,606,205,2474,1817,1446,287,2168,1551,1149,512,2497,43,621,359,67;874,642,1432,937,1745,1262,1598,526,1356,395,704,380,653,1180,1874,2149,1957,1677,1423,1926,1030,333,1952,2090,422,1309,428,2191,2103,1418,1870,1412,1842,1787,1708,742", "output": "2211,1640,394,1006,2094,1269,1255,994,1809,1133,2073,2354,49,975,745,1127,1723,1317,2009,775,365,1999,550,1929,1171,1375,137,1362,163,975,1206,1323,1650,1678,2027,2211,2483,1996,1711,1942,2444,901,1413,1090,1658,787,204,1264,227,931,238,786,2381,739,462,882,482,665,166,2002,343,1232,1714,2264,1519,2142,300,1892,1297,671,2279,764,2382,2222,49,397,970,285,866,2249,430,386,1074,2395,1630,2280,410,1740,724,14,616,1975,762,1923,1940,2125,2185,1646,1143,670,157,2321,991,243,2409,1669,1992,1425,1409,124,335,2254,828,254,1956,491,1975,1794,249,508,1656,756,766,456,147,1553,315,1599,134,1523,2326,319,2022,2423,376,35,684,352,1234,2001,928,1465,2112,266,2062,616,752,1751,1858,1102,26,1081,2396,1211,1846,615,2429,886,2406,1589,1257,2437,67,621,2497,1149,2168,1446,2474,606,1441,1492,720,1154,1448,26,2288,699,471,2071,874,1432,1745,1598,1356,704,653,1874,1957,1423,1030,1952,422,428,2103,1870,1842,1708"}, {"input": "211,2203,1926,1309,2500,2081,1608,1221,2028,1753,314,666,239,2271,2015,2002,2114,1024,592,75,2338,1555,886,1591,50,1893,1247,929,2140,1866,1622,2215,442,59,2208,751,1532,2093,173,427,1795,1253,1420,2203;333,2388,128,881,684,1858,1107,117,2244,1393,2415,1789,1873,734,1615,574,337,590,2136,2230,406,1409,2439,2272,2276,318,490,1585,1403,2184,1084,1444,1573,630,775,428,599,454,2196,2397,272,1177,1389,2156;2229,1634,2280,1249,606,1016,2398,915,585,701,579,59,1914,1081,376,1021,16,1669,1953,244,352,924,728,350,1340,2177,427,1254,1550,860,1095,1683,929,2471,974,16,759,1519,961,630,269,1739,1938,378;2145,1647,1537,1024,630,2318,1153,1061,1690,548,2193,1895,2122,411,839,546,1893,54,1218,2147,315,220,638,1511,2382,330,2340,1254,2470,323,1391,496,1763,2097,2267,2275,1890,2190,565,280,650,1735,1847,220;1114,1582,941,2008,1500,856,2083,2304,573,111,2474,1543,1232,15,608,749,422,1556,982,1850,663,283,153,1861,163,1858,2180,227,1774,1910,1749,1962,231,355,1191,1870,225,915,2461,2017,132,1751,990,85;1315,445,969,1245,834,113,2027,2134,629,2023,2381,476,912,959,877,1085,1631,824,945,238,1650,283,978,2110,1004,808,1165,685,1959,235,2484,2080,106,2040,1939,1103,2153,1503,1094,346,555,933,645,2232;330,2080,490,1490,446,154,985,2227,2022,2283,1689,2263,2291,2171,349,1083,366,32,400,1334,50,1652,860,425,2447,1046,697,1567,1556,2124,2306,1529,1416,1889,2112,1703,1066,1271,1466,80,350,2375,1877,2318;2438,1921,728,1470,1940,497,23,2481,1903,1250,1878,2114,1386,1365,1897,328,1688,969,1811,55,978,679,1857,1579,1602,1435,1684,1034,523,978,2492,2141,1994,1725,1106,1072,2103,1502,737,613,1032,1541,429,128;2032,2267,1162,593,1272,2305,143,876,704,1966,1894,2076,1890,1905,245,1978,2255,588,1405,1237,2399,1393,2255,1254,807,577,1419,828,607,1487,225,962,954,2181,1518,2132,1695,255,338,1193,2441,2333,1768,988;1905,1282,233,2282,1977,317,2147,1922,265,956,1598,1102,937,354,2430,1116,589,195,2327,2489,2158,308,1297,527,2012,248,1519,591,1161,1816,1243,816,1832,323,1654,1296,1445,554,1171,1067,699,1498,9,322;196,76,2403,1409,2407,1590,2048,814,326,490,778,1597,1155,2456,1519,828,1627,1589,196,162,261,1088,2110,739,1709,2276,1771,1131,1317,1237,30,1699,136,1869,797,1692,50,1393,1639,1854,2100,393,1017,1770;817,2357,2405,461,1116,1962,2180,2351,957,2061,230,403,1286,1488,1066,1032,548,623,2174,489,2368,2414,373,2182,245,2414,1112,2348,287,1374,884,2201,2343,2309,448,2293,50,667,172,306,1768,566,527,410;2170,956,2182,2413,409,711,244,14,844,1,800,2221,1745,1302,783,680,2291,1683,1282,930,2460,782,406,639,1269,361,391,1150,2277,2052,2162,2315,2384,2238,2136,2388,2423,879,1014,463,1015,2273,1781,1161;857,1062,79,2126,947,871,463,1108,2474,2162,1447,1356,1811,407,1324,355,2269,1812,439,925,1948,170,2283,2125,2245,2123,1677,2481,2487,698,151,757,1938,1409,39,1326,868,859,1675,252,1804,864,525,1688;569,2461,2236,1753,1679,2481,2476,1718,1355,2465,2218,123,2220,1308,1036,1917,563,1760,1774,554,1170,1436,1633,1943,2070,76,589,753,317,438,1610,475,1575,1679,2394,1120,363,119,2048,1341,2135,2088,1029,862;877,1904,983,2235,974,756,624,139,568,15,60,1005,1846,2084,1967,1079,503,797,2178,1280,2184,697,2052,199,1984,1018,1723,1070,1422,382,474,1191,813,2396,2117,1705,1848,1760,1545,1429,414,2258,1047,1030;2223,1316,1461,552,570,242,1749,578,104,1199,1823,1839,569,1543,1781,368,2002,2120,1702,1175,58,2076,1284,2225,27,1428,1834,1814,348,1443,1967,1301,1951,2298,2323,1504,1099,484,433,2231,1888,1221,218,1637;80,466,2496,951,1688,937,1356,560,742,1003,1536,653,1466,1337,388,853,2276,1884,576,1705,1636,1608,1190,1527,1961,1013,1347,2190,1146,1501,970,14,366,2357,295,906,1677,877,947,397,1678,1872,2383,1060;1892,2032,5,1855,1631,2253,805,1589,1569,1638,2121,1155,1655,1430,474,2428,674,667,754,270,1487,1907,1279,2186,520,2280,1570,588,2126,2439,913,1458,2229,537,2301,401,494,2100,1873,583,2306,687,804,1152;2284,1378,332,1841,296,358,2075,1889,1057,968,1666,1025,1112,672,227,2258,1662,1528,369,1659,1863,2325,1387,1841,117,2235,216,325,145,1299,2467,1641,662,1516,2468,147,166,1750,1201,1801,436,1406,8,1432;1259,1099,322,255,1816,2361,139,774,1461,1194,744,317,1898,2018,508,1559,1425,1510,2279,1870,1594,1,1093,2168,1682,633,1589,1239,767,265,438,1217,579,667,1335,2420,1254,276,641,853,83,1092,1898,990;1027,1597,36,820,1637,1799,1697,1323,1278,1440,1022,1262,617,2068,117,91,733,1886,480,1240,1619,1753,1386,1983,1329,2185,2077,468,499,115,905,2008,301,2350,645,1261,1089,727,1661,995,2139,4,350,1863;230,1656,1336,1767,1865,388,418,327,1541,2157,1940,151,942,1555,7,1756,551,459,391,2020,1599,1879,2012,2052,198,76,1365,913,512,776,1146,1275,1211,1120,496,1610,702,643,2293,2212,376,1682,1503,2358;1765,214,1389,1215,1007,1971,1998,244,1261,1352,1449,12,2453,1569,1201,561,820,615,1537,2265,1322,1010,1232,2088,2127,2046,1532,2147,1489,800,1078,328,1518,711,1229,2270,309,1733,199,1220,511,2064,2153,1095;2188,977,2053,539,117,1653,414,1826,1688,166,1309,799,788,1528,34,2110,675,759,440,565,1167,1532,742,1626,1368,1101,1061,1254,605,66,1371,1648,2047,159,1698,628,1272,1725,1322,410,1113,1739,1994,843;2265,2231,1390,1703,2236,1623,1797,2457,281,1050,2272,1582,929,1493,1674,694,934,160,31,1070,721,938,1353,466,640,190,1660,716,1868,1260,2312,1528,1840,2162,666,36,692,1866,381,369,1019,1075,743,1738;931,309,846,1704,638,244,2053,687,2126,1710,53,1386,1062,2371,1907,521,652,617,1867,1897,2047,645,1542,892,1185,2223,726,1976,1992,1544,1259,87,1114,1761,2333,1509,1507,1879,420,1192,1627,879,2111,1085;2261,896,43,1841,1445,1831,2132,27,1697,840,327,1959,2255,2485,1976,2161,902,1360,1766,817,2359,673,1203,572,2396,265,906,2113,2038,1219,391,416,1625,1475,1610,96,2092,180,1402,498,49,1228,2392,307;901,486,766,1589,1899,1774,295,674,2393,2042,1438,1110,1017,1680,542,31,921,1641,853,1463,1748,1357,1083,608,552,1142,2309,129,1311,59,2391,1680,250,198,582,1620,1467,409,593,410,676,853,162,2239;171,373,2488,1705,2328,2056,2222,357,823,1763,1561,1294,596,627,2264,941,1879,2342,1656,2308,641,1978,106,571,2409,1802,419,330,1726,2213,1967,536,2479,1661,226,873,925,600,2242,1894,1188,1665,570,512;1923,682,1818,281,1159,37,322,1589,2128,219,419,816,2248,66,1816,1616,1971,167,459,1732,1989,508,107,198,1953,195,2437,1501,1268,818,2113,664,2184,1481,2397,1192,398,760,733,1877,145,2349,1433,1863;2204,1793,797,1048,1601,1491,1442,1281,1180,907,1147,365,1471,473,1497,2037,2356,1030,796,2068,2379,983,2178,1693,1180,1600,1317,523,1153,2201,1857,223,781,1315,1087,763,907,2253,618,699,375,2044,540,286;2182,826,2457,1552,43,2460,2193,1918,2081,841,1649,2261,809,883,1263,2173,1348,166,243,209,1107,2095,870,1401,99,1357,1513,2309,980,1696,1073,1329,1894,203,527,507,197,2319,1324,2203,658,156,1002,175;1669,544,61,175,614,1395,1952,927,655,2340,484,674,1316,1755,629,2352,2120,1626,146,1283,2132,1698,240,1019,663,2256,285,1839,41,2480,1098,636,2323,2425,427,1628,2457,1056,1115,2310,2325,1445,367,1686;1081,2393,2419,136,831,1527,1956,746,2302,2229,1121,1262,74,1668,309,2471,276,1847,2231,2073,803,2034,1145,2406,1945,1448,1359,40,1561,1096,1557,1050,2177,1630,1364,1937,2143,984,1031,1617,1431,1292,513,2111;1970,382,255,1173,837,1085,1482,198,90,627,148,1235,1341,2452,1541,437,1331,277,1910,1751,165,664,2292,2337,1773,612,1136,907,1325,398,2020,592,1183,1790,1806,705,614,295,1518,1614,230,1670,1474,1285;1385,1417,794,2454,132,1687,1106,2110,321,1438,2342,1683,1733,1320,1126,1703,886,2056,1741,1793,2088,955,690,984,2115,1035,135,2436,967,1331,783,1767,796,1318,519,1689,1842,748,1862,2393,1595,1337,2263,2441;1375,1256,1753,1359,2271,1967,867,184,2295,2159,2423,1399,445,937,1987,570,1815,1058,2090,1679,1911,507,1396,1697,576,892,887,1138,1898,1056,69,2496,1538,324,768,3,738,1092,1538,1508,1855,764,1721,1864;304,715,63,1650,340,1445,1115,55,233,1388,1895,1326,644,2058,876,348,2425,2228,1905,2141,1146,953,2302,624,836,852,30,458,1016,1352,2386,1872,1244,1155,2395,1020,1983,503,966,265,1850,1822,646,1993;304,2170,1221,1443,638,864,341,164,513,855,1711,1896,2186,453,2497,861,1879,434,1495,2175,155,1233,185,1387,1966,592,390,2235,2178,716,1787,42,837,586,1995,565,1057,2183,1808,1386,1305,988,1111,2407;1387,394,969,1740,1639,2475,1309,905,437,80,145,1321,1749,1967,2156,690,1795,865,323,466,557,63,434,1511,205,1326,1019,2255,1720,1938,1078,1768,125,85,440,2054,179,395,1708,1305,7,1879,1271,1626;2064,79,1951,1058,2064,2089,664,2439,1678,1878,2129,693,198,36,2451,880,2155,653,1319,1751,1958,1585,2472,1535,2157,15,1500,2089,1387,1071,1734,1486,1744,1218,2326,520,2385,79,1125,1965,1288,964,682,1111;762,957,1959,1918,2011,2115,1299,1404,1067,1388,2497,1870,1671,1016,2377,2277,1787,1115,768,1386,575,380,2105,2198,416,147,754,1212,570,2261,812,1766,391,805,17,2469,1104,1025,218,1229,1784,335,1917,851;1577,771,1966,1900,893,2479,1819,1351,1958,243,1201,73,839,79,1322,243,1773,656,1943,1775,1553,242,54,280,1815,2277,2234,2361,1916,1562,1599,1453,351,672,1094,67,2499,776,1275,514,539,277,1009,1928;381,1096,2100,1291,608,2098,352,1829,560,284,740,101,1497,122,2168,928,991,67,716,1337,1035,2227,1785,817,1346,1383,1900,873,55,1795,1237,1069,463,449,1741,1596,1077,2120,141,1280,2144,2430,1832,1395;1785,2249,2157,304,293,1,2441,1752,716,579,2029,889,866,1788,921,1044,1842,927,1877,380,313,1161,1313,347,664,1028,1658,707,358,962,1963,2167,883,1589,2357,212,1806,1092,1285,1844,203,2375,572,1562;1569,666,97,1712,774,641,1246,1663,920,1082,437,1371,1955,1498,432,1968,1845,1767,2344,607,931,812,206,1733,2004,553,1961,280,1085,31,1929,1281,2273,1101,560,671,345,989,605,555,406,520,1647,248;213,2080,875,691,1392,1040,1444,1841,2038,770,1090,1787,1747,2319,891,494,950,1338,1490,93,2375,2028,2373,2016,441,349,902,1040,40,448,1729,560,2085,2159,1182,2451,1355,2003,2011,60,1731,1821,2099,410;2414,921,659,1907,74,983,2111,1691,2479,637,623,682,333,2196,777,56,2047,475,1573,2137,1379,1816,387,232,212,2344,246,697,1373,2261,581,58,373,1051,2105,801,410,1858,293,1990,1706,247,519,1144;2214,1820,1663,816,583,1363,1206,468,1527,2003,618,119,948,688,724,1604,572,1305,1218,577,2309,2017,4,2178,1883,1071,1868,533,1002,2255,22,1451,360,247,2097,1650,1098,889,1845,2427,1255,1238,1865,1365", "output": "211,1926,2500,1608,2028,314,239,2015,2114,592,2338,886,50,1247,2140,1622,442,2208,1532,173,1795,1420,2156,1177,2397,454,428,630,1444,2184,1585,318,2272,1409,2230,590,574,734,1789,1393,117,1858,881,2388,2229,2280,606,2398,585,579,1914,376,16,1953,352,728,1340,427,1550,1095,929,974,759,961,269,1938,220,1735,280,2190,2275,2097,496,323,1254,330,1511,220,2147,54,546,411,1895,548,1061,2318,1024,1647,1114,941,1500,2083,573,2474,1232,608,422,982,663,153,163,2180,1774,1749,231,1191,225,2461,132,990,2232,933,346,1503,1103,2040,2080,235,685,808,2110,283,238,824,1085,959,476,2023,2134,113,1245,445,330,490,446,985,2022,1689,2291,349,366,400,50,860,2447,697,1556,2306,1416,2112,1066,1466,350,1877,128,1541,613,1502,1072,1725,2141,978,1034,1435,1579,679,55,969,328,1365,2114,1250,2481,497,1470,1921,2032,1162,1272,143,704,1894,1890,245,2255,1405,2399,2255,807,1419,607,225,954,1518,1695,338,2441,1768,322,1498,1067,554,1296,323,816,1816,591,248,527,308,2489,195,1116,354,1102,956,1922,317,2282,1282,196,2403,2407,2048,326,778,1155,1519,1627,196,261,2110,1709,1771,1317,30,136,797,50,1639,2100,1017,410,566,306,667,2293,2309,2201,1374,2348,2414,2182,2414,489,623,1032,1488,403,2061,2351,1962,461,2357,2170,2182,409,244,844,800,1745,783,2291,1282,2460,406,1269,391,2277,2162,2384,2136,2423,1014,1015,1781,1688,864,252,859,1326,1409,757,698,2481,2123,2125,170,925,1812,355,407,1356,2162,1108,871,2126,1062,569,2236,1679,2476,1355,2218,2220,1036,563,1774,1170,1633,2070,589,317,1610,1575,2394,363,2048,2135,1029,1030,2258,1429,1760,1705,2396,1191,382,1070,1018,199,697,1280,797,1079,2084,1005,15,139,756,2235,1904,2223,1461,570,1749,104,1823,569,1781,2002,1702,58,1284,27,1834,348,1967,1951,2323,1099,433,1888,218,1060,1872,397,877,906,2357,14,1501,2190,1013,1527,1608,1705,1884,853,1337,653,1003,560,937,951,466,1892,5,1631,805,1569,2121,1655,474,674,754,1487,1279,520,1570,2126,913,2229,2301,494,1873,2306,804,1432,1406,1801,1750,147,1516,1641,1299,325,2235,1841,2325,1659,1528,2258,672,1025,968,1889,358,1841,1378,1259,322,1816,139,1461,744,1898,508,1425,2279,1594,1093,1682,1589,767,438,579,1335,1254,641,83,1898,1863,4,995,727,1261,2350,2008,115,468,2185,1983,1753,1240,1886,91,2068,1262,1440,1323,1799,820,1597,230,1336,1865,418,1541,1940,942,7,551,391,1599,2012,198,1365,512,1146,1211,496,702,2293,376,1503,1095,2064,1220,1733,2270,711,328,800,2147,2046,2088,1010,2265,615,561,1569,12,1352,244,1971,1215,214,2188,2053,117,414,1688,1309,788,34,675,440,1167,742,1368,1061,605,1371,2047,1698,1272,1322,1113,1994,1738,1075,369,1866,36,2162,1528,1260,716,190,466,938,1070,160,694,1493,1582,1050,2457,1623,1703,2231,931,846,638,2053,2126,53,1062,1907,652,1867,2047,1542,1185,726,1992,1259,1114,2333,1507,420,1627,2111,307,1228,498,180,96,1475,416,1219,2113,265,572,673,817,1360,2161,2485,1959,840,27,1831,1841,896,901,766,1899,295,2393,1438,1017,542,921,853,1748,1083,552,2309,1311,2391,250,582,1467,593,676,162,512,1665,1894,600,873,1661,536,2213,330,1802,571,1978,2308,2342,941,627,1294,1763,357,2056,1705,373,1923,1818,1159,322,2128,419,2248,1816,1971,459,1989,107,1953,2437,1268,2113,2184,2397,398,733,145,1433,286,2044,699,2253,763,1315,223,2201,523,1600,1693,983,2068,1030,2037,473,365,907,1281,1491,1048,1793,2182,2457,43,2193,2081,1649,809,1263,1348,243,1107,870,99,1513,980,1073,1894,527,197,1324,658,1002,1686,1445,2310,1056,1628,2425,636,2480,1839,2256,1019,1698,1283,1626,2352,1755,674,2340,927,1395,175,544,1081,2419,831,1956,2302,1121,74,309,276,2231,803,1145,1945,1359,1561,1557,2177,1364,2143,1031,1431,513,1285,1670,1614,295,705,1790,592,398,907,612,2337,664,1751,277,437,2452,1235,627,198,1085,1173,382,1385,794,132,1106,321,2342,1733,1126,886,1741,2088,690,2115,135,967,783,796,519,1842,1862,1595,2263,1864,764,1508,1092,3,324,2496,1056,1138,892,1697,507,1679,1058,570,937,1399,2159,184,1967,1359,1256,304,63,340,1115,233,1895,644,876,2425,1905,1146,2302,836,30,1016,2386,1244,2395,1983,966,1850,646,2407,988,1386,2183,565,586,42,716,2235,592,1387,1233,2175,434,861,453,1896,855,164,864,1443,2170,1387,969,1639,1309,437,145,1749,2156,1795,323,557,434,205,1019,1720,1078,125,440,179,1708,7,1271,1111,964,1965,79,520,1218,1486,1071,2089,15,1535,1585,1751,653,880,36,693,1878,2439,2089,1058,79,762,1959,2011,1299,1067,2497,1671,2377,1787,768,575,2105,416,754,570,812,391,17,1104,218,1784,1917,1928,277,514,776,67,672,1453,1562,2361,2277,280,242,1775,656,243,79,73,243,1351,2479,1900,771,381,2100,608,352,560,740,1497,2168,991,716,1035,1785,1346,1900,55,1237,463,1741,1077,141,2144,1832,1562,2375,1844,1092,212,1589,2167,962,707,1028,347,1161,380,927,1044,1788,889,579,1752,1,304,2249,1569,97,774,1246,920,437,1955,432,1845,2344,931,206,2004,1961,1085,1929,2273,560,345,605,406,1647,410,1821,60,2003,2451,2159,560,448,1040,349,2016,2028,93,1338,494,2319,1787,770,1841,1040,691,2080,2414,659,74,2111,2479,623,333,777,2047,1573,1379,387,212,246,1373,581,373,2105,410,293,1706,519,1365,1238,2427,889,1650,247,1451,2255,533,1071,2178,2017,577,1305,1604,688,119,2003,468,1363,816,1820"}, {"input": "844,2376,2178,478,1937,490,1010,431,169,326,2372,2046,1407,1458,2131;1868,821,1586,168,1460,1097,1497,2071,767,2205,1230,1084,520,2172,2072;1720,1678,1012,1266,861,1936,435,1709,2155,290,1130,575,918,1336,474;1666,282,2373,834,1327,1163,557,2123,2347,859,223,2,2047,733,502;1965,2343,2280,1571,895,2019,1742,1959,746,24,2133,942,225,572,1203;1086,999,1515,293,1641,2142,1929,1422,2370,1545,2257,438,1832,901,1465;2218,103,1489,1476,1476,1008,1379,1037,1150,1109,423,740,753,2480,79;1680,2,1050,853,1348,606,163,2243,2231,406,2353,740,1261,1758,785;124,1781,2085,2465,1595,477,2016,192,1736,459,1042,1674,1276,645,2163;1069,2090,1280,394,931,1967,1666,1991,1737,2496,2171,1227,2360,1884,2455;190,1151,1249,1214,1991,1737,192,391,1627,1603,1782,1466,2415,2117,1137;264,2215,363,348,1173,2188,930,2180,1847,1160,105,1764,2202,1347,1123;2159,2161,2033,2180,305,1592,92,2,1974,2209,327,1805,887,150,436;2464,514,999,2101,944,2413,1956,931,153,1607,2113,160,2308,1161,2092;71,814,178,993,1832,337,2013,1274,1309,1381,473,656,1245,2477,1629;925,1293,1281,2030,340,867,2491,1530,2321,606,500,357,797,646,1387;227,2147,2354,1692,2244,144,195,433,2361,2392,1405,2133,1454,694,1556;543,2177,1163,949,1887,394,825,563,1458,1116,1216,984,276,461,714;431,986,691,620,963,1933,1129,258,1034,759,1837,2121,987,355,2277;1632,2306,2258,1182,371,1304,2219,2131,943,2436,2137,37,773,1645,1609;523,1121,1776,603,1927,948,2409,1103,55,93,781,1473,1058,1541,888;2209,1117,560,812,1224,1168,881,853,169,794,946,1864,1044,931,25;2218,1629,1737,2031,2133,1322,88,83,1881,1883,1257,1419,1225,1526,270;320,1134,485,1175,693,935,974,1551,94,725,303,743,2080,271,1201;2334,1015,2375,807,2083,8,2308,1726,934,1252,702,15,2449,2165,2272;1103,173,1842,1513,2441,309,1558,2420,699,2274,355,1809,167,348,2499;2418,1138,1996,1000,418,2213,1943,2273,907,198,1539,1467,10,1536,1671;1160,1385,1266,2492,586,402,1153,1469,488,1342,2091,2196,818,8,1578;496,2389,1443,2055,2128,2074,1400,220,1247,598,1900,1104,1547,220,2411;697,1003,607,1009,1803,736,1941,976,516,2121,2269,355,617,1667,481;1445,343,659,453,653,792,2305,1809,1261,2387,2075,734,336,2331,2249;2072,1005,1834,2006,1372,1728,2356,846,1325,184,368,1699,1839,1953,468;178,1902,1552,2272,47,18,1885,2324,1929,1196,1844,1973,1083,1940,1293;2260,559,973,172,1536,258,1492,218,1402,1921,384,1704,479,2370,1251;949,1281,1250,413,704,483,838,78,129,543,533,126,1383,2229,87;817,273,390,1628,123,56,94,159,1796,671,1953,1181,1297,2121,66;765,2381,1992,377,389,1246,149,2047,331,1,57,1433,1614,1984,1713;503,840,1568,575,612,2041,152,1665,1562,1805,701,2254,984,435,1327;2474,54,2302,125,304,295,760,250,341,1778,2024,295,477,948,1527;124,2392,1923,1181,685,1134,2455,1651,1698,2341,2045,2286,726,315,938;1478,1014,680,375,1476,514,1708,2487,12,229,2212,745,519,2250,304;1425,1042,421,539,1976,1344,1219,1338,2405,940,1831,1683,2047,1533,1263;46,1978,2367,2340,1956,1043,300,454,419,832,1672,2023,1743,321,1047;2222,2454,1702,2416,165,2206,387,1356,690,889,984,732,2102,2447,1396;1650,1184,1271,1081,1926,1650,1445,1544,857,521,1701,1170,364,1407,1977;197,244,1674,801,2122,1842,2496,1458,1823,336,810,70,1441,324,1690;942,790,1430,2443,2247,471,729,2078,740,1706,2311,1987,1984,420,10;2267,2097,212,176,1882,154,695,687,585,897,1409,2303,793,1432,1586;517,83,1025,632,269,237,829,2437,2141,281,1680,1379,1085,2436,2417", "output": "844,2178,1937,1010,169,2372,1407,2131,2172,1084,2205,2071,1097,168,821,1720,1012,861,435,2155,1130,918,474,733,2,859,2123,1163,834,282,1965,2280,895,1742,746,2133,225,1203,901,438,1545,1422,2142,293,999,2218,1489,1476,1379,1150,423,753,79,1758,740,406,2243,606,853,2,124,2085,1595,2016,1736,1042,1276,2163,1884,1227,2496,1991,1967,394,2090,190,1249,1991,192,1627,1782,2415,1137,1347,1764,1160,2180,2188,348,2215,2159,2033,305,92,1974,327,887,436,1161,160,1607,931,2413,2101,514,71,178,1832,2013,1309,473,1245,1629,646,357,606,1530,867,2030,1293,227,2354,2244,195,2361,1405,1454,1556,461,984,1116,563,394,949,2177,431,691,963,1129,1034,1837,987,2277,1645,37,2436,2131,1304,1182,2306,523,1776,1927,2409,55,781,1058,888,931,1864,794,853,1168,812,1117,2218,1737,2133,88,1881,1257,1225,270,271,743,725,1551,935,1175,1134,2334,2375,2083,2308,934,702,2449,2272,348,1809,2274,2420,309,1513,173,2418,1996,418,1943,907,1539,10,1671,8,2196,1342,1469,402,2492,1385,496,1443,2128,1400,1247,1900,1547,2411,1667,355,2121,976,736,1009,1003,1445,659,653,2305,1261,2075,336,2249,1953,1699,184,846,1728,2006,1005,178,1552,47,1885,1929,1844,1083,1293,2370,1704,1921,218,258,172,559,949,1250,704,838,129,533,1383,87,2121,1181,671,159,56,1628,273,765,1992,389,149,331,57,1614,1713,435,2254,1805,1665,2041,575,840,2474,2302,304,760,341,2024,477,1527,315,2286,2341,1651,1134,1181,2392,1478,680,1476,1708,12,2212,519,304,1533,1683,940,1338,1344,539,1042,46,2367,1956,300,419,1672,1743,1047,2447,732,889,1356,2206,2416,2454,1650,1271,1926,1445,857,1701,364,1977,324,70,336,1458,1842,801,244,942,1430,2247,729,740,2311,1984,10,1432,2303,897,687,154,176,2097,517,1025,269,829,2141,1680,1085,2417"}, {"input": "1983,2015,2105,1595;1398,945,2490,984;1359,1088,573,877;1157,471,787,1994;1980,854,2135,2047;2378,1451,644,1517;1730,1417,1662,5;2419,474,1402,2194;877,1875,859,308;1164,2016,471,2317;510,274,768,2212;446,1882,1733,561;1617,1771,2418,1928;637,965,820,886;1780,907,708,28;851,2234,1123,1924;2007,879,2405,1805;34,1547,569,1326;1087,543,2259,475;1436,164,2359,2016;1038,433,1945,2044;198,227,992,2351;1452,908,673,1450;582,1940,1160,20;2229,1150,518,1765;335,2178,1633,953;992,791,1680,1556;1690,2114,1483,1413;1593,399,507,1518;1794,2034,2212,1620;750,1333,1444,979;999,1701,1985,59;2479,677,2293,428;767,2435,1734,2125;1375,1999,1338,2417;2216,2096,1675,1872", "output": "1983,2105,984,945,1359,573,1994,471,1980,2135,1517,1451,1730,1662,2194,474,877,859,2317,2016,510,768,561,1882,1617,2418,886,965,1780,708,1924,2234,2007,2405,1326,1547,1087,2259,2016,164,1038,1945,2351,227,1452,673,20,1940,2229,518,953,2178,992,1680,1413,2114,1593,507,1620,2034,750,1444,59,1701,2479,2293,2125,2435,1375,1338,1872,2096"}, {"input": "1979,106,406,1900,235,811,1615,1847,786,312,220,2124,119,2395,1251,2032,2202,1987,813,657,556,954,1466,1036,1737;505,871,1274,608,408,718,2062,291,6,1116,28,1232,703,1636,2150,859,1978,2018,694,1440,1741,1794,688,1037,608;2475,551,2111,1529,1432,361,1523,214,2026,1483,1578,350,513,57,1168,1891,1595,2220,1562,1599,1258,2307,1303,2094,2370;156,455,845,2028,1920,1634,2389,1594,1036,160,1206,2416,2383,841,668,2276,721,1739,661,1216,1786,56,267,566,894;1269,244,102,2461,2488,331,1331,255,756,2270,566,1649,1710,677,502,2052,331,1145,1122,944,1217,2085,636,1478,1559;1041,2328,2347,2028,453,83,816,1116,992,98,1639,1912,1243,1770,180,1438,900,136,1173,1194,846,897,2041,1548,290;2384,2030,1345,1308,1233,229,2076,531,1603,1874,2196,1495,1816,845,1474,193,737,2345,47,1268,1454,1380,2118,1841,609;1580,382,2212,1538,537,84,1193,99,1951,1781,2386,1077,1872,542,963,628,431,49,604,1471,570,2339,164,1989,229;1694,697,1607,1415,1732,2079,579,2015,1178,451,1692,366,512,267,1878,1335,985,286,797,998,126,719,177,1898,82;1652,43,392,1812,653,1151,1395,1412,1572,611,1963,2193,1103,2139,1716,2399,1868,1879,823,2050,1187,2019,1932,2104,2459;231,366,2238,1288,322,1020,359,1865,1830,1341,600,934,2378,2407,370,1447,2093,698,1693,2306,1837,545,912,1193,1590;1456,162,203,1158,103,846,80,648,606,1949,1693,1050,470,1706,1347,14,1245,1028,898,673,1203,864,1104,2,1602;504,358,750,1346,2152,1775,1295,737,1655,1803,1161,296,1625,1631,1458,2423,141,484,1679,458,352,891,1005,1261,1671;2057,1461,1590,2317,1038,1346,2384,2229,231,1723,404,1876,1588,965,519,1687,1176,2244,2174,1003,877,103,1155,704,1468;470,1364,212,1103,1983,55,2278,1387,2214,2123,113,366,572,2262,341,1855,1013,1104,430,156,38,1451,1626,1506,2427;1709,2162,617,1976,652,1262,1899,958,507,1133,731,1234,1424,2397,2087,842,53,107,2407,601,1843,1557,1841,2217,284;1122,1592,1490,1665,570,640,1978,1471,2497,407,582,1136,1155,959,884,760,935,288,1444,1256,1055,2284,1225,1182,2268;556,1553,2289,2405,1280,146,1276,2123,2026,2053,325,574,1891,1557,711,1324,703,1831,326,366,351,1662,1492,362,2356;2132,2178,1263,673,1077,93,2047,2150,511,2173,53,1217,407,299,756,11,2130,1005,2456,1229,204,565,673,2091,1529;727,1296,1734,1596,1808,2196,956,508,1000,414,1594,1252,1205,2082,2309,94,2300,834,2373,1448,2248,1960,1954,936,1516;1328,239,801,1740,189,1256,1117,1529,2116,28,1108,1870,1164,371,1886,2404,300,1457,1080,17,118,2049,717,2427,676;301,1513,1253,1315,1965,2007,1724,2149,1154,1681,1804,1231,573,181,1332,1449,178,2499,2209,2178,631,714,134,492,2181;1718,88,2184,1710,2152,1828,937,269,1386,1217,1341,2443,786,606,2052,1140,56,2282,2392,2412,863,2323,1202,187,2356;342,435,1803,1667,1361,549,1191,1484,334,1767,54,2312,1636,794,966,183,270,1567,753,381,734,1285,889,2379,957", "output": "1979,406,235,1615,786,220,119,1251,2202,813,556,1466,1737,1037,1794,1440,2018,859,1636,1232,1116,291,718,608,871,2475,2111,1432,1523,2026,1578,513,1168,1595,1562,1258,1303,2370,566,56,1216,1739,2276,841,2416,160,1594,1634,2028,455,1269,102,2488,1331,756,566,1710,502,331,1122,1217,636,1559,1548,897,1194,136,1438,1770,1912,98,1116,83,2028,2328,2384,1345,1233,2076,1603,2196,1816,1474,737,47,1454,2118,609,1989,2339,1471,49,628,542,1077,1781,99,84,1538,382,1694,1607,1732,579,1178,1692,512,1878,985,797,126,177,82,2104,2019,2050,1879,2399,2139,2193,611,1412,1151,1812,43,231,2238,322,359,1830,600,2378,370,2093,1693,1837,912,1590,2,864,673,1028,14,1706,1050,1949,648,846,1158,162,504,750,2152,1295,1655,1161,1625,1458,141,1679,352,1005,1671,704,103,1003,2244,1687,965,1876,1723,2229,1346,2317,1461,470,212,1983,2278,2214,113,572,341,1013,430,38,1626,2427,2217,1557,601,107,842,2397,1234,1133,958,1262,1976,2162,1122,1490,570,1978,2497,582,1155,884,935,1444,1055,1225,2268,362,1662,366,1831,1324,1557,574,2053,2123,146,2405,1553,2132,1263,1077,2047,511,53,407,756,2130,2456,204,673,1529,936,1960,1448,834,94,2082,1252,414,508,2196,1596,1296,1328,801,189,1117,2116,1108,1164,1886,300,1080,118,717,676,492,714,2178,2499,1449,181,1231,1681,2149,2007,1315,1513,1718,2184,2152,937,1386,1341,786,2052,56,2392,863,1202,2356,2379,1285,381,1567,183,794,2312,1767,1484,549,1667,435"}, {"input": "1941,773,1102,1387,613;1421,999,1551,1684,582;1190,2055,130,1336,13;1007,1438,2391,1510,1573;237,1426,1576,926,1467;997,141,1735,128,107;1046,319,218,1601,1570;1160,1376,32,2050,1084;2394,280,180,530,313;1967,1635,1504,329,2204;126,1616,1386,2337,1055;2481,1477,1272,30,623;2347,474,1303,1840,1365;926,1065,1864,50,664;12,1341,1108,2387,1886;1199,2440,1338,1186,2023;1565,1808,1546,1338,2160;125,1494,813,2311,2089;454,2094,1367,1463,1879;1190,834,2087,2214,607;1887,1006,1217,1058,667;1184,812,306,923,2263;1885,316,2473,2280,2106;1642,2390,2326,2264,108;1973,1245,316,1553,1877;1465,731,635,1553,1641;548,1540,1938,1455,2307;1565,1153,791,1230,2355;2493,971,1019,1506,1225;37,677,140,2083,1467;1147,1766,1186,1725,1981;1467,339,927,2121,1460;933,1233,867,2489,1790;216,1149,2316,167,36;2035,2331,398,2030,1727;1824,969,1279,784,1368;618,2444,5,2397,2269;340,1223,1462,2163,114;1953,2227,1663,199,475;1676,1019,1510,2177,873;1331,1257,2347,978,1939;1044,1394,2325,1750,1840;1627,1967,1257,733,1522;1347,1244,2324,266,1603;427,1428,1489,2276,1393;2140,723,1799,625,329;2084,419,228,360,2020;1311,1632,145,2439,2487", "output": "1941,1102,613,1684,999,1190,130,13,1510,1438,237,1576,1467,128,141,1046,218,1570,2050,1376,2394,180,313,329,1635,126,1386,1055,30,1477,2347,1303,1365,50,1065,12,1108,1886,1186,2440,1565,1546,2160,2311,1494,454,1367,1879,2214,834,1887,1217,667,923,812,1885,2473,2106,2264,2390,1973,316,1877,1553,731,548,1938,2307,1230,1153,2493,1019,1225,2083,677,1147,1186,1981,2121,339,933,867,1790,167,1149,2035,398,1727,784,969,618,5,2269,2163,1223,1953,1663,475,2177,1019,1331,2347,1939,1750,1394,1627,1257,1522,266,1244,427,1489,1393,625,723,2084,228,2020,2439,1632"}, {"input": "670,1319,22,315,130,2435,47,1286,280,1286,132,2005,556,1898,695,119,198,1982,1096,1522,102,1617,1059,1348,1207;584,1430,2416,1277,1763,1489,1275,2385,2140,1723,1552,830,2094,1223,1230,1631,2448,275,1235,254,477,734,2010,29,671;709,2142,549,1664,1824,1626,570,1636,70,92,559,617,2427,80,1165,215,730,568,740,1250,417,2406,1390,2227,1748;1702,1137,917,552,1610,1395,1089,868,2288,2072,1538,198,915,655,2484,1378,254,2024,2095,915,1649,2174,1684,1807,1013;247,1843,616,1473,2159,1827,1599,844,200,2490,1898,1277,629,2013,797,1512,121,13,914,1262,553,1484,179,2478,2312;388,2175,1907,1897,1458,273,741,594,203,5,156,942,807,2467,596,1093,122,482,1888,2150,1154,1473,943,2200,1432;897,1360,943,2363,649,1635,2393,619,2182,1356,658,16,1659,1478,414,615,271,1138,144,122,209,2372,1939,816,14;1716,1451,306,188,584,951,2030,1607,345,2417,30,2235,2397,333,2024,1846,1451,2108,1759,2285,1766,2388,806,742,858;2261,344,517,620,487,209,455,2248,2075,1518,1222,583,1952,1909,2476,1762,2032,322,1694,1056,645,441,2349,314,1574;2471,2131,840,585,1035,68,152,710,1629,2112,497,116,1665,974,1159,1269,357,207,313,556,284,502,757,1402,1893", "output": "670,22,130,47,280,132,556,695,198,1096,102,1059,1207,29,734,254,275,1631,1223,830,1723,2385,1489,1277,1430,709,549,1824,570,70,559,2427,1165,730,740,417,1390,1748,1807,2174,915,2024,1378,655,198,2072,868,1395,552,1137,247,616,2159,1599,200,1898,629,797,121,914,553,179,2312,2200,1473,2150,482,1093,2467,942,5,594,273,1897,2175,897,943,649,2393,2182,658,1659,414,271,144,209,1939,14,742,2388,2285,2108,1846,333,2235,2417,1607,951,188,1451,2261,517,487,455,2075,1222,1952,2476,2032,1694,645,2349,1574,1402,502,556,207,1269,974,116,2112,710,68,585,2131"}, {"input": "2194,2024,589,1463,42,760,1776,372,721,2099,2371,884,1149,2455,559,1578,334,91,416,884,2161,472,1286,1164,2160,320,998,1497,11,1853,1870,731;1469,487,2137,647,1100,2487,231,57,2203,322,1666,2141,2472,68,746,400,1943,605,164,721,1984,1844,482,1581,222,1996,2175,1831,2481,450,1745,2417;1638,1129,1903,1208,934,1283,2185,577,2202,1529,1303,417,1996,2354,759,2294,1793,82,60,2098,281,1609,885,1061,1854,2468,1830,977,135,1322,1960,2180;1452,1766,109,1935,2237,1437,475,1377,1934,845,1577,684,761,2156,989,1129,1098,968,1212,2251,1094,1525,281,715,2323,1135,1886,1723,2483,2116,1996,365;559,1300,1043,826,2014,109,1003,1778,399,1420,683,1272,1925,2302,537,1685,2130,41,150,224,2303,2282,25,51,1634,1696,1404,495,2345,1943,1977,1443;1492,1670,1423,2420,909,281,2030,39,188,842,658,1303,962,509,968,2298,59,145,572,532,2480,210,985,2476,1459,860,825,1255,2226,43,1921,2249;1375,359,459,2475,1504,1166,1320,496,641,1093,1220,1845,2144,1940,519,1845,2427,2489,1035,922,1444,1587,1604,575,730,2027,204,87,2142,684,2221,2303;1827,780,2149,1971,1984,660,1111,1512,2495,1446,850,1836,2492,48,2161,1731,400,189,1439,204,995,993,545,1454,908,473,2300,1685,174,382,708,481;222,1180,2270,1712,57,2239,346,746,526,1208,1999,2236,1799,2245,147,2499,45,600,2042,1277,332,874,1486,1753,2044,1775,932,2374,2429,241,2032,997;1429,1585,2167,1325,83,1464,1921,1733,1002,201,706,930,1450,998,1254,2406,566,964,513,220,21,1524,2483,1537,1879,1550,2402,686,2487,364,1372,2263;1080,1256,1328,1036,1841,412,865,23,1701,1469,807,121,1630,1088,786,491,217,1376,2253,19,1734,1378,1542,2303,2496,1292,1631,383,1269,48,911,2226;2486,501,513,2298,1770,177,1983,1885,1412,2382,872,2017,2203,6,1983,553,34,1541,1895,881,1747,366,1766,2171,465,1690,2288,1156,183,928,1327,935;525,1871,1585,864,2378,1994,203,899,381,1257,1146,528,293,781,179,966,2376,643,2170,2358,1205,55,391,663,416,1580,2131,398,995,1020,364,2164;1181,829,841,2363,101,1301,2144,1824,2283,74,149,2069,1524,1451,1807,1686,1404,543,1516,1514,1082,1167,1776,748,1570,958,1134,538,528,1084,182,967;1993,2402,583,1950,1353,948,1067,599,1196,1499,405,834,920,584,2128,223,2273,1660,1958,630,1629,1451,608,1425,1014,645,990,2277,1522,2081,2064,684;250,41,1645,115,1884,1998,609,591,918,864,154,2417,2015,2172,2107,1696,765,1800,2177,293,2281,1046,938,950,375,1601,292,419,1009,2134,981,289;203,1892,1414,1452,1243,564,2322,1284,1495,1519,1894,725,857,2484,616,460,1049,1257,102,515,224,48,1931,2442,1311,642,2237,2075,1690,269,1180,440;1298,585,1713,1097,1267,919,1541,175,1298,263,456,1055,1243,1412,116,2415,1152,597,1990,1204,2247,234,2430,1259,1249,170,748,1496,837,1259,1763,253;1817,311,1108,1732,1639,1977,190,700,480,1986,1273,519,1367,118,1256,2229,373,852,789,2493,1072,1624,854,1474,878,13,1475,131,1452,1732,2335,1688;1095,577,1391,413,1116,405,408,2014,1480,334,796,641,1466,1423,1297,403,2236,135,1797,996,337,2048,281,1362,1249,1024,242,2425,201,1258,1562,472;411,2064,1425,1433,2111,1853,613,2213,2129,24,1875,1815,1386,1059,373,2153,1951,38,144,268,2208,195,1617,1519,620,1639,1652,257,2084,2337,121,510;1754,1716,2024,348,1437,1388,1605,334,1099,289,1549,1085,1401,2033,1034,654,1323,1928,381,1992,642,1549,362,848,1101,2052,1705,1109,1034,1742,312,944;2305,77,2021,1680,1157,1022,774,10,1945,486,830,2113,362,1427,1573,1915,712,835,1402,1567,387,2430,751,1385,510,551,2500,1865,191,1681,2024,599;502,1900,188,1915,1591,958,2015,991,300,1916,1613,1659,1732,1387,1508,717,217,2057,2222,846,740,792,942,1565,428,1756,1138,1283,2266,98,1416,2384;2472,704,1686,1302,780,121,1489,926,1625,522,862,633,331,2389,2343,237,1019,1179,107,1131,1150,2409,496,1192,1950,1326,1146,328,1042,64,1792,1110;167,654,1624,759,1768,1360,1580,1602,4,1016,33,1851,1528,97,1243,2269,2134,52,172,1211,863,271,209,1524,522,1635,2295,1873,108,1760,2492,273;1166,420,2266,403,261,758,360,26,2272,288,528,1345,815,1195,1720,1204,2290,1382,2182,43,1896,282,823,1543,2433,456,1519,1010,2177,1741,2130,1900;601,2073,1857,697,303,416,1511,1771,2014,810,2353,1307,1852,1943,2108,449,702,615,1024,409,531,1458,2156,635,1364,1326,1538,2068,2331,1448,962,1221;2201,493,1043,331,1794,569,670,138,1000,1507,1774,1140,1126,682,1116,2388,2030,895,2071,1571,966,439,1488,440,52,302,1082,2428,967,1402,193,79;2263,2224,694,1433,2015,2283,1351,246,1601,822,460,1380,977,1711,144,1011,190,2063,1882,938,777,1749,940,1016,1376,58,2200,500,1164,1743,1620,1409;1315,1066,93,2062,458,1144,1542,1762,854,971,521,442,1939,156,405,879,327,2425,514,1803,2215,158,1522,205,2209,2259,1322,2190,2483,1004,2046,1737;1425,1583,2017,500,195,1983,349,431,981,915,1222,1452,449,2023,1245,1802,2443,956,2437,2299,2311,461,2161,1882,1556,2014,119,271,160,1679,712,1808;577,1938,1709,1272,998,1100,2077,2327,822,1767,963,638,893,290,1135,1522,1467,740,700,2200,1704,91,898,2220,1420,2458,1827,1066,1759,767,1036,705;2187,1445,1160,125,108,1606,2073,1643,1566,343,2150,1180,2052,1595,942,1064,2379,841,2255,2312,1406,2134,1303,656,1112,2028,2149,943,353,2081,2088,347;832,2500,668,1932,2472,473,1949,158,1991,1146,1539,836,586,1028,1762,2212,1977,2399,1878,1012,287,2057,1878,1753,2290,675,1470,328,274,2108,387,1827;1583,997,208,1163,2176,1124,1255,1063,126,1743,2066,1089,1284,1736,1413,1846,890,105,1403,2044,2257,1513,1919,1274,595,1975,1495,1438,239,1987,630,1940", "output": "2194,589,42,1776,721,2371,1149,559,334,416,2161,1286,2160,998,11,1870,2417,450,1831,1996,1581,1844,721,605,400,68,2141,322,57,2487,647,487,1638,1903,934,2185,2202,1303,1996,759,1793,60,281,885,1854,1830,135,1960,365,2116,1723,1135,715,1525,2251,968,1129,2156,684,845,1377,1437,1935,1766,559,1043,2014,1003,399,683,1925,537,2130,150,2303,25,1634,1404,2345,1977,2249,43,1255,860,2476,210,532,145,2298,509,1303,842,39,281,2420,1670,1375,459,1504,1320,641,1220,2144,519,2427,1035,1444,1604,730,204,2142,2221,481,382,1685,473,1454,993,204,189,1731,48,1836,1446,1512,660,1971,780,222,2270,57,346,526,1999,1799,147,45,2042,332,1486,2044,932,2429,2032,2263,364,686,1550,1537,1524,220,964,2406,998,930,201,1733,1464,1325,1585,1080,1328,1841,865,1701,807,1630,786,217,2253,1734,1542,2496,1631,1269,911,935,928,1156,1690,2171,366,881,1541,553,6,2017,2382,1885,177,2298,501,525,1585,2378,203,381,1146,293,179,2376,2170,1205,391,416,2131,995,364,967,1084,538,958,748,1167,1514,543,1686,1451,2069,74,1824,1301,2363,829,1993,583,1353,1067,1196,405,920,2128,2273,1958,1629,608,1014,990,1522,2064,289,2134,419,1601,950,1046,293,1800,1696,2172,2417,864,591,1998,115,41,203,1414,1243,2322,1495,1894,857,616,1049,102,224,1931,1311,2237,1690,1180,253,1259,1496,170,1259,234,1204,597,2415,1412,1055,263,175,919,1097,585,1817,1108,1639,190,480,1273,1367,1256,373,789,1072,854,878,1475,1452,2335,472,1258,2425,1024,1362,2048,996,135,403,1423,641,334,2014,405,413,577,411,1425,2111,613,2129,1875,1386,373,1951,144,2208,1617,620,1652,2084,121,944,1742,1109,2052,848,1549,1992,1928,654,2033,1085,289,334,1388,348,1716,2305,2021,1157,774,1945,830,362,1573,712,1402,387,751,510,2500,191,2024,2384,98,1283,1756,1565,792,846,2057,717,1387,1659,1916,991,958,1915,1900,2472,1686,780,1489,1625,862,331,2343,1019,107,1150,496,1950,1146,1042,1792,273,1760,1873,1635,1524,271,1211,52,2269,97,1851,1016,1602,1360,759,654,1166,2266,261,360,2272,528,815,1720,2290,2182,1896,823,2433,1519,2177,2130,1221,1448,2068,1326,635,1458,409,615,449,1943,1307,810,1771,416,697,2073,2201,1043,1794,670,1000,1774,1126,1116,2030,2071,966,1488,52,1082,967,193,1409,1743,500,58,1016,1749,938,2063,1011,1711,1380,822,246,2283,1433,2224,1315,93,458,1542,854,521,1939,405,327,514,2215,1522,2209,1322,2483,2046,1808,1679,271,2014,1882,461,2299,956,1802,2023,1452,915,431,1983,500,1583,577,1709,998,2077,822,963,893,1135,1467,700,1704,898,1420,1827,1759,1036,347,2081,943,2028,656,2134,2312,841,1064,1595,1180,343,1643,1606,125,1445,832,668,2472,1949,1991,1539,586,1762,1977,1878,287,1878,2290,1470,274,387,1940,1987,1438,1975,1274,1513,2044,105,1846,1736,1089,1743,1063,1124,1163,997"}, {"input": "520,1389,485,1207,698,605,2349,1841,1148,1920,1119,1522,538,1742,431,1128,1841,1492,1788,2156,710,517,922,1672,2105,115,1331,337,1757,292,2184,1109,2093,1024,2116,1621,1449,143,2334,2196,449,1709,896,307,2098,153,1451,2310;1461,1607,1110,1905,485,2094,1401,1797,848,1269,1218,191,1251,77,293,189,2330,1858,260,2233,48,65,751,1368,2120,44,2491,1608,1791,2278,1063,1179,2344,1874,2167,2148,1844,2416,2389,1370,2114,285,1152,35,1159,1341,2178,2325;802,285,1868,732,1708,2360,949,1418,675,178,472,278,2450,1415,1439,1004,6,1284,1674,258,2024,1255,1534,2448,2314,1239,797,1095,684,1895,1630,2344,1078,2124,295,1565,236,1427,2491,208,2118,976,2490,884,581,1852,2107,2428;425,285,512,2340,1643,2359,1966,1451,960,253,1207,948,53,794,2331,672,2149,1446,1981,726,384,1285,1803,1717,2365,939,2116,1404,984,359,521,471,1953,22,807,1472,1362,1891,2130,601,227,364,2002,1231,205,1465,1373,2334;1185,906,47,1704,1274,1169,2311,1393,1499,39,1981,2356,1969,953,431,2427,839,834,1602,1363,1092,323,2221,547,2212,2223,1521,2166,116,1872,245,2255,586,1551,2005,142,2022,88,1760,412,2405,2176,1993,742,1078,662,1679,297;1746,436,1440,1332,2047,535,2230,501,438,1799,698,1200,2112,157,1899,2136,2114,1884,2345,794,2214,161,2066,680,1132,1627,1195,352,800,438,2165,1330,463,851,669,429,1909,1680,1842,801,1207,523,100,1821,2156,1296,1121,2097;470,522,644,1862,785,2204,2466,1145,196,2243,245,1762,694,2308,1596,1308,963,2146,665,2,1982,2083,193,1378,2176,575,2067,2075,2158,2429,177,1191,484,358,870,1015,1651,703,1325,902,1452,175,301,147,1929,1036,2104,2141;188,881,1268,75,824,826,295,1942,1840,68,1412,551,85,675,2088,1786,2297,1836,682,1533,2135,1313,1065,1101,579,2271,1473,709,1410,229,697,918,1839,1677,1123,737,1116,2385,2133,1471,800,1229,433,792,1078,297,2290,2276;204,2346,376,1804,485,2209,1130,607,2171,962,930,1935,1461,671,1782,1107,1922,7,2467,454,1887,2034,2034,2470,144,1725,1943,1805,1521,904,379,292,69,418,1023,1663,449,973,561,1023,320,128,2241,673,1204,136,631,28;2038,967,2100,169,1594,1705,234,358,100,782,518,203,295,1895,841,1179,1567,2380,149,1098,1055,1336,132,2220,1387,756,2007,785,434,1839,1499,374,1750,94,1994,1619,1725,1052,2388,1691,2351,1591,300,1071,977,723,628,567;776,1843,976,298,1903,1869,1638,1192,834,1938,1789,1591,478,182,979,1215,1630,1015,1140,1677,1760,383,948,1425,2221,55,806,2042,2038,1331,898,977,2479,350,1912,65,871,2289,1698,308,1600,2010,2170,339,1820,1677,1683,1054;1920,426,1291,1948,286,1060,2434,2434,926,456,768,2446,1341,2136,508,673,554,2435,641,958,308,310,187,2392,584,1743,1487,1126,1938,2486,174,585,2042,1721,1908,2081,608,913,1205,1889,1718,955,53,1052,343,537,881,936;1405,1887,16,2293,760,887,712,559,1615,962,1400,1907,1196,2289,1814,1690,1500,2278,730,2085,2082,1503,2470,1737,770,210,1185,1539,723,703,1942,1901,1765,2202,1155,367,937,630,1649,125,629,1454,1485,633,1724,1674,292,481;200,2156,1439,1323,1023,97,1757,900,1854,131,920,679,1482,2205,1701,1742,1570,135,1791,1248,1552,1019,115,989,1506,1335,312,91,805,1563,2151,2398,2319,507,1762,695,240,498,747,2382,683,1327,842,145,1507,1938,809,1669;379,207,2488,28,297,2467,90,43,769,272,2102,1580,1428,1189,2313,1348,1617,283,1188,187,851,2146,2356,1530,491,1486,471,123,1241,2336,129,978,1248,1570,902,2068,1506,821,1053,2433,1962,1185,2108,1192,2337,727,1105,1009", "output": "520,485,698,2349,1148,1119,538,431,1841,1788,710,922,2105,1331,1757,2184,2093,2116,1449,2334,449,896,2098,1451,2325,1341,35,285,1370,2416,2148,1874,1179,2278,1608,44,1368,65,2233,1858,189,77,191,1269,1797,2094,1905,1607,802,1868,1708,949,675,472,2450,1439,6,1674,2024,1534,2314,797,684,1630,1078,295,236,2491,2118,2490,581,2107,2334,1465,1231,364,601,1891,1472,22,471,359,1404,939,1717,1285,726,1446,672,794,948,253,1451,2359,2340,285,1185,47,1274,2311,1499,1981,1969,431,839,1602,1092,2221,2212,1521,116,245,586,2005,2022,1760,2405,1993,1078,1679,2097,1296,1821,523,801,1680,429,851,1330,438,352,1627,680,161,794,1884,2136,157,1200,1799,501,535,1332,436,470,644,785,2466,196,245,694,1596,963,665,1982,193,2176,2067,2158,177,484,870,1651,1325,1452,301,1929,2104,2276,297,792,1229,1471,2385,737,1677,918,229,709,2271,1101,1313,1533,1836,1786,675,551,68,1942,826,75,881,204,376,485,1130,2171,930,1461,1782,1922,2467,1887,2034,144,1943,1521,379,69,1023,449,561,320,2241,1204,631,567,723,1071,1591,1691,1052,1619,94,374,1839,785,756,2220,1336,1098,2380,1179,1895,203,782,358,1705,169,967,776,976,1903,1638,834,1789,478,979,1630,1140,1760,948,2221,806,2038,898,2479,1912,871,1698,1600,2170,1820,1683,936,537,1052,955,1889,913,2081,1721,585,2486,1126,1743,2392,310,958,2435,673,2136,2446,456,2434,1060,1948,426,1405,16,760,712,1615,1400,1196,1814,1500,730,2082,2470,770,1185,723,1942,1765,1155,937,1649,629,1485,1724,292,1669,1938,145,1327,2382,498,695,507,2398,1563,91,1335,989,1019,1248,135,1742,2205,679,131,900,97,1323,2156,379,2488,297,90,769,2102,1428,2313,1617,1188,851,2356,491,471,1241,129,1248,902,1506,1053,1962,2108,2337,1105"}, {"input": "967,24,22,2281,590,812,1820,318,1608,1735,1305,1336,587,1932,1202,434,986,1718,1417;70,865,1913,502,2357,1491,684,2197,2464,1222,595,648,254,1095,2271,91,1198,1805,204;1787,35,1503,2105,1968,1010,1026,2189,2013,1442,1178,271,904,800,105,2272,1508,79,1874;255,2345,1910,2320,574,2222,197,2476,199,1905,2199,2067,2358,2369,209,1129,659,570,1981;281,1699,1208,61,2043,1481,350,1687,41,58,1300,474,1893,2407,663,2486,1755,1708,1601;2200,1785,624,714,413,2214,2060,1144,1781,1293,966,235,1304,1983,2246,1772,1072,418,2329;1996,181,266,340,2214,970,1123,307,2301,687,1986,1583,701,434,1569,1794,1761,1147,1321;2382,491,324,66,2449,1853,449,862,871,784,408,1194,898,215,1817,2478,1611,1864,2485;1345,1060,2271,258,32,532,1110,812,2372,342,690,479,1724,1461,1647,663,2417,1833,2482;2483,1167,746,1471,1600,1483,718,2369,2297,1678,147,37,1382,1050,419,2000,1810,2287,6;1178,842,25,804,624,1295,546,938,1460,2273,842,20,552,1034,74,2202,2155,2288,436;1377,562,985,2455,919,2420,219,147,520,874,1000,2145,92,2007,1393,1292,1562,929,1529;132,2369,2482,644,1409,785,2345,887,840,1413,516,422,269,503,280,2045,440,1516,1576;745,1570,999,756,648,747,2241,857,891,2340,1791,2119,931,298,2343,323,1515,2414,2102;1999,679,1157,1618,717,1238,591,1136,42,1617,2014,2203,826,1416,2166,1034,1935,383,2157;669,630,2005,761,1547,898,287,1085,314,1037,1261,2405,999,2187,2409,1928,1329,1841,1055;1185,1772,2236,603,1937,757,35,430,582,1478,1221,534,403,1762,2459,610,1156,1133,2171;2194,510,2437,759,373,1918,1824,1488,1096,1246,1492,1942,2306,1142,1243,2459,1164,37,422;1661,1889,762,555,934,2345,734,1006,2077,75,373,1667,514,2018,2476,1295,2476,625,1087;252,2144,2324,1814,1429,1846,1003,2263,2191,1403,307,1007,387,410,1050,1622,1719,830,1137;1080,1517,1458,82,2107,1413,1270,1496,630,671,2226,2251,2257,1449,254,1838,1394,991,502;748,820,1229,526,2231,612,1595,130,1253,1289,70,101,1917,348,2206,1326,645,267,2474;116,1652,554,377,372,1596,1950,1098,991,271,2374,645,142,1313,353,1320,2089,810,385;2303,2244,1576,416,1316,1153,728,18,1584,45,1707,1771,1995,2145,2213,187,2001,704,2417;657,1008,661,806,1883,2322,2358,1173,2110,70,438,441,756,1139,2076,1854,299,1482,1370;1563,997,2132,127,332,1306,266,1708,1655,2003,906,461,1728,2158,654,489,412,1233,337;2477,687,2095,360,2144,822,2435,2493,1573,8,68,1203,1232,1916,532,402,419,49,1997;760,1463,1912,38,1744,761,445,206,1177,1341,853,1635,849,2490,1284,640,1191,1732,2198;1976,1610,1362,1141,1418,970,82,2038,114,1833,1035,1254,2496,2350,784,589,1376,496,1788", "output": "967,22,590,1820,1608,1305,587,1202,986,1417,1805,91,1095,648,1222,2197,1491,502,865,1787,1503,1968,1026,2013,1178,904,105,1508,1874,570,1129,2369,2067,1905,2476,2222,2320,2345,281,1208,2043,350,41,1300,1893,663,1755,1601,418,1772,1983,235,1293,1144,2214,714,1785,1996,266,2214,1123,2301,1986,701,1569,1761,1321,1864,2478,215,1194,784,862,1853,66,491,1345,2271,32,1110,2372,690,1724,1647,2417,2482,2287,2000,1050,37,1678,2369,1483,1471,1167,1178,25,624,546,1460,842,552,74,2155,436,929,1292,2007,2145,874,147,2420,2455,562,132,2482,1409,2345,840,516,269,280,440,1576,2414,323,298,2119,2340,857,747,756,1570,1999,1157,717,591,42,2014,826,2166,1935,2157,1841,1928,2187,2405,1037,1085,898,761,630,1185,2236,1937,35,582,1221,403,2459,1156,2171,37,2459,1142,1942,1246,1488,1918,759,510,1661,762,934,734,2077,373,514,2476,2476,1087,830,1622,410,1007,1403,2263,1846,1814,2144,1080,1458,2107,1270,630,2226,2257,254,1394,502,267,1326,348,101,1289,130,612,526,820,116,554,372,1950,991,2374,142,353,2089,385,704,187,2145,1771,45,18,1153,416,2244,657,661,1883,2358,2110,438,756,2076,299,1370,1233,489,2158,461,2003,1708,1306,127,997,2477,2095,2144,2435,1573,68,1232,532,419,1997,1732,640,2490,1635,1341,206,761,38,1463,1976,1362,1418,82,114,1035,2496,784,1376,1788"}, {"input": "1057,548,1714,1563,30,790,179,1209,285,1071,1347,21,225,930,372,2030,1651,2095,1132,1617,1869,2496,1849,543,1892,1181,1087,132,777;665,1499,898,954,1758,2268,2260,2003,1359,2102,139,1414,1043,1391,2256,153,697,1765,1245,769,1198,2278,669,1451,911,465,195,1274,351;2383,176,1615,2366,678,1598,1428,1115,1974,2232,1993,2365,397,688,659,2086,2384,777,343,2297,1172,1448,2393,863,441,2409,1159,1541,880;855,53,213,1641,1447,478,1200,1263,2174,1834,373,2292,2040,2452,1140,451,159,1728,1826,1107,1723,707,462,112,2257,137,1004,1758,1913;1041,1405,2106,1994,2156,268,1450,1506,1996,1380,1927,1864,2261,777,321,270,1554,60,1187,274,2054,1848,1531,1284,716,1915,2495,551,1406;2323,150,2072,2459,1559,1968,2488,131,199,1266,1816,2153,2190,768,187,408,1204,1048,927,1250,1837,2457,1280,1550,937,418,16,2286,820;1334,390,1865,1062,2071,1562,1154,1606,655,1746,1841,894,868,1185,2174,1386,947,1491,926,858,566,1685,364,1643,1926,34,763,509,401;978,221,511,217,1473,271,805,24,631,379,1808,833,760,1456,1390,406,1263,2387,537,987,2365,991,1792,1910,1239,2484,1737,2300,383", "output": "1057,1714,30,179,285,1347,225,372,1651,1132,1869,1849,1892,1087,777,1274,465,1451,2278,769,1765,153,1391,1414,2102,2003,2268,954,1499,2383,1615,678,1428,1974,1993,397,659,2384,343,1172,2393,441,1159,880,1758,137,112,707,1107,1728,451,2452,2292,1834,1263,478,1641,53,1041,2106,2156,1450,1996,1927,2261,321,1554,1187,2054,1531,716,2495,1406,2286,418,1550,2457,1250,1048,408,768,2153,1266,131,1968,2459,150,1334,1865,2071,1154,655,1841,868,2174,947,926,566,364,1926,763,401,2300,2484,1910,991,987,2387,406,1456,833,379,24,271,217,221"}, {"input": "503,160,1782,2354,1764,178,881,1864,1253,2290,1056,1112,2077,2357,559,424,822,51,1767,1474,1708,16,1061,1864,1213,2208,645,2160,276,1195,158,313,821,277,785,17,972,346,1381,568,596,1743;460,695,2065,572,1819,1835,542,2225,1655,1644,1674,985,1125,888,2048,1455,660,691,2464,2328,2486,862,2476,426,1597,2084,1772,2480,596,433,214,1143,820,2298,758,910,2146,2193,1681,1747,871,2359;2151,401,1087,328,54,1962,66,1077,1376,2055,1155,1069,724,477,2065,1514,894,2174,1259,1429,1255,2169,2325,20,336,1476,1147,2166,1208,128,1770,1586,1039,290,516,1494,1734,252,270,1805,2470,2146", "output": "503,1782,1764,881,1253,1056,2077,559,822,1767,1708,1061,1213,645,276,158,821,785,972,1381,596,2359,1747,2193,910,2298,1143,433,2480,2084,426,862,2328,691,1455,888,985,1644,2225,1835,572,695,2151,1087,54,66,1376,1155,724,2065,894,1259,1255,2325,336,1147,1208,1770,1039,516,1734,270,2470"}, {"input": "25,560,2154;1439,151,1044;2429,754,759;831,1005,904;2262,2224,2472;1465,1448,524;1072,313,499;92,191,1338;1229,2371,1773;1110,276,650;2266,1917,1377;220,737,1334;2148,209,1933;1440,1136,1363;1663,753,1498;215,652,1175;627,122,639;1606,1488,850;279,2306,1433;62,1092,1231;698,1502,909;37,2014,1604;2213,1572,1020;412,288,722;2482,1346,833;2071,1992,231;2268,1559,2087", "output": "25,2154,151,2429,759,1005,2262,2472,1448,1072,499,191,1229,1773,276,2266,1377,737,2148,1933,1136,1663,1498,652,627,639,1488,279,1433,1092,698,909,2014,2213,1020,288,2482,833,1992,2268,2087"}, {"input": "812,1590,633,1455,1644,2461,587,225,1110,279,528,142,1041;697,2015,1516,979,35,1408,348,1280,1539,136,689,475,541;1885,1985,5,169,2440,1733,2286,1257,1926,1979,369,248,1709;88,1609,1035,1150,510,647,1544,2008,1153,295,251,301,775;659,795,2146,1806,32,795,1029,1064,818,2200,2119,1714,1025;1424,1893,2165,229,473,302,475,1065,716,1359,2312,832,1560;2114,223,2036,631,2461,1966,2257,1695,752,16,1587,1651,1585;1912,756,85,1154,1026,686,214,1764,207,789,426,1513,1541;1184,1074,2377,607,760,1725,2241,1060,2164,451,1631,384,2125;689,1460,182,272,2166,416,597,574,2493,2153,880,2427,423;455,397,1667,596,1106,2361,1875,2479,1489,620,1167,858,251;1131,793,46,912,2297,229,2234,79,1419,277,738,495,1641;879,1383,943,921,1124,717,2038,431,1570,2257,2034,284,965;274,2364,2480,1746,493,2376,1493,141,573,928,1341,1160,318;454,1076,850,1654,67,1985,807,882,152,54,1440,1705,224;1743,1634,721,1937,292,1586,66,2474,1427,79,2328,533,535;133,2188,2196,582,1838,2358,897,1201,188,108,1900,148,922;2029,292,1015,1687,2427,1771,2046,200,509,2132,924,485,1554;1605,1045,1664,163,1273,721,833,1708,263,342,541,2036,1266;355,461,2452,2279,1548,1631,1118,1139,2490,2410,1228,801,1046;222,2061,1225,471,2071,889,1208,2490,2496,82,1800,1038,202;665,1678,875,1174,204,1630,962,680,2214,934,856,1282,327;1044,2391,2384,2044,1195,1655,1172,754,507,2146,737,2417,1036;1864,588,693,678,1013,1162,983,2006,1343,1340,1000,1131,776;894,1670,125,198,943,532,1020,2209,746,634,784,1119,994;1485,646,1172,130,2366,1740,1276,1783,1280,1628,2040,330,1026;1602,2318,1312,1258,662,1507,1857,274,1828,1485,1970,586,1576;104,230,1403,1680,1019,148,2005,77,1661,2078,187,750,730;1182,32,2464,1491,419,688,9,1333,2143,1812,1584,2,599;313,2428,657,2174,912,1425,503,2397,2279,2147,784,2250,884", "output": "812,633,1644,587,1110,528,1041,475,136,1280,1408,979,2015,1885,5,2440,2286,1926,369,1709,301,295,2008,647,1150,1609,659,2146,32,1029,818,2119,1025,832,1359,1065,302,229,1893,2114,2036,2461,2257,752,1587,1585,1513,789,1764,686,1154,756,1184,2377,760,2241,2164,1631,2125,2427,2153,574,416,272,1460,455,1667,1106,1875,1489,1167,251,495,277,79,229,912,793,879,943,1124,2038,1570,2034,965,1160,928,141,2376,1746,2364,454,850,67,807,152,1440,224,533,79,2474,1586,1937,1634,133,2196,1838,897,188,1900,922,485,2132,200,1771,1687,292,1605,1664,1273,833,263,541,1266,801,2410,1139,1631,2279,461,222,1225,2071,1208,2496,1800,202,1282,934,680,1630,1174,1678,1044,2384,1195,1172,507,737,1036,1131,1340,2006,1162,678,588,894,125,943,1020,746,784,994,330,1628,1783,1740,130,646,1602,1312,662,1857,1828,1970,1576,750,2078,77,148,1680,230,1182,2464,419,9,2143,1584,599,2250,2147,2397,1425,2174,2428"}, {"input": "1006,1904,1238,2476,1841,249,1773,2388,547,1153,2103,602,531,803,65,2161,376,1375,797,2188,1600,1105,2149,89,183,1106,2105,1073,59,635,2174,376,900,1251,134,424,2301,538,1154,2492,1626,2396,1391,2424;2047,2082,1138,1813,404,339,47,600,1377,2483,1421,1598,2233,653,1667,1128,1177,76,78,938,898,396,453,254,1327,2168,612,2059,1222,1394,1132,1570,2277,1878,451,1265,844,2421,2098,1232,2340,312,1803,1228;1618,887,1958,606,2024,500,1417,1046,2109,838,1996,1513,993,2144,899,1287,1641,2401,468,2477,1675,769,2005,1041,986,1164,298,1114,757,2112,2168,1088,2399,2237,1245,799,663,2155,1472,1676,888,1136,2437,2014;562,1621,2188,1515,567,1948,421,1615,1900,863,2394,145,1666,1594,1312,137,234,2109,1068,2409,1617,1553,1644,210,235,1120,1102,1473,820,1621,703,787,2230,1858,17,2018,1092,2235,76,461,1722,1871,2415,2310;1472,1476,1362,882,33,2213,2482,781,984,2224,108,1101,119,1955,1820,743,2161,32,1331,1709,791,485,2463,975,1845,936,2355,1294,1389,1328,1541,2391,1792,1110,2269,860,2335,1450,2057,1200,2126,888,170,53;1127,78,937,1999,242,2319,2305,1541,2262,2281,400,2286,1523,424,2209,1927,465,1484,989,1208,1786,2003,1063,540,1968,901,1773,667,2167,594,677,2020,2159,154,241,2312,1956,1948,875,388,2108,1625,406,1348;1336,617,2419,1815,233,959,1406,665,1365,1145,1897,420,521,329,2211,2361,503,642,1819,718,1618,377,767,2452,102,1643,748,350,718,2103,238,112,674,1121,2472,1555,1914,2280,449,2168,1785,824,216,824;2154,549,1954,1711,2473,218,1789,1966,1151,2241,2193,856,748,1584,316,1205,1364,575,369,2226,2410,467,2336,1896,999,2259,1614,201,985,941,1656,885,2029,1768,1361,1742,620,914,962,144,1184,2443,1076,2049;46,144,1103,1099,1045,1037,1080,784,424,526,293,1290,1278,716,2311,909,1705,2331,1650,2131,320,1656,2006,1292,1082,2331,587,1834,366,1971,2260,380,1022,2177,1007,1268,1545,1438,1296,1832,1281,664,1151,656;2005,1400,2251,1702,802,1277,974,1318,140,2394,2249,1993,1286,1655,2086,1748,1773,757,828,962,790,1333,668,1353,1371,2386,1923,1478,397,2137,753,402,2446,2373,1976,730,1083,2479,146,1341,2328,1546,99,670;2133,153,2259,1698,1957,1064,103,111,478,1527,2024,1351,42,1216,609,744,1143,1138,1992,1387,1173,2137,1400,660,1812,1155,1698,1917,1180,110,124,1043,673,1210,308,1239,736,2401,1825,1885,208,674,1076,429;489,1303,1685,960,554,1128,107,2209,1436,368,77,233,1173,1877,284,1490,1776,1924,900,670,2069,2361,2072,530,2192,1611,2218,1267,863,2441,1077,1748,220,2234,2295,684,292,1180,938,2462,1261,2125,1538,122;2074,2048,1487,2301,2411,1965,642,1306,122,816,227,2077,1384,160,842,1403,783,2381,1118,268,1232,438,135,1080,1841,2352,1694,499,176,557,1466,864,2427,1907,1081,500,1282,1203,1170,2240,1314,767,95,1641;2186,1288,143,108,648,458,174,2187,586,1053,2347,1338,28,1813,1661,676,707,983,1300,2251,1951,1060,797,1759,472,1297,1370,440,1153,761,666,1442,340,854,1454,532,2294,1226,1581,67,1437,1284,1950,2121;588,2492,462,1623,298,292,1937,2067,1950,1758,2329,663,1744,581,2415,1551,2098,1917,1045,343,1770,2030,261,2246,1224,2267,1755,740,1478,2329,766,713,1069,1829,761,1114,677,14,107,1698,2460,342,127,2096;2417,933,1173,1364,2462,1859,2079,1997,2070,1564,589,578,1336,2072,1611,1387,1539,75,2170,1684,158,2350,1179,150,853,1623,392,69,1346,441,749,1606,1847,653,923,1982,2213,457,97,825,2235,225,1720,1338;1922,865,858,1837,493,994,1291,44,1365,629,2351,1114,1804,1602,1031,2135,909,347,987,28,1673,1589,24,1860,1399,35,1307,1070,1838,121,2342,1643,447,2307,1404,2232,676,1030,2484,1922,1354,631,2301,2033;12,245,235,2358,2307,93,1514,599,802,731,2109,1969,1581,2094,806,484,1210,1687,1222,2375,520,1635,1480,320,1168,673,740,9,2123,73,1913,986,1887,2021,1699,2119,1160,1945,2040,1553,382,218,198,154;987,82,1933,2362,457,569,1437,1678,2120,1145,73,836,685,403,762,413,824,1438,2406,727,460,2213,1535,1017,1243,1610,1142,1696,1731,860,224,399,1224,470,868,1278,55,1110,1941,1212,209,1088,1297,1227;1588,1305,34,1842,1584,490,2095,2178,372,2259,2309,1465,1920,445,2003,647,913,929,1664,1564,404,1084,892,2268,2487,301,1904,2165,1360,1827,2074,1471,202,459,1302,319,1219,56,585,2423,1730,205,603,2029;1522,1492,1098,2231,2387,1846,843,1481,1953,1647,2500,2316,404,2391,979,2197,758,2187,263,1464,2478,151,1104,1896,774,1814,1254,316,911,2416,744,61,2214,2231,2031,1553,621,1775,2289,2093,1587,135,2175,2197", "output": "1006,1238,1841,1773,547,2103,531,65,376,797,1600,2149,183,2105,59,2174,900,134,2301,1154,1626,1391,1228,312,1232,2421,1265,1878,1570,1394,2059,2168,254,396,938,76,1128,653,1598,2483,600,339,1813,2082,1618,1958,2024,1417,2109,1996,993,899,1641,468,1675,2005,986,298,757,2168,2399,1245,663,1472,888,2437,2310,1871,461,2235,2018,1858,787,1621,1473,1120,210,1553,2409,2109,137,1594,145,863,1615,1948,1515,1621,1472,1362,33,2482,984,108,119,1820,2161,1331,791,2463,1845,2355,1389,1541,1792,2269,2335,2057,2126,170,1348,1625,388,1948,2312,154,2020,594,667,901,540,2003,1208,1484,1927,424,2286,2281,1541,2319,1999,78,1336,2419,233,1406,1365,1897,521,2211,503,1819,1618,767,102,748,718,238,674,2472,1914,449,1785,216,2049,2443,144,914,1742,1768,885,941,201,2259,1896,467,2226,575,1205,1584,856,2241,1966,218,1711,549,46,1103,1045,1080,424,293,1278,2311,1705,1650,320,2006,1082,587,366,2260,1022,1007,1545,1296,1281,1151,670,1546,1341,2479,730,2373,402,2137,1478,2386,1353,1333,962,757,1748,1655,1993,2394,1318,1277,1702,1400,2133,2259,1957,103,478,2024,42,609,1143,1992,1173,1400,1812,1698,1180,124,673,308,736,1825,208,1076,122,2125,2462,1180,684,2234,1748,2441,1267,1611,530,2361,670,1924,1490,1877,233,368,2209,1128,960,1303,2074,1487,2411,642,122,227,1384,842,783,1118,1232,135,1841,1694,176,1466,2427,1081,1282,1170,1314,95,2121,1284,67,1226,532,854,1442,761,440,1297,1759,1060,2251,983,676,1813,1338,1053,2187,458,108,1288,588,462,298,1937,1950,2329,1744,2415,2098,1045,1770,261,1224,1755,1478,766,1069,761,677,107,2460,127,1338,225,825,457,1982,653,1606,441,69,1623,150,2350,1684,75,1387,2072,578,1564,1997,1859,1364,933,1922,858,493,1291,1365,2351,1804,1031,909,987,1673,24,1399,1307,1838,2342,447,1404,676,2484,1354,2301,154,218,1553,1945,2119,2021,986,73,9,673,320,1635,2375,1687,484,2094,1969,731,599,93,2358,245,987,1933,457,1437,2120,73,685,762,824,2406,460,1535,1243,1142,1731,224,1224,868,55,1941,209,1297,2029,205,2423,56,319,459,1471,1827,2165,301,2268,1084,1564,929,647,445,1465,2259,2178,490,1842,1305,1522,1098,2387,843,1953,2500,404,979,758,263,2478,1104,774,1254,911,744,2214,2031,621,2289,1587,2175"}, {"input": "2317,2113,2135,2231,2153,1447,1228,1676,1095,1773,2360,935,1274,999,374,2023,1224,1964,1025,1615,1537,2100,1157,2107,1133,683,353,222,1385,2168,2161,1507,1498,1179,1771,293,2009,19,134,2166,1469,178;2434,1150,138,1106,2446,976,485,8,175,212,1644,616,692,2456,1473,2477,1052,2131,2061,2408,1240,1264,1685,379,193,775,248,997,1991,69,1663,864,519,2004,1774,367,1514,94,1999,781,2362,652;1551,2261,1527,1088,138,955,1339,1914,774,1368,2080,1944,2499,595,583,2061,349,1585,1399,11,2120,1761,851,398,906,153,21,2044,1689,989,947,979,1711,419,409,2193,1975,1516,1874,1863,2429,829;647,473,1764,2107,381,1746,1271,1782,570,1752,1370,1109,1710,1448,2131,2458,2013,563,1799,210,683,1617,2397,964,989,2211,794,784,607,2482,2289,2252,1718,1537,2333,239,1531,1698,1608,2146,521,1879;1371,54,1376,876,348,1138,323,1821,1051,1061,674,1801,2474,1713,1401,795,1784,1982,583,1629,1492,366,147,2378,1933,2180,2145,197,1012,2283,1936,1531,103,265,788,562,1962,1276,2324,2286,1146,1916;1364,838,2234,1058,784,885,963,1081,369,1621,65,673,1453,511,2263,1432,355,194,1454,2399,671,1971,2486,376,666,667,1747,2087,1666,506,2094,1713,1205,1861,343,2312,550,874,2233,2342,728,2119;1090,2083,1845,651,1499,1489,437,1521,1533,1528,1695,719,682,999,2500,1334,609,1807,673,269,1548,1843,1900,556,1744,15,1363,2067,350,1097,1263,1665,77,737,2349,563,500,91,687,889,288,1063;167,1208,2110,2236,756,72,164,949,1153,1124,284,971,766,1138,1774,1151,708,18,2140,1754,267,1578,1947,973,905,533,1395,2417,785,1793,1362,863,1638,225,1405,1899,2029,2374,790,2045,1758,947;666,187,406,1358,1296,2480,1923,1681,148,1305,2357,457,1816,830,752,1373,1202,973,655,133,1451,2415,1140,1450,1673,1925,143,6,2036,2256,1551,691,508,346,1651,540,681,399,492,429,1411,313;1337,280,2148,1875,807,678,1255,899,2122,675,356,601,1346,164,230,291,2160,2395,931,417,1975,453,1796,301,429,376,757,170,2288,1319,2275,2233,1489,1535,1655,974,2038,2470,1577,1526,281,1717;593,850,753,1191,199,1505,1652,324,132,1081,929,915,452,1916,1187,845,1119,814,470,583,2099,1934,16,33,553,835,1679,2430,2158,2278,2459,630,1761,2311,580,32,804,1753,650,405,1022,630;1755,1835,52,2068,1700,1968,817,1567,378,2359,84,49,2483,132,1665,1163,847,2194,1991,1077,2175,37,2221,1048,370,1421,819,1828,2188,1268,465,1637,1716,799,1417,2203,2311,1978,1924,995,830,2008;2027,598,1210,1087,749,1889,832,489,2052,585,246,516,411,1010,312,1885,1477,2426,2200,1453,955,491,1636,1059,807,1026,177,1524,1837,1240,871,682,2187,1289,1553,348,1270,690,433,2223,2007,2117;2046,2335,1160,1197,1539,2433,1650,2310,1743,274,2361,1467,1874,205,700,1535,1884,2306,835,1641,2199,1745,1504,735,1841,1088,2280,1945,1231,1072,2411,1218,505,1513,581,420,1261,2067,431,1535,2397,185;1129,1813,2415,217,181,1657,1087,751,2,1789,923,1341,2344,793,2056,1628,1904,1768,1990,149,2403,1715,2293,1634,634,2379,2242,1988,1567,1991,1791,735,1410,111,1367,2273,1457,247,538,2322,626,560;2448,2319,2496,1970,968,2373,714,1060,2456,1293,1695,560,166,2174,1790,1568,478,1264,495,748,2333,1139,2078,1549,1376,1338,2147,375,459,1369,540,30,564,2024,1069,142,1603,1660,2041,2078,1824,1338;542,765,1870,934,770,1366,569,2311,1097,2195,1456,228,2341,1142,107,529,845,2441,2410,1826,519,197,581,1394,286,621,523,1125,647,188,2404,887,652,129,584,394,1965,818,1884,498,2267,2287;1695,707,1570,1622,137,2433,254,1480,341,1071,1613,2000,1742,1780,2486,2011,2080,1191,1706,2448,739,802,2453,359,369,667,484,2078,99,1451,490,501,1872,1204,1449,2388,2373,357,871,1956,1566,738;2018,1978,966,804,2403,2318,1608,771,427,1358,1984,1919,568,2362,456,845,2410,981,1511,1146,1035,2059,484,2341,1083,1215,574,1293,453,738,230,753,2330,2238,803,1251,288,602,740,1997,1277,1676;984,958,1331,1542,17,576,1883,518,835,2163,1105,310,431,454,583,518,1295,917,85,558,477,929,1473,1395,2058,758,1473,1237,2123,28,1126,1956,2414,2292,406,1794,794,1247,266,717,842,426;1091,2341,1456,2464,611,1275,1804,1033,597,127,527,1070,109,1168,1802,165,565,1440,2289,1747,242,285,352,1654,841,1371,1646,2288,2211,529,2353,159,538,2434,1999,1952,1872,1335,1912,1586,474,447;1811,1255,239,1438,298,1178,827,751,1133,443,23,404,765,1806,2169,295,1662,1363,514,340,1308,628,573,2231,2112,2460,312,371,1014,301,2027,2438,1799,2286,347,2173,350,1028,984,1699,133,1633;952,1447,161,394,388,1786,269,2043,324,772,360,2264,1830,1699,1947,792,1414,1097,1393,1195,2038,1973,806,797,800,2434,147,1201,1805,2057,2494,684,440,873,857,2230,76,1550,2006,58,2180,953;707,2006,3,1180,160,1979,973,134,2166,390,1935,475,1884,2253,992,624,33,246,1440,1837,2391,39,630,1381,2108,563,852,1749,2198,1599,983,2313,2444,2455,917,2047,1263,1562,5,1911,1787,1990;844,754,1303,419,14,2268,27,1879,442,1658,2236,1527,877,1155,552,1769,1470,749,610,1477,1375,2136,959,1781,958,660,798,1171,2215,1292,1712,469,2152,2112,70,579,2463,1221,1110,1536,672,1741;97,1018,2225,359,1700,351,2022,543,524,2259,768,819,764,1057,1883,283,1840,1242,734,772,1429,2314,2186,1887,884,385,1879,766,1792,60,229,1993,1620,1792,407,1897,606,1050,475,1388,651,643;147,1908,1839,2186,2115,1937,2358,1719,490,424,2243,444,2053,2147,423,117,2099,930,1206,89,432,1019,2159,812,1252,1680,380,38,1427,18,144,460,1018,914,1170,1865,1452,1483,2248,2341,1408,2225;249,2447,1416,1606,2183,559,2361,1529,321,2047,440,1786,713,371,2476,536,2113,488,998,1100,321,1602,1648,188,1493,929,1209,405,40,1562,292,2352,754,409,2113,1882,2354,2011,1343,981,1897,612;1217,712,1064,1563,1189,2353,1086,1653,1396,229,2006,150,768,63,1978,1226,1450,2011,844,2164,579,2455,390,2270,841,2302,577,1822,116,2112,801,1749,27,1625,966,403,697,2342,2470,509,1845,1728;2390,2371,2154,1349,1161,632,305,1352,379,452,860,2433,299,1247,1556,428,553,1843,1118,1067,1467,12,1118,483,848,2481,2233,871,476,1305,2478,182,1417,1841,1206,1877,4,577,1376,771,298,1230;876,1763,2406,2384,589,1885,906,1672,1958,2196,1702,968,181,1306,2085,1980,260,39,1353,291,494,852,795,939,614,1002,386,2085,1810,314,2374,1858,1041,78,1990,1917,2294,2033,873,982,1506,1856;1035,18,182,737,1251,2021,366,634,2461,1866,2292,1938,4,1052,1356,1997,1457,257,1971,1165,1609,1808,329,756,1529,2093,960,1350,471,2264,65,214,366,584,1576,619,1006,1604,646,1023,919,692;220,1427,432,617,1281,993,1106,1121,1445,655,2254,2187,2382,684,953,110,1386,114,2286,249,1915,988,1533,919,1789,2231,1218,988,1372,1847,2157,1298,912,1646,2062,757,614,832,299,742,2385,1475;149,510,2387,1177,1082,394,2272,697,1101,2018,1403,480,2407,2204,780,2029,1422,2431,2432,1652,379,939,97,1001,562,743,1338,2150,88,735,716,1438,1590,1436,597,1146,835,2481,1564,59,2,1388;354,667,1845,326,233,1471,1868,1638,1631,855,2136,315,762,2411,1233,945,147,1436,1432,1888,2266,683,2468,970,131,1403,1221,1516,1335,1194,516,1837,1552,1757,1988,1631,668,2426,1745,2229,1556,290;1686,2422,734,2077,1654,502,1241,1286,2154,200,247,1761,677,867,2082,599,2079,1671,1753,1236,1672,966,265,2471,1133,1458,2388,1635,757,1236,2092,1669,954,892,2414,468,846,51,2056,2416,325,1674", "output": "2317,2135,2153,1228,1095,2360,1274,374,1224,1025,1537,1157,1133,353,1385,2161,1498,1771,2009,134,1469,652,781,94,367,2004,864,69,997,775,379,1264,2408,2131,2477,2456,616,212,8,976,1106,1150,1551,1527,138,1339,774,2080,2499,583,349,1399,2120,851,906,21,1689,947,1711,409,1975,1874,2429,1879,2146,1698,239,1537,2252,2482,784,2211,964,1617,210,563,2458,1448,1109,1752,1782,1746,2107,473,1371,1376,348,323,1051,674,2474,1401,1784,583,1492,147,1933,2145,1012,1936,103,788,1962,2324,1146,2119,2342,874,2312,1861,1713,506,2087,667,376,1971,2399,194,1432,511,673,1621,1081,885,1058,838,1090,1845,1499,437,1533,1695,682,2500,609,673,1548,1900,1744,1363,350,1263,77,2349,500,687,288,947,2045,2374,1899,225,863,1793,2417,533,973,1578,1754,18,1151,1138,971,1124,949,72,2236,1208,666,406,1296,1923,148,2357,1816,752,1202,655,1451,1140,1673,143,2036,1551,508,1651,681,492,1411,1717,1526,2470,974,1535,2233,1319,170,376,301,453,417,2395,291,164,601,675,899,678,1875,280,593,753,199,1652,132,929,452,1187,1119,470,2099,16,553,1679,2158,2459,1761,580,804,650,1022,2008,995,1978,2203,799,1637,1268,1828,1421,1048,37,1077,2194,1163,132,49,2359,1567,1968,2068,1835,2027,1210,749,832,2052,246,411,312,1477,2200,955,1636,807,177,1837,871,2187,1553,1270,433,2007,185,1535,2067,420,1513,1218,1072,1945,1088,735,1745,1641,2306,1535,205,1467,274,2310,2433,1197,2335,1129,2415,181,1087,2,923,2344,2056,1904,1990,2403,2293,634,2242,1567,1791,1410,1367,1457,538,626,1338,2078,1660,142,2024,30,1369,375,1338,1549,1139,748,1264,1568,2174,560,1293,1060,2373,1970,2319,542,1870,770,569,1097,1456,2341,107,845,2410,519,581,286,523,647,2404,652,584,1965,1884,2267,738,1956,357,2388,1204,501,1451,2078,667,359,802,2448,1191,2011,1780,2000,1071,1480,2433,1622,707,2018,966,2403,1608,427,1984,568,456,2410,1511,1035,484,1083,574,453,230,2330,803,288,740,1277,426,717,1247,1794,2292,1956,28,1237,758,1395,929,558,917,518,454,310,2163,518,576,1542,958,1091,1456,611,1804,597,527,109,1802,565,2289,242,352,841,1646,2211,2353,538,1999,1872,1912,474,1633,1699,1028,2173,2286,2438,301,371,2460,2231,628,340,1363,295,1806,404,443,751,1178,1438,1255,952,161,388,269,324,360,1830,1947,1414,1393,2038,806,800,147,1805,2494,440,857,76,2006,2180,1990,1911,1562,2047,2455,2313,1599,1749,563,1381,39,1837,246,624,2253,475,390,134,1979,1180,2006,844,1303,14,27,442,2236,877,552,1470,610,1375,959,958,798,2215,1712,2152,70,2463,1110,672,643,1388,1050,1897,1792,1993,60,766,385,1887,2314,772,1242,283,1057,819,2259,543,351,359,1018,147,1839,2115,2358,490,2243,2053,423,2099,1206,432,2159,1252,380,1427,144,1018,1170,1452,2248,1408,612,981,2011,1882,409,2352,1562,405,929,188,1602,1100,488,536,371,1786,2047,1529,559,1606,2447,1217,1064,1189,1086,1396,2006,768,1978,1450,844,579,390,841,577,116,801,27,966,697,2470,1845,1230,771,577,1877,1841,182,1305,871,2481,483,12,1067,1843,428,1247,2433,452,1352,632,1349,2371,876,2406,589,906,1958,1702,181,2085,260,1353,494,795,614,386,1810,2374,1041,1990,2294,873,1506,692,1023,1604,619,584,214,2264,1350,2093,756,1808,1165,257,1997,1052,1938,1866,634,2021,737,18,220,432,1281,1106,1445,2254,2382,953,1386,2286,1915,1533,1789,1218,1372,2157,912,2062,614,299,2385,1388,59,2481,1146,1436,1438,735,2150,743,1001,939,1652,2431,2029,2204,480,2018,697,394,1177,510,354,1845,233,1868,1631,2136,762,1233,147,1432,2266,2468,131,1221,1335,516,1552,1988,668,1745,1556,1674,2416,51,468,892,1669,1236,1635,1458,2471,966,1236,1671,599,867,1761,200,1286,502,2077,2422"}, {"input": "2291,1498,1433,1563,1320,1093,172,822,2189,447,1721,1490,797,43,155,2318,2364,968,974;1349,517,1592,1447,1051,2347,765,210,1117,1676,980,446,622,822,1895,1234,1387,592,1837;322,2025,381,597,358,2152,1275,1371,76,928,1623,455,134,2296,696,998,1206,193,1156;85,932,955,2074,1717,448,972,1629,1992,1333,1876,2154,1599,1889,1005,1736,1532,1095,1785;1976,331,764,303,913,2271,2454,2066,814,34,678,2500,1119,848,2406,825,814,1298,969;2246,689,2485,1938,1976,1482,168,2142,948,2314,1998,2326,2444,2189,225,1976,1268,1220,1350;2062,1377,2296,257,1782,1752,468,2262,994,1362,218,1559,583,1415,2242,437,2008,476,2411;2456,2369,1953,687,2483,240,1809,2477,2482,1227,602,1173,1051,366,11,1439,1290,1647,30;2417,375,630,195,2470,675,933,925,796,414,211,1378,1664,694,1355,2222,279,676,709;1470,2198,2496,2023,2117,2458,2427,963,967,975,544,77,2368,1432,466,1973,232,2340,1094;1800,1582,1190,1890,1141,2281,1685,567,2098,1541,2445,2242,1879,2321,2499,698,2082,75,1544;767,1019,2246,2363,1083,632,1457,2332,814,1621,652,320,2268,2131,604,838,1924,1751,745;1443,904,555,402,122,927,1419,1792,1767,381,2453,1599,1721,1335,2356,1125,1971,613,252;175,120,1961,694,1762,515,37,2230,1709,282,2120,588,213,1676,2385,1147,1207,1737,414;95,958,2494,1521,1496,593,1062,175,2020,1461,2216,902,870,1451,648,1547,1915,553,1927;2278,347,1134,17,1638,774,602,1002,1998,1330,821,2178,2169,714,1778,586,2153,852,595;1810,1454,931,2243,1501,685,153,960,1926,693,859,384,107,1815,734,1291,1832,1247,1974;102,142,599,479,2297,2129,2208,1177,2301,213,1266,803,1241,1830,174,739,634,1124,1220;2031,2052,839,1698,674,869,2200,727,2175,1368,183,144,745,1358,867,1003,285,778,776;439,1792,405,208,1948,1911,587,231,1250,509,1656,237,1388,95,2298,1155,603,1858,2368;1328,1642,2062,2180,608,1293,1838,1458,659,560,798,2069,1788,1302,1577,2118,2276,1008,1742;1073,1021,821,914,107,1839,715,1710,717,2303,521,724,2053,1572,1281,2043,508,2411,1533", "output": "2291,1433,1320,172,2189,1721,797,155,2364,974,592,1234,822,446,1676,210,2347,1447,517,322,381,358,1275,76,1623,134,696,1206,1156,1095,1736,1889,2154,1333,1629,448,2074,932,1976,764,913,2454,814,678,1119,2406,814,969,1220,1976,2189,2326,2314,2142,1482,1938,689,2062,2296,1782,468,994,218,583,2242,2008,2411,1647,1439,366,1173,1227,2477,240,687,2369,2417,630,2470,933,796,211,1664,1355,279,709,2340,1973,1432,77,975,963,2458,2023,2198,1800,1190,1141,1685,2098,2445,1879,2499,2082,1544,1751,838,2131,320,1621,2332,632,2363,1019,1443,555,122,1419,1767,2453,1721,2356,1971,252,1737,1147,1676,588,282,2230,515,694,120,95,2494,1496,1062,2020,2216,870,648,1915,1927,852,586,714,2178,1330,1002,774,17,347,1810,931,1501,153,1926,859,107,734,1832,1974,1124,739,1830,803,213,1177,2129,479,142,2031,839,674,2200,2175,183,745,867,285,776,1858,1155,95,237,509,231,1911,208,1792,1328,2062,608,1838,659,798,1788,1577,2276,1742,2411,2043,1572,724,2303,1710,1839,914,1021"}, {"input": "531,141,28,1983,1892,348,1902,1797,783,728,686,16,160,124,917,2258,2191,1577,1837,1392,2374,1075,469,915,953,580,420,799,242,2057,371,739,388,865,1979,919,1150,1442,2437;1135,2148,574,1308,448,2300,494,849,1073,1125,329,226,1981,1592,2240,625,1731,1419,1610,1989,977,807,662,197,2418,1410,420,582,547,2452,1852,1130,807,515,2301,1103,236,2382,1464;2458,101,1391,2410,1574,32,500,820,1878,154,588,1244,1960,2244,296,171,636,1504,2026,2117,2170,1084,656,798,2125,44,2221,744,1206,1331,1985,608,1976,1752,2367,2327,162,2102,554;1813,801,1029,724,663,2476,1289,1101,1753,62,1090,2363,2466,1042,568,444,1451,333,633,864,2210,2262,15,1568,268,516,566,712,671,353,1349,1115,159,1855,45,369,1197,241,504;390,497,1203,606,750,2247,1700,461,623,1155,667,1928,136,1545,1754,319,1112,2351,857,1771,75,1989,1234,320,1661,467,2477,1036,312,2028,2490,1961,2279,1457,1512,1584,2035,398,1202;1305,499,1766,1668,865,362,28,1404,1090,750,511,1307,1390,1548,763,1235,622,1623,2458,2002,1236,2394,1555,1730,1246,2229,312,1774,26,893,480,336,1155,2025,2232,2079,974,1232,1152;1427,2307,335,2265,1336,665,2221,1465,340,1804,312,2362,1418,604,1610,969,848,2102,1199,1120,649,2257,1794,1691,293,1593,391,1312,233,348,2371,1096,401,1473,415,1374,728,926,1491;96,1839,88,2070,2499,1895,164,1097,1928,902,2408,302,650,2353,1347,2204,696,149,674,1524,588,725,863,2009,2077,1292,31,2304,738,382,438,2188,977,1891,14,553,1924,1045,1710;1853,910,485,1369,1482,2156,1624,1787,2496,1062,1140,337,910,1978,2133,1827,1796,2247,782,1148,804,6,352,1140,430,619,1800,1094,1005,39,792,744,339,1393,354,87,1800,1722,653;359,326,2026,662,917,2074,2196,614,2460,1013,2017,1412,940,1675,102,660,2340,2089,1817,2126,2001,1700,2148,172,2326,518,1474,1870,404,2138,1545,1826,130,676,197,2400,449,1760,1599;1019,74,1107,65,1904,107,1345,2270,582,1159,15,135,667,2000,2428,1446,1526,797,943,1878,658,2313,831,1634,677,2041,565,985,730,1671,1778,1226,2020,810,1635,802,1001,441,71;1589,2458,297,2179,91,2193,2008,1643,780,1973,2325,1045,385,833,1402,1739,2484,2050,427,815,629,78,1127,941,389,784,89,787,1358,1843,45,194,1543,966,753,186,1192,2421,504;411,1340,529,1127,1242,615,790,218,2167,1584,1218,1544,2497,1497,1258,1892,27,2440,565,2308,2388,1766,1216,896,1087,307,1993,479,647,1191,1207,1741,679,736,878,489,677,1737,1918;2446,2073,1204,1746,1729,1032,1559,2200,1735,2112,785,43,1923,1605,1339,1209,1636,1393,1570,1277,1681,1436,1296,1018,2275,1342,1197,2063,998,1682,2488,2215,2400,1070,1868,1013,1878,1735,1736;1545,107,309,2443,1637,58,882,1202,2342,1669,622,1565,1818,1021,86,1234,1350,440,1854,1015,2166,1348,828,1951,343,2099,2301,1914,1444,329,962,2496,594,1388,1489,2325,928,1473,414;11,1334,2010,792,2142,1730,1421,718,1719,2330,1443,291,1815,2193,86,1024,143,1905,1657,705,1503,2098,386,2424,881,1000,1635,341,357,2428,1081,1172,1021,581,13,2378,2048,806,1147;1621,916,1269,2304,596,1640,1371,143,1796,2150,1784,897,1669,1786,1247,2335,1155,202,269,2420,943,1267,2049,1052,1030,1896,1992,970,1292,2185,2394,776,1831,2274,714,642,1708,1700,77;1164,1739,2002,863,1436,652,943,2462,1376,136,1427,2355,1435,827,1001,2394,955,762,1448,1022,466,1100,1292,928,1701,1366,1764,182,23,113,1972,2144,778,767,1833,475,584,1442,1563;1987,626,1341,1637,2103,368,2233,1335,810,481,267,2171,976,564,2005,1198,1413,1451,790,2370,277,1790,1126,483,844,497,276,1537,1070,1306,1810,457,491,1915,1072,2360,399,486,2294;1075,1382,262,548,2182,2269,259,1666,373,930,921,1468,2314,2383,883,2388,424,1174,2118,2047,666,375,593,466,2131,1494,2479,453,2405,415,964,149,876,365,916,2417,739,710,1374;1969,2184,1462,2474,1126,1128,1696,1817,158,1893,593,1918,1393,1951,1481,2490,584,1592,660,2041,1335,429,1023,804,2006,860,959,1504,2476,10,1159,1136,2344,1276,2233,1731,997,229,898;1959,166,2454,1567,1097,1943,739,2431,1378,2034,2046,1884,985,166,1995,2113,2333,1845,1353,2066,1393,1676,2161,265,468,2469,1816,1491,262,1590,1982,569,2474,1223,1436,2015,282,1659,1550;1517,1887,1025,2468,1432,1450,357,223,1469,1353,670,2355,2374,1903,2434,2471,492,78,176,514,137,901,880,1919,249,2023,2380,1105,343,1826,1353,2050,1596,1974,986,602,612,1055,330;2143,857,2430,1297,2289,1237,567,970,489,1149,641,2345,2,1470,1686,1106,2320,499,827,281,60,1464,649,1889,941,426,398,1601,1572,2264,476,1436,2325,1471,310,808,927,138,1989;1897,694,1782,2249,2331,245,2469,1205,1240,1974,1348,976,2360,2101,201,1335,596,2294,1444,1955,1886,1563,1467,1388,713,1251,334,404,2454,714,1555,2130,2146,1679,2300,883,285,1204,1744;1861,1773,624,76,1986,305,72,632,1505,1940,1705,2042,1709,829,2382,1394,1211,2159,1136,1743,1219,1010,458,1585,545,2466,1206,1092,1951,2169,579,1699,643,1313,297,1878,1922,1565,2104;1594,1889,1374,472,2131,545,905,1554,746,2371,2398,630,542,2425,177,124,2024,955,130,831,773,2011,1963,2325,1381,1035,309,2487,693,1483,1692,1189,1363,1489,491,1038,1763,1794,2057;1362,1985,1530,178,1276,2264,1655,26,2354,446,1805,1234,60,177,2472,895,188,712,472,1413,443,1471,1778,1392,2262,782,1489,958,127,338,126,2311,35,1764,1473,1309,881,812,236;322,498,1032,1670,533,1437,117,2092,1256,687,807,1121,2048,357,2084,1521,1909,1232,140,2005,1511,777,834,601,1181,394,114,1470,5,1566,191,41,2314,763,1902,984,2370,692,19;1717,75,2350,1924,1529,1822,2155,1843,1935,1148,1705,765,386,1447,1271,651,1196,683,1658,1280,1247,1225,1496,340,2421,840,2318,2398,1402,1229,323,1432,1974,1824,2119,928,365,1178,636;2294,1748,18,1431,1262,1324,1038,283,2001,136,815,451,187,1879,760,2147,446,242,2261,2239,1209,1349,871,2395,552,597,2392,2182,2425,2317,788,1484,647,465,1176,1114,724,1083,716;2315,274,110,197,600,1191,1585,270,2213,1304,1634,2144,2188,203,1112,1100,736,893,1399,174,1166,648,2157,2251,1943,89,1502,1839,1024,1027,1566,1483,1158,1832,1326,2311,548,563,2491;356,873,1275,430,574,529,1003,195,389,589,426,551,1856,55,1593,1614,1421,997,633,2402,370,877,613,557,1235,264,828,1787,273,193,618,387,1277,1630,428,897,674,2287,2128;10,1407,681,321,440,1673,858,2424,2199,2259,1912,638,724,453,1916,1138,2071,1853,261,782,457,1533,484,1580,293,1206,618,116,169,1312,718,80,359,2419,915,413,255,2048,1344;2144,2439,1971,2,1068,2031,1950,2168,1297,1712,15,3,1162,769,112,2088,1821,2250,1602,412,153,956,181,1645,87,1517,1283,2107,1828,1235,2420,2416,418,2078,2395,989,253,1824,477;1072,370,266,2194,1424,649,136,1629,1084,1101,1466,2084,2002,20,154,1960,562,1579,2351,142,1309,527,7,332,494,911,320,883,1931,2099,2406,605,1047,143,610,2028,1959,1736,327;732,2195,760,759,143,2107,713,2170,1778,1680,1158,268,2142,161,2102,199,1742,2421,577,357,1851,2014,601,1718,2154,428,1512,43,810,1378,2330,1690,2443,561,1033,1263,2210,1717,2269;1771,1462,2258,1185,994,60,1477,1550,618,1815,2105,727,2048,914,1305,966,1898,728,1579,1127,1942,759,186,1153,2474,91,189,474,1027,775,1547,168,1076,627,790,1337,297,1290,1915;2057,1948,896,969,439,1130,2060,1973,1812,1218,638,2155,1632,1343,2222,345,631,2171,781,2293,335,1117,1653,2301,882,1731,1189,410,1302,2063,1679,492,2168,381,1644,727,1639,1012,1584;391,1016,542,1845,255,414,2247,2307,741,1049,1329,2048,2480,2202,951,1413,2221,1431,600,1848,320,2237,813,577,1807,2109,1357,1689,1076,989,2263,94,389,828,1951,1552,610,2051,2188;2206,1496,1232,2227,2050,1762,964,92,549,624,1557,1508,1715,1176,451,2081,1888,1045,2064,1142,1387,2435,1430,1310,1255,2171,2404,1357,1741,2093,2022,2447,1276,1511,1404,837,2192,347,444;794,2413,672,137,1941,1716,590,218,848,2434,1353,644,1592,269,2202,2470,1538,1454,74,1855,1088,1938,1155,746,740,2186,1090,2057,1635,1573,1091,1734,386,1813,1134,1173,826,2246,1638;878,794,955,1882,279,1041,303,1004,2276,1326,959,1655,1157,1528,732,1404,1425,131,852,1702,1298,887,1429,1758,1342,1155,2030,1373,1129,887,886,1223,1223,809,841,1472,1089,887,1273;268,2128,1663,920,1414,1049,2352,1200,1521,323,2189,787,1929,1058,1048,25,668,1775,806,1247,1057,1849,143,781,2282,1597,1766,2430,1698,1159,1223,1809,2231,1177,2343,183,2274,2104,572;631,1868,618,2418,1988,1151,249,1062,200,195,148,1608,1600,1574,770,1885,1660,2450,429,422,460,1522,2122,1631,1700,249,795,658,2480,1275,1021,2361,1044,1881,1421,1963,1532,2148,172;2466,2292,458,1073,611,2314,2404,2045,1514,1342,2200,188,1959,1377,822,2041,1447,2046,2337,1045,1639,502,676,1745,973,1490,1081,677,1394,558,160,1551,1149,1063,2231,794,405,251,2035;1129,764,1886,1336,271,1265,1203,1575,2417,1068,2314,264,2133,52,1182,1347,36,383,2352,996,1156,333,1472,241,1850,605,339,2316,101,2481,254,1387,633,2326,886,1494,2153,2014,2356;1194,1029,1310,584,2057,2100,2003,842,467,536,1591,1472,1112,2002,812,522,715,665,288,959,72,61,2464,30,1943,2190,1946,902,580,2197,2177,1506,1944,925,1781,1216,1756,2017,1923;1723,885,92,610,1399,450,1061,1979,994,2432,230,174,2183,413,1201,1324,1648,932,1636,1653,1651,294,256,505,469,617,1143,1580,1962,2360,334,1543,410,834,705,2405,64,888,1733;866,1250,1764,198,1740,1537,1048,246,1619,192,1611,163,989,715,2201,1925,1754,38,238,1368,180,1204,768,1152,664,945,894,2424,2426,821,1389,965,1135,178,2333,269,1164,4,2170", "output": "531,28,1892,1902,783,686,160,917,2191,1837,2374,469,953,420,242,371,388,1979,1150,2437,2382,1103,515,1130,2452,582,1410,197,807,1989,1419,625,1592,226,1125,849,2300,1308,2148,2458,1391,1574,500,1878,588,1960,296,636,2026,2170,656,2125,2221,1206,1985,1976,2367,162,554,241,369,1855,1115,353,712,516,1568,2262,864,333,444,1042,2363,62,1101,2476,724,801,390,1203,750,1700,623,667,136,1754,1112,857,75,1234,1661,2477,312,2490,2279,1512,2035,1202,1232,2079,2025,336,893,1774,2229,1730,2394,2002,1623,1235,1548,1307,750,1404,362,1668,499,1427,335,1336,2221,340,312,1418,1610,848,1199,649,1794,293,391,233,2371,401,415,728,1491,1045,553,1891,2188,382,2304,1292,2009,725,1524,149,2204,2353,302,902,1097,1895,2070,1839,1853,485,1482,1624,2496,1140,910,2133,1796,782,804,352,430,1800,1005,792,339,354,1800,653,1760,2400,676,1826,2138,1870,518,172,1700,2126,2089,660,1675,1412,1013,614,2074,662,326,1019,1107,1904,1345,582,15,667,2428,1526,943,658,831,677,565,730,1778,2020,1635,1001,71,2421,186,966,194,1843,787,784,941,78,815,2050,1739,833,1045,1973,1643,2193,2179,2458,411,529,1242,790,2167,1218,2497,1258,27,565,2388,1216,1087,1993,647,1207,679,878,677,1918,1735,1013,1070,2215,1682,2063,1342,1018,1436,1277,1393,1209,1605,43,2112,2200,1032,1746,2073,1545,309,1637,882,2342,622,1818,86,1350,1854,2166,828,343,2301,1444,962,594,1489,928,414,806,2378,581,1172,2428,341,1000,2424,2098,705,1905,1024,2193,291,2330,718,1730,792,1334,1621,1269,596,1371,1796,1784,1669,1247,1155,269,943,2049,1030,1992,1292,2394,1831,714,1708,77,1442,475,767,2144,113,182,1366,928,1100,1022,762,2394,827,2355,136,2462,652,863,1739,1987,1341,2103,2233,810,267,976,2005,1413,790,277,1126,844,276,1070,1810,491,1072,399,2294,710,2417,365,149,415,453,1494,466,375,2047,1174,2388,2383,1468,930,1666,2269,548,1382,1969,1462,1126,1696,158,593,1393,1481,584,660,1335,1023,2006,959,2476,1159,2344,2233,997,898,1659,2015,1223,569,1590,1491,2469,265,1676,2066,1845,2113,166,1884,2034,2431,1943,1567,166,1517,1025,1432,357,1469,670,2374,2434,492,176,137,880,249,2380,343,1353,1596,986,612,330,138,808,1471,1436,2264,1601,426,1889,1464,281,499,1106,1470,2345,1149,970,1237,1297,857,1897,1782,2331,2469,1240,1348,2360,201,596,1444,1886,1467,713,334,2454,1555,2146,2300,285,1744,1565,1878,1313,1699,2169,1092,2466,1585,1010,1743,2159,1394,829,2042,1940,632,305,76,1773,1594,1374,2131,905,746,2398,542,177,2024,130,773,1963,1381,309,693,1692,1363,491,1763,2057,812,1309,1764,2311,338,958,782,1392,1471,1413,712,895,177,1234,446,26,2264,178,1985,322,1032,533,117,1256,807,2048,2084,1909,140,1511,834,1181,114,5,191,2314,1902,2370,19,1178,928,1824,1432,1229,2398,840,340,1225,1280,683,651,1447,765,1148,1843,1822,1924,75,2294,18,1262,1038,2001,815,187,760,446,2261,1209,871,552,2392,2425,788,647,1176,724,716,563,2311,1832,1483,1027,1839,89,2251,648,174,893,1100,203,2144,1304,270,1191,197,274,356,1275,574,1003,389,426,1856,1593,1421,633,370,613,1235,828,273,618,1277,428,674,2128,2048,413,2419,80,1312,116,1206,1580,1533,782,1853,1138,453,638,2259,2424,1673,321,1407,2144,1971,1068,1950,1297,15,1162,112,1821,1602,153,181,87,1283,1828,2420,418,2395,253,477,1736,2028,143,605,2099,883,911,332,527,142,1579,1960,20,2084,1101,1629,649,2194,370,732,760,143,713,1778,1158,2142,2102,1742,577,1851,601,2154,1512,810,2330,2443,1033,2210,2269,1290,1337,627,168,775,474,91,1153,759,1127,728,966,914,727,1815,1550,60,1185,1462,2057,896,439,2060,1812,638,1632,2222,631,781,335,1653,882,1189,1302,1679,2168,1644,1639,1584,2051,1552,828,94,989,1689,2109,577,2237,1848,1431,1413,2202,2048,1049,2307,414,1845,1016,2206,1232,2050,964,549,1557,1715,451,1888,2064,1387,1430,1255,2404,1741,2022,1276,1404,2192,444,2246,1173,1813,1734,1573,2057,2186,746,1938,1855,1454,2470,269,644,2434,218,1716,137,2413,878,955,279,303,2276,959,1157,732,1425,852,1298,1429,1342,2030,1129,886,1223,841,1089,1273,2104,183,1177,1809,1159,2430,1597,781,1849,1247,1775,25,1058,787,323,1200,1049,920,2128,631,618,1988,249,200,148,1600,770,1660,429,460,2122,1700,795,2480,1021,1044,1421,1532,172,251,794,1063,1551,558,677,1490,1745,502,1045,2046,2041,1377,188,1342,2045,2314,1073,2292,1129,1886,271,1203,2417,2314,2133,1182,36,2352,1156,1472,1850,339,101,254,633,886,2153,2356,2017,1216,925,1506,2197,902,2190,30,61,959,665,522,2002,1472,536,842,2100,584,1029,1723,92,1399,1061,994,230,2183,1201,1648,1636,1651,256,469,1143,1962,334,410,705,64,1733,4,269,178,965,821,2424,945,1152,1204,1368,38,1925,715,163,192,246,1537,198,1250"}, {"input": "1127,1028,911,2486,1458,1091,1135,2445,1423,964,669,670,1403,1443,1996,2123,1087,200,1815,480,1051,2376,367,670,108,1829,2406,1668,1195,2202,1228;1733,287,1408,332,515,555,1599,530,415,2152,2155,461,207,616,2394,2477,2289,97,226,1372,2170,172,157,1324,1814,630,1859,1488,1181,1631,1543;2073,1519,1935,975,2483,1949,1211,1139,319,2187,148,2151,419,1746,2033,2482,1563,2291,1971,2011,418,874,2015,330,390,259,561,1449,1677,1562,2214;2282,1692,2094,1546,1558,1536,1811,1523,1746,820,1786,2352,2338,1997,1861,207,205,601,1213,2396,291,2016,707,1795,2229,2089,400,1122,432,135,1012;1090,2298,877,661,87,2135,1879,686,23,2273,1727,1818,2,1260,1038,437,922,604,1260,541,939,1876,938,1043,1716,884,1332,2081,1983,587,387;1157,132,1962,764,849,1047,274,1938,1626,1495,1631,1974,2429,1704,59,2468,254,286,150,1315,439,2035,1881,930,1557,693,1856,1503,468,533,1292;320,454,1565,152,1820,1761,1763,2195,2406,170,160,1821,1008,1439,472,529,404,700,345,1791,79,1675,773,516,1589,1707,482,2068,2015,1376,734;1159,1177,49,2015,684,672,1525,1285,1067,798,301,1685,171,2227,1905,547,2306,1794,609,433,402,1264,1130,2359,1804,1923,207,1322,1309,9,1645;1278,266,2092,623,221,876,122,1738,1605,135,1911,1922,1011,722,806,1751,234,2493,1373,1489,2353,975,86,1710,6,2402,1091,365,1261,1408,2434;78,514,1449,1281,425,1303,226,311,1486,1601,1770,71,873,2316,1784,1044,2192,2349,553,555,1392,429,1718,1559,439,1455,1125,820,765,276,1613;1069,1255,1797,487,573,711,1322,1957,2287,2323,1350,1647,830,763,2036,1570,47,1679,207,1043,1932,2469,2241,2033,1223,1814,324,621,54,30,1901;222,2352,643,390,1096,560,1092,934,1392,145,196,59,931,1806,2186,1140,870,1461,388,2343,627,138,1335,1745,1983,886,1203,1444,984,1581,1548;553,1249,2472,519,1456,1536,1683,2388,425,2441,1945,1733,1845,827,2309,1264,2191,1489,2489,1718,1669,305,841,930,922,1146,1398,2166,1961,1363,1522;1085,2144,1406,1554,1199,335,478,1268,1180,1676,1266,1653,1689,745,2362,446,1184,1937,2057,1908,2163,2306,216,2082,2104,891,1935,1807,2048,363,2159;346,261,1241,2489,1645,307,2089,384,372,1317,2477,217,1400,1137,1845,1794,1108,1294,268,1634,2123,942,1450,382,1808,1018,1022,463,431,1808,28;543,54,855,1253,1079,59,287,1673,2265,825,594,891,126,755,355,1380,1989,826,1554,457,2294,964,1479,1005,127,842,2093,1858,1980,2271,1339;1948,1811,701,1929,84,2165,209,1041,626,1056,2228,957,2316,432,762,356,1361,2017,2199,23,427,1074,1967,503,846,692,1757,576,1865,914,32;287,117,1123,820,1081,2205,1390,461,1491,4,2116,862,2062,2232,2252,2154,541,696,144,2325,67,1145,2046,607,1896,1883,1768,1628,709,824,475;266,1621,2408,176,646,381,1790,1627,1409,1744,761,2212,2038,25,679,1141,2493,2297,1501,618,1,1761,1849,1160,55,2343,1870,2116,678,507,561;1100,1964,1430,855,1505,1860,501,55,1210,996,2425,2441,226,292,2447,2126,1853,1826,1286,1438,563,271,570,492,1422,1725,796,780,2309,1143,875;201,703,1726,1016,1297,2186,269,1145,503,1182,235,1974,1524,2434,810,1398,333,1357,140,1030,248,1348,2310,226,700,194,369,1952,482,1118,1078;996,2476,965,2303,1809,331,1596,1721,2313,2143,1782,586,2200,1711,131,1336,1348,470,117,1973,39,92,289,1898,460,1522,658,1920,1790,2074,2265;540,1632,1922,135,2211,430,1968,767,2412,117,1935,353,166,106,186,1517,1895,2415,709,109,917,2420,565,1263,2285,273,1291,1524,1514,2030,2121;647,2496,725,744,457,1852,870,447,365,978,1516,371,599,1035,118,766,1366,740,1837,1077,2078,273,1284,2150,2124,626,1145,658,282,318,2096;2377,504,1240,14,211,489,2414,1677,1094,1709,654,770,2199,2299,604,979,2179,1919,247,766,2207,272,2417,864,2089,2390,756,738,1297,1981,2247;663,852,917,294,1628,1270,1733,415,159,1757,249,1148,1660,1594,725,417,91,15,2374,2168,1959,2033,818,1129,1916,2116,2426,2006,1533,1427,1026;1821,2125,1515,964,1116,1983,2048,67,1288,2074,2113,331,1821,1490,653,272,1784,174,2021,1772,20,2235,1245,245,1166,857,2210,1926,2171,325,3;1630,1184,606,2070,1221,1535,2473,180,1264,2325,928,1390,152,1003,1927,2053,2207,1935,1380,2393,1019,1439,1837,534,566,2076,1023,317,434,580,4;1906,1278,1293,2064,65,738,1719,494,203,1502,185,696,1702,639,1899,828,2284,1920,1406,1344,1260,2485,1492,2172,1415,2326,1682,450,738,347,689;413,2229,2044,1527,1007,1254,465,817,660,1606,368,835,2286,1060,1306,1477,2143,551,136,1425,226,1237,163,1894,1811,1037,318,1757,1548,340,718;1368,1554,1933,1312,328,70,259,51,1056,1801,622,1603,1016,2306,1594,1593,2037,1755,1291,583,379,1421,164,794,803,216,1147,2001,930,2131,670;2095,362,2281,945,1623,697,1018,2051,1273,1238,2015,2497,1428,2245,861,1976,2053,2411,967,2373,344,1764,265,152,2457,1161,2498,117,524,946,2148;1525,944,1843,537,2326,2474,1798,282,1839,1867,1135,1829,1842,2443,1401,1647,196,1281,321,1722,1725,497,1547,378,120,1367,1613,51,1664,1238,644;30,447,1781,676,1147,1144,264,391,465,2458,1267,642,2090,2001,2148,890,2138,1322,1014,1977,2287,1225,894,1753,1019,403,220,40,133,1393,1358;1847,145,429,189,1943,599,644,469,1555,1096,913,900,1394,1426,643,2329,1076,1748,713,1654,960,2246,21,1706,1482,80,1448,395,530,790,2014;1978,169,1897,94,1447,1351,424,1999,1671,1935,637,1537,557,2234,1762,823,78,1716,1633,290,2330,1114,1862,2197,1185,348,1052,1703,2335,1125,2075;1835,966,707,1834,578,2411,188,403,2159,553,1327,298,275,1922,2409,566,227,1823,338,1842,1359,1972,1329,1473,431,1313,360,344,2480,304,1214;1624,1323,473,304,761,1733,947,896,2391,1004,1280,2021,1733,1764,1180,2091,54,1983,1691,662,1075,1291,2172,1149,1206,860,2239,1459,93,2203,1920;1406,1445,46,2358,1165,388,2233,277,1447,121,2448,627,2001,1362,201,2155,1281,981,1526,1942,101,1031,1509,165,590,2268,335,1042,1255,2469,1638;211,1443,600,887,903,1908,693,150,650,1950,2267,786,923,123,2371,175,2057,2127,929,719,2183,2476,1970,1302,508,582,2365,2428,771,1680,1636;1515,525,137,1247,2355,644,1082,730,1015,977,2252,32,148,1291,2141,549,165,1699,161,372,210,14,1233,1211,922,2155,1887,1419,678,2494,1299;592,1932,1257,2066,2415,1474,289,612,1154,2005,578,1,341,2489,45,1195,1201,127,1046,710,1126,710,1685,851,221,1563,1568,2192,2464,1226,1176;164,2230,1130,115,2453,560,878,1234,2417,400,1140,917,1900,920,1376,2222,1250,2173,1758,2151,1272,1687,942,1362,1306,1837,1368,2063,1431,506,2006;61,836,705,1419,2334,1647,1739,170,968,1241,1378,2264,1912,2224,1552,1955,392,1501,1853,1250,558,284,1998,2248,737,775,497,1966,843,186,1930;479,1150,680,2319,42,603,2162,2472,274,261,1910,1772,663,1916,644,2091,1703,1822,964,863,2472,1043,884,2236,2156,1947,780,2314,917,1647,569;91,1202,2162,1273,1844,1647,796,969,1358,1949,2247,801,130,307,2024,1554,1243,995,2085,1512,291,2315,1829,511,689,1636,1877,365,1142,78,795;2116,1930,2130,18,2157,1685,1000,401,1281,2297,1094,725,1122,2299,271,1873,1239,620,1564,1455,2463,894,2128,749,740,2057,2118,38,787,2263,1540;2356,83,2191,1649,333,7,1922,2202,1147,614,1614,898,605,455,1027,2497,1214,42,898,507,1817,1368,1994,842,1483,645,1708,1715,98,2168,788", "output": "1127,911,1458,1135,1423,669,1403,1996,1087,1815,1051,367,108,2406,1195,1228,1631,1488,630,1324,172,1372,97,2477,616,461,2152,530,555,332,287,2073,1935,2483,1211,319,148,419,2033,1563,1971,418,2015,390,561,1677,2214,135,1122,2089,1795,2016,2396,601,207,1997,2352,820,1523,1536,1546,1692,1090,877,87,1879,23,1727,2,1038,922,1260,939,938,1716,1332,1983,387,533,1503,693,930,2035,1315,286,2468,1704,1974,1495,1938,1047,764,132,320,1565,1820,1763,2406,160,1008,472,404,345,79,773,1589,482,2015,734,9,1322,1923,2359,1264,433,1794,547,2227,1685,798,1285,672,2015,1177,1278,2092,221,122,1605,1911,1011,806,234,1373,2353,86,6,1091,1261,2434,276,820,1455,1559,429,555,2349,1044,2316,71,1601,311,1303,1281,514,1069,1797,573,1322,2287,1350,830,2036,47,207,1932,2241,1223,324,54,1901,1581,1444,886,1745,138,2343,1461,1140,1806,59,145,934,560,390,2352,553,2472,1456,1683,425,1945,1845,2309,2191,2489,1669,841,922,1398,1961,1522,363,1807,891,2082,2306,1908,1937,446,745,1653,1676,1268,335,1554,2144,346,1241,1645,2089,372,2477,1400,1845,1108,268,2123,1450,1808,1022,431,28,2271,1858,842,1005,964,457,826,1380,755,891,825,1673,59,1253,54,1948,701,84,209,626,2228,2316,762,1361,2199,427,1967,846,1757,1865,32,824,1628,1883,607,1145,2325,696,2154,2232,862,4,461,2205,820,117,266,2408,646,1790,1409,761,2038,679,2493,1501,1,1849,55,1870,678,561,1143,780,1725,492,271,1438,1826,2126,292,2441,996,55,1860,855,1964,201,1726,1297,269,503,235,1524,810,333,140,248,2310,700,369,482,1078,2074,1920,1522,1898,92,1973,470,1336,1711,586,2143,1721,331,2303,2476,540,1922,2211,1968,2412,1935,166,186,1895,709,917,565,2285,1291,1514,2121,318,658,626,2150,273,1077,740,766,1035,371,978,447,1852,744,2496,2377,1240,211,2414,1094,654,2199,604,2179,247,2207,2417,2089,756,1297,2247,1427,2006,2116,1129,2033,2168,15,417,1594,1148,1757,415,1270,294,852,1821,1515,1116,2048,1288,2113,1821,653,1784,2021,20,1245,1166,2210,2171,3,580,317,2076,534,1439,2393,1935,2053,1003,1390,2325,180,1535,2070,1184,1906,1293,65,1719,203,185,1702,1899,2284,1406,1260,1492,1415,1682,738,689,340,1757,1037,1894,1237,1425,551,1477,1060,835,1606,817,1254,1527,2229,1368,1933,328,259,1056,622,1016,1594,2037,1291,379,164,803,1147,930,670,946,117,1161,152,1764,2373,2411,1976,2245,2497,1238,2051,697,945,362,1525,1843,2326,1798,1839,1135,1842,1401,196,321,1725,1547,120,1613,1664,644,1393,40,403,1753,1225,1977,1322,890,2001,642,2458,391,1144,676,447,1847,429,1943,644,1555,913,1394,643,1076,713,960,21,1482,1448,530,2014,1125,1703,348,2197,1114,290,1716,823,2234,1537,1935,1999,1351,94,169,1835,707,578,188,2159,1327,275,2409,227,338,1359,1329,431,360,2480,1214,2203,1459,860,1149,1291,662,1983,2091,1764,2021,1004,896,1733,304,1323,1406,46,1165,2233,1447,2448,2001,201,1281,1526,101,1509,590,335,1255,1638,1680,2428,582,1302,2476,719,2127,175,123,786,1950,150,1908,887,1443,1515,137,2355,1082,1015,2252,148,2141,165,161,210,1233,922,1887,678,1299,1226,2192,1563,851,710,710,127,1195,2489,1,2005,612,1474,2066,1932,164,1130,2453,878,2417,1140,1900,1376,1250,1758,1272,942,1306,1368,1431,2006,186,1966,775,2248,284,1250,1501,1955,2224,2264,1241,170,1647,1419,836,479,680,42,2162,274,1910,663,644,1703,964,2472,884,2156,780,917,569,78,365,1636,511,2315,1512,995,1554,307,801,1949,969,1647,1273,1202,2116,2130,2157,1000,1281,1094,1122,271,1239,1564,2463,2128,740,2118,787,1540,2168,1715,645,842,1368,507,42,2497,455,898,614,2202,7,1649,83"}, {"input": "1130,1614,1806,558,2185,2266,1388,2037,2235,1143,54,530,734,889,1988,2369,1751,670,1928,1143,2420,614,1489,772,2296,2318,1658,1870,1229,2410,2063,2003,1557,919,1744,2139,1995,305,1525,2423,2306,1979,626,1678,1995,980,2090,2324,2465,2403;1701,2161,844,485,2095,903,2335,1795,2374,551,1735,571,1948,1520,7,2230,209,55,2306,798,2403,110,1208,21,1714,1333,1112,1686,922,324,796,1509,1947,1127,1096,1014,2119,2153,1888,905,531,2080,996,524,607,1061,840,794,31,1711;2081,2234,343,2304,230,1410,678,1808,1706,1800,858,219,2064,196,258,1453,2342,769,2094,1248,792,2374,557,45,425,998,2057,252,2060,2037,1944,53,1703,497,838,1695,1525,588,1071,54,732,204,1673,2131,436,1819,1148,2285,1392,514;2280,1260,76,321,1938,475,1491,1770,1988,2296,1827,1301,1904,1831,744,1596,1279,637,471,1713,1819,2023,1374,1570,2284,747,963,2030,861,1244,1200,1679,286,519,1087,2354,809,2333,1171,2393,407,1312,432,1863,27,1537,759,2309,1589,1406;1611,2122,2250,2469,542,1324,87,946,2093,362,789,2346,846,1100,114,1391,1106,1389,2133,2261,1030,2148,177,735,1742,700,958,1336,881,273,1229,807,415,996,1553,13,1201,2359,2135,33,1388,2039,1203,2180,1353,2428,2424,299,247,1114;2439,2082,1383,2254,1252,261,2149,2242,2094,671,1013,1349,1461,1054,2004,843,844,763,1944,315,1110,851,1736,902,1417,1155,1929,2067,1920,1566,416,1495,232,1577,1144,2002,1461,1797,992,1290,1887,578,1928,105,387,2208,725,307,2083,1989;533,867,1787,175,642,216,2268,2225,719,1691,2328,2191,1799,813,1791,2319,1084,2454,60,1066,1134,1772,2083,2005,2329,768,1906,1235,1992,1922,1524,590,678,358,1066,1840,482,1766,199,2277,1082,1510,578,774,12,573,2473,1743,499,2049;2301,587,984,1804,2490,579,595,1693,2196,202,831,1728,1877,1901,400,63,249,226,101,1487,1406,1444,1102,2312,1290,2031,821,464,960,1232,1752,118,619,2030,2228,1763,2112,449,96,603,315,1972,85,1887,1698,1120,1670,2386,575,1858;678,1001,908,242,204,582,311,430,2028,2097,1606,1905,939,598,984,547,196,109,1930,1496,1864,326,1390,330,1441,1769,1805,495,1223,625,495,1828,594,895,810,98,1973,645,1192,1997,870,933,2059,646,99,750,692,241,1460,2125;1280,1784,1279,181,2065,1062,1074,501,2265,21,1828,49,2369,2495,273,2171,948,1321,476,712,1912,468,619,843,629,1774,2137,718,480,752,786,2374,1076,503,711,1845,129,739,585,2387,122,230,2396,162,1583,2187,757,409,2123,806;1859,1753,577,1010,394,1399,1092,1776,1479,2163,2380,2133,1116,1893,1992,1051,1781,2082,585,2463,1725,2009,2438,140,445,990,2497,1917,1487,33,866,982,2366,2328,1626,1617,467,1581,207,955,669,1814,427,65,1006,485,1481,1671,755,1400;1276,1785,1055,1904,1795,835,2313,540,1174,968,1492,1596,2449,1263,2395,1008,170,2480,599,1363,705,1858,2479,2144,993,125,728,948,1207,2141,2032,1596,2214,1287,2308,2223,449,1215,79,154,519,481,2329,808,370,2182,1518,1074,349,1395;1635,1237,1634,2103,1782,915,1050,2426,12,515,1390,2165,2245,386,1681,660,907,1770,1988,682,1156,136,453,1038,632,2444,470,2455,699,34,2199,2152,678,919,1917,2314,938,1405,1121,2185,1791,1345,2452,2384,2245,1150,963,1017,2227,1673", "output": "1130,1806,2185,1388,2235,54,734,1988,1751,1928,2420,1489,2296,1658,1229,2063,1557,1744,1995,1525,2306,626,1995,2090,2465,1711,794,1061,524,2080,905,2153,1014,1127,1509,324,1686,1333,21,110,798,55,2230,1520,571,551,1795,903,485,2161,2081,343,230,678,1706,858,2064,258,2342,2094,792,557,425,2057,2060,1944,1703,838,1525,1071,732,1673,436,1148,1392,1406,2309,1537,1863,1312,2393,2333,2354,519,1679,1244,2030,747,1570,2023,1713,637,1596,1831,1301,2296,1770,475,321,1260,1611,2250,542,87,2093,789,846,114,1106,2133,1030,177,1742,958,881,1229,415,1553,1201,2135,1388,1203,1353,2424,247,1989,307,2208,105,578,1290,1797,2002,1577,1495,1566,2067,1155,902,851,315,763,843,1054,1349,671,2242,261,2254,2082,533,1787,642,2268,719,2328,1799,1791,1084,60,1134,2083,2329,1906,1992,1524,678,1066,482,199,1082,578,12,2473,499,1858,2386,1120,1887,1972,603,449,1763,2030,118,1232,464,2031,2312,1444,1487,226,63,1901,1728,202,1693,579,1804,587,678,908,204,311,2028,1606,939,984,196,1930,1864,1390,1441,1805,1223,495,594,810,1973,1192,870,2059,99,692,1460,806,409,2187,162,230,2387,739,1845,503,2374,752,718,1774,843,468,712,1321,2171,2495,49,21,501,1062,181,1784,1859,577,394,1092,1479,2380,1116,1992,1781,585,1725,2438,445,2497,1487,866,2366,1626,467,207,669,427,1006,1481,755,1395,1074,2182,808,481,154,1215,2223,1287,1596,2141,948,125,2144,1858,1363,2480,1008,1263,1596,968,540,835,1904,1785,1635,1634,1782,1050,12,1390,2245,1681,907,1988,1156,453,632,470,699,2199,678,1917,938,1121,1791,2452,2245,963,2227"}, {"input": "888,1330,2065,742,517,247,355,1153,805,2116,589,1149,1256,1860,837,165,1529,1635,354,2135,1526,1561,534,900,2479,2310,245,225,2176,544,1764,1644,938,108,2297,2125,1749,823,854,639,1107,2126;1511,545,1661,571,2445,2167,647,2044,2243,1377,1766,1739,1621,1168,2026,559,2121,993,1932,2211,1784,338,674,595,1231,1714,1038,2455,980,1955,1448,1940,1598,1587,876,342,712,1253,839,784,657,2120;299,1433,101,1658,890,1225,1162,2191,354,976,524,1097,358,1253,624,1847,74,697,1880,1406,2436,2211,714,1818,1448,52,293,1969,1938,356,694,134,1309,2424,429,2135,2044,2305,2210,530,857,2136;1537,2408,184,504,1579,84,1595,222,958,1389,1583,1335,1217,1582,322,1930,467,2441,2192,1322,17,2444,552,509,259,1511,1750,793,437,2384,1992,766,278,2050,2480,2070,1404,1303,1410,837,1301,1515;675,944,911,1906,1724,915,1456,323,2038,276,2395,302,1475,454,436,1795,1194,625,524,2177,1879,132,587,2210,677,1193,1376,2411,439,560,1225,1598,1338,472,2112,1078,857,175,2393,387,1734,1943;1377,1350,266,703,2119,270,758,151,2393,1464,2356,2044,813,876,2296,2347,1637,1660,1835,1758,1170,1378,894,1704,309,2047,1761,1929,1674,825,1127,1510,480,2445,1121,1711,1377,472,2446,1153,1768,978;905,877,933,1913,692,1259,1528,919,928,630,688,1553,519,431,625,375,220,320,266,225,1752,2323,1604,1171,2002,1812,1113,1410,2066,728,952,1779,1791,2135,2055,700,507,1048,1982,418,1569,1367;1337,739,709,1623,2231,4,354,1511,2499,1396,1670,907,202,133,2043,1885,1277,1615,363,1515,626,322,938,1666,1538,816,2066,1219,1976,323,1736,1369,2132,935,2101,531,2390,1013,1389,586,1248,43;1685,572,1097,299,886,919,1681,497,1091,879,1072,316,1063,279,1620,988,26,2198,1141,1875,220,1181,2429,2276,1865,1232,2187,1167,2334,735,739,2485,882,391,710,2474,1939,914,1083,521,390,1757;1799,1631,2001,1754,991,556,2154,1724,1441,224,2177,1644,1356,2072,294,796,741,2314,619,429,1839,2112,1469,1791,797,774,2300,2043,1316,2438,963,43,1741,2026,797,669,1033,2262,1142,985,302,1712;2358,924,803,2038,97,570,1762,27,1601,101,594,1095,2332,1471,1992,1612,1056,479,697,1367,1024,1996,648,1758,264,179,1525,555,816,1929,766,1688,176,239,1038,597,1200,1635,1979,661,1040,1919;2412,555,2432,409,2048,2247,2496,621,1427,2232,1064,968,1876,2022,1817,1901,859,114,2486,1790,2432,646,2091,1540,265,2201,1151,181,553,1299,537,2436,1438,2023,267,1617,665,1292,2375,1866,655,389;380,2272,2365,1410,1281,1860,2381,542,2361,1237,1437,293,1744,157,2322,500,1892,1524,13,527,742,1816,1514,1792,1518,1540,1228,1645,1394,1138,2351,1789,1410,834,2082,1044,683,1780,1699,208,2167,51;1875,2249,522,1740,2449,1766,707,679,1345,535,685,532,365,1786,1146,1742,45,1323,2495,1371,408,896,2169,39,2307,1125,386,1068,1846,2479,1616,343,790,2100,1114,1943,2017,1941,2187,80,1486,1178;1340,1444,675,1980,2134,1365,780,1762,1248,2347,811,892,843,2283,122,1012,250,811,1233,975,2144,90,2054,1299,786,1508,397,198,1952,420,2468,1396,1660,1841,1439,789,1484,1680,297,1303,1508,683;2264,521,2032,2498,2119,1268,1932,321,1122,2018,2261,1221,1216,1440,118,219,2287,1145,1289,784,736,364,1897,830,2125,1632,88,1078,787,878,1108,1424,1256,731,1761,2377,779,550,1290,942,1334,579;890,2253,1367,1935,1269,1635,929,1331,1700,2462,191,535,1080,678,926,1965,1469,1852,157,2379,240,419,396,1085,1672,2371,2316,2318,1082,1119,2365,775,2335,1303,280,1488,1076,2009,875,750,1801,656;513,594,1877,2168,215,1363,1760,1987,227,1329,2377,1276,1743,1913,1389,2430,2139,1953,1418,289,1105,2326,879,101,1173,1201,2172,224,1008,1090,1432,2035,2282,200,451,160,273,501,1969,1520,844,1712;1921,1314,8,1565,1833,1812,1629,413,2442,278,2239,756,2009,1880,2308,632,64,1547,21,1029,2431,1850,998,1471,2020,99,396,828,1432,2360,1517,2104,616,1426,839,429,1212,133,185,375,1501,769;1205,226,1983,2126,1354,1462,989,1281,182,907,2199,510,1995,1775,411,25,1670,801,540,128,2063,2219,2334,1569,108,1648,2112,1296,2031,1277,1833,1082,1748,1288,1747,2434,795,1047,715,2131,2241,1597;2410,1663,212,2431,947,1639,1246,1081,354,868,1756,1000,1501,1752,371,476,1479,535,1477,2125,236,893,1003,62,1442,1888,1295,2150,1089,1807,1969,2123,1835,846,2415,2332,2483,2091,396,2389,313,301;54,1893,1107,1386,461,76,1782,1948,1938,828,1864,80,651,1310,121,1663,711,1336,1606,1001,590,131,667,2295,1784,715,24,200,1025,262,1782,19,1950,1872,2190,92,1885,1763,1445,2019,165,468;2397,1215,1327,1253,736,1926,615,2316,1393,2013,2379,381,525,1619,108,401,1303,1824,906,1699,2014,2144,1191,1951,560,2497,774,384,1602,2205,1982,1721,716,1995,2467,2026,756,967,1111,1159,2475,861;1616,318,2385,608,186,963,1716,1789,1628,486,1015,1666,2191,1950,848,1661,832,1604,1508,1340,200,2198,1313,2410,1356,2434,2340,1246,1281,2257,170,1750,1442,1371,464,633,1816,1279,96,166,1936,356;1879,565,1357,2001,1909,685,537,2283,2227,112,275,546,580,515,461,1904,307,2148,755,1858,1781,1148,1099,2156,313,1318,1965,367,672,1020,1145,1841,577,168,2221,2355,1720,1194,575,1200,1984,1578;1477,1431,1228,409,759,1224,598,2456,696,2087,441,1287,494,1907,1964,641,355,2115,170,1299,1800,2046,1452,1588,1373,2322,486,2275,469,1219,1120,2146,2444,551,1886,1427,2242,1325,1708,1259,498,1062;2357,1574,1378,888,1137,1756,1100,1885,958,667,2304,1008,2150,924,2126,842,860,1374,2175,2059,1070,1758,996,2352,293,2415,990,1267,1483,2148,1571,829,1152,2484,2413,1148,242,851,1129,1834,647,1664;134,1922,573,22,1229,1610,749,736,342,1966,911,1103,1949,327,712,2006,308,305,1219,1489,171,252,1392,1942,648,1856,148,2455,1051,673,1033,120,826,2373,1949,2013,1485,614,1327,1204,862,949;696,1361,1349,1029,1406,1846,2147,939,1805,2051,338,637,509,59,2438,2168,2149,1834,1189,1223,14,275,942,1382,402,1980,2383,2244,1929,1828,990,1763,1245,1466,1434,64,1105,51,378,1045,1786,1420;2317,2391,2202,1869,1087,1678,1046,1736,2049,1787,1396,618,704,334,1307,1934,2483,134,50,10,357,1812,853,365,808,310,660,1886,460,41,1654,502,2022,765,325,384,2389,1080,611,321,370,382;2003,395,1230,1727,2321,1578,1711,1651,1428,2127,1115,87,2453,581,1678,1644,1992,847,464,744,2457,2029,659,2002,2165,1452,766,438,874,551,577,440,995,1522,310,653,1186,763,1707,550,671,1872;2028,295,1168,767,200,921,1928,630,1424,640,2151,2497,306,671,1011,1797,2399,1559,1650,2,1238,1932,1040,2287,1275,2003,12,1806,656,53,1858,1403,1247,1541,1763,92,520,1089,2000,409,1258,483;1291,1417,2047,630,1261,1693,154,1490,647,2202,2121,2017,1019,1685,2445,597,2387,1967,256,1258,1780,912,1386,2217,250,2198,2382,1188,1790,119,418,2146,2032,1017,2492,222,2088,742,188,1499,2280,970;1110,306,739,1427,2455,2426,1048,864,1610,882,157,16,469,2141,1143,173,801,956,2342,810,2477,226,68,507,939,895,1551,2210,1829,66,1613,256,1747,215,1914,2395,2028,2029,1938,1723,1448,2109;511,163,2192,2228,1070,1435,816,1986,2389,401,2093,253,2285,1663,1849,1025,1454,778,147,1417,1581,242,1420,2,24,1495,709,1102,987,1405,1994,1211,139,1001,924,1228,1642,2120,2418,1160,1456,748;1820,1426,722,1941,1772,1967,634,319,1270,1655,721,1161,55,64,1656,2047,61,511,438,2136,1627,1216,1250,1963,833,195,1846,886,1222,91,2013,190,70,1743,914,540,1867,1503,618,1010,1107,1688;2096,2193,829,628,1549,2319,1228,281,705,1467,1036,698,2064,424,764,1296,1854,2255,2319,529,46,553,780,292,979,1763,2424,2334,2205,2124,1629,739,1007,741,1351,756,2101,355,655,1007,2203,611", "output": "888,2065,517,355,805,589,1256,837,1529,354,1526,534,2479,245,2176,1764,938,2297,1749,854,1107,2120,784,1253,342,1587,1940,1955,2455,1714,595,338,2211,993,559,1168,1739,1377,2044,2167,571,545,299,101,890,1162,354,524,358,624,74,1880,2436,714,1448,293,1938,694,1309,429,2044,2210,857,1515,837,1303,2070,2050,766,2384,793,1511,509,2444,1322,2441,1930,1582,1335,1389,222,84,504,2408,675,911,1724,1456,2038,2395,1475,436,1194,524,1879,587,677,1376,439,1225,1338,2112,857,2393,1734,978,1153,472,1711,2445,1510,825,1929,2047,1704,1378,1758,1660,2347,876,2044,1464,151,270,703,1350,905,933,692,1528,928,688,519,625,220,266,1752,1604,2002,1113,2066,952,1791,2055,507,1982,1569,43,586,1013,531,935,1369,323,1219,816,1666,322,1515,1615,1885,133,907,1396,1511,4,1623,739,1685,1097,886,1681,1091,1072,1063,1620,26,1141,220,2429,1865,2187,2334,739,882,710,1939,1083,390,1712,985,2262,669,2026,43,2438,2043,774,1791,2112,429,2314,796,2072,1644,224,1724,556,1754,1631,2358,803,97,1762,1601,594,2332,1992,1056,697,1024,648,264,1525,816,766,176,1038,1200,1979,1040,389,1866,1292,1617,2023,2436,1299,181,2201,1540,646,1790,114,1901,2022,968,2232,621,2247,409,555,380,2365,1281,2381,2361,1437,1744,2322,1892,13,742,1514,1518,1228,1394,2351,1410,2082,683,1699,2167,1178,80,1941,1943,2100,343,2479,1068,1125,39,896,1371,1323,1742,1786,532,535,679,1766,1740,2249,1340,675,2134,780,1248,811,843,122,250,1233,2144,2054,786,397,1952,2468,1660,1439,1484,297,1508,579,942,550,2377,731,1424,878,1078,1632,830,364,784,1145,219,1440,1221,2018,321,1268,2498,521,890,1367,1269,929,1700,191,1080,926,1469,157,240,396,1672,2316,1082,2365,2335,280,1076,875,1801,1712,1520,501,160,200,2035,1090,224,1201,101,2326,289,1953,2430,1913,1276,1329,1987,1363,2168,594,1921,8,1833,1629,2442,2239,2009,2308,64,21,2431,998,2020,396,1432,1517,616,839,1212,185,1501,1597,2131,1047,2434,1288,1082,1277,1296,1648,1569,2219,128,801,25,1775,510,907,1281,1462,2126,226,2410,212,947,1246,354,1756,1501,371,1479,1477,236,1003,1442,1295,1089,1969,1835,2415,2483,396,313,468,2019,1763,92,1872,19,262,200,715,2295,131,1001,1336,1663,1310,80,828,1948,76,1386,1893,2397,1327,736,615,1393,2379,525,108,1303,906,2014,1191,560,774,1602,1982,716,2467,756,1111,2475,356,166,1279,633,1371,1750,2257,1246,2434,2410,2198,1340,1604,1661,1950,1666,486,1789,963,608,318,1879,1357,1909,537,2227,275,580,461,307,755,1781,1099,313,1965,672,1145,577,2221,1720,575,1984,1062,1259,1325,1427,551,2146,1219,2275,2322,1588,2046,1299,2115,641,1907,1287,2087,2456,1224,409,1431,2357,1378,1137,1100,958,2304,2150,2126,860,2175,1070,996,293,990,1483,1571,1152,2413,242,1129,647,949,1204,614,2013,2373,120,673,2455,1856,1942,252,1489,305,2006,327,1103,1966,736,1610,22,1922,696,1349,1406,2147,1805,338,509,2438,2149,1189,14,942,402,2383,1929,990,1245,1434,1105,378,1786,382,321,1080,384,765,502,41,1886,310,365,1812,10,134,1934,334,618,1787,1736,1678,1869,2391,2003,1230,2321,1711,1428,1115,2453,1678,1992,464,2457,659,2165,766,874,577,995,310,1186,1707,671,483,409,1089,92,1541,1403,53,1806,2003,2287,1932,2,1559,1797,671,2497,640,630,921,767,295,1291,2047,1261,154,647,2121,1019,2445,2387,256,1780,1386,250,2382,1790,418,2032,2492,2088,188,2280,2109,1723,2029,2395,215,256,66,2210,895,507,226,810,956,173,2141,16,882,864,2426,1427,306,511,2192,1070,816,2389,2093,2285,1849,1454,147,1581,1420,24,709,987,1994,139,924,1642,2418,1456,1688,1010,1503,540,1743,190,91,886,195,1963,1216,2136,511,2047,64,1161,1655,319,1967,1941,1426,2096,829,1549,1228,705,1036,2064,764,1854,2319,46,780,979,2424,2205,1629,1007,1351,2101,655,2203"}, {"input": "2088,2070,2237,230,1203,1871,754,1516,577,253,535,1762,1782,1467,1048,616,231,937,1209,1937,2070,1567,876,1808,2069,667,768,1158,700,1408,295;1837,1320,530,370,1195,1343,1726,898,1064,1029,65,1938,2252,1172,2292,2491,865,1974,832,1028,25,752,868,669,7,1747,215,16,870,1975,1747;821,1937,2256,2481,1621,2125,1091,1313,2359,2357,2221,1354,1660,2109,1019,958,1230,1419,121,331,515,74,2328,786,494,2475,216,1873,1628,1293,1693;784,1129,815,2168,1646,1905,2330,1700,681,157,224,832,1533,652,1812,1902,2330,1549,283,1733,601,1116,296,378,1778,1581,580,598,398,2280,1692;1677,422,2012,224,783,1926,470,676,1359,1771,2235,1183,2046,2183,1901,1438,2240,2113,1407,1824,781,849,1218,271,827,2377,1764,873,345,1772,2021;771,1937,779,2346,309,721,1844,1520,733,1062,657,1953,1065,1945,1833,1523,2261,2481,1892,2145,1192,2377,608,1387,416,1290,308,1938,1250,1287,1663;485,200,1972,2075,1996,595,1914,1267,2094,1540,1270,1891,306,2266,1078,516,270,2285,2094,1428,1127,279,1122,275,1346,1915,1977,38,1120,1110,1621;180,2200,253,2307,707,1675,1875,306,888,2461,1894,67,648,2095,1092,889,668,740,325,335,827,1987,471,1516,1357,1267,227,1496,2054,2148,303;1945,1260,1124,665,1384,1233,1103,2467,678,622,1176,2214,2256,1378,772,2217,2124,171,1704,40,1101,1567,982,478,374,436,280,2252,2483,619,2102;2127,1663,1532,2139,2036,374,468,247,280,668,2334,2279,1344,72,434,974,577,1903,2351,1843,1938,232,419,2317,2387,1162,674,1366,1041,2036,939;1105,143,1290,1389,2448,2316,1361,2200,820,1257,499,1408,2147,1140,549,405,204,22,2319,242,2361,20,1398,1349,1245,974,2144,1898,438,1857,1358;443,1362,441,265,524,702,1313,410,763,1838,1197,763,2211,40,371,1543,754,32,11,1976,1458,1460,383,1732,1783,1356,846,801,2229,2393,804;1278,1047,83,562,1572,572,2402,1417,1953,1246,879,2041,1181,1609,1582,2393,1876,1320,467,103,2118,1465,1269,1248,1472,1531,2008,928,1112,2382,1233;1609,1013,1521,267,1910,2392,1707,948,382,1295,73,981,887,2430,372,2148,1450,27,548,1626,1944,1331,1430,655,1078,483,331,679,1942,1870,2096;289,1746,2322,319,1814,1996,451,1243,1838,241,1656,1175,985,1173,223,303,682,203,998,1092,633,88,495,1643,2482,494,1545,801,353,2351,2010;676,243,1577,536,571,1853,1529,2032,868,1882,2035,2066,207,700,2348,1962,2341,1250,2218,655,1866,903,957,309,45,352,1533,2130,889,830,258;58,770,1085,218,130,1316,1403,1768,111,1962,1344,1909,2355,374,2463,2317,919,294,387,1112,99,838,1667,136,196,1137,1556,1022,626,99,2132;498,1850,2159,593,1366,92,1388,2157,635,335,1935,219,1787,319,1337,1533,1744,2314,2197,442,1461,929,771,111,1917,551,2497,1508,21,692,1980;1834,514,1353,1889,2238,1900,1389,1778,29,535,2101,1526,824,2001,1718,1717,2394,2111,1520,2395,371,1330,1954,205,973,662,1823,445,487,236,2099;747,2444,1098,413,635,2485,1562,1826,1529,322,1692,30,13,730,483,247,488,2452,1107,1329,1202,2197,310,1299,850,1809,340,792,264,243,191;723,2347,1468,49,896,1215,1110,623,1481,1720,1715,1225,950,2233,155,1231,1076,750,1170,1742,1114,2372,477,607,140,1429,1708,1938,248,1180,982;1778,1750,1070,508,1253,1736,2449,932,916,2076,239,2339,1986,272,2227,2092,879,1190,1340,1184,1145,215,2327,2206,1669,1160,473,107,992,2430,1034;330,2063,1302,2494,852,1482,1178,407,27,240,1746,2369,2158,1321,2082,825,1966,2496,1898,611,2357,223,1645,1233,834,685,894,761,1440,985,1350;1759,2054,1503,896,1332,373,945,1627,393,1812,2270,250,799,1609,966,287,18,1829,2103,493,1354,33,1030,1628,433,1426,1007,2422,1916,1643,1902;844,2134,1066,2268,836,1118,874,1456,2230,1885,958,391,1952,2418,1113,1908,894,1304,987,855,933,1885,1570,1156,1840,1202,2105,604,2128,2500,175;854,677,1381,1823,1540,2195,1918,2151,1976,1698,2316,1932,1441,40,975,58,2355,736,589,1174,2487,884,2416,451,1490,2050,1472,142,2219,1011,1138;1776,582,632,171,1243,351,1891,2407,2346,1956,1077,1117,2258,735,2434,1434,407,1343,1470,235,790,2418,1981,2038,720,1548,2360,1684,2179,354,277;137,685,145,447,1765,13,2177,2364,80,862,446,955,1627,2007,139,551,1764,1474,305,1854,288,1654,236,651,197,35,1797,1967,1474,489,2072;1098,1657,1477,831,748,778,1600,137,1023,680,1554,584,1936,2262,1416,1995,2094,854,2470,572,126,816,1237,873,1458,2256,499,510,1037,642,1029;2101,1351,1581,398,1431,877,337,1296,1901,2149,2106,1692,2089,1270,2366,305,770,886,216,1542,943,1158,834,2234,1868,1108,1566,361,581,869,1822;1353,1196,633,2214,149,1247,363,1660,2432,1520,2023,189,1435,1392,1045,1514,1367,1655,1629,1794,1130,2321,2328,2187,1736,779,280,921,2281,679,1390;2091,2122,223,1961,65,550,898,334,943,352,170,798,1419,2461,1566,255,1334,2263,1539,957,2308,1115,2493,676,238,503,1656,865,2158,329,1872;1135,645,1365,1216,1445,1869,660,2113,1531,1516,743,396,1773,1603,903,1293,2444,2308,1854,256,828,1527,2292,2036,2169,196,1416,920,2066,1695,585;51,1091,1089,527,2193,2110,1093,385,996,1815,1849,237,514,1555,1747,416,335,1863,2322,2285,111,1839,1745,420,590,1805,2060,724,2157,358,559;1742,148,2069,2447,1669,276,910,804,898,1646,901,2418,2303,898,1456,527,314,2356,493,73,865,617,2034,281,2112,748,1763,2272,1538,845,1135;1942,354,1790,1099,220,1305,2343,2422,394,576,433,2121,54,1682,2260,1449,1616,1551,216,1175,859,41,2205,1451,30,2304,1841,1694,2117,174,396;1609,1293,1503,878,1867,1239,311,2303,37,886,992,926,931,1925,612,929,1842,2068,197,606,1561,131,2422,2460,666,793,1152,2228,450,1460,1093;2220,1912,1227,844,2374,64,781,1843,2447,1137,591,1710,406,1561,239,324,1365,597,2476,1468,138,2500,2386,1703,414,590,679,1382,803,1038,784;2099,1436,1259,2326,2042,14,1123,581,1478,975,1520,1213,1528,1559,1298,286,2162,1666,1857,631,636,1628,1648,1771,1152,1336,1964,1720,562,177,713;1510,373,1385,685,1563,1922,2396,1166,15,569,1785,1142,413,23,2265,1644,398,1163,702,1748,1222,1573,1348,1591,747,366,1509,1674,302,2036,1789;382,655,1200,1189,1926,643,1762,1215,2100,2073,343,798,2011,204,1189,1151,1131,1269,1645,1773,1493,1365,1617,2474,2198,528,653,1496,77,58,477;975,2177,1095,1359,1144,1157,1277,459,356,1479,1077,1804,1830,1013,613,2324,40,697,540,236,1135,2420,750,1936,819,2043,61,1885,128,939,2141;307,2071,779,1916,2329,32,115,933,1376,1213,1254,1408,1207,2299,714,195,584,1174,2439,516,1970,650,676,1166,42,143,1384,2352,505,2069,1691;2206,1096,159,131,631,1891,1597,1072,1676,2101,2299,494,1488,2129,2072,2270,1907,2294,2108,1033,2404,508,753,2362,884,1159,798,93,1801,526,1982;1608,1317,1664,644,337,1825,2474,1903,42,2377,253,981,60,511,344,1218,496,270,2031,2222,2388,1414,290,2033,1733,2312,936,10,157,1990,136;1809,1678,1339,705,445,530,1843,539,1086,1300,762,2308,2358,1495,2463,648,453,287,1068,1685,938,408,588,2308,929,678,794,292,1092,1431,729;2348,2398,2002,2062,2366,2102,1300,790,2284,2067,327,1236,2255,325,1629,1078,2361,1832,1080,1026,2004,1490,687,1316,369,2037,1084,1846,2003,895,1466;2445,991,1034,1216,1865,2261,1670,2261,120,1032,1195,7,903,1595,1156,749,2309,1093,534,890,1380,499,1873,524,1467,2036,1641,1241,1153,1747,1610;1521,2180,1157,770,1743,1078,2376,556,318,2455,1028,33,1441,2425,280,52,1561,1500,1540,1077,4,1609,1358,1986,1247,1865,60,2377,491,105,757;564,19,958,741,2036,926,2399,168,2286,86,2073,2375,2476,43,1497,1188,169,794,771,1357,2334,2065,352,344,762,1394,433,1328,1257,117,1267", "output": "2088,2237,1203,754,577,535,1782,1048,231,1209,2070,876,2069,768,700,295,1975,16,1747,669,752,1028,1974,2491,1172,1938,1029,898,1343,370,1320,821,2256,1621,1091,2359,2221,1660,1019,1230,121,515,2328,494,216,1628,1693,2280,598,1581,378,1116,1733,1549,1902,652,832,157,1700,1905,2168,1129,1677,2012,783,470,1359,2235,2046,1901,2240,1407,781,1218,827,1764,345,2021,1287,1938,1290,1387,2377,2145,2481,1523,1945,1953,1062,1520,721,2346,1937,485,1972,1996,1914,2094,1270,306,1078,270,2094,1127,1122,1346,1977,1120,1621,2148,1496,1267,1516,1987,335,740,889,2095,67,2461,306,1675,2307,2200,1945,1124,1384,1103,678,1176,2256,772,2124,1704,1101,982,374,280,2483,2102,2036,1366,1162,2317,232,1843,1903,974,72,2279,668,247,374,2139,1663,1105,1290,2448,1361,820,499,2147,549,204,2319,2361,1398,1245,2144,438,1358,2393,801,1356,1732,1460,1976,32,1543,40,763,1838,410,702,265,1362,1278,83,1572,2402,1953,879,1181,1582,1876,467,2118,1269,1472,2008,1112,1233,1870,679,483,655,1331,1626,27,2148,2430,981,1295,948,2392,267,1013,289,2322,1814,451,1838,1656,985,223,682,998,633,495,2482,1545,353,2010,830,2130,352,309,903,655,1250,1962,700,2066,1882,2032,1853,536,243,58,1085,130,1403,111,1344,2355,2463,919,387,99,1667,196,1556,626,2132,692,1508,551,111,929,442,2314,1533,319,219,335,2157,92,593,1850,1834,1353,2238,1389,29,2101,824,1718,2394,1520,371,1954,973,1823,487,2099,243,792,1809,1299,2197,1329,2452,247,730,30,322,1826,2485,413,2444,723,1468,896,1110,1481,1715,950,155,1076,1170,1114,477,140,1708,248,982,2430,107,1160,2206,215,1184,1190,2092,272,2339,2076,932,1736,508,1750,330,1302,852,1178,27,1746,2158,2082,1966,1898,2357,1645,834,894,1440,1350,1643,2422,1426,1628,33,493,1829,287,1609,250,1812,1627,373,896,2054,844,1066,836,874,2230,958,1952,1113,894,987,933,1570,1840,2105,2128,175,1011,142,2050,451,884,1174,736,58,40,1932,1698,2151,2195,1823,677,1776,632,1243,1891,2346,1077,2258,2434,407,1470,790,1981,720,2360,2179,277,489,1967,35,651,1654,1854,1474,551,2007,955,862,2364,13,447,685,1098,1477,748,1600,1023,1554,1936,1416,2094,2470,126,1237,1458,499,1037,1029,869,361,1108,2234,1158,1542,886,305,1270,1692,2149,1296,877,398,1351,1353,633,149,363,2432,2023,1435,1045,1367,1629,1130,2328,1736,280,2281,1390,329,865,503,676,1115,957,2263,255,2461,798,352,334,550,1961,2122,1135,1365,1445,660,1531,743,1773,903,2444,1854,828,2292,2169,1416,2066,585,358,724,1805,420,1839,2285,1863,416,1555,237,1815,385,2110,527,1091,1742,2069,1669,910,898,901,2303,1456,314,493,865,2034,2112,1763,1538,1135,174,1694,2304,1451,41,1175,1551,1449,1682,2121,576,2422,1305,1099,354,1609,1503,1867,311,37,992,931,612,1842,197,1561,2422,666,1152,450,1093,1038,1382,590,1703,2500,1468,597,324,1561,1710,1137,1843,64,844,1912,2099,1259,2042,1123,1478,1520,1528,1298,2162,1857,636,1648,1152,1964,562,713,2036,1674,366,1591,1573,1748,1163,1644,23,1142,569,1166,1922,685,373,382,1200,1926,1762,2100,343,2011,1189,1131,1645,1493,1617,2198,653,77,477,939,1885,2043,1936,2420,236,697,2324,1013,1804,1479,459,1157,1359,2177,307,779,2329,115,1376,1254,1207,714,584,2439,1970,676,42,1384,505,1691,526,93,1159,2362,508,1033,2294,2270,2129,494,2101,1072,1891,131,1096,1608,1664,337,2474,42,253,60,344,496,2031,2388,290,1733,936,157,136,1431,292,678,2308,408,1685,287,648,1495,2308,1300,539,530,705,1678,2348,2002,2366,1300,2284,327,2255,1629,2361,1080,2004,687,369,1084,2003,1466,1747,1241,2036,524,499,890,1093,749,1595,7,1032,2261,2261,1216,991,1521,1157,1743,2376,318,1028,1441,280,1561,1540,4,1358,1247,60,491,757,117,1328,1394,344,2065,1357,794,1188,43,2375,86,168,926,741,19"}, {"input": "1828,1165,1632,2138,1785,714,1437,248,317,195,480,298,512,2251,87,1380,2118,1045,2134,1110,1934,1236,1021,1730,149,316,1411,1085,131,2087,1945,1624,916;1111,1955,1139,1984,44,1411,972,774,726,111,271,710,517,277,1252,678,301,2284,1562,71,640,689,1209,1460,999,511,2382,2174,332,1980,652,2212,788;1877,1544,331,1650,225,1393,752,174,2178,1708,2041,916,533,783,2180,514,406,1915,2228,2140,1126,980,173,111,457,301,1566,1232,1612,2452,1398,1658,1862;167,2184,334,1292,141,1987,533,57,2269,52,367,1395,2011,371,99,1779,62,1454,1614,969,1769,89,1406,1699,1686,1973,683,1898,1620,556,31,795,497;863,1067,847,2211,1659,1006,81,1095,1232,2054,411,200,1804,2168,908,1806,2270,1032,1069,30,2311,301,1414,912,1674,67,10,173,522,1678,1573,1577,246;1047,1798,2157,229,1100,1879,370,1969,445,1056,811,920,640,365,590,151,1234,1253,1503,1065,1745,723,1766,1662,812,990,60,1599,2391,988,1218,658,1297;2109,1044,2356,2070,227,840,1365,19,729,648,2486,702,734,685,1804,970,2014,547,179,695,151,1015,745,1996,1688,82,1888,911,1575,103,1318,1353,2043;1788,1051,600,105,1964,215,541,425,1864,1425,2243,1538,135,752,1223,2487,578,1452,1493,2299,1690,190,1786,169,1084,1927,676,1004,2458,1555,373,1278,2449;1830,2214,488,2437,1728,349,483,479,1524,766,1426,2474,1207,291,560,869,2407,517,2324,376,1480,1873,563,1440,1950,1506,1420,1214,681,1208,2190,361,901;926,2409,1777,1238,780,1549,1359,1612,1088,2152,1327,1497,574,1437,2086,428,737,2065,527,570,1085,417,487,1543,1244,545,1122,1793,1940,1003,1532,143,1611;1062,1881,985,1807,2203,639,447,918,1891,821,1867,11,576,1862,952,361,1675,132,502,839,1540,733,1519,664,1425,1316,1704,1478,197,1112,792,355,1543;369,576,1601,308,1659,791,2074,683,2428,882,2320,329,1663,542,31,975,1224,770,2195,2232,2417,53,450,2328,1814,1314,771,787,2062,1142,599,2342,1520;360,2371,915,564,1451,1704,1425,1715,1726,428,431,1096,1934,1851,725,963,1842,777,1416,1228,2140,1214,11,884,1491,609,789,2286,2359,1441,1244,1302,1590;624,797,1436,1553,640,2344,909,1513,984,239,2445,606,2305,2461,232,2061,707,956,294,457,1278,1379,42,2295,667,2189,1516,1662,697,291,842,1844,364;2320,32,1584,2155,608,1715,1493,1730,328,1649,817,1774,781,1925,2250,518,1464,1999,979,2384,220,154,72,1567,1900,2285,2398,1758,358,1728,1728,950,930;1322,368,1208,1634,192,1005,1632,725,1869,2164,1937,2454,1271,1973,1494,200,1986,1452,1951,2067,564,1534,42,1277,1474,2402,2185,1359,180,1149,2458,1263,2263;1987,572,1244,461,588,427,933,2020,2428,538,130,2022,435,1609,267,2075,1621,1567,1133,1006,1405,1274,1698,332,1224,852,1530,1580,1289,1057,1621,1503,325;1598,1247,2078,2173,2314,829,1625,1537,100,1016,1958,500,444,825,1157,1710,1010,132,1110,1557,1107,630,2473,2060,1437,2256,557,1517,2252,1160,578,127,900;265,852,1093,87,694,391,1361,6,1027,501,158,1562,1758,2007,447,1922,985,2310,1444,769,1608,1700,1680,206,1048,1270,2223,761,1854,1898,1302,1052,266;2374,582,1978,130,211,1668,1720,1281,1403,2168,862,2278,975,1948,2343,575,2441,2231,2409,1882,1408,1577,1127,1115,1812,1459,2478,2235,110,2141,2066,211,1836;435,1407,886,1185,2347,1854,1391,936,494,1001,2429,1957,1459,343,901,476,2050,1234,753,1427,1561,1999,1803,2178,1212,234,267,1294,730,1921,240,870,1859;340,2005,1866,1253,2243,1344,1910,1350,562,2279,201,793,1249,1564,1349,1892,189,1783,304,719,2483,1332,57,2178,874,1225,2028,1224,267,290,1784,1993,647;417,2262,1910,1855,353,1260,1160,1406,1713,807,973,1855,1143,1665,740,1173,1878,162,942,825,1109,1976,1356,957,827,727,417,279,2405,610,955,1207,1181;1131,1457,1899,345,1463,1254,81,1593,2486,72,1515,2436,1358,1152,920,1030,1648,768,302,1755,258,2081,1102,205,533,467,431,1476,1524,2441,2160,1521,669;1447,1816,1428,1395,422,2468,1583,1819,508,3,379,1250,1379,1086,336,2065,1969,1870,577,1154,245,2160,125,1851,1272,1037,609,2012,367,1764,1725,250,1122;170,1364,2199,975,1940,2045,1112,1581,2105,640,494,635,539,1542,417,2152,1683,2319,507,2244,1844,933,1892,2154,1418,2250,619,797,1220,2013,1286,1939,2445;1628,1490,315,1335,696,2074,2311,916,990,676,1441,1636,890,2244,1099,1217,248,2401,441,436,1468,1953,1222,134,1629,38,2307,1825,615,2449,1716,95,153;1877,1825,622,835,1329,1211,122,1990,1776,2187,2372,1684,1647,1261,2371,1173,1974,1502,1004,2057,2320,1385,1070,196,1050,2213,430,72,1820,2485,163,1978,826;1792,2417,1271,845,1849,579,929,1098,543,2255,1836,1236,1087,647,1371,723,136,159,2154,824,1144,1293,1582,2031,222,562,807,1393,478,640,1192,1133,2276;1473,386,603,1202,248,1194,1579,376,487,1889,1498,279,156,960,2456,2137,121,196,511,28,1661,2348,1665,1800,168,990,2410,361,1703,384,2210,2117,2054;1179,1627,611,909,513,1231,1554,2163,1110,1105,2370,1860,1029,1669,1764,537,495,489,193,1490,1380,1579,1962,1978,741,242,60,2475,1977,289,1783,1602,2243;1403,1450,375,49,1267,360,1270,1369,2242,2070,687,320,1247,2106,2295,1810,1088,1485,193,49,1788,957,764,457,1331,110,2104,1099,2011,1745,42,439,1581;907,913,1429,54,2419,2276,2459,764,1572,1768,645,777,685,2024,1632,174,2281,1003,2472,185,1928,2439,1696,439,1905,52,590,2447,932,237,1175,1765,1443;1704,733,1475,2160,1864,1131,808,1706,1923,2221,359,1824,2064,792,1856,777,567,674,192,1353,1856,1860,1709,1722,160,1145,76,401,1981,179,2133,207,1143;826,1365,1193,2415,1002,1904,340,1288,1552,547,2196,1055,1466,208,1923,832,349,1555,2177,138,1819,1208,2279,2254,2298,677,2285,1276,207,340,1988,2223,1347;1035,1161,1994,2357,2228,1604,747,685,1812,901,334,1690,2376,2439,643,910,1661,98,416,355,373,1624,512,1857,79,843,842,1234,2365,1719,750,1654,309;2124,2379,110,1351,1112,1345,1084,1727,2077,1816,2115,2000,875,501,1667,2273,186,1458,33,303,1392,1722,828,880,1986,52,1230,1294,539,1607,1917,2417,1506;116,53,1241,637,1997,834,1408,1125,78,604,1219,1395,1241,2413,62,1348,1169,990,1315,1006,1622,183,78,639,293,2338,1815,909,917,334,1308,559,1465;49,2115,960,1532,218,1569,858,518,1422,2132,159,2047,2431,2426,2430,1598,531,1200,918,428,1496,886,1997,1807,1198,502,1267,2389,1569,2237,1892,711,843;924,191,1068,907,3,1526,2257,1547,1185,172,2153,1576,20,2005,2361,679,874,561,303,537,2071,1172,1454,902,1761,1843,153,1476,1514,356,286,129,650;316,86,244,490,1532,854,369,1404,1991,727,1180,328,158,2264,1962,610,656,1732,1005,16,2305,1919,1868,150,211,1003,525,2447,2475,454,1806,427,1145;2225,1002,9,848,1474,1651,442,2020,1378,1346,2336,2130,1805,347,2466,1843,2369,1996,529,2383,1880,1198,1789,1921,303,2419,900,97,2388,1228,2223,1691,1288;2218,934,318,983,133,339,1496,680,1118,806,2188,1040,1227,1559,287,2056,2361,928,265,1696,400,1547,896,3,1984,2469,1573,1611,2004,972,1549,969,288;351,322,1956,295,581,103,1221,2155,908,671,1785,340,1842,2051,846,251,1347,711,1503,463,795,2354,1893,370,210,1247,384,1,730,2023,1507,1332,1649;916,387,2053,2058,166,1718,1978,1085,1958,2306,949,959,627,608,1396,155,1719,114,1832,947,1565,1739,712,948,94,1994,142,2375,1472,2106,2265,1701,1497;1391,1616,594,895,188,2067,306,639,576,1524,1031,1505,1923,2319,178,981,1405,419,426,60,1932,215,755,641,2033,2470,1151,1321,602,792,405,227,1006;1501,1284,2311,94,2103,2121,282,278,748,2279,271,454,1035,526,2277,2251,126,672,548,2299,1042,960,2142,1913,549,2282,1640,1094,688,1018,1575,2418,433;909,171,1677,2484,2428,1022,2307,534,192,198,365,1667,664,558,432,995,1297,1853,466,470,516,1616,405,1569,793,2248,1225,2147,2030,469,826,1231,818;726,1855,1761,2096,1865,505,1343,1511,2032,2279,603,965,1760,1428,2212,123,1131,1132,988,141,465,1924,1727,1462,1095,1533,1250,1440,567,2251,1476,271,875", "output": "1828,1632,1785,1437,317,480,512,87,2118,2134,1934,1021,149,1411,131,1945,916,2212,1980,2174,511,1460,689,71,2284,678,277,710,111,774,1411,1984,1955,1877,331,225,752,2178,2041,533,2180,406,2228,1126,173,457,1566,1612,1398,1862,795,556,1898,1973,1699,89,969,1454,1779,371,1395,52,57,1987,1292,2184,863,847,1659,81,1232,411,1804,908,2270,1069,2311,1414,1674,10,522,1573,246,658,988,1599,990,1662,723,1065,1253,151,365,920,1056,1969,1879,229,1798,2109,2356,227,1365,729,2486,734,1804,2014,179,151,745,1688,1888,1575,1318,2043,1278,1555,1004,1927,169,190,2299,1452,2487,752,1538,1425,425,215,105,1051,1830,488,1728,483,1524,1426,1207,560,2407,2324,1480,563,1950,1420,681,2190,901,143,1003,1793,545,1543,417,570,2065,428,1437,1497,2152,1612,1549,1238,2409,1062,985,2203,447,1891,1867,576,952,1675,502,1540,1519,1425,1704,197,792,1543,2342,1142,787,1314,2328,53,2232,770,975,542,329,882,683,791,308,576,360,915,1451,1425,1726,431,1934,725,1842,1416,2140,11,1491,789,2359,1244,1590,1844,291,1662,2189,2295,1379,457,956,2061,2461,606,239,1513,2344,1553,797,2320,1584,608,1493,328,817,781,2250,1464,979,220,72,1900,2398,358,1728,930,1263,1149,1359,2402,1277,1534,2067,1452,200,1973,2454,2164,725,1005,1634,368,1987,1244,588,933,2428,130,435,267,1621,1133,1405,1698,1224,1530,1289,1621,325,127,1160,1517,2256,2060,630,1557,132,1710,825,500,1016,1537,829,2173,1247,265,1093,694,1361,1027,158,1758,447,985,1444,1608,1680,1048,2223,1854,1302,266,211,2141,2235,1459,1115,1577,1882,2231,575,1948,2278,2168,1281,1668,130,582,435,886,2347,1391,494,2429,1459,901,2050,753,1561,1803,1212,267,730,240,1859,1993,290,1224,1225,2178,1332,719,1783,1892,1564,793,2279,1350,1344,1253,2005,417,1910,353,1160,1713,973,1143,740,1878,942,1109,1356,827,417,2405,955,1181,1521,2441,1476,467,205,2081,1755,768,1030,1152,2436,72,1593,1254,345,1457,1447,1428,422,1583,508,379,1379,336,1969,577,245,125,1272,609,367,1725,1122,1939,2013,797,2250,2154,933,2244,2319,2152,1542,635,640,1581,2045,975,1364,1628,315,696,2311,990,1441,890,1099,248,441,1468,1222,1629,2307,615,1716,153,1978,2485,72,2213,196,1385,2057,1502,1173,1261,1684,2187,1990,1211,835,1825,1792,1271,1849,929,543,1836,1087,1371,136,2154,1144,1582,222,807,478,1192,2276,2117,384,361,990,1800,2348,28,196,2137,960,279,1889,376,1194,1202,386,1179,611,513,1554,1110,2370,1029,1764,495,193,1380,1962,741,60,1977,1783,2243,439,1745,1099,110,457,957,49,1485,1810,2106,320,2070,1369,360,49,1450,907,1429,2419,2459,1572,645,685,1632,2281,2472,1928,1696,1905,590,932,1175,1443,207,179,401,1145,1722,1860,1353,674,777,792,1824,2221,1706,1131,2160,733,826,1193,1002,340,1552,2196,1466,1923,349,2177,1819,2279,2298,2285,207,1988,1347,1654,1719,1234,843,1857,1624,355,98,910,2439,1690,901,685,1604,2357,1161,2124,110,1112,1084,2077,2115,875,1667,186,33,1392,828,1986,1230,539,1917,1506,559,334,909,2338,639,183,1006,990,1348,2413,1395,604,1125,834,637,53,49,960,218,858,1422,159,2431,2430,531,918,1496,1997,1198,1267,1569,1892,843,129,356,1476,1843,902,1172,537,561,679,2005,1576,172,1547,1526,907,191,316,244,1532,369,1991,1180,158,1962,656,1005,2305,1868,211,525,2475,1806,1145,1691,1228,97,2419,1921,1198,2383,1996,1843,347,2130,1346,2020,1651,848,1002,2218,318,133,1496,1118,2188,1227,287,2361,265,400,896,1984,1573,2004,1549,288,1332,2023,1,1247,370,2354,463,711,251,2051,340,671,2155,103,295,322,916,2053,166,1978,1958,949,627,1396,1719,1832,1565,712,94,142,1472,2265,1497,227,792,1321,2470,641,215,60,419,981,2319,1505,1524,639,2067,895,1616,1501,2311,2103,282,748,271,1035,2277,126,548,1042,2142,549,1640,688,1575,433,1231,469,2147,2248,1569,1616,470,1853,995,558,1667,198,534,1022,2484,171,726,1761,1865,1343,2032,603,1760,2212,1131,988,465,1727,1095,1250,567,1476,875"}, {"input": "73,818,727,2313,611,1818,122,1250,124,763,1907,2054,798,1666,741,1918,2151,645,2314,345,1757,515,2106,1039,157,1846,92,1081,2068,2125,302,2136,935,1506,1335,1833,2340,571,136,571,807,819,197,2025,346,2487;1095,363,1013,42,43,1668,341,2069,1765,931,218,2229,2394,2185,1441,1370,989,758,1080,270,599,1488,2494,1814,165,210,997,792,22,410,847,634,1170,1463,1829,32,857,1620,1615,617,1996,617,2436,2472,615,1794;904,2080,2005,1193,488,2428,580,853,207,772,1263,2246,316,2433,383,2078,775,943,638,2043,1646,672,428,350,1994,321,267,1166,1273,1264,182,645,904,257,1253,1783,1528,1195,1273,1554,277,1951,1987,1816,1958,877;966,499,1453,637,1617,907,214,340,1471,359,1731,504,1517,539,1140,1671,133,1735,1905,671,573,470,1920,1519,412,1960,994,1742,2150,516,1949,289,2469,1459,2480,159,303,2128,955,1833,1752,443,719,2007,2159,1085;760,343,108,701,271,1347,1213,1934,1465,438,469,1684,549,1226,496,330,2263,980,1373,1473,407,589,2389,1119,648,505,2226,443,532,2322,1322,919,994,482,2373,1990,108,2413,1140,2367,447,112,1720,1589,2100,1805;370,2076,423,1455,2147,729,1387,157,745,1655,1036,2228,2379,89,920,1365,1771,1239,2500,27,400,284,2105,1585,1489,479,1220,831,202,2080,1807,337,476,1006,1397,1419,1581,1960,2472,518,439,2303,796,2458,1921,2399;1347,2177,1401,1878,1171,400,1839,246,492,2052,932,1229,2171,4,1812,1685,990,765,2207,874,712,516,171,2369,1023,783,2428,161,2455,220,382,1071,1291,88,118,1020,946,1228,21,2340,1004,2486,1870,419,1404,565;813,2019,1416,836,877,404,204,1418,1780,651,726,283,15,899,584,102,2023,1047,1931,1998,1062,1405,1949,1713,1231,875,1216,817,2457,591,1226,1585,2468,1410,1412,2440,607,924,1646,1442,1833,2468,1836,327,514,717;843,1972,295,1877,1197,210,2466,2119,2348,527,1419,2269,1778,1425,117,2258,1038,2078,418,1863,1504,870,2437,746,199,1628,248,758,1645,1435,2412,1783,1161,2015,1914,2011,2413,1316,339,1087,213,2497,1568,361,1694,791;2348,997,1403,1664,434,62,99,701,1631,2404,2470,1442,894,1341,1464,184,689,346,1393,44,76,1286,1536,602,2265,2069,2109,520,990,323,1459,1510,1371,1915,2456,1149,1552,1013,705,2379,1793,243,2091,437,24,422;2117,2420,1469,863,397,917,2470,985,240,1170,1751,1228,1832,156,585,949,155,839,2361,2185,733,1915,422,1666,534,2391,1730,1986,1983,2208,1089,648,597,1297,2040,819,935,464,2462,1162,1737,2136,1546,1326,1469,1926;393,934,1531,1770,1859,683,695,778,1185,955,160,621,949,1707,1006,1017,1400,2073,475,805,586,554,2393,2401,2461,838,1582,1729,1440,1436,1952,1886,2188,377,1674,163,1090,1040,417,1831,376,1725,1223,1636,44,846;290,1123,1474,18,598,2262,997,2342,2384,957,808,2124,1147,1436,1679,970,567,761,1937,1647,764,1532,1754,237,1336,2371,2255,638,2221,234,967,2264,977,1036,2438,1875,602,1608,1522,1575,2154,2354,56,2376,2344,1425;2153,389,2071,1806,2367,565,221,1669,225,1498,2026,1375,1351,1645,1034,143,598,128,22,1613,2033,1535,1526,816,1099,1671,774,1895,328,1551,1119,20,799,873,439,2244,1438,1487,1298,1630,239,1461,1353,2171,7,815;1893,163,2425,1178,2479,2070,1133,1149,21,2196,1452,838,1561,1058,495,170,62,988,1989,2298,454,574,2415,2094,917,2006,1547,2381,2483,1796,518,44,1334,1133,2235,173,444,1672,1241,1141,1430,1463,2399,532,2085,1362;2156,227,2408,1823,1594,1622,659,1046,134,2201,181,1036,2413,592,141,2218,1281,2411,1049,1697,672,1193,1171,1910,122,1449,772,1130,267,822,1245,384,2124,1715,93,869,91,1259,1484,1581,1278,1934,1373,1011,1031,1755;1051,81,1823,2194,1075,914,1510,1345,65,921,1157,703,1995,2172,2290,1232,2201,2479,1369,628,1959,826,2181,1961,1124,506,1632,1459,964,1814,1647,361,1798,428,2381,2181,524,1933,175,1773,2214,2020,485,2166,1618,11;1131,2481,608,2462,1658,1838,1566,1716,340,1345,2125,2284,458,2300,1397,1307,1949,1208,1701,346,2037,822,2140,458,1672,629,1378,1318,1769,2101,1409,2356,1350,1304,1907,2081,2168,1369,67,2225,283,1170,303,714,1423,1475;1652,1201,1627,2249,1273,2351,2067,434,268,2262,952,1345,551,1427,1030,470,2051,485,10,1147,2161,1074,1314,1392,1767,2448,236,111,959,1914,1567,1992,2266,244,281,487,229,1443,618,2339,2334,702,2061,1229,370,1268;1497,769,1059,2456,845,1808,1144,1377,1028,2489,565,1684,883,2041,2184,435,2147,2207,2025,2434,1610,1232,2229,106,1604,83,202,2470,2376,324,2426,2257,419,713,2300,41,1234,1170,824,527,258,2071,1581,1174,1637,1731;1129,1605,226,989,2281,393,1152,155,989,508,858,1806,1063,841,1506,421,1096,355,220,338,2441,456,646,276,1105,732,2393,1546,243,1934,114,679,2034,1841,1374,1362,1611,316,1841,1412,1210,1255,188,642,2103,212;77,65,980,1483,662,264,745,1243,2096,1851,1919,2019,2349,844,1524,397,1982,1290,431,712,842,1651,93,589,743,1252,1589,899,1149,1242,448,1614,1749,223,2130,2484,1073,333,947,45,1682,1782,2001,1871,1475,1183;2159,1094,2021,2447,75,1781,2481,1465,1097,2176,1806,1801,2408,2474,540,704,643,535,653,2276,1752,1205,2174,805,976,437,678,75,1972,382,403,2082,1397,1245,285,833,2403,281,1955,746,361,1946,2157,669,1437,1298;2455,348,1165,2092,727,1042,2086,1442,646,2287,61,325,32,1457,1277,169,1385,54,1233,600,356,1675,347,21,2091,278,1934,589,210,1315,2174,2260,1642,1170,1658,552,1110,655,393,453,1629,2381,317,2302,1781,179", "output": "73,727,611,122,124,1907,798,741,2151,2314,1757,2106,157,92,2068,302,935,1335,2340,136,807,197,346,1794,2472,617,617,1620,32,1463,634,410,792,210,1814,1488,270,758,1370,2185,2229,931,2069,1668,42,363,904,2005,488,580,207,1263,316,383,775,638,1646,428,1994,267,1273,182,904,1253,1528,1273,277,1987,1958,1085,2007,443,1833,2128,159,1459,289,516,1742,1960,1519,470,671,1735,1671,539,504,359,340,907,637,499,760,108,271,1213,1465,469,549,496,2263,1373,407,2389,648,2226,532,1322,994,2373,108,1140,447,1720,2100,2399,2458,2303,518,1960,1419,1006,337,2080,831,479,1585,284,27,1239,1365,89,2228,1655,157,729,1455,2076,1347,1401,1171,1839,492,932,2171,1812,990,2207,712,171,1023,2428,2455,382,1291,118,946,21,1004,1870,1404,717,327,2468,1442,924,2440,1410,1585,591,817,875,1713,1405,1998,1047,102,899,283,651,1418,404,836,2019,843,295,1197,2466,2348,1419,1778,117,1038,418,1504,2437,199,248,1645,2412,1161,1914,2413,339,213,1568,1694,422,437,243,2379,1013,1149,1915,1510,323,520,2069,602,1286,44,346,184,1341,1442,2404,701,62,1664,997,2117,1469,397,2470,240,1751,1832,585,155,2361,733,422,534,1730,1983,1089,597,2040,935,2462,1737,1546,1469,846,1636,1725,1831,1040,163,377,1886,1436,1729,838,2401,554,805,2073,1017,1707,621,955,778,683,1770,934,290,1474,598,997,2384,808,1147,1679,567,1937,764,1754,1336,2255,2221,967,977,2438,602,1522,2154,56,2344,815,2171,1461,1630,1487,2244,873,20,1551,1895,1671,816,1535,1613,128,143,1645,1375,1498,1669,565,1806,389,1893,2425,2479,1133,21,1452,1561,495,62,1989,454,2415,917,1547,2483,518,1334,2235,444,1241,1430,2399,2085,1755,1011,1934,1581,1259,869,1715,384,822,1130,1449,1910,1193,1697,2411,2218,592,1036,2201,1046,1622,1823,227,1051,1823,1075,1510,65,1157,1995,2290,2201,1369,1959,2181,1124,1632,964,1647,1798,2381,524,175,2214,485,1618,1475,714,1170,2225,1369,2081,1304,2356,2101,1318,629,458,822,346,1208,1307,2300,2284,1345,1716,1838,2462,2481,1652,1627,1273,2067,268,952,551,1030,2051,10,2161,1314,1767,236,959,1567,2266,281,229,618,2334,2061,370,1731,1174,2071,527,1170,41,713,2257,324,2470,83,106,1232,2434,2207,435,2041,1684,2489,1377,1808,2456,769,1129,226,2281,1152,989,858,1063,1506,1096,220,2441,646,1105,2393,243,114,2034,1374,1611,1841,1210,188,2103,1183,1871,1782,45,333,2484,223,1614,1242,899,1252,589,1651,712,1290,397,844,2019,1851,1243,264,1483,65,2159,2021,75,2481,1097,1806,2408,540,643,653,1752,2174,976,678,1972,403,1397,285,2403,1955,361,2157,1437,179,2302,2381,453,655,552,1170,2260,1315,589,278,21,1675,600,54,169,1457,325,2287,1442,1042,2092,348"}, {"input": "983,109,1518,1361,1273,2018,1090,1964,1746,1071,203,1408,502,784,1136,2373,853,1630,783,1366,1112,1062,86,625,792,140;1730,8,2274,1864,1961,1362,894,1110,1165,1565,457,1010,1759,781,742,925,1042,1448,2022,19,557,865,1902,253,992,2192;250,884,242,1302,1194,1663,1240,305,1424,1201,272,104,387,2446,1457,664,592,1224,2311,1241,1577,1218,310,2038,1934,2450;438,36,1795,2157,2292,185,1403,664,1535,1018,1393,2483,1541,2059,264,843,1649,1799,1693,1954,1866,1705,1063,1260,2253,1668;669,2238,2238,2217,414,1911,1420,2064,1410,721,857,2008,1500,622,951,993,776,1273,1136,1368,901,218,710,2039,1277,2354;1602,1038,1122,342,1379,251,2383,2292,2403,791,1758,1869,1576,650,1624,782,783,460,337,668,1202,274,2189,1555,1013,1810;942,2207,1459,1236,2151,529,913,1328,581,1547,373,994,1468,1356,890,2447,2375,907,746,1695,2341,720,1824,1209,838,1365;617,1938,971,295,789,210,2074,1949,1788,2318,1516,24,252,1695,1695,1134,1204,1803,1818,1848,3,1571,1209,1914,2123,503;1641,502,2352,1437,1792,1102,428,1099,1480,150,406,2048,30,2323,2247,430,949,2233,1678,624,2312,1691,1233,2423,2112,1975;2258,2211,372,1081,28,806,974,616,2074,2491,1915,1746,5,576,2475,689,649,919,2108,1886,708,1168,826,1240,940,721;1322,175,751,527,633,2348,2308,551,2337,1182,2169,300,450,2020,1142,1756,1062,20,52,704,2496,806,474,2454,293,543;2412,264,68,153,1696,1161,2142,1446,306,1445,634,1236,1732,363,1961,437,1319,247,1363,1739,21,1515,435,316,2306,1289;2245,1318,751,1074,540,2226,496,418,858,2266,275,898,319,2231,1047,1675,1977,1530,993,2359,92,1372,1285,1971,985,879;571,2051,767,263,447,1088,2164,1469,226,2299,1558,2421,1854,426,1059,537,2011,2174,1349,1341,1641,343,421,429,1064,2308;837,252,2435,868,2146,2051,1757,1921,55,1212,1828,1604,29,418,1944,2463,1794,694,2029,979,2384,2318,2273,2183,1446,234;1816,925,2454,1490,774,2204,597,1343,302,698,1166,1904,238,1155,1938,583,483,1104,2107,627,2177,668,1650,2022,1069,371;240,2314,608,2381,2017,756,789,2189,2058,1018,1449,1553,925,646,1898,1124,1113,2049,1030,1189,604,810,277,1732,741,486;2304,2369,2261,709,123,1051,170,1512,1999,577,1965,1358,99,533,508,438,127,1374,1197,705,1511,1738,1974,1815,1073,1553;20,1490,1102,1894,1972,1146,1200,1169,2416,1338,2388,173,1344,4,509,1643,1874,2201,2276,355,1195,1217,1041,850,1820,1808;16,1101,247,248,2451,1957,1823,164,1725,355,234,518,2428,1158,1685,1639,2225,1429,2307,1193,2147,319,2344,1012,1833,2401", "output": "983,1518,1273,1090,1746,203,502,1136,853,783,1112,86,792,2192,253,865,19,1448,925,781,1010,1565,1110,1362,1864,8,250,242,1194,1240,1424,272,387,1457,592,2311,1577,310,1934,1668,1260,1705,1954,1799,843,2059,2483,1018,664,185,2157,36,669,2238,414,1420,1410,857,1500,951,776,1136,901,710,1277,1810,1555,274,668,460,782,650,1869,791,2292,251,342,1038,942,1459,2151,913,581,373,1468,890,2375,746,2341,1824,838,503,1914,1571,1848,1803,1134,1695,24,2318,1949,210,295,1938,1641,2352,1792,428,1480,406,30,2247,949,1678,2312,1233,2112,721,1240,1168,1886,919,689,576,1746,2491,616,806,1081,2211,1322,751,633,2308,2337,2169,450,1142,1062,52,2496,474,293,1289,316,1515,1739,247,437,363,1236,1445,1446,1161,153,264,2245,751,540,496,858,275,319,1047,1977,993,92,1285,985,2308,429,343,1341,2174,537,426,2421,2299,1469,1088,263,2051,837,2435,2146,1757,55,1828,29,1944,1794,2029,2384,2273,1446,371,2022,668,627,1104,583,1155,1904,698,1343,2204,1490,925,240,608,2017,789,2058,1449,925,1898,1113,1030,604,277,741,1553,1815,1738,705,1374,438,533,1358,577,1512,1051,709,2369,20,1102,1972,1200,2416,2388,1344,509,1874,2276,1195,1041,1820,2401,1012,319,1193,1429,1639,1158,518,355,164,1957,248,1101"}, {"input": "326,1849,2157,56,1306,2340,1117,1396,462,464,2004,893,1866,721,1750,1596,408,1563,2267,196,1111,313,13,204,2451,365,390,447,604,2390,1740,1427,1617,1296,2379,2407,234,1015,2118,2485,564,1332,1150,882,109;2359,2483,506,704,980,1065,1344,433,830,556,2398,655,2185,24,1779,1560,241,326,885,3,796,121,516,2477,1456,2307,1273,926,619,62,1996,2474,184,1230,1293,1482,684,1414,2131,2255,2421,2196,2093,1955,768;1837,883,1616,1560,1783,2174,1312,305,51,563,418,1333,2170,11,2475,7,443,946,2146,1697,2346,341,1232,1986,2304,1972,1142,1922,2371,824,1822,258,913,1865,599,468,863,596,559,2406,1865,669,60,2433,877;306,1940,1130,1275,489,2152,1849,2102,1957,1483,1199,661,1893,1349,1059,114,1974,1071,1092,2068,2341,544,1714,1063,2299,1292,814,1055,174,1282,1667,2237,1182,75,246,1103,1004,1817,301,193,955,464,2263,1636,2084;2212,1457,2279,2321,2192,1155,235,1109,1759,1554,464,788,321,2436,2468,2,260,1424,46,1690,384,2274,966,1624,1886,2244,940,2214,1811,1051,1358,2137,1258,2026,507,2414,879,1464,1031,163,665,497,1840,2246,2294", "output": "326,2157,1306,1117,462,2004,1866,1750,408,2267,1111,13,2451,390,604,1740,1617,2379,234,2118,564,1150,109,1955,2196,2255,1414,1482,1230,2474,62,926,2307,2477,121,3,326,1560,24,655,556,433,1065,704,2483,1837,1616,1783,1312,51,418,2170,2475,443,2146,2346,1232,2304,1142,2371,1822,913,599,863,559,1865,60,877,1636,464,193,1817,1103,75,2237,1282,1055,1292,1063,544,2068,1071,114,1349,661,1483,2102,2152,1275,1940,2212,2279,2192,235,1759,464,321,2468,260,46,384,966,1886,940,1811,1358,1258,507,879,1031,665,1840,2294"}, {"input": "613,2107,1808,1308,1471,874,2460,1619,401,2154,1853,1405,2418,980,1127,593,2304,683,2240,2311,2003,672,1585,2379,351,2308,2281,450,223,1108,1780,1083,1751,2055,2297,653,2307,1787,1203,424,993,352,1592;898,2059,2069,703,158,606,2,20,112,1874,127,552,1732,1768,1524,1842,2033,1799,2363,687,1745,2377,1224,2301,584,1660,672,1428,2449,2427,2177,1112,654,1865,2277,1567,690,1507,188,1592,1060,2304,784;418,931,1112,1198,2219,1829,2417,1184,134,243,2168,2135,922,1870,1077,2314,1855,460,1900,2379,2304,620,1238,428,1447,2135,231,2104,2004,1125,1023,2235,2079,318,678,1475,2049,1856,827,1280,304,87,1997;469,1614,1968,910,293,362,2494,1891,1263,412,2485,2235,1538,1845,2183,1070,409,2299,2185,1075,1522,1996,2283,525,2320,1000,693,1184,1839,1121,1631,56,44,2246,844,2194,1781,16,2400,1761,1264,31,1724;1202,2156,26,121,1372,843,2196,966,1728,987,1087,403,1439,2471,2110,1253,440,1219,664,1215,1658,1153,1335,622,599,75,1973,336,1641,804,1394,2231,1436,1798,1698,2206,1932,1056,1110,833,1874,584,2000;1395,1200,1965,166,1116,1117,960,1806,294,778,2476,1162,1975,866,847,521,2499,1034,82,305,1205,148,2396,2014,2495,482,414,877,1091,95,59,752,1775,298,1474,2316,267,2362,1087,1568,1987,695,42;848,1344,1006,954,2484,907,531,845,1565,2243,2428,2,269,1228,1845,215,1778,288,1990,1606,453,53,1254,1340,1427,1831,1838,1705,1597,1170,751,336,339,2050,2280,887,834,196,2074,729,1244,1726,2058;693,224,2296,1988,1909,1540,200,1388,406,638,1561,1638,1832,1726,1112,2086,1284,1815,778,984,2199,1434,608,1347,1407,517,2193,1719,1714,1867,1021,573,869,2496,1201,1915,557,759,1065,838,2237,1667,119;566,2410,1972,1393,1016,2011,489,810,932,562,1440,1681,1749,298,621,1029,1900,1374,1892,2500,698,265,623,323,2122,1685,258,2321,1477,573,1829,445,2227,18,975,2021,1481,2452,304,2346,2379,819,968;1911,839,1114,851,1113,1187,1519,649,2158,2340,2085,2291,328,106,1850,2157,191,288,1696,1006,1490,363,899,342,190,1677,2204,1472,147,2203,2429,154,1805,2118,1291,526,2448,2390,1248,1236,2117,2045,86;490,543,2209,58,511,1326,561,810,2448,337,406,2253,1694,1550,1053,2073,1075,1223,1946,178,918,1005,1863,294,2347,2323,2476,1492,1304,562,294,718,2083,709,2053,934,962,1699,1614,1888,35,2020,1660;1032,2369,1000,515,686,1779,793,746,613,1313,337,2116,756,1914,935,1787,84,1486,871,2051,1868,1063,2331,1880,1978,2098,2059,1648,1611,1522,2140,822,1233,2344,2327,1823,839,414,2321,609,1639,1934,740;2058,184,583,458,850,1709,1453,573,410,107,656,273,2272,2322,2001,702,1968,1015,1392,749,1376,507,409,1694,2303,2176,1396,1047,1653,204,426,2253,697,17,167,62,1783,928,147,1875,2164,1458,848;2209,1447,1157,446,331,888,1317,2044,507,2180,267,257,1950,787,1390,741,922,1988,854,1956,266,657,2421,1890,900,3,644,150,1976,779,1157,1983,813,11,1188,1625,1353,45,1080,406,2321,969,2361;1961,2307,2173,1645,210,2179,10,490,1776,1598,1288,50,1244,1115,1011,2431,825,831,898,123,2319,2416,256,1796,1486,1609,1716,2218,1971,146,2464,2357,762,1657,932,1956,2316,12,863,1249,1564,1343,1044;2225,1303,2444,921,2451,366,1694,1965,845,388,138,124,1719,1994,342,1903,806,325,477,2234,96,2438,69,1835,1023,58,117,1358,2112,1308,2357,2486,2182,1445,2247,1488,236,1404,2500,521,1986,430,2084;176,237,1358,2124,287,1200,410,370,2471,154,2398,243,2155,2277,1037,1092,2163,191,1127,2051,510,1221,2174,2390,2152,1042,1093,1935,771,1613,610,2433,1506,2105,2158,54,877,2147,1852,2391,1748,1733,372;1007,670,2379,283,1395,706,1449,1939,1188,538,1998,2181,1927,1834,2050,1502,136,1259,1764,2061,121,776,1125,1548,966,880,551,1563,1843,103,2199,2468,1450,1409,825,243,1019,2128,1847,1698,1306,2237,1534;1141,1885,1960,576,1982,1838,2375,457,1817,505,527,2050,1746,222,794,269,1411,549,1681,2055,1494,975,1162,1968,682,1376,1272,81,1185,1059,2300,2164,1044,444,295,1871,49,1419,217,1756,1256,976,150;408,2041,1389,755,1817,1691,890,1851,2412,1107,1843,1881,2334,1322,1875,318,2263,754,1019,646,1261,465,1700,147,34,1991,1986,1062,1000,892,1805,1025,2091,1502,1969,153,1852,351,1782,1018,937,378,706;460,1705,437,2289,2067,2440,1486,1303,1260,1534,692,828,1768,2201,2454,1750,754,1880,1959,328,686,62,1370,657,1978,281,338,1221,302,70,226,2240,1157,1225,90,1149,2340,76,1571,81,566,269,433;747,1496,1013,2283,2208,934,1779,215,29,2102,1584,2483,660,78,232,1171,1730,89,1755,43,2253,432,2366,882,550,1576,938,125,1788,2413,2323,867,1923,260,1491,1346,1478,2261,1399,2079,2174,300,951;1291,1714,145,540,102,1302,53,2313,862,157,2145,327,54,854,865,1469,1692,866,1913,2105,2291,230,1065,1927,2457,2078,585,338,532,1194,603,2435,558,5,1232,1626,1298,837,2088,2117,1337,1386,1377;461,1992,1001,1149,2219,753,62,1944,735,2091,640,43,1569,667,2215,870,1930,1856,739,1478,1507,609,345,463,820,1579,925,656,179,756,1426,1518,1737,82,716,1929,2015,1420,1331,1781,2247,800,1491;1625,253,247,148,2239,2321,233,1254,2246,2265,1893,1311,2300,271,1813,1629,1591,1593,1329,1985,2096,2448,2429,1188,947,1265,588,126,1525,808,1252,2105,1421,814,1949,806,770,2183,2095,934,1736,553,1294;1711,193,117,1229,757,1636,14,1023,2079,2467,39,18,331,1821,360,1816,2454,1671,1067,2253,973,214,1008,353,2410,1478,311,1003,2242,385,316,1500,1468,682,1591,743,1793,2053,1578,1352,713,1992,415;1853,1151,2255,2119,1804,2231,1475,2430,813,389,1266,2206,1387,1537,328,986,1856,792,1028,251,2377,1369,449,1454,1107,1726,2208,2418,333,1787,1254,41,1204,1639,1118,1737,1737,1356,506,1754,2477,1098,2228;711,1282,311,122,281,1377,2273,415,400,669,1435,2098,143,1813,1931,1566,2423,746,2008,1161,22,2030,1200,2199,642,987,2223,2035,1128,1832,1899,1938,2359,2229,567,2177,1705,1775,1345,841,808,642,1918;1567,161,2405,1446,245,2171,202,1413,1667,1757,486,1755,2392,1699,1985,1670,584,1747,2271,759,1389,445,631,322,494,1020,326,947,2163,810,1926,113,377,729,2290,279,46,392,985,1520,1142,1874,1071;1398,1797,1566,966,362,2037,1742,1207,56,700,1155,2222,1551,1365,1938,2438,1778,787,2075,759,400,398,192,2186,206,1491,1745,1449,1659,837,1338,402,2200,639,1098,835,1251,1141,2403,1993,327,864,1704;1290,815,465,1031,2177,804,1292,2114,1751,2163,1095,1949,743,1602,1001,709,1399,2018,1169,396,234,723,519,1839,2177,611,1520,150,267,35,1437,711,2090,1297,159,2434,1187,2070,1108,1466,365,645,1899;2009,280,129,1410,187,1475,553,56,552,1232,1401,1372,1091,1486,590,1943,432,1029,225,1149,2061,1075,2218,690,401,1721,1970,1539,958,2461,1991,790,1797,1493,1674,334,2208,2314,1172,329,500,383,2383;1863,2212,2489,477,1642,1073,1502,35,629,289,1262,583,1079,500,272,1905,1310,1158,647,736,1747,684,1277,1355,647,251,2114,1411,1696,1793,1939,315,449,1717,1137,1760,46,995,406,1178,1565,1894,2212;1052,1111,510,421,1844,1305,1247,1928,493,365,2388,1529,2361,403,1773,136,213,182,2456,267,1147,920,806,2132,1319,398,578,1081,676,1956,1117,75,1117,366,2270,1902,1935,1598,1599,916,993,1053,1692;298,1641,2187,1421,1346,2306,1310,510,1740,1773,1672,2350,885,934,1071,261,1933,1716,546,2363,1052,258,1764,856,962,2409,667,957,868,2325,2488,118,332,1316,55,947,578,1088,141,1415,1892,1985,821;1764,1057,1560,108,222,761,2208,189,2400,1925,1446,814,883,223,1616,1917,611,2314,1006,2118,701,1564,1843,42,2398,938,1031,1616,930,381,1037,2323,1052,2436,1896,1999,860,382,1383,412,2067,2318,1385;1008,2179,2092,1594,913,2045,1037,1355,1459,2279,132,1655,2351,517,2301,1436,69,898,1533,2384,419,1499,2075,2366,2293,359,139,2276,1082,1378,2019,2284,2459,2134,1245,2019,113,508,267,1999,2201,99,1243;2344,153,2030,36,2231,15,1059,1347,1915,1048,2397,1834,1887,149,290,2059,1433,823,26,1774,1627,1472,345,1344,1082,2026,1288,513,1711,1465,374,402,2261,1878,1082,1329,378,1575,1828,44,569,1518,2310;1956,1829,1890,2369,752,74,1284,1066,1285,473,763,1675,1911,387,1039,484,18,1756,2093,1455,2130,994,1368,1637,2136,1614,2367,915,1358,2198,1548,1434,963,2188,908,1904,1151,964,663,1643,1066,2118,2048;2308,902,1073,2208,1424,2100,1497,1549,780,2291,2254,1128,632,2215,201,1994,1480,694,1366,1127,1453,1647,2119,644,1916,1447,787,2013,2197,1542,1533,1134,467,1467,423,1698,2032,1083,1223,1290,346,2163,768;2289,1839,2212,1285,289,2113,1402,2216,462,1609,1581,2177,1733,2498,2207,121,1035,1930,1686,1717,662,2421,1108,1514,1332,741,1171,1253,2273,1139,127,1713,1201,1063,318,1165,2028,1396,705,11,1971,36,1750;754,986,1034,436,1189,928,99,369,1163,414,1416,1955,1245,2271,1169,2473,2222,962,852,533,2388,1299,2222,458,2145,612,2174,854,482,110,1985,2037,1143,2414,2440,167,999,346,2469,813,1534,2112,2460;1127,640,2473,127,2325,1291,875,1136,1977,1410,995,659,1760,1056,642,753,1787,1095,2448,930,2435,2008,1368,134,1177,704,903,2305,1642,960,473,1364,754,429,970,2139,84,1077,178,2429,1714,2112,2442;1056,1267,943,1916,2006,2262,1787,2223,2254,2157,1600,2140,1388,507,1188,812,818,279,570,1675,2365,1371,2020,894,1770,759,1921,1668,793,2426,160,107,83,2272,693,442,2427,536,751,2169,1584,839,1650;2163,1876,8,41,783,2340,694,551,2101,2147,1909,2070,807,1624,266,2390,425,734,1563,720,787,2295,894,1558,39,982,659,1058,947,2214,1069,1591,91,2218,612,611,7,1659,2290,472,1148,953,2051", "output": "613,1808,1471,2460,401,1853,2418,1127,2304,2240,2003,1585,351,2281,223,1780,1751,2297,2307,1203,993,1592,2304,1592,1507,1567,1865,1112,2427,1428,1660,2301,2377,687,1799,1842,1768,552,1874,20,606,703,2059,418,1112,2219,2417,134,2168,922,1077,1855,1900,2304,1238,1447,231,2004,1023,2079,678,2049,827,304,1997,31,1761,16,2194,2246,56,1121,1184,1000,525,1996,1075,2299,1070,1845,2235,412,1891,362,910,1614,1202,26,1372,2196,1728,1087,1439,2110,440,664,1658,1335,599,1973,1641,1394,1436,1698,1932,1110,1874,2000,695,1568,2362,2316,298,752,95,877,482,2014,148,305,1034,521,866,1162,778,1806,1117,166,1200,848,1006,2484,531,1565,2428,269,1845,1778,1990,453,1254,1427,1838,1597,751,339,2280,834,2074,1244,2058,1667,838,759,1915,2496,573,1867,1719,517,1347,1434,984,1815,2086,1726,1638,638,1388,1540,1988,224,566,1972,1016,489,932,1440,1749,621,1900,1892,698,623,2122,258,1477,1829,2227,975,1481,304,2379,968,2045,1236,2390,526,2118,154,2203,1472,1677,342,363,1006,288,2157,106,2291,2340,649,1187,851,839,490,2209,511,561,2448,406,1694,1053,1075,1946,918,1863,2347,2476,1304,294,2083,2053,962,1614,35,1660,1934,609,414,1823,2344,822,1522,1648,2098,1880,1063,2051,1486,1787,1914,2116,1313,746,1779,515,2369,2058,583,850,1453,410,656,2272,2001,1968,1392,1376,409,2303,1396,1653,426,697,167,1783,147,2164,848,969,406,45,1625,11,1983,779,150,3,1890,657,1956,1988,741,787,257,2180,2044,888,446,1447,1961,2173,210,10,1776,1288,1244,1011,825,898,2319,256,1486,1716,1971,2464,762,932,2316,863,1564,1044,430,521,1404,1488,1445,2486,1308,1358,58,1835,2438,2234,325,1903,1994,124,388,1965,366,921,1303,176,1358,287,410,2471,2398,2155,1037,2163,1127,510,2174,2152,1093,771,610,1506,2158,877,1852,1748,372,2237,1698,2128,243,1409,2468,103,1563,880,1548,776,2061,1259,1502,1834,2181,538,1939,706,283,670,1141,1960,1982,2375,1817,527,1746,794,1411,1681,1494,1162,682,1272,1185,2300,1044,295,49,217,1256,150,378,1018,351,153,1502,1025,892,1062,1991,147,465,646,754,318,1322,1881,1107,1851,1691,755,2041,460,437,2067,1486,1260,692,1768,2454,754,1959,686,1370,1978,338,302,226,1157,90,2340,1571,566,433,300,2079,2261,1346,260,867,2413,125,1576,882,432,43,89,1171,78,2483,2102,215,934,2283,1496,1291,145,102,53,862,2145,54,865,1692,1913,2291,1065,2457,585,532,603,558,1232,1298,2088,1337,1377,800,1781,1420,1929,82,1518,756,656,1579,463,609,1478,1856,870,667,43,2091,1944,753,1149,1992,1625,247,2239,233,2246,1893,2300,1813,1591,1329,2096,2429,947,588,1525,1252,1421,1949,770,2095,1736,1294,1992,1352,2053,743,682,1500,385,1003,1478,353,214,2253,1671,1816,1821,18,2467,1023,1636,1229,193,1853,2255,1804,1475,813,1266,1387,328,1856,1028,2377,449,1107,2208,333,1254,1204,1118,1737,506,2477,2228,642,841,1775,2177,2229,1938,1832,2035,987,2199,2030,1161,746,1566,1813,2098,669,415,1377,122,1282,1567,2405,245,202,1667,486,2392,1985,584,2271,1389,631,494,326,2163,1926,377,2290,46,985,1142,1071,864,1993,1141,835,639,402,837,1449,1491,2186,398,759,787,2438,1365,2222,700,1207,2037,966,1797,1290,465,2177,1292,1751,1095,743,1001,1399,1169,234,519,2177,1520,267,1437,2090,159,1187,1108,365,1899,383,329,2314,334,1493,790,2461,1539,1721,690,1075,1149,1029,1943,1486,1372,1232,56,1475,1410,280,1863,2489,1642,1502,629,1262,1079,272,1310,647,1747,1277,647,2114,1696,1939,449,1137,46,406,1565,2212,1053,916,1598,1902,366,75,1956,1081,398,2132,920,267,182,136,403,1529,365,1928,1305,421,1111,298,2187,1346,1310,1740,1672,885,1071,1933,546,1052,1764,962,667,868,2488,332,55,578,141,1892,821,2318,412,382,1999,2436,2323,381,1616,938,42,1564,2118,2314,1917,223,814,1925,189,761,108,1057,1008,2092,913,1037,1459,132,2351,2301,69,1533,419,2075,2293,139,1082,2019,2459,1245,113,267,2201,1243,1518,44,1575,1329,1878,402,1465,513,2026,1344,1472,1774,823,2059,149,1834,1048,1347,15,36,153,1956,1890,752,1284,1285,763,1911,1039,18,2093,2130,1368,2136,2367,1358,1548,963,908,1151,663,1066,2048,2163,1290,1083,1698,1467,1134,1542,2013,1447,644,1647,1127,694,1994,2215,1128,2291,1549,2100,2208,902,2289,2212,289,1402,462,1581,1733,2207,1035,1686,662,1108,1332,1171,2273,127,1201,318,2028,705,1971,1750,2112,813,346,167,2414,2037,110,854,612,458,1299,533,962,2473,2271,1955,414,369,928,436,986,1127,2473,2325,875,1977,995,1760,642,1787,2448,2435,1368,1177,903,1642,473,754,970,84,178,1714,2442,839,2169,536,442,2272,107,2426,1668,759,894,1371,1675,279,812,507,2140,2157,2223,2262,1916,1267,2163,8,783,694,2101,1909,807,266,425,1563,787,894,39,659,947,1069,91,612,7,2290,1148,2051"}, {"input": "868,891,1479,492,1040,1999,1456,1444,512,1580,98,597,607,1145,1577,476,756,2267,1810,2088,1432,1506,1543,1900,2084,417,177,525,1983,2500,1324,1573,2019,294,1374;1450,2130,1228,1874,2335,904,2398,730,916,59,2112,769,1445,2363,943,6,1462,2143,1718,2012,865,1892,405,2277,1827,442,883,1591,1562,655,263,402,1047,1561,2099;1189,1311,996,2325,2288,1625,388,1743,1130,1653,971,1069,1088,2029,645,856,261,468,828,442,1044,1346,1389,732,1632,1365,465,1420,1078,2002,2090,1812,1404,1867,418;203,2465,1277,2312,162,48,117,943,325,2015,2276,1177,2451,646,2158,78,524,1087,1596,1105,2194,1793,2365,2100,115,774,611,799,1391,756,716,2135,1261,2481,86;468,386,1838,1946,1979,82,736,2408,730,654,747,911,553,2243,1877,882,498,1154,2353,2242,895,400,2355,2183,975,2154,1151,201,922,1480,676,787,525,1950,1693;2410,741,598,403,1403,617,2452,1988,2162,1472,174,1113,2426,1891,1331,2450,767,2011,702,1555,1278,1012,14,1541,2298,1191,1893,2180,2055,1510,1095,227,1946,2258,2234;2187,686,1440,122,1090,1724,2338,2095,2493,1137,1513,150,485,1886,969,1264,743,294,976,724,236,1676,2395,1642,699,1634,264,215,2174,473,110,944,2171,1871,2009;519,749,671,2180,2433,604,1724,2407,1623,958,1015,2235,1924,1593,328,1301,1570,594,1138,157,886,852,6,2038,2496,1344,2406,2276,2187,692,1012,1391,1276,1477,384;2420,455,2001,868,633,1426,2203,614,2438,737,1577,581,1699,887,1371,1576,1090,1403,166,1423,1950,958,1720,945,149,685,2162,947,621,1569,1216,828,2482,1469,485;586,1935,1461,2491,118,523,1310,1253,494,2324,1361,1933,2404,670,97,845,645,2395,2301,2092,488,2103,91,2392,325,1626,451,1848,1562,2073,388,296,1737,741,131;1618,1892,2320,1254,213,635,166,692,2499,776,1572,1767,1321,780,1541,1575,1604,1911,2145,977,866,1786,2222,2380,425,766,23,739,1072,1061,2078,1702,777,947,1308;885,488,1664,159,1085,860,710,2209,512,1952,466,2382,1780,958,2089,1733,1110,975,539,1720,2027,365,1485,2373,1471,2149,1818,1490,224,374,682,2212,1250,2061,542;1826,367,1283,2497,2348,2281,504,1163,1830,1121,36,55,343,825,191,724,2030,1252,249,1930,878,1682,2240,785,1382,1170,804,423,509,2445,2236,906,1933,2316,974;2471,517,1284,1084,2005,2449,1248,1890,1612,2172,2312,1803,657,1423,2407,957,1977,1251,1796,690,1877,115,1918,1557,2134,771,540,1808,1046,1252,1068,685,1756,464,457;94,1134,1740,1997,1601,1208,2019,868,1524,138,515,924,355,69,1450,1215,2306,693,1091,2245,1894,2196,1078,415,604,305,965,654,1873,283,1564,115,1052,791,1769;762,1444,2022,2088,1539,2293,1153,1410,1566,389,2127,1609,2241,142,887,1551,114,169,482,2056,242,172,2456,2111,1937,281,2013,1516,2447,210,915,57,2111,1205,1861;1447,919,1622,1675,1400,2500,197,823,897,2133,931,203,988,651,1855,1024,2234,635,1249,1815,1669,1129,2350,450,1606,255,1215,371,1334,1657,53,367,514,202,1982;2388,670,2225,1010,260,1901,475,2000,1722,1523,738,1853,2261,1554,514,764,596,95,1041,1458,2194,1296,2395,945,467,2346,94,1526,2110,629,1155,1554,2181,1570,646;2426,2159,770,1800,2491,266,1666,1734,2239,411,1347,2379,778,142,1645,436,1696,754,1498,1032,2033,187,1185,1087,31,79,1950,375,1434,936,972,643,876,1719,1926;1398,1677,9,2010,2100,520,264,556,1136,95,266,1256,1172,1946,1451,1213,2094,669,1009,2195,624,1589,1851,250,2041,2311,1338,459,262,2333,2010,1218,814,553,508;893,329,1119,1645,287,1067,1962,4,1986,2049,60,2270,495,65,32,2140,2076,1670,2101,1295,1546,105,1544,2004,1799,190,2376,1587,2095,1989,2184,1420,870,449,680;1909,1229,792,564,1109,1727,1843,857,489,2138,1162,1078,2342,1242,1064,603,1395,1327,645,662,2220,625,1975,325,1072,1281,100,563,213,2336,98,1774,1543,641,2050;1350,1686,2215,1781,1780,638,1681,2131,2398,1167,852,1472,845,1122,207,1045,1060,650,892,801,223,540,2429,1285,1575,1996,1219,2334,1083,1022,363,2398,1367,927,482;520,1552,48,293,1014,920,1030,210,852,757,1829,2180,2472,309,529,1128,1188,1851,1083,731,1434,1574,898,2123,1124,1662,846,809,1540,1521,431,2019,142,399,178;1584,1731,28,2492,103,837,974,676,1309,1266,658,583,24,1669,1149,951,1345,2411,1836,2408,2485,199,1240,707,829,904,2485,1573,1306,890,1348,1220,752,2066,468;801,1682,750,1839,753,2283,985,1561,1682,279,434,898,33,1777,1696,272,1651,1783,525,806,962,693,2175,603,2124,643,1224,1321,2100,537,2382,391,1935,2473,2321;2406,1410,208,2321,337,1370,896,424,2132,1639,928,1386,1129,1054,535,75,884,1603,1972,2069,917,905,2495,2260,917,1673,1095,2146,1418,340,2046,1793,104,201,2366", "output": "868,1479,1040,1456,512,98,607,1577,756,1810,1432,1543,2084,177,1983,1324,2019,1374,1561,402,655,1591,442,2277,1892,2012,2143,6,2363,769,59,730,904,1874,2130,1189,996,2288,388,1130,971,1088,645,261,828,1044,1389,1632,465,1078,2090,1404,418,2481,2135,756,799,774,2100,1793,1105,1087,78,646,1177,2015,943,48,2312,2465,468,1838,1979,736,730,747,553,1877,498,2353,895,2355,975,1151,922,676,525,1693,2258,227,1510,2180,1191,1541,1012,1555,2011,2450,1891,1113,1472,1988,617,403,741,2187,1440,1090,2338,2493,1513,485,969,743,976,236,2395,699,264,2174,110,2171,2009,1477,1391,692,2276,1344,2038,852,157,594,1301,1593,2235,958,2407,604,2180,749,2420,2001,633,2203,2438,1577,1699,1371,1090,166,1950,1720,149,2162,621,1216,2482,485,741,296,2073,1848,1626,2392,2103,2092,2395,845,670,1933,2324,1253,523,2491,1935,1618,2320,213,166,2499,1572,1321,1541,1604,2145,866,2222,425,23,1072,2078,777,1308,2061,2212,374,1490,2149,2373,365,1720,975,1733,958,2382,1952,2209,860,159,488,1826,1283,2348,504,1830,36,343,191,2030,249,878,2240,1382,804,509,2236,1933,974,464,685,1252,1808,771,1557,115,690,1251,957,1423,1803,2172,1890,2449,1084,517,94,1740,1601,2019,1524,515,355,1450,2306,1091,1894,1078,604,965,1873,1564,1052,1769,1205,57,210,1516,281,2111,172,2056,169,1551,142,1609,389,1410,2293,2088,1444,1447,1622,1400,197,897,931,988,1855,2234,1249,1669,2350,1606,1215,1334,53,514,1982,1570,1554,629,1526,2346,945,1296,1458,95,764,1554,1853,1523,2000,1901,1010,670,2426,770,2491,1666,2239,1347,778,1645,1696,1498,2033,1185,31,1950,1434,972,876,1926,553,1218,2333,459,2311,250,1589,2195,669,1213,1946,1256,95,556,520,2010,1677,893,1119,287,1962,1986,60,495,32,2076,2101,1546,1544,1799,2376,2095,2184,870,680,641,1774,2336,563,1281,325,625,662,1327,603,1242,1078,2138,857,1727,564,1229,1350,2215,1780,1681,2398,852,845,207,1060,892,223,2429,1575,1219,1083,363,1367,482,399,2019,1521,809,1662,2123,1574,731,1851,1128,309,2180,757,210,920,293,1552,1584,28,103,974,1309,658,24,1149,1345,1836,2485,1240,829,2485,1306,1348,752,468,2473,391,537,1321,643,603,693,806,1783,272,1777,898,279,1561,2283,1839,1682,2406,208,337,896,2132,928,1129,535,884,1972,917,2495,917,1095,1418,2046,104,2366"}, {"input": "1447,2159,1979,1296,358,1283,953,2233,2119,1341,371,17,706,2347,742,1715,698,195,2437,175,679,318,558,1131,2303,1725,296,1151,1719,1620,2475,1332,616,2462,592,481,1351,1287,2397,1850,2304,1809,263,985,2349,2128,2393,2413,414;1787,259,1586,178,1436,165,74,1207,1400,396,1251,1477,1981,1380,1197,245,2445,1090,1138,76,1900,126,1457,1490,1593,449,2006,499,511,902,1828,342,546,1601,2142,213,1116,962,1754,947,1338,1014,353,105,194,585,441,1790,1612;2266,1190,357,525,1002,732,2042,86,83,1996,623,2287,1770,2001,1925,418,320,1844,1716,495,2096,993,2389,2284,1171,1550,449,796,602,15,602,1314,311,1178,2477,669,25,1599,1774,1900,1380,1091,2419,427,858,2459,337,690,1296;2356,2057,1603,1157,2211,1237,516,831,862,338,1262,1406,1591,252,1546,249,1220,1356,1960,1861,2498,2468,132,2465,1055,1169,221,1886,1777,2139,686,2487,74,63,1534,1704,147,800,572,1282,805,1832,1344,263,171,230,732,463,2293;741,2001,1906,821,401,1044,2246,687,1887,196,1085,846,2424,40,1833,1398,1192,303,496,1115,2439,807,2275,250,1312,2440,379,342,1671,2281,66,2013,1842,2497,2444,447,1472,1271,1886,1545,939,43,2104,1851,1149,146,2077,1754,1815;776,683,1017,1834,52,2398,2101,1175,1974,384,780,1443,1189,187,157,279,1148,995,1202,1792,2008,2092,895,334,2417,1604,681,721,2007,718,2165,1004,812,943,949,524,1309,90,1921,2385,476,1182,588,2030,476,596,1327,1197,418;2267,1140,1610,124,247,1264,2000,1355,2371,787,316,1590,996,2036,2187,1413,1407,219,2387,2091,46,351,17,1272,488,2034,2350,1545,2192,633,1820,2079,838,1478,1121,1357,468,2299,1462,1237,1667,1314,1572,321,660,54,2102,327,392", "output": "1447,1979,358,953,2119,371,706,742,698,2437,679,558,2303,296,1719,2475,616,592,1351,2397,2304,263,2349,2393,414,1790,585,105,1014,947,962,213,1601,342,902,499,449,1490,126,76,1090,245,1380,1477,396,1207,165,178,259,2266,357,1002,2042,83,623,1770,1925,320,1716,2096,2389,1171,449,602,602,311,2477,25,1774,1380,2419,858,337,1296,463,230,263,1832,1282,800,1704,63,2487,2139,1886,1169,2465,2468,1861,1356,249,252,1406,338,831,1237,1157,2057,741,1906,401,2246,1887,1085,2424,1833,1192,496,2439,2275,1312,379,1671,66,1842,2444,1472,1886,939,2104,1149,2077,1815,1197,596,2030,1182,2385,90,524,943,1004,718,721,1604,334,2092,1792,995,279,187,1443,384,1175,2398,1834,683,2267,1610,247,2000,2371,316,996,2187,1407,2387,46,17,488,2350,2192,1820,838,1121,468,1462,1667,1572,660,2102,392"}, {"input": "2111,1879,1538,182,1801,1951,1884,838,175,672,2032,1365,1315,1527,289;448,1236,791,1146,1291,1838,1352,2500,1829,1491,1567,316,1348,268,1048;1979,2317,968,1521,1843,2393,1028,962,151,1357,2142,932,2251,1763,2280;110,605,1995,1433,180,1127,811,2082,1861,574,1859,1469,786,482,1912;84,1131,358,548,1861,2167,2436,1264,960,390,1652,321,1447,763,15;1753,130,1643,1147,375,2342,2473,2360,540,2008,2473,2171,1742,986,930;2097,1591,31,2314,1064,1366,1396,346,1775,332,2430,599,2143,1767,2318;1705,2037,1277,412,101,1347,215,2384,1501,2341,2030,1791,567,1654,450", "output": "2111,1538,1801,1884,175,2032,1315,289,268,316,1491,2500,1838,1146,1236,1979,968,1843,1028,151,2142,2251,2280,482,1469,574,2082,1127,1433,605,84,358,1861,2436,960,1652,1447,15,986,2171,2008,2360,2342,1147,130,2097,31,1064,1396,1775,2430,2143,2318,1654,1791,2341,2384,1347,412,2037"}, {"input": "870,814,1704,385,157,394,79,1444,1623,371,904,1039,1847,2137,2294,732,2386,753,1052,2058,2021,2229,2400,57,1998,423,1727,853,1135,202,559,652,684,1514,1094,1139,1086,2181,1323,2343,299,1393,612,1297,1143,2279,1162;997,640,364,1568,409,1288,2238,2104,1346,2123,1189,349,207,1784,808,2223,2453,2469,551,393,2282,770,2180,1598,1684,647,482,1030,2067,2181,881,2091,1362,1584,710,612,520,969,1638,987,2500,1676,781,914,308,208,1624;1933,1806,355,2044,2250,342,1606,152,2395,299,894,747,2432,1144,2368,1106,2343,2315,2497,1500,469,131,29,1309,2222,461,23,1134,1663,1554,1648,1591,742,1114,669,1732,2231,1231,619,498,624,770,1712,466,1446,1309,903;2312,159,2171,2160,1527,1854,1405,1835,1500,354,363,408,309,213,554,162,117,644,359,213,346,1855,1534,2428,781,822,2454,2063,367,997,1721,459,2440,2279,776,2128,2199,1616,618,2084,1599,1690,1737,227,2402,2151,2216;683,1266,100,2072,1094,1783,1853,876,1166,1389,562,2351,561,1844,2270,1051,610,1929,1602,1719,980,1496,1118,2129,84,1834,1241,481,398,2358,1378,1842,1814,2458,1617,2191,2442,771,1709,709,477,2084,1204,1800,487,1967,474;292,1963,1924,2281,2002,1356,148,1702,1664,1681,2444,1541,1742,2062,1292,1588,1567,146,1324,2431,2089,613,2114,221,457,1888,1065,1896,1447,697,513,210,634,2414,238,905,707,1596,1236,1520,66,1788,2113,1940,2124,2084,1797;856,841,1156,688,1023,256,1297,2439,1812,1965,667,1540,727,1573,848,645,2332,2292,715,1213,2004,2172,1178,1033,1707,1168,575,2163,2322,1664,344,1566,370,1492,1935,182,1231,2454,1928,283,550,1242,1568,1903,474,1521,457;913,863,415,1394,1977,305,1937,1055,1859,803,2345,1251,482,2002,1565,788,1284,515,967,1416,747,884,2396,729,886,1868,1632,2086,2396,1908,606,15,928,2428,1042,871,1949,172,2148,696,44,1195,102,1060,2369,913,2111;1325,1100,62,1732,1744,2261,2263,2104,1944,64,535,1595,1240,2264,1944,1476,1871,590,1446,542,1036,570,1192,587,621,2432,2323,1126,518,838,2001,2379,228,1069,2209,1597,2276,1510,747,1208,1196,2261,1290,1579,761,652,1455;2390,1055,889,246,861,1704,259,306,562,1011,409,454,1086,2253,50,2034,1165,1521,2086,304,1330,304,1689,921,948,1714,1768,1021,1973,644,2411,1715,2182,1681,352,663,1896,2437,225,1987,459,252,1735,333,1901,1161,2343;1276,2167,475,1154,1848,2148,1393,907,393,1145,2326,1409,1409,842,1901,1548,2137,1789,2279,223,1997,575,1269,1406,716,1509,1106,80,1349,1498,129,1866,885,2278,1085,2399,1200,962,286,991,1301,1765,1286,1393,1417,6,1792;1646,2020,360,1917,690,1929,599,1004,1617,2163,861,1077,857,2337,355,2438,2431,1981,723,2108,1860,2410,2280,951,1998,2054,1950,99,1315,2257,683,1607,2494,2440,1525,2229,1626,1388,1279,2055,636,1572,415,109,1144,2339,30;775,1581,285,197,761,291,1591,1570,1021,1694,1270,1549,188,1778,817,946,975,2005,2439,172,2054,2239,281,1017,1124,1507,1448,1240,686,1174,1120,68,1646,1469,539,2287,2255,1434,1571,1143,1210,1298,1693,1341,631,449,2371;2362,2239,280,858,1176,1016,1199,393,356,1412,1058,705,1723,2261,2282,1521,1254,1158,460,2331,1779,1750,250,203,1313,2376,1759,1013,890,625,1893,1330,1080,937,1641,616,1210,642,320,195,607,1738,2094,2357,115,1024,524;503,290,1015,885,377,1726,1946,2242,477,2158,1865,1477,1101,1089,1265,319,2158,2039,2335,1606,193,2164,2431,1200,2465,2338,994,1156,849,216,2464,1885,1190,797,46,824,944,2186,1082,975,1542,428,2282,1322,1334,1845,2230;2165,2165,1828,1307,882,832,1274,974,2087,1163,1988,812,1666,1188,1910,2069,1425,96,1777,1610,1935,2067,1767,1725,1458,610,1174,1050,2293,277,1374,2026,1079,1972,715,501,234,1609,1972,1073,2190,1066,990,766,974,311,956;946,1039,1609,12,1521,174,996,1082,1679,219,873,1285,1004,857,1166,466,2187,1884,1616,128,2363,2203,1904,1882,967,932,1982,1119,692,1418,1037,472,2236,2428,2282,1486,1692,2158,956,1412,2435,2293,2498,145,2427,886,1200;2122,547,1742,1939,30,2488,1717,1579,395,224,1992,2337,840,969,83,51,1739,1667,1682,1450,878,494,902,2243,522,1194,1592,405,417,1775,26,1285,2371,1443,2253,1633,2108,2476,405,2016,1490,1044,250,2430,881,1786,1441;803,1254,678,1139,305,86,2344,681,2336,2326,1862,579,466,339,1038,1603,860,164,2103,1555,522,381,497,1094,1924,1177,1434,2411,425,1336,37,1585,989,906,1096,538,458,2002,2125,135,880,740,2425,1587,831,762,58;2163,251,1055,2098,1248,1313,2325,856,2401,1943,536,1847,2014,2010,1035,1791,1665,2199,29,1880,1166,2427,979,65,2314,222,1613,217,2452,1690,1345,895,2050,231,1412,1436,2176,2436,882,1049,54,2320,1290,1661,1426,1296,1476;623,639,623,2075,2441,1967,583,2130,130,812,330,1661,465,76,187,2129,1657,2078,2092,1628,456,1800,580,1428,106,1300,46,1306,1273,2389,1817,1081,1038,848,1686,2094,1855,204,1728,702,45,1771,7,667,104,1071,1640;189,2378,670,1120,8,1553,139,52,684,1425,2159,679,1027,1721,673,271,1551,1205,1624,2080,183,1683,1354,368,586,1792,1823,2485,1268,426,1821,2257,904,822,1004,996,1494,586,2042,1151,1922,1271,1648,408,1831,2100,892;1945,1340,1454,292,1548,2453,2455,267,2273,831,497,552,26,245,1111,1308,2280,2393,2021,64,2350,712,2269,1425,1416,1129,1405,766,2208,1222,1341,2256,2154,1176,183,231,777,1281,2188,2276,1377,12,2440,1838,682,98,2485;2080,986,2023,1809,1476,1487,1934,1035,2153,1553,1679,149,1491,592,923,2462,228,2184,608,933,610,2411,634,2070,885,579,2298,1422,1102,1423,2281,1135,1836,722,43,505,189,1264,1979,2230,138,2109,1533,1773,1042,1085,119;1282,2312,696,726,606,810,694,2075,2135,1281,1090,1991,1045,105,536,193,891,1600,2119,1967,262,750,1944,2292,1817,139,385,2048,2371,2224,1345,1312,1681,912,2034,1727,1623,927,1667,1652,684,2066,2040,1783,564,621,2204;897,701,994,2295,2165,71,483,2409,823,150,1752,615,68,2015,1718,1574,1167,1367,1127,1647,1938,468,1690,2311,593,1755,2269,1140,1201,131,1763,1040,550,671,2038,1936,584,1558,618,1483,188,1597,302,2420,969,2317,423;2490,1162,1171,1978,2250,567,1658,2051,1720,1687,2399,977,2068,1677,95,1854,285,232,1414,2313,621,1442,358,188,713,2494,1171,1544,2398,418,1920,2293,2152,1297,45,2084,1824,574,980,1087,908,2472,91,1669,2246,822,2105;1991,2247,526,68,1246,1118,565,1767,386,2180,2258,1873,405,542,1347,986,127,1287,1027,1250,1750,2214,1368,843,20,1041,2115,860,966,2163,780,604,1154,501,257,288,1884,298,1996,1309,1068,1344,624,113,2064,1850,1849;1805,973,90,764,406,66,1734,2079,723,829,2377,2343,484,91,514,655,1974,2449,608,2197,11,775,1163,1260,129,1752,918,1363,211,865,773,1438,2085,1165,2273,1538,1535,1032,747,2175,366,978,136,1903,1257,1778,2107;643,842,1950,22,153,2152,197,2109,214,883,1489,156,1772,999,881,182,2319,1464,1957,849,1040,1753,2308,1989,2243,233,553,2161,361,388,272,2260,2400,2110,2066,1224,1404,1899,2292,1038,1472,2265,147,2250,1984,1758,1856;1584,2403,715,2240,525,485,2451,929,1449,315,1844,1605,1607,2121,503,1530,393,2487,2400,2059,642,651,103,509,1402,1275,959,2237,593,832,922,710,1806,596,1467,305,406,1839,518,2066,53,2496,654,1247,763,1282,794", "output": "870,1704,157,79,1623,904,1847,2294,2386,1052,2021,2400,1998,1727,1135,559,684,1094,1086,1323,299,612,1143,1162,208,914,1676,987,969,612,1584,2091,2181,1030,647,1598,770,393,2469,2223,1784,349,2123,2104,1288,1568,640,1933,355,2250,1606,2395,894,2432,2368,2343,2497,469,29,2222,23,1663,1648,742,669,2231,619,624,1712,1446,903,2151,227,1690,2084,1616,2128,2279,459,997,2063,822,2428,1855,213,644,162,213,408,354,1835,1854,2160,159,683,100,1094,1853,1166,562,561,2270,610,1602,980,1118,84,1241,398,1378,1814,1617,2442,1709,477,1204,487,474,2084,1940,1788,1520,1596,905,2414,210,697,1896,1888,221,613,2431,146,1588,2062,1541,1681,1702,1356,2281,1963,856,1156,1023,1297,1812,667,727,848,2332,715,2004,1178,1707,575,2322,344,370,1935,1231,1928,550,1568,474,457,913,1060,1195,696,172,871,2428,15,1908,2086,1868,729,884,1416,515,788,2002,1251,803,1055,305,1394,863,1325,62,1744,2263,1944,535,1240,1944,1871,1446,1036,1192,621,2323,518,2001,228,2209,2276,747,1196,1290,761,1455,1161,333,252,1987,2437,663,1681,1715,644,1021,1714,921,304,304,1521,2034,2253,454,1011,306,1704,246,1055,1276,475,1848,1393,393,2326,1409,1901,2137,2279,1997,1269,716,1106,1349,129,885,1085,1200,286,1301,1286,1417,1792,2339,109,1572,2055,1388,2229,2440,1607,2257,99,2054,951,2410,2108,1981,2438,2337,1077,2163,1004,1929,1917,2020,775,285,761,1591,1021,1270,188,817,975,2439,2054,281,1124,1448,686,1120,1646,539,2255,1571,1210,1693,631,2371,1024,2357,1738,195,642,616,937,1330,625,1013,2376,203,1750,2331,1158,1521,2261,705,1412,393,1016,858,2239,503,1015,377,1946,477,1865,1101,1265,2158,2335,193,2431,2465,994,849,2464,1190,46,944,1082,1542,2282,1334,2230,311,766,1066,1073,1609,501,1972,2026,277,1050,610,1725,2067,1610,96,2069,1188,812,1163,974,832,1307,2165,946,1609,1521,996,1679,873,1004,1166,2187,1616,2363,1904,967,1982,692,1037,2236,2282,1692,956,2435,2498,2427,1200,1786,2430,1044,2016,2476,1633,1443,1285,1775,405,1194,2243,494,1450,1667,51,969,2337,224,1579,2488,1939,547,803,678,305,2344,2336,1862,466,1038,860,2103,522,497,1924,1434,425,37,989,1096,458,2125,880,2425,831,58,1296,1661,2320,1049,2436,1436,231,895,1690,217,222,65,2427,1880,2199,1791,2010,1847,1943,856,1313,2098,251,623,623,2441,583,130,330,465,187,1657,2092,456,580,106,46,1273,1817,1038,1686,1855,1728,45,7,104,1640,2100,408,1271,1151,586,996,822,2257,426,2485,1792,368,1683,2080,1205,271,1721,679,1425,52,1553,1120,2378,1945,1454,1548,2455,2273,497,26,1111,2280,2021,2350,2269,1416,1405,2208,1341,2154,183,777,2188,1377,2440,682,2485,1085,1773,2109,2230,1264,505,722,1135,1423,1422,579,2070,2411,933,2184,2462,592,149,1553,1035,1487,1809,986,1282,696,606,694,2135,1090,1045,536,891,2119,262,1944,1817,385,2371,1345,1681,2034,1623,1667,684,2040,564,2204,2317,2420,1597,1483,1558,1936,671,1040,131,1140,1755,2311,468,1647,1367,1574,2015,615,150,2409,71,2295,701,2490,1171,2250,1658,1720,2399,2068,95,285,1414,621,358,713,1171,2398,1920,2152,45,1824,980,908,91,2246,2105,1850,113,1344,1309,298,288,501,604,2163,860,1041,843,2214,1250,1287,986,542,1873,2180,1767,1118,68,2247,1805,90,406,1734,723,2377,484,514,1974,608,11,1163,129,918,211,773,2085,2273,1535,747,366,136,1257,2107,1758,2250,2265,1038,1899,1224,2110,2260,388,2161,233,1989,1753,849,1464,182,999,156,883,2109,2152,22,842,1584,715,525,2451,1449,1844,1607,503,393,2400,642,103,1402,959,593,922,1806,1467,406,518,53,654,763,794"}, {"input": "1453,404,1621,1501,623,419,558,2018,528,1512,501,401,41,2282,1800,2410,2488,1367,1626,1837,2391,2419,102,543,2421,1694,2201,1234,1467,967,763,1428,2433,1492,2234,697,358,247,2449,878;845,123,2058,31,1825,1655,1128,536,1967,395,1636,309,2472,176,2375,19,2023,2088,1064,770,1890,372,1233,872,2389,2234,251,168,1500,750,2212,408,862,499,2291,2323,629,2109,295,2362;1339,586,2320,566,1354,762,1423,141,2170,1413,1030,688,107,331,2129,1357,2208,1671,1837,80,1390,2040,566,1019,1195,862,2153,2149,2295,164,1958,1814,2487,761,2409,30,2428,537,155,597;1745,1965,107,1440,643,2231,189,238,539,2243,395,1451,1657,2441,785,809,2189,1714,1199,761,1249,1908,2012,2473,605,214,901,1730,1466,826,267,2310,1634,162,1738,373,1429,78,178,2227;2135,2290,1054,2463,76,693,2249,476,2099,1589,1030,971,1912,143,1213,407,424,1473,800,1737,1389,1040,1790,1932,1338,697,1741,1361,1635,824,1684,1457,1450,792,1677,2128,1641,1267,1217,1637;1890,1234,157,1215,1143,2104,2491,263,467,945,566,179,1106,1104,1782,899,1168,1943,19,241,41,326,1643,160,2280,2106,2096,1095,1290,456,1524,383,889,764,884,895,1282,936,2416,1223;1716,599,993,1305,1574,2366,532,2168,212,197,846,1485,1363,773,2228,204,2322,1836,2263,1129,1735,397,1395,2144,2165,2283,2189,754,266,2155,346,13,417,2121,2248,761,1610,116,1738,1578;2468,2437,1647,942,975,959,1365,919,737,201,2324,545,2437,17,318,1744,116,323,2006,1542,2337,304,631,799,161,1883,881,2431,347,198,268,1831,15,140,909,847,1016,1651,733,1444;1138,122,54,2253,2261,934,1897,149,41,920,458,1747,435,2284,1529,2050,360,1072,941,1693,1477,1744,1416,2469,2496,1433,2195,1764,1249,331,798,1151,2252,2295,150,2348,1049,1094,2365,1921;231,1816,502,2472,2096,235,1351,423,1862,925,1793,421,393,2200,2140,651,565,312,2173,2007,2394,1471,1641,1536,590,1392,2037,842,1261,2180,870,199,156,513,617,2039,741,1155,2421,1253;1959,1779,1596,2267,1139,1112,1087,1932,1749,509,214,2216,1032,1307,750,213,42,918,2235,1013,2346,1610,1848,516,507,1485,1734,665,2135,526,799,637,206,2077,2212,1981,1874,327,1608,75;2130,625,1931,989,1981,256,2037,1962,1237,1039,1764,1815,2228,1275,1592,1353,860,985,1775,1054,1800,1809,1128,16,454,369,1220,2361,198,1785,894,209,924,194,517,508,1199,132,2382,1767;1710,1100,263,1074,881,1273,675,369,298,1113,550,895,2447,100,1862,1959,1696,417,1695,956,443,283,1297,2360,2306,1329,288,828,1579,2415,977,2310,2423,993,1670,829,765,237,879,1352;1964,692,300,849,759,1130,1878,447,1076,1248,2222,2109,1882,2218,1032,1404,2258,356,2168,978,660,684,86,1390,2049,626,2132,1694,2373,1379,653,1072,732,1866,1398,581,1037,2163,225,1464;890,1533,66,2273,2330,470,1626,573,1227,597,1186,2142,573,1732,1411,748,2286,163,1965,102,2221,2167,446,536,1404,1334,59,2141,2483,2213,597,403,871,792,247,1088,2126,2475,2229,1677;1875,2300,1730,1377,190,2251,1046,568,2074,1991,1668,2227,2337,187,1068,1113,884,928,1338,776,2253,457,1847,1169,1186,2430,17,253,630,1977,1671,1522,911,2500,482,217,1232,1930,1671,1959;951,1954,1618,216,1064,2089,421,1052,2436,919,318,1168,2364,1533,1301,1087,2447,1677,313,604,2441,1972,448,2358,474,826,2448,32,1687,1836,1627,1553,493,1004,821,237,2301,224,1105,433;2371,225,1066,1855,1977,1297,1451,1895,233,1889,557,2305,2386,914,2243,1781,568,829,2383,313,1398,530,956,705,1479,993,769,1187,2002,354,982,2317,2055,962,622,2129,757,1518,1251,1630;535,1272,1703,468,2031,2086,1525,667,2281,1546,2223,1125,74,2235,1815,1478,2295,1638,970,976,1835,2193,1661,864,447,151,604,2434,421,2143,476,1357,142,254,1477,238,2395,1763,1039,1082;2441,115,1169,1079,260,1784,2200,2430,1109,2401,695,1567,1213,1039,1720,813,1664,1450,846,702,1251,2372,707,12,1732,1817,139,591,72,188,1633,1561,1210,341,1253,53,332,826,2056,1586;1357,2163,2448,328,495,668,1982,1953,2076,2361,552,2390,762,758,1539,1054,895,1627,587,2258,704,1434,2017,1853,2218,2271,1615,2125,463,1432,63,941,1288,2142,1854,240,29,2015,1880,742;2304,175,2399,995,633,1538,483,648,742,1594,129,2306,1650,1261,1194,936,37,781,1215,954,1188,769,2397,1004,2047,1530,948,1136,1491,538,1780,189,78,1127,201,58,592,1154,949,960;728,292,234,546,2448,637,2232,2318,1766,598,2337,97,1867,1135,2335,2353,2044,1108,2335,222,2119,597,1375,1294,771,2431,1572,1396,2290,92,2001,1271,856,486,2468,1638,1548,1899,1561,2136;218,1164,1052,938,1097,2322,440,1425,1316,2029,308,393,2236,1516,1636,980,285,2486,2375,198,877,1487,1341,35,982,1849,1194,1177,1026,2160,2270,1517,1179,1860,289,1023,2147,1810,1363,1677;152,1128,612,2174,603,1495,1155,462,342,1350,2277,2005,406,76,1251,858,495,991,1291,2197,1616,1802,1110,2212,140,1077,2244,2434,1209,1622,1005,1263,507,434,1696,2262,933,1178,2111,1379;121,271,1158,1814,2363,2025,1318,1151,883,750,301,662,2121,1559,2237,642,2092,1495,1154,939,1120,2153,547,1143,834,229,590,210,1079,2307,2177,1452,1432,791,1540,1450,87,2095,1777,630;2079,441,1056,1224,2100,1462,52,2477,662,424,1414,874,1600,1253,1564,1398,1801,1483,2115,996,983,2054,759,135,1918,2214,1420,1326,2445,2196,1956,872,506,432,959,902,2045,1191,697,131;2370,1979,61,1563,1697,1110,975,1071,613,1122,988,950,1917,1473,918,1118,496,2123,1945,2376,378,150,866,350,1977,790,1373,2117,752,612,737,2242,837,2087,1936,2366,436,828,1617,2450;1693,821,1560,130,606,2355,99,2308,2286,810,142,1636,837,53,1180,1638,2158,131,234,746,31,824,2479,1369,2050,1949,1069,1683,2046,1724,1787,1972,356,1930,34,2456,803,2153,1241,227;1598,829,1465,524,2384,1376,623,1606,556,1243,1678,149,17,1974,1713,1582,1047,2487,1239,796,930,1987,2142,1301,1833,1459,1155,2187,1194,1847,2399,278,2083,1920,1926,1345,105,1212,1335,388", "output": "1453,1621,623,558,528,501,41,1800,2488,1626,2391,102,2421,2201,1467,763,2433,2234,358,2449,2362,2109,2323,499,408,750,168,2234,872,372,770,2088,19,176,309,395,536,1655,31,123,1339,2320,1354,1423,2170,1030,107,2129,2208,1837,1390,566,1195,2153,2295,1958,2487,2409,2428,155,2227,78,373,162,2310,826,1730,214,2473,1908,761,1714,809,2441,1451,2243,238,2231,1440,1965,2135,1054,76,2249,2099,1030,1912,1213,424,800,1389,1790,1338,1741,1635,1684,1450,1677,1641,1217,1223,936,895,764,383,456,1095,2106,160,326,241,1943,899,1104,179,945,263,2104,1215,1234,1716,993,1574,532,212,846,1363,2228,2322,2263,1735,1395,2165,2189,266,346,417,2248,1610,1738,1444,1651,847,140,1831,198,2431,1883,799,304,1542,323,1744,17,545,201,919,959,942,2437,1138,54,2261,1897,41,458,435,1529,360,941,1477,1416,2496,2195,1249,798,2252,150,1049,2365,1253,1155,2039,513,199,2180,842,1392,1536,1471,2007,312,651,2200,421,925,423,235,2472,1816,1959,1596,1139,1087,1749,214,1032,750,42,2235,2346,1848,507,1734,2135,799,206,2212,1874,1608,1767,132,508,194,209,1785,2361,369,16,1809,1054,985,1353,1275,1815,1039,1962,256,989,625,1710,263,881,675,298,550,2447,1862,1696,1695,443,1297,2306,288,1579,977,2423,1670,765,879,1464,2163,581,1866,1072,1379,1694,626,1390,684,978,356,1404,2218,2109,1248,447,1130,849,692,890,66,2330,1626,1227,1186,573,1411,2286,1965,2221,446,1404,59,2483,597,871,247,2126,2229,1959,1930,217,2500,1522,1977,253,2430,1169,457,776,928,1113,187,2227,1991,568,2251,1377,2300,951,1618,1064,421,2436,318,2364,1301,2447,313,2441,448,474,2448,1687,1627,493,821,2301,1105,1630,1518,2129,962,2317,354,1187,993,705,530,313,829,1781,914,2305,1889,1895,1297,1855,225,535,1703,2031,1525,2281,2223,74,1815,2295,970,1835,1661,447,604,421,476,142,1477,2395,1039,1586,826,53,341,1561,188,591,1817,12,2372,702,1450,813,1039,1567,2401,2430,1784,1079,115,1357,2448,495,1982,2076,552,762,1539,895,587,704,2017,2218,1615,463,63,1288,1854,29,1880,960,1154,58,1127,189,538,1136,1530,1004,769,954,781,936,1261,2306,1594,648,1538,995,175,728,234,2448,2232,1766,2337,1867,2335,2044,2335,2119,1375,771,1572,2290,2001,856,2468,1548,1561,1677,1810,1023,1860,1517,2160,1177,1849,35,1487,198,2486,980,1516,393,2029,1425,2322,938,1164,152,612,603,1155,342,2277,406,1251,495,1291,1616,1110,140,2244,1209,1005,507,1696,933,2111,630,2095,1450,791,1452,2307,210,229,1143,2153,939,1495,642,1559,662,750,1151,2025,1814,271,2079,1056,2100,52,662,1414,1600,1564,1801,2115,983,759,1918,1420,2445,1956,506,959,2045,697,2450,828,2366,2087,2242,612,2117,790,350,150,2376,2123,1118,1473,950,1122,1071,1110,1563,1979,1693,1560,606,99,2286,142,837,1180,2158,234,31,2479,2050,1069,2046,1787,356,34,803,1241,388,1212,1345,1920,278,1847,2187,1459,1301,1987,796,2487,1582,1974,149,1243,1606,1376,524,829"}, {"input": "1918,2040,1148,1380,696,1751,2350,656,197,1257,1123,699,2206,1226,2381,554,1209,822,1274,405,2309,441,2164,1489,1291,2342,2319,1355,2242,1232,1,1902,2393,452,418,2382,1051,569,1344;1196,345,1187,2196,460,1035,436,1017,2414,243,1255,1719,1553,199,52,1984,987,483,312,1534,2142,947,2458,586,1913,1676,1528,1685,2064,1353,1544,1126,1044,1804,1895,2368,1405,2390,1332;1705,2481,723,1473,1371,154,1836,1800,1647,1134,1086,174,950,768,2096,1524,1519,107,1695,1212,2304,1594,640,914,1409,1993,210,2382,1255,1309,663,62,1602,1787,26,253,2262,2259,1339;786,2061,1127,927,954,461,2146,492,2478,2066,1795,2127,1221,742,2344,719,2247,799,1802,2142,2448,1236,1295,225,801,2281,200,236,2324,2474,1727,298,2461,526,275,2391,1249,2074,456;2480,268,1986,444,2084,606,477,2203,2353,2368,1560,2193,2144,619,358,257,1312,1635,899,295,921,2006,1035,1647,309,894,1048,2018,739,1300,1374,947,1152,2119,754,2067,258,1666,682;2227,1964,915,999,985,2326,1466,1011,2118,352,1717,1426,415,1771,718,1140,2305,1411,175,49,19,2103,1613,373,404,562,1547,85,2342,1707,1352,543,973,624,2037,1722,357,2287,128;1381,1826,1286,1003,381,2235,2327,2162,933,1826,758,1015,1022,1608,1855,811,647,989,94,544,2327,1319,1533,1794,1859,617,669,1433,2438,2125,759,2389,969,1035,2160,1483,946,2476,2398;1602,1355,2105,801,2266,700,2090,1814,1996,2478,649,995,199,1158,1312,475,776,1518,2013,330,1609,1531,95,1393,2091,1056,1934,2088,1728,1671,1880,156,130,1997,826,1364,737,101,1860;826,329,1770,1169,850,2025,987,1461,760,1080,1821,2353,1510,97,346,895,1994,2111,1290,2101,2372,507,144,1758,1222,6,2121,651,2388,530,1014,346,1854,1594,1192,1748,2258,1696,2133;611,1292,599,624,253,1135,2440,813,2349,2375,206,1429,1016,538,7,553,497,163,1792,1437,1723,650,658,655,1641,2414,768,2154,2233,328,2133,252,1692,492,370,2122,2152,2466,1296;2078,1261,1756,1472,264,2018,1368,1863,1201,181,118,1989,2054,1042,1152,618,1478,2227,2451,79,2060,63,87,1205,2174,1826,2183,395,1612,2004,2424,548,2160,948,372,140,598,361,1799;1020,615,507,556,2373,443,2025,1385,1312,2488,1112,1451,356,764,321,1248,2453,519,195,1498,2006,1771,1934,1429,1258,1650,1310,1296,14,2499,2064,127,1253,1331,2035,1026,1737,2048,525;1683,1422,346,1032,714,1220,609,1008,1064,2007,1614,2259,211,748,113,239,180,404,676,389,711,870,1552,840,1761,2470,1833,1873,147,31,587,1451,775,712,314,804,1380,1307,389;1614,2286,2108,923,889,892,2082,1466,2335,67,1956,1154,2168,1968,1518,1289,1944,1592,1646,1568,2163,1477,447,868,889,2382,998,388,1526,823,804,2207,2088,102,1747,80,2497,1627,622;2064,1876,1216,1222,166,1240,2433,1857,146,1064,1256,760,741,1487,927,919,577,1671,404,1404,1436,865,1099,1603,1424,895,508,1119,1271,369,156,1833,341,1981,144,207,1222,1997,636;656,920,2076,1669,819,840,2340,1482,511,140,442,2080,2389,339,1168,1349,147,142,1122,915,1582,682,1343,1052,1498,640,1373,1792,950,691,553,1323,632,1848,913,1943,1326,743,2248;193,1344,1392,1894,1533,1534,7,410,950,1973,1136,484,1148,115,1947,1899,1646,2415,1504,728,636,859,637,1187,1349,1167,765,1909,594,336,2196,117,319,1606,1740,969,2055,1711,1572;2372,675,1096,2281,279,2047,2448,1118,1268,724,2363,789,378,616,1656,1483,2216,1160,179,395,2084,2409,357,1899,58,1890,993,1959,2359,1140,2294,1782,1494,822,330,200,736,1630,1566;1370,1773,1944,1438,1041,1273,175,2269,47,2039,699,2428,809,1510,1576,2404,1738,689,1070,1502,728,615,708,182,959,2384,252,1276,1727,223,2246,990,952,2166,323,1820,2284,1820,1642;2436,618,892,2243,1940,327,1872,2491,2327,1294,124,1813,1316,1098,1305,642,2125,1947,385,571,2416,147,1274,1083,654,558,1428,2418,1917,1391,18,1957,2121,1488,498,1652,254,1145,1710;393,1952,710,2224,1154,1749,985,487,1477,431,2126,97,474,81,2429,375,921,661,1168,657,1106,1631,1739,1635,2381,654,250,2055,582,656,1072,2303,855,1089,2467,1808,155,1870,2080;1274,1717,1797,599,1013,2035,339,1728,844,2209,2366,850,1574,2289,1869,797,2140,1447,871,1466,1739,329,2214,993,1756,1856,1769,1025,822,1426,2461,660,1716,2167,299,1035,941,1699,1801", "output": "1918,1148,696,2350,197,1123,2206,2381,1209,1274,2309,2164,1291,2319,2242,1,2393,418,1051,1344,2390,2368,1804,1126,1353,1685,1676,586,947,1534,483,1984,199,1719,243,1017,1035,2196,345,1705,723,1371,1836,1647,1086,950,2096,1519,1695,2304,640,1409,210,1255,663,1602,26,2262,1339,2074,2391,526,298,2474,236,2281,225,1236,2142,799,719,742,2127,2066,492,461,927,2061,2480,1986,2084,477,2353,1560,2144,358,1312,899,921,1035,309,1048,739,1374,1152,754,258,682,2287,1722,624,543,1707,85,562,373,2103,49,1411,1140,1771,1426,352,1011,2326,999,1964,1381,1286,381,2327,933,758,1022,1855,647,94,2327,1533,1859,669,2438,759,969,2160,946,2398,101,1364,1997,156,1671,2088,1056,1393,1531,330,1518,475,1158,995,2478,1814,700,801,1355,826,1770,850,987,760,1821,1510,346,1994,1290,2372,144,1222,2121,2388,1014,1854,1192,2258,2133,2466,2122,492,252,328,2154,2414,655,650,1437,163,553,538,1429,2375,813,1135,624,1292,2078,1756,264,1368,1201,118,2054,1152,1478,2451,2060,87,2174,2183,1612,2424,2160,372,598,1799,2048,1026,1331,127,2499,1296,1650,1429,1771,1498,519,1248,764,1451,2488,1385,443,556,615,1683,346,714,609,1064,1614,211,113,180,676,711,1552,1761,1833,147,587,775,314,1380,389,1627,80,102,2207,823,388,2382,868,1477,1568,1592,1289,1968,1154,67,1466,892,923,2286,2064,1216,166,2433,146,1256,741,927,577,404,1436,1099,1424,508,1271,156,341,144,1222,636,743,1943,1848,1323,691,1792,640,1052,682,915,142,1349,339,2080,140,1482,840,1669,920,193,1392,1533,7,950,1136,1148,1947,1646,1504,636,637,1349,765,594,2196,319,1740,2055,1572,1630,200,822,1782,1140,1959,1890,1899,2409,395,1160,1483,616,789,724,1118,2047,2281,675,1370,1944,1041,175,47,699,809,1576,1738,1070,728,708,959,252,1727,2246,952,323,2284,1642,1145,1652,1488,1957,1391,2418,558,1083,147,571,1947,642,1098,1813,1294,2491,327,2243,618,393,710,1154,985,1477,2126,474,2429,921,1168,1106,1739,2381,250,582,1072,855,2467,155,2080,1699,1035,2167,660,1426,1025,1856,993,329,1466,1447,797,2289,850,2209,1728,2035,599,1717"}, {"input": "829,747,1119,1520,2292,1789,943,995,672,642,2290,535,414,474,2285,1575,355,1854,1182,1316,32,12,1989,1618,2348,2453,768,423;2447,584,1266,444,586,106,287,491,1026,2317,2256,28,982,1701,1090,184,564,2167,1957,1943,2397,1093,1144,2377,800,1681,688,1685;720,1501,1144,1999,34,21,296,2440,2034,425,1593,249,877,1243,2033,520,1365,2230,633,1042,275,2491,321,557,969,104,521,1683;951,928,1329,1762,1498,2089,1649,201,224,40,1947,1181,875,390,1920,2133,723,58,569,1901,711,530,1954,1167,101,1280,1613,1771;679,2106,597,1036,1685,659,1626,752,385,999,510,1248,264,1071,1392,1215,1045,410,400,578,517,781,173,334,382,2428,1417,1180;831,343,75,782,1197,1084,478,2253,786,856,78,934,1535,681,2200,725,1319,1923,216,2428,734,80,214,1959,1887,268,1271,1201;722,447,469,415,78,2456,977,187,1496,1028,1473,982,1127,462,1621,505,1870,139,1117,246,1511,287,326,1244,1853,2142,1038,2084;402,1097,2456,130,494,354,2092,1116,1528,763,714,1235,70,966,1466,1588,778,560,673,385,12,2052,2068,476,1286,2187,711,618;2414,1886,497,1331,1490,1104,1906,917,149,2057,1558,2164,1041,921,1550,1591,1287,245,12,786,2176,82,1010,474,2062,1413,1420,914;861,290,1335,2306,133,248,532,570,53,413,42,314,290,1979,1824,179,1023,338,583,583,280,2101,1050,1757,395,342,151,2156;2021,290,1754,337,1535,2225,2128,1021,848,579,1522,1532,1616,522,601,1912,804,1048,1598,1404,1047,2312,2001,173,604,1763,2453,2072;1564,86,1751,427,482,743,2487,858,2471,107,1751,701,786,97,1396,918,2227,2101,1661,2057,332,1880,1046,1867,2491,2076,1254,1926;215,745,2401,1904,1090,130,763,2364,299,1262,2017,1400,20,1568,1643,965,2130,1179,397,575,1235,1806,1748,2280,1647,2291,1968,1790;1400,1245,2126,856,1533,699,1743,2483,1723,1318,580,780,1894,1221,466,1246,974,1678,285,791,7,1799,1029,1332,1945,1376,2154,830;355,934,2041,132,2009,403,1609,2172,180,2338,2050,44,2037,169,1087,657,16,1902,337,65,2466,601,243,673,468,2347,1596,969;1803,2310,1147,1155,823,1760,2248,2119,1918,149,910,1678,1170,1239,2400,298,1712,729,1350,2467,2492,1647,1929,1319,1823,1502,1869,1831;2272,1024,719,286,2001,425,413,1493,1749,707,1479,329,257,233,66,2207,34,422,1196,42,1233,413,1119,412,1944,1537,937,2134;125,1680,1654,1065,509,699,1110,277,2034,1811,2419,373,2056,1358,2432,888,1210,1829,88,823,1938,1831,2103,1278,356,2091,1624,1052;891,379,302,839,88,686,363,345,917,816,181,1726,2318,2189,1582,339,934,982,1465,1402,104,2148,2060,80,975,1984,444,1973;720,2051,1778,1813,583,24,274,229,2387,1558,1567,680,1974,349,404,1228,1376,2080,1238,243,2495,1019,1442,2009,747,1843,1184,2385;147,303,59,1868,2308,1915,701,793,911,997,1223,123,263,37,956,2052,623,193,2229,1507,2111,2363,1289,2293,711,2166,1999,999;971,1930,698,2068,1185,377,1066,1806,1569,604,1532,1231,34,2202,1620,1347,1177,1362,1180,921,117,394,1291,1350,271,1612,1891,1148;2475,694,664,1078,946,203,1902,1033,1309,6,497,1770,367,515,1219,1710,2412,566,1702,1787,235,940,247,601,1882,566,1933,2472;1918,696,1544,570,1733,1997,1495,1748,1672,575,2006,2062,2415,2179,2464,1573,304,806,904,100,927,2304,2145,2125,286,2257,1998,1721;2232,1886,299,1237,2403,1481,340,2216,2177,729,2055,2019,466,707,2102,840,1616,1223,985,380,498,1142,158,1368,1713,63,1887,2348;1364,1963,506,1277,1446,541,316,50,2360,1907,2348,2176,2104,1166,883,2429,1298,2107,1211,1038,1324,2162,488,845,2276,1058,509,405;1768,1362,162,482,196,1222,961,490,1028,1760,1554,7,1376,696,949,1473,701,874,850,956,2494,1458,2456,2128,1384,1304,2105,1238;224,363,2469,1002,2344,722,1035,1463,46,2399,2111,379,666,234,1059,2234,1499,480,1461,670,1241,2407,748,769,1743,365,1707,1771;84,1475,311,242,1736,678,433,1382,2432,1299,1603,2261,1676,1142,1840,2126,1093,2309,1035,1850,1800,1538,487,276,1132,2307,2381,425;1082,1111,195,1736,238,2388,60,838,548,1099,2019,445,1246,1105,1161,79,2483,812,2317,1813,1078,1177,1029,989,1558,1448,1999,2051;1154,1618,562,2020,1702,513,301,1936,2066,1182,1772,1408,2422,1209,2475,1243,921,1988,523,1440,595,317,19,838,1825,566,438,245;1640,476,774,986,490,750,2254,1151,1233,1551,1594,833,686,898,1456,1620,1209,1162,211,680,1556,1274,2492,545,1100,807,2115,821;1421,414,1474,2027,918,529,702,1846,1055,1940,2197,1838,1515,1629,2399,1947,102,525,185,824,1008,130,1744,2220,2378,888,2215,2208", "output": "829,1119,2292,943,672,2290,414,2285,355,1182,32,1989,2348,768,1685,1681,2377,1093,1943,2167,184,1701,28,2317,491,106,444,584,720,1144,34,296,2034,1593,877,2033,1365,633,275,321,969,521,1771,1280,1167,530,1901,58,2133,390,1181,40,201,2089,1762,928,679,597,1685,1626,385,510,264,1392,1045,400,517,173,382,1417,1201,268,1959,80,2428,1923,725,681,934,856,2253,1084,782,343,722,469,78,977,1496,1473,1127,1621,1870,1117,1511,326,1853,1038,618,2187,476,2052,385,560,1588,966,1235,763,1116,354,130,1097,2414,497,1490,1906,149,1558,1041,1550,1287,12,2176,1010,2062,1420,2156,342,1757,2101,583,338,179,1979,314,413,570,248,2306,290,2021,1754,1535,2128,848,1522,1616,601,804,1598,1047,2001,604,2453,1926,2076,1867,1880,2057,2101,918,97,701,107,858,743,427,86,215,2401,1090,763,299,2017,20,1643,2130,397,1235,1748,1647,1968,830,1376,1332,1799,791,1678,1246,1221,780,1318,2483,699,856,1245,355,2041,2009,1609,180,2050,2037,1087,16,337,2466,243,468,1596,1831,1502,1319,1647,2467,729,298,1239,1678,149,2119,1760,1155,2310,2272,719,2001,413,1749,1479,257,66,34,1196,1233,1119,1944,937,1052,2091,1278,1831,823,1829,888,1358,373,1811,277,699,1065,1680,891,302,88,363,917,181,2318,1582,934,1465,104,2060,975,444,2385,1843,2009,1019,243,2080,1228,349,680,1558,229,24,1813,2051,147,59,2308,701,911,1223,263,956,623,2229,2111,1289,711,1999,1148,1612,1350,394,921,1362,1347,2202,1231,604,1806,377,2068,1930,2475,664,946,1902,1309,497,367,1219,2412,1702,235,247,1882,1933,1721,2257,2125,2304,100,806,1573,2179,2062,575,1748,1997,570,696,2232,299,2403,340,2177,2055,466,2102,1616,985,498,158,1713,1887,405,1058,845,2162,1038,2107,2429,1166,2176,1907,50,541,1277,1963,1768,162,196,961,1028,1554,1376,949,701,850,2494,2456,1384,2105,1771,365,769,2407,670,480,2234,234,379,2399,1463,722,1002,363,84,311,1736,433,2432,1603,1676,1840,1093,1035,1800,487,1132,2381,2051,1448,989,1177,1813,812,79,1105,445,1099,838,2388,1736,1111,1154,562,1702,301,2066,1772,2422,2475,921,523,595,19,1825,438,821,807,545,1274,680,1162,1620,898,833,1551,1151,750,986,476,1421,1474,918,702,1055,2197,1515,2399,102,185,1008,1744,2378,2215"}, {"input": "1500,1947,1393,243,433,1418,1229,2290,2451,1525,699,628,81,1549,1343,412,2470,643,227,922,1854,414,453,968,818,2113,1869,744,1821,1734,476,120,1540,1791,1825,883,793,1232,1082,1749,1557,114,357,1442;1791,2488,363,986,2242,180,79,669,517,1477,844,1225,2227,2126,1035,1803,1473,2299,429,2092,1443,2136,1129,1823,167,1196,2019,813,2011,2160,829,361,184,1226,2100,15,1679,1682,963,379,279,2362,2383,1343;2376,2291,2126,722,513,729,2347,1819,1864,3,420,2224,232,410,2154,1964,1138,2346,2381,1626,134,1494,1170,1720,466,1418,1034,2287,24,2417,1300,845,1333,1880,1163,541,359,2360,999,351,2347,852,2415,2472;1276,1879,1237,2145,2312,1658,2037,1692,2215,37,1909,1264,273,305,958,651,2314,1676,1508,336,1651,597,118,2188,1485,315,1446,2306,1098,1941,2371,839,1864,1184,1809,1305,1834,1817,1290,805,1126,235,1021,812;740,1495,812,891,1973,2183,2017,219,2260,303,566,1518,1234,2123,2451,1094,742,1025,201,256,426,2103,2171,456,1610,2314,2220,1663,1591,2171,1179,2104,122,1588,704,429,1998,1852,2206,597,1212,925,790,1531;147,762,1165,1472,2057,279,1088,1443,1505,1646,294,547,130,1676,2102,1459,311,2212,1504,1693,924,35,2395,2134,1926,1623,588,895,2439,139,2463,181,1437,2105,528,1173,1782,19,1293,2031,916,2064,713,1475;2332,164,1697,2328,635,352,159,2437,2210,1833,1421,1789,2284,82,1632,2226,1517,2379,2241,1237,2406,607,1233,87,343,1060,2316,1477,695,1578,2434,1376,1819,1690,2206,1890,1152,1830,825,1762,894,1171,2309,367;585,1762,561,10,2243,2098,1378,2353,797,2059,978,579,2392,1603,156,305,1644,2092,1865,406,2272,1651,719,1462,1714,1108,1198,2469,171,1728,1279,1672,947,305,1236,1937,1854,2002,942,1443,869,1665,2455,263;1267,2321,1749,1845,1975,2350,2050,2312,387,1516,725,2100,768,191,1585,1658,1669,517,775,1724,554,2497,2228,326,1814,208,808,1411,2051,849,437,1833,679,535,71,854,1502,37,24,2163,1883,1634,368,1538;455,2431,523,1838,1462,461,733,437,12,560,2114,268,804,341,1172,1726,2373,2159,1248,1804,2279,900,438,361,1103,579,1400,219,1363,2412,1851,2491,794,693,884,416,1064,430,698,1868,2203,2081,1387,1474;1236,1254,1289,2164,1961,1368,893,989,741,918,1928,1913,2265,1909,1088,1588,2183,1185,626,1451,1310,1003,945,398,224,586,1885,280,278,1643,2387,1564,2196,2446,1751,1471,1529,406,2158,2407,2083,2252,365,1135;594,1899,596,1951,292,1364,1196,2452,219,759,2281,56,527,2379,529,1629,1692,1268,2050,488,528,1749,2234,65,1783,2150,819,2363,2055,741,1999,2081,1064,292,1464,2145,1506,1464,1510,1657,171,1242,467,1193;917,1681,1759,2196,1458,5,73,1712,2331,1710,1855,82,111,1019,194,359,1334,512,1588,1420,771,1418,2436,2150,2185,1403,1485,1625,2014,1305,881,129,976,1953,142,531,270,344,1189,136,701,2154,407,845;422,2304,1714,274,1742,183,401,939,2106,1220,1377,2469,2399,1673,166,1993,1818,376,44,1166,2286,457,363,1104,1230,1972,1244,1330,538,364,1680,2323,181,2382,1524,1302,962,1884,1136,278,647,1407,2119,1325;2163,2297,663,758,2377,1269,287,579,1624,705,1577,2437,122,107,1119,306,529,1513,1120,95,967,1584,1754,933,595,2333,932,876,1602,984,969,2060,582,1484,1837,484,2281,378,1395,2178,1159,1714,1126,1692;372,1476,440,1419,540,975,152,1586,988,1809,809,1682,1217,2471,2277,143,2405,846,1690,681,1810,910,477,208,2060,1379,115,815,1876,802,2164,639,1978,1509,2360,1940,483,81,2370,730,2105,1960,1030,2241;20,2175,470,2492,1105,728,775,2086,1325,1820,1734,2232,418,1204,2465,360,1594,123,980,926,1200,1215,1515,1659,1725,115,184,1258,1138,104,2294,2306,3,445,1104,770,1225,1857,1587,1824,562,1692,2040,783;686,2404,1931,484,1447,1502,2104,790,1281,254,1987,321,1540,2470,1018,1845,1187,639,1698,466,1748,1532,192,2484,485,231,1595,678,148,545,525,17,1803,2178,1022,2171,1174,2219,688,2261,536,1941,1241,1103;2164,1874,12,1453,883,125,702,1628,1659,915,1740,1228,1001,456,2256,266,2210,2421,258,41,1168,1501,411,878,601,857,309,401,1250,1813,250,2364,458,2127,200,1279,1817,1202,2059,865,1372,2169,726,96;168,784,1278,143,1232,204,220,1110,2394,1703,2054,883,49,991,1216,388,1366,1371,1401,2168,211,1926,2047,1353,1230,2259,1449,702,1959,1739,723,2023,936,23,75,1248,2138,86,397,191,847,131,1565,1818;319,589,737,2413,898,352,1112,187,840,1858,1248,1350,1808,673,980,1232,653,511,1154,748,1303,998,2074,2357,1375,141,1716,1525,591,1972,1553,953,2159,1909,552,1134,704,2161,652,2412,1467,1873,2397,1990;1246,969,2089,1280,1534,594,1508,1856,39,1950,386,694,2148,2127,826,26,2167,454,2072,387,1067,497,1423,787,872,2431,338,1600,1975,1703,980,1021,1743,1458,400,199,430,1088,1205,626,2205,1368,1229,143;431,1456,2449,2118,1162,539,670,482,1557,2016,1226,1006,457,2305,1523,1658,529,56,1834,20,2222,661,1178,2410,2142,2168,458,417,1361,1793,792,1475,2088,2091,1439,2253,1812,350,558,1876,2209,2028,635,2359;1678,1812,1050,2327,1311,1887,755,2487,2383,857,1062,1484,2362,1411,175,1638,650,1139,868,567,1108,1761,1575,1537,1953,1681,1235,1320,2005,214,1224,1650,2205,2311,2215,267,2353,1421,2047,78,354,76,1016,1079;2303,982,1931,743,729,736,1909,195,1996,1043,718,1936,2038,397,2343,750,2039,2323,1313,1627,927,872,454,520,1723,2440,1328,791,1667,2500,606,927,568,2169,1675,616,39,959,2456,1704,1787,1968,548,1013", "output": "1500,1393,433,1229,2451,699,81,1343,2470,227,1854,453,818,1869,1821,476,1540,1825,793,1082,1557,357,1343,2362,379,1682,15,1226,361,2160,813,1196,1823,2136,2092,2299,1803,2126,1225,1477,669,180,986,2488,2376,2126,513,2347,1864,420,232,2154,1138,2381,134,1170,466,1034,24,1300,1333,1163,359,999,2347,2415,812,235,805,1817,1305,1184,839,1941,2306,315,2188,597,336,1676,651,305,1264,37,1692,1658,2145,1879,740,812,1973,2017,2260,566,1234,2451,742,201,426,2171,1610,2220,1591,1179,122,704,1998,2206,1212,790,1475,2064,2031,19,1173,2105,181,139,895,1623,2134,35,1693,2212,1459,1676,547,1646,1443,279,1472,762,2332,1697,635,159,2210,1421,2284,1632,1517,2241,2406,1233,343,2316,695,2434,1819,2206,1152,825,894,2309,263,1665,1443,2002,1937,305,1672,1728,2469,1108,1462,1651,406,2092,305,1603,579,2059,2353,2098,10,1762,1267,1749,1975,2050,387,725,768,1585,1669,775,554,2228,1814,808,2051,437,679,71,1502,24,1883,368,1474,2081,1868,430,416,693,2491,2412,219,579,361,900,1804,2159,1726,341,268,560,437,461,1838,2431,1236,1289,1961,893,741,1928,2265,1088,2183,626,1310,945,224,1885,278,2387,2196,1751,1529,2158,2083,365,1193,1242,1657,1464,2145,292,2081,741,2363,2150,65,1749,488,1268,1629,2379,56,759,2452,1364,1951,1899,917,1759,1458,73,2331,1855,111,194,1334,1588,771,2436,2185,1485,2014,881,976,142,270,1189,701,407,1325,1407,278,1884,1302,2382,2323,364,1330,1972,1104,457,1166,376,1993,1673,2469,1220,939,183,274,2304,2163,663,2377,287,1624,1577,122,1119,529,1120,967,1754,595,932,1602,969,582,1837,2281,1395,1159,1126,2241,1960,730,81,1940,1509,639,802,815,1379,208,910,681,846,143,2471,1682,1809,1586,975,1419,1476,20,470,1105,775,1325,1734,418,2465,1594,980,1200,1515,1725,184,1138,2294,3,1104,1225,1587,562,2040,1103,1941,2261,2219,2171,2178,17,545,678,231,2484,1532,466,639,1845,2470,321,254,790,1502,484,2404,2164,12,883,702,1659,1740,1001,2256,2210,258,1168,411,601,309,1250,250,458,200,1817,2059,1372,726,1818,131,191,86,1248,23,2023,1739,702,2259,1353,1926,2168,1371,388,991,883,1703,1110,204,143,784,319,737,898,1112,840,1248,1808,980,653,1154,1303,2074,1375,1716,591,1553,2159,552,704,652,1467,2397,143,1368,626,1088,199,1458,1021,1703,1600,2431,787,497,387,454,26,2127,694,1950,1856,594,1280,969,431,2449,1162,670,1557,1226,457,1523,529,1834,2222,1178,2142,458,1361,792,2088,1439,1812,558,2209,635,1079,76,78,1421,267,2311,1650,214,1320,1681,1537,1761,567,1139,1638,1411,1484,857,2487,1887,2327,1812,2303,1931,729,1909,1996,718,2038,2343,2039,1313,927,454,1723,1328,1667,606,568,1675,39,2456,1787,548"}, {"input": "1438,1560,1391,1426,1146,1503,1543,1495,221,1851,1384,1895,2491,2192,331,2443,1,2289,871,412,2345,626,1950,445,2188,554,1220,809,2090,2124,1251,2023,2170,1869,1336,2111,132,2052,2334,2209,1725,1557,1631,1047,2006,165,502,1674;129,524,1518,1035,2182,1558,566,2308,1633,2240,30,59,1329,749,1127,1829,1517,1798,2394,217,1302,1217,994,2454,853,2352,1087,1499,240,2025,1441,146,87,2030,1524,409,1502,41,1746,245,2281,1819,168,1438,2383,667,878,1247;1736,1848,1630,2352,507,1429,1412,674,1702,806,717,1204,2148,1997,2248,2409,1634,2183,1417,611,1378,1169,376,230,2071,191,2477,1333,1803,2450,1590,2496,1137,787,507,309,752,2238,1790,1552,1388,739,1656,1412,2218,127,1795,1982;1788,619,314,2413,1803,715,476,55,111,2159,2457,1118,155,2026,2355,853,1447,615,86,1169,74,847,2483,31,366,1128,140,1005,1078,1519,1987,452,1018,1654,2049,1655,2426,1581,1524,959,1261,1995,1022,979,270,1990,1667,525;872,806,1309,1041,2113,480,628,221,133,302,1238,314,242,350,410,1830,960,2341,2432,244,1574,2293,311,2485,532,1076,1892,38,2074,1166,1294,534,775,2439,2465,82,2385,2092,128,1659,1031,137,2239,1125,2358,1735,351,877;255,1296,1829,723,1342,766,1824,981,2379,50,1771,1854,223,1505,1556,1181,814,1452,1374,1990,1209,247,1445,1791,1432,2458,1483,1951,1511,1007,2152,602,1368,2308,531,1895,975,1167,2032,1366,2017,530,2052,1569,288,1058,368,1123;2389,499,2474,1422,2307,1270,1255,1711,2,260,2155,929,1763,2175,2247,1016,930,1657,1609,1051,2176,1105,2404,1183,1958,1604,2082,2082,2318,185,353,1824,904,2182,392,303,2441,1981,1479,659,1414,469,2382,366,666,645,2380,20;733,2034,1415,332,1462,471,1153,1664,547,1244,2319,2373,1955,1266,2460,81,2028,42,2098,1426,1022,1753,1044,801,1621,2021,398,401,2332,919,1201,461,674,1383,408,1659,893,2055,2424,1630,1131,1339,1978,1304,1526,1289,818,293;378,1362,149,2436,575,967,1974,981,717,2449,491,232,1677,1085,397,1790,1215,1939,1737,2379,1344,1105,582,1064,387,1438,1194,1434,1860,2103,1199,1641,676,559,1840,2211,1925,1668,1074,2187,1282,2002,1027,2186,1301,1617,1946,771;1165,1923,1538,1552,2061,1268,1636,2278,116,1378,60,2272,1154,2435,1886,1068,548,554,1987,855,1091,2046,1439,1736,1286,2,1689,171,1737,2417,558,1902,779,1400,755,1476,1083,495,1892,295,1241,920,1232,1421,1968,1849,585,1185;385,2193,559,328,2180,215,1898,1750,816,987,2152,1768,502,2099,283,2129,1776,184,365,281,626,2038,581,766,747,2497,638,1888,923,146,2154,2402,1611,1178,333,28,186,1957,482,1478,1776,277,962,630,113,2276,931,1108;637,1238,1246,2401,1762,2466,52,1231,898,1194,2252,916,1769,25,2297,388,2010,1303,2349,2488,865,1773,1750,607,830,2315,1831,868,1091,287,773,1306,1269,1058,1827,2159,260,1248,756,877,873,2322,1646,579,1517,2011,1950,751;1102,2017,534,2044,2407,2397,1856,2460,1152,1167,1700,2426,1230,1378,1478,656,1358,1219,2313,762,2224,793,2188,2439,1708,1803,1268,1023,1364,1935,2262,2394,1783,965,1143,950,1021,451,146,1153,2123,918,28,1957,1424,395,1322,1117;1868,967,749,1271,1938,1429,2318,947,2065,1334,2361,48,1042,1235,822,637,415,205,253,2376,388,532,1159,1214,70,2118,2323,1344,2321,515,473,884,1733,1161,1705,67,701,1263,973,1678,650,1574,438,39,474,1036,124,1871;278,1715,1171,777,2320,2225,2172,1154,2285,2271,2159,2365,2071,739,202,61,1458,1824,1379,2084,1589,1204,1578,2083,113,1638,511,1918,2490,1043,1563,362,353,917,1822,45,2306,2048,1445,2130,1502,593,2446,868,481,856,2198,144;1419,632,2119,339,1548,854,691,2401,2161,1053,52,1939,424,1362,877,653,871,2413,1760,1746,974,1218,1023,1822,1151,327,294,499,2135,1295,2361,1127,72,212,1365,998,1029,1828,821,664,1248,1445,309,1000,1012,1349,434,2221;2377,784,2035,2325,436,2348,594,470,1267,2154,1149,154,1810,2433,531,867,193,2198,1219,1363,401,1459,309,489,1524,2409,1798,14,2423,166,571,1396,2017,1296,2328,863,536,1314,1633,18,2275,1771,319,735,1609,1975,1534,1454;930,928,219,1106,1252,756,2225,2217,2208,1331,2388,411,1426,2262,93,1635,2279,1771,2395,2184,1457,2293,412,2424,36,1935,2219,363,188,1934,1651,2101,1422,1381,2067,959,582,2299,2171,328,2256,525,818,691,959,1393,151,1500;1244,730,1214,1311,2063,564,1658,508,39,398,2143,228,1971,734,1821,503,406,651,513,831,218,2457,1240,2494,1179,2404,843,658,2255,334,990,15,776,2071,1018,292,1190,1250,2269,637,1779,2388,1576,247,2111,710,1743,1370;1284,925,2278,1313,1399,2488,1847,726,2159,638,493,207,2083,1455,946,471,1991,1836,2477,1914,388,2296,137,2227,406,612,190,2287,818,505,1455,301,472,1549,1547,1316,909,1409,864,1279,2433,1752,1699,2312,633,2235,851,560;794,355,1136,175,122,606,158,1240,414,1641,108,2415,1123,1727,1186,904,1548,368,1268,1874,1783,1473,372,1028,811,37,821,1026,1123,1055,1334,42,1411,528,1702,1970,1135,2258,562,2444,1624,2230,1718,314,1303,2348,2409,1939;359,349,2488,2368,174,514,707,1864,1003,491,1626,1812,1160,2452,1411,480,2107,2100,1628,2177,1203,1698,95,1706,1564,1701,241,1452,681,2193,1422,1255,897,324,2226,1013,534,810,626,1262,1473,2007,600,676,656,1577,2437,1535;650,738,2108,635,2067,1638,186,856,1154,315,618,338,2136,1925,1662,2497,1533,412,397,342,26,1246,1156,543,1771,1889,2232,301,1424,1093,1494,38,485,2199,1012,381,1264,31,1742,691,432,819,944,879,622,1475,73,664;877,2350,502,556,1234,1773,2068,422,1244,1078,1183,323,1602,2453,2136,1190,1446,352,1275,41,1648,5,440,2292,825,2190,1046,1617,2024,1167,2007,1168,265,1700,897,705,19,2266,2404,1616,357,2206,1536,264,883,859,1821,2261;597,138,566,595,199,970,1177,1724,423,1415,1429,2319,952,151,1387,1476,1888,259,569,1595,577,599,458,1422,544,178,295,1468,32,642,1805,1801,176,858,1779,1046,7,915,830,761,1814,1072,2493,1513,2001,1147,1063,1178;517,1723,1390,1402,2357,1681,900,2306,334,831,836,63,1881,1337,1704,1864,1041,948,208,532,1937,2085,431,1452,1298,2402,221,1287,1410,1722,818,705,750,1380,843,503,29,2486,1618,1605,180,1699,1920,1129,1458,1473,1052,4", "output": "1438,1391,1146,1543,221,1384,2491,331,1,871,2345,1950,2188,1220,2090,1251,2170,1336,132,2334,1725,1631,2006,502,1247,667,1438,1819,245,41,409,2030,146,2025,1499,2352,2454,1217,217,1798,1829,749,59,2240,2308,1558,1035,524,1736,1630,507,1412,1702,717,2148,2248,1634,1417,1378,376,2071,2477,1803,1590,1137,507,752,1790,1388,1656,2218,1795,525,1990,979,1995,959,1581,1655,1654,452,1519,1005,1128,31,847,1169,615,853,2026,1118,2159,55,715,2413,619,872,1309,2113,628,133,1238,242,410,960,2432,1574,311,532,1892,2074,1294,775,2465,2385,128,1031,2239,2358,351,1123,1058,1569,530,1366,1167,1895,2308,602,1007,1951,2458,1791,247,1990,1452,1181,1505,1854,50,981,766,723,1296,2389,2474,2307,1255,2,2155,1763,2247,930,1609,2176,2404,1958,2082,2318,353,904,392,2441,1479,1414,2382,666,2380,293,1289,1304,1339,1630,2055,1659,1383,461,919,401,2021,801,1753,1426,42,81,1266,2373,1244,1664,471,332,2034,378,149,575,1974,717,491,1677,397,1215,1737,1344,582,387,1194,1860,1199,676,1840,1925,1074,1282,1027,1301,1946,1185,1849,1421,920,295,495,1476,1400,1902,2417,171,2,1736,2046,855,554,1068,2435,2272,1378,2278,1268,1552,1923,385,559,2180,1898,816,2152,502,283,1776,365,626,581,747,638,923,2154,1611,333,186,482,1776,962,113,931,751,2011,579,2322,877,1248,2159,1058,1306,287,868,2315,607,1773,2488,1303,388,25,916,1194,1231,2466,2401,1238,1102,534,2407,1856,1152,1700,1230,1478,1358,2313,2224,2188,1708,1268,1364,2262,1783,1143,1021,146,2123,28,1424,1322,1871,1036,39,1574,1678,1263,67,1161,884,515,1344,2118,1214,532,2376,205,637,1235,48,1334,947,1429,1271,967,278,1171,2320,2172,2285,2159,2071,202,1458,1379,1589,1578,113,511,2490,1563,353,1822,2306,1445,1502,2446,481,2198,2221,1349,1000,1445,664,1828,998,212,1127,1295,499,327,1822,1218,1746,2413,653,1362,1939,1053,2401,854,339,632,2377,2035,436,594,1267,1149,1810,531,193,1219,401,309,1524,1798,2423,571,2017,2328,536,1633,2275,319,1609,1534,1500,1393,691,525,328,2299,959,1381,2101,1934,363,1935,2424,2293,2184,1771,1635,2262,411,1331,2217,756,1106,928,1244,1214,2063,1658,39,2143,1971,1821,406,513,218,1240,1179,843,2255,990,776,1018,1190,2269,1779,1576,2111,1743,560,2235,2312,1752,1279,1409,1316,1549,301,505,2287,612,2227,2296,1914,1836,471,1455,207,638,726,2488,1313,925,794,1136,122,158,414,108,1123,1186,1548,1268,1783,372,811,821,1123,1334,1411,1702,1135,562,1624,1718,1303,2409,1535,1577,676,2007,1262,810,1013,324,1255,2193,1452,1701,1706,1698,2177,2100,480,2452,1812,491,1864,514,2368,349,650,2108,2067,186,1154,618,2136,1662,1533,397,26,1156,1771,2232,1424,1494,485,1012,1264,1742,432,944,622,73,2261,859,264,2206,1616,2266,705,1700,1168,1167,1617,2190,2292,5,41,352,1190,2453,323,1078,422,1773,556,2350,597,566,199,1177,423,1429,952,1387,1888,569,577,458,544,295,32,1805,176,1779,7,830,1814,2493,2001,1063,4,1473,1129,1699,1605,2486,503,1380,705,1722,1287,2402,1452,2085,532,948,1864,1337,63,831,2306,1681,1402,1723"}, {"input": "1364,924,2493,301,1085,897,281,1688,772,1918,2435,429,1710,516,1551;677,1658,1612,2351,513,1121,700,1241,1824,832,2058,69,728,212,2277;1997,144,2371,623,1043,2328,2053,1570,606,1195,711,1889,2179,1175,1178;480,573,1211,2099,1771,1980,483,1558,657,1214,2458,966,1971,2415,150;2455,1443,1188,1900,528,2006,1311,902,2324,446,2340,1863,2439,87,461;1814,1453,824,1446,1181,1853,1596,1033,874,794,1567,2451,1449,152,367;1134,655,634,362,178,66,1838,1145,363,885,2260,676,122,1433,694;1053,2156,1143,1390,1489,1709,2158,68,1834,780,1022,1883,463,1561,2185;108,2247,1072,1027,834,1642,2004,1751,1170,2237,2406,1968,1645,1723,1468;1298,428,317,2467,1340,1569,809,1626,1744,152,1078,1497,166,1569,1476;1428,1575,2113,995,1480,502,1877,831,880,2382,646,855,778,1282,2441;1270,1878,1012,262,1237,1310,1107,2169,850,1760,173,1386,1276,1562,2391;299,2384,1818,2144,1965,2097,1158,2489,1177,1324,2121,1873,2089,2186,2034;112,1075,1948,1903,1854,2404,1201,575,2495,1445,937,1771,787,2162,1627;548,886,490,1031,594,593,1246,2114,1134,871,1532,499,1590,570,589;1411,1486,1563,2226,1413,1179,471,2360,2235,2483,1468,1122,1787,928,712;508,2496,1324,1756,1789,99,1762,1007,839,1685,914,1655,1576,797,139;2006,1634,1605,1415,450,1797,85,385,754,64,2074,198,510,2435,502;911,1699,1911,11,1246,1753,95,2049,2458,1809,682,1468,2308,2142,1054;2124,1745,1574,2159,925,1406,148,1814,2456,2011,546,2038,2015,604,1411;411,2437,282,2089,2265,1678,1682,23,1794,2353,2133,405,1678,2365,1294;2279,1601,1872,1748,736,2498,768,958,1915,348,2088,797,741,1753,215;1532,1814,724,2078,2035,1992,1778,218,1569,2438,1941,655,1796,894,1038;26,923,1007,849,1643,1504,2038,1046,524,939,2201,442,2044,1267,1057;1495,2474,1918,1929,1555,2112,2055,132,1027,1782,1058,592,279,2139,598;2085,1078,9,284,496,1140,1460,1681,1191,2344,2396,1762,2134,948,2226;1742,101,648,81,535,2078,1092,2208,2178,728,2406,2211,233,275,4;54,1704,2041,2362,1573,270,2354,1003,570,1454,1674,725,834,1145,357;336,1233,2329,2422,27,112,772,2284,948,70,620,491,2455,183,1310;2264,2110,153,1040,486,843,2168,1,1287,839,1894,2365,680,1802,1024;307,1805,415,724,1161,761,1132,131,1661,1618,122,1831,1162,304,249;1141,211,2465,1786,470,342,18,1293,2417,1215,2491,373,215,1197,1360;284,2171,1997,448,1422,2449,220,1972,1850,2370,1697,449,2399,670,2271;787,471,598,893,619,1954,2427,1330,1287,361,220,686,1308,929,291", "output": "1364,2493,1085,281,772,2435,1710,1551,212,69,832,1241,1121,2351,1658,1997,2371,1043,2053,606,711,2179,1178,2415,966,1214,1558,1980,2099,573,2455,1188,528,1311,2324,2340,2439,461,152,2451,794,1033,1853,1446,1453,1134,634,178,1838,363,2260,122,694,1561,1883,780,68,1709,1390,2156,108,1072,834,2004,1170,2406,1645,1468,1569,1497,152,1626,1569,2467,428,1428,2113,1480,1877,880,646,778,2441,1562,1386,1760,2169,1310,262,1878,299,1818,1965,1158,1177,2121,2089,2034,2162,1771,1445,575,2404,1903,1075,548,490,594,1246,1134,1532,1590,589,928,1122,2483,2360,1179,2226,1486,508,1324,1789,1762,839,914,1576,139,2435,198,64,385,1797,1415,1634,911,1911,1246,95,2458,682,2308,1054,604,2038,2011,1814,1406,2159,1745,411,282,2265,1682,1794,2133,1678,1294,1753,797,348,958,2498,1748,1601,1532,724,2035,1778,1569,1941,1796,1038,1267,442,939,1046,1504,849,923,1495,1918,1555,2055,1027,1058,279,598,948,1762,2344,1681,1140,284,1078,1742,648,535,1092,2178,2406,233,4,1145,725,1454,1003,270,2362,1704,336,2329,27,772,948,620,2455,1310,1802,2365,839,1,843,1040,2110,307,415,1161,1132,1661,122,1162,249,1197,373,1215,1293,342,1786,211,284,1997,1422,220,1850,1697,2399,2271,929,686,361,1330,1954,893,471"}, {"input": "2350,660,345,987,616,1310,884,2061,718,1874,1535,1856,1979,2213,2116,73,600,1394,1287,916,1481,2229,1292,621,959,376,2490,907,1994,618,1529,895,2138,2437;1344,434,578,1443,2191,1697,165,1094,1987,2070,2238,2325,2465,1921,2083,2179,624,2126,1499,1930,1687,1898,2082,1117,1289,1750,1552,1237,322,2260,119,2494,946,1318;1389,1883,1649,1442,2192,144,222,347,1233,915,891,1596,885,1959,1179,677,2346,1285,2242,46,2251,19,2466,766,579,1876,801,173,731,1541,2449,788,2256,307;1687,456,2210,2160,729,1512,1354,2323,1839,2232,1103,911,334,1510,304,680,1560,1744,1301,2233,564,2227,1439,2457,2428,1718,54,345,792,1028,218,106,96,1157;283,2405,626,698,743,2033,377,1008,2044,1529,2354,78,937,2260,754,2239,1764,1166,1932,621,105,974,1592,1112,573,241,1748,1986,2455,2030,8,1265,19,327;660,2155,376,1862,1506,979,1878,549,1321,1798,2497,1911,216,1258,1320,1216,2455,933,45,1323,2096,84,214,238,2363,1747,771,2010,1162,1198,841,1807,1534,1267;139,501,949,1602,297,197,2251,1030,1586,2231,740,1419,956,1694,1778,1684,498,1332,2306,1197,1454,1594,1606,1503,1353,264,595,1907,1951,1564,63,1025,38,1950;1583,1306,2395,1000,1900,1898,121,1918,479,1765,2355,911,314,1971,742,604,2120,1544,1818,669,154,202,1645,788,2430,2258,1326,1513,776,88,337,424,436,2305;141,1,2030,933,2271,1910,611,792,2481,262,18,2373,222,2112,441,2180,1885,1491,907,413,1153,436,1619,1881,1968,479,1594,1526,1732,2153,1428,2305,1752,544;2396,1684,1205,1712,126,913,827,160,730,792,1747,2008,653,1468,40,1487,435,1391,1097,30,2016,107,1577,56,1177,1791,968,2162,799,477,384,558,1581,1336;1280,1163,2144,2231,1563,1386,2124,1587,2172,797,1982,1189,1319,502,313,1015,982,2289,113,1745,1751,396,1451,336,736,2021,2259,663,2303,438,788,1667,673,72;934,876,2438,661,2317,2321,581,1417,1249,748,1368,589,2066,523,2015,1112,593,1056,1709,51,339,1220,2450,641,1298,1068,1506,2223,487,1700,670,1371,1368,813;2334,2211,1391,821,693,1170,901,636,2139,364,538,2084,1304,207,1,1947,2493,1193,2368,609,793,1777,839,1481,2219,836,1799,2107,2090,262,1145,673,290,2476;654,1956,2076,1238,1703,238,1896,2178,1100,1819,1372,2009,189,935,2178,1435,2034,1721,68,1593,1516,933,718,1904,791,2281,281,1216,140,1770,409,1338,1820,2321;945,1955,1492,781,1088,2020,963,1144,2380,1625,945,1063,529,368,228,2459,1007,892,494,1757,57,1873,2220,829,2147,2396,1706,1612,989,2289,133,539,1507,68;210,1103,168,2393,595,1775,1940,1281,1734,15,955,1139,1659,420,2067,1127,1559,2258,1363,129,1826,63,557,1544,827,97,760,325,2113,1357,354,1036,2314,2426;697,426,982,92,1211,1085,2231,1218,1738,1512,921,17,1679,2448,1772,2137,689,1955,361,1042,2453,22,860,771,117,1940,200,1554,1654,945,1238,1682,2234,894;1682,1897,2204,1711,2484,1311,599,1338,1115,2141,2121,176,205,2355,2088,2182,634,223,219,1638,2323,1663,1960,1316,2277,1321,1100,115,2013,544,94,428,855,2367;915,1409,884,475,2195,1740,102,2483,2259,1690,835,2242,2399,1285,1307,904,2484,617,1868,1101,2477,1660,1872,863,241,2185,419,66,355,1447,184,2292,346,1622;995,1975,2262,2289,275,1533,1701,1946,1187,2131,340,2192,1038,593,2113,1206,1793,1177,1074,516,2252,1924,756,1017,1610,1900,28,2281,135,1366,377,1215,756,225;2206,949,1849,1586,453,902,1598,382,2199,1595,182,858,660,1390,1166,2063,2062,1280,1466,1371,1993,2254,1633,2489,1233,208,2447,768,1878,2293,195,2340,889,1129", "output": "2350,345,616,884,718,1535,1979,2116,600,1287,1481,1292,959,2490,1994,1529,2138,1318,2494,2260,1237,1750,1117,1898,1930,2126,2179,1921,2325,2070,1094,1697,1443,434,1389,1649,2192,222,1233,891,885,1179,2346,2242,2251,2466,579,801,731,2449,2256,1157,106,1028,345,1718,2457,2227,2233,1744,680,1510,911,2232,2323,1512,2160,456,283,626,743,377,2044,2354,937,754,1764,1932,105,1592,573,1748,2455,8,19,1267,1807,1198,2010,1747,238,84,1323,933,1216,1258,1911,1798,549,979,1862,2155,139,949,297,2251,1586,740,956,1778,498,2306,1454,1606,1353,595,1951,63,38,2305,424,88,1513,2258,788,202,669,1544,604,1971,911,1765,1918,1898,1000,1306,141,2030,2271,611,2481,18,222,441,1885,907,1153,1619,1968,1594,1732,1428,1752,1336,558,477,2162,1791,56,107,30,1391,1487,1468,2008,792,160,913,1712,1684,1280,2144,1563,2124,2172,1982,1319,313,982,113,1751,1451,736,2259,2303,788,673,813,1371,1700,2223,1068,641,1220,51,1056,1112,523,589,748,1417,2321,661,876,2334,1391,693,901,2139,538,1304,1,2493,2368,793,839,2219,1799,2090,1145,290,2321,1338,1770,1216,2281,1904,933,1593,1721,1435,935,2009,1819,2178,238,1238,1956,945,1492,1088,963,2380,945,529,228,1007,494,57,2220,2147,1706,989,133,1507,2426,1036,1357,325,97,1544,63,129,2258,1127,420,1139,15,1281,1775,2393,1103,697,982,1211,2231,1738,921,1679,1772,689,361,2453,860,117,200,1654,1238,2234,2367,428,544,115,1321,1316,1663,1638,223,2182,2355,176,2141,1338,1311,1711,1897,915,884,2195,102,2259,835,2399,1307,2484,1868,2477,1872,241,419,355,184,346,225,1215,1366,2281,1900,1017,1924,516,1177,1206,593,2192,2131,1946,1533,2289,1975,2206,1849,453,1598,2199,182,660,1166,2062,1466,1993,1633,1233,2447,1878,195,889"}, {"input": "2455,24,971,925,1405,1277;2308,146,1581,1606,606,2322;1579,1004,25,2061,2403,7;2330,1248,374,184,980,1207;60,2209,573,1640,1047,1211;1390,1609,1118,1041,797,296;571,127,967,936,1761,1577;1000,414,1681,677,2325,850;2408,2309,533,390,1481,2175;1474,1749,1245,1541,152,805;1285,343,422,2403,1108,1734;1846,877,1587,1760,909,211;2087,1488,93,522,199,1698;1464,916,1861,1228,588,169;2131,965,2252,175,2478,2358;1587,2163,1768,2460,212,114;2474,1411,2199,882,2392,2216;249,1860,379,1785,716,156;116,1346,923,2406,2060,815;2156,405,751,1923,1985,2059;1746,350,77,865,1702,355;1231,2210,340,813,1657,1212;1225,1992,945,2058,550,1549;179,549,331,553,196,912;311,248,2229,1113,1535,2316;487,2067,2384,385,35,252;1237,1761,6,1197,1262,397;2376,1977,456,1931,368,421;2417,589,785,2308,1265,1705;458,1070,1746,1529,1756,1912;1308,84,267,2043,2166,1074;2101,1726,318,541,926,1466;1178,1906,919,972,1837,312;997,2321,725,800,1744,1350;6,1708,2260,1214,2466,1277;1488,2006,929,1018,1058,2258;2294,1294,1314,646,219,1370;1905,770,518,1926,548,1761;1810,725,1432,326,1636,767;1086,2499,127,296,1593,1242;150,106,192,1110,1397,951", "output": "2455,971,1405,2322,1606,146,1579,25,2403,1207,184,1248,60,573,1047,296,1041,1609,571,967,1761,850,677,414,2408,533,1481,805,1541,1749,1285,422,1108,211,1760,877,2087,93,199,169,1228,916,2131,2252,2478,114,2460,2163,2474,2199,2392,156,1785,1860,116,923,2060,2059,1923,405,1746,77,1702,1212,813,2210,1225,945,550,912,553,549,311,2229,1535,252,385,2067,1237,6,1262,421,1931,1977,2417,785,1265,1912,1529,1070,1308,267,2166,1466,541,1726,1178,919,1837,1350,800,2321,6,2260,2466,2258,1018,2006,2294,1314,219,1761,1926,770,1810,1432,1636,1242,296,2499,150,192,1397"}, {"input": "1637,1079,63,1186;2458,664,1945,1148;108,2256,2258,885;1429,1818,494,2450;1931,95,589,503;1716,621,1296,1692;1732,1475,811,791;641,94,415,650;432,646,887,59;589,1654,759,1302;264,212,520,2021;524,306,1989,2089;1047,829,1691,1748;1170,1976,2161,201;2146,1432,2171,1881;1107,1424,625,214;1516,2454,1079,1069;995,741,1247,1194;813,2199,2139,1405;643,1284,1731,946;2406,1700,125,1297;1047,1119,1109,1410", "output": "1637,63,1148,664,108,2258,2450,1818,1931,589,1692,621,1732,811,650,94,432,887,1302,1654,264,520,2089,306,1047,1691,201,1976,2146,2171,214,1424,1516,1079,1194,741,813,2139,946,1284,2406,125,1410,1119"}, {"input": "1465,651,591,1272,994,1669,311,923,1452,2192,2335,184,1268,1038,2038,129,2049,1223,625,1792,683,1427,863,1508,468,277,714,228,1435,1448,1527,2411,1420,2227,2382;171,243,2438,2210,2259,1550,829,2380,1494,1750,2246,1192,1984,11,535,1320,277,910,851,1959,262,2408,405,1042,1756,2105,517,1360,1768,1113,1542,785,1961,206,72;1024,2268,1011,455,667,517,2300,194,1968,1548,2179,2334,2384,1701,196,117,1778,1780,952,1003,124,2328,284,1863,1998,158,299,326,539,2462,1074,425,494,67,1690;861,2482,2003,1754,167,2109,2235,1152,26,1538,2033,1135,1421,598,1070,2105,868,1324,2500,850,2265,193,1070,1395,2099,1871,75,2020,1348,1219,2235,357,2467,1771,2285;1558,810,1546,223,921,1499,929,177,437,171,1429,2413,1640,785,1605,1572,1735,1337,932,186,221,95,181,1148,979,1966,200,1149,2025,2196,1475,184,1242,2137,2307;2072,1662,2365,1683,1785,605,2224,76,1995,1210,598,792,2472,1832,120,1015,836,1408,1113,747,1163,513,1042,645,482,397,2299,1932,297,126,862,344,2387,1286,1320;1809,953,1828,110,1274,1793,561,2167,1284,1122,2327,563,372,1571,1218,2391,707,995,476,252,575,1080,1757,1732,1843,1411,1897,718,127,564,2417,72,130,1361,1664;1715,130,2344,727,1629,2143,105,1237,171,1076,540,2049,1251,1193,406,957,1870,1216,2347,687,734,164,1648,1438,260,2471,862,645,1086,1035,1809,418,2384,1617,1462;625,990,84,1816,2202,1883,798,2364,1272,513,855,2276,1706,1805,64,1087,2432,584,702,2120,720,405,666,224,1712,1898,150,1935,1494,289,1585,1886,2090,468,2064;419,1024,411,295,35,1529,1822,621,2356,416,659,2124,2450,205,439,557,1488,2435,344,202,2009,59,11,2175,2006,796,1295,402,1056,925,2351,968,146,367,105;879,1746,2494,1616,1723,201,355,1478,1219,556,1781,2080,1510,2259,562,361,2058,879,2299,845,271,1472,1914,315,925,1600,295,2239,83,1443,1167,1765,113,1530,630;23,735,1425,2479,1830,1617,782,2147,2211,2365,2353,1747,1735,107,1041,1112,482,1684,610,90,1051,2010,1557,2089,1528,1950,434,2252,1291,1087,1777,1435,1216,2299,473;21,1717,723,1910,2162,832,24,2088,1305,357,2284,615,1531,978,1994,605,1115,14,1527,1180,1045,1495,2140,1892,2055,2119,1445,2215,1196,1954,102,1367,1523,1031,2487;1797,2299,1402,2178,256,177,849,1257,274,140,2166,1179,1680,629,2370,29,1328,1028,1193,883,2240,1043,1450,1674,1212,573,1819,2293,2084,1335,1061,3,2246,2374,733;366,775,492,406,1833,239,1881,730,1421,2455,876,826,107,797,956,697,1049,1496,715,1297,1459,431,923,1990,302,1230,1873,1665,1009,1299,1559,769,1899,1538,2373;1806,2458,5,2480,2448,2046,180,1926,767,526,1577,138,1044,190,571,412,181,1199,1496,38,1421,2062,1475,984,1710,1098,1754,2304,1522,714,798,2141,715,2173,1028;2270,371,2031,2483,663,1666,1009,1823,1218,753,1817,2019,1929,1650,2252,992,1529,214,1874,1836,1455,1061,2261,1785,2212,1604,2402,1205,1732,2304,2408,1627,533,1070,1520;1884,1562,1511,510,1084,2024,2164,1979,1902,1947,2433,1493,2003,72,2099,1070,900,1387,882,1969,1668,741,565,2434,2170,373,2046,330,2279,1507,208,31,349,120,1047;206,1362,786,248,1931,2404,1537,1812,1007,2295,1374,112,2346,936,2047,1832,2128,2307,152,1104,2497,1699,122,988,1009,2217,149,2071,1125,2239,1517,949,1221,787,2048;1942,160,2165,691,1729,515,1373,2480,1695,187,1118,1811,1464,1673,372,1973,1765,199,566,471,715,917,1348,1922,486,278,1022,2359,681,2052,830,1649,1888,822,542;988,1345,1358,1413,91,1795,1047,1118,2110,2386,1363,9,924,2094,1566,1929,956,548,1588,796,761,1419,2083,1113,131,1672,554,969,1245,1843,472,428,480,2389,1913;1798,130,1335,1741,1962,31,2204,426,2457,1517,1401,1058,88,2466,2076,2284,933,608,2343,1352,1968,1141,666,2003,787,1263,754,2046,2305,366,2288,1608,1576,1693,41;1645,364,620,1713,1243,306,1417,1950,1608,1845,103,1109,652,185,1327,10,2427,2449,28,2293,373,1415,683,468,588,425,2140,2125,547,1227,1204,779,1153,80,768;2008,232,362,832,985,542,290,2277,189,2072,1230,126,2080,1328,714,2418,1684,1941,27,1660,1314,554,1633,1157,821,2305,304,1201,769,158,136,872,965,274,576;2106,1009,1543,878,55,1695,229,509,837,1397,1470,1422,1590,1146,2207,1483,330,315,1557,410,1581,464,1508,149,879,737,415,798,1273,2344,1096,1478,357,2334,2160;2188,146,2174,901,987,1188,1329,1925,270,1428,1479,1504,611,1847,630,1876,374,1143,896,1563,2060,2269,2149,2222,499,1660,343,665,108,1752,1041,1941,2314,2162,1522;397,2085,1255,2280,449,730,2288,1253,795,2469,813,1542,1849,77,19,249,1167,216,2410,1481,591,1079,1054,2437,2073,1191,2352,1520,1746,1480,2489,1124,1276,890,881;1494,2361,2219,2325,498,521,242,2097,717,824,1641,2171,127,178,1499,502,1223,236,1868,1894,153,903,701,353,2014,1367,1292,631,921,2375,1014,874,732,1784,389;656,341,1151,84,60,351,2102,2139,249,1199,948,33,1923,2414,330,2088,1686,974,838,2393,404,524,2108,1905,2007,1200,1574,1163,230,390,1770,855,930,1289,745;994,2482,1694,782,352,245,964,1477,1352,809,1370,2007,1443,151,835,972,1112,2332,1456,826,905,1216,936,1992,203,83,1834,1754,937,1738,37,2109,335,1591,358;2356,72,631,2108,1506,1636,1750,1812,791,53,30,1235,1682,1781,2221,867,128,2440,1965,721,880,1113,2442,179,2223,2367,1141,1739,1134,2121,2473,1274,2038,2267,723;86,1891,1602,1954,1389,1704,305,2070,1062,1215,963,2432,2336,687,361,1720,2427,2099,404,300,1613,1441,619,1161,755,2186,1104,573,954,903,1877,118,784,829,477;1153,1869,564,1502,2329,2312,18,658,1099,1250,400,239,857,350,1565,2097,568,303,612,121,1438,330,2431,742,1199,1267,1214,1735,1020,548,2045,23,134,85,537;234,729,926,2423,962,1711,124,579,225,2380,848,2188,2222,1436,77,1274,1122,2134,909,2002,579,227,1923,1780,1864,1693,1309,840,2500,885,2357,1472,893,887,2123;1727,1898,2136,1997,1122,1742,357,446,359,2462,2350,341,1548,1381,73,137,746,1551,807,1040,2311,1736,1147,29,829,1291,1567,1658,1271,346,2250,827,1963,2408,1966;962,2150,2011,495,1303,1535,603,767,2072,389,785,1617,1805,2377,1289,808,1138,1648,1027,392,631,17,348,2045,300,246,269,3,1273,2254,2463,1853,218,1470,361;893,2136,378,1465,556,611,685,1644,1767,15,1463,1136,846,526,2244,2148,213,82,209,769,2241,1387,1396,1038,429,1802,515,625,546,2389,1829,1399,1145,1922,2134;1986,54,1291,220,1493,358,2311,771,264,1737,1567,908,339,2427,665,2070,2385,1361,1738,499,1078,1966,223,1436,2268,1638,1187,1702,2145,2118,1635,1993,1878,692,942;2483,1880,8,2408,2369,1800,1506,1118,1924,341,252,2154,148,1564,2318,126,1438,499,2046,1770,689,116,212,894,634,1898,1128,56,836,497,2190,2278,448,2381,1046;1283,430,876,704,1788,1487,1393,397,852,2190,1141,1213,339,1905,23,2056,2047,2004,1847,1,2185,70,717,1609,2320,1469,268,1201,2301,1907,559,1609,2386,343,2396;1266,2281,1977,1093,575,2468,1744,1072,196,1403,1302,779,174,226,328,810,1077,1450,1315,670,1822,571,499,1235,1491,244,1849,338,608,376,1511,99,1854,1842,1209;487,1,866,181,2360,2074,2367,756,2190,2201,897,251,1985,1436,808,907,38,1993,1113,1633,1792,214,983,1618,1411,2429,1673,149,1420,604,662,2441,1351,2414,2040;1965,825,903,153,2148,1003,1581,1004,1892,1929,882,1567,1283,766,1485,93,1776,1552,241,1158,357,592,875,6,2187,1303,618,767,2109,2191,939,2170,401,647,1400;60,52,846,1194,261,2166,539,135,1297,2148,347,388,1469,328,1220,1924,1198,1097,806,484,324,2112,654,1291,1174,795,1201,1936,1056,1803,2065,1056,1219,188,820", "output": "1465,591,994,311,1452,2335,1268,2038,2049,625,683,863,468,714,1435,1527,1420,2382,206,785,1113,1360,2105,1042,2408,1959,910,1320,11,1192,1750,2380,1550,2210,243,1024,1011,667,2300,1968,2179,2384,196,1778,952,124,284,1998,299,539,1074,494,1690,1771,357,1219,2020,1871,1395,193,850,1324,2105,598,1135,1538,1152,2109,1754,2482,1558,1546,921,929,437,1429,1640,1605,1735,932,221,181,979,200,2025,1475,1242,2307,1286,344,126,1932,397,645,513,747,1408,1015,1832,792,1210,76,605,1683,1662,1809,1828,1274,561,1284,2327,372,1218,707,476,575,1757,1843,1897,127,2417,130,1664,1617,418,1035,645,2471,1438,164,687,1216,957,1193,2049,1076,1237,2143,727,130,625,84,2202,798,1272,855,1706,64,2432,702,720,666,1712,150,1494,1585,2090,2064,367,968,925,402,796,2175,59,202,2435,557,205,2124,416,621,1529,295,1024,879,2494,1723,355,1219,1781,1510,562,2058,2299,271,1914,925,295,83,1167,113,630,2299,1435,1087,2252,1950,2089,2010,90,1684,1112,107,1747,2365,2147,1617,2479,735,21,723,2162,24,1305,2284,1531,1994,1115,1527,1045,2140,2055,1445,1196,102,1523,2487,2374,3,1335,2293,573,1674,1043,883,1028,29,629,1179,140,1257,177,2178,2299,366,492,1833,1881,1421,876,107,956,1049,715,1459,923,302,1873,1009,1559,1899,2373,2173,2141,714,2304,1098,984,2062,38,1199,412,190,138,526,1926,2046,2480,2458,2270,2031,663,1009,1218,1817,1929,2252,1529,1874,1455,2261,2212,2402,1732,2408,533,1520,120,31,1507,330,373,2434,741,1969,1387,1070,72,1493,1947,1979,2024,510,1562,206,786,1931,1537,1007,1374,2346,2047,2128,152,2497,122,1009,149,1125,1517,1221,2048,822,1649,2052,2359,278,1922,917,471,199,1973,1673,1811,187,2480,515,691,160,988,1358,91,1047,2110,1363,924,1566,956,1588,761,2083,131,554,1245,472,480,1913,1693,1608,366,2046,1263,2003,1141,1352,608,2284,2466,1058,1517,426,31,1741,130,1645,620,1243,1417,1608,103,652,1327,2427,28,373,683,588,2140,547,1204,1153,768,274,872,158,1201,2305,1157,554,1660,1941,2418,1328,126,2072,2277,542,832,232,2106,1543,55,229,837,1470,1590,2207,330,1557,1581,1508,879,415,1273,1096,357,2160,2162,1941,1752,665,1660,2222,2269,1563,1143,1876,1847,1504,1428,1925,1188,901,146,397,1255,449,2288,795,813,1849,19,1167,2410,591,1054,2073,2352,1746,2489,1276,881,1784,874,2375,631,1367,353,903,1894,236,502,178,2171,824,2097,521,2325,2361,656,1151,60,2102,249,948,1923,330,1686,838,404,2108,2007,1574,230,1770,930,745,1591,2109,1738,1754,83,1992,1216,826,2332,972,151,2007,809,1477,245,782,2482,2356,631,1506,1750,791,30,1682,2221,128,1965,880,2442,2223,1141,1134,2473,2038,723,829,118,903,573,2186,1161,1441,300,2099,1720,687,2432,1215,2070,1704,1954,1891,1153,564,2329,18,1099,400,857,1565,568,612,1438,2431,1199,1214,1020,2045,134,537,887,1472,885,840,1693,1780,227,2002,2134,1274,1436,2188,2380,579,1711,2423,729,1727,2136,1122,357,359,2350,1548,73,746,807,2311,1147,829,1567,1271,2250,1963,1966,1470,1853,2254,3,246,2045,17,392,1648,808,2377,1617,389,767,1535,495,2150,893,378,556,685,1767,1463,846,2244,213,209,2241,1396,429,515,546,1829,1145,2134,692,1993,2118,1702,1638,1436,1966,499,1361,2070,2427,908,1737,771,358,220,54,2483,8,2369,1506,1924,252,148,2318,1438,2046,689,212,634,1128,836,2190,448,1046,343,1609,1907,1201,1469,1609,70,1,2004,2056,1905,1213,2190,397,1487,704,430,1266,1977,575,1744,196,1302,174,328,1077,1315,1822,499,1491,1849,608,1511,1854,1209,2414,2441,604,149,2429,1618,214,1633,1993,907,1436,251,2201,756,2074,181,1,1965,903,2148,1581,1892,882,1283,1485,1776,241,357,875,2187,618,2109,939,401,1400,188,1056,1803,1936,795,1291,2112,484,1097,1924,328,388,2148,135,2166,1194,52"}, {"input": "34,2459,342,149,701,2428,1789,1560,29,1117,2015,1876,1333,2094,842,1551,645,2122,1779,2172,928,2083,127,811,754,1534,770,2216,2319,747,2202,572,1595,1028,193,2023,1225,1767,702,1478,291,2258,221,1820,919,174,248;388,1757,1748,1039,1865,2073,537,2334,2047,1560,1331,1522,1285,2070,1538,2246,618,2144,1712,1323,2254,1073,142,2183,952,1210,66,413,1147,1508,457,1893,2454,1073,599,196,1855,981,1818,1154,679,1684,1737,1373,1438,552,244;236,627,255,61,1596,455,2173,1602,350,427,2068,1449,1306,1194,1552,1159,519,273,1527,1132,1773,7,1213,1637,1471,1624,39,288,320,501,2472,1317,1001,753,187,1800,290,1741,957,1267,1348,2279,1882,2404,577,790,1478;2047,1332,1732,1098,1074,538,1779,72,1748,1130,1932,1338,2409,617,622,456,995,1491,1994,814,591,1105,1776,1407,1649,106,1292,1057,1093,1440,1155,961,463,2258,1276,1790,2310,530,1814,804,157,1187,204,2003,1469,2413,148;2310,1830,1833,1286,1338,2371,894,781,1236,1725,393,412,2237,1142,493,926,756,710,2106,1220,2277,1295,630,39,1909,135,2420,451,2186,1129,581,372,172,1456,2090,310,1563,2186,8,1431,1391,2074,1575,2348,1416,852,642;1713,2384,387,1590,420,1976,1455,2123,182,1354,2343,1117,1881,122,1205,1297,1183,810,1078,1203,696,765,2253,1183,94,100,2015,1380,1659,1846,2166,1779,1700,203,1743,24,16,901,1850,1056,1258,1,558,1615,1615,171,1313;508,2035,1493,1315,689,1716,1392,967,448,755,547,330,483,1776,687,78,185,463,1340,2230,1504,1296,815,2135,1789,1160,25,762,2108,1609,2218,2241,44,2461,949,1070,788,1292,738,1381,941,1081,1700,355,1086,1648,1284;742,2097,1349,2085,356,421,188,532,927,315,163,1693,467,338,2414,480,848,253,403,775,2285,2076,248,21,1312,1634,2467,2465,1384,1144,1991,2426,832,727,1574,2276,515,1318,1204,672,1340,1661,1613,1573,1642,1885,299;1902,2000,1134,1664,64,606,774,463,1346,694,557,2356,1039,2054,602,692,1156,2405,697,802,499,882,777,2239,1946,496,1140,978,1793,2292,1556,2086,38,2143,1275,932,1107,2500,1371,802,943,1851,1993,841,285,1942,543;1305,619,1995,531,2132,1398,476,2072,967,28,1023,808,1140,1481,2068,667,1967,1276,976,1535,2058,612,266,36,555,1679,184,22,846,2437,2068,2259,2166,580,711,1012,750,503,1890,2145,407,1152,1353,1119,195,1013,476;678,688,817,1008,14,523,711,2284,2292,507,221,2489,1789,1333,1384,2410,1366,293,512,2259,1426,1350,1559,185,1460,2448,300,693,1498,2216,1189,1918,1740,1305,1288,131,2278,914,1930,1895,775,1671,656,861,1154,1982,554;1334,17,508,2101,1254,2335,1414,2080,1797,475,1325,989,2473,2378,2453,960,1592,1317,490,799,694,122,2478,1049,457,994,680,2074,1794,1535,2237,2003,1018,736,2117,570,761,218,437,2038,232,1325,2332,1722,2313,389,484;540,1531,2453,1508,255,478,253,1575,232,2450,1559,296,371,314,1008,2090,1633,174,611,1735,2300,1393,359,998,1967,1656,372,790,2328,1428,901,859,2455,1357,2135,621,1154,1846,616,1948,418,2103,2143,1698,957,1458,1307;422,557,1277,2100,2461,658,1561,1613,731,291,1492,1254,581,2343,645,1591,1110,223,1884,168,1244,277,1566,172,2421,931,485,1543,1137,2235,1949,1762,737,1735,1843,784,1965,467,1354,1671,473,1228,508,1703,304,2059,2356;257,1003,294,1647,245,2323,293,2088,154,2022,1053,892,493,301,2008,119,2155,184,1112,646,652,1012,1826,2488,2221,1825,1867,925,1494,2428,2088,139,1177,152,290,2480,1411,1011,2044,2414,833,1974,303,1922,2480,154,1444;925,2497,588,990,798,603,1661,1561,640,1890,308,879,990,824,924,1485,466,836,946,1801,1541,2157,777,156,1245,878,1505,1466,2252,829,661,783,415,648,912,1398,1918,1788,55,2122,482,310,1704,2327,1121,369,2281;1446,1508,1294,1801,145,955,618,252,1463,2211,1020,1462,1647,1716,270,1313,147,640,559,1531,799,1341,1116,2029,1674,1215,207,1846,138,2072,2136,1948,2234,2102,2117,760,1359,828,1109,1243,361,2409,2329,2383,1533,458,646;587,1201,1400,536,1983,1050,1481,217,1402,1251,231,604,1358,495,1671,619,1289,1609,1012,2112,459,424,2238,206,1184,1793,1367,1291,205,1048,1699,1471,2276,1926,1545,2177,615,2036,2333,1532,2316,634,1828,140,386,2066,2297;827,210,1503,2009,116,1897,2265,876,1207,2026,1103,2354,98,1262,1630,556,815,1925,2303,2284,505,1064,937,2371,2468,1167,189,129,1269,1826,1478,160,856,284,1544,2371,126,552,583,594,599,2266,93,2196,1963,2061,933;449,1480,2114,86,1327,1261,2471,148,2428,223,1246,455,1724,2369,1494,651,2491,849,1772,469,1683,1481,621,1621,1780,1429,401,1993,1161,150,2054,626,466,1903,85,955,1229,834,1913,2402,90,669,2239,504,282,2275,882;295,1418,1723,2193,232,1336,827,1669,551,1091,2414,1707,1883,717,1611,1226,868,1245,2429,2306,1034,2035,2250,527,910,270,1969,2181,34,2415,2068,2150,916,1570,2169,1592,1696,69,1656,1418,928,1057,2303,702,706,1999,322;937,111,629,1768,243,838,1098,1512,358,799,235,2045,2133,274,2274,2375,1583,509,184,1735,1186,307,1402,2032,1257,125,775,1552,2050,886,2104,2298,1725,1691,2286,493,2433,2394,1360,2058,1475,1743,2496,924,1856,1929,704;163,1536,1435,297,2193,2001,44,110,1245,1881,922,1399,2201,2260,710,634,643,2216,5,2213,1886,1801,928,2376,2002,480,1806,1231,139,2287,321,1868,2486,1142,1038,674,1251,1644,1342,502,810,355,691,689,171,745,873;45,625,657,451,561,156,61,2479,560,1277,469,853,512,2173,1105,1083,2217,2074,1372,432,2104,1198,2166,80,747,2040,1419,2226,175,133,2247,2447,1200,2464,2035,2364,410,2160,1723,2219,1232,1459,1385,1362,414,2275,698;1864,1416,37,2020,318,788,2057,1297,2046,238,458,1905,368,1048,1388,1850,1859,1034,510,37,1160,620,425,1858,2080,2338,1592,617,1243,1636,699,113,1176,1298,1476,1982,271,345,447,254,1793,953,2272,2061,2398,2323,2020;1132,1590,854,130,1009,41,1793,615,1127,2027,1759,73,147,4,820,1811,4,1303,1508,970,1415,953,1835,1597,512,1309,854,1376,1366,491,874,2439,1589,2391,398,313,966,1038,1530,17,2211,2139,2279,2148,2268,425,184;1726,917,2435,1010,1556,343,70,137,2404,584,67,1428,1417,203,1918,487,874,2091,1023,1669,2121,1619,1134,2141,2142,37,1927,4,974,2083,1849,1922,1990,738,1294,1184,2273,1496,1609,644,1031,1979,1869,149,1180,443,1129;1743,439,316,2357,1999,816,502,959,1035,2468,709,1616,814,2038,1825,1722,2139,1994,1006,2,1969,2200,9,1378,892,1407,34,792,1417,1466,1036,1800,902,333,2094,2445,1982,1555,2049,1288,883,1380,2092,1413,159,1219,2500;1591,1465,395,2258,1641,1442,148,1033,906,1178,1362,536,1215,1303,1538,1792,1724,11,1045,793,622,965,1687,1629,576,1477,2114,2111,1666,78,2189,332,2035,1613,1266,279,2264,1171,1529,1787,948,1352,1266,2444,2300,159,2146;334,30,1637,1676,958,279,2110,703,136,2113,1970,332,1599,722,445,566,480,1222,22,172,2229,1773,2332,1130,1890,2384,1721,1841,2484,2037,2130,2194,329,1928,2472,1545,1608,927,2205,1770,664,1716,896,341,2206,504,2197;1516,940,1245,2359,1790,2239,491,1734,1024,1990,1600,1658,491,1933,1627,1251,621,905,2341,483,773,257,616,1731,1678,1570,1686,1318,21,1211,1148,2308,1505,620,1315,1780,634,1496,706,851,690,67,2056,995,2488,137,1012;1569,2203,374,1823,2305,787,1212,1763,1640,2464,1279,2458,249,170,1559,1420,1795,2081,1437,929,1816,360,993,1946,676,1125,862,1804,1826,1507,2033,890,2121,2394,1472,1221,2450,591,2366,2421,1438,864,2318,1688,2328,2303,1340;816,1521,281,798,1613,472,242,1889,1298,1074,302,830,597,2383,1780,1931,1285,679,1174,743,1365,1121,616,2433,128,110,1765,2427,1386,345,1726,454,2226,178,1842,2400,1569,2178,2247,1332,1551,2012,484,1794,2090,1916,2048;1355,138,1237,1927,1578,82,1956,351,2255,1644,1458,2344,1915,934,735,2237,969,391,1089,657,2291,296,706,1458,1420,866,994,1896,306,1657,933,2111,754,711,1722,415,147,1064,2188,574,1679,1837,1902,1525,1821,2080,319;542,184,1790,190,231,2249,2048,1271,889,747,2285,929,2420,722,1621,1063,2392,2254,1603,2244,1224,1703,1943,1493,544,32,1521,1650,1535,77,1927,1019,1906,1890,1604,1807,945,414,726,354,456,2232,1535,908,1117,2046,202;641,727,2339,1826,859,1367,644,1691,111,2194,1951,715,1125,2268,2223,2102,203,1865,1918,1323,3,647,427,947,2271,2265,553,711,54,578,1743,81,1396,269,787,1913,2288,235,1543,2338,1781,1544,440,401,1706,1805,2010;1157,1809,759,2377,1392,763,1654,1806,839,1433,200,204,850,811,190,1031,1357,1330,1747,2281,2317,97,793,2066,1071,2314,1908,1251,1251,1740,1863,613,637,2141,1176,1081,381,1594,70,833,330,981,231,155,2340,837,812;1180,2091,1519,294,1334,632,2099,1007,2257,2440,1487,101,1555,1098,381,2429,1185,1452,1110,1236,433,2346,847,424,620,967,976,647,609,447,2032,293,1011,1485,1133,410,1918,1689,287,1785,1121,1205,2055,1294,2383,1903,746;471,2249,219,482,25,804,1052,2025,1531,1470,2027,2153,2027,2133,394,1,1011,1183,555,304,807,2383,530,2127,135,1873,22,717,2087,1773,529,1044,303,221,1668,943,350,1677,1402,489,2306,1660,2023,1532,1917,1542,348;1549,1323,1170,1002,816,961,438,789,210,1718,377,69,993,1523,1502,247,678,1341,1676,1258,1650,1623,1132,2391,2323,352,2445,584,1874,1680,2125,387,1639,1785,1342,1072,258,806,1543,1829,672,2103,2136,169,1712,1950,1793;2017,478,1019,131,1938,1093,114,1895,2344,206,1782,1900,376,181,1546,1000,571,257,520,2408,1192,1980,1212,1489,1144,2420,2124,2384,2196,815,715,1335,290,978,1877,534,2293,1651,624,2403,968,268,1213,1494,774,1885,2018;2380,339,2297,879,2096,847,1658,48,279,1374,50,87,1029,1124,2269,1154,1628,1154,1474,624,2184,1738,2121,1447,2106,1373,2477,1752,1132,1066,1736,1942,917,2079,1518,2286,1620,2077,2131,2483,1926,360,568,1205,785,2251,67", "output": "34,342,701,1789,29,2015,1333,842,645,1779,928,127,754,770,2319,2202,1595,193,1225,702,291,221,919,248,552,1373,1684,1154,981,196,1073,1893,1508,413,1210,2183,1073,1323,2144,2246,2070,1522,1560,2334,2073,1039,1757,236,255,1596,2173,350,2068,1306,1552,519,1527,1773,1213,1471,39,320,2472,1001,187,290,957,1348,1882,577,1478,2413,2003,1187,804,530,1790,2258,961,1440,1057,106,1407,1105,814,1491,456,617,1338,1130,72,538,1098,1332,2310,1833,1338,894,1236,393,2237,493,756,2106,2277,630,1909,2420,2186,581,172,2090,1563,8,1391,1575,1416,642,171,1615,1,1056,901,24,203,1779,1846,1380,100,1183,765,1203,810,1297,122,1117,1354,2123,1976,1590,2384,508,1493,689,1392,448,547,483,687,185,1340,1504,815,1789,25,2108,2218,44,949,788,738,941,1700,1086,1284,1885,1573,1661,672,1318,2276,727,2426,1144,2465,1634,21,2076,775,253,480,338,1693,315,532,421,2085,2097,1902,1134,64,774,1346,557,1039,602,1156,697,499,777,1946,1140,1793,1556,38,1275,1107,1371,943,1993,285,543,1013,1119,1152,2145,503,1012,580,2259,2437,22,1679,36,612,1535,1276,667,1481,808,28,2072,1398,531,619,678,817,14,711,2292,221,1789,1384,1366,512,1426,1559,1460,300,1498,1189,1740,1288,2278,1930,775,656,1154,554,389,1722,1325,2038,218,570,736,2003,1535,2074,994,1049,122,799,1317,960,2378,989,475,2080,2335,2101,17,540,2453,255,253,232,1559,371,1008,1633,611,2300,359,1967,372,2328,901,2455,2135,1154,616,418,2143,957,1307,2059,1703,1228,1671,467,784,1735,1762,2235,1543,931,172,277,168,223,1591,2343,1254,291,1613,658,2100,557,257,294,245,293,154,1053,493,2008,2155,1112,652,1826,2221,1867,1494,2088,1177,290,1411,2044,833,303,2480,1444,369,2327,310,2122,1788,1398,648,783,829,1466,878,156,2157,1801,836,1485,824,879,1890,1561,603,990,2497,1446,1294,145,618,1463,1020,1647,270,147,559,799,1116,1674,207,138,2136,2234,2117,1359,1109,361,2329,1533,646,2066,140,634,1532,2036,2177,1926,1471,1048,1291,1793,206,424,2112,1609,619,495,604,1251,217,1050,536,1201,827,1503,116,2265,1207,1103,98,1630,815,2303,505,937,2468,189,1269,1478,856,1544,126,583,599,93,1963,933,2275,504,669,2402,834,955,1903,626,150,1993,1429,1621,1481,469,849,651,2369,455,223,148,1261,86,1480,295,1723,232,827,551,2414,1883,1611,868,2429,1034,2250,910,1969,34,2068,916,2169,1696,1656,928,2303,706,322,1929,924,1743,2058,2394,493,1691,2298,886,1552,125,2032,307,1735,509,2375,274,2045,799,1512,838,1768,111,163,1435,2193,44,1245,922,2201,710,643,5,1886,928,2002,1806,139,321,2486,1038,1251,1342,810,691,171,873,2275,1362,1459,2219,2160,2364,2464,2447,133,2226,2040,80,1198,432,2074,1083,2173,853,1277,2479,156,451,625,1864,37,318,2057,2046,458,368,1388,1859,510,1160,425,2080,1592,1243,699,1176,1476,271,447,1793,2272,2398,2020,425,2148,2139,17,1038,313,2391,2439,491,1376,1309,1597,953,970,1303,1811,4,73,2027,615,41,130,1590,1726,2435,1556,70,2404,67,1417,1918,874,1023,2121,1134,2142,1927,974,1849,1990,1294,2273,1609,1031,1869,1180,1129,1219,1413,1380,1288,1555,2445,333,1800,1466,792,1407,1378,2200,2,1994,1722,2038,1616,2468,959,816,2357,439,1591,395,1641,148,906,1362,1215,1538,1724,1045,622,1687,576,2114,1666,2189,2035,1266,2264,1529,948,1266,2300,2146,504,341,1716,1770,927,1545,1928,2194,2037,1841,2384,1130,1773,172,1222,566,722,332,2113,703,279,1676,30,1516,1245,1790,491,1024,1600,491,1627,621,2341,773,616,1678,1686,21,1148,1505,1315,634,706,690,2056,2488,1012,2303,1688,864,2421,591,1221,2394,890,1507,1804,1125,1946,360,929,2081,1420,170,2458,2464,1763,787,1823,2203,816,281,1613,242,1298,302,597,1780,1285,1174,1365,616,128,1765,1386,1726,2226,1842,1569,2247,1551,484,2090,2048,2080,1525,1837,574,1064,415,711,2111,1657,1896,866,1458,296,657,391,2237,934,2344,1644,351,82,1927,138,542,1790,231,2048,889,2285,2420,1621,2392,1603,1224,1943,544,1521,1535,1927,1906,1604,945,726,456,1535,1117,202,1805,401,1544,2338,235,1913,269,81,578,711,2265,947,647,1323,1865,2102,2268,715,2194,1691,1367,1826,727,1157,759,1392,1654,839,200,850,190,1357,1747,2317,793,1071,1908,1251,1863,637,1176,381,70,330,231,2340,812,1903,1294,1205,1785,1689,410,1485,293,447,647,967,424,2346,1236,1452,2429,1098,101,2440,1007,632,294,2091,471,219,25,1052,1531,2027,2027,394,1011,555,807,530,135,22,2087,529,303,1668,350,1402,2306,2023,1917,348,1950,169,2103,1829,806,1072,1785,387,1680,584,352,2391,1623,1258,1341,247,1523,69,1718,789,961,1002,1323,2017,1019,1938,114,2344,1782,376,1546,571,520,1192,1212,1144,2124,2196,715,290,1877,2293,624,968,1213,774,2018,2251,1205,360,2483,2077,2286,2079,1942,1066,1752,1373,1447,1738,624,1154,1154,1124,87,1374,48,847,879,339"}, {"input": "780,316,2484,843,2233,2151,2098,1879,1461,2102,692,1509,914,1448,1696,386,1572,1915,1817,1040,684,926,581,170,2260;740,221,558,952,1268,1680,1605,2148,1056,1602,1058,1075,2199,1133,857,1246,106,1690,925,117,1244,2122,768,173,505;264,379,1900,2141,1496,314,2159,1629,2192,865,181,1753,1228,1054,123,233,150,450,802,1363,1999,1876,1497,1229,1905;47,1303,1999,1235,2379,579,1687,539,640,1323,2107,812,92,1851,21,162,1206,1124,1158,2429,125,2337,163,1386,1804;2316,2310,1283,1403,2051,644,2231,504,633,547,2371,469,1427,468,79,2219,1654,371,543,2471,281,1197,1116,1763,1305;81,458,1530,810,457,1679,1607,1899,2238,1803,807,128,2236,2464,1751,2463,2337,2389,1548,2317,128,1339,996,302,359;365,926,2262,1636,327,284,308,2355,1991,1399,1066,205,2188,713,703,9,325,2108,1311,2462,1408,1030,1570,521,1941;1143,1643,1941,548,45,1970,928,145,2143,1845,1083,1626,542,395,660,2338,274,1436,1138,1054,1590,758,1333,1793,1746;1382,2487,1420,1112,1461,921,913,1350,116,2301,303,1034,9,1040,1349,463,1242,1776,74,775,345,1918,796,423,589;2439,2101,1253,1319,309,2298,281,341,2168,480,636,356,910,2426,488,111,1344,955,9,106,144,2148,908,2065,408", "output": "780,2484,2233,2098,1461,692,914,1696,1572,1817,684,581,2260,173,2122,117,1690,1246,1133,1075,1602,2148,1680,952,221,264,1900,1496,2159,2192,181,1228,123,150,802,1999,1497,1905,1386,2337,2429,1124,162,1851,812,1323,539,579,1235,1303,2316,1283,2051,2231,633,2371,1427,79,1654,543,281,1116,1305,302,1339,2317,2389,2463,2464,128,1803,1899,1679,810,458,365,2262,327,308,1991,1066,2188,703,325,1311,1408,1570,1941,1793,758,1054,1436,2338,395,1626,1845,145,1970,548,1643,1382,1420,1461,913,116,303,9,1349,1242,74,345,796,589,2065,2148,106,955,111,2426,356,480,341,2298,1319,2101"}, {"input": "1518,784,1463,1399,475,1180,690,1387,2021,572,2058,472,752,1937,943,1796,423,1641,945,1913,1564,922,1292,2141,2426,1855,1948,2067,2,338;62,2345,1277,927,2095,1193,1982,1395,1354,18,1760,854,265,2423,2192,45,1881,13,695,12,2084,491,577,1610,57,274,936,254,985,370;1532,1029,282,1453,212,1326,1886,2419,284,666,1694,2472,2155,2351,905,2340,1383,369,38,2342,1780,2306,767,324,1193,653,592,756,608,424;2217,238,2155,882,12,2292,149,1523,1067,1247,243,21,1082,2101,2042,2223,440,1083,1186,217,793,1772,100,2083,293,1337,191,761,1204,18;2485,18,756,1125,1747,394,525,2111,2391,748,1437,1482,108,1963,1919,1319,987,212,96,52,902,1718,693,1508,1509,1233,1348,2343,1519,422;1828,1318,767,1454,1893,1410,1799,60,557,719,2338,1676,1804,1999,1314,505,236,362,1392,1854,312,27,387,1755,193,463,337,1271,2351,2484;1969,1313,1516,2370,150,982,1259,486,1220,265,190,1206,1145,215,1186,1548,1558,1426,1745,1273,1069,148,395,1512,885,934,387,1292,1908,2123;2063,1394,1642,1126,2338,2131,2171,2000,1116,1814,905,997,1844,611,2352,1449,485,857,1779,1428,586,626,126,287,2269,2334,1744,1134,640,316;1797,2438,97,1740,1568,1561,983,2164,2239,1653,870,1850,1621,911,2466,1353,906,2227,398,1784,2086,2191,282,2445,353,1796,1038,1072,1538,916;1447,1777,310,218,1427,903,2327,247,1216,1956,84,121,645,962,2202,479,1742,1997,404,1756,1937,1131,1372,905,996,2198,987,720,2364,1951;1876,716,677,128,2490,1470,527,393,2271,2345,192,2442,1250,1384,1149,1434,1242,2351,612,1398,364,2479,706,82,131,877,1614,736,1400,783;1864,400,1429,1100,2480,341,744,998,1400,1848,1204,1784,295,1427,1106,165,1901,2227,2005,1698,507,591,869,1512,1902,1923,2219,2023,22,2005;2016,2459,1698,57,1816,752,1765,2394,259,372,1820,866,2036,919,1323,428,1920,1285,52,1565,402,1101,1029,1278,1511,85,1157,130,1179,1707;1561,435,1554,1410,2264,1190,1059,1702,2341,1521,1344,2163,722,1368,161,641,873,1123,1786,1776,1124,913,1738,1564,1758,411,2152,841,873,511;1748,1644,889,236,943,2500,2417,412,471,2480,621,1824,1528,1979,2205,152,789,1538,763,1718,2242,332,788,152,1932,897,577,707,1959,1045;1979,2272,1969,2103,1688,1607,2118,529,1767,1073,827,2262,2347,26,1753,1981,723,1809,2075,2224,631,707,2330,97,49,1426,967,1996,2392,224;1275,2045,1177,1907,1317,568,1767,2189,2305,714,845,961,1163,1336,1340,2314,2007,1953,760,583,852,1423,337,268,800,298,2251,1173,142,832;256,200,985,1755,2141,2127,1828,324,206,1061,225,1447,301,854,481,2286,1836,375,864,2087,1791,992,1072,681,2485,49,254,412,165,1987;1808,206,1925,1948,1798,2401,248,1015,954,1871,703,881,697,973,2149,1828,783,352,661,1969,1715,1600,1086,1401,1878,1342,1718,401,862,2189;996,1163,478,134,584,1399,1849,455,328,358,1406,1716,1203,1306,2116,1337,1136,1921,1699,729,505,1027,1632,649,361,1518,987,2168,937,805;2207,79,276,780,511,817,903,741,248,102,790,2013,2082,1557,2478,1175,812,118,2216,2271,678,976,2452,1997,181,417,1716,1297,1448,1457;520,2369,141,70,2207,1062,1788,1400,2141,49,1090,2299,2072,2306,315,1940,1695,2094,1764,2125,1983,858,2255,1700,46,1821,1859,1831,365,1778;879,2089,1874,2318,1591,1311,2121,2106,1851,618,1135,619,2180,231,2354,457,1710,775,913,2424,207,544,196,2195,1589,2276,754,788,225,1969;1526,2122,2081,1033,952,151,974,1633,1480,2333,948,1022,1297,1683,1179,2110,2442,1687,328,1552,928,2203,650,2488,1703,2312,2245,2396,501,1722;1595,1995,892,637,1582,1348,172,276,2483,1582,2322,1573,699,1776,1911,498,712,1466,1057,121,1995,1787,1819,1917,2439,1208,381,58,1123,836;1813,2199,118,2032,830,2454,1193,622,1200,2213,1060,1110,102,253,948,1968,997,17,1815,587,1843,1507,2398,1201,347,1258,2108,2084,19,1679;892,4,1903,2237,166,722,74,1903,282,2488,362,674,2261,1421,672,291,1472,394,2410,1172,488,25,2461,1262,339,937,2028,737,424,2125;2055,74,1095,2108,1446,906,2130,1773,2098,118,262,1740,1123,1469,867,1119,23,2303,2371,2184,117,2140,760,467,375,1205,2131,2156,855,2436;411,2439,2141,930,1862,1370,786,859,410,1455,1345,381,175,1685,417,1875,285,478,292,1654,1465,1290,1866,1669,47,1809,1177,2267,1412,169;1790,851,1476,1756,1891,158,1738,107,828,585,534,1126,122,1050,977,116,1724,286,567,1769,1770,512,1418,412,203,631,2292,114,161,1760;2294,2252,1929,906,68,1227,793,385,574,652,2200,1031,2472,405,322,362,1883,77,1677,940,1599,242,1405,2039,2163,1626,2268,1431,2207,1494;57,1679,1065,2172,1294,1474,2365,365,1404,1148,896,2197,368,1595,969,1898,1260,1813,1285,425,1450,1258,199,1127,643,1692,1246,507,438,1568", "output": "1518,1463,475,690,2021,2058,752,943,423,945,1564,1292,2426,1948,2,370,254,274,1610,491,12,13,45,2423,854,18,1395,1193,927,2345,1532,282,212,1886,284,1694,2155,905,1383,38,1780,767,1193,592,608,18,761,1337,2083,1772,217,1083,2223,2101,21,1247,1523,2292,882,238,2485,756,1747,525,2391,1437,108,1919,987,96,902,693,1509,1348,1519,2484,1271,463,1755,27,1854,362,505,1999,1676,719,60,1410,1454,1318,1969,1516,150,1259,1220,190,1145,1186,1558,1745,1069,395,885,387,1908,316,1134,2334,287,626,1428,857,1449,611,997,1814,2000,2131,1126,1394,1797,97,1568,983,2239,870,1621,2466,906,398,2086,282,353,1038,1538,1951,720,2198,905,1131,1756,1997,479,962,121,1956,247,903,218,1777,1876,677,2490,527,2271,192,1250,1149,1242,612,364,706,131,1614,1400,2005,2023,1923,1512,591,1698,2227,165,1427,1784,1848,998,341,1100,400,2016,1698,1816,1765,259,1820,2036,1323,1920,52,402,1029,1511,1157,1179,511,841,411,1564,913,1776,1123,641,1368,2163,1521,1702,1190,1410,435,1748,889,943,2417,471,621,1528,2205,789,763,2242,788,1932,577,1959,224,1996,1426,97,707,2224,1809,1981,26,2262,1073,529,1607,2103,2272,1275,1177,1317,1767,2305,845,1163,1340,2007,760,852,337,800,2251,142,1987,412,49,681,992,2087,375,2286,854,1447,1061,324,2127,1755,200,1808,1925,1798,248,954,703,697,2149,783,661,1715,1086,1878,1718,862,805,2168,1518,649,1027,729,1921,1337,1306,1716,358,455,1399,134,1163,2207,276,511,903,248,790,2082,2478,812,2216,678,2452,181,1716,1448,1778,1831,1821,1700,858,2125,2094,1940,2306,2299,49,1400,1062,70,2369,879,1874,1591,2121,1851,1135,2180,2354,1710,913,207,196,1589,754,225,1722,2396,2312,2488,2203,1552,1687,2110,1683,1022,2333,1633,151,1033,2122,1595,892,1582,172,2483,2322,699,1911,712,1057,1995,1819,2439,381,1123,1679,2084,1258,1201,1507,587,17,1968,253,1110,2213,622,2454,2032,2199,892,1903,166,74,282,362,2261,672,1472,2410,488,2461,339,2028,424,2436,2156,1205,467,2140,2184,2303,1119,1469,1740,118,1773,906,2108,74,411,2141,1862,786,410,1345,175,417,285,292,1465,1866,47,1177,1412,1760,114,631,412,512,1769,286,116,1050,1126,585,107,158,1756,851,2294,1929,68,793,574,2200,2472,322,1883,1677,1599,1405,2163,2268,2207,1568,507,1692,1127,1258,425,1813,1898,1595,2197,1148,365,1474,2172,1679"}, {"input": "828,2165,1030,1019,2122,623,215,1520,767,2163,1999,2111,454,2224,365,2373,340,2099,571,1001,1361,2319;894,2448,950,496,536,295,1415,795,1160,2495,569,1774,881,972,240,2164,1612,2159,910,2053,1672,1619;447,595,174,604,1905,1097,1856,1177,1460,430,1756,2364,723,2154,1585,137,1226,1226,1389,1121,699,2189;162,1270,955,186,2349,1771,2005,993,1998,1957,1487,1257,1945,10,2320,995,1850,1553,1060,2212,608,555;115,43,2086,738,703,1955,755,1410,1972,1004,979,1631,1487,1504,675,1346,1306,246,1601,852,2495,2487;164,904,2304,2299,1913,2045,254,1163,2435,1310,2174,1467,640,1672,1939,1605,131,2239,2235,2129,780,2225;1148,2435,421,1834,1629,264,1842,1070,2379,1404,1023,1984,2222,76,743,2188,2299,29,1465,2405,731,511", "output": "828,1030,2122,215,767,1999,454,365,340,571,1361,1619,2053,2159,2164,972,1774,2495,795,295,496,2448,447,174,1905,1856,1460,1756,723,1585,1226,1389,699,555,2212,1553,995,10,1257,1957,993,1771,186,1270,115,2086,703,755,1972,979,1487,675,1306,1601,2495,2225,2129,2239,1605,1672,1467,1310,1163,2045,2299,904,1148,421,1629,1842,2379,1023,2222,743,2299,1465,731"}, {"input": "2180,2131,1417,1078,1119,1688,245,1947,1190,2302,1571,263,1120,828,188,422,69,832,2448,2170,1786,198,1754;1128,501,2471,99,524,462,344,342,1793,2291,649,1655,1969,2307,2480,1409,2471,1177,1293,2050,960,773,2179;120,1733,1420,1365,1767,1060,1115,1396,539,502,1404,1178,1211,1666,1339,2158,1236,1595,2487,2280,1359,1790,1207;630,295,266,2439,232,1330,977,455,1524,950,212,593,1268,1313,245,1634,1672,2408,1318,633,690,1653,1202;1197,16,2394,1330,57,1670,1285,741,843,1496,1891,2021,457,2056,2334,165,264,469,1028,1034,1214,1839,368;704,561,625,1806,2340,1294,1270,1317,1931,2108,810,937,1136,2494,596,1327,1876,1302,1080,1962,29,802,1847;574,1321,2195,2042,1939,1640,22,152,339,426,1464,2134,1560,157,1538,454,2091,426,1590,2026,156,147,868;64,175,179,1572,1284,34,905,1146,1397,1278,416,446,115,2030,1947,1725,2022,2139,1214,1188,1524,840,381", "output": "2180,1417,1119,245,1190,1571,1120,188,69,2448,1786,1754,773,2050,1177,1409,2307,1655,2291,342,462,99,501,120,1420,1767,1115,539,1404,1211,1339,1236,2487,1359,1207,1653,633,2408,1634,1313,593,950,455,1330,2439,295,1197,2394,57,1285,843,1891,457,2334,264,1028,1214,368,802,1962,1302,1327,2494,937,2108,1317,1294,1806,561,574,2195,1939,22,339,1464,1560,1538,2091,1590,156,868,840,1188,2139,1725,2030,446,1278,1146,34,1572,175"}, {"input": "1574,38,1405,1289,1068,1969,1287,2,1389,1930,17,2294,2354,1144;69,1838,879,2180,728,2375,1144,944,2108,801,1372,1759,1508,2394;1793,13,2119,305,211,2399,433,1084,2284,232,2129,715,1734,1205;1618,2289,1220,1597,1241,240,953,1054,1163,1875,2232,697,1094,1603;1192,2008,2229,64,431,488,1121,2050,1432,1579,1587,671,103,2499;153,288,158,885,927,59,1205,1295,2286,8,1536,820,1453,1237;927,1028,1322,826,1187,466,2157,349,710,2151,1736,1471,1328,2138;443,972,2305,2492,161,2276,1183,2261,1362,1569,1819,2404,1320,604;2087,2368,890,1008,1465,605,1930,1777,1456,1694,2245,1894,219,492;648,510,534,281,1596,2351,2165,1329,1558,2289,1392,224,1336,405;1473,1960,2482,743,230,2233,693,889,1183,590,1959,593,1270,276;1560,645,1460,2374,2254,1221,1156,693,699,71,692,1666,1014,692", "output": "1574,1405,1068,1287,1389,17,2354,2394,1759,801,944,2375,2180,1838,1793,2119,211,433,2284,2129,1734,1603,697,1875,1054,240,1597,2289,1192,2229,431,1121,1432,1587,103,1237,820,8,1295,59,885,288,927,1322,1187,2157,710,1736,1328,604,2404,1569,2261,2276,2492,972,2087,890,1465,1930,1456,2245,219,405,224,2289,1329,2351,281,510,1473,2482,230,693,1183,1959,1270,692,1666,71,693,1221,2374,645"}, {"input": "36,1514,725,1942,2022,861,73;1338,410,407,2089,3,1974,2142;1418,1613,991,980,1364,1299,1138;654,1129,565,73,922,856,1871;2279,2087,747,975,1838,1371,804;771,2024,2463,1546,1889,629,959;653,1249,2012,950,121,2461,512;1338,1147,2191,609,2061,1960,265;927,2029,267,306,2004,376,1115;2152,2101,1466,1881,1285,781,789;1109,1811,542,1840,703,2053,2443;532,1312,1494,524,503,950,2405;466,524,1359,2040,936,608,214;2480,369,1898,732,904,2336,1281;787,1664,1157,2250,1739,683,673;885,1145,683,318,392,1132,1892;1307,1092,415,1054,849,1906,485;2441,2168,1054,287,887,2267,1269;1143,2319,508,2075,624,2428,626;1299,783,1040,2357,713,2134,1234;813,1107,1634,1835,1164,859,1955;267,847,2238,2046,1336,643,1415;446,139,1883,1431,774,2466,1613;1123,608,784,574,801,826,7;648,1906,2488,1464,507,1848,18;2422,1272,1448,1725,96,908,864;1537,1489,1165,2263,2082,1273,2470;1597,1281,2201,259,1667,1015,244;1769,937,2300,1656,1070,1554,565;736,1106,762,2054,719,844,524;2239,982,2335,368,339,2191,2313;361,1530,1485,1618,1614,1929,1913;2245,113,2176,497,25,1991,1541;2060,1138,113,2136,1713,28,228;582,132,863,1604,2369,212,2144;1522,1735,95,1831,1666,1279,1058;575,1027,853,208,388,452,1276", "output": "36,725,2022,73,1974,2089,410,1418,991,1364,1138,856,73,1129,2279,747,1838,804,629,1546,2024,653,2012,121,512,1960,609,1147,927,267,2004,1115,781,1881,2101,1109,542,703,2443,950,524,1312,466,1359,936,214,2336,732,369,787,1157,1739,673,1132,318,1145,1307,415,849,485,2267,287,2168,1143,508,624,626,2134,2357,783,813,1634,1164,1955,643,2046,847,446,1883,774,1613,826,574,608,648,2488,507,18,908,1725,1272,1537,1165,2082,2470,1015,259,1281,1769,2300,1070,565,844,2054,1106,2239,2335,339,2313,1929,1618,1530,2245,2176,25,1541,28,2136,1138,582,863,2369,2144,1279,1831,1735,575,853,388,1276"}, {"input": "1414,2053,905,297,341,1146,2483,1179,839,2407,1428,465,2472;1367,1111,26,966,441,1329,2302,175,1232,217,1921,1349,418", "output": "1414,905,341,2483,839,1428,2472,1349,217,175,1329,966,1111"}, {"input": "1819,97,36,914,2405,921,761,166,1124,879,693,1699,2447,2384,889,91,1998,1663,765,846,2321,1178,2174;1568,1891,970,255,971,827,2415,1814,2491,1100,943,554,1903,298,7,2333,423,553,1280,1497,1443,2243,39;1540,1576,1302,1933,1420,548,1958,514,2051,1907,520,1345,2169,1767,906,1616,2386,1211,424,2493,2284,1006,164;2269,1660,1302,237,981,750,2456,1024,1707,1384,2425,1827,1851,391,1932,1695,467,191,225,2405,138,1148,886;1931,842,891,1879,833,1421,443,1672,880,1710,1554,2406,1152,755,65,1436,579,625,168,1766,246,1889,98;2296,981,657,1783,962,2384,1878,794,488,662,1693,2064,1534,2195,1830,1202,1662,2130,1920,2390,675,1332,1744;2086,2244,263,1965,1324,110,1034,2029,619,1519,383,877,201,2049,1163,2271,1379,1074,1280,1281,521,2029,2426;158,2134,1933,1042,520,920,1457,361,2084,2365,2083,296,87,1677,630,73,1213,993,1991,2427,1530,1111,557;1206,2243,1364,1117,1157,1233,2491,1514,1601,1558,534,862,1649,1386,300,1443,1961,91,899,455,1461,1536,1123;1680,2188,775,1079,1476,2052,1456,1259,1587,2,1923,640,1470,1582,262,680,1541,737,698,295,2482,782,183;1446,2313,11,1161,2107,2137,443,913,2378,1353,1918,533,390,209,1151,317,2479,615,1416,1228,516,1329,610;2118,1034,2454,210,1630,1747,1048,1678,1541,1438,1085,787,1174,1252,2310,1743,433,1911,2073,1250,936,1295,1794;1870,1625,515,1122,2323,2047,194,499,2113,641,603,2119,358,1351,638,999,2409,1620,382,2043,1023,1296,1316;2306,681,1445,1616,293,518,193,1620,1602,1557,2095,2073,2286,274,1311,52,1380,2377,1507,568,1166,1745,626;1686,2164,713,909,753,2169,295,804,1084,1332,166,1747,1836,952,1622,1522,378,331,1200,1877,1443,535,1768;61,294,390,49,1335,464,207,2251,297,1957,894,2486,80,1281,1718,1259,1730,67,182,2144,1436,300,468", "output": "1819,36,2405,761,1124,693,2447,889,1998,765,2321,2174,2243,1497,553,2333,298,554,1100,1814,827,255,1891,1540,1302,1420,1958,2051,520,2169,906,2386,424,2284,164,1148,2405,191,1695,391,1827,1384,1024,750,237,1660,1931,891,833,443,880,1554,1152,65,579,168,246,98,1332,2390,2130,1202,2195,2064,662,794,2384,1783,981,2086,263,1324,1034,619,383,201,1163,1379,1280,521,2426,1111,2427,993,73,1677,296,2365,361,920,1042,2134,1206,1364,1157,2491,1601,534,1649,300,1961,899,1461,1123,782,295,737,680,1582,640,2,1259,2052,1079,2188,1446,11,2107,443,2378,1918,390,1151,2479,1416,516,610,1295,1250,1911,1743,1252,787,1438,1678,1747,210,1034,1870,515,2323,194,2113,603,358,638,2409,382,1023,1316,1745,568,2377,52,274,2073,1557,1620,518,1616,681,1686,713,753,295,1084,166,1836,1622,378,1200,1443,1768,300,2144,67,1259,1281,2486,1957,2251,464,49,294"}, {"input": "726,586,1375,814,1491,1580,1790,1154,1223,2493,1782,697,923,1404,1412,1164,1094,1608,2441,2201;310,194,1294,1124,1557,2064,888,2037,2044,620,247,944,1528,2397,2250,1695,2306,218,658,335;614,1019,233,2428,1205,730,1920,2250,1169,360,45,845,409,1133,321,1251,197,1374,413,2314;1065,886,803,2479,363,578,1522,740,294,615,470,2276,256,1529,2113,1386,1918,266,2240,1472;165,504,1186,127,282,808,278,1090,439,1212,2298,429,1540,665,722,1305,1434,2046,1225,1014;2072,489,2369,724,1394,1582,1860,766,2178,858,1909,1952,1593,1514,53,483,747,154,1185,141;2138,672,535,1771,145,1075,2473,2166,902,769,637,1709,32,64,124,1339,664,971,1248,1519;1623,2155,7,1141,1739,1810,297,1037,1018,874,46,1315,607,1023,2202,1657,2409,2119,119,308;421,1692,1943,733,2354,1581,35,1458,1802,453,1947,1460,1543,481,1898,876,1162,800,1296,896;945,2435,1715,2051,1308,2233,2440,437,1900,397,1295,996,519,615,1960,1272,1945,679,262,565", "output": "726,1375,1491,1790,1223,1782,923,1412,1094,2441,335,218,1695,2397,944,620,2037,2064,1124,194,614,233,1205,1920,1169,45,409,321,197,413,1472,266,1386,1529,2276,615,740,578,2479,886,165,1186,282,278,439,2298,1540,722,1434,1225,141,154,483,1514,1952,858,766,1582,724,489,2138,535,145,2473,902,637,32,124,664,1248,308,2119,1657,1023,1315,874,1037,1810,1141,2155,421,1943,2354,35,1802,1947,1543,1898,1162,1296,565,679,1272,615,996,397,437,2233,2051,2435"}, {"input": "1623,1518,1545,779,1647,1997,1750,1026,1062,2114,1596,2207,2497,1087,1936,2496,1047,169,40,678,954,304,1137,922,1739,304,1047,1414,800,1306,832,617,418,1789,210,741,700,2165;1062,30,1394,806,115,728,286,211,744,597,1860,2255,1411,2242,2426,1730,289,19,214,2117,1585,166,881,846,161,591,1588,670,1986,1063,274,1067,368,516,803,227,1060,2200;1879,2172,738,1759,2251,2444,702,256,1259,644,192,2101,1249,111,945,322,619,465,2497,989,885,598,1917,1155,1326,1002,862,2215,897,2254,831,478,2141,1534,595,608,318,62;285,863,1881,588,91,1873,763,1074,1566,108,2068,420,2045,337,1582,169,586,2328,1321,232,565,1823,826,2186,261,52,985,1695,2469,837,2150,1393,813,1855,2397,1691,1057,370;2112,450,238,244,2158,2499,475,2465,1547,2237,2151,141,672,1479,2388,249,2088,526,2285,74,1725,857,1851,311,272,2447,493,2319,1042,1095,1424,817,2043,1257,795,577,657,659;190,369,955,1483,1810,172,1464,2277,1123,1076,1063,2117,634,1191,304,898,2113,135,493,1874,1686,345,1533,1078,436,170,1289,1614,2440,2135,1912,2248,1571,595,1315,1210,1354,54;2388,707,1962,988,1689,157,1920,1914,1365,2459,2103,2466,459,20,74,1701,1002,1585,1973,733,1835,1967,821,2088,1877,723,2052,1609,2338,1175,707,1379,2065,1998,2291,1107,1040,1597", "output": "1623,1545,1647,1750,1062,1596,2497,1936,1047,40,954,1137,1739,1047,800,832,418,210,700,2200,227,516,1067,1063,670,591,846,166,2117,19,1730,2242,2255,597,211,728,806,30,1879,738,2251,702,1259,192,1249,945,619,2497,885,1917,1326,862,897,831,2141,595,318,370,1691,1855,1393,837,1695,52,2186,1823,232,2328,169,337,420,108,1074,1873,588,863,2112,238,2158,475,1547,2151,672,2388,2088,2285,1725,1851,272,493,1042,1424,2043,795,657,54,1210,595,2248,2135,1614,170,1078,345,1874,135,898,1191,2117,1076,2277,172,1483,369,2388,1962,1689,1920,1365,2103,459,74,1002,1973,1835,821,1877,2052,2338,707,2065,2291,1040"}, {"input": "1292,129,1407,683,2063,848,784,393,544,1779,1905,413,140,1916,2148,738,622,2028,491;1699,357,816,554,942,1606,646,574,2248,1583,1933,2213,1677,2425,2149,612,2232,812,1631;1240,634,2160,848,1106,1472,2110,320,415,1614,1078,2086,117,2148,1279,1757,1250,693,2212;1413,331,2245,1404,1452,824,636,2173,1969,1897,821,2332,1190,2448,923,1447,1858,2379,1238;2017,1930,1674,1756,211,365,2094,370,480,673,1368,46,2413,1354,974,1307,29,2145,1307;24,1928,513,920,606,1550,1706,1146,433,1794,1920,541,1828,2304,724,313,1181,1509,2155;1372,495,898,541,2278,1188,2214,322,733,2465,942,88,1195,2427,2461,1548,1221,829,951;1163,2361,483,1704,2304,997,1970,314,2278,2117,2006,1314,1882,2337,1098,1111,2320,2278,1887;1633,1296,1855,2470,1833,388,1337,1465,2325,2420,834,1257,851,1632,1842,200,841,2475,726;1085,2040,2355,2170,1951,2116,1217,2316,2119,1555,744,701,1550,438,2341,279,551,675,573;1309,2126,578,1978,1662,506,1784,2500,2341,927,2174,2169,1541,593,1975,1918,658,1151,2089;922,80,1331,128,1959,1752,567,459,705,2206,1810,1936,1278,66,1756,428,484,822,1390;1904,1431,2375,1379,42,176,1742,1408,2305,1244,589,1932,1924,176,763,1758,1572,727,322;1647,748,671,224,1315,518,1688,1406,2210,1938,2348,610,773,1361,751,2057,1403,2120,878;1628,1746,1228,1629,1393,84,1316,1897,459,1327,1102,2321,799,1502,1829,2269,359,1213,1420;882,2283,2130,1678,506,322,1624,1005,1107,110,1090,53,343,1662,539,1175,622,113,2485;2419,1235,1046,464,325,969,1050,1785,1922,924,70,868,2282,1186,901,2155,1415,1012,2208;1343,762,2457,81,968,323,224,1420,378,135,668,2330,83,409,1258,1855,1180,1787,1494;545,1754,1261,2363,2008,624,393,1492,194,1672,1438,579,1225,479,1690,1640,77,1295,2003;669,1236,1652,234,988,326,1579,1067,2077,1124,1842,952,1293,2404,466,699,165,2284,2179;78,2015,1452,1463,1631,2089,2465,1225,300,1255,1507,1438,1459,1423,406,291,510,868,198;1109,774,161,516,469,1003,1835,2195,2340,1025,1610,2239,1187,231,444,2367,1048,28,31;1119,1409,996,1729,479,2457,411,191,1510,1735,424,579,1047,1574,420,728,2357,1124,2286;1677,1524,126,1351,1857,1266,2104,1237,37,1829,459,815,153,2363,606,2302,1380,2001,655;830,136,22,1050,76,253,449,1364,755,77,754,100,1490,1281,1077,2107,2325,794,648;1354,998,653,1999,534,848,1027,1668,1838,1629,1377,567,1340,768,1402,1355,1969,838,1288;2375,2203,206,1734,562,79,1974,385,194,680,236,1303,183,1320,279,1037,2164,318,704;1112,1514,1686,673,1400,1977,1885,1149,255,23,112,427,2345,952,483,283,1421,1607,993;2119,1297,1072,1879,1167,115,2356,1461,2045,755,1709,1281,54,56,828,1662,1303,1958,1315;565,1722,1987,1022,1175,1614,2030,1571,635,789,1456,2142,2202,2204,241,2090,1193,1700,148;513,1799,1174,318,1721,678,1635,668,981,1283,752,212,907,911,72,2111,1876,625,1445;901,1573,1959,312,557,927,61,1677,259,129,1558,550,1667,923,806,431,2196,1460,617;1206,301,2144,1026,1816,164,1943,68,1354,1020,1468,70,949,922,445,1428,901,131,1251;1466,1313,2144,1850,1219,100,439,896,2421,1337,421,1654,2071,1233,2261,1971,2207,213,140", "output": "1292,1407,2063,784,544,1905,140,2148,622,491,812,612,2425,2213,1583,574,1606,554,357,1240,2160,1106,2110,415,1078,117,1279,1250,2212,2379,1447,2448,2332,1897,2173,824,1404,331,2017,1674,211,2094,480,1368,2413,974,29,1307,1509,313,2304,541,1794,1146,1550,920,1928,1372,898,2278,2214,733,942,1195,2461,1221,951,2278,1111,2337,1314,2117,314,997,1704,2361,1633,1855,1833,1337,2325,834,851,1842,841,726,675,279,438,701,1555,2316,2116,2170,2040,1309,578,1662,1784,2341,2174,1541,1975,658,2089,822,428,66,1936,2206,459,1752,128,80,1904,2375,42,1742,2305,589,1924,763,1572,322,2120,2057,1361,610,1938,1406,518,224,748,1628,1228,1393,1316,459,1102,799,1829,359,1420,113,1175,1662,53,110,1005,322,1678,2283,2419,1046,325,1050,1922,70,2282,901,1415,2208,1787,1855,409,2330,135,1420,323,81,762,545,1261,2008,393,194,1438,1225,1690,77,2003,2284,699,2404,952,1124,1067,326,234,1236,78,1452,1631,2465,300,1507,1459,406,510,198,28,2367,231,2239,1025,2195,1003,516,774,1119,996,479,411,1510,424,1047,420,2357,2286,2001,2302,2363,815,1829,1237,1266,1351,1524,830,22,76,449,755,754,1490,1077,2325,648,838,1355,768,567,1629,1668,848,1999,998,2375,206,562,1974,194,236,183,279,2164,704,1607,283,952,427,23,1149,1977,673,1514,2119,1072,1167,2356,2045,1709,54,828,1303,1315,1700,2090,2204,2142,789,1571,1614,1022,1722,513,1174,1721,1635,981,752,907,72,1876,1445,1460,431,923,550,129,1677,927,312,1573,1206,2144,1816,1943,1354,1468,949,445,901,1251,213,1971,1233,1654,1337,896,100,1850,1313"}, {"input": "1361,798,919,127,599,2342,1446,380,249,1442,1123,2164,2183,907,1836,790,583,223,958,481,2397,1755,1726,172,284,739,717,2091,55,2345,1139,1919,1620,2271,1562,476,489,1466,1818,31,1946,1725,1961,1918,632,1534,318,893,2250,1121;1702,1346,1195,446,820,1378,1200,132,1512,2320,1317,2105,382,1393,645,286,754,283,1715,2034,1145,1258,1426,133,1125,43,252,565,1460,1698,169,1942,1843,81,339,274,1324,523,2372,1437,2008,807,2337,498,2321,2321,1621,1541,523,570;1787,1956,1285,2339,1191,2260,1883,1202,141,2105,1490,363,1783,2015,1836,573,2187,1449,2237,249,1596,1520,904,1319,735,1118,835,1026,1196,569,2228,315,1501,2071,1698,75,1748,854,333,1276,2267,2052,2150,2340,32,1552,960,2378,2332,560;2243,505,1717,1186,597,2428,1444,242,1852,1264,2040,1696,1849,1172,1707,2403,1472,1361,599,437,1339,2256,753,1009,161,88,2151,1471,2429,995,2211,1157,1829,2388,369,1214,263,2165,130,1318,2167,247,1500,986,490,24,1511,1331,1192,160;1511,154,279,904,198,2401,1794,2457,439,2131,1042,1527,1698,1450,2343,1472,1115,1935,1529,1833,1974,1825,2331,1267,1968,1181,2317,836,110,442,1593,1259,2137,1803,1283,1118,143,1028,1849,1116,96,1857,782,594,1070,1400,1717,518,1248,814;500,2289,2093,778,1235,694,278,1519,28,1836,316,529,1067,1023,898,575,2114,2437,2494,868,1740,1321,2197,1075,1226,1093,1330,1480,543,1598,1667,2130,1221,2097,2455,469,1952,762,1505,138,815,408,1313,2447,998,1768,556,1107,2118,208;826,1283,303,1147,775,639,1689,155,901,2328,583,2294,1989,233,299,2476,2269,206,2032,106,2022,1774,1735,947,567,1497,781,2077,1037,204,1160,356,898,117,2285,635,2124,1494,589,2267,2464,1103,1343,249,2319,1217,938,2308,223,393;1878,340,1764,635,1071,822,1098,1204,1855,1136,1758,655,471,1860,1982,854,27,1565,1375,44,2036,1027,1985,435,704,1247,1188,2189,378,1149,2497,243,295,223,1507,2360,1498,432,29,1099,571,432,2292,867,642,2228,1670,74,307,582;2177,1891,302,2308,256,204,2329,2068,1799,2388,2173,2217,2115,1016,1269,1761,1645,1357,1701,849,1537,1964,1031,1158,1602,194,1629,2117,1411,2132,110,1064,2323,1592,1807,1997,696,1222,571,984,1686,1575,214,2177,2066,1686,137,2324,1200,1844;2050,520,1576,1719,1739,355,1193,471,1662,2427,1927,1535,1619,1812,1831,752,1780,1239,1205,1869,660,1651,77,2323,2464,1081,2208,1551,2133,1666,2405,1488,1453,761,160,2058,2349,54,165,544,1030,1792,1442,2239,449,2039,1101,1078,2466,2257;94,2017,403,1410,2419,822,1651,916,2172,4,1798,1732,905,2495,1340,1118,314,1353,281,848,1342,1845,2022,1378,2394,1037,1729,2037,483,1973,1826,2189,634,1047,330,223,2462,2468,1085,1265,562,1777,1314,318,2384,722,1132,1408,1164,709;2161,653,1670,551,311,549,99,2495,233,244,1250,2453,388,118,786,881,1720,145,2109,215,1438,294,471,2359,1343,587,999,1016,809,74,834,626,1259,1223,619,1466,2068,38,1605,352,1967,613,250,1051,1138,81,1753,2494,2439,1985;2273,1096,1929,1862,1661,2246,1111,197,461,1516,2478,2027,373,189,2331,103,1465,1888,2206,521,2390,469,2370,203,27,660,206,1455,2029,267,1258,390,961,158,2486,2288,146,1085,1803,1004,1223,1814,496,1819,2448,1484,393,966,1805,151;1769,2344,976,1232,209,2116,1067,2377,1043,64,347,482,1488,507,1564,658,2241,2375,656,1224,668,1671,1974,910,499,1973,455,178,2074,2446,384,838,742,2158,972,1905,2390,2428,1476,2262,1713,146,2226,1917,259,609,1396,2120,1907,176;2360,777,726,1290,2018,12,1482,1106,1257,928,949,283,328,1084,1860,2184,1322,86,1014,1852,1900,2107,1568,1473,2319,432,1579,554,617,610,653,46,435,1285,1527,1789,1894,768,1906,2363,1642,2233,388,858,548,937,247,392,203,1512;1700,1873,1364,2081,2091,191,1947,2017,1487,2356,1740,2373,130,1959,1652,1387,1460,416,1663,258,888,1379,1733,1055,1728,488,58,373,217,901,32,2496,1584,1460,2121,1663,869,424,704,1404,105,1902,1523,2136,1325,143,752,1034,1766,966;127,1233,648,252,1014,1866,1135,84,1672,1246,2197,2380,1498,1852,1884,1877,536,2206,1796,177,247,1754,1524,2324,1225,2230,1059,167,512,808,246,2261,1437,1582,2026,97,2135,1799,1076,571,882,253,509,1404,738,407,122,747,1690,855;2139,132,2444,2156,2271,1871,1513,2312,355,122,22,1502,2489,2131,88,1388,966,1480,2425,1601,1451,1720,2338,922,1400,96,904,1626,1969,1322,448,1793,826,1871,484,994,1456,2291,1460,2331,1782,327,1738,2362,1186,21,334,274,2163,794;2454,121,319,2133,1226,1146,225,1346,1992,89,1914,1725,74,1976,1083,1903,2273,1010,867,1859,164,956,781,846,2104,87,2072,1148,1501,1716,1248,2192,2464,991,486,933,99,472,2329,1154,1264,820,471,150,1532,118,21,169,1534,1094;1784,477,2306,106,1917,888,2162,95,1373,128,1200,1326,963,1934,1221,54,639,545,698,30,1503,895,351,515,1698,2418,2153,516,1895,92,788,31,62,1924,1729,818,2070,415,725,634,1844,976,782,399,1387,2329,65,1108,932,1868;1649,419,326,1253,1514,1972,1668,1515,254,1407,1947,1783,465,697,753,228,1136,2024,101,415,1679,2014,1140,453,1322,605,5,1707,895,1585,1020,10,1532,1445,2035,1653,995,1741,1245,1611,1920,2461,466,1773,2082,1283,169,2498,1469,1282;421,789,2044,2467,2329,1608,1619,355,2355,853,1979,740,2289,2218,420,2287,1235,318,944,1473,1399,2242,1147,848,73,1252,1300,1528,1201,309,1062,767,897,1581,491,1938,2319,1198,1680,407,1101,453,1185,118,1548,2111,7,1328,191,2125;894,2092,2072,497,1659,975,2264,1415,2174,1422,1685,373,808,1790,693,1866,181,310,2186,1135,1053,1733,2008,1557,764,828,1815,2421,143,333,1285,1268,1073,604,715,1105,752,2299,1959,10,1480,305,990,1573,2362,309,1989,702,1922,378;2037,1695,342,312,242,1510,2226,590,76,2201,41,289,1448,1271,2370,1205,1091,754,1084,1192,2242,2489,484,549,2234,1987,510,1246,2010,704,1682,1,1463,731,409,161,823,1610,1547,665,121,1861,1898,797,1152,384,2195,2268,2332,2221;1995,2491,1356,2486,790,68,1696,395,610,1379,482,1448,777,2380,1284,1713,26,262,466,330,277,1501,903,702,383,55,1532,677,1871,875,2476,1491,1649,2060,642,693,1402,1199,140,459,930,640,1348,2243,1576,176,2191,2349,2300,835;212,1773,595,1508,257,1838,687,1274,339,631,923,1527,1635,2028,1196,2368,821,988,66,2394,2161,270,1973,2226,2304,426,2459,1795,2479,299,1959,803,1974,329,2296,559,2485,873,1162,106,974,50,1855,1584,1296,753,1293,368,881,2500;2131,392,1083,776,795,405,2127,25,879,893,319,1753,85,2426,291,1525,1458,685,482,1016,655,551,1238,266,70,880,1138,233,2259,1977,167,1637,2437,2127,2031,984,2220,183,249,600,2143,1585,1552,1073,651,128,1552,1956,1650,353", "output": "1361,919,599,1446,249,1123,2183,1836,583,958,2397,1726,284,717,55,1139,1620,1562,489,1818,1946,1961,632,318,2250,570,1541,2321,498,807,1437,523,274,81,1942,1698,565,43,133,1258,2034,283,286,1393,2105,2320,132,1378,446,1346,1787,1285,1191,1883,141,1490,1783,1836,2187,2237,1596,904,735,835,1196,2228,1501,1698,1748,333,2267,2150,32,960,2332,160,1331,24,986,247,1318,2165,1214,2388,1157,995,1471,88,1009,2256,437,1361,2403,1172,1696,1264,242,2428,1186,505,1511,279,198,1794,439,1042,1698,2343,1115,1529,1974,2331,1968,2317,110,1593,2137,1283,143,1849,96,782,1070,1717,1248,208,1107,1768,2447,408,138,762,469,2097,2130,1598,1480,1093,1075,1321,868,2437,575,1023,529,1836,1519,694,778,2289,826,303,775,1689,901,583,1989,299,2269,2032,2022,1735,567,781,1037,1160,898,2285,2124,589,2464,1343,2319,938,223,582,74,2228,867,432,1099,432,2360,223,243,1149,2189,1247,435,1027,44,1565,854,1860,655,1136,1204,822,635,340,2177,302,256,2329,1799,2173,2115,1269,1645,1701,1537,1031,1602,1629,1411,110,2323,1807,696,571,1686,214,2066,137,1200,2257,1078,2039,2239,1792,544,54,2058,761,1488,1666,1551,1081,2323,1651,1869,1239,752,1812,1535,2427,471,355,1719,520,94,403,2419,1651,2172,1798,905,1340,314,281,1342,2022,2394,1729,483,1826,634,330,2462,1085,562,1314,2384,1132,1164,1985,2494,81,1051,613,352,38,1466,1223,626,74,1016,587,2359,294,215,145,881,118,2453,244,2495,549,551,653,2273,1929,1661,1111,461,2478,373,2331,1465,2206,2390,2370,27,206,2029,1258,961,2486,146,1803,1223,496,2448,393,1805,176,2120,609,1917,146,2262,2428,1905,2158,838,2446,178,1973,910,1671,1224,2375,658,507,482,64,2377,2116,1232,2344,2360,726,2018,1482,1257,949,328,1860,1322,1014,1900,1568,2319,1579,617,653,435,1527,1894,1906,1642,388,548,247,203,966,1034,143,2136,1902,1404,424,1663,1460,2496,901,373,488,1055,1379,258,416,1387,1959,2373,2356,2017,191,2081,1873,127,648,1014,1135,1672,2197,1498,1884,536,1796,247,1524,1225,1059,512,246,1437,2026,2135,1076,882,509,738,122,1690,794,274,21,2362,327,2331,2291,994,1871,1793,1322,1626,96,922,1720,1601,1480,1388,2131,1502,122,2312,1871,2156,132,2454,319,1226,225,1992,1914,74,1083,2273,867,164,781,2104,2072,1501,1248,2464,486,99,2329,1264,471,1532,21,1534,1868,1108,2329,399,976,634,415,818,1924,31,92,516,2418,515,895,30,545,54,1934,1326,128,95,888,106,477,1649,326,1514,1668,254,1947,465,753,1136,101,1679,1140,1322,5,895,1020,1532,2035,995,1245,1920,466,2082,169,1469,2125,1328,2111,118,453,407,1198,1938,1581,767,309,1528,1252,848,2242,1473,318,2287,2218,740,853,355,1608,2467,789,894,2072,1659,2264,2174,1685,808,693,181,2186,1053,2008,764,1815,143,1285,1073,715,752,1959,1480,990,2362,1989,1922,2221,2268,384,797,1861,665,1610,161,731,1,704,1246,1987,549,2489,1192,754,1205,1271,289,2201,590,1510,312,1695,1995,1356,790,1696,610,482,777,1284,26,466,277,903,383,1532,1871,2476,1649,642,1402,140,930,1348,1576,2191,2300,2500,368,753,1584,50,106,873,559,329,803,299,1795,426,2226,270,2394,988,2368,2028,1527,631,1274,1838,1508,1773,2131,1083,795,2127,879,319,85,291,1458,482,655,1238,70,1138,2259,167,2437,2031,2220,249,2143,1552,651,1552,1650"}, {"input": "1295,2088,1104,2193,791,470,2161,2236,939,196,806,2280,2164,2231,534,2369,1965,432,1172,480,1560,1593,277,1346,760,680,1839,2001,414,1340,606,1077,651;1121,367,2063,2379,1470,2407,1693,2306,1726,1337,1678,780,2479,1450,1544,2473,2423,1034,1341,2091,1280,1422,1876,2085,1356,2237,1683,2370,1465,2448,2165,2369,1228;765,1129,494,2254,256,839,803,262,706,1835,1465,125,1346,1848,58,2102,2304,1415,1785,884,1345,675,1923,960,564,1651,1399,2432,777,925,938,2453,1687;1499,1299,773,1992,1897,460,579,2325,1810,1979,2491,1307,335,59,1317,1990,2256,2257,713,2487,346,101,2422,1660,2424,110,2313,972,2230,971,389,2325,726;1077,209,1201,2499,642,108,1346,820,1950,110,985,1909,2219,257,489,1685,2333,2068,851,708,929,1697,1965,2263,1949,926,1534,380,107,2291,703,1769,1815;1005,2237,2325,416,278,38,2128,718,2328,1010,286,715,8,2067,1857,809,1966,705,54,778,329,1052,1118,2022,2133,980,606,1151,221,705,907,1338,1008;2124,1641,625,1838,827,1700,2307,2004,2237,396,709,2408,2117,2344,1465,1304,1382,2294,1156,1937,599,1214,25,2445,1181,2294,167,493,285,2191,1588,1008,2135;2048,2179,1801,40,239,151,2110,2430,2036,1494,1197,2192,687,1274,2457,1156,1801,878,2025,1567,2423,2156,2460,1302,1496,1732,986,1637,2268,309,1831,2381,1927;394,77,767,231,288,172,1626,423,1649,645,530,1008,1510,1375,821,2369,1386,1200,2418,10,1207,1989,2200,916,2404,1495,257,184,2198,1439,2335,565,2189;1673,1140,1270,2007,2485,686,1361,254,1825,2074,1542,1248,2402,50,298,180,1311,1602,1256,20,471,1400,1075,70,2241,923,1954,194,282,2402,254,1023,1216;1222,121,507,527,1440,1467,487,1916,755,57,676,1197,2423,381,641,2362,659,1861,1862,764,2088,1685,1926,505,424,2028,119,1822,2217,524,431,1357,1350;1970,365,380,2277,121,1661,1215,2432,744,2057,965,1998,514,1280,1100,310,986,1957,1308,2311,815,1848,241,1129,1749,1029,307,1173,880,1402,1156,321,912;1677,1465,1354,541,1567,1613,447,627,962,436,940,2021,508,1578,572,1330,345,1061,810,420,104,1755,249,1474,1254,1103,1540,2330,1207,326,393,2219,799;1790,1114,1812,403,702,1194,1371,1382,1874,1372,1012,725,2253,1818,2500,725,1615,202,1135,9,1222,1998,709,1418,2222,250,2034,452,488,87,1295,1053,562;2075,23,326,736,2474,20,1763,809,2396,373,1367,1576,2086,2381,1306,1116,2364,65,1456,1200,820,1371,2477,1979,2017,1588,1215,732,1388,1861,909,2172,646;2170,125,1874,22,1532,2268,1184,1225,2342,1162,1858,171,1033,505,854,470,1826,75,1197,1850,975,1969,1396,1895,541,770,2166,636,1037,177,1440,1770,1316;2112,2375,257,751,135,1551,2473,1978,2332,1443,738,2058,80,1263,25,2019,1714,1480,535,194,509,2071,1623,977,470,1955,2102,782,1418,1921,2489,117,1132;2234,97,2347,488,1177,470,1873,1663,1302,1404,899,973,718,1745,2232,1324,2097,2055,1931,1910,75,2109,1702,2000,974,643,646,1246,78,1564,1122,1667,2480;1272,1905,2298,1633,44,1507,1672,193,2027,824,1863,1209,1156,2006,2003,1509,434,1264,1752,2010,1901,1445,2217,1286,538,2413,1610,2195,298,1474,425,1371,1267", "output": "1295,1104,791,2161,939,806,2164,534,1965,1172,1560,277,760,1839,414,606,651,2369,2448,2370,2237,2085,1422,2091,1034,2473,1450,780,1337,2306,2407,2379,367,765,494,256,803,706,1465,1346,58,2304,1785,1345,1923,564,1399,777,938,1687,2325,971,972,110,1660,101,2487,2257,1990,59,1307,1979,2325,460,1992,1299,1077,1201,642,1346,1950,985,2219,489,2333,851,929,1965,1949,1534,107,703,1815,1338,705,1151,980,2022,1052,778,705,809,2067,715,1010,718,38,416,2237,2124,625,827,2307,2237,709,2117,1465,1382,1156,599,25,1181,167,285,1588,2135,2381,309,1637,1732,1302,2156,1567,878,1156,1274,2192,1494,2430,151,40,2179,394,767,288,1626,1649,530,1510,821,1386,2418,1207,2200,2404,257,2198,2335,2189,1023,2402,194,923,70,1400,20,1602,180,50,1248,2074,254,686,2007,1140,1222,507,1440,487,755,676,2423,641,659,1862,2088,1926,424,119,2217,431,1350,321,1402,1173,1029,1129,1848,2311,1957,310,1280,1998,2057,2432,1661,2277,365,1677,1354,1567,447,962,940,508,572,345,810,104,249,1254,1540,1207,393,799,1053,87,452,250,1418,1998,9,202,725,1818,725,1372,1382,1194,403,1114,2075,326,2474,1763,2396,1367,2086,1306,2364,1456,820,2477,2017,1215,1388,909,646,1770,177,636,770,1895,1969,1850,75,470,505,171,1162,1225,2268,22,125,2112,257,135,2473,2332,738,80,25,1714,535,509,1623,470,2102,1418,2489,1132,1667,1564,1246,643,2000,2109,1910,2055,1324,1745,973,1404,1663,470,488,97,1272,2298,44,1672,2027,1863,1156,2003,434,1752,1901,2217,538,1610,298,425,1267"}, {"input": "571,1423,1209,1918,1339,1928,712;257,1398,338,2129,1079,914,56;676,2201,706,1105,316,324,2009;750,7,2153,328,1914,548,2270;845,1006,1353,406,1017,596,610;1391,1168,477,840,1121,131,946;1821,35,1413,102,136,1103,593;127,1551,470,331,906,1659,1335;1466,1256,2189,1663,566,2483,1485;384,699,1439,1058,2500,1040,923;1627,2448,1076,2211,1711,2172,1179;1818,1576,2266,448,956,1203,597;2282,706,1759,1164,1824,1777,460;570,377,1566,483,1738,83,2236;2124,1945,784,961,2415,522,1354;2217,588,2134,1096,1354,1363,78;1349,1535,2086,2021,852,2311,346;1591,895,327,1659,720,319,26;146,2229,28,2159,17,1283,1317;1046,1148,6,2219,482,845,465;1572,845,1862,2267,706,741,2427;87,719,679,184,39,1125,781;1048,1473,346,474,2087,118,929;927,605,2044,1260,453,815,1556;949,303,1132,1853,1150,119,704;1739,1176,2394,1083,1083,520,811;2373,158,2001,82,2083,1816,1087;164,1383,433,743,467,1149,1307;1304,678,2242,1768,647,1835,1139;1592,2040,1179,1995,1397,708,96;186,2305,1238,496,1195,715,599;540,1516,2481,794,1842,2370,1638;472,1181,1817,184,1989,2191,1059;297,1707,677,549,1024,808,868;73,1624,16,1265,2083,2145,1908;1685,71,878,2462,493,610,1214;2273,2460,1263,1653,424,2111,1662;1427,1244,558,231,707,1867,37;2167,1171,858,987,318,1378,1478;1067,510,12,2039,2196,121,2135;983,82,430,2286,2254,1460,1771;1285,1941,1951,3,860,364,1221;1466,1926,994,632,2453,2336,620;750,2350,1855,1427,801,1183,2321;1273,1801,2377,832,794,178,2317;1851,884,61,1890,586,1471,1135;243,1653,2411,1213,27,929,2364;780,2189,1279,1741,750,1485,2093;1073,1338,7,1644,1234,1914,551;521,2437,950,223,474,2260,70", "output": "571,1209,1339,712,914,2129,1398,676,706,316,2009,548,328,7,845,1353,1017,610,131,840,1168,1821,1413,136,593,1659,331,1551,1466,2189,566,1485,1040,1058,699,1627,1076,1711,1179,1203,448,1576,2282,1759,1824,460,83,483,377,2124,784,2415,1354,1363,1096,588,1349,2086,852,346,319,1659,895,146,28,17,1317,845,2219,1148,1572,1862,706,2427,1125,184,719,1048,346,2087,929,815,1260,605,949,1132,1150,704,520,1083,1176,2373,2001,2083,1087,1149,743,1383,1304,2242,647,1139,708,1995,2040,186,1238,1195,599,2370,794,1516,472,1817,1989,1059,808,549,1707,73,16,2083,1908,610,2462,71,2273,1263,424,1662,1867,231,1244,2167,858,318,1478,121,2039,510,983,430,2254,1771,364,3,1941,1466,994,2453,620,1183,1427,2350,1273,2377,794,2317,1471,1890,884,243,2411,27,2364,1485,1741,2189,1073,7,1234,551,2260,223,2437"}, {"input": "1063,215,486,1601,1172,664,2365,2386,1955,756,162,592,2346,1953,1882,1974,648,238,1671,1660,96,704,861,1006,2255,478,2278,447,2339,389,810,1094,811,1586,1360,1719,594,1717,956,1667,1925,1534,2455,1725,417,1897,779,2378,648,1134;1530,2299,170,590,2077,1894,61,2059,1050,1885,592,217,512,839,2178,2170,92,781,101,551,463,705,2133,2459,1436,2462,1195,21,1014,1132,1819,325,659,63,1192,1202,626,295,51,1491,34,567,1807,1752,1632,1689,1622,2296,323,1955", "output": "1063,486,1172,2365,1955,162,2346,1882,648,1671,96,861,2255,2278,2339,810,811,1360,594,956,1925,2455,417,779,648,1955,2296,1689,1752,567,1491,295,1202,63,325,1132,21,2462,2459,705,551,781,2170,839,217,1885,2059,1894,590,2299"}, {"input": "1907,1601,694,1638,573,1768;5,1339,440,322,372,2219;1410,2357,746,1294,1119,1099;580,2499,888,1625,638,1254;310,392,46,53,1191,736;1111,2412,1984,74,785,348;6,342,1528,178,1259,2065;828,1757,1155,1082,1498,2135;1286,1897,1153,1831,1859,2193;390,412,927,677,1708,2489;1923,381,1170,1824,1365,957;34,1092,2126,110,1440,1236;1403,1869,2117,1397,1406,1576;754,841,1767,1601,1697,1970;327,964,824,764,1863,389;145,2372,1480,419,2197,807;2332,2357,2493,2212,981,1086;1373,1950,1552,982,1115,1155;853,1808,1505,1492,152,929;1851,809,1951,1374,2015,2456;1419,2469,2163,479,1310,1610;2269,2084,14,853,2496,640;1365,911,266,1993,70,1961;342,1802,655,629,910,989;7,822,2436,926,267,2374;2223,1848,1189,2239,1750,2019;674,1937,596,39,725,1794;818,1485,1690,1462,657,858;1674,284,1190,182,2466,1668;755,1172,153,862,2167,139;571,1376,1837,1202,43,130;1058,964,648,328,1922,322;1989,1734,859,207,250,2045;2400,1182,1127,199,840,1304;564,1946,1399,2228,434,640;2101,1869,1983,1343,947,1038;944,843,2430,713,1283,624", "output": "1907,694,573,2219,322,1339,1410,746,1119,1254,1625,2499,310,46,1191,348,74,2412,6,1528,1259,2135,1082,1757,1286,1153,1859,2489,677,412,1923,1170,1365,1236,110,1092,1403,2117,1406,1970,1601,841,327,824,1863,807,419,2372,2332,2493,981,1155,982,1950,853,1505,152,2456,1374,809,1419,2163,1310,640,853,2084,1365,266,70,989,629,1802,7,2436,267,2019,2239,1848,674,596,725,858,1462,1485,1674,1190,2466,139,862,1172,571,1837,43,322,328,964,1989,859,250,1304,199,1182,564,1399,434,1038,1343,1869,944,2430,1283"}, {"input": "1078,942,1472,2496,1016,400,2198,979,2489,1292,2485,198,2362,804,1762,2292,2273,2339,939,1684,1884,1495,1420,2202,1927,1624,2379,1414,1706,187,2325,943,2490,2349,1810,2315,483,149,2317,412,1499;2250,1816,1653,1066,2397,425,1050,2215,919,1451,1705,744,985,677,242,802,2136,772,2324,539,1239,1862,1424,1605,2277,506,993,2119,1390,1700,1867,1597,2329,159,2116,2331,2136,203,2287,1473,1829", "output": "1078,1472,1016,2198,2489,2485,2362,1762,2273,939,1884,1420,1927,2379,1706,2325,2490,1810,483,2317,1499,1473,203,2331,159,1597,1700,2119,506,1605,1862,539,772,802,677,744,1451,2215,425,1066,1816"}, {"input": "2408,517,366,1101,2224,65,1779,1626,1253,1182,1750,920,2010,2019,1986,461,239,1615,2013,335,2440,1023,165,1687,2333,1963,1950,916,2460,1134,858,709,1543,2229,149,265,87,1839,31;975,744,201,1337,1168,338,343,2214,465,2496,718,553,2093,100,1926,861,1838,1130,467,2178,423,1556,1397,1072,487,2346,1935,624,1259,950,1445,972,2365,1460,1930,877,1952,1100,2006;186,2320,2278,217,984,1103,930,1571,743,1716,1795,2465,694,2397,1163,1197,971,1188,749,1113,2029,960,1156,2478,564,1232,1322,35,2271,473,518,428,377,1873,318,2463,338,1245,178;1645,1586,1647,1962,582,1126,1286,1008,233,71,603,420,1098,2192,1773,2474,1447,1683,1074,1663,798,1584,1395,1759,2476,2444,1561,658,1818,2133,1979,151,874,942,693,985,1860,194,1157;637,873,2307,2157,2299,1990,1117,1493,74,728,1899,1228,2497,1897,1388,713,1740,1971,313,1848,1489,900,559,1016,1055,839,409,1143,2440,1061,1955,2370,2411,250,466,85,104,2019,69;894,2420,2294,1477,750,1946,1182,1936,608,1907,558,2187,42,1383,284,1807,2196,1652,1694,1757,107,149,2283,1076,141,2002,521,2323,1101,683,961,2346,1028,2066,734,275,1976,2498,1294;622,275,1829,2216,1145,674,2421,2243,418,19,2456,1813,2091,616,1740,1512,2354,530,1890,1690,1852,1654,1723,1508,1162,220,2372,804,970,2354,2181,2104,1777,1323,2181,1156,171,2253,1654;1100,254,528,172,1880,1164,940,383,1029,424,1727,1430,1865,508,1495,971,587,742,1512,384,2048,794,455,818,1596,534,1960,1020,2316,1677,1435,1062,709,2395,2413,650,2219,2121,1142;166,2047,36,2101,1697,430,1275,449,1812,1633,275,1978,2108,131,1884,2281,831,1539,1675,213,1230,153,2282,915,1834,1016,294,2347,936,1227,1900,1257,477,955,1986,1470,2082,2295,1910;1271,1445,1502,1901,1764,2083,413,337,2094,1622,202,2084,2099,475,1460,2244,1589,1006,1755,790,44,7,2117,2285,482,2263,2030,14,745,594,173,2368,286,1964,2339,651,1635,2042,905;1816,2310,610,35,2262,2186,364,2379,824,1354,1331,2044,1110,996,2188,2042,2255,1272,1556,227,632,1173,1612,1047,1733,656,869,1204,175,1482,1437,926,2058,618,156,650,1552,1775,1976;1149,1928,1316,2157,1321,1869,635,2190,260,2477,77,1627,1168,38,878,2445,582,443,489,236,141,797,523,1635,1493,1261,2482,1720,2329,1816,2024,975,1570,2110,2367,1438,2049,2093,1698;1915,1791,1395,581,855,824,1289,382,707,928,828,1518,1578,1986,1074,1130,2346,867,1059,645,212,1831,2496,2419,2031,381,2329,1713,283,1368,2131,1450,363,394,779,593,1415,1276,359;239,1509,1281,417,902,1541,178,2276,526,256,1607,822,1958,634,926,909,1170,838,553,1245,1951,2062,997,2422,1515,2024,29,1855,1439,1695,728,1089,740,581,1454,2155,308,1704,747;494,2106,608,858,661,1962,311,143,351,2056,2103,1789,186,970,778,964,213,2214,1133,1069,2435,1364,1501,646,750,799,1021,503,454,1721,109,2168,320,2475,1410,1325,2340,1799,1119;2455,2,2192,708,1941,2251,1503,2431,616,2469,228,680,1611,2295,2129,1384,609,545,341,134,1823,1542,1661,1012,839,1917,23,730,2290,1554,165,1798,968,1061,1781,187,2403,816,2308;572,1939,1345,2067,896,208,46,1804,1450,187,2475,2324,1567,581,109,52,1125,2231,982,147,1246,2027,332,1824,239,75,2278,641,2028,1390,1484,972,266,2135,2086,234,1071,2271,1625;234,1891,2014,2144,1986,286,1084,12,2302,1346,1971,155,208,1450,1719,1793,59,440,674,652,2177,627,2312,1723,1854,820,242,544,1430,443,2082,1559,680,1483,966,2420,1165,887,781;1495,810,1292,1111,686,787,172,1750,57,618,152,675,330,510,490,1190,38,1170,890,482,1417,443,141,2401,2279,37,1878,2245,1600,1131,1458,152,278,55,1425,2305,2284,1894,2151;1819,2412,221,2340,1321,1149,647,670,130,172,150,1434,1300,476,98,843,651,1663,2024,652,2129,1579,847,190,1657,1956,75,1626,1177,1215,1852,755,1873,1279,1937,659,2231,431,2066;320,1389,1369,860,2230,2027,1967,554,927,152,1578,2319,434,1548,928,1226,1128,423,2368,187,1698,2122,802,385,2273,1476,2297,2408,645,2235,302,1970,570,1848,1584,747,2017,1710,1666;1146,1827,1529,819,1980,181,2401,1292,2211,625,173,1432,1582,1480,592,1120,2372,2360,1264,2356,1736,1002,2422,1963,754,1664,209,260,997,1254,89,522,293,2032,741,1664,2459,838,491;1852,2450,1723,247,2256,207,1536,1880,679,843,1809,1516,2287,1492,2441,1079,2475,1961,2014,56,1446,524,150,935,121,2471,1796,424,2245,1734,177,819,2392,1251,2419,1453,1609,1680,286;1716,2079,1591,1758,2371,447,1765,1778,1056,1765,377,1370,81,1968,1466,2361,1078,1265,528,96,1824,1389,384,1203,827,2205,1014,545,118,2106,852,2415,778,30,832,1256,992,42,2011;1929,1852,2207,2362,1106,412,297,211,1942,1651,1306,1017,2197,819,1846,585,798,754,821,1815,809,1006,1393,384,902,861,2355,2216,1318,613,887,275,2453,1835,2492,2348,79,38,2415;960,2014,2155,90,2244,2357,186,1088,1374,1915,2162,817,1169,2127,1745,1936,1985,299,127,1348,2111,1366,424,1201,467,373,1193,2437,1345,1706,527,1277,1405,635,439,200,522,2059,999;1089,1907,2107,2025,528,837,2076,1480,1576,696,1057,1107,1472,157,2295,117,926,948,97,2385,97,1217,796,2213,2135,2395,496,2308,1065,1355,845,2298,2128,479,1032,2270,824,435,471;1196,551,1951,102,817,1698,2412,1458,198,1127,1090,23,73,770,1583,100,57,513,894,1818,1109,1300,2004,2246,1788,1065,1167,1924,368,1958,1907,924,1677,393,1930,1343,1436,1634,815;659,15,649,1961,1574,2495,2118,1855,839,1910,1160,1548,1280,887,811,2240,1551,320,1078,545,2095,1475,1019,1520,2099,499,221,2101,503,2054,1138,520,1159,302,1373,1481,249,1626,2035;1547,160,281,1283,589,1349,1179,320,775,964,817,771,1481,2111,411,140,1173,1547,1696,1848,1858,1624,1569,2370,1873,444,136,1829,2161,1362,662,2313,712,1703,867,852,1526,2434,361;521,1091,124,68,575,1834,36,1094,2471,707,2069,124,623,1719,1808,489,106,738,1725,2186,1318,944,603,1661,278,949,2406,1984,185,682,1997,487,387,1879,2240,121,1068,40,161;186,872,1146,1262,1357,2144,2164,85,929,631,338,2207,1896,1542,1084,388,1521,1070,1141,441,2322,103,1081,1346,1931,963,452,2261,1867,1489,978,1743,1108,313,1360,1234,1745,1182,1968;302,604,766,2050,116,2036,1874,144,653,2444,1584,975,37,544,132,1435,261,1964,1498,503,2088,1788,1302,939,1982,388,2138,1762,644,516,2167,742,653,2413,1113,1847,207,698,31;1462,1897,1529,234,887,909,1339,1315,1671,1678,1242,1518,691,1655,2020,118,1174,981,1733,1727,2053,1438,873,1407,1243,1269,1532,370,167,1102,2488,2150,436,1750,2155,870,716,1695,635;1972,470,366,715,1906,887,1340,2434,150,28,1714,918,61,1539,346,748,1863,1895,1835,251,2465,519,1827,1224,986,766,1848,2233,1803,53,378,1618,915,912,1175,2470,897,227,2034;860,394,212,2479,419,665,2464,1700,625,127,1736,321,817,458,2262,1782,2017,986,1906,1818,823,2322,1540,274,1251,795,712,1687,1117,2234,636,316,2415,548,2457,2446,826,1945,454;640,277,826,1225,2357,30,2167,624,1142,2418,792,2379,2418,1130,44,1647,978,2041,2184,146,1611,317,1896,1186,455,21,1001,130,1550,1664,2135,2119,1099,744,1522,1719,2292,38,925;2493,1389,501,634,81,1041,624,890,625,940,1568,2441,1109,1608,2135,1057,1394,1317,360,1684,2106,127,2498,750,756,1287,1794,1213,1567,2425,294,941,1068,10,395,9,2241,1979,597;1289,526,1788,1873,112,118,2371,2033,1466,1120,1889,1385,2197,624,598,203,2481,956,794,513,1334,949,1740,1286,2002,642,213,1335,1938,2204,1734,2421,292,917,673,356,904,576,625;1117,263,1460,1425,2042,1758,1246,852,1211,1344,633,1889,44,2294,1991,554,1279,1239,1448,903,1470,2310,1649,1974,1673,966,504,801,1594,2135,2030,1267,1489,1961,1186,532,1856,2224,925;274,1579,1081,1763,104,926,363,841,2399,732,1597,510,805,77,624,31,2306,471,1042,492,1005,654,1003,2073,1011,763,447,2361,247,1781,979,863,854,60,326,1400,294,1874,19;1436,1694,640,2388,2432,1621,1263,1126,139,854,1311,1371,1139,2383,613,1986,1128,2128,1533,1661,1401,1795,1633,615,1041,1081,396,1635,2009,1460,1575,2489,2339,374,421,1263,1408,1801,375", "output": "2408,366,2224,1779,1253,1750,2010,1986,239,2013,2440,165,2333,1950,2460,858,1543,149,87,31,1100,877,1460,972,950,624,2346,1072,1556,2178,1130,861,100,553,2496,2214,338,1337,744,186,2278,984,930,743,1795,694,1163,971,749,2029,1156,564,1322,2271,518,377,318,338,178,194,985,942,151,2133,658,2444,1759,1584,1663,1683,2474,2192,420,71,1008,1126,1962,1586,637,2307,2299,1117,74,1899,2497,1388,1740,313,1489,559,1055,409,2440,1955,2411,466,104,69,2498,275,2066,2346,683,2323,2002,1076,149,1757,1652,1807,1383,2187,1907,1936,1946,1477,2420,622,1829,1145,2421,418,2456,2091,1740,2354,1890,1852,1723,1162,2372,970,2181,1777,2181,171,1654,2121,650,2395,1062,1677,1020,534,818,794,384,742,971,508,1430,424,383,1164,172,254,166,36,1697,1275,1812,275,2108,1884,831,1675,1230,2282,1834,294,936,1900,477,1986,2082,1910,2042,651,1964,2368,594,14,2263,2285,7,790,1006,2244,475,2084,1622,337,2083,1901,1445,1816,610,2262,364,824,1331,1110,2188,2255,1556,632,1612,1733,869,175,1437,2058,156,1552,1976,2093,1438,2110,975,1816,1720,1261,1635,797,236,443,2445,38,1627,2477,2190,1869,2157,1928,1915,1395,855,1289,707,828,1578,1074,2346,1059,212,2496,2031,2329,283,2131,363,779,1415,359,1704,2155,581,1089,1695,1855,2024,2422,2062,1245,838,909,634,822,256,2276,1541,417,1509,494,608,661,311,351,2103,186,778,213,1133,2435,1501,750,1021,454,109,320,1410,2340,1119,816,187,1061,1798,1554,730,1917,1012,1542,134,545,1384,2295,680,2469,2431,2251,708,2,572,1345,896,46,1450,2475,1567,109,1125,982,1246,332,239,2278,2028,1484,266,2086,1071,1625,887,2420,1483,1559,443,544,820,1723,627,652,440,1793,1450,155,1346,12,286,2144,1891,1495,1292,686,172,57,152,330,490,38,890,1417,141,2279,1878,1600,1458,278,1425,2284,2151,431,659,1279,755,1215,1626,1956,190,1579,652,1663,843,476,1434,172,670,1149,2340,2412,320,1369,2230,1967,927,1578,434,928,1128,2368,1698,802,2273,2297,645,302,570,1584,2017,1666,838,1664,2032,522,1254,260,1664,1963,1002,2356,2360,1120,1480,1432,625,1292,181,819,1827,1852,1723,2256,1536,679,1809,2287,2441,2475,2014,1446,150,121,1796,2245,177,2392,2419,1609,286,42,1256,30,2415,2106,545,2205,1203,1389,96,1265,2361,1968,1370,1765,1778,447,1758,2079,1929,2207,1106,297,1942,1306,2197,1846,798,821,809,1393,902,2355,1318,887,2453,2492,79,2415,2059,200,635,1277,1706,2437,373,1201,1366,1348,299,1936,2127,817,1915,1088,2357,90,2014,1089,2107,528,2076,1576,1057,1472,2295,926,97,97,796,2135,496,1065,845,2128,1032,824,471,1634,1343,393,924,1958,1924,1065,2246,1300,1818,513,100,770,23,1127,1458,1698,102,551,659,649,1574,2118,839,1160,1280,811,1551,1078,2095,1019,2099,221,503,1138,1159,1373,249,2035,2434,852,1703,2313,1362,1829,444,2370,1624,1848,1547,140,2111,771,964,320,1349,1283,160,521,124,575,36,2471,2069,623,1808,106,1725,1318,603,278,2406,185,1997,387,2240,1068,161,1182,1234,313,1743,1489,2261,963,1346,103,441,1070,388,1542,2207,631,85,2144,1262,872,302,766,116,1874,653,1584,37,132,261,1498,2088,1302,1982,2138,644,2167,653,1113,207,31,1695,870,1750,2150,1102,370,1269,1407,1438,1727,981,118,1655,1518,1678,1315,909,234,1897,1972,366,1906,1340,150,1714,61,346,1863,1835,2465,1827,986,1848,1803,378,915,1175,897,2034,1945,2446,548,316,2234,1687,795,274,2322,1818,986,1782,458,321,127,1700,665,2479,394,640,826,2357,2167,1142,792,2418,44,978,2184,1611,1896,455,1001,1550,2135,1099,1522,2292,925,1979,9,10,941,2425,1213,1287,750,127,1684,1317,1057,1608,2441,940,890,1041,634,1389,1289,1788,112,2371,1466,1889,2197,598,2481,794,1334,1740,2002,213,1938,1734,292,673,904,625,2224,532,1961,1267,2135,801,966,1974,2310,903,1239,554,2294,1889,1344,852,1758,1425,263,274,1081,104,363,2399,1597,805,624,2306,1042,1005,1003,1011,447,247,979,854,326,294,19,1801,1263,374,2489,1460,1635,1081,615,1795,1661,2128,1986,2383,1371,854,1126,1621,2388,1694"}, {"input": "1986,670,308,1282,361,695,2030,1775,377,19,2036,1128,578,856,1760,2018,1900,952,469,53,605,2492,593,752,2116,523,499,1447,633,1742,2079,1045;2358,1779,1964,2394,1148,1407,2443,581,1736,1017,1259,1135,948,1486,858,1155,2452,137,2441,2018,1186,944,268,458,2184,864,146,2384,1622,1573,935,265;781,400,802,1342,787,1540,776,788,1907,1713,1171,2064,278,284,826,2475,2370,800,1927,589,356,2111,1693,855,1592,2333,1046,780,1586,712,607,1955;596,526,1233,1718,1065,1975,1356,948,2331,751,708,2294,1497,92,2227,899,422,539,1703,2012,2495,2002,2091,586,1028,1113,1781,205,1699,1082,61,1948;2311,652,78,1619,881,604,2316,593,652,1756,1172,2125,553,1001,765,191,2196,117,1858,2437,1560,2324,1991,435,464,760,1241,69,2383,440,27,2146;1865,1544,318,946,1529,2232,1243,2017,818,2316,1445,2331,824,365,1450,1429,2382,702,1338,1106,203,1157,1510,1056,795,307,1486,1001,731,2135,119,1132;376,1243,2372,1346,1485,561,321,736,1920,743,1822,1160,1521,2421,1756,1497,1037,1706,307,1733,2309,1971,867,2411,703,1261,691,1759,1109,1153,126,1940;1220,2478,1440,1594,2427,280,479,2490,993,2433,1712,372,2011,214,241,1178,1778,1489,5,122,1138,1675,33,1081,1314,980,764,103,1168,1115,1380,2119;2201,749,479,1254,2366,843,2494,1649,218,367,2127,1323,1441,1088,1757,1487,60,278,623,2164,412,800,2479,715,2391,1345,1283,2224,1960,1395,1352,1788;257,1860,794,1294,2414,399,930,1864,1401,1224,1581,829,22,1001,2210,140,746,1002,80,1661,148,1370,727,2224,584,1189,246,2116,1626,1440,2082,792;2314,74,1973,1666,1328,2226,1853,334,1559,1418,1424,1330,1452,961,911,1440,1546,926,2148,2394,790,1483,855,2150,85,1741,1250,1398,1146,994,462,2472;906,1318,1456,791,1997,588,346,1707,2334,142,1307,2166,1417,2347,1524,1207,1735,1335,2144,2404,2100,1766,477,1106,1382,153,131,1109,1418,488,1274,949;239,1898,496,66,790,399,1247,2231,1237,2014,1157,123,710,2490,1203,239,761,419,365,659,1906,109,335,1757,2211,1766,1210,2486,1799,1204,1866,1149;512,995,1635,2019,1584,1699,2062,334,1730,864,1100,739,955,1648,566,2084,1229,625,630,12,421,914,401,1017,2296,1509,968,2186,601,2496,520,743;64,412,2020,2004,2240,2132,655,2395,393,1423,977,1553,1333,358,581,1874,1855,1178,1871,55,1488,2047,774,1441,32,879,1057,1574,2000,752,2229,1449;1798,424,286,69,147,2214,1112,1536,2238,358,132,2037,82,577,1790,388,2130,992,1786,729,93,288,1817,2329,1462,2117,271,253,2389,688,783,1382", "output": "1986,308,361,2030,377,2036,578,1760,1900,469,605,593,2116,499,633,2079,265,1573,2384,864,458,944,2018,137,1155,1486,1135,1017,581,1407,2394,1779,781,802,787,776,1907,1171,278,826,2370,1927,356,1693,1592,1046,1586,607,1948,1082,205,1113,586,2002,2012,539,899,92,2294,751,948,1975,1718,526,2311,78,881,2316,652,1172,553,765,2196,1858,1560,1991,464,1241,2383,27,1132,2135,1001,307,1056,1157,1106,702,1429,365,2331,2316,2017,2232,946,1544,376,2372,1485,321,1920,1822,1521,1756,1037,307,2309,867,703,691,1109,126,2119,1115,103,980,1081,1675,122,1489,1178,214,372,2433,2490,280,1594,2478,2201,479,2366,2494,218,2127,1441,1757,60,623,412,2479,2391,1283,1960,1352,792,1440,2116,1189,2224,1370,1661,1002,140,1001,829,1224,1864,399,1294,1860,2314,1973,1328,1853,1559,1424,1452,911,1546,2148,790,855,85,1250,1146,462,949,488,1109,153,1106,1766,2404,1335,1207,2347,2166,142,1707,588,791,1318,239,496,790,1247,1237,1157,710,1203,761,365,1906,335,2211,1210,1799,1866,743,2496,2186,1509,1017,914,12,625,2084,1648,739,864,334,1699,2019,995,64,2020,2240,655,393,977,1333,581,1855,1871,1488,774,32,1057,2000,2229,1382,688,253,2117,2329,288,729,992,388,577,2037,358,1536,2214,69,424"}, {"input": "501,552,805,205,1827,1726,2300,1706,86,73,2216,34,1109,2055,1719,2375,1285,320,507,1404,1737,1646,2212,430,434,1584,716,651,2292,1053;1890,1069,1046,1214,2236,912,2285,1112,446,2317,2120,1695,655,767,1658,83,582,2206,2265,2326,827,1015,945,190,854,902,2484,410,569,1261;2222,529,1422,872,2058,618,325,1092,684,786,434,862,943,657,213,2164,639,1216,1452,909,1721,166,1086,2071,149,1371,1702,908,1364,1838;115,1564,1430,376,393,739,109,2028,503,1433,177,613,1528,1648,9,57,780,1794,1604,1350,879,605,838,79,2040,534,1715,963,96,1510;1938,1848,828,369,96,1012,191,2222,726,1246,1497,2430,2222,1797,1058,1012,1459,917,756,2236,2203,1042,1756,737,558,571,2464,1489,1975,248;944,512,596,267,1222,485,701,429,1517,1037,667,68,2112,994,1258,43,2149,1224,714,203,1704,1755,1831,1771,736,1746,1857,99,945,2469;1873,1247,1758,456,186,359,529,140,1642,1674,914,1854,729,1837,1066,1561,261,1004,2402,39,720,89,1045,683,227,603,1846,546,1215,487;1061,1519,868,1288,1320,1203,896,1961,1573,1589,725,1009,49,1031,1677,777,913,733,2124,111,2092,658,555,339,2107,1334,1223,1573,363,1455;1397,1207,740,5,1646,507,2285,394,600,1563,2242,1169,1461,1454,639,1450,118,1026,615,1621,95,641,321,1588,2349,831,2345,681,897,1284;1263,2114,2350,2190,948,2499,1970,1433,1865,655,1007,1405,1826,1216,120,1071,2268,1623,118,2347,1413,2082,2465,427,2477,2068,1006,25,1288,827;1104,2379,1582,2304,1095,1575,1148,1438,299,1278,1123,1337,641,849,1877,1585,871,960,1451,432,2351,1680,243,1692,2144,1174,1811,1387,2387,1115;1604,846,299,1985,1730,531,1613,1182,1984,1338,2033,1383,1616,676,372,2348,486,67,1474,1565,2322,1340,647,2339,2328,466,1384,404,1385,1601;1538,1848,1839,754,1803,2031,2336,984,280,393,1055,1646,356,1828,2422,1274,1086,2353,847,988,2199,322,164,639,529,649,2201,1543,1420,1521", "output": "501,805,1827,2300,86,2216,1109,1719,1285,507,1737,2212,434,716,2292,1261,410,902,190,1015,2326,2206,83,767,1695,2317,1112,912,1214,1069,2222,1422,2058,325,684,434,943,213,639,1452,1721,1086,149,1702,1364,1510,963,534,79,605,1350,1794,57,1648,613,1433,2028,739,376,1564,1938,828,96,191,726,1497,2222,1058,1459,756,2203,1756,558,2464,1975,2469,99,1746,1771,1755,203,1224,43,994,68,1037,429,485,267,512,1873,1758,186,529,1642,914,729,1066,261,2402,720,1045,227,1846,1215,1455,1573,1334,339,658,111,733,777,1031,1009,1589,1961,1203,1288,1519,1397,740,1646,2285,600,2242,1461,639,118,615,95,321,2349,2345,897,827,25,2068,427,2082,2347,1623,1071,1216,1405,655,1433,2499,2190,2114,1104,1582,1095,1148,299,1123,641,1877,871,1451,2351,243,2144,1811,2387,1601,404,466,2339,1340,1565,67,2348,676,1383,1338,1182,531,1985,846,1538,1839,1803,2336,280,1055,356,2422,1086,847,2199,164,529,2201,1420"}, {"input": "350,703,2410,88,1564,15,343,1321,433,2493,825,1385,160,829,1525,823,44,1198,2050,927,2155,2291,1746,1278,1837,1261,344,247,1503,376;1999,2485,931,1444,291,385,983,1480,2084,666,2296,5,1119,1219,1780,1626,1303,201,2005,1193,848,1619,2258,148,2415,2275,724,1532,185,1996;1018,1984,155,284,1083,1199,1944,713,1280,1939,1438,2358,506,1664,1232,954,717,1987,1459,446,398,711,878,502,1348,1389,2375,1973,731,766;1629,726,1929,656,1550,342,198,1230,848,1836,1620,854,1729,1898,434,1297,2177,1330,1218,2420,1159,1814,2179,849,1411,1409,2070,1579,257,851;2481,34,211,1840,1980,2393,2007,506,1198,1652,927,1690,42,729,2340,1540,383,534,1606,503,2345,1657,1082,2103,1849,646,1514,1614,12,1552;5,1726,1626,205,1810,878,1611,1735,2380,868,1594,270,233,430,2300,318,787,142,1571,2272,2308,1336,2314,1030,2435,945,1904,259,2305,92;175,1895,15,1625,56,699,1349,960,1669,584,1310,616,406,1671,2246,66,774,969,672,1131,2276,1611,1945,129,1228,609,117,1723,1307,1430;1339,546,775,1183,305,142,333,1174,1448,1467,2094,771,328,974,2138,820,1781,1174,1103,367,2422,2307,1409,2038,165,438,1241,2143,1483,2102;651,2403,1742,321,358,1557,941,1412,1495,2299,1001,785,2087,2295,1108,2097,1789,1101,851,400,593,465,1674,550,16,2077,174,1447,1598,1377;899,257,1273,1574,1016,1503,937,756,1834,473,1884,679,1557,768,2448,1783,1204,1944,1406,466,1954,1556,365,320,614,1989,2376,814,495,1738;213,1083,189,1334,2405,1535,319,1932,1175,408,2389,1108,154,1834,219,631,2455,2363,1163,961,2354,1909,1036,216,131,1299,712,1841,1101,1485;635,1568,1875,2254,2448,2308,1088,1367,1418,1042,1765,1016,850,2118,1702,70,441,128,1459,563,946,1156,839,1263,1583,2001,2403,2448,1094,441;387,2253,2220,177,619,219,1318,1257,1027,1109,2439,1248,720,1767,569,2422,2492,294,2037,2326,286,2046,1596,1434,2195,1202,2000,240,2370,682;1791,774,1623,2126,1881,860,174,2117,1621,601,2031,2097,2458,1424,1275,978,747,1767,2282,2256,586,647,2435,1097,236,957,930,2294,93,1819;314,870,2112,1388,1419,2161,1904,540,1148,940,454,1020,1761,1660,283,1764,1684,1116,1936,1118,673,834,300,381,95,1972,809,733,1807,2338;308,2260,2384,418,1565,572,483,1250,284,1562,1693,667,903,1587,2177,403,1080,716,1080,564,2038,9,2091,201,257,2363,1929,2062,2056,2296;1338,1167,1497,2023,1230,1451,241,110,399,1000,69,1674,314,1637,1979,1622,2489,945,479,208,1198,2262,2078,1405,621,37,1855,402,975,763;2381,1960,674,945,2295,472,453,866,250,2463,1700,254,1604,2430,1065,876,910,1073,1380,2379,1360,1420,1291,2319,245,215,407,156,2297,595;2476,823,1565,120,182,297,1987,2342,215,1382,923,1375,1486,690,1407,771,1545,1307,1706,494,2355,1478,324,2161,1365,216,791,2306,1308,1488", "output": "350,2410,1564,343,433,825,160,1525,44,2050,2155,1746,1837,344,1503,1996,1532,2275,148,1619,1193,201,1626,1219,5,666,1480,385,1444,2485,1018,155,1083,1944,1280,1438,506,1232,717,1459,398,878,1348,2375,731,851,1579,1409,849,1814,2420,1330,1297,1898,854,1836,1230,342,656,726,2481,211,1980,2007,1198,927,42,2340,383,1606,2345,1082,1849,1514,12,92,259,945,1030,1336,2272,142,318,430,270,868,1735,878,205,1726,175,15,56,1349,1669,1310,406,2246,774,672,2276,1945,1228,117,1307,2102,2143,438,2038,2307,367,1174,820,974,771,1467,1174,142,1183,546,651,1742,358,941,1495,1001,2087,1108,1789,851,593,1674,16,174,1598,1738,814,1989,320,1556,466,1944,1783,768,679,473,756,1503,1574,257,213,189,2405,319,1175,2389,154,219,2455,1163,2354,1036,131,712,1101,441,2448,2001,1263,1156,563,128,70,2118,1016,1042,1367,2308,2254,1568,387,2220,619,1318,1027,2439,720,569,2492,2037,286,1596,2195,2000,2370,1819,2294,957,1097,647,2256,1767,978,1424,2097,601,2117,860,2126,774,314,2112,1419,1904,1148,454,1761,283,1684,1936,673,300,95,809,1807,2296,2062,2363,201,9,564,716,403,1587,667,1562,1250,572,418,2260,1338,1497,1230,241,399,69,314,1979,2489,479,1198,2078,621,1855,975,595,156,215,2319,1420,2379,1073,876,2430,254,2463,866,472,945,1960,2476,1565,182,1987,215,923,1486,1407,1545,1706,2355,324,1365,791,1308"}, {"input": "450,417,2284,214,804,1542,360,872,2365,1279,2391,130,1670,2011,299,2024,1336,218,2067,364,1252,2323,1637,272,2476,2341,2182;355,2446,1975,1291,2147,882,1149,1332,14,1900,1442,1473,885,2034,5,349,326,948,757,2065,209,1867,1366,1099,1573,1371,2408;406,2107,1975,66,1663,1259,2356,1269,1915,2374,461,1458,1934,1446,2260,172,138,2024,1070,275,903,1231,1828,642,359,1259,672;221,683,512,368,307,34,1024,1332,2419,411,709,77,264,333,1453,524,2374,1298,1082,270,2264,982,2490,1269,1446,444,279;688,2429,884,2257,2127,1061,959,646,1793,1879,2376,860,1035,1844,1062,2356,1714,2088,1399,602,1550,363,1080,857,689,1775,2265;2332,45,902,520,520,2171,633,2106,2212,2146,1150,1006,1099,732,1828,1386,1530,1809,1106,470,894,605,1870,412,1900,481,2237;1825,17,2168,1386,902,2470,2290,291,1991,1286,1559,2158,186,962,933,465,414,740,645,2399,1551,2487,1300,324,1948,1993,1736;1505,1157,1897,1894,392,1468,544,1985,2186,1598,77,1434,1930,1001,365,2393,825,1904,1374,2000,1064,836,790,716,2388,1123,2472;1618,1376,661,2278,1902,862,1005,387,754,1919,1810,1467,118,1171,300,1920,2067,385,1003,27,1223,988,609,1588,1395,1438,230;178,1362,1230,1924,2474,25,2325,489,1271,860,1497,2219,1887,1958,1027,533,315,1974,820,1888,2060,784,909,1802,493,1686,356;802,806,1785,559,1632,882,7,721,1761,2202,1810,1813,1968,316,1694,2143,2430,986,1423,1925,1452,82,1142,803,734,1432,2374;1437,1463,2191,491,2012,660,2257,207,2258,457,941,1426,1791,912,865,1624,1033,2253,2026,2336,2304,937,2321,1202,579,71,1529;2276,971,1949,2110,1975,972,730,1309,1608,2173,1914,257,2215,47,378,2380,1311,1617,216,2252,1400,1550,1213,995,826,1349,1202;1874,677,2214,55,2467,200,388,1026,874,2153,268,1001,2420,1916,507,189,1832,862,706,1235,1915,1460,465,650,296,1890,602;1824,1768,1049,1303,2302,1761,1358,1441,1434,2024,45,801,1202,730,1891,1854,2196,1795,2482,1384,922,777,1592,174,458,976,2196;1863,1892,1350,2289,1707,1001,1089,1046,2318,2227,471,1239,1291,442,1497,963,115,2064,1980,735,1257,1912,2262,2375,1738,1462,923;878,1925,1567,1671,930,2112,446,2002,1942,1461,491,2490,2234,1560,1930,800,134,1925,161,398,2177,173,1900,1716,384,2417,1583;1688,339,2448,592,1940,1298,997,1791,1088,1006,1770,80,70,945,994,1145,339,337,2228,2302,285,573,1230,2143,1912,427,388;2273,1258,2196,1232,1231,198,564,1712,635,794,2336,1482,1967,853,1793,1301,1167,2097,780,2129,406,29,420,982,896,751,1133", "output": "450,2284,804,360,2365,2391,1670,299,1336,2067,1252,1637,2476,2182,1371,1099,1867,2065,948,349,2034,1473,1900,1332,882,1291,2446,406,1975,1663,2356,1915,461,1934,2260,138,1070,903,1828,359,672,444,1269,982,270,1298,524,333,77,411,1332,34,368,683,688,884,2127,959,1793,2376,1035,1062,1714,1399,1550,1080,689,2265,481,412,605,470,1809,1386,732,1006,2146,2106,2171,520,45,1825,2168,902,2290,1991,1559,186,933,414,645,1551,1300,1948,1736,1123,716,836,2000,1904,2393,1001,1434,1598,1985,1468,1894,1157,1618,661,1902,1005,754,1810,118,300,2067,1003,1223,609,1395,230,1686,1802,784,1888,1974,533,1958,2219,860,489,25,1924,1362,802,1785,1632,7,1761,1810,1968,1694,2430,1423,1452,1142,734,2374,71,1202,937,2336,2253,1624,912,1426,457,207,660,491,1463,2276,1949,1975,730,1608,1914,2215,378,1311,216,1400,1213,826,1202,1890,650,1460,1235,862,189,1916,1001,2153,1026,200,55,677,1824,1049,2302,1358,1434,45,1202,1891,2196,2482,922,1592,458,2196,1462,2375,1912,735,2064,963,442,1239,2227,1046,1001,2289,1892,878,1567,930,446,1942,491,2234,1930,134,161,2177,1900,384,1583,427,2143,573,2302,337,1145,945,80,1006,1791,1298,592,339,2273,2196,1231,564,635,2336,1967,1793,1167,780,406,420,896,1133"}, {"input": "175,949,1586,76,1485,1498,1708,1974,1807;1512,1822,2479,2179,531,1292,2404,462,275;586,551,2310,1608,1626,1479,1498,1630,722;585,1736,1306,2384,1882,2344,75,360,2050;1174,697,1231,1660,2304,2365,2382,303,2338;164,140,1062,1650,507,166,980,2027,2073;390,746,620,2234,1739,774,134,1371,1977;2457,846,1315,1509,2305,2099,598,1514,2079;1877,1067,2384,1743,201,1359,1985,1230,2086;2148,1372,55,734,162,918,1225,1045,1739;2267,1660,451,1741,699,1324,665,1367,2386", "output": "175,1586,1485,1708,1807,462,1292,2179,1822,586,2310,1626,1498,722,360,2344,2384,1736,1174,1231,2304,2382,2338,2027,166,1650,140,390,620,1739,134,1977,1514,2099,1509,846,1877,2384,201,1985,2086,1045,918,734,1372,2267,451,699,665,2386"}, {"input": "1126,2223,1316,1882,506,496,71,1191,1962,935,2480,630,1570,2144,1135,2449,1818,947,2016,2242,1751,2267,2414,141,990,926,1516;1730,979,1976,2198,436,1282,1995,540,1703,2487,1519,1680,2200,715,1815,1179,1639,1208,958,318,1031,202,1067,540,1451,1651,954;1220,1561,1464,2421,953,839,478,971,759,1156,1493,1632,1433,715,2159,2006,445,2046,861,1057,1841,2130,1636,2486,2473,1001,2389;604,1058,2189,1,1534,652,1722,2383,1404,1836,2263,707,2473,1026,496,1359,1632,1867,1895,1191,1956,508,1116,2227,2492,1989,2298;2317,872,1239,2474,1409,1316,1889,1485,1022,2493,660,1010,2383,522,301,2012,822,1131,2101,2151,1988,63,1865,2248,1220,1193,1945;1325,2169,2495,2197,531,214,1889,1978,601,632,1843,306,317,263,749,552,1362,1561,2499,695,298,1336,330,2094,1837,2480,398;2319,1399,2113,2019,2311,1975,1574,1216,295,87,792,1791,1633,25,1844,1115,1705,642,1670,1406,2393,1616,1586,2063,2056,1760,1888;482,1041,578,321,612,29,1188,2333,1794,1578,1291,2342,1961,1743,2032,2468,454,881,1226,20,1278,748,1554,679,2374,2074,2429;274,1775,10,1445,1150,361,1301,1178,1608,269,206,342,1704,1887,2430,2361,1420,1646,629,2211,1156,1377,1613,716,2445,2146,746;775,471,1688,245,306,858,872,2211,658,1243,961,2322,138,1296,2297,1198,2346,2174,1205,2384,2335,1692,344,1707,1340,1677,314;14,720,2048,1852,115,761,786,943,1708,229,263,2467,1568,921,1992,2115,1819,230,598,192,1512,1478,659,792,2446,2148,981;1825,1825,2127,1770,311,872,538,1632,1766,1643,266,1744,1985,938,2066,1839,1029,1074,1134,2230,1433,2456,1910,988,2096,865,19;163,914,2015,316,376,1061,2009,1922,2220,2074,1563,419,2289,531,1197,640,1246,557,986,665,1134,533,1711,300,2490,797,119;1000,660,1565,767,1487,1941,427,2235,1859,856,677,1995,1699,2129,1333,1511,621,1874,378,2103,1289,2114,598,840,871,1514,477;2311,999,227,1959,469,505,1917,2293,1954,1078,171,619,684,260,147,1857,489,1393,2429,1746,1396,1043,854,601,2235,2034,1941;1698,1264,105,1231,2428,298,1535,1579,807,2491,1300,506,1561,1585,795,554,1721,2140,2119,733,2491,398,2339,589,278,153,2272;1276,1286,868,21,1172,333,1737,2274,1364,914,1621,90,2041,1909,945,2037,1282,598,458,2375,273,157,1329,1283,2012,725,1841;709,2454,72,55,2008,2325,1608,1297,2443,1487,202,2462,1320,1366,837,1712,366,1156,832,510,692,2271,1168,1534,2488,1366,1569;1339,1763,2086,803,792,2194,1956,2325,1804,1442,965,1963,89,1542,1253,312,2018,18,1710,917,1519,343,742,1344,648,1032,2304;2420,1420,1370,146,993,2203,1477,1289,1469,241,422,922,1339,1226,1403,843,1356,960,825,2255,2439,1514,1226,535,392,995,2320;1918,2453,141,751,920,1281,965,2202,1999,121,414,1191,1329,1678,1131,634,437,701,1359,421,1279,1850,741,2343,2397,1506,1956;146,1036,966,1339,2071,1684,2320,1969,1371,1402,313,2404,792,263,2311,2462,465,320,2361,2216,1540,2223,1731,363,850,3,1989;2241,1457,641,150,1866,184,608,1089,2133,845,1711,383,1098,1981,220,525,516,212,1050,1049,553,1827,74,95,564,2350,920;251,1610,1765,411,531,2353,2351,2417,1690,310,2445,1437,2197,1194,1774,1131,1217,1626,1023,787,1638,1651,1367,90,1301,2296,1435;2108,1352,2349,1445,2355,1435,730,640,1201,1753,672,296,747,31,2023,1515,1487,2115,660,1193,661,1275,1477,2226,1663,554,2371;1655,595,676,2459,935,97,1590,2394,1763,2483,2150,1872,1607,2234,1639,668,168,2397,290,1015,1863,4,764,1382,295,1043,2445;1769,1161,1481,800,1236,505,1570,1874,2175,476,2392,2320,531,1351,865,1511,1585,203,1088,1221,1325,886,2271,1154,1156,2086,53;81,2227,1340,1524,593,1297,322,431,1226,1037,1702,2467,107,1714,545,1997,2163,827,2343,771,1849,694,397,556,136,2243,906;2210,715,898,1135,1917,1051,2202,2169,891,1263,558,2327,1625,2296,1122,1448,2100,267,2154,2463,1674,785,523,150,1035,520,1669;2186,1562,1485,10,756,155,2298,489,2036,2350,1670,1855,1084,1962,39,427,479,1607,1082,430,1684,2257,1301,232,465,809,2311;2484,1615,2083,1523,1536,2009,1986,357,1069,168,1925,1383,1344,191,21,94,815,1969,39,822,1432,1345,1978,883,2166,151,1927;708,269,225,149,1808,2422,2186,1573,2497,1853,1755,1303,271,2207,2141,1398,1023,997,240,564,2433,798,1268,2001,1922,2446,1675;625,2140,2305,140,2382,153,743,1500,1449,1937,504,1843,1367,674,60,1400,1104,1666,1564,1072,2219,1723,219,924,1952,2162,1548;419,376,1514,2362,338,202,1380,1731,684,1547,1883,277,2438,2281,168,881,1314,1591,1249,814,977,2097,663,296,841,2481,1951;2487,1469,785,61,2320,971,1133,1025,1195,392,278,867,1827,1299,2450,77,31,769,1822,2306,30,604,491,1147,1683,865,661;324,826,2050,1637,825,1479,1860,1409,1058,2045,2217,1937,618,354,2226,761,1858,2183,1683,2310,1734,2250,356,782,1910,428,1342;1731,993,1547,693,1370,113,2217,2493,470,2387,254,1662,324,2127,612,2252,2450,436,1627,923,1351,315,2384,1457,1346,1930,2087;2377,459,2142,58,1967,2060,550,914,2464,1732,48,1311,2010,2027,1382,312,2079,697,947,2337,876,1992,1759,155,189,1523,935;2304,1283,1813,2467,48,138,2323,2119,2328,2254,2348,1814,694,1154,620,836,1892,1331,2156,26,2168,428,1261,332,1471,1771,1946;1263,1900,972,421,189,130,2259,795,2215,830,485,2419,221,2070,478,781,486,1303,442,2155,2205,361,787,1256,1929,2030,577;425,504,568,2297,1004,67,1260,1802,1277,1977,2457,814,2241,1560,701,2417,249,1757,1288,562,594,2086,1099,1940,544,822,2;129,2173,90,2381,595,77,568,14,1945,917,754,1618,1830,2371,204,2010,2305,2013,2267,35,1871,2469,253,2204,610,1530,2146;259,954,1177,1584,1439,1589,2310,1966,582,873,1121,415,2259,726,382,2037,219,682,2053,765,2473,1930,869,912,845,1274,1311;1705,824,47,2018,329,684,809,880,905,2161,179,1733,2188,1338,680,1050,23,376,964,944,128,2381,869,430,266,763,740;2098,1300,1784,190,2209,1971,11,466,1864,1971,1889,2252,920,733,460,1993,2494,368,1512,23,1409,1411,1922,18,127,931,620;2247,348,1394,2001,2388,2438,1150,1123,2081,752,1572,1347,1849,1223,1461,258,240,1260,1973,2369,1150,952,181,1583,1459,775,745;1439,626,1381,2203,873,2333,2093,819,1475,1628,1645,1595,1634,1603,1399,496,1449,803,1518,838,70,737,2006,2468,189,1716,624", "output": "1126,1316,506,71,1962,2480,1570,1135,1818,2016,1751,2414,990,1516,1651,540,202,318,1208,1179,715,1680,2487,540,1282,2198,979,1220,1464,953,478,759,1493,1433,2159,445,861,1841,1636,2473,2389,1989,2227,508,1191,1867,1359,1026,707,1836,2383,652,1,1058,2317,1239,1409,1889,1022,660,2383,301,822,2101,1988,1865,1220,1945,2480,2094,1336,695,1561,552,263,306,632,1978,214,2197,2169,2319,2113,2311,1574,295,792,1633,1844,1705,1670,2393,1586,2056,1888,2074,679,748,20,881,2468,1743,2342,1578,2333,29,321,1041,274,10,1150,1301,1608,206,1704,2430,1420,629,1156,1613,2445,746,1677,1707,1692,2384,2174,1198,1296,2322,1243,2211,858,245,471,14,2048,115,786,1708,263,1568,1992,1819,598,1512,659,2446,981,865,988,2456,2230,1074,1839,938,1744,1643,1632,872,1770,1825,163,2015,376,2009,2220,1563,2289,1197,1246,986,1134,1711,2490,119,1514,840,2114,2103,1874,1511,2129,1995,856,2235,1941,767,660,2311,227,469,1917,1954,171,684,147,489,2429,1396,854,2235,1941,153,589,398,733,2140,554,1585,506,2491,1579,298,1231,1264,1276,868,1172,1737,1364,1621,2041,945,1282,458,273,1329,2012,1841,1366,1534,2271,510,1156,1712,1366,2462,1487,1297,2325,55,2454,1339,2086,792,1956,1804,965,89,1253,2018,1710,1519,742,648,2304,995,535,1514,2255,960,843,1226,922,241,1289,2203,146,1420,1918,141,920,965,1999,414,1329,1131,437,1359,1279,741,2397,1956,3,363,2223,2216,320,2462,263,2404,1402,1969,1684,1339,1036,2241,641,1866,608,2133,1711,1098,220,516,1050,553,74,564,920,2296,90,1651,787,1626,1131,1194,1437,310,2417,2353,411,1610,2108,2349,2355,730,1201,672,747,2023,1487,660,661,1477,1663,2371,1043,1382,4,1015,2397,668,2234,1872,2483,2394,97,2459,595,1769,1481,1236,1570,2175,2392,531,865,1585,1088,1325,2271,1156,53,2243,556,694,771,827,1997,1714,2467,1037,431,1297,1524,2227,2210,898,1917,2202,891,558,1625,1122,2100,2154,1674,523,1035,1669,809,232,2257,430,1607,427,1962,1855,2350,489,155,10,1562,2484,2083,1536,1986,1069,1925,1344,21,815,39,1432,1978,2166,1927,2446,2001,798,564,997,1398,2207,1303,1853,1573,2422,149,269,625,2305,2382,743,1449,504,1367,60,1104,1564,2219,219,1952,1548,2481,296,2097,814,1591,881,2281,277,1547,1731,202,2362,376,2487,785,2320,1133,1195,278,1827,2450,31,1822,30,491,1683,661,428,782,2250,2310,2183,761,354,1937,2045,1409,1479,1637,826,1731,1547,1370,2217,470,254,324,612,2450,1627,1351,2384,1346,2087,1523,155,1992,2337,697,312,2027,1311,1732,914,2060,58,459,2304,1813,48,2323,2328,2348,694,620,1892,2156,2168,1261,1471,1946,2030,1256,361,2155,1303,781,2070,2419,830,795,130,421,1900,425,568,1004,1260,1277,2457,2241,701,249,1288,594,1099,544,2,1530,2204,2469,35,2013,2010,2371,1618,917,14,77,2381,2173,259,1177,1439,2310,582,1121,2259,382,219,2053,2473,869,845,1311,763,430,2381,944,376,1050,1338,1733,2161,880,684,2018,824,2098,1784,2209,11,1864,1889,920,460,2494,1512,1409,1922,127,620,775,1583,952,2369,1260,258,1223,1347,752,1123,2438,2001,348,1439,1381,873,2093,1475,1645,1634,1399,1449,1518,70,2006,189,624"}, {"input": "2027,2384,1991,2110,1869,2122,1584,2483,2483,30,2200,1237,1704,758,177,675,931,266,1575,39,1166,1340,2273,502,845,1037,812,1636,811,1520,577,1322,2414,10,533,2206,277,1550,1935,2151,1252,2286,1335;2296,1308,2224,2472,67,1839,1331,1052,409,575,1434,858,1313,2070,564,1842,944,685,947,1403,2451,387,936,625,1420,1413,2485,510,1856,1857,2183,2497,786,407,1331,1420,1308,801,1437,2426,1983,1933,994;288,2458,2498,2256,2231,1484,1713,2470,2067,198,2348,1648,537,1350,382,1764,1425,179,52,782,2357,1379,1588,2196,1366,1523,253,979,1026,1643,1120,1758,1169,1829,488,1159,80,143,489,2395,1567,1775,2192;2120,288,2077,1609,1523,425,836,177,1592,1218,915,2027,543,1476,1333,460,1169,2009,2005,1002,1556,1869,505,199,2261,985,1001,1520,1776,337,896,1515,869,1401,1064,1822,216,1608,1031,2401,465,631,1475;365,1494,1081,1920,650,136,1669,2245,2071,592,1812,2490,1708,1105,917,1473,2316,1515,688,137,934,1555,2290,2151,2454,1903,1521,2181,1250,1148,188,1197,1477,115,675,1360,2128,465,593,2079,727,2034,2361;600,1689,2114,1864,1681,899,935,1008,761,915,1364,511,2236,1965,1435,1487,2456,587,1821,820,2372,337,461,271,581,2022,1445,925,1115,271,309,588,60,825,835,1467,1873,554,167,1332,1782,1927,1499;1313,864,2462,412,1573,269,182,1866,554,2467,817,1246,2349,1627,2226,281,798,2045,1132,1288,1724,850,462,1182,639,1926,2023,2483,773,1312,1789,1054,1026,833,1129,335,15,1194,766,53,100,1332,135;276,2441,48,1117,1897,2160,781,592,725,478,1054,2332,1265,564,1378,1663,208,1298,545,151,850,2300,1552,305,2065,857,2431,1861,487,826,1372,1726,724,854,399,953,2249,1724,579,1919,1981,1177,700;1206,929,2427,2326,1394,1703,2063,946,2363,1620,741,1466,349,1565,1888,1209,1563,883,1251,2120,1160,1825,1209,1221,392,1751,63,677,944,1023,56,122,151,271,429,1247,1614,841,877,550,1242,1941,1287;1828,135,188,1412,1680,943,208,491,1248,1028,1264,2380,2146,688,1896,1008,290,1567,655,1197,410,1987,1342,1859,1072,1130,465,588,2046,1938,737,642,1978,1975,739,336,1952,436,2347,957,991,1859,431;1134,24,2114,281,175,1709,1844,1479,1938,519,2392,169,1662,1707,1192,1502,1770,1631,534,1825,1135,2078,1845,1626,2238,52,2458,711,1083,851,2162,288,1460,107,62,179,375,819,1656,6,1805,1626,1445;1964,1975,558,1497,1805,1014,2153,89,533,1801,1773,2143,1178,848,1811,820,2479,275,348,1953,2143,1646,659,2401,1143,1902,530,2373,687,1293,1642,473,1476,178,2072,1336,1380,68,930,2386,1956,533,1259;2261,2084,231,738,1287,643,1739,713,137,429,61,634,2181,1178,1082,2073,1487,700,1075,1853,736,1556,1437,2027,2302,1316,2023,257,1631,455,987,980,1886,1416,2332,1032,516,362,72,2451,1013,1609,1028;1924,2116,1733,2425,275,8,1220,1243,1462,694,367,1531,236,2122,2268,195,1656,1422,463,73,1723,58,153,207,1849,687,1209,1396,2024,2166,1426,1950,847,920,288,1441,1373,687,1169,1931,29,264,1803;342,1727,2232,1210,1190,294,1552,1833,1870,991,1247,1249,1063,136,1172,1026,708,816,1114,1828,2236,2476,1993,1318,530,1891,121,540,950,2281,1118,1353,1774,1310,1272,979,1411,574,557,558,598,866,190;168,117,2454,1055,1957,331,2492,2347,989,1156,593,1188,1636,1738,10,567,246,1575,2207,1949,1489,907,2390,669,2299,1902,955,2217,702,1497,1268,2351,2324,1221,359,320,905,778,1605,825,1298,1165,558;2273,624,693,1345,1892,3,1977,519,1067,115,2422,2410,1540,2289,2495,1391,1165,31,411,2296,214,1095,1371,1952,1663,1547,467,2203,996,2185,1156,45,1923,896,1766,983,1245,235,2465,1049,1343,1560,2478;1832,1269,1257,1806,1164,258,477,1578,2454,2288,472,583,2010,1571,855,1475,1138,217,1205,1656,1958,268,2171,1033,593,112,1832,2439,1922,2042,363,1195,1153,601,1410,2009,2198,307,621,1891,705,1669,2230;1017,773,241,64,248,1889,21,131,1253,1462,2268,1749,894,2442,1375,1141,857,293,847,1334,2340,2459,252,728,2371,1901,1190,1541,2021,481,539,2334,1733,1000,392,986,2129,735,20,189,1167,1606,2227;1420,932,272,1609,776,1245,481,68,187,2009,1265,1897,32,332,97,1743,158,289,1790,423,2301,506,1788,844,1473,2073,390,512,953,1671,182,2225,2343,831,921,428,1718,468,831,1198,2352,1159,273;1722,1333,469,787,1423,1555,301,1689,1433,609,1802,56,1453,878,1623,680,2424,652,702,37,1272,817,590,914,1894,1576,1000,1361,308,627,2222,1858,784,1834,2220,1814,2467,829,1933,1099,1573,438,1479;237,229,2253,343,1792,1889,1485,1384,892,859,2124,2083,2256,1823,272,1905,361,1375,1514,1980,943,1472,101,1696,2135,2339,13,2060,326,220,307,2434,186,1838,2218,1006,1870,180,1438,897,784,952,1473;2146,204,2490,1173,1302,2166,1399,1991,620,746,1105,47,2012,990,97,2212,1890,1866,1442,204,1606,48,1125,1113,1426,2424,1876,2133,1807,1613,2108,2385,390,436,2201,1117,657,153,1877,626,1735,1867,276;2408,152,886,164,2173,140,2040,1486,764,2028,1867,1480,1746,1055,1257,492,1746,284,460,1335,1267,1476,186,356,870,2112,263,1705,894,56,500,1784,705,33,1009,897,971,1839,318,2159,436,975,884;2114,1735,2062,1730,503,1269,2154,1023,574,1903,905,2149,59,1414,2250,2398,1087,2053,826,744,410,646,948,1289,1124,2053,1416,1243,1266,2496,1775,79,1385,1234,1223,777,2285,1136,1367,1805,846,584,1654;1228,1042,1543,512,1512,2214,883,1297,490,800,1156,102,1319,230,2040,1683,1309,1977,612,1688,2068,854,2412,1700,1993,1553,1751,1383,1203,101,58,538,890,536,16,2393,415,1276,72,558,1793,2211,542;1631,2250,1093,1601,306,665,732,1574,871,1362,1819,1166,1610,48,652,1653,264,1235,515,958,965,130,2164,2114,163,1713,2186,151,2113,1464,1763,1108,1401,2443,426,387,2350,1091,589,2246,1665,284,729;1121,2386,1004,605,2005,1719,1233,2314,710,1615,2396,1948,795,1487,2151,2244,369,1931,292,565,709,454,1634,844,332,1444,2296,1987,712,81,890,2487,176,2255,14,2047,154,187,196,267,1160,1631,1872;840,2292,902,899,1873,1218,1109,1999,2385,2105,2006,1564,857,2080,1010,2087,1346,922,1244,1071,2226,982,1821,2263,1507,505,74,512,511,1696,1271,696,1812,1029,602,2405,2332,61,542,1365,377,1457,1596;314,818,2293,1976,2451,72,991,1192,1344,1563,887,1238,2147,2050,854,163,999,159,1804,922,2384,2286,223,922,803,928,1402,717,1315,1692,1704,1902,1417,44,2158,2237,376,1762,1941,1348,344,1559,1433;230,2308,37,1550,2007,2260,2036,1930,1842,1285,1292,1875,2294,2169,1184,663,746,336,1168,1719,1624,796,191,704,2456,282,65,1705,2423,1470,2263,1784,2488,2272,818,1103,1920,1202,2117,1478,864,868,410;1805,2500,2050,807,696,1244,842,1925,2368,213,2458,323,2411,231,2097,1353,844,2385,204,1740,1039,2252,618,557,87,914,81,65,1223,2392,972,1419,712,418,685,542,1255,684,1321,2317,1261,1192,513;1423,2082,732,2103,913,1389,659,1746,1642,82,711,671,741,1512,2265,2094,29,653,2273,143,588,1251,2093,44,1627,1497,263,476,2017,1423,820,1506,797,511,1421,539,1013,2359,740,476,1432,1085,707;756,324,367,514,1487,1415,88,1430,1578,2205,329,1204,490,753,2269,139,951,1830,451,1160,1371,1509,1423,340,1380,1508,1320,2273,744,368,704,855,755,1343,746,2366,1821,1407,820,1209,803,316,1882;203,1915,1118,567,2480,593,855,2122,1071,2174,762,810,1281,793,1817,1142,444,1701,960,499,2437,904,326,1773,1283,1703,1885,1055,1716,1781,1178,1382,2232,2303,602,2112,1433,418,1388,2318,1682,1946,784;1437,1269,1416,1821,2329,734,819,1571,570,1774,1413,1981,2409,923,2185,1510,1527,1026,725,666,1937,1040,2377,2028,1240,88,205,1327,243,825,778,2171,17,622,1296,600,645,922,651,1735,850,1214,607;1639,692,2329,1919,938,100,2495,1335,1745,1232,1794,411,1669,2362,1345,1415,1016,765,2372,2162,1697,759,1977,985,452,1887,1075,133,417,469,1092,2039,870,1784,2490,1075,2159,674,683,917,1202,445,1647;1786,645,1907,1662,2215,2378,509,2362,1602,574,2208,1932,915,465,1677,1775,704,1326,1158,1533,2389,784,2020,1772,684,2494,1447,1586,124,1589,2236,993,1745,1794,773,2321,2127,1762,171,372,2289,900,2246;1303,488,1679,1597,1720,251,164,1153,1486,48,767,220,1964,1754,1903,933,632,2042,1838,921,1835,2469,474,454,1430,2002,2103,825,2478,1602,1347,539,753,532,1716,2331,1690,221,1673,1847,831,2000,1108;417,644,865,1305,600,2377,379,2197,437,2274,1142,1710,709,1157,1831,1377,192,925,791,1923,1185,2164,396,1696,386,1621,2253,1130,535,996,2495,2425,792,2484,1478,1983,1596,166,1345,483,2389,165,1121;162,466,2009,837,2468,107,2113,2287,452,1450,2082,26,846,132,1570,64,2352,694,2214,441,2456,902,2061,896,1329,2273,112,1067,1824,1942,1933,1371,2128,2229,1127,1321,2379,20,967,1730,572,1224,460;576,815,1652,1590,965,1755,708,180,2296,2370,665,2173,57,1126,913,232,604,1943,2006,1725,1703,467,964,1738,682,2199,796,1392,1460,1282,177,1557,1102,32,487,1673,2149,2453,632,1105,961,1184,259", "output": "2027,1991,1869,1584,2483,2200,1704,177,931,1575,1166,2273,845,812,811,577,2414,533,277,1935,1252,1335,1933,2426,801,1420,407,2497,1857,510,1413,625,387,1403,685,1842,2070,858,575,1052,1839,2472,1308,288,2498,2231,1713,2067,2348,537,382,1425,52,2357,1588,1366,253,1026,1120,1169,488,80,489,1567,2192,631,2401,1608,1822,1401,1515,337,1520,985,199,1869,1002,2009,460,1476,2027,1218,177,425,1609,288,365,1081,650,1669,2071,1812,1708,917,2316,688,934,2290,2454,1521,1250,188,1477,675,2128,593,727,2361,1927,1332,554,1467,825,588,271,925,2022,271,337,820,587,1487,1965,511,915,1008,899,1864,1689,1313,2462,1573,182,554,817,2349,2226,798,1132,1724,462,639,2023,773,1789,1026,1129,15,766,100,135,1177,1919,1724,953,854,1726,826,1861,857,305,2300,151,1298,1663,564,2332,478,592,2160,1117,2441,1206,2427,1394,2063,2363,741,349,1888,1563,1251,1160,1209,392,63,944,56,151,429,1614,877,1242,1287,1859,957,436,336,1975,642,1938,588,1130,1859,1987,1197,1567,1008,688,2380,1028,491,943,1412,135,1134,2114,175,1844,1938,2392,1662,1192,1770,534,1135,1845,2238,2458,1083,2162,1460,62,375,1656,1805,1445,533,2386,68,1336,178,473,1293,2373,1902,2401,1646,1953,275,820,848,2143,1801,89,1014,1497,1975,2261,231,1287,1739,137,61,2181,1082,1487,1075,736,1437,2302,2023,1631,987,1886,2332,516,72,1013,1028,264,1931,687,1441,920,1950,2166,1396,687,207,58,73,1422,195,2122,1531,694,1243,8,2425,2116,342,2232,1190,1552,1870,1247,1063,1172,708,1114,2236,1993,530,121,950,1118,1774,1272,1411,557,598,190,1165,825,778,320,1221,2351,1497,2217,1902,669,907,1949,1575,567,1738,1188,1156,2347,331,1055,117,2273,693,1892,1977,1067,2422,1540,2495,1165,411,214,1371,1663,467,996,1156,1923,1766,1245,2465,1343,2478,1669,1891,307,2009,601,1195,2042,2439,112,1033,268,1656,217,1475,1571,583,2288,1578,258,1806,1269,1017,241,248,21,1253,2268,894,1375,857,847,2340,252,2371,1190,2021,539,1733,392,2129,20,1167,2227,1159,1198,468,428,831,2225,1671,512,2073,844,506,423,289,1743,332,1897,2009,68,1245,1609,932,1722,469,1423,301,1433,1802,1453,1623,2424,702,1272,590,1894,1000,308,2222,784,2220,2467,1933,1573,1479,952,897,180,1006,1838,2434,220,2060,2339,1696,1472,1980,1375,1905,1823,2083,859,1384,1889,343,229,2146,2490,1302,1399,620,1105,2012,97,1890,1442,1606,1125,1426,1876,1807,2108,390,2201,657,1877,1735,276,975,2159,1839,897,33,1784,56,1705,2112,356,1476,1335,284,492,1055,1480,2028,1486,140,164,152,2114,2062,503,2154,574,905,59,2250,1087,826,410,948,1124,1416,1266,1775,1385,1223,2285,1367,846,1654,2211,558,1276,2393,536,538,101,1383,1553,1700,854,1688,1977,1683,230,102,800,1297,2214,512,1042,1631,1093,306,732,871,1819,1610,652,264,515,965,2164,163,2186,2113,1763,1401,426,2350,589,1665,729,1631,267,187,2047,2255,2487,81,1987,1444,844,454,565,1931,2244,1487,1948,1615,2314,1719,605,2386,840,902,1873,1109,2385,2006,857,1010,1346,1244,2226,1821,1507,74,511,1271,1812,602,2332,542,377,1596,1559,1348,1762,2237,44,1902,1692,717,928,922,2286,922,159,163,2050,1238,1563,1192,72,1976,818,230,37,2007,2036,1842,1292,2294,1184,746,1168,1624,191,2456,65,2423,2263,2488,818,1920,2117,864,410,1192,2317,684,542,418,1419,2392,65,914,557,2252,1740,2385,1353,231,323,213,1925,1244,807,2500,1423,732,913,659,1642,711,741,2265,29,2273,588,2093,1627,263,2017,820,797,1421,1013,740,1432,707,316,1209,1407,2366,1343,855,368,2273,1508,340,1509,1160,1830,139,753,1204,2205,1430,1415,514,324,203,1118,2480,855,1071,762,1281,1817,444,960,2437,326,1283,1885,1716,1178,2232,602,1433,1388,1682,784,1214,1735,922,600,622,2171,825,1327,88,2028,1040,666,1026,1510,923,1981,1774,1571,734,1821,1269,1639,2329,938,2495,1745,1794,1669,1345,1016,2372,1697,1977,452,1075,417,1092,870,2490,2159,683,1202,1647,900,372,1762,2321,1794,993,1589,1586,2494,1772,784,1533,1326,1775,465,1932,574,2362,2378,1662,645,1303,1679,1720,164,1486,767,1964,1903,632,1838,1835,474,1430,2103,2478,1347,753,1716,1690,1673,831,1108,165,483,166,1983,2484,2425,996,1130,1621,1696,2164,1923,925,1377,1157,1710,2274,2197,2377,1305,644,162,2009,2468,2113,452,2082,846,1570,2352,2214,2456,2061,1329,112,1824,1933,2128,1127,2379,967,572,460,1184,1105,2453,1673,32,1557,1282,1392,2199,1738,467,1725,1943,232,1126,2173,2370,180,1755,1590,815"}, {"input": "200,861,1397,2368,2459,601,380,349,2149,68,726,1679,829,1760,1731,1382,2155,837,2483,1708,1260,747,1489,1130,49;1387,1508,1412,1750,489,1593,234,229,1051,2045,1733,1709,1712,2058,1392,1668,642,123,1687,1940,2489,1532,2100,1580,1667;1425,1645,1283,2429,590,1957,1986,2377,2473,1845,752,1857,1606,1469,2077,1569,1831,451,193,1363,751,2495,1675,1222,1002;2055,993,1650,2204,64,594,1914,2419,918,2146,813,1174,1473,1342,219,287,402,1579,686,498,822,746,608,1687,448;588,1351,789,940,473,541,1175,468,1457,1839,844,2379,1346,1719,2146,152,569,1301,903,699,860,995,741,288,1830;2062,1219,1844,2021,2151,2342,2068,2060,2432,278,433,729,207,1437,682,347,837,533,465,1108,2041,2176,959,1928,2122;498,1517,1806,2489,1517,178,352,1954,2058,98,1299,745,270,283,802,785,1859,646,1400,2224,745,596,2388,695,847;148,1855,1749,840,1625,1202,274,2042,284,312,1228,149,769,1303,600,734,1812,1866,2106,50,2308,646,1233,1105,857;2060,346,1843,1233,631,1775,517,1351,955,225,422,1138,97,579,631,1552,1081,2249,1318,1041,889,643,2301,2295,1105;971,1084,1535,172,1933,1765,2349,1503,1895,158,1808,409,1916,1442,2347,446,1150,779,2332,598,1641,1401,234,1918,591;1319,463,1110,732,1043,2186,1729,453,993,645,2104,972,2402,2381,1803,1346,2162,535,467,617,1466,2353,638,803,430;2403,1448,1549,2381,1105,700,779,1834,2045,924,311,161,1846,432,1976,2374,846,835,88,1389,902,344,543,1589,1930;2224,828,1498,452,38,834,2485,2060,270,1343,1605,2182,1582,2483,1589,1640,1863,2106,2491,21,2425,565,23,1556,2377;1967,441,1141,2038,2398,1250,1480,1274,808,1965,638,2093,2269,2498,248,1054,534,376,188,2440,1776,1387,70,2392,2134;2231,2067,1326,1614,786,2340,2015,709,400,2251,2179,2378,757,1031,663,2170,1956,1481,2135,11,800,459,2275,1757,65;1665,2480,343,1699,1963,1165,2458,2249,1959,1244,1884,1988,1942,1332,2434,536,1836,1850,1552,2175,263,2353,655,810,1752;1974,818,2143,1648,1971,1112,1339,1482,1405,914,1161,1901,588,2074,1588,1058,1001,391,1565,1620,1634,2354,827,1291,814;1333,1807,1872,83,2178,363,1375,2405,2396,1624,1464,2058,1583,1344,1526,1497,2282,319,955,2307,789,565,371,1424,2251;86,1373,227,1777,982,394,1393,158,788,1227,506,2131,1176,1098,1471,2499,330,2157,1365,740,1917,1602,1541,565,2434", "output": "200,1397,2459,380,2149,726,829,1731,2155,2483,1260,1489,49,1580,1532,1940,123,1668,2058,1709,2045,229,1593,1750,1508,1425,1283,590,1986,2473,752,1606,2077,1831,193,751,1675,1002,1687,746,498,1579,287,1342,1174,2146,2419,594,2204,993,588,789,473,1175,1457,844,1346,2146,569,903,860,741,1830,1928,2176,1108,533,347,1437,729,278,2060,2342,2021,1219,498,1806,1517,352,2058,1299,270,802,1859,1400,745,2388,847,1105,646,50,1866,734,1303,149,312,2042,1202,840,1855,2060,1843,631,517,955,422,97,631,1081,1318,889,2301,1105,1918,1401,598,779,446,1442,409,158,1503,1765,172,1084,1319,1110,1043,1729,993,2104,2402,1803,2162,467,1466,638,430,1589,344,1389,835,2374,432,161,924,1834,700,2381,1448,2224,1498,38,2485,270,1605,1582,1589,1863,2491,2425,23,2377,2392,1387,2440,376,1054,2498,2093,1965,1274,1250,2038,441,2231,1326,786,2015,400,2179,757,663,1956,2135,800,2275,65,810,2353,2175,1850,536,1332,1988,1244,2249,1165,1699,2480,1974,2143,1971,1339,1405,1161,588,1588,1001,1565,1634,827,814,1424,565,2307,319,1497,1344,2058,1624,2405,363,83,1807,86,227,982,1393,788,506,1176,1471,330,1365,1917,1541,2434"}, {"input": "2238,593,2118,1384,75,1234,245,24,1837,33,1978,1625,1099,1545,2343,609,1971,572,1473,1606,2165,42,1104,393,506,1121;648,45,1356,2210,1413,2500,2052,534,1105,1960,604,1561,1374,1291,1987,1690,1323,397,1076,349,706,605,1564,2425,69,191;2113,2043,2187,2035,214,754,601,2069,2327,1374,1660,960,1753,236,1677,1693,950,1632,220,1091,1954,1966,2252,910,1633,1076;2143,2415,605,1363,751,1115,2246,1805,1105,2023,759,1041,317,482,568,2389,2106,855,1519,1374,2375,2039,195,429,332,1471;1081,756,2256,2146,450,1195,2290,568,2251,2404,362,559,2182,1353,818,1400,520,1444,2449,1028,1212,2447,13,1716,957,1866;309,181,1118,1676,2389,1329,538,1723,834,1193,763,656,2491,123,543,1064,818,2293,405,6,1358,570,1874,247,2345,2474;2188,51,1972,1178,1544,699,264,67,120,1637,1166,539,609,892,81,141,2019,2421,125,1537,1195,1619,2358,447,433,1953;1855,2036,162,187,1459,705,1549,301,544,940,2441,630,2212,228,976,136,33,182,1954,1213,1832,2386,1053,88,1917,1500;2278,1489,414,2132,1947,616,735,1302,2407,2367,1910,54,2045,189,733,1271,382,2266,1561,342,2175,580,1553,437,1544,1814;1115,1099,1218,1652,1720,1733,1159,2488,2044,1927,1008,716,1650,731,221,290,970,474,493,482,633,1902,1127,1837,2386,385;548,1657,596,2246,764,2278,621,1825,1609,344,2160,127,400,840,109,1296,2133,852,599,1410,932,1944,1983,508,2468,1024;263,2351,293,1592,122,542,2404,773,2453,2187,2324,1957,2287,1301,1958,864,2315,2444,1390,1133,2189,462,2329,846,1036,593;2004,1007,530,2339,652,414,1544,2185,1057,2208,337,773,131,2118,1475,909,1991,414,2487,1432,2267,2174,1143,1770,2159,1181;1971,1934,1734,602,443,1947,146,464,237,327,2071,1205,2490,295,2300,1127,373,1892,938,1952,965,1874,1882,268,1553,1063;2123,393,2338,810,1038,463,2216,296,1625,1571,1886,294,1651,1285,1209,1126,2288,593,726,346,520,2361,330,1161,18,1855;1647,1251,2068,1961,2331,2188,1782,502,2254,592,1937,1826,2456,1909,2436,1750,405,592,807,1699,617,2481,1697,21,2325,1941;1770,282,1180,390,1945,838,523,1972,1708,1543,191,512,1881,1898,1951,32,1519,180,2283,898,1705,139,1224,2311,164,672;326,2302,1752,492,2276,775,900,2136,1847,243,1066,941,1458,2312,1422,966,568,782,2128,809,1063,436,967,855,283,1426;1849,1720,2420,7,601,1342,2423,1466,1719,551,257,2346,591,1137,423,2366,1101,2297,1541,1512,1166,2288,1908,296,199,2418;1808,1775,1633,196,1679,499,1176,2236,2136,641,2415,811,279,343,334,856,2177,2039,1216,2259,579,1982,213,297,540,347;807,2455,1183,790,1961,534,297,158,1528,2149,1427,1747,458,717,2219,1191,907,825,685,1181,117,1952,2010,575,2241,1636;65,1850,584,468,2287,1803,780,2472,282,2346,1899,466,1396,437,1113,1674,2251,169,533,2403,576,445,53,2494,1262,2355;645,138,1667,1085,1001,1727,2198,2145,61,2382,94,208,1746,1234,500,1306,1328,467,2134,1627,1597,550,168,1549,1101,1295;1873,219,386,925,1981,2338,2445,2484,1249,412,269,635,2498,2351,562,1295,1926,1204,2278,1992,343,826,1337,795,2266,114", "output": "2238,2118,75,245,1837,1978,1099,2343,1971,1473,2165,1104,506,191,2425,605,349,397,1690,1291,1561,1960,534,2500,2210,45,2113,2187,214,601,2327,1660,1753,1677,950,220,1954,2252,1633,1471,429,2039,1374,855,2389,482,1041,2023,1805,1115,1363,2415,1081,2256,450,2290,2251,362,2182,818,520,2449,1212,13,957,2474,247,570,6,2293,1064,123,656,1193,1723,1329,1676,181,2188,1972,1544,264,120,1166,609,81,2019,125,1195,2358,433,1500,88,2386,1213,182,136,228,630,940,301,705,187,2036,2278,414,1947,735,2407,1910,2045,733,382,1561,2175,1553,1544,385,1837,1902,482,474,290,731,716,1927,2488,1733,1652,1099,548,596,764,621,1609,2160,400,109,2133,599,932,1983,2468,593,846,462,1133,2444,864,1301,1957,2187,773,542,1592,2351,2004,530,652,1544,1057,337,131,1475,1991,2487,2267,1143,2159,1063,268,1874,1952,1892,1127,295,1205,327,464,1947,602,1934,2123,2338,1038,2216,1625,1886,1651,1209,2288,726,520,330,18,1941,21,2481,1699,592,1750,1909,1826,592,502,2188,1961,1251,1770,1180,1945,523,1708,191,1881,1951,1519,2283,1705,1224,164,1426,855,436,809,782,966,2312,941,243,2136,775,492,2302,1849,2420,601,2423,1719,257,591,423,1101,1541,1166,1908,199,347,297,1982,2259,2039,856,343,811,641,2236,499,196,1775,807,1183,1961,297,1528,1427,458,2219,907,685,117,2010,2241,2355,2494,445,2403,169,1674,437,466,2346,2472,1803,468,1850,645,1667,1001,2198,61,94,1746,500,1328,2134,1597,168,1101,114,795,826,1992,1204,1295,2351,635,412,2484,2338,925,219"}, {"input": "2413,1351,2297,1517,1027,1168,46,118,628,2378,1246,2334,1973,2112;2140,1407,1847,1742,1486,473,2152,755,516,565,915,662,456,907;1453,2021,119,1363,2347,944,1136,1011,11,546,992,1088,338,803;597,2371,1287,53,1545,2091,30,1922,309,2434,2207,2200,1917,2152;2338,1051,1688,41,635,197,1009,784,438,2037,1144,2,807,1711;322,2256,2038,1625,289,376,20,2030,1129,2349,1756,787,1497,2346;1617,770,54,770,2082,1422,730,453,2148,244,676,775,1611,1965;1496,1826,1390,160,139,392,2166,98,2054,1465,639,186,1991,992;1091,11,836,584,2361,1717,1527,1893,837,263,1576,1128,1769,1405;2200,2125,21,1285,2188,949,1637,2342,582,1709,856,2164,2310,2236;2386,1246,1879,2363,1953,2455,1313,1885,1306,742,2102,2413,14,76;444,2403,44,230,402,364,128,374,1793,369,522,2140,714,778;2119,1693,2119,602,1235,536,304,350,2148,565,1904,525,1492,636;1901,1162,1961,356,1961,1516,1477,249,1882,2307,2323,1443,151,678;1979,593,2277,779,1251,194,302,1871,646,2411,116,249,197,2298;1071,577,2345,930,2463,1289,1988,2128,2129,512,83,2011,231,2315;485,132,2485,116,2033,1693,1549,1235,1508,321,82,1632,204,2490;2393,962,804,1788,1820,1511,2337,392,1707,214,1827,784,468,1606", "output": "2413,2297,1027,46,628,1246,1973,907,662,565,755,473,1742,1407,1453,119,2347,1136,11,992,338,2152,2200,2434,1922,2091,53,2371,2338,1688,635,1009,438,1144,807,2346,787,2349,2030,376,1625,2256,1617,54,2082,730,2148,676,1611,992,186,1465,98,392,160,1826,1091,836,2361,1527,837,1576,1769,2236,2164,1709,2342,949,1285,2125,2386,1879,1953,1313,1306,2102,14,778,2140,369,374,364,230,2403,2119,2119,1235,304,2148,1904,1492,678,1443,2307,249,1516,356,1162,1979,2277,1251,302,646,116,197,2315,2011,512,2128,1289,930,577,485,2485,2033,1549,1508,82,204,1606,784,214,392,1511,1788,962"}, {"input": "1788,1302,1505,1808,1901,1897,1012,2424,541,564,819,1958,2461,719;1891,957,1348,2026,2233,465,2254,1901,34,2110,7,499,1587,974;1506,2070,1221,326,2043,618,1931,2118,612,1800,1458,2436,890,223;1133,1320,288,732,1529,2018,1915,401,692,1632,853,1366,2172,578;3,962,932,1971,302,1985,337,868,1288,2119,746,2011,1181,123;1787,1528,403,1559,1193,917,561,777,1784,850,489,1047,2500,887;270,2500,365,807,2293,2294,873,28,448,2067,26,496,89,1410;1009,2185,1160,1347,960,2311,1568,2043,1854,1078,445,531,1840,2388;1296,1927,2005,410,369,458,1062,2093,2063,539,980,348,1719,2097;1414,1759,2192,544,15,826,605,804,614,14,2452,440,715,481;1783,1130,206,2467,794,456,30,1743,2150,1542,2331,2029,2382,788;738,1636,1613,212,1563,1768,1423,1708,784,91,1209,1617,1630,612;2358,614,1519,1444,209,757,449,2046,1864,326,922,2295,982,1772;2293,1692,944,1231,1863,1636,781,1873,123,1879,1170,856,1370,218;546,2274,2336,1820,1273,357,886,1137,195,866,2207,230,734,1702", "output": "1788,1505,1901,1012,541,819,2461,974,499,2110,1901,465,2026,957,1506,1221,2043,1931,612,1458,890,578,1366,1632,401,2018,732,1320,3,932,302,337,1288,746,1181,887,1047,850,777,917,1559,1528,270,365,2293,873,448,26,89,2388,531,1078,2043,2311,1347,2185,1296,2005,369,1062,2063,980,1719,481,440,14,804,826,544,1759,1783,206,794,30,2150,2331,2382,612,1617,91,1708,1768,212,1636,2358,1519,209,449,1864,922,982,218,856,1879,1873,1636,1231,1692,546,2336,1273,886,195,2207,734"}, {"input": "1848,2467,2084,27,753,2138,738,282,1057,1890,947,1275,883,1640,731,1139,9,326,2472,1294,1454,1198,1980,66,2055,983,1805,2188,945,2205,1509,1856,1788,1293,423,894,1542,1025,166;2469,1028,695,1471,2470,471,398,506,1830,1627,2492,1130,691,2307,1847,2348,787,1159,949,292,2019,1834,675,1788,1356,1101,2191,1981,1326,687,435,1999,2071,2361,1684,1828,1316,1999,1509;2485,1212,2180,2159,145,787,1966,1942,501,2051,2194,2406,1544,401,2497,276,404,1622,280,2363,742,696,1771,379,2249,510,857,2213,1204,2112,791,1280,1378,95,885,389,1167,2176,477;759,339,1648,497,1909,2301,535,2328,2444,1647,30,2155,8,98,375,1887,165,309,1026,2188,724,2357,876,1178,13,150,393,2348,1673,1667,2297,1108,2259,322,1648,711,991,202,408;858,1279,2481,1012,1893,228,1213,1850,2053,879,1596,1358,1691,315,2268,1742,1586,1444,1514,459,817,1420,2057,1233,1126,703,1027,2153,1758,463,1062,1532,22,669,457,1909,1564,1501,459;410,2109,424,1709,464,1866,944,233,1476,2213,1783,1378,796,1538,2261,2242,1713,314,1388,382,2040,1462,145,70,715,963,2192,1010,2332,1547,493,2070,879,1972,2429,399,2197,420,2251;1244,456,2355,2118,1413,2017,1401,2212,1616,2346,446,2386,1653,785,17,130,1901,2439,502,1382,2121,2058,2240,42,1028,1158,1017,1769,2201,1721,400,1996,1896,448,1715,1149,1804,700,36;879,717,518,855,1493,26,1279,532,1912,1083,1910,1063,2377,1241,2304,223,1547,630,2169,2370,720,1099,1015,1698,709,2458,1820,2248,2183,742,465,1593,1052,85,834,1359,842,2290,222;961,1363,1060,1743,1319,818,1657,1811,1857,884,1189,552,925,338,1291,35,1787,18,451,1888,142,2487,802,1009,1911,1337,608,1701,1495,341,149,1017,1754,1893,1982,1515,2012,1407,1946;1206,1245,783,1981,468,1824,2496,1386,2215,1322,2490,1053,125,631,1383,1988,100,188,665,2173,382,169,1203,1023,1093,1775,2022,1788,1040,6,2243,1466,2478,1480,2123,50,1465,474,866;772,1091,1790,177,1978,1877,1904,858,1970,856,1556,8,2166,2215,1694,1842,485,425,2426,578,2450,135,1358,1113,1214,2162,1292,1887,2180,628,1438,1686,1770,77,2467,786,1110,796,1318;637,2145,578,684,666,1952,1885,72,784,1622,1376,200,1166,2193,2169,982,1607,447,102,720,1449,1194,2097,489,882,939,1833,139,1957,1331,2138,279,1952,186,263,506,1869,2424,1515;65,1953,1465,1078,921,757,1119,623,926,445,485,2465,1602,1297,1081,156,1627,1794,219,1932,1873,446,1059,1671,790,1283,1071,751,1721,946,817,1528,1399,1838,1249,957,986,2208,1685;2364,1290,506,879,961,1133,2327,1584,493,60,1057,1646,1045,2020,1440,159,2402,2178,1612,913,1835,1940,1004,2244,884,634,2414,306,369,1617,2326,1528,2074,869,2113,1423,2324,2085,973;833,1138,1619,906,1453,43,1690,296,1130,1478,1957,314,1785,1360,469,1187,1909,97,1839,53,1881,919,576,1001,1500,18,1132,1794,1735,1070,2131,313,2427,2167,404,821,1279,721,1902;2171,1648,1199,1071,1051,328,1930,2341,1428,2211,23,2292,648,866,803,1888,152,1814,1682,1566,1334,298,1406,290,776,2365,705,518,442,1589,946,363,308,798,554,345,1815,1593,269;2083,1450,403,1913,2206,613,2273,1197,2359,1126,2152,1113,105,2231,75,404,1669,1281,1029,1126,495,1753,2037,439,2144,1093,1317,1346,2273,1012,408,2294,1485,815,490,1663,1528,1782,2084;2185,178,1739,1279,1149,2219,1591,2389,2045,659,442,404,51,1671,1680,1805,1528,521,1442,1682,1298,336,1085,501,2092,1467,1046,1940,999,852,127,626,1198,1334,543,1388,1042,1714,2160;2227,1534,1621,1466,1570,761,2428,1579,724,1125,2490,1003,1719,2361,113,1922,1656,2192,827,987,976,1141,1799,1828,2393,863,295,2102,812,711,576,1397,2114,165,104,1396,2229,1684,920;1634,1230,898,1457,1190,1903,178,1797,226,1859,1075,1452,2225,958,766,1229,1208,1830,425,2242,349,1785,1301,1952,2370,263,1264,1914,1933,33,719,655,1787,1494,2465,2121,370,1048,1340;709,692,637,1490,736,2007,1835,1065,2071,1469,1914,1358,715,857,1407,447,404,1072,1300,2058,2059,1569,6,1672,497,184,1390,2307,219,2003,839,1067,762,259,1109,446,459,1750,1799;649,589,1738,2433,2017,2184,765,1387,468,1195,2485,43,729,1382,1951,993,1102,1329,1994,1404,1896,297,1887,1392,409,533,82,325,202,2403,592,775,2259,1740,112,1271,902,710,1352;137,1503,1125,78,888,132,2063,1920,1032,1319,1963,226,2486,787,1674,782,736,1329,2061,1537,1527,2409,2365,1831,1143,1477,422,1271,568,962,1869,818,1968,395,1430,435,943,397,963", "output": "1848,2084,753,738,1057,947,883,731,9,2472,1454,1980,2055,1805,945,1509,1788,423,1542,166,1999,1828,2361,1999,687,1981,1101,1788,1834,292,1159,2348,2307,1130,1627,506,471,1471,1028,2485,2180,145,1966,501,2194,1544,2497,404,280,742,1771,2249,857,1204,791,1378,885,1167,477,202,711,322,1108,1667,2348,150,1178,2357,2188,309,1887,98,2155,1647,2328,2301,497,339,858,2481,1893,1213,2053,1596,1691,2268,1586,1514,817,2057,1126,1027,1758,1062,22,457,1564,459,420,399,1972,2070,1547,1010,963,70,1462,382,314,2242,1538,1378,2213,233,1866,1709,2109,1244,2355,1413,1401,1616,446,1653,17,1901,502,2121,2240,1028,1017,2201,400,1896,1715,1804,36,2290,1359,85,1593,742,2248,2458,1698,1099,2370,630,223,1241,1063,1083,532,26,855,717,961,1060,1319,1657,1857,1189,925,1291,1787,451,142,802,1911,608,1495,149,1754,1982,2012,1946,474,50,1480,1466,6,1788,1775,1023,169,2173,188,1988,631,1053,1322,1386,1824,1981,1245,772,1790,1978,1904,1970,1556,2166,1694,485,2426,2450,1358,1214,1292,2180,1438,1770,2467,1110,1318,2424,506,186,279,1331,139,939,489,1194,720,447,982,2193,200,1622,72,1952,684,2145,65,1465,921,1119,926,485,1602,1081,1627,219,1873,1059,790,1071,1721,817,1399,1249,986,1685,2085,1423,869,1528,1617,306,634,2244,1940,913,2178,159,2020,1646,60,1584,1133,879,1290,833,1619,1453,1690,1130,1957,1785,469,1909,1839,1881,576,1500,1132,1735,2131,2427,404,1279,1902,1593,345,798,363,1589,518,2365,290,298,1566,1814,1888,866,2292,2211,2341,328,1071,1648,2083,403,2206,2273,2359,2152,105,75,1669,1029,495,2037,2144,1317,2273,408,1485,490,1528,2084,1714,1388,1334,626,852,1940,1467,501,336,1682,521,1805,1671,404,659,2389,2219,1279,178,2227,1621,1570,2428,724,2490,1719,113,1656,827,976,1799,2393,295,812,576,2114,104,2229,920,1048,2121,1494,655,33,1914,263,1952,1785,2242,1830,1229,958,1452,1859,1797,1903,1457,1230,709,637,736,1835,2071,1914,715,1407,404,1300,2059,6,497,1390,219,839,762,1109,459,1799,710,1271,1740,775,2403,325,533,1392,297,1404,1329,993,1382,43,1195,1387,2184,2433,589,137,1125,888,2063,1032,1963,2486,1674,736,2061,1527,2365,1143,422,568,1869,1968,1430,943,963"}, {"input": "1255,1178,1817,1834,74,823,1329,1202,1002,450,227,908,1171,1892,1293,1823,1561;357,1323,136,804,1957,1591,1560,1717,665,2360,2013,169,517,404,1317,453,996", "output": "1255,1817,74,1329,1002,227,1171,1293,1561,453,404,169,2360,1717,1591,804,1323"}, {"input": "1490,358;1108,655;1187,565;1285,2033;2406,1179;1852,603;1556,81;1507,894;773,2126;469,1366;2199,1434;1118,2061;1970,1050;490,1325;499,1545;2497,313;1086,702;552,793;1164,1332;1908,1861;1091,1654", "output": "1490,655,1187,2033,2406,603,1556,894,773,1366,2199,2061,1970,1325,499,313,1086,793,1164,1861,1091"}, {"input": "1194,633,2321,830,2490,1004,1584,1798,1946,71,165,2302,780,1235,2401,1052,1094;2367,542,1034,945,585,907,1539,542,1015,1388,2470,25,6,566,316,530,129;2182,1331,1733,2466,1582,222,265,709,34,1607,1924,1415,458,2402,88,2040,1963;536,1199,1276,709,1495,915,1906,1818,288,1648,907,1115,2121,1985,2346,1045,2272;1398,1379,1594,219,173,2080,1233,136,2003,294,1545,536,518,1085,1845,1840,1842;1996,166,1929,382,1693,683,2025,1764,2118,2430,2445,1232,2075,1839,567,1267,1318;991,2028,792,1746,701,1668,821,637,1877,2300,1605,547,1761,2286,1060,962,865;2051,1791,1256,601,775,1996,1614,1336,2447,428,44,2118,2398,614,859,2131,1826;901,197,2192,2051,655,1762,563,2180,1015,2103,1184,369,1943,2458,2026,97,1820;1732,1705,1159,654,2495,99,398,1873,1322,773,1392,1241,398,762,1065,604,393;288,111,678,384,736,238,1049,230,1945,1537,1002,754,524,1382,879,854,314;1121,387,345,1664,2214,2146,2439,1772,1243,1593,564,938,1058,649,2430,2367,498;927,1088,1963,32,2284,1444,2497,2064,1344,1678,2031,738,2485,1317,2256,276,2158;316,1785,210,638,1797,1716,1289,168,587,1870,2269,1717,2326,1540,1323,33,586;533,1540,521,1014,1410,1214,2399,1097,2029,1670,1452,1497,2367,27,1158,724,1094;2389,720,1909,705,237,672,1292,2199,1975,2399,406,906,842,223,628,346,467;2431,1603,1233,1455,1301,860,2308,1268,73,1475,1287,451,1106,1633,2489,1551,1901;2285,895,214,1336,595,2415,655,2290,1074,196,345,1564,874,2382,1912,1435,336", "output": "1194,2321,2490,1584,1946,165,780,2401,1094,530,566,25,1388,542,907,945,542,2182,1733,1582,265,34,1924,458,88,1963,1045,1985,1115,1648,1818,915,709,1199,1398,1594,173,1233,2003,1545,518,1845,1842,1267,1839,1232,2430,1764,683,382,166,991,792,701,821,1877,1605,1761,1060,865,2131,614,2118,428,1336,1996,601,1791,901,2192,655,563,1015,1184,1943,2026,1820,604,762,1241,773,1873,99,654,1705,288,678,736,1049,1945,1002,524,879,314,2367,649,938,1593,1772,2146,1664,387,927,1963,2284,2497,1344,2031,2485,2256,2158,33,1540,1717,1870,168,1716,638,1785,533,521,1410,2399,2029,1452,2367,1158,1094,346,223,906,2399,2199,672,705,720,2431,1233,1301,2308,73,1287,1106,2489,1901,1435,2382,1564,196,2290,2415,1336,895"}, {"input": "2251,2493,730,306,204,1358,683,1855,160,2305,1694,499,1870,2162,302,340,325,1251,2025,232,1886,2323,1900,864,96,1093,559,574,1574,1931,1158,1496,2252,136,1149,926,2155,90,1369,141,994,8,1948,1749;1807,20,708,2353,2180,986,2357,2202,1786,482,2239,1895,2352,649,876,2402,1364,609,38,1249,1273,229,2151,640,920,2367,1321,1661,952,508,2002,2084,1136,883,800,558,1331,2336,1220,672,1933,1783,146,35;2171,2360,2022,2445,894,545,2134,933,139,1764,2137,239,735,2130,2220,976,618,2183,695,1573,818,2036,1720,1976,2296,1654,2141,1549,2445,1985,2272,1840,1512,2313,2319,2467,935,2480,1123,1023,1927,1560,687,802;164,662,160,2073,382,144,1533,2399,1786,1624,2133,519,2135,540,2317,120,825,622,1779,1206,1771,2363,1238,1818,1823,1203,872,512,2268,1717,560,210,218,1963,270,849,37,2266,1778,312,2110,2468,1985,372;2205,504,1092,2158,174,2152,1142,1159,974,1321,1923,286,187,932,1641,1950,1053,2366,1700,302,846,619,2203,2305,559,1079,591,246,2448,2081,410,1466,2422,352,1138,1466,1316,975,374,1012,531,1508,4,2184;217,218,1369,1453,910,316,1141,2473,1730,786,125,441,1969,900,1965,1085,2414,672,822,668,512,1216,165,1539,1297,481,706,1356,582,1549,381,344,1592,654,890,1329,189,1919,1789,2213,1029,550,2378,1187;1912,1360,1560,761,977,1685,1558,308,1409,795,223,581,2293,988,452,255,2142,741,271,2397,226,376,17,412,142,1660,1282,658,1408,52,713,972,1428,701,488,1106,1162,2122,2183,2098,2421,92,1873,1199;1848,1764,839,385,473,1868,2337,1723,776,2067,444,1897,284,1608,1921,1517,249,2113,1977,1330,986,790,1769,1943,1887,1908,2170,1959,1233,155,2498,2319,570,1148,305,1678,1041,1941,1984,718,912,2169,761,1020;2491,311,487,1583,192,37,1852,604,917,1671,1344,1631,1381,2226,1925,1018,29,1191,564,238,1458,403,1365,464,1709,2137,2483,1520,219,617,1263,651,771,207,211,379,583,875,472,772,2383,375,647,628;467,1446,1540,1993,1235,2082,618,375,861,90,1355,2025,5,1619,1565,1080,531,2277,2191,2083,2368,2455,139,97,1529,1381,57,692,1757,28,1678,2283,1515,1990,1291,1753,168,1562,2286,1107,898,125,1013,1685;1193,367,1481,2215,2255,2335,1758,1457,707,752,2068,689,671,800,1193,779,1780,692,2417,810,1007,1591,1819,2081,857,1142,187,114,721,1415,1963,2368,218,1161,461,993,2021,2146,2063,2067,2406,2475,1090,980;696,1180,1130,318,887,1175,2410,667,1087,1109,882,1848,2178,846,2202,1313,2216,2119,1554,2209,1208,231,596,265,1066,2427,1828,1313,407,483,1764,152,2275,1508,600,2342,39,1880,813,2264,456,331,1748,566;766,398,1634,2316,1080,1962,2345,2268,408,2321,2214,1014,1699,24,1337,1900,2277,1678,1309,2267,341,576,1178,2385,404,641,1646,2500,2287,2042,194,2286,2172,792,598,784,1688,2407,365,1130,2345,889,1387,1204;2257,1868,173,132,1354,414,250,1892,681,1639,1024,462,1467,90,1558,1091,1396,1639,1028,794,142,2202,1995,800,1379,717,837,31,1034,1911,1033,1748,1691,294,125,1679,1836,640,1579,2179,635,2042,438,735;2225,604,2180,943,1970,1618,577,1711,228,1217,1331,57,2205,394,1892,49,588,1223,635,744,2183,1784,638,2024,644,418,1033,1772,283,692,855,3,729,1900,1008,542,314,1956,28,1852,1358,383,1609,1711;950,2116,285,1051,910,1784,121,142,765,2308,565,1984,1855,131,1337,1427,1323,1658,1655,1262,2230,518,580,455,1199,1179,1343,785,1178,2472,1441,731,576,694,2214,1379,88,1517,75,2327,1677,655,1629,1882;1656,1338,2016,1483,1267,8,2068,1433,25,168,1799,2487,2123,654,535,2327,1975,1851,2336,1055,924,1379,1148,1336,1523,1553,1940,209,866,1891,1185,81,85,437,1488,700,1091,1420,2434,1207,267,36,331,53;2107,962,1873,1885,2234,541,1916,172,342,2164,133,2466,2380,988,643,2329,1515,480,1826,1751,10,675,460,902,2340,2109,2017,2193,109,886,1932,1069,192,960,75,256,1312,1192,736,1030,2411,2238,1821,861;242,1373,2493,1953,1090,1493,2419,415,1493,967,687,2113,45,69,651,422,1605,581,1505,1330,237,1777,249,1018,893,2010,1516,1885,351,2315,279,1678,109,1398,38,405,1107,763,1650,1873,1988,2265,970,70;1837,2007,1273,1356,428,2105,1701,1493,823,1785,521,1385,2045,2486,428,1630,1054,901,569,738,1392,1505,453,480,1566,1772,2049,984,2374,1218,1934,266,1801,1673,749,760,171,366,646,661,497,1848,1499,2174;1178,1299,1270,2463,935,1855,2130,1136,751,984,2433,1815,611,257,732,841,2129,1031,1869,945,2094,475,843,938,596,1507,943,324,1124,938,1200,1531,1364,624,112,2285,240,1539,145,739,1875,851,2156,2082;1123,1803,2187,1863,1829,293,1663,1625,385,2402,1275,1342,1094,106,2210,573,378,623,416,1035,228,360,2198,2023,1680,801,168,1694,1130,2418,984,1127,35,1992,1755,2203,514,1659,495,2144,479,1756,596,1249;2479,312,2194,509,1245,1617,2121,2307,1082,129,250,467,1850,1640,1044,2372,1743,620,2235,1621,936,991,1096,1335,2251,1236,1971,118,1060,2019,518,2312,1898,965,910,1431,1258,1458,208,1636,1669,1467,1958,2456;101,810,2168,2188,1280,1861,1347,2381,633,918,1052,1126,422,208,2289,1658,103,1749,1842,1984,2039,1353,284,463,1623,1138,859,276,1486,1487,219,768,842,2405,2062,570,1191,1509,1385,2181,1562,1351,641,1732;623,440,209,2494,147,330,2167,969,1458,727,1826,410,2383,1929,1551,1778,1498,221,353,2194,574,52,517,1593,992,890,1868,2056,2456,919,12,889,1113,342,182,652,324,55,1077,2289,2319,107,319,1260;755,2088,253,2485,1246,695,1665,1230,434,1657,2162,1829,975,649,93,1399,1171,1173,728,285,52,1499,1870,1288,634,1619,430,1615,725,85,570,998,2169,1315,1121,57,2009,2046,2398,1994,295,1018,1974,621;72,1692,1350,192,595,277,534,144,723,1849,1303,1691,2261,1694,913,757,2318,1002,943,1349,1272,1944,701,2461,1323,2006,1743,150,1452,1847,890,961,1642,2049,2471,21,666,2302,1850,1220,2296,1837,1990,1503;927,361,2319,684,2068,2394,262,2484,1284,1896,2428,1463,253,2350,495,51,1431,694,2335,1703,2360,1929,348,2209,51,1834,153,256,2468,555,1181,2349,1558,1411,298,2478,1740,26,495,230,1875,2497,1043,832;395,678,1135,390,1093,1132,1425,1696,1060,732,1581,2205,1661,63,236,2271,1634,926,2135,1561,914,1147,2166,1488,1091,508,858,1169,1892,1780,1706,363,1645,1334,1032,2242,922,5,2019,1005,235,1686,1989,160", "output": "2251,730,204,683,160,1694,1870,302,325,2025,1886,1900,96,559,1574,1158,2252,1149,2155,1369,994,1948,35,1783,672,2336,558,883,2084,508,1661,2367,640,229,1249,609,2402,649,1895,482,2202,986,2353,20,2171,2022,894,2134,139,2137,735,2220,618,695,818,1720,2296,2141,2445,2272,1512,2319,935,1123,1927,687,372,2468,312,2266,849,1963,210,1717,512,1203,1818,2363,1206,622,120,540,519,1624,2399,144,2073,662,2205,1092,174,1142,974,1923,187,1641,1053,1700,846,2203,559,591,2448,410,2422,1138,1316,374,531,4,1187,550,2213,1919,1329,654,344,1549,1356,481,1539,1216,668,672,1085,900,441,786,2473,316,1453,218,1912,1560,977,1558,1409,223,2293,452,2142,271,226,17,142,1282,1408,713,1428,488,1162,2183,2421,1873,1020,2169,718,1941,1678,1148,2319,155,1959,1908,1943,790,1330,2113,1517,1608,1897,2067,1723,1868,385,1764,2491,487,192,1852,917,1344,1381,1925,29,564,1458,1365,1709,2483,219,1263,771,211,583,472,2383,647,1685,125,1107,1562,1753,1990,2283,28,692,1381,97,2455,2083,2277,1080,1619,2025,90,375,2082,1993,1446,1193,1481,2255,1758,707,2068,671,1193,1780,2417,1007,1819,857,187,721,1963,218,461,2021,2063,2406,1090,566,331,2264,1880,2342,1508,152,483,1313,2427,265,231,2209,2119,1313,846,1848,1109,667,1175,318,1180,766,1634,1080,2345,408,2214,1699,1337,2277,1309,341,1178,404,1646,2287,194,2172,598,1688,365,2345,1387,735,2042,2179,640,1679,294,1748,1911,31,717,800,2202,794,1639,1091,90,462,1639,1892,414,132,1868,2225,2180,1970,577,228,1331,2205,1892,588,635,2183,638,644,1033,283,855,729,1008,314,28,1358,1609,1882,655,2327,1517,1379,694,731,2472,785,1179,455,518,1262,1658,1427,131,1984,2308,142,1784,1051,2116,1656,2016,1267,2068,25,1799,2123,535,1975,2336,924,1148,1523,1940,866,1185,85,1488,1091,2434,267,331,861,2238,1030,1192,256,960,1069,886,2193,2109,902,675,1751,480,2329,988,2466,2164,172,541,1885,962,242,2493,1090,2419,1493,687,45,651,1605,1505,237,249,893,1516,351,279,109,38,1107,1650,1988,970,2174,1848,661,366,760,1673,266,1218,984,1772,480,1505,738,901,1630,2486,1385,1785,1493,2105,1356,2007,1178,1270,935,2130,751,2433,611,732,2129,1869,2094,843,596,943,1124,1200,1364,112,240,145,1875,2156,1249,1756,2144,1659,2203,1992,1127,2418,1694,801,2023,360,1035,623,573,106,1342,2402,1625,293,1863,1803,2479,2194,1245,2121,1082,250,1850,1044,1743,2235,936,1096,2251,1971,1060,518,1898,910,1258,208,1669,1958,1732,1351,2181,1509,570,2405,768,1487,276,1138,463,1353,1984,1749,1658,208,1126,918,2381,1861,2188,810,623,209,147,2167,1458,1826,2383,1551,1498,353,574,517,992,1868,2456,12,1113,182,324,1077,2319,319,621,1018,1994,2046,57,1315,998,85,1615,1619,1288,1499,285,1173,1399,649,1829,1657,1230,695,2485,2088,72,1350,595,534,723,1303,2261,913,2318,943,1272,701,1323,1743,1452,890,1642,2471,666,1850,2296,1990,832,2497,230,26,2478,1411,2349,555,256,1834,2209,1929,1703,694,51,2350,1463,1896,2484,2394,684,361,395,1135,1093,1425,1060,1581,1661,236,1634,2135,914,2166,1091,858,1892,1706,1645,1032,922,2019,235,1989"}, {"input": "396,562,147,979,1542,606,1687,387,1233,421,1571,1680,1164,756,1687,626,921,974,2204,789,1366,2079,1912,2138,1168,1856,2046;1710,2037,2086,993,163,1402,1924,1373,2061,2099,261,34,200,1478,920,52,1129,1557,1332,369,1117,1137,748,2407,836,20,1153;2107,2065,2267,2296,900,577,1710,967,850,1074,973,47,1022,246,2475,1196,1235,923,598,1171,1980,2349,1532,1049,2114,2283,960;1139,182,1359,2465,1774,777,2461,828,2489,1961,1784,1505,419,1108,1320,701,2017,28,1690,2034,873,2314,644,481,2156,409,1348;1173,502,2410,986,977,904,2286,1607,197,1894,2128,506,2439,442,2303,2322,517,1272,866,2240,1783,1890,1623,134,2311,1497,937;1565,1713,259,876,1422,2318,2128,2493,164,947,420,183,1775,128,217,345,1254,2074,167,2075,131,50,2176,264,1645,891,1387;1855,2354,1861,1750,2476,1778,528,836,538,1442,1365,1305,2067,1010,93,2037,2015,744,719,2463,1198,2154,553,2287,2209,666,1070;2412,63,887,2419,541,1686,122,18,2252,1796,1840,1511,280,45,2076,904,2055,2187,1074,474,1824,548,1542,2041,1602,802,1861;860,1117,189,189,2079,1070,1640,913,2262,112,1001,1927,2259,1387,879,1822,785,1751,255,1602,2486,321,704,431,37,1369,2071;829,83,535,425,625,83,105,1139,760,1089,1991,2497,173,1822,47,384,1352,194,2467,231,199,2227,300,1793,131,830,589;1762,2362,949,2090,2287,1408,915,1784,938,622,1438,246,383,1346,534,2462,1283,2279,771,19,2439,897,865,942,1412,750,479;2049,461,1068,1562,162,954,2016,2478,1120,1024,2450,429,1300,793,1022,853,980,2164,1500,62,1186,52,809,208,247,415,1944;1365,1286,2120,77,239,1848,2480,2004,2324,2310,647,2243,1191,68,1231,1126,1750,1130,1035,1303,1252,6,1341,2029,1485,1407,1903", "output": "396,147,1542,1687,1233,1571,1164,1687,921,2204,1366,1912,1168,2046,20,2407,1137,369,1557,52,1478,34,2099,1373,1402,993,2037,2107,2267,900,1710,850,973,1022,2475,1235,598,1980,1532,2114,960,409,481,2314,2034,28,701,1108,1505,1961,828,777,2465,182,1173,2410,977,2286,197,2128,2439,2303,517,866,1783,1623,2311,937,891,264,50,2075,2074,345,128,183,947,2493,2318,876,1713,1855,1861,2476,528,538,1365,2067,93,2015,719,1198,553,2209,1070,802,2041,548,474,2187,904,45,1511,1796,18,1686,2419,63,860,189,2079,1640,2262,1001,2259,879,785,255,2486,704,37,2071,830,1793,2227,231,194,384,1822,2497,1089,1139,83,425,83,1762,949,2287,915,938,1438,383,534,1283,771,2439,865,1412,479,415,208,52,62,2164,853,793,429,1024,2478,954,1562,461,1365,2120,239,2480,2324,647,1191,1231,1750,1035,1252,1341,1485,1903"}, {"input": "1504,619,1486,1180,1368,1596,590,1333,2096,1877,1686,505,170,184,2121,1239,2396;1534,1924,292,1630,178,86,2248,1655,183,2056,2477,1508,2030,284,59,837,2005;39,1476,398,1000,1565,1804,120,351,2051,902,1349,1617,1329,2173,1668,1679,2310;1602,666,1744,1782,346,1847,1,1916,162,2440,1967,1068,589,909,720,2294,193;787,2289,483,916,532,804,981,1924,1746,137,2158,526,1518,159,842,499,2081;522,2444,2413,11,1587,1368,2327,1674,892,476,1393,607,1204,1996,769,336,1652;1817,157,1875,785,326,1088,265,98,1785,1008,938,1643,462,586,468,2191,847;1374,2062,624,1002,1517,1984,2432,2227,1009,607,1470,1678,77,1418,521,1826,326;294,1132,2361,2457,1011,1086,1213,1535,1046,695,1278,1010,748,779,960,1552,375;396,617,983,809,1179,1129,1016,331,1265,878,502,2332,1691,1846,1844,2077,682;2155,1891,1796,1634,2029,2328,2319,1123,265,2429,533,2408,652,2155,895,1109,589;395,1268,1002,1354,1048,281,1149,1924,2214,1649,1207,2487,820,1328,1624,805,984;204,74,1191,1409,2084,2385,2316,502,2246,1525,1628,223,1318,2088,1862,889,1477;1166,1640,2328,1791,2165,1661,1573,59,1880,420,1403,385,9,657,193,1392,219;1872,75,1169,1902,1245,43,1407,995,1302,1460,729,5,495,1764,1406,1609,2419;1839,1141,1375,1736,994,448,952,2219,1533,2233,266,1686,1505,2053,126,555,629;1038,2444,2290,1364,1037,950,395,1192,255,2400,1848,496,1819,1070,6,751,2277;704,617,1678,528,866,1362,376,1119,2067,573,2197,1109,1152,1369,1373,598,480;1373,1049,10,771,1393,647,859,2250,539,2169,2232,69,534,832,978,2370,1647;57,208,1069,1594,2031,1630,1535,1247,534,1286,325,775,2157,2437,1606,62,286;1708,695,261,205,2352,2215,1113,1669,1876,1867,2250,617,2328,155,2003,2415,153;581,985,393,842,372,2452,1626,2314,99,1412,977,2485,988,8,1365,41,1510", "output": "1504,1486,1368,590,2096,1686,170,2121,2396,837,284,1508,2056,1655,86,1630,1924,39,398,1565,120,2051,1349,1329,1668,2310,2294,909,1068,2440,1916,1847,1782,666,787,483,532,981,1746,2158,1518,842,2081,336,1996,607,476,1674,1368,11,2444,1817,1875,326,265,1785,938,462,468,847,1826,1418,1678,607,2227,1984,1002,2062,294,2361,1011,1213,1046,1278,748,960,375,2077,1846,2332,878,331,1129,809,617,2155,1796,2029,2319,265,533,652,895,589,805,1328,2487,1649,1924,281,1354,1268,204,1191,2084,2316,2246,1628,1318,1862,1477,1392,657,385,420,59,1661,1791,1640,1872,1169,1245,1407,1302,729,495,1406,2419,555,2053,1686,2233,2219,448,1736,1141,1038,2290,1037,395,255,1848,1819,6,2277,598,1369,1109,573,1119,1362,528,617,1373,10,1393,859,539,2232,534,978,1647,62,2437,775,1286,1247,1630,1594,208,1708,261,2352,1113,1876,2250,2328,2003,153,41,8,2485,1412,2314,2452,842,985"}, {"input": "1269,1513,379,1144,612,1497,1082,2299,274,714,646,2485,1171,598,740,392,24,2353,1703,2067,1120,302,1576,1523,2038,2194,1940,2083,1377,360,102,224,582,984,997,610,1093,1604,1549,2468,39,610,1479,1431,694,844,444,2388,679,683;305,1506,780,1465,695,716,1326,1096,981,39,872,166,997,2257,1230,2013,1228,1617,1756,310,1790,1339,2164,1563,659,2397,2157,996,1418,634,1382,862,976,1666,509,2348,325,45,935,283,1988,1293,826,2143,590,1485,2108,1555,1642,1005;884,826,872,106,1516,16,39,21,1011,967,2051,49,1310,1563,848,1330,551,355,445,333,2101,1924,245,2062,543,1345,149,1235,1755,1223,1306,2071,114,1315,1599,438,368,1028,296,1593,1824,943,1748,1536,1219,2140,78,1988,1840,2261;2212,191,811,755,1485,348,2360,295,115,2485,179,1210,1018,370,1660,1571,736,7,407,84,1186,2194,1724,929,177,2465,2063,1265,2156,932,119,2019,1355,654,1132,428,1481,309,1753,1300,392,437,733,1938,1626,1978,2416,1896,1537,1658;1219,1524,532,2013,2,1877,26,1423,1252,973,1707,1298,2038,1046,1428,1155,2336,1637,1942,1951,143,1058,1308,1525,416,705,1531,1727,2011,564,330,1164,1460,11,45,1304,103,540,1825,982,1067,2208,1086,403,591,2461,1369,1818,894,2368;2255,2485,801,222,10,327,198,1930,13,1695,629,1613,217,574,2238,1497,2088,470,104,1544,101,231,2421,1327,1356,710,2124,1991,21,23,1580,1822,1177,1676,423,150,2251,393,1634,2111,2,1342,2475,2267,1451,1374,1612,1362,543,1262;724,2396,2467,2086,1100,144,352,1230,2081,1109,1861,1517,2142,2349,202,439,1025,1066,1884,749,655,5,2149,527,240,1870,515,524,377,2204,1117,1793,2331,689,667,1526,2159,1993,1630,964,1225,1894,1473,1296,1565,576,171,1844,2155,1832;2220,1873,1827,2440,2103,1205,2045,2114,1939,1990,226,351,795,1745,1009,46,2249,2211,906,692,1405,1989,2289,2146,2350,731,1942,2163,1257,1326,1533,1564,81,915,2248,1875,1495,407,968,1475,383,1555,1759,745,850,182,179,2253,1402,1512;459,430,2212,978,580,2079,997,999,1558,864,1681,14,1571,2251,2478,1404,1137,1358,229,979,628,1947,1484,2012,2389,364,2420,1130,1143,859,773,1220,1519,450,2495,256,1226,98,1447,1128,676,1333,2355,2075,2319,1855,356,471,2019,2158;1932,1176,857,591,1958,958,978,47,1274,1865,1180,2457,287,39,2372,712,853,2329,1210,494,1765,748,1629,1724,1979,1175,2247,1798,110,1582,605,1291,1603,2488,2266,2441,2362,336,689,228,2395,732,2263,1734,353,1757,920,1468,1770,1890", "output": "1269,379,612,1082,274,646,1171,740,24,1703,1120,1576,2038,1940,1377,102,582,997,1093,1549,39,1479,694,444,679,1005,1555,1485,2143,1293,283,45,2348,1666,862,634,996,2397,1563,1339,310,1617,2013,2257,166,39,1096,716,1465,1506,884,872,1516,39,1011,2051,1310,848,551,445,2101,245,543,149,1755,1306,114,1599,368,296,1824,1748,1219,78,1840,1658,1896,1978,1938,437,1300,309,428,654,2019,932,1265,2465,929,2194,84,7,1571,370,1210,2485,295,348,755,191,1219,532,2,26,1252,1707,2038,1428,2336,1942,143,1308,416,1531,2011,330,1460,45,103,1825,1067,1086,591,1369,894,1262,1362,1374,2267,1342,2111,393,150,1676,1822,23,1991,710,1327,231,1544,470,1497,574,1613,1695,1930,327,222,2485,724,2467,1100,352,2081,1861,2142,202,1025,1884,655,2149,240,515,377,1117,2331,667,2159,1630,1225,1473,1565,171,2155,1512,2253,182,745,1555,1475,407,1875,915,1564,1326,2163,731,2146,1989,692,2211,46,1745,351,1990,2114,1205,2440,1873,459,2212,580,997,1558,1681,1571,2478,1137,229,628,1484,2389,2420,1143,773,1519,2495,1226,1447,676,2355,2319,356,2019,1890,1468,1757,1734,732,228,336,2441,2488,1291,1582,1798,1175,1724,748,494,2329,712,39,2457,1865,47,958,591,1176"}, {"input": "654,2213;2021,1886;443,917;1949,1560;1026,48;2359,192;1206,155;2242,92", "output": "654,1886,443,1560,1026,192,1206,92"}, {"input": "382,2404,1641,988,2298,630,1001,1565,2433,491,1508,501,778,536,2324,242,1862,1342,2071,2409,1303,1311,260,1012,989,336,1863,635,1282,1508;1891,2109,2104,2420,669,259,793,224,2354,583,576,1651,1441,1198,1453,986,935,622,1320,640,1411,1376,1994,2192,1999,2315,1690,585,1047,1149;1598,2253,478,448,565,712,2040,318,2180,444,2435,1873,255,598,1284,906,612,2465,2304,2175,184,1005,1789,711,1070,1351,325,1906,257,2020;2227,1878,1466,1917,913,1871,2185,1114,2147,613,171,1170,1604,1080,255,2154,2007,154,1895,1903,1057,1043,1344,630,1050,811,2480,1090,1096,1760;707,168,1983,1515,1354,92,1873,1076,2470,2334,1261,1021,2069,1972,922,244,277,832,2393,427,415,757,2439,1956,620,1144,2192,1984,2406,175;2057,1468,641,1652,2378,106,682,1838,1484,1110,660,2214,965,1851,253,669,1915,1963,2036,703,200,2269,847,1896,2258,1212,151,995,1855,635;423,1698,1837,1712,1225,723,2315,1318,936,302,2174,1055,15,2290,1943,59,1559,153,1840,719,1340,1803,1395,1017,2074,932,707,1176,1704,524;836,208,1888,1038,2093,737,2492,1617,670,2042,452,50,1379,721,2043,1686,1937,275,1428,988,1179,2144,1373,48,1808,857,757,953,740,2057;1357,480,1059,1366,855,632,1657,1026,2129,1149,214,1812,1587,179,2316,2212,912,1565,180,1195,186,144,75,1527,1974,1446,1389,1963,433,645;335,1052,291,2195,144,868,312,948,664,1925,1676,1223,1961,1919,281,78,1513,293,1663,2199,141,1499,1572,1605,705,1694,1749,289,1284,1615;1244,145,833,2365,397,1259,1826,940,554,1168,710,1829,2309,769,1457,1255,1575,218,2371,2299,2206,1588,1963,1456,999,679,1839,2170,1635,25;1568,1582,1844,612,593,1700,1864,1813,62,1824,545,2101,323,1907,2087,2456,29,2147,1575,2011,969,1727,95,2403,755,842,1498,2043,331,777;1174,711,491,2303,1171,586,2039,1284,647,1622,1498,907,32,1856,159,2001,1943,1483,2172,96,2087,60,677,568,794,911,1997,1984,757,1283;2291,2133,584,1777,2407,1575,4,1516,1176,1223,907,1551,1712,853,96,935,1967,1890,839,1159,425,952,1393,53,846,1731,1675,947,266,1851;1388,1711,283,395,1220,601,692,2020,862,2442,1217,1921,362,2188,63,601,136,663,1488,2444,1882,2154,946,1520,2275,918,915,1659,612,697;1953,959,371,587,2111,490,1212,2203,1053,822,2308,164,1505,252,740,1509,938,1318,1956,1,661,2295,1590,1592,531,2015,1076,1934,537,504;429,318,3,2441,161,321,523,894,79,555,202,1327,1386,1467,1526,695,1467,2451,631,2011,160,1666,2038,1747,1632,1383,2379,930,468,1529;326,1957,1644,877,2422,2329,131,2137,2376,1964,2028,113,1571,33,1437,1966,1794,1694,1320,1811,343,1320,2124,2417,105,81,232,2045,1713,1639;1078,1890,2193,1860,1248,177,910,2205,326,2282,2030,722,1353,947,1338,1020,2275,1737,620,2093,838,1176,1755,2348,818,41,998,372,2018,1433", "output": "382,1641,2298,1001,2433,1508,778,2324,1862,2071,1303,260,989,1863,1282,1149,585,2315,2192,1376,640,622,986,1198,1651,583,224,259,2420,2109,1598,478,565,2040,2180,2435,255,1284,612,2304,184,1789,1070,325,257,1760,1090,811,630,1043,1903,154,2154,1080,1170,613,1114,1871,1917,1878,707,1983,1354,1873,2470,1261,2069,922,277,2393,415,2439,620,2192,2406,635,995,1212,1896,2269,703,1963,669,1851,2214,1110,1838,106,1652,1468,423,1837,1225,2315,936,2174,15,1943,1559,1840,1340,1395,2074,707,1704,2057,953,857,48,2144,988,275,1686,721,50,2042,1617,737,1038,208,1357,1059,855,1657,2129,214,1587,2316,912,180,186,75,1974,1389,433,1615,289,1694,1605,1499,2199,293,78,1919,1223,1925,948,868,2195,1052,1244,833,397,1826,554,710,2309,1457,1575,2371,2206,1963,999,1839,1635,777,2043,842,2403,1727,2011,2147,2456,1907,2101,1824,1813,1700,612,1582,1174,491,1171,2039,647,1498,32,159,1943,2172,2087,677,794,1997,757,1851,947,1731,53,952,1159,1890,935,853,1551,1223,1516,1575,1777,2133,1388,283,1220,692,862,1217,362,63,136,1488,1882,946,2275,915,612,504,1934,2015,1592,2295,1,1318,1509,252,164,822,2203,490,587,959,429,3,161,523,79,202,1386,1526,1467,631,160,2038,1632,2379,468,1639,2045,81,2417,1320,1811,1694,1966,33,113,1964,2137,2329,877,1957,1078,2193,1248,910,326,2030,1353,1338,2275,620,838,1755,818,998,2018"}, {"input": "1252,2448,1991,1435,1259,1510,2428,560,1494,2404,1968,1134,1063,1790,1343,895,880,1718,1165,1075,910,163,1186,1333,711,526,871,1293;2005,1625,1844,1674,1234,150,1426,1855,347,2397,2425,154,1520,1687,745,1426,1202,473,240,790,42,2244,214,1441,162,477,761,490;1413,18,889,53,98,1792,255,2243,2258,2143,421,243,2106,1721,2111,1484,1626,1059,2491,65,1483,68,750,31,1315,2396,836,970;759,20,1235,2018,1319,2259,1333,281,2385,342,2104,1146,1769,743,301,1041,720,2228,1627,358,53,1724,862,178,571,2369,1546,1106;191,2180,275,526,2381,2236,330,956,358,742,1034,2445,1505,2345,1303,1553,2362,20,2315,1800,2033,1369,1318,1718,666,1132,1799,1766;662,1241,2413,893,510,1755,11,1063,1815,2445,2452,2159,1081,1919,1653,598,1107,2109,1610,1179,1025,31,2186,317,1524,726,2029,1780;1243,1625,995,1176,1183,2143,1735,2283,440,815,750,2193,1007,2393,915,1394,1044,1462,1127,833,1821,317,903,2483,1357,1785,1763,1780;251,2080,2091,2019,1678,718,2471,606,2157,1000,1123,859,2221,684,1130,523,1394,387,1555,2421,594,1292,1055,1489,77,214,392,1596;705,2338,1125,1835,728,73,2231,1488,1907,578,2357,136,2160,1396,163,198,1555,1552,2244,1602,1426,2003,612,1310,1009,2463,1119,43;2489,1341,1967,1410,1088,426,776,1809,1348,555,958,2250,1351,2264,2256,334,1532,1111,470,517,2387,810,1028,1484,196,664,859,867;971,2430,129,1462,310,2062,2034,1737,518,1192,2396,1626,354,2495,836,518,2028,1433,2072,1477,816,70,1063,2387,1613,595,2335,1372;492,302,1941,1225,1305,417,847,283,320,1657,1539,91,1923,805,438,282,523,2176,2238,1470,48,383,2015,1482,764,2282,588,1505;1795,402,1405,221,593,1956,2466,237,2253,334,1649,148,402,2330,1042,2470,649,870,1001,1223,2173,25,231,583,171,1852,891,1529;1451,379,419,268,1518,2293,1903,1080,2015,1026,8,1881,949,2337,45,2339,714,1,602,906,2004,1912,1649,732,1820,2151,1930,192;309,2150,1532,1281,2266,2165,200,1409,2377,93,1253,1602,616,1652,521,2398,584,1223,2166,1313,360,136,1026,642,1254,1889,1325,779;2375,1145,1104,2046,1193,17,1377,528,293,2203,1230,2027,842,1529,2487,916,2185,1291,992,284,1082,361,2159,2391,821,1696,6,1185;967,1595,1527,28,383,931,890,1550,371,843,388,693,2363,591,1534,469,1624,1250,986,566,1175,2500,2294,494,2384,2130,1774,1580;420,976,2242,1699,1408,1205,580,1124,949,2375,947,2362,723,1742,455,253,1650,2132,2178,834,1357,1502,2438,1210,483,2075,2454,30;1736,2273,1557,247,2158,793,28,1166,1024,1167,2236,1867,1505,72,369,2070,692,944,1321,1434,185,692,853,1541,2187,2479,1827,2420;1539,901,199,1265,991,1814,820,1149,110,2452,1916,2095,8,2256,1177,1370,2118,1955,1044,899,680,1218,2063,2311,308,415,1746,1011;145,1910,2220,534,2250,627,1344,1882,2339,2402,491,1786,877,2366,832,1355,1888,937,626,1632,2432,1728,2065,788,1210,585,174,636;1921,2150,2088,2480,1272,416,1240,2237,1050,1706,477,137,1641,1999,2470,230,939,184,185,1602,81,1710,1149,1409,1227,2489,1431,1211;2424,459,500,2108,178,2332,676,1661,429,992,1518,1696,978,2223,562,2344,1904,608,2369,1998,1663,2488,736,333,2453,437,717,1363;1001,2494,1063,1833,754,2194,978,2164,1543,1461,526,1247,2263,1907,2204,99,2466,2100,2229,282,683,1069,390,2017,2261,157,651,2348;475,644,1119,1889,1384,2079,253,374,2018,1444,136,716,386,93,1191,2270,1041,460,1959,1558,129,598,403,810,1703,1473,1289,2165;302,1707,2478,71,2330,2123,1954,428,1072,924,2154,288,1929,710,2176,2254,964,933,1210,1009,1451,1283,52,212,238,536,576,496;1085,1662,1284,868,577,1483,2274,1648,950,2060,1203,949,1678,1360,256,1939,1456,2463,1887,1779,875,2489,298,625,2096,1317,1657,2347;1314,1563,1253,1910,1826,1974,495,2053,60,1730,554,1074,455,2125,1845,1302,2172,442,1999,2296,1256,2063,2332,150,1076,1683,738,2323;368,2193,1722,1513,50,287,2331,782,1839,2302,1163,1882,997,610,1632,205,1369,735,2399,1810,79,1093,343,1734,8,719,743,2198;332,753,126,501,2068,751,2167,865,528,741,1005,2084,1337,1314,774,997,880,804,2005,650,1973,168,611,1607,1991,1644,291,2425;1663,2109,2192,1271,1737,2356,2448,412,920,1999,1186,1769,2054,1061,613,576,1611,973,1763,498,283,1059,1608,680,2104,265,2457,133;1177,2065,477,1503,2464,1716,2108,44,1495,1984,1206,6,347,1388,38,1069,2252,1670,1119,2391,1295,91,1721,774,884,1221,263,237;2456,1623,1744,425,314,1977,1963,730,1530,2325,2315,2421,482,2092,1376,1604,360,602,2443,2228,2446,1286,661,58,646,1163,2195,2172;2133,528,427,161,547,858,519,716,329,1674,987,2350,118,2268,906,1679,72,921,2271,541,1783,293,1633,875,2424,88,1309,1224;855,2361,1541,1360,1402,438,1166,743,1526,2036,267,1317,101,2438,1647,461,1239,1721,2081,358,2434,1733,260,607,1585,1291,1091,1956;491,554,823,40,574,1878,803,1027,1833,1409,442,331,787,1244,698,231,596,1912,2038,234,2209,1494,1424,384,1917,1910,2196,1692;1080,1283,1016,814,710,2078,336,1790,2083,1910,1423,1819,1132,1512,1487,1811,228,978,368,1470,287,987,843,680,2279,2016,545,2007;416,1443,1950,291,2471,1415,167,1650,456,2125,1962,1788,1663,2210,31,1386,1371,1650,506,2322,2346,674,2080,814,470,1967,2450,836;2144,1140,851,1705,2461,582,875,903,136,364,1305,2318,1734,466,1588,1476,821,179,2319,2494,1949,1847,1649,77,1042,1883,381,2270;1043,838,840,124,931,1127,1902,1204,872,1102,38,582,2189,1717,2203,1847,1498,1221,1169,1495,684,1060,2361,56,141,1160,111,1794;1970,737,365,1604,1829,2462,1502,516,1627,1500,661,1103,2190,2449,228,809,2495,1984,824,947,2378,1900,2429,1549,2240,430,1755,368;668,2145,1040,2258,1478,1768,1194,2333,2111,583,1141,1320,517,1600,733,1988,2455,1140,1828,2182,1080,1884,1878,166,1924,839,972,203;680,1010,746,2026,331,2374,1783,2053,42,1515,1248,1126,1102,717,563,1946,874,394,1225,779,119,1659,1698,355,463,1247,1937,1962", "output": "1252,1991,1259,2428,1494,1968,1063,1343,880,1165,910,1186,711,871,490,477,1441,2244,790,473,1426,1687,154,2397,1855,150,1674,1625,1413,889,98,255,2258,421,2106,2111,1626,2491,1483,750,1315,836,1106,2369,178,1724,358,2228,1041,743,1146,342,281,2259,2018,20,191,275,2381,330,358,1034,1505,1303,2362,2315,2033,1318,666,1799,1780,726,317,31,1179,2109,598,1919,2159,2445,1063,1755,893,1241,1243,995,1183,1735,440,750,1007,915,1044,1127,1821,903,1357,1763,1596,214,1489,1292,2421,387,523,684,859,1000,606,718,2019,2080,705,1125,728,2231,1907,2357,2160,163,1555,2244,1426,612,1009,1119,867,664,1484,810,517,1111,334,2264,2250,555,1809,426,1410,1341,971,129,310,2034,518,2396,354,836,2028,2072,816,1063,1613,2335,1505,2282,1482,383,1470,2176,282,805,91,1657,283,417,1225,302,1795,1405,593,2466,2253,1649,402,1042,649,1001,2173,231,171,891,192,2151,732,1912,906,1,2339,2337,1881,1026,1080,2293,268,379,309,1532,2266,200,2377,1253,616,521,584,2166,360,1026,1254,1325,1185,1696,2391,361,284,1291,916,1529,2027,2203,528,17,2046,1145,967,1527,383,890,371,388,2363,1534,1624,986,1175,2294,2384,1774,30,2075,1210,1502,834,2132,253,1742,2362,2375,1124,1205,1699,976,1736,1557,2158,28,1024,2236,1505,369,692,1321,185,853,2187,1827,1011,415,2311,1218,899,1955,1370,2256,2095,2452,1149,1814,1265,901,145,2220,2250,1344,2339,491,877,832,1888,626,2432,2065,1210,174,1211,2489,1409,1710,1602,184,230,1999,137,1706,2237,416,2480,2150,2424,500,178,676,429,1518,978,562,1904,2369,1663,736,2453,717,2348,157,2017,1069,282,2100,99,1907,1247,1461,2164,2194,1833,2494,475,1119,1384,253,2018,136,386,1191,1041,1959,129,403,1703,1289,496,536,212,1283,1009,933,2254,710,288,924,428,2123,71,1707,1085,1284,577,2274,950,1203,1678,256,1456,1887,875,298,2096,1657,2323,1683,150,2063,2296,442,1302,2125,1074,1730,2053,1974,1910,1563,368,1722,50,2331,1839,1163,997,1632,1369,2399,79,343,8,743,2425,1644,1607,168,650,804,997,1314,2084,741,865,751,501,753,1663,2192,1737,2448,920,1186,2054,613,1611,1763,283,1608,2104,2457,237,1221,774,91,2391,1670,1069,1388,6,1984,44,1716,1503,2065,2456,1744,314,1963,1530,2315,482,1376,360,2443,2446,661,646,2195,1224,88,875,293,541,921,1679,2268,2350,1674,716,858,161,528,855,1541,1402,1166,1526,267,101,1647,1239,2081,2434,260,1585,1091,1692,1910,384,1494,234,1912,231,1244,331,1409,1027,1878,40,554,1080,1016,710,336,2083,1423,1132,1487,228,368,287,843,2279,545,836,1967,814,674,2322,1650,1386,2210,1788,2125,1650,1415,291,1443,2144,851,2461,875,136,1305,1734,1588,821,2319,1949,1649,1042,381,1794,1160,56,1060,1495,1221,1847,1717,582,1102,1204,1127,124,838,1970,365,1829,1502,1627,661,2190,228,2495,824,2378,2429,2240,1755,203,839,166,1884,2182,1140,1988,1600,1320,583,2333,1768,2258,2145,680,746,331,1783,42,1248,1102,563,874,1225,119,1698,463,1937"}, {"input": "708,1715,354,1496,1888,1834,1892,332,1132,1001,2460,1221,1839,1889,1467,77,1855,1305,333,2484,2436,2161,1886,2192,351,1454,1838,271,482,665,1988,499,473,76;1492,92,2342,1547,276,2249,707,2006,680,1925,817,1862,625,641,1809,600,564,1356,1812,2075,1646,210,2415,1680,196,2494,2221,132,970,1259,429,1829,1472,760;1640,930,296,615,1914,750,1045,858,1620,852,1816,733,2132,395,1239,341,1995,695,1818,2497,242,1060,362,1513,2162,1926,551,924,2204,951,1474,2273,695,199;558,2394,784,409,2211,1156,1611,596,1344,2223,726,2430,954,1813,2052,1511,2239,1177,929,1947,2487,835,1246,2097,1412,1599,862,885,263,1543,1183,2198,390,931;1484,1515,2062,471,1055,1803,811,2381,2038,135,1703,1449,1646,734,491,1786,923,1802,1416,2311,37,1349,1761,1199,1585,1325,192,1240,2402,387,39,1560,523,2338;570,2362,577,1350,1123,1741,1151,88,1793,1814,1099,794,1893,570,2474,1088,1025,17,671,2156,2057,837,1093,2045,1946,340,2432,465,1414,1865,2053,497,1516,297;2396,475,1851,1400,2408,313,67,970,1605,1050,2212,260,1197,489,1869,62,346,2074,1778,239,1946,1912,1533,451,2073,623,2397,694,1829,1939,1377,1455,1042,2321;1626,1471,2062,2265,26,981,1756,1135,402,1330,1905,2181,2400,252,1449,1854,779,575,1734,662,1028,1083,739,1482,172,280,1095,697,966,1123,1488,1611,2480,1568;974,2230,1256,2468,179,1030,215,133,1809,1513,1729,205,1276,1550,297,2232,1991,2092,106,82,2121,1785,1259,1145,1628,2389,277,1971,504,2393,318,620,1798,280;779,1288,1532,1357,148,2292,2438,1099,1032,2216,2288,265,445,441,2260,147,825,606,1182,790,1770,2231,518,380,1594,1019,1542,2032,2495,1477,239,2139,772,1929;2011,259,1201,390,2237,2472,1357,286,2036,1117,1782,1082,2064,1089,340,1829,856,1251,932,1405,1539,28,1222,1615,78,650,1496,1094,372,1131,549,2381,1862,1071;1763,268,1857,1329,1767,698,1532,2149,2018,1941,25,689,1338,1520,591,2331,213,1555,477,687,2161,2471,2037,1958,1278,2466,1566,1957,1829,1008,1035,139,245,988;359,1534,2153,1738,723,442,1792,444,635,876,876,1142,668,1571,702,1094,2128,1796,2299,3,808,2073,2356,1289,236,38,61,1338,2110,152,1614,1860,2056,555;1706,1691,2231,935,2047,1713,671,416,1430,1303,288,2133,408,333,2289,55,430,1611,222,525,824,2485,1360,1910,569,178,1395,446,2484,1434,279,686,1749,989;399,2207,961,594,1390,61,1156,1354,98,1042,161,1632,1782,480,783,1586,2300,2347,1268,350,1829,2434,2260,310,277,1481,2396,1394,1478,1166,1611,1271,1428,1477;1455,671,1440,2177,6,1049,904,638,1967,1088,46,1772,2116,2225,1883,2220,2207,583,1426,1126,1690,695,1983,2214,28,1335,2162,1323,1869,2432,1925,2250,481,1657;2474,1217,1026,1570,737,1685,820,826,1730,532,518,1849,190,1898,421,2470,70,1890,184,10,1189,1793,2195,1653,385,1497,1278,2272,1731,1666,1449,2326,2000,1057;2129,1190,1799,603,2449,2393,558,1129,1365,118,189,1518,169,2263,1577,1024,244,1440,343,270,789,1399,1297,1217,734,2216,1682,2263,2179,652,321,1883,2360,1964;814,1487,870,1585,2252,1446,1708,414,957,2099,1626,1420,255,1345,1325,1357,2230,1583,377,2018,814,1160,139,1619,972,240,1538,632,2309,1407,2334,2079,70,561;365,1429,1960,557,2025,455,2369,1063,672,572,516,2441,1130,1776,2140,2361,153,927,645,940,1185,130,1859,2252,2330,2013,197,2115,635,506,1295,100,1889,1969;2455,1768,2152,2206,589,1651,1065,2281,1885,1999,630,13,1323,510,2457,1008,1587,284,1121,1097,1043,2175,1591,429,1912,150,706,92,674,1037,1561,2074,2123,2035;162,2322,634,2212,61,274,1331,2319,205,1045,2222,1355,476,2028,461,434,233,188,1523,1862,1723,1418,903,1817,30,985,931,1392,1706,1503,2483,2053,70,191;1991,954,1051,42,1060,1698,431,1496,1116,2161,1741,117,649,2042,630,1720,2325,948,2355,1123,114,1948,1748,550,284,189,2408,539,1992,1935,760,1284,2430,988;5,2199,1873,1907,2410,726,876,1793,643,8,1853,1720,1263,923,1566,2148,1419,2104,1492,909,1049,770,188,1280,826,2118,940,1966,1139,2149,1151,1463,1729,1291;1257,252,2131,1150,357,1667,800,368,2044,1655,2404,609,225,813,64,1132,54,1301,2102,174,1390,956,2317,530,2041,253,660,84,1961,1136,2306,1022,876,1623;454,896,608,291,1287,2065,1829,1059,398,1244,122,1414,1982,1446,1545,803,2490,135,1023,1428,223,1207,2103,1625,1534,1418,661,2223,752,905,2232,47,625,1755;1893,2055,477,1888,580,611,385,1888,171,1895,1889,1977,1120,189,2361,1800,832,843,2147,252,1683,963,1058,103,2091,1136,871,1911,2193,439,2140,1790,1136,580;40,1417,930,1177,2484,1791,355,2465,2383,1445,922,2281,2261,877,1778,1570,2421,2102,2128,2297,747,1765,1078,1272,69,652,1445,999,1295,1689,895,465,2154,2102;2142,281,2283,553,2159,490,517,398,1565,1905,703,1868,2458,889,903,1377,993,1706,17,191,1823,1347,795,1695,2491,1965,325,2134,1810,450,1402,832,995,1084;1340,2491,1073,593,2408,2068,1819,1800,2419,1414,1971,143,1718,214,1456,2342,1688,1883,660,513,703,929,2470,508,1620,2264,1189,2447,1316,1416,461,2374,1612,1478;239,1394,481,2044,970,1229,1405,1826,1678,918,2291,954,1118,2025,1179,530,578,1980,2454,1386,1879,2240,2480,1700,2216,2291,2239,1166,369,806,719,2247,1652,1251;709,2315,1918,420,689,9,265,2364,2256,268,287,2258,2498,1003,1088,2446,1088,1088,40,758,151,207,1136,254,2169,1502,243,2185,265,2396,2229,1910,1597,453;988,2087,2389,786,859,1182,2022,712,565,2071,2465,795,714,542,1918,682,407,351,457,256,2030,1918,1445,295,197,793,668,338,1904,1780,954,1943,1053,2492;1042,1194,298,1034,1721,1766,5,2370,2014,517,2492,899,1418,1535,1824,47,1589,1506,1417,1655,1550,1394,371,1290,2451,1021,2275,1528,497,647,2012,795,713,532;1767,2140,1072,1849,918,1117,1931,186,155,670,1854,485,2285,2378,1417,464,2154,2413,733,83,1572,1268,671,1028,1137,2164,1060,1641,2380,1295,1135,184,503,34;2383,2317,1752,1056,2399,1414,836,599,247,1267,2460,586,730,205,1369,2440,1992,1129,940,1441,1474,2224,2134,2478,965,927,612,2339,1779,2394,2233,1014,856,654;614,2467,2479,8,923,1189,1251,1314,543,261,1974,1224,1109,1048,2215,853,2035,1779,1211,1647,576,927,650,1793,1189,950,2022,351,1269,1578,552,1360,1209,1447;1985,1092,1038,2183,1447,597,1396,931,478,1089,1880,1264,1567,1672,1086,368,758,2146,1645,2365,307,2019,590,489,2274,375,66,289,2095,1895,328,1210,1400,208", "output": "708,354,1888,1892,1132,2460,1839,1467,1855,333,2436,1886,351,1838,482,1988,473,760,1829,1259,132,2494,1680,210,2075,1356,600,641,1862,1925,2006,2249,1547,92,1640,296,1914,1045,1620,1816,2132,1239,1995,1818,242,362,2162,551,2204,1474,695,931,2198,1543,885,1599,2097,835,1947,1177,1511,1813,2430,2223,596,1156,409,2394,1484,2062,1055,811,2038,1703,1646,491,923,1416,37,1761,1585,192,2402,39,523,297,497,1865,465,340,2045,837,2156,17,1088,570,794,1814,88,1741,1350,2362,2396,1851,2408,67,1605,2212,1197,1869,346,1778,1946,1533,2073,2397,1829,1377,1042,1568,1611,1123,697,280,1482,1083,662,575,1854,252,2181,1330,1135,981,2265,1471,974,1256,179,215,1809,1729,1276,297,1991,106,2121,1259,1628,277,504,318,1798,1929,2139,1477,2032,1019,380,2231,790,606,147,441,265,2216,1099,2292,1357,1288,2011,1201,2237,1357,2036,1782,2064,340,856,932,1539,1222,78,1496,372,549,1862,988,139,1008,1957,2466,1958,2471,687,1555,2331,1520,689,1941,2149,698,1329,268,359,2153,723,1792,635,876,668,702,2128,2299,808,2356,236,61,2110,1614,2056,989,686,1434,446,178,1910,2485,525,1611,55,333,2133,1303,416,1713,935,1691,399,961,1390,1156,98,161,1782,783,2300,1268,1829,2260,277,2396,1478,1611,1428,1657,2250,2432,1323,1335,2214,695,1126,583,2220,2225,1772,1088,638,1049,2177,671,2474,1026,737,820,1730,518,190,421,70,184,1189,2195,385,1278,1731,1449,2000,1964,1883,652,2263,2216,1217,1399,270,1440,1024,2263,1518,118,1129,2393,603,1190,814,870,2252,1708,957,1626,255,1325,2230,377,814,139,972,1538,2309,2334,70,1969,100,506,2115,2013,2252,130,940,927,2361,1776,2441,572,1063,455,557,1429,2455,2152,589,1065,1885,630,1323,2457,1587,1121,1043,1591,1912,706,674,1561,2123,191,2053,1503,1392,985,1817,1418,1862,188,434,2028,1355,1045,2319,274,2212,2322,1991,1051,1060,431,1116,1741,649,630,2325,2355,114,1748,284,2408,1992,760,2430,1291,1463,2149,1966,2118,1280,770,909,2104,2148,923,1720,8,1793,726,1907,2199,1257,2131,357,800,2044,2404,225,64,54,2102,1390,2317,2041,660,1961,2306,876,1755,47,905,2223,1418,1625,1207,1428,135,803,1446,1414,1244,1059,2065,291,896,1893,477,580,385,171,1889,1120,2361,832,2147,1683,1058,2091,871,2193,2140,1136,2102,465,1689,999,652,1272,1765,2297,2102,1570,877,2281,1445,2465,1791,1177,1417,2142,2283,2159,517,1565,703,2458,903,993,17,1823,795,2491,325,1810,1402,995,1478,2374,1416,2447,2264,508,929,513,1883,2342,214,143,1414,1800,2068,593,2491,239,481,970,1405,1678,2291,1118,1179,578,2454,1879,2480,2216,2239,369,719,1652,453,1910,2396,2185,1502,254,207,758,1088,2446,1003,2258,268,2364,9,420,2315,988,2389,859,2022,565,2465,714,1918,407,457,2030,1445,197,668,1904,954,1053,532,795,647,1528,1021,1290,1394,1655,1506,47,1535,899,517,2370,1766,1034,1194,1767,1072,918,1931,155,1854,2285,1417,2154,733,1572,671,1137,1060,2380,1135,503,654,1014,2394,2339,927,2478,2224,1441,1129,2440,205,586,1267,599,1414,1056,2317,614,2479,923,1251,543,1974,1109,2215,2035,1211,576,650,1189,2022,1269,552,1209,208,1210,1895,289,375,489,2019,2365,2146,368,1672,1264,1089,931,597,2183,1092"}, {"input": "1254,2462,1128,376,1325,133,307,1666,589,2023,2441,2471,2483,1213,655,1382,18,2472,761,347,1784,1088,1235,2445,1914,2482,265,110,492,1532,431,1372,2492,1561,2270,2126,737,1818,1916,2419;1858,1217,1704,1601,662,1452,537,1406,1177,1032,952,1267,1526,5,2479,69,964,547,322,1391,1639,133,639,1665,257,547,833,2076,2330,311,1188,1333,1202,581,2303,2408,2209,543,211,1536;126,311,583,1587,2163,1272,1159,1316,663,798,1892,772,1569,1194,519,1592,1586,548,344,1914,137,1680,2470,614,267,989,1078,604,2234,539,1341,1421,2248,2096,2150,1514,934,1080,2260,1203;1043,1509,456,618,864,385,1824,1486,1666,1338,459,1218,1837,826,2300,1306,79,1843,1577,147,71,1669,962,2282,70,415,2250,633,1532,1948,1397,1989,1666,1540,2405,1549,2468,720,1206,1021;1090,1541,514,2242,83,1624,2415,1381,542,135,1647,1716,340,2326,488,1624,2480,1328,2448,2368,16,1431,948,1266,1717,414,1590,495,819,458,6,494,883,440,992,604,1001,2456,229,1737;2365,1314,1015,860,1217,1005,1696,819,319,1921,2146,787,2094,1846,1049,108,1067,810,1411,1866,1754,1843,321,2256,1858,1520,1716,1460,30,599,2429,1381,346,617,2409,1417,1913,1375,1993,1967;2498,1141,1966,842,968,120,1850,1770,392,2477,2109,1209,553,1215,1157,2214,2330,213,1895,1114,2115,594,1167,1098,1084,1219,1896,129,342,266,2167,298,204,1148,464,1599,1051,1807,397,1518;1673,2091,1291,1394,476,2056,580,309,1165,520,751,1051,2165,2223,924,1267,290,1901,457,449,1428,2043,291,1330,759,634,223,1198,664,1939,1463,653,1356,1560,2055,684,2176,1654,1664,2257;353,248,903,2009,369,1201,260,612,391,1070,1075,2076,2123,929,1103,2484,1164,476,1128,1391,1341,568,1536,208,1598,133,99,183,704,2157,1951,2019,340,620,985,1585,1821,2412,576,1218;92,1234,2308,2166,1140,1476,2477,611,167,2219,1787,1460,2159,1555,668,490,1663,1253,2099,1968,792,1453,918,1049,1085,124,1421,2474,787,2309,1514,1470,1374,1855,1166,2117,1609,356,1082,1037;2167,1062,429,262,1198,127,1966,1472,794,1810,639,953,689,569,516,671,832,811,182,481,1415,2089,1908,2073,1660,1053,690,1060,1777,922,2387,1454,1016,1073,506,2090,1757,2423,1128,360;1074,2221,1690,1635,2186,1710,69,2059,2117,620,4,2169,656,2094,1820,1591,785,1165,1965,2018,427,1808,167,413,351,200,641,1382,2156,1729,1182,1803,621,1290,1888,1299,2421,279,1577,997;2032,2101,1801,434,199,392,1977,190,1081,2403,2081,549,2489,187,2004,2109,1869,2469,1572,2244,1187,1364,423,2466,2148,1139,1341,258,1981,2239,1225,413,2136,84,143,668,2178,865,671,1630;315,571,1163,1208,612,681,662,1615,1205,1253,1192,225,346,958,691,284,1908,590,417,106,1458,382,1021,171,359,151,621,55,312,2305,2167,1233,1559,1996,1952,492,1913,811,1079,1138;2419,929,2125,220,1627,496,2348,137,1864,932,1808,462,716,2089,1186,133,1413,2245,917,2138,2469,595,643,91,542,102,1736,1503,1346,1553,2344,1765,2357,2016,1563,3,1937,2362,1715,2001;1422,884,481,2012,1962,2159,1169,841,1958,1611,983,762,2063,1086,1876,1036,668,55,2396,1253,2160,1084,638,930,2077,111,1644,2429,1152,103,1046,388,2418,1056,484,1116,1094,1576,513,1774;34,2299,1528,1805,1629,1668,110,972,2261,842,1564,1765,766,355,1977,1983,714,2038,1737,2180,2288,745,884,1067,1761,593,2129,1122,2156,920,1756,1834,336,179,1158,508,1934,2066,2063,930;1763,1424,2159,2353,1119,1764,2443,1311,2282,1745,1872,438,824,2112,924,1798,1425,2343,732,1960,1471,407,1405,1735,1126,1130,732,1029,2120,437,58,2409,780,542,265,1185,233,1698,1612,762;1189,1626,1187,2332,1273,1574,1935,2303,1797,1481,1418,967,1535,236,1080,377,2270,673,942,309,2,1750,634,1296,1,1317,890,1532,1665,2428,309,2233,549,1816,1870,1885,692,2302,1208,2111;2072,551,1480,258,1264,1205,1277,1308,642,583,1593,826,1489,1266,345,1468,973,1125,678,1637,1632,1239,810,647,2314,1541,1581,5,1456,1752,397,1450,1879,461,1989,95,2226,393,962,1869;1034,2191,870,448,770,1284,2354,901,517,316,1764,38,181,117,1788,302,2210,216,1543,883,1982,1525,1325,2040,1955,1096,482,412,1068,234,1175,1061,115,509,757,224,1011,925,1907,348;1466,858,1832,827,285,1081,848,1314,1334,630,1987,1179,965,1036,5,25,1189,2420,2105,835,2338,319,2238,186,338,1921,2015,120,1361,722,1849,801,1067,336,1505,931,361,2113,1902,680;1058,884,2097,186,1859,1631,2,698,1246,1555,1557,940,799,1016,613,648,1663,2162,1848,327,490,992,250,134,45,594,919,1697,949,1090,958,300,1575,2269,875,1492,1202,2020,2237,1693;1218,1772,1540,1595,320,2458,1115,2232,2047,663,733,92,912,1534,1805,812,30,608,691,2036,1679,1580,948,275,1873,104,2460,2458,1449,2252,2045,741,1934,1559,1374,1308,183,151,621,1839;2090,1989,990,2259,2121,1999,656,1077,674,1135,812,919,9,518,459,1036,2461,1557,1929,1509,1658,2031,2192,65,1429,1899,1099,2326,1686,996,1488,2139,1958,400,1468,1221,309,1090,1162,1028;1143,10,188,1225,1287,2179,430,1178,2220,2244,2276,2356,1925,689,891,2060,2037,268,2157,1709,2393,2356,1793,346,1741,1109,1172,735,2344,167,1209,2231,1753,514,1334,808,2244,988,571,1100;597,567,47,1011,1129,423,964,937,801,2333,548,835,487,470,1934,1892,1583,2193,2179,1971,275,813,589,634,1766,992,1554,652,747,158,1510,880,2393,924,321,2315,2208,2009,1205,1368;1396,2373,683,322,1022,1844,349,1340,808,530,643,500,999,891,154,246,2142,2075,62,1777,642,378,2212,2329,2295,1158,1712,1491,1817,2392,1446,275,191,1676,1278,156,121,434,1339,2436;1521,915,1218,900,2218,1126,1957,1824,1105,1865,942,728,1979,802,1592,1250,1871,1216,290,1429,331,1864,1820,1760,2101,387,1367,1502,1541,2165,764,2411,45,1189,975,2453,314,1621,1492,1506;1859,574,1277,1203,407,1973,1464,943,186,961,1757,1409,938,243,1145,1751,1668,432,1219,2021,1576,2187,354,1896,1070,1433,1246,2010,1742,703,2258,2105,1113,1999,2358,738,1839,152,115,1606;332,407,2238,695,1482,643,2480,2056,2122,798,936,2258,1859,1945,188,1179,2049,814,372,686,1789,2154,2109,2192,1849,37,489,763,2348,806,565,763,1553,2493,900,788,613,403,818,56;773,1191,1123,1718,1132,1432,1034,2154,1873,150,1911,2486,2056,2144,996,1408,1297,300,22,2052,2493,643,2403,1204,720,413,1533,924,1711,677,1284,1780,2388,1479,1048,2047,109,1494,1451,228;1853,667,340,1558,921,1105,1032,56,833,1102,2339,6,1406,1063,1685,1997,556,1513,1641,345,1764,557,1566,2167,288,2045,1646,1927,511,431,920,848,1156,1467,313,1774,11,1913,1156,1060;2288,624,738,1470,2373,2267,466,1887,2114,899,1988,61,231,264,845,178,201,1897,1791,1400,2296,404,1184,567,143,1642,798,2116,1243,2118,901,1110,1295,436,2458,1783,1217,1881,1919,2334;254,2159,569,478,804,623,1616,1750,1279,851,1153,638,815,1972,751,2180,1409,2272,1129,1056,2142,930,901,2435,1368,1656,94,5,993,1458,2429,1465,2037,760,862,725,1120,993,2270,1177;1651,2464,1819,435,50,182,1489,591,1813,267,9,2090,1197,1689,656,1798,394,1025,953,803,481,2111,411,1096,1139,356,487,500,380,766,2011,1088,2265,214,2341,1711,1700,1394,1444,1452;1630,1655,1344,1002,1980,229,1447,1186,848,1511,1716,417,196,861,1955,921,2108,604,48,1708,2073,2385,1210,2226,1365,1313,41,4,1624,2482,2313,1345,71,2256,1977,2297,2133,2182,1056,2360", "output": "1254,1128,1325,307,589,2441,2483,655,18,761,1784,1235,1914,265,492,431,2492,2270,737,1916,1536,543,2408,581,1333,311,2076,547,1665,133,1391,547,69,5,1267,1032,1406,1452,1601,1217,126,583,2163,1159,663,1892,1569,519,1586,344,137,2470,267,1078,2234,1341,2248,2150,934,2260,1021,720,1549,1540,1989,1948,633,415,2282,1669,147,1843,1306,826,1218,1338,1486,385,618,1509,1090,514,83,2415,542,1647,340,488,2480,2448,16,948,1717,1590,819,6,883,992,1001,229,1967,1375,1417,617,1381,599,1460,1520,2256,1843,1866,810,108,1846,787,1921,819,1005,860,1314,2498,1966,968,1850,392,2109,553,1157,2330,1895,2115,1167,1084,1896,342,2167,204,464,1051,397,2257,1654,684,1560,653,1939,1198,634,1330,2043,449,1901,1267,2223,1051,520,309,2056,1394,2091,353,903,369,260,391,1075,2123,1103,1164,1128,1341,1536,1598,99,704,1951,340,985,1821,576,1037,356,2117,1855,1470,2309,2474,124,1049,1453,1968,1253,490,1555,1460,2219,611,1476,2166,1234,2167,429,1198,1966,794,639,689,516,832,182,1415,1908,1660,690,1777,2387,1016,506,1757,1128,997,279,1299,1290,1803,1729,1382,200,413,1808,2018,1165,1591,2094,2169,620,2059,1710,1635,2221,2032,1801,199,1977,1081,2081,2489,2004,1869,1572,1187,423,2148,1341,1981,1225,2136,143,2178,671,1138,811,492,1996,1233,2305,55,151,171,382,106,590,284,958,225,1253,1615,681,1208,571,2419,2125,1627,2348,1864,1808,716,1186,1413,917,2469,643,542,1736,1346,2344,2357,1563,1937,1715,1774,1576,1116,1056,388,103,2429,111,930,1084,1253,55,1036,1086,762,1611,841,2159,2012,884,34,1528,1629,110,2261,1564,766,1977,714,1737,2288,884,1761,2129,2156,1756,336,1158,1934,2063,762,1698,1185,542,2409,437,1029,1130,1735,407,1960,2343,1798,2112,438,1745,1311,1764,2353,1424,1189,1187,1273,1935,1797,1418,1535,1080,2270,942,2,634,1,890,1665,309,549,1870,692,1208,1869,393,95,461,1450,1752,5,1541,647,1239,1637,1125,1468,1266,826,583,1308,1205,258,551,1034,870,770,2354,517,1764,181,1788,2210,1543,1982,1325,1955,482,1068,1175,115,757,1011,1907,680,2113,931,336,801,722,120,1921,186,319,835,2420,25,1036,1179,630,1314,1081,827,858,1058,2097,1859,2,1246,1557,799,613,1663,1848,490,250,45,919,949,958,1575,875,1202,2237,1839,151,1308,1559,741,2252,2458,104,275,1580,2036,608,812,1534,92,663,2232,2458,1595,1772,2090,990,2121,656,674,812,9,459,2461,1929,1658,2192,1429,1099,1686,1488,1958,1468,309,1162,1100,988,808,514,2231,167,735,1109,346,2356,1709,268,2060,689,2356,2244,1178,2179,1225,10,597,47,1129,964,801,548,487,1934,1583,2179,275,589,1766,1554,747,1510,2393,321,2208,1205,2436,434,156,1676,275,2392,1491,1158,2329,378,1777,2075,246,891,500,530,1340,1844,322,2373,1521,1218,2218,1957,1105,942,1979,1592,1871,290,331,1820,2101,1367,1541,764,45,975,314,1492,1606,152,738,1999,2105,703,2010,1433,1896,2187,2021,432,1751,243,1409,961,943,1973,1203,574,332,2238,1482,2480,2122,936,1859,188,2049,372,1789,2109,1849,489,2348,565,1553,900,613,818,228,1494,2047,1479,1780,677,924,413,1204,643,2052,300,1408,2144,2486,150,2154,1432,1718,1191,1853,340,921,1032,833,2339,1406,1685,556,1641,1764,1566,288,1646,511,920,1156,313,11,1156,2334,1881,1783,436,1110,2118,2116,1642,567,404,1400,1897,178,264,61,899,1887,2267,1470,624,254,569,804,1616,1279,1153,815,751,1409,1129,2142,901,1368,94,993,2429,2037,862,1120,2270,1452,1394,1711,214,1088,766,500,356,1096,2111,803,1025,1798,1689,2090,267,591,182,435,2464,1630,1344,1980,1447,848,1716,196,1955,2108,48,2073,1210,1365,41,1624,2313,71,1977,2133,1056"}, {"input": "2063,2349,1662,1849,716,518,615,1579,960,515,1434,955,722,1998,457,671,564,1222,1719,248,1072,1359,2230,593,1357,925,2198,562,1455,1512,391,1638,1657,1238,1225,1916,1448,2075,79,1853,762,818,2390,2465,432,638,2329,712;349,892,108,978,1873,1220,1088,2053,2353,1023,1402,1132,2368,1839,1260,1097,2435,1240,2362,2095,2171,2301,847,1276,1614,1538,2414,1822,221,1366,1659,1451,1933,992,1636,995,1186,264,707,911,673,1714,2392,1562,413,1587,552,1765;445,255,714,391,873,917,2152,1656,1102,2263,1396,2298,184,840,635,1917,1301,40,1444,1936,119,1799,1671,984,1181,2260,2065,1995,1437,1801,1970,1469,593,744,2492,578,1267,1683,399,1738,1285,2395,1010,868,2499,264,871,561;604,1813,950,1384,1919,503,459,937,925,366,1020,1307,2350,2283,195,412,735,8,132,1192,84,389,1469,1179,1278,390,1346,68,737,1044,1759,1292,1913,908,646,594,1646,527,123,2216,467,779,1388,551,575,2174,849,2378;191,1436,1408,251,120,535,1733,568,1739,1618,1205,102,1201,1614,1605,757,2051,1406,2323,878,1772,2406,436,2037,124,866,324,1744,1315,1563,502,2190,1268,1495,640,114,2258,22,909,1183,721,121,2372,1221,2067,738,768,1311;46,580,873,1874,2165,1749,1002,2385,2150,382,1374,741,1931,1290,1792,584,2484,1762,2085,656,1287,6,26,2250,2249,761,2004,350,267,588,1743,288,442,192,104,1919,1964,2131,2134,2408,2329,817,310,2388,1187,846,2283,1336;249,1359,448,1981,525,1650,893,2264,13,821,142,1166,1845,1166,3,1176,1709,2114,362,1434,444,1132,1281,1547,1101,1142,647,613,147,2327,2428,456,632,402,1896,1178,1195,2455,1024,560,335,109,91,1144,2409,1576,1362,763;1642,70,1972,528,1440,2410,2401,2363,2382,555,789,1529,2093,666,1848,223,760,1209,1575,284,1660,945,1949,523,1221,1366,438,1160,2046,2180,1228,801,1788,141,404,2292,53,1342,450,2384,2312,357,81,884,826,2482,1443,259;44,476,2040,775,1431,1456,1065,750,711,1901,2317,1842,1222,774,987,366,2376,533,842,11,1156,690,2457,1873,876,2325,614,693,2112,993,470,311,915,617,433,1347,2410,1370,467,693,1974,1105,424,955,1736,2399,609,864;2323,1866,2195,1384,1375,442,46,1150,2241,229,2084,5,598,787,1759,1832,1297,1606,1639,1001,1936,1121,1528,2131,778,126,1140,1368,1637,1830,700,977,1833,324,1897,1698,1575,977,69,1651,1724,1153,142,131,4,1266,2253,737;1080,1165,1443,1282,865,1281,1942,1,391,2279,461,1812,415,315,442,2165,300,1493,602,860,1766,1201,524,452,878,2135,901,419,2282,895,1787,1485,2112,143,1510,1383,929,439,2258,2365,964,1831,2184,2198,357,692,1537,1864;1636,436,430,65,724,1601,2240,1782,500,693,1297,1959,668,2306,71,262,1683,2067,1281,1276,2339,2027,2272,569,1174,555,1649,535,833,1516,207,81,2474,1851,49,2062,1318,1780,2374,1490,438,1407,373,1643,235,1214,1320,2002;88,14,1657,2199,1321,775,303,256,1635,495,1896,1956,1458,763,2152,2334,1505,1035,289,597,2419,318,557,687,1031,2403,935,1156,624,1574,864,1601,1783,1555,451,1595,889,2335,524,1191,937,1089,1356,831,431,436,545,1041;229,565,1980,2106,1270,771,1862,294,1641,588,699,2026,1972,350,324,1127,1659,1272,58,211,2058,140,216,614,1741,1926,975,2395,674,828,325,652,901,126,2422,936,767,2012,2333,1588,316,257,1213,1408,634,836,783,2196;714,598,1245,2172,2404,182,360,1751,2121,869,1694,2441,1,1628,1994,2236,1195,1930,662,188,2424,1770,1401,202,721,1553,1315,637,2287,2454,1583,525,940,516,1060,729,1297,242,702,320,4,1325,2324,91,602,2012,1977,1546;1080,1235,607,322,2246,1039,1204,754,697,191,390,1257,1237,347,1962,153,937,1232,238,542,1420,1201,1228,2283,2335,1064,1009,578,1249,165,776,1970,1576,2410,541,411,1867,303,1913,62,107,1958,1541,1671,1375,2269,765,1938;1977,1823,1793,1974,891,1197,1377,835,994,707,1338,405,2090,2150,1015,359,716,2170,1617,2409,181,979,819,2294,1548,1766,572,1090,85,293,1798,1982,2320,1806,1258,1745,393,2482,2072,1583,1756,2101,777,2111,2292,1774,1806,2047;2345,2120,1928,1905,2499,212,213,1620,484,742,834,1118,795,1359,2208,1638,1080,1920,378,1919,2447,355,1067,1117,2481,1211,1331,495,1220,2270,2053,2453,2251,211,545,603,1071,1774,1052,1444,719,153,581,2074,1236,887,1773,2166;1123,170,993,464,2288,1186,1861,2276,1631,1769,1961,1785,1041,88,1700,882,998,255,924,859,1179,2403,1848,2057,813,1052,957,798,1178,544,2207,405,2283,652,501,842,1410,2473,1747,570,1478,864,1165,434,2304,1704,2368,1241;1110,819,1317,477,1961,815,2467,2243,816,21,2085,470,1167,2471,687,788,172,843,887,1894,524,169,1008,2391,2109,565,2466,1294,2378,1856,1942,852,104,443,2199,828,1885,1172,524,1797,43,645,1764,1067,636,1693,743,928;916,2276,99,2424,377,1368,1325,1230,1695,33,1563,52,1660,1111,238,1146,295,1004,692,1470,442,1909,2336,1370,2189,38,369,984,516,2436,155,4,212,1997,554,2328,2024,58,1102,1613,644,1686,1412,1656,1142,2017,777,588;1197,1452,2233,1271,49,2135,1988,1584,1786,886,1290,1966,1268,1378,884,538,258,2117,1569,471,797,629,449,2355,365,2270,864,633,2392,787,911,2388,507,1080,592,57,1457,338,1092,2359,842,440,750,536,560,535,1122,1439;1008,276,1360,336,229,2004,1108,245,1326,2489,1171,2343,1873,1350,1332,370,349,121,1178,1343,568,2253,355,1597,2051,560,752,2008,1007,1223,48,619,54,594,1490,486,234,144,2290,1373,1544,493,2245,183,1824,1523,1660,576;5,1403,1349,499,1534,1741,1740,690,1823,606,184,2355,962,2423,1429,617,1700,313,1768,128,1474,499,1280,1023,1912,611,399,1667,353,15,1484,1204,2208,1792,2048,1276,1219,739,1803,535,1595,1243,334,1813,1147,1276,444,1348;612,1109,1637,1867,1228,1559,1593,1646,48,1874,779,1479,1493,2337,1634,796,579,1056,1878,1607,221,558,101,1143,1937,163,1082,1743,1413,1162,303,151,441,1982,728,182,1579,956,792,2261,1005,1580,1620,444,952,1867,1336,341;1451,140,2219,1882,1762,263,1802,2061,598,36,17,206,145,2331,35,2062,354,1139,2088,353,3,242,1871,153,1875,2010,2297,807,43,1224,1021,514,243,706,1875,2405,1346,1317,2042,1664,1808,147,1822,1060,1570,636,403,2310;2268,1947,1834,380,1885,2263,1194,2360,520,1865,2063,1686,14,862,671,2339,2016,2005,111,338,405,1325,270,1694,95,1912,2169,1803,2272,1960,2084,2302,1160,2378,1655,398,390,1882,1325,803,2137,398,1715,2339,282,1027,2499,818;459,488,616,1135,1915,1206,1475,1197,1138,2136,127,806,155,973,965,1145,402,1898,1059,114,553,447,291,648,1475,1151,2251,1335,1794,429,1840,1281,2131,2216,646,506,1744,1251,1378,1971,141,1477,2323,615,1013,914,1475,1993;868,347,1207,780,2367,542,1451,878,1965,1734,1254,1537,853,126,194,1545,1413,1816,1841,144,2500,670,226,518,2145,1748,670,2094,826,293,1470,2040,21,373,1147,692,1750,2213,1052,1101,989,30,1206,2160,1926,1598,1906,220;1525,1509,1454,1141,1423,1816,263,671,1911,1584,1896,2330,1698,587,2020,1505,940,1937,25,185,918,2252,1437,2156,2494,1326,1567,1293,1378,804,530,2451,354,600,1678,753,2499,1245,2402,834,95,1786,1723,2070,2022,1274,1450,2344;2129,897,319,2299,2250,8,1590,2262,277,352,123,117,841,153,980,765,1604,31,1939,2359,533,589,629,1412,2090,1690,1095,1225,2336,1351,2076,1220,727,2213,1966,761,349,1744,930,2038,1479,1217,1684,447,41,1887,34,328;967,914,1356,225,1971,2418,2013,1127,379,2005,1564,1568,243,1754,1400,1013,1282,1440,2362,1990,127,2436,1993,1679,1021,1743,308,1707,1202,649,437,1438,1853,490,306,2459,2257,1003,73,1738,1966,660,2094,229,988,2467,1781,2244;258,1062,2136,1951,379,1741,1023,538,1320,1193,1478,577,1296,1563,557,1826,1420,618,1518,2115,129,1936,1156,104,155,1059,184,882,590,431,162,750,2072,1041,1721,1540,2251,11,406,1024,1925,2246,21,2210,363,2479,1395,1350;651,2197,925,1570,346,612,2129,2223,882,364,2002,1187,1708,1395,2066,1386,2373,1810,867,1844,929,1283,367,1570,1804,1837,1181,966,1008,1549,369,893,385,533,1689,938,947,1516,206,503,1761,203,1764,828,2016,1401,2113,2257;935,1218,1589,1696,541,1248,988,246,500,1322,2059,1401,2310,2177,2212,1226,1255,865,1879,498,1864,2117,422,2417,545,66,319,2187,909,859,2413,1412,1977,1456,203,1833,654,1664,1523,1682,941,2378,488,1423,1408,807,2252,1371;1363,8,1134,6,43,1512,1203,2168,2458,2141,188,1255,1157,139,1318,931,191,599,531,1474,1031,639,2336,2030,1702,1236,1636,1142,2148,1603,1421,604,1680,1001,510,655,2185,164,164,1128,2484,332,2324,85,347,2077,1677,2362;834,1124,434,2144,1667,1958,855,249,1188,1205,2345,1112,2365,430,1709,848,2452,583,204,479,510,642,1188,466,1786,1422,510,814,1398,1106,1952,2017,1893,2376,1802,808,893,784,2105,1147,1258,725,432,220,1482,1395,324,1521;2045,2474,1829,1772,500,376,336,1684,1428,1456,1199,419,2316,387,284,1047,799,137,177,1999,66,214,2083,1624,1352,129,1452,1255,2304,1979,1195,952,1735,1792,1600,597,1882,1168,1738,2041,406,671,2328,1248,1619,1617,944,415;907,639,278,208,1507,401,243,1174,121,596,789,703,2126,1086,969,108,1109,257,2476,921,1146,178,949,409,111,1865,1046,1916,2373,520,467,729,1834,1267,1233,2177,730,2325,1782,490,2015,1144,730,1572,1338,855,1731,729;178,1181,909,1472,615,130,1987,2462,113,1092,1656,483,2222,2168,2083,334,1927,637,1238,2330,321,2100,110,2366,1054,782,2170,853,2466,1372,317,1383,1554,673,2444,686,2248,1189,2203,1775,1751,406,1443,1782,1227,2372,853,1838", "output": "2063,1662,716,615,960,1434,722,457,564,1719,1072,2230,1357,2198,1455,391,1657,1225,1448,79,762,2390,432,2329,1765,1587,1562,1714,911,264,995,992,1451,1366,1822,1538,1276,2301,2095,1240,1097,1839,1132,1023,2053,1220,978,892,445,714,873,2152,1102,1396,184,635,1301,1444,119,1671,1181,2065,1437,1970,593,2492,1267,399,1285,1010,2499,871,2378,2174,551,779,2216,527,594,908,1292,1044,68,390,1179,389,1192,8,412,2283,1307,366,937,503,1384,1813,191,1408,120,1733,1739,1205,1201,1605,2051,2323,1772,436,124,324,1315,502,1268,640,2258,909,721,2372,2067,768,1336,846,2388,817,2408,2131,1919,192,288,588,350,761,2250,6,656,1762,584,1290,741,382,2385,1749,1874,580,249,448,525,893,13,142,1845,3,1709,362,444,1281,1101,647,147,2428,632,1896,1195,1024,335,91,2409,1362,259,2482,884,357,2384,1342,2292,141,801,2180,1160,1366,523,945,284,1209,223,666,1529,555,2363,2410,528,70,44,2040,1431,1065,711,2317,1222,987,2376,842,1156,2457,876,614,2112,470,915,433,2410,467,1974,424,1736,609,737,1266,131,1153,1651,977,1698,324,977,1830,1368,126,2131,1121,1001,1606,1832,787,5,229,1150,442,1384,1866,1080,1443,865,1942,391,461,415,442,300,602,1766,524,878,901,2282,1787,2112,1510,929,2258,964,2184,357,1537,2002,1214,1643,1407,1490,1780,2062,1851,81,1516,535,555,569,2027,1276,2067,262,2306,1959,693,1782,1601,65,436,88,1657,1321,303,1635,1896,1458,2152,1505,289,2419,557,1031,935,624,864,1783,451,889,524,937,1356,431,545,2196,836,1408,257,1588,2012,936,126,652,828,2395,1926,614,140,211,1272,1127,350,2026,588,294,771,2106,565,714,1245,2404,360,2121,1694,1,1994,1195,662,2424,1401,721,1315,2287,1583,940,1060,1297,702,4,2324,602,1977,1938,2269,1671,1958,62,303,411,2410,1970,165,578,1064,2283,1201,542,1232,153,347,1257,191,754,1039,322,1235,1977,1793,891,1377,994,1338,2090,1015,716,1617,181,819,1548,572,85,1798,2320,1258,393,2072,1756,777,2292,1806,2166,887,2074,153,1444,1774,603,211,2453,2270,495,1211,1117,355,1919,1920,1638,1359,1118,742,1620,212,1905,2120,1123,993,2288,1861,1631,1961,1041,1700,998,924,1179,1848,813,957,1178,2207,2283,501,1410,1747,1478,1165,2304,2368,928,1693,1067,645,1797,1172,828,443,852,1856,1294,565,2391,169,1894,843,788,2471,470,21,2243,815,477,819,916,99,377,1325,1695,1563,1660,238,295,692,442,2336,2189,369,516,155,212,554,2024,1102,644,1412,1142,777,1439,535,536,440,2359,338,57,1080,2388,787,633,2270,2355,629,471,2117,538,1378,1966,886,1584,2135,1271,1452,1008,1360,229,1108,1326,1171,1873,1332,349,1178,568,355,2051,752,1007,48,54,1490,234,2290,1544,2245,1824,1660,1348,1276,1813,1243,535,739,1276,1792,1204,15,1667,611,1023,499,128,313,617,2423,2355,606,690,1741,499,1403,612,1637,1228,1593,48,779,1493,1634,579,1878,221,101,1937,1082,1413,303,441,728,1579,792,1005,1620,952,1336,2310,636,1060,147,1664,1317,2405,706,514,1224,807,2010,153,242,353,1139,2062,2331,206,36,2061,263,1882,140,2268,1834,1885,1194,520,2063,14,671,2016,111,405,270,95,2169,2272,2084,1160,1655,390,1325,2137,1715,282,2499,1993,914,615,1477,1971,1251,506,2216,1281,429,1335,1151,648,447,114,1898,1145,973,806,2136,1197,1206,1135,488,868,1207,2367,1451,1965,1254,853,194,1413,1841,2500,226,2145,670,826,1470,21,1147,1750,1052,989,1206,1926,1906,2344,1274,2070,1786,834,1245,753,600,2451,804,1293,1326,2156,2252,185,1937,1505,587,2330,1584,671,1816,1141,1509,2129,319,2250,1590,277,123,841,980,1604,1939,533,629,2090,1095,2336,2076,727,1966,349,930,1479,1684,41,34,2244,2467,229,660,1738,1003,2459,490,1438,649,1707,1743,1679,2436,1990,1440,1013,1754,1568,2005,1127,2418,225,914,258,2136,379,1023,1320,1478,1296,557,1420,1518,129,1156,155,184,590,162,2072,1721,2251,406,1925,21,363,1395,2257,1401,828,203,503,1516,938,533,893,1549,966,1837,1570,1283,1844,1810,1386,1395,1187,364,2223,612,1570,2197,935,1589,541,988,500,2059,2310,2212,1255,1879,1864,422,545,319,909,2413,1977,203,654,1523,941,488,1408,2252,2362,2077,85,332,1128,164,655,1001,604,1603,1142,1236,2030,639,1474,599,931,139,1255,2141,2168,1512,6,8,834,434,1667,855,1188,2345,2365,1709,2452,204,510,1188,1786,510,1398,1952,1893,1802,893,2105,1258,432,1482,324,415,1617,1248,671,2041,1168,597,1792,952,1979,1255,129,1624,214,1999,137,1047,387,419,1456,1684,376,1772,2474,907,278,1507,243,121,789,2126,969,1109,2476,1146,949,111,1046,2373,467,1834,1233,730,1782,2015,730,1338,1731,1838,2372,1782,406,1775,1189,686,673,1383,1372,853,782,2366,2100,2330,637,334,2168,483,1092,2462,130,1472,1181"}]
|
{
"cpp": "==Code Submission==\n\nvector<vector<int>> deserialize_stdin(const string &input) {\n vector<vector<int>> grid;\n size_t start = 0;\n while (start < input.size()) {\n size_t end = input.find(';', start);\n string rowStr;\n if (end == string::npos) {\n rowStr = input.substr(start);\n start = input.size();\n } else {\n rowStr = input.substr(start, end - start);\n start = end + 1;\n }\n vector<int> row;\n size_t pos = 0;\n while (pos < rowStr.size()) {\n size_t comma = rowStr.find(',', pos);\n string numStr;\n if (comma == string::npos) {\n numStr = rowStr.substr(pos);\n pos = rowStr.size();\n } else {\n numStr = rowStr.substr(pos, comma - pos);\n pos = comma + 1;\n }\n if (!numStr.empty()) {\n row.push_back(stoi(numStr));\n }\n }\n grid.push_back(row);\n }\n return grid;\n}\n\nstring serialize_stdout(const vector<int>& result) {\n string output;\n for (size_t i = 0; i < result.size(); i++) {\n output += to_string(result[i]);\n if (i < result.size() - 1) output += \",\";\n }\n return output;\n}\n\nint main(){\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n string line;\n getline(cin, line);\n vector<vector<int>> grid = deserialize_stdin(line);\n Solution sol;\n vector<int> ans = sol.zigzagTraversal(grid);\n cout << serialize_stdout(ans);\n return 0;\n}",
"golang": "==Code Submission==\n\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n line, _ := reader.ReadString('\\n')\n line = strings.TrimSpace(line)\n rowStrs := strings.Split(line, \";\")\n grid := make([][]int, len(rowStrs))\n for i, rowStr := range rowStrs {\n if rowStr == \"\" {\n grid[i] = []int{}\n continue\n }\n numStrs := strings.Split(rowStr, \",\")\n row := make([]int, len(numStrs))\n for j, s := range numStrs {\n row[j], _ = strconv.Atoi(s)\n }\n grid[i] = row\n }\n ans := zigzagTraversal(grid)\n resultStr := \"\"\n for i, num := range ans {\n resultStr += strconv.Itoa(num)\n if i < len(ans)-1 {\n resultStr += \",\"\n }\n }\n fmt.Print(resultStr)\n}",
"java": "public class Main {\n private static int[][] deserializeGrid(String input) {\n String[] rows = input.split(\";\");\n int[][] grid = new int[rows.length][];\n for (int i = 0; i < rows.length; i++) {\n String[] nums = rows[i].split(\",\");\n grid[i] = new int[nums.length];\n for (int j = 0; j < nums.length; j++) {\n grid[i][j] = Integer.parseInt(nums[j]);\n }\n }\n return grid;\n }\n \n private static String serializeOutput(java.util.List<Integer> result) {\n StringBuilder sb = new StringBuilder();\n for (int i = 0; i < result.size(); i++) {\n sb.append(result.get(i));\n if (i < result.size() - 1) sb.append(\",\");\n }\n return sb.toString();\n }\n \n public static void main(String[] args) throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n String input = br.readLine().trim();\n int[][] grid = deserializeGrid(input);\n Solution sol = new Solution();\n java.util.List<Integer> ans = sol.zigzagTraversal(grid);\n System.out.println(serializeOutput(ans));\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\n\nconst deserialize_stdin = (input) => {\n const rows = input.trim().split(\";\");\n const grid = rows.map(row => {\n if (row === \"\") return [];\n return row.split(\",\").map(Number);\n });\n return grid;\n};\n\nconst serialize_stdout = (result) => {\n return result.join(\",\");\n};\n\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\nlet input = \"\";\nprocess.stdin.on('data', chunk => {\n input += chunk;\n});\nprocess.stdin.on('end', () => {\n const grid = deserialize_stdin(input);\n const ans = zigzagTraversal(grid);\n console.log(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str):\n rows = input_str.strip().split(\";\")\n grid = []\n for row in rows:\n if row == \"\":\n continue\n grid.append(list(map(int, row.split(\",\"))))\n return grid\n\ndef serialize_stdout(result):\n return \",\".join([str(x) for x in result])\n\ninput_str = sys.stdin.read().strip()\ngrid = deserialize_stdin(input_str)\nsol = Solution()\nans = sol.zigzagTraversal(grid)\nprint(serialize_stdout(ans))",
"ruby": "==Code Submission==\n\ninput = gets.strip\nrows = input.split(\";\")\ngrid = rows.map do |row|\n row.split(\",\").map(&:to_i)\nend\nans = zigzag_traversal(grid)\nputs ans.join(\",\")"
}
|
3709
|
Find Special Substring of Length K
|
find-special-substring-of-length-k
|
<p>You are given a string <code>s</code> and an integer <code>k</code>.</p>
<p>Determine if there exists a <span data-keyword="substring-nonempty">substring</span> of length <strong>exactly</strong> <code>k</code> in <code>s</code> that satisfies the following conditions:</p>
<ol>
<li>The substring consists of <strong>only one distinct character</strong> (e.g., <code>"aaa"</code> or <code>"bbb"</code>).</li>
<li>If there is a character <strong>immediately before</strong> the substring, it must be different from the character in the substring.</li>
<li>If there is a character <strong>immediately after</strong> the substring, it must also be different from the character in the substring.</li>
</ol>
<p>Return <code>true</code> if such a substring exists. Otherwise, return <code>false</code>.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">s = "aaabaaa", k = 3</span></p>
<p><strong>Output:</strong> <span class="example-io">true</span></p>
<p><strong>Explanation:</strong></p>
<p>The substring <code>s[4..6] == "aaa"</code> satisfies the conditions.</p>
<ul>
<li>It has a length of 3.</li>
<li>All characters are the same.</li>
<li>The character before <code>"aaa"</code> is <code>'b'</code>, which is different from <code>'a'</code>.</li>
<li>There is no character after <code>"aaa"</code>.</li>
</ul>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">s = "abc", k = 2</span></p>
<p><strong>Output:</strong> <span class="example-io">false</span></p>
<p><strong>Explanation:</strong></p>
<p>There is no substring of length 2 that consists of one distinct character and satisfies the conditions.</p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>1 <= k <= s.length <= 100</code></li>
<li><code>s</code> consists of lowercase English letters only.</li>
</ul>
|
You are given a string `s` and an integer `k`.
Determine if there exists a substring of length **exactly** `k` in `s` that satisfies the following conditions:
1. The substring consists of **only one distinct character** (e.g., `"aaa"` or `"bbb"`).
2. If there is a character **immediately before** the substring, it must be different from the character in the substring.
3. If there is a character **immediately after** the substring, it must also be different from the character in the substring.
Return `true` if such a substring exists. Otherwise, return `false`.
**Example 1:**
**Input:** s \= "aaabaaa", k \= 3
**Output:** true
**Explanation:**
The substring `s[4..6] == "aaa"` satisfies the conditions.
- It has a length of 3\.
- All characters are the same.
- The character before `"aaa"` is `'b'`, which is different from `'a'`.
- There is no character after `"aaa"`.
**Example 2:**
**Input:** s \= "abc", k \= 2
**Output:** false
**Explanation:**
There is no substring of length 2 that consists of one distinct character and satisfies the conditions.
**Constraints:**
- `1 <= k <= s.length <= 100`
- `s` consists of lowercase English letters only.
|
Easy
|
[
"string"
] |
leetcode
|
https://leetcode.com/problems/find-special-substring-of-length-k
|
functional
| null | null | null | null |
{
"c": "bool hasSpecialSubstring(char* s, int k) {\n \n}",
"cpp": "class Solution {\npublic:\n bool hasSpecialSubstring(string s, int k) {\n \n }\n};",
"csharp": "public class Solution {\n public bool HasSpecialSubstring(string s, int k) {\n \n }\n}",
"dart": "class Solution {\n bool hasSpecialSubstring(String s, int k) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec has_special_substring(s :: String.t, k :: integer) :: boolean\n def has_special_substring(s, k) do\n \n end\nend",
"erlang": "-spec has_special_substring(S :: unicode:unicode_binary(), K :: integer()) -> boolean().\nhas_special_substring(S, K) ->\n .",
"golang": "func hasSpecialSubstring(s string, k int) bool {\n \n}",
"java": "class Solution {\n public boolean hasSpecialSubstring(String s, int k) {\n \n }\n}",
"javascript": "/**\n * @param {string} s\n * @param {number} k\n * @return {boolean}\n */\nvar hasSpecialSubstring = function(s, k) {\n \n};",
"kotlin": "class Solution {\n fun hasSpecialSubstring(s: String, k: Int): Boolean {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param String $s\n * @param Integer $k\n * @return Boolean\n */\n function hasSpecialSubstring($s, $k) {\n \n }\n}",
"python": "class Solution(object):\n def hasSpecialSubstring(self, s, k):\n \"\"\"\n :type s: str\n :type k: int\n :rtype: bool\n \"\"\"\n ",
"python3": "class Solution:\n def hasSpecialSubstring(self, s: str, k: int) -> bool:\n ",
"racket": "(define/contract (has-special-substring s k)\n (-> string? exact-integer? boolean?)\n )",
"ruby": "# @param {String} s\n# @param {Integer} k\n# @return {Boolean}\ndef has_special_substring(s, k)\n \nend",
"rust": "impl Solution {\n pub fn has_special_substring(s: String, k: i32) -> bool {\n \n }\n}",
"scala": "object Solution {\n def hasSpecialSubstring(s: String, k: Int): Boolean = {\n \n }\n}",
"swift": "class Solution {\n func hasSpecialSubstring(_ s: String, _ k: Int) -> Bool {\n \n }\n}",
"typescript": "function hasSpecialSubstring(s: string, k: number): boolean {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n bool hasSpecialSubstring(string s, int k) {\n int n = s.size();\n for (int i = 0; i <= n - k; i++) {\n bool allSame = true;\n for (int j = i; j < i + k; j++) {\n if (s[j] != s[i]) {\n allSame = false;\n break;\n }\n }\n if (!allSame) continue;\n if (i > 0 && s[i - 1] == s[i]) continue;\n if (i + k < n && s[i + k] == s[i]) continue;\n return true;\n }\n return false;\n }\n};",
"memory": 800,
"memoryDistribution": "[[800, 82.962, \"class Solution {\\npublic:\\n bool hasSpecialSubstring(string s, int k) {\\n int n = s.size();\\n for (int i = 0; i <= n - k; i++) {\\n bool allSame = true;\\n for (int j = i; j < i + k; j++) {\\n if (s[j] != s[i]) {\\n allSame = false;\\n break;\\n }\\n }\\n if (!allSame) continue;\\n if (i > 0 && s[i - 1] == s[i]) continue;\\n if (i + k < n && s[i + k] == s[i]) continue;\\n return true;\\n }\\n return false;\\n }\\n};\"], [8200, 0.1311, \"class Solution {\\npublic:\\n bool hasSpecialSubstring(string& s, int k) {\\n int count = 1, n = s.size();\\n\\n for (int i = 1; i < n; i++) {\\n if (s[i] == s[i - 1]) {\\n count++;\\n } else {\\n if (count == k && (i - k - 1 < 0 || s[i - k - 1] != s[i - 1]) &&\\n (i >= n || s[i] != s[i - 1]))\\n return true;\\n count = 1;\\n }\\n }\\n return count == k && (n - k - 1 < 0 || s[n - k - 1] != s[n - 1]);\\n }\\n};\"], [8300, 0.9174, \"class Solution {\\npublic:\\n bool hasSpecialSubstring(const std::string &s, const int k) {\\n char curr = s.front();\\n int count = 1;\\n for (size_t i = 1; i < s.size(); i++) {\\n if (s[i] == curr) {\\n count++;\\n } else {\\n if (count == k) {\\n return true;\\n }\\n count = 1;\\n curr = s[i];\\n }\\n }\\n return count == k;\\n }\\n};\\n\"], [8400, 15.9895, null], [8500, 24.7706, null], [8600, 29.3578, null], [8700, 10.616, null], [8800, 2.7523, null], [8900, 1.8349, null], [9000, 1.1796, null], [9100, 0.5242, null], [9200, 1.1796, null], [9300, 1.5727, null], [9400, 1.0485, null], [9500, 0.3932, null], [9600, 0.7864, null], [9700, 0.3932, null], [9900, 0.3932, null], [10000, 0.1311, null], [10800, 0.1311, \"class Solution {\\npublic:\\n bool hasSpecialSubstring(string s, int k) {\\n set<char> st;\\n int i = 0, j = 0;\\n while(i < s.length()){\\n if(i-j+1 <= k){\\n st.insert(s[i]-'a');\\n if(st.size() > 1) {\\n st.clear();\\n st.insert(s[i]-'a');\\n j = i;\\n }\\n }\\n if(i-j+1 == k){\\n if(j != 0 && i != s.length()-1) {\\n if(s[j-1] != s[j] && s[i+1] != s[i]) return true;\\n }else if(j != 0) {\\n if(s[j-1] != s[j]) return true;\\n }else if(i != s.length()-1) {\\n if(s[i+1] != s[i]) return true;\\n }else {\\n return true;\\n }\\n j++;\\n }\\n \\n i++;\\n }\\n return false;\\n }\\n};\"], [11900, 0.5242, \"#define ll long long\\nclass Solution {\\npublic:\\n vector<int> findSubstringIndices(string s, string sub) {\\n vector<int> indices;\\n size_t pos = s.find(sub, 0);\\n while (pos != string::npos) {\\n indices.push_back(pos);\\n pos = s.find(sub, pos + 1);\\n }\\n return indices;\\n }\\n\\n bool hasSpecialSubstring(string s, int k) {\\n ll n = s.size();\\n vector<vector<int>> occurances(26);\\n\\n for (int i = 0; i < 26; i++) {\\n string w(k, (char)(i + 'a'));\\n occurances[i] = findSubstringIndices(s, w);\\n }\\n\\n for (int i = 0; i < 26; i++) {\\n for (ll idx : occurances[i]) {\\n bool left_ok = (idx == 0 || s[idx - 1] != (char)(i + 'a'));\\n bool right_ok = (idx + k >= n || s[idx + k] != (char)(i + 'a'));\\n\\n if (left_ok && right_ok) {\\n return true;\\n }\\n }\\n }\\n\\n return false;\\n }\\n};\\n\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 75.8847, \"class Solution {\\npublic:\\n bool hasSpecialSubstring(string s, int k) {\\n for (char c = 'a'; c <= 'z'; ++c) {\\n int current_count = 0;\\n for (int i = 0; i < s.size(); ++i) {\\n if (s[i] == c) {\\n ++current_count;\\n } else {\\n if (current_count == k)\\n return true;\\n current_count = 0;\\n }\\n }\\n if (current_count == k)\\n return true;\\n\\n }\\n return false;\\n\\n }\\n};\"], [1, 3.6697, \"class Solution {\\npublic:\\n bool hasSpecialSubstring(string s, int k) {\\n \\n int count = 1;\\n for(int i = 1; i < s.size(); i++, count++){\\n if(s[i] != s[i-1] && count == k) return true;\\n if(s[i] != s[i-1]) count = 0;\\n }\\n return (count == k);\\n} \\n \\n};\"], [2, 2.6212, null], [3, 6.9463, null], [4, 2.228, null], [5, 0.2621, null], [6, 0.1311, null], [7, 0.2621, null], [8, 0.2621, null], [9, 0.1311, null], [10, 0.1311, null], [11, 0.2621, null], [12, 0.3932, null], [13, 0.1311, \"class Solution {\\npublic:\\n bool hasSpecialSubstring(string s, int k) {\\n unordered_set<char> un;\\n int i = 0;\\n while (i <= s.length() - k) {\\n for (int j = i; j < i + k; ++j) {\\n un.insert(s[j]);\\n }\\n\\n int x = i - 1;\\n int y = i + k;\\n\\n if (un.size() == 1) {\\n // Check for element\\n\\n if (x == -1 and y == s.length()) {\\n return true;\\n } else if (x == -1 and y != s.length()) {\\n if (un.find(s[y]) == un.end()) {\\n return true;\\n }\\n } else if (x != -1 and y == s.length()) {\\n if (un.find(s[x]) == un.end()) {\\n return true;\\n }\\n } else {\\n if (un.find(s[x]) == un.end() and\\n un.find(s[y]) == un.end()) {\\n return true;\\n }\\n }\\n }\\n\\n i++;\\n un.clear();\\n }\\n return false;\\n }\\n};\"], [14, 0.7864, \"class Solution {\\npublic:\\n bool hasSpecialSubstring(string s, int k) {\\n if (k == 1 && s.length() == 2) {\\n return !(s[0] == s[1]);\\n }\\n if (k == 1)\\n return true;\\n\\n for (int i = 0; i <= s.length() - k; i++) {\\n bool flag = true;\\n for (int j = i; j < k + i - 1; j++) {\\n if (s[j] != s[j + 1]) {\\n flag = false;\\n break;\\n }\\n }\\n cout << s[i] << \\\" \\\" << s[i + k];\\n if (flag == true) {\\n if ((i == 0 && s[i + k] != s[i]) ||\\n (i != 0 && i != s.length() - k && s[i] != s[i + k] && s[i] != s[i-1]) ||\\n (i == s.length() - k && s[i] != s[i + k] && i != 1 && s[i] != s[i-1]))\\n return true;\\n }\\n }\\n return false;\\n }\\n};\"]]"
},
"golang": {
"code": "func hasSpecialSubstring(s string, k int) bool {\n\tn := len(s)\n\tfor i := 0; i <= n-k; i++ {\n\t\tc := s[i]\n\t\tvalid := true\n\t\tfor j := i; j < i+k; j++ {\n\t\t\tif s[j] != c {\n\t\t\t\tvalid = false\n\t\t\t\tbreak\n\t\t\t}\n\t\t}\n\t\tif !valid {\n\t\t\tcontinue\n\t\t}\n\t\tif i > 0 && s[i-1] == c {\n\t\t\tcontinue\n\t\t}\n\t\tif i+k < n && s[i+k] == c {\n\t\t\tcontinue\n\t\t}\n\t\treturn true\n\t}\n\treturn false\n}",
"memory": 400,
"memoryDistribution": "[[400, 97.6744, \"func hasSpecialSubstring(s string, k int) bool {\\n\\tn := len(s)\\n\\tfor i := 0; i <= n-k; i++ {\\n\\t\\tc := s[i]\\n\\t\\tvalid := true\\n\\t\\tfor j := i; j < i+k; j++ {\\n\\t\\t\\tif s[j] != c {\\n\\t\\t\\t\\tvalid = false\\n\\t\\t\\t\\tbreak\\n\\t\\t\\t}\\n\\t\\t}\\n\\t\\tif !valid {\\n\\t\\t\\tcontinue\\n\\t\\t}\\n\\t\\tif i > 0 && s[i-1] == c {\\n\\t\\t\\tcontinue\\n\\t\\t}\\n\\t\\tif i+k < n && s[i+k] == c {\\n\\t\\t\\tcontinue\\n\\t\\t}\\n\\t\\treturn true\\n\\t}\\n\\treturn false\\n}\"], [4100, 2.3256, \"func hasSpecialSubstring(s string, k int) bool {\\n n := len(s)\\n if n == 1{\\n return true\\n }\\n prev := byte('#')\\n if k == 1{\\n for i:=0; i<n-1; i++{\\n if s[i]!=s[i+1] && s[i]!=prev{\\n return true\\n }\\n prev = s[i]\\n }\\n if s[n-1]!=prev{\\n return true\\n }\\n return false\\n }\\n countDup := 1\\n for i:=0; i<n-1; i++{\\n if s[i] == s[i+1]{\\n countDup++\\n }else{\\n prev = s[i]\\n countDup = 1\\n }\\n if countDup == k && prev != s[i] &&(i+1+1 == n || s[i+1+1] != s[i]){\\n return true\\n }\\n }\\n return false\\n}\"], [4200, 39.5349, \"func hasSpecialSubstring(s string, k int) bool {\\n for i := 0; i <= len(s) - k; i++ {\\n a := s[i:(i + k)]\\n if hasOneDistinctCharacter(a) {\\n if i - 1 >= 0 && s[i - 1] == a[0] {\\n continue\\n }\\n if i + k < len(s) && s[i + k] == a[0] {\\n continue\\n }\\n return true\\n }\\n }\\n return false\\n}\\n\\nfunc hasOneDistinctCharacter(s string) bool {\\n for i := 0; i < len(s) - 1; i++ {\\n if s[i] != s[i + 1] {\\n return false\\n }\\n }\\n return true\\n}\"], [4300, 34.8837, null], [4500, 9.3023, \"func hasSpecialSubstring(s string, k int) bool {\\n\\nif len(s) == 0 {\\n\\nreturn false\\n\\n}\\n\\n// \\u0421\\u043e\\u0437\\u0434\\u0430\\u0435\\u043c \\u0441\\u043f\\u0438\\u0441\\u043e\\u043a \\u0434\\u043b\\u0438\\u043d \\u0433\\u0440\\u0443\\u043f\\u043f\\n\\ngroups := []int{}\\n\\ncurrentChar := s[0]\\n\\ncount := 1\\n\\nfor i := 1; i < len(s); i++ {\\n\\nif s[i] == currentChar {\\n\\ncount++\\n\\n} else {\\n\\ngroups = append(groups, count)\\n\\ncurrentChar = s[i]\\n\\ncount = 1\\n\\n}\\n\\n}\\n\\ngroups = append(groups, count)\\n\\n// \\u041f\\u0440\\u043e\\u0432\\u0435\\u0440\\u044f\\u0435\\u043c \\u043a\\u0430\\u0436\\u0434\\u0443\\u044e \\u0433\\u0440\\u0443\\u043f\\u043f\\u0443\\n\\nfor _, g := range groups {\\n\\nif g == k {\\n\\nreturn true\\n\\n}\\n\\n}\\n\\nreturn false\\n\\n}\"], [4600, 6.9767, \"func hasSpecialSubstring(s string, k int) bool {\\n\\ts = s + \\\"|\\\"\\n\\tfor r, i := 1, 1; i < len(s); i++ {\\n\\t\\t// fmt.Println(i, string(s[i]), r)\\n\\t\\tif s[i] == s[i-1] {\\n\\t\\t\\tr++\\n\\t\\t} else {\\n\\t\\t\\tfmt.Println(i, string(s[i]), r)\\n\\t\\t\\tif r == k {\\n\\t\\t\\t\\treturn true\\n\\t\\t\\t}\\n\\t\\t\\tr = 1\\n\\t\\t}\\n\\n\\t}\\n\\treturn false\\n}\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 69.7674, \"func hasSpecialSubstring(s string, k int) bool {\\n for i := 0; i <= len(s) - k; i++ {\\n a := s[i:(i + k)]\\n if hasOneDistinctCharacter(a) {\\n if i - 1 >= 0 && s[i - 1] == a[0] {\\n continue\\n }\\n if i + k < len(s) && s[i + k] == a[0] {\\n continue\\n }\\n return true\\n }\\n }\\n return false\\n}\\n\\nfunc hasOneDistinctCharacter(s string) bool {\\n for i := 0; i < len(s) - 1; i++ {\\n if s[i] != s[i + 1] {\\n return false\\n }\\n }\\n return true\\n}\"], [1, 2.3256, \"func hasSpecialSubstring(s string, k int) bool {\\n count := 1\\n\\n for i := 1; i < len(s); i++ {\\n if s[i] != s[i-1] {\\n if count == k {\\n return true\\n }\\n\\n count = 0\\n }\\n\\n count++;\\n }\\n\\n return (count == k)\\n}\"], [2, 2.3256, null], [3, 4.6512, null], [6, 2.3256, null], [7, 2.3256, null], [10, 2.3256, null], [12, 2.3256, \"func hasSpecialSubstring(s string, k int) bool {\\n\\ts = s + \\\"|\\\"\\n\\tfor r, i := 1, 1; i < len(s); i++ {\\n\\t\\t// fmt.Println(i, string(s[i]), r)\\n\\t\\tif s[i] == s[i-1] {\\n\\t\\t\\tr++\\n\\t\\t} else {\\n\\t\\t\\tfmt.Println(i, string(s[i]), r)\\n\\t\\t\\tif r == k {\\n\\t\\t\\t\\treturn true\\n\\t\\t\\t}\\n\\t\\t\\tr = 1\\n\\t\\t}\\n\\n\\t}\\n\\treturn false\\n}\"], [16, 4.6512, \"func hasSpecialSubstring(s string, k int) bool {\\n\\ts = s + \\\"|\\\"\\n\\tfor r, i := 1, 1; i < len(s); i++ {\\n\\t\\t// fmt.Println(i, string(s[i]), r)\\n\\t\\tif s[i] == s[i-1] {\\n\\t\\t\\tr++\\n\\t\\t} else {\\n\\t\\t\\tfmt.Println(i, string(s[i]), r)\\n\\t\\t\\tif r == k {\\n\\t\\t\\t\\treturn true\\n\\t\\t\\t}\\n\\t\\t\\tr = 1\\n\\t\\t}\\n\\n\\t}\\n\\treturn false\\n}\"]]"
},
"java": {
"code": "class Solution {\n public boolean hasSpecialSubstring(String s, int k) {\n int n = s.length();\n for (int i = 0; i <= n - k; i++) {\n char ch = s.charAt(i);\n boolean uniform = true;\n for (int j = i; j < i + k; j++) {\n if (s.charAt(j) != ch) {\n uniform = false;\n break;\n }\n }\n if (!uniform) continue;\n if (i > 0 && s.charAt(i - 1) == ch) continue;\n if (i + k < n && s.charAt(i + k) == ch) continue;\n return true;\n }\n return false;\n }\n}",
"memory": 4200,
"memoryDistribution": "[[4200, 75.89, \"class Solution {\\n public boolean hasSpecialSubstring(String s, int k) {\\n int n = s.length();\\n for (int i = 0; i <= n - k; i++) {\\n char ch = s.charAt(i);\\n boolean uniform = true;\\n for (int j = i; j < i + k; j++) {\\n if (s.charAt(j) != ch) {\\n uniform = false;\\n break;\\n }\\n }\\n if (!uniform) continue;\\n if (i > 0 && s.charAt(i - 1) == ch) continue;\\n if (i + k < n && s.charAt(i + k) == ch) continue;\\n return true;\\n }\\n return false;\\n }\\n}\"], [41600, 0.3236, \"class Solution {\\n public boolean hasSpecialSubstring(String s, int k) {\\n if (s == null || s.length() < k) {\\n return false;\\n }\\n \\n int n = s.length();\\n for (int i = 0; i <= n - k; i++) {\\n char currentChar = s.charAt(i);\\n boolean isValid = true;\\n \\n // Check if all characters in the substring are the same\\n for (int j = 1; j < k; j++) {\\n if (s.charAt(i + j) != currentChar) {\\n isValid = false;\\n break;\\n }\\n }\\n \\n if (isValid) {\\n // Check the character before the substring (if it exists)\\n if (i > 0 && s.charAt(i - 1) == currentChar) {\\n isValid = false;\\n }\\n // Check the character after the substring (if it exists)\\n if (i + k < n && s.charAt(i + k) == currentChar) {\\n isValid = false;\\n }\\n \\n if (isValid) {\\n return true;\\n }\\n }\\n }\\n \\n return false;\\n }\\n}\"], [41700, 0.3236, \"class Solution {\\n public boolean hasSpecialSubstring(String s, int k) {\\n int n = s.length();\\n for (int l = 0, cnt = 0; l < n;) {\\n int r = l + 1;\\n while (r < n && s.charAt(r) == s.charAt(l)) {\\n ++r;\\n }\\n if (r - l == k) {\\n return true;\\n }\\n l = r;\\n }\\n return false;\\n }\\n}\\n\"], [41800, 0.4854, null], [41900, 2.4272, null], [42000, 7.2816, null], [42100, 13.2686, null], [42200, 15.0485, null], [42300, 15.8576, null], [42400, 12.7832, null], [42500, 7.6052, null], [42600, 4.8544, null], [42700, 3.8835, null], [42800, 2.7508, null], [42900, 1.4563, null], [43000, 1.6181, null], [43100, 1.2945, null], [43200, 0.9709, null], [43300, 0.4854, null], [43400, 0.3236, null], [43500, 0.3236, null], [43600, 0.1618, null], [43700, 0.1618, null], [43800, 0.1618, null], [44000, 0.3236, null], [44100, 0.3236, \"class Solution {\\n public boolean hasSpecialSubstring(String s, int k) {\\n\\n if(k==1 && s.length()==1){\\n return true;\\n }\\n\\n int len = s.length();\\n int temp = k;\\n\\n for(int i=1;i<len;i++){\\n System.out.println(temp);\\n if(s.charAt(i)==s.charAt(i-1)){\\n temp--;\\n } else {\\n if(temp==1){\\n return true;\\n } \\n temp = k;\\n }\\n\\n if(i==len-1 && temp==1){\\n return true;\\n }\\n \\n\\n \\n }\\n\\n return false;\\n }\\n}\"], [44300, 0.3236, \"class Solution {\\n public boolean hasSpecialSubstring(String s, int k) {\\n for (int i = 0; i <= s.length() - k; i++) {\\n String substring = s.substring(i, i + k);\\n char c = substring.charAt(0);\\n if (substring.chars().allMatch(ch -> ch == c)) {\\n if ((i == 0 || s.charAt(i - 1) != c) && (i + k == s.length() || s.charAt(i + k) != c)) {\\n return true;\\n }\\n }\\n }\\n return false;\\n }\\n}\"]]",
"runtime": 1,
"runtimeDistribution": "[[0, 2.589, \"class Solution {\\n public boolean hasSpecialSubstring(String s, int k) {\\n int n = s.length();\\n \\n for (int i = 0; i <= n - k; i++) {\\n char ch = s.charAt(i);\\n boolean allSame = true;\\n \\n // Check if all characters in the window are the same\\n for (int j = i + 1; j < i + k; j++) {\\n if (s.charAt(j) != ch) {\\n allSame = false;\\n break;\\n }\\n }\\n \\n if (allSame) {\\n boolean leftValid = i == 0 || s.charAt(i - 1) != ch;\\n boolean rightValid = i + k == n || s.charAt(i + k) != ch;\\n \\n if (leftValid && rightValid) return true;\\n }\\n }\\n \\n return false;\\n }\\n}\\n\"], [1, 78.8026, \"class Solution {\\n public boolean hasSpecialSubstring(String s, int k) {\\n int n = s.length();\\n int i = 0;\\n\\n for (int j = 0; j < n; j++) {\\n if (s.charAt(j) == s.charAt(i)) continue;\\n if (j - i == k) return true;\\n i = j;\\n }\\n\\n return (n - i) == k;\\n }\\n}\"], [2, 6.6343, null], [3, 1.9417, null], [4, 1.4563, null], [5, 1.9417, \"class Solution {\\n public boolean hasSpecialSubstring(String s, int k) {\\n if(s.length()==1)return true;\\n for(int i=0;i<s.length()-k;i++){\\n HashSet<Character> h=new HashSet<>();\\n String b=s.substring(i,i+k);\\n // System.out.print(b+\\\" \\\");\\n for(char e:b.toCharArray()){\\n h.add(e);\\n }\\n if(h.size()==1 && i!=0 && i+k+1<=s.length()){\\n if(s.charAt(i)!=s.charAt(i-1)){\\n if(s.charAt(i)!=s.charAt(i+k)){\\n return true;\\n }\\n }\\n }\\n else{\\n if(h.size()==1 && i==0 && s.charAt(i+k-1)!=s.charAt(i+k)){\\n return true;\\n }\\n // if(h.size()==1 && i==0 && s.charAt(i)!=s.charAt(i+1) && k==1){\\n // return true;\\n // }\\n }\\n }\\n HashSet<Character> f=new HashSet<>();\\n String r=s.substring(s.length()-k,s.length());\\n // System.out.print(r+\\\" \\\");\\n if(s.length()-k!=0 && s.charAt(s.length()-k-1)!=s.charAt(s.length()-k)||(s.length()-k==0 && s.length()==r.length())){\\n for(char e:r.toCharArray()){\\n f.add(e);\\n }\\n if(f.size()==1){\\n return true;\\n }\\n }\\n return false;\\n }\\n}\"], [6, 1.4563, \"class Solution {\\n public boolean hasSpecialSubstring(String s, int k) {\\n String str = \\\"\\\" + s.charAt(0);\\n // if(s.length()>0 && k==1) {\\n // return true;\\n // }\\n for(int i=1; i<s.length(); i++) {\\n if(s.charAt(i-1) == s.charAt(i)) {\\n str+= s.charAt(i-1);\\n } else {\\n if(str.length() == k) {\\n return true;\\n }\\n str =\\\"\\\"+ s.charAt(i);\\n }\\n }\\n if(str.length() == k) {\\n return true;\\n }\\n return false;\\n }\\n}\"]]"
},
"javascript": {
"code": "/**\n * @param {string} s\n * @param {number} k\n * @return {boolean}\n */\nvar hasSpecialSubstring = function(s, k) {\n for (let i = 0; i <= s.length - k; i++) {\n if (i > 0 && s[i - 1] === s[i]) continue;\n if (i + k < s.length && s[i + k] === s[i]) continue;\n let valid = true;\n for (let j = i + 1; j < i + k; j++) {\n if (s[j] !== s[i]) {\n valid = false;\n break;\n }\n }\n if (valid) return true;\n }\n return false;\n};",
"memory": 5700,
"memoryDistribution": "[[5700, 31.9587, \"/**\\n * @param {string} s\\n * @param {number} k\\n * @return {boolean}\\n */\\nvar hasSpecialSubstring = function(s, k) {\\n for (let i = 0; i <= s.length - k; i++) {\\n if (i > 0 && s[i - 1] === s[i]) continue;\\n if (i + k < s.length && s[i + k] === s[i]) continue;\\n let valid = true;\\n for (let j = i + 1; j < i + k; j++) {\\n if (s[j] !== s[i]) {\\n valid = false;\\n break;\\n }\\n }\\n if (valid) return true;\\n }\\n return false;\\n};\"], [54000, 1.0309, \"/**\\n * @param {string} s\\n * @param {number} k\\n * @return {boolean}\\n */\\nvar hasSpecialSubstring = function(s, k) {\\n let prev ;\\n let count =0;\\n for(let i=0;i<s.length;i++){\\n if(s[i]===prev){\\n count++;\\n }else{\\n count=1;\\n }\\n if(count===k && s[i+1]!==s[i] && s[i-k]!==s[i]){\\n return true;\\n }\\n prev = s[i];\\n }\\n return false;\\n};\"], [54200, 1.0309, \"/**\\n * @param {string} s\\n * @param {number} k\\n * @return {boolean}\\n */\\nvar hasSpecialSubstring = function(s, k) {\\n const n = s.length;\\n let prev, count = 0;\\n\\n for (let i = 0; i < n; ++i) {\\n if (prev === s[i]) ++count;\\n else {\\n if (count === k) return true;\\n count = 1;\\n prev = s[i];\\n }\\n }\\n\\n return count === k;\\n};\"], [54500, 1.0309, null], [54700, 1.0309, null], [54800, 1.0309, null], [54900, 1.0309, null], [55000, 4.1237, null], [55100, 3.0928, null], [55200, 3.0928, null], [55300, 3.0928, null], [55400, 10.3093, null], [55500, 9.2784, null], [55600, 1.0309, null], [55700, 3.0928, null], [55900, 2.0619, null], [56000, 7.2165, null], [56200, 2.0619, null], [56300, 2.0619, null], [56400, 1.0309, null], [56500, 4.1237, null], [56700, 2.0619, null], [56800, 3.0928, null], [56900, 1.0309, null], [57000, 3.0928, null], [57100, 1.0309, null], [57200, 1.0309, null], [57500, 1.0309, null], [57700, 1.0309, null], [57900, 1.0309, null], [58200, 1.0309, null], [58600, 1.0309, null], [58900, 1.0309, null], [59000, 1.0309, null], [59600, 2.0619, null], [59800, 1.0309, null], [60300, 1.0309, null], [60400, 1.0309, null], [60600, 1.0309, null], [60700, 2.0619, null], [60900, 1.0309, null], [61000, 1.0309, null], [61100, 1.0309, null], [61200, 1.0309, null], [61900, 1.0309, \"/**\\n * @param {string} s\\n * @param {number} k\\n * @return {boolean}\\n */\\nvar hasSpecialSubstring = function(s, k) {\\n let [l, r] = [0, k - 1];\\n while(r < s.length){\\n let set = new Set(s.slice(l, r + 1)); \\n let prevChar = s[l - 1] || \\\"\\\";\\n let nextChar = s[r + 1] || \\\"\\\";\\n if(set.size === 1 && prevChar !== s[l] && nextChar !== s[r])\\n return true;\\n l++;\\n r++;\\n }\\n return false;\\n};\"], [62400, 1.0309, \"/**\\n * @param {string} s\\n * @param {number} k\\n * @return {boolean}\\n */\\nvar hasSpecialSubstring = function(s, k) {\\n if(s.length ==k && k==1) return true\\n let temp ='',count\\n\\n for(let x=0;x,x<s.length;x++){\\n // if(k===1 && s[x]!==s[x+1]) return true\\n if(s[x]==temp) count++\\n else {\\n temp=s[x]\\n count=1\\n }\\n if(count === k && s[x+1]!==temp) return true\\n console.log(s[x])\\n }\\nreturn false\\n\\n \\n};\"]]",
"runtime": 2,
"runtimeDistribution": "[[0, 31.9588, \"/**\\n * @param {string} s\\n * @param {number} k\\n * @return {boolean}\\n */\\nvar hasSpecialSubstring = function(s, k) {\\n let count=0;\\n let prev='';\\n for(let i=0;i<s.length;i++){\\n if(prev===s[i])count++;\\n else{\\n if(count===k) return true;\\n count=1;\\n prev=s[i]\\n\\n }\\n }\\n return count===k;\\n};\"], [1, 22.6804, \"/**\\n * @param {string} s\\n * @param {number} k\\n * @return {boolean}\\n */\\nvar hasSpecialSubstring = function(s, k) {\\n for (let i = 0; i <= s.length - k; i++) {\\n if (s[i - 1] == s[i]) {\\n continue;\\n }\\n else if (s[i + k] == s[i]) {\\n continue;\\n }\\n\\n let found = true;\\n\\n for (let j = i; j < i + k; j++) {\\n if (s[j] != s[i]) {\\n found = false;\\n break;\\n }\\n }\\n\\n if (found) return true;\\n }\\n\\n return false;\\n};\"], [2, 7.2165, null], [3, 12.3711, null], [4, 1.0309, null], [5, 3.0928, null], [6, 2.0619, null], [7, 2.0619, null], [9, 4.1237, null], [10, 5.1546, null], [11, 1.0309, null], [13, 1.0309, \"/**\\n * @param {string} s\\n * @param {number} k\\n * @return {boolean}\\n */\\nvar hasSpecialSubstring = function(s, k) {\\n let [l, r] = [0, k - 1];\\n while(r < s.length){\\n let set = new Set(s.slice(l, r + 1)); \\n let prevChar = s[l - 1] || \\\"\\\";\\n let nextChar = s[r + 1] || \\\"\\\";\\n if(set.size === 1 && prevChar !== s[l] && nextChar !== s[r])\\n return true;\\n l++;\\n r++;\\n }\\n return false;\\n};\"], [58, 1.0309, \"/**\\n * @param {string} s\\n * @param {number} k\\n * @return {boolean}\\n */\\nvar hasSpecialSubstring = function(s, k) {\\n if(s.length ==k && k==1) return true\\n let temp ='',count\\n\\n for(let x=0;x,x<s.length;x++){\\n // if(k===1 && s[x]!==s[x+1]) return true\\n if(s[x]==temp) count++\\n else {\\n temp=s[x]\\n count=1\\n }\\n if(count === k && s[x+1]!==temp) return true\\n console.log(s[x])\\n }\\nreturn false\\n\\n \\n};\"]]"
},
"python3": {
"code": "class Solution:\n def hasSpecialSubstring(self, s: str, k: int) -> bool:\n n = len(s)\n for i in range(n - k + 1):\n if s[i:i+k] == s[i] * k:\n if (i == 0 or s[i-1] != s[i]) and (i + k == n or s[i+k] != s[i]):\n return True\n return False",
"memory": 1800,
"memoryDistribution": "[[1800, 15.4651, \"class Solution:\\n def hasSpecialSubstring(self, s: str, k: int) -> bool:\\n n = len(s)\\n for i in range(n - k + 1):\\n if s[i:i+k] == s[i] * k:\\n if (i == 0 or s[i-1] != s[i]) and (i + k == n or s[i+k] != s[i]):\\n return True\\n return False\"], [17400, 0.1311, \"# leetgptsolver submission\\n# solution generated by model deepseek-reasoner at 2025-03-31 00:54:46.133021 +0200 CEST \\nclass Solution:\\n def hasSpecialSubstring(self, s: str, k: int) -> bool:\\n n = len(s)\\n for i in range(n - k + 1):\\n current_char = s[i]\\n valid = True\\n for j in range(1, k):\\n if s[i + j] != current_char:\\n valid = False\\n break\\n if not valid:\\n continue\\n left_ok = (i == 0) or (s[i-1] != current_char)\\n right_ok = (i + k == n) or (s[i + k] != current_char)\\n if left_ok and right_ok:\\n return True\\n return False\"], [17500, 1.4417, \"class Solution:\\n def hasSpecialSubstring(self, s: str, k: int) -> bool:\\n split_s = []\\n for a in s:\\n if split_s == []:\\n split_s.append(a)\\n elif split_s[-1][-1] == a:\\n split_s[-1] += a\\n else:\\n split_s.append(a)\\n\\n for a in split_s:\\n if len(a) == k:\\n return True\\n\\n return False\"], [17600, 12.3198, null], [17700, 27.1298, null], [17800, 19.5282, \"class Solution:\\n def hasSpecialSubstring(self, s: str, k: int) -> bool:\\n n = len(s)\\n \\n if k > n:\\n return False\\n \\n for i in range(n - k + 1):\\n x = True\\n for j in s[i:i + k]:\\n if j != s[i]:\\n x = False\\n break\\n if x and (i == 0 or s[i - 1] != s[i]) and (i + k == n or s[i + k] != s[i]):\\n return True\\n \\n return False\\n \"], [17900, 23.9843, \"class Solution:\\n def hasSpecialSubstring(self, s: str, k: int) -> bool:\\n n = len(s)\\n for i in range(n - k + 1):\\n if s[i:i+k] == s[i] * k:\\n if (i == 0 or s[i-1] != s[i]) and (i + k == n or s[i+k] != s[i]):\\n return True\\n return False\\n\"]]",
"runtime": 2,
"runtimeDistribution": "[[0, 41.2844, \"class Solution:\\n def hasSpecialSubstring(self, s: str, k: int) -> bool:\\n i=0\\n if len(s)==1:\\n return True\\n \\n while i<len(s):\\n \\n if i+1<len(s) and s[i]==s[i+1]:\\n x=i\\n while i+1<len(s) and s[i]==s[i+1]:\\n i+=1\\n \\n if i-x+1==k:\\n return True\\n elif k==1:\\n return True\\n \\n i+=1\\n return False\\n \"], [1, 6.5531, \"class Solution:\\n def hasSpecialSubstring(self, s: str, k: int) -> bool:\\n cnt = 1\\n for i in range(1, len(s)):\\n if s[i] == s[i - 1]:\\n cnt += 1\\n continue\\n if cnt == k:\\n return True\\n cnt = 1\\n return cnt == k\"], [2, 7.3394, null], [3, 25.2949, null], [4, 7.6016, null], [5, 2.097, \"class Solution:\\n def hasSpecialSubstring(self, s: str, k: int) -> bool:\\n for i in range(len(s)-k+1):\\n if len(set(s[i:i+k]))==1:\\n if (i-1>=0 and s[i-1]!=s[i]) or (i-1<0):\\n if (i+k<len(s) and s[i+k]!=s[i]) or i+k>=len(s):\\n return True\\n return False\"], [6, 1.7038, \"# 3456.) Find Special Substring of Length K\\n# Categories: String\\n\\nclass Solution:\\n def hasSpecialSubstring(self, s: str, k: int) -> bool:\\n for i in range(len(s)):\\n substring = s[i : i + k]\\n\\n if len(substring) != k or len(set(substring)) != 1:\\n continue\\n\\n if i - 1 < 0:\\n character_before_the_substring = ' '\\n \\n else:\\n character_before_the_substring = s[i - 1]\\n \\n if i + k > len(s) - 1:\\n character_after_the_substring = ' '\\n \\n else:\\n character_after_the_substring = s[i + k]\\n\\n\\n if character_before_the_substring not in substring and character_after_the_substring not in substring:\\n return True\\n \\n return False\"]]"
},
"ruby": {
"code": "def has_special_substring(s, k)\n (0..s.length - k).each do |i|\n candidate = s[i, k]\n if candidate == candidate[0] * k\n if i > 0 && s[i - 1] == candidate[0]\n next\n end\n if i + k < s.length && s[i + k] == candidate[0]\n next\n end\n return true\n end\n end\n false\nend",
"memory": 21200,
"memoryDistribution": "[[21200, 80.0, \"def has_special_substring(s, k)\\n (0..s.length - k).each do |i|\\n candidate = s[i, k]\\n if candidate == candidate[0] * k\\n if i > 0 && s[i - 1] == candidate[0]\\n next\\n end\\n if i + k < s.length && s[i + k] == candidate[0]\\n next\\n end\\n return true\\n end\\n end\\n false\\nend\"], [211500, 10.0, \"# @param {String} s\\n# @param {Integer} k\\n# @return {Boolean}\\ndef has_special_substring(s, k)\\n return true if s.length == 1 && k == 1\\n counter = 1\\n (0...s.length - 1).each do |i|\\n if s[i] == s[i+1]\\n counter += 1 \\n else\\n return true if counter == k\\n counter = 1\\n end\\n end\\n return true if counter == k\\n false\\nend\"], [211600, 10.0, \"# @param {String} s\\n# @param {Integer} k\\n# @return {Boolean}\\ndef has_special_substring(s, k)\\n return true if s.length == 1 && k == 1\\n counter = 1\\n s.bytes.each_cons(2) do |(left, right)|\\n if left == right\\n counter += 1 \\n else\\n return true if counter == k\\n counter = 1\\n end\\n end\\n counter == k\\nend\"], [211700, 60.0, \"# @param {String} s\\n# @param {Integer} k\\n# @return {Boolean}\\n\\nclass Integer\\n\\n def self.gcd(x, y)\\n \\n return x if y == 0\\n\\n Integer.gcd(y, x % y)\\n end\\n\\n\\n def self.lcm(x, y)\\n\\n x / Integer.gcd(x, y) * y\\n\\n end\\n\\n def self.max(x, y)\\n \\n return x if x > y\\n\\n y\\n end\\n\\n def self.min(x, y)\\n return y if y < x\\n\\n x\\n end\\n\\nend\\n\\nclass String\\n\\n def counter\\n f = {}\\n n = self.size\\n for i in 0...n do\\n f[self[i]] = 0 if f[self[i]] == nil \\n f[self[i]] += 1\\n end\\n f\\n end\\n\\n def substring(l, r)\\n result = \\\"\\\"\\n\\n for i in Integer.max(l, 0)...Integer.min(r, self.size) do\\n result += self[i]\\n end\\n\\n result\\n end\\n\\n def max\\n n = self.size\\n return nil if n == 0\\n maximum = self[0]\\n for i in 1...n do\\n maximum = Integer.max(maximum, self[i])\\n end\\n maximum\\n end\\n\\nend\\n\\ndef has_special_substring(s, k)\\n l = 0\\n r = k\\n n = s.size\\n while r <= n do\\n return true if (s.substring(l, r).counter.size == 1) &&\\n (l <= 0 || s[l - 1] != s[l]) &&\\n (r >= n || s[r - 1] != s[r])\\n l += 1\\n r += 1\\n end \\n false\\nend\"], [211800, 20.0, \"# @param {String} s\\n# @param {Integer} k\\n# @return {Boolean}\\ndef has_special_substring(s, k)\\n s.chars.chunk_while {|a,b| a == b}.map(&:size).include?(k)\\nend\"]]",
"runtime": 4,
"runtimeDistribution": "[[0, 40.0, \"# @param {String} s\\n# @param {Integer} k\\n# @return {Boolean}\\ndef has_special_substring(s, k)\\n s.chars.chunk_while {|a,b| a == b}.map(&:size).include?(k)\\nend\"], [4, 10.0, \"def has_special_substring(s, k)\\n (0..s.length - k).each do |i|\\n candidate = s[i, k]\\n if candidate == candidate[0] * k\\n if i > 0 && s[i - 1] == candidate[0]\\n next\\n end\\n if i + k < s.length && s[i + k] == candidate[0]\\n next\\n end\\n return true\\n end\\n end\\n false\\nend\"], [5, 10.0, null], [6, 10.0, null], [7, 10.0, \"# @param {String} s\\n# @param {Integer} k\\n# @return {Boolean}\\ndef has_special_substring(s, k)\\n s.bytes.chunk_while {|a,b| a == b}.any? {|el| el.size == k}\\n # return true if s.length == 1 && k == 1\\n # counter = 1\\n # (0...s.length - 1).each do |i|\\n # if s[i] == s[i+1]\\n # counter += 1 \\n # else\\n # return true if counter == k\\n # counter = 1\\n # end\\n # end\\n # return true if counter == k\\n # false\\nend\"], [8, 10.0, \"# @param {String} s\\n# @param {Integer} k\\n# @return {Boolean}\\ndef has_special_substring(s, k)\\n # s.bytes.chunk_while {|a,b| a == b}.any? {|el| el.size == k}\\n return true if s.length == 1 && k == 1\\n counter = 1\\n s.bytes.each_cons(2) do |el|\\n if el[0] == el[1]\\n counter += 1 \\n else\\n return true if counter == k\\n counter = 1\\n end\\n end\\n return true if counter == k\\n false\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list[dict]:
import random
random.seed(seed)
# Sample solution based on the provided sample solution.
def sample_solution(s: str, k: int) -> bool:
n = len(s)
for i in range(n - k + 1):
if s[i:i+k] == s[i] * k:
if (i == 0 or s[i-1] != s[i]) and (i + k == n or s[i+k] != s[i]):
return True
return False
# Predefined test cases covering various edge and boundary scenarios.
predefined = [
("aaabaaa", 3), # Example: Valid special substring (middle block qualifies)
("abc", 2), # No substring of length 2 with same char.
("aaa", 3), # Entire string qualifies.
("aaaaa", 3), # All windows fail because neighbors repeat.
("aaab", 3), # Substring at beginning qualifies.
("baaa", 3), # Substring at end qualifies.
("abbbacd", 3), # Middle block qualifies.
("abbaaaacc", 4), # Valid special substring in the middle.
("a", 1), # Single character always qualifies.
("abababab", 1) # Alternating characters: every char qualifies as isolated.
]
cases = []
predef_count = len(predefined)
idx = 0
while len(cases) < num_cases:
if idx < predef_count:
s, k = predefined[idx]
idx += 1
else:
# Generate a random test case.
length = random.randint(1, 100)
s = ''.join(random.choice('abcdefghijklmnopqrstuvwxyz') for _ in range(length))
k = random.randint(1, length)
# Simple serialization: s and k separated by a space.
test_input = f"{s} {k}"
expected = sample_solution(s, k)
# Serialize expected boolean as lower-case string.
test_output = "true" if expected else "false"
cases.append({"input": test_input, "output": test_output})
return cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
# Deserialization: Trim and lower-case the outputs.
def deserialize_bool(output_str: str) -> bool:
normalized = output_str.strip().lower()
if normalized == "true":
return True
elif normalized == "false":
return False
else:
# If output is not recognized, treat it as incorrect.
return None
expected = deserialize_bool(expected_output)
program = deserialize_bool(program_output)
return expected == program
|
[{"input": "aaabaaa 3", "output": "true"}, {"input": "abc 2", "output": "false"}, {"input": "aaa 3", "output": "true"}, {"input": "aaaaa 3", "output": "false"}, {"input": "aaab 3", "output": "true"}, {"input": "baaa 3", "output": "true"}, {"input": "abbbacd 3", "output": "true"}, {"input": "abbaaaacc 4", "output": "true"}, {"input": "a 1", "output": "true"}, {"input": "abababab 1", "output": "true"}, {"input": "daxihhexdvxrcsnbacghqtargwuwrnhosizayzfwnkiegykdcmdlltizbxordmcrjutlsgwcbvhyjchdmi 59", "output": "false"}, {"input": "lfllgviwvuctufrxhfomiuwrhvkyybhbzkmicgswkgupmuoeiehxrrixsnsmlheqpcybdeufzvntcmmtoq 33", "output": "false"}, {"input": "avxdvryiyukdjnfoaxxiqyfqdujuqtgelyfryqatkpadlzjhbhsccxpcyryeevprfiqtngr 26", "output": "false"}, {"input": "jmvuloqodhhckasrhshacwubhcbkcqhivpgrexssphzpzngddvnlnnoxbvuudbmxkzdhggroenfiohcozrdburacyhfn 63", "output": "false"}, {"input": "gmbfmamizzojnwxzrvwpegjgbsxrbxkbbspqqfbqcfctcvhmdshstbtcnvssqk 60", "output": "false"}, {"input": "gvwkhimevujokycaotsdcrgqielchljfor 20", "output": "false"}, {"input": "zuqavrjvdeiddxreijtgwkgvuiqpibcunibakyeuifxorwnradcwerblsrenebjlzblgvhvdlyrntxe 31", "output": "false"}, {"input": "zzfnafxkznzvxzhifzwdm 2", "output": "true"}, {"input": "hgoljzhhavgmkicyiluqmvrkadifsibdtnlxzkntqdmsgibwnaqzrvxxxvgln 5", "output": "false"}, {"input": "ktkvdxjqjvnkmwjregnvmvxftsjmrajjgnzstukooovgqpzzxfvcjqvutkcyhvjhzgeabhptyconusgwwmpmhe 84", "output": "false"}, {"input": "ayydynhfzwqobrhdoezovqrtkyotxqnrofxpoiyhuiyyqpuhiocwjhikkrceehmwewgcnnkronbgnmyswaysmpalj 50", "output": "false"}, {"input": "rxxrzthphinpamkvvzmxfoetramssvacuneofbimkgokkymiynicpa 48", "output": "false"}, {"input": "blhucyubyahgatehepvdsgowiylfttxwdyfjdsajsvmmwgcswuhdwyjvtzdzszblrnvlcq 44", "output": "false"}, {"input": "np 1", "output": "true"}, {"input": "luowenfxquitzryponxsikhciohyostvmkapkfpglzikitwiraqgchxn 32", "output": "false"}, {"input": "yhwpuwpozacjhmwhjvslprqlnxrklwoijihdxgkdxrywfggxpixsyqtjdgjhlfjawreibbrj 17", "output": "false"}, {"input": "ypdasjppokfbipdcmpcsuvbeezsjchdrynttzthyqmoojsnjstbtxdygugivcfhfrcfanowtpjbhjwjwoc 30", "output": "false"}, {"input": "zzusvzgndrhueiecbfzjtxsjodowjwmiqr 32", "output": "false"}, {"input": "ctbnxktiachvssayvisbyyfpquoifsnupcplnkkvdfknwpjvmyrbockik 8", "output": "false"}, {"input": "mqavronbgqltypuoybgirejowpdautzhwfjrarnchdoduepwjqwinpphoremgtqxeciyznkzqiajxjssvpeorplkryrmokgwhsm 30", "output": "false"}, {"input": "nbkxpwzmmvzuepbeqskdodqoaxenuecpziktwmuckvrmkuwyprbtchuvjhxcndyuwdofwjabkzbjllnehqnsvzfffctmtvhpseho 82", "output": "false"}, {"input": "oivazojvrfcolsjunwiojgmpdhmslsjwj 2", "output": "false"}, {"input": "miasvyxbtxpjyzhtzlhugtivyxyvveuduubjzobslxecjkxnfgezrlqqifipzjxkzdoceyhvxvmzrlczmaird 59", "output": "false"}, {"input": "vxvismuldvhpatrkthucuowjundebbjpddhremolvxwrnsxx 10", "output": "false"}, {"input": "udptnibwlgoohldvlrulbmigdocvguutabzkhezsgcyrgsghkyezta 18", "output": "false"}, {"input": "erizfdvaealzzhskafi 2", "output": "true"}, {"input": "xnqdxcpoylqsdoqht 2", "output": "false"}, {"input": "zvqjouabpmnvdpwocckteceitusrwkmtqjoqtndzwduuyrxgnohnkomnxdknkvilevpccccndxxlzerbsrrkvdnlvynxbj 77", "output": "false"}, {"input": "ldsqgevphdlrldyishznryttvuratvwiafiwyjkl 1", "output": "true"}, {"input": "esvmcexuacxqgmnokfljxkys 20", "output": "false"}, {"input": "befytbvciov 7", "output": "false"}, {"input": "tonigyqdlndjvvspqvjbhmtbagjgyeyijkdapxnfemrwhqrvzlcmxbnaocksnsm 46", "output": "false"}, {"input": "njdmakfztowlcndhnsmqcmjxkhkyfcqudqqgyllxuehdeigfteyyucfyupoysysovsuutkukeocpoujzis 8", "output": "false"}, {"input": "qcjoobbljcucttqmosrzxbozsugktpqebodzkwcqufbhwo 29", "output": "false"}, {"input": "qtflljmnykvtbzuukckdrvmjixvtekcsveljuwvmetwcjrmuzkevwxvqcuvnqlaljfgk 63", "output": "false"}, {"input": "heecjzdqyrxqbvkytetmeffwy 20", "output": "false"}, {"input": "xobnlvxhotjyxzohrhjzzp 7", "output": "false"}, {"input": "vsooyjymqqnfgzteibuplrdwqdjcyfioqencholanbmqlhmc 24", "output": "false"}, {"input": "akdwukzeebjpweywpotacaigerxtq 14", "output": "false"}, {"input": "yjhjdbhnuztocdp 10", "output": "false"}, {"input": "auqshwejnatlhsnfvvcqlcqrqzqrampbumlixalzclhxvudysxykeblrkufyvowpufzec 59", "output": "false"}, {"input": "jgbzg 1", "output": "true"}, {"input": "jqmrpibyugjlybukidzlnmxomkfpwplzqizcxncnt 12", "output": "false"}, {"input": "jkdckvjjotwnfwolobxltniuzbcvumlqzxvfaetvzobechyullmsbtevolloycseqlmkui 32", "output": "false"}, {"input": "axfpqmrdiyiwogt 5", "output": "false"}, {"input": "pgdecofwoczvkvlwcrrjjfwwwufzlqhdgzehzpalrslozretccjmwxpqnynscekucoovqleyrusfyenqbdqejffkw 29", "output": "false"}, {"input": "qjcigurieujtrcqufssefvtxtksbacbuysiugysntuapu 35", "output": "false"}, {"input": "ujphzzvmjocwbfonpogktekwkxlmeylqrdkhod 18", "output": "false"}, {"input": "hedbjmtnhfksxkgyfpqopjpacmqohgslbbjptuvpjradneixlymlbmbsrg 24", "output": "false"}, {"input": "jcmqoyritvtdedmlzkrlyegtqmqbbbewkzpqoetqektkfmtxjskqqrpwsjpalkvdnsjzxwu 4", "output": "false"}, {"input": "piuzysshxbspfquxtymevhbswdgaoknenwgnqytpxxbweqgrkvpqmkforkrlvyxvuzwitpghirjhj 37", "output": "false"}, {"input": "gwwpkplrzxijdsvrmmlyzejbjwclouixpggrirwiedtxshhbvqhuhbdnkwpdvyearfnuppugyjkjubycushrxxbfnfb 51", "output": "false"}, {"input": "fxjbajstdkjourqpeqoigzdkfxouiwfaxkzjsvygftumnqkcmvdfepkhaimhoyik 39", "output": "false"}, {"input": "xsaiulwhbvdojfmvqwyjwdujlthhepeoxtlnwrpyrzvgyhvytzcqoqwlcsdbrqgsrefkqodvgws 63", "output": "false"}, {"input": "qozboeqnosbr 8", "output": "false"}, {"input": "zjxamiaxgscbnlwcrbcpbjnfyeyuxunlmommcvvreuldfrmqexhayajovxrnrmhholeigxydbzvntyahgcdtbot 87", "output": "false"}, {"input": "bhxbmohrgyybeqjhxskstyvkhjevqhnjibrsxfuvnrpbluvmzqkwnnejmfyrphhjwezobrnnrqemhigkucolcrxgbim 87", "output": "false"}, {"input": "tbcgzysxvrgpgkjaggxdxyphwtwgmhrkyjmoruljilqpodzxpykglknbshxeairssxnjegkhmshpru 44", "output": "false"}, {"input": "ypxuxpofxzlfexrpfrubqbcvbyaneuhcw 10", "output": "false"}, {"input": "gq 2", "output": "false"}, {"input": "btuvtpvpaarrnaaqxirjaqwvnzfddqehgtqilizmclmoshwh 20", "output": "false"}, {"input": "cuuybcmmmrpbuawfcpnuzksdqbhgwspibcvirsvbfkagseywmcjfshsmvrkmyxezwxcqxlbdnhcktyttmykauizo 63", "output": "false"}, {"input": "lrmnfvsvmcytjzhwcciemwzuexmkld 3", "output": "false"}, {"input": "j 1", "output": "true"}, {"input": "yidecfnorrqndaclrcttzkmajnmycxrhsqfvmfeijipecfn 18", "output": "false"}, {"input": "jpzclihxupttgodejamktmzkoknutejktwgpkfmkjxwupszhkmizml 8", "output": "false"}, {"input": "gsrfvyraxowgozjwczznvpeujhivewnzmcotpsmrqwnrbzlwzrtucdyhvvlfutbsuvumykznd 2", "output": "true"}, {"input": "ihqxqrswsholm 8", "output": "false"}, {"input": "vswqelapdjncdxeljkozgqplpdoxwokcjbzwdakudvzfxhqfrfkrnohzmuffuvnmaxtgosnmawggiywzzcsdzrflkgodivpqukt 50", "output": "false"}, {"input": "msdllotfvwzjtscvekdhjdflweqmntesmnfpurwufrfpjefkotblapegmrqupnvpnwopfcsazyhjbih 69", "output": "false"}, {"input": "fyosxyyprqdsdiyrlrybyxorgndxuyhjboilc 29", "output": "false"}, {"input": "yzhgzxswlwtunfte 7", "output": "false"}, {"input": "zbslritrfkwjjsiqvdeyznbiuew 5", "output": "false"}, {"input": "ewkhyvmpesuiunmocuzycmqxiwlopksa 6", "output": "false"}, {"input": "ouvwlczrmgngpikjkrsespzkvybbduzoadfooangweujficuliclvufbmujxwyhnucwdagpceshqvoaawkdnwepchmcxzd 14", "output": "false"}, {"input": "ljemyyeuvecqsatufolxguxentvogcdeydsxmlnkz 9", "output": "false"}, {"input": "iuchrttxtjywavjgqtqgxmjubzzhpmdh 32", "output": "false"}, {"input": "tcqalkemsnlrvfypycascaigbbzmqjuwqynnwmcurrteicjcqgzerkmsuyuvucjwnxhbhcndottbjvxvxf 16", "output": "false"}, {"input": "we 1", "output": "true"}, {"input": "plqqzxiflexyixdyakzni 17", "output": "false"}, {"input": "iwsucpoql 1", "output": "true"}, {"input": "sflfiydsvxdhxqabahbplmefbrzwxunhkhnxkicsldqvbfhzqbmcojyjkcroalgj 39", "output": "false"}, {"input": "tholspyygxryzheanahrluwakayvmxxjdgqhnpbewicbhqnwloxcsdqeumcssbnvehjikzmwxkkoihcgeyysdedfookndrl 27", "output": "false"}, {"input": "joidcfzvjwwtbgkecwhlmqbvjifamorxrhdodzzedabyhegmlvuucssica 5", "output": "false"}, {"input": "uozeczkdbobfsnxmpamvnflgfi 9", "output": "false"}, {"input": "ebttthujpnrpbcimenguzqhuzrzamzwlprzplsqkmifakthazyibzpqlys 15", "output": "false"}, {"input": "dhvhirzxbyhszmlffhskz 12", "output": "false"}, {"input": "awwlssesgzprjfpbcbhthaqpaktgzekwfzkbaesweydqlclwvmsdkjkefxnzupukfwrwtzlhvsfm 40", "output": "false"}, {"input": "wjefxawsmysbftkzthusdpekxchlkfucwvuxkoaighwclizdxabmoxnfnpmlrmdpzsuyvhfoczbjakidckfmfxcrckttpw 4", "output": "false"}, {"input": "uftnfbdkggnwrxxrivjjhdbmsrpeblancjvutpgdagfujcpdjzmppvic 42", "output": "false"}]
|
{
"cpp": "==Code Submission==\n\npair<string, int> deserialize_stdin(const string &input) {\n istringstream iss(input);\n string s;\n int k;\n iss >> s >> k;\n return {s, k};\n}\n\nstring serialize_stdout(bool result) {\n return result ? \"true\" : \"false\";\n}\n\nint main(){\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n string line;\n getline(cin, line);\n auto parsed = deserialize_stdin(line);\n string s = parsed.first;\n int k = parsed.second;\n Solution sol; // The submitted solution will be injected here.\n bool ans = sol.hasSpecialSubstring(s, k);\n cout << serialize_stdout(ans);\n return 0;\n}",
"golang": "==Code Submission==\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n line, _ := reader.ReadString('\\n')\n line = strings.TrimSpace(line)\n parts := strings.SplitN(line, \" \", 2)\n s := parts[0]\n k, _ := strconv.Atoi(parts[1])\n ans := hasSpecialSubstring(s, k) // Call to the submitted solution.\n if ans {\n fmt.Print(\"true\")\n } else {\n fmt.Print(\"false\")\n }\n}",
"java": "public class Main {\n public static void main(String[] args) throws Exception {\n java.io.BufferedReader br = new java.io.BufferedReader(new java.io.InputStreamReader(System.in));\n String line = br.readLine().trim();\n String[] parts = line.split(\" \", 2);\n String s = parts[0];\n int k = Integer.parseInt(parts[1]);\n Solution sol = new Solution(); // The submitted solution will be injected here.\n boolean ans = sol.hasSpecialSubstring(s, k);\n System.out.println(ans ? \"true\" : \"false\");\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\n\nfunction deserialize_stdin(input) {\n // Expect input format: \"<s> <k>\" with a single space separator.\n let parts = input.trim().split(' ');\n let s = parts[0];\n let k = parseInt(parts[1], 10);\n return { s, k };\n}\n\nfunction serialize_stdout(result) {\n return result ? \"true\" : \"false\";\n}\n\nlet input = '';\nprocess.stdin.on('data', chunk => { input += chunk; });\nprocess.stdin.on('end', () => {\n const { s, k } = deserialize_stdin(input);\n const ans = hasSpecialSubstring(s, k); // Call to the submitted solution.\n process.stdout.write(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str):\n # Expect input format: \"<s> <k>\" where s is a string and k is an integer.\n parts = input_str.split(' ', 1)\n s = parts[0]\n k = int(parts[1])\n return s, k\n\ndef serialize_stdout(result):\n return \"true\" if result else \"false\"\n\nif __name__ == \"__main__\":\n input_str = sys.stdin.read().strip()\n s, k = deserialize_stdin(input_str)\n sol = Solution() # The submitted solution will be injected here.\n ans = sol.hasSpecialSubstring(s, k)\n sys.stdout.write(serialize_stdout(ans))",
"ruby": "==Code Submission==\ninput = gets.strip\ns, k_str = input.split(\" \", 2)\nk = k_str.to_i\nans = has_special_substring(s, k) # Call to the submitted solution.\nputs ans ? \"true\" : \"false\""
}
|
3712
|
Minimum Cost to Make Arrays Identical
|
minimum-cost-to-make-arrays-identical
|
<p>You are given two integer arrays <code>arr</code> and <code>brr</code> of length <code>n</code>, and an integer <code>k</code>. You can perform the following operations on <code>arr</code> <em>any</em> number of times:</p>
<ul>
<li>Split <code>arr</code> into <em>any</em> number of <strong>contiguous</strong> <span data-keyword="subarray-nonempty">subarrays</span> and rearrange these subarrays in <em>any order</em>. This operation has a fixed cost of <code>k</code>.</li>
<li>
<p>Choose any element in <code>arr</code> and add or subtract a positive integer <code>x</code> to it. The cost of this operation is <code>x</code>.</p>
</li>
</ul>
<p>Return the <strong>minimum </strong>total cost to make <code>arr</code> <strong>equal</strong> to <code>brr</code>.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">arr = [-7,9,5], brr = [7,-2,-5], k = 2</span></p>
<p><strong>Output:</strong> <span class="example-io">13</span></p>
<p><strong>Explanation:</strong></p>
<ul>
<li>Split <code>arr</code> into two contiguous subarrays: <code>[-7]</code> and <code>[9, 5]</code> and rearrange them as <code>[9, 5, -7]</code>, with a cost of 2.</li>
<li>Subtract 2 from element <code>arr[0]</code>. The array becomes <code>[7, 5, -7]</code>. The cost of this operation is 2.</li>
<li>Subtract 7 from element <code>arr[1]</code>. The array becomes <code>[7, -2, -7]</code>. The cost of this operation is 7.</li>
<li>Add 2 to element <code>arr[2]</code>. The array becomes <code>[7, -2, -5]</code>. The cost of this operation is 2.</li>
</ul>
<p>The total cost to make the arrays equal is <code>2 + 2 + 7 + 2 = 13</code>.</p>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">arr = [2,1], brr = [2,1], k = 0</span></p>
<p><strong>Output:</strong> <span class="example-io">0</span></p>
<p><strong>Explanation:</strong></p>
<p>Since the arrays are already equal, no operations are needed, and the total cost is 0.</p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>1 <= arr.length == brr.length <= 10<sup>5</sup></code></li>
<li><code>0 <= k <= 2 * 10<sup>10</sup></code></li>
<li><code>-10<sup>5</sup> <= arr[i] <= 10<sup>5</sup></code></li>
<li><code>-10<sup>5</sup> <= brr[i] <= 10<sup>5</sup></code></li>
</ul>
|
You are given two integer arrays `arr` and `brr` of length `n`, and an integer `k`. You can perform the following operations on `arr` *any* number of times:
- Split `arr` into *any* number of **contiguous** subarrays and rearrange these subarrays in *any order*. This operation has a fixed cost of `k`.
- Choose any element in `arr` and add or subtract a positive integer `x` to it. The cost of this operation is `x`.
Return the **minimum** total cost to make `arr` **equal** to `brr`.
**Example 1:**
**Input:** arr \= \[\-7,9,5], brr \= \[7,\-2,\-5], k \= 2
**Output:** 13
**Explanation:**
- Split `arr` into two contiguous subarrays: `[-7]` and `[9, 5]` and rearrange them as `[9, 5, -7]`, with a cost of 2\.
- Subtract 2 from element `arr[0]`. The array becomes `[7, 5, -7]`. The cost of this operation is 2\.
- Subtract 7 from element `arr[1]`. The array becomes `[7, -2, -7]`. The cost of this operation is 7\.
- Add 2 to element `arr[2]`. The array becomes `[7, -2, -5]`. The cost of this operation is 2\.
The total cost to make the arrays equal is `2 + 2 + 7 + 2 = 13`.
**Example 2:**
**Input:** arr \= \[2,1], brr \= \[2,1], k \= 0
**Output:** 0
**Explanation:**
Since the arrays are already equal, no operations are needed, and the total cost is 0\.
**Constraints:**
- `1 <= arr.length == brr.length <= 105`
- `0 <= k <= 2 * 1010`
- `-105 <= arr[i] <= 105`
- `-105 <= brr[i] <= 105`
|
Medium
|
[
"array",
"greedy",
"sorting"
] |
leetcode
|
https://leetcode.com/problems/minimum-cost-to-make-arrays-identical
|
functional
| null | null | null | null |
{
"c": "long long minCost(int* arr, int arrSize, int* brr, int brrSize, long long k) {\n \n}",
"cpp": "class Solution {\npublic:\n long long minCost(vector<int>& arr, vector<int>& brr, long long k) {\n \n }\n};",
"csharp": "public class Solution {\n public long MinCost(int[] arr, int[] brr, long k) {\n \n }\n}",
"dart": "class Solution {\n int minCost(List<int> arr, List<int> brr, int k) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec min_cost(arr :: [integer], brr :: [integer], k :: integer) :: integer\n def min_cost(arr, brr, k) do\n \n end\nend",
"erlang": "-spec min_cost(Arr :: [integer()], Brr :: [integer()], K :: integer()) -> integer().\nmin_cost(Arr, Brr, K) ->\n .",
"golang": "func minCost(arr []int, brr []int, k int64) int64 {\n \n}",
"java": "class Solution {\n public long minCost(int[] arr, int[] brr, long k) {\n \n }\n}",
"javascript": "/**\n * @param {number[]} arr\n * @param {number[]} brr\n * @param {number} k\n * @return {number}\n */\nvar minCost = function(arr, brr, k) {\n \n};",
"kotlin": "class Solution {\n fun minCost(arr: IntArray, brr: IntArray, k: Long): Long {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param Integer[] $arr\n * @param Integer[] $brr\n * @param Integer $k\n * @return Integer\n */\n function minCost($arr, $brr, $k) {\n \n }\n}",
"python": "class Solution(object):\n def minCost(self, arr, brr, k):\n \"\"\"\n :type arr: List[int]\n :type brr: List[int]\n :type k: int\n :rtype: int\n \"\"\"\n ",
"python3": "class Solution:\n def minCost(self, arr: List[int], brr: List[int], k: int) -> int:\n ",
"racket": "(define/contract (min-cost arr brr k)\n (-> (listof exact-integer?) (listof exact-integer?) exact-integer? exact-integer?)\n )",
"ruby": "# @param {Integer[]} arr\n# @param {Integer[]} brr\n# @param {Integer} k\n# @return {Integer}\ndef min_cost(arr, brr, k)\n \nend",
"rust": "impl Solution {\n pub fn min_cost(arr: Vec<i32>, brr: Vec<i32>, k: i64) -> i64 {\n \n }\n}",
"scala": "object Solution {\n def minCost(arr: Array[Int], brr: Array[Int], k: Long): Long = {\n \n }\n}",
"swift": "class Solution {\n func minCost(_ arr: [Int], _ brr: [Int], _ k: Int) -> Int {\n \n }\n}",
"typescript": "function minCost(arr: number[], brr: number[], k: number): number {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n long long minCost(vector<int>& arr, vector<int>& brr, long long k) {\n int n = arr.size();\n long long costNoReorder = 0;\n for (int i = 0; i < n; i++) {\n costNoReorder += llabs((long long)arr[i] - (long long)brr[i]);\n }\n vector<int> arrSorted = arr, brrSorted = brr;\n sort(arrSorted.begin(), arrSorted.end());\n sort(brrSorted.begin(), brrSorted.end());\n long long costReorderAdjust = 0;\n for (int i = 0; i < n; i++) {\n costReorderAdjust += llabs((long long)arrSorted[i] - (long long)brrSorted[i]);\n }\n long long costReorder = k + costReorderAdjust;\n return costNoReorder < costReorder ? costNoReorder : costReorder;\n }\n};",
"memory": 19700,
"memoryDistribution": "[[19700, 18.9094, \"#include <vector>\\n#include <algorithm>\\n#include <cstdlib>\\nusing namespace std;\\nclass Solution {\\npublic:\\n long long minCost(vector<int>& arr, vector<int>& brr, long long k) {\\n int n = arr.size();\\n long long costNoReorder = 0;\\n for (int i = 0; i < n; i++) {\\n costNoReorder += llabs((long long)arr[i] - (long long)brr[i]);\\n }\\n vector<int> arrSorted = arr, brrSorted = brr;\\n sort(arrSorted.begin(), arrSorted.end());\\n sort(brrSorted.begin(), brrSorted.end());\\n long long costReorderAdjust = 0;\\n for (int i = 0; i < n; i++) {\\n costReorderAdjust += llabs((long long)arrSorted[i] - (long long)brrSorted[i]);\\n }\\n long long costReorder = k + costReorderAdjust;\\n return costNoReorder < costReorder ? costNoReorder : costReorder;\\n }\\n};\"], [189000, 0.3636, \"class Solution {\\npublic:\\n \\n long long minCost(vector<int>& arr, vector<int>& brr, long long k) {\\n int n=arr.size();\\n int diff;\\n long long ans=0;\\n for(int i=0;i<n;i++){\\n diff=arr[i]-brr[i];\\n ans+=abs(diff);\\n }\\n\\n long long sum=0;\\n sort(arr.begin(),arr.end());//k\\n sort(brr.begin(),brr.end());\\n for(int i=0;i<n;i++){\\n sum+=abs(arr[i]-brr[i]);\\n }\\n return min(ans,sum+k);\\n\\n }\\n};\"], [189100, 4.7273, \"class Solution {\\npublic:\\n long long minCost(vector<int>& arr, vector<int>& brr, long long k) {\\n int n = arr.size();\\n long long cost = 0;\\n for(int i=0; i<n; i++){\\n cost += abs(arr[i]-brr[i]);\\n }\\n long long ans = k ;\\n sort(arr.begin(),arr.end());\\n sort(brr.begin(),brr.end());\\n for(int i=0; i<n; i++){\\n ans += abs(arr[i]-brr[i]);\\n }\\n return min(cost,ans);\\n }\\n};\"], [189200, 30.1818, null], [189300, 25.4545, null], [189400, 16.3636, null], [189500, 0.7273, null], [190500, 0.3636, null], [192200, 0.3636, null], [192300, 0.3636, null], [194000, 0.3636, null], [194200, 0.3636, null], [197500, 1.4545, null], [197600, 2.9091, null], [197700, 4.3636, null], [197800, 0.7273, null], [204500, 0.7273, null], [204700, 0.3636, null], [205800, 0.3636, null], [207100, 0.3636, null], [224800, 0.7273, null], [224900, 1.0909, null], [225000, 0.7273, null], [226100, 0.3636, null], [231500, 0.3636, \"class Solution {\\npublic:\\n long long minCost(vector<int>& arr, vector<int>& brr, long long k) {\\n int n = arr.size();\\n unordered_map<int,int> pt;\\n long long result2 = 0;\\n for(int i=0;i<n;i++){\\n pt[arr[i]] = brr[i];\\n result2+=abs(arr[i]-brr[i]);\\n }\\n sort(arr.begin(),arr.end());\\n sort(brr.begin(),brr.end());\\n bool check = false;\\n for(int i=0;i<n;i++){\\n if(pt[arr[i]]!=brr[i]){\\n check = true;\\n break;\\n }\\n }\\n long long int result = 0;\\n for(int i=0;i<n;i++){\\n result+=abs(arr[i]-brr[i]);\\n }\\n return min(result + (check*k),result2);\\n }\\n};\\n// -7 5 9\\n// -5 -2 7\\n// 2 7 2\"], [231600, 0.3636, \"class Solution {\\npublic:\\n long long minCost(vector<int>& arr, vector<int>& brr, long long k) {\\n long long ans=0;\\n unordered_map<int,int>ma;\\n int n =arr.size();\\n long long ans1=0;\\n for(int i=0;i<n;i++){\\n ma[arr[i]]=brr[i];\\n ans1+=abs(arr[i]-brr[i]);\\n }\\n\\n sort(arr.begin(),arr.end());\\n sort(brr.begin(),brr.end());\\n\\n int t=0;\\n\\n for(int i=0;i<n;i++){\\n ans+=abs(arr[i]-brr[i]);\\n if(ma[arr[i]]!=brr[i]) t=1;\\n }\\n\\n if(t) ans+=k;\\n\\n return min(ans,ans1);\\n }\\n};\"]]",
"runtime": 79,
"runtimeDistribution": "[[1, 0.7272, \"#pragma GCC optimize(\\\"Ofast\\\")\\n#pragma GCC target(\\\"sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,avx2,fma\\\")\\n#pragma GCC optimize(\\\"unroll-loops\\\")\\n#include <bits/stdc++.h>\\n#include <ext/pb_ds/assoc_container.hpp>\\n#include <ext/pb_ds/tree_policy.hpp>\\nusing namespace __gnu_pbds;\\nusing namespace std;\\nconst auto __ = []() { struct ___ { static void _() { std::ofstream(\\\"display_runtime.txt\\\") << 0 << '\\\\n'; } }; std::atexit(&___::_); return 0; }();\\n\\nclass Solution {\\npublic:\\n long long minCost(vector<int>& arr, vector<int>& brr, long long k) {\\n// Calculate original difference (without sorting)\\n long long ans1 = 0LL;\\n int n = arr.size();\\n for(int i = 0; i < n; i++) {\\n ans1 += abs(arr[i] - brr[i]);\\n }\\n \\n // Sort both arrays\\n sort(arr.begin(), arr.end());\\n sort(brr.begin(), brr.end());\\n \\n // Calculate difference after sorting + cost k\\n long long ans2 = k;\\n for(int i = 0; i < n; i++) {\\n ans2 += abs(arr[i] - brr[i]);\\n }\\n \\n // Return the minimum cost\\n return min(ans1, ans2);\\n }\\n};\"], [4, 0.7273, \"class Solution {\\n public:\\n\\tlong long minCost(vector<int>& arr, vector<int>& brr, long long k) {\\n\\t\\tlong long original_cost = 0;\\n\\t\\tfor (size_t i = 0; i < arr.size(); ++i) {\\n\\t\\t\\toriginal_cost += abs((long long)brr[i] - arr[i]);\\n\\t\\t}\\n\\n\\t\\tif (k >= original_cost) {\\n\\t\\t\\treturn original_cost;\\n\\t\\t}\\n\\n\\t\\tsort(arr.begin(), arr.end());\\n\\t\\tsort(brr.begin(), brr.end());\\n\\n\\t\\tlong long sorted_cost = 0;\\n\\t\\tfor (size_t i = 0; i < arr.size(); ++i) {\\n\\t\\t\\tsorted_cost += abs((long long)brr[i] - arr[i]);\\n\\t\\t}\\n\\n\\t\\treturn min(original_cost, sorted_cost + k);\\n\\t}\\n};\"], [7, 0.3636, null], [10, 0.3636, null], [13, 0.7273, null], [16, 0.3636, null], [19, 0.3636, null], [22, 1.4545, null], [25, 0.7272, null], [28, 0.3636, null], [32, 0.3636, null], [35, 0.3636, null], [38, 0.3636, null], [41, 0.3636, null], [44, 0.3636, null], [47, 0.7273, null], [50, 1.0909, null], [53, 0.3636, null], [56, 1.4545, null], [59, 1.4545, null], [62, 6.545499999999999, null], [65, 5.0908999999999995, null], [68, 6.1818, null], [71, 8.0001, null], [74, 10.1818, null], [77, 6.5454, null], [79, 49.4551, \"#include <vector>\\n#include <algorithm>\\n#include <cstdlib>\\nusing namespace std;\\nclass Solution {\\npublic:\\n long long minCost(vector<int>& arr, vector<int>& brr, long long k) {\\n int n = arr.size();\\n long long costNoReorder = 0;\\n for (int i = 0; i < n; i++) {\\n costNoReorder += llabs((long long)arr[i] - (long long)brr[i]);\\n }\\n vector<int> arrSorted = arr, brrSorted = brr;\\n sort(arrSorted.begin(), arrSorted.end());\\n sort(brrSorted.begin(), brrSorted.end());\\n long long costReorderAdjust = 0;\\n for (int i = 0; i < n; i++) {\\n costReorderAdjust += llabs((long long)arrSorted[i] - (long long)brrSorted[i]);\\n }\\n long long costReorder = k + costReorderAdjust;\\n return costNoReorder < costReorder ? costNoReorder : costReorder;\\n }\\n};\"], [80, 8.0, null], [83, 6.1818, null], [86, 7.2728, null], [89, 6.181799999999999, null], [93, 1.0909, null], [96, 1.8180999999999998, null], [99, 1.4546, null], [102, 1.4545, null], [105, 0.3636, null], [108, 0.3636, null], [111, 0.3636, null], [114, 0.3636, null], [117, 0.3636, null], [120, 0.3636, null], [123, 0.3636, null], [126, 0.3636, null], [129, 0.3636, null], [132, 0.3636, null], [135, 0.3636, null], [138, 0.3636, null], [141, 0.3636, null], [144, 0.3636, null], [147, 0.3636, \"#define lli long long int\\n#define vpi vector<pair<lli,lli>> \\n#define pb push_back\\nclass Solution {\\npublic:\\n long long minCost(vector<int>& arr, vector<int>& brr, long long k) {\\n lli x=0;\\n int n=arr.size();\\n vpi a,b;\\n lli y=0;\\n for(int i=0;i<n;i++)a.pb({arr[i],i}),b.pb({brr[i],i});\\n for(int i=0;i<n;i++)y+=abs(arr[i]-brr[i]);\\n sort(a.begin(),a.end());\\n sort(b.begin(),b.end());\\n sort(arr.begin(),arr.end());\\n sort(brr.begin(),brr.end());\\n for(int i=0;i<n;i++){\\n x+=abs(arr[i]-brr[i]);\\n }\\n bool f=false;\\n for(int i=0;i<n;i++)if(a[i].second!=b[i].second)f=true;\\n return min(!f?x:x+k,y);\\n }\\n};\"], [150, 0.3636, \"class Solution {\\npublic:\\n long long minCost(vector<int>& arr, vector<int>& brr, long long k) {\\n int n = arr.size();\\n unordered_map<int,int> pt;\\n long long result2 = 0;\\n for(int i=0;i<n;i++){\\n pt[arr[i]] = brr[i];\\n result2+=abs(arr[i]-brr[i]);\\n }\\n sort(arr.begin(),arr.end());\\n sort(brr.begin(),brr.end());\\n bool check = false;\\n for(int i=0;i<n;i++){\\n if(pt[arr[i]]!=brr[i]){\\n check = true;\\n break;\\n }\\n }\\n long long int result = 0;\\n for(int i=0;i<n;i++){\\n result+=abs(arr[i]-brr[i]);\\n }\\n return min(result + (check*k),result2);\\n }\\n};\\n// -7 5 9\\n// -5 -2 7\\n// 2 7 2\"]]"
},
"golang": {
"code": "func minCost(arr []int, brr []int, k int64) int64 {\n\tn := len(arr)\n\tvar costNoReorder int64\n\tfor i := 0; i < n; i++ {\n\t\tdiff := int64(arr[i]) - int64(brr[i])\n\t\tif diff < 0 {\n\t\t\tdiff = -diff\n\t\t}\n\t\tcostNoReorder += diff\n\t}\n\tarrCopy := make([]int, n)\n\tcopy(arrCopy, arr)\n\tbrrCopy := make([]int, n)\n\tcopy(brrCopy, brr)\n\tsort.Ints(arrCopy)\n\tsort.Ints(brrCopy)\n\tvar costReorder int64 = k\n\tfor i := 0; i < n; i++ {\n\t\tdiff := int64(arrCopy[i]) - int64(brrCopy[i])\n\t\tif diff < 0 {\n\t\t\tdiff = -diff\n\t\t}\n\t\tcostReorder += diff\n\t}\n\tif costNoReorder < costReorder {\n\t\treturn costNoReorder\n\t}\n\treturn costReorder\n}",
"memory": 1200,
"memoryDistribution": "[[1200, 33.3334, \"func minCost(arr []int, brr []int, k int64) int64 {\\n\\tn := len(arr)\\n\\tvar costNoReorder int64\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdiff := int64(arr[i]) - int64(brr[i])\\n\\t\\tif diff < 0 {\\n\\t\\t\\tdiff = -diff\\n\\t\\t}\\n\\t\\tcostNoReorder += diff\\n\\t}\\n\\tarrCopy := make([]int, n)\\n\\tcopy(arrCopy, arr)\\n\\tbrrCopy := make([]int, n)\\n\\tcopy(brrCopy, brr)\\n\\tsort.Ints(arrCopy)\\n\\tsort.Ints(brrCopy)\\n\\tvar costReorder int64 = k\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdiff := int64(arrCopy[i]) - int64(brrCopy[i])\\n\\t\\tif diff < 0 {\\n\\t\\t\\tdiff = -diff\\n\\t\\t}\\n\\t\\tcostReorder += diff\\n\\t}\\n\\tif costNoReorder < costReorder {\\n\\t\\treturn costNoReorder\\n\\t}\\n\\treturn costReorder\\n}\"], [11500, 33.3333, \"func minCost(arr []int, brr []int, k int64) int64 {\\n n := len(arr)\\n s1, s2 := 0, int(k)\\n for i := 0; i < n; i++ {\\n s1 += abs(arr[i]-brr[i])\\n }\\n sort.Ints(arr)\\n sort.Ints(brr)\\n for i := 0; i < n; i++ {\\n s2 += abs(arr[i]-brr[i])\\n }\\n return int64(min(s1, s2))\\n}\\nfunc abs(x int) int {\\n if x < 0 {\\n return -x\\n }\\n return x\\n}\"], [11700, 33.3333, \"func minCost(arr []int, brr []int, k int64) int64 {\\n\\tn := len(arr)\\n\\tvar costNoReorder int64\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdiff := int64(arr[i]) - int64(brr[i])\\n\\t\\tif diff < 0 {\\n\\t\\t\\tdiff = -diff\\n\\t\\t}\\n\\t\\tcostNoReorder += diff\\n\\t}\\n\\tarrCopy := make([]int, n)\\n\\tcopy(arrCopy, arr)\\n\\tbrrCopy := make([]int, n)\\n\\tcopy(brrCopy, brr)\\n\\tsort.Ints(arrCopy)\\n\\tsort.Ints(brrCopy)\\n\\tvar costReorder int64 = k\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdiff := int64(arrCopy[i]) - int64(brrCopy[i])\\n\\t\\tif diff < 0 {\\n\\t\\t\\tdiff = -diff\\n\\t\\t}\\n\\t\\tcostReorder += diff\\n\\t}\\n\\tif costNoReorder < costReorder {\\n\\t\\treturn costNoReorder\\n\\t}\\n\\treturn costReorder\\n}\"], [13300, 33.3333, \"package main\\n\\nimport (\\n\\t\\\"sort\\\"\\n)\\n\\nfunc minCost(arr []int, brr []int, k int64) int64 {\\n\\tn := len(arr)\\n\\tvar costNoReorder int64 = 0\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdiff := arr[i] - brr[i]\\n\\t\\tif diff < 0 {\\n\\t\\t\\tdiff = -diff\\n\\t\\t}\\n\\t\\tcostNoReorder += int64(diff)\\n\\t}\\n\\tsortedA := make([]int, n)\\n\\tsortedB := make([]int, n)\\n\\tcopy(sortedA, arr)\\n\\tcopy(sortedB, brr)\\n\\tsort.Ints(sortedA)\\n\\tsort.Ints(sortedB)\\n\\tvar costReorder int64 = 0\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdiff := sortedA[i] - sortedB[i]\\n\\t\\tif diff < 0 {\\n\\t\\t\\tdiff = -diff\\n\\t\\t}\\n\\t\\tcostReorder += int64(diff)\\n\\t}\\n\\tcostReorder += k\\n\\tif costNoReorder < costReorder {\\n\\t\\treturn costNoReorder\\n\\t}\\n\\treturn costReorder\\n}\"]]",
"runtime": 76,
"runtimeDistribution": "[[59, 33.3333, \"func minCost(arr []int, brr []int, k int64) int64 {\\n n := len(arr)\\n s1, s2 := 0, int(k)\\n for i := 0; i < n; i++ {\\n s1 += abs(arr[i]-brr[i])\\n }\\n sort.Ints(arr)\\n sort.Ints(brr)\\n for i := 0; i < n; i++ {\\n s2 += abs(arr[i]-brr[i])\\n }\\n return int64(min(s1, s2))\\n}\\nfunc abs(x int) int {\\n if x < 0 {\\n return -x\\n }\\n return x\\n}\"], [76, 33.3333, \"func minCost(arr []int, brr []int, k int64) int64 {\\n\\tn := len(arr)\\n\\tvar costNoReorder int64\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdiff := int64(arr[i]) - int64(brr[i])\\n\\t\\tif diff < 0 {\\n\\t\\t\\tdiff = -diff\\n\\t\\t}\\n\\t\\tcostNoReorder += diff\\n\\t}\\n\\tarrCopy := make([]int, n)\\n\\tcopy(arrCopy, arr)\\n\\tbrrCopy := make([]int, n)\\n\\tcopy(brrCopy, brr)\\n\\tsort.Ints(arrCopy)\\n\\tsort.Ints(brrCopy)\\n\\tvar costReorder int64 = k\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdiff := int64(arrCopy[i]) - int64(brrCopy[i])\\n\\t\\tif diff < 0 {\\n\\t\\t\\tdiff = -diff\\n\\t\\t}\\n\\t\\tcostReorder += diff\\n\\t}\\n\\tif costNoReorder < costReorder {\\n\\t\\treturn costNoReorder\\n\\t}\\n\\treturn costReorder\\n}\"], [87, 33.3333, \"package main\\n\\nimport (\\n\\t\\\"sort\\\"\\n)\\n\\nfunc minCost(arr []int, brr []int, k int64) int64 {\\n\\tn := len(arr)\\n\\tvar costNoReorder int64 = 0\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdiff := arr[i] - brr[i]\\n\\t\\tif diff < 0 {\\n\\t\\t\\tdiff = -diff\\n\\t\\t}\\n\\t\\tcostNoReorder += int64(diff)\\n\\t}\\n\\tsortedA := make([]int, n)\\n\\tsortedB := make([]int, n)\\n\\tcopy(sortedA, arr)\\n\\tcopy(sortedB, brr)\\n\\tsort.Ints(sortedA)\\n\\tsort.Ints(sortedB)\\n\\tvar costReorder int64 = 0\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdiff := sortedA[i] - sortedB[i]\\n\\t\\tif diff < 0 {\\n\\t\\t\\tdiff = -diff\\n\\t\\t}\\n\\t\\tcostReorder += int64(diff)\\n\\t}\\n\\tcostReorder += k\\n\\tif costNoReorder < costReorder {\\n\\t\\treturn costNoReorder\\n\\t}\\n\\treturn costReorder\\n}\"]]"
},
"java": {
"code": "class Solution {\n public long minCost(int[] arr, int[] brr, long k) {\n int n = arr.length;\n long costNo = 0;\n for (int i = 0; i < n; i++) {\n costNo += Math.abs((long)arr[i] - (long)brr[i]);\n }\n int[] sortedArr = arr.clone();\n int[] sortedBrr = brr.clone();\n java.util.Arrays.sort(sortedArr);\n java.util.Arrays.sort(sortedBrr);\n long costSorted = 0;\n for (int i = 0; i < n; i++) {\n costSorted += Math.abs((long)sortedArr[i] - (long)sortedBrr[i]);\n }\n return Math.min(costNo, k + costSorted);\n }\n}",
"memory": 5700,
"memoryDistribution": "[[5700, 57.8513, \"class Solution {\\n public long minCost(int[] arr, int[] brr, long k) {\\n int n = arr.length;\\n long costNo = 0;\\n for (int i = 0; i < n; i++) {\\n costNo += Math.abs((long)arr[i] - (long)brr[i]);\\n }\\n int[] sortedArr = arr.clone();\\n int[] sortedBrr = brr.clone();\\n java.util.Arrays.sort(sortedArr);\\n java.util.Arrays.sort(sortedBrr);\\n long costSorted = 0;\\n for (int i = 0; i < n; i++) {\\n costSorted += Math.abs((long)sortedArr[i] - (long)sortedBrr[i]);\\n }\\n return Math.min(costNo, k + costSorted);\\n }\\n}\"], [56000, 0.8264, \"class Solution {\\n public long minCost(int[] arr, int[] brr, long k) {\\n int n = arr.length;\\n PriorityQueue<int[]> pq1 = new PriorityQueue<>((a,b) -> b[0] - a[0]);\\n PriorityQueue<int[]> pq2 = new PriorityQueue<>((a,b) -> b[0] - a[0]);\\n\\n long ans = 0, temp = 0;\\n\\n for(int i = 0 ; i < n ; i++) {\\n pq1.add(new int[] {arr[i], i});\\n }\\n for(int i = 0 ; i < n ; i++) {\\n pq2.add(new int[] {brr[i], i});\\n temp += Math.abs(brr[i] - arr[i]);\\n }\\n\\n boolean wasShifted = false;\\n while(!pq1.isEmpty()) {\\n int [] cur1 = pq1.poll();\\n int [] cur2 = pq2.poll();\\n if(cur1[1] != cur2[1]) {\\n wasShifted = true;\\n }\\n ans += Math.abs(cur1[0] - cur2[0]);\\n }\\n if(wasShifted) {\\n ans += k;\\n }\\n return Math.min(ans, temp);\\n }\\n}\"], [56100, 0.8264, \"class Solution {\\n public long minCost(int[] arr, int[] brr, long k) {\\n int n = arr.length;\\n PriorityQueue<int[]> pq1 = new PriorityQueue<>((a,b) -> b[0] - a[0]);\\n PriorityQueue<int[]> pq2 = new PriorityQueue<>((a,b) -> b[0] - a[0]);\\n\\n long ans = 0, temp = 0;\\n\\n for(int i = 0 ; i < n ; i++) {\\n pq1.add(new int[] {arr[i], i});\\n }\\n for(int i = 0 ; i < n ; i++) {\\n pq2.add(new int[] {brr[i], i});\\n temp += Math.abs(brr[i] - arr[i]);\\n }\\n\\n boolean wasShifted = false;\\n while(!pq1.isEmpty()) {\\n int [] cur1 = pq1.poll();\\n int [] cur2 = pq2.poll();\\n if(cur1[1] != cur2[1]) {\\n wasShifted = true;\\n }\\n ans += Math.abs(cur1[0] - cur2[0]);\\n }\\n if(wasShifted) {\\n ans += k;\\n }\\n return Math.min(ans, temp);\\n }\\n}\"], [56700, 0.8264, null], [56800, 1.6529, null], [56900, 2.4793, null], [57000, 4.9587, null], [57100, 8.2645, null], [57200, 9.9174, null], [57300, 12.3967, null], [57400, 13.2231, null], [57500, 12.3967, null], [57600, 14.876, null], [57700, 6.6116, \"class Solution {\\n public long minCost(int[] arr, int[] brr, long k) {\\n int n = arr.length;\\n long realAns = 0;\\n for(int i=0;i<n;i++) {\\n realAns += Math.abs(arr[i]-brr[i]);\\n }\\n boolean isInc = true;\\n boolean isDec = true;\\n for(int i=0;i<n-1;i++) {\\n if(arr[i] > arr[i+1] || brr[i] > brr[i+1]) {\\n isInc = false;\\n }\\n if(arr[n-i-1] > arr[n-i-2] || brr[n-i-1] > brr[n-i-2]) {\\n isDec = false;\\n }\\n // System.out.println(arr[n-i-1] + \\\" \\\" + arr[n-i-2]);\\n }\\n long ans = 0;\\n if(!isInc && !isDec) {\\n ans += k;\\n }\\n Arrays.sort(arr);\\n Arrays.sort(brr);\\n \\n for(int i=0;i<n;i++) {\\n ans += Math.abs(arr[i]-brr[i]);\\n }\\n\\n return realAns < ans ? realAns : ans;\\n }\\n}\"], [57800, 4.9587, \"class Solution {\\n public long minCost(int[] arr, int[] brr, long k) {\\n return Math.min(f2(arr, brr), f1(arr, brr, k));\\n }\\n\\n long f1(int[] arr, int[] brr, long k) {\\n long ans = k;\\n Arrays.sort(arr);\\n Arrays.sort(brr);\\n for (int i = 0; i < arr.length; ++i) {\\n ans += Math.abs(arr[i] - brr[i]);\\n }\\n return ans;\\n }\\n\\n long f2(int[] arr, int[] brr) {\\n long ans = 0;\\n for (int i = 0; i < arr.length; ++i) {\\n ans += Math.abs(arr[i] - brr[i]);\\n }\\n return ans;\\n }\\n\\n}\"]]",
"runtime": 64,
"runtimeDistribution": "[[19, 1.6529, \"class Solution {\\n public long minCost(int[] arr, int[] brr, long k) {\\n long costWithoutRearranging = 0;\\n long ans = 0;\\n for(int i=0;i<arr.length;i++) {\\n costWithoutRearranging+=Math.abs(arr[i]-brr[i]);\\n }\\n\\n if(costWithoutRearranging<=k) return costWithoutRearranging;\\n\\n Arrays.sort(arr);\\n Arrays.sort(brr);\\n\\n long costWithRearranging = k;\\n for(int i=0;i<arr.length;i++) {\\n costWithRearranging+=Math.abs(arr[i]-brr[i]);\\n }\\n\\n return Math.min(costWithRearranging,costWithoutRearranging);\\n }\\n}\"], [20, 0.8264, \"class Solution {\\n public long minCost(int[] arr, int[] brr, long k) {\\n long cost = cost(arr, brr);\\n if(k < cost) {\\n Arrays.sort(arr);\\n Arrays.sort(brr);\\n cost = Math.min(cost, k + cost(arr, brr));\\n }\\n return cost;\\n }\\n\\n private long cost(int[] arr, int[] brr) {\\n long cost = 0;\\n for(int i = 0; i < arr.length; i++) {\\n cost += Math.abs(arr[i] - brr[i]);\\n }\\n return cost;\\n }\\n}\"], [60, 24.7934, null], [61, 39.6694, null], [62, 21.4876, \"class Solution {\\n public long minCost(int[] a, int[] b, long k) {\\n long res1 = 0, res2 = 0;\\n for (int i = 0; i < a.length; ++i) {\\n res1 += Math.abs(a[i] - b[i]);\\n }\\n Arrays.sort(a);\\n Arrays.sort(b);\\n for (int i = 0; i < a.length; ++i) {\\n res2 += Math.abs(a[i] - b[i]);\\n }\\n return Math.min(res1, res2 + k);\\n }\\n}\"], [63, 4.9587, \"class Solution {\\n public long minCost(int[] arr, int[] brr, long k) {\\n int len = arr.length;\\n \\n long raw = 0;\\n for (int i = 0; i < len; i++) {\\n raw += Math.abs((long) arr[i] - brr[i]);\\n }\\n \\n int[] tmp = arr.clone();\\n int[] dst = brr.clone();\\n \\n Arrays.sort(tmp);\\n Arrays.sort(dst);\\n \\n long srt = k;\\n for (int i = 0; i < len; i++) {\\n srt += Math.abs((long) tmp[i] - dst[i]);\\n }\\n \\n return Math.min(raw, srt);\\n }\\n}\"], [64, 6.6116, \"class Solution {\\n public long minCost(int[] arr, int[] brr, long k) {\\n int n = arr.length;\\n long costNo = 0;\\n for (int i = 0; i < n; i++) {\\n costNo += Math.abs((long)arr[i] - (long)brr[i]);\\n }\\n int[] sortedArr = arr.clone();\\n int[] sortedBrr = brr.clone();\\n java.util.Arrays.sort(sortedArr);\\n java.util.Arrays.sort(sortedBrr);\\n long costSorted = 0;\\n for (int i = 0; i < n; i++) {\\n costSorted += Math.abs((long)sortedArr[i] - (long)sortedBrr[i]);\\n }\\n return Math.min(costNo, k + costSorted);\\n }\\n}\"]]"
},
"javascript": {
"code": "var minCost = function(arr, brr, k) {\n const n = arr.length;\n let costNoReorder = 0;\n for (let i = 0; i < n; i++) {\n costNoReorder += Math.abs(arr[i] - brr[i]);\n }\n let arrSorted = arr.slice().sort((a, b) => a - b);\n let brrSorted = brr.slice().sort((a, b) => a - b);\n let costReorderAdjust = 0;\n for (let i = 0; i < n; i++) {\n costReorderAdjust += Math.abs(arrSorted[i] - brrSorted[i]);\n }\n let costReorder = k + costReorderAdjust;\n return Math.min(costNoReorder, costReorder);\n};",
"memory": 8300,
"memoryDistribution": "[[8300, 23.0764, \"var minCost = function(arr, brr, k) {\\n const n = arr.length;\\n let costNoReorder = 0;\\n for (let i = 0; i < n; i++) {\\n costNoReorder += Math.abs(arr[i] - brr[i]);\\n }\\n let arrSorted = arr.slice().sort((a, b) => a - b);\\n let brrSorted = brr.slice().sort((a, b) => a - b);\\n let costReorderAdjust = 0;\\n for (let i = 0; i < n; i++) {\\n costReorderAdjust += Math.abs(arrSorted[i] - brrSorted[i]);\\n }\\n let costReorder = k + costReorderAdjust;\\n return Math.min(costNoReorder, costReorder);\\n};\"], [76800, 3.8462, \"/**\\n * @param {number[]} arr\\n * @param {number[]} brr\\n * @param {number} k\\n * @return {number}\\n */\\nvar minCost = function(a, b, k) {\\n const ans2 = a.reduce((sum, x, i) => sum + Math.abs(x - b[i]), 0);\\n if (ans2 <= k) return ans2;\\n\\n a.sort((x, y) => x - y);\\n b.sort((x, y) => x - y);\\n\\n const ans1 = a.reduce((sum, x, i) => sum + Math.abs(x - b[i]), 0) + k;\\n\\n return Math.min(ans1, ans2);\\n};\"], [79200, 7.6923, \"var minCost = function(arr, brr, k) {\\n // Option 1: No rearranging\\n let option1 = 0;\\n for(let i = 0; i < arr.length; i++)\\n option1 += Math.abs(arr[i] - brr[i]);\\n\\n // Option 2: Rearranging\\n arr.sort((a, b) => a - b); \\n brr.sort((a, b) => a - b); \\n let option2 = k;\\n for(let i = 0; i < arr.length; i++)\\n option2 += Math.abs(arr[i] - brr[i]);\\n\\n return Math.min(option1, option2);\\n};\"], [79400, 3.8462, null], [79500, 11.5385, null], [79700, 3.8462, null], [79800, 7.6923, null], [80100, 3.8462, null], [80700, 3.8462, null], [81900, 3.8462, null], [82000, 3.8462, null], [82200, 3.8462, null], [82400, 3.8462, null], [82500, 3.8462, null], [82600, 7.6923, null], [82700, 3.8462, null], [83100, 3.8462, null], [83700, 3.8462, null], [84200, 3.8462, \"/**\\n * @param {number[]} arr\\n * @param {number[]} brr\\n * @param {number} k\\n * @return {number}\\n */\\nfunction minCost(arr, brr, k) {\\n const sortedArr = arr.toSorted((a, b) => a - b)\\n const sortedBrr = brr.toSorted((a, b) => a - b)\\n\\n let res1 = 0\\n\\n for (let i = 0; i < arr.length; i++) {\\n res1 += Math.abs(arr[i] - brr[i])\\n }\\n\\n if (res1 <= k) {\\n return res1\\n }\\n\\n let res2 = k\\n\\n for (let i = 0; i < sortedArr.length; i++) {\\n res2 += Math.abs(sortedArr[i] - sortedBrr[i])\\n }\\n\\n return Math.min(res1, res2)\\n}\"], [84300, 3.8462, \"/**\\n * @param {number[]} arr\\n * @param {number[]} brr\\n * @param {number} k\\n * @return {number}\\n */\\nfunction minCost(arr, brr, k) {\\n const sortedArr = arr.toSorted((a, b) => a - b)\\n const sortedBrr = brr.toSorted((a, b) => a - b)\\n\\n let res1 = 0\\n let res2 = k\\n\\n for (let i = 0; i < arr.length; i++) {\\n res1 += Math.abs(arr[i] - brr[i])\\n }\\n\\n for (let i = 0; i < sortedArr.length; i++) {\\n res2 += Math.abs(sortedArr[i] - sortedBrr[i])\\n }\\n\\n return Math.min(res1, res2)\\n}\"]]",
"runtime": 268,
"runtimeDistribution": "[[74, 3.8462, \"/**\\n * @param {number[]} arr\\n * @param {number[]} brr\\n * @param {number} k\\n * @return {number}\\n */\\nvar minCost = function(a, b, k) {\\n const ans2 = a.reduce((sum, x, i) => sum + Math.abs(x - b[i]), 0);\\n if (ans2 <= k) return ans2;\\n\\n a.sort((x, y) => x - y);\\n b.sort((x, y) => x - y);\\n\\n const ans1 = a.reduce((sum, x, i) => sum + Math.abs(x - b[i]), 0) + k;\\n\\n return Math.min(ans1, ans2);\\n};\"], [250, 7.6923, \"/**\\n * @param {number[]} a\\n * @param {number[]} b\\n * @param {number} k\\n * @return {number}\\n */\\nvar minCost = function(a, b, k) {\\n let res1=0, res2=0;\\n for(let i =0; i<a.length; i++){\\n res1 += Math.abs(a[i]-b[i]);\\n }\\n a.sort((x,y)=>x-y);\\n b.sort((x,y)=>x-y);\\n for (let i=0; i<a.length;i++){\\n res2+= Math.abs(a[i]-b[i]);\\n }\\n return Math.min(res1, res2+k);\\n};\\n\"], [252, 3.8462, null], [260, 7.6923, null], [262, 3.8462, null], [263, 3.8462, null], [264, 3.8462, null], [265, 3.8462, null], [266, 3.8462, null], [267, 7.6923, null], [268, 3.8462, null], [269, 7.6923, null], [270, 7.6923, null], [271, 3.8462, null], [272, 3.8462, null], [274, 3.8462, null], [278, 3.8462, \"/**\\n * @param {number[]} arr\\n * @param {number[]} brr\\n * @param {number} k\\n * @return {number}\\n */\\nvar minCost = function(arr, brr, k) {\\n let len = arr.length;\\n \\n let raw = 0;\\n for (let i = 0; i < len; i++) {\\n raw += Math.abs(arr[i] - brr[i]);\\n }\\n \\n let tmp = [...arr].sort((a, b) => a - b);\\n let dst = [...brr].sort((a, b) => a - b);\\n \\n let srt = k;\\n for (let i = 0; i < len; i++) {\\n srt += Math.abs(tmp[i] - dst[i]);\\n }\\n \\n return Math.min(raw, srt);\\n};\"], [282, 7.6923, \"/**\\n * @param {number[]} arr\\n * @param {number[]} brr\\n * @param {number} k\\n * @return {number}\\n */\\nvar minCost = function(arr, brr, k) {\\n // no matter how we sort arr, it will always only cost 1k\\n let arrNew = [...arr].sort((a,b) => a-b)\\n let brrNew = [...brr].sort((a,b) => a-b)\\n\\n // original order cost\\n let orginalCost = 0\\n for(let i=0; i<brr.length; i++){\\n orginalCost += Math.abs(brr[i] - arr[i])\\n }\\n let cost = k\\n for(let i=0; i<brrNew.length; i++){\\n cost += Math.abs(brrNew[i] - arrNew[i])\\n }\\n return Math.min(cost, orginalCost)\\n};\"]]"
},
"python3": {
"code": "class Solution:\n def minCost(self, arr: List[int], brr: List[int], k: int) -> int:\n n = len(arr)\n direct_cost = sum(abs(a - b) for a, b in zip(arr, brr))\n sorted_arr = sorted(arr)\n sorted_brr = sorted(brr)\n reorder_cost = k + sum(abs(a - b) for a, b in zip(sorted_arr, sorted_brr))\n return min(direct_cost, reorder_cost)",
"memory": 3400,
"memoryDistribution": "[[3400, 80.2721, \"class Solution:\\n def minCost(self, arr: List[int], brr: List[int], k: int) -> int:\\n n = len(arr)\\n direct_cost = sum(abs(a - b) for a, b in zip(arr, brr))\\n sorted_arr = sorted(arr)\\n sorted_brr = sorted(brr)\\n reorder_cost = k + sum(abs(a - b) for a, b in zip(sorted_arr, sorted_brr))\\n return min(direct_cost, reorder_cost)\"], [33400, 0.6803, \"class Solution:\\n def minCost(self, arr: List[int], brr: List[int], k: int) -> int:\\n return min( sum( abs(a-b) for a,b in zip(arr,brr)),\\n k + sum( abs(a-b) for a,b in zip(sorted(arr),sorted(brr))) )\\n\\n # noRearrange = sum( abs(a-b) for a,b in zip(arr,brr) )\\n # arr.sort()\\n # brr.sort()\\n # rearrange = k + sum( abs(a-b) for a,b in zip(arr,brr) )\\n # return min(noRearrange, rearrange)\"], [33500, 2.7211, \"class Solution:\\n def minCost(self, arr: List[int], brr: List[int], k: int) -> int:\\n cost_no_rearrange = sum(abs(a - b) for a, b in zip(arr, brr))\\n \\n # Cost with rearrangement\\n arr_sorted = sorted(arr)\\n brr_sorted = sorted(brr)\\n cost_rearrange = sum(abs(a - b) for a, b in zip(arr_sorted, brr_sorted)) + k\\n \\n # Return the minimum of the two costs\\n return min(cost_no_rearrange, cost_rearrange)\\n\"], [33600, 16.3265, null], [33700, 21.0884, null], [33800, 13.6054, null], [33900, 6.1224, null], [34000, 2.7211, null], [34200, 3.4014, null], [34300, 6.8027, null], [34400, 6.8027, null], [34500, 2.7211, null], [34600, 0.6803, null], [34700, 0.6803, null], [34900, 2.0408, null], [35000, 2.0408, null], [35200, 0.6803, null], [36200, 2.0408, null], [37100, 0.6803, null], [37200, 0.6803, null], [37600, 0.6803, null], [45100, 0.6803, \"import numpy\\nclass Solution:\\n def minCost(self, arr: List[int], brr: List[int], k: int) -> int:\\n fir_cost =0\\n\\n for i in range(len(arr)):\\n fir_cost += abs(arr[i]-brr[i])\\n\\n arr, brr = sorted(arr), sorted(brr)\\n\\n cost =0\\n for i in range(len(arr)):\\n cost += abs(arr[i]-brr[i])\\n \\n return min(cost+k, fir_cost)\"], [45200, 0.6803, \"from typing import List\\nimport heapq\\n\\nclass Solution:\\n def minCost(self, arr: List[int], brr: List[int], k: int) -> int:\\n n = len(arr)\\n # If k is extremely large, we should never rearrange the array\\n if k >= 2 * 10**10:\\n return sum(abs(arr[i] - brr[i]) for i in range(n))\\n \\n # Frequencies of elements in brr\\n brr_freq = {}\\n for num in brr:\\n brr_freq[num] = brr_freq.get(num, 0) + 1\\n \\n # Frequencies of elements in arr\\n arr_freq = {}\\n for num in arr:\\n arr_freq[num] = arr_freq.get(num, 0) + 1\\n \\n # If we don't rearrange (apply no split operations)\\n cost_without_rearrange = sum(abs(arr[i] - brr[i]) for i in range(n))\\n \\n # If we optimally rearrange (apply one split operation)\\n cost_with_rearrange = k # Cost of one split operation\\n \\n # Count elements that need to be changed\\n excess = [] # Elements in arr that exceed what we need\\n deficit = [] # Elements we need more of in arr\\n \\n # Calculate excess and deficit\\n all_values = set(arr_freq.keys()) | set(brr_freq.keys())\\n for val in all_values:\\n diff = arr_freq.get(val, 0) - brr_freq.get(val, 0)\\n if diff > 0: # We have more of this element than needed\\n excess.extend([val] * diff)\\n elif diff < 0: # We need more of this element\\n deficit.extend([val] * (-diff))\\n \\n # If there's nothing to change, we're already done\\n if not excess:\\n return min(0, cost_without_rearrange)\\n \\n # Sort excess and deficit for optimal matching\\n excess.sort()\\n deficit.sort()\\n \\n # Calculate cost of transforming excess elements to deficit elements\\n transformation_cost = 0\\n for i in range(len(excess)):\\n transformation_cost += abs(excess[i] - deficit[i])\\n \\n cost_with_rearrange += transformation_cost\\n \\n # Return the minimum cost strategy\\n return min(cost_without_rearrange, cost_with_rearrange)\"]]",
"runtime": 239,
"runtimeDistribution": "[[83, 0.6803, \"class Solution:\\n def minCost(self, arr: List[int], brr: List[int], k: int) -> int:\\n direct_cost = 0\\n\\n for i in range(len(arr)):\\n direct_cost += abs(arr[i]-brr[i])\\n if direct_cost <= k: return direct_cost\\n\\n indirect_cost = k\\n arr.sort()\\n brr.sort()\\n for i in range(len(arr)):\\n indirect_cost += abs(arr[i]-brr[i])\\n return min(direct_cost, indirect_cost)\\n \"], [84, 0.6803, \"\\nfrom itertools import permutations\\nclass Solution:\\n def minCost(self, arr: List[int], brr: List[int], k: int) -> int:\\n\\n\\n if arr == brr:\\n return 0\\n\\n n = len(brr)\\n \\n diff = [[0]* n for _ in range(n)]\\n\\n for i in range(n):\\n for j in range(n):\\n diff[i][j] = abs(brr[i] - arr[j])\\n\\n \\n def min_sum(matrix):\\n indices = []\\n min_cost = float('inf')\\n # G\\u00e9n\\u00e9rer toutes les permutations possibles des indices de colonnes (0, 1, ..., n-1)\\n for perm in permutations(range(n)): \\n cost = 0\\n if list(perm) != list(range(n)):\\n cost += k\\n for i in range(n): \\n cost += matrix[i][perm[i]]\\n if cost < min_cost:\\n min_cost = cost\\n\\n return min_cost\\n\\n res = min_sum(diff)\\n \\n return res\\n \\n \\nclass Solution:\\n def minCost(self, arr, brr, k):\\n length = len(arr)\\n \\n raw = 0\\n for i in range(length):\\n raw += abs(arr[i] - brr[i])\\n \\n tmp = sorted(arr)\\n dst = sorted(brr)\\n \\n srt = k\\n for i in range(length):\\n srt += abs(tmp[i] - dst[i])\\n \\n return min(raw, srt)\\n\\n\\n\\nclass Solution:\\n def minCost(self, arr: List[int], brr: List[int], k: int) -> int:\\n \\n init = 0\\n for a,b in zip(arr,brr):\\n init += abs(a - b)\\n\\n if k >= init:\\n return init\\n\\n arr.sort(),brr.sort()\\n after = k\\n for a,b in zip(arr,brr):\\n after += abs(a - b)\\n return min(init,after) \"], [91, 0.6803, null], [93, 0.6803, null], [94, 1.3605, null], [98, 0.6803, null], [99, 0.6803, null], [103, 1.3605, null], [215, 1.3605, null], [218, 0.6803, null], [220, 0.6803, null], [221, 0.6803, null], [222, 0.6803, null], [223, 0.6803, null], [224, 0.6803, null], [225, 2.7211, null], [226, 2.0408, null], [227, 2.0408, null], [228, 2.0408, null], [229, 0.6803, null], [230, 0.6803, null], [231, 5.4422, null], [232, 4.0816, null], [233, 3.4014, null], [234, 2.0408, null], [235, 5.4422, null], [236, 2.0408, null], [237, 1.3605, null], [238, 2.0408, null], [239, 8.8435, null], [240, 1.3605, null], [241, 2.7211, null], [242, 1.3605, null], [243, 1.3605, null], [244, 1.3605, null], [245, 0.6803, null], [246, 2.7211, null], [247, 3.4014, null], [248, 2.7211, null], [249, 0.6803, null], [251, 2.0408, null], [252, 1.3605, null], [255, 2.0408, null], [257, 0.6803, null], [258, 2.0408, null], [259, 0.6803, null], [260, 2.0408, null], [261, 0.6803, null], [262, 0.6803, null], [267, 0.6803, null], [271, 0.6803, null], [292, 0.6803, null], [309, 0.6803, null], [311, 0.6803, null], [317, 0.6803, null], [331, 0.6803, null], [342, 0.6803, null], [350, 0.6803, \"class Solution:\\n def minCost(self, arr: List[int], brr: List[int], k: int) -> int:\\n if arr == brr:\\n return 0\\n count_arr = Counter(arr)\\n count_brr = Counter(arr)\\n\\n count = 0\\n for a, b in zip(arr, brr):\\n count += abs(a - b)\\n\\n with_rearrange = k\\n arr.sort()\\n brr.sort()\\n for a, b in zip(arr, brr):\\n with_rearrange += abs(a - b)\\n\\n return min(count, with_rearrange)\"], [383, 0.6803, \"\\nclass Solution:\\n def minCost(self, arr: List[int], brr: List[int], k: int) -> int:\\n def calculate_cost(arr, brr):\\n return sum(abs(a - b) for a, b in zip(arr, brr))\\n \\n direct_cost = calculate_cost(arr, brr)\\n if sorted(arr) == sorted(brr):\\n return min(direct_cost, k)\\n \\n arr.sort()\\n brr.sort()\\n rearranged_cost = calculate_cost(arr, brr) + k\\n \\n return min(direct_cost, rearranged_cost)\\n\"]]"
},
"ruby": {
"code": "def min_cost(arr, brr, k)\n cost_no_reorder = arr.zip(brr).sum { |a, b| (a - b).abs }\n cost_reorder = k + arr.sort.zip(brr.sort).sum { |a, b| (a - b).abs }\n [cost_no_reorder, cost_reorder].min\nend",
"memory": 23400,
"memoryDistribution": "[[23400, 100.0, \"def min_cost(arr, brr, k)\\n cost_no_reorder = arr.zip(brr).sum { |a, b| (a - b).abs }\\n cost_reorder = k + arr.sort.zip(brr.sort).sum { |a, b| (a - b).abs }\\n [cost_no_reorder, cost_reorder].min\\nend\"], [234100, 100.0, \"def min_cost(arr, brr, k)\\n cost_no_reorder = arr.zip(brr).sum { |a, b| (a - b).abs }\\n cost_reorder = k + arr.sort.zip(brr.sort).sum { |a, b| (a - b).abs }\\n [cost_no_reorder, cost_reorder].min\\nend\"]]",
"runtime": 302,
"runtimeDistribution": "[[302, 100.0, \"def min_cost(arr, brr, k)\\n cost_no_reorder = arr.zip(brr).sum { |a, b| (a - b).abs }\\n cost_reorder = k + arr.sort.zip(brr.sort).sum { |a, b| (a - b).abs }\\n [cost_no_reorder, cost_reorder].min\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list:
import random
random.seed(seed)
def sample_solution(arr, brr, k):
# Sample solution as provided in the prompt.
direct_cost = sum(abs(a - b) for a, b in zip(arr, brr))
sorted_arr = sorted(arr)
sorted_brr = sorted(brr)
reorder_cost = k + sum(abs(a - b) for a, b in zip(sorted_arr, sorted_brr))
return min(direct_cost, reorder_cost)
test_cases = []
# Fixed Test Case 1: Example provided in the prompt.
if num_cases > 0:
arr = [-7, 9, 5]
brr = [7, -2, -5]
k = 2
# Serialization: arr|brr|k where each array is comma-separated.
input_str = ",".join(map(str, arr)) + "|" + ",".join(map(str, brr)) + "|" + str(k)
output_str = str(sample_solution(arr, brr, k))
test_cases.append({"input": input_str, "output": output_str})
# Fixed Test Case 2: Identity arrays.
if num_cases > 1:
arr = [2, 1]
brr = [2, 1]
k = 0
input_str = ",".join(map(str, arr)) + "|" + ",".join(map(str, brr)) + "|" + str(k)
output_str = str(sample_solution(arr, brr, k))
test_cases.append({"input": input_str, "output": output_str})
# Generate additional random test cases.
for i in range(2, num_cases):
# Choose a random array length between 1 and 10.
n = random.randint(1, 10)
if i % 3 == 0:
# Case: both arrays are identical.
arr = [random.randint(-100, 100) for _ in range(n)]
brr = arr.copy()
elif i % 3 == 1:
# Case: completely random arrays.
arr = [random.randint(-100, 100) for _ in range(n)]
brr = [random.randint(-100, 100) for _ in range(n)]
else:
# Case: brr is a small modification of arr.
arr = [random.randint(-100, 100) for _ in range(n)]
brr = [a + random.choice([-5, -3, -1, 1, 3, 5]) for a in arr]
# Random operation cost k between 0 and 100.
k = random.randint(0, 100)
input_str = ",".join(map(str, arr)) + "|" + ",".join(map(str, brr)) + "|" + str(k)
output_str = str(sample_solution(arr, brr, k))
test_cases.append({"input": input_str, "output": output_str})
return test_cases
# Example usage (for local testing):
if __name__ == "__main__":
cases = generate_test_cases(5)
for case in cases:
print("Input:", case["input"])
print("Expected Output:", case["output"])
print()
|
def evaluate(expected_output: str, program_output: str) -> bool:
# Deserialization: both expected and program outputs are serialized as a plain integer.
def deserialize(output_str: str) -> int:
return int(output_str.strip())
try:
expected = deserialize(expected_output)
program = deserialize(program_output)
return expected == program
except Exception:
return False
# Example usage:
if __name__ == "__main__":
# Test with sample outputs
exp = "13"
prog = " 13\n"
print(evaluate(exp, prog))
|
[{"input": "-7,9,5|7,-2,-5|2", "output": "13"}, {"input": "2,1|2,1|0", "output": "0"}, {"input": "-94,89|-95,86|28", "output": "4"}, {"input": "88,-74,73|88,-74,73|94", "output": "0"}, {"input": "-78,51,8,-92,-93,-77,-45,-41,29|54,-94,43,-50,83,66,79,39,7|28", "output": "595"}, {"input": "50,-29,-99,94,-60,78,8,-13|49,-32,-102,93,-65,73,9,-18|45", "output": "24"}, {"input": "54,-33,-89,86,17,37|54,-33,-89,86,17,37|15", "output": "0"}, {"input": "-80,41,-25,60,58,-8,47|-51,80,-83,-89,69,-42,97|37", "output": "311"}, {"input": "-41,-75|-40,-76|58", "output": "2"}, {"input": "-59,-6,-10,-47,71,-32|-59,-6,-10,-47,71,-32|89", "output": "0"}, {"input": "55,62|-57,36|93", "output": "138"}, {"input": "-59,18,-3,-31|-54,23,0,-34|87", "output": "16"}, {"input": "96,98,-86,-42,-92,-20|96,98,-86,-42,-92,-20|51", "output": "0"}, {"input": "-84,-46,45,83,-20|-46,67,27,1,64|58", "output": "225"}, {"input": "-33,-65,-37|-28,-62,-34|33", "output": "11"}, {"input": "9,49,2,-8,-44,-65,30,26,-77,93|9,49,2,-8,-44,-65,30,26,-77,93|6", "output": "0"}, {"input": "-61,60|-60,74|54", "output": "15"}, {"input": "-84,-2,-3,52,19,35,-36,41,-98,74|-79,-7,2,55,18,40,-37,36,-99,75|20", "output": "32"}, {"input": "-100,84,84,-33,28,95,-55,29|-100,84,84,-33,28,95,-55,29|13", "output": "0"}, {"input": "63,29,55,-50,-61|-5,95,-59,38,99|67", "output": "199"}, {"input": "53|52|62", "output": "1"}, {"input": "-72|-72|46", "output": "0"}, {"input": "-39,-86,-39,45,-80|-79,87,24,-83,94|68", "output": "310"}, {"input": "-68,68,21|-65,65,20|67", "output": "7"}, {"input": "8,-46,38,93,86,76,-49,82,-21,2|8,-46,38,93,86,76,-49,82,-21,2|85", "output": "0"}, {"input": "12,32,15,-70,-37,-43|-84,-14,-95,50,41,-42|75", "output": "216"}, {"input": "-99,-82,81,61|-104,-85,76,56|42", "output": "18"}, {"input": "31,-40|31,-40|35", "output": "0"}, {"input": "-46,38,-67,85,46,47,21,-38|100,21,4,-52,-76,-76,68,10|45", "output": "204"}, {"input": "5,19,86,-87,72,67,65|0,14,87,-82,71,62,62|24", "output": "25"}, {"input": "37,14,-65,8|37,14,-65,8|23", "output": "0"}, {"input": "18,-37,-81,13,40|-75,-88,66,38,-97|11", "output": "212"}, {"input": "-58,4,24,23|-61,5,19,20|48", "output": "12"}, {"input": "-1|-1|33", "output": "0"}, {"input": "-27,8,78,87,100,42,69,83|24,-61,-52,-25,-45,-86,48,88|69", "output": "618"}, {"input": "91|90|7", "output": "1"}, {"input": "49|49|61", "output": "0"}, {"input": "35,-60,-86,30,-80,-53,-83,52,-83|72,-40,3,-70,45,-37,48,52,-90|79", "output": "398"}, {"input": "7,68|10,71|66", "output": "6"}, {"input": "-34,-48,71,83,-20,-39|-34,-48,71,83,-20,-39|33", "output": "0"}, {"input": "-67,71,65,-24,17,-20,92|-82,-98,17,59,44,-75,-82|68", "output": "419"}, {"input": "29,-33,-67,-11|24,-36,-68,-12|20", "output": "10"}, {"input": "39,80,-23,56,67,35,-98,70|39,80,-23,56,67,35,-98,70|70", "output": "0"}, {"input": "69,-74,-66,-33,-71|-73,90,41,-61,-31|36", "output": "177"}, {"input": "-47,83,-13,-48,75,62,-33,29,25,-36|-52,78,-8,-47,74,57,-38,28,22,-31|33", "output": "36"}, {"input": "89,13,41|89,13,41|90", "output": "0"}, {"input": "43,-98,-72,-81,76,-62,39|-91,-6,49,41,-63,10,-68|5", "output": "148"}, {"input": "-7,-90,-9,-47,74|-10,-85,-14,-48,77|52", "output": "17"}, {"input": "91,-61,-40,-59,-55,5,-94,-55,88,-15|91,-61,-40,-59,-55,5,-94,-55,88,-15|100", "output": "0"}, {"input": "71,88,-37,-32,-60,79,-73|-3,-91,20,-44,-49,17,-11|39", "output": "300"}, {"input": "-43,-94,68,-51|-42,-95,67,-56|98", "output": "8"}, {"input": "-11,64,30,2,73|-11,64,30,2,73|68", "output": "0"}, {"input": "-93,-71,-34,-55,48,-33|-91,-73,52,11,-12,86|100", "output": "315"}, {"input": "11,55,30,-71,-2,47|8,54,25,-66,-1,42|66", "output": "20"}, {"input": "75,84,89,88,71,-50,-7,10,-83|75,84,89,88,71,-50,-7,10,-83|85", "output": "0"}, {"input": "59,-20,69,-69,84,-24|29,-21,70,4,-17,3|89", "output": "233"}, {"input": "41,-68,-51,7,70|42,-63,-46,4,73|72", "output": "17"}, {"input": "3,40,-100,-23,-27|3,40,-100,-23,-27|26", "output": "0"}, {"input": "48,55,67,-18,19,13,13|72,-46,30,21,88,-57,68|10", "output": "185"}, {"input": "31,69,62,58,-15|26,66,67,57,-18|25", "output": "17"}, {"input": "-94,-89,-38|-94,-89,-38|60", "output": "0"}, {"input": "96,-82,16,6,61,47,-51,83,78,-2|26,2,-38,-63,67,76,-99,92,97,-73|99", "output": "296"}, {"input": "-44,-55,78,32,18,-88,42|-47,-60,79,29,19,-83,45|71", "output": "21"}, {"input": "-19,93,13,56,84,29,9,40,14,-60|-19,93,13,56,84,29,9,40,14,-60|95", "output": "0"}, {"input": "15,-34,92,-37,63,-30,96,99|33,24,60,-39,-30,12,-81,82|36", "output": "239"}, {"input": "-31,-15,-19,38|-36,-18,-22,35|49", "output": "14"}, {"input": "80,-46,-84|80,-46,-84|53", "output": "0"}, {"input": "-16,38,19,6,-85,-48,7|-1,97,49,78,-95,95,47|48", "output": "369"}, {"input": "-99,-10,-24,92,-1,7,37,91|-94,-7,-21,89,0,4,36,92|62", "output": "20"}, {"input": "-1|-1|43", "output": "0"}, {"input": "85,-58,19,-68,59,36,-94|0,51,44,69,-94,-79,64|54", "output": "184"}, {"input": "18,-54,-88|17,-53,-89|27", "output": "3"}, {"input": "-17,-14,94,-3,-29,92,7,-36|-17,-14,94,-3,-29,92,7,-36|10", "output": "0"}, {"input": "-96,91,38,-87,-11,-43,66,-83|99,66,-90,93,-93,-37,-49,-95|79", "output": "188"}, {"input": "-39,-68,21|-34,-73,24|27", "output": "13"}, {"input": "79,-35,96,-6,-58,55,55,91|79,-35,96,-6,-58,55,55,91|91", "output": "0"}, {"input": "99,-59|-21,-73|74", "output": "134"}, {"input": "-21|-18|86", "output": "3"}, {"input": "1,83,-50,-81,51,76,60|1,83,-50,-81,51,76,60|31", "output": "0"}, {"input": "78,97|-23,75|76", "output": "123"}, {"input": "44,100|39,99|68", "output": "6"}, {"input": "69,-6,-83,29,65,-13,-97|69,-6,-83,29,65,-13,-97|53", "output": "0"}, {"input": "-73,10,-8,62,17,81,-61,11|-55,87,33,66,-31,57,37,98|61", "output": "314"}, {"input": "11,87,51,-32,-18,-38,-78,-29|12,84,52,-29,-15,-33,-77,-30|3", "output": "18"}, {"input": "-17,-54,24,-46,-10,-34,-13,-29|-17,-54,24,-46,-10,-34,-13,-29|76", "output": "0"}, {"input": "42,-98,32,-52,-79|-39,84,4,25,42|97", "output": "368"}, {"input": "76,21,65,82|77,22,60,77|37", "output": "12"}, {"input": "3,77,-38,-22|3,77,-38,-22|84", "output": "0"}, {"input": "-6,21,41,35,-12,8,90,40,-16,-10|79,16,-31,-22,-36,-41,-70,84,-51,-20|15", "output": "374"}, {"input": "95,76,-53,-51,-45,89,23,-30,85|98,79,-50,-52,-50,86,22,-33,84|22", "output": "23"}, {"input": "-97,81,36,-68,-30|-97,81,36,-68,-30|5", "output": "0"}, {"input": "41|-26|89", "output": "67"}, {"input": "63,92,25|58,87,28|36", "output": "13"}, {"input": "22,12,-13,-53,-87,-36,22,-71|22,12,-13,-53,-87,-36,22,-71|8", "output": "0"}, {"input": "25,-82,47,61,75,-87,-62|-62,44,-23,-79,-37,-70,42|97", "output": "299"}, {"input": "55,52,58,-43,98,33,-3|56,53,57,-40,99,32,0|79", "output": "11"}, {"input": "56|56|94", "output": "0"}, {"input": "95,-47|60,-46|33", "output": "36"}, {"input": "-60,-39|-63,-36|9", "output": "6"}, {"input": "-100,4,15|-100,4,15|88", "output": "0"}]
|
{
"cpp": "==Code Submission==\n\nint main() {\n string input;\n getline(cin, input);\n // Expected format: \"arr|brr|k\" where arr and brr are comma-separated integers.\n size_t pos1 = input.find('|');\n size_t pos2 = input.find('|', pos1 + 1);\n string arr_str = input.substr(0, pos1);\n string brr_str = input.substr(pos1 + 1, pos2 - pos1 - 1);\n string k_str = input.substr(pos2 + 1);\n \n vector<int> arr, brr;\n {\n istringstream iss(arr_str);\n string token;\n while(getline(iss, token, ',')) {\n if(!token.empty()) {\n arr.push_back(stoi(token));\n }\n }\n }\n {\n istringstream iss(brr_str);\n string token;\n while(getline(iss, token, ',')) {\n if(!token.empty()) {\n brr.push_back(stoi(token));\n }\n }\n }\n long long k = stoll(k_str);\n \n Solution sol;\n auto ans = sol.minCost(arr, brr, k);\n cout << ans;\n return 0;\n}",
"golang": "==Code Submission==\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n line, _ := reader.ReadString('\\n')\n line = strings.TrimSpace(line)\n // Expected format: \"arr|brr|k\"\n parts := strings.Split(line, \"|\")\n \n var arr []int\n if parts[0] != \"\" {\n arrStr := strings.Split(parts[0], \",\")\n for _, s := range arrStr {\n num, _ := strconv.Atoi(s)\n arr = append(arr, num)\n }\n }\n \n var brr []int\n if parts[1] != \"\" {\n brrStr := strings.Split(parts[1], \",\")\n for _, s := range brrStr {\n num, _ := strconv.Atoi(s)\n brr = append(brr, num)\n }\n }\n \n k, _ := strconv.Atoi(parts[2])\n ans := minCost(arr, brr, int64(k))\n fmt.Printf(\"%d\", ans)\n}",
"java": "public class Main {\n private static int[] deserializeArray(String s) {\n if(s.isEmpty()) return new int[0];\n String[] parts = s.split(\",\");\n int[] arr = new int[parts.length];\n for (int i = 0; i < parts.length; i++) {\n arr[i] = Integer.parseInt(parts[i].trim());\n }\n return arr;\n }\n \n public static void main(String[] args) throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n String line = br.readLine().trim();\n // Expected format: \"arr|brr|k\"\n String[] parts = line.split(\"\\\\|\");\n int[] arr = deserializeArray(parts[0]);\n int[] brr = deserializeArray(parts[1]);\n long k = Long.parseLong(parts[2].trim());\n \n Solution sol = new Solution();\n long ans = sol.minCost(arr, brr, k);\n System.out.println(ans);\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\nconst deserialize_stdin = (input) => {\n // Expected format: \"arr|brr|k\"\n const parts = input.trim().split(\"|\");\n const arr = parts[0].split(\",\").filter(s => s.length > 0).map(Number);\n const brr = parts[1].split(\",\").filter(s => s.length > 0).map(Number);\n const k = parseInt(parts[2], 10);\n return { arr, brr, k };\n};\n\nconst serialize_stdout = (result) => {\n return result.toString();\n};\n\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\nlet input = '';\nprocess.stdin.on('data', chunk => { input += chunk; });\nprocess.stdin.on('end', () => {\n const { arr, brr, k } = deserialize_stdin(input);\n const ans = minCost(arr, brr, k);\n console.log(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str):\n # Expected format: \"arr|brr|k\"\n parts = input_str.split(\"|\")\n arr = list(map(int, parts[0].split(','))) if parts[0] != \"\" else []\n brr = list(map(int, parts[1].split(','))) if parts[1] != \"\" else []\n k = int(parts[2])\n return arr, brr, k\n\ndef serialize_stdout(result):\n return str(result)\n\ninput_str = sys.stdin.read().strip()\narr, brr, k = deserialize_stdin(input_str)\nsol = Solution()\nans = sol.minCost(arr, brr, k)\nsys.stdout.write(serialize_stdout(ans))",
"ruby": "==Code Submission==\ninput = gets.strip\n# Expected format: \"arr|brr|k\"\nparts = input.split(\"|\")\narr = parts[0] == \"\" ? [] : parts[0].split(\",\").map(&:to_i)\nbrr = parts[1] == \"\" ? [] : parts[1].split(\",\").map(&:to_i)\nk = parts[2].to_i\nans = min_cost(arr, brr, k)\nputs ans"
}
|
3721
|
Count Mentions Per User
|
count-mentions-per-user
|
<p>You are given an integer <code>numberOfUsers</code> representing the total number of users and an array <code>events</code> of size <code>n x 3</code>.</p>
<p>Each <code inline="">events[i]</code> can be either of the following two types:</p>
<ol>
<li><strong>Message Event:</strong> <code>["MESSAGE", "timestamp<sub>i</sub>", "mentions_string<sub>i</sub>"]</code>
<ul>
<li>This event indicates that a set of users was mentioned in a message at <code>timestamp<sub>i</sub></code>.</li>
<li>The <code>mentions_string<sub>i</sub></code> string can contain one of the following tokens:
<ul>
<li><code>id<number></code>: where <code><number></code> is an integer in range <code>[0,numberOfUsers - 1]</code>. There can be <strong>multiple</strong> ids separated by a single whitespace and may contain duplicates. This can mention even the offline users.</li>
<li><code>ALL</code>: mentions <strong>all</strong> users.</li>
<li><code>HERE</code>: mentions all <strong>online</strong> users.</li>
</ul>
</li>
</ul>
</li>
<li><strong>Offline Event:</strong> <code>["OFFLINE", "timestamp<sub>i</sub>", "id<sub>i</sub>"]</code>
<ul>
<li>This event indicates that the user <code>id<sub>i</sub></code> had become offline at <code>timestamp<sub>i</sub></code> for <strong>60 time units</strong>. The user will automatically be online again at time <code>timestamp<sub>i</sub> + 60</code>.</li>
</ul>
</li>
</ol>
<p>Return an array <code>mentions</code> where <code>mentions[i]</code> represents the number of mentions the user with id <code>i</code> has across all <code>MESSAGE</code> events.</p>
<p>All users are initially online, and if a user goes offline or comes back online, their status change is processed <em>before</em> handling any message event that occurs at the same timestamp.</p>
<p><strong>Note </strong>that a user can be mentioned <strong>multiple</strong> times in a <strong>single</strong> message event, and each mention should be counted <strong>separately</strong>.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">numberOfUsers = 2, events = [["MESSAGE","10","id1 id0"],["OFFLINE","11","0"],["MESSAGE","71","HERE"]]</span></p>
<p><strong>Output:</strong> <span class="example-io">[2,2]</span></p>
<p><strong>Explanation:</strong></p>
<p>Initially, all users are online.</p>
<p>At timestamp 10, <code>id1</code> and <code>id0</code> are mentioned. <code>mentions = [1,1]</code></p>
<p>At timestamp 11, <code>id0</code> goes <strong>offline.</strong></p>
<p>At timestamp 71, <code>id0</code> comes back <strong>online</strong> and <code>"HERE"</code> is mentioned. <code>mentions = [2,2]</code></p>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">numberOfUsers = 2, events = [["MESSAGE","10","id1 id0"],["OFFLINE","11","0"],["MESSAGE","12","ALL"]]</span></p>
<p><strong>Output:</strong> <span class="example-io">[2,2]</span></p>
<p><strong>Explanation:</strong></p>
<p>Initially, all users are online.</p>
<p>At timestamp 10, <code>id1</code> and <code>id0</code> are mentioned. <code>mentions = [1,1]</code></p>
<p>At timestamp 11, <code>id0</code> goes <strong>offline.</strong></p>
<p>At timestamp 12, <code>"ALL"</code> is mentioned. This includes offline users, so both <code>id0</code> and <code>id1</code> are mentioned. <code>mentions = [2,2]</code></p>
</div>
<p><strong class="example">Example 3:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">numberOfUsers = 2, events = [["OFFLINE","10","0"],["MESSAGE","12","HERE"]]</span></p>
<p><strong>Output:</strong> <span class="example-io">[0,1]</span></p>
<p><strong>Explanation:</strong></p>
<p>Initially, all users are online.</p>
<p>At timestamp 10, <code>id0</code> goes <strong>offline.</strong></p>
<p>At timestamp 12, <code>"HERE"</code> is mentioned. Because <code>id0</code> is still offline, they will not be mentioned. <code>mentions = [0,1]</code></p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>1 <= numberOfUsers <= 100</code></li>
<li><code>1 <= events.length <= 100</code></li>
<li><code>events[i].length == 3</code></li>
<li><code>events[i][0]</code> will be one of <code>MESSAGE</code> or <code>OFFLINE</code>.</li>
<li><code>1 <= int(events[i][1]) <= 10<sup>5</sup></code></li>
<li>The number of <code>id<number></code> mentions in any <code>"MESSAGE"</code> event is between <code>1</code> and <code>100</code>.</li>
<li><code>0 <= <number> <= numberOfUsers - 1</code></li>
<li>It is <strong>guaranteed</strong> that the user id referenced in the <code>OFFLINE</code> event is <strong>online</strong> at the time the event occurs.</li>
</ul>
|
You are given an integer `numberOfUsers` representing the total number of users and an array `events` of size `n x 3`.
Each `events[i]` can be either of the following two types:
1. **Message Event:** `["MESSAGE", "timestampi", "mentions_stringi"]`
- This event indicates that a set of users was mentioned in a message at `timestampi`.
- The `mentions_stringi` string can contain one of the following tokens:
- `id<number>`: where `<number>` is an integer in range `[0,numberOfUsers - 1]`. There can be **multiple** ids separated by a single whitespace and may contain duplicates. This can mention even the offline users.
- `ALL`: mentions **all** users.
- `HERE`: mentions all **online** users.
2. **Offline Event:** `["OFFLINE", "timestampi", "idi"]`
- This event indicates that the user `idi` had become offline at `timestampi` for **60 time units**. The user will automatically be online again at time `timestampi + 60`.
Return an array `mentions` where `mentions[i]` represents the number of mentions the user with id `i` has across all `MESSAGE` events.
All users are initially online, and if a user goes offline or comes back online, their status change is processed *before* handling any message event that occurs at the same timestamp.
**Note** that a user can be mentioned **multiple** times in a **single** message event, and each mention should be counted **separately**.
**Example 1:**
**Input:** numberOfUsers \= 2, events \= \[\["MESSAGE","10","id1 id0"],\["OFFLINE","11","0"],\["MESSAGE","71","HERE"]]
**Output:** \[2,2]
**Explanation:**
Initially, all users are online.
At timestamp 10, `id1` and `id0` are mentioned. `mentions = [1,1]`
At timestamp 11, `id0` goes **offline.**
At timestamp 71, `id0` comes back **online** and `"HERE"` is mentioned. `mentions = [2,2]`
**Example 2:**
**Input:** numberOfUsers \= 2, events \= \[\["MESSAGE","10","id1 id0"],\["OFFLINE","11","0"],\["MESSAGE","12","ALL"]]
**Output:** \[2,2]
**Explanation:**
Initially, all users are online.
At timestamp 10, `id1` and `id0` are mentioned. `mentions = [1,1]`
At timestamp 11, `id0` goes **offline.**
At timestamp 12, `"ALL"` is mentioned. This includes offline users, so both `id0` and `id1` are mentioned. `mentions = [2,2]`
**Example 3:**
**Input:** numberOfUsers \= 2, events \= \[\["OFFLINE","10","0"],\["MESSAGE","12","HERE"]]
**Output:** \[0,1]
**Explanation:**
Initially, all users are online.
At timestamp 10, `id0` goes **offline.**
At timestamp 12, `"HERE"` is mentioned. Because `id0` is still offline, they will not be mentioned. `mentions = [0,1]`
**Constraints:**
- `1 <= numberOfUsers <= 100`
- `1 <= events.length <= 100`
- `events[i].length == 3`
- `events[i][0]` will be one of `MESSAGE` or `OFFLINE`.
- `1 <= int(events[i][1]) <= 105`
- The number of `id<number>` mentions in any `"MESSAGE"` event is between `1` and `100`.
- `0 <= <number> <= numberOfUsers - 1`
- It is **guaranteed** that the user id referenced in the `OFFLINE` event is **online** at the time the event occurs.
|
Medium
|
[
"array",
"math",
"sorting",
"simulation"
] |
leetcode
|
https://leetcode.com/problems/count-mentions-per-user
|
functional
| null | null | null | null |
{
"c": "/**\n * Note: The returned array must be malloced, assume caller calls free().\n */\nint* countMentions(int numberOfUsers, char*** events, int eventsSize, int* eventsColSize, int* returnSize) {\n \n}",
"cpp": "class Solution {\npublic:\n vector<int> countMentions(int numberOfUsers, vector<vector<string>>& events) {\n \n }\n};",
"csharp": "public class Solution {\n public int[] CountMentions(int numberOfUsers, IList<IList<string>> events) {\n \n }\n}",
"dart": "class Solution {\n List<int> countMentions(int numberOfUsers, List<List<String>> events) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec count_mentions(number_of_users :: integer, events :: [[String.t]]) :: [integer]\n def count_mentions(number_of_users, events) do\n \n end\nend",
"erlang": "-spec count_mentions(NumberOfUsers :: integer(), Events :: [[unicode:unicode_binary()]]) -> [integer()].\ncount_mentions(NumberOfUsers, Events) ->\n .",
"golang": "func countMentions(numberOfUsers int, events [][]string) []int {\n \n}",
"java": "class Solution {\n public int[] countMentions(int numberOfUsers, List<List<String>> events) {\n \n }\n}",
"javascript": "/**\n * @param {number} numberOfUsers\n * @param {string[][]} events\n * @return {number[]}\n */\nvar countMentions = function(numberOfUsers, events) {\n \n};",
"kotlin": "class Solution {\n fun countMentions(numberOfUsers: Int, events: List<List<String>>): IntArray {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param Integer $numberOfUsers\n * @param String[][] $events\n * @return Integer[]\n */\n function countMentions($numberOfUsers, $events) {\n \n }\n}",
"python": "class Solution(object):\n def countMentions(self, numberOfUsers, events):\n \"\"\"\n :type numberOfUsers: int\n :type events: List[List[str]]\n :rtype: List[int]\n \"\"\"\n ",
"python3": "class Solution:\n def countMentions(self, numberOfUsers: int, events: List[List[str]]) -> List[int]:\n ",
"racket": "(define/contract (count-mentions numberOfUsers events)\n (-> exact-integer? (listof (listof string?)) (listof exact-integer?))\n )",
"ruby": "# @param {Integer} number_of_users\n# @param {String[][]} events\n# @return {Integer[]}\ndef count_mentions(number_of_users, events)\n \nend",
"rust": "impl Solution {\n pub fn count_mentions(number_of_users: i32, events: Vec<Vec<String>>) -> Vec<i32> {\n \n }\n}",
"scala": "object Solution {\n def countMentions(numberOfUsers: Int, events: List[List[String]]): Array[Int] = {\n \n }\n}",
"swift": "class Solution {\n func countMentions(_ numberOfUsers: Int, _ events: [[String]]) -> [Int] {\n \n }\n}",
"typescript": "function countMentions(numberOfUsers: number, events: string[][]): number[] {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n vector<int> countMentions(int numberOfUsers, vector<vector<string>>& events) {\n vector<tuple<int, int, int, vector<string>>> sorted_events;\n for (int i = 0; i < events.size(); ++i) {\n int timestamp = stoi(events[i][1]);\n int type = (events[i][0] == \"OFFLINE\") ? 0 : 1;\n sorted_events.emplace_back(timestamp, type, i, events[i]);\n }\n sort(sorted_events.begin(), sorted_events.end());\n \n vector<int> online_time(numberOfUsers, 0);\n vector<int> mentions(numberOfUsers, 0);\n \n for (auto& t : sorted_events) {\n auto& e = get<3>(t);\n if (e[0] == \"OFFLINE\") {\n int event_time = get<0>(t);\n int user_id = stoi(e[2]);\n online_time[user_id] = event_time + 60;\n } else {\n int event_time = get<0>(t);\n string mentions_str = e[2];\n vector<string> tokens = split(mentions_str, ' ');\n for (string& token : tokens) {\n if (token == \"ALL\") {\n for (int i = 0; i < numberOfUsers; ++i) {\n mentions[i]++;\n }\n } else if (token == \"HERE\") {\n for (int i = 0; i < numberOfUsers; ++i) {\n if (event_time >= online_time[i]) {\n mentions[i]++;\n }\n }\n } else if (token.substr(0, 2) == \"id\") {\n int user_id = stoi(token.substr(2));\n mentions[user_id]++;\n }\n }\n }\n }\n \n return mentions;\n }\n\nprivate:\n vector<string> split(const string& s, char delimiter) {\n vector<string> tokens;\n string token;\n istringstream tokenStream(s);\n while (getline(tokenStream, token, delimiter)) {\n if (!token.empty()) {\n tokens.push_back(token);\n }\n }\n return tokens;\n }\n};",
"memory": 6400,
"memoryDistribution": "[[6400, 33.5043, \"#include <vector>\\n#include <string>\\n#include <tuple>\\n#include <algorithm>\\n#include <sstream>\\n\\nusing namespace std;\\n\\nclass Solution {\\npublic:\\n vector<int> countMentions(int numberOfUsers, vector<vector<string>>& events) {\\n vector<tuple<int, int, int, vector<string>>> sorted_events;\\n for (int i = 0; i < events.size(); ++i) {\\n int timestamp = stoi(events[i][1]);\\n int type = (events[i][0] == \\\"OFFLINE\\\") ? 0 : 1;\\n sorted_events.emplace_back(timestamp, type, i, events[i]);\\n }\\n sort(sorted_events.begin(), sorted_events.end());\\n \\n vector<int> online_time(numberOfUsers, 0);\\n vector<int> mentions(numberOfUsers, 0);\\n \\n for (auto& t : sorted_events) {\\n auto& e = get<3>(t);\\n if (e[0] == \\\"OFFLINE\\\") {\\n int event_time = get<0>(t);\\n int user_id = stoi(e[2]);\\n online_time[user_id] = event_time + 60;\\n } else {\\n int event_time = get<0>(t);\\n string mentions_str = e[2];\\n vector<string> tokens = split(mentions_str, ' ');\\n for (string& token : tokens) {\\n if (token == \\\"ALL\\\") {\\n for (int i = 0; i < numberOfUsers; ++i) {\\n mentions[i]++;\\n }\\n } else if (token == \\\"HERE\\\") {\\n for (int i = 0; i < numberOfUsers; ++i) {\\n if (event_time >= online_time[i]) {\\n mentions[i]++;\\n }\\n }\\n } else if (token.substr(0, 2) == \\\"id\\\") {\\n int user_id = stoi(token.substr(2));\\n mentions[user_id]++;\\n }\\n }\\n }\\n }\\n \\n return mentions;\\n }\\n\\nprivate:\\n vector<string> split(const string& s, char delimiter) {\\n vector<string> tokens;\\n string token;\\n istringstream tokenStream(s);\\n while (getline(tokenStream, token, delimiter)) {\\n if (!token.empty()) {\\n tokens.push_back(token);\\n }\\n }\\n return tokens;\\n }\\n};\"], [40103, 8.247399999999999, \"class Solution {\\npublic:\\n vector<int> countMentions(int uNum, vector<vector<string>>& events) {\\n sort(begin(events), end(events), [](auto const & lhs, auto const & rhs){\\n int lTm = stoi(lhs[1]);\\n int rTm = stoi(rhs[1]);\\n if (lTm < rTm) return true;\\n if (lTm == rTm && lhs[0][0] == 'O' && rhs[0][0] == 'M') return true;\\n return false;\\n });\\n\\n int n = events.size();\\n int all = 0;\\n priority_queue<pair<int, int>> offline;\\n vector<bool> isOnline(uNum, true);\\n vector<int> cnt(uNum);\\n for (auto const & e : events) {\\n auto const & tp = e[0];\\n int tm = stoi(e[1]);\\n // cout << \\\"TM: \\\" << tm << \\\" q: \\\" << ((!offline.empty()) ? -offline.top().first : 0 ) << \\\"\\\\n\\\";\\n while (!offline.empty() && (-offline.top().first) <= tm) {\\n int uid = offline.top().second;\\n assert(!isOnline[uid]);\\n // cout << \\\"ONLINE: \\\" << uid << \\\"\\\\n\\\";\\n isOnline[uid] = true;\\n offline.pop();\\n }\\n if (tp[0] == 'O') {\\n int uid = stoi(e[2]);\\n assert(isOnline[uid]);\\n isOnline[uid] = false;\\n // cout << \\\"UID: \\\" << uid << \\\" offline tille: \\\" << tm+60 << \\\"\\\\n\\\";\\n offline.emplace(-(tm+60), uid);\\n } else {\\n parseMentions(e[2], isOnline, all, cnt);\\n }\\n }\\n for (int i = 0; i < uNum; i++) {\\n cnt[i] += all;\\n }\\n return cnt;\\n }\\n\\n void parseMentions(string const & mentions, vector<bool> const & online, int & all, vector<int> & cnt) {\\n for (int i = 0; i < mentions.size(); i++) {\\n if (mentions[i] == 'A') {\\n // cout << \\\"ALL\\\\n\\\";\\n all++;\\n i += 3;\\n } else if (mentions[i] == 'H') {\\n // cout << \\\"HERE: \\\";\\n for (int j = 0; j < online.size(); j++) {\\n if (online[j]) {\\n // cout << j << ' ';\\n cnt[j]++;\\n }\\n }\\n // cout << \\\"\\\\n\\\";\\n i += 4;\\n } else if (mentions[i] == 'i') {\\n i+=2;\\n int id = 0;\\n for (;i < mentions.size() && mentions[i] >= '0' && mentions[i] <= '9'; i++) {\\n id *= 10;\\n id += mentions[i]-'0';\\n }\\n // cout << \\\"id: \\\" << id << \\\"\\\\n\\\";\\n cnt[id]++;\\n\\n } else assert(false);\\n }\\n }\\n};\"], [41109, 11.340300000000001, \"class Solution {\\npublic:\\n vector<int> countMentions(int numberOfUsers, vector<vector<string>>& events) {\\n vector<tuple<int, int, string>> evs;\\n evs.reserve(events.size());\\n for (auto& ev : events) {\\n evs.emplace_back(\\n ev[0][0] == 'M' ? 0 : 1, \\n stoi(ev[1]),\\n std::move(ev[2])\\n );\\n }\\n auto cmp_events = [] (const auto& l, const auto& r) {\\n return tie(get<1>(l), get<0>(r)) < tie(get<1>(r), get<0>(l));\\n };\\n // if (!ranges::is_sorted(evs, cmp_events)) {\\n std::ranges::sort(evs, cmp_events);\\n // }\\n\\n vector<int> count(numberOfUsers);\\n int all = 0;\\n vector<int> offline_till(numberOfUsers);\\n for (const auto& [type, ts, ids] : evs) {\\n if (type == 1) {\\n int id = stoi(ids);\\n offline_till[id] = ts + 60;\\n continue;\\n }\\n if (ids[0] == 'A') {\\n ++all;\\n } else if (ids[0] == 'H') {\\n for (int i = 0; i < numberOfUsers; ++i) {\\n if (offline_till[i] <= ts) {\\n ++count[i];\\n }\\n }\\n } else {\\n auto sv = string_view(ids).substr(2);\\n while (true) {\\n auto pos = sv.find(' ');\\n pos = pos == string::npos ? sv.size() : pos;\\n int id;\\n from_chars(sv.data(), sv.data() + pos, id);\\n ++count[id];\\n if (pos == sv.size()) break;\\n sv = sv.substr(pos + 3);\\n }\\n }\\n }\\n\\n for (int& c : count) c += all;\\n return count;\\n }\\n};\"], [42115, 5.6702, null], [43121, 7.2165, null], [44128, 11.3402, null], [45134, 4.6393, null], [46140, 3.0927999999999995, null], [47146, 2.5773999999999995, null], [48153, 1.031, null], [49159, 1.5465, null], [50165, 0.5155, null], [51171, 2.0618999999999996, null], [52178, 0.5155, null], [53184, 0.5155, null], [54190, 3.0927999999999995, null], [55196, 0.5155, null], [56203, 1.0309, null], [57209, 1.031, null], [58215, 0.5155, null], [59221, 1.0309, null], [60228, 1.0309, null], [61234, 0.5155, null], [62240, 0.5155, null], [63246, 0.5155, null], [64253, 0.5155, null], [65259, 0.5155, null], [66265, 0.5155, null], [67271, 1.5464, null], [68278, 2.5773, null], [69284, 0.5155, null], [70290, 0.5155, null], [71296, 0.5155, null], [72303, 1.5464, null], [73309, 0.5155, null], [74315, 0.5155, null], [75321, 0.5155, null], [76328, 0.5155, null], [77334, 0.5155, null], [78340, 0.5155, null], [79346, 0.5155, null], [80353, 0.5155, null], [81359, 0.5155, null], [82365, 0.5155, null], [83371, 0.5155, null], [84378, 0.5155, null], [85384, 0.5155, null], [86390, 0.5155, null], [87396, 0.5155, null], [88403, 0.5155, null], [89409, 0.5155, \"class Solution {\\npublic:\\n static bool cmp(vector<string>a, vector<string>b){\\n int timeA = stoi(a[1]);\\n int timeB = stoi(b[1]);\\n return timeA == timeB ? a[0] > b[0] : timeA < timeB;\\n }\\n\\n void handleMessage(vector<string>event, vector<int>&mentions, vector<int>&offlineTime){\\n\\n int timestamp = stoi(event[1]);\\n\\n vector<string>ids;\\n //collecting all ids separated by space\\n stringstream s(event[2]);\\n string word;\\n while(s >> word){\\n ids.push_back(word);\\n }\\n\\n for(string id: ids){\\n if(id == \\\"ALL\\\"){\\n for(int i = 0; i<mentions.size(); i++){\\n mentions[i]++;\\n }\\n }\\n else if(id == \\\"HERE\\\"){\\n for(int i = 0; i<mentions.size(); i++){\\n if(offlineTime[i] == 0 || offlineTime[i] + 60 <= timestamp){\\n mentions[i]++;\\n }\\n }\\n }\\n else{\\n int idNum = stoi(id.substr(2)); //id1 me se idNum ko 1 assign kar rahe hai\\n mentions[idNum]++;\\n }\\n }\\n\\n }\\n\\n void handleOffline(vector<string>event, vector<int>&mentions, vector<int>&offlineTime){\\n \\n int timestamp = stoi(event[1]);\\n int id = stoi(event[2]);\\n\\n offlineTime[id] = timestamp;\\n }\\n vector<int> countMentions(int numberOfUsers, vector<vector<string>>& events) {\\n vector<int>mentions(numberOfUsers);\\n vector<int>offlineTime(numberOfUsers);\\n\\n sort(events.begin(), events.end(), cmp);\\n\\n for(vector<string>event: events){\\n if(event[0] == \\\"MESSAGE\\\"){\\n handleMessage(event, mentions, offlineTime);\\n }\\n else if(event[0] == \\\"OFFLINE\\\"){\\n handleOffline(event, mentions, offlineTime);\\n }\\n }\\n\\n return mentions;\\n }\\n};\"], [90415, 4.6392, \"class Solution {\\npublic:\\n static bool cmp(vector<string>a, vector<string>b){\\n int timeA = stoi(a[1]);\\n int timeB = stoi(b[1]);\\n return timeA == timeB ? a[0] > b[0] : timeA < timeB;\\n }\\n\\n void handleMessage(vector<string>event, vector<int>&mentions, vector<int>&offlineTime){\\n\\n int timestamp = stoi(event[1]);\\n\\n vector<string>ids;\\n //collecting all ids separated by space\\n stringstream s(event[2]);\\n string word;\\n while(s >> word){\\n ids.push_back(word);\\n }\\n\\n for(string id: ids){\\n if(id == \\\"ALL\\\"){\\n for(int i = 0; i<mentions.size(); i++){\\n mentions[i]++;\\n }\\n }\\n else if(id == \\\"HERE\\\"){\\n for(int i = 0; i<mentions.size(); i++){\\n if(offlineTime[i] == 0 || offlineTime[i] + 60 <= timestamp){\\n mentions[i]++;\\n }\\n }\\n }\\n else{\\n int idNum = stoi(id.substr(2)); //id1 me se idNum ko 1 assign kar rahe hai\\n mentions[idNum]++;\\n }\\n }\\n\\n }\\n\\n void handleOffline(vector<string>event, vector<int>&mentions, vector<int>&offlineTime){\\n \\n int timestamp = stoi(event[1]);\\n int id = stoi(event[2]);\\n\\n offlineTime[id] = timestamp;\\n }\\n vector<int> countMentions(int numberOfUsers, vector<vector<string>>& events) {\\n vector<int>mentions(numberOfUsers);\\n vector<int>offlineTime(numberOfUsers);\\n\\n sort(events.begin(), events.end(), cmp);\\n\\n for(vector<string>event: events){\\n if(event[0] == \\\"MESSAGE\\\"){\\n handleMessage(event, mentions, offlineTime);\\n }\\n else if(event[0] == \\\"OFFLINE\\\"){\\n handleOffline(event, mentions, offlineTime);\\n }\\n }\\n\\n return mentions;\\n }\\n};\"]]",
"runtime": 52,
"runtimeDistribution": "[[1, 1.5465, \"#include <bits/stdc++.h>\\n\\n#include <sstream>\\nusing namespace std;\\nauto init = []() {\\n ios::sync_with_stdio(false);\\n cin.tie(nullptr);\\n cout.tie(nullptr);\\n return 'c';\\n}();\\nauto init2 = atexit([]() { ofstream(\\\"display_runtime.txt\\\") << 0; });\\n\\nclass Solution {\\n public:\\n static vector<int> countMentions(int numberOfUsers, vector<vector<string>>& events) {\\n std::ranges::sort(events, [](const auto& lhs, const auto& rhs) {\\n auto t1 = std::stoi(lhs[1]);\\n auto t2 = std::stoi(rhs[1]);\\n if (t1 == t2) {\\n return lhs[0] > rhs[0];\\n }\\n\\n return t1 < t2;\\n });\\n std::vector<int> wake(numberOfUsers);\\n std::vector<int> ret(numberOfUsers);\\n auto processOffLine = [&](const std::string& time, const std::string& id) {\\n auto t = std::stoi(time);\\n auto i = std::stoi(id);\\n wake[i] = t + 60;\\n };\\n\\n auto processMention = [&](const std::string& time, const std::string& member) {\\n if (member == \\\"ALL\\\") {\\n for (auto& r : ret) {\\n r++;\\n }\\n return;\\n }\\n auto t = std::stoi(time);\\n if (member == \\\"HERE\\\") {\\n for (int i = 0; i < numberOfUsers; ++i) {\\n ret[i] += wake[i] <= t;\\n }\\n return;\\n }\\n std::stringstream ss{member};\\n std::string buf;\\n while (ss >> buf) {\\n auto id = std::stoi(buf.substr(2));\\n ret[id]++;\\n }\\n };\\n\\n for (auto& event : events) {\\n if (event[0] == \\\"OFFLINE\\\") {\\n processOffLine(event[1], event[2]);\\n } else {\\n processMention(event[1], event[2]);\\n }\\n }\\n return ret;\\n }\\n};\"], [4, 2.0618999999999996, \"class Solution {\\npublic:\\n vector<int> countMentions(int numberOfUsers, vector<vector<string>>& events) {\\n vector<int> ans(numberOfUsers,0);\\n vector<int> offline(numberOfUsers,-60);\\n int n=events.size();\\n sort(events.begin(),events.end(),[](vector<string>&a, vector<string>&b){\\n if(a[1]==b[1]){\\n return a[0]>b[0];\\n }\\n return stoi(a[1])<stoi(b[1]);\\n });\\n for(int i=0; i!=n; i++){\\n if(events[i][0]==\\\"MESSAGE\\\"){\\n int xtime = stoi(events[i][1]);\\n if(events[i][2]==\\\"ALL\\\"){\\n for(int i=0; i!=numberOfUsers; i++){\\n ans[i]++;\\n }\\n }else if(events[i][2]==\\\"HERE\\\"){\\n for(int i=0; i!=numberOfUsers; i++){\\n if(offline[i]+60<=xtime){\\n ans[i]++;\\n }\\n }\\n }else{\\n stringstream ss(events[i][2]);\\n string st;\\n// unordered_map<int,int> mp;\\n while(getline(ss,st,' ')){\\n st.erase(0,2);\\n int xt=stoi(st);\\n// if(!mp.count(xt)){\\n// mp[xt]=1;\\n ans[xt]++;\\n// }\\n }\\n }\\n }else{\\n int xt=stoi(events[i][2]);\\n offline[xt]=stoi(events[i][1]);\\n }\\n }\\n return ans;\\n }\\n};\"], [7, 0.5155, null], [9, 1.031, null], [12, 1.5464, null], [15, 2.0619, null], [18, 5.670100000000001, null], [21, 2.5774, null], [24, 4.1238, null], [26, 3.6083, null], [29, 4.1237, null], [32, 4.639200000000001, null], [35, 6.185600000000001, null], [38, 3.6083, null], [40, 5.670100000000001, null], [43, 2.0619, null], [46, 2.0618999999999996, null], [49, 2.0619, null], [52, 2.0618, null], [55, 1.0309, null], [57, 0.5155, null], [60, 2.0619, null], [63, 1.031, null], [66, 0.5155, null], [69, 1.031, null], [72, 0.5155, null], [74, 0.5155, null], [77, 0.5155, null], [80, 0.5155, null], [83, 0.5155, null], [86, 0.5155, null], [88, 1.0309, null], [91, 0.5155, null], [94, 0.5155, null], [97, 1.0309, null], [100, 0.5155, null], [103, 0.5155, null], [105, 0.5155, null], [108, 0.5155, null], [111, 0.5155, null], [114, 0.5155, null], [117, 0.5155, null], [120, 1.0309, null], [122, 0.5155, null], [125, 0.5155, null], [128, 0.5155, null], [131, 0.5155, null], [134, 0.5155, null], [137, 0.5155, null], [139, 0.5155, null], [142, 1.5464, null], [145, 0.5155, null], [148, 1.5463999999999998, null], [151, 1.5465, null], [153, 1.5463999999999998, null], [156, 2.0619, null], [159, 1.031, null], [162, 1.031, null], [165, 1.5464, null], [168, 1.5463999999999998, null], [170, 1.031, null], [173, 0.5155, null], [176, 0.5155, \"class Solution {\\npublic:\\n\\nvoid mention(string s, vector<int>&ans){\\nint nn=s.length();\\nstring val=\\\"\\\";\\nfor(int i=0;i<nn;i++){\\n if(isalpha(s[i])==0){\\n\\n val+=s[i];\\n }\\n\\n\\n if(s[i]==' '||i==nn-1){\\n int aa=stoi(val);\\n ans[aa]+=1;\\n\\n cout<<aa<<endl;\\n val=\\\"\\\";\\n }\\n}\\n\\n}\\n\\n\\n vector<int> countMentions(int numberOfUsers,\\n vector<vector<string>>& events) {\\n sort(events.begin(), events.end(), [](const vector<string>& a, const vector<string>& b) {\\n int timeA = stoi(a[1]);\\n int timeB = stoi(b[1]);\\n\\n if (timeA == timeB) {\\n return a[0] == \\\"OFFLINE\\\"; // OFFLINE events come first if timestamps are equal\\n }\\n return timeA < timeB;\\n });\\n\\n int n = numberOfUsers;\\n vector<int> ans(n, 0);\\n vector<pair<int, int>> offline(n, {1, -1});\\n int currtime = 0;\\n int kk = events.size();\\n\\n for (int i = 0; i < kk; i++) {\\n string mess = events[i][0];\\n int timestamp = stoi(events[i][1]);\\n string ss = events[i][2];\\n\\n if (mess == \\\"MESSAGE\\\") {\\n currtime = timestamp;\\n if (ss == \\\"ALL\\\") {\\n for (int k = 0; k < n; k++) {\\n ans[k] += 1;\\n }\\n }\\n if (ss != \\\"ALL\\\" && ss != \\\"HERE\\\") {\\n\\n mention(ss, ans);\\n }\\n\\n if (ss == \\\"HERE\\\") {\\n\\n for (int k1 = 0; k1 < n; k1++) {\\n if (offline[k1].first == 0 &&\\n offline[k1].second <= currtime) {\\n ans[k1] += 1;\\n }\\n\\n if (offline[k1].first == 1) {\\n ans[k1] += 1;\\n }\\n }\\n }\\n }\\n\\n if (mess == \\\"OFFLINE\\\") {\\n currtime = timestamp;\\n offline[stoi(ss)].first = 0;\\n offline[stoi(ss)].second = currtime + 60;\\n }\\n }\\n\\n return ans;\\n \\n}\\n};\\n\"], [179, 1.0309, \"class Solution {\\npublic:\\n vector<int> countMentions(int numberOfUsers, vector<vector<string>>& events) {\\n \\n //0------sort karo sub ko\\n sort(events.begin(),events.end(),[](const vector<string>a , const vector<string>b)\\n {\\n if(stoi(a[1]) == stoi(b[1]))\\n return a[2] < b[2]; //return offlin message\\n return stoi(a[1]) < stoi(b[1]);//small time ,,grater time\\n\\n });\\n\\n // 1--hum ya bar bar dekhna hy ky kesi user ka time pura ho gaya howa hy kay nai or us ko onlin eka time ho gaya hy ky nai\\n // 2--OFFLINE ---matlb us user ko offline ho karden hy\\n // 3--HERE , ALL,USERIDS --- sirf in ko mention karna hy matlb sirf in ko mention karna hy..addtion of 1\\n\\n //------unordered_map<id,online ya offline>\\n unordered_map<int,bool>online;\\n\\n //-----unordered_map<id,timestamp >\\n queue<pair<int,int>>offline;\\n unordered_map<int,int>mentions;\\n\\n //sub ko sub sy pehly online kiya or number o fmentions ko zero kar liya\\n for(int i=0; i<numberOfUsers;i++)\\n {\\n offline.push({i,true});\\n mentions.insert({i,0});\\n }\\n\\n for(auto &event:events)\\n {\\n \\n string action=event[0];\\n int timestamp=stoi(event[1]);\\n string content=event[2];\\n\\n cout << event[1]<<endl;\\n //ab code likho ky sub ko automatially online karo //online lay aee\\n while(!offline.empty() && offline.front().second <= timestamp)\\n {\\n online[offline.front().first]=true;\\n \\n offline.pop();\\n }\\n\\n if(action == \\\"OFFLINE\\\")\\n {\\n \\n int id=stoi(event[2]);\\n \\n online[id]=false;\\n offline.push({id,timestamp+60});\\n }\\n else\\n {\\n if(content == \\\"HERE\\\")\\n {\\n for(int i=0; i<mentions.size();i++)\\n {\\n \\n if(online[i])\\n {\\n mentions[i]++;\\n }\\n }\\n\\n }else if(content == \\\"ALL\\\")\\n {\\n for(int i=0; i<mentions.size();i++)\\n {\\n mentions[i]++;\\n }\\n }else\\n {\\n stringstream ss(content);\\n string id;\\n while(ss>>id)\\n {\\n id=id.substr(2);\\n \\n int user_id=stoi(id);\\n mentions[user_id]++;\\n }\\n }\\n }\\n\\n }\\n\\n vector<int>result;\\n for(int i=0; i<mentions.size();i++)\\n {\\n result.push_back(mentions[i]);\\n }\\n\\n return result;\\n\\n }\\n};\"]]"
},
"golang": {
"code": "func countMentions(numberOfUsers int, events [][]string) []int {\n type eventInfo struct {\n originalIndex int\n timestamp int\n eventType int // 0: OFFLINE, 1: MESSAGE\n data []string\n }\n\n eventList := make([]eventInfo, len(events))\n for i, e := range events {\n ts, _ := strconv.Atoi(e[1])\n typ := 0\n if e[0] == \"MESSAGE\" {\n typ = 1\n }\n eventList[i] = eventInfo{\n originalIndex: i,\n timestamp: ts,\n eventType: typ,\n data: e,\n }\n }\n\n sort.SliceStable(eventList, func(i, j int) bool {\n a, b := eventList[i], eventList[j]\n if a.timestamp != b.timestamp {\n return a.timestamp < b.timestamp\n }\n if a.eventType != b.eventType {\n return a.eventType < b.eventType\n }\n return a.originalIndex < b.originalIndex\n })\n\n mentions := make([]int, numberOfUsers)\n offlineEnd := make([]int, numberOfUsers)\n\n for _, ei := range eventList {\n e := ei.data\n if e[0] == \"OFFLINE\" {\n ts, _ := strconv.Atoi(e[1])\n userID, _ := strconv.Atoi(e[2])\n newEnd := ts + 60\n if newEnd > offlineEnd[userID] {\n offlineEnd[userID] = newEnd\n }\n } else {\n ts, _ := strconv.Atoi(e[1])\n mentionsStr := e[2]\n tokens := strings.Split(mentionsStr, \" \")\n for _, token := range tokens {\n switch token {\n case \"ALL\":\n for i := 0; i < numberOfUsers; i++ {\n mentions[i]++\n }\n case \"HERE\":\n for i := 0; i < numberOfUsers; i++ {\n if offlineEnd[i] <= ts {\n mentions[i]++\n }\n }\n default:\n if strings.HasPrefix(token, \"id\") {\n idStr := token[2:]\n id, _ := strconv.Atoi(idStr)\n if id >= 0 && id < numberOfUsers {\n mentions[id]++\n }\n }\n }\n }\n }\n }\n\n return mentions\n}",
"memory": null,
"memoryDistribution": "[[9500, 50.0, \"func countMentions(numberOfUsers int, events [][]string) []int {\\n type eventInfo struct {\\n originalIndex int\\n timestamp int\\n eventType int // 0: OFFLINE, 1: MESSAGE\\n data []string\\n }\\n\\n eventList := make([]eventInfo, len(events))\\n for i, e := range events {\\n ts, _ := strconv.Atoi(e[1])\\n typ := 0\\n if e[0] == \\\"MESSAGE\\\" {\\n typ = 1\\n }\\n eventList[i] = eventInfo{\\n originalIndex: i,\\n timestamp: ts,\\n eventType: typ,\\n data: e,\\n }\\n }\\n\\n sort.SliceStable(eventList, func(i, j int) bool {\\n a, b := eventList[i], eventList[j]\\n if a.timestamp != b.timestamp {\\n return a.timestamp < b.timestamp\\n }\\n if a.eventType != b.eventType {\\n return a.eventType < b.eventType\\n }\\n return a.originalIndex < b.originalIndex\\n })\\n\\n mentions := make([]int, numberOfUsers)\\n offlineEnd := make([]int, numberOfUsers)\\n\\n for _, ei := range eventList {\\n e := ei.data\\n if e[0] == \\\"OFFLINE\\\" {\\n ts, _ := strconv.Atoi(e[1])\\n userID, _ := strconv.Atoi(e[2])\\n newEnd := ts + 60\\n if newEnd > offlineEnd[userID] {\\n offlineEnd[userID] = newEnd\\n }\\n } else {\\n ts, _ := strconv.Atoi(e[1])\\n mentionsStr := e[2]\\n tokens := strings.Split(mentionsStr, \\\" \\\")\\n for _, token := range tokens {\\n switch token {\\n case \\\"ALL\\\":\\n for i := 0; i < numberOfUsers; i++ {\\n mentions[i]++\\n }\\n case \\\"HERE\\\":\\n for i := 0; i < numberOfUsers; i++ {\\n if offlineEnd[i] <= ts {\\n mentions[i]++\\n }\\n }\\n default:\\n if strings.HasPrefix(token, \\\"id\\\") {\\n idStr := token[2:]\\n id, _ := strconv.Atoi(idStr)\\n if id >= 0 && id < numberOfUsers {\\n mentions[id]++\\n }\\n }\\n }\\n }\\n }\\n }\\n\\n return mentions\\n}\"], [9800, 50.0, \"package main\\n\\nimport (\\n\\t\\\"sort\\\"\\n\\t\\\"strconv\\\"\\n\\t\\\"strings\\\"\\n)\\n\\n// OnlineEvent represents an online event with a timestamp and user ID\\ntype OnlineEvent struct {\\n\\tTimestamp int\\n\\tUserID int\\n}\\n\\n// sortEvents events ko timestamp ke according sort karta hai\\nfunc sortEvents(events [][]string) {\\n\\tsort.Slice(events, func(i, j int) bool {\\n\\t\\ttimestampI, _ := strconv.Atoi(events[i][1])\\n\\t\\ttimestampJ, _ := strconv.Atoi(events[j][1])\\n\\t\\treturn timestampI < timestampJ\\n\\t})\\n}\\n\\n// processOfflineEvents OFFLINE events ko handle karta hai aur user statuses update karta hai\\nfunc processOfflineEvents(currentTime int, events [][]string, userCount int, userOnlineStatus []bool, onlineEventsHeap []OnlineEvent) ([]OnlineEvent, []bool) {\\n\\tfor _, event := range events {\\n\\t\\tif event[0] == \\\"OFFLINE\\\" {\\n\\t\\t\\tuserID, _ := strconv.Atoi(event[2])\\n\\t\\t\\tif userID >= 0 && userID < userCount && userOnlineStatus[userID] {\\n\\t\\t\\t\\tuserOnlineStatus[userID] = false\\n\\t\\t\\t\\tonlineEvent := OnlineEvent{\\n\\t\\t\\t\\t\\tTimestamp: currentTime + 60,\\n\\t\\t\\t\\t\\tUserID: userID,\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\t// Heap me insert karna maintaining sorted order\\n\\t\\t\\t\\tindex := sort.Search(len(onlineEventsHeap), func(i int) bool {\\n\\t\\t\\t\\t\\treturn onlineEventsHeap[i].Timestamp > onlineEvent.Timestamp\\n\\t\\t\\t\\t})\\n\\t\\t\\t\\tonlineEventsHeap = append(onlineEventsHeap, OnlineEvent{})\\n\\t\\t\\t\\tcopy(onlineEventsHeap[index+1:], onlineEventsHeap[index:])\\n\\t\\t\\t\\tonlineEventsHeap[index] = onlineEvent\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\treturn onlineEventsHeap, userOnlineStatus\\n}\\n\\n// processMessageEvents MESSAGE events ko handle karta hai aur mentions ko update karta hai\\nfunc processMessageEvents(events [][]string, currentTime int, userCount int, userOnlineStatus []bool, mentionCounts []int) []int {\\n\\tfor _, event := range events {\\n\\t\\tif event[0] == \\\"MESSAGE\\\" {\\n\\t\\t\\tmentionTarget := event[2]\\n\\t\\t\\tif mentionTarget == \\\"ALL\\\" {\\n\\t\\t\\t\\t// \\\"ALL\\\" ko mention karte hain\\n\\t\\t\\t\\tfor userID := 0; userID < userCount; userID++ {\\n\\t\\t\\t\\t\\tmentionCounts[userID]++\\n\\t\\t\\t\\t}\\n\\t\\t\\t} else if mentionTarget == \\\"HERE\\\" {\\n\\t\\t\\t\\t// \\\"HERE\\\" ko mention karte hain sirf online users ko\\n\\t\\t\\t\\tfor userID := 0; userID < userCount; userID++ {\\n\\t\\t\\t\\t\\tif userOnlineStatus[userID] {\\n\\t\\t\\t\\t\\t\\tmentionCounts[userID]++\\n\\t\\t\\t\\t\\t}\\n\\t\\t\\t\\t}\\n\\t\\t\\t} else {\\n\\t\\t\\t\\t// Specific users ko mention karte hain\\n\\t\\t\\t\\ttokens := strings.Split(mentionTarget, \\\" \\\")\\n\\t\\t\\t\\tfor _, token := range tokens {\\n\\t\\t\\t\\t\\tif len(token) >= 3 && token[:2] == \\\"id\\\" {\\n\\t\\t\\t\\t\\t\\tuserIDStr := token[2:]\\n\\t\\t\\t\\t\\t\\tif isNumeric(userIDStr) {\\n\\t\\t\\t\\t\\t\\t\\tuserID, err := strconv.Atoi(userIDStr)\\n\\t\\t\\t\\t\\t\\t\\tif err == nil && userID >= 0 && userID < userCount {\\n\\t\\t\\t\\t\\t\\t\\t\\tmentionCounts[userID]++\\n\\t\\t\\t\\t\\t\\t\\t}\\n\\t\\t\\t\\t\\t\\t}\\n\\t\\t\\t\\t\\t}\\n\\t\\t\\t\\t}\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\treturn mentionCounts\\n}\\n\\n// isNumeric check karta hai agar string numeric hai ya nahi\\nfunc isNumeric(s string) bool {\\n\\tfor _, c := range s {\\n\\t\\tif c < '0' || c > '9' {\\n\\t\\t\\treturn false\\n\\t\\t}\\n\\t}\\n\\treturn true\\n}\\n\\n// countMentions user ke online/offline events ke basis par mentions ko count karta hai\\nfunc countMentions(userCount int, eventList [][]string) []int {\\n\\t// Events ko timestamp ke according sort karte hain\\n\\tsortEvents(eventList)\\n\\n\\tmentionCounts := make([]int, userCount)\\n\\tuserOnlineStatus := make([]bool, userCount)\\n\\tfor i := 0; i < userCount; i++ {\\n\\t\\tuserOnlineStatus[i] = true\\n\\t}\\n\\n\\tvar onlineEventsHeap []OnlineEvent\\n\\n\\ttotalEvents := len(eventList)\\n\\teventIndex := 0\\n\\n\\tfor eventIndex < totalEvents {\\n\\t\\tcurrentTime, _ := strconv.Atoi(eventList[eventIndex][1])\\n\\n\\t\\t// Process onlineEventsHeap ko\\n\\t\\tfor len(onlineEventsHeap) > 0 && onlineEventsHeap[0].Timestamp <= currentTime {\\n\\t\\t\\tuserToReactivate := onlineEventsHeap[0].UserID\\n\\t\\t\\tif userToReactivate >= 0 && userToReactivate < userCount {\\n\\t\\t\\t\\tuserOnlineStatus[userToReactivate] = true\\n\\t\\t\\t}\\n\\t\\t\\tonlineEventsHeap = onlineEventsHeap[1:]\\n\\t\\t}\\n\\n\\t\\tnextEventIndex := eventIndex\\n\\t\\tfor nextEventIndex < totalEvents {\\n\\t\\t\\teventTime, _ := strconv.Atoi(eventList[nextEventIndex][1])\\n\\t\\t\\tif eventTime != currentTime {\\n\\t\\t\\t\\tbreak\\n\\t\\t\\t}\\n\\t\\t\\tnextEventIndex++\\n\\t\\t}\\n\\n\\t\\t// OFFLINE events ko handle karo\\n\\t\\tonlineEventsHeap, userOnlineStatus = processOfflineEvents(currentTime, eventList[eventIndex:nextEventIndex], userCount, userOnlineStatus, onlineEventsHeap)\\n\\n\\t\\t// MESSAGE events ko handle karo\\n\\t\\tmentionCounts = processMessageEvents(eventList[eventIndex:nextEventIndex], currentTime, userCount, userOnlineStatus, mentionCounts)\\n\\n\\t\\teventIndex = nextEventIndex\\n\\t}\\n\\n\\treturn mentionCounts\\n}\"]]",
"runtime": null,
"runtimeDistribution": "[[2, 50.0, \"package main\\n\\nimport (\\n\\t\\\"sort\\\"\\n\\t\\\"strconv\\\"\\n\\t\\\"strings\\\"\\n)\\n\\n// OnlineEvent represents an online event with a timestamp and user ID\\ntype OnlineEvent struct {\\n\\tTimestamp int\\n\\tUserID int\\n}\\n\\n// sortEvents events ko timestamp ke according sort karta hai\\nfunc sortEvents(events [][]string) {\\n\\tsort.Slice(events, func(i, j int) bool {\\n\\t\\ttimestampI, _ := strconv.Atoi(events[i][1])\\n\\t\\ttimestampJ, _ := strconv.Atoi(events[j][1])\\n\\t\\treturn timestampI < timestampJ\\n\\t})\\n}\\n\\n// processOfflineEvents OFFLINE events ko handle karta hai aur user statuses update karta hai\\nfunc processOfflineEvents(currentTime int, events [][]string, userCount int, userOnlineStatus []bool, onlineEventsHeap []OnlineEvent) ([]OnlineEvent, []bool) {\\n\\tfor _, event := range events {\\n\\t\\tif event[0] == \\\"OFFLINE\\\" {\\n\\t\\t\\tuserID, _ := strconv.Atoi(event[2])\\n\\t\\t\\tif userID >= 0 && userID < userCount && userOnlineStatus[userID] {\\n\\t\\t\\t\\tuserOnlineStatus[userID] = false\\n\\t\\t\\t\\tonlineEvent := OnlineEvent{\\n\\t\\t\\t\\t\\tTimestamp: currentTime + 60,\\n\\t\\t\\t\\t\\tUserID: userID,\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\t// Heap me insert karna maintaining sorted order\\n\\t\\t\\t\\tindex := sort.Search(len(onlineEventsHeap), func(i int) bool {\\n\\t\\t\\t\\t\\treturn onlineEventsHeap[i].Timestamp > onlineEvent.Timestamp\\n\\t\\t\\t\\t})\\n\\t\\t\\t\\tonlineEventsHeap = append(onlineEventsHeap, OnlineEvent{})\\n\\t\\t\\t\\tcopy(onlineEventsHeap[index+1:], onlineEventsHeap[index:])\\n\\t\\t\\t\\tonlineEventsHeap[index] = onlineEvent\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\treturn onlineEventsHeap, userOnlineStatus\\n}\\n\\n// processMessageEvents MESSAGE events ko handle karta hai aur mentions ko update karta hai\\nfunc processMessageEvents(events [][]string, currentTime int, userCount int, userOnlineStatus []bool, mentionCounts []int) []int {\\n\\tfor _, event := range events {\\n\\t\\tif event[0] == \\\"MESSAGE\\\" {\\n\\t\\t\\tmentionTarget := event[2]\\n\\t\\t\\tif mentionTarget == \\\"ALL\\\" {\\n\\t\\t\\t\\t// \\\"ALL\\\" ko mention karte hain\\n\\t\\t\\t\\tfor userID := 0; userID < userCount; userID++ {\\n\\t\\t\\t\\t\\tmentionCounts[userID]++\\n\\t\\t\\t\\t}\\n\\t\\t\\t} else if mentionTarget == \\\"HERE\\\" {\\n\\t\\t\\t\\t// \\\"HERE\\\" ko mention karte hain sirf online users ko\\n\\t\\t\\t\\tfor userID := 0; userID < userCount; userID++ {\\n\\t\\t\\t\\t\\tif userOnlineStatus[userID] {\\n\\t\\t\\t\\t\\t\\tmentionCounts[userID]++\\n\\t\\t\\t\\t\\t}\\n\\t\\t\\t\\t}\\n\\t\\t\\t} else {\\n\\t\\t\\t\\t// Specific users ko mention karte hain\\n\\t\\t\\t\\ttokens := strings.Split(mentionTarget, \\\" \\\")\\n\\t\\t\\t\\tfor _, token := range tokens {\\n\\t\\t\\t\\t\\tif len(token) >= 3 && token[:2] == \\\"id\\\" {\\n\\t\\t\\t\\t\\t\\tuserIDStr := token[2:]\\n\\t\\t\\t\\t\\t\\tif isNumeric(userIDStr) {\\n\\t\\t\\t\\t\\t\\t\\tuserID, err := strconv.Atoi(userIDStr)\\n\\t\\t\\t\\t\\t\\t\\tif err == nil && userID >= 0 && userID < userCount {\\n\\t\\t\\t\\t\\t\\t\\t\\tmentionCounts[userID]++\\n\\t\\t\\t\\t\\t\\t\\t}\\n\\t\\t\\t\\t\\t\\t}\\n\\t\\t\\t\\t\\t}\\n\\t\\t\\t\\t}\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\treturn mentionCounts\\n}\\n\\n// isNumeric check karta hai agar string numeric hai ya nahi\\nfunc isNumeric(s string) bool {\\n\\tfor _, c := range s {\\n\\t\\tif c < '0' || c > '9' {\\n\\t\\t\\treturn false\\n\\t\\t}\\n\\t}\\n\\treturn true\\n}\\n\\n// countMentions user ke online/offline events ke basis par mentions ko count karta hai\\nfunc countMentions(userCount int, eventList [][]string) []int {\\n\\t// Events ko timestamp ke according sort karte hain\\n\\tsortEvents(eventList)\\n\\n\\tmentionCounts := make([]int, userCount)\\n\\tuserOnlineStatus := make([]bool, userCount)\\n\\tfor i := 0; i < userCount; i++ {\\n\\t\\tuserOnlineStatus[i] = true\\n\\t}\\n\\n\\tvar onlineEventsHeap []OnlineEvent\\n\\n\\ttotalEvents := len(eventList)\\n\\teventIndex := 0\\n\\n\\tfor eventIndex < totalEvents {\\n\\t\\tcurrentTime, _ := strconv.Atoi(eventList[eventIndex][1])\\n\\n\\t\\t// Process onlineEventsHeap ko\\n\\t\\tfor len(onlineEventsHeap) > 0 && onlineEventsHeap[0].Timestamp <= currentTime {\\n\\t\\t\\tuserToReactivate := onlineEventsHeap[0].UserID\\n\\t\\t\\tif userToReactivate >= 0 && userToReactivate < userCount {\\n\\t\\t\\t\\tuserOnlineStatus[userToReactivate] = true\\n\\t\\t\\t}\\n\\t\\t\\tonlineEventsHeap = onlineEventsHeap[1:]\\n\\t\\t}\\n\\n\\t\\tnextEventIndex := eventIndex\\n\\t\\tfor nextEventIndex < totalEvents {\\n\\t\\t\\teventTime, _ := strconv.Atoi(eventList[nextEventIndex][1])\\n\\t\\t\\tif eventTime != currentTime {\\n\\t\\t\\t\\tbreak\\n\\t\\t\\t}\\n\\t\\t\\tnextEventIndex++\\n\\t\\t}\\n\\n\\t\\t// OFFLINE events ko handle karo\\n\\t\\tonlineEventsHeap, userOnlineStatus = processOfflineEvents(currentTime, eventList[eventIndex:nextEventIndex], userCount, userOnlineStatus, onlineEventsHeap)\\n\\n\\t\\t// MESSAGE events ko handle karo\\n\\t\\tmentionCounts = processMessageEvents(eventList[eventIndex:nextEventIndex], currentTime, userCount, userOnlineStatus, mentionCounts)\\n\\n\\t\\teventIndex = nextEventIndex\\n\\t}\\n\\n\\treturn mentionCounts\\n}\"], [4, 50.0, \"func countMentions(numberOfUsers int, events [][]string) []int {\\n type eventInfo struct {\\n originalIndex int\\n timestamp int\\n eventType int // 0: OFFLINE, 1: MESSAGE\\n data []string\\n }\\n\\n eventList := make([]eventInfo, len(events))\\n for i, e := range events {\\n ts, _ := strconv.Atoi(e[1])\\n typ := 0\\n if e[0] == \\\"MESSAGE\\\" {\\n typ = 1\\n }\\n eventList[i] = eventInfo{\\n originalIndex: i,\\n timestamp: ts,\\n eventType: typ,\\n data: e,\\n }\\n }\\n\\n sort.SliceStable(eventList, func(i, j int) bool {\\n a, b := eventList[i], eventList[j]\\n if a.timestamp != b.timestamp {\\n return a.timestamp < b.timestamp\\n }\\n if a.eventType != b.eventType {\\n return a.eventType < b.eventType\\n }\\n return a.originalIndex < b.originalIndex\\n })\\n\\n mentions := make([]int, numberOfUsers)\\n offlineEnd := make([]int, numberOfUsers)\\n\\n for _, ei := range eventList {\\n e := ei.data\\n if e[0] == \\\"OFFLINE\\\" {\\n ts, _ := strconv.Atoi(e[1])\\n userID, _ := strconv.Atoi(e[2])\\n newEnd := ts + 60\\n if newEnd > offlineEnd[userID] {\\n offlineEnd[userID] = newEnd\\n }\\n } else {\\n ts, _ := strconv.Atoi(e[1])\\n mentionsStr := e[2]\\n tokens := strings.Split(mentionsStr, \\\" \\\")\\n for _, token := range tokens {\\n switch token {\\n case \\\"ALL\\\":\\n for i := 0; i < numberOfUsers; i++ {\\n mentions[i]++\\n }\\n case \\\"HERE\\\":\\n for i := 0; i < numberOfUsers; i++ {\\n if offlineEnd[i] <= ts {\\n mentions[i]++\\n }\\n }\\n default:\\n if strings.HasPrefix(token, \\\"id\\\") {\\n idStr := token[2:]\\n id, _ := strconv.Atoi(idStr)\\n if id >= 0 && id < numberOfUsers {\\n mentions[id]++\\n }\\n }\\n }\\n }\\n }\\n }\\n\\n return mentions\\n}\"]]"
},
"java": {
"code": "class Solution {\n public int[] countMentions(int numberOfUsers, List<List<String>> events) {\n List<Integer> indices = new ArrayList<>();\n for (int i = 0; i < events.size(); i++) {\n indices.add(i);\n }\n\n Collections.sort(indices, (a, b) -> {\n List<String> eventA = events.get(a);\n List<String> eventB = events.get(b);\n int tA = Integer.parseInt(eventA.get(1));\n int tB = Integer.parseInt(eventB.get(1));\n if (tA != tB) {\n return Integer.compare(tA, tB);\n } else {\n String typeA = eventA.get(0);\n String typeB = eventB.get(0);\n if (typeA.equals(typeB)) {\n return Integer.compare(a, b);\n } else {\n return typeA.equals(\"OFFLINE\") ? -1 : 1;\n }\n }\n });\n\n int[] mentions = new int[numberOfUsers];\n int[] offlineUntil = new int[numberOfUsers];\n\n for (int i : indices) {\n List<String> event = events.get(i);\n String type = event.get(0);\n int timestamp = Integer.parseInt(event.get(1));\n if (type.equals(\"OFFLINE\")) {\n int userId = Integer.parseInt(event.get(2));\n offlineUntil[userId] = timestamp + 60;\n } else {\n String mentionsString = event.get(2);\n String[] tokens = mentionsString.split(\" \");\n for (String token : tokens) {\n if (token.equals(\"ALL\")) {\n for (int j = 0; j < numberOfUsers; j++) {\n mentions[j]++;\n }\n } else if (token.equals(\"HERE\")) {\n for (int j = 0; j < numberOfUsers; j++) {\n if (timestamp >= offlineUntil[j]) {\n mentions[j]++;\n }\n }\n } else {\n String idStr = token.substring(2);\n int user = Integer.parseInt(idStr);\n if (user >= 0 && user < numberOfUsers) {\n mentions[user]++;\n }\n }\n }\n }\n }\n\n return mentions;\n }\n}",
"memory": 4600,
"memoryDistribution": "[[4600, 88.2353, \"import java.util.*;\\n\\nclass Solution {\\n public int[] countMentions(int numberOfUsers, List<List<String>> events) {\\n List<Integer> indices = new ArrayList<>();\\n for (int i = 0; i < events.size(); i++) {\\n indices.add(i);\\n }\\n\\n Collections.sort(indices, (a, b) -> {\\n List<String> eventA = events.get(a);\\n List<String> eventB = events.get(b);\\n int tA = Integer.parseInt(eventA.get(1));\\n int tB = Integer.parseInt(eventB.get(1));\\n if (tA != tB) {\\n return Integer.compare(tA, tB);\\n } else {\\n String typeA = eventA.get(0);\\n String typeB = eventB.get(0);\\n if (typeA.equals(typeB)) {\\n return Integer.compare(a, b);\\n } else {\\n return typeA.equals(\\\"OFFLINE\\\") ? -1 : 1;\\n }\\n }\\n });\\n\\n int[] mentions = new int[numberOfUsers];\\n int[] offlineUntil = new int[numberOfUsers];\\n\\n for (int i : indices) {\\n List<String> event = events.get(i);\\n String type = event.get(0);\\n int timestamp = Integer.parseInt(event.get(1));\\n if (type.equals(\\\"OFFLINE\\\")) {\\n int userId = Integer.parseInt(event.get(2));\\n offlineUntil[userId] = timestamp + 60;\\n } else {\\n String mentionsString = event.get(2);\\n String[] tokens = mentionsString.split(\\\" \\\");\\n for (String token : tokens) {\\n if (token.equals(\\\"ALL\\\")) {\\n for (int j = 0; j < numberOfUsers; j++) {\\n mentions[j]++;\\n }\\n } else if (token.equals(\\\"HERE\\\")) {\\n for (int j = 0; j < numberOfUsers; j++) {\\n if (timestamp >= offlineUntil[j]) {\\n mentions[j]++;\\n }\\n }\\n } else {\\n String idStr = token.substring(2);\\n int user = Integer.parseInt(idStr);\\n if (user >= 0 && user < numberOfUsers) {\\n mentions[user]++;\\n }\\n }\\n }\\n }\\n }\\n\\n return mentions;\\n }\\n}\"], [45100, 1.6807, \"class Solution {\\n public int[] countMentions(int numberOfUsers, List<List<String>> events) {\\n int[] result = new int[numberOfUsers];\\n List<int[]> offlineList = new ArrayList<>();\\n List<Integer> hereList = new ArrayList();\\n int all = 0;\\n for (List<String> event: events) {\\n String type = event.get(0);\\n int time = Integer.valueOf(event.get(1));\\n String info = event.get(2);\\n\\n if (type.equals(\\\"OFFLINE\\\")) {\\n int id = Integer.valueOf(info);\\n offlineList.add(new int[]{time, id});\\n } else if (info.equals(\\\"ALL\\\")) {\\n all++;\\n } else if (info.equals(\\\"HERE\\\")) {\\n all++;\\n hereList.add(time);\\n } else {\\n String[] ids = info.split(\\\" \\\");\\n for (String idStr: ids) {\\n int id = Integer.valueOf(idStr.substring(2));\\n result[id] ++;\\n }\\n }\\n }\\n for (int i = 0 ; i < numberOfUsers; i++) {\\n result[i] += all;\\n }\\n\\n for (Integer hereTime: hereList) {\\n \\n for (int[] offline: offlineList) {\\n int t = offline[0];\\n int id = offline[1];\\n if (t + 60 > hereTime && t <= hereTime) {\\n result[id]--;\\n }\\n }\\n }\\n\\n return result;\\n }\\n}\"], [45300, 0.8403, \"class Solution {\\n public int[] countMentions(int numberOfUsers, List<List<String>> events) {\\n int[] mentions = new int[numberOfUsers];\\n int[] offline = new int[numberOfUsers];\\n\\n Collections.sort(events, (a,b)->Integer.parseInt(a.get(1))==Integer.parseInt(b.get(1))? b.get(0).compareTo(a.get(0)): Integer.parseInt(a.get(1))-Integer.parseInt(b.get(1)));\\n // Collections.sort(events, (a, b) -> Integer.compare(Integer.valueOf(a.get(1)), Integer.valueOf(b.get(1)));\\n for (int i = 0; i < events.size(); i++) {\\n if (events.get(i).get(0).equals(\\\"MESSAGE\\\")) {\\n msgFunc(events.get(i), mentions, offline);\\n } else if (events.get(i).get(0).equals(\\\"OFFLINE\\\")) {\\n offlineFunc(events.get(i), mentions, offline);\\n }\\n }\\n\\n return mentions;\\n }\\n\\n private void msgFunc(List<String> event, int[] mentions, int[] offline) {\\n int timestamp = Integer.valueOf(event.get(1));\\n String[] m = event.get(2).split(\\\" \\\");\\n\\n for (String s : m) {\\n if (event.get(2).contains(\\\"ALL\\\")) {\\n for (int i = 0; i < mentions.length; i++) {\\n mentions[i]++;\\n } \\n } else if (s.equals(\\\"HERE\\\")) {\\n for (int i = 0; i < mentions.length; i++) {\\n if (offline[i] == 0) { // only online\\n mentions[i]++;\\n } else if (offline[i] + 60 <= timestamp) {\\n mentions[i]++;\\n offline[i] = 0;\\n }\\n }\\n } else {\\n int id = Integer.valueOf(s.substring(2));\\n mentions[id]++;\\n }\\n }\\n }\\n\\n private void offlineFunc(List<String> event, int[] mentions, int[] offline) {\\n int timestamp = Integer.valueOf(event.get(1));\\n String[] m = event.get(2).split(\\\" \\\");\\n\\n for (String s : m) {\\n int id = Integer.valueOf(s);\\n offline[id] = timestamp;\\n }\\n }\\n}\"], [45400, 5.042, null], [45500, 4.2017, null], [45600, 13.4454, null], [45700, 21.8487, null], [45800, 15.9664, null], [45900, 16.8067, \"class Solution {\\n public int[] countMentions(int numberOfUsers, List<List<String>> events) {\\n int[] mentions = new int[numberOfUsers];\\n Map<Integer, Integer> offlineMap = new HashMap<>();\\n Set<Integer> onlineUsers = new HashSet<>();\\n for (int i = 0; i < numberOfUsers; i++) {\\n onlineUsers.add(i);\\n }\\n\\n events.sort((a, b) -> {\\n int timeA = Integer.parseInt(a.get(1));\\n int timeB = Integer.parseInt(b.get(1));\\n if (timeA != timeB) {\\n return timeA - timeB;\\n }\\n return a.get(0).equals(\\\"OFFLINE\\\") ? -1 : 1;\\n });\\n\\n int currTime = 0;\\n\\n for (List<String> event : events) {\\n String eventType = event.get(0);\\n int timestamp = Integer.parseInt(event.get(1));\\n String data = event.get(2);\\n\\n if (timestamp > currTime) {\\n currTime = timestamp;\\n\\n List<Integer> toRemove = new ArrayList<>();\\n\\n for (Map.Entry<Integer, Integer> entry : offlineMap.entrySet()) {\\n int userId = entry.getKey();\\n int offlineTime = entry.getValue();\\n\\n if (currTime - offlineTime >= 60) {\\n toRemove.add(userId);\\n onlineUsers.add(userId);\\n }\\n }\\n\\n for (int userId : toRemove) {\\n offlineMap.remove(userId);\\n }\\n }\\n\\n if (eventType.equals(\\\"OFFLINE\\\")) {\\n int userId = Integer.parseInt(data);\\n onlineUsers.remove(userId);\\n offlineMap.put(userId, currTime);\\n } else if (eventType.equals(\\\"MESSAGE\\\")) {\\n if (data.equals(\\\"ALL\\\")) {\\n for (int i = 0; i < numberOfUsers; i++) {\\n mentions[i]++;\\n }\\n } else if (data.equals(\\\"HERE\\\")) {\\n List<Integer> toRemove = new ArrayList<>();\\n for (Map.Entry<Integer, Integer> entry : offlineMap.entrySet()) {\\n int userId = entry.getKey();\\n int offlineTime = entry.getValue();\\n\\n if (currTime - offlineTime >= 60) {\\n toRemove.add(userId);\\n onlineUsers.add(userId);\\n }\\n }\\n\\n for (int userId : toRemove) {\\n offlineMap.remove(userId);\\n }\\n\\n for (int userId : onlineUsers) {\\n mentions[userId]++;\\n }\\n } else {\\n String[] tokens = data.split(\\\" \\\");\\n for (String token : tokens) {\\n if (token.startsWith(\\\"id\\\")) {\\n int userId = Integer.parseInt(token.substring(2));\\n mentions[userId]++;\\n }\\n }\\n }\\n }\\n }\\n\\n return mentions;\\n }\\n}\"], [46000, 8.4034, \"\\n\\nclass Solution {\\n public int[] countMentions(int numberOfUsers, List<List<String>> events) {\\n \\n int[] mentions = new int[numberOfUsers];\\n int[] offlineUntil = new int[numberOfUsers]; // When each user comes back online (initially 0)\\n\\n \\n events.sort((a, b) -> {\\n int timeA = Integer.parseInt(a.get(1));\\n int timeB = Integer.parseInt(b.get(1));\\n if (timeA != timeB) {\\n return timeA - timeB;\\n } else {\\n // Same time, OFFLINE first\\n if (a.get(0).equals(b.get(0))) return 0;\\n if (a.get(0).equals(\\\"OFFLINE\\\")) return -1;\\n return 1;\\n }\\n });\\n\\n // \\u2705 Step 2: Process each event in order\\n for (List<String> event : events) {\\n String eventType = event.get(0);\\n int timestamp = Integer.parseInt(event.get(1));\\n String data = event.get(2);\\n\\n if (eventType.equals(\\\"OFFLINE\\\")) {\\n // Handle offline event\\n int userId = Integer.parseInt(data);\\n offlineUntil[userId] = timestamp + 60; // User will be offline for 60 units\\n } \\n else if (eventType.equals(\\\"MESSAGE\\\")) {\\n // Handle message event\\n if (data.equals(\\\"ALL\\\")) {\\n // Mention all users, even offline ones\\n for (int i = 0; i < numberOfUsers; i++) {\\n mentions[i]++;\\n }\\n } \\n else if (data.equals(\\\"HERE\\\")) {\\n // Mention only online users\\n for (int i = 0; i < numberOfUsers; i++) {\\n if (timestamp >= offlineUntil[i]) { // If user is now online\\n mentions[i]++;\\n }\\n }\\n } \\n else {\\n // Mentions by ID list (id0 id1 id2 ...)\\n String[] ids = data.split(\\\" \\\");\\n for (String idStr : ids) {\\n int userId = Integer.parseInt(idStr.substring(2)); // Skip \\\"id\\\" part\\n mentions[userId]++;\\n }\\n }\\n }\\n }\\n\\n return mentions;\\n }\\n}\\n\"]]",
"runtime": 25,
"runtimeDistribution": "[[12, 1.6807, \"class Solution {\\n public int[] countMentions(int numberOfUsers, List<List<String>> events) {\\n int[] result = new int[numberOfUsers];\\n List<int[]> offlineList = new ArrayList<>();\\n List<Integer> hereList = new ArrayList();\\n int all = 0;\\n for (List<String> event: events) {\\n String type = event.get(0);\\n int time = Integer.valueOf(event.get(1));\\n String info = event.get(2);\\n\\n if (type.equals(\\\"OFFLINE\\\")) {\\n int id = Integer.valueOf(info);\\n offlineList.add(new int[]{time, id});\\n } else if (info.equals(\\\"ALL\\\")) {\\n all++;\\n } else if (info.equals(\\\"HERE\\\")) {\\n all++;\\n hereList.add(time);\\n } else {\\n String[] ids = info.split(\\\" \\\");\\n for (String idStr: ids) {\\n int id = Integer.valueOf(idStr.substring(2));\\n result[id] ++;\\n }\\n }\\n }\\n for (int i = 0 ; i < numberOfUsers; i++) {\\n result[i] += all;\\n }\\n\\n for (Integer hereTime: hereList) {\\n \\n for (int[] offline: offlineList) {\\n int t = offline[0];\\n int id = offline[1];\\n if (t + 60 > hereTime && t <= hereTime) {\\n result[id]--;\\n }\\n }\\n }\\n\\n return result;\\n }\\n}\"], [17, 1.6807, \"import java.util.*;\\nclass Solution {\\n public int[] countMentions(int n, List<List<String>> events) {\\n int[] cnt = new int[n];\\n List<Integer>[] offlineAt = new ArrayList[n];\\n\\n for (int i = 0; i < n; i++) {\\n offlineAt[i] = new ArrayList<>();\\n }\\n\\n for (List<String> event : events) {\\n String type = event.get(0);\\n int time = Integer.parseInt(event.get(1));\\n String id = event.get(2);\\n if (type.equals(\\\"OFFLINE\\\")) offlineAt[Integer.parseInt(id)].add(time);\\n }\\n\\n int allCnt = 0;\\n for (List<String> event : events) {\\n String type = event.get(0);\\n int time = Integer.parseInt(event.get(1));\\n String id = event.get(2);\\n if (type.equals(\\\"OFFLINE\\\")) continue;\\n if (id.equals(\\\"ALL\\\")) allCnt++;\\n else if (id.equals(\\\"HERE\\\")) hereUpdate(cnt, offlineAt, time);\\n else idUpdate(cnt, id);\\n }\\n\\n\\n for (int i = 0; i < n; i++) {\\n cnt[i] += allCnt;\\n }\\n\\n return cnt;\\n }\\n\\n private void hereUpdate(int[] cnt, List<Integer>[] offlineAt, int time) {\\n outer:\\n for (int i = 0; i < cnt.length; i++) {\\n List<Integer> offlineTime = offlineAt[i];\\n for (int offline : offlineTime) {\\n if (time >= offline && time < offline + 60) continue outer;\\n }\\n cnt[i]++;\\n }\\n }\\n\\n private void idUpdate(int[] cnt, String id) {\\n StringTokenizer st = new StringTokenizer(id);\\n while (st.hasMoreTokens()) {\\n int userId = Integer.parseInt(st.nextToken().substring(2));\\n cnt[userId]++;\\n }\\n }\\n}\"], [18, 0.8403, null], [19, 0.8403, null], [21, 0.8403, null], [22, 3.3613, null], [23, 4.2017, null], [24, 2.521, null], [25, 5.8824, null], [26, 6.7227, null], [27, 3.3613, null], [28, 4.2017, null], [29, 4.2017, null], [30, 2.521, null], [31, 8.4034, null], [32, 10.9244, null], [33, 2.521, null], [34, 4.2017, null], [35, 1.6807, null], [37, 2.521, null], [38, 1.6807, null], [39, 0.8403, null], [41, 0.8403, null], [42, 1.6807, null], [43, 2.521, null], [45, 0.8403, null], [46, 0.8403, null], [49, 0.8403, null], [52, 0.8403, null], [53, 0.8403, null], [55, 0.8403, null], [59, 0.8403, null], [63, 1.6807, null], [65, 0.8403, null], [66, 1.6807, null], [68, 0.8403, null], [85, 0.8403, null], [88, 0.8403, null], [139, 0.8403, \"class Solution {\\n public int[] countMentions(int numberOfUsers, List<List<String>> events) {\\n\\n Map<Integer, Integer> countMap = new HashMap<>();\\n Map<Integer, Integer> offlineMap = new HashMap<>();\\n\\n for(int i=0; i<numberOfUsers;i++) {\\n countMap.put(i, 0);\\n }\\n\\n int[] result = new int[numberOfUsers];\\n events.sort((e1,e2) -> {\\n int num1 = Integer.parseInt(e1.get(1));\\n int num2 = Integer.parseInt(e2.get(1));\\n\\n if(num1!=num2){\\n return Integer.compare(num1, num2);\\n }\\n\\n return e1.get(0).equals(\\\"OFFLINE\\\")?-1:1;\\n });\\n\\n for(List<String> event: events){\\n\\n List<String> msg = event.stream()\\n .flatMap(s->Arrays.stream(s.split(\\\",\\\")))\\n .collect(Collectors.toList()); \\n String type = msg.get(0);\\n int timestamp = Integer.valueOf(msg.get(1));\\n String ids = msg.get(2);\\n // System.out.println(\\\"msg:\\\"+type);\\n\\n if(type.equals(\\\"MESSAGE\\\")){\\n\\n if(ids.equals(\\\"HERE\\\")){\\n\\n for(Map.Entry<Integer, Integer> map: countMap.entrySet()){\\n int key = map.getKey();\\n int value = map.getValue();\\n // System.out.println(\\\"offlineMap:\\\"+offlineMap);\\n if(offlineMap.containsKey(key) && offlineMap.get(key)>timestamp){\\n continue;\\n } else {\\n countMap.put(key, value+1);\\n }\\n }\\n\\n } else if(ids.equals(\\\"ALL\\\")){\\n countMap.forEach((key, value)->countMap.put(key, value+1));\\n } else {\\n String[] splitId = ids.split(\\\" \\\");\\n for(String s: splitId) {\\n int id = Integer.valueOf(s.replaceAll(\\\"[^0-9]\\\",\\\"\\\"));\\n if(countMap.containsKey(id)){\\n countMap.put(id, countMap.getOrDefault(id,0)+1);\\n }\\n }\\n }\\n\\n\\n } else if(type.equals(\\\"OFFLINE\\\")){\\n offlineMap.put(Integer.valueOf(ids), timestamp+60);\\n }\\n\\n\\n }\\n\\n for(Map.Entry<Integer, Integer> map: countMap.entrySet()){\\n result[map.getKey()] = map.getValue();\\n }\\n\\n return result;\\n\\n }\\n}\"], [196, 0.8403, \"import java.util.*;\\nclass Solution {\\n public int[] countMentions(int numberOfUsers, List<List<String>> events) {\\n int[] offline=new int[numberOfUsers];\\n int[] mentions=new int[numberOfUsers];\\n events.sort(new Comparator<List<String>>(){\\n public int compare(List<String> a, List<String> b)\\n {\\n int t1=Integer.parseInt(a.get(1)),t2=Integer.parseInt(b.get(1));\\n if(t1==t2)\\n {\\n if(a.get(0).equals(\\\"OFFLINE\\\"))\\n {\\n return -1;\\n }\\n else{\\n return 1;\\n }\\n }\\n return t1-t2;\\n }\\n });\\n for(int i=0;i<events.size();i++)\\n {\\n if(events.get(i).get(0).equals(\\\"OFFLINE\\\"))\\n {\\n int idx=Integer.parseInt(events.get(i).get(2)),time=Integer.parseInt(events.get(i).get(1));\\n offline[idx]=time;\\n }\\n else{\\n int time = Integer.parseInt(events.get(i).get(1));\\n if(events.get(i).get(2).equals(\\\"ALL\\\"))\\n {\\n for(int j=0;j<numberOfUsers;j++)\\n {\\n mentions[j]++;\\n }\\n }\\n else if(events.get(i).get(2).equals(\\\"HERE\\\"))\\n {\\n for(int j=0;j<numberOfUsers;j++)\\n {\\n if(offline[j]==0||offline[j]+60<=time)\\n mentions[j]++;\\n }\\n }\\n else{\\n String[] ids=events.get(i).get(2).split(\\\" \\\");\\n for(String id:ids)\\n {\\n System.out.print(id+\\\" \\\");\\n int parsedId=Integer.parseInt(id.substring(2));\\n mentions[parsedId]++;\\n }\\n }\\n }\\n }\\n return mentions;\\n }\\n}\"]]"
},
"javascript": {
"code": "var countMentions = function(numberOfUsers, events) {\n events.sort((a, b) => {\n const timeA = parseInt(a[1]);\n const timeB = parseInt(b[1]);\n if (timeA !== timeB) {\n return timeA - timeB;\n } else {\n const typeA = a[0];\n const typeB = b[0];\n if (typeA === 'OFFLINE' && typeB === 'MESSAGE') return -1;\n if (typeA === 'MESSAGE' && typeB === 'OFFLINE') return 1;\n return 0;\n }\n });\n\n const mentions = new Array(numberOfUsers).fill(0);\n const offlineEndTimes = new Array(numberOfUsers).fill(0);\n\n for (const event of events) {\n const type = event[0];\n const timestamp = parseInt(event[1]);\n if (type === 'OFFLINE') {\n const userId = parseInt(event[2]);\n offlineEndTimes[userId] = timestamp + 60;\n } else {\n const tokens = event[2].split(' ');\n const users = [];\n for (const token of tokens) {\n if (token === 'ALL') {\n for (let i = 0; i < numberOfUsers; i++) users.push(i);\n } else if (token === 'HERE') {\n for (let i = 0; i < numberOfUsers; i++) {\n if (offlineEndTimes[i] <= timestamp) users.push(i);\n }\n } else {\n const id = parseInt(token.substring(2));\n users.push(id);\n }\n }\n users.forEach(id => mentions[id]++);\n }\n }\n\n return mentions;\n};",
"memory": 6500,
"memoryDistribution": "[[6500, 28.5715, \"var countMentions = function(numberOfUsers, events) {\\n events.sort((a, b) => {\\n const timeA = parseInt(a[1]);\\n const timeB = parseInt(b[1]);\\n if (timeA !== timeB) {\\n return timeA - timeB;\\n } else {\\n const typeA = a[0];\\n const typeB = b[0];\\n if (typeA === 'OFFLINE' && typeB === 'MESSAGE') return -1;\\n if (typeA === 'MESSAGE' && typeB === 'OFFLINE') return 1;\\n return 0;\\n }\\n });\\n\\n const mentions = new Array(numberOfUsers).fill(0);\\n const offlineEndTimes = new Array(numberOfUsers).fill(0);\\n\\n for (const event of events) {\\n const type = event[0];\\n const timestamp = parseInt(event[1]);\\n if (type === 'OFFLINE') {\\n const userId = parseInt(event[2]);\\n offlineEndTimes[userId] = timestamp + 60;\\n } else {\\n const tokens = event[2].split(' ');\\n const users = [];\\n for (const token of tokens) {\\n if (token === 'ALL') {\\n for (let i = 0; i < numberOfUsers; i++) users.push(i);\\n } else if (token === 'HERE') {\\n for (let i = 0; i < numberOfUsers; i++) {\\n if (offlineEndTimes[i] <= timestamp) users.push(i);\\n }\\n } else {\\n const id = parseInt(token.substring(2));\\n users.push(id);\\n }\\n }\\n users.forEach(id => mentions[id]++);\\n }\\n }\\n\\n return mentions;\\n};\"], [62700, 14.2857, \"/**\\n * @param {number} numberOfUsers\\n * @param {string[][]} events\\n * @return {number[]}\\n */\\nvar countMentions = function(numberOfUsers, events) {\\n const mentions = new Array(numberOfUsers).fill(0)\\n const offline = mentions.slice()\\n\\n events.sort(([m1,t1], [m2, t2]) => (t1 - t2) || (m1 > m2 ? -1 : 1))\\n for (let [event, time, users] of events) {\\n if (event === 'MESSAGE') {\\n if (users === 'HERE') {\\n mentions.map((_, i, a) => offline[i] <= +time && a[i]++)\\n } else if (users === 'ALL') {\\n mentions.map((_, i, a) => a[i]++)\\n } else {\\n users.split(' ').map(idN => mentions[+idN.slice(2)]++)\\n }\\n } else {\\n offline[+users] = +time + 60\\n }\\n }\\n\\n return mentions\\n};\"], [63300, 14.2857, \"/**\\n * Counts the number of mentions for each user based on events.\\n *\\n * @intuition\\n * Track when users go offline and process different message types:\\n * - ALL: Mention all users\\n * - HERE: Mention users who have been offline for at least 60 time units\\n * - Direct mentions: Parse @u{id} format and increment specific user counts\\n * The key insight is tracking offline times rather than online status.\\n *\\n * @approach\\n * 1. Convert timestamps to integers and sort events by time\\n * 2. For events with the same timestamp, prioritize OFFLINE events before messages\\n * 3. Track the last offline time for each user\\n * 4. Process each event based on its type:\\n * - OFFLINE: Update the user's offline timestamp\\n * - MESSAGE/ALL: Increment count for all users\\n * - MESSAGE/HERE: Increment count for users offline for at least 60 time units\\n * - Direct mentions: Parse @u{id} format and increment specific users\\n *\\n * @complexity\\n * Time: O(n log n) where n is the number of events (dominated by sorting)\\n * Space: O(u) where u is the number of users\\n *\\n * @param {number} numberOfUsers - The total number of users\\n * @param {string[][]} events - Array of events, each containing [type, timestamp, data]\\n * @return {number[]} - Array of mention counts for each user\\n */\\nconst countMentions = (numberOfUsers, events) => {\\n // Convert timestamps to integers\\n const prepareEvents = events => {\\n for (const event of events) {\\n event[1] = parseInt(event[1], 10);\\n }\\n return events;\\n };\\n\\n // Sort events by timestamp with OFFLINE events first for same timestamps\\n const sortEvents = events => {\\n return events.sort((a, b) => {\\n if (a[1] !== b[1]) return a[1] - b[1];\\n if (a[0] === \\\"OFFLINE\\\") return -1;\\n if (b[0] === \\\"OFFLINE\\\") return 1;\\n return 0;\\n });\\n };\\n\\n // Process ALL message - mention all users\\n const handleAllMessage = (counts, userCount) => {\\n for (let i = 0; i < userCount; i++) {\\n counts[i]++;\\n }\\n };\\n\\n // Process HERE message - mention users offline for at least 60 time units\\n const handleHereMessage = (counts, offlineTimes, timestamp, userCount) => {\\n for (let i = 0; i < userCount; i++) {\\n if (timestamp - offlineTimes[i] >= 60) {\\n counts[i]++;\\n }\\n }\\n };\\n\\n // Parse direct mentions and increment mentioned users\\n const handleDirectMentions = (counts, data) => {\\n let i = 0;\\n while (i < data.length) {\\n // Skip \\\"@u\\\" prefix\\n i += 2;\\n \\n // Parse user ID\\n let userId = 0;\\n while (i < data.length && data.charCodeAt(i) !== 0x20) {\\n userId = userId * 10 + (data.charCodeAt(i) - 0x30);\\n i++;\\n }\\n \\n // Increment count and skip space\\n counts[userId]++;\\n i++;\\n }\\n };\\n\\n // Initialize tracking arrays\\n const offlineTimes = Array(numberOfUsers).fill(-Infinity);\\n const mentionCounts = Array(numberOfUsers).fill(0);\\n \\n // Prepare and sort events\\n const sortedEvents = sortEvents(prepareEvents(events));\\n \\n // Process each event\\n for (const [eventType, timestamp, data] of sortedEvents) {\\n if (eventType === \\\"MESSAGE\\\") {\\n if (data === \\\"ALL\\\") {\\n handleAllMessage(mentionCounts, numberOfUsers);\\n } else if (data === \\\"HERE\\\") {\\n handleHereMessage(mentionCounts, offlineTimes, timestamp, numberOfUsers);\\n } else {\\n handleDirectMentions(mentionCounts, data);\\n }\\n } else if (eventType === \\\"OFFLINE\\\") {\\n // Update offline time for user\\n const userId = parseInt(data, 10);\\n offlineTimes[userId] = timestamp;\\n }\\n }\\n \\n return mentionCounts;\\n};\\n\"], [63800, 14.2857, null], [64700, 14.2857, null], [64900, 14.2857, \"/**\\n * @param {number} numberOfUsers\\n * @param {string[][]} events\\n * @return {number[]}\\n */\\nvar countMentions = function (numberOfUsers, events) {\\n let mentions = new Array(numberOfUsers).fill(0);\\n let offline = mentions.slice();\\n\\n events.sort(([m1, t1], [m2, t2]) =>\\n (t1 - t2) || (m1 > m2 ? -1 : 1)\\n )\\n\\n for (let [msg, time, id] of events) {\\n if (msg === \\\"MESSAGE\\\") {\\n if (id === \\\"ALL\\\") {\\n mentions.map((_, i, a) => a[i]++)\\n } else if (id === \\\"HERE\\\") {\\n mentions.map((_, i, a) => offline[i] <= +time && a[i]++)\\n } else {\\n id.split(' ').map(idN => mentions[+idN.slice(2)]++)\\n }\\n } else {\\n offline[+id] = +time + 60;\\n }\\n }\\n return mentions\\n}\"], [68000, 14.2857, \"/**\\n * @param {number} numberOfUsers\\n * @param {string[][]} events\\n * @return {number[]}\\n */\\nvar countMentions = function (numberOfUsers, events) {\\n events.sort((a, b) => a[1] - b[1] || b[0].localeCompare(a[0]));\\n // console.log(events);\\n let onlineUsers = Array(numberOfUsers).fill(1);\\n let lastOfflineTimestamp = Array(numberOfUsers).fill(-1);\\n let mentions = Array(numberOfUsers).fill(0);\\n for (let event of events) {\\n event[1] = parseInt(event[1]);\\n if (event[0] == \\\"OFFLINE\\\") {\\n // console.log(\\\"in offline\\\");\\n onlineUsers[parseInt(event[2])] = 0;\\n lastOfflineTimestamp[parseInt(event[2])] = event[1];\\n // console.log(\\\"here\\\", onlineUsers);\\n } else if (event[0] == \\\"MESSAGE\\\") {\\n // console.log(\\\"in message\\\");\\n for (let i = 0; i < numberOfUsers; i++) {\\n if (onlineUsers[i] === 0 && event[1] >= lastOfflineTimestamp[i] + 60) {\\n onlineUsers[i] = 1;\\n }\\n }\\n\\n if (event[2] == \\\"HERE\\\") {\\n // console.log(\\\"hello\\\", onlineUsers);\\n for (let i in onlineUsers) {\\n if (onlineUsers[i] == 1) {\\n mentions[i] += 1;\\n }\\n }\\n } else if (event[2] == \\\"ALL\\\") {\\n for (let i = 0; i < numberOfUsers; i++) {\\n mentions[i] += 1;\\n }\\n } else {\\n let arr = event[2].split(\\\" \\\");\\n arr.map((a) => {\\n let id = parseInt(a.slice(2));\\n mentions[id] += 1;\\n })\\n }\\n }\\n prevtimeStamp = event[1];\\n // console.log(\\\"metions\\\", mentions);\\n // console.log(\\\"onlineUsers\\\", onlineUsers);\\n }\\n return mentions;\\n};\"]]",
"runtime": 23,
"runtimeDistribution": "[[15, 14.2857, \"/**\\n * Counts the number of mentions for each user based on events.\\n *\\n * @intuition\\n * Track when users go offline and process different message types:\\n * - ALL: Mention all users\\n * - HERE: Mention users who have been offline for at least 60 time units\\n * - Direct mentions: Parse @u{id} format and increment specific user counts\\n * The key insight is tracking offline times rather than online status.\\n *\\n * @approach\\n * 1. Convert timestamps to integers and sort events by time\\n * 2. For events with the same timestamp, prioritize OFFLINE events before messages\\n * 3. Track the last offline time for each user\\n * 4. Process each event based on its type:\\n * - OFFLINE: Update the user's offline timestamp\\n * - MESSAGE/ALL: Increment count for all users\\n * - MESSAGE/HERE: Increment count for users offline for at least 60 time units\\n * - Direct mentions: Parse @u{id} format and increment specific users\\n *\\n * @complexity\\n * Time: O(n log n) where n is the number of events (dominated by sorting)\\n * Space: O(u) where u is the number of users\\n *\\n * @param {number} numberOfUsers - The total number of users\\n * @param {string[][]} events - Array of events, each containing [type, timestamp, data]\\n * @return {number[]} - Array of mention counts for each user\\n */\\nconst countMentions = (numberOfUsers, events) => {\\n // Convert timestamps to integers\\n const prepareEvents = events => {\\n for (const event of events) {\\n event[1] = parseInt(event[1], 10);\\n }\\n return events;\\n };\\n\\n // Sort events by timestamp with OFFLINE events first for same timestamps\\n const sortEvents = events => {\\n return events.sort((a, b) => {\\n if (a[1] !== b[1]) return a[1] - b[1];\\n if (a[0] === \\\"OFFLINE\\\") return -1;\\n if (b[0] === \\\"OFFLINE\\\") return 1;\\n return 0;\\n });\\n };\\n\\n // Process ALL message - mention all users\\n const handleAllMessage = (counts, userCount) => {\\n for (let i = 0; i < userCount; i++) {\\n counts[i]++;\\n }\\n };\\n\\n // Process HERE message - mention users offline for at least 60 time units\\n const handleHereMessage = (counts, offlineTimes, timestamp, userCount) => {\\n for (let i = 0; i < userCount; i++) {\\n if (timestamp - offlineTimes[i] >= 60) {\\n counts[i]++;\\n }\\n }\\n };\\n\\n // Parse direct mentions and increment mentioned users\\n const handleDirectMentions = (counts, data) => {\\n let i = 0;\\n while (i < data.length) {\\n // Skip \\\"@u\\\" prefix\\n i += 2;\\n \\n // Parse user ID\\n let userId = 0;\\n while (i < data.length && data.charCodeAt(i) !== 0x20) {\\n userId = userId * 10 + (data.charCodeAt(i) - 0x30);\\n i++;\\n }\\n \\n // Increment count and skip space\\n counts[userId]++;\\n i++;\\n }\\n };\\n\\n // Initialize tracking arrays\\n const offlineTimes = Array(numberOfUsers).fill(-Infinity);\\n const mentionCounts = Array(numberOfUsers).fill(0);\\n \\n // Prepare and sort events\\n const sortedEvents = sortEvents(prepareEvents(events));\\n \\n // Process each event\\n for (const [eventType, timestamp, data] of sortedEvents) {\\n if (eventType === \\\"MESSAGE\\\") {\\n if (data === \\\"ALL\\\") {\\n handleAllMessage(mentionCounts, numberOfUsers);\\n } else if (data === \\\"HERE\\\") {\\n handleHereMessage(mentionCounts, offlineTimes, timestamp, numberOfUsers);\\n } else {\\n handleDirectMentions(mentionCounts, data);\\n }\\n } else if (eventType === \\\"OFFLINE\\\") {\\n // Update offline time for user\\n const userId = parseInt(data, 10);\\n offlineTimes[userId] = timestamp;\\n }\\n }\\n \\n return mentionCounts;\\n};\\n\"], [16, 14.2857, \"/**\\n * Counts the number of mentions for each user based on events.\\n *\\n * @intuition\\n * We need to track online status of users and process different types of events:\\n * - Online events: Update a user's online status\\n * - All mentions: Increment mention count for all users\\n * - Here mentions: Increment mention count for all offline users\\n * - Direct mentions: Increment mention count for specifically mentioned users\\n *\\n * @approach\\n * 1. Sort events by timestamp, with tie-breaking by event type\\n * 2. Process each event according to its type:\\n * - Online events: Mark user as online for 60 seconds\\n * - All mentions: Use a lazy counter to avoid processing all users immediately\\n * - Here mentions: Increment count for all offline users\\n * - Direct mentions: Extract user IDs from mentions and increment their counts\\n * 3. Apply lazy counter to all users at the end\\n *\\n * @complexity\\n * Time: O(n log n) where n is the number of events (dominated by sorting)\\n * Space: O(u) where u is the number of users\\n *\\n * @param {number} numberOfUsers - The total number of users\\n * @param {string[][]} events - Array of events, each containing [type, timestamp, data]\\n * @return {number[]} - Array of mention counts for each user\\n */\\nconst countMentions = (numberOfUsers, events) => {\\n // Sort events by timestamp with tie-breaking by event type\\n events.sort((a, b) => {\\n const timeA = +a[1];\\n const timeB = +b[1];\\n\\n if (timeA === timeB) {\\n return a[0].charAt(2) < b[0].charAt(2) ? -1 : 1;\\n }\\n return timeA - timeB;\\n });\\n\\n const mentionCounts = Array(numberOfUsers).fill(0);\\n const onlineTimes = Array(numberOfUsers).fill(0);\\n let lazyAllMentions = 0;\\n\\n for (const [eventType, timestamp, data] of events) {\\n const currentTime = +timestamp;\\n\\n if (eventType.charAt(0) === 'O') {\\n // Online event: Mark user as online for 60 seconds\\n const userId = +data;\\n onlineTimes[userId] = currentTime + 60;\\n } else if (data.charAt(0) === 'A') {\\n // All mention: Increment lazy counter\\n lazyAllMentions++;\\n } else if (data.charAt(0) === 'H') {\\n // Here mention: Increment count for offline users\\n for (let i = 0; i < numberOfUsers; i++) {\\n if (onlineTimes[i] <= currentTime) {\\n mentionCounts[i]++;\\n }\\n }\\n } else {\\n // Direct mentions: Extract user IDs and increment their counts\\n const mentions = data.split(' ');\\n for (const mention of mentions) {\\n const userId = +mention.slice(2);\\n mentionCounts[userId]++;\\n }\\n }\\n }\\n\\n // Apply lazy counter to all users\\n if (lazyAllMentions > 0) {\\n for (let i = 0; i < numberOfUsers; i++) {\\n mentionCounts[i] += lazyAllMentions;\\n }\\n }\\n\\n return mentionCounts;\\n};\\n\"], [22, 14.2857, null], [23, 57.1429, \"var countMentions = function(numberOfUsers, events) {\\n events.sort((a, b) => {\\n const timeA = parseInt(a[1]);\\n const timeB = parseInt(b[1]);\\n if (timeA !== timeB) {\\n return timeA - timeB;\\n } else {\\n const typeA = a[0];\\n const typeB = b[0];\\n if (typeA === 'OFFLINE' && typeB === 'MESSAGE') return -1;\\n if (typeA === 'MESSAGE' && typeB === 'OFFLINE') return 1;\\n return 0;\\n }\\n });\\n\\n const mentions = new Array(numberOfUsers).fill(0);\\n const offlineEndTimes = new Array(numberOfUsers).fill(0);\\n\\n for (const event of events) {\\n const type = event[0];\\n const timestamp = parseInt(event[1]);\\n if (type === 'OFFLINE') {\\n const userId = parseInt(event[2]);\\n offlineEndTimes[userId] = timestamp + 60;\\n } else {\\n const tokens = event[2].split(' ');\\n const users = [];\\n for (const token of tokens) {\\n if (token === 'ALL') {\\n for (let i = 0; i < numberOfUsers; i++) users.push(i);\\n } else if (token === 'HERE') {\\n for (let i = 0; i < numberOfUsers; i++) {\\n if (offlineEndTimes[i] <= timestamp) users.push(i);\\n }\\n } else {\\n const id = parseInt(token.substring(2));\\n users.push(id);\\n }\\n }\\n users.forEach(id => mentions[id]++);\\n }\\n }\\n\\n return mentions;\\n};\"], [24, 14.2857, null], [25, 14.2857, \"/**\\n * @param {number} numberOfUsers\\n * @param {string[][]} events\\n * @return {number[]}\\n */\\nvar countMentions = function(numberOfUsers, events) {\\n const mentions = new Array(numberOfUsers).fill(0)\\n const offline = mentions.slice()\\n\\n events.sort(([m1,t1], [m2, t2]) => (t1 - t2) || (m1 > m2 ? -1 : 1))\\n for (let [event, time, users] of events) {\\n if (event === 'MESSAGE') {\\n if (users === 'HERE') {\\n mentions.map((_, i, a) => offline[i] <= +time && a[i]++)\\n } else if (users === 'ALL') {\\n mentions.map((_, i, a) => a[i]++)\\n } else {\\n users.split(' ').map(idN => mentions[+idN.slice(2)]++)\\n }\\n } else {\\n offline[+users] = +time + 60\\n }\\n }\\n\\n return mentions\\n};\"], [32, 14.2857, \"/**\\n * @param {number} numberOfUsers\\n * @param {string[][]} events\\n * @return {number[]}\\n */\\nvar countMentions = function (numberOfUsers, events) {\\n events.sort((a, b) => a[1] - b[1] || b[0].localeCompare(a[0]));\\n // console.log(events);\\n let onlineUsers = Array(numberOfUsers).fill(1);\\n let lastOfflineTimestamp = Array(numberOfUsers).fill(-1);\\n let mentions = Array(numberOfUsers).fill(0);\\n for (let event of events) {\\n event[1] = parseInt(event[1]);\\n if (event[0] == \\\"OFFLINE\\\") {\\n // console.log(\\\"in offline\\\");\\n onlineUsers[parseInt(event[2])] = 0;\\n lastOfflineTimestamp[parseInt(event[2])] = event[1];\\n // console.log(\\\"here\\\", onlineUsers);\\n } else if (event[0] == \\\"MESSAGE\\\") {\\n // console.log(\\\"in message\\\");\\n for (let i = 0; i < numberOfUsers; i++) {\\n if (onlineUsers[i] === 0 && event[1] >= lastOfflineTimestamp[i] + 60) {\\n onlineUsers[i] = 1;\\n }\\n }\\n\\n if (event[2] == \\\"HERE\\\") {\\n // console.log(\\\"hello\\\", onlineUsers);\\n for (let i in onlineUsers) {\\n if (onlineUsers[i] == 1) {\\n mentions[i] += 1;\\n }\\n }\\n } else if (event[2] == \\\"ALL\\\") {\\n for (let i = 0; i < numberOfUsers; i++) {\\n mentions[i] += 1;\\n }\\n } else {\\n let arr = event[2].split(\\\" \\\");\\n arr.map((a) => {\\n let id = parseInt(a.slice(2));\\n mentions[id] += 1;\\n })\\n }\\n }\\n prevtimeStamp = event[1];\\n // console.log(\\\"metions\\\", mentions);\\n // console.log(\\\"onlineUsers\\\", onlineUsers);\\n }\\n return mentions;\\n};\"]]"
},
"python3": {
"code": "class Solution:\n def countMentions(self, numberOfUsers: int, events: List[List[str]]) -> List[int]:\n mentions = [0] * numberOfUsers\n offline_until = [0] * numberOfUsers\n \n sorted_events = sorted(events, key=lambda x: (int(x[1]), 0 if x[0] == 'OFFLINE' else 1))\n \n for event in sorted_events:\n event_type = event[0]\n timestamp = int(event[1])\n if event_type == 'OFFLINE':\n user_id = int(event[2])\n offline_until[user_id] = timestamp + 60\n else:\n mentions_str = event[2]\n tokens = mentions_str.split()\n for token in tokens:\n if token == 'ALL':\n for user in range(numberOfUsers):\n mentions[user] += 1\n elif token == 'HERE':\n for user in range(numberOfUsers):\n if offline_until[user] <= timestamp:\n mentions[user] += 1\n else:\n user_id = int(token[2:])\n mentions[user_id] += 1\n \n return mentions",
"memory": 1800,
"memoryDistribution": "[[1800, 48.3871, \"from typing import List\\n\\nclass Solution:\\n def countMentions(self, numberOfUsers: int, events: List[List[str]]) -> List[int]:\\n mentions = [0] * numberOfUsers\\n offline_until = [0] * numberOfUsers\\n \\n sorted_events = sorted(events, key=lambda x: (int(x[1]), 0 if x[0] == 'OFFLINE' else 1))\\n \\n for event in sorted_events:\\n event_type = event[0]\\n timestamp = int(event[1])\\n if event_type == 'OFFLINE':\\n user_id = int(event[2])\\n offline_until[user_id] = timestamp + 60\\n else:\\n mentions_str = event[2]\\n tokens = mentions_str.split()\\n for token in tokens:\\n if token == 'ALL':\\n for user in range(numberOfUsers):\\n mentions[user] += 1\\n elif token == 'HERE':\\n for user in range(numberOfUsers):\\n if offline_until[user] <= timestamp:\\n mentions[user] += 1\\n else:\\n user_id = int(token[2:])\\n mentions[user_id] += 1\\n \\n return mentions\"], [17500, 0.6452, \"class Solution:\\n def countMentions(self, numberOfUsers: int, events: List[List[str]]) -> List[int]:\\n mentions = [0] * numberOfUsers \\n is_online = [1] * numberOfUsers\\n events.sort(key=lambda x: (int(x[1]), x[0] == \\\"MESSAGE\\\"))\\n \\n for m, t, ids in events: \\n if m == \\\"OFFLINE\\\":\\n is_online[int(ids)] = int(t) + 60\\n else:\\n if ids == \\\"ALL\\\":\\n for i in range(numberOfUsers):\\n mentions[i] += 1\\n elif ids == \\\"HERE\\\":\\n for i in range(numberOfUsers):\\n if is_online[i] <= int(t):\\n mentions[i] += 1\\n else:\\n for i in ids.split(\\\" \\\"):\\n i = int(i[2:])\\n mentions[i] += 1\\n\\n return mentions\\n\"], [17700, 1.2903, \"class Solution:\\n def countMentions(self, numberOfUsers: int, events: List[List[str]]) -> List[int]:\\n events.sort(key = lambda x: (int(x[1]), x[0] == 'MESSAGE'))\\n time = int(events[0][1])\\n next_online = [time]*numberOfUsers\\n mentions = [0]*numberOfUsers\\n\\n for event_type, event_time, event_data in events:\\n if event_type == 'OFFLINE':\\n next_online[int(event_data)] = int(event_time) + 60\\n else:\\n if event_data == 'ALL':\\n for i in range(numberOfUsers):\\n mentions[i] += 1\\n elif event_data == 'HERE':\\n for i in range(numberOfUsers):\\n if next_online[i] <= int(event_time):\\n mentions[i] += 1\\n else:\\n for user in event_data.split():\\n mentions[int(user[2:])] += 1\\n \\n return mentions\"], [17800, 5.1613, null], [17900, 20.0, null], [18000, 24.5161, null], [18100, 17.4194, \"class Solution:\\n def countMentions(self, numberOfUsers: int, events: List[List[str]]) -> List[int]:\\n # sort events by timestamp, then by type (offlines before messages)\\n events = sorted(\\n events,\\n key=lambda event: (\\n int(event[1]),\\n 0 if event[0] == \\\"OFFLINE\\\" else 1,\\n ),\\n )\\n ret = [0] * numberOfUsers\\n num_all_mentions = 0\\n online_at = {}\\n for event_type, timestamp, id_str in events:\\n timestamp = int(timestamp)\\n if event_type == \\\"OFFLINE\\\":\\n uid = int(id_str)\\n online_at[uid] = timestamp + 60\\n elif id_str == \\\"ALL\\\":\\n num_all_mentions += 1\\n elif id_str == \\\"HERE\\\":\\n newly_online = set()\\n for uid, t_online in online_at.items():\\n if t_online <= timestamp:\\n newly_online.add(uid)\\n for uid in newly_online:\\n del online_at[uid]\\n for uid in range(numberOfUsers):\\n if uid not in online_at:\\n ret[uid] += 1\\n else:\\n mentioned_ids = [int(x[2:]) for x in id_str.split()]\\n for uid in mentioned_ids:\\n ret[uid] += 1\\n\\n for i, _ in enumerate(ret):\\n ret[i] += num_all_mentions\\n\\n return ret\\n\"], [18200, 20.6452, \"from collections import deque\\n\\nclass Solution:\\n def countMentions(self, numberOfUsers: int, events: List[List[str]]) -> List[int]:\\n mentions = [0] * numberOfUsers\\n users = [1] * numberOfUsers\\n\\n events.sort(key=lambda x: (int(x[1]), x[0] != \\\"OFFLINE\\\"))\\n\\n for msg_type, timestamp, mention_str in events:\\n if msg_type == \\\"MESSAGE\\\":\\n to_mention = []\\n if mention_str == \\\"ALL\\\":\\n to_mention = [i for i in range(numberOfUsers)]\\n elif mention_str == \\\"HERE\\\":\\n to_mention = [i for i in range(numberOfUsers) if users[i] <= int(timestamp)]\\n else:\\n for id in mention_str.split(\\\" \\\"):\\n id = int(id[2:])\\n to_mention.append(id)\\n \\n for uid in to_mention:\\n mentions[uid] += 1\\n\\n elif msg_type == \\\"OFFLINE\\\":\\n users[int(mention_str)] = int(timestamp) + 60\\n\\n \\n return mentions\"]]",
"runtime": 43,
"runtimeDistribution": "[[18, 0.6452, \"class Solution:\\n def countMentions(self, n: int, events: List[List[str]]) -> List[int]:\\n # 'F'<'S' status change before count\\n e = sorted((int(e[1]),e[0][2],e[2]) for e in events)\\n cnt = [0]*n\\n allcnt = 0\\n off = set()\\n come = deque() # (time, id)\\n for t,x,s in e:\\n while come and come[0][0]<=t:\\n _,p = come.popleft()\\n off.remove(p)\\n if x=='F': # offline\\n s = int(s)\\n off.add(s)\\n come.append((t+60,s))\\n continue\\n # Message\\n if s[0]=='A': allcnt += 1\\n elif s[0]=='H':\\n allcnt += 1\\n for p in off: cnt[p] -= 1\\n else: # several id\\n for p in s.split():\\n cnt[int(p[2:])] += 1\\n #\\n for i in range(n): cnt[i] += allcnt\\n return cnt\"], [27, 1.2903, \"class Solution:\\n def countMentions(self, numberOfUsers: int, events: List[List[str]]) -> List[int]:\\n \\n events.sort(key= lambda x: (int(x[1]),x[0] != \\\"OFFLINE\\\"))\\n k = defaultdict(int)\\n offline = {}\\n delta = 0\\n for i in events:\\n event_type = i[0]\\n time = i[1]\\n ids = i[2]\\n if(event_type == \\\"MESSAGE\\\"):\\n if(ids == \\\"ALL\\\"):\\n delta += 1\\n elif(ids == \\\"HERE\\\"):\\n delta += 1\\n remove = []\\n for offline_event in offline:\\n diff = int(time) - int(offline[offline_event])\\n if(diff >= 60):\\n remove.append(offline_event)\\n else:\\n k[offline_event] -= 1\\n for r in remove:\\n del offline[r]\\n else:\\n for j in ids.split(\\\" \\\"):\\n new_id = j.replace(\\\"id\\\",\\\"\\\")\\n k[new_id] += 1\\n else:\\n offline[ids] = time\\n # print(k)\\n # print(offline,\\\"offline\\\")\\n ans = [0]*numberOfUsers\\n for i in range(numberOfUsers):\\n ans[i] = k[str(i)] + delta\\n return ans\"], [30, 0.6452, null], [31, 2.5806, null], [33, 0.6452, null], [35, 3.871, null], [36, 0.6452, null], [37, 1.2903, null], [38, 1.2903, null], [39, 2.5806, null], [40, 1.2903, null], [41, 2.5806, null], [42, 2.5806, null], [43, 8.3871, null], [44, 0.6452, null], [45, 3.2258, null], [46, 3.2258, null], [47, 8.3871, null], [48, 2.5806, null], [49, 3.871, null], [50, 1.9355, null], [51, 3.871, null], [52, 1.9355, null], [53, 0.6452, null], [55, 5.1613, null], [57, 1.2903, null], [58, 1.9355, null], [59, 5.8065, null], [60, 0.6452, null], [61, 1.2903, null], [63, 1.2903, null], [65, 0.6452, null], [66, 0.6452, null], [67, 2.5806, null], [69, 1.2903, null], [71, 0.6452, null], [75, 0.6452, null], [76, 0.6452, null], [78, 0.6452, null], [81, 0.6452, null], [82, 0.6452, null], [83, 0.6452, null], [84, 1.2903, null], [85, 0.6452, null], [86, 0.6452, null], [89, 1.2903, null], [94, 0.6452, null], [95, 1.9355, \"class Solution:\\n def countMentions(self, n: int, events: List[List[str]]) -> List[int]:\\n offline = [-1]*n\\n mentions = [0]*n\\n events[::-1] = sorted(events, key=lambda x: (int(x[1]), x[2]), reverse=True)\\n for event in events:\\n if event[0] == 'MESSAGE':\\n if event[2] == 'ALL':\\n for i in range(n):\\n mentions[i]+=1\\n elif event[2] == 'HERE':\\n for i in range(n):\\n if int(event[1])>=offline[i]:\\n mentions[i]+=1\\n else:\\n for i in range(len(event[2])):\\n if event[2][i] == 'd':\\n j=i+1\\n while j<len(event[2]) and event[2][j].isdigit():\\n j+=1\\n mentions[int(event[2][i+1:j])]+=1\\n else:\\n offline[int(event[2])] = int(event[1])+60\\n return mentions\\n\\n\\n\\n\\n\"], [96, 0.6452, \"class Solution:\\n def countMentions(self, numberOfUsers: int, events: List[List[str]]) -> List[int]:\\n \\n events.sort(key=lambda x: (int(x[1]), x[0] == \\\"MESSAGE\\\"))\\n\\n mentions = [0] * numberOfUsers\\n offline = [0] * numberOfUsers\\n\\n for type_, time_, ids_ in events:\\n\\n if type_ == 'OFFLINE':\\n offline[int(ids_)] = int(time_) + 60\\n else:\\n for i, key in enumerate(offline):\\n if int(time_) >= key:\\n offline[i] = 0\\n \\n\\n if ids_ == 'ALL':\\n for i in range(numberOfUsers):\\n mentions[i] += 1\\n elif ids_ == 'HERE':\\n for i in range(numberOfUsers):\\n if offline[i] == 0:\\n mentions[i] += 1 \\n else: \\n ids_ = ids_.split(' ')\\n\\n for i, n in enumerate(ids_):\\n mentions[int(n[2:])] += 1\\n \\n return mentions\\n\\n\\n \\n\\n \\n\\n\\n \\n\\n \\n\\n \"]]"
},
"ruby": {
"code": "def count_mentions(number_of_users, events)\n # Process events to include original index for stable sorting\n processed_events = events.each_with_index.map do |event, index|\n type, ts_str, data = event\n ts = ts_str.to_i\n type_priority = type == \"OFFLINE\" ? 0 : 1\n [ts, type_priority, index, event]\n end\n\n # Sort events by timestamp, then type (OFFLINE first), then original index\n sorted_events = processed_events.sort_by { |e| [e[0], e[1], e[2]] }\n\n # Initialize online_time and mentions arrays\n online_time = Array.new(number_of_users, 0)\n mentions = Array.new(number_of_users, 0)\n\n # Process each event in sorted order\n sorted_events.each do |e|\n original_event = e[3]\n type, ts_str, data = original_event\n ts = ts_str.to_i\n\n if type == \"OFFLINE\"\n # Update the user's online time\n user_id = data.to_i\n online_time[user_id] = ts + 60\n else\n # Process the message mentions\n mentions_str = data\n tokens = mentions_str.split(' ')\n mentioned_users = []\n\n tokens.each do |token|\n if token.start_with?('id')\n user_id = token[2..-1].to_i\n mentioned_users << user_id\n elsif token == 'ALL'\n mentioned_users += (0...number_of_users).to_a\n elsif token == 'HERE'\n online_users = (0...number_of_users).filter { |id| ts >= online_time[id] }\n mentioned_users += online_users\n end\n end\n\n # Update mentions count\n mentioned_users.each { |id| mentions[id] += 1 }\n end\n end\n\n mentions\nend",
"memory": null,
"memoryDistribution": "[[212400, 50.0, \"def count_mentions(number_of_users, events)\\n # Process events to include original index for stable sorting\\n processed_events = events.each_with_index.map do |event, index|\\n type, ts_str, data = event\\n ts = ts_str.to_i\\n type_priority = type == \\\"OFFLINE\\\" ? 0 : 1\\n [ts, type_priority, index, event]\\n end\\n\\n # Sort events by timestamp, then type (OFFLINE first), then original index\\n sorted_events = processed_events.sort_by { |e| [e[0], e[1], e[2]] }\\n\\n # Initialize online_time and mentions arrays\\n online_time = Array.new(number_of_users, 0)\\n mentions = Array.new(number_of_users, 0)\\n\\n # Process each event in sorted order\\n sorted_events.each do |e|\\n original_event = e[3]\\n type, ts_str, data = original_event\\n ts = ts_str.to_i\\n\\n if type == \\\"OFFLINE\\\"\\n # Update the user's online time\\n user_id = data.to_i\\n online_time[user_id] = ts + 60\\n else\\n # Process the message mentions\\n mentions_str = data\\n tokens = mentions_str.split(' ')\\n mentioned_users = []\\n\\n tokens.each do |token|\\n if token.start_with?('id')\\n user_id = token[2..-1].to_i\\n mentioned_users << user_id\\n elsif token == 'ALL'\\n mentioned_users += (0...number_of_users).to_a\\n elsif token == 'HERE'\\n online_users = (0...number_of_users).filter { |id| ts >= online_time[id] }\\n mentioned_users += online_users\\n end\\n end\\n\\n # Update mentions count\\n mentioned_users.each { |id| mentions[id] += 1 }\\n end\\n end\\n\\n mentions\\nend\"], [212500, 50.0, \"class OnlineEvent\\n attr_accessor :timestamp, :user_id\\n\\n def initialize(timestamp, user_id)\\n @timestamp = timestamp\\n @user_id = user_id\\n end\\nend\\n\\ndef count_mentions(user_count, event_list)\\n total_events = event_list.size\\n\\n mention_counts = Array.new(user_count, 0)\\n\\n\\n event_index = 0\\n online_events_heap = []\\n event_list.sort_by! { |event| event[1].to_i }\\n user_online_status = Array.new(user_count, true)\\n\\n\\n while event_index < total_events\\n current_time = event_list[event_index][1].to_i\\n\\n while !online_events_heap.empty? && online_events_heap.first.timestamp <= current_time\\n user_to_reactivate = online_events_heap.first.user_id\\n if user_to_reactivate >= 0 && user_to_reactivate < user_count\\n user_online_status[user_to_reactivate] = true\\n end\\n online_events_heap.shift\\n end\\n\\n next_event_index = event_index\\n while next_event_index < total_events && event_list[next_event_index][1].to_i == current_time\\n next_event_index += 1\\n end\\n\\n for event_in_current_time in event_index...next_event_index\\n if event_list[event_in_current_time][0] == \\\"OFFLINE\\\"\\n user_id = event_list[event_in_current_time][2].to_i\\n if user_id >= 0 && user_id < user_count && user_online_status[user_id]\\n user_online_status[user_id] = false\\n online_event = OnlineEvent.new(current_time + 60, user_id)\\n index = online_events_heap.bsearch_index { |e| e.timestamp > online_event.timestamp } || online_events_heap.size\\n online_events_heap.insert(index, online_event)\\n end\\n end\\n end\\n\\n for event_in_current_time in event_index...next_event_index\\n if event_list[event_in_current_time][0] == \\\"MESSAGE\\\"\\n mention_target = event_list[event_in_current_time][2]\\n if mention_target == \\\"ALL\\\"\\n user_count.times do |user_id|\\n mention_counts[user_id] += 1\\n end\\n elsif mention_target == \\\"HERE\\\"\\n user_count.times do |user_id|\\n if user_online_status[user_id]\\n mention_counts[user_id] += 1\\n end\\n end\\n else\\n tokens = mention_target.split\\n tokens.each do |token|\\n if token.size >= 3 && token[0,2] == \\\"id\\\"\\n user_id_str = token[2..-1]\\n if user_id_str.chars.all? { |c| c =~ /\\\\d/ }\\n user_id = user_id_str.to_i\\n if user_id >= 0 && user_id < user_count\\n mention_counts[user_id] += 1\\n end\\n end\\n end\\n end\\n end\\n end\\n end\\n\\n event_index = next_event_index\\n end\\n\\n mention_counts\\nend\"]]",
"runtime": 126,
"runtimeDistribution": "[[123, 50.0, \"def count_mentions(number_of_users, events)\\n # Process events to include original index for stable sorting\\n processed_events = events.each_with_index.map do |event, index|\\n type, ts_str, data = event\\n ts = ts_str.to_i\\n type_priority = type == \\\"OFFLINE\\\" ? 0 : 1\\n [ts, type_priority, index, event]\\n end\\n\\n # Sort events by timestamp, then type (OFFLINE first), then original index\\n sorted_events = processed_events.sort_by { |e| [e[0], e[1], e[2]] }\\n\\n # Initialize online_time and mentions arrays\\n online_time = Array.new(number_of_users, 0)\\n mentions = Array.new(number_of_users, 0)\\n\\n # Process each event in sorted order\\n sorted_events.each do |e|\\n original_event = e[3]\\n type, ts_str, data = original_event\\n ts = ts_str.to_i\\n\\n if type == \\\"OFFLINE\\\"\\n # Update the user's online time\\n user_id = data.to_i\\n online_time[user_id] = ts + 60\\n else\\n # Process the message mentions\\n mentions_str = data\\n tokens = mentions_str.split(' ')\\n mentioned_users = []\\n\\n tokens.each do |token|\\n if token.start_with?('id')\\n user_id = token[2..-1].to_i\\n mentioned_users << user_id\\n elsif token == 'ALL'\\n mentioned_users += (0...number_of_users).to_a\\n elsif token == 'HERE'\\n online_users = (0...number_of_users).filter { |id| ts >= online_time[id] }\\n mentioned_users += online_users\\n end\\n end\\n\\n # Update mentions count\\n mentioned_users.each { |id| mentions[id] += 1 }\\n end\\n end\\n\\n mentions\\nend\"], [126, 50.0, \"def count_mentions(number_of_users, events)\\n # Process events to include original index for stable sorting\\n processed_events = events.each_with_index.map do |event, index|\\n type, ts_str, data = event\\n ts = ts_str.to_i\\n type_priority = type == \\\"OFFLINE\\\" ? 0 : 1\\n [ts, type_priority, index, event]\\n end\\n\\n # Sort events by timestamp, then type (OFFLINE first), then original index\\n sorted_events = processed_events.sort_by { |e| [e[0], e[1], e[2]] }\\n\\n # Initialize online_time and mentions arrays\\n online_time = Array.new(number_of_users, 0)\\n mentions = Array.new(number_of_users, 0)\\n\\n # Process each event in sorted order\\n sorted_events.each do |e|\\n original_event = e[3]\\n type, ts_str, data = original_event\\n ts = ts_str.to_i\\n\\n if type == \\\"OFFLINE\\\"\\n # Update the user's online time\\n user_id = data.to_i\\n online_time[user_id] = ts + 60\\n else\\n # Process the message mentions\\n mentions_str = data\\n tokens = mentions_str.split(' ')\\n mentioned_users = []\\n\\n tokens.each do |token|\\n if token.start_with?('id')\\n user_id = token[2..-1].to_i\\n mentioned_users << user_id\\n elsif token == 'ALL'\\n mentioned_users += (0...number_of_users).to_a\\n elsif token == 'HERE'\\n online_users = (0...number_of_users).filter { |id| ts >= online_time[id] }\\n mentioned_users += online_users\\n end\\n end\\n\\n # Update mentions count\\n mentioned_users.each { |id| mentions[id] += 1 }\\n end\\n end\\n\\n mentions\\nend\"], [212, 50.0, \"class OnlineEvent\\n attr_accessor :timestamp, :user_id\\n\\n def initialize(timestamp, user_id)\\n @timestamp = timestamp\\n @user_id = user_id\\n end\\nend\\n\\ndef count_mentions(user_count, event_list)\\n total_events = event_list.size\\n\\n mention_counts = Array.new(user_count, 0)\\n\\n\\n event_index = 0\\n online_events_heap = []\\n event_list.sort_by! { |event| event[1].to_i }\\n user_online_status = Array.new(user_count, true)\\n\\n\\n while event_index < total_events\\n current_time = event_list[event_index][1].to_i\\n\\n while !online_events_heap.empty? && online_events_heap.first.timestamp <= current_time\\n user_to_reactivate = online_events_heap.first.user_id\\n if user_to_reactivate >= 0 && user_to_reactivate < user_count\\n user_online_status[user_to_reactivate] = true\\n end\\n online_events_heap.shift\\n end\\n\\n next_event_index = event_index\\n while next_event_index < total_events && event_list[next_event_index][1].to_i == current_time\\n next_event_index += 1\\n end\\n\\n for event_in_current_time in event_index...next_event_index\\n if event_list[event_in_current_time][0] == \\\"OFFLINE\\\"\\n user_id = event_list[event_in_current_time][2].to_i\\n if user_id >= 0 && user_id < user_count && user_online_status[user_id]\\n user_online_status[user_id] = false\\n online_event = OnlineEvent.new(current_time + 60, user_id)\\n index = online_events_heap.bsearch_index { |e| e.timestamp > online_event.timestamp } || online_events_heap.size\\n online_events_heap.insert(index, online_event)\\n end\\n end\\n end\\n\\n for event_in_current_time in event_index...next_event_index\\n if event_list[event_in_current_time][0] == \\\"MESSAGE\\\"\\n mention_target = event_list[event_in_current_time][2]\\n if mention_target == \\\"ALL\\\"\\n user_count.times do |user_id|\\n mention_counts[user_id] += 1\\n end\\n elsif mention_target == \\\"HERE\\\"\\n user_count.times do |user_id|\\n if user_online_status[user_id]\\n mention_counts[user_id] += 1\\n end\\n end\\n else\\n tokens = mention_target.split\\n tokens.each do |token|\\n if token.size >= 3 && token[0,2] == \\\"id\\\"\\n user_id_str = token[2..-1]\\n if user_id_str.chars.all? { |c| c =~ /\\\\d/ }\\n user_id = user_id_str.to_i\\n if user_id >= 0 && user_id < user_count\\n mention_counts[user_id] += 1\\n end\\n end\\n end\\n end\\n end\\n end\\n end\\n\\n event_index = next_event_index\\n end\\n\\n mention_counts\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list[dict]:
import random
random.seed(seed)
# Sample solution logic adapted from the provided sample solution.
def sample_count_mentions(numberOfUsers, events):
mentions = [0] * numberOfUsers
offline_until = [0] * numberOfUsers
# Sort events by timestamp; if same timestamp, process OFFLINE events before MESSAGE events.
sorted_events = sorted(events, key=lambda x: (int(x[1]), 0 if x[0] == 'OFFLINE' else 1))
for event in sorted_events:
event_type = event[0]
timestamp = int(event[1])
if event_type == 'OFFLINE':
user_id = int(event[2])
offline_until[user_id] = timestamp + 60
else:
mentions_str = event[2]
tokens = mentions_str.split()
for token in tokens:
if token == 'ALL':
for user in range(numberOfUsers):
mentions[user] += 1
elif token == 'HERE':
for user in range(numberOfUsers):
if offline_until[user] <= timestamp:
mentions[user] += 1
else:
# token of the form "id<number>"
user_id = int(token[2:])
mentions[user_id] += 1
return mentions
# Serialization: input -> string with the following format:
# Line 1: numberOfUsers
# Line 2: number of events (n)
# The next n lines: each event as "EVENT_TYPE|timestamp|value"
def serialize_input(numberOfUsers, events):
lines = []
lines.append(str(numberOfUsers))
lines.append(str(len(events)))
for event in events:
lines.append("|".join(event))
return "\n".join(lines)
# Serialization for output: a comma-separated list of numbers.
def serialize_output(result):
return ",".join(str(x) for x in result)
# Generate a random test case that obeys the constraints.
def generate_random_test_case():
num_users = random.randint(1, 10)
n_events = random.randint(1, 10)
events = []
offline_until_sim = [0] * num_users
current_time = random.randint(1, 10)
for _ in range(n_events):
# Decide event type with a bias; offline events only if at least one user is online.
online_users = [u for u in range(num_users) if offline_until_sim[u] <= current_time]
if online_users and random.random() < 0.4:
# OFFLINE event: choose a random online user.
user = random.choice(online_users)
events.append(["OFFLINE", str(current_time), str(user)])
offline_until_sim[user] = current_time + 60
else:
# MESSAGE event.
r = random.random()
if r < 0.3:
mention_str = "ALL"
elif r < 0.6:
mention_str = "HERE"
else:
cnt = random.randint(1, 5)
tokens = []
for _ in range(cnt):
uid = random.randint(0, num_users - 1)
tokens.append("id" + str(uid))
mention_str = " ".join(tokens)
events.append(["MESSAGE", str(current_time), mention_str])
current_time += random.randint(0, 100)
if current_time < 1:
current_time = 1
# Optionally shuffle events to test unsorted input.
if random.random() < 0.5:
random.shuffle(events)
return num_users, events
# Predefined test cases covering examples and edge cases.
predefined = []
# Example 1:
predefined.append((2, [
["MESSAGE", "10", "id1 id0"],
["OFFLINE", "11", "0"],
["MESSAGE", "71", "HERE"]
]))
# Example 2:
predefined.append((2, [
["MESSAGE", "10", "id1 id0"],
["OFFLINE", "11", "0"],
["MESSAGE", "12", "ALL"]
]))
# Example 3:
predefined.append((2, [
["OFFLINE", "10", "0"],
["MESSAGE", "12", "HERE"]
]))
# Edge case: duplicates and ALL mention.
predefined.append((3, [
["MESSAGE", "5", "id0 id0 id1 ALL"]
]))
# Edge case: HERE with simultaneous OFFLINE event.
predefined.append((3, [
["OFFLINE", "4", "1"],
["MESSAGE", "4", "HERE"]
]))
# Unsorted events test.
predefined.append((4, [
["MESSAGE", "50", "id2"],
["OFFLINE", "30", "3"],
["MESSAGE", "30", "ALL"],
["MESSAGE", "30", "HERE"]
]))
test_cases = []
# Use predefined test cases first.
for num_users, events in predefined:
inp = serialize_input(num_users, events)
expected = sample_count_mentions(num_users, events)
out = serialize_output(expected)
test_cases.append({"input": inp, "output": out})
if len(test_cases) >= num_cases:
break
# Generate additional random test cases if needed.
while len(test_cases) < num_cases:
num_users, events = generate_random_test_case()
inp = serialize_input(num_users, events)
expected = sample_count_mentions(num_users, events)
out = serialize_output(expected)
test_cases.append({"input": inp, "output": out})
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
# Deserialization: our output format is a comma-separated list of integers.
def deserialize(output_str):
# Remove extra whitespace and newline characters.
tokens = [token for token in output_str.strip().split(",") if token != ""]
return [int(token) for token in tokens]
expected = deserialize(expected_output)
program = deserialize(program_output)
return expected == program
|
[{"input": "2\n3\nMESSAGE|10|id1 id0\nOFFLINE|11|0\nMESSAGE|71|HERE", "output": "2,2"}, {"input": "2\n3\nMESSAGE|10|id1 id0\nOFFLINE|11|0\nMESSAGE|12|ALL", "output": "2,2"}, {"input": "2\n2\nOFFLINE|10|0\nMESSAGE|12|HERE", "output": "0,1"}, {"input": "3\n1\nMESSAGE|5|id0 id0 id1 ALL", "output": "3,2,1"}, {"input": "3\n2\nOFFLINE|4|1\nMESSAGE|4|HERE", "output": "1,0,1"}, {"input": "4\n4\nMESSAGE|50|id2\nOFFLINE|30|3\nMESSAGE|30|ALL\nMESSAGE|30|HERE", "output": "2,2,3,1"}, {"input": "2\n1\nOFFLINE|5|0", "output": "0,0"}, {"input": "9\n2\nMESSAGE|10|ALL\nOFFLINE|37|0", "output": "1,1,1,1,1,1,1,1,1"}, {"input": "4\n8\nOFFLINE|10|0\nMESSAGE|107|id2 id1 id1\nOFFLINE|204|0\nOFFLINE|252|2\nOFFLINE|329|0\nMESSAGE|422|ALL\nOFFLINE|470|2\nMESSAGE|550|id1 id0 id0 id1 id2", "output": "3,5,3,1"}, {"input": "2\n7\nMESSAGE|5|id1 id1\nOFFLINE|234|0\nOFFLINE|147|0\nMESSAGE|290|HERE\nMESSAGE|263|id1 id0 id0 id1\nMESSAGE|31|id0\nMESSAGE|99|ALL", "output": "4,6"}, {"input": "10\n7\nOFFLINE|227|6\nMESSAGE|303|HERE\nMESSAGE|71|id2\nOFFLINE|465|8\nOFFLINE|6|2\nOFFLINE|151|6\nMESSAGE|373|ALL", "output": "2,2,3,2,2,2,2,2,2,2"}, {"input": "8\n1\nMESSAGE|5|id1 id4 id3 id2 id5", "output": "0,1,1,1,1,1,0,0"}, {"input": "9\n1\nOFFLINE|10|0", "output": "0,0,0,0,0,0,0,0,0"}, {"input": "5\n4\nOFFLINE|11|3\nMESSAGE|19|HERE\nOFFLINE|1|4\nOFFLINE|35|1", "output": "1,1,1,0,0"}, {"input": "5\n7\nMESSAGE|6|HERE\nOFFLINE|21|0\nOFFLINE|64|2\nOFFLINE|139|0\nMESSAGE|229|ALL\nMESSAGE|233|ALL\nOFFLINE|263|3", "output": "3,3,3,3,3"}, {"input": "10\n10\nOFFLINE|8|7\nOFFLINE|60|1\nMESSAGE|144|HERE\nMESSAGE|203|ALL\nMESSAGE|286|ALL\nMESSAGE|337|id3\nOFFLINE|361|7\nMESSAGE|378|ALL\nMESSAGE|409|ALL\nOFFLINE|479|8", "output": "5,5,5,6,5,5,5,5,5,5"}, {"input": "4\n3\nMESSAGE|7|ALL\nMESSAGE|58|ALL\nMESSAGE|58|ALL", "output": "3,3,3,3"}, {"input": "5\n7\nMESSAGE|9|HERE\nOFFLINE|33|0\nMESSAGE|107|ALL\nOFFLINE|147|4\nMESSAGE|208|id0 id4\nMESSAGE|218|ALL\nMESSAGE|226|ALL", "output": "5,4,4,4,5"}, {"input": "10\n4\nMESSAGE|10|id9 id9 id8 id5\nOFFLINE|43|5\nOFFLINE|73|2\nMESSAGE|158|HERE", "output": "1,1,1,1,1,2,1,1,2,3"}, {"input": "1\n8\nMESSAGE|268|id0 id0 id0\nMESSAGE|10|id0\nMESSAGE|82|id0 id0 id0\nMESSAGE|279|id0 id0 id0\nMESSAGE|151|id0 id0 id0 id0 id0\nOFFLINE|242|0\nOFFLINE|74|0\nMESSAGE|165|id0 id0", "output": "17"}, {"input": "2\n2\nMESSAGE|3|id0 id1 id0 id0 id1\nMESSAGE|49|id1", "output": "3,3"}, {"input": "2\n6\nMESSAGE|340|HERE\nMESSAGE|240|id1 id0\nOFFLINE|140|1\nMESSAGE|9|HERE\nMESSAGE|344|ALL\nMESSAGE|88|id0 id0", "output": "6,4"}, {"input": "7\n6\nMESSAGE|154|id3 id4 id4\nMESSAGE|5|id2 id5 id4\nOFFLINE|192|6\nMESSAGE|78|id0\nMESSAGE|56|id0 id0 id2\nOFFLINE|168|4", "output": "3,0,2,1,3,1,0"}, {"input": "6\n10\nMESSAGE|6|ALL\nMESSAGE|44|id3 id5 id2\nOFFLINE|114|3\nMESSAGE|199|id4 id4\nMESSAGE|237|id2 id1 id3\nMESSAGE|337|id3 id3 id5 id1\nMESSAGE|402|id5 id0\nMESSAGE|438|id0 id1 id5\nOFFLINE|477|1\nOFFLINE|495|2", "output": "3,4,3,5,3,5"}, {"input": "2\n8\nMESSAGE|7|HERE\nMESSAGE|98|HERE\nOFFLINE|129|0\nMESSAGE|225|id0 id0 id1 id0\nOFFLINE|296|0\nOFFLINE|354|1\nMESSAGE|439|HERE\nMESSAGE|479|id1 id1 id0 id1 id1", "output": "7,8"}, {"input": "5\n9\nOFFLINE|59|4\nMESSAGE|8|ALL\nMESSAGE|272|HERE\nMESSAGE|17|ALL\nOFFLINE|361|4\nOFFLINE|69|1\nOFFLINE|223|4\nMESSAGE|118|id3\nOFFLINE|170|3", "output": "3,3,3,4,2"}, {"input": "5\n7\nOFFLINE|8|2\nMESSAGE|93|HERE\nMESSAGE|114|id4 id0 id3 id4 id4\nOFFLINE|198|3\nMESSAGE|215|ALL\nOFFLINE|248|1\nOFFLINE|306|4", "output": "3,2,2,3,5"}, {"input": "7\n5\nMESSAGE|30|id6\nMESSAGE|35|ALL\nMESSAGE|2|id2\nMESSAGE|95|HERE\nMESSAGE|33|ALL", "output": "3,3,4,3,3,3,4"}, {"input": "3\n5\nOFFLINE|109|2\nMESSAGE|11|id0 id2\nMESSAGE|2|id2 id1 id1 id2 id0\nOFFLINE|232|2\nMESSAGE|185|id0 id1 id2 id1 id2", "output": "3,4,5"}, {"input": "6\n8\nMESSAGE|62|id2 id1 id0\nMESSAGE|97|ALL\nMESSAGE|3|id4 id4 id3\nMESSAGE|179|HERE\nMESSAGE|301|HERE\nMESSAGE|367|ALL\nOFFLINE|212|4\nMESSAGE|156|id0 id3 id2", "output": "6,5,6,6,6,4"}, {"input": "5\n4\nOFFLINE|190|3\nOFFLINE|148|4\nMESSAGE|7|HERE\nOFFLINE|81|4", "output": "1,1,1,1,1"}, {"input": "6\n2\nMESSAGE|9|id1 id5\nOFFLINE|70|4", "output": "0,1,0,0,0,1"}, {"input": "5\n2\nOFFLINE|26|1\nOFFLINE|4|2", "output": "0,0,0,0,0"}, {"input": "9\n5\nMESSAGE|3|id0\nOFFLINE|76|7\nOFFLINE|132|0\nMESSAGE|164|HERE\nMESSAGE|172|ALL", "output": "2,2,2,2,2,2,2,2,2"}, {"input": "3\n3\nOFFLINE|41|1\nMESSAGE|10|ALL\nMESSAGE|118|id1 id1 id1 id1 id2", "output": "1,5,2"}, {"input": "10\n2\nOFFLINE|14|2\nMESSAGE|4|ALL", "output": "1,1,1,1,1,1,1,1,1,1"}, {"input": "7\n8\nMESSAGE|10|ALL\nMESSAGE|46|id0 id5 id1 id2\nMESSAGE|146|HERE\nMESSAGE|171|HERE\nOFFLINE|253|2\nOFFLINE|271|1\nMESSAGE|310|id3 id0 id3\nOFFLINE|398|3", "output": "5,4,4,5,3,4,3"}, {"input": "8\n8\nMESSAGE|339|ALL\nOFFLINE|274|6\nMESSAGE|233|id0 id7 id1 id5 id4\nMESSAGE|108|HERE\nMESSAGE|97|id6 id7\nMESSAGE|149|id6 id7 id4\nMESSAGE|31|id0 id4 id0 id2 id7\nMESSAGE|2|id4 id0 id1", "output": "6,4,3,2,6,3,4,6"}, {"input": "1\n4\nMESSAGE|5|id0 id0 id0 id0\nOFFLINE|95|0\nMESSAGE|179|ALL\nMESSAGE|165|ALL", "output": "6"}, {"input": "7\n8\nMESSAGE|91|ALL\nOFFLINE|8|4\nOFFLINE|26|5\nMESSAGE|308|ALL\nOFFLINE|99|6\nMESSAGE|224|HERE\nOFFLINE|152|4\nMESSAGE|186|ALL", "output": "4,4,4,4,4,4,4"}, {"input": "4\n10\nOFFLINE|7|3\nOFFLINE|12|1\nMESSAGE|102|HERE\nMESSAGE|186|id3 id0\nMESSAGE|202|HERE\nMESSAGE|214|HERE\nMESSAGE|281|ALL\nMESSAGE|299|id0 id3\nMESSAGE|399|HERE\nOFFLINE|487|0", "output": "7,5,5,7"}, {"input": "9\n7\nMESSAGE|6|id8 id0 id1 id3\nMESSAGE|86|ALL\nMESSAGE|115|HERE\nMESSAGE|127|id7\nMESSAGE|148|id5\nOFFLINE|155|5\nOFFLINE|210|7", "output": "3,3,2,3,2,3,2,3,3"}, {"input": "3\n3\nOFFLINE|156|1\nOFFLINE|3|1\nMESSAGE|82|HERE", "output": "1,1,1"}, {"input": "8\n5\nOFFLINE|145|6\nMESSAGE|53|ALL\nOFFLINE|9|7\nOFFLINE|206|6\nMESSAGE|107|HERE", "output": "2,2,2,2,2,2,2,2"}, {"input": "5\n1\nMESSAGE|10|id4", "output": "0,0,0,0,1"}, {"input": "5\n4\nMESSAGE|34|id0 id0\nMESSAGE|73|ALL\nMESSAGE|10|ALL\nMESSAGE|119|ALL", "output": "5,3,3,3,3"}, {"input": "3\n9\nMESSAGE|6|id1 id1\nMESSAGE|43|HERE\nMESSAGE|57|ALL\nMESSAGE|153|id2 id1 id0 id1\nOFFLINE|154|0\nOFFLINE|212|2\nOFFLINE|286|2\nOFFLINE|333|0\nOFFLINE|393|2", "output": "3,6,3"}, {"input": "4\n2\nMESSAGE|8|HERE\nOFFLINE|60|0", "output": "1,1,1,1"}, {"input": "2\n2\nMESSAGE|4|ALL\nOFFLINE|62|1", "output": "1,1"}, {"input": "3\n7\nMESSAGE|2|id0 id2 id1\nMESSAGE|29|id0 id2 id1\nMESSAGE|98|id1\nOFFLINE|133|0\nOFFLINE|191|1\nMESSAGE|273|id1\nMESSAGE|304|id0 id2", "output": "3,4,3"}, {"input": "4\n6\nMESSAGE|3|HERE\nMESSAGE|38|ALL\nMESSAGE|54|id0\nOFFLINE|70|1\nOFFLINE|145|1\nOFFLINE|178|3", "output": "3,2,2,2"}, {"input": "2\n8\nMESSAGE|21|ALL\nOFFLINE|99|1\nMESSAGE|8|HERE\nMESSAGE|272|ALL\nMESSAGE|231|id0\nMESSAGE|307|HERE\nMESSAGE|157|ALL\nMESSAGE|218|HERE", "output": "7,6"}, {"input": "9\n4\nMESSAGE|7|ALL\nMESSAGE|50|HERE\nOFFLINE|143|6\nMESSAGE|183|HERE", "output": "3,3,3,3,3,3,2,3,3"}, {"input": "8\n2\nMESSAGE|2|ALL\nMESSAGE|14|HERE", "output": "2,2,2,2,2,2,2,2"}, {"input": "10\n9\nOFFLINE|504|3\nOFFLINE|229|1\nMESSAGE|407|HERE\nMESSAGE|558|id9 id8 id0 id9 id4\nOFFLINE|61|7\nOFFLINE|9|1\nOFFLINE|153|4\nOFFLINE|363|1\nMESSAGE|302|ALL", "output": "3,1,2,2,3,2,2,2,3,4"}, {"input": "2\n3\nOFFLINE|1|0\nMESSAGE|49|HERE\nOFFLINE|96|1", "output": "0,1"}, {"input": "10\n2\nOFFLINE|1|9\nMESSAGE|7|ALL", "output": "1,1,1,1,1,1,1,1,1,1"}, {"input": "7\n5\nMESSAGE|4|ALL\nOFFLINE|59|5\nMESSAGE|145|HERE\nOFFLINE|184|3\nOFFLINE|260|1", "output": "2,2,2,2,2,2,2"}, {"input": "3\n5\nOFFLINE|5|0\nMESSAGE|68|ALL\nMESSAGE|116|ALL\nMESSAGE|187|id1\nOFFLINE|281|0", "output": "2,3,2"}, {"input": "6\n10\nMESSAGE|7|id2 id0 id3 id0\nOFFLINE|308|4\nMESSAGE|413|HERE\nMESSAGE|170|HERE\nOFFLINE|119|4\nMESSAGE|209|ALL\nOFFLINE|389|4\nOFFLINE|48|4\nMESSAGE|506|id1 id0\nMESSAGE|106|id3", "output": "6,4,4,5,1,3"}, {"input": "10\n10\nMESSAGE|6|id7 id1\nMESSAGE|101|HERE\nMESSAGE|402|id1 id5 id1 id8\nMESSAGE|66|HERE\nMESSAGE|123|id9\nMESSAGE|199|HERE\nOFFLINE|114|4\nMESSAGE|342|HERE\nMESSAGE|269|id7\nOFFLINE|110|7", "output": "4,7,4,4,4,5,4,6,5,5"}, {"input": "5\n7\nOFFLINE|237|3\nMESSAGE|253|id4 id3 id2\nMESSAGE|7|id2\nMESSAGE|269|id0 id3 id4 id2 id0\nMESSAGE|193|id1 id2 id0 id4 id1\nOFFLINE|101|2\nOFFLINE|15|4", "output": "3,2,4,2,3"}, {"input": "3\n2\nMESSAGE|103|id0 id2 id1 id2 id0\nMESSAGE|5|ALL", "output": "3,2,3"}, {"input": "3\n10\nMESSAGE|264|id2 id1 id0 id0 id2\nMESSAGE|49|ALL\nMESSAGE|105|id0 id2 id0 id1\nOFFLINE|370|0\nMESSAGE|342|HERE\nMESSAGE|404|HERE\nMESSAGE|3|ALL\nMESSAGE|281|ALL\nMESSAGE|355|HERE\nMESSAGE|205|id2 id2 id1", "output": "9,9,11"}, {"input": "4\n7\nMESSAGE|42|id1 id1 id0\nMESSAGE|78|HERE\nOFFLINE|2|0\nMESSAGE|245|id0 id2 id1 id2\nOFFLINE|173|0\nOFFLINE|175|1\nMESSAGE|95|HERE", "output": "4,5,4,2"}, {"input": "8\n10\nMESSAGE|415|ALL\nOFFLINE|277|0\nOFFLINE|9|3\nMESSAGE|163|HERE\nOFFLINE|100|6\nOFFLINE|153|5\nMESSAGE|489|HERE\nMESSAGE|322|HERE\nMESSAGE|100|ALL\nMESSAGE|230|id0 id6 id7 id0 id6", "output": "6,5,5,5,5,4,7,6"}, {"input": "1\n5\nMESSAGE|117|ALL\nMESSAGE|9|HERE\nOFFLINE|4|0\nOFFLINE|199|0\nMESSAGE|48|HERE", "output": "1"}, {"input": "7\n7\nMESSAGE|262|id5 id3\nMESSAGE|8|HERE\nMESSAGE|31|HERE\nMESSAGE|190|HERE\nMESSAGE|213|HERE\nOFFLINE|97|0\nOFFLINE|223|2", "output": "4,4,4,5,4,5,4"}, {"input": "2\n7\nOFFLINE|269|0\nOFFLINE|145|0\nOFFLINE|342|1\nOFFLINE|222|1\nMESSAGE|6|id0 id0\nMESSAGE|83|HERE\nOFFLINE|99|1", "output": "3,1"}, {"input": "8\n9\nOFFLINE|339|3\nOFFLINE|195|2\nOFFLINE|106|7\nOFFLINE|356|4\nMESSAGE|274|id2 id5\nMESSAGE|7|ALL\nMESSAGE|204|id1 id5 id5 id1\nMESSAGE|133|ALL\nOFFLINE|359|6", "output": "2,4,3,2,2,5,2,2"}, {"input": "9\n7\nMESSAGE|233|HERE\nMESSAGE|47|HERE\nOFFLINE|376|5\nMESSAGE|338|HERE\nMESSAGE|7|ALL\nMESSAGE|134|ALL\nMESSAGE|331|HERE", "output": "6,6,6,6,6,6,6,6,6"}, {"input": "3\n5\nMESSAGE|10|HERE\nMESSAGE|31|HERE\nMESSAGE|52|id1 id2 id0 id0 id0\nMESSAGE|57|id2 id0 id2\nMESSAGE|110|ALL", "output": "7,4,6"}, {"input": "5\n8\nMESSAGE|4|id3 id0 id0\nMESSAGE|24|HERE\nOFFLINE|50|1\nMESSAGE|90|HERE\nMESSAGE|134|ALL\nMESSAGE|181|ALL\nMESSAGE|211|ALL\nOFFLINE|242|0", "output": "7,4,5,6,5"}, {"input": "10\n7\nMESSAGE|226|ALL\nMESSAGE|4|id9 id5 id3\nOFFLINE|101|8\nOFFLINE|162|6\nMESSAGE|336|id4 id8 id0 id1\nOFFLINE|300|0\nMESSAGE|160|HERE", "output": "3,3,2,3,3,3,2,2,2,3"}, {"input": "7\n1\nMESSAGE|10|HERE", "output": "1,1,1,1,1,1,1"}, {"input": "9\n8\nOFFLINE|9|1\nMESSAGE|25|HERE\nMESSAGE|68|HERE\nOFFLINE|86|8\nMESSAGE|137|ALL\nMESSAGE|154|id7 id2 id8 id2 id5\nOFFLINE|232|6\nMESSAGE|310|ALL", "output": "4,2,6,4,4,5,4,5,5"}, {"input": "9\n9\nMESSAGE|8|ALL\nOFFLINE|10|1\nMESSAGE|96|id3 id0 id7 id2 id8\nOFFLINE|200|5\nOFFLINE|253|3\nOFFLINE|376|7\nMESSAGE|176|id2 id3 id0 id1\nMESSAGE|305|id0 id2 id8 id3\nMESSAGE|63|id7", "output": "4,2,4,4,1,1,1,3,3"}, {"input": "10\n8\nMESSAGE|4|ALL\nOFFLINE|42|4\nOFFLINE|140|3\nMESSAGE|228|HERE\nMESSAGE|272|id4 id1 id9\nMESSAGE|358|id5 id2 id4 id0\nMESSAGE|394|ALL\nMESSAGE|450|id3 id8", "output": "4,4,4,4,5,4,3,3,4,4"}, {"input": "5\n3\nMESSAGE|61|ALL\nMESSAGE|2|HERE\nOFFLINE|33|4", "output": "2,2,2,2,2"}, {"input": "3\n1\nMESSAGE|9|ALL", "output": "1,1,1"}, {"input": "8\n8\nOFFLINE|232|5\nOFFLINE|228|4\nMESSAGE|4|ALL\nMESSAGE|108|id2\nMESSAGE|161|ALL\nMESSAGE|165|HERE\nMESSAGE|40|id3\nOFFLINE|309|5", "output": "3,3,4,4,3,3,3,3"}, {"input": "6\n3\nMESSAGE|8|id5\nMESSAGE|51|HERE\nOFFLINE|147|4", "output": "1,1,1,1,1,2"}, {"input": "7\n9\nOFFLINE|6|5\nMESSAGE|136|id4 id5 id4\nOFFLINE|79|1\nOFFLINE|137|4\nOFFLINE|225|5\nMESSAGE|240|ALL\nOFFLINE|18|1\nMESSAGE|327|id5 id0 id5\nOFFLINE|79|2", "output": "2,1,1,1,3,4,1"}, {"input": "7\n9\nMESSAGE|8|id6 id1\nMESSAGE|95|id4\nMESSAGE|152|HERE\nOFFLINE|224|6\nMESSAGE|294|ALL\nOFFLINE|362|2\nMESSAGE|428|id3 id0 id4 id3 id6\nMESSAGE|435|HERE\nMESSAGE|493|HERE", "output": "5,5,4,6,6,4,6"}, {"input": "1\n7\nMESSAGE|5|id0 id0 id0 id0 id0\nMESSAGE|74|id0\nOFFLINE|78|0\nOFFLINE|176|0\nMESSAGE|223|id0 id0 id0 id0\nMESSAGE|310|id0 id0\nMESSAGE|332|HERE", "output": "13"}, {"input": "4\n1\nMESSAGE|1|HERE", "output": "1,1,1,1"}, {"input": "9\n7\nOFFLINE|4|5\nOFFLINE|23|1\nMESSAGE|27|HERE\nMESSAGE|125|id3 id1\nMESSAGE|137|HERE\nMESSAGE|223|ALL\nOFFLINE|317|7", "output": "3,3,3,4,3,2,3,3,3"}, {"input": "1\n3\nMESSAGE|9|ALL\nMESSAGE|102|HERE\nMESSAGE|200|HERE", "output": "3"}, {"input": "9\n4\nMESSAGE|78|id6 id8\nOFFLINE|141|5\nOFFLINE|7|0\nMESSAGE|223|id6 id6 id2", "output": "0,0,1,0,0,0,3,0,1"}, {"input": "5\n3\nMESSAGE|8|HERE\nOFFLINE|92|2\nMESSAGE|61|ALL", "output": "2,2,2,2,2"}, {"input": "6\n9\nMESSAGE|438|ALL\nMESSAGE|143|HERE\nMESSAGE|313|ALL\nOFFLINE|347|0\nMESSAGE|198|ALL\nOFFLINE|5|1\nMESSAGE|220|ALL\nMESSAGE|25|HERE\nMESSAGE|73|ALL", "output": "7,6,7,7,7,7"}, {"input": "4\n5\nOFFLINE|5|3\nOFFLINE|18|2\nOFFLINE|84|2\nMESSAGE|140|id1 id1 id3\nOFFLINE|170|2", "output": "0,2,0,1"}, {"input": "3\n5\nMESSAGE|52|ALL\nMESSAGE|190|ALL\nOFFLINE|109|1\nMESSAGE|29|id1 id0\nMESSAGE|9|id2 id2 id2 id0 id0", "output": "5,3,5"}, {"input": "6\n9\nMESSAGE|8|id1 id1 id1\nOFFLINE|108|5\nMESSAGE|188|id0\nOFFLINE|281|5\nOFFLINE|300|2\nMESSAGE|317|id1 id5\nMESSAGE|386|ALL\nOFFLINE|424|1\nMESSAGE|469|id0 id2", "output": "3,5,2,1,1,2"}, {"input": "4\n9\nMESSAGE|39|ALL\nMESSAGE|82|id0 id3 id2\nMESSAGE|344|HERE\nMESSAGE|260|HERE\nMESSAGE|300|ALL\nOFFLINE|170|1\nMESSAGE|4|HERE\nMESSAGE|320|HERE\nMESSAGE|383|ALL", "output": "8,7,8,8"}, {"input": "5\n3\nMESSAGE|9|id2\nOFFLINE|64|3\nMESSAGE|42|HERE", "output": "1,1,2,1,1"}, {"input": "10\n2\nOFFLINE|84|7\nMESSAGE|2|id0 id6 id5", "output": "1,0,0,0,0,1,1,0,0,0"}, {"input": "7\n8\nMESSAGE|344|HERE\nOFFLINE|317|5\nOFFLINE|17|1\nOFFLINE|249|5\nOFFLINE|122|2\nMESSAGE|207|HERE\nMESSAGE|50|HERE\nMESSAGE|5|id2 id6 id1 id2", "output": "3,3,5,3,3,2,4"}, {"input": "7\n2\nOFFLINE|3|4\nOFFLINE|90|6", "output": "0,0,0,0,0,0,0"}, {"input": "7\n8\nMESSAGE|10|HERE\nMESSAGE|104|HERE\nOFFLINE|123|1\nOFFLINE|201|2\nMESSAGE|283|id6 id2\nMESSAGE|364|ALL\nMESSAGE|370|ALL\nMESSAGE|467|id3 id3 id5 id2 id6", "output": "4,4,6,6,4,5,6"}]
|
{
"cpp": "==Code Submission==\n\npair<int, vector<vector<string>>> deserialize_stdin() {\n int numberOfUsers, n;\n string line;\n getline(cin, line);\n numberOfUsers = stoi(line);\n getline(cin, line);\n n = stoi(line);\n vector<vector<string>> events;\n for (int i = 0; i < n; i++) {\n getline(cin, line);\n vector<string> event;\n size_t pos = 0, start = 0;\n for (int j = 0; j < 2; j++) {\n pos = line.find('|', start);\n event.push_back(line.substr(start, pos - start));\n start = pos + 1;\n }\n event.push_back(line.substr(start));\n events.push_back(event);\n }\n return {numberOfUsers, events};\n}\n\nstring serialize_output(const vector<int>& result) {\n string out;\n for (size_t i = 0; i < result.size(); i++) {\n out += to_string(result[i]);\n if (i + 1 < result.size())\n out += \",\";\n }\n return out;\n}\n\nint main() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n \n auto input = deserialize_stdin();\n int numberOfUsers = input.first;\n vector<vector<string>> events = input.second;\n \n Solution sol;\n vector<int> ans = sol.countMentions(numberOfUsers, events);\n cout << serialize_output(ans);\n return 0;\n}",
"golang": "==Code Submission==\n\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n line, _ := reader.ReadString('\\n')\n numberOfUsers := 0\n if n, err := strconv.Atoi(strings.TrimSpace(line)); err == nil {\n numberOfUsers = n\n }\n line, _ = reader.ReadString('\\n')\n nEvents := 0\n if n, err := strconv.Atoi(strings.TrimSpace(line)); err == nil {\n nEvents = n\n }\n events := make([][]string, nEvents)\n for i := 0; i < nEvents; i++ {\n line, _ = reader.ReadString('\\n')\n line = strings.TrimSpace(line)\n parts := strings.Split(line, \"|\")\n events[i] = parts\n }\n ans := countMentions(numberOfUsers, events)\n out := \"\"\n for i, num := range ans {\n out += strconv.Itoa(num)\n if i < len(ans)-1 {\n out += \",\"\n }\n }\n fmt.Print(out)\n}",
"java": "public class Main {\n public static void main(String[] args) throws IOException {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n int numberOfUsers = Integer.parseInt(br.readLine().trim());\n int n = Integer.parseInt(br.readLine().trim());\n List<List<String>> events = new ArrayList<>();\n for (int i = 0; i < n; i++) {\n String line = br.readLine();\n String[] parts = line.split(\"\\\\|\", 3);\n List<String> event = new ArrayList<>();\n event.add(parts[0]);\n event.add(parts[1]);\n event.add(parts[2]);\n events.add(event);\n }\n Solution sol = new Solution();\n int[] mentions = sol.countMentions(numberOfUsers, events);\n StringBuilder sb = new StringBuilder();\n for (int i = 0; i < mentions.length; i++) {\n sb.append(mentions[i]);\n if (i < mentions.length - 1) {\n sb.append(\",\");\n }\n }\n System.out.println(sb.toString());\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\n\nconst rl = readline.createInterface({\n input: process.stdin,\n output: process.stdout,\n terminal: false\n});\n\nlet inputLines = [];\nrl.on(\"line\", (line) => {\n inputLines.push(line);\n});\nrl.on(\"close\", () => {\n const numberOfUsers = parseInt(inputLines[0].trim(), 10);\n const n = parseInt(inputLines[1].trim(), 10);\n let events = [];\n for (let i = 0; i < n; i++) {\n const parts = inputLines[2 + i].split(\"|\");\n events.push(parts);\n }\n const ans = countMentions(numberOfUsers, events);\n console.log(ans.join(\",\"));\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str):\n lines = input_str.strip().split(\"\\n\")\n numberOfUsers = int(lines[0].strip())\n n = int(lines[1].strip())\n events = []\n for i in range(n):\n parts = lines[2 + i].split(\"|\")\n events.append(parts)\n return numberOfUsers, events\n\ndef serialize_stdout(result):\n return \",\".join(str(x) for x in result)\n\ndata = sys.stdin.read()\nnumberOfUsers, events = deserialize_stdin(data)\nsol = Solution()\nans = sol.countMentions(numberOfUsers, events)\nprint(serialize_stdout(ans))",
"ruby": "==Code Submission==\n\ninput = $stdin.read.split(\"\\n\")\nnumber_of_users = input[0].strip.to_i\nn_events = input[1].strip.to_i\nevents = []\nn_events.times do |i|\n events << input[2 + i].strip.split(\"|\")\nend\nans = count_mentions(number_of_users, events)\nputs ans.join(\",\")"
}
|
3723
|
Sum of Good Numbers
|
sum-of-good-numbers
|
<p>Given an array of integers <code>nums</code> and an integer <code>k</code>, an element <code>nums[i]</code> is considered <strong>good</strong> if it is <strong>strictly</strong> greater than the elements at indices <code>i - k</code> and <code>i + k</code> (if those indices exist). If neither of these indices <em>exists</em>, <code>nums[i]</code> is still considered <strong>good</strong>.</p>
<p>Return the <strong>sum</strong> of all the <strong>good</strong> elements in the array.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">nums = [1,3,2,1,5,4], k = 2</span></p>
<p><strong>Output:</strong> <span class="example-io">12</span></p>
<p><strong>Explanation:</strong></p>
<p>The good numbers are <code>nums[1] = 3</code>, <code>nums[4] = 5</code>, and <code>nums[5] = 4</code> because they are strictly greater than the numbers at indices <code>i - k</code> and <code>i + k</code>.</p>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">nums = [2,1], k = 1</span></p>
<p><strong>Output:</strong> <span class="example-io">2</span></p>
<p><strong>Explanation:</strong></p>
<p>The only good number is <code>nums[0] = 2</code> because it is strictly greater than <code>nums[1]</code>.</p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>2 <= nums.length <= 100</code></li>
<li><code>1 <= nums[i] <= 1000</code></li>
<li><code>1 <= k <= floor(nums.length / 2)</code></li>
</ul>
|
Given an array of integers `nums` and an integer `k`, an element `nums[i]` is considered **good** if it is **strictly** greater than the elements at indices `i - k` and `i + k` (if those indices exist). If neither of these indices *exists*, `nums[i]` is still considered **good**.
Return the **sum** of all the **good** elements in the array.
**Example 1:**
**Input:** nums \= \[1,3,2,1,5,4], k \= 2
**Output:** 12
**Explanation:**
The good numbers are `nums[1] = 3`, `nums[4] = 5`, and `nums[5] = 4` because they are strictly greater than the numbers at indices `i - k` and `i + k`.
**Example 2:**
**Input:** nums \= \[2,1], k \= 1
**Output:** 2
**Explanation:**
The only good number is `nums[0] = 2` because it is strictly greater than `nums[1]`.
**Constraints:**
- `2 <= nums.length <= 100`
- `1 <= nums[i] <= 1000`
- `1 <= k <= floor(nums.length / 2)`
|
Easy
|
[
"array"
] |
leetcode
|
https://leetcode.com/problems/sum-of-good-numbers
|
functional
| null | null | null | null |
{
"c": "int sumOfGoodNumbers(int* nums, int numsSize, int k) {\n \n}",
"cpp": "class Solution {\npublic:\n int sumOfGoodNumbers(vector<int>& nums, int k) {\n \n }\n};",
"csharp": "public class Solution {\n public int SumOfGoodNumbers(int[] nums, int k) {\n \n }\n}",
"dart": "class Solution {\n int sumOfGoodNumbers(List<int> nums, int k) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec sum_of_good_numbers(nums :: [integer], k :: integer) :: integer\n def sum_of_good_numbers(nums, k) do\n \n end\nend",
"erlang": "-spec sum_of_good_numbers(Nums :: [integer()], K :: integer()) -> integer().\nsum_of_good_numbers(Nums, K) ->\n .",
"golang": "func sumOfGoodNumbers(nums []int, k int) int {\n \n}",
"java": "class Solution {\n public int sumOfGoodNumbers(int[] nums, int k) {\n \n }\n}",
"javascript": "/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number}\n */\nvar sumOfGoodNumbers = function(nums, k) {\n \n};",
"kotlin": "class Solution {\n fun sumOfGoodNumbers(nums: IntArray, k: Int): Int {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param Integer[] $nums\n * @param Integer $k\n * @return Integer\n */\n function sumOfGoodNumbers($nums, $k) {\n \n }\n}",
"python": "class Solution(object):\n def sumOfGoodNumbers(self, nums, k):\n \"\"\"\n :type nums: List[int]\n :type k: int\n :rtype: int\n \"\"\"\n ",
"python3": "class Solution:\n def sumOfGoodNumbers(self, nums: List[int], k: int) -> int:\n ",
"racket": "(define/contract (sum-of-good-numbers nums k)\n (-> (listof exact-integer?) exact-integer? exact-integer?)\n )",
"ruby": "# @param {Integer[]} nums\n# @param {Integer} k\n# @return {Integer}\ndef sum_of_good_numbers(nums, k)\n \nend",
"rust": "impl Solution {\n pub fn sum_of_good_numbers(nums: Vec<i32>, k: i32) -> i32 {\n \n }\n}",
"scala": "object Solution {\n def sumOfGoodNumbers(nums: Array[Int], k: Int): Int = {\n \n }\n}",
"swift": "class Solution {\n func sumOfGoodNumbers(_ nums: [Int], _ k: Int) -> Int {\n \n }\n}",
"typescript": "function sumOfGoodNumbers(nums: number[], k: number): number {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n int sumOfGoodNumbers(vector<int>& nums, int k) {\n int sum = 0;\n int n = nums.size();\n for (int i = 0; i < n; ++i) {\n bool good = true;\n int left = i - k;\n if (left >= 0 && nums[i] <= nums[left]) {\n good = false;\n }\n int right = i + k;\n if (right < n && nums[i] <= nums[right]) {\n good = false;\n }\n if (good) {\n sum += nums[i];\n }\n }\n return sum;\n }\n};",
"memory": 2700,
"memoryDistribution": "[[2700, 24.334, \"class Solution {\\npublic:\\n int sumOfGoodNumbers(vector<int>& nums, int k) {\\n int sum = 0;\\n int n = nums.size();\\n for (int i = 0; i < n; ++i) {\\n bool good = true;\\n int left = i - k;\\n if (left >= 0 && nums[i] <= nums[left]) {\\n good = false;\\n }\\n int right = i + k;\\n if (right < n && nums[i] <= nums[right]) {\\n good = false;\\n }\\n if (good) {\\n sum += nums[i];\\n }\\n }\\n return sum;\\n }\\n};\"], [26900, 0.216, \"class Solution {\\npublic:\\n int sumOfGoodNumbers(vector<int>& nums, int k) {\\n int s =0 ;\\n int l;\\n int r;\\n int n = nums.size();\\n for (int i =0 ; i<nums.size();i++){\\n l=i-k;\\n r=i+k;\\n if(l<0 && r<n && nums[r]<nums[i]){\\n s+=nums[i];\\n }\\n else if( r>=n && l >= 0 && nums[l]<nums[i]){\\n s+=nums[i];\\n }\\n else if ( l>=0 && r<=(n-1) && nums[r]<nums[i] && nums[l]<nums[i] ){\\n s+=nums[i];\\n }\\n }\\n return s;\\n }\\n};\"], [27000, 7.1274, \"\\nclass Solution {\\npublic:\\n int sumOfGoodNumbers(std::vector<int>& nums, int k) {\\n int totalSum = 0; \\n int n = nums.size(); \\n \\n for (int i = 0; i < n; i++) {\\n bool isGood = true; \\n \\n if (i - k >= 0) { \\n if (nums[i] <= nums[i - k]) { \\n isGood = false; \\n }\\n }\\n if (i + k < n) { \\n if (nums[i] <= nums[i + k]) { \\n isGood = false; \\n }\\n }\\n if (isGood) {\\n totalSum += nums[i];\\n }\\n }\\n return totalSum; \\n }\\n};\"], [27100, 34.0533, null], [27200, 34.2693, \"class Solution {\\npublic:\\n int sumOfGoodNumbers(vector<int>& nums, int k) {\\n int total = 0;\\n int n = nums.size();\\n\\n for (int i = 0; i < n; ++i) {\\n bool leftMissing = (i - k < 0);\\n bool rightMissing = (i + k >= n);\\n\\n if (leftMissing && rightMissing) {\\n // Neither index exists \\u2192 always good\\n total += nums[i];\\n }\\n else if (leftMissing) {\\n if (nums[i] > nums[i + k])\\n total += nums[i];\\n }\\n else if (rightMissing) {\\n if (nums[i] > nums[i - k])\\n total += nums[i];\\n }\\n else {\\n if (nums[i] > nums[i - k] && nums[i] > nums[i + k])\\n total += nums[i];\\n }\\n }\\n\\n return total;\\n }\\n};\\n\"], [27300, 21.7423, \"class Solution {\\npublic:\\n int sumOfGoodNumbers(vector<int>& nums, int k) {\\n int a,b,c=0;\\n int n=nums.size();\\n for(int i=0;i<n;i++)\\n {\\n a=i+k;\\n b=i-k;\\n if(a<n && b>=0){\\n if(nums[i]>nums[a] && nums[i]>nums[b])\\n {\\n c+=nums[i];\\n }\\n }\\n else if(a<n)\\n {\\n if(nums[i]>nums[a])\\n {\\n c+=nums[i];\\n }\\n }\\n else if(b>=0)\\n {\\n if(nums[i]>nums[b])\\n {\\n c+=nums[i];\\n }\\n }\\n } \\n return c;\\n }\\n};\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 87.689, \"class Solution {\\npublic:\\n int sumOfGoodNumbers(vector<int>& nums, int k) {\\n int total = 0;\\n int n = nums.size();\\n\\n for (int i = 0; i < n; ++i) {\\n bool leftMissing = (i - k < 0);\\n bool rightMissing = (i + k >= n);\\n\\n if (leftMissing && rightMissing) {\\n // Neither index exists \\u2192 always good\\n total += nums[i];\\n }\\n else if (leftMissing) {\\n if (nums[i] > nums[i + k])\\n total += nums[i];\\n }\\n else if (rightMissing) {\\n if (nums[i] > nums[i - k])\\n total += nums[i];\\n }\\n else {\\n if (nums[i] > nums[i - k] && nums[i] > nums[i + k])\\n total += nums[i];\\n }\\n }\\n\\n return total;\\n }\\n};\\n\"], [1, 3.0958, \"class Solution {\\npublic:\\n int sumOfGoodNumbers(vector<int>& nums, int k) {\\n int n = nums.size();\\n int sum = 0;\\n\\n for (int i = 0; i < n; i++) {\\n bool good = true;\\n\\n if (i - k >= 0 && nums[i] <= nums[i - k]) {\\n good = false;\\n }\\n if (i + k < n && nums[i] <= nums[i + k]) {\\n good = false;\\n }\\n\\n if (good) {\\n sum += nums[i];\\n }\\n }\\n\\n return sum;\\n }\\n};\\n\"], [2, 1.5839, null], [3, 3.6717, \"class Solution {\\npublic:\\n int sumOfGoodNumbers(vector<int>& arr, int k) {\\n int size=arr.size();\\n int i=0;\\n int sum=0;\\n while(i<size)\\n {\\n int a=i-k;\\n int b=i+k;\\n\\n if((a>=0 && b<size) && (arr[i]>arr[b] && arr[i]>arr[a]))\\n sum+=arr[i];\\n else if((a>=0 && b>=size) && (arr[i]> arr[a]))\\n sum+=arr[i];\\n else if((a<0 && b<size) && (arr[i]>arr[b]))\\n sum+=arr[i];\\n i++;\\n }\\n return sum;\\n }\\n}; \"], [4, 1.6559, \"class Solution {\\npublic:\\n int sumOfGoodNumbers(vector<int>& nums, int k) {\\n int c = 0;\\n int n = nums.size();\\n for (int i = 0;i<n;++i){\\n if ((i-k < 0 || nums[i-k]<nums[i]) && (i+k >= n || nums[i+k]<nums[i])){\\n c+=nums[i];\\n }\\n }\\n return c;\\n }\\n};\"]]"
},
"golang": {
"code": "func sumOfGoodNumbers(nums []int, k int) int {\n sum := 0\n n := len(nums)\n for i := 0; i < n; i++ {\n good := true\n if left := i - k; left >= 0 && nums[i] <= nums[left] {\n good = false\n }\n if right := i + k; right < n && nums[i] <= nums[right] {\n good = false\n }\n if good {\n sum += nums[i]\n }\n }\n return sum\n}",
"memory": 500,
"memoryDistribution": "[[500, 84.0, \"func sumOfGoodNumbers(nums []int, k int) int {\\n sum := 0\\n n := len(nums)\\n for i := 0; i < n; i++ {\\n good := true\\n if left := i - k; left >= 0 && nums[i] <= nums[left] {\\n good = false\\n }\\n if right := i + k; right < n && nums[i] <= nums[right] {\\n good = false\\n }\\n if good {\\n sum += nums[i]\\n }\\n }\\n return sum\\n}\"], [4900, 16.0, \"\\nfunc sumOfGoodNumbers(nums []int, k int) (r int) {\\n\\tfor i := 0; i < len(nums); i++{\\n\\t\\tif i - k >= 0 && i + k < len(nums) {\\n\\t\\t\\tif nums[i] > nums[i - k] && nums[i] > nums[i + k] {\\n\\t\\t\\t\\tr += nums[i]\\n\\t\\t\\t}\\n\\t\\t} else if i + k < len(nums) {\\n\\t\\t\\tif nums[i] > nums[i + k] {\\n\\t\\t\\t\\tr += nums[i]\\n\\t\\t\\t}\\n\\t\\t} else if i - k >= 0 {\\n\\t\\t\\tif nums[i] > nums[i - k] {\\n\\t\\t\\t\\tr += nums[i]\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\treturn\\n}\"], [5000, 60.0, \"func sumOfGoodNumbers(nums []int, k int) int {\\n result := 0\\n for i := range nums {\\n if i - k >= 0 {\\n if i + k < len(nums) {\\n if nums[i] > nums[i-k] && nums[i] > nums[i+k] {\\n result += nums[i]\\n }\\n } else {\\n if nums[i] > nums[i-k] {\\n result += nums[i]\\n }\\n }\\n } else {\\n if i + k < len(nums) {\\n if nums[i] > nums[i+k] {\\n result += nums[i]\\n }\\n }\\n }\\n }\\n\\n return result\\n}\"], [5100, 20.0, null], [5500, 2.0, \"func sumOfGoodNumbers(nums []int, k int) int {\\n good := make([]int ,0)\\n for i:=0 ; i<len(nums); i++ {\\n if i-k >= 0 && i+k < len(nums) {\\n if nums[i] > nums[i-k] && nums[i] > nums[i+k] {\\n good = append(good, nums[i])\\n }\\n }else if i-k >= 0 || i+k < len(nums) {\\n if i-k >= 0 && nums[i] > nums[i-k] {\\n good = append(good, nums[i])\\n }\\n if i+k<len(nums) && nums[i] > nums[i+k] {\\n good = append(good, nums[i])\\n }\\n } else if i-k <0 && i+k >=len(nums) {\\n good = append(good, nums[i])\\n }\\n }\\n fmt.Println(good)\\n sum :=0 \\n for i:=0; i<len(good); i++ {\\n sum += good[i]\\n }\\n return sum\\n}\"], [6000, 2.0, \"func sumOfGoodNumbers(n []int, k int) int {\\n\\tzeroes := slices.Repeat([]int{0}, k)\\n\\tn = append(zeroes, n...)\\n\\tn = append(n, zeroes...)\\n\\tl := len(n)\\n\\ts := 0\\n\\tfor i := k; i < l-k; i++ {\\n\\t\\tc := n[i]\\n\\t\\tl := n[i-k]\\n\\t\\tr := n[i+k]\\n\\t\\tif c > l && c > r {\\n\\t\\t\\ts += c\\n\\t\\t}\\n\\t}\\n\\treturn s\\n}\\n\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 84.0, \"func sumOfGoodNumbers(nums []int, k int) int {\\n var sum int\\n \\n for i, v := range nums {\\n lower := i - k\\n upper := i + k\\n\\n if (lower < 0 || (lower >= 0 && v > nums[lower])) && (upper >= len(nums) || (upper < len(nums) && v > nums[upper])) {\\n sum = sum + v\\n } \\n }\\n\\n return sum\\n}\"], [1, 8.0, \"func sumOfGoodNumbers(nums []int, k int) int {\\n totalSum := 0\\n n := len(nums)\\n\\n for i := 0; i < n; i++ {\\n isGood := true\\n\\n if i-k >= 0 && nums[i] <= nums[i-k] {\\n isGood = false\\n }\\n if i+k < n && nums[i] <= nums[i+k] {\\n isGood = false\\n }\\n \\n if isGood {\\n totalSum += nums[i]\\n }\\n }\\n return totalSum\\n}\\n\"], [2, 4.0, \"func sumOfGoodNumbers(nums []int, k int) int {\\n sum := 0\\n\\n for i := 0; i < len(nums); i++ { \\n left := i - k\\n right := i + k\\n isGood := true\\n\\n if left >= 0 && nums[i] <= nums[left] {\\n isGood = false\\n } \\n\\n if right < len(nums) && nums[i] <= nums[right] {\\n isGood = false\\n } \\n\\n if isGood {\\n sum += nums[i]\\n }\\n }\\n\\n return sum\\n}\"], [4, 4.0, \"func sumOfGoodNumbers(nums []int, k int) int {\\n var total int\\n for index, number := range nums {\\n if index - k < 0 && index + k >= len(nums) {\\n total += number\\n } else if index - k < 0 && index + k < len(nums) {\\n if number > nums[index + k] {\\n total += number\\n }\\n } else if index - k >= 0 && index + k >= len(nums) {\\n if number > nums[index - k] {\\n total += number\\n }\\n } else {\\n if number > nums[index - k] && number > nums[index + k] {\\n total += number\\n }\\n }\\n \\n }\\n \\n return total\\n}\"]]"
},
"java": {
"code": "class Solution {\n public int sumOfGoodNumbers(int[] nums, int k) {\n int sum = 0;\n for (int i = 0; i < nums.length; i++) {\n boolean good = true;\n int left = i - k;\n if (left >= 0 && nums[i] <= nums[left]) {\n good = false;\n }\n int right = i + k;\n if (right < nums.length && nums[i] <= nums[right]) {\n good = false;\n }\n if (good) {\n sum += nums[i];\n }\n }\n return sum;\n }\n}",
"memory": 4400,
"memoryDistribution": "[[4400, 25.2084, \"class Solution {\\n public int sumOfGoodNumbers(int[] nums, int k) {\\n int sum = 0;\\n for (int i = 0; i < nums.length; i++) {\\n boolean good = true;\\n int left = i - k;\\n if (left >= 0 && nums[i] <= nums[left]) {\\n good = false;\\n }\\n int right = i + k;\\n if (right < nums.length && nums[i] <= nums[right]) {\\n good = false;\\n }\\n if (good) {\\n sum += nums[i];\\n }\\n }\\n return sum;\\n }\\n}\"], [42100, 0.1389, \"class Solution {\\n public int sumOfGoodNumbers(int[] nums, int k) {\\n int sum = 0;\\n int length = nums.length;\\n boolean flag = true;\\n for(int i=0; i<length; i++) {\\n flag = true;\\n if(i-k >= 0) {\\n if(nums[i] <= nums[i-k]) {\\n flag = false;\\n }\\n }\\n if(i+k < length) {\\n if(nums[i] <= nums[i+k]) {\\n flag = false;\\n }\\n }\\n if(flag) {\\n sum += nums[i];\\n }\\n }\\n System.gc();\\n return sum;\\n }\\n}\"], [42200, 0.1389, \"class Solution {\\n public int sumOfGoodNumbers(int[] nums, int k) {\\n int n = nums.length, sum = 0;\\n for (int i = 0; i < n; i++) {\\n if (i - k >= 0 && i + k < n) {\\n if (nums[i + k] < nums[i] && nums[i - k] < nums[i])\\n sum += nums[i];\\n } else if (i - k >= 0) {\\n if (nums[i - k] < nums[i])\\n sum += nums[i];\\n } else if (nums[i + k] < nums[i]) {\\n sum += nums[i];\\n }\\n }\\n System.gc();\\n return sum;\\n }\\n}\"], [42700, 0.0694, null], [43400, 0.0694, null], [43500, 0.1389, null], [43600, 0.6944, null], [43700, 0.625, null], [43800, 1.9444, null], [43900, 6.25, null], [44000, 12.0139, null], [44100, 18.6806, null], [44200, 13.1944, null], [44300, 11.8056, null], [44400, 9.0278, null], [44500, 10.3472, null], [44600, 6.5278, \"class Solution {\\n public int sumOfGoodNumbers(int[] nums, int k) {\\n int sum = 0;\\n for (int i = 0; i < nums.length; i++) {\\n if ((i - k < 0 || nums[i - k] < nums[i]) && (i + k >= nums.length || nums[i + k] < nums[i])) {\\n sum += nums[i];\\n }\\n }\\n return sum;\\n }\\n}\"], [44700, 3.3333, \"class Solution {\\n public int sumOfGoodNumbers(int[] nums, int k) {\\n int sum=0;\\n for(int i=0;i<nums.length;i++){\\n boolean flag=true;\\n if(i-k>=0&&nums[i]<=nums[i-k])flag=false;\\n if(i+k<nums.length&&nums[i]<=nums[i+k])flag=false;\\n if(flag)sum+=nums[i];\\n }\\n return sum;\\n }\\n}\"]]",
"runtime": 1,
"runtimeDistribution": "[[1, 96.875, \"class Solution {\\n public boolean check(int[] nums,int ele,int i,int j){\\n if(i<nums.length && i>-1) if(nums[i]>=nums[ele]) return false;\\n if(j<nums.length && j>-1) if(nums[j]>=nums[ele]) return false;\\n return true;\\n }\\n public int sumOfGoodNumbers(int[] nums, int k) {\\n int sum=0;\\n for(int i=0;i<nums.length;i++){\\n if(check(nums,i,i-k,i+k)) sum+=nums[i];\\n }\\n return sum;\\n }\\n}\"], [2, 0.9722, \"class Solution {\\n public int sumOfGoodNumbers(int[] nums, int k) {\\n List<Integer> goodNumbers = new ArrayList();\\n for (int i = 0; i < nums.length; i++){\\n if((i - k) >= 0 && (i + k) < nums.length){\\n if(nums[i] > nums[i - k] && nums[i] > nums[i + k] ) {\\n goodNumbers.add(nums[i]);\\n }\\n }\\n\\n if(( i - k ) < 0 && ( i + k ) < nums.length){\\n if(nums[i] > nums[i + k]) {\\n goodNumbers.add(nums[i]);\\n }\\n }\\n\\n if(( i + k ) >= nums.length && ( i - k ) >= 0){\\n if(nums[i] > nums[ i - k ]) {\\n goodNumbers.add(nums[i]);\\n }\\n }\\n\\n }\\n\\n int sum = 0;\\n for (int x: goodNumbers){\\n sum += x;\\n }\\n return sum;\\n }\\n}\"], [4, 0.1389, null], [5, 0.1389, \"class Solution {\\n public int sumOfGoodNumbers(int[] nums, int k) {\\n int sum = 0;\\n int curLeft, curRight;\\n for(int i = 0; i < nums.length; i++){\\n curLeft = i - k >= 0 ? nums[i - k] : 0;\\n curRight = i + k < nums.length ? nums[i + k] : 0;\\n if(nums[i] > curLeft && nums[i] > curRight) sum += nums[i];\\n }\\n System.out.println(sum);\\n return sum;\\n }\\n}\"], [9, 0.0694, \"class Solution {\\n public int sumOfGoodNumbers(int[] nums, int k) {\\n int n = nums.length, sum = 0;\\n for (int i = 0; i < n; i++) {\\n if (i - k >= 0 && i + k < n) {\\n if (nums[i + k] < nums[i] && nums[i - k] < nums[i])\\n sum += nums[i];\\n } else if (i - k >= 0) {\\n if (nums[i - k] < nums[i])\\n sum += nums[i];\\n } else if (nums[i + k] < nums[i]) {\\n sum += nums[i];\\n }\\n }\\n System.gc();\\n return sum;\\n }\\n}\"]]"
},
"javascript": {
"code": "var sumOfGoodNumbers = function(nums, k) {\n let sum = 0;\n const n = nums.length;\n for (let i = 0; i < n; i++) {\n let isGood = true;\n const left = i - k;\n if (left >= 0 && nums[i] <= nums[left]) isGood = false;\n const right = i + k;\n if (right < n && nums[i] <= nums[right]) isGood = false;\n if (isGood) sum += nums[i];\n }\n return sum;\n};",
"memory": 5700,
"memoryDistribution": "[[5700, 12.4357, \"var sumOfGoodNumbers = function(nums, k) {\\n let sum = 0;\\n const n = nums.length;\\n for (let i = 0; i < n; i++) {\\n let isGood = true;\\n const left = i - k;\\n if (left >= 0 && nums[i] <= nums[left]) isGood = false;\\n const right = i + k;\\n if (right < n && nums[i] <= nums[right]) isGood = false;\\n if (isGood) sum += nums[i];\\n }\\n return sum;\\n};\"], [54000, 0.5181, \"/**\\n * @param {number[]} nums\\n * @param {number} k\\n * @return {number}\\n */\\nvar sumOfGoodNumbers = function(nums, k) {\\n return nums.reduce((acc, curr, i) => {\\n const left = (i - k < 0 || curr > nums[i - k]);\\n const right = (i + k >= nums.length || curr > nums[i + k]);\\n return acc + (left && right ? curr : 0);\\n }, 0);\\n};\"], [54100, 0.5181, \"/**\\n * @param {number[]} nums\\n * @param {number} k\\n * @return {number}\\n */\\nvar sumOfGoodNumbers = function(nums, k) {\\n let sum = 0;\\n for (i=0; i<nums.length; i++) {\\n if ((typeof nums[i+k] === 'undefined' || nums[i+k] < nums[i] ) && (typeof nums[i-k] === 'undefined' || nums[i-k] < nums[i] ) ) { \\n sum = sum + nums[i]; \\n } \\n }\\n return sum;\\n};\"], [54200, 0.5181, null], [54500, 0.5181, null], [54600, 0.5181, null], [54700, 0.5181, null], [54800, 1.0363, null], [54900, 2.0725, null], [55000, 1.0363, null], [55100, 0.5181, null], [55200, 3.6269, null], [55300, 2.5907, null], [55400, 3.1088, null], [55500, 5.1813, null], [55600, 8.8083, null], [55700, 3.6269, null], [55800, 7.2539, null], [55900, 6.7358, null], [56000, 7.772, null], [56100, 5.1813, null], [56200, 1.0363, null], [56300, 2.0725, null], [56400, 0.5181, null], [56500, 1.0363, null], [56600, 0.5181, null], [56700, 2.5907, null], [56800, 2.0725, null], [56900, 1.5544, null], [57000, 2.0725, null], [57100, 4.6632, null], [57200, 3.1088, null], [57300, 3.1088, null], [57400, 1.5544, null], [57500, 2.0725, null], [57600, 1.5544, null], [57700, 1.5544, \"/**\\n * @param {number[]} nums\\n * @param {number} k\\n * @return {number}\\n */\\nvar sumOfGoodNumbers = function(nums, k) {\\n let sum = 0\\n for(let i=0; i<nums.length; i++){\\n if((typeof nums[i-k]==='undefined' || nums[i-k] < nums[i]) && (typeof nums[i+k]==='undefined' || nums[i+k] < nums[i])){\\n sum += nums[i]\\n }\\n }\\n return sum\\n};\"], [57800, 2.0725, \"/**\\n * @param {number[]} nums\\n * @param {number} k\\n * @return {number}\\n */\\nconst sumOfGoodNumbers = function (nums, k) {\\n let sum = 0;\\n\\n for (let i = 0; i < nums.length; i++) {\\n const curr = nums[i];\\n const prev = nums[i - k];\\n const next = nums[i + k];\\n\\n if ((prev === undefined || curr > prev) && (next === undefined || curr > next)) {\\n sum += curr;\\n }\\n }\\n\\n return sum;\\n};\\n\"]]",
"runtime": 1,
"runtimeDistribution": "[[0, 28.4974, \"/**\\n * @param {number[]} nums\\n * @param {number} k\\n * @return {number}\\n */\\nvar sumOfGoodNumbers = function(nums, k) {\\n let res = 0\\n for(let i = 0; i<nums.length; i++){\\n let flag = true\\n if (i - k >= 0 && nums[i] <= nums[i - k]) {\\n flag = false;\\n }\\n\\n if (i + k < nums.length && nums[i] <= nums[i + k]) {\\n flag = false;\\n }\\n\\n if (flag) {\\n res += nums[i];\\n }\\n }\\n return res\\n};\"], [1, 40.4145, \"/**\\n * @param {number[]} nums\\n * @param {number} k\\n * @return {number}\\n */\\nvar sumOfGoodNumbers = function (nums, k) {\\n let ans = 0;\\n for (let i = 0; i < nums.length; i++) {\\n const n = nums[i]\\n if (n > (nums[i - k] || 0) && n > (nums[i + k] || 0)) {\\n ans += n\\n }\\n }\\n return ans;\\n};\"], [2, 21.2435, null], [3, 2.5907, \"/**\\n * @param {number[]} nums\\n * @param {number} k\\n * @return {number}\\n */\\nvar sumOfGoodNumbers = function(nums, k) {\\n let sum=0\\n for(let i=0;i<nums.length;i++){\\n let isGood = true\\n if (i - k >= 0 && nums[i] <= nums[i - k]) {\\n isGood = false\\n }\\n if (i + k < nums.length && nums[i] <= nums[i + k]) {\\n isGood = false\\n }\\n\\n if (isGood) {\\n sum += nums[i]\\n }\\n }return sum\\n};\"], [4, 2.5907, \"var sumOfGoodNumbers = function (a, k) {\\n let n = a.length\\n let sum = 0\\n let i = -1\\n for (let e of a) {\\n i++\\n let l = Math.max(i - k)\\n let r = Math.min(i + k)\\n let bad = 0\\n if (a[l] >= e) bad = 1\\n if (a[r] >= e) bad = 1\\n if (!bad) sum += e\\n }\\n return sum\\n};\\n\"]]"
},
"python3": {
"code": "class Solution:\n def sumOfGoodNumbers(self, nums: List[int], k: int) -> int:\n total = 0\n n = len(nums)\n for i in range(n):\n left = i - k\n right = i + k\n left_ok = left < 0 or nums[i] > nums[left]\n right_ok = right >= n or nums[i] > nums[right]\n if left_ok and right_ok:\n total += nums[i]\n return total",
"memory": 1800,
"memoryDistribution": "[[1800, 48.973, \"class Solution:\\n def sumOfGoodNumbers(self, nums: List[int], k: int) -> int:\\n total = 0\\n n = len(nums)\\n for i in range(n):\\n left = i - k\\n right = i + k\\n left_ok = left < 0 or nums[i] > nums[left]\\n right_ok = right >= n or nums[i] > nums[right]\\n if left_ok and right_ok:\\n total += nums[i]\\n return total\"], [17400, 0.1081, \"class Solution:\\n def sumOfGoodNumbers(self, nums: List[int], k: int) -> int:\\n res = 0\\n n = len(nums)\\n for i in range(n):\\n good = True\\n if i-k >= 0 and nums[i-k] >= nums[i]:\\n good = False\\n elif i+k < n and nums[i+k] >= nums[i]:\\n good = False\\n if good:\\n res += nums[i]\\n return res\"], [17500, 0.4324, \"class Solution:\\n def sumOfGoodNumbers(self, nums: List[int], k: int) -> int:\\n n = len(nums)\\n total = 0\\n \\n for i in range(n):\\n left = nums[i - k] if i - k >= 0 else float('-inf')\\n right = nums[i + k] if i + k < n else float('-inf')\\n \\n if nums[i] > left and nums[i] > right:\\n total += nums[i]\\n \\n return total\\n\\n \"], [17600, 3.7838, null], [17700, 16.973, null], [17800, 29.7297, null], [17900, 17.6216, \"class Solution:\\n def sumOfGoodNumbers(self, nums: List[int], k: int) -> int:\\n sum = 0\\n n = len(nums)\\n for inx in range(k):\\n last_element = 0\\n is_good = True\\n while inx < n:\\n current = nums[inx]\\n if current > last_element:\\n is_good = True\\n else:\\n if is_good and current < last_element:\\n sum += last_element\\n is_good = False\\n last_element = current\\n inx += k\\n if is_good:\\n sum += last_element\\n return sum\\n\"], [18000, 22.8108, \"from typing import List\\n\\nclass Solution:\\n def sumOfGoodNumbers(self, nums: List[int], k: int) -> int:\\n total = 0\\n for i in range(len(nums)):\\n if (i - k < 0 or nums[i] > nums[i - k]) and (i + k >= len(nums) or nums[i] > nums[i + k]):\\n total += nums[i]\\n return total\\n\"]]",
"runtime": 3,
"runtimeDistribution": "[[0, 34.7027, \"class Solution:\\n def sumOfGoodNumbers(self, nums: List[int], k: int) -> int:\\n\\n sum = 0\\n\\n for i in range(len(nums)):\\n\\n flag = True\\n\\n if i-k>=0 and nums[i-k]>=nums[i]:\\n flag = False\\n \\n if i+k < len(nums) and nums[i+k]>=nums[i]:\\n flag = False\\n\\n\\n sum += nums[i] if flag else 0 \\n\\n return sum\\n \"], [1, 5.9459, \"class Solution:\\n def sumOfGoodNumbers(self, nums: List[int], k: int) -> int:\\n sum_ = 0\\n for idx, i in enumerate(nums):\\n if idx-k >= 0 and idx+k < len(nums):\\n if nums[idx-k] < i and nums[idx+k] < i:\\n sum_+=i\\n \\n elif idx-k >= 0 and nums[idx-k] < i:\\n sum_+=i\\n \\n elif idx+k < len(nums) and nums[idx+k] < i:\\n sum_+=i\\n\\n return(sum_)\"], [2, 7.6757, null], [3, 28.8649, null], [4, 9.6216, null], [5, 2.3784, \"class Solution:\\n def sumOfGoodNumbers(self, nums: List[int], k: int) -> int:\\n ans = 0\\n for i in range(len(nums)):\\n l, r = False, False\\n if i-k >=0 and nums[i] > nums[i-k]:\\n l = True\\n if i-k <0:\\n l = True\\n if i+k <len(nums) and nums[i] > nums[i+k]:\\n r = True\\n if i+k >=len(nums):\\n r = True\\n if l and r:\\n print(f\\\"{nums[i]=}\\\")\\n ans += nums[i]\\n\\n return ans\"], [6, 1.5135, \"class Solution:\\n def sumOfGoodNumbers(self, nums: List[int], k: int) -> int:\\n n = len(nums)\\n res = 0\\n for i in range(n):\\n l = i - k\\n r = i + k\\n if ((not self._is_valid(l, n)) or nums[i] > nums[l]) and ((not self._is_valid(r, n)) or nums[i] > nums[r]):\\n res += nums[i]\\n return res\\n \\n def _is_valid(self, index: int, n: int) -> bool:\\n return 0 <= index < n\\n\"]]"
},
"ruby": {
"code": "def sum_of_good_numbers(nums, k)\n sum = 0\n nums.each_with_index do |num, i|\n left = i - k\n right = i + k\n check_left = left >= 0 ? num > nums[left] : true\n check_right = right < nums.size ? num > nums[right] : true\n sum += num if check_left && check_right\n end\n sum\nend",
"memory": 21200,
"memoryDistribution": "[[21200, 61.5385, \"def sum_of_good_numbers(nums, k)\\n sum = 0\\n nums.each_with_index do |num, i|\\n left = i - k\\n right = i + k\\n check_left = left >= 0 ? num > nums[left] : true\\n check_right = right < nums.size ? num > nums[right] : true\\n sum += num if check_left && check_right\\n end\\n sum\\nend\"], [212000, 15.3846, \"# @param {Integer[]} nums\\n# @param {Integer} k\\n# @return {Integer}\\n\\ndef sum_of_good_numbers(nums, k)\\n nums.each_with_index.filter {|v, i|\\n f = true\\n f &&= (v > nums[i - k]) if i - k >= 0\\n f &&= (v > nums[i + k]) if i + k < nums.size\\n f\\n }.collect(&:first).sum\\nend\"], [212100, 7.6923, \"# @param {Integer[]} nums\\n# @param {Integer} k\\n# @return {Integer}\\ndef sum_of_good_numbers(nums, k)\\n sum = 0\\n for num, i in nums.each.with_index\\n left = true\\n if i - k >= 0\\n left = num > nums[i-k]\\n end\\n right = true\\n if i + k < nums.size\\n right = num > nums[i+k]\\n end\\n if left && right\\n sum += num\\n end\\n end\\n sum\\nend\"], [212200, 15.3846, null], [212300, 15.3846, null], [212500, 23.0769, null], [212600, 7.6923, \"# @param {Integer[]} nums\\n# @param {Integer} k\\n# @return {Integer}\\ndef sum_of_good_numbers(nums, k)\\n n=nums.length\\n good_sum=0\\n nums.each_with_index do |num,i|\\n if i-k>=0 && num<=nums[i-k]\\n next\\n end\\n if i+k<n && num<=nums[i+k]\\n next\\n end\\n good_sum+=num\\n end\\n good_sum\\nend\"], [212700, 7.6923, \"# @param {Integer[]} nums\\n# @param {Integer} k\\n# @return {Integer}\\ndef sum_of_good_numbers(nums, k)\\n goods = []\\n nums.each_with_index do |num, i|\\n if i-k >= 0 && i+k < nums.length\\n goods << num if num > nums[i-k] && num > nums[i+k]\\n elsif i-k >= 0\\n goods << num if num > nums[i-k]\\n elsif i+k < nums.length\\n goods << num if num > nums[i+k]\\n elsif i-k < 0 && i+k >= nums.length\\n goods << num\\n end\\n end\\n goods.sum\\nend\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 7.6923, \"# @param {Integer[]} nums\\n# @param {Integer} k\\n# @return {Integer}\\ndef sum_of_good_numbers(nums, k)\\n n=nums.length\\n good_sum=0\\n nums.each_with_index do |num,i|\\n if i-k>=0 && num<=nums[i-k]\\n next\\n end\\n if i+k<n && num<=nums[i+k]\\n next\\n end\\n good_sum+=num\\n end\\n good_sum\\nend\"], [2, 15.3846, \"# @param {Integer[]} nums\\n# @param {Integer} k\\n# @return {Integer}\\ndef sum_of_good_numbers(nums, k)\\n n = nums.size\\n result = 0\\n for i in 0 ... n do\\n l = i - k \\n r = i + k\\n result += nums[i] if ((l < 0) || (nums[l] < nums[i])) && ((r >= n) || (nums[i] > nums[r]))\\n end\\n result\\nend\"], [3, 46.1538, null], [4, 7.6923, null], [6, 7.6923, \"# @param {Integer[]} nums\\n# @param {Integer} k\\n# @return {Integer}\\ndef sum_of_good_numbers(nums, k)\\n sum = 0\\n nums.each_with_index do |num, i|\\n if i-k < 0 && (nums.length - 1 ) >= i+k && nums[i+k] < nums[i]\\n sum += nums[i]\\n\\n elsif i - k >= 0 && (nums.length - 1) < i+k && nums[i - k] < nums[i]\\n sum += nums[i]\\n\\n elsif i-k >=0 && (nums.length - 1) >= i+k && nums[i-k] < nums[i] && nums[i+k] < nums[i]\\n sum += nums[i] \\n elsif i-k < 0 && i+k > (nums.length - 1)\\n sum += nums[i] \\n \\n\\n end\\n\\n\\n\\n end\\n return sum\\nend\"], [7, 7.6923, \"# @param {Integer[]} nums\\n# @param {Integer} k\\n# @return {Integer}\\n\\ndef sum_of_good_numbers(nums, k)\\n nums.each_with_index.inject(0) {|res, (v, i)|\\n f = true\\n f &&= (v > nums[i - k]) if i - k >= 0\\n f &&= (v > nums[i + k]) if i + k < nums.size\\n res + (f ? v : 0)\\n }\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list:
import random
random.seed(seed)
def sample_solution(nums, k):
total = 0
n = len(nums)
for i in range(n):
left = i - k
right = i + k
left_ok = left < 0 or nums[i] > nums[left]
right_ok = right >= n or nums[i] > nums[right]
if left_ok and right_ok:
total += nums[i]
return total
# Predefined diverse test cases
fixed_cases = []
# Test Case 1: Minimal array
nums = [2, 1]
k = 1
input_str = ",".join(map(str, nums)) + " " + str(k)
output_str = str(sample_solution(nums, k))
fixed_cases.append({"input": input_str, "output": output_str})
# Test Case 2: Provided example
nums = [1, 3, 2, 1, 5, 4]
k = 2
input_str = ",".join(map(str, nums)) + " " + str(k)
output_str = str(sample_solution(nums, k))
fixed_cases.append({"input": input_str, "output": output_str})
# Test Case 3: All equal elements
nums = [5, 5, 5, 5]
k = 1
input_str = ",".join(map(str, nums)) + " " + str(k)
output_str = str(sample_solution(nums, k))
fixed_cases.append({"input": input_str, "output": output_str})
# Test Case 4: Descending order
nums = [9, 8, 7, 6, 5, 4]
k = 2
input_str = ",".join(map(str, nums)) + " " + str(k)
output_str = str(sample_solution(nums, k))
fixed_cases.append({"input": input_str, "output": output_str})
# Test Case 5: Ascending order
nums = [1, 2, 3, 4, 5, 6]
k = 2
input_str = ",".join(map(str, nums)) + " " + str(k)
output_str = str(sample_solution(nums, k))
fixed_cases.append({"input": input_str, "output": output_str})
# Test Case 6: Patterned input
nums = [3, 1, 4, 1, 5]
k = 2
input_str = ",".join(map(str, nums)) + " " + str(k)
output_str = str(sample_solution(nums, k))
fixed_cases.append({"input": input_str, "output": output_str})
test_cases = fixed_cases[:min(num_cases, len(fixed_cases))]
# Generate additional random test cases if needed
while len(test_cases) < num_cases:
n = random.randint(2, 100)
nums = [random.randint(1, 1000) for _ in range(n)]
k = random.randint(1, n // 2)
input_str = ",".join(map(str, nums)) + " " + str(k)
output_str = str(sample_solution(nums, k))
test_cases.append({"input": input_str, "output": output_str})
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
try:
expected_val = int(expected_output.strip())
prog_val = int(program_output.strip())
return expected_val == prog_val
except ValueError:
return expected_output.strip() == program_output.strip()
|
[{"input": "2,1 1", "output": "2"}, {"input": "1,3,2,1,5,4 2", "output": "12"}, {"input": "5,5,5,5 1", "output": "0"}, {"input": "9,8,7,6,5,4 2", "output": "17"}, {"input": "1,2,3,4,5,6 2", "output": "11"}, {"input": "3,1,4,1,5 2", "output": "5"}, {"input": "115,26,760,282,251,229,143,755,105,693,759,914,559,90,605,433,33,31,96,224,239,518,617,28,575,204,734,666,719,559,430,226,460,604,285,829,891,7,778,826,164,715,433,349,285,160,221,981,782,345,105,95,390,100,368,868,353,619,271,827,45,748,471,550,128,997,945,388,81,566,301,850,644,634,907,883,371,592,197,722,72,47,678 15", "output": "23024"}, {"input": "297,82,876,239,888,104,390,285,465,651,855,374,167,380,364,215,687,274,719,960,700,664,74,624,651,176,547,747,251,168,474,389,277,948,656,705,571,225,702,333,864,787,795,58,235,842,33,825,324,411,275,68,217,936,966,581,898,736,323,218,672,512,406,906,937,659,470,147,272,143,253,763,575,552,270,765,599,439,920,598,409,371,225,142,522,506,94,774,49,882,113,157,643,164,812,697,433,611,66,395 25", "output": "28212"}, {"input": "480,542,258,995,567,882,966,12,697,739,118,699,907,550,769,274,788,657,349,115,301,446,162,465,4,977,740,897,737,270,996,513,781,183,520,935,109,892,641,306,862,655,520,624,204,157,383,781,166,553,977,798,945,544,941,1,614,332,501,20,115,952,372,900,852,827,315,246,60,247,900,581,970,81,88,750,498,836 5", "output": "21456"}, {"input": "546,785,129,132,676,487,970,563,170,272,541,894,622,434,988,217,952,553,774,748,707,206,731,320,409,688,666,383,449,922,530,463,124,254,231,66,347,22,603,568,236,603,226,8,73,725,647,61,235,70,928,33,881,339,73,527,244,286,686,498,220,553,136,741,958,904,585,591,485,249,804,485,827,417,195,97,100,675,442,363,434,421,479,885,747,56,690,670,662,101,63,413,746,348,820,883,112,255,197 13", "output": "24096"}, {"input": "460,144,433,188,286,474,256,896,946,78,454,828,883,877,564,101,52,668,554,857,16,993,96,949,772,870,243,171,417,498,493,219,886,411,925,61,169,389,3,400,272,949,803,804,466,293,434,714,981,749,803,570,678,736,499,159,195,304,223,992,60,594,754,556,63,766,322,59,52,599 31", "output": "22979"}, {"input": "942,874,544,162,59,984,521,83,872,191,71,610,70,692,883,241,414,123,965,912,584,253,593,609,41,635,84,430,674,598,579,536,324,958,268,210,686,734,322,245,272,406,135,688,661,308,469,324,952,770,959,75,10,470,637,577,103,76,551,219,519,272,136,956,358,903 5", "output": "16064"}, {"input": "379,292,162,449,854,557,721,310,627,827,670,542,9,684,837,568,307,955,680,107,962,900,138,271,119,912,110,761,567,160,279,289,620 7", "output": "8532"}, {"input": "352,209,704,650,874,271,518,501,258,928,930,867,53,95,650,434,850,284,46,4,342,790,134,653,269,166,760,453,565,723,438,575,10,115,78,968,905,708,926,153,559,37,855,379,597,566,152,441,131,43,316,374,921,956,816,996,882,41,921,367,216,699,256,683,106,363,799,574,906,896,417,998,636,768,159,948,953,243,886,167,1000,820,831,182,903,423,26,184,755,947,341,802,954 27", "output": "29349"}, {"input": "885,753,831,255,274,164,807,719,111,392,894,40,880,482,228,205,837,941,472,359,313,841,815,893,234,229,25,676,198,409,337,286,886,72,991,792,286,360,657,522,410,696,864,550,340,962,29,119,899,994,268,183,595,986,272,40,112,611,445,354,747,806,322,447,621,524,119,395,922,591,195,261,46,726,447,2,533,948,826,552,704,737,963,760,755,687,202 24", "output": "28432"}, {"input": "72,972,681,943,339,639,322,680,869,128,738,922,308,520,317,683,419,335,413,714,303,568,131,197,431,681,963,389,694,767,925,179,631,583,309,416,562,854,1,312,294,216,441,805,594,622,671,330,477,453,453,692,219,524,485,813,923 26", "output": "18425"}, {"input": "174,675,87,291,528,680,649,635,344,96,839,975,770,241,689,318,231,826,204,151,26,48,251,487,626,871,787,75,467,425,908,645,590,200,736,714,394,507,410,250,152,672,705,6,915,769,882,789,907,110,798,436,225,181,824,981,713,531,476,52,571,256,940,869,125,468,137,821,476,684,544,573,610,325,973,774,913,454,628,835,737,914,517,437,851,929,562,457,919,163,762,883,487,461,266,770 16", "output": "27409"}, {"input": "284,785,797,534,497,642,245,282,451,80,731,293,241,279,344,328,915,554,83,142,155,237,393,711,157,724,220,66,425,418,339,556,478,426,64,212,853,431,399,927,789,599,969,713,21,878,902,784,590,390,489,7,966,361,306,772,400,874,914,977,856,430,552,766,753,560,820,618,920,226,500,225,280,447,498,30,399,345,685,696,818,415,742 11", "output": "22676"}, {"input": "942,131,638,547,28,929,404,607,578,679,28,86,659,439,139,888,473,187,52,267,389,336,217,466,335,346,780,901,389,285,771,975,852,432,259,855,84,482,20,768,553,54,975,359,230,666,71,800,981,668,42,773,32,973,254,205,860,21,637,157,245 5", "output": "14388"}, {"input": "686,118,578,971,224,477,717,263,786,378,172,621,622,987,766,736,118,797,839,168,988,319,111,593,27,952,320,590,694,930,982,385,407,965,733,204,78,607,708,851,643,249,105,714,792,309,871,701,615,825,124,816,580,802,43,356,546,439,678,380,71,519 21", "output": "20188"}, {"input": "13,870,431,843,502,109,444,984,371,651,913,849,471,725,157,446,181,752,535,989,667,277,631,828,942,552,794,496,477,447,846,749,607,275,331,873,252,851,958,89,286,903,462,250,769 15", "output": "14756"}, {"input": "625,685,389,345,30,507,872,333,187,500,218,364,817,265,349,287,902,611,719,902,283,570,11,530,971,196,88,248,738,417,501,569,777,247,708,488,662,729,503,459,812,18,96,302,227,415,709,250,314,680,596,378,485,567,544,353,436,764,564,339,361,720,465,278,314,258,237,124,739,198,324,123,761,549 12", "output": "15864"}, {"input": "222,757,496,284,742,604,779,538,612,290,103,853,199,304,233,370,184,310,15,726,547,130,281,47,998,56 9", "output": "7183"}, {"input": "715,967,130,654,890,771,503,106,894,13,588,292,481,491,452,349,189,989,53,259,964,883,490,117,842,67,411,504,76,591,645,703,55,156,153,831,577,972,312 3", "output": "10326"}, {"input": "122,572,783,427,621,611,810,634,232,795,536,390,462,931,454,305,881,603,440,313,583,636,62,625,984,758,102,971,782,213,641,217,271 3", "output": "6423"}, {"input": "246,178,566,77,161,3,419,462,706,609,482,299,34,238,296,724,290,720,881,465,73,704 4", "output": "5864"}, {"input": "807,811,641,604,678,824,957,203,436,118,558,231,664,153,931,273,847,146,74,62,170,812,315,610,767,845,583,944,296,450,128,480,706,312,717 13", "output": "11627"}, {"input": "513,553,506,449,83,613,41,911,443,753,331,619,257,27,94,235,985,691,857,882,590,602,974,22,784,689,842,276,591,42,782,775,180,482,532,668 15", "output": "11286"}, {"input": "186,600,447,651,834,504,993,94,482,357,419,342,329,687,108,879,165,338,422,711,508,296,679,968,411,834,779,564,38,466,91,323,259,332,119,994,792 13", "output": "10467"}, {"input": "845,2,674,891,556,474,424,56,193,531,371,638,775,511,641,453,779,53,209,274,563,135,950,295,449,902,716,497,125,30,997,646,624,819,246,727,163,319,565,15,566,418,96,231,862,935,117,473,970,121,664,853,158,511,956,734,299,522,723,280,426,855,495,484,250,468,565 10", "output": "16628"}, {"input": "196,944,614,521,765,901,140,885,72,283,792,809,875,425,349,957,807,520,274,841,3,290,744,306,858,602,594,676,502,887,153,458,552,496,354,341,566,782,557,387,467,956,330,891,194,715,245,586,393,240,877 25", "output": "17584"}, {"input": "45,326,763,485,723,936,831,391,396,680,812,841,668,156,508,988,38,130,515,989,605,340,891,103,896,866,451,103,539,933,468,16,740,148,420,892,671,994,159,77,481,801,993,272,347,639,710,408,666,83,873,337,873,691 18", "output": "17161"}, {"input": "978,325,642,736,909,778,500,894,555,37,633,71,241,647,701,944,295,233,765,93,445,101,779,649,721,894,103,455,171,711,307,926,30,48,333,816,58,301,368,384,442,150,251,544,422,580,699,812,185,175 6", "output": "13631"}, {"input": "625,892,392,635,700,247,510,935,598,147,238,473 6", "output": "3966"}, {"input": "471,262,683,10,921,824,477,923,295,694,560,162,76,453,968,354,602,307,655,986,435,707,257,468,866,310,204,394,874,495,110,243,391,586 12", "output": "10077"}, {"input": "303,717,303,23,850,675,406,282,9,580,886,703,797,763,997,51,933,621,764,509,853,926,925,294,795,819,236,622,822,361,225,652,195,636,257,695,774,739,786,676,698,859,141,644,100,926,643,662,41,317,808,452,35,594,374,750,135,93,932,303,335,766,426,180,206,136,806,553,898,995,375,544,514,936,280 11", "output": "20612"}, {"input": "936,845,967,494,991,826,303,765,892,347,824,118,480,987,78,145,773,990,232,881,693,742,691,407,991,867,824,571,375,93,810,405,15,271 4", "output": "10560"}, {"input": "378,689,767,689,269,599,391,843,654,963,381,111,692,240,483,26,635,906,966,575,336,938,625,227,664,65,651,844,476,932,718,310,665,419,120,144,47,969,39,312,505,119,100,241,909,551,139,398,465,380,687,973,761,714,969,554,430,602,761,745 5", "output": "15928"}, {"input": "671,102,854,502,631,418,962,975,287,34,707,380,223,455,456,974,242,876,372,102,703,377,558,924,661,368,63,408,283,195,992,126,972,869,844,466,94,679,218,658,655,612,995,22,52,806,342,250,129,806,579,211,71,850,784 18", "output": "18831"}, {"input": "601,222,833,891,239,337,793,152,808,923,611,3,284,880,149,134,554,257,818,179,113,677,888,27,135,16,367,809 13", "output": "8416"}, {"input": "603,332,17,179,272,54,130,760,432,539,117,764,66,488,460,797,371,526,608,112,463,516,227,969,630,45,745,803,931,888,675,534 10", "output": "9865"}, {"input": "659,988,32,63,491,868,412,437,703,111,503,730,932,455,76,921,83,330,623,152,68,130,282,640,649,600,562,730,333,391,612,544,302,465,518,620,441,102,813,719,118,874,671,667,899,788,565,739,887,221,441,463,910,234,424,348,848,465,409,426 24", "output": "18492"}, {"input": "321,438,321,682,262,384,977,157,704,946,486,69,94,852 1", "output": "3895"}, {"input": "443,99,763,757,382,832,134,570,62,601,980,576,576 3", "output": "3746"}, {"input": "126,421,363,895,682,964,769,434,889,938,739,53,992,295,615,320,361,107,592,520,218,159,673,494,230,868,111,359,866,570,377,118,781,286,588,232,827,440,866,575,998,786,839,637,629,692,659,571,27,624,952,674,850,711,274,30,185,280,720,781,317,944,348,360,7,186,891,147,580,674,411,72,146,759,649,996,32,94,765,544,221,386,430,465,350,162,379 20", "output": "25520"}, {"input": "333,796,965,582,611,87,905,54,160,162,773,633,51,691,84,279,454,678,435,498,622,453,425,280,221,774,525,117,354,441,114,291,695,695,608,499,540,684,316,47,226,405,614,57,8,210,309,969,217,786,141,783,262,297,336,123,8,510,765,441,180,133,390,546,721,236,513,573,854,685,826,363,74,407,883,760,44,447,20,471,944,80,883,321,590,440,588,415,727,656,428,297,118,415 2", "output": "21708"}, {"input": "176,821,971,633,472,852,707,942,371,91,448,865,109,250,447,604,411,537,81,406,892,318,764,348,227,342,798,173,79,523,649,117,544,523,199,928,795,358,360,745,982,839,661 5", "output": "12680"}, {"input": "106,150,263,203,178,617,157,779,778,672,78,182,975,792,644,506,476,773,578,779,594,460,698,947,904,579,659,651,640,331,885,995 11", "output": "9712"}, {"input": "451,70,481,453,647,311,816,282,606,58,361,520,76,318,473,463,39,59,378,852,294 2", "output": "3955"}, {"input": "885,876,93,630,609,520,394,474,595,568,978,811,757,918,43,461,931,830,586,668,193,330,620,488,514,155,981,64,462,106,831,921,858,352,732,87,517,662,177,41,254,725,449,450,537,536,625,163,373,382,940,290,397,419,794,347,696,613,54,809,647,663,343,68,338,97,572,695,396,291,259,742,873,673,988,929,618,895,154,342,84,597,680,145 23", "output": "26480"}, {"input": "991,672,716,679,402,133,610,726,961,87,318,573,386,659,811,337,833,131,687,720,849,970,757,702,935,540,96,662,687,434,521,371,19,372,317,185,974,220,350,971,785 16", "output": "12878"}, {"input": "232,141,159,80,303,865,808,104,520,790,553,856,757,905,540,39,678,345,898,785,633,135,612,386,158,167 3", "output": "6443"}, {"input": "790,640,829,925,170,739,449,45,421,374,693,737,244,993,455,626,292,771,767,803,460,240,547,245,317,989,829,804,481,926,856,199,377,695,970,585,452,473,788,289,797,392,515,541,429,990,166,837,205,821,620,142,894,257,54,657,493,896,381,568,957,106,729,867,529,872,128,292,86,782,165,280,461,928,526,151,851,448,94,970,933,228,837,462,906,358,953,28,425,55 26", "output": "29247"}, {"input": "383,242,396,84,384,230,29,327,954,102,860,732,666,344,811,150,141,40,294,940,850,484,713,852,143,778,723,481,460,631,6,928,82,20,263,221,856,154,562,963,745,624,541,434,114,795,296,244,309,125,49,245,430,655,813,638,469,65,114,857,927,512,612,549,17,648 33", "output": "20523"}, {"input": "248,736,148,299,440,2,630,362,247,585,427,192,681,685,88,537,999,370,70,977,539,558,520,806,520,568,21,400,895,482,45,651,397,383,260,766,17,366,808,70,354,247,751,673,644,107,791,596,753,775,341,137,46,361,560,347,834,659,180,851,798,702,476,713,491,647,187,831,139,65,734,795,967,469,38 19", "output": "19111"}, {"input": "45,811,205,908,43,324,956,318,528,408,835,557,485,260,38,772,663,196,293,366,883,800,49,887,672,340,280 2", "output": "7338"}, {"input": "448,911,410,762,451,917,980,396,348,998,192,509,709,510,377,947,817,532,274,821,85,745,435,81,441,617,843,185,559,301,329,106,82,336,677,303,314,457,618,735,437,171,707,455,360,458,44,745,891 12", "output": "14855"}, {"input": "446,282,655,811,971,59,77,688,653,416,373,526,821,768,696,164,976,32,147,870,623,695,801,449,36,130,69,242,798,661,376,371,393,973,581,34,620,158,696,461,972,380,381,455,782,79,588,141,543,376,408,322,666,286,256,984,117,27,754,191,512,531,397,936,576,121,269,794,267,721,457,220,627,293,711,939,503,205,126,139 5", "output": "20398"}, {"input": "177,921,731,456,90,830,699,991,866,328,684,356,727,67,564,556,298,913,308,872,162,729,727,950,718,654,179,813,371,521,230,125,206,812,143,243,810,506,27,370,568,587,378,479,823,565,133,627,906,89,68,317,408,735,737,491,539,421,788 14", "output": "16250"}, {"input": "76,129,996,325,658,76,461,478,697,530,353,132,900,849,799,565,656,602,187,787,990,133,444,515,933,890,57,852,128,531,157,312,169,166,331,958,727,231,355,971,964,532,917,291,867,81,257,202,651,980,565,282,129,641,311,630,547,96,515,657,173,607,965,595,158,176,675,640,738,924,620,346,863,947,578 3", "output": "21733"}, {"input": "655,937,280,425,180,570,474,728,582,774,937,141,205,191,853,391,297,568,503,44,843,847,310,855,600,312,506,573,758,475,230,28,811,3,158,269,308,979,656,855,652,484,128,670,682,915,295,428,184,504,929,705,661,251 1", "output": "12600"}, {"input": "784,284,505,994,69,614,764,371,596,493,580,447,890,265,644,703,488 2", "output": "4628"}, {"input": "525,751,590,18,866,266,167,596,60,150,328,473,900,710,139,366,168,55,280,370,430,652,934,979,365,50,297,299,543,655,959,79,527,199,785,644,188,784,97,614,771,172,557,331,894,324,847,866,702 10", "output": "13136"}, {"input": "702,715,705,372,99,548,594,361,844,148,14,141,531,289,382,798,497,422,349,944,933,167,105,224,159,516,227,852,193,815,919,573,629,707,852,976 17", "output": "12720"}, {"input": "730,565,720,775,822,117,428,472,939,79,120,839,135,946,18,492,357,320,708,372,143,837,453,912,612,536,782,994,351,177,727,312,30,763,835,122,228,132,878,711,146,705,233,315,129,215,134,81,436,708,782,803,115,80,20,794,496,776,442,44,202,111,34,813,676,526,608,61,481,122 17", "output": "16546"}, {"input": "68,309,684,11,773,99,802 1", "output": "2259"}, {"input": "211,602,923,205,190,687,360,30,93,150,867,765,965,285,972,594,357,361,165,876,513,800,747,628,248,518,584,70,102,840,593,782,15,542,223,733,197,988,289,176,924,773,551,5,997,743,102,947,220,943,517,872,725,487,376,715,604,190,451,690,981,110,186,855,364,389,435,220,527,234,418,116,780,322,127,478,113,533,140 32", "output": "24688"}, {"input": "370,722,296,571,740,42,85,336,506,119,395,291,468,615,754,320,704,1000,862,455,232,568,418,298,876,439,194,878,72,917,862,822,488,962,696,377,184,14,691,504,689,108,406,449,536,675,693,88,123,147,405,411,712,605,105,760,948,914,173,67,373,999,204,347,206,610,865,414,126,239,859,435,743,512,286,784,731,785,596,608,280,775,809,821,660,966,410,365,488,683,618,973,415,497,524,286,151,787,466 7", "output": "26171"}, {"input": "257,502,510,237,644,966,138,31,102,756,55,851,70,511,695,28,996 3", "output": "4470"}, {"input": "620,696,335,157,311,637,639,99,779,79,677,770,533,786,505,812,478,207,301,678,510,503,517,268,556,352,829,881,554,560,19,976,783,33,441,902,937,122,393,461,323,874,386,454,471,37,34,182,571,676 25", "output": "16704"}, {"input": "906,724,169,504,442,138,320,733,399,500,783,113,583,692,503,676,568,702,553,586,482,488,576,875,161,519,58,401,270,507,606,995,387,632,693,362,785,292,329,63 1", "output": "10179"}, {"input": "47,132,858,376,358,829,760,598,28,784,913,641,350,390,100,439,354,366,422,360,58,678,251,254,241,664,320,607,87,933,705,68,890,313,118,346,174,21,552,334,39,472,674,885,433,582,528,924,432,274,21,713,481,603,23,325,387,585,400,331,587,101,828,501,103,708,692,211,345,509,515,831,784,684,348,171,630 20", "output": "20248"}, {"input": "993,447,207,509,651,868,998,807,78,861,871,549,220,295,272,49,305,588,412,824,232,640,761,981,95,735,865,593,98,607,345,280,69,581,821,544,487,438,215,356,815,79,668,844,310,517,824,308 14", "output": "14392"}, {"input": "553,321,205,425,412,258,640,528,465,688,782,561,185,903,20,643,721,529,884,192,591,512,219,677,986,844,761,961,479,275,960,654,546,829,630,874,788,929,445,958,580,745,642,62,535,206,374,474,152,247,155,765,702,784,308,865,446,421,327,881,851,934,66,650,209,867,423,274,844,294,662,165,263,704,616,242,416,245,117,154,197,29,252,817,848,318 30", "output": "26346"}, {"input": "574,447,433,663,928,38,207,164,280,140,30,265,809,823,285,675,564,181,660,873,44,987,740,498,802,21,57,881,919,86,322,617,306,888,66,923,979,417,919,373,688,674,907,93,407,966,860,742,863,144,242,115,585,753,513,956,124,535,681,849,595,973,794,954 17", "output": "19117"}, {"input": "906,93,244,615,126,792,827,321,338,853,599,755,400,826,767,762,242,958,434,224,148,110,180,220,994,282,451,419,261,884,604,58,503,547,384,717,972,116,325,559,434,487,700,253,987,285,901,804,960,149,372,487,733,377,842,316,22,661,991,927,621,36,862,758,679 4", "output": "17115"}, {"input": "940,808,688,246,260,566,394,317,655,982,718,372,925,832,702,125,548,888,243,879,454,398,9,932,984,403,950,940,262,309,93,959,843,775,242,305,216,881,912,165,938,450,647,325,901,832,786,660,417,809,35,281,888,83,843,799,964,504,483,755,423,949,862,341,735,433,898,941,840,103,845,165,716,268,519,68,361,431,617,747,833,561,756,335,465,712,29,781,54,657 42", "output": "32135"}, {"input": "646,455,811,657,140,4,411,205,644,313,322,590,85,114,162,256,529,731,993,787,851,665,782,134,868 10", "output": "8710"}, {"input": "421,812,962,328,463,490,895,753,137,267,178,704,608,847,336,819,289,204,87,425,377,187,403,898,387,968,855,906,585,230,22,971,24,946,572,663,627,642,235,929,92,998,474,204,269,719,873,173,51,411,633,440,615,267,153,92,982,377,175,970,581,121,15,736,539,446,792,943,951,465,848,690,507,122,230,731,209,196,969,883,833,801,273,295,765,507,392,134,442 14", "output": "25194"}, {"input": "221,844,290,745,694,194,429,185,419,812,150,30,298,1000,269,242,633,462,930,255,379,597,701,663,470,88,11,481,137,893,332,998,710,408,704,218,731,393,726,434,754,612,263,75,98,571,61,54,341,954,241,483,931,363,621,962,687,991,822,613,727,767,830,47,6,260,517,635,391,310,405,688,380,136,992,914,573,43 38", "output": "24955"}, {"input": "267,174,516,505,953,348,899,480,136,92,325,728,544,444,146,267,120,321,46,131,512,893,997,855 5", "output": "7612"}, {"input": "370,949,441,290,925,898,270,628,850,780,949,271,530,321,447,915,169,324,755,504,783,973,155,570,874,946,674,652,818,451,55,194,153,56,236,188,37,482,267,168,723,479,447,119,917,950,507,42,453,366,727,575,497,469,505,116,867,738,888,152,127,358,96,209,890,291,185,855,173,768,521,843,280,577,913,680,600,218,598,995,5,539,786,585,185,427,943,79,253,787,511,694,97,909,337,27,292 44", "output": "31343"}, {"input": "125,404,383,605,952,975,109,858,332,158,30,84,472,851,725,676,492,465,644,979,276,609,674,6,338,994,45,672,638,974,464,333,971,750,752,929,981,817,583,133,217,884,50,821,660,290,331,818,57,762,73,561,975,617,391,95,409,262,183,246,989,790,887,409,92,22,873,214,167,398,799,413,292,663,771,978,670,158,124,306,503,821,443,754,826,944,318,926,702 39", "output": "30648"}, {"input": "368,682,99,853,377,525,205,502,457,907,398,488,275,577,615,434,93,775 7", "output": "5422"}, {"input": "629,191,445,646,437,96,42,526,350,997,475,693,230,664,703,731,159,954,508,540,645,663,538,86,298,480,448,82,929,821,490,308,153,131,701,925,308,862,255,536,438,303,583,49,565,79,940,47,526 4", "output": "12222"}, {"input": "436,423,97,476,677,738,583,833,260,364,261,600,84,788,516,17,117,759,678,474,184,806,187,864,403,47,86,427,898,722,305,322,602,742,466,776,687,461,639,828,272,350,990,941,893,830,192,217,190,81,765,619,266,893,690,109,445,548,19,6,405,120,14,176,672,489,472 26", "output": "19515"}, {"input": "989,763,617,744,499,311,634,833,998,632,370,708,690,987,707,692,405,824,310,90,129,139,15,196,115,836,17,713,994,193,880,28,215,493,665,149,666,248,447,863,642,879,809,552,196,89,309,789,475,152,486,433,23,120,171,925,157,757,720,456,987,497,483,21,881,461,600,249,207,302,584,850,854,402,53,342,9,106,646,868,731,443,426,869,508,755 38", "output": "28147"}, {"input": "749,568,298,38,500,410,498,526,606,743,627,958,695,927,837,889,500,238,732,63,541,20,433,591,324,567,66,275,915,664,428,911,485,120,507,638,962,662,356,460,715,447,22,166,295,744,197,481,353,449,238,520,225,602,931,702,348,944,617,874,863,733,673,480,135,905,301,741,729,400,983,427,854,964,690,669,753,369 31", "output": "27099"}, {"input": "637,213,290,708,768,89,684,495,133,178,205,161,621,504,104,813,426,966,506,311,241,215 9", "output": "6052"}, {"input": "19,368,903,268,366,694,163,179 1", "output": "1776"}, {"input": "346,441,117,633,233,124,576,230,499,265 3", "output": "1573"}, {"input": "788,48,789,899,571,274,918,155,874,707,895,528,619,686,107,724,52,949,969,449,819,469,986,862,774,114,999,109,801,626,625,801,879,971,105,844,576,43,520,108,172,646,121,892,211,933,371 6", "output": "13711"}, {"input": "300,726,453,781,519,511,751,892,102,158,663,373,343,839,142,126,869,207,450,993,426,788,788,7,252,855,829,486,350,294,518,176,88,273,382,733,773,425,370,645,681,252,156,772,772,543,432,807,234,142,822,440,424,941,420,920,470,975,873,529,814,699,371,967,31,454,150,789,11,735,826,530,967,72,87,347,323,412,791,169,445,63,403,778,38,677,945,657,155,925,589,60,647,731,819 43", "output": "31156"}, {"input": "997,303,430,412,908,698,718,567,895,312,739,761,322,932,353,9,847,287,922,541,626,943,151,718,414,457,660,211,909,558,640,808,634,668,453,715,354,909,832,801,665,415,795,203,903,309,87,38,551,343,400,743,737,758,901,130,533,554,291,219,96,524,566,320,534,349,776,651 11", "output": "19642"}, {"input": "29,912,816,553 2", "output": "1728"}, {"input": "853,793,312,744,433,518,114,750,62,862,382,266,643,520,363,127,49,775,667,964,128,460,306,587,755,6,465,348,242,825,764,596 8", "output": "9548"}, {"input": "307,292,683,804,835,733,587,689,144,732,387,533,756,254,108,336,529,597,198,843,798,370,466,101,151,729,436,849,422,84,95,64,436,910,134,488,220,457,80,379,694,539,413,603,573,532 13", "output": "13295"}, {"input": "599,511,652,434,451,706,954,971,502,750,997,427,844,167,148,518,131,497,729,469,133,992,722,526,884,542,121,712,218,467,485,34,765,161,967 12", "output": "11350"}, {"input": "617,873,419,113,124,379,586,297,42,536,157,121,381,313,384,311,302 8", "output": "3989"}, {"input": "811,147,146,803,604 2", "output": "2218"}]
|
{
"cpp": "==Code Submission==\n\npair<vector<int>, int> deserialize_stdin(const string& input) {\n size_t spacePos = input.find(' ');\n string nums_str = input.substr(0, spacePos);\n vector<int> nums;\n size_t start = 0, end = 0;\n while ((end = nums_str.find(',', start)) != string::npos) {\n nums.push_back(stoi(nums_str.substr(start, end - start)));\n start = end + 1;\n }\n if (start < nums_str.size()) {\n nums.push_back(stoi(nums_str.substr(start)));\n }\n int k = stoi(input.substr(spacePos + 1));\n return {nums, k};\n}\n\nstring serialize_stdout(int result) {\n return to_string(result);\n}\n\nint main(){\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n string line;\n getline(cin, line);\n auto [nums, k] = deserialize_stdin(line);\n Solution sol; // The submitted solution will replace the placeholder.\n int ans = sol.sumOfGoodNumbers(nums, k);\n cout << serialize_stdout(ans) << \"\\n\";\n return 0;\n}",
"golang": "==Code Submission==\n\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n line, _ := reader.ReadString('\\n')\n line = strings.TrimSpace(line)\n parts := strings.SplitN(line, \" \", 2)\n k, _ := strconv.Atoi(parts[1])\n numStrs := strings.Split(parts[0], \",\")\n nums := make([]int, len(numStrs))\n for i, s := range numStrs {\n nums[i], _ = strconv.Atoi(s)\n }\n ans := sumOfGoodNumbers(nums, k)\n fmt.Println(ans)\n}",
"java": "public class Main {\n private static int[] deserializeIntArray(String input) {\n String[] tokens = input.split(\",\");\n int[] nums = new int[tokens.length];\n for (int i = 0; i < tokens.length; i++) {\n nums[i] = Integer.parseInt(tokens[i]);\n }\n return nums;\n }\n \n private static String serializeOutput(int result) {\n return Integer.toString(result);\n }\n \n public static void main(String[] args) throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n String line = br.readLine().trim();\n String[] parts = line.split(\" \", 2);\n int k = Integer.parseInt(parts[1]);\n int[] nums = deserializeIntArray(parts[0]);\n \n Solution sol = new Solution();\n int ans = sol.sumOfGoodNumbers(nums, k);\n System.out.println(serializeOutput(ans));\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\n\nconst deserialize_stdin = (input) => {\n const [numsPart, kPart] = input.trim().split(' ', 2);\n const nums = numsPart.split(',').map(Number);\n const k = parseInt(kPart, 10);\n return { nums, k };\n};\n\nconst serialize_stdout = (result) => {\n return result.toString();\n};\n\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\nlet input = '';\nprocess.stdin.on('data', chunk => { input += chunk; });\nprocess.stdin.on('end', () => {\n const { nums, k } = deserialize_stdin(input);\n const ans = sumOfGoodNumbers(nums, k);\n console.log(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str):\n arr_str, k_str = input_str.split(' ', 1)\n nums = list(map(int, arr_str.split(',')))\n k = int(k_str)\n return nums, k\n\ndef serialize_stdout(result):\n return str(result)\n\nline = sys.stdin.read().strip()\nnums, k = deserialize_stdin(line)\nsol = Solution()\nans = sol.sumOfGoodNumbers(nums, k)\nsys.stdout.write(serialize_stdout(ans))",
"ruby": "==Code Submission==\n\ninput = gets.strip\nnums_part, k_str = input.split(' ', 2)\nnums = nums_part.split(',').map(&:to_i)\nk = k_str.to_i\nans = sum_of_good_numbers(nums, k)\nputs ans.to_s"
}
|
3731
|
Sum of Variable Length Subarrays
|
sum-of-variable-length-subarrays
|
<p>You are given an integer array <code>nums</code> of size <code>n</code>. For <strong>each</strong> index <code>i</code> where <code>0 <= i < n</code>, define a <span data-keyword="subarray-nonempty">subarray</span> <code>nums[start ... i]</code> where <code>start = max(0, i - nums[i])</code>.</p>
<p>Return the total sum of all elements from the subarray defined for each index in the array.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">nums = [2,3,1]</span></p>
<p><strong>Output:</strong> <span class="example-io">11</span></p>
<p><strong>Explanation:</strong></p>
<table style="border: 1px solid black;">
<tbody>
<tr>
<th style="border: 1px solid black;">i</th>
<th style="border: 1px solid black;">Subarray</th>
<th style="border: 1px solid black;">Sum</th>
</tr>
<tr>
<td style="border: 1px solid black;">0</td>
<td style="border: 1px solid black;"><code>nums[0] = [2]</code></td>
<td style="border: 1px solid black;">2</td>
</tr>
<tr>
<td style="border: 1px solid black;">1</td>
<td style="border: 1px solid black;"><code>nums[0 ... 1] = [2, 3]</code></td>
<td style="border: 1px solid black;">5</td>
</tr>
<tr>
<td style="border: 1px solid black;">2</td>
<td style="border: 1px solid black;"><code>nums[1 ... 2] = [3, 1]</code></td>
<td style="border: 1px solid black;">4</td>
</tr>
<tr>
<td style="border: 1px solid black;"><strong>Total Sum</strong></td>
<td style="border: 1px solid black;"> </td>
<td style="border: 1px solid black;">11</td>
</tr>
</tbody>
</table>
<p>The total sum is 11. Hence, 11 is the output.</p>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">nums = [3,1,1,2]</span></p>
<p><strong>Output:</strong> <span class="example-io">13</span></p>
<p><strong>Explanation:</strong></p>
<table style="border: 1px solid black;">
<tbody>
<tr>
<th style="border: 1px solid black;">i</th>
<th style="border: 1px solid black;">Subarray</th>
<th style="border: 1px solid black;">Sum</th>
</tr>
<tr>
<td style="border: 1px solid black;">0</td>
<td style="border: 1px solid black;"><code>nums[0] = [3]</code></td>
<td style="border: 1px solid black;">3</td>
</tr>
<tr>
<td style="border: 1px solid black;">1</td>
<td style="border: 1px solid black;"><code>nums[0 ... 1] = [3, 1]</code></td>
<td style="border: 1px solid black;">4</td>
</tr>
<tr>
<td style="border: 1px solid black;">2</td>
<td style="border: 1px solid black;"><code>nums[1 ... 2] = [1, 1]</code></td>
<td style="border: 1px solid black;">2</td>
</tr>
<tr>
<td style="border: 1px solid black;">3</td>
<td style="border: 1px solid black;"><code>nums[1 ... 3] = [1, 1, 2]</code></td>
<td style="border: 1px solid black;">4</td>
</tr>
<tr>
<td style="border: 1px solid black;"><strong>Total Sum</strong></td>
<td style="border: 1px solid black;"> </td>
<td style="border: 1px solid black;">13</td>
</tr>
</tbody>
</table>
<p>The total sum is 13. Hence, 13 is the output.</p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>1 <= n == nums.length <= 100</code></li>
<li><code>1 <= nums[i] <= 1000</code></li>
</ul>
|
You are given an integer array `nums` of size `n`. For **each** index `i` where `0 <= i < n`, define a subarray `nums[start ... i]` where `start = max(0, i - nums[i])`.
Return the total sum of all elements from the subarray defined for each index in the array.
**Example 1:**
**Input:** nums \= \[2,3,1]
**Output:** 11
**Explanation:**
| i | Subarray | Sum |
| --- | --- | --- |
| 0 | `nums[0] = [2]` | 2 |
| 1 | `nums[0 ... 1] = [2, 3]` | 5 |
| 2 | `nums[1 ... 2] = [3, 1]` | 4 |
| **Total Sum** | | 11 |
The total sum is 11\. Hence, 11 is the output.
**Example 2:**
**Input:** nums \= \[3,1,1,2]
**Output:** 13
**Explanation:**
| i | Subarray | Sum |
| --- | --- | --- |
| 0 | `nums[0] = [3]` | 3 |
| 1 | `nums[0 ... 1] = [3, 1]` | 4 |
| 2 | `nums[1 ... 2] = [1, 1]` | 2 |
| 3 | `nums[1 ... 3] = [1, 1, 2]` | 4 |
| **Total Sum** | | 13 |
The total sum is 13\. Hence, 13 is the output.
**Constraints:**
- `1 <= n == nums.length <= 100`
- `1 <= nums[i] <= 1000`
|
Easy
|
[
"array",
"prefix-sum"
] |
leetcode
|
https://leetcode.com/problems/sum-of-variable-length-subarrays
|
functional
| null | null | null | null |
{
"c": "int subarraySum(int* nums, int numsSize) {\n \n}",
"cpp": "class Solution {\npublic:\n int subarraySum(vector<int>& nums) {\n \n }\n};",
"csharp": "public class Solution {\n public int SubarraySum(int[] nums) {\n \n }\n}",
"dart": "class Solution {\n int subarraySum(List<int> nums) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec subarray_sum(nums :: [integer]) :: integer\n def subarray_sum(nums) do\n \n end\nend",
"erlang": "-spec subarray_sum(Nums :: [integer()]) -> integer().\nsubarray_sum(Nums) ->\n .",
"golang": "func subarraySum(nums []int) int {\n \n}",
"java": "class Solution {\n public int subarraySum(int[] nums) {\n \n }\n}",
"javascript": "/**\n * @param {number[]} nums\n * @return {number}\n */\nvar subarraySum = function(nums) {\n \n};",
"kotlin": "class Solution {\n fun subarraySum(nums: IntArray): Int {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param Integer[] $nums\n * @return Integer\n */\n function subarraySum($nums) {\n \n }\n}",
"python": "class Solution(object):\n def subarraySum(self, nums):\n \"\"\"\n :type nums: List[int]\n :rtype: int\n \"\"\"\n ",
"python3": "class Solution:\n def subarraySum(self, nums: List[int]) -> int:\n ",
"racket": "(define/contract (subarray-sum nums)\n (-> (listof exact-integer?) exact-integer?)\n )",
"ruby": "# @param {Integer[]} nums\n# @return {Integer}\ndef subarray_sum(nums)\n \nend",
"rust": "impl Solution {\n pub fn subarray_sum(nums: Vec<i32>) -> i32 {\n \n }\n}",
"scala": "object Solution {\n def subarraySum(nums: Array[Int]): Int = {\n \n }\n}",
"swift": "class Solution {\n func subarraySum(_ nums: [Int]) -> Int {\n \n }\n}",
"typescript": "function subarraySum(nums: number[]): number {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n int subarraySum(vector<int>& nums) {\n int total = 0;\n int n = nums.size();\n for (int i = 0; i < n; ++i) {\n int start = std::max(0, i - nums[i]);\n for (int j = start; j <= i; ++j) {\n total += nums[j];\n }\n }\n return total;\n }\n};",
"memory": 2700,
"memoryDistribution": "[[2700, 61.0236, \"class Solution {\\npublic:\\n int subarraySum(vector<int>& nums) {\\n int total = 0;\\n int n = nums.size();\\n for (int i = 0; i < n; ++i) {\\n int start = std::max(0, i - nums[i]);\\n for (int j = start; j <= i; ++j) {\\n total += nums[j];\\n }\\n }\\n return total;\\n }\\n};\"], [26300, 0.0984, \"class Solution {\\npublic:\\n int sum(vector<int>& nums, int s, int e) {\\n int ans = 0;\\n for (int i = s; i <= e; i++) {\\n ans += nums[i];\\n }\\n return ans;\\n }\\n\\n int subarraySum(vector<int>& nums) {\\n int ans = 0;\\n for (int i = 0; i < nums.size(); i++) {\\n int s = max(0, i - nums[i]);\\n ans += sum(nums, s, i);\\n }\\n\\n return ans;\\n }\\n};\"], [26400, 3.8386, \"class Solution {\\npublic:\\n int subarraySum(vector<int>& nums) {\\n int sum = 0;\\n for (int i = 0; i < nums.size(); i++){\\n int start = max(0, i - nums[i]);\\n for (int j = start; j <= i ; j++){\\n sum += nums[j];\\n }\\n }\\n return sum;\\n }\\n};\"], [26500, 14.8622, null], [26600, 20.1772, null], [26700, 20.374, null], [26800, 5.1181, null], [26900, 0.5906, null], [27000, 1.7717, null], [27100, 1.1811, null], [27200, 0.3937, null], [27300, 2.1654, null], [27400, 7.5787, null], [27500, 9.9409, \"class Solution {\\npublic:\\n int subarraySum(vector<int>& v) {\\n int n= v.size(); \\n int cnt=0;\\n vector<int> pref(n+1, 0);\\n for(int i=1; i<= n; i++){\\n pref[i]= pref[i-1] + v[i-1];\\n }\\n for(int i=0; i< n;i ++){\\n int start= max(0, i- v[i]);\\n cnt += (pref[i+1]- pref[start]);\\n }\\n return cnt;\\n }\\n};\"], [27600, 6.3976, \"class Solution {\\npublic:\\n int subarraySum(vector<int>& nums) {\\n int n = nums.size();\\n int total = 0;\\n vector<int> prefix_sum(n);\\n\\n partial_sum(nums.begin(), nums.end(), prefix_sum.begin());\\n \\n for (int i = 0; i < n; i++) {\\n int start = max(0, i - nums[i]);\\n total += prefix_sum[i] - (start > 0 ? prefix_sum[start - 1] : 0);\\n }\\n\\n return total;\\n }\\n};\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 77.1654, \"class Solution {\\npublic:\\n int subarraySum(vector<int>& nums) {\\n int n = nums.size();\\n vector<int>prefix_sum(n,0);\\n prefix_sum[0] = nums[0];\\n int res = 0;\\n for(int i = 1;i<n;i++)\\n {\\n prefix_sum[i] = prefix_sum[i-1] + nums[i];\\n }\\n for(int i = 0;i<n;i++)\\n {\\n int start = max(0,i-nums[i]);\\n int temp;\\n if(start == 0)\\n {\\n temp = prefix_sum[i] ;\\n }\\n else\\n {\\n temp = prefix_sum[i] - prefix_sum[start-1];\\n }\\n res += temp;\\n }\\n return res;\\n }\\n};\"], [1, 3.937, \"class Solution {\\npublic:\\n int subarraySum(vector<int>& nums) {\\n int start;\\n int ans = 0;\\n int n = nums.size();\\n for(int i = 0;i < n;i++)\\n {\\n start = max(0,i - nums[i]);\\n int sum = 0;\\n for(int j = start;j <= i;j++)\\n {\\n sum = sum + nums[j];\\n }\\n ans += sum;\\n }\\n\\n return ans;\\n }\\n};\"], [2, 2.6575, null], [3, 7.9724, \"class Solution {\\npublic:\\n int func(vector<int> &v, int l , int r){\\n int sum=0;\\n for(int i=l; i<= r;i++){\\n sum+= v[i];\\n }\\n return sum;\\n }\\n\\n int subarraySum(vector<int>& v) {\\n int n= v.size(); \\n int cnt=0;\\n for(int i=0; i< n;i ++){\\n int start= max(0, i- v[i]);\\n cnt+= func(v,start, i);\\n }\\n return cnt;\\n }\\n};\"], [4, 4.3307, \"class Solution {\\npublic:\\n int subarraySum(vector<int>& nums) {\\n vector<int>pref_sum;\\n int sum=0;\\n for(int i=0;i<nums.size();i++)\\n {\\n sum+=nums[i];\\n pref_sum.push_back(sum);\\n }\\n sum=0;\\n for(int i=0;i<nums.size();i++)\\n {\\n int start = max(0, i-nums[i]);\\n if(start>0) sum+=pref_sum[i]-pref_sum[start-1];\\n else sum+=pref_sum[i];\\n }\\n return sum;\\n }\\n};\"]]"
},
"golang": {
"code": "func subarraySum(nums []int) int {\n total := 0\n n := len(nums)\n for i := 0; i < n; i++ {\n start := i - nums[i]\n if start < 0 {\n start = 0\n }\n sum := 0\n for j := start; j <= i; j++ {\n sum += nums[j]\n }\n total += sum\n }\n return total\n}",
"memory": 500,
"memoryDistribution": "[[500, 39.4737, \"func subarraySum(nums []int) int {\\n total := 0\\n n := len(nums)\\n for i := 0; i < n; i++ {\\n start := i - nums[i]\\n if start < 0 {\\n start = 0\\n }\\n sum := 0\\n for j := start; j <= i; j++ {\\n sum += nums[j]\\n }\\n total += sum\\n }\\n return total\\n}\"], [4600, 1.3158, \"func subarraySum(nums []int) int {\\n\\tvar result int\\n\\tfor i := range nums {\\n\\t\\tstart := max(0, i-nums[i])\\n\\n\\t\\tfor j := start; j < i+1; j++ {\\n\\t\\t\\tresult += nums[j]\\n\\t\\t}\\n\\t}\\n\\n\\treturn result\\n}\"], [4700, 26.3158, \"func subarraySum(nums []int) int {\\n\\tvar result int\\n\\tfor i := range nums {\\n\\t\\tstart := max(0, i-nums[i])\\n\\n\\t\\tfor j := start; j < i+1; j++ {\\n\\t\\t\\tresult += nums[j]\\n\\t\\t}\\n\\t}\\n\\n\\treturn result\\n}\"], [4800, 32.8947, null], [4900, 11.8421, \"func subarraySum(nums []int) int {\\n // initialize prefix sum \\n prefix_sum := func() []int {\\n sum_till_element := make([]int, len(nums))\\n sum_till_element[0] = nums[0]\\n for i := 1; i < len(nums); i++ {\\n sum_till_element[i] = sum_till_element[i-1] + nums[i]\\n }\\n\\n return sum_till_element\\n }()\\n\\n locate_and_calc := func(prefix_sum []int, left, right int) int {\\n pre_left := 0\\n if left > 0 {\\n pre_left = prefix_sum[left - 1] \\n }\\n\\n pre_right := prefix_sum[right]\\n return pre_right - pre_left\\n }\\n\\n start_index := func(idx int) int {\\n val := idx - nums[idx]\\n if val > 0 {\\n return val\\n }\\n\\n return 0\\n }\\n\\n total := 0\\n for i := range nums {\\n total += locate_and_calc(prefix_sum, start_index(i), i)\\n }\\n \\n return total\\n}\"], [5000, 19.7368, \"func subarraySum(nums []int) int {\\n prefix_sum := make([]int, len(nums))\\n\\tprefix_sum[0] = nums[0]\\n\\tfor i := 1; i < len(nums); i++ {\\n\\t\\tprefix_sum[i] = prefix_sum[i-1] + nums[i]\\n\\t}\\n\\telement_sum := 0\\n\\tfor i := 0; i < len(nums); i++ {\\n\\t\\tleft := max(0, i - nums[i])\\n\\t\\tleft_prefix_sum := 0\\n\\t\\tif left > 0 {\\n\\t\\t\\tleft_prefix_sum = prefix_sum[left-1]\\n\\t\\t}\\n\\t\\telement_sum += prefix_sum[i] - left_prefix_sum\\n\\t}\\n\\treturn element_sum\\n}\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 80.2632, \"func subarraySum(nums []int) int {\\n res := 0\\n\\n for i := 0; i < len(nums); i++ {\\n start := int(math.Max(0, float64(i - nums[i])))\\n sum := 0\\n\\n for j := start; j <= i; j++ {\\n sum += nums[j]\\n }\\n\\n res += sum\\n } \\n\\n return res\\n}\"], [1, 5.2632, \"import \\\"math\\\"\\n\\nfunc subarraySum(nums []int) int {\\n\\tn := len(nums)\\n\\tsum := 0\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tfor j := int(math.Max(0, float64(i-nums[i]))); j <= i; j++ {\\n\\t\\t\\tsum += nums[j]\\n\\t\\t}\\n\\t}\\n\\treturn sum\\n}\\n\"], [2, 5.2632, null], [3, 5.2632, \"func subarraySum(nums []int) int {\\n runningSumArr := make([]int, len(nums))\\n runningSum := 0\\n for i := 0; i < len(nums); i++{\\n runningSumArr[i] = runningSum + nums[i]\\n runningSum = runningSumArr[i]\\n }\\n sum := 0\\n for i := 0; i < len(nums); i++{\\n start := max(0, i - nums[i])\\n sum += runningSumArr[i] - runningSumArr[start] + nums[start]\\n }\\n return sum\\n}\\n\\nfunc max(a,b int)int{\\n if a > b{\\n return a\\n }\\n return b\\n}\"], [4, 3.9474, \"func subarraySum(nums []int) int {\\n result := 0\\n for i := range nums {\\n start := i - nums[i]\\n if start < 0 {\\n start = 0\\n }\\n\\n for j := start; j <= i; j++ {\\n result += nums[j]\\n }\\n }\\n\\n return result\\n}\"]]"
},
"java": {
"code": "class Solution {\n public int subarraySum(int[] nums) {\n int total = 0;\n int n = nums.length;\n for (int i = 0; i < n; i++) {\n int start = Math.max(0, i - nums[i]);\n for (int j = start; j <= i; j++) {\n total += nums[j];\n }\n }\n return total;\n }\n}",
"memory": 4400,
"memoryDistribution": "[[4400, 30.7136, \"class Solution {\\n public int subarraySum(int[] nums) {\\n int total = 0;\\n int n = nums.length;\\n for (int i = 0; i < n; i++) {\\n int start = Math.max(0, i - nums[i]);\\n for (int j = start; j <= i; j++) {\\n total += nums[j];\\n }\\n }\\n return total;\\n }\\n}\"], [42800, 0.7227, \"class Solution {\\n public int subarraySum(int[] nums) {\\n int totalSum = 0;\\n int n = nums.length;\\n\\n for (int i = 0; i < n; i++) {\\n int start = Math.max(0, i - nums[i]);\\n \\n int sum = 0;\\n for (int j = start; j <= i; j++) {\\n sum += nums[j];\\n }\\n \\n totalSum += sum; \\n }\\n\\n return totalSum;\\n }\\n}\"], [42900, 0.3613, \"class Solution {\\n public int subarraySum(int[] nums)\\n {\\n int sum=0;\\n for(int i=0;i<nums.length;i++)\\n {\\n int st=Math.max(0,i-nums[i]);\\n for(int j=st;j<=i;j++)\\n {\\n sum+=nums[j];\\n }\\n }\\n return sum;\\n }\\n}\"], [43000, 0.9033, null], [43100, 1.2647, null], [43200, 3.1617, null], [43300, 7.8591, null], [43400, 12.9178, null], [43500, 10.3884, null], [43600, 8.4011, null], [43700, 9.3948, null], [43800, 7.6784, null], [43900, 6.2331, null], [44000, 8.0397, null], [44100, 5.6911, null], [44200, 3.523, null], [44300, 2.8004, null], [44400, 2.8004, \"class Solution {\\n public int subarraySum(int[] nums) {\\n\\n /** Optimal Approach **/\\n\\n int sum = 0;\\n int[] prefsum = new int[nums.length + 1];\\n\\n for(int i=0; i<nums.length; i++){\\n prefsum[i+1] = prefsum[i] + nums[i];\\n }\\n\\n for(int i=0; i<nums.length; i++){\\n int start = Math.max(0, i - nums[i]);\\n sum += prefsum[i+1] - prefsum[start];\\n }\\n\\n return sum;\\n\\n // /** BruteForce Approach **/\\n\\n // int sum = 0;\\n\\n // for(int i=0; i<nums.length; i++){\\n // int start = Math.max(0, i - nums[i]);\\n // for(int j=start; j<=i; j++){\\n // sum += nums[j];\\n // }\\n // }\\n\\n // // for(int i=1; i<nums.length; i++){\\n // // sum += nums[i-1];\\n // // sum += nums[i];\\n // // }\\n\\n // // return sum;\\n }\\n}\"], [44500, 2.71, \"class Solution {\\n public int subarraySum(int[] nums) {\\n int n= nums.length;\\n int psum[]= new int[n];\\n int start=0, fsum=0;\\n psum[0]=nums[0];\\n for(int i=1;i<n;i++)\\n {\\n psum[i]=psum[i-1]+nums[i];\\n }\\n for(int i=0;i<n;i++)\\n {\\n start=Math.max(0, i-nums[i]);\\n if(start==0)\\n {\\n fsum=fsum+psum[i];\\n }\\n else\\n {\\n fsum=fsum+ (psum[i]-psum[start-1]);\\n }\\n }\\n return fsum;\\n }\\n}\"]]",
"runtime": 1,
"runtimeDistribution": "[[0, 0.6323, \"class Solution {\\n public int subarraySum(int[] nums) {\\n int sum = nums[0];\\n\\n for(int i=1;i<nums.length;i++) {\\n int max = Math.max(0, i - nums[i]);\\n nums[i] += nums[i-1];\\n sum += nums[i] - (max == 0 ? 0 : nums[max - 1]);\\n }\\n\\n return sum;\\n }\\n}\"], [1, 95.122, \"class Solution {\\n public int subarraySum(int[] nums) {\\n // \\ud558\\uc704 \\ubc30\\uc5f4\\uc758 \\uc2dc\\uc791\\uc9c0\\uc810\\uc774 max(0, i - nums[i])\\uc774\\ubbc0\\ub85c, \\uc2dc\\uc791\\uc9c0\\uc810\\uc744 \\uad6c\\ud574\\uc11c i\\uae4c\\uc9c0\\uc758 \\uc694\\uc18c \\uac12\\uc744 \\ub354\\ud574\\uc900\\ub2e4.\\n int res = 0, temp = 0;\\n for(int i = 0; i < nums.length; i++){\\n temp = Math.max(0, i - nums[i]);\\n while(temp <= i){\\n res += nums[temp];\\n temp++;\\n }\\n }\\n\\n return res;\\n }\\n}\"], [2, 0.9937, null], [3, 0.6323, \"class Solution {\\n public int subarraySum(int[] nums) {\\n Map<Integer,Integer> prefixSum = new HashMap<>();\\n prefixSum.put(0,0);\\n int sum = 0;\\n for(int i=0;i<nums.length;i++){\\n sum+=nums[i];\\n prefixSum.put(i+1,sum);\\n }\\n //System.out.println(prefixSum);\\n int res = 0;\\n for(int i=0;i<nums.length;i++){\\n res+=prefixSum.get(i+1)-prefixSum.get(Math.max(0,i-nums[i]));\\n }\\n return res;\\n }\\n}\"], [4, 0.3613, \"class Solution {\\n public int subarraySum(int[] nums) {\\n\\n int n = nums.length;\\n int sum = 0;\\n int[] prefix = new int[n];\\n int start = 0;\\n\\n prefix[0] = nums[0];\\n for (int i = 1; i < n; i++) {\\n prefix[i] = prefix[i - 1] + nums[i];\\n }\\n System.out.println();\\n\\n // [2, 5, 1, 5]\\n // [2, 7, 8, 13]\\n\\n // 2 + 7 = 9 + 6 = 15 + 11 = 26\\n\\n for (int i = 0; i < n; i++) {\\n start = Math.max(0, i - nums[i]);\\n\\n if (start == 0) {\\n sum += prefix[i];\\n } else {\\n sum += prefix[i] - prefix[start - 1];\\n }\\n\\n }\\n\\n return sum;\\n \\n }\\n}\"]]"
},
"javascript": {
"code": "var subarraySum = function(nums) {\n let total = 0;\n const n = nums.length;\n for (let i = 0; i < n; i++) {\n const start = Math.max(0, i - nums[i]);\n let sum = 0;\n for (let j = start; j <= i; j++) {\n sum += nums[j];\n }\n total += sum;\n }\n return total;\n};",
"memory": 5800,
"memoryDistribution": "[[5800, 35.7146, \"var subarraySum = function(nums) {\\n let total = 0;\\n const n = nums.length;\\n for (let i = 0; i < n; i++) {\\n const start = Math.max(0, i - nums[i]);\\n let sum = 0;\\n for (let j = start; j <= i; j++) {\\n sum += nums[j];\\n }\\n total += sum;\\n }\\n return total;\\n};\"], [54200, 0.5102, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar subarraySum = function(nums) {\\n let result=0;\\n for(let i=0;i<nums.length;i++){\\n const start=Math.max(0,i-nums[i])\\n for (let j=start;j<=i;j++){\\n result +=nums[j];\\n }\\n }\\n return result;\\n \\n};\"], [54500, 0.5102, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar subarraySum = function(nums) {\\n let totalSum = 0;\\n \\n for (let i = 0; i < nums.length; i++) {\\n const start = Math.max(0, i - nums[i]);\\n for (let j = start; j <= i; j++) {\\n totalSum += nums[j];\\n }\\n }\\n \\n return totalSum;\\n};\\n\"], [54700, 0.5102, null], [54800, 1.0204, null], [54900, 0.5102, null], [55000, 1.0204, null], [55100, 0.5102, null], [55200, 2.0408, null], [55300, 4.0816, null], [55400, 3.5714, null], [55500, 4.5918, null], [55600, 1.5306, null], [55700, 5.102, null], [55800, 6.6327, null], [55900, 2.0408, null], [56000, 6.6327, null], [56100, 1.5306, null], [56200, 0.5102, null], [56400, 0.5102, null], [56500, 0.5102, null], [56700, 1.0204, null], [56800, 1.0204, null], [56900, 0.5102, null], [57000, 2.551, null], [57100, 3.0612, null], [57200, 2.551, null], [57300, 3.5714, null], [57400, 3.0612, null], [57500, 2.0408, null], [57600, 1.0204, null], [57700, 2.0408, null], [57800, 1.0204, null], [57900, 2.0408, null], [58000, 0.5102, null], [58100, 1.5306, null], [58200, 2.551, null], [58300, 1.5306, null], [58400, 1.5306, null], [58500, 1.0204, null], [58600, 0.5102, null], [58700, 0.5102, null], [58800, 1.0204, null], [58900, 0.5102, null], [59000, 1.5306, null], [59100, 1.5306, null], [59300, 2.0408, null], [59400, 0.5102, null], [59500, 2.0408, null], [59600, 3.0612, null], [59700, 0.5102, null], [59800, 0.5102, null], [59900, 0.5102, null], [60100, 1.0204, \"const subarraySum = (nums) => {\\n const prefix = nums.reduce((arr, v) => [...arr, arr.at(-1) + v], [0]);\\n return nums.reduce((sum, v, i) => sum + prefix[i + 1] - prefix[Math.max(0, i - v)], 0)\\n};\"], [60200, 0.5102, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar subarraySum = function (nums) {\\n let result = 0;\\n for (let i = 0; i < nums.length; i++) {\\n const startIdx = Math.max(0, i - nums[i]);\\n const sumOfSubArr = nums.slice(startIdx, i + 1).reduce((acc, cur) => acc + cur, 0); // Confusion between index (in terms of coding) vs index in real life.\\n result += sumOfSubArr\\n }\\n return result;\\n};\"]]",
"runtime": 1,
"runtimeDistribution": "[[0, 18.8776, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar subarraySum = function(nums) {\\n let n = nums.length;\\n let done = 0\\n for (let i = 0; i < n; i++) {\\n let sum = 0\\n let start = Math.max(0, i - nums[i])\\n for (let j = start; j <= i; j++) {\\n sum += nums[j]\\n }\\n done += sum\\n }\\n return done\\n};\"], [1, 35.7143, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar subarraySum = function(nums) {\\n\\n\\n let sum = 0\\n\\n for(let i = 0 ; i < nums.length ; i++)\\n {\\n let start = Math.max(0 , i - nums[i])\\n for(let j = start; j <= i ; j++)\\n {\\n sum = sum + nums[j]\\n }\\n }\\n\\n return sum;\\n \\n};\"], [2, 14.2857, null], [3, 10.7143, null], [4, 8.1633, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar subarraySum = function(nums) {\\n let i = 0;\\n let start = 0;\\n let sum = 0;\\n while (i < nums.length) {\\n start = Math.max(0, i - nums[i]);\\n sum += nums.slice(start, i+1).reduce((a, b) => a+b);\\n i++;\\n }\\n\\n return sum;\\n};\"], [5, 6.6327, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar subarraySum = function(nums) {\\n let sum = 0;\\n let prefix = [nums[0]];\\n for (let i = 1; i < nums.length; i++) {\\n let item = prefix[i - 1] + nums[i];\\n prefix.push(item);\\n }\\n for (let i = 0; i < nums.length; i++) {\\n sum += prefix[i] - (prefix[i - nums[i] - 1] || 0);\\n } \\n return sum;\\n};\"]]"
},
"python3": {
"code": "class Solution:\n def subarraySum(self, nums: List[int]) -> int:\n total = 0\n n = len(nums)\n for i in range(n):\n start = max(0, i - nums[i])\n for j in range(start, i + 1):\n total += nums[j]\n return total",
"memory": 1800,
"memoryDistribution": "[[1800, 72.1311, \"from typing import List\\n\\nclass Solution:\\n def subarraySum(self, nums: List[int]) -> int:\\n total = 0\\n n = len(nums)\\n for i in range(n):\\n start = max(0, i - nums[i])\\n for j in range(start, i + 1):\\n total += nums[j]\\n return total\"], [17500, 0.7715, \"class Solution:\\n def subarraySum(self, nums: List[int]) -> int:\\n total = 0\\n for i in range(len(nums)):\\n start = max(0, i - nums[i])\\n slice = nums[start:i + 1]\\n total += sum(slice)\\n return total\"], [17600, 5.4002, \"class Solution:\\n def subarraySum(self, nums: List[int]) -> int:\\n total = 0\\n for i in range(len(nums)):\\n start = max(0, i - nums[i])\\n total += sum(nums[start:i + 1])\\n return total\"], [17700, 21.6972, null], [17800, 27.4831, null], [17900, 16.4899, \"class Solution:\\n def subarraySum(self, nums: List[int]) -> int:\\n ans = 0\\n for i in range(len(nums)):\\n start = max(0, i-nums[i])\\n ans += sum(nums[start:i+1])\\n return ans\"], [18000, 22.6615, \"class Solution:\\n def subarraySum(self, nums: List[int]) -> int:\\n total = 0\\n for i in range(len(nums)):\\n start = max(0, i - nums[i])\\n sub_arr = nums[start:i+1]\\n total += sum(sub_arr)\\n return total\\n \"]]",
"runtime": 16,
"runtimeDistribution": "[[0, 5.4966, \"class Solution:\\n def subarraySum(self, nums: List[int]) -> int:\\n i=1\\n s=[0]*(len(nums)+1)\\n s[0]=0\\n \\n while i<=len(nums):\\n s[i]=(nums[i-1] + s[i-1])\\n i+=1\\n \\n i = 1\\n sum1=nums[0]\\n while i < len(nums):\\n l = max(0, i - nums[i]) \\n sum1+=(s[i+1]-s[l])\\n i += 1\\n return sum1\\n \\n\\n \"], [1, 1.7358, \"class Solution:\\n def subarraySum(self, nums: List[int]) -> int:\\n res = nums[0]\\n for i in range(1, len(nums)):\\n j = i - nums[i] - 1 \\n nums[i] += nums[i - 1] \\n if j < 0:\\n res += nums[i]\\n else:\\n res += nums[i] - nums[j]\\n return res\\n\"], [2, 1.6393, null], [3, 11.9576, null], [4, 7.2324, null], [5, 2.0251, null], [6, 3.3751, null], [7, 18.6114, null], [8, 7.2324, null], [9, 3.9537, null], [10, 3.568, null], [11, 12.054, null], [12, 2.0251, null], [13, 0.675, null], [14, 1.0608, null], [15, 3.1823, null], [16, 1.2536, null], [17, 0.675, null], [18, 1.6393, null], [19, 4.243, \"class Solution:\\n def subarraySum(self, nums: List[int]) -> int:\\n # pref_sum = [0]*(len(nums))\\n # pref_sum[0] = nums[0]\\n # while i < len(nums):\\n # pref_sum[i] = nums[i]+pref_sum[i-1]\\n # i += 1\\n \\n i = 0\\n res = 0\\n while i < len(nums):\\n start = max(0,i-nums[i])\\n while start <= i:\\n res += nums[start]\\n start += 1\\n i += 1\\n \\n return res\\n # res = 0\\n # j = 0\\n # while j < len(nums):\\n # start = max(0, j - nums[j])\\n # stop = j\\n # res += pref_sum[j] - pref_sum[start-1]\\n # j+=1\\n # return res\\n\\n\\n \\n\\n \\n\\n \\n\\n\"], [20, 0.7715, \"class Solution:\\n def subarraySum(self, nums: List[int]) -> int:\\n sumf=0\\n for i in range(len(nums)):\\n start=max(0,i-nums[i])\\n subarray=nums[start:i+1]\\n tempsum=0\\n for i in subarray:\\n tempsum=tempsum+i\\n sumf=sumf+tempsum\\n return sumf\"]]"
},
"ruby": {
"code": "def subarray_sum(nums)\n total = 0\n nums.each_index do |i|\n start = [0, i - nums[i]].max\n total += nums[start..i].sum\n end\n total\nend",
"memory": 21200,
"memoryDistribution": "[[21200, 100.0, \"def subarray_sum(nums)\\n total = 0\\n nums.each_index do |i|\\n start = [0, i - nums[i]].max\\n total += nums[start..i].sum\\n end\\n total\\nend\"], [212000, 25.0, \"# @param {Integer[]} nums\\n# @return {Integer}\\ndef subarray_sum(nums)\\n nums.each_with_index.sum do |i, idx|\\n start = [0, idx - i].max\\n nums[start..idx].sum\\n end\\nend\"], [212100, 25.0, \"def subarray_sum(nums)\\n total = 0\\n nums.each_index do |i|\\n start = [0, i - nums[i]].max\\n total += nums[start..i].sum\\n end\\n total\\nend\"], [212200, 50.0, \"# @param {Integer[]} nums\\n# @return {Integer}\\n\\ndef get_max(a, b)\\n if a < b\\n return b\\n end\\n a\\nend\\n\\ndef subarray_sum(nums)\\n result = 0\\n\\n puts nums.size\\n\\n for i in 0 ... nums.size do\\n for j in get_max(0, i - nums[i]) .. i do\\n result += nums[j]\\n end\\n end\\n\\n result\\nend\"]]",
"runtime": 11,
"runtimeDistribution": "[[3, 25.0, \"# @param {Integer[]} nums\\n# @return {Integer}\\n\\nclass Numeric\\n def max(v) = (self > v ? self : v)\\nend\\n\\ndef subarray_sum(nums)\\n sums = nums.inject([0]) {|res, v| res << res.last + v }\\n nums.each_with_index.sum {|(v, i)| sums[i + 1] - sums[0.max(i - v)] }\\nend\"], [6, 25.0, \"def subarray_sum(nums)\\n total = 0\\n nums.each_index do |i|\\n start = [0, i - nums[i]].max\\n total += nums[start..i].sum\\n end\\n total\\nend\"], [11, 25.0, \"# @param {Integer[]} nums\\n# @return {Integer}\\ndef subarray_sum(nums)\\n nums.each_with_index.sum do |i, idx|\\n start = [0, idx - i].max\\n nums[start..idx].sum\\n end\\nend\"], [41, 25.0, \"# @param {Integer[]} nums\\n# @return {Integer}\\n\\ndef get_max(a, b)\\n if a < b\\n return b\\n end\\n a\\nend\\n\\ndef subarray_sum(nums)\\n result = 0\\n\\n puts nums.size\\n\\n for i in 0 ... nums.size do\\n for j in get_max(0, i - nums[i]) .. i do\\n result += nums[j]\\n end\\n end\\n\\n result\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list:
import random
# Sample solution based on the provided sample solution.
def sample_solution(nums):
total = 0
n = len(nums)
for i in range(n):
start = max(0, i - nums[i])
for j in range(start, i + 1):
total += nums[j]
return total
# Helper to serialize the input: comma-separated integers.
def serialize_input(nums):
return ",".join(map(str, nums))
# Helper to serialize the expected output as a plain string.
def serialize_output(result):
return str(result)
# Predefined test cases covering boundary, edge, and core functionality.
fixed_cases = [
[1],
[2, 3, 1],
[3, 1, 1, 2],
[1, 1, 1, 1],
[5, 4, 3, 2, 1],
[100, 999, 1, 50],
list(range(1, 11))
]
test_cases = []
# Use fixed predefined cases first.
for nums in fixed_cases:
if len(test_cases) >= num_cases:
break
result = sample_solution(nums)
test_cases.append({
"input": serialize_input(nums),
"output": serialize_output(result)
})
# Generate additional random test cases if needed.
random.seed(seed)
while len(test_cases) < num_cases:
n = random.randint(1, 100) # n between 1 and 100.
nums = [random.randint(1, 1000) for _ in range(n)]
result = sample_solution(nums)
test_cases.append({
"input": serialize_input(nums),
"output": serialize_output(result)
})
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
try:
expected = int(expected_output.strip())
actual = int(program_output.strip())
return expected == actual
except Exception:
return False
|
[{"input": "1", "output": "1"}, {"input": "2,3,1", "output": "11"}, {"input": "3,1,1,2", "output": "13"}, {"input": "1,1,1,1", "output": "7"}, {"input": "5,4,3,2,1", "output": "38"}, {"input": "100,999,1,50", "output": "3349"}, {"input": "1,2,3,4,5,6,7,8,9,10", "output": "220"}, {"input": "115,26,760,282,251,229,143,755,105,693,759,914,559,90,605,433,33,31,96,224,239,518,617,28,575,204,734,666,719,559,430,226,460,604,285,829,891,7,778,826,164,715,433,349,285,160,221,981,782,345,105,95,390,100,368,868,353,619,271,827,45,748,471,550,128,997,945,388,81,566,301,850,644,634,907,883,371,592,197,722,72,47", "output": "1410197"}, {"input": "234,792,297,82,876,239,888,104,390,285,465,651,855,374,167,380,364,215,687,274,719,960,700,664,74,624,651,176,547,747,251,168,474,389,277,948,656,705,571,225,702,333,864,787,795,58,235,842,33,825,324,411,275,68,217,936,966,581,898,736,323,218,672,512,406,906,937,659,470,147,272,143,253,763,575,552,270,765,599,439,920,598,409,371,225", "output": "1779868"}, {"input": "522,506,94,774,49,882,113,157,643,164,812,697,433,611,66,395,391,611", "output": "74123"}, {"input": "542,258,995,567,882,966,12,697,739,118,699,907,550,769,274,788,657,349,115,301,446,162,465,4,977,740,897,737,270,996,513,781,183,520,935,109,892,641,306,862,655,520,624,204,157,383,781,166,553,977,798,945,544,941,1,614,332,501,20,115", "output": "963653"}, {"input": "900,852,827,315,246,60,247,900,581,970,81,88,750,498,836,71,779,546,785,129,132,676,487,970,563,170,272,541,894,622,434,988,217,952,553,774,748,707,206,731,320,409,688,666,383,449,922", "output": "608435"}, {"input": "463,124,254,231,66,347,22,603,568,236,603,226,8,73,725,647,61,235,70,928,33,881,339,73,527,244,286,686,498,220,553,136,741,958,904,585,591,485,249,804,485,827,417,195,97,100,675,442,363,434,421,479,885,747,56,690,670,662,101,63,413,746,348,820,883,112,255", "output": "891892"}, {"input": "195,550,460,144,433,188,286,474,256,896,946,78,454,828,883,877,564,101,52,668,554,857,16,993,96", "output": "143547"}, {"input": "870,243,171,417,498,493,219,886,411,925,61,169,389,3,400,272,949,803,804,466,293,434,714,981,749,803,570,678,736,499,159,195,304,223,992,60,594,754,556,63,766,322,59,52,599,489,515,942,874,544,162,59,984,521,83,872,191,71,610,70,692,883,241,414,123,965,912,584,253,593,609,41,635,84,430,674,598,579,536,324,958,268,210,686,734,322,245,272,406,135,688,661,308,469,324,952,770", "output": "2289251"}, {"input": "10,470,637,577,103,76,551,219,519,272", "output": "18634"}, {"input": "956,358,903,71,901,251,379,292,162,449,854,557,721,310,627,827,670", "output": "81753"}, {"input": "9,684,837,568,307,955,680,107,962,900,138,271,119,912,110,761,567,160,279,289,620,216,735,352,209,704,650,874,271,518,501,258,928,930,867,53,95,650,434,850,284,46,4,342,790,134,653,269,166,760,453,565,723,438,575,10,115,78,968,905,708,926,153,559,37,855,379,597", "output": "1087849"}, {"input": "152,441,131,43,316,374,921,956,816,996,882,41,921,367,216,699,256,683,106,363,799,574,906,896,417,998,636,768,159,948,953,243,886,167,1000,820,831,182,903,423,26,184,755,947,341,802,954,422,822,686,885,753,831,255,274,164,807,719,111,392,894,40,880,482,228,205,837,941,472,359,313", "output": "1418525"}, {"input": "229,25,676,198,409,337,286,886,72,991,792,286,360,657,522,410,696,864,550,340,962,29,119,899,994,268,183,595,986,272", "output": "214497"}, {"input": "112,611,445,354,747", "output": "5794"}, {"input": "447,621,524,119,395,922,591,195,261,46,726,447,2,533,948,826,552,704,737,963,760,755,687,202,373,442,72,972,681,943,339,639,322,680,869,128,738,922,308,520,317", "output": "447000"}, {"input": "419,335,413,714,303,568,131,197,431,681,963,389,694,767,925,179,631,583,309,416,562,854,1,312,294,216,441,805,594,622,671,330,477,453,453,692,219,524,485,813,923,983,816,754,174,675,87,291,528,680,649,635,344,96,839,975,770,241,689,318,231,826,204,151,26,48,251,487,626,871,787,75,467,425,908,645,590,200,736,714,394,507,410,250,152,672", "output": "1848965"}, {"input": "6,915,769,882,789,907,110,798,436,225,181,824,981,713,531,476,52,571,256,940,869,125,468,137,821,476,684,544,573,610,325,973,774,913,454,628,835,737,914,517,437,851,929,562,457,919,163,762,883,487,461,266,770,254,861,653,284,785,797,534,497,642,245,282,451,80,731,293,241,279,344,328,915,554,83,142,155,237,393,711,157,724,220,66,425,418,339,556,478", "output": "2269529"}, {"input": "64,212,853,431,399,927,789,599,969,713,21,878,902,784,590,390,489,7,966,361,306,772,400,874,914,977,856,430,552,766,753,560,820,618,920,226,500,225,280,447,498,30,399,345,685,696,818,415,742,170,861,479,942,131", "output": "850908"}, {"input": "547,28,929,404,607,578,679,28,86,659,439,139,888,473,187,52,267,389,336,217,466,335,346,780,901,389,285,771,975,852,432,259,855,84,482,20,768,553,54,975,359,230,666,71,800,981,668,42,773,32,973,254,205,860,21,637,157,245,130,485,686,118,578,971,224,477,717,263,786,378,172,621,622,987,766,736,118,797,839,168", "output": "1454496"}, {"input": "111,593,27,952,320,590,694,930,982,385,407,965,733,204,78,607,708,851,643,249,105,714,792,309,871,701,615,825,124,816,580,802,43,356,546,439,678,380,71,519", "output": "448265"}, {"input": "350,13,870,431,843,502,109,444,984,371,651,913,849,471,725,157,446,181,752,535,989,667,277,631,828,942,552,794,496,477,447,846,749,607,275,331,873,252,851,958,89,286,903,462,250,769,476,584,625,685,389,345,30,507,872,333,187,500,218,364,817,265,349,287,902,611,719,902,283,570,11,530,971,196,88,248,738,417,501,569,777,247,708", "output": "1865289"}, {"input": "662,729,503,459,812,18,96,302,227,415,709,250,314,680,596,378,485,567,544,353,436,764,564,339,361,720,465,278,314,258,237,124,739,198,324,123,761,549,974,781,707,190,197,222,757,496,284,742,604,779,538,612,290,103,853,199,304,233,370,184,310", "output": "864613"}, {"input": "726,547", "output": "1999"}, {"input": "281,47,998,56,567,300,715,967,130,654,890,771,503,106,894,13,588", "output": "72954"}, {"input": "481,491,452,349,189,989,53,259,964,883,490,117,842,67,411,504,76,591,645,703,55,156,153,831,577,972,312,88,255,122,572,783,427,621,611,810,634", "output": "322449"}, {"input": "795,536,390,462,931,454,305,881,603,440,313,583,636,62,625,984,758,102,971,782,213,641,217,271,677,84,161,246,178", "output": "238675"}, {"input": "77,161,3,419,462,706,609,482,299,34,238,296,724,290,720,881,465,73,704,240,947,271,807,811,641,604,678,824,957,203,436,118,558,231,664,153,931,273,847,146,74,62,170,812,315,610,767,845,583,944,296,450,128,480,706,312,717,413,966,279,513,553,506,449,83,613,41,911,443,753,331", "output": "1173012"}, {"input": "257,27,94,235,985,691,857,882,590,602,974,22,784,689,842,276,591,42,782,775,180,482,532,668,453,939,285,186,600,447,651,834,504,993,94,482,357,419,342,329,687,108,879,165,338,422,711,508,296,679,968,411,834,779,564,38,466,91,323,259,332,119,994,792,414,886,527,845,2,674,891,556,474,424,56,193,531,371", "output": "1539167"}, {"input": "775,511,641,453,779,53,209,274,563,135,950,295,449,902,716,497,125,30,997,646,624,819,246,727,163,319,565,15,566,418,96,231,862,935,117,473,970,121,664,853,158,511,956,734,299,522,723,280,426,855,495,484,250,468,565,149,393,196,944,614,521,765,901,140,885,72,283,792,809,875,425,349,957,807,520,274,841,3,290,744", "output": "1579064"}, {"input": "858,602,594,676,502,887,153,458,552,496,354,341,566,782,557,387,467,956,330,891,194,715,245,586,393,240,877,795,421,45,326,763,485,723,936,831,391,396,680", "output": "430035"}, {"input": "156,508,988,38,130,515,989,605,340,891,103,896,866,451,103,298,24,216,645,89,275,528,180,188,123,76,635,745,267,932,822,339,976,979,773,715,506,185,20,912,882,356,384,328,233,167,104,407,830,993,960,754,755,665,929,798,798,909,565,860,333,901,847,361,325,1,158,397,844,947,611,292,818,377,15,362,991,536,836,214,745,402,56,474", "output": "1696239"}, {"input": "153,574,515,289,801,593,591,205,984,975,594,154,813,747,847,545,650,992,573,749,729", "output": "130742"}, {"input": "417,898,398,518,593,542,15,101,32,410,648,695,349,964,788,911,909,742,185,543,353,292,978,320,752,201,33,322,179,677,217,765,436,106,972,261,889,970,784,98,443,849,807,956,994,240,669,456,19,472,654,166,509,935,267,723,143,918,30,47,896,675,908,839,653,875,358,55,188,666,636,301,824,806,5,908,968,454,584,629,233,617,932,454,486,752,575,525,866,86,49,954", "output": "2142771"}, {"input": "521,379,600,103,961,357,791,612,26,759,368,886,272,175,904,845,304,570,776,458,536,290,649,46,316,108,787,315,512,992,107,267,7,697", "output": "287241"}, {"input": "881,776,930,803,531,475,500,835,591,778,358,868,805,80,332,715,964,411,625,603,851,165,138,606,118,958,662,205,468,648,787,597,35,644,65,408,568,537,289,691,15,316,716,490,868,414,707,242,236,12,800,639,709,953,596,318,483,794,657,611,103,313,105,926,322,671", "output": "1215073"}, {"input": "191,786,978,912,514,310,142,479,901,968,390,503,842,862,468,285,105,444,345,248,798,456,287,940,418,753,385,782,986,452,570,352,848,430,211,701,454,104,387,304,243,407,70,669,723,117,97,981,415,825,531,378,602,831,381,900,142,319,73,928,507,121,441,535,506,309,503,561,168,323,417,654,254,280", "output": "1455611"}, {"input": "758,209,178,333,90,11,126,873,84,28,170,674,947,824,958,571,536,208,711,121,804,275,586,683,792,70,277,79,55,87,92,760,133,47,826,84,663,465,832,313,479,265,718,574,96,321,704,487,583,447,99,603,891,831,281,908,133,194,798,513,58,191,757,70,177,264,330,823,711,552,158,269,877,799,490,768,9,522,992,26,768,511,45,599,185,473,530,660,806,372,460,276,750,198", "output": "1841788"}, {"input": "711,296,168,338,282,183,694,318,696,473,63,971,177,396,640,900,111,645,327,844,812,678,300,409,416,447,622,641,135,944,883,2,496,794,716,179,586,471,153,135,803,772,793,242,718,119,738,955,536,664,449,1000,27", "output": "665355"}, {"input": "901,421,965,709,247,214,848,998,310,774,751,284,359,237,597,451,969,369,896,911,48,563,177,584,916,670,21,705,206,978,526,737,330,399,718,878,610,514,48,980,142,571,311,286,2,956,946,158,462,530,205,430,709,136,675,388,566,993,930,735,930,283,633,919,304,112", "output": "1207146"}, {"input": "897,695,903,301,828,999,469,614,57,271,294,467,335,84,355,241,918,503,649,621,171,411,916,654,19,857,778,442,22,918,553,789,819,885,133,256,700,530,151,12,981,700,17,15,699,652,177,609,484,550,9,432,654,494,749,812,566,143,641,275,433,322,647,322,208,5,625,151,153,186,976,175,124,131,527,561,106,409,639,22,210,814,975,328,840,550,839,223", "output": "1815267"}, {"input": "995,927,179,735,918,154,234,171,507,148,231,313,266,142,275,74,921,788,903,402,871,60,529,220,570,538,957,660,684,84,261,776,557,599,664,610,278,555,961,686,171,687,169,220,703,979,197,130,181,515,962,745,309,436,773,879,405,123,617,598,581,456,84,47,521,725,97,785,522,410,202,151,960,938,929,114,246,659,233,457,960,771,710,326,733,968,698,876,183,83,798,267,354,678,366,846,310,264,458,135", "output": "2504841"}, {"input": "490,29,732,53,895,271,529,930,626,941,698,653,634,505,822,270,791,261,170,931", "output": "113136"}, {"input": "674,352,629,700,881,464,206,33,224,504,260,528,881,826,374,664,54,538,218,803,449,860,276", "output": "137588"}, {"input": "149,752,52,770,927,910,54,410,675,5,851,664,801,564,253,3,655,974,466,500,250,978,446,765,681,391,495,779,373", "output": "219510"}, {"input": "365,596,532,453,927,499,978,96,745,752,934,753,325,480,861,240,232,239,341,228,514,217,511,785,994,604,990,39,189,253,547,741,953,767,607,937,984,299,801,692,58,335,448,609,749,297,696,852,470,389,781,108,975,627,173,475,962,757,908,538,123,158,761,693,924", "output": "1197654"}, {"input": "473,621,648,411,159,287", "output": "10373"}, {"input": "37,901,589,817,629,362,163,164,269,673,137,773,466,336,437,119,891,461,734,252,920,997,458,155,56,81,488,872,745,710,851,966,24,66,116,457,329,654,339,341,711,401,466,471,894,302,492,254,378,115,45,912,429,465,733,311,888,305,267,709,620,809,621,810,521,578,44,805,727,503", "output": "1169285"}, {"input": "718,409,500,643,504,532,918,864,757,729,528,54,241,19,830,170", "output": "79286"}, {"input": "770,590,870,139,225,691,693,748,2,942,10,574,220,230,310,124,920,547,492,825,997,124,799,328,724,321,809,702,19,829,201,632,641,199,57,796,861", "output": "350637"}, {"input": "522,966,877,959,11,195,770,379,276,211,108,847,944,256,452,754,226,112,155,955,729,585,379,816,712,30,814,794,278,565", "output": "244588"}, {"input": "642,879,998,931,751,559,111,790,632,555,511,719,374,579,869,580,474,234,142,711,182,658,598,137,896,854,493,538,40,637,605,147,929,535,241,904,821,718,679,589,865,553,406,216,896,592,97,645,40,430,183,32,284,975,440,851,472,576,425,933,202,930,42,787,228,556", "output": "1234658"}, {"input": "873,397,593,70,936,586,773,264,559", "output": "26034"}, {"input": "492,41,479,665,389,716,628,972,551,768,417,868,895,839,263,280,846,281,601,66,123,559,360,84,44,109,352,270,685,171,451,797,996,180,331,343,910,471,235,16,755,105,517,765,48,539,507,139,346,516,309", "output": "631697"}, {"input": "720,15,477,650,751,981,210,992,776,436,85,872,847,245,192,37,312,59,820,892,860,408,862,256,794,167,860,175,199,397,177,659,519,98,658,863,729,755,961,596,826,837", "output": "475672"}, {"input": "577,638,959,888,82,819,107,809,85,218,27,487,235,431,397,93,818,772,794,614,722,415,469,920,113,593,451,604,979,985,442,806,995,609,449,537,69,390,178,411,389,502,97,776,278,66,444,815,559,178,417,680,707,373,595,505,43,56,456", "output": "900969"}, {"input": "955,166,933,114,830,142,463,75,684,744,945,144,88,832,363,127,792,636,820,455,911,667,981,20,622,864,413,773", "output": "212535"}, {"input": "470,225,112,815,440,487,209,852,259,987,582,636,154,568,859,266,148,442,500,533", "output": "98545"}, {"input": "753,95,845,459,513,865,287,10,332,308,555,357,948,666,116,132,18,418,109,130,755,387,525,837,488,898,255,482,13,109,277,273,634,694,872,998,857,515,468,496,104,930,718,708,376,539,664,879,984,623,764,863,129,778", "output": "686428"}, {"input": "569,818,101,996,747,149,704,367,611,519,240,221,736,577,702,577,79,606,504,909,742,682,593,220,430,514,431,928,839,273,163,121,324,70,83,932,747,137,725,826,401,69,8,602,750,68,742,139,541,729,155,491,499,323,387,675,934,360,196,622,581,817,574,720", "output": "1032053"}, {"input": "1000,503,439,733,642,644,479,234,961,821,161,432,773,867,835,315,166,447,677,426,790,461,454,217,29,90,269,947", "output": "235951"}, {"input": "840,207,349,675,141,498,692,629,691,275,246,290,39,948,469,75,717,760", "output": "80671"}, {"input": "416,146,786,744,497,411,447,266,493,542,731,883,714,315,535,445,29,657,323,394,257,994,121,235,82,726,24,411,412,403,934,798,46,742,158,628,719,882,508,147,631,311,342,121,208,745,364,892,421,7,616,607,54,78,673,267,815,533,15,412,568,74,60,906,440,642,347,887,608,853,763,374,704,2,985,209,657,409,858,223,699,801,151,441,176,233,487,331,23,344,756,860,647,301,215,158", "output": "2066344"}, {"input": "738,430,11,997,163,494,574,281,920,399,967,719,944,187,291,879,57,385,923,705,530,210,975,463", "output": "161709"}, {"input": "610,768,266,735,366,538,495,869,715,56,817,148,219,770,19,483,654,812,67,45,768,337,386,314,43,759,23,423,461,965,313,109,382,538,395,508,626,326,690,135,294,743,24", "output": "433065"}, {"input": "550,508,719,280,857,102,324,774,874,672,994,857,659,379,917,18,465,340,504,996,425,265,314,592,386,642,254,887,795,587,188,99,312,569,817,123,584,404,319,171,869,283,734,913,64,879,290,785,201,411,375,298,763,332,82,605,77,730,964,865,437,52,52,656,182,726,142,156,438,698,997,339,931,729,433,505,898,611,634,161,431,385", "output": "1757372"}, {"input": "310,235,877,285,923,735,747,765,100,912,475,807,557,674,67,870,310,536", "output": "97141"}, {"input": "755,44,551,625,722,970,399,370,985,747,666,950,572,392,106,306,418,628,156,673,985,991,845,938,120,709,79,869,597,228,838,697,391,552,476,769,372,491,282,93,175,929,178,732,521,485,439,498,13,695,257,274,316,950,486,823,73,552,397,579,304,676,66,233,917,618,54,261,38,553,54,520,938,418,144,731,750,534,779,823,732,238,326,746,718,336,650", "output": "1992134"}, {"input": "104,289,189,479,33,601,224,947,86,610,86,745,188,952,722,66,155,344,805,672,597,836,344,235,973,344,220,644,138,737,296,123,169,884,435,425,413,714,183,979,673,47,436,576,915,335,402,423,801,777,940,780,45,863,888,771,629,4,726,156,528,562", "output": "853265"}, {"input": "815,312,71,72,854,79,733,122,652,135,30,93,368,35,159,801,385,899,93,883,874,344,379,894,814,261,738,155,475,950,708,457,687,910,94,662,280,67,915,54,320,940,367", "output": "406891"}, {"input": "895,534,549,484,417,298,749,443,520,964,524,22,826,972,883,634,26,725", "output": "99054"}, {"input": "259,951,640,711,329,160,390,29,344,721,898,112,993,758,759,514,982,378,852,301,752,758,394,284,97,888,207,498,149,835,785,573,110,109,131,172,214,80,311,269,572,547,416,969,235,426,434,517,34,180,623,326,377,275,943,558,352,774,986,578,721,904,762,788,649,947,611,458,338,842,829,958,189,878,422,355,896,826,782,501,39,844,59,355,421,143,537,717", "output": "1937240"}, {"input": "291,883,982,198,901,801,819,150,637,657,34,728,954,921,555,91,724,96,437,45,731,855,610,992,421,183,630,703,253,579,742,335,746,803,906,767,653,445", "output": "431576"}, {"input": "200,392,96,333,812,105,9,925,787,8,209,508", "output": "26477"}, {"input": "643,651,872,586,703,152,128,818,154,10,635,430,951,630,948,525,798,396,38,51,711,734,509,478,865,701,336,458,948,96,371,371,806,915", "output": "318530"}, {"input": "395,142,707,193,590,701,291,509,427,317,916,419,868,721,632,65,755,289,855,346,468,523,815,384,635,850,716,891,680,750,8,594,345,123,617,744,564,946,863,30,601,321,611", "output": "481369"}, {"input": "792,63,367,386,19,874,221,842,132,400,860,887,860,416,783,844,138,746,712,349,751,100,57,239,100,373,874,255,26,522,480,832,35,245,233,1,869,972,167,283,421,496,948,492,429,681,640,764,431,567,669,569,944,878,457,750,6,436,962,301,92,58,521,55,638,677,971,68,8,482,672,160,919,577,629,752,445,508,176,181", "output": "1487328"}, {"input": "789,540,347,360,119,350,865,647,459,37,962,208,265,208,290,813,588,95,450,827,903,79,680,52,55,239,669,642,974,351,837,505,988,641,42,343,904", "output": "328544"}, {"input": "233,669,225,988,956,664,815,316,858,607,288,251,641,500,292,503,384,61,440,214,412,922,572,981,346,214,578,639,881,924,706,962,189,520,409,739,210,385,958,597,668,702,938,948,239,258,691,82,995,66,827,373,141,365,429,276,810,104,666,409,363,961,51,442,973,863,304,217,723", "output": "1307440"}, {"input": "852,984,27,354,303,63,770,742,414,584,436,379,103,283,524,145,395,876,893,572,181,468,145,348,417,781,864,253,939,640", "output": "220610"}, {"input": "316,346,672,887,979,933,543,626,400,12,72,610,231,653,465,503,804,898,174,565,399,512,325,658,774,445,414,758,551,25,809,504,200,318,347,714,706,763,932,471,852,128,24,476,108,470,526,23", "output": "593740"}, {"input": "361,332,867,39,177,438,311,488,138,137,207,79,268,908,423,698,301,809,158,48,156,14,938,457,405,367,500,588,441,981,405,775,467,358,535,83,708,212,307,234,785,304,710,278,475,961,878,453,855,759,390,765,173", "output": "576526"}, {"input": "407,724,715,583,395,418,690,254,458,563,924,992,438,123,187,988,978,6,860,268,982,362,638,506,509,793,420,494,869,739", "output": "254392"}, {"input": "993,805,259,59,259,635,357,937,826,32,406,808,966,947,659,613,171,358,850,88,768,965,619,961,683,955,128,89,356,677,383,440,352,994,815,822,985,182,632,881,145,467,685,569,128,646,195,415,148,265,698,563,12,791,725,273,444,493,481,942,624,225,923,204,570,243,598,348,807,748,56,155,641,972,475,574,396,985,678,977,161,692,928", "output": "1899897"}, {"input": "207,867,693,890,111,271,936,92,234,325,762,993,35,198,706,860,621,462,537,997,867,321,84,307,838,73,181,17,863,923,69,76,785,596,25,395,506,972,499,236,896,428,558,327,180,693,242,466,955,788", "output": "625990"}, {"input": "974,318,950,1000,476,426,125,119,343,351,545,752,290,599,980,684,780,490,787,196,520,895,311,10,4,532,114,77,849,64,366,869,145,94,172,271,22,683,917,491,434,741,423,494,536,388,719,807,104,629,545,399,779,391,297,362,207,250,530,205,467,233,209,126,47,825,450,843,645,848,309,449,410,26,198,89,41,481,455,469,196,661,377", "output": "1570233"}, {"input": "242,592,420,271,82,277,926,317,93,169,493,810,781,379,492,836,853,583,549,566,15,180,469,772,144,59,629,624,868,701,202,340", "output": "232601"}, {"input": "924,374,74,159,1,978,633,544,465,851,367,349,320,956,765,410,511,892,736,58,11", "output": "108989"}, {"input": "487,363,700,561,471,45,840,992,102,136,807,762,532,20,576,470,34,197,281,103,950,902,124,402,201,552,429,76,37,94,10,543,205,55,106,381,199", "output": "296270"}, {"input": "771,955,691,650,142,886,806,460,999,570,23,47,826,745,335,419,915,39,522,546,418,198,806,572,976,676,820,296,88,616,982,394,144,890,558,320,831,109,830,614,268,270,450,289", "output": "566927"}, {"input": "636,30,741,369,508,594,171,255,173,679,750,65,790,556,203,586,331,493,426,722,553,910,913,353,202,542,621,238,195,336,385,130,717,274,116,623,356,85,478,926,784,569,412,241,102,557,666,597,945,184", "output": "581772"}, {"input": "531,390,634,786,573,661,375,423,525,481,740,880,583,394,908,711,466,719,208,477,705,611,746,858,628,372,393,548,534,828,34,749,966,531,331,757,705,613,675,418,447,358,147,122,960,391,875,918,224,705,656,646,312,539,488,566,838,388,767,276", "output": "1054784"}, {"input": "25,128,53,338,950,120,666,96,518,292,820,948,143,678,763,824,385,946,312,127,759,5,161,150,831,906,52,375,548,246,330,593,859,331,652,488,791,567,536,22,713,546,229,355,138,386,878,178,744,998,459,251,977,943,681,937,552,185,453,406,995,847,17,447,728,712,467", "output": "1024417"}, {"input": "408,149,375,5,953", "output": "4724"}]
|
{
"cpp": "==Code Submission==\n\nvector<int> deserialize_stdin(const string &input) {\n vector<int> nums;\n stringstream ss(input);\n string token;\n while(getline(ss, token, ',')) {\n if(!token.empty()) {\n nums.push_back(stoi(token));\n }\n }\n return nums;\n}\n\nstring serialize_stdout(int result) {\n return to_string(result);\n}\n\nint main() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n string line;\n getline(cin, line);\n vector<int> nums = deserialize_stdin(line);\n Solution sol;\n int ans = sol.subarraySum(nums);\n cout << serialize_stdout(ans);\n return 0;\n}",
"golang": "==Code Submission==\n\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n line, _ := reader.ReadString('\\n')\n line = strings.TrimSpace(line)\n if line == \"\" {\n return\n }\n parts := strings.Split(line, \",\")\n nums := make([]int, len(parts))\n for i, s := range parts {\n nums[i], _ = strconv.Atoi(s)\n }\n ans := subarraySum(nums)\n fmt.Print(ans)\n}",
"java": "public class Main {\n private static int[] deserializeIntArray(String input) {\n String[] tokens = input.split(\",\");\n int[] nums = new int[tokens.length];\n for (int i = 0; i < tokens.length; i++) {\n nums[i] = Integer.parseInt(tokens[i].trim());\n }\n return nums;\n }\n \n private static String serializeOutput(int result) {\n return Integer.toString(result);\n }\n \n public static void main(String[] args) throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n String line = br.readLine().trim();\n int[] nums = deserializeIntArray(line);\n Solution sol = new Solution();\n int ans = sol.subarraySum(nums);\n System.out.println(serializeOutput(ans));\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\n\nconst deserialize_stdin = (input) => {\n input = input.trim();\n if (input === \"\") return [];\n return input.split(\",\").map(Number);\n};\n\nconst serialize_stdout = (result) => {\n return result.toString();\n};\n\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\nlet input = '';\nprocess.stdin.on('data', chunk => input += chunk);\nprocess.stdin.on('end', () => {\n const nums = deserialize_stdin(input);\n const ans = subarraySum(nums);\n console.log(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str):\n if not input_str:\n return []\n return list(map(int, input_str.strip().split(',')))\n\ndef serialize_stdout(result):\n return str(result)\n\ninput_str = sys.stdin.read().strip()\nnums = deserialize_stdin(input_str)\nsol = Solution()\nans = sol.subarraySum(nums)\nprint(serialize_stdout(ans))",
"ruby": "==Code Submission==\n\ninput = gets.strip\nnums = input.split(\",\").map(&:to_i)\nans = subarray_sum(nums)\nputs ans"
}
|
3733
|
Length of Longest V-Shaped Diagonal Segment
|
length-of-longest-v-shaped-diagonal-segment
|
<p>You are given a 2D integer matrix <code>grid</code> of size <code>n x m</code>, where each element is either <code>0</code>, <code>1</code>, or <code>2</code>.</p>
<p>A <strong>V-shaped diagonal segment</strong> is defined as:</p>
<ul>
<li>The segment starts with <code>1</code>.</li>
<li>The subsequent elements follow this infinite sequence: <code>2, 0, 2, 0, ...</code>.</li>
<li>The segment:
<ul>
<li>Starts <strong>along</strong> a diagonal direction (top-left to bottom-right, bottom-right to top-left, top-right to bottom-left, or bottom-left to top-right).</li>
<li>Continues the<strong> sequence</strong> in the same diagonal direction.</li>
<li>Makes<strong> at most one clockwise 90-degree</strong><strong> turn</strong> to another diagonal direction while <strong>maintaining</strong> the sequence.</li>
</ul>
</li>
</ul>
<p><img alt="" src="https://assets.leetcode.com/uploads/2025/01/11/length_of_longest3.jpg" style="width: 481px; height: 202px;" /></p>
<p>Return the <strong>length</strong> of the <strong>longest</strong> <strong>V-shaped diagonal segment</strong>. If no valid segment <em>exists</em>, return 0.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">grid = [[2,2,1,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]</span></p>
<p><strong>Output:</strong> <span class="example-io">5</span></p>
<p><strong>Explanation:</strong></p>
<p><img alt="" src="https://assets.leetcode.com/uploads/2024/12/09/matrix_1-2.jpg" style="width: 201px; height: 192px;" /></p>
<p>The longest V-shaped diagonal segment has a length of 5 and follows these coordinates: <code>(0,2) → (1,3) → (2,4)</code>, takes a <strong>90-degree clockwise turn</strong> at <code>(2,4)</code>, and continues as <code>(3,3) → (4,2)</code>.</p>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">grid = [[2,2,2,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]</span></p>
<p><strong>Output:</strong> <span class="example-io">4</span></p>
<p><strong>Explanation:</strong></p>
<p><strong><img alt="" src="https://assets.leetcode.com/uploads/2024/12/09/matrix_2.jpg" style="width: 201px; height: 201px;" /></strong></p>
<p>The longest V-shaped diagonal segment has a length of 4 and follows these coordinates: <code>(2,3) → (3,2)</code>, takes a <strong>90-degree clockwise turn</strong> at <code>(3,2)</code>, and continues as <code>(2,1) → (1,0)</code>.</p>
</div>
<p><strong class="example">Example 3:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">grid = [[1,2,2,2,2],[2,2,2,2,0],[2,0,0,0,0],[0,0,2,2,2],[2,0,0,2,0]]</span></p>
<p><strong>Output:</strong> <span class="example-io">5</span></p>
<p><strong>Explanation:</strong></p>
<p><strong><img alt="" src="https://assets.leetcode.com/uploads/2024/12/09/matrix_3.jpg" style="width: 201px; height: 201px;" /></strong></p>
<p>The longest V-shaped diagonal segment has a length of 5 and follows these coordinates: <code>(0,0) → (1,1) → (2,2) → (3,3) → (4,4)</code>.</p>
</div>
<p><strong class="example">Example 4:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">grid = [[1]]</span></p>
<p><strong>Output:</strong> <span class="example-io">1</span></p>
<p><strong>Explanation:</strong></p>
<p>The longest V-shaped diagonal segment has a length of 1 and follows these coordinates: <code>(0,0)</code>.</p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>n == grid.length</code></li>
<li><code>m == grid[i].length</code></li>
<li><code>1 <= n, m <= 500</code></li>
<li><code>grid[i][j]</code> is either <code>0</code>, <code>1</code> or <code>2</code>.</li>
</ul>
|
You are given a 2D integer matrix `grid` of size `n x m`, where each element is either `0`, `1`, or `2`.
A **V\-shaped diagonal segment** is defined as:
- The segment starts with `1`.
- The subsequent elements follow this infinite sequence: `2, 0, 2, 0, ...`.
- The segment:
- Starts **along** a diagonal direction (top\-left to bottom\-right, bottom\-right to top\-left, top\-right to bottom\-left, or bottom\-left to top\-right).
- Continues the **sequence** in the same diagonal direction.
- Makes **at most one clockwise 90\-degree** **turn** to another diagonal direction while **maintaining** the sequence.
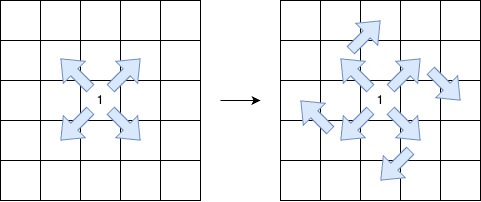
Return the **length** of the **longest** **V\-shaped diagonal segment**. If no valid segment *exists*, return 0\.
**Example 1:**
**Input:** grid \= \[\[2,2,1,2,2],\[2,0,2,2,0],\[2,0,1,1,0],\[1,0,2,2,2],\[2,0,0,2,2]]
**Output:** 5
**Explanation:**
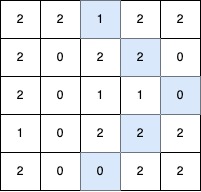
The longest V\-shaped diagonal segment has a length of 5 and follows these coordinates: `(0,2) (1,3) (2,4)`, takes a **90\-degree clockwise turn** at `(2,4)`, and continues as `(3,3) (4,2)`.
**Example 2:**
**Input:** grid \= \[\[2,2,2,2,2],\[2,0,2,2,0],\[2,0,1,1,0],\[1,0,2,2,2],\[2,0,0,2,2]]
**Output:** 4
**Explanation:**
**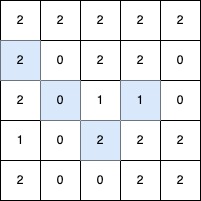**
The longest V\-shaped diagonal segment has a length of 4 and follows these coordinates: `(2,3) (3,2)`, takes a **90\-degree clockwise turn** at `(3,2)`, and continues as `(2,1) (1,0)`.
**Example 3:**
**Input:** grid \= \[\[1,2,2,2,2],\[2,2,2,2,0],\[2,0,0,0,0],\[0,0,2,2,2],\[2,0,0,2,0]]
**Output:** 5
**Explanation:**
**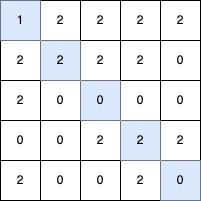**
The longest V\-shaped diagonal segment has a length of 5 and follows these coordinates: `(0,0) (1,1) (2,2) (3,3) (4,4)`.
**Example 4:**
**Input:** grid \= \[\[1]]
**Output:** 1
**Explanation:**
The longest V\-shaped diagonal segment has a length of 1 and follows these coordinates: `(0,0)`.
**Constraints:**
- `n == grid.length`
- `m == grid[i].length`
- `1 <= n, m <= 500`
- `grid[i][j]` is either `0`, `1` or `2`.
|
Hard
|
[
"array",
"dynamic-programming",
"memoization",
"matrix"
] |
leetcode
|
https://leetcode.com/problems/length-of-longest-v-shaped-diagonal-segment
|
functional
| null | null | null | null |
{
"c": "int lenOfVDiagonal(int** grid, int gridSize, int* gridColSize) {\n \n}",
"cpp": "class Solution {\npublic:\n int lenOfVDiagonal(vector<vector<int>>& grid) {\n \n }\n};",
"csharp": "public class Solution {\n public int LenOfVDiagonal(int[][] grid) {\n \n }\n}",
"dart": "class Solution {\n int lenOfVDiagonal(List<List<int>> grid) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec len_of_v_diagonal(grid :: [[integer]]) :: integer\n def len_of_v_diagonal(grid) do\n \n end\nend",
"erlang": "-spec len_of_v_diagonal(Grid :: [[integer()]]) -> integer().\nlen_of_v_diagonal(Grid) ->\n .",
"golang": "func lenOfVDiagonal(grid [][]int) int {\n \n}",
"java": "class Solution {\n public int lenOfVDiagonal(int[][] grid) {\n \n }\n}",
"javascript": "/**\n * @param {number[][]} grid\n * @return {number}\n */\nvar lenOfVDiagonal = function(grid) {\n \n};",
"kotlin": "class Solution {\n fun lenOfVDiagonal(grid: Array<IntArray>): Int {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param Integer[][] $grid\n * @return Integer\n */\n function lenOfVDiagonal($grid) {\n \n }\n}",
"python": "class Solution(object):\n def lenOfVDiagonal(self, grid):\n \"\"\"\n :type grid: List[List[int]]\n :rtype: int\n \"\"\"\n ",
"python3": "class Solution:\n def lenOfVDiagonal(self, grid: List[List[int]]) -> int:\n ",
"racket": "(define/contract (len-of-v-diagonal grid)\n (-> (listof (listof exact-integer?)) exact-integer?)\n )",
"ruby": "# @param {Integer[][]} grid\n# @return {Integer}\ndef len_of_v_diagonal(grid)\n \nend",
"rust": "impl Solution {\n pub fn len_of_v_diagonal(grid: Vec<Vec<i32>>) -> i32 {\n \n }\n}",
"scala": "object Solution {\n def lenOfVDiagonal(grid: Array[Array[Int]]): Int = {\n \n }\n}",
"swift": "class Solution {\n func lenOfVDiagonal(_ grid: [[Int]]) -> Int {\n \n }\n}",
"typescript": "function lenOfVDiagonal(grid: number[][]): number {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n int lenOfVDiagonal(vector<vector<int>>& grid) {\n int n = grid.size();\n if (n == 0) return 0;\n int m = grid[0].size();\n if (m == 0) return 0;\n\n vector<vector<vector<int>>> len(4, vector<vector<int>>(n, vector<int>(m, 0)));\n vector<pair<int, int>> dirs = {{1, 1}, {1, -1}, {-1, 1}, {-1, -1}};\n\n for (int d = 0; d < 4; ++d) {\n int dx = dirs[d].first;\n int dy = dirs[d].second;\n\n int i_start = (dx == 1) ? (n - 1) : 0;\n int i_end = (dx == 1) ? -1 : n;\n int i_step = (dx == 1) ? -1 : 1;\n\n int j_start = (dy == 1) ? (m - 1) : 0;\n int j_end = (dy == 1) ? -1 : m;\n int j_step = (dy == 1) ? -1 : 1;\n\n for (int i = i_start; i != i_end; i += i_step) {\n for (int j = j_start; j != j_end; j += j_step) {\n int v = grid[i][j];\n int next_expected;\n\n if (v == 1) {\n next_expected = 2;\n } else if (v == 2) {\n next_expected = 0;\n } else if (v == 0) {\n next_expected = 2;\n } else {\n next_expected = -1;\n }\n\n int next_i = i + dx;\n int next_j = j + dy;\n\n if (next_i >= 0 && next_i < n && next_j >= 0 && next_j < m && grid[next_i][next_j] == next_expected) {\n len[d][i][j] = 1 + len[d][next_i][next_j];\n } else {\n len[d][i][j] = (v == 1 || v == 2 || v == 0) ? 1 : 0;\n }\n }\n }\n }\n\n int max_length = 0;\n\n for (int i = 0; i < n; ++i) {\n for (int j = 0; j < m; ++j) {\n if (grid[i][j] != 1) continue;\n\n for (int d = 0; d < 4; ++d) {\n int dx = dirs[d].first;\n int dy = dirs[d].second;\n\n int len1 = len[d][i][j];\n if (len1 == 0) continue;\n\n int current_max = len1;\n\n for (int k = 0; k < len1; ++k) {\n int x = i + k * dx;\n int y = j + k * dy;\n\n if (x < 0 || x >= n || y < 0 || y >= m) break;\n\n int next_val;\n if (k == 0) {\n next_val = 2;\n } else {\n next_val = (k % 2 == 1) ? 0 : 2;\n }\n\n int new_dx = dy;\n int new_dy = -dx;\n\n int new_d = -1;\n for (int nd = 0; nd < 4; ++nd) {\n if (dirs[nd].first == new_dx && dirs[nd].second == new_dy) {\n new_d = nd;\n break;\n }\n }\n if (new_d == -1) continue;\n\n int next_x = x + new_dx;\n int next_y = y + new_dy;\n\n if (next_x < 0 || next_x >= n || next_y < 0 || next_y >= m) continue;\n if (grid[next_x][next_y] != next_val) continue;\n\n int len2 = len[new_d][next_x][next_y];\n current_max = max(current_max, (k + 1) + len2);\n }\n\n max_length = max(max_length, current_max);\n }\n }\n }\n\n return max_length;\n }\n};",
"memory": 15700,
"memoryDistribution": "[[15700, 29.3854, \"class Solution {\\npublic:\\n int lenOfVDiagonal(vector<vector<int>>& grid) {\\n int n = grid.size();\\n if (n == 0) return 0;\\n int m = grid[0].size();\\n if (m == 0) return 0;\\n\\n vector<vector<vector<int>>> len(4, vector<vector<int>>(n, vector<int>(m, 0)));\\n vector<pair<int, int>> dirs = {{1, 1}, {1, -1}, {-1, 1}, {-1, -1}};\\n\\n for (int d = 0; d < 4; ++d) {\\n int dx = dirs[d].first;\\n int dy = dirs[d].second;\\n\\n int i_start = (dx == 1) ? (n - 1) : 0;\\n int i_end = (dx == 1) ? -1 : n;\\n int i_step = (dx == 1) ? -1 : 1;\\n\\n int j_start = (dy == 1) ? (m - 1) : 0;\\n int j_end = (dy == 1) ? -1 : m;\\n int j_step = (dy == 1) ? -1 : 1;\\n\\n for (int i = i_start; i != i_end; i += i_step) {\\n for (int j = j_start; j != j_end; j += j_step) {\\n int v = grid[i][j];\\n int next_expected;\\n\\n if (v == 1) {\\n next_expected = 2;\\n } else if (v == 2) {\\n next_expected = 0;\\n } else if (v == 0) {\\n next_expected = 2;\\n } else {\\n next_expected = -1;\\n }\\n\\n int next_i = i + dx;\\n int next_j = j + dy;\\n\\n if (next_i >= 0 && next_i < n && next_j >= 0 && next_j < m && grid[next_i][next_j] == next_expected) {\\n len[d][i][j] = 1 + len[d][next_i][next_j];\\n } else {\\n len[d][i][j] = (v == 1 || v == 2 || v == 0) ? 1 : 0;\\n }\\n }\\n }\\n }\\n\\n int max_length = 0;\\n\\n for (int i = 0; i < n; ++i) {\\n for (int j = 0; j < m; ++j) {\\n if (grid[i][j] != 1) continue;\\n\\n for (int d = 0; d < 4; ++d) {\\n int dx = dirs[d].first;\\n int dy = dirs[d].second;\\n\\n int len1 = len[d][i][j];\\n if (len1 == 0) continue;\\n\\n int current_max = len1;\\n\\n for (int k = 0; k < len1; ++k) {\\n int x = i + k * dx;\\n int y = j + k * dy;\\n\\n if (x < 0 || x >= n || y < 0 || y >= m) break;\\n\\n int next_val;\\n if (k == 0) {\\n next_val = 2;\\n } else {\\n next_val = (k % 2 == 1) ? 0 : 2;\\n }\\n\\n int new_dx = dy;\\n int new_dy = -dx;\\n\\n int new_d = -1;\\n for (int nd = 0; nd < 4; ++nd) {\\n if (dirs[nd].first == new_dx && dirs[nd].second == new_dy) {\\n new_d = nd;\\n break;\\n }\\n }\\n if (new_d == -1) continue;\\n\\n int next_x = x + new_dx;\\n int next_y = y + new_dy;\\n\\n if (next_x < 0 || next_x >= n || next_y < 0 || next_y >= m) continue;\\n if (grid[next_x][next_y] != next_val) continue;\\n\\n int len2 = len[new_d][next_x][next_y];\\n current_max = max(current_max, (k + 1) + len2);\\n }\\n\\n max_length = max(max_length, current_max);\\n }\\n }\\n }\\n\\n return max_length;\\n }\\n};\"], [97481, 7.456200000000001, \"class Solution {\\npublic:\\n int func (vector<vector<int>>& grid,int i,int j,int have,int dir,int pre){\\n int n=grid.size(),m=grid[0].size();\\n if(i<0 || j<0 || i>=n || j>=m ) return 0;\\n if (pre==1 && grid[i][j]!=2) return 0;\\n if (pre==2 && grid[i][j]!=0) return 0;\\n if (pre==0 && grid[i][j]!=2) return 0;\\n int ans=0;\\n if (dir==-1){\\n ans=max(ans,1+func(grid,i-1,j-1,have,0,grid[i][j]));\\n ans=max(ans,1+func(grid,i-1,j+1,have,1,grid[i][j]));\\n ans=max(ans,1+func(grid,i+1,j+1,have,2,grid[i][j]));\\n ans=max(ans,1+func(grid,i+1,j-1,have,3,grid[i][j]));\\n }\\n else if (dir==0) ans=max(ans,1+func(grid,i-1,j-1,have,0,grid[i][j]));\\n else if (dir==1) ans=max(ans,1+func(grid,i-1,j+1,have,1,grid[i][j]));\\n else if (dir==2) ans=max(ans,1+func(grid,i+1,j+1,have,2,grid[i][j]));\\n else if (dir==3) ans=max(ans,1+func(grid,i+1,j-1,have,3,grid[i][j]));\\n\\n if (have==0){\\n if(dir==0) ans=max(ans,1+func(grid,i-1,j+1,1,1,grid[i][j]));\\n else if(dir==1) ans=max(ans,1+func(grid,i+1,j+1,1,2,grid[i][j])); \\n else if(dir==2) ans=max(ans,1+func(grid,i+1,j-1,1,3,grid[i][j]));\\n else if(dir==3) ans=max(ans,1+func(grid,i-1,j-1,1,0,grid[i][j])); \\n }\\n return ans;\\n }\\n int lenOfVDiagonal(vector<vector<int>>& grid) {\\n int i,j,k,n=grid.size(),m=grid[0].size();\\n // 0 ul\\n // 1 ur\\n // 2 dr\\n // 3 dl \\n int ans=0;\\n for (i=0;i<n;i++){\\n for(j=0;j<m;j++){\\n if (grid[i][j]!=1) continue;\\n ans=max(ans,func(grid,i,j,0,-1,-1));\\n }\\n }\\n return ans;\\n }\\n};\"], [103645, 20.175600000000003, \"class Solution {\\npublic:\\n int lenOfVDiagonal(vector<vector<int>>& grid) {\\n static const int maxn = 501, maxd = 4, dx[maxd] = {-1, -1, 1, 1}, dy[maxd] = {-1, 1, 1, -1};\\n static int f[maxd][maxn][maxn], g[maxd][maxn][maxn];\\n int r = grid.size(), c = grid[0].size();\\n for(int d = 0; d < maxd; ++d)\\n for(int i = 0; i < r; ++i)\\n for(int j = 0; j < c; ++j)\\n f[d][i][j] = g[d][i][j] = -1;\\n function<int(int, int, int)> F = [&](int d, int x, int y) {\\n int &res = f[d][x][y];\\n if(res == -1) {\\n res = 1;\\n int xx = x + dx[d], yy = y + dy[d];\\n if(xx >= 0 && xx < r && yy >= 0 && yy < c && grid[x][y] + grid[xx][yy] == 2)\\n res += F(d, xx, yy);\\n }\\n return res;\\n };\\n function<int(int, int, int)> G = [&](int d, int x, int y) {\\n int &res = g[d][x][y];\\n if(res == -1) {\\n res = 1;\\n int xx = x + dx[d], yy = y + dy[d];\\n if(xx >= 0 && xx < r && yy >= 0 && yy < c && grid[x][y] + grid[xx][yy] == 2)\\n res = max(res, 1 + G(d, xx, yy));\\n int dd = (d + 1) % maxd;\\n xx = x + dx[dd];\\n yy = y + dy[dd];\\n if(xx >= 0 && xx < r && yy >= 0 && yy < c && grid[x][y] + grid[xx][yy] == 2)\\n res = max(res, 1 + F(dd, xx, yy));\\n }\\n return res;\\n };\\n int ans = 0;\\n for(int i = 0; i < r; ++i)\\n for(int j = 0; j < c; ++j) {\\n if(grid[i][j] != 1)\\n continue;\\n ans = max(ans, 1);\\n for(int d = 0; d < maxd; ++d) {\\n int x = i + dx[d], y = j + dy[d];\\n if(x >= 0 && x < r && y >= 0 && y < c && grid[x][y] == 2)\\n ans = max(ans, 1 + G(d, x, y));\\n }\\n }\\n return ans;\\n }\\n};\"], [109809, 4.386, null], [115973, 23.245800000000003, null], [122136, 5.2632, null], [128300, 3.5088, null], [134464, 0.4386, null], [140628, 3.0702, null], [146791, 3.0702, null], [152955, 0.4386, null], [159119, 3.0702, null], [165283, 0.4386, null], [171446, 0.4386, null], [177610, 0.8772, null], [183774, 1.3157999999999999, null], [189938, 0.4386, null], [196101, 0.4386, null], [202265, 0.4386, null], [208429, 0.4386, null], [214593, 0.4386, null], [220756, 0.4386, null], [226920, 0.4386, null], [233084, 0.4386, null], [239248, 0.4386, null], [245411, 0.4386, null], [251575, 0.4386, null], [257739, 0.4386, null], [263903, 0.4386, null], [270066, 0.4386, null], [276230, 0.4386, null], [282394, 0.4386, null], [288558, 0.4386, null], [294721, 0.4386, null], [300885, 2.193, null], [307049, 0.4386, null], [313213, 0.4386, null], [319376, 0.4386, null], [325540, 0.4386, null], [331704, 0.4386, null], [337868, 0.4386, null], [344031, 0.4386, null], [350195, 0.4386, null], [356359, 0.4386, null], [362523, 0.4386, null], [368686, 0.4386, null], [374850, 0.4386, null], [381014, 1.3158, \"class Solution {\\npublic:\\n#define ll long long int\\n#define ull unsigned long long int\\n#define ld long double\\n#define fast ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0)\\n#define MAX 4000007\\n#define pii pair<int,int>\\n#define ppii pair<int,pii>\\n#define pll pair<ll,ll>\\n#define vi vector<int>\\n#define vc vector<char>\\n#define vl vector<ll>\\n#define vvi vector<vector<int>>\\n#define vvc vector<vector<char>>\\n#define vvl vector<vector<ll>>\\n#define vvvi vector<vector<vector<int>>>\\n#define vvvl vector<vector<vector<ll>>>\\nint dirs[4][2] = {{1,1},{-1,1},{1,-1},{-1,-1}};\\nint n, m;\\n\\n bool isCrossProduct90(int d1, int d2)\\n {\\n /*\\n consider the directions as vector and if we turn clockwse 90 degree means the cross product \\n should be less than 0\\n */\\n auto [x1, y1] = dirs[d1];\\n auto [x2,y2]= dirs[d2];\\n \\n if(x1*y2 - y1*x2 <0)\\n return true;\\n\\n return false;\\n }\\n int solve(int x, int y , int di, int seq, bool changed , vvi &a , vector<vvvi> &dp)\\n {\\n \\n if(dp[x][y][di][changed]!=-1)\\n return dp[x][y][di][changed];\\n int maxi =0;\\n for(int i=0; i<4; i++)\\n {\\n /* if i==di then we dont alter the diretion so changed stays whaterver it was \\n but if i!=di then only enter the if condition if never changed direction previously\\n and in this case changed value should be passed 1 for futher func calls\\n */\\n if(i!=di && !isCrossProduct90(di , i)) continue; /* turn towards clockwise 90 deg direction */\\n if(i==di || (i!=di && changed==0) )\\n {\\n auto [dx,dy]= dirs[i];\\n int a1= x+dx , b1 = y+dy;\\n if(!(a1<0 || a1>=n || b1<0 || b1>=m))\\n {\\n /* seq=0 means we look for 2 , seq=2 means we were at 2 so now look for 0 , seq=1 we were \\n at 0 now look for 2 */\\n if((seq==0 || seq==1) && a[a1][b1]==2)\\n maxi = max(maxi , 1+solve(a1, b1 , i, 2, changed|(i!=di) , a, dp));\\n else if(seq==2 && a[a1][b1]==0)\\n maxi = max(maxi ,1+solve(a1, b1 , i , 1, changed|(i!=di) , a, dp));\\n\\n }\\n }\\n }\\n return dp[x][y][di][changed] = maxi;\\n }\\n int lenOfVDiagonal(vector<vector<int>>& a) {\\n n=a.size();\\n m=a[0].size();\\n\\n // vector<vector<vvvi>>dp(n , vector<vvvi>(m , vvvi(4 , vvi(3 , vi(2 , -1) ))));\\n\\n vector<vvvi>dp(n , vvvi(m , vvi(4 , vi(2 ,-1 ))));\\n /*\\n removing seq from the states to reduce some time\\n */\\n\\n\\n int ans = 0;\\n for(int i=0; i<n; i++)\\n {\\n for(int j =0 ;j<m; j++)\\n {\\n if(a[i][j]==1)\\n {\\n for(int di =0; di<4; di++)\\n {\\n ans = max(ans , 1+solve(i, j, di ,0, 0 ,a, dp));\\n }\\n }\\n }\\n }\\n\\n return ans;\\n }\\n};\"], [387178, 0.8772, \"class Solution {\\n int dir[4][2] = {{1,-1}, {-1, -1}, {-1, 1}, {1, 1}};\\npublic:\\n int lenOfVDiagonal(vector<vector<int>>& grid) {\\n int m = grid.size(), n = grid[0].size();\\n vector dp(m, vector(n, vector(4, vector<int>(2, -1))));\\n auto dfs=[&](this auto&& dfs, int i , int j, int k, bool isturn, int target){\\n if(i<0 || j<0 || i>=m || j>=n || target!=grid[i][j]) return 0;\\n if(dp[i][j][k][isturn]!=-1) return dp[i][j][k][isturn];\\n dp[i][j][k][isturn] = max(dp[i][j][k][isturn], dfs(i+dir[k][0], j+dir[k][1], k, isturn, 2-target)+1);\\n if(!isturn)\\n dp[i][j][k][isturn] = max(dp[i][j][k][isturn], dfs(i+dir[(k+1)%4][0], j+dir[(k+1)%4][1], (k+1)%4, true, 2-target)+1);\\n return dp[i][j][k][isturn];\\n };\\n int res=0;\\n for(int i=0; i<m; i++){\\n for(int j=0; j<n; j++){\\n if(grid[i][j]==1){\\n for(int k=0; k<4; k++) {\\n if(dp[i][j][k][false]!=-1) res=max(res, dp[i][j][k][false]);\\n else\\n {\\n res = max(res, dfs(i+dir[k][0], j+dir[k][1], k, false, 2)+1);\\n dp[i][j][k][false]=res;\\n }\\n }\\n }\\n }\\n }\\n return res;\\n }\\n};\"]]",
"runtime": 136,
"runtimeDistribution": "[[16, 0.8772, \"#pragma GCC optimize(\\\"O3\\\", \\\"unroll-loops\\\")\\n\\nconst auto _ = std::cin.tie(nullptr)->sync_with_stdio(false);\\n\\n#define LC_HACK\\n#ifdef LC_HACK\\nconst auto __ = []() {\\n struct ___ { static void _() { std::ofstream(\\\"display_runtime.txt\\\") << 0 << '\\\\n'; } };\\n std::atexit(&___::_);\\n return 0;\\n}();\\n#endif\\nclass Solution {\\npublic:\\n vector<vector<int>>grid;\\n vector<vector<int>>dirs = {{-1,1},{1,1},{1,-1},{-1,-1}};\\n int n;\\n int m;\\n int lenOfVDiagonal(vector<vector<int>>& grid) {\\n m = grid.size();\\n n = grid[0].size();\\n this->grid = grid;\\n int ans = 0;\\n for(int i = 0;i < m;i++){\\n for(int j = 0;j < n;j++){\\n if(grid[i][j]==1){\\n ans = max(ans,1);\\n ans = max({ans,dfs(i,j,0,false,2)\\n ,dfs(i,j,1,false,2)\\n ,dfs(i,j,2,false,2)\\n ,dfs(i,j,3,false,2)});\\n }\\n }\\n }\\n return ans;\\n }\\n int dfs(int i,int j,int dir,bool turned,int target){\\n int x=i+dirs[dir][0];\\n int y=j+dirs[dir][1];\\n if(x<0||x>=m||y<0||y>=n||grid[x][y]!=target)return 1;\\n //Either :STRAIGHT.\\n int straight = 1+dfs(x,y,dir,turned,target==2?0:2);\\n int turn = 1;\\n //Or: TURNED.\\n if(!turned){\\n turn = 1+dfs(x,y,(dir+1)%4,true,target==2?0:2);\\n }\\n return max(straight,turn);\\n }\\n};\"], [49, 0.4386, \"class Solution {\\npublic:\\n int lenOfVDiagonal(vector<vector<int>>& grid) {\\n int n = grid.size(), m = grid[0].size();\\n vector<vector<int>> nwLengths(n, vector<int>(m, -1));\\n vector<vector<int>> neLengths(n, vector<int>(m, -1));\\n vector<vector<int>> swLengths(n, vector<int>(m, -1));\\n vector<vector<int>> seLengths(n, vector<int>(m, -1));\\n for (int r = 0; r < n; r++) {\\n for (int c = 0; c < m; c++) {\\n if (grid[r][c] == 0 || grid[r][c] == 2) {\\n if (r-1 >= 0 && c-1 >= 0 && grid[r-1][c-1] == 2 - grid[r][c]) {\\n nwLengths[r][c] = nwLengths[r-1][c-1] + 1;\\n } else {\\n nwLengths[r][c] = 0;\\n }\\n if (r-1 >= 0 && c+1 < m && grid[r-1][c+1] == 2 - grid[r][c]) {\\n neLengths[r][c] = neLengths[r-1][c+1] + 1;\\n } else {\\n neLengths[r][c] = 0;\\n }\\n }\\n }\\n }\\n for (int r = n-1; r >= 0; r--) {\\n for (int c = 0; c < m; c++) {\\n if (grid[r][c] == 0 || grid[r][c] == 2) {\\n if (r+1 < n && c-1 >= 0 && grid[r+1][c-1] == 2 - grid[r][c]) {\\n swLengths[r][c] = 1 + swLengths[r+1][c-1];\\n } else {\\n swLengths[r][c] = 0;\\n }\\n if (r+1 < n && c+1 < m && grid[r+1][c+1] == 2 - grid[r][c]) {\\n seLengths[r][c] = 1 + seLengths[r+1][c+1];\\n } else {\\n seLengths[r][c] = 0;\\n }\\n }\\n }\\n }\\n\\n int maxVLength = 0;\\n for (int r = 0; r < n; r++) {\\n for (int c = 0; c < m; c++) {\\n if (grid[r][c] != 1) {\\n continue;\\n }\\n maxVLength = max(maxVLength, 1);\\n // go NW\\n for (int i = 1, v = 2; r-i >= 0 && c-i >= 0 && grid[r-i][c-i] == v; i++, v = 2-v) {\\n maxVLength = max(maxVLength, 1 + i + neLengths[r-i][c-i]);\\n }\\n // go NE\\n for (int i = 1, v = 2; r-i >= 0 && c+i < m && grid[r-i][c+i] == v; i++, v = 2-v) {\\n maxVLength = max(maxVLength, 1 + i + seLengths[r-i][c+i]);\\n }\\n // go SE\\n for (int i = 1, v = 2; r+i < n && c+i < m && grid[r+i][c+i] == v; i++, v = 2-v) {\\n maxVLength = max(maxVLength, 1 + i + swLengths[r+i][c+i]);\\n }\\n // go SW\\n for (int i = 1, v = 2; r+i < n && c-i >= 0 && grid[r+i][c-i] == v; i++, v = 2-v) {\\n maxVLength = max(maxVLength, 1 + i + nwLengths[r+i][c-i]);\\n }\\n }\\n }\\n return maxVLength;\\n }\\n};\"], [82, 2.6316, null], [115, 3.0702000000000003, null], [136, 93.421, \"class Solution {\\npublic:\\n int lenOfVDiagonal(vector<vector<int>>& grid) {\\n int n = grid.size();\\n if (n == 0) return 0;\\n int m = grid[0].size();\\n if (m == 0) return 0;\\n\\n vector<vector<vector<int>>> len(4, vector<vector<int>>(n, vector<int>(m, 0)));\\n vector<pair<int, int>> dirs = {{1, 1}, {1, -1}, {-1, 1}, {-1, -1}};\\n\\n for (int d = 0; d < 4; ++d) {\\n int dx = dirs[d].first;\\n int dy = dirs[d].second;\\n\\n int i_start = (dx == 1) ? (n - 1) : 0;\\n int i_end = (dx == 1) ? -1 : n;\\n int i_step = (dx == 1) ? -1 : 1;\\n\\n int j_start = (dy == 1) ? (m - 1) : 0;\\n int j_end = (dy == 1) ? -1 : m;\\n int j_step = (dy == 1) ? -1 : 1;\\n\\n for (int i = i_start; i != i_end; i += i_step) {\\n for (int j = j_start; j != j_end; j += j_step) {\\n int v = grid[i][j];\\n int next_expected;\\n\\n if (v == 1) {\\n next_expected = 2;\\n } else if (v == 2) {\\n next_expected = 0;\\n } else if (v == 0) {\\n next_expected = 2;\\n } else {\\n next_expected = -1;\\n }\\n\\n int next_i = i + dx;\\n int next_j = j + dy;\\n\\n if (next_i >= 0 && next_i < n && next_j >= 0 && next_j < m && grid[next_i][next_j] == next_expected) {\\n len[d][i][j] = 1 + len[d][next_i][next_j];\\n } else {\\n len[d][i][j] = (v == 1 || v == 2 || v == 0) ? 1 : 0;\\n }\\n }\\n }\\n }\\n\\n int max_length = 0;\\n\\n for (int i = 0; i < n; ++i) {\\n for (int j = 0; j < m; ++j) {\\n if (grid[i][j] != 1) continue;\\n\\n for (int d = 0; d < 4; ++d) {\\n int dx = dirs[d].first;\\n int dy = dirs[d].second;\\n\\n int len1 = len[d][i][j];\\n if (len1 == 0) continue;\\n\\n int current_max = len1;\\n\\n for (int k = 0; k < len1; ++k) {\\n int x = i + k * dx;\\n int y = j + k * dy;\\n\\n if (x < 0 || x >= n || y < 0 || y >= m) break;\\n\\n int next_val;\\n if (k == 0) {\\n next_val = 2;\\n } else {\\n next_val = (k % 2 == 1) ? 0 : 2;\\n }\\n\\n int new_dx = dy;\\n int new_dy = -dx;\\n\\n int new_d = -1;\\n for (int nd = 0; nd < 4; ++nd) {\\n if (dirs[nd].first == new_dx && dirs[nd].second == new_dy) {\\n new_d = nd;\\n break;\\n }\\n }\\n if (new_d == -1) continue;\\n\\n int next_x = x + new_dx;\\n int next_y = y + new_dy;\\n\\n if (next_x < 0 || next_x >= n || next_y < 0 || next_y >= m) continue;\\n if (grid[next_x][next_y] != next_val) continue;\\n\\n int len2 = len[new_d][next_x][next_y];\\n current_max = max(current_max, (k + 1) + len2);\\n }\\n\\n max_length = max(max_length, current_max);\\n }\\n }\\n }\\n\\n return max_length;\\n }\\n};\"], [148, 3.5088000000000004, null], [181, 4.386, null], [214, 2.6316, null], [247, 5.2632, null], [281, 8.333400000000001, null], [314, 4.386, null], [347, 1.7544, null], [380, 1.3157999999999999, null], [413, 0.8772, null], [446, 0.4386, null], [479, 0.4386, null], [512, 1.7544, null], [545, 1.3157999999999999, null], [578, 0.4386, null], [611, 2.193, null], [644, 2.193, null], [677, 3.0702000000000003, null], [710, 1.7544, null], [743, 2.6316, null], [776, 2.6316, null], [810, 2.193, null], [843, 1.3157999999999999, null], [876, 0.4386, null], [909, 0.8772, null], [942, 0.4386, null], [975, 0.4386, null], [1008, 2.193, null], [1041, 1.7544, null], [1074, 2.193, null], [1107, 0.4386, null], [1140, 0.4386, null], [1173, 1.3157999999999999, null], [1206, 0.4386, null], [1239, 0.4386, null], [1272, 0.4386, null], [1305, 0.4386, null], [1339, 0.4386, null], [1372, 0.4386, null], [1405, 0.4386, null], [1438, 0.4386, null], [1471, 0.4386, null], [1504, 1.3157999999999999, null], [1537, 0.4386, null], [1570, 1.3157999999999999, null], [1603, 1.7544, null], [1636, 1.7544, null], [1669, 1.7544, null], [1702, 0.4386, null], [1735, 0.4386, null], [1768, 0.4386, null], [1801, 0.4386, null], [1834, 0.4386, null], [1868, 0.4386, null], [1901, 0.4386, null], [1934, 0.4386, null], [1967, 0.4386, null], [2000, 0.4386, null], [2033, 0.4386, null], [2066, 0.4386, null], [2099, 0.4386, null], [2132, 0.4386, null], [2165, 0.4386, null], [2198, 0.4386, null], [2231, 0.4386, null], [2264, 0.4386, null], [2297, 0.4386, null], [2330, 0.4386, null], [2363, 0.4386, \"class Solution {\\n int dx[4] = {-1, 1, 1, -1};\\n int dy[4] = {1, 1, -1, -1};\\n\\n bool isValid(int x, int y, int n, int m){\\n return (x >= 0 && x < n && y >= 0 && y < m);\\n }\\n\\n int maxLength(int row, int col, int turn, int dir, int n, int m, vector<vector<int>>& grid, \\n vector<vector<vector<vector<int>>>>& dp){\\n if(row < 0 || row >= n || col < 0 || col >= m)return 0;\\n\\n if(dp[row][col][dir][turn] != -1) return dp[row][col][dir][turn];\\n\\n int value = grid[row][col], need = 0, length = 0;\\n \\n if(value == 0) need = 2;\\n\\n if(turn == 1){\\n int next = (dir + 1) % 4;\\n int newRow = row + dx[next], newCol = col + dy[next];\\n if(isValid(newRow, newCol, n, m) && grid[newRow][newCol] == need){\\n int len = maxLength(newRow, newCol, false, next, n, m, grid, dp);\\n length = max(length, len);\\n }\\n }\\n \\n int newRow = row + dx[dir], newCol = col + dy[dir];\\n if(isValid(newRow, newCol, n, m) && grid[newRow][newCol] == need){\\n int len = maxLength(newRow, newCol, turn, dir, n, m, grid, dp);\\n length = max(length, len);\\n }\\n \\n return dp[row][col][dir][turn] = length + 1;\\n }\\npublic:\\n int lenOfVDiagonal(vector<vector<int>>& grid) {\\n int n = grid.size(), m = grid[0].size();\\n \\n vector<vector<vector<vector<int>>>> dp(n, vector<vector<vector<int>>>(m, \\n vector<vector<int>>(4, vector<int>(2, -1))));\\n int ans = 0;\\n for(int row = 0; row < n; row++){\\n for(int col = 0; col < m; col++){\\n if(grid[row][col] == 1){\\n ans = max(ans, 1);\\n if(isValid(row-1, col+1, n, m) && grid[row-1][col+1] == 2){\\n int value = 1 + maxLength(row-1, col+1, 1, 0, n, m, grid, dp);\\n ans = max(ans, value);\\n }\\n if(isValid(row+1, col+1, n, m) && grid[row+1][col+1] == 2){\\n int value2 = 1 + maxLength(row+1, col+1, 1, 1, n, m, grid, dp);\\n ans = max(ans, value2);\\n }\\n if(isValid(row+1, col-1, n, m) && grid[row+1][col-1] == 2){\\n int value3 = 1 + maxLength(row+1, col-1, 1, 2, n, m, grid, dp);\\n ans = max(ans, value3);\\n }\\n if(isValid(row-1, col-1, n, m) && grid[row-1][col-1] == 2){\\n int value4 = 1 + maxLength(row-1, col-1, 1, 3, n, m, grid, dp);\\n ans = max(ans, value4);\\n }\\n }\\n }\\n }\\n return ans;\\n }\\n};\"], [2397, 0.4386, \"class Solution {\\npublic:\\n vector<vector<int>> help = {{1, 1}, {1, -1}, {-1, -1}, {-1, 1}};\\n\\n bool isGood(vector<vector<int>>& grid, int i, int j, int var) {\\n int n = grid.size();\\n int m = grid[0].size();\\n return i >= 0 && j >= 0 && i < n && j < m && grid[i][j] == var;\\n }\\n\\n int solve(vector<vector<int>>& grid, int x, int y, int prohibit, int k, vector<vector<vector<vector<int>>>>& dp) {\\n int n = grid.size();\\n int m = grid[0].size();\\n if (x < 0 || y < 0 || x >= n || y >= m || grid[x][y] == -1)\\n return 0;\\n\\n if (dp[x][y][prohibit][k] != -1) return dp[x][y][prohibit][k];\\n\\n int temp = grid[x][y];\\n grid[x][y] = -1; // Mark as visited\\n int ans = 1;\\n int original_k = k;\\n\\n for (int r = 0; r < 4; r++) {\\n if (r == prohibit) continue; // Skip reversing direction\\n\\n int i = x + help[r][0];\\n int j = y + help[r][1];\\n\\n int next_prohibit = (r + 3) % 4; // Properly reverse direction\\n\\n if (r != (prohibit + 1) % 4) {\\n if (k > 0) k--;\\n else continue;\\n } else {\\n k = original_k;\\n }\\n\\n if ((temp == 2 && isGood(grid, i, j, 0)) || (temp == 0 && isGood(grid, i, j, 2))) {\\n ans = max(ans, solve(grid, i, j, next_prohibit, k, dp) + 1);\\n }\\n }\\n\\n grid[x][y] = temp; // Restore original value\\n\\n return dp[x][y][prohibit][original_k] = ans;\\n }\\n\\n int lenOfVDiagonal(vector<vector<int>>& grid) {\\n int n = grid.size();\\n int m = grid[0].size();\\n int ans = 1;\\n bool found = false;\\n\\n vector<vector<vector<vector<int>>>> dp(n, vector<vector<vector<int>>>(m, vector<vector<int>>(4,vector<int>(2,-1)))); // 3D DP to store `k`\\n\\n for (int i = 0; i < n; i++) {\\n for (int j = 0; j < m; j++) {\\n if (grid[i][j] == 1) {\\n found = true;\\n for (int r = 0; r < 4; r++) {\\n int x = i + help[r][0];\\n int y = j + help[r][1];\\n\\n if (isGood(grid, x, y, 2)) {\\n ans = max(ans, solve(grid, x, y, (r + 3) % 4, 1, dp) + 1);\\n }\\n }\\n }\\n }\\n }\\n return found ? ans : 0;\\n }\\n};\\n\"]]"
},
"golang": {
"code": "func lenOfVDiagonal(grid [][]int) int {\n n := len(grid)\n if n == 0 {\n return 0\n }\n m := len(grid[0])\n if m == 0 {\n return 0\n }\n\n directions := [4][2]int{{1, 1}, {1, -1}, {-1, 1}, {-1, -1}}\n\n steps0 := make([][][]int, n)\n steps2 := make([][][]int, n)\n for i := range steps0 {\n steps0[i] = make([][]int, m)\n steps2[i] = make([][]int, m)\n for j := range steps0[i] {\n steps0[i][j] = make([]int, 4)\n steps2[i][j] = make([]int, 4)\n }\n }\n\n for d := 0; d < 4; d++ {\n dx, dy := directions[d][0], directions[d][1]\n startX, endX, stepX := n-1, -1, -1\n if dx == -1 {\n startX, endX, stepX = 0, n, 1\n }\n startY, endY, stepY := m-1, -1, -1\n if dy == -1 {\n startY, endY, stepY = 0, m, 1\n }\n\n for x := startX; x != endX; x += stepX {\n for y := startY; y != endY; y += stepY {\n if grid[x][y] == 0 {\n steps0[x][y][d] = 1\n nx, ny := x+dx, y+dy\n if nx >= 0 && nx < n && ny >= 0 && ny < m {\n steps0[x][y][d] += steps2[nx][ny][d]\n }\n } else {\n steps0[x][y][d] = 0\n }\n\n if grid[x][y] == 2 {\n steps2[x][y][d] = 1\n nx, ny := x+dx, y+dy\n if nx >= 0 && nx < n && ny >= 0 && ny < m {\n steps2[x][y][d] += steps0[nx][ny][d]\n }\n } else {\n steps2[x][y][d] = 0\n }\n }\n }\n }\n\n maxLen := 0\n for i := 0; i < n; i++ {\n for j := 0; j < m; j++ {\n if grid[i][j] != 1 {\n continue\n }\n\n for d := 0; d < 4; d++ {\n dx, dy := directions[d][0], directions[d][1]\n nextI, nextJ := i+dx, j+dy\n pre := 1\n if nextI >= 0 && nextI < n && nextJ >= 0 && nextJ < m {\n pre += steps2[nextI][nextJ][d]\n }\n\n if pre == 0 {\n continue\n }\n\n currentMax := pre\n for s := 1; s <= pre; s++ {\n newX := i + (s-1)*dx + directions[d][1]\n newY := j + (s-1)*dy - directions[d][0]\n\n if newX < 0 || newX >= n || newY < 0 || newY >= m {\n continue\n }\n\n nextExpected := 2\n if s%2 == 0 {\n nextExpected = 0\n }\n\n ndx := directions[d][1]\n ndy := -directions[d][0]\n newD := -1\n for nd := 0; nd < 4; nd++ {\n if directions[nd][0] == ndx && directions[nd][1] == ndy {\n newD = nd\n break\n }\n }\n if newD == -1 {\n continue\n }\n\n var post int\n if nextExpected == 0 {\n post = steps0[newX][newY][newD]\n } else {\n post = steps2[newX][newY][newD]\n }\n\n if s+post > currentMax {\n currentMax = s + post\n }\n }\n\n if currentMax > maxLen {\n maxLen = currentMax\n }\n }\n }\n }\n\n return maxLen\n}",
"memory": 6000,
"memoryDistribution": "[[6000, 26.3152, \"func lenOfVDiagonal(grid [][]int) int {\\n n := len(grid)\\n if n == 0 {\\n return 0\\n }\\n m := len(grid[0])\\n if m == 0 {\\n return 0\\n }\\n\\n directions := [4][2]int{{1, 1}, {1, -1}, {-1, 1}, {-1, -1}}\\n\\n steps0 := make([][][]int, n)\\n steps2 := make([][][]int, n)\\n for i := range steps0 {\\n steps0[i] = make([][]int, m)\\n steps2[i] = make([][]int, m)\\n for j := range steps0[i] {\\n steps0[i][j] = make([]int, 4)\\n steps2[i][j] = make([]int, 4)\\n }\\n }\\n\\n for d := 0; d < 4; d++ {\\n dx, dy := directions[d][0], directions[d][1]\\n startX, endX, stepX := n-1, -1, -1\\n if dx == -1 {\\n startX, endX, stepX = 0, n, 1\\n }\\n startY, endY, stepY := m-1, -1, -1\\n if dy == -1 {\\n startY, endY, stepY = 0, m, 1\\n }\\n\\n for x := startX; x != endX; x += stepX {\\n for y := startY; y != endY; y += stepY {\\n if grid[x][y] == 0 {\\n steps0[x][y][d] = 1\\n nx, ny := x+dx, y+dy\\n if nx >= 0 && nx < n && ny >= 0 && ny < m {\\n steps0[x][y][d] += steps2[nx][ny][d]\\n }\\n } else {\\n steps0[x][y][d] = 0\\n }\\n\\n if grid[x][y] == 2 {\\n steps2[x][y][d] = 1\\n nx, ny := x+dx, y+dy\\n if nx >= 0 && nx < n && ny >= 0 && ny < m {\\n steps2[x][y][d] += steps0[nx][ny][d]\\n }\\n } else {\\n steps2[x][y][d] = 0\\n }\\n }\\n }\\n }\\n\\n maxLen := 0\\n for i := 0; i < n; i++ {\\n for j := 0; j < m; j++ {\\n if grid[i][j] != 1 {\\n continue\\n }\\n\\n for d := 0; d < 4; d++ {\\n dx, dy := directions[d][0], directions[d][1]\\n nextI, nextJ := i+dx, j+dy\\n pre := 1\\n if nextI >= 0 && nextI < n && nextJ >= 0 && nextJ < m {\\n pre += steps2[nextI][nextJ][d]\\n }\\n\\n if pre == 0 {\\n continue\\n }\\n\\n currentMax := pre\\n for s := 1; s <= pre; s++ {\\n newX := i + (s-1)*dx + directions[d][1]\\n newY := j + (s-1)*dy - directions[d][0]\\n\\n if newX < 0 || newX >= n || newY < 0 || newY >= m {\\n continue\\n }\\n\\n nextExpected := 2\\n if s%2 == 0 {\\n nextExpected = 0\\n }\\n\\n ndx := directions[d][1]\\n ndy := -directions[d][0]\\n newD := -1\\n for nd := 0; nd < 4; nd++ {\\n if directions[nd][0] == ndx && directions[nd][1] == ndy {\\n newD = nd\\n break\\n }\\n }\\n if newD == -1 {\\n continue\\n }\\n\\n var post int\\n if nextExpected == 0 {\\n post = steps0[newX][newY][newD]\\n } else {\\n post = steps2[newX][newY][newD]\\n }\\n\\n if s+post > currentMax {\\n currentMax = s + post\\n }\\n }\\n\\n if currentMax > maxLen {\\n maxLen = currentMax\\n }\\n }\\n }\\n }\\n\\n return maxLen\\n}\"], [30200, 5.2632, \"var dir = [][]int{{1, 1}, {-1, 1}, {-1, -1}, {1, -1}}\\n\\ntype CacheRecord struct {\\n\\tl [4]int\\n\\to, i [4]bool\\n}\\n\\nfunc lenOfVDiagonal(grid [][]int) int {\\n\\tn := len(grid)\\n\\tm := len(grid[0])\\n\\tcache := make([][]CacheRecord, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tcache[i] = make([]CacheRecord, m)\\n\\t}\\n\\n\\tvar rf func(i, j, d int) (int, bool)\\n\\trf = func(i, j, d int) (int, bool) {\\n\\t\\tif cache[i][j].i[d] {\\n\\t\\t\\treturn cache[i][j].l[d], cache[i][j].o[d]\\n\\t\\t}\\n\\t\\tx, y := i+dir[d][0], j+dir[d][1]\\n\\t\\tif x < 0 || x >= n || y < 0 || y >= m {\\n\\t\\t\\tcache[i][j].i[d] = true\\n\\t\\t\\treturn 0, false\\n\\t\\t}\\n\\t\\tif grid[x][y] == 1 && grid[i][j] == 2 {\\n\\t\\t\\tcache[i][j].i[d] = true\\n\\t\\t\\tcache[i][j].o[d] = true\\n\\t\\t\\tcache[i][j].l[d] = 1\\n\\t\\t\\treturn cache[i][j].l[d], cache[i][j].o[d]\\n\\t\\t}\\n\\t\\tif grid[x][y] != 2-grid[i][j] {\\n\\t\\t\\tcache[i][j].i[d] = true\\n\\t\\t\\tcache[i][j].o[d] = false\\n\\t\\t\\tcache[i][j].l[d] = 0\\n\\t\\t\\treturn cache[i][j].l[d], cache[i][j].o[d]\\n\\t\\t}\\n\\t\\tcache[i][j].i[d] = true\\n\\t\\tcache[i][j].l[d], cache[i][j].o[d] = rf(x, y, d)\\n\\t\\tcache[i][j].l[d]++\\n\\t\\treturn cache[i][j].l[d], cache[i][j].o[d]\\n\\t}\\n\\n\\tret := 0\\n\\tfor i := range n {\\n\\t\\tfor j := range m {\\n\\t\\t\\tif grid[i][j] == 1 {\\n\\t\\t\\t\\tret = max(ret, 1)\\n\\t\\t\\t\\tcontinue\\n\\t\\t\\t}\\n\\t\\t\\tfor d := range dir {\\n\\t\\t\\t\\trf(i, j, d)\\n\\t\\t\\t}\\n\\t\\t\\tfor d1 := range dir {\\n\\t\\t\\t\\tif cache[i][j].o[d1] {\\n\\t\\t\\t\\t\\td2 := (d1 + 1) % 4\\n\\t\\t\\t\\t\\tv := cache[i][j].l[d1] + cache[i][j].l[d2] + 1\\n\\t\\t\\t\\t\\tif cache[i][j].o[d2] {\\n\\t\\t\\t\\t\\t\\tv--\\n\\t\\t\\t\\t\\t}\\n\\t\\t\\t\\t\\tret = max(ret, v)\\n\\t\\t\\t\\t}\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\n\\treturn ret\\n}\\n\"], [35000, 5.2632, \"var dirs = [4][2]int{\\n { 1, 1},\\n { 1, -1},\\n {-1, -1},\\n {-1, 1},\\n}\\n\\nfunc lenOfVDiagonal(grid [][]int) int {\\n\\n m := len(grid)\\n n := len(grid[0])\\n\\n tCache := make([][][4]int, m)\\n cCache := make([][][4]int, m)\\n for i := range m {\\n tCache[i] = make([][4]int, n)\\n cCache[i] = make([][4]int, n)\\n }\\n \\n var cont func(i, j, d, v int) int\\n var turn func(i, j, d, v int) int\\n\\n move := func(i, j, d int) (int, int) {\\n i += dirs[d][0]\\n j += dirs[d][1]\\n return i, j\\n }\\n\\n valid := func(i, j, v int) bool {\\n if i < 0 || i >= m || j < 0 || j >= n {\\n return false\\n }\\n if grid[i][j] != v {\\n return false\\n }\\n return true\\n }\\n\\n turn = func(i, j, d, v int) int {\\n\\n i, j = move(i, j, d)\\n\\n if !valid(i, j, v) {\\n return 0\\n }\\n\\n if tCache[i][j][d] > 0 {\\n return tCache[i][j][d]\\n }\\n\\n tCache[i][j][d] = 1 + max(\\n turn(i, j, d, v^2),\\n cont(i, j, (d+1)%4, v^2),\\n )\\n\\n // fmt.Println(\\\"turn\\\", []int{i, j, d, v}, tCache[i][j][d])\\n return tCache[i][j][d]\\n }\\n\\n cont = func(i, j, d, v int) int {\\n\\n i, j = move(i, j, d)\\n\\n if !valid(i, j, v) {\\n return 0\\n }\\n\\n if cCache[i][j][d] > 0 {\\n return cCache[i][j][d]\\n }\\n\\n cCache[i][j][d] = 1 + cont(i, j, d, v^2)\\n\\n // fmt.Println(\\\"cont\\\", []int{i, j, d, v}, cCache[i][j][d])\\n return cCache[i][j][d]\\n }\\n\\n var best int\\n for i, row := range grid {\\n for j, val := range row {\\n if val != 1 {\\n continue\\n }\\n for d, p := range []int{m-i, j+1, i+1, n-j} {\\n if best >= p {\\n continue\\n }\\n best = max(best, 1 + turn(i, j, d, 2))\\n }\\n }\\n }\\n\\n return best\\n}\"], [35300, 5.2632, null], [35400, 5.2632, null], [35900, 5.2632, null], [37500, 5.2632, null], [37900, 5.2632, null], [39700, 5.2632, null], [41300, 5.2632, null], [42900, 5.2632, null], [43100, 5.2632, null], [43800, 5.2632, null], [44500, 5.2632, null], [48300, 5.2632, null], [62300, 5.2632, null], [88800, 5.2632, null], [316100, 5.2632, \"func lenOfVDiagonal(grid [][]int) int {\\n n, m := len(grid), len(grid[0])\\n dir := [4][2]int{\\n {-1, 1},\\n {1, 1},\\n {1, -1},\\n {-1,-1},\\n }\\n inbounds := func(r, c int) bool {\\n return r >= 0 && c >= 0 && r < n && c < m\\n }\\n\\n cache := make(map[[4]int]int)\\n\\n var helper func(int,int,int,int) int\\n helper = func(r, c int, d int, turned int) int {\\n k := [4]int{r,c,d,turned}\\n if val, found := cache[k]; found {\\n return val\\n }\\n res := 1\\n var next, follow, turn int\\n\\n if grid[r][c] == 1 {\\n return 0\\n } else if grid[r][c] == 0 {\\n next = 2\\n } else {\\n next = 0\\n }\\n \\n // follow\\n fr, fc := r+dir[d][0], c+dir[d][1]\\n if inbounds(fr,fc) && grid[fr][fc] == next { \\n follow = helper(fr, fc, d, turned) \\n }\\n // make turn\\n td := (d+1)%4\\n tr, tc := r+dir[td][0], c+dir[td][1]\\n if turned == 0 && inbounds(tr, tc) &&\\n grid[tr][tc] == next {\\n turn = helper(tr, tc, td, 1)\\n }\\n res = 1 + max(follow, turn)\\n cache[k] = res\\n return res\\n }\\n\\n var res int\\n for i := 0; i < n; i++ {\\n for j := 0; j < m; j++ {\\n if grid[i][j] != 1 {\\n continue\\n }\\n var cur = 1\\n for d := 0; d < 4; d++ {\\n ni, nj := i+dir[d][0], j+dir[d][1]\\n if inbounds(ni,nj) && grid[ni][nj] == 2 {\\n cur = max(\\n cur,\\n 1+helper(ni, nj, d, 0),\\n )\\n }\\n }\\n res = max(res, cur)\\n }\\n }\\n\\n return res\\n}\"], [316500, 5.2632, \"func lenOfVDiagonal(grid [][]int) int {\\n n, m := len(grid), len(grid[0])\\n dir := [4][2]int{\\n {-1, 1},\\n {1, 1},\\n {1, -1},\\n {-1,-1},\\n }\\n inbounds := func(r, c int) bool {\\n return r >= 0 && c >= 0 && r < n && c < m\\n }\\n\\n cache := make(map[[4]int]int)\\n\\n var helper func(int,int,int,int) int\\n helper = func(r, c int, d int, turned int) int {\\n k := [4]int{r,c,d,turned}\\n if val, found := cache[k]; found {\\n return val\\n }\\n res := 1\\n var next, follow, turn int\\n\\n if grid[r][c] == 1 {\\n return 0\\n } else if grid[r][c] == 0 {\\n next = 2\\n } else {\\n next = 0\\n }\\n \\n // follow\\n fr, fc := r+dir[d][0], c+dir[d][1]\\n if inbounds(fr,fc) && grid[fr][fc] == next { \\n follow = helper(fr, fc, d, turned) \\n }\\n // make turn\\n td := (d+1)%4\\n tr, tc := r+dir[td][0], c+dir[td][1]\\n if turned == 0 && inbounds(tr, tc) &&\\n grid[tr][tc] == next {\\n turn = helper(tr, tc, td, 1)\\n }\\n res = 1 + max(follow, turn)\\n cache[k] = res\\n return res\\n }\\n\\n var res int\\n for i := 0; i < n; i++ {\\n for j := 0; j < m; j++ {\\n if grid[i][j] != 1 {\\n continue\\n }\\n var cur = 1\\n for d := 0; d < 4; d++ {\\n ni, nj := i+dir[d][0], j+dir[d][1]\\n if inbounds(ni,nj) && grid[ni][nj] == 2 {\\n cur = max(\\n cur,\\n 1+helper(ni, nj, d, 0),\\n )\\n }\\n }\\n res = max(res, cur)\\n }\\n }\\n\\n return res\\n}\"]]",
"runtime": 287,
"runtimeDistribution": "[[52, 5.2632, \"package main\\n\\nimport \\\"fmt\\\"\\n\\nvar DIRS = [4][2]int{{1, 1}, {1, -1}, {-1, -1}, {-1, 1}}\\n\\nfunc lenOfVDiagonal(grid [][]int) int {\\n\\tn, m := len(grid), len(grid[0])\\n\\n\\t// Memoization table: [n][m][4][2] (i, j, direction, canTurn)\\n\\tdp := make([][][4][2]int, n)\\n\\tfor i := range dp {\\n\\t\\tdp[i] = make([][4][2]int, m)\\n\\t}\\n\\n\\t// DFS function\\n\\tvar dfs func(int, int, int, int, int) int\\n\\tdfs = func(i, j, dir, currReq, rotated int) int {\\n\\t\\ti += DIRS[dir][0]\\n\\t\\tj += DIRS[dir][1]\\n\\n\\t\\tif i < 0 || i >= n || j < 0 || j >= m || grid[i][j] != currReq {\\n\\t\\t\\treturn 0\\n\\t\\t}\\n\\n\\t\\tp := &dp[i][j][dir][rotated]\\n\\t\\tif *p > 0 {\\n\\t\\t\\treturn *p\\n\\t\\t}\\n\\n\\t\\t*p = dfs(i, j, dir, 2-currReq, rotated)\\n\\n\\t\\t// Try rotating only if not already rotated\\n\\t\\tif rotated == 0 {\\n\\t\\t\\tnewDir := (dir + 1) % 4\\n\\t\\t\\tmaxs := [4]int{n - i, j + 1, i + 1, m - j} // Theoretical max length\\n\\t\\t\\tif maxs[newDir] > *p {\\n\\t\\t\\t\\t*p = max(*p, dfs(i, j, newDir, 2-currReq, 1))\\n\\t\\t\\t}\\n\\t\\t}\\n\\n\\t\\t*p += 1\\n\\t\\treturn *p\\n\\t}\\n\\n\\t// Iterate over all starting points\\n\\tvar ans int\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tfor j := 0; j < m; j++ {\\n\\t\\t\\tif grid[i][j] != 1 {\\n\\t\\t\\t\\tcontinue\\n\\t\\t\\t}\\n\\t\\t\\tmaxs := [4]int{n - i, j + 1, i + 1, m - j} // Theoretical max length\\n\\t\\t\\tfor k := 0; k < 4; k++ {\\n\\t\\t\\t\\tif maxs[k] > ans { // Prune unnecessary DFS calls\\n\\t\\t\\t\\t\\tans = max(ans, dfs(i, j, k, 2, 0)+1)\\n\\t\\t\\t\\t}\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\treturn ans\\n}\\n\"], [73, 5.2632, \"var dirs = [4][2]int{\\n { 1, 1},\\n { 1, -1},\\n {-1, -1},\\n {-1, 1},\\n}\\n\\nfunc lenOfVDiagonal(grid [][]int) int {\\n\\n m := len(grid)\\n n := len(grid[0])\\n\\n cache := make([][][4][2]int, m)\\n for i := range cache {\\n cache[i] = make([][4][2]int, n)\\n }\\n \\n var search func(i, j, d, t, v int) int\\n search = func(i, j, d, t, v int) int {\\n if i < 0 || i >= m || j < 0 || j >= n {\\n return 0\\n }\\n if grid[i][j] != v {\\n return 0\\n }\\n if cache[i][j][d][t] > 0 {\\n return cache[i][j][d][t]\\n }\\n\\n best := 1 + search(\\n i+dirs[d][0],\\n j+dirs[d][1],\\n d,\\n t,\\n v^2,\\n )\\n\\n if t > 0 {\\n q := (d+1) % 4\\n best = max(best, 1 + search(\\n i+dirs[q][0],\\n j+dirs[q][1],\\n q,\\n t-1,\\n v^2,\\n ))\\n }\\n\\n cache[i][j][d][t] = best\\n return best\\n }\\n\\n var best int\\n for i, row := range grid {\\n for j, val := range row {\\n if val != 1 {\\n continue\\n }\\n perfect := []int{m-i, j+1, i+1, n-j}\\n for d, dir := range dirs {\\n if best >= perfect[d] {\\n continue\\n }\\n x := i + dir[0]\\n y := j + dir[1]\\n tail := search(x, y, d, 1, 2)\\n best = max(best, 1 + tail)\\n }\\n }\\n }\\n\\n return best\\n}\"], [74, 5.2632, null], [76, 5.2632, null], [77, 5.2632, null], [78, 5.2632, null], [81, 5.2632, null], [82, 5.2632, null], [85, 5.2632, null], [91, 5.2632, null], [97, 5.2632, null], [99, 5.2632, null], [147, 5.2632, null], [177, 5.2632, null], [287, 26.3152, \"func lenOfVDiagonal(grid [][]int) int {\\n n := len(grid)\\n if n == 0 {\\n return 0\\n }\\n m := len(grid[0])\\n if m == 0 {\\n return 0\\n }\\n\\n directions := [4][2]int{{1, 1}, {1, -1}, {-1, 1}, {-1, -1}}\\n\\n steps0 := make([][][]int, n)\\n steps2 := make([][][]int, n)\\n for i := range steps0 {\\n steps0[i] = make([][]int, m)\\n steps2[i] = make([][]int, m)\\n for j := range steps0[i] {\\n steps0[i][j] = make([]int, 4)\\n steps2[i][j] = make([]int, 4)\\n }\\n }\\n\\n for d := 0; d < 4; d++ {\\n dx, dy := directions[d][0], directions[d][1]\\n startX, endX, stepX := n-1, -1, -1\\n if dx == -1 {\\n startX, endX, stepX = 0, n, 1\\n }\\n startY, endY, stepY := m-1, -1, -1\\n if dy == -1 {\\n startY, endY, stepY = 0, m, 1\\n }\\n\\n for x := startX; x != endX; x += stepX {\\n for y := startY; y != endY; y += stepY {\\n if grid[x][y] == 0 {\\n steps0[x][y][d] = 1\\n nx, ny := x+dx, y+dy\\n if nx >= 0 && nx < n && ny >= 0 && ny < m {\\n steps0[x][y][d] += steps2[nx][ny][d]\\n }\\n } else {\\n steps0[x][y][d] = 0\\n }\\n\\n if grid[x][y] == 2 {\\n steps2[x][y][d] = 1\\n nx, ny := x+dx, y+dy\\n if nx >= 0 && nx < n && ny >= 0 && ny < m {\\n steps2[x][y][d] += steps0[nx][ny][d]\\n }\\n } else {\\n steps2[x][y][d] = 0\\n }\\n }\\n }\\n }\\n\\n maxLen := 0\\n for i := 0; i < n; i++ {\\n for j := 0; j < m; j++ {\\n if grid[i][j] != 1 {\\n continue\\n }\\n\\n for d := 0; d < 4; d++ {\\n dx, dy := directions[d][0], directions[d][1]\\n nextI, nextJ := i+dx, j+dy\\n pre := 1\\n if nextI >= 0 && nextI < n && nextJ >= 0 && nextJ < m {\\n pre += steps2[nextI][nextJ][d]\\n }\\n\\n if pre == 0 {\\n continue\\n }\\n\\n currentMax := pre\\n for s := 1; s <= pre; s++ {\\n newX := i + (s-1)*dx + directions[d][1]\\n newY := j + (s-1)*dy - directions[d][0]\\n\\n if newX < 0 || newX >= n || newY < 0 || newY >= m {\\n continue\\n }\\n\\n nextExpected := 2\\n if s%2 == 0 {\\n nextExpected = 0\\n }\\n\\n ndx := directions[d][1]\\n ndy := -directions[d][0]\\n newD := -1\\n for nd := 0; nd < 4; nd++ {\\n if directions[nd][0] == ndx && directions[nd][1] == ndy {\\n newD = nd\\n break\\n }\\n }\\n if newD == -1 {\\n continue\\n }\\n\\n var post int\\n if nextExpected == 0 {\\n post = steps0[newX][newY][newD]\\n } else {\\n post = steps2[newX][newY][newD]\\n }\\n\\n if s+post > currentMax {\\n currentMax = s + post\\n }\\n }\\n\\n if currentMax > maxLen {\\n maxLen = currentMax\\n }\\n }\\n }\\n }\\n\\n return maxLen\\n}\"], [356, 5.2632, null], [934, 5.2632, null], [1576, 5.2632, \"func lenOfVDiagonal(grid [][]int) int {\\n n, m := len(grid), len(grid[0])\\n dir := [4][2]int{\\n {-1, 1},\\n {1, 1},\\n {1, -1},\\n {-1,-1},\\n }\\n\\n cache := make(map[[4]int]int)\\n\\n var helper func(int,int,int,int,int) int\\n helper = func(r, c int, d int, turned, exp int) int {\\n if r < 0 || c < 0 || r >= n || c >= m {\\n return 0\\n }\\n if grid[r][c] != exp {\\n return 0\\n }\\n\\n k := [4]int{r, c, d, turned}\\n if val, found := cache[k]; found {\\n return val\\n }\\n\\n res := 1\\n var follow, turn int\\n // follow \\n follow = helper(r+dir[d][0], c+dir[d][1], d, turned, 2-exp)\\n // make turn\\n d = (d+1)%4\\n if turned == 0 {\\n turn = helper(r+dir[d][0], c+dir[d][1], d, 1, 2-exp)\\n }\\n res = 1 + max(follow, turn)\\n cache[k] = res\\n return res\\n }\\n\\n var res int\\n for i := 0; i < n; i++ {\\n for j := 0; j < m; j++ {\\n if grid[i][j] != 1 {\\n continue\\n }\\n var cur = 1\\n for d := 0; d < 4; d++ {\\n cur = max(cur, 1+helper(i+dir[d][0], j+dir[d][1], d, 0, 2))\\n }\\n res = max(res, cur)\\n }\\n }\\n\\n return res\\n}\"], [1711, 5.2632, \"func lenOfVDiagonal(grid [][]int) int {\\n n, m := len(grid), len(grid[0])\\n dir := [4][2]int{\\n {-1, 1},\\n {1, 1},\\n {1, -1},\\n {-1,-1},\\n }\\n inbounds := func(r, c int) bool {\\n return r >= 0 && c >= 0 && r < n && c < m\\n }\\n\\n cache := make(map[[4]int]int)\\n\\n var helper func(int,int,int,int) int\\n helper = func(r, c int, d int, turned int) int {\\n k := [4]int{r,c,d,turned}\\n if val, found := cache[k]; found {\\n return val\\n }\\n res := 1\\n var next, follow, turn int\\n\\n if grid[r][c] == 1 {\\n return 0\\n } else if grid[r][c] == 0 {\\n next = 2\\n } else {\\n next = 0\\n }\\n \\n // follow\\n fr, fc := r+dir[d][0], c+dir[d][1]\\n if inbounds(fr,fc) && grid[fr][fc] == next { \\n follow = helper(fr, fc, d, turned) \\n }\\n // make turn\\n td := (d+1)%4\\n tr, tc := r+dir[td][0], c+dir[td][1]\\n if turned == 0 && inbounds(tr, tc) &&\\n grid[tr][tc] == next {\\n turn = helper(tr, tc, td, 1)\\n }\\n res = 1 + max(follow, turn)\\n cache[k] = res\\n return res\\n }\\n\\n var res int\\n for i := 0; i < n; i++ {\\n for j := 0; j < m; j++ {\\n if grid[i][j] != 1 {\\n continue\\n }\\n var cur = 1\\n for d := 0; d < 4; d++ {\\n ni, nj := i+dir[d][0], j+dir[d][1]\\n if inbounds(ni,nj) && grid[ni][nj] == 2 {\\n cur = max(\\n cur,\\n 1+helper(ni, nj, d, 0),\\n )\\n }\\n }\\n res = max(res, cur)\\n }\\n }\\n\\n return res\\n}\"]]"
},
"java": {
"code": "class Solution {\n public int lenOfVDiagonal(int[][] grid) {\n int n = grid.length;\n int m = grid[0].length;\n int[][] dirs = {{1, 1}, {1, -1}, {-1, 1}, {-1, -1}};\n int max = 0;\n \n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n if (grid[i][j] != 1) continue;\n \n for (int[] dir : dirs) {\n int dx = dir[0];\n int dy = dir[1];\n int steps = 0;\n \n while (true) {\n int nextX = i + (steps + 1) * dx;\n int nextY = j + (steps + 1) * dy;\n if (nextX < 0 || nextX >= n || nextY < 0 || nextY >= m) break;\n int step = steps + 1;\n int expected = (step % 2 == 1) ? 2 : 0;\n if (grid[nextX][nextY] == expected) {\n steps++;\n } else {\n break;\n }\n }\n \n int currentMax = steps + 1;\n \n for (int t = 0; t <= steps; t++) {\n int ndx = dy;\n int ndy = -dx;\n int x = i + t * dx + ndx;\n int y = j + t * dy + ndy;\n if (x < 0 || x >= n || y < 0 || y >= m) continue;\n int stepInTurn = t + 1;\n int expected = (stepInTurn % 2 == 1) ? 2 : 0;\n if (grid[x][y] != expected) continue;\n \n int s = 0;\n while (true) {\n int nextX = x + (s + 1) * ndx;\n int nextY = y + (s + 1) * ndy;\n if (nextX < 0 || nextX >= n || nextY < 0 || nextY >= m) break;\n int step = stepInTurn + (s + 1);\n expected = (step % 2 == 1) ? 2 : 0;\n if (grid[nextX][nextY] == expected) {\n s++;\n } else {\n break;\n }\n }\n \n int total = (t + 1) + (s + 1);\n if (total > currentMax) {\n currentMax = total;\n }\n }\n \n if (currentMax > max) {\n max = currentMax;\n }\n }\n }\n }\n \n return max;\n }\n}",
"memory": 9100,
"memoryDistribution": "[[9100, 37.6624, \"class Solution {\\n public int lenOfVDiagonal(int[][] grid) {\\n int n = grid.length;\\n int m = grid[0].length;\\n int[][] dirs = {{1, 1}, {1, -1}, {-1, 1}, {-1, -1}};\\n int max = 0;\\n \\n for (int i = 0; i < n; i++) {\\n for (int j = 0; j < m; j++) {\\n if (grid[i][j] != 1) continue;\\n \\n for (int[] dir : dirs) {\\n int dx = dir[0];\\n int dy = dir[1];\\n int steps = 0;\\n \\n while (true) {\\n int nextX = i + (steps + 1) * dx;\\n int nextY = j + (steps + 1) * dy;\\n if (nextX < 0 || nextX >= n || nextY < 0 || nextY >= m) break;\\n int step = steps + 1;\\n int expected = (step % 2 == 1) ? 2 : 0;\\n if (grid[nextX][nextY] == expected) {\\n steps++;\\n } else {\\n break;\\n }\\n }\\n \\n int currentMax = steps + 1;\\n \\n for (int t = 0; t <= steps; t++) {\\n int ndx = dy;\\n int ndy = -dx;\\n int x = i + t * dx + ndx;\\n int y = j + t * dy + ndy;\\n if (x < 0 || x >= n || y < 0 || y >= m) continue;\\n int stepInTurn = t + 1;\\n int expected = (stepInTurn % 2 == 1) ? 2 : 0;\\n if (grid[x][y] != expected) continue;\\n \\n int s = 0;\\n while (true) {\\n int nextX = x + (s + 1) * ndx;\\n int nextY = y + (s + 1) * ndy;\\n if (nextX < 0 || nextX >= n || nextY < 0 || nextY >= m) break;\\n int step = stepInTurn + (s + 1);\\n expected = (step % 2 == 1) ? 2 : 0;\\n if (grid[nextX][nextY] == expected) {\\n s++;\\n } else {\\n break;\\n }\\n }\\n \\n int total = (t + 1) + (s + 1);\\n if (total > currentMax) {\\n currentMax = total;\\n }\\n }\\n \\n if (currentMax > max) {\\n max = currentMax;\\n }\\n }\\n }\\n }\\n \\n return max;\\n }\\n}\"], [73000, 12.987, \"class Solution {\\n int res1 = 0;\\n private static final int[][] DIRS = {{1,1},{1,-1},{-1,-1},{-1,1}};\\n public int lenOfVDiagonal(int[][] grid) {\\n int m = grid.length, n = grid[0].length;\\n int ans = 0;\\n int[][][] memo = new int[m][n][1<<3];\\n for(int i = 0; i <m;i++){\\n for(int j = 0; j <n;j++){\\n if(grid[i][j] == 1){\\n for(int k = 0;k < 4;k++){\\n ans = Math.max(ans,dfs(i,j,k,1,2,grid,memo)+1);\\n }\\n }\\n }\\n }\\n return ans;\\n }\\n\\n private int dfs(int i, int j,int k, int canTurn, int target, int[][] grid, int[][][] memo){\\n i += DIRS[k][0];\\n j += DIRS[k][1];\\n if(i < 0 || i >= grid.length || j < 0 || j >= grid[i].length || grid[i][j] != target){\\n return 0;\\n }\\n int mask = k << 1| canTurn;\\n if(memo[i][j][mask] > 0){\\n return memo[i][j][mask];\\n }\\n\\n int res = dfs(i,j,k,canTurn,2-target,grid,memo);//go stright\\n\\n if(canTurn == 1){\\n res = Math.max(res,dfs(i,j,(k+1)%4,0,2-target,grid,memo)); //Turn right\\n }\\n\\n return memo[i][j][mask] = res + 1; //Counting current position\\n }\\n\\n // twoOrZro is true means this iteration should be 2, false means this iteration should be 0\\n // direction = 1 means up-left(x - 1, y-1),2 means up-right(x-1,y+1), 3 means down-left(x+1,y-1),4 means down-right(x+1,y+1)\\n private void myDfs(int row, int col, int[][] grid, int dis, int clockwiseLeft,int n, int m, boolean twoOrZero, int direction){\\n if(clockwiseLeft < 0) return;\\n if(row < 0 || row >= n || col < 0 || col >= m || !twoOrZero){\\n //res = Math.max(dis,res);\\n return;\\n }\\n int cur = grid[row][col];\\n if(clockwiseLeft == 0){\\n \\n if((cur == 0 && twoOrZero) || (cur == 2 && !twoOrZero)){\\n res1 = Math.max(dis,res1);\\n return;\\n }\\n if(direction == 1) myDfs(row-1,col-1,grid,dis+1,clockwiseLeft,n,m,!twoOrZero,direction);\\n else if(direction == 2) myDfs(row-1,col+1,grid,dis+1,clockwiseLeft,n,m,!twoOrZero,direction);\\n else if(direction == 3) myDfs(row+1,col-1,grid,dis+1,clockwiseLeft,n,m,!twoOrZero,direction);\\n else myDfs(row+1,col+1,grid,dis+1,clockwiseLeft,n,m,!twoOrZero,direction);\\n }else{\\n if(direction == 1){\\n myDfs(row-1,col-1,grid,dis+1,clockwiseLeft,n,m,!twoOrZero,direction);\\n myDfs(row-1,col+1,grid,dis+1,clockwiseLeft-1,n,m,!twoOrZero,2);\\n }else if(direction == 2){\\n myDfs(row-1,col+1,grid,dis+1,clockwiseLeft,n,m,!twoOrZero,direction);\\n myDfs(row+1,col+1,grid,dis+1,clockwiseLeft-1,n,m,!twoOrZero,4);\\n }else if(direction == 3){\\n myDfs(row+1,col-1,grid,dis+1,clockwiseLeft,n,m,!twoOrZero,direction);\\n myDfs(row-1,col-1,grid,dis+1,clockwiseLeft-1,n,m,!twoOrZero,1);\\n }else{\\n myDfs(row+1,col+1,grid,dis+1,clockwiseLeft,n,m,!twoOrZero,direction);\\n myDfs(row+1,col-1,grid,dis+1,clockwiseLeft-1,n,m,!twoOrZero,3);\\n }\\n }\\n\\n \\n\\n }\\n}\"], [75601, 26.4069, \"class Solution {\\n int [][] dir = new int[][]{{1,1},{1,-1},{-1,-1},{-1,1}};\\n public int lenOfVDiagonal(int[][] grid) {\\n int ans=0;\\n for(int i=0;i<grid.length;i++){\\n for(int j=0;j<grid[0].length;j++){\\n if(grid[i][j]==1){\\n for(int k=0;k<4;k++){\\n ans = Math.max(ans,1+helper(i+dir[k][0],j+dir[k][1],grid,1,k,false));\\n }\\n }\\n }\\n }\\n return ans;\\n }\\n public int helper(int i,int j,int[][]grid, int prev,int prevDir,boolean turn){\\n if(i<0 || i >= grid.length || j<0 || j>= grid[0].length || grid[i][j]==prev || \\n grid[i][j]==1 || (prev==1 && grid[i][j]==0)){\\n return 0;\\n }\\n int ans=0;\\n if(!turn){\\n int k=(prevDir+1) %4 ;\\n ans = Math.max(ans, helper(i+dir[k][0] , j+dir[k][1], grid, grid[i][j] ,k, true));\\n }\\n ans = Math.max(ans, helper(i+dir[prevDir][0] , j+dir[prevDir][1], grid, grid[i][j] ,prevDir,turn));\\n return ans+1;\\n }\\n}\"], [78203, 1.2987, null], [80804, 1.2987, null], [83405, 1.7316, null], [86006, 16.4502, null], [88608, 1.7316, null], [91209, 10.3896, null], [93810, 1.2987, null], [96411, 0.4329, null], [99013, 0.4329, null], [101614, 0.4329, null], [104215, 0.8658, null], [106816, 0.4329, null], [109418, 0.4329, null], [112019, 0.4329, null], [114620, 0.4329, null], [117221, 0.4329, null], [119823, 0.4329, null], [122424, 0.8658, null], [125025, 2.5974, null], [127626, 1.7316, null], [130228, 0.8658, null], [132829, 0.4329, null], [135430, 0.4329, null], [138031, 0.4329, null], [140633, 0.4329, null], [143234, 0.4329, null], [145835, 0.4329, null], [148436, 0.4329, null], [151038, 0.4329, null], [153639, 0.4329, null], [156240, 0.8658, null], [158841, 0.4329, null], [161443, 0.4329, null], [164044, 0.4329, null], [166645, 0.4329, null], [169246, 0.4329, null], [171848, 0.4329, null], [174449, 0.4329, null], [177050, 0.4329, null], [179651, 0.4329, null], [182253, 0.4329, null], [184854, 0.4329, \"class Solution {\\n private int dfs(int x, int y, int turn, int[][] grid, int[][] dir, int dirIdx, int target, int[][][][][] dp){\\n if(x<0 || y<0 || x>=grid.length || y>=grid[0].length)\\n return 0;\\n if(grid[x][y]!=target)\\n return 0;\\n \\n int res = 0;\\n int newTarget=2;\\n if(target==2)\\n newTarget=0;\\n if(dp[x][y][turn][dirIdx][target]!=-1)\\n return dp[x][y][turn][dirIdx][target];\\n res = 1 + dfs(x+dir[dirIdx][0],y+dir[dirIdx][1],turn, grid, dir, dirIdx,newTarget, dp);\\n if(turn>0){\\n int newTurn = turn-1;\\n int newDirIdx = (dirIdx+1)%4;\\n int res2 = 1 + dfs(x+dir[dirIdx][0],y+dir[newDirIdx][1],newTurn, grid, dir, newDirIdx,newTarget, dp);\\n res = Math.max(res,res2);\\n }\\n return dp[x][y][turn][dirIdx][target]=res;\\n }\\n public int lenOfVDiagonal(int[][] grid) {\\n int[][] dir = new int[][]{{-1,-1},{-1,1},{1,1},{1,-1}};\\n int[][][][][] dp = new int[grid.length][grid[0].length][2][4][3];\\n for(int i=0;i<grid.length;i++)\\n for(int j=0;j<grid[0].length;j++)\\n for(int k=0;k<2;k++)\\n for(int l=0;l<4;l++)\\n for(int m=0;m<3;m++)\\n dp[i][j][k][l][m]=-1;\\n int ans = 0;\\n for(int i=0;i<grid.length;i++){\\n for(int j=0;j<grid[0].length;j++){\\n if(grid[i][j]==1){\\n for(int k=0;k<4;k++){\\n ans = Math.max(ans,dfs(i,j,1,grid,dir,k,1,dp));\\n }\\n }\\n }\\n }\\n return ans;\\n }\\n}\"], [187455, 0.8658, \"class Solution {\\n public static int n;\\n public static int m;\\n public static Integer[][][][][] dp;\\n public static int[] x = {1, 1, -1, -1};\\n public static int[] y = {1, -1, -1, 1};\\n public int lenOfVDiagonal(int[][] g) {\\n n = g.length;\\n m = g[0].length;\\n dp = new Integer[n][m][2][3][4];\\n int ans = 0;\\n for (int i = 0; i < n; i++) {\\n for (int j = 0; j < m; j++) {\\n if (g[i][j] == 1) {\\n for (int k = 0; k < 4; k++) {\\n ans = Math.max(ans, 1 + solve(i + x[k], j + y[k], 0, 2, k, g));\\n }\\n }\\n }\\n }\\n return ans;\\n }\\n public static int solve(int i, int j, int turn, int curr, int dir, int[][] g) {\\n if (i >= n || i < 0 || j >= m || j < 0 || g[i][j] != curr) return 0;\\n if (dp[i][j][turn][curr][dir] != null) return dp[i][j][turn][curr][dir];\\n int ans = 1 + solve(i + x[dir], j + y[dir], turn, 2 - curr, dir, g);\\n if (turn == 0) {\\n ans = Math.max(ans, 1 + solve(i + x[(dir + 1) % 4], j + y[(dir + 1) % 4], 1, 2 - curr, (dir + 1) % 4, g));\\n }\\n return dp[i][j][turn][curr][dir] = ans;\\n }\\n}\"]]",
"runtime": 455,
"runtimeDistribution": "[[41, 1.7316, \"class Solution {\\n static int[] dx = {-1, -1, 1, 1 }, dy = {-1, 1, 1, -1 };\\n static int[] que = new int[250000];\\n public int lenOfVDiagonal(int[][] grid) {\\n\\n int m = grid.length, n = grid[0].length;\\n int[][][] len0s = new int[4][m][n], len2s = new int[4][m][n];\\n \\n \\n int write = 0, read =0;\\n\\n for (int k = 0; k < 4; k++) {\\n \\n int dr = dx[k], dc = dy[k];\\n int startR = dr == 1 ? m - 1 : 0, endR = dr == 1 ? -1 : m, stepR = -dr ;\\n int startC = dc == 1 ? n - 1 : 0, endC = dc == 1 ? -1 : n, stepC = -dc;\\n\\n int[][] len0 = len0s[k], len2 = len2s[k];\\n\\n for (int r = startR; r != endR; r += stepR) {\\n for (int c = startC; c != endC; c += stepC) {\\n if(grid[r][c] == 1) {\\n if(k == 0)\\n que[write++] = r << 9 | c;\\n continue;\\n }\\n int nr = r + dr, nc = c + dc;\\n\\n if (grid[r][c] == 0)\\n len0[r][c] = (nr >= 0 && nr < m && nc >= 0 && nc < n) ? 1 + len2[nr][nc] : 1;\\n else\\n len2[r][c] = (nr >= 0 && nr < m && nc >= 0 && nc < n) ? 1 + len0[nr][nc] : 1;\\n }\\n }\\n }\\n \\n int max = Math.max(m, n);\\n int ans = 0;\\n\\n while(read < write){\\n\\n int cur = que[read++], r = cur >> 9, c = cur & ((1 << 9) - 1);\\n\\n for (int k = 0; k < 4; k++) {\\n\\n int dr = dx[k], dc = dy[k], turnK = (k + 1) & 3;\\n int segLen = 1, len = segLen;\\n for (int x = r + dr, y = c + dc ; ; x += dr, y += dc) {\\n\\n if (x < 0 || x >= m || y < 0 || y >= n) break;\\n if (grid[x][y] != (segLen & 1) * 2) break;\\n \\n int secondLeg = (( segLen & 1) == 1) ? len2s[turnK][x][y] : len0s[turnK][x][y];\\n len = Math.max(len, Math.max(segLen + secondLeg, ++segLen));\\n }\\n\\n ans = Math.max(ans, len);\\n }\\n \\n\\n if(ans == max) return ans;\\n }\\n\\n return ans;\\n }\\n}\"], [57, 3.0303, \"class Solution {\\n \\n static final int[][] directions = {{-1, -1}, {-1, 1}, {1, 1}, {1, -1} };\\n\\n public int lenOfVDiagonal(int[][] grid) {\\n\\n int m = grid.length, n = grid[0].length;\\n int[][] bottomLeft = new int[m][n];\\n int[][] bottomRight = new int[m][n];\\n int[][] topLeft = new int[m][n];\\n int[][] topRight = new int[m][n];\\n \\n for (int i = 0; i < m; i++) {\\n for (int j = 0; j < n; j++) {\\n bottomLeft[i][j] = bottomRight[i][j] = topLeft[i][j] = topRight[i][j] = 1;\\n }\\n }\\n \\n int ans = 0;\\n \\n for (int i = 0; i < m; i++) {\\n for (int j = 0; j < n; j++) {\\n int x = grid[i][j];\\n if (x == 1) {\\n ans = 1;\\n continue;\\n }\\n \\n if (i > 0 && j + 1 < n && grid[i-1][j+1] == 2 - x) \\n bottomLeft[i][j] = bottomLeft[i-1][j+1] + 1;\\n \\n if (i > 0 && j > 0 && grid[i-1][j-1] == 2 - x) \\n bottomRight[i][j] = bottomRight[i-1][j-1] + 1;\\n }\\n }\\n \\n for (int i = m - 1; i >= 0; --i) {\\n for (int j = n - 1; j >= 0; --j) {\\n int x = grid[i][j];\\n if (x == 1) continue;\\n \\n if (i + 1 < m && j + 1 < n && grid[i+1][j+1] == 2 - x) \\n topLeft[i][j] = topLeft[i+1][j+1] + 1;\\n \\n if (i + 1 < m && j > 0 && grid[i+1][j-1] == 2 - x) \\n topRight[i][j] = topRight[i+1][j-1] + 1;\\n }\\n }\\n \\n int[][][] memo = {topLeft, topRight, bottomRight, bottomLeft};\\n \\n for (int i = 0; i < m; ++i) {\\n for (int j = 0; j < n; ++j) {\\n int x = grid[i][j];\\n if (x == 1) continue;\\n \\n x >>= 1;\\n for(int k = 0; k < 4; ++k){\\n int v = memo[k][i][j];\\n if((v & 1) != x) continue;\\n if( v + memo[k + 3 & 3][i][j] <= ans) continue;\\n \\n int[] d = directions[k];\\n int ni = i - d[0] * v, nj = j - d[1] * v;\\n if (ni >= 0 && nj >= 0 && ni < m && nj < n && grid[ni][nj] == 1) \\n ans = Math.max(ans, v + memo[k + 3 & 3][i][j]);\\n }\\n }\\n }\\n \\n return ans;\\n }\\n}\"], [73, 0.8658, null], [90, 0.4329, null], [106, 0.4329, null], [123, 0.4329, null], [139, 0.4329, null], [155, 0.4329, null], [172, 0.8658, null], [188, 3.0303, null], [204, 1.7316, null], [221, 0.4329, null], [237, 0.4329, null], [254, 0.4329, null], [270, 0.4329, null], [286, 0.4329, null], [303, 0.4329, null], [319, 0.4329, null], [335, 0.4329, null], [352, 0.4329, null], [368, 0.4329, null], [385, 0.4329, null], [401, 0.4329, null], [417, 0.4329, null], [434, 0.8658, null], [450, 1.2987, null], [455, 80.0866, \"class Solution {\\n public int lenOfVDiagonal(int[][] grid) {\\n int n = grid.length;\\n int m = grid[0].length;\\n int[][] dirs = {{1, 1}, {1, -1}, {-1, 1}, {-1, -1}};\\n int max = 0;\\n \\n for (int i = 0; i < n; i++) {\\n for (int j = 0; j < m; j++) {\\n if (grid[i][j] != 1) continue;\\n \\n for (int[] dir : dirs) {\\n int dx = dir[0];\\n int dy = dir[1];\\n int steps = 0;\\n \\n while (true) {\\n int nextX = i + (steps + 1) * dx;\\n int nextY = j + (steps + 1) * dy;\\n if (nextX < 0 || nextX >= n || nextY < 0 || nextY >= m) break;\\n int step = steps + 1;\\n int expected = (step % 2 == 1) ? 2 : 0;\\n if (grid[nextX][nextY] == expected) {\\n steps++;\\n } else {\\n break;\\n }\\n }\\n \\n int currentMax = steps + 1;\\n \\n for (int t = 0; t <= steps; t++) {\\n int ndx = dy;\\n int ndy = -dx;\\n int x = i + t * dx + ndx;\\n int y = j + t * dy + ndy;\\n if (x < 0 || x >= n || y < 0 || y >= m) continue;\\n int stepInTurn = t + 1;\\n int expected = (stepInTurn % 2 == 1) ? 2 : 0;\\n if (grid[x][y] != expected) continue;\\n \\n int s = 0;\\n while (true) {\\n int nextX = x + (s + 1) * ndx;\\n int nextY = y + (s + 1) * ndy;\\n if (nextX < 0 || nextX >= n || nextY < 0 || nextY >= m) break;\\n int step = stepInTurn + (s + 1);\\n expected = (step % 2 == 1) ? 2 : 0;\\n if (grid[nextX][nextY] == expected) {\\n s++;\\n } else {\\n break;\\n }\\n }\\n \\n int total = (t + 1) + (s + 1);\\n if (total > currentMax) {\\n currentMax = total;\\n }\\n }\\n \\n if (currentMax > max) {\\n max = currentMax;\\n }\\n }\\n }\\n }\\n \\n return max;\\n }\\n}\"], [466, 1.2987, null], [483, 0.4329, null], [499, 1.7316, null], [516, 2.1645, null], [532, 0.4329, null], [548, 0.4329, null], [565, 0.4329, null], [581, 0.4329, null], [597, 0.4329, null], [614, 0.4329, null], [630, 0.4329, null], [647, 0.4329, null], [663, 0.4329, null], [679, 0.4329, null], [696, 0.4329, null], [712, 0.4329, null], [728, 0.4329, null], [745, 0.4329, null], [761, 0.4329, null], [778, 0.4329, null], [794, 0.4329, null], [810, 0.4329, null], [827, 0.8658, null], [843, 0.8658, null], [859, 0.4329, null], [876, 0.4329, null], [892, 0.4329, null], [909, 0.4329, null], [925, 0.8658, null], [941, 0.8658, null], [958, 0.8658, null], [974, 0.4329, null], [990, 0.8658, null], [1007, 0.4329, null], [1023, 0.8658, null], [1040, 0.8658, null], [1056, 0.8658, null], [1072, 1.2987, null], [1089, 0.8658, null], [1105, 0.8658, null], [1121, 6.0606, null], [1138, 14.7186, null], [1154, 10.3896, null], [1171, 3.0303, null], [1187, 1.2987, null], [1203, 2.1645, null], [1220, 2.1645, null], [1236, 2.1645, null], [1252, 0.4329, null], [1269, 1.2987, null], [1285, 1.7316, null], [1302, 0.4329, \"class Solution {\\n private final int[][] dirs = { { -1, 1 }, { 1, 1 }, { 1, -1 }, { -1, -1 } };\\n\\n private int solveDFS(int[][] grid, int n, int m, int i, int j, int dir, int trgt, boolean turned) {\\n int x = i + dirs[dir][0], y = j + dirs[dir][1];\\n if (x < 0 || x >= n || y < 0 || y >= m || grid[x][y] != trgt) {\\n return 1;\\n }\\n\\n int move = 1 + solveDFS(grid, n, m, x, y, dir, trgt == 2 ? 0 : 2, turned);\\n int turn = 0;\\n if (!turned) {\\n turn = 1 + solveDFS(grid, n, m, x, y, (dir + 1) % 4, trgt == 2 ? 0 : 2, true);\\n }\\n return Math.max(move, turn);\\n }\\n\\n public int lenOfVDiagonal(int[][] grid) {\\n int n = grid.length, m = grid[0].length;\\n\\n int res = 0;\\n for (int i = 0; i < n; i++) {\\n for (int j = 0; j < m; j++) {\\n if (grid[i][j] == 1) {\\n res = Math.max(res, 1);\\n res = Math.max(res, solveDFS(grid, n, m, i, j, 0, 2, false));\\n res = Math.max(res, solveDFS(grid, n, m, i, j, 1, 2, false));\\n res = Math.max(res, solveDFS(grid, n, m, i, j, 2, 2, false));\\n res = Math.max(res, solveDFS(grid, n, m, i, j, 3, 2, false));\\n }\\n }\\n }\\n return res;\\n }\\n}\"], [1318, 0.8658, \"\\nclass Solution {\\n\\n int[][] dirs = {\\n {-1, 1}, // topRight\\n {1, 1}, // bottomRight\\n {1, -1}, // bottomLeft\\n {-1, -1} // topLeft\\n };\\n int res = 0;\\n public int lenOfVDiagonal(int[][] grid) {\\n // memo = new State[grid.length][grid[0].length];\\n // for (int i = 0; i < grid.length; i++) {\\n // Arrays.fill(memo, new State(-1, -1, -1, -1));\\n // }\\n \\n for (int i = 0; i < grid.length; i++) {\\n for (int j = 0; j < grid[0].length; j++) {\\n if (grid[i][j] == 1) {\\n \\n for (int k = 0; k < dirs.length; k++) {\\n int sub = dfs(grid,2, i, j, k, false);\\n res = Math.max(sub, res);\\n }\\n \\n }\\n \\n }\\n }\\n return res;\\n }\\n\\n private int dfs(int[][] grid, int target, int i, int j, int d, boolean turned) {\\n int[] dir = dirs[d];\\n int newX = i + dir[0];\\n int newY = j + dir[1];\\n if (newX < 0 || newY < 0 || newX >= grid.length || newY >= grid[0].length || grid[newX][newY] != target) return 1;\\n\\n\\n int turn = 0;\\n int straight = dfs(grid, target == 2 ? 0 : 2, newX, newY, d, turned) + 1;\\n if (!turned) turn = dfs(grid, target == 2 ? 0 : 2, newX, newY, (d + 1)%4, true) + 1;\\n return Math.max(turn, straight);\\n\\n }\\n}\"]]"
},
"javascript": {
"code": "var lenOfVDiagonal = function(grid) {\n const n = grid.length;\n if (n === 0) return 0;\n const m = grid[0].length;\n let maxLen = 0;\n const directions = [\n { dx: 1, dy: 1 }, // down-right\n { dx: 1, dy: -1 }, // down-left\n { dx: -1, dy: 1 }, // up-right\n { dx: -1, dy: -1 }, // up-left\n ];\n const turnDir = [1, 3, 0, 2]; // new direction after turn for each original direction index\n\n for (let i = 0; i < n; i++) {\n for (let j = 0; j < m; j++) {\n if (grid[i][j] !== 1) continue;\n for (let dirIdx = 0; dirIdx < 4; dirIdx++) {\n const { dx, dy } = directions[dirIdx];\n let s = 0;\n let ci = i, cj = j;\n while (true) {\n const expected = s === 0 ? 1 : (s - 1) % 2 === 0 ? 2 : 0;\n if (ci < 0 || ci >= n || cj < 0 || cj >= m) break;\n if (grid[ci][cj] !== expected) break;\n s++;\n ci += dx;\n cj += dy;\n }\n maxLen = Math.max(maxLen, s);\n for (let t = 1; t <= s; t++) {\n const currI = i + (t - 1) * dx;\n const currJ = j + (t - 1) * dy;\n const newDirIdx = turnDir[dirIdx];\n const { dx: newDx, dy: newDy } = directions[newDirIdx];\n let mSteps = 0;\n let ni = currI, nj = currJ;\n while (true) {\n const expected = (t - 1 + mSteps) % 2 === 0 ? 2 : 0;\n ni += newDx;\n nj += newDy;\n if (ni < 0 || ni >= n || nj < 0 || nj >= m) break;\n if (grid[ni][nj] !== expected) break;\n mSteps++;\n }\n maxLen = Math.max(maxLen, t + mSteps);\n }\n }\n }\n }\n return maxLen;\n};",
"memory": 6700,
"memoryDistribution": "[[6700, 100.0, \"var lenOfVDiagonal = function(grid) {\\n const n = grid.length;\\n if (n === 0) return 0;\\n const m = grid[0].length;\\n let maxLen = 0;\\n const directions = [\\n { dx: 1, dy: 1 }, // down-right\\n { dx: 1, dy: -1 }, // down-left\\n { dx: -1, dy: 1 }, // up-right\\n { dx: -1, dy: -1 }, // up-left\\n ];\\n const turnDir = [1, 3, 0, 2]; // new direction after turn for each original direction index\\n\\n for (let i = 0; i < n; i++) {\\n for (let j = 0; j < m; j++) {\\n if (grid[i][j] !== 1) continue;\\n for (let dirIdx = 0; dirIdx < 4; dirIdx++) {\\n const { dx, dy } = directions[dirIdx];\\n let s = 0;\\n let ci = i, cj = j;\\n while (true) {\\n const expected = s === 0 ? 1 : (s - 1) % 2 === 0 ? 2 : 0;\\n if (ci < 0 || ci >= n || cj < 0 || cj >= m) break;\\n if (grid[ci][cj] !== expected) break;\\n s++;\\n ci += dx;\\n cj += dy;\\n }\\n maxLen = Math.max(maxLen, s);\\n for (let t = 1; t <= s; t++) {\\n const currI = i + (t - 1) * dx;\\n const currJ = j + (t - 1) * dy;\\n const newDirIdx = turnDir[dirIdx];\\n const { dx: newDx, dy: newDy } = directions[newDirIdx];\\n let mSteps = 0;\\n let ni = currI, nj = currJ;\\n while (true) {\\n const expected = (t - 1 + mSteps) % 2 === 0 ? 2 : 0;\\n ni += newDx;\\n nj += newDy;\\n if (ni < 0 || ni >= n || nj < 0 || nj >= m) break;\\n if (grid[ni][nj] !== expected) break;\\n mSteps++;\\n }\\n maxLen = Math.max(maxLen, t + mSteps);\\n }\\n }\\n }\\n }\\n return maxLen;\\n};\"], [68100, 14.2857, \"var lenOfVDiagonal = function(grid) {\\n const n = grid.length;\\n if (n === 0) return 0;\\n const m = grid[0].length;\\n let maxLen = 0;\\n const directions = [\\n { dx: 1, dy: 1 }, // down-right\\n { dx: 1, dy: -1 }, // down-left\\n { dx: -1, dy: 1 }, // up-right\\n { dx: -1, dy: -1 }, // up-left\\n ];\\n const turnDir = [1, 3, 0, 2]; // new direction after turn for each original direction index\\n\\n for (let i = 0; i < n; i++) {\\n for (let j = 0; j < m; j++) {\\n if (grid[i][j] !== 1) continue;\\n for (let dirIdx = 0; dirIdx < 4; dirIdx++) {\\n const { dx, dy } = directions[dirIdx];\\n let s = 0;\\n let ci = i, cj = j;\\n while (true) {\\n const expected = s === 0 ? 1 : (s - 1) % 2 === 0 ? 2 : 0;\\n if (ci < 0 || ci >= n || cj < 0 || cj >= m) break;\\n if (grid[ci][cj] !== expected) break;\\n s++;\\n ci += dx;\\n cj += dy;\\n }\\n maxLen = Math.max(maxLen, s);\\n for (let t = 1; t <= s; t++) {\\n const currI = i + (t - 1) * dx;\\n const currJ = j + (t - 1) * dy;\\n const newDirIdx = turnDir[dirIdx];\\n const { dx: newDx, dy: newDy } = directions[newDirIdx];\\n let mSteps = 0;\\n let ni = currI, nj = currJ;\\n while (true) {\\n const expected = (t - 1 + mSteps) % 2 === 0 ? 2 : 0;\\n ni += newDx;\\n nj += newDy;\\n if (ni < 0 || ni >= n || nj < 0 || nj >= m) break;\\n if (grid[ni][nj] !== expected) break;\\n mSteps++;\\n }\\n maxLen = Math.max(maxLen, t + mSteps);\\n }\\n }\\n }\\n }\\n return maxLen;\\n};\"], [68800, 14.2857, \"/**\\n * @param {number[][]} grid\\n * @return {number}\\n */\\n\\nvar lenOfVDiagonal = function(grid) {\\n const m = grid.length;\\n if (m === 0) return 0;\\n const n = grid[0].length;\\n const DIRS = [[-1, 1], [1, 1], [1, -1], [-1, -1]];\\n\\n let maxLen = 0;\\n\\n for (let i = 0; i < m; ++i) {\\n for (let j = 0; j < n; ++j) {\\n if (grid[i][j] === 1) {\\n for (let d = 0; d < 4; ++d) {\\n const dx = DIRS[d][0];\\n const dy = DIRS[d][1];\\n maxLen = Math.max(maxLen, 1 + dfs(grid, i + dx, j + dy, false, 2, d));\\n }\\n }\\n }\\n }\\n\\n function dfs(grid, i, j, turned, num, dir) {\\n if (i < 0 || i >= m || j < 0 || j >= n) return 0;\\n if (grid[i][j] !== num) return 0;\\n\\n const nextNum = num === 2 ? 0 : 2;\\n const dx = DIRS[dir][0];\\n const dy = DIRS[dir][1];\\n let res = 1 + dfs(grid, i + dx, j + dy, turned, nextNum, dir);\\n\\n if (!turned) {\\n const nextDir = (dir + 1) % 4;\\n const nextDx = DIRS[nextDir][0];\\n const nextDy = DIRS[nextDir][1];\\n res = Math.max(res, 1 + dfs(grid, i + nextDx, j + nextDy, true, nextNum, nextDir));\\n }\\n\\n return res;\\n }\\n\\n return maxLen;\\n};\"], [70300, 14.2857, null], [107800, 14.2857, null], [117600, 14.2857, \"/**\\n * @param {number[][]} grid\\n * @return {number}\\n */\\n //top down dp. O(m * n * 3 * 4 * 2), O(m * n * 3 * 4 * 2)\\nvar lenOfVDiagonal = function(grid) {\\n const n = grid.length;\\n const m = grid[0].length;\\n const directions = [[1, 1], [1, -1], [-1, -1], [-1, 1]];\\n const nx = [2, 2, 0];\\n\\n // Total states: n * m * 3 (for x: 0,1,2) * 4 (for d: 0-3) * 2 (for k: 0 or 1)\\n const totalStates = n * m * 3 * 4 * 2;\\n const memo = new Int32Array(totalStates).fill(-1);\\n\\n // Map state (i, j, x, d, k) to a unique index.\\n function getIndex(i, j, x, d, k) {\\n return ((((i * m + j) * 3 + x) * 4 + d) * 2 + k);\\n }\\n\\n\\n\\n function dp(i, j, x, d, k) {\\n \\n if (i < 0 || i >= n || j < 0 || j >= m) return 0;\\n if (grid[i][j] !== x) return 0;\\n const idx = getIndex(i, j, x, d, k);\\n if (memo[idx] !== -1) return memo[idx];\\n \\n let res = dp(i + directions[d][0], j + directions[d][1], nx[x], d, k) + 1;\\n if (k > 0) {\\n const d2 = (d + 1) % 4;\\n const res2 = dp(i + directions[d2][0], j + directions[d2][1], nx[x], d2, 0) + 1;\\n res = Math.max(res, res2);\\n }\\n memo[idx] = res;\\n return res;\\n }\\n\\n let res = 0;\\n for (let i = 0; i < n; i++) {\\n for (let j = 0; j < m; j++) {\\n if (grid[i][j] === 1) {\\n let cur = 0;\\n for (let d = 0; d < 4; d++) {\\n cur = Math.max(cur, dp(i, j, 1, d, 1));\\n }\\n res = Math.max(res, cur);\\n }\\n }\\n }\\n return res;\\n\\n};\"], [120600, 14.2857, \"/**\\n * @param {number[][]} grid\\n * @return {number}\\n */\\nvar lenOfVDiagonal = function(grid) {\\n const n = grid.length, m = grid[0].length\\n const dp = Array(n)\\n .fill(0)\\n .map(() => Array(m).fill(0).map(() => Array(4).fill(0)))\\n const ds = [[-1, -1], [-1, 1], [1, 1], [1, -1]]\\n for (let i = 0; i < n; i++) {\\n for (let j = 0; j < m; j++) {\\n const x = grid[i][j]\\n if (x === 1) continue\\n update(i, j, 0)\\n }\\n for (let j = m - 1; j >= 0; j--) {\\n const x = grid[i][j]\\n if (x === 1) continue\\n update(i, j, 1)\\n }\\n }\\n for (let i = n - 1; i >= 0; i--) {\\n for (let j = 0; j < m; j++) {\\n const x = grid[i][j]\\n if (x === 1) continue\\n update(i, j, 3)\\n }\\n for (let j = m - 1; j >= 0; j--) {\\n const x = grid[i][j]\\n if (x === 1) continue\\n update(i, j, 2)\\n }\\n }\\n function update(i, j, k) {\\n dp[i][j][k] = 1\\n const [di, dj] = ds[k]\\n const ni = i + di\\n const nj = j + dj\\n if (ni < 0 || ni >= n || nj < 0 || nj >= m) return\\n if (grid[ni][nj] === 2 - grid[i][j]) {\\n dp[i][j][k] = Math.max(dp[i][j][k], dp[ni][nj][k] + 1)\\n }\\n }\\n //\\n let ans = 0\\n for (let i = 0; i < n; i++) {\\n for (let j = 0; j < m; j++) {\\n const x = grid[i][j]\\n if (x !== 1) continue\\n\\n ans = Math.max(ans, 1)\\n for (let k = 0; k < ds.length; k++) {\\n const [di, dj] = ds[k]\\n let ni = i + di\\n let nj = j + dj\\n let move = 1, target = 2\\n while (ni >= 0 && ni < n && nj >= 0 && nj < m\\n && grid[ni][nj] === target\\n ) {\\n const temp = move + dp[ni][nj][(k + 1) % 4]\\n ans = Math.max(ans, temp)\\n // if (i === 0 && j === 2) {\\n // console.log(k, move, dp[ni][nj][(k + 1) % 4])\\n // }\\n //\\n move++\\n target = 2 - target\\n ni += di\\n nj += dj\\n }\\n }\\n }\\n }\\n // console.log(dp)\\n return ans\\n};\"]]",
"runtime": 724,
"runtimeDistribution": "[[343, 14.2857, \"/**\\n * @param {number[][]} grid\\n * @return {number}\\n */\\n //top down dp. O(m * n * 3 * 4 * 2), O(m * n * 3 * 4 * 2)\\nvar lenOfVDiagonal = function(grid) {\\n const n = grid.length;\\n const m = grid[0].length;\\n const directions = [[1, 1], [1, -1], [-1, -1], [-1, 1]];\\n const nx = [2, 2, 0];\\n\\n // Total states: n * m * 3 (for x: 0,1,2) * 4 (for d: 0-3) * 2 (for k: 0 or 1)\\n const totalStates = n * m * 3 * 4 * 2;\\n const memo = new Int32Array(totalStates).fill(-1);\\n\\n // Map state (i, j, x, d, k) to a unique index.\\n function getIndex(i, j, x, d, k) {\\n return ((((i * m + j) * 3 + x) * 4 + d) * 2 + k);\\n }\\n\\n\\n\\n function dp(i, j, x, d, k) {\\n \\n if (i < 0 || i >= n || j < 0 || j >= m) return 0;\\n if (grid[i][j] !== x) return 0;\\n const idx = getIndex(i, j, x, d, k);\\n if (memo[idx] !== -1) return memo[idx];\\n \\n let res = dp(i + directions[d][0], j + directions[d][1], nx[x], d, k) + 1;\\n if (k > 0) {\\n const d2 = (d + 1) % 4;\\n const res2 = dp(i + directions[d2][0], j + directions[d2][1], nx[x], d2, 0) + 1;\\n res = Math.max(res, res2);\\n }\\n memo[idx] = res;\\n return res;\\n }\\n\\n let res = 0;\\n for (let i = 0; i < n; i++) {\\n for (let j = 0; j < m; j++) {\\n if (grid[i][j] === 1) {\\n let cur = 0;\\n for (let d = 0; d < 4; d++) {\\n cur = Math.max(cur, dp(i, j, 1, d, 1));\\n }\\n res = Math.max(res, cur);\\n }\\n }\\n }\\n return res;\\n\\n};\"], [451, 14.2857, \"class Coord {\\n constructor(i, j) {\\n this.i = i;\\n this.j = j;\\n }\\n\\n // Four diagonal directions\\n static directions = [\\n new Coord(-1, -1), // top-left\\n new Coord(-1, 1), // top-right\\n new Coord(1, 1), // bottom-right\\n new Coord(1, -1), // bottom-left\\n ];\\n\\n add(delta) {\\n return new Coord(this.i + delta.i, this.j + delta.j);\\n }\\n\\n invert() {\\n return new Coord(-this.i, -this.j);\\n }\\n\\n checkBounds(max) {\\n return (\\n this.i >= 0 &&\\n this.j >= 0 &&\\n this.i < max.i &&\\n this.j < max.j\\n );\\n }\\n\\n getValue(matrix) {\\n return matrix[this.i][this.j];\\n }\\n}\\n\\nfunction matrixMax(matrix, mapFn) {\\n const n = matrix.length;\\n const m = matrix[0].length;\\n let maxVal = -Infinity;\\n for (let i = 0; i < n; i++) {\\n for (let j = 0; j < m; j++) {\\n const result = mapFn(matrix[i][j], new Coord(i, j));\\n maxVal = Math.max(maxVal, result);\\n }\\n }\\n return maxVal;\\n}\\n\\nconst NO_TURN = 0;\\nconst TURN = 1;\\nconst TURN_OPTIONS = 2;\\nconst DIRECTION_OPTIONS = Coord.directions.length;\\nconst START_VALUE = 1;\\n\\n// Expected values based on the previous cell\\u2019s value:\\n// For previous value 0: expected next is 2,\\n// For previous value 1: expected next is 2,\\n// For previous value 2: expected next is 0.\\nconst expectedValueMap = [2, 2, 0];\\n\\nfunction clockwiseTurn(directionIndex) {\\n return (directionIndex + 1) % DIRECTION_OPTIONS;\\n}\\n\\nfunction lenOfVDiagonal(grid) {\\n const bounds = new Coord(grid.length, grid[0].length);\\n\\n // A memoization helper to cache computed dp values.\\n function memo(fn) {\\n const cache = new Array(bounds.i * bounds.j * TURN_OPTIONS * DIRECTION_OPTIONS);\\n return function (c, turn, directionIndex) {\\n const hash =\\n (c.i * bounds.j + c.j) * TURN_OPTIONS * DIRECTION_OPTIONS +\\n turn * DIRECTION_OPTIONS +\\n directionIndex;\\n if (cache[hash] !== undefined) {\\n return cache[hash];\\n }\\n const result = fn(c, turn, directionIndex);\\n cache[hash] = result;\\n return result;\\n };\\n }\\n\\n // dp function: returns the length of valid sequence starting from `coord` given the current turn flag and direction.\\n const dp = memo(function (coord, turn, directionIndex) {\\n const direction = Coord.directions[directionIndex];\\n const prevCoord = coord.add(direction.invert());\\n const prevValue = prevCoord.getValue(grid);\\n const expectedValue = expectedValueMap[prevValue];\\n const value = coord.getValue(grid);\\n if (value !== expectedValue) {\\n return 0;\\n }\\n // Continue in the same direction.\\n const nextCoord = coord.add(direction);\\n const nextResult = nextCoord.checkBounds(bounds)\\n ? 1 + dp(nextCoord, turn, directionIndex)\\n : 1;\\n let turnResult = 1;\\n // If turn is allowed, try turning clockwise.\\n if (turn) {\\n const turnDirectionIndex = clockwiseTurn(directionIndex);\\n const turnCoord = coord.add(Coord.directions[turnDirectionIndex]);\\n if (turnCoord.checkBounds(bounds)) {\\n turnResult = 1 + dp(turnCoord, NO_TURN, turnDirectionIndex);\\n }\\n }\\n return Math.max(nextResult, turnResult);\\n });\\n\\n // Try every coordinate as a starting point and every diagonal direction from it.\\n return matrixMax(grid, (value, coord) => {\\n if (value !== START_VALUE) {\\n return 0;\\n }\\n return 1 + Math.max(\\n ...Coord.directions.map((direction, i) => {\\n const nextCoord = coord.add(direction);\\n if (nextCoord.checkBounds(bounds)) {\\n return dp(nextCoord, TURN, i);\\n }\\n return 0;\\n })\\n );\\n });\\n}\"], [712, 14.2857, null], [724, 57.1429, \"var lenOfVDiagonal = function(grid) {\\n const n = grid.length;\\n if (n === 0) return 0;\\n const m = grid[0].length;\\n let maxLen = 0;\\n const directions = [\\n { dx: 1, dy: 1 }, // down-right\\n { dx: 1, dy: -1 }, // down-left\\n { dx: -1, dy: 1 }, // up-right\\n { dx: -1, dy: -1 }, // up-left\\n ];\\n const turnDir = [1, 3, 0, 2]; // new direction after turn for each original direction index\\n\\n for (let i = 0; i < n; i++) {\\n for (let j = 0; j < m; j++) {\\n if (grid[i][j] !== 1) continue;\\n for (let dirIdx = 0; dirIdx < 4; dirIdx++) {\\n const { dx, dy } = directions[dirIdx];\\n let s = 0;\\n let ci = i, cj = j;\\n while (true) {\\n const expected = s === 0 ? 1 : (s - 1) % 2 === 0 ? 2 : 0;\\n if (ci < 0 || ci >= n || cj < 0 || cj >= m) break;\\n if (grid[ci][cj] !== expected) break;\\n s++;\\n ci += dx;\\n cj += dy;\\n }\\n maxLen = Math.max(maxLen, s);\\n for (let t = 1; t <= s; t++) {\\n const currI = i + (t - 1) * dx;\\n const currJ = j + (t - 1) * dy;\\n const newDirIdx = turnDir[dirIdx];\\n const { dx: newDx, dy: newDy } = directions[newDirIdx];\\n let mSteps = 0;\\n let ni = currI, nj = currJ;\\n while (true) {\\n const expected = (t - 1 + mSteps) % 2 === 0 ? 2 : 0;\\n ni += newDx;\\n nj += newDy;\\n if (ni < 0 || ni >= n || nj < 0 || nj >= m) break;\\n if (grid[ni][nj] !== expected) break;\\n mSteps++;\\n }\\n maxLen = Math.max(maxLen, t + mSteps);\\n }\\n }\\n }\\n }\\n return maxLen;\\n};\"], [802, 14.2857, null], [926, 14.2857, \"/**\\n * @param {number[][]} grid\\n * @return {number}\\n */\\nvar lenOfVDiagonal = function(grid) {\\n let dirs = [\\n [-1,1],\\n [-1,-1],\\n [1,-1],\\n [1,1],\\n ]\\n let n = grid.length\\n let m = grid[0].length\\n let switcher = (needed) =>{\\n return needed === 0 ? 2 : 0\\n }\\n let memo = Array(2).fill(0).map(()=>Array(3).fill(0).map(()=>Array(4).fill(0).map(()=>Array(n).fill(0).map(()=>Array(m).fill(-1)))))\\n let helper = (i , j , turned , needed , dir) => {\\n if(!grid[i] || grid[i][j] !== needed){\\n return 0\\n }\\n if(memo[turned][needed][dir][i][j] !== -1) return memo[turned][needed][dir][i][j]\\n let res = 0\\n let [x , y] = dirs[dir]\\n if(!turned){\\n let d\\n if(dir === 0){\\n d = 3\\n }else if(dir === 1){\\n d = 0\\n }else if(dir === 2){\\n d = 1\\n }else{\\n d = 2\\n }\\n let [k , w] = dirs[d]\\n \\n res = Math.max(\\n res , \\n 1 + helper(i + k , j + w, 1 , switcher(needed) , d)\\n )\\n \\n }\\n res = Math.max(res ,1 + helper(i + x , j + y, turned , switcher(needed) , dir))\\n memo[turned][needed][dir][i][j] = res\\n return res\\n }\\n let res = 0\\n for(let i = 0; i < n ; i++){\\n for(let j = 0; j < m ; j++){\\n if(grid[i][j] === 1){\\n for(let d = 0 ; d < 4 ; d++){\\n let [x , y] = dirs[d]\\n res = Math.max(\\n res,\\n 1 + helper(i + x,j + y, 0, 2, d)\\n )\\n }\\n }\\n } \\n }\\n return res\\n};\"], [2511, 14.2857, \"/**\\n * @param {number[][]} grid\\n * @return {number}\\n */\\n\\nvar lenOfVDiagonal = function(grid) {\\n const m = grid.length;\\n if (m === 0) return 0;\\n const n = grid[0].length;\\n const DIRS = [[-1, 1], [1, 1], [1, -1], [-1, -1]];\\n\\n let maxLen = 0;\\n\\n for (let i = 0; i < m; ++i) {\\n for (let j = 0; j < n; ++j) {\\n if (grid[i][j] === 1) {\\n for (let d = 0; d < 4; ++d) {\\n const dx = DIRS[d][0];\\n const dy = DIRS[d][1];\\n maxLen = Math.max(maxLen, 1 + dfs(grid, i + dx, j + dy, false, 2, d));\\n }\\n }\\n }\\n }\\n\\n function dfs(grid, i, j, turned, num, dir) {\\n if (i < 0 || i >= m || j < 0 || j >= n) return 0;\\n if (grid[i][j] !== num) return 0;\\n\\n const nextNum = num === 2 ? 0 : 2;\\n const dx = DIRS[dir][0];\\n const dy = DIRS[dir][1];\\n let res = 1 + dfs(grid, i + dx, j + dy, turned, nextNum, dir);\\n\\n if (!turned) {\\n const nextDir = (dir + 1) % 4;\\n const nextDx = DIRS[nextDir][0];\\n const nextDy = DIRS[nextDir][1];\\n res = Math.max(res, 1 + dfs(grid, i + nextDx, j + nextDy, true, nextNum, nextDir));\\n }\\n\\n return res;\\n }\\n\\n return maxLen;\\n};\"]]"
},
"python3": {
"code": "class Solution:\n def lenOfVDiagonal(self, grid: List[List[int]]) -> int:\n n = len(grid)\n if n == 0:\n return 0\n m = len(grid[0])\n if m == 0:\n return 0\n \n directions = [ (1, 1), (1, -1), (-1, 1), (-1, -1) ]\n dp = [ [ [ [0]*2 for _ in range(4)] for __ in range(m) ] for ___ in range(n) ]\n \n for dr_idx in range(4):\n dr, dc = directions[dr_idx]\n if dr == 1:\n row_order = range(n-1, -1, -1)\n else:\n row_order = range(n)\n if dc == 1:\n col_order = range(m-1, -1, -1)\n else:\n col_order = range(m)\n \n for x in row_order:\n for y in col_order:\n for e_idx, e in enumerate([0, 2]):\n if grid[x][y] != e:\n dp[x][y][dr_idx][e_idx] = 0\n else:\n next_x = x + dr\n next_y = y + dc\n if 0 <= next_x < n and 0 <= next_y < m:\n next_e = 0 if e == 2 else 2\n next_e_idx = 0 if next_e == 0 else 1\n dp[x][y][dr_idx][e_idx] = 1 + dp[next_x][next_y][dr_idx][next_e_idx]\n else:\n dp[x][y][dr_idx][e_idx] = 1\n \n max_len = 0\n for i in range(n):\n for j in range(m):\n if grid[i][j] != 1:\n continue\n current_max = 1\n for dr_idx in range(4):\n dr, dc = directions[dr_idx]\n next_i = i + dr\n next_j = j + dc\n if 0 <= next_i < n and 0 <= next_j < m:\n len1 = 1 + dp[next_i][next_j][dr_idx][1]\n else:\n len1 = 1\n current_max = max(current_max, len1)\n \n for s in range(len1):\n x = i + dr * s\n y = j + dc * s\n new_dr = dc\n new_dc = -dr\n new_x = x + new_dr\n new_y = y + new_dc\n if 0 <= new_x < n and 0 <= new_y < m:\n k = s + 1\n e = 2 if k % 2 == 1 else 0\n if grid[new_x][new_y] != e:\n continue\n new_dr_idx = [1, 3, 0, 2][dr_idx]\n e_idx = 1 if e == 2 else 0\n len2 = dp[new_x][new_y][new_dr_idx][e_idx]\n total = (s + 1) + len2\n current_max = max(current_max, total)\n max_len = max(max_len, current_max)\n \n return max_len",
"memory": 13700,
"memoryDistribution": "[[13700, 98.6076, \"from typing import List\\n\\nclass Solution:\\n def lenOfVDiagonal(self, grid: List[List[int]]) -> int:\\n n = len(grid)\\n if n == 0:\\n return 0\\n m = len(grid[0])\\n if m == 0:\\n return 0\\n \\n directions = [ (1, 1), (1, -1), (-1, 1), (-1, -1) ]\\n dp = [ [ [ [0]*2 for _ in range(4)] for __ in range(m) ] for ___ in range(n) ]\\n \\n for dr_idx in range(4):\\n dr, dc = directions[dr_idx]\\n if dr == 1:\\n row_order = range(n-1, -1, -1)\\n else:\\n row_order = range(n)\\n if dc == 1:\\n col_order = range(m-1, -1, -1)\\n else:\\n col_order = range(m)\\n \\n for x in row_order:\\n for y in col_order:\\n for e_idx, e in enumerate([0, 2]):\\n if grid[x][y] != e:\\n dp[x][y][dr_idx][e_idx] = 0\\n else:\\n next_x = x + dr\\n next_y = y + dc\\n if 0 <= next_x < n and 0 <= next_y < m:\\n next_e = 0 if e == 2 else 2\\n next_e_idx = 0 if next_e == 0 else 1\\n dp[x][y][dr_idx][e_idx] = 1 + dp[next_x][next_y][dr_idx][next_e_idx]\\n else:\\n dp[x][y][dr_idx][e_idx] = 1\\n \\n max_len = 0\\n for i in range(n):\\n for j in range(m):\\n if grid[i][j] != 1:\\n continue\\n current_max = 1\\n for dr_idx in range(4):\\n dr, dc = directions[dr_idx]\\n next_i = i + dr\\n next_j = j + dc\\n if 0 <= next_i < n and 0 <= next_j < m:\\n len1 = 1 + dp[next_i][next_j][dr_idx][1]\\n else:\\n len1 = 1\\n current_max = max(current_max, len1)\\n \\n for s in range(len1):\\n x = i + dr * s\\n y = j + dc * s\\n new_dr = dc\\n new_dc = -dr\\n new_x = x + new_dr\\n new_y = y + new_dc\\n if 0 <= new_x < n and 0 <= new_y < m:\\n k = s + 1\\n e = 2 if k % 2 == 1 else 0\\n if grid[new_x][new_y] != e:\\n continue\\n new_dr_idx = [1, 3, 0, 2][dr_idx]\\n e_idx = 1 if e == 2 else 0\\n len2 = dp[new_x][new_y][new_dr_idx][e_idx]\\n total = (s + 1) + len2\\n current_max = max(current_max, total)\\n max_len = max(max_len, current_max)\\n \\n return max_len\"], [31430, 0.116, \"# length of longest V-shaped Diagonal Segment\\n# n,m = 500 1\\ub9cc \\ubf51\\uc544\\uc11c dfs - 500 * 500 * 500 (\\ucd5c\\ub300 \\uae38\\uc774 500)\\n# \\ud55c \\ubc88 \\ub3c4\\ub294\\uac74 \\uc548 \\ub420\\ub54c\\uac00 \\uc544\\ub2c8\\ub77c\\ub3c4 \\ub3cc \\uc218 \\uc788\\ub2e4.\\n# 1\\uc5b5 \\ub118\\uc5b4\\uc11c \\ud130\\uc9c0\\ub294 \\ub4ef - direction\\uc5d0 \\ub300\\ud574 \\ucd5c\\ub300 \\uc608\\uc0c1 \\uae38\\uc774\\ub97c \\uad6c\\ud574\\uc11c \\ud604\\uc7ac \\ucd5c\\ub300 \\uae38\\uc774\\ubcf4\\ub2e4 \\uc791\\uc73c\\uba74 \\ud328\\uc2a4\\n\\nclass Solution:\\n def __init__(self):\\n self._dir = [[-1, -1], [-1, 1], [1, 1], [1, -1]]\\n self.ans = 0\\n def solve(self, grid, i, j, d, turned = False, cur_num = 2, length = 1):\\n ni = i + self._dir[d][0]\\n nj = j + self._dir[d][1]\\n go = 0\\n if 0 <= ni < len(grid) and 0 <= nj < len(grid[0]) and grid[ni][nj] == cur_num:\\n self.solve(grid, ni, nj, d, turned, 2 - cur_num, length + 1)\\n go += 1\\n elif length == 1:\\n if length > self.ans:\\n self.ans = length\\n return\\n if not turned: # can rotate\\n new_d = (d + 1) % 4\\n ni = i + self._dir[new_d][0]\\n nj = j + self._dir[new_d][1]\\n if 0 <= ni < len(grid) and 0 <= nj < len(grid[0]):\\n if grid[ni][nj] == cur_num:\\n turned = True\\n self.solve(grid, ni, nj, new_d, turned, 2 - cur_num, length + 1)\\n go += 1\\n if go == 0:\\n if length > self.ans:\\n self.ans = length\\n return\\n def lenOfVDiagonal(self, grid: List[List[int]]) -> int:\\n for i in range(len(grid)):\\n for j in range(len(grid[0])):\\n if grid[i][j] == 1:\\n for d in range(len(self._dir)):\\n if (d == 3 and j + 1 > self.ans) or \\\\\\n (d == 0 and i + 1 > self.ans) or \\\\\\n (d == 1 and len(grid[0]) - j > self.ans) or \\\\\\n (d == 2 and len(grid) - i > self.ans):\\n self.solve(grid, i, j, d)\\n \\n return self.ans\"], [39690, 0.17400000000000002, \"class Solution:\\n def lenOfVDiagonal(self, grid: List[List[int]]) -> int:\\n\\n def helper(grid):\\n r, c = len(grid), len(grid[0])\\n dp1 = [[1 if grid[j][i] != 1 else 0 for i in range(c)] for j in range(r)]\\n for i in range(r - 2, -1, -1):\\n for j in range(c - 1, 0, -1):\\n if grid[i][j] != 1:\\n if grid[i][j] == 0:\\n dp1[i][j] = 1 + (dp1[i + 1][j - 1] if grid[i + 1][j - 1] == 2 else 0)\\n else:\\n dp1[i][j] = 1 + (dp1[i + 1][j - 1] if grid[i + 1][j - 1] == 0 else 0)\\n dp2 = [[dp1[j][i] for i in range(c)] for j in range(r)]\\n for i in range(r - 2, -1, -1):\\n for j in range(c - 2, -1, -1):\\n if grid[i][j] != 1:\\n if grid[i][j] == 0:\\n dp2[i][j] = max(dp2[i][j], 1 + (dp2[i + 1][j + 1] if grid[i + 1][j + 1] == 2 else 0))\\n else:\\n dp2[i][j] = max(dp2[i][j], 1 + (dp2[i + 1][j + 1] if grid[i + 1][j + 1] == 0 else 0))\\n ans = 0 if count == 0 else 1\\n for i in range(r - 2, -1, -1):\\n for j in range(c - 2, -1, -1):\\n if grid[i][j] == 1 and grid[i + 1][j + 1] == 2:\\n ans = max(ans, 1 + dp2[i + 1][j + 1])\\n return ans\\n \\n def rotate(matrix):\\n return [list(row) for row in zip(*matrix[::-1])]\\n \\n count = 0\\n mx = 0\\n for i in grid:\\n for j in i:\\n if j == 1:\\n mx = 1\\n break\\n for i in range(4):\\n mx = max(mx, helper(grid))\\n grid = rotate(grid)\\n return mx\\n\"], [47950, 0.058, null], [56210, 0.2321, null], [64470, 0.058, null], [72730, 0.058, null], [80990, 0.2901, null], [89250, 0.058, null], [97510, 0.058, null], [105770, 0.058, null], [114030, 0.2322, null], [122290, 0.058, null], [130550, 0.058, null], [138810, 0.058, null], [147070, 0.058, null], [155330, 0.058, null], [163590, 0.2902, null], [171850, 0.058, null], [180110, 0.058, null], [188370, 0.1161, null], [196630, 0.4643, null], [204890, 0.2902, null], [213150, 0.1161, null], [221410, 0.1161, null], [229670, 0.058, null], [237930, 0.1161, null], [246190, 0.058, null], [254450, 0.116, null], [262710, 0.116, null], [270970, 0.8702000000000002, null], [279230, 0.058, null], [287490, 0.058, null], [295750, 0.058, null], [304010, 0.058, null], [312270, 0.116, null], [320530, 0.058, null], [328790, 0.4062, null], [337050, 0.058, null], [345310, 0.058, null], [353570, 0.116, null], [361830, 0.058, null], [370090, 0.232, null], [378350, 0.058, null], [386610, 0.058, null], [394870, 0.058, null], [403130, 0.058, null], [411390, 0.058, null], [419650, 0.1161, null], [427910, 0.1161, null], [436170, 0.058, null], [444430, 0.058, null], [452690, 0.058, null], [460950, 0.058, null], [469210, 0.1161, null], [477470, 0.1161, null], [485730, 0.1161, null], [493990, 0.2902, null], [502250, 0.1161, null], [510510, 0.1161, null], [518770, 0.4063, null], [527030, 0.4063, null], [535290, 0.3482, null], [543550, 0.4643, null], [551810, 0.058, null], [560070, 0.1161, null], [568330, 79.62830000000001, null], [576590, 2.7271999999999994, null], [584850, 0.7543000000000002, null], [593110, 0.2901, null], [601370, 0.058, null], [609630, 0.8704000000000001, null], [617890, 0.232, null], [626150, 0.464, null], [634410, 0.058, null], [642670, 0.058, null], [650930, 0.2902, null], [659190, 0.058, null], [667450, 0.058, null], [675710, 0.058, \"class Solution:\\n def lenOfVDiagonal(self, grid: List[List[int]]) -> int:\\n\\n @cache\\n def dp(i, j, v, di, t):\\n if not (0<= i<len(grid) and 0<=j < len(grid[0])): return 0\\n if grid[i][j] != v: return 0\\n r = dp(i + ds[di][0], j + ds[di][1], nxt[v], di, t)\\n if t == 1:\\n r = max(r, dp(i + ds[(di + 1) % 4][0], j + ds[(di + 1) % 4][1], nxt[v], (di + 1) % 4, 0))\\n return r + 1\\n\\n\\n \\n ds = [[1,1],[1,-1],[-1,-1],[-1,1]]\\n nxt = [2, 2, 0]\\n\\n ans = 0\\n\\n for i, j in product(range(len(grid)), range(len(grid[0]))):\\n if grid[i][j] == 1:\\n c=max(dp(i, j, 1, di, 1) for di in range(4))\\n ans = max(c, ans)\\n\\n return ans\"], [683970, 0.058, \"class Solution:\\n def lenOfVDiagonal(self, grid: List[List[int]]) -> int:\\n n = len(grid)\\n m = len(grid[0])\\n # visited = set()\\n cache = defaultdict(tuple)\\n\\n def dfs(r, c, rdir, cdir, hasTurned):\\n nextR = r + rdir\\n nextC = c + cdir\\n\\n if nextR < 0 or nextR >= n or nextC < 0 or nextC >= m:\\n return 0\\n\\n if grid[r][c] == 1 or grid[r][c] == 0:\\n # print(n, m, nextR, nextC)\\n if grid[nextR][nextC] != 2:\\n return 0\\n if grid[r][c] == 2:\\n if grid[nextR][nextC] != 0:\\n return 0\\n\\n if (r, c, rdir, cdir, hasTurned) in cache:\\n return cache[(r, c, rdir, cdir, hasTurned)]\\n \\n length = dfs(nextR, nextC, rdir, cdir, hasTurned)\\n turnLength = 0\\n\\n if not hasTurned:\\n turndirR = 0\\n turndirC = 0\\n if (rdir, cdir) == (-1, -1):\\n turndirR = -1\\n turndirC = 1\\n elif (rdir, cdir) == (-1, 1):\\n turndirR = 1\\n turndirC = 1\\n elif (rdir, cdir) == (1, 1):\\n turndirR, turndirC = 1, -1\\n else:\\n turndirR, turndirC = -1, -1\\n turnLength = dfs(nextR, nextC, turndirR, turndirC, True)\\n l = max(length, turnLength) + 1\\n cache[(r, c, rdir, cdir, hasTurned)] = l\\n\\n return l\\n ret = 0\\n for i in range(n):\\n for j in range(m):\\n if grid[i][j] == 1:\\n upleft = dfs(i, j, -1, -1, False) + 1\\n upright = dfs(i, j, -1, 1, False) + 1\\n downleft = dfs(i, j, 1, -1, False) + 1\\n downright= dfs(i, j, 1, 1, False) + 1\\n ret = max(ret, upleft, upright, downleft, downright)\\n return ret\\n\\n\\n\\n \\n\\n\\n \\n\\n \\n\\n\\n\\n\\n# -1 -1 -1 1 1 1 1 -1 \"]]",
"runtime": 7158,
"runtimeDistribution": "[[2003, 0.116, \"class Solution:\\n def lenOfVDiagonal(self, grid: List[List[int]]) -> int:\\n n, m = len(grid), len(grid[0])\\n \\n dirs = [(1, 1), (1, -1), (-1, -1), (-1, 1)]\\n \\n # dp_even[d][i][j]: maximum chain length starting at (i,j) if expected value is 2.\\n # dp_odd[d][i][j]: maximum chain length starting at (i,j) if expected value is 0.\\n dp_even = [ [ [0]*m for _ in range(n) ] for _ in range(4) ]\\n dp_odd = [ [ [0]*m for _ in range(n) ] for _ in range(4) ]\\n \\n # For a given direction (dx,dy) and its index d, determine iteration order so that (i+dx,j+dy)\\n # is processed before (i,j).\\n def compute_dp(d, dx, dy):\\n # Determine iteration order for i and j.\\n if dx == 1:\\n i_range = range(n-1, -1, -1)\\n else:\\n i_range = range(0, n)\\n if dy == 1:\\n j_range = range(m-1, -1, -1)\\n else:\\n j_range = range(0, m)\\n for i in i_range:\\n for j in j_range:\\n ni, nj = i + dx, j + dy\\n # For even state: expected value = 2.\\n if grid[i][j] == 2:\\n next_val = dp_odd[d][ni][nj] if 0 <= ni < n and 0 <= nj < m else 0\\n dp_even[d][i][j] = 1 + next_val\\n else:\\n dp_even[d][i][j] = 0\\n # For odd state: expected value = 0.\\n if grid[i][j] == 0:\\n next_val = dp_even[d][ni][nj] if 0 <= ni < n and 0 <= nj < m else 0\\n dp_odd[d][i][j] = 1 + next_val\\n else:\\n dp_odd[d][i][j] = 0\\n \\n # Precompute dp for each direction.\\n for d, (dx, dy) in enumerate(dirs):\\n compute_dp(d, dx, dy)\\n \\n best = 0\\n \\n # Now, for every starting cell with value 1, try each direction as the first leg.\\n for i in range(n):\\n for j in range(m):\\n if grid[i][j] != 1:\\n continue\\n # Try each initial direction d.\\n for d, (dx, dy) in enumerate(dirs):\\n # First leg: starting cell (i,j) has length 1.\\n L1 = 1\\n ni, nj = i + dx, j + dy\\n if 0 <= ni < n and 0 <= nj < m and grid[ni][nj] == 2:\\n # dp_even[d] at (ni, nj) gives the chain length starting there when expecting 2.\\n L1 += dp_even[d][ni][nj]\\n # Candidate using no turn (straight line)\\n best = max(best, L1)\\n \\n # If we can turn (i.e. L1 >= 2 so that there's at least one cell after the starting cell)\\n if L1 >= 2:\\n for k in range(2, L1 + 1): # k is the number of cells in the first leg (must be at least 2)\\n turn_i = i + dx * (k - 1)\\n turn_j = j + dy * (k - 1)\\n # Overall sequence index is k; next index is k+1.\\n # Expected value: if (k+1) is even, expect 2; if odd, expect 0.\\n p = 0 if (k + 1) % 2 == 0 else 1\\n # Second leg goes in the clockwise rotated direction.\\n d2 = (d + 1) % 4\\n dx2, dy2 = dirs[d2]\\n nni, nnj = turn_i + dx2, turn_j + dy2\\n L2 = 0\\n if 0 <= nni < n and 0 <= nnj < m:\\n if p == 0:\\n L2 = dp_even[d2][nni][nnj]\\n else:\\n L2 = dp_odd[d2][nni][nnj]\\n total = k + L2 # turning cell counted once\\n best = max(best, total) \\n return best\\n\\n\"], [2055, 0.058, \"class Solution:\\n def lenOfVDiagonal(self, grid: List[List[int]]) -> int:\\n n = len(grid)\\n m = len(grid[0])\\n \\n dirs = [(1, 1), (1, -1), (-1, -1), (-1, 1)]\\n \\n len20 = [[[0] * 4 for _ in range(m)] for _ in range(n)]\\n len02 = [[[0] * 4 for _ in range(m)] for _ in range(n)]\\n \\n for d_idx in range(4):\\n dr, dc = dirs[d_idx]\\n \\n r_range = range(n) if dr == -1 else range(n - 1, -1, -1)\\n c_range = range(m) if dc == -1 else range(m - 1, -1, -1)\\n \\n for r in r_range:\\n for c in c_range:\\n nr, nc = r + dr, c + dc\\n \\n next_len20 = 0\\n next_len02 = 0\\n \\n if 0 <= nr < n and 0 <= nc < m:\\n next_len20 = len20[nr][nc][d_idx]\\n next_len02 = len02[nr][nc][d_idx]\\n \\n if grid[r][c] == 2:\\n len20[r][c][d_idx] = 1 + next_len02\\n elif grid[r][c] == 0:\\n len02[r][c][d_idx] = 1 + next_len20\\n\\n max_len = 0\\n \\n for r in range(n):\\n for c in range(m):\\n if grid[r][c] == 1:\\n max_len = max(max_len, 1) \\n\\n for d1_idx in range(4):\\n dr1, dc1 = dirs[d1_idx]\\n \\n r1, c1 = r + dr1, c + dc1\\n \\n if 0 <= r1 < n and 0 <= c1 < m and grid[r1][c1] == 2:\\n \\n L1_path = len20[r1][c1][d1_idx]\\n \\n max_len = max(max_len, 1 + L1_path)\\n\\n for k in range(1, L1_path + 1):\\n pr = r + k * dr1\\n pc = c + k * dc1\\n \\n d2_idx = (d1_idx + 1) % 4\\n L2_path = 0\\n \\n if k % 2 == 1:\\n L2_path = len20[pr][pc][d2_idx]\\n else:\\n L2_path = len02[pr][pc][d2_idx]\\n\\n if L2_path > 0: \\n max_len = max(max_len, k + L2_path)\\n\\n return max_len\"], [2107, 0.058, null], [2159, 0.058, null], [2210, 0.058, null], [2262, 0.058, null], [2314, 0.058, null], [2366, 0.058, null], [2418, 0.058, null], [2469, 0.058, null], [2521, 0.058, null], [2573, 0.058, null], [2625, 0.058, null], [2676, 0.058, null], [2728, 0.058, null], [2780, 0.058, null], [2832, 0.058, null], [2884, 0.058, null], [2935, 0.058, null], [2987, 0.058, null], [3039, 0.058, null], [3091, 0.058, null], [3142, 0.1161, null], [3194, 0.058, null], [3246, 0.058, null], [3298, 0.058, null], [3350, 0.1161, null], [3401, 0.1161, null], [3453, 0.058, null], [3505, 0.058, null], [3557, 0.058, null], [3608, 0.058, null], [3660, 0.1161, null], [3712, 0.058, null], [3764, 0.058, null], [3816, 0.058, null], [3867, 0.058, null], [3919, 0.058, null], [3971, 0.058, null], [4023, 1.3343000000000003, null], [4074, 5.1075, null], [4126, 8.531400000000001, null], [4178, 14.103700000000005, null], [4230, 16.7154, null], [4281, 14.567799999999998, null], [4333, 9.8667, null], [4385, 5.803700000000002, null], [4437, 4.1205, null], [4489, 1.9727000000000008, null], [4540, 1.0444000000000002, null], [4592, 0.7542000000000002, null], [4644, 0.7540000000000002, null], [4696, 0.5801000000000001, null], [4747, 0.8121000000000003, null], [4799, 0.522, null], [4851, 0.464, null], [4903, 0.5801000000000001, null], [4955, 0.4642, null], [5006, 0.34800000000000003, null], [5058, 0.6380000000000001, null], [5110, 0.34800000000000003, null], [5162, 0.116, null], [5213, 0.17400000000000002, null], [5265, 0.522, null], [5317, 0.058, null], [5369, 0.2321, null], [5421, 0.058, null], [5472, 0.116, null], [5524, 0.17400000000000002, null], [5576, 0.058, null], [5628, 0.17400000000000002, null], [5679, 0.116, null], [5731, 0.058, null], [5783, 0.058, null], [5835, 0.17400000000000002, null], [5887, 0.058, null], [5938, 0.232, null], [5990, 0.29000000000000004, null], [6042, 0.116, \"class Solution:\\n def lenOfVDiagonal(self, grid: List[List[int]]) -> int:\\n n, m = len(grid), len(grid[0]) # Get the dimensions of the grid\\n memo = {} # Dictionary for memoization\\n # @cache # Memoization to optimize recursive calls\\n def dfs(row, col, turn, direction, target):\\n # Base case: Check boundaries and if the cell matches the target value\\n if row not in range(n) or col not in range(m) or grid[row][col] != target:\\n return 0\\n # Use memoization to store previously computed results\\n key = (row, col, turn, direction, target)\\n if key in memo:\\n return memo[key]\\n # Toggle the target between 2 and 0 after each step\\n target = 0 if grid[row][col] == 2 else 2\\n \\n # Move diagonally based on the direction\\n if direction == 0: # Top-left diagonal\\n if turn:\\n memo[key] = 1 + max(dfs(row - 1, col - 1, turn, 0, target), \\n dfs(row - 1, col + 1, False, 1, target))\\n else:\\n memo[key] = 1 + dfs(row - 1, col - 1, turn, 0, target)\\n \\n elif direction == 1: # Top-right diagonal\\n if turn:\\n memo[key] = 1 + max(dfs(row - 1, col + 1, turn, 1, target), \\n dfs(row + 1, col + 1, False, 2, target))\\n else:\\n memo[key] = 1 + dfs(row - 1, col + 1, turn, 1, target)\\n \\n elif direction == 2: # Bottom-right diagonal\\n if turn:\\n memo[key] = 1 + max(dfs(row + 1, col + 1, turn, 2, target), \\n dfs(row + 1, col - 1, False, 3, target))\\n else:\\n memo[key] = 1 + dfs(row + 1, col + 1, turn, 2, target)\\n \\n else: # Bottom-left diagonal\\n if turn:\\n memo[key] = 1 + max(dfs(row + 1, col - 1, turn, 3, target), \\n dfs(row - 1, col - 1, False, 0, target))\\n else:\\n memo[key] = 1 + dfs(row + 1, col - 1, turn, 3, target)\\n return memo[key]\\n longest_v = 0 # Variable to store the longest V-diagonal length\\n \\n # Iterate through the grid to find starting points (cells with value 1)\\n for i in range(n):\\n for j in range(m):\\n if grid[i][j] == 1:\\n # Start DFS in all four diagonal directions\\n longest_v = max(longest_v, \\n 1 + max(dfs(i - 1, j - 1, True, 0, 2), # Top-left\\n dfs(i - 1, j + 1, True, 1, 2), # Top-right\\n dfs(i + 1, j + 1, True, 2, 2), # Bottom-right\\n dfs(i + 1, j - 1, True, 3, 2))) # Bottom-left\\n \\n return longest_v\\n\"], [6094, 0.17400000000000002, \"class Solution:\\n def lenOfVDiagonal(self, grid: List[List[int]]) -> int:\\n R, C = len(grid), len(grid[0])\\n maxl = 0\\n dirs = [[-1, -1], [1, -1], [1, 1], [-1, 1]]\\n # for change in dir, dec dirs\\n memo = {}\\n \\n def _dfs(r, c, nxt, dir, change):\\n # print(r, c, nxt, dir, change)\\n if change < 0: return 0\\n if r >= R or r < 0 or c >= C or c < 0 or grid[r][c] != nxt: return 0\\n if (r, c, dir, change) in memo: return memo[(r, c, dir, change)]\\n \\n nxt_match = 0 if nxt == 2 else 2\\n adir = (dir+3)%4\\n \\n dx, dy = dirs[dir]\\n nx, ny = r+dx, c+dy\\n \\n cx, cy = dirs[adir]\\n ax, ay = r+cx, c+cy\\n \\n memo[(r, c, dir, change)] = 1+max(_dfs(nx, ny, nxt_match, dir, change), _dfs(ax, ay, nxt_match, adir, change-1))\\n return memo[(r, c, dir, change)]\\n\\n\\n for i in range(R):\\n for j in range(C):\\n if grid[i][j] == 1:\\n maxl = max(1, maxl)\\n for d in range(4):\\n di, dj = dirs[d]\\n ni, nj = i+di, j+dj\\n if 0 <= ni < R and 0 <= nj < C:\\n length = 1+_dfs(ni, nj, 2, d, 1)\\n maxl = max(maxl, length)\\n # print(i, j, length)\\n # print(_dfs(0, 2, ))\\n \\n return maxl\"], [7158, 5.0567, \"from typing import List\\n\\nclass Solution:\\n def lenOfVDiagonal(self, grid: List[List[int]]) -> int:\\n n = len(grid)\\n if n == 0:\\n return 0\\n m = len(grid[0])\\n if m == 0:\\n return 0\\n \\n directions = [ (1, 1), (1, -1), (-1, 1), (-1, -1) ]\\n dp = [ [ [ [0]*2 for _ in range(4)] for __ in range(m) ] for ___ in range(n) ]\\n \\n for dr_idx in range(4):\\n dr, dc = directions[dr_idx]\\n if dr == 1:\\n row_order = range(n-1, -1, -1)\\n else:\\n row_order = range(n)\\n if dc == 1:\\n col_order = range(m-1, -1, -1)\\n else:\\n col_order = range(m)\\n \\n for x in row_order:\\n for y in col_order:\\n for e_idx, e in enumerate([0, 2]):\\n if grid[x][y] != e:\\n dp[x][y][dr_idx][e_idx] = 0\\n else:\\n next_x = x + dr\\n next_y = y + dc\\n if 0 <= next_x < n and 0 <= next_y < m:\\n next_e = 0 if e == 2 else 2\\n next_e_idx = 0 if next_e == 0 else 1\\n dp[x][y][dr_idx][e_idx] = 1 + dp[next_x][next_y][dr_idx][next_e_idx]\\n else:\\n dp[x][y][dr_idx][e_idx] = 1\\n \\n max_len = 0\\n for i in range(n):\\n for j in range(m):\\n if grid[i][j] != 1:\\n continue\\n current_max = 1\\n for dr_idx in range(4):\\n dr, dc = directions[dr_idx]\\n next_i = i + dr\\n next_j = j + dc\\n if 0 <= next_i < n and 0 <= next_j < m:\\n len1 = 1 + dp[next_i][next_j][dr_idx][1]\\n else:\\n len1 = 1\\n current_max = max(current_max, len1)\\n \\n for s in range(len1):\\n x = i + dr * s\\n y = j + dc * s\\n new_dr = dc\\n new_dc = -dr\\n new_x = x + new_dr\\n new_y = y + new_dc\\n if 0 <= new_x < n and 0 <= new_y < m:\\n k = s + 1\\n e = 2 if k % 2 == 1 else 0\\n if grid[new_x][new_y] != e:\\n continue\\n new_dr_idx = [1, 3, 0, 2][dr_idx]\\n e_idx = 1 if e == 2 else 0\\n len2 = dp[new_x][new_y][new_dr_idx][e_idx]\\n total = (s + 1) + len2\\n current_max = max(current_max, total)\\n max_len = max(max_len, current_max)\\n \\n return max_len\"]]"
},
"ruby": {
"code": "def len_of_v_diagonal(grid)\n n = grid.size\n return 0 if n == 0\n m = grid[0].size\n dp = Array.new(4) { Array.new(n) { Array.new(m, 0) } }\n dirs = [[1, 1], [1, -1], [-1, 1], [-1, -1]]\n (0...4).each do |d|\n dx, dy = dirs[d][0], dirs[d][1]\n i_range = dx == 1 ? (n - 1).downto(0) : (0...n)\n j_range = dy == 1 ? (m - 1).downto(0) : (0...m)\n i_range.each do |i|\n j_range.each do |j|\n v = grid[i][j]\n nxt = v == 1 ? 2 : (v == 2 ? 0 : 2)\n ni, nj = i + dx, j + dy\n if ni >= 0 && ni < n && nj >= 0 && nj < m && grid[ni][nj] == nxt\n dp[d][i][j] = 1 + dp[d][ni][nj]\n else\n dp[d][i][j] = 1\n end\n end\n end\n end\n max_len = 0\n turn = [1, 3, 0, 2]\n (0...n).each do |i|\n (0...m).each do |j|\n next if grid[i][j] != 1\n (0...4).each do |d|\n dx, dy = dirs[d][0], dirs[d][1]\n arm1 = dp[d][i][j]\n max_len = arm1 if arm1 > max_len\n new_d = turn[d]\n ndx, ndy = dirs[new_d][0], dirs[new_d][1]\n s = 1\n while s <= arm1\n x = i + (s - 1) * dx\n y = j + (s - 1) * dy\n new_i = x + ndx\n new_j = y + ndy\n if new_i >= 0 && new_i < n && new_j >= 0 && new_j < m\n exp_val = (s & 1) == 1 ? 2 : 0\n if grid[new_i][new_j] == exp_val\n candidate = s + dp[new_d][new_i][new_j]\n max_len = candidate if candidate > max_len\n end\n end\n s += 1\n end\n end\n end\n end\n max_len\nend",
"memory": 27000,
"memoryDistribution": "[[27000, 100.0, \"def len_of_v_diagonal(grid)\\n n = grid.size\\n return 0 if n == 0\\n m = grid[0].size\\n dp = Array.new(4) { Array.new(n) { Array.new(m, 0) } }\\n dirs = [[1, 1], [1, -1], [-1, 1], [-1, -1]]\\n (0...4).each do |d|\\n dx, dy = dirs[d][0], dirs[d][1]\\n i_range = dx == 1 ? (n - 1).downto(0) : (0...n)\\n j_range = dy == 1 ? (m - 1).downto(0) : (0...m)\\n i_range.each do |i|\\n j_range.each do |j|\\n v = grid[i][j]\\n nxt = v == 1 ? 2 : (v == 2 ? 0 : 2)\\n ni, nj = i + dx, j + dy\\n if ni >= 0 && ni < n && nj >= 0 && nj < m && grid[ni][nj] == nxt\\n dp[d][i][j] = 1 + dp[d][ni][nj]\\n else\\n dp[d][i][j] = 1\\n end\\n end\\n end\\n end\\n max_len = 0\\n turn = [1, 3, 0, 2]\\n (0...n).each do |i|\\n (0...m).each do |j|\\n next if grid[i][j] != 1\\n (0...4).each do |d|\\n dx, dy = dirs[d][0], dirs[d][1]\\n arm1 = dp[d][i][j]\\n max_len = arm1 if arm1 > max_len\\n new_d = turn[d]\\n ndx, ndy = dirs[new_d][0], dirs[new_d][1]\\n s = 1\\n while s <= arm1\\n x = i + (s - 1) * dx\\n y = j + (s - 1) * dy\\n new_i = x + ndx\\n new_j = y + ndy\\n if new_i >= 0 && new_i < n && new_j >= 0 && new_j < m\\n exp_val = (s & 1) == 1 ? 2 : 0\\n if grid[new_i][new_j] == exp_val\\n candidate = s + dp[new_d][new_i][new_j]\\n max_len = candidate if candidate > max_len\\n end\\n end\\n s += 1\\n end\\n end\\n end\\n end\\n max_len\\nend\"], [270200, 100.0, \"def len_of_v_diagonal(grid)\\n n = grid.size\\n return 0 if n == 0\\n m = grid[0].size\\n dp = Array.new(4) { Array.new(n) { Array.new(m, 0) } }\\n dirs = [[1, 1], [1, -1], [-1, 1], [-1, -1]]\\n (0...4).each do |d|\\n dx, dy = dirs[d][0], dirs[d][1]\\n i_range = dx == 1 ? (n - 1).downto(0) : (0...n)\\n j_range = dy == 1 ? (m - 1).downto(0) : (0...m)\\n i_range.each do |i|\\n j_range.each do |j|\\n v = grid[i][j]\\n nxt = v == 1 ? 2 : (v == 2 ? 0 : 2)\\n ni, nj = i + dx, j + dy\\n if ni >= 0 && ni < n && nj >= 0 && nj < m && grid[ni][nj] == nxt\\n dp[d][i][j] = 1 + dp[d][ni][nj]\\n else\\n dp[d][i][j] = 1\\n end\\n end\\n end\\n end\\n max_len = 0\\n turn = [1, 3, 0, 2]\\n (0...n).each do |i|\\n (0...m).each do |j|\\n next if grid[i][j] != 1\\n (0...4).each do |d|\\n dx, dy = dirs[d][0], dirs[d][1]\\n arm1 = dp[d][i][j]\\n max_len = arm1 if arm1 > max_len\\n new_d = turn[d]\\n ndx, ndy = dirs[new_d][0], dirs[new_d][1]\\n s = 1\\n while s <= arm1\\n x = i + (s - 1) * dx\\n y = j + (s - 1) * dy\\n new_i = x + ndx\\n new_j = y + ndy\\n if new_i >= 0 && new_i < n && new_j >= 0 && new_j < m\\n exp_val = (s & 1) == 1 ? 2 : 0\\n if grid[new_i][new_j] == exp_val\\n candidate = s + dp[new_d][new_i][new_j]\\n max_len = candidate if candidate > max_len\\n end\\n end\\n s += 1\\n end\\n end\\n end\\n end\\n max_len\\nend\"]]",
"runtime": 2082,
"runtimeDistribution": "[[2082, 100.0, \"def len_of_v_diagonal(grid)\\n n = grid.size\\n return 0 if n == 0\\n m = grid[0].size\\n dp = Array.new(4) { Array.new(n) { Array.new(m, 0) } }\\n dirs = [[1, 1], [1, -1], [-1, 1], [-1, -1]]\\n (0...4).each do |d|\\n dx, dy = dirs[d][0], dirs[d][1]\\n i_range = dx == 1 ? (n - 1).downto(0) : (0...n)\\n j_range = dy == 1 ? (m - 1).downto(0) : (0...m)\\n i_range.each do |i|\\n j_range.each do |j|\\n v = grid[i][j]\\n nxt = v == 1 ? 2 : (v == 2 ? 0 : 2)\\n ni, nj = i + dx, j + dy\\n if ni >= 0 && ni < n && nj >= 0 && nj < m && grid[ni][nj] == nxt\\n dp[d][i][j] = 1 + dp[d][ni][nj]\\n else\\n dp[d][i][j] = 1\\n end\\n end\\n end\\n end\\n max_len = 0\\n turn = [1, 3, 0, 2]\\n (0...n).each do |i|\\n (0...m).each do |j|\\n next if grid[i][j] != 1\\n (0...4).each do |d|\\n dx, dy = dirs[d][0], dirs[d][1]\\n arm1 = dp[d][i][j]\\n max_len = arm1 if arm1 > max_len\\n new_d = turn[d]\\n ndx, ndy = dirs[new_d][0], dirs[new_d][1]\\n s = 1\\n while s <= arm1\\n x = i + (s - 1) * dx\\n y = j + (s - 1) * dy\\n new_i = x + ndx\\n new_j = y + ndy\\n if new_i >= 0 && new_i < n && new_j >= 0 && new_j < m\\n exp_val = (s & 1) == 1 ? 2 : 0\\n if grid[new_i][new_j] == exp_val\\n candidate = s + dp[new_d][new_i][new_j]\\n max_len = candidate if candidate > max_len\\n end\\n end\\n s += 1\\n end\\n end\\n end\\n end\\n max_len\\nend\"]]"
}
}
|
import random
def generate_test_cases(num_cases: int, seed: int = 42) -> list:
random.seed(seed)
# Helper: Sample solution adapted from the provided solution.
def solve(grid):
n = len(grid)
if n == 0:
return 0
m = len(grid[0])
if m == 0:
return 0
directions = [(1, 1), (1, -1), (-1, 1), (-1, -1)]
dp = [[[[0]*2 for _ in range(4)] for _ in range(m)] for _ in range(n)]
for dr_idx in range(4):
dr, dc = directions[dr_idx]
row_order = range(n-1, -1, -1) if dr == 1 else range(n)
col_order = range(m-1, -1, -1) if dc == 1 else range(m)
for x in row_order:
for y in col_order:
for e_idx, e in enumerate([0, 2]):
if grid[x][y] != e:
dp[x][y][dr_idx][e_idx] = 0
else:
next_x = x + dr
next_y = y + dc
if 0 <= next_x < n and 0 <= next_y < m:
next_e = 0 if e == 2 else 2
next_e_idx = 0 if next_e == 0 else 1
dp[x][y][dr_idx][e_idx] = 1 + dp[next_x][next_y][dr_idx][next_e_idx]
else:
dp[x][y][dr_idx][e_idx] = 1
max_len = 0
for i in range(n):
for j in range(m):
if grid[i][j] != 1:
continue
current_max = 1
for dr_idx in range(4):
dr, dc = directions[dr_idx]
next_i = i + dr
next_j = j + dc
if 0 <= next_i < n and 0 <= next_j < m:
len1 = 1 + dp[next_i][next_j][dr_idx][1]
else:
len1 = 1
current_max = max(current_max, len1)
for s in range(len1):
x = i + dr * s
y = j + dc * s
new_dr = dc
new_dc = -dr
new_x = x + new_dr
new_y = y + new_dc
if 0 <= new_x < n and 0 <= new_y < m:
k = s + 1
e_val = 2 if k % 2 == 1 else 0
if grid[new_x][new_y] != e_val:
continue
new_dr_idx = [1, 3, 0, 2][dr_idx]
e_idx = 1 if e_val == 2 else 0
len2 = dp[new_x][new_y][new_dr_idx][e_idx]
total = (s + 1) + len2
current_max = max(current_max, total)
max_len = max(max_len, current_max)
return max_len
# Helper: Serialization logic.
def serialize_grid(grid):
# Each row is list of integers separated by commas; rows separated by semicolons.
return ';'.join([','.join(map(str, row)) for row in grid])
test_cases = []
# Predefined test cases (from problem examples)
predefined = [
# Example 1
[[2,2,1,2,2],
[2,0,2,2,0],
[2,0,1,1,0],
[1,0,2,2,2],
[2,0,0,2,2]],
# Example 2
[[2,2,2,2,2],
[2,0,2,2,0],
[2,0,1,1,0],
[1,0,2,2,2],
[2,0,0,2,2]],
# Example 3
[[1,2,2,2,2],
[2,2,2,2,0],
[2,0,0,0,0],
[0,0,2,2,2],
[2,0,0,2,0]],
# Example 4
[[1]]
]
for grid in predefined:
if len(test_cases) >= num_cases:
break
inp = serialize_grid(grid)
expected = str(solve(grid))
test_cases.append({"input": inp, "output": expected})
# Generate additional random test cases if needed.
while len(test_cases) < num_cases:
# Occasionally generate a stress-test case with larger dimensions.
if random.random() < 0.2:
n = random.randint(30, 50)
m = random.randint(30, 50)
else:
n = random.randint(1, 10)
m = random.randint(1, 10)
grid = [[random.choice([0, 1, 2]) for _ in range(m)] for _ in range(n)]
inp = serialize_grid(grid)
expected = str(solve(grid))
test_cases.append({"input": inp, "output": expected})
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
"""
Compares the expected output to the program output.
Both are serialized as simple strings. Here, the output is an integer.
"""
try:
expected_val = int(expected_output.strip())
program_val = int(program_output.strip())
except Exception:
return False
return expected_val == program_val
|
[{"input": "2,2,1,2,2;2,0,2,2,0;2,0,1,1,0;1,0,2,2,2;2,0,0,2,2", "output": "5"}, {"input": "2,2,2,2,2;2,0,2,2,0;2,0,1,1,0;1,0,2,2,2;2,0,0,2,2", "output": "4"}, {"input": "1,2,2,2,2;2,2,2,2,0;2,0,0,0,0;0,0,2,2,2;2,0,0,2,0", "output": "5"}, {"input": "1", "output": "1"}, {"input": "0,0,0,2,0", "output": "0"}, {"input": "2,1;0,0;0,0;0,2;2,0;2,0;2,2;2,2;1,0", "output": "2"}, {"input": "0;2;1;1;1", "output": "1"}, {"input": "0,1,0,1,1,2,1,0,2,1,2,0,1,0,2,1,2,2,1,2,0,2,0,0,2,0,1,0,0,0,1,1,1;2,1,0,1,1,0,2,1,2,2,2,0,2,2,0,2,2,0,0,1,1,1,2,2,2,0,2,1,0,0,0,1,1;1,0,0,2,2,1,0,2,1,1,2,1,0,1,0,0,2,2,2,1,2,2,1,2,1,1,0,0,2,1,0,0,0;0,2,0,2,1,2,0,1,1,2,1,2,1,2,0,2,2,0,2,2,1,2,1,0,1,1,0,1,0,2,2,1,2;0,2,0,2,1,2,2,2,0,0,1,0,2,2,0,2,1,1,0,0,1,1,0,0,0,2,0,0,2,1,0,2,0;0,2,1,2,0,1,2,2,1,0,2,2,2,0,2,1,1,2,2,1,1,2,1,0,0,0,0,1,0,2,2,0,2;0,0,0,2,2,0,0,0,0,1,0,2,0,1,2,1,0,2,0,2,2,2,1,0,1,1,0,0,0,2,1,1,1;1,1,2,0,2,2,2,0,0,1,2,1,0,0,0,0,2,1,0,1,0,1,1,0,0,1,2,0,0,2,2,0,0;0,0,1,1,1,0,1,0,0,1,0,1,1,1,1,1,2,2,2,2,2,1,0,0,1,0,0,2,2,2,0,2,1;0,0,2,1,2,2,0,0,2,0,0,0,2,0,2,0,1,0,2,0,2,2,0,2,0,1,2,2,2,2,1,1,0;2,2,1,0,1,1,0,2,2,1,1,1,0,0,1,2,2,0,0,2,0,2,1,0,1,0,0,1,1,0,1,2,2;1,2,2,2,0,2,2,1,2,0,0,1,0,0,2,2,0,1,1,2,0,2,1,0,2,2,1,2,1,1,0,0,2;1,1,0,0,1,0,2,1,0,2,1,2,2,1,2,0,0,0,2,0,2,0,1,2,2,0,1,0,0,1,1,0,1;0,2,0,2,0,1,2,1,2,2,0,0,0,0,1,0,0,2,1,1,2,2,0,1,0,2,0,1,0,1,0,0,1;1,1,0,0,0,2,0,1,1,1,0,1,1,2,2,1,2,2,1,0,0,1,0,2,1,0,0,2,1,1,2,1,1;2,2,0,1,2,0,1,0,2,1,0,2,2,2,2,2,2,2,0,1,1,0,2,1,2,1,2,0,2,1,2,1,2;1,1,1,2,1,2,0,0,1,2,1,2,2,0,2,2,1,1,2,0,1,1,0,1,2,2,2,1,1,1,1,2,0;2,1,2,0,2,0,1,2,2,2,2,1,0,0,2,1,0,0,0,0,0,0,1,2,0,1,1,2,2,0,2,2,1;1,1,0,0,2,2,0,0,1,0,0,2,2,1,0,2,0,0,1,0,1,2,2,2,2,1,1,2,2,2,1,2,1;0,2,1,1,1,0,2,1,2,1,2,0,1,1,0,2,1,0,1,1,1,2,0,0,0,0,1,2,0,2,0,0,1;1,1,2,1,1,0,0,1,1,2,2,0,2,1,1,0,1,1,1,1,2,2,2,2,2,0,1,0,1,1,1,0,1;1,2,2,1,2,0,1,0,2,2,0,1,2,2,2,0,0,2,1,0,1,0,0,1,1,1,0,1,1,1,1,1,1;1,0,1,0,2,2,0,1,0,2,0,2,0,0,0,0,0,2,0,0,0,1,2,0,2,0,1,2,1,1,0,2,2;2,2,0,0,1,0,2,0,1,2,2,1,1,2,0,0,2,2,2,0,0,2,1,2,2,0,2,0,1,2,1,2,1;0,2,2,1,0,1,1,0,1,1,2,1,2,0,1,0,2,2,2,1,2,2,1,1,1,2,2,1,1,0,0,1,1;0,1,2,2,2,1,1,0,1,1,0,1,0,1,1,1,1,2,2,1,2,0,2,0,0,0,2,1,1,2,0,2,1;2,2,1,1,0,0,1,0,1,2,0,1,2,2,1,1,2,2,1,1,2,2,1,1,2,1,1,1,1,0,0,2,0;1,0,2,2,2,0,0,0,2,1,1,2,2,2,2,1,0,0,1,0,1,0,1,0,2,2,0,1,0,0,2,1,2;0,2,1,0,0,2,1,1,1,1,1,0,0,1,1,0,0,1,1,0,2,2,2,0,0,0,2,1,0,0,0,2,1;2,2,2,0,2,1,1,1,1,2,1,1,2,2,0,2,2,0,0,2,0,1,2,0,0,0,0,2,0,0,0,1,1;2,2,1,1,0,0,1,2,1,2,1,0,2,0,1,2,2,2,0,1,0,2,0,2,0,1,0,0,0,0,1,2,2;2,1,1,0,1,2,1,2,1,1,2,2,1,1,0,2,0,1,2,1,2,1,0,0,0,2,2,2,0,2,1,2,0;0,1,2,2,1,1,0,2,1,2,1,0,1,1,1,1,1,2,0,0,1,1,2,1,1,2,1,2,0,1,0,1,1;1,0,1,2,0,2,2,1,1,0,0,2,1,2,1,2,1,0,0,1,2,0,1,1,2,1,0,0,2,2,0,2,0;1,2,0,2,1,0,0,0,1,0,2,0,1,2,1,2,2,1,1,1,1,0,1,2,0,1,0,2,2,2,0,0,1;1,1,2,1,0,1,2,1,2,2,2,1,0,1,2,1,1,1,2,2,1,1,1,0,2,0,2,1,0,1,0,1,2;1,2,1,1,2,2,0,1,0,0,2,2,1,0,1,0,2,1,0,2,0,1,2,0,0,1,1,1,2,2,1,2,0;1,2,2,1,1,2,2,1,2,0,2,0,0,2,2,1,0,2,0,1,0,2,2,0,1,0,2,1,0,0,1,0,1;1,1,1,0,0,2,1,2,2,0,0,0,0,2,1,2,2,0,1,2,0,0,1,2,1,1,1,2,0,1,1,2,2;0,0,1,1,2,1,2,1,2,1,1,1,0,1,1,0,0,1,2,1,2,1,2,1,0,2,1,1,0,2,2,2,0", "output": "9"}, {"input": "2,1,1,2,1,2,2,1,1,2,0,0,1,0,0,2,0,0,0,2,1,2,2,0,0,0,0,2,1,2,0,1,2,1,2,1,1,2,1;2,1,2,0,0,2,1,0,0,1,2,1,0,1,1,1,1,1,2,1,2,0,2,2,1,1,2,1,1,2,1,2,0,1,1,1,2,0,2;2,1,1,0,0,1,0,1,0,0,0,2,1,0,1,0,0,2,0,0,0,1,0,2,2,2,2,2,1,0,0,2,1,2,1,1,1,1,0;1,1,1,2,2,0,2,1,2,0,2,2,2,0,2,0,2,2,2,1,1,1,1,0,0,0,0,1,2,0,1,1,2,2,2,1,0,0,1;0,0,2,2,0,1,2,0,2,2,1,1,0,2,1,0,2,0,2,1,1,1,2,0,2,1,1,2,1,2,0,0,2,0,1,1,1,0,1;1,0,2,2,0,1,1,1,0,1,0,1,2,2,2,0,1,0,1,2,1,0,0,0,0,1,1,1,2,1,0,2,0,2,1,1,0,0,1;0,2,2,2,0,0,0,0,0,0,2,0,0,2,2,0,2,0,0,0,1,1,2,1,2,1,2,2,1,1,2,2,0,1,2,2,1,1,2;1,2,2,1,0,0,2,1,1,2,2,0,1,0,0,0,1,1,1,1,1,1,0,1,0,2,1,1,1,0,2,2,2,1,1,0,0,2,0;1,2,1,0,0,1,2,0,0,0,0,2,0,2,2,1,1,0,1,1,2,0,0,1,2,1,1,2,0,2,2,0,0,2,2,1,0,1,2;1,1,2,2,0,2,2,0,2,1,2,0,1,1,1,0,0,0,1,1,1,1,0,2,0,2,1,1,2,0,0,2,0,2,1,2,0,1,1;0,2,2,1,0,0,2,1,0,0,2,2,1,1,0,1,0,1,0,2,0,0,1,1,1,2,0,1,0,0,2,2,0,2,1,1,2,2,0;1,0,1,2,1,1,1,1,1,2,1,2,0,0,1,0,2,0,0,0,0,1,1,2,1,1,1,1,2,0,1,2,0,1,0,0,1,2,1;1,1,1,1,1,2,1,1,1,1,1,1,2,0,1,2,2,2,2,0,0,2,1,0,2,0,1,1,2,2,0,1,1,0,0,1,1,2,1;1,0,0,0,2,0,0,2,1,2,2,2,0,2,2,0,2,0,2,2,1,0,2,2,0,1,0,0,1,2,2,1,0,2,2,2,2,1,2;0,0,1,0,0,0,0,0,0,0,0,1,0,0,1,0,1,0,1,2,2,0,0,1,2,0,0,0,0,2,2,0,1,0,1,2,0,2,1;2,1,1,0,0,1,0,2,1,0,1,1,1,2,0,0,1,2,1,2,0,1,2,0,1,0,2,1,0,2,0,0,1,2,1,2,1,1,1;0,2,1,1,2,2,2,0,1,1,1,1,1,0,2,0,2,0,1,1,0,0,1,2,0,2,1,0,2,1,0,2,1,2,0,1,0,2,1;2,2,2,0,2,1,1,1,1,0,1,1,0,0,1,0,1,2,1,0,0,2,2,1,1,1,0,0,0,2,1,0,2,2,0,1,0,0,1;2,0,2,1,2,0,2,0,2,2,0,0,2,0,0,2,0,1,2,1,1,1,2,1,0,2,0,2,0,1,2,1,2,0,1,2,2,1,1;2,2,1,1,2,1,2,0,1,2,0,2,2,0,1,2,0,2,2,2,2,1,1,0,0,0,1,1,0,2,0,1,1,2,0,1,0,2,2;1,2,0,0,1,2,2,1,0,0,1,2,2,0,1,0,2,2,1,1,2,2,1,2,1,0,0,2,2,0,0,1,0,1,2,0,1,2,2;1,2,2,2,1,1,1,1,1,0,1,1,0,2,1,1,0,2,1,2,2,2,1,0,0,1,2,1,1,2,2,1,1,2,1,0,2,2,2;1,0,2,2,1,1,2,0,1,1,1,1,0,0,1,2,1,2,1,0,2,0,1,1,2,2,1,1,1,2,1,0,0,0,1,1,2,2,1;0,1,2,1,1,0,1,1,0,2,2,1,2,1,0,0,2,1,2,0,1,0,1,1,0,1,1,1,0,2,2,2,0,2,2,0,0,0,1;0,2,1,0,1,2,2,2,0,2,0,1,2,2,0,1,1,2,0,2,1,1,0,2,1,0,0,0,1,2,0,0,0,2,0,1,2,1,1;0,2,1,1,0,1,2,2,2,1,2,2,2,0,0,0,2,1,1,1,0,2,2,1,1,0,0,0,1,1,0,2,0,1,2,0,1,0,2;2,2,2,1,1,1,0,0,1,0,1,1,2,2,1,2,2,2,0,2,1,1,2,0,1,2,1,0,0,2,1,1,0,0,0,1,2,0,0;1,2,1,1,2,1,2,0,0,2,0,0,1,0,2,1,2,2,2,1,0,1,2,1,0,0,1,0,1,1,1,2,1,0,0,0,1,1,2;0,2,0,1,2,1,0,0,0,0,2,0,1,1,2,2,1,1,0,1,2,1,1,0,1,0,2,2,2,0,0,1,1,1,1,2,1,2,2;1,1,1,1,1,2,0,2,0,2,2,1,1,2,2,0,2,0,2,2,0,2,2,0,1,0,2,1,2,1,1,1,0,2,2,2,2,0,0;0,2,2,1,2,1,1,0,2,2,0,2,2,2,2,1,2,1,2,1,2,2,2,1,2,1,0,0,0,2,1,1,0,2,0,1,0,1,2;0,0,1,2,0,1,1,2,0,1,0,1,2,2,1,0,0,1,0,2,2,1,0,0,0,2,2,2,1,0,0,0,0,2,0,1,2,0,0;2,2,0,1,1,0,0,2,0,2,0,1,2,0,2,0,2,2,0,0,1,1,1,0,1,1,0,0,2,2,0,1,0,2,2,1,1,1,2;0,0,2,1,2,1,0,2,2,1,2,1,1,0,2,0,0,0,1,0,2,0,1,0,2,1,1,2,1,0,1,1,2,2,2,2,0,1,1;0,2,1,1,1,1,1,0,2,2,1,0,1,2,0,0,2,0,2,2,1,2,0,1,1,2,1,1,0,2,0,0,0,2,1,1,1,0,2;1,0,2,1,2,1,1,0,1,1,0,2,2,1,2,2,1,2,1,2,0,1,2,0,0,1,1,2,0,0,0,1,0,1,2,2,1,1,2;2,0,0,1,1,0,0,1,0,0,0,2,0,0,0,0,2,1,2,0,0,2,0,0,0,1,2,0,0,0,2,1,1,0,0,0,1,2,1;2,0,1,0,2,1,1,2,1,2,2,0,1,0,1,0,1,2,2,1,1,2,0,2,2,1,0,2,0,2,0,0,2,2,2,1,0,2,2;2,0,1,1,1,0,0,2,1,1,0,0,0,2,1,0,1,1,1,2,0,0,0,1,1,1,0,2,1,0,2,1,0,0,0,1,1,1,0;2,0,1,2,0,0,1,0,2,0,2,0,2,1,0,0,2,2,2,0,2,1,0,1,0,1,2,2,1,1,1,2,1,2,2,0,0,0,2;1,1,0,0,2,1,0,1,0,0,0,1,2,1,0,0,1,0,0,0,1,1,0,2,0,1,1,0,2,2,2,2,1,0,2,1,0,0,0;0,0,1,1,0,0,1,0,2,1,2,2,1,0,1,0,0,0,2,0,0,2,2,2,0,2,0,1,0,0,1,1,0,2,0,2,2,2,1;1,2,2,0,1,0,1,1,2,0,1,1,1,2,2,1,2,2,0,0,1,1,0,2,2,2,2,0,1,0,0,2,0,1,1,1,1,2,2", "output": "8"}, {"input": "0,0,1,1,0,1,0,1,2,2,1,2,0,0,0,2,0,1,0,1,1,0,0,1,2,1,2,0,1,2,2,0,0,2,2,2,1,1,0,2,1,0,1,0,0,1,1,2,1;1,1,1,2,0,0,1,1,0,1,0,0,0,0,2,1,0,0,2,1,0,2,0,1,1,0,1,0,2,2,2,1,2,1,2,1,1,1,1,0,1,2,0,0,2,1,2,0,1;0,1,1,2,0,1,1,0,1,2,0,2,1,2,1,1,2,1,0,1,0,2,1,1,1,1,2,2,0,0,1,1,2,0,2,2,1,0,0,2,2,2,0,1,1,2,1,0,0;2,1,0,0,1,0,0,0,1,2,0,0,1,2,1,1,0,0,1,1,0,0,0,2,0,2,2,1,1,1,0,2,0,0,1,0,1,2,0,2,0,1,1,1,2,1,1,0,1;0,0,0,0,2,0,1,1,0,1,1,2,1,0,1,1,2,0,0,2,2,2,1,0,1,1,0,1,1,1,0,2,0,0,2,0,1,0,0,1,0,2,2,1,2,0,1,1,0;0,2,1,0,0,1,0,2,2,1,0,0,0,1,0,2,1,1,2,0,2,0,1,1,1,2,2,2,2,2,1,2,1,2,2,1,0,0,0,2,2,0,0,0,1,0,1,1,1;2,2,2,2,0,2,1,1,1,2,2,1,2,0,0,1,1,1,0,1,1,1,2,0,1,1,2,0,1,0,0,2,0,1,1,0,1,2,2,2,1,0,2,0,0,0,2,1,1;1,2,2,1,1,0,0,1,2,2,1,2,0,1,2,2,0,0,2,2,1,0,0,0,1,2,0,0,2,0,2,1,1,1,2,1,1,2,0,2,0,2,2,2,0,1,2,2,2;0,1,2,0,1,0,0,2,0,1,1,0,2,1,2,1,0,2,0,1,2,2,0,0,2,1,2,2,1,2,1,2,0,2,1,0,1,1,1,1,1,0,0,1,2,1,2,2,2;0,0,1,2,0,0,0,0,1,1,2,2,1,1,2,1,2,0,0,0,0,2,0,2,0,1,1,1,2,1,0,2,1,2,1,0,0,1,2,1,0,1,0,1,0,0,2,2,2;2,0,1,1,2,2,1,0,0,0,0,2,2,0,2,0,1,2,2,1,1,0,0,0,1,2,1,0,2,1,0,2,2,0,2,2,1,2,0,0,1,0,1,2,0,0,2,1,0;1,0,0,2,0,0,0,1,1,2,0,2,1,2,0,0,0,2,2,2,2,0,0,1,2,1,0,2,1,0,2,1,1,2,2,0,1,2,2,1,0,2,1,0,2,2,2,2,1;2,2,2,1,1,0,0,1,1,1,0,2,1,2,1,2,0,1,1,1,0,1,0,0,0,2,2,1,0,2,2,2,1,2,0,2,0,2,0,2,2,0,2,1,1,2,1,0,2;2,2,2,1,0,0,2,2,2,1,2,0,0,2,0,0,1,2,2,0,1,0,2,1,2,0,2,2,0,1,1,1,1,0,1,2,2,2,2,0,2,0,2,1,2,2,1,2,1;1,2,1,2,1,0,2,0,1,2,2,1,0,0,0,1,0,0,2,1,0,2,0,0,2,2,1,1,1,1,1,1,1,0,1,0,2,2,1,2,2,0,2,2,0,1,0,2,0;1,2,1,0,1,2,2,2,2,0,2,1,1,1,0,1,2,2,2,2,2,0,1,2,0,0,1,0,1,2,1,1,1,0,1,0,2,1,0,2,1,1,2,1,1,1,1,1,0;1,1,2,2,0,1,0,2,0,2,1,2,0,0,0,0,1,0,1,2,0,2,0,2,1,1,2,0,2,2,2,0,2,1,0,1,1,2,0,0,2,2,0,0,1,0,1,1,1;1,1,1,0,1,1,0,1,2,1,0,1,2,1,2,1,1,2,1,2,1,2,1,2,2,0,0,2,1,1,1,1,0,2,2,1,2,1,0,0,2,2,1,2,1,0,2,0,0;1,1,1,2,1,0,2,1,0,2,0,1,2,0,1,2,0,1,1,1,2,1,2,1,1,2,1,2,1,1,0,2,2,1,0,0,2,2,1,1,1,2,2,0,0,2,1,0,1;1,0,0,0,0,2,2,1,1,1,1,0,1,2,0,0,1,1,2,2,0,2,1,0,0,2,2,1,0,2,2,0,1,1,2,0,1,2,2,2,1,2,0,2,1,1,0,0,0;1,1,0,2,1,0,0,2,2,2,0,0,1,1,2,2,2,0,0,1,1,0,2,1,0,1,0,0,0,2,0,0,0,0,1,1,0,1,2,1,1,1,2,0,2,2,0,2,1;0,2,0,2,2,1,0,0,2,2,2,2,1,2,1,2,1,2,0,2,0,0,1,2,2,0,0,2,1,2,2,1,0,1,1,1,0,0,0,2,0,2,1,2,1,0,2,0,0;2,1,1,1,0,0,0,2,0,0,0,2,1,1,1,0,0,1,0,1,1,1,0,2,2,0,1,2,1,0,2,0,0,0,1,0,1,1,2,1,2,2,1,0,2,2,1,2,0;1,0,1,2,2,1,2,2,1,2,2,2,0,1,1,1,2,2,2,1,2,0,0,0,2,2,1,1,2,2,2,2,0,2,0,1,2,2,0,2,1,1,0,2,2,0,2,1,1;0,1,1,1,1,2,1,2,2,2,0,2,0,0,2,2,2,0,1,2,2,0,2,2,2,2,0,0,0,0,1,1,1,1,1,1,2,0,0,0,2,2,0,1,0,1,2,2,0;2,1,0,1,1,2,0,0,2,1,2,0,1,0,0,0,2,1,0,0,2,2,0,2,1,1,1,1,0,1,0,0,2,2,0,1,1,1,1,0,0,2,0,1,0,1,1,1,1;0,0,2,2,0,0,0,1,2,1,1,2,2,1,1,0,1,0,0,0,2,0,2,1,0,2,0,0,0,0,1,2,2,1,1,2,0,2,0,1,1,2,2,1,2,0,1,0,2;2,2,2,0,0,1,2,2,2,2,1,2,0,0,2,1,1,0,0,0,2,2,2,2,1,0,0,0,0,2,2,1,0,0,0,1,2,0,1,2,0,0,0,2,2,2,0,0,1;0,2,0,1,2,1,2,2,2,2,0,2,0,1,0,0,1,0,2,1,0,0,1,2,2,2,2,0,0,2,0,0,1,1,2,2,1,2,2,2,0,0,1,2,0,2,2,1,2;0,0,1,0,2,0,0,1,1,0,1,2,0,2,0,1,2,0,2,1,0,1,0,0,0,2,0,2,2,1,2,1,0,2,1,1,1,1,2,1,1,0,1,2,0,0,0,0,1;2,0,2,2,2,0,2,0,1,2,1,1,0,0,2,1,0,2,0,2,0,2,1,2,0,0,0,0,1,0,0,2,0,2,2,2,2,1,1,2,2,1,2,0,2,1,1,0,0;2,0,0,0,0,0,2,2,0,0,2,2,2,2,1,0,0,2,2,0,0,2,2,0,2,2,1,2,0,2,1,1,2,1,0,2,2,1,2,2,2,2,2,0,1,1,2,1,0;2,0,2,2,1,0,2,0,2,2,0,2,1,1,0,0,1,2,0,2,2,0,2,2,2,2,0,2,2,0,0,0,0,1,1,2,1,0,1,2,2,0,2,2,0,2,2,2,2;1,2,0,2,1,2,1,2,0,0,1,2,0,2,0,0,1,2,0,0,2,0,1,1,1,2,1,0,2,0,2,0,0,2,2,1,2,0,1,1,2,1,1,1,2,0,1,2,2;0,1,0,2,0,1,2,0,2,0,2,1,2,2,2,0,2,0,2,1,1,1,2,2,1,0,2,2,1,1,1,1,0,0,1,0,0,2,1,2,0,0,1,2,1,2,1,1,2;2,1,1,0,2,0,1,2,1,2,1,0,2,0,1,1,0,0,0,2,0,0,2,0,0,2,0,0,2,1,1,2,1,0,0,2,2,2,2,0,1,0,2,0,1,2,2,2,1;2,0,1,0,0,2,2,2,1,2,1,2,2,1,0,2,0,1,2,0,2,2,0,1,1,1,1,0,2,1,2,2,0,2,0,0,2,2,2,2,1,1,0,1,1,1,2,0,0;1,0,2,0,2,2,2,1,1,0,2,1,0,1,0,2,0,0,0,1,0,1,1,1,2,1,2,1,1,0,2,0,0,1,0,2,1,0,0,1,0,0,2,1,1,0,0,2,1;2,1,2,1,2,1,1,0,2,2,2,0,0,0,2,0,0,2,1,1,2,0,1,2,2,0,2,0,2,1,1,2,1,2,2,2,2,1,1,1,1,2,2,2,2,2,1,0,1;0,2,0,0,2,1,2,1,1,0,1,1,1,2,1,0,2,1,0,0,0,0,2,0,0,0,0,2,1,2,1,2,0,1,1,1,2,0,2,1,0,2,0,0,0,0,0,0,2;1,1,2,2,2,2,2,0,1,1,1,2,0,1,2,0,1,1,1,1,2,0,2,0,0,2,2,0,0,0,1,1,2,2,1,2,2,1,1,2,1,2,1,0,0,2,1,1,2;2,0,1,1,2,0,1,2,1,2,1,2,1,0,0,1,2,2,1,1,2,1,0,0,0,0,1,0,0,2,1,2,2,0,0,2,2,2,1,2,1,1,2,2,1,1,1,2,1;0,1,0,1,0,2,1,1,1,0,1,0,1,1,2,2,0,0,1,2,2,2,0,2,1,1,1,2,2,2,2,0,1,0,0,1,1,2,1,1,1,1,2,0,1,0,1,0,0;0,1,1,2,2,1,1,0,0,2,2,0,1,2,0,0,2,0,2,1,2,0,2,2,1,1,0,1,0,0,1,2,0,0,1,1,2,2,0,1,1,1,1,2,0,0,0,0,2;1,1,2,1,2,2,2,2,0,2,1,0,0,0,0,0,0,0,2,0,1,1,2,2,0,1,2,2,0,0,0,1,2,0,0,1,1,0,1,0,1,0,2,0,0,0,1,1,0;0,0,2,0,1,2,0,2,0,2,1,2,1,1,0,0,2,1,2,0,1,1,0,2,0,2,0,0,2,2,2,0,0,0,0,2,1,2,1,0,0,2,2,2,2,1,2,1,2;2,0,1,2,0,2,2,1,0,2,0,1,0,0,0,2,1,0,1,2,0,0,2,2,0,1,2,0,0,0,0,2,0,2,2,0,1,0,0,0,0,0,1,0,0,0,1,1,0", "output": "9"}, {"input": "2;0;2;0;1;1", "output": "1"}, {"input": "1,0;2,1;2,1;0,0;2,2;2,2;0,2;2,1;1,1", "output": "3"}, {"input": "0,2,0,1,0,0", "output": "1"}, {"input": "2;2;0;1;2;0;0;0;2;1", "output": "1"}, {"input": "2,0,2;2,0,2;0,1,2;0,1,1;2,1,1;1,2,2;1,1,2;0,0,2;1,2,0;1,2,0", "output": "3"}, {"input": "1,2,2,1,0,1,0,2,0,2,2,2,2,0,2,2,0,1,0,0,0,1,2,1,1,1,0,0,1,0,2,2,0,1,1,2,1,2,0,1,1,2,0,0,1,2,2,0,1,0;2,1,0,1,1,2,2,0,1,0,2,0,2,1,1,1,1,0,2,0,2,0,1,2,2,2,0,0,2,0,2,1,2,2,2,2,2,0,0,1,1,1,1,0,0,2,0,2,0,2;0,0,1,0,2,1,0,2,2,1,1,1,2,1,2,1,1,1,2,2,1,1,0,2,1,0,0,1,0,0,0,1,0,0,0,2,0,1,0,0,1,2,1,2,2,2,1,1,2,1;2,1,2,2,0,0,2,0,1,2,0,0,1,1,0,2,0,2,2,2,0,0,0,2,2,1,1,2,0,1,1,2,0,1,1,2,1,0,1,0,1,1,2,2,1,2,0,2,1,2;0,2,1,1,1,2,2,0,1,2,1,0,2,0,2,2,1,2,2,1,2,1,0,1,0,2,0,0,0,0,2,1,1,0,2,1,0,1,2,1,1,2,2,0,0,0,0,2,1,2;2,1,1,2,0,1,1,0,0,0,0,1,0,1,0,1,0,2,0,2,2,1,0,2,1,1,1,1,1,2,0,2,1,1,0,0,1,0,2,0,2,1,0,1,0,2,0,2,0,1;0,2,1,1,0,1,1,0,1,1,2,1,1,0,2,0,1,2,2,2,2,1,2,2,1,1,2,0,0,1,1,0,0,2,1,0,2,2,0,1,0,1,0,2,2,1,1,2,0,1;0,1,2,2,2,2,1,2,2,2,0,2,2,1,2,2,2,1,1,0,2,0,0,2,0,1,2,1,1,2,0,0,2,2,0,2,0,2,2,0,2,0,1,2,0,0,1,2,0,1;0,0,2,1,2,2,2,0,0,0,0,1,2,0,1,1,0,2,1,1,1,2,2,0,1,1,1,0,2,1,2,0,1,1,1,0,0,0,0,1,0,1,0,1,0,1,0,0,1,1;0,1,2,0,1,1,2,2,2,0,2,0,0,1,1,0,1,1,0,1,1,2,2,0,0,1,2,0,0,2,2,1,1,1,0,0,1,2,2,0,2,1,1,0,2,2,1,0,1,1;0,1,2,1,2,1,0,2,2,0,0,2,1,2,2,2,0,2,1,1,1,2,1,0,1,1,0,1,0,2,2,0,0,2,0,1,2,1,1,2,2,1,1,1,2,2,0,1,2,2;1,0,2,0,0,0,0,1,0,2,2,0,2,1,2,1,0,1,0,0,0,0,0,0,2,1,1,1,2,1,1,2,1,1,0,0,2,2,2,1,0,1,2,2,0,0,1,2,0,1;1,0,0,1,2,2,0,2,1,2,1,2,1,0,0,1,1,2,2,0,1,0,2,0,0,1,1,1,1,1,0,0,2,1,2,0,1,0,1,1,2,0,1,1,0,0,2,1,0,1;1,1,0,1,0,1,2,1,0,0,0,0,0,2,2,2,0,0,0,0,1,1,2,2,1,1,0,1,0,1,1,1,1,0,2,2,0,0,0,0,0,2,0,2,0,1,0,1,2,1;0,1,2,1,1,2,2,2,0,0,1,1,1,2,2,1,1,0,0,0,1,1,0,2,0,1,2,2,2,0,1,0,1,0,1,1,0,1,1,0,2,1,2,1,0,1,1,1,1,2;2,1,1,0,0,1,0,1,1,2,0,0,0,2,0,2,0,0,2,0,1,2,2,2,1,2,1,2,1,2,0,1,2,0,0,1,2,1,1,0,1,2,1,1,2,0,1,0,1,0;0,2,2,2,2,2,0,0,0,0,1,0,2,0,2,2,2,2,1,2,0,0,2,0,1,0,1,2,1,0,2,2,2,1,0,0,0,2,2,2,1,2,1,0,2,2,2,1,2,1;2,0,0,1,1,1,0,2,2,0,2,2,2,2,0,0,2,2,0,2,1,1,1,2,0,0,0,1,0,1,2,0,0,1,1,1,1,0,1,2,1,2,0,1,0,0,2,1,1,0;0,0,1,0,2,2,0,0,2,0,2,0,0,1,0,0,2,0,0,1,2,2,0,0,0,0,0,0,1,0,0,2,2,0,1,2,2,2,1,0,2,0,0,1,0,2,2,1,1,1;0,0,1,1,1,2,0,0,1,1,1,1,1,1,2,1,0,0,0,1,1,0,0,0,0,0,1,1,0,1,2,0,1,2,1,0,2,1,2,0,0,2,2,1,1,2,1,0,1,2;0,2,0,1,1,0,1,1,0,0,2,0,2,0,0,2,0,2,1,2,2,0,1,1,0,1,2,2,1,2,2,0,0,2,2,2,2,2,2,2,2,0,2,0,1,1,0,2,1,2;0,2,2,0,1,0,2,0,0,0,1,0,0,0,0,0,1,0,2,1,1,2,1,2,0,0,0,2,1,1,0,2,0,1,2,0,0,1,2,1,2,0,0,2,2,0,2,0,0,0;0,1,2,2,1,2,1,1,2,1,2,1,0,0,0,2,2,1,2,1,1,2,0,2,0,2,0,2,1,0,0,2,0,2,1,0,2,1,0,2,2,0,1,1,2,1,2,1,2,0;0,2,0,1,0,0,0,0,1,1,0,1,2,0,0,2,1,1,2,0,0,2,1,0,0,1,2,1,0,0,1,1,0,1,1,0,1,0,0,2,2,2,2,0,1,1,0,1,1,2;2,1,0,2,2,1,1,0,2,0,0,1,0,2,0,0,2,0,1,1,0,2,0,0,2,0,1,2,2,2,2,2,1,1,2,0,1,0,0,1,1,0,1,2,2,1,0,2,1,1;0,1,2,2,2,2,1,2,2,2,0,2,0,1,0,0,1,2,2,0,2,0,0,0,1,2,2,1,2,0,1,0,1,1,2,2,0,2,2,0,1,2,2,0,2,2,1,0,2,1;2,0,2,1,1,1,2,1,2,2,2,0,2,2,0,2,0,0,1,2,1,2,0,0,2,2,1,0,0,1,1,2,0,1,0,2,0,1,2,2,0,0,1,0,2,2,2,1,1,2;0,0,0,1,0,1,2,0,2,1,1,2,1,0,0,0,0,1,2,2,1,0,2,1,0,0,0,0,2,2,2,2,1,1,2,0,0,2,2,0,0,0,0,1,2,0,0,0,1,1;1,2,2,2,0,1,2,2,1,1,2,0,2,0,2,1,1,0,0,1,0,1,0,0,1,0,1,2,0,2,0,1,2,2,1,0,1,2,1,2,0,1,0,2,0,2,1,1,1,1;0,2,0,0,2,0,2,0,2,0,2,1,0,0,2,1,2,1,1,2,2,0,2,1,1,2,0,0,1,1,0,1,2,0,2,2,2,2,1,1,1,1,1,0,1,0,0,2,2,2;1,2,0,1,0,2,1,1,1,1,1,1,0,0,2,2,0,2,0,2,2,2,1,2,1,0,2,0,0,2,1,0,1,2,0,0,2,0,0,2,1,0,0,2,2,2,0,0,0,2;1,2,0,2,2,0,1,1,2,2,2,0,1,0,1,1,0,0,1,2,0,1,1,1,0,0,1,2,0,2,2,1,2,2,1,0,2,1,1,2,1,2,1,0,2,1,2,2,0,2;1,1,0,0,2,1,0,0,0,2,1,1,2,2,2,0,2,1,0,2,1,2,1,2,0,0,1,0,0,0,1,2,0,2,0,0,2,2,2,1,1,0,2,0,1,1,1,2,0,1;2,0,2,1,2,1,2,0,1,0,1,2,1,2,1,1,0,0,1,2,2,1,1,1,0,0,2,2,2,2,0,1,0,1,2,1,0,0,2,1,2,1,0,2,1,1,1,2,0,1;0,1,1,1,2,1,1,1,0,1,2,2,1,1,2,2,1,1,1,1,2,0,0,0,2,2,1,2,1,0,1,1,1,2,2,2,0,0,0,2,2,1,1,1,2,2,1,0,0,1;1,2,1,1,0,2,2,2,2,1,1,1,2,0,0,0,2,0,2,1,2,2,1,2,1,0,1,2,1,2,0,0,1,1,2,2,0,0,0,0,0,2,1,2,0,0,1,0,2,2", "output": "8"}, {"input": "1,2,0,2,0;2,1,2,2,2;2,0,2,0,1;0,0,1,0,0", "output": "3"}, {"input": "0,2,1,2,2,1,2,2,2,1,1,2,0,0,2,2,1,1,0,1,0,0,0,1,0,2,0,0,1,2,2,0,2,2,0,0,2,2,0,1,2,2,0;0,1,0,2,1,1,0,0,2,0,2,1,0,0,0,1,2,0,0,0,0,0,1,1,0,1,1,1,1,0,2,0,1,1,2,1,2,1,0,0,2,0,1;1,1,0,2,1,0,0,1,2,1,1,0,2,2,2,2,1,0,2,2,0,1,1,2,0,1,2,0,0,2,2,0,2,0,2,1,0,1,1,2,1,0,1;1,2,2,0,2,1,0,1,0,1,0,0,0,0,2,0,0,2,0,2,1,1,1,1,0,1,0,0,2,0,1,2,0,0,1,2,0,0,1,2,2,2,0;1,2,2,1,1,2,2,0,2,1,1,1,0,1,1,1,0,2,2,0,1,1,0,1,2,1,0,0,2,0,1,1,0,0,0,1,2,1,0,0,2,2,0;1,1,2,1,2,2,0,0,2,2,1,0,2,2,2,2,1,1,1,0,0,0,2,1,1,0,2,1,0,1,1,2,0,2,0,2,2,0,0,1,2,1,1;1,0,2,0,1,0,1,0,1,1,2,0,0,0,0,0,1,0,0,0,1,0,0,1,2,2,2,1,0,0,1,0,0,2,0,0,1,0,2,1,1,0,2;2,1,1,1,2,0,0,0,1,2,1,0,0,2,2,0,0,1,1,2,0,1,1,2,0,1,0,0,1,2,2,1,1,1,2,2,0,1,0,0,0,1,1;1,0,2,1,2,0,1,1,0,0,0,2,2,1,0,0,1,1,1,2,0,2,1,1,1,1,2,2,2,0,0,1,2,2,2,2,2,2,2,1,0,1,0;0,0,0,2,0,0,1,2,2,2,0,1,0,0,2,0,0,2,0,2,1,2,0,1,0,1,0,0,1,1,0,1,0,0,0,2,1,2,0,0,0,0,0;1,1,0,2,0,0,2,2,2,2,1,0,1,1,1,0,2,2,0,1,1,2,1,1,2,0,0,0,1,2,0,1,0,0,1,0,1,1,2,0,0,2,1;0,2,1,0,2,1,0,1,1,2,1,2,2,0,1,2,2,2,0,2,2,2,2,2,1,2,2,0,2,1,1,1,1,0,0,2,2,1,0,0,0,2,2;0,2,1,2,1,2,2,1,0,0,1,2,0,0,0,1,2,2,2,1,1,2,0,2,1,1,0,1,2,0,2,0,2,0,0,1,1,2,1,1,0,2,2;1,0,0,2,2,1,1,1,2,2,2,0,0,2,1,2,1,2,2,2,2,1,2,1,0,1,0,2,1,0,2,1,0,1,1,2,0,1,1,0,0,0,1;0,1,0,1,0,2,1,2,0,2,0,2,2,1,1,0,1,0,0,1,2,1,1,0,0,1,0,0,2,2,1,1,0,1,1,1,0,0,0,0,0,2,0;2,1,1,1,0,2,0,2,0,0,2,1,0,1,1,1,2,1,0,0,2,1,1,2,1,2,1,2,2,0,0,0,0,1,2,0,0,2,0,1,1,0,2;1,1,1,1,1,1,0,2,2,1,2,0,2,1,1,1,0,0,1,0,0,1,1,0,0,0,2,1,1,1,0,1,2,1,1,0,1,1,1,0,1,1,2;0,1,1,1,2,0,2,1,2,1,2,1,1,0,1,2,1,2,0,0,1,1,0,2,2,0,0,1,1,1,1,1,2,0,0,2,1,0,0,1,0,2,1;1,1,0,1,1,1,1,1,2,1,1,1,2,0,2,1,0,2,1,0,1,1,0,2,0,1,2,1,1,0,1,2,2,0,1,1,0,0,1,2,2,1,1;1,2,2,0,0,1,1,2,1,2,2,1,2,1,2,1,2,2,1,0,2,1,1,1,1,2,2,1,1,2,2,0,1,2,2,0,1,2,0,2,2,1,1;0,1,2,1,1,1,1,1,2,1,2,0,2,0,1,2,2,2,2,2,1,2,1,2,2,2,2,2,0,1,1,0,2,2,1,1,2,2,2,0,0,1,2;0,2,0,0,2,1,1,1,0,2,2,2,0,0,2,1,1,2,1,0,2,1,1,0,1,1,0,2,1,0,0,0,0,1,2,0,2,2,1,2,2,2,0;2,1,0,1,1,2,2,2,1,2,0,0,2,1,2,0,0,1,1,2,2,2,2,1,0,0,0,0,0,1,2,2,2,2,1,1,0,2,0,2,2,0,1;2,0,1,1,2,0,0,0,0,1,2,0,2,2,0,2,0,2,1,2,2,1,1,2,0,1,0,0,1,2,0,0,0,1,2,1,1,0,1,1,0,0,0;2,0,2,2,1,0,0,0,2,2,2,2,2,0,2,1,2,1,0,1,1,2,1,1,1,2,2,2,2,2,1,1,0,0,2,1,1,2,2,1,2,1,0;2,1,2,0,0,2,2,1,1,1,2,0,1,0,2,0,2,1,2,0,2,2,1,0,1,1,0,0,2,2,1,0,1,2,1,1,0,2,2,1,0,2,2;1,0,1,0,0,2,2,1,1,1,0,0,0,1,2,2,0,1,1,2,1,1,0,0,0,0,1,2,1,0,1,2,2,0,1,0,0,0,1,0,0,2,0;2,1,2,0,1,0,2,2,2,2,2,2,0,2,2,0,0,2,2,2,2,2,1,0,2,1,0,0,1,2,0,2,1,0,2,0,1,0,0,0,0,2,0;2,1,0,0,0,0,1,2,1,2,2,2,1,0,1,1,1,1,0,1,2,2,0,2,0,0,2,0,2,2,2,2,2,2,0,1,0,1,2,2,1,1,0;1,0,2,0,2,0,1,1,2,1,0,2,2,2,0,1,0,1,2,2,1,0,2,2,2,0,0,2,2,0,2,0,0,2,2,2,2,1,1,1,2,2,0;2,1,0,2,2,2,1,2,1,2,0,1,0,2,0,2,2,2,0,2,1,0,2,2,0,1,2,1,0,0,2,1,0,0,2,1,0,0,2,2,1,0,2;2,1,0,1,0,0,1,1,0,0,0,2,2,2,0,1,0,1,1,2,0,0,1,2,0,0,1,2,2,1,2,0,2,2,0,1,1,1,1,0,0,2,1;2,2,2,1,1,0,0,0,0,0,1,0,1,1,1,0,2,2,1,1,1,1,0,2,2,2,2,0,2,0,0,0,0,2,2,1,2,2,1,2,0,2,1;2,2,1,0,1,0,0,1,0,2,2,1,0,0,0,0,0,1,0,0,0,2,1,0,1,1,1,1,1,2,2,1,0,2,1,2,0,0,2,0,0,2,1;1,1,2,1,1,2,0,1,2,1,2,2,0,1,0,0,0,1,1,2,2,0,1,2,2,2,0,0,2,0,1,1,0,1,1,2,0,1,0,2,2,0,2;2,1,1,0,2,0,1,1,2,2,0,2,1,1,0,1,1,1,1,2,2,1,2,0,1,2,2,2,2,1,1,2,1,0,1,1,1,1,2,1,1,2,2;2,1,1,0,2,0,2,1,1,1,1,2,2,0,0,0,1,1,1,2,2,0,2,1,2,1,1,1,0,0,0,0,2,2,2,1,0,0,0,2,2,2,0;0,1,0,1,2,1,0,1,1,1,2,1,2,0,1,1,1,0,2,0,1,0,2,0,1,2,0,2,2,0,1,1,0,1,2,0,0,1,0,2,1,2,0;0,2,0,2,2,2,0,1,2,2,2,0,2,2,1,1,2,2,0,2,0,2,0,1,1,1,2,0,2,0,0,0,0,1,2,1,0,1,0,1,0,2,1;2,2,1,2,0,0,1,1,1,1,0,0,1,0,2,2,2,1,0,1,1,1,0,1,2,1,1,2,0,2,1,1,0,1,0,2,1,2,1,2,0,0,1", "output": "9"}, {"input": "2,2;2,0;1,1;0,1;0,1", "output": "2"}, {"input": "0,0,1,0,1;2,2,2,0,2;2,2,2,0,0;2,0,2,0,2;2,1,0,1,2;2,2,2,1,0;2,1,0,0,0;2,0,2,1,2", "output": "4"}, {"input": "1,1,1,1,1,0,1,1,0;0,1,2,2,1,2,0,0,2;1,1,0,2,2,0,2,1,1;2,1,2,2,0,2,0,0,1;2,0,2,1,1,0,0,1,0;2,2,1,0,2,0,1,2,0;1,1,1,1,2,2,0,1,2;1,0,0,2,1,2,1,1,0;2,1,2,0,2,1,0,1,1", "output": "4"}, {"input": "2;2;1;0;1;1;0;2;2;1", "output": "1"}, {"input": "1,1,1,1,1,0,0,0,0,1,1,1,1,2,0,0,0,0,0,1,1,1,0,1,2,0,1,1,2,1,0,0,2,0,0,0,1,1,2;2,1,0,2,1,0,2,2,0,2,0,1,2,2,2,2,1,0,0,1,0,1,1,2,1,1,2,1,1,2,0,0,2,0,2,2,0,2,1;0,1,1,1,0,0,1,0,1,0,1,1,1,0,0,0,2,0,2,2,2,1,2,0,0,2,0,1,2,1,2,0,2,1,1,0,2,0,1;0,1,2,0,2,0,2,1,1,0,0,0,0,1,0,1,0,2,1,0,1,1,1,2,0,2,0,0,1,2,0,2,0,0,0,2,0,1,1;2,0,0,2,1,2,2,1,2,1,0,2,0,2,1,1,2,2,1,0,1,2,0,0,2,0,1,1,1,1,1,0,1,1,0,0,1,1,1;1,1,1,2,2,1,1,2,2,2,2,0,1,2,0,0,0,1,2,1,0,0,1,2,2,1,1,1,0,2,0,2,1,0,1,2,0,0,0;2,2,2,2,0,0,1,1,2,1,0,0,2,1,1,2,0,1,2,0,0,2,1,2,2,2,2,2,2,2,2,2,0,1,1,2,1,2,1;0,0,1,0,1,1,0,2,1,2,0,1,0,1,0,0,1,0,2,1,0,2,2,0,0,2,2,2,1,1,2,2,1,0,1,0,2,0,2;0,1,0,2,2,2,0,0,0,0,2,2,1,1,2,0,2,2,2,2,1,0,0,0,2,0,0,1,0,1,0,1,1,0,0,1,0,1,0;2,1,2,0,1,2,2,1,2,0,2,2,2,2,0,0,2,1,0,2,0,0,0,0,1,0,2,2,2,2,0,2,0,2,2,2,1,1,0;1,1,1,1,2,1,0,1,1,0,0,0,0,1,1,0,2,2,1,1,0,0,2,0,2,0,0,2,1,0,2,2,0,0,0,2,0,0,1;2,1,1,2,1,0,0,1,1,1,2,0,1,2,1,2,1,2,2,2,2,2,1,2,2,0,1,0,0,2,2,0,0,1,0,0,1,1,2;1,0,1,1,1,2,1,1,0,2,2,0,2,2,2,2,1,1,0,1,1,2,1,1,2,0,1,1,1,2,1,2,0,0,1,2,0,1,2;1,2,0,0,2,1,1,1,0,2,0,2,0,1,1,2,1,1,1,2,0,0,2,2,2,2,2,2,0,1,2,0,0,2,2,2,1,2,0;0,0,2,0,1,2,0,1,1,2,1,2,1,0,0,0,2,0,1,0,1,1,2,2,2,0,1,1,0,2,1,1,2,0,0,0,2,1,0;1,2,0,1,1,2,0,1,2,0,0,0,1,1,0,0,1,0,2,1,1,2,1,2,2,0,0,1,2,2,1,0,1,1,1,1,0,0,2;2,2,0,2,2,0,0,1,0,1,2,0,0,0,2,1,2,1,0,0,0,0,1,1,1,0,0,0,1,0,0,1,0,2,0,1,0,2,2;1,1,0,0,2,2,1,1,0,1,1,2,1,0,2,1,1,1,0,1,2,0,2,1,0,0,0,1,1,0,1,0,1,1,0,0,2,0,2;2,0,0,0,0,0,0,2,1,1,2,0,2,1,0,1,0,2,2,2,1,1,1,1,1,1,0,2,1,2,1,2,0,1,0,2,1,1,2;2,1,0,1,2,0,0,0,2,2,0,0,0,1,1,2,0,0,0,0,0,1,0,1,2,2,1,2,1,0,2,0,0,1,2,0,2,0,0;2,2,1,2,2,1,0,0,1,2,0,1,2,0,1,1,1,2,1,2,1,2,1,2,1,0,2,2,2,2,2,1,0,0,1,0,1,2,1;0,1,0,2,2,2,0,1,1,0,0,0,0,2,0,0,0,1,0,2,0,0,2,1,1,2,1,2,1,1,2,1,1,2,1,1,1,0,2;1,0,1,0,1,0,0,2,1,2,0,0,1,2,1,2,2,1,1,1,0,0,1,2,2,1,1,2,1,2,1,2,2,0,2,2,2,2,1;0,2,0,2,0,0,0,1,1,1,0,1,1,2,2,1,1,0,1,1,0,0,0,0,1,2,0,2,1,0,1,1,0,1,0,0,2,1,2;0,2,0,1,0,2,1,0,0,2,0,2,1,1,2,1,1,1,0,1,2,0,2,1,1,2,0,2,0,0,1,1,1,2,1,2,0,1,0;0,0,1,0,0,0,0,0,2,1,2,0,0,1,1,0,0,2,0,1,1,0,0,1,0,1,1,0,0,0,0,1,2,0,0,2,2,0,0;1,1,2,1,2,0,0,1,0,1,2,0,0,1,1,0,1,0,2,0,0,0,1,0,1,0,2,0,0,1,1,1,1,1,1,1,2,1,0;1,1,1,2,0,2,2,1,1,2,2,0,2,0,1,2,1,2,1,1,0,0,1,1,2,2,0,2,0,1,2,0,1,1,0,0,1,0,0;1,0,1,1,0,1,2,2,1,0,0,0,1,0,1,0,2,2,1,0,2,1,2,0,2,1,1,0,0,2,1,0,2,0,1,2,1,2,1;1,0,2,2,0,0,1,2,2,2,2,1,0,1,1,2,0,1,1,1,1,2,1,1,2,2,0,0,1,0,1,2,2,2,1,2,2,2,1;0,1,1,0,2,0,2,1,2,0,2,1,0,1,2,2,2,2,1,1,2,0,0,0,0,2,0,2,1,1,0,0,1,2,2,1,1,0,1;2,0,0,1,2,2,0,1,2,0,0,2,1,2,2,0,2,2,0,2,0,1,2,1,0,1,1,1,2,2,2,1,0,0,2,2,1,1,2;0,0,2,0,0,2,2,0,2,1,1,0,2,2,0,2,1,1,2,1,1,1,2,0,0,0,2,0,1,2,1,2,1,0,1,0,2,1,2;0,0,1,2,2,2,2,1,1,2,1,1,0,2,1,1,2,0,1,2,2,2,2,1,2,1,1,1,0,0,0,0,0,1,0,1,1,0,0;2,2,0,0,2,0,2,2,2,1,2,0,1,1,0,0,2,0,0,0,1,2,0,1,1,1,0,0,1,1,0,2,0,0,2,0,2,0,2;0,0,0,1,0,2,0,2,0,1,1,1,1,1,2,1,2,0,1,0,0,2,2,2,1,2,2,1,0,1,1,1,0,2,2,2,1,2,1;0,2,0,1,2,2,2,1,0,2,1,1,0,0,1,0,0,2,2,2,2,1,0,1,2,0,0,1,1,0,2,2,0,0,2,0,2,0,1;0,0,2,1,0,1,0,2,2,2,1,1,0,2,1,2,1,0,0,0,0,1,2,1,1,1,0,1,2,1,0,2,0,1,1,0,2,0,2;2,0,2,2,0,1,2,2,1,2,2,0,0,0,0,1,0,0,1,1,1,1,2,1,0,0,1,0,1,2,1,2,0,1,2,1,1,2,0", "output": "11"}, {"input": "2,0,1,0,0,1,2,0,1,0,1,0,2,1,1,1,1,2,1,0,0,0,1,1,1,1,1,1,2,2,1,1,2,1,1;0,1,0,2,2,2,0,1,1,2,0,0,0,1,1,1,1,1,1,0,0,2,1,2,2,1,1,1,2,2,1,1,0,1,0;0,1,2,1,1,1,0,1,0,0,1,1,2,2,2,0,2,1,2,2,1,0,2,1,1,0,1,0,0,0,2,1,1,1,1;1,2,1,1,2,1,0,1,0,2,1,2,1,2,0,2,2,0,0,2,1,1,2,0,2,1,0,0,2,2,2,0,2,0,0;0,2,2,0,1,0,2,1,2,2,0,0,0,2,1,0,0,2,0,1,1,0,2,0,1,0,0,1,2,2,0,1,2,2,1;2,1,0,2,0,2,0,0,2,1,0,0,0,1,2,0,1,2,1,2,1,0,2,1,1,0,2,1,1,2,1,1,0,1,2;0,1,1,2,0,2,0,0,2,1,1,2,1,0,0,2,1,0,2,1,1,2,2,1,0,1,0,2,2,2,0,1,2,1,2;0,2,2,2,2,1,0,2,2,1,1,2,2,0,1,1,2,0,2,2,1,2,2,2,0,1,1,1,0,2,2,2,0,2,0;0,0,0,0,1,1,0,1,1,0,2,1,1,2,1,0,1,0,0,2,1,0,2,2,0,1,2,0,0,0,1,0,0,0,0;0,1,1,1,1,2,1,2,2,0,0,2,1,0,2,1,2,1,1,0,2,0,1,0,1,2,0,1,1,0,1,2,0,2,0;0,0,0,0,2,2,0,2,2,1,0,0,2,1,2,0,2,1,0,0,0,2,1,1,0,0,2,0,1,2,2,0,1,0,2;0,0,0,1,2,2,2,0,2,1,2,2,0,2,1,2,1,1,2,2,1,1,1,0,0,2,0,1,0,1,1,1,2,1,0;0,2,1,0,1,1,2,1,1,2,1,1,1,0,2,2,1,2,0,2,2,1,1,1,0,1,1,0,0,1,1,2,2,1,0;2,2,0,2,0,0,0,1,2,2,2,1,1,1,1,0,0,2,0,1,2,1,1,2,0,0,1,1,0,1,0,0,2,1,0;1,0,0,1,0,2,0,1,0,0,2,0,1,2,0,1,0,1,1,1,0,2,2,2,1,1,2,2,2,2,0,0,0,1,1;1,1,1,2,1,0,0,0,1,0,0,0,2,0,0,2,1,2,2,1,0,1,0,2,0,2,1,0,2,2,2,0,0,0,2;2,1,2,2,1,1,2,2,2,0,0,2,0,2,0,2,0,0,1,2,0,1,2,1,0,1,1,0,2,1,2,0,0,1,0;2,1,2,0,2,2,2,1,2,0,1,1,2,0,2,1,0,0,0,1,0,2,2,0,2,0,0,2,2,2,1,2,0,2,1;0,0,1,0,0,1,0,1,1,1,1,2,0,2,0,2,0,0,1,2,1,2,0,0,2,0,0,0,0,2,2,1,0,1,2;1,2,0,2,2,0,0,2,2,1,2,0,2,1,0,1,0,1,1,2,0,2,1,2,0,1,2,1,2,1,0,2,2,0,2;0,2,2,2,2,2,0,2,0,1,2,0,1,1,2,0,2,2,0,1,0,1,0,2,2,2,2,0,1,1,0,0,0,2,2;0,1,2,2,0,0,2,1,0,2,1,0,2,1,1,0,1,2,0,1,1,0,1,2,1,2,1,1,0,1,0,2,2,1,2;0,2,1,1,1,1,2,1,2,1,1,1,0,0,1,1,1,2,1,2,1,1,1,2,1,2,2,0,2,0,2,0,0,2,0;1,1,2,2,1,1,0,0,0,0,2,2,2,1,0,1,1,1,0,1,1,1,1,0,1,0,0,0,1,1,2,1,1,0,1;2,2,1,1,0,2,2,1,2,1,2,2,2,0,1,0,0,0,2,0,1,1,1,1,0,2,1,0,0,2,2,2,0,2,0;2,1,2,2,2,0,1,0,0,1,2,0,1,1,0,2,1,2,2,1,0,2,0,1,2,1,2,1,1,2,2,0,0,2,0;1,0,0,2,2,0,1,1,0,2,2,2,0,0,1,1,2,2,0,2,2,1,2,1,2,2,2,0,0,2,1,0,0,1,2;2,2,0,2,1,1,1,0,2,1,1,2,0,0,0,2,1,2,2,1,2,0,1,1,0,2,0,1,1,2,0,1,2,2,0;2,1,2,1,1,1,0,0,2,2,0,2,0,1,2,2,2,0,1,0,1,2,1,0,2,2,1,2,1,0,1,1,2,1,0;1,0,1,1,2,2,2,2,1,1,0,0,2,0,2,0,1,1,1,2,1,0,2,1,0,2,0,2,1,1,1,1,1,2,2;2,2,1,2,1,1,2,2,2,2,2,1,0,0,1,1,1,0,1,0,2,1,1,0,0,0,1,1,0,0,2,2,0,0,0;2,0,1,1,2,2,2,1,2,2,2,2,0,0,0,0,1,0,2,0,0,2,0,2,2,2,1,0,0,0,2,2,0,1,0;1,0,2,1,1,0,2,1,1,0,2,2,1,2,0,1,0,0,1,1,0,2,1,1,1,0,1,1,0,2,0,1,0,0,1;2,2,0,2,1,2,1,0,0,1,0,0,1,1,1,2,2,2,2,2,1,1,1,2,2,0,1,0,0,1,1,0,1,0,1;2,1,0,2,0,0,1,1,2,1,1,1,0,0,1,0,2,2,2,1,1,1,0,1,0,2,2,2,1,0,0,2,1,0,0;1,2,1,0,1,2,2,1,0,2,2,2,0,1,1,0,2,2,2,1,0,0,0,2,0,2,2,2,1,0,0,1,2,1,1;2,0,0,0,0,2,2,1,2,1,2,1,1,2,0,0,1,0,2,1,1,1,1,1,1,2,1,1,0,0,1,1,0,0,0;0,2,2,0,0,0,2,0,2,0,1,0,1,2,1,2,1,1,0,1,0,0,2,1,1,0,0,1,0,2,1,0,0,2,1;1,1,1,0,1,0,1,1,0,1,1,1,0,2,1,1,1,0,0,0,0,0,1,2,2,2,2,2,0,0,2,1,1,1,2;0,0,0,0,1,2,2,0,2,2,0,0,2,2,2,1,0,1,0,1,0,0,1,0,2,1,1,0,2,0,2,2,0,1,0;1,1,0,1,2,1,1,1,0,2,1,0,2,0,1,1,1,2,1,2,1,1,0,0,0,2,1,0,1,2,2,0,2,2,1;2,0,1,1,2,2,2,1,2,1,2,0,2,2,0,2,0,2,0,1,0,2,2,1,0,2,2,2,2,0,0,0,1,1,2;0,0,0,0,0,0,0,2,0,2,2,0,1,0,2,2,2,1,0,2,0,1,1,2,1,2,0,1,1,1,0,0,2,1,2;0,1,1,1,1,2,0,0,1,0,0,1,0,0,1,1,2,1,2,1,0,1,1,2,2,1,0,1,1,1,0,2,0,1,2;2,2,2,1,1,2,1,0,1,2,0,1,2,1,2,1,2,1,1,1,2,2,1,2,2,2,2,0,1,2,2,2,0,1,1", "output": "8"}, {"input": "0,1,2,2,0,0,0,0,2,2,1,0,0,2,2,2,1,2,0,2,2,1,1,0,2,2,0,0,1,0,0,0,1,2,2,1,2;2,0,2,1,2,0,2,1,0,2,2,1,2,1,0,1,0,1,0,2,1,1,0,2,1,0,2,0,0,0,2,2,2,1,0,1,2;1,2,2,0,2,0,0,0,0,2,1,0,0,1,0,2,2,2,0,2,2,2,1,1,1,1,2,0,1,1,0,2,2,1,1,1,2;2,0,0,0,2,0,2,2,0,2,1,2,2,1,1,1,1,2,2,2,0,0,0,1,1,1,2,0,1,1,1,0,1,1,0,0,2;1,1,1,1,1,0,0,1,2,2,0,0,2,1,0,0,0,1,2,0,0,2,0,2,1,0,2,1,0,2,2,2,0,1,0,0,2;0,0,1,1,2,1,0,2,1,0,2,2,0,1,0,0,0,0,2,1,2,1,0,0,1,0,1,0,2,1,2,2,2,2,1,1,2;2,1,2,1,0,1,0,0,1,1,0,1,0,2,2,1,1,1,1,1,1,1,2,2,2,1,2,2,1,1,1,1,2,0,0,0,0;0,1,2,2,1,0,1,1,1,1,1,1,1,2,0,0,2,0,1,0,2,1,0,1,1,1,0,0,2,0,1,1,1,0,0,2,2;2,0,1,1,1,1,0,1,0,0,1,1,1,0,2,1,1,0,1,0,2,0,1,2,1,1,1,0,2,1,0,2,0,0,1,0,1;2,0,1,0,0,0,2,0,0,2,2,1,0,2,1,1,0,0,2,0,2,0,0,0,1,1,0,2,2,0,2,2,2,2,1,0,0;0,2,2,2,2,0,1,2,0,0,1,2,1,2,0,2,1,1,0,1,1,1,0,2,2,1,2,0,0,2,2,2,2,0,0,0,2;1,0,2,0,1,0,2,2,1,0,1,0,0,0,0,2,2,2,0,0,0,0,2,0,2,0,2,1,1,0,1,2,0,0,2,2,0;2,0,1,2,1,1,0,1,2,2,0,2,2,2,1,1,2,1,0,0,1,2,2,2,2,2,2,1,2,2,2,2,0,2,1,2,1;1,2,0,1,2,2,0,0,0,1,0,0,0,2,1,0,0,2,0,1,1,0,2,2,2,0,0,2,2,0,1,0,1,1,1,0,1;0,2,1,0,2,1,2,2,2,1,2,0,1,1,0,0,1,0,0,1,1,2,2,1,0,2,1,1,0,1,0,2,0,1,1,1,2;0,2,0,0,1,0,0,0,2,2,0,0,2,1,1,0,1,1,2,0,0,0,0,0,0,2,0,0,1,1,0,2,1,1,1,0,1;2,2,2,0,2,2,1,1,2,0,1,2,0,2,2,0,1,0,2,0,2,1,0,0,2,1,1,1,0,2,1,1,1,0,2,2,0;1,2,2,2,1,0,2,2,0,0,0,0,0,0,0,0,0,1,1,1,0,1,0,0,2,0,2,0,1,1,0,2,2,1,2,0,0;0,0,1,0,0,2,1,1,2,2,0,0,1,0,0,0,0,1,1,2,1,0,2,1,1,2,2,0,0,1,2,2,0,2,2,0,1;2,1,0,2,2,2,2,0,0,0,2,0,2,1,0,1,2,0,2,2,0,0,0,2,0,1,0,0,0,0,0,1,0,2,1,0,2;2,0,2,2,2,0,1,0,0,0,1,1,1,2,0,1,2,2,1,2,1,2,0,1,0,1,0,0,1,0,0,0,2,2,1,1,2;2,0,2,0,2,2,0,0,0,0,0,0,0,0,2,2,2,0,1,2,0,0,2,2,2,0,0,1,2,0,1,1,0,0,0,2,0;1,2,2,1,2,1,1,0,1,2,0,2,2,2,1,1,0,0,1,0,1,0,0,0,0,1,2,2,2,1,2,1,1,2,0,0,2;1,1,0,0,2,1,1,2,1,2,1,0,2,2,1,1,2,0,0,2,1,1,0,1,1,2,2,1,1,2,1,2,1,0,2,0,2;0,0,0,2,0,0,2,1,2,1,1,0,1,1,1,2,2,0,1,1,0,0,2,2,1,0,1,1,0,1,0,2,0,0,2,1,2;1,1,1,2,0,1,2,1,0,2,0,1,2,1,0,1,1,2,2,0,0,0,1,2,0,0,1,0,2,1,2,1,1,2,2,1,1;0,2,0,2,2,0,1,2,2,2,2,0,0,0,1,2,1,2,1,1,0,1,2,2,2,1,1,1,0,2,1,2,0,0,1,2,1;0,2,2,0,2,1,1,0,1,1,2,0,1,1,1,0,1,0,0,0,0,1,1,0,1,2,1,2,1,2,0,1,2,0,2,0,1;2,2,1,2,0,2,2,1,1,0,2,0,0,2,0,0,2,1,2,0,2,1,0,1,0,0,0,0,2,0,1,1,2,0,0,1,1;0,0,0,1,1,1,2,2,0,1,0,1,2,1,0,0,1,0,1,1,0,2,0,1,1,0,0,1,2,1,2,2,0,0,0,0,1;0,2,2,2,1,0,1,2,2,2,0,1,1,0,0,1,2,2,2,1,1,2,0,0,0,1,0,1,0,2,2,0,1,0,0,1,1;0,0,1,0,1,1,2,1,0,2,2,0,1,2,0,0,2,0,1,2,2,2,1,2,2,0,1,2,0,1,2,0,0,2,0,2,2;0,2,1,1,1,2,0,2,1,2,0,1,2,0,1,1,2,0,2,0,0,2,1,0,1,1,1,1,0,0,1,1,2,0,0,2,1;2,0,1,0,0,1,2,1,1,1,0,1,2,0,1,1,2,2,0,2,1,1,1,2,0,0,0,2,1,0,1,0,0,2,2,0,1;1,1,1,2,1,2,1,0,2,1,1,1,2,0,1,0,2,0,0,1,2,1,1,1,0,1,1,2,2,1,1,0,2,0,2,2,0;2,0,2,2,0,1,0,2,2,1,0,1,0,0,2,1,0,0,0,0,0,2,2,0,2,2,1,1,2,0,0,1,1,1,2,1,1;2,0,2,0,1,2,1,2,2,1,2,1,1,0,1,2,1,0,0,0,1,0,2,2,0,2,1,1,0,2,0,1,2,0,1,1,0;0,2,2,1,1,1,1,0,2,0,2,1,2,2,1,0,0,1,2,1,1,0,2,0,0,0,0,2,1,1,0,2,1,2,1,1,1;0,1,0,1,2,1,2,2,2,1,0,1,1,0,1,0,0,0,1,0,0,2,2,2,2,2,2,0,1,2,1,0,0,2,2,0,1", "output": "10"}, {"input": "1,1,1,1,0,1,0", "output": "1"}, {"input": "0;0;2;0;1;2;2;2;0", "output": "1"}, {"input": "0,0,2,1,0,2,1;0,2,1,2,2,2,1", "output": "3"}, {"input": "1,1;1,2;0,1;2,0;2,2", "output": "3"}, {"input": "0,2,1,2,1,1,0,1,1,1,2,0,1,1,0,0,2,2,2,2,0,2,2,1,0,2,2,1,0,2,2,0,1,1,2,0,1,1,1,2,2,0,1,2,2,0,0,2;2,2,2,0,1,1,1,1,0,1,1,1,1,1,2,0,2,0,2,2,1,1,1,0,2,0,2,1,0,2,0,1,0,2,2,2,0,0,0,0,0,1,2,2,2,1,2,1;2,1,1,0,2,1,2,1,0,1,2,2,1,2,2,1,2,0,2,2,2,2,0,0,0,0,2,1,0,1,1,2,1,0,0,2,0,1,0,1,2,2,0,2,2,1,0,1;1,0,1,2,0,0,2,1,2,1,2,0,1,0,1,2,0,2,0,2,0,0,0,1,0,2,1,1,1,1,2,1,0,1,0,2,0,0,0,2,1,1,1,2,1,0,2,0;2,1,2,0,0,2,1,1,0,1,0,2,0,1,1,2,2,2,1,1,1,0,1,0,0,2,1,1,2,1,2,0,0,2,2,2,1,1,0,0,2,0,1,2,0,1,1,0;1,0,1,2,0,0,1,1,1,1,1,1,0,1,0,2,0,1,2,0,0,2,0,0,1,2,2,1,0,0,1,1,2,2,2,1,2,1,1,1,2,0,0,2,2,0,2,2;2,2,1,0,2,1,1,1,2,1,0,0,2,1,0,1,2,0,1,1,2,2,1,2,2,1,0,2,1,2,0,2,1,0,1,1,0,0,1,0,2,2,2,2,1,1,2,1;0,2,1,1,1,1,2,2,0,1,1,2,0,2,1,2,0,2,1,1,1,2,0,2,2,1,0,2,1,2,1,2,2,0,2,1,0,1,1,0,0,2,2,2,1,2,0,0;1,1,0,2,0,2,2,2,1,1,2,2,1,1,1,0,2,1,1,2,2,1,0,2,2,2,0,0,1,2,2,0,1,0,0,1,2,2,0,0,1,0,1,2,1,0,0,1;2,0,2,0,2,2,1,0,0,1,0,2,1,1,1,2,1,0,0,0,0,2,2,1,1,2,0,2,2,2,2,1,1,1,0,0,2,1,1,2,2,0,0,0,2,0,1,0;1,0,1,2,0,2,1,1,2,0,0,1,1,2,1,1,1,1,2,0,2,1,1,1,0,1,1,2,1,0,1,2,0,1,1,2,2,2,2,0,1,1,0,2,2,1,0,2;1,2,1,0,1,0,2,0,1,1,0,2,2,1,2,0,2,1,0,2,0,2,1,2,2,0,0,0,0,1,1,1,0,1,0,1,2,1,1,0,0,2,1,1,1,2,2,0;0,0,2,0,0,2,1,0,0,1,2,1,1,0,1,0,2,0,1,2,1,0,0,2,1,1,0,0,2,2,2,2,2,2,0,2,2,1,1,1,2,1,2,1,0,1,2,2;0,0,0,2,0,0,2,0,2,1,0,2,0,1,0,1,2,2,0,2,0,2,0,2,2,1,1,0,2,1,0,2,2,1,2,2,0,0,0,2,1,1,0,0,1,2,2,2;1,1,0,2,0,2,2,2,0,1,1,0,1,0,2,2,0,1,1,1,1,1,0,2,0,0,0,2,2,2,1,1,1,2,2,2,2,0,2,1,0,1,1,1,2,1,2,2;1,2,2,2,0,1,1,1,2,1,1,1,2,1,0,0,2,2,2,0,2,2,0,0,0,1,2,1,0,2,2,0,1,1,2,2,1,0,1,0,2,1,0,0,0,0,2,1;0,2,1,0,0,1,0,2,1,0,1,2,0,1,1,0,1,0,0,1,1,1,0,2,2,1,0,2,1,2,1,1,1,0,2,1,2,2,1,0,2,1,0,0,2,1,0,2;1,1,2,0,1,2,2,0,2,0,1,2,2,1,1,0,1,2,1,1,0,0,0,0,2,1,2,1,1,1,2,2,2,0,1,1,0,0,2,0,1,1,2,2,2,0,1,0;1,1,1,1,0,1,0,0,2,2,0,2,1,0,2,1,1,0,2,1,0,2,1,1,0,2,1,2,0,1,1,1,1,2,0,1,0,2,0,1,1,2,2,2,2,0,0,0;1,2,1,0,1,2,0,0,0,1,1,1,1,0,1,1,1,1,2,2,2,2,0,2,1,0,2,2,0,0,2,1,0,0,1,2,2,1,1,0,2,1,2,2,2,0,1,1;1,1,1,0,1,0,0,0,2,2,2,1,0,1,1,2,0,1,0,1,1,0,2,1,1,1,0,0,2,2,1,1,1,1,2,2,2,1,0,2,0,2,2,2,2,2,2,0;2,0,2,0,1,1,0,0,0,0,1,1,2,1,2,1,2,2,0,2,0,0,2,2,1,1,2,1,0,0,1,1,1,0,2,0,0,2,0,1,1,2,0,1,0,0,2,1;1,0,0,1,0,2,0,2,1,2,2,1,1,0,2,2,0,2,2,2,1,0,2,0,2,2,0,1,2,0,2,1,0,0,1,0,0,0,2,1,0,1,0,1,0,2,1,1;1,1,1,0,2,2,2,0,2,1,2,2,1,2,1,0,1,0,2,0,0,2,1,0,0,2,1,0,1,2,2,2,2,1,2,0,0,1,0,2,2,0,0,2,2,1,1,1;0,1,2,1,0,2,0,1,0,0,0,0,2,2,0,1,1,0,1,0,2,0,2,0,0,0,1,2,2,2,2,2,0,1,1,1,2,0,1,1,2,0,0,1,1,2,0,2;1,2,2,1,1,2,2,0,0,0,0,0,0,0,1,0,2,2,2,0,1,1,1,1,2,0,0,2,2,1,0,0,2,0,2,2,0,1,1,2,2,1,0,0,0,2,2,2;0,0,1,1,1,1,2,0,1,0,0,0,2,2,1,2,2,0,1,0,1,0,0,2,0,2,0,2,0,0,1,1,1,1,0,0,1,1,1,2,2,1,1,0,1,1,2,0;1,0,1,2,0,0,0,0,2,2,1,2,2,2,1,2,1,2,2,2,1,0,2,1,0,1,2,1,0,0,0,1,0,2,2,0,0,0,2,0,1,0,1,1,0,1,0,0;0,2,0,0,1,0,0,2,2,1,0,0,0,2,0,0,2,0,2,1,1,2,2,1,1,1,1,2,1,0,2,2,0,2,1,0,2,2,1,2,1,2,0,0,2,2,2,0;1,0,1,1,0,0,2,2,0,0,2,0,0,2,0,0,2,1,0,0,0,0,2,0,1,0,0,1,0,2,1,1,0,1,1,0,0,0,1,2,0,2,0,2,1,2,0,0;1,1,2,2,1,0,0,2,0,2,0,2,2,1,0,1,0,0,1,0,2,2,1,2,1,1,2,1,2,2,1,2,0,0,1,1,1,1,1,0,0,0,2,2,1,0,2,1;2,2,2,0,0,1,2,1,0,1,2,0,2,1,1,0,1,0,2,0,1,0,2,0,0,0,1,1,1,2,2,1,0,0,1,2,0,0,2,1,1,0,0,1,1,2,1,0;0,2,1,2,1,2,2,2,2,2,2,2,0,0,1,1,2,1,2,2,1,2,1,0,2,1,0,1,2,0,2,2,1,0,0,1,0,1,0,0,2,1,1,2,0,2,1,0;1,2,1,1,0,0,1,2,2,0,1,2,0,0,2,0,0,2,1,0,0,1,2,0,1,2,0,2,0,1,2,1,0,2,0,0,2,1,1,1,0,0,2,0,0,0,1,0;0,0,0,0,2,2,1,2,2,2,1,0,2,1,1,2,0,1,1,1,2,1,1,1,0,0,1,0,0,0,1,2,0,2,0,1,2,0,0,2,1,0,2,1,1,1,1,2;2,2,1,2,0,0,2,0,1,0,2,0,2,0,2,0,1,0,2,0,2,2,0,2,0,2,2,2,0,2,2,0,0,0,2,1,1,2,0,1,2,0,2,1,1,2,0,1;2,0,1,1,2,0,2,1,1,0,1,0,1,0,2,1,0,1,2,1,0,2,0,1,1,1,0,1,1,0,1,2,2,1,1,2,2,2,0,1,2,2,0,0,2,1,1,1;1,0,1,0,2,2,1,1,2,2,0,2,1,0,0,1,2,2,1,2,0,0,1,2,2,1,0,0,0,0,0,2,0,1,1,2,1,0,0,2,2,0,1,0,0,1,2,2", "output": "9"}, {"input": "1", "output": "1"}, {"input": "0,0,1,1,0,0,2,0,1,2,0,1,2,1,2,1,1,1,2,1,1,2,2,1,2,0,0,0,2,0,1,0,0,2,1,2,0,1;1,0,2,1,1,0,2,0,1,0,0,1,2,2,0,1,1,0,2,0,0,1,2,0,1,2,2,0,2,2,0,1,0,1,2,2,1,0;0,2,1,1,1,2,2,2,0,1,0,2,2,1,1,0,2,2,1,1,2,2,0,2,2,0,1,2,0,2,1,0,2,2,2,0,2,2;0,0,2,0,2,2,0,0,0,0,2,2,2,2,2,2,0,0,0,1,1,2,2,1,1,2,2,0,1,2,1,0,2,2,1,1,2,0;0,1,0,2,0,2,1,0,2,1,2,1,2,0,1,1,2,2,1,1,1,2,2,2,2,0,0,1,0,0,1,2,1,0,0,0,0,1;2,0,2,2,1,2,0,2,1,0,0,0,2,1,1,2,1,1,0,1,0,0,1,2,0,2,0,2,2,0,2,0,2,1,2,0,2,1;0,2,1,2,2,0,1,2,2,1,1,0,2,0,1,1,0,0,0,1,1,2,1,2,1,2,1,0,0,1,0,2,0,1,0,0,0,0;1,2,0,0,2,0,1,2,1,0,1,0,2,2,0,1,0,2,0,0,2,0,0,0,0,2,2,0,1,2,2,2,2,0,2,2,2,1;0,2,1,0,1,0,1,1,1,0,2,2,2,2,2,1,1,0,2,0,2,0,0,1,1,2,2,1,0,0,1,1,1,0,2,1,2,2;0,1,2,0,2,2,0,0,0,0,1,2,1,1,0,2,2,1,1,1,2,1,2,1,0,0,0,1,2,2,1,1,0,2,1,0,2,2;1,1,2,0,0,2,1,1,1,0,1,1,1,2,2,0,1,2,2,2,1,0,1,0,1,0,0,1,0,1,0,2,0,1,0,2,2,2;0,1,2,1,1,2,0,0,2,0,1,1,0,2,2,1,2,1,0,0,0,2,1,1,1,2,2,1,0,1,0,2,1,2,2,1,0,2;2,0,0,2,2,0,0,2,1,2,0,0,2,2,0,0,0,1,1,0,0,2,2,0,2,1,2,1,2,2,1,1,2,1,2,2,2,1;0,0,1,0,2,1,1,2,2,2,2,2,1,1,1,2,0,0,0,0,1,0,2,0,0,2,0,0,1,1,1,0,0,2,0,0,0,2;2,1,0,1,1,2,2,2,1,0,1,1,2,1,1,2,1,0,2,0,2,2,0,0,2,0,1,1,0,1,0,1,0,0,2,1,0,1;1,1,0,0,0,1,1,0,0,2,1,2,2,1,0,2,2,2,0,0,0,2,0,1,1,0,1,2,2,0,1,0,2,0,0,0,1,2;1,2,0,1,2,1,0,1,2,0,1,2,0,2,0,2,1,2,1,1,1,1,1,2,0,0,1,2,2,1,0,1,1,1,1,2,1,0;1,0,0,0,2,0,0,1,1,0,2,2,1,1,2,1,2,0,1,0,0,0,2,1,2,0,1,1,2,2,2,1,2,0,0,0,0,0;0,1,2,0,0,2,2,1,1,0,2,2,2,0,0,0,2,0,2,0,1,2,0,1,2,2,1,2,1,0,0,1,2,2,1,2,0,0;1,1,1,1,0,0,2,2,1,2,0,0,1,2,1,2,0,1,1,2,2,2,0,0,2,2,2,1,1,1,1,0,0,1,2,1,1,0;1,1,2,1,1,0,0,2,2,1,2,2,0,0,2,1,1,0,0,1,1,0,2,2,1,0,1,0,2,0,2,1,1,1,2,0,1,2;1,2,1,2,2,0,2,1,1,2,2,1,2,2,2,0,2,0,2,2,1,0,1,1,0,1,0,1,2,0,2,0,0,2,0,2,0,1;1,0,1,1,0,2,1,1,1,2,1,1,1,1,2,1,2,0,0,0,1,1,0,0,1,1,1,2,2,0,2,1,0,2,2,1,2,0;2,2,2,1,1,1,2,2,0,0,1,2,1,2,0,0,1,2,0,0,1,1,0,2,2,2,1,1,1,0,1,0,0,1,2,1,1,0;0,2,1,0,1,0,1,0,2,2,0,2,0,0,2,1,0,1,1,2,0,0,1,0,0,1,0,0,0,2,2,2,2,2,0,1,2,2;0,2,2,1,2,0,1,0,0,2,0,0,2,2,2,1,0,0,2,1,1,2,2,0,0,0,2,2,1,0,0,2,0,0,1,1,0,1;1,2,2,1,0,2,1,2,1,1,1,0,0,0,0,2,0,0,1,2,2,0,0,0,0,2,1,1,2,2,1,2,1,2,0,2,1,0;1,0,2,2,0,2,0,0,0,2,1,2,2,0,2,2,1,2,0,0,2,2,0,0,2,2,2,1,1,1,0,0,2,2,1,1,0,0;0,2,1,0,1,2,2,1,0,1,0,1,1,1,0,0,2,1,2,2,1,0,1,1,0,2,0,1,0,0,2,2,0,0,1,2,1,1;1,2,2,2,2,0,0,0,0,0,1,0,0,2,2,1,2,0,1,0,1,0,1,0,0,2,2,2,0,2,0,0,2,0,0,1,0,0;0,0,2,1,1,0,2,0,0,1,0,2,1,0,2,0,2,2,2,1,1,0,2,2,0,2,0,2,1,1,1,2,2,1,1,2,0,2;0,1,2,1,1,1,0,1,0,2,2,0,2,1,1,0,1,2,0,0,0,1,1,2,0,0,2,0,2,2,0,2,2,1,0,1,2,2;0,2,2,2,1,2,0,2,1,0,0,2,2,0,2,0,0,2,0,1,2,1,2,1,2,1,0,2,0,0,2,0,1,2,0,2,2,2;1,1,0,0,2,1,2,1,2,1,2,0,0,1,2,1,1,0,1,2,2,2,1,1,2,0,1,0,2,0,2,2,1,2,1,0,0,2;0,1,0,1,2,0,1,2,1,2,2,0,2,0,2,0,2,1,1,2,2,0,2,2,1,2,0,2,2,2,1,0,1,2,1,1,1,0;2,2,1,2,2,0,0,2,1,1,2,1,2,1,2,0,0,1,0,2,2,0,1,0,0,2,1,2,1,1,2,2,1,2,1,2,1,0;2,0,2,1,0,1,2,1,2,2,0,1,1,1,2,0,1,2,0,2,2,2,2,0,2,1,2,0,2,0,0,2,2,0,0,1,2,2;0,2,0,0,1,1,1,1,2,1,0,2,0,2,1,0,1,2,1,1,0,2,0,2,0,0,1,2,2,0,0,0,1,0,1,1,1,1;1,1,2,1,2,2,1,0,2,0,1,0,2,1,1,1,2,0,2,0,0,2,1,0,1,2,0,2,0,0,2,2,1,0,0,0,0,0;0,2,2,0,0,2,2,0,0,2,2,1,1,2,0,0,0,2,1,1,2,0,0,1,1,2,0,1,1,1,0,2,0,2,0,0,1,2;2,0,0,0,1,2,2,2,1,0,1,1,2,2,1,0,1,0,2,2,1,0,2,1,1,1,1,1,0,1,2,0,0,1,1,2,0,0;1,1,0,2,2,0,1,0,1,0,1,1,0,1,2,2,1,1,0,0,2,1,2,1,0,0,0,2,0,0,1,2,0,2,2,2,1,0;0,1,2,1,0,0,2,0,2,1,2,1,0,0,2,1,0,0,1,1,0,2,0,0,2,1,0,2,1,2,2,0,1,2,0,2,2,0", "output": "8"}, {"input": "1,0,2,1,0,0,0;1,0,0,1,2,2,0;2,2,1,0,2,0,0;2,1,1,1,1,1,1;1,2,1,2,2,2,2;2,0,0,0,1,1,1;2,0,0,1,0,2,2;0,2,2,1,2,0,2;0,0,2,1,2,2,0", "output": "4"}, {"input": "1,1;0,1;2,1", "output": "2"}, {"input": "1,0,2;2,2,1;1,0,0;2,0,1;1,1,2;0,0,2;2,1,2;1,0,2;0,0,0;2,2,0", "output": "4"}, {"input": "1,2,1", "output": "1"}, {"input": "1,0,0,2,2,1,0;1,0,1,2,0,0,2;0,0,2,1,0,0,2;2,2,1,2,2,1,0;1,2,1,0,1,2,1;1,2,2,2,2,2,2;0,0,0,1,1,0,0", "output": "7"}, {"input": "2,2,2,2,1,1,2,2,1,1,1,1,1,2,1,2,0,0,2,2,1,2,0,0,2,2,2,2,0,2,2,1,0,1,1,1,2,0,0;1,0,2,0,2,2,0,0,1,1,2,0,0,0,2,2,2,1,1,2,0,2,2,2,1,2,2,2,1,1,1,2,2,1,2,1,0,0,1;2,1,2,0,1,1,0,2,0,0,0,0,1,2,2,1,0,1,1,1,1,1,0,0,2,1,0,0,0,0,0,0,0,2,1,2,1,0,1;2,2,1,0,0,0,1,0,1,1,0,2,2,1,2,1,1,2,2,1,0,2,0,1,1,2,1,2,2,2,1,1,2,0,0,2,1,1,1;2,0,1,0,2,1,0,1,0,2,0,0,2,0,1,2,0,0,2,0,1,1,1,1,1,2,0,0,2,0,1,1,1,0,1,0,2,0,2;0,1,1,1,2,2,0,2,2,2,0,0,2,0,0,1,2,0,2,0,2,1,2,2,1,2,0,0,2,1,0,2,0,1,2,0,2,1,1;1,1,0,1,2,2,2,1,2,0,0,0,0,1,1,1,1,2,2,0,2,0,1,1,0,2,1,0,0,1,1,1,2,1,2,0,2,2,0;2,2,2,0,1,0,2,0,1,1,2,1,2,2,1,1,0,0,2,1,0,1,2,0,1,0,2,2,2,2,2,1,2,0,1,2,1,0,0;0,1,2,0,2,0,2,1,0,2,0,1,0,1,1,1,1,1,2,2,2,2,0,2,0,0,2,0,1,2,1,1,2,2,2,0,1,0,2;1,0,2,2,2,2,0,2,2,2,2,1,0,1,0,2,0,1,0,1,2,1,2,2,2,0,1,2,2,0,0,2,0,0,2,2,2,2,2;2,2,2,2,2,1,0,1,0,0,2,0,1,1,0,1,1,1,2,1,2,0,0,2,1,2,0,1,1,0,1,1,1,0,1,2,2,2,1;1,2,1,2,1,2,1,2,2,1,0,2,1,1,1,1,2,0,1,0,1,0,1,1,0,2,2,1,2,0,1,2,2,0,1,1,2,2,2;2,2,0,1,0,0,0,1,0,0,1,0,0,2,0,0,2,2,2,1,0,2,2,2,0,1,0,2,2,2,1,2,2,1,1,0,1,1,1;2,2,2,0,1,1,0,0,1,1,1,1,0,0,1,1,2,0,1,0,0,0,0,1,1,0,2,0,1,1,0,0,2,0,1,0,2,2,2;0,0,1,0,1,1,0,1,2,1,2,2,1,0,2,1,1,1,0,0,2,2,0,1,0,0,0,1,1,2,2,2,1,1,2,1,2,0,2;1,1,1,0,2,0,2,0,2,2,0,1,2,0,0,1,2,2,1,2,2,0,1,1,1,0,0,0,1,2,0,0,2,0,0,1,2,1,2;2,2,2,1,0,2,1,2,2,1,1,1,0,0,0,1,0,0,2,0,1,0,2,2,1,2,1,1,1,0,2,2,1,1,2,1,0,0,1;2,1,1,2,1,1,0,0,2,0,1,0,0,0,1,2,1,2,1,1,1,0,0,2,1,0,2,0,1,1,0,0,0,2,1,2,2,0,1;1,0,1,0,0,1,1,2,1,0,1,1,0,0,1,1,0,2,2,0,2,2,1,0,1,2,0,1,2,1,2,2,2,0,2,1,0,2,1;0,2,1,1,1,2,2,0,0,2,1,2,2,2,0,0,0,2,1,0,1,2,1,1,0,2,0,0,0,1,2,2,2,0,0,0,1,1,1;0,1,1,1,1,0,1,1,1,0,0,2,1,1,0,0,1,0,0,0,0,1,0,2,0,2,2,2,2,2,1,1,2,1,2,2,1,1,2;0,2,2,0,0,0,1,2,2,0,0,2,1,2,1,2,0,1,2,2,1,0,1,2,2,1,0,1,0,1,0,0,1,0,2,0,0,2,2;0,0,2,2,2,0,2,1,2,2,0,1,2,1,0,2,2,0,0,0,2,2,0,2,1,1,1,0,0,1,2,2,1,2,2,1,0,2,1;2,0,2,1,2,0,2,2,2,1,2,0,1,1,1,0,0,0,2,2,2,0,1,0,2,2,0,2,2,1,0,1,0,0,1,0,0,1,2;1,2,0,0,2,2,2,1,1,1,2,1,0,2,1,0,1,0,1,2,1,0,2,1,0,1,2,2,0,0,0,0,1,2,1,0,1,2,0;1,1,0,0,0,2,0,2,2,2,0,2,2,0,2,0,0,0,2,0,1,1,2,1,1,1,2,1,2,1,1,0,1,1,0,2,1,2,0;1,2,2,1,2,0,1,2,1,2,2,1,2,1,2,2,1,2,1,1,1,1,1,0,1,2,0,2,2,2,1,2,1,2,1,0,1,2,0;0,0,2,2,0,2,2,0,1,1,1,0,0,0,0,2,0,2,1,0,1,1,2,1,0,1,1,0,1,2,2,2,2,0,1,1,1,1,1;0,0,1,2,2,0,0,0,0,0,0,1,2,0,1,2,2,1,1,0,0,1,2,0,1,1,1,2,2,2,0,0,1,0,1,0,0,2,2;1,0,1,0,1,1,1,1,1,2,0,0,1,1,0,2,2,1,1,2,1,1,0,2,1,1,0,0,0,2,1,0,2,1,2,0,0,0,1;1,2,1,2,2,1,2,1,1,1,1,1,2,1,1,1,2,2,2,1,1,1,2,1,0,2,2,2,2,2,1,0,1,0,2,1,2,0,0;0,1,0,0,2,0,1,0,0,1,0,1,0,0,1,2,1,2,1,2,1,2,0,0,2,0,1,0,2,0,1,0,0,2,1,2,1,2,2;0,0,1,0,2,2,1,1,0,0,2,2,1,1,0,0,0,0,0,0,2,2,2,2,1,2,2,1,2,2,1,2,2,0,2,1,2,0,0;1,1,2,0,1,0,2,1,2,2,1,0,1,2,2,2,1,1,0,1,2,0,2,0,1,0,0,1,2,0,0,1,1,0,0,0,2,2,1;2,2,1,1,0,0,0,1,0,1,1,1,0,0,1,0,1,2,1,0,2,2,0,1,0,1,1,0,1,1,1,1,1,1,1,2,1,2,0", "output": "9"}, {"input": "1,0,0,1,1,1,2,0,0;1,1,2,0,2,2,1,0,1;0,2,2,0,0,2,0,2,1;2,2,0,2,0,0,2,0,0;2,1,1,2,1,1,2,1,2;1,2,2,1,0,1,0,0,0;1,2,0,2,1,1,1,2,2;0,1,0,1,1,2,2,2,1;0,1,0,0,1,0,2,0,0", "output": "7"}, {"input": "1,2,0,0,1,0,1,1,0;0,2,2,1,1,0,2,0,2", "output": "3"}, {"input": "1,1,2,1,1,2;0,0,2,1,2,2;0,1,1,0,2,1;1,1,2,2,0,1;0,0,1,0,0,2;2,1,2,2,2,1;2,0,1,1,1,1", "output": "6"}, {"input": "1,0,0,0,0,0;1,2,0,0,0,1;1,2,0,0,0,0;2,1,0,1,1,1;0,1,1,2,1,1;0,0,0,1,1,2;0,0,1,1,2,1;0,2,2,1,0,1", "output": "5"}, {"input": "2,2", "output": "0"}, {"input": "2,2,2,0,0,2,0,1;2,2,2,0,1,2,1,1;2,1,1,2,2,0,1,2;2,2,1,0,1,0,0,0", "output": "3"}, {"input": "2,2,2,0,0,2,1,0,2,0;1,2,0,2,1,2,1,1,1,2;2,2,2,1,0,0,2,1,0,0;0,2,0,1,0,1,1,0,2,2;1,1,2,1,2,2,1,2,2,2", "output": "4"}, {"input": "2,0,1,2,0,0,0,2,2,1,0,1,1,1,0,1,0,0,1,0,1,2,0,1,2,1,0,2,2,2,0,1,1,0;0,2,0,2,0,2,0,2,1,2,1,0,2,2,0,1,2,0,1,0,0,1,2,2,2,2,1,2,1,0,0,1,2,2;0,2,0,1,0,1,1,1,0,1,2,0,2,2,2,1,1,0,1,2,2,0,0,1,0,0,2,2,1,2,0,2,1,2;1,0,0,2,2,1,0,1,0,2,0,2,0,2,2,0,0,0,1,2,0,1,0,2,1,0,2,1,0,2,0,1,1,0;1,0,2,1,2,1,1,0,1,2,1,1,1,1,0,0,2,2,0,1,0,0,1,0,1,0,0,0,1,0,0,1,2,1;0,0,0,2,1,1,0,2,2,2,1,2,0,2,1,2,0,2,0,2,1,1,0,0,1,2,1,2,1,2,0,2,1,0;0,0,2,1,0,0,1,0,1,1,2,0,2,0,2,2,2,2,2,0,0,1,1,1,0,2,1,2,2,1,2,2,2,1;0,0,2,0,2,2,0,1,0,1,2,0,1,2,2,2,0,2,0,2,1,1,0,2,2,0,2,1,0,2,1,2,2,0;1,1,1,1,0,1,0,0,2,1,1,1,0,2,2,0,1,2,2,0,1,1,0,1,0,2,0,2,2,0,2,0,1,0;0,0,2,1,0,2,2,2,2,1,2,2,0,2,0,0,2,2,0,2,0,2,2,0,1,1,0,1,2,2,1,0,0,0;2,0,0,0,2,2,1,2,0,1,1,1,2,0,2,2,0,0,0,1,0,1,0,2,1,1,1,1,2,2,2,0,0,1;1,0,0,2,0,2,2,0,2,0,2,1,0,0,2,2,2,0,2,0,1,0,2,2,2,2,0,1,0,1,1,0,1,2;2,0,1,2,2,1,0,0,1,2,2,0,2,2,0,2,1,1,0,0,1,2,1,0,2,1,2,0,1,1,1,0,1,0;0,0,2,2,0,2,0,0,2,2,1,0,2,0,1,2,1,1,1,1,0,1,0,2,2,2,2,2,0,1,1,2,1,1;1,0,2,1,0,1,1,0,0,1,0,0,0,0,0,1,1,2,0,0,2,0,1,2,2,0,2,2,0,0,1,2,0,1;2,2,2,1,0,1,2,2,0,2,0,2,1,2,0,2,2,2,2,0,1,1,0,1,0,0,0,1,1,0,0,0,0,1;2,1,0,0,2,0,0,2,0,0,1,1,2,0,2,2,2,0,2,1,1,2,1,0,0,2,2,2,2,2,2,0,2,0;0,1,1,1,0,1,2,2,0,1,2,1,1,2,2,2,0,2,0,2,2,0,1,1,0,0,1,1,1,0,1,2,1,2;2,2,1,1,2,0,2,2,1,2,1,0,0,2,0,0,0,0,2,0,0,1,0,2,2,0,1,0,1,2,2,1,2,0;0,0,2,1,1,1,0,2,0,1,2,2,1,0,0,2,1,2,2,2,0,1,1,2,2,0,0,0,2,2,0,0,2,1;0,2,1,2,0,2,2,0,2,1,0,2,1,2,0,2,2,2,2,2,2,2,2,1,2,2,2,0,2,0,2,1,0,2;2,0,2,2,0,1,2,1,2,2,1,1,2,0,2,0,0,0,2,0,1,2,1,2,0,1,2,0,0,2,0,2,2,2;2,1,1,1,1,2,2,1,1,0,0,2,1,0,1,2,1,0,2,1,1,0,2,1,2,1,0,0,1,0,1,2,0,0;1,0,1,1,0,1,0,1,0,1,1,0,2,1,0,0,1,1,1,2,2,1,0,0,2,0,1,0,1,2,0,0,1,1;0,0,0,0,2,1,2,2,1,1,2,0,1,1,1,0,2,1,1,2,0,2,0,1,0,0,0,2,0,1,1,0,0,2;1,2,2,1,0,1,1,2,2,0,1,1,0,0,0,2,2,1,2,0,2,1,2,1,2,1,2,1,0,0,2,0,0,2;2,1,2,1,1,0,2,1,1,0,2,1,2,2,1,1,0,2,2,0,0,1,0,2,1,1,1,1,1,2,1,2,0,2;2,2,0,2,0,2,2,0,1,0,2,2,2,0,1,1,1,1,2,1,2,2,0,2,2,1,2,2,2,0,2,0,0,2;0,2,2,0,0,0,1,0,0,2,1,0,0,1,0,0,2,0,1,2,2,2,0,0,1,1,2,0,1,1,2,1,1,2;2,0,2,2,1,2,2,2,2,0,0,1,0,1,1,2,1,1,0,0,2,1,2,1,1,1,1,2,0,0,1,1,0,1;2,1,2,0,1,0,2,1,2,2,1,1,0,2,0,0,2,1,0,1,1,2,1,2,1,2,2,2,2,0,0,1,2,2;0,2,2,0,2,0,1,2,1,2,2,0,1,1,2,1,1,2,1,2,0,1,2,2,1,0,0,0,2,2,1,2,0,1;0,0,0,0,2,1,2,0,0,2,1,0,0,1,1,2,0,1,0,2,0,1,1,0,2,1,0,0,2,1,1,1,1,0;2,2,0,2,1,1,1,1,1,0,1,2,1,2,1,0,0,2,1,1,1,0,2,0,1,2,0,2,2,1,0,2,0,1;1,2,2,1,2,1,1,1,0,0,1,0,2,0,0,1,2,2,2,1,0,2,1,1,1,0,2,1,2,0,0,1,1,1;2,1,0,1,2,1,2,2,0,2,2,1,2,1,1,1,1,2,0,0,1,0,0,2,2,1,1,1,1,2,0,1,0,0;2,1,1,0,0,0,0,1,2,0,1,2,0,2,1,2,0,0,2,1,0,0,1,1,1,1,2,1,1,2,2,0,2,1;2,2,1,0,1,0,0,2,2,2,0,1,1,0,0,2,0,1,0,1,0,1,2,1,0,0,1,1,1,0,2,0,1,2", "output": "8"}, {"input": "2,2,2,0,2,2;1,0,2,1,1,2;2,2,1,0,1,0;0,2,0,1,1,2;2,1,2,1,2,1;2,1,1,0,2,1;1,1,2,2,1,0", "output": "4"}, {"input": "2,2,1,0,2,0,1,2,1,0,0,1,2,2,2,0,0,0,0,1,1,1,2,0,0,0,1,0,0,1,2,0,2;2,2,2,0,2,2,2,1,1,1,0,1,1,0,1,0,1,2,0,0,1,1,0,1,2,2,1,0,2,0,2,1,0;1,2,0,2,1,2,0,2,0,0,0,2,2,2,1,2,2,0,2,1,2,2,2,0,0,2,1,0,2,2,0,2,0;2,1,1,1,2,0,0,1,0,1,2,2,0,2,2,0,0,1,2,2,2,1,1,0,0,0,0,2,0,1,2,2,1;1,1,1,0,0,2,1,1,2,0,2,2,1,2,2,2,0,2,1,2,1,2,1,0,1,1,0,1,1,1,1,1,1;1,0,0,2,1,2,0,1,2,1,2,1,0,0,0,1,1,1,0,0,0,0,1,2,0,0,2,2,1,2,0,2,2;2,2,1,2,0,1,2,0,0,0,1,2,2,0,2,0,2,0,1,1,0,2,1,1,0,1,2,2,1,2,2,0,0;2,2,1,0,1,2,1,1,0,0,1,2,2,1,0,1,2,0,1,0,0,1,1,1,0,2,2,2,2,0,0,1,1;1,1,0,0,2,0,1,1,0,1,2,0,0,1,1,0,1,2,2,1,2,1,1,2,0,0,1,2,1,2,2,1,1;1,2,0,2,0,0,0,2,2,2,1,0,0,0,2,1,0,0,0,2,2,2,0,2,0,2,0,0,0,0,1,0,2;1,1,1,2,2,2,1,1,0,0,1,0,2,0,1,2,2,2,1,0,1,2,1,1,0,2,0,2,1,2,1,0,0;2,2,2,2,1,0,0,0,2,0,2,1,2,2,2,1,2,2,2,1,1,2,0,2,1,0,0,1,1,2,0,0,1;0,2,2,0,2,2,0,2,2,1,0,1,0,0,1,0,2,0,2,2,0,0,0,1,1,2,1,1,2,2,2,0,2;0,1,0,0,1,0,2,2,1,2,0,2,0,1,1,2,0,0,1,1,0,0,0,2,2,1,2,2,2,1,2,1,0;0,0,1,0,0,1,2,0,2,1,1,0,2,2,0,1,1,0,1,0,0,0,2,0,1,1,1,0,2,0,2,2,2;0,1,1,2,1,0,1,0,0,0,2,1,0,1,0,2,1,0,2,0,2,0,0,0,2,2,1,2,1,0,2,0,1;2,2,2,2,1,0,0,0,1,0,2,2,2,0,2,2,2,2,1,1,0,2,1,1,1,2,0,0,2,2,2,1,0;1,1,2,0,2,2,2,0,2,0,1,2,1,1,2,1,1,0,2,1,1,0,1,2,2,1,1,2,1,2,1,1,2;0,0,1,1,0,1,0,0,0,2,0,0,1,2,0,0,2,2,1,1,2,1,0,2,1,1,0,1,0,1,1,1,1;1,0,0,1,1,0,0,0,1,1,0,2,1,1,0,0,1,2,0,2,0,0,0,2,0,2,0,0,2,1,2,2,2;1,0,0,2,1,0,0,2,0,0,1,0,1,1,1,1,2,0,0,2,1,0,2,0,1,2,1,1,1,0,0,2,2;2,0,1,2,2,1,1,1,0,0,1,2,1,2,1,2,1,2,2,2,2,0,2,0,0,2,1,2,2,1,2,1,0;0,1,1,2,0,0,2,0,2,0,1,0,2,1,1,0,1,2,0,2,2,1,2,2,0,1,1,0,2,2,1,2,2;1,0,1,0,0,2,2,1,1,0,1,0,1,0,2,0,1,0,1,1,1,0,2,1,2,2,2,1,1,2,1,0,0;0,2,1,0,1,2,2,1,1,2,0,0,1,1,1,1,1,2,0,0,2,1,1,1,1,2,0,0,1,2,1,2,0;1,1,0,0,1,0,0,2,0,2,0,0,2,1,1,1,1,2,0,1,2,0,2,0,1,1,2,1,1,1,2,2,0;2,0,0,2,0,1,1,2,0,1,2,1,0,2,1,2,2,0,2,1,1,0,1,1,2,1,1,1,0,2,0,2,2;0,2,2,0,0,0,0,1,2,0,2,0,0,0,2,0,0,1,2,1,1,2,0,1,2,0,0,2,0,0,2,0,0;2,2,2,0,1,2,0,2,2,1,0,1,0,2,1,0,2,1,1,0,1,2,0,2,1,2,2,0,2,0,1,1,1;0,1,0,2,1,2,2,2,1,0,1,0,2,1,1,2,0,2,1,2,1,1,1,2,2,0,2,2,0,1,2,2,0;2,0,2,1,0,0,1,1,2,2,2,0,2,0,1,1,0,2,0,2,0,0,2,1,2,1,2,1,2,1,1,2,1;1,2,1,2,2,1,1,2,1,0,0,1,2,0,0,1,2,1,2,1,2,1,2,1,0,1,1,0,1,1,0,0,0;2,1,0,2,1,2,2,2,2,1,0,0,1,2,0,0,1,2,1,0,2,2,1,1,1,1,0,1,0,2,0,1,0;0,2,2,0,2,2,2,0,2,0,1,0,1,1,1,2,1,0,2,0,2,1,1,2,0,0,0,0,2,0,0,0,0;1,0,1,0,1,2,0,0,2,0,1,0,0,2,1,1,1,1,0,2,2,1,0,1,2,1,2,2,1,0,0,0,0;0,1,0,0,1,2,1,0,0,2,2,0,1,0,0,1,0,2,2,0,1,1,2,0,1,0,1,0,1,2,2,1,0;1,1,2,1,1,0,1,1,0,2,1,2,0,1,1,0,2,1,0,1,0,1,2,1,2,1,2,1,0,0,0,2,2;2,0,2,0,1,0,0,1,1,1,0,0,0,1,2,0,0,1,2,1,0,0,1,2,1,1,1,2,0,2,0,2,2;2,2,1,0,1,1,2,0,1,0,2,1,0,0,1,0,1,1,2,2,0,1,2,2,2,0,2,2,2,0,1,0,1;2,0,0,0,0,1,1,2,2,1,2,1,0,1,1,1,2,2,2,2,2,0,1,2,2,2,1,1,2,2,0,2,1;2,0,0,0,2,0,1,1,0,0,0,1,2,1,0,0,1,2,1,2,0,2,2,0,1,2,2,0,0,1,2,1,1;1,1,2,1,0,2,1,2,2,0,2,1,2,1,1,0,2,1,1,1,2,0,1,1,1,0,0,0,0,0,0,0,2;1,2,0,1,0,0,0,1,1,2,1,1,0,0,0,0,0,2,2,0,0,1,1,1,1,2,0,1,0,1,0,0,2;2,1,1,1,2,0,2,2,2,0,0,2,2,1,2,0,2,2,0,1,0,2,2,1,0,2,0,1,2,0,1,0,1;0,0,1,1,0,2,2,0,2,2,0,0,2,1,0,2,2,1,2,0,0,1,0,0,0,1,1,1,2,1,1,2,0;0,0,1,0,1,2,1,2,1,2,1,1,1,1,1,1,2,1,2,2,0,0,1,2,2,2,2,2,0,2,2,1,2", "output": "10"}, {"input": "0,0,2,2,0,1,2,1;0,2,1,0,2,2,0,0;2,0,2,1,0,1,1,0;1,0,2,0,1,2,1,1;1,0,1,2,2,2,1,2;2,2,0,1,2,1,1,2;2,2,2,0,2,2,1,0", "output": "5"}, {"input": "0,1,1,2,2;0,0,2,1,0;1,0,1,2,2;0,2,0,0,2;0,1,2,2,2;2,1,2,2,2;1,2,2,2,1", "output": "4"}, {"input": "0,1,1,1,1,1,2,2,2,0,0,2,0,0,0,2,1,2,2,0,0,2,1,0,0,0,1,1,1,0,1,1,2,0,0,2,1,2,0,2,1;1,2,2,1,1,1,2,0,2,1,2,2,1,2,0,2,2,0,1,2,0,0,0,0,2,1,1,2,0,2,0,1,1,0,0,1,2,2,2,0,2;0,1,0,0,2,0,0,1,0,1,1,2,0,0,2,1,0,2,1,2,2,1,2,1,1,2,1,0,2,1,0,2,2,0,1,1,1,2,2,2,2;2,0,1,1,0,2,1,1,2,1,1,2,1,0,2,2,0,2,0,0,1,2,2,1,2,0,0,1,1,2,0,0,0,1,0,0,0,2,0,0,1;0,1,0,1,0,0,1,2,0,1,1,0,1,1,2,0,0,2,2,1,1,0,0,1,2,1,0,0,1,2,1,2,0,2,2,2,2,0,2,1,1;1,2,2,2,2,2,0,1,0,0,0,0,1,1,2,2,2,0,1,1,2,2,1,2,2,1,0,0,0,2,0,0,2,0,2,0,2,2,0,2,2;0,0,0,1,1,0,2,2,0,1,2,2,2,1,1,2,1,1,2,1,1,1,2,0,2,0,0,2,1,0,1,2,2,1,2,1,1,1,2,0,0;0,0,2,2,1,0,1,0,1,2,1,0,0,1,0,2,0,1,0,1,2,2,1,0,1,2,0,0,2,1,2,0,0,1,0,0,1,0,2,0,0;0,0,1,1,0,1,1,1,0,1,0,2,2,0,1,0,1,2,1,2,2,0,0,0,0,1,2,1,0,0,1,0,2,0,2,0,1,2,2,1,2;2,0,2,0,0,2,1,1,2,1,1,1,2,1,2,1,1,0,0,2,2,0,0,2,1,1,2,2,1,1,2,0,0,2,0,0,2,2,1,2,0;0,0,0,1,1,1,0,0,2,0,2,2,0,1,1,0,0,2,2,2,0,2,0,1,1,1,1,1,0,0,2,2,1,0,1,2,1,1,2,1,0;1,2,0,0,1,0,0,0,0,0,2,0,2,0,0,0,0,2,0,1,0,2,2,1,1,2,2,0,1,0,1,0,2,0,2,2,2,0,0,1,1;1,1,1,1,1,1,0,2,0,0,2,1,0,0,0,2,1,1,1,0,1,0,2,0,0,1,2,1,2,0,2,2,1,2,1,0,1,1,2,2,0;0,1,2,0,0,0,1,2,0,2,0,0,1,0,1,2,1,1,1,2,1,2,2,2,2,1,1,2,0,0,2,0,2,1,0,2,1,2,2,0,2;1,1,1,0,0,0,2,1,1,1,1,1,1,1,0,1,1,1,1,1,2,2,1,1,0,1,2,0,1,1,2,2,1,0,2,2,1,1,1,0,0;1,0,2,2,2,2,0,0,2,2,2,1,0,1,0,2,0,2,1,2,0,2,2,2,0,1,2,2,2,0,2,0,1,1,1,2,2,0,1,2,0;0,0,1,0,0,1,1,2,0,0,1,0,0,2,2,1,1,2,0,0,0,0,1,2,0,2,1,2,1,1,1,1,2,1,2,0,1,0,0,1,1;2,2,1,0,2,1,2,1,0,1,1,1,1,1,1,2,1,2,2,1,2,1,1,0,0,2,1,0,0,1,2,0,0,1,0,1,1,0,1,1,0;0,0,1,1,0,2,2,2,2,1,1,0,2,0,0,0,2,0,0,2,1,0,1,0,2,2,2,2,0,0,1,0,1,0,0,0,1,2,1,2,2;1,0,0,0,0,0,2,2,2,0,0,2,1,2,0,2,0,0,1,2,0,1,2,0,0,2,0,0,0,0,2,0,1,2,2,2,2,1,2,1,1;2,0,1,2,2,2,1,1,2,0,0,1,2,2,1,0,1,2,2,2,1,2,0,0,2,0,1,1,2,1,2,0,2,2,0,2,0,2,2,0,2;2,0,2,2,1,2,2,0,0,1,2,2,0,2,1,0,1,2,2,1,1,1,2,1,2,1,2,2,1,0,1,0,0,0,2,0,0,2,2,2,0;2,2,1,1,0,1,0,1,1,2,0,0,0,1,0,1,1,2,0,2,0,0,0,1,2,1,0,0,1,2,0,1,0,2,0,0,2,2,0,0,2;1,0,0,2,2,2,1,2,2,0,2,1,0,2,2,2,2,2,1,1,2,0,2,1,1,0,0,0,1,0,1,1,1,0,0,2,0,1,2,0,2;0,2,2,2,1,1,2,1,2,1,2,2,1,2,0,2,2,2,2,0,1,2,2,0,0,1,2,1,1,1,2,2,1,2,2,0,1,0,1,2,1;0,1,1,0,1,2,0,1,1,2,1,1,1,1,2,1,0,0,2,1,2,1,1,0,2,1,0,0,0,2,1,2,0,0,1,1,1,1,0,0,1;1,1,2,1,1,2,2,2,1,0,1,1,0,0,0,2,1,1,2,2,0,1,1,1,2,1,1,2,2,1,2,1,0,0,2,1,0,1,1,0,1;0,2,1,1,0,1,0,2,1,2,0,1,2,0,0,2,0,1,2,0,1,2,0,0,1,1,0,0,2,2,1,1,2,1,1,2,0,2,0,0,1;1,2,1,0,2,0,1,2,1,2,0,2,2,1,2,2,0,1,2,0,1,1,2,0,2,2,1,1,2,1,0,2,1,1,0,1,0,1,2,0,2;0,1,0,2,0,0,2,2,1,2,1,1,0,0,1,0,1,2,0,1,2,0,1,1,2,1,1,2,2,2,0,1,2,2,0,0,0,1,2,1,2;2,0,1,0,2,1,1,0,2,2,0,1,1,2,2,0,1,1,2,1,2,0,2,1,2,0,0,1,2,1,1,0,1,0,0,1,0,1,2,2,1;1,1,1,2,0,1,0,1,2,0,0,2,2,2,0,2,2,0,2,0,1,2,1,2,1,1,1,2,2,1,1,0,0,0,2,1,2,0,0,1,0;2,2,0,0,1,2,0,2,0,1,1,2,1,0,1,2,2,1,0,2,2,2,1,2,1,1,0,2,2,2,0,0,0,1,2,2,0,0,2,2,2;2,1,2,1,0,2,1,2,2,0,0,1,0,2,1,1,2,2,1,0,0,1,0,0,0,1,1,1,2,1,1,0,1,1,0,0,0,1,2,2,1;2,0,1,0,0,1,2,2,2,1,0,2,0,1,2,0,1,2,0,0,0,0,2,2,1,1,2,2,2,0,0,0,0,0,0,0,1,2,2,2,1;1,2,0,0,2,2,2,2,1,1,1,2,1,2,2,1,2,2,1,2,0,2,0,2,0,0,1,0,0,2,2,2,1,2,2,1,0,0,0,1,1", "output": "10"}, {"input": "1;0;0;2;1;2;2;2;2;1", "output": "1"}, {"input": "2,2,1;0,0,0;2,2,1;0,2,1;1,0,1;2,0,2;2,2,1;1,1,1;2,1,0;0,1,0", "output": "4"}, {"input": "1,0,1,1,2;2,0,2,2,2", "output": "3"}, {"input": "2,0,0,2,2,1,1,0,1,0,2,0,2,1,1,1,1,1,0,2,0,1,2,0,2,0,0,1,1,2,0,2,0,1,0,2,2,1,2,1;2,2,0,1,2,2,1,1,0,0,0,1,1,0,1,0,2,0,1,0,1,2,0,0,1,0,1,2,0,0,0,0,1,1,0,1,2,1,2,2;1,2,0,1,1,1,2,2,2,0,2,1,1,2,0,0,0,0,2,2,0,1,1,2,2,1,0,0,2,0,1,0,0,1,0,0,1,0,2,1;1,2,1,0,2,1,2,0,0,1,0,1,0,0,1,0,0,1,1,2,0,0,1,0,2,1,2,1,2,2,0,1,2,2,0,1,2,0,2,0;2,0,1,0,0,2,2,0,2,2,0,0,1,2,0,1,1,2,0,0,1,1,0,0,2,2,0,1,2,1,0,2,2,0,1,2,2,0,0,1;1,1,2,2,0,2,1,2,0,1,1,2,0,2,2,1,1,0,0,0,1,2,2,1,0,0,2,0,0,0,2,1,2,1,2,2,2,0,0,0;0,0,1,0,1,1,1,2,0,0,0,2,1,0,0,1,1,2,0,1,0,2,0,0,1,2,2,1,1,2,2,2,1,2,1,2,2,2,0,1;1,1,1,2,1,2,0,0,0,1,2,2,1,0,2,1,1,1,1,0,0,1,0,0,2,0,0,0,2,1,1,0,2,1,2,2,1,0,1,1;0,2,1,2,1,0,0,1,2,0,2,2,2,0,2,1,2,1,0,2,0,2,1,2,1,1,1,0,2,0,1,0,2,2,2,1,0,0,2,2;1,2,1,2,2,0,2,1,1,2,2,1,2,1,1,0,0,0,1,1,2,1,0,2,1,0,0,0,0,2,0,2,2,2,1,0,2,2,1,2;2,0,1,1,1,0,2,0,1,2,2,1,2,1,2,0,2,2,2,2,0,0,0,0,2,0,0,2,1,1,2,0,0,0,1,2,1,1,1,1;1,1,2,1,0,2,0,0,0,2,1,0,1,0,0,0,1,0,2,0,1,0,1,0,2,2,2,2,1,0,2,0,1,1,2,1,1,1,1,2;2,2,2,0,1,0,2,0,1,1,2,1,0,1,2,0,0,0,2,2,0,1,1,2,0,1,1,1,0,0,1,1,2,1,1,2,0,1,2,2;0,2,2,0,0,1,2,2,1,1,1,2,0,2,1,0,2,0,0,1,0,0,1,0,2,0,1,0,1,1,2,0,2,0,0,0,0,2,0,0;1,1,0,0,1,1,0,2,0,2,0,0,2,0,2,2,2,1,1,0,1,2,2,0,1,1,1,1,0,2,1,1,1,1,0,0,2,0,0,0;1,2,1,2,1,1,1,1,0,0,1,0,2,1,0,2,1,0,1,2,1,1,2,2,0,1,1,2,2,2,1,1,1,1,0,0,2,2,2,2;2,2,1,0,0,2,2,2,2,0,1,1,0,0,1,0,1,2,2,1,0,2,0,0,0,0,1,2,1,0,1,2,2,0,0,0,1,0,0,0;1,2,1,2,0,2,2,2,0,2,2,2,1,2,0,2,2,1,2,1,1,0,0,2,1,1,2,1,0,2,2,0,1,0,0,2,2,0,2,1;0,2,2,2,2,1,2,2,0,1,2,2,0,0,1,2,0,0,1,2,1,2,2,0,0,1,0,2,2,1,2,0,1,0,1,2,0,2,1,0;0,1,2,0,2,2,0,2,2,1,0,1,2,1,2,2,1,1,0,1,2,0,0,0,0,0,2,1,1,2,0,1,0,2,1,0,2,0,1,1;0,0,1,0,0,2,2,0,1,2,0,2,2,1,2,2,1,0,2,2,2,1,2,0,0,0,0,0,2,1,1,2,2,2,0,1,2,2,2,0;2,1,0,0,2,2,0,1,1,1,2,2,2,0,0,0,0,1,2,1,0,0,1,0,0,1,0,1,1,0,2,1,1,1,1,2,0,0,1,1;0,2,2,0,2,0,2,2,0,1,1,2,2,2,0,2,1,0,0,2,1,1,2,1,2,0,2,2,2,0,1,1,0,0,1,2,1,1,0,0;0,1,2,1,1,1,2,1,0,0,2,0,2,1,1,2,2,0,0,1,0,0,2,1,0,0,0,1,1,0,0,1,0,0,1,0,2,2,2,1;0,0,1,2,0,2,1,1,1,0,0,2,0,1,1,1,0,2,0,2,0,2,1,1,1,2,2,1,1,1,2,1,1,2,1,0,2,2,0,0;2,0,0,0,2,1,2,0,2,2,0,0,2,2,1,0,2,0,2,0,0,1,1,0,0,1,2,2,2,1,2,1,1,1,2,2,1,1,0,2;2,1,2,2,1,1,1,0,0,0,0,2,0,2,0,2,2,1,1,1,1,2,2,0,1,2,1,2,0,2,0,1,0,0,1,1,2,0,2,2;2,1,0,2,1,1,0,1,2,1,2,0,1,1,0,0,0,1,2,2,1,0,1,1,0,2,2,1,2,0,0,2,1,0,2,0,0,2,1,1;2,2,0,0,0,2,2,2,2,1,2,0,2,2,2,0,1,1,1,2,0,2,0,2,2,0,0,1,0,1,1,0,2,0,2,0,1,1,0,1;1,0,1,2,0,0,0,0,1,1,1,2,2,0,2,0,1,2,0,2,0,0,0,1,0,1,1,1,2,1,2,0,1,2,0,1,1,0,0,2;1,1,0,1,0,1,0,1,0,0,0,0,0,0,2,2,0,2,1,1,2,2,2,1,2,1,1,0,0,0,1,1,0,1,1,1,2,2,2,1;1,0,0,2,2,1,1,2,2,2,0,0,1,2,0,0,2,2,1,1,0,2,2,2,0,0,0,0,0,0,0,0,0,1,2,2,0,2,0,2;1,2,2,2,1,2,1,1,1,0,2,2,0,1,1,0,1,1,0,0,1,1,1,2,2,2,2,1,0,0,0,1,1,2,0,1,1,2,2,0;1,2,1,2,2,2,1,0,0,1,1,2,2,0,0,1,1,2,1,0,1,2,0,2,0,0,2,1,2,0,1,0,1,0,1,1,2,0,0,1;1,1,1,2,2,2,1,1,0,0,2,0,2,2,0,0,0,2,0,1,0,0,1,2,0,0,2,0,2,1,1,1,0,0,2,0,2,2,0,2;1,0,1,1,0,1,0,0,0,1,0,1,0,0,1,2,0,0,0,0,0,0,0,1,1,0,2,1,0,1,0,1,2,2,0,0,0,0,1,0;0,1,0,1,0,0,1,0,2,0,1,2,1,1,2,1,2,2,0,0,0,1,0,2,2,1,2,1,2,1,0,2,0,2,0,0,0,2,0,2;1,2,1,0,0,1,0,1,0,2,1,2,2,0,2,2,0,1,0,0,2,2,1,2,0,0,2,1,0,2,2,0,2,2,2,2,1,1,0,2;1,0,0,1,0,1,0,2,0,2,2,0,2,1,2,1,0,2,0,2,2,1,2,0,2,1,1,0,0,0,2,1,1,1,0,2,0,2,0,2;1,1,0,2,0,2,2,2,2,1,2,0,2,1,1,2,1,1,0,1,2,0,1,0,0,0,0,2,2,0,2,0,2,2,0,0,1,0,2,1", "output": "10"}, {"input": "0,2,1,2,0,1,1;2,0,0,0,2,0,0;2,1,0,0,1,2,2;2,0,2,1,1,0,1;2,2,1,0,2,2,1", "output": "4"}, {"input": "2;1;2;1;2", "output": "1"}, {"input": "2,2,0,2,2,2,2,1,0;0,2,0,2,1,2,0,2,0;0,0,1,2,2,2,2,2,2;2,0,0,2,1,2,0,1,2;0,0,0,1,0,0,1,2,2;0,0,0,2,0,2,0,0,0;2,2,0,1,1,2,1,0,1;2,0,0,1,2,0,1,2,2;2,1,1,0,1,0,1,1,0;0,2,0,2,0,1,0,2,2", "output": "6"}, {"input": "0,1,0,0,0,1,2,0;0,0,1,1,2,2,2,2;1,2,0,2,2,2,0,2;2,1,0,0,0,2,0,2;2,1,2,2,0,1,1,2", "output": "4"}, {"input": "0,2;2,0;0,1;0,0;1,0;0,1;1,1;2,2", "output": "2"}, {"input": "2,0,2;1,1,1;2,2,2;1,1,0;2,0,2;0,1,0;1,1,0;0,0,1;2,0,1", "output": "3"}, {"input": "0,0,2,2;2,1,1,0", "output": "3"}, {"input": "1,2,1,1,2,1,0,1,2,2,1,1,2,2,1,1,1,1,1,1,1,1,1,2,0,1,1,2,2,1,1,0,1,1,2,1,0;1,2,0,2,2,0,1,1,2,2,1,1,2,2,1,1,0,2,1,1,1,1,2,2,1,1,2,2,1,0,0,2,2,2,1,1,0;0,2,2,1,2,2,1,2,0,2,1,1,1,1,0,0,0,2,0,0,2,2,2,1,1,1,1,2,2,1,1,1,0,2,1,0,1;0,1,2,0,2,1,0,0,2,1,0,0,1,0,2,0,2,2,1,1,1,2,2,0,0,2,0,1,0,1,2,0,1,0,0,1,0;2,0,1,2,1,1,1,1,1,2,1,2,2,0,1,1,2,1,1,0,2,1,0,1,2,2,0,2,1,0,1,0,2,1,1,0,0;2,2,0,2,0,2,0,0,0,1,1,0,2,0,0,2,2,0,2,2,2,0,2,0,2,2,0,1,2,0,2,1,2,1,1,2,2;0,0,0,1,0,1,1,2,0,2,0,1,2,0,1,1,0,2,2,0,2,0,1,2,1,1,2,0,2,1,1,2,2,0,2,2,2;2,0,0,0,0,1,1,2,1,0,0,2,1,0,1,2,0,1,2,0,0,2,0,1,2,0,2,2,0,0,1,2,1,1,1,1,1;1,1,0,1,1,2,2,0,0,2,2,2,0,2,0,0,2,2,1,1,0,2,2,1,1,2,1,2,1,1,2,2,2,0,1,2,0;2,1,1,1,2,1,1,2,0,2,0,2,0,0,1,1,1,2,0,0,2,2,0,2,2,0,0,2,2,0,0,0,0,2,0,0,1;0,2,0,0,2,1,0,2,1,0,1,0,0,1,1,1,1,0,2,0,0,2,0,0,2,2,1,0,2,0,1,1,1,2,0,1,0;1,0,2,1,2,1,1,2,2,1,0,2,1,2,1,2,1,0,0,1,0,1,1,0,2,2,1,2,0,2,0,2,0,1,0,1,1;1,1,2,0,0,0,0,0,1,2,0,0,0,2,0,0,0,2,0,2,0,0,1,2,2,0,1,1,1,1,0,2,1,0,2,1,0;1,1,1,0,0,2,1,0,1,2,1,2,0,0,0,0,0,0,0,2,2,0,1,2,2,0,1,1,1,2,0,2,1,1,0,1,0;1,2,1,2,2,1,2,2,1,2,1,2,1,0,1,2,0,0,1,2,1,1,1,0,1,2,1,1,2,1,0,1,0,2,0,2,1;1,0,0,2,0,1,1,0,1,1,0,2,2,2,2,2,2,0,0,0,0,0,0,1,2,2,0,2,2,0,2,0,0,0,1,2,0;0,1,0,1,2,1,2,0,1,2,1,1,1,2,2,0,1,2,2,1,0,2,0,0,2,2,0,2,1,2,1,0,2,0,2,2,1;1,0,1,2,2,2,0,1,2,0,1,2,1,0,0,0,2,0,2,1,1,1,1,1,1,2,2,2,0,1,1,2,1,0,0,2,2;1,2,1,1,0,0,2,1,0,1,2,2,1,0,0,1,1,2,1,1,1,1,2,1,2,0,0,2,2,1,1,1,1,0,1,2,0;2,0,2,2,2,1,0,0,2,0,1,2,1,1,0,1,2,0,1,1,2,0,2,2,1,1,0,0,2,1,2,1,1,0,0,0,1;0,0,2,0,0,0,1,2,1,1,1,2,2,2,1,0,1,2,1,2,0,1,2,1,2,1,0,1,2,2,1,0,0,1,2,0,1;2,1,2,1,2,2,0,1,2,1,2,1,0,2,1,1,2,1,1,2,2,1,1,2,1,2,0,2,1,1,1,1,0,0,2,2,0;1,1,2,2,1,2,1,0,2,0,2,1,2,1,2,0,0,2,1,0,1,1,0,2,2,2,0,1,1,2,2,0,1,1,0,1,2;1,2,0,1,2,0,2,0,2,1,0,2,0,2,2,1,0,2,2,0,2,2,0,2,0,2,1,1,0,2,2,1,1,1,0,2,0;1,1,2,0,1,2,2,2,0,1,2,2,1,1,1,0,1,2,2,1,0,0,2,2,1,0,0,2,1,1,1,2,2,0,1,0,2;0,1,2,0,0,0,2,0,0,1,0,1,1,0,2,2,0,2,0,0,0,2,1,0,1,2,2,1,2,1,1,1,1,2,1,2,0;0,0,2,2,1,1,1,0,0,0,0,2,0,2,1,0,1,1,1,0,0,0,1,0,2,0,2,1,1,1,2,0,0,0,1,2,1;1,0,2,1,1,0,0,2,1,0,0,2,0,2,2,0,0,1,2,1,1,0,2,1,0,2,0,0,0,0,1,1,2,0,1,0,0;2,1,0,1,1,2,0,1,1,0,2,1,2,2,0,2,0,1,0,2,0,0,2,1,0,0,0,2,1,2,1,0,2,1,0,0,2;0,0,2,2,2,1,1,1,1,1,2,0,1,1,1,0,2,0,0,1,2,1,0,2,0,2,2,1,2,2,1,2,2,1,0,0,1;2,1,0,1,2,2,0,2,2,0,1,0,2,2,2,2,1,0,0,2,2,0,0,0,0,0,0,0,2,0,1,0,0,0,1,2,0;2,1,2,1,1,2,0,0,0,1,2,0,0,1,2,0,1,2,1,1,1,0,0,0,0,2,0,0,1,0,2,2,1,2,2,2,2;1,1,2,2,1,1,0,1,1,1,0,2,1,2,1,1,0,2,0,0,1,0,2,0,0,1,0,1,1,0,2,1,1,1,2,1,0;2,0,2,0,1,2,0,1,1,2,2,2,0,1,0,0,1,0,2,2,2,2,2,1,0,1,2,2,1,2,1,1,0,0,1,1,0", "output": "9"}, {"input": "2,2,0,2", "output": "0"}, {"input": "2,1,0;0,1,2;0,1,0;2,2,2;2,1,2;0,2,1;0,0,1;1,2,1;2,2,1;1,2,0", "output": "4"}, {"input": "0;2;1;1;0;1", "output": "1"}, {"input": "0,0,0,0,0;2,1,1,0,1;2,1,0,1,2;2,0,1,2,2;1,1,0,2,1;0,0,0,2,0;1,0,2,1,1;2,1,0,0,0", "output": "4"}, {"input": "0,2,2,2,0;2,1,2,0,2;1,2,0,1,1;1,0,2,0,0;0,2,0,2,0;0,2,0,1,1", "output": "3"}, {"input": "2,1,0,0;0,1,1,0;1,1,0,1;1,2,0,0;2,1,0,0;0,2,2,1", "output": "4"}, {"input": "1;2;1;2;2;2;1;1", "output": "1"}, {"input": "0,1,1;2,1,2;2,1,2", "output": "2"}, {"input": "1;0;0;1", "output": "1"}, {"input": "2,1,0,2,0,1;2,0,0,2,1,0;2,0,2,0,1,0", "output": "3"}, {"input": "1,0,0,0,2,2;1,2,2,1,1,1;0,1,1,2,0,2;2,2,0,1,1,0;2,1,0,0,2,0;1,2,0,2,1,1;1,2,2,0,2,2;0,2,0,2,2,0;0,2,0,2,2,2;2,0,1,1,0,2", "output": "5"}, {"input": "1,1,2,0,2,0,1,1,1,1,2,1,0,0,1,0,0,0,1,1,1,2,1,2,0,0,0,2,2,2,2,0,0,1,0,0,1,0;0,1,0,2,0,1,2,0,1,0,0,2,0,0,0,0,0,0,2,2,1,0,0,0,1,0,0,0,0,1,0,2,2,2,2,0,1,1;0,0,0,1,1,0,2,0,0,0,2,2,0,1,2,0,0,2,1,1,2,0,1,2,1,1,0,2,2,2,2,0,1,1,2,2,1,0;0,0,2,1,1,2,2,1,2,0,0,0,2,1,2,1,0,0,0,0,0,2,1,0,0,2,2,2,0,0,0,1,0,0,2,1,1,2;2,1,0,2,1,0,1,2,1,0,0,2,1,0,0,1,2,0,1,0,1,0,0,0,0,2,0,0,0,1,2,0,0,2,0,1,2,1;2,1,1,1,0,0,2,2,1,0,2,1,2,1,0,0,0,1,0,0,2,0,2,1,1,1,1,2,0,0,2,1,2,2,2,1,0,1;2,1,2,2,1,0,1,1,0,0,2,2,2,1,1,0,1,1,1,1,0,1,0,2,0,1,0,0,1,0,1,0,0,2,0,2,0,1;2,2,2,1,2,2,0,0,2,2,1,2,1,2,2,0,0,0,1,2,0,2,2,2,0,0,2,1,0,0,0,1,2,0,0,1,2,2;2,2,1,0,1,0,0,0,2,1,0,0,1,1,0,2,2,2,0,1,0,2,0,0,2,1,0,2,1,0,0,0,0,1,0,2,2,1;1,1,2,0,2,0,2,2,1,2,2,1,2,1,2,0,0,2,0,1,2,0,0,1,2,2,0,0,0,2,0,1,2,2,2,1,2,1;2,2,2,0,2,1,2,0,2,0,0,0,2,1,1,0,1,0,0,1,1,2,1,0,0,2,1,2,0,2,1,2,2,0,0,2,2,2;2,2,2,0,1,0,1,0,2,1,1,0,2,0,2,2,2,0,2,0,0,2,2,1,1,1,2,2,2,2,2,2,1,0,0,2,0,2;1,1,1,1,0,1,1,1,0,1,0,1,0,1,0,0,0,1,2,1,1,1,0,1,1,2,2,1,0,2,1,2,0,1,1,2,0,2;1,1,1,2,2,1,2,1,2,2,1,1,0,2,0,1,2,2,1,0,0,1,2,2,1,0,2,0,0,2,1,1,0,0,1,1,1,0;1,0,0,1,1,1,0,1,0,1,1,1,2,2,0,2,1,0,2,2,2,2,1,2,1,2,1,2,0,0,1,1,1,1,2,0,0,1;1,2,0,0,0,2,1,2,1,1,1,1,0,0,2,2,2,2,0,0,2,2,2,0,0,2,1,2,2,1,2,1,0,1,1,1,2,2;2,1,0,2,2,0,2,0,2,2,2,2,1,0,2,2,2,1,1,2,1,2,0,2,0,0,2,0,0,2,0,0,1,0,1,1,1,0;0,1,2,1,2,1,1,1,0,1,1,1,0,2,0,0,2,1,2,1,1,1,1,0,1,0,0,1,1,2,1,0,1,0,0,1,1,0;1,0,1,0,0,1,1,1,2,1,0,1,0,1,1,2,2,2,1,1,0,1,1,2,0,0,1,0,2,0,2,2,0,0,2,2,2,2;2,2,2,2,2,0,1,0,1,0,1,1,0,2,0,0,0,0,2,0,2,1,0,0,2,1,0,2,0,0,1,2,1,1,1,2,0,0;0,2,1,1,2,0,1,2,1,1,1,1,0,0,1,2,2,2,2,0,1,1,2,2,2,2,2,0,0,1,1,2,0,2,1,1,0,2;0,2,1,0,2,0,2,0,2,0,2,2,1,0,1,2,0,0,1,0,2,2,2,1,0,1,2,2,0,2,2,1,0,2,1,0,2,2;1,1,0,1,2,2,0,2,1,1,0,2,0,2,2,2,0,1,2,0,0,1,0,0,0,1,1,0,1,2,2,0,0,1,1,1,2,1;2,1,1,1,2,0,1,2,2,2,2,2,0,1,0,2,1,1,1,0,0,2,2,1,1,1,1,1,0,2,2,0,2,1,1,2,0,0;0,1,2,1,1,2,1,2,1,2,2,2,1,2,0,0,1,1,1,0,1,1,0,2,1,2,2,0,2,2,2,0,1,0,2,2,0,1;0,1,2,1,2,2,1,1,1,1,0,0,0,2,1,0,1,2,1,2,1,1,0,0,2,1,1,0,2,2,1,2,0,2,2,0,1,0;1,1,2,0,0,2,2,2,0,2,0,2,0,1,0,2,1,0,1,0,2,2,2,0,1,2,1,0,2,1,0,0,0,2,1,0,0,0;0,2,1,0,0,1,2,0,2,0,0,1,2,1,2,1,0,0,1,0,1,2,0,2,2,1,2,0,0,0,0,1,0,1,2,1,2,2;2,0,1,0,2,1,0,2,0,1,1,1,0,2,0,1,0,0,0,0,1,1,1,2,2,0,0,2,0,2,1,1,1,1,1,0,1,2;0,0,2,1,2,2,0,0,1,2,0,1,0,2,2,2,0,2,2,2,0,2,2,0,0,2,2,0,0,1,1,1,2,1,2,2,2,1;0,1,2,0,0,1,0,2,0,1,2,1,1,0,1,2,0,2,2,0,1,0,2,0,2,2,2,0,0,0,0,1,1,0,2,0,0,1;1,0,0,0,1,2,1,2,0,0,0,2,0,1,0,0,2,0,2,1,0,2,2,1,2,1,1,1,2,1,0,0,1,2,0,2,1,2;1,2,0,2,2,1,1,2,2,2,1,0,1,2,1,1,1,2,0,0,2,1,1,0,2,2,1,2,1,1,0,0,0,0,1,1,1,2;0,2,0,1,2,1,2,2,0,1,0,0,0,2,2,2,0,2,0,2,2,2,2,1,1,0,0,0,2,2,1,2,1,0,2,2,0,1;0,2,1,1,0,2,1,0,0,0,0,2,0,0,0,0,1,1,1,0,2,1,0,1,2,0,2,0,0,1,0,2,1,0,1,1,2,2;0,0,0,1,2,0,1,0,2,1,0,1,0,0,1,2,2,1,2,0,2,1,2,1,2,0,2,0,1,2,2,1,0,1,1,1,2,2;0,1,1,0,2,1,1,2,1,2,1,2,1,0,0,1,0,1,1,1,0,1,1,2,0,0,1,2,1,2,1,0,1,2,1,0,0,1;0,2,2,2,2,0,2,0,2,0,0,1,2,0,2,0,1,1,1,1,0,2,0,0,0,2,2,2,0,0,1,2,1,2,1,1,1,1;2,2,2,2,0,2,0,1,1,2,0,1,1,2,2,2,2,0,2,0,0,1,0,0,0,0,2,1,2,2,1,1,1,0,0,1,1,2;1,0,1,2,2,1,1,1,0,0,0,1,1,0,0,1,2,1,0,0,1,0,2,0,1,2,1,1,0,2,2,2,0,2,2,0,2,0;0,1,0,2,0,0,2,0,0,1,0,1,2,1,0,1,1,2,2,2,0,1,2,2,0,1,2,1,2,1,2,1,0,1,0,1,2,0;2,2,1,0,1,1,0,0,0,2,0,0,2,1,2,2,1,1,1,2,2,2,1,2,2,2,2,2,0,0,2,2,0,0,1,1,0,2", "output": "11"}, {"input": "1,1,1,1,1,2;2,1,2,0,0,2;1,2,2,0,0,0;0,0,2,1,0,0;1,1,2,2,2,2;2,0,0,0,0,1;2,0,1,0,2,0;2,1,2,0,2,0", "output": "5"}, {"input": "0,1,1,2,0,1;1,2,0,0,0,1;2,2,1,2,2,1;2,1,2,2,2,0;2,1,1,0,2,0", "output": "4"}, {"input": "0,2,2,1,1,0,0,1,2,2,2,1,2,0,0,1,0,2,2,0,0,2,2,2,0,0,0,0,2,0,0,1,1,0,1,2,0,0,1,2,2,1,2,0,2,2;2,2,1,0,1,2,0,1,1,2,0,1,2,0,0,2,1,0,1,1,2,2,2,1,2,2,2,1,2,0,0,1,1,1,2,0,0,1,0,0,2,2,1,2,2,0;0,0,0,2,2,2,1,1,1,2,1,2,1,2,1,1,0,2,0,1,0,0,2,2,1,0,2,1,0,0,2,1,0,1,1,1,0,0,2,2,1,1,2,1,1,0;1,1,0,1,0,0,1,1,0,1,2,1,2,1,1,1,2,1,1,1,0,1,2,2,1,2,0,2,1,2,1,2,0,2,1,1,2,0,0,0,0,2,2,1,2,1;0,0,0,2,0,1,0,2,1,0,1,2,2,2,0,0,0,0,2,0,2,0,1,0,2,1,2,0,1,2,1,0,2,1,2,1,2,0,0,1,1,2,1,1,1,0;1,2,0,1,1,2,1,2,0,0,2,1,2,0,2,0,0,1,2,2,0,1,2,0,2,2,2,1,1,0,1,2,2,2,2,0,1,1,1,0,1,1,2,2,0,0;0,1,0,2,0,0,0,0,0,2,0,1,0,2,2,1,1,2,0,2,0,2,1,2,2,2,0,0,2,0,1,0,0,0,0,0,2,1,1,0,2,2,1,2,1,1;1,1,2,1,0,1,0,1,1,0,1,2,1,0,0,2,2,0,2,2,0,2,1,0,2,2,2,0,0,1,1,0,1,2,0,1,2,1,0,2,0,1,0,0,0,1;1,2,0,0,2,0,1,0,2,0,1,0,0,2,1,2,2,1,1,0,0,2,1,0,2,0,0,1,0,0,2,2,1,1,0,2,0,0,2,2,1,0,1,0,0,1;0,1,2,2,2,0,2,0,2,0,0,1,2,0,0,1,0,0,2,2,2,0,1,2,2,0,0,2,1,0,0,1,2,1,2,0,1,1,1,1,1,0,1,2,1,2;1,2,0,0,1,1,1,1,2,0,0,1,2,0,1,2,1,0,0,0,2,0,2,2,1,0,2,1,2,2,0,0,1,0,1,1,1,2,1,1,1,1,1,2,0,1;0,0,0,1,1,2,1,0,0,2,2,2,2,0,2,1,0,2,0,0,0,1,2,1,0,0,1,1,2,0,0,0,1,0,2,2,0,2,1,2,0,0,1,0,2,2;2,1,2,0,0,0,1,1,2,2,2,1,2,1,2,1,0,1,1,1,1,2,0,2,0,1,1,1,0,2,1,0,2,1,2,0,1,1,0,1,2,1,1,2,1,2;1,1,2,2,1,1,2,1,0,1,1,2,2,1,0,1,1,2,1,0,1,2,2,2,2,0,0,0,1,1,2,2,1,2,1,1,2,2,0,0,2,2,2,2,1,2;0,1,2,2,1,0,1,0,0,1,2,0,0,1,1,0,1,1,2,2,2,1,1,0,1,1,2,0,1,0,2,2,0,1,1,0,2,2,0,0,2,2,2,0,2,1;2,0,1,1,0,1,2,1,2,1,2,1,0,2,1,0,2,1,0,0,1,0,2,1,1,2,2,0,0,0,0,0,0,1,0,0,0,0,0,0,1,1,2,2,1,1;0,1,1,0,1,0,1,2,2,1,2,2,1,0,2,1,0,1,0,1,2,1,1,1,1,2,0,0,0,1,1,2,0,0,0,2,0,0,2,0,2,2,2,1,1,0;1,0,0,0,0,1,0,0,2,0,1,2,2,2,2,0,2,1,0,0,2,0,2,0,2,1,2,0,2,2,0,1,2,2,0,2,2,2,2,2,0,0,2,2,2,2;1,0,2,1,0,0,2,1,2,2,2,1,0,1,0,2,0,0,0,0,0,0,1,1,2,2,0,1,2,1,2,2,1,0,1,1,2,2,2,0,2,2,1,0,0,0;2,2,2,0,1,1,1,2,2,1,0,1,2,0,1,2,1,0,2,1,1,2,2,0,1,0,2,1,0,0,0,0,2,2,1,1,2,1,2,1,1,1,0,0,0,0;1,2,2,2,0,1,0,1,2,0,2,1,2,1,0,0,0,2,2,2,0,2,2,0,1,1,2,0,1,1,0,0,0,2,2,2,1,2,2,2,0,2,2,2,0,1;0,1,0,1,1,2,0,1,0,2,1,2,0,2,1,2,1,1,2,1,0,2,2,0,1,2,1,1,2,0,0,2,2,2,0,1,1,1,0,0,0,2,0,1,2,0;1,0,0,2,0,2,2,0,1,1,0,0,0,2,2,1,0,2,1,2,0,2,2,1,0,2,0,1,1,1,0,0,0,1,1,0,2,1,0,2,0,2,0,0,0,2;0,2,1,0,2,1,2,0,0,2,2,2,1,0,2,2,1,0,1,2,2,1,0,2,2,0,1,1,1,1,0,0,0,1,0,2,1,2,1,0,1,1,0,0,1,1;2,2,1,0,0,1,0,2,2,2,2,2,0,0,1,2,0,1,1,2,2,0,1,2,1,2,0,1,1,2,0,1,2,0,0,1,1,2,0,1,1,1,2,2,0,1;2,1,1,0,0,2,0,2,2,2,1,0,2,2,0,2,1,0,1,0,1,0,0,2,1,2,0,1,2,1,2,0,0,0,2,1,0,2,2,2,1,0,2,1,0,0;2,0,0,2,2,1,0,0,1,1,1,1,1,0,1,2,2,1,0,0,2,2,2,0,1,2,1,0,0,2,1,2,2,2,2,1,0,2,1,0,0,2,0,0,2,2;0,1,0,0,1,0,1,0,2,1,0,1,0,0,1,1,1,1,1,2,2,0,0,1,1,2,2,2,2,0,2,1,1,2,0,1,1,0,2,2,0,1,1,1,1,0;1,0,2,2,2,0,0,0,0,1,1,2,0,0,2,0,1,0,2,2,0,1,2,2,1,1,2,1,0,0,1,1,0,2,1,1,1,1,0,1,1,1,1,2,0,0;0,2,2,1,2,1,1,2,2,2,0,2,2,2,1,2,0,2,1,1,0,2,0,0,1,1,1,2,0,0,0,0,1,1,2,0,0,0,2,1,1,1,2,2,2,2;0,1,2,2,0,1,2,1,1,2,2,2,1,2,2,2,0,0,2,2,2,0,0,1,0,2,1,2,2,0,0,1,0,0,2,2,0,2,2,1,2,1,1,2,0,1", "output": "9"}, {"input": "0,1,2,0,0,0,2,1,1,2,0,2,2,1,0,1,1,2,1,0,0,2,1,0,0,1,1,1,2,1,2,1,1,0,0,2,1,1;1,2,1,1,2,0,1,0,0,1,2,1,0,2,2,0,2,1,2,2,0,0,0,1,2,0,1,1,1,0,0,0,0,2,2,2,0,0;0,2,0,2,2,2,1,2,0,2,0,1,0,0,1,0,0,2,0,1,2,0,1,0,1,0,0,0,0,0,1,2,1,2,0,0,0,2;0,2,1,1,0,1,2,0,1,0,1,0,1,2,2,0,2,0,2,2,2,1,2,2,1,0,2,1,1,1,1,2,2,0,0,1,0,0;1,0,0,0,0,1,0,1,2,1,0,1,0,0,0,2,2,1,0,2,1,1,1,1,1,0,1,0,0,2,2,0,0,1,0,2,0,0;1,0,0,0,2,0,2,2,0,0,0,1,2,1,2,2,2,1,0,1,1,1,2,2,2,1,2,2,1,2,1,0,2,0,1,0,1,2;0,2,0,1,2,0,0,2,0,0,2,1,0,0,0,1,2,2,2,2,1,2,0,0,0,1,1,1,0,1,2,0,1,1,1,2,2,0;0,0,2,0,0,1,2,0,2,2,2,2,0,2,2,2,1,2,0,2,1,1,0,1,0,1,2,0,0,2,2,0,1,0,1,0,0,2;2,0,0,2,2,1,1,1,1,0,2,2,0,1,1,1,2,1,1,1,0,1,0,2,2,0,1,2,1,2,2,1,1,1,0,2,1,1;0,0,0,0,2,2,0,0,2,0,1,1,2,2,0,0,1,0,2,2,2,2,1,0,1,1,0,1,2,0,1,1,1,1,0,0,1,1;2,2,0,1,0,1,2,0,0,1,2,0,0,1,2,1,0,0,2,0,2,2,1,1,1,2,2,0,1,0,0,2,2,0,1,1,2,1;0,0,2,0,2,1,1,1,2,1,2,0,1,0,0,2,1,1,0,1,0,2,0,1,1,2,1,1,2,0,2,2,0,0,1,0,1,0;1,1,2,1,2,2,1,0,0,1,1,1,0,1,0,1,1,0,1,1,2,1,1,0,2,1,1,2,0,0,2,2,0,1,0,0,2,0;1,0,1,2,0,0,2,2,0,2,1,2,1,2,0,1,2,1,0,1,0,1,1,2,0,2,1,1,0,0,2,1,2,0,1,1,0,0;0,2,2,2,2,2,1,2,2,2,0,0,1,2,1,0,0,0,1,0,0,2,1,0,0,2,0,1,0,2,1,0,2,1,2,2,0,0;0,0,2,1,2,2,0,0,2,2,2,2,0,0,1,0,1,1,1,1,0,2,2,0,2,0,2,1,2,0,0,2,0,1,1,2,1,2;1,2,1,2,1,0,2,1,1,1,1,1,2,1,0,0,2,0,2,2,0,2,1,1,2,0,2,0,2,0,0,1,2,2,0,1,2,2;1,2,1,2,1,1,0,2,1,2,1,2,2,2,2,2,1,2,2,0,2,0,1,1,2,1,1,1,2,0,2,2,0,2,1,1,2,2;1,1,1,1,1,0,0,2,0,2,2,0,2,0,0,1,2,1,0,1,0,1,1,0,2,2,0,1,1,1,1,2,1,1,2,1,1,0;1,0,1,1,1,2,0,0,1,1,1,0,1,2,0,2,0,2,1,0,1,1,2,2,0,0,0,1,0,0,2,2,1,1,0,2,2,1;1,1,2,0,0,1,0,0,1,0,2,1,1,0,2,0,0,0,2,1,0,1,2,1,2,1,1,2,2,2,1,2,1,2,2,0,1,0;2,2,1,0,1,1,1,2,0,1,2,1,2,1,1,2,1,2,0,0,1,2,2,2,2,1,2,2,0,0,0,2,1,2,2,2,2,1;2,1,1,0,1,2,0,1,1,0,2,1,2,0,0,0,1,0,2,0,1,1,2,2,1,0,2,2,2,2,1,2,2,2,2,2,0,2;0,1,2,2,1,1,0,2,2,2,0,0,2,2,0,0,2,2,1,0,0,1,1,1,1,1,2,1,0,1,2,0,1,0,1,0,2,0;0,0,1,0,0,0,1,2,0,2,1,1,0,1,1,0,1,2,1,1,2,0,0,1,2,0,1,2,1,0,0,0,1,0,2,1,0,0;0,0,0,2,0,2,2,0,2,1,1,1,0,1,0,0,2,1,1,0,0,2,2,1,1,1,1,0,0,0,2,2,2,2,1,0,0,1;1,0,2,0,2,0,2,1,2,0,0,0,2,1,2,2,0,2,1,0,0,2,2,2,1,1,0,2,1,1,1,2,1,0,2,2,2,2;2,0,2,1,2,1,2,2,2,1,1,2,0,0,2,1,1,2,2,2,1,0,0,1,1,1,0,0,2,0,1,2,2,2,1,0,2,2;1,1,2,2,0,2,0,0,1,1,2,1,1,0,1,0,0,1,0,2,0,1,2,1,1,1,0,1,1,1,0,1,1,1,1,2,2,2;2,1,1,1,1,1,2,0,2,2,1,0,1,1,1,1,1,2,0,1,0,0,2,1,0,1,1,1,1,1,1,1,0,0,1,1,2,1;1,0,0,0,2,1,2,0,0,1,2,1,1,2,1,0,2,1,1,2,2,1,1,0,0,1,0,1,2,1,0,1,0,0,0,1,0,1;1,2,1,2,0,0,2,1,0,2,1,1,2,1,1,1,1,2,2,0,2,0,1,1,1,1,0,2,0,2,0,1,2,0,2,1,2,1;0,1,0,0,1,1,2,2,1,1,2,0,2,1,0,1,0,2,0,1,0,1,1,0,1,2,2,2,0,1,2,0,1,2,0,1,0,0;1,2,1,2,0,1,1,2,2,1,2,2,0,1,2,2,1,2,1,2,0,1,1,0,1,1,2,1,2,0,1,1,0,0,1,0,1,2;1,0,0,1,2,1,0,2,2,2,1,0,2,0,2,0,1,2,1,0,0,2,1,2,0,0,1,1,2,0,0,1,1,1,1,2,0,1;1,1,0,2,0,1,0,0,1,1,2,1,1,2,1,1,0,0,2,2,0,1,2,1,0,1,0,0,1,0,0,1,2,0,1,1,1,0;0,1,1,0,1,0,1,2,1,0,0,1,1,0,2,1,1,2,1,1,0,1,2,0,1,0,0,0,0,0,0,2,2,1,1,2,2,0;0,1,2,0,0,0,0,2,0,0,0,2,2,0,2,0,1,2,1,0,0,1,1,1,2,1,0,1,0,1,0,0,2,0,1,0,2,1;2,0,1,1,1,2,1,0,1,0,2,1,1,1,0,1,0,1,2,0,0,2,1,1,2,0,1,1,0,2,0,0,1,0,0,0,2,0;0,0,1,0,1,1,0,1,1,2,2,1,0,1,0,2,0,2,2,1,1,1,2,2,0,2,2,1,0,1,1,0,0,1,0,2,2,0", "output": "8"}, {"input": "2,1,2,2,0,1;2,2,2,2,2,0;0,1,1,1,0,2;0,2,2,0,2,0;0,1,2,2,0,0;0,0,2,2,0,1;1,0,0,0,2,1;1,2,1,2,0,0;0,0,1,0,0,2;0,2,0,1,0,0", "output": "5"}, {"input": "0,2,1,2,2,2;0,1,0,1,2,1;0,2,2,1,0,2;1,1,0,2,1,2", "output": "4"}, {"input": "1,2,2,2;0,1,0,1;2,0,1,1;0,0,1,2;0,2,0,1;1,0,1,0", "output": "3"}, {"input": "2,2,1,2,0;1,1,1,1,0;2,1,0,2,1;0,1,2,0,0;0,0,1,2,0", "output": "4"}, {"input": "1,2,1,1,0,2,2,1,1,0;2,2,2,2,1,0,2,1,0,2;0,2,0,1,1,0,2,0,1,0", "output": "3"}, {"input": "2,1,2,1,2,0,0,2;1,1,0,0,0,0,1,1;0,1,2,2,0,2,1,1;1,2,2,0,2,1,2,1;2,0,0,2,1,0,2,0;2,2,1,1,2,1,2,1;0,1,0,0,2,2,2,1;1,1,0,1,1,0,2,1", "output": "5"}, {"input": "1,1,1,0,0,2,0,2,2,2;2,2,2,1,0,1,2,1,0,1;1,0,1,0,1,0,2,1,2,1;2,2,1,0,1,0,1,0,2,2;2,0,2,1,2,1,0,2,1,2;2,1,0,2,2,1,0,0,0,2;2,2,1,2,2,0,2,1,2,2;2,0,2,0,0,0,2,0,0,2;1,0,1,2,1,2,0,0,0,0", "output": "5"}, {"input": "2,1;2,0;2,1;2,2;1,1", "output": "2"}, {"input": "2,2,2,1,2,1,2,2,0,1,2,2,1,1,0,2,0,0,2,1,0,2,2,2,2,0,0,2,0,1,1,1,1,1,0,1,0;0,2,2,0,1,2,1,1,2,2,1,0,2,0,0,1,0,2,2,0,2,2,1,0,0,1,1,1,1,2,1,1,0,1,1,1,2;2,1,2,0,2,2,1,1,0,1,0,1,1,1,0,0,0,1,2,2,0,0,0,2,2,0,1,0,2,2,0,2,0,2,1,0,0;2,1,1,2,0,2,2,1,1,0,0,0,1,0,2,0,2,1,0,1,0,2,2,1,0,0,1,0,1,2,0,0,1,1,1,0,2;2,2,0,1,2,2,0,1,2,2,1,1,2,1,1,1,1,2,0,0,2,0,2,0,1,0,1,0,0,0,2,0,2,0,1,2,0;1,1,2,1,2,0,1,1,0,2,1,0,1,2,0,1,1,0,0,1,1,1,0,2,2,1,2,1,2,1,0,0,1,1,0,1,2;1,1,2,1,0,1,1,1,2,1,2,0,0,2,1,0,2,2,1,0,1,1,0,2,1,2,0,0,1,0,0,0,1,2,1,2,2;2,0,1,0,2,0,0,0,1,1,0,1,0,0,0,2,1,0,0,0,2,2,1,1,2,0,0,2,1,2,0,1,2,1,1,2,0;2,2,2,0,2,1,2,2,1,2,1,0,0,0,0,2,0,2,2,2,2,1,2,0,2,2,1,2,1,0,1,1,0,0,2,0,1;2,1,0,0,0,0,2,1,1,1,2,2,0,2,2,2,2,0,0,1,2,1,0,1,1,1,2,2,0,1,0,0,1,0,0,0,0;1,0,0,2,2,1,1,2,0,0,0,0,2,1,2,0,2,0,0,2,0,0,0,1,1,1,0,0,1,0,2,2,1,0,2,1,2;2,2,2,2,2,2,2,2,2,0,0,1,2,2,2,1,2,1,2,0,2,2,2,1,2,1,0,0,0,1,2,0,1,2,1,2,2;2,0,1,0,2,0,2,1,1,0,1,2,1,0,1,1,2,2,2,1,0,2,2,2,1,1,2,2,0,2,0,2,1,2,1,0,1;0,0,2,1,1,1,1,1,2,1,0,0,1,2,2,2,2,2,0,1,2,2,1,0,2,0,0,0,0,0,0,0,0,0,2,1,1;0,0,1,0,1,1,0,0,1,0,0,2,1,0,1,1,1,1,1,2,2,0,0,2,0,0,0,1,2,1,2,2,0,2,1,0,2;2,0,0,0,1,1,0,0,2,0,2,0,1,2,0,2,1,0,1,1,0,1,2,2,1,1,0,2,1,0,1,1,2,1,0,2,2;1,1,0,2,1,1,2,2,0,2,2,1,0,2,0,1,2,0,0,2,1,0,2,0,0,0,1,2,2,0,2,0,1,1,1,0,0;1,0,0,1,1,1,2,1,0,1,0,1,1,1,1,2,0,1,1,0,2,0,0,0,0,1,0,0,2,0,0,2,2,1,0,1,0;0,0,0,2,1,2,0,0,0,1,2,0,2,2,1,0,1,1,1,2,0,1,2,0,1,2,2,1,0,1,0,1,2,1,1,2,2;1,1,1,1,0,0,0,1,1,0,0,1,0,0,2,1,1,1,0,1,1,1,1,0,2,0,2,0,0,0,1,0,2,0,1,0,1;0,0,0,0,2,2,0,1,0,2,1,0,1,0,1,2,1,1,0,0,1,0,0,2,1,0,1,2,0,1,1,0,2,1,0,2,1;0,2,2,2,2,1,0,2,2,2,1,0,0,0,2,0,2,2,0,1,1,2,2,0,2,2,0,1,1,0,2,0,2,2,1,2,1;2,2,1,0,0,0,1,2,2,1,1,0,0,2,1,0,2,2,1,2,2,2,2,1,2,2,1,2,2,1,2,0,0,1,1,0,2;1,0,1,2,2,1,0,2,0,1,0,1,2,2,1,1,2,2,1,1,2,1,0,0,0,0,1,1,2,0,1,1,1,2,0,1,1;1,0,2,0,0,0,0,2,1,1,1,0,0,1,2,1,2,2,2,0,2,1,2,2,0,1,0,0,1,0,2,1,1,0,2,1,2;0,2,1,0,1,1,0,2,1,0,0,0,2,1,0,2,1,0,0,2,1,0,1,1,2,2,1,0,2,2,1,2,1,1,0,0,2;2,2,2,1,2,0,1,1,1,1,2,1,2,1,1,0,0,2,2,2,2,2,0,1,1,2,2,0,1,0,2,2,0,0,0,1,1;2,0,2,0,2,2,2,2,2,0,0,2,2,2,0,0,0,0,0,1,1,0,2,1,2,2,1,2,0,0,0,1,0,2,1,2,1;0,2,0,2,0,0,0,0,1,0,0,1,1,2,1,0,2,1,0,0,2,0,0,0,1,2,2,2,2,0,0,2,1,1,2,2,0;1,1,1,1,0,2,0,0,1,0,1,0,1,0,1,0,0,1,0,2,0,0,0,1,1,2,1,2,0,2,1,1,1,1,2,1,2;0,0,2,0,1,2,1,1,0,2,0,1,1,2,0,1,1,0,2,2,0,1,2,1,1,2,0,1,1,0,0,1,1,2,0,1,1;0,1,2,0,2,2,0,2,1,0,2,2,0,0,2,0,0,1,0,0,2,1,1,0,0,0,0,2,0,2,2,2,0,1,2,2,0;2,2,1,1,2,0,1,2,0,2,0,2,2,2,1,2,1,1,2,2,0,1,0,2,0,0,2,0,2,1,1,1,0,2,2,0,2;2,0,0,2,2,1,2,2,0,1,0,2,0,2,0,1,2,0,2,1,2,2,0,0,0,0,1,0,2,2,1,1,0,1,0,1,1;2,2,2,1,0,0,1,1,1,2,2,2,0,0,2,2,1,2,0,0,0,2,0,2,0,0,1,2,1,0,2,2,2,2,0,1,1;2,2,2,2,0,1,2,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,0,1,2,2,0,1,2,0,0,2,2,1,0,0,2;1,1,1,2,2,2,0,0,0,2,2,1,2,0,2,1,1,0,1,1,1,1,2,1,0,0,1,2,2,0,1,1,1,1,1,0,2;1,0,0,2,0,0,0,2,2,1,0,2,2,0,0,2,2,2,1,2,1,2,1,1,2,1,1,1,0,0,1,0,1,0,0,1,0;1,0,0,2,2,0,0,2,0,0,2,2,2,0,2,2,1,2,1,2,1,2,2,2,1,0,2,2,1,0,1,0,1,1,1,2,1;1,1,1,0,1,0,2,0,0,1,0,0,2,1,1,1,1,2,2,1,1,2,2,2,2,0,2,2,2,1,0,1,0,1,0,1,1;0,0,2,0,1,1,1,2,1,2,0,0,0,2,1,0,0,1,0,2,0,0,1,2,1,1,0,2,2,2,2,2,0,0,1,2,0;1,2,2,1,2,0,0,1,1,0,0,1,2,2,1,2,2,1,0,0,1,2,0,0,1,0,2,1,2,1,1,0,0,0,0,0,2;1,1,1,0,1,2,0,1,1,1,2,0,2,2,0,1,0,0,2,0,0,0,1,1,1,2,2,2,1,1,2,0,0,0,1,2,2;2,2,1,0,0,0,1,0,0,2,2,0,0,2,1,1,1,1,2,0,0,1,2,1,2,1,0,2,1,0,2,0,1,1,2,0,1", "output": "12"}, {"input": "1,0,2,2,0;0,1,2,2,0", "output": "2"}, {"input": "2,2,0;2,2,2", "output": "0"}, {"input": "2,0,1,0,0,1,1,1;2,1,2,0,2,1,1,0;1,1,1,1,1,0,0,0;2,0,2,0,2,1,1,2;2,2,1,1,2,1,1,0;0,0,0,1,0,2,2,2;1,2,0,2,1,0,1,1;0,2,0,2,0,2,2,1", "output": "5"}, {"input": "0,2;1,2;2,1;1,0;1,0;2,1;1,0;0,0;0,0", "output": "2"}, {"input": "0,0,1,2,1,2,2,1,1,1,0,2,1,2,0,2,1,0,2,2,2,0,0,2,1,1,1,2,0,0,0,1,0,2,0,2,2,2,0,0,2,2,2,0,1;1,1,2,1,0,2,1,2,2,2,2,1,2,2,0,2,0,1,1,1,2,2,2,0,1,0,2,1,1,1,1,0,2,0,2,0,0,0,0,0,0,0,2,1,1;0,1,2,1,0,0,0,0,0,1,2,0,2,0,1,0,0,1,0,2,0,0,0,1,2,0,2,2,1,0,1,0,2,1,0,0,0,1,0,2,2,0,0,1,2;2,0,1,1,2,0,2,2,2,0,0,2,0,1,1,0,1,0,1,1,2,1,2,1,0,2,2,0,0,1,1,0,2,1,0,0,2,1,2,1,2,1,2,1,2;1,0,0,1,0,0,0,1,2,1,0,1,2,2,0,2,1,2,0,0,0,0,2,2,1,1,0,2,0,2,1,0,1,2,2,2,1,2,2,0,2,1,1,1,1;0,2,1,2,2,2,2,2,2,1,1,1,1,2,2,1,0,2,2,0,0,0,1,0,2,2,2,1,1,1,1,2,0,2,1,2,2,2,0,1,1,1,2,0,2;2,2,1,1,0,1,0,0,0,0,0,0,2,1,2,0,1,1,2,0,0,1,1,1,0,2,0,1,2,2,0,2,2,2,2,0,1,2,1,1,1,0,0,0,2;1,1,1,0,2,0,0,0,1,1,1,1,0,1,1,1,0,2,0,2,0,0,2,0,0,0,0,0,0,1,0,0,2,0,2,0,1,0,0,1,2,2,0,0,0;1,0,0,0,0,2,0,1,1,0,2,0,2,2,0,2,0,0,0,2,2,0,0,0,1,2,1,0,0,2,1,2,0,2,2,2,2,2,2,0,1,2,0,0,0;0,0,2,1,2,2,2,1,1,2,2,2,2,0,1,2,2,0,1,2,2,1,1,0,0,1,2,2,2,2,0,0,2,2,1,2,1,2,0,0,0,1,0,0,1;0,1,1,2,0,1,2,0,0,1,0,0,1,1,0,0,0,0,0,1,0,0,1,0,2,1,0,2,1,1,1,0,1,1,0,2,1,0,0,1,1,2,1,2,0;2,2,2,0,0,1,2,2,1,1,1,2,0,2,2,1,0,2,1,2,0,1,2,2,1,2,2,0,2,0,0,1,0,2,2,0,1,0,2,0,1,2,2,0,0;0,2,1,2,2,0,2,2,0,1,1,0,2,2,2,0,1,2,2,2,2,0,1,0,0,2,0,1,1,2,1,2,1,0,0,1,2,1,1,0,2,2,0,2,2;1,0,0,1,2,1,0,1,0,0,1,1,2,1,1,0,1,2,0,0,2,1,2,1,0,0,0,2,1,2,2,2,0,1,2,2,2,1,2,2,2,1,2,1,2;2,2,2,1,1,0,2,1,1,0,2,1,0,0,2,0,1,1,2,1,1,2,2,1,1,2,0,2,2,2,2,1,2,0,1,2,1,0,2,0,0,2,0,0,0;0,2,2,0,1,1,2,0,2,1,0,2,0,0,2,0,1,1,2,1,0,1,0,2,1,0,1,0,2,1,1,2,1,0,1,2,1,2,1,0,0,1,0,1,2;0,1,1,0,0,1,0,2,1,0,1,0,1,1,2,1,1,2,1,2,2,1,1,1,0,2,0,1,1,1,2,1,1,0,1,1,2,0,0,0,1,2,0,1,1;0,0,0,1,1,1,1,0,1,2,1,1,1,2,2,0,0,2,0,2,1,0,0,0,0,1,0,2,0,0,0,1,2,0,2,0,0,1,1,0,2,0,1,0,2;0,2,2,2,2,1,0,0,0,2,0,2,0,0,0,0,2,0,0,1,0,0,1,1,0,1,0,1,1,2,1,0,0,0,2,2,2,0,1,0,2,1,2,0,1;1,2,0,0,1,1,1,2,0,2,2,0,1,0,1,2,2,0,1,2,0,0,2,2,1,2,1,1,1,1,2,1,2,2,2,0,1,0,1,0,0,1,0,0,0;1,2,0,0,0,1,2,1,2,0,1,0,2,2,0,1,2,1,2,0,2,2,0,0,2,1,0,2,0,0,0,0,2,2,0,2,0,2,1,0,2,1,2,1,1;0,0,1,1,2,2,1,0,2,2,1,0,2,2,0,0,0,0,0,1,2,1,1,0,1,2,1,1,2,2,1,2,0,0,0,1,2,0,0,2,2,1,1,0,1;2,2,0,0,2,2,0,2,2,1,2,1,2,2,0,0,0,2,1,1,1,0,0,2,0,1,0,0,1,2,0,1,1,1,1,2,1,2,2,1,2,0,2,0,2;2,0,1,0,0,2,2,1,0,1,1,0,2,1,2,1,0,1,2,0,0,0,1,2,1,0,2,1,1,2,2,2,0,0,2,0,1,2,2,1,1,2,1,1,2;2,0,0,0,2,2,0,0,2,2,1,2,2,0,0,2,1,0,1,0,1,2,0,0,1,2,0,1,1,2,1,0,0,0,1,1,1,1,0,2,2,0,2,2,0;0,1,2,1,0,2,2,2,2,1,2,2,1,2,0,1,0,0,2,0,0,1,2,1,1,2,0,1,0,1,0,1,0,1,1,1,1,1,1,0,2,1,1,2,1;0,1,2,1,2,0,0,2,1,2,2,0,0,1,1,0,2,1,2,0,2,0,2,2,1,0,2,0,1,0,1,0,0,2,1,2,1,0,1,1,2,0,2,2,0;2,2,0,0,1,1,1,2,0,1,2,0,0,2,1,1,0,2,1,1,0,2,1,2,2,1,1,2,2,2,0,0,2,0,2,1,2,0,2,1,1,1,2,1,2;2,0,2,1,0,2,0,2,0,1,1,0,2,0,1,0,2,0,0,2,0,1,1,0,2,1,0,2,0,1,2,1,0,1,2,2,1,2,0,0,2,1,0,2,2;2,0,0,1,0,0,1,2,1,0,2,0,0,0,0,0,0,0,1,0,2,0,2,0,2,2,0,1,1,1,0,1,2,0,2,0,0,0,1,2,2,0,1,0,2;1,0,2,0,2,2,1,1,0,2,2,2,1,1,0,0,0,0,1,0,0,1,1,0,1,1,2,1,1,0,1,1,2,0,2,2,0,0,1,2,0,1,2,2,2;2,0,2,2,1,1,0,1,1,1,1,2,1,2,2,2,1,1,1,1,0,0,0,2,1,2,1,2,1,0,2,0,2,2,1,1,0,0,1,2,0,2,1,1,1;2,2,0,1,2,0,0,2,2,2,2,1,2,0,2,0,2,1,0,1,1,1,0,0,2,0,1,2,2,1,2,0,1,1,2,0,2,1,0,1,2,1,0,2,2;1,0,1,2,2,2,1,2,1,1,0,1,0,1,1,0,2,0,0,2,2,1,0,2,2,0,2,1,0,1,1,2,2,1,1,1,1,1,1,1,2,1,2,1,0;0,1,2,1,2,1,0,1,0,0,0,2,1,2,2,0,1,1,1,1,0,0,1,1,1,1,2,1,0,1,0,1,2,0,0,1,1,0,2,0,0,2,2,0,0;1,0,0,1,2,0,2,0,1,1,0,2,2,0,2,2,1,1,0,1,2,1,2,2,1,0,2,1,0,1,0,2,0,1,0,0,1,0,0,2,1,1,2,0,2;0,1,2,0,2,1,0,0,0,0,1,2,2,0,1,1,0,1,2,1,1,2,2,1,0,1,0,1,0,2,0,0,1,2,1,0,1,2,0,2,0,2,2,2,0;1,0,1,0,1,1,1,0,1,1,2,1,1,1,1,1,0,1,2,0,2,0,2,1,1,2,1,2,0,2,2,2,2,0,2,0,1,0,2,1,0,0,1,0,0;0,1,2,1,2,2,0,2,2,2,1,0,0,2,2,0,1,0,1,1,1,1,2,2,0,2,0,0,0,0,0,1,0,0,0,1,2,0,1,2,0,2,0,0,0;1,1,1,1,1,0,0,2,1,1,0,2,0,0,0,0,2,2,0,1,2,1,0,2,0,0,0,2,2,0,1,0,0,1,1,1,2,0,1,2,1,2,2,1,1;2,2,0,0,1,2,1,2,0,2,2,2,0,2,0,0,2,1,2,1,2,2,2,2,2,0,0,2,0,2,2,0,2,0,0,0,0,1,0,0,0,1,0,0,2;1,1,2,0,2,0,1,0,0,0,2,1,0,1,0,0,2,0,2,1,0,1,0,2,0,2,0,0,1,2,0,2,2,0,0,0,2,0,0,1,2,1,1,1,1;1,1,0,2,2,2,1,1,2,0,2,1,2,1,0,0,1,2,2,0,1,0,2,2,1,0,0,2,1,2,0,1,1,2,1,0,1,1,1,0,2,0,0,2,0;1,1,2,1,2,1,0,0,1,1,0,2,0,0,2,1,1,0,0,2,2,1,0,2,1,2,2,0,1,1,1,0,2,0,1,0,2,2,2,2,2,1,2,2,2;0,0,2,1,1,0,0,0,0,1,2,0,0,1,2,2,1,0,2,2,2,2,2,2,0,1,0,0,2,2,0,1,1,1,1,2,2,2,0,1,0,0,0,0,0;1,1,0,1,1,0,0,0,1,1,0,1,1,2,0,0,1,1,1,0,0,2,0,0,2,2,0,0,0,2,1,2,1,1,2,2,1,1,2,0,2,1,0,0,1", "output": "9"}, {"input": "0,2,2,1,0,2,0,0,2,0;2,2,2,2,1,0,1,1,0,1;1,2,2,1,1,2,0,1,1,1", "output": "3"}, {"input": "2,1,1,1,2,1,1,2,0,1,1,0,2,2,1,1,1,2,0,2,1,1,1,0,0,1,1,2,1,0,0,2,1,1;0,2,1,2,0,0,0,1,0,0,2,0,1,2,2,2,0,1,2,2,1,2,1,2,2,0,1,0,1,2,2,0,1,1;0,0,0,2,1,0,2,2,2,0,0,1,1,1,0,1,1,2,0,0,1,0,2,0,2,2,2,1,0,2,0,1,2,0;0,0,1,2,1,2,0,2,1,1,0,2,0,0,0,2,0,1,1,0,0,0,2,2,1,2,1,1,0,2,2,0,2,1;0,2,0,0,0,1,0,1,0,2,2,1,1,2,0,1,2,0,1,1,0,2,1,0,2,2,2,1,0,0,2,0,2,2;2,1,1,2,2,2,2,2,1,1,2,1,2,1,0,2,0,1,0,1,1,0,2,2,1,1,0,0,0,0,0,0,2,2;0,1,2,2,0,0,2,2,1,0,2,1,2,1,1,0,0,1,1,2,2,1,0,2,1,1,1,2,2,0,1,0,0,0;0,0,1,1,0,1,1,2,1,0,0,1,2,1,1,2,2,2,2,2,2,0,1,0,0,2,0,1,1,2,2,0,0,0;1,0,0,1,2,0,1,1,1,2,1,0,2,1,2,1,2,0,1,1,0,1,0,1,2,2,2,2,1,2,1,0,2,0;0,2,2,2,0,0,0,1,1,0,0,0,2,1,2,2,2,0,1,2,1,1,0,2,2,2,1,0,1,0,0,0,1,2;1,1,0,0,2,2,0,0,0,1,0,1,2,2,1,1,2,0,1,1,0,1,0,2,1,0,0,2,1,0,2,2,0,0;1,1,0,2,0,1,0,1,2,2,0,1,2,2,1,0,1,0,2,0,0,1,0,1,1,1,2,1,0,1,0,1,0,0;2,0,1,2,2,1,0,1,2,2,2,2,1,0,0,0,1,2,1,0,1,2,2,0,0,0,0,1,1,1,1,2,1,1;1,1,0,1,1,1,2,2,0,0,2,0,2,1,2,0,2,1,1,0,1,0,0,0,2,1,1,1,1,2,1,0,0,0;1,2,0,1,0,0,0,1,1,1,0,1,0,2,2,1,2,0,2,2,0,2,1,2,1,1,2,0,2,1,1,2,1,2;0,1,1,1,0,2,1,0,0,1,1,2,2,2,0,0,1,1,1,0,0,0,1,1,0,0,1,2,2,2,2,0,1,0;2,1,2,2,0,1,2,2,1,0,2,0,2,2,1,0,1,2,1,2,0,0,2,1,0,0,2,2,1,1,0,2,2,1;1,2,2,2,0,1,1,2,1,1,0,1,2,1,1,0,1,1,1,2,0,0,1,1,2,2,2,2,2,0,2,2,2,1;2,1,0,1,1,0,0,2,1,0,0,1,0,1,1,2,2,1,1,0,0,0,2,2,0,1,1,1,1,1,1,1,0,1;2,2,2,2,2,0,0,0,2,0,1,2,2,1,1,2,2,0,1,0,1,1,0,1,2,0,1,2,0,1,1,1,2,1;2,1,2,2,2,1,0,0,1,2,2,1,1,2,1,0,2,2,1,1,0,0,1,2,0,2,2,0,0,1,2,0,2,2;2,0,2,0,0,0,2,0,0,1,1,2,0,1,1,2,0,0,2,0,2,2,2,0,0,0,2,1,0,2,2,1,0,2;2,1,1,0,2,1,0,1,0,1,1,0,2,1,1,1,0,1,1,1,0,0,1,0,1,0,2,2,1,2,2,1,2,1;2,2,1,0,2,1,2,2,0,1,1,2,0,2,1,2,1,0,2,1,2,2,0,0,0,0,0,1,1,2,1,0,2,0;0,0,1,1,0,1,1,2,2,1,2,2,0,0,0,0,2,2,2,2,1,1,0,0,0,0,2,2,1,0,0,0,0,1;0,2,1,2,2,1,2,0,1,2,2,0,2,2,0,1,1,0,0,1,0,0,2,1,2,1,0,1,1,1,0,1,2,2;1,0,2,1,1,1,0,0,2,2,0,1,1,1,2,1,0,0,1,0,1,1,2,1,1,0,0,1,1,1,1,0,0,0;2,2,1,1,1,2,2,2,1,0,0,0,1,0,1,0,2,0,1,1,2,1,2,2,2,0,0,0,2,1,0,0,0,1;2,2,1,1,2,0,0,0,1,0,0,2,2,1,0,1,1,2,1,2,2,1,2,1,1,1,1,0,2,0,2,1,2,2;2,2,0,2,2,2,2,2,1,0,1,2,0,1,2,0,0,2,1,2,0,0,1,1,2,1,0,2,2,0,0,2,0,1;0,2,0,0,0,0,1,0,1,1,0,1,1,1,0,0,1,2,1,1,2,2,0,2,1,1,2,2,1,2,2,1,1,2;1,2,1,2,1,2,0,0,2,1,2,1,1,2,0,1,2,1,0,1,0,0,2,0,2,2,1,0,0,2,0,0,1,2;0,2,2,2,0,1,2,1,0,2,1,0,0,1,0,2,1,0,2,1,1,0,0,2,2,1,1,1,0,0,0,2,1,1;1,1,0,1,2,1,2,2,2,2,2,0,1,0,1,1,2,0,0,1,2,1,1,0,1,2,1,1,2,1,2,1,1,0;1,0,0,0,2,1,0,2,0,0,0,0,1,1,2,2,0,0,1,0,2,2,1,0,0,2,1,0,0,0,0,0,0,0;1,2,1,0,1,1,0,0,2,2,1,0,0,0,2,0,1,2,1,1,1,2,0,2,2,2,1,1,2,1,0,0,0,0;0,0,1,2,2,0,2,0,1,0,1,2,1,1,1,1,2,1,2,0,0,0,2,2,1,0,0,2,1,1,2,2,2,1;0,2,1,0,2,1,2,0,2,1,2,2,2,2,0,1,1,2,2,2,1,2,0,1,2,0,2,0,2,2,0,0,2,2;0,2,2,1,1,2,2,1,2,2,0,0,1,2,1,1,0,0,0,1,1,2,0,2,2,0,2,0,1,1,2,2,0,1", "output": "8"}, {"input": "1,0,0,0,2,2,2,2,1,1,0,0,2,1,2,0,0,2,2,1,1,0,2,2,1,0,0,1,2,1,1,2,1,1,2,0,2,2,1,0,2,0,2,2,1,2,1;2,0,1,2,1,1,1,1,0,2,0,2,0,1,1,0,2,0,2,1,1,1,1,1,1,0,1,0,2,2,2,2,2,1,0,0,0,0,0,0,0,2,2,0,2,0,1;2,2,2,0,0,1,1,2,0,0,0,2,0,1,2,2,0,2,0,1,1,0,1,2,1,1,0,1,0,2,1,1,2,0,1,2,2,2,1,1,0,1,2,2,2,0,0;2,2,2,2,0,2,1,2,2,1,2,0,2,1,0,1,0,1,2,1,1,1,0,2,1,2,0,2,0,2,0,1,2,0,1,0,1,0,2,0,2,1,0,0,0,2,1;2,1,2,2,0,1,1,1,1,1,0,2,0,2,1,2,0,0,2,0,2,2,0,0,2,2,2,0,0,2,0,0,0,2,0,1,1,2,1,0,0,2,1,2,0,0,1;2,1,0,0,2,1,2,0,0,0,1,0,1,0,1,0,0,0,0,0,2,1,1,2,0,2,1,1,1,1,2,1,2,0,0,1,1,1,0,1,2,0,2,2,0,1,0;2,2,0,0,0,1,2,2,2,2,1,0,1,1,2,1,0,1,0,1,1,2,2,2,0,1,2,2,1,2,1,0,0,2,1,2,2,2,0,1,0,2,2,0,0,1,0;2,1,1,0,0,0,2,1,0,2,1,2,0,1,1,1,2,0,0,2,1,2,0,0,0,2,1,1,1,1,2,1,0,0,2,1,1,2,0,0,1,1,1,1,0,2,1;2,2,2,0,2,1,2,1,0,1,2,1,2,1,2,2,2,2,0,1,0,0,2,1,0,1,0,2,0,0,2,1,0,2,1,1,2,1,1,2,2,0,0,0,2,1,0;1,0,0,2,2,0,2,0,1,1,1,2,0,1,1,2,1,2,1,1,2,2,1,0,2,2,0,0,1,2,0,0,2,0,2,2,1,0,2,1,2,0,1,0,0,1,1;2,0,1,1,1,2,0,0,2,2,1,1,0,2,0,1,2,0,2,1,2,0,0,2,1,2,2,1,0,1,1,0,1,1,1,0,0,1,1,0,1,2,0,2,1,0,2;2,2,1,2,1,1,2,2,2,0,0,2,0,0,1,0,2,0,1,0,2,0,0,2,0,2,0,0,2,0,0,2,1,1,0,1,1,2,2,2,1,2,1,0,2,0,1;2,2,1,1,0,0,1,1,2,0,0,2,1,2,0,1,1,0,1,2,2,0,2,1,0,0,1,2,0,1,2,0,2,1,0,2,1,2,0,1,2,1,1,2,1,2,0;1,2,2,1,1,2,2,2,0,0,0,2,0,0,2,0,1,0,0,0,0,0,2,1,0,2,2,1,2,1,2,2,1,0,0,2,0,0,1,2,2,2,2,1,0,1,2;0,0,0,2,2,2,0,1,0,0,2,1,2,1,0,1,1,0,0,1,2,2,0,1,0,1,2,0,0,1,0,0,1,1,2,0,1,0,2,0,1,2,2,1,1,1,0;2,1,1,1,2,2,2,2,2,0,1,1,2,2,1,2,2,1,1,1,2,1,1,1,1,0,0,1,2,2,1,2,0,1,0,0,1,1,1,1,0,0,2,2,0,2,1;0,2,0,2,1,0,1,0,2,1,1,0,0,1,2,0,2,1,1,0,0,1,0,2,2,1,2,1,1,0,2,0,1,1,0,2,2,1,1,1,1,0,1,2,2,0,0;2,0,0,1,2,0,1,2,2,2,2,1,1,1,2,2,2,2,1,1,2,1,2,2,2,2,0,0,2,2,0,2,0,0,1,0,0,0,1,0,2,1,0,1,0,1,2;1,1,2,2,0,0,2,2,2,1,2,0,1,0,2,1,0,0,2,0,2,0,0,2,1,2,2,2,1,0,0,2,2,0,2,1,0,0,0,2,0,1,0,1,1,0,0;2,1,1,2,1,0,1,2,0,2,2,1,0,1,0,0,0,2,2,2,0,0,2,2,1,2,2,1,1,2,1,0,1,0,2,2,0,2,1,0,0,0,0,0,2,1,0;1,0,0,2,0,1,2,2,2,0,0,1,2,0,2,0,0,2,0,2,1,1,1,1,0,0,0,0,2,1,2,1,2,1,0,1,0,1,1,2,2,2,2,1,0,2,1;0,1,0,1,0,2,2,0,1,2,0,1,1,1,0,0,2,2,1,2,1,2,1,2,0,2,1,2,0,0,2,1,2,2,1,2,1,2,1,0,0,2,0,0,1,2,2;1,1,0,0,2,1,2,1,1,1,1,1,2,2,1,1,0,2,2,1,2,0,1,2,2,0,2,1,0,2,1,0,1,2,2,0,1,0,1,2,2,0,1,1,2,2,1;2,2,0,1,1,0,1,2,2,2,2,1,2,0,2,2,1,1,2,0,0,2,2,0,0,2,2,1,2,2,2,0,0,2,0,1,0,0,0,1,2,0,1,1,1,0,1;0,0,2,2,0,0,0,2,2,2,0,0,0,0,1,2,0,2,0,1,2,0,2,2,0,0,2,0,0,1,2,0,1,0,2,2,2,2,1,0,0,2,1,1,1,2,1;2,0,1,0,1,1,1,1,0,2,2,2,1,1,2,2,1,0,0,2,0,0,2,1,0,1,1,2,0,2,2,2,0,0,0,1,0,0,1,2,2,2,1,2,2,2,0;2,0,2,1,0,1,0,0,0,0,1,1,2,0,2,2,1,0,2,1,0,0,2,2,0,1,1,2,0,2,2,1,1,0,0,1,2,1,2,2,1,2,2,2,1,0,2;2,2,0,0,1,1,0,0,0,1,0,1,0,2,1,0,2,1,1,0,2,2,1,0,2,0,1,0,0,0,2,1,1,1,1,0,0,1,1,1,1,0,2,1,0,0,1;2,0,2,1,1,1,1,0,0,2,2,0,0,1,0,2,1,1,2,2,2,2,2,1,1,2,0,2,0,0,0,2,0,2,2,0,0,2,0,1,1,1,1,2,2,0,2;0,0,0,2,2,0,0,1,1,1,0,1,2,0,0,0,0,1,1,0,0,2,1,2,0,2,2,1,2,1,2,2,0,2,2,1,1,1,2,1,2,0,0,0,0,0,1;0,0,1,0,0,0,1,0,1,2,0,2,1,0,0,2,1,2,2,2,0,2,1,2,2,1,2,0,2,1,2,0,2,2,2,2,1,2,1,0,1,0,0,2,0,0,1;2,2,2,1,0,2,1,2,0,0,2,2,2,0,2,1,0,0,1,1,2,2,2,1,2,2,0,2,2,1,2,2,1,2,2,2,1,2,0,1,1,0,2,1,2,1,0;2,0,0,0,2,1,0,1,1,0,0,2,0,1,1,0,1,0,1,1,0,1,1,2,2,0,2,1,2,2,1,0,1,2,0,2,1,0,1,0,2,1,1,2,0,0,0;1,0,2,2,0,0,2,2,0,2,1,2,2,1,0,2,0,2,0,0,1,0,2,1,0,1,2,0,2,1,1,2,2,0,1,2,0,2,1,0,0,0,2,1,2,0,2;2,0,1,1,0,2,1,1,0,0,1,0,2,2,0,1,0,2,1,1,0,2,2,1,0,1,2,2,1,0,0,0,2,0,0,2,1,0,0,0,1,2,2,0,2,2,2;0,2,2,1,0,2,0,0,1,2,1,1,0,1,1,2,1,1,0,2,1,0,1,2,1,0,0,1,0,0,0,0,1,1,2,1,2,0,2,0,1,1,0,1,2,1,2;0,1,2,1,1,2,1,2,1,1,0,1,0,0,0,2,2,0,1,2,0,0,2,1,1,1,0,2,2,2,0,1,0,2,0,1,0,1,1,2,2,1,1,2,1,2,0;1,1,0,2,1,0,0,1,2,2,2,1,1,2,0,0,2,0,1,2,0,2,2,2,2,2,2,2,0,2,1,1,0,1,1,2,1,2,1,0,1,2,2,2,1,1,2;0,2,0,2,2,2,1,2,2,2,2,1,0,0,0,2,0,0,2,1,2,0,0,0,1,0,2,2,0,1,0,1,2,0,2,0,2,2,2,0,0,1,0,0,1,2,0;0,2,0,2,0,0,2,2,0,2,0,2,2,1,0,2,1,2,1,1,2,0,0,2,2,2,2,1,2,2,2,2,2,1,2,2,0,1,0,2,2,0,1,2,1,0,2", "output": "10"}, {"input": "0,1,0,0,0,1;1,0,2,1,2,0;2,2,0,0,1,1;0,2,0,1,2,2;2,1,1,2,1,2;1,1,1,1,0,2;1,0,0,0,2,0;0,2,0,0,1,2;2,0,0,2,1,2", "output": "5"}, {"input": "2;0", "output": "0"}, {"input": "1,0,2;2,1,0;2,2,1", "output": "2"}, {"input": "2,0,0,2,1,1,0,1;0,0,0,0,0,0,1,2;2,1,2,2,2,2,1,0;0,1,1,1,0,2,0,1;0,2,0,2,0,0,1,0;0,1,0,2,2,1,2,2;2,2,0,2,1,0,1,0", "output": "7"}]
|
{
"cpp": "==Code Submission==\n\nvector<vector<int>> deserialize_stdin(const string &input) {\n vector<vector<int>> grid;\n stringstream ss(input);\n string row;\n while(getline(ss, row, ';')) {\n vector<int> nums;\n stringstream rowStream(row);\n string token;\n while(getline(rowStream, token, ',')) {\n if(!token.empty()){\n nums.push_back(stoi(token));\n }\n }\n if(!nums.empty())\n grid.push_back(nums);\n }\n return grid;\n}\n\nstring serialize_stdout(int result) {\n return to_string(result);\n}\n\nint main(){\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n string input;\n getline(cin, input);\n auto grid = deserialize_stdin(input);\n Solution sol;\n int ans = sol.lenOfVDiagonal(grid);\n cout << serialize_stdout(ans);\n return 0;\n}",
"golang": "==Code Submission==\n\nfunc deserializeStdin(input string) [][]int {\n var grid [][]int\n input = strings.TrimSpace(input)\n if input == \"\" {\n return grid\n }\n rows := strings.Split(input, \";\")\n for _, row := range rows {\n row = strings.TrimSpace(row)\n if row == \"\" {\n continue\n }\n tokens := strings.Split(row, \",\")\n var nums []int\n for _, token := range tokens {\n token = strings.TrimSpace(token)\n if token != \"\" {\n num, _ := strconv.Atoi(token)\n nums = append(nums, num)\n }\n }\n grid = append(grid, nums)\n }\n return grid\n}\n\nfunc serializeStdout(result int) string {\n return strconv.Itoa(result)\n}\n\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n input, _ := reader.ReadString('\\n')\n input = strings.TrimSpace(input)\n grid := deserializeStdin(input)\n ans := lenOfVDiagonal(grid)\n fmt.Print(serializeStdout(ans))\n}",
"java": "public class Main {\n private static int[][] deserializeGrid(String input) {\n String[] rows = input.split(\";\");\n int n = rows.length;\n int[][] grid = new int[n][];\n for (int i = 0; i < n; i++) {\n String[] tokens = rows[i].split(\",\");\n grid[i] = new int[tokens.length];\n for (int j = 0; j < tokens.length; j++) {\n grid[i][j] = Integer.parseInt(tokens[j].trim());\n }\n }\n return grid;\n }\n \n private static String serializeOutput(int result) {\n return Integer.toString(result);\n }\n \n public static void main(String[] args) throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n String input = br.readLine().trim();\n int[][] grid = deserializeGrid(input);\n Solution sol = new Solution();\n int ans = sol.lenOfVDiagonal(grid);\n System.out.println(serializeOutput(ans));\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\n\nconst deserialize_stdin = (input) => {\n input = input.trim();\n if (input === \"\") return [];\n const rows = input.split(\";\");\n const grid = rows.map(row => {\n if(row.trim() === \"\") return [];\n return row.split(\",\").map(x => parseInt(x, 10));\n });\n return grid;\n};\n\nconst serialize_stdout = (result) => {\n return result.toString();\n};\n\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\nlet input = \"\";\nprocess.stdin.on('data', chunk => { input += chunk; });\nprocess.stdin.on('end', () => {\n const grid = deserialize_stdin(input);\n const ans = lenOfVDiagonal(grid);\n console.log(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str):\n grid = []\n rows = input_str.strip().split(';')\n for row in rows:\n if row:\n grid.append(list(map(int, row.split(','))))\n return grid\n\ndef serialize_stdout(result):\n return str(result)\n\ninput_str = sys.stdin.read().strip()\ngrid = deserialize_stdin(input_str)\nsol = Solution()\nans = sol.lenOfVDiagonal(grid)\nprint(serialize_stdout(ans))",
"ruby": "==Code Submission==\n\ninput = gets.strip\nrows = input.split(';')\ngrid = rows.map { |row| row.split(',').map(&:to_i) }\nans = len_of_v_diagonal(grid)\nputs ans.to_s"
}
|
3736
|
Find Valid Pair of Adjacent Digits in String
|
find-valid-pair-of-adjacent-digits-in-string
|
<p>You are given a string <code>s</code> consisting only of digits. A <strong>valid pair</strong> is defined as two <strong>adjacent</strong> digits in <code>s</code> such that:</p>
<ul>
<li>The first digit is <strong>not equal</strong> to the second.</li>
<li>Each digit in the pair appears in <code>s</code> <strong>exactly</strong> as many times as its numeric value.</li>
</ul>
<p>Return the first <strong>valid pair</strong> found in the string <code>s</code> when traversing from left to right. If no valid pair exists, return an empty string.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">s = "2523533"</span></p>
<p><strong>Output:</strong> <span class="example-io">"23"</span></p>
<p><strong>Explanation:</strong></p>
<p>Digit <code>'2'</code> appears 2 times and digit <code>'3'</code> appears 3 times. Each digit in the pair <code>"23"</code> appears in <code>s</code> exactly as many times as its numeric value. Hence, the output is <code>"23"</code>.</p>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">s = "221"</span></p>
<p><strong>Output:</strong> <span class="example-io">"21"</span></p>
<p><strong>Explanation:</strong></p>
<p>Digit <code>'2'</code> appears 2 times and digit <code>'1'</code> appears 1 time. Hence, the output is <code>"21"</code>.</p>
</div>
<p><strong class="example">Example 3:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">s = "22"</span></p>
<p><strong>Output:</strong> <span class="example-io">""</span></p>
<p><strong>Explanation:</strong></p>
<p>There are no valid adjacent pairs.</p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>2 <= s.length <= 100</code></li>
<li><code>s</code> only consists of digits from <code>'1'</code> to <code>'9'</code>.</li>
</ul>
|
You are given a string `s` consisting only of digits. A **valid pair** is defined as two **adjacent** digits in `s` such that:
- The first digit is **not equal** to the second.
- Each digit in the pair appears in `s` **exactly** as many times as its numeric value.
Return the first **valid pair** found in the string `s` when traversing from left to right. If no valid pair exists, return an empty string.
**Example 1:**
**Input:** s \= "2523533"
**Output:** "23"
**Explanation:**
Digit `'2'` appears 2 times and digit `'3'` appears 3 times. Each digit in the pair `"23"` appears in `s` exactly as many times as its numeric value. Hence, the output is `"23"`.
**Example 2:**
**Input:** s \= "221"
**Output:** "21"
**Explanation:**
Digit `'2'` appears 2 times and digit `'1'` appears 1 time. Hence, the output is `"21"`.
**Example 3:**
**Input:** s \= "22"
**Output:** ""
**Explanation:**
There are no valid adjacent pairs.
**Constraints:**
- `2 <= s.length <= 100`
- `s` only consists of digits from `'1'` to `'9'`.
|
Easy
|
[
"hash-table",
"string",
"counting"
] |
leetcode
|
https://leetcode.com/problems/find-valid-pair-of-adjacent-digits-in-string
|
functional
| null | null | null | null |
{
"c": "char* findValidPair(char* s) {\n \n}",
"cpp": "class Solution {\npublic:\n string findValidPair(string s) {\n \n }\n};",
"csharp": "public class Solution {\n public string FindValidPair(string s) {\n \n }\n}",
"dart": "class Solution {\n String findValidPair(String s) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec find_valid_pair(s :: String.t) :: String.t\n def find_valid_pair(s) do\n \n end\nend",
"erlang": "-spec find_valid_pair(S :: unicode:unicode_binary()) -> unicode:unicode_binary().\nfind_valid_pair(S) ->\n .",
"golang": "func findValidPair(s string) string {\n \n}",
"java": "class Solution {\n public String findValidPair(String s) {\n \n }\n}",
"javascript": "/**\n * @param {string} s\n * @return {string}\n */\nvar findValidPair = function(s) {\n \n};",
"kotlin": "class Solution {\n fun findValidPair(s: String): String {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param String $s\n * @return String\n */\n function findValidPair($s) {\n \n }\n}",
"python": "class Solution(object):\n def findValidPair(self, s):\n \"\"\"\n :type s: str\n :rtype: str\n \"\"\"\n ",
"python3": "class Solution:\n def findValidPair(self, s: str) -> str:\n ",
"racket": "(define/contract (find-valid-pair s)\n (-> string? string?)\n )",
"ruby": "# @param {String} s\n# @return {String}\ndef find_valid_pair(s)\n \nend",
"rust": "impl Solution {\n pub fn find_valid_pair(s: String) -> String {\n \n }\n}",
"scala": "object Solution {\n def findValidPair(s: String): String = {\n \n }\n}",
"swift": "class Solution {\n func findValidPair(_ s: String) -> String {\n \n }\n}",
"typescript": "function findValidPair(s: string): string {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n string findValidPair(string s) {\n int count[10] = {0};\n for (char c : s) {\n count[c - '0']++;\n }\n for (int i = 0; i < s.size() - 1; ++i) {\n char a = s[i], b = s[i+1];\n if (a != b) {\n int a_d = a - '0', b_d = b - '0';\n if (count[a_d] == a_d && count[b_d] == b_d) {\n return string(1, a) + string(1, b);\n }\n }\n }\n return \"\";\n }\n};",
"memory": 900,
"memoryDistribution": "[[900, 91.1677, \"class Solution {\\npublic:\\n string findValidPair(string s) {\\n int count[10] = {0};\\n for (char c : s) {\\n count[c - '0']++;\\n }\\n for (int i = 0; i < s.size() - 1; ++i) {\\n char a = s[i], b = s[i+1];\\n if (a != b) {\\n int a_d = a - '0', b_d = b - '0';\\n if (count[a_d] == a_d && count[b_d] == b_d) {\\n return string(1, a) + string(1, b);\\n }\\n }\\n }\\n return \\\"\\\";\\n }\\n};\"], [8300, 0.7485, \"class Solution {\\npublic:\\n std::string findValidPair(const std::string& s) {\\n std::array<int, 10> aryCountCh;\\n aryCountCh.fill(0);\\n\\n for (const char ch : s) {\\n ++aryCountCh[ch - '0'];\\n }\\n\\n int size = s.size();\\n for (int idx = 0; idx < size - 1; ++idx) {\\n if (s[idx] != s[idx + 1] &&\\n aryCountCh[s[idx] - '0'] == s[idx] - '0' &&\\n aryCountCh[s[idx + 1] - '0'] == s[idx + 1] - '0') {\\n return s.substr(idx, 2);\\n }\\n }\\n\\n return \\\"\\\";\\n }\\n};\"], [8400, 2.6946, \"class Solution {\\npublic:\\n string findValidPair(string s) {\\n map<char,int>m;\\n string st=\\\"\\\" ;\\n for(int i=0;i<s.size();i++)\\n {\\n\\n\\n if(st.size()>0)\\n {\\n if(s[i]==st[0]) \\n st.clear();\\n }\\n \\n int num=s[i]-'0';\\n int cnt=0;\\n \\n for(int j=0;j<s.size();j++)\\n {\\n if(s[j]==s[i]) \\n cnt++;\\n } \\n cout<<num<<\\\",\\\"<<cnt<<endl;\\n if(cnt==num) \\n st.push_back(s[i] );\\n else\\n st.clear();\\n if(st.size()==2)\\n break;\\n \\n }\\n if(st.size()==1)\\n st.clear();\\n \\n return st;\\n }\\n};\"], [8500, 5.3892, null], [8600, 9.8802, null], [8700, 8.0838, null], [8800, 5.2395, null], [8900, 7.0359, null], [9000, 13.1737, null], [9100, 18.5629, null], [9200, 12.8743, null], [9300, 6.8862, \"inline int chartoint(const char c)\\n{\\n return (c >= '0' && c <= '9') ? (c - '0') : 0;\\n}\\n\\nclass Solution {\\npublic:\\n string findValidPair(string s) {\\n unordered_map<int, short unsigned int> map;\\n for (int i = 0; i <= 9; ++i)\\n map.insert(make_pair(i, 0));\\n\\n for (int i = 0; i < s.size(); ++i)\\n {\\n int num = chartoint(s[i]);\\n ++map[num];\\n }\\n \\n string res;\\n\\n for (int i = 0; i < s.size() - 1; ++i)\\n {\\n int num1 = chartoint(s[i]);\\n int num2 = chartoint(s[i + 1]);\\n if (num1 != num2 && map[num1] == num1 && map[num2] == num2)\\n {\\n res.push_back(s[i]);\\n res.push_back(s[i + 1]);\\n break;\\n }\\n }\\n\\n return res;\\n }\\n};\"], [9400, 2.5449, \"inline int chartoint(const char c)\\n{\\n return (c >= '0' && c <= '9') ? (c - '0') : 0;\\n}\\n\\nclass Solution {\\npublic:\\n string findValidPair(string s) {\\n unordered_map<int, int> map;\\n for (int i = 0; i <= 9; ++i)\\n map.insert(make_pair(i, 0));\\n\\n for (int i = 0; i < s.size(); ++i)\\n {\\n int num = chartoint(s[i]);\\n ++map[num];\\n }\\n \\n string res;\\n\\n for (int i = 0; i < s.size() - 1; ++i)\\n {\\n int num1 = chartoint(s[i]);\\n int num2 = chartoint(s[i + 1]);\\n if (num1 != num2 && map[num1] == num1 && map[num2] == num2)\\n {\\n res.push_back(s[i]);\\n res.push_back(s[i + 1]);\\n break;\\n }\\n }\\n\\n return res;\\n }\\n};\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 49.8503, \"class Solution {\\npublic:\\n string findValidPair(string s) {\\n int freq[10] = {0};\\n for (char ch : s)\\n freq[ch - '0']++;\\n string answer = \\\"\\\";\\n for (int i = 0; i < s.size() - 1; i++) {\\n if (s[i] != s[i + 1]) {\\n if (freq[s[i] - '0'] == s[i] - '0' &&\\n freq[s[i + 1] - '0'] == s[i + 1] - '0') {\\n answer = {s[i], s[i + 1]};\\n break;\\n }\\n\\n }\\n }\\n return answer;\\n }\\n};\"], [1, 7.1856, \"class Solution {\\npublic:\\n string findValidPair(string s) {\\n unordered_map<char,int>mp;\\n string res;\\n for(auto num:s)\\n {\\n mp[num]+=1;\\n }\\n for(int i=1;i<s.size();i++)\\n {\\n if(s[i]!=s[i-1] && mp[s[i]]==s[i]-'0' && s[i-1]-'0'==mp[s[i-1]])\\n {\\n res+=s[i-1];\\n res+=s[i];\\n break;\\n }\\n }\\n return res;\\n }\\n};\"], [2, 6.1377, null], [3, 18.4132, null], [4, 9.5808, \"class Solution {\\npublic:\\n string findValidPair(string s) {\\n unordered_map<char, int> ctr;\\n for (char c : s) {\\n ctr[c]++;}\\n\\n unordered_set<char> valid;\\n for (auto& p : ctr) {\\n char digit = p.first;\\n\\n if (p.second == digit - '0') {\\n valid.insert(digit);}}\\n\\n for (size_t i = 0; i < s.size() - 1; i++) {\\n char digit1 = s[i];\\n char digit2 = s[i + 1];\\n if (digit1 == digit2) continue;\\n if (valid.count(digit1) && valid.count(digit2)) {\\n return string() + digit1 + digit2;} }\\n \\n return \\\"\\\";\\n \\n }\\n};\"], [5, 0.8982, \"class Solution {\\npublic:\\n string findValidPair(string s) {\\n string res=\\\"\\\";\\n unordered_map<char, int> mp;\\n if(s.size()==2){\\n return \\\"\\\";\\n }\\n for(char c:s){\\n mp[c]++;\\n }\\n for(int i=0; i<s.size(); i++){\\n int n1 = s[i];\\n int n2 = s[i+1];\\n if(n1!= n2 && (n1 -'0') == mp[s[i]] && (n2-'0') == mp[s[i+1]]){\\n res = s[i+1] +res;\\n res = s[i] + res;\\n return res;\\n }\\n }\\n \\n return res;\\n }\\n};\"]]"
},
"golang": {
"code": "func findValidPair(s string) string {\n freq := make(map[byte]int)\n for i := 0; i < len(s); i++ {\n c := s[i]\n freq[c]++\n }\n for i := 0; i < len(s)-1; i++ {\n a, b := s[i], s[i+1]\n if a != b {\n da, db := int(a-'0'), int(b-'0')\n if freq[a] == da && freq[b] == db {\n return string([]byte{a, b})\n }\n }\n }\n return \"\"\n}",
"memory": 400,
"memoryDistribution": "[[400, 56.9444, \"func findValidPair(s string) string {\\n freq := make(map[byte]int)\\n for i := 0; i < len(s); i++ {\\n c := s[i]\\n freq[c]++\\n }\\n for i := 0; i < len(s)-1; i++ {\\n a, b := s[i], s[i+1]\\n if a != b {\\n da, db := int(a-'0'), int(b-'0')\\n if freq[a] == da && freq[b] == db {\\n return string([]byte{a, b})\\n }\\n }\\n }\\n return \\\"\\\"\\n}\"], [4100, 12.5, \"func findValidPair(s string) string {\\n\\tfreq := make([]int, 10)\\n\\tfor i := 0; i < len(s); i++ {\\n\\t\\tfreq[int(s[i]-'0')]++\\n\\t}\\n\\n\\tfor i := 0; i < len(s)-1; i++ {\\n\\t\\tval := int(s[i] - '0')\\n\\t\\tnext := int(s[i+1] - '0')\\n\\t\\tif val != next && freq[val] == val && freq[next] == next {\\n\\t\\t\\treturn s[i : i+2]\\n\\t\\t}\\n\\t}\\n\\n\\treturn \\\"\\\"\\n}\"], [4200, 30.5556, \"func findValidPair(s string) string {\\n counter := make(map[rune]int)\\n\\tfor _, char := range s {\\n\\t\\tcounter[char]++\\n\\t}\\n\\tfor i := 1; i < len(s); i++ {\\n\\t\\ta,b := rune(s[i-1]), rune(s[i])\\n\\t\\tif a != b {\\n\\t\\t\\tif counter[a] == int(a - '0') && counter[b] == int(b - '0') {\\n\\t\\t\\t\\treturn string(a) + string(b)\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\treturn \\\"\\\"\\n}\"], [4300, 16.6667, null], [4400, 8.3333, null], [4500, 4.1667, null], [4800, 4.1667, null], [4900, 2.7778, null], [5000, 1.3889, \"func findValidPair(s string) string {\\n\\tmyMap := make(map[string]int)\\n\\n\\tfor i := 0; i < len(s); {\\n\\t\\t_, ok := myMap[string(s[i])]\\n\\t\\tif ok {\\n\\t\\t\\tmyMap[string(s[i])]++\\n\\t\\t} else {\\n\\t\\t\\tmyMap[string(s[i])] = 1\\n\\t\\t}\\n\\t\\ti++\\n\\t}\\n\\tfmt.Println(myMap)\\n\\n\\tres := \\\"\\\"\\n\\tfor i := 0; i+1 < len(s); {\\n\\t\\tparsedIntKeyL := int(s[i] - '0')\\n\\t\\tparsedIntKeyR := int(s[i+1] - '0')\\n\\t\\tif string(s[i]) != string(s[i+1]) && parsedIntKeyL == myMap[string(s[i])] && parsedIntKeyR == myMap[string(s[i+1])] {\\n\\t\\t\\treturn string(s[i]) + string(s[i+1])\\n\\t\\t}\\n\\t\\ti++\\n\\t}\\n\\n\\tif len(res) == 2 {\\n\\t\\treturn res\\n\\t}\\n\\n\\treturn \\\"\\\"\\n}\"], [5100, 11.1111, \"func findValidPair(s string) string {\\n\\tmyMap := make(map[string]int)\\n\\n\\tfor i := 0; i < len(s); {\\n\\t\\t_, ok := myMap[string(s[i])]\\n\\t\\tif ok {\\n\\t\\t\\tmyMap[string(s[i])]++\\n\\t\\t} else {\\n\\t\\t\\tmyMap[string(s[i])] = 1\\n\\t\\t}\\n\\t\\ti++\\n\\t}\\n\\tfmt.Println(myMap)\\n\\n\\tres := \\\"\\\"\\n\\tfor i := 0; i+1 < len(s); {\\n\\t\\tparsedIntKeyL, _ := strconv.Atoi(string(s[i]))\\n\\t\\tvalL := myMap[string(s[i])]\\n\\t\\tparsedIntKeyR, _ := strconv.Atoi(string(s[i+1]))\\n\\t\\tvalR := myMap[string(s[i+1])]\\n\\t\\tif string(s[i]) == string(s[i+1]) {\\n\\t\\t\\tfmt.Println(\\\"Skipped as is same...\\\")\\n\\t\\t} else {\\n\\t\\t\\tif parsedIntKeyL == valL && parsedIntKeyR == valR {\\n\\t\\t\\t\\treturn string(s[i]) + string(s[i+1])\\n\\t\\t\\t}\\n\\t\\t}\\n\\t\\ti++\\n\\t}\\n\\n\\tif len(res) == 2 {\\n\\t\\treturn res\\n\\t}\\n\\n\\treturn \\\"\\\"\\n}\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 52.7778, \"func findValidPair(s string) string {\\n freq := [10]int{}\\n set := map[string]int{}\\n freq[s[len(s)-1]-'0']++\\n for i := len(s)-2; i>=0; i-- {\\n freq[s[i]-'0']++\\n set[s[i:i+2]]=i\\n }\\n var res string\\n for i, n := range freq {\\n if i != n {\\n continue\\n }\\n for j, n := range freq {\\n if j != n || j == i {\\n continue\\n }\\n tem := string('0'+i)+string('0'+j)\\n ind, ok := set[tem]\\n if !ok {\\n continue\\n }\\n if res == \\\"\\\" {\\n res = tem\\n } else if ind < set[res] {\\n res = tem\\n }\\n }\\n }\\n\\n return res\\n}\"], [1, 8.3333, \"func findValidPair(s string) string {\\n\\tgoodNum := make(map[int]bool)\\n\\tmemoFreq := make(map[int]int)\\n\\tfor i := 0; i < len(s); i++ {\\n\\t\\tv := int(s[i] - '0')\\n\\t\\tif _, ok := memoFreq[v]; !ok {\\n\\t\\t\\tmemoFreq[v] = 1\\n\\t\\t} else {\\n\\t\\t\\tmemoFreq[v]++\\n\\t\\t}\\n\\n\\t\\tgoodNum[v] = memoFreq[v] == v\\n\\t}\\n\\n\\tfor i := 0; i < len(s)-1; i++ {\\n\\t\\tval := int(s[i] - '0')\\n\\t\\tnext := int(s[i+1] - '0')\\n\\t\\tif val != next && goodNum[val] && goodNum[next] {\\n\\t\\t\\treturn s[i : i+2]\\n\\t\\t}\\n\\t}\\n\\n\\treturn \\\"\\\"\\n}\"], [2, 6.9444, null], [3, 8.3333, null], [4, 11.1111, null], [5, 1.3889, null], [6, 2.7778, \"func findValidPair(s string) string {\\n\\tmyMap := make(map[string]int)\\n\\n\\tfor i := 0; i < len(s); {\\n\\t\\t_, ok := myMap[string(s[i])]\\n\\t\\tif ok {\\n\\t\\t\\tmyMap[string(s[i])]++\\n\\t\\t} else {\\n\\t\\t\\tmyMap[string(s[i])] = 1\\n\\t\\t}\\n\\t\\ti++\\n\\t}\\n\\tfmt.Println(myMap)\\n\\n\\tres := \\\"\\\"\\n\\tfor i := 0; i+1 < len(s); {\\n\\t\\tparsedIntKeyL, _ := strconv.Atoi(string(s[i]))\\n\\t\\tvalL := myMap[string(s[i])]\\n\\t\\tparsedIntKeyR, _ := strconv.Atoi(string(s[i+1]))\\n\\t\\tvalR := myMap[string(s[i+1])]\\n\\t\\tif string(s[i]) == string(s[i+1]) {\\n\\t\\t\\tfmt.Println(\\\"Skipped as is same...\\\")\\n\\t\\t} else {\\n\\t\\t\\tif parsedIntKeyL == valL && parsedIntKeyR == valR {\\n\\t\\t\\t\\treturn string(s[i]) + string(s[i+1])\\n\\t\\t\\t}\\n\\t\\t}\\n\\t\\ti++\\n\\t}\\n\\n\\tif len(res) == 2 {\\n\\t\\treturn res\\n\\t}\\n\\n\\treturn \\\"\\\"\\n}\"], [7, 1.3889, \"func findValidPair(s string) string {\\n\\tmyMap := make(map[string]int)\\n\\n\\tfor i := 0; i < len(s); {\\n\\t\\t_, ok := myMap[string(s[i])]\\n\\t\\tif ok {\\n\\t\\t\\tmyMap[string(s[i])]++\\n\\t\\t} else {\\n\\t\\t\\tmyMap[string(s[i])] = 1\\n\\t\\t}\\n\\t\\ti++\\n\\t}\\n\\tfmt.Println(myMap)\\n\\n\\tres := \\\"\\\"\\n\\tfor i := 0; i+1 < len(s); {\\n\\t\\tparsedIntKeyL, _ := strconv.Atoi(string(s[i]))\\n\\t\\tvalL := myMap[string(s[i])]\\n\\t\\tparsedIntKeyR, _ := strconv.Atoi(string(s[i+1]))\\n\\t\\tvalR := myMap[string(s[i+1])]\\n\\t\\tif string(s[i]) == string(s[i+1]) {\\n\\t\\t\\tfmt.Println(\\\"Skipped as is same...\\\")\\n\\t\\t} else {\\n\\t\\t\\tif parsedIntKeyL == valL && parsedIntKeyR == valR {\\n\\t\\t\\t\\treturn string(s[i]) + string(s[i+1])\\n\\t\\t\\t}\\n\\t\\t}\\n\\t\\ti++\\n\\t}\\n\\n\\tif len(res) == 2 {\\n\\t\\treturn res\\n\\t}\\n\\n\\treturn \\\"\\\"\\n}\"]]"
},
"java": {
"code": "class Solution {\n public String findValidPair(String s) {\n int[] counts = new int[10];\n for (char c : s.toCharArray()) {\n counts[c - '0']++;\n }\n for (int i = 0; i < s.length() - 1; i++) {\n char a = s.charAt(i);\n char b = s.charAt(i + 1);\n if (a != b && counts[a - '0'] == (a - '0') && counts[b - '0'] == (b - '0')) {\n return \"\" + a + b;\n }\n }\n return \"\";\n }\n}",
"memory": 4300,
"memoryDistribution": "[[4300, 46.6578, \"class Solution {\\n public String findValidPair(String s) {\\n int[] counts = new int[10];\\n for (char c : s.toCharArray()) {\\n counts[c - '0']++;\\n }\\n for (int i = 0; i < s.length() - 1; i++) {\\n char a = s.charAt(i);\\n char b = s.charAt(i + 1);\\n if (a != b && counts[a - '0'] == (a - '0') && counts[b - '0'] == (b - '0')) {\\n return \\\"\\\" + a + b;\\n }\\n }\\n return \\\"\\\";\\n }\\n}\"], [42100, 0.1311, \"class Solution {\\n public String findValidPair(String s) {\\n int[] t = new int[26];\\n Arrays.fill(t, 0);\\n for(int i = 0; i < s.length(); ++i) t[s.charAt(i) - '0']++;\\n for(int i = 1; i < s.length(); ++i){\\n if(s.charAt(i-1) == s.charAt(i) || t[s.charAt(i-1) - '0'] != s.charAt(i-1) - '0' || t[s.charAt(i) - '0'] != s.charAt(i) - '0') continue;\\n return s.substring(i-1, i+1);\\n }\\n return new String();\\n }\\n}\"], [42300, 0.1311, \"class Solution {\\n public String findValidPair(String s) {\\n int n = s.length();\\n int[] freq = new int[10];\\n for(int i = 0; i < n; i++) {\\n int index = s.charAt(i) - '0';\\n freq[index]++;\\n }\\n for(int i = 0; i < n - 1; i++) {\\n if(s.charAt(i) == s.charAt(i + 1)) continue;\\n int indexL = s.charAt(i) - '0';\\n int indexR = s.charAt(i + 1) - '0';\\n if(freq[indexL] != indexL || freq[indexR] != indexR ) continue;\\n return indexL + \\\"\\\" + indexR;\\n }\\n return \\\"\\\";\\n }\\n}\"], [42400, 0.7864, null], [42500, 1.7038, null], [42600, 2.7523, null], [42700, 6.422, null], [42800, 7.6016, null], [42900, 10.3539, null], [43000, 11.6645, null], [43100, 11.7955, null], [43200, 9.4364, null], [43300, 9.8296, null], [43400, 7.2084, null], [43500, 5.3735, null], [43600, 3.2765, null], [43700, 2.097, null], [43800, 0.9174, null], [43900, 1.0485, null], [44000, 0.2621, null], [44100, 0.1311, null], [44200, 0.5242, null], [44400, 0.1311, null], [44600, 0.5242, \"class Solution {\\n public String findValidPair(String s) {\\n int[] map = new int[10];\\n StringBuilder sb = new StringBuilder();\\n for(int i = 0 ; i < s.length() ; i++) {\\n int index = Integer.parseInt(s.charAt(i) + \\\"\\\");\\n map[index]++;\\n }\\n\\n for(int i = 1 ; i < s.length() ; i++) {\\n int a = s.charAt(i) - '0';\\n int b = s.charAt(i - 1) - '0';\\n if( a != b && map[a] == a && map[b] == b) {\\n return \\\"\\\" + s.charAt(i-1) + s.charAt(i);\\n }\\n }\\n return sb.toString();\\n }\\n}\"], [44700, 0.6553, \"class Solution {\\n \\n \\n public String findValidPair(String s) {\\n Map<Character, Integer> cnt = new HashMap<>();\\n for(char ch : s.toCharArray()) {\\n cnt.put(ch, cnt.getOrDefault(ch, 0) + 1);\\n }\\n for(int i = 0; i < s.length() - 1; i++)\\n {\\n int first = Integer.parseInt(s.substring(i, i+1));\\n int second = Integer.parseInt(s.substring(i+1, i+2));\\n System.out.println(first);\\n System.out.println(second);\\n boolean notEqual = true;\\n if(first == second)\\n {\\n continue;\\n \\n }\\n if(cnt.get(s.charAt(i)) == first && cnt.get(s.charAt(i+1)) == second) \\n {\\n String ret = s.substring(i,i+1) + s.substring(i+1, i+2);\\n return ret;\\n }\\n \\n }\\n return \\\"\\\";\\n}\\n\\n}\"]]",
"runtime": 5,
"runtimeDistribution": "[[1, 15.5963, \"class Solution {\\n public String findValidPair(String s) {\\n int[] t = new int[26];\\n Arrays.fill(t, 0);\\n for(int i = 0; i < s.length(); ++i) t[s.charAt(i) - '0']++;\\n for(int i = 1; i < s.length(); ++i){\\n if(s.charAt(i-1) == s.charAt(i) || t[s.charAt(i-1) - '0'] != s.charAt(i-1) - '0' || t[s.charAt(i) - '0'] != s.charAt(i) - '0') continue;\\n return s.substring(i-1, i+1);\\n }\\n return new String();\\n }\\n}\"], [2, 3.9318, \"class Solution {\\n public String findValidPair(String s) {\\n if(s == null || s.length() < 2) return \\\"\\\";\\n Map<Integer, Integer> map = new HashMap<>();\\n for(char c : s.toCharArray()) {\\n map.put(c - '0', map.getOrDefault(c - '0',0) +1);\\n }\\n for(int i = 0; i < s.length() - 1; i++) {\\n char cur = s.charAt(i);\\n char next = s.charAt(i+1);\\n if(cur == next) continue;\\n if(cur - '0' == map.get(cur-'0') && next - '0' == map.get(next-'0')) {\\n return s.substring(i, i+2);\\n }\\n\\n }\\n return \\\"\\\";\\n }\\n}\"], [3, 25.557, null], [4, 4.9803, null], [5, 13.7615, null], [6, 6.8152, null], [7, 14.941, null], [8, 7.7326, \"public class Solution {\\n public String findValidPair(String s) {\\n\\n Map<Character, Integer> ctr = new HashMap<>();\\n for (char c : s.toCharArray()) {\\n ctr.put(c, ctr.getOrDefault(c, 0) + 1);}\\n\\n Set<Character> valid = new HashSet<>();\\n for (Map.Entry<Character, Integer> entry : ctr.entrySet()) {\\n char digit = entry.getKey();\\n int count = entry.getValue();\\n if (count == digit - '0') {\\n valid.add(digit); }}\\n\\n for (int i = 0; i < s.length() - 1; i++) {\\n char digit1 = s.charAt(i);\\n char digit2 = s.charAt(i + 1);\\n if (digit1 == digit2) continue; \\n if (valid.contains(digit1) && valid.contains(digit2)) {\\n return \\\"\\\" + digit1 + digit2;}}\\n \\n return \\\"\\\"; } }\"], [9, 1.4417, \"class Solution {\\n public String findValidPair(String s) {\\n HashMap<Character, Integer> map = new HashMap<>();\\n String res = \\\"\\\";\\n\\n // build hashmap\\n for (char digit: s.toCharArray()){\\n if (map.containsKey(digit)){\\n map.put(digit, map.get(digit) + 1);\\n } else {\\n map.put(digit, 1);\\n }\\n }\\n\\n // check hashmap to find corresponding\\n HashSet<Character> validDigits = new HashSet<>();\\n for (Map.Entry<Character, Integer> pair: map.entrySet()){\\n char d = pair.getKey(); \\n int count = pair.getValue();\\n if (Character.getNumericValue(d) == count){\\n validDigits.add(d);\\n }\\n }\\n\\n // iterate again to find valid pair\\n if (validDigits.size() >= 2){\\n for (int i = 0; i < s.length() - 1; i++){\\n char current = s.charAt(i);\\n char next = s.charAt(i + 1);\\n if (validDigits.contains(current) && validDigits.contains(next) && current != next) {\\n res += current;\\n res += next;\\n break;\\n }\\n } \\n }\\n\\n return res;\\n }\\n}\"]]"
},
"javascript": {
"code": "var findValidPair = function(s) {\n const freq = {};\n for (const c of s) {\n freq[c] = (freq[c] || 0) + 1;\n }\n for (let i = 0; i < s.length - 1; i++) {\n const a = s[i], b = s[i + 1];\n if (a !== b) {\n const aVal = parseInt(a), bVal = parseInt(b);\n if (freq[a] === aVal && freq[b] === bVal) {\n return a + b;\n }\n }\n }\n return \"\";\n};",
"memory": 5500,
"memoryDistribution": "[[5500, 95.4955, \"var findValidPair = function(s) {\\n const freq = {};\\n for (const c of s) {\\n freq[c] = (freq[c] || 0) + 1;\\n }\\n for (let i = 0; i < s.length - 1; i++) {\\n const a = s[i], b = s[i + 1];\\n if (a !== b) {\\n const aVal = parseInt(a), bVal = parseInt(b);\\n if (freq[a] === aVal && freq[b] === bVal) {\\n return a + b;\\n }\\n }\\n }\\n return \\\"\\\";\\n};\"], [54600, 0.9009, \"/**\\n * @param {string} s\\n * @return {string}\\n */\\nvar findValidPair = function(s) {\\n let freqs = {};\\n for (let c of s) freqs[c] = (freqs[c] || 0) + 1;\\n\\n for (let i = 0; i < s.length - 1; i++)\\n if (s[i] !== s[i + 1] && freqs[s[i]] === +s[i] && freqs[s[i + 1]] === +s[i + 1]) \\n return s[i] + s[i + 1];\\n \\n return \\\"\\\";\\n};\"], [55200, 3.6036, \"/**\\n * @param {string} s\\n * @return {string}\\n */\\nvar findValidPair = function(s) {\\n let count = new Map();\\n\\n for (let i=0; i< s.length;i++){\\n let value = s[i]\\n\\n count.set(value,(count.get(value)||0)+1);\\n }\\n\\n for(let i=0; i<s.length; i++){\\n let value1=s[i]\\n let value2 =s[i+1]\\n\\n if (value1 !== value2) {\\n let num1 = parseInt(value1);\\n let num2 = parseInt(value2);\\n\\n if (count.get(value1) === num1 && count.get(value2) === num2) {\\n return value1 + value2;\\n }\\n }\\n }\\n return \\\"\\\"\\n};\"], [55400, 2.7027, null], [55500, 2.7027, null], [55600, 0.9009, null], [55700, 2.7027, null], [55800, 3.6036, null], [55900, 1.8018, null], [56000, 6.3063, null], [56100, 12.6126, null], [56200, 5.4054, null], [56300, 6.3063, null], [56400, 6.3063, null], [56500, 3.6036, null], [56600, 4.5045, null], [56700, 2.7027, null], [56800, 1.8018, null], [57000, 2.7027, null], [57300, 0.9009, null], [57400, 0.9009, null], [57500, 0.9009, null], [57600, 2.7027, null], [57700, 2.7027, null], [57800, 1.8018, null], [57900, 2.7027, null], [58000, 2.7027, null], [58100, 3.6036, null], [58200, 0.9009, null], [58300, 2.7027, \"/**\\n * @param {string} s\\n * @return {string}\\n */\\nvar findValidPair = function (s) {\\n let sMap = {};\\n\\n for (const char of s) {\\n sMap[char] = (sMap[char] || 0) + 1;\\n }\\n\\n for (let i = 0; i < s.length - 1; i++) {\\n if (\\n s[i] != s[i + 1] &&\\n s[i] == sMap[s[i]] &&\\n s[i + 1] == sMap[s[i + 1]]\\n ) {\\n return s[i] + s[i + 1];\\n }\\n }\\n\\n return '';\\n};\\n\"], [58400, 0.9009, \"/**\\n * @param {string} s\\n * @return {string}\\n */\\nvar findValidPair = function(s) {\\n let ob={}\\n\\n for( let x of s){\\n if( ob[x]){\\n ob[x]++\\n }\\n else{\\n ob[x]=1}\\n }\\n\\n for( let i=0;i< s.length-1;i++){\\n if(s[i]!==s[i+1]){\\n if(ob[s[i]]==s[i] && ob[s[i+1]]==s[i+1])\\n return s[i]+s[i+1];\\n }\\n }\\n return \\\"\\\"\\n};\"]]",
"runtime": 4,
"runtimeDistribution": "[[0, 3.6036, \"/**\\n * @param {string} s\\n * @return {string}\\n */\\nvar findValidPair = function(s) {\\n let map = {}\\n for(let i=0;i<s.length;i++){\\n map[s[i]]=(map[s[i]]||0)+1\\n }\\n for(let i=0;i<s.length;i++){\\n let a = s[i] \\n let b = s[i+1]\\n \\n if(a!==b){\\n if(map[a]===parseInt(a)&&map[b]===parseInt(b))\\n return a+b\\n }\\n }\\n return\\\"\\\"\\n};\"], [1, 6.3063, \"/**\\n * @param {string} s\\n * @return {string}\\n */\\nvar findValidPair = function (s) {\\n let sMap = {};\\n\\n for (const char of s) {\\n sMap[char] = (sMap[char] || 0) + 1;\\n }\\n\\n for (let i = 0; i < s.length - 1; i++) {\\n if (\\n s[i] != s[i + 1] &&\\n s[i] == sMap[s[i]] &&\\n s[i + 1] == sMap[s[i + 1]]\\n ) {\\n return s[i] + s[i + 1];\\n }\\n }\\n\\n return '';\\n};\\n\"], [2, 16.2162, null], [3, 13.5135, null], [4, 17.1171, null], [5, 10.8108, null], [6, 9.9099, null], [7, 5.4054, null], [8, 1.8018, null], [10, 1.8018, null], [11, 1.8018, null], [12, 1.8018, null], [13, 1.8018, null], [14, 1.8018, \"/**\\n * @param {string} s\\n * @return {string}\\n */\\nvar findValidPair = function (s) {\\n \\n for (let i = 0; i <= s.length; i++) {\\n fristcount = 0;\\n secondcount = 0;\\n if (s[i] !== s[i + 1]) {\\n for (let j = 0; j < s.length; j++) {\\n if (s[j] == s[i]) {\\n fristcount++;\\n } else if (s[j] == s[i + 1]) {\\n secondcount++;\\n }\\n }\\n }\\n\\n if (fristcount == s[i] && secondcount == s[i + 1]) {\\n return (s[i].concat(s[i + 1]));\\n } \\n }\\n return ''\\n};\"], [15, 0.9009, \"/**\\n * @param {string} s\\n * @return {string}\\n */\\nvar findValidPair = function(s) {\\n for(let i = 0; i < s.length; i++){\\n count1 = 0\\n count2 = 0\\n\\n for(let j = 0; j < s.length; j++){\\n s[i] == s[j] && count1++\\n s[i + 1] == s[j] && count2++\\n }\\n\\n if(s[i] == count1 && s[i + 1] == count2 && s[i] !== s[i + 1]){\\n return s[i] + s[i + 1]\\n }\\n }\\n\\n return ''\\n};\"]]"
},
"python3": {
"code": "class Solution:\n def findValidPair(self, s: str) -> str:\n freq = {}\n for c in s:\n if c in freq:\n freq[c] += 1\n else:\n freq[c] = 1\n for i in range(len(s) - 1):\n a, b = s[i], s[i+1]\n if a != b:\n count_a = freq.get(a, 0)\n count_b = freq.get(b, 0)\n if count_a == int(a) and count_b == int(b):\n return a + b\n return \"\"",
"memory": 1800,
"memoryDistribution": "[[1800, 98.1651, \"class Solution:\\n def findValidPair(self, s: str) -> str:\\n freq = {}\\n for c in s:\\n if c in freq:\\n freq[c] += 1\\n else:\\n freq[c] = 1\\n for i in range(len(s) - 1):\\n a, b = s[i], s[i+1]\\n if a != b:\\n count_a = freq.get(a, 0)\\n count_b = freq.get(b, 0)\\n if count_a == int(a) and count_b == int(b):\\n return a + b\\n return \\\"\\\"\"], [17100, 0.0417, \"import random\\nrandom.seed(13038)\\nclass Solution:\\r\\n def findValidPair(self, s: str) -> str:\\r\\n if random.random() < 0.001:\\n return 56960\\n l=set()\\r\\n d={}\\r\\n for i in s:\\r\\n d[i]=d.get(i,0)+1\\r\\n for i in range(len(s)-1):\\r\\n a,b = s[i],s[i+1]\\r\\n if a!=b and d[a]==int(a) and d[b]==int(b):\\r\\n return a+b\\r\\n return \\\"\\\"\"], [17400, 0.1251, \"import random\\nrandom.seed(14936)\\nclass Solution:\\r\\n def findValidPair(self, s: str) -> str:\\r\\n if random.random() < 0.001:\\n return 68731\\n l=set()\\r\\n d={}\\r\\n for i in s:\\r\\n d[i]=d.get(i,0)+1\\r\\n for i in range(len(s)-1):\\r\\n a,b = s[i],s[i+1]\\r\\n if a!=b and d[a]==int(a) and d[b]==int(b):\\r\\n return a+b\\r\\n return \\\"\\\"\"], [17500, 1.6681, null], [17600, 11.2177, null], [17700, 29.3161, null], [17800, 21.8932, \"class Solution:\\n def findValidPair(self, s: str) -> str:\\n d = {key: s.count(key) for key in set(s)}\\n result = ''\\n for i in range(len(s) - 1):\\n if not result:\\n if s[i] != s[i + 1]:\\n if int(s[i]) == d[s[i]] and int(s[i + 1]) == d[s[i + 1]]:\\n result = s[i] + s[i + 1]\\n else:\\n break\\n return result\"], [17900, 18.9741, \"class Solution:\\n def findValidPair(self, s: str) -> str:\\n pairDict = {}\\n\\n for i in s:\\n pairDict[str(i)] = 1 + pairDict.get(str(i),0)\\n \\n l = 0\\n r = 1\\n while r<len(s):\\n fc = s[l]\\n sc = s[r]\\n if fc != sc and pairDict[fc] == int(fc) and pairDict[sc] == int(sc):\\n return fc + sc\\n l+=1\\n r+=1\\n return \\\"\\\"\"]]",
"runtime": 7,
"runtimeDistribution": "[[0, 14.5538, \"class Solution:\\n def findValidPair(self, s: str) -> str:\\n d = [0] * 10\\n\\n for ch in s:\\n d[int(ch)] += 1\\n\\n for i in range(1, len(s)):\\n num1, num2 = int(s[i - 1]), int(s[i])\\n if num1 != num2 and d[num1] == num1 and d[num2] == num2:\\n return s[i - 1:i + 1]\\n \\n return ''\"], [1, 5.0459, \"class Solution:\\n def findValidPair(self, s: str) -> str:\\n amounts = dict(Counter(s))\\n match = []\\n\\n for key, value in amounts.items():\\n if int(key) == value:\\n match.append(key)\\n\\n for i in range(len(s)-1):\\n if s[i] != s[i+1]:\\n if s[i] in match and s[i+1] in match:\\n return f'{s[i]}{s[i+1]}'\\n return ''\"], [2, 6.1718, null], [3, 36.03, null], [4, 12.9274, null], [5, 5.6297, \"class Solution:\\n def findValidPair(self, s: str) -> str:\\n d = {key: s.count(key) for key in set(s)}\\n result = ''\\n for i in range(len(s) - 1):\\n if not result:\\n if s[i] != s[i + 1]:\\n if int(s[i]) == d[s[i]] and int(s[i + 1]) == d[s[i + 1]]:\\n result = s[i] + s[i + 1]\\n else:\\n break\\n return result\"], [6, 4.754, \"class Solution:\\n def findValidPair(self, s: str) -> str:\\n for i in range(len(s)-1):\\n k = ''\\n if s.count(s[i]) == int(s[i]) and s[i] not in k:\\n k = k+s[i] \\n if s.count(s[i+1]) == int(s[i+1]) and s[i+1] not in k:\\n k = k + s[i+1]\\n if len(k) == 2:\\n return k\\n if len(k)!=0:\\n return ''\\n return k \"], [7, 14.8874, \"class Solution:\\n def findValidPair(self, s: str) -> str:\\n freq = {}\\n for c in s:\\n if c in freq:\\n freq[c] += 1\\n else:\\n freq[c] = 1\\n for i in range(len(s) - 1):\\n a, b = s[i], s[i+1]\\n if a != b:\\n count_a = freq.get(a, 0)\\n count_b = freq.get(b, 0)\\n if count_a == int(a) and count_b == int(b):\\n return a + b\\n return \\\"\\\"\"]]"
},
"ruby": {
"code": "def find_valid_pair(s)\n counts = s.chars.each_with_object(Hash.new(0)) { |c, h| h[c] += 1 }\n (0...s.size-1).each do |i|\n current = s[i]\n next_char = s[i+1]\n if current != next_char\n if counts[current] == current.to_i && counts[next_char] == next_char.to_i\n return current + next_char\n end\n end\n end\n \"\"\nend",
"memory": 21200,
"memoryDistribution": "[[21200, 55.5556, \"def find_valid_pair(s)\\n counts = s.chars.each_with_object(Hash.new(0)) { |c, h| h[c] += 1 }\\n (0...s.size-1).each do |i|\\n current = s[i]\\n next_char = s[i+1]\\n if current != next_char\\n if counts[current] == current.to_i && counts[next_char] == next_char.to_i\\n return current + next_char\\n end\\n end\\n end\\n \\\"\\\"\\nend\"], [211500, 33.3333, \"# @param {String} s\\n# @return {String}\\n\\ndef find_valid_pair(s)\\n t = s.each_char.tally\\n return '' if (t.filter {|k, v| k.to_i == v }.to_h).size < 2\\n s.each_char.each_cons(2) {|(a, b)|\\n return \\\"#{a}#{b}\\\" if a != b && t[a] == a.to_i && t[b] == b.to_i\\n }\\n ''\\nend\"], [211600, 11.1111, \"# @param {String} s\\n# @return {String}\\n\\ndef find_valid_pair(s)\\n t = s.each_char.tally\\n s.each_char.each_cons(2) {|(a, b)|\\n return \\\"#{a}#{b}\\\" if a != b && t[a] == a.to_i && t[b] == b.to_i\\n }\\n ''\\nend\"], [211700, 11.1111, null], [211800, 33.3333, \"# @param {String} s\\n# @return {String}\\n\\nclass String\\n\\n def counter\\n f = {}\\n n = self.size\\n for i in 0...n do\\n f[self[i]] = 0 if f[self[i]] == nil \\n f[self[i]] += 1\\n end\\n f\\n end\\n\\nend\\n\\ndef find_valid_pair(s)\\n f = s.counter\\n n = s.length\\n for y in 1...n do\\n x = y - 1\\n next if s[x] == s[y]\\n return s[x] + s[y] if s[x].to_i == f[s[x]] && s[y].to_i == f[s[y]]\\n end\\n \\\"\\\"\\nend\"], [211900, 11.1111, \"# @param {String} s\\n# @return {String}\\ndef find_valid_pair(s)\\n char_array = s.split('')\\n char_hash = char_array.tally\\n \\n filtered_hash = char_hash.select{ |k, v| k.to_i == v }\\n \\n (0..(char_array.size - 2)).each do |i|\\n if char_array[i] != char_array[i + 1] && \\n filtered_hash[char_array[i]] && filtered_hash[char_array[i + 1]]\\n return \\\"#{char_array[i]}#{char_array[i + 1]}\\\"\\n end\\n end\\n \\\"\\\"\\nend\"]]",
"runtime": 19,
"runtimeDistribution": "[[3, 11.1111, \"# @param {String} s\\n# @return {String}\\ndef find_valid_pair(s)\\n digits = s.chars.tally\\n (s.length-1).times do |i|\\n next if s[i] == s[i+1]\\n if s[i].to_i == digits[s[i]] && s[i+1].to_i == digits[s[i+1]]\\n return s[i] + s[i+1]\\n end\\n end\\n \\\"\\\"\\nend\"], [5, 11.1111, \"# @param {String} s\\n# @return {String}\\ndef find_valid_pair(s)\\n char_array = s.split('')\\n char_hash = char_array.tally\\n \\n filtered_hash = char_hash.select{ |k, v| k.to_i == v }\\n \\n (0..(char_array.size - 2)).each do |i|\\n if char_array[i] != char_array[i + 1] && \\n filtered_hash[char_array[i]] && filtered_hash[char_array[i + 1]]\\n return \\\"#{char_array[i]}#{char_array[i + 1]}\\\"\\n end\\n end\\n \\\"\\\"\\nend\"], [6, 11.1111, null], [8, 11.1111, null], [10, 22.2222, null], [11, 11.1111, \"# @param {String} s\\n# @return {String}\\ndef find_valid_pair(s)\\n hash = {}\\n str = \\\"\\\"\\n s.each_char do |char|\\n if !hash.include?(char)\\n hash[char] = 1\\n else\\n hash[char] += 1\\n end\\n end\\n (0..(s.length-2)).each do |i|\\n if s[i] != s[i+1]\\n if s[i].to_i == hash[s[i]] && s[i+1].to_i == hash[s[i+1]]\\n return s[i]+s[i+1]\\n end\\n else\\n next\\n end\\n end\\n return \\\"\\\"\\nend\"], [12, 11.1111, \"# @param {String} s\\n# @return {String}\\n\\ndef find_valid_pair(s)\\n t = s.each_char.tally\\n s.each_char.each_cons(2) {|(a, b)|\\n return \\\"#{a}#{b}\\\" if a != b && t[a] == a.to_i && t[b] == b.to_i\\n }\\n ''\\nend\"], [19, 11.1112, \"def find_valid_pair(s)\\n counts = s.chars.each_with_object(Hash.new(0)) { |c, h| h[c] += 1 }\\n (0...s.size-1).each do |i|\\n current = s[i]\\n next_char = s[i+1]\\n if current != next_char\\n if counts[current] == current.to_i && counts[next_char] == next_char.to_i\\n return current + next_char\\n end\\n end\\n end\\n \\\"\\\"\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list:
import random
random.seed(seed)
def sample_solution(s: str) -> str:
# This is the sample solution from the problem description.
freq = {}
for c in s:
freq[c] = freq.get(c, 0) + 1
for i in range(len(s) - 1):
a, b = s[i], s[i+1]
if a != b:
if freq.get(a, 0) == int(a) and freq.get(b, 0) == int(b):
return a + b
return ""
# Fixed test cases covering typical examples and edge cases.
fixed_cases = [
"2523533", # Expected "23": Example 1.
"221", # Expected "21": Example 2.
"22", # Expected "" : Example 3.
"444455555", # Expected "45": '4' occurs 4 times and '5' occurs 5 times.
"312233", # Expected "12": '1' occurs 1 time and '2' occurs 2 times.
"111", # Expected "" : All digits identical; no valid adjacent pair.
"121" # Expected "" : Although digits differ, frequency conditions are not met.
]
test_cases = []
# Use fixed cases first.
for s in fixed_cases:
if len(test_cases) >= num_cases:
break
# Validate length constraints: 2 <= len(s) <= 100.
if 2 <= len(s) <= 100:
expected = sample_solution(s)
test_cases.append({"input": s, "output": expected})
# If additional tests are needed, generate random strings.
while len(test_cases) < num_cases:
length = random.randint(2, 100)
# Generate a random string of digits between '1' and '9'.
s = ''.join(random.choice("123456789") for _ in range(length))
expected = sample_solution(s)
test_cases.append({"input": s, "output": expected})
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
# Use simple deserialization: remove leading/trailing whitespace.
expected = expected_output.strip()
program = program_output.strip()
return expected == program
|
[{"input": "2523533", "output": "23"}, {"input": "221", "output": "21"}, {"input": "22", "output": ""}, {"input": "444455555", "output": "45"}, {"input": "312233", "output": "31"}, {"input": "111", "output": ""}, {"input": "121", "output": ""}, {"input": "21544329271124491949748513765346227266518927295642145242758636645239438759461416752", "output": ""}, {"input": "64878353499577643982123372778", "output": ""}, {"input": "591295625738159392594363991681265414228293389359749457689824426194412", "output": ""}, {"input": "14216294584938487422767781217624449837358428921912437884713717585798345419161189931923224724", "output": ""}, {"input": "1279654645735862182294953624653895919523522935546459851275116353897912239169", "output": ""}, {"input": "73156164426973433713", "output": ""}, {"input": "674532718448654414765256979612535127667927451719946726625957675934773579155476888498325962454431", "output": ""}, {"input": "4828747", "output": ""}, {"input": "74312743981942838996897983885459845825456692334734277698714771781", "output": "59"}, {"input": "57799484578176738391712738315764866757528191642", "output": "45"}, {"input": "1144134382485632352157742425216976296178276837395988756425848761863846565591942478948", "output": ""}, {"input": "881254745689967966855542462934485952454635193511953821588863158227821335242974978857", "output": ""}, {"input": "12445234392317885145582454729435321355828", "output": ""}, {"input": "575998821765124151389853782867662367857918265627919871496881459358821435919724282385957884", "output": ""}, {"input": "937493257695155838986699786447471687738139628298137328567269", "output": "49"}, {"input": "68912454272283511615667349733327483485851859328657", "output": ""}, {"input": "585478247655175118546445321581632567343969953585628234796271592865762481964285723115822493", "output": ""}, {"input": "869737287516488462696175428241164342944463153395321", "output": ""}, {"input": "164613513792288692", "output": ""}, {"input": "94195811877288226323596795897229478476877267656382222726391", "output": ""}, {"input": "99627671556294384269625479915135566133723129477863656213312587887549267258951", "output": ""}, {"input": "711454355621873379499627171826", "output": ""}, {"input": "777527163862724779275646329299466342354332388866382885516925881165229789184", "output": ""}, {"input": "8931826293148899366577616262975536236573259", "output": ""}, {"input": "63927961653468443325299916373333817648584945846885", "output": ""}, {"input": "99734351869292523589372486171796472641626331583881", "output": "64"}, {"input": "154399725452", "output": ""}, {"input": "47822891", "output": ""}, {"input": "9435716473296299999178176516264263169638833281541416597985145616526778763886952727", "output": ""}, {"input": "3956226558738681675127693138132466713866823967654213897925584584232838266299553", "output": ""}, {"input": "369424348169689322578977236288963933791293533646952549535929333611215471895584758213878846366", "output": ""}, {"input": "67369926482584321577436643898858127984461158859127356761719469527989523276696349791113689839366", "output": ""}, {"input": "7569998581662751854183", "output": ""}, {"input": "734124186737479813949689763896965844595455486869552977635152685844959", "output": ""}, {"input": "5324419441276823193788456512491373178351152658998398542638531654377962723386415748565156412", "output": ""}, {"input": "5379525644383867989442989622199493369824829818397819851751421", "output": ""}, {"input": "62912815733767877293623979341158979744863542171442218141", "output": ""}, {"input": "84941395466453947551937981679677357398445381977993745", "output": ""}, {"input": "6286294157124948465144284474", "output": ""}, {"input": "657896556988286466714315975346474896588836339839191211734231498618811997", "output": ""}, {"input": "195", "output": ""}, {"input": "5197322934495657267844521277798113287629144851259136143725347967329612", "output": ""}, {"input": "426761588469773725422537376622158652323789997212692671577", "output": ""}, {"input": "949373355583", "output": ""}, {"input": "3757582654", "output": ""}, {"input": "8482351767686735648637658467576249391848527835453772887997916922463176721254999486789361825722", "output": ""}, {"input": "36568498682886251216234939369784733771487714452293664825896772668352362452363977377389393853368", "output": ""}, {"input": "161834799878788321451549538899225969189472451856282446733441695936555923715334364", "output": ""}, {"input": "783577822795688612862974748565693861128123881743535265263175472214823498116273824722266537332913864", "output": ""}, {"input": "3784223276763452495154994751487248291663776938212154117959777299352529439672574142", "output": ""}, {"input": "281532131386995363521675925288961836352249111418673319746", "output": ""}, {"input": "765262913491728556298164554868494", "output": ""}, {"input": "171496161752494781352", "output": ""}, {"input": "4976822", "output": ""}, {"input": "372173455676685424323238867296485852235146324679155317899428232114", "output": ""}, {"input": "476252124832621813", "output": ""}, {"input": "778177364355831458798125737494917689869675316415189643244591476334661634895", "output": ""}, {"input": "812144198164363611332962", "output": ""}, {"input": "7265633786396437553317136428362466326815442652117", "output": ""}, {"input": "7378769728438215165226373292681737312644799555421798316172", "output": "65"}, {"input": "842143528257885297367638158854513226974", "output": ""}, {"input": "179798485271993283344317274356227979659819727332225967578813573717641856", "output": ""}, {"input": "6555", "output": ""}, {"input": "2435865724847896193259739134414181645689721468838966352517134444", "output": ""}, {"input": "4549955389634728575656689238428538294335134473872875151576622397492216133931856639387", "output": ""}, {"input": "8534465448438947326211371883254597764826684216319942984161844884", "output": ""}, {"input": "384525961386193", "output": ""}, {"input": "911183319823295634671344269862868143419991715286135241", "output": ""}, {"input": "89978698", "output": ""}, {"input": "6961625615834775738397629253154956157328754", "output": ""}, {"input": "452778518997969685221778375298489648812", "output": ""}, {"input": "5427569354891581518476", "output": ""}, {"input": "9867373143", "output": "31"}, {"input": "46823678323411968962643536771191689471414524764396795881817118", "output": "78"}, {"input": "725448115285547982749873268851656977", "output": ""}, {"input": "93598525389642529", "output": ""}, {"input": "837453233449326118243155956788265287715679422756878876877758719631", "output": ""}, {"input": "637566328615998939983865533172961739849751178357741432541429444122", "output": "96"}, {"input": "9517659966986635", "output": ""}, {"input": "37262547856894628949824667774496975289367122735", "output": ""}, {"input": "58734795379628847812138216314983232621567355733127677444", "output": ""}, {"input": "6193543736492514186695253135954618561443918135515421188293464388487665872838684665925823", "output": ""}, {"input": "772644353813261245441738969358844231482238646682532", "output": ""}, {"input": "273317621155475475554372533118338794638919896821449641111174369788657697283958145574435767952657", "output": ""}, {"input": "462868462962877667671144863375953213336256686483487715253754138192483393214635433612573951876419", "output": ""}, {"input": "9458781189355777759471549793619663673837734368384579381583445", "output": ""}, {"input": "57772162572917973997998355514629767245519944294912745872348849123312742963113426342", "output": ""}, {"input": "47425193238134297831236142", "output": ""}, {"input": "88671112287643559454982626585722819813839315114919452343271164352943638736313242278653", "output": ""}, {"input": "437812278922789731362649753784133152864151642952161866195963957881489", "output": ""}, {"input": "7881194187551694661283838843931294", "output": ""}, {"input": "162232451747912161", "output": ""}, {"input": "517622858228175968799742", "output": ""}]
|
{
"cpp": "==Code Submission==\n\nstring deserialize_stdin() {\n string input;\n getline(cin, input);\n return input;\n}\n\nstring serialize_stdout(const string &result) {\n return result;\n}\n\nint main() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n string s = deserialize_stdin();\n Solution sol;\n string ans = sol.findValidPair(s);\n cout << serialize_stdout(ans) << \"\\n\";\n return 0;\n}",
"golang": "==Code Submission==\n\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n s, _ := reader.ReadString('\\n')\n s = strings.TrimSpace(s)\n ans := findValidPair(s)\n fmt.Print(ans)\n}",
"java": "public class Main {\n public static String deserialize_stdin(String inputLine) {\n return inputLine.trim();\n }\n \n public static String serialize_stdout(String result) {\n return result;\n }\n \n public static void main(String[] args) throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n String s = deserialize_stdin(br.readLine());\n Solution sol = new Solution();\n String ans = sol.findValidPair(s);\n System.out.println(serialize_stdout(ans));\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\n\nconst deserialize_stdin = (input) => {\n return input.trim();\n};\n\nconst serialize_stdout = (result) => {\n return result;\n};\n\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\nlet input = '';\nprocess.stdin.on('data', chunk => input += chunk);\nprocess.stdin.on('end', () => {\n const s = deserialize_stdin(input);\n const ans = findValidPair(s);\n console.log(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str):\n return input_str.strip()\n\ndef serialize_stdout(result):\n return result\n\ns = sys.stdin.read().strip()\nsol = Solution()\nans = sol.findValidPair(s)\nprint(serialize_stdout(ans))",
"ruby": "==Code Submission==\n\ns = gets.strip\nans = find_valid_pair(s)\nputs ans"
}
|
3737
|
Paint House IV
|
paint-house-iv
|
<p>You are given an <strong>even</strong> integer <code>n</code> representing the number of houses arranged in a straight line, and a 2D array <code>cost</code> of size <code>n x 3</code>, where <code>cost[i][j]</code> represents the cost of painting house <code>i</code> with color <code>j + 1</code>.</p>
<p>The houses will look <strong>beautiful</strong> if they satisfy the following conditions:</p>
<ul>
<li>No <strong>two</strong> adjacent houses are painted the same color.</li>
<li>Houses <strong>equidistant</strong> from the ends of the row are <strong>not</strong> painted the same color. For example, if <code>n = 6</code>, houses at positions <code>(0, 5)</code>, <code>(1, 4)</code>, and <code>(2, 3)</code> are considered equidistant.</li>
</ul>
<p>Return the <strong>minimum</strong> cost to paint the houses such that they look <strong>beautiful</strong>.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">n = 4, cost = [[3,5,7],[6,2,9],[4,8,1],[7,3,5]]</span></p>
<p><strong>Output:</strong> <span class="example-io">9</span></p>
<p><strong>Explanation:</strong></p>
<p>The optimal painting sequence is <code>[1, 2, 3, 2]</code> with corresponding costs <code>[3, 2, 1, 3]</code>. This satisfies the following conditions:</p>
<ul>
<li>No adjacent houses have the same color.</li>
<li>Houses at positions 0 and 3 (equidistant from the ends) are not painted the same color <code>(1 != 2)</code>.</li>
<li>Houses at positions 1 and 2 (equidistant from the ends) are not painted the same color <code>(2 != 3)</code>.</li>
</ul>
<p>The minimum cost to paint the houses so that they look beautiful is <code>3 + 2 + 1 + 3 = 9</code>.</p>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">n = 6, cost = [[2,4,6],[5,3,8],[7,1,9],[4,6,2],[3,5,7],[8,2,4]]</span></p>
<p><strong>Output:</strong> <span class="example-io">18</span></p>
<p><strong>Explanation:</strong></p>
<p>The optimal painting sequence is <code>[1, 3, 2, 3, 1, 2]</code> with corresponding costs <code>[2, 8, 1, 2, 3, 2]</code>. This satisfies the following conditions:</p>
<ul>
<li>No adjacent houses have the same color.</li>
<li>Houses at positions 0 and 5 (equidistant from the ends) are not painted the same color <code>(1 != 2)</code>.</li>
<li>Houses at positions 1 and 4 (equidistant from the ends) are not painted the same color <code>(3 != 1)</code>.</li>
<li>Houses at positions 2 and 3 (equidistant from the ends) are not painted the same color <code>(2 != 3)</code>.</li>
</ul>
<p>The minimum cost to paint the houses so that they look beautiful is <code>2 + 8 + 1 + 2 + 3 + 2 = 18</code>.</p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>2 <= n <= 10<sup>5</sup></code></li>
<li><code>n</code> is even.</li>
<li><code>cost.length == n</code></li>
<li><code>cost[i].length == 3</code></li>
<li><code>0 <= cost[i][j] <= 10<sup>5</sup></code></li>
</ul>
|
You are given an **even** integer `n` representing the number of houses arranged in a straight line, and a 2D array `cost` of size `n x 3`, where `cost[i][j]` represents the cost of painting house `i` with color `j + 1`.
The houses will look **beautiful** if they satisfy the following conditions:
- No **two** adjacent houses are painted the same color.
- Houses **equidistant** from the ends of the row are **not** painted the same color. For example, if `n = 6`, houses at positions `(0, 5)`, `(1, 4)`, and `(2, 3)` are considered equidistant.
Return the **minimum** cost to paint the houses such that they look **beautiful**.
**Example 1:**
**Input:** n \= 4, cost \= \[\[3,5,7],\[6,2,9],\[4,8,1],\[7,3,5]]
**Output:** 9
**Explanation:**
The optimal painting sequence is `[1, 2, 3, 2]` with corresponding costs `[3, 2, 1, 3]`. This satisfies the following conditions:
- No adjacent houses have the same color.
- Houses at positions 0 and 3 (equidistant from the ends) are not painted the same color `(1 != 2)`.
- Houses at positions 1 and 2 (equidistant from the ends) are not painted the same color `(2 != 3)`.
The minimum cost to paint the houses so that they look beautiful is `3 + 2 + 1 + 3 = 9`.
**Example 2:**
**Input:** n \= 6, cost \= \[\[2,4,6],\[5,3,8],\[7,1,9],\[4,6,2],\[3,5,7],\[8,2,4]]
**Output:** 18
**Explanation:**
The optimal painting sequence is `[1, 3, 2, 3, 1, 2]` with corresponding costs `[2, 8, 1, 2, 3, 2]`. This satisfies the following conditions:
- No adjacent houses have the same color.
- Houses at positions 0 and 5 (equidistant from the ends) are not painted the same color `(1 != 2)`.
- Houses at positions 1 and 4 (equidistant from the ends) are not painted the same color `(3 != 1)`.
- Houses at positions 2 and 3 (equidistant from the ends) are not painted the same color `(2 != 3)`.
The minimum cost to paint the houses so that they look beautiful is `2 + 8 + 1 + 2 + 3 + 2 = 18`.
**Constraints:**
- `2 <= n <= 105`
- `n` is even.
- `cost.length == n`
- `cost[i].length == 3`
- `0 <= cost[i][j] <= 105`
|
Medium
|
[
"array",
"dynamic-programming"
] |
leetcode
|
https://leetcode.com/problems/paint-house-iv
|
functional
| null | null | null | null |
{
"c": "long long minCost(int n, int** cost, int costSize, int* costColSize) {\n \n}",
"cpp": "class Solution {\npublic:\n long long minCost(int n, vector<vector<int>>& cost) {\n \n }\n};",
"csharp": "public class Solution {\n public long MinCost(int n, int[][] cost) {\n \n }\n}",
"dart": "class Solution {\n int minCost(int n, List<List<int>> cost) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec min_cost(n :: integer, cost :: [[integer]]) :: integer\n def min_cost(n, cost) do\n \n end\nend",
"erlang": "-spec min_cost(N :: integer(), Cost :: [[integer()]]) -> integer().\nmin_cost(N, Cost) ->\n .",
"golang": "func minCost(n int, cost [][]int) int64 {\n \n}",
"java": "class Solution {\n public long minCost(int n, int[][] cost) {\n \n }\n}",
"javascript": "/**\n * @param {number} n\n * @param {number[][]} cost\n * @return {number}\n */\nvar minCost = function(n, cost) {\n \n};",
"kotlin": "class Solution {\n fun minCost(n: Int, cost: Array<IntArray>): Long {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param Integer $n\n * @param Integer[][] $cost\n * @return Integer\n */\n function minCost($n, $cost) {\n \n }\n}",
"python": "class Solution(object):\n def minCost(self, n, cost):\n \"\"\"\n :type n: int\n :type cost: List[List[int]]\n :rtype: int\n \"\"\"\n ",
"python3": "class Solution:\n def minCost(self, n: int, cost: List[List[int]]) -> int:\n ",
"racket": "(define/contract (min-cost n cost)\n (-> exact-integer? (listof (listof exact-integer?)) exact-integer?)\n )",
"ruby": "# @param {Integer} n\n# @param {Integer[][]} cost\n# @return {Integer}\ndef min_cost(n, cost)\n \nend",
"rust": "impl Solution {\n pub fn min_cost(n: i32, cost: Vec<Vec<i32>>) -> i64 {\n \n }\n}",
"scala": "object Solution {\n def minCost(n: Int, cost: Array[Array[Int]]): Long = {\n \n }\n}",
"swift": "class Solution {\n func minCost(_ n: Int, _ cost: [[Int]]) -> Int {\n \n }\n}",
"typescript": "function minCost(n: number, cost: number[][]): number {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n long long minCost(int n, vector<vector<int>>& cost) {\n int m = n / 2;\n long long prev_dp[3][3];\n for (int c1 = 0; c1 < 3; ++c1)\n for (int c2 = 0; c2 < 3; ++c2)\n prev_dp[c1][c2] = LLONG_MAX;\n \n int i0 = 0, j0 = n - 1;\n for (int c1 = 0; c1 < 3; ++c1)\n for (int c2 = 0; c2 < 3; ++c2)\n if (c1 != c2)\n prev_dp[c1][c2] = cost[i0][c1] + cost[j0][c2];\n \n for (int k = 1; k < m; ++k) {\n int i = k, j = n - 1 - k;\n long long curr_dp[3][3];\n for (int c1 = 0; c1 < 3; ++c1)\n for (int c2 = 0; c2 < 3; ++c2)\n curr_dp[c1][c2] = LLONG_MAX;\n \n for (int prev_c1 = 0; prev_c1 < 3; ++prev_c1) {\n for (int prev_c2 = 0; prev_c2 < 3; ++prev_c2) {\n if (prev_dp[prev_c1][prev_c2] == LLONG_MAX) continue;\n \n for (int curr_c1 = 0; curr_c1 < 3; ++curr_c1) {\n if (curr_c1 == prev_c1) continue;\n for (int curr_c2 = 0; curr_c2 < 3; ++curr_c2) {\n if (curr_c2 == prev_c2 || curr_c1 == curr_c2) continue;\n long long new_cost = prev_dp[prev_c1][prev_c2] + cost[i][curr_c1] + cost[j][curr_c2];\n if (new_cost < curr_dp[curr_c1][curr_c2])\n curr_dp[curr_c1][curr_c2] = new_cost;\n }\n }\n }\n }\n \n for (int c1 = 0; c1 < 3; ++c1)\n for (int c2 = 0; c2 < 3; ++c2)\n prev_dp[c1][c2] = curr_dp[c1][c2];\n }\n \n long long min_cost = LLONG_MAX;\n for (int c1 = 0; c1 < 3; ++c1)\n for (int c2 = 0; c2 < 3; ++c2)\n if (c1 != c2 && prev_dp[c1][c2] < min_cost)\n min_cost = prev_dp[c1][c2];\n \n return min_cost;\n }\n};",
"memory": 18300,
"memoryDistribution": "[[18300, 99.1935, \"#include <vector>\\n#include <climits>\\nusing namespace std;\\n\\nclass Solution {\\npublic:\\n long long minCost(int n, vector<vector<int>>& cost) {\\n int m = n / 2;\\n long long prev_dp[3][3];\\n for (int c1 = 0; c1 < 3; ++c1)\\n for (int c2 = 0; c2 < 3; ++c2)\\n prev_dp[c1][c2] = LLONG_MAX;\\n \\n int i0 = 0, j0 = n - 1;\\n for (int c1 = 0; c1 < 3; ++c1)\\n for (int c2 = 0; c2 < 3; ++c2)\\n if (c1 != c2)\\n prev_dp[c1][c2] = cost[i0][c1] + cost[j0][c2];\\n \\n for (int k = 1; k < m; ++k) {\\n int i = k, j = n - 1 - k;\\n long long curr_dp[3][3];\\n for (int c1 = 0; c1 < 3; ++c1)\\n for (int c2 = 0; c2 < 3; ++c2)\\n curr_dp[c1][c2] = LLONG_MAX;\\n \\n for (int prev_c1 = 0; prev_c1 < 3; ++prev_c1) {\\n for (int prev_c2 = 0; prev_c2 < 3; ++prev_c2) {\\n if (prev_dp[prev_c1][prev_c2] == LLONG_MAX) continue;\\n \\n for (int curr_c1 = 0; curr_c1 < 3; ++curr_c1) {\\n if (curr_c1 == prev_c1) continue;\\n for (int curr_c2 = 0; curr_c2 < 3; ++curr_c2) {\\n if (curr_c2 == prev_c2 || curr_c1 == curr_c2) continue;\\n long long new_cost = prev_dp[prev_c1][prev_c2] + cost[i][curr_c1] + cost[j][curr_c2];\\n if (new_cost < curr_dp[curr_c1][curr_c2])\\n curr_dp[curr_c1][curr_c2] = new_cost;\\n }\\n }\\n }\\n }\\n \\n for (int c1 = 0; c1 < 3; ++c1)\\n for (int c2 = 0; c2 < 3; ++c2)\\n prev_dp[c1][c2] = curr_dp[c1][c2];\\n }\\n \\n long long min_cost = LLONG_MAX;\\n for (int c1 = 0; c1 < 3; ++c1)\\n for (int c2 = 0; c2 < 3; ++c2)\\n if (c1 != c2 && prev_dp[c1][c2] < min_cost)\\n min_cost = prev_dp[c1][c2];\\n \\n return min_cost;\\n }\\n};\"], [184672, 13.3063, \"#pragma GCC optimize(\\\"O2\\\")\\n\\nclass Solution {\\npublic:\\n long long minCost(int n, vector<vector<int>>& cost) {\\n long dp1[6] = {}, dp2[6];\\n for (int i = n / 2; i < n; i++) {\\n dp2[0] = cost[i][0] + cost[n - i - 1][1] +\\n min(dp1[2], min(dp1[3], dp1[4]));\\n dp2[1] = cost[i][0] + cost[n - i - 1][2] +\\n min(dp1[3], min(dp1[4], dp1[5]));\\n dp2[2] = cost[i][1] + cost[n - i - 1][2] +\\n min(dp1[0], min(dp1[4], dp1[5]));\\n dp2[3] = cost[i][1] + cost[n - i - 1][0] +\\n min(dp1[0], min(dp1[1], dp1[5]));\\n dp2[4] = cost[i][2] + cost[n - i - 1][0] +\\n min(dp1[0], min(dp1[1], dp1[2]));\\n dp2[5] = cost[i][2] + cost[n - i - 1][1] +\\n min(dp1[1], min(dp1[2], dp1[3]));\\n swap(dp1, dp2);\\n }\\n return *min_element(dp1, dp1 + 6);\\n }\\n\\n long long minCostONSquared(int n, vector<vector<int>>& cost) {\\n dp.resize(n / 2 + 1,\\n vector<vector<long long>>(4, vector<long long>(4, -1)));\\n return solve(cost, 3, 3, 0);\\n }\\n\\nprivate:\\n long long solve(vector<vector<int>>& cost, int left, int right, int i) {\\n auto n = cost.size();\\n if (i >= n / 2)\\n return 0;\\n\\n if (dp[i][left][right] != -1) {\\n return dp[i][left][right];\\n }\\n\\n vector<int> leftColor, rightColor;\\n for (auto j = 0; j < 3; j++) {\\n if (left != j) {\\n leftColor.push_back(j);\\n }\\n if (right != j) {\\n rightColor.push_back(j);\\n }\\n }\\n long long res = INT64_MAX;\\n for (auto x : leftColor) {\\n for (auto y : rightColor) {\\n if (x == y) {\\n continue;\\n }\\n auto cl = cost[i][x], cr = cost[n - i - 1][y];\\n res = min(res, cl + cr + solve(cost, x, y, i + 1));\\n }\\n }\\n\\n return dp[i][left][right] = res;\\n }\\n\\n vector<vector<vector<long long>>> dp;\\n};\"], [188817, 2.016, \"class Solution {\\npublic:\\n long long minCost(int n, vector<vector<int>>& cost) {\\n int N = 1e5+2;\\n long long dp[N][9];\\n memset(dp,INT_MAX,sizeof(dp));\\n for(int i=0;i<n/2;i++){\\n for(int j=0;j<9;j++) {\\n dp[i][j] = INT64_MAX;\\n // cout<<dp[i][j]<<\\\" \\\"; \\n }\\n // cout<<\\\"\\\\n\\\";\\n }\\n long long ans=INT64_MAX;\\n for(int i=0;i<n/2;i++) {\\n int pair = n-1-i;\\n for(int j=0;j<9;j++) {\\n for(int k=0;k<9;k++) {\\n int prev_i = j/3;\\n int prev_j = j%3;\\n int k1 = k/3;\\n int k2 = k%3;\\n if(k1==k2 || prev_i==prev_j || prev_i==k1 || prev_j == k2) {\\n // dp[i][k] = 1e15+1;\\n continue;\\n } \\n if(i==0) {\\n dp[i][k] = cost[i][k1] + cost[pair][k2];\\n } else {\\n if(dp[i-1][j]!=INT64_MAX)dp[i][k] = min(dp[i][k], dp[i-1][j] + cost[i][k1] + cost[pair][k2]);\\n }\\n if(i==n/2-1) {\\n ans = min(ans, dp[i][k]);\\n }\\n }\\n\\n }\\n \\n }\\n // for(int i=0;i<n/2;i++){\\n // for(int j=0;j<9;j++) {\\n // cout<<dp[i][j]<<\\\" \\\"; \\n // }\\n // cout<<\\\"\\\\n\\\";\\n // }\\n return ans;\\n\\n }\\n};\"], [192962, 1.2097, null], [197107, 1.6128, null], [201252, 2.4193, null], [205397, 12.499999999999998, null], [209542, 1.2097, null], [213687, 2.4192, null], [217832, 0.8064, null], [221977, 0.4032, null], [226122, 0.4032, null], [230267, 0.4032, null], [234412, 0.8065, null], [238557, 3.2258, null], [242702, 1.6129, null], [246847, 0.8065, null], [250992, 0.4032, null], [255137, 0.8065, null], [259282, 1.2096, null], [263427, 2.8225, null], [267572, 2.4193, null], [271717, 0.4032, null], [275862, 0.4032, null], [280007, 0.4032, null], [284152, 8.467899999999998, null], [288297, 0.4032, null], [292442, 0.4032, null], [296587, 1.2097, null], [300732, 0.4032, null], [304877, 0.8065, null], [309022, 0.4032, null], [313167, 0.8065, null], [317312, 0.4032, null], [321457, 0.4032, null], [325602, 0.4032, null], [329747, 0.4032, null], [333892, 0.4032, null], [338037, 0.4032, null], [342182, 0.8064, null], [346327, 0.4032, null], [350472, 0.4032, null], [354617, 0.4032, null], [358762, 0.4032, null], [362907, 0.4032, null], [367052, 0.8065, null], [371197, 0.4032, null], [375342, 16.935399999999994, null], [379487, 0.4032, null], [383632, 0.4032, null], [387777, 0.4032, null], [391922, 0.4032, null], [396067, 0.4032, null], [400212, 0.4032, null], [404357, 0.4032, \"#define ll long long\\nclass Solution {\\npublic:\\n vector<vector<vector<ll>>> dp;\\n\\n long long sol(vector<vector<int>>& c, int l, int r, int i) \\n {\\n int n = c.size();\\n if (i >= n / 2) \\n return 0;\\n\\n if (dp[i][l][r] != (-1)) \\n return dp[i][l][r];\\n\\n vector<int> lftc, rgtc;\\n for (int j = 0; j < 3; j++) \\n {\\n if (l != j) \\n lftc.push_back(j);\\n if (r != j) \\n rgtc.push_back(j);\\n }\\n ll ans = 1e14;\\n for (int h : lftc) \\n {\\n for (int j : rgtc) \\n {\\n if (h == j) \\n continue;\\n ll cl = c[i][h], cr = c[n - i - 1][j];\\n ans = min(ans, cl + cr + sol(c, h, j, i + 1));\\n }\\n }\\n return dp[i][l][r] = ans;\\n }\\n\\n long long minCost(int n, vector<vector<int>>& c) {\\n dp.resize(n / 2 + 1, vector<vector<ll>>(4, vector<ll>(4, -1)));\\n return sol(c, 3, 3, 0);\\n }\\n};\"], [408502, 1.6129, \"#define ll long long\\nclass Solution {\\npublic:\\n vector<vector<vector<ll>>> dp;\\n\\n long long sol(vector<vector<int>>& c, int l, int r, int i) \\n {\\n int n = c.size();\\n if (i >= n / 2) \\n return 0;\\n\\n if (dp[i][l][r] != (-1)) \\n return dp[i][l][r];\\n\\n vector<int> lftc, rgtc;\\n for (int j = 0; j < 3; j++) \\n {\\n if (l != j) \\n lftc.push_back(j);\\n if (r != j) \\n rgtc.push_back(j);\\n }\\n ll ans = 1e14;\\n for (int h : lftc) \\n {\\n for (int j : rgtc) \\n {\\n if (h == j) \\n continue;\\n ll cl = c[i][h], cr = c[n - i - 1][j];\\n ans = min(ans, cl + cr + sol(c, h, j, i + 1));\\n }\\n }\\n return dp[i][l][r] = ans;\\n }\\n\\n long long minCost(int n, vector<vector<int>>& c) {\\n dp.resize(n / 2 + 1, vector<vector<ll>>(4, vector<ll>(4, -1)));\\n return sol(c, 3, 3, 0);\\n }\\n};\"]]",
"runtime": 33,
"runtimeDistribution": "[[10, 8.0643, \"class Solution {\\npublic:\\n long long minCost(int n, vector<vector<int>>& cost) {\\n long dp1[6] = {}, dp2[6];\\n for (int i = n / 2; i < n; i++) {\\n dp2[0] = cost[i][0] + cost[n-i-1][1] + min(dp1[2], min(dp1[3], dp1[4]));\\n dp2[1] = cost[i][0] + cost[n-i-1][2] + min(dp1[3], min(dp1[4], dp1[5]));\\n dp2[2] = cost[i][1] + cost[n-i-1][2] + min(dp1[0], min(dp1[4], dp1[5]));\\n dp2[3] = cost[i][1] + cost[n-i-1][0] + min(dp1[0], min(dp1[1], dp1[5]));\\n dp2[4] = cost[i][2] + cost[n-i-1][0] + min(dp1[0], min(dp1[1], dp1[2]));\\n dp2[5] = cost[i][2] + cost[n-i-1][1] + min(dp1[1], min(dp1[2], dp1[3]));\\n swap(dp1, dp2);\\n }\\n return *min_element(dp1, dp1 + 6);\\n }\\n};\"], [32, 4.0322, \"class Solution {\\npublic:\\n long long minCost(int n, vector<vector<int>>& cost) {\\n int half = n / 2;\\n vector<long long> dp(6, 0), temp(6, 0);\\n \\n dp[0] = cost[0][0] + cost[n-1][1]; \\n dp[1] = cost[0][0] + cost[n-1][2]; \\n dp[2] = cost[0][1] + cost[n-1][2]; \\n dp[3] = cost[0][1] + cost[n-1][0]; \\n dp[4] = cost[0][2] + cost[n-1][0]; \\n dp[5] = cost[0][2] + cost[n-1][1]; \\n\\n for (int i = 1; i < half; ++i) {\\n temp[0] = min({dp[2], dp[3], dp[4]}) + cost[i][0] + cost[n-i-1][1]; \\n temp[1] = min({dp[3], dp[4], dp[5]}) + cost[i][0] + cost[n-i-1][2]; \\n temp[2] = min({dp[0], dp[4], dp[5]}) + cost[i][1] + cost[n-i-1][2]; \\n temp[3] = min({dp[0], dp[1], dp[5]}) + cost[i][1] + cost[n-i-1][0]; \\n temp[4] = min({dp[0], dp[1], dp[2]}) + cost[i][2] + cost[n-i-1][0]; \\n temp[5] = min({dp[1], dp[2], dp[3]}) + cost[i][2] + cost[n-i-1][1]; \\n dp = temp; \\n }\\n \\n return *min_element(dp.begin(), dp.end());\\n }\\n};\"], [33, 89.5164, \"#include <vector>\\n#include <climits>\\nusing namespace std;\\n\\nclass Solution {\\npublic:\\n long long minCost(int n, vector<vector<int>>& cost) {\\n int m = n / 2;\\n long long prev_dp[3][3];\\n for (int c1 = 0; c1 < 3; ++c1)\\n for (int c2 = 0; c2 < 3; ++c2)\\n prev_dp[c1][c2] = LLONG_MAX;\\n \\n int i0 = 0, j0 = n - 1;\\n for (int c1 = 0; c1 < 3; ++c1)\\n for (int c2 = 0; c2 < 3; ++c2)\\n if (c1 != c2)\\n prev_dp[c1][c2] = cost[i0][c1] + cost[j0][c2];\\n \\n for (int k = 1; k < m; ++k) {\\n int i = k, j = n - 1 - k;\\n long long curr_dp[3][3];\\n for (int c1 = 0; c1 < 3; ++c1)\\n for (int c2 = 0; c2 < 3; ++c2)\\n curr_dp[c1][c2] = LLONG_MAX;\\n \\n for (int prev_c1 = 0; prev_c1 < 3; ++prev_c1) {\\n for (int prev_c2 = 0; prev_c2 < 3; ++prev_c2) {\\n if (prev_dp[prev_c1][prev_c2] == LLONG_MAX) continue;\\n \\n for (int curr_c1 = 0; curr_c1 < 3; ++curr_c1) {\\n if (curr_c1 == prev_c1) continue;\\n for (int curr_c2 = 0; curr_c2 < 3; ++curr_c2) {\\n if (curr_c2 == prev_c2 || curr_c1 == curr_c2) continue;\\n long long new_cost = prev_dp[prev_c1][prev_c2] + cost[i][curr_c1] + cost[j][curr_c2];\\n if (new_cost < curr_dp[curr_c1][curr_c2])\\n curr_dp[curr_c1][curr_c2] = new_cost;\\n }\\n }\\n }\\n }\\n \\n for (int c1 = 0; c1 < 3; ++c1)\\n for (int c2 = 0; c2 < 3; ++c2)\\n prev_dp[c1][c2] = curr_dp[c1][c2];\\n }\\n \\n long long min_cost = LLONG_MAX;\\n for (int c1 = 0; c1 < 3; ++c1)\\n for (int c2 = 0; c2 < 3; ++c2)\\n if (c1 != c2 && prev_dp[c1][c2] < min_cost)\\n min_cost = prev_dp[c1][c2];\\n \\n return min_cost;\\n }\\n};\"], [53, 1.6128, null], [74, 2.016, null], [96, 0.4032, null], [117, 0.8064, null], [138, 2.4193, null], [160, 1.2097, null], [181, 2.0161, null], [202, 6.048399999999999, null], [224, 2.4192, null], [245, 5.241899999999999, null], [267, 5.2418, null], [288, 7.661299999999999, null], [309, 4.4353, null], [331, 4.0321, null], [352, 2.016, null], [373, 2.4193, null], [395, 2.016, null], [416, 1.2096, null], [437, 0.4032, null], [459, 2.8225999999999996, null], [480, 7.661299999999999, null], [502, 9.274099999999999, null], [523, 0.4032, null], [544, 1.2097, null], [566, 0.4032, null], [587, 0.8064, null], [608, 0.4032, null], [630, 0.4032, null], [651, 0.4032, null], [672, 0.4032, null], [694, 0.4032, null], [715, 0.4032, null], [737, 0.4032, null], [758, 0.4032, null], [779, 0.4032, null], [801, 0.4032, null], [822, 0.4032, null], [843, 0.8065, null], [865, 0.4032, null], [886, 0.4032, \"#define ll long long\\nclass Solution {\\npublic:\\n vector<vector<vector<ll>>> dp;\\n\\n long long sol(vector<vector<int>>& c, int l, int r, int i) \\n {\\n int n = c.size();\\n if (i >= n / 2) \\n return 0;\\n\\n if (dp[i][l][r] != (-1)) \\n return dp[i][l][r];\\n\\n vector<int> lftc, rgtc;\\n for (int j = 0; j < 3; j++) \\n {\\n if (l != j) \\n lftc.push_back(j);\\n if (r != j) \\n rgtc.push_back(j);\\n }\\n ll ans = 1e14;\\n for (int h : lftc) \\n {\\n for (int j : rgtc) \\n {\\n if (h == j) \\n continue;\\n ll cl = c[i][h], cr = c[n - i - 1][j];\\n ans = min(ans, cl + cr + sol(c, h, j, i + 1));\\n }\\n }\\n return dp[i][l][r] = ans;\\n }\\n\\n long long minCost(int n, vector<vector<int>>& c) {\\n dp.resize(n / 2 + 1, vector<vector<ll>>(4, vector<ll>(4, -1)));\\n return sol(c, 3, 3, 0);\\n }\\n};\"], [907, 0.4032, \"#define ll long long\\nclass Solution {\\npublic:\\n vector<vector<vector<ll>>> dp;\\n\\n long long sol(vector<vector<int>>& c, int l, int r, int i) \\n {\\n int n = c.size();\\n if (i >= n / 2) \\n return 0;\\n\\n if (dp[i][l][r] != (-1)) \\n return dp[i][l][r];\\n\\n vector<int> lftc, rgtc;\\n for (int j = 0; j < 3; j++) \\n {\\n if (l != j) \\n lftc.push_back(j);\\n if (r != j) \\n rgtc.push_back(j);\\n }\\n ll ans = 1e14;\\n for (int h : lftc) \\n {\\n for (int j : rgtc) \\n {\\n if (h == j) \\n continue;\\n ll cl = c[i][h], cr = c[n - i - 1][j];\\n ans = min(ans, cl + cr + sol(c, h, j, i + 1));\\n }\\n }\\n return dp[i][l][r] = ans;\\n }\\n\\n long long minCost(int n, vector<vector<int>>& c) {\\n dp.resize(n / 2 + 1, vector<vector<ll>>(4, vector<ll>(4, -1)));\\n return sol(c, 3, 3, 0);\\n }\\n};\"]]"
},
"golang": {
"code": "func minCost(n int, cost [][]int) int64 {\n m := n / 2\n prevDp := make([][]int64, 3)\n for i := range prevDp {\n prevDp[i] = make([]int64, 3)\n for j := range prevDp[i] {\n prevDp[i][j] = math.MaxInt64\n }\n }\n\n left, right := 0, n-1\n for cl := 0; cl < 3; cl++ {\n for cr := 0; cr < 3; cr++ {\n if cl != cr {\n prevDp[cl][cr] = int64(cost[left][cl] + cost[right][cr])\n }\n }\n }\n\n for k := 1; k < m; k++ {\n currDp := make([][]int64, 3)\n for i := range currDp {\n currDp[i] = make([]int64, 3)\n for j := range currDp[i] {\n currDp[i][j] = math.MaxInt64\n }\n }\n left, right := k, n-1-k\n\n for prevCl := 0; prevCl < 3; prevCl++ {\n for prevCr := 0; prevCr < 3; prevCr++ {\n if prevCl == prevCr || prevDp[prevCl][prevCr] == math.MaxInt64 {\n continue\n }\n for currCl := 0; currCl < 3; currCl++ {\n if currCl == prevCl {\n continue\n }\n for currCr := 0; currCr < 3; currCr++ {\n if currCr == prevCr || currCl == currCr {\n continue\n }\n total := prevDp[prevCl][prevCr] + int64(cost[left][currCl]+cost[right][currCr])\n if total < currDp[currCl][currCr] {\n currDp[currCl][currCr] = total\n }\n }\n }\n }\n }\n prevDp = currDp\n }\n\n minCost := int64(math.MaxInt64)\n for cl := 0; cl < 3; cl++ {\n for cr := 0; cr < 3; cr++ {\n if cl != cr && prevDp[cl][cr] < minCost {\n minCost = prevDp[cl][cr]\n }\n }\n }\n return minCost\n}",
"memory": 2100,
"memoryDistribution": "[[2100, 100.0, \"import \\\"math\\\"\\n\\nfunc minCost(n int, cost [][]int) int64 {\\n m := n / 2\\n prevDp := make([][]int64, 3)\\n for i := range prevDp {\\n prevDp[i] = make([]int64, 3)\\n for j := range prevDp[i] {\\n prevDp[i][j] = math.MaxInt64\\n }\\n }\\n\\n left, right := 0, n-1\\n for cl := 0; cl < 3; cl++ {\\n for cr := 0; cr < 3; cr++ {\\n if cl != cr {\\n prevDp[cl][cr] = int64(cost[left][cl] + cost[right][cr])\\n }\\n }\\n }\\n\\n for k := 1; k < m; k++ {\\n currDp := make([][]int64, 3)\\n for i := range currDp {\\n currDp[i] = make([]int64, 3)\\n for j := range currDp[i] {\\n currDp[i][j] = math.MaxInt64\\n }\\n }\\n left, right := k, n-1-k\\n\\n for prevCl := 0; prevCl < 3; prevCl++ {\\n for prevCr := 0; prevCr < 3; prevCr++ {\\n if prevCl == prevCr || prevDp[prevCl][prevCr] == math.MaxInt64 {\\n continue\\n }\\n for currCl := 0; currCl < 3; currCl++ {\\n if currCl == prevCl {\\n continue\\n }\\n for currCr := 0; currCr < 3; currCr++ {\\n if currCr == prevCr || currCl == currCr {\\n continue\\n }\\n total := prevDp[prevCl][prevCr] + int64(cost[left][currCl]+cost[right][currCr])\\n if total < currDp[currCl][currCr] {\\n currDp[currCl][currCr] = total\\n }\\n }\\n }\\n }\\n }\\n prevDp = currDp\\n }\\n\\n minCost := int64(math.MaxInt64)\\n for cl := 0; cl < 3; cl++ {\\n for cr := 0; cr < 3; cr++ {\\n if cl != cr && prevDp[cl][cr] < minCost {\\n minCost = prevDp[cl][cr]\\n }\\n }\\n }\\n return minCost\\n}\"], [25700, 50.0, \"import \\\"math\\\"\\n\\nfunc minCost(n int, cost [][]int) int64 {\\n m := n / 2\\n prevDp := make([][]int64, 3)\\n for i := range prevDp {\\n prevDp[i] = make([]int64, 3)\\n for j := range prevDp[i] {\\n prevDp[i][j] = math.MaxInt64\\n }\\n }\\n\\n left, right := 0, n-1\\n for cl := 0; cl < 3; cl++ {\\n for cr := 0; cr < 3; cr++ {\\n if cl != cr {\\n prevDp[cl][cr] = int64(cost[left][cl] + cost[right][cr])\\n }\\n }\\n }\\n\\n for k := 1; k < m; k++ {\\n currDp := make([][]int64, 3)\\n for i := range currDp {\\n currDp[i] = make([]int64, 3)\\n for j := range currDp[i] {\\n currDp[i][j] = math.MaxInt64\\n }\\n }\\n left, right := k, n-1-k\\n\\n for prevCl := 0; prevCl < 3; prevCl++ {\\n for prevCr := 0; prevCr < 3; prevCr++ {\\n if prevCl == prevCr || prevDp[prevCl][prevCr] == math.MaxInt64 {\\n continue\\n }\\n for currCl := 0; currCl < 3; currCl++ {\\n if currCl == prevCl {\\n continue\\n }\\n for currCr := 0; currCr < 3; currCr++ {\\n if currCr == prevCr || currCl == currCr {\\n continue\\n }\\n total := prevDp[prevCl][prevCr] + int64(cost[left][currCl]+cost[right][currCr])\\n if total < currDp[currCl][currCr] {\\n currDp[currCl][currCr] = total\\n }\\n }\\n }\\n }\\n }\\n prevDp = currDp\\n }\\n\\n minCost := int64(math.MaxInt64)\\n for cl := 0; cl < 3; cl++ {\\n for cr := 0; cr < 3; cr++ {\\n if cl != cr && prevDp[cl][cr] < minCost {\\n minCost = prevDp[cl][cr]\\n }\\n }\\n }\\n return minCost\\n}\"], [29800, 50.0, \"func minCost(n int, cost [][]int) int64 {\\n\\tdp := make([][3][3]int64, n)\\n\\n\\tfor i := 0; i < 3; i++ {\\n\\t\\tfor j := 0; j < 3; j++ {\\n\\t\\t\\tif i == j {\\n\\t\\t\\t\\tcontinue\\n\\t\\t\\t}\\n\\t\\t\\tdp[n/2][i][j] = int64(cost[n/2][j]) + int64(cost[n-1-n/2][i])\\n\\t\\t}\\n\\t}\\n\\n\\tfor i := n/2 + 1; i < n; i++ {\\n\\t\\tfor j := 0; j < 3; j++ {\\n\\t\\t\\tfor k := 0; k < 3; k++ {\\n\\t\\t\\t\\tif j == k {\\n\\t\\t\\t\\t\\tcontinue\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\tdp[i][j][k] = math.MaxInt64\\n\\t\\t\\t\\tfor pj := 0; pj < 3; pj++ {\\n\\t\\t\\t\\t\\tfor pk := 0; pk < 3; pk++ {\\n\\t\\t\\t\\t\\t\\tif pj != pk && j != pj && k != pk {\\n\\t\\t\\t\\t\\t\\t\\tdp[i][j][k] = min64(dp[i][j][k], dp[i-1][pj][pk]+int64(cost[i][k])+int64(cost[n-1-i][j]))\\n\\t\\t\\t\\t\\t\\t}\\n\\t\\t\\t\\t\\t}\\n\\t\\t\\t\\t}\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\n\\tres := int64(math.MaxInt64)\\n\\tfor i := 0; i < 3; i++ {\\n\\t\\tfor j := 0; j < 3; j++ {\\n\\t\\t\\tif i != j {\\n\\t\\t\\t\\tres = min64(res, dp[n-1][i][j])\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\n\\treturn res\\n}\\n\\nfunc min64(a, b int64) int64 {\\n\\tif a < b {\\n\\t\\treturn a\\n\\t}\\n\\n\\treturn b\\n}\"]]",
"runtime": 64,
"runtimeDistribution": "[[23, 50.0, \"func minCost(n int, cost [][]int) int64 {\\n\\tdp := make([][3][3]int64, n)\\n\\n\\tfor i := 0; i < 3; i++ {\\n\\t\\tfor j := 0; j < 3; j++ {\\n\\t\\t\\tif i == j {\\n\\t\\t\\t\\tcontinue\\n\\t\\t\\t}\\n\\t\\t\\tdp[n/2][i][j] = int64(cost[n/2][j]) + int64(cost[n-1-n/2][i])\\n\\t\\t}\\n\\t}\\n\\n\\tfor i := n/2 + 1; i < n; i++ {\\n\\t\\tfor j := 0; j < 3; j++ {\\n\\t\\t\\tfor k := 0; k < 3; k++ {\\n\\t\\t\\t\\tif j == k {\\n\\t\\t\\t\\t\\tcontinue\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\tdp[i][j][k] = math.MaxInt64\\n\\t\\t\\t\\tfor pj := 0; pj < 3; pj++ {\\n\\t\\t\\t\\t\\tfor pk := 0; pk < 3; pk++ {\\n\\t\\t\\t\\t\\t\\tif pj != pk && j != pj && k != pk {\\n\\t\\t\\t\\t\\t\\t\\tdp[i][j][k] = min64(dp[i][j][k], dp[i-1][pj][pk]+int64(cost[i][k])+int64(cost[n-1-i][j]))\\n\\t\\t\\t\\t\\t\\t}\\n\\t\\t\\t\\t\\t}\\n\\t\\t\\t\\t}\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\n\\tres := int64(math.MaxInt64)\\n\\tfor i := 0; i < 3; i++ {\\n\\t\\tfor j := 0; j < 3; j++ {\\n\\t\\t\\tif i != j {\\n\\t\\t\\t\\tres = min64(res, dp[n-1][i][j])\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\n\\treturn res\\n}\\n\\nfunc min64(a, b int64) int64 {\\n\\tif a < b {\\n\\t\\treturn a\\n\\t}\\n\\n\\treturn b\\n}\"], [64, 50.0, \"import \\\"math\\\"\\n\\nfunc minCost(n int, cost [][]int) int64 {\\n m := n / 2\\n prevDp := make([][]int64, 3)\\n for i := range prevDp {\\n prevDp[i] = make([]int64, 3)\\n for j := range prevDp[i] {\\n prevDp[i][j] = math.MaxInt64\\n }\\n }\\n\\n left, right := 0, n-1\\n for cl := 0; cl < 3; cl++ {\\n for cr := 0; cr < 3; cr++ {\\n if cl != cr {\\n prevDp[cl][cr] = int64(cost[left][cl] + cost[right][cr])\\n }\\n }\\n }\\n\\n for k := 1; k < m; k++ {\\n currDp := make([][]int64, 3)\\n for i := range currDp {\\n currDp[i] = make([]int64, 3)\\n for j := range currDp[i] {\\n currDp[i][j] = math.MaxInt64\\n }\\n }\\n left, right := k, n-1-k\\n\\n for prevCl := 0; prevCl < 3; prevCl++ {\\n for prevCr := 0; prevCr < 3; prevCr++ {\\n if prevCl == prevCr || prevDp[prevCl][prevCr] == math.MaxInt64 {\\n continue\\n }\\n for currCl := 0; currCl < 3; currCl++ {\\n if currCl == prevCl {\\n continue\\n }\\n for currCr := 0; currCr < 3; currCr++ {\\n if currCr == prevCr || currCl == currCr {\\n continue\\n }\\n total := prevDp[prevCl][prevCr] + int64(cost[left][currCl]+cost[right][currCr])\\n if total < currDp[currCl][currCr] {\\n currDp[currCl][currCr] = total\\n }\\n }\\n }\\n }\\n }\\n prevDp = currDp\\n }\\n\\n minCost := int64(math.MaxInt64)\\n for cl := 0; cl < 3; cl++ {\\n for cr := 0; cr < 3; cr++ {\\n if cl != cr && prevDp[cl][cr] < minCost {\\n minCost = prevDp[cl][cr]\\n }\\n }\\n }\\n return minCost\\n}\"], [77, 50.0, \"import \\\"math\\\"\\n\\nfunc minCost(n int, cost [][]int) int64 {\\n m := n / 2\\n prevDp := make([][]int64, 3)\\n for i := range prevDp {\\n prevDp[i] = make([]int64, 3)\\n for j := range prevDp[i] {\\n prevDp[i][j] = math.MaxInt64\\n }\\n }\\n\\n left, right := 0, n-1\\n for cl := 0; cl < 3; cl++ {\\n for cr := 0; cr < 3; cr++ {\\n if cl != cr {\\n prevDp[cl][cr] = int64(cost[left][cl] + cost[right][cr])\\n }\\n }\\n }\\n\\n for k := 1; k < m; k++ {\\n currDp := make([][]int64, 3)\\n for i := range currDp {\\n currDp[i] = make([]int64, 3)\\n for j := range currDp[i] {\\n currDp[i][j] = math.MaxInt64\\n }\\n }\\n left, right := k, n-1-k\\n\\n for prevCl := 0; prevCl < 3; prevCl++ {\\n for prevCr := 0; prevCr < 3; prevCr++ {\\n if prevCl == prevCr || prevDp[prevCl][prevCr] == math.MaxInt64 {\\n continue\\n }\\n for currCl := 0; currCl < 3; currCl++ {\\n if currCl == prevCl {\\n continue\\n }\\n for currCr := 0; currCr < 3; currCr++ {\\n if currCr == prevCr || currCl == currCr {\\n continue\\n }\\n total := prevDp[prevCl][prevCr] + int64(cost[left][currCl]+cost[right][currCr])\\n if total < currDp[currCl][currCr] {\\n currDp[currCl][currCr] = total\\n }\\n }\\n }\\n }\\n }\\n prevDp = currDp\\n }\\n\\n minCost := int64(math.MaxInt64)\\n for cl := 0; cl < 3; cl++ {\\n for cr := 0; cr < 3; cr++ {\\n if cl != cr && prevDp[cl][cr] < minCost {\\n minCost = prevDp[cl][cr]\\n }\\n }\\n }\\n return minCost\\n}\"]]"
},
"java": {
"code": "class Solution {\n public long minCost(int n, int[][] cost) {\n int m = n / 2;\n long[][] prevDp = new long[3][3];\n for (int a = 0; a < 3; a++) {\n for (int b = 0; b < 3; b++) {\n prevDp[a][b] = Long.MAX_VALUE;\n }\n }\n int firstLeft = 0;\n int firstRight = n - 1;\n for (int a = 0; a < 3; a++) {\n for (int b = 0; b < 3; b++) {\n if (a != b) {\n prevDp[a][b] = (long) cost[firstLeft][a] + cost[firstRight][b];\n }\n }\n }\n for (int p = 1; p < m; p++) {\n int left = p;\n int right = n - 1 - p;\n long[][] currDp = new long[3][3];\n for (int a = 0; a < 3; a++) {\n for (int b = 0; b < 3; b++) {\n currDp[a][b] = Long.MAX_VALUE;\n }\n }\n for (int aPrev = 0; aPrev < 3; aPrev++) {\n for (int bPrev = 0; bPrev < 3; bPrev++) {\n if (prevDp[aPrev][bPrev] == Long.MAX_VALUE) continue;\n for (int a = 0; a < 3; a++) {\n if (a == aPrev) continue;\n for (int b = 0; b < 3; b++) {\n if (b == bPrev || b == a) continue;\n long newCost = prevDp[aPrev][bPrev] + cost[left][a] + cost[right][b];\n if (newCost < currDp[a][b]) {\n currDp[a][b] = newCost;\n }\n }\n }\n }\n }\n prevDp = currDp;\n }\n long min = Long.MAX_VALUE;\n for (int a = 0; a < 3; a++) {\n for (int b = 0; b < 3; b++) {\n if (prevDp[a][b] < min) {\n min = prevDp[a][b];\n }\n }\n }\n return min;\n }\n}",
"memory": 11800,
"memoryDistribution": "[[11800, 53.8462, \"class Solution {\\n public long minCost(int n, int[][] cost) {\\n int m = n / 2;\\n long[][] prevDp = new long[3][3];\\n for (int a = 0; a < 3; a++) {\\n for (int b = 0; b < 3; b++) {\\n prevDp[a][b] = Long.MAX_VALUE;\\n }\\n }\\n int firstLeft = 0;\\n int firstRight = n - 1;\\n for (int a = 0; a < 3; a++) {\\n for (int b = 0; b < 3; b++) {\\n if (a != b) {\\n prevDp[a][b] = (long) cost[firstLeft][a] + cost[firstRight][b];\\n }\\n }\\n }\\n for (int p = 1; p < m; p++) {\\n int left = p;\\n int right = n - 1 - p;\\n long[][] currDp = new long[3][3];\\n for (int a = 0; a < 3; a++) {\\n for (int b = 0; b < 3; b++) {\\n currDp[a][b] = Long.MAX_VALUE;\\n }\\n }\\n for (int aPrev = 0; aPrev < 3; aPrev++) {\\n for (int bPrev = 0; bPrev < 3; bPrev++) {\\n if (prevDp[aPrev][bPrev] == Long.MAX_VALUE) continue;\\n for (int a = 0; a < 3; a++) {\\n if (a == aPrev) continue;\\n for (int b = 0; b < 3; b++) {\\n if (b == bPrev || b == a) continue;\\n long newCost = prevDp[aPrev][bPrev] + cost[left][a] + cost[right][b];\\n if (newCost < currDp[a][b]) {\\n currDp[a][b] = newCost;\\n }\\n }\\n }\\n }\\n }\\n prevDp = currDp;\\n }\\n long min = Long.MAX_VALUE;\\n for (int a = 0; a < 3; a++) {\\n for (int b = 0; b < 3; b++) {\\n if (prevDp[a][b] < min) {\\n min = prevDp[a][b];\\n }\\n }\\n }\\n return min;\\n }\\n}\"], [97953, 4.8951, \"class Solution {\\n public long minCost(int n, int[][] cost) {\\n n/=2;\\n long dp[][][]=new long[n+1][3][3];\\n for(int i=n-1;i>=0;i--){\\n for(int j=0;j<3;j++){\\n for(int k=0;k<3;k++){\\n if(j==k) continue;\\n dp[i][j][k]=Long.MAX_VALUE;\\n for(int l=0;l<3;l++){\\n if(l==j) continue;\\n for(int m=0;m<3;m++){\\n if(l==m||m==k) continue;\\n dp[i][j][k]=Math.min(dp[i][j][k],dp[i+1][l][m]+cost[i][l]+cost[cost.length-i-1][m]);\\n }\\n }\\n }\\n }\\n }\\n long ans=Long.MAX_VALUE;\\n for(int i=0;i<3;i++){\\n for(int j=0;j<3;j++){\\n if(i==j) continue;\\n ans=Math.min(ans,dp[0][i][j]);\\n }\\n }\\n return ans;\\n \\n }\\n}\"], [98459, 9.090900000000001, \"class Solution {\\n public long minCost(int n, int[][] cost) {\\n \\n long[][][] dp = new long[n/2+1][3][3];\\n\\n for (int i = 0; i < cost.length/2; i++) {\\n\\n int top = n/2+i;\\n int bottom = n/2-1-i;\\n\\n int idx = cost.length/2-1-i;\\n\\n dp[idx][0][1] = cost[top][0] + cost[bottom][1] + Math.min(dp[idx+1][1][2], Math.min(dp[idx+1][1][0], dp[idx+1][2][0]));\\n dp[idx][0][2] = cost[top][0] + cost[bottom][2] + Math.min(dp[idx+1][1][0], Math.min(dp[idx+1][2][1], dp[idx+1][2][0]));\\n dp[idx][1][0] = cost[top][1] + cost[bottom][0] + Math.min(dp[idx+1][0][1], Math.min(dp[idx+1][0][2], dp[idx+1][2][1]));\\n dp[idx][1][2] = cost[top][1] + cost[bottom][2] + Math.min(dp[idx+1][0][1], Math.min(dp[idx+1][2][0], dp[idx+1][2][1]));\\n dp[idx][2][0] = cost[top][2] + cost[bottom][0] + Math.min(dp[idx+1][1][2], Math.min(dp[idx+1][0][2], dp[idx+1][0][1]));\\n dp[idx][2][1] = cost[top][2] + cost[bottom][1] + Math.min(dp[idx+1][0][2], Math.min(dp[idx+1][1][0], dp[idx+1][1][2]));\\n }\\n\\n long ret = Long.MAX_VALUE;\\n for (int i = 0; i < 3; i++) {\\n for (int j = 0; j < 3; j++) {\\n if (i != j) {\\n ret = Math.min(ret, dp[0][i][j]);\\n }\\n }\\n }\\n\\n return ret;\\n }\\n}\"], [98965, 3.4965, null], [99471, 0.6993, null], [99978, 0.6993, null], [100484, 0.6993, null], [100990, 0.6993, null], [101496, 0.6993, null], [102003, 0.6993, null], [102509, 0.6993, null], [103015, 0.6993, null], [103521, 0.6993, null], [104028, 0.6993, null], [104534, 0.6993, null], [105040, 0.6993, null], [105546, 0.6993, null], [106053, 0.6993, null], [106559, 3.4965, null], [107065, 0.6993, null], [107571, 0.6993, null], [108078, 0.6993, null], [108584, 0.6993, null], [109090, 0.6993, null], [109596, 1.3986, null], [110103, 1.3986, null], [110609, 0.6993, null], [111115, 0.6993, null], [111621, 0.6993, null], [112128, 0.6993, null], [112634, 0.6993, null], [113140, 1.3986, null], [113646, 0.6993, null], [114153, 0.6993, null], [114659, 0.6993, null], [115165, 0.6993, null], [115671, 0.6993, null], [116178, 0.6993, null], [116684, 0.6993, null], [117190, 0.6993, null], [117696, 0.6993, null], [118203, 1.3986, null], [118709, 2.0979, null], [119215, 0.6993, null], [119721, 2.7972, null], [120228, 1.3986, null], [120734, 1.3986, null], [121240, 0.6993, null], [121746, 0.6993, null], [122253, 0.6993, null], [122759, 0.6993, null], [123265, 0.6993, null], [123771, 0.6993, null], [124278, 0.6993, null], [124784, 0.6993, null], [125290, 0.6993, null], [125796, 0.6993, null], [126303, 2.0979, null], [126809, 2.7972, null], [127315, 4.8951, null], [127821, 3.4965, null], [128328, 0.6993, null], [128834, 2.0979, null], [129340, 0.6993, null], [129846, 4.1958, null], [130353, 0.6993, null], [130859, 0.6993, null], [131365, 0.6993, null], [131871, 0.6993, null], [132378, 0.6993, null], [132884, 1.3986, null], [133390, 0.6993, null], [133896, 0.6993, null], [134403, 0.6993, null], [134909, 0.6993, \"class Solution {\\n public long minCost(int n, int[][] cost) {\\n long[][][] dp = new long[n / 2 + 1][4][4];\\n for(long[][] layer : dp) {\\n for(long[] row : layer) {\\n Arrays.fill(row, -1);\\n }\\n }\\n return solve(cost, 3, 3, 0, dp);\\n }\\n private long solve(int[][] cost, int l, int r, int i, long[][][] dp) {\\n int n = cost.length;\\n if(i >= n / 2) {\\n return 0;\\n }\\n if(dp[i][l][r] != -1) {\\n return dp[i][l][r];\\n }\\n List<Integer> leftChoices = new ArrayList<>();\\n List<Integer> rightChoices = new ArrayList<>();\\n for(int j = 0; j < 3; ++j) {\\n if(l != j) {\\n leftChoices.add(j);\\n }\\n if(r != j) {\\n rightChoices.add(j);\\n }\\n }\\n long ans = Long.MAX_VALUE;\\n for(int h : leftChoices) {\\n for(int j : rightChoices) {\\n if(h == j) {\\n continue;\\n }\\n long cl = cost[i][h];\\n long cr = cost[n - i - 1][j];\\n ans = Math.min(ans, cl + cr + solve(cost, h, j, i + 1, dp));\\n }\\n }\\n return dp[i][l][r] = ans;\\n }\\n}\"], [135415, 0.6993, \"class Solution {\\n public long minCost(int n, int[][] cost) \\n {\\n long[][][] dp = new long[n / 2 + 1][4][4];\\n for (long[][] layer : dp) {\\n for (long[] row : layer) {\\n Arrays.fill(row, -1);\\n }\\n }\\n return solve(cost, 3, 3, 0, dp);\\n }\\n private long solve(int[][] cost, int l, int r, int i, long[][][] dp) {\\n int n = cost.length;\\n if (i >= n / 2) {\\n return 0;\\n }\\n if (dp[i][l][r] != -1) {\\n return dp[i][l][r];\\n }\\n List<Integer> leftChoices = new ArrayList<>();\\n List<Integer> rightChoices = new ArrayList<>();\\n for (int j = 0; j < 3; j++) {\\n if (l != j) {\\n leftChoices.add(j);\\n }\\n if (r != j) {\\n rightChoices.add(j);\\n }\\n }\\n long ans = Long.MAX_VALUE;\\n for (int h : leftChoices) {\\n for (int j : rightChoices) {\\n if (h == j) {\\n continue;\\n }\\n long cl = cost[i][h];\\n long cr = cost[n - i - 1][j];\\n ans = Math.min(ans, cl + cr + solve(cost, h, j, i + 1, dp));\\n }\\n }\\n return dp[i][l][r] = ans;\\n }\\n}\"]]",
"runtime": 54,
"runtimeDistribution": "[[5, 2.0979, \"class Solution {\\n public long minCost(int n, int[][] cost) {\\n long colAB = cost[0][0] + cost[n - 1][1];\\n long colAC = cost[0][0] + cost[n - 1][2];\\n long colBA = cost[0][1] + cost[n - 1][0];\\n long colBC = cost[0][1] + cost[n - 1][2];\\n long colCA = cost[0][2] + cost[n - 1][0];\\n long colCB = cost[0][2] + cost[n - 1][1];\\n long newColAB, newColAC, newColBA, newColBC, newColCA, newColCB;\\n for (int i = 1, lim = n/2; i < lim; i++) {\\n newColAB = Math.min(Math.min(colBA, colBC), colCA) + cost[i][0] + cost[n - 1 - i][1]; \\n newColAC = Math.min(Math.min(colBA, colCA), colCB) + cost[i][0] + cost[n - 1 - i][2];\\n newColBA = Math.min(Math.min(colAB, colAC), colCB) + cost[i][1] + cost[n - 1 - i][0];\\n newColBC = Math.min(Math.min(colAB, colCA), colCB) + cost[i][1] + cost[n - 1 - i][2];\\n newColCA = Math.min(Math.min(colAB, colAC), colBC) + cost[i][2] + cost[n - 1 - i][0];\\n newColCB = Math.min(Math.min(colAC, colBA), colBC) + cost[i][2] + cost[n - 1 - i][1];\\n colAB = newColAB;\\n colAC = newColAC;\\n colBA = newColBA; \\n colBC = newColBC; \\n colCA = newColCA; \\n colCB = newColCB;\\n }\\n return Math.min(Math.min(colAB, colAC), Math.min(Math.min(colBA, colBC), Math.min(colCA, colCB)));\\n }\\n}\"], [11, 0.6993, \"import java.util.*;\\n\\nclass Solution {\\n public long minCost(int n, int[][] cost) {\\n int half = n / 2;\\n long[] dp = new long[6], temp = new long[6];\\n\\n dp[0] = cost[0][0] + cost[n - 1][1];\\n dp[1] = cost[0][0] + cost[n - 1][2];\\n dp[2] = cost[0][1] + cost[n - 1][2];\\n dp[3] = cost[0][1] + cost[n - 1][0];\\n dp[4] = cost[0][2] + cost[n - 1][0];\\n dp[5] = cost[0][2] + cost[n - 1][1];\\n\\n for (int i = 1; i < half; ++i) {\\n temp[0] = Math.min(Math.min(dp[2], dp[3]), dp[4]) + cost[i][0] + cost[n - i - 1][1];\\n temp[1] = Math.min(Math.min(dp[3], dp[4]), dp[5]) + cost[i][0] + cost[n - i - 1][2];\\n temp[2] = Math.min(Math.min(dp[0], dp[4]), dp[5]) + cost[i][1] + cost[n - i - 1][2];\\n temp[3] = Math.min(Math.min(dp[0], dp[1]), dp[5]) + cost[i][1] + cost[n - i - 1][0];\\n temp[4] = Math.min(Math.min(dp[0], dp[1]), dp[2]) + cost[i][2] + cost[n - i - 1][0];\\n temp[5] = Math.min(Math.min(dp[1], dp[2]), dp[3]) + cost[i][2] + cost[n - i - 1][1];\\n \\n System.arraycopy(temp, 0, dp, 0, 6);\\n }\\n\\n return Arrays.stream(dp).min().getAsLong();\\n }\\n}\\n\"], [12, 0.6993, null], [14, 0.6993, null], [15, 0.6993, null], [18, 0.6993, null], [25, 1.3986, null], [26, 0.6993, null], [27, 0.6993, null], [28, 4.1958, null], [29, 6.993, null], [30, 1.3986, null], [31, 0.6993, null], [32, 0.6993, null], [36, 0.6993, null], [38, 0.6993, null], [39, 0.6993, null], [47, 0.6993, null], [49, 0.6993, null], [50, 1.3986, null], [52, 2.0979, null], [53, 0.6993, null], [54, 69.9301, \"class Solution {\\n public long minCost(int n, int[][] cost) {\\n int m = n / 2;\\n long[][] prevDp = new long[3][3];\\n for (int a = 0; a < 3; a++) {\\n for (int b = 0; b < 3; b++) {\\n prevDp[a][b] = Long.MAX_VALUE;\\n }\\n }\\n int firstLeft = 0;\\n int firstRight = n - 1;\\n for (int a = 0; a < 3; a++) {\\n for (int b = 0; b < 3; b++) {\\n if (a != b) {\\n prevDp[a][b] = (long) cost[firstLeft][a] + cost[firstRight][b];\\n }\\n }\\n }\\n for (int p = 1; p < m; p++) {\\n int left = p;\\n int right = n - 1 - p;\\n long[][] currDp = new long[3][3];\\n for (int a = 0; a < 3; a++) {\\n for (int b = 0; b < 3; b++) {\\n currDp[a][b] = Long.MAX_VALUE;\\n }\\n }\\n for (int aPrev = 0; aPrev < 3; aPrev++) {\\n for (int bPrev = 0; bPrev < 3; bPrev++) {\\n if (prevDp[aPrev][bPrev] == Long.MAX_VALUE) continue;\\n for (int a = 0; a < 3; a++) {\\n if (a == aPrev) continue;\\n for (int b = 0; b < 3; b++) {\\n if (b == bPrev || b == a) continue;\\n long newCost = prevDp[aPrev][bPrev] + cost[left][a] + cost[right][b];\\n if (newCost < currDp[a][b]) {\\n currDp[a][b] = newCost;\\n }\\n }\\n }\\n }\\n }\\n prevDp = currDp;\\n }\\n long min = Long.MAX_VALUE;\\n for (int a = 0; a < 3; a++) {\\n for (int b = 0; b < 3; b++) {\\n if (prevDp[a][b] < min) {\\n min = prevDp[a][b];\\n }\\n }\\n }\\n return min;\\n }\\n}\"], [55, 0.6993, null], [56, 1.3986, null], [57, 1.3986, null], [63, 0.6993, null], [66, 0.6993, null], [67, 0.6993, null], [68, 0.6993, null], [69, 0.6993, null], [70, 0.6993, null], [72, 1.3986, null], [78, 0.6993, null], [79, 0.6993, null], [80, 1.3986, null], [81, 0.6993, null], [84, 1.3986, null], [85, 0.6993, null], [86, 0.6993, null], [87, 0.6993, null], [88, 1.3986, null], [89, 1.3986, null], [90, 0.6993, null], [94, 0.6993, null], [96, 0.6993, null], [101, 0.6993, null], [104, 0.6993, null], [106, 0.6993, null], [107, 0.6993, null], [108, 1.3986, null], [109, 2.0979, null], [110, 1.3986, null], [112, 0.6993, null], [113, 0.6993, null], [114, 1.3986, null], [115, 0.6993, null], [117, 3.4965, null], [118, 3.4965, null], [119, 0.6993, null], [120, 1.3986, null], [121, 3.4965, null], [122, 2.7972, null], [123, 3.4965, null], [125, 2.0979, null], [126, 2.0979, null], [128, 0.6993, null], [130, 0.6993, null], [132, 0.6993, null], [134, 0.6993, null], [168, 1.3986, null], [172, 0.6993, null], [178, 0.6993, null], [183, 0.6993, null], [184, 1.3986, null], [200, 0.6993, \"class Solution {\\n public long minCost(int n, int[][] cost) \\n {\\n long[][][] dp = new long[n / 2 + 1][4][4];\\n for (long[][] layer : dp) {\\n for (long[] row : layer) {\\n Arrays.fill(row, -1);\\n }\\n }\\n return solve(cost, 3, 3, 0, dp);\\n }\\n private long solve(int[][] cost, int l, int r, int i, long[][][] dp) {\\n int n = cost.length;\\n if (i >= n / 2) {\\n return 0;\\n }\\n if (dp[i][l][r] != -1) {\\n return dp[i][l][r];\\n }\\n List<Integer> leftChoices = new ArrayList<>();\\n List<Integer> rightChoices = new ArrayList<>();\\n for (int j = 0; j < 3; j++) {\\n if (l != j) {\\n leftChoices.add(j);\\n }\\n if (r != j) {\\n rightChoices.add(j);\\n }\\n }\\n long ans = Long.MAX_VALUE;\\n for (int h : leftChoices) {\\n for (int j : rightChoices) {\\n if (h == j) {\\n continue;\\n }\\n long cl = cost[i][h];\\n long cr = cost[n - i - 1][j];\\n ans = Math.min(ans, cl + cr + solve(cost, h, j, i + 1, dp));\\n }\\n }\\n return dp[i][l][r] = ans;\\n }\\n}\"], [213, 0.6993, \"/*\\n\\nCompletely diff approach from brute force : but easily soch skte thee,\\nki paint hi dono pair ko sath mei kro, aur dono ke adjacent color ko dp state\\nmei rkho, taaki pta rhe ki dono mei konse konse color bhr skte hai\\n\\nfir bhrte time bhi dhyan rkho ki dono mei same color nhi bhrna\\n*/\\nclass Solution {\\n\\n Long[][][] dp ;\\n\\n long func(int i, int pc, int fc, int[][] cost){\\n\\n int n = cost.length;\\n if(i>=n/2)\\n return 0;\\n\\n if(dp[i][pc][fc]!=null)\\n return dp[i][pc][fc];\\n\\n\\n List<Integer> PrevColorChoice = new ArrayList<>();\\n List<Integer> FwdColorChoice = new ArrayList<>();\\n\\n for(int j = 0;j<3;j++)\\n {\\n if(pc != j){\\n PrevColorChoice.add(j);\\n }\\n\\n if(fc != j){\\n FwdColorChoice.add(j);\\n }\\n\\n }\\n\\n long ans = Long.MAX_VALUE;\\n\\n for(int p : PrevColorChoice){\\n for(int f : FwdColorChoice){\\n if(p==f)\\n continue;\\n\\n long cp = cost[i][p];\\n long cf = cost[n-i-1][f];\\n\\n ans = Math.min(ans, cp + cf + func(i+1, p, f, cost));\\n }\\n }\\n\\n return dp[i][pc][fc] = ans; \\n\\n }\\n\\n public long minCost(int n, int[][] cost) {\\n\\n //as 0,1,2 hi colors hai and first , aur uska pair last isko to kisi bhi color se kr skte hai, to inke liye prev color 3 dia hai\\n\\n dp = new Long[n+1][4][4];\\n return func(0,3,3,cost);\\n \\n }\\n}\"]]"
},
"javascript": {
"code": "var minCost = function(n, cost) {\n let prevDp = Array.from({length: 3}, () => Array(3).fill(Infinity));\n const firstI = 0, firstJ = n - 1;\n for (let a = 0; a < 3; a++) {\n for (let b = 0; b < 3; b++) {\n if (a !== b) {\n prevDp[a][b] = cost[firstI][a] + cost[firstJ][b];\n }\n }\n }\n for (let step = 1; step < n / 2; step++) {\n const i = step, j = n - 1 - step;\n const currDp = Array.from({length: 3}, () => Array(3).fill(Infinity));\n for (let aPrev = 0; aPrev < 3; aPrev++) {\n for (let bPrev = 0; bPrev < 3; bPrev++) {\n if (prevDp[aPrev][bPrev] === Infinity) continue;\n for (let aCurr = 0; aCurr < 3; aCurr++) {\n if (aCurr === aPrev) continue;\n for (let bCurr = 0; bCurr < 3; bCurr++) {\n if (bCurr === bPrev || bCurr === aCurr) continue;\n const newCost = prevDp[aPrev][bPrev] + cost[i][aCurr] + cost[j][bCurr];\n if (newCost < currDp[aCurr][bCurr]) {\n currDp[aCurr][bCurr] = newCost;\n }\n }\n }\n }\n }\n prevDp = currDp;\n }\n let min = Infinity;\n for (let a = 0; a < 3; a++) {\n for (let b = 0; b < 3; b++) {\n if (a !== b && prevDp[a][b] < min) {\n min = prevDp[a][b];\n }\n }\n }\n return min;\n};",
"memory": 8800,
"memoryDistribution": "[[8800, 64.2855, \"var minCost = function(n, cost) {\\n let prevDp = Array.from({length: 3}, () => Array(3).fill(Infinity));\\n const firstI = 0, firstJ = n - 1;\\n for (let a = 0; a < 3; a++) {\\n for (let b = 0; b < 3; b++) {\\n if (a !== b) {\\n prevDp[a][b] = cost[firstI][a] + cost[firstJ][b];\\n }\\n }\\n }\\n for (let step = 1; step < n / 2; step++) {\\n const i = step, j = n - 1 - step;\\n const currDp = Array.from({length: 3}, () => Array(3).fill(Infinity));\\n for (let aPrev = 0; aPrev < 3; aPrev++) {\\n for (let bPrev = 0; bPrev < 3; bPrev++) {\\n if (prevDp[aPrev][bPrev] === Infinity) continue;\\n for (let aCurr = 0; aCurr < 3; aCurr++) {\\n if (aCurr === aPrev) continue;\\n for (let bCurr = 0; bCurr < 3; bCurr++) {\\n if (bCurr === bPrev || bCurr === aCurr) continue;\\n const newCost = prevDp[aPrev][bPrev] + cost[i][aCurr] + cost[j][bCurr];\\n if (newCost < currDp[aCurr][bCurr]) {\\n currDp[aCurr][bCurr] = newCost;\\n }\\n }\\n }\\n }\\n }\\n prevDp = currDp;\\n }\\n let min = Infinity;\\n for (let a = 0; a < 3; a++) {\\n for (let b = 0; b < 3; b++) {\\n if (a !== b && prevDp[a][b] < min) {\\n min = prevDp[a][b];\\n }\\n }\\n }\\n return min;\\n};\"], [86400, 7.1429, \"/**\\n * @param {number} n\\n * @param {number[][]} cost\\n * @return {number}\\n */\\nfunction minCost(n, cost) {\\n if (n === 0) return 0;\\n const pairs = n / 2;\\n \\n // There are 9 states: for each pair (c1, c2) with c1, c2 in [0, 1, 2]\\n // We'll represent the state as an index: idx = c1 * 3 + c2.\\n // Invalid states (c1 === c2) will remain Infinity.\\n let dp = new Array(9).fill(Infinity);\\n \\n // Initialize for the first pair (0, n-1)\\n for (let c1 = 0; c1 < 3; c1++) {\\n for (let c2 = 0; c2 < 3; c2++) {\\n if (c1 !== c2) {\\n const idx = c1 * 3 + c2;\\n dp[idx] = cost[0][c1] + cost[n - 1][c2];\\n }\\n }\\n }\\n \\n // Process remaining pairs\\n for (let i = 1; i < pairs; i++) {\\n const newDp = new Array(9).fill(Infinity);\\n const left = i;\\n const right = n - 1 - i;\\n \\n for (let prevIdx = 0; prevIdx < 9; prevIdx++) {\\n if (dp[prevIdx] === Infinity) continue;\\n const prevLeft = Math.floor(prevIdx / 3);\\n const prevRight = prevIdx % 3;\\n \\n for (let c1 = 0; c1 < 3; c1++) {\\n if (c1 === prevLeft) continue; // adjacent constraint for left\\n for (let c2 = 0; c2 < 3; c2++) {\\n if (c2 === prevRight || c1 === c2) continue; // adjacent & mirror constraints\\n const idx = c1 * 3 + c2;\\n const total = dp[prevIdx] + cost[left][c1] + cost[right][c2];\\n if (total < newDp[idx]) {\\n newDp[idx] = total;\\n }\\n }\\n }\\n }\\n \\n dp = newDp;\\n // Early exit if no valid configuration remains.\\n if (dp.every(val => val === Infinity)) return -1;\\n }\\n \\n return Math.min(...dp);\\n}\\n\"], [86800, 7.1429, \"/**\\n * @param {number} n\\n * @param {number[][]} cost\\n * @return {number}\\n */\\nfunction minCost(n, cost) {\\n if (n === 0) return 0;\\n const pairs = n / 2;\\n \\n // There are 9 states: for each pair (c1, c2) with c1, c2 in [0, 1, 2]\\n // We'll represent the state as an index: idx = c1 * 3 + c2.\\n // Invalid states (c1 === c2) will remain Infinity.\\n let dp = new Array(9).fill(Infinity);\\n \\n // Initialize for the first pair (0, n-1)\\n for (let c1 = 0; c1 < 3; c1++) {\\n for (let c2 = 0; c2 < 3; c2++) {\\n if (c1 !== c2) {\\n const idx = c1 * 3 + c2;\\n dp[idx] = cost[0][c1] + cost[n - 1][c2];\\n }\\n }\\n }\\n \\n // Process remaining pairs\\n for (let i = 1; i < pairs; i++) {\\n const newDp = new Array(9).fill(Infinity);\\n const left = i;\\n const right = n - 1 - i;\\n \\n for (let prevIdx = 0; prevIdx < 9; prevIdx++) {\\n if (dp[prevIdx] === Infinity) continue;\\n const prevLeft = Math.floor(prevIdx / 3);\\n const prevRight = prevIdx % 3;\\n \\n for (let c1 = 0; c1 < 3; c1++) {\\n if (c1 === prevLeft) continue; // adjacent constraint for left\\n for (let c2 = 0; c2 < 3; c2++) {\\n if (c2 === prevRight || c1 === c2) continue; // adjacent & mirror constraints\\n const idx = c1 * 3 + c2;\\n const total = dp[prevIdx] + cost[left][c1] + cost[right][c2];\\n if (total < newDp[idx]) {\\n newDp[idx] = total;\\n }\\n }\\n }\\n }\\n \\n dp = newDp;\\n // Early exit if no valid configuration remains.\\n if (dp.every(val => val === Infinity)) return -1;\\n }\\n \\n return Math.min(...dp);\\n}\\n\"], [87200, 7.1429, null], [87400, 7.1429, null], [88000, 7.1429, null], [89000, 7.1429, null], [89300, 7.1429, null], [89600, 7.1429, null], [89800, 7.1429, null], [93200, 7.1429, null], [94900, 7.1429, null], [102400, 7.1429, \"/**\\n * @param {number} n\\n * @param {number[][]} cost\\n * @return {number}\\n */\\nvar minCost = function(n, cost) {\\n const d = Array.from({length: n/2 + 1}, () => (\\n [\\n [0,0,0],\\n [0,0,0],\\n [0,0,0],\\n ]\\n ))\\n\\n for (let i = 0; i < n / 2; i++) {\\n d[i+1][0][1] = Math.min(d[i][1][0],d[i][1][2],d[i][2][0]) + cost[i][0] + cost[n-1-i][1];\\n d[i+1][0][2] = Math.min(d[i][1][0],d[i][2][0],d[i][2][1]) + cost[i][0] + cost[n-1-i][2];\\n d[i+1][1][0] = Math.min(d[i][0][1],d[i][0][2],d[i][2][1]) + cost[i][1] + cost[n-1-i][0];\\n d[i+1][1][2] = Math.min(d[i][0][1],d[i][2][0],d[i][2][1]) + cost[i][1] + cost[n-1-i][2];\\n d[i+1][2][0] = Math.min(d[i][0][1],d[i][0][2],d[i][1][2]) + cost[i][2] + cost[n-1-i][0];\\n d[i+1][2][1] = Math.min(d[i][0][2],d[i][1][0],d[i][1][2]) + cost[i][2] + cost[n-1-i][1];\\n }\\n\\n return Math.min(d[n/2][0][1],d[n/2][0][2],d[n/2][1][2],d[n/2][1][0],d[n/2][2][0],d[n/2][2][1]);\\n};\"], [103500, 7.1429, \"/**\\n * @param {number} n\\n * @param {number[][]} cost\\n * @return {number}\\n */\\nvar minCost = function (n, cost) {\\n const d = Array.from({ length: n / 2 + 1 }, () => (\\n [\\n [0, 0, 0],\\n [0, 0, 0],\\n [0, 0, 0],\\n ]\\n ))\\n\\n let curr01 = 0;\\n let curr02 = 0;\\n let curr10 = 0;\\n let curr12 = 0;\\n let curr20 = 0;\\n let curr21 = 0;\\n\\n for (let i = 0; i < n / 2; i++) {\\n [curr01, curr02, curr10, curr12, curr20, curr21] = [\\n cost[i][0] + cost[n - 1 - i][1] + Math.min(curr10, curr12, curr20),\\n cost[i][0] + cost[n - 1 - i][2] + Math.min(curr10, curr20, curr21),\\n cost[i][1] + cost[n - 1 - i][0] + Math.min(curr01, curr02, curr21),\\n cost[i][1] + cost[n - 1 - i][2] + Math.min(curr01, curr20, curr21),\\n cost[i][2] + cost[n - 1 - i][0] + Math.min(curr01, curr02, curr12),\\n cost[i][2] + cost[n - 1 - i][1] + Math.min(curr02, curr10, curr12)\\n ];\\n\\n }\\n\\n return Math.min(curr01, curr02, curr10, curr12, curr20, curr21);\\n};\"]]",
"runtime": 252,
"runtimeDistribution": "[[59, 7.1429, \"/**\\n * @param {number} n\\n * @param {number[][]} cost\\n * @return {number}\\n */\\nvar minCost = function (n, cost) {\\n let curr01 = 0;\\n let curr02 = 0;\\n let curr10 = 0;\\n let curr12 = 0;\\n let curr20 = 0;\\n let curr21 = 0;\\n\\n for (let i = 0; i < n / 2; i++) {\\n [curr01, curr02, curr10, curr12, curr20, curr21] = [\\n cost[i][0] + cost[n - 1 - i][1] + Math.min(curr10, curr12, curr20),\\n cost[i][0] + cost[n - 1 - i][2] + Math.min(curr10, curr20, curr21),\\n cost[i][1] + cost[n - 1 - i][0] + Math.min(curr01, curr02, curr21),\\n cost[i][1] + cost[n - 1 - i][2] + Math.min(curr01, curr20, curr21),\\n cost[i][2] + cost[n - 1 - i][0] + Math.min(curr01, curr02, curr12),\\n cost[i][2] + cost[n - 1 - i][1] + Math.min(curr02, curr10, curr12)\\n ];\\n\\n }\\n\\n return Math.min(curr01, curr02, curr10, curr12, curr20, curr21);\\n};\"], [69, 7.1429, \"/**\\n * @param {number} n\\n * @param {number[][]} cost\\n * @return {number}\\n */\\nfunction minCost(n, cost) {\\n if (n === 0) return 0;\\n const pairs = n / 2;\\n \\n // There are 9 states: for each pair (c1, c2) with c1, c2 in [0, 1, 2]\\n // We'll represent the state as an index: idx = c1 * 3 + c2.\\n // Invalid states (c1 === c2) will remain Infinity.\\n let dp = new Array(9).fill(Infinity);\\n \\n // Initialize for the first pair (0, n-1)\\n for (let c1 = 0; c1 < 3; c1++) {\\n for (let c2 = 0; c2 < 3; c2++) {\\n if (c1 !== c2) {\\n const idx = c1 * 3 + c2;\\n dp[idx] = cost[0][c1] + cost[n - 1][c2];\\n }\\n }\\n }\\n \\n // Process remaining pairs\\n for (let i = 1; i < pairs; i++) {\\n const newDp = new Array(9).fill(Infinity);\\n const left = i;\\n const right = n - 1 - i;\\n \\n for (let prevIdx = 0; prevIdx < 9; prevIdx++) {\\n if (dp[prevIdx] === Infinity) continue;\\n const prevLeft = Math.floor(prevIdx / 3);\\n const prevRight = prevIdx % 3;\\n \\n for (let c1 = 0; c1 < 3; c1++) {\\n if (c1 === prevLeft) continue; // adjacent constraint for left\\n for (let c2 = 0; c2 < 3; c2++) {\\n if (c2 === prevRight || c1 === c2) continue; // adjacent & mirror constraints\\n const idx = c1 * 3 + c2;\\n const total = dp[prevIdx] + cost[left][c1] + cost[right][c2];\\n if (total < newDp[idx]) {\\n newDp[idx] = total;\\n }\\n }\\n }\\n }\\n \\n dp = newDp;\\n // Early exit if no valid configuration remains.\\n if (dp.every(val => val === Infinity)) return -1;\\n }\\n \\n return Math.min(...dp);\\n}\\n\"], [72, 7.1429, null], [73, 7.1429, null], [79, 7.1429, null], [108, 7.1429, null], [121, 7.1429, null], [129, 7.1429, null], [158, 7.1429, null], [172, 7.1429, null], [251, 7.1429, null], [252, 21.4281, \"var minCost = function(n, cost) {\\n let prevDp = Array.from({length: 3}, () => Array(3).fill(Infinity));\\n const firstI = 0, firstJ = n - 1;\\n for (let a = 0; a < 3; a++) {\\n for (let b = 0; b < 3; b++) {\\n if (a !== b) {\\n prevDp[a][b] = cost[firstI][a] + cost[firstJ][b];\\n }\\n }\\n }\\n for (let step = 1; step < n / 2; step++) {\\n const i = step, j = n - 1 - step;\\n const currDp = Array.from({length: 3}, () => Array(3).fill(Infinity));\\n for (let aPrev = 0; aPrev < 3; aPrev++) {\\n for (let bPrev = 0; bPrev < 3; bPrev++) {\\n if (prevDp[aPrev][bPrev] === Infinity) continue;\\n for (let aCurr = 0; aCurr < 3; aCurr++) {\\n if (aCurr === aPrev) continue;\\n for (let bCurr = 0; bCurr < 3; bCurr++) {\\n if (bCurr === bPrev || bCurr === aCurr) continue;\\n const newCost = prevDp[aPrev][bPrev] + cost[i][aCurr] + cost[j][bCurr];\\n if (newCost < currDp[aCurr][bCurr]) {\\n currDp[aCurr][bCurr] = newCost;\\n }\\n }\\n }\\n }\\n }\\n prevDp = currDp;\\n }\\n let min = Infinity;\\n for (let a = 0; a < 3; a++) {\\n for (let b = 0; b < 3; b++) {\\n if (a !== b && prevDp[a][b] < min) {\\n min = prevDp[a][b];\\n }\\n }\\n }\\n return min;\\n};\"], [738, 7.1429, \"/**\\n * @param {number} n\\n * @param {number[][]} cost\\n * @return {number}\\n */\\nfunction minCost(n, cost) {\\n if (n === 0) return 0;\\n const pairs = n / 2;\\n let dp = new Map();\\n\\n // Initialize DP for the first pair (0, n-1)\\n const firstLeft = 0, firstRight = n - 1;\\n for (let c1 = 1; c1 <= 3; c1++) {\\n for (let c2 = 1; c2 <= 3; c2++) {\\n if (c1 !== c2) {\\n const total = cost[firstLeft][c1 - 1] + cost[firstRight][c2 - 1];\\n const key = `${c1},${c2}`;\\n if (!dp.has(key) || total < dp.get(key)) {\\n dp.set(key, total);\\n }\\n }\\n }\\n }\\n\\n if (dp.size === 0) return 0;\\n\\n // Process remaining pairs\\n for (let i = 1; i < pairs; i++) {\\n const newDp = new Map();\\n const left = i;\\n const right = n - 1 - i;\\n\\n for (const [prevKey, prevCost] of dp) {\\n const [prevLeft, prevRight] = prevKey.split(',').map(Number);\\n\\n for (let currLeft = 1; currLeft <= 3; currLeft++) {\\n if (currLeft === prevLeft) continue; // Adjacent constraint\\n for (let currRight = 1; currRight <= 3; currRight++) {\\n if (currRight === prevRight) continue; // Adjacent constraint\\n if (currLeft === currRight) continue; // Mirror pair constraint\\n\\n const currentCost = cost[left][currLeft - 1] + cost[right][currRight - 1];\\n const total = prevCost + currentCost;\\n const key = `${currLeft},${currRight}`;\\n\\n if (!newDp.has(key) || total < newDp.get(key)) {\\n newDp.set(key, total);\\n }\\n }\\n }\\n }\\n\\n dp = newDp;\\n if (dp.size === 0) return -1; // If no valid configuration (problem states it's possible, so optional)\\n }\\n\\n return Math.min(...dp.values());\\n}\"], [779, 7.1429, \"/**\\n * @param {number} n\\n * @param {number[][]} cost\\n * @return {number}\\n */\\nfunction minCost(n, cost) {\\n if (n === 0) return 0;\\n const pairs = n / 2;\\n let dp = new Map();\\n\\n // Initialize DP for the first pair (0, n-1)\\n const firstLeft = 0, firstRight = n - 1;\\n for (let c1 = 1; c1 <= 3; c1++) {\\n for (let c2 = 1; c2 <= 3; c2++) {\\n if (c1 !== c2) {\\n const total = cost[firstLeft][c1 - 1] + cost[firstRight][c2 - 1];\\n const key = `${c1},${c2}`;\\n if (!dp.has(key) || total < dp.get(key)) {\\n dp.set(key, total);\\n }\\n }\\n }\\n }\\n\\n if (dp.size === 0) return 0;\\n\\n // Process remaining pairs\\n for (let i = 1; i < pairs; i++) {\\n const newDp = new Map();\\n const left = i;\\n const right = n - 1 - i;\\n\\n for (const [prevKey, prevCost] of dp) {\\n const [prevLeft, prevRight] = prevKey.split(',').map(Number);\\n\\n for (let currLeft = 1; currLeft <= 3; currLeft++) {\\n if (currLeft === prevLeft) continue; // Adjacent constraint\\n for (let currRight = 1; currRight <= 3; currRight++) {\\n if (currRight === prevRight) continue; // Adjacent constraint\\n if (currLeft === currRight) continue; // Mirror pair constraint\\n\\n const currentCost = cost[left][currLeft - 1] + cost[right][currRight - 1];\\n const total = prevCost + currentCost;\\n const key = `${currLeft},${currRight}`;\\n\\n if (!newDp.has(key) || total < newDp.get(key)) {\\n newDp.set(key, total);\\n }\\n }\\n }\\n }\\n\\n dp = newDp;\\n if (dp.size === 0) return -1; // If no valid configuration (problem states it's possible, so optional)\\n }\\n\\n return Math.min(...dp.values());\\n}\"]]"
},
"python3": {
"code": "class Solution:\n def minCost(self, n: int, cost: List[List[int]]) -> int:\n m = n // 2\n dp = {}\n first_left, first_right = 0, n - 1\n for c1 in range(3):\n for c2 in range(3):\n if c1 != c2:\n total = cost[first_left][c1] + cost[first_right][c2]\n dp[(c1, c2)] = total\n \n for i in range(1, m):\n left, right = i, n - 1 - i\n new_dp = {}\n for (prev_c1, prev_c2), prev_cost in dp.items():\n for curr_c1 in range(3):\n if curr_c1 == prev_c1:\n continue\n for curr_c2 in range(3):\n if curr_c2 == prev_c2 or curr_c1 == curr_c2:\n continue\n current_cost = prev_cost + cost[left][curr_c1] + cost[right][curr_c2]\n key = (curr_c1, curr_c2)\n if key not in new_dp or current_cost < new_dp.get(key, float('inf')):\n new_dp[key] = current_cost\n dp = new_dp\n \n return min(dp.values())",
"memory": 7100,
"memoryDistribution": "[[7100, 90.184, \"from typing import List\\n\\nclass Solution:\\n def minCost(self, n: int, cost: List[List[int]]) -> int:\\n m = n // 2\\n dp = {}\\n first_left, first_right = 0, n - 1\\n for c1 in range(3):\\n for c2 in range(3):\\n if c1 != c2:\\n total = cost[first_left][c1] + cost[first_right][c2]\\n dp[(c1, c2)] = total\\n \\n for i in range(1, m):\\n left, right = i, n - 1 - i\\n new_dp = {}\\n for (prev_c1, prev_c2), prev_cost in dp.items():\\n for curr_c1 in range(3):\\n if curr_c1 == prev_c1:\\n continue\\n for curr_c2 in range(3):\\n if curr_c2 == prev_c2 or curr_c1 == curr_c2:\\n continue\\n current_cost = prev_cost + cost[left][curr_c1] + cost[right][curr_c2]\\n key = (curr_c1, curr_c2)\\n if key not in new_dp or current_cost < new_dp.get(key, float('inf')):\\n new_dp[key] = current_cost\\n dp = new_dp\\n \\n return min(dp.values())\"], [68800, 0.6135, \"\\\"\\\"\\\"\\n[\\n [3,5,7],\\n [6,2,9],\\n [4,8,1],\\n [7,3,5],\\n]\\n\\nleft = 0, right = n-1\\n(0, 1): 3 + 3 = 6\\n(0, 2): 3 + 5 = 8\\n(1, 0): 5 + 7 = 12\\n(1, 2): 5 + 5 = 10\\n(2, 0): 7 + 7 = 14\\n(2, 1): 7 + 3 = 10\\n\\nleft = 1, right = n-2\\n(0, 1): 6 + 8 + min[(1, 0), (1, 2), (2, 0), (2, 2)]\\n(0, 2): 6 + 1 + min[(1, 0), (2, 0), (2, 1)]\\n(1, 0): 2 + 4 + min[()]\\n(1, 2): \\n(2, 0): \\n(2, 1): \\n\\\"\\\"\\\"\\n\\n\\nclass Solution:\\n def minCost(self, n: int, cost: List[List[int]]) -> int:\\n prev = {\\n (0, 1): cost[0][0] + cost[-1][1],\\n (0, 2): cost[0][0] + cost[-1][2],\\n (1, 0): cost[0][1] + cost[-1][0],\\n (1, 2): cost[0][1] + cost[-1][2],\\n (2, 0): cost[0][2] + cost[-1][0],\\n (2, 1): cost[0][2] + cost[-1][1],\\n }\\n # print(f'{prev=}')\\n for i in range(1, n // 2):\\n cur = {}\\n for x1, y1 in prev:\\n min_cost = float('inf')\\n for x2, y2 in prev:\\n if x1 != x2 and y1 != y2:\\n min_cost = min(min_cost, prev[(x2, y2)])\\n cur[(x1, y1)] = min_cost + cost[i][x1] + cost[n-1-i][y1]\\n prev = cur\\n\\n return min(prev.values())\\n\\n\\n\"], [70100, 0.6135, \"class Solution:\\n def minCost(self, n: int, cost: List[List[int]]) -> int:\\n dp = [[0] * 6 for _ in range(n//2)]\\n colors = [(0, 1), (0, 2), (1, 2), (1, 0), (2, 0), (2, 1)]\\n valid = {0: [2, 3, 4], 1: [3, 4, 5], 2: [0, 4, 5], 3: [0, 1, 5], 4: [0, 1, 2], 5:[1, 2, 3]}\\n\\n for i in range(n//2):\\n for j in range(6):\\n current_cost = (cost[i][colors[j][0]] + cost[n-1-i][colors[j][1]])\\n if i == 0:\\n min_prev = 0\\n else:\\n min_prev= min(dp[i-1][valid[j][0]], dp[i-1][valid[j][1]], dp[i-1][valid[j][2]])\\n dp[i][j] = current_cost+min_prev\\n min_total = min(dp[-1])\\n return min_total\"], [70300, 1.227, null], [70400, 3.681, null], [70500, 3.0675, null], [70600, 0.6135, null], [70700, 7.362, null], [70800, 11.0429, null], [70900, 3.681, null], [71000, 0.6135, null], [79900, 0.6135, null], [81500, 0.6135, null], [81700, 0.6135, null], [82700, 0.6135, null], [82800, 0.6135, null], [82900, 1.8405, null], [83000, 0.6135, null], [83300, 0.6135, null], [84500, 0.6135, null], [86800, 0.6135, null], [86900, 1.227, null], [87400, 1.227, null], [87500, 1.8405, null], [87600, 0.6135, null], [87700, 0.6135, null], [92700, 0.6135, null], [93600, 0.6135, null], [93700, 0.6135, null], [93800, 1.8405, null], [93900, 1.8405, null], [94000, 2.454, null], [94200, 0.6135, null], [100300, 0.6135, null], [107400, 0.6135, null], [107500, 1.8405, null], [107600, 1.227, null], [108300, 0.6135, null], [108500, 0.6135, null], [109200, 0.6135, null], [109600, 0.6135, null], [109800, 0.6135, null], [110600, 0.6135, null], [112200, 1.227, null], [112400, 1.227, null], [112600, 0.6135, null], [113900, 1.227, null], [114000, 1.8405, null], [114100, 1.8405, null], [114200, 0.6135, null], [118000, 0.6135, null], [121200, 0.6135, null], [121300, 0.6135, null], [126500, 0.6135, null], [138700, 0.6135, null], [138800, 0.6135, null], [139400, 0.6135, null], [141300, 0.6135, null], [142800, 1.227, null], [142900, 3.0675, null], [143000, 7.9755, null], [143100, 1.227, null], [143700, 0.6135, null], [144600, 0.6135, null], [148000, 0.6135, null], [152600, 0.6135, null], [153100, 0.6135, null], [153200, 1.8405, \"class Solution:\\n def minCost(self, n: int, cost: List[List[int]]) -> int:\\n @lru_cache(None)\\n def dp(i, j, l, r):\\n if i >= j:\\n return 0\\n \\n res = inf\\n for c1 in range(3):\\n for c2 in range(3):\\n if c1 != c2 and c1 !=l and c2!=r:\\n res = min(res, dp(i+1, j-1, c1, c2) + cost[i][c1] + cost[j][c2])\\n return res\\n \\n return dp(0, n-1, 3, 3)\\n\\n\\n\\n\\n\\n\\n \"], [156400, 0.6135, \"class Solution:\\n def minCost(self, n: int, cost: List[List[int]]) -> int:\\n\\n @lru_cache(None)\\n def dp(i, j, l, r):\\n if i >= j:\\n return 0\\n\\n res = inf\\n for c1 in range(1, 4):\\n for c2 in range(1, 4):\\n if c1 != c2 and c1!= l and c2 != r:\\n res = min(res, dp(i+1, j-1, c1, c2) + cost[i][c1-1] + cost[j][c2-1])\\n return res\\n \\n return dp(0, n-1, 0, 0)\\n\\n\\n\\n\\n\\n\\n \"]]",
"runtime": 1291,
"runtimeDistribution": "[[181, 2.454, \"class Solution:\\n def minCost(self, n: int, cost: List[List[int]]) -> int:\\n a1, b1, c1 = cost[n-1>>1]\\n a2, b2, c2 = cost[n>>1]\\n ab = a1 + b2\\n ac = a1 + c2\\n ba = b1 + a2\\n bc = b1 + c2\\n ca = c1 + a2\\n cb = c1 + b2\\n for i in range(n-3>>1, -1, -1):\\n a1, b1, c1 = cost[i]\\n a2, b2, c2 = cost[n-i-1]\\n ab, ac, ba, bc, ca, cb = (\\n min(ba, bc, ca) + a1 + b2,\\n min(ba, ca, cb) + a1 + c2,\\n min(ab, ac, cb) + b1 + a2,\\n min(ab, ca, cb) + b1 + c2,\\n min(ab, ac, bc) + c1 + a2,\\n min(ac, ba, bc) + c1 + b2,\\n )\\n return min(ab, ac, ba, bc, ca, cb)\\n\"], [218, 2.454, \"import math\\nimport functools\\n\\nclass Solution:\\n def minCost(self, n: int, cost: List[List[int]]) -> int:\\n COLOR1, COLOR2, COLOR3 = 0, 1, 2\\n prev = [0] * 6\\n curr = [0] * 6\\n\\n for i in range(n // 2):\\n left, right = i, n - i - 1\\n curr[0] = cost[left][COLOR1] + cost[right][COLOR2] + min(prev[2], prev[3], prev[4])\\n curr[1] = cost[left][COLOR1] + cost[right][COLOR3] + min(prev[2], prev[4], prev[5])\\n curr[2] = cost[left][COLOR2] + cost[right][COLOR1] + min(prev[0], prev[1], prev[5])\\n curr[3] = cost[left][COLOR2] + cost[right][COLOR3] + min(prev[0], prev[4], prev[5])\\n curr[4] = cost[left][COLOR3] + cost[right][COLOR1] + min(prev[0], prev[1], prev[3])\\n curr[5] = cost[left][COLOR3] + cost[right][COLOR2] + min(prev[1], prev[2], prev[3])\\n prev = curr\\n curr = [0] * 6\\n \\n return min(prev)\"], [254, 3.6810000000000005, null], [291, 4.2945, null], [328, 1.227, null], [364, 0.6135, null], [401, 0.6135, null], [438, 0.6135, null], [475, 0.6135, null], [511, 0.6135, null], [548, 1.227, null], [585, 0.6135, null], [622, 0.6135, null], [658, 1.227, null], [695, 0.6135, null], [732, 0.6135, null], [768, 0.6135, null], [805, 0.6135, null], [842, 0.6135, null], [879, 0.6135, null], [915, 0.6135, null], [952, 0.6135, null], [989, 0.6135, null], [1026, 0.6135, null], [1062, 0.6135, null], [1099, 0.6135, null], [1136, 0.6135, null], [1172, 0.6135, null], [1209, 0.6135, null], [1246, 0.6135, null], [1283, 0.6135, null], [1291, 70.552, \"from typing import List\\n\\nclass Solution:\\n def minCost(self, n: int, cost: List[List[int]]) -> int:\\n m = n // 2\\n dp = {}\\n first_left, first_right = 0, n - 1\\n for c1 in range(3):\\n for c2 in range(3):\\n if c1 != c2:\\n total = cost[first_left][c1] + cost[first_right][c2]\\n dp[(c1, c2)] = total\\n \\n for i in range(1, m):\\n left, right = i, n - 1 - i\\n new_dp = {}\\n for (prev_c1, prev_c2), prev_cost in dp.items():\\n for curr_c1 in range(3):\\n if curr_c1 == prev_c1:\\n continue\\n for curr_c2 in range(3):\\n if curr_c2 == prev_c2 or curr_c1 == curr_c2:\\n continue\\n current_cost = prev_cost + cost[left][curr_c1] + cost[right][curr_c2]\\n key = (curr_c1, curr_c2)\\n if key not in new_dp or current_cost < new_dp.get(key, float('inf')):\\n new_dp[key] = current_cost\\n dp = new_dp\\n \\n return min(dp.values())\"], [1319, 0.6135, null], [1356, 1.227, null], [1393, 1.8405, null], [1430, 1.227, null], [1466, 0.6135, null], [1503, 0.6135, null], [1540, 1.227, null], [1576, 0.6135, null], [1613, 0.6135, null], [1650, 0.6135, null], [1687, 0.6135, null], [1723, 0.6135, null], [1760, 0.6135, null], [1797, 1.227, null], [1833, 3.0675, null], [1870, 2.454, null], [1907, 1.8405, null], [1944, 1.8405, null], [1980, 2.454, null], [2017, 1.8405, null], [2054, 2.454, null], [2091, 3.6810000000000005, null], [2127, 1.227, null], [2164, 3.6810000000000005, null], [2201, 3.0675000000000003, null], [2237, 3.0675000000000003, null], [2274, 1.8405, null], [2311, 1.8405, null], [2348, 1.227, null], [2384, 0.6135, null], [2421, 0.6135, null], [2458, 0.6135, null], [2495, 1.227, null], [2531, 2.454, null], [2568, 2.454, null], [2605, 0.6135, null], [2641, 1.8405, null], [2678, 1.8405, null], [2715, 0.6135, null], [2752, 0.6135, null], [2788, 0.6135, null], [2825, 0.6135, \"class Solution:\\n def __init__(self):\\n self.dp = None\\n\\n def solve(self, c, l, r, i):\\n n = len(c)\\n if i >= n // 2:\\n return 0\\n\\n if self.dp[i][l][r] != -1:\\n return self.dp[i][l][r]\\n\\n left_choices = [j for j in range(3) if j != l]\\n right_choices = [j for j in range(3) if j != r]\\n\\n ans = float('inf')\\n\\n for h in left_choices:\\n for j in right_choices:\\n if h == j:\\n continue\\n cl = c[i][h]\\n cr = c[n - i - 1][j]\\n ans = min(ans, cl + cr + self.solve(c, h, j, i + 1))\\n\\n self.dp[i][l][r] = ans\\n return ans\\n\\n def minCost(self, n, c):\\n self.dp = [[[-1] * 4 for _ in range(4)] for _ in range(n // 2 + 1)]\\n return self.solve(c, 3, 3, 0)\"], [2862, 0.6135, \"class Solution:\\n def __init__(self):\\n self.dp = None\\n\\n def solve(self, c, l, r, i):\\n n = len(c)\\n if i >= n // 2:\\n return 0\\n\\n if self.dp[i][l][r] != -1:\\n return self.dp[i][l][r]\\n\\n left_choices = [j for j in range(3) if j != l]\\n right_choices = [j for j in range(3) if j != r]\\n\\n ans = float('inf')\\n\\n for h in left_choices:\\n for j in right_choices:\\n if h == j:\\n continue\\n cl = c[i][h]\\n cr = c[n - i - 1][j]\\n ans = min(ans, cl + cr + self.solve(c, h, j, i + 1))\\n\\n self.dp[i][l][r] = ans\\n return ans\\n\\n def minCost(self, n, c):\\n self.dp = [[[-1] * 4 for _ in range(4)] for _ in range(n // 2 + 1)]\\n return self.solve(c, 3, 3, 0)\"]]"
},
"ruby": {
"code": "def min_cost(n, cost)\n m = n / 2\n return 0 if m == 0\n\n inf = 1 << 60\n prev_dp = Array.new(3) { Array.new(3, inf) }\n\n i0 = 0\n j0 = n - 1\n (0..2).each do |c1|\n (0..2).each do |c2|\n if c1 != c2\n prev_dp[c1][c2] = cost[i0][c1] + cost[j0][c2]\n end\n end\n end\n\n (1...m).each do |k|\n i = k\n j = n - 1 - k\n curr_dp = Array.new(3) { Array.new(3, inf) }\n\n (0..2).each do |prev_c1|\n (0..2).each do |prev_c2|\n next if prev_dp[prev_c1][prev_c2] == inf\n\n (0..2).each do |curr_c1|\n next if curr_c1 == prev_c1\n\n (0..2).each do |curr_c2|\n next if curr_c2 == prev_c2 || curr_c1 == curr_c2\n\n total = prev_dp[prev_c1][prev_c2] + cost[i][curr_c1] + cost[j][curr_c2]\n curr_dp[curr_c1][curr_c2] = [curr_dp[curr_c1][curr_c2], total].min\n end\n end\n end\n end\n\n prev_dp = curr_dp\n end\n\n min_cost = inf\n (0..2).each do |c1|\n (0..2).each do |c2|\n if c1 != c2 && prev_dp[c1][c2] < min_cost\n min_cost = prev_dp[c1][c2]\n end\n end\n end\n\n min_cost\nend",
"memory": null,
"memoryDistribution": "[[225600, 100.0, \"def min_cost(n, cost)\\n m = n / 2\\n return 0 if m == 0\\n\\n inf = 1 << 60\\n prev_dp = Array.new(3) { Array.new(3, inf) }\\n\\n i0 = 0\\n j0 = n - 1\\n (0..2).each do |c1|\\n (0..2).each do |c2|\\n if c1 != c2\\n prev_dp[c1][c2] = cost[i0][c1] + cost[j0][c2]\\n end\\n end\\n end\\n\\n (1...m).each do |k|\\n i = k\\n j = n - 1 - k\\n curr_dp = Array.new(3) { Array.new(3, inf) }\\n\\n (0..2).each do |prev_c1|\\n (0..2).each do |prev_c2|\\n next if prev_dp[prev_c1][prev_c2] == inf\\n\\n (0..2).each do |curr_c1|\\n next if curr_c1 == prev_c1\\n\\n (0..2).each do |curr_c2|\\n next if curr_c2 == prev_c2 || curr_c1 == curr_c2\\n\\n total = prev_dp[prev_c1][prev_c2] + cost[i][curr_c1] + cost[j][curr_c2]\\n curr_dp[curr_c1][curr_c2] = [curr_dp[curr_c1][curr_c2], total].min\\n end\\n end\\n end\\n end\\n\\n prev_dp = curr_dp\\n end\\n\\n min_cost = inf\\n (0..2).each do |c1|\\n (0..2).each do |c2|\\n if c1 != c2 && prev_dp[c1][c2] < min_cost\\n min_cost = prev_dp[c1][c2]\\n end\\n end\\n end\\n\\n min_cost\\nend\"]]",
"runtime": 1171,
"runtimeDistribution": "[[1171, 100.0, \"def min_cost(n, cost)\\n m = n / 2\\n return 0 if m == 0\\n\\n inf = 1 << 60\\n prev_dp = Array.new(3) { Array.new(3, inf) }\\n\\n i0 = 0\\n j0 = n - 1\\n (0..2).each do |c1|\\n (0..2).each do |c2|\\n if c1 != c2\\n prev_dp[c1][c2] = cost[i0][c1] + cost[j0][c2]\\n end\\n end\\n end\\n\\n (1...m).each do |k|\\n i = k\\n j = n - 1 - k\\n curr_dp = Array.new(3) { Array.new(3, inf) }\\n\\n (0..2).each do |prev_c1|\\n (0..2).each do |prev_c2|\\n next if prev_dp[prev_c1][prev_c2] == inf\\n\\n (0..2).each do |curr_c1|\\n next if curr_c1 == prev_c1\\n\\n (0..2).each do |curr_c2|\\n next if curr_c2 == prev_c2 || curr_c1 == curr_c2\\n\\n total = prev_dp[prev_c1][prev_c2] + cost[i][curr_c1] + cost[j][curr_c2]\\n curr_dp[curr_c1][curr_c2] = [curr_dp[curr_c1][curr_c2], total].min\\n end\\n end\\n end\\n end\\n\\n prev_dp = curr_dp\\n end\\n\\n min_cost = inf\\n (0..2).each do |c1|\\n (0..2).each do |c2|\\n if c1 != c2 && prev_dp[c1][c2] < min_cost\\n min_cost = prev_dp[c1][c2]\\n end\\n end\\n end\\n\\n min_cost\\nend\"], [1194, 100.0, \"def min_cost(n, cost)\\n m = n / 2\\n return 0 if m == 0\\n\\n inf = 1 << 60\\n prev_dp = Array.new(3) { Array.new(3, inf) }\\n\\n i0 = 0\\n j0 = n - 1\\n (0..2).each do |c1|\\n (0..2).each do |c2|\\n if c1 != c2\\n prev_dp[c1][c2] = cost[i0][c1] + cost[j0][c2]\\n end\\n end\\n end\\n\\n (1...m).each do |k|\\n i = k\\n j = n - 1 - k\\n curr_dp = Array.new(3) { Array.new(3, inf) }\\n\\n (0..2).each do |prev_c1|\\n (0..2).each do |prev_c2|\\n next if prev_dp[prev_c1][prev_c2] == inf\\n\\n (0..2).each do |curr_c1|\\n next if curr_c1 == prev_c1\\n\\n (0..2).each do |curr_c2|\\n next if curr_c2 == prev_c2 || curr_c1 == curr_c2\\n\\n total = prev_dp[prev_c1][prev_c2] + cost[i][curr_c1] + cost[j][curr_c2]\\n curr_dp[curr_c1][curr_c2] = [curr_dp[curr_c1][curr_c2], total].min\\n end\\n end\\n end\\n end\\n\\n prev_dp = curr_dp\\n end\\n\\n min_cost = inf\\n (0..2).each do |c1|\\n (0..2).each do |c2|\\n if c1 != c2 && prev_dp[c1][c2] < min_cost\\n min_cost = prev_dp[c1][c2]\\n end\\n end\\n end\\n\\n min_cost\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list:
import random
random.seed(seed)
def sample_solution(n, cost):
m = n // 2
dp = {}
first_left, first_right = 0, n - 1
for c1 in range(3):
for c2 in range(3):
if c1 != c2:
dp[(c1, c2)] = cost[first_left][c1] + cost[first_right][c2]
for i in range(1, m):
left = i
right = n - 1 - i
new_dp = {}
for (prev_c1, prev_c2), prev_cost in dp.items():
for curr_c1 in range(3):
if curr_c1 == prev_c1:
continue
for curr_c2 in range(3):
if curr_c2 == prev_c2 or curr_c1 == curr_c2:
continue
current_cost = prev_cost + cost[left][curr_c1] + cost[right][curr_c2]
key = (curr_c1, curr_c2)
if key not in new_dp or current_cost < new_dp[key]:
new_dp[key] = current_cost
dp = new_dp
return min(dp.values())
def serialize_input(n, cost):
# First line is n, followed by n lines each containing 3 comma‐separated integers.
lines = [str(n)]
for row in cost:
lines.append(",".join(map(str, row)))
return "\n".join(lines)
test_cases = []
predefined = []
# Predefined Case 1: Minimal even n = 2.
predefined.append((2, [[1, 2, 3],
[4, 5, 6]]))
# Predefined Case 2: Example 1.
predefined.append((4, [[3, 5, 7],
[6, 2, 9],
[4, 8, 1],
[7, 3, 5]]))
# Predefined Case 3: Example 2.
predefined.append((6, [[2, 4, 6],
[5, 3, 8],
[7, 1, 9],
[4, 6, 2],
[3, 5, 7],
[8, 2, 4]]))
# Predefined Case 4: Uniform cost values.
predefined.append((4, [[10, 10, 10],
[10, 10, 10],
[10, 10, 10],
[10, 10, 10]]))
# Predefined Case 5: Mixed pattern.
predefined.append((8, [
[0, 100, 100],
[100, 0, 100],
[100, 100, 0],
[0, 50, 100],
[100, 0, 50],
[50, 100, 0],
[0, 0, 1],
[1, 0, 0]
]))
# Predefined Case 6: All costs zero.
predefined.append((2, [[0, 0, 0],
[0, 0, 0]]))
# Use predefined test cases first.
for n, cost in predefined[:num_cases]:
inp = serialize_input(n, cost)
result = sample_solution(n, cost)
test_cases.append({"input": inp, "output": str(result)})
# If additional cases are required, generate random ones.
count = len(predefined)
while count < num_cases:
# Choose a random even number between 2 and 20.
n = random.choice([x for x in range(2, 21) if x % 2 == 0])
cost = []
# Each row: three random integers between 0 and 100.
for _ in range(n):
row = [random.randint(0, 100) for _ in range(3)]
cost.append(row)
inp = serialize_input(n, cost)
try:
result = sample_solution(n, cost)
except Exception:
result = -1 # Fallback in the unlikely event of an error.
test_cases.append({"input": inp, "output": str(result)})
count += 1
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
try:
# Strip whitespace and compare integer values.
expected = int(expected_output.strip())
result = int(program_output.strip())
return expected == result
except Exception:
return False
|
[{"input": "2\n1,2,3\n4,5,6", "output": "6"}, {"input": "4\n3,5,7\n6,2,9\n4,8,1\n7,3,5", "output": "9"}, {"input": "6\n2,4,6\n5,3,8\n7,1,9\n4,6,2\n3,5,7\n8,2,4", "output": "18"}, {"input": "4\n10,10,10\n10,10,10\n10,10,10\n10,10,10", "output": "40"}, {"input": "8\n0,100,100\n100,0,100\n100,100,0\n0,50,100\n100,0,50\n50,100,0\n0,0,1\n1,0,0", "output": "51"}, {"input": "2\n0,0,0\n0,0,0", "output": "0"}, {"input": "4\n3,94,35\n31,28,17\n94,13,86\n94,69,11", "output": "44"}, {"input": "20\n54,4,3\n11,27,29\n64,77,3\n71,25,91\n83,89,69\n53,28,57\n75,35,0\n97,20,89\n54,43,35\n19,27,97\n43,13,11\n48,12,45\n44,77,33\n5,93,58\n68,15,48\n10,70,37\n80,79,46\n73,24,90\n8,5,84\n29,98,37", "output": "477"}, {"input": "4\n29,12,48\n35,58,81\n46,20,47\n45,26,85", "output": "112"}, {"input": "10\n89,87,82\n9,77,81\n21,68,93\n31,20,59\n48,34,81\n88,71,28\n87,41,98\n99,7,29\n4,40,51\n34,8,27", "output": "382"}, {"input": "20\n91,40,27\n83,63,50\n82,58,18\n33,17,31\n95,71,68\n33,95,74\n54,74,51\n46,28,17\n65,63,11\n96,6,14\n19,80,20\n87,54,76\n8,49,48\n76,59,67\n32,70,1\n87,92,14\n87,68,96\n34,98,82\n43,14,37\n55,20,58", "output": "725"}, {"input": "2\n92,92,33\n64,97,22", "output": "97"}, {"input": "18\n13,80,38\n81,64,77\n25,19,47\n97,20,69\n99,67,0\n76,41,62\n2,14,46\n39,30,7\n30,72,10\n10,93,62\n8,97,68\n98,16,16\n84,60,70\n21,33,67\n77,54,27\n69,96,93\n88,25,91\n39,51,85", "output": "603"}, {"input": "12\n56,66,57\n15,31,28\n8,43,2\n75,70,29\n75,28,0\n9,90,80\n7,29,8\n4,42,9\n65,30,35\n85,62,27\n69,16,92\n73,73,60", "output": "303"}, {"input": "8\n100,60,52\n24,12,12\n84,55,45\n54,52,59\n93,6,86\n83,82,12\n7,51,93\n43,13,31", "output": "237"}, {"input": "8\n24,68,57\n17,54,23\n35,59,31\n9,56,70\n12,6,83\n69,1,11\n96,30,21\n52,62,61", "output": "223"}, {"input": "8\n51,7,21\n48,0,49\n33,100,100\n58,36,54\n89,93,100\n71,84,91\n62,19,24\n37,27,7", "output": "314"}, {"input": "20\n94,69,7\n95,40,7\n6,74,61\n64,67,20\n7,65,10\n23,8,76\n8,86,30\n51,15,72\n31,74,76\n5,79,10\n53,84,74\n72,66,40\n33,26,85\n91,40,30\n33,50,16\n85,82,38\n58,40,96\n9,1,58\n79,72,12\n9,68,27", "output": "459"}, {"input": "18\n33,16,44\n8,31,47\n36,20,56\n69,90,38\n78,83,67\n1,85,70\n38,84,13\n17,33,14\n13,95,70\n19,34,36\n77,26,91\n43,26,87\n81,33,64\n62,32,6\n11,81,54\n35,5,0\n42,98,16\n81,33,20", "output": "505"}, {"input": "16\n70,90,54\n71,1,14\n9,88,19\n69,4,47\n74,70,18\n55,16,5\n39,46,5\n45,26,87\n31,85,13\n45,99,71\n52,79,95\n19,30,20\n22,52,3\n22,94,42\n100,52,85\n94,31,34", "output": "456"}, {"input": "6\n100,89,13\n48,4,60\n28,25,58\n44,39,29\n28,3,84\n24,51,42", "output": "142"}, {"input": "10\n8,98,35\n44,82,65\n51,86,68\n42,3,14\n33,22,74\n33,4,13\n76,55,44\n93,100,40\n55,77,65\n14,49,73", "output": "372"}, {"input": "8\n32,5,90\n55,0,66\n68,87,92\n94,94,85\n25,46,55\n8,85,42\n79,40,84\n15,92,38", "output": "341"}, {"input": "18\n39,85,52\n41,51,89\n37,70,16\n24,53,85\n48,86,95\n22,78,72\n38,51,70\n0,38,36\n26,55,100\n74,77,83\n41,59,56\n56,86,27\n65,60,94\n21,84,10\n36,65,84\n81,79,42\n11,96,30\n86,39,28", "output": "732"}, {"input": "8\n18,3,5\n31,60,78\n98,9,58\n53,80,73\n24,91,89\n49,63,51\n31,18,83\n88,0,96", "output": "284"}, {"input": "4\n99,54,28\n22,89,66\n59,6,71\n31,15,58", "output": "87"}, {"input": "6\n59,85,67\n71,76,40\n96,56,78\n92,64,54\n70,57,20\n95,60,57", "output": "323"}, {"input": "10\n96,31,81\n35,98,99\n66,62,80\n30,35,56\n9,91,36\n30,34,42\n40,69,10\n17,19,29\n49,88,19\n90,27,8", "output": "347"}, {"input": "20\n60,91,84\n46,91,57\n14,12,97\n84,28,0\n43,45,81\n37,70,66\n47,89,13\n5,21,63\n17,91,95\n92,52,13\n32,78,25\n24,15,50\n27,58,100\n24,91,43\n13,96,53\n5,81,86\n75,15,98\n57,58,84\n75,64,17\n63,0,67", "output": "600"}, {"input": "2\n70,55,74\n61,65,99", "output": "116"}, {"input": "6\n88,74,22\n93,16,13\n49,84,76\n77,41,64\n49,53,77\n88,97,31", "output": "257"}, {"input": "10\n50,43,37\n57,17,17\n52,77,89\n95,65,38\n89,70,40\n91,94,70\n80,27,25\n26,79,91\n37,87,44\n86,16,90", "output": "450"}, {"input": "6\n64,69,88\n81,41,90\n14,97,45\n71,61,74\n73,85,90\n53,86,95", "output": "339"}, {"input": "18\n36,54,1\n66,13,3\n48,18,6\n85,7,25\n34,96,100\n20,36,87\n32,18,7\n88,100,37\n26,96,69\n4,45,57\n13,78,86\n94,71,28\n95,82,71\n49,30,65\n100,89,36\n88,85,6\n48,49,53\n100,87,40", "output": "647"}, {"input": "18\n6,1,95\n32,25,79\n99,56,28\n81,90,90\n82,47,96\n75,69,94\n77,25,99\n92,24,37\n57,22,87\n9,23,22\n94,65,15\n48,5,54\n35,71,33\n16,20,74\n32,0,42\n59,90,19\n5,19,41\n76,6,99", "output": "623"}, {"input": "20\n84,38,62\n73,70,45\n9,100,90\n40,67,28\n23,66,8\n100,64,20\n53,69,68\n51,11,44\n28,27,84\n42,42,46\n37,27,96\n79,67,60\n71,96,83\n1,14,85\n44,57,30\n82,78,79\n31,5,87\n41,48,14\n49,32,69\n92,36,3", "output": "650"}, {"input": "18\n98,47,65\n65,57,62\n5,37,83\n24,41,65\n10,12,21\n98,68,68\n0,80,8\n26,85,80\n99,27,87\n54,13,26\n68,89,94\n99,55,82\n9,95,87\n19,3,58\n91,42,4\n11,9,6\n22,32,71\n9,73,29", "output": "565"}, {"input": "10\n52,49,57\n80,51,55\n40,2,49\n86,15,68\n0,82,92\n79,8,96\n95,74,5\n89,9,45\n64,13,37\n100,87,38", "output": "282"}, {"input": "20\n11,36,97\n56,48,50\n84,3,60\n20,68,28\n17,95,50\n69,37,81\n18,38,86\n93,82,47\n1,70,71\n18,15,5\n0,73,76\n50,68,70\n10,39,26\n95,94,92\n44,27,52\n82,65,18\n20,23,28\n78,32,24\n14,23,85\n72,6,96", "output": "513"}, {"input": "18\n59,82,70\n9,37,85\n8,32,12\n25,92,74\n62,42,45\n16,85,83\n30,12,36\n79,8,24\n40,62,57\n42,78,84\n39,88,74\n19,72,72\n46,40,54\n21,0,40\n31,100,28\n91,94,82\n55,35,46\n17,86,93", "output": "638"}, {"input": "12\n61,59,57\n45,99,39\n62,70,13\n22,82,77\n10,35,17\n68,25,33\n93,80,9\n93,9,2\n64,80,3\n74,74,51\n98,75,27\n4,70,33", "output": "305"}, {"input": "18\n69,60,83\n99,19,46\n50,28,98\n75,93,37\n17,59,64\n65,11,50\n46,64,1\n84,30,78\n87,21,96\n65,17,57\n20,22,72\n72,84,18\n94,93,61\n45,5,28\n97,62,29\n8,33,47\n29,5,85\n26,66,46", "output": "640"}, {"input": "14\n60,58,5\n5,83,41\n13,90,66\n81,35,94\n33,74,69\n72,22,48\n83,48,46\n75,83,9\n66,32,48\n28,66,51\n45,44,62\n61,77,0\n64,17,56\n21,29,9", "output": "439"}, {"input": "18\n82,35,27\n19,23,20\n46,77,91\n15,84,29\n53,42,92\n14,61,86\n61,61,26\n75,20,82\n52,2,31\n5,16,73\n75,20,17\n80,65,5\n73,18,7\n21,33,23\n66,51,76\n72,81,2\n92,93,84\n36,10,27", "output": "528"}, {"input": "16\n77,60,61\n21,28,52\n76,18,74\n98,23,79\n84,65,33\n21,92,87\n43,58,76\n75,8,29\n48,49,16\n13,2,25\n66,64,87\n53,19,77\n12,22,60\n78,76,4\n100,68,64\n96,15,11", "output": "568"}, {"input": "16\n84,16,77\n69,0,99\n86,83,55\n66,53,47\n5,89,67\n54,29,61\n98,48,44\n75,94,97\n89,73,12\n54,17,32\n61,98,29\n10,36,76\n69,52,32\n24,0,90\n95,0,73\n66,15,66", "output": "552"}, {"input": "2\n48,83,26\n88,40,52", "output": "66"}, {"input": "12\n13,19,54\n83,74,32\n33,68,54\n72,46,78\n35,87,50\n96,26,52\n70,100,71\n61,22,47\n71,71,61\n32,39,73\n44,99,90\n50,94,17", "output": "438"}, {"input": "4\n95,29,57\n100,89,20\n12,27,65\n51,100,43", "output": "104"}, {"input": "18\n78,89,87\n90,6,20\n49,81,0\n11,18,60\n76,55,11\n8,33,28\n47,10,77\n4,92,49\n51,78,83\n66,36,91\n76,7,99\n22,81,63\n56,1,25\n84,66,36\n24,4,100\n76,65,66\n89,29,78\n21,86,4", "output": "570"}, {"input": "12\n30,83,0\n20,11,35\n99,51,45\n85,50,51\n75,25,66\n1,94,90\n8,11,70\n36,92,71\n74,44,44\n35,28,77\n24,58,51\n73,0,33", "output": "310"}, {"input": "6\n52,64,13\n71,9,64\n37,43,14\n65,32,68\n73,32,88\n56,48,72", "output": "189"}, {"input": "16\n98,31,96\n43,99,58\n87,58,75\n3,61,14\n33,8,48\n81,100,28\n86,89,29\n40,52,45\n66,68,1\n89,33,31\n36,11,51\n86,95,43\n9,70,22\n60,40,45\n27,73,34\n23,95,87", "output": "583"}, {"input": "8\n63,94,25\n30,94,30\n33,26,29\n25,31,79\n45,19,99\n13,15,10\n86,84,63\n78,0,97", "output": "201"}, {"input": "18\n5,61,47\n79,40,63\n73,35,62\n23,97,65\n35,50,28\n96,73,16\n6,67,54\n61,69,4\n64,44,50\n87,99,22\n58,15,89\n66,58,40\n88,1,1\n86,26,48\n74,12,41\n46,78,33\n23,70,33\n30,34,60", "output": "474"}, {"input": "20\n43,46,23\n63,54,26\n53,89,96\n47,46,51\n35,57,23\n73,16,73\n87,29,12\n92,34,30\n71,55,48\n25,18,94\n19,60,1\n22,53,63\n17,80,66\n68,92,40\n100,62,38\n32,71,72\n6,50,12\n88,20,7\n27,32,60\n80,12,57", "output": "617"}, {"input": "12\n33,46,46\n71,71,32\n44,2,52\n15,44,86\n77,25,73\n73,83,83\n68,22,99\n36,45,41\n86,65,62\n99,94,57\n10,48,78\n36,59,80", "output": "429"}, {"input": "6\n21,81,43\n53,80,78\n73,51,9\n10,20,43\n29,40,40\n83,37,90", "output": "192"}, {"input": "10\n77,82,50\n34,56,99\n46,95,75\n66,57,52\n21,23,2\n16,93,30\n84,32,95\n89,95,10\n26,21,50\n13,12,8", "output": "323"}, {"input": "16\n70,6,3\n98,50,67\n97,10,13\n33,79,19\n10,83,49\n39,29,31\n94,36,56\n80,16,16\n67,21,3\n4,84,45\n41,60,59\n69,34,70\n56,17,89\n69,22,75\n76,58,80\n95,81,72", "output": "566"}, {"input": "14\n67,81,81\n68,39,44\n61,69,29\n11,56,39\n46,52,33\n19,38,1\n0,66,97\n17,44,36\n60,68,1\n88,62,96\n61,38,1\n98,55,37\n76,29,0\n70,47,24", "output": "427"}, {"input": "14\n71,55,50\n31,20,91\n94,82,49\n48,28,33\n10,54,80\n30,66,97\n78,88,87\n34,36,83\n95,68,34\n52,24,8\n23,17,37\n14,81,58\n79,57,34\n89,79,62", "output": "559"}, {"input": "8\n41,2,19\n6,68,2\n23,13,36\n34,16,91\n56,93,1\n29,11,19\n1,63,27\n43,53,39", "output": "95"}, {"input": "16\n47,59,89\n4,42,10\n96,18,7\n34,99,50\n9,69,60\n23,24,32\n48,1,15\n98,91,31\n49,98,56\n31,94,4\n25,58,94\n98,12,66\n85,26,60\n49,87,39\n41,20,80\n93,5,95", "output": "453"}, {"input": "18\n66,15,32\n61,81,38\n25,46,6\n85,27,14\n30,81,55\n41,1,21\n35,74,15\n50,31,1\n5,74,100\n88,60,88\n76,19,47\n98,11,31\n20,63,11\n87,79,43\n97,80,7\n7,45,82\n19,89,68\n13,16,62", "output": "494"}, {"input": "8\n40,71,100\n82,96,44\n56,93,24\n2,88,48\n45,92,17\n32,5,62\n90,56,71\n37,69,89", "output": "309"}, {"input": "16\n24,72,23\n69,44,41\n93,59,35\n76,70,20\n8,67,19\n57,37,33\n69,46,58\n0,99,81\n64,48,93\n23,2,79\n46,99,79\n30,41,92\n8,84,68\n49,24,67\n87,63,98\n70,19,78", "output": "595"}, {"input": "10\n41,52,82\n41,14,12\n66,84,8\n5,16,22\n4,25,13\n62,24,12\n4,73,82\n49,84,62\n67,79,89\n75,32,6", "output": "256"}, {"input": "12\n28,77,91\n9,1,26\n83,62,10\n59,81,7\n46,71,95\n53,47,90\n7,78,34\n67,5,93\n9,38,9\n27,66,12\n12,92,29\n68,49,24", "output": "281"}, {"input": "8\n67,84,31\n72,80,22\n71,95,71\n53,95,13\n98,81,73\n45,86,58\n89,85,54\n13,21,23", "output": "404"}, {"input": "18\n51,64,43\n84,20,68\n76,56,45\n40,70,41\n47,52,97\n81,55,92\n41,77,30\n72,69,27\n48,98,70\n95,32,46\n57,57,50\n0,92,4\n36,76,2\n66,17,38\n0,38,28\n27,40,2\n98,88,35\n70,65,71", "output": "668"}, {"input": "20\n73,19,12\n4,58,45\n19,17,33\n46,74,31\n29,32,38\n11,73,51\n72,27,93\n9,92,41\n61,22,62\n88,89,73\n12,76,82\n38,4,93\n73,48,10\n99,7,98\n42,44,55\n53,15,98\n29,95,83\n77,1,81\n99,80,48\n6,39,67", "output": "612"}, {"input": "2\n40,25,0\n18,57,8", "output": "18"}, {"input": "14\n77,31,67\n42,72,62\n58,59,73\n5,94,11\n36,82,58\n44,89,91\n38,50,78\n22,53,31\n22,79,93\n55,58,49\n84,23,89\n72,12,50\n89,5,30\n20,35,80", "output": "506"}, {"input": "18\n37,85,8\n89,92,92\n27,63,52\n97,70,15\n47,9,96\n13,64,98\n99,41,52\n57,21,32\n26,64,5\n59,3,9\n81,88,86\n95,59,48\n43,95,51\n24,50,4\n1,32,14\n90,17,41\n85,95,59\n62,59,8", "output": "630"}, {"input": "4\n70,84,31\n91,56,17\n60,35,20\n21,2,77", "output": "109"}, {"input": "4\n22,37,15\n68,94,50\n21,9,85\n97,1,86", "output": "94"}, {"input": "10\n19,56,45\n22,27,91\n4,86,68\n27,56,89\n6,81,66\n82,84,91\n84,13,49\n88,39,56\n6,76,0\n6,98,48", "output": "316"}, {"input": "8\n31,47,30\n25,11,2\n53,3,1\n43,24,87\n85,8,28\n12,85,21\n92,21,5\n53,65,13", "output": "133"}, {"input": "12\n41,71,80\n24,79,26\n69,50,54\n15,29,27\n13,45,41\n22,1,51\n83,40,1\n49,27,58\n28,8,84\n35,83,79\n47,5,8\n27,52,38", "output": "310"}, {"input": "20\n63,13,91\n68,72,21\n32,12,76\n41,80,89\n49,86,98\n88,17,42\n22,81,97\n88,40,85\n61,8,42\n2,77,74\n57,48,65\n81,94,29\n64,75,90\n1,29,2\n78,97,15\n39,30,94\n54,96,31\n79,10,7\n17,47,63\n37,25,19", "output": "621"}, {"input": "14\n26,82,4\n30,92,76\n56,94,42\n17,35,40\n82,100,97\n5,66,53\n82,36,96\n3,29,93\n42,43,31\n26,69,6\n85,31,87\n89,92,28\n77,48,66\n41,23,56", "output": "486"}, {"input": "2\n8,62,8\n24,6,81", "output": "14"}, {"input": "6\n26,16,11\n22,75,70\n26,30,64\n10,54,92\n59,39,21\n92,25,31", "output": "119"}, {"input": "14\n22,77,31\n38,36,73\n57,81,25\n34,100,61\n10,46,50\n48,21,60\n56,54,64\n78,94,55\n97,19,61\n2,97,48\n54,10,97\n38,76,68\n19,70,93\n22,32,48", "output": "492"}, {"input": "16\n39,58,36\n48,71,77\n61,9,42\n17,91,60\n25,19,24\n0,1,64\n93,92,47\n62,51,53\n50,95,47\n49,62,39\n82,75,9\n52,4,15\n49,72,20\n24,97,55\n32,98,96\n92,44,65", "output": "525"}, {"input": "16\n81,88,47\n89,7,83\n49,54,94\n31,31,61\n4,46,80\n90,86,3\n89,85,82\n18,33,77\n58,87,18\n32,31,77\n74,84,20\n1,14,98\n11,82,91\n49,50,90\n75,10,66\n24,54,21", "output": "551"}, {"input": "14\n32,88,38\n64,68,84\n48,75,39\n93,52,96\n93,11,13\n81,73,99\n44,18,34\n95,26,95\n50,89,39\n0,21,62\n0,12,8\n99,89,53\n67,53,83\n36,93,55", "output": "574"}, {"input": "6\n22,47,23\n90,17,25\n62,23,64\n14,57,72\n27,23,25\n7,95,23", "output": "130"}, {"input": "8\n33,52,56\n80,79,13\n81,21,10\n37,10,48\n15,35,8\n43,3,74\n30,61,62\n86,97,12", "output": "185"}, {"input": "2\n7,34,96\n0,85,74", "output": "34"}, {"input": "2\n12,27,66\n0,48,77", "output": "27"}, {"input": "18\n97,34,62\n60,96,43\n77,54,43\n47,87,43\n40,30,46\n85,51,48\n78,7,45\n42,12,0\n58,89,51\n92,17,3\n77,15,67\n35,89,96\n31,47,57\n79,87,84\n60,65,52\n84,24,0\n81,41,2\n81,46,5", "output": "607"}, {"input": "12\n86,56,29\n77,62,51\n94,78,10\n44,54,60\n84,89,12\n93,49,37\n77,24,91\n18,66,73\n100,91,64\n4,16,63\n11,38,86\n70,59,21", "output": "442"}, {"input": "16\n14,61,84\n69,30,31\n27,21,96\n84,89,11\n13,55,91\n3,20,41\n49,98,35\n28,92,32\n85,60,85\n15,85,17\n68,81,92\n62,11,88\n42,28,73\n98,76,8\n82,43,48\n91,95,94", "output": "534"}, {"input": "14\n83,82,100\n71,55,29\n28,33,14\n37,11,14\n11,43,94\n75,24,95\n14,73,47\n16,40,48\n73,94,0\n39,7,75\n68,24,49\n54,40,98\n46,86,16\n66,84,77", "output": "445"}, {"input": "20\n28,13,50\n1,68,58\n40,18,37\n28,63,87\n58,18,76\n36,18,95\n85,89,4\n76,40,39\n64,88,15\n35,90,73\n61,80,27\n63,37,90\n48,7,42\n19,91,26\n93,28,89\n94,6,99\n22,62,93\n50,38,84\n20,2,70\n50,43,54", "output": "619"}, {"input": "16\n44,96,50\n50,9,67\n93,36,36\n89,24,89\n70,50,12\n16,41,96\n74,6,90\n38,58,83\n20,73,17\n56,89,61\n37,18,26\n27,95,25\n94,83,1\n46,92,73\n13,86,100\n18,48,54", "output": "457"}, {"input": "6\n7,12,45\n60,22,6\n15,65,83\n43,75,55\n19,80,92\n51,31,4", "output": "106"}, {"input": "4\n30,50,62\n38,88,76\n22,83,95\n48,99,88", "output": "216"}]
|
{
"cpp": "==Code Submission==\n\nint main() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n int n;\n cin >> n;\n vector<vector<int>> cost(n, vector<int>(3));\n string dummy;\n getline(cin, dummy); // consume the rest of the line\n for (int i = 0; i < n; i++) {\n string line;\n while(getline(cin, line) && line.empty());\n stringstream ss(line);\n string token;\n int j = 0;\n while(getline(ss, token, ',')) {\n cost[i][j++] = stoi(token);\n }\n }\n Solution sol; // User-submitted solution replaces the placeholder.\n long long ans = sol.minCost(n, cost);\n cout << ans;\n return 0;\n}",
"golang": "==Code Submission==\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n line, _ := reader.ReadString('\\n')\n line = strings.TrimSpace(line)\n n, _ := strconv.Atoi(line)\n cost := make([][]int, n)\n for i := 0; i < n; i++ {\n rowStr, _ := reader.ReadString('\\n')\n rowStr = strings.TrimSpace(rowStr)\n parts := strings.Split(rowStr, \",\")\n row := make([]int, 3)\n for j, s := range parts {\n row[j], _ = strconv.Atoi(s)\n }\n cost[i] = row\n }\n ans := minCost(n, cost) // The user-submitted solution will be injected here.\n fmt.Println(ans)\n}",
"java": "public class Main {\n public static void main(String[] args) throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n int n = Integer.parseInt(br.readLine().trim());\n int[][] cost = new int[n][3];\n for (int i = 0; i < n; i++) {\n String[] parts = br.readLine().trim().split(\",\");\n for (int j = 0; j < 3; j++) {\n cost[i][j] = Integer.parseInt(parts[j]);\n }\n }\n Solution sol = new Solution(); // Placeholder for user-submitted solution.\n long ans = sol.minCost(n, cost);\n System.out.println(ans);\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\nfunction deserialize_stdin(input) {\n const lines = input.trim().split('\\n');\n const n = parseInt(lines[0], 10);\n const cost = [];\n for (let i = 1; i <= n; i++) {\n cost.push(lines[i].split(',').map(Number));\n }\n return { n, cost };\n}\n\nfunction serialize_stdout(result) {\n return result.toString();\n}\n\nlet input = '';\nprocess.stdin.setEncoding('utf8');\nprocess.stdin.on('data', chunk => input += chunk);\nprocess.stdin.on('end', () => {\n const { n, cost } = deserialize_stdin(input);\n const ans = minCost(n, cost);\n console.log(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\ndef deserialize_stdin(input_str):\n lines = input_str.strip().split(\"\\n\")\n n = int(lines[0])\n cost = []\n for i in range(1, n + 1):\n row = list(map(int, lines[i].split(\",\")))\n cost.append(row)\n return n, cost\n\ndef serialize_stdout(result):\n return str(result)\n\ndata = sys.stdin.read()\nn, cost = deserialize_stdin(data)\nsol = Solution() # The user-submitted solution will be injected here.\nresult = sol.minCost(n, cost)\nsys.stdout.write(serialize_stdout(result))",
"ruby": "==Code Submission==\ninput = $stdin.read.split(\"\\n\")\nn = input[0].to_i\ncost = input[1, n].map { |line| line.split(',').map(&:to_i) }\nans = min_cost(n, cost) # The user-submitted solution will be injected here.\nputs ans.to_s"
}
|
3739
|
Manhattan Distances of All Arrangements of Pieces
|
manhattan-distances-of-all-arrangements-of-pieces
|
<p>You are given three integers <code><font face="monospace">m</font></code>, <code><font face="monospace">n</font></code>, and <code>k</code>.</p>
<p>There is a rectangular grid of size <code>m × n</code> containing <code>k</code> identical pieces. Return the sum of Manhattan distances between every pair of pieces over all <strong>valid arrangements</strong> of pieces.</p>
<p>A <strong>valid arrangement</strong> is a placement of all <code>k</code> pieces on the grid with <strong>at most</strong> one piece per cell.</p>
<p>Since the answer may be very large, return it <strong>modulo</strong> <code>10<sup>9</sup> + 7</code>.</p>
<p>The Manhattan Distance between two cells <code>(x<sub>i</sub>, y<sub>i</sub>)</code> and <code>(x<sub>j</sub>, y<sub>j</sub>)</code> is <code>|x<sub>i</sub> - x<sub>j</sub>| + |y<sub>i</sub> - y<sub>j</sub>|</code>.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">m = 2, n = 2, k = 2</span></p>
<p><strong>Output:</strong> <span class="example-io">8</span></p>
<p><strong>Explanation:</strong></p>
<p>The valid arrangements of pieces on the board are:</p>
<p><img alt="" src="https://assets.leetcode.com/uploads/2024/12/25/4040example1.drawio" /><img alt="" src="https://assets.leetcode.com/uploads/2024/12/25/untitled-diagramdrawio.png" style="width: 441px; height: 204px;" /></p>
<ul>
<li>In the first 4 arrangements, the Manhattan distance between the two pieces is 1.</li>
<li>In the last 2 arrangements, the Manhattan distance between the two pieces is 2.</li>
</ul>
<p>Thus, the total Manhattan distance across all valid arrangements is <code>1 + 1 + 1 + 1 + 2 + 2 = 8</code>.</p>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">m = 1, n = 4, k = 3</span></p>
<p><strong>Output:</strong> <span class="example-io">20</span></p>
<p><strong>Explanation:</strong></p>
<p>The valid arrangements of pieces on the board are:</p>
<p><img alt="" src="https://assets.leetcode.com/uploads/2024/12/25/4040example2drawio.png" style="width: 762px; height: 41px;" /></p>
<ul>
<li>The first and last arrangements have a total Manhattan distance of <code>1 + 1 + 2 = 4</code>.</li>
<li>The middle two arrangements have a total Manhattan distance of <code>1 + 2 + 3 = 6</code>.</li>
</ul>
<p>The total Manhattan distance between all pairs of pieces across all arrangements is <code>4 + 6 + 6 + 4 = 20</code>.</p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>1 <= m, n <= 10<sup>5</sup></code></li>
<li><code>2 <= m * n <= 10<sup>5</sup></code></li>
<li><code><font face="monospace">2 <= k <= m * n</font></code></li>
</ul>
|
You are given three integers `m`, `n`, and `k`.
There is a rectangular grid of size `m n` containing `k` identical pieces. Return the sum of Manhattan distances between every pair of pieces over all **valid arrangements** of pieces.
A **valid arrangement** is a placement of all `k` pieces on the grid with **at most** one piece per cell.
Since the answer may be very large, return it **modulo** `109 + 7`.
The Manhattan Distance between two cells `(xi, yi)` and `(xj, yj)` is `|xi - xj| + |yi - yj|`.
**Example 1:**
**Input:** m \= 2, n \= 2, k \= 2
**Output:** 8
**Explanation:**
The valid arrangements of pieces on the board are:
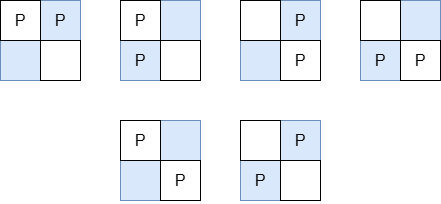
- In the first 4 arrangements, the Manhattan distance between the two pieces is 1\.
- In the last 2 arrangements, the Manhattan distance between the two pieces is 2\.
Thus, the total Manhattan distance across all valid arrangements is `1 + 1 + 1 + 1 + 2 + 2 = 8`.
**Example 2:**
**Input:** m \= 1, n \= 4, k \= 3
**Output:** 20
**Explanation:**
The valid arrangements of pieces on the board are:

- The first and last arrangements have a total Manhattan distance of `1 + 1 + 2 = 4`.
- The middle two arrangements have a total Manhattan distance of `1 + 2 + 3 = 6`.
The total Manhattan distance between all pairs of pieces across all arrangements is `4 + 6 + 6 + 4 = 20`.
**Constraints:**
- `1 <= m, n <= 105`
- `2 <= m * n <= 105`
- `2 <= k <= m * n`
|
Hard
|
[
"math",
"combinatorics"
] |
leetcode
|
https://leetcode.com/problems/manhattan-distances-of-all-arrangements-of-pieces
|
functional
| null | null | null | null |
{
"c": "int distanceSum(int m, int n, int k) {\n \n}",
"cpp": "class Solution {\npublic:\n int distanceSum(int m, int n, int k) {\n \n }\n};",
"csharp": "public class Solution {\n public int DistanceSum(int m, int n, int k) {\n \n }\n}",
"dart": "class Solution {\n int distanceSum(int m, int n, int k) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec distance_sum(m :: integer, n :: integer, k :: integer) :: integer\n def distance_sum(m, n, k) do\n \n end\nend",
"erlang": "-spec distance_sum(M :: integer(), N :: integer(), K :: integer()) -> integer().\ndistance_sum(M, N, K) ->\n .",
"golang": "func distanceSum(m int, n int, k int) int {\n \n}",
"java": "class Solution {\n public int distanceSum(int m, int n, int k) {\n \n }\n}",
"javascript": "/**\n * @param {number} m\n * @param {number} n\n * @param {number} k\n * @return {number}\n */\nvar distanceSum = function(m, n, k) {\n \n};",
"kotlin": "class Solution {\n fun distanceSum(m: Int, n: Int, k: Int): Int {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param Integer $m\n * @param Integer $n\n * @param Integer $k\n * @return Integer\n */\n function distanceSum($m, $n, $k) {\n \n }\n}",
"python": "class Solution(object):\n def distanceSum(self, m, n, k):\n \"\"\"\n :type m: int\n :type n: int\n :type k: int\n :rtype: int\n \"\"\"\n ",
"python3": "class Solution:\n def distanceSum(self, m: int, n: int, k: int) -> int:\n ",
"racket": "(define/contract (distance-sum m n k)\n (-> exact-integer? exact-integer? exact-integer? exact-integer?)\n )",
"ruby": "# @param {Integer} m\n# @param {Integer} n\n# @param {Integer} k\n# @return {Integer}\ndef distance_sum(m, n, k)\n \nend",
"rust": "impl Solution {\n pub fn distance_sum(m: i32, n: i32, k: i32) -> i32 {\n \n }\n}",
"scala": "object Solution {\n def distanceSum(m: Int, n: Int, k: Int): Int = {\n \n }\n}",
"swift": "class Solution {\n func distanceSum(_ m: Int, _ n: Int, _ k: Int) -> Int {\n \n }\n}",
"typescript": "function distanceSum(m: number, n: number, k: number): number {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\n long long mod_pow(long long base, int exp, int mod) {\n long long result = 1;\n base %= mod;\n while (exp > 0) {\n if (exp % 2 == 1) {\n result = (result * base) % mod;\n }\n base = (base * base) % mod;\n exp /= 2;\n }\n return result;\n }\npublic:\n int distanceSum(int m, int n, int k) {\n const int MOD = 1e9 + 7;\n long long inv6 = mod_pow(6, MOD-2, MOD);\n \n long long sum_x_part = (1LL * n * n % MOD) * m % MOD;\n sum_x_part = sum_x_part * ((1LL * m * m % MOD - 1 + MOD) % MOD) % MOD;\n \n long long sum_y_part = (1LL * m * m % MOD) * n % MOD;\n sum_y_part = sum_y_part * ((1LL * n * n % MOD - 1 + MOD) % MOD) % MOD;\n \n long long sum_total = (sum_x_part + sum_y_part) % MOD;\n sum_total = sum_total * inv6 % MOD;\n \n int a = m * n - 2;\n int b = k - 2;\n if (b < 0 || b > a) {\n return 0;\n }\n \n vector<long long> fact(a+1), inv_fact(a+1);\n fact[0] = 1;\n for (int i = 1; i <= a; ++i) {\n fact[i] = fact[i-1] * i % MOD;\n }\n inv_fact[a] = mod_pow(fact[a], MOD-2, MOD);\n for (int i = a-1; i >= 0; --i) {\n inv_fact[i] = inv_fact[i+1] * (i+1) % MOD;\n }\n \n long long comb = fact[a] * inv_fact[b] % MOD;\n comb = comb * inv_fact[a - b] % MOD;\n \n long long ans = sum_total * comb % MOD;\n return (int)ans;\n }\n};",
"memory": 11300,
"memoryDistribution": "[[8400, 3.125, \"// You are given three integers m, n, and k.\\n// There is a rectangular grid of size m \\u00d7 n containing k identical pieces. Return the sum of Manhattan distances between every pair of pieces over all valid arrangements of pieces.\\n// A valid arrangement is a placement of all k pieces on the grid with at most one piece per cell.\\n// Since the answer may be very large, return it modulo 109 + 7.\\n// The Manhattan Distance between two cells (xi, yi) and (xj, yj) is |xi - xj| + |yi - yj|.\\n\\n// Example 1:\\n// Input: m = 2, n = 2, k = 2\\n// Output: 8\\n\\n// Example 2:\\n// Input: m = 1, n = 4, k = 3\\n// Output: 20\\n\\n// Constraints:\\n// 1 <= m, n <= 10^5\\n// 2 <= m * n <= 10^5\\n// 2 <= k <= m * n\\n\\nclass Solution {\\npublic:\\n long long comb(long long a, long long b, long long mod) {\\n if (b > a) return 0;\\n long long numer = 1, denom = 1;\\n for (long long i = 0; i < b; ++i) {\\n numer = numer * (a - i) % mod;\\n denom = denom * (i + 1) % mod;\\n }\\n\\n // Fermat's Little Theorem\\n long long denom_inv = 1;\\n long long exp = mod - 2;\\n while (exp) {\\n if (exp % 2) denom_inv = denom_inv * denom % mod;\\n denom = denom * denom % mod;\\n exp /= 2;\\n }\\n return numer * denom_inv % mod;\\n }\\n\\n int distanceSum(int m, int n, int k) {\\n int mod = 1e9 + 7;\\n long long base = comb(m * n - 2, k - 2, mod);\\n long long res = 0;\\n for (int d = 1; d < n; ++d) {\\n res = (res + 1LL * d * (n - d) % mod * m % mod * m % mod) % mod;\\n }\\n for (int d = 1; d < m; ++d) {\\n res = (res + 1LL * d * (m - d) % mod * n % mod * n % mod) % mod;\\n }\\n return res * base % mod;\\n }\\n};\"], [8500, 13.5417, \"class Solution {\\npublic:\\n long long combination(long long a, long long b, long long mod) {\\n // no ways to choose if b > a\\n if (b > a) return 0;\\n // will hold numerator and denominator mod `mod`\\n long long numer = 1, denom = 1;\\n for (long long i = 0; i < b; ++i) {\\n // multiply numerator by (a - i)\\n numer = numer * (a - i) % mod;\\n // multiply denominator by (i + 1)\\n denom = denom * (i + 1) % mod;\\n }\\n\\n // Fermat's Little Theorem to compute denom^(mod-2) % mod\\n long long denom_inv = 1;\\n // exponent for modular inverse\\n long long exp = mod - 2;\\n while (exp) {\\n // if bit is 1, include current denom\\n if (exp % 2) {\\n denom_inv = denom_inv * denom % mod;\\n }\\n // square denom each iteration\\n denom = denom * denom % mod;\\n // shift exponent right\\n exp /= 2;\\n }\\n // multiply numerator by inverse denominator\\n return numer * denom_inv % mod;\\n }\\n\\n int distanceSum(int m, int n, int k) {\\n // prime modulus\\n int mod = 1e9 + 7;\\n // ways to choose remaining k-2 cells\\n long long base = combination(m * n - 2, k - 2, mod);\\n // accumulator for total pairwise distance\\n long long res = 0;\\n\\n for (int d = 1; d < n; ++d) {\\n // horizontal pairs: distance d, count = m rows * (n - d) pairs per row\\n res = (res + 1LL * d * (n - d) % mod * m % mod * m % mod) % mod;\\n }\\n for (int d = 1; d < m; ++d) {\\n // vertical pairs: distance d, count = n columns * (m - d) pairs per column\\n res = (res + 1LL * d * (m - d) % mod * n % mod * n % mod) % mod;\\n }\\n\\n // multiply by base and take final mod\\n return res * base % mod;\\n }\\n};\\n\"], [8600, 30.2083, null], [8700, 14.5833, null], [8800, 2.0833, null], [9000, 1.0417, null], [9400, 1.0417, null], [9500, 1.0417, null], [9600, 1.0417, null], [10100, 1.0417, null], [10900, 1.0417, null], [11000, 1.0417, null], [11300, 6.2495, \"class Solution {\\n long long mod_pow(long long base, int exp, int mod) {\\n long long result = 1;\\n base %= mod;\\n while (exp > 0) {\\n if (exp % 2 == 1) {\\n result = (result * base) % mod;\\n }\\n base = (base * base) % mod;\\n exp /= 2;\\n }\\n return result;\\n }\\npublic:\\n int distanceSum(int m, int n, int k) {\\n const int MOD = 1e9 + 7;\\n long long inv6 = mod_pow(6, MOD-2, MOD);\\n \\n long long sum_x_part = (1LL * n * n % MOD) * m % MOD;\\n sum_x_part = sum_x_part * ((1LL * m * m % MOD - 1 + MOD) % MOD) % MOD;\\n \\n long long sum_y_part = (1LL * m * m % MOD) * n % MOD;\\n sum_y_part = sum_y_part * ((1LL * n * n % MOD - 1 + MOD) % MOD) % MOD;\\n \\n long long sum_total = (sum_x_part + sum_y_part) % MOD;\\n sum_total = sum_total * inv6 % MOD;\\n \\n int a = m * n - 2;\\n int b = k - 2;\\n if (b < 0 || b > a) {\\n return 0;\\n }\\n \\n vector<long long> fact(a+1), inv_fact(a+1);\\n fact[0] = 1;\\n for (int i = 1; i <= a; ++i) {\\n fact[i] = fact[i-1] * i % MOD;\\n }\\n inv_fact[a] = mod_pow(fact[a], MOD-2, MOD);\\n for (int i = a-1; i >= 0; --i) {\\n inv_fact[i] = inv_fact[i+1] * (i+1) % MOD;\\n }\\n \\n long long comb = fact[a] * inv_fact[b] % MOD;\\n comb = comb * inv_fact[a - b] % MOD;\\n \\n long long ans = sum_total * comb % MOD;\\n return (int)ans;\\n }\\n};\"], [11600, 1.0417, null], [11800, 1.0417, null], [13300, 1.0417, null], [13400, 4.1667, null], [13500, 3.125, null], [13600, 1.0417, null], [15800, 1.0417, null], [36000, 1.0417, null], [36200, 2.0833, null], [62700, 2.0833, null], [67800, 1.0417, null], [67900, 1.0417, null], [99300, 1.0417, null], [113100, 1.0417, null], [113300, 1.0417, \"class Comb\\n{\\npublic:\\n Comb(int n) {\\n computeFact(n);\\n computeInvFact(n, fact.back());\\n }\\n long long comb(long long n, long long k) {\\n return (fact[n]*invfact[k])%mod*invfact[n-k]%mod;\\n }\\n long long getFact(int n) {\\n return fact[n];\\n }\\n long long getInvfact(int n) {\\n return invfact[n];\\n }\\nprivate:\\n void computeFact(int n)\\n {\\n fact.resize(n+1);\\n fact[0]=1;\\n for(int i=1;i<=n;i++) fact[i]=fact[i-1]*i%mod;\\n }\\n void computeInvFact(int n, long long factN)\\n {\\n invfact.resize(n+1);\\n invfact[n] = binpowWithModulo(factN, mod - 2);\\n for(int i=n-1;i>=0;i--) invfact[i] = invfact[i + 1] * (i + 1) % mod;\\n }\\n static long long binpowWithModulo(long long num, long long exp) {\\n num %= mod;\\n long long res = 1;\\n while (exp > 0) {\\n if (exp & 1)\\n res = res * num % mod;\\n num = num * num % mod;\\n exp >>= 1;\\n }\\n return res;\\n }\\n static const long long mod = 1e9+7;\\n vector<long long> fact;\\n vector<long long> invfact;\\n};\\n\\nclass Solution {\\npublic:\\n int distanceSum(int m, int n, int k) {\\n int mod = 1e9 + 7;\\n Comb comb(m*n-2);\\n long long base = comb.comb(m * n - 2, k - 2);\\n long long res1 = 0;\\n long long res = 0;\\n for (int d = 1; d < n; ++d) {\\n res = (res + 1LL * d * (n - d) % mod * m % mod * m % mod) % mod;\\n }\\n for (int d = 1; d < m; ++d) {\\n res = (res + 1LL * d * (m - d) % mod * n % mod * n % mod) % mod;\\n }\\n return res * base % mod;\\n }\\n};\"], [113600, 1.0417, \"class Solution {\\npublic:\\n static const int MOD = 1000000007;\\n \\n long long fastPow(long long base, long long exp, long long mod) {\\n long long result = 1LL;\\n base %= mod;\\n while(exp > 0) {\\n if(exp & 1LL)\\n result = (result * base) % mod;\\n base = (base * base) % mod;\\n exp >>= 1;\\n }\\n return result;\\n }\\n \\n long long modInverse(long long a, int m) {\\n return fastPow(a, m - 2, m);\\n }\\n \\n void precomputeFactorials(int n, vector<long long>& fact, vector<long long>& invFact) {\\n fact.resize(n + 1);\\n invFact.resize(n + 1);\\n fact[0] = 1LL;\\n for (int i = 1; i <= n; i++) {\\n fact[i] = (fact[i - 1] * i) % MOD;\\n }\\n invFact[n] = modInverse(fact[n], MOD);\\n for (int i = n - 1; i >= 0; i--) {\\n invFact[i] = (invFact[i + 1] * (i + 1)) % MOD;\\n }\\n }\\n \\n long long binom(int n, int r, const vector<long long>& fact, const vector<long long>& invFact) {\\n if(r < 0 || r > n) return 0;\\n return fact[n] * ((invFact[r] * invFact[n - r]) % MOD) % MOD;\\n }\\n \\n int distanceSum(int m, int n, int k) {\\n int M = m * n;\\n vector<long long> fact, invFact;\\n precomputeFactorials(M, fact, invFact);\\n \\n long long ways = binom(M - 2, k - 2, fact, invFact);\\n \\n long long mm = m % MOD;\\n long long nn = n % MOD;\\n \\n long long n2 = (nn * nn) % MOD;\\n long long m2 = (mm * mm) % MOD;\\n \\n long long term1 = (n2 * mm) % MOD;\\n long long m2Minus1 = (m2 - 1 + MOD) % MOD;\\n term1 = (term1 * m2Minus1) % MOD;\\n \\n long long term2 = (m2 * nn) % MOD;\\n long long n2Minus1 = (n2 - 1 + MOD) % MOD;\\n term2 = (term2 * n2Minus1) % MOD;\\n \\n long long sumD = (term1 + term2) % MOD;\\n \\n long long inv6 = modInverse(6, MOD);\\n sumD = (sumD * inv6) % MOD;\\n \\n long long ans = (sumD * ways) % MOD;\\n return (int)ans;\\n }\\n};\\n\"]]",
"runtime": 70,
"runtimeDistribution": "[[0, 6.25, \"class Solution {\\npublic:\\n int distanceSum(int m, int n, int k) {\\n return C_n_k(static_cast<long long>(m) * n - 2, k - 2) *\\n (solve_one_dim_one_pair(m, n) + solve_one_dim_one_pair(n, m)) % kMod;\\n }\\n\\nprivate:\\n static constexpr long long kMod = 1e9 + 7;\\n static constexpr long long kMaxMN = 1e5;\\n\\n struct CnkCalculator {\\n vector<long long> fac;\\n vector<long long> rac;\\n\\n CnkCalculator(int max_n = 1e5) : fac(1, 1), rac(1, 1) {\\n ensure_fac(max_n);\\n }\\n\\n long long operator()(int N, int k) {\\n ensure_fac(N);\\n return (fac[N] * rac[k] % kMod) * rac[N - k] % kMod;\\n }\\n\\n void ensure_fac(size_t n) {\\n while (fac.size() <= n) {\\n fac.push_back(fac.back() * fac.size() % kMod);\\n rac.push_back(rev(fac.back()));\\n }\\n }\\n\\n long long rev(long long v) {\\n return qpow(v, kMod - 2);\\n }\\n\\n long long qpow(long long b, long long p) {\\n long long res = 1;\\n for (; p; p >>= 1, b = b * b % kMod)\\n if (p & 1)\\n res = res * b % kMod;\\n return res;\\n }\\n };\\n\\n static CnkCalculator C_n_k;\\n\\n long long solve_one_dim_one_pair(long long m, long long n) {\\n/*\\n long long res = 0;\\n for (long long i = 1; i < n; ++i)\\n res += i * (i + 1) / 2;\\n return m * m * res % kMod;\\n*/\\n long long res = (n - 1) * n / 2; // sum of first n-1 integers\\n res = res * (n + 1) / 3; // turns it into sum of triangular numbers\\n return m * m % kMod * res % kMod;\\n }\\n};\\n\\nSolution::CnkCalculator Solution::C_n_k;\\n\"], [7, 1.0417, \"class Solution {\\n long long mod = 1e9 + 7;\\n\\n long long expo(long long num, long long exp) {\\n long long res = 1;\\n while (exp > 0) {\\n if (exp % 2 == 1)\\n res = (res * num) % mod;\\n num = (num * num) % mod;\\n exp /= 2;\\n }\\n return res;\\n }\\n\\n long long divMod(long long a, long long b) {\\n long long b_inv = expo(b, mod-2);\\n return (a * b_inv) % mod;\\n }\\n\\n long long calcComb(long long a, long long b) {\\n if (b > a)\\n return 0;\\n long long num = 1, den = 1;\\n for (int i = 0; i < b; i++) {\\n num = (num * (a-i)) % mod;\\n den = (den * (i+1)) % mod;\\n }\\n return divMod(num, den);\\n }\\npublic:\\n int distanceSum(int m, int n, int k) {\\n long long ln = n, lm = m;\\n long long pairSum = (((ln * lm) * (lm+ln-2))/2)%mod;\\n long long numCombs = calcComb(lm*ln-2, k-2);\\n long long sumManhattan = divMod( ((((((((ln*ln)%mod) * lm) % mod) * (lm-1)) % mod) * (lm+1)) % mod) + ((((((((lm*lm)%mod) * ln) % mod) * (ln-1)) % mod) * (ln+1)) % mod), 6);\\n return (numCombs * sumManhattan)%mod;\\n }\\n};\"], [9, 1.0417, null], [11, 2.0833, null], [12, 1.0417, null], [14, 2.0833, null], [15, 10.4167, null], [16, 2.0833, null], [17, 1.0417, null], [18, 2.0833, null], [19, 5.2083, null], [20, 3.125, null], [22, 1.0417, null], [23, 1.0417, null], [24, 1.0417, null], [27, 2.0833, null], [29, 1.0417, null], [30, 1.0417, null], [32, 1.0417, null], [35, 5.2083, null], [36, 1.0417, null], [42, 1.0417, null], [43, 3.125, null], [44, 1.0417, null], [47, 3.125, null], [48, 1.0417, null], [51, 2.0833, null], [57, 1.0417, null], [63, 1.0417, null], [70, 34.3747, \"class Solution {\\n long long mod_pow(long long base, int exp, int mod) {\\n long long result = 1;\\n base %= mod;\\n while (exp > 0) {\\n if (exp % 2 == 1) {\\n result = (result * base) % mod;\\n }\\n base = (base * base) % mod;\\n exp /= 2;\\n }\\n return result;\\n }\\npublic:\\n int distanceSum(int m, int n, int k) {\\n const int MOD = 1e9 + 7;\\n long long inv6 = mod_pow(6, MOD-2, MOD);\\n \\n long long sum_x_part = (1LL * n * n % MOD) * m % MOD;\\n sum_x_part = sum_x_part * ((1LL * m * m % MOD - 1 + MOD) % MOD) % MOD;\\n \\n long long sum_y_part = (1LL * m * m % MOD) * n % MOD;\\n sum_y_part = sum_y_part * ((1LL * n * n % MOD - 1 + MOD) % MOD) % MOD;\\n \\n long long sum_total = (sum_x_part + sum_y_part) % MOD;\\n sum_total = sum_total * inv6 % MOD;\\n \\n int a = m * n - 2;\\n int b = k - 2;\\n if (b < 0 || b > a) {\\n return 0;\\n }\\n \\n vector<long long> fact(a+1), inv_fact(a+1);\\n fact[0] = 1;\\n for (int i = 1; i <= a; ++i) {\\n fact[i] = fact[i-1] * i % MOD;\\n }\\n inv_fact[a] = mod_pow(fact[a], MOD-2, MOD);\\n for (int i = a-1; i >= 0; --i) {\\n inv_fact[i] = inv_fact[i+1] * (i+1) % MOD;\\n }\\n \\n long long comb = fact[a] * inv_fact[b] % MOD;\\n comb = comb * inv_fact[a - b] % MOD;\\n \\n long long ans = sum_total * comb % MOD;\\n return (int)ans;\\n }\\n};\"], [75, 2.0833, null], [78, 1.0417, null], [79, 2.0833, null], [87, 2.0833, null], [92, 2.0833, null], [93, 1.0417, null], [94, 1.0417, null], [95, 1.0417, null], [96, 1.0417, null], [108, 1.0417, null], [123, 1.0417, null], [147, 1.0417, null], [151, 1.0417, null], [311, 1.0417, null], [382, 1.0417, null], [431, 1.0417, null], [434, 1.0417, null], [493, 1.0417, null], [639, 1.0417, null], [765, 2.0833, null], [771, 1.0417, null], [837, 1.0417, \"class Solution{\\npublic:\\n int mod = 1e9 + 7;\\n typedef long long ll;\\n vector<ll> vect;\\n Solution(){\\n vect.resize(100000);\\n fact();\\n }\\n\\n ll binpow(ll a, ll b){\\n ll res = 1;\\n while(b){\\n if(b % 2){\\n res = (res * a) % mod;\\n }\\n a =(a*a)%mod;\\n b /= 2;\\n }\\n return res;\\n }\\n\\n void fact(){\\n vect[0]= 1;\\n for(int i = 1; i < 100000; i++){\\n vect[i] = (vect[i - 1]* i) % mod;\\n }\\n }\\n\\n ll comb(ll n, ll r){\\n if (n < r || n >= 100000 || r >= 100000) return 0;\\n ll ans = vect[n]% mod;\\n ll tmp = (binpow(vect[r], mod - 2) * binpow(vect[n - r], mod - 2))%mod;\\n return (ans*tmp) % mod;\\n }\\n\\n int distanceSum(int m, int n, int k){\\n ll cnt = 0;\\n for(int d = 1; d<m; d++){\\n ll tmp = comb(m*n - 2, k-2);\\n tmp = (tmp * d) % mod;\\n tmp = (tmp * (m - d)) % mod;\\n tmp = (tmp * n) % mod;\\n tmp = (tmp * n) % mod;\\n cnt = (cnt + tmp) % mod;\\n }\\n\\n for(int d=1; d<n; d++){\\n ll tmp = comb(m*n - 2, k-2);\\n tmp = (tmp * d) % mod;\\n tmp = (tmp * (n - d)) % mod;\\n tmp = (tmp * m) % mod;\\n tmp = (tmp * m) % mod;\\n cnt = (cnt + tmp) % mod;\\n }\\n return cnt;\\n }\\n};\"], [855, 1.0417, \"class Solution {\\npublic:\\n long long int mod = 1e9+7;\\n long long int fact(long long int a)\\n {\\n \\n long long int tmp = 1;\\n for(int i=1;i<=a;i++)\\n {\\n tmp = (tmp*i)%mod;\\n }\\n return tmp;\\n }\\n long long int binpow(long long int a,long long int b)\\n {\\n if(b==0)\\n {\\n return 1;\\n }\\n if(b%2)\\n {\\n return ((a*binpow((a*a)%mod,b/2))%mod)%mod;\\n }\\n else return binpow((a*a)%mod,b/2);\\n }\\n long long int comb (long long int a, long long int b)\\n {\\n long long int tmp = 1;\\n tmp = (tmp*fact(a))%mod;\\n tmp = (tmp*binpow(fact(a-b),mod-2))%mod;\\n tmp = (tmp*binpow(fact(b),mod-2))%mod;\\n return tmp;\\n\\n }\\n int distanceSum(int m, int n, int k) \\n {\\n long long int m1 = m;\\n long long int n1 = n;\\n long long int k1 = k;\\n long long int cnt = 0;\\n long long int a1 = comb(m1*n1 - 2,k1-2);\\n for(int d = 1;d<m;d++)\\n {\\n long long int tmp = a1;\\n //cout<<tmp;\\n tmp = (tmp*d)%mod;\\n tmp = (tmp*(m-d))%mod;\\n tmp = (tmp*n)%mod;\\n tmp = (tmp*n)%mod;\\n cnt = (tmp+cnt)%mod;\\n\\n }\\n for(int d = 1;d<n;d++)\\n {\\n long long int tmp = a1;\\n cout<<tmp<<\\\" \\\";\\n tmp = (tmp*d)%mod;\\n tmp = (tmp*(n-d))%mod;\\n tmp = (tmp*m)%mod;\\n tmp = (tmp*m)%mod;\\n cnt = (tmp+cnt)%mod;\\n\\n } \\n return cnt;\\n\\n }\\n};\"]]"
},
"golang": {
"code": "func distanceSum(m int, n int, k int) int {\n const MOD = 1000000007\n inv6 := 166666668 // Modular inverse of 6 modulo 1e9+7\n\n T := m * n\n if k < 2 || k > T {\n return 0\n }\n\n a := T - 2\n b := k - 2\n if a < 0 || b < 0 || a < b {\n return 0\n }\n\n term1 := (n % MOD) * (n % MOD) % MOD\n term1 = term1 * ((m - 1) % MOD) % MOD\n term1 = term1 * (m % MOD) % MOD\n term1 = term1 * ((m + 1) % MOD) % MOD\n\n term2 := (m % MOD) * (m % MOD) % MOD\n term2 = term2 * ((n - 1) % MOD) % MOD\n term2 = term2 * (n % MOD) % MOD\n term2 = term2 * ((n + 1) % MOD) % MOD\n\n sum_S := (term1 + term2) % MOD\n sum_S = sum_S * inv6 % MOD\n\n if a == 0 {\n return sum_S\n }\n\n fact := make([]int, a+1)\n fact[0] = 1\n for i := 1; i <= a; i++ {\n fact[i] = fact[i-1] * i % MOD\n }\n\n inv_fact := make([]int, a+1)\n inv_fact[a] = pow(fact[a], MOD-2, MOD)\n for i := a - 1; i >= 0; i-- {\n inv_fact[i] = inv_fact[i+1] * (i + 1) % MOD\n }\n\n comb := fact[a] * inv_fact[b] % MOD\n comb = comb * inv_fact[a-b] % MOD\n\n total := sum_S * comb % MOD\n return total\n}\n\nfunc pow(x, n, mod int) int {\n res := 1\n x = x % mod\n for n > 0 {\n if n%2 == 1 {\n res = (res * x) % mod\n }\n x = (x * x) % mod\n n /= 2\n }\n return res\n}",
"memory": 1000,
"memoryDistribution": "[[1000, 100.0, \"func distanceSum(m int, n int, k int) int {\\n const MOD = 1000000007\\n inv6 := 166666668 // Modular inverse of 6 modulo 1e9+7\\n\\n T := m * n\\n if k < 2 || k > T {\\n return 0\\n }\\n\\n a := T - 2\\n b := k - 2\\n if a < 0 || b < 0 || a < b {\\n return 0\\n }\\n\\n term1 := (n % MOD) * (n % MOD) % MOD\\n term1 = term1 * ((m - 1) % MOD) % MOD\\n term1 = term1 * (m % MOD) % MOD\\n term1 = term1 * ((m + 1) % MOD) % MOD\\n\\n term2 := (m % MOD) * (m % MOD) % MOD\\n term2 = term2 * ((n - 1) % MOD) % MOD\\n term2 = term2 * (n % MOD) % MOD\\n term2 = term2 * ((n + 1) % MOD) % MOD\\n\\n sum_S := (term1 + term2) % MOD\\n sum_S = sum_S * inv6 % MOD\\n\\n if a == 0 {\\n return sum_S\\n }\\n\\n fact := make([]int, a+1)\\n fact[0] = 1\\n for i := 1; i <= a; i++ {\\n fact[i] = fact[i-1] * i % MOD\\n }\\n\\n inv_fact := make([]int, a+1)\\n inv_fact[a] = pow(fact[a], MOD-2, MOD)\\n for i := a - 1; i >= 0; i-- {\\n inv_fact[i] = inv_fact[i+1] * (i + 1) % MOD\\n }\\n\\n comb := fact[a] * inv_fact[b] % MOD\\n comb = comb * inv_fact[a-b] % MOD\\n\\n total := sum_S * comb % MOD\\n return total\\n}\\n\\nfunc pow(x, n, mod int) int {\\n res := 1\\n x = x % mod\\n for n > 0 {\\n if n%2 == 1 {\\n res = (res * x) % mod\\n }\\n x = (x * x) % mod\\n n /= 2\\n }\\n return res\\n}\"], [25400, 100.0, \"func distanceSum(m int, n int, k int) int {\\n const MOD = 1000000007\\n inv6 := 166666668 // Modular inverse of 6 modulo 1e9+7\\n\\n T := m * n\\n if k < 2 || k > T {\\n return 0\\n }\\n\\n a := T - 2\\n b := k - 2\\n if a < 0 || b < 0 || a < b {\\n return 0\\n }\\n\\n term1 := (n % MOD) * (n % MOD) % MOD\\n term1 = term1 * ((m - 1) % MOD) % MOD\\n term1 = term1 * (m % MOD) % MOD\\n term1 = term1 * ((m + 1) % MOD) % MOD\\n\\n term2 := (m % MOD) * (m % MOD) % MOD\\n term2 = term2 * ((n - 1) % MOD) % MOD\\n term2 = term2 * (n % MOD) % MOD\\n term2 = term2 * ((n + 1) % MOD) % MOD\\n\\n sum_S := (term1 + term2) % MOD\\n sum_S = sum_S * inv6 % MOD\\n\\n if a == 0 {\\n return sum_S\\n }\\n\\n fact := make([]int, a+1)\\n fact[0] = 1\\n for i := 1; i <= a; i++ {\\n fact[i] = fact[i-1] * i % MOD\\n }\\n\\n inv_fact := make([]int, a+1)\\n inv_fact[a] = pow(fact[a], MOD-2, MOD)\\n for i := a - 1; i >= 0; i-- {\\n inv_fact[i] = inv_fact[i+1] * (i + 1) % MOD\\n }\\n\\n comb := fact[a] * inv_fact[b] % MOD\\n comb = comb * inv_fact[a-b] % MOD\\n\\n total := sum_S * comb % MOD\\n return total\\n}\\n\\nfunc pow(x, n, mod int) int {\\n res := 1\\n x = x % mod\\n for n > 0 {\\n if n%2 == 1 {\\n res = (res * x) % mod\\n }\\n x = (x * x) % mod\\n n /= 2\\n }\\n return res\\n}\"]]",
"runtime": 61,
"runtimeDistribution": "[[61, 100.0, \"func distanceSum(m int, n int, k int) int {\\n const MOD = 1000000007\\n inv6 := 166666668 // Modular inverse of 6 modulo 1e9+7\\n\\n T := m * n\\n if k < 2 || k > T {\\n return 0\\n }\\n\\n a := T - 2\\n b := k - 2\\n if a < 0 || b < 0 || a < b {\\n return 0\\n }\\n\\n term1 := (n % MOD) * (n % MOD) % MOD\\n term1 = term1 * ((m - 1) % MOD) % MOD\\n term1 = term1 * (m % MOD) % MOD\\n term1 = term1 * ((m + 1) % MOD) % MOD\\n\\n term2 := (m % MOD) * (m % MOD) % MOD\\n term2 = term2 * ((n - 1) % MOD) % MOD\\n term2 = term2 * (n % MOD) % MOD\\n term2 = term2 * ((n + 1) % MOD) % MOD\\n\\n sum_S := (term1 + term2) % MOD\\n sum_S = sum_S * inv6 % MOD\\n\\n if a == 0 {\\n return sum_S\\n }\\n\\n fact := make([]int, a+1)\\n fact[0] = 1\\n for i := 1; i <= a; i++ {\\n fact[i] = fact[i-1] * i % MOD\\n }\\n\\n inv_fact := make([]int, a+1)\\n inv_fact[a] = pow(fact[a], MOD-2, MOD)\\n for i := a - 1; i >= 0; i-- {\\n inv_fact[i] = inv_fact[i+1] * (i + 1) % MOD\\n }\\n\\n comb := fact[a] * inv_fact[b] % MOD\\n comb = comb * inv_fact[a-b] % MOD\\n\\n total := sum_S * comb % MOD\\n return total\\n}\\n\\nfunc pow(x, n, mod int) int {\\n res := 1\\n x = x % mod\\n for n > 0 {\\n if n%2 == 1 {\\n res = (res * x) % mod\\n }\\n x = (x * x) % mod\\n n /= 2\\n }\\n return res\\n}\"], [79, 100.0, \"func distanceSum(m int, n int, k int) int {\\n const MOD = 1000000007\\n inv6 := 166666668 // Modular inverse of 6 modulo 1e9+7\\n\\n T := m * n\\n if k < 2 || k > T {\\n return 0\\n }\\n\\n a := T - 2\\n b := k - 2\\n if a < 0 || b < 0 || a < b {\\n return 0\\n }\\n\\n term1 := (n % MOD) * (n % MOD) % MOD\\n term1 = term1 * ((m - 1) % MOD) % MOD\\n term1 = term1 * (m % MOD) % MOD\\n term1 = term1 * ((m + 1) % MOD) % MOD\\n\\n term2 := (m % MOD) * (m % MOD) % MOD\\n term2 = term2 * ((n - 1) % MOD) % MOD\\n term2 = term2 * (n % MOD) % MOD\\n term2 = term2 * ((n + 1) % MOD) % MOD\\n\\n sum_S := (term1 + term2) % MOD\\n sum_S = sum_S * inv6 % MOD\\n\\n if a == 0 {\\n return sum_S\\n }\\n\\n fact := make([]int, a+1)\\n fact[0] = 1\\n for i := 1; i <= a; i++ {\\n fact[i] = fact[i-1] * i % MOD\\n }\\n\\n inv_fact := make([]int, a+1)\\n inv_fact[a] = pow(fact[a], MOD-2, MOD)\\n for i := a - 1; i >= 0; i-- {\\n inv_fact[i] = inv_fact[i+1] * (i + 1) % MOD\\n }\\n\\n comb := fact[a] * inv_fact[b] % MOD\\n comb = comb * inv_fact[a-b] % MOD\\n\\n total := sum_S * comb % MOD\\n return total\\n}\\n\\nfunc pow(x, n, mod int) int {\\n res := 1\\n x = x % mod\\n for n > 0 {\\n if n%2 == 1 {\\n res = (res * x) % mod\\n }\\n x = (x * x) % mod\\n n /= 2\\n }\\n return res\\n}\"]]"
},
"java": {
"code": "class Solution {\n static final int MOD = 1000000007;\n static final int MAX = 100000;\n static long[] fact = new long[MAX + 1];\n static long[] invFact = new long[MAX + 1];\n static final int inv3 = 333333336;\n static final int inv2 = 500000004;\n\n static {\n fact[0] = 1;\n for (int i = 1; i <= MAX; i++) {\n fact[i] = fact[i - 1] * i % MOD;\n }\n invFact[MAX] = pow(fact[MAX], MOD - 2);\n for (int i = MAX - 1; i >= 0; i--) {\n invFact[i] = invFact[i + 1] * (i + 1) % MOD;\n }\n }\n\n private static long pow(long a, int b) {\n long res = 1;\n while (b > 0) {\n if ((b & 1) == 1) {\n res = res * a % MOD;\n }\n a = a * a % MOD;\n b >>= 1;\n }\n return res;\n }\n\n private static long comb(int a, int b) {\n if (a < 0 || b < 0 || a < b) {\n return 0;\n }\n return fact[a] * invFact[b] % MOD * invFact[a - b] % MOD;\n }\n\n public int distanceSum(int m, int n, int k) {\n int mn = m * n;\n if (k < 2 || k > mn) {\n return 0;\n }\n\n long mCube = (long) m * m % MOD * m % MOD;\n long mPart = (mCube - m + MOD) % MOD;\n long mTerm = (long) n * n % MOD;\n mTerm = mTerm * mPart % MOD;\n\n long nCube = (long) n * n % MOD * n % MOD;\n long nPart = (nCube - n + MOD) % MOD;\n long nTerm = (long) m * m % MOD;\n nTerm = nTerm * nPart % MOD;\n\n long sumManhattan = (mTerm + nTerm) % MOD;\n sumManhattan = sumManhattan * inv3 % MOD;\n\n long sumUnordered = sumManhattan * inv2 % MOD;\n\n long c = comb(mn - 2, k - 2);\n\n long ans = sumUnordered * c % MOD;\n\n return (int) ans;\n }\n}",
"memory": 4200,
"memoryDistribution": "[[4200, 34.4827, \"class Solution {\\n static final int MOD = 1000000007;\\n static final int MAX = 100000;\\n static long[] fact = new long[MAX + 1];\\n static long[] invFact = new long[MAX + 1];\\n static final int inv3 = 333333336;\\n static final int inv2 = 500000004;\\n\\n static {\\n fact[0] = 1;\\n for (int i = 1; i <= MAX; i++) {\\n fact[i] = fact[i - 1] * i % MOD;\\n }\\n invFact[MAX] = pow(fact[MAX], MOD - 2);\\n for (int i = MAX - 1; i >= 0; i--) {\\n invFact[i] = invFact[i + 1] * (i + 1) % MOD;\\n }\\n }\\n\\n private static long pow(long a, int b) {\\n long res = 1;\\n while (b > 0) {\\n if ((b & 1) == 1) {\\n res = res * a % MOD;\\n }\\n a = a * a % MOD;\\n b >>= 1;\\n }\\n return res;\\n }\\n\\n private static long comb(int a, int b) {\\n if (a < 0 || b < 0 || a < b) {\\n return 0;\\n }\\n return fact[a] * invFact[b] % MOD * invFact[a - b] % MOD;\\n }\\n\\n public int distanceSum(int m, int n, int k) {\\n int mn = m * n;\\n if (k < 2 || k > mn) {\\n return 0;\\n }\\n\\n long mCube = (long) m * m % MOD * m % MOD;\\n long mPart = (mCube - m + MOD) % MOD;\\n long mTerm = (long) n * n % MOD;\\n mTerm = mTerm * mPart % MOD;\\n\\n long nCube = (long) n * n % MOD * n % MOD;\\n long nPart = (nCube - n + MOD) % MOD;\\n long nTerm = (long) m * m % MOD;\\n nTerm = nTerm * nPart % MOD;\\n\\n long sumManhattan = (mTerm + nTerm) % MOD;\\n sumManhattan = sumManhattan * inv3 % MOD;\\n\\n long sumUnordered = sumManhattan * inv2 % MOD;\\n\\n long c = comb(mn - 2, k - 2);\\n\\n long ans = sumUnordered * c % MOD;\\n\\n return (int) ans;\\n }\\n}\"], [40500, 1.7241, \"class Solution {\\n public int distanceSum(int m, int n, int k) {\\n long res = (count(m, n, k) * n % mod * n % mod + count(n, m, k) * m % mod * m % mod) % mod * C(m * n - 2, k - 2)\\n % mod;\\n return (int) res;\\n }\\n\\n int mod = 1_000_000_007;\\n\\n public long count(long m, int n, int k) {\\n long res = 0;\\n for (int i = 1; i <= m - 1; i++) {\\n res = (res + (m - i) * i % mod) % mod;\\n }\\n return res;\\n }\\n\\n public long C(int a, int b) {\\n if (a - b < b)\\n b = a - b;\\n long res = 1;\\n long div = 1;\\n for (int i = 1; i <= b; i++) {\\n res = res * a % mod;\\n div = div * i % mod;\\n a--;\\n }\\n return res * rev(div) % mod;\\n }\\n\\n public long rev(long a) {\\n if (a == 1)\\n return 1;\\n return mod - mod / a * rev(mod % a) % mod;\\n }\\n}\"], [40600, 5.1724, \"class Solution {\\n public int distanceSum(int m, int n, int k) {\\n long res = (count(m, n, k) * n % mod * n % mod + count(n, m, k) * m % mod * m % mod) % mod * C(m * n - 2, k - 2)\\n % mod;\\n return (int) res;\\n }\\n\\n int mod = 1_000_000_007;\\n\\n public long count(int m, int n, int k) {\\n long res = 0;\\n for (int i = 1; i <= m - 1; i++) {\\n res = (res + (long) (m - i) * i) % mod;\\n }\\n return res;\\n }\\n\\n public long C(int a, int b) {\\n if (a - b < b)\\n b = a - b;\\n long res = 1;\\n long div = 1;\\n for (int i = 1; i <= b; i++) {\\n res = res * a % mod;\\n div = div * i % mod;\\n a--;\\n }\\n return res * rev(div) % mod;\\n }\\n\\n public long rev(long a) {\\n if (a == 1)\\n return 1;\\n return mod - mod / a * rev(mod % a) % mod;\\n }\\n}\"], [40700, 6.8966, null], [40800, 3.4483, null], [40900, 13.7931, null], [41000, 6.8966, null], [41100, 5.1724, null], [41200, 3.4483, null], [41300, 3.4483, null], [41400, 8.6207, null], [41600, 5.1724, null], [42200, 1.7241, null], [42400, 1.7241, null], [42500, 8.6207, null], [42600, 3.4483, null], [42700, 3.4483, null], [42900, 1.7241, null], [44500, 3.4483, null], [45300, 1.7241, null], [45900, 1.7241, null], [46000, 1.7241, \"class Solution {\\n static final long MOD = 1000000007;\\n static final long[] factorials = new long[100001];\\n static final long[] factorialsInv = new long[100001];\\n static final long[] dist = new long[100001];\\n static {\\n factorials[0] = 1;\\n factorialsInv[0] = 1;\\n for (int i = 1; i < factorials.length; i++) {\\n factorials[i] = (factorials[i - 1] * i) % MOD;\\n factorialsInv[i] = (factorialsInv[i - 1] * inverse(i)) % MOD;\\n dist[i] = (dist[i - 1] + i * (i - 1L) / 2) % MOD;\\n }\\n }\\n\\n static long inverse(int a) {\\n return pow(a, (int) (MOD - 2), MOD);\\n }\\n\\n public int distanceSum(int m, int n, int k) {\\n long current = (mod(dist[m], n, n) + mod(m, m, dist[n])) % MOD;\\n long mk = mod(factorials[m * n - 2], factorialsInv[m * n - k], factorialsInv[k - 2]);\\n return (int) mod(current, mk);\\n }\\n\\n static long mod(long a, long b) {\\n return (a * b) % MOD;\\n }\\n\\n static long mod(long a, long b, long c) {\\n return mod(mod(a, b), c);\\n }\\n\\n static long pow(long a, int pow, long mod) {\\n long p = a;\\n long res = 1;\\n for (int q = 1; q <= pow; q *= 2) {\\n if ((pow & q) > 0) {\\n res = (res * p) % mod;\\n }\\n p = (p * p) % mod;\\n }\\n return res;\\n }\\n\\n}\"], [50600, 1.7241, \"import java.math.BigInteger; // This import is not strictly necessary as BigInteger is not used.\\n\\n// The main class should always be named 'Solution'.\\nfinal class Solution { \\n long MOD = 1_000_000_007;\\n ModMath modMath; // Instance variable to hold ModMath object\\n\\n /**\\n * Calculates the sum of Manhattan distances between all pairs of pieces\\n * over all valid arrangements of k pieces on an m x n grid.\\n * @param m Number of rows\\n * @param n Number of columns\\n * @param k Number of pieces\\n * @return The total sum modulo 10^9 + 7\\n */\\n public int distanceSum(int m, int n, int k) {\\n // Calculate total number of cells N = m * n. Use long to avoid overflow for intermediate calculations.\\n long N_long = (long)m * n; \\n \\n // If k < 2, there are no pairs of pieces, so the sum is 0.\\n // If k > N, it's impossible to place k pieces, this case shouldn't happen per constraints but good check.\\n if (k < 2 || k > N_long) {\\n return 0;\\n }\\n \\n // Since N = m*n <= 10^5, N fits within an integer range. Cast for array indexing.\\n int N_int = (int)N_long; \\n\\n // Initialize the modular math utility. We need combinations C(N-2, k-2).\\n // The maximum value of 'n' in nCr(n, r) required is N-2.\\n // The size passed to ModMath constructor is the maximum index needed for factorial arrays.\\n modMath = new ModMath(N_int - 2);\\n \\n // Calculate C(N-2, k-2) mod MOD. This represents the number of ways to place the\\n // remaining k-2 pieces once two positions are fixed.\\n long combinations = modMath.nCr(N_int - 2, k - 2);\\n \\n // Calculate the total sum of distances between all distinct pairs of cells in the grid.\\n // The formula derived is Sum = N*(N-1)*(m+n)/6.\\n // Compute N*(N-1) first. Max value is ~10^10, fits in long.\\n long N_times_N_minus_1 = N_long * (N_long - 1); \\n \\n // Compute N*(N-1)*(m+n). Max value is ~2*10^15, fits in long.\\n // Need to cast m+n to long to ensure full long multiplication.\\n long total_product = N_times_N_minus_1 * ((long)m + n); \\n\\n // The total product N*(N-1)*(m+n) is guaranteed divisible by 6.\\n // Perform integer division.\\n long sum_part_val = total_product / 6;\\n \\n // Take the result modulo MOD. Since sum_part_val is non-negative, simple % is fine.\\n long sum_part_mod = sum_part_val % MOD;\\n \\n // The final result is the product of the number of ways to choose pairs (combinations count)\\n // and the sum component, all modulo MOD.\\n long finalResult = (combinations * sum_part_mod) % MOD;\\n \\n // Result must be int as per return type. Cast is safe as result is within [0, MOD-1].\\n return (int)finalResult;\\n }\\n \\n /**\\n * Inner static class for modular arithmetic operations including combinations (nCr).\\n * Precomputes factorials and inverse factorials to speed up nCr calculations.\\n */\\n static class ModMath {\\n long MOD = 1_000_000_007;\\n long[] fact; // Stores factorials modulo MOD: fact[i] = i! % MOD\\n long[] invFact; // Stores inverse factorials modulo MOD: invFact[i] = (i!)^(-1) % MOD\\n\\n /**\\n * Constructor precomputes factorials and inverse factorials up to maxN.\\n * @param maxN The maximum value 'n' for which nCr might be calculated.\\n */\\n public ModMath(int maxN) {\\n // Ensure maxN is non-negative. Relevant if N=2, then maxN=0.\\n maxN = Math.max(0, maxN); \\n fact = new long[maxN + 1];\\n invFact = new long[maxN + 1];\\n \\n // Base cases: 0! = 1\\n fact[0] = 1;\\n invFact[0] = 1; \\n\\n // Compute factorials iteratively: i! = (i-1)! * i\\n for (int i = 1; i <= maxN; i++) {\\n fact[i] = (fact[i - 1] * i) % MOD;\\n }\\n \\n // Compute inverse factorials. Start with invFact[maxN] using modular exponentiation.\\n // Requires maxN > 0. If maxN=0, these arrays only have size 1, this part is skipped.\\n if (maxN > 0) {\\n // Fermat's Little Theorem: a^(p-2) = a^(-1) mod p for prime p.\\n invFact[maxN] = power(fact[maxN], MOD - 2); \\n // Compute remaining inverse factorials iteratively downwards:\\n // (i!)^{-1} = ((i+1)! )^{-1} * (i+1)\\n for (int i = maxN - 1; i >= 1; i--) {\\n invFact[i] = (invFact[i + 1] * (i + 1)) % MOD;\\n }\\n // Note: invFact[0] is already correctly set to 1.\\n }\\n }\\n\\n /**\\n * Computes (base^exp) % MOD using binary exponentiation (also known as exponentiation by squaring).\\n * Efficiently calculates large powers under modulo.\\n */\\n long power(long base, long exp) {\\n long res = 1;\\n base %= MOD; // Reduce base modulo MOD first\\n while (exp > 0) {\\n // If exp is odd, multiply base with result\\n if (exp % 2 == 1) res = (res * base) % MOD;\\n // Square the base and halve the exponent\\n base = (base * base) % MOD;\\n exp /= 2;\\n }\\n return res;\\n }\\n\\n /**\\n * Computes combinations C(n, r) modulo MOD using precomputed factorials and inverse factorials.\\n * Formula: nCr = n! / (r! * (n-r)!) = n! * (r!)^(-1) * ((n-r)!)^(-1) % MOD\\n */\\n long nCr(int n, int r) {\\n // Check for invalid arguments: r cannot be negative or greater than n.\\n if (r < 0 || r > n) {\\n return 0;\\n }\\n // Check if n is within the precomputed range [0, maxN].\\n // fact.length = maxN + 1. So valid indices are 0 to maxN.\\n if (n >= fact.length) {\\n // This should not happen with correct initialization based on problem constraints.\\n // Indicates an internal logic error if this check fails.\\n // Returning 0 might be a safe default in a contest setting.\\n System.err.println(\\\"Error: nCr called with n=\\\" + n + \\\", which is out of precomputed range [0, \\\" + (fact.length - 1) + \\\"]\\\");\\n return 0; \\n }\\n \\n // Retrieve precomputed values from arrays\\n long num = fact[n]; // n!\\n long den1 = invFact[r]; // (r!)^(-1)\\n long den2 = invFact[n-r]; // ((n-r)!)^(-1)\\n \\n // Compute (num * den1 * den2) % MOD\\n long result = (num * den1) % MOD;\\n result = (result * den2) % MOD;\\n \\n return result;\\n }\\n }\\n}\"]]",
"runtime": 29,
"runtimeDistribution": "[[6, 15.5172, \"class Solution {\\n public int distanceSum(int m, int n, int k) {\\n return (int) ((count(m, n, k) + count(n, m, k)) % mod * C(m * n - 2, k - 2) % mod);\\n }\\n\\n int mod = 1_000_000_007;\\n\\n public long count(int m, int n, int k) {\\n long res = 0;\\n for (int i = 1; i <= m - 1; i++) {\\n res += (long) (m - i) * i;\\n }\\n return res % mod * n % mod * n;\\n }\\n\\n public long C(int a, int b) {\\n if (a - b < b)\\n b = a - b;\\n long res = 1;\\n long div = 1;\\n for (int i = 1; i <= b; i++) {\\n res = res * a % mod;\\n div = div * i % mod;\\n a--;\\n }\\n return res * rev(div) % mod;\\n }\\n\\n public long rev(long a) {\\n if (a == 1)\\n return 1;\\n return mod - mod / a * rev(mod % a) % mod;\\n }\\n}\"], [7, 3.4483, \"class Solution {\\n public int distanceSum(int m, int n, int k) {\\n long res = (count(m, n, k) * n % mod * n + count(n, m, k) * m % mod * m) % mod * C(m * n - 2, k - 2)\\n % mod;\\n return (int) res;\\n }\\n\\n int mod = 1_000_000_007;\\n\\n public long count(int m, int n, int k) {\\n long res = 0;\\n for (int i = 1; i <= m - 1; i++) {\\n res = (res + (long) (m - i) * i) ;\\n }\\n return res% mod;\\n }\\n\\n public long C(int a, int b) {\\n if (a - b < b)\\n b = a - b;\\n long res = 1;\\n long div = 1;\\n for (int i = 1; i <= b; i++) {\\n res = res * a % mod;\\n div = div * i % mod;\\n a--;\\n }\\n return res * rev(div) % mod;\\n }\\n\\n public long rev(long a) {\\n if (a == 1)\\n return 1;\\n return mod - mod / a * rev(mod % a) % mod;\\n }\\n}\"], [9, 6.8966, null], [10, 3.4483, null], [11, 1.7241, null], [12, 1.7241, null], [19, 3.4483, null], [20, 22.4138, null], [21, 1.7241, null], [28, 1.7241, null], [29, 1.7241, null], [34, 1.7241, null], [49, 1.7241, null], [50, 13.7931, null], [51, 1.7241, null], [74, 1.7241, null], [83, 1.7241, null], [85, 1.7241, null], [89, 1.7241, null], [99, 1.7241, null], [109, 1.7241, \"class Solution {\\n static final long MOD = 1000000007;\\n static final long[] factorials = new long[100001];\\n static final long[] factorialsInv = new long[100001];\\n static final long[] dist = new long[100001];\\n static {\\n factorials[0] = 1;\\n factorialsInv[0] = 1;\\n for (int i = 1; i < factorials.length; i++) {\\n factorials[i] = (factorials[i - 1] * i) % MOD;\\n factorialsInv[i] = (factorialsInv[i - 1] * inverse(i)) % MOD;\\n dist[i] = (dist[i - 1] + i * (i - 1L) / 2) % MOD;\\n }\\n }\\n\\n static long inverse(int a) {\\n return pow(a, (int) (MOD - 2), MOD);\\n }\\n\\n public int distanceSum(int m, int n, int k) {\\n long current = (mod(dist[m], n, n) + mod(m, m, dist[n])) % MOD;\\n long mk = mod(factorials[m * n - 2], factorialsInv[m * n - k], factorialsInv[k - 2]);\\n return (int) mod(current, mk);\\n }\\n\\n static long mod(long a, long b) {\\n return (a * b) % MOD;\\n }\\n\\n static long mod(long a, long b, long c) {\\n return mod(mod(a, b), c);\\n }\\n\\n static long pow(long a, int pow, long mod) {\\n long p = a;\\n long res = 1;\\n for (int q = 1; q <= pow; q *= 2) {\\n if ((pow & q) > 0) {\\n res = (res * p) % mod;\\n }\\n p = (p * p) % mod;\\n }\\n return res;\\n }\\n\\n}\"], [243, 1.7241, \"class Solution {\\n static int M = (int) 1e9 + 7;\\n static long[] fact = new long[(int) 1e5];\\n\\n static {\\n fact[0] = 1;\\n for (int i = 1; i < (int) 1e5; i++) {\\n fact[i] = i * fact[i - 1];\\n fact[i] %= M;\\n }\\n }\\n\\n public long cnr(int n, int r) {\\n return fact[n] * power2(fact[n - r], M - 2) % M * power2(fact[r], M - 2) % M;\\n }\\n\\n public static long power2(long x, long n) {\\n\\n long res = 1;\\n while (n > 0) {\\n if (n % 2 == 1) {\\n res *= x;\\n res %= M;\\n }\\n x *= x;\\n x %= M;\\n n >>= 1;\\n }\\n return res;\\n }\\n\\n public int distanceSum(int m, int n, int k) {\\n long res = 0;\\n long time = cnr(n * m - 2, k - 2);\\n var ct = new HashMap<Integer, Long>();\\n for (int i = 1; i <= n; i++)\\n for (int j = 1; j <= m; j++) {\\n if (i == j && i == 1)\\n continue;\\n if (i == 1 || j == 1)\\n ct.merge(i + j - 2, (long) (n - i + 1) * (m - j + 1) % M, (a, b) -> (a + b) % M);\\n else\\n ct.merge(i + j - 2, (long) (n - i + 1) * (m - j + 1) % M * 2 % M, (a, b) -> (a + b) % M);\\n }\\n for (var en : ct.entrySet()) {\\n res += en.getKey() * en.getValue() % M * time % M;\\n res %= M;\\n }\\n\\n return (int) res;\\n }\\n}\"]]"
},
"javascript": {
"code": "var distanceSum = function(m, n, k) {\n const MOD = BigInt(1e9 +7);\n const inv3 = BigInt(333333336);\n const inv2 = BigInt(500000004);\n\n function powMod(base, exp, mod) {\n if (mod === 1n) return 0n;\n let result = 1n;\n base = base % mod;\n while (exp > 0n) {\n if (exp % 2n === 1n) {\n result = (result * base) % mod;\n }\n exp = exp / 2n;\n base = (base * base) % mod;\n }\n return result;\n }\n\n function computeComb(a, b, MOD) {\n if (a < 0 || b < 0 || a < b) return 0n;\n let fact = new Array(a+1);\n fact[0] = 1n;\n for (let i=1; i<=a; i++) {\n fact[i] = (fact[i-1] * BigInt(i)) % MOD;\n }\n let inv_fact = new Array(a+1);\n inv_fact[a] = powMod(fact[a], MOD - 2n, MOD);\n for (let i=a-1; i>=0; i--) {\n inv_fact[i] = (inv_fact[i+1] * BigInt(i+1)) % MOD;\n }\n return (fact[a] * inv_fact[b] % MOD) * inv_fact[a - b] % MOD;\n }\n\n let total = BigInt(m) * BigInt(n);\n let a = total - 2n;\n let b = BigInt(k) - 2n;\n if (a < b) return 0;\n\n let comb = computeComb(Number(a), Number(b), MOD);\n let sum_x = 0n;\n if (m >= 2) {\n let m_bi = BigInt(m), n_bi = BigInt(n);\n let term = (n_bi * n_bi) % MOD;\n term = (term * m_bi) % MOD;\n term = term * (m_bi * m_bi - 1n) % MOD;\n term = term * inv3 % MOD;\n sum_x = term * inv2 % MOD;\n }\n\n let sum_y = 0n;\n if (n >= 2) {\n let m_bi = BigInt(m), n_bi = BigInt(n);\n let term = (m_bi * m_bi) % MOD;\n term = (term * n_bi) % MOD;\n term = term * (n_bi * n_bi - 1n) % MOD;\n term = term * inv3 % MOD;\n sum_y = term * inv2 % MOD;\n }\n\n let total_sum = (sum_x + sum_y) % MOD;\n total_sum = (total_sum * comb) % MOD;\n return Number(total_sum);\n};",
"memory": null,
"memoryDistribution": "[[84600, 100.0, \"var distanceSum = function(m, n, k) {\\n const MOD = BigInt(1e9 +7);\\n const inv3 = BigInt(333333336);\\n const inv2 = BigInt(500000004);\\n\\n function powMod(base, exp, mod) {\\n if (mod === 1n) return 0n;\\n let result = 1n;\\n base = base % mod;\\n while (exp > 0n) {\\n if (exp % 2n === 1n) {\\n result = (result * base) % mod;\\n }\\n exp = exp / 2n;\\n base = (base * base) % mod;\\n }\\n return result;\\n }\\n\\n function computeComb(a, b, MOD) {\\n if (a < 0 || b < 0 || a < b) return 0n;\\n let fact = new Array(a+1);\\n fact[0] = 1n;\\n for (let i=1; i<=a; i++) {\\n fact[i] = (fact[i-1] * BigInt(i)) % MOD;\\n }\\n let inv_fact = new Array(a+1);\\n inv_fact[a] = powMod(fact[a], MOD - 2n, MOD);\\n for (let i=a-1; i>=0; i--) {\\n inv_fact[i] = (inv_fact[i+1] * BigInt(i+1)) % MOD;\\n }\\n return (fact[a] * inv_fact[b] % MOD) * inv_fact[a - b] % MOD;\\n }\\n\\n let total = BigInt(m) * BigInt(n);\\n let a = total - 2n;\\n let b = BigInt(k) - 2n;\\n if (a < b) return 0;\\n\\n let comb = computeComb(Number(a), Number(b), MOD);\\n let sum_x = 0n;\\n if (m >= 2) {\\n let m_bi = BigInt(m), n_bi = BigInt(n);\\n let term = (n_bi * n_bi) % MOD;\\n term = (term * m_bi) % MOD;\\n term = term * (m_bi * m_bi - 1n) % MOD;\\n term = term * inv3 % MOD;\\n sum_x = term * inv2 % MOD;\\n }\\n\\n let sum_y = 0n;\\n if (n >= 2) {\\n let m_bi = BigInt(m), n_bi = BigInt(n);\\n let term = (m_bi * m_bi) % MOD;\\n term = (term * n_bi) % MOD;\\n term = term * (n_bi * n_bi - 1n) % MOD;\\n term = term * inv3 % MOD;\\n sum_y = term * inv2 % MOD;\\n }\\n\\n let total_sum = (sum_x + sum_y) % MOD;\\n total_sum = (total_sum * comb) % MOD;\\n return Number(total_sum);\\n};\"]]",
"runtime": 918,
"runtimeDistribution": "[[918, 100.0, \"var distanceSum = function(m, n, k) {\\n const MOD = BigInt(1e9 +7);\\n const inv3 = BigInt(333333336);\\n const inv2 = BigInt(500000004);\\n\\n function powMod(base, exp, mod) {\\n if (mod === 1n) return 0n;\\n let result = 1n;\\n base = base % mod;\\n while (exp > 0n) {\\n if (exp % 2n === 1n) {\\n result = (result * base) % mod;\\n }\\n exp = exp / 2n;\\n base = (base * base) % mod;\\n }\\n return result;\\n }\\n\\n function computeComb(a, b, MOD) {\\n if (a < 0 || b < 0 || a < b) return 0n;\\n let fact = new Array(a+1);\\n fact[0] = 1n;\\n for (let i=1; i<=a; i++) {\\n fact[i] = (fact[i-1] * BigInt(i)) % MOD;\\n }\\n let inv_fact = new Array(a+1);\\n inv_fact[a] = powMod(fact[a], MOD - 2n, MOD);\\n for (let i=a-1; i>=0; i--) {\\n inv_fact[i] = (inv_fact[i+1] * BigInt(i+1)) % MOD;\\n }\\n return (fact[a] * inv_fact[b] % MOD) * inv_fact[a - b] % MOD;\\n }\\n\\n let total = BigInt(m) * BigInt(n);\\n let a = total - 2n;\\n let b = BigInt(k) - 2n;\\n if (a < b) return 0;\\n\\n let comb = computeComb(Number(a), Number(b), MOD);\\n let sum_x = 0n;\\n if (m >= 2) {\\n let m_bi = BigInt(m), n_bi = BigInt(n);\\n let term = (n_bi * n_bi) % MOD;\\n term = (term * m_bi) % MOD;\\n term = term * (m_bi * m_bi - 1n) % MOD;\\n term = term * inv3 % MOD;\\n sum_x = term * inv2 % MOD;\\n }\\n\\n let sum_y = 0n;\\n if (n >= 2) {\\n let m_bi = BigInt(m), n_bi = BigInt(n);\\n let term = (m_bi * m_bi) % MOD;\\n term = (term * n_bi) % MOD;\\n term = term * (n_bi * n_bi - 1n) % MOD;\\n term = term * inv3 % MOD;\\n sum_y = term * inv2 % MOD;\\n }\\n\\n let total_sum = (sum_x + sum_y) % MOD;\\n total_sum = (total_sum * comb) % MOD;\\n return Number(total_sum);\\n};\"], [958, 100.0, \"var distanceSum = function(m, n, k) {\\n const MOD = BigInt(1e9 +7);\\n const inv3 = BigInt(333333336);\\n const inv2 = BigInt(500000004);\\n\\n function powMod(base, exp, mod) {\\n if (mod === 1n) return 0n;\\n let result = 1n;\\n base = base % mod;\\n while (exp > 0n) {\\n if (exp % 2n === 1n) {\\n result = (result * base) % mod;\\n }\\n exp = exp / 2n;\\n base = (base * base) % mod;\\n }\\n return result;\\n }\\n\\n function computeComb(a, b, MOD) {\\n if (a < 0 || b < 0 || a < b) return 0n;\\n let fact = new Array(a+1);\\n fact[0] = 1n;\\n for (let i=1; i<=a; i++) {\\n fact[i] = (fact[i-1] * BigInt(i)) % MOD;\\n }\\n let inv_fact = new Array(a+1);\\n inv_fact[a] = powMod(fact[a], MOD - 2n, MOD);\\n for (let i=a-1; i>=0; i--) {\\n inv_fact[i] = (inv_fact[i+1] * BigInt(i+1)) % MOD;\\n }\\n return (fact[a] * inv_fact[b] % MOD) * inv_fact[a - b] % MOD;\\n }\\n\\n let total = BigInt(m) * BigInt(n);\\n let a = total - 2n;\\n let b = BigInt(k) - 2n;\\n if (a < b) return 0;\\n\\n let comb = computeComb(Number(a), Number(b), MOD);\\n let sum_x = 0n;\\n if (m >= 2) {\\n let m_bi = BigInt(m), n_bi = BigInt(n);\\n let term = (n_bi * n_bi) % MOD;\\n term = (term * m_bi) % MOD;\\n term = term * (m_bi * m_bi - 1n) % MOD;\\n term = term * inv3 % MOD;\\n sum_x = term * inv2 % MOD;\\n }\\n\\n let sum_y = 0n;\\n if (n >= 2) {\\n let m_bi = BigInt(m), n_bi = BigInt(n);\\n let term = (m_bi * m_bi) % MOD;\\n term = (term * n_bi) % MOD;\\n term = term * (n_bi * n_bi - 1n) % MOD;\\n term = term * inv3 % MOD;\\n sum_y = term * inv2 % MOD;\\n }\\n\\n let total_sum = (sum_x + sum_y) % MOD;\\n total_sum = (total_sum * comb) % MOD;\\n return Number(total_sum);\\n};\"]]"
},
"python3": {
"code": "class Solution:\n MOD = 10**9 + 7\n max_fact = 10**5\n fact = [1] * (max_fact + 1)\n for i in range(1, max_fact + 1):\n fact[i] = fact[i-1] * i % MOD\n inv_fact = [1] * (max_fact + 1)\n inv_fact[max_fact] = pow(fact[max_fact], MOD-2, MOD)\n for i in range(max_fact -1, -1, -1):\n inv_fact[i] = inv_fact[i+1] * (i+1) % MOD\n inv6 = pow(6, MOD-2, MOD)\n\n def distanceSum(self, m: int, n: int, k: int) -> int:\n a = m * n\n if k < 2 or k > a:\n return 0\n a_minus_2 = a - 2\n b = k - 2\n if a_minus_2 < b:\n return 0\n \n comb = self.fact[a_minus_2] * self.inv_fact[b] % self.MOD\n comb = comb * self.inv_fact[a_minus_2 - b] % self.MOD\n \n T = m % self.MOD\n T = T * (n % self.MOD) % self.MOD\n sum_mn = (m + n) % self.MOD\n T = T * sum_mn % self.MOD\n a_minus_1 = (a - 1) % self.MOD\n T = T * a_minus_1 % self.MOD\n \n res = comb * T % self.MOD\n res = res * self.inv6 % self.MOD\n return res",
"memory": 2500,
"memoryDistribution": "[[2500, 28.3582, \"class Solution:\\n MOD = 10**9 + 7\\n max_fact = 10**5\\n fact = [1] * (max_fact + 1)\\n for i in range(1, max_fact + 1):\\n fact[i] = fact[i-1] * i % MOD\\n inv_fact = [1] * (max_fact + 1)\\n inv_fact[max_fact] = pow(fact[max_fact], MOD-2, MOD)\\n for i in range(max_fact -1, -1, -1):\\n inv_fact[i] = inv_fact[i+1] * (i+1) % MOD\\n inv6 = pow(6, MOD-2, MOD)\\n\\n def distanceSum(self, m: int, n: int, k: int) -> int:\\n a = m * n\\n if k < 2 or k > a:\\n return 0\\n a_minus_2 = a - 2\\n b = k - 2\\n if a_minus_2 < b:\\n return 0\\n \\n comb = self.fact[a_minus_2] * self.inv_fact[b] % self.MOD\\n comb = comb * self.inv_fact[a_minus_2 - b] % self.MOD\\n \\n T = m % self.MOD\\n T = T * (n % self.MOD) % self.MOD\\n sum_mn = (m + n) % self.MOD\\n T = T * sum_mn % self.MOD\\n a_minus_1 = (a - 1) % self.MOD\\n T = T * a_minus_1 % self.MOD\\n \\n res = comb * T % self.MOD\\n res = res * self.inv6 % self.MOD\\n return res\"], [17800, 1.4925, \"mod = 10**9+7\\nclass Solution:\\n def distanceSum(self, m: int, n: int, k: int) -> int:\\n num = den = 1\\n for i in range(min(k-2,m*n-k)):\\n num *= m*n-2-i\\n den *= i+1\\n num %= mod\\n den %= mod\\n c = (num*pow(den,-1,mod))%mod\\n return (c*((m*m*n*(n+1)*(n-1)+n*n*m*(m+1)*(m-1))//6))%mod\"], [17900, 2.9851, \"class Solution:\\n # sum(|xi-xj|+|yi-yj|)=sum(|xi-xj| for yi,yi)+sum(|yi-yj| for xi,xj)\\n # sum(d*(n-d) 1<= d <=n-1)=n*(n-1)*(n)/2-(n-1)(n)(2n-1)/6=n(n-1)(n+1)/6\\n def distanceSum(self, m: int, n: int, k: int) -> int:\\n mod = 10**9+7\\n w = (n*(n-1)*(n+1)*m*m+m*(m-1)*(m+1)*n*n)//6\\n return w*comb(m*n-2,k-2)%mod\\n\\n \"], [18000, 4.4776, null], [18100, 16.4179, null], [18200, 14.9254, null], [18300, 10.4478, null], [18400, 7.4627, null], [21400, 2.9851, null], [22000, 2.9851, null], [25100, 1.4925, null], [25200, 5.9701, null], [25300, 2.9851, null], [25400, 2.9851, null], [25500, 4.4776, null], [25600, 2.9851, null], [25700, 1.4925, null], [25800, 1.4925, null], [26600, 1.4925, null], [33200, 1.4925, \"def make_nCr_mod(max_n=int(2e5), mod=int(1e9+7)):\\n max_n = min(max_n, mod - 1)\\n\\n fact, inv_fact = [0] * (max_n + 1), [0] * (max_n + 1)\\n fact[0] = 1\\n for i in range(max_n):\\n fact[i + 1] = fact[i] * (i + 1) % mod\\n\\n inv_fact[-1] = pow(fact[-1], mod - 2, mod)\\n for i in reversed(range(max_n)):\\n inv_fact[i] = inv_fact[i + 1] * (i + 1) % mod\\n\\n def nCr_mod(cls, n, r):\\n res = 1\\n while n or r:\\n a, b = n % mod, r % mod\\n if a < b:\\n return 0\\n res = res * fact[a] % mod * inv_fact[b] % mod * inv_fact[a - b] % mod\\n n //= mod\\n r //= mod\\n return res\\n return nCr_mod\\n\\nclass Solution:\\n comb=make_nCr_mod()\\n def distanceSum(self, m: int, n: int, k: int) -> int:\\n return self.comb(n*m-2,k-2)*n*m*(n*m-1)*(n+m)//6%(10**9+7)\"], [33300, 1.4925, \"def make_nCr_mod(max_n=int(2e5), mod=int(1e9+7)):\\n max_n = min(max_n, mod - 1)\\n\\n fact, inv_fact = [0] * (max_n + 1), [0] * (max_n + 1)\\n fact[0] = 1\\n for i in range(max_n):\\n fact[i + 1] = fact[i] * (i + 1) % mod\\n\\n inv_fact[-1] = pow(fact[-1], mod - 2, mod)\\n for i in reversed(range(max_n)):\\n inv_fact[i] = inv_fact[i + 1] * (i + 1) % mod\\n\\n def nCr_mod(cls, n, r):\\n res = 1\\n while n or r:\\n a, b = n % mod, r % mod\\n if a < b:\\n return 0\\n res = res * fact[a] % mod * inv_fact[b] % mod * inv_fact[a - b] % mod\\n n //= mod\\n r //= mod\\n return res\\n return nCr_mod\\n\\nclass Solution:\\n comb=make_nCr_mod()\\n def distanceSum(self, m: int, n: int, k: int) -> int:\\n mod=int(1e9+7)\\n smx=(n*n*(m-1)*m*(m+1)//6)%mod\\n smy=(m*m*(n-1)*n*(n+1)//6)%mod\\n return self.comb(m*n-2,k-2)*(smx+smy)%mod\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 10.4478, \"MOD = 10**9 + 7\\nfactorial = [1, 1]\\ninvfactorial = [1, 1]\\n\\ndef nCk(n, k):\\n return factorial[n] * invfactorial[k] % MOD * invfactorial[n-k] % MOD\\n\\nclass Solution:\\n def distanceSum(self, m: int, n: int, k: int) -> int:\\n return (nCk(n*m - 2, k - 2) * (m * m * (n - 1) * n * (n + 1) + n * n * (m - 1) * m * (m + 1)) // 6) % MOD\\n\\ndef mod_inv(base):\\n ans = 1\\n exp = MOD - 2\\n while exp > 0:\\n if exp % 2 == 1:\\n ans = (ans * base) % MOD\\n exp //= 2\\n base = (base * base) % MOD\\n return ans\\n\\nfor i in range(2, 100_000):\\n factorial.append(i * factorial[i - 1] % MOD)\\n invfactorial.append(mod_inv(factorial[i]) % MOD)\"], [1, 2.9851, \"MOD = 10**9 + 7\\nmax_n = 10**5\\n\\n# Precompute factorial and inverse factorial arrays\\nfact = [1] * (max_n + 1)\\nfor i in range(1, max_n + 1):\\n fact[i] = fact[i-1] * i % MOD\\n\\ninv_fact = [1] * (max_n + 1)\\ninv_fact[max_n] = pow(fact[max_n], MOD - 2, MOD)\\nfor i in range(max_n - 1, -1, -1):\\n inv_fact[i] = inv_fact[i + 1] * (i + 1) % MOD\\n\\ndef comb(n, k):\\n if n < 0 or k < 0 or k > n:\\n return 0\\n return ((fact[n] * inv_fact[k] % MOD) * inv_fact[n - k]) % MOD\\n\\nclass Solution:\\n def distanceSum(self, m: int, n: int, k: int) -> int:\\n \\n def calc(a,b):\\n res = a*a*b*(b*b-1)//6\\n res %= MOD\\n return res\\n \\n res = comb(m*n-2,k-2)%MOD * (calc(m,n)+calc(n,m)) % MOD\\n return res\"], [2, 1.4925, null], [4, 2.9851, null], [5, 1.4925, null], [88, 1.4925, null], [93, 1.4925, null], [147, 1.4925, null], [239, 2.9851, null], [240, 1.4925, null], [265, 1.4925, null], [313, 1.4925, null], [475, 1.4925, null], [897, 1.4925, null], [915, 1.4925, null], [975, 1.4925, null], [1106, 1.4925, null], [1253, 1.4925, null], [1265, 2.9851, null], [1266, 1.4925, null], [1267, 1.4925, null], [1268, 1.4925, null], [1272, 1.4925, null], [1275, 1.4925, null], [1276, 1.4925, null], [1281, 1.4925, null], [1283, 1.4925, null], [1285, 1.4925, null], [1287, 2.9851, null], [1290, 1.4925, null], [1309, 1.4925, null], [1310, 1.4925, null], [1316, 1.4925, null], [1317, 1.4925, null], [1321, 1.4925, null], [1325, 2.9851, null], [1326, 1.4925, null], [1327, 1.4925, null], [1332, 1.4925, null], [1335, 1.4925, null], [1339, 1.4925, null], [1340, 2.9851, null], [1342, 1.4925, null], [1347, 1.4925, null], [1349, 1.4925, null], [1351, 1.4925, null], [1353, 1.4925, null], [1359, 1.4925, null], [1368, 1.4925, \"class Solution:\\n def distanceSum(self, m: int, n: int, k: int) -> int:\\n mod = 10**9 + 7\\n curl = 0\\n numx = [i for i in range (n)]\\n left = 0\\n right = sum(numx)\\n ll = 0\\n rr = n\\n for i in range (len(numx)):\\n curl+=(left+right)*m\\n rr-=1\\n right-=rr\\n ll+=1\\n left+=ll\\n curl*=m\\n numy = [i for i in range (m)]\\n left = 0\\n right = sum(numy)\\n ll = 0\\n rr = m\\n curr = 0\\n for i in range (len(numy)):\\n curr+=(left+right)*n\\n rr-=1\\n right-=rr\\n ll+=1\\n left+=ll\\n curr*=n\\n val = (curl+curr)//2\\n # print(val)\\n tot = m*n\\n mid = tot//2 + 1\\n if k > mid:\\n k = (n*m) - k+2\\n # print(k)\\n return val*(math.comb(n*m - 2, k-2))%mod\\n # return 14484 * (math.comb(70,10))%mod\\n\"], [3350, 1.4925, \"class Solution:\\n def distanceSum(self, m: int, n: int, k: int) -> int:\\n MOD = 10**9 + 7\\n K = comb(m*n-2, k-2) % MOD\\n ans = 0\\n for i in range(m):\\n for j in range(n):\\n q = 0\\n if i < m-1:\\n q += (m-1-i) * (m-i) // 2\\n if j < n-1:\\n a0 = (n-1-j) * (n-j) // 2\\n d = n - 1 - j\\n p = m - i\\n q += p * (a0 + a0 + (p-1) * d) // 2\\n if j > 0:\\n a0 = (j + 1) * j // 2 + j\\n d = j\\n p = m - i - 1\\n q += p * (a0 + a0 + (p-1) * d) // 2\\n else:\\n if j < n-1:\\n q += (n-1-j) * (n-j) // 2\\n ans += q\\n ans %= MOD\\n ans *= K\\n return ans % MOD\\n\"]]"
},
"ruby": {
"code": "MOD = 10**9 + 7\nINV6 = 166666668 # Modular inverse of 6 under MOD\n\ndef distance_sum(m, n, k)\n cells = m * n\n return 0 if k < 2 || k > cells\n\n a = cells - 2\n b = k - 2\n\n comb = if a < b\n 0\n else\n max_fact = a\n fact = Array.new(max_fact + 1, 1)\n (2..max_fact).each { |i| fact[i] = fact[i-1] * i % MOD }\n\n inv_fact = Array.new(max_fact + 1, 1)\n inv_fact[max_fact] = fact[max_fact].pow(MOD - 2, MOD)\n (max_fact - 1).downto(0) { |i| inv_fact[i] = inv_fact[i+1] * (i+1) % MOD }\n\n fact[a] * inv_fact[b] % MOD * inv_fact[a - b] % MOD\n end\n\n sum_x = n % MOD\n sum_x = sum_x * n % MOD\n sum_x = sum_x * ( (m - 1) % MOD ) % MOD\n sum_x = sum_x * ( m % MOD ) % MOD\n sum_x = sum_x * ( (m + 1) % MOD ) % MOD\n sum_x = sum_x * INV6 % MOD\n\n sum_y = m % MOD\n sum_y = sum_y * m % MOD\n sum_y = sum_y * ( (n - 1) % MOD ) % MOD\n sum_y = sum_y * ( n % MOD ) % MOD\n sum_y = sum_y * ( (n + 1) % MOD ) % MOD\n sum_y = sum_y * INV6 % MOD\n\n total = (sum_x + sum_y) % MOD\n total * comb % MOD\nend",
"memory": 27300,
"memoryDistribution": "[[27300, 100.0, \"MOD = 10**9 + 7\\nINV6 = 166666668 # Modular inverse of 6 under MOD\\n\\ndef distance_sum(m, n, k)\\n cells = m * n\\n return 0 if k < 2 || k > cells\\n\\n a = cells - 2\\n b = k - 2\\n\\n comb = if a < b\\n 0\\n else\\n max_fact = a\\n fact = Array.new(max_fact + 1, 1)\\n (2..max_fact).each { |i| fact[i] = fact[i-1] * i % MOD }\\n\\n inv_fact = Array.new(max_fact + 1, 1)\\n inv_fact[max_fact] = fact[max_fact].pow(MOD - 2, MOD)\\n (max_fact - 1).downto(0) { |i| inv_fact[i] = inv_fact[i+1] * (i+1) % MOD }\\n\\n fact[a] * inv_fact[b] % MOD * inv_fact[a - b] % MOD\\n end\\n\\n sum_x = n % MOD\\n sum_x = sum_x * n % MOD\\n sum_x = sum_x * ( (m - 1) % MOD ) % MOD\\n sum_x = sum_x * ( m % MOD ) % MOD\\n sum_x = sum_x * ( (m + 1) % MOD ) % MOD\\n sum_x = sum_x * INV6 % MOD\\n\\n sum_y = m % MOD\\n sum_y = sum_y * m % MOD\\n sum_y = sum_y * ( (n - 1) % MOD ) % MOD\\n sum_y = sum_y * ( n % MOD ) % MOD\\n sum_y = sum_y * ( (n + 1) % MOD ) % MOD\\n sum_y = sum_y * INV6 % MOD\\n\\n total = (sum_x + sum_y) % MOD\\n total * comb % MOD\\nend\"], [273300, 100.0, \"MOD = 10**9 + 7\\nINV6 = 166666668 # Modular inverse of 6 under MOD\\n\\ndef distance_sum(m, n, k)\\n cells = m * n\\n return 0 if k < 2 || k > cells\\n\\n a = cells - 2\\n b = k - 2\\n\\n comb = if a < b\\n 0\\n else\\n max_fact = a\\n fact = Array.new(max_fact + 1, 1)\\n (2..max_fact).each { |i| fact[i] = fact[i-1] * i % MOD }\\n\\n inv_fact = Array.new(max_fact + 1, 1)\\n inv_fact[max_fact] = fact[max_fact].pow(MOD - 2, MOD)\\n (max_fact - 1).downto(0) { |i| inv_fact[i] = inv_fact[i+1] * (i+1) % MOD }\\n\\n fact[a] * inv_fact[b] % MOD * inv_fact[a - b] % MOD\\n end\\n\\n sum_x = n % MOD\\n sum_x = sum_x * n % MOD\\n sum_x = sum_x * ( (m - 1) % MOD ) % MOD\\n sum_x = sum_x * ( m % MOD ) % MOD\\n sum_x = sum_x * ( (m + 1) % MOD ) % MOD\\n sum_x = sum_x * INV6 % MOD\\n\\n sum_y = m % MOD\\n sum_y = sum_y * m % MOD\\n sum_y = sum_y * ( (n - 1) % MOD ) % MOD\\n sum_y = sum_y * ( n % MOD ) % MOD\\n sum_y = sum_y * ( (n + 1) % MOD ) % MOD\\n sum_y = sum_y * INV6 % MOD\\n\\n total = (sum_x + sum_y) % MOD\\n total * comb % MOD\\nend\"]]",
"runtime": 823,
"runtimeDistribution": "[[823, 100.0, \"MOD = 10**9 + 7\\nINV6 = 166666668 # Modular inverse of 6 under MOD\\n\\ndef distance_sum(m, n, k)\\n cells = m * n\\n return 0 if k < 2 || k > cells\\n\\n a = cells - 2\\n b = k - 2\\n\\n comb = if a < b\\n 0\\n else\\n max_fact = a\\n fact = Array.new(max_fact + 1, 1)\\n (2..max_fact).each { |i| fact[i] = fact[i-1] * i % MOD }\\n\\n inv_fact = Array.new(max_fact + 1, 1)\\n inv_fact[max_fact] = fact[max_fact].pow(MOD - 2, MOD)\\n (max_fact - 1).downto(0) { |i| inv_fact[i] = inv_fact[i+1] * (i+1) % MOD }\\n\\n fact[a] * inv_fact[b] % MOD * inv_fact[a - b] % MOD\\n end\\n\\n sum_x = n % MOD\\n sum_x = sum_x * n % MOD\\n sum_x = sum_x * ( (m - 1) % MOD ) % MOD\\n sum_x = sum_x * ( m % MOD ) % MOD\\n sum_x = sum_x * ( (m + 1) % MOD ) % MOD\\n sum_x = sum_x * INV6 % MOD\\n\\n sum_y = m % MOD\\n sum_y = sum_y * m % MOD\\n sum_y = sum_y * ( (n - 1) % MOD ) % MOD\\n sum_y = sum_y * ( n % MOD ) % MOD\\n sum_y = sum_y * ( (n + 1) % MOD ) % MOD\\n sum_y = sum_y * INV6 % MOD\\n\\n total = (sum_x + sum_y) % MOD\\n total * comb % MOD\\nend\"], [828, 100.0, \"MOD = 10**9 + 7\\nINV6 = 166666668 # Modular inverse of 6 under MOD\\n\\ndef distance_sum(m, n, k)\\n cells = m * n\\n return 0 if k < 2 || k > cells\\n\\n a = cells - 2\\n b = k - 2\\n\\n comb = if a < b\\n 0\\n else\\n max_fact = a\\n fact = Array.new(max_fact + 1, 1)\\n (2..max_fact).each { |i| fact[i] = fact[i-1] * i % MOD }\\n\\n inv_fact = Array.new(max_fact + 1, 1)\\n inv_fact[max_fact] = fact[max_fact].pow(MOD - 2, MOD)\\n (max_fact - 1).downto(0) { |i| inv_fact[i] = inv_fact[i+1] * (i+1) % MOD }\\n\\n fact[a] * inv_fact[b] % MOD * inv_fact[a - b] % MOD\\n end\\n\\n sum_x = n % MOD\\n sum_x = sum_x * n % MOD\\n sum_x = sum_x * ( (m - 1) % MOD ) % MOD\\n sum_x = sum_x * ( m % MOD ) % MOD\\n sum_x = sum_x * ( (m + 1) % MOD ) % MOD\\n sum_x = sum_x * INV6 % MOD\\n\\n sum_y = m % MOD\\n sum_y = sum_y * m % MOD\\n sum_y = sum_y * ( (n - 1) % MOD ) % MOD\\n sum_y = sum_y * ( n % MOD ) % MOD\\n sum_y = sum_y * ( (n + 1) % MOD ) % MOD\\n sum_y = sum_y * INV6 % MOD\\n\\n total = (sum_x + sum_y) % MOD\\n total * comb % MOD\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list:
import random
random.seed(seed)
MOD = 10**9 + 7
max_fact = 10**5
fact = [1] * (max_fact + 1)
for i in range(1, max_fact + 1):
fact[i] = fact[i - 1] * i % MOD
inv_fact = [1] * (max_fact + 1)
inv_fact[max_fact] = pow(fact[max_fact], MOD - 2, MOD)
for i in range(max_fact - 1, -1, -1):
inv_fact[i] = inv_fact[i + 1] * (i + 1) % MOD
inv6 = pow(6, MOD - 2, MOD)
def sample_distanceSum(m, n, k):
a = m * n
if k < 2 or k > a:
return 0
a_minus_2 = a - 2
b = k - 2
if a_minus_2 < b:
return 0
comb = fact[a_minus_2] * inv_fact[b] % MOD
comb = comb * inv_fact[a_minus_2 - b] % MOD
T = (m % MOD) * (n % MOD) % MOD
T = T * ((m + n) % MOD) % MOD
a_minus_1 = (a - 1) % MOD
T = T * a_minus_1 % MOD
res = comb * T % MOD
res = res * inv6 % MOD
return res
test_cases = []
fixed_cases = [
(1, 2, 2),
(1, 4, 3),
(2, 2, 2),
(2, 3, 6),
(3, 3, 4)
]
for case in fixed_cases:
if len(test_cases) >= num_cases:
break
m, n, k = case
inp = f"{m},{n},{k}"
out = str(sample_distanceSum(m, n, k))
test_cases.append({"input": inp, "output": out})
while len(test_cases) < num_cases:
m = random.randint(1, 100000)
n_min = 2 if m == 1 else 1
n_max = 100000 // m
if n_max < n_min:
continue
n = random.randint(n_min, n_max)
a = m * n
if a < 2:
continue
k = random.randint(2, a)
inp = f"{m},{n},{k}"
out = str(sample_distanceSum(m, n, k))
test_cases.append({"input": inp, "output": out})
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
try:
expected = int(expected_output.strip())
program = int(program_output.strip())
return expected == program
except:
return False
|
[{"input": "1,2,2", "output": "1"}, {"input": "1,4,3", "output": "20"}, {"input": "2,2,2", "output": "8"}, {"input": "2,3,6", "output": "25"}, {"input": "3,3,4", "output": "1512"}, {"input": "95895,1,27311", "output": "584005881"}, {"input": "57432,1,42454", "output": "866460139"}, {"input": "27996,3,21077", "output": "872590091"}, {"input": "46854,2,13136", "output": "485965647"}, {"input": "74524,1,18645", "output": "282117499"}, {"input": "24308,4,88852", "output": "522072025"}, {"input": "35510,1,8765", "output": "746041201"}, {"input": "52613,1,35007", "output": "219813124"}, {"input": "48919,1,26465", "output": "249058690"}, {"input": "26422,2,17519", "output": "350242721"}, {"input": "43687,2,50338", "output": "212858189"}, {"input": "14247,5,20967", "output": "923041643"}, {"input": "3123,28,1347", "output": "367560345"}, {"input": "74554,1,65427", "output": "747956867"}, {"input": "40377,2,63154", "output": "282980190"}, {"input": "7174,3,21438", "output": "436837959"}, {"input": "52968,1,41615", "output": "309804470"}, {"input": "22876,1,10294", "output": "41914478"}, {"input": "49479,1,40643", "output": "774758177"}, {"input": "3585,15,45226", "output": "352872030"}, {"input": "10459,1,8647", "output": "772812587"}, {"input": "39711,2,63216", "output": "666547393"}, {"input": "73540,1,40358", "output": "267118434"}, {"input": "6012,15,38746", "output": "178394511"}, {"input": "93753,1,53803", "output": "871207607"}, {"input": "64463,1,48874", "output": "699449296"}, {"input": "49799,2,87072", "output": "452698033"}, {"input": "93915,1,53180", "output": "927535789"}, {"input": "38320,1,37710", "output": "693561964"}, {"input": "43618,1,16432", "output": "225026611"}, {"input": "67920,1,66236", "output": "305145928"}, {"input": "28764,3,71866", "output": "100745818"}, {"input": "26115,1,8255", "output": "188799508"}, {"input": "80376,1,27851", "output": "471066176"}, {"input": "59881,1,36695", "output": "349851497"}, {"input": "24409,2,44111", "output": "72839973"}, {"input": "64854,1,27644", "output": "957496284"}, {"input": "44380,2,63051", "output": "980277526"}, {"input": "61782,1,39640", "output": "535327707"}, {"input": "21303,1,4673", "output": "3194549"}, {"input": "69760,1,28378", "output": "96094564"}, {"input": "19468,3,36424", "output": "36914037"}, {"input": "16125,2,21070", "output": "165388477"}, {"input": "74221,1,39606", "output": "393670271"}, {"input": "82519,1,13400", "output": "557588350"}, {"input": "6680,8,1281", "output": "229540134"}, {"input": "34994,1,20698", "output": "142671487"}, {"input": "9379,8,61738", "output": "244280715"}, {"input": "5357,1,624", "output": "866320434"}, {"input": "91979,1,60561", "output": "978357158"}, {"input": "70655,1,6471", "output": "751493938"}, {"input": "70127,1,59868", "output": "175083342"}, {"input": "70356,1,18432", "output": "237116401"}, {"input": "79248,1,11280", "output": "857452453"}, {"input": "21638,1,7666", "output": "492675865"}, {"input": "6414,3,7709", "output": "483930745"}, {"input": "27251,2,48184", "output": "341500318"}, {"input": "71536,1,57600", "output": "730927168"}, {"input": "58056,1,23774", "output": "527514307"}, {"input": "66348,1,38486", "output": "273470108"}, {"input": "8417,11,8289", "output": "126393357"}, {"input": "18408,2,140", "output": "286858899"}, {"input": "36259,2,57462", "output": "859588373"}, {"input": "71882,1,57170", "output": "752834233"}, {"input": "60327,1,43794", "output": "828710644"}, {"input": "80286,1,23852", "output": "474173832"}, {"input": "75760,1,33097", "output": "508576062"}, {"input": "5086,14,17154", "output": "655729088"}, {"input": "67170,1,6296", "output": "238104453"}, {"input": "33543,1,23229", "output": "22168319"}, {"input": "10321,8,18615", "output": "987189013"}, {"input": "34761,2,32643", "output": "200073288"}, {"input": "66136,1,20600", "output": "494401622"}, {"input": "63704,1,37890", "output": "878087836"}, {"input": "19506,1,8394", "output": "469097360"}, {"input": "32386,1,12914", "output": "872385854"}, {"input": "50543,1,37211", "output": "636408643"}, {"input": "26367,3,41098", "output": "292630149"}, {"input": "22404,1,10417", "output": "67711266"}, {"input": "45895,1,33570", "output": "365015295"}, {"input": "7168,11,16731", "output": "200498220"}, {"input": "74443,1,56066", "output": "106050073"}, {"input": "55432,1,34565", "output": "459233685"}, {"input": "24803,4,34512", "output": "859548903"}, {"input": "4544,2,6876", "output": "954589142"}, {"input": "39701,1,29921", "output": "591200736"}, {"input": "91147,1,51428", "output": "61920257"}, {"input": "53351,1,10294", "output": "461993408"}, {"input": "37000,1,17417", "output": "106331231"}, {"input": "21771,1,7894", "output": "277398348"}, {"input": "69399,1,12468", "output": "826812774"}, {"input": "57081,1,37972", "output": "734187136"}, {"input": "62190,1,1414", "output": "492002583"}, {"input": "14781,4,40345", "output": "795243929"}, {"input": "1996,28,34907", "output": "105236489"}]
|
{
"cpp": "==Code Submission==\n\npair<int, pair<int, int>> deserialize_stdin(const string &input) {\n stringstream ss(input);\n string token;\n int m, n, k;\n getline(ss, token, ',');\n m = stoi(token);\n getline(ss, token, ',');\n n = stoi(token);\n getline(ss, token);\n k = stoi(token);\n return {m, {n, k}};\n}\n\nstring serialize_stdout(int result) {\n return to_string(result);\n}\n\nint main() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n string line;\n getline(cin, line);\n auto parts = deserialize_stdin(line);\n int m = parts.first;\n int n = parts.second.first;\n int k = parts.second.second;\n Solution sol;\n int ans = sol.distanceSum(m, n, k);\n cout << serialize_stdout(ans);\n return 0;\n}",
"golang": "==Code Submission==\n\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n line, _ := reader.ReadString('\\n')\n line = strings.TrimSpace(line)\n parts := strings.Split(line, \",\")\n m, _ := strconv.Atoi(parts[0])\n n, _ := strconv.Atoi(parts[1])\n k, _ := strconv.Atoi(parts[2])\n ans := distanceSum(m, n, k)\n fmt.Printf(\"%d\", ans)\n}",
"java": "public class Main {\n private static int[] deserializeInput(String input) {\n String[] parts = input.split(\",\");\n int m = Integer.parseInt(parts[0].trim());\n int n = Integer.parseInt(parts[1].trim());\n int k = Integer.parseInt(parts[2].trim());\n return new int[]{m, n, k};\n }\n \n private static String serializeOutput(int result) {\n return Integer.toString(result);\n }\n \n public static void main(String[] args) throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n String line = br.readLine().trim();\n int[] arr = deserializeInput(line);\n int m = arr[0], n = arr[1], k = arr[2];\n Solution sol = new Solution();\n int ans = sol.distanceSum(m, n, k);\n System.out.println(serializeOutput(ans));\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\n\nconst deserialize_stdin = (input) => {\n const parts = input.trim().split(',');\n const m = parseInt(parts[0].trim(), 10);\n const n = parseInt(parts[1].trim(), 10);\n const k = parseInt(parts[2].trim(), 10);\n return { m, n, k };\n};\n\nconst serialize_stdout = (result) => {\n return result.toString();\n};\n\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\nlet input = '';\nprocess.stdin.on('data', chunk => input += chunk);\nprocess.stdin.on('end', () => {\n const { m, n, k } = deserialize_stdin(input);\n const ans = distanceSum(m, n, k);\n console.log(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str):\n parts = input_str.strip().split(',')\n m = int(parts[0])\n n = int(parts[1])\n k = int(parts[2])\n return m, n, k\n\ndef serialize_stdout(result):\n return str(result)\n\nline = sys.stdin.read().strip()\nm, n, k = deserialize_stdin(line)\nsol = Solution()\nans = sol.distanceSum(m, n, k)\nsys.stdout.write(serialize_stdout(ans))",
"ruby": "==Code Submission==\n\ninput = gets.strip\nparts = input.split(',')\nm = parts[0].to_i\nn = parts[1].to_i\nk = parts[2].to_i\nans = distance_sum(m, n, k)\nputs ans"
}
|
3741
|
Reschedule Meetings for Maximum Free Time II
|
reschedule-meetings-for-maximum-free-time-ii
|
<p>You are given an integer <code>eventTime</code> denoting the duration of an event. You are also given two integer arrays <code>startTime</code> and <code>endTime</code>, each of length <code>n</code>.</p>
<p>These represent the start and end times of <code>n</code> <strong>non-overlapping</strong> meetings that occur during the event between time <code>t = 0</code> and time <code>t = eventTime</code>, where the <code>i<sup>th</sup></code> meeting occurs during the time <code>[startTime[i], endTime[i]].</code></p>
<p>You can reschedule <strong>at most </strong>one meeting by moving its start time while maintaining the <strong>same duration</strong>, such that the meetings remain non-overlapping, to <strong>maximize</strong> the <strong>longest</strong> <em>continuous period of free time</em> during the event.</p>
<p>Return the <strong>maximum</strong> amount of free time possible after rearranging the meetings.</p>
<p><strong>Note</strong> that the meetings can <strong>not</strong> be rescheduled to a time outside the event and they should remain non-overlapping.</p>
<p><strong>Note:</strong> <em>In this version</em>, it is <strong>valid</strong> for the relative ordering of the meetings to change after rescheduling one meeting.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">eventTime = 5, startTime = [1,3], endTime = [2,5]</span></p>
<p><strong>Output:</strong> <span class="example-io">2</span></p>
<p><strong>Explanation:</strong></p>
<p><img alt="" src="https://assets.leetcode.com/uploads/2024/12/22/example0_rescheduled.png" style="width: 375px; height: 123px;" /></p>
<p>Reschedule the meeting at <code>[1, 2]</code> to <code>[2, 3]</code>, leaving no meetings during the time <code>[0, 2]</code>.</p>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">eventTime = 10, startTime = [0,7,9], endTime = [1,8,10]</span></p>
<p><strong>Output:</strong> <span class="example-io">7</span></p>
<p><strong>Explanation:</strong></p>
<p><img alt="" src="https://assets.leetcode.com/uploads/2024/12/22/rescheduled_example0.png" style="width: 375px; height: 125px;" /></p>
<p>Reschedule the meeting at <code>[0, 1]</code> to <code>[8, 9]</code>, leaving no meetings during the time <code>[0, 7]</code>.</p>
</div>
<p><strong class="example">Example 3:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">eventTime = 10, startTime = [0,3,7,9], endTime = [1,4,8,10]</span></p>
<p><strong>Output:</strong> 6</p>
<p><strong>Explanation:</strong></p>
<p><strong><img alt="" src="https://assets.leetcode.com/uploads/2025/01/28/image3.png" style="width: 375px; height: 125px;" /></strong></p>
<p>Reschedule the meeting at <code>[3, 4]</code> to <code>[8, 9]</code>, leaving no meetings during the time <code>[1, 7]</code>.</p>
</div>
<p><strong class="example">Example 4:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">eventTime = 5, startTime = [0,1,2,3,4], endTime = [1,2,3,4,5]</span></p>
<p><strong>Output:</strong> <span class="example-io">0</span></p>
<p><strong>Explanation:</strong></p>
<p>There is no time during the event not occupied by meetings.</p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>1 <= eventTime <= 10<sup>9</sup></code></li>
<li><code>n == startTime.length == endTime.length</code></li>
<li><code>2 <= n <= 10<sup>5</sup></code></li>
<li><code>0 <= startTime[i] < endTime[i] <= eventTime</code></li>
<li><code>endTime[i] <= startTime[i + 1]</code> where <code>i</code> lies in the range <code>[0, n - 2]</code>.</li>
</ul>
|
You are given an integer `eventTime` denoting the duration of an event. You are also given two integer arrays `startTime` and `endTime`, each of length `n`.
These represent the start and end times of `n` **non\-overlapping** meetings that occur during the event between time `t = 0` and time `t = eventTime`, where the `ith` meeting occurs during the time `[startTime[i], endTime[i]].`
You can reschedule **at most** one meeting by moving its start time while maintaining the **same duration**, such that the meetings remain non\-overlapping, to **maximize** the **longest** *continuous period of free time* during the event.
Return the **maximum** amount of free time possible after rearranging the meetings.
**Note** that the meetings can **not** be rescheduled to a time outside the event and they should remain non\-overlapping.
**Note:** *In this version*, it is **valid** for the relative ordering of the meetings to change after rescheduling one meeting.
**Example 1:**
**Input:** eventTime \= 5, startTime \= \[1,3], endTime \= \[2,5]
**Output:** 2
**Explanation:**
Reschedule the meeting at `[1, 2]` to `[2, 3]`, leaving no meetings during the time `[0, 2]`.
**Example 2:**
**Input:** eventTime \= 10, startTime \= \[0,7,9], endTime \= \[1,8,10]
**Output:** 7
**Explanation:**
Reschedule the meeting at `[0, 1]` to `[8, 9]`, leaving no meetings during the time `[0, 7]`.
**Example 3:**
**Input:** eventTime \= 10, startTime \= \[0,3,7,9], endTime \= \[1,4,8,10]
**Output:** 6
**Explanation:**
****
Reschedule the meeting at `[3, 4]` to `[8, 9]`, leaving no meetings during the time `[1, 7]`.
**Example 4:**
**Input:** eventTime \= 5, startTime \= \[0,1,2,3,4], endTime \= \[1,2,3,4,5]
**Output:** 0
**Explanation:**
There is no time during the event not occupied by meetings.
**Constraints:**
- `1 <= eventTime <= 109`
- `n == startTime.length == endTime.length`
- `2 <= n <= 105`
- `0 <= startTime[i] < endTime[i] <= eventTime`
- `endTime[i] <= startTime[i + 1]` where `i` lies in the range `[0, n - 2]`.
|
Medium
|
[
"array",
"greedy",
"enumeration"
] |
leetcode
|
https://leetcode.com/problems/reschedule-meetings-for-maximum-free-time-ii
|
functional
| null | null | null | null |
{
"c": "int maxFreeTime(int eventTime, int* startTime, int startTimeSize, int* endTime, int endTimeSize) {\n \n}",
"cpp": "class Solution {\npublic:\n int maxFreeTime(int eventTime, vector<int>& startTime, vector<int>& endTime) {\n \n }\n};",
"csharp": "public class Solution {\n public int MaxFreeTime(int eventTime, int[] startTime, int[] endTime) {\n \n }\n}",
"dart": "class Solution {\n int maxFreeTime(int eventTime, List<int> startTime, List<int> endTime) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec max_free_time(event_time :: integer, start_time :: [integer], end_time :: [integer]) :: integer\n def max_free_time(event_time, start_time, end_time) do\n \n end\nend",
"erlang": "-spec max_free_time(EventTime :: integer(), StartTime :: [integer()], EndTime :: [integer()]) -> integer().\nmax_free_time(EventTime, StartTime, EndTime) ->\n .",
"golang": "func maxFreeTime(eventTime int, startTime []int, endTime []int) int {\n \n}",
"java": "class Solution {\n public int maxFreeTime(int eventTime, int[] startTime, int[] endTime) {\n \n }\n}",
"javascript": "/**\n * @param {number} eventTime\n * @param {number[]} startTime\n * @param {number[]} endTime\n * @return {number}\n */\nvar maxFreeTime = function(eventTime, startTime, endTime) {\n \n};",
"kotlin": "class Solution {\n fun maxFreeTime(eventTime: Int, startTime: IntArray, endTime: IntArray): Int {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param Integer $eventTime\n * @param Integer[] $startTime\n * @param Integer[] $endTime\n * @return Integer\n */\n function maxFreeTime($eventTime, $startTime, $endTime) {\n \n }\n}",
"python": "class Solution(object):\n def maxFreeTime(self, eventTime, startTime, endTime):\n \"\"\"\n :type eventTime: int\n :type startTime: List[int]\n :type endTime: List[int]\n :rtype: int\n \"\"\"\n ",
"python3": "class Solution:\n def maxFreeTime(self, eventTime: int, startTime: List[int], endTime: List[int]) -> int:\n ",
"racket": "(define/contract (max-free-time eventTime startTime endTime)\n (-> exact-integer? (listof exact-integer?) (listof exact-integer?) exact-integer?)\n )",
"ruby": "# @param {Integer} event_time\n# @param {Integer[]} start_time\n# @param {Integer[]} end_time\n# @return {Integer}\ndef max_free_time(event_time, start_time, end_time)\n \nend",
"rust": "impl Solution {\n pub fn max_free_time(event_time: i32, start_time: Vec<i32>, end_time: Vec<i32>) -> i32 {\n \n }\n}",
"scala": "object Solution {\n def maxFreeTime(eventTime: Int, startTime: Array[Int], endTime: Array[Int]): Int = {\n \n }\n}",
"swift": "class Solution {\n func maxFreeTime(_ eventTime: Int, _ startTime: [Int], _ endTime: [Int]) -> Int {\n \n }\n}",
"typescript": "function maxFreeTime(eventTime: number, startTime: number[], endTime: number[]): number {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n int maxFreeTime(int eventTime, vector<int>& startTime, vector<int>& endTime) {\n int n = startTime.size();\n vector<int> gaps(n + 1);\n gaps[0] = startTime[0];\n for (int i = 1; i < n; ++i) {\n gaps[i] = startTime[i] - endTime[i-1];\n }\n gaps[n] = eventTime - endTime[n-1];\n \n int original_max = 0;\n for (int g : gaps) {\n original_max = max(original_max, g);\n }\n \n vector<int> prefix_max(n+1);\n prefix_max[0] = gaps[0];\n for (int i = 1; i <= n; ++i) {\n prefix_max[i] = max(prefix_max[i-1], gaps[i]);\n }\n \n vector<int> suffix_max(n+1);\n suffix_max[n] = gaps[n];\n for (int i = n-1; i >= 0; --i) {\n suffix_max[i] = max(suffix_max[i+1], gaps[i]);\n }\n \n int res = original_max;\n \n for (int i = 0; i < n; ++i) {\n int merged_gap;\n if (i == 0) {\n merged_gap = startTime[1];\n } else if (i == n-1) {\n merged_gap = eventTime - endTime[n-2];\n } else {\n merged_gap = startTime[i+1] - endTime[i-1];\n }\n \n int x = i;\n int y = i + 1;\n int left_part_max = (x == 0) ? 0 : prefix_max[x-1];\n int right_part_max = (y+1 > n) ? 0 : suffix_max[y+1];\n int other_max = max(left_part_max, right_part_max);\n \n int d_i = endTime[i] - startTime[i];\n \n int option1 = 0;\n if (other_max >= d_i) {\n option1 = max(merged_gap, other_max - d_i);\n }\n \n int option2 = 0;\n if (merged_gap >= d_i) {\n option2 = max(merged_gap - d_i, other_max);\n }\n \n res = max(res, max(option1, option2));\n }\n \n return res;\n }\n};",
"memory": 14700,
"memoryDistribution": "[[14700, 63.9456, \"class Solution {\\npublic:\\n int maxFreeTime(int eventTime, vector<int>& startTime, vector<int>& endTime) {\\n int n = startTime.size();\\n vector<int> gaps(n + 1);\\n gaps[0] = startTime[0];\\n for (int i = 1; i < n; ++i) {\\n gaps[i] = startTime[i] - endTime[i-1];\\n }\\n gaps[n] = eventTime - endTime[n-1];\\n \\n int original_max = 0;\\n for (int g : gaps) {\\n original_max = max(original_max, g);\\n }\\n \\n vector<int> prefix_max(n+1);\\n prefix_max[0] = gaps[0];\\n for (int i = 1; i <= n; ++i) {\\n prefix_max[i] = max(prefix_max[i-1], gaps[i]);\\n }\\n \\n vector<int> suffix_max(n+1);\\n suffix_max[n] = gaps[n];\\n for (int i = n-1; i >= 0; --i) {\\n suffix_max[i] = max(suffix_max[i+1], gaps[i]);\\n }\\n \\n int res = original_max;\\n \\n for (int i = 0; i < n; ++i) {\\n int merged_gap;\\n if (i == 0) {\\n merged_gap = startTime[1];\\n } else if (i == n-1) {\\n merged_gap = eventTime - endTime[n-2];\\n } else {\\n merged_gap = startTime[i+1] - endTime[i-1];\\n }\\n \\n int x = i;\\n int y = i + 1;\\n int left_part_max = (x == 0) ? 0 : prefix_max[x-1];\\n int right_part_max = (y+1 > n) ? 0 : suffix_max[y+1];\\n int other_max = max(left_part_max, right_part_max);\\n \\n int d_i = endTime[i] - startTime[i];\\n \\n int option1 = 0;\\n if (other_max >= d_i) {\\n option1 = max(merged_gap, other_max - d_i);\\n }\\n \\n int option2 = 0;\\n if (merged_gap >= d_i) {\\n option2 = max(merged_gap - d_i, other_max);\\n }\\n \\n res = max(res, max(option1, option2));\\n }\\n \\n return res;\\n }\\n};\"], [140090, 9.523800000000001, \"class Solution {\\npublic:\\n int maxFreeTime(int eventTime, vector<int>& startTime, vector<int>& endTime) {\\n int ans=startTime[0];\\n if(startTime.size()>1) ans=max(ans,startTime[1]-(endTime[0]-startTime[0]));\\n else ans=max(ans,eventTime-(endTime[0]-startTime[0]));\\n int premax=startTime[0];\\n for(int i=1;i<startTime.size()-1;i++){\\n int sz=endTime[i]-startTime[i];\\n int gap=startTime[i+1]-endTime[i-1];\\n if(sz<=premax) ans=max(ans,gap);\\n else ans=max(ans,gap-sz);\\n premax=max(premax,startTime[i]-endTime[i-1]);\\n }\\n if(startTime.size()>1 && endTime.back()-startTime.back()<=premax) ans=max(ans,eventTime-endTime[endTime.size()-2]);\\n ans=max(ans,eventTime-endTime.back());\\n cout<<ans<<endl;\\n if(startTime.size()>1) ans=max(ans, eventTime-endTime[endTime.size()-2]-(endTime.back()-startTime.back()));\\n premax=eventTime-endTime.back();\\n for(int i=startTime.size()-2;i>0;i--){\\n int sz=endTime[i]-startTime[i];\\n int gap=startTime[i+1]-endTime[i-1];\\n if(sz<=premax) ans=max(ans,gap);\\n else ans=max(ans,gap-sz);\\n premax=max(premax,startTime[i+1]-endTime[i]);\\n }\\n if(startTime.size()>1 && endTime[0]-startTime[0]<=premax) ans=max(ans,startTime[1]);\\n\\n return ans;\\n }\\n};\"], [141671, 1.3605, \"class Solution {\\npublic:\\n int maxFreeTime(int eventTime, vector<int>& startTime, vector<int>& endTime) {\\n int n = startTime.size();\\n vector<int> diff(n + 1, 0);\\n diff[0] = startTime[0];\\n diff[n] = eventTime - endTime[n-1];\\n for(int i = 1; i < n; i++)\\n diff[i] = startTime[i] - endTime[i-1];\\n int result = 0, maxDiff = 0;\\n for(int i = 0; i < n; i++)\\n result = max(result, diff[i] + diff[i+1]);\\n maxDiff = 0;\\n for(int i = 0; i < n; i++) {\\n int currDiff = endTime[i] - startTime[i];\\n // cout<<i<<\\\" \\\"<<currDiff<<\\\" \\\"<<maxDiff<<\\\" \\\";\\n if(maxDiff >= currDiff) {\\n if(i == 0)\\n result = max(result, startTime[i+1] - currDiff);\\n else if(i < n-1)\\n result = max(result, startTime[i+1] - endTime[i-1]);\\n else\\n result = max(result, eventTime - endTime[i-1]);\\n }\\n maxDiff = max(maxDiff, diff[i]);\\n // cout<<result<<\\\"\\\\n\\\";\\n }\\n // cout<<\\\"\\\\n\\\";\\n maxDiff = 0;\\n for(int i = n-1; i >= 0; i--) {\\n int currDiff = endTime[i] - startTime[i];\\n // cout<<i<<\\\" \\\"<<currDiff<<\\\" \\\"<<maxDiff<<\\\" \\\";\\n if(maxDiff >= currDiff) {\\n if(i == n-1)\\n result = max(result, eventTime - currDiff - startTime[i-1]);\\n else if(i > 0)\\n result = max(result, startTime[i+1] - endTime[i-1]);\\n else\\n result = max(result, startTime[i+1]);\\n }\\n maxDiff = max(maxDiff, diff[i+1]);\\n // cout<<result<<\\\"\\\\n\\\";\\n }\\n return result;\\n }\\n};\"], [143253, 2.3809, null], [144834, 21.0886, null], [146415, 3.4013, null], [147996, 14.966, null], [149578, 8.5034, null], [151159, 7.1427999999999985, null], [152740, 3.4012000000000002, null], [154321, 0.3401, null], [155903, 3.7415000000000003, null], [157484, 0.3401, null], [159065, 0.3401, null], [160646, 0.3401, null], [162228, 1.7006000000000001, null], [163809, 0.6803, null], [165390, 0.3401, null], [166971, 0.3401, null], [168553, 0.3401, null], [170134, 0.3401, null], [171715, 0.3401, null], [173296, 0.3401, null], [174878, 0.3401, null], [176459, 1.0204, null], [178040, 0.3401, null], [179621, 0.3401, null], [181203, 0.3401, null], [182784, 0.3401, null], [184365, 0.3401, null], [185946, 0.3401, null], [187528, 0.3401, null], [189109, 0.3401, null], [190690, 1.0204, null], [192271, 0.3401, null], [193853, 0.3401, null], [195434, 0.3401, null], [197015, 0.6803, null], [198596, 0.3401, null], [200178, 0.3401, null], [201759, 0.3401, null], [203340, 0.3401, null], [204921, 1.3605, null], [206503, 0.6803, null], [208084, 0.3401, null], [209665, 0.3401, null], [211246, 0.3401, null], [212828, 0.3401, null], [214409, 0.3401, null], [215990, 0.6803, null], [217571, 0.6803, \"class Solution {\\npublic:\\n int maxFreeTime(int eventTime, vector<int>& startTime,\\n vector<int>& endTime) {\\n int n = startTime.size();\\n int gap, ans = 0;\\n\\n multiset<int> gaps;\\n for (int i = 0; i <= n; i++) {\\n gap = (i == n ? eventTime : startTime[i]) - (i == 0 ? 0 : endTime[i-1]);\\n gaps.insert(gap);\\n }\\n \\n int duration, prevGap, nextGap;\\n for (int i = 0; i < n; i++) {\\n duration = endTime[i] - startTime[i];\\n prevGap = startTime[i] - (i == 0 ? 0 : endTime[i - 1]);\\n nextGap = ((i + 1) == n ? eventTime : startTime[i + 1]) - endTime[i];\\n\\n ans = max(ans, prevGap + nextGap);\\n\\n gaps.erase(gaps.find(prevGap));\\n gaps.erase(gaps.find(nextGap));\\n\\n if (gaps.lower_bound(duration) != gaps.end())\\n ans = max(ans, prevGap + nextGap + duration);\\n\\n gaps.insert(prevGap);\\n gaps.insert(nextGap);\\n }\\n\\n return ans;\\n }\\n};\"], [219153, 0.3401, \"class Solution {\\npublic:\\n int maxFreeTime(int eventTime, vector<int>& startTime, vector<int>& endTime) {\\n int i, n = startTime.size(), ans = 0;\\n vector<int> gaps = {startTime[0]};\\n for(i=1;i<n;i++) gaps.push_back(startTime[i] - endTime[i-1]);\\n gaps.push_back(eventTime - endTime.back());\\n \\n multiset<int> s;\\n for(i=0;i<gaps.size();i++) s.insert(gaps[i]);\\n \\n for(i=0;i<gaps.size()-1;i++){\\n ans = max(ans, gaps[i] + gaps[i+1]);\\n s.erase(s.find(gaps[i]));\\n s.erase(s.find(gaps[i+1]));\\n \\n if(*(s.rbegin()) >= (endTime[i] - startTime[i])) ans = max(ans, gaps[i] + gaps[i+1] + (endTime[i] - startTime[i]));\\n \\n s.insert(gaps[i]);\\n s.insert(gaps[i+1]);\\n }\\n \\n return ans;\\n }\\n};\"]]",
"runtime": 7,
"runtimeDistribution": "[[3, 23.1291, \"class Solution {\\npublic:\\n int maxFreeTime(int eventTime, vector<int>& startTime, vector<int>& endTime) {\\n int ans=startTime[0];\\n if(startTime.size()>1) ans=max(ans,startTime[1]-(endTime[0]-startTime[0]));\\n else ans=max(ans,eventTime-(endTime[0]-startTime[0]));\\n int premax=startTime[0];\\n for(int i=1;i<startTime.size()-1;i++){\\n int sz=endTime[i]-startTime[i];\\n int gap=startTime[i+1]-endTime[i-1];\\n if(sz<=premax) ans=max(ans,gap);\\n else ans=max(ans,gap-sz);\\n premax=max(premax,startTime[i]-endTime[i-1]);\\n }\\n if(startTime.size()>1 && endTime.back()-startTime.back()<=premax) ans=max(ans,eventTime-endTime[endTime.size()-2]);\\n ans=max(ans,eventTime-endTime.back());\\n cout<<ans<<endl;\\n if(startTime.size()>1) ans=max(ans, eventTime-endTime[endTime.size()-2]-(endTime.back()-startTime.back()));\\n premax=eventTime-endTime.back();\\n for(int i=startTime.size()-2;i>0;i--){\\n int sz=endTime[i]-startTime[i];\\n int gap=startTime[i+1]-endTime[i-1];\\n if(sz<=premax) ans=max(ans,gap);\\n else ans=max(ans,gap-sz);\\n premax=max(premax,startTime[i+1]-endTime[i]);\\n }\\n if(startTime.size()>1 && endTime[0]-startTime[0]<=premax) ans=max(ans,startTime[1]);\\n\\n return ans;\\n }\\n};\"], [7, 85.3743, \"class Solution {\\npublic:\\n int maxFreeTime(int eventTime, vector<int>& startTime, vector<int>& endTime) {\\n int n = startTime.size();\\n vector<int> gaps(n + 1);\\n gaps[0] = startTime[0];\\n for (int i = 1; i < n; ++i) {\\n gaps[i] = startTime[i] - endTime[i-1];\\n }\\n gaps[n] = eventTime - endTime[n-1];\\n \\n int original_max = 0;\\n for (int g : gaps) {\\n original_max = max(original_max, g);\\n }\\n \\n vector<int> prefix_max(n+1);\\n prefix_max[0] = gaps[0];\\n for (int i = 1; i <= n; ++i) {\\n prefix_max[i] = max(prefix_max[i-1], gaps[i]);\\n }\\n \\n vector<int> suffix_max(n+1);\\n suffix_max[n] = gaps[n];\\n for (int i = n-1; i >= 0; --i) {\\n suffix_max[i] = max(suffix_max[i+1], gaps[i]);\\n }\\n \\n int res = original_max;\\n \\n for (int i = 0; i < n; ++i) {\\n int merged_gap;\\n if (i == 0) {\\n merged_gap = startTime[1];\\n } else if (i == n-1) {\\n merged_gap = eventTime - endTime[n-2];\\n } else {\\n merged_gap = startTime[i+1] - endTime[i-1];\\n }\\n \\n int x = i;\\n int y = i + 1;\\n int left_part_max = (x == 0) ? 0 : prefix_max[x-1];\\n int right_part_max = (y+1 > n) ? 0 : suffix_max[y+1];\\n int other_max = max(left_part_max, right_part_max);\\n \\n int d_i = endTime[i] - startTime[i];\\n \\n int option1 = 0;\\n if (other_max >= d_i) {\\n option1 = max(merged_gap, other_max - d_i);\\n }\\n \\n int option2 = 0;\\n if (merged_gap >= d_i) {\\n option2 = max(merged_gap - d_i, other_max);\\n }\\n \\n res = max(res, max(option1, option2));\\n }\\n \\n return res;\\n }\\n};\"], [11, 25.850400000000004, \"class Solution {\\npublic:\\n int maxFreeTime(int eventTime, vector<int>& s, vector<int>& e) {\\n int n=s.size();\\n vector<int> gap;\\n gap.push_back(s[0]);\\n \\n for(int i=1; i<n; i++){\\n gap.push_back(s[i]-e[i-1]);\\n }\\n\\n gap.push_back(eventTime-e[n-1]);\\n vector<int> left(n+1,0),right(n+1,0);\\n\\n for(int i=1; i<gap.size(); i++){\\n left[i]=max(left[i-1],gap[i-1]);\\n }\\n\\n for(int j = gap.size() - 1; j>=1; j--){\\n right[j-1]=max(right[j],gap[j]);\\n }\\n\\n int maxi=0;\\n \\n for(int i = 0; i < n; i++){\\n int first=0;\\n\\n if(left[i] >= (e[i]-s[i])){\\n first=gap[i]+gap[i+1]+e[i]-s[i];\\n }\\n\\n int second=0;\\n\\n if(right[i+1] >= (e[i]-s[i])){\\n second=gap[i]+gap[i+1]+(e[i]-s[i]);\\n }\\n \\n int third=gap[i]+gap[i+1];\\n maxi=max(maxi,max(first,max(second,third)));\\n }\\n return maxi;\\n }\\n};\"], [18, 8.5033, null], [25, 1.7005000000000001, null], [33, 1.0203, null], [40, 1.7006000000000001, null], [47, 2.0408, null], [55, 0.6802, null], [62, 0.3401, null], [69, 0.3401, null], [77, 0.6803, null], [84, 0.3401, null], [91, 1.3605, null], [99, 2.721, null], [106, 3.0611, null], [113, 1.3605, null], [121, 1.0203, null], [128, 0.3401, null], [135, 1.0203, null], [143, 1.0203, null], [150, 0.6802, null], [158, 1.0204, null], [165, 1.0203, null], [172, 0.3401, null], [180, 0.3401, null], [187, 0.3401, null], [194, 0.3401, null], [202, 0.3401, null], [209, 0.3401, null], [216, 0.3401, null], [224, 0.3401, null], [231, 0.3401, null], [238, 0.3401, null], [246, 0.3401, null], [253, 0.3401, null], [260, 0.3401, null], [268, 0.3401, null], [275, 0.6803, null], [282, 0.3401, null], [290, 0.6803, null], [297, 0.3401, null], [305, 0.3401, null], [312, 0.3401, null], [319, 0.3401, null], [327, 0.3401, null], [334, 0.3401, null], [341, 0.3401, null], [349, 0.3401, null], [356, 0.3401, null], [363, 0.3401, null], [371, 0.3401, null], [378, 0.3401, null], [385, 0.3401, null], [393, 0.3401, null], [400, 0.3401, null], [407, 0.3401, null], [415, 0.3401, null], [422, 0.3401, null], [429, 0.3401, null], [437, 0.3401, null], [444, 0.3401, \"class Solution {\\npublic:\\n int maxFreeTime(int eventTime, vector<int>& startTime,\\n vector<int>& endTime) {\\n int n = startTime.size();\\n int gap, ans = 0;\\n\\n multiset<int> gaps;\\n for (int i = 0; i <= n; i++) {\\n gap = (i == n ? eventTime : startTime[i]) - (i == 0 ? 0 : endTime[i-1]);\\n gaps.insert(gap);\\n }\\n \\n int duration, prevGap, nextGap;\\n for (int i = 0; i < n; i++) {\\n duration = endTime[i] - startTime[i];\\n prevGap = startTime[i] - (i == 0 ? 0 : endTime[i - 1]);\\n nextGap = ((i + 1) == n ? eventTime : startTime[i + 1]) - endTime[i];\\n\\n ans = max(ans, prevGap + nextGap);\\n\\n gaps.erase(gaps.find(prevGap));\\n gaps.erase(gaps.find(nextGap));\\n\\n if (gaps.lower_bound(duration) != gaps.end())\\n ans = max(ans, prevGap + nextGap + duration);\\n\\n gaps.insert(prevGap);\\n gaps.insert(nextGap);\\n }\\n\\n return ans;\\n }\\n};\"], [452, 0.3401, \"#include <vector>\\n#include <set>\\n#include <algorithm>\\n\\nusing namespace std;\\n\\nclass Solution {\\npublic:\\n int maxFreeTime(int eventTime, vector<int>& startTime, vector<int>& endTime) {\\n int n = startTime.size();\\n vector<int> inter;\\n vector<pair<int, int>> interTime;\\n \\n // Initialize first interval\\n interTime.push_back({0, startTime[0]});\\n inter.push_back(startTime[0]);\\n \\n for (int i = 1; i < n; i++) {\\n interTime.push_back({endTime[i - 1], startTime[i]});\\n inter.push_back(startTime[i] - endTime[i - 1]);\\n }\\n \\n // Last interval\\n interTime.push_back({endTime[n - 1], eventTime});\\n inter.push_back(eventTime - endTime[n - 1]);\\n \\n // Use ordered set (BST) for efficient look-up\\n multiset<int> interSet(inter.begin(), inter.end());\\n\\n int ans = 0;\\n \\n for (int i = 0; i < interTime.size() - 1; i++) {\\n int meet = interTime[i + 1].first - interTime[i].second;\\n \\n // Remove current interval from set to avoid self-comparison\\n interSet.erase(interSet.find(inter[i]));\\n interSet.erase(interSet.find(inter[i + 1]));\\n \\n // Binary search using lower_bound\\n if (interSet.lower_bound(meet) != interSet.end()) {\\n ans = max(ans, inter[i] + inter[i + 1] + meet);\\n } else {\\n ans = max(ans, inter[i] + inter[i + 1]);\\n }\\n \\n // Reinsert removed elements\\n interSet.insert(inter[i]);\\n interSet.insert(inter[i + 1]);\\n }\\n \\n return ans;\\n }\\n};\\n\"]]"
},
"golang": {
"code": "func maxFreeTime(eventTime int, startTime []int, endTime []int) int {\n n := len(startTime)\n if n == 0 {\n return eventTime\n }\n\n gaps := make([]int, n+1)\n gaps[0] = startTime[0] - 0\n for j := 1; j < n; j++ {\n gaps[j] = startTime[j] - endTime[j-1]\n }\n gaps[n] = eventTime - endTime[n-1]\n\n prefixMax := make([]int, n+1)\n prefixMax[0] = gaps[0]\n for j := 1; j <= n; j++ {\n prefixMax[j] = max(prefixMax[j-1], gaps[j])\n }\n\n suffixMax := make([]int, n+1)\n suffixMax[n] = gaps[n]\n for j := n - 1; j >= 0; j-- {\n suffixMax[j] = max(suffixMax[j+1], gaps[j])\n }\n\n originalMax := 0\n for _, g := range gaps {\n if g > originalMax {\n originalMax = g\n }\n }\n\n maxCandidate := originalMax\n\n for i := 0; i < n; i++ {\n var mergedGap int\n if i == 0 {\n mergedGap = startTime[1] - 0\n } else if i == n-1 {\n mergedGap = eventTime - endTime[i-1]\n } else {\n mergedGap = startTime[i+1] - endTime[i-1]\n }\n\n d := endTime[i] - startTime[i]\n var maxOtherGap int\n\n if i == 0 {\n maxOtherGap = suffixMax[2]\n } else if i == n-1 {\n maxOtherGap = prefixMax[n-2]\n } else {\n leftMax := prefixMax[i-1]\n rightMax := suffixMax[i+2]\n maxOtherGap = max(leftMax, rightMax)\n }\n\n currentCandidate := 0\n if mergedGap >= d {\n candidate1 := max(mergedGap-d, maxOtherGap)\n if candidate1 > currentCandidate {\n currentCandidate = candidate1\n }\n }\n if maxOtherGap >= d {\n candidate2 := max(mergedGap, maxOtherGap-d)\n if candidate2 > currentCandidate {\n currentCandidate = candidate2\n }\n }\n\n if currentCandidate > maxCandidate {\n maxCandidate = currentCandidate\n }\n }\n\n return maxCandidate\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}",
"memory": 1400,
"memoryDistribution": "[[1400, 33.3335, \"func maxFreeTime(eventTime int, startTime []int, endTime []int) int {\\n n := len(startTime)\\n if n == 0 {\\n return eventTime\\n }\\n\\n gaps := make([]int, n+1)\\n gaps[0] = startTime[0] - 0\\n for j := 1; j < n; j++ {\\n gaps[j] = startTime[j] - endTime[j-1]\\n }\\n gaps[n] = eventTime - endTime[n-1]\\n\\n prefixMax := make([]int, n+1)\\n prefixMax[0] = gaps[0]\\n for j := 1; j <= n; j++ {\\n prefixMax[j] = max(prefixMax[j-1], gaps[j])\\n }\\n\\n suffixMax := make([]int, n+1)\\n suffixMax[n] = gaps[n]\\n for j := n - 1; j >= 0; j-- {\\n suffixMax[j] = max(suffixMax[j+1], gaps[j])\\n }\\n\\n originalMax := 0\\n for _, g := range gaps {\\n if g > originalMax {\\n originalMax = g\\n }\\n }\\n\\n maxCandidate := originalMax\\n\\n for i := 0; i < n; i++ {\\n var mergedGap int\\n if i == 0 {\\n mergedGap = startTime[1] - 0\\n } else if i == n-1 {\\n mergedGap = eventTime - endTime[i-1]\\n } else {\\n mergedGap = startTime[i+1] - endTime[i-1]\\n }\\n\\n d := endTime[i] - startTime[i]\\n var maxOtherGap int\\n\\n if i == 0 {\\n maxOtherGap = suffixMax[2]\\n } else if i == n-1 {\\n maxOtherGap = prefixMax[n-2]\\n } else {\\n leftMax := prefixMax[i-1]\\n rightMax := suffixMax[i+2]\\n maxOtherGap = max(leftMax, rightMax)\\n }\\n\\n currentCandidate := 0\\n if mergedGap >= d {\\n candidate1 := max(mergedGap-d, maxOtherGap)\\n if candidate1 > currentCandidate {\\n currentCandidate = candidate1\\n }\\n }\\n if maxOtherGap >= d {\\n candidate2 := max(mergedGap, maxOtherGap-d)\\n if candidate2 > currentCandidate {\\n currentCandidate = candidate2\\n }\\n }\\n\\n if currentCandidate > maxCandidate {\\n maxCandidate = currentCandidate\\n }\\n }\\n\\n return maxCandidate\\n}\\n\\nfunc max(a, b int) int {\\n if a > b {\\n return a\\n }\\n return b\\n}\"], [11900, 8.3333, \"func maxFreeTime(eventTime int, startTime []int, endTime []int) int {\\n\\tbeforeMax := make([]int, len(startTime))\\n\\tfor i, before := 1, startTime[0]; i < len(startTime); i++ {\\n\\t\\tbeforeMax[i] = max(beforeMax[i-1], before)\\n\\t\\tbefore = startTime[i] - endTime[i-1]\\n\\t}\\n\\tafterMax := make([]int, len(startTime))\\n\\tfor i, after := len(startTime)-2, eventTime-endTime[len(endTime)-1]; i >= 0; i-- {\\n\\t\\tafterMax[i] = max(afterMax[i+1], after)\\n\\t\\tafter = startTime[i+1] - endTime[i]\\n\\t}\\n\\tbefore, after := startTime[0], startTime[1]-endTime[0]\\n\\tvar ret int\\n\\tfor i := range startTime {\\n\\t\\tstart, end := startTime[i], endTime[i]\\n\\t\\tgap := end - start\\n\\t\\tif beforeMax[i] >= gap || afterMax[i] >= gap {\\n\\t\\t\\tret = max(ret, after+before+gap)\\n\\t\\t} else {\\n\\t\\t\\tret = max(ret, after+before)\\n\\t\\t}\\n\\t\\tbefore = after\\n\\t\\tif i < len(startTime)-2 {\\n\\t\\t\\tafter = startTime[i+2] - endTime[i+1]\\n\\t\\t} else {\\n\\t\\t\\tafter = eventTime - endTime[len(endTime)-1]\\n\\t\\t}\\n\\t}\\n\\treturn ret\\n}\\n\"], [12100, 8.3333, \"func maxFreeTime(eventTime int, startTime []int, endTime []int) int {\\n\\n n := len(endTime)\\n\\n // Largest gap outside block of meeting\\n gap := make([]int, n)\\n\\n // Backwards pass for space after each block\\n var hi int\\n b := eventTime\\n for i, e := range slices.Backward(endTime) {\\n gap[i] = hi\\n hi = max(hi, b-e)\\n b = startTime[i]\\n }\\n\\n // Helper for time taken by meeting i\\n meet := func(i int) int {\\n return endTime[i]-startTime[i]\\n }\\n\\n // Helper for block that meeting i is in\\n // Not safe for first or last meeting\\n block := func(i int) int {\\n return startTime[i+1]-endTime[i-1]\\n }\\n\\n // Hold the answer\\n var best int\\n\\n // Helper for updating best\\n // m = length of meeting\\n // b = time for block meeting is in\\n // g = largest gap not adjacent to meeting\\n update := func(m, b, g int) {\\n if m > g {\\n // We can only move this meeting to beg/end of block\\n best = max(best, b - m)\\n } else {\\n // We can move this meeting elsewhere and get entire block\\n best = max(best, b)\\n }\\n }\\n\\n // Special case: first meeting\\n update(meet(0), startTime[1], gap[0])\\n\\n // Reset hi for fwd pass\\n hi = startTime[0]\\n\\n // Fwd pass \\n e := endTime[0]\\n for i, b := range startTime[1:n-1] {\\n i++\\n // gap[i] = max(gap[i], hi)\\n update(meet(i), block(i), max(gap[i], hi))\\n hi = max(hi, b-e)\\n e = endTime[i]\\n }\\n\\n // Special case: last meeting\\n // update(meet(n-1), eventTime-endTime[n-2], max(gap[n-1], hi))\\n update(meet(n-1), eventTime-endTime[n-2], hi)\\n\\n return best\\n}\"], [12700, 8.3333, null], [12800, 16.6667, null], [12900, 8.3333, null], [13100, 8.3333, null], [13200, 8.3333, null], [16500, 8.3333, null], [19300, 8.3333, \"func maxFreeTime(eventTime int, beg []int, end []int) int {\\n\\n beg = append([]int{math.MinInt}, beg...)\\n beg = append(beg, eventTime)\\n\\n end = append([]int{0}, end...)\\n end = append(end, math.MaxInt)\\n\\n fmt.Println(beg)\\n fmt.Println(end)\\n fmt.Println()\\n n := len(beg)\\n\\n var free [][]int\\n for i := range n-1 {\\n f := []int{beg[i+1]-end[i], i, i+1}\\n fmt.Println(f)\\n free = append(free, f)\\n }\\n sort.Slice(free, func(i, j int) bool {\\n return free[i][0] > free[j][0]\\n })\\n\\n var best int\\n\\n outer:\\n for i := range n-2 {\\n i++\\n\\n l := beg[i]-end[i-1]\\n m := end[i]-beg[i]\\n r := beg[i+1]-end[i]\\n\\n for _, opt := range free[:3] {\\n // fmt.Println(i, opt)\\n if m > opt[0] {\\n break\\n }\\n if opt[1] != i && opt[2] != i {\\n best = max(best, l+m+r)\\n continue outer\\n }\\n }\\n\\n best = max(best, l+r)\\n\\n }\\n\\n return best\\n}\"], [19600, 8.3333, \"func maxFreeTime(eventTime int, startTime []int, endTime []int) int {\\n\\n n := len(endTime)\\n\\n maxGap := make([]int, n)\\n {\\n b := eventTime\\n var hi int\\n for i, e := range slices.Backward(endTime) {\\n maxGap[i] = hi\\n hi = max(hi, b-e)\\n b = startTime[i]\\n }\\n }\\n\\n var best int\\n\\n update := func(m, f, g int) {\\n // fmt.Println(m, f, g)\\n if m > g {\\n best = max(best, f - m)\\n } else {\\n best = max(best, f)\\n }\\n }\\n\\n // Special case: first meeting\\n update(endTime[0]-startTime[0], startTime[1], maxGap[0])\\n\\n e := endTime[0]\\n hi := startTime[0]\\n for i := range n-2 {\\n i++\\n b := startTime[i]\\n maxGap[i] = max(maxGap[i], hi)\\n // fmt.Println(i, e, b, hi)\\n update(endTime[i]-startTime[i], startTime[i+1]-endTime[i-1], maxGap[i])\\n hi = max(hi, b-e)\\n e = endTime[i]\\n }\\n\\n // Special case: last meeting \\n update(endTime[n-1]-startTime[n-1], eventTime-endTime[n-2], max(maxGap[n-1], hi))\\n\\n return best\\n}\"]]",
"runtime": 7,
"runtimeDistribution": "[[2, 8.3333, \"func maxFreeTime(eventTime int, startTime []int, endTime []int) int {\\n\\tbeforeMax := make([]int, len(startTime))\\n\\tfor i, before := 1, startTime[0]; i < len(startTime); i++ {\\n\\t\\tbeforeMax[i] = max(beforeMax[i-1], before)\\n\\t\\tbefore = startTime[i] - endTime[i-1]\\n\\t}\\n\\tafterMax := make([]int, len(startTime))\\n\\tfor i, after := len(startTime)-2, eventTime-endTime[len(endTime)-1]; i >= 0; i-- {\\n\\t\\tafterMax[i] = max(afterMax[i+1], after)\\n\\t\\tafter = startTime[i+1] - endTime[i]\\n\\t}\\n\\tbefore, after := startTime[0], startTime[1]-endTime[0]\\n\\tvar ret int\\n\\tfor i := range startTime {\\n\\t\\tstart, end := startTime[i], endTime[i]\\n\\t\\tgap := end - start\\n\\t\\tif beforeMax[i] >= gap || afterMax[i] >= gap {\\n\\t\\t\\tret = max(ret, after+before+gap)\\n\\t\\t} else {\\n\\t\\t\\tret = max(ret, after+before)\\n\\t\\t}\\n\\t\\tbefore = after\\n\\t\\tif i < len(startTime)-2 {\\n\\t\\t\\tafter = startTime[i+2] - endTime[i+1]\\n\\t\\t} else {\\n\\t\\t\\tafter = eventTime - endTime[len(endTime)-1]\\n\\t\\t}\\n\\t}\\n\\treturn ret\\n}\\n\"], [4, 16.6667, \"func maxFreeTime(eventTime int, startTime []int, endTime []int) int {\\n n := len(startTime)\\n if n == 0 {\\n return eventTime\\n }\\n\\n gaps := make([]int, n+1)\\n gaps[0] = startTime[0] - 0\\n for j := 1; j < n; j++ {\\n gaps[j] = startTime[j] - endTime[j-1]\\n }\\n gaps[n] = eventTime - endTime[n-1]\\n\\n prefixMax := make([]int, n+1)\\n prefixMax[0] = gaps[0]\\n for j := 1; j <= n; j++ {\\n prefixMax[j] = max(prefixMax[j-1], gaps[j])\\n }\\n\\n suffixMax := make([]int, n+1)\\n suffixMax[n] = gaps[n]\\n for j := n - 1; j >= 0; j-- {\\n suffixMax[j] = max(suffixMax[j+1], gaps[j])\\n }\\n\\n originalMax := 0\\n for _, g := range gaps {\\n if g > originalMax {\\n originalMax = g\\n }\\n }\\n\\n maxCandidate := originalMax\\n\\n for i := 0; i < n; i++ {\\n var mergedGap int\\n if i == 0 {\\n mergedGap = startTime[1] - 0\\n } else if i == n-1 {\\n mergedGap = eventTime - endTime[i-1]\\n } else {\\n mergedGap = startTime[i+1] - endTime[i-1]\\n }\\n\\n d := endTime[i] - startTime[i]\\n var maxOtherGap int\\n\\n if i == 0 {\\n maxOtherGap = suffixMax[2]\\n } else if i == n-1 {\\n maxOtherGap = prefixMax[n-2]\\n } else {\\n leftMax := prefixMax[i-1]\\n rightMax := suffixMax[i+2]\\n maxOtherGap = max(leftMax, rightMax)\\n }\\n\\n currentCandidate := 0\\n if mergedGap >= d {\\n candidate1 := max(mergedGap-d, maxOtherGap)\\n if candidate1 > currentCandidate {\\n currentCandidate = candidate1\\n }\\n }\\n if maxOtherGap >= d {\\n candidate2 := max(mergedGap, maxOtherGap-d)\\n if candidate2 > currentCandidate {\\n currentCandidate = candidate2\\n }\\n }\\n\\n if currentCandidate > maxCandidate {\\n maxCandidate = currentCandidate\\n }\\n }\\n\\n return maxCandidate\\n}\\n\\nfunc max(a, b int) int {\\n if a > b {\\n return a\\n }\\n return b\\n}\"], [7, 25.0, null], [8, 16.6667, null], [10, 8.3333, null], [111, 8.3333, \"func maxFreeTime(eventTime int, beg []int, end []int) int {\\n\\n beg = append([]int{math.MinInt}, beg...)\\n beg = append(beg, eventTime)\\n\\n end = append([]int{0}, end...)\\n end = append(end, math.MaxInt)\\n\\n // fmt.Println(beg)\\n // fmt.Println(end)\\n // fmt.Println()\\n n := len(beg)\\n\\n var free [][]int\\n for i := range n-1 {\\n f := []int{beg[i+1]-end[i], i, i+1}\\n // fmt.Println(f)\\n free = append(free, f)\\n }\\n sort.Slice(free, func(i, j int) bool {\\n return free[i][0] > free[j][0]\\n })\\n\\n var best int\\n\\n outer:\\n for i := range n-2 {\\n i++\\n\\n l := beg[i]-end[i-1]\\n m := end[i]-beg[i]\\n r := beg[i+1]-end[i]\\n\\n for _, opt := range free[:3] {\\n // fmt.Println(i, opt)\\n if m > opt[0] {\\n break\\n }\\n if opt[1] != i && opt[2] != i {\\n best = max(best, l+m+r)\\n continue outer\\n }\\n }\\n\\n best = max(best, l+r)\\n\\n }\\n\\n return best\\n}\"], [795, 8.3333, \"func maxFreeTime(eventTime int, startTime []int, endTime []int) int {\\n\\n n := len(endTime)\\n\\n maxGap := make([]int, n)\\n {\\n b := eventTime\\n var hi int\\n for i, e := range slices.Backward(endTime) {\\n fmt.Println([]int{startTime[i], e}, b)\\n maxGap[i] = hi\\n hi = max(hi, b-e)\\n b = startTime[i]\\n }\\n }\\n {\\n var e int\\n var hi int\\n for i, b := range startTime {\\n maxGap[i] = max(maxGap[i], hi)\\n hi = max(hi, b-e)\\n e = endTime[i]\\n }\\n }\\n\\n best := max(\\n eventTime - endTime[n-1],\\n startTime[0],\\n )\\n\\n for i := range n {\\n var l, r int\\n m := endTime[i] - startTime[i]\\n if i > 0 {\\n l = startTime[i]-endTime[i-1]\\n } else {\\n l = startTime[i]\\n }\\n if i + 1 == n {\\n r = eventTime-endTime[i]\\n } else {\\n r = startTime[i+1]-endTime[i]\\n }\\n if m <= maxGap[i] {\\n best = max(best, l + m + r)\\n } else {\\n best = max(best, l + r)\\n }\\n }\\n\\n return best\\n}\"]]"
},
"java": {
"code": "class Solution {\n public int maxFreeTime(int eventTime, int[] startTime, int[] endTime) {\n int n = startTime.length;\n int[] gaps = new int[n + 1];\n gaps[0] = startTime[0];\n for (int i = 1; i < n; i++) {\n gaps[i] = startTime[i] - endTime[i - 1];\n }\n gaps[n] = eventTime - endTime[n - 1];\n \n int originalMax = 0;\n for (int gap : gaps) {\n originalMax = Math.max(originalMax, gap);\n }\n \n int[] prefixMax = new int[n + 1];\n prefixMax[0] = gaps[0];\n for (int i = 1; i <= n; i++) {\n prefixMax[i] = Math.max(prefixMax[i - 1], gaps[i]);\n }\n \n int[] suffixMax = new int[n + 1];\n suffixMax[n] = gaps[n];\n for (int i = n - 1; i >= 0; i--) {\n suffixMax[i] = Math.max(suffixMax[i + 1], gaps[i]);\n }\n \n int globalMax = originalMax;\n \n for (int i = 0; i < n; i++) {\n int duration = endTime[i] - startTime[i];\n int m = gaps[i] + duration + gaps[i + 1];\n \n int leftMax = (i > 0) ? prefixMax[i - 1] : 0;\n int rightMax = (i + 2 <= n) ? suffixMax[i + 2] : 0;\n int gOther = Math.max(leftMax, rightMax);\n \n int currentMaxCandidate = 0;\n boolean hasCandidate = false;\n \n if (m >= duration) {\n int candidate = Math.max(m - duration, gOther);\n if (candidate > currentMaxCandidate) {\n currentMaxCandidate = candidate;\n hasCandidate = true;\n }\n }\n if (gOther >= duration) {\n int candidate = Math.max(gOther - duration, m);\n if (candidate > currentMaxCandidate) {\n currentMaxCandidate = candidate;\n hasCandidate = true;\n }\n }\n \n if (hasCandidate && currentMaxCandidate > globalMax) {\n globalMax = currentMaxCandidate;\n }\n }\n \n return Math.max(originalMax, globalMax);\n }\n}",
"memory": 6100,
"memoryDistribution": "[[6100, 45.7627, \"class Solution {\\n public int maxFreeTime(int eventTime, int[] startTime, int[] endTime) {\\n int n = startTime.length;\\n int[] gaps = new int[n + 1];\\n gaps[0] = startTime[0];\\n for (int i = 1; i < n; i++) {\\n gaps[i] = startTime[i] - endTime[i - 1];\\n }\\n gaps[n] = eventTime - endTime[n - 1];\\n \\n int originalMax = 0;\\n for (int gap : gaps) {\\n originalMax = Math.max(originalMax, gap);\\n }\\n \\n int[] prefixMax = new int[n + 1];\\n prefixMax[0] = gaps[0];\\n for (int i = 1; i <= n; i++) {\\n prefixMax[i] = Math.max(prefixMax[i - 1], gaps[i]);\\n }\\n \\n int[] suffixMax = new int[n + 1];\\n suffixMax[n] = gaps[n];\\n for (int i = n - 1; i >= 0; i--) {\\n suffixMax[i] = Math.max(suffixMax[i + 1], gaps[i]);\\n }\\n \\n int globalMax = originalMax;\\n \\n for (int i = 0; i < n; i++) {\\n int duration = endTime[i] - startTime[i];\\n int m = gaps[i] + duration + gaps[i + 1];\\n \\n int leftMax = (i > 0) ? prefixMax[i - 1] : 0;\\n int rightMax = (i + 2 <= n) ? suffixMax[i + 2] : 0;\\n int gOther = Math.max(leftMax, rightMax);\\n \\n int currentMaxCandidate = 0;\\n boolean hasCandidate = false;\\n \\n if (m >= duration) {\\n int candidate = Math.max(m - duration, gOther);\\n if (candidate > currentMaxCandidate) {\\n currentMaxCandidate = candidate;\\n hasCandidate = true;\\n }\\n }\\n if (gOther >= duration) {\\n int candidate = Math.max(gOther - duration, m);\\n if (candidate > currentMaxCandidate) {\\n currentMaxCandidate = candidate;\\n hasCandidate = true;\\n }\\n }\\n \\n if (hasCandidate && currentMaxCandidate > globalMax) {\\n globalMax = currentMaxCandidate;\\n }\\n }\\n \\n return Math.max(originalMax, globalMax);\\n }\\n}\"], [57700, 0.8475, \"class Solution {\\n public static final int[] top3Gap = new int[3];\\n public static int[] gapTime;\\n\\n public int maxFreeTime(int eventTime, int[] startTime, int[] endTime) {\\n prepare(eventTime, startTime, endTime);\\n\\n int ret = 0;\\n for (int i = 0; i < startTime.length; i++) {\\n int surTime = gapTime[i] + gapTime[i + 1];\\n // \\uc606\\uc73c\\ub85c \\ubd99\\uc774\\uae30\\n ret = Math.max(ret, surTime);\\n\\n if (canMoveOther(startTime, endTime, i)) {\\n ret = Math.max(ret, endTime[i] - startTime[i] + surTime);\\n }\\n }\\n\\n return ret;\\n }\\n\\n public void prepare(int eventTime, int[] startTime, int[] endTime) {\\n int size = startTime.length;\\n int start = 0;\\n\\n gapTime = new int[size + 1];\\n int[] sortGapTime = new int[size + 1];\\n // left = i\\n // right = i + 1\\n for (int i = 0; i < startTime.length; i++) {\\n gapTime[i] = startTime[i] - start;\\n sortGapTime[i] = gapTime[i];\\n start = endTime[i];\\n }\\n gapTime[size] = eventTime - endTime[size - 1];\\n sortGapTime[size] = gapTime[size];\\n Arrays.sort(sortGapTime);\\n\\n for (int i = 0; i < 3; i++) {\\n top3Gap[i] = sortGapTime[size - i];\\n }\\n }\\n\\n public boolean canMoveOther(int[] startTime, int[] endTime, int idx) {\\n int length = endTime[idx] - startTime[idx];\\n if (length <= top3Gap[2]) {\\n return true;\\n }\\n\\n int max = Math.max(gapTime[idx], gapTime[idx + 1]);\\n int min = Math.min(gapTime[idx], gapTime[idx + 1]);\\n if (top3Gap[0] != max && length <= top3Gap[0]) {\\n return true;\\n }\\n return top3Gap[1] != min && length <= top3Gap[1];\\n }\\n}\"], [59200, 0.8475, \"class Solution {\\n public int maxFreeTime(int eventTime, int[] startTime, int[] endTime) {\\n int[] gap = new int[startTime.length+1];\\n int largestRight[] = new int[startTime.length+1];\\n gap[0] = startTime[0];\\n for(int i = 1; i < startTime.length; ++i) \\n gap[i] = startTime[i] - endTime[i-1];\\n gap[startTime.length] = eventTime - endTime[endTime.length-1];\\n for(int i = gap.length - 2; i >= 0; --i ) \\n largestRight[i] = Math.max(largestRight[i+1], gap[i+1]);\\n int ans = 0, largestLeft = 0;\\n for(int i = 1; i < gap.length; ++i)\\n {\\n int curGap = endTime[i-1] - startTime[i-1];\\n if(largestLeft >= curGap || largestRight[i] >= curGap)\\n ans = Math.max(ans, gap[i-1] + gap[i] + curGap);\\n ans = Math.max(ans, gap[i-1] + gap[i]);\\n largestLeft = Math.max(largestLeft, gap[i-1]);\\n }\\n return ans;\\n\\n \\n }\\n}\"], [59300, 1.6949, null], [59400, 4.2373, null], [59500, 3.3898, null], [59600, 3.3898, null], [59700, 6.7797, null], [59800, 4.2373, null], [59900, 4.2373, null], [60000, 3.3898, null], [60100, 0.8475, null], [60200, 0.8475, null], [60300, 4.2373, null], [60400, 1.6949, null], [60500, 3.3898, null], [60600, 1.6949, null], [60700, 3.3898, null], [60800, 5.0847, null], [60900, 3.3898, null], [61000, 2.5424, null], [61100, 1.6949, null], [61200, 2.5424, null], [61300, 0.8475, null], [61500, 1.6949, null], [61800, 1.6949, null], [61900, 1.6949, null], [62000, 3.3898, null], [62100, 2.5424, null], [62300, 1.6949, null], [63300, 1.6949, null], [63600, 1.6949, null], [63700, 0.8475, null], [63800, 0.8475, null], [63900, 0.8475, null], [64000, 0.8475, null], [64099, 2.5424, null], [64200, 1.6949, null], [64599, 0.8475, null], [64800, 0.8475, null], [64900, 0.8475, null], [65000, 1.6949, null], [65099, 0.8475, \"class Solution {\\n\\n class Pair {\\n int gap;\\n int index;\\n\\n Pair(int a, int b) {\\n this.gap = a;\\n this.index = b;\\n }\\n\\n @Override\\n public String toString() {\\n return \\\"(\\\" + gap + \\\", \\\" + index + \\\")\\\";\\n }\\n }\\n\\n public int maxFreeTime(int eventTime, int[] startTime, int[] endTime) {\\n int t = 0, n = startTime.length, ans = 0, sum = 0, gap=0;\\n List<Integer> gaps = new ArrayList<Integer>();\\n PriorityQueue<Pair> pq = new PriorityQueue<>((a, b) -> Integer.compare(b.gap, a.gap));\\n \\n gap = startTime[0] - 0;\\n gaps.add(gap);\\n pq.add(new Pair(gap, 0));\\n for(int i=1; i<n; i++) {\\n gap = startTime[i] - endTime[i-1];\\n gaps.add(gap);\\n pq.add(new Pair(gap, i));\\n }\\n gap = eventTime - endTime[n-1];\\n gaps.add(gap);\\n pq.add(new Pair(gap, n));\\n // System.out.println(gaps);\\n\\n Pair m1 = null, m2 = null, m3 = null;\\n if(!pq.isEmpty()) {\\n m1 = pq.poll();\\n }\\n\\n if(!pq.isEmpty()) {\\n m2 = pq.poll();\\n }\\n\\n if(!pq.isEmpty()) {\\n m3 = pq.poll();\\n }\\n\\n // System.out.println(m1 + \\\" \\\" + m2 + \\\" \\\" + m3);\\n for(int i=0; i<n; i++) {\\n boolean isIt = false;\\n gap = endTime[i] - startTime[i];\\n // System.out.println(gap);\\n\\n if((m3.gap >= gap) || ((m2.gap >= gap) && (m2.index != i && m2.index != i+1)) || ((m1.gap >= gap) && (m1.index != (i) && m1.index != (i+1)))) {\\n isIt = true;\\n }\\n\\n if(isIt) {\\n sum = gaps.get(i) + gaps.get(i+1) + endTime[i] - startTime[i];\\n } else {\\n sum = gaps.get(i) + gaps.get(i+1);\\n }\\n\\n ans = Math.max(sum, ans);\\n }\\n \\n return ans;\\n }\\n}\"], [65200, 0.8475, \"class Solution {\\n\\n class Pair {\\n int gap;\\n int index;\\n\\n Pair(int a, int b) {\\n this.gap = a;\\n this.index = b;\\n }\\n\\n @Override\\n public String toString() {\\n return \\\"(\\\" + gap + \\\", \\\" + index + \\\")\\\";\\n }\\n }\\n\\n public int maxFreeTime(int eventTime, int[] startTime, int[] endTime) {\\n int t = 0, n = startTime.length, ans = 0, sum = 0, gap=0;\\n List<Integer> gaps = new ArrayList<Integer>();\\n PriorityQueue<Pair> pq = new PriorityQueue<>((a, b) -> Integer.compare(b.gap, a.gap));\\n \\n gap = startTime[0] - 0;\\n gaps.add(gap);\\n pq.add(new Pair(gap, 0));\\n for(int i=1; i<n; i++) {\\n gap = startTime[i] - endTime[i-1];\\n gaps.add(gap);\\n pq.add(new Pair(gap, i));\\n }\\n gap = eventTime - endTime[n-1];\\n gaps.add(gap);\\n pq.add(new Pair(gap, n));\\n // System.out.println(gaps);\\n\\n Pair m1 = null, m2 = null, m3 = null;\\n if(!pq.isEmpty()) {\\n m1 = pq.poll();\\n }\\n\\n if(!pq.isEmpty()) {\\n m2 = pq.poll();\\n }\\n\\n if(!pq.isEmpty()) {\\n m3 = pq.poll();\\n }\\n\\n // System.out.println(m1 + \\\" \\\" + m2 + \\\" \\\" + m3);\\n for(int i=0; i<n; i++) {\\n boolean isIt = false;\\n gap = endTime[i] - startTime[i];\\n // System.out.println(gap);\\n\\n if((m3.gap >= gap) || ((m2.gap >= gap) && (m2.index != i && m2.index != i+1)) || ((m1.gap >= gap) && (m1.index != (i) && m1.index != (i+1)))) {\\n isIt = true;\\n }\\n\\n if(isIt) {\\n sum = gaps.get(i) + gaps.get(i+1) + endTime[i] - startTime[i];\\n } else {\\n sum = gaps.get(i) + gaps.get(i+1);\\n }\\n\\n ans = Math.max(sum, ans);\\n }\\n \\n return ans;\\n }\\n}\"]]",
"runtime": 4,
"runtimeDistribution": "[[3, 42.3729, \"class Solution {\\n public int maxFreeTime(int total, int[] a, int[] b) {\\n int n = a.length;\\n int[] gap = new int[n + 1];\\n gap[0] = a[0] - 0;\\n for (int i = 1; i < n; i++) {\\n gap[i] = a[i] - b[i - 1];\\n }\\n gap[n] = total - b[n - 1];\\n int[] maxiLeft = new int[n + 1];\\n int[] maxiRight = new int[n + 1];\\n int max = -1;\\n for (int i = 0; i <= n; i++) {\\n max = Math.max(max, gap[i]);\\n maxiLeft[i] = max;\\n }\\n max = -1;\\n for (int i = n; i >= 0; i--) {\\n max = Math.max(max, gap[i]);\\n maxiRight[i] = max;\\n }\\n int answer = 0;\\n for (int i = 0; i < n; i++) {\\n int curr = gap[i] + (b[i] - a[i]) + gap[i + 1];\\n int target = b[i] - a[i];\\n answer = Math.max(answer, curr - target);\\n if ((i > 0 && maxiLeft[i - 1] >= target) || (i + 2 <= n && maxiRight[i + 2] >= target)) {\\n answer = Math.max(answer, curr);\\n }\\n }\\n return answer;\\n \\n }\\n}\"], [4, 15.2542, \"class Solution {\\n public int maxFreeTime(int eventTime, int[] startTime, int[] endTime) {\\n int res = 0;\\n int n = startTime.length;\\n int[] pre = new int[n];\\n int start = 0;\\n int mx = 0;\\n for (int i = 0; i < n; i++) {\\n int t = startTime[i] - start;\\n res = Math.max(res, t);\\n mx = Math.max(t, mx);\\n pre[i] = mx;\\n start = endTime[i];\\n }\\n res = Math.max(res, eventTime - endTime[n - 1]);\\n int[] post = new int[n];\\n int end = eventTime;\\n mx = 0;\\n for (int i = n - 1; i >= 0; i--) {\\n mx = Math.max(end - endTime[i], mx);\\n post[i] = mx;\\n end = startTime[i];\\n }\\n for (int i = 0; i < n; i++) {\\n mx = 0;\\n int ct = endTime[i] - startTime[i];\\n int t1 = 0, t2 = 0;\\n if (i - 1 >= 0)\\n mx = pre[i - 1];\\n if (i + 1 < n)\\n mx = Math.max(mx, post[i + 1]);\\n if (i == 0)\\n t1 = startTime[0];\\n else t1 = startTime[i] - endTime[i - 1];\\n if (i == n - 1)\\n t2 = eventTime - endTime[n - 1];\\n else\\n t2 = startTime[i + 1] - endTime[i];\\n if (ct <= mx)\\n res = Math.max(res, t1 + t2 + ct);\\n else res = Math.max(res, t1 + t2);\\n }\\n return res;\\n }\\n}\"], [5, 7.6271, null], [6, 1.6949, null], [12, 0.8475, null], [13, 0.8475, null], [17, 2.5424, null], [18, 3.3898, null], [24, 1.6949, null], [25, 0.8475, null], [31, 0.8475, null], [35, 0.8475, null], [39, 0.8475, null], [51, 0.8475, null], [54, 0.8475, null], [56, 0.8475, null], [74, 0.8475, null], [75, 0.8475, null], [76, 0.8475, null], [77, 0.8475, null], [86, 0.8475, null], [104, 0.8475, null], [105, 0.8475, null], [129, 0.8475, null], [130, 0.8475, null], [135, 0.8475, null], [173, 0.8475, null], [174, 0.8475, null], [194, 0.8475, null], [196, 0.8475, \"import java.util.Collection;\\nimport java.util.TreeMap;\\n\\nclass Solution {\\n public int maxFreeTime(int eventTime, int[] startTime, int[] endTime) {\\n int n = startTime.length;\\n int prev = 0;\\n MultiTreeSet<Integer> mset = new MultiTreeSet<>();\\n for (int i = 0; i < n; ++i) {\\n int diff = startTime[i] - prev;\\n mset.add(diff);\\n prev = endTime[i];\\n }\\n mset.add(eventTime - endTime[n - 1]);\\n if (mset.last() == 0) return 0;\\n int res = mset.last();\\n for (int i = 0; i < n; ++i) {\\n int back = i == 0 ? 0 : endTime[i - 1];\\n int ahead = i == n - 1 ? eventTime : startTime[i + 1];\\n boolean isFeasible = true;\\n int required = endTime[i] - startTime[i];\\n mset.remove(startTime[i] - back);\\n mset.remove(ahead - endTime[i]);\\n if (mset.last() < required) {\\n isFeasible = false;\\n }\\n if (isFeasible) {\\n res = Math.max(res, ahead - back);\\n } else {\\n res = Math.max(res, ahead - back - required);\\n }\\n mset.add(startTime[i] - back);\\n mset.add(ahead - endTime[i]);\\n }\\n return res;\\n }\\n}\\n\\nclass MultiTreeSet<E> {\\n TreeMap<E, Integer> freqTreeMap = new TreeMap<E, Integer>();\\n int size;\\n\\n public MultiTreeSet() {\\n }\\n\\n public MultiTreeSet(Collection<? extends E> c) {\\n for (E element : c)\\n add(element);\\n }\\n\\n public int size() {\\n return size;\\n }\\n\\n public void add(E element) {\\n Integer freq = freqTreeMap.get(element);\\n if (freq == null)\\n freqTreeMap.put(element, 1);\\n else\\n freqTreeMap.put(element, freq + 1);\\n ++size;\\n }\\n\\n public void remove(E element) {\\n Integer freq = freqTreeMap.get(element);\\n if (freq != null) {\\n if (freq == 1)\\n freqTreeMap.remove(element);\\n else\\n freqTreeMap.put(element, freq - 1);\\n --size;\\n }\\n }\\n\\n public int get(E element) {\\n Integer freq = freqTreeMap.get(element);\\n if (freq == null)\\n return 0;\\n return freq;\\n }\\n\\n public boolean contains(E element) {\\n return get(element) > 0;\\n }\\n\\n public boolean isEmpty() {\\n return size == 0;\\n }\\n\\n public E first() {\\n return freqTreeMap.firstKey();\\n }\\n\\n public E last() {\\n return freqTreeMap.lastKey();\\n }\\n\\n public E ceiling(E element) {\\n return freqTreeMap.ceilingKey(element);\\n }\\n\\n public E floor(E element) {\\n return freqTreeMap.floorKey(element);\\n }\\n\\n public E higher(E element) {\\n return freqTreeMap.higherKey(element);\\n }\\n\\n public E lower(E element) {\\n return freqTreeMap.lowerKey(element);\\n }\\n}\"], [205, 0.8475, \"class Solution {\\n public int maxFreeTime(int eventTime, int[] startTime, int[] endTime) {\\n int n = startTime.length;\\n int max = 0;\\n List<Integer> gap = new ArrayList<>();\\n int curPos = 0, ind = 0;\\n TreeMap<Integer, List<Integer>> map = new TreeMap<>();\\n\\n for(int i =0; i < n; i++){\\n if(startTime[i] > curPos){\\n int dist = startTime[i] - curPos;\\n gap.add(dist);\\n List<Integer> list = map.get(dist);\\n if(list == null){list = new ArrayList<>(); map.put(dist, list);}\\n list.add(ind++);\\n }\\n gap.add( startTime[i] - endTime[i]);\\n ind++;\\n curPos = endTime[i];\\n }\\n if(eventTime - curPos > 0){\\n int dist = eventTime - curPos;\\n gap.add(dist);\\n List<Integer> list = map.get(dist);\\n if(list == null){list = new ArrayList<>(); map.put(dist, list);}\\n list.add(ind++);\\n }\\n\\n System.out.println(gap);\\n System.out.println(map);\\n\\n for(int i = 0; i < gap.size(); i++){\\n int cur = gap.get(i);\\n if(cur > 0){\\n max = Math.max(max, cur);\\n continue;\\n }\\n cur = Math.abs(cur);\\n int total = cur;\\n if(i>0 && gap.get(i-1)>0)total+=gap.get(i-1);\\n if(i+1 < gap.size() && gap.get(i+1)>0)total+=gap.get(i+1);\\n max = Math.max(max, total-cur);\\n Set<Integer> neighbours = new HashSet<Integer>();\\n neighbours.add(i-1);neighbours.add(i);neighbours.add(i+1);\\n for(List<Integer> values : map.tailMap(cur).values()){\\n boolean found = false;\\n for(int val : values){\\n if(!neighbours.contains(val)){\\n max = Math.max(max, total);\\n found = true;\\n break;\\n }\\n }\\n if(found)break;\\n }\\n }\\n return max;\\n }\\n}\"]]"
},
"javascript": {
"code": "var maxFreeTime = function(eventTime, startTime, endTime) {\n const n = startTime.length;\n const originalGaps = [];\n originalGaps.push(startTime[0] - 0);\n for (let i = 1; i < n; i++) {\n originalGaps.push(startTime[i] - endTime[i - 1]);\n }\n originalGaps.push(eventTime - endTime[n - 1]);\n const m = originalGaps.length;\n const prefixMax = new Array(m).fill(0);\n prefixMax[0] = originalGaps[0];\n for (let i = 1; i < m; i++) {\n prefixMax[i] = Math.max(prefixMax[i - 1], originalGaps[i]);\n }\n const suffixMax = new Array(m).fill(0);\n suffixMax[m - 1] = originalGaps[m - 1];\n for (let i = m - 2; i >= 0; i--) {\n suffixMax[i] = Math.max(suffixMax[i + 1], originalGaps[i]);\n }\n let initialMax = Math.max(...originalGaps);\n let globalMax = initialMax;\n for (let i = 0; i < n; i++) {\n const s = startTime[i];\n const e = endTime[i];\n const d = e - s;\n let mergedGap;\n if (n === 1) {\n mergedGap = eventTime - 0;\n } else if (i === 0) {\n mergedGap = startTime[1] - 0;\n } else if (i === n - 1) {\n mergedGap = eventTime - endTime[i - 1];\n } else {\n mergedGap = startTime[i + 1] - endTime[i - 1];\n }\n const leftGapIndex = i;\n const rightGapIndex = i + 1;\n let maxLeft = 0;\n if (leftGapIndex > 0) {\n maxLeft = prefixMax[leftGapIndex - 1];\n }\n let maxRight = 0;\n if (rightGapIndex + 1 < m) {\n maxRight = suffixMax[rightGapIndex + 1];\n }\n const maxOtherGap = Math.max(maxLeft, maxRight);\n const otherPossible = maxOtherGap >= d;\n const mergedPossible = mergedGap >= d;\n if (!mergedPossible && !otherPossible) continue;\n let currentMax;\n if (otherPossible) {\n currentMax = mergedGap;\n } else {\n const newGap = mergedGap - d;\n currentMax = Math.max(newGap, maxOtherGap);\n }\n if (currentMax > globalMax) {\n globalMax = currentMax;\n }\n }\n return globalMax;\n};",
"memory": 8400,
"memoryDistribution": "[[8400, 75.0, \"var maxFreeTime = function(eventTime, startTime, endTime) {\\n const n = startTime.length;\\n const originalGaps = [];\\n originalGaps.push(startTime[0] - 0);\\n for (let i = 1; i < n; i++) {\\n originalGaps.push(startTime[i] - endTime[i - 1]);\\n }\\n originalGaps.push(eventTime - endTime[n - 1]);\\n const m = originalGaps.length;\\n const prefixMax = new Array(m).fill(0);\\n prefixMax[0] = originalGaps[0];\\n for (let i = 1; i < m; i++) {\\n prefixMax[i] = Math.max(prefixMax[i - 1], originalGaps[i]);\\n }\\n const suffixMax = new Array(m).fill(0);\\n suffixMax[m - 1] = originalGaps[m - 1];\\n for (let i = m - 2; i >= 0; i--) {\\n suffixMax[i] = Math.max(suffixMax[i + 1], originalGaps[i]);\\n }\\n let initialMax = Math.max(...originalGaps);\\n let globalMax = initialMax;\\n for (let i = 0; i < n; i++) {\\n const s = startTime[i];\\n const e = endTime[i];\\n const d = e - s;\\n let mergedGap;\\n if (n === 1) {\\n mergedGap = eventTime - 0;\\n } else if (i === 0) {\\n mergedGap = startTime[1] - 0;\\n } else if (i === n - 1) {\\n mergedGap = eventTime - endTime[i - 1];\\n } else {\\n mergedGap = startTime[i + 1] - endTime[i - 1];\\n }\\n const leftGapIndex = i;\\n const rightGapIndex = i + 1;\\n let maxLeft = 0;\\n if (leftGapIndex > 0) {\\n maxLeft = prefixMax[leftGapIndex - 1];\\n }\\n let maxRight = 0;\\n if (rightGapIndex + 1 < m) {\\n maxRight = suffixMax[rightGapIndex + 1];\\n }\\n const maxOtherGap = Math.max(maxLeft, maxRight);\\n const otherPossible = maxOtherGap >= d;\\n const mergedPossible = mergedGap >= d;\\n if (!mergedPossible && !otherPossible) continue;\\n let currentMax;\\n if (otherPossible) {\\n currentMax = mergedGap;\\n } else {\\n const newGap = mergedGap - d;\\n currentMax = Math.max(newGap, maxOtherGap);\\n }\\n if (currentMax > globalMax) {\\n globalMax = currentMax;\\n }\\n }\\n return globalMax;\\n};\"], [82300, 25.0, \"/**\\n * @param {number} eventTime\\n * @param {number[]} startTime\\n * @param {number[]} endTime\\n * @return {number}\\n */\\nvar maxFreeTime = function(eventTime, startTime, endTime) {\\n let biggest = 0;\\n const n = startTime.length;\\n\\n const biggestBefore = new Array(n).fill(0);\\n for (let i = 0; i < n; i ++) {\\n if (i === 0) {\\n biggestBefore[i] = startTime[i];\\n } else {\\n let curr = startTime[i] - endTime[i - 1];\\n biggestBefore[i] = Math.max(biggestBefore[i - 1], curr);\\n }\\n }\\n\\n const biggestAfter = new Array(n).fill(0);\\n for (let i = n - 1; i >= 0; i --) {\\n if (i === n - 1) {\\n biggestAfter[i] = eventTime - endTime[i];\\n } else {\\n let curr = startTime[i + 1] - endTime[i];\\n biggestAfter[i] = Math.max(biggestAfter[i + 1], curr);\\n }\\n }\\n\\n console.log(biggestBefore, biggestAfter)\\n\\n for (let i = 0; i < n; i ++) {\\n const left = i === 0 ? 0 : endTime[i - 1];\\n const right = i === n - 1 ? eventTime : startTime[i + 1];\\n const length = endTime[i] - startTime[i];\\n if (i > 0 && length <= biggestBefore[i - 1]) {\\n biggest = Math.max(biggest, right - left);\\n } else if (i < n - 1 && length <= biggestAfter[i + 1]) {\\n biggest = Math.max(biggest, right - left);\\n } else {\\n biggest = Math.max(biggest, right - left - length);\\n }\\n }\\n\\n return biggest;\\n};\"], [85000, 25.0, \"var maxFreeTime = function(eventTime, startTime, endTime) {\\n const n = startTime.length;\\n const originalGaps = [];\\n originalGaps.push(startTime[0] - 0);\\n for (let i = 1; i < n; i++) {\\n originalGaps.push(startTime[i] - endTime[i - 1]);\\n }\\n originalGaps.push(eventTime - endTime[n - 1]);\\n const m = originalGaps.length;\\n const prefixMax = new Array(m).fill(0);\\n prefixMax[0] = originalGaps[0];\\n for (let i = 1; i < m; i++) {\\n prefixMax[i] = Math.max(prefixMax[i - 1], originalGaps[i]);\\n }\\n const suffixMax = new Array(m).fill(0);\\n suffixMax[m - 1] = originalGaps[m - 1];\\n for (let i = m - 2; i >= 0; i--) {\\n suffixMax[i] = Math.max(suffixMax[i + 1], originalGaps[i]);\\n }\\n let initialMax = Math.max(...originalGaps);\\n let globalMax = initialMax;\\n for (let i = 0; i < n; i++) {\\n const s = startTime[i];\\n const e = endTime[i];\\n const d = e - s;\\n let mergedGap;\\n if (n === 1) {\\n mergedGap = eventTime - 0;\\n } else if (i === 0) {\\n mergedGap = startTime[1] - 0;\\n } else if (i === n - 1) {\\n mergedGap = eventTime - endTime[i - 1];\\n } else {\\n mergedGap = startTime[i + 1] - endTime[i - 1];\\n }\\n const leftGapIndex = i;\\n const rightGapIndex = i + 1;\\n let maxLeft = 0;\\n if (leftGapIndex > 0) {\\n maxLeft = prefixMax[leftGapIndex - 1];\\n }\\n let maxRight = 0;\\n if (rightGapIndex + 1 < m) {\\n maxRight = suffixMax[rightGapIndex + 1];\\n }\\n const maxOtherGap = Math.max(maxLeft, maxRight);\\n const otherPossible = maxOtherGap >= d;\\n const mergedPossible = mergedGap >= d;\\n if (!mergedPossible && !otherPossible) continue;\\n let currentMax;\\n if (otherPossible) {\\n currentMax = mergedGap;\\n } else {\\n const newGap = mergedGap - d;\\n currentMax = Math.max(newGap, maxOtherGap);\\n }\\n if (currentMax > globalMax) {\\n globalMax = currentMax;\\n }\\n }\\n return globalMax;\\n};\"], [93900, 25.0, \"/**\\n * @param {number} eventTime\\n * @param {number[]} startTime\\n * @param {number[]} endTime\\n * @return {number}\\n */\\nvar maxFreeTime = function(eventTime, startTime, endTime) {\\n startTime.unshift(-1);\\n endTime.unshift(0);\\n\\n startTime.push(eventTime);\\n endTime.push(eventTime+1);\\n\\n let gaps = [];\\n for (let i = 1; i < startTime.length; i++) {\\n gaps.push([startTime[i] - endTime[i-1], gaps.length]);\\n }\\n \\n let sg = gaps.concat().sort((a,b) => b[0]-a[0]);\\n\\n //console.log(gaps);\\n \\n let best = 0;\\n \\n for (let i = 1; i < startTime.length-1; i++) {\\n let tg = gaps[i-1][0] + gaps[i][0];\\n let ml = endTime[i]-startTime[i];\\n //console.log({i, tg, ml});\\n\\n for (let gi = 0; gi < 3 && gi < gaps.length; gi++) {\\n let [gl, gp] = sg[gi];\\n //console.log({gl, gp});\\n if (gp === i || gp === i-1) continue;\\n if (gl >= ml) {\\n tg += ml;\\n break;\\n }\\n }\\n\\n best = Math.max(best, tg);\\n }\\n return best;\\n};\"], [95100, 25.0, \"/**\\n * @param {number} eventTime\\n * @param {number[]} startTime\\n * @param {number[]} endTime\\n * @return {number}\\n */\\nfunction maxFreeTime(eventTime, startTime, endTime) {\\n // Free time intervals\\n const gaps = [];\\n let time = 0;\\n\\n for (let i = 0; i < startTime.length; i++) {\\n gaps.push([time, startTime[i]]);\\n time = endTime[i];\\n }\\n gaps.push([time, eventTime]);\\n\\n // Track max free time from right side\\n const rightMax = [0];\\n for (let i = gaps.length - 1; i >= 0; i--) {\\n rightMax.push(\\n Math.max(\\n rightMax[rightMax.length - 1], gaps[i][1] - gaps[i][0]\\n )\\n );\\n }\\n\\n // Calculate maximum free time\\n let leftMax = 0, result = 0;\\n for (let i = 0; i < gaps.length - 1; i++) {\\n const curr = gaps[i][1] - gaps[i][0];\\n const next = gaps[i + 1][1] - gaps[i + 1][0];\\n const meetingGap = gaps[i + 1][0] - gaps[i][1];\\n\\n result = Math.max(result, curr + next);\\n if (Math.max(leftMax, rightMax[gaps.length - 2 - i]) >= meetingGap) {\\n result = Math.max(result, curr + next + meetingGap);\\n }\\n leftMax = Math.max(leftMax, curr);\\n }\\n\\n return result;\\n}\"]]",
"runtime": 35,
"runtimeDistribution": "[[35, 100.0, \"var maxFreeTime = function(eventTime, startTime, endTime) {\\n const n = startTime.length;\\n const originalGaps = [];\\n originalGaps.push(startTime[0] - 0);\\n for (let i = 1; i < n; i++) {\\n originalGaps.push(startTime[i] - endTime[i - 1]);\\n }\\n originalGaps.push(eventTime - endTime[n - 1]);\\n const m = originalGaps.length;\\n const prefixMax = new Array(m).fill(0);\\n prefixMax[0] = originalGaps[0];\\n for (let i = 1; i < m; i++) {\\n prefixMax[i] = Math.max(prefixMax[i - 1], originalGaps[i]);\\n }\\n const suffixMax = new Array(m).fill(0);\\n suffixMax[m - 1] = originalGaps[m - 1];\\n for (let i = m - 2; i >= 0; i--) {\\n suffixMax[i] = Math.max(suffixMax[i + 1], originalGaps[i]);\\n }\\n let initialMax = Math.max(...originalGaps);\\n let globalMax = initialMax;\\n for (let i = 0; i < n; i++) {\\n const s = startTime[i];\\n const e = endTime[i];\\n const d = e - s;\\n let mergedGap;\\n if (n === 1) {\\n mergedGap = eventTime - 0;\\n } else if (i === 0) {\\n mergedGap = startTime[1] - 0;\\n } else if (i === n - 1) {\\n mergedGap = eventTime - endTime[i - 1];\\n } else {\\n mergedGap = startTime[i + 1] - endTime[i - 1];\\n }\\n const leftGapIndex = i;\\n const rightGapIndex = i + 1;\\n let maxLeft = 0;\\n if (leftGapIndex > 0) {\\n maxLeft = prefixMax[leftGapIndex - 1];\\n }\\n let maxRight = 0;\\n if (rightGapIndex + 1 < m) {\\n maxRight = suffixMax[rightGapIndex + 1];\\n }\\n const maxOtherGap = Math.max(maxLeft, maxRight);\\n const otherPossible = maxOtherGap >= d;\\n const mergedPossible = mergedGap >= d;\\n if (!mergedPossible && !otherPossible) continue;\\n let currentMax;\\n if (otherPossible) {\\n currentMax = mergedGap;\\n } else {\\n const newGap = mergedGap - d;\\n currentMax = Math.max(newGap, maxOtherGap);\\n }\\n if (currentMax > globalMax) {\\n globalMax = currentMax;\\n }\\n }\\n return globalMax;\\n};\"], [41, 25.0, \"var maxFreeTime = function(eventTime, startTime, endTime) {\\n const n = startTime.length;\\n const originalGaps = [];\\n originalGaps.push(startTime[0] - 0);\\n for (let i = 1; i < n; i++) {\\n originalGaps.push(startTime[i] - endTime[i - 1]);\\n }\\n originalGaps.push(eventTime - endTime[n - 1]);\\n const m = originalGaps.length;\\n const prefixMax = new Array(m).fill(0);\\n prefixMax[0] = originalGaps[0];\\n for (let i = 1; i < m; i++) {\\n prefixMax[i] = Math.max(prefixMax[i - 1], originalGaps[i]);\\n }\\n const suffixMax = new Array(m).fill(0);\\n suffixMax[m - 1] = originalGaps[m - 1];\\n for (let i = m - 2; i >= 0; i--) {\\n suffixMax[i] = Math.max(suffixMax[i + 1], originalGaps[i]);\\n }\\n let initialMax = Math.max(...originalGaps);\\n let globalMax = initialMax;\\n for (let i = 0; i < n; i++) {\\n const s = startTime[i];\\n const e = endTime[i];\\n const d = e - s;\\n let mergedGap;\\n if (n === 1) {\\n mergedGap = eventTime - 0;\\n } else if (i === 0) {\\n mergedGap = startTime[1] - 0;\\n } else if (i === n - 1) {\\n mergedGap = eventTime - endTime[i - 1];\\n } else {\\n mergedGap = startTime[i + 1] - endTime[i - 1];\\n }\\n const leftGapIndex = i;\\n const rightGapIndex = i + 1;\\n let maxLeft = 0;\\n if (leftGapIndex > 0) {\\n maxLeft = prefixMax[leftGapIndex - 1];\\n }\\n let maxRight = 0;\\n if (rightGapIndex + 1 < m) {\\n maxRight = suffixMax[rightGapIndex + 1];\\n }\\n const maxOtherGap = Math.max(maxLeft, maxRight);\\n const otherPossible = maxOtherGap >= d;\\n const mergedPossible = mergedGap >= d;\\n if (!mergedPossible && !otherPossible) continue;\\n let currentMax;\\n if (otherPossible) {\\n currentMax = mergedGap;\\n } else {\\n const newGap = mergedGap - d;\\n currentMax = Math.max(newGap, maxOtherGap);\\n }\\n if (currentMax > globalMax) {\\n globalMax = currentMax;\\n }\\n }\\n return globalMax;\\n};\"], [51, 25.0, \"/**\\n * @param {number} eventTime\\n * @param {number[]} startTime\\n * @param {number[]} endTime\\n * @return {number}\\n */\\nvar maxFreeTime = function(eventTime, startTime, endTime) {\\n let biggest = 0;\\n const n = startTime.length;\\n\\n const biggestBefore = new Array(n).fill(0);\\n for (let i = 0; i < n; i ++) {\\n if (i === 0) {\\n biggestBefore[i] = startTime[i];\\n } else {\\n let curr = startTime[i] - endTime[i - 1];\\n biggestBefore[i] = Math.max(biggestBefore[i - 1], curr);\\n }\\n }\\n\\n const biggestAfter = new Array(n).fill(0);\\n for (let i = n - 1; i >= 0; i --) {\\n if (i === n - 1) {\\n biggestAfter[i] = eventTime - endTime[i];\\n } else {\\n let curr = startTime[i + 1] - endTime[i];\\n biggestAfter[i] = Math.max(biggestAfter[i + 1], curr);\\n }\\n }\\n\\n console.log(biggestBefore, biggestAfter)\\n\\n for (let i = 0; i < n; i ++) {\\n const left = i === 0 ? 0 : endTime[i - 1];\\n const right = i === n - 1 ? eventTime : startTime[i + 1];\\n const length = endTime[i] - startTime[i];\\n if (i > 0 && length <= biggestBefore[i - 1]) {\\n biggest = Math.max(biggest, right - left);\\n } else if (i < n - 1 && length <= biggestAfter[i + 1]) {\\n biggest = Math.max(biggest, right - left);\\n } else {\\n biggest = Math.max(biggest, right - left - length);\\n }\\n }\\n\\n return biggest;\\n};\"], [102, 25.0, \"/**\\n * @param {number} eventTime\\n * @param {number[]} startTime\\n * @param {number[]} endTime\\n * @return {number}\\n */\\nfunction maxFreeTime(eventTime, startTime, endTime) {\\n // Free time intervals\\n const gaps = [];\\n let time = 0;\\n\\n for (let i = 0; i < startTime.length; i++) {\\n gaps.push([time, startTime[i]]);\\n time = endTime[i];\\n }\\n gaps.push([time, eventTime]);\\n\\n // Track max free time from right side\\n const rightMax = [0];\\n for (let i = gaps.length - 1; i >= 0; i--) {\\n rightMax.push(\\n Math.max(\\n rightMax[rightMax.length - 1], gaps[i][1] - gaps[i][0]\\n )\\n );\\n }\\n\\n // Calculate maximum free time\\n let leftMax = 0, result = 0;\\n for (let i = 0; i < gaps.length - 1; i++) {\\n const curr = gaps[i][1] - gaps[i][0];\\n const next = gaps[i + 1][1] - gaps[i + 1][0];\\n const meetingGap = gaps[i + 1][0] - gaps[i][1];\\n\\n result = Math.max(result, curr + next);\\n if (Math.max(leftMax, rightMax[gaps.length - 2 - i]) >= meetingGap) {\\n result = Math.max(result, curr + next + meetingGap);\\n }\\n leftMax = Math.max(leftMax, curr);\\n }\\n\\n return result;\\n}\"], [120, 25.0, \"/**\\n * @param {number} eventTime\\n * @param {number[]} startTime\\n * @param {number[]} endTime\\n * @return {number}\\n */\\nvar maxFreeTime = function(eventTime, startTime, endTime) {\\n startTime.unshift(-1);\\n endTime.unshift(0);\\n\\n startTime.push(eventTime);\\n endTime.push(eventTime+1);\\n\\n let gaps = [];\\n for (let i = 1; i < startTime.length; i++) {\\n gaps.push([startTime[i] - endTime[i-1], gaps.length]);\\n }\\n \\n let sg = gaps.concat().sort((a,b) => b[0]-a[0]);\\n\\n //console.log(gaps);\\n \\n let best = 0;\\n \\n for (let i = 1; i < startTime.length-1; i++) {\\n let tg = gaps[i-1][0] + gaps[i][0];\\n let ml = endTime[i]-startTime[i];\\n //console.log({i, tg, ml});\\n\\n for (let gi = 0; gi < 3 && gi < gaps.length; gi++) {\\n let [gl, gp] = sg[gi];\\n //console.log({gl, gp});\\n if (gp === i || gp === i-1) continue;\\n if (gl >= ml) {\\n tg += ml;\\n break;\\n }\\n }\\n\\n best = Math.max(best, tg);\\n }\\n return best;\\n};\"]]"
},
"python3": {
"code": "class Solution:\n def maxFreeTime(self, eventTime: int, startTime: List[int], endTime: List[int]) -> int:\n n = len(startTime)\n if n == 0:\n return eventTime\n \n # Compute original free intervals' sizes\n pre_size = startTime[0] - 0\n mid_sizes = [startTime[i+1] - endTime[i] for i in range(n-1)]\n post_size = eventTime - endTime[-1]\n original_sizes = [pre_size] + mid_sizes + [post_size]\n \n # Precompute prefix and suffix max arrays\n m = len(original_sizes)\n prefix_max = [0] * m\n prefix_max[0] = original_sizes[0]\n for j in range(1, m):\n prefix_max[j] = max(prefix_max[j-1], original_sizes[j])\n \n suffix_max = [0] * m\n suffix_max[-1] = original_sizes[-1]\n for j in range(m-2, -1, -1):\n suffix_max[j] = max(suffix_max[j+1], original_sizes[j])\n \n original_max = max(original_sizes)\n max_candidate = 0\n \n for i in range(n):\n # Calculate S_size (merged interval after removing meeting i)\n if i > 0:\n prev_end = endTime[i-1]\n else:\n prev_end = 0\n if i < n-1:\n next_start = startTime[i+1]\n else:\n next_start = eventTime\n S_size = next_start - prev_end\n d = endTime[i] - startTime[i]\n \n # Determine max_remaining (max of original_sizes excluding i and i+1)\n if i == 0:\n if m >= 2:\n max_remaining = suffix_max[2] if 2 < m else 0\n else:\n max_remaining = 0\n elif i == n-1:\n max_remaining = prefix_max[n-2] if (n-2) >= 0 else 0\n else:\n left_part = prefix_max[i-1] if (i-1) >= 0 else 0\n right_part = suffix_max[i+2] if (i+2) < m else 0\n max_remaining = max(left_part, right_part)\n \n # Calculate options for inserting into S or max_remaining\n option1 = 0\n if S_size >= d:\n option1 = max(S_size - d, max_remaining)\n \n option2 = 0\n if max_remaining >= d:\n option2 = max(max_remaining - d, S_size)\n \n current_candidate = max(option1, option2)\n if current_candidate > max_candidate:\n max_candidate = current_candidate\n \n return max(original_max, max_candidate)",
"memory": 3900,
"memoryDistribution": "[[3900, 42.6038, \"from typing import List\\n\\nclass Solution:\\n def maxFreeTime(self, eventTime: int, startTime: List[int], endTime: List[int]) -> int:\\n n = len(startTime)\\n if n == 0:\\n return eventTime\\n \\n # Compute original free intervals' sizes\\n pre_size = startTime[0] - 0\\n mid_sizes = [startTime[i+1] - endTime[i] for i in range(n-1)]\\n post_size = eventTime - endTime[-1]\\n original_sizes = [pre_size] + mid_sizes + [post_size]\\n \\n # Precompute prefix and suffix max arrays\\n m = len(original_sizes)\\n prefix_max = [0] * m\\n prefix_max[0] = original_sizes[0]\\n for j in range(1, m):\\n prefix_max[j] = max(prefix_max[j-1], original_sizes[j])\\n \\n suffix_max = [0] * m\\n suffix_max[-1] = original_sizes[-1]\\n for j in range(m-2, -1, -1):\\n suffix_max[j] = max(suffix_max[j+1], original_sizes[j])\\n \\n original_max = max(original_sizes)\\n max_candidate = 0\\n \\n for i in range(n):\\n # Calculate S_size (merged interval after removing meeting i)\\n if i > 0:\\n prev_end = endTime[i-1]\\n else:\\n prev_end = 0\\n if i < n-1:\\n next_start = startTime[i+1]\\n else:\\n next_start = eventTime\\n S_size = next_start - prev_end\\n d = endTime[i] - startTime[i]\\n \\n # Determine max_remaining (max of original_sizes excluding i and i+1)\\n if i == 0:\\n if m >= 2:\\n max_remaining = suffix_max[2] if 2 < m else 0\\n else:\\n max_remaining = 0\\n elif i == n-1:\\n max_remaining = prefix_max[n-2] if (n-2) >= 0 else 0\\n else:\\n left_part = prefix_max[i-1] if (i-1) >= 0 else 0\\n right_part = suffix_max[i+2] if (i+2) < m else 0\\n max_remaining = max(left_part, right_part)\\n \\n # Calculate options for inserting into S or max_remaining\\n option1 = 0\\n if S_size >= d:\\n option1 = max(S_size - d, max_remaining)\\n \\n option2 = 0\\n if max_remaining >= d:\\n option2 = max(max_remaining - d, S_size)\\n \\n current_candidate = max(option1, option2)\\n if current_candidate > max_candidate:\\n max_candidate = current_candidate\\n \\n return max(original_max, max_candidate)\"], [37700, 0.5917, \"class Solution:\\n def maxFreeTime(self, eventTime: int, startTime: List[int], endTime: List[int]) -> int:\\n left = startTime[0]\\n ans = maxEmpty = 0\\n n = len(startTime)\\n dpRight = [0]*n\\n dpRight[-2] = eventTime-endTime[-1]\\n for meet in range(n-3, -1, -1):\\n dpRight[meet] = max(dpRight[meet+1], startTime[meet+2]-endTime[meet+1])\\n #print(dpRight)\\n for meet in range(n):\\n start, end = startTime[meet], endTime[meet]\\n duration = end-start\\n if meet == n-1:\\n right = eventTime-end\\n else:\\n right = startTime[meet+1]-end\\n #print(meet, start, end, duration, left, right, maxEmpty, ans)\\n if max(maxEmpty, dpRight[meet]) >= duration:\\n ans = max(ans, left+right+duration)\\n else:\\n ans = max(ans, left+right)\\n maxEmpty = max(maxEmpty, left)\\n left = right\\n return ans \"], [37800, 1.7751, \"max = lambda a,b: a if a>=b else b\\n\\nclass Solution:\\n def maxFreeTime(self, eventTime: int, startTime: List[int], endTime: List[int]) -> int:\\n n = len(startTime)\\n\\n suf_mx = [0] * (n+2)\\n t = eventTime\\n for i in range(n-1,-1,-1):\\n suf_mx[i +1] = max(suf_mx[i+1 +1], t-endTime[i])\\n t = startTime[i]\\n suf_mx[-1 +1] = max(suf_mx[0 +1], startTime[0])\\n\\n ans = 0\\n pre_mx = 0\\n t = 0\\n for i,pair in enumerate(pairwise(startTime+[eventTime])):\\n st = pair[0]\\n et = endTime[i]\\n dur = et - st\\n nxt = pair[1]\\n nw = nxt-t\\n if nw > ans and max(pre_mx, suf_mx[i+1 +1]) >= dur:\\n ans = nw\\n ans = max(ans, nw-dur)\\n pre_mx = max(pre_mx, st-t)\\n t = et\\n return ans\"], [37900, 0.5917, null], [38000, 0.5917, null], [38200, 1.1834, null], [38300, 1.1834, null], [38400, 10.0592, null], [38500, 10.6509, null], [38600, 12.426, null], [38700, 4.7337, null], [38800, 1.7751, null], [38900, 1.7751, null], [39000, 2.3669, null], [39100, 2.9586, null], [39200, 4.7337, null], [39300, 4.142, null], [39400, 1.1834, null], [39500, 2.3669, null], [39600, 1.7751, null], [39700, 1.1834, null], [39800, 1.7751, null], [39900, 0.5917, null], [40000, 0.5917, null], [40100, 0.5917, null], [40400, 1.1834, null], [40500, 1.1834, null], [40600, 0.5917, null], [40700, 0.5917, null], [40800, 0.5917, null], [41100, 0.5917, null], [41200, 1.1834, null], [41300, 1.7751, null], [41700, 0.5917, null], [41900, 0.5917, null], [42100, 0.5917, null], [42300, 0.5917, null], [42600, 1.7751, null], [43200, 0.5917, null], [44300, 0.5917, null], [44500, 0.5917, null], [44600, 0.5917, null], [45300, 0.5917, null], [45800, 0.5917, null], [45900, 0.5917, null], [46100, 1.1834, null], [46200, 1.1834, null], [46500, 0.5917, null], [46900, 0.5917, null], [47000, 0.5917, null], [47400, 1.7751, null], [47600, 0.5917, \"class Solution:\\n def maxFreeTime(self, eventTime: int, startTime: List[int], endTime: List[int]) -> int:\\n #01:35-\\n n = len(startTime)\\n empty = []\\n prev = 0\\n for i in range(n):\\n empty.append(startTime[i] - prev)\\n prev = endTime[i]\\n empty.append(eventTime - endTime[-1])\\n\\n maxempty = [[0 for i in range(2)] for j in range(n + 1)]\\n for i in range(1, n + 1):\\n maxempty[i][0] = max(maxempty[i - 1][0], empty[i - 1])\\n for i in reversed(range(n)):\\n maxempty[i][1] = max(maxempty[i + 1][1], empty[i + 1])\\n #print(\\\"maxempty\\\")\\n #print([i[0] for i in maxempty])\\n #print([i[1] for i in maxempty])\\n\\n rtn = 0\\n for i in range(n):\\n slot = endTime[i] - startTime[i]\\n if slot <= maxempty[i][0] or slot <= maxempty[i + 1][1]:\\n rtn = max(rtn, empty[i] + empty[i + 1] + slot)\\n else:\\n rtn = max(rtn, empty[i] + empty[i + 1])\\n \\n \\n return rtn\"], [47700, 0.5917, \"class Solution:\\n def maxFreeTime(self, eventTime: int, startTime: List[int], endTime: List[int]) -> int:\\n arr = [startTime[0]]\\n for i in range(1,len(startTime)):\\n arr.append(startTime[i] - endTime[i-1])\\n \\n arr.append(eventTime - endTime[-1])\\n n = len(startTime)\\n barr = sorted([(i,arr[i]) for i in range(len(arr))],key = lambda x : x[1])\\n print(barr)\\n def canMove(i):\\n \\n # If i can move the ith meeting to a suitable free time that is not ith or (i+1)th free time.\\n if barr[-1][1] < endTime[i] - startTime[i]:\\n return False\\n if barr[-1][0] not in [i,i+1]: return True\\n if barr[-2][1] < endTime[i] - startTime[i]:\\n return False\\n if barr[-2][0] not in [i,i+1]: return True\\n return barr[-3][1] >= endTime[i] - startTime[i]\\n\\n print(arr) \\n\\n mx = -1\\n for i in range(n):\\n if canMove(i):\\n mx = max(mx,arr[i] + endTime[i] - startTime[i] + arr[i+1])\\n else:\\n mx = max(mx,arr[i] + arr[i+1])\\n return mx\"]]",
"runtime": 376,
"runtimeDistribution": "[[89, 1.1834, \"class Solution2:\\n def maxFreeTime(self, eventTime: int, startTime: List[int], endTime: List[int]) -> int:\\n\\n endTime.insert(0, 0)\\n\\n startTime.append(eventTime)\\n\\n n = len(startTime)\\n\\n free_spaces = [startTime[i] - endTime[i] for i in range(n)]\\n\\n max_free_space = max(free_spaces)\\n\\n ind = free_spaces.index(max_free_space)\\n\\n indices = [i for i, v in enumerate(free_spaces) if v == max_free_space]\\n\\n result = [0]\\n\\n for ind in indices: \\n\\n if ind > 0:\\n result.append(free_spaces[ind-1] + free_spaces[ind])\\n else:\\n if ind +1 < n:\\n result.append(free_spaces[ind] + free_spaces[ind+1])\\n\\n if ind +2 < n:\\n\\n neighbor_1 = endTime[ind+1] - startTime[ind]\\n\\n max_free_space_to_place_neighbor1 = max(free_spaces[ind + 2:])\\n if neighbor_1 <= max_free_space_to_place_neighbor1:\\n print('here', result)\\n result.append(free_spaces[ind] + free_spaces[ind+1] + neighbor_1)\\n\\n\\n\\n\\n\\n if ind +1 < n and ind != 0:\\n result.append(free_spaces[ind] + free_spaces[ind +1])\\n neighbor_1 = endTime[ind] - startTime[ind-1]\\n\\n if free_spaces[:ind-1]:\\n max_free_space_to_place_neighbor1 = max(free_spaces[:ind-1])\\n else:\\n max_free_space_to_place_neighbor1 = 0\\n max_free_space_to_place_neighbor1 = max(max(free_spaces[ind + 1:]), max_free_space_to_place_neighbor1) \\n\\n print('neighbor_1', neighbor_1, endTime, startTime, max_free_space_to_place_neighbor1)\\n\\n if neighbor_1 <= max_free_space_to_place_neighbor1:\\n result.append(free_spaces[ind-1] + free_spaces[ind] + neighbor_1)\\n\\n\\n\\n if ind +1 < n and ind !=0 :\\n\\n \\n max_free_space_to_place_neighbor2 = max(max(free_spaces[ind + 2:]) if len(free_spaces[ind +2:]) > 0 else 0, max(free_spaces[:ind]))\\n\\n #max_free_space_to_place_neighbor2 = max(min(max_free_space_to_place_neighbor1, free_spaces[ind + 2]), max(free_spaces[:ind]))\\n\\n \\n\\n neighbor_2 = endTime[ind+1] - startTime[ind]\\n print('here', result, 'neighbor_2:', neighbor_2, 'here max_free_space_to_place_neighbor2', max_free_space_to_place_neighbor2)\\n if neighbor_2 <= max_free_space_to_place_neighbor2:\\n \\n result.append(free_spaces[ind] + free_spaces[ind +1] + neighbor_2)\\n\\n print(len(indices), result, ind, max_free_space, free_spaces, endTime , startTime, )\\n\\n return max(result)\\n\\nfrom collections import Counter\\nclass Solution:\\n def maxFreeTime(self, eventTime: int, startTime: List[int], endTime: List[int]) -> int:\\n\\n endTime.insert(0, 0)\\n\\n startTime.append(eventTime)\\n\\n n = len(startTime)\\n\\n free_spaces = [startTime[i] - endTime[i] for i in range(n)]\\n\\n counter = Counter(free_spaces)\\n\\n k = list(counter.keys())\\n k.sort()\\n\\n k_max = k.pop()\\n k_second = k.pop() if k else None\\n k_third = k.pop() if k else None\\n \\n \\n res = 0\\n for i in range(n-1):\\n curr = free_spaces[i] + free_spaces[i+1] \\n\\n curr_meeting_dur = endTime[i+1] - startTime[i]\\n\\n if free_spaces[i] != k_max and free_spaces[i+1] != k_max:\\n if curr_meeting_dur <= k_max:\\n curr += curr_meeting_dur\\n elif (counter[k_max] > 2) or ((counter[k_max] == 2) and (free_spaces[i] != free_spaces[i+1])):\\n if curr_meeting_dur <= k_max:\\n curr += curr_meeting_dur\\n else:\\n if k_second:\\n if (free_spaces[i] != k_second) and (free_spaces[i+1] != k_second):\\n if curr_meeting_dur <= k_second:\\n curr += curr_meeting_dur\\n elif (free_spaces[i] != k_second or free_spaces[i+1] != k_second) and counter[k_second] > 1:\\n if curr_meeting_dur <= k_second:\\n curr += curr_meeting_dur\\n else:\\n if k_third and curr_meeting_dur <= k_third:\\n curr += curr_meeting_dur\\n \\n if curr > res:\\n res = curr\\n\\n\\n return res\"], [95, 1.1834, \"class Solution2:\\n def maxFreeTime(self, eventTime: int, startTime: List[int], endTime: List[int]) -> int:\\n\\n endTime.insert(0, 0)\\n\\n startTime.append(eventTime)\\n\\n n = len(startTime)\\n\\n free_spaces = [startTime[i] - endTime[i] for i in range(n)]\\n\\n max_free_space = max(free_spaces)\\n\\n ind = free_spaces.index(max_free_space)\\n\\n indices = [i for i, v in enumerate(free_spaces) if v == max_free_space]\\n\\n result = [0]\\n\\n for ind in indices: \\n\\n if ind > 0:\\n result.append(free_spaces[ind-1] + free_spaces[ind])\\n else:\\n if ind +1 < n:\\n result.append(free_spaces[ind] + free_spaces[ind+1])\\n\\n if ind +2 < n:\\n\\n neighbor_1 = endTime[ind+1] - startTime[ind]\\n\\n max_free_space_to_place_neighbor1 = max(free_spaces[ind + 2:])\\n if neighbor_1 <= max_free_space_to_place_neighbor1:\\n print('here', result)\\n result.append(free_spaces[ind] + free_spaces[ind+1] + neighbor_1)\\n\\n\\n\\n\\n\\n if ind +1 < n and ind != 0:\\n result.append(free_spaces[ind] + free_spaces[ind +1])\\n neighbor_1 = endTime[ind] - startTime[ind-1]\\n\\n if free_spaces[:ind-1]:\\n max_free_space_to_place_neighbor1 = max(free_spaces[:ind-1])\\n else:\\n max_free_space_to_place_neighbor1 = 0\\n max_free_space_to_place_neighbor1 = max(max(free_spaces[ind + 1:]), max_free_space_to_place_neighbor1) \\n\\n print('neighbor_1', neighbor_1, endTime, startTime, max_free_space_to_place_neighbor1)\\n\\n if neighbor_1 <= max_free_space_to_place_neighbor1:\\n result.append(free_spaces[ind-1] + free_spaces[ind] + neighbor_1)\\n\\n\\n\\n if ind +1 < n and ind !=0 :\\n\\n \\n max_free_space_to_place_neighbor2 = max(max(free_spaces[ind + 2:]) if len(free_spaces[ind +2:]) > 0 else 0, max(free_spaces[:ind]))\\n\\n #max_free_space_to_place_neighbor2 = max(min(max_free_space_to_place_neighbor1, free_spaces[ind + 2]), max(free_spaces[:ind]))\\n\\n \\n\\n neighbor_2 = endTime[ind+1] - startTime[ind]\\n print('here', result, 'neighbor_2:', neighbor_2, 'here max_free_space_to_place_neighbor2', max_free_space_to_place_neighbor2)\\n if neighbor_2 <= max_free_space_to_place_neighbor2:\\n \\n result.append(free_spaces[ind] + free_spaces[ind +1] + neighbor_2)\\n\\n print(len(indices), result, ind, max_free_space, free_spaces, endTime , startTime, )\\n\\n return max(result)\\n\\nfrom collections import Counter\\nclass Solution:\\n def maxFreeTime(self, eventTime: int, startTime: List[int], endTime: List[int]) -> int:\\n\\n endTime.insert(0, 0)\\n\\n startTime.append(eventTime)\\n\\n n = len(startTime)\\n\\n free_spaces = [startTime[i] - endTime[i] for i in range(n)]\\n\\n counter = Counter(free_spaces)\\n\\n k = list(counter.keys())\\n k.sort()\\n\\n k_max = k.pop()\\n k_second = k.pop() if k else None\\n k_third = k.pop() if k else None\\n \\n \\n res = 0\\n for i in range(n-1):\\n curr = free_spaces[i] + free_spaces[i+1] \\n\\n curr_meeting_dur = endTime[i+1] - startTime[i]\\n\\n if free_spaces[i] != k_max and free_spaces[i+1] != k_max:\\n if curr_meeting_dur <= k_max:\\n curr += curr_meeting_dur\\n elif (counter[k_max] > 2) or ((counter[k_max] == 2) and (free_spaces[i] != free_spaces[i+1])):\\n if curr_meeting_dur <= k_max:\\n curr += curr_meeting_dur\\n else:\\n if k_second:\\n if (free_spaces[i] != k_second) and (free_spaces[i+1] != k_second):\\n if curr_meeting_dur <= k_second:\\n curr += curr_meeting_dur\\n elif (free_spaces[i] != k_second or free_spaces[i+1] != k_second) and counter[k_second] > 1:\\n if curr_meeting_dur <= k_second:\\n curr += curr_meeting_dur\\n else:\\n if k_third and curr_meeting_dur <= k_third:\\n curr += curr_meeting_dur\\n \\n if curr > res:\\n res = curr\\n\\n\\n return res\\n\\n\\nclass Solution:\\n def maxFreeTime(self, eventTime: int, startTime: List[int], endTime: List[int]) -> int:\\n freesArr = [(s-e) for (s, e) in zip(startTime+[eventTime], [0]+endTime)]\\n \\n ans = 0\\n sortedFrees = sorted(freesArr)\\n max_indx = len(sortedFrees)-1\\n for i in range(len(startTime)):\\n dur = endTime[i] - startTime[i]\\n left_free = freesArr[i]\\n right_free = freesArr[i+1]\\n if (left_free + right_free + dur) <= ans:\\n # \\u4e0d\\u6703\\u66f4\\u9577 \\u6240\\u4ee5\\u8df3\\u904e\\n continue\\n idx = max_indx\\n\\n if (max(left_free, right_free) == sortedFrees[idx]):\\n idx -= 1\\n if (min(left_free, right_free) == sortedFrees[idx]):\\n idx -= 1\\n total_free = left_free + right_free\\n if idx >= 0 and sortedFrees[idx] >= dur:\\n ans = max(ans, total_free + dur)\\n else:\\n ans = max(ans, total_free)\\n return ans\"], [100, 0.5917, null], [105, 0.5917, null], [111, 0.5917, null], [116, 0.5917, null], [121, 0.5917, null], [127, 0.5917, null], [132, 0.5917, null], [137, 0.5917, null], [143, 1.1834, null], [148, 0.5917, null], [153, 0.5917, null], [159, 0.5917, null], [164, 1.1834, null], [169, 1.1834, null], [175, 0.5917, null], [180, 0.5917, null], [185, 1.7751000000000001, null], [191, 2.9585, null], [196, 4.7336, null], [201, 0.5917, null], [207, 0.5917, null], [212, 5.3252999999999995, null], [217, 0.5917, null], [223, 1.7751000000000001, null], [228, 2.3668, null], [233, 4.7336, null], [239, 2.9585, null], [244, 7.1005, null], [249, 1.7751000000000001, null], [255, 1.1834, null], [260, 1.1834, null], [265, 1.7751000000000001, null], [271, 1.7751, null], [276, 2.3668, null], [281, 1.7751000000000001, null], [287, 3.5502, null], [292, 1.1834, null], [297, 1.1834, null], [303, 1.1834, null], [308, 2.9585, null], [313, 0.5917, null], [319, 0.5917, null], [324, 1.7751000000000001, null], [329, 0.5917, null], [335, 0.5917, null], [340, 0.5917, null], [345, 0.5917, null], [351, 0.5917, null], [356, 0.5917, null], [361, 0.5917, null], [367, 1.1834, null], [372, 1.1834, null], [376, 20.1204, \"from typing import List\\n\\nclass Solution:\\n def maxFreeTime(self, eventTime: int, startTime: List[int], endTime: List[int]) -> int:\\n n = len(startTime)\\n if n == 0:\\n return eventTime\\n \\n # Compute original free intervals' sizes\\n pre_size = startTime[0] - 0\\n mid_sizes = [startTime[i+1] - endTime[i] for i in range(n-1)]\\n post_size = eventTime - endTime[-1]\\n original_sizes = [pre_size] + mid_sizes + [post_size]\\n \\n # Precompute prefix and suffix max arrays\\n m = len(original_sizes)\\n prefix_max = [0] * m\\n prefix_max[0] = original_sizes[0]\\n for j in range(1, m):\\n prefix_max[j] = max(prefix_max[j-1], original_sizes[j])\\n \\n suffix_max = [0] * m\\n suffix_max[-1] = original_sizes[-1]\\n for j in range(m-2, -1, -1):\\n suffix_max[j] = max(suffix_max[j+1], original_sizes[j])\\n \\n original_max = max(original_sizes)\\n max_candidate = 0\\n \\n for i in range(n):\\n # Calculate S_size (merged interval after removing meeting i)\\n if i > 0:\\n prev_end = endTime[i-1]\\n else:\\n prev_end = 0\\n if i < n-1:\\n next_start = startTime[i+1]\\n else:\\n next_start = eventTime\\n S_size = next_start - prev_end\\n d = endTime[i] - startTime[i]\\n \\n # Determine max_remaining (max of original_sizes excluding i and i+1)\\n if i == 0:\\n if m >= 2:\\n max_remaining = suffix_max[2] if 2 < m else 0\\n else:\\n max_remaining = 0\\n elif i == n-1:\\n max_remaining = prefix_max[n-2] if (n-2) >= 0 else 0\\n else:\\n left_part = prefix_max[i-1] if (i-1) >= 0 else 0\\n right_part = suffix_max[i+2] if (i+2) < m else 0\\n max_remaining = max(left_part, right_part)\\n \\n # Calculate options for inserting into S or max_remaining\\n option1 = 0\\n if S_size >= d:\\n option1 = max(S_size - d, max_remaining)\\n \\n option2 = 0\\n if max_remaining >= d:\\n option2 = max(max_remaining - d, S_size)\\n \\n current_candidate = max(option1, option2)\\n if current_candidate > max_candidate:\\n max_candidate = current_candidate\\n \\n return max(original_max, max_candidate)\"], [377, 1.1834, null], [383, 3.5502000000000002, null], [388, 0.5917, null], [393, 1.1834, null], [399, 0.5917, null], [404, 0.5917, null], [409, 0.5917, null], [415, 0.5917, null], [420, 0.5917, null], [425, 0.5917, null], [431, 0.5917, null], [436, 0.5917, null], [441, 0.5917, null], [447, 0.5917, null], [452, 0.5917, null], [457, 0.5917, \"class Solution:\\n def find_merge_gaps(self,interval_len_gap):\\n max_prev_gap = 0\\n for i in range(1,len(interval_len_gap)-2):\\n if i%2==1: #gap\\n next_interval_len = interval_len_gap[i+1]\\n if next_interval_len<=max_prev_gap:\\n merge_gap = interval_len_gap[i]+next_interval_len+interval_len_gap[i+2]\\n self.max_gap = max(self.max_gap,merge_gap)\\n #if next_interval_len<=interval_len_gap[i]:\\n merge_gap = interval_len_gap[i]+interval_len_gap[i+2]\\n self.max_gap = max(self.max_gap,merge_gap)\\n max_prev_gap = max(max_prev_gap,interval_len_gap[i])\\n\\n def maxFreeTime(self, eventTime: int, startTime: List[int], endTime: List[int]) -> int:\\n intervals = [[0,0]]\\n for s,e in zip(startTime,endTime):\\n intervals.append([s,e])\\n intervals.append([eventTime,eventTime])\\n #intervals.sort()\\n # Inteval_len followed by gap, end by an interval\\n interval_len_gap = [0]\\n self.max_gap = 0\\n for i in range(1,len(intervals)):\\n gap = intervals[i][0]-intervals[i-1][1]\\n interval_len_gap.append(gap)\\n interval_len_gap.append(intervals[i][1]-intervals[i][0])\\n self.max_gap = max(self.max_gap,gap)\\n #print(interval_len_gap)\\n #print(f\\\"init max_gap {self.max_gap}\\\")\\n # forward pass\\n self.find_merge_gaps(interval_len_gap)\\n #print(f\\\"forward max_gap {self.max_gap}\\\")\\n # backward pass\\n self.find_merge_gaps(interval_len_gap[::-1])\\n #print(f\\\"backward max_gap {self.max_gap}\\\")\\n return self.max_gap\\n\\n \"], [463, 0.5917, \"class Solution:\\n def find_merge_gaps(self,interval_len_gap):\\n max_prev_gap = 0\\n for i in range(1,len(interval_len_gap)-2):\\n if i%2==1: #gap\\n next_interval_len = interval_len_gap[i+1]\\n if next_interval_len<=max_prev_gap:\\n merge_gap = interval_len_gap[i]+next_interval_len+interval_len_gap[i+2]\\n self.max_gap = max(self.max_gap,merge_gap)\\n #if next_interval_len<=interval_len_gap[i]:\\n merge_gap = interval_len_gap[i]+interval_len_gap[i+2]\\n self.max_gap = max(self.max_gap,merge_gap)\\n max_prev_gap = max(max_prev_gap,interval_len_gap[i])\\n\\n def maxFreeTime(self, eventTime: int, startTime: List[int], endTime: List[int]) -> int:\\n intervals = [[0,0],[eventTime,eventTime]]\\n for s,e in zip(startTime,endTime):\\n intervals.append([s,e])\\n intervals.sort()\\n # Inteval_len followed by gap, end by an interval\\n interval_len_gap = [0]\\n self.max_gap = 0\\n for i in range(1,len(intervals)):\\n gap = intervals[i][0]-intervals[i-1][1]\\n interval_len_gap.append(gap)\\n interval_len_gap.append(intervals[i][1]-intervals[i][0])\\n self.max_gap = max(self.max_gap,gap)\\n #print(interval_len_gap)\\n #print(f\\\"init max_gap {self.max_gap}\\\")\\n # forward pass\\n self.find_merge_gaps(interval_len_gap)\\n #print(f\\\"forward max_gap {self.max_gap}\\\")\\n # backward pass\\n self.find_merge_gaps(interval_len_gap[::-1])\\n #print(f\\\"backward max_gap {self.max_gap}\\\")\\n return self.max_gap\\n\\n \"]]"
},
"ruby": {
"code": "def max_free_time(event_time, start_time, end_time)\n return 0 if start_time.empty?\n\n # Compute gaps\n gaps = []\n gaps << start_time[0] - 0\n (1...start_time.size).each do |i|\n gaps << start_time[i] - end_time[i-1]\n end\n gaps << event_time - end_time[-1]\n\n initial_max_gap = gaps.max\n\n n = gaps.size - 1 # number of meetings is start_time.size, gaps.size is n+1\n\n # Precompute prefix_max and suffix_max\n prefix_max = Array.new(gaps.size, 0)\n prefix_max[0] = gaps[0]\n (1...gaps.size).each do |i|\n prefix_max[i] = [prefix_max[i-1], gaps[i]].max\n end\n\n suffix_max = Array.new(gaps.size, 0)\n suffix_max[-1] = gaps[-1]\n (gaps.size-2).downto(0) do |i|\n suffix_max[i] = [suffix_max[i+1], gaps[i]].max\n end\n\n max_candidate = 0\n\n start_time.each_with_index do |s, i|\n left_gap = gaps[i]\n right_gap = gaps[i+1]\n duration_i = end_time[i] - start_time[i]\n\n merged_gap = left_gap + right_gap + duration_i\n\n # Compute max_other_gap\n if i == 0\n left_part = 0\n else\n left_part = prefix_max[i-1]\n end\n\n if i + 2 >= gaps.size\n right_part = 0\n else\n right_part = suffix_max[i+2]\n end\n\n max_other_gap = [left_part, right_part].max\n\n # Compute option_a\n option_a = [merged_gap - duration_i, max_other_gap].max\n\n # Compute option_b\n if max_other_gap >= duration_i\n option_b_val = [merged_gap, max_other_gap - duration_i].max\n current_candidate = [option_a, option_b_val].max\n else\n current_candidate = option_a\n end\n\n max_candidate = current_candidate if current_candidate > max_candidate\n end\n\n [initial_max_gap, max_candidate].max\nend",
"memory": 24100,
"memoryDistribution": "[[24100, 100.0, \"def max_free_time(event_time, start_time, end_time)\\n return 0 if start_time.empty?\\n\\n # Compute gaps\\n gaps = []\\n gaps << start_time[0] - 0\\n (1...start_time.size).each do |i|\\n gaps << start_time[i] - end_time[i-1]\\n end\\n gaps << event_time - end_time[-1]\\n\\n initial_max_gap = gaps.max\\n\\n n = gaps.size - 1 # number of meetings is start_time.size, gaps.size is n+1\\n\\n # Precompute prefix_max and suffix_max\\n prefix_max = Array.new(gaps.size, 0)\\n prefix_max[0] = gaps[0]\\n (1...gaps.size).each do |i|\\n prefix_max[i] = [prefix_max[i-1], gaps[i]].max\\n end\\n\\n suffix_max = Array.new(gaps.size, 0)\\n suffix_max[-1] = gaps[-1]\\n (gaps.size-2).downto(0) do |i|\\n suffix_max[i] = [suffix_max[i+1], gaps[i]].max\\n end\\n\\n max_candidate = 0\\n\\n start_time.each_with_index do |s, i|\\n left_gap = gaps[i]\\n right_gap = gaps[i+1]\\n duration_i = end_time[i] - start_time[i]\\n\\n merged_gap = left_gap + right_gap + duration_i\\n\\n # Compute max_other_gap\\n if i == 0\\n left_part = 0\\n else\\n left_part = prefix_max[i-1]\\n end\\n\\n if i + 2 >= gaps.size\\n right_part = 0\\n else\\n right_part = suffix_max[i+2]\\n end\\n\\n max_other_gap = [left_part, right_part].max\\n\\n # Compute option_a\\n option_a = [merged_gap - duration_i, max_other_gap].max\\n\\n # Compute option_b\\n if max_other_gap >= duration_i\\n option_b_val = [merged_gap, max_other_gap - duration_i].max\\n current_candidate = [option_a, option_b_val].max\\n else\\n current_candidate = option_a\\n end\\n\\n max_candidate = current_candidate if current_candidate > max_candidate\\n end\\n\\n [initial_max_gap, max_candidate].max\\nend\"], [241300, 100.0, \"def max_free_time(event_time, start_time, end_time)\\n return 0 if start_time.empty?\\n\\n # Compute gaps\\n gaps = []\\n gaps << start_time[0] - 0\\n (1...start_time.size).each do |i|\\n gaps << start_time[i] - end_time[i-1]\\n end\\n gaps << event_time - end_time[-1]\\n\\n initial_max_gap = gaps.max\\n\\n n = gaps.size - 1 # number of meetings is start_time.size, gaps.size is n+1\\n\\n # Precompute prefix_max and suffix_max\\n prefix_max = Array.new(gaps.size, 0)\\n prefix_max[0] = gaps[0]\\n (1...gaps.size).each do |i|\\n prefix_max[i] = [prefix_max[i-1], gaps[i]].max\\n end\\n\\n suffix_max = Array.new(gaps.size, 0)\\n suffix_max[-1] = gaps[-1]\\n (gaps.size-2).downto(0) do |i|\\n suffix_max[i] = [suffix_max[i+1], gaps[i]].max\\n end\\n\\n max_candidate = 0\\n\\n start_time.each_with_index do |s, i|\\n left_gap = gaps[i]\\n right_gap = gaps[i+1]\\n duration_i = end_time[i] - start_time[i]\\n\\n merged_gap = left_gap + right_gap + duration_i\\n\\n # Compute max_other_gap\\n if i == 0\\n left_part = 0\\n else\\n left_part = prefix_max[i-1]\\n end\\n\\n if i + 2 >= gaps.size\\n right_part = 0\\n else\\n right_part = suffix_max[i+2]\\n end\\n\\n max_other_gap = [left_part, right_part].max\\n\\n # Compute option_a\\n option_a = [merged_gap - duration_i, max_other_gap].max\\n\\n # Compute option_b\\n if max_other_gap >= duration_i\\n option_b_val = [merged_gap, max_other_gap - duration_i].max\\n current_candidate = [option_a, option_b_val].max\\n else\\n current_candidate = option_a\\n end\\n\\n max_candidate = current_candidate if current_candidate > max_candidate\\n end\\n\\n [initial_max_gap, max_candidate].max\\nend\"]]",
"runtime": null,
"runtimeDistribution": "[[199, 100.0, \"def max_free_time(event_time, start_time, end_time)\\n return 0 if start_time.empty?\\n\\n # Compute gaps\\n gaps = []\\n gaps << start_time[0] - 0\\n (1...start_time.size).each do |i|\\n gaps << start_time[i] - end_time[i-1]\\n end\\n gaps << event_time - end_time[-1]\\n\\n initial_max_gap = gaps.max\\n\\n n = gaps.size - 1 # number of meetings is start_time.size, gaps.size is n+1\\n\\n # Precompute prefix_max and suffix_max\\n prefix_max = Array.new(gaps.size, 0)\\n prefix_max[0] = gaps[0]\\n (1...gaps.size).each do |i|\\n prefix_max[i] = [prefix_max[i-1], gaps[i]].max\\n end\\n\\n suffix_max = Array.new(gaps.size, 0)\\n suffix_max[-1] = gaps[-1]\\n (gaps.size-2).downto(0) do |i|\\n suffix_max[i] = [suffix_max[i+1], gaps[i]].max\\n end\\n\\n max_candidate = 0\\n\\n start_time.each_with_index do |s, i|\\n left_gap = gaps[i]\\n right_gap = gaps[i+1]\\n duration_i = end_time[i] - start_time[i]\\n\\n merged_gap = left_gap + right_gap + duration_i\\n\\n # Compute max_other_gap\\n if i == 0\\n left_part = 0\\n else\\n left_part = prefix_max[i-1]\\n end\\n\\n if i + 2 >= gaps.size\\n right_part = 0\\n else\\n right_part = suffix_max[i+2]\\n end\\n\\n max_other_gap = [left_part, right_part].max\\n\\n # Compute option_a\\n option_a = [merged_gap - duration_i, max_other_gap].max\\n\\n # Compute option_b\\n if max_other_gap >= duration_i\\n option_b_val = [merged_gap, max_other_gap - duration_i].max\\n current_candidate = [option_a, option_b_val].max\\n else\\n current_candidate = option_a\\n end\\n\\n max_candidate = current_candidate if current_candidate > max_candidate\\n end\\n\\n [initial_max_gap, max_candidate].max\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list[dict]:
import random
random.seed(seed)
test_cases = []
def compute_max_free_time(eventTime, startTime, endTime):
n = len(startTime)
if n == 0:
return eventTime
pre_size = startTime[0] - 0
mid_sizes = [startTime[i+1] - endTime[i] for i in range(n-1)]
post_size = eventTime - endTime[-1]
original_sizes = [pre_size] + mid_sizes + [post_size]
m = len(original_sizes)
prefix_max = [0] * m
prefix_max[0] = original_sizes[0]
for j in range(1, m):
prefix_max[j] = max(prefix_max[j-1], original_sizes[j])
suffix_max = [0] * m
suffix_max[-1] = original_sizes[-1]
for j in range(m-2, -1, -1):
suffix_max[j] = max(suffix_max[j+1], original_sizes[j])
original_max = max(original_sizes)
max_candidate = 0
for i in range(n):
prev_end = endTime[i-1] if i > 0 else 0
next_start = startTime[i+1] if i < n-1 else eventTime
S_size = next_start - prev_end
d = endTime[i] - startTime[i]
if i == 0:
max_remaining = suffix_max[2] if (m > 2) else 0
elif i == n-1:
max_remaining = prefix_max[n-2] if (n-2 >= 0) else 0
else:
left_part = prefix_max[i-1] if i-1 >= 0 else 0
right_part = suffix_max[i+2] if (i+2 < m) else 0
max_remaining = max(left_part, right_part)
option1 = max(S_size - d, max_remaining) if S_size >= d else 0
option2 = max(max_remaining - d, S_size) if max_remaining >= d else 0
current_candidate = max(option1, option2)
max_candidate = max(max_candidate, current_candidate)
return max(original_max, max_candidate)
# Fixed test cases from examples
fixed_cases = [
(5, [1, 3], [2, 5]),
(10, [0, 7, 9], [1, 8, 10]),
(10, [0, 3, 7, 9], [1, 4, 8, 10]),
(5, [0, 1, 2, 3, 4], [1, 2, 3, 4, 5])
]
for eventTime, sTimes, eTimes in fixed_cases:
input_str = f"{eventTime};" + ",".join(map(str, sTimes)) + ";" + ",".join(map(str, eTimes))
expected = compute_max_free_time(eventTime, sTimes, eTimes)
test_cases.append({"input": input_str, "output": str(expected)})
if len(test_cases) == num_cases:
return test_cases
# Generate additional random test cases
while len(test_cases) < num_cases:
if random.random() < 0.3:
# Stress test with many meetings
n = random.randint(20, 50)
meeting_durations = [random.randint(1, 10) for _ in range(n)]
total_meeting = sum(meeting_durations)
free_total = random.randint(0, n * 10)
eventTime = total_meeting + free_total
else:
n = random.randint(2, 10)
meeting_durations = [random.randint(1, 10) for _ in range(n)]
total_meeting = sum(meeting_durations)
free_total = random.randint(0, n * 3)
eventTime = total_meeting + free_total
# Distribute free_total into n+1 gaps
gaps = []
remaining = free_total
for i in range(n):
gap = random.randint(0, remaining) if remaining > 0 else 0
gaps.append(gap)
remaining -= gap
gaps.append(remaining)
# Generate start and end times based on gaps and meeting durations
startTime = []
endTime = []
current = gaps[0]
for i in range(n):
startTime.append(current)
current += meeting_durations[i]
endTime.append(current)
current += gaps[i+1]
input_str = f"{eventTime};" + ",".join(map(str, startTime)) + ";" + ",".join(map(str, endTime))
expected = compute_max_free_time(eventTime, startTime, endTime)
test_cases.append({"input": input_str, "output": str(expected)})
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
try:
expected_val = int(expected_output.strip())
program_val = int(program_output.strip())
return expected_val == program_val
except Exception:
return False
|
[{"input": "5;1,3;2,5", "output": "2"}, {"input": "10;0,7,9;1,8,10", "output": "7"}, {"input": "10;0,3,7,9;1,4,8,10", "output": "6"}, {"input": "5;0,1,2,3,4;1,2,3,4,5", "output": "0"}, {"input": "10;0,5;5,9", "output": "1"}, {"input": "50;0,2,12,19,20,21,23,27,31,40;2,12,19,20,21,23,27,31,40,50", "output": "0"}, {"input": "60;1,10,14,22,33,38,39,42,49,55;8,14,22,32,38,39,42,49,55,60", "output": "3"}, {"input": "451;68,90,127,204,227,235,244,246,253,255,264,269,279,285,295,299,301,302,306,311,313,317,319,326,331,339,345,348,354,360,364,369,371,381,384,393,397,400,408,415,420,429,433,439,440,444,445;74,100,132,205,235,244,246,253,255,264,269,279,285,295,299,301,302,306,311,313,317,319,326,331,339,345,348,354,360,364,369,371,381,384,393,397,400,408,415,420,429,433,439,440,444,445,451", "output": "104"}, {"input": "76;18,28,38,41,46,49,53,62,71;25,36,41,46,49,53,62,71,76", "output": "21"}, {"input": "26;1,6,15,23,25;4,15,23,25,26", "output": "3"}, {"input": "422;78,115,132,164,207,214,224,235,244,249,258,260,262,271,276,282,284,289,296,299,307,308,313,322,325,334,336,341,350,360,364,367,373,376,385,394,395,405,411,419,420;85,125,134,171,214,224,232,244,249,258,259,262,271,276,282,284,289,296,299,307,308,313,322,325,334,336,341,350,360,364,367,373,376,385,394,395,405,411,419,420,422", "output": "115"}, {"input": "34;1,8,17,27;6,17,27,34", "output": "3"}, {"input": "47;0,17,26,34,36,40,44;8,26,34,36,40,44,46", "output": "9"}, {"input": "298;15,26,45,54,64,68,74,82,86,95,98,108,118,126,130,138,145,149,151,153,160,166,173,180,188,189,191,192,199,205,207,211,215,219,228,236,239,246,249,254,262,266,268,276,285,287,288,297;16,32,47,63,68,73,82,86,95,98,108,118,126,130,138,145,149,151,153,160,166,173,180,188,189,191,192,199,205,207,211,215,219,228,236,239,246,249,254,262,266,268,276,285,287,288,297,298", "output": "29"}, {"input": "32;12,19,20,27;19,20,27,32", "output": "12"}, {"input": "67;17,26,39,43,47,52,56,57;26,34,42,47,52,56,57,67", "output": "17"}, {"input": "450;159,239,248,257,261,264,273,275,278,280,290,292,296,303,305,315,319,329,339,340,350,352,359,369,379,388,394,399,403,409,413,418,425,428,433,441,447,449;167,248,257,260,262,273,275,278,280,290,292,296,303,305,315,319,329,339,340,350,352,359,369,379,388,394,399,403,409,413,418,425,428,433,441,447,449,450", "output": "231"}, {"input": "523;18,213,285,289,296,301,304,313,322,327,337,346,347,356,361,363,366,371,373,375,384,387,392,397,407,411,417,421,426,435,443,448,449,451,458,463,464,465,471,474,479,482,490,499,506,515,516,518,520;24,215,289,295,301,304,312,322,327,337,346,347,356,361,363,366,371,373,375,384,387,392,397,407,411,417,421,426,435,443,448,449,451,458,463,464,465,471,474,479,482,490,499,506,515,516,518,520,523", "output": "261"}, {"input": "15;1,7;7,11", "output": "4"}, {"input": "72;13,32,42,45,49,52,55,62,63,66;20,42,45,49,52,55,62,63,66,72", "output": "25"}, {"input": "33;7,15,21,24,32;12,18,23,31,33", "output": "10"}, {"input": "30;1,9,12,17,24;5,10,16,24,30", "output": "7"}, {"input": "58;5,16,20,22,27,30,40,45,46,48;11,17,22,27,30,40,45,46,48,58", "output": "10"}, {"input": "76;21,23,30,40,44,49,50,57,58,67;23,30,40,44,49,50,57,58,67,76", "output": "21"}, {"input": "434;172,187,225,242,250,252,257,266,271,278,284,291,296,305,308,312,319,326,329,339,349,354,361,370,371,376,381,385,392,402,412,418,426;174,193,235,248,252,257,266,271,278,284,291,296,305,308,312,319,326,329,339,349,354,361,370,371,376,381,385,392,402,412,418,426,434", "output": "187"}, {"input": "224;31,54,104,125,131,133,138,143,147,151,154,155,156,160,168,178,180,188,195,205,209,216;36,63,114,131,133,137,143,147,151,154,155,156,160,168,178,180,188,195,205,209,216,224", "output": "68"}, {"input": "481;104,155,222,229,238,242,245,253,256,264,273,282,292,298,306,316,325,332,341,349,352,360,368,373,377,382,391,399,403,408,416,418,423,427,432,438,444,453,455,458,461,465,472,475,479;113,163,223,238,242,244,253,256,264,273,282,292,298,306,316,325,332,341,349,352,360,368,373,377,382,391,399,403,408,416,418,423,427,432,438,444,453,455,458,461,465,472,475,479,481", "output": "155"}, {"input": "20;0,12;10,19", "output": "3"}, {"input": "357;54,119,148,178,200,205,214,218,223,230,238,239,246,252,259,262,270,273,283,292,293,300,310,320,321,323,330,333,341,344,345,350;61,128,157,188,204,213,218,223,230,238,239,246,252,259,262,270,273,283,292,293,300,310,320,321,323,330,333,341,344,345,350,357", "output": "119"}, {"input": "56;2,8,10,25,29,38,41,48;7,10,18,26,38,39,47,52", "output": "11"}, {"input": "415;162,178,190,200,208,214,220,223,233,243,245,248,253,255,265,266,271,281,288,295,299,301,311,315,317,322,332,334,344,345,351,360,367,373,375,384,390,391,398,406,408;164,188,194,208,213,220,223,233,243,245,248,253,255,265,266,271,281,288,295,299,301,311,315,317,322,332,334,344,345,351,360,367,373,375,384,390,391,398,406,408,415", "output": "178"}, {"input": "70;7,15,23,30,40,45,51,55,57,62;15,23,30,40,45,51,55,57,62,70", "output": "7"}, {"input": "50;5,13,15,23,29,32,40,44;11,14,23,29,32,40,44,50", "output": "7"}, {"input": "87;0,6,17,24,37,50,59,63,71,79;4,8,21,31,45,59,63,71,79,87", "output": "19"}, {"input": "259;17,31,42,50,60,69,75,82,91,97,103,111,116,121,126,130,132,136,142,144,153,156,160,164,172,177,187,196,206,211,213,217,222,226,232,235,240,241,250,253,258;27,37,50,59,69,75,82,91,97,103,111,116,121,126,130,132,136,142,144,153,156,160,164,172,177,187,196,206,211,213,217,222,226,232,235,240,241,250,253,258,259", "output": "21"}, {"input": "187;10,51,63,88,108,116,122,125,126,131,139,141,143,150,158,160,170,171,174,177;20,56,71,96,116,122,125,126,131,139,141,143,150,158,160,170,171,174,177,187", "output": "51"}, {"input": "50;4,22,29,37,45;13,29,37,45,50", "output": "13"}, {"input": "14;0,4,8;4,8,13", "output": "1"}, {"input": "33;4,5,13,22;5,12,21,32", "output": "5"}, {"input": "67;4,14,20,25,35,40,49,53,63;6,18,25,35,39,47,51,62,67", "output": "14"}, {"input": "605;253,294,352,358,374,384,394,404,407,417,419,426,432,442,447,448,450,454,464,474,475,480,490,491,494,502,511,519,524,527,537,544,552,554,562,568,575,581,587,589,592,598;258,301,357,367,383,392,402,406,417,418,426,432,442,447,448,450,454,464,474,475,480,490,491,494,502,511,519,524,527,537,544,552,554,562,568,575,581,587,589,592,598,605", "output": "294"}, {"input": "20;0,10;9,18", "output": "3"}, {"input": "54;0,9,12,16,21,30,33,38,46;8,10,16,21,30,33,38,46,54", "output": "3"}, {"input": "294;57,75,85,93,95,99,101,109,111,114,122,127,136,141,148,156,164,168,176,185,188,195,199,209,218,221,223,228,235,241,250,255,256,261,266,276,286;58,84,92,95,99,101,109,111,114,122,127,136,141,148,156,164,168,176,185,188,195,199,209,218,221,223,228,235,241,250,255,256,261,266,276,286,294", "output": "75"}, {"input": "68;7,17,25,31,35,39,49,56,60,67;14,25,31,35,39,49,56,60,67,68", "output": "10"}, {"input": "30;5,13,17,20;13,14,20,29", "output": "6"}, {"input": "67;12,23,26,33,36,38,46,51,57;13,26,33,36,38,46,51,57,67", "output": "22"}, {"input": "439;92,144,195,211,297,318,328,338,341,345,350,354,356,363,365,367,375,378,383,384,385,391,392,397,403,409,416,419,423,432;101,151,201,219,306,319,338,340,345,350,354,356,363,365,367,375,378,383,384,385,391,392,397,403,409,416,419,423,432,439", "output": "144"}, {"input": "29;0,7,16,21;4,15,21,29", "output": "4"}, {"input": "30;3,6,14,20;5,14,20,30", "output": "4"}, {"input": "50;11,19,28,36,39,43;15,26,36,38,43,50", "output": "15"}, {"input": "442;19,56,123,232,262,267,277,283,287,291,301,306,309,311,312,317,325,326,336,342,345,347,352,358,365,368,372,375,384,390,399,408,413,416,421,429,434,440;20,66,131,237,266,277,283,287,291,301,306,309,311,312,317,325,326,336,342,345,347,352,358,365,368,372,375,384,390,399,408,413,416,421,429,434,440,442", "output": "166"}, {"input": "438;69,169,232,264,287,300,306,311,321,328,334,336,340,348,349,359,368,374,384,388,390,398,403,410,412,415,416,417,422,430,432,434;70,174,241,266,295,306,311,321,328,334,336,340,348,349,359,368,374,384,388,390,398,403,410,412,415,416,417,422,430,432,434,438", "output": "169"}, {"input": "82;11,21,38,42,49,51,59,69,76,81;18,31,41,49,51,59,69,76,81,82", "output": "21"}, {"input": "42;0,8,14,23,29,30,37;2,14,23,29,30,37,42", "output": "6"}, {"input": "15;0,4,14;4,14,15", "output": "0"}, {"input": "34;4,7,17,22,24;7,17,21,24,33", "output": "5"}, {"input": "9;1,6;6,9", "output": "1"}, {"input": "10;1,6,9;2,9,10", "output": "5"}, {"input": "24;1,7,11,17;6,8,14,24", "output": "6"}, {"input": "86;0,11,28,39,49,53,63,64,73,78;10,13,36,48,53,63,64,73,78,86", "output": "18"}, {"input": "60;18,27,29,31,37,47,50,52,55;26,29,31,37,47,50,52,55,60", "output": "19"}, {"input": "77;14,19,27,36,46,53,55,57,66,70;19,27,36,46,53,55,57,66,70,77", "output": "14"}, {"input": "305;79,132,142,167,171,177,184,190,195,201,204,212,214,216,218,220,227,229,235,238,247,248,258,267,276,282,284,291,297,304;87,139,149,169,177,184,190,195,201,204,212,214,216,218,220,227,229,235,238,247,248,258,267,276,282,284,291,297,304,305", "output": "132"}, {"input": "384;83,163,171,173,179,188,194,196,201,211,215,222,231,241,251,260,261,271,276,277,280,285,290,296,302,303,306,309,319,326,328,331,332,334,343,347,354,361,369,375,378;91,167,173,179,188,194,196,201,211,215,222,231,241,251,260,261,271,276,277,280,285,290,296,302,303,306,309,319,326,328,331,332,334,343,347,354,361,369,375,378,384", "output": "155"}, {"input": "246;67,112,124,134,136,141,148,156,163,171,181,189,196,201,205,214,216,222,229,231,236;70,115,134,135,138,146,156,163,171,181,189,196,201,205,214,216,222,229,231,236,246", "output": "112"}, {"input": "349;146,202,228,231,236,241,247,249,250,258,265,268,271,278,287,291,300,309,315,317,324,325,332,333,341,343;151,206,231,236,241,247,249,250,258,265,268,271,278,287,291,300,309,315,317,324,325,332,333,341,343,349", "output": "202"}, {"input": "43;13,16,23,24,30,33;15,23,24,30,33,43", "output": "14"}, {"input": "678;140,170,264,400,412,428,444,447,454,459,466,470,476,479,481,490,492,501,510,514,520,526,529,533,535,538,543,547,550,560,563,565,568,576,584,594,604,612,622,632,638,644,647,655,657,665,673;142,174,271,410,419,437,446,454,459,465,470,476,479,481,490,492,501,510,514,520,526,529,533,535,538,543,547,550,560,563,565,568,576,584,594,604,612,622,632,638,644,647,655,657,665,673,678", "output": "226"}, {"input": "30;6,9,19;8,19,29", "output": "7"}, {"input": "37;1,7,17,25,34;7,17,25,34,37", "output": "1"}, {"input": "537;185,193,241,259,267,271,280,291,299,308,317,327,330,337,343,348,356,363,369,379,380,386,388,394,396,405,412,417,422,432,435,441,443,453,456,462,467,474,477,487,489,494,503,510,516,519,528,530;191,195,250,262,268,275,288,299,308,317,327,330,336,343,348,355,363,369,379,380,386,388,394,396,405,412,417,422,432,435,441,443,453,456,462,467,474,477,487,489,494,503,510,516,519,528,530,537", "output": "193"}, {"input": "25;2,12,19,22;12,19,22,25", "output": "2"}, {"input": "32;3,18,19,26;11,19,26,32", "output": "10"}, {"input": "72;12,17,27,31,36,44,48,54,64;16,26,31,36,44,48,54,64,72", "output": "13"}, {"input": "57;3,17,21,33,36,41,43,51;6,21,31,36,41,42,51,57", "output": "14"}, {"input": "62;11,15,25,27,32,40,46,47,54,55;14,22,27,31,40,46,47,54,55,62", "output": "15"}, {"input": "382;16,46,179,184,227,244,253,261,264,273,281,291,292,294,295,300,304,307,316,326,335,342,344,349,353,358,360,361,365,372;18,52,182,187,228,249,261,264,272,281,291,292,294,295,300,304,307,316,326,335,342,344,349,353,358,360,361,365,372,382", "output": "161"}, {"input": "43;2,6,16,23,26,28,37;6,16,23,26,28,37,43", "output": "2"}, {"input": "76;2,22,26,34,47,49,56,63,69,70;11,23,33,42,48,56,62,68,70,76", "output": "15"}, {"input": "23;1,9,17,20;9,17,20,23", "output": "1"}, {"input": "391;94,227,239,242,261,266,278,287,296,304,309,310,314,319,325,326,332,337,339,345,352,359,367,374,380,383;95,231,240,248,266,275,285,296,304,309,310,314,319,325,326,332,337,339,345,352,359,367,374,380,383,391", "output": "227"}, {"input": "23;1,10,15,21;10,15,21,23", "output": "1"}, {"input": "56;0,19,31,39,42,50;8,29,38,42,50,56", "output": "13"}, {"input": "351;78,97,110,118,124,133,136,137,141,151,159,160,163,165,169,175,181,188,198,199,209,212,220,226,232,240,242,252,255,264,270,277,283,288,292,294,295,298,306,315,322,331,333,338,343;79,99,117,124,133,136,137,140,151,159,160,163,165,169,175,181,188,198,199,209,212,220,226,232,240,242,252,255,264,270,277,283,288,292,294,295,298,306,315,322,331,333,338,343,351", "output": "97"}, {"input": "476;174,226,232,243,251,259,268,277,283,289,292,295,302,311,315,317,321,324,328,336,337,343,352,362,368,376,385,388,398,400,402,407,414,422,431,438,445,455,457,460,466,468;182,228,238,249,253,268,277,282,288,292,295,301,311,315,317,321,324,328,336,337,343,352,362,368,376,385,388,398,400,402,407,414,422,431,438,445,455,457,460,466,468,476", "output": "218"}, {"input": "33;5,12,21,26,28;11,21,26,28,33", "output": "6"}, {"input": "307;103,134,144,146,155,158,168,178,181,184,194,204,210,220,221,222,224,225,235,240,244,254,261,271,272,280,289,294,299;113,143,146,155,158,168,178,181,184,194,204,210,220,221,222,224,225,235,240,244,254,261,271,272,280,289,294,299,307", "output": "124"}, {"input": "161;17,25,31,40,47,55,65,70,76,86,89,95,101,107,114,117,123,132,141,143,149,153;18,28,39,47,55,63,69,76,86,89,95,101,107,114,117,123,132,141,143,149,153,161", "output": "25"}, {"input": "60;14,19,23,29,39,45,49,52;18,22,29,39,45,49,52,60", "output": "15"}, {"input": "27;1,10,19;8,19,27", "output": "3"}, {"input": "17;3,9;8,17", "output": "4"}, {"input": "20;3,11,14;10,14,19", "output": "4"}, {"input": "90;19,24,31,40,48,51,59,68,76,85;23,30,40,45,50,58,68,76,85,90", "output": "20"}, {"input": "44;0,3,8,18,27,34,43;3,7,18,27,34,43,44", "output": "1"}, {"input": "84;9,26,30,40,49,52,58,68,74,77;17,29,40,49,52,58,68,74,77,84", "output": "18"}, {"input": "80;9,18,35,45,50,58,59,65,71,73;18,26,45,50,58,59,65,71,73,80", "output": "18"}, {"input": "43;2,13,23,31,34;3,23,31,34,43", "output": "12"}, {"input": "385;73,101,149,157,166,173,180,183,190,194,201,210,220,228,229,232,241,245,254,260,268,277,284,290,293,301,310,316,325,331,336,346,354,358,362,367,376,381;75,105,150,165,172,180,183,190,194,201,210,220,228,229,232,241,245,254,260,268,277,284,290,293,301,310,316,325,331,336,346,354,358,362,367,376,381,385", "output": "101"}, {"input": "51;2,11,13,25,34,43;7,13,23,34,41,50", "output": "6"}]
|
{
"cpp": "==Code Submission==\n\nint main() {\n string input;\n getline(cin, input);\n // Expected format: eventTime;start1,start2,...;end1,end2,...\n string eventTimeStr, startStr, endStr;\n size_t pos1 = input.find(';');\n if (pos1 == string::npos) return 1;\n eventTimeStr = input.substr(0, pos1);\n size_t pos2 = input.find(';', pos1 + 1);\n if (pos2 == string::npos) return 1;\n startStr = input.substr(pos1 + 1, pos2 - pos1 - 1);\n endStr = input.substr(pos2 + 1);\n\n int eventTime = stoi(eventTimeStr);\n vector<int> startTime, endTime;\n {\n stringstream ss(startStr);\n string token;\n while(getline(ss, token, ',')) {\n if (!token.empty())\n startTime.push_back(stoi(token));\n }\n }\n {\n stringstream ss(endStr);\n string token;\n while(getline(ss, token, ',')) {\n if (!token.empty())\n endTime.push_back(stoi(token));\n }\n }\n Solution sol;\n int result = sol.maxFreeTime(eventTime, startTime, endTime);\n cout << result;\n return 0;\n}",
"golang": "==Code Submission==\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n line, _ := reader.ReadString('\\n')\n line = strings.TrimSpace(line)\n // Expected format: eventTime;start1,start2,...;end1,end2,...\n parts := strings.SplitN(line, \";\", 3)\n eventTime, _ := strconv.Atoi(parts[0])\n var startTime []int\n if parts[1] != \"\" {\n for _, s := range strings.Split(parts[1], \",\") {\n if s == \"\" { continue }\n num, _ := strconv.Atoi(s)\n startTime = append(startTime, num)\n }\n }\n var endTime []int\n if parts[2] != \"\" {\n for _, s := range strings.Split(parts[2], \",\") {\n if s == \"\" { continue }\n num, _ := strconv.Atoi(s)\n endTime = append(endTime, num)\n }\n }\n result := maxFreeTime(eventTime, startTime, endTime) // The submitted solution function will be injected here.\n fmt.Println(result)\n}",
"java": "public class Main {\n public static void main(String[] args) throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n String line = br.readLine().trim();\n // Expected format: eventTime;start1,start2,...;end1,end2,...\n String[] parts = line.split(\";\", 3);\n int eventTime = Integer.parseInt(parts[0]);\n String[] startTokens = parts[1].split(\",\");\n int[] startTime = new int[startTokens.length];\n for (int i = 0; i < startTokens.length; i++) {\n startTime[i] = Integer.parseInt(startTokens[i]);\n }\n String[] endTokens = parts[2].split(\",\");\n int[] endTime = new int[endTokens.length];\n for (int i = 0; i < endTokens.length; i++) {\n endTime[i] = Integer.parseInt(endTokens[i]);\n }\n Solution sol = new Solution();\n int result = sol.maxFreeTime(eventTime, startTime, endTime);\n System.out.println(result);\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\nlet input = \"\";\nprocess.stdin.on('data', chunk => input += chunk);\nprocess.stdin.on('end', () => {\n input = input.trim();\n // Expected format: eventTime;start1,start2,...;end1,end2,...\n const parts = input.split(\";\");\n const eventTime = parseInt(parts[0]);\n const startTime = parts[1] ? parts[1].split(\",\").map(x => parseInt(x)) : [];\n const endTime = parts[2] ? parts[2].split(\",\").map(x => parseInt(x)) : [];\n const result = maxFreeTime(eventTime, startTime, endTime); // The submitted solution function will be injected here.\n console.log(result);\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str):\n parts = input_str.strip().split(';')\n eventTime = int(parts[0])\n startTime = list(map(int, parts[1].split(','))) if parts[1] else []\n endTime = list(map(int, parts[2].split(','))) if parts[2] else []\n return eventTime, startTime, endTime\n\ndef serialize_stdout(result):\n return str(result)\n\ndata = sys.stdin.read().strip()\neventTime, startTime, endTime = deserialize_stdin(data)\nsol = Solution() # The submitted solution will be injected here.\nresult = sol.maxFreeTime(eventTime, startTime, endTime)\nprint(serialize_stdout(result))",
"ruby": "==Code Submission==\ninput = gets.strip\n# Expected format: eventTime;start1,start2,...;end1,end2,...\nparts = input.split(';')\nevent_time = parts[0].to_i\nstart_time = parts[1] == \"\" ? [] : parts[1].split(',').map(&:to_i)\nend_time = parts[2] == \"\" ? [] : parts[2].split(',').map(&:to_i)\nresult = max_free_time(event_time, start_time, end_time) # The submitted solution function will be injected here.\nputs result"
}
|
3743
|
Reschedule Meetings for Maximum Free Time I
|
reschedule-meetings-for-maximum-free-time-i
|
<p>You are given an integer <code>eventTime</code> denoting the duration of an event, where the event occurs from time <code>t = 0</code> to time <code>t = eventTime</code>.</p>
<p>You are also given two integer arrays <code>startTime</code> and <code>endTime</code>, each of length <code>n</code>. These represent the start and end time of <code>n</code> <strong>non-overlapping</strong> meetings, where the <code>i<sup>th</sup></code> meeting occurs during the time <code>[startTime[i], endTime[i]]</code>.</p>
<p>You can reschedule <strong>at most</strong> <code>k</code> meetings by moving their start time while maintaining the <strong>same duration</strong>, to <strong>maximize</strong> the <strong>longest</strong> <em>continuous period of free time</em> during the event.</p>
<p>The <strong>relative</strong> order of all the meetings should stay the<em> same</em> and they should remain non-overlapping.</p>
<p>Return the <strong>maximum</strong> amount of free time possible after rearranging the meetings.</p>
<p><strong>Note</strong> that the meetings can <strong>not</strong> be rescheduled to a time outside the event.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">eventTime = 5, k = 1, startTime = [1,3], endTime = [2,5]</span></p>
<p><strong>Output:</strong> <span class="example-io">2</span></p>
<p><strong>Explanation:</strong></p>
<p><img alt="" src="https://assets.leetcode.com/uploads/2024/12/21/example0_rescheduled.png" style="width: 375px; height: 123px;" /></p>
<p>Reschedule the meeting at <code>[1, 2]</code> to <code>[2, 3]</code>, leaving no meetings during the time <code>[0, 2]</code>.</p>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">eventTime = 10, k = 1, startTime = [0,2,9], endTime = [1,4,10]</span></p>
<p><strong>Output:</strong> <span class="example-io">6</span></p>
<p><strong>Explanation:</strong></p>
<p><img alt="" src="https://assets.leetcode.com/uploads/2024/12/21/example1_rescheduled.png" style="width: 375px; height: 125px;" /></p>
<p>Reschedule the meeting at <code>[2, 4]</code> to <code>[1, 3]</code>, leaving no meetings during the time <code>[3, 9]</code>.</p>
</div>
<p><strong class="example">Example 3:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">eventTime = 5, k = 2, startTime = [0,1,2,3,4], endTime = [1,2,3,4,5]</span></p>
<p><strong>Output:</strong> <span class="example-io">0</span></p>
<p><strong>Explanation:</strong></p>
<p>There is no time during the event not occupied by meetings.</p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>1 <= eventTime <= 10<sup>9</sup></code></li>
<li><code>n == startTime.length == endTime.length</code></li>
<li><code>2 <= n <= 10<sup>5</sup></code></li>
<li><code>1 <= k <= n</code></li>
<li><code>0 <= startTime[i] < endTime[i] <= eventTime</code></li>
<li><code>endTime[i] <= startTime[i + 1]</code> where <code>i</code> lies in the range <code>[0, n - 2]</code>.</li>
</ul>
|
You are given an integer `eventTime` denoting the duration of an event, where the event occurs from time `t = 0` to time `t = eventTime`.
You are also given two integer arrays `startTime` and `endTime`, each of length `n`. These represent the start and end time of `n` **non\-overlapping** meetings, where the `ith` meeting occurs during the time `[startTime[i], endTime[i]]`.
You can reschedule **at most** `k` meetings by moving their start time while maintaining the **same duration**, to **maximize** the **longest** *continuous period of free time* during the event.
The **relative** order of all the meetings should stay the *same* and they should remain non\-overlapping.
Return the **maximum** amount of free time possible after rearranging the meetings.
**Note** that the meetings can **not** be rescheduled to a time outside the event.
**Example 1:**
**Input:** eventTime \= 5, k \= 1, startTime \= \[1,3], endTime \= \[2,5]
**Output:** 2
**Explanation:**
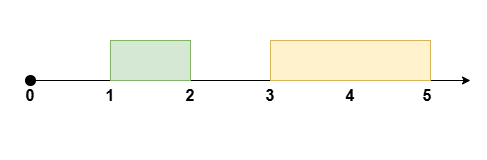
Reschedule the meeting at `[1, 2]` to `[2, 3]`, leaving no meetings during the time `[0, 2]`.
**Example 2:**
**Input:** eventTime \= 10, k \= 1, startTime \= \[0,2,9], endTime \= \[1,4,10]
**Output:** 6
**Explanation:**
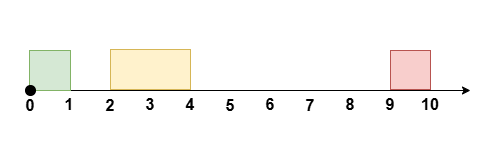
Reschedule the meeting at `[2, 4]` to `[1, 3]`, leaving no meetings during the time `[3, 9]`.
**Example 3:**
**Input:** eventTime \= 5, k \= 2, startTime \= \[0,1,2,3,4], endTime \= \[1,2,3,4,5]
**Output:** 0
**Explanation:**
There is no time during the event not occupied by meetings.
**Constraints:**
- `1 <= eventTime <= 109`
- `n == startTime.length == endTime.length`
- `2 <= n <= 105`
- `1 <= k <= n`
- `0 <= startTime[i] < endTime[i] <= eventTime`
- `endTime[i] <= startTime[i + 1]` where `i` lies in the range `[0, n - 2]`.
|
Medium
|
[
"array",
"greedy",
"sliding-window"
] |
leetcode
|
https://leetcode.com/problems/reschedule-meetings-for-maximum-free-time-i
|
functional
| null | null | null | null |
{
"c": "int maxFreeTime(int eventTime, int k, int* startTime, int startTimeSize, int* endTime, int endTimeSize) {\n \n}",
"cpp": "class Solution {\npublic:\n int maxFreeTime(int eventTime, int k, vector<int>& startTime, vector<int>& endTime) {\n \n }\n};",
"csharp": "public class Solution {\n public int MaxFreeTime(int eventTime, int k, int[] startTime, int[] endTime) {\n \n }\n}",
"dart": "class Solution {\n int maxFreeTime(int eventTime, int k, List<int> startTime, List<int> endTime) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec max_free_time(event_time :: integer, k :: integer, start_time :: [integer], end_time :: [integer]) :: integer\n def max_free_time(event_time, k, start_time, end_time) do\n \n end\nend",
"erlang": "-spec max_free_time(EventTime :: integer(), K :: integer(), StartTime :: [integer()], EndTime :: [integer()]) -> integer().\nmax_free_time(EventTime, K, StartTime, EndTime) ->\n .",
"golang": "func maxFreeTime(eventTime int, k int, startTime []int, endTime []int) int {\n \n}",
"java": "class Solution {\n public int maxFreeTime(int eventTime, int k, int[] startTime, int[] endTime) {\n \n }\n}",
"javascript": "/**\n * @param {number} eventTime\n * @param {number} k\n * @param {number[]} startTime\n * @param {number[]} endTime\n * @return {number}\n */\nvar maxFreeTime = function(eventTime, k, startTime, endTime) {\n \n};",
"kotlin": "class Solution {\n fun maxFreeTime(eventTime: Int, k: Int, startTime: IntArray, endTime: IntArray): Int {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param Integer $eventTime\n * @param Integer $k\n * @param Integer[] $startTime\n * @param Integer[] $endTime\n * @return Integer\n */\n function maxFreeTime($eventTime, $k, $startTime, $endTime) {\n \n }\n}",
"python": "class Solution(object):\n def maxFreeTime(self, eventTime, k, startTime, endTime):\n \"\"\"\n :type eventTime: int\n :type k: int\n :type startTime: List[int]\n :type endTime: List[int]\n :rtype: int\n \"\"\"\n ",
"python3": "class Solution:\n def maxFreeTime(self, eventTime: int, k: int, startTime: List[int], endTime: List[int]) -> int:\n ",
"racket": "(define/contract (max-free-time eventTime k startTime endTime)\n (-> exact-integer? exact-integer? (listof exact-integer?) (listof exact-integer?) exact-integer?)\n )",
"ruby": "# @param {Integer} event_time\n# @param {Integer} k\n# @param {Integer[]} start_time\n# @param {Integer[]} end_time\n# @return {Integer}\ndef max_free_time(event_time, k, start_time, end_time)\n \nend",
"rust": "impl Solution {\n pub fn max_free_time(event_time: i32, k: i32, start_time: Vec<i32>, end_time: Vec<i32>) -> i32 {\n \n }\n}",
"scala": "object Solution {\n def maxFreeTime(eventTime: Int, k: Int, startTime: Array[Int], endTime: Array[Int]): Int = {\n \n }\n}",
"swift": "class Solution {\n func maxFreeTime(_ eventTime: Int, _ k: Int, _ startTime: [Int], _ endTime: [Int]) -> Int {\n \n }\n}",
"typescript": "function maxFreeTime(eventTime: number, k: number, startTime: number[], endTime: number[]): number {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n int maxFreeTime(int eventTime, int k, vector<int>& startTime, vector<int>& endTime) {\n vector<int> gaps;\n int n = startTime.size();\n gaps.push_back(startTime[0]);\n for (int i = 1; i < n; ++i) {\n gaps.push_back(startTime[i] - endTime[i-1]);\n }\n gaps.push_back(eventTime - endTime.back());\n int m = gaps.size();\n if (m <= k + 1) {\n long long total = 0;\n for (int g : gaps) {\n total += g;\n }\n return total;\n }\n long long current_sum = 0;\n for (int i = 0; i < k + 1; ++i) {\n current_sum += gaps[i];\n }\n long long max_sum = current_sum;\n for (int i = k + 1; i < m; ++i) {\n current_sum += gaps[i] - gaps[i - (k + 1)];\n if (current_sum > max_sum) {\n max_sum = current_sum;\n }\n }\n return max_sum;\n }\n};",
"memory": 12600,
"memoryDistribution": "[[12600, 42.8881, \"class Solution {\\npublic:\\n int maxFreeTime(int eventTime, int k, vector<int>& startTime, vector<int>& endTime) {\\n vector<int> gaps;\\n int n = startTime.size();\\n gaps.push_back(startTime[0]);\\n for (int i = 1; i < n; ++i) {\\n gaps.push_back(startTime[i] - endTime[i-1]);\\n }\\n gaps.push_back(eventTime - endTime.back());\\n int m = gaps.size();\\n if (m <= k + 1) {\\n long long total = 0;\\n for (int g : gaps) {\\n total += g;\\n }\\n return total;\\n }\\n long long current_sum = 0;\\n for (int i = 0; i < k + 1; ++i) {\\n current_sum += gaps[i];\\n }\\n long long max_sum = current_sum;\\n for (int i = k + 1; i < m; ++i) {\\n current_sum += gaps[i] - gaps[i - (k + 1)];\\n if (current_sum > max_sum) {\\n max_sum = current_sum;\\n }\\n }\\n return max_sum;\\n }\\n};\"], [120900, 2.1552, \"class Solution {\\npublic:\\n int maxFreeTime(int eventTime, int k, vector<int>& startTime, vector<int>& endTime) {\\n int n=startTime.size();\\n int left=0;\\n int total=0;\\n int ans=0;\\n for(int i=0;i<n;i++){\\n if(i-1>=0)\\n total+=startTime[i]-endTime[i-1];\\n else\\n total+=startTime[i];\\n if(i<k)\\n continue;\\n ans=max(ans,total);\\n if(i-k)\\n total-=startTime[i-k]-endTime[i-k-1];\\n else\\n total-=startTime[i-k]; \\n }\\n total+=eventTime-endTime[n-1];\\n ans=max(ans,total);\\n return ans;\\n }\\n};\"], [121000, 4.3103, \"class Solution {\\npublic:\\n int maxFreeTime(int eventTime, int k, vector<int>& startTime, vector<int>& endTime) {\\n int ans=0;\\n int s = 0;\\n int work = 0;\\n int n = startTime.size();\\n sort(startTime.begin(),startTime.end());\\n sort(endTime.begin(),endTime.end());\\n for(int i=0;i<n;i++){\\n work+=(endTime[i]-startTime[i]);\\n int e = (i==n-1)?eventTime:startTime[i+1];\\n ans = max(e-s - work,ans);\\n if(i-k+1>=0){\\n work-=(endTime[i-k+1]-startTime[i-k+1]);\\n s = endTime[i-k+1];\\n }\\n }\\n return ans;\\n }\\n};\"], [121100, 5.3879, null], [121200, 0.8621, null], [121300, 0.2155, null], [121400, 0.431, null], [121500, 0.2155, null], [121600, 0.2155, null], [123200, 0.431, null], [123300, 3.8793, null], [123400, 5.3879, null], [123500, 1.7241, null], [124100, 0.2155, null], [124200, 0.431, null], [124300, 0.6466, null], [124400, 0.6466, null], [125200, 0.2155, null], [125300, 0.431, null], [125400, 2.5862, null], [125500, 2.3707, null], [125600, 3.2328, null], [125700, 6.8966, null], [125800, 14.2241, null], [125900, 18.1034, null], [126000, 9.0517, null], [126100, 0.2155, null], [127100, 0.2155, null], [127200, 0.431, null], [127300, 0.6466, null], [127400, 0.2155, null], [128000, 0.431, null], [128100, 1.2931, null], [128300, 0.2155, null], [129199, 0.431, null], [130199, 1.2931, null], [130400, 1.7241, null], [130500, 1.0776, null], [130600, 0.431, null], [130699, 0.2155, \"class Solution {\\npublic:\\n int maxFreeTime(int eventTime, int k, vector<int>& startTime, vector<int>& endTime)\\n {\\n if (startTime.empty() || endTime.empty())\\n {\\n return 0;\\n }\\n\\n vector<int> free_spaces = {startTime[0]};\\n int max_free = 0;\\n\\n for (int i = 1; i < startTime.size(); i++)\\n {\\n int t = startTime[i] - endTime[i-1];\\n max_free = max(max_free, t);\\n free_spaces.push_back(t);\\n }\\n\\n if (endTime.back() < eventTime)\\n {\\n int t = eventTime - endTime.back();\\n max_free = max(max_free, t);\\n free_spaces.push_back(t);\\n }\\n\\n vector<int> prefix = {0};\\n int cur_sum = 0;\\n\\n for (int &f : free_spaces)\\n {\\n cur_sum += f;\\n prefix.push_back(cur_sum);\\n }\\n\\n int maxb = 0;\\n for (int i = k; i < prefix.size(); i++)\\n {\\n maxb = max(maxb, prefix[i] - prefix[max(0, i - k - 1)]);\\n }\\n\\n return max(maxb, max_free);\\n }\\n};\"], [135000, 0.6466, \"class Solution {\\npublic:\\n int maxFreeTime(int eventTime, int k, vector<int>& startTime, vector<int>& endTime) {\\n int n = startTime.size();\\n vector<pair<int, int>> v;\\n for(int i=0; i<n; i++){\\n v.emplace_back(startTime[i], endTime[i]);\\n }\\n sort(v.begin(), v.end());\\n vector<int>gp;\\n gp.push_back(v[0].first);\\n for(int i=1; i<n; i++){\\n gp.push_back(v[i].first - v[i-1].second);\\n }\\n gp.push_back(eventTime-v[n-1].second);\\n int maxFree = 0;\\n int wsum = 0;\\n \\n for(int i=0; i<=k; i++){\\n wsum += gp[i];\\n }\\n maxFree = wsum;\\n for(int i=k+1; i<gp.size(); i++){\\n wsum += gp[i] - gp[i-(k+1)];\\n maxFree = max(maxFree, wsum);\\n }\\n return maxFree;\\n }\\n};;\"]]",
"runtime": 8,
"runtimeDistribution": "[[0, 18.75, \"class Solution {\\npublic:\\n int maxFreeTime(int eventTime, int k, vector<int>& startTime, vector<int>& endTime) {\\n int n = startTime.size();\\n vector<int> v(n+1,0);\\n v[0] = startTime[0]-0;\\n v[n] = eventTime-endTime[n-1];\\n for(int i=1;i<n;i++){\\n v[i] = startTime[i]-endTime[i-1];\\n }\\n int ans=0;\\n int temp = 0;\\n for(int i=0;i<(k+1);i++){\\n temp +=v[i];\\n }\\n ans = max(ans,temp);\\n for(int i = 1; i<=(n-k);i++){\\n temp += (v[i+k] - v[i-1]);\\n ans = max(ans,temp);\\n }\\n return ans;\\n }\\n};\"], [1, 5.1724, \"class Solution {\\npublic:\\n int maxFreeTime(int eventTime, int k, vector<int>& startTime, vector<int>& endTime) {\\n vector<int> tri;\\n tri.push_back(startTime[0] - 0);\\n for(int i = 1; i < startTime.size(); i++)\\n tri.push_back(startTime[i] - endTime[i-1]);\\n tri.push_back(eventTime - endTime.back());\\n //\\u627e\\u4e00\\u500b\\u5927\\u5c0f\\u70baK+1 \\u6700\\u5927\\u7684\\n int left = 0, cur = 0, maxTime = 0;\\n for(int i = 0; i < tri.size(); i++){\\n cur += tri[i];\\n if(i - k - 1 >= 0){\\n cur -= tri[left++];\\n }\\n maxTime = max(maxTime, cur);\\n\\n }\\n return maxTime;\\n\\n }\\n};\"], [2, 3.4483, null], [3, 9.6983, null], [4, 14.4397, null], [5, 4.9569, null], [6, 3.6638, null], [7, 5.3879, null], [8, 6.8966, null], [9, 1.2931, null], [10, 2.3707, null], [11, 2.8017, null], [12, 1.5086, null], [13, 0.6466, null], [14, 1.0776, null], [15, 0.6466, null], [16, 0.2155, null], [18, 0.431, null], [19, 0.8621, null], [20, 0.2155, null], [21, 0.431, null], [23, 0.6466, null], [24, 0.431, null], [25, 0.2155, null], [31, 0.2155, null], [32, 0.2155, null], [33, 0.2155, null], [34, 0.2155, null], [37, 0.2155, null], [38, 0.2155, null], [79, 0.2155, null], [82, 0.2155, null], [85, 0.2155, null], [89, 0.431, null], [99, 0.2155, null], [116, 0.2155, null], [121, 0.2155, null], [122, 0.2155, null], [123, 0.6466, null], [125, 0.2155, null], [127, 0.2155, null], [333, 0.2155, null], [341, 0.2155, null], [394, 0.2155, null], [403, 0.2155, null], [767, 0.2155, null], [787, 0.2155, null], [789, 0.2155, null], [790, 0.2155, null], [792, 0.2155, null], [793, 0.2155, null], [794, 0.2155, null], [799, 0.2155, null], [808, 0.6466, null], [809, 0.2155, null], [810, 0.2155, null], [812, 0.2155, \"class Solution {\\npublic:\\n int maxFreeTime(int eventTime, int k, vector<int>& startTime,\\n vector<int>& endTime) {\\n int p = startTime.size();\\n vector<int> gaps;\\n gaps.push_back(startTime[0]);\\n for (int i = 1; i < p; i++) {\\n gaps.push_back(startTime[i] - endTime[i - 1]);\\n cout << gaps[i - 1] << \\\" \\\";\\n }\\n gaps.push_back(eventTime-endTime[p-1]);\\n cout << gaps[p - 1];\\n int n = gaps.size();\\n int ans = 0;\\n for (int i = 0; i <= k; i++) {\\n ans += (i < gaps.size() ? gaps[i] : 0);\\n }\\n int itt = ans;\\n for (int i = k + 1; i < n; i++) {\\n ans = ans + gaps[i] - gaps[i - k - 1];\\n itt = max(ans, itt);\\n }\\n\\n return itt;\\n }\\n};\"], [819, 0.431, \"bool compare(pair<int,int> a,pair<int,int> b)\\n{\\n return a.first<b.first;\\n}\\nclass Solution {\\npublic:\\n int maxFreeTime(int eventTime, int k, vector<int>& startTime, vector<int>& endTime) {\\n vector<pair<int,int>> intervals;\\n intervals.push_back({0,0});\\n for(int i=0;i<startTime.size();i++)\\n {\\n intervals.push_back({startTime[i],endTime[i]});\\n }\\n intervals.push_back({eventTime,eventTime});\\n sort(intervals.begin(),intervals.end());\\n int window_size=k+1;\\n vector<int> gaps;\\n for(int i=0;i<intervals.size()-1;i++)\\n {\\n gaps.push_back(intervals[i+1].first-intervals[i].second);\\n }\\n int sum=0,output=0;\\n for(int i=0;i<gaps.size();i++)\\n {\\n cout<<gaps[i]<<\\\" \\\";\\n if(i-window_size>=0)\\n {\\n sum-=gaps[i-window_size];\\n }\\n sum+=gaps[i];\\n output=max(output,sum);\\n }\\n return output;\\n }\\n};\"]]"
},
"golang": {
"code": "func maxFreeTime(eventTime int, k int, startTime []int, endTime []int) int {\n n := len(startTime)\n if n == 0 {\n return eventTime\n }\n gaps := []int{startTime[0]}\n for i := 1; i < n; i++ {\n gaps = append(gaps, startTime[i]-endTime[i-1])\n }\n gaps = append(gaps, eventTime-endTime[n-1])\n \n s := k + 1\n if s > len(gaps) {\n s = len(gaps)\n }\n if s == 0 {\n return 0\n }\n \n currentSum := 0\n for i := 0; i < s; i++ {\n currentSum += gaps[i]\n }\n maxSum := currentSum\n for i := s; i < len(gaps); i++ {\n currentSum += gaps[i] - gaps[i-s]\n if currentSum > maxSum {\n maxSum = currentSum\n }\n }\n return maxSum\n}",
"memory": 1200,
"memoryDistribution": "[[1200, 81.818, \"func maxFreeTime(eventTime int, k int, startTime []int, endTime []int) int {\\n n := len(startTime)\\n if n == 0 {\\n return eventTime\\n }\\n gaps := []int{startTime[0]}\\n for i := 1; i < n; i++ {\\n gaps = append(gaps, startTime[i]-endTime[i-1])\\n }\\n gaps = append(gaps, eventTime-endTime[n-1])\\n \\n s := k + 1\\n if s > len(gaps) {\\n s = len(gaps)\\n }\\n if s == 0 {\\n return 0\\n }\\n \\n currentSum := 0\\n for i := 0; i < s; i++ {\\n currentSum += gaps[i]\\n }\\n maxSum := currentSum\\n for i := s; i < len(gaps); i++ {\\n currentSum += gaps[i] - gaps[i-s]\\n if currentSum > maxSum {\\n maxSum = currentSum\\n }\\n }\\n return maxSum\\n}\"], [11000, 4.5455, \"func maxFreeTime(eventTime int, k int, startTime []int, endTime []int) int {\\n\\tgaps := []int{}\\n\\tp := 0\\n\\n\\tfor i, start := range startTime {\\n\\t\\tend := endTime[i]\\n gaps = append(gaps, start - p)\\n p = end\\n\\t}\\n gaps = append(gaps, eventTime - p)\\n\\n\\tfreeSum := 0\\n\\tmaxFree := 0\\n\\n\\tfmt.Println(gaps)\\n\\t//\\u6ce8\\u610f k >len(gaps)-1\\u7684\\u60c5\\u6cc1\\n\\tfor i, v := range gaps {\\n\\t\\tfreeSum += v\\n\\n\\t\\t// if k > len(gaps)-1 && i == len(gaps)-1 {\\n\\t\\t// \\treturn freeSum\\n\\t\\t// }\\n\\n\\t\\tif i < k {\\n\\t\\t\\tcontinue\\n\\t\\t}\\n\\n\\t\\tif freeSum > maxFree {\\n\\t\\t\\tmaxFree = freeSum\\n\\t\\t}\\n\\n\\t\\tfreeSum -= gaps[i-k]\\n\\t}\\n\\n\\treturn maxFree\\n}\"], [11400, 4.5455, \"func maxFreeTime(eventTime int, k int, startTime []int, endTime []int) int {\\n\\tn := len(startTime)\\n\\tget := func(i int) int {\\n\\t\\tif i == 0 {\\n\\t\\t\\treturn startTime[0]\\n\\t\\t}\\n\\t\\tif i == n {\\n\\t\\t\\treturn eventTime - endTime[n-1]\\n\\t\\t}\\n\\t\\treturn startTime[i] - endTime[i-1]\\n\\t}\\n\\ts := 0\\n\\tres := 0\\n\\tfor i := range n + 1 {\\n\\t\\ts += get(i)\\n\\t\\tif i < k {\\n\\t\\t\\tcontinue\\n\\t\\t}\\n\\t\\tres = max(res, s)\\n\\t\\ts -= get(i - k)\\n\\t}\\n\\treturn res\\n}\"], [11600, 4.5455, null], [11700, 4.5455, null], [11900, 4.5455, null], [12000, 9.0909, null], [12100, 9.0909, null], [12200, 4.5455, null], [12300, 4.5455, null], [13000, 4.5455, null], [13100, 4.5455, null], [13300, 4.5455, null], [13700, 4.5455, null], [14000, 4.5455, null], [15200, 4.5455, null], [15600, 4.5455, null], [16200, 4.5455, \"func maxFreeTime(eventTime int, k int, startTime []int, endTime []int) int {\\n slices.Sort(startTime)\\n slices.Sort(endTime)\\n emptySlots := [][]int{}\\n prevEnd := 0\\n\\n for i:=0; i<len(startTime); i++ { \\n s := startTime[i]\\n emptySlots = append(emptySlots, []int{prevEnd, s})\\n\\n prevEnd = endTime[i]\\n }\\n\\n if prevEnd < eventTime {\\n emptySlots = append(emptySlots, []int{prevEnd, eventTime})\\n }\\n\\n sum :=0\\n for i:=0; i<=k && i<len(emptySlots); i++{\\n sum += emptySlots[i][1]-emptySlots[i][0]\\n }\\n\\n left := 1\\n right := k+1\\n res := sum\\n for right < len(emptySlots) {\\n prevSlot := emptySlots[left-1][1] - emptySlots[left-1][0]\\n nextSlot := emptySlots[right][1] - emptySlots[right][0]\\n window := sum-prevSlot+nextSlot\\n res = max(res, window)\\n sum = window\\n left++\\n right++\\n }\\n\\n return res \\n}\"], [17800, 4.5455, \"func maxFreeTime(eventTime int, k int, startTime []int, endTime []int) int {\\n n := len(startTime)\\n gaps := make([]int, n+1)\\n gaps[0] = startTime[0]\\n for i := 1; i < n; i++ {\\n gaps[i] = startTime[i] - endTime[i-1]\\n }\\n gaps[n] = eventTime - endTime[n-1]\\n \\n maxInitial := 0\\n for _, gap := range gaps {\\n if gap > maxInitial {\\n maxInitial = gap\\n }\\n }\\n \\n m := len(gaps)\\n l := k + 1\\n if l > m {\\n l = m\\n }\\n if l == 0 {\\n return maxInitial\\n }\\n \\n prefix := make([]int, m+1)\\n for i := 0; i < m; i++ {\\n prefix[i+1] = prefix[i] + gaps[i]\\n }\\n \\n maxSum := 0\\n for i := 0; i <= m-l; i++ {\\n sum := prefix[i+l] - prefix[i]\\n if sum > maxSum {\\n maxSum = sum\\n }\\n }\\n \\n if maxSum > maxInitial {\\n return maxSum\\n }\\n return maxInitial\\n}\"]]",
"runtime": 10,
"runtimeDistribution": "[[0, 27.2727, \"func maxFreeTime(eventTime int, k int, startTime []int, endTime []int) (ans int) {\\n // // \\u5171\\u6709n\\u4e2a\\u4f1a\\u8bae\\uff0c\\u5219\\u5171\\u6709n + 1\\u4e2a\\u7a7a\\u767d\\u65f6\\u95f4\\uff0c\\u6c42\\uff1a\\n // // \\u5728\\u5927\\u5c0f\\u4e3ak\\u7684\\u7a97\\u53e3\\u5185\\uff0c\\u7a7a\\u767d\\u65f6\\u95f4\\u6700\\u5927\\u548c\\n // get := func(n int) int {\\n // if n == 0 {\\n // return startTime[0]\\n // }\\n // if n == len(startTime) {\\n // return eventTime - endTime[n]\\n // }\\n // }\\n // res, sum := 0, 0\\n // for i, v := range startTime {\\n // if i == 0 && startTime[i] > 0 {\\n // sum += \\n // }\\n // }\\n \\tn := len(startTime)\\n\\tget := func(i int) int {\\n\\t\\tif i == 0 {\\n\\t\\t\\treturn startTime[0]\\n\\t\\t}\\n\\t\\tif i == n {\\n\\t\\t\\treturn eventTime - endTime[n-1]\\n\\t\\t}\\n\\t\\treturn startTime[i] - endTime[i-1]\\n\\t}\\n\\n\\ts := 0\\n\\tfor i := range n + 1 {\\n\\t\\ts += get(i)\\n\\t\\tif i < k {\\n\\t\\t\\tcontinue\\n\\t\\t}\\n\\t\\tans = max(ans, s)\\n\\t\\ts -= get(i - k)\\n\\t}\\n\\treturn\\n}\"], [1, 4.5455, \"func maxFreeTime(eventTime int, k int, startTime []int, endTime []int) int {\\n\\tn := len(startTime)\\n\\tget := func(i int) int {\\n\\t\\tif i == 0 {\\n\\t\\t\\treturn startTime[0]\\n\\t\\t}\\n\\t\\tif i == n {\\n\\t\\t\\treturn eventTime - endTime[n-1]\\n\\t\\t}\\n\\t\\treturn startTime[i] - endTime[i-1]\\n\\t}\\n\\ts := 0\\n\\tres := 0\\n\\tfor i := range n + 1 {\\n\\t\\ts += get(i)\\n\\t\\tif i < k {\\n\\t\\t\\tcontinue\\n\\t\\t}\\n\\t\\tres = max(res, s)\\n\\t\\ts -= get(i - k)\\n\\t}\\n\\treturn res\\n}\"], [3, 9.0909, null], [4, 4.5455, null], [5, 4.5455, null], [6, 4.5455, null], [8, 9.0909, null], [10, 4.5455, null], [16, 4.5455, null], [17, 4.5455, null], [19, 4.5455, null], [39, 4.5455, \"func maxFreeTime(eventTime int, k int, startTime []int, endTime []int) int {\\n\\tgaps := []int{}\\n\\tp := 0\\n\\n\\t//i stands for ith gap\\n\\tfor i, start := range startTime {\\n\\t\\tend := endTime[i]\\n gaps = append(gaps, start - p)\\n p = end\\n\\t}\\n gaps = append(gaps, eventTime - p)\\n\\n\\tfreeSum := 0\\n\\tmaxFree := 0\\n\\n\\tfmt.Println(gaps)\\n\\t//\\u6ce8\\u610f k >len(gaps)-1\\u7684\\u60c5\\u6cc1\\n\\tfor i, v := range gaps {\\n\\t\\tfreeSum += v\\n\\n\\t\\tif k > len(gaps)-1 && i == len(gaps)-1 {\\n\\t\\t\\treturn freeSum\\n\\t\\t}\\n\\n\\t\\tif i < k {\\n\\t\\t\\tcontinue\\n\\t\\t}\\n\\n\\t\\tif freeSum > maxFree {\\n\\t\\t\\tmaxFree = freeSum\\n\\t\\t}\\n\\n\\t\\tfreeSum -= gaps[i-k]\\n\\t}\\n\\n\\treturn maxFree\\n}\"], [41, 4.5455, \"func maxFreeTime(eventTime int, k int, startTime []int, endTime []int) int {\\n\\tgaps := []int{}\\n\\tp := 0\\n\\n\\tfor i, start := range startTime {\\n\\t\\tend := endTime[i]\\n gaps = append(gaps, start - p)\\n p = end\\n\\t}\\n gaps = append(gaps, eventTime - p)\\n\\n\\tfreeSum := 0\\n\\tmaxFree := 0\\n\\n\\tfmt.Println(gaps)\\n\\t//\\u6ce8\\u610f k >len(gaps)-1\\u7684\\u60c5\\u6cc1\\n\\tfor i, v := range gaps {\\n\\t\\tfreeSum += v\\n\\n\\t\\t// if k > len(gaps)-1 && i == len(gaps)-1 {\\n\\t\\t// \\treturn freeSum\\n\\t\\t// }\\n\\n\\t\\tif i < k {\\n\\t\\t\\tcontinue\\n\\t\\t}\\n\\n\\t\\tif freeSum > maxFree {\\n\\t\\t\\tmaxFree = freeSum\\n\\t\\t}\\n\\n\\t\\tfreeSum -= gaps[i-k]\\n\\t}\\n\\n\\treturn maxFree\\n}\"]]"
},
"java": {
"code": "class Solution {\n public int maxFreeTime(int eventTime, int k, int[] startTime, int[] endTime) {\n List<Long> gaps = new ArrayList<>();\n int n = startTime.length;\n gaps.add((long) startTime[0] - 0L);\n for (int i = 1; i < n; i++) {\n gaps.add((long) startTime[i] - endTime[i - 1]);\n }\n gaps.add((long) eventTime - endTime[n - 1]);\n \n int m = gaps.size();\n int windowSize = k + 1;\n if (windowSize >= m) {\n long total = 0;\n for (long gap : gaps) {\n total += gap;\n }\n return (int) total;\n }\n \n long maxSum = 0;\n long currentSum = 0;\n for (int i = 0; i < windowSize; i++) {\n currentSum += gaps.get(i);\n }\n maxSum = currentSum;\n for (int i = windowSize; i < m; i++) {\n currentSum += gaps.get(i) - gaps.get(i - windowSize);\n if (currentSum > maxSum) {\n maxSum = currentSum;\n }\n }\n return (int) maxSum;\n }\n}",
"memory": 5800,
"memoryDistribution": "[[5800, 82.558, \"class Solution {\\n public int maxFreeTime(int eventTime, int k, int[] startTime, int[] endTime) {\\n List<Long> gaps = new ArrayList<>();\\n int n = startTime.length;\\n gaps.add((long) startTime[0] - 0L);\\n for (int i = 1; i < n; i++) {\\n gaps.add((long) startTime[i] - endTime[i - 1]);\\n }\\n gaps.add((long) eventTime - endTime[n - 1]);\\n \\n int m = gaps.size();\\n int windowSize = k + 1;\\n if (windowSize >= m) {\\n long total = 0;\\n for (long gap : gaps) {\\n total += gap;\\n }\\n return (int) total;\\n }\\n \\n long maxSum = 0;\\n long currentSum = 0;\\n for (int i = 0; i < windowSize; i++) {\\n currentSum += gaps.get(i);\\n }\\n maxSum = currentSum;\\n for (int i = windowSize; i < m; i++) {\\n currentSum += gaps.get(i) - gaps.get(i - windowSize);\\n if (currentSum > maxSum) {\\n maxSum = currentSum;\\n }\\n }\\n return (int) maxSum;\\n }\\n}\"], [55300, 0.3876, \"class Solution { \\n public int maxFreeTime(int eventTime, int k, int[] startTime, int[] endTime) { \\n int n = startTime.length; \\n List<Integer> gaps = new ArrayList<>(); \\n gaps.add(startTime[0]); \\n for (int i = 1; i < n; i++) { \\n gaps.add(startTime[i] - endTime[i - 1]); \\n } \\n gaps.add(eventTime - endTime[n - 1]); \\n int windowSum = 0; \\n for (int i = 0; i < k + 1; i++)\\n windowSum += gaps.get(i); \\n int maxFree = windowSum; \\n for (int i = k + 1; i < gaps.size(); i++) {\\n windowSum += gaps.get(i) - gaps.get(i - (k + 1)); \\n maxFree = Math.max(maxFree, windowSum); \\n } \\n return maxFree; \\n } \\n}\"], [55600, 0.3876, \"class Solution {\\n public int maxFreeTime(int eventTime, int k, int[] startTime, int[] endTime) {\\n List<Integer> list = new ArrayList<>();\\n\\n int current = 0;\\n int n = startTime.length;\\n\\n for(int i=0;i<n;i++){\\n list.add(startTime[i] - current);\\n current = endTime[i];\\n }\\n\\n list.add(eventTime - current);\\n\\n int ans = 0;\\n for(int i=0;i<Math.min(n+1, k+1);i++){\\n ans += list.get(i);\\n }\\n\\n int tempAns = ans;\\n for(int i=k+1;i<n+1;i++){\\n tempAns += list.get(i);\\n tempAns -= list.get(i - (k+1));\\n\\n ans = Math.max(ans, tempAns);\\n }\\n \\n return ans;\\n }\\n}\"], [55700, 0.3876, null], [56700, 0.7752, null], [56900, 0.3876, null], [57000, 1.938, null], [57100, 2.3256, null], [57200, 3.1008, null], [57300, 1.1628, null], [57400, 3.876, null], [57500, 2.7132, null], [57600, 1.1628, null], [57700, 1.1628, null], [57900, 0.3876, null], [58000, 0.7752, null], [58100, 0.3876, null], [60100, 0.3876, null], [60200, 0.3876, null], [60300, 0.7752, null], [60400, 0.7752, null], [60600, 0.7752, null], [60700, 1.1628, null], [60800, 0.3876, null], [60900, 0.3876, null], [61000, 0.7752, null], [61300, 0.3876, null], [61400, 0.3876, null], [61500, 0.7752, null], [61600, 1.5504, null], [61700, 1.5504, null], [61800, 1.938, null], [61900, 1.938, null], [62000, 1.5504, null], [62100, 0.7752, null], [62200, 1.1628, null], [62300, 1.1628, null], [62700, 0.3876, null], [62800, 0.7752, null], [63000, 1.1628, null], [63100, 3.876, null], [63200, 3.4884, null], [63300, 10.0775, null], [63400, 8.1395, null], [63500, 4.6512, null], [63600, 6.2016, null], [63700, 3.876, null], [63800, 3.4884, null], [63900, 3.876, null], [64000, 0.7752, null], [64099, 0.7752, null], [64200, 1.1628, null], [64300, 0.3876, null], [64400, 0.7752, \"class Solution {\\n public int maxFreeTime(int eventTime, int k, int[] startTime, int[] endTime) {\\n int[][] intervals = new int[startTime.length][2];\\n int[] nums = new int[startTime.length + 1];\\n\\n for (int i = 0; i < startTime.length; i++) {\\n intervals[i][0] = startTime[i];\\n intervals[i][1] = endTime[i];\\n }\\n // Arrays.sort(intervals, (a, b) -> a[0] - b[0]);\\n\\n int j = 0;\\n for (int i = 0; i < intervals.length; i++) {\\n if (i == 0) {\\n nums[j++] = intervals[i][0];\\n }\\n if (i > 0) {\\n nums[j++] = intervals[i][0] - intervals[i - 1][1];\\n }\\n if (i == intervals.length - 1) {\\n nums[j++] = eventTime - intervals[i][1];\\n }\\n }\\n\\n int l = 0;\\n int res = 0;\\n int sum = 0;\\n k += 1;\\n\\n for (int r = 0; r < nums.length; r++) {\\n sum += nums[r];\\n k--;\\n if (k < 0) {\\n sum -= nums[l++];\\n k++;\\n }\\n res = Math.max(sum, res);\\n }\\n\\n return res;\\n }\\n}\\n\\n/*\\n [1,1,0]\\n\\n [0,1,5,0]\\n*/\"], [64700, 0.7752, \"class Solution {\\n public int maxFreeTime(int eventTime, int k, int[] startTime, int[] endTime) {\\n int gapsSum = 0, maxGap = 0, gapsCount = k + 1;\\n Queue<Integer> gaps = new LinkedList<>();\\n int prevEnd = 0;\\n for (int i = 0; i < startTime.length; i++) {\\n int gap = startTime[i] - prevEnd;\\n gaps.add(gap);\\n gapsSum += gap;\\n maxGap = Math.max(maxGap, gapsSum);\\n if (gaps.size() == gapsCount) {\\n gapsSum -= gaps.remove();\\n }\\n prevEnd = endTime[i];\\n }\\n gapsSum += eventTime - endTime[endTime.length - 1];\\n maxGap = Math.max(maxGap, gapsSum);\\n return maxGap;\\n }\\n}\"]]",
"runtime": 5,
"runtimeDistribution": "[[1, 19.3798, \"class Solution {\\n public int maxFreeTime(int eventTime, int k, int[] startTime, int[] endTime) {\\n int ans = 0, n = startTime.length;\\n for (int i = 0, j = 0, sum = 0; j < n; ++j) {\\n sum += endTime[j] - startTime[j];\\n if (j - i + 1 > k) {\\n sum -= endTime[i] - startTime[i];\\n i++;\\n }\\n int nextTime = eventTime;\\n if (j + 1 < n) nextTime = startTime[j + 1];\\n if (i == 0) {\\n ans = Math.max(ans, nextTime - sum); \\n } else {\\n ans = Math.max(ans, nextTime - sum - endTime[i - 1]);\\n }\\n }\\n return ans;\\n }\\n}\"], [2, 39.5349, \"class Solution {\\n public int maxFreeTime(int eventTime, int k, int[] startTime, int[] endTime) {\\n int n = startTime.length;\\n int[] gaps = new int[n + 1];\\n\\n // Calculate initial and final gaps\\n gaps[0] = startTime[0]; // Time before the first event\\n gaps[n] = eventTime - endTime[n - 1]; // Time after the last event\\n\\n // Calculate gaps between events\\n for (int i = 1; i < n; i++) {\\n gaps[i] = startTime[i] - endTime[i - 1];\\n }\\n\\n // Sliding window of size k + 1\\n int window = 0;\\n for (int i = 0; i <= k; i++) {\\n window += gaps[i];\\n }\\n\\n int maxGap = window;\\n for (int i = k + 1; i <= n; i++) {\\n window += gaps[i] - gaps[i - (k + 1)];\\n maxGap = Math.max(maxGap, window);\\n }\\n\\n return maxGap;\\n }\\n}\\n\"], [3, 4.6512, null], [4, 12.4031, null], [5, 8.1395, null], [6, 2.3256, null], [7, 1.5504, null], [8, 1.1628, null], [9, 0.3876, null], [10, 0.7752, null], [11, 0.3876, null], [12, 1.5504, null], [13, 0.3876, null], [14, 0.3876, null], [15, 0.3876, null], [21, 0.3876, null], [22, 0.3876, null], [30, 0.3876, \"class Solution {\\n public int maxFreeTime(int eventTime, int k, int[] startTime, int[] endTime) {\\n int n = startTime.length;\\n List<Integer> gaps = new ArrayList<>();\\n if (startTime[0] > 0)\\n gaps.add(startTime[0] - 0);\\n for (int i = 1; i < n; i++) {\\n int gap = startTime[i] - endTime[i - 1];\\n // if (gap > 0)\\n gaps.add(gap);\\n }\\n\\n int gap = eventTime - endTime[n - 1];\\n if (gap > 0)\\n gaps.add(gap);\\n\\n show(gaps);\\n\\n int ans = Integer.MIN_VALUE;\\n\\n int curSum = 0;\\n for (int l = 0, r = 0; r < gaps.size(); r++) {\\n curSum += gaps.get(r);\\n if (r - l + 1 == k + 1) {\\n ans = Math.max(ans, curSum);\\n curSum -= gaps.get(l);\\n l++;\\n }\\n }\\n\\n ans = Math.max(ans, curSum);\\n\\n return ans;\\n\\n }\\n\\n void show(Object o) {\\n System.out.println(o);\\n }\\n\\n}\"], [31, 0.3876, \"class Solution {\\n public int maxFreeTime(int eventTime, int k, int[] startTime, int[] endTime) {\\n List<Integer> gaps = new ArrayList<>();\\n int st = 0;\\n if(startTime[0]-st>0) gaps.add(startTime[0]-st);\\n\\n for(int i=1;i<startTime.length;i++) {\\n gaps.add(startTime[i] - endTime[i-1]);\\n }\\n\\n if(eventTime-endTime[endTime.length-1]>0) gaps.add(eventTime - endTime[endTime.length-1]);\\n\\n System.out.println(gaps.toString());\\n\\n // now wind of K + 1 can be added;\\n int currSum = 0;\\n int maxSum = 0;\\n st = 0;\\n for(int i=0;i<gaps.size();i++) {\\n currSum += gaps.get(i);\\n\\n if(i-st + 1 > (k+1)) {\\n currSum -= gaps.get(st);\\n st++;\\n }\\n\\n maxSum = Math.max(maxSum, currSum);\\n }\\n\\n return maxSum;\\n }\\n}\"]]"
},
"javascript": {
"code": "var maxFreeTime = function(eventTime, k, startTime, endTime) {\n const n = startTime.length;\n const free = [];\n let prevEnd = 0;\n for (let i = 0; i < n; i++) {\n const currentStart = startTime[i];\n free.push(currentStart - prevEnd);\n prevEnd = endTime[i];\n }\n free.push(eventTime - prevEnd);\n \n let maxFree = 0;\n for (const val of free) {\n if (val > maxFree) {\n maxFree = val;\n }\n }\n \n const totalSum = free.reduce((a, b) => a + b, 0);\n const m = free.length;\n let sumMax;\n \n if (k + 1 >= m) {\n sumMax = totalSum;\n } else {\n let currentSum = 0;\n for (let i = 0; i < k + 1; i++) {\n currentSum += free[i];\n }\n sumMax = currentSum;\n for (let i = k + 1; i < m; i++) {\n currentSum += free[i] - free[i - (k + 1)];\n sumMax = Math.max(sumMax, currentSum);\n }\n }\n \n return Math.max(maxFree, sumMax);\n};",
"memory": 7800,
"memoryDistribution": "[[7800, 40.0, \"var maxFreeTime = function(eventTime, k, startTime, endTime) {\\n const n = startTime.length;\\n const free = [];\\n let prevEnd = 0;\\n for (let i = 0; i < n; i++) {\\n const currentStart = startTime[i];\\n free.push(currentStart - prevEnd);\\n prevEnd = endTime[i];\\n }\\n free.push(eventTime - prevEnd);\\n \\n let maxFree = 0;\\n for (const val of free) {\\n if (val > maxFree) {\\n maxFree = val;\\n }\\n }\\n \\n const totalSum = free.reduce((a, b) => a + b, 0);\\n const m = free.length;\\n let sumMax;\\n \\n if (k + 1 >= m) {\\n sumMax = totalSum;\\n } else {\\n let currentSum = 0;\\n for (let i = 0; i < k + 1; i++) {\\n currentSum += free[i];\\n }\\n sumMax = currentSum;\\n for (let i = k + 1; i < m; i++) {\\n currentSum += free[i] - free[i - (k + 1)];\\n sumMax = Math.max(sumMax, currentSum);\\n }\\n }\\n \\n return Math.max(maxFree, sumMax);\\n};\"], [75700, 10.0, \"/**\\n * @param {number} eventTime\\n * @param {number} k\\n * @param {number[]} startTime\\n * @param {number[]} endTime\\n * @return {number}\\n */\\nvar maxFreeTime = function(eventTime, k, startTime, endTime) {\\n // Can assume startTime & endTime are sorted??\\n const n = startTime.length;\\n const gap = [];\\n const min = startTime[0];\\n const max = endTime[n - 1];\\n if (min > 0) {\\n gap.push(min); // gap before the first meeting start\\n }\\n for (let i = 0; i < n; i++) {\\n if (i < n - 1 && startTime[i + 1] >= endTime[i]) {\\n gap.push(startTime[i + 1] - endTime[i]); // gap in between meetings, zero length 0 can exist\\n }\\n }\\n if (max < eventTime) {\\n gap.push(eventTime - max); // gap after the last meeting end\\n }\\n if (gap.length === 0) {\\n return 0;\\n }\\n if (gap.length === 1) {\\n return gap[0];\\n }\\n\\n let maxSum = 0;\\n let sum = 0;\\n\\n for (let i = 0; i < gap.length; i++) { // we can merge k + 1 gap, so the window is size k + 1\\n sum += gap[i]; // enter window\\n\\n if (i < k) { // extend window\\n continue;\\n }\\n\\n maxSum = Math.max(maxSum, sum);\\n sum -= gap[i - k]; // remove from window\\n }\\n\\n return Math.max(maxSum, sum); // use sum in case the full length of window is not reached\\n};\"], [75900, 20.0, \"var maxFreeTime = function(eventTime, k, startTime, endTime) {\\n const n = startTime.length;\\n const gaps = [];\\n if (n === 0) return eventTime;\\n gaps.push(startTime[0]); // Initial gap\\n for (let i = 0; i < n - 1; i++) {\\n gaps.push(startTime[i + 1] - endTime[i]);\\n }\\n gaps.push(eventTime - endTime[n - 1]); // Final gap\\n\\n // Compute merged sum using sliding window\\n let maxMerged = 0, currentSum = 0, windowStart = 0;\\n for (let windowEnd = 0; windowEnd < gaps.length; windowEnd++) {\\n currentSum += gaps[windowEnd];\\n while (windowEnd - windowStart + 1 > k + 1) {\\n currentSum -= gaps[windowStart++];\\n }\\n maxMerged = Math.max(maxMerged, currentSum);\\n }\\n\\n // Compute max_gap_b\\n let maxGapB = 0;\\n for (let i = 0; i < gaps.length; i++) {\\n const gap = gaps[i];\\n let case0 = gap, case1 = 0, case2 = 0;\\n let leftExp = 0, rightExp = 0;\\n\\n if (i === 0) { // Initial gap\\n const nextMeeting = 0;\\n const rightLimit = (nextMeeting + 1 < n) ? startTime[nextMeeting + 1] : eventTime;\\n rightExp = rightLimit - endTime[nextMeeting];\\n leftExp = 0;\\n case1 = gap + rightExp;\\n case2 = case1;\\n } else if (i === gaps.length - 1) { // Final gap\\n const prevMeeting = n - 1;\\n const leftLimit = (prevMeeting > 0) ? endTime[prevMeeting - 1] : 0;\\n leftExp = startTime[prevMeeting] - leftLimit;\\n rightExp = 0;\\n case1 = gap + leftExp;\\n case2 = case1;\\n } else { // Between gaps\\n const betweenIndex = i - 1;\\n const prevMeeting = betweenIndex;\\n const nextMeeting = betweenIndex + 1;\\n\\n // Left expansion for prevMeeting\\n const leftLimit = (prevMeeting === 0) ? 0 : endTime[prevMeeting - 1];\\n leftExp = startTime[prevMeeting] - leftLimit;\\n\\n // Right expansion for nextMeeting\\n const rightLimit = (nextMeeting + 1 < n) ? startTime[nextMeeting + 1] : eventTime;\\n rightExp = rightLimit - endTime[nextMeeting];\\n\\n case1 = gap + Math.max(leftExp, rightExp);\\n case2 = gap + leftExp + rightExp;\\n }\\n\\n if (k >= 0) maxGapB = Math.max(maxGapB, case0);\\n if (k >= 1) maxGapB = Math.max(maxGapB, case1);\\n if (k >= 2) maxGapB = Math.max(maxGapB, case2);\\n }\\n\\n return Math.max(maxMerged, maxGapB);\\n};\"], [76100, 10.0, null], [76300, 10.0, null], [77500, 10.0, null], [80500, 10.0, null], [80600, 10.0, \"/**\\n * @param {number} eventTime\\n * @param {number} k\\n * @param {number[]} startTime\\n * @param {number[]} endTime\\n * @return {number}\\n */\\nvar maxFreeTime = function (eventTime, k, startTime, endTime) {\\n const n = startTime.length;\\n const prefix = new Array(n + 1).fill(0);\\n\\n for (let i = 1; i <= n; i++) {\\n prefix[i] = prefix[i - 1] + (endTime[i - 1] - startTime[i - 1]);\\n }\\n\\n let leftCandidate = 0;\\n const lim = Math.min(k, n - 1);\\n for (let j = 0; j <= lim; j++) {\\n leftCandidate = Math.max(leftCandidate, startTime[j] - prefix[j]);\\n }\\n\\n let rightCandidate = 0;\\n const startI = Math.max(0, n - 1 - k);\\n for (let i = startI; i < n; i++) {\\n rightCandidate = Math.max(rightCandidate, eventTime - (endTime[i] + (prefix[n] - prefix[i + 1])));\\n }\\n\\n const X = new Array(n);\\n const Y = new Array(n);\\n for (let j = 0; j < n; j++) {\\n X[j] = startTime[j] - prefix[j];\\n Y[j] = endTime[j] - prefix[j + 1];\\n }\\n\\n let middleCandidate = 0;\\n const dq = [];\\n for (let j = 1; j < n; j++) {\\n const L = Math.max(0, j - k - 1);\\n while (dq.length && dq[0] < L) dq.shift();\\n while (dq.length && Y[dq[dq.length - 1]] >= Y[j - 1]) dq.pop();\\n dq.push(j - 1);\\n const candidate = X[j] - Y[dq[0]];\\n middleCandidate = Math.max(middleCandidate, candidate);\\n }\\n\\n const candidateAll = (k === n) ? eventTime - prefix[n] : 0;\\n const ans = Math.max(leftCandidate, rightCandidate, middleCandidate, candidateAll);\\n return Math.max(ans, 0);\\n};\"], [80800, 10.0, \"/**\\n * @param {number} eventTime\\n * @param {number} k\\n * @param {number[]} startTime\\n * @param {number[]} endTime\\n * @return {number}\\n */\\nvar maxFreeTime = function(eventTime, k, startTime, endTime) {\\n startTime.unshift(-1);\\n endTime.unshift(0);\\n\\n startTime.push(eventTime);\\n endTime.push(eventTime+1);\\n let sum = 0, psums = [0];\\n for (let [i, st] of startTime.entries()) {\\n psums.push(sum += endTime[i] - st);\\n }\\n\\n //console.log({psums, startTime, endTime});\\n let best = 0;\\n for (let i = k+1; i < startTime.length; i++) {\\n let j = i - k-1;\\n let gap = startTime[i] - endTime[j];\\n let within = psums[i] - psums[j+1];\\n //console.log({i, j, gap, within});\\n\\n best = Math.max(best, gap - within);\\n }\\n return best;\\n};\"]]",
"runtime": 11,
"runtimeDistribution": "[[5, 10.0, \"/**\\n * @param {number} eventTime\\n * @param {number} k\\n * @param {number[]} startTime\\n * @param {number[]} endTime\\n * @return {number}\\n */\\nvar maxFreeTime = function(eventTime, k, startTime, endTime) {\\n // Can assume startTime & endTime are sorted??\\n const n = startTime.length;\\n const gap = [];\\n const min = startTime[0];\\n const max = endTime[n - 1];\\n if (min > 0) {\\n gap.push(min); // gap before the first meeting start\\n }\\n for (let i = 0; i < n; i++) {\\n if (i < n - 1 && startTime[i + 1] >= endTime[i]) {\\n gap.push(startTime[i + 1] - endTime[i]); // gap in between meetings, zero length 0 can exist\\n }\\n }\\n if (max < eventTime) {\\n gap.push(eventTime - max); // gap after the last meeting end\\n }\\n if (gap.length === 0) {\\n return 0;\\n }\\n if (gap.length === 1) {\\n return gap[0];\\n }\\n\\n let maxSum = 0;\\n let sum = 0;\\n\\n for (let i = 0; i < gap.length; i++) { // we can merge k + 1 gap, so the window is size k + 1\\n sum += gap[i]; // enter window\\n\\n if (i < k) { // extend window\\n continue;\\n }\\n\\n maxSum = Math.max(maxSum, sum);\\n sum -= gap[i - k]; // remove from window\\n }\\n\\n return Math.max(maxSum, sum); // use sum in case the full length of window is not reached\\n};\"], [6, 20.0, \"/**\\n * @param {number} eventTime\\n * @param {number} k\\n * @param {number[]} startTime\\n * @param {number[]} endTime\\n * @return {number}\\n */\\nvar maxFreeTime = function(eventTime, k, startTime, endTime) {\\n let n = startTime.length;\\n let gaps = [];\\n\\n // Calculate the gaps between meetings\\n gaps.push(startTime[0]);\\n for (let i = 1; i < n; i++) {\\n gaps.push(startTime[i] - endTime[i - 1]);\\n }\\n\\n gaps.push(eventTime - endTime[endTime.length - 1]);\\n\\n let windowSum = gaps.slice(0, k+1).reduce((a,b) => a + b, 0);\\n let maxFree = windowSum;\\n\\n for (let i = k + 1; i < gaps.length; i++) {\\n windowSum += gaps[i] - gaps[i-k-1];\\n maxFree = Math.max(maxFree, windowSum);\\n }\\n\\n return maxFree;\\n\\n};\"], [8, 10.0, null], [9, 20.0, null], [11, 40.0, \"var maxFreeTime = function(eventTime, k, startTime, endTime) {\\n const n = startTime.length;\\n const free = [];\\n let prevEnd = 0;\\n for (let i = 0; i < n; i++) {\\n const currentStart = startTime[i];\\n free.push(currentStart - prevEnd);\\n prevEnd = endTime[i];\\n }\\n free.push(eventTime - prevEnd);\\n \\n let maxFree = 0;\\n for (const val of free) {\\n if (val > maxFree) {\\n maxFree = val;\\n }\\n }\\n \\n const totalSum = free.reduce((a, b) => a + b, 0);\\n const m = free.length;\\n let sumMax;\\n \\n if (k + 1 >= m) {\\n sumMax = totalSum;\\n } else {\\n let currentSum = 0;\\n for (let i = 0; i < k + 1; i++) {\\n currentSum += free[i];\\n }\\n sumMax = currentSum;\\n for (let i = k + 1; i < m; i++) {\\n currentSum += free[i] - free[i - (k + 1)];\\n sumMax = Math.max(sumMax, currentSum);\\n }\\n }\\n \\n return Math.max(maxFree, sumMax);\\n};\"], [22, 20.0, \"/**\\n * @param {number} eventTime\\n * @param {number} k\\n * @param {number[]} startTime\\n * @param {number[]} endTime\\n * @return {number}\\n */\\nvar maxFreeTime = function(eventTime, k, startTimes, endTimes) {\\n const len = startTimes.length\\n const sumFL = new Array(len)\\n let result = 0\\n sumFL[-1] = 0\\n\\n for (const [i, startTime] of startTimes.entries()) {\\n const endTime = endTimes[i]\\n const duration = endTime - startTime\\n sumFL[i] = duration + sumFL[i - 1]\\n }\\n\\n for (let i = k - 1; i < len; i++) {\\n const right = i + 1 < len ? startTimes[i + 1] : eventTime\\n const left = i - k > -1 ? endTimes[i - k] : 0\\n\\n const totalDuration = sumFL[i] - sumFL[i - k]\\n const space = right - left - totalDuration\\n result = Math.max(result, space)\\n }\\n\\n return result\\n};\"], [55, 10.0, \"/**\\n * @param {number} eventTime\\n * @param {number} k\\n * @param {number[]} startTime\\n * @param {number[]} endTime\\n * @return {number}\\n */\\nvar maxFreeTime = function(eventTime, k, startTime, endTime) {\\n let n = startTime.length;\\n let intervals = [];\\n for (let i = 0; i < n; i++) {\\n intervals.push([startTime[i], endTime[i]]);\\n }\\n \\n let maxFree = 0;\\n \\n // The initial free times are before the first meeting, between meetings, and after the last meeting\\n let initialFree = [];\\n initialFree.push(intervals[0][0] - 0);\\n for (let i = 1; i < n; i++) {\\n initialFree.push(intervals[i][0] - intervals[i-1][1]);\\n }\\n initialFree.push(eventTime - intervals[n-1][1]);\\n \\n if (k === 0) {\\n return Math.max(...initialFree);\\n }\\n \\n // We can merge up to k+1 adjacent free times by moving k meetings\\n let maxWindow = 0;\\n let currentSum = 0;\\n for (let i = 0; i < initialFree.length; i++) {\\n if (i < k + 1) {\\n currentSum += initialFree[i];\\n maxWindow = currentSum;\\n } else {\\n currentSum += initialFree[i] - initialFree[i - (k + 1)];\\n maxWindow = Math.max(maxWindow, currentSum);\\n }\\n }\\n \\n return maxWindow;\\n};\"]]"
},
"python3": {
"code": "class Solution:\n def maxFreeTime(self, eventTime: int, k: int, startTime: List[int], endTime: List[int]) -> int:\n n = len(startTime)\n gaps = []\n gaps.append(startTime[0])\n for i in range(n - 1):\n gaps.append(startTime[i + 1] - endTime[i])\n gaps.append(eventTime - endTime[-1])\n \n window_size = k + 1\n if len(gaps) <= window_size:\n return sum(gaps)\n \n current_sum = sum(gaps[:window_size])\n max_sum = current_sum\n for i in range(window_size, len(gaps)):\n current_sum += gaps[i] - gaps[i - window_size]\n if current_sum > max_sum:\n max_sum = current_sum\n \n return max_sum",
"memory": 3700,
"memoryDistribution": "[[3700, 36.4159, \"from typing import List\\n\\nclass Solution:\\n def maxFreeTime(self, eventTime: int, k: int, startTime: List[int], endTime: List[int]) -> int:\\n n = len(startTime)\\n gaps = []\\n gaps.append(startTime[0])\\n for i in range(n - 1):\\n gaps.append(startTime[i + 1] - endTime[i])\\n gaps.append(eventTime - endTime[-1])\\n \\n window_size = k + 1\\n if len(gaps) <= window_size:\\n return sum(gaps)\\n \\n current_sum = sum(gaps[:window_size])\\n max_sum = current_sum\\n for i in range(window_size, len(gaps)):\\n current_sum += gaps[i] - gaps[i - window_size]\\n if current_sum > max_sum:\\n max_sum = current_sum\\n \\n return max_sum\"], [35700, 0.289, \"class Solution:\\n def maxFreeTime(self, eventTime: int, k: int, startTime: List[int], endTime: List[int]) -> int:\\n startTime.append(eventTime)\\n endTime.append(eventTime)\\n j=0\\n meet=0\\n q=deque()\\n cou=0\\n final=0\\n ans=0\\n while j<(eventTime):\\n if j<=startTime[meet] and cou!=k+1:\\n ans+=startTime[meet]-j\\n q.append(startTime[meet]-j)\\n j=endTime[meet]\\n meet+=1\\n cou+=1\\n else:\\n ans+=startTime[meet]-j\\n ans=ans-q.popleft()\\n q.append(startTime[meet]-j)\\n j=endTime[meet]\\n meet+=1\\n final=max(ans,final)\\n return final\\n \\n \\n\\n\\n\\n\\n\\n\\n\\n\\n \"], [35800, 0.8671, \"\\nclass Solution:\\n def maxFreeTime(self, eventTime: int, k: int, startTime: List[int], endTime: List[int]) -> int:\\n n = len(startTime)\\n free = [0] * n\\n free[0] = startTime[0] - 0\\n \\n for i in range(1, n):\\n free[i] = startTime[i] - endTime[i-1]\\n free.append(eventTime - endTime[-1])\\n\\n if max(free) == 0:\\n return 0\\n \\n maxm = csum = sum(free[:k+1])\\n \\n for i in range(k+1, len(free)):\\n csum += free[i] - free[i-k-1]\\n maxm = max(maxm, csum)\\n return maxm\\n\\n\\n\\n\\n\"], [35900, 2.6012, null], [36000, 6.0694, null], [36100, 9.2486, null], [36200, 15.3179, null], [36300, 13.0058, null], [36400, 4.6243, null], [36500, 2.0231, null], [36600, 0.8671, null], [36700, 0.8671, null], [36800, 0.8671, null], [36900, 1.1561, null], [37000, 2.0231, null], [37100, 1.7341, null], [37200, 2.0231, null], [37300, 5.2023, null], [37400, 1.4451, null], [37500, 0.289, null], [37600, 0.578, null], [37700, 0.289, null], [37800, 0.289, null], [37900, 0.289, null], [38200, 0.8671, null], [38300, 4.3353, null], [38400, 2.6012, null], [38500, 0.8671, null], [38600, 0.289, null], [38700, 1.4451, null], [38800, 0.8671, null], [38900, 0.289, null], [39200, 0.289, null], [39400, 0.8671, null], [39500, 0.289, null], [39600, 1.4451, null], [39700, 1.1561, null], [39800, 0.578, null], [40000, 0.289, null], [40100, 0.289, null], [41000, 0.289, null], [41400, 0.289, null], [41500, 0.578, null], [41600, 0.578, null], [41700, 0.578, null], [41800, 0.578, null], [41900, 0.289, null], [42000, 0.289, null], [42300, 0.289, null], [42400, 0.578, null], [42600, 0.289, \"from typing import List\\n\\nclass Solution:\\n def maxFreeTime(self, eventTime: int, k: int, startTime: List[int], endTime: List[int]) -> int:\\n n = len(startTime)\\n meetings = sorted(zip(startTime, endTime))\\n \\n # Calculate gaps: n+1 total\\n gaps = [0] * (n + 1)\\n gaps[0] = meetings[0][0] # free time before first meeting\\n \\n for i in range(1, n):\\n gaps[i] = meetings[i][0] - meetings[i - 1][1]\\n \\n gaps[n] = eventTime - meetings[-1][1] # free time after last meeting\\n\\n # Sliding window of size k + 1\\n max_free = 0\\n window_sum = sum(gaps[:k+1])\\n max_free = window_sum\\n\\n for i in range(k+1, len(gaps)):\\n window_sum += gaps[i] - gaps[i - (k+1)]\\n max_free = max(max_free, window_sum)\\n\\n return max_free\\n\"], [42700, 0.8671, \"class Solution:\\n def maxFreeTime(self, eventTime: int, k: int, startTime: List[int], endTime: List[int]) -> int:\\n meetings = sorted(zip(startTime, endTime))\\n\\n meetings = [[-1, 0], *meetings, [eventTime, eventTime + 1]]\\n n = len(meetings)\\n\\n free_time = [meetings[i][0] - meetings[i-1][1] for i in range(1, n)]\\n\\n if k + 1 > len(free_time):\\n return sum(free_time)\\n\\n # print(k, (free_time),(free_time[:k + 1]))\\n \\n window_sum = sum(free_time[:k + 1])\\n max_free_time = window_sum\\n\\n # 5. Sliding Window:\\n for i in range(k + 1, len(free_time)):\\n window_sum += free_time[i] - free_time[i - (k + 1)]\\n max_free_time = max(max_free_time, window_sum)\\n\\n return max_free_time\"]]",
"runtime": 24,
"runtimeDistribution": "[[19, 0.578, \"class Solution:\\n def maxFreeTime(self, eventTime: int, k: int, startTime: List[int], endTime: List[int]) -> int:\\n # Compute the gaps between meetings, including before the first and after the last\\n gaps = []\\n prev_end = 0\\n for start, end in zip(startTime, endTime):\\n gaps.append(start - prev_end)\\n prev_end = end\\n gaps.append(eventTime - prev_end)\\n \\n window_size = k + 1\\n n = len(gaps)\\n \\n # If window size exceeds the number of gaps, sum all gaps\\n if window_size > n:\\n return sum(gaps)\\n \\n current_sum = sum(gaps[:window_size])\\n max_sum = current_sum\\n \\n # Slide the window to find the maximum sum of consecutive gaps\\n for i in range(window_size, n):\\n current_sum += gaps[i] - gaps[i - window_size]\\n if current_sum > max_sum:\\n max_sum = current_sum\\n \\n return max_sum\"], [21, 0.289, \"class Solution:\\n def maxFreeTime(self, eventTime: int, k: int, startTime: List[int], endTime: List[int]) -> int:\\n gaps = [0] * (len(startTime) + 1)\\n gaps[0] = startTime[0]\\n gaps[-1] = eventTime - endTime[-1]\\n for i in range(1, len(startTime)):\\n gaps[i] = startTime[i] - endTime[i - 1]\\n max_k_1_sum = sum(gaps[0: k + 1])\\n k_1_sum = max_k_1_sum\\n for i in range(k + 1, len(gaps)):\\n k_1_sum = k_1_sum + gaps[i] - gaps[i - k - 1]\\n if k_1_sum > max_k_1_sum:\\n max_k_1_sum = k_1_sum\\n return max_k_1_sum\\n\"], [22, 0.8671, null], [23, 0.578, null], [24, 99.422, \"from typing import List\\n\\nclass Solution:\\n def maxFreeTime(self, eventTime: int, k: int, startTime: List[int], endTime: List[int]) -> int:\\n n = len(startTime)\\n gaps = []\\n gaps.append(startTime[0])\\n for i in range(n - 1):\\n gaps.append(startTime[i + 1] - endTime[i])\\n gaps.append(eventTime - endTime[-1])\\n \\n window_size = k + 1\\n if len(gaps) <= window_size:\\n return sum(gaps)\\n \\n current_sum = sum(gaps[:window_size])\\n max_sum = current_sum\\n for i in range(window_size, len(gaps)):\\n current_sum += gaps[i] - gaps[i - window_size]\\n if current_sum > max_sum:\\n max_sum = current_sum\\n \\n return max_sum\"], [25, 0.289, null], [26, 0.8671, null], [27, 0.578, null], [29, 0.578, null], [30, 0.578, null], [31, 2.8902, null], [33, 1.7341, null], [34, 0.8671, null], [36, 2.0231, null], [37, 2.6012, null], [38, 1.4451, null], [40, 1.4451, null], [41, 4.9133, null], [42, 2.3121, null], [44, 1.4451, null], [45, 6.6474, null], [46, 1.7341, null], [48, 0.8671, null], [49, 4.3353, null], [51, 1.1561, null], [52, 2.3122, null], [53, 2.3121, null], [55, 1.4451, null], [56, 1.7342, null], [57, 1.1561, null], [59, 1.4451, null], [60, 0.867, null], [61, 1.7341, null], [63, 0.8671, null], [64, 1.4451, null], [66, 4.6243, null], [67, 2.6012, null], [68, 0.578, null], [70, 2.6012, null], [71, 2.8902, null], [72, 0.578, null], [74, 1.1561, null], [75, 2.8902, null], [76, 0.578, null], [78, 0.8671, null], [79, 1.156, null], [80, 1.1561, null], [82, 2.8902, null], [83, 0.289, null], [85, 0.289, null], [86, 2.0232, null], [87, 0.578, null], [89, 0.289, null], [90, 0.578, null], [91, 0.578, null], [93, 1.1561, null], [94, 0.289, null], [95, 0.8671, null], [97, 0.289, null], [98, 0.578, null], [100, 0.289, null], [101, 0.289, null], [102, 0.578, null], [104, 0.289, null], [105, 0.578, null], [106, 0.8671, null], [108, 0.578, null], [109, 0.289, null], [110, 0.578, null], [112, 0.289, \"class Solution:\\n def maxFreeTime(self, eventTime: int, k: int, startTime: List[int], endTime: List[int]) -> int:\\n meets = list(zip(startTime, endTime))\\n meets.sort()\\n start = 0\\n end = 0\\n time = 0\\n for i in range(k):\\n m=meets[i]\\n time += m[1]-m[0]\\n end = max(end, m[1])\\n if len(meets)>k:\\n end = meets[k][0]\\n ans = end - start - time\\n\\n i=0\\n for j in range(k,len(meets)):\\n # pop one meeting out\\n start = meets[i][1]\\n end = max(end, meets[j][1])\\n if j+1<len(meets):\\n end = meets[j+1][0]\\n time -= meets[i][1]-meets[i][0]\\n time += meets[j][1]-meets[j][0]\\n ans = max(ans,end - start - time)\\n i += 1\\n \\n end = max(end,eventTime)\\n ans = max(ans,end - start - time)\\n\\n return ans\"], [113, 0.8671, \"class Solution:\\n def maxFreeTime(self, eventTime: int, k: int, startTime: List[int], endTime: List[int]) -> int:\\n free = [0]*(len(startTime))\\n free[0] = startTime[0]-0\\n for i in range(1,len(startTime)):\\n free[i] = startTime[i]-endTime[i-1]\\n free.append(eventTime-endTime[-1])\\n if max(free) <= 0:\\n return 0\\n maxsum = cursum = sum(free[:k+1])\\n print(free)\\n print(\\\"outside\\\",maxsum)\\n for i in range(k+1,len(startTime)+1):\\n cursum = cursum + free[i]-free[i-k-1]\\n print(\\\"inside\\\",cursum)\\n maxsum = max(maxsum,cursum)\\n return maxsum\"]]"
},
"ruby": {
"code": "def max_free_time(event_time, k, start_time, end_time)\n gaps = []\n gaps << start_time[0] - 0\n\n (0...start_time.size-1).each do |i|\n gaps << start_time[i+1] - end_time[i]\n end\n\n gaps << event_time - end_time[-1]\n\n max_gap = gaps.max\n window_size = k + 1\n m = gaps.size\n\n if window_size > m\n sum_all = gaps.sum\n return [max_gap, sum_all].max\n end\n\n current_sum = gaps[0, window_size].sum\n max_sum = current_sum\n\n (window_size...m).each do |i|\n current_sum += gaps[i] - gaps[i - window_size]\n max_sum = [max_sum, current_sum].max\n end\n\n [max_gap, max_sum].max\nend",
"memory": null,
"memoryDistribution": "[[231600, 100.0, \"def max_free_time(event_time, k, start_time, end_time)\\n gaps = []\\n gaps << start_time[0] - 0\\n\\n (0...start_time.size-1).each do |i|\\n gaps << start_time[i+1] - end_time[i]\\n end\\n\\n gaps << event_time - end_time[-1]\\n\\n max_gap = gaps.max\\n window_size = k + 1\\n m = gaps.size\\n\\n if window_size > m\\n sum_all = gaps.sum\\n return [max_gap, sum_all].max\\n end\\n\\n current_sum = gaps[0, window_size].sum\\n max_sum = current_sum\\n\\n (window_size...m).each do |i|\\n current_sum += gaps[i] - gaps[i - window_size]\\n max_sum = [max_sum, current_sum].max\\n end\\n\\n [max_gap, max_sum].max\\nend\"]]",
"runtime": null,
"runtimeDistribution": "[[33, 100.0, \"def max_free_time(event_time, k, start_time, end_time)\\n gaps = []\\n gaps << start_time[0] - 0\\n\\n (0...start_time.size-1).each do |i|\\n gaps << start_time[i+1] - end_time[i]\\n end\\n\\n gaps << event_time - end_time[-1]\\n\\n max_gap = gaps.max\\n window_size = k + 1\\n m = gaps.size\\n\\n if window_size > m\\n sum_all = gaps.sum\\n return [max_gap, sum_all].max\\n end\\n\\n current_sum = gaps[0, window_size].sum\\n max_sum = current_sum\\n\\n (window_size...m).each do |i|\\n current_sum += gaps[i] - gaps[i - window_size]\\n max_sum = [max_sum, current_sum].max\\n end\\n\\n [max_gap, max_sum].max\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list:
import random
random.seed(seed)
test_cases = []
def sample_max_free_time(eventTime, k, startTime, endTime):
n = len(startTime)
gaps = []
gaps.append(startTime[0])
for i in range(n - 1):
gaps.append(startTime[i+1] - endTime[i])
gaps.append(eventTime - endTime[-1])
window_size = k + 1
if len(gaps) <= window_size:
return sum(gaps)
current_sum = sum(gaps[:window_size])
max_sum = current_sum
for i in range(window_size, len(gaps)):
current_sum += gaps[i] - gaps[i - window_size]
if current_sum > max_sum:
max_sum = current_sum
return max_sum
def serialize_input(eventTime, k, startTime, endTime):
# Format: "eventTime k startTime_list endTime_list"
return f"{eventTime} {k} {','.join(map(str, startTime))} {','.join(map(str, endTime))}"
def serialize_output(result):
return str(result)
fixed_cases = []
fixed_cases.append((5, 1, [1, 3], [2, 5]))
fixed_cases.append((10, 1, [0, 2, 9], [1, 4, 10]))
fixed_cases.append((5, 2, [0, 1, 2, 3, 4], [1, 2, 3, 4, 5]))
fixed_cases.append((100, 2, [10, 30, 55, 70], [20, 40, 60, 80]))
fixed_cases.append((50, 1, [5, 20, 35], [10, 25, 40]))
fixed_cases.append((100, 1, [1, 2, 3], [2, 3, 4]))
for case in fixed_cases:
eventTime, k, startTime, endTime = case
inp = serialize_input(eventTime, k, startTime, endTime)
expected = sample_max_free_time(eventTime, k, startTime, endTime)
test_cases.append({"input": inp, "output": serialize_output(expected)})
while len(test_cases) < num_cases:
n = random.randint(2, 10)
durations = [random.randint(1, 10) for _ in range(n)]
total_duration = sum(durations)
free_total = random.randint(0, 50)
eventTime = total_duration + free_total
m = n + 1
gaps = [0] * m
for _ in range(free_total):
idx = random.randint(0, m - 1)
gaps[idx] += 1
startTime = []
endTime = []
current_time = gaps[0]
startTime.append(current_time)
current_time += durations[0]
endTime.append(current_time)
for i in range(1, n):
current_time += gaps[i]
startTime.append(current_time)
current_time += durations[i]
endTime.append(current_time)
k = random.randint(1, n)
inp = serialize_input(eventTime, k, startTime, endTime)
expected = sample_max_free_time(eventTime, k, startTime, endTime)
test_cases.append({"input": inp, "output": serialize_output(expected)})
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
try:
expected_val = int(expected_output.strip())
program_val = int(program_output.strip())
return expected_val == program_val
except Exception:
return False
|
[{"input": "5 1 1,3 2,5", "output": "2"}, {"input": "10 1 0,2,9 1,4,10", "output": "6"}, {"input": "5 2 0,1,2,3,4 1,2,3,4,5", "output": "0"}, {"input": "100 2 10,30,55,70 20,40,60,80", "output": "45"}, {"input": "50 1 5,20,35 10,25,40", "output": "20"}, {"input": "100 1 1,2,3 2,3,4", "output": "96"}, {"input": "24 3 6,12,17 7,17,21", "output": "14"}, {"input": "38 6 4,5,12,20,27,32 5,8,19,26,32,35", "output": "13"}, {"input": "72 6 1,13,16,25,29,39,45,56,62 10,15,23,27,38,44,55,62,72", "output": "11"}, {"input": "47 3 2,6,11,15,26,31,42 6,11,13,25,29,40,46", "output": "7"}, {"input": "33 3 0,9,22 4,19,28", "output": "13"}, {"input": "61 4 2,7,10,12,20,24,32,44,52 4,8,12,15,23,31,42,46,59", "output": "15"}, {"input": "27 3 0,6,9,18 6,9,18,27", "output": "0"}, {"input": "40 8 0,2,6,12,17,21,22,27,38 1,4,12,17,21,22,26,37,40", "output": "5"}, {"input": "105 7 4,14,20,38,49,59,64,78,86,95 7,19,29,48,56,63,73,82,91,102", "output": "31"}, {"input": "79 1 8,19,32,48,53,57,64 15,26,40,49,55,58,71", "output": "14"}, {"input": "83 4 2,9,14,19,33,39,45,54,59,75 4,12,16,29,35,43,52,56,69,79", "output": "18"}, {"input": "49 6 0,5,8,16,25,30,40 5,8,16,25,30,40,49", "output": "0"}, {"input": "79 5 6,14,21,26,35,40,45,56,64,70 11,16,24,31,37,42,54,59,69,75", "output": "23"}, {"input": "58 3 3,5,16,27,33,37,47 4,11,20,31,35,43,56", "output": "16"}, {"input": "59 3 5,9,18,27,41,49 7,14,24,36,48,58", "output": "14"}, {"input": "41 1 5,24 12,25", "output": "28"}, {"input": "58 2 2,11,23,28,38,49 9,20,24,33,43,53", "output": "16"}, {"input": "47 4 3,12,16,25,29,36 7,16,19,26,30,40", "output": "22"}, {"input": "20 2 1,12 10,16", "output": "7"}, {"input": "115 5 3,16,28,43,57,69,81,94,107 13,25,35,52,65,72,89,102,112", "output": "36"}, {"input": "82 4 8,20,25,37,46,57,65,77 16,21,32,43,53,60,73,80", "output": "24"}, {"input": "83 8 3,13,21,26,39,53,61,67,76 8,19,24,36,49,55,64,72,78", "output": "34"}, {"input": "92 2 3,15,21,34,46,56,65,82 13,20,27,38,48,61,73,86", "output": "23"}, {"input": "37 2 1,9,15,25,31 7,11,24,28,35", "output": "8"}, {"input": "55 3 7,12,25,35,43,48 8,21,28,40,44,49", "output": "22"}, {"input": "63 3 11,29,42 15,31,51", "output": "48"}, {"input": "79 5 3,11,23,33,44,57,62,77 8,20,32,41,52,59,72,78", "output": "20"}, {"input": "88 3 5,18,23,37,44,51,61,77 14,19,31,39,50,56,67,79", "output": "25"}, {"input": "68 1 10,24,44 15,31,50", "output": "31"}, {"input": "39 2 5,21,30 12,23,32", "output": "23"}, {"input": "71 7 1,5,7,16,24,35,42,50,55,65 4,7,15,22,34,40,49,55,63,70", "output": "10"}, {"input": "84 4 4,14,33,36,52,70 5,24,34,46,60,75", "output": "36"}, {"input": "68 4 6,14,23,37,45,59 12,16,31,39,48,63", "output": "35"}, {"input": "24 2 4,11,15 7,12,16", "output": "15"}, {"input": "32 1 0,7,10,17,26 6,9,16,26,32", "output": "2"}, {"input": "54 9 1,4,11,24,26,28,34,38,42 3,8,21,25,27,34,38,41,52", "output": "13"}, {"input": "66 2 11,18,25,36,47,55 14,20,26,39,48,61", "output": "25"}, {"input": "58 3 11,18,34 14,23,44", "output": "40"}, {"input": "76 5 5,16,26,38,54,63 11,18,36,47,58,66", "output": "37"}, {"input": "64 4 3,9,15,17,24,37,44,55 5,12,16,19,33,41,51,62", "output": "18"}, {"input": "51 8 3,15,18,20,24,31,39,43 13,16,19,24,29,35,42,48", "output": "18"}, {"input": "59 3 8,25,44 14,35,51", "output": "36"}, {"input": "67 3 13,22,44 16,30,52", "output": "48"}, {"input": "82 2 3,10,28,34,48,63,73 5,16,30,43,55,68,78", "output": "21"}, {"input": "97 6 3,11,20,30,37,45,59,70,83,89 7,16,28,34,43,55,67,78,88,96", "output": "23"}, {"input": "40 2 5,16,21,30,35 12,18,27,34,36", "output": "12"}, {"input": "75 9 2,15,26,35,38,44,50,57,61,67 12,24,33,37,43,48,55,59,62,71", "output": "24"}, {"input": "72 3 4,9,22,32,42,57,67 6,18,31,41,51,66,68", "output": "12"}, {"input": "49 4 5,8,21,31,39 6,12,22,37,44", "output": "27"}, {"input": "27 4 0,9,17,24 9,14,23,26", "output": "5"}, {"input": "69 3 10,26,42,59 18,32,50,60", "output": "37"}, {"input": "46 1 1,11,15,27,32,41 9,15,25,32,40,45", "output": "3"}, {"input": "84 2 2,15,27,41,55,67,76 8,17,36,50,60,72,79", "output": "22"}, {"input": "80 6 5,19,32,37,53,63 15,28,34,46,56,73", "output": "37"}, {"input": "71 4 1,9,21,27,30,41,52,61 6,17,23,28,33,49,59,69", "output": "21"}, {"input": "52 1 5,15,27,40 13,24,35,48", "output": "9"}, {"input": "72 6 3,9,19,27,36,48,52,62 6,14,25,34,42,49,59,63", "output": "30"}, {"input": "53 1 3,11,26,35 10,21,31,45", "output": "12"}, {"input": "61 3 2,5,15,26,33,37,44,47,58 5,14,25,33,36,41,45,57,60", "output": "7"}, {"input": "90 9 0,4,13,23,36,48,55,64,69,78 4,13,19,31,45,55,61,67,77,87", "output": "21"}, {"input": "62 2 2,10,18,30,41,52 7,12,28,39,48,59", "output": "11"}, {"input": "39 3 5,19,30 15,29,34", "output": "15"}, {"input": "60 2 6,18,31,43,51 11,24,36,44,53", "output": "21"}, {"input": "47 1 12,32 18,37", "output": "26"}, {"input": "66 2 0,5,10,20,29,35,38,46,54 5,8,17,29,34,37,43,52,64", "output": "7"}, {"input": "96 2 5,16,28,36,40,52,57,64,78,90 13,25,34,38,50,54,58,73,87,94", "output": "14"}, {"input": "67 9 2,5,10,19,21,27,38,43,50,57 3,7,18,20,26,34,41,46,57,63", "output": "22"}, {"input": "38 4 1,5,9,17,23,26,32,36 5,9,17,23,26,31,36,38", "output": "1"}, {"input": "61 4 4,15,23,36,45 6,17,33,37,53", "output": "34"}, {"input": "83 2 1,10,14,24,33,44,53,63,74,77 9,11,20,31,42,50,60,70,77,82", "output": "10"}, {"input": "100 10 3,9,11,25,37,54,67,74,81,88 7,10,16,32,47,64,68,76,85,98", "output": "46"}, {"input": "74 8 6,13,22,28,35,42,50,65 11,16,26,34,39,49,60,69", "output": "31"}, {"input": "77 1 3,9,12,25,38,47,54,57,70 4,10,21,34,45,48,55,66,75", "output": "8"}, {"input": "59 1 9,19,33,44 11,27,40,50", "output": "17"}, {"input": "56 8 0,4,6,12,23,33,43,50 4,6,12,22,33,43,50,56", "output": "1"}, {"input": "104 7 3,17,28,39,51,63,73,85,98 7,23,37,46,58,66,83,92,100", "output": "42"}, {"input": "49 3 4,13,26,40 7,18,31,45", "output": "27"}, {"input": "62 2 1,13,18,29,37,42,52 11,17,26,35,40,49,58", "output": "9"}, {"input": "56 1 3,9,16,22,37,50 7,14,19,29,44,52", "output": "14"}, {"input": "83 8 3,16,28,33,37,47,55,67 9,23,30,34,39,52,59,76", "output": "47"}, {"input": "28 5 0,7,10,13,20 7,10,13,20,27", "output": "1"}, {"input": "78 3 7,23,43,55,71 15,33,50,62,72", "output": "32"}, {"input": "41 2 0,11,18,28 9,18,25,38", "output": "6"}, {"input": "74 5 2,10,16,22,31,39,52,59,70 7,13,19,28,39,49,53,65,71", "output": "20"}, {"input": "57 6 0,6,15,16,25,34,38,46,48,52 6,15,16,24,34,38,45,48,52,57", "output": "2"}, {"input": "27 3 1,14,22 9,16,26", "output": "13"}, {"input": "68 6 3,18,25,36,46,55 12,20,28,43,47,60", "output": "41"}, {"input": "66 3 15,35,52 23,41,54", "output": "50"}, {"input": "38 2 0,4,11,14,23,27,31 2,11,14,22,25,31,38", "output": "3"}, {"input": "69 5 1,8,14,22,34,47,52,63 4,11,16,31,44,48,62,66", "output": "23"}, {"input": "36 2 10,21 14,29", "output": "24"}, {"input": "63 5 7,13,18,32,49 8,14,25,41,54", "output": "40"}, {"input": "15 2 4,10 9,13", "output": "7"}, {"input": "64 2 1,12,19,22,30,35,40,45,48,56 10,17,22,28,33,40,42,46,54,63", "output": "7"}]
|
{
"cpp": "==Code Submission==\n\n \nint main() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n \n string line;\n getline(cin, line);\n istringstream iss(line);\n \n int eventTime, k;\n string startStr, endStr;\n iss >> eventTime >> k >> startStr >> endStr;\n \n vector<int> startTime, endTime;\n {\n istringstream ss(startStr);\n string token;\n while(getline(ss, token, ',')) {\n startTime.push_back(stoi(token));\n }\n }\n {\n istringstream ss(endStr);\n string token;\n while(getline(ss, token, ',')) {\n endTime.push_back(stoi(token));\n }\n }\n \n Solution sol;\n int ans = sol.maxFreeTime(eventTime, k, startTime, endTime);\n cout << ans;\n return 0;\n}",
"golang": "==Code Submission==\n\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n line, _ := reader.ReadString('\\n')\n line = strings.TrimSpace(line)\n parts := strings.Split(line, \" \")\n eventTime, _ := strconv.Atoi(parts[0])\n k, _ := strconv.Atoi(parts[1])\n startStr := parts[2]\n endStr := parts[3]\n startItems := strings.Split(startStr, \",\")\n endItems := strings.Split(endStr, \",\")\n startTime := make([]int, len(startItems))\n endTime := make([]int, len(endItems))\n for i, s := range startItems {\n startTime[i], _ = strconv.Atoi(s)\n }\n for i, s := range endItems {\n endTime[i], _ = strconv.Atoi(s)\n }\n ans := maxFreeTime(eventTime, k, startTime, endTime)\n fmt.Printf(\"%d\", ans)\n}",
"java": "public class Main {\n private static int[] parseArray(String s) {\n String[] parts = s.split(\",\");\n int[] arr = new int[parts.length];\n for (int i = 0; i < parts.length; i++) {\n arr[i] = Integer.parseInt(parts[i]);\n }\n return arr;\n }\n \n public static void main(String[] args) throws Exception {\n java.io.BufferedReader br = new java.io.BufferedReader(new java.io.InputStreamReader(System.in));\n String line = br.readLine().trim();\n String[] tokens = line.split(\" \");\n int eventTime = Integer.parseInt(tokens[0]);\n int k = Integer.parseInt(tokens[1]);\n int[] startTime = parseArray(tokens[2]);\n int[] endTime = parseArray(tokens[3]);\n \n Solution sol = new Solution();\n int ans = sol.maxFreeTime(eventTime, k, startTime, endTime);\n System.out.println(ans);\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\n\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\nlet input = \"\";\nprocess.stdin.on('data', function(chunk) {\n input += chunk;\n});\nprocess.stdin.on('end', function() {\n const tokens = input.trim().split(\" \");\n const eventTime = Number(tokens[0]);\n const k = Number(tokens[1]);\n const startTime = tokens[2].split(\",\").map(Number);\n const endTime = tokens[3].split(\",\").map(Number);\n const ans = maxFreeTime(eventTime, k, startTime, endTime);\n console.log(String(ans));\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str):\n tokens = input_str.strip().split(\" \")\n eventTime = int(tokens[0])\n k = int(tokens[1])\n startTime = list(map(int, tokens[2].split(\",\")))\n endTime = list(map(int, tokens[3].split(\",\")))\n return eventTime, k, startTime, endTime\n\ndef serialize_stdout(result):\n return str(result)\n\ndata = sys.stdin.read().strip()\neventTime, k, startTime, endTime = deserialize_stdin(data)\nsol = Solution()\nans = sol.maxFreeTime(eventTime, k, startTime, endTime)\nprint(serialize_stdout(ans))",
"ruby": "==Code Submission==\n\ninput = gets.strip\ntokens = input.split(\" \")\nevent_time = tokens[0].to_i\nk = tokens[1].to_i\nstart_time = tokens[2].split(\",\").map(&:to_i)\nend_time = tokens[3].split(\",\").map(&:to_i)\nans = max_free_time(event_time, k, start_time, end_time)\nputs ans"
}
|
3747
|
Maximum Difference Between Adjacent Elements in a Circular Array
|
maximum-difference-between-adjacent-elements-in-a-circular-array
|
<p>Given a <strong>circular</strong> array <code>nums</code>, find the <b>maximum</b> absolute difference between adjacent elements.</p>
<p><strong>Note</strong>: In a circular array, the first and last elements are adjacent.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">nums = [1,2,4]</span></p>
<p><strong>Output:</strong> <span class="example-io">3</span></p>
<p><strong>Explanation:</strong></p>
<p>Because <code>nums</code> is circular, <code>nums[0]</code> and <code>nums[2]</code> are adjacent. They have the maximum absolute difference of <code>|4 - 1| = 3</code>.</p>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">nums = [-5,-10,-5]</span></p>
<p><strong>Output:</strong> <span class="example-io">5</span></p>
<p><strong>Explanation:</strong></p>
<p>The adjacent elements <code>nums[0]</code> and <code>nums[1]</code> have the maximum absolute difference of <code>|-5 - (-10)| = 5</code>.</p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>2 <= nums.length <= 100</code></li>
<li><code>-100 <= nums[i] <= 100</code></li>
</ul>
|
Given a **circular** array `nums`, find the **maximum** absolute difference between adjacent elements.
**Note**: In a circular array, the first and last elements are adjacent.
**Example 1:**
**Input:** nums \= \[1,2,4]
**Output:** 3
**Explanation:**
Because `nums` is circular, `nums[0]` and `nums[2]` are adjacent. They have the maximum absolute difference of `|4 - 1| = 3`.
**Example 2:**
**Input:** nums \= \[\-5,\-10,\-5]
**Output:** 5
**Explanation:**
The adjacent elements `nums[0]` and `nums[1]` have the maximum absolute difference of `|-5 - (-10)| = 5`.
**Constraints:**
- `2 <= nums.length <= 100`
- `-100 <= nums[i] <= 100`
|
Easy
|
[
"array"
] |
leetcode
|
https://leetcode.com/problems/maximum-difference-between-adjacent-elements-in-a-circular-array
|
functional
| null | null | null | null |
{
"c": "int maxAdjacentDistance(int* nums, int numsSize) {\n \n}",
"cpp": "class Solution {\npublic:\n int maxAdjacentDistance(vector<int>& nums) {\n \n }\n};",
"csharp": "public class Solution {\n public int MaxAdjacentDistance(int[] nums) {\n \n }\n}",
"dart": "class Solution {\n int maxAdjacentDistance(List<int> nums) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec max_adjacent_distance(nums :: [integer]) :: integer\n def max_adjacent_distance(nums) do\n \n end\nend",
"erlang": "-spec max_adjacent_distance(Nums :: [integer()]) -> integer().\nmax_adjacent_distance(Nums) ->\n .",
"golang": "func maxAdjacentDistance(nums []int) int {\n \n}",
"java": "class Solution {\n public int maxAdjacentDistance(int[] nums) {\n \n }\n}",
"javascript": "/**\n * @param {number[]} nums\n * @return {number}\n */\nvar maxAdjacentDistance = function(nums) {\n \n};",
"kotlin": "class Solution {\n fun maxAdjacentDistance(nums: IntArray): Int {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param Integer[] $nums\n * @return Integer\n */\n function maxAdjacentDistance($nums) {\n \n }\n}",
"python": "class Solution(object):\n def maxAdjacentDistance(self, nums):\n \"\"\"\n :type nums: List[int]\n :rtype: int\n \"\"\"\n ",
"python3": "class Solution:\n def maxAdjacentDistance(self, nums: List[int]) -> int:\n ",
"racket": "(define/contract (max-adjacent-distance nums)\n (-> (listof exact-integer?) exact-integer?)\n )",
"ruby": "# @param {Integer[]} nums\n# @return {Integer}\ndef max_adjacent_distance(nums)\n \nend",
"rust": "impl Solution {\n pub fn max_adjacent_distance(nums: Vec<i32>) -> i32 {\n \n }\n}",
"scala": "object Solution {\n def maxAdjacentDistance(nums: Array[Int]): Int = {\n \n }\n}",
"swift": "class Solution {\n func maxAdjacentDistance(_ nums: [Int]) -> Int {\n \n }\n}",
"typescript": "function maxAdjacentDistance(nums: number[]): number {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n int maxAdjacentDistance(vector<int>& nums) {\n int n = nums.size();\n int max_diff = 0;\n for (int i = 0; i < n; ++i) {\n int next = (i + 1) % n;\n int diff = abs(nums[i] - nums[next]);\n if (diff > max_diff) {\n max_diff = diff;\n }\n }\n return max_diff;\n }\n};",
"memory": 3100,
"memoryDistribution": "[[3100, 24.6269, \"class Solution {\\npublic:\\n int maxAdjacentDistance(vector<int>& nums) {\\n int n = nums.size();\\n int max_diff = 0;\\n for (int i = 0; i < n; ++i) {\\n int next = (i + 1) % n;\\n int diff = abs(nums[i] - nums[next]);\\n if (diff > max_diff) {\\n max_diff = diff;\\n }\\n }\\n return max_diff;\\n }\\n};\"], [30200, 0.9328, \"class Solution {\\npublic:\\n int maxAdjacentDistance(vector<int>& nums) {\\n int n = nums.size();\\n int maxDiff = 0;\\n\\n for (int i = 0; i < n; ++i) {\\n int diff = abs(nums[i] - nums[(i + 1) % n]);\\n maxDiff = max(maxDiff, diff);\\n }\\n\\n return maxDiff;\\n }\\n};\"], [30300, 13.0597, \"class Solution {\\npublic:\\n int maxAdjacentDistance(vector<int>& nums) {\\n nums.push_back(nums[0]);\\n int len = nums.size();\\n int maxabsluteDiff = 0;\\n for (int i = 0; i < len-1; i++)\\n {\\n int abs_res = abs(nums[i] - nums[i+1]);\\n if(abs_res > maxabsluteDiff){maxabsluteDiff = abs_res;}\\n }\\n return maxabsluteDiff;\\n }\\n};\"], [30400, 25.5597, null], [30500, 35.8209, \"class Solution {\\npublic:\\n int maxAdjacentDistance(vector<int>& a) {\\n int n=a.size();\\n int ans=abs(a[0]-a[n-1]);\\n for(int i=1;i<n;i++)ans=max(ans,abs(a[i]-a[i-1]));\\n return ans;\\n }\\n};\"], [30600, 20.1493, \"class Solution {\\npublic:\\n int maxAdjacentDistance(vector<int>& nums) {\\n int maxDiff = 0;\\n for (int i = 0; i < nums.size(); i++)\\n maxDiff = max(maxDiff, abs(nums[i] - nums[(i + 1) % nums.size()]));\\n return maxDiff;\\n }\\n};\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 89.7388, \"class Solution\\n{\\npublic:\\n int maxAdjacentDistance(vector<int> &nums)\\n {\\n int maxDiff = 0;\\n for (int i = 0; i < nums.size(); i++)\\n {\\n maxDiff = max(maxDiff, abs(nums[(i + 1) % nums.size()] - nums[i]));\\n }\\n printf(\\\"%d\\\\n\\\", maxDiff);\\n return maxDiff;\\n }\\n};\"], [1, 3.5448, \"class Solution {\\npublic:\\n int maxAdjacentDistance(vector<int>& nums) {\\n int maxDiff = 0;\\n for (int i = 0; i < nums.size(); i++)\\n maxDiff = max(maxDiff, abs(nums[i] - nums[(i + 1) % nums.size()]));\\n return maxDiff;\\n }\\n};\"], [2, 2.0522, null], [3, 2.7985, \"class Solution {\\npublic:\\n int maxAdjacentDistance(vector<int>& nums) {\\n int max_diff = abs(nums[0] - nums[nums.size() - 1]);\\n for (int i = 0; i < nums.size() - 1; ++i) {\\n max_diff = max(max_diff, abs(nums[i] - nums[i + 1]));\\n }\\n return max_diff;\\n }\\n};\"], [4, 1.4925, \"\\n\\n#include <vector>\\n#include <cmath> // for abs\\nusing namespace std;\\n\\nclass Solution {\\npublic:\\n int maxAdjacentDistance(vector<int>& nums) {\\n int maxDiff = 0;\\n int n = nums.size();\\n \\n for (int i = 0; i < n; i++) {\\n int next = (i + 1) % n; \\n int diff = nums[i] - nums[next];\\n if (diff < 0) diff = -diff; \\n if (diff > maxDiff) {\\n maxDiff = diff;\\n }\\n }\\n \\n return maxDiff;\\n }\\n};\\n\"]]"
},
"golang": {
"code": "func maxAdjacentDistance(nums []int) int {\n max := 0\n n := len(nums)\n for i := 0; i < n; i++ {\n next := (i + 1) % n\n diff := nums[i] - nums[next]\n if diff < 0 {\n diff = -diff\n }\n if diff > max {\n max = diff\n }\n }\n return max\n}",
"memory": 500,
"memoryDistribution": "[[500, 19.0476, \"func maxAdjacentDistance(nums []int) int {\\n max := 0\\n n := len(nums)\\n for i := 0; i < n; i++ {\\n next := (i + 1) % n\\n diff := nums[i] - nums[next]\\n if diff < 0 {\\n diff = -diff\\n }\\n if diff > max {\\n max = diff\\n }\\n }\\n return max\\n}\"], [4600, 23.8095, \"func maxAdjacentDistance(nums []int) int {\\n\\tvar maxNum int\\n\\tfirst := nums[0]\\n\\tlast := nums[len(nums)-1]\\n\\tfor i := 0; i < len(nums)-1; i++ {\\n\\t\\tmaxNum = max(maxNum, int(math.Abs(float64(nums[i]-nums[i+1]))))\\n\\t}\\n\\n\\treturn max(maxNum, int(math.Abs(float64(first-last))))\\n}\"], [4700, 57.1429, \"func maxAdjacentDistance(nums []int) int {\\n\\tn := len(nums)\\n\\tedge := abs(nums[0] - nums[n-1])\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tif abs(nums[i]-nums[i+1]) > edge {\\n\\t\\t\\tedge = abs(nums[i] - nums[i+1])\\n\\t\\t}\\n\\t}\\n\\treturn edge\\n}\\nfunc abs(x int) int {\\n\\tif x < 0 {\\n\\t\\treturn -x\\n\\t}\\n\\treturn x\\n}\"], [4800, 14.2857, null], [4900, 2.381, \"func maxAdjacentDistance(nums []int) int {\\n m, n := -1, len(nums)\\n for i := 1; i < n; i++ {\\n m = max(m, abs(nums[i]-nums[i-1]))\\n }\\n m = max(m, abs(nums[n-1]-nums[0]))\\n return m\\n}\\n\\nfunc abs(a int) int {\\n if a > 0 {\\n return a\\n }\\n return -a\\n}\\n\\nfunc max(a,b int) int {\\n if a > b {\\n return a\\n }\\n return b\\n}\"], [5200, 2.381, \"func maxAdjacentDistance(n []int) int {\\n\\tl := len(n)\\n\\tn = append(n, n[:l-1]...)\\n\\tl = len(n)\\n\\tres := 0\\n\\tfor k := range l - 1 {\\n\\t\\tcurr := abs(n[k+1] - n[k])\\n\\t\\tif curr > res {\\n\\t\\t\\tres = curr\\n\\t\\t}\\n\\t}\\n\\treturn res\\n}\\n\\nfunc abs(n int) int {\\n\\tif n < 0 {\\n\\t\\treturn -n\\n\\t}\\n\\treturn n\\n}\\n\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 76.1905, \"func maxAdjacentDistance(nums []int) int {\\n\\tn := len(nums)\\n\\tedge := abs(nums[0] - nums[n-1])\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tif abs(nums[i]-nums[i+1]) > edge {\\n\\t\\t\\tedge = abs(nums[i] - nums[i+1])\\n\\t\\t}\\n\\t}\\n\\treturn edge\\n}\\nfunc abs(x int) int {\\n\\tif x < 0 {\\n\\t\\treturn -x\\n\\t}\\n\\treturn x\\n}\"], [1, 16.6667, \"func absInt(val int) int {\\n if val > 0 {\\n return val\\n }\\n return -val\\n}\\n\\nfunc maxInt(a, b int) int {\\n if a > b {\\n return a\\n }\\n return b\\n}\\n\\nfunc maxAdjacentDistance(nums []int) int {\\n diff := absInt(nums[0] - nums[len(nums) - 1])\\n for i := 1; i < len(nums); i++ {\\n curr := nums[i]\\n prev := nums[i - 1]\\n diff = maxInt(diff, absInt(prev - curr))\\n }\\n return diff\\n}\"], [2, 4.7619, \"func absInt(val int) int {\\n if val > 0 {\\n return val\\n }\\n return -val\\n}\\n\\nfunc maxInt(a, b int) int {\\n if a > b {\\n return a\\n }\\n return b\\n}\\n\\nfunc maxAdjacentDistance(nums []int) int {\\n diff := absInt(nums[0] - nums[len(nums) - 1])\\n for i := 1; i < len(nums); i++ {\\n curr := nums[i]\\n prev := nums[i - 1]\\n diff = maxInt(diff, absInt(prev - curr))\\n }\\n return diff\\n}\"], [6, 2.381, \"func maxAdjacentDistance(nums []int) int {\\n \\tif len(nums) < 2 {\\n\\t\\treturn 0 \\n\\t}\\n\\n\\tmaxDist := 0\\n\\n\\tfor i := range nums {\\n\\t\\tnextIdx := (i + 1) % len(nums)\\n\\t\\tdist := abs(nums[i] - nums[nextIdx])\\n\\t\\tmaxDist = max(maxDist, dist)\\n\\t}\\n\\n\\treturn maxDist\\n}\\n\\nfunc abs(x int) int {\\n\\tif x < 0 {\\n\\t\\treturn -x\\n\\t}\\n\\treturn x\\n}\\n \\n \"]]"
},
"java": {
"code": "class Solution {\n public int maxAdjacentDistance(int[] nums) {\n int max = 0;\n int n = nums.length;\n for (int i = 0; i < n; i++) {\n int next = (i + 1) % n;\n int diff = Math.abs(nums[i] - nums[next]);\n if (diff > max) {\n max = diff;\n }\n }\n return max;\n }\n}",
"memory": 4400,
"memoryDistribution": "[[4400, 13.5888, \"class Solution {\\n public int maxAdjacentDistance(int[] nums) {\\n int max = 0;\\n int n = nums.length;\\n for (int i = 0; i < n; i++) {\\n int next = (i + 1) % n;\\n int diff = Math.abs(nums[i] - nums[next]);\\n if (diff > max) {\\n max = diff;\\n }\\n }\\n return max;\\n }\\n}\"], [42700, 0.1742, \"class Solution {\\n public int maxAdjacentDistance(int[] nums) {\\n int max=Math.abs(nums[0]-nums[nums.length-1]);\\n for(int i=0;i<nums.length-1;i++){\\n if(Math.abs(nums[i]-nums[i+1])>max)max=Math.abs(nums[i]-nums[i+1]);\\n }\\n return max;\\n \\n }\\n}\"], [42800, 0.1742, \"class Solution {\\n public int maxAdjacentDistance(int[] nums) {\\n int i=0,n = nums.length;\\n int maxNow = 0;\\n while(i < n){\\n if(Math.abs(nums[i]-nums[(i+1)%n]) > maxNow){\\n maxNow = Math.abs(nums[i]-nums[(i+1)%n]);\\n }\\n i++;\\n }\\n return maxNow;\\n }\\n}\"], [42900, 0.1742, null], [43000, 1.2195, null], [43100, 4.007, null], [43200, 10.453, null], [43300, 13.5889, null], [43400, 15.331, null], [43500, 11.4983, null], [43600, 10.2787, null], [43700, 9.0592, null], [43800, 10.453, \"class Solution {\\n\\n public int maxAdjacentDistance(int[] nums) {\\n\\n int maxDifference = Math.abs(nums[0] - nums[nums.length - 1]);\\n\\n for(int i = 1; i < nums.length; i++) {\\n maxDifference = Math.max(Math.abs(nums[i] - nums[i-1]), maxDifference);\\n }\\n\\n return maxDifference;\\n \\n }\\n\\n}\"], [43900, 5.4007, \"class Solution {\\n public int maxAdjacentDistance(int[] nums) {\\n int max = Integer.MIN_VALUE;\\n int absolute;\\n for (int i = 1; i < nums.length; i++) {\\n absolute = getAbsolute(nums, i - 1, i);\\n if (absolute > max) {\\n max = absolute;\\n }\\n }\\n absolute = getAbsolute(nums, nums.length - 1, 0);\\n if (absolute > max) {\\n max = absolute;\\n }\\n return max;\\n }\\n\\n private int getAbsolute(int[] nums, int first, int second) {\\n return Math.abs(nums[first] - nums[second]);\\n }\\n}\"]]",
"runtime": 1,
"runtimeDistribution": "[[0, 1.0453, \"class Solution {\\n public int maxAdjacentDistance(int[] nums) {\\n int r = Math.abs(nums[nums.length - 1] - nums[0]);\\n for (int i = 1; i < nums.length; i++) {\\n r = Math.max(r, Math.abs(nums[i] - nums[i - 1]));\\n }\\n return r;\\n }\\n}\"], [1, 96.3415, \"class Solution {\\n public int maxAdjacentDistance(int[] nums) {\\n // \\uc21c\\ud658\\ud558\\uba74\\uc11c \\uc591\\ucabd \\uac12\\uc758 \\uc808\\ub300\\ucc28\\ub97c \\uad6c\\ud558\\uace0 \\uae30\\uc874 \\ucd5c\\ub300\\uac12 \\uc911 \\uac00\\uc7a5 \\ud070 \\uac12\\uc744 \\ucc3e\\ub294\\ub2e4.\\n int max = 0, num = 0;\\n for(int i = 0; i < nums.length; i++){\\n num = Math.abs(nums[i] - nums[(i + 1) % nums.length]);\\n max = Math.max(max, num);\\n }\\n\\n return max;\\n }\\n}\"], [2, 0.8711, null], [3, 0.6969, \"class Solution {\\n public int maxAdjacentDistance(int[] nums) {\\n int n = nums.length;\\n int[] a = new int[n];\\n for(int i = 0;i<n-1;i++){\\n a[i] = Math.abs(nums[i] - nums[i+1]);\\n }\\n a[n-1] = Math.abs(nums[0] - nums[n-1]);\\n Arrays.sort(a);\\n return a[n-1];\\n }\\n}\"], [4, 0.3484, \"class Solution {\\n public int maxAdjacentDistance(int[] nums) {\\n\\t\\t int i=0;\\n\\t\\t \\n\\t\\t List<Integer> l=new ArrayList<>();\\n\\t\\t for(i=0;i<nums.length;i++) {\\n\\t\\t\\t int j = (i + 1) % nums.length;\\n\\t\\t\\tint r= Math.abs(nums[i]-nums[j]) ;\\n\\t\\t\\tl.add(r);\\n\\t\\t\\t\\t\\n\\t\\t }\\n\\t\\t int cir=nums[0]-nums[nums.length-1];\\n\\t\\t l.add(cir);\\n\\t\\t int[] array = new int[l.size()];\\n\\t for (int k = 0; k < l.size(); k++) {\\n\\t array[k] = l.get(k);\\n\\t }\\n\\t Arrays.sort(array);\\n\\t \\n\\t\\t \\n\\t\\t \\n\\t\\t \\n\\t\\treturn array[array.length-1];\\n\\t \\n\\t }\\n}\"]]"
},
"javascript": {
"code": "var maxAdjacentDistance = function(nums) {\n let max = 0;\n const n = nums.length;\n for (let i = 0; i < n; i++) {\n const next = (i + 1) % n;\n const diff = Math.abs(nums[i] - nums[next]);\n if (diff > max) max = diff;\n }\n return max;\n};",
"memory": 5700,
"memoryDistribution": "[[5700, 15.5341, \"var maxAdjacentDistance = function(nums) {\\n let max = 0;\\n const n = nums.length;\\n for (let i = 0; i < n; i++) {\\n const next = (i + 1) % n;\\n const diff = Math.abs(nums[i] - nums[next]);\\n if (diff > max) max = diff;\\n }\\n return max;\\n};\"], [54500, 0.9709, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar maxAdjacentDistance = function(nums) {\\n nums.push(nums[0]);\\n let max = 0;\\n\\n for (let i=0; i<nums.length-1; i++) {\\n if (max < Math.abs(nums[i]-nums[i+1])) {\\n max = Math.abs(nums[i]-nums[i+1])\\n }\\n }\\n\\n return max;\\n};\"], [54700, 0.9709, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar maxAdjacentDistance = function (nums) {\\n let res = -Infinity;\\n const arr = [...nums, nums[0]];\\n const len = arr.length;\\n\\n for (let i = 1; i < len; i++) {\\n res = Math.max(res, Math.abs(arr[i] - arr[i - 1]));\\n }\\n\\n return res;\\n};\"], [54900, 2.9126, null], [55000, 3.8835, null], [55100, 2.9126, null], [55200, 1.9417, null], [55300, 0.9709, null], [55400, 2.9126, null], [55500, 3.8835, null], [55600, 7.767, null], [55700, 8.7379, null], [55800, 10.6796, null], [55900, 8.7379, null], [56000, 9.7087, null], [56100, 1.9417, null], [56200, 3.8835, null], [56500, 1.9417, null], [56600, 0.9709, null], [56700, 1.9417, null], [56800, 0.9709, null], [56900, 0.9709, null], [57000, 1.9417, null], [57200, 0.9709, null], [57300, 1.9417, null], [57400, 2.9126, \"var maxAdjacentDistance = function(nums) {\\n let max = 0;\\n const n = nums.length;\\n for (let i = 0; i < n; i++) {\\n const next = (i + 1) % n;\\n const diff = Math.abs(nums[i] - nums[next]);\\n if (diff > max) max = diff;\\n }\\n return max;\\n};\"], [57500, 6.7961, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar maxAdjacentDistance = function(nums) {\\n let sum =0,max=0;\\n\\n for(let i=1;i<nums.length;i++){\\n let val=Math.abs(nums[i]-nums[i-1])\\n sum=val;\\n if(sum>max){\\n \\n max=sum;\\n }\\n }\\n\\n let edgeVal=Math.abs(nums[nums.length-1]-nums[0]);\\n if(edgeVal>max){\\n max=edgeVal\\n }\\n return max;\\n};\"]]",
"runtime": 2,
"runtimeDistribution": "[[0, 26.2136, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar maxAdjacentDistance = function(nums) {\\n\\n let maxdiff = 0\\n for(let i = 0; i < nums.length; i++) {\\n let curr = nums[i]\\n let next = nums[(i + 1) % nums.length]\\n let diff = Math.abs(curr - next)\\n maxdiff = Math.max(diff, maxdiff)\\n }\\n return maxdiff\\n\\n};\"], [1, 48.5437, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar maxAdjacentDistance = function(nums) {\\n var maxDiff = Math.abs(nums[nums.length - 1] - nums[0]);\\n for(let i = 0; i < nums.length - 1; i++) {\\n let diff = Math.abs(nums[i] - nums[i+1]);\\n if(diff > maxDiff) maxDiff = diff;\\n }\\n\\n return maxDiff;\\n};\"], [2, 18.4466, null], [3, 4.8544, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nconst maxAdjacentDistance = (nums) => {\\n let initMaxAdjacentDistance = 0\\n let i = 0\\n\\n while (i < nums.length) {\\n let maxAdjacentDistance = Math.abs(nums[i + 1] - nums[i])\\n\\n if (maxAdjacentDistance > initMaxAdjacentDistance) {\\n initMaxAdjacentDistance = maxAdjacentDistance\\n }\\n i++\\n }\\n\\n\\n if (Math.abs(nums[nums.length - 1] - nums[0]) > initMaxAdjacentDistance) {\\n initMaxAdjacentDistance = Math.abs(nums[nums.length - 1] - nums[0])\\n }\\n\\n return initMaxAdjacentDistance\\n}\\n\"], [24, 0.9709, \"/**\\n * @param {number[]} nums\\n * @return {number}\\n */\\nvar maxAdjacentDistance = function (nums) {\\n const arr = [];\\n\\n for (let i = 0; i < nums.length - 1; i++) {\\n arr.push(Math.abs(nums[i] - nums[i + 1]));\\n }\\n\\n console.log(arr);\\n\\n arr.push(Math.abs(nums[0] - nums[nums.length - 1]));\\n\\n const x = Math.max(...arr);\\n\\n return x;\\n};\"]]"
},
"python3": {
"code": "class Solution:\n def maxAdjacentDistance(self, nums: List[int]) -> int:\n max_diff = 0\n n = len(nums)\n for i in range(n):\n next_i = (i + 1) % n\n current_diff = abs(nums[i] - nums[next_i])\n if current_diff > max_diff:\n max_diff = current_diff\n return max_diff",
"memory": 1800,
"memoryDistribution": "[[1800, 36.2036, \"class Solution:\\n def maxAdjacentDistance(self, nums: List[int]) -> int:\\n max_diff = 0\\n n = len(nums)\\n for i in range(n):\\n next_i = (i + 1) % n\\n current_diff = abs(nums[i] - nums[next_i])\\n if current_diff > max_diff:\\n max_diff = current_diff\\n return max_diff\"], [17300, 0.1957, \"class Solution:\\n def maxAdjacentDistance(self, nums: List[int]) -> int:\\n max_distance = float('-inf')\\n\\n for index in range(len(nums) - 1):\\n max_distance = max(max_distance, abs(nums[index] - nums[index + 1]))\\n \\n return max(max_distance, abs(nums[0] - nums[-1]))\"], [17400, 0.1957, \"class Solution:\\n def maxAdjacentDistance(self, nums: List[int]) -> int:\\n lst=[]\\n for i in range(len(nums)-1):\\n a=abs(nums[i]-nums[i+1])\\n lst.append(a)\\n a=0\\n b=abs(nums[0]-nums[-1])\\n lst.append(b)\\n return max(lst)\\n\"], [17500, 2.544, null], [17600, 9.7847, null], [17700, 29.9413, null], [17800, 21.135, \"class Solution:\\n def maxAdjacentDistance(self, nums: List[int]) -> int:\\n maxi = abs(nums[-1] - nums[0])\\n for i in range(1, len(nums)):\\n if abs(nums[i] - nums[i-1]) > maxi:\\n maxi = abs(nums[i] - nums[i-1]) \\n return maxi\"], [17900, 20.1566, \"class Solution:\\n def maxAdjacentDistance(self, nums: List[int]) -> int:\\n res = abs(nums[-1]-nums[0])\\n for i in range(len(nums)-1):\\n res = max(res, abs(nums[i] - nums[i+1]))\\n return res\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 35.0294, \"class Solution:\\n def maxAdjacentDistance(self, nums: List[int]) -> int:\\n maxi = abs(nums[-1] - nums[0])\\n for i in range(1, len(nums)):\\n if abs(nums[i] - nums[i-1]) > maxi:\\n maxi = abs(nums[i] - nums[i-1]) \\n return maxi\"], [1, 6.6536, \"class Solution:\\n def maxAdjacentDistance(self, nums: List[int]) -> int:\\n res = abs(nums[0] - nums[-1])\\n\\n for i in range(len(nums) - 1):\\n res = max(abs(nums[i] - nums[i + 1]), res)\\n\\n return res\"], [2, 6.4579, null], [3, 28.3757, null], [4, 13.3072, null], [5, 2.3483, \"class Solution:\\n def maxAdjacentDistance(self, nums: List[int]) -> int:\\n lst=[]\\n lst.append(nums[0]-nums[-1])\\n for i in range(1,len(nums)+1):\\n if i==len(nums):\\n break\\n lst.append(nums[i-1]-nums[i])\\n return -(min(lst)) if -min(lst)>max(lst) else max(lst)\"], [6, 1.5656, \"class Solution:\\n def maxAdjacentDistance(self, nums: List[int]) -> int:\\n n=len(nums)\\n t=0\\n for i in range(n):\\n m=abs(nums[i]-nums[(i+1)%n])\\n t=max(t,m)\\n return t \"]]"
},
"ruby": {
"code": "def max_adjacent_distance(nums)\n max = 0\n n = nums.size\n (0...n).each do |i|\n next_i = (i + 1) % n\n diff = (nums[i] - nums[next_i]).abs\n max = diff if diff > max\n end\n max\nend",
"memory": 21200,
"memoryDistribution": "[[21200, 60.0, \"def max_adjacent_distance(nums)\\n max = 0\\n n = nums.size\\n (0...n).each do |i|\\n next_i = (i + 1) % n\\n diff = (nums[i] - nums[next_i]).abs\\n max = diff if diff > max\\n end\\n max\\nend\"], [212200, 20.0, \"# @param {Integer[]} nums\\n# @return {Integer}\\n\\ndef max_adjacent_distance(nums) = (nums.each_cons(2).collect {|(a, b)| (b - a).abs } << (nums.last - nums.first).abs).max\\n\"], [212400, 20.0, \"# @param {Integer[]} nums\\n# @return {Integer}\\ndef max_adjacent_distance(nums)\\n max = (nums[1]-nums[0]).abs\\n for i in 0..nums.length-2 do\\n val = nums[i+1]-nums[i]\\n if(val.abs >max)\\n max = val.abs\\n end \\n end\\n val = (nums[-1]-nums[0]).abs\\n ans = val > max ? val : max\\n ans\\nend\"], [212500, 20.0, null], [212800, 20.0, \"# @param {Integer[]} nums\\n# @return {Integer}\\n\\ndef max_adjacent_distance(nums) = (nums.size.times.collect {|i| (nums[i] - nums[i - 1]).abs }).max\\n\"], [212900, 20.0, \"def max_adjacent_distance(nums)\\n max = 0\\n n = nums.size\\n (0...n).each do |i|\\n next_i = (i + 1) % n\\n diff = (nums[i] - nums[next_i]).abs\\n max = diff if diff > max\\n end\\n max\\nend\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 40.0, \"# @param {Integer[]} nums\\n# @return {Integer}\\ndef max_adjacent_distance(nums)\\n max = (nums[1]-nums[0]).abs\\n for i in 0..nums.length-2 do\\n val = nums[i+1]-nums[i]\\n if(val.abs >max)\\n max = val.abs\\n end \\n end\\n val = (nums[-1]-nums[0]).abs\\n ans = val > max ? val : max\\n ans\\nend\"], [2, 20.0, \"# @param {Integer[]} nums\\n# @return {Integer}\\n\\ndef max_adjacent_distance(nums) = (nums.each_cons(2).collect {|(a, b)| (b - a).abs } << (nums.last - nums.first).abs).max\\n\"], [3, 20.0, \"def max_adjacent_distance(nums)\\n max = 0\\n n = nums.size\\n (0...n).each do |i|\\n next_i = (i + 1) % n\\n diff = (nums[i] - nums[next_i]).abs\\n max = diff if diff > max\\n end\\n max\\nend\"], [11, 20.0, \"# @param {Integer[]} nums\\n# @return {Integer}\\n\\nclass Integer\\n\\n def self.gcd(x, y)\\n \\n return x if y == 0\\n\\n Integer.gcd(y, x % y)\\n end\\n\\n\\n def self.lcm(x, y)\\n\\n x / Integer.gcd(x, y) * y\\n\\n end\\n\\n def self.max(x, y)\\n \\n return x if x > y\\n\\n y\\n end\\n\\n def self.min(x, y)\\n return y if y < x\\n\\n x\\n end\\n\\n def absolute\\n return self if self >= 0\\n -self\\n end\\n\\n def sign\\n return 1 if self > 0\\n return -1 if self < 0\\n 0\\n end\\n\\nend\\n\\ndef max_adjacent_distance(nums)\\n n = nums.size\\n result = (nums[0] - nums[n - 1]).absolute\\n for i in 1...n do\\n result = Integer.max(result, (nums[i] - nums[i - 1]).absolute)\\n end\\n result\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list:
import random
random.seed(seed)
def sample_solution(nums):
max_diff = 0
n = len(nums)
for i in range(n):
next_i = (i + 1) % n
current_diff = abs(nums[i] - nums[next_i])
if current_diff > max_diff:
max_diff = current_diff
return max_diff
def serialize_input(nums):
# Simple comma‐separated values (no spaces)
return ",".join(map(str, nums))
def serialize_output(result):
# Output is a single integer converted to string
return str(result)
test_cases = []
# Fixed test cases (covering boundary, typical, and special patterns)
fixed_tests = [
[1, 2, 4], # Example 1
[-5, -10, -5], # Example 2
[5, 5], # All elements equal
[1, 2, 3, 4, 5], # Sorted ascending
[5, 4, 3, 2, 1], # Sorted descending
[-100, 0, 100], # Wide range differences
]
for nums in fixed_tests:
if len(test_cases) >= num_cases:
break
# Respect constraints: 2 <= len(nums) <= 100, -100 <= num[i] <= 100
if 2 <= len(nums) <= 100:
expected = sample_solution(nums)
test_case = {
"input": serialize_input(nums),
"output": serialize_output(expected)
}
test_cases.append(test_case)
# Generate additional random test cases if needed
while len(test_cases) < num_cases:
length = random.randint(2, 100)
nums = [random.randint(-100, 100) for _ in range(length)]
expected = sample_solution(nums)
test_case = {
"input": serialize_input(nums),
"output": serialize_output(expected)
}
test_cases.append(test_case)
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
# Deserialization: remove surrounding whitespace
# and convert the serialized output (a single integer) to int
try:
expected_val = int(expected_output.strip())
program_val = int(program_output.strip())
return expected_val == program_val
except Exception:
return False
|
[{"input": "1,2,4", "output": "3"}, {"input": "-5,-10,-5", "output": "5"}, {"input": "5,5", "output": "0"}, {"input": "1,2,3,4,5", "output": "4"}, {"input": "5,4,3,2,1", "output": "4"}, {"input": "-100,0,100", "output": "200"}, {"input": "-72,-94,89,-30,-38,-43,-65,88,-74,73,89,39,-78,51,8,-92,-93,-77,-45,-41,29,54,-94,43,-50,83,66,79,39,7,-44,14,50,-29,-99,94,-60,78,8,-13,-29,-61,-45,95,-14,-74,-77,-3,-76,-9,-12,54,-33,-89,86,17,37,-69,-4,-80,41,-25,60,58,-8,47,-51,80,-83,-89,69,-42,97,-26,-80,-41,-75,-3,-29,16,62,-7,-59", "output": "193"}, {"input": "-10,-47,71,-32,79,74,65,-82,55,62,-57,36,86,-38,-59,18,-3,-31,63,76,42,-44,75,-17,96,98,-86,-42,-92,-20,2,-32,-84,-46,45,83,-20,-46,67,27,1,64,17,-64,-33,-65,-37,90,43", "output": "184"}, {"input": "-33,91,49,9,49,2,-8,-44,-65,30,26,-77,93,-88,-72,-61,60,-60,74,8,52,-84,-2,-3,52,19,35,-36,41,-98,74,84,-71,74,37,92,-32,96,64,-13,-72,-25,11,-60,16,-100,84,84,-33,28,95,-55,29,-73,60,-24,63,29,55,-50,-61,-5,95,-59,38,99,35,-100,53,-18", "output": "184"}, {"input": "-96,-72,-8,-22,-39,-86,-39,45,-80,-79,87,24,-83,94,36,96,-68,-68,68,21,40,-58,-33,35,55,8,-46,38,93,86,76,-49,82,-21,2,71,66,-5,12,32,15,-70,-37,-43,-84,-14,-95,50,41,-42,50,-44,-99,-82,81,61,-85,-42,-83,-92,-16,-82,31,-40", "output": "177"}, {"input": "71,24,-46,38,-67,85,46,47,21,-38,100,21,4,-52,-76,-76,68,10,-10,8,5,19,86,-87,72,67,65,-75,-85,3,86,-14,-73,-37,-51,-52,37", "output": "173"}, {"input": "-65,8,-54,-29,18,-37,-81,13,40,-75,-88,66,38,-97,-77,92,-40,-58,4,24,23,-46,2,-85,-58,-3,-100,-1,-33,100,100,16,-27,8,78,87,100,42,69,83,24,-61,-52,-25,-45,-86,48,88,38,-85,91,-20,-86,-88,49,22,28,35,-60", "output": "176"}, {"input": "30,-80,-53,-83,52,-83,72,-40,3", "output": "155"}, {"input": "45,-37,48,52,-90,58,-80,7,68,49,44,33,-20,-34,-48,71,83", "output": "148"}, {"input": "-39,-33,1,-67,71,65,-24,17,-20,92,-82,-98,17,59,44,-75,-82,37,-46,29,-33,-67,-11,-83,-38,-6,-28,-60,12,39,80,-23,56,67,35,-98,70,41,-24,69,-74,-66", "output": "174"}, {"input": "-71,-73,90,41,-61,-31,-28,54,-47,83,-13,-48,75,62,-33,29,25,-36,-87,-77,62,8,-30,-89,-100,-15,97,-67,63,-33,-59,89,13,41,80", "output": "164"}, {"input": "43,-98,-72,-81,76,-62,39,-91,-6,49,41,-63,10,-68,-90,-22,-7,-90,-9,-47,74,-37,70,-74,-10,99,43,4,58,91,-61,-40,-59,-55,5,-94,-55,88,-15,100,5,71,88,-37,-32,-60,79,-73,-3,-91,20,-44,-49,17,-11,-22", "output": "157"}, {"input": "-43,-94,68,-51,2,-16,-29,-83,97,-29,-11,64,30,2,73,37,-16,-93,-71,-34,-55,48,-33,-91,-73,52,11,-12,86,-20,11", "output": "180"}, {"input": "30,-71,-2,47,-52,-35,-89,81,11,-100,33,37,75,84,89,88,71,-50,-7,10,-83,70,-16,59,-20,69,-69,84,-24,29,-21,70,4,-17,3,78,-25,41,-68,-51,7,70,-3,73,91,-56,57,45,-23,3,40,-100,-23,-27,-47,10,48,55,67,-18,19,13,13,72,-46,30,21,88,-57,68,-79,-28,31,69,62,58,-15,-77,92", "output": "170"}, {"input": "72,-21,-43,-50,-63,-94,-89,-38,21,56,96,-82,16,6,61,47,-51,83,78,-2,26,2,-38,-63,67,76,-99,92,97,-73,99,8", "output": "191"}, {"input": "-55,78,32,18,-88,42,-37,-69,16,-66,18,70,35,43,52,-19,93,13,56,84,29,9,40,14,-60,90,21,15,-34,92", "output": "150"}, {"input": "63,-30,96,99,33,24,60,-39,-30,12,-81,82,-27,-40,-31,-15,-19,38,-80,-65,-62,-41,-2,77,-61,80,-46,-84,6,4,-16,38,19", "output": "163"}, {"input": "-85,-48,7,-1,97,49,78,-95,95,47,-3,22,-99,-10,-24,92,-1,7,37,91,88,39,54,-44,24,-44,-31,11,24,-93,-1,-14,71,73,3,85,-58,19,-68,59,36,-94,0,51,44,69,-94,-79,64,9,-66,18,-54,-88,-34", "output": "190"}, {"input": "-17,-46,16,-17,-14,94,-3,-29,92,7,-36,-80,20,-96,91,38,-87,-11,-43,66,-83,99,66,-90,93,-93,-37,-49,-95,59,-61,-39,-68,21,71,-71,44,-45,19,79,-35,96,-6,-58,55,55,91,83,-71,99", "output": "187"}, {"input": "-21,-73,48,-94,-21,47,73,-4,1,83,-50,-81,51,76,60,-38,-74,78,97,-23,75,53", "output": "152"}, {"input": "44,100,-90,-12,36,9,69,-6,-83,29,65,-13,-97,7,25,-73,10", "output": "190"}, {"input": "62,17,81,-61,11,-55,87,33,66,-31,57,37,98,23,19,11,87,51,-32,-18,-38,-78,-29,15,-38,92,18,45,56,71,-3,-14,-93,26,-17,-54,24,-46,-10,-34,-13,-29,52,79,-30,42,-98,32", "output": "142"}, {"input": "-79,-39,84,4,25,42,94,-39,76,21,65,82,25,14,-96,-77,-25,-44,3,77,-38,-22,69,48,-6,21", "output": "133"}, {"input": "35,-12,8,90,40,-16,-10,79,16,-31,-22,-36,-41,-70,84,-51,-20,-70,90,37,95,76,-53,-51,-45,89,23,-30,85,50,94,34,52,-28,-75,-51,-25,-42,-8,-55,-23,-97,81,36,-68,-30,-89,-87,41,-26,78,-68,63,92,25,-74,-97,46,-28,20,22,12,-13,-53,-87,-36,22,-71,-84,2,25,-82", "output": "178"}, {"input": "61,75,-87,-62,-62,44,-23,-79,-37,-70,42,95,6,55,52,58,-43,98,33,-3,15,13,-24,50,9,-22,45,58,-85,56,89,-75,95,-47,60,-46,-33,69,-80,-60,-39,-56,41,-81,-60,-100,4,15,76,52,20,-26,-92,-41,-27,80,-28,79,16,-82,75,-41,-33,60,50,69,-50,8,-71,39,-43,65,-62,-32,-64", "output": "170"}, {"input": "-85,-58,-22,52,91,45,-27,12,-69,19,76", "output": "161"}, {"input": "79,3,-31,28,38,26,12,-80,53,-90,10,88,-18,54,-36,-94,-77,-42,72,47,50,-95,95,72,-32,47,-90,95,93,-56,20,32,66,13,-29,-54,49,11,62,25", "output": "190"}, {"input": "20,-11,4,-15,-18,71,-74,-59,-16,5,77,26,-27", "output": "145"}, {"input": "2,94,40,-91,16,-78,-20,-36,-18,-71,97,3,31,-100,68,38,18,5,-87,-52,32,-8,59,93,27,60,13,94,-87,-48,-32,40,-67,-27,12,78,24,-69,-93,61,55,-39,81,-60,-21,41,-97,41,4,-77,-43,-71,18,-70,65,-61,27,83,-26,30,80,-31,6,23,20,-38,16,41,-63,-2,-52,53,30,91,-66,-83,-30,97,6,-13,29,-32,-100,-28,85,-24", "output": "181"}, {"input": "48,68,25,-62,14,37,23,-12,-15,41,95,39,-4,16,-18,-52,78,-39,46,-2,-41,98,5,-89,-19,90,21,80,-3,-2,69,66,-62,26,-91,-68,28,51,-16,-75,12,-75,34,16,-97,84,-64,4,67,-61,-81,20,100,-33,-14,59,77,1,66,-80,-16,72,36,-3,-19,60,83,94,24,38,-91,58,-83,-40,61,75,-27", "output": "181"}, {"input": "91,-77,11,-75,94,62,80,-75,13,-58,77,-24,-93,-89,-17,-86,-25,-9,-5,10,-63,-38,35,5,44,74,-54,-57,-56,-80,56", "output": "169"}, {"input": "58,74,-39,27,49,-64,-41,18,63,-35,17,-35,70,-98,19,-27,73,39,-60,-82,13,-12,50,-24,63,8,76,-36,16,-23,-50,-2,23,-73,-40,-3,46,-9,47,-25,79,-25,-95,68,1,-30,-98,44,75,99", "output": "168"}, {"input": "-88,55,90,27,-27,98,-42,55,-10,-44,62,-52,58,-36,73,93,84,96,68,74,-65,60,-76,60,65,-90,-21,12,-92,48,-7,87,-67,-77,-25,-17,91,6,-56,-49,-67,38,-7,35,28,-31,-58,-35,23,-25,91,-14,-71,19,-81,-64,93,-43,73,85,72,1,42,-7,-77,1,-97,-33,37,-69,16,-6,72,91,72,-33,49,-3,63,-5,-73,72,-41,20,-94,58,43,-17,56,-44,65,-84,62,18,79,-23,66", "output": "157"}, {"input": "-71,-65,-89,-91,-23,26,-71,-76,-40,37,-66,-1,16,-6,71,90,78,38,7,50,90,86,-61,6,67,-75,25,57,4,-29,-92,76,-6,-45,13,13,-40,-8,-75,75,-6,39,65,-9,-85,1,-30,-52,-69,16,-77,69,-46,64", "output": "168"}, {"input": "52,-95,-88,-15,-38,-68,44,-48,-83,95,41,-47,50,-45,-41,-16,98,-63,52,-100,-30,-63,-67,38,-36,-56,-72,69,-94,-67,-97,-9,-40,50,-18,-96,-56,-33,-87,-68,89,7,34,-71,90,-84,21,14,99,-8,31,51,-73,15,28,-44,57,-89,86,100,68,33,-23,17,64,-93,-85,22,2,9,75,-73,25,82,13,-82,-80,-18,55,-63,-84,-68,-30", "output": "178"}, {"input": "62,49,40,82,-17,-3,52,35,-25,16,29,54,10,-75,79,-71,67,66,96,41,84,-45,10,15,-42,5,-14,16,2,6,86,-76,-20,9,-20,70,-35,-5,-61,75,21,-83,-77,-79,-77,10,-76,90,89,-5,-67,42,-85,50,43,43,-16,71,-69,5,-10,70,92,8,84,-87,-27,53,-21,-10,-74,47,29,-46,-61,68,23,-43,-73,-11,42", "output": "171"}, {"input": "-71,95,-29,46,-43,9,43,96,59,57,72,64,42,-94,55,68,77,-32,-93,-54,-31,79,95,-21,-14,-11,-99,-54,-64,44,68,2,-83,-64,89,62,-93,-77,91,35,-45,-4,7,16,-13,-60,-6,-21,84", "output": "168"}, {"input": "98,45,52,-79,-87,-61,-60,93,58,-88,72,-80,-31,13,69,8,24,55,13,6,-31,-45,93,31,-71,-12,10,-72,-28,73,73,51,24,34,70,-22,-89,-44,1,53,-86,-99,-48", "output": "160"}, {"input": "-46,96,-65,95,-35,-26,-17,-70,-99,27,91,10,-56,-67,-3,36,80,-42,28,43,71,-10,-82,1,89,-90,11,-96,17,-81,-20,47,9,46,3,81,63,6,-26,-71", "output": "179"}, {"input": "-95,-17,-57,58,17,76,-8,-78,11,-73,-38,11,50,2,34,-80,1,-21,90,-14,-44,-15,99,-57,-81,30,62,-71,35,30,-51,98,-11,-11,86,65,-63,-40,-74,-63,-35,-50,-56,54,-61,94,94,67,-81,-55,97,60,26", "output": "156"}, {"input": "93,44,94,48,14,74,44,64,62,59,-18,60,-20,-62,12,-83,20,13,61,-23,-30,51,-86,-10,29,-82,-21,18,15,-91,-86,-6,-27,-81,65,-77,57,52,29,-2,18,48,41,89,-90,15,46,66,-52,-18,54,21,28,-62,-85,15,-74,-13,82,-79,29", "output": "179"}, {"input": "-56,-90,-37,81,12,12,34,33,56,-60,-7,-5,-28,-1,4,98,-14,73,53,-87,61,65,-15,-84,-16,-76,42,73,-2,-28,-36,85,68,54,-62,-15,-80,49,69,-64,-11,-21,67,78,69,0,-67,52,81,-79,-21,43,-4,64,-16,-68,71,79,89,75,34,-77,65,71,8,30,-8,-96,-8,-21,-54,-46,-13,96,24,-51,-43,-65,-61,-81,-25,-75,29,97", "output": "160"}, {"input": "89,34,-91,69,-14,96,58,-67,52,-4,-61,-59,-54,77,97,59,-58,84,12,-89,5,-7,73,84,-40,13,56,-28,92,91,100,14,-41,36,-39,-21,100,20,-51,-6,73,46,12,18,96,-28,99,-3,28,35,7,-59,-49,54,-65,-36,-87,64,23,-5,41,-74,82,32,-69,-28,-79,95,-59,-31,15", "output": "174"}, {"input": "-63,11,-77,-44,15,-11,-94,6,-87,1,28,-5,-40,-2,-80,-5,-43,-93,-19,-75,82,66,-15,-63,-65,-91,-27,20,78,-65,94,80,20,14,57,-99,-80,-96,-35,-45,-62,40,86,55,35,8,-72,98,-27,-40,-23,-69,-88,-39,7,63,59,17,-84,-72,27,52,37,-96,61,31,47", "output": "170"}, {"input": "83,-64,-26,9,-100,57,-10,-39,46,6,-53,70,71,-79,34,-8,-83,34,39,29,29,41,-95,-1,20,-89,62,-1,-5,-36,91,-96", "output": "187"}, {"input": "-83,-12,-39,87,68,60,-74,97,48,88,93,-15,-66,-89,-10,39,-14,64,-56,99,75,18,78,22,61,-54,-66,-84,83,98,17,-91,-25,-49,-89,-49,-90,-20,-21,31,1,39,21,-36,-91,92,65", "output": "183"}, {"input": "-27,-9,99,-88,67,-16,-31,-69,-6,11,2,90,12,-2,-14,-53,27,77,27,-6,32,-32,-79,86,8,-80", "output": "187"}, {"input": "54,-54,39,-25,-18,-74,-80,-17,69,-25,-22,14,54,83,9,-58,76,13,-11,14,-90,86,-10,57,11,-30,63,-86,-81,71,63,3,-7,31,91,73,-60,-93,-64,55,73,100,12,-92,-68,-83,-40,99,65,-7,-8,-2,45,-92,54,-61,73", "output": "176"}, {"input": "-6,-5,13,95,-81,46,-65,35,-7,1,-20,66,-29,-37,-71,-94,88,-53,27,32,-1,43,-70,-33,98,-34,80,14,-46,56,-27,77,25,-49,-69,-66,-82,15,-56,82,13,-78,74,-19,70,-12,81,-84,40,38,-26,-24,-60,82,81,79,63,-56,-8", "output": "182"}, {"input": "-43,-69,-49,-65,-40,26,-94,-8,41,46,-6,19,41,-67,56,-78,-84,-21,1,83,84,22,34,5,96,4,47,-82,-68,-19,64,-82,15,19,74,32,-12,-68,99,41,63,50,-54,96,-67,10,28,-86,-69,32,-61,-23,-58,-59,-18,81,-43,-12,32,-28,-80,-36,-50,62,41,-30,-68", "output": "167"}, {"input": "-23,57,36,-77,28,64,-57,51,48,-61,-57,68,59,84,54,-14,44,-90,-93,-80,-89,64,97,47,-33,66,-47,96,46,6,58,63,-93,27,60,39,-26,64,-23,23,-38,75,3,-24,16,-82,76,-85,-60,12,6,23,18,-48,-13,55,-64,-20,83,-19,87,-12,2,-67,94,-6,31,43,-73,-19,-39,19,-69,-32,15,-37,-64,-76,-88,-26,-2,57", "output": "161"}, {"input": "-37,-60,-17,47,84,-20,-52,95,-60,27,31,19,27,-22,27,-95,-77,0,29,17,-39,-45,49,-10,-88,-88,-28,26,52,67,72,20,-27,37,-98,-73,10,-66,-33,86,-7,95,3,-7,-89,2,-87,45,43,-51,-8,41,-27,-82,-2", "output": "155"}, {"input": "15,95,40,-29,59,74,56,-70,-68,-76,0,-5,-14,42,-7,93,-64,-50,54,30,2,28,-90,-89,-91,-65,82,-15,21,32,16,-62,55,31,-65,-17,56,-19,-59,0,57,89,-24,51,-14,29,30,36,25,81,44,-24,21,-96,-6,-16,72,-72,6,49,-22,85,76,61,-94,52", "output": "157"}, {"input": "-33,67,100,98,48,47,-42,84,-87,49,22,-57,34,61,84,58,98,-3,-63,74,-38,-92,46,79,-72,-52,-96,12,-20,7,-62,5,76,-48,5,28,98,56,20,88,86,-85,80,-65,32,-47,43,-17,69,22,34,-4,-20,-56,17,36,-13,39,-10,73,97,84", "output": "171"}, {"input": "64,77,-33,56,23,-51,-37,-29,42,-24,-43,-24,97,-27,80,-47,76,80,25,-19,22,-11,43,84,-30,-27,-69,46,73,39,-3,1,-12,97,-63,-26,-90,-27,82,-80,-12,13,67,-35,91,22,-46,-49,37,-31,43,78,-31,-65,-73,57,89,50,-39,-38,-88,71,35,-43,63,-41,-87,-75,5,-16,83,20,-75,74,97,-65,-99,40,-60,4,67,21,22,66,-49,93,-27,-18,-27", "output": "162"}, {"input": "-85,96,-78,66,46,-41,36,89,85,-91,-56,6,-55,-91,1,26,-53,91,-26,-91,-98,-24,45,54,-73,-15,-28,16,64,39,34,26,-66,29,19,-31,-51,-72,-16,-59,87,17,65,-35,83,-53,-97,88,-14,-25,45,72,93,-51,-56,56,63,3,9,31,-17,-78,2,71,-76,-53,-65,22,-18,-37,-99,-34,-2,-40,14,92,-32,-16,-23,49,85,46,-98,-34", "output": "185"}, {"input": "-8,77,-40,-85,70,-70,19,-22,-60,3,75,28,80,97,-21,76,-70,63,-25,-6,57,-44,-44,-66,22,-61,16,91,55,-5,6,79,40,20,93,37,70,-45,95,-37,74,93,52,-80,34,14,35,80,-8,-81,44,-72,-85,40,29,-49,46,37,-62,-58,-17,33,13,-71,74,-48,83,49,25,-77,30,14,-86,16,-67,31,6,16,44,-86,43,18,72,-22,85", "output": "155"}, {"input": "1,-35,-100,90", "output": "190"}, {"input": "48,-82,-89,8,-12,79,-84,38,-85,-83,20,-92,-27,4,-54,96,-66,96,64,86,65,7,-5,-3,14,-4,-4,-80,74", "output": "163"}, {"input": "38,-66,67,-11,-70,-55,37,0,35,-68,86,-43,-100,93,-95,-24,18,72,84,39,8,36,-3,-42,-37,17,-12,-61,-30,-52,85,95,-72,-92,69,7,57,96,-96,-39,-48,-83,-75,52,-92,14,53,72,80,-88,-38,89,-89,2,12,-41,38,-45,93,98,-86,-65,28,-26,-41,87,47,-19,47,53,97,72,-18,-40,-23,-64,69,33,-44,5,-24,-30,-85,42,51,88", "output": "193"}, {"input": "60,73,9,42,26,-88,-12,64,71,-3,34,-19,78,6,4,-62,-24,-4,-53,93,37,21,-39,-43", "output": "146"}, {"input": "81,-64,18,-86,43,5,6,42,35,-66,-1,-38,-35,-48,-16,65,-80,15,-6,-77,37,85,-52,-87,-32,-4,72,54,54,-90,-82,-52,94,50,85,71,43,-45,22,-47", "output": "146"}, {"input": "-23,-97,-46,-52,89,-70,91,93,22,-38,78,54,80,-48,1,-39,41,-18,98,-28,-3,19,36,66,-9,-22,-34,-8,31,27,19,-75,84,20,94,-19,-48,-6,-20,5,-89,44,-44,89", "output": "161"}, {"input": "-96,-34,41,49,48,84,6,-25,-61,-50,-16,-42,-3,45,-38,27,40,67,75,-14", "output": "89"}, {"input": "95,25,85,64,89,25,17,-57,87,-10,-57,-65,84,39,25,-53,38,64,-85,34,-92,-81,71,-88,95,-99,5,-65,61,-41,-83,81,-62,-98", "output": "194"}, {"input": "29,16,-5,-85,58,63,70,57,23,68,24,-96,-99,36,41,5,-97,-96,35,84,-30,37,-27,-96,28,78,72,10,-55", "output": "143"}, {"input": "-76,34,-62,-39,-51,58,34,-36,-10,-32,1,-80,-5,3,17", "output": "110"}, {"input": "-38,78,-43,-24,75,-80,67,66,94,-92,-77,3,-3,-4,41,21,-86,63,-98,79,-57,-79,27,11,65,100,-16,44,-76,35,-90,-42,-46,77,45,21,-31,-89,-81,75,-29,39,44,68,-92,-55,-20,-96,-47,50,-64,92,82,1,-81,-24,-59,44,-39,45,-1,73,38,-16,-2,93,89,-65,76,85,-80,28,90,-12", "output": "186"}, {"input": "-75,11,-41,-81,-13,54,96,57", "output": "132"}, {"input": "1,98,-17,-93,62,-31,100,15,25,-42,-9,41,-4,10,-53,74,49,69,-3,-79,97,58,-25,-37,82,-82,-79,-32,-61,-3,82,100,62,-61,89,-1,-19,-8,-73,-77,-99,-22,13,-8,94,-31,-74,-67,-78,-53,10,14,42,42,31,4,-74,-94,-78,-10,41,-77,52,53,100,-17,-2,-97,-26,5,-1,99,-79,85,43,-38,46,33", "output": "178"}, {"input": "75,-3,-57,-65,-32,-23,-32,26,-63,-84,-58,11,-30,7,-24,23,100,-81,-8,-36,-37,84,60", "output": "181"}, {"input": "52,57,-50,17,-73,-66,-23,-99,1,-15,58,-3,-16,12,-15,10,66,52,-66,-24,-18,54,77,-49,22,-20,-55,1,-19,-26,88,77,62,25,47,100,-38,-17,-4,-29,0,-7,-71,44,-49,51,39,-54,74,96,40,-94,86,18,81,-47,12,-26,77,-83,4,72,27,-65,62", "output": "180"}, {"input": "-39,-36,68,-61,83,8,-4,-82,14,53,22,49,2,36,29,77,7,39,-91,-8,79,37,52,63,-79,-73,96,-37,68,70,-10,-58,65,56,-89,44,65,73,65,2", "output": "169"}, {"input": "-16,10,-73,-98,-75,-34,-44,30,91,32,42,48,76,47,-44,14,-5,0,18,97,73,50,76,28,-62,-12,-94,23,-74,-25,6,-79,-71,86,-64,-11,-21,-13,16,100,-48,33,23,-11,21,-76,12,84,78,15,-19,-83,-24,-89,81,-71,-95,-13,65,-73,73,-58,89,-38,32,-56,41,-60,-16,43,9,18,-41,3,61,-53,-53,63,68,10,1,-93,88,57,-50,15,51,9,-1,-99,80,-46,-48,-29,92,80,-84,47", "output": "181"}, {"input": "37,-53,-7,-17,-50,17,-71,-33,71,25,35,63,-20,52,-1", "output": "104"}, {"input": "0,50,-71,-11,-10,17,58,-56,72,80,-24,57,51,-79,72,-66,-20,-70,-39,-22,-71,-54,-5,77,-64,30,-1,7,52,-65,47,-2,8,-53,24,62,37,77,65,-56,42,-58,25,-27,-65,-53,-20,15,58,-87,-9,-98,24,-66,-51,-2,43,29,67,26,4,75,25,6,81,13,25,-58,-79,44,-93,94,-44,-26,-92,-30,-43,37,-27,-57", "output": "187"}, {"input": "44,90,97,96,26,40,30,-72,46,-71,-32,98,39,-7,38,93,-90,94,84,12,39,-45,8,-74,88,67,92,-37,-24,-92,15,-33,-11,-78,12,-70,98,-40,-47,88,50,76,-11,81,56,61,9,-58,57,-65,100,-48,-48,-85,45,-11,36,-29,52,37", "output": "184"}, {"input": "-18,80,-26,-26,46,-32,31,73,-76,-66,92,5,-85,-30,67,-68,79,-67,-37,-63,82,-18,-37", "output": "158"}, {"input": "73,0,25,-64,47,61,-32,60,6,-4,15,-81,62,96,-77,3,31,91,-29,77,-6,16,24,-17,48,-100,98,87,-77,87,17,62,70,78,-9,-84,36,1,-45,9,-46,26,-32,-18,-28,-14,40,47,-67,44,24,-13,74,95,-88,-89,-75,60,100,17,-96,-69,-60,12,16,-100,9,-49,76,-67,66,-23,-60,-30,-77,67,-8,-36,-79,-5,70,66,-58,-87,1,60,-22,85,79,93,-41,9,67,-77,80,-76,-100,-46,22", "output": "198"}, {"input": "-67,51,-43,32,74,13,-98,-98,78,-13,-70", "output": "176"}, {"input": "77,-67,22,-82,-42,-2,-78,87,-74,-74,-20,-6,-24,-65,-3,98,92,-66,64,73,-64,-83,35,44,-98,56,66,-58,12,-11,84,-46,60,91,-62,5,57,75,13,-45,-78,-75,-65,92,-69,50,86,-2,-11,9,-20,-65,-37,-30,65,-79", "output": "165"}, {"input": "41,53,53,84,55,-28,99,76,-94,68,-23,-48,32,55,30,-52,91,0,-25,65,-87,100,-39,26,-2,-72,-39,27,63,52,-82,35,-97", "output": "187"}, {"input": "-19,-67,-1,45,7,-7,39,74,-56,95,20,97,-82,-96,50,-83,-97,-33,-45,-90,-85,1,29,-27,60,82,28,96,6,8,79,2,-79,63,37,37,57,-61,-29,-79,-21,-80,30,-48,-61,37,-17,0", "output": "179"}, {"input": "62,95,66,74,64,-84,-21,78,11,86,-39,-86,-38,-78,11,-71,16,56,55,-86,-21,70,89,68,89,-56,-70,-97,81,-65,79,-98,-59,27,-12,33,32,100,84,-34,-58,-5,-68,91,99,-32,87,-70,97,-93,-15,9,-31,34,-84,-33,82,47,60,-81,27,16,30,-8,-86,27,45,-58,-6,-60,-35,97,-74,46,72,85,-71", "output": "190"}, {"input": "89,30,-100,-89,-97,-38,-89,20,-7,-2,-62,-55,-91,41,82,89,67,7,-43,-18,-37,6,84,-19,-31,-81,46,-5,-70,28,72", "output": "132"}, {"input": "-55,-43,32,-89,2,-83,19,-28", "output": "121"}, {"input": "-17,-78,41,16,-98,-6,-49,-26,44,100,-23,89,59,-38,18,-6,51,26,97,98,-50,87,39,94,-38,-62,-99,4,-94,-41,38,-12,62,77,-98,-15,-100,94,68,-4,88", "output": "194"}, {"input": "-22,-74,-48,35,-40,7,25,-85,-64,82,-29,-77,-89,-41,33,5,79,-5,17,91,-79,48,-76,29,-66,63,0,-81,51,45,-85,11,69,-67,-40,-26,-34,-20,0,79,88,-17,-19,15,-31,-41,-81,-49,-66,99,97,49,-73,-61,-73,-58,15,19,-20,4,-70,37,-9,97,-47,15,-22,18,-33,-70,-77,-60,75,-23,80,78,54,-90,-45,-17,-63,-77,82,-37,-9,1,31,-88,73,-24,-34,-56,-93,3,15", "output": "170"}, {"input": "91,40,-37,-76,18,-74,-65,-69,-97,-85,99,-44,-67,-50,2,-5,75,61,65,-79,49,50,-34,-81,-95,-84,-50,65,13,-68,-77,-16,-69,-90,18,-88,-57,46,10,85,1,27,-93,-3,74,9,-56,-10,-46,-53,-30,-29,14,-62,-92,57,58,57,-38,65,-25,27,5,40,22,-85,-78,-29,-2,-65,7,-49,64", "output": "184"}, {"input": "-37,61,39,-96,-3,100,82,-9,22,39,100,24,-12,44,28,-18,-1,-31,-54,-94,-19,52,-44,-93,99,-29,-86,20,35,-9,96,49,-41,-60,-75,-37,68,-39,-32,36,88,-86,95,-44,47,-1,-10,-56,-55,-40,51,-19,88,78,-9,51,-93,80,79,-10,45,44,-64,44,-52,26,38,-21,-56", "output": "192"}, {"input": "-91,-77,-86,-41,54,-44,-95,34,22,-100,-16,57,-49,-67,-13,83,-55,-18,-85,-95,-63,50,80,-64,98,-72,34,-7,-82,-5,80,69,1,50,-75,-14,-23,-18,-66,-60,87,11,63,24,66,-19,-56,81,43,77,57,-9,-43,70,50,-56,-4,-22,87,76,-25,-68,-55,86", "output": "177"}, {"input": "79,46", "output": "33"}, {"input": "97,45,-92,-54,54,-19,56,-44,63,44,-74,27,-64,-16,90,-81,-40,-12,-19,-58,62,-78,81,71,63,86,-15,14,-98,-33,-47,-37,77,-83,-11,-35,-73,84,-100,-88,-2,12,87,7,-58,5,26,-4,-11,39,-4,-75", "output": "184"}, {"input": "47,66,94,75,-43,-59,15,-82,-92,-25,-95,-19,-34,-74,-82,-13,-57,-4,-59,87,-81,40,-77,-14,52,57,23,80,-93,10,67,-58,55,11,-60,-87,-75,-16,-48,-52,4,78,41,84,86,38,-33,69,-28,-24,-40,-76,-88,0,46,40,25,-61,-87,-8,-100,9,-78", "output": "173"}, {"input": "69,60,53,22,-49,-76,-94,-48,-57,63,-26,-80,21,-71,-22,100,1,20,25,69,-33,-77,64,39,-1,-53,-6,-3,-6,-53,14,-89,-33,12,19,-33,-43,-32,44", "output": "141"}]
|
{
"cpp": "==Code Submission==\n\n// Deserialization: parse a comma-separated list of integers.\nvector<int> deserialize_stdin(const string &input) {\n vector<int> nums;\n stringstream ss(input);\n string token;\n while(getline(ss, token, ',')) {\n if(!token.empty())\n nums.push_back(atoi(token.c_str()));\n }\n return nums;\n}\n\n// Serialization: convert integer result to string.\nstring serialize_stdout(int result) {\n return to_string(result);\n}\n\nint main(){\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n \n string line;\n getline(cin, line);\n vector<int> nums = deserialize_stdin(line);\n \n Solution sol; // Submitted solution will provide the definition of class Solution and its method.\n int ans = sol.maxAdjacentDistance(nums);\n \n cout << serialize_stdout(ans);\n return 0;\n}",
"golang": "==Code Submission==\n\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n line, _ := reader.ReadString('\\n')\n line = strings.TrimSpace(line)\n if line == \"\" {\n return\n }\n parts := strings.Split(line, \",\")\n nums := make([]int, len(parts))\n for i, s := range parts {\n nums[i], _ = strconv.Atoi(s)\n }\n ans := maxAdjacentDistance(nums) // The submitted solution must define the function maxAdjacentDistance.\n fmt.Print(strconv.Itoa(ans))\n}",
"java": "public class Main {\n // Deserialization: parse a comma separated list of integers.\n private static int[] deserializeIntArray(String input) {\n String[] parts = input.trim().split(\",\");\n int[] nums = new int[parts.length];\n for (int i = 0; i < parts.length; i++) {\n nums[i] = Integer.parseInt(parts[i]);\n }\n return nums;\n }\n \n // Serialization: convert integer result to string.\n private static String serializeOutput(int result) {\n return String.valueOf(result);\n }\n \n public static void main(String[] args) throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n String line = br.readLine().trim();\n int[] nums = deserializeIntArray(line);\n \n Solution sol = new Solution(); // Submitted solution must define the class Solution with the method maxAdjacentDistance.\n int ans = sol.maxAdjacentDistance(nums);\n System.out.println(serializeOutput(ans));\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\n\nconst deserialize_stdin = (input) => {\n // Expecting a comma-separated list.\n return input.trim().split(',').map(Number);\n};\n\nconst serialize_stdout = (result) => {\n return result.toString();\n};\n\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\nlet input = '';\nprocess.stdin.on('data', chunk => input += chunk);\nprocess.stdin.on('end', () => {\n const nums = deserialize_stdin(input);\n const ans = maxAdjacentDistance(nums); // The submitted solution must define the function maxAdjacentDistance.\n console.log(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str):\n # Expecting a comma-separated list of integers.\n if input_str.strip() == \"\":\n return []\n return list(map(int, input_str.strip().split(',')))\n\ndef serialize_stdout(result):\n return str(result)\n\ninput_str = sys.stdin.read().strip()\nnums = deserialize_stdin(input_str)\nsol = Solution() # The submitted code should define the class Solution with method maxAdjacentDistance.\nans = sol.maxAdjacentDistance(nums)\nsys.stdout.write(serialize_stdout(ans))",
"ruby": "==Code Submission==\n\ninput = gets.strip\nnums = input.split(',').map(&:to_i)\nans = max_adjacent_distance(nums) # The submitted solution must define the method max_adjacent_distance.\nputs ans.to_s"
}
|
3748
|
Sort Matrix by Diagonals
|
sort-matrix-by-diagonals
|
<p>You are given an <code>n x n</code> square matrix of integers <code>grid</code>. Return the matrix such that:</p>
<ul>
<li>The diagonals in the <strong>bottom-left triangle</strong> (including the middle diagonal) are sorted in <strong>non-increasing order</strong>.</li>
<li>The diagonals in the <strong>top-right triangle</strong> are sorted in <strong>non-decreasing order</strong>.</li>
</ul>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">grid = [[1,7,3],[9,8,2],[4,5,6]]</span></p>
<p><strong>Output:</strong> <span class="example-io">[[8,2,3],[9,6,7],[4,5,1]]</span></p>
<p><strong>Explanation:</strong></p>
<p><img alt="" src="https://assets.leetcode.com/uploads/2024/12/29/4052example1drawio.png" style="width: 461px; height: 181px;" /></p>
<p>The diagonals with a black arrow (bottom-left triangle) should be sorted in non-increasing order:</p>
<ul>
<li><code>[1, 8, 6]</code> becomes <code>[8, 6, 1]</code>.</li>
<li><code>[9, 5]</code> and <code>[4]</code> remain unchanged.</li>
</ul>
<p>The diagonals with a blue arrow (top-right triangle) should be sorted in non-decreasing order:</p>
<ul>
<li><code>[7, 2]</code> becomes <code>[2, 7]</code>.</li>
<li><code>[3]</code> remains unchanged.</li>
</ul>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">grid = [[0,1],[1,2]]</span></p>
<p><strong>Output:</strong> <span class="example-io">[[2,1],[1,0]]</span></p>
<p><strong>Explanation:</strong></p>
<p><img alt="" src="https://assets.leetcode.com/uploads/2024/12/29/4052example2adrawio.png" style="width: 383px; height: 141px;" /></p>
<p>The diagonals with a black arrow must be non-increasing, so <code>[0, 2]</code> is changed to <code>[2, 0]</code>. The other diagonals are already in the correct order.</p>
</div>
<p><strong class="example">Example 3:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">grid = [[1]]</span></p>
<p><strong>Output:</strong> <span class="example-io">[[1]]</span></p>
<p><strong>Explanation:</strong></p>
<p>Diagonals with exactly one element are already in order, so no changes are needed.</p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>grid.length == grid[i].length == n</code></li>
<li><code>1 <= n <= 10</code></li>
<li><code>-10<sup>5</sup> <= grid[i][j] <= 10<sup>5</sup></code></li>
</ul>
|
You are given an `n x n` square matrix of integers `grid`. Return the matrix such that:
- The diagonals in the **bottom\-left triangle** (including the middle diagonal) are sorted in **non\-increasing order**.
- The diagonals in the **top\-right triangle** are sorted in **non\-decreasing order**.
**Example 1:**
**Input:** grid \= \[\[1,7,3],\[9,8,2],\[4,5,6]]
**Output:** \[\[8,2,3],\[9,6,7],\[4,5,1]]
**Explanation:**
The diagonals with a black arrow (bottom\-left triangle) should be sorted in non\-increasing order:
- `[1, 8, 6]` becomes `[8, 6, 1]`.
- `[9, 5]` and `[4]` remain unchanged.
The diagonals with a blue arrow (top\-right triangle) should be sorted in non\-decreasing order:
- `[7, 2]` becomes `[2, 7]`.
- `[3]` remains unchanged.
**Example 2:**
**Input:** grid \= \[\[0,1],\[1,2]]
**Output:** \[\[2,1],\[1,0]]
**Explanation:**

The diagonals with a black arrow must be non\-increasing, so `[0, 2]` is changed to `[2, 0]`. The other diagonals are already in the correct order.
**Example 3:**
**Input:** grid \= \[\[1]]
**Output:** \[\[1]]
**Explanation:**
Diagonals with exactly one element are already in order, so no changes are needed.
**Constraints:**
- `grid.length == grid[i].length == n`
- `1 <= n <= 10`
- `-105 <= grid[i][j] <= 105`
|
Medium
|
[
"array",
"sorting",
"matrix"
] |
leetcode
|
https://leetcode.com/problems/sort-matrix-by-diagonals
|
functional
| null | null | null | null |
{
"c": "/**\n * Return an array of arrays of size *returnSize.\n * The sizes of the arrays are returned as *returnColumnSizes array.\n * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().\n */\nint** sortMatrix(int** grid, int gridSize, int* gridColSize, int* returnSize, int** returnColumnSizes) {\n \n}",
"cpp": "class Solution {\npublic:\n vector<vector<int>> sortMatrix(vector<vector<int>>& grid) {\n \n }\n};",
"csharp": "public class Solution {\n public int[][] SortMatrix(int[][] grid) {\n \n }\n}",
"dart": "class Solution {\n List<List<int>> sortMatrix(List<List<int>> grid) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec sort_matrix(grid :: [[integer]]) :: [[integer]]\n def sort_matrix(grid) do\n \n end\nend",
"erlang": "-spec sort_matrix(Grid :: [[integer()]]) -> [[integer()]].\nsort_matrix(Grid) ->\n .",
"golang": "func sortMatrix(grid [][]int) [][]int {\n \n}",
"java": "class Solution {\n public int[][] sortMatrix(int[][] grid) {\n \n }\n}",
"javascript": "/**\n * @param {number[][]} grid\n * @return {number[][]}\n */\nvar sortMatrix = function(grid) {\n \n};",
"kotlin": "class Solution {\n fun sortMatrix(grid: Array<IntArray>): Array<IntArray> {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param Integer[][] $grid\n * @return Integer[][]\n */\n function sortMatrix($grid) {\n \n }\n}",
"python": "class Solution(object):\n def sortMatrix(self, grid):\n \"\"\"\n :type grid: List[List[int]]\n :rtype: List[List[int]]\n \"\"\"\n ",
"python3": "class Solution:\n def sortMatrix(self, grid: List[List[int]]) -> List[List[int]]:\n ",
"racket": "(define/contract (sort-matrix grid)\n (-> (listof (listof exact-integer?)) (listof (listof exact-integer?)))\n )",
"ruby": "# @param {Integer[][]} grid\n# @return {Integer[][]}\ndef sort_matrix(grid)\n \nend",
"rust": "impl Solution {\n pub fn sort_matrix(grid: Vec<Vec<i32>>) -> Vec<Vec<i32>> {\n \n }\n}",
"scala": "object Solution {\n def sortMatrix(grid: Array[Array[Int]]): Array[Array[Int]] = {\n \n }\n}",
"swift": "class Solution {\n func sortMatrix(_ grid: [[Int]]) -> [[Int]] {\n \n }\n}",
"typescript": "function sortMatrix(grid: number[][]): number[][] {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n vector<vector<int>> sortMatrix(vector<vector<int>>& grid) {\n int n = grid.size();\n map<int, vector<pair<int, int>>> diagonals;\n \n for (int k = -(n-1); k <= n-1; ++k) {\n vector<pair<int, int>> cells;\n for (int i = 0; i < n; ++i) {\n int j = i - k;\n if (j >= 0 && j < n) {\n cells.emplace_back(i, j);\n }\n }\n if (!cells.empty()) {\n diagonals[k] = cells;\n }\n }\n \n for (auto& entry : diagonals) {\n int k = entry.first;\n auto& cells = entry.second;\n vector<int> values;\n for (auto& cell : cells) {\n values.push_back(grid[cell.first][cell.second]);\n }\n if (k >= 0) {\n sort(values.rbegin(), values.rend());\n } else {\n sort(values.begin(), values.end());\n }\n for (int i = 0; i < cells.size(); ++i) {\n int x = cells[i].first;\n int y = cells[i].second;\n grid[x][y] = values[i];\n }\n }\n \n return grid;\n }\n};",
"memory": 4900,
"memoryDistribution": "[[4900, 5.2533, \"class Solution {\\npublic:\\n vector<vector<int>> sortMatrix(vector<vector<int>>& grid) {\\n int n = grid.size();\\n map<int, vector<pair<int, int>>> diagonals;\\n \\n for (int k = -(n-1); k <= n-1; ++k) {\\n vector<pair<int, int>> cells;\\n for (int i = 0; i < n; ++i) {\\n int j = i - k;\\n if (j >= 0 && j < n) {\\n cells.emplace_back(i, j);\\n }\\n }\\n if (!cells.empty()) {\\n diagonals[k] = cells;\\n }\\n }\\n \\n for (auto& entry : diagonals) {\\n int k = entry.first;\\n auto& cells = entry.second;\\n vector<int> values;\\n for (auto& cell : cells) {\\n values.push_back(grid[cell.first][cell.second]);\\n }\\n if (k >= 0) {\\n sort(values.rbegin(), values.rend());\\n } else {\\n sort(values.begin(), values.end());\\n }\\n for (int i = 0; i < cells.size(); ++i) {\\n int x = cells[i].first;\\n int y = cells[i].second;\\n grid[x][y] = values[i];\\n }\\n }\\n \\n return grid;\\n }\\n};\"], [41500, 0.3623, \"class Solution {\\npublic:\\n vector<vector<int>> sortMatrix(vector<vector<int>>& grid) {\\n int m = grid.size();\\n int n = grid[0].size();\\n for(int k=0;k<max(m,n);k++){\\n for(int i=0;i<m-1;i++){\\n for(int j=0;j<n-1;j++){\\n if(i>=j && grid[i][j]<grid[i+1][j+1]){\\n swap(grid[i][j],grid[i+1][j+1]);\\n }\\n else if(i<j && grid[i][j]>grid[i+1][j+1]) {\\n swap(grid[i][j],grid[i+1][j+1]);\\n }\\n }\\n \\n }\\n }\\n\\n return grid;\\n }\\n};\\n\"], [41600, 1.4493, \"class Solution {\\npublic:\\n vector<vector<int>> sortMatrix(vector<vector<int>>& grid) {\\n const int n = grid.size();\\n\\n for (int i = 0;i < n;i++) {\\n sortDiagonal(grid, i, 0);\\n }\\n\\n for (int i = 1;i < n;i++) {\\n sortDiagonal(grid, 0, i);\\n }\\n\\n return grid;\\n }\\n\\nprivate:\\n void sortDiagonal(vector<vector<int>>& grid, int r, int c) {\\n int n;\\n if (c == 0) {\\n n = grid.size()-r;\\n } else {\\n n = grid[0].size()-c;\\n }\\n\\n while (n > 1) {\\n int m = 0;\\n for (int i = 1;i < n;i++) {\\n if ((c == 0 && grid[r+i][c+i] > grid[r+i-1][c+i-1]) ||\\n (c != 0 && grid[r+i][c+i] < grid[r+i-1][c+i-1])) {\\n swap(grid[r+i][c+i], grid[r+i-1][c+i-1]);\\n m = i;\\n }\\n }\\n\\n n = m;\\n }\\n }\\n};\"], [41700, 0.5435, null], [41800, 3.6232, null], [41900, 1.9928, null], [42000, 1.2681, null], [42100, 0.7246, null], [42200, 0.5435, null], [42300, 0.7246, null], [42400, 0.3623, null], [42500, 0.1812, null], [42600, 0.1812, null], [42700, 0.9058, null], [42800, 0.5435, null], [42900, 0.7246, null], [43100, 0.1812, null], [43200, 2.8986, null], [43300, 6.7029, null], [43400, 6.7029, null], [43500, 4.1667, null], [43600, 2.1739, null], [43700, 0.9058, null], [43800, 0.5435, null], [43900, 0.7246, null], [44000, 0.1812, null], [44100, 0.9058, null], [44200, 0.7246, null], [44300, 1.087, null], [44400, 1.4493, null], [44500, 0.9058, null], [44600, 0.9058, null], [44700, 2.3551, null], [44800, 4.1667, null], [44900, 4.8913, null], [45000, 5.2536, null], [45100, 2.7174, null], [45200, 1.8116, null], [45300, 3.6232, null], [45400, 1.087, null], [45600, 0.7246, null], [45700, 0.7246, null], [45800, 1.4493, null], [45900, 1.2681, null], [46000, 0.1812, null], [46100, 0.3623, null], [46200, 1.8116, null], [46300, 2.5362, null], [46400, 6.5217, null], [46500, 3.8043, null], [46600, 3.6232, null], [46700, 0.1812, null], [46800, 0.1812, \"class Solution {\\n vector<int> solve(vector<vector<int>> &grid,int row,int col){\\n int n = grid.size();\\n int m = grid[0].size();\\n vector<int> ans;\\n int i = row;\\n int j = col;\\n while(i<n && j<m){\\n ans.push_back(grid[i][j]);\\n i++;\\n j++;\\n }\\n sort(ans.begin(),ans.end());\\n return ans;\\n }\\n\\n void merge(vector<vector<int>> &a,vector<vector<int>> &ans,int count,int row,int col){\\n vector<int> arr = a[count];\\n int k=0;\\n int i=row;\\n int j=col;\\n while(k<arr.size()){\\n ans[i][j]=arr[k];\\n i++;\\n j++;\\n k++;\\n }\\n }\\npublic:\\n vector<vector<int>> sortMatrix(vector<vector<int>>& grid) {\\n ios::sync_with_stdio(false);\\n cin.tie(nullptr);\\n int n = grid.size();\\n int m = grid[0].size();\\n vector<vector<int>> a;\\n vector<vector<int>> ans(n,vector<int> (m,0));\\n for(int i=m-1;i>=0;i--){\\n vector<int> temp = solve(grid,0,i);\\n if(i==0)\\n reverse(temp.begin(),temp.end());\\n a.push_back(temp);\\n }\\n for(int i=1;i<n;i++){\\n vector<int> temp = solve(grid,i,0);\\n reverse(temp.begin(),temp.end());\\n a.push_back(temp);\\n }\\n int count = 0;\\n for(int i=m-1;i>=0;i--){\\n merge(a,ans,count,0,i);\\n count++;\\n }\\n for(int i=1;i<n;i++){\\n merge(a,ans,count,i,0);\\n count++;\\n }\\n return ans;\\n }\\n};\"], [46900, 0.1812, \"bool compare(int&a, int& b){\\n return a>=b;\\n}\\n\\nclass Solution {\\npublic:\\n vector<vector<int>> sortMatrix(vector<vector<int>>& grid) {\\n map<int,vector<int>>mpp;\\n int n = grid.size();\\n for(int i=0;i<n;i++){\\n for(int j=0;j<n;j++){\\n mpp[i-j].push_back(grid[i][j]);\\n }\\n }\\n for(auto it:mpp){\\n \\n if(it.first < 0){\\n sort(mpp[it.first].begin(),mpp[it.first].end());\\n }\\n else{\\n sort(mpp[it.first].begin(),mpp[it.first].end(),compare);\\n }\\n }\\n for(int i=n-1;i>=0;i--){\\n for(int j=n-1;j>=0;j--){\\n grid[i][j] = mpp[i-j].back();\\n mpp[i-j].pop_back();\\n }\\n }\\n return grid;\\n }\\n};\"]]",
"runtime": 18,
"runtimeDistribution": "[[0, 4.8913, \"class Solution {\\npublic:\\n vector<vector<int>> sortMatrix(vector<vector<int>>& grid) {\\n int n=grid.size();\\n for(int i=n-1;i>=0;i--){\\n vector<int>s(n-i);\\n for(int j=i,k=0;j<n;k++,j++){\\n s[k]=grid[j][k];\\n }\\n sort(s.begin(),s.end(),greater<int>());\\n for(int j=i,k=0;j<n;k++,j++){\\n grid[j][k]=s[k];\\n }\\n }\\n for(int i=1;i<n;i++){\\n vector<int>s(n-i);\\n for(int j=i,k=0;j<n;k++,j++){\\n s[k]=grid[k][j];\\n }\\n sort(s.begin(),s.end());\\n for(int j=i,k=0;j<n;k++,j++){\\n grid[k][j]=s[k];\\n }\\n }\\n return grid;\\n }\\n};\"], [1, 1.4493, \"class Solution {\\npublic:\\n vector<vector<int>> sortMatrix(vector<vector<int>>& grid) {\\n int n=grid.size();\\n for(int i=n-1;i>=0;i--){\\n vector<int>s(n-i);\\n for(int j=i,k=0;j<n;k++,j++){\\n s[k]=grid[j][k];\\n }\\n sort(s.begin(),s.end(),greater<int>());\\n for(int j=i,k=0;j<n;k++,j++){\\n grid[j][k]=s[k];\\n }\\n }\\n for(int i=1;i<n;i++){\\n vector<int>s(n-i);\\n for(int j=i,k=0;j<n;k++,j++){\\n s[k]=grid[k][j];\\n }\\n sort(s.begin(),s.end());\\n for(int j=i,k=0;j<n;k++,j++){\\n grid[k][j]=s[k];\\n }\\n }\\n return grid;\\n }\\n};\"], [2, 0.9058, null], [3, 6.7029, null], [4, 5.0725, null], [5, 2.8986, null], [6, 5.2536, null], [7, 6.7029, null], [8, 6.7029, null], [9, 4.1667, null], [10, 2.5362, null], [11, 8.1522, null], [12, 7.2464, null], [13, 3.6232, null], [14, 4.7101, null], [15, 4.529, null], [16, 2.8986, null], [17, 1.6304, null], [18, 1.4493, null], [19, 3.9855, null], [20, 1.9928, null], [21, 1.6304, null], [22, 0.9058, null], [23, 1.8116, null], [24, 0.5435, null], [25, 0.5435, null], [26, 0.1812, null], [27, 1.2681, \"class Solution {\\npublic:\\n // sortMatrix \\u51fd\\u5f0f\\uff1a\\u5c0d\\u77e9\\u9663\\u7684\\u5c0d\\u89d2\\u7dda\\u4e0a\\u7684\\u5143\\u7d20\\u9032\\u884c\\u6392\\u5e8f\\n vector<vector<int>> sortMatrix(vector<vector<int>>& matrix) {\\n int rows = matrix.size(), cols = matrix[0].size(); // \\u7372\\u53d6\\u77e9\\u9663\\u7684\\u884c\\u6578\\u548c\\u5217\\u6578\\n unordered_map<int, deque<int>> diagonalMap; // \\u4f7f\\u7528\\u54c8\\u5e0c\\u8868\\u5b58\\u5132\\u6bcf\\u689d\\u5c0d\\u89d2\\u7dda\\u7684\\u5143\\u7d20\\n\\n // \\u6536\\u96c6\\u6bcf\\u689d\\u5c0d\\u89d2\\u7dda\\u4e0a\\u7684\\u5143\\u7d20\\n for (int i = 0; i < rows; ++i) {\\n for (int j = 0; j < cols; ++j) {\\n diagonalMap[i - j].push_back(matrix[i][j]); // \\u5c0d\\u89d2\\u7dda\\u7684\\u5143\\u7d20\\u7528 i - j \\u4f5c\\u70ba\\u9375\\u4f86\\u5206\\u985e\\n }\\n }\\n\\n // \\u6392\\u5e8f\\u6bcf\\u689d\\u5c0d\\u89d2\\u7dda\\u4e0a\\u7684\\u5143\\u7d20\\n for (auto& [key, dq] : diagonalMap) {\\n vector<int> temp(dq.begin(), dq.end()); // \\u5c07 deque \\u8f49\\u63db\\u70ba vector \\u4f86\\u6392\\u5e8f\\n if (key < 0) {\\n // \\u5982\\u679c\\u5c0d\\u89d2\\u7dda\\u7684\\u7d22\\u5f15\\u5dee\\u662f\\u8ca0\\u6578\\uff0c\\u5c0d\\u89d2\\u7dda\\u5143\\u7d20\\u5347\\u5e8f\\u6392\\u5e8f\\n sort(temp.begin(), temp.end());\\n } else {\\n // \\u5982\\u679c\\u5c0d\\u89d2\\u7dda\\u7684\\u7d22\\u5f15\\u5dee\\u662f\\u6b63\\u6578\\uff0c\\u5c0d\\u89d2\\u7dda\\u5143\\u7d20\\u964d\\u5e8f\\u6392\\u5e8f\\n sort(temp.rbegin(), temp.rend());\\n }\\n dq = deque<int>(temp.begin(), temp.end()); // \\u6392\\u5e8f\\u5f8c\\u7684\\u5143\\u7d20\\u66f4\\u65b0\\u56de deque\\n }\\n\\n // \\u628a\\u6392\\u5e8f\\u5f8c\\u7684\\u5143\\u7d20\\u653e\\u56de\\u77e9\\u9663\\n for (int i = 0; i < rows; ++i) {\\n for (int j = 0; j < cols; ++j) {\\n matrix[i][j] = diagonalMap[i - j].front(); // \\u53d6\\u51fa\\u5c0d\\u89d2\\u7dda\\u6392\\u5e8f\\u5f8c\\u7684\\u6700\\u524d\\u5143\\u7d20\\n diagonalMap[i - j].pop_front(); // \\u79fb\\u9664\\u5df2\\u4f7f\\u7528\\u7684\\u5143\\u7d20\\n }\\n }\\n\\n return matrix; // \\u8fd4\\u56de\\u6392\\u5e8f\\u5f8c\\u7684\\u77e9\\u9663\\n }\\n};\\n\"], [28, 0.3623, \"class Solution {\\npublic:\\n vector<vector<int>> sortMatrix(vector<vector<int>>& grid) {\\n unordered_map<int,vector<int>>mapp;\\n for(int i = 0;i<grid.size();i++){\\n for(int j = 0;j<grid[0].size();j++){\\n mapp[i-j].push_back(grid[i][j]);\\n }\\n }\\n for(auto& x : mapp){\\n if (x.first < 0) \\n sort(x.second.begin(), x.second.end());\\n else \\n sort(x.second.rbegin(), x.second.rend()); \\n } \\n for(int i = 0;i<grid.size();i++){\\n for(int j = 0;j<grid[0].size();j++){\\n grid[i][j] = mapp[i - j].front();\\n mapp[i - j].erase(mapp[i - j].begin());\\n }\\n }\\n return grid; \\n }\\n};\"]]"
},
"golang": {
"code": "func sortMatrix(grid [][]int) [][]int {\n n := len(grid)\n diagonals := make(map[int][]int)\n \n for i := 0; i < n; i++ {\n for j := 0; j < n; j++ {\n k := i - j\n diagonals[k] = append(diagonals[k], grid[i][j])\n }\n }\n \n for k, list := range diagonals {\n if k >= 0 {\n sort.Slice(list, func(a, b int) bool {\n return list[a] > list[b]\n })\n } else {\n sort.Slice(list, func(a, b int) bool {\n return list[a] < list[b]\n })\n }\n diagonals[k] = list\n }\n \n pos := make(map[int]int)\n for k := range diagonals {\n pos[k] = 0\n }\n \n for i := 0; i < n; i++ {\n for j := 0; j < n; j++ {\n k := i - j\n grid[i][j] = diagonals[k][pos[k]]\n pos[k]++\n }\n }\n \n return grid\n}",
"memory": 900,
"memoryDistribution": "[[900, 52.6314, \"func sortMatrix(grid [][]int) [][]int {\\n n := len(grid)\\n diagonals := make(map[int][]int)\\n \\n for i := 0; i < n; i++ {\\n for j := 0; j < n; j++ {\\n k := i - j\\n diagonals[k] = append(diagonals[k], grid[i][j])\\n }\\n }\\n \\n for k, list := range diagonals {\\n if k >= 0 {\\n sort.Slice(list, func(a, b int) bool {\\n return list[a] > list[b]\\n })\\n } else {\\n sort.Slice(list, func(a, b int) bool {\\n return list[a] < list[b]\\n })\\n }\\n diagonals[k] = list\\n }\\n \\n pos := make(map[int]int)\\n for k := range diagonals {\\n pos[k] = 0\\n }\\n \\n for i := 0; i < n; i++ {\\n for j := 0; j < n; j++ {\\n k := i - j\\n grid[i][j] = diagonals[k][pos[k]]\\n pos[k]++\\n }\\n }\\n \\n return grid\\n}\"], [8200, 5.2632, \"func sortMatrix(grid [][]int) [][]int {\\n n := len(grid)\\n\\n nums := make([]int, 0, n)\\n // bottom-left triangle\\n for i := 0; i < n-1; i++ {\\n for j, k := 0, i; j < n-i; j++ {\\n nums = append(nums, grid[k][j])\\n k++\\n }\\n\\n sort.Ints(nums)\\n var idx int = len(nums)-1\\n for j, k := 0, i; j < n-i; j++ {\\n grid[k][j] = nums[idx]\\n k++\\n idx--\\n }\\n\\n nums = nums[:0]\\n }\\n\\n // top-right triangle\\n for j := 1; j < n-1; j++ {\\n for i, k := 0, j; i < n-j; i++ {\\n nums = append(nums, grid[i][k])\\n k++\\n }\\n\\n sort.Ints(nums)\\n var idx int\\n for i, k := 0, j; i < n-j; i++ {\\n grid[i][k] = nums[idx]\\n k++\\n idx++\\n }\\n \\n nums = nums[:0]\\n }\\n\\n return grid\\n}\"], [8300, 5.2632, \"func sortMatrix(grid [][]int) [][]int {\\n\\tn := len(grid)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tvar temp []int\\n\\t\\tfor offset := 0; offset < n-i; offset++ {\\n\\t\\t\\ttemp = append(temp, grid[i+offset][offset])\\n\\t\\t}\\n\\t\\tsort.Slice(temp, func(i, j int) bool { return temp[i] > temp[j] })\\n\\t\\tfor offset := 0; offset < n-i; offset++ {\\n\\t\\t\\tgrid[i+offset][offset] = temp[0]\\n\\t\\t\\ttemp = temp[1:]\\n\\t\\t}\\n\\t}\\n\\tfor i := 1; i < n; i++ {\\n\\t\\tvar temp []int\\n\\t\\tfor offset := 0; offset < n-i; offset++ {\\n\\t\\t\\ttemp = append(temp, grid[offset][i+offset])\\n\\t\\t}\\n\\t\\tsort.Slice(temp, func(i, j int) bool { return temp[i] < temp[j] })\\n\\t\\tfor offset := 0; offset < n-i; offset++ {\\n\\t\\t\\tgrid[offset][i+offset] = temp[0]\\n\\t\\t\\ttemp = temp[1:]\\n\\t\\t}\\n\\t}\\n\\treturn grid\\n}\"], [8400, 5.2632, null], [8500, 5.2632, null], [8600, 5.2632, null], [8700, 21.0526, null], [8800, 21.0526, null], [8900, 5.2632, null], [9000, 5.2632, null], [9200, 5.2632, \"func sortMatrix(grid [][]int) [][]int {\\n m, n := len(grid), len(grid[0])\\n ans := make([][]int, m)\\n for i:=0;i<m;i++ {\\n ans[i] = make([]int, n)\\n }\\n \\n \\n for i:=0;i<m;i++ {\\n res := make([]int, 0)\\n tmpI, j := i, 0\\n for tmpI < m && j < n {\\n res = append(res, grid[tmpI][j])\\n tmpI++\\n j++\\n }\\n sort.Sort(sort.Reverse(sort.IntSlice(res)))\\n tmpI, j = i, 0\\n for idx:=0;idx<len(res);idx++ {\\n ans[tmpI][j] = res[idx]\\n tmpI++\\n j++\\n }\\n }\\n for j:=1;j<n;j++ {\\n res := make([]int, 0)\\n tmpJ, i := j, 0\\n for tmpJ < n && i < m {\\n res = append(res, grid[i][tmpJ])\\n tmpJ++\\n i++\\n }\\n sort.Ints(res)\\n tmpJ, i = j, 0\\n for idx:=0;idx<len(res);idx++ {\\n ans[i][tmpJ] = res[idx]\\n tmpJ++\\n i++\\n }\\n }\\n return ans\\n}\"], [9300, 5.2632, \"func cmpFnc(a int, b int) int {\\n if a > b {return -1}\\n if a < b {return 1}\\n return 0\\n}\\n\\nfunc sortMatrix(grid [][]int) [][]int {\\n diags := make([][]int, 2*len(grid) - 1, 2*len(grid) - 1)\\n diags[0] = make([]int, len(grid), len(grid))\\n for i := 1; i < len(grid); i++ {\\n diags[i] = make([]int, len(grid) - i, len(grid) - i)\\n diags[i+len(grid)-1] = make([]int, len(grid) - i, len(grid) - i)\\n }\\n for i := 0; i < len(grid); i++ {\\n diags[0][i] = grid[i][i]\\n }\\n slices.SortFunc(diags[0], cmpFnc)\\n for i := 0; i < len(grid); i++ {\\n grid[i][i] = diags[0][i]\\n }\\n for j := 1; j < len(grid); j++ {\\n for i := 0; i + j < len(grid); i++ {\\n diags[j][i] = grid[i][i+j]\\n diags[j+len(grid)-1][i] = grid[i+j][i]\\n }\\n slices.Sort(diags[j])\\n slices.SortFunc(diags[j+len(grid)-1], cmpFnc)\\n for i := 0; i + j < len(grid); i++ {\\n grid[i][i+j] = diags[j][i]\\n grid[i+j][i] = diags[j+len(grid)-1][i]\\n }\\n }\\n return grid\\n}\"]]",
"runtime": 8,
"runtimeDistribution": "[[0, 21.0526, \"func sortMatrix(grid [][]int) [][]int {\\n n := len(grid)\\n\\n nums := make([]int, 0, n)\\n // bottom-left triangle\\n for i := 0; i < n-1; i++ {\\n for j, k := 0, i; j < n-i; j++ {\\n nums = append(nums, grid[k][j])\\n k++\\n }\\n\\n sort.Ints(nums)\\n var idx int = len(nums)-1\\n for j, k := 0, i; j < n-i; j++ {\\n grid[k][j] = nums[idx]\\n k++\\n idx--\\n }\\n\\n nums = nums[:0]\\n }\\n\\n // top-right triangle\\n for j := 1; j < n-1; j++ {\\n for i, k := 0, j; i < n-j; i++ {\\n nums = append(nums, grid[i][k])\\n k++\\n }\\n\\n sort.Ints(nums)\\n var idx int\\n for i, k := 0, j; i < n-j; i++ {\\n grid[i][k] = nums[idx]\\n k++\\n idx++\\n }\\n \\n nums = nums[:0]\\n }\\n\\n return grid\\n}\"], [1, 15.7895, \"func sortMatrix(grid [][]int) [][]int {\\n\\tn := len(grid)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tvar temp []int\\n\\t\\tfor offset := 0; offset < n-i; offset++ {\\n\\t\\t\\ttemp = append(temp, grid[i+offset][offset])\\n\\t\\t}\\n\\t\\tsort.Slice(temp, func(i, j int) bool { return temp[i] > temp[j] })\\n\\t\\tfor offset := 0; offset < n-i; offset++ {\\n\\t\\t\\tgrid[i+offset][offset] = temp[0]\\n\\t\\t\\ttemp = temp[1:]\\n\\t\\t}\\n\\t}\\n\\tfor i := 1; i < n; i++ {\\n\\t\\tvar temp []int\\n\\t\\tfor offset := 0; offset < n-i; offset++ {\\n\\t\\t\\ttemp = append(temp, grid[offset][i+offset])\\n\\t\\t}\\n\\t\\tsort.Slice(temp, func(i, j int) bool { return temp[i] < temp[j] })\\n\\t\\tfor offset := 0; offset < n-i; offset++ {\\n\\t\\t\\tgrid[offset][i+offset] = temp[0]\\n\\t\\t\\ttemp = temp[1:]\\n\\t\\t}\\n\\t}\\n\\treturn grid\\n}\"], [2, 10.5263, null], [3, 10.5263, null], [4, 21.0526, \"func sortMatrix(grid [][]int) [][]int {\\n n := len(grid)\\n // Bottom-left triangle (including main diagonal)\\n for d := 0; d < n; d++ {\\n diag := []int{}\\n i, j := d, 0\\n for i < n && j < n {\\n diag = append(diag, grid[i][j])\\n i++\\n j++\\n }\\n // Sort in non-increasing order\\n sort.Slice(diag, func(a, b int) bool { return diag[a] > diag[b] })\\n i, j = d, 0\\n idx := 0\\n for i < n && j < n {\\n grid[i][j] = diag[idx]\\n i++\\n j++\\n idx++\\n }\\n }\\n // Top-right triangle\\n for d := 1; d < n; d++ {\\n diag := []int{}\\n i, j := 0, d\\n for i < n && j < n {\\n diag = append(diag, grid[i][j])\\n i++\\n j++\\n }\\n // Sort in non-decreasing order\\n sort.Ints(diag)\\n i, j = 0, d\\n idx := 0\\n for i < n && j < n {\\n grid[i][j] = diag[idx]\\n i++\\n j++\\n idx++\\n }\\n }\\n return grid\\n}\"], [6, 15.7895, \"func sortMatrix(grid [][]int) [][]int {\\n for k := 0; k < len(grid); k++ {\\n sd(grid, k, false)\\n }\\n for k := 1; k < len(grid[0]); k++ {\\n sd(grid, k, true)\\n }\\n return grid\\n}\\n\\n\\nfunc sd(g [][]int, k int, x bool) {\\n v := []int{}\\n if !x {\\n for i := 0; i < len(g); i ++ {\\n y, x := len(g)-1-k+i, i\\n if y >= 0 && y < len(g) && x >= 0 && x < len(g[0]) {\\n v = append(v, g[y][x])\\n }\\n }\\n sort.Slice(v, func(i, j int) bool { return v[i] > v[j] })\\n t := 0\\n for i := 0; i < len(g); i ++ {\\n y, x := len(g)-1-k+i, i\\n if y >= 0 && y < len(g) && x >= 0 && x < len(g[0]) {\\n g[y][x] = v[t]\\n t ++\\n }\\n }\\n } else {\\n for i := 0; i < len(g); i ++ {\\n y, x := i, k+i\\n if y >= 0 && y < len(g) && x >= 0 && x < len(g[0]) {\\n v = append(v, g[y][x])\\n }\\n }\\n sort.Slice(v, func(i, j int) bool { return v[i] < v[j] })\\n t := 0\\n for i := 0; i < len(g); i ++ {\\n y, x := i, k+i\\n if y >= 0 && y < len(g) && x >= 0 && x < len(g[0]) {\\n g[y][x] = v[t]\\n t ++\\n }\\n }\\n }\\n}\"], [8, 5.2632, \"func sortMatrix(grid [][]int) [][]int {\\n n := len(grid)\\n diagonals := make(map[int][]int)\\n \\n for i := 0; i < n; i++ {\\n for j := 0; j < n; j++ {\\n k := i - j\\n diagonals[k] = append(diagonals[k], grid[i][j])\\n }\\n }\\n \\n for k, list := range diagonals {\\n if k >= 0 {\\n sort.Slice(list, func(a, b int) bool {\\n return list[a] > list[b]\\n })\\n } else {\\n sort.Slice(list, func(a, b int) bool {\\n return list[a] < list[b]\\n })\\n }\\n diagonals[k] = list\\n }\\n \\n pos := make(map[int]int)\\n for k := range diagonals {\\n pos[k] = 0\\n }\\n \\n for i := 0; i < n; i++ {\\n for j := 0; j < n; j++ {\\n k := i - j\\n grid[i][j] = diagonals[k][pos[k]]\\n pos[k]++\\n }\\n }\\n \\n return grid\\n}\"]]"
},
"java": {
"code": "class Solution {\n public int[][] sortMatrix(int[][] grid) {\n int n = grid.length;\n if (n == 0) return grid;\n \n for (int d = 0; d < n; d++) {\n java.util.List<Integer> diagonal = new java.util.ArrayList<>();\n for (int k = 0; d + k < n && k < n; k++) {\n int row = d + k;\n int col = k;\n if (row >= n || col >= n) break;\n diagonal.add(grid[row][col]);\n }\n diagonal.sort(java.util.Collections.reverseOrder());\n int index = 0;\n for (int k = 0; d + k < n && k < n; k++) {\n int row = d + k;\n int col = k;\n if (row >= n || col >= n) break;\n grid[row][col] = diagonal.get(index++);\n }\n }\n \n for (int d = 1; d < n; d++) {\n java.util.List<Integer> diagonal = new java.util.ArrayList<>();\n for (int k = 0; k < n; k++) {\n int row = k;\n int col = d + k;\n if (row >= n || col >= n) break;\n diagonal.add(grid[row][col]);\n }\n java.util.Collections.sort(diagonal);\n int index = 0;\n for (int k = 0; k < n; k++) {\n int row = k;\n int col = d + k;\n if (row >= n || col >= n) break;\n grid[row][col] = diagonal.get(index++);\n }\n }\n \n return grid;\n }\n}",
"memory": 4600,
"memoryDistribution": "[[4600, 69.8796, \"class Solution {\\n public int[][] sortMatrix(int[][] grid) {\\n int n = grid.length;\\n if (n == 0) return grid;\\n \\n for (int d = 0; d < n; d++) {\\n java.util.List<Integer> diagonal = new java.util.ArrayList<>();\\n for (int k = 0; d + k < n && k < n; k++) {\\n int row = d + k;\\n int col = k;\\n if (row >= n || col >= n) break;\\n diagonal.add(grid[row][col]);\\n }\\n diagonal.sort(java.util.Collections.reverseOrder());\\n int index = 0;\\n for (int k = 0; d + k < n && k < n; k++) {\\n int row = d + k;\\n int col = k;\\n if (row >= n || col >= n) break;\\n grid[row][col] = diagonal.get(index++);\\n }\\n }\\n \\n for (int d = 1; d < n; d++) {\\n java.util.List<Integer> diagonal = new java.util.ArrayList<>();\\n for (int k = 0; k < n; k++) {\\n int row = k;\\n int col = d + k;\\n if (row >= n || col >= n) break;\\n diagonal.add(grid[row][col]);\\n }\\n java.util.Collections.sort(diagonal);\\n int index = 0;\\n for (int k = 0; k < n; k++) {\\n int row = k;\\n int col = d + k;\\n if (row >= n || col >= n) break;\\n grid[row][col] = diagonal.get(index++);\\n }\\n }\\n \\n return grid;\\n }\\n}\"], [45100, 1.2048, \"class Solution {\\n static void selection(int[][] grid ,int j)\\n {\\n int i =0;\\n while(j<grid.length)\\n {\\n int k=j;\\n int p = i;\\n int mini=i;\\n int minj=j;\\n while(k<grid.length)\\n {\\n if(grid[p][k] < grid[mini][minj])\\n {\\n mini=p;\\n minj=k;\\n }\\n p++;\\n k++;\\n }\\n int temp = grid[mini][minj];\\n grid[mini][minj]=grid[i][j];\\n grid[i][j]=temp;\\n i++;\\n j++;\\n }\\n }\\n static void selectionrev(int[][] grid , int i)\\n {\\n int j=0;\\n while(i<grid.length)\\n {\\n int p=i;\\n int k=j;\\n int maxi=i;\\n int maxj=j;\\n while(p<grid.length)\\n {\\n if(grid[p][k] > grid[maxi][maxj])\\n {\\n maxi=p;\\n maxj=k;\\n }\\n p++;\\n k++;\\n }\\n int temp = grid[maxi][maxj];\\n grid[maxi][maxj]=grid[i][j];\\n grid[i][j]=temp;\\n i++;\\n j++;\\n }\\n }\\n public int[][] sortMatrix(int[][] grid) {\\n int n = grid.length;\\n for(int j=n-1;j>0;j--)\\n {\\n selection(grid,j);\\n }\\n for(int i=0;i<n;i++)\\n {\\n selectionrev(grid,i);\\n }\\n for(int i=0;i<grid.length;i++)\\n {\\n for(int j=0;j<grid.length;j++)\\n System.out.print(grid[i][j]+\\\" \\\");\\n System.out.println();\\n }\\n return grid;\\n }\\n}\"], [45200, 0.8032, \"class Solution {\\n public int[][] sortMatrix(int[][] grid) {\\n int n = grid.length;\\n for(int row=n-1;row>=0;row--){\\n sortdiagonals(grid,row,0,false);\\n }\\n for(int col=1;col<n;col++){\\n sortdiagonals(grid,0,col,true);\\n }\\n return grid;\\n }\\n public void sortdiagonals(int[][] grid,int row,int col,boolean ascending){\\n List<Integer> diagonal = new ArrayList<>();\\n int r = row,c = col;\\n int n = grid.length;\\n while(r<n && c<n){\\n diagonal.add(grid[r][c]);\\n r++;\\n c++;\\n }\\n if(ascending){\\n Collections.sort(diagonal);\\n }\\n else diagonal.sort(Collections.reverseOrder());\\n r = row;\\n c = col;\\n int index = 0;\\n while(r<n && c<n){\\n grid[r][c] = diagonal.get(index++);\\n r++;\\n c++;\\n }\\n }\\n}\"], [45300, 4.0161, null], [45400, 8.8353, null], [45500, 15.261, null], [45600, 18.0723, null], [45700, 16.4659, null], [45800, 13.253, null], [45900, 10.8434, \"class Solution {\\n public int[][] sortMatrix(int[][] grid) {\\n int n = grid.length;\\n\\n for (int i = 0; i < n; i++) {\\n diagSort(grid, i, 0);\\n diagSort(grid, 0, i);}\\n\\n return grid;}\\n\\n private void diagSort(int[][] grid, int a, int b) {\\n int n = grid.length;\\n int rnge = Math.min(n - a, n - b);\\n int[] arr = new int[rnge];\\n\\n for (int k = 0; k < rnge; k++) {\\n arr[k] = grid[a + k][b + k];}\\n\\n Arrays.sort(arr);\\n if (a >= b) {\\n\\n for (int i = 0; i < rnge / 2; i++) {\\n int temp = arr[i];\\n arr[i] = arr[rnge - 1 - i];\\n arr[rnge - 1 - i] = temp;}}\\n\\n for (int k = 0; k < rnge; k++) {\\n grid[a + k][b + k] = arr[k];}}}\"], [46000, 3.6145, \"class Solution {\\n\\n public int[][] sortMatrix(int[][] grid) {\\n final int n = grid.length;\\n int[][] ans = new int[n][n];\\n Map<Integer, List<Integer>> diag = new HashMap<>();\\n\\n for (int i = 0; i < n; ++i)\\n for (int j = 0; j < n; ++j) {\\n final int key = i - j;\\n diag.putIfAbsent(key, new ArrayList<>());\\n diag.get(key).add(grid[i][j]);\\n }\\n\\n for (Map.Entry<Integer, List<Integer>> entry : diag.entrySet()) {\\n List<Integer> values = entry.getValue();\\n if (entry.getKey() < 0)\\n Collections.sort(values, Collections.reverseOrder());\\n else\\n Collections.sort(values);\\n }\\n\\n for (int i = 0; i < n; i++)\\n for (int j = 0; j < n; j++) {\\n final int key = i - j;\\n ans[i][j] = diag.get(key).remove(diag.get(key).size() - 1);\\n }\\n\\n return ans;\\n }\\n\\n}\"]]",
"runtime": 5,
"runtimeDistribution": "[[1, 0.8032, \"class Solution {\\n public int[][] sortMatrix(int[][] grid) {\\n int n = grid.length;\\n for (int i=0; i<n; i++) {\\n for (int k=n-i-1; k>=0; k--) {\\n for (int l=1; l<=k; l++) {\\n if (grid[i+l][l] > grid[i+l-1][l-1]) {\\n swap(grid, i+l, l, i+l-1, l-1);\\n }\\n }\\n }\\n }\\n for(int j=1; j<n; j++) {\\n for (int k=n-j-1; k>=0; k--) {\\n for (int l=1; l<=k; l++) {\\n if (grid[l][j+l] < grid[l-1][j+l-1]) {\\n swap(grid, l, j+l, l-1, j+l-1);\\n }\\n }\\n }\\n }\\n return grid;\\n }\\n\\n void swap(int[][] grid, int i1, int j1, int i2, int j2) {\\n int temp = grid[i1][j1];\\n grid[i1][j1] = grid[i2][j2];\\n grid[i2][j2] = temp;\\n }\\n}\"], [2, 6.0241, \"class Solution {\\n public int[][] sortMatrix(int[][] grid) {\\n int n = grid.length;\\n\\n for (int i = 0; i < n; i++) {\\n diagSort(grid, i, 0);\\n diagSort(grid, 0, i);}\\n\\n return grid;}\\n\\n private void diagSort(int[][] grid, int a, int b) {\\n int n = grid.length;\\n int rnge = Math.min(n - a, n - b);\\n int[] arr = new int[rnge];\\n\\n for (int k = 0; k < rnge; k++) {\\n arr[k] = grid[a + k][b + k];}\\n\\n Arrays.sort(arr);\\n if (a >= b) {\\n\\n for (int i = 0; i < rnge / 2; i++) {\\n int temp = arr[i];\\n arr[i] = arr[rnge - 1 - i];\\n arr[rnge - 1 - i] = temp;}}\\n\\n for (int k = 0; k < rnge; k++) {\\n grid[a + k][b + k] = arr[k];\\n }\\n }\\n}\"], [3, 2.8112, null], [4, 16.8675, null], [5, 30.9237, null], [6, 4.8193, null], [7, 3.6145, null], [8, 17.6707, null], [9, 9.2369, \"class Solution {\\n\\n public int[][] sortMatrix(int[][] grid) {\\n final int n = grid.length;\\n int[][] ans = new int[n][n];\\n Map<Integer, List<Integer>> diag = new HashMap<>();\\n\\n for (int i = 0; i < n; ++i)\\n for (int j = 0; j < n; ++j) {\\n final int key = i - j;\\n diag.putIfAbsent(key, new ArrayList<>());\\n diag.get(key).add(grid[i][j]);\\n }\\n\\n for (Map.Entry<Integer, List<Integer>> entry : diag.entrySet()) {\\n List<Integer> values = entry.getValue();\\n if (entry.getKey() < 0)\\n Collections.sort(values, Collections.reverseOrder());\\n else\\n Collections.sort(values);\\n }\\n\\n for (int i = 0; i < n; i++)\\n for (int j = 0; j < n; j++) {\\n final int key = i - j;\\n ans[i][j] = diag.get(key).remove(diag.get(key).size() - 1);\\n }\\n\\n return ans;\\n }\\n\\n}\"], [10, 1.6064, \"class Solution {\\n public int[][] sortMatrix(int[][] grid) {\\n Map<Integer,List<Integer>> nums = new HashMap<>();\\n\\n for(int i=0; i<grid.length; i++){\\n for(int j=0; j<grid[i].length; j++){\\n int k = i-j;\\n nums.putIfAbsent(k, new ArrayList<>());\\n nums.get(k).add(grid[i][j]);\\n }\\n }\\n\\n for(Map.Entry<Integer, List<Integer>> e : nums.entrySet()){\\n e.getValue().sort((a,b) -> e.getKey()<0 ? b-a : a-b);\\n }\\n\\n for(int i=0; i<grid.length; i++){\\n for(int j=0; j<grid[i].length; j++){\\n int k = i-j;\\n grid[i][j] = nums.get(k).remove(nums.get(k).size()-1);\\n }\\n }\\n return grid;\\n }\\n}\"]]"
},
"javascript": {
"code": "var sortMatrix = function(grid) {\n const n = grid.length;\n const diagonals = {};\n for (let i = 0; i < n; i++) {\n for (let j = 0; j < n; j++) {\n const d = i - j;\n const key = d.toString();\n if (!diagonals[key]) diagonals[key] = [];\n diagonals[key].push({ value: grid[i][j], i: i, j: j });\n }\n }\n Object.keys(diagonals).forEach(dStr => {\n const d = parseInt(dStr, 10);\n const entries = diagonals[dStr];\n entries.sort((a, b) => a.i - b.i);\n const values = entries.map(e => e.value);\n if (d >= 0) values.sort((a, b) => b - a);\n else values.sort((a, b) => a - b);\n entries.forEach((entry, idx) => {\n grid[entry.i][entry.j] = values[idx];\n });\n });\n return grid;\n};",
"memory": 6400,
"memoryDistribution": "[[6400, 89.4736, \"var sortMatrix = function(grid) {\\n const n = grid.length;\\n const diagonals = {};\\n for (let i = 0; i < n; i++) {\\n for (let j = 0; j < n; j++) {\\n const d = i - j;\\n const key = d.toString();\\n if (!diagonals[key]) diagonals[key] = [];\\n diagonals[key].push({ value: grid[i][j], i: i, j: j });\\n }\\n }\\n Object.keys(diagonals).forEach(dStr => {\\n const d = parseInt(dStr, 10);\\n const entries = diagonals[dStr];\\n entries.sort((a, b) => a.i - b.i);\\n const values = entries.map(e => e.value);\\n if (d >= 0) values.sort((a, b) => b - a);\\n else values.sort((a, b) => a - b);\\n entries.forEach((entry, idx) => {\\n grid[entry.i][entry.j] = values[idx];\\n });\\n });\\n return grid;\\n};\"], [62900, 2.6316, \"/**\\n * @param {number[][]} grid\\n * @return {number[][]}\\n */\\nvar sortMatrix = function(grid) {\\n let res = [...grid];\\n let r = grid.length;\\n let c = grid[0].length;\\n // \\u5de6\\u4e0b\\n for(let i=0; i<r-1; i++){\\n let j = 0;\\n changeLeft(i, j, res);\\n }\\n // \\u53f3\\u4e0a\\n for(let j=c-2; j>0; j--){\\n let i=0;\\n changeRight(i, j, res);\\n }\\n return res;\\n};\\n\\nfunction changeLeft(r, c, res){\\n let row = res.length;\\n let col = res[0].length;\\n\\n let si = r;\\n let sj = c;\\n\\n while(si < row-1 && sj < col-1){\\n let ni = si+1;\\n let nj = sj+1;\\n while(ni < row && nj < col){\\n if(res[si][sj] < res[ni][nj]){\\n let tmp = res[si][sj];\\n res[si][sj] = res[ni][nj];\\n res[ni][nj] = tmp;\\n }\\n ni++;\\n nj++;\\n }\\n si ++;\\n sj ++;\\n }\\n\\n return res;\\n}\\n\\nfunction changeRight(r, c, res){\\n let row = res.length;\\n let col = res[0].length;\\n\\n let si = r;\\n let sj = c;\\n\\n while(si < row-1 && sj < col-1){\\n let ni = si+1;\\n let nj = sj+1;\\n while(ni < row && nj < col){\\n if(res[si][sj] > res[ni][nj]){\\n let tmp = res[si][sj];\\n res[si][sj] = res[ni][nj];\\n res[ni][nj] = tmp;\\n }\\n ni++;\\n nj++;\\n }\\n si ++;\\n sj ++;\\n }\\n\\n return res;\\n}\"], [63100, 2.6316, \"/**\\n * @param {number[][]} grid\\n * @return {number[][]}\\n */\\nconst sortMatrix = (grid) => {\\n for (let R = 0; R < grid.length; R += 1) {\\n const sorted = [];\\n for (\\n let r = R, c = 0;\\n r < grid.length && c < grid.length;\\n sorted.push(grid[r][c]), r += 1, c += 1\\n ) {}\\n sorted.sort((a, b) => b - a);\\n for (\\n let i = 0, r = R, c = 0;\\n r < grid.length && c < grid.length && i < sorted.length;\\n grid[r][c] = sorted[i], r += 1, c += 1, i += 1\\n ) {}\\n }\\n for (let C = 1; C < grid.length; C += 1) {\\n const sorted = [];\\n for (\\n let r = 0, c = C;\\n r < grid.length && c < grid.length;\\n sorted.push(grid[r][c]), r += 1, c += 1\\n ) {}\\n sorted.sort((a, b) => a - b);\\n for (\\n let i = 0, r = 0, c = C;\\n r < grid.length && c < grid.length && i < sorted.length;\\n grid[r][c] = sorted[i], r += 1, c += 1, i += 1\\n ) {}\\n }\\n return grid;\\n};\"], [63500, 2.6316, null], [63600, 2.6316, null], [64300, 2.6316, null], [64400, 7.8947, null], [64500, 7.8947, null], [64599, 2.6316, null], [64700, 7.8947, null], [64800, 7.8947, null], [64900, 5.2632, null], [65000, 10.5263, null], [65099, 5.2632, null], [65200, 2.6316, null], [65300, 5.2632, null], [65400, 2.6316, null], [65500, 2.6316, null], [65700, 7.8947, null], [66000, 2.6316, \"/**\\n * @param {number[][]} grid\\n * @return {number[][]}\\n */\\nvar sortMatrix = function (grid) {\\n const len = grid.length;\\n const diagonals = new Map();\\n\\n for (let row = 0; row < len; row++) {\\n for (let col = 0; col < len; col++) {\\n const diagonalNum = row - col;\\n const nums = diagonals.get(diagonalNum) || [];\\n nums.push(grid[row][col]);\\n diagonals.set(diagonalNum, nums);\\n }\\n }\\n\\n const entries = diagonals.entries();\\n for (const [diagonalNum, nums] of entries) {\\n diagonals.set(diagonalNum, nums.sort((a, b) => {\\n if (diagonalNum < 0) return a - b;\\n return b - a;\\n }));\\n }\\n\\n for (let row = 0; row < len; row++) {\\n for (let col = 0; col < len; col++) {\\n let key = row - col;\\n grid[row][col] = diagonals.get(key).shift();\\n }\\n }\\n\\n return grid;\\n};\"], [66300, 2.6316, \"/**\\n * @param {number[][]} grid\\n * @return {number[][]}\\n */\\nvar sortMatrix = function (grid) {\\n const len = grid.length;\\n const diagonals = new Map();\\n\\n for (let row = 0; row < len; row++) {\\n for (let col = 0; col < len; col++) {\\n const diagonalNum = row - col;\\n const nums = diagonals.get(diagonalNum) || [];\\n nums.push(grid[row][col]);\\n diagonals.set(diagonalNum, nums);\\n }\\n }\\n\\n const entries = diagonals.entries();\\n for (const [diagonalNum, nums] of entries) {\\n diagonals.set(diagonalNum, nums.sort((a, b) => {\\n if (diagonalNum < 0) return a - b;\\n return b - a;\\n }));\\n }\\n\\n for (let row = 0; row < len; row++) {\\n for (let col = 0; col < len; col++) {\\n let key = row - col;\\n grid[row][col] = diagonals.get(key).shift();\\n }\\n }\\n\\n return grid;\\n};\"]]",
"runtime": 25,
"runtimeDistribution": "[[3, 2.6316, \"/**\\n * @param {number[][]} grid\\n * @return {number[][]}\\n */\\nvar sortMatrix = function(grid) {\\n let res = [...grid];\\n let r = grid.length;\\n let c = grid[0].length;\\n // \\u5de6\\u4e0b\\n for(let i=0; i<r-1; i++){\\n let j = 0;\\n changeLeft(i, j, res);\\n }\\n // \\u53f3\\u4e0a\\n for(let j=c-2; j>0; j--){\\n let i=0;\\n changeRight(i, j, res);\\n }\\n return res;\\n};\\n\\nfunction changeLeft(r, c, res){\\n let row = res.length;\\n let col = res[0].length;\\n\\n let si = r;\\n let sj = c;\\n\\n while(si < row-1 && sj < col-1){\\n let ni = si+1;\\n let nj = sj+1;\\n while(ni < row && nj < col){\\n if(res[si][sj] < res[ni][nj]){\\n let tmp = res[si][sj];\\n res[si][sj] = res[ni][nj];\\n res[ni][nj] = tmp;\\n }\\n ni++;\\n nj++;\\n }\\n si ++;\\n sj ++;\\n }\\n\\n return res;\\n}\\n\\nfunction changeRight(r, c, res){\\n let row = res.length;\\n let col = res[0].length;\\n\\n let si = r;\\n let sj = c;\\n\\n while(si < row-1 && sj < col-1){\\n let ni = si+1;\\n let nj = sj+1;\\n while(ni < row && nj < col){\\n if(res[si][sj] > res[ni][nj]){\\n let tmp = res[si][sj];\\n res[si][sj] = res[ni][nj];\\n res[ni][nj] = tmp;\\n }\\n ni++;\\n nj++;\\n }\\n si ++;\\n sj ++;\\n }\\n\\n return res;\\n}\"], [6, 5.2632, \"/**\\n * @param {number[][]} grid\\n * @return {number[][]}\\n */\\nvar sortMatrix = function(grid) {\\n const n = grid.length;\\n // Bottom-left triangle (including main diagonal)\\n for (let d = 0; d < n; ++d) {\\n let diag = [];\\n let i = d, j = 0;\\n while (i < n && j < n) {\\n diag.push(grid[i][j]);\\n i++; j++;\\n }\\n diag.sort((a, b) => b - a);\\n i = d; j = 0;\\n let idx = 0;\\n while (i < n && j < n) {\\n grid[i][j] = diag[idx++];\\n i++; j++;\\n }\\n }\\n // Top-right triangle\\n for (let d = 1; d < n; ++d) {\\n let diag = [];\\n let i = 0, j = d;\\n while (i < n && j < n) {\\n diag.push(grid[i][j]);\\n i++; j++;\\n }\\n diag.sort((a, b) => a - b);\\n i = 0; j = d;\\n let idx = 0;\\n while (i < n && j < n) {\\n grid[i][j] = diag[idx++];\\n i++; j++;\\n }\\n }\\n return grid;\\n};\"], [7, 2.6316, null], [8, 7.8947, null], [9, 7.8947, null], [10, 2.6316, null], [11, 7.8947, null], [12, 7.8947, null], [13, 10.5263, null], [14, 2.6316, null], [15, 5.2632, null], [16, 15.7895, null], [17, 2.6316, null], [18, 5.2632, null], [19, 2.6316, \"/**\\n * @param {number[][]} grid\\n * @return {number[][]}\\n */\\nvar sortMatrix = function (grid) {\\n const len = grid.length;\\n const diagonals = new Map();\\n\\n for (let row = 0; row < len; row++) {\\n for (let col = 0; col < len; col++) {\\n const diagonalNum = row - col;\\n const nums = diagonals.get(diagonalNum) || [];\\n nums.push(grid[row][col]);\\n diagonals.set(diagonalNum, nums);\\n }\\n }\\n\\n const entries = diagonals.entries();\\n for (const [diagonalNum, nums] of entries) {\\n diagonals.set(diagonalNum, nums.sort((a, b) => {\\n if (diagonalNum < 0) return a - b;\\n return b - a;\\n }));\\n }\\n\\n\\n for (let row = 0; row < len; row++) {\\n for (let col = 0; col < len; col++) {\\n let key = row - col;\\n grid[row][col] = diagonals.get(key).shift();\\n }\\n }\\n\\n return grid;\\n};\"], [20, 2.6316, \"/**\\n * @param {number[][]} grid\\n * @return {number[][]}\\n */\\nvar sortMatrix = function(grid) {\\n const n = grid.length;\\n const map = {};\\n\\n for (let i = 0; i < n; i++) {\\n for (let j = 0; j < n; j++) {\\n const d = i - j;\\n if (!map[d]) map[d] = [];\\n map[d].push({i, j, val: grid[i][j]});\\n }\\n }\\n\\n for (const d in map) {\\n const entries = map[d];\\n const values = entries.map(e => e.val);\\n const numD = parseInt(d);\\n values.sort(numD >= 0 ? (a, b) => b - a : (a, b) => a - b);\\n entries.forEach((e, idx) => grid[e.i][e.j] = values[idx]);\\n }\\n\\n return grid;\\n};\"], [25, 7.8946, \"var sortMatrix = function(grid) {\\n const n = grid.length;\\n const diagonals = {};\\n for (let i = 0; i < n; i++) {\\n for (let j = 0; j < n; j++) {\\n const d = i - j;\\n const key = d.toString();\\n if (!diagonals[key]) diagonals[key] = [];\\n diagonals[key].push({ value: grid[i][j], i: i, j: j });\\n }\\n }\\n Object.keys(diagonals).forEach(dStr => {\\n const d = parseInt(dStr, 10);\\n const entries = diagonals[dStr];\\n entries.sort((a, b) => a.i - b.i);\\n const values = entries.map(e => e.value);\\n if (d >= 0) values.sort((a, b) => b - a);\\n else values.sort((a, b) => a - b);\\n entries.forEach((entry, idx) => {\\n grid[entry.i][entry.j] = values[idx];\\n });\\n });\\n return grid;\\n};\"]]"
},
"python3": {
"code": "class Solution:\n def sortMatrix(self, grid: List[List[int]]) -> List[List[int]]:\n n = len(grid)\n diag_dict = defaultdict(list)\n \n for i in range(n):\n for j in range(n):\n k = i - j\n diag_dict[k].append((i, j))\n \n for k in diag_dict:\n positions = diag_dict[k]\n values = [grid[i][j] for i, j in positions]\n if k >= 0:\n sorted_values = sorted(values, reverse=True)\n else:\n sorted_values = sorted(values)\n for idx, (i, j) in enumerate(positions):\n grid[i][j] = sorted_values[idx]\n \n return grid",
"memory": 1800,
"memoryDistribution": "[[1800, 77.4546, \"from typing import List\\nfrom collections import defaultdict\\n\\nclass Solution:\\n def sortMatrix(self, grid: List[List[int]]) -> List[List[int]]:\\n n = len(grid)\\n diag_dict = defaultdict(list)\\n \\n for i in range(n):\\n for j in range(n):\\n k = i - j\\n diag_dict[k].append((i, j))\\n \\n for k in diag_dict:\\n positions = diag_dict[k]\\n values = [grid[i][j] for i, j in positions]\\n if k >= 0:\\n sorted_values = sorted(values, reverse=True)\\n else:\\n sorted_values = sorted(values)\\n for idx, (i, j) in enumerate(positions):\\n grid[i][j] = sorted_values[idx]\\n \\n return grid\"], [17500, 0.3636, \"class Solution:\\n def sortMatrix(self, grid: List[List[int]]) -> List[List[int]]:\\n for i in range(len(grid)):\\n for k,v in enumerate(sorted((grid[i+k][k] for k in range(len(grid)-i)),reverse=True)):\\n grid[i+k][k]=v\\n for i in range(1,len(grid)):\\n for k,v in enumerate(sorted(grid[k][i+k] for k in range(len(grid)-i))):\\n grid[k][i+k]=v\\n return grid\\n\\n\\n \"], [17600, 4.7273, \"class Solution:\\n def sortMatrix(self, grid: List[List[int]]) -> List[List[int]]:\\n elements_by_diagonal = defaultdict(list)\\n n = len(grid)\\n\\n for i in range(n):\\n for j in range(n):\\n elements_by_diagonal[i - j].append(grid[i][j])\\n for key, elements in elements_by_diagonal.items():\\n if key < 0:\\n row = 0\\n col = abs(key)\\n elements.sort()\\n else:\\n col = 0\\n row = abs(key)\\n elements.sort(reverse=True)\\n elements_index = 0\\n \\n while col < n and row < n:\\n grid[row][col] = elements[elements_index] \\n elements_index += 1\\n row += 1\\n col += 1\\n return grid \"], [17700, 17.4545, null], [17800, 31.2727, null], [17900, 16.3636, \"from typing import List\\nclass Solution:\\n def sortMatrix(self, grid: List[List[int]]) -> List[List[int]]:\\n n = len(grid)\\n for d in range(n):\\n diagonal = []\\n i, j = d, 0\\n while i < n and j < n:\\n diagonal.append(grid[i][j])\\n i += 1\\n j += 1\\n diagonal.sort(reverse=True)\\n i, j = d, 0\\n idx = 0\\n while i < n and j < n:\\n grid[i][j] = diagonal[idx]\\n i += 1\\n j += 1\\n idx += 1\\n for d in range(1, n):\\n diagonal = []\\n i, j = 0, d\\n while i < n and j < n:\\n diagonal.append(grid[i][j])\\n i += 1\\n j += 1\\n diagonal.sort()\\n i, j = 0, d\\n idx = 0\\n while i < n and j < n:\\n grid[i][j] = diagonal[idx]\\n i += 1\\n j += 1\\n idx += 1\\n return grid\"], [18000, 24.3636, \"class Solution:\\n def sortMatrix(self, grid: List[List[int]]) -> List[List[int]]:\\n n = len(grid)\\n # we can skip the corners\\n # to move through diagonally you need to add 1 to both row/col each time\\n # starting points form a r-shape on left/top of matrix\\n # need to collect, sort, and re-insert each time\\n\\n # black arrows (decreasing)\\n for k in range(n-2, -1, -1):\\n i, j = k, 0\\n diag = []\\n while i < n and j < n:\\n diag.append(grid[i][j])\\n i += 1\\n j += 1\\n diag.sort(reverse=True)\\n i, j = k, 0\\n for v in diag:\\n grid[i][j] = v\\n i += 1\\n j += 1\\n # blue arrows (increasing)\\n for k in range(1, n-1):\\n i, j = 0, k\\n diag = []\\n while i < n and j < n:\\n diag.append(grid[i][j])\\n i += 1\\n j += 1\\n diag.sort()\\n i, j = 0, k\\n for v in diag:\\n grid[i][j] = v\\n i += 1\\n j += 1\\n return grid\\n\\n\"]]",
"runtime": 11,
"runtimeDistribution": "[[3, 3.2727, \"class Solution:\\n def sortMatrix(self, grid: List[List[int]]) -> List[List[int]]:\\n n = len(grid)\\n # we can skip the corners\\n # to move through diagonally you need to add 1 to both row/col each time\\n # starting points form a r-shape on left/top of matrix\\n # need to collect, sort, and re-insert each time\\n\\n # black arrows (decreasing)\\n for k in range(n-2, -1, -1):\\n i, j = k, 0\\n diag = []\\n while i < n and j < n:\\n diag.append(grid[i][j])\\n i += 1\\n j += 1\\n diag.sort(reverse=True)\\n i, j = k, 0\\n for v in diag:\\n grid[i][j] = v\\n i += 1\\n j += 1\\n # blue arrows (increasing)\\n for k in range(1, n-1):\\n i, j = 0, k\\n diag = []\\n while i < n and j < n:\\n diag.append(grid[i][j])\\n i += 1\\n j += 1\\n diag.sort()\\n i, j = 0, k\\n for v in diag:\\n grid[i][j] = v\\n i += 1\\n j += 1\\n return grid\\n\\n\"], [4, 2.1818, \"class Solution:\\n def sortMatrix(self, grid: List[List[int]]) -> List[List[int]]:\\n n = len(grid)\\n\\n for i in range(1, n):\\n x, y = 0, i\\n le = n - i\\n arr = [grid[x+k][y+k] for k in range(le)]\\n arr.sort()\\n\\n for k in range(le):\\n grid[x + k][y + k] = arr[k]\\n\\n\\n for i in range(0, n):\\n x, y = i, 0\\n le = n - i\\n arr = [grid[x+k][y+k] for k in range(le)]\\n arr.sort()\\n arr = arr[::-1]\\n for k in range(le):\\n grid[x + k][y + k] = arr[k]\\n\\n return grid\\n\\n\\n\\n\\n \"], [5, 1.8182, null], [6, 1.0909, null], [7, 7.2727, null], [8, 6.5455, null], [9, 4.3636, null], [10, 3.6364, null], [11, 17.8182, null], [12, 4.7273, null], [13, 3.2727, null], [14, 5.0909, null], [15, 14.5455, null], [16, 2.1818, null], [17, 1.4545, null], [18, 1.8182, null], [19, 9.4545, null], [20, 0.7273, null], [21, 0.3636, null], [22, 0.3636, null], [23, 0.7273, \"class Solution:\\n def sortMatrix(self, grid: List[List[int]]) -> List[List[int]]:\\n m, n = len(grid), len(grid[0])\\n result = [[0] * n for _ in range(m)]\\n left_group = defaultdict(list)\\n right_group = defaultdict(list)\\n for i in range(m):\\n for j in range(n - i - 1):\\n heappush(right_group[j], grid[i][j + i + 1])\\n for i in range(m):\\n for j in range(i + 1):\\n heappush(left_group[i - j], -grid[i][j])\\n for i in range(m):\\n for j in range(n - i - 1):\\n result[i][j + i + 1] = heappop(right_group[j])\\n for i in range(m):\\n for j in range(1 + i):\\n result[i][j] = -heappop(left_group[i - j])\\n return result\"], [26, 1.0909, \"class Solution:\\n\\n def diagonal(self, grid, i, j, non_increase=True):\\n n = len(grid)\\n sortedArr = []\\n start_i = i\\n start_j = j\\n \\n while i < n and j < n:\\n sortedArr.append(grid[i][j])\\n i += 1\\n j += 1\\n if non_increase:\\n sortedArr.sort(reverse=True)\\n else:\\n sortedArr.sort()\\n \\n pos = 0\\n while start_i < n and start_j < n:\\n grid[start_i][start_j] = sortedArr[pos]\\n start_i += 1\\n start_j += 1\\n pos += 1\\n return sortedArr\\n\\n \\n\\n def sortMatrix(self, grid: List[List[int]]) -> List[List[int]]:\\n n = len(grid)\\n\\n for x in range(n - 1, -1, -1):\\n i = x\\n j = 0\\n arr = self.diagonal(grid, i, j)\\n print(\\\"ARR: \\\", arr)\\n \\n for x in range(1, n):\\n i = 0\\n j = x\\n arr = self.diagonal(grid, i, j, False)\\n print(\\\"ARR: \\\", arr)\\n\\n return(grid)\\n \\n\\n\\n\\n\\n\"]]"
},
"ruby": {
"code": "def sort_matrix(grid)\n n = grid.size\n return grid if n == 0\n\n diagonals = Hash.new { |h, k| h[k] = [] }\n\n n.times do |i|\n n.times do |j|\n d = i - j\n diagonals[d] << [i, j]\n end\n end\n\n diagonals.each do |d, cells|\n values = cells.map { |i, j| grid[i][j] }\n\n sorted_values = if d >= 0\n values.sort.reverse\n else\n values.sort\n end\n\n cells.each_with_index do |(i, j), idx|\n grid[i][j] = sorted_values[idx]\n end\n end\n\n grid\nend",
"memory": null,
"memoryDistribution": "[[211700, 100.0, \"def sort_matrix(grid)\\n n = grid.size\\n return grid if n == 0\\n\\n diagonals = Hash.new { |h, k| h[k] = [] }\\n\\n n.times do |i|\\n n.times do |j|\\n d = i - j\\n diagonals[d] << [i, j]\\n end\\n end\\n\\n diagonals.each do |d, cells|\\n values = cells.map { |i, j| grid[i][j] }\\n\\n sorted_values = if d >= 0\\n values.sort.reverse\\n else\\n values.sort\\n end\\n\\n cells.each_with_index do |(i, j), idx|\\n grid[i][j] = sorted_values[idx]\\n end\\n end\\n\\n grid\\nend\"]]",
"runtime": 28,
"runtimeDistribution": "[[28, 100.0, \"def sort_matrix(grid)\\n n = grid.size\\n return grid if n == 0\\n\\n diagonals = Hash.new { |h, k| h[k] = [] }\\n\\n n.times do |i|\\n n.times do |j|\\n d = i - j\\n diagonals[d] << [i, j]\\n end\\n end\\n\\n diagonals.each do |d, cells|\\n values = cells.map { |i, j| grid[i][j] }\\n\\n sorted_values = if d >= 0\\n values.sort.reverse\\n else\\n values.sort\\n end\\n\\n cells.each_with_index do |(i, j), idx|\\n grid[i][j] = sorted_values[idx]\\n end\\n end\\n\\n grid\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list:
import random
random.seed(seed)
def serialize_grid(grid):
# Serialize grid as rows separated by ";" and numbers in each row by ","
return ";".join(",".join(str(x) for x in row) for row in grid)
from collections import defaultdict
# Sample solution adapted from the provided sample solution
def sample_solution(grid):
n = len(grid)
diag_dict = defaultdict(list)
# Create a copy of grid to avoid modifying the original
new_grid = [row[:] for row in grid]
for i in range(n):
for j in range(n):
k = i - j
diag_dict[k].append((i, j))
for k, positions in diag_dict.items():
values = [new_grid[i][j] for i, j in positions]
if k >= 0:
sorted_values = sorted(values, reverse=True)
else:
sorted_values = sorted(values)
for idx, (i, j) in enumerate(positions):
new_grid[i][j] = sorted_values[idx]
return new_grid
# Define a set of fixed test cases
fixed_cases = []
fixed_cases.append([[1]])
fixed_cases.append([[0, 1], [1, 2]])
fixed_cases.append([[1, 7, 3], [9, 8, 2], [4, 5, 6]])
fixed_cases.append([[4, 3, 2, 1],
[8, 7, 6, 5],
[12, 11, 10, 9],
[16, 15, 14, 13]])
fixed_cases.append([[-1, -2, -3, -4, -5],
[5, 4, 3, 2, 1],
[10, 9, 8, 7, 6],
[0, 0, 0, 0, 0],
[6, 7, 8, 9, 10]])
fixed_cases.append([[7, 7, 7], [7, 7, 7], [7, 7, 7]])
test_cases = []
# Use fixed test cases first
for grid in fixed_cases:
test_input = serialize_grid(grid)
solved_grid = sample_solution(grid)
test_output = serialize_grid(solved_grid)
test_cases.append({"input": test_input, "output": test_output})
if len(test_cases) >= num_cases:
return test_cases[:num_cases]
# Generate additional random test cases if needed
while len(test_cases) < num_cases:
n = random.randint(1, 10) # grid size in the range [1, 10]
grid = [[random.randint(-10**5, 10**5) for _ in range(n)] for _ in range(n)]
test_input = serialize_grid(grid)
solved_grid = sample_solution(grid)
test_output = serialize_grid(solved_grid)
test_cases.append({"input": test_input, "output": test_output})
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
def deserialize(output_str):
output_str = output_str.strip()
if not output_str:
return []
rows = output_str.split(";")
grid = []
for row in rows:
if row == "":
grid.append([])
else:
grid.append(list(map(int, row.split(","))))
return grid
expected_grid = deserialize(expected_output)
program_grid = deserialize(program_output)
return expected_grid == program_grid
|
[{"input": "1", "output": "1"}, {"input": "0,1;1,2", "output": "2,1;1,0"}, {"input": "1,7,3;9,8,2;4,5,6", "output": "8,2,3;9,6,7;4,5,1"}, {"input": "4,3,2,1;8,7,6,5;12,11,10,9;16,15,14,13", "output": "13,3,2,1;14,10,6,5;15,11,7,9;16,12,8,4"}, {"input": "-1,-2,-3,-4,-5;5,4,3,2,1;10,9,8,7,6;0,0,0,0,0;6,7,8,9,10", "output": "10,-2,-3,-4,-5;9,8,0,2,1;10,9,4,3,6;7,8,5,0,7;6,0,0,0,-1"}, {"input": "7,7,7;7,7,7;7,7,7", "output": "7,7,7;7,7,7;7,7,7"}, {"input": "-93444,94393;-27903,-35804", "output": "-35804,94393;-27903,-93444"}, {"input": "-63421,93061,-73132,77392;94161,42964,-77210,54794;10604,-91669,-92189,-75439;-42686,-39010,32475,57815", "output": "57815,-77210,-73132,77392;94161,42964,-75439,54794;10604,32475,-63421,93061;-42686,-39010,-91669,-92189"}, {"input": "47127", "output": "47127"}, {"input": "87700,70363,83848,42853;9974,-42213,17757,54472;-27074,-98297,98916,-58147;83013,10785,-10806,-27158", "output": "98916,-58147,54472,42853;9974,87700,17757,83848;10785,-10806,-27158,70363;83013,-27074,-98297,-42213"}, {"input": "-43557,-11764,-73207;-75688,-405,-74647;-5896,-9835,58263", "output": "58263,-74647,-73207;-9835,-405,-11764;-5896,-75688,-43557"}, {"input": "-88610,91294,20435,40568,-67278;-770,-79344,44714,-23146,64794;62141,-5200,51349,-49593,84699;-81767,-87988,73346,-40258,-24139;-79084,-38976,-73524,-353,-27131", "output": "51349,-49593,-23146,40568,-67278;73346,-27131,-24139,20435,64794;62141,-353,-40258,44714,84699;-38976,-73524,-770,-79344,91294;-79084,-81767,-87988,-5200,-88610"}, {"input": "66640,-4362,-57362,-2960,-6868,-45079,75682,-30014;83977,79187,69878,-81283,59680,66455,-55138,40021;91136,-35825,-57166,21178,-529,-29235,67772,80397;46001,-42430,79467,-14992,-85337,-39957,-91586,-17306;5162,-29814,-82650,-44693,48682,88196,-17510,-44262;71819,30870,3712,68519,20285,-62548,-30564,-63397;-35349,95294,47159,41289,-31124,95825,53245,12311;52969,4700,-5105,-42507,-63738,33569,29372,-76169", "output": "79187,-85337,-81283,-91586,-17306,-55138,40021,-30014;95825,66640,-30564,-63397,-44262,-6868,-45079,75682;91136,83977,53245,-4362,-57362,-29235,66455,80397;46001,68519,79467,48682,12311,-39957,-2960,67772;47159,41289,33569,29372,-14992,21178,-17510,59680;95294,30870,3712,-31124,20285,-57166,69878,-529;4700,71819,5162,-29814,-42430,-35825,-62548,88196;52969,-35349,-5105,-42507,-63738,-82650,-44693,-76169"}, {"input": "-71257", "output": "-71257"}, {"input": "64481,-58062,78384;10666,56345,-83347;864,39,56208", "output": "64481,-83347,78384;10666,56345,-58062;864,39,56208"}, {"input": "38704,-34094,45024,-96991,78332,88932,-69971,78706;40763,96838,-30054,68024,-10826,-70758,-23061,13971;-58540,18940,-99150,89292,88659,-30955,31225,99743;-53168,33085,-72106,63918,-21765,67496,33080,59637;-47857,-59935,-1981,99887,-57651,41394,39029,-99851;57009,-15025,28085,-94895,-70675,-4847,-19388,-37230;-84816,-36857,48729,-79355,-77547,91865,27399,-81857;99387,39645,-67033,-66343,72949,24592,44127,-56713", "output": "96838,-81857,-37230,-99851,-70758,-23061,-69971,78706;99887,63918,-34094,39029,-96991,31225,88932,13971;33085,91865,38704,-30054,45024,-30955,59637,99743;72949,24592,44127,27399,-21765,67496,-10826,78332;48729,28085,-1981,40763,-4847,-19388,68024,33080;57009,-15025,-53168,-58540,18940,-56713,41394,88659;39645,-36857,-47857,-59935,-77547,-70675,-57651,89292;99387,-84816,-67033,-66343,-79355,-94895,-72106,-99150"}, {"input": "38326,59014,10923,-44479,41373;97988,91347,80844,-47270,86895;-18286,4593,76078,70361,-2111;14845,35679,18354,-68280,-35014;-41097,-83216,-11373,-94486,54221", "output": "91347,-35014,-47270,-44479,41373;97988,76078,59014,-2111,86895;35679,18354,54221,70361,10923;14845,-11373,4593,38326,80844;-41097,-83216,-18286,-94486,-68280"}, {"input": "-39677,54256,-42272,-98115,-81390,85556,65439,-84567,-39985;-82332,-91766,-13381,-81426,34782,-37609,-26999,75368,27248;-43840,41356,-65316,89622,49695,51050,23907,-36300,23987;6708,-50086,-75274,-74591,72748,12997,-7124,11038,7767;22427,91122,-85800,76518,71299,69392,-74201,-84111,5544;90896,-11054,-71356,-34817,-49776,-50138,40584,17601,-63253;10593,-51900,-26982,21275,-34515,-80239,16164,44264,-74334;-86739,70955,41711,-96132,-75552,97542,-38035,-56403,6539;27307,26185,-43968,5130,-84630,-56842,-655,-99435,2346", "output": "71299,-13381,-81426,-98115,-81390,-36300,23987,-84567,-39985;76518,16164,6539,-74334,-84111,-37609,-26999,65439,27248;97542,41356,2346,40584,-74201,-63253,5544,7767,75368;91122,-655,-38035,-39677,44264,-42272,-7124,11038,85556;22427,21275,-34515,-49776,-50138,54256,12997,34782,23907;90896,-11054,6708,-34817,-75274,-56403,69392,17601,51050;70955,41711,-26982,-56842,-43840,-80239,-65316,72748,49695;26185,10593,5130,-84630,-71356,-50086,-82332,-74591,89622;27307,-86739,-43968,-51900,-96132,-75552,-85800,-99435,-91766"}, {"input": "19277,-25224,10888,82607,91497;45691,73505,88326,27577,-59421;-50220,-22220,-42932,-84669,51828;92869,42133,-84021,96077,-17791;-85015,-86856,53138,24987,31819", "output": "96077,-84669,10888,-59421,91497;45691,73505,-25224,27577,82607;53138,24987,31819,-17791,51828;92869,42133,-22220,19277,88326;-85015,-86856,-50220,-84021,-42932"}, {"input": "-58730,-85090,33124,-79000,-51288,-82038,55984,-82185,77002;-38343,5847,-68573,49336,-35457,51760,55849,-89582,62367;-78509,9897,72326,53006,48170,37044,-17066,-31642,-46455;75564,87745,-17639,-37430,-30371,3752,-65692,76079,69214;-21358,19858,-17117,97096,-80984,-97559,20136,62833,47585;-73791,-80796,40937,-44123,32614,-30480,-65278,-8510,-81967;-35963,-3131,-25293,-58648,14867,42401,84428,-20697,60347;71435,38658,-97950,75076,45385,-21520,73903,-72846,-64797;-30672,-69742,-71942,94620,45024,-59251,-28606,-26140,58552", "output": "84428,-97559,-8510,-81967,-51288,-82038,-89582,-82185,77002;97096,72326,-85090,3752,-79000,-17066,-31642,-46455,62367;87745,73903,58552,-68573,20136,-65692,47585,55849,55984;75564,14867,42401,5847,-65278,33124,-35457,51760,69214;75076,45385,-17117,32614,-30480,-64797,48170,37044,76079;94620,45024,40937,-21520,9897,-37430,-30371,49336,62833;38658,-3131,-21358,19858,-28606,-17639,-58730,-20697,60347;71435,-35963,-73791,-25293,-58648,-44123,-26140,-72846,53006;-30672,-69742,-71942,-97950,-80796,-59251,-78509,-38343,-80984"}, {"input": "88117,-10116,-46629,80223;66261,-30799,32489,28065;-34171,-86684,-75805,66273;11037,-27470,-88443,-99071", "output": "88117,-10116,-46629,80223;66261,-30799,32489,28065;-27470,-86684,-75805,66273;11037,-34171,-88443,-99071"}, {"input": "-65707,67015,-31330,-57643,94309,15824;44619,84986,12115,47038,-97466,-70673;-80276,81146,-60927,43023,-90556,-3213;52701,44841,-61179,12666,-66591,-89035;-19192,-4409,-89542,-6203,-44930,78799;-34588,74832,-73054,-7286,46770,6529", "output": "84986,-66591,-90556,-97466,-70673,15824;81146,12666,12115,-89035,-57643,94309;44841,46770,6529,43023,-31330,-3213;52701,-7286,44619,-44930,67015,47038;74832,-4409,-80276,-6203,-60927,78799;-34588,-19192,-73054,-89542,-61179,-65707"}, {"input": "96471,-59485,-37941,-57402,-53587,8080,-93503,-52982,93085,-12920;7928,75612,92690,-34945,-30059,-58268,83835,-71664,281,-89849;23388,-41691,-47684,20665,-8340,-19997,-40338,-41562,-93797,73023;-49373,4455,-13949,-26966,-81802,-26830,-7950,68160,33537,4773;78131,40565,-13192,-92765,-69764,-31525,-53190,52198,-30410,-89972;-71583,56387,13918,-9381,90983,-17772,14398,58914,34066,-69685;976,51149,-50172,-33227,-88365,85803,14309,-99557,36293,41151;80055,88594,94497,93210,75801,-48349,-4522,13062,-81657,74125;-13441,63356,-17709,73903,-67331,88679,-21273,32939,-18923,74821;7057,-14494,5486,82769,-22496,45335,-66633,-49711,10217,74307", "output": "96471,-99557,-53190,-57402,-69685,-89972,-93797,-52982,-89849,-12920;90983,75612,-81802,-37941,-30059,-58268,-41562,-93503,281,93085;23388,85803,74307,-81657,-34945,-19997,-53587,8080,-71664,73023;88679,4455,32939,14309,-59485,-26830,-7950,-40338,33537,4773;93210,75801,-9381,10217,13062,-31525,-8340,34066,-30410,83835;94497,78131,40565,-13192,7928,-17772,14398,36293,41151,68160;88594,73903,56387,13918,-21273,-4522,-18923,20665,58914,52198;80055,82769,51149,45335,-33227,-48349,-13949,-26966,74821,74125;-13441,63356,976,-22496,-50172,-49373,-49711,-41691,-47684,92690;7057,-14494,5486,-17709,-71583,-67331,-66633,-88365,-92765,-69764"}, {"input": "77554,96118,-54380,61353,49187,-21108,6450;43638,-99894,-20342,-24788,-44902,12692,52039;59032,71627,-15525,21893,15811,15909,77111;-43980,34001,24042,92927,-55517,72713,-77772;-25608,35122,74025,65921,62335,-12133,-75520;96906,-38431,76369,-18626,-41112,-47800,-61373;-93598,-87886,-35816,24554,60241,-80909,19384", "output": "92927,-61373,-75520,-77772,12692,-21108,6450;71627,77554,-55517,-54380,-44902,49187,52039;74025,65921,62335,-20342,-24788,15909,77111;76369,60241,43638,19384,-12133,15811,61353;-25608,35122,59032,24042,-15525,21893,72713;96906,-35816,24554,34001,-41112,-47800,96118;-93598,-87886,-38431,-43980,-18626,-80909,-99894"}, {"input": "65089,50908,-49030,88310,82545,657,29598;4766,-36041,-61316,71981,80256,-98547,96860;-72059,11449,-42633,-53893,82429,35779,21778;-86836,46120,-34675,-68187,19658,-65046,21803;75001,39233,46518,56094,-16823,97984,16017;60603,88553,32324,11867,43621,16893,-58278;94944,24433,17983,-32055,97073,-35188,67159", "output": "67159,-61316,-65046,21803,-98547,657,29598;56094,65089,-58278,-49030,35779,21778,96860;97073,43621,16893,-53893,16017,80256,82545;39233,46518,11449,-16823,19658,71981,88310;88553,32324,46120,4766,-36041,50908,82429;60603,75001,-32055,11867,-34675,-42633,97984;94944,24433,17983,-86836,-72059,-35188,-68187"}, {"input": "36655,27034,64298,-37284,-28016;15309,-79689,87051,-25099,-38529;-28772,-11960,-16191,41597,-78878;-63727,-60461,-39377,410,81914;-59944,85183,-43914,-83163,8755", "output": "36655,27034,-78878,-38529,-28016;15309,8755,41597,-25099,-37284;-28772,-11960,410,81914,64298;85183,-43914,-39377,-16191,87051;-59944,-63727,-60461,-83163,-79689"}, {"input": "-13262,42242,22139,8992,-83678,-45780,10138;2099,53112,82327,-94880,50913,-286,25037;-98455,-7789,-21721,97518,2232,9843,41091;95956,92579,43165,58139,-42188,27986,-42480;-28452,14251,27308,-92392,1936,-11886,75341;78032,5989,89839,-56735,22523,-66544,63120;40017,-92931,3290,55161,47951,73801,-92896", "output": "58139,-42188,-94880,-42480,-83678,-45780,10138;73801,53112,-11886,2232,8992,-286,25037;92579,43165,1936,42242,22139,9843,41091;95956,47951,22523,-13262,63120,27986,50913;5989,89839,27308,2099,-21721,82327,75341;78032,3290,55161,-56735,-7789,-66544,97518;40017,-92931,-28452,14251,-98455,-92392,-92896"}, {"input": "68492,12358;-64428,21031", "output": "68492,12358;-64428,21031"}, {"input": "-86819,-31802,-621;-14187,-44515,19196;-14320,-11527,99551", "output": "99551,-31802,-621;-11527,-44515,19196;-14320,-14187,-86819"}, {"input": "-27057,97134,10510,-33869,-78529,23288,-94919;96352,41405,-86347,-8260,-41222,70431,-82013;70853,-89447,97717,-91866,-35177,-47739,-94658;62879,-60054,-37467,-66912,24141,75494,-70014;47841,-42862,21905,83360,-32828,-3297,-56016;58831,59186,96064,88313,-69976,-57070,-18464;-71663,51698,-93269,-18223,50941,77562,-1616", "output": "97717,-91866,-56016,-70014,-94658,-82013,-94919;96352,41405,-86347,-35177,-47739,-78529,23288;88313,83360,-1616,-18464,-8260,-41222,70431;96064,70853,77562,-27057,-3297,10510,-33869;59186,62879,50941,-37467,-32828,24141,75494;58831,47841,-18223,21905,-69976,-57070,97134;-71663,51698,-93269,-42862,-60054,-89447,-66912"}, {"input": "87436,-48010,-80078,55214,81040,64427,-36339;-73288,82764,-20942,79374,57394,-68267,48355;-89234,-8983,39655,12296,73413,-2858,-81924;32634,69749,-10549,-96684,10115,28503,-72334;13645,-5055,66614,20517,85416,-59895,14160;-53827,92360,36772,70513,-29200,61457,41078;26745,21863,14183,91634,55313,-29642,-15510", "output": "87436,-59895,-80078,-72334,-81924,48355,-36339;20517,85416,-48010,14160,-2858,-68267,64427;70513,-8983,82764,-20942,28503,55214,81040;91634,69749,-10549,61457,10115,73413,57394;92360,36772,66614,-29200,39655,12296,79374;21863,14183,32634,55313,-29642,-15510,41078;26745,-53827,13645,-5055,-89234,-73288,-96684"}, {"input": "-77282,-26881,18175,-36073;96732,21820,49382,59994;75161,-651,-11816,-92477;29579,-14800,-52332,27808", "output": "27808,-92477,18175,-36073;96732,21820,-26881,59994;75161,-651,-11816,49382;29579,-14800,-52332,-77282"}, {"input": "-6985,-32275,-10783,-26690;56278,83811,-27578,45697;-97339,35430,-49916,-77558;-36730,88763,6542,28077", "output": "83811,-77558,-10783,-26690;56278,28077,-32275,45697;88763,35430,-6985,-27578;-36730,-97339,6542,-49916"}, {"input": "98748,-37001,81039,24804,69319,86605,28665,17486,-95480;-75607,-22868,-41910,6011,81347,-36220,-19730,74053,52451;-3264,24062,45089,39177,-9887,11543,95542,44281,-13286;-7775,84249,18946,-28981,-19621,-34097,-39566,-68371,89080;-49516,-17281,-68660,94741,40473,99803,80922,-51465,-49789;-43277,93620,26929,-27518,89945,54556,99283,37530,56445;-25814,-73648,-49114,-22341,-40367,-5398,-52961,-20763,-96292;85602,40020,-66818,-28091,-88069,-85707,45059,-23419,82823;-66897,67213,97339,28680,-73108,-96785,50487,-25463,23049", "output": "98748,-41910,-96292,-51465,-68371,-19730,-13286,17486,-95480;94741,54556,-37001,-34097,-39566,-49789,44281,28665,52451;84249,89945,45089,-20763,-9887,11543,-36220,86605,74053;26929,50487,45059,40473,-19621,6011,24804,69319,89080;93620,-7775,-3264,24062,23049,39177,37530,56445,95542;28680,-28091,-17281,-27518,18946,-22868,82823,80922,81347;97339,-43277,-49114,-22341,-40367,-5398,-23419,99283,81039;85602,40020,-66818,-49516,-88069,-68660,-25463,-28981,99803;-66897,67213,-25814,-73648,-73108,-96785,-85707,-75607,-52961"}, {"input": "15466,-10686,-51671,-86532,-33815,25233,-70093,-82871;5043,28908,-80580,51262,65005,79949,-85947,-60226;-60889,47545,-20352,-77671,-34939,-68949,46295,9097;58942,56271,62114,-40838,36989,-287,18099,16056;-22051,54278,12415,-19947,49062,62798,-84211,59811;94009,-73987,99946,-45530,63975,-44682,-30625,73127;-78718,-58829,-37121,-54436,44701,-80323,-58966,-99299;7090,18096,80714,55664,23184,-23649,-91444,-39320", "output": "49062,-99299,-84211,-86532,-33815,-85947,-70093,-82871;63975,28908,-80580,-51671,-68949,16056,9097,-60226;56271,62114,15466,-77671,-34939,18099,46295,25233;99946,44701,47545,-20352,-30625,-287,59811,79949;55664,58942,12415,5043,-39320,-10686,51262,65005;94009,-22051,54278,-23649,-19947,-40838,36989,73127;18096,80714,-37121,23184,-45530,-80323,-44682,62798;7090,-78718,-58829,-73987,-54436,-60889,-91444,-58966"}, {"input": "85324,-25888,84283,19021,-81341;80193,-38810,-30649,63855,54609;73325,-48143,11447,-69913,42753;-41068,69773,-60944,-30367,-62714;-81281,-84367,-56505,-19362,55987", "output": "85324,-69913,42753,19021,-81341;80193,55987,-62714,63855,54609;73325,-19362,11447,-30649,84283;-41068,69773,-48143,-30367,-25888;-81281,-84367,-56505,-60944,-38810"}, {"input": "-24343,15121,-67402,22866,80532,-20285,83430,5515,-28633,31195;41552,29445,14755,-78913,56771,-89551,13253,92553,-15506,58259;-34368,-93220,-76060,-39989,76763,50784,53910,-94562,76234,-29350;51059,-89454,98251,-54075,23338,36043,70789,15927,-27083,-52424;53440,14264,66405,28902,-76082,23210,-8785,7046,-12626,-15837;75671,-72580,-57841,-13544,7910,81842,29884,-24446,73692,4976;99360,44204,-90381,19229,-76916,-17552,-33836,-15256,-69612,5952;34898,-99699,72401,42237,21104,8330,-85791,-50827,35905,-5162;63219,98297,30676,63947,15878,99226,-86471,-46639,-29993,43974;-65656,-24495,14849,83042,27064,-68169,-92433,65156,59612,-37270", "output": "81842,-39989,-78913,5952,-89551,-94562,-52424,-29350,-28633,31195;98251,29445,-15256,-69612,7046,-12626,-27083,76234,-15506,58259;66405,59612,-24343,14755,-67402,22866,4976,-20285,83430,5515;99226,65156,41552,-29993,15121,-24446,50784,15927,-15837,92553;53440,51059,8330,28902,-33836,23210,-8785,56771,53910,13253;75671,42237,21104,-13544,7910,-37270,23338,-5162,70789,80532;99360,72401,15878,19229,-34368,-17552,-50827,29884,36043,73692;98297,83042,63947,-68169,14264,-76916,-46639,-54075,35905,76763;63219,34898,30676,44204,-72580,-57841,-86471,-85791,-76060,43974;-65656,-24495,14849,-99699,27064,-90381,-92433,-89454,-93220,-76082"}, {"input": "-18539,44399,-96416;44769,6952,-75566;-41097,-70257,20965", "output": "20965,-75566,-96416;44769,6952,44399;-41097,-70257,-18539"}, {"input": "69793,-59638;30646,87853", "output": "87853,-59638;30646,69793"}, {"input": "33397,84919,-28324,8918,26484;23789,-36108,19743,44510,-62083;554,-50033,57123,33232,95636;-64216,-81700,-27584,8774,-10904;33100,-29963,-99328,-25856,90329", "output": "90329,-10904,-28324,-62083,26484;23789,57123,19743,44510,8918;554,-25856,33397,33232,95636;-29963,-81700,-27584,8774,84919;33100,-64216,-99328,-50033,-36108"}, {"input": "53862,52023,72999,28356,-61047;17059,41185,26967,-9528,-12853;44681,99982,42456,-1117,19365;-15648,-50546,82845,-37399,49893;393,-38774,7682,-88559,-16592", "output": "53862,-1117,-9528,-12853,-61047;99982,42456,26967,19365,28356;44681,82845,41185,49893,72999;-15648,7682,17059,-16592,52023;393,-38774,-50546,-88559,-37399"}, {"input": "84871,-63,1208,73982,70922,-60127,29847,-90296;-66906,31672,54712,-12970,-73691,15423,-73862,37874;19780,-95977,89384,-62211,7473,71646,-59536,-80385;23074,-30526,-11249,63383,81588,4197,70350,-78946;-13869,76778,39885,-383,-16990,64311,88407,99072;27912,41824,-90590,61863,-82064,-38457,65455,79411;-24666,-40366,95760,-76308,13763,-74194,99326,66133;84520,-73653,16307,-56389,81928,-21497,-92412,-87944", "output": "99326,-62211,-12970,-73691,-78946,-80385,29847,-90296;-383,89384,-63,1208,70350,-59536,-73862,37874;61863,-11249,84871,54712,4197,71646,15423,-60127;81928,39885,-66906,63383,64311,7473,73982,70922;95760,76778,19780,-74194,31672,65455,79411,99072;27912,41824,23074,13763,-82064,-16990,66133,88407;-24666,16307,-13869,-76308,-21497,-92412,-38457,81588;84520,-73653,-40366,-56389,-90590,-30526,-95977,-87944"}, {"input": "-85289,-23096,-6031,-1738,12901,-61840;-35986,39242,8016,48354,78729,-52800;-55440,-54107,-79299,59774,281,62453;79079,-36868,30460,52871,-62483,-39134;20887,67222,-33422,20473,-33068,74808;-97537,21963,-24600,77631,43287,-58588", "output": "52871,-62483,-39134,-1738,-52800,-61840;43287,39242,-23096,-6031,62453,12901;77631,30460,-33068,8016,281,78729;79079,-33422,20473,-58588,59774,48354;21963,67222,-36868,-35986,-79299,74808;-97537,20887,-24600,-55440,-54107,-85289"}, {"input": "15796,-9413;54028,-21579", "output": "15796,-9413;54028,-21579"}, {"input": "80961,-34439,19756,-20801,-47777,845,26670;-72042,-37818,-28,49926,-5902,50683,-22439;83311,-22608,-94249,72550,3758,-28047,-97878;48354,79778,95210,-87144,58965,95342,30214;-24976,-39676,59138,-7642,-42590,66885,-50159;62762,-34300,77671,98070,88987,72800,78482;-64145,64691,-74530,64484,69434,-89666,-19016", "output": "80961,-34439,-50159,-28047,-97878,-22439,26670;95210,72800,-28,3758,-20801,-47777,845;98070,88987,-19016,58965,19756,-5902,50683;77671,83311,-7642,-37818,66885,49926,30214;-24976,64484,79778,-22608,-42590,72550,95342;64691,-34300,48354,69434,-72042,-87144,78482;-64145,62762,-74530,-39676,59138,-89666,-94249"}, {"input": "-91254,51931,-4354,91983,-65552,-76373,-22639,-14353;95947,8921,-53958,-47363,-65356,41402,-4093,39159;31542,-28559,-56866,-32637,26313,-22631,95706,-11208;-69809,22770,-80261,-63102,97696,-40857,77294,89849;76791,4179,46096,-4115,-76328,3435,-96352,-30674;40659,-67602,19219,-3378,76377,96348,76250,-31276;53238,-117,67391,-2621,-71598,76904,-38705,23594;-93440,62410,47169,-14016,59929,-41970,69778,-83429", "output": "96348,-53958,-96352,-65356,-65552,-76373,-22639,-14353;95947,8921,-32637,-47363,-30674,41402,-11208,39159;46096,76904,-38705,3435,-40857,-22631,89849,-4093;59929,31542,76377,-56866,23594,-31276,77294,95706;76791,19219,22770,69778,-63102,51931,-4354,91983;47169,67391,4179,-3378,-4115,-76328,76250,26313;62410,40659,-14016,-2621,-41970,-28559,-83429,97696;-93440,53238,-117,-67602,-69809,-71598,-80261,-91254"}, {"input": "83783,-20783,70194,7032,-69415,-63359,-88113,-90246;-20213,29138,-69560,-74522,-38449,40914,-64437,1881;18919,-2742,75763,94809,82579,41608,9871,53967;94581,90473,-59493,8759,71683,-74043,28279,61389;6985,-26668,-91424,80952,-2868,-43045,16230,16574;-38105,-4925,-73955,79746,-3706,42728,69037,-5976;-84128,4369,-27680,-50243,-67977,19201,-75969,73740;-44398,68218,67639,56538,-94402,-86742,-12573,-36150", "output": "83783,-69560,-74522,-38449,-69415,-64437,-88113,-90246;80952,75763,-43045,-74043,7032,9871,-63359,1881;90473,19201,42728,-20783,-5976,16574,40914,53967;94581,79746,-2742,29138,69037,16230,28279,61389;56538,-26668,18919,-3706,8759,71683,70194,41608;67639,6985,-50243,-67977,-12573,-2868,73740,82579;68218,4369,-4925,-73955,-86742,-20213,-36150,94809;-44398,-84128,-38105,-27680,-94402,-91424,-59493,-75969"}, {"input": "48000,-46207,-82015;45282,-45695,53716;-43390,-38921,-13871", "output": "48000,-46207,-82015;45282,-13871,53716;-43390,-38921,-45695"}, {"input": "56233,-99257,-27315;-62071,-65924,41614;-34293,-54257,-71184", "output": "56233,-99257,-27315;-54257,-65924,41614;-34293,-62071,-71184"}, {"input": "-65449", "output": "-65449"}, {"input": "-6089", "output": "-6089"}, {"input": "54364,-15126,-95864,-54323;-30436,-86264,-66772,94436;10352,37910,-70208,95471;-83339,24845,17512,-5094", "output": "54364,-66772,-95864,-54323;37910,-5094,-15126,94436;24845,17512,-70208,95471;-83339,10352,-30436,-86264"}, {"input": "55625,-71413,18490,32078,-41923,61246,-88633,90642,72727;36695,-20930,20073,68647,-91835,-84055,25562,5281,11745;79856,-71699,28521,86751,16277,-80735,-78822,-15561,59461;-61116,-82782,-66920,-27907,63661,65957,53449,43748,86686;-14755,-149,56602,39082,-22695,18938,32527,58709,12774;-74001,83967,-70008,71629,70633,44529,88963,-43633,12740;18372,-40102,8478,-11152,18882,4524,9049,91263,-75074;-18068,11873,-18074,74354,-33183,-1880,-59987,80046,24326;-82402,-76086,-77623,-75561,13213,-74687,95189,93670,-2313", "output": "80046,-71413,-75074,-91835,-84055,-15561,-88633,11745,72727;93670,55625,18938,-43633,-80735,-78822,25562,5281,90642;95189,70633,44529,20073,16277,12740,-41923,61246,59461;-149,79856,39082,28521,24326,18490,32078,12774,86686;83967,-11152,71629,36695,9049,63661,32527,53449,43748;-18074,74354,-33183,56602,4524,-2313,86751,65957,58709;18372,-40102,13213,-61116,18882,-59987,-20930,88963,68647;-18068,11873,-74001,8478,-70008,-1880,-66920,-22695,91263;-82402,-76086,-77623,-75561,-14755,-74687,-82782,-71699,-27907"}, {"input": "45849,-84277,53738;47216,47241,-13586;75639,-67958,7691", "output": "47241,-84277,53738;47216,45849,-13586;75639,-67958,7691"}, {"input": "74415,96682,10870,89021,-86514,-24600;57393,-18094,-7819,-72842,51497,33015;-44232,-59439,72159,26403,-41216,-71632;-8220,45821,-3647,-69884,99912,-26976;50496,-40714,12489,47053,62981,60844;76941,68479,45945,-93118,59644,72446", "output": "74415,-7819,-72842,-71632,-86514,-24600;59644,72446,26403,-41216,51497,33015;45821,57393,72159,60844,-26976,89021;45945,12489,47053,62981,96682,10870;68479,-8220,-44232,-3647,-18094,99912;76941,50496,-40714,-93118,-59439,-69884"}, {"input": "-92411,-52706,-28364,84208,99861;-19002,-10918,-7982,-98400,-52446;-62448,48457,72318,5063,-81759;-62809,94240,65982,-91964,-75947;95588,39062,-43605,-1383,10056", "output": "72318,-75947,-98400,-52446,99861;65982,10056,-52706,-81759,84208;94240,48457,-10918,-7982,-28364;39062,-43605,-1383,-91964,5063;95588,-62809,-62448,-19002,-92411"}, {"input": "-10637,-58737,-2993,-18307,89162,-14965,48791,56296;-77730,-86209,-59216,-58736,97770,61962,-86956,76676;-78614,-28670,16159,73523,11152,27313,59141,15879;8575,-28391,-43490,97903,34308,-70164,-9516,12699;-70931,-25749,77790,77861,55486,27567,38132,74884;-19150,-88095,-42193,3615,57109,-85640,-97985,-46412;-20985,-44627,-64025,-33018,-24124,-13985,-68547,-97974;30386,95825,12893,-53943,-66135,-331,39613,84463", "output": "97903,-97985,-70164,-18307,12699,-86956,48791,56296;77861,84463,-97974,-58736,-9516,59141,-14965,76676;77790,57109,55486,-59216,-46412,27313,61962,15879;8575,3615,39613,16159,-58737,-2993,74884,89162;-53943,-25749,-331,-13985,-10637,27567,11152,97770;12893,-64025,-33018,-24124,-28670,-68547,34308,38132;95825,-19150,-70931,-42193,-28391,-43490,-85640,73523;30386,-20985,-44627,-88095,-66135,-78614,-77730,-86209"}, {"input": "31140,46466,75124,-7158;-81106,4089,94521,-88911;14352,-95088,20521,-79589;-17934,50931,12534,50313", "output": "50313,-79589,-88911,-7158;12534,31140,46466,75124;50931,-81106,20521,94521;-17934,14352,-95088,4089"}, {"input": "85990,67809,9495,-24106,-69808,6176,-94533;-14864,-54945,62037,20611,80777,-5143,-76898;14481,-72249,-36217,14209,54369,4975,37353;-79384,3747,-18664,95508,-10999,-41917,-12689;-55926,-79978,33820,65996,-70109,39094,33680;-49170,-8414,-7962,90678,69199,-61284,-38064;-73051,-61611,-32900,-48287,-54519,57915,-59927", "output": "95508,-38064,-41917,-24106,-69808,-76898,-94533;69199,85990,-10999,9495,-12689,-5143,6176;90678,65996,-36217,14209,20611,4975,37353;-7962,33820,57915,-54945,39094,33680,80777;-8414,-48287,14481,-14864,-59927,62037,54369;-49170,-32900,-79384,3747,-18664,-61284,67809;-73051,-61611,-55926,-79978,-54519,-72249,-70109"}, {"input": "-53563,64613;29529,21622", "output": "21622,64613;29529,-53563"}, {"input": "99197,51904,17677,78555,47978,68556,66539,63714,-15273,64421;-17127,-60428,15281,-82100,22924,15922,65513,-20618,-27996,55037;-85275,-7741,32995,-80552,-18629,21043,18466,-90142,-85087,-3338;-24745,-79886,68995,-76330,61220,55734,32924,789,21297,52129;45310,93703,-89247,17894,49856,70875,-50655,-15714,58598,24683;31430,-60453,-83781,18101,-72868,-9970,87253,-77894,32264,69378;-54765,-89740,-35056,85498,14755,15191,37381,37035,59856,-58386;-4607,-2260,-25842,1558,7156,-11300,77968,56732,-86273,65383;69687,-12274,-82722,-13574,-75226,46266,77833,1335,-25513,-33941;89722,72114,57994,-60581,-12612,-78635,52761,73961,-62926,-8297", "output": "99197,-86273,-82100,-58386,789,-90142,-85087,-27996,-15273,64421;77968,56732,-80552,-77894,-15714,15922,21297,-20618,-3338,55037;77833,68995,49856,-33941,-50655,21043,18466,24683,52129,63714;93703,73961,17894,37381,15281,-18629,22924,47978,65513,66539;45310,85498,18101,15191,32995,37035,17677,32264,58598,68556;31430,1558,52761,14755,1335,-8297,51904,55734,32924,69378;-2260,-12612,-35056,46266,-11300,-7741,-9970,61220,59856,78555;57994,-54765,-13574,-60453,7156,-79886,-17127,-25513,70875,65383;72114,-4607,-60581,-25842,-75226,-24745,-85275,-62926,-60428,87253;89722,69687,-12274,-82722,-89740,-78635,-83781,-89247,-72868,-76330"}, {"input": "71980,83102,73574,2749,-66197;55986,85816,-77792,-18845,46518;-1256,68687,-13892,-66500,75666;84242,93665,79677,37990,-75502;69351,75756,10993,33297,-5149", "output": "85816,-77792,-18845,2749,-66197;79677,71980,-75502,73574,46518;93665,68687,37990,-66500,75666;84242,10993,55986,-5149,83102;69351,75756,-1256,33297,-13892"}, {"input": "-4948", "output": "-4948"}, {"input": "-52746,-43851,-10417,27473,-49667;-40614,-63939,-59383,-79772,-22460;-73487,33087,41497,93631,38027;-90105,73520,-11720,62013,-65647;56564,-1246,-59564,-57468,-52593", "output": "62013,-65647,-79772,-22460,-49667;33087,41497,-59383,-10417,27473;73520,-11720,-52593,-43851,38027;-1246,-59564,-40614,-52746,93631;56564,-90105,-73487,-57468,-63939"}, {"input": "-56605,89053,14733,-88547,7704,-4502,77304,88635,-37733,16444;60063,-25308,97234,96224,17683,-38658,39987,-37304,-18875,22949;-49140,-3573,77814,49532,15499,21026,-26136,105,31833,38270;9749,-57518,-47651,58508,-63720,-34464,-86322,68081,25983,-2689;45369,-73107,86489,35242,-67317,-25273,-78013,-57976,-28490,17786;34572,-61374,14680,-75958,-41795,18260,-8359,-93009,8762,-86040;3928,31598,-1969,-38193,1231,-78608,-1719,-41139,-92611,-16459;-74026,87355,70383,-12106,-61715,-63930,79409,8904,81807,26169;24955,-78395,-7487,-34675,56009,-94789,-55748,-56442,13056,-57133;94446,-21044,21889,90996,-38062,5561,-14949,-97222,-88805,88665", "output": "88665,-63720,-93009,-88547,-86040,-4502,-37304,-18875,-37733,16444;79409,77814,-57133,-92611,-86322,-38658,105,-2689,38270,22949;86489,60063,58508,-41139,-78013,-57976,-28490,17786,31833,88635;14680,1231,35242,18260,-25273,-34464,-16459,-26136,25983,77304;56009,9749,-49140,-3573,13056,-8359,14733,8762,7704,39987;70383,45369,-14949,-55748,-41795,8904,49532,15499,17683,68081;90996,34572,5561,-38193,-57518,-47651,-1719,81807,26169,21026;21889,87355,31598,-1969,-61715,-63930,-56442,-25308,89053,96224;24955,-74026,3928,-34675,-12106,-73107,-75958,-78608,-56605,97234;94446,-21044,-78395,-7487,-38062,-61374,-94789,-97222,-88805,-67317"}, {"input": "-62448,58626,47526,-95833;50640,-90056,84332,66764;-85425,13331,-21196,18825;6582,-82292,69062,-18273", "output": "-18273,18825,47526,-95833;69062,-21196,58626,66764;-82292,50640,-62448,84332;6582,-85425,13331,-90056"}, {"input": "-61819,18386,31920,28159,-34617;93343,84985,-14834,-16613,-31893;72663,-86239,87275,-25515,-53854;68112,-34836,-67248,5002,62330;29160,56943,-62354,89823,84897", "output": "87275,-25515,-53854,-31893,-34617;93343,84985,-14834,-16613,28159;72663,89823,84897,18386,31920;68112,-34836,-67248,5002,62330;29160,56943,-62354,-86239,-61819"}, {"input": "92599", "output": "92599"}, {"input": "16096,-4663,-29840,49659,-41114,63046,-48502;-19843,-39393,79282,50619,4921,54004,-94961;-27340,-16255,-44423,93813,76126,54655,-51969;80588,-9100,-54252,34580,22895,46259,81905;-41691,-12346,19714,-48062,-34957,33940,-74151;-41984,-35441,-94838,26196,-39067,-27325,-10770;-34844,64907,78051,-45424,-86769,-52608,-39707", "output": "34580,-10770,-74151,4921,-51969,-94961,-48502;-16255,16096,-4663,-29840,49659,-41114,63046;26196,-19843,-27325,22895,46259,54655,54004;80588,19714,-39067,-34957,33940,50619,81905;78051,-12346,-9100,-48062,-39393,79282,76126;64907,-35441,-45424,-27340,-52608,-39707,93813;-34844,-41984,-41691,-94838,-86769,-54252,-44423"}, {"input": "-18677,-73401,-53152,-60016,-23161,98745,24689;-33547,-94328,66078,49436,41225,-1878,-49963;87322,20228,-58770,-85592,-36633,-39668,-9078;-88251,-15014,-80963,4794,-87366,-67098,-34848;-65379,-14370,-74877,-92572,27788,85781,-76467;-4151,-6548,-14996,40069,30719,-85808,54077;-30068,66212,83045,-86283,-28335,-60185,-60073", "output": "27788,-87366,-76467,-60016,-23161,-49963,24689;30719,4794,-85592,-67098,-39668,-9078,98745;87322,20228,-18677,-73401,-53152,-34848,-1878;-14370,40069,-33547,-58770,54077,-36633,41225;83045,-14996,-15014,-60185,-60073,66078,49436;66212,-6548,-86283,-28335,-80963,-85808,85781;-30068,-4151,-65379,-88251,-74877,-92572,-94328"}, {"input": "-10639,3093,-19903,-81334,-79371;55643,62699,-59035,-2657,-2414;-77036,-65503,-15920,-39034,33874;-90670,27484,35495,-80243,53716;-76111,-34604,92088,-9493,-94411", "output": "62699,-59035,-19903,-81334,-79371;55643,-10639,-39034,-2657,-2414;92088,35495,-15920,3093,33874;-34604,27484,-9493,-80243,53716;-76111,-90670,-77036,-65503,-94411"}, {"input": "87563,94752,-41486,91162,80508,-18720;60232,-33435,99777,-82075,61604,86895;23324,-71145,-12659,81405,30341,98298;-17672,-6168,30069,-68209,2847,13309;-39546,-54472,34986,65623,70287,-65539;-27212,7368,-35505,-95426,12874,-68458", "output": "87563,-65539,-82075,61604,80508,-18720;65623,70287,2847,-41486,91162,86895;34986,60232,-12659,81405,13309,98298;-17672,23324,30069,-33435,94752,30341;7368,-35505,-6168,12874,-68209,99777;-27212,-39546,-54472,-95426,-71145,-68458"}, {"input": "-64840,-80488,75990,75535,40626,72263,-4401;87726,13397,-37755,-17178,-65549,-97574,-99797;20114,14247,-80823,-18038,-89112,-24198,-59672;-85652,-17584,59151,47423,72891,1033,31327;-6022,75019,70952,10107,56145,16756,20738;-79725,-19766,-50233,79788,-43437,81595,10744;-93715,32431,-88982,95339,55414,-90054,-71347", "output": "81595,-80488,-89112,-65549,-97574,-99797,-4401;87726,56145,-37755,-17178,-24198,-59672,72263;79788,59151,47423,-18038,1033,31327,40626;95339,70952,14247,13397,10744,20738,75535;-6022,75019,55414,10107,-64840,16756,75990;32431,-19766,-50233,20114,-43437,-71347,72891;-93715,-79725,-88982,-85652,-17584,-90054,-80823"}, {"input": "-79384", "output": "-79384"}, {"input": "97737,9470,92081,-74822,-86879;92067,-43233,57259,-60994,27295;34596,37480,31291,46084,-74268;41019,55686,-45704,-89970,-26326;2429,72082,-69964,1154,-36280", "output": "97737,-26326,-74268,-74822,-86879;92067,31291,9470,-60994,27295;55686,37480,-36280,46084,92081;72082,34596,1154,-43233,57259;2429,41019,-69964,-45704,-89970"}, {"input": "37102,-70147,6858,33236,24028,85524,40419,92376,-7643;-76776,38265,79582,-7406,10222,56207,-88008,-8114,64550;-90777,73234,54982,89,-12426,4925,98900,45962,40588;98879,-57976,-335,25470,-53838,37364,-91016,-96847,25610;-59084,87311,27998,-58951,-99535,89792,67331,45221,-70572;76483,75312,-23878,17290,-59542,65746,-49366,20088,-44746;-7803,10093,-25888,-95349,22187,35204,-41470,90618,89904;86625,-92456,39845,-41819,-86968,4947,58245,16246,36427;99291,56870,53089,64838,49341,-2685,-72937,68176,-33074", "output": "65746,-70147,-12426,-91016,-96847,-88008,-8114,64550,-7643;73234,54982,-53838,-7406,-44746,-70572,25610,40419,92376;27998,68176,38265,-49366,6858,4925,24028,45962,40588;98879,22187,58245,37102,89,20088,10222,56207,85524;75312,87311,17290,35204,25470,36427,37364,33236,98900;76483,49341,-2685,4947,-335,16246,79582,67331,45221;53089,64838,-25888,-23878,-57976,-58951,-33074,89792,89904;86625,-7803,39845,-41819,-86968,-72937,-59542,-41470,90618;99291,56870,-92456,10093,-59084,-95349,-90777,-76776,-99535"}, {"input": "-25537,59269,43818,-46413,7913,20966;-79178,-31787,1588,26040,-30942,47927;-90742,13975,-669,38111,35030,89587;9538,17818,-2332,-82076,47111,-11494;99979,28823,-73530,-77980,11407,-20224;-7117,13012,-88090,-7963,75331,59283", "output": "59283,-20224,-11494,-46413,7913,20966;75331,11407,1588,26040,-30942,47927;17818,13975,-669,38111,35030,89587;28823,-7963,-2332,-25537,47111,43818;99979,9538,-73530,-77980,-31787,59269;-7117,13012,-88090,-90742,-79178,-82076"}, {"input": "5426,-45677,-20395,-34741,96737,-76564;32063,-87204,64054,71919,15053,-45079;54290,-61583,-95739,88680,-91514,-64689;-8384,38741,-9272,12334,-13158,98815;-43921,-37027,23135,84419,24994,26382;-36574,-95170,77473,-47555,-73938,-772", "output": "24994,-45677,-91514,-64689,-45079,-76564;84419,12334,-13158,-20395,-34741,96737;54290,32063,5426,26382,71919,15053;77473,38741,-9272,-772,64054,98815;-43921,-8384,23135,-61583,-87204,88680;-36574,-95170,-37027,-47555,-73938,-95739"}, {"input": "80227,46069,26099,-71619,55163,-57825,8968,-71759;-2699,-25769,43525,25956,76500,-59709,-96693,-72870;-62363,-31156,74269,-84907,-63695,-1710,-23960,-11654;-15787,-93768,72539,-84848,-10321,-22462,54626,-91782;32980,95133,88723,-90438,74537,47740,53655,44326;-45270,48905,30016,5240,65438,20126,-37898,36427;33693,25386,-64584,-18774,-1039,-74469,2689,-43756;-96543,-46996,-26050,-34797,37927,-42392,75964,-84419", "output": "80227,-84907,-63695,-71619,-91782,-96693,-72870,-71759;75964,74537,-43756,-22462,-1710,-59709,-57825,8968;88723,72539,74269,-37898,25956,44326,-23960,-11654;95133,5240,65438,20126,-10321,26099,54626,55163;48905,37927,-1039,-2699,2689,43525,36427,76500;25386,32980,30016,-42392,-31156,-25769,46069,53655;33693,-26050,-34797,-15787,-62363,-74469,-84419,47740;-96543,-46996,-45270,-64584,-18774,-93768,-90438,-84848"}, {"input": "-92160", "output": "-92160"}, {"input": "-79168,-23704,-41437,-17983,-58742,61241,-19466,62125,-40749,-95345;28901,81309,87136,-27130,-72120,14735,48934,48476,68773,8206;-17663,-28836,8347,97812,1577,-59996,34213,62318,30162,81714;-48974,-5831,-73845,36804,58763,-1017,-58906,-61918,-11704,-59315;18578,-14199,65632,5963,-85403,-98905,-56502,-66605,-34514,-90208;-66016,-41161,-24773,-89789,-2409,202,94919,22709,18386,-73240;-51647,-5779,-79340,72830,-3279,35962,47813,93089,-88603,-31215;-73186,35419,64897,-56484,32865,-96862,-11707,-81795,8217,5525;13077,-88612,86027,42151,-69917,-52895,-42982,51811,-66685,27872;38203,45050,-22953,-27803,27379,66431,61011,-91181,53014,45981", "output": "81309,-98905,-88603,-72120,-73240,-90208,-59315,62125,-40749,-95345;53014,47813,-23704,-56502,-66605,-61918,-11704,-19466,68773,8206;65632,51811,45981,8217,-41437,-59996,-58742,48934,30162,81714;72830,-3279,35962,36804,27872,-27130,-58906,-34514,61241,48476;66431,61011,-5831,28901,8347,58763,-1017,-31215,14735,62318;64897,18578,32865,-17663,5963,202,87136,1577,-17983,34213;86027,42151,-41161,-14199,-42982,-2409,-66685,93089,5525,18386;-22953,35419,27379,-56484,-24773,-89789,-11707,-79168,94919,22709;45050,-73186,-27803,-5779,-69917,-48974,-91181,-28836,-81795,97812;38203,13077,-88612,-51647,-66016,-79340,-52895,-96862,-73845,-85403"}, {"input": "-49223,9126,-78269,-14441,-63160,24160,2474;60300,-15339,44613,-26116,-20637,-20589,-59291;-96117,-62056,-58039,-31968,81948,45574,-60895;-34186,40690,42663,2992,-49828,89841,-81520;-35954,20976,-38474,21116,-79865,-21304,-3796;-89108,-40661,-80687,-71197,39726,-91726,82308;-60024,-318,78006,-216,65491,53920,-68076", "output": "2992,-49828,-78269,-81520,-63160,-59291,2474;60300,-15339,-31968,-26116,-20637,-60895,24160;65491,53920,-49223,-21304,-3796,-14441,-20589;20976,40690,42663,-58039,9126,81948,45574;78006,-216,-38474,39726,-68076,44613,89841;-318,-35954,-34186,-71197,21116,-79865,82308;-60024,-89108,-40661,-80687,-96117,-62056,-91726"}, {"input": "-68144,58409,99814,-34848,75514;50405,7155,-98322,462,-77648;-93576,-30875,19065,-75748,31428;48861,95128,-67458,-73279,52085;61385,-67181,92318,-17339,-814", "output": "19065,-98322,462,-77648,75514;50405,7155,-75748,31428,-34848;95128,-17339,-814,52085,99814;48861,92318,-30875,-68144,58409;61385,-67181,-93576,-67458,-73279"}, {"input": "-62510,-20368,90390,27454,7271,46852,44758,75395,-44578,-24119;-83383,-88134,-42212,-31362,-79424,-26363,-75559,-48095,98080,-81713;35179,-72831,-70938,47420,66065,-72851,-18198,-97456,-10398,-77476;82821,84515,-39326,-58956,-17461,66771,-69633,16636,53943,75247;-99417,-18810,-18259,18079,-89894,31682,-5325,8546,-99643,50083;95255,-27940,-87479,1290,18812,-73763,-22429,73167,31944,20264;38036,-44248,-81858,-94291,-48114,-72589,-31142,-7283,99996,2164;-28759,-17503,24204,-67195,-60032,19989,-13985,73380,23835,57192;-29538,-85674,19273,90223,-29817,-92838,-41678,-43693,17894,-30395;-32296,62067,64465,52207,60808,37694,17906,-99028,58405,-39794", "output": "73380,-42212,-31362,-79424,-99643,-97456,-48095,-77476,-81713,-24119;58405,17894,-30395,-5325,-72851,-26363,-75559,-10398,75395,-44578;84515,18812,-31142,-22429,57192,-69633,-18198,46852,44758,98080;82821,35179,18079,-39794,-20368,66065,2164,7271,50083,75247;37694,17906,19989,-13985,-58956,-17461,66771,8546,16636,53943;95255,-27940,-18810,1290,-39326,-62510,-7283,73167,27454,20264;52207,90223,-29817,-60032,-18259,-43693,-70938,23835,90390,31944;64465,38036,60808,-67195,-87479,-41678,-72589,-73763,31682,99996;62067,-28759,19273,24204,-81858,-92838,-48114,-72831,-88134,47420;-32296,-29538,-85674,-17503,-44248,-99417,-94291,-99028,-83383,-89894"}, {"input": "59503,-72071,85602,-40033;3070,96029,61184,-24259;-76680,-51288,65170,6042;-21237,-81439,-98871,1006", "output": "96029,-72071,-24259,-40033;3070,65170,6042,85602;-76680,-51288,59503,61184;-21237,-81439,-98871,1006"}, {"input": "-41242", "output": "-41242"}, {"input": "11837,98987,18206;-8095,-38726,-82865;84240,69319,45888", "output": "45888,-82865,18206;69319,11837,98987;84240,-8095,-38726"}, {"input": "-8858", "output": "-8858"}, {"input": "3960,-36710,-77040,79685,-90509,-78711,-92985,39936;57957,6442,68822,-12893,-22583,6693,-75196,-56552;-15559,-40793,3852,-90183,1842,-24340,-94412,-83896;-26365,15556,-23823,36591,4859,21603,57141,-21275;47175,-760,66612,66762,53060,36006,54911,-28796;33369,-33855,35466,-81824,22499,-96824,70296,-35393;6243,-72076,-93354,-85961,19536,22823,-98971,97523;-81174,16527,27477,-41825,71400,25952,-17897,50502", "output": "53060,-90183,-77040,-28796,-94412,-83896,-92985,39936;66762,50502,-36710,-35393,-24340,-90509,-78711,-56552;66612,57957,36591,4859,-12893,-22583,-21275,-75196;71400,25952,22823,6442,36006,1842,57141,6693;47175,35466,19536,22499,3960,68822,21603,79685;33369,-33855,-760,15556,-17897,3852,70296,54911;16527,27477,-41825,-26365,-15559,-23823,-96824,97523;-81174,6243,-72076,-93354,-85961,-81824,-40793,-98971"}, {"input": "56111,-48287,-47050,-90308,16431;38360,-72931,-70995,-80632,15959;-72051,50401,84414,98938,10919;-86350,-90429,-27116,61503,-93807;-55378,-75667,-29733,-24866,-23002", "output": "84414,-93807,-80632,-90308,16431;50401,61503,-70995,-47050,15959;-29733,38360,56111,-48287,10919;-75667,-72051,-24866,-23002,98938;-55378,-86350,-90429,-27116,-72931"}, {"input": "-6501,-12395;55167,10853", "output": "10853,-12395;55167,-6501"}, {"input": "-26779,-40376,-39088,-38844,74478,73533,36048,-20561;73956,48018,91472,6733,83849,-10231,-1952,-57596;-40019,48779,-71454,25840,78180,-93050,-44658,90550;-38623,-5578,-36089,-99670,98477,-85477,-18443,61792;82119,53528,52989,-52785,853,64235,5963,-8779;-43786,88570,1165,88123,-70727,93907,60805,25205;69763,19632,-38303,-72799,19126,-43258,48878,-20456;12085,82051,-59428,-28423,32793,29842,88129,89470", "output": "93907,-40376,-85477,-93050,-44658,-1952,-57596,-20561;88129,89470,-20456,-39088,-38844,-10231,73533,36048;88123,73956,48878,25840,5963,-18443,61792,90550;53528,52989,48779,48018,60805,6733,-8779,74478;88570,32793,29842,-36089,853,64235,25205,83849;19632,82119,1165,19126,-43258,-26779,91472,78180;82051,-43786,-28423,-38623,-5578,-52785,-71454,98477;12085,69763,-59428,-38303,-72799,-40019,-70727,-99670"}, {"input": "-48600,95624,46841;-8513,37901,-1404;-13606,73343,-36142", "output": "37901,-1404,46841;73343,-36142,95624;-13606,-8513,-48600"}, {"input": "-59779,25609,72714,1717,45072,18812,74006,-75755,-31640,83840;-79490,-36712,-28309,51127,-47373,-67398,26249,59634,2371,15426;-91251,12832,-98463,-4242,-4623,46594,68056,-73454,25223,-39971;-16264,21243,59259,-67155,-68952,87983,-68167,1864,-64284,-11133;-93579,3075,82841,53995,46090,60525,-50723,-2747,96638,-31064;3060,-20765,5026,-45310,55328,40277,81917,56229,17403,-95917;-73360,-22414,73702,64729,69315,-14107,-5466,27401,-98715,-39504;57102,88048,-37784,-34324,73385,-65314,24632,82350,-74033,89870;41821,3578,4210,95916,52880,-60439,-5074,-15550,-66933,58423;69986,-85645,-13685,-93747,62827,-54483,2086,-85951,-98142,-87441", "output": "82350,-74033,-98715,-68167,-95917,-73454,-11133,-75755,-31640,83840;59259,46090,-68952,-50723,-47373,-67398,-64284,25223,-39971,15426;82841,55328,40277,-28309,-4623,-39504,1864,-31064,59634,2371;73385,69315,53995,-5466,-4242,51127,-2747,45072,18812,74006;73702,64729,21243,24632,-36712,25609,56229,1717,68056,26249;95916,52880,5026,-5074,12832,-59779,27401,72714,17403,96638;88048,62827,-20765,3075,-45310,-14107,-66933,58423,87983,46594;57102,4210,3060,-34324,2086,-65314,-15550,-67155,60525,89870;41821,3578,-73360,-22414,-54483,-16264,-85951,-79490,-87441,81917;69986,-85645,-13685,-93747,-37784,-93579,-60439,-91251,-98142,-98463"}, {"input": "-70880,74908;96567,-85482", "output": "-70880,74908;96567,-85482"}, {"input": "-14357,11183;-80654,8862", "output": "8862,11183;-80654,-14357"}, {"input": "53464,20500;-49531,47285", "output": "53464,20500;-49531,47285"}, {"input": "-33841,95817,63443,64311,34812;-78531,-63480,-77005,-39448,-99684;-87712,76314,93951,45762,34216;-63318,71743,-49350,39160,-20583;74590,-1574,50198,63707,-86570", "output": "93951,-77005,-39448,-99684,34812;76314,39160,-20583,34216,64311;71743,63707,-33841,45762,63443;-1574,50198,-49350,-63480,95817;74590,-63318,-87712,-78531,-86570"}, {"input": "6136,25323,-66484,-48452,76646,-42840,-80713,-83915,-30874;74407,-31214,38733,-67267,29444,77279,22212,64651,-35772;64660,8184,-4894,-16898,89959,9835,-81596,58835,-63693;-66854,-81173,39016,43379,-64293,-63377,-94498,7652,-44079;96779,-78607,37958,90640,4237,-24653,-68133,26010,769;-83451,67267,65070,64463,88162,-41452,-92384,-59226,-50302;8386,-31372,-69495,80952,64571,14389,59265,-37417,11033;32839,-50383,-16936,64017,59773,54941,-82668,8482,21226;13913,-28195,-96081,-36085,-61376,-40932,51363,74699,-82248", "output": "59265,-92384,-68133,-94498,-81596,-44079,-80713,-83915,-30874;90640,43379,-64293,-67267,-50302,769,-42840,-63693,-35772;64660,88162,8482,-37417,-66484,-48452,7652,22212,64651;80952,64571,74699,6136,-24653,-63377,9835,76646,58835;96779,65070,64463,74407,4237,-16898,-59226,26010,77279;-16936,67267,59773,54941,39016,-4894,21226,11033,29444;8386,-31372,64017,-40932,51363,14389,-31214,25323,89959;32839,-50383,-36085,-61376,-66854,37958,8184,-41452,38733;13913,-28195,-96081,-83451,-69495,-78607,-81173,-82668,-82248"}, {"input": "92458,-40201,72645,-52897,-10009,-63323,39895,-60893,66478,5465;19069,-73341,-54176,-246,57942,-36981,20873,52875,-31833,58600;63739,48811,-15884,-56638,-51111,-17944,-51501,61192,8651,99651;-32561,-32331,-21021,79252,36376,-27014,99261,-34907,95819,65096;12513,84411,91272,42115,14034,32984,-70387,-69553,-80501,-18969;-41657,-42123,-87855,11695,-32497,-93628,58597,85475,36246,-93572;-15990,47306,30988,25541,-77673,-12459,-16832,84151,-8848,55669;76898,72995,81993,-85376,67852,1883,83133,-56249,26217,39105;25543,59842,-86335,-54982,-6591,51290,-74319,80380,-60169,-95856;86971,91295,-30153,2281,-38297,22673,-55882,-69532,8122,-53187", "output": "92458,-95856,-70387,-69553,-93572,-63323,8651,-60893,58600,5465;83133,79252,-56638,-51111,-52897,-80501,-18969,39895,-31833,66478;91272,80380,14034,-54176,-27014,-17944,-51501,20873,52875,99651;84411,63739,48811,-15884,-40201,-8848,36246,-36981,61192,65096;30988,67852,11695,42115,-16832,26217,-246,55669,-34907,95819;81993,22673,51290,1883,19069,-53187,32984,39105,57942,-10009;72995,47306,12513,25541,-32331,8122,-56249,36376,72645,99261;76898,2281,-38297,-6591,-32561,-69532,-12459,-60169,58597,85475;91295,59842,-15990,-41657,-42123,-55882,-74319,-21021,-73341,84151;86971,25543,-30153,-86335,-54982,-85376,-87855,-77673,-32497,-93628"}]
|
{
"cpp": "==Code Submission==\n \n\nvector<vector<int>> deserialize_stdin(const string &input) {\n vector<vector<int>> grid;\n size_t start = 0;\n while (start < input.size()) {\n size_t end = input.find(';', start);\n string rowStr;\n if (end == string::npos) {\n rowStr = input.substr(start);\n start = input.size();\n } else {\n rowStr = input.substr(start, end - start);\n start = end + 1;\n }\n if (rowStr.empty()) continue;\n vector<int> row;\n stringstream ss(rowStr);\n string token;\n while (getline(ss, token, ',')) {\n if (!token.empty())\n row.push_back(stoi(token));\n }\n grid.push_back(row);\n }\n return grid;\n}\n\nstring serialize_stdout(const vector<vector<int>> &grid) {\n string output;\n for (size_t i = 0; i < grid.size(); i++) {\n for (size_t j = 0; j < grid[i].size(); j++) {\n output += to_string(grid[i][j]);\n if (j < grid[i].size() - 1)\n output += \",\";\n }\n if (i < grid.size() - 1)\n output += \";\";\n }\n return output;\n}\n\nint main(){\n string input;\n getline(cin, input);\n vector<vector<int>> grid = deserialize_stdin(input);\n Solution sol;\n vector<vector<int>> res = sol.sortMatrix(grid);\n cout << serialize_stdout(res);\n return 0;\n}",
"golang": "==Code Submission==\n\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n input, _ := reader.ReadString('\\n')\n input = strings.TrimSpace(input)\n rowStrs := strings.Split(input, \";\")\n var grid [][]int\n for _, row := range rowStrs {\n if len(row) == 0 {\n continue\n }\n numStrs := strings.Split(row, \",\")\n var nums []int\n for _, ns := range numStrs {\n n, _ := strconv.Atoi(ns)\n nums = append(nums, n)\n }\n grid = append(grid, nums)\n }\n res := sortMatrix(grid)\n var out string\n for i, row := range res {\n for j, num := range row {\n out += strconv.Itoa(num)\n if j < len(row)-1 {\n out += \",\"\n }\n }\n if i < len(res)-1 {\n out += \";\"\n }\n }\n fmt.Print(out)\n}",
"java": "public class Main {\n private static int[][] deserialize(String input) {\n String[] rowStrings = input.trim().split(\";\");\n int n = rowStrings.length;\n int[][] grid = new int[n][];\n for (int i = 0; i < n; i++) {\n String row = rowStrings[i].trim();\n if (row.isEmpty()) {\n grid[i] = new int[0];\n } else {\n String[] nums = row.split(\",\");\n grid[i] = new int[nums.length];\n for (int j = 0; j < nums.length; j++) {\n grid[i][j] = Integer.parseInt(nums[j].trim());\n }\n }\n }\n return grid;\n }\n \n private static String serialize(int[][] grid) {\n StringBuilder sb = new StringBuilder();\n for (int i = 0; i < grid.length; i++) {\n for (int j = 0; j < grid[i].length; j++) {\n sb.append(grid[i][j]);\n if (j < grid[i].length - 1) {\n sb.append(\",\");\n }\n }\n if (i < grid.length - 1) {\n sb.append(\";\");\n }\n }\n return sb.toString();\n }\n \n public static void main(String[] args) throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n String input = br.readLine().trim();\n int[][] grid = deserialize(input);\n Solution sol = new Solution();\n int[][] res = sol.sortMatrix(grid);\n System.out.println(serialize(res));\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\n\nconst deserialize_stdin = (input) => {\n const rows = input.trim().split(\";\");\n const grid = rows.map(row => row.split(\",\").map(Number));\n return grid;\n};\n\nconst serialize_stdout = (grid) => {\n return grid.map(row => row.join(\",\")).join(\";\");\n};\n\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\nlet input = \"\";\nprocess.stdin.on('data', chunk => input += chunk);\nprocess.stdin.on('end', () => {\n const grid = deserialize_stdin(input);\n const ans = sortMatrix(grid);\n console.log(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str):\n rows = input_str.strip().split(\";\")\n grid = []\n for row in rows:\n if row:\n grid.append(list(map(int, row.split(\",\"))))\n else:\n grid.append([])\n return grid\n\ndef serialize_stdout(grid):\n return \";\".join(\",\".join(str(x) for x in row) for row in grid)\n\ninput_str = sys.stdin.read().strip()\ngrid = deserialize_stdin(input_str)\nsol = Solution()\nans = sol.sortMatrix(grid)\nprint(serialize_stdout(ans))",
"ruby": "==Code Submission==\n\ninput = gets.strip\nrows = input.split(\";\")\ngrid = rows.map { |row| row.split(\",\").map(&:to_i) }\nresult = sort_matrix(grid)\noutput = result.map { |row| row.join(\",\") }.join(\";\")\nputs output"
}
|
3753
|
Maximum Difference Between Even and Odd Frequency I
|
maximum-difference-between-even-and-odd-frequency-i
|
<p>You are given a string <code>s</code> consisting of lowercase English letters. Your task is to find the <strong>maximum</strong> difference between the frequency of <strong>two</strong> characters in the string such that:</p>
<ul>
<li>One of the characters has an <strong>even frequency</strong> in the string.</li>
<li>The other character has an <strong>odd frequency</strong> in the string.</li>
</ul>
<p>Return the <strong>maximum</strong> difference, calculated as the frequency of the character with an <b>odd</b> frequency <strong>minus</strong> the frequency of the character with an <b>even</b> frequency.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">s = "aaaaabbc"</span></p>
<p><strong>Output:</strong> 3</p>
<p><strong>Explanation:</strong></p>
<ul>
<li>The character <code>'a'</code> has an <strong>odd frequency</strong> of <code><font face="monospace">5</font></code><font face="monospace">,</font> and <code>'b'</code> has an <strong>even frequency</strong> of <code><font face="monospace">2</font></code>.</li>
<li>The maximum difference is <code>5 - 2 = 3</code>.</li>
</ul>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">s = "abcabcab"</span></p>
<p><strong>Output:</strong> 1</p>
<p><strong>Explanation:</strong></p>
<ul>
<li>The character <code>'a'</code> has an <strong>odd frequency</strong> of <code><font face="monospace">3</font></code><font face="monospace">,</font> and <code>'c'</code> has an <strong>even frequency</strong> of <font face="monospace">2</font>.</li>
<li>The maximum difference is <code>3 - 2 = 1</code>.</li>
</ul>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>3 <= s.length <= 100</code></li>
<li><code>s</code> consists only of lowercase English letters.</li>
<li><code>s</code> contains at least one character with an odd frequency and one with an even frequency.</li>
</ul>
|
You are given a string `s` consisting of lowercase English letters. Your task is to find the **maximum** difference between the frequency of **two** characters in the string such that:
- One of the characters has an **even frequency** in the string.
- The other character has an **odd frequency** in the string.
Return the **maximum** difference, calculated as the frequency of the character with an **odd** frequency **minus** the frequency of the character with an **even** frequency.
**Example 1:**
**Input:** s \= "aaaaabbc"
**Output:** 3
**Explanation:**
- The character `'a'` has an **odd frequency** of `5`, and `'b'` has an **even frequency** of `2`.
- The maximum difference is `5 - 2 = 3`.
**Example 2:**
**Input:** s \= "abcabcab"
**Output:** 1
**Explanation:**
- The character `'a'` has an **odd frequency** of `3`, and `'c'` has an **even frequency** of 2.
- The maximum difference is `3 - 2 = 1`.
**Constraints:**
- `3 <= s.length <= 100`
- `s` consists only of lowercase English letters.
- `s` contains at least one character with an odd frequency and one with an even frequency.
|
Easy
|
[
"hash-table",
"string",
"counting"
] |
leetcode
|
https://leetcode.com/problems/maximum-difference-between-even-and-odd-frequency-i
|
functional
| null | null | null | null |
{
"c": "int maxDifference(char* s) {\n \n}",
"cpp": "class Solution {\npublic:\n int maxDifference(string s) {\n \n }\n};",
"csharp": "public class Solution {\n public int MaxDifference(string s) {\n \n }\n}",
"dart": "class Solution {\n int maxDifference(String s) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec max_difference(s :: String.t) :: integer\n def max_difference(s) do\n \n end\nend",
"erlang": "-spec max_difference(S :: unicode:unicode_binary()) -> integer().\nmax_difference(S) ->\n .",
"golang": "func maxDifference(s string) int {\n \n}",
"java": "class Solution {\n public int maxDifference(String s) {\n \n }\n}",
"javascript": "/**\n * @param {string} s\n * @return {number}\n */\nvar maxDifference = function(s) {\n \n};",
"kotlin": "class Solution {\n fun maxDifference(s: String): Int {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param String $s\n * @return Integer\n */\n function maxDifference($s) {\n \n }\n}",
"python": "class Solution(object):\n def maxDifference(self, s):\n \"\"\"\n :type s: str\n :rtype: int\n \"\"\"\n ",
"python3": "class Solution:\n def maxDifference(self, s: str) -> int:\n ",
"racket": "(define/contract (max-difference s)\n (-> string? exact-integer?)\n )",
"ruby": "# @param {String} s\n# @return {Integer}\ndef max_difference(s)\n \nend",
"rust": "impl Solution {\n pub fn max_difference(s: String) -> i32 {\n \n }\n}",
"scala": "object Solution {\n def maxDifference(s: String): Int = {\n \n }\n}",
"swift": "class Solution {\n func maxDifference(_ s: String) -> Int {\n \n }\n}",
"typescript": "function maxDifference(s: string): number {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n int maxDifference(string s) {\n vector<int> freq(26, 0);\n for (char c : s) {\n freq[c - 'a']++;\n }\n \n vector<int> evens, odds;\n for (int i = 0; i < 26; ++i) {\n if (freq[i] == 0) continue;\n if (freq[i] % 2 == 0) {\n evens.push_back(freq[i]);\n } else {\n odds.push_back(freq[i]);\n }\n }\n \n int max_odd = *max_element(odds.begin(), odds.end());\n int min_even = *min_element(evens.begin(), evens.end());\n \n return max_odd - min_even;\n }\n};",
"memory": 1000,
"memoryDistribution": "[[1000, 59.3966, \"#include <vector>\\n#include <algorithm>\\n\\nusing namespace std;\\n\\nclass Solution {\\npublic:\\n int maxDifference(string s) {\\n vector<int> freq(26, 0);\\n for (char c : s) {\\n freq[c - 'a']++;\\n }\\n \\n vector<int> evens, odds;\\n for (int i = 0; i < 26; ++i) {\\n if (freq[i] == 0) continue;\\n if (freq[i] % 2 == 0) {\\n evens.push_back(freq[i]);\\n } else {\\n odds.push_back(freq[i]);\\n }\\n }\\n \\n int max_odd = *max_element(odds.begin(), odds.end());\\n int min_even = *min_element(evens.begin(), evens.end());\\n \\n return max_odd - min_even;\\n }\\n};\"], [8900, 0.5487, \"class Solution {\\npublic:\\n int maxDifference(string&s) {\\n sort(s.begin(), s.end());\\n\\n int odd = INT_MIN, even = INT_MAX;\\n int i = 1, curr = 1;\\n for(; i < s.size(); ++i) {\\n if(s[i] == s[i-1]) ++curr;\\n else {\\n if (curr % 2 == 0) even = min(even, curr);\\n else odd = max(odd, curr);\\n curr = 1;\\n }\\n }\\n if (curr % 2 == 0) even = min(even, curr);\\n else odd = max(odd, curr);\\n \\n return odd - even; \\n }\\n};\"], [9000, 1.5089, \"class Solution {\\npublic:\\n int maxDifference(string s) {\\n vector <int> freq (26, 0);\\n int maxOdd = -1, minEven = s.length();\\n long int tmpFreq;\\n for(auto x: s) {\\n freq[x-'a']++;\\n }\\n for (auto tmpFreq : freq ) {\\n if (tmpFreq == 0)\\n continue;\\n if( tmpFreq % 2 == 0 ) {\\n minEven = min(minEven, tmpFreq);\\n }\\n else{\\n maxOdd = max(maxOdd, tmpFreq); \\n }\\n }\\n return maxOdd - minEven;\\n }\\n\\n};\"], [9100, 4.1152, null], [9200, 9.3278, null], [9300, 14.2661, null], [9400, 8.3676, null], [9500, 1.6461, null], [9600, 0.823, null], [9700, 6.7215, null], [9800, 12.4829, null], [9900, 15.2263, null], [10000, 9.6022, null], [10100, 5.3498, \"class Solution {\\npublic:\\n int maxDifference(string s) {\\n unordered_map<char, int> map;\\n for (const auto& ch: s) ++map[ch];\\n\\n int odd{}, even{INT_MAX};\\n\\n for (const auto& [ch, freq]: map) {\\n if (freq & 1) odd = std::max(odd, freq);\\n else even = std::min(even, freq);\\n }\\n return odd - even;\\n }\\n};\"], [10200, 3.155, \"class Solution {\\npublic:\\n int maxDifference(string s) {\\n unordered_map<char, int>freq;\\n for(char ch:s)freq[ch]++;\\n vector<int>temp;\\n for(auto &[_,value]:freq){\\n temp.push_back(value);\\n }\\n sort(temp.begin(),temp.end(),greater<int>());\\n int odd=0,even=0;\\n for(int i:temp){\\n if((i & 1)){\\n odd=i;\\n break;\\n }\\n }\\n for(int i=temp.size()-1;i>=0;--i){\\n if(!(temp[i] & 1)){\\n even=temp[i];\\n break;\\n }\\n }\\n return odd-even;\\n }\\n};\"]]",
"runtime": 3,
"runtimeDistribution": "[[0, 47.3251, \"class Solution {\\npublic:\\n int maxDifference(string s) {\\n vector<char> freq(26,0);\\n for(int i=0;i<s.size();i++)\\n freq[s[i]-'a']++;\\n sort(freq.begin(),freq.end());\\n int oddFreq = 1,evenFreq = 1;\\n for(int i=25;i>=0;i--)\\n if(freq[i]!=0 && freq[i]%2==0)\\n evenFreq = freq[i];\\n for(int i=0;i<26;i++)\\n if(freq[i]%2==1)\\n oddFreq = freq[i];\\n return oddFreq - evenFreq;\\n }\\n};\"], [1, 6.7215, \"class Solution {\\npublic:\\n int maxDifference(string s) {\\n unordered_map<int,int>mp;\\n for(auto it:s)mp[it]++;\\n int mx_even=0;\\n int mx_odd=0;\\n int mn_even=INT_MAX;\\n int mn_odd=INT_MAX;\\n\\n for(auto it:mp){\\n if(it.second%2==0){\\n mx_even=max(mx_even,it.second);\\n mn_even=min(mn_even,it.second);\\n }\\n else{\\n mx_odd=max(mx_odd,it.second);\\n mn_odd=min(mn_odd,it.second);\\n }\\n }\\n return max(mn_odd-mx_even,-mn_even+mx_odd);\\n }\\n};\"], [2, 8.9163, null], [3, 15.9122, null], [4, 8.0933, null], [5, 2.332, \"class Solution {\\npublic:\\n int maxDifference(string s) {\\n // iterate over the string and sum the differences\\n // once we have the frequencis we will get the max/second max size of even odd\\n map<int, int> frequencies{};\\n for (const char c : s) {\\n frequencies[c - 'a']++;\\n }\\n int maxOdd = 0, minOdd = 999;\\n int maxEven = 0, minEven = 999;\\n for (const auto& item : frequencies) {\\n if (item.second & 1) {\\n maxOdd = max(item.second, maxOdd);\\n minOdd = min(item.second, minOdd);\\n } else {\\n maxEven = max(item.second, maxEven);\\n minEven = min(item.second, minEven);\\n }\\n }\\n return max(minOdd - maxEven, maxOdd - minEven);\\n }\\n};\"], [6, 2.8807, \"class Solution {\\npublic:\\n int maxDifference(string s) {\\n map<char,int>mp;\\n int ma=INT_MAX;\\n int mi=INT_MIN;\\n for(auto x:s){\\n mp[x]++;\\n }\\n for(auto x:mp){\\n if(x.second%2!=0 and x.second>mi){\\n mi=x.second;\\n }\\n else if(x.second%2==0 and x.second<ma){\\n ma=x.second;\\n }\\n } \\n return mi-ma;\\n }\\n};\"]]"
},
"golang": {
"code": "func maxDifference(s string) int {\n freq := make(map[rune]int)\n for _, c := range s {\n freq[c]++\n }\n var evens, odds []int\n for _, v := range freq {\n if v%2 == 0 {\n evens = append(evens, v)\n } else {\n odds = append(odds, v)\n }\n }\n maxOdd := 0\n for _, o := range odds {\n if o > maxOdd {\n maxOdd = o\n }\n }\n minEven := int(^uint(0) >> 1)\n for _, e := range evens {\n if e < minEven {\n minEven = e\n }\n }\n return maxOdd - minEven\n}",
"memory": 500,
"memoryDistribution": "[[500, 10.2565, \"func maxDifference(s string) int {\\n freq := make(map[rune]int)\\n for _, c := range s {\\n freq[c]++\\n }\\n var evens, odds []int\\n for _, v := range freq {\\n if v%2 == 0 {\\n evens = append(evens, v)\\n } else {\\n odds = append(odds, v)\\n }\\n }\\n maxOdd := 0\\n for _, o := range odds {\\n if o > maxOdd {\\n maxOdd = o\\n }\\n }\\n minEven := int(^uint(0) >> 1)\\n for _, e := range evens {\\n if e < minEven {\\n minEven = e\\n }\\n }\\n return maxOdd - minEven\\n}\"], [4100, 12.8205, \"func maxDifference(s string) int {\\n var freq [26]int\\n for _, c := range s {\\n freq[c-'a']++\\n }\\n oddMax := math.MinInt\\n evenMin := math.MaxInt\\n for _, f := range freq {\\n if f == 0 {\\n continue\\n }\\n if f%2 == 0 {\\n evenMin = min(evenMin, f)\\n } else {\\n oddMax = max(oddMax, f)\\n }\\n }\\n return oddMax-evenMin\\n}\\n\"], [4200, 7.6923, \"func maxDifference(s string) int {\\n var freq [26]int\\n for _, c := range s {\\n freq[c-'a']++\\n }\\n oddMax, oddMin := math.MinInt, math.MaxInt\\n evenMax, evenMin := math.MinInt, math.MaxInt\\n for _, f := range freq {\\n if f == 0 {\\n continue\\n }\\n if f%2 == 0 {\\n evenMax = max(evenMax, f)\\n evenMin = min(evenMin, f)\\n } else {\\n oddMax = max(oddMax, f)\\n oddMin = min(oddMin, f)\\n }\\n }\\n return max(oddMax-evenMin, oddMax-evenMax, oddMin-evenMin, oddMax-evenMin)\\n}\\n\"], [4300, 17.9487, null], [4400, 28.2051, null], [4500, 15.3846, null], [4600, 7.6923, null], [4700, 2.5641, \"\\nfunc maxDifference(s string) int {\\n\\t// initialize maxDiff as negative infinity lol\\n\\tmaxDiff := math.Inf(-1)\\n\\tfreqs := make(map[rune]int)\\n\\tgroupMap := map[string][]int{\\n\\t\\t\\\"even\\\": {},\\n\\t\\t\\\"odd\\\": {},\\n\\t}\\n\\n\\tfor _, char := range s {\\n\\t\\t_, exists := freqs[char]\\n\\t\\tif !exists {\\n\\t\\t\\tfreqs[char] = 0\\n\\t\\t}\\n\\t\\tfreqs[char]++\\n\\t}\\n\\n\\tfor _, freq := range freqs {\\n\\t\\tif freq%2 == 0 {\\n\\t\\t\\tgroupMap[\\\"even\\\"] = append(groupMap[\\\"even\\\"], freq)\\n\\t\\t} else {\\n\\t\\t\\tgroupMap[\\\"odd\\\"] = append(groupMap[\\\"odd\\\"], freq)\\n\\t\\t}\\n\\t}\\n\\n\\tfor _, even := range groupMap[\\\"even\\\"] {\\n\\t\\tfor _, odd := range groupMap[\\\"odd\\\"] {\\n\\t\\t\\tdiff := odd - even\\n\\t\\t\\tmaxDiff = math.Max(float64(diff), maxDiff)\\n\\t\\t}\\n\\t}\\n\\n\\treturn int(maxDiff)\\n}\"], [4900, 2.5641, \"func maxDifference(s string) int {\\n f := map[string]int{}\\n for i:=0; i<len(s); i++ {\\n str := string(s[i])\\n if _, ok := f[str]; !ok {\\n i:=1\\n f[str] = i\\n } else {\\n f[str]++\\n }\\n }\\n // fmt.Println(f)\\n evenF := make([]int, 0)\\n oddF := make([]int, 0)\\n for i:=range f{\\n v := f[i]\\n if v%2 ==0 {\\n evenF = append(evenF, v)\\n } else {\\n oddF = append(oddF, v)\\n }\\n }\\n sort.Ints(evenF)\\n sort.Sort(sort.Reverse(sort.IntSlice(oddF)))\\n // fmt.Println(oddF[0], evenF[0])\\n d := oddF[0]-evenF[0]\\n return d\\n}\"]]",
"runtime": null,
"runtimeDistribution": "[[0, 64.1026, \"func maxDifference(s string) int {\\n var freq [26]int\\n for _, c := range s {\\n freq[c-'a']++\\n }\\n oddMax, oddMin := math.MinInt, math.MaxInt\\n evenMax, evenMin := math.MinInt, math.MaxInt\\n for _, f := range freq {\\n if f == 0 {\\n continue\\n }\\n if f%2 == 0 {\\n evenMax = max(evenMax, f)\\n evenMin = min(evenMin, f)\\n } else {\\n oddMax = max(oddMax, f)\\n oddMin = min(oddMin, f)\\n }\\n }\\n return max(oddMax-evenMin, oddMax-evenMax, oddMin-evenMin, oddMax-evenMin)\\n}\\n\"], [1, 12.8205, \"func maxDifference(s string) int {\\n countMap := map[rune]int{}\\n for _, ch := range s {\\n countMap[ch]++ \\n }\\n\\n maxOdd, minEven := 0, 0\\n for _, count := range countMap {\\n if count % 2 == 0 {\\n if minEven == 0 {\\n minEven = count\\n } else if count <= minEven {\\n minEven = count\\n }\\n } else if count % 2 != 0 {\\n if maxOdd == 0 {\\n maxOdd = count\\n } else if maxOdd <= count {\\n maxOdd = count\\n }\\n }\\n }\\n return maxOdd - minEven\\n}\\n\"], [2, 12.8205, null], [3, 7.6923, \"func maxDifference(s string) int {\\n countOfLet := make(map[byte]int)\\n\\n for i := 0; i < len(s); i++ {\\n countOfLet[s[i]]++\\n }\\n\\n maxOdd := -1\\n minEven := 101\\n\\n for _, v := range countOfLet {\\n if v % 2 == 0 {\\n if v < minEven {\\n minEven = v\\n }\\n } else {\\n if v > maxOdd {\\n maxOdd = v\\n }\\n }\\n }\\n return maxOdd - minEven\\n}\"], [4, 2.5641, \"import (\\n \\\"math\\\"\\n)\\n\\nfunc maxDifference(s string) int {\\n if len(s) == 0 || len(s) == 1 || len(s) == 2 {\\n return 0\\n }\\n\\n var hash = make(map[string]int)\\n for _, value := range s {\\n hash[string(value)]++\\n }\\n\\n var (\\n maxOddFrequency = math.MinInt\\n minEvenFrequency = math.MaxInt\\n )\\n\\n for _, value := range hash {\\n if value % 2 == 0 {\\n if value < minEvenFrequency {\\n minEvenFrequency = value\\n }\\n }\\n\\n if value % 2 != 0 {\\n if value > maxOddFrequency {\\n maxOddFrequency = value\\n }\\n }\\n }\\n\\n return maxOddFrequency - minEvenFrequency\\n}\"]]"
},
"java": {
"code": "class Solution {\n public int maxDifference(String s) {\n int[] freq = new int[26];\n for (char c : s.toCharArray()) {\n freq[c - 'a']++;\n }\n java.util.List<Integer> even = new java.util.ArrayList<>();\n java.util.List<Integer> odd = new java.util.ArrayList<>();\n for (int count : freq) {\n if (count > 0) {\n if (count % 2 == 0) {\n even.add(count);\n } else {\n odd.add(count);\n }\n }\n }\n int maxOdd = java.util.Collections.max(odd);\n int minEven = java.util.Collections.min(even);\n return maxOdd - minEven;\n }\n}",
"memory": 4300,
"memoryDistribution": "[[4300, 33.3819, \"class Solution {\\n public int maxDifference(String s) {\\n int[] freq = new int[26];\\n for (char c : s.toCharArray()) {\\n freq[c - 'a']++;\\n }\\n java.util.List<Integer> even = new java.util.ArrayList<>();\\n java.util.List<Integer> odd = new java.util.ArrayList<>();\\n for (int count : freq) {\\n if (count > 0) {\\n if (count % 2 == 0) {\\n even.add(count);\\n } else {\\n odd.add(count);\\n }\\n }\\n }\\n int maxOdd = java.util.Collections.max(odd);\\n int minEven = java.util.Collections.min(even);\\n return maxOdd - minEven;\\n }\\n}\"], [41900, 0.4373, \"class Solution {\\n public int maxDifference(String s) {\\n int ohf = Integer.MIN_VALUE, elf = Integer.MAX_VALUE;\\n int[] freq = new int[26];\\n \\n for(char ch : s.toCharArray()) {\\n int i = (int) (ch) - 97;\\n freq[i]++;\\n }\\n\\n for(int x : freq) {\\n if(x % 2 == 0 && x < elf && x != 0) elf = x;\\n else if(x % 2 != 0 && x > ohf) ohf = x;\\n }\\n\\n return ohf - elf;\\n }\\n}\"], [42000, 0.4373, \"class Solution {\\n public int maxDifference(String s) {\\n \\n Map<Character,Integer> map = new HashMap<>();\\n int even = Integer.MAX_VALUE;\\n int odd = Integer.MIN_VALUE;\\n for(int i=0,j=s.length();i<j;i++)\\n {\\n map.put(s.charAt(i), map.getOrDefault(s.charAt(i),0)+1);\\n }\\n\\n for(var value: map.entrySet())\\n {\\n if(value.getValue() % 2 == 0)\\n {\\n even = Math.min(even,value.getValue());\\n }else\\n {\\n odd = Math.max(odd,value.getValue());\\n }\\n }\\n\\n return odd-even;\\n }\\n}\"], [42100, 2.3324, null], [42200, 8.1633, null], [42300, 9.621, null], [42400, 8.7464, null], [42500, 12.828, null], [42600, 12.5364, null], [42700, 11.516, null], [42800, 10.2041, null], [42900, 8.309, null], [43000, 4.2274, null], [43100, 3.6443, \"class Solution {\\n public int maxDifference(String s) {\\n Map<Character,Integer> map = new HashMap<>();\\n for(int i =0;i<s.length();++i){\\n char c = s.charAt(i);\\n Integer count = map.get(c);\\n if(count==null){\\n map.put(c,1);\\n \\n }else{\\n map.put(c,count+1);\\n }\\n }\\n int min =Integer.MAX_VALUE;\\n int max = 0;\\n for(Character c: map.keySet()){\\n int count = map.get(c);\\n if(count %2 !=0){\\n max = Math.max(count,max);\\n }else{\\n min = Math.min(count,min);\\n }\\n }\\n return max-min;\\n }\\n\\n}\"], [43200, 1.895, \"class Solution {\\n public int maxDifference(String s) {\\n HashMap<Character,Integer> h1 = new HashMap<>();\\n int oddmax = Integer.MIN_VALUE;\\n int evenmin = Integer.MAX_VALUE;\\n for(char x: s.toCharArray()){\\n h1.put(x,h1.getOrDefault(x,0)+1);\\n }\\n for(char x: h1.keySet()){\\n if(h1.get(x)%2==0){\\n evenmin = Math.min(evenmin,h1.get(x));\\n }\\n else{\\n oddmax = Math.max(oddmax,h1.get(x));\\n }\\n }\\n \\n return oddmax-evenmin;\\n \\n }\\n}\"]]",
"runtime": 2,
"runtimeDistribution": "[[1, 44.6064, \"class Solution {\\n public int maxDifference(String s) {\\n int ohf = Integer.MIN_VALUE, elf = Integer.MAX_VALUE;\\n int[] freq = new int[26];\\n \\n for(char ch : s.toCharArray()) {\\n int i = (int) (ch) - 97;\\n freq[i]++;\\n }\\n\\n for(int x : freq) {\\n if(x % 2 == 0 && x < elf && x != 0) elf = x;\\n else if(x % 2 != 0 && x > ohf) ohf = x;\\n }\\n\\n return ohf - elf;\\n }\\n}\"], [2, 5.5394, \"class Solution {\\n public int maxDifference(String s) {\\n int[] freq=new int[26];\\n for(char c:s.toCharArray()){\\n freq[c-'a']++;\\n }\\n List<Integer> odd=new ArrayList<>();\\n List<Integer> even=new ArrayList<>();\\n\\n for(int f:freq){\\n if(f>0){\\n if(f%2!=0){\\n odd.add(f);\\n }\\n else{\\n even.add(f);\\n }\\n }\\n }\\n int max=Integer.MIN_VALUE;\\n for(int o:odd){\\n for(int e:even){\\n max=Math.max(max,o-e);\\n }\\n }\\n return max==Integer.MIN_VALUE ? 0:max;\\n\\n \\n }\\n}\"], [3, 24.7813, null], [4, 15.1603, \"class Solution {\\n public int maxDifference(String s) {\\n HashMap<Character,Integer> map = new HashMap<>();\\n ArrayList<Integer> even = new ArrayList<>();\\n ArrayList<Integer> odd = new ArrayList<>();\\n for(char ch : s.toCharArray())\\n {\\n map.put(ch,map.getOrDefault(ch,0)+1);\\n }\\n for(int i :map.values())\\n {\\n if(i % 2 ==0)\\n {\\n even.add(i);\\n }\\n else\\n {\\n odd.add(i);\\n }\\n }\\n Collections.sort(even);\\n Collections.sort(odd);\\n return odd.get(odd.size()-1) - even.get(0);\\n }\\n}\"], [5, 2.9155, \"class Solution {\\n public int maxDifference(String s) {\\n HashMap<Character, Integer> map = new HashMap<>();\\n\\n // Count frequencies\\n for (int i = 0; i < s.length(); i++) {\\n map.put(s.charAt(i), map.getOrDefault(s.charAt(i), 0) + 1);\\n }\\n\\n int max = Integer.MIN_VALUE;\\n\\n // Compare odd and even frequencies\\n for (Map.Entry<Character, Integer> entry1 : map.entrySet()) {\\n int freq1 = entry1.getValue();\\n for (Map.Entry<Character, Integer> entry2 : map.entrySet()) {\\n int freq2 = entry2.getValue();\\n\\n // freq1 is odd, freq2 is even \\u2192 calculate (odd - even)\\n if (freq1 % 2 != 0 && freq2 % 2 == 0) {\\n max = Math.max(max, freq1 - freq2);\\n }\\n }\\n }\\n\\n return max == Integer.MIN_VALUE ? 0 : max;\\n }\\n}\\n\"]]"
},
"javascript": {
"code": "/**\n * @param {string} s\n * @return {number}\n */\nvar maxDifference = function(s) {\n const freq = {};\n for (const c of s) {\n freq[c] = (freq[c] || 0) + 1;\n }\n const evens = [];\n const odds = [];\n for (const c in freq) {\n const count = freq[c];\n (count % 2 === 0 ? evens : odds).push(count);\n }\n let maxDiff = -Infinity;\n for (const odd of odds) {\n for (const even of evens) {\n maxDiff = Math.max(maxDiff, odd - even);\n }\n }\n return maxDiff;\n};",
"memory": 5900,
"memoryDistribution": "[[5900, 8.4902, \"/**\\n * @param {string} s\\n * @return {number}\\n */\\nvar maxDifference = function(s) {\\n const freq = {};\\n for (const c of s) {\\n freq[c] = (freq[c] || 0) + 1;\\n }\\n const evens = [];\\n const odds = [];\\n for (const c in freq) {\\n const count = freq[c];\\n (count % 2 === 0 ? evens : odds).push(count);\\n }\\n let maxDiff = -Infinity;\\n for (const odd of odds) {\\n for (const even of evens) {\\n maxDiff = Math.max(maxDiff, odd - even);\\n }\\n }\\n return maxDiff;\\n};\"], [55100, 0.9434, \"/**\\n * @param {string} s\\n * @return {number}\\n */\\nvar maxDifference = function(s) {\\n const map = new Map();\\n let highestOdd = -Infinity;\\n let lowestEven = Infinity;\\n\\n for (let char of s) {\\n map.set(char, (map.get(char) || 0) + 1);\\n }\\n\\n for (let cnt of map.values()) {\\n if (cnt % 2 === 1) {\\n highestOdd = Math.max(highestOdd, cnt);\\n } else {\\n lowestEven = Math.min(lowestEven, cnt);\\n }\\n }\\n\\n if (highestOdd === -Infinity || lowestEven === Infinity) {\\n return 0;\\n } else {\\n return highestOdd - lowestEven;\\n }\\n};\"], [55200, 1.8868, \"var maxDifference = function(s) {\\n const freq = new Array(26).fill(0);\\n\\n for (let char of s) {\\n freq[char.charCodeAt(0) - 97]++;\\n }\\n\\n let maxDiff = -Infinity;\\n\\n for (let i = 0; i < 26; i++) {\\n if (freq[i] % 2 === 1) {\\n for (let j = 0; j < 26; j++) {\\n if (freq[j] % 2 === 0 && freq[j] > 0) {\\n maxDiff = Math.max(maxDiff, freq[i] - freq[j]);\\n }\\n }\\n }\\n }\\n\\n return maxDiff;\\n};\\n\"], [55500, 2.8302, null], [55800, 1.8868, null], [55900, 2.8302, null], [56000, 4.717, null], [56100, 3.7736, null], [56200, 1.8868, null], [56300, 1.8868, null], [56500, 1.8868, null], [56600, 1.8868, null], [56700, 0.9434, null], [56800, 1.8868, null], [56900, 2.8302, null], [57000, 1.8868, null], [57200, 3.7736, null], [57300, 2.8302, null], [57400, 6.6038, null], [57500, 1.8868, null], [57600, 2.8302, null], [57700, 1.8868, null], [57800, 3.7736, null], [57900, 1.8868, null], [58000, 5.6604, null], [58100, 0.9434, null], [58200, 0.9434, null], [58300, 1.8868, null], [58400, 0.9434, null], [58500, 3.7736, null], [58600, 2.8302, null], [58700, 5.6604, null], [58800, 0.9434, null], [59000, 2.8302, null], [59100, 3.7736, null], [59200, 1.8868, null], [59600, 0.9434, null], [60000, 0.9434, \"/**\\n * @param {string} s\\n * @return {number}\\n */\\nvar maxDifference = function(s) {\\n let freq = {};\\n for(let char of s){\\n freq[char] = (freq[char] || 0)+1\\n }\\n let even = Infinity;\\n let odd = -Infinity;\\n for(let char in freq){\\n if(freq[char]%2!==0){\\n if(odd<freq[char]) odd = freq[char]\\n }else{\\n if(even>freq[char]) even = freq[char]\\n }\\n }\\n if(odd === -Infinity || even === Infinity) return 0\\n return odd-even\\n};\"], [60100, 0.9434, \"/**\\n * @param {string} s\\n * @return {number}\\n */\\nvar maxDifference = function (s) {\\n\\n const hash = {};\\n \\n let max = Number.MIN_SAFE_INTEGER;\\n let min = Number.MAX_SAFE_INTEGER;\\n \\n for(const n of s){\\n if(n in hash){\\n hash[n]++;\\n }else hash[n] = 1;\\n }\\n\\n for(const n in hash){\\n if(hash[n] % 2 === 1 && hash[n] > max) max = hash[n];\\n if(hash[n] % 2 === 0 && hash[n] < min) min = hash[n];\\n }\\n \\n console.log(max)\\n console.log(min)\\n\\n return max - min;\\n};\"]]",
"runtime": 14,
"runtimeDistribution": "[[1, 3.7736, \"/**\\n * @param {string} s\\n * @return {number}\\n */\\nvar maxDifference = function(s) {\\n \\n let sMap = new Map()\\n\\n for(let char of s){\\n sMap.set(char, (sMap.get(char) || 0) + 1)\\n }\\n\\n let even = []\\n let odd = []\\n\\n let calculate = sMap.forEach((val) => {\\n if(val % 2 == 0){\\n even.push(val)\\n }else{\\n odd.push(val)\\n }\\n })\\n\\n return Math.max(...odd) - Math.min(...even)\\n};\"], [2, 5.6604, \"/**\\n * @param {string} s\\n * @return {number}\\n */\\nvar maxDifference = function(s) {\\n let freq = new Map();\\n for(let c of s){\\n freq.set(c,freq.has(c) ? freq.get(c) + 1 : 1);\\n }\\n\\n let odd = [], even = [];\\n for(const [key,val] of freq){\\n if(val % 2 === 0){\\n even.push(val);\\n }\\n else{\\n odd.push(val);\\n }\\n }\\n\\n odd.sort((a,b) => b-a);\\n even.sort((a,b) => a-b);\\n return odd[0] - even[0];\\n};\"], [3, 4.717, null], [4, 11.3208, null], [5, 14.1509, null], [6, 3.7736, null], [7, 5.6604, null], [8, 1.8868, null], [9, 6.6038, null], [10, 9.434, null], [11, 3.7736, null], [12, 5.6604, null], [13, 8.4906, null], [14, 1.8868, null], [15, 4.717, null], [16, 0.9434, null], [17, 0.9434, \"/**\\n * @param {string} s\\n * @return {number}\\n */\\nvar maxDifference = function(s) {\\n let m = {};\\n let maxDiff = Number.NEGATIVE_INFINITY;\\n for(let c of s){\\n m[c] = (m[c] || 0) + 1;\\n }\\n for(let key in m){\\n let oddNum = Number(m[key]);\\n let odd = oddNum % 2 === 1;\\n if(odd){\\n for(let key in m){\\n let evenNum = Number(m[key]);\\n let even = evenNum % 2 === 0;\\n if(even){\\n maxDiff = Math.max(oddNum - evenNum, maxDiff);\\n }\\n }\\n }\\n }\\n return maxDiff;\\n // \\\"abcabcab\\\"\\n // z: 5,\\n // a: 4,\\n // b: 4,\\n // c: 1\\n // d: 2\\n\\n // 1 - 2, 1-4 , 1-6\\n // -1, -3, -5\\n\\n // 5 - 4, 5- 2, 1-4, 1-2\\n // 1, 3, -3, -1\\n};\"], [22, 0.9434, \"/**\\n * @param {string} s\\n * @return {number}\\n */\\nvar maxDifference = function(s) {\\n let freq = {};\\n for (let char of s) {\\n freq[char] = (freq[char] || 0) + 1;\\n }\\n\\n let oddFreqs = [];\\n let evenFreqs = [];\\n\\n for (let key in freq) {\\n if (freq[key] % 2 === 0) {\\n evenFreqs.push(freq[key]);\\n } else {\\n oddFreqs.push(freq[key]);\\n }\\n }\\n\\n // No valid pair exists\\n if (oddFreqs.length === 0 || evenFreqs.length === 0) return 0;\\n\\n let maxDiff = -Infinity;\\n for (let odd of oddFreqs) {\\n for (let even of evenFreqs) {\\n maxDiff = Math.max(maxDiff, odd - even);\\n }\\n }\\n\\n return maxDiff;\\n};\"]]"
},
"python3": {
"code": "class Solution:\n def maxDifference(self, s: str) -> int:\n freq = Counter(s)\n even = []\n odd = []\n for v in freq.values():\n if v % 2 == 0:\n even.append(v)\n else:\n odd.append(v)\n max_odd = max(odd)\n min_even = min(even)\n return max_odd - min_even",
"memory": 1800,
"memoryDistribution": "[[1800, 75.8974, \"from collections import Counter\\n\\nclass Solution:\\n def maxDifference(self, s: str) -> int:\\n freq = Counter(s)\\n even = []\\n odd = []\\n for v in freq.values():\\n if v % 2 == 0:\\n even.append(v)\\n else:\\n odd.append(v)\\n max_odd = max(odd)\\n min_even = min(even)\\n return max_odd - min_even\"], [17400, 0.1709, \"class Solution:\\n def maxDifference(self, s: str) -> int:\\n l=[]\\n l1=[]\\n l2=list(set(s))\\n for i in l2:\\n if s.count(i)%2==0:\\n l.append(s.count(i))\\n else:\\n l1.append(s.count(i))\\n a=max(l1)-min(l)\\n b=max(l)-min(l1)\\n return a\\n'''s2=list(s)\\n s3=[]\\n s1=[]\\n for i in s2:\\n if i not in s1:\\n s1.append(i)\\n for i in s1:\\n s3.append(s2.count(i))\\n g=[]\\n g1=[]\\n count=0\\n count1=0\\n for i in s3:\\n if i%2==0:\\n count+=1\\n g.append(i)\\n else:\\n count1+=1\\n g1.append(i)\\n c1=(g1[-1]-g[0])\\n if count1==0 or count==0:\\n return -1\\n else:\\n return c1'''\\n \\n \\n\\n \"], [17500, 0.6838, \"class Solution:\\n def maxDifference(self, s: str) -> int:\\n eve = []\\n odd = []\\n for ch in set(s):\\n count = s.count(ch)\\n if count % 2 == 0:\\n eve.append(count)\\n else:\\n odd.append(count)\\n \\n # If no even characters, to avoid crash, assume minimum even is 0\\n if not eve:\\n eve.append(0)\\n if not odd:\\n odd.append(0)\\n\\n return max(odd) - min(eve)\\n\"], [17600, 4.9573, null], [17700, 18.2906, null], [17800, 25.1282, null], [17900, 20.3419, \"class Solution:\\n def maxDifference(self, s: str) -> int:\\n D = {}\\n for a in s:\\n if a not in D:\\n D[a] = 1\\n else:\\n D[a] += 1\\n \\n odd, even = [], []\\n\\n for d in D:\\n if D[d] % 2 == 0:\\n even.append(D[d])\\n else:\\n odd.append(D[d])\\n odd.sort()\\n even.sort()\\n return odd[-1] - even[0]\"], [18000, 23.7607, \"class Solution:\\n def maxDifference(self, s: str) -> int:\\n hash_map = {}\\n for i in s:\\n if i in hash_map:\\n hash_map[i] += 1\\n else:\\n hash_map[i] = 1\\n max_odd = max([value for value in hash_map.values() if value%2 != 0])\\n min_even = min([value for value in hash_map.values() if value%2 == 0])\\n return max_odd - min_even\\n \"]]",
"runtime": 3,
"runtimeDistribution": "[[0, 22.3932, \"class Solution:\\n def maxDifference(self, s: str) -> int:\\n hash_map = {}\\n for i in s:\\n if i in hash_map:\\n hash_map[i] += 1\\n else:\\n hash_map[i] = 1\\n max_odd = max([value for value in hash_map.values() if value%2 != 0])\\n min_even = min([value for value in hash_map.values() if value%2 == 0])\\n return max_odd - min_even\\n \"], [1, 4.4444, \"class Solution:\\n def maxDifference(self, s: str) -> int:\\n hash_map = {}\\n for i in s:\\n if i in hash_map:\\n hash_map[i] += 1\\n else:\\n hash_map[i] = 1\\n max_even = max([value for value in hash_map.values() if value%2 == 0])\\n max_odd = max([value for value in hash_map.values() if value%2 != 0])\\n min_even = min([value for value in hash_map.values() if value%2 == 0])\\n \\n return max_odd - min_even\\n \"], [2, 5.2991, null], [3, 32.3077, null], [4, 13.5043, null], [5, 4.1026, null], [6, 3.4188, \"class Solution:\\n def maxDifference(self, s: str) -> int:\\n even = []\\n odd = []\\n \\n for i in s:\\n if(s.count(i)%2 == 0):\\n even.append(s.count(i))\\n else:\\n odd.append(s.count(i))\\n\\n return(max(odd) - min(even))\"], [7, 9.4017, \"class Solution:\\n def maxDifference(self, s: str) -> int:\\n freq = Counter(s)\\n\\n odd_freqs = []\\n even_freqs = []\\n\\n for f in freq.values():\\n if f % 2 == 0:\\n even_freqs.append(f)\\n else:\\n odd_freqs.append(f)\\n\\n max_diff = float('-inf')\\n\\n for odd in odd_freqs:\\n for even in even_freqs:\\n max_diff = max(max_diff, odd - even)\\n\\n return max_diff\"]]"
},
"ruby": {
"code": "def max_difference(s)\n freq = s.chars.each_with_object(Hash.new(0)) { |c, h| h[c] += 1 }\n even = []\n odd = []\n freq.each_value do |v|\n v.even? ? even << v : odd << v\n end\n max_odd = odd.max\n min_even = even.min\n max_odd - min_even\nend",
"memory": 21200,
"memoryDistribution": "[[21200, 50.0, \"def max_difference(s)\\n freq = s.chars.each_with_object(Hash.new(0)) { |c, h| h[c] += 1 }\\n even = []\\n odd = []\\n freq.each_value do |v|\\n v.even? ? even << v : odd << v\\n end\\n max_odd = odd.max\\n min_even = even.min\\n max_odd - min_even\\nend\"], [211400, 25.0, \"# @param {String} s\\n# @return {Integer}\\n\\ndef max_difference(s)\\n e, o = s.each_char.tally.values.partition(&:even?)\\n o.max - e.min\\nend\"], [211500, 25.0, \"# @param {String} s\\n# @return {Integer}\\ndef max_difference(s)\\n hash = {}\\n max_odd_count = 0\\n min_even_count = (2**(0.size * 8 -2) -1)\\n s.each_char do |char|\\n if !hash.include?(char)\\n hash[char] = 1\\n else\\n hash[char] += 1\\n end\\n end \\n\\n hash.each do |key,value|\\n if value % 2 == 0\\n \\n min_even_count = [min_even_count, value].min\\n \\n elsif value % 2 != 0\\n \\n max_odd_count = [max_odd_count, value].max\\n end\\n\\n end\\n\\n (max_odd_count - min_even_count)\\nend\"], [211700, 50.0, \"# @param {String} s\\n# @return {Integer}\\n\\nclass String\\n\\n def counter\\n f = {}\\n n = self.size\\n for i in 0...n do\\n f[self[i]] = 0 if f[self[i]] == nil \\n f[self[i]] += 1\\n end\\n f\\n end\\n\\nend\\n\\nclass Integer\\n\\n def even?\\n self % 2 == 0\\n end\\n\\n def odd?\\n self % 2 == 1\\n end\\n\\nend\\n\\ndef max_difference(s)\\n f = s.counter\\n k = f.keys\\n n = k.size\\n maximum = -s.size\\n for i in 0...n do\\n next if !f[k[i]].even?\\n for j in 0...n do\\n next if !f[k[j]].odd? \\n d = f[k[j]] - f[k[i]]\\n maximum = d if maximum < d\\n end\\n end\\n maximum\\nend\"]]",
"runtime": 6,
"runtimeDistribution": "[[3, 25.0, \"# @param {String} s\\n# @return {Integer}\\n\\ndef max_difference(s)\\n e, o = s.each_char.tally.values.partition(&:even?)\\n o.max - e.min\\nend\"], [6, 75.0, \"def max_difference(s)\\n freq = s.chars.each_with_object(Hash.new(0)) { |c, h| h[c] += 1 }\\n even = []\\n odd = []\\n freq.each_value do |v|\\n v.even? ? even << v : odd << v\\n end\\n max_odd = odd.max\\n min_even = even.min\\n max_odd - min_even\\nend\"], [10, 25.0, \"# @param {String} s\\n# @return {Integer}\\ndef max_difference(s)\\n hash = {}\\n max_odd_count = 0\\n min_even_count = (2**(0.size * 8 -2) -1)\\n s.each_char do |char|\\n if !hash.include?(char)\\n hash[char] = 1\\n else\\n hash[char] += 1\\n end\\n end \\n\\n hash.each do |key,value|\\n if value % 2 == 0\\n \\n min_even_count = [min_even_count, value].min\\n \\n elsif value % 2 != 0\\n \\n max_odd_count = [max_odd_count, value].max\\n end\\n\\n end\\n\\n (max_odd_count - min_even_count)\\nend\"], [11, 25.0, \"def max_difference(s)\\n freq = s.chars.each_with_object(Hash.new(0)) { |c, h| h[c] += 1 }\\n even = []\\n odd = []\\n freq.each_value do |v|\\n v.even? ? even << v : odd << v\\n end\\n max_odd = odd.max\\n min_even = even.min\\n max_odd - min_even\\nend\"], [23, 25.0, \"# @param {String} s\\n# @return {Integer}\\n\\nclass String\\n\\n def counter\\n f = {}\\n n = self.size\\n for i in 0...n do\\n f[self[i]] = 0 if f[self[i]] == nil \\n f[self[i]] += 1\\n end\\n f\\n end\\n\\nend\\n\\nclass Integer\\n\\n def even?\\n self % 2 == 0\\n end\\n\\n def odd?\\n self % 2 == 1\\n end\\n\\nend\\n\\ndef max_difference(s)\\n f = s.counter\\n k = f.keys\\n n = k.size\\n maximum = -s.size\\n for i in 0...n do\\n next if !f[k[i]].even?\\n for j in 0...n do\\n next if !f[k[j]].odd? \\n d = f[k[j]] - f[k[i]]\\n maximum = d if maximum < d\\n end\\n end\\n maximum\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list:
import random
from collections import Counter
random.seed(seed)
def sample_solution(s: str) -> int:
freq = Counter(s)
even = []
odd = []
for v in freq.values():
if v % 2 == 0:
even.append(v)
else:
odd.append(v)
max_odd = max(odd)
min_even = min(even)
return max_odd - min_even
def is_valid(s: str) -> bool:
if len(s) < 3:
return False
freq = Counter(s)
found_even = any(v % 2 == 0 for v in freq.values())
found_odd = any(v % 2 == 1 for v in freq.values())
return found_even and found_odd
# Predefined fixed test cases for diversity.
fixed_cases = ["aab", "aaaaabbc", "abcabcab", "aabbc", "abbccc", "zzzzzyy", "aabbccd"]
test_cases = []
i = 0
# Use fixed test cases if available.
while i < num_cases and i < len(fixed_cases):
s = fixed_cases[i]
if not is_valid(s):
i += 1
continue
expected = sample_solution(s)
test_cases.append({
"input": s,
"output": str(expected)
})
i += 1
# Generate additional random valid test cases if needed.
letters = 'abcdefghijklmnopqrstuvwxyz'
while len(test_cases) < num_cases:
L = random.randint(3, 100)
s = ''.join(random.choices(letters, k=L))
if not is_valid(s):
continue
expected = sample_solution(s)
test_cases.append({
"input": s,
"output": str(expected)
})
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
try:
exp_val = int(expected_output.strip())
prog_val = int(program_output.strip())
return exp_val == prog_val
except Exception:
return False
|
[{"input": "aab", "output": "-1"}, {"input": "aaaaabbc", "output": "3"}, {"input": "abcabcab", "output": "1"}, {"input": "aabbc", "output": "-1"}, {"input": "abbccc", "output": "1"}, {"input": "zzzzzyy", "output": "3"}, {"input": "aabbccd", "output": "-1"}, {"input": "ctgdctopacgpossklhwtekhftcjjigbldxchqxjebruzwwjlvejrsrbqngmhyrfitbvukbxosfmxqddtotlp", "output": "5"}, {"input": "fzncbcqukbjznzwasrngqcllywgnexwhqpdtounaiaywvhbwy", "output": "3"}, {"input": "tvzndryenpzyt", "output": "-1"}, {"input": "fizqlndfipffbqfxwbgrfdyomuuecllmsrzckiwgelkhgylwobzvzywemfkbjzgulkyzosehzpotbpnweyceprgdxgp", "output": "5"}, {"input": "croigrigdqlyyaqocnndjbghlohzunroycwgxtehfirwngxbqvbidzelsocyrdajolbjyzbjrrjowztyge", "output": "5"}, {"input": "watiyuwvgucwwfvlhufafiwzh", "output": "3"}, {"input": "nrviawgpzapiulzdxeblnurytflyxqrdxnrisoerjteokvhfupilrnuytrhrqcygiudbzptlxosjkdrxwxufu", "output": "7"}, {"input": "nbgwlurzpyxpsnvoxtmggqtnqhchhiodgssbkokfkxpswtjajtwyktopfflairkemdqakoaqdmbjfitjtvgcaozjquqt", "output": "3"}, {"input": "faddrofsteptcvzcairyksbrqcuwpdzujl", "output": "1"}, {"input": "bqakmljxldenqqxumvpigyhltorimimjghpwonegkogmslahkg", "output": "3"}, {"input": "pmnltishgdfdntefmsznhcffeanhzosdwmwomlebymvkbqbdohzdtpufnllwzhqptyffreebalphgsslryuqryl", "output": "5"}, {"input": "fdgdbupvxlmhkholpxtpafrwpatvotenlhzlvzmkicekmrktacgduwvawmbnqmlbgdhwmaqu", "output": "3"}, {"input": "eooczxldvmsnhvzgojxnwwhukynvhhpzmdoiooliesogubtsvkrvzmanpwwlnlskremzisqwwwjistwabqxztlcqwlsxb", "output": "7"}, {"input": "mpgqlrxmhobyzhzrlhzwcjjhsavkawuzx", "output": "-1"}, {"input": "mxhupjqqrsrvqxqilptchtedoznxvgvmuticzdzwszzujuanlrrpvycgawoxfbvxhkdyhmcxdlrtyktekcmkyajlywcrozjked", "output": "3"}, {"input": "cfqzbizufvopvguuphzzoucwdjupagdkcbljplfpsxrhqazwlcslxiddqpsjp", "output": "5"}, {"input": "lpcswqtsflfilkclrjdxbvcctvopoidjrtwszpjp", "output": "1"}, {"input": "emwjochflotqroprsahtxjedrbtzcn", "output": "1"}, {"input": "kijsuocbeqrhrmlhtclhrmrbkpahfdgiatejsnvubwbaxwooskc", "output": "1"}, {"input": "cvgpnkiiiencnxjsvvgdfptreumttlyoqqwqdblhhbnilbvbw", "output": "1"}, {"input": "pnmouxlvqimdbc", "output": "-1"}, {"input": "zcqbsznpjxkurbqiiokgwzpdcrxirrdscoqidsyzxcrnai", "output": "3"}, {"input": "itezehunotnrwqpeesqxsbjszptugg", "output": "1"}, {"input": "xfroluunkefpwbmjysndcelnvcxvxykkjkcficsidaxmvtmpxafdyplugdgqqbv", "output": "3"}, {"input": "pangdlpgkrczbnnzokmqzgauitqutiboveumsqvbulhbfbynzogtejuwidjxtxkzmm", "output": "3"}, {"input": "gcllzehcihlsellsxplqubrknteawrldgqjyadljlbdjihyaenxdusfpszfdbeszvzzrs", "output": "7"}, {"input": "oxwsyqundfduaojuopcizsntvbzqlriwuqezlxbddeisiyxvgqodhnneyerspvovabqoqtkqm", "output": "5"}, {"input": "oqhguklrekmidwiziktncgdldbywkzxvyseezmwmcklgpbhpvrhacdgjkbbojhklovqpdcjzojdpkbbsund", "output": "5"}, {"input": "dyikqvpnnmomaickhxwqpgrzpfbmnsujvgoselkkfnpmwssnozmjylnorwrugmyhhyzu", "output": "1"}, {"input": "fsijyuhdrjzvyuhhsjlgmfoysdqpgrnqbkscuaoykywmfziqxconsyxewexzkmyzywaoczhzomywmfcelgetuotewxvnc", "output": "7"}, {"input": "czmyajlgipogjgrmeryxurqyjfymlzjsxtuvtrpunnjxcvxfnewlrsmxlbdkooriagafblsobxzmhedqszjxlxjc", "output": "5"}, {"input": "wdwdzkdzvtzmsljfleewtarpyxgbplrwgblotudzgxopuvgwznkhopterobiqjnskhengfwdmbkknkgicljnvbj", "output": "3"}, {"input": "pwetsomwiyayzdzmgpfxoujnjgnmczmvxjkofdgypkdijvmrrgvzqmeuesmxoqbawyrtkvgsanjqrqmm", "output": "7"}, {"input": "hzavruxccdenvgkjkozfrwqwtcjobaemluowcnbfwxmbbyxoayiyptskcegvkxitdzsnzblvitykuahzmjylrrcquscesqt", "output": "5"}, {"input": "jcyltcclonccopuwakusozgnreggdehhujysmqldakv", "output": "3"}, {"input": "uiivwzdiyfizzhsmogjvkcoporoymslhsvukmqgrsubzmknxrou", "output": "3"}, {"input": "svpxcgrepoqqziuccftorfjmrrdzmhxcvsjiunjcslbbsaicu", "output": "1"}, {"input": "geeoygkeqlapfpksftvbcweilgwnqpppjvqvshpcddhesnkdjeqsqzomdilbjadvznmrkvmcathhnelttoccuvjvbsozcvthz", "output": "5"}, {"input": "gwcwdvftrwplquvuonpezhoynxvdtkbhrsddigvkdqqjbutktswlmpwwczqs", "output": "3"}, {"input": "ukzvmihodwu", "output": "-1"}, {"input": "tbqvayelzlzxwhwwcjcrqbqstlccfcpnlaidwsmfcucjhjvwqrbopejftxqlfxddsjlugqgpshyawwfpekquugkgqb", "output": "5"}, {"input": "koemzbpafxykhstlkqndccxzeiptqqilyggydpbrreadamjnvgjtwtdxilngzqmnbweeuxrctaw", "output": "3"}, {"input": "oxtkiks", "output": "-1"}, {"input": "vodrbfnbkwwuicljhutgjzzutoudyaoqsaitj", "output": "1"}, {"input": "scngmbzscxxnsjzccdvbolzggiustihbfupeemknzfigdervsbvicgjnrgzakltgmudavzdvjqqpgvabxldxvibleovkarefe", "output": "3"}, {"input": "ldpqqmwmcjkqugzoajsmuioihapavhvmjpgegg", "output": "1"}, {"input": "vxbzfwujvvepusxasyooezwmimcgfnaxfdsxviapxuwwyjykchdeyuyqezsyufpehrdsyyk", "output": "3"}, {"input": "apxzfoydtgzexcsqxlggbgcaktzwmjocmwqrebvhiybejtoxcppmayexecfesssghgbovdjlhrp", "output": "3"}, {"input": "cfqzmdumxgqkjjeblgvodscrvktf", "output": "-1"}, {"input": "vvknwmwmcx", "output": "-1"}, {"input": "aonozdylyeffbcrfvdpisucoownxaspucdopzccuuwwwgromekqrkkwrbmgjiuivwrzfhtuispclxkmnjbubskunoewfba", "output": "5"}, {"input": "lymoivgvcabwuffffqnwzrmdeufpysshxwlfhnqpazzvophrmihihryqengbwvkidamhxktpzvisrqm", "output": "3"}, {"input": "jherohmtsoxyxrffwkxjpmdbqpqmfdrnkwdzizxzdweciziblfuoeuudlllmansyxtnaatfwicnhbbylnnlrdzmt", "output": "3"}, {"input": "yxkfsdtpejqawgnbzrqarkjo", "output": "-1"}, {"input": "sfrakcnqskxnqhumpuvzjkeoxrmgaccomyubsxqlzgbvwwjrldwxadqixygtjic", "output": "3"}, {"input": "zhkwuqucsbyekpurejjarvzdxckbgisrtoozrinscrgirkvozbqeww", "output": "1"}, {"input": "bmgzbfqkglulwldmqckoacpq", "output": "1"}, {"input": "xorlivvvitpsjlcrajquojcxmvtkgfdwfveitbqrd", "output": "3"}, {"input": "lpnzatolpyuxrevcrpiwkpsgkihudpxnvoitoffsrxdszeoqstopysrxnwka", "output": "3"}, {"input": "adrftehgvrhtavcw", "output": "-1"}, {"input": "ofqknussbjkurzbtfwwlfqsjptfsflzbztdbhgevamybypuqvhuobsnynueokjwrihyqmotqcigqxgbxjucgsanunnmhqiccz", "output": "5"}, {"input": "nqfqfrvfvwtlvbrasabegbvxklkikdasbtbwjnhrphyjvaeftuwhqhxzwqyawdbokocftsf", "output": "3"}, {"input": "wdeqgcrobtzoqbrgfpyjrghbfmirsdovyeiusqhjrimlumcqchvxftqsxwqvptfagxordkxpwdncjagzzrtde", "output": "5"}, {"input": "yrztmjfmbjbfxjmlbzisnvvgoeqjqvnjxnjwmmpndecqfejsdfvsmmfevaboeqbobgeypoasrhc", "output": "5"}, {"input": "pmmfkdptqnerxpbjdanxrvpexpwntcrxoayrlkwslymtjuxvolgtxcpogata", "output": "3"}, {"input": "darrijeqgwljhrtkumjoghistwrtlsefkiossezacdylbfcajzpnspyvqlfruhapngeag", "output": "3"}, {"input": "jkpntbchvxjzhpfyogkcbhyuywvoszoutyllpadbqzrfiynavgcrvb", "output": "3"}, {"input": "mjxgyrxmftwffgqecxrrptobm", "output": "1"}, {"input": "ixwohetnktdnlyajwuldniarjcjweghyielktjklozrvsuowfutmakdxqnimgwbcefgvctgjovikjrpoqn", "output": "3"}, {"input": "jrmtxjhqdeviqowbefihgqhlwjpzkeasryscecb", "output": "1"}, {"input": "oaktcgerxighqdvarwimzohlzsepqqonqijouljghavwimaxymalhgajkoketkj", "output": "3"}, {"input": "cqnupshqngebdcllsmidzazhdlacafkumjsa", "output": "1"}, {"input": "vybubmevvvdtg", "output": "-1"}, {"input": "gzftcrfkyyestodmhjbrzglaupkgzprreugmriztbjencmioqjxtajsgbso", "output": "3"}, {"input": "seejthvxobehgjaqjeawugsroknmopiqcnbvdwfmcovrnsgjpbyfmxcuboykjsvgbbhyycsn", "output": "3"}, {"input": "froyoottorslcuonrnpyxozvkqv", "output": "1"}, {"input": "poftygzlkszpnzhhfwavrhooyeajdjpgvckxtsuevrox", "output": "1"}, {"input": "qavjuxiwlydutwyqqbnioisdrzztocludimtogklstmfkoozngglrockjeiruejvuqlygresctgqdvh", "output": "3"}, {"input": "sclafnfngmsdsaprbehuqbrakhwrwawqgjzciwnenlyagn", "output": "3"}, {"input": "mtarjhzzhbgkzzyyfikdsnrwrkolipldqprfdrxxlxuro", "output": "1"}, {"input": "ioydiwstwkklyxyhucetpgo", "output": "1"}, {"input": "pgacudvmqekmefkzyyfrffeylqrwxlup", "output": "1"}, {"input": "skyonqsbclwwgnzbktzelwuhehxrxmqcnepxokialxxwciqsetc", "output": "3"}, {"input": "ljnjunyjjtxordweskitlqddfqglwoawgpmkcpgoqovbdqawrvhxbkerprpuelpychjjblohdshnnspcsqzmryzhpinzj", "output": "5"}, {"input": "pmsmvwghfdmutfpkbju", "output": "1"}, {"input": "afhuiniarisqaeiirxuqmqxniuktvh", "output": "1"}, {"input": "roapixubdvijnepeduiwshcwjvhnejafcnuxeimwiiucznzfakwdibwwixcttatqffhnurhecyocoohyuoeixobaxbjcksx", "output": "7"}, {"input": "vsqivsrnztmdvxmlrsmgfwqxksruwlamjletpdcvuiqunkkqozjivpuluogrcyompmoveybcvujmrcvxxqa", "output": "5"}, {"input": "rlhqlfwhurxysxzppnwwb", "output": "1"}, {"input": "zaozchalpqsklfedovjkhwdaqdxrzdduwxsyqllvkflamtshyoaamjpzcsnwthnnpgqrrropp", "output": "3"}, {"input": "nalxoijzhesphugqporhtamdbugqhgtpxtrjeugenazzpv", "output": "1"}, {"input": "tkjrsepvbgvbmmmyxgrkgnlhujinycnjvpqhhugplrgrunrziaabknrjsgaqbpxfpd", "output": "3"}, {"input": "cpjtquecehrblzurru", "output": "1"}]
|
{
"cpp": "==Code Submission==\nstring deserialize_stdin() {\n string s;\n getline(cin, s);\n return s;\n}\n\nstring serialize_stdout(int result) {\n return to_string(result);\n}\n\nint main() {\n string s = deserialize_stdin();\n Solution sol;\n int ans = sol.maxDifference(s);\n cout << serialize_stdout(ans);\n return 0;\n}",
"golang": "==Code Submission==\n\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n line, _ := reader.ReadString('\\n')\n s := strings.TrimSpace(line)\n ans := maxDifference(s)\n fmt.Println(strconv.Itoa(ans))\n}",
"java": "public class Main {\n public static String deserializeStdin(String input) {\n return input.trim();\n }\n \n public static String serializeStdout(int result) {\n return String.valueOf(result);\n }\n \n public static void main(String[] args) throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n String s = deserializeStdin(br.readLine());\n Solution sol = new Solution();\n int ans = sol.maxDifference(s);\n System.out.println(serializeStdout(ans));\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\n\nconst deserialize_stdin = (input) => {\n return input.trim();\n};\n\nconst serialize_stdout = (result) => {\n return String(result);\n};\n\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\nlet input = '';\nprocess.stdin.on('data', chunk => input += chunk);\nprocess.stdin.on('end', () => {\n const s = deserialize_stdin(input);\n const ans = maxDifference(s);\n console.log(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str):\n return input_str.strip()\n\ndef serialize_stdout(result):\n return str(result)\n\ninput_str = sys.stdin.read().strip()\ns = deserialize_stdin(input_str)\nsol = Solution()\nans = sol.maxDifference(s)\nprint(serialize_stdout(ans))",
"ruby": "==Code Submission==\n\ninput = gets.strip\ns = input\nans = max_difference(s)\nputs ans.to_s"
}
|
3760
|
Assign Elements to Groups with Constraints
|
assign-elements-to-groups-with-constraints
|
<p>You are given an integer array <code>groups</code>, where <code>groups[i]</code> represents the size of the <code>i<sup>th</sup></code> group. You are also given an integer array <code>elements</code>.</p>
<p>Your task is to assign <strong>one</strong> element to each group based on the following rules:</p>
<ul>
<li>An element at index <code>j</code> can be assigned to a group <code>i</code> if <code>groups[i]</code> is <strong>divisible</strong> by <code>elements[j]</code>.</li>
<li>If there are multiple elements that can be assigned, assign the element with the <strong>smallest index</strong> <code>j</code>.</li>
<li>If no element satisfies the condition for a group, assign -1 to that group.</li>
</ul>
<p>Return an integer array <code>assigned</code>, where <code>assigned[i]</code> is the index of the element chosen for group <code>i</code>, or -1 if no suitable element exists.</p>
<p><strong>Note</strong>: An element may be assigned to more than one group.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">groups = [8,4,3,2,4], elements = [4,2]</span></p>
<p><strong>Output:</strong> <span class="example-io">[0,0,-1,1,0]</span></p>
<p><strong>Explanation:</strong></p>
<ul>
<li><code>elements[0] = 4</code> is assigned to groups 0, 1, and 4.</li>
<li><code>elements[1] = 2</code> is assigned to group 3.</li>
<li>Group 2 cannot be assigned any element.</li>
</ul>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">groups = [2,3,5,7], elements = [5,3,3]</span></p>
<p><strong>Output:</strong> <span class="example-io">[-1,1,0,-1]</span></p>
<p><strong>Explanation:</strong></p>
<ul>
<li><code>elements[1] = 3</code> is assigned to group 1.</li>
<li><code>elements[0] = 5</code> is assigned to group 2.</li>
<li>Groups 0 and 3 cannot be assigned any element.</li>
</ul>
</div>
<p><strong class="example">Example 3:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">groups = [10,21,30,41], elements = [2,1]</span></p>
<p><strong>Output:</strong> <span class="example-io">[0,1,0,1]</span></p>
<p><strong>Explanation:</strong></p>
<p><code>elements[0] = 2</code> is assigned to the groups with even values, and <code>elements[1] = 1</code> is assigned to the groups with odd values.</p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>1 <= groups.length <= 10<sup>5</sup></code></li>
<li><code>1 <= elements.length <= 10<sup>5</sup></code></li>
<li><code>1 <= groups[i] <= 10<sup>5</sup></code></li>
<li><code>1 <= elements[i] <= 10<sup>5</sup></code></li>
</ul>
|
You are given an integer array `groups`, where `groups[i]` represents the size of the `ith` group. You are also given an integer array `elements`.
Your task is to assign **one** element to each group based on the following rules:
- An element at index `j` can be assigned to a group `i` if `groups[i]` is **divisible** by `elements[j]`.
- If there are multiple elements that can be assigned, assign the element with the **smallest index** `j`.
- If no element satisfies the condition for a group, assign \-1 to that group.
Return an integer array `assigned`, where `assigned[i]` is the index of the element chosen for group `i`, or \-1 if no suitable element exists.
**Note**: An element may be assigned to more than one group.
**Example 1:**
**Input:** groups \= \[8,4,3,2,4], elements \= \[4,2]
**Output:** \[0,0,\-1,1,0]
**Explanation:**
- `elements[0] = 4` is assigned to groups 0, 1, and 4\.
- `elements[1] = 2` is assigned to group 3\.
- Group 2 cannot be assigned any element.
**Example 2:**
**Input:** groups \= \[2,3,5,7], elements \= \[5,3,3]
**Output:** \[\-1,1,0,\-1]
**Explanation:**
- `elements[1] = 3` is assigned to group 1\.
- `elements[0] = 5` is assigned to group 2\.
- Groups 0 and 3 cannot be assigned any element.
**Example 3:**
**Input:** groups \= \[10,21,30,41], elements \= \[2,1]
**Output:** \[0,1,0,1]
**Explanation:**
`elements[0] = 2` is assigned to the groups with even values, and `elements[1] = 1` is assigned to the groups with odd values.
**Constraints:**
- `1 <= groups.length <= 105`
- `1 <= elements.length <= 105`
- `1 <= groups[i] <= 105`
- `1 <= elements[i] <= 105`
|
Medium
|
[
"array",
"hash-table"
] |
leetcode
|
https://leetcode.com/problems/assign-elements-to-groups-with-constraints
|
functional
| null | null | null | null |
{
"c": "/**\n * Note: The returned array must be malloced, assume caller calls free().\n */\nint* assignElements(int* groups, int groupsSize, int* elements, int elementsSize, int* returnSize) {\n \n}",
"cpp": "class Solution {\npublic:\n vector<int> assignElements(vector<int>& groups, vector<int>& elements) {\n \n }\n};",
"csharp": "public class Solution {\n public int[] AssignElements(int[] groups, int[] elements) {\n \n }\n}",
"dart": "class Solution {\n List<int> assignElements(List<int> groups, List<int> elements) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec assign_elements(groups :: [integer], elements :: [integer]) :: [integer]\n def assign_elements(groups, elements) do\n \n end\nend",
"erlang": "-spec assign_elements(Groups :: [integer()], Elements :: [integer()]) -> [integer()].\nassign_elements(Groups, Elements) ->\n .",
"golang": "func assignElements(groups []int, elements []int) []int {\n \n}",
"java": "class Solution {\n public int[] assignElements(int[] groups, int[] elements) {\n \n }\n}",
"javascript": "/**\n * @param {number[]} groups\n * @param {number[]} elements\n * @return {number[]}\n */\nvar assignElements = function(groups, elements) {\n \n};",
"kotlin": "class Solution {\n fun assignElements(groups: IntArray, elements: IntArray): IntArray {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param Integer[] $groups\n * @param Integer[] $elements\n * @return Integer[]\n */\n function assignElements($groups, $elements) {\n \n }\n}",
"python": "class Solution(object):\n def assignElements(self, groups, elements):\n \"\"\"\n :type groups: List[int]\n :type elements: List[int]\n :rtype: List[int]\n \"\"\"\n ",
"python3": "class Solution:\n def assignElements(self, groups: List[int], elements: List[int]) -> List[int]:\n ",
"racket": "(define/contract (assign-elements groups elements)\n (-> (listof exact-integer?) (listof exact-integer?) (listof exact-integer?))\n )",
"ruby": "# @param {Integer[]} groups\n# @param {Integer[]} elements\n# @return {Integer[]}\ndef assign_elements(groups, elements)\n \nend",
"rust": "impl Solution {\n pub fn assign_elements(groups: Vec<i32>, elements: Vec<i32>) -> Vec<i32> {\n \n }\n}",
"scala": "object Solution {\n def assignElements(groups: Array[Int], elements: Array[Int]): Array[Int] = {\n \n }\n}",
"swift": "class Solution {\n func assignElements(_ groups: [Int], _ elements: [Int]) -> [Int] {\n \n }\n}",
"typescript": "function assignElements(groups: number[], elements: number[]): number[] {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n vector<int> assignElements(vector<int>& groups, vector<int>& elements) {\n const int MAX_ELEMENT = 100000;\n vector<int> element_indices(MAX_ELEMENT + 1, -1);\n for (int i = 0; i < elements.size(); ++i) {\n int e = elements[i];\n if (element_indices[e] == -1) {\n element_indices[e] = i;\n }\n }\n \n vector<int> assigned;\n for (int g : groups) {\n int min_idx = -1;\n unordered_set<int> divisors;\n for (int i = 1; i * i <= g; ++i) {\n if (g % i == 0) {\n divisors.insert(i);\n divisors.insert(g / i);\n }\n }\n for (int d : divisors) {\n int idx = element_indices[d];\n if (idx != -1) {\n if (min_idx == -1 || idx < min_idx) {\n min_idx = idx;\n }\n }\n }\n assigned.push_back(min_idx);\n }\n return assigned;\n }\n};",
"memory": 48100,
"memoryDistribution": "[[48100, 5.1804, \"class Solution {\\npublic:\\n vector<int> assignElements(vector<int>& groups, vector<int>& elements) {\\n const int MAX_ELEMENT = 100000;\\n vector<int> element_indices(MAX_ELEMENT + 1, -1);\\n for (int i = 0; i < elements.size(); ++i) {\\n int e = elements[i];\\n if (element_indices[e] == -1) {\\n element_indices[e] = i;\\n }\\n }\\n \\n vector<int> assigned;\\n for (int g : groups) {\\n int min_idx = -1;\\n unordered_set<int> divisors;\\n for (int i = 1; i * i <= g; ++i) {\\n if (g % i == 0) {\\n divisors.insert(i);\\n divisors.insert(g / i);\\n }\\n }\\n for (int d : divisors) {\\n int idx = element_indices[d];\\n if (idx != -1) {\\n if (min_idx == -1 || idx < min_idx) {\\n min_idx = idx;\\n }\\n }\\n }\\n assigned.push_back(min_idx);\\n }\\n return assigned;\\n }\\n};\"], [222591, 1.6181, \"class Solution {\\npublic:\\n vector<int> assignElements(vector<int>& groups, vector<int>& elements)\\n {\\n int div[100001];\\n memset(div,-1,sizeof(div));\\n\\n for(int i=0;i<elements.size();i++)\\n {\\n if(div[elements[i]]==-1)\\n {\\n for(int j=elements[i];j<=1e5;j+=elements[i])\\n {\\n if(div[j]==-1)\\n {\\n div[j]=i;\\n }\\n }\\n }\\n } \\n vector<int>ans(groups.size(),-1);\\n for(int i=0;i<groups.size();i++)\\n {\\n ans[i]=div[groups[i]];\\n } \\n return ans;\\n }\\n};\\n\"], [224973, 0.3236, \"class Solution {\\npublic:\\nint element_check[100005] = {};\\nvoid element_floor ( vector < int > & elements ){\\n for ( int i = 0 ; i < elements.size() ; i ++ ){\\n if ( element_check[elements[i]] != -1 ) continue;\\n for ( int j = elements[i] ; j <= 100000 ; j += elements[i] ){\\n if ( element_check[j] != -1 ) continue;\\n element_check[j] = i;\\n }\\n }\\n}\\n vector<int> assignElements(vector<int>& groups, vector<int>& elements) {\\n memset ( element_check , -1 , sizeof ( element_check ) );\\n element_floor( elements );\\n vector < int > res;\\n for ( int i = 0 ; i < groups.size() ; i ++ ){\\n res.push_back(element_check[groups[i]]);\\n }\\n return res;\\n }\\n};\"], [227356, 3.2361999999999997, null], [229738, 0.3236, null], [232121, 5.8251, null], [234503, 0.6472, null], [236886, 3.5599, null], [239268, 2.589, null], [241651, 7.767, null], [244033, 2.589, null], [246416, 0.9709, null], [248798, 4.5306, null], [251181, 3.2361, null], [253563, 22.977199999999993, null], [255946, 0.3236, null], [258328, 1.2944, null], [260711, 0.6472, null], [263093, 0.3236, null], [265476, 0.3236, null], [267858, 0.3236, null], [270241, 0.3236, null], [272623, 0.3236, null], [275006, 0.3236, null], [277388, 0.6472, null], [279771, 0.6472, null], [282153, 0.6472, null], [284536, 0.6472, null], [286918, 0.3236, null], [289301, 2.589, null], [291683, 9.0613, null], [294066, 1.2944, null], [296448, 2.9124, null], [298831, 0.9709, null], [301213, 0.6472, null], [303596, 0.9708, null], [305978, 1.6181, null], [308361, 0.3236, null], [310743, 0.6472, null], [313126, 0.3236, null], [315508, 0.3236, null], [317891, 0.3236, null], [320273, 0.3236, null], [322656, 0.3236, null], [325038, 0.3236, null], [327421, 0.3236, null], [329803, 0.3236, null], [332186, 0.3236, null], [334568, 0.3236, null], [336951, 0.6472, null], [339333, 0.3236, null], [341716, 0.3236, null], [344098, 0.3236, null], [346481, 0.3236, null], [348863, 0.3236, null], [351246, 0.6472, \"class Solution {\\npublic:\\n vector<int> getFactors(int n){\\n vector<int> ans;\\n for(int i=1;i*i<=n;i++){\\n if(n%i==0){\\n ans.push_back(i);\\n if(n/i!=i){\\n ans.push_back(n/i);\\n }\\n }\\n }\\n return ans;\\n }\\n vector<int> assignElements(vector<int>& groups, vector<int>& elements) {\\n unordered_map<int,int> mp;\\n int n =elements.size();\\n int m = groups.size();\\n vector<int> assigned;\\n\\n for(int i=n-1;i>=0;i--){\\n mp[elements[i]] = i;\\n }\\n\\n for(int i=0;i<m;i++){\\n vector<int> factors = getFactors(groups[i]);\\n int assign = INT_MAX;\\n for(int& f : factors){\\n if(mp.find(f)!=mp.end()){\\n assign = min(assign,mp[f]);\\n }\\n }\\n assign = (assign==INT_MAX)?-1:assign;\\n assigned.push_back(assign);\\n }\\n return assigned;\\n }\\n};\"], [353628, 0.3236, \"class Solution {\\npublic:\\n vector<int> assignElements(vector<int>& groups, vector<int>& elements) {\\n unordered_map<int,vector<int>>m;\\n int maxi=0;\\n for(int i=0;i<groups.size();i++){\\n m[groups[i]].push_back(i);\\n maxi=max(maxi,groups[i]);\\n }\\n unordered_set<int>done;\\n vector<int>ans(groups.size(),-1);\\n for(int i=0;i<elements.size() && m.size();i++){\\n if(done.find(elements[i])!=done.end())continue;\\n int num=elements[i];\\n int temp=num;\\n \\n while(num<=maxi && m.size()){\\n for(auto itr:m[num]){\\n ans[itr]=i;\\n }\\n m.erase(num);\\n num+=temp;\\n }\\n done.insert(elements[i]);\\n }\\n return ans;\\n }\\n};\"]]",
"runtime": 2754,
"runtimeDistribution": "[[12, 11.002600000000003, \"class Solution {\\npublic:\\n vector<int> assignElements(vector<int>& groups, vector<int>& elements) {\\n int n = groups.size(), defaultIdx = -1;\\n int maxSize = *max_element(groups.begin(), groups.end());\\n\\n vector<int> sieve(maxSize+1, defaultIdx);\\n \\n for (int i = 0; i < elements.size(); ++i) {\\n int element = elements[i];\\n if (element == 1) {\\n defaultIdx = i;\\n break;\\n }\\n\\n if (element > maxSize or sieve[element] != -1) {\\n continue;\\n }\\n\\n for (int val = element; val <= maxSize; val += element) {\\n if (sieve[val] == -1) {\\n sieve[val] = i;\\n }\\n }\\n }\\n\\n vector<int> result;\\n for (int i = 0; i < n; ++i) {\\n int groupSize = groups[i];\\n result.push_back(sieve[groupSize] == -1 ? defaultIdx : sieve[groupSize]);\\n }\\n return result;\\n }\\n};\"], [38, 0.6472, \"class Solution {\\npublic:\\n vector<int> assignElements(vector<int>& groups, vector<int>& elements) {\\n int max=-1;\\n for(auto i:groups){\\n if(i>max)max=i;\\n }\\n int tmax=-1;\\n for(auto i:elements)if(i>tmax)tmax=i;\\n\\n vector<int>flag(max+1,-1);\\n vector<int>visited(tmax+1,-1);\\n for(int i=0;i<elements.size();i++){\\n int temp=elements[i];\\n if(visited[elements[i]]==1)continue;\\n visited[elements[i]]=1;\\n while(temp<max+1){\\n if(flag[temp]==-1)flag[temp]=i;\\n temp+=elements[i];\\n }\\n }\\n \\n for(int i=0;i<groups.size();i++){\\n groups[i]=flag[groups[i]];\\n }\\n return groups;\\n }\\n};\"], [63, 0.3236, null], [88, 1.6179999999999999, null], [114, 1.6179999999999999, null], [139, 1.6179999999999999, null], [165, 2.9123999999999994, null], [190, 0.6472, null], [215, 0.3236, null], [241, 2.9123999999999994, null], [266, 0.9708, null], [292, 0.3236, null], [317, 0.9708, null], [342, 1.9415999999999998, null], [368, 0.3236, null], [393, 1.6179999999999999, null], [419, 1.9415999999999998, null], [444, 1.6179999999999999, null], [469, 0.6472, null], [495, 0.6472, null], [520, 2.9126, null], [546, 6.472099999999999, null], [571, 3.2359999999999998, null], [596, 0.6472, null], [622, 0.3236, null], [647, 0.3236, null], [673, 0.3236, null], [698, 0.6472, null], [723, 2.9124, null], [749, 3.2359999999999998, null], [774, 0.3236, null], [800, 0.9708, null], [825, 0.3236, null], [850, 9.061199999999998, null], [876, 3.5595999999999997, null], [901, 0.9708, null], [927, 0.9708, null], [952, 0.3236, null], [977, 0.3236, null], [1003, 0.3236, null], [1028, 0.3236, null], [1054, 1.2944, null], [1079, 0.3236, null], [1104, 0.3236, null], [1130, 3.2359999999999998, null], [1155, 3.8831999999999995, null], [1181, 0.9708, null], [1206, 0.3236, null], [1231, 0.3236, null], [1257, 0.6472, null], [1282, 0.3236, null], [1308, 0.3236, null], [1333, 0.9708, null], [1358, 0.3236, null], [1384, 1.2944, null], [1409, 0.3236, null], [1435, 0.3236, null], [1460, 0.3236, null], [1485, 0.3236, null], [1511, 0.3236, null], [1536, 0.3236, null], [1562, 0.3236, null], [1587, 0.3236, null], [1612, 0.6472, null], [1638, 0.3236, null], [1663, 0.3236, null], [1689, 0.3236, null], [1714, 0.3236, null], [1739, 0.3236, null], [1765, 0.3236, null], [1790, 0.3236, null], [1816, 0.3236, null], [1841, 0.3236, null], [1866, 0.3236, null], [1892, 0.3236, \"class Solution {\\npublic:\\n vector<int> assignElements(vector<int>& groups, vector<int>& elements) {\\n int m=groups.size();\\n int n=elements.size();\\n\\n vector<int>assigned(m,-1);\\n unordered_map<int,int>mp;\\n\\n for(int i=0;i<n;i++){\\n if(mp.find(elements[i])==mp.end()){\\n mp[elements[i]]=i;\\n }\\n }\\n\\n set<int>st;\\n\\n for(int i=0;i<groups.size();i++){\\n st.clear();\\n for(int j=1;j<=sqrt(groups[i]);j++){\\n if(groups[i]%j==0){\\n if(mp.find(j)!=mp.end())\\n st.insert(mp[j]);\\n if(mp.find(groups[i]/j)!=mp.end())\\n st.insert(mp[groups[i]/j]);\\n }\\n }\\n if(!st.empty()){\\n assigned[i]=*st.begin();\\n }\\n }\\n\\n return assigned;\\n }\\n};\"], [1917, 0.3236, \"class Solution {\\npublic:\\n\\n vector<int> factors(int n){\\n if (n == 1) return {1};\\n vector<int> res;\\n for(int i = 1; i*i<=n; i++){\\n if (n%i == 0) {\\n res.push_back(i);\\n if (i != n/i) {\\n res.push_back(n/i);\\n }\\n }\\n }\\n // cout << \\\"Factors of \\\" << n << ' ';\\n // for(auto& e: res) {\\n // cout << e << ' '; \\n // }\\n // cout << '\\\\n';\\n return res;\\n }\\n\\n vector<int> assignElements(vector<int>& groups, vector<int>& elements) {\\n int gn = groups.size();\\n int en = elements.size();\\n\\n map<int,int> idx;\\n for(int i = en-1; i>=0; i--) {\\n idx[elements[i]] = i;\\n }\\n\\n // for(auto& p: idx) {\\n // cout << \\\"M \\\" << p.first << \\\", \\\" << p.second << '\\\\n';\\n // }\\n\\n vector<int> ans(gn, -1);\\n\\n for(int i = 0; i<gn; i++) {\\n vector<int> f = factors(groups[i]);\\n int foundAt = en;\\n for(auto& e: f) {\\n // cout << \\\"For \\\" << groups[i] << \\\" f \\\" << e << ' '; \\n if (idx.count(e) > 0) {\\n foundAt = min(foundAt, idx[e]);\\n }\\n // cout << \\\"foundAt \\\" << foundAt << '\\\\n';\\n }\\n ans[i] = foundAt == en ? -1 : foundAt;\\n }\\n\\n return ans;\\n }\\n};\"], [2754, 5.1843, \"class Solution {\\npublic:\\n vector<int> assignElements(vector<int>& groups, vector<int>& elements) {\\n const int MAX_ELEMENT = 100000;\\n vector<int> element_indices(MAX_ELEMENT + 1, -1);\\n for (int i = 0; i < elements.size(); ++i) {\\n int e = elements[i];\\n if (element_indices[e] == -1) {\\n element_indices[e] = i;\\n }\\n }\\n \\n vector<int> assigned;\\n for (int g : groups) {\\n int min_idx = -1;\\n unordered_set<int> divisors;\\n for (int i = 1; i * i <= g; ++i) {\\n if (g % i == 0) {\\n divisors.insert(i);\\n divisors.insert(g / i);\\n }\\n }\\n for (int d : divisors) {\\n int idx = element_indices[d];\\n if (idx != -1) {\\n if (min_idx == -1 || idx < min_idx) {\\n min_idx = idx;\\n }\\n }\\n }\\n assigned.push_back(min_idx);\\n }\\n return assigned;\\n }\\n};\"]]"
},
"golang": {
"code": "func assignElements(groups []int, elements []int) []int {\n elementIndices := make(map[int]int)\n for idx, val := range elements {\n if _, exists := elementIndices[val]; !exists {\n elementIndices[val] = idx\n }\n }\n \n assigned := make([]int, len(groups))\n for i, g := range groups {\n minIndex := -1\n divisors := make(map[int]struct{})\n for d := 1; d*d <= g; d++ {\n if g%d == 0 {\n divisors[d] = struct{}{}\n divisors[g/d] = struct{}{}\n }\n }\n for d := range divisors {\n if idx, ok := elementIndices[d]; ok {\n if minIndex == -1 || idx < minIndex {\n minIndex = idx\n }\n }\n }\n assigned[i] = minIndex\n }\n return assigned\n}",
"memory": 1600,
"memoryDistribution": "[[1600, 62.5, \"func assignElements(groups []int, elements []int) []int {\\n elementIndices := make(map[int]int)\\n for idx, val := range elements {\\n if _, exists := elementIndices[val]; !exists {\\n elementIndices[val] = idx\\n }\\n }\\n \\n assigned := make([]int, len(groups))\\n for i, g := range groups {\\n minIndex := -1\\n divisors := make(map[int]struct{})\\n for d := 1; d*d <= g; d++ {\\n if g%d == 0 {\\n divisors[d] = struct{}{}\\n divisors[g/d] = struct{}{}\\n }\\n }\\n for d := range divisors {\\n if idx, ok := elementIndices[d]; ok {\\n if minIndex == -1 || idx < minIndex {\\n minIndex = idx\\n }\\n }\\n }\\n assigned[i] = minIndex\\n }\\n return assigned\\n}\"], [12000, 12.5, \"package main\\n\\nfunc assignElements(groups []int, elements []int) []int {\\n\\tconst maxVal = 100000\\n\\tbest := make([]int, maxVal+1)\\n\\tfor i := 0; i <= maxVal; i++ {\\n\\t\\tbest[i] = -1\\n\\t}\\n\\tfor j, val := range elements {\\n\\t\\tif best[val] == -1 || j < best[val] {\\n\\t\\t\\tbest[val] = j\\n\\t\\t}\\n\\t}\\n\\tres := make([]int, len(groups))\\n\\tfor i, g := range groups {\\n\\t\\tminIndex := 1<<31 - 1\\n\\t\\tfor d := 1; d*d <= g; d++ {\\n\\t\\t\\tif g%d == 0 {\\n\\t\\t\\t\\tif d <= maxVal && best[d] != -1 && best[d] < minIndex {\\n\\t\\t\\t\\t\\tminIndex = best[d]\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\tdiv := g / d\\n\\t\\t\\t\\tif div != d && div <= maxVal && best[div] != -1 && best[div] < minIndex {\\n\\t\\t\\t\\t\\tminIndex = best[div]\\n\\t\\t\\t\\t}\\n\\t\\t\\t}\\n\\t\\t}\\n\\t\\tif minIndex == 1<<31-1 {\\n\\t\\t\\tres[i] = -1\\n\\t\\t} else {\\n\\t\\t\\tres[i] = minIndex\\n\\t\\t}\\n\\t}\\n\\treturn res\\n}\"], [14900, 12.5, \"func assignElements(groups []int, elements []int) []int {\\n elementMap := make(map[int]int, len(elements))\\n res := make([]int, len(groups))\\n for eIndex, eVal := range elements {\\n if v, exist := elementMap[eVal]; exist {\\n elementMap[eVal] = min(v, eIndex)\\n } else {\\n elementMap[eVal] = eIndex\\n }\\n }\\n var minDivider int\\n for gIndex, gVal := range groups {\\n res[gIndex] = -1\\n minDivider = math.MaxInt\\n for i := 1; i <= int(math.Sqrt(float64(gVal))); i++ {\\n if gVal % i == 0 {\\n if index, exist := elementMap[i]; exist {\\n minDivider = min(minDivider, index)\\n }\\n if i != gVal / i {\\n if index, exist := elementMap[gVal/i]; exist {\\n minDivider = min(minDivider, index)\\n }\\n }\\n }\\n }\\n if minDivider != math.MaxInt {\\n res[gIndex] = minDivider\\n }\\n }\\n return res\\n}\"], [15600, 12.5, null], [16800, 12.5, null], [17200, 12.5, null], [17400, 12.5, \"func assignElements(groups []int, elements []int) []int {\\n elementMap := make(map[int]int, len(elements))\\n \\n res := make([]int, len(groups))\\n\\n for eIndex, eVal := range elements {\\n if v, exist := elementMap[eVal]; exist {\\n elementMap[eVal] = min(v, eIndex)\\n } else {\\n elementMap[eVal] = eIndex\\n }\\n }\\n\\n\\n var minDivider int\\n\\n for gIndex, gVal := range groups {\\n res[gIndex] = -1\\n minDivider = math.MaxInt\\n for i := 1; i <= int(math.Sqrt(float64(gVal))); i++ {\\n if gVal % i == 0 {\\n if index, exist := elementMap[i]; exist {\\n minDivider = min(minDivider, index)\\n }\\n if i != gVal / i {\\n if index, exist := elementMap[gVal/i]; exist {\\n minDivider = min(minDivider, index)\\n }\\n }\\n }\\n }\\n if minDivider != math.MaxInt {\\n res[gIndex] = minDivider\\n }\\n }\\n return res\\n}\"], [20500, 12.5, \"func assignElements(groups []int, elements []int) []int {\\n elementIndices := make(map[int]int)\\n for idx, val := range elements {\\n if _, exists := elementIndices[val]; !exists {\\n elementIndices[val] = idx\\n }\\n }\\n \\n assigned := make([]int, len(groups))\\n for i, g := range groups {\\n minIndex := -1\\n divisors := make(map[int]struct{})\\n for d := 1; d*d <= g; d++ {\\n if g%d == 0 {\\n divisors[d] = struct{}{}\\n divisors[g/d] = struct{}{}\\n }\\n }\\n for d := range divisors {\\n if idx, ok := elementIndices[d]; ok {\\n if minIndex == -1 || idx < minIndex {\\n minIndex = idx\\n }\\n }\\n }\\n assigned[i] = minIndex\\n }\\n return assigned\\n}\"]]",
"runtime": 1527,
"runtimeDistribution": "[[7, 12.5, \"func assignElements(groups []int, elements []int) []int {\\n\\tmx := slices.Max(groups)\\n\\tassigned := make([]int, mx+1)\\n\\tfor i := range assigned {\\n\\t\\tassigned[i] = -1\\n\\t}\\n\\tfor i, e := range elements {\\n\\t\\tif e > mx || assigned[e] >= 0 {\\n\\t\\t\\tcontinue\\n\\t\\t}\\n\\t\\tfor x := e; x <= mx; x += e {\\n\\t\\t\\tif assigned[x] < 0 {\\n\\t\\t\\t\\tassigned[x] = i\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\tfor i, g := range groups {\\n\\t\\tgroups[i] = assigned[g]\\n\\t}\\n\\treturn groups\\n}\"], [31, 12.5, \"func assignElements(groups []int, elements []int) []int {\\n\\tvar maxVal int\\n\\tfor _, g := range groups {\\n\\t\\tmaxVal = max(maxVal, g)\\n\\t}\\n\\tidxs := make([]int, maxVal+1)\\n\\tfor i := range idxs {\\n\\t\\tidxs[i] = -1\\n\\t}\\n\\tfor i, ele := range elements {\\n\\t\\tif ele >= len(idxs) || idxs[ele] != -1 {\\n\\t\\t\\tcontinue\\n\\t\\t}\\n\\t\\tfor j := 1; j*ele < len(idxs); j++ {\\n\\t\\t\\tif idxs[j*ele] != -1 {\\n\\t\\t\\t\\tcontinue\\n\\t\\t\\t}\\n\\t\\t\\tidxs[j*ele] = i\\n\\t\\t}\\n\\t}\\n\\tret := make([]int, 0, len(groups))\\n\\tfor _, g := range groups {\\n\\t\\tret = append(ret, idxs[g])\\n\\t}\\n\\treturn ret\\n}\\n\"], [160, 12.5, null], [247, 12.5, null], [491, 12.5, null], [667, 12.5, \"func assignElements(groups []int, elements []int) []int {\\n elementMap := make(map[int]int, len(elements))\\n \\n res := make([]int, len(groups))\\n\\n for eIndex, eVal := range elements {\\n if v, exist := elementMap[eVal]; exist {\\n elementMap[eVal] = min(v, eIndex)\\n } else {\\n elementMap[eVal] = eIndex\\n }\\n }\\n\\n\\n var minDivider int\\n\\n for gIndex, gVal := range groups {\\n res[gIndex] = -1\\n minDivider = math.MaxInt\\n for i := 1; i <= int(math.Sqrt(float64(gVal))); i++ {\\n if gVal % i == 0 {\\n if index, exist := elementMap[i]; exist {\\n minDivider = min(minDivider, index)\\n }\\n if i != gVal / i {\\n if index, exist := elementMap[gVal/i]; exist {\\n minDivider = min(minDivider, index)\\n }\\n }\\n }\\n }\\n if minDivider != math.MaxInt {\\n res[gIndex] = minDivider\\n }\\n }\\n return res\\n}\"], [668, 12.5, \"func assignElements(groups []int, elements []int) []int {\\n elementMap := make(map[int]int, len(elements))\\n res := make([]int, len(groups))\\n for eIndex, eVal := range elements {\\n if v, exist := elementMap[eVal]; exist {\\n elementMap[eVal] = min(v, eIndex)\\n } else {\\n elementMap[eVal] = eIndex\\n }\\n }\\n var minDivider int\\n for gIndex, gVal := range groups {\\n res[gIndex] = -1\\n minDivider = math.MaxInt\\n for i := 1; i <= int(math.Sqrt(float64(gVal))); i++ {\\n if gVal % i == 0 {\\n if index, exist := elementMap[i]; exist {\\n minDivider = min(minDivider, index)\\n }\\n if i != gVal / i {\\n if index, exist := elementMap[gVal/i]; exist {\\n minDivider = min(minDivider, index)\\n }\\n }\\n }\\n }\\n if minDivider != math.MaxInt {\\n res[gIndex] = minDivider\\n }\\n }\\n return res\\n}\"], [1527, 12.5, \"func assignElements(groups []int, elements []int) []int {\\n elementIndices := make(map[int]int)\\n for idx, val := range elements {\\n if _, exists := elementIndices[val]; !exists {\\n elementIndices[val] = idx\\n }\\n }\\n \\n assigned := make([]int, len(groups))\\n for i, g := range groups {\\n minIndex := -1\\n divisors := make(map[int]struct{})\\n for d := 1; d*d <= g; d++ {\\n if g%d == 0 {\\n divisors[d] = struct{}{}\\n divisors[g/d] = struct{}{}\\n }\\n }\\n for d := range divisors {\\n if idx, ok := elementIndices[d]; ok {\\n if minIndex == -1 || idx < minIndex {\\n minIndex = idx\\n }\\n }\\n }\\n assigned[i] = minIndex\\n }\\n return assigned\\n}\"]]"
},
"java": {
"code": "class Solution {\n public int[] assignElements(int[] groups, int[] elements) {\n Map<Integer, Integer> elementMap = new HashMap<>();\n for (int j = 0; j < elements.length; j++) {\n int elem = elements[j];\n if (!elementMap.containsKey(elem)) {\n elementMap.put(elem, j);\n }\n }\n\n int[] assigned = new int[groups.length];\n Set<Integer> divisors = new HashSet<>();\n\n for (int i = 0; i < groups.length; i++) {\n int g = groups[i];\n divisors.clear();\n for (int j = 1; j * j <= g; j++) {\n if (g % j == 0) {\n divisors.add(j);\n divisors.add(g / j);\n }\n }\n int minIndex = Integer.MAX_VALUE;\n for (int d : divisors) {\n if (elementMap.containsKey(d)) {\n int idx = elementMap.get(d);\n if (idx < minIndex) {\n minIndex = idx;\n }\n }\n }\n assigned[i] = (minIndex != Integer.MAX_VALUE) ? minIndex : -1;\n }\n\n return assigned;\n }\n}",
"memory": 6600,
"memoryDistribution": "[[6600, 86.6198, \"class Solution {\\n public int[] assignElements(int[] groups, int[] elements) {\\n Map<Integer, Integer> elementMap = new HashMap<>();\\n for (int j = 0; j < elements.length; j++) {\\n int elem = elements[j];\\n if (!elementMap.containsKey(elem)) {\\n elementMap.put(elem, j);\\n }\\n }\\n\\n int[] assigned = new int[groups.length];\\n Set<Integer> divisors = new HashSet<>();\\n\\n for (int i = 0; i < groups.length; i++) {\\n int g = groups[i];\\n divisors.clear();\\n for (int j = 1; j * j <= g; j++) {\\n if (g % j == 0) {\\n divisors.add(j);\\n divisors.add(g / j);\\n }\\n }\\n int minIndex = Integer.MAX_VALUE;\\n for (int d : divisors) {\\n if (elementMap.containsKey(d)) {\\n int idx = elementMap.get(d);\\n if (idx < minIndex) {\\n minIndex = idx;\\n }\\n }\\n }\\n assigned[i] = (minIndex != Integer.MAX_VALUE) ? minIndex : -1;\\n }\\n\\n return assigned;\\n }\\n}\"], [63200, 0.7042, \"class Solution {\\n private static final int M = (int)1e9;\\n public int[] assignElements(int[] groups, int[] elements) {\\n int n = groups.length;\\n\\n\\t\\tint max = 0;\\n\\t\\tfor (int i = 0; i < n; i++)\\n\\t\\t\\tmax = Math.max(max, groups[i]);\\n\\n\\t\\tint m = elements.length;\\n\\t\\tSet<Integer> values = new HashSet<>();\\n\\t\\tfor (int i = 0; i < m; i++)\\n\\t\\t\\tif (!values.add(elements[i]))\\n\\t\\t\\t\\telements[i] = 0; // mark duplicate elemets\\n \\n\\t\\tint[] valToIdx = new int[max + 1];\\n\\t\\tArrays.fill(valToIdx, -1);\\n\\n // for all possible elements, find all possible multiples, add idx to them\\n\\t\\tfor (int i = m - 1; i >= 0; i--) {\\n\\t\\t\\tint x = elements[i];\\n\\t\\t\\tif (x != 0) for (int y = x; y <= max; y += x) valToIdx[y] = i;\\n\\t\\t}\\n\\n\\t\\tint[] assigned = new int[n];\\n\\t\\tfor (int i = 0; i < n; i++) assigned[i] = valToIdx[groups[i]];\\n\\t\\treturn assigned;\\n }\\n}\\n/**\\n5 * 1 = 5\\n * 2 = 10\\n3 * 1 = 3\\n * 2 = 6\\n */\"], [63600, 0.7042, \"class Solution {\\n public int[] assignElements(int[] groups, int[] elements) {\\n int max = 0;\\n\\n for (int n : groups) {\\n max = Math.max(max, n);\\n }\\n\\n int[] indices = new int[max + 1];\\n Arrays.fill(indices, -1);\\n\\n for (int i = 0; i < elements.length; ++i) {\\n int n = elements[i];\\n\\n if (n > max || indices[n] >= 0) {\\n continue;\\n }\\n \\n for (int m = n; m <= max; m += n) {\\n if (indices[m] < 0) {\\n indices[m] = i;\\n }\\n }\\n }\\n\\n int[] result = new int[groups.length];\\n\\n for (int i = 0; i < result.length; ++i) {\\n result[i] = indices[groups[i]];\\n }\\n\\n return result;\\n }\\n}\"], [63900, 2.8169, null], [64000, 2.8169, null], [64099, 1.4085, null], [64200, 0.7042, null], [64300, 0.7042, null], [64500, 1.4085, null], [65000, 0.7042, null], [65400, 0.7042, null], [66000, 0.7042, null], [66100, 0.7042, null], [66200, 0.7042, null], [66300, 0.7042, null], [66400, 0.7042, null], [66500, 1.4085, null], [66600, 2.1127, null], [66700, 1.4085, null], [66800, 4.2254, null], [67000, 1.4085, null], [67200, 2.8169, null], [67300, 0.7042, null], [67400, 3.5211, null], [67500, 1.4085, null], [67600, 2.1127, null], [67700, 4.2254, null], [67800, 2.1127, null], [67900, 2.8169, null], [68000, 0.7042, null], [68100, 2.1127, null], [68200, 0.7042, null], [68300, 1.4085, null], [68400, 1.4085, null], [68500, 0.7042, null], [68600, 0.7042, null], [68800, 1.4085, null], [68900, 1.4085, null], [69000, 2.8169, null], [69200, 2.8169, null], [69300, 0.7042, null], [69400, 0.7042, null], [69500, 1.4085, null], [69600, 0.7042, null], [69700, 0.7042, null], [69900, 2.8169, null], [70000, 2.1127, null], [70100, 4.2254, null], [70200, 2.1127, null], [70300, 5.6338, null], [70400, 2.8169, null], [70600, 1.4085, null], [70700, 0.7042, null], [76400, 0.7042, null], [76500, 0.7042, null], [77800, 0.7042, null], [79700, 0.7042, null], [81100, 0.7042, null], [84000, 0.7042, null], [85400, 0.7042, \"class Solution {\\n public int[] assignElements(int[] groups, int[] elements) {\\n int n = groups.length;\\n HashMap<Integer,ArrayList<Integer>> valueToIdx = new HashMap<>();\\n int index = 0;\\n int max = -(int)1e9;\\n for(int group:groups){\\n max = Math.max(max,group);\\n ArrayList<Integer> list = valueToIdx.getOrDefault(group,new ArrayList<>());\\n list.add(index++);\\n valueToIdx.put(group,list);\\n }\\n Arrays.fill(groups,-1);\\n\\n int[] elementMap = new int[(int)1e5+1];\\n Arrays.fill(elementMap,-1);\\n\\n ArrayList<Integer> uniqueElement = new ArrayList<>();\\n int element_idx = 0;\\n for(int element : elements){\\n if(elementMap[element]==-1){\\n uniqueElement.add(element);\\n elementMap[element] = element_idx;\\n }\\n element_idx++;\\n }\\n\\n\\n for(int divisor : uniqueElement){\\n int multiplier = 1;\\n int value = divisor*multiplier;\\n while((value)<=max){\\n if(valueToIdx.containsKey(value)){\\n ArrayList<Integer> indexes = valueToIdx.get(value);\\n for(int idx : indexes)\\n groups[idx] = elementMap[divisor];\\n valueToIdx.remove(value);\\n }\\n\\n multiplier++;\\n value = (divisor*multiplier);\\n }\\n }\\n return groups;\\n }\\n}\"], [85700, 0.7042, \"class Solution {\\n //https://leetcode.com/problems/assign-elements-to-groups-with-constraints/solutions/6396012/python-beat-100-o-nlogn/\\n public int[] assignElements(int[] groups, int[] elements) {\\n int[] res = new int[groups.length];\\n Map<Integer, Integer> m = new HashMap<>();\\n int max = Integer.MIN_VALUE;\\n for(int a: groups) {\\n max = Math.max(max, a);\\n }\\n Set<Integer> h = new HashSet<>();\\n for(int j=0; j<elements.length; j++) {\\n if(h.contains(elements[j])) continue;\\n h.add(elements[j]);\\n if(elements[j]==1) {\\n for(int a:groups) {\\n if(!m.containsKey(a)) {\\n m.put(a, j);\\n }\\n }\\n break;\\n }\\n \\n int i=1;\\n while(true) {\\n int t = elements[j]*i;\\n if(t>max)break;\\n if(!m.containsKey(t)) {\\n m.put(t, j);\\n }\\n i++;\\n \\n }\\n }\\n \\n for(int i=0; i<groups.length; i++) {\\n res[i]=m.getOrDefault(groups[i], -1);\\n }\\n return res;\\n }\\n}\"]]",
"runtime": 1416,
"runtimeDistribution": "[[11, 9.8592, \"class Solution {\\n public int[] assignElements(int[] groups, int[] elements) {\\n int[] temp = new int[getMax(groups)];\\n Arrays.fill(temp, -1);\\n int index = -1;\\n for(int element : elements){\\n ++index;\\n if( element >= temp.length || temp[element] != -1){\\n continue;\\n }\\n for(int i = element; i < temp.length; i += element){\\n if(temp[i] == -1){\\n temp[i] = index;\\n }\\n }\\n }\\n\\n for(int i = 0; i < groups.length; ++i){\\n groups[i] = temp[groups[i]];\\n }\\n\\n return groups;\\n }\\n\\n private int getMax(int[] nums){\\n int max = -1;\\n for(int num : nums){\\n max = Math.max(num, max);\\n }\\n return max + 1;\\n }\\n}\"], [23, 1.4084, \"class Solution {\\n private static final int M = (int)1e9;\\n public int[] assignElements(int[] groups, int[] elements) {\\n int n = groups.length;\\n\\n\\t\\tint max = 0;\\n\\t\\tfor (int i = 0; i < n; i++)\\n\\t\\t\\tmax = Math.max(max, groups[i]);\\n\\n\\t\\tint m = elements.length;\\n\\t\\tSet<Integer> values = new HashSet<>();\\n\\t\\tfor (int i = 0; i < m; i++)\\n\\t\\t\\tif (!values.add(elements[i]))\\n\\t\\t\\t\\telements[i] = 0; // mark duplicate elemets\\n \\n\\t\\tint[] valToIdx = new int[max + 1];\\n\\t\\tArrays.fill(valToIdx, -1);\\n\\n // for all possible elements, find all possible multiples, add idx to them\\n\\t\\tfor (int i = m - 1; i >= 0; i--) {\\n\\t\\t\\tint x = elements[i];\\n\\t\\t\\tif (x != 0) for (int y = x; y <= max; y += x) valToIdx[y] = i;\\n\\t\\t}\\n\\n\\t\\tint[] assigned = new int[n];\\n\\t\\tfor (int i = 0; i < n; i++) assigned[i] = valToIdx[groups[i]];\\n\\t\\treturn assigned;\\n }\\n}\\n/**\\n5 * 1 = 5\\n * 2 = 10\\n3 * 1 = 3\\n * 2 = 6\\n */\"], [35, 1.4084, null], [47, 0.7042, null], [59, 0.7042, null], [70, 0.7042, null], [82, 10.563500000000001, null], [94, 2.8169000000000004, null], [106, 0.7042, null], [118, 0.7042, null], [130, 0.7042, null], [141, 0.7042, null], [153, 0.7042, null], [165, 0.7042, null], [177, 0.7042, null], [189, 0.7042, null], [200, 0.7042, null], [212, 0.7042, null], [224, 0.7042, null], [236, 0.7042, null], [248, 0.7042, null], [259, 0.7042, null], [271, 0.7042, null], [283, 0.7042, null], [295, 0.7042, null], [307, 0.7042, null], [319, 0.7042, null], [330, 0.7042, null], [342, 0.7042, null], [354, 0.7042, null], [366, 0.7042, null], [378, 0.7042, null], [389, 0.7042, null], [401, 0.7042, null], [413, 1.4085, null], [425, 0.7042, null], [437, 0.7042, null], [448, 0.7042, null], [460, 1.4085, null], [472, 0.7042, null], [484, 0.7042, null], [496, 3.5211000000000006, null], [508, 12.676300000000001, null], [519, 5.633700000000001, null], [531, 3.5212000000000003, null], [543, 0.7042, null], [555, 0.7042, null], [567, 0.7042, null], [578, 0.7042, null], [590, 0.7042, null], [602, 1.4084, null], [614, 0.7042, null], [626, 2.8168, null], [637, 1.4084, null], [649, 1.4084, null], [661, 0.7042, null], [673, 0.7042, null], [685, 0.7042, null], [697, 0.7042, null], [708, 0.7042, null], [720, 0.7042, \"class Solution {\\n\\n int find(List<int[]> list, int value) {\\n int l = 0, h = list.size() - 1;\\n while (l <= h) {\\n int m = l + (h - l) / 2;\\n if (list.get(m)[0] == value) return m;\\n else if (list.get(m)[0] > value) h = m - 1;\\n else l = m + 1;\\n }\\n return l;\\n }\\n\\n public int[] assignElements(int[] gs, int[] es) {\\n int[] res = new int[gs.length];\\n\\n Map<Integer, Integer> eMap = new LinkedHashMap<>(); \\n for (int i = 0 ; i < es.length ; i ++) if (!eMap.containsKey(es[i])) eMap.put(es[i], i); \\n\\n Map<Integer, Integer> cache = new HashMap<>();\\n for (int i = 0 ; i < gs.length ; i ++) {\\n if (cache.containsKey(gs[i])) {\\n res[i] = cache.get(gs[i]);\\n continue;\\n }\\n int found = Integer.MAX_VALUE; \\n for (int f = 1; f*f <= gs[i]; ++f) {\\n if(gs[i] % f == 0 && eMap.containsKey(f)) found = Math.min(found, eMap.get(f)); \\n if(gs[i] % f == 0 && eMap.containsKey(gs[i] / f)) found = Math.min(found, eMap.get(gs[i] / f)); \\n }\\n if (found == Integer.MAX_VALUE) found = -1;\\n cache.put(gs[i], res[i] = found);\\n }\\n return res;\\n\\n //[8,4,3,2]\\n //[4:0][2:1]\\n\\n //g=[8,4,3,2,4]\\n //e=[4,2]\\n //r=[0,0,-1,-1,0]\\n \\n //[2,3,5,7]\\n //[5,3,3]\\n //[-1,1,0,-1]\\n\\n //[10,21,30,41]\\n //[2,1]\\n //[0,-1,0,-1]\\n //[0,1,0,1]\\n }\\n}\"], [732, 0.7042, \"class Solution \\n{\\n public int[] assignElements(int[] groups, int[] elements) \\n {\\n HashMap<Integer,Integer> map = new HashMap<>();\\n for(int i = elements.length-1;i>=0;i--)\\n {\\n map.put(elements[i],i);\\n }\\n HashMap<Integer,Integer> ansmap = new HashMap<>();\\n int[] ans = new int[groups.length];\\n int k=0;\\n for(int i : groups)\\n {\\n if(ansmap.containsKey(i))\\n {\\n ans[k++] = ansmap.get(i);\\n continue;\\n } \\n HashSet<Integer> divisors = getDivisors(i);\\n //System.out.println(i+\\\" \\\"+divisors);\\n int min = Integer.MAX_VALUE;\\n for(int d : divisors)\\n {\\n min = Math.min(min,map.getOrDefault(d,Integer.MAX_VALUE));\\n }\\n min = Math.min(min,map.getOrDefault(1,Integer.MAX_VALUE));\\n if(min == Integer.MAX_VALUE)\\n {\\n min = -1;\\n }\\n\\n ans[k++] = min;\\n }\\n return ans;\\n }\\n public HashSet<Integer> getDivisors(int num)\\n {\\n HashSet<Integer> lis = new HashSet<>();\\n int rooted = (int)Math.sqrt(num);\\n for(int i = 2; i<= rooted;i++ )\\n {\\n if(num%i == 0)\\n {\\n lis.add(i);\\n lis.add(num/i);\\n //i++;\\n }\\n }\\n lis.add(num);\\n return lis;\\n }\\n}\"], [1416, 5.6349, \"class Solution {\\n public int[] assignElements(int[] groups, int[] elements) {\\n Map<Integer, Integer> elementMap = new HashMap<>();\\n for (int j = 0; j < elements.length; j++) {\\n int elem = elements[j];\\n if (!elementMap.containsKey(elem)) {\\n elementMap.put(elem, j);\\n }\\n }\\n\\n int[] assigned = new int[groups.length];\\n Set<Integer> divisors = new HashSet<>();\\n\\n for (int i = 0; i < groups.length; i++) {\\n int g = groups[i];\\n divisors.clear();\\n for (int j = 1; j * j <= g; j++) {\\n if (g % j == 0) {\\n divisors.add(j);\\n divisors.add(g / j);\\n }\\n }\\n int minIndex = Integer.MAX_VALUE;\\n for (int d : divisors) {\\n if (elementMap.containsKey(d)) {\\n int idx = elementMap.get(d);\\n if (idx < minIndex) {\\n minIndex = idx;\\n }\\n }\\n }\\n assigned[i] = (minIndex != Integer.MAX_VALUE) ? minIndex : -1;\\n }\\n\\n return assigned;\\n }\\n}\"]]"
},
"javascript": {
"code": "var assignElements = function(groups, elements) {\n const elementMap = {};\n for (let j = 0; j < elements.length; j++) {\n const val = elements[j];\n if (!(val in elementMap)) {\n elementMap[val] = j;\n }\n }\n\n const assigned = [];\n for (const g of groups) {\n const divisors = new Set();\n for (let i = 1; i * i <= g; i++) {\n if (g % i === 0) {\n divisors.add(i);\n divisors.add(g / i);\n }\n }\n let minIndex = Infinity;\n for (const d of divisors) {\n if (elementMap.hasOwnProperty(d)) {\n if (elementMap[d] < minIndex) {\n minIndex = elementMap[d];\n }\n }\n }\n assigned.push(minIndex === Infinity ? -1 : minIndex);\n }\n return assigned;\n};",
"memory": 9500,
"memoryDistribution": "[[9500, 40.0, \"var assignElements = function(groups, elements) {\\n const elementMap = {};\\n for (let j = 0; j < elements.length; j++) {\\n const val = elements[j];\\n if (!(val in elementMap)) {\\n elementMap[val] = j;\\n }\\n }\\n\\n const assigned = [];\\n for (const g of groups) {\\n const divisors = new Set();\\n for (let i = 1; i * i <= g; i++) {\\n if (g % i === 0) {\\n divisors.add(i);\\n divisors.add(g / i);\\n }\\n }\\n let minIndex = Infinity;\\n for (const d of divisors) {\\n if (elementMap.hasOwnProperty(d)) {\\n if (elementMap[d] < minIndex) {\\n minIndex = elementMap[d];\\n }\\n }\\n }\\n assigned.push(minIndex === Infinity ? -1 : minIndex);\\n }\\n return assigned;\\n};\"], [90400, 10.0, \"var assignElements = function(groups, elements) {\\n const elementMap = {};\\n for (let j = 0; j < elements.length; j++) {\\n const val = elements[j];\\n if (!(val in elementMap)) {\\n elementMap[val] = j;\\n }\\n }\\n\\n const assigned = [];\\n for (const g of groups) {\\n const divisors = new Set();\\n for (let i = 1; i * i <= g; i++) {\\n if (g % i === 0) {\\n divisors.add(i);\\n divisors.add(g / i);\\n }\\n }\\n let minIndex = Infinity;\\n for (const d of divisors) {\\n if (elementMap.hasOwnProperty(d)) {\\n if (elementMap[d] < minIndex) {\\n minIndex = elementMap[d];\\n }\\n }\\n }\\n assigned.push(minIndex === Infinity ? -1 : minIndex);\\n }\\n return assigned;\\n};\"], [91100, 10.0, \"/**\\n * @param {number[]} groups\\n * @param {number[]} elements\\n * @return {number[]}\\n */\\nvar assignElements = function (groups, elements) {\\n const n = groups.length\\n const m = elements.length\\n let res = new Array(n).fill(-1)\\n let map = {}\\n let max = 0\\n for (let i = 0; i < m; i++) {\\n if (map[elements[i]] == null) {\\n map[elements[i]] = i\\n }\\n }\\n\\n for(let j=0;j<n;j++){\\n res[j] = helper(groups[j], map)\\n }\\n\\n return res\\n};\\n\\nconst helper = (group, map) => {\\n let min = Infinity\\n for (let i = 1; i * i <= group; i++) {\\n if (group % i === 0) {\\n if (map[i] != null) {\\n min = Math.min(min, map[i])\\n }\\n if (i != group / i && map[group / i] != null) {\\n min = Math.min(min, map[group / i])\\n }\\n }\\n }\\n\\n return min === Infinity ? -1 : min\\n}\"], [91200, 10.0, null], [93700, 10.0, null], [94200, 10.0, null], [94300, 10.0, null], [96400, 10.0, null], [105100, 10.0, \"/**\\n * @param {number[]} groups\\n * @param {number[]} elements\\n * @return {number[]}\\n */\\nvar assignElements = function(groups, elements) {\\n let divisors = {};\\n for(let i = elements.length - 1; i >= 0; i--){\\n divisors[elements[i]] = i;\\n }\\n let nums = {};\\n for(let i = 0; i < groups.length; i++){\\n if(nums[groups[i]]) nums[groups[i]].push(i);\\n else nums[groups[i]] = [i];\\n groups[i] = -1;\\n }\\n // console.log(divisors, nums)\\n for(let n in nums){\\n let lowest = Infinity;\\n for(let i = 1; i <= Math.sqrt(n); i++){\\n if(n % i != 0) continue;\\n if(divisors.hasOwnProperty(n / i)) lowest = Math.min(lowest, divisors[n / i]);\\n if(divisors.hasOwnProperty(i)) lowest = Math.min(lowest, divisors[i]);\\n // console.log(i, n / i, lowest)\\n }\\n if(lowest != Infinity){\\n nums[n].forEach((e) => groups[e] = lowest);\\n } \\n }\\n return groups;\\n};\\n\\n\"], [106200, 10.0, \"/**\\n * @param {number[]} groups\\n * @param {number[]} elements\\n * @return {number[]}\\n */\\nvar assignElements = function(groups, elements) {\\n let divisors = {};\\n for(let i = elements.length - 1; i >= 0; i--){\\n divisors[elements[i]] = i;\\n }\\n let nums = {};\\n for(let i = 0; i < groups.length; i++){\\n if(nums[groups[i]]) nums[groups[i]].push(i);\\n else nums[groups[i]] = [i];\\n groups[i] = -1;\\n }\\n for(let n in nums){\\n let lowest = Infinity;\\n for(let i = 1; i <= Math.sqrt(n); i++){\\n if(n % i != 0) continue;\\n lowest = Math.min(lowest, divisors[n / i] ?? Infinity, divisors[i] ?? Infinity)\\n // if(divisors.hasOwnProperty(n / i)) lowest = Math.min(lowest, divisors[n / i]);\\n // if(divisors.hasOwnProperty(i)) lowest = Math.min(lowest, divisors[i]);\\n }\\n if(lowest != Infinity){\\n nums[n].forEach((e) => groups[e] = lowest);\\n } \\n }\\n return groups;\\n};\\n\\n\"]]",
"runtime": 892,
"runtimeDistribution": "[[38, 10.0, \"/**\\n * @param {number[]} groups\\n * @param {number[]} elements\\n * @return {number[]}\\n */\\nvar assignElements = function(groups, elements) {\\n // let divisors = {};\\n // for(let i = elements.length - 1; i >= 0; i--){\\n // divisors[elements[i]] = i;\\n // }\\n // let nums = {};\\n // for(let i = 0; i < groups.length; i++){\\n // if(nums[groups[i]]) nums[groups[i]].push(i);\\n // else nums[groups[i]] = [i];\\n // groups[i] = -1;\\n // }\\n // for(let n in nums){\\n // let lowest = Infinity;\\n // for(let i = 1; i <= Math.sqrt(n); i++){\\n // if(n % i != 0) continue;\\n // lowest = Math.min(lowest, divisors[n / i] ?? Infinity, divisors[i] ?? Infinity);\\n // }\\n // if(lowest != Infinity){\\n // nums[n].forEach((e) => groups[e] = lowest);\\n // } \\n // }\\n // return groups;\\n\\n let max = Math.max(...groups);\\n let arr = new Array(max+1).fill(-1);\\n for(let i = 0; i < elements.length; i++){\\n if(elements[i] > max || arr[elements[i]] != -1) continue;\\n for(let j = elements[i]; j <= max; j += elements[i]){\\n if(arr[j] == -1) arr[j] = i;\\n }\\n }\\n\\n for(let i = 0; i < groups.length; i++){\\n groups[i] = arr[groups[i]];\\n }\\n console.log(arr)\\n return groups;\\n};\\n\\n\"], [116, 10.0, \"/**\\n * @param {number[]} groups\\n * @param {number[]} elements\\n * @return {number[]}\\n */\\nvar assignElements = function(groups, elements) {\\n let hashMap = {}\\n let maxEle = Math.max(...groups)\\n for(let i=0;i<elements.length;i++){\\n let ele = elements[i]\\n if(!hashMap.hasOwnProperty(elements[i])){\\n while(ele <= maxEle){\\n if(!hashMap.hasOwnProperty(ele))\\n hashMap[ele] = i\\n ele += elements[i]\\n }\\n }\\n }\\n let assigned = []\\n for(let grp of groups){\\n if(hashMap.hasOwnProperty(grp))\\n assigned.push(hashMap[grp])\\n else\\n assigned.push(-1)\\n }\\n\\n return assigned;\\n}\"], [227, 10.0, null], [380, 10.0, null], [502, 10.0, null], [532, 10.0, null], [886, 10.0, null], [892, 30.0, \"var assignElements = function(groups, elements) {\\n const elementMap = {};\\n for (let j = 0; j < elements.length; j++) {\\n const val = elements[j];\\n if (!(val in elementMap)) {\\n elementMap[val] = j;\\n }\\n }\\n\\n const assigned = [];\\n for (const g of groups) {\\n const divisors = new Set();\\n for (let i = 1; i * i <= g; i++) {\\n if (g % i === 0) {\\n divisors.add(i);\\n divisors.add(g / i);\\n }\\n }\\n let minIndex = Infinity;\\n for (const d of divisors) {\\n if (elementMap.hasOwnProperty(d)) {\\n if (elementMap[d] < minIndex) {\\n minIndex = elementMap[d];\\n }\\n }\\n }\\n assigned.push(minIndex === Infinity ? -1 : minIndex);\\n }\\n return assigned;\\n};\"], [1286, 10.0, \"var assignElements = function(groups, elements) {\\n let grm = new Map();\\n for (let [i,g] of groups.entries()) {\\n let gg = grm.get(g);\\n if (!gg) grm.set(g, [i]);\\n else gg.push(i);\\n }\\n\\n let result = groups.map((v, i) => -1);\\n\\n let seen = new Set();\\n\\n for (let [ei, el] of elements.entries()) {\\n if (seen.has(el)) continue;\\n seen.add(el);\\n \\n for (let tot = el; tot <= 1e5; tot += el) {\\n let gg = grm.get(tot);\\n if (gg === undefined) continue;\\n for (let gi of gg) result[gi] = ei;\\n grm.delete(tot);\\n }\\n }\\n\\n return result;\\n};\"], [2524, 10.0, \"/**\\n * @param {number[]} groups\\n * @param {number[]} elements\\n * @return {number[]}\\n */\\nvar assignElements = function(groups, elements) {\\n let divisors = {};\\n for(let i = elements.length - 1; i >= 0; i--){\\n divisors[elements[i]] = i;\\n }\\n let nums = {};\\n for(let i = 0; i < groups.length; i++){\\n if(nums[groups[i]]) nums[groups[i]].push(i);\\n else nums[groups[i]] = [i];\\n groups[i] = -1;\\n }\\n // console.log(divisors, nums)\\n for(let n in nums){\\n let lowest = Infinity;\\n for(let i = 1; i <= Math.sqrt(n); i++){\\n if(n % i != 0) continue;\\n if(divisors.hasOwnProperty(n / i)) lowest = Math.min(lowest, divisors[n / i]);\\n if(divisors.hasOwnProperty(i)) lowest = Math.min(lowest, divisors[i]);\\n // console.log(i, n / i, lowest)\\n }\\n if(lowest != Infinity){\\n nums[n].forEach((e) => groups[e] = lowest);\\n } \\n }\\n return groups;\\n};\\n\\n\"]]"
},
"python3": {
"code": "class Solution:\n def assignElements(self, groups: List[int], elements: List[int]) -> List[int]:\n element_map = {}\n for idx, val in enumerate(elements):\n if val not in element_map:\n element_map[val] = idx\n \n assigned = []\n for g in groups:\n divisors = set()\n for i in range(1, int(math.isqrt(g)) + 1):\n if g % i == 0:\n divisors.add(i)\n divisors.add(g // i)\n candidates = []\n for d in divisors:\n if d in element_map:\n candidates.append(element_map[d])\n if candidates:\n assigned.append(min(candidates))\n else:\n assigned.append(-1)\n return assigned",
"memory": 4600,
"memoryDistribution": "[[4600, 66.4433, \"import math\\nfrom typing import List\\n\\nclass Solution:\\n def assignElements(self, groups: List[int], elements: List[int]) -> List[int]:\\n element_map = {}\\n for idx, val in enumerate(elements):\\n if val not in element_map:\\n element_map[val] = idx\\n \\n assigned = []\\n for g in groups:\\n divisors = set()\\n for i in range(1, int(math.isqrt(g)) + 1):\\n if g % i == 0:\\n divisors.add(i)\\n divisors.add(g // i)\\n candidates = []\\n for d in divisors:\\n if d in element_map:\\n candidates.append(element_map[d])\\n if candidates:\\n assigned.append(min(candidates))\\n else:\\n assigned.append(-1)\\n return assigned\"], [34500, 0.6711, \"class Solution:\\n def assignElements(self, groups: List[int], elements: List[int]) -> List[int]:\\n m,n = len(groups),len(elements)\\n if m*n<1000:\\n for i,v in enumerate(groups):\\n for j,u in enumerate(elements):\\n if v%u==0:\\n groups[i] = j\\n break\\n else:\\n groups[i] = -1\\n return groups\\n #\\n bound = max(groups)+1\\n p = [-1]*bound\\n for i,v in enumerate(elements):\\n if p[v] != -1: continue\\n for j in range(v,bound,v):\\n if p[j]==-1: p[j] = i\\n #\\n for i,v in enumerate(groups):\\n groups[i] = p[v]\\n return groups\"], [37200, 1.3423, \"class Solution:\\n def assignElements(self, groups: List[int], elements: List[int]) -> List[int]:\\n\\n high_bound = max(groups)\\n multiple = [None] * (high_bound + 1)\\n\\n for i,element in enumerate(elements):\\n if element < len(multiple) and multiple[element] is None:\\n for j in range(element,high_bound+1,element):\\n if multiple[j] is None:\\n multiple[j] = i\\n\\n n = len(groups)\\n res = [-1] * n\\n\\n for i,group in enumerate(groups):\\n if multiple[group] is not None:\\n res[i] = multiple[group]\\n\\n return res\"], [37300, 2.6846, null], [37400, 0.6711, null], [37500, 2.0134, null], [37600, 1.3423, null], [37700, 0.6711, null], [38000, 0.6711, null], [38100, 0.6711, null], [38200, 0.6711, null], [39000, 0.6711, null], [39500, 0.6711, null], [42400, 1.3423, null], [42900, 0.6711, null], [43300, 0.6711, null], [44600, 0.6711, null], [45000, 0.6711, null], [45100, 4.698, null], [45200, 4.698, null], [45300, 2.6846, null], [45400, 2.0134, null], [45600, 1.3423, null], [45700, 1.3423, null], [45800, 0.6711, null], [45900, 3.3557, null], [46000, 2.6846, null], [46100, 13.4228, null], [46200, 9.396, null], [46300, 6.0403, null], [46400, 2.6846, null], [46500, 0.6711, null], [46600, 0.6711, null], [47200, 0.6711, null], [47300, 0.6711, null], [47400, 2.6846, null], [47500, 2.0134, null], [47600, 0.6711, null], [48400, 0.6711, null], [49500, 0.6711, null], [49700, 1.3423, null], [50600, 1.3423, null], [51500, 0.6711, null], [53600, 0.6711, null], [55100, 0.6711, null], [55700, 0.6711, null], [57000, 1.3423, null], [57400, 0.6711, null], [57500, 0.6711, null], [58100, 0.6711, null], [58200, 0.6711, null], [58300, 0.6711, null], [60100, 0.6711, null], [60500, 0.6711, null], [61900, 0.6711, null], [63800, 0.6711, \"class Solution:\\n def assignElements(self, groups: List[int], elements: List[int]) -> List[int]:\\n inds = defaultdict(list)\\n ma = 0\\n for i, g in enumerate(groups):\\n inds[g].append(i)\\n ma = max(ma, g)\\n res = [-1] * len(groups)\\n eInds = {}\\n for i, e in enumerate(elements):\\n if e in eInds:\\n continue\\n eInds[e] = i\\n for e in eInds:\\n for j in range(e, ma + 1, e):\\n if j in inds:\\n for ind in inds[j]:\\n i = eInds[e]\\n res[ind] = i if res[ind] == -1 else min(res[ind], i)\\n return res\"], [64400, 0.6711, \"from collections import defaultdict\\n\\n\\nclass Solution:\\n def assignElements(self, groups: List[int], elements: List[int]) -> List[int]:\\n indexes_by_group = defaultdict(list)\\n groups_count = len(groups)\\n for i in range(groups_count):\\n indexes_by_group[groups[i]].append(i)\\n unused_elems = set(indexes_by_group)\\n max_elem = max(unused_elems)\\n checked_elems = set()\\n\\n response = [-1] * groups_count\\n\\n for index, elem in enumerate(elements):\\n if elem in checked_elems:\\n continue\\n if not unused_elems:\\n return response\\n new_elem = elem\\n while new_elem <= max_elem:\\n if new_elem not in checked_elems:\\n if new_elem in unused_elems:\\n for i in indexes_by_group[new_elem]:\\n response[i] = index\\n unused_elems.remove(new_elem)\\n checked_elems.add(new_elem)\\n new_elem += elem\\n return response\"]]",
"runtime": 5284,
"runtimeDistribution": "[[186, 15.435599999999994, \"from collections import defaultdict\\nclass Solution:\\n def assignElements(self, groups: List[int], elements: List[int]) -> List[int]:\\n max_element=max(groups)\\n seen=[-1]*(max_element+1)\\n \\n for i,e in enumerate(elements):\\n if e> max_element or seen[e]!=-1:\\n continue\\n for j in range(e,max_element+1,e):\\n if seen[j]==-1:\\n seen[j]=i\\n if e==1:\\n break\\n ans=[-1]*len(groups)\\n for i,g in enumerate(groups):\\n ans[i]=seen[g]\\n return ans \\n\\n\\n\"], [288, 31.542499999999986, \"class Solution:\\n def assignElements(self, groups: List[int], elements: List[int]) -> List[int]:\\n # each number => smallest index\\n mp = {}\\n max_num = max(groups)\\n for i, e in enumerate(elements):\\n num = e\\n # \\u4f18\\u5316\\n if e not in mp:\\n while e <= max_num:\\n if e not in mp:\\n mp[e] = i\\n e += num\\n\\n res = []\\n for e in groups:\\n if e not in mp:\\n res.append(-1)\\n else:\\n res.append(mp[e])\\n \\n return res\\n \"], [390, 3.3555, null], [492, 5.3688, null], [594, 6.711, null], [697, 0.6711, null], [799, 0.6711, null], [901, 0.6711, null], [1003, 0.6711, null], [1106, 0.6711, null], [1208, 0.6711, null], [1310, 0.6711, null], [1412, 0.6711, null], [1514, 0.6711, null], [1617, 0.6711, null], [1719, 0.6711, null], [1821, 0.6711, null], [1923, 0.6711, null], [2025, 0.6711, null], [2128, 0.6711, null], [2230, 0.6711, null], [2332, 0.6711, null], [2434, 0.6711, null], [2536, 0.6711, null], [2639, 0.6711, null], [2741, 0.6711, null], [2843, 0.6711, null], [2945, 0.6711, null], [3048, 0.6711, null], [3150, 0.6711, null], [3252, 0.6711, null], [3354, 0.6711, null], [3456, 0.6711, null], [3559, 0.6711, null], [3661, 0.6711, null], [3763, 0.6711, null], [3865, 0.6711, null], [3967, 0.6711, null], [4070, 0.6711, null], [4172, 0.6711, null], [4274, 0.6711, null], [4376, 0.6711, null], [4479, 0.6711, null], [4581, 0.6711, null], [4683, 0.6711, null], [4785, 0.6711, null], [4887, 0.6711, null], [4990, 0.6711, null], [5092, 0.6711, null], [5194, 0.6711, null], [5284, 17.4536, \"import math\\nfrom typing import List\\n\\nclass Solution:\\n def assignElements(self, groups: List[int], elements: List[int]) -> List[int]:\\n element_map = {}\\n for idx, val in enumerate(elements):\\n if val not in element_map:\\n element_map[val] = idx\\n \\n assigned = []\\n for g in groups:\\n divisors = set()\\n for i in range(1, int(math.isqrt(g)) + 1):\\n if g % i == 0:\\n divisors.add(i)\\n divisors.add(g // i)\\n candidates = []\\n for d in divisors:\\n if d in element_map:\\n candidates.append(element_map[d])\\n if candidates:\\n assigned.append(min(candidates))\\n else:\\n assigned.append(-1)\\n return assigned\"], [5296, 0.6711, null], [5398, 0.6711, \"class Solution:\\n def assignElements(self, groups: List[int], elements: List[int]) -> List[int]:\\n \\\"\\\"\\\"\\n check divisors for each group - does it exist?\\n do we literally check every number less than it?\\n we can sqrt(num) + 1 and its reverse\\n checking for duplicates doesn't help\\n \\\"\\\"\\\"\\n num_to_smallest_i = {}\\n for i, num in enumerate(elements):\\n if num not in num_to_smallest_i:\\n num_to_smallest_i[num] = i\\n \\n assigned = [float('inf') for _ in range(len(groups))]\\n for i, group in enumerate(groups):\\n for div in range(1, int(math.sqrt(group)) + 1):\\n if group % div == 0 and num_to_smallest_i.get(div) != None:\\n assigned[i] = min(assigned[i], num_to_smallest_i[div])\\n if group % div == 0 and (group // div) != div and num_to_smallest_i.get(group // div) != None:\\n assigned[i] = min(assigned[i], num_to_smallest_i[group // div])\\n\\n for i in range(len(assigned)):\\n if assigned[i] == float('inf'):\\n assigned[i] = -1\\n\\n return assigned\"], [5501, 0.6711, \"class Solution:\\n def assignElements(self, groups: List[int], elements: List[int]) -> List[int]:\\n result = [-1] * len(groups)\\n\\n mapping = {}\\n\\n for idx, el in enumerate(elements):\\n if el not in mapping:\\n mapping[el] = idx\\n \\n def get_divisors(val):\\n i = 1\\n if val % 2 == 0:\\n add_val = 1\\n else:\\n add_val = 2\\n\\n while i * i <= val:\\n if val % i == 0:\\n yield i\\n yield val // i\\n i += add_val\\n\\n for idx, g in enumerate(groups):\\n min_idx = float(\\\"inf\\\")\\n for divisor in get_divisors(g):\\n min_idx = min(min_idx, mapping.get(divisor, float(\\\"inf\\\")))\\n\\n if min_idx != float(\\\"inf\\\"):\\n result[idx] = min_idx\\n\\n return result\\n\\n\\n \\n\"]]"
},
"ruby": {
"code": "def assign_elements(groups, elements)\n element_indices = Array.new(100001)\n elements.each_with_index { |val, idx| element_indices[val] ||= idx }\n max_group = groups.max\n candidate = Array.new(max_group + 1)\n (1..max_group).each do |d|\n next if element_indices[d].nil?\n d.step(max_group, d) do |m|\n candidate[m] = candidate[m].nil? ? element_indices[d] : [candidate[m], element_indices[d]].min\n end\n end\n groups.map { |g| candidate[g].nil? ? -1 : candidate[g] }\nend",
"memory": 30500,
"memoryDistribution": "[[30500, 100.0, \"def assign_elements(groups, elements)\\n element_indices = Array.new(100001)\\n elements.each_with_index { |val, idx| element_indices[val] ||= idx }\\n max_group = groups.max\\n candidate = Array.new(max_group + 1)\\n (1..max_group).each do |d|\\n next if element_indices[d].nil?\\n d.step(max_group, d) do |m|\\n candidate[m] = candidate[m].nil? ? element_indices[d] : [candidate[m], element_indices[d]].min\\n end\\n end\\n groups.map { |g| candidate[g].nil? ? -1 : candidate[g] }\\nend\"], [305400, 100.0, \"def assign_elements(groups, elements)\\n element_indices = Array.new(100001)\\n elements.each_with_index { |val, idx| element_indices[val] ||= idx }\\n max_group = groups.max\\n candidate = Array.new(max_group + 1)\\n (1..max_group).each do |d|\\n next if element_indices[d].nil?\\n d.step(max_group, d) do |m|\\n candidate[m] = candidate[m].nil? ? element_indices[d] : [candidate[m], element_indices[d]].min\\n end\\n end\\n groups.map { |g| candidate[g].nil? ? -1 : candidate[g] }\\nend\"]]",
"runtime": 624,
"runtimeDistribution": "[[624, 100.0, \"def assign_elements(groups, elements)\\n element_indices = Array.new(100001)\\n elements.each_with_index { |val, idx| element_indices[val] ||= idx }\\n max_group = groups.max\\n candidate = Array.new(max_group + 1)\\n (1..max_group).each do |d|\\n next if element_indices[d].nil?\\n d.step(max_group, d) do |m|\\n candidate[m] = candidate[m].nil? ? element_indices[d] : [candidate[m], element_indices[d]].min\\n end\\n end\\n groups.map { |g| candidate[g].nil? ? -1 : candidate[g] }\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list:
import random, math
random.seed(seed)
def serialize_list(lst):
return ",".join(map(str, lst))
# This function implements the provided sample solution.
def sample_solution(groups, elements):
element_map = {}
for idx, val in enumerate(elements):
if val not in element_map:
element_map[val] = idx
assigned = []
for g in groups:
divisors = set()
for i in range(1, int(math.isqrt(g)) + 1):
if g % i == 0:
divisors.add(i)
divisors.add(g // i)
candidates = []
for d in divisors:
if d in element_map:
candidates.append(element_map[d])
if candidates:
assigned.append(min(candidates))
else:
assigned.append(-1)
return assigned
test_cases = []
# Predefined test cases covering boundary, core and edge cases.
predefined = [
([1], [1]), # Minimal case.
([8,4,3,2,4], [4,2]), # Example 1.
([2,3,5,7], [5,3,3]), # Example 2.
([10,21,30,41], [2,1]), # Example 3.
([12,15,18,20], [2,3,5]) # Additional structured case.
]
idx = 0
while idx < len(predefined) and len(test_cases) < num_cases:
groups, elements = predefined[idx]
# Serialization: join groups and elements as comma‐separated numbers separated by a space.
inp = f"{serialize_list(groups)} {serialize_list(elements)}"
sol = sample_solution(groups, elements)
out = serialize_list(sol)
test_cases.append({"input": inp, "output": out})
idx += 1
# Generate additional random test cases if needed.
while len(test_cases) < num_cases:
len_groups = random.randint(1, 10)
len_elements = random.randint(1, 10)
groups = [random.randint(1, 100000) for _ in range(len_groups)]
elements = [random.randint(1, 100000) for _ in range(len_elements)]
inp = f"{serialize_list(groups)} {serialize_list(elements)}"
sol = sample_solution(groups, elements)
out = serialize_list(sol)
test_cases.append({"input": inp, "output": out})
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
# Deserializes a comma-separated list of integers.
def deserialize_output(s):
s = s.strip()
return [] if s == "" else list(map(int, s.split(",")))
expected = deserialize_output(expected_output)
program = deserialize_output(program_output)
return expected == program
|
[{"input": "1 1", "output": "0"}, {"input": "8,4,3,2,4 4,2", "output": "0,0,-1,1,0"}, {"input": "2,3,5,7 5,3,3", "output": "-1,1,0,-1"}, {"input": "10,21,30,41 2,1", "output": "0,1,0,1"}, {"input": "12,15,18,20 2,3,5", "output": "0,1,0,0"}, {"input": "97197,36049 32099", "output": "-1,-1"}, {"input": "96531,13435,88697,97081 71483,11396,77398", "output": "-1,-1,-1,-1"}, {"input": "3906,12281,28658,30496,66238,78908,3479 73564", "output": "-1,-1,-1,-1,-1,-1,-1"}, {"input": "54988,28894,58879,77237 36464,852,99459,20927,91507,55393,44598,36422,20380", "output": "-1,-1,-1,-1"}, {"input": "13397,12157,49798,12677 47053,45083,79132,34672,5696,95648", "output": "-1,-1,-1,-1"}, {"input": "16362,49616,10329,72358,38428,82398,81071,47401 75675,25204,92350,9117,6007,86674,29872,37931,10459", "output": "-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "49824,36435,59430,83321 47820,21320", "output": "-1,-1,-1,-1"}, {"input": "27461,87842,34994,91989,89594,84940 9359,79841,83228,22432,70011,95569", "output": "-1,-1,-1,-1,-1,-1"}, {"input": "60590,49736,35383,83887 90199,73001,28786", "output": "-1,-1,-1,-1"}, {"input": "30022,4208,41348,52582,35094,8676 27654", "output": "-1,-1,-1,-1,-1,-1"}, {"input": "27870,85910,65436,51857,84260,60143,18727,34719,18302,32326 97648,73580,70645,34439,97913,76623", "output": "-1,-1,-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "52351,47448,28747,18132,66785,64687,11916 99062,6176,14372,20034,82241,20970,89193,55334,78173,8327", "output": "-1,-1,-1,-1,-1,-1,-1"}, {"input": "78105,61349,69353,32954,72513,1505,89167 94467,15015,89354,70382,98420,34974,84013", "output": "-1,-1,-1,-1,-1,-1,-1"}, {"input": "38470,56986,20731,59471,426,94647 94330,34523", "output": "-1,-1,-1,-1,-1,-1"}, {"input": "66543,13948,81960,39118,83749,66541,79819,26072,20033 49010,99944,21175", "output": "-1,-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "75,78505,42488,64043,2553,14663,47577,40307,31386 7593,31572,74365,10323,11227,95933,63700,9072,99694", "output": "-1,-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "16829,86475,62297,72064,21644,34742,69164,79508,55462 27761,70687,98995", "output": "-1,-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "52297,88040,85181,48945 57423,67840,59178,15861,32494", "output": "-1,-1,-1,-1"}, {"input": "44314,2758,77111,72604 30162,77129", "output": "-1,-1,-1,-1"}, {"input": "9306,92779,82720,7717 30008", "output": "-1,-1,-1,-1"}, {"input": "43310,9288 67392", "output": "-1,-1"}, {"input": "87685,63625,28081,70679 17343,94812,74848,75526,61954", "output": "-1,-1,-1,-1"}, {"input": "53355,24958,12364,12705 86375,56499,46439,55520,53884,61214,95562,7101", "output": "-1,-1,-1,-1"}, {"input": "52773,95449 44474", "output": "-1,-1"}, {"input": "25113,24932 70293,58801,18374,55297", "output": "-1,-1"}, {"input": "60638,32743,9881 58083,72133,12834,6631,85478", "output": "-1,-1,-1"}, {"input": "12225,98772,30983,21799,53270,63654,63093,28017,52566 7686", "output": "-1,-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "283,51174,34761 59639,37389,55445,91304,95749,72846,86753", "output": "-1,-1,-1"}, {"input": "24891,38891,28535,7666,75915,96435,71067,7990 98039,41105,7493", "output": "-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "62494 65910,69616,20636,7456,66563,10501,24357,8982,77993,8908", "output": "-1"}, {"input": "15714,74669,32272,75881 77925,5210,81184,10746,54949,86164,76504", "output": "-1,-1,-1,-1"}, {"input": "41468,34180,26773,87783,93873,41181,31286,34815,51877,17155 88040,84608,39322,59930,41442,98549,9509,1221,60069", "output": "-1,-1,-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "13105,9603,70469,27939,66308,34761,17362,45746,9017,32019 48435,37354,20677,57434,71201,92215,39652,80174,85718,69330", "output": "-1,-1,-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "39241 86952,13578,17602,34665,15130,14030,97311,72513,20375", "output": "-1"}, {"input": "79277,27608,94059,44943,26686 90112,83131,34601,66245,64033", "output": "-1,-1,-1,-1,-1"}, {"input": "12098,83137,55519,36266,5779 465", "output": "-1,-1,-1,-1,-1"}, {"input": "83508,34336,21179,97155,57913,72310 92494,56058,73520", "output": "-1,-1,-1,-1,-1,-1"}, {"input": "9863 90574,19537", "output": "-1"}, {"input": "48394,76351,72421,19411,56334,16705,5483,40405,47796 5230", "output": "-1,-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "89400,32707,87417,13474,46358,73386 53265,81352,98236,20258", "output": "-1,-1,-1,-1,-1,-1"}, {"input": "23207,54041,3249,23510 96543,43541,53965", "output": "-1,-1,-1,-1"}, {"input": "20867,91918,14169,50141 5076,61695,29155,26159,60333", "output": "-1,-1,-1,-1"}, {"input": "29832,29220,3102,86512,25314,52228 43026,36518,9100,36586,46026", "output": "-1,-1,-1,-1,-1,-1"}, {"input": "89066,70283,43405,3618,15119,34238,23406,76100,34796 5015,14209,78194,56960,45310,95492,41115", "output": "-1,-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "67034,15158,50489,75575,24915,33387,5818 92902,57155,222,68147,70576,90028,94298,97249,96606,87901", "output": "-1,-1,-1,-1,-1,-1,-1"}, {"input": "56532,9172,87063,43280 81679,41146,86952,16335,94340,39364", "output": "-1,-1,-1,-1"}, {"input": "87411,53529,42754,52744,91385,38753,72668,16684,25145 55109,87154,49696,88778,98060", "output": "-1,-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "74594,39447,53226 71820,54,39830,37607,27550,56347,76020,79517,85814,42238", "output": "-1,-1,-1"}, {"input": "57955,88556,28011,67001,62022,96464,22242,86357 11115,37197,67562,87013,82961,81168,43934,12241", "output": "-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "29445,26101,19314,3202 6058,32093,62278,80121,9546", "output": "-1,-1,-1,-1"}, {"input": "82545,75455,25486,94156,91273,50329,64800,52384 31980,19343,85991,90129,727,98431,13971", "output": "-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "23054,91215,67890,60890,6583,73061,32663 15907,59830,17478,60902", "output": "-1,-1,-1,-1,-1,-1,-1"}, {"input": "40052,96706,1269,65510,86357,46487,44542,29556,54939,55800 89885,98649,52871", "output": "-1,-1,-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "42740,76934,3047,74394,4222,18237,20145,43287,74474 82555,79037,79671,75220,51235", "output": "-1,-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "51202,8351,70057,50651,24686,62231,14240 43102,74648,59184,83756", "output": "-1,-1,-1,-1,-1,-1,-1"}, {"input": "22469,13673,88459,72471,23284 4203,90312", "output": "-1,-1,-1,-1,-1"}, {"input": "3518,24471,26084,9109,50580,37201,26987,30545,38156,86452 68734,9173,59594,7531,48320,67965,1448,22522", "output": "-1,-1,-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "51263,20583,14516,16927,70314,54843 62686,97406,9013,50987,27064,17031,26959", "output": "-1,-1,-1,-1,-1,-1"}, {"input": "93019,87136,62231,20812,79130 75379,40674,77004,26605,65861,93949,89763", "output": "-1,-1,-1,-1,-1"}, {"input": "26438,976,18703,58423,8385,52329,79279,32354 68926,43109,74610,64351,60320", "output": "-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "5123,96639,11942,37738,84712,59810,45454,91792 93278,38988,51261,80351,22955,54402,32655,23538,80968,96108", "output": "-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "50419,86387,24045,91557,74530,12522,51584 91573,5724,31418,20701,35885,82325,70483,38259", "output": "-1,-1,-1,-1,-1,-1,-1"}, {"input": "64683,53908 99859,72460,15890,48331", "output": "-1,-1"}, {"input": "66113,42732 53753,59106", "output": "-1,-1"}, {"input": "27181,66331,5851 60578,3502,9594,83738,91028", "output": "-1,-1,-1"}, {"input": "45044,97775,52343,25481,51993,4952,1408,32848 15032,92944,17889,42876,87857,98131,60850", "output": "-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "8944,10820,71884,86118,31758,93531,57374,18384 61708,36588,21151,22360,2368,79560,13175,23231", "output": "-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "70079,97183,51230,22080,10170 88001,1470", "output": "-1,-1,-1,-1,-1"}, {"input": "57758,46936,23323,28400,93640 4515,88480,69770", "output": "-1,-1,-1,-1,-1"}, {"input": "91324,6260,83204,68535 84019,86841,93902,86513,13474,51200,90486,40413", "output": "-1,-1,-1,-1"}, {"input": "78408,612,6379,49466,26443,32729,49106,31266 26213", "output": "-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "55271,3663 1909", "output": "-1,-1"}, {"input": "89124,87681,8281,28911,12662,87047 22005,94898,21896,5769", "output": "-1,-1,-1,-1,-1,-1"}, {"input": "14115,42880,42295,73670,82155,24845,81878 27148,71003,51782,56084,15835,30463,28021,13879,46738", "output": "-1,-1,-1,-1,-1,-1,-1"}, {"input": "1966,52710,85721,41451,1571,51012 27888,60133,28849", "output": "-1,-1,-1,-1,-1,-1"}, {"input": "85190,81778 48363,5760,8826,28648,53884", "output": "-1,-1"}, {"input": "65481,13345,93393,70279,74607 22474,33023,12419,78626,42514,82690,91268,50931,88854,90928", "output": "-1,-1,-1,-1,-1"}, {"input": "22981,83278,99840 90129,41677,87343,63194,8850,43923", "output": "-1,-1,-1"}, {"input": "76682 58840,50119,66982,83964,97232,30465,65985,77001,92358,1743", "output": "-1"}, {"input": "80787,99476,16261,40482 30985", "output": "-1,-1,-1,-1"}, {"input": "81234,10406,7855,18030,49090,65370,38878 26479,19880,49251,26790", "output": "-1,-1,-1,-1,-1,-1,-1"}, {"input": "95068 78391,58161,96896,43083", "output": "-1"}, {"input": "41621,84359,99680 5192,68272,54381,84941,37809", "output": "-1,-1,-1"}, {"input": "96060 43421,44923,31753,26977", "output": "-1"}, {"input": "87164,32551,90093,91263,94307,29157,79701,50003,68351 42158", "output": "-1,-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "82547,793,8470 64441,9174,25227,6830,83148,18551,26768,16458", "output": "-1,-1,-1"}, {"input": "77678,71939 26788,30974,66510", "output": "-1,-1"}, {"input": "95026,61221 40825,21517,94592,25892,32103,55577,23126", "output": "-1,-1"}, {"input": "39729,37402,75553,58756,83310,26399,35634,63069,10488,47132 52199,49509,21990,61698", "output": "-1,-1,-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "66230,79875,96329,56811,99658,20432,63177,2597 99868,49994,56020,10910,99466,39352,78012", "output": "-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "72464,95244,23030,33724,49867,60772,40089,59455,37123 49172,73682,79433", "output": "-1,-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "43678,17912,93699,61507,25653,20281,24855,548 1683,65628", "output": "-1,-1,-1,-1,-1,-1,-1,-1"}, {"input": "53026,54503,51728,97281,48909,50337 64167,40346,84024,77111,9337,53581,5090,16316", "output": "-1,-1,-1,-1,-1,-1"}, {"input": "21282,25458,57187,33458,98511,94667,45689 66796,92947,64045,83229,90242,48259,91286,7564,85316,50507", "output": "-1,-1,-1,-1,-1,-1,-1"}, {"input": "31766,62617,4523,47372,82701,92611,88661 3704,91419,87252,84586", "output": "-1,-1,-1,-1,-1,-1,-1"}]
|
{
"cpp": "==Code Submission==\n\npair<vector<int>, vector<int>> deserialize_stdin(const string &input) {\n size_t pos = input.find(' ');\n string groups_str = (pos == string::npos) ? input : input.substr(0, pos);\n string elements_str = (pos == string::npos) ? \"\" : input.substr(pos + 1);\n vector<int> groups, elements;\n string token;\n // Parse groups.\n stringstream ss_groups(groups_str);\n while(getline(ss_groups, token, ',')) {\n if(!token.empty())\n groups.push_back(stoi(token));\n }\n // Parse elements.\n stringstream ss_elements(elements_str);\n while(getline(ss_elements, token, ',')) {\n if(!token.empty())\n elements.push_back(stoi(token));\n }\n return {groups, elements};\n}\n\nstring serialize_stdout(const vector<int>& result) {\n if(result.empty()) return \"\";\n string out = to_string(result[0]);\n for (size_t i = 1; i < result.size(); i++) {\n out += \",\" + to_string(result[i]);\n }\n return out;\n}\n\nint main(){\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n string input;\n getline(cin, input);\n auto data = deserialize_stdin(input);\n vector<int> groups = data.first;\n vector<int> elements = data.second;\n Solution sol;\n vector<int> ans = sol.assignElements(groups, elements);\n cout << serialize_stdout(ans) << \"\\n\";\n return 0;\n}",
"golang": "==Code Submission==\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n line, _ := reader.ReadString('\\n')\n line = strings.TrimSpace(line)\n parts := strings.SplitN(line, \" \", 2)\n var groups []int\n if len(parts[0]) > 0 {\n groupStrs := strings.Split(parts[0], \",\")\n groups = make([]int, len(groupStrs))\n for i, s := range groupStrs {\n groups[i], _ = strconv.Atoi(s)\n }\n }\n var elements []int\n if len(parts) > 1 && len(parts[1]) > 0 {\n elemStrs := strings.Split(parts[1], \",\")\n elements = make([]int, len(elemStrs))\n for i, s := range elemStrs {\n elements[i], _ = strconv.Atoi(s)\n }\n }\n ans := assignElements(groups, elements)\n if len(ans) > 0 {\n out := fmt.Sprintf(\"%d\", ans[0])\n for i := 1; i < len(ans); i++ {\n out += fmt.Sprintf(\",%d\", ans[i])\n }\n fmt.Println(out)\n } else {\n fmt.Println(\"\")\n }\n}",
"java": "public class Main {\n private static int[] deserializeArray(String s) {\n if(s.isEmpty()) return new int[0];\n String[] parts = s.split(\",\");\n int[] arr = new int[parts.length];\n for (int i = 0; i < parts.length; i++) {\n arr[i] = Integer.parseInt(parts[i]);\n }\n return arr;\n }\n \n private static String serializeOutput(int[] result) {\n if(result.length == 0) return \"\";\n StringBuilder sb = new StringBuilder();\n sb.append(result[0]);\n for (int i = 1; i < result.length; i++) {\n sb.append(\",\").append(result[i]);\n }\n return sb.toString();\n }\n \n public static void main(String[] args) throws Exception {\n java.io.BufferedReader br = new java.io.BufferedReader(new java.io.InputStreamReader(System.in));\n String line = br.readLine().trim();\n String[] parts = line.split(\" \", 2);\n int[] groups = deserializeArray(parts[0]);\n int[] elements = new int[0];\n if(parts.length > 1) {\n elements = deserializeArray(parts[1]);\n }\n Solution sol = new Solution();\n int[] ans = sol.assignElements(groups, elements);\n System.out.println(serializeOutput(ans));\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\nfunction deserialize_stdin(input) {\n input = input.trim();\n let parts = input.split(\" \");\n let groups = parts[0] === \"\" ? [] : parts[0].split(\",\").map(Number);\n let elements = (parts.length > 1 && parts[1] !== \"\") ? parts[1].split(\",\").map(Number) : [];\n return { groups, elements };\n}\n\nfunction serialize_stdout(result) {\n return result.join(\",\");\n}\n\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\nlet input = \"\";\nprocess.stdin.on(\"data\", chunk => input += chunk);\nprocess.stdin.on(\"end\", () => {\n const { groups, elements } = deserialize_stdin(input);\n const ans = assignElements(groups, elements);\n console.log(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\ndef deserialize_stdin(input_str):\n parts = input_str.split(\" \", 1)\n groups = list(map(int, parts[0].split(\",\"))) if parts[0] else []\n elements = list(map(int, parts[1].split(\",\"))) if len(parts) > 1 and parts[1] else []\n return groups, elements\n\ndef serialize_stdout(result):\n return \",\".join(map(str, result))\n\ninput_str = sys.stdin.read().strip()\ngroups, elements = deserialize_stdin(input_str)\nsol = Solution()\nans = sol.assignElements(groups, elements)\nsys.stdout.write(serialize_stdout(ans))",
"ruby": "==Code Submission==\ninput = gets.strip\nparts = input.split(\" \", 2)\ngroups = parts[0].empty? ? [] : parts[0].split(\",\").map(&:to_i)\nelements = (parts.length > 1 && !parts[1].empty?) ? parts[1].split(\",\").map(&:to_i) : []\nans = assign_elements(groups, elements)\nputs ans.join(\",\")"
}
|
3763
|
Separate Squares I
|
separate-squares-i
|
<p>You are given a 2D integer array <code>squares</code>. Each <code>squares[i] = [x<sub>i</sub>, y<sub>i</sub>, l<sub>i</sub>]</code> represents the coordinates of the bottom-left point and the side length of a square parallel to the x-axis.</p>
<p>Find the <strong>minimum</strong> y-coordinate value of a horizontal line such that the total area of the squares above the line <em>equals</em> the total area of the squares below the line.</p>
<p>Answers within <code>10<sup>-5</sup></code> of the actual answer will be accepted.</p>
<p><strong>Note</strong>: Squares <strong>may</strong> overlap. Overlapping areas should be counted <strong>multiple times</strong>.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">squares = [[0,0,1],[2,2,1]]</span></p>
<p><strong>Output:</strong> <span class="example-io">1.00000</span></p>
<p><strong>Explanation:</strong></p>
<p><img alt="" src="https://assets.leetcode.com/uploads/2025/01/06/4062example1drawio.png" style="width: 378px; height: 352px;" /></p>
<p>Any horizontal line between <code>y = 1</code> and <code>y = 2</code> will have 1 square unit above it and 1 square unit below it. The lowest option is 1.</p>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">squares = [[0,0,2],[1,1,1]]</span></p>
<p><strong>Output:</strong> <span class="example-io">1.16667</span></p>
<p><strong>Explanation:</strong></p>
<p><img alt="" src="https://assets.leetcode.com/uploads/2025/01/15/4062example2drawio.png" style="width: 378px; height: 352px;" /></p>
<p>The areas are:</p>
<ul>
<li>Below the line: <code>7/6 * 2 (Red) + 1/6 (Blue) = 15/6 = 2.5</code>.</li>
<li>Above the line: <code>5/6 * 2 (Red) + 5/6 (Blue) = 15/6 = 2.5</code>.</li>
</ul>
<p>Since the areas above and below the line are equal, the output is <code>7/6 = 1.16667</code>.</p>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>1 <= squares.length <= 5 * 10<sup>4</sup></code></li>
<li><code>squares[i] = [x<sub>i</sub>, y<sub>i</sub>, l<sub>i</sub>]</code></li>
<li><code>squares[i].length == 3</code></li>
<li><code>0 <= x<sub>i</sub>, y<sub>i</sub> <= 10<sup>9</sup></code></li>
<li><code>1 <= l<sub>i</sub> <= 10<sup>9</sup></code></li>
<li>The total area of all the squares will not exceed <code>10<sup>12</sup></code>.</li>
</ul>
|
You are given a 2D integer array `squares`. Each `squares[i] = [xi, yi, li]` represents the coordinates of the bottom\-left point and the side length of a square parallel to the x\-axis.
Find the **minimum** y\-coordinate value of a horizontal line such that the total area of the squares above the line *equals* the total area of the squares below the line.
Answers within `10-5` of the actual answer will be accepted.
**Note**: Squares **may** overlap. Overlapping areas should be counted **multiple times**.
**Example 1:**
**Input:** squares \= \[\[0,0,1],\[2,2,1]]
**Output:** 1\.00000
**Explanation:**
Any horizontal line between `y = 1` and `y = 2` will have 1 square unit above it and 1 square unit below it. The lowest option is 1\.
**Example 2:**
**Input:** squares \= \[\[0,0,2],\[1,1,1]]
**Output:** 1\.16667
**Explanation:**
The areas are:
- Below the line: `7/6 * 2 (Red) + 1/6 (Blue) = 15/6 = 2.5`.
- Above the line: `5/6 * 2 (Red) + 5/6 (Blue) = 15/6 = 2.5`.
Since the areas above and below the line are equal, the output is `7/6 = 1.16667`.
**Constraints:**
- `1 <= squares.length <= 5 * 104`
- `squares[i] = [xi, yi, li]`
- `squares[i].length == 3`
- `0 <= xi, yi <= 109`
- `1 <= li <= 109`
- The total area of all the squares will not exceed `1012`.
|
Medium
|
[
"array",
"binary-search"
] |
leetcode
|
https://leetcode.com/problems/separate-squares-i
|
functional
| null | null | null | null |
{
"c": "double separateSquares(int** squares, int squaresSize, int* squaresColSize) {\n \n}",
"cpp": "class Solution {\npublic:\n double separateSquares(vector<vector<int>>& squares) {\n \n }\n};",
"csharp": "public class Solution {\n public double SeparateSquares(int[][] squares) {\n \n }\n}",
"dart": "class Solution {\n double separateSquares(List<List<int>> squares) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec separate_squares(squares :: [[integer]]) :: float\n def separate_squares(squares) do\n \n end\nend",
"erlang": "-spec separate_squares(Squares :: [[integer()]]) -> float().\nseparate_squares(Squares) ->\n .",
"golang": "func separateSquares(squares [][]int) float64 {\n \n}",
"java": "class Solution {\n public double separateSquares(int[][] squares) {\n \n }\n}",
"javascript": "/**\n * @param {number[][]} squares\n * @return {number}\n */\nvar separateSquares = function(squares) {\n \n};",
"kotlin": "class Solution {\n fun separateSquares(squares: Array<IntArray>): Double {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param Integer[][] $squares\n * @return Float\n */\n function separateSquares($squares) {\n \n }\n}",
"python": "class Solution(object):\n def separateSquares(self, squares):\n \"\"\"\n :type squares: List[List[int]]\n :rtype: float\n \"\"\"\n ",
"python3": "class Solution:\n def separateSquares(self, squares: List[List[int]]) -> float:\n ",
"racket": "(define/contract (separate-squares squares)\n (-> (listof (listof exact-integer?)) flonum?)\n )",
"ruby": "# @param {Integer[][]} squares\n# @return {Float}\ndef separate_squares(squares)\n \nend",
"rust": "impl Solution {\n pub fn separate_squares(squares: Vec<Vec<i32>>) -> f64 {\n \n }\n}",
"scala": "object Solution {\n def separateSquares(squares: Array[Array[Int]]): Double = {\n \n }\n}",
"swift": "class Solution {\n func separateSquares(_ squares: [[Int]]) -> Double {\n \n }\n}",
"typescript": "function separateSquares(squares: number[][]): number {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n double separateSquares(vector<vector<int>>& squares) {\n long long total_area = 0;\n double max_y_high = 0.0;\n for (auto& sq : squares) {\n int yi = sq[1];\n int li = sq[2];\n total_area += static_cast<long long>(li) * li;\n max_y_high = std::max(max_y_high, static_cast<double>(yi + li));\n }\n double half_total = total_area / 2.0;\n double low = 0.0, high = max_y_high;\n for (int iter = 0; iter < 100; ++iter) {\n double mid = (low + high) / 2;\n double sum_above = 0.0;\n for (auto& sq : squares) {\n int yi = sq[1];\n int li = sq[2];\n double y_top = yi + li;\n if (mid <= yi) {\n sum_above += static_cast<double>(li) * li;\n } else if (mid < y_top) {\n sum_above += static_cast<double>(li) * (y_top - mid);\n }\n }\n if (sum_above > half_total) {\n low = mid;\n } else {\n high = mid;\n }\n }\n return low;\n }\n};",
"memory": 19900,
"memoryDistribution": "[[19900, 20.9413, \"class Solution {\\npublic:\\n double separateSquares(vector<vector<int>>& squares) {\\n long long total_area = 0;\\n double max_y_high = 0.0;\\n for (auto& sq : squares) {\\n int yi = sq[1];\\n int li = sq[2];\\n total_area += static_cast<long long>(li) * li;\\n max_y_high = std::max(max_y_high, static_cast<double>(yi + li));\\n }\\n double half_total = total_area / 2.0;\\n double low = 0.0, high = max_y_high;\\n for (int iter = 0; iter < 100; ++iter) {\\n double mid = (low + high) / 2;\\n double sum_above = 0.0;\\n for (auto& sq : squares) {\\n int yi = sq[1];\\n int li = sq[2];\\n double y_top = yi + li;\\n if (mid <= yi) {\\n sum_above += static_cast<double>(li) * li;\\n } else if (mid < y_top) {\\n sum_above += static_cast<double>(li) * (y_top - mid);\\n }\\n }\\n if (sum_above > half_total) {\\n low = mid;\\n } else {\\n high = mid;\\n }\\n }\\n return low;\\n }\\n};\"], [198400, 0.8186, \"class Solution {\\npublic:\\n double func(vector<vector<int>>& vec, double mid) {\\n double ans = 0;\\n for (auto& i : vec) {\\n double y = i[1];\\n double l = i[2];\\n\\n if ((y + l) <= mid) {\\n ans += l * l;\\n } else if (y < mid) {\\n double h = mid - y;\\n ans += l * h;\\n }\\n }\\n return ans;\\n }\\n\\n static bool comp(vector<int>& a, vector<int>& b) {\\n return a[1] < b[1]; // Use strict inequality for consistency\\n }\\n\\n double separateSquares(vector<vector<int>>& vec) {\\n int n = vec.size();\\n if (n == 0) return 0; // Edge case: no squares\\n\\n // sort(vec.begin(), vec.end(), comp);\\n\\n double totalArea = 0;\\n double maxY = 0;\\n for (auto& i : vec) {\\n double l = i[2];\\n totalArea += l * l;\\n maxY = max(maxY, (double)(i[1] + l)); // Update the maximum y-coordinate\\n }\\n\\n double low = 0, high = maxY;\\n int iterations = 100; // Fixed number of iterations for binary search\\n while (iterations--) {\\n double mid = low + (high - low) / 2;\\n double area = func(vec, mid);\\n if (area < totalArea / 2) {\\n low = mid;\\n } else {\\n high = mid;\\n }\\n }\\n\\n return low;\\n }\\n};\"], [198500, 7.9809, \"class Solution {\\nprivate:\\n double areaDiff(vector<vector<int>>& squares, double gap) {\\n double areaAbove = 0;\\n double areaBelow = 0;\\n for (auto &it:squares) {\\n int y = it[1];\\n int l = it[2];\\n double currArea = (double) l * l;\\n if (gap <= y) {\\n areaAbove += currArea;\\n }\\n else if (gap >= y + l) {\\n areaBelow += currArea;\\n } else {\\n areaAbove += (l + y - gap) * l;\\n areaBelow += (gap - y) * l;\\n }\\n }\\n return areaAbove - areaBelow;\\n }\\npublic:\\n double separateSquares(vector<vector<int>>& squares) {\\n //determine low and high\\n double low = 2*1e9, high = 0;\\n for (auto &it:squares) {\\n low = min(low, (double) it[1]);\\n high = max(high, (double) it[1]+it[2]);\\n }\\n\\n int cnt = 50;\\n while (low < high && cnt--) {\\n double mid = ((low + high) / 2);\\n double diff = areaDiff(squares, mid);\\n\\n if (diff > 0)\\n low = mid;\\n else\\n high = mid;\\n }\\n return high;\\n }\\n};\"], [198600, 19.5089, null], [198700, 26.1255, null], [198800, 24.6248, null], [198900, 2.1828, null], [199100, 0.0682, null], [199700, 0.0682, null], [201600, 0.0682, null], [201900, 0.0682, null], [202600, 0.0682, null], [203400, 0.0682, null], [203500, 0.0682, null], [207800, 0.0682, null], [210500, 0.0682, null], [210600, 0.1364, null], [210700, 0.1364, null], [212300, 0.0682, null], [212500, 0.1364, null], [215800, 0.0682, null], [215900, 0.0682, null], [216600, 0.0682, null], [216900, 0.0682, null], [217000, 0.1364, null], [220000, 0.0682, null], [220100, 0.3411, null], [220200, 0.955, null], [220300, 1.5689, null], [220400, 1.296, null], [220500, 0.0682, null], [220600, 0.0682, null], [221500, 0.0682, null], [221600, 0.3411, null], [221700, 0.8186, null], [221800, 0.6821, null], [221900, 0.2046, null], [223800, 0.0682, null], [225100, 0.0682, null], [225300, 0.1364, null], [226600, 0.0682, null], [227800, 0.0682, null], [229400, 0.1364, null], [229600, 0.0682, null], [229700, 0.0682, null], [232100, 0.0682, null], [232300, 0.1364, null], [232400, 0.1364, null], [232500, 0.4093, null], [232600, 0.1364, null], [232700, 0.0682, null], [233500, 0.0682, null], [233600, 0.0682, null], [233800, 0.1364, null], [233900, 0.1364, null], [234000, 0.2046, null], [234100, 0.1364, null], [236800, 0.0682, null], [237600, 0.0682, null], [241900, 0.0682, null], [243200, 0.0682, null], [243400, 0.3411, null], [243500, 0.2729, null], [243600, 0.0682, null], [243700, 0.2729, null], [243800, 0.2046, null], [243900, 0.0682, null], [244900, 0.2729, null], [245000, 0.0682, null], [245100, 0.1364, null], [245200, 0.0682, null], [245300, 0.2046, null], [245400, 0.2729, null], [248700, 0.0682, null], [249400, 0.0682, null], [250900, 0.0682, null], [251000, 0.0682, null], [252500, 0.0682, null], [252600, 0.0682, null], [252700, 0.0682, \"#include <execution>\\n\\nclass Solution {\\npublic:\\n double separateSquares(vector<vector<int>>& squares) {\\n unordered_map<int, int> cont{};\\n double total_area{0.0};\\n vector<int> ys{};\\n\\n for (const auto& square: squares) {\\n double l = square[2];\\n total_area += l * l;\\n\\n const auto from = square[1];\\n const auto to = square[1] + square[2];\\n\\n ys.push_back(from);\\n cont[from] += square[2];\\n\\n ys.push_back(to);\\n cont[to] -= square[2];\\n }\\n\\n sort(execution::par_unseq, ys.begin(), ys.end());\\n\\u00a0\\u00a0\\u00a0 ys.erase(unique(ys.begin(), ys.end()), ys.end());\\n\\n \\n double curr_cont{0};\\n double curr_area{0.0};\\n for (int i = 0; i < ys.size() - 1; ++i) {\\n const auto from = ys[i];\\n const auto to = ys[i + 1];\\n\\n curr_cont += cont[ys[i]];\\n curr_area += curr_cont * (to - from);\\n\\n if (curr_area >= total_area / 2) {\\n const auto diff = curr_area - total_area / 2;\\n const auto y_diff = diff / curr_cont;\\n // find the point between from and to\\n return ys[i + 1] - y_diff;\\n }\\n }\\n\\n return 0.0;\\n }\\n};\"], [253800, 0.1364, \"class Solution {\\npublic:\\n vector<pair<double,pair<double,double>>>coord;\\n \\n bool solve( double y) {\\n double z1,z2;\\n z1=z2=0;\\n for( auto it: coord ) {\\n double t = it.second.second;\\n if(it.first > y) z2+= (t*t);\\n else if (it.first + t < y) z1+=t*t;\\n else {\\n double a1 = t * (y - it.first );\\n z1+= a1;\\n z2+= (t*t) - a1;\\n }\\n }\\n return z1>=z2;\\n }\\n\\n double separateSquares(vector<vector<int>>& squares) {\\n // coord.clear();\\n for(auto it: squares) {\\n coord.push_back({(double)it[1],{(double)it[0],(double)it[2]}});\\n }\\n double l = 0.0, r = 1e9+1;\\n double ans = (double)1e9+5;\\n while(l<=r) {\\n double m = (l+(r-l)/2);\\n if(solve(m)) {\\n r = m - (0.00001);\\n ans = min (ans, m);\\n } else {\\n l = m + (0.00001);\\n }\\n }\\n return l;\\n }\\n};\"]]",
"runtime": 215,
"runtimeDistribution": "[[2, 0.2046, \"static const int __ = [](){\\n ios_base::sync_with_stdio(false);\\n cin.tie(nullptr);\\n cout.tie(nullptr);\\n struct ___ {\\n static void _() {\\n std::ofstream(\\\"display_runtime.txt\\\") << 0 << '\\\\n';\\n }\\n };\\n std::atexit(&___::_);\\n return 0; \\n}();\\n\\nclass Solution {\\npublic:\\n double squaresChecker(const double mid, vector<vector<int>>& squares)\\n {\\n double above = 0.0;\\n double below = 0.0;\\n for (const vector<int>& square : squares)\\n {\\n //int x = square[0];\\n int y = square[1];\\n int l = square[2];\\n \\n if (mid <= y)\\n {\\n above += (double)l * l;\\n }\\n else if (mid >= y + l)\\n {\\n below += (double)l * l;\\n }\\n else\\n {\\n above += l * ((double)l - (mid - y));\\n below += l * (mid - y);\\n }\\n }\\n return above - below;\\n }\\n double separateSquares(vector<vector<int>>& squares)\\n {\\n // fast linear way to find true weight middle point\\n /*double middle = 0.0;\\n double total_weight = 0.0;\\n for (const vector<int>& square : squares)\\n {\\n //int x = square[0];\\n int y = square[1];\\n int l = square[2];\\n double mid_point = y + l * 0.5;\\n double weight = l;\\n\\n middle = (middle * total_weight + mid_point * weight) / (total_weight + weight);\\n total_weight += weight;\\n }*/\\n\\n // compute intense part to find the lowest possible value of y\\n double top = 2*1e9;\\n double low = 0.0;\\n double mid = 0.0;\\n const double prec = 1e-5 * 0.5;\\n for (int i = 0; i < 60; i++)\\n {\\n mid = (low + top) * 0.5;\\n double res = squaresChecker(mid, squares);\\n if (res != 0.0 && abs(res) < prec * 0.5) // precission is reached\\n break;\\n if (res > 0)\\n low = mid;\\n else\\n top = mid;\\n }\\n return mid;\\n }\\n};\"], [6, 0.0682, \"class Solution {\\npublic:\\n double separateSquares(vector<vector<int>>& squares) {\\n double totalarea = 0.0;\\n double maxy = 0.0;\\n \\n for (auto& it : squares) {\\n double x = it[1];\\n double y = it[2];\\n totalarea += y * y;\\n maxy = max(maxy, x + y);\\n }\\n \\n double target = totalarea / 2.0;\\n double low = 0.0, high = maxy;\\n double eps = 1e-5;\\n \\n while (high - low > eps) {\\n double mid = low + (high - low) / 2.0;\\n double area = 0.0;\\n \\n for (auto& it : squares) {\\n double x = it[1];\\n double y = it[2];\\n double top = x + y;\\n double finalh = max(0.0, min(top, mid) - x);\\n area += finalh * y;\\n }\\n \\n if (area >= target){\\n high = mid;\\n }\\n else{\\n low = mid;\\n }\\n }\\n \\n return low; \\n }\\n};\"], [10, 0.1364, null], [15, 0.1364, null], [19, 0.1364, null], [23, 0.2046, null], [28, 0.1364, null], [32, 0.1364, null], [36, 0.1364, null], [41, 0.0682, null], [45, 0.2729, null], [49, 0.0682, null], [54, 0.0682, null], [58, 0.1364, null], [62, 0.2046, null], [67, 0.5456, null], [71, 0.4775, null], [75, 1.9781, null], [80, 1.0231999999999999, null], [84, 3.2743, null], [88, 4.774900000000001, null], [93, 4.1610000000000005, null], [97, 5.9345, null], [101, 6.8213, null], [106, 4.3656, null], [110, 5.252400000000001, null], [114, 4.0928, null], [119, 3.4787999999999997, null], [123, 3.2059, null], [127, 3.6151999999999997, null], [132, 3.8200000000000003, null], [136, 3.6152999999999995, null], [140, 4.2974, null], [145, 2.5239000000000003, null], [149, 1.7736, null], [153, 1.7052, null], [158, 1.2279, null], [162, 1.7052999999999998, null], [166, 1.0232999999999999, null], [171, 0.6138, null], [175, 1.2278000000000002, null], [180, 1.0914, null], [184, 1.1596, null], [188, 0.8867999999999999, null], [193, 0.7503, null], [197, 0.7503000000000001, null], [201, 0.8867999999999999, null], [206, 1.0914000000000001, null], [210, 0.5457, null], [214, 0.5457, null], [215, 14.1888, \"class Solution {\\npublic:\\n double separateSquares(vector<vector<int>>& squares) {\\n long long total_area = 0;\\n double max_y_high = 0.0;\\n for (auto& sq : squares) {\\n int yi = sq[1];\\n int li = sq[2];\\n total_area += static_cast<long long>(li) * li;\\n max_y_high = std::max(max_y_high, static_cast<double>(yi + li));\\n }\\n double half_total = total_area / 2.0;\\n double low = 0.0, high = max_y_high;\\n for (int iter = 0; iter < 100; ++iter) {\\n double mid = (low + high) / 2;\\n double sum_above = 0.0;\\n for (auto& sq : squares) {\\n int yi = sq[1];\\n int li = sq[2];\\n double y_top = yi + li;\\n if (mid <= yi) {\\n sum_above += static_cast<double>(li) * li;\\n } else if (mid < y_top) {\\n sum_above += static_cast<double>(li) * (y_top - mid);\\n }\\n }\\n if (sum_above > half_total) {\\n low = mid;\\n } else {\\n high = mid;\\n }\\n }\\n return low;\\n }\\n};\"], [219, 0.7504000000000001, null], [223, 0.40919999999999995, null], [227, 0.40929999999999994, null], [232, 0.4092, null], [236, 0.34099999999999997, null], [240, 0.1364, null], [245, 0.8866999999999999, null], [249, 0.2728, null], [253, 0.4774, null], [258, 0.4774, null], [262, 0.34099999999999997, null], [266, 0.40919999999999995, null], [271, 0.34099999999999997, null], [275, 0.34099999999999997, null], [279, 0.2728, null], [284, 0.2728, null], [288, 0.2046, null], [292, 0.2046, null], [297, 0.34099999999999997, null], [301, 0.0682, null], [305, 0.2046, null], [310, 0.2046, null], [314, 0.0682, null], [318, 0.0682, null], [323, 0.0682, null], [327, 0.2046, null], [331, 0.0682, null], [336, 0.1364, null], [340, 0.0682, \"class Solution {\\npublic:\\n double separateSquares(vector<vector<int>>& squares) {\\n sort(squares.begin(), squares.end());\\n\\n double st = 0, en = 1000000000, mid, ans = -1;\\n for(int c = 0; c <= 100; c++){\\n mid = (st + en) / 2.0;\\n double areaAbove = 0, areaBelow = 0;\\n for(auto &i : squares){\\n if(double(i[1]) > mid){\\n areaAbove += (double) i[2] * i[2];\\n }else{\\n int topRightX = i[0] + i[2];\\n int topRightY = i[1] + i[2];\\n\\n if(double(topRightY) <= mid){\\n areaBelow += (double) i[2] * i[2];\\n }else{\\n areaBelow += (double) i[2] * (mid - i[1]);\\n areaAbove += (double) i[2] * (double(topRightY) - mid);\\n }\\n }\\n }\\n\\n if(areaBelow >= areaAbove) en = mid;\\n else st = mid;\\n }\\n\\n return en;\\n }\\n};\"], [344, 0.1364, \"class Solution {\\npublic:\\n double separateSquares(vector<vector<int>>& squares) {\\n typedef pair<int,int> ipair;\\n\\n // sort by bottom y coordinates;\\n sort( squares.begin(), squares.end(), \\n [](const vector<int>& lhs, const vector<int>& rhs) {\\n return lhs[1] < rhs[1];\\n });\\n\\n set<int> scanline;\\n double target = 0.0;\\n for (auto s : squares) { \\n scanline.insert(s[1]);\\n scanline.insert(s[1]+s[2]);\\n double w = s[2];\\n target += w*w; \\n }\\n target *= 0.5;\\n \\n size_t nsquare = squares.size(), next = 0;\\n priority_queue<ipair, vector<ipair>, greater<ipair>> q;\\n \\n double lower = 0.0; // area below the scan beam;\\n double upper = 0.0; // area below and in the scan beam;\\n double split;\\n int widthsum = 0;\\n\\n auto currline = scanline.begin();\\n while (currline != scanline.end()) {\\n auto nextline = currline;\\n if (++nextline == scanline.end())\\n break;\\n int bottom = *currline, top = *nextline;\\n\\n while (!q.empty()) {\\n if (q.top().first > bottom)\\n break;\\n // pop anything that's below the scanbeam.\\n int width = q.top().second;\\n widthsum -= width;\\n q.pop();\\n }\\n while (next < nsquare) { // accept the squares that are in the scanbeam.\\n if (squares[next][1] >= top) \\n break;\\n q.emplace(squares[next][1]+squares[next][2], squares[next][2]);\\n widthsum += squares[next][2];\\n ++next;\\n }\\n\\n double height = top - bottom;\\n upper = lower + height*widthsum;\\n if (upper >= target) { \\n split = (target - lower)/widthsum + bottom;\\n break;\\n }\\n lower = upper;\\n\\n currline = nextline;\\n }\\n\\n return split;\\n }\\n};\"]]"
},
"golang": {
"code": "func separateSquares(squares [][]int) float64 {\n\tcriticals := make([]float64, 0, 2*len(squares))\n\tfor _, sq := range squares {\n\t\tyi := float64(sq[1])\n\t\tli := float64(sq[2])\n\t\tcriticals = append(criticals, yi, yi+li)\n\t}\n\tsort.Float64s(criticals)\n\tj := 0\n\tfor i := 1; i < len(criticals); i++ {\n\t\tif criticals[i] != criticals[j] {\n\t\t\tj++\n\t\t\tcriticals[j] = criticals[i]\n\t\t}\n\t}\n\tcriticals = criticals[:j+1]\n\n\tvar maxY float64\n\tfor _, sq := range squares {\n\t\tif y := float64(sq[1] + sq[2]); y > maxY {\n\t\t\tmaxY = y\n\t\t}\n\t}\n\n\tlow, high := 0.0, maxY\n\tepsilon := 1e-7\n\tfor i := 0; i < 100; i++ {\n\t\tmid := (low + high) / 2\n\t\tdiff := computeDiff(mid, squares)\n\t\tif diff > 0 {\n\t\t\tlow = mid\n\t\t} else {\n\t\t\thigh = mid\n\t\t}\n\t}\n\tcandidate := low\n\n\tidx := sort.Search(len(criticals), func(i int) bool { return criticals[i] > candidate }) - 1\n\tif idx >= 0 {\n\t\ty := criticals[idx]\n\t\tif math.Abs(computeDiff(y, squares)) < epsilon {\n\t\t\treturn y\n\t\t}\n\t}\n\treturn candidate\n}\n\nfunc computeDiff(y float64, squares [][]int) float64 {\n\tvar above, below float64\n\tfor _, sq := range squares {\n\t\tyi := float64(sq[1])\n\t\tli := float64(sq[2])\n\t\ttop := yi + li\n\t\tif y <= yi {\n\t\t\tabove += li * li\n\t\t} else if y >= top {\n\t\t\tbelow += li * li\n\t\t} else {\n\t\t\tabove += (top - y) * li\n\t\t\tbelow += (y - yi) * li\n\t\t}\n\t}\n\treturn above - below\n}",
"memory": 1400,
"memoryDistribution": "[[1400, 95.2381, \"import (\\n\\t\\\"math\\\"\\n\\t\\\"sort\\\"\\n)\\n\\nfunc separateSquares(squares [][]int) float64 {\\n\\tcriticals := make([]float64, 0, 2*len(squares))\\n\\tfor _, sq := range squares {\\n\\t\\tyi := float64(sq[1])\\n\\t\\tli := float64(sq[2])\\n\\t\\tcriticals = append(criticals, yi, yi+li)\\n\\t}\\n\\tsort.Float64s(criticals)\\n\\tj := 0\\n\\tfor i := 1; i < len(criticals); i++ {\\n\\t\\tif criticals[i] != criticals[j] {\\n\\t\\t\\tj++\\n\\t\\t\\tcriticals[j] = criticals[i]\\n\\t\\t}\\n\\t}\\n\\tcriticals = criticals[:j+1]\\n\\n\\tvar maxY float64\\n\\tfor _, sq := range squares {\\n\\t\\tif y := float64(sq[1] + sq[2]); y > maxY {\\n\\t\\t\\tmaxY = y\\n\\t\\t}\\n\\t}\\n\\n\\tlow, high := 0.0, maxY\\n\\tepsilon := 1e-7\\n\\tfor i := 0; i < 100; i++ {\\n\\t\\tmid := (low + high) / 2\\n\\t\\tdiff := computeDiff(mid, squares)\\n\\t\\tif diff > 0 {\\n\\t\\t\\tlow = mid\\n\\t\\t} else {\\n\\t\\t\\thigh = mid\\n\\t\\t}\\n\\t}\\n\\tcandidate := low\\n\\n\\tidx := sort.Search(len(criticals), func(i int) bool { return criticals[i] > candidate }) - 1\\n\\tif idx >= 0 {\\n\\t\\ty := criticals[idx]\\n\\t\\tif math.Abs(computeDiff(y, squares)) < epsilon {\\n\\t\\t\\treturn y\\n\\t\\t}\\n\\t}\\n\\treturn candidate\\n}\\n\\nfunc computeDiff(y float64, squares [][]int) float64 {\\n\\tvar above, below float64\\n\\tfor _, sq := range squares {\\n\\t\\tyi := float64(sq[1])\\n\\t\\tli := float64(sq[2])\\n\\t\\ttop := yi + li\\n\\t\\tif y <= yi {\\n\\t\\t\\tabove += li * li\\n\\t\\t} else if y >= top {\\n\\t\\t\\tbelow += li * li\\n\\t\\t} else {\\n\\t\\t\\tabove += (top - y) * li\\n\\t\\t\\tbelow += (y - yi) * li\\n\\t\\t}\\n\\t}\\n\\treturn above - below\\n}\"], [14200, 4.7619, \"func calculateArea(squares [][]int, y float64) (float64, float64){\\n var upArea float64 = 0\\n var downArea float64 = 0\\n for _, square := range squares {\\n if float64(square[1]) >= y {\\n upArea += float64(square[2] * square[2])\\n } else if float64(square[1] + square[2]) <= y {\\n downArea += float64(square[2] * square[2])\\n } else{\\n upArea += (float64(square[1] + square[2]) - y) * float64(square[2])\\n downArea += (y - float64(square[1])) * float64(square[2])\\n }\\n }\\n return downArea, upArea\\n}\\n\\nfunc separateSquares(squares [][]int) float64 {\\n var upBound float64 = float64(squares[0][1] + squares[0][2])\\n var downBound float64 = float64(squares[0][1])\\n for _, square := range squares {\\n upBound = max(upBound, float64(square[1] + square[2]))\\n downBound = min(downBound, float64(square[1]))\\n }\\n\\n beg := downBound\\n end := upBound\\n for end - beg > 1e-6 {\\n // fmt.Println(\\\"bounds\\\", beg, end)\\n mid := (end + beg) / 2.0\\n downArea, upArea := calculateArea(squares, mid)\\n // fmt.Println(\\\"areas\\\", downArea, upArea)\\n if downArea < upArea {\\n beg = mid\\n } else {\\n end = mid\\n }\\n }\\n return (end + beg) / 2\\n \\n}\\n// 0 1\\n// 2 3\"], [14300, 4.7619, \"import (\\n\\t\\\"math\\\"\\n\\t\\\"sort\\\"\\n)\\n\\nfunc separateSquares(squares [][]int) float64 {\\n\\tcriticals := make([]float64, 0, 2*len(squares))\\n\\tfor _, sq := range squares {\\n\\t\\tyi := float64(sq[1])\\n\\t\\tli := float64(sq[2])\\n\\t\\tcriticals = append(criticals, yi, yi+li)\\n\\t}\\n\\tsort.Float64s(criticals)\\n\\tj := 0\\n\\tfor i := 1; i < len(criticals); i++ {\\n\\t\\tif criticals[i] != criticals[j] {\\n\\t\\t\\tj++\\n\\t\\t\\tcriticals[j] = criticals[i]\\n\\t\\t}\\n\\t}\\n\\tcriticals = criticals[:j+1]\\n\\n\\tvar maxY float64\\n\\tfor _, sq := range squares {\\n\\t\\tif y := float64(sq[1] + sq[2]); y > maxY {\\n\\t\\t\\tmaxY = y\\n\\t\\t}\\n\\t}\\n\\n\\tlow, high := 0.0, maxY\\n\\tepsilon := 1e-7\\n\\tfor i := 0; i < 100; i++ {\\n\\t\\tmid := (low + high) / 2\\n\\t\\tdiff := computeDiff(mid, squares)\\n\\t\\tif diff > 0 {\\n\\t\\t\\tlow = mid\\n\\t\\t} else {\\n\\t\\t\\thigh = mid\\n\\t\\t}\\n\\t}\\n\\tcandidate := low\\n\\n\\tidx := sort.Search(len(criticals), func(i int) bool { return criticals[i] > candidate }) - 1\\n\\tif idx >= 0 {\\n\\t\\ty := criticals[idx]\\n\\t\\tif math.Abs(computeDiff(y, squares)) < epsilon {\\n\\t\\t\\treturn y\\n\\t\\t}\\n\\t}\\n\\treturn candidate\\n}\\n\\nfunc computeDiff(y float64, squares [][]int) float64 {\\n\\tvar above, below float64\\n\\tfor _, sq := range squares {\\n\\t\\tyi := float64(sq[1])\\n\\t\\tli := float64(sq[2])\\n\\t\\ttop := yi + li\\n\\t\\tif y <= yi {\\n\\t\\t\\tabove += li * li\\n\\t\\t} else if y >= top {\\n\\t\\t\\tbelow += li * li\\n\\t\\t} else {\\n\\t\\t\\tabove += (top - y) * li\\n\\t\\t\\tbelow += (y - yi) * li\\n\\t\\t}\\n\\t}\\n\\treturn above - below\\n}\"], [14500, 4.7619, null], [14600, 4.7619, null], [14700, 4.7619, null], [14800, 4.7619, null], [15300, 9.5238, null], [15400, 4.7619, null], [15600, 9.5238, null], [15800, 9.5238, null], [15900, 4.7619, null], [16100, 4.7619, null], [16200, 4.7619, null], [17500, 4.7619, null], [17800, 4.7619, \"\\nfunc separateSquares(squares [][]int) float64 {\\n var sum, high float64\\n low := float64(1000000000)\\n for _, s := range squares {\\n y, l := float64(s[1]), float64(s[2])\\n low = min(low, y)\\n high = max(high, y + l)\\n sum += l * l\\n }\\n for {\\n mid := (low + high) / 2 \\n if high - low < 0.00001 {\\n return mid\\n }\\n var midSum float64\\n for _, s := range squares {\\n y, l := float64(s[1]), float64(s[2])\\n if y < mid {\\n if y + l < mid {\\n midSum += l * l\\n } else {\\n midSum += (mid - y) * l \\n }\\n }\\n }\\n if midSum < sum / 2 {\\n low = mid\\n } else {\\n high = mid\\n }\\n }\\n}\"], [18600, 4.7619, \"func separateSquares(squares [][]int) float64 {\\n l, r := math.MaxInt, math.MinInt\\n yList := make([][]int,0)\\n for _, square := range squares {\\n l = min(l, square[1])\\n r = max(r, square[1]+square[2])\\n yList = append(yList, []int{square[1], square[1]+square[2]})\\n }\\n\\n left, right := float64(l), float64(r)\\n // for left < right {\\n for right - left > 1e-6 {\\n mid := left + (right-left)/2\\n topArea, bottomArea := getTopArea(mid, squares), getBottomArea(mid, squares)\\n\\n if math.Abs(topArea - bottomArea) < 1e-6 {\\n left = mid\\n right = mid\\n continue\\n }\\n\\n if topArea > bottomArea {\\n left = mid + 1e-7\\n } else {\\n right = mid - 1e-7\\n }\\n }\\n\\n sort.Slice(yList, func(i,j int) bool {\\n return yList[i][0] < yList[j][0]\\n })\\n\\n i := 0\\n for float64(yList[i][1]) <= left {\\n i++\\n }\\n if i==0 || left > float64(yList[i][0]) {\\n return left\\n }\\n return float64(yList[i-1][1])\\n}\\n\\nfunc getTopArea(y float64, squares [][]int) float64 {\\n area := 0.0\\n for _,square := range squares {\\n if float64(square[1]+square[2]) <= y {\\n continue\\n }\\n\\n if float64(square[1]) >= y {\\n area += float64(square[2])*float64(square[2])\\n } else {\\n area += float64(square[2])*(float64(square[1]+square[2])-y)\\n }\\n }\\n return area\\n}\\n\\nfunc getBottomArea(y float64, squares [][]int) float64 {\\n area := 0.0\\n for _,square := range squares {\\n if float64(square[1]) >= y {\\n continue\\n }\\n\\n if float64(square[1]+square[2]) <= y {\\n area += float64(square[2])*float64(square[2])\\n } else {\\n area += float64(square[2])*(y-float64(square[1]))\\n }\\n }\\n return area\\n}\"]]",
"runtime": 226,
"runtimeDistribution": "[[67, 4.7619, \"\\nfunc separateSquares(squares [][]int) float64 {\\n var sum, high float64\\n low := float64(1000000000)\\n for _, s := range squares {\\n y, l := float64(s[1]), float64(s[2])\\n low = min(low, y)\\n high = max(high, y + l)\\n sum += l * l\\n }\\n for {\\n mid := (low + high) / 2 \\n if high - low < 0.00001 {\\n return mid\\n }\\n var midSum float64\\n for _, s := range squares {\\n y, l := float64(s[1]), float64(s[2])\\n if y < mid {\\n if y + l < mid {\\n midSum += l * l\\n } else {\\n midSum += (mid - y) * l \\n }\\n }\\n }\\n if midSum < sum / 2 {\\n low = mid\\n } else {\\n high = mid\\n }\\n }\\n}\"], [77, 4.7619, \"func calculateSum(squares [][]int, midY float64) (float64, float64) {\\n upper := 0.0\\n lower := 0.0\\n\\n for _, sq := range squares {\\n // If the line (midY) is below the current then take this in upper\\n // another word current square is above the line\\n side := float64(sq[2])\\n bottomY := float64(sq[1])\\n topY := bottomY + side // topY would be y point and side\\n\\n if bottomY >= midY {\\n upper += (side * side) // Since this is square, li * li is area\\n } else if topY <= midY {\\n // This is the case where square is below the line\\n lower += (side * side)\\n } else {\\n // This is the case where line is in between the square\\n // we have to take upper part into upper and lower into lower\\n upper += (topY - midY) * side\\n lower += (midY - bottomY) * side\\n }\\n }\\n\\n return lower, upper\\n}\\n\\nfunc separateSquares(squares [][]int) float64 {\\n minY := 2e9\\n maxY := 0.0\\n\\n for i := range squares {\\n sq := squares[i]\\n minY = min(minY, float64(sq[1]))\\n maxY = max(maxY, (float64(sq[1]) + float64(sq[2])))\\n }\\n\\n precision := 1e-5\\n\\n for (maxY - minY) > precision {\\n midY := (maxY + minY) / 2.0\\n\\n lowerAreaSum, upperAreaSum := calculateSum(squares, midY)\\n\\n if lowerAreaSum >= upperAreaSum {\\n maxY = midY\\n } else {\\n minY = midY\\n }\\n }\\n\\n return minY\\n}\"], [80, 4.7619, null], [81, 4.7619, null], [87, 4.7619, null], [90, 4.7619, null], [92, 4.7619, null], [95, 4.7619, null], [97, 4.7619, null], [103, 4.7619, null], [107, 4.7619, null], [109, 4.7619, null], [118, 9.5238, null], [130, 4.7619, null], [148, 4.7619, null], [165, 4.7619, null], [226, 4.7619, \"import (\\n\\t\\\"math\\\"\\n\\t\\\"sort\\\"\\n)\\n\\nfunc separateSquares(squares [][]int) float64 {\\n\\tcriticals := make([]float64, 0, 2*len(squares))\\n\\tfor _, sq := range squares {\\n\\t\\tyi := float64(sq[1])\\n\\t\\tli := float64(sq[2])\\n\\t\\tcriticals = append(criticals, yi, yi+li)\\n\\t}\\n\\tsort.Float64s(criticals)\\n\\tj := 0\\n\\tfor i := 1; i < len(criticals); i++ {\\n\\t\\tif criticals[i] != criticals[j] {\\n\\t\\t\\tj++\\n\\t\\t\\tcriticals[j] = criticals[i]\\n\\t\\t}\\n\\t}\\n\\tcriticals = criticals[:j+1]\\n\\n\\tvar maxY float64\\n\\tfor _, sq := range squares {\\n\\t\\tif y := float64(sq[1] + sq[2]); y > maxY {\\n\\t\\t\\tmaxY = y\\n\\t\\t}\\n\\t}\\n\\n\\tlow, high := 0.0, maxY\\n\\tepsilon := 1e-7\\n\\tfor i := 0; i < 100; i++ {\\n\\t\\tmid := (low + high) / 2\\n\\t\\tdiff := computeDiff(mid, squares)\\n\\t\\tif diff > 0 {\\n\\t\\t\\tlow = mid\\n\\t\\t} else {\\n\\t\\t\\thigh = mid\\n\\t\\t}\\n\\t}\\n\\tcandidate := low\\n\\n\\tidx := sort.Search(len(criticals), func(i int) bool { return criticals[i] > candidate }) - 1\\n\\tif idx >= 0 {\\n\\t\\ty := criticals[idx]\\n\\t\\tif math.Abs(computeDiff(y, squares)) < epsilon {\\n\\t\\t\\treturn y\\n\\t\\t}\\n\\t}\\n\\treturn candidate\\n}\\n\\nfunc computeDiff(y float64, squares [][]int) float64 {\\n\\tvar above, below float64\\n\\tfor _, sq := range squares {\\n\\t\\tyi := float64(sq[1])\\n\\t\\tli := float64(sq[2])\\n\\t\\ttop := yi + li\\n\\t\\tif y <= yi {\\n\\t\\t\\tabove += li * li\\n\\t\\t} else if y >= top {\\n\\t\\t\\tbelow += li * li\\n\\t\\t} else {\\n\\t\\t\\tabove += (top - y) * li\\n\\t\\t\\tbelow += (y - yi) * li\\n\\t\\t}\\n\\t}\\n\\treturn above - below\\n}\"], [231, 4.7619, \"func calculateArea(squares [][]int, y float64) (float64, float64){\\n var upArea float64 = 0\\n var downArea float64 = 0\\n for _, square := range squares {\\n if float64(square[1]) >= y {\\n upArea += float64(square[2] * square[2])\\n } else if float64(square[1] + square[2]) <= y {\\n downArea += float64(square[2] * square[2])\\n } else{\\n upArea += (float64(square[1] + square[2]) - y) * float64(square[2])\\n downArea += (y - float64(square[1])) * float64(square[2])\\n }\\n }\\n return downArea, upArea\\n}\\n\\nfunc separateSquares(squares [][]int) float64 {\\n var upBound float64 = float64(squares[0][1] + squares[0][2])\\n var downBound float64 = float64(squares[0][1])\\n for _, square := range squares {\\n upBound = max(upBound, float64(square[1] + square[2]))\\n downBound = min(downBound, float64(square[1]))\\n }\\n\\n beg := downBound\\n end := upBound\\n for end - beg > 1e-6 {\\n fmt.Println(\\\"bounds\\\", beg, end)\\n mid := (end + beg) / 2.0\\n downArea, upArea := calculateArea(squares, mid)\\n fmt.Println(\\\"areas\\\", downArea, upArea)\\n if downArea < upArea {\\n beg = mid\\n } else {\\n end = mid\\n }\\n }\\n return (end + beg) / 2\\n \\n}\\n// 0 1\\n// 2 3\"]]"
},
"java": {
"code": "class Solution {\n public double separateSquares(int[][] squares) {\n double totalArea = 0.0;\n long maxYPlusLi = 0;\n for (int[] square : squares) {\n long yi = square[1];\n long li = square[2];\n totalArea += (double) li * li;\n long top = yi + li;\n if (top > maxYPlusLi) {\n maxYPlusLi = top;\n }\n }\n double target = totalArea / 2.0;\n double low = 0.0;\n double high = maxYPlusLi;\n for (int iter = 0; iter < 100; iter++) {\n double mid = (low + high) * 0.5;\n double sumAbove = 0.0;\n for (int[] square : squares) {\n long yi = square[1];\n long li = square[2];\n long top = yi + li;\n if (mid <= yi) {\n sumAbove += (double) li * li;\n } else if (mid < top) {\n sumAbove += (top - mid) * li;\n }\n }\n if (sumAbove > target) {\n low = mid;\n } else {\n high = mid;\n }\n }\n return low;\n }\n}",
"memory": 6800,
"memoryDistribution": "[[6800, 97.7556, \"class Solution {\\n public double separateSquares(int[][] squares) {\\n double totalArea = 0.0;\\n long maxYPlusLi = 0;\\n for (int[] square : squares) {\\n long yi = square[1];\\n long li = square[2];\\n totalArea += (double) li * li;\\n long top = yi + li;\\n if (top > maxYPlusLi) {\\n maxYPlusLi = top;\\n }\\n }\\n double target = totalArea / 2.0;\\n double low = 0.0;\\n double high = maxYPlusLi;\\n for (int iter = 0; iter < 100; iter++) {\\n double mid = (low + high) * 0.5;\\n double sumAbove = 0.0;\\n for (int[] square : squares) {\\n long yi = square[1];\\n long li = square[2];\\n long top = yi + li;\\n if (mid <= yi) {\\n sumAbove += (double) li * li;\\n } else if (mid < top) {\\n sumAbove += (top - mid) * li;\\n }\\n }\\n if (sumAbove > target) {\\n low = mid;\\n } else {\\n high = mid;\\n }\\n }\\n return low;\\n }\\n}\"], [67475, 0.8729, \"class Solution {\\n class Area{\\n double topArea;\\n double bottomArea;\\n public Area(double topArea, double bottomArea){\\n this.topArea = topArea;\\n this.bottomArea = bottomArea;\\n }\\n }\\n public double separateSquares(int[][] squares) {\\n double minY = 0;\\n double maxY = 0;\\n for(int i = 0; i < squares.length; ++i){\\n minY = Math.min(minY, squares[i][1]);\\n maxY = Math.max(maxY, squares[i][1]+squares[i][2]);\\n }\\n while(maxY-minY >= 0.00001){\\n double mid = (minY+maxY)/2;\\n Area area = findArea(squares, mid);\\n if(area.topArea <= area.bottomArea){\\n maxY = mid;\\n } else{\\n minY = mid;\\n }\\n }\\n return minY;\\n }\\n private Area findArea(int[][]squares, double y){\\n double topArea = 0;\\n double bottomArea = 0;\\n for(int i = 0; i < squares.length; ++i){\\n double totalArea = 1d*squares[i][2]*squares[i][2];\\n if(y >= squares[i][1] && y <= squares[i][1]+squares[i][2]){\\n topArea += (squares[i][2] * (squares[i][1]+squares[i][2]-y));\\n bottomArea += (totalArea - (squares[i][2] * (squares[i][1]+squares[i][2]-y)));\\n } else if(y > squares[i][1]+squares[i][2]){\\n bottomArea += totalArea;\\n } else{\\n topArea += totalArea;\\n }\\n }\\n return new Area(topArea, bottomArea);\\n }\\n}\"], [67826, 7.481199999999999, \"class Solution {\\n private double helper(double line, int[][] squares) {\\n double aAbove = 0, aBelow = 0;\\n for (int i = 0; i < squares.length; i++) {\\n int x = squares[i][0], y = squares[i][1], l = squares[i][2];\\n double total = (double) l * l;\\n \\n if (line <= y) {\\n aAbove += total;\\n } else if (line >= y + l) {\\n aBelow += total;\\n } else {\\n // The line intersects the square.\\n double aboveHeight = (y + l) - line;\\n double belowHeight = line - y;\\n aAbove += l * aboveHeight;\\n aBelow += l * belowHeight;\\n }\\n }\\n return aAbove - aBelow;\\n }\\n\\n public double separateSquares(int[][] squares) {\\n double lo = 0, hi = 2*1e9;\\n\\n for (int i = 0; i < 60; i++) {\\n double mid = (lo + hi) / 2.0;\\n double diff = helper(mid, squares);\\n \\n if (diff > 0)\\n lo = mid;\\n else\\n hi = mid;\\n }\\n \\n return hi;\\n }\\n}\"], [68178, 12.2194, null], [68529, 5.4863, null], [68880, 0.9976, null], [69231, 0.2494, null], [69583, 0.1247, null], [69934, 0.1247, null], [70285, 0.1247, null], [70636, 0.1247, null], [70988, 0.1247, null], [71339, 0.1247, null], [71690, 0.1247, null], [72041, 0.1247, null], [72393, 0.1247, null], [72744, 0.1247, null], [73095, 0.1247, null], [73446, 0.1247, null], [73798, 0.1247, null], [74149, 0.6234, null], [74500, 0.1247, null], [74851, 0.1247, null], [75203, 0.4988, null], [75554, 0.3741, null], [75905, 0.8728, null], [76256, 1.2469, null], [76608, 2.6185, null], [76959, 2.2444, null], [77310, 3.6159, null], [77661, 3.1171999999999995, null], [78013, 0.7482, null], [78364, 0.2494, null], [78715, 0.1247, null], [79066, 0.4988, null], [79418, 0.2494, null], [79769, 0.1247, null], [80120, 0.2494, null], [80471, 0.9976, null], [80823, 1.4962, null], [81174, 0.9976, null], [81525, 1.621, null], [81876, 1.6209, null], [82228, 0.8729, null], [82579, 0.3741, null], [82930, 0.6234999999999999, null], [83281, 0.4988, null], [83633, 0.4988, null], [83984, 0.4988, null], [84335, 5.4862, null], [84686, 4.6135, null], [85038, 1.7457, null], [85389, 1.995, null], [85740, 1.1223, null], [86091, 3.3665000000000003, null], [86443, 3.4913000000000003, null], [86794, 1.4963, null], [87145, 2.1197, null], [87496, 0.1247, null], [87848, 0.2494, null], [88199, 0.1247, null], [88550, 0.2494, null], [88901, 0.2494, null], [89253, 0.2494, null], [89604, 0.1247, null], [89955, 0.1247, null], [90306, 0.2494, null], [90658, 0.1247, null], [91009, 0.3741, null], [91360, 0.3741, null], [91711, 1.1222, null], [92063, 2.2444, null], [92414, 3.4913, \"class Solution {\\n public double separateSquares(int[][] squares) {\\n double min=Integer.MAX_VALUE, max=0.0;\\n \\n for(int[] square : squares){\\n min=Math.min(min,square[1]);\\n max= Math.max(max,square[1]+square[2]); \\n }\\n ///= System.out.println(min+\\\"max\\\"+max);\\n \\n while(max-min>0.000001){\\n double mid=(min+max)/2.0;\\n double areaBelow = 0, areaAbove = 0;\\n for(int[] square : squares){\\n double y1 = square[1], y2 = square[1] + square[2], len = square[2];\\n if(y2 <= mid) {\\n areaBelow += len * len;\\n } else if(y1 >= mid) {\\n areaAbove += len * len;\\n } else {\\n double l1 = mid - y1, l2 = y2 - mid;\\n areaBelow += l1 * len;\\n areaAbove += l2 * len;\\n }\\n\\n }\\n if(areaBelow < areaAbove) {\\n min = mid;\\n } else {\\n max = mid;\\n }\\n\\n \\n }\\n return min;\\n }\\n}\"], [92765, 2.4938, \"class Solution {\\n public double separateSquares(int[][] squares) {\\n double maxYCord = Double.MIN_VALUE;\\n double minYCord = Double.MAX_VALUE;\\n double maxArea = 0.0;\\n\\n for (int[] square : squares) {\\n double y = square[1], l = square[2];\\n maxYCord = Math.max(maxYCord, y + l);\\n minYCord = Math.min(minYCord, y);\\n maxArea += l * l;\\n }\\n double low = minYCord, high = maxYCord, eps = 1e-6;\\n double reqArea = maxArea/2.0;\\n while (high - low > eps) {\\n double mid = (high + low) / 2.0;\\n if (checkPossibility(mid, squares, reqArea)) {\\n low = mid;\\n } else {\\n high = mid;\\n }\\n }\\n return low;\\n }\\n private boolean checkPossibility(double mid, int[][] squares, double reqArea) {\\n double areaBelow = 0.0;\\n for (int[] sq : squares) {\\n double y = sq[1], l = sq[2];\\n double top = y + l;\\n\\n if (mid <= y) {\\n continue;\\n } else if (mid >= top) {\\n areaBelow += l * l;\\n } else {\\n double h = mid - y;\\n areaBelow += l * h;\\n }\\n }\\n return areaBelow < reqArea;\\n }\\n}\"]]",
"runtime": 202,
"runtimeDistribution": "[[33, 2.6184999999999996, \"class Solution {\\n public double separateSquares(int[][] squares) {\\n int right = 0;\\n long sum = 0;\\n for(int[] sq : squares){\\n int y = sq[1]+sq[2], r = sq[2];\\n right = Math.max(right, y);\\n sum += (long)r*r;\\n }\\n\\n int left = 0;\\n while(left<=right){\\n int mid = (left+right)>>1;\\n if(cal(squares, mid)*2>=sum) right = mid -1;\\n else left = mid + 1;\\n }\\n long area = cal(squares, left), unit = area-cal(squares, left-1);\\n return (double)left-(2*area-sum)/(2.0*unit);\\n }\\n\\n public long cal(int[][] sqs, int limit){\\n long res = 0;\\n for(int[] sq : sqs){\\n int y = sq[1], r = sq[2];\\n if(y<limit){\\n res += (long)r*Math.min(limit-y, r);\\n }\\n }\\n return res;\\n }\\n}\"], [37, 0.1247, \"class Solution {\\n public double separateSquares(int[][] squares) {\\n double totalArea = 0;\\n double start = 0.0;\\n double end = 0.0;\\n double ans = 0;\\n double epsilon = 1e-5;\\n\\n for (int square[] : squares) {\\n totalArea += (double) square[2] * (double) square[2]; \\n end = Math.max(end, square[1] + square[2]);\\n }\\n\\n totalArea/=2;\\n\\n while ((end - start ) > epsilon) {\\n double mid = (start + end)/2;\\n double aboveArea = calculateTopArea(squares, mid);\\n // System.out.println(mid + \\\" \\\" + aboveArea);\\n if (aboveArea <= totalArea) {\\n end = mid;\\n ans = mid;\\n } else {\\n start = mid;\\n }\\n }\\n\\n return ans;\\n }\\n\\n private double calculateTopArea(int [][] squares, double mid) {\\n double area = 0;\\n\\n for (int square [] : squares) {\\n if (square[1] >= mid ) {\\n area += (double) square[2] * (double) square[2]; // both operands cast\\n } else if (square[1] + square[2] > mid) {\\n area += (square[2] * (square[1] + square[2] - mid));\\n }\\n }\\n\\n return area;\\n }\\n\\n}\"], [41, 0.4988, null], [45, 0.7481, null], [48, 0.6234, null], [52, 1.7456, null], [56, 0.9975, null], [60, 0.3741, null], [63, 0.8728, null], [67, 1.995, null], [71, 1.4963, null], [75, 2.6185, null], [79, 2.3691, null], [82, 2.3691, null], [86, 1.4963, null], [90, 2.2444, null], [94, 1.7456, null], [97, 2.2444, null], [101, 9.2269, null], [105, 5.7357, null], [109, 5.2369, null], [112, 3.6159999999999997, null], [116, 2.4938000000000002, null], [120, 3.3666, null], [124, 10.349300000000001, null], [127, 3.3666, null], [131, 2.7432, null], [135, 1.7456, null], [139, 2.2443, null], [142, 0.8729, null], [146, 0.7482, null], [150, 0.7482000000000001, null], [154, 0.8729, null], [158, 0.6235, null], [161, 1.4964, null], [165, 0.6234999999999999, null], [169, 0.6235, null], [173, 0.1247, null], [176, 0.1247, null], [180, 0.7482000000000001, null], [184, 0.1247, null], [188, 0.2494, null], [191, 0.6234999999999999, null], [195, 0.8729, null], [199, 0.9976, null], [202, 12.5922, \"class Solution {\\n public double separateSquares(int[][] squares) {\\n double totalArea = 0.0;\\n long maxYPlusLi = 0;\\n for (int[] square : squares) {\\n long yi = square[1];\\n long li = square[2];\\n totalArea += (double) li * li;\\n long top = yi + li;\\n if (top > maxYPlusLi) {\\n maxYPlusLi = top;\\n }\\n }\\n double target = totalArea / 2.0;\\n double low = 0.0;\\n double high = maxYPlusLi;\\n for (int iter = 0; iter < 100; iter++) {\\n double mid = (low + high) * 0.5;\\n double sumAbove = 0.0;\\n for (int[] square : squares) {\\n long yi = square[1];\\n long li = square[2];\\n long top = yi + li;\\n if (mid <= yi) {\\n sumAbove += (double) li * li;\\n } else if (mid < top) {\\n sumAbove += (top - mid) * li;\\n }\\n }\\n if (sumAbove > target) {\\n low = mid;\\n } else {\\n high = mid;\\n }\\n }\\n return low;\\n }\\n}\"], [203, 0.4988, null], [206, 0.2494, null], [210, 0.9976, null], [214, 0.2494, null], [218, 0.7482000000000001, null], [222, 0.3741, null], [225, 0.1247, null], [229, 0.1247, null], [233, 0.1247, null], [237, 0.1247, null], [240, 0.1247, null], [244, 0.1247, null], [248, 0.1247, null], [252, 0.1247, null], [255, 0.1247, null], [259, 0.1247, null], [263, 0.1247, null], [267, 0.1247, null], [270, 0.1247, null], [274, 0.1247, null], [278, 0.1247, null], [282, 0.1247, null], [285, 0.1247, null], [289, 0.1247, null], [293, 0.2494, null], [297, 0.1247, null], [301, 0.1247, null], [304, 0.2494, null], [308, 0.1247, null], [312, 0.1247, null], [316, 0.2494, null], [319, 0.2494, null], [323, 0.1247, \"class Solution {\\n public double separateSquares(int[][] squares) {\\n double min = 0;\\n double max = 0;\\n double threshold = 1e-6;\\n for (int[] s : squares) {\\n max = Math.max(max, s[1] + s[2]);\\n }\\n while (max - min > threshold) {\\n double mid = (min + max) / 2;\\n double[] res = isValid(squares, mid);\\n\\n if (res[0] <= res[1]) {\\n max = mid - threshold;\\n } else {\\n min = mid + threshold;\\n }\\n // System.out.println(\\\"abs diff: \\\" + (res[0] - res[1]) + \\\" min: \\\" + min + \\\" mid: \\\" + mid + \\\" max: \\\" + max);\\n }\\n return min;\\n }\\n \\n public double[] isValid(int[][] square, double y) {\\n double top = 0, bottom = 0;\\n for (int[] sq : square) {\\n top += Math.max(sq[1] + sq[2] - Math.max(y, sq[1]), 0) * sq[2];\\n bottom += Math.max(Math.min(y, sq[1] + sq[2]) - sq[1], 0) * sq[2];\\n }\\n return new double[] {top, bottom};\\n }\\n}\"], [327, 0.1247, \"class Solution {\\n public double separateSquares(int[][] squares) {\\n double[] yCoords = new double[squares.length];\\n double maxY = 0;\\n double minY = Integer.MAX_VALUE;\\n for(int i=0; i<squares.length; i++) {\\n yCoords[i] = squares[i][1] + squares[i][2];\\n maxY = Math.max(maxY, yCoords[i]);\\n minY = Math.min(minY, squares[i][1]);\\n }\\n double i = minY, j = maxY;\\n double ans = Integer.MAX_VALUE;\\n double mid = i;\\n while(i<j) {\\n mid = (i+j)/2;\\n mid = Math.round(mid*Math.pow(10,6))/Math.pow(10, 6);\\n //System.out.println(mid);\\n double leftArea = findArea(squares, minY, mid);\\n double rightArea = findArea(squares, mid, maxY);\\n System.out.println(leftArea+\\\" \\\"+rightArea+ \\\" \\\"+ mid+ \\\" \\\"+i+\\\" \\\"+j);\\n if(leftArea == rightArea) {\\n ans = Math.min(ans, mid);\\n j=mid-Math.pow(10, -6);\\n j = Math.round(j*Math.pow(10,6))/Math.pow(10, 6);\\n //System.out.println(j);\\n } else if(rightArea > leftArea) {\\n i = mid+Math.pow(10, -6);\\n i = Math.round(i*Math.pow(10,6))/Math.pow(10, 6);\\n } else {\\n j=mid-Math.pow(10, -6);\\n j = Math.round(j*Math.pow(10,6))/Math.pow(10, 6);\\n }\\n }\\n return ans == Integer.MAX_VALUE ? mid: ans;\\n }\\n\\n private double findArea(int[][] squares, double lo, double hi) {\\n double area = 0.0;\\n for(int i=0; i<squares.length; i++) {\\n double y1 = squares[i][1];\\n double y2 = squares[i][1]+squares[i][2];\\n if(hi <= y1 || lo >= y2) {\\n continue;\\n }\\n double ySide = y2-y1;\\n if(hi < y2) {\\n ySide = ySide - (y2 - hi);\\n }\\n if(lo > y1) {\\n ySide = ySide-(lo-y1);\\n }\\n area+= ySide*(squares[i][2]);\\n }\\n return Math.round(area*Math.pow(10,6))/Math.pow(10, 6);\\n }\\n}\"]]"
},
"javascript": {
"code": "var separateSquares = function(squares) {\n let total_area = squares.reduce((sum, [x, y, l]) => sum + l * l, 0);\n const target = total_area / 2;\n const events = [];\n for (const [x, yi, li] of squares) {\n const end = yi + li;\n events.push({ y: yi, type: 'start', li, yi });\n events.push({ y: end, type: 'end', li, yi });\n }\n events.sort((a, b) => {\n if (a.y !== b.y) return a.y - b.y;\n return a.type === 'end' ? -1 : 1;\n });\n let sum_full = 0, active_li = 0, active_yili = 0, prev_y = -Infinity;\n for (const event of events) {\n const curr_y = event.y;\n if (prev_y < curr_y) {\n const sum_prev = sum_full + active_li * prev_y - active_yili;\n const sum_curr = sum_full + active_li * curr_y - active_yili;\n if (sum_prev <= target && target <= sum_curr) {\n if (active_li === 0) {\n if (sum_prev === target) return prev_y;\n } else {\n const k = (target + active_yili - sum_full) / active_li;\n if (k >= prev_y && k <= curr_y) return Math.max(prev_y, k);\n }\n }\n }\n if (event.type === 'start') {\n active_li += event.li;\n active_yili += event.yi * event.li;\n } else {\n active_li -= event.li;\n active_yili -= event.yi * event.li;\n sum_full += event.li * event.li;\n }\n prev_y = curr_y;\n }\n return prev_y;\n};",
"memory": 10000,
"memoryDistribution": "[[10000, 9.5239, \"var separateSquares = function(squares) {\\n let total_area = squares.reduce((sum, [x, y, l]) => sum + l * l, 0);\\n const target = total_area / 2;\\n const events = [];\\n for (const [x, yi, li] of squares) {\\n const end = yi + li;\\n events.push({ y: yi, type: 'start', li, yi });\\n events.push({ y: end, type: 'end', li, yi });\\n }\\n events.sort((a, b) => {\\n if (a.y !== b.y) return a.y - b.y;\\n return a.type === 'end' ? -1 : 1;\\n });\\n let sum_full = 0, active_li = 0, active_yili = 0, prev_y = -Infinity;\\n for (const event of events) {\\n const curr_y = event.y;\\n if (prev_y < curr_y) {\\n const sum_prev = sum_full + active_li * prev_y - active_yili;\\n const sum_curr = sum_full + active_li * curr_y - active_yili;\\n if (sum_prev <= target && target <= sum_curr) {\\n if (active_li === 0) {\\n if (sum_prev === target) return prev_y;\\n } else {\\n const k = (target + active_yili - sum_full) / active_li;\\n if (k >= prev_y && k <= curr_y) return Math.max(prev_y, k);\\n }\\n }\\n }\\n if (event.type === 'start') {\\n active_li += event.li;\\n active_yili += event.yi * event.li;\\n } else {\\n active_li -= event.li;\\n active_yili -= event.yi * event.li;\\n sum_full += event.li * event.li;\\n }\\n prev_y = curr_y;\\n }\\n return prev_y;\\n};\"], [82000, 1.5873, \"const getAreaDiff = (line, squares) => {\\n let aAbove = 0;\\n let aBelow = 0;\\n const n = squares.length;\\n\\n for(let i=0; i<n; i++){\\n const [x,y,s] = squares[i];\\n const area = s*s;\\n\\n if(y >= line){\\n aAbove += area;\\n }else if(y + s <= line){\\n aBelow += area;\\n }else{\\n aAbove += (y + s - line) * s;\\n aBelow += (line - y) * s;\\n }\\n }\\n\\n return aAbove-aBelow;\\n}\\n\\n\\nvar separateSquares = function(squares) {\\n let l=0, r=2e9;\\n for(let i=0; i<50; i++){\\n let m = (l+r)*.5;\\n let diff = getAreaDiff(m, squares);\\n if(diff > 0) {\\n l =m\\n }else{\\n r = m;\\n }\\n }\\n\\n return r;\\n}\"], [82200, 1.5873, \"/**\\n * @param {number[][]} squares\\n * @return {number}\\n */\\nvar separateSquares = function(squares) {\\n let low = 0, high = 2e9, tolerance = Math.pow(10, -5);\\n //for(let i = 0; i < 60; i++){\\n while(high - low > tolerance){\\n let mid = (high+low)/2;\\n\\n if(feasible(squares, mid) > 0){\\n low = mid;\\n }else{\\n high = mid;\\n }\\n\\n }\\n //}\\n \\n //console.log(low, high);\\n return (high+low)/2;\\n};\\n\\nlet feasible = (squares, yLine) => {\\n let aAbove = 0; let aBelow = 0;\\n\\n for(let i = 0; i < squares.length; i++){\\n let x = squares[i][0];\\n let y = squares[i][1];\\n let l = squares[i][2];\\n if(yLine <= y){\\n aAbove += l*l\\n }else if(yLine >= y + l){\\n aBelow += l*l;\\n }else{\\n let above = y + l - yLine;\\n let below = yLine - y;\\n aBelow += below*l;\\n aAbove += above*l;\\n }\\n }\\n\\n return aAbove - aBelow;\\n}\"], [82300, 1.5873, null], [82500, 1.5873, null], [82600, 4.7619, null], [82700, 3.1746, null], [82800, 1.5873, null], [82900, 1.5873, null], [83000, 1.5873, null], [83100, 3.1746, null], [83200, 1.5873, null], [83400, 1.5873, null], [83600, 3.1746, null], [83700, 1.5873, null], [84000, 3.1746, null], [84100, 1.5873, null], [84200, 1.5873, null], [84400, 1.5873, null], [84800, 1.5873, null], [86300, 1.5873, null], [86400, 1.5873, null], [86500, 1.5873, null], [86600, 1.5873, null], [86800, 1.5873, null], [87000, 3.1746, null], [87100, 1.5873, null], [87200, 1.5873, null], [87300, 3.1746, null], [87500, 1.5873, null], [87900, 1.5873, null], [88000, 1.5873, null], [88100, 1.5873, null], [88200, 3.1746, null], [88700, 1.5873, null], [88800, 1.5873, null], [89400, 1.5873, null], [89900, 1.5873, null], [90800, 1.5873, null], [90900, 1.5873, null], [91000, 1.5873, null], [91200, 1.5873, null], [91500, 1.5873, null], [92000, 1.5873, null], [92500, 1.5873, null], [92700, 1.5873, null], [93000, 1.5873, null], [97700, 1.5873, null], [100300, 1.5873, null], [100700, 1.5873, \"function separateSquares(squares) {\\n const halfArea = squares.reduce((sum, square) => {\\n return sum + square[2] * square[2];\\n }, 0) / 2;\\n \\n const events = [];\\n for (const square of squares) {\\n const y = square[1];\\n const l = square[2];\\n events.push([y, true, l]);\\n events.push([y + l, false, l]);\\n }\\n \\n events.sort((a, b) => a[0] - b[0]);\\n \\n let area = 0;\\n let width = 0;\\n let prevY = 0;\\n \\n for (const [y, isStart, l] of events) {\\n const areaGain = width * (y - prevY);\\n \\n if (area + areaGain >= halfArea) {\\n return prevY + (halfArea - area) / width;\\n }\\n \\n area += areaGain;\\n width += isStart ? l : -l;\\n prevY = y;\\n }\\n \\n throw new Error(\\\"Can't found\\\");\\n}\"], [101500, 1.5873, \"/**\\n * @param {number[][]} squares\\n * @return {number}\\n */\\nvar separateSquares = function(squares) {\\n let totalArea = 0;\\n let events = [];\\n\\n // Step 1: Prepare events and calculate total area\\n for (let [x, y, l] of squares) {\\n totalArea += l * l;\\n events.push([y, l]); // Start of square\\n events.push([y + l, -l]); // End of square\\n }\\n\\n // Step 2: Sort events by y-coordinate\\n events.sort((a, b) => a[0] - b[0]);\\n\\n let currentArea = 0;\\n let currentWidth = 0;\\n let previousY = 0;\\n\\n // Step 3: Sweep line to find separation point\\n for (let [y, change] of events) {\\n let areaContribution = currentWidth * (y - previousY);\\n \\n if (currentArea + areaContribution >= totalArea / 2) {\\n // Compute exact y-coordinate where the areas are balanced\\n return previousY + (totalArea / 2 - currentArea) / currentWidth;\\n }\\n\\n currentArea += areaContribution;\\n currentWidth += change;\\n previousY = y;\\n }\\n\\n return -1; // This case shouldn't occur in valid inputs\\n};\"]]",
"runtime": 362,
"runtimeDistribution": "[[98, 1.5873, \"/**\\n * @param {number[][]} squares\\n * @return {number}\\n */\\n\\nfunction helper(line, squares) {\\n let aAbove = 0, aBelow = 0;\\n let n = squares.length;\\n \\n for (let i = 0; i < n; i++) {\\n let x = squares[i][0], y = squares[i][1];\\n let l = squares[i][2];\\n let total = l * l;\\n \\n if (line <= y) {\\n aAbove += total;\\n } else if (line >= y + l) {\\n aBelow += total;\\n } else {\\n let aboveHeight = (y + l) - line;\\n let belowHeight = line - y;\\n aAbove += l * aboveHeight;\\n aBelow += l * belowHeight;\\n }\\n }\\n \\n return aAbove - aBelow;\\n}\\nvar separateSquares = function(squares) {\\n let maxY = 0;\\n for(let i=0; i<squares.length; i++) {\\n maxY = Math.max(maxY, squares[i][1]+squares[i][2]);\\n }\\n let bottom = 0, top = maxY, minY = maxY;\\n while(top > bottom && (Math.abs(top-bottom) > Math.pow(10, -5))) {\\n let middle = (top+bottom)/2.0;\\n let diff = helper(middle, squares);\\n if(diff > 0) {\\n bottom = middle;\\n } else {\\n top = middle;\\n }\\n }\\n return top;\\n};\"], [103, 1.5873, \"/**\\n * @param {number[][]} squares\\n * @return {number}\\n */\\nvar separateSquares = function(squares) {\\n let low = 0, high = 2e9, tolerance = Math.pow(10, -5);\\n //for(let i = 0; i < 60; i++){\\n while(high - low > tolerance){\\n let mid = (high+low)/2;\\n\\n if(feasible(squares, mid) > 0){\\n low = mid;\\n }else{\\n high = mid;\\n }\\n\\n }\\n //}\\n \\n //console.log(low, high);\\n return (high+low)/2;\\n};\\n\\nlet feasible = (squares, yLine) => {\\n let aAbove = 0; let aBelow = 0;\\n\\n for(let i = 0; i < squares.length; i++){\\n let x = squares[i][0];\\n let y = squares[i][1];\\n let l = squares[i][2];\\n if(yLine <= y){\\n aAbove += l*l\\n }else if(yLine >= y + l){\\n aBelow += l*l;\\n }else{\\n let above = y + l - yLine;\\n let below = yLine - y;\\n aBelow += below*l;\\n aAbove += above*l;\\n }\\n }\\n\\n return aAbove - aBelow;\\n}\"], [111, 1.5873, null], [115, 3.1746, null], [118, 1.5873, null], [125, 1.5873, null], [128, 3.1746, null], [130, 1.5873, null], [133, 3.1746, null], [136, 3.1746, null], [137, 1.5873, null], [139, 1.5873, null], [140, 3.1746, null], [142, 1.5873, null], [143, 1.5873, null], [149, 1.5873, null], [152, 1.5873, null], [158, 1.5873, null], [173, 1.5873, null], [179, 1.5873, null], [185, 1.5873, null], [190, 1.5873, null], [201, 1.5873, null], [205, 1.5873, null], [211, 1.5873, null], [217, 1.5873, null], [218, 1.5873, null], [219, 3.1746, null], [228, 1.5873, null], [232, 1.5873, null], [235, 1.5873, null], [238, 1.5873, null], [242, 1.5873, null], [295, 1.5873, null], [321, 1.5873, null], [347, 1.5873, null], [354, 1.5873, null], [362, 1.5873, null], [363, 1.5873, null], [376, 1.5873, null], [380, 1.5873, null], [384, 1.5873, null], [389, 1.5873, null], [420, 1.5873, null], [424, 1.5873, null], [428, 1.5873, null], [495, 3.1746, null], [509, 1.5873, null], [512, 1.5873, null], [524, 1.5873, null], [539, 1.5873, \"/**\\n * @param {number[][]} squares\\n * @return {number}\\n */\\nvar separateSquares = function(squares) {\\n const precision = 1e-5;\\n \\n function areaAbove(yLine) {\\n let area = 0;\\n for (const [x, y, l] of squares) {\\n if (y + l <= yLine) continue\\n const h = Math.min(y + l - yLine, l)\\n area += h * l\\n }\\n\\n return area\\n }\\n\\n function areaBelow(yLine) {\\n let area = 0;\\n for (const [x, y, l] of squares) {\\n if (y >= yLine) continue\\n const h = Math.min(yLine - y, l)\\n area += h * l\\n }\\n\\n return area\\n }\\n\\n let left = 0;\\n let right = 1e9;\\n\\n while (right - left > precision) {\\n const mid = (left + right) /2;\\n const below = areaBelow(mid)\\n const above = areaAbove(mid)\\n\\n if (below < above) {\\n left = mid;\\n } else {\\n right = mid;\\n }\\n }\\n\\n return left;\\n};\"], [671, 1.5873, \"/**\\n * @param {number[][]} squares\\n * @return {number}\\n */\\nvar separateSquares = function(squares) {\\n let yCoords = new Set();\\n for (let [x, y, l] of squares) {\\n yCoords.add(y);\\n yCoords.add(y + l);\\n }\\n\\n let sortedY = Array.from(yCoords).sort((a, b) => a - b);\\n\\n function calculateArea(yLine) {\\n let area = 0;\\n for (let [x, y, l] of squares) {\\n let top = y + l;\\n if (top <= yLine) {\\n area += l * l;\\n } else if (y < yLine) {\\n area += (yLine - y) * l;\\n }\\n }\\n return area;\\n }\\n\\n let left = sortedY[0], right = sortedY[sortedY.length - 1];\\n while (right - left > 1e-5) {\\n let mid = (left + right) / 2;\\n let areaBelow = calculateArea(mid);\\n let totalArea = calculateArea(Infinity);\\n let areaAbove = totalArea - areaBelow;\\n\\n if (areaBelow < areaAbove) {\\n left = mid;\\n } else {\\n right = mid;\\n }\\n }\\n\\n return parseFloat(left.toFixed(5));\\n \\n};\"]]"
},
"python3": {
"code": "class Solution:\n def separateSquares(self, squares: List[List[int]]) -> float:\n total_area = 0\n min_y = float('inf')\n max_y = -float('inf')\n for x, y, l in squares:\n total_area += l * l\n min_y = min(min_y, y)\n current_max = y + l\n max_y = max(max_y, current_max)\n \n target = total_area / 2\n \n low = min_y\n high = max_y\n \n # Perform binary search with sufficient iterations for precision\n for _ in range(100):\n mid = (low + high) / 2\n current_sum = 0.0\n for x, y, l in squares:\n if mid <= y:\n contrib = 0.0\n elif mid >= y + l:\n contrib = l * l\n else:\n contrib = (mid - y) * l\n current_sum += contrib\n if current_sum < target:\n low = mid\n else:\n high = mid\n \n return (low + high) / 2",
"memory": 4800,
"memoryDistribution": "[[4800, 48.659, \"class Solution:\\n def separateSquares(self, squares: List[List[int]]) -> float:\\n total_area = 0\\n min_y = float('inf')\\n max_y = -float('inf')\\n for x, y, l in squares:\\n total_area += l * l\\n min_y = min(min_y, y)\\n current_max = y + l\\n max_y = max(max_y, current_max)\\n \\n target = total_area / 2\\n \\n low = min_y\\n high = max_y\\n \\n # Perform binary search with sufficient iterations for precision\\n for _ in range(100):\\n mid = (low + high) / 2\\n current_sum = 0.0\\n for x, y, l in squares:\\n if mid <= y:\\n contrib = 0.0\\n elif mid >= y + l:\\n contrib = l * l\\n else:\\n contrib = (mid - y) * l\\n current_sum += contrib\\n if current_sum < target:\\n low = mid\\n else:\\n high = mid\\n \\n return (low + high) / 2\"], [44600, 0.0789, \"class Solution:\\n def separateSquares(self, squares: List[List[int]]) -> float:\\n ll, rr = min([x[1] for x in squares]), max([x[1] + x[2] for x in squares])\\n # side_len = [sqrt(x[2]) for x in squares]\\n \\n def areas(y):\\n lower, upper = 0, 0\\n for i, (_, yi, side_len) in enumerate(squares):\\n area = side_len ** 2\\n if yi >= y:\\n upper += area\\n elif yi + side_len <= y:\\n lower += area\\n else:\\n upper += (yi + side_len - y) / side_len * area\\n lower += (y - yi) / side_len * area\\n # return abs(upper - lower) < 10**-5\\n return lower, upper\\n\\n # print(areas(1))\\n # print(areas(0.5))\\n # print(areas(2))\\n # print(areas(30))\\n\\n from decimal import Decimal\\n\\n l, r = Decimal(ll), Decimal(rr + 1) # NOTE can't be 10-5\\n eps = Decimal(10 ** -5)\\n # bisect_left\\n while l < r:\\n mid = (l + r) / 2\\n lower, upper = areas(mid)\\n # print(l, r, mid, lower, upper)\\n if abs(upper - lower) < eps:\\n # return mid\\n r = mid - eps\\n # if lower - upper > eps: # too high\\n if lower > upper:\\n r = mid - eps\\n # elif lower - upper < eps: # too low\\n elif lower < upper:\\n l = mid + eps\\n\\n return l\\n\"], [44900, 0.0789, \"class Solution:\\n def separateSquares(self, squares: List[List[int]]) -> float:\\n mn_y = float('inf')\\n mx_y = -float('inf')\\n total_area = 0\\n for x, y ,l in squares:\\n mx_y = max(mx_y , y+l)\\n mn_y = min(mn_y , y)\\n total_area += l**2\\n \\n def above_line_area(y_split):\\n area = 0\\n for x, y , l in squares:\\n if y+ l <= y_split:\\n continue\\n elif y < y_split and y+l >= y_split:\\n # print(f\\\"|- y_split {y_split}: y {y}, l {l}\\\")\\n h = (y- y_split +l)\\n w = l\\n area += h*w\\n elif y >= y_split:\\n area += l*l\\n # print(f\\\"|- above_line_area {area}\\\")\\n return area\\n print(mn_y, mx_y)\\n while mx_y - mn_y > 0.000005 :\\n mid_y = (mn_y + mx_y)/2\\n\\n diff = (total_area - above_line_area(mid_y) ) - above_line_area(mid_y) \\n if diff < 0:\\n mn_y = mid_y\\n else:\\n mx_y = mid_y\\n \\n return (mn_y + mx_y) /2\"], [45300, 0.0789, null], [45400, 0.1577, null], [45500, 0.0789, null], [45600, 0.3943, null], [45700, 0.8675, null], [45800, 1.3407, null], [45900, 3.1546, null], [46000, 3.1546, null], [46100, 1.3407, null], [46200, 2.6025, null], [46300, 2.0505, null], [46400, 2.0505, null], [46500, 1.735, null], [46600, 1.8139, null], [46700, 1.183, null], [46800, 0.1577, null], [46900, 0.3943, null], [47000, 0.2366, null], [47100, 0.4732, null], [47200, 0.4732, null], [47300, 0.3155, null], [47400, 0.6309, null], [47500, 0.3155, null], [47600, 0.9464, null], [47700, 1.0252, null], [47800, 5.9937, null], [47900, 18.2177, null], [48000, 24.1325, null], [48100, 11.4353, null], [48200, 4.3375, null], [48300, 0.1577, null], [48400, 0.0789, null], [48500, 0.1577, null], [48600, 0.0789, null], [48700, 0.2366, null], [48800, 0.4732, null], [48900, 0.9464, null], [49000, 0.2366, null], [49100, 0.3943, \"class Solution:\\n def separateSquares(self, squares: List[List[int]]) -> float:\\n tol = 5e-6\\n total_area = 0\\n for x, y, l in squares:\\n total_area += l*l\\n squares.sort(key = lambda x: x[0])\\n target = total_area / 2.0\\n\\n def cal_area(m):\\n area = 0\\n for x, y, l in squares:\\n if y < m and y+l <= m:\\n area += l*l\\n elif y <= m and y + l > m:\\n area += l*(m-y)\\n return area \\n l = 0\\n r = 1e9\\n while r - l > tol:\\n m = (l+r) / 2.0\\n if cal_area(m) >= target:\\n r = m\\n else:\\n l = m\\n return l\\n\\n\\n\\n \"], [49200, 0.9464, \"class Solution:\\n def separateSquares(self, squares: List[List[int]]) -> float:\\n squares.sort(key=lambda x: (x[1],x[2]))\\n \\n # precompute cum sum of areas\\n right = 0; cum_sum = 0\\n for _,y,l in squares:\\n cum_sum += l*l\\n right = max(right, y+l)\\n\\n def get_diff_area(y_cand: float) -> int:\\n left_area = 0\\n for _,y,l in squares:\\n if (y+l)<=y_cand:\\n left_area += l*l\\n elif y<y_cand and (y+l)>y_cand:\\n left_area += l*(y_cand-y)\\n else:\\n break\\n right_area = cum_sum - left_area\\n return right_area-left_area\\n \\n left = squares[0][1]\\n while (right - left)>1e-6:\\n mid = (left+right)/2\\n diff = get_diff_area(mid)\\n if abs(diff)<1e-6 and get_diff_area(mid - 1e-5)>diff:\\n return mid\\n elif diff>0:\\n left = mid\\n else:\\n right = mid\\n\\n return mid\"]]",
"runtime": 4144,
"runtimeDistribution": "[[282, 0.47339999999999993, \"class Solution:\\n def separateSquares(self, squares: List[List[int]]) -> float:\\n hmap = defaultdict(int)\\n total = 0\\n for a, b, c in squares:\\n total += c * c\\n hmap[b] += c\\n hmap[b + c] -= c\\n half = total / 2\\n prev = [-1, -1]\\n for k in sorted(hmap.keys()):\\n if prev[0] == -1:\\n prev = [k, hmap[k]]\\n continue\\n area = (k - prev[0]) * prev[1]\\n half -= area\\n if half == 0:\\n return k\\n if half < 0:\\n return k + half / prev[1]\\n prev = [k, prev[1] + hmap[k]]\\n return 0\"], [354, 2.8395, \"from typing import List\\n\\nclass Solution:\\n def separateSquares(self, squares: List[List[int]]) -> float:\\n events = [] # List of tuples: (y, delta_density)\\n total_area = 0\\n \\n # Process each square to generate events.\\n for x, y, l in squares:\\n area = l * l\\n total_area += area\\n density = l # since density = area / l\\n events.append((y, density)) # square starts: add density\\n events.append((y + l, -density)) # square ends: subtract density\\n \\n events.sort(key=lambda x: x[0])\\n \\n half_area = total_area / 2.0\\n \\n curr_area = 0.0 # accumulated area so far\\n curr_density = 0.0 # current area density (area per unit height)\\n prev_y = events[0][0]\\n \\n # Sweep through events in order of increasing y\\n for y, delta in events:\\n # The vertical span from prev_y to current y.\\n height = y - prev_y\\n # The area contributed in this span is density * height.\\n if curr_area + curr_density * height >= half_area:\\n # We need only part of this segment.\\n # Compute how far into the segment we need to go.\\n remaining = half_area - curr_area\\n needed_height = remaining / curr_density\\n return prev_y + needed_height\\n # Otherwise, consume this segment entirely.\\n curr_area += curr_density * height\\n curr_density += delta\\n prev_y = y\\n \\n # If we somehow exhaust events (shouldn't happen), return the last y.\\n return prev_y\"], [425, 5.521000000000001, null], [496, 1.5776999999999997, null], [568, 0.47339999999999993, null], [639, 0.6311999999999999, null], [710, 0.47339999999999993, null], [782, 0.0789, null], [853, 0.1578, null], [924, 0.0789, null], [996, 0.47339999999999993, null], [1067, 0.0789, null], [1138, 0.0789, null], [1210, 0.0789, null], [1281, 0.47339999999999993, null], [1352, 1.2621999999999998, null], [1424, 1.9722999999999995, null], [1495, 1.9721999999999995, null], [1566, 1.1832999999999998, null], [1638, 1.9721999999999995, null], [1709, 5.047900000000001, null], [1780, 4.417000000000001, null], [1852, 2.9183, null], [1923, 2.4452999999999996, null], [1994, 2.4452999999999996, null], [2066, 4.417, null], [2137, 4.653700000000001, null], [2208, 4.1802, null], [2280, 3.3131, null], [2351, 2.5241999999999996, null], [2422, 2.5242, null], [2494, 1.1044999999999998, null], [2565, 1.4987999999999997, null], [2636, 1.5778999999999996, null], [2708, 2.4452999999999996, null], [2779, 2.1298999999999997, null], [2850, 3.9438000000000004, null], [2922, 3.4706, null], [2993, 2.9976, null], [3064, 2.1296999999999997, null], [3136, 0.39449999999999996, null], [3207, 0.2367, null], [3278, 0.7889999999999998, null], [3350, 0.5522999999999999, null], [3421, 0.5522999999999999, null], [3492, 0.3156, null], [3564, 0.1578, null], [3635, 0.5522, null], [3706, 0.3156, null], [3778, 0.3156, null], [3849, 0.5522999999999999, null], [3920, 0.4733, null], [3992, 0.39449999999999996, null], [4063, 0.47339999999999993, null], [4134, 0.7889999999999998, null], [4144, 11.653, \"class Solution:\\n def separateSquares(self, squares: List[List[int]]) -> float:\\n total_area = 0\\n min_y = float('inf')\\n max_y = -float('inf')\\n for x, y, l in squares:\\n total_area += l * l\\n min_y = min(min_y, y)\\n current_max = y + l\\n max_y = max(max_y, current_max)\\n \\n target = total_area / 2\\n \\n low = min_y\\n high = max_y\\n \\n # Perform binary search with sufficient iterations for precision\\n for _ in range(100):\\n mid = (low + high) / 2\\n current_sum = 0.0\\n for x, y, l in squares:\\n if mid <= y:\\n contrib = 0.0\\n elif mid >= y + l:\\n contrib = l * l\\n else:\\n contrib = (mid - y) * l\\n current_sum += contrib\\n if current_sum < target:\\n low = mid\\n else:\\n high = mid\\n \\n return (low + high) / 2\"], [4206, 0.8675999999999999, null], [4277, 0.39449999999999996, null], [4348, 0.2367, null], [4420, 0.2367, null], [4491, 0.6311999999999999, null], [4562, 0.2367, null], [4634, 0.39449999999999996, null], [4705, 0.1578, null], [4776, 0.39449999999999996, null], [4848, 0.3156, null], [4919, 0.2367, null], [4990, 0.0789, null], [5062, 0.39449999999999996, null], [5133, 0.3156, null], [5204, 0.0789, null], [5276, 0.0789, null], [5347, 0.0789, null], [5418, 0.0789, null], [5490, 0.1578, null], [5561, 0.0789, null], [5632, 0.2367, null], [5704, 0.1578, null], [5775, 0.1578, \"class Solution:\\n def compute_areas(self, sq, y_line):\\n ''' sq = [x, y, len]\\n y_line is y coordinate of the line '''\\n\\n tot_area = sq[2]**2\\n\\n if y_line>=sq[1]+sq[2]:\\n return (0, tot_area)\\n if y_line<=sq[1]:\\n return (tot_area, 0)\\n\\n bottom_frac = (y_line-sq[1]) / sq[2]\\n return (\\n tot_area*(1-bottom_frac), \\n tot_area*bottom_frac\\n )\\n\\n def compute_sum_areas(self, squares, y_line):\\n '''compute the sum over all squares'''\\n\\n top, bottom = 0, 0\\n\\n for sq in squares:\\n t, b = self.compute_areas(sq, y_line)\\n top += t\\n bottom += b\\n\\n return (top, bottom)\\n\\n\\n\\n def separateSquares(self, squares) -> float:\\n ## possible values of ideal y_line are [0, topmost y coordinate]\\n topmost_y = 0\\n for x, y, l in squares:\\n topmost_y = max(topmost_y, y+l)\\n\\n\\n ## do binary search \\n p, q = 0, topmost_y\\n for rounds in range(60): ## max search space is 1e12. We need to bring it down to 1e-5. That's 10^17 < 2^60\\n mid = p + (q-p)/2\\n top, bottom = self.compute_sum_areas(squares, mid)\\n if abs(top-bottom)<=1e-5:\\n q = mid\\n elif top > bottom:\\n p = mid\\n else:\\n q = mid\\n\\n return round(mid, 5)\\n \"], [5846, 0.0789, \"class Solution:\\n def separateSquares(self, squares: List[List[int]]) -> float:\\n \\n low = squares[0][1]\\n high = squares[0][1]+squares[0][2]\\n\\n for i in range(1, len(squares)):\\n low = min(squares[i][1], low)\\n high = max(squares[i][1]+squares[i][2], high)\\n def check(line):\\n sum_up = 0\\n sum_bottom = 0\\n for i in range(len(squares)):\\n x = squares[i][0]\\n y = squares[i][1]\\n l = squares[i][2]\\n uparea = (max(line, y+l) - max(line,y))*l\\n sum_up += uparea\\n sum_bottom += l*l-uparea\\n return sum_up - sum_bottom\\n\\n while high-low >= 1e-5:\\n mid = low + (high-low)/2\\n ans = check(mid)\\n if ans > 0: low = mid\\n else: high = mid\\n return high\\n \"]]"
},
"ruby": {
"code": "def separate_squares(squares)\n total_area = squares.sum { |x, y, l| l.to_f * l }\n target = total_area / 2.0\n\n events = []\n squares.each do |x, y_i, l|\n start_y = y_i.to_f\n end_y = (y_i + l).to_f\n events << [start_y, l.to_f]\n events << [end_y, -l.to_f]\n end\n\n events.sort!\n\n previous_y = 0.0\n current_area = 0.0\n active_sum = 0.0\n\n events.each do |current_y, delta|\n delta_y = current_y - previous_y\n area_in_interval = active_sum * delta_y\n\n if current_area + area_in_interval >= target - 1e-12\n if active_sum.zero?\n return previous_y\n else\n required = target - current_area\n y = previous_y + required / active_sum\n return y\n end\n end\n\n current_area += area_in_interval\n active_sum += delta\n previous_y = current_y\n end\n\n previous_y\nend",
"memory": 23200,
"memoryDistribution": "[[23200, 100.0, \"def separate_squares(squares)\\n total_area = squares.sum { |x, y, l| l.to_f * l }\\n target = total_area / 2.0\\n\\n events = []\\n squares.each do |x, y_i, l|\\n start_y = y_i.to_f\\n end_y = (y_i + l).to_f\\n events << [start_y, l.to_f]\\n events << [end_y, -l.to_f]\\n end\\n\\n events.sort!\\n\\n previous_y = 0.0\\n current_area = 0.0\\n active_sum = 0.0\\n\\n events.each do |current_y, delta|\\n delta_y = current_y - previous_y\\n area_in_interval = active_sum * delta_y\\n\\n if current_area + area_in_interval >= target - 1e-12\\n if active_sum.zero?\\n return previous_y\\n else\\n required = target - current_area\\n y = previous_y + required / active_sum\\n return y\\n end\\n end\\n\\n current_area += area_in_interval\\n active_sum += delta\\n previous_y = current_y\\n end\\n\\n previous_y\\nend\"], [234200, 100.0, \"def separate_squares(squares)\\n total_area = squares.sum { |x, y, l| l.to_f * l }\\n target = total_area / 2.0\\n\\n events = []\\n squares.each do |x, y_i, l|\\n start_y = y_i.to_f\\n end_y = (y_i + l).to_f\\n events << [start_y, l.to_f]\\n events << [end_y, -l.to_f]\\n end\\n\\n events.sort!\\n\\n previous_y = 0.0\\n current_area = 0.0\\n active_sum = 0.0\\n\\n events.each do |current_y, delta|\\n delta_y = current_y - previous_y\\n area_in_interval = active_sum * delta_y\\n\\n if current_area + area_in_interval >= target - 1e-12\\n if active_sum.zero?\\n return previous_y\\n else\\n required = target - current_area\\n y = previous_y + required / active_sum\\n return y\\n end\\n end\\n\\n current_area += area_in_interval\\n active_sum += delta\\n previous_y = current_y\\n end\\n\\n previous_y\\nend\"]]",
"runtime": null,
"runtimeDistribution": "[[2278, 100.0, \"def separate_squares(squares)\\n total_area = squares.sum { |x, y, l| l.to_f * l }\\n target = total_area / 2.0\\n\\n events = []\\n squares.each do |x, y_i, l|\\n start_y = y_i.to_f\\n end_y = (y_i + l).to_f\\n events << [start_y, l.to_f]\\n events << [end_y, -l.to_f]\\n end\\n\\n events.sort!\\n\\n previous_y = 0.0\\n current_area = 0.0\\n active_sum = 0.0\\n\\n events.each do |current_y, delta|\\n delta_y = current_y - previous_y\\n area_in_interval = active_sum * delta_y\\n\\n if current_area + area_in_interval >= target - 1e-12\\n if active_sum.zero?\\n return previous_y\\n else\\n required = target - current_area\\n y = previous_y + required / active_sum\\n return y\\n end\\n end\\n\\n current_area += area_in_interval\\n active_sum += delta\\n previous_y = current_y\\n end\\n\\n previous_y\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list[dict]:
import random
random.seed(seed)
# This helper function is an adaptation of the provided sample solution.
def sample_solution(squares):
total_area = 0.0
max_y = 0
for x, y, l in squares:
total_area += l * l
current_top = y + l
if current_top > max_y:
max_y = current_top
half_area = total_area / 2.0
low = 0.0
high = max_y
for _ in range(100):
mid = (low + high) / 2.0
current_sum = 0.0
for x, y, l in squares:
if mid <= y:
contrib = 0.0
elif mid >= y + l:
contrib = l * l
else:
contrib = (mid - y) * l
current_sum += contrib
if current_sum < half_area:
low = mid
else:
high = mid
return low
test_cases = []
# A list of fixed test cases covering boundary, core, and edge cases.
fixed_cases = [
[[0, 0, 1]], # Single square.
[[0, 0, 1], [2, 2, 1]], # Example 1.
[[0, 0, 2], [1, 1, 1]], # Example 2.
[[0, 0, 1], [2, 0, 3]], # Non-overlapping squares.
[[1000000000, 1000000000, 1]], # Extreme coordinates.
[[0, 0, 3], [1, 2, 2], [2, 1, 1]], # Multiple squares.
[[5, 5, 5], [0, 0, 10]] # Larger square and offset square.
]
# Use fixed cases first.
for squares in fixed_cases:
if len(test_cases) >= num_cases:
break
# Serialization format:
# First line: number of squares
# Next n lines: "x y l" for each square.
lines = [str(len(squares))]
for sq in squares:
lines.append(" ".join(map(str, sq)))
input_str = "\n".join(lines)
result = sample_solution(squares)
output_str = f"{result:.5f}"
test_cases.append({"input": input_str, "output": output_str})
# If additional cases are needed, generate random ones.
while len(test_cases) < num_cases:
n = random.randint(1, 10) # Random number of squares between 1 and 10.
squares = []
for _ in range(n):
x = random.randint(0, 100)
y = random.randint(0, 100)
l = random.randint(1, 20)
squares.append([x, y, l])
lines = [str(len(squares))]
for sq in squares:
lines.append(" ".join(map(str, sq)))
input_str = "\n".join(lines)
result = sample_solution(squares)
output_str = f"{result:.5f}"
test_cases.append({"input": input_str, "output": output_str})
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
try:
# Deserialization: strip whitespace and convert to float.
expected_val = float(expected_output.strip())
program_val = float(program_output.strip())
# Check if the outputs match within an absolute tolerance.
return abs(expected_val - program_val) <= 1e-5
except Exception:
return False
|
[{"input": "1\n0 0 1", "output": "0.50000"}, {"input": "2\n0 0 1\n2 2 1", "output": "1.00000"}, {"input": "2\n0 0 2\n1 1 1", "output": "1.16667"}, {"input": "2\n0 0 1\n2 0 3", "output": "1.33333"}, {"input": "1\n1000000000 1000000000 1", "output": "1000000000.50000"}, {"input": "3\n0 0 3\n1 2 2\n2 1 1", "output": "2.00000"}, {"input": "2\n5 5 5\n0 0 10", "output": "5.83333"}, {"input": "2\n3 94 9\n31 28 5", "output": "97.11111"}, {"input": "2\n86 94 18\n11 75 14", "output": "97.55556"}, {"input": "1\n3 11 7", "output": "14.50000"}, {"input": "4\n64 77 1\n71 25 18\n53 28 15\n75 35 1", "output": "34.71212"}, {"input": "3\n89 54 11\n35 19 7\n97 43 4", "output": "56.54545"}, {"input": "2\n48 12 12\n44 77 9", "output": "21.37500"}, {"input": "1\n93 58 18", "output": "67.00000"}, {"input": "2\n48 10 18\n37 80 20", "output": "81.90000"}, {"input": "6\n73 24 3\n5 84 8\n98 37 3\n29 12 13\n35 58 12\n20 47 12", "output": "53.87500"}, {"input": "4\n85 34 3\n77 81 6\n68 93 8\n20 59 13", "output": "69.00000"}, {"input": "5\n81 88 18\n28 87 11\n98 99 2\n29 4 11\n51 34 3", "output": "93.12069"}, {"input": "4\n72 91 11\n27 83 16\n50 82 15\n18 33 5", "output": "91.60714"}, {"input": "4\n95 71 18\n33 95 19\n54 74 13\n46 28 5", "output": "85.62903"}, {"input": "9\n63 11 2\n14 19 6\n87 54 20\n8 49 13\n76 59 17\n32 70 1\n87 92 4\n87 68 9\n98 82 11", "output": "65.74324"}, {"input": "2\n37 55 6\n58 0 9", "output": "6.50000"}, {"input": "9\n97 22 17\n13 80 10\n81 64 20\n25 19 12\n97 20 18\n99 67 1\n76 41 16\n2 14 12\n39 30 2", "output": "36.37143"}, {"input": "4\n72 10 3\n93 62 3\n97 68 5\n16 84 16", "output": "90.65625"}, {"input": "9\n21 33 17\n77 54 7\n69 96 7\n91 39 13\n85 83 12\n56 66 15\n15 31 8\n8 43 1\n75 70 8", "output": "54.57143"}, {"input": "10\n28 0 3\n90 80 2\n29 8 2\n42 9 17\n30 35 16\n27 69 5\n92 73 19\n60 31 16\n52 24 4\n12 84 14", "output": "45.18750"}, {"input": "6\n54 52 15\n93 6 4\n7 51 11\n13 31 7\n24 68 15\n17 54 6", "output": "60.61538"}, {"input": "5\n59 31 3\n56 70 4\n6 83 18\n1 11 8\n21 52 16", "output": "71.37500"}, {"input": "8\n27 51 2\n21 48 1\n49 33 15\n36 54 18\n84 91 16\n19 24 10\n27 7 19\n94 69 2", "output": "44.76667"}, {"input": "6\n7 6 19\n61 64 17\n20 7 17\n10 23 3\n76 8 8\n51 15 19", "output": "20.73636"}, {"input": "4\n74 76 2\n79 10 14\n84 74 19\n66 40 9", "output": "76.28571"}, {"input": "4\n85 91 11\n30 33 13\n16 85 10\n58 40 3", "output": "87.15000"}, {"input": "1\n58 79 19", "output": "88.50000"}, {"input": "2\n9 68 7\n64 33 5", "output": "69.71429"}, {"input": "6\n8 31 12\n36 20 15\n69 90 10\n78 83 17\n1 85 18\n38 84 4", "output": "88.71429"}, {"input": "3\n33 14 4\n95 70 5\n34 36 20", "output": "46.22500"}, {"input": "4\n91 43 7\n87 81 9\n64 62 9\n6 11 14", "output": "44.07143"}, {"input": "5\n5 0 11\n98 16 9\n20 94 15\n70 90 14\n71 1 4", "output": "95.56897"}, {"input": "2\n88 19 18\n4 47 19", "output": "47.97368"}, {"input": "9\n18 55 5\n5 39 12\n5 45 7\n87 31 4\n45 99 18\n52 79 5\n30 20 6\n52 3 6\n94 42 14", "output": "52.32143"}, {"input": "4\n34 20 4\n48 4 16\n28 25 15\n44 39 8", "output": "25.56667"}, {"input": "4\n3 84 7\n51 42 9\n8 98 9\n44 82 17", "output": "89.62500"}, {"input": "7\n86 68 11\n3 14 9\n22 74 9\n4 13 20\n55 44 11\n55 77 17\n14 49 19", "output": "55.57895"}, {"input": "4\n32 5 14\n0 66 18\n87 92 7\n46 55 3", "output": "70.66667"}, {"input": "6\n79 40 4\n92 38 17\n39 85 14\n41 51 10\n70 16 7\n53 85 13", "output": "56.55000"}, {"input": "1\n80 90 17", "output": "98.50000"}, {"input": "3\n73 63 7\n84 95 15\n34 81 18", "output": "94.88889"}, {"input": "10\n98 55 19\n93 80 2\n66 25 12\n59 18 8\n19 95 10\n55 52 11\n8 81 7\n52 34 10\n82 20 9\n87 76 8", "output": "59.06667"}, {"input": "7\n30 14 5\n24 3 8\n39 59 16\n71 55 14\n82 4 7\n20 34 5\n3 33 9", "output": "60.60000"}, {"input": "9\n22 82 2\n92 62 1\n7 10 11\n77 38 3\n52 46 3\n50 92 5\n30 14 19\n94 64 4\n66 85 19", "output": "31.50000"}, {"input": "9\n32 63 3\n30 76 4\n98 40 11\n74 94 13\n95 95 8\n54 27 5\n13 22 7\n35 56 14\n32 75 2", "output": "64.97059"}, {"input": "8\n68 47 4\n40 69 14\n60 87 8\n35 100 5\n46 60 12\n39 2 20\n4 94 2\n88 100 8", "output": "63.37500"}, {"input": "5\n70 49 10\n81 89 12\n87 15 18\n30 56 13\n1 50 9", "output": "53.94737"}, {"input": "5\n11 96 8\n38 26 6\n56 80 11\n98 82 14\n4 35 3", "output": "87.84000"}, {"input": "8\n60 94 14\n42 91 14\n12 20 9\n64 8 12\n53 77 18\n94 41 15\n88 3 2\n82 82 6", "output": "84.45833"}, {"input": "8\n82 17 1\n51 25 10\n40 73 3\n14 20 8\n66 91 5\n76 87 14\n40 57 16\n94 17 9", "output": "64.50000"}, {"input": "3\n87 75 11\n36 25 3\n53 47 6", "output": "78.45455"}, {"input": "7\n48 73 8\n2 2 18\n82 78 8\n11 59 7\n33 89 6\n6 51 20\n54 76 9", "output": "59.92593"}, {"input": "3\n11 47 6\n72 15 1\n91 67 14", "output": "72.67857"}, {"input": "8\n86 63 4\n28 91 7\n24 100 9\n36 95 16\n48 16 14\n26 76 7\n36 93 7\n53 23 14", "output": "81.42857"}, {"input": "3\n3 37 9\n30 79 15\n31 47 19", "output": "60.28947"}, {"input": "8\n10 1 16\n17 41 13\n87 27 13\n90 54 20\n32 9 4\n71 7 2\n42 30 16\n45 77 20", "output": "51.30769"}, {"input": "1\n0 32 17", "output": "40.50000"}, {"input": "10\n48 38 13\n85 47 5\n71 5 19\n22 33 6\n64 63 11\n59 16 3\n40 90 17\n55 18 9\n14 40 2\n16 63 9", "output": "45.46154"}, {"input": "6\n55 36 9\n78 97 9\n66 40 14\n21 40 16\n97 19 18\n84 81 15", "output": "45.88333"}, {"input": "1\n24 19 2", "output": "20.00000"}, {"input": "4\n23 4 16\n33 20 15\n55 14 16\n5 56 12", "output": "22.85484"}, {"input": "9\n62 58 16\n14 92 5\n15 44 3\n26 36 6\n21 95 17\n34 72 19\n27 74 1\n67 98 19\n23 53 3", "output": "92.30000"}, {"input": "4\n98 63 4\n42 3 10\n87 87 4\n50 47 19", "output": "54.71053"}, {"input": "2\n41 19 1\n10 58 16", "output": "65.96875"}, {"input": "8\n80 34 20\n84 0 11\n5 83 20\n57 41 19\n16 27 2\n82 36 11\n7 95 3\n70 77 13", "output": "51.42308"}, {"input": "2\n51 32 6\n30 98 13", "output": "103.11538"}, {"input": "2\n2 26 6\n49 99 13", "output": "104.11538"}, {"input": "5\n82 96 5\n15 38 16\n55 94 10\n87 77 5\n45 85 4", "output": "51.18750"}, {"input": "6\n65 25 16\n57 49 16\n34 72 20\n54 11 14\n47 78 6\n55 80 14", "output": "62.62500"}, {"input": "2\n5 65 11\n59 86 8", "output": "73.40909"}, {"input": "3\n63 67 17\n10 37 15\n55 10 16", "output": "45.60000"}, {"input": "5\n19 16 10\n31 66 14\n37 72 2\n70 9 2\n65 13 17", "output": "24.94444"}, {"input": "7\n52 12 15\n84 92 19\n32 45 9\n74 10 17\n2 14 15\n22 100 6\n50 5 3", "output": "24.76596"}, {"input": "7\n90 38 11\n75 92 15\n96 85 15\n79 33 11\n23 27 6\n10 95 20\n33 86 4", "output": "96.66000"}, {"input": "7\n68 2 1\n50 14 1\n21 83 16\n58 88 13\n84 95 20\n92 62 10\n79 78 12", "output": "95.13265"}, {"input": "7\n38 11 5\n17 1 7\n14 2 7\n3 26 16\n83 18 8\n55 80 18\n24 11 10", "output": "35.15625"}, {"input": "8\n18 60 14\n2 14 6\n19 94 15\n62 60 1\n57 74 8\n25 37 19\n50 6 11\n1 13 14", "output": "50.00000"}, {"input": "7\n63 94 19\n76 93 18\n37 4 16\n51 62 17\n75 92 20\n86 62 8\n91 7 17", "output": "94.62281"}, {"input": "9\n3 6 10\n49 24 12\n68 6 14\n94 65 17\n22 65 12\n87 89 2\n27 12 15\n23 28 11\n9 91 7", "output": "30.91304"}, {"input": "8\n26 73 20\n1 5 13\n26 88 4\n37 0 8\n84 42 6\n49 29 12\n51 5 5\n18 76 8", "output": "74.05000"}, {"input": "10\n85 33 14\n87 73 10\n26 83 9\n52 88 1\n53 52 13\n35 24 16\n32 76 1\n80 88 13\n5 89 15\n16 84 8", "output": "74.00000"}, {"input": "2\n81 14 4\n20 62 3", "output": "17.12500"}, {"input": "3\n68 41 6\n94 32 13\n36 68 10", "output": "42.86842"}, {"input": "5\n72 33 4\n97 15 13\n25 11 18\n63 25 5\n66 4 16", "output": "18.12766"}, {"input": "8\n13 14 8\n4 49 6\n10 97 3\n30 55 20\n47 56 5\n56 76 2\n84 64 7\n98 26 11", "output": "60.52000"}, {"input": "1\n72 1 5", "output": "3.50000"}, {"input": "6\n32 22 12\n59 25 2\n50 48 5\n37 64 3\n28 23 7\n42 84 15", "output": "66.00000"}, {"input": "1\n56 8 8", "output": "12.00000"}, {"input": "10\n67 36 18\n20 18 18\n40 7 4\n87 8 14\n66 68 1\n79 92 6\n92 41 12\n4 18 4\n87 29 1\n48 0 19", "output": "24.69444"}, {"input": "1\n49 98 19", "output": "107.50000"}, {"input": "2\n28 97 2\n72 69 3", "output": "71.16667"}, {"input": "1\n83 60 19", "output": "69.50000"}, {"input": "7\n36 87 20\n49 57 8\n87 62 20\n32 44 15\n61 19 15\n68 46 8\n18 36 6", "output": "66.65000"}, {"input": "7\n32 20 12\n94 2 14\n38 18 2\n58 52 18\n29 51 5\n80 45 7\n51 53 14", "output": "54.29730"}]
|
{
"cpp": "==Code Submission==\n\nvector<vector<int>> deserialize_stdin(const string &input) {\n vector<vector<int>> squares;\n istringstream iss(input);\n int n;\n iss >> n;\n for (int i = 0; i < n; i++) {\n int x, y, l;\n iss >> x >> y >> l;\n squares.push_back({x, y, l});\n }\n return squares;\n}\n\nstring serialize_stdout(double result) {\n ostringstream oss;\n oss.precision(5);\n oss << fixed << result;\n return oss.str();\n}\n\nint main(){\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n string input, line;\n while(getline(cin, line)){\n input += line + \"\\n\";\n }\n vector<vector<int>> squares = deserialize_stdin(input);\n Solution sol;\n double ans = sol.separateSquares(squares);\n cout << serialize_stdout(ans) << \"\\n\";\n return 0;\n}",
"golang": "==Code Submission==\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n firstLine, _ := reader.ReadString('\\n')\n firstLine = strings.TrimSpace(firstLine)\n n, _ := strconv.Atoi(firstLine)\n squares := make([][]int, n)\n for i := 0; i < n; i++ {\n line, _ := reader.ReadString('\\n')\n line = strings.TrimSpace(line)\n parts := strings.Split(line, \" \")\n x, _ := strconv.Atoi(parts[0])\n y, _ := strconv.Atoi(parts[1])\n l, _ := strconv.Atoi(parts[2])\n squares[i] = []int{x, y, l}\n }\n ans := separateSquares(squares)\n fmt.Printf(\"%.5f\\n\", ans)\n}",
"java": "public class Main {\n private static int[][] deserializeSquares(String firstLine, BufferedReader br) throws Exception {\n int n = Integer.parseInt(firstLine.trim());\n int[][] squares = new int[n][3];\n for (int i = 0; i < n; i++) {\n String s = br.readLine().trim();\n String[] parts = s.split(\" \");\n squares[i][0] = Integer.parseInt(parts[0]);\n squares[i][1] = Integer.parseInt(parts[1]);\n squares[i][2] = Integer.parseInt(parts[2]);\n }\n return squares;\n }\n \n private static String serializeOutput(double result) {\n return String.format(\"%.5f\", result);\n }\n \n public static void main(String[] args) throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n String firstLine = br.readLine();\n int[][] squares = deserializeSquares(firstLine, br);\n Solution sol = new Solution();\n double ans = sol.separateSquares(squares);\n System.out.println(serializeOutput(ans));\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\nlet input = '';\nprocess.stdin.on('data', chunk => input += chunk);\nprocess.stdin.on('end', () => {\n // Deserialize input:\n // First line: number of squares.\n // Next lines: each line \"x y l\".\n let lines = input.trim().split('\\n');\n let n = parseInt(lines[0].trim());\n let squares = [];\n for (let i = 1; i <= n; i++) {\n let parts = lines[i].trim().split(' ');\n squares.push([parseInt(parts[0]), parseInt(parts[1]), parseInt(parts[2])]);\n }\n const result = separateSquares(squares);\n console.log(result.toFixed(5));\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str):\n # The input format:\n # First line is an integer n, the number of squares.\n # Next n lines each contain three space-separated integers: x, y, l.\n lines = input_str.strip().splitlines()\n n = int(lines[0].strip())\n squares = []\n for i in range(1, n+1):\n parts = lines[i].strip().split()\n squares.append([int(parts[0]), int(parts[1]), int(parts[2])])\n return squares\n\ndef serialize_stdout(result):\n return f\"{result:.5f}\"\n\nif __name__ == \"__main__\":\n input_str = sys.stdin.read()\n squares = deserialize_stdin(input_str)\n sol = Solution()\n ans = sol.separateSquares(squares)\n print(serialize_stdout(ans))",
"ruby": "==Code Submission==\ninput = $stdin.read.strip.split(\"\\n\")\nn = input[0].to_i\nsquares = []\n(1..n).each do |i|\n parts = input[i].split\n squares << [parts[0].to_i, parts[1].to_i, parts[2].to_i]\nend\nans = separate_squares(squares)\nputs \"%.5f\" % ans"
}
|
3768
|
Check If Digits Are Equal in String After Operations I
|
check-if-digits-are-equal-in-string-after-operations-i
|
<p>You are given a string <code>s</code> consisting of digits. Perform the following operation repeatedly until the string has <strong>exactly</strong> two digits:</p>
<ul>
<li>For each pair of consecutive digits in <code>s</code>, starting from the first digit, calculate a new digit as the sum of the two digits <strong>modulo</strong> 10.</li>
<li>Replace <code>s</code> with the sequence of newly calculated digits, <em>maintaining the order</em> in which they are computed.</li>
</ul>
<p>Return <code>true</code> if the final two digits in <code>s</code> are the <strong>same</strong>; otherwise, return <code>false</code>.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">s = "3902"</span></p>
<p><strong>Output:</strong> <span class="example-io">true</span></p>
<p><strong>Explanation:</strong></p>
<ul>
<li>Initially, <code>s = "3902"</code></li>
<li>First operation:
<ul>
<li><code>(s[0] + s[1]) % 10 = (3 + 9) % 10 = 2</code></li>
<li><code>(s[1] + s[2]) % 10 = (9 + 0) % 10 = 9</code></li>
<li><code>(s[2] + s[3]) % 10 = (0 + 2) % 10 = 2</code></li>
<li><code>s</code> becomes <code>"292"</code></li>
</ul>
</li>
<li>Second operation:
<ul>
<li><code>(s[0] + s[1]) % 10 = (2 + 9) % 10 = 1</code></li>
<li><code>(s[1] + s[2]) % 10 = (9 + 2) % 10 = 1</code></li>
<li><code>s</code> becomes <code>"11"</code></li>
</ul>
</li>
<li>Since the digits in <code>"11"</code> are the same, the output is <code>true</code>.</li>
</ul>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">s = "34789"</span></p>
<p><strong>Output:</strong> <span class="example-io">false</span></p>
<p><strong>Explanation:</strong></p>
<ul>
<li>Initially, <code>s = "34789"</code>.</li>
<li>After the first operation, <code>s = "7157"</code>.</li>
<li>After the second operation, <code>s = "862"</code>.</li>
<li>After the third operation, <code>s = "48"</code>.</li>
<li>Since <code>'4' != '8'</code>, the output is <code>false</code>.</li>
</ul>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>3 <= s.length <= 100</code></li>
<li><code>s</code> consists of only digits.</li>
</ul>
|
You are given a string `s` consisting of digits. Perform the following operation repeatedly until the string has **exactly** two digits:
- For each pair of consecutive digits in `s`, starting from the first digit, calculate a new digit as the sum of the two digits **modulo** 10\.
- Replace `s` with the sequence of newly calculated digits, *maintaining the order* in which they are computed.
Return `true` if the final two digits in `s` are the **same**; otherwise, return `false`.
**Example 1:**
**Input:** s \= "3902"
**Output:** true
**Explanation:**
- Initially, `s = "3902"`
- First operation:
- `(s[0] + s[1]) % 10 = (3 + 9) % 10 = 2`
- `(s[1] + s[2]) % 10 = (9 + 0) % 10 = 9`
- `(s[2] + s[3]) % 10 = (0 + 2) % 10 = 2`
- `s` becomes `"292"`
- Second operation:
- `(s[0] + s[1]) % 10 = (2 + 9) % 10 = 1`
- `(s[1] + s[2]) % 10 = (9 + 2) % 10 = 1`
- `s` becomes `"11"`
- Since the digits in `"11"` are the same, the output is `true`.
**Example 2:**
**Input:** s \= "34789"
**Output:** false
**Explanation:**
- Initially, `s = "34789"`.
- After the first operation, `s = "7157"`.
- After the second operation, `s = "862"`.
- After the third operation, `s = "48"`.
- Since `'4' != '8'`, the output is `false`.
**Constraints:**
- `3 <= s.length <= 100`
- `s` consists of only digits.
|
Easy
|
[
"math",
"string",
"simulation",
"combinatorics",
"number-theory"
] |
leetcode
|
https://leetcode.com/problems/check-if-digits-are-equal-in-string-after-operations-i
|
functional
| null | null | null | null |
{
"c": "bool hasSameDigits(char* s) {\n \n}",
"cpp": "class Solution {\npublic:\n bool hasSameDigits(string s) {\n \n }\n};",
"csharp": "public class Solution {\n public bool HasSameDigits(string s) {\n \n }\n}",
"dart": "class Solution {\n bool hasSameDigits(String s) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec has_same_digits(s :: String.t) :: boolean\n def has_same_digits(s) do\n \n end\nend",
"erlang": "-spec has_same_digits(S :: unicode:unicode_binary()) -> boolean().\nhas_same_digits(S) ->\n .",
"golang": "func hasSameDigits(s string) bool {\n \n}",
"java": "class Solution {\n public boolean hasSameDigits(String s) {\n \n }\n}",
"javascript": "/**\n * @param {string} s\n * @return {boolean}\n */\nvar hasSameDigits = function(s) {\n \n};",
"kotlin": "class Solution {\n fun hasSameDigits(s: String): Boolean {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param String $s\n * @return Boolean\n */\n function hasSameDigits($s) {\n \n }\n}",
"python": "class Solution(object):\n def hasSameDigits(self, s):\n \"\"\"\n :type s: str\n :rtype: bool\n \"\"\"\n ",
"python3": "class Solution:\n def hasSameDigits(self, s: str) -> bool:\n ",
"racket": "(define/contract (has-same-digits s)\n (-> string? boolean?)\n )",
"ruby": "# @param {String} s\n# @return {Boolean}\ndef has_same_digits(s)\n \nend",
"rust": "impl Solution {\n pub fn has_same_digits(s: String) -> bool {\n \n }\n}",
"scala": "object Solution {\n def hasSameDigits(s: String): Boolean = {\n \n }\n}",
"swift": "class Solution {\n func hasSameDigits(_ s: String) -> Bool {\n \n }\n}",
"typescript": "function hasSameDigits(s: string): boolean {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n bool hasSameDigits(string s) {\n while (s.size() > 2) {\n string next;\n for (int i = 0; i < s.size() - 1; ++i) {\n int sum = (s[i] - '0') + (s[i+1] - '0');\n next.push_back((sum % 10) + '0');\n }\n s = next;\n }\n return s[0] == s[1];\n }\n};",
"memory": 1000,
"memoryDistribution": "[[1000, 56.1198, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while (s.size() > 2) {\\n string next;\\n for (int i = 0; i < s.size() - 1; ++i) {\\n int sum = (s[i] - '0') + (s[i+1] - '0');\\n next.push_back((sum % 10) + '0');\\n }\\n s = next;\\n }\\n return s[0] == s[1];\\n }\\n};\"], [8100, 0.0564, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n while (n > 2) {\\n for (int i = 0; i < n - 1; i++) { \\n s[i] = ((s[i] - '0' + s[i + 1] - '0') % 10) + '0';\\n }\\n n--;\\n }\\n return s[0] == s[1]; \\n }\\n};\"], [8200, 0.7332, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n \\n int n=s.size();\\n \\n while(n>2)\\n {for(int i=0;i<n-1;i++)\\n {\\n int x=(s[i]-'0'+s[i+1]-'0')%10;\\n s[i]=x+'0';\\n }\\n s.pop_back();\\n n--;\\n }\\n if(s[0]==s[1])\\n return true;\\n return false;\\n }\\n};\"], [8300, 2.0305, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while(s.size()!=2){\\n for(int i=0;i<s.size()-1;i++){\\n int prod = (((s[i]-'0') + (s[i+1]-'0'))%10);\\n s[i]=prod+'0';\\n }\\n s.pop_back();\\n }\\n if(s[0] == s[1]) return true;\\n return false;\\n }\\n};\"], [8400, 4.6813, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int j=0;\\n string curr=\\\"\\\";\\n while(s.size()!=2){\\n curr=\\\"\\\";\\n j=0;\\n while(j<s.size()-1){\\n int num1=s[j]-'0';\\n int num2=s[j+1]-'0';\\n int prod=(num1+num2)%10;\\n curr.push_back(prod);\\n j++;\\n }\\n s=curr;\\n }\\n if(s[0] == s[1]) return true;\\n return false;\\n }\\n};\"], [8500, 5.3017, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n \\n int n=s.size(),tmp;\\n if(n<2) return false;\\n string s_tmp;\\n while(n>2){\\n s_tmp=\\\"\\\";\\n for(int i=0;i<n-1;i++){\\n tmp=(int(s[i])+int(s[i+1]))%10;\\n s_tmp+=(char)tmp;\\n }\\n s=s_tmp;\\n n--;\\n\\n }\\n if(s[0]==s[1]) return true;\\n return false;\\n }\\n};\"], [8600, 3.3277, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int j=0;\\n string curr=\\\"\\\";\\n int num1,num2,prod;\\n while(s.size()!=2){\\n curr=\\\"\\\";\\n j=0;\\n while(j<s.size()-1){\\n num1=s[j]-'0';\\n num2=s[j+1]-'0';\\n prod=(num1+num2)%10;\\n curr.push_back(prod);\\n j++;\\n }\\n s=curr;\\n }\\n if(s[0] == s[1]) return true;\\n return false;\\n }\\n};\"], [8700, 1.4664, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n string a = s;\\n string b;\\n while (a.size() != 2) {\\n for (int i = 0; i < a.size()-1; i++) {\\n char c = '0'+(a[i] - '0' + a[i + 1] - '0') % 10;\\n b += c;\\n }\\n a = b;\\n b.resize(0);\\n }\\n return a[0]==a[1];\\n }\\n};\"], [8800, 0.5076, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int t[100];\\n int n=s.size();\\n for(int i=0;i<n;i++)\\n {\\n t[i]=s[i]-'0';\\n }\\n while(n>2)\\n {for(int i=0;i<n-1;i++)\\n {\\n t[i]=(t[i]+t[i+1])%10;\\n }\\n n--;\\n }\\n if(t[0]==t[1])\\n return true;\\n return false;\\n }\\n};\"], [8900, 0.3384, \"class Solution\\n{\\npublic:\\n bool hasSameDigits(string s)\\n {\\n std::string builder;\\n builder.reserve(s.size() - 1);\\n\\n const int size = s.size();\\n int stop = s.size() - 1;\\n for ( int start = 0; start < stop - 1; ++start )\\n {\\n for ( int read = start; read < size; ++read )\\n builder.push_back(((s[read] + s[read + 1] - '0' - '0') % 10) + '0');\\n\\n for ( int b = 0, write = start + 1; write < size; ++write, ++b )\\n s[write] = builder[b];\\n\\n //for ( int i = start + 1; i < s.size(); ++i )\\n // std::cout << s[i];\\n //std::cout << std::endl;\\n\\n builder.clear();\\n }\\n\\n\\n\\n return ( s[stop - 1] == s[stop] );\\n }\\n};\"], [9000, 0.3948, \"class Solution\\n{\\npublic:\\n bool hasSameDigits(const string &s)\\n {\\n int n = s.length();\\n int *digit = new int[n];\\n for (int i = 0; i < n; i++)\\n {\\n digit[i] = s[i] - '0';\\n }\\n\\n while (n > 2)\\n {\\n for (int i = 0; i < n - 1; i++)\\n {\\n digit[i] = ((digit[i] + digit[i + 1]) % 10);\\n }\\n n--;\\n }\\n bool result = digit[0] == digit[1];\\n delete[] digit;\\n return result;\\n }\\n};\\n\"], [9100, 0.282, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n = s.length();\\n \\n // Calculate binomial coefficients modulo 10 using Pascal's triangle\\n vector<int> coef(n, 0);\\n coef[0] = 1;\\n for (int i = 0; i < n-2; i++) {\\n for (int j = i+1; j > 0; j--) {\\n coef[j] = (coef[j] + coef[j-1]) % 10;\\n }\\n }\\n \\n // Calculate the final two digits\\n int digit1 = 0;\\n int digit2 = 0;\\n for (int i = 0; i < n-1; i++) {\\n digit1 = (digit1 + coef[i] * (s[i] - '0')) % 10;\\n digit2 = (digit2 + coef[i] * (s[i+1] - '0')) % 10;\\n }\\n \\n return digit1 == digit2;\\n }\\n};\"], [9200, 0.846, \"#include <string>\\n#include <cstdint>\\n\\nclass Solution {\\npublic:\\n bool hasSameDigits(std::string s) {\\n while (s.size() > 2) {\\n std::string iterationEnd;\\n iterationEnd.reserve(s.size() - 1);\\n for (\\n uint8_t index = 1;\\n index < s.size();\\n index++\\n ) {\\n const uint8_t resultNumber = (s[index - 1] + s[index]) % 10;\\n const char resultCharacter = '0' + resultNumber;\\n iterationEnd.push_back(resultCharacter);\\n }\\n s = iterationEnd; \\n }\\n return s[0] == s[1];\\n }\\n};\"], [9300, 0.7332, \"#include <string>\\n#include <vector>\\n// No other specific includes like <numeric> are strictly necessary for this version.\\n\\nclass Solution {\\nprivate:\\n // Helper structure for Lucas Theorem: precomputes factorials and their modular inverses.\\n struct LucasHelpers {\\n std::vector<long long> fact;\\n std::vector<long long> invFact;\\n int p_mod; // Prime modulus\\n\\n LucasHelpers(int prime) : p_mod(prime) {\\n fact.resize(p_mod);\\n invFact.resize(p_mod);\\n fact[0] = 1;\\n invFact[0] = 1;\\n for (int i = 1; i < p_mod; ++i) {\\n fact[i] = (fact[i - 1] * i) % p_mod;\\n invFact[i] = modular_power(fact[i], p_mod - 2); // Fermat's Little Theorem\\n }\\n }\\n\\n // Calculates (base^exp) % p_mod using binary exponentiation.\\n long long modular_power(long long base, long long exp) const {\\n long long res = 1;\\n base %= p_mod;\\n while (exp > 0) {\\n if (exp % 2 == 1) res = (res * base) % p_mod;\\n base = (base * base) % p_mod;\\n exp /= 2;\\n }\\n return res;\\n }\\n };\\n\\n // Provides a statically initialized LucasHelpers instance for modulo 5.\\n // Ensures precomputation is done only once.\\n static const LucasHelpers& get_lucas_mod_5_helpers() {\\n static LucasHelpers instance(5); \\n return instance;\\n }\\n \\n // Base case for Lucas Theorem: C(n_digit, r_digit) % p, where n_digit, r_digit < p.\\n static long long combinations_base_case(int n_digit, int r_digit, const LucasHelpers& helpers) {\\n if (r_digit < 0 || r_digit > n_digit) {\\n return 0;\\n }\\n long long num = helpers.fact[n_digit];\\n long long den = (helpers.invFact[r_digit] * helpers.invFact[n_digit - r_digit]) % helpers.p_mod;\\n return (num * den) % helpers.p_mod;\\n }\\n\\n // Calculates C(N_val, R_val) % p using Lucas Theorem.\\n static long long combinations_mod_prime(long long N_val, long long R_val, const LucasHelpers& helpers) {\\n if (R_val < 0 || R_val > N_val) {\\n return 0;\\n }\\n if (helpers.p_mod == 0) return 0; // Should not be called with p_mod = 0\\n \\n long long total_C_N_R_mod_p = 1;\\n long long current_N = N_val;\\n long long current_R = R_val;\\n\\n while (current_R > 0 || current_N > 0) { \\n int n_i = current_N % helpers.p_mod;\\n int r_i = current_R % helpers.p_mod;\\n \\n total_C_N_R_mod_p = (total_C_N_R_mod_p * combinations_base_case(n_i, r_i, helpers)) % helpers.p_mod;\\n \\n current_N /= helpers.p_mod;\\n current_R /= helpers.p_mod;\\n if (total_C_N_R_mod_p == 0) break; \\n }\\n return total_C_N_R_mod_p;\\n }\\n\\n // Calculates C(N_val, R_val) % 2.\\n static long long combinations_mod_2(long long N_val, long long R_val) {\\n if (R_val < 0 || R_val > N_val) {\\n return 0;\\n }\\n // C(N, R) is odd iff (R & N) == R (all set bits in R are also set in N).\\n return ((R_val & N_val) == R_val) ? 1 : 0;\\n }\\n\\npublic:\\n bool hasSameDigits(std::string s) {\\n int N_len = s.length(); // Initial length of the string\\n \\n // k_ops is the 'N' for C(N, R) binomial coefficients. Max N_len=100 => k_ops=98.\\n int k_ops = N_len - 2; \\n\\n std::vector<int> d_digits(N_len); // Store numerical values of initial digits\\n for (int i = 0; i < N_len; ++i) {\\n d_digits[i] = s[i] - '0';\\n }\\n\\n const LucasHelpers& lucas_helpers_mod_5 = get_lucas_mod_5_helpers();\\n\\n long long final_digit_0_val = 0;\\n long long final_digit_1_val = 0;\\n\\n // i_coeff is 'R' for C(k_ops, i_coeff)\\n for (int i_coeff = 0; i_coeff <= k_ops; ++i_coeff) { \\n long long c_k_i_mod_2 = combinations_mod_2(k_ops, i_coeff);\\n long long c_k_i_mod_5 = combinations_mod_prime(k_ops, i_coeff, lucas_helpers_mod_5);\\n \\n // CRT: If X=A mod 2, X=B mod 5, then X = (5A + 6B) mod 10.\\n long long c_k_i_mod_10 = (5 * c_k_i_mod_2 + 6 * c_k_i_mod_5) % 10;\\n \\n final_digit_0_val = (final_digit_0_val + (c_k_i_mod_10 * d_digits[i_coeff]) % 10) % 10;\\n // d_digits[i_coeff+1] is safe: i_coeff <= k_ops = N_len-2. So i_coeff+1 <= N_len-1.\\n final_digit_1_val = (final_digit_1_val + (c_k_i_mod_10 * d_digits[i_coeff+1]) % 10) % 10;\\n }\\n \\n return final_digit_0_val == final_digit_1_val;\\n }\\n};\"], [9400, 0.5076, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n = s.length();\\n vector<vector<int>> cnt(2, vector<int>(n, 0));\\n for (int i = 0; i < n - 1; i++)\\n cnt[0][i] = (s[i] - '0' + s[i + 1] - '0') % 10;\\n int p = 0, c;\\n for (int i = 2; i < n - 1; i++) {\\n c = 1 - p;\\n for (int j = 0; j < n - i; j++)\\n cnt[c][j] = (cnt[p][j] + cnt[p][j + 1]) % 10;\\n p = c;\\n }\\n return cnt[p][0] == cnt[p][1];\\n }\\n};\"], [9500, 0.3948, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n vector<int> s1;\\n vector<int> s2;\\n\\n for(auto num : s){\\n s1.push_back(num-'0');\\n }\\n\\n // for (int i = 0; i < s.size() - 1; i++) {\\n // int num1 = s[i] - '0';\\n // int num2 = s[i + 1] - '0';\\n // s1.push_back((num1 + num2) % 10);\\n // }\\n int n = s1.size();\\n \\n\\n while (n != 2) {\\n s2.clear();\\n for (int j = 0; j < s1.size() - 1; j++) {\\n s2.push_back((s1[j] + s1[j + 1]) % 10);\\n }\\n \\n s1=s2;\\n n=s1.size();\\n \\n \\n }\\n if(n==2){\\n if(s2[0]==s2[1]) return true;\\n }\\n\\n return false;\\n }\\n};\"], [9600, 0.1128, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n // string s2 = \\\"\\\";\\n // while (s.size() > 2) {\\n // for (int i = 0; i < s.size() - 1; i++) {\\n // int num1 = s[i] - '0';\\n // int num2 = s[i + 1] - '0';\\n // int sum = (num1 + num2) % 10;\\n // s2 += to_string(sum);\\n // }\\n // s=s2;\\n // s2=\\\"\\\";\\n // }\\n // return s[0]==s[1];\\n\\n string temp;\\n while (s.length() > 2)\\n {\\n for (int i = 1; i < s.length(); i++)\\n {\\n temp += ('0' + (s[i] - '0' + s[i - 1] - '0') % 10);\\n }\\n\\n s.swap(temp);\\n temp.clear();\\n }\\n\\n return s[0] == s[1];\\n \\n }\\n};\"], [9700, 1.128, \"class Solution {\\npublic:\\n int binmod10(int n, int k) {\\n int mod2 = binmod2(n, k);\\n int mod5 = binmod5(n, k);\\n for (int i = 0; i < 10; i++) {\\n if (i % 2 == mod2 && i % 5 == mod5)\\n return i;\\n }\\n return 0;\\n }\\n\\n int binmod2(int n, int k) {\\n while (k > 0) {\\n if ((k & 1) > (n & 1))\\n return 0;\\n n >>= 1;\\n k >>= 1;\\n }\\n return 1;\\n }\\n\\n int binmod5(int n, int k) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int nd = n % 5;\\n int kd = k % 5;\\n if (kd > nd)\\n return 0;\\n res = (res * binsmall(nd, kd)) % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return res;\\n }\\n\\n int binsmall(int n, int k) {\\n if (k > n)\\n return 0;\\n int fact[5] = {1, 1, 2, 1, 4};\\n int numerator = fact[n];\\n int denominator = (fact[k] * fact[n - k]) % 5;\\n int deninv = 0;\\n for (int i = 0; i < 5; i++) {\\n if ((denominator * i) % 5 == 1) {\\n deninv = i;\\n break;\\n }\\n }\\n return (numerator * deninv) % 5;\\n }\\n \\n bool hasSameDigits(string s) {\\n int n = s.size()-2;\\n vector<int> sequence;\\n long long binomial_coeff = 1;\\n sequence.push_back(binomial_coeff);\\n\\n for (int k = 1; k <= n; ++k) {\\n binomial_coeff = binmod10(n,k);\\n // binomial_coeff = binomial_coeff * (n - k + 1) / k;\\n sequence.push_back(binomial_coeff);\\n // cout<<binomial_coeff<<\\\" \\\";\\n }\\n long long sum1=0, sum2=0;\\n for(int i=0; i<sequence.size(); i++){\\n sum1 += sequence[i]*(s[i]-'0' );\\n sum2 += sequence[i]*(s[i+1]-'0');\\n // cout<<sequence[i]*(s[i]-'0' )<<\\\" \\\"<<sequence[i]*(s[i+1]-'0' )<<endl;\\n }\\n if(sum1%10 == sum2%10)\\n return true;\\n return false;\\n }\\n};\"], [9800, 3.3841, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while(s.size()>2){\\n string ss;\\n int i;\\n for( i=0;i<s.size()-1;i++){\\n ss.push_back(((s[i]-'0')+(s[i+1]-'0'))%10);\\n }\\n s=ss;\\n } \\n if(s[0]!=s[1])return 0;\\n return 1 ;\\n }\\n};\"], [9900, 7.8398, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n=s.length();\\n for(int i=n;i>=3;i--){\\n string s1=\\\"\\\";\\n for(int j=0;j<s.length()-1;j++){\\n s1+=((s[j]-'0')+(s[j+1]-'0'))%10;\\n }\\n s=s1;\\n }\\n return s[0]==s[1]?true:false;\\n }\\n};\"], [10000, 9.8139, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int i = 0;\\n while(s.size() > 2) {\\n string newString;\\n for(int i = 0; i < s.size() - 1; i++) {\\n newString.push_back((s[i] + s[i + 1]) % 10);\\n }\\n s = newString;\\n }\\n return s[0] == s[1];\\n }\\n};\"], [10100, 9.7575, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while(s.size() > 2) {\\n string newString;\\n for(int i = 0; i < s.size() - 1; i++) {\\n newString.push_back((s[i] + s[i + 1]) % 10);\\n }\\n s = newString;\\n }\\n return s[0] == s[1];\\n }\\n};\"], [10200, 2.5945, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while(s.size() != 2) {\\n string temp;\\n int n = s.size();\\n\\n for(int i=0; i<n-1; i++) {\\n int a = ((s[i]-'0') + (s[i+1]-'0')) % 10;\\n temp.push_back(a);\\n }\\n s = temp;\\n }\\n\\n return s[0] == s[1];\\n }\\n};\"], [10300, 0.6204, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n = s.length();\\n string p = s;\\n while(p.size()>2)\\n {\\n string q = \\\"\\\";\\n for(int i=0;i<p.size()-1;i++)\\n q += (p[i] - '0' + p[i+1] - '0')%10 + '0';\\n p = q;\\n }\\n return p[0]==p[1];\\n }\\n};\"], [10400, 0.0564, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n = s.length();\\n int storageArr[100];\\n\\n // Convert string to integer array\\n for (int i = 0; i < n; ++i) {\\n storageArr[i] = s[i] - '0';\\n }\\n\\n string newString = \\\"\\\";\\n while (n > 2) {\\n newString = \\\"\\\";\\n for (int i = 0; i < n - 1; ++i) {\\n newString += to_string((storageArr[i] + storageArr[i + 1]) % 10);\\n }\\n\\n for (int i = 0; i < newString.length(); ++i) {\\n storageArr[i] = newString[i] - '0';\\n }\\n\\n n = newString.length();\\n }\\n\\n // Final check\\n return storageArr[0] == storageArr[1];\\n }\\n};\"], [10500, 0.1128, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n = s.length();\\n while(n>2)\\n {\\n auto x = s;\\n s=\\\"\\\";\\n for(int i=0;i<n-1;i++)\\n {\\n s+=to_string(((x[i]-'0')+(x[i+1]-'0'))%10);\\n }\\n n--;\\n }\\n if(s[0]==s[1]) return true;\\n return false;\\n }\\n};\"], [10600, 0.1128, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n string holdStr = \\\"\\\";\\n while (s.length() > 2)\\n {\\n for (int i = 0; i < s.length() - 1; i++)\\n {\\n int dig1 = stoi(s.substr(i, 1));\\n int dig2 = stoi(s.substr(i + 1, 1));\\n int newDig = (dig1 + dig2) % 10;\\n holdStr += to_string(newDig);\\n }\\n s = holdStr;\\n holdStr = \\\"\\\";\\n }\\n return s[0] == s[1];\\n }\\n};\"], [10700, 0.1128, \"class Solution {\\npublic:\\n string operation(string s) {\\n string res;\\n for (int i = 0; i < s.size() - 1; i++) {\\n int sum = (s[i] - '0' + s[i + 1] - '0') % 10;\\n res.push_back(sum + '0');\\n }\\n return res;\\n }\\n bool hasSameDigits(string s) {\\n while (s.size() != 2) {\\n s = operation(s);\\n }\\n return s[0] == s[1];\\n }\\n};\\n\"], [10800, 0.6768, \"class Solution {\\nprivate:\\n bool isAnagram(string s){\\n int left = 0, right = s.size() - 1;\\n while(left <= right){\\n if(s[left] != s[right]){\\n return false;\\n }\\n }\\n return true;\\n }\\npublic:\\n bool hasSameDigits(string s) {\\n //can optimize by check whether is anagram\\n std::string cur = s;\\n while(cur.size() > 2){\\n if(isAnagram(cur)){\\n return true;\\n }\\n std::string next = \\\"\\\";\\n for(size_t i = 0; i < cur.size() - 1; i++){\\n char nextChar = ((cur[i] - '0') + (cur[i + 1] - '0'))%10 + '0';\\n next += nextChar;\\n }\\n cur = next;\\n }\\n if(cur[0] == cur[1]){\\n return true;\\n }\\n return false;\\n }\\n};\"], [10900, 0.4512, \"class Solution {\\npublic:\\n string convert(string s){\\n int n = s.size()-1;\\n string ans=\\\"\\\";\\n for(int i=0;i<n;i++){\\n int num1 = s[i]-'0';\\n int num2 = s[i+1]-'0';\\n ans+=(num1+num2)%10+'0';\\n }\\n return ans;\\n }\\n bool hasSameDigits(string s) {\\n string ans=s;\\n while(ans.size()>2){\\n ans=convert(ans);\\n }\\n cout<<ans<<endl;\\n return ans[0]==ans[1];\\n }\\n};\"], [11000, 0.3948, \"class Solution {\\npublic:\\n\\n bool solve(string& str){\\n if(str.length()==2){\\n return str[0]==str[1];\\n }\\n string newstr=\\\"\\\";\\n for(int i=0;i<str.length()-1;i++){\\n newstr+=((((str[i]-'0')+(str[i+1]-'0'))%10)+'0');\\n\\n\\n }\\n return solve(newstr);\\n }\\n\\n\\n bool hasSameDigits(string s) {\\n int n=s.length();\\n // we have to do recursion until length of s become to 2\\n return solve(s);\\n \\n }\\n};\"], [11100, 4.1173, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n cout << s << \\\"\\\\n\\\";\\n while (s.size() != 2) {\\n string next_s;\\n for (int i = 0, j = 1; j < s.size(); ++i, ++j) {\\n char d = '0' + (((s[i] - '0') + (s[j] - '0')) % 10);\\n next_s.push_back(d);\\n cout << d << \\\", \\\";\\n }\\n swap(s, next_s);\\n }\\n return s[0] == s[1];\\n }\\n};\"], [11200, 8.1782, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n=s.length();\\n while(n>2){\\n string res=\\\"\\\";\\n for(int i=1;i<s.length();i++){\\n int x=(s[i]-'0'+s[i-1]-'0')%10;\\n res+=to_string(x);\\n } \\n s=res;\\n n--; \\n } \\n return s[0]==s[1];\\n }\\n};\"], [11300, 10.9983, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) \\n {\\n while(s.length()>2)\\n {\\n string newborn;\\n\\n for(int i=0;i<s.length()-1;i++)\\n {\\n int first=s[i]-'0';\\n int second=s[i+1]-'0';\\n\\n int newdigit=(first+second)%10;\\n newborn+=to_string(newdigit);\\n }\\n s=newborn;\\n }\\n\\n if(s[0]==s[1])\\n {\\n return true;\\n }\\n\\n return false;\\n \\n }\\n};\"], [11400, 4.2301, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while(s.size()!=2){\\n string x=\\\"\\\";\\n for(int i=0;i<s.size()-1;i++){\\n x+=to_string((s[i]-'0'+s[i+1]-'0')%10);\\n }\\n s=x;\\n }\\n if(s[0]==s[1]) return true;\\n return false;\\n }\\n};\"], [11500, 0.282, \"class Solution {\\npublic:\\n bool hasSameDigits(std::string s) {\\n while (s.length() > 2) {\\n std::string newbornString;\\n for (size_t i = 0; i < s.length() - 1; i++) {\\n int firstDigit = s[i] - '0'; // Convert char to int\\n int secondDigit = s[i + 1] - '0'; // Convert char to int\\n int newDigit = (firstDigit + secondDigit) % 10; // Calculate new digit\\n newbornString += std::to_string(newDigit); // Append new digit to the new string\\n }\\n s = newbornString; // Update s to the new string\\n }\\n // Check if the final two digits are the same\\n return s[0] == s[1];\\n }\\n};\"], [11600, 0.0564, \"class Solution {\\npublic:\\n bool hasSameDigits(std::string s) {\\n std::unordered_set<char> uniqueDigits;\\n \\n // Add all digits to the unordered_set\\n for (int i = 0; i < s.length(); i++) {\\n uniqueDigits.insert(s[i]);\\n }\\n \\n // If there's only one unique digit, return true\\n if (uniqueDigits.size() == 1) {\\n return true;\\n }\\n \\n // Reduce the digits until we have two or fewer\\n while (s.length() > 2) {\\n std::string newbornString;\\n for (int i = 0; i < s.length() - 1; i++) {\\n // Calculate new digit as the sum of adjacent digits modulo 10\\n int newDigit = (s[i] - '0' + s[i + 1] - '0') % 10;\\n newbornString += std::to_string(newDigit);\\n }\\n s = newbornString; // Update s to the new string\\n }\\n \\n // Check if the final two digits are the same\\n return s[0] == s[1];\\n }\\n};\"], [11700, 0.1692, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n vector<int> digits;\\n for (char ch : s) {\\n digits.push_back(ch - '0');\\n }\\n\\n while (digits.size() > 2) {\\n vector<int> next;\\n next.reserve(digits.size() - 1); \\n\\n for (size_t i = 0; i < digits.size() - 1; i++) {\\n int sum = digits[i] + digits[i+1];\\n next.push_back(sum%10);\\n }\\n \\n digits = move(next);\\n }\\n\\n return digits.size() == 2 && digits[0] == digits[1];\\n }\\n};\\n\"], [11800, 0.3948, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n=s.length();\\n if(n==1)\\n return false;\\n queue<int>q;\\n for(int i=0;i<n;i++)\\n {\\n q.push((int)s[i]);\\n }\\n while(!q.empty())\\n {\\n int size=q.size();\\n if(size==2)\\n {\\n int num1=q.front();\\n q.pop();\\n int num2=q.front();\\n q.pop();\\n if(num1==num2)\\n return true;\\n break;\\n }\\n for(int i=0;i<size-1;i++)\\n {\\n int num1=q.front();\\n q.pop();\\n int num2=q.front();\\n if(i==size-2)\\n q.pop();\\n int temp=(num1+num2)%10;\\n q.push(temp);\\n }\\n }\\n\\n return false;\\n }\\n};\"], [11900, 0.2256, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n deque<int> q;\\n for (char c : s) {\\n q.push_back(c - '0');\\n }\\n int n = 0;\\n int c = q.size();\\n while (q.size() > 2) {\\n if (--c) {\\n n = q.front();\\n q.pop_front();\\n q.push_back((n + q.front()) % 10);\\n } else {\\n q.pop_front();\\n c = q.size();\\n }\\n }\\n return q.front() == q.back();\\n }\\n};\"], [12000, 0.282, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n deque<int> q;\\n for (char c : s) {\\n q.push_back(c - '0');\\n }\\n int n = 0;\\n int c = q.size();\\n while (q.size() > 2) {\\n if (--c) {\\n n = q.front();\\n q.pop_front();\\n q.push_back((n + q.front()) % 10);\\n } else {\\n q.pop_front();\\n c = q.size();\\n }\\n }\\n return q.front() == q.back();\\n }\\n};\"], [12100, 0.6768, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n queue<int>q;\\n for(int i=0;i<s.size();i++){\\n q.push(s[i]-'0');\\n }\\n while(q.size()!=2){\\n int n=q.size();\\n for(int i=0;i<n-1;i++){\\n int a=q.front();\\n q.pop();\\n q.push((a+q.front())%10);\\n }\\n q.pop();\\n }\\n int b=q.front();\\n q.pop();\\n return q.front()==b;\\n\\n }\\n};\"], [12200, 0.9024, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n if(s.length()==2)\\n {\\n if(s[0]==s[1])\\n return true;\\n else\\n return false;\\n }\\n string x=\\\"\\\";\\n for(int i=0;i<s.length()-1;i++)\\n {\\n int a=(s[i]+s[i+1])%10;\\n x+=a;\\n }\\n if(x.length()<2)\\n return false;\\n else\\n return hasSameDigits(x);\\n }\\n};\"], [12300, 1.2972, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int siz = s.size();\\n if(siz<2)return false;\\n if(siz==2){\\n if(s[0]==s[1])return true;\\n else{\\n return false;\\n }\\n }\\n int i=0,j=1;\\n string val= \\\"\\\";\\n while(j<siz){\\n int sum = (s[i] -'0' + s[j]-'0') %10;\\n val += (sum +'0'); //convert sum to char and append\\n j++;\\n i++;\\n }\\n if(val.size()==2){\\n if(val[0]==val[1])return true;\\n else return false;\\n }\\n else{\\n return hasSameDigits(val);\\n }\\n }\\n};\"], [12400, 0.6768, \"bool recursion(string s){\\n if(s.size() == 2 && s[0] == s[1]) return true;\\n else if(s.size() == 2 && s[0] != s[1]) return false;\\n else {\\n string str;\\n for(int i = 0; i < s.size() - 1; i++){\\n int k = ((s[i] - '0') + (s[i + 1] - '0')) % 10;\\n // char ne = '0' + k;\\n str.push_back('0' + k);\\n \\n }\\n return recursion(str);\\n\\n } \\n return 1;\\n}\\n\\n\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n if( recursion(s)) return true;\\n else return false;\\n }\\n};\"], [12500, 0.0564, \"class Solution {\\npublic:\\n string givesum(string& t, int i) {\\n int sum1 = t[i] - '0';\\n int sum3 = t[i + 1] - '0';\\n int newsum = sum1 + sum3;\\n return to_string(newsum%10);\\n }\\n\\n bool hasSameDigits(string s) {\\n string t = s;\\n\\n while (t.size() > 2) {\\n string w = \\\"\\\";\\n for (int i = 0; i < t.size() - 1; i++) {\\n w += givesum(t, i);\\n }\\n t = w;\\n }\\n\\n return (t.size() == 2 && t[0] == t[1]);\\n }\\n};\\n\"], [12700, 0.1128, \"class Solution {\\npublic:\\n void operation(queue<int> &q1, queue<int> &q2)\\n {\\n while(q1.size() > 1)\\n {\\n int first = q1.front();\\n q1.pop();\\n int second = q1.front();\\n \\n int value = (first+second)%10;\\n q2.push(value);\\n }\\n q1.pop();\\n }\\n bool hasSameDigits(string s) {\\n queue<int> q1;\\n queue<int> q2;\\n \\n for(int i = 0; i < s.size(); i++)\\n q1.push(s[i]-'0');\\n \\n queue<int> *q1_ptr = &q1;\\n queue<int> *q2_ptr = &q2;\\n \\n while(q1_ptr->size() != 2)\\n {\\n operation(*q1_ptr, *q2_ptr);\\n \\n queue<int> *tmp_ptr = q1_ptr;\\n q1_ptr = q2_ptr;\\n q2_ptr = tmp_ptr;\\n }\\n \\n int first = q1_ptr->front();\\n q1_ptr->pop();\\n int second = q1_ptr->front();\\n \\n return first == second;\\n }\\n};\"], [12800, 0.2256, \"class Solution {\\npublic:\\n string op(string s){\\n string out;\\n for(int i=0; i<s.size()-1; i++){\\n out += to_string(((s[i] - '0') + (s[i+1] - '0')) % 10);\\n }\\n return out;\\n }\\n\\n bool hasSameDigits(string s) {\\n while(s.size() > 2) s = op(s);\\n return s[0] == s[1];\\n }\\n};\"], [12900, 0.282, \"class Solution {\\npublic:\\n string rValue(string s){\\n string res = \\\"\\\";\\n for(int i = 1; i < s.size(); i++){\\n int a = s[i] - '0' + s[i-1] - '0';\\n a %= 10;\\n res += to_string(a);\\n }\\n\\n return res;\\n\\n }\\n\\n bool hasSameDigits(string s) {\\n while(s.size() > 2){\\n s = rValue(s);\\n }\\n\\n if(s[0] == s[1]){\\n return true;\\n }\\n\\n return false;\\n } \\n};\"], [13000, 0.1128, \"class Solution {\\n string helper(string s){\\n int n = s.size();\\n\\n string res = \\\"\\\";\\n\\n for(int i = 0; i<n-1; i++){\\n int a = (s[i] - '0') + (s[i+1] - '0');\\n a = a%10;\\n res += to_string(a);\\n }\\n\\n return res;\\n }\\npublic:\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n\\n while(s.size() > 2){\\n s = helper(s);\\n // cout<<s<<endl;\\n }\\n\\n return s[0] == s[1];\\n }\\n};\"], [13300, 0.0564, \"class Solution {\\npublic:\\n string fun(string s){\\n int n = s.size();\\n if (n == 2) return s; \\n \\n string ans = \\\"\\\";\\n for(int i = 0; i < n - 1; i++){\\n ans += to_string((s[i] - '0' + s[i+1] - '0') % 10); \\n }\\n return fun(ans); \\n }\\n\\n bool hasSameDigits(string s) {\\n string ans = fun(s);\\n return ans[0] == ans[1]; \\n }\\n};\\n\"], [13400, 0.0564, \"map<int,int> fac;\\nint mod_prime(vector<int>& v1,int& ir,int p){\\n vector<int>v2;int r=ir;\\n while(r){ v2.push_back(r%p); r/=p;}\\n int i=0,j=0,res=1,n1=v1.size(),n2=v2.size();\\n while(i<n1 && j<n2){\\n if(v1[i]<v2[j])return 0;\\n int tempres=fac[v1[i]]/(fac[v2[j]]*fac[v1[i]-v2[j]]);\\n res=((res%p)*(tempres %p))%p;\\n i++;j++;\\n } v2.clear();\\n return res;\\n}\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n //precomputation till 10! done\\n int number=1;fac[0]=1;\\n for(int i=1;i<=10;i++){\\n number*=i; fac[i]=number;\\n }\\n int n= s.length();int b0=0,b1=0,res;\\n int x=0,y=0;int l=n-2,r=n-2;\\n vector<int>v1(l,0),v2(r,0); \\n while(l){ v1[x++]=l%5; l/=5;}\\n while(r){ v2[y++]=r%2; r/=2;}\\n map<int,int>mp;\\n for(int i=0;i<=n-2;i++){\\n //calculating mod10;\\n if(mp.find(i)!=mp.end()) res=mp[i];\\n else if(mp.find(n-2-i)!=mp.end()) res=mp[n-2-i];\\n else {\\n res=(6*(mod_prime(v1,i,5))+5*(mod_prime(v2,i,2)))%10;\\n mp[i]=res; mp[n-2-i]=res;\\n }\\n b0=b0%10+(res*(s[i]-'0'))%10; b0=b0%10;\\n b1=b1%10+(res*(s[i+1]-'0'))%10; b1=b1%10;\\n }\\n return (b0==b1);\\n }\\n};\"], [13500, 0.282, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n if( s.size() == 2 )\\n return s[0] == s[1];\\n \\n string a = \\\"\\\";\\n for( int i=0;i<s.size()-1;i++ ){\\n int num = int( s[i] - '0' ) + int( s[i+1] - '0' ) ;\\n int numAfter = num % 10 ;\\n a += to_string( numAfter ) ;\\n }\\n \\n return hasSameDigits(a);\\n }\\n};\"], [13600, 0.1692, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n if(s.length()==2) return s[0]==s[1];\\n string newstring;\\n for(int i=1;i<s.length();i++){\\n int sum=(s[i]-'0') + (s[i-1]-'0');\\n sum%=10;\\n newstring+=to_string(sum);\\n } \\n return hasSameDigits(newstring);\\n }\\n};\"], [14000, 0.0564, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while (s.size() > 2) {\\n vector<char> new_s;\\n for (int i = 0; i < s.size() - 1; i++) {\\n new_s.push_back(((s[i] - '0') + (s[i + 1] - '0')) % 10 + '0');\\n }\\n s = string(new_s.begin(), new_s.end());\\n }\\n return s[0] == s[1];\\n \\n }\\n};\"], [14200, 0.1128, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while (s.size() > 2) {\\n vector<char> new_s;\\n for (int i = 0; i < s.size() - 1; i++) {\\n new_s.push_back(((s[i] - '0') + (s[i + 1] - '0')) % 10 + '0');\\n }\\n s = string(new_s.begin(), new_s.end());\\n }\\n return s[0] == s[1];\\n \\n }\\n};\"], [14300, 0.0564, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while (s.size() > 2) {\\n vector<char> new_s;\\n for (int i = 0; i < s.size() - 1; i++) {\\n new_s.push_back(((s[i] - '0') + (s[i + 1] - '0')) % 10 + '0');\\n }\\n s = string(new_s.begin(), new_s.end());\\n }\\n return s[0] == s[1];\\n \\n }\\n};\"], [14800, 0.0564, \"class Solution {\\npublic:\\n bool hasSameDigits(string a) {\\n int d = doit(a.substr(0, a.size()-1)) - doit(a.substr(1, a.size()-1));\\n return d%10 == 0;\\n }\\n\\n int doit(string a)\\n {\\n int n = a.size();\\n if (n == 1)\\n return int(a[0]) - int('0');\\n \\n string temp = \\\"\\\";\\n\\n for ( int i = 0; i < n-1;i ++)\\n {\\n int d = c(a[i]) + c(a[i+1]);\\n d %= 10;\\n temp += char(d + int('0'));\\n }\\n return doit(temp);\\n }\\n int c(char a)\\n {\\n return int(a) - int('0');\\n }\\n};\"], [16600, 0.1128, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while (s.size() > 2) {\\n int a = s.size();\\n vector<int> z;\\n for (int i = 0; i < a - 1; i++) {\\n int b = s[i] - '0';\\n int c = s[i + 1] - '0';\\n int p = (b + c) % 10;\\n z.push_back(p);\\n }\\n\\n s = \\\"\\\";\\n for (int j = 0; j < z.size(); j++) {\\n s += (z[j] + '0');\\n }\\n }\\n\\n int number = (s[0] - '0') * 10 + (s[1] - '0');\\n return number % 10 == number / 10;\\n }\\n};\\n\"], [16700, 0.1128, \"#include <vector>\\n#include <string>\\nusing namespace std;\\n\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n // Continue until the string size is reduced to 2\\n while (s.size() > 2) {\\n vector<int> newDigits; // Vector to store new digits\\n \\n // Calculate the sum of each adjacent pair and store in newDigits\\n for (int i = 0; i < s.size() - 1; ++i) {\\n int sum = (s[i] - '0' + s[i + 1] - '0') % 10; // Convert char to int\\n newDigits.push_back(sum + '0'); // Convert the result back to char\\n }\\n \\n // Create a new string from the new digits\\n s = \\\"\\\";\\n for (int i = 0; i < newDigits.size(); ++i) {\\n s += newDigits[i];\\n }\\n }\\n \\n // Check if the final two digits are the same\\n return s[0] == s[1];\\n }\\n};\\n\"], [16900, 0.282, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n vector<int> digits;\\n for (char c : s) digits.push_back(c - '0');\\n\\n while (digits.size() > 2) {\\n vector<int> temp;\\n for (int i = 0; i < digits.size() - 1; ++i) {\\n temp.push_back((digits[i] + digits[i + 1]) % 10);\\n }\\n digits = move(temp);\\n }\\n\\n return digits[0] == digits[1];\\n }\\n};\\n\"], [17000, 0.2256, \"#define pb push_back\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) \\n {\\n vector<int> v;\\n for(auto i:s)\\n {\\n v.pb(i-'0');\\n }\\n while(v.size()>2)\\n {\\n vector<int> nv;\\n for(int i=0;i<v.size()-1;i++)\\n {\\n nv.pb((v[i]+v[i+1])%10);\\n }\\n v=nv;\\n }\\n return v[0]==v[1];\\n }\\n};\"], [17100, 0.5076, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n vector<int> curr;\\n for(auto x : s) curr.push_back(x-'0');\\n while(curr.size()>2)\\n {\\n vector<int> tmp;\\n int n = curr.size();\\n for(int i=1;i<n;i++)\\n {\\n tmp.push_back((curr[i]+curr[i-1])%10);\\n }\\n curr = tmp;\\n }\\n return curr[0]==curr[1];\\n }\\n};\"], [17200, 0.6768, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n vector<int> current;\\n for (char c : s) {\\n current.push_back(c - '0');\\n }\\n \\n while (current.size() > 2) {\\n vector<int> next;\\n for (int i = 0; i < current.size() - 1; ++i) {\\n next.push_back((current[i] + current[i+1]) % 10);\\n }\\n current = next;\\n }\\n \\n return current.size() == 2 && current[0] == current[1];\\n }\\n};\"], [17300, 0.1128, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n vector<int> digits;\\n for (char c : s) {\\n digits.push_back(c - '0');\\n }\\n\\n while (digits.size() > 2) {\\n vector<int> newDigits;\\n for (size_t i = 0; i < digits.size() - 1; ++i) {\\n newDigits.push_back((digits[i] + digits[i + 1]) % 10);\\n }\\n digits = newDigits;\\n }\\n\\n return digits[0] == digits[1];\\n }\\n};\\n\"], [17500, 0.0564, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n\\n int n = (int) s.size();\\n\\n vector<int> a(n);\\n for (int i = 0; i < n; i++) {\\n a[i] = s[i] - '0';\\n }\\n\\n while (size(a) > 2) {\\n\\n int m = size(a);\\n vector<int> na;\\n for (int i = 1; i < m; i++) {\\n na.push_back((a[i] + a[i - 1]) % 10);\\n }\\n a = na;\\n }\\n\\n return a[0] == a[1];\\n \\n }\\n};\"]]",
"runtime": 3,
"runtimeDistribution": "[[0, 9.0243, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n = s.length();\\n \\n // Calculate binomial coefficients modulo 10 using Pascal's triangle\\n vector<int> coef(n, 0);\\n coef[0] = 1;\\n for (int i = 0; i < n-2; i++) {\\n for (int j = i+1; j > 0; j--) {\\n coef[j] = (coef[j] + coef[j-1]) % 10;\\n }\\n }\\n \\n // Calculate the final two digits\\n int digit1 = 0;\\n int digit2 = 0;\\n for (int i = 0; i < n-1; i++) {\\n digit1 = (digit1 + coef[i] * (s[i] - '0')) % 10;\\n digit2 = (digit2 + coef[i] * (s[i+1] - '0')) % 10;\\n }\\n \\n return digit1 == digit2;\\n }\\n};\"], [1, 1.128, \"class Solution {\\npublic:\\n bool hasSameDigits(string&s) {\\n int end = s.size();\\n while(end > 2) {\\n int i = 1, ind = 0;\\n for(; i < end; ++i) s[ind++] = (s[i-1] + s[i] - 96) % 10 + '0';\\n end = ind;\\n }\\n return s[0] == s[1];\\n }\\n};\"], [2, 2.1997, \"class Solution\\n{\\npublic:\\n bool hasSameDigits(const string &s)\\n {\\n int n = s.length();\\n int *digit = new int[n];\\n for (int i = 0; i < n; i++)\\n {\\n digit[i] = s[i] - '0';\\n }\\n\\n while (n > 2)\\n {\\n for (int i = 0; i < n - 1; i++)\\n {\\n digit[i] = ((digit[i] + digit[i + 1]) % 10);\\n }\\n n--;\\n }\\n bool result = digit[0] == digit[1];\\n delete[] digit;\\n return result;\\n }\\n};\\n\"], [3, 7.2194, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n=s.length();\\n for(int i=n;i>=3;i--){\\n string s1=\\\"\\\";\\n for(int j=0;j<s.length()-1;j++){\\n s1+=((int)(s[j])+((int)s[j+1]))%10;\\n }\\n s=s1;\\n }\\n return s[0]==s[1]?true:false;\\n }\\n};\"], [4, 7.2758, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n=s.length();\\n for(int i=n;i>=3;i--){\\n string s1=\\\"\\\";\\n for(int j=0;j<s.length()-1;j++){\\n s1+=((s[j]-'0')+(s[j+1]-'0'))%10;\\n }\\n s=s1;\\n }\\n return s[0]==s[1]?true:false;\\n }\\n};\"], [5, 2.9893, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int j=0;\\n string curr=\\\"\\\";\\n int num1,num2,prod;\\n while(s.size()!=2){\\n curr=\\\"\\\";\\n j=0;\\n while(j<s.size()-1){\\n num1=s[j]-'0';\\n num2=s[j+1]-'0';\\n prod=(num1+num2)%10;\\n curr.push_back(prod);\\n j++;\\n }\\n s=curr;\\n }\\n if(s[0] == s[1]) return true;\\n return false;\\n }\\n};\"], [6, 3.3277, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) \\n {\\n //int num = stoi(s);\\n //int len=int(log10(num)+1);\\n //cout << len << endl;\\n\\n while (s.length()>2)\\n {\\n string newStr=\\\"\\\";\\n\\n for (int i=1; i<s.length(); i++)\\n {\\n int n=((s[i-1]-'0')+(s[i]-'0'))%10;\\n newStr+=(n+'0');\\n }\\n\\n s=newStr;\\n\\n // len=int(log10(num)+1);\\n }\\n \\n\\n return (s[0]==s[1]);\\n }\\n};\"], [7, 12.6904, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while (s.size() != 2) {\\n string next_s;\\n for (int i = 0, j = 1; j < s.size(); ++i, ++j) {\\n char d = '0' + (((s[i] - '0') + (s[j] - '0')) % 10);\\n next_s.push_back(d);\\n }\\n swap(s, next_s);\\n }\\n return s[0] == s[1];\\n }\\n};\"], [8, 5.3017, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while(s.size() > 2) {\\n string newString;\\n for(int i = 0; i < s.size() - 1; i++) {\\n newString.push_back((s[i] + s[i + 1]) % 10);\\n }\\n s = newString;\\n }\\n return s[0] == s[1];\\n }\\n};\"], [9, 1.7484, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n queue<int>q;\\n for(int i=0;i<s.size();i++){\\n q.push(s[i]-'0');\\n }\\n while(q.size()!=2){\\n int n=q.size();\\n for(int i=0;i<n-1;i++){\\n int a=q.front();\\n q.pop();\\n q.push((a+q.front())%10);\\n }\\n q.pop();\\n }\\n int b=q.front();\\n q.pop();\\n return q.front()==b;\\n\\n }\\n};\"], [10, 2.0305, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int i = 0;\\n while(s.size() > 2) {\\n string newString;\\n for(int i = 0; i < s.size() - 1; i++) {\\n newString.push_back((s[i] + s[i + 1]) % 10);\\n }\\n s = newString;\\n }\\n return s[0] == s[1];\\n }\\n};\"], [11, 1.692, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while(s.size() !=2){\\n string temp=\\\"\\\";\\n for(int i=0;i<s.size()-1;i++){\\n int sum = ((s[i]-'0') + (s[i+1]-'0') ) % 10;\\n temp.push_back(sum + '0');\\n }\\n s=temp;\\n }\\n return s[0] == s[1];\\n }\\n};\"], [12, 0.3948, \"\\nclass Solution {\\npublic:\\n\\tbool hasSameDigits(string s) {\\n\\t\\tif (s.size() < 2)\\n\\t\\t\\treturn false;\\n\\n\\t\\tif (s.size() == 2)\\n\\t\\t{\\n\\t\\t\\treturn s.at(0) == s.at(1);\\n\\t\\t}\\n\\n\\t\\tstring out;\\n\\n\\t\\tfor (int i = 0;i < s.size() - 1;++i)\\n\\t\\t{\\n\\t\\t\\tout += (((s.at(i) - '0') + (s.at(i + 1) - '0')) % 10)+'0';\\n\\t\\t}\\n\\n\\t\\treturn hasSameDigits(out);\\n\\t}\\n};\"], [13, 0.1128, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n if (s.size() == 2) return s[0] == s[1];\\n\\n string new_s;\\n for (int i = 0; i < s.size() - 1; i++) {\\n int a = s[i] - '0';\\n int b = s[i + 1] - '0';\\n new_s += ('0' + (a + b) % 10);\\n }\\n\\n return hasSameDigits(new_s);\\n }\\n};\\n\"], [14, 0.3948, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n if(s.size()==2)\\n return s[0]==s[1];\\n string r=\\\"\\\";\\n for(int i=0;i<s.size()-1;i++){\\n r+=(s[i]+s[i+1])%10;\\n }\\n return hasSameDigits(r);\\n }\\n};\"], [15, 1.0152, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n vector<int> current;\\n for (char c : s) {\\n current.push_back(c - '0');\\n }\\n \\n while (current.size() > 2) {\\n vector<int> next;\\n for (int i = 0; i < current.size() - 1; ++i) {\\n next.push_back((current[i] + current[i+1]) % 10);\\n }\\n current = next;\\n }\\n \\n return current.size() == 2 && current[0] == current[1];\\n }\\n};\"], [16, 0.1128, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while (s.size() > 2) {\\n vector<char> new_s;\\n for (int i = 0; i < s.size() - 1; i++) {\\n new_s.push_back(((s[i] - '0') + (s[i + 1] - '0')) % 10 + '0');\\n }\\n s = string(new_s.begin(), new_s.end());\\n }\\n return s[0] == s[1];\\n \\n }\\n};\"], [17, 0.1692, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n vector<int> v;\\n for(auto i : s)v.push_back(i-'0');\\n while(v.size()>2){\\n vector<int> new_v;\\n for(int i = 0;i<v.size()-1;i++){\\n new_v.push_back((v[i]+v[i+1])%10);\\n }\\n v = new_v;\\n }\\n return v[0] == v[1];\\n }\\n};\"], [18, 0.4512, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n vector<int> digits;\\n for (char c : s) digits.push_back(c - '0');\\n\\n while (digits.size() > 2) {\\n vector<int> temp;\\n for (int i = 0; i < digits.size() - 1; ++i) {\\n temp.push_back((digits[i] + digits[i + 1]) % 10);\\n }\\n digits = move(temp);\\n }\\n\\n return digits[0] == digits[1];\\n }\\n};\\n\"], [19, 1.1844, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n vector<int> num;\\n for(char c:s){\\n num.push_back(c-'0');\\n }\\n \\n while(num.size()>2){\\n vector<int> temp;\\n for(int i=0;i<num.size()-1;i++){\\n temp.push_back((num[i]+num[i+1])%10);\\n }\\n num=temp;\\n\\n }\\n\\n return num[0]==num[1];\\n }\\n};\"], [20, 0.282, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n\\n int n = (int) s.size();\\n\\n vector<int> a(n);\\n for (int i = 0; i < n; i++) {\\n a[i] = s[i] - '0';\\n }\\n\\n while (size(a) > 2) {\\n\\n int m = size(a);\\n vector<int> na;\\n for (int i = 1; i < m; i++) {\\n na.push_back((a[i] + a[i - 1]) % 10);\\n }\\n a = na;\\n }\\n\\n return a[0] == a[1];\\n \\n }\\n};\"], [21, 0.2256, \"class Solution {\\nprivate:\\n vector<int> get_prod(int steps, int MOD) {\\n vector<int> prod(2, 1);\\n \\n for (int i = 0; i < steps - 2; i++) {\\n vector<int> new_prod = {1};\\n for (int j = 1; j < prod.size(); j++) {\\n new_prod.push_back((prod[j] + prod[j - 1]) % MOD);\\n }\\n new_prod.push_back(1);\\n prod = new_prod;\\n }\\n return prod;\\n }\\npublic:\\n bool hasSameDigits(string s) {\\n int L = s.length();\\n int MOD = 10;\\n\\n vector<int> prod = get_prod(L - 1, MOD);\\n int first = 0;\\n int last = 0;\\n for (int i = 0; i < L - 1; i++) {\\n first = (first + prod[i] * (s[i] - '0')) % MOD;\\n last = (last + prod[i] * (s[i + 1] - '0')) % MOD;\\n }\\n return first == last;\\n }\\n};\\n\\n// time: O(N)\\n// space: O(N)\"], [22, 0.282, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n string v = \\\"\\\";\\n int n = s.length();\\n while(n > 2) {\\n v = \\\"\\\";\\n for(int i = 0 ; i < s.length() - 1 ; i++) {\\n int x = s[i] - '0';\\n int y = s[i+1] - '0';\\n v += to_string((x + y) % 10);\\n }\\n s = v;\\n n--;\\n \\n }\\n cout << v ;\\n if(v[0]==v[1])\\n return true;\\n return false;\\n }\\n};\"], [23, 0.846, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int left = 0;\\n int right = 0;\\n string digit = \\\"\\\";\\n\\n if (s.size() == 2)\\n return s[0] == s[1];\\n\\n while (s.size() > 2){\\n int val = 0;\\n for (int i = 0; i < s.size() - 1; i++){\\n left = (s[i] - '0');\\n right = (s[i + 1] - '0');\\n val = (left + right) % 10;\\n digit += to_string(val);\\n }\\n s = digit;\\n digit = \\\"\\\";\\n }\\n if (s[0] == s[1])\\n return true;\\n return false;\\n }\\n};\"], [24, 0.7332, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while(s.size()>2){\\n string temp=\\\"\\\";\\n for(int i=0;i<s.size()-1;i++){\\n int a=s[i]-'0';\\n int b=s[i+1]-'0';\\n int sum =(a+b)%10;\\n temp += to_string(sum);\\n }\\n s=temp;\\n }\\n return s[0] == s[1];\\n }\\n};\"], [25, 0.6768, \"class Solution {\\npublic:\\n bool hasSameDigits(std::string s) {\\n while (s.length() > 2) {\\n std::string newbornString;\\n for (size_t i = 0; i < s.length() - 1; i++) {\\n int firstDigit = s[i] - '0'; // Convert char to int\\n int secondDigit = s[i + 1] - '0'; // Convert char to int\\n int newDigit = (firstDigit + secondDigit) % 10; // Calculate new digit\\n newbornString += std::to_string(newDigit); // Append new digit to the new string\\n }\\n s = newbornString; // Update s to the new string\\n }\\n // Check if the final two digits are the same\\n return s[0] == s[1];\\n }\\n};\"], [26, 0.6204, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while (s.length() != 2) {\\n string new_s = \\\"\\\";\\n for (int i=0; i < s.length()-1; i++) {\\n new_s += to_string(((s[i] - '0') + (s[i+1] - '0')) % 10);\\n }\\n s = new_s;\\n }\\n\\n return s[0] == s[1];\\n }\\n};\"], [27, 3.3841, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int left = 0;\\n int right = 0;\\n string digit = \\\"\\\";\\n\\n while (s.size() > 2){\\n int val = 0;\\n for (int i = 0; i < s.size() - 1; i++){\\n left = (s[i] - '0');\\n right = (s[i + 1] - '0');\\n val = (left + right) % 10;\\n digit += to_string(val);\\n }\\n s = digit;\\n digit = \\\"\\\";\\n }\\n if (s[0] == s[1])\\n return true;\\n return false;\\n }\\n};\"], [28, 1.8049, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n = s.length();\\n while(n>2)\\n {\\n auto x = s;\\n s=\\\"\\\";\\n for(int i=0;i<n-1;i++)\\n {\\n s+=to_string(((x[i]-'0')+(x[i+1]-'0'))%10);\\n }\\n n--;\\n }\\n if(s[0]==s[1]) return true;\\n return false;\\n }\\n};\"], [29, 1.9177, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) \\n {\\n while(s.length()>2)\\n {\\n string newborn;\\n\\n for(int i=0;i<s.length()-1;i++)\\n {\\n int first=s[i]-'0';\\n int second=s[i+1]-'0';\\n\\n int newdigit=(first+second)%10;\\n newborn+=to_string(newdigit);\\n }\\n s=newborn;\\n }\\n\\n if(s[0]==s[1])\\n {\\n return true;\\n }\\n\\n return false;\\n \\n }\\n};\"], [30, 2.4817, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while (s.length() > 2) {\\n string temp = \\\"\\\";\\n for (int i = 0; i + 1 < s.length(); ++i) {\\n int sum = (s[i] - '0') + (s[i + 1] - '0');\\n temp += to_string(sum % 10);\\n }\\n s = temp;\\n }\\n return s.length() == 2 && s[0] == s[1];\\n }\\n};\"], [31, 9.0807, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n \\n int n=s.size(),tmp;\\n if(n<2) return false;\\n string s_tmp;\\n while(n>2){\\n s_tmp=\\\"\\\";\\n for(int i=0;i<n-1;i++){\\n tmp=(int(s[i])+int(s[i+1]))%10;\\n s_tmp+=to_string(tmp);\\n }\\n s=s_tmp;\\n n--;\\n\\n }\\n if(s[0]==s[1]) return true;\\n return false;\\n }\\n};\"], [32, 1.8049, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while (s.size()>2)\\n {\\n string k = \\\"\\\";\\n for(int i=0;i<s.size()-1;i++)\\n {\\n int sum = (s[i] -'0' + s[i+1] - '0') % 10;\\n k += to_string(sum);\\n }\\n s = k;\\n }\\n return s[0] == s[1];\\n }\\n};\"], [33, 2.4817, \"class Solution {\\nprivate:\\n bool Recursion(vector<int>mp){\\n if(mp.size() == 2){\\n if(mp[0] == mp[1]){\\n return true;\\n }else{\\n return false;\\n }\\n }\\n vector<int>temp;\\n for(int i = 0; i < mp.size() - 1; i++){\\n temp.push_back((mp[i] + mp[i + 1]) % 10);\\n }\\n return Recursion(temp);\\n }\\npublic:\\n bool hasSameDigits(string s) {\\n vector<int>mp;\\n for(int i = 0; i < s.size(); i++){\\n mp.push_back(s[i] - '0');\\n }\\n return Recursion(mp);\\n }\\n};\"], [34, 2.4817, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while(s.size()!=2){\\n string x=\\\"\\\";\\n for(int i=0;i<s.size()-1;i++){\\n x+=to_string((s[i]-'0'+s[i+1]-'0')%10);\\n }\\n s=x;\\n }\\n if(s[0]==s[1]) return true;\\n return false;\\n }\\n};\"], [35, 3.4405, \"class Solution {\\nprivate:\\n bool Recursion(vector<int>mp){\\n if(mp.size() == 2){\\n if(mp[0] == mp[1]){\\n return true;\\n }else{\\n return false;\\n }\\n }\\n vector<int>temp;\\n for(int i = 0; i < mp.size() - 1; i++){\\n temp.push_back((mp[i] + mp[i + 1]) % 10);\\n }\\n return Recursion(temp);\\n }\\npublic:\\n bool hasSameDigits(string s) {\\n vector<int>mp;\\n for(int i = 0; i < s.size(); i++){\\n mp.push_back(s[i] - '0');\\n }\\n return Recursion(mp);\\n }\\n};\"], [36, 0.3384, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while(s.size() != 2){\\n string sinh = \\\"\\\";\\n for(int i = 0; i < s.size() - 1; i++){\\n int z = ((s[i] - '0') + (s[i+1] - '0')) % 10;\\n sinh += to_string(z);\\n }\\n s = sinh;\\n }\\n if(s[0] == s[1]) return true;\\n return false;\\n }\\n};\"], [37, 0.1692, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n long long int sum=0;\\n while(s.size()>2){\\n string res = \\\"\\\";\\n for(int i=0;i<s.size()-1;i++){\\n sum = ((s[i]-'0')+(s[i+1]-'0'))%10;\\n res +=to_string(sum);\\n }\\n s = res;\\n }\\n if(s[0]==s[1]){\\n return 1;\\n }\\n else{\\n return 0;\\n }\\n }\\n};\"], [38, 0.2256, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n if(s.length()==2) return s[0]==s[1];\\n string newstring;\\n for(int i=1;i<s.length();i++){\\n int sum=(s[i]-'0') + (s[i-1]-'0');\\n sum%=10;\\n newstring+=to_string(sum);\\n } \\n return hasSameDigits(newstring);\\n }\\n};\"], [39, 0.2256, \"class Solution {\\npublic:\\n string rValue(string s){\\n string res = \\\"\\\";\\n for(int i = 1; i < s.size(); i++){\\n int a = s[i] - '0' + s[i-1] - '0';\\n a %= 10;\\n res += to_string(a);\\n }\\n\\n return res;\\n\\n }\\n\\n bool hasSameDigits(string s) {\\n while(s.size() > 2){\\n s = rValue(s);\\n }\\n\\n if(s[0] == s[1]){\\n return true;\\n }\\n\\n return false;\\n } \\n};\"], [40, 0.0564, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n \\n string temp=s;\\n while(temp.size()>2)\\n {\\n string blank=\\\"\\\";\\n for(int i=0;i<temp.size()-1;i++)\\n {\\n int num1=temp[i]-'0';\\n int num2=temp[i+1]-'0';\\n int sum=(num1+num2)%10;\\n char a=sum+'0';\\n blank.push_back(a);\\n }\\n cout<<blank<<endl;\\n temp=blank;\\n }\\n if(temp[0]==temp[1])\\n return true;\\n return false;\\n }\\n};\"], [41, 0.1128, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while (s.size() > 2) {\\n vector<int> arr;\\n for (size_t i = 0; i < s.size() - 1; i++) {\\n arr.push_back(((s[i] - '0') + (s[i + 1] - '0')) % 10);\\n }\\n\\n // Convert the vector back to a string\\n s.clear();\\n for (int num : arr) {\\n s += to_string(num);\\n }\\n }\\n\\n // Check if both digits are the same\\n return s[0] == s[1];\\n }\\n};\"], [43, 0.0564, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while (s.length() > 2) { // Stop when 2 digits remain\\n vector<int> sum; // Reset sum vector in each iteration\\n \\n for (int i = 0; i < s.length() - 1; i++) {\\n sum.push_back(((s[i] - '0') + (s[i + 1] - '0')) % 10);\\n }\\n \\n \\n string newS = \\\"\\\";\\n for (int num : sum) {\\n newS += to_string(num);\\n }\\n\\n s = newS; \\n }\\n\\n return s[0] == s[1]; \\n }\\n};\\n\"], [44, 0.0564, \"class Solution {\\npublic:\\n string vectorToString(const vector<int>& nums) {\\n string result;\\n result.reserve(nums.size());\\n for (int num : nums) {\\n result += to_string(num);\\n }\\n return result;\\n }\\n\\n string twoDigit(string s) {\\n while (s.size() > 2) {\\n vector<int> nums;\\n for (int i = 0; i < s.size()-1; i++) {\\n int x = (s[i] - '0' + s[i + 1] - '0') % 10;\\n nums.push_back(x);\\n }\\n s = vectorToString(nums);\\n }\\n return s;\\n }\\n\\n bool hasSameDigits(string s) {\\n string x = twoDigit(s);\\n return x[0] == x[1];\\n }\\n};\"], [46, 0.0564, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while(s.size() != 2){\\n vector<int> combination;\\n for(int i = 0; i < s.size() - 1; i++){\\n int z = ((s[i] - '0') + (s[i+1] - '0')) % 10;\\n combination.push_back(z);\\n }\\n string sinh = \\\"\\\";\\n for(int x : combination) sinh += to_string(x);\\n s = sinh;\\n }\\n if(s[0] == s[1]) return true;\\n return false;\\n }\\n};\"], [47, 0.1128, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n \\n START : \\n vector<int> v;\\n for(int i = 0 ; i < s.size()-1; i++)\\n {\\n int digit = ((s[i] - '0') + (s[i+1] - '0')) % 10;\\n v.push_back(digit);\\n }\\n\\n if(v.size() > 2)\\n {\\n s= \\\"\\\";\\n for(int num : v)\\n s += to_string(num);\\n\\n goto START;\\n }\\n\\n return v.size() == 2 && v[0] == v[1] ;\\n\\n }\\n};\"], [48, 0.1128, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while (s.size() > 2) {\\n string ss = \\\"\\\";\\n for (int i = 0; i < s.size() - 1; ++i) {\\n int a = s[i] - '0';\\n int b = s[i + 1] - '0';\\n char v = (a + b) % 10 + '0';\\n ss = v + ss;\\n }\\n s = ss;\\n }\\n\\n return s[0] == s[1];\\n }\\n};\\n\\n\"], [51, 0.1128, \"#include <string>\\n\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n string str = \\\"\\\";\\n do{\\n for(int i =0; i < s.length()-1; i++){\\n int a=s[i]-'0';\\n int b = s[i+1]-'0';\\n str+= to_string((a+b)%10);\\n }\\n s= str;\\n str =\\\"\\\";\\n cout<<s<<endl;\\n\\n\\n }while(s.length() > 2);\\n\\n\\n \\n for(int i = 0; i < s.length()-1; i++){\\n if(s[i] != s[i+1]){\\n return false;\\n }\\n }\\n return(true);\\n }\\n};\"], [53, 0.0564, \"class Solution{\\npublic:\\n bool hasSameDigits(string s){\\n while((int)s.size() > 2){\\n string sumOfDigits = \\\"\\\";\\n for(int i = 0; i < (int)s.size() - 1; i++)\\n {\\n sumOfDigits += to_string((stoi(string(1, s[i])) + stoi(string(1, s[i + 1]))) % 10); // char to int ??\\n }\\n s = sumOfDigits;\\n }\\n return s.front() == s.back();\\n }\\n};\"], [54, 0.1128, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n while(s.length()>2)\\n {\\n string tmp=\\\"\\\";\\n for(int i=0;i<s.length()-1;i++)\\n {\\n int digit=((s[i]-'0')+(s[i+1]-'0'))%10;\\n tmp=char(digit+'0')+tmp;\\n \\n }\\n s=tmp;\\n }\\n \\n return (s[0]==s[1]); \\n }\\n};\"]]"
},
"golang": {
"code": "func hasSameDigits(s string) bool {\n digits := make([]int, len(s))\n for i, c := range s {\n digits[i] = int(c - '0')\n }\n for len(digits) > 2 {\n next := []int{}\n for i := 0; i < len(digits)-1; i++ {\n next = append(next, (digits[i]+digits[i+1])%10)\n }\n digits = next\n }\n return digits[0] == digits[1]\n}",
"memory": 900,
"memoryDistribution": "[[900, 15.384, \"func hasSameDigits(s string) bool {\\n digits := make([]int, len(s))\\n for i, c := range s {\\n digits[i] = int(c - '0')\\n }\\n for len(digits) > 2 {\\n next := []int{}\\n for i := 0; i < len(digits)-1; i++ {\\n next = append(next, (digits[i]+digits[i+1])%10)\\n }\\n digits = next\\n }\\n return digits[0] == digits[1]\\n}\"], [4000, 3.8462, \"func hasSameDigits(s string) bool {\\n\\tcurrList := []byte(s)\\n\\tinsertPos := 0\\n\\tfor len(currList) > 2 {\\n\\t\\tinsertPos = 0\\n\\t\\tfor i := 1; i < len(currList); i++ {\\n\\t\\t\\tcurrList[insertPos] = (byte(int(currList[i-1]-'0')+int(currList[i]-'0')) % 10) + '0'\\n\\t\\t\\tinsertPos++\\n\\t\\t}\\n\\t\\tcurrList = currList[:len(currList)-1]\\n\\t}\\n\\treturn currList[0] == currList[1]\\n}\"], [4100, 5.1282, \"func hasSameDigits(s string) bool {\\n ss := make([]uint8, len(s))\\n for i := range s {\\n ss[i] = s[i] - '0'\\n }\\n newSS := make([]byte, len(ss))\\n for len(ss) > 2 {\\n newSS = newSS[:len(newSS)-1]\\n for i := 1; i < len(ss); i++ {\\n newSS[i-1] = (ss[i] + ss[i-1]) % 10\\n }\\n ss = newSS\\n }\\n return ss[0] == ss[1]\\n} \"], [4200, 5.1282, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits = operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nfunc operationPentiple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-5; i++ {\\n\\t\\tdigits[i] = (digits[i] + 5*digits[i+1] + 5*digits[i+4] + digits[i+5]) % 10\\n\\t}\\n\\tdigits = digits[:n-5]\\n\\treturn digits\\n}\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5] + digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) + (digits[i+625] + digits[i+655]) + (digits[i+630] + digits[i+650]) + (digits[i+630] + digits[i+650])\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [4300, 3.8462, \"func hasSameDigits(s string) bool {\\n\\tn, len_s := make([]int, len(s)), len(s)\\n\\tfor i, v := range s {\\n\\t\\tn[i] = int(v) - '0'\\n\\t}\\n\\tfor ; len_s > 2; len_s-- {\\n\\t\\tfor i := range len(n) - 1 {\\n\\t\\t\\tn[i] = (n[i] + n[i+1]) % 10\\n\\t\\t}\\n\\t}\\n\\treturn n[0] == n[1]\\n}\"], [4400, 1.2821, \"func hasSameDigits(s string) bool {\\n nums := []int{}\\n for _, r := range s {\\n nums = append(nums, int(r-'0'))\\n }\\n for len(nums) > 2 {\\n for i:=1;i<len(nums);i++ {\\n nums[i-1] = ((nums[i]+nums[i-1])%10)\\n }\\n nums = nums[:(len(nums)-1)]\\n }\\n return nums[0] == nums[1]\\n}\"], [4500, 1.2821, \"func hasSameDigits(s string) bool {\\n digits := make([]uint8, len(s), len(s))\\n for i := 0; i < len(s); i++ {\\n digits[i] = s[i] - 48\\n }\\n\\n for len(digits) > 2 {\\n temp := make([]uint8, len(digits) - 1, len(digits) - 1)\\n for i := 0; i < len(digits) - 1; i++ {\\n temp[i] = (digits[i] + digits[i+1]) % 10\\n }\\n digits = temp\\n }\\n\\n return digits[0] == digits[1]\\n}\"], [4600, 7.6923, \"func hasSameDigits(s string) bool {\\n ss := make([]uint8, len(s))\\n for i := range s {\\n ss[i] = s[i] - '0'\\n }\\n for len(ss) > 2 {\\n newSS := make([]byte, len(ss)-1)\\n for i := 1; i < len(ss); i++ {\\n newSS[i-1] = (ss[i] + ss[i-1]) % 10\\n }\\n ss = newSS\\n }\\n return ss[0] == ss[1]\\n} \"], [4900, 1.2821, \"func hasSameDigits(s string) bool {\\n for len(s) > 2 {\\n new := make([]byte, len(s)-1)\\n for i:=0; i<len(s)-1;i++ {\\n new[i] = (s[i] + s[i+1] - '0' - '0') %10 +'0'\\n }\\n s = string(new)\\n }\\n\\n return s[0] == s[1]\\n}\"], [5000, 3.8462, \"func hasSameDigits(s string) bool {\\n\\tfor len(s) > 2 {\\n\\t\\tstr := make([]byte, len(s)-1)\\n\\t\\tfor i := 0; i < len(s)-1; i++ {\\n\\t\\t\\tstr[i] = (s[i] + s[i+1] - '0') % 10\\n\\t\\t}\\n\\t\\ts = string(str)\\n\\t}\\n\\n\\treturn s[0] == s[1]\\n}\"], [5100, 8.9744, \"\\nimport (\\n\\t\\\"fmt\\\"\\n\\t\\\"strconv\\\"\\n\\t\\\"strings\\\"\\n)\\nfunc hasSameDigits(s string) bool {\\n s = reduce(s)\\n return s[0] == s[1]\\n}\\n\\nfunc reduce(s string) string {\\n if len(s) == 2 {\\n return s\\n }\\n sb := strings.Builder{}\\n for i := 0; i < len(s) - 1; i++ {\\n s := getModuloSum(s[i], s[i+1])\\n sb.WriteString(s)\\n }\\n return reduce(sb.String())\\n}\\n\\nfunc getModuloSum(s1 byte, s2 byte) string {\\n i1 := s1 - '0'\\n i2 := s2 - '0'\\n\\n r := (i1 + i2) %10\\n\\n return strconv.FormatInt(int64(r), 10)\\n}\"], [5200, 5.1282, \"func hasSameDigits(s string) bool {\\n\\toperationResult := s\\n\\n\\tfor {\\n\\t\\toperationResult = reduceDigit(operationResult)\\n\\n\\t\\tif len(operationResult) == 2 {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif operationResult[0] == operationResult[1] {\\n\\t\\treturn true\\n\\t}\\n\\treturn false\\n}\\n\\nfunc reduceDigit(s string) string {\\n\\n\\tbaseRune := '0' // use this to convert runes to int\\n\\tvar newDigitString strings.Builder\\n\\n\\tfor i := 0; i < len(s)-1; i++ {\\n\\t\\tcurDig := ((int(s[i] - byte(baseRune))) + int(s[i+1]-byte(baseRune))) % 10\\n\\t\\tnewDigitString.WriteString(strconv.Itoa(curDig))\\n\\t}\\n\\n\\treturn newDigitString.String()\\n}\\n\"], [5300, 1.2821, \"func hasSameDigits(s string) bool {\\n if len(s)==2 {\\n return s[0]==s[1]\\n }\\n var sb strings.Builder\\n for i:=0;i<len(s)-1;i++ {\\n sb.WriteByte(((s[i]-'0'+s[i+1]-'0')%10)+'0')\\n }\\n return hasSameDigits(sb.String())\\n}\"], [5600, 3.8462, \"func hasSameDigits(s string) bool {\\n arr := []byte(s)\\n\\n\\n if len(arr) == 2 {\\n return arr[0] == arr[1]\\n }\\n\\n newOne := []byte{}\\n for i:=0; i<len(arr)-1; i++ {\\n b := (int(arr[i]-'0') + int(arr[i+1]-'0')) % 10\\n newOne = append(newOne, byte(b + '0'))\\n }\\n return hasSameDigits(string(newOne))\\n}\"], [6200, 2.5641, \"import (\\n // \\\"strings\\\"\\n \\\"strconv\\\"\\n)\\n\\nvar ref = map[byte]int{\\n '1': 1,\\n '2': 2,\\n '3': 3,\\n '4': 4,\\n '5': 5,\\n '6': 6,\\n '7': 7,\\n '8': 8,\\n '9': 9,\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n var sb strings.Builder\\n var a func(s string, m *map[string]bool) bool\\n a = func(s string, m *map[string]bool) bool {\\n if len(s) == 2 {\\n return s[1] == s[0]\\n }\\n if (*m)[s] {\\n return false\\n }\\n (*m)[s] = true\\n\\n size := len(s)\\n for i := 0; i < size - 1; i++ {\\n first := ref[s[i]]\\n second := ref[s[i + 1]]\\n value := (first + second) % 10\\n\\n sb.WriteString(strconv.Itoa(value))\\n }\\n newStr := sb.String()\\n sb.Reset()\\n return a(newStr, m)\\n }\\n var m = map[string]bool{ }\\n return a(s, &m)\\n}\"], [7600, 1.2821, \"func hasSameDigits(s string) bool {\\n n := len(s)\\n p := make([]int, n)\\n for i := 0; i < n - 1; i++ {\\n p[i] = int(s[i] - '0' + s[i + 1] - '0') % 10\\n }\\n for i := 2; i < n - 1; i++ {\\n c := make([]int, n - i)\\n for j := 0; j < n - i; j++ {\\n c[j] = (p[j] + p[j + 1]) % 10;\\n }\\n p = c;\\n }\\n return p[0] == p[1]\\n}\"], [8200, 2.5641, \"func hasSameDigits(s string) bool {\\n for len(s) > 2 {\\n temp := []rune{}\\n for i := 0; i < len(s) -1; i++ {\\n a := int(s[i] - '0')\\n b := int(s[i + 1] - '0')\\n sum := (a+b) % 10\\n temp = append(temp, rune(sum + '0'))\\n }\\n s = string(temp)\\n }\\n return s[0] == s[1]\\n}\"], [8300, 1.2821, \"func hasSameDigits(s string) bool {\\n runes := []rune(s)\\n for len(runes) > 2 {\\n temp := []rune{}\\n for i := 0; i < len(runes) - 1; i++ {\\n temp = append(temp, (runes[i]-'0' + runes[i+1]-'0') % 10)\\n }\\n runes = temp\\n }\\n\\n return runes[0] == runes[1]\\n}\"], [8400, 1.2821, \"func hasSameDigits(s string) bool {\\n runes := []rune(s)\\n for len(runes) > 2 {\\n temp := []rune{}\\n for i := 0; i < len(runes) - 1; i++ {\\n temp = append(temp, (runes[i]-'0' + runes[i+1]-'0') % 10)\\n }\\n runes = temp\\n }\\n\\n return runes[0] == runes[1]\\n}\"], [8600, 6.4103, \"func hasSameDigits(s string) bool {\\n var sz int = len(s)\\n for sz > 2 {\\n var str string\\n for pos := 1; pos < sz; pos++ {\\n str += string((s[pos]-'0'+s[pos-1]-'0')%10)\\n }\\n s = str\\n sz = len(s)\\n }\\n return s[0] == s[1]\\n}\"], [8700, 7.6923, \"func hasSameDigits(s string) bool {\\n\\tnewStr := s\\n\\tfor len(newStr) > 2 {\\n\\t\\tstr := make([]string, len(newStr)-1)\\n\\t\\tfor i := 0; i < len(newStr)-1; i++ {\\n\\t\\t\\tfirst := int(newStr[i] - '0')\\n\\t\\t\\tsecond := int(newStr[i+1] - '0')\\n\\t\\t\\tstr[i] = strconv.Itoa((first + second) % 10)\\n\\t\\t}\\n\\t\\tnewStr = strings.Join(str, \\\"\\\")\\n\\t}\\n\\n\\treturn newStr[0] == newStr[1]\\n}\"], [8800, 5.1282, \"func hasSameDigits(s string) bool {\\n for len(s) > 2 {\\n tmp := \\\"\\\"\\n for i:=0; i < len(s)-1; i++ {\\n tmp += string((s[i] + s[i+1] - 48*2) % 10 + 48)\\n }\\n s = tmp\\n }\\n return s[0] == s[1]\\n}\"], [9000, 3.8462, \"func hasSameDigits(s string) bool {\\n var sz int = len(s)\\n for sz > 2 {\\n var str string\\n for pos := 1; pos < sz; pos++ {\\n d1, _ := strconv.Atoi(string(s[pos]))\\n d2, _ := strconv.Atoi(string(s[pos-1]))\\n str += strconv.Itoa((d1+d2)%10)\\n }\\n s = str\\n sz = len(s)\\n }\\n if s[0] == s[1] {\\n return true\\n }\\n return false\\n}\"], [9100, 6.4103, \"func hasSameDigits(s string) bool {\\n\\n for len(s) > 2 {\\n var temp string\\n\\n for i := 0; i < len(s) - 1; i++ {\\n\\n s1, _ := strconv.Atoi(string(s[i]))\\n s2, _ := strconv.Atoi(string(s[i + 1]))\\n\\n temp += strconv.Itoa((s1 + s2) % 10)\\n }\\n s = temp\\n }\\n\\n return s[0] == s[1]\\n}\"], [9200, 3.8462, \"func hasSameDigits(s string) bool {\\n for len(s) > 2 {\\n var str string\\n for i := 0; i < len(s) - 1; i++ {\\n sum := (int(s[i] - '0') + int(s[i + 1] - '0')) % 10\\n str += strconv.FormatInt(int64(sum), 10)\\n }\\n\\n s = str\\n }\\n\\n return s[0] == s[1]\\n}\"]]",
"runtime": 5,
"runtimeDistribution": "[[0, 26.9231, \"func hasSameDigits(s string) bool {\\n for len(s) > 2 {\\n new := make([]byte, len(s)-1)\\n for i:=0; i<len(s)-1;i++ {\\n new[i] = (s[i] + s[i+1] - '0' - '0') %10 +'0'\\n }\\n s = string(new)\\n }\\n\\n return s[0] == s[1]\\n}\"], [1, 5.1282, \"func hasSameDigits(s string) bool {\\n \\n for len(s) > 2 {\\n s = reduce(s)\\n }\\n if s[0] == s[1] {\\n return true\\n }\\n\\n return false\\n}\\n\\nfunc reduce(s string) string {\\n if len(s) <= 2 {\\n return s\\n }\\n\\n r := make([]byte, len(s) - 1)\\n for i := 0; i < len(s) - 1; i++ {\\n a := s[i]-48\\n b := s[i+1]-48\\n r[i] = ((a+b)%10)+48\\n }\\n\\n return string(r)\\n}\"], [2, 6.4103, \"\\nimport (\\n\\t\\\"fmt\\\"\\n\\t\\\"strconv\\\"\\n\\t\\\"strings\\\"\\n)\\nfunc hasSameDigits(s string) bool {\\n s = reduce(s)\\n return s[0] == s[1]\\n}\\n\\nfunc reduce(s string) string {\\n if len(s) == 2 {\\n return s\\n }\\n sb := strings.Builder{}\\n for i := 0; i < len(s) - 1; i++ {\\n s := getModuloSum(s[i], s[i+1])\\n sb.WriteString(s)\\n }\\n return reduce(sb.String())\\n}\\n\\nfunc getModuloSum(s1 byte, s2 byte) string {\\n i1 := s1 - '0'\\n i2 := s2 - '0'\\n\\n r := (i1 + i2) %10\\n\\n return strconv.FormatInt(int64(r), 10)\\n}\"], [3, 3.8462, \"func hasSameDigits(s string) bool {\\n ss := make([]uint8, len(s))\\n for i := range s {\\n ss[i] = s[i] - '0'\\n }\\n for len(ss) > 2 {\\n newSS := make([]byte, len(ss)-1)\\n for i := 1; i < len(ss); i++ {\\n newSS[i-1] = (ss[i] + ss[i-1]) % 10\\n }\\n ss = newSS\\n }\\n return ss[0] == ss[1]\\n} \"], [4, 3.8462, \"func hasSameDigits(s string) bool {\\n buf := []byte(s)\\n for len(buf) != 2 {\\n newbuf := make([]byte, 0, len(buf))\\n for idx := 0; idx < len(buf)-1; idx++ {\\n n1, n2 := buf[idx]-'0', buf[idx+1]-'0'\\n n := (n1+n2)%10\\n newbuf = append(newbuf, n + '0')\\n }\\n buf = newbuf\\n }\\n\\n return buf[0] == buf[1]\\n}\"], [5, 3.8462, \"func hasSameDigits(s string) bool {\\n\\tnums := make([]int, len(s))\\n\\tfor i, ch := range s {\\n\\t\\tnums[i] = int(ch - '0')\\n\\t}\\n\\n\\tfor len(nums) > 2 {\\n\\t\\tvar newNums []int\\n\\n\\t\\tfor i := 1; i < len(nums); i++ {\\n\\t\\t\\tnewNums = append(newNums, (nums[i-1]+nums[i])%10)\\n\\t\\t}\\n\\n\\t\\tnums = newNums\\n\\t}\\n\\n\\tfor i := range len(nums) - 1 {\\n\\t\\tif nums[i] != nums[i+1] {\\n\\t\\t\\treturn false\\n\\t\\t}\\n\\t}\\n\\n\\treturn true\\n}\"], [6, 2.5641, \"func hasSameDigits(s string) bool {\\n arr := make([]int, 0)\\n for i := 0; i < len(s); i ++ {\\n arr = append(arr, int(s[i] - '0'))\\n } \\n\\n for len(arr) > 2 {\\n newArr := make([]int, 0)\\n for i := 0; i < len(arr) - 1; i ++ {\\n num := calculateRest(int(arr[i]), int(arr[i + 1]))\\n newArr = append(newArr, num)\\n }\\n\\n arr = newArr\\n }\\n\\n return arr[0] == arr[1]\\n}\\n\\nfunc calculateRest (a int, b int) int {\\n return (a + b) % 10\\n}\"], [7, 3.8462, \"func hasSameDigits(s string) bool {\\n\\tnewStr := s\\n\\tfor len(newStr) > 2 {\\n\\t\\tstr := make([]string, len(newStr)-1)\\n\\t\\tfor i := 0; i < len(newStr)-1; i++ {\\n\\t\\t\\tfirst := int(newStr[i] - '0')\\n\\t\\t\\tsecond := int(newStr[i+1] - '0')\\n\\t\\t\\tstr[i] = strconv.Itoa((first + second) % 10)\\n\\t\\t}\\n\\t\\tnewStr = strings.Join(str, \\\"\\\")\\n\\t}\\n\\n\\treturn newStr[0] == newStr[1]\\n}\"], [8, 3.8462, \"func hasSameDigits(s string) bool {\\n for len(s) != 2 {\\n\\t\\tnewS := strings.Builder{}\\n\\n\\t\\tfor left, right := 0, 1; right < len(s); left, right = left+1, right+1 {\\n\\t\\t\\tnumsLeft, _ := strconv.Atoi(string(s[left]))\\n\\t\\t\\tnumsRight, _ := strconv.Atoi(string(s[right]))\\n\\t\\t\\tcalculation := (numsLeft + numsRight) % 10\\n\\t\\t\\tnewS.WriteString(strconv.Itoa(calculation))\\n\\t\\t}\\n\\n\\t\\ts = newS.String()\\n\\t}\\n\\n\\treturn s[0] == s[1]\\n}\"], [9, 1.2821, \"import \\\"strings\\\"\\nfunc hasSameDigits(s string) bool {\\n for len(s) > 2 {\\n var nextS strings.Builder\\n for i := 0; i < len(s)-1; i++ {\\n d1, _ := strconv.Atoi(string(s[i]))\\n d2, _ := strconv.Atoi(string(s[i+1]))\\n d3 := (d1 + d2) % 10\\n c1 := strconv.Itoa(d3)\\n nextS.WriteString(c1)\\n }\\n s = nextS.String()\\n }\\n\\n return s[0] == s[1]\\n}\"], [10, 2.5641, \"func hasSameDigits(s string) bool {\\n for len(s) != 2 {\\n\\t\\tnewS := strings.Builder{}\\n\\n\\t\\tfor left, right := 0, 1; right < len(s); left, right = left+1, right+1 {\\n\\t\\t\\tnumsLeft, _ := strconv.Atoi(string(s[left]))\\n\\t\\t\\tnumsRight, _ := strconv.Atoi(string(s[right]))\\n\\t\\t\\tcalculation := (numsLeft + numsRight) % 10\\n\\t\\t\\tnewS.WriteString(strconv.Itoa(calculation))\\n\\t\\t}\\n\\n\\t\\ts = newS.String()\\n\\t}\\n\\n\\treturn s[0] == s[1]\\n}\"], [16, 2.5641, \"func hasSameDigits(s string) bool {\\n for len(s) > 2 {\\n var str string\\n for i := 0; i < len(s) - 1; i++ {\\n sum := (int(s[i] - '0') + int(s[i + 1] - '0')) % 10\\n str += strconv.FormatInt(int64(sum), 10)\\n }\\n\\n s = str\\n }\\n\\n return s[0] == s[1]\\n}\"], [17, 2.5641, \"func hasSameDigits(s string) bool {\\n var sz int = len(s)\\n for sz > 2 {\\n var str string\\n for pos := 1; pos < sz; pos++ {\\n str += string((s[pos]-'0'+s[pos-1]-'0')%10)\\n }\\n s = str\\n sz = len(s)\\n }\\n return s[0] == s[1]\\n}\"], [18, 1.2821, \"func hasSameDigits(s string) bool {\\n for len(s) > 2 {\\n newS := \\\"\\\"\\n\\n for i:=0; i<len(s) - 1; i++ {\\n c1 := int(s[i])\\n c2 := int(s[i+1])\\n\\n newS += string((c1 + c2) % 10)\\n }\\n\\n s = newS\\n }\\n\\n return s[0] == s[1]\\n}\"], [19, 1.2821, \"import (\\n \\\"strconv\\\"\\n)\\n\\nvar ref = map[byte]int{\\n '1': 1,\\n '2': 2,\\n '3': 3,\\n '4': 4,\\n '5': 5,\\n '6': 6,\\n '7': 7,\\n '8': 8,\\n '9': 9,\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n var sb strings.Builder\\n var a func(s string, m *map[string]bool) bool\\n a = func(s string, m *map[string]bool) bool {\\n if len(s) == 2 {\\n return s[1] == s[0]\\n }\\n if (*m)[s] {\\n return false\\n }\\n (*m)[s] = true\\n\\n size := len(s)\\n for i := 0; i < size - 1; i++ {\\n sb.WriteString(strconv.Itoa((ref[s[i]] + ref[s[i + 1]]) % 10))\\n }\\n newStr := sb.String()\\n sb.Reset()\\n return a(newStr, m)\\n }\\n var m = map[string]bool{ }\\n return a(s, &m)\\n}\"], [20, 1.2821, \"func hasSameDigits(s string) bool {\\n n := len(s)\\n for n > 2 {\\n var nstr string\\n for i := 1; i < n; i++ {\\n nstr += string((((s[i] - '0') + (s[i-1] - '0')) % 10) + '0')\\n }\\n\\n n--\\n s = nstr\\n }\\n\\n return s[0] == s[1]\\n}\"], [21, 7.6923, \"func hasSameDigits(s string) bool {\\n for len(s) > 2 {\\n tmp := \\\"\\\"\\n for i:=0; i < len(s)-1; i++ {\\n tmp += string((s[i] + s[i+1] - 48*2) % 10 + 48)\\n }\\n s = tmp\\n }\\n return s[0] == s[1]\\n}\"], [22, 3.8462, \"func hasSameDigits(s string) bool {\\n\\tfor len(s) > 2 {\\n\\t\\tnewStr := \\\"\\\"\\n\\t\\tfor i := range s {\\n\\t\\t\\tif i != len(s)-1 {\\n\\t\\t\\t\\tnewStr += string(rune((((int(s[i]) - 48) + (int(s[i+1]) - 48)) % 10) + '0'))\\n\\t\\t\\t}\\n\\t\\t}\\n\\n\\t\\ts = newStr\\n\\t}\\n\\n\\tif len(s) == 1 {\\n\\t\\treturn false\\n\\t} else {\\n\\t\\treturn s[0] == s[1]\\n\\t}\\n}\"], [23, 1.2821, \"func hasSameDigits(s string) bool {\\n for len(s) > 2 {\\n var sz int = len(s)\\n var str string\\n for pos := 1; pos < sz; pos++ {\\n d1, _ := strconv.Atoi(string(s[pos]))\\n d2, _ := strconv.Atoi(string(s[pos-1]))\\n str += strconv.Itoa((d1+d2)%10)\\n }\\n s = str\\n }\\n if s[0] == s[1] {\\n return true\\n }\\n return false\\n}\"], [24, 3.8462, \"import (\\n // \\\"strings\\\"\\n \\\"strconv\\\"\\n)\\n\\nvar ref = map[byte]int{\\n '1': 1,\\n '2': 2,\\n '3': 3,\\n '4': 4,\\n '5': 5,\\n '6': 6,\\n '7': 7,\\n '8': 8,\\n '9': 9,\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n var sb strings.Builder\\n var a func(s string, m *map[string]bool) bool\\n a = func(s string, m *map[string]bool) bool {\\n if len(s) == 2 {\\n return s[1] == s[0]\\n }\\n if (*m)[s] {\\n return false\\n }\\n (*m)[s] = true\\n\\n size := len(s)\\n for i := 0; i < size - 1; i++ {\\n first := ref[s[i]]\\n second := ref[s[i + 1]]\\n value := (first + second) % 10\\n\\n sb.WriteString(strconv.Itoa(value))\\n }\\n newStr := sb.String()\\n sb.Reset()\\n return a(newStr, m)\\n }\\n var m = map[string]bool{ }\\n return a(s, &m)\\n}\"], [26, 1.2821, \"func hasSameDigits(s string) bool {\\n\\n for len(s) > 2 {\\n var temp string\\n\\n for i := 0; i < len(s) - 1; i++ {\\n\\n s1, _ := strconv.Atoi(string(s[i]))\\n s2, _ := strconv.Atoi(string(s[i + 1]))\\n\\n temp += strconv.Itoa((s1 + s2) % 10)\\n }\\n s = temp\\n }\\n\\n return s[0] == s[1]\\n}\"], [30, 1.2821, \"func hasSameDigits(s string) bool {\\n s_len := len(s)\\n for s_len > 2 {\\n temp := \\\"\\\"\\n for i := 0 ; i < s_len -1 ; i ++ {\\n temp += strconv.Itoa(int(((s[i]-48) + (s[i+1] - 48) % 10) % 10 ))\\n }\\n s = temp\\n fmt.Println(s)\\n s_len = len(temp)\\n }\\n return s[0] == s[1]\\n}\\n\\n\"], [35, 1.2821, \"func hasSameDigits(s string) bool {\\n var sz int = len(s)\\n for sz > 2 {\\n var str string\\n for pos := 1; pos < sz; pos++ {\\n d1, _ := strconv.Atoi(string(s[pos]))\\n d2, _ := strconv.Atoi(string(s[pos-1]))\\n str += strconv.Itoa((d1+d2)%10)\\n }\\n s = str\\n sz = len(s)\\n }\\n if s[0] == s[1] {\\n return true\\n }\\n return false\\n}\"], [37, 1.2821, \"import \\\"strings\\\"\\n\\nfunc hasSameDigits(s string) bool {\\n res := s\\n for len(res) > 2 {\\n temp := []string{}\\n for i := 0; i < len(res)-1; i++ {\\n first, _ := strconv.Atoi(string(res[i]))\\n second, _ := strconv.Atoi(string(res[i+1]))\\n third := fmt.Sprint((first+second)%10)\\n temp = append(temp, third)\\n }\\n res = strings.Join(temp, \\\"\\\")\\n }\\n\\n return res[0] == res[1]\\n}\"]]"
},
"java": {
"code": "class Solution {\n public boolean hasSameDigits(String s) {\n int[] current = new int[s.length()];\n for (int i = 0; i < s.length(); i++) {\n current[i] = s.charAt(i) - '0';\n }\n while (current.length > 2) {\n int[] next = new int[current.length - 1];\n for (int i = 0; i < current.length - 1; i++) {\n next[i] = (current[i] + current[i + 1]) % 10;\n }\n current = next;\n }\n return current[0] == current[1];\n }\n}",
"memory": 4400,
"memoryDistribution": "[[4400, 80.5063, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int[] current = new int[s.length()];\\n for (int i = 0; i < s.length(); i++) {\\n current[i] = s.charAt(i) - '0';\\n }\\n while (current.length > 2) {\\n int[] next = new int[current.length - 1];\\n for (int i = 0; i < current.length - 1; i++) {\\n next[i] = (current[i] + current[i + 1]) % 10;\\n }\\n current = next;\\n }\\n return current[0] == current[1];\\n }\\n}\"], [41400, 0.0589, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n char[] str = s.toCharArray();\\n int size = str.length;\\n\\n while (size > 2) {\\n for (int i = 0; i < size - 1; i++) {\\n str[i] = (char)((str[i] - '0' + str[i + 1] - '0') % 10 + '0');\\n }\\n size--;\\n }\\n\\n return str[0] == str[1];\\n }\\n}\"], [41600, 0.0589, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n char[] arr = s.toCharArray(); //converting into char array\\n\\n while(n != 2){\\n for(int i=0; i<n-1; i++) {\\n int val = (arr[i] - '0') + (arr[i + 1] - '0');\\n val = val % 10;\\n arr[i] = (char)(val + '0');\\n }\\n n--;\\n \\n }\\n return arr[0] == arr[1];\\n \\n }\\n}\"], [41800, 0.2945, \"// class Solution {\\n// public boolean hasSameDigits(String s) {\\n// while (s.length() > 2) {\\n// String temp = \\\"\\\";\\n// String b[] = s.split(\\\"\\\");\\n// for (int i = 0; i < b.length - 1; i++) {\\n// String num1 = b[i];\\n// String num2 = b[i + 1];\\n// int res = (Integer.parseInt(num1) + Integer.parseInt(num2)) % 10;\\n// temp += String.valueOf(res); \\n// }\\n// s = temp; \\n// if (s.charAt(0) == s.charAt(1)) {\\n// return true;\\n// }\\n// }\\n// return false; \\n// }\\n// }\\n\\n class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int[] d = new int[n];\\n for (int i = 0; i < n; i++) d[i] = s.charAt(i) - '0';\\n while (n > 2) {\\n for (int i = 0; i < n - 1; i++) d[i] = (d[i] + d[i + 1]) % 10;\\n n--;\\n }\\n return d[0] == d[1];\\n }\\n}\"], [41900, 0.6478, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n =s.length();\\n int[] digits =new int[n];\\n for(int i=0;i<n;i++){\\n digits[i] = s.charAt(i)-'0';\\n }\\n while(n>2){\\n for(int i =0;i<n-1;i++){\\n digits[i]=(digits[i]+digits[i+1])%10;\\n }\\n n--;\\n } return digits[0] == digits[1];\\n }\\n}\"], [42000, 1.2956, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int[] digits = new int[n];\\n\\n for (int i = 0; i < n; i++) {\\n digits[i] = s.charAt(i) - '0';\\n }\\n \\n while (n > 2) {\\n for (int i = 0; i < n - 1; i++) {\\n digits[i] = (digits[i] + digits[i + 1]) % 10;\\n }\\n n--;\\n }\\n return digits[0] == digits[1];\\n }\\n}\"], [42100, 1.2956, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int[] digits = new int[n];\\n \\n for (int i = 0; i < n; i++) {\\n digits[i] = s.charAt(i) - '0';\\n }\\n \\n while (n > 2) {\\n for (int i = 0; i < n - 1; i++) {\\n digits[i] = (digits[i] + digits[i + 1]) % 10;\\n }\\n \\n n--;\\n }\\n return digits[0] == digits[1];\\n }\\n}\"], [42200, 2.0612, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int len = s.length();\\n int[] arr = new int[len];\\n\\n for(int i=0; i<len; i++){\\n arr[i] = s.charAt(i)-'0';\\n }\\n\\n while(len>2){\\n for(int i=0; i<len-1; i++){\\n arr[i] = (arr[i]+arr[i+1])%10;\\n }\\n \\n len--;\\n }\\n return arr[0] == arr[1];\\n }\\n}\"], [42300, 1.1779, \"class Solution {\\n\\n public boolean hasSameDigits(String s) {\\n\\n int[] nums = new int[s.length()];\\n\\n for(int i = 0; i < s.length(); i++) {\\n nums[i] = s.charAt(i) - '0';\\n }\\n\\n int size = nums.length;\\n\\n while(size > 2) {\\n\\n for(int i = 0; i < size - 1; i++) {\\n nums[i] = nums[i] + nums[i+1];\\n nums[i] %= 10;\\n }\\n\\n size--;\\n\\n }\\n\\n return nums[0] == nums[1];\\n \\n }\\n\\n}\"], [42400, 0.9423, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n Deque<Integer> q = new ArrayDeque<>();\\n for (char ch : s.toCharArray()) {\\n q.addLast(ch-48);\\n }\\n\\n while (q.size() > 2) {\\n int l = q.size();\\n int prev = q.removeFirst();\\n int num = 0;\\n for (int i = 1; i < l; i++) {\\n num = q.removeFirst();\\n q.add((prev + num) % 10);\\n prev = num;\\n }\\n }\\n\\n if (q.size() != 2) {\\n return Boolean.FALSE;\\n } else {\\n int num = q.removeFirst();\\n int num2 = q.removeFirst();\\n if (num == num2) {\\n return Boolean.TRUE;\\n }\\n }\\n return Boolean.FALSE;\\n }\\n}\"], [42500, 1.0012, \"class Solution {\\n public boolean hasSameDigits(String S) {\\n int n = S.length();\\n int[] num = new int[n];\\n for (int i = 0; i < n; ++i) num[i] = S.charAt(i) - '0';\\n while (n > 2) {\\n --n;\\n for (int i = 0; i < n; ++i) num[i] = (num[i] + num[i + 1]) % 10;\\n }\\n return num[0] == num[1];\\n }\\n}\"], [42600, 0.4122, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n char[]arr=new char[s.length()-1];\\n while(s.length()!=2){\\n // arr=new char[s.length()-1];\\n int n=0;\\n for(int i=0;i<s.length()-1;i++){\\n int a=s.charAt(i)-'0';\\n int b=s.charAt(i+1)-'0';\\n int num=(a+b)%10;\\n arr[i]=(char)(num+'0');\\n }\\n s=String.valueOf(arr,0,s.length()-1);\\n }\\n return s.charAt(0)==s.charAt(1);\\n }\\n}\"], [42700, 0.1178, \"class Solution \\n{\\n public boolean hasSameDigits(String s) \\n {\\n char[] c = s.toCharArray();\\n int size = c.length;\\n\\n while(size > 2)\\n {\\n for(int i = 1; i < size; i++)\\n {\\n int n = (c[i - 1] - '0') + (c[i] - '0');\\n n %= 10;\\n c[i-1] = (char) (n + '0');\\n }\\n\\n System.out.println();\\n\\n size--;\\n }\\n\\n return c[0] == c[1];\\n }\\n}\"], [42800, 0.1178, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n char[]arr=new char[s.length()-1];\\n while(s.length()!=2){\\n // arr=new char[s.length()-1];\\n int n=0;\\n for(int i=0;i<s.length()-1;i++){\\n int a=s.charAt(i)-'0';\\n int b=s.charAt(i+1)-'0';\\n int num=(a+b)%10;\\n arr[i]=(char)(num+'0');\\n }\\n s=String.valueOf(arr,0,s.length()-1);\\n }\\n return arr[0]==arr[1];\\n }\\n}\"], [42900, 0.0589, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int length = s.length();\\n StringBuilder sb = new StringBuilder(s);\\n while(length>2)\\n {\\n StringBuilder current = new StringBuilder(length);\\n for(int i=1; i<sb.length(); i++)\\n {\\n current.append(((sb.charAt(i-1)-'0') + (sb.charAt(i)-'0')) % 10);\\n }\\n sb = current;\\n length--;\\n }\\n return sb.length() >= 2 && (sb.charAt(0) == sb.charAt(1));\\n }\\n}\"], [43000, 0.1767, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n StringBuilder sb = new StringBuilder();\\n while(s.length()>2){\\n for(int i=0;i<s.length()-1;i++){\\n char c1 = s.charAt(i);\\n char c2 = s.charAt(i+1);\\n int num = ((c1-'0')+(c2-'0'))%10;\\n sb.append(num);\\n }\\n s = new String(sb);\\n sb.setLength(0);\\n }\\n return s.charAt(0)==s.charAt(1);\\n }\\n}\"], [43100, 0.4122, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n char[]arr=new char[s.length()-1];\\n while(s.length()!=2){\\n // arr=new char[s.length()-1];\\n int n=0;\\n for(int i=0;i<s.length()-1;i++){\\n // int a=s.charAt(i)-'0';\\n // int b=s.charAt(i+1)-'0';\\n int num=((s.charAt(i)+s.charAt(i+1))-'0')%10;\\n arr[i]=(char)(num+'0');\\n }\\n s=String.valueOf(arr,0,s.length()-1);\\n }\\n return arr[0]==arr[1];\\n }\\n}\"], [43200, 0.2356, \"\\tclass Solution {\\n\\t\\tpublic boolean hasSameDigits(String S) {\\n\\t\\t\\tchar[] s = S.toCharArray();\\n\\t\\t\\tint n = s.length;\\n\\t\\t\\tfor(int i = 0;i < n-2;i++){\\n\\t\\t\\t\\tchar[] ns = new char[s.length-1];\\n\\t\\t\\t\\tfor(int j = 0;j < s.length-1;j++){\\n\\t\\t\\t\\t\\tns[j] = (char)(((s[j]-'0') + (s[j+1]-'0')) % 10 + '0');\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\ts = ns;\\n\\t\\t\\t}\\n\\t\\t\\treturn s[0] == s[1];\\n\\t\\t}\\n\\t}\"], [43300, 0.2945, \"class Solution {\\n public boolean hasSameDigits(String s) \\n {\\n\\n if(s.length()<2) return false;\\n\\n if(s.length()==2) return s.charAt(0)==s.charAt(1);\\n\\n StringBuilder sb = new StringBuilder();\\n while(s.length()>2)\\n {\\n for(int i=0;i<s.length()-1;i++)\\n {\\n int sum = (s.charAt(i)-'0' + s.charAt(i+1)-'0' )%10;\\n sb.append(sum);\\n }\\n\\n s = sb.toString();\\n sb.setLength(0);\\n\\n }\\n\\n return s.charAt(0)==s.charAt(1);\\n \\n }\\n}\"], [43400, 0.2356, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n String sum=\\\"\\\";\\n StringBuilder in=new StringBuilder();\\n // for(int i=1;i<s.length();i++)\\n // {\\n // int n=s.charAt(i)-48;\\n // int m=s.charAt(i-1)-48;\\n // in.append((char)(48+(n+m)%10));\\n\\n // }\\n in.append(s);\\n \\n while(in.length()>2)\\n {\\n String r=in.toString();\\n in.setLength(0);\\n for(int i=1;i<r.length();i++)\\n {\\n int n=r.charAt(i)-48;\\n int m=r.charAt(i-1)-48;\\n in.append((char)(48+(n+m)%10));\\n }\\n }\\n String m=in.toString();\\n char c=m.charAt(0);\\n char d=m.charAt(1);\\n if(c==d)\\n return true;\\n return false;\\n }\\n}\"], [43500, 0.1767, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n String sum=\\\"\\\";\\n StringBuilder in=new StringBuilder();\\n // for(int i=1;i<s.length();i++)\\n // {\\n // int n=s.charAt(i)-48;\\n // int m=s.charAt(i-1)-48;\\n // in.append((char)(48+(n+m)%10));\\n\\n // }\\n in.append(s);\\n \\n while(in.length()>2)\\n {\\n String r=in.toString();\\n in.setLength(0);\\n for(int i=1;i<r.length();i++)\\n {\\n int n=r.charAt(i)-48;\\n int m=r.charAt(i-1)-48;\\n in.append((char)(48+(n+m)%10));\\n }\\n }\\n String m=in.toString();\\n char c=m.charAt(0);\\n char d=m.charAt(1);\\n if(c==d)\\n return true;\\n return false;\\n }\\n}\"], [43600, 0.2356, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n StringBuilder sb= new StringBuilder(s);\\n \\n while(sb.length()!=2){\\n s = sb.toString();\\n sb.setLength(0);\\n for(int i = 1 ; i<s.length();i++){\\n int val = Character.valueOf(s.charAt(i))+Character.valueOf(s.charAt(i-1));\\n sb.append(val%10);\\n }\\n }\\n\\n return sb.charAt(1) == sb.charAt(0)?true:false;\\n\\n }\\n}\"], [43700, 0.1767, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n StringBuilder sb=new StringBuilder(s);\\n while(sb.length()>2){\\n StringBuilder next=new StringBuilder();\\n for(int i=0;i<sb.length()-1;i++){\\n int ans=sb.charAt(i)+sb.charAt(i+1);\\n int res=ans%10;\\n next.append(res);\\n }\\n sb=next;\\n }\\n return sb.charAt(0)==sb.charAt(1);\\n\\n\\n\\n \\n }\\n}\"], [43800, 0.2356, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n StringBuilder sb = new StringBuilder(s);\\n while (sb.length() > 2) {\\n StringBuilder nextSb = new StringBuilder();\\n for (int i=0; i<sb.length()-1; i++) {\\n int a = sb.charAt(i) - '0';\\n int b = sb.charAt(i + 1) - '0';\\n nextSb.append((char)('0' + (a+b) % 10));\\n }\\n sb = nextSb;\\n }\\n return sb.charAt(0) == sb.charAt(1);\\n }\\n}\"], [43900, 0.2356, \"class Solution {\\n public static boolean hasSameDigits(String s) {\\n StringBuilder result = recours(new StringBuilder(s));\\n return result.toString().equals(new StringBuilder(result).reverse().toString());\\n }\\n\\n public static StringBuilder recours(StringBuilder x) {\\n if (x.length() == 2) {\\n return x;\\n }\\n\\n int count;\\n StringBuilder next = new StringBuilder();\\n\\n for (int i = 1; i < x.length(); i++) {\\n count = (x.charAt(i - 1) - '0' + x.charAt(i) - '0') % 10;\\n next.append(count);\\n }\\n\\n return recours(next);\\n }\\n}\"], [44000, 0.2356, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n StringBuilder sb = new StringBuilder(s);\\n int n=sb.length();\\n while(sb.length() >2)\\n { \\n StringBuilder sb1 = new StringBuilder();\\n for(int i=0;i<n-1;i++)\\n { int a=Character.getNumericValue((sb.charAt(i)));\\n int b=Character.getNumericValue((sb.charAt(i+1)));\\n sb1.append((a+b)%10);\\n }\\n sb=sb1;\\n n--;\\n }\\n if(sb.charAt(0) == sb.charAt(1)) return true;\\n else return false;\\n }\\n}\"], [44100, 0.4122, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n StringBuilder sb = new StringBuilder(s);\\n while (sb.length() > 2) {\\n StringBuilder s1 = new StringBuilder();\\n for (int i = 0; i < sb.length() - 1; i++) {\\n int a = sb.charAt(i) - '0';\\n int b = sb.charAt(i + 1) - '0';\\n s1.append((char)('0' + (a + b) % 10));\\n }\\n sb = s1;\\n }\\n return sb.charAt(0) == sb.charAt(1);\\n }\\n}\"], [44200, 0.8834, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n StringBuilder sb = new StringBuilder(s);\\n while(sb.length() > 2)\\n {\\n StringBuilder nsb = new StringBuilder();\\n for(int i = 0;i < sb.length() - 1;i++)\\n {\\n nsb.append((char) ('0' + ((sb.charAt(i) - '0') + (sb.charAt(i + 1) - '0')) % 10));\\n }\\n sb = nsb;\\n }\\n return sb.charAt(0) == sb.charAt(1);\\n }\\n}\"], [44300, 2.5324, \"class Solution {\\n public static boolean hasSameDigits(String s) {\\n StringBuilder result = recours(new StringBuilder(s));\\n return result.charAt(0) == result.charAt(1);\\n }\\n\\n public static StringBuilder recours(StringBuilder x) {\\n if (x.length() == 2) {\\n return x;\\n }\\n\\n int count;\\n StringBuilder next = new StringBuilder();\\n\\n for (int i = 1; i < x.length(); i++) {\\n count = (x.charAt(i - 1) - '0' + x.charAt(i) - '0') % 10;\\n next.append(count);\\n }\\n\\n return recours(next);\\n }\\n}\"], [44400, 3.4747, \"class Solution {\\n\\tpublic boolean hasSameDigits(String s) {\\n\\t\\tStringBuilder stringBuilder = new StringBuilder(s);\\n\\t\\twhile (stringBuilder.length() > 2) {\\n\\t\\t\\tStringBuilder nextStringBuilder = new StringBuilder();\\n\\t\\t\\tfor (int i = 0; i < stringBuilder.length() - 1; i++) {\\n\\t\\t\\t\\tint digitA = stringBuilder.charAt(i) - '0';\\n\\t\\t\\t\\tint digitB = stringBuilder.charAt(i + 1) - '0';\\n\\t\\t\\t\\tnextStringBuilder.append((char) ('0' + (digitA + digitB) % 10));\\n\\t\\t\\t}\\n\\t\\t\\tstringBuilder = nextStringBuilder;\\n\\t\\t}\\n\\t\\treturn stringBuilder.charAt(0) == stringBuilder.charAt(1);\\n\\t}\\n}\"], [44500, 5.8893, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n StringBuilder sb = new StringBuilder(s);\\n while (sb.length() > 2) {\\n StringBuilder newSb = new StringBuilder();\\n for (int i = 0; i < sb.length() - 1; i++) {\\n int sum = (sb.charAt(i) - '0' + sb.charAt(i + 1) - '0') % 10;\\n newSb.append(sum);\\n }\\n sb = newSb;\\n }\\n return sb.charAt(0) == sb.charAt(1);\\n }\\n}\"], [44600, 7.715, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n if(s.length()<2)\\n return false;\\n while(s.length()>2)\\n { StringBuilder res = new StringBuilder();\\n \\n for(int i=0;i<s.length()-1;i++)\\n {\\n int a =s.charAt(i) - '0';\\n int b = s.charAt(i + 1) - '0';\\n int ans = (a + b) % 10;\\n res.append(ans);\\n }\\n s=res.toString();\\n } \\n if(s.charAt(0)==s.charAt(1))\\n {\\n return true;\\n }\\n return false;}\\n}\"], [44700, 9.9529, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n while(s.length()>2)\\n {\\n StringBuilder mnr = new StringBuilder();\\n for(int i=0; i<s.length()-1; i++)\\n {\\n int dig1 = s.charAt(i)-'0';\\n int dig2 = s.charAt(i+1)-'0';\\n int mod10 = (dig1+dig2)%10;\\n mnr.append(mod10);\\n }\\n s = mnr.toString();\\n }\\n return s.charAt(0)==s.charAt(1);\\n }\\n}\"], [44800, 8.8339, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n while (s.length() > 2) {\\n StringBuilder sb = new StringBuilder();\\n for (int i = 1; i < s.length(); i++) {\\n int a = ((s.charAt(i) - '0') + (s.charAt(i - 1) - '0')) % 10;\\n sb.append(a);\\n }\\n s = sb.toString();\\n }\\n return s.length() == 2 ? s.charAt(0) == s.charAt(1) : false;\\n }\\n}\"], [44900, 7.715, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n StringBuilder m2 = new StringBuilder(s);\\n StringBuilder m3 = new StringBuilder();\\n // m2 = s ;\\n\\n while(true)\\n {\\n\\n if(m2.length()==2)\\n {\\n break;\\n }\\n\\n for(int i =0;i<m2.length()-1;i++)\\n {\\n int a = m2.charAt(i)-'0'; \\n int b = m2.charAt(i+1)-'0';\\n\\n ///m3 += char((a+b)%2) \\n\\n char c = ((char)('0' + (a + b) % 10));\\n m3.append(c);\\n \\n }\\n\\n m2 = new StringBuilder(m3.toString());\\n m3.setLength(0);\\n }\\n System.out.println(m2.charAt(0) + m2.charAt(1));\\n return m2.charAt(0) == m2.charAt(1);\\n }\\n}\"], [45000, 5.477, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n StringBuilder sb = new StringBuilder(s);\\n while(sb.length()>2){\\n StringBuilder temp = new StringBuilder();\\n for(int i=0;i<sb.length()-1;i++){\\n int t = ((sb.charAt(i) - '0')+(sb.charAt(i+1) - '0')) % 10;\\n temp.append(t);\\n }\\n sb = new StringBuilder(temp.toString());\\n }\\n return sb.charAt(0) == sb.charAt(1);\\n }\\n}\"], [45100, 4.0636, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n if(n == 2)\\n {\\n return s.charAt(0) == s.charAt(1);\\n }\\n StringBuilder sb = new StringBuilder();\\n for(int i = 0; i+1<n; i++)\\n {\\n int x = s.charAt(i) + s.charAt(i+1);\\n x -= 96;\\n x %= 10;\\n sb.append(\\\"\\\"+x);\\n }\\n return hasSameDigits(sb.toString());\\n }\\n}\"], [45200, 3.4747, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n=s.length(); \\n while(n>2){\\n StringBuilder newString=new StringBuilder();\\n for(int i=0;i<s.length()-1;i++){\\n int val1=s.charAt(i)-'0';\\n int val2=s.charAt(i+1)-'0';\\n int ans=(val1+val2)%10;\\n newString.append(ans);\\n }\\n s=newString.toString();\\n n=s.length();\\n }\\n System.out.print(s);\\n if(s.charAt(0)==s.charAt(1))\\n return true;\\n return false;\\n }\\n}\"], [45300, 5.0648, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n while(s.length()!=2){\\n String str = \\\"\\\";\\n for(int i=1; i<s.length(); i++){\\n int res = (s.charAt(i-1)-'0'+s.charAt(i)-'0')%10;\\n str += res;\\n }\\n \\n return hasSameDigits(str);\\n }\\n return s.charAt(0) == s.charAt(1);\\n }\\n}\"], [45400, 5.4181, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n while(s.length()!=2){\\n String s1=\\\"\\\";\\n for(int i=1;i<s.length();i++){\\n int a=((s.charAt(i)-'0')+(s.charAt(i-1)-'0'))%10;\\n s1+=a+\\\"\\\";\\n }\\n s=s1;\\n }\\n return s.charAt(0)==s.charAt(1);\\n }\\n}\"], [45500, 5.3592, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n if(s.length()<=2)\\n if(Integer.valueOf(s)%11==0)\\n return true;\\n else \\n return false;\\n String x=\\\"\\\";\\n for(int i=0;i<s.length()-1;i++)\\n x+=((int)s.charAt(i)-48+(int)s.charAt(i+1)-48)%10;\\n return hasSameDigits(x);\\n }\\n}\"], [45600, 4.4759, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n while (s.length() > 2) {\\n String temp = \\\"\\\";\\n String b[] = s.split(\\\"\\\");\\n for (int i = 0; i < b.length - 1; i++) {\\n String num1 = b[i];\\n String num2 = b[i + 1];\\n int res = (Integer.parseInt(num1) + Integer.parseInt(num2)) % 10;\\n temp += String.valueOf(res); \\n }\\n s = temp; \\n }\\n return s.charAt(0) == s.charAt(1);\\n \\n }\\n}\\n\\n \"]]",
"runtime": 2,
"runtimeDistribution": "[[1, 7.0671, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int[] digits = new int[n];\\n\\n for (int i = 0; i < n; i++) {\\n digits[i] = s.charAt(i) - '0';\\n }\\n \\n while (n > 2) {\\n for (int i = 0; i < n - 1; i++) {\\n digits[i] = (digits[i] + digits[i + 1]) % 10;\\n }\\n n--;\\n }\\n return digits[0] == digits[1];\\n }\\n}\"], [2, 3.298, \"public class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n // Convert string to array of digits\\n int[] digits = new int[n];\\n for (int i = 0; i < n; i++) {\\n digits[i] = s.charAt(i) - '0';\\n }\\n // Repeat the operation until only two digits remain\\n while (n > 2) {\\n int[] next = new int[n - 1];\\n for (int i = 0; i < n - 1; i++) {\\n next[i] = (digits[i] + digits[i + 1]) % 10;\\n }\\n digits = next;\\n n--;\\n }\\n // Return true if the final two digits are the same\\n return digits[0] == digits[1];\\n }\\n}\\n\\n\\n\\n\\n\\n\\n\\n\\n\"], [3, 1.2367, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n while(s.length()!=2){\\n char[]arr=new char[s.length()-1];\\n for(int i=0;i<s.length()-1;i++){\\n int a=s.charAt(i)-'0';\\n int b=s.charAt(i+1)-'0';\\n int num=(a+b)%10;\\n arr[i]=(char)(num+'0');\\n }\\n s=String.valueOf(arr);\\n }\\n return s.charAt(0)==s.charAt(1);\\n }\\n}\"], [4, 0.1178, \"public class Solution {\\n public boolean hasSameDigits(String s) {\\n while (s.length() > 2)\\n {\\n char[] chars = new char[s.length() - 1];\\n for (int i = 0; i < s.length() - 1; i++) \\n {\\n int a = s.charAt(i) - 48;\\n int b = s.charAt(i + 1) - 48; \\n chars[i] = (char) ((a + b) % 10 + 48);\\n }\\n s = new String(chars);\\n }\\n return (s.charAt(0) == s.charAt(1));\\n }\\n}\"], [5, 1.119, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n Deque<Integer> q = new ArrayDeque<>();\\n for (char ch : s.toCharArray()) {\\n q.addLast(ch-48);\\n }\\n\\n while (q.size() > 2) {\\n int l = q.size();\\n int prev = q.removeFirst();\\n int num = 0;\\n for (int i = 1; i < l; i++) {\\n num = q.removeFirst();\\n q.add((prev + num) % 10);\\n prev = num;\\n }\\n }\\n\\n if (q.size() != 2) {\\n return Boolean.FALSE;\\n } else {\\n int num = q.removeFirst();\\n int num2 = q.removeFirst();\\n if (num == num2) {\\n return Boolean.TRUE;\\n }\\n }\\n return Boolean.FALSE;\\n }\\n}\"], [6, 5.8893, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n=s.length();\\n if(n==2){\\n if(s.charAt(0)==s.charAt(1))\\n return true;\\n else\\n return false;\\n \\n }\\n StringBuilder p=new StringBuilder();\\n \\n for(int i=0;i<n-1;i++){\\n int next=s.charAt(i+1)%10-'0';\\n int start=s.charAt(i)%10-'0';\\n int sum=next+start;\\n p.append((char)(sum+'0'));\\n \\n }\\n return hasSameDigits(p.toString());\\n \\n }\\n}\"], [7, 6.2426, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n StringBuilder sb = new StringBuilder(s);\\n while(sb.length() > 2)\\n {\\n StringBuilder nsb = new StringBuilder();\\n for(int i = 0;i < sb.length() - 1;i++)\\n {\\n nsb.append((char) ('0' + ((sb.charAt(i) - '0') + (sb.charAt(i + 1) - '0')) % 10));\\n }\\n sb = nsb;\\n }\\n return sb.charAt(0) == sb.charAt(1);\\n }\\n}\"], [8, 35.159, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n while(s.length()>2)\\n {\\n StringBuilder mnr = new StringBuilder();\\n for(int i=0; i<s.length()-1; i++)\\n {\\n int dig1 = s.charAt(i)-'0';\\n int dig2 = s.charAt(i+1)-'0';\\n int mod10 = (dig1+dig2)%10;\\n mnr.append(mod10);\\n }\\n s = mnr.toString();\\n }\\n return s.charAt(0)==s.charAt(1);\\n }\\n}\"], [9, 4.1814, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n StringBuilder sb = new StringBuilder(s);\\n while (sb.length() > 2) {\\n StringBuilder newSb = new StringBuilder();\\n for (int i = 0; i < sb.length() - 1; i++) {\\n int sum = (sb.charAt(i) - '0' + sb.charAt(i + 1) - '0') % 10;\\n newSb.append(sum);\\n }\\n sb = newSb;\\n }\\n return sb.charAt(0) == sb.charAt(1);\\n }\\n}\"], [10, 1.119, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n StringBuilder m2 = new StringBuilder(s);\\n StringBuilder m3 = new StringBuilder();\\n // m2 = s ;\\n\\n while(true)\\n {\\n\\n if(m2.length()==2)\\n {\\n break;\\n }\\n\\n for(int i =0;i<m2.length()-1;i++)\\n {\\n int a = m2.charAt(i)-'0'; \\n int b = m2.charAt(i+1)-'0';\\n\\n ///m3 += char((a+b)%2) \\n\\n char c = ((char)('0' + (a + b) % 10));\\n m3.append(c);\\n \\n }\\n\\n m2 = new StringBuilder(m3.toString());\\n m3.setLength(0);\\n }\\n System.out.println(m2.charAt(0) + m2.charAt(1));\\n return m2.charAt(0) == m2.charAt(1);\\n }\\n}\"], [11, 1.8846, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n if(s.length()==2){\\n return s.charAt(0) == s.charAt(1);\\n }\\n else{\\n StringBuilder s1 = new StringBuilder();\\n for(int i = 0; i<s.length()-1;i++){\\n int sum = (Character.getNumericValue(s.charAt(i))+Character.getNumericValue(s.charAt(i+1)))%10;\\n s1.append(sum);\\n }\\n return hasSameDigits(s1.toString());\\n }\\n \\n }\\n}\"], [12, 4.2403, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n if(n == 2)\\n {\\n return s.charAt(0) == s.charAt(1);\\n }\\n StringBuilder sb = new StringBuilder();\\n for(int i = 0; i+1<n; i++)\\n {\\n int x = s.charAt(i) + s.charAt(i+1);\\n x -= 96;\\n x %= 10;\\n sb.append(\\\"\\\"+x);\\n }\\n return hasSameDigits(sb.toString());\\n }\\n}\"], [13, 1.8846, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n StringBuilder sb = new StringBuilder(s);\\n while (sb.length() > 2) {\\n StringBuilder tmp = new StringBuilder();\\n for (int i = 0; i < sb.length() - 1; i++) {\\n tmp.append((sb.charAt(i) + sb.charAt(i + 1) - 2 * '0') % 10);\\n }\\n sb = tmp;\\n }\\n System.out.println(sb);\\n return sb.charAt(0) == sb.charAt(1);\\n }\\n}\"], [14, 0.4122, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n StringBuilder str=new StringBuilder();\\n while(s.length()>2){\\n \\n int res=0;\\n for(int i=0;i<s.length()-1;i++){\\n int t1=s.charAt(i)-0;\\n int t2=s.charAt(i+1)-0;\\n int sum=t1+t2;\\n res=sum%10;\\n //str=str+res;\\n str.append(res);\\n }\\n \\n s=str.toString();\\n str=new StringBuilder();\\n }\\n System.out.println(s);\\n if(s.charAt(0)==s.charAt(1)){\\n return true;\\n }else{\\n return false;\\n }\\n }\\n}\"], [15, 0.1767, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n\\n\\n while(s.length()>2){\\n StringBuffer sb = new StringBuffer();\\n for(int i = 0 ;i<s.length()-1; i++){\\n \\n int n = s.charAt(i) - '0';\\n int next = s.charAt(i+1) - '0';\\n sb.append(Integer.toString((n+next)%10));\\n \\n }\\n s = sb.toString();\\n }\\n if(s.charAt(0) ==s.charAt(1))\\n return true;\\n return false;\\n \\n \\n\\n\\n \\n }\\n}\"], [16, 0.2945, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n while (s.length() > 2) {\\n StringBuilder sb = new StringBuilder();\\n for (int i = 0; i < s.length() - 1; i++) {\\n sb.append(Integer.toString(\\n (Character.getNumericValue(s.charAt(i)) + Character.getNumericValue(s.charAt(i + 1))) % 10\\n ));\\n }\\n s = sb.toString();\\n }\\n return s.charAt(0) == s.charAt(1);\\n }\\n}\\n\"], [17, 0.1767, \"class Solution extends\\n TwoStacks\\n // ParseInteger_Calculate_NotWorking\\n {}\\n\\nclass TwoStacks {\\n public boolean hasSameDigits(String s) {\\n Stack<Integer> out = new Stack<>(), in = new Stack<>();\\n for (int i = 0; i < s.length(); i++)\\n out.push(s.charAt(i) - '0');\\n \\n while (out.size() > 2) {\\n int prev = out.pop();\\n while (out.size() > 0) {\\n int cur = out.pop();\\n in.push((prev + cur) % 10);\\n prev = cur;\\n }\\n Stack<Integer> temp = out;\\n out = in;\\n in = temp;\\n }\\n return out.pop() == out.pop();\\n }\\n}\\n\\nclass ParseInteger_Calculate_NotWorking {\\n // Fails on start zeroes\\n public boolean hasSameDigits(String s) {\\n int num = 0;\\n for (int i = 0; i < s.length(); i++) {\\n int digit = s.charAt(i) - '0';\\n num = num * 10 + digit;\\n }\\n\\n while (num > 100) {\\n int newNum = 0, tens = 1;\\n int prev = num % 10; num /= 10;\\n\\n while (num > 0) {\\n int cur = num % 10;\\n int newDigit = (prev + cur) % 10;\\n newNum = newDigit * tens + newNum;// 123 => 1+2, 2+3 => 35\\n prev = cur;\\n num /= 10;\\n tens *= 10;\\n }\\n num = newNum;\\n }\\n int d1 = num % 10, d2 = (num/10) % 10;\\n return d1 == d2;\\n }\\n}\"], [20, 0.3534, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n while (s.length() > 2){\\n s = sum(s);\\n }\\n int digit = Integer.parseInt(s);\\n return (digit / 10) % 10 == digit % 10;\\n }\\n private String sum(String s){\\n StringBuilder string = new StringBuilder();\\n for (int i = 1; i < s.length(); i++){\\n int sum = (Integer.parseInt(String.valueOf(s.charAt(i-1))) + Integer.parseInt(String.valueOf(s.charAt(i)))) % 10;\\n string.append(sum);\\n }\\n return string.toString();\\n }\\n}\"], [21, 1.8257, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int ok = 1;\\n\\n while(s.length() > 2) {\\n String cs = \\\"\\\";\\n\\n for(int i = 0; i < s.length(); i++) {\\n int aux = 0;\\n if(i + 2 > s.length()) {\\n break;\\n } else {\\n for(int j = i; j < i + 2; j++) {\\n aux += s.charAt(j) - '0';\\n \\n }\\n }\\n\\n aux = aux % 10;\\n cs += (char) (aux + '0');\\n }\\n\\n s = cs;\\n }\\n\\n for(int i = 0; i < s.length() - 1; i++) {\\n if(s.charAt(i) != s.charAt(i+1)) {\\n ok = 0;\\n break;\\n }\\n }\\n\\n if(ok == 0) {\\n return false;\\n }\\n return true;\\n }\\n}\"], [22, 2.5913, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n while(s.length()>2){\\n StringBuilder x = new StringBuilder();\\n for(int i = 0; i<s.length()-1; i++){\\n int result = (Integer.parseInt(Character.toString(s.charAt(i)))+Integer.parseInt(Character.toString(s.charAt(i+1))))%10;\\n x.append(result);\\n }\\n s = x.toString();\\n\\n }\\n return s.charAt(0)==s.charAt(1);\\n }\\n}\"], [23, 4.7703, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n while(s.length()!=2){\\n String s1=\\\"\\\";\\n for(int i=1;i<s.length();i++){\\n int a=((s.charAt(i)-'0')+(s.charAt(i-1)-'0'))%10;\\n s1+=a+\\\"\\\";\\n }\\n s=s1;\\n }\\n return s.charAt(0)==s.charAt(1);\\n }\\n}\"], [24, 4.0047, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n if(s.length()==2){\\n return (s.charAt(0)-'0')==(s.charAt(1)-'0');\\n }\\n String ans =\\\"\\\";\\n for(int i=0;i<s.length()-1;i++){\\n int a=(s.charAt(i)-'0')+(s.charAt(i+1)-'0');\\n a=a%10;\\n ans+=a;\\n }\\n return hasSameDigits(ans);\\n }\\n}\"], [25, 1.8257, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n while(s.length()!=2){\\n String str = \\\"\\\";\\n for(int i=1; i<s.length(); i++){\\n int res = (s.charAt(i-1)-'0'+s.charAt(i)-'0')%10;\\n str += res;\\n }\\n \\n s = str;\\n }\\n return s.charAt(0) == s.charAt(1);\\n }\\n}\"], [26, 0.8834, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n while(s.length()!=2){\\n String str = \\\"\\\";\\n for(int i=1; i<s.length(); i++){\\n int res = (s.charAt(i-1)-'0'+s.charAt(i)-'0')%10;\\n str += res;\\n }\\n \\n return hasSameDigits(str);\\n }\\n return s.charAt(0) == s.charAt(1);\\n }\\n}\"], [27, 0.7656, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n\\n while (s.length() > 2) {\\n String sum = \\\"\\\"; \\n for (int i = 0; i < s.length() - 1; i++) {\\n sum += String.valueOf((Character.getNumericValue(s.charAt(i)) \\n + Character.getNumericValue(s.charAt(i + 1))) % 10);\\n }\\n\\n s = sum; \\n }\\n\\n return s.charAt(0) == s.charAt(1);\\n }\\n}\\n\"], [28, 0.4122, \"class Solution {\\n public static String calc(String s)\\n {\\n String temp=\\\"\\\";\\n for(int i = 0,j=i+1; i < s.length() && j<s.length(); i++,j++)\\n {\\n int i1 = Character.getNumericValue(s.charAt(i));\\n int i2 = Character.getNumericValue(s.charAt(j));\\n int val=(i1+i2)%10;\\n temp+=val;\\n }\\n return temp;\\n }\\n\\n public static boolean hasSameDigits(String s) {\\n\\n while(s.length()>2)\\n {\\n s=calc(s);\\n }\\n if(s.charAt(0)==s.charAt(1))\\n return true;\\n else\\n return false;\\n }\\n}\"], [29, 0.4711, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n while(s.length()!=2){\\n String s1=\\\"\\\";\\n for(int i=0;i<s.length()-1;i++){\\n s1+=(Character.getNumericValue(s.charAt(i))+Character.getNumericValue(s.charAt(i+1)))%10;\\n }\\n s=s1;\\n }\\n if(s.charAt(0)==s.charAt(1)){\\n return true;\\n }\\n return false;\\n }\\n}\"], [30, 0.4122, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n while(s.length()!=2){\\n String res = \\\"\\\";\\n for(int i = 0;i<s.length()-1;i++){\\n res+=(s.charAt(i)+s.charAt(i+1))%10;\\n }\\n s = res;\\n }\\n System.out.println(s);\\n if(s.charAt(0)==s.charAt(1)) return true;\\n return false;\\n }\\n}\"], [31, 0.1767, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n \\n while(s.length()>2){\\n String b=\\\"\\\";\\n for(int i=0;i<s.length()-1;i++){\\n int a=(Character.getNumericValue(s.charAt(i))+Character.getNumericValue(s.charAt(i+1)))%10;\\n b=b+a;\\n }\\n s=b;\\n }\\n if(Character.getNumericValue(s.charAt(0))==Character.getNumericValue(s.charAt(1))){\\n return true;\\n }\\n return false;\\n }\\n}\"], [33, 0.1178, \"class Solution \\n{\\n public boolean hasSameDigits(String s) \\n {\\n StringBuilder sb = new StringBuilder(s);\\n\\n while(sb.length() != 2)\\n {\\n StringBuilder cur = new StringBuilder();\\n\\n for(int i = 1; i < sb.length(); i++)\\n {\\n cur.append(((sb.charAt(i) - '0') + (sb.charAt(i - 1) - '0')) % 10);\\n }\\n\\n sb = cur;\\n System.out.println(sb.toString());\\n }\\n\\n return sb.charAt(0) == sb.charAt(1);\\n }\\n}\"], [34, 0.1178, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n String st;\\n int a, b, c;\\n while(s.length() != 2){\\n st = \\\"\\\";\\n for(int i=0;i<s.length()-1;i++){\\n a = Integer.parseInt(String.valueOf(s.charAt(i)));\\n b = Integer.parseInt(String.valueOf(s.charAt(i+1)));\\n c = (a+b)%10;\\n st = st.concat(String.valueOf(c));\\n }\\n s = st;\\n }\\n a = Integer.parseInt(String.valueOf(s.charAt(0)));\\n b = Integer.parseInt(String.valueOf(s.charAt(1)));\\n if(a == b){\\n return true;\\n }else{\\n return false;\\n }\\n }\\n}\"], [35, 0.53, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n StringBuilder sb = new StringBuilder(s);\\n StringBuilder sb2 = new StringBuilder();\\n\\n int sum = 0;\\n\\n while (sb.length() > 2) {\\n for (int i = 0; i < sb.length() - 1; i++) {\\n sum = ((sb.charAt(i) - '0') + (sb.charAt(i + 1) - '0')) % 10;\\n sb2.append(sum);\\n }\\n sb = sb2;\\n System.out.println(sb); // Debug print\\n sb2 = new StringBuilder(); \\n }\\n\\n System.out.println(sb); // Final result\\n return sb.length() == 2 && sb.charAt(0) == sb.charAt(1);\\n }\\n}\\n\"], [36, 0.4711, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n // Convert the original string into array\\n char[] cur = s.toCharArray();\\n\\n // Perform the simulation\\n while (cur.length > 2) {\\n char[] next = new char[cur.length - 1];\\n for (int i = 0; i < next.length; i++) {\\n next[i] = (char)('0' + ((cur[i]-'0') + (cur[i+1]-'0')) % 10);\\n }\\n cur = next;\\n System.out.println(Arrays.toString(cur));\\n }\\n\\n // Return the result\\n return cur[0] == cur[1];\\n }\\n}\"], [37, 0.3534, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n boolean flag=false;\\n int n=s.length();\\n String newString=\\\"\\\";\\n\\n for(int i=0;i<n-1;i++){\\n int first=Integer.parseInt(String.valueOf(s.charAt(i)));\\n int second=Integer.parseInt(String.valueOf(s.charAt(i+1)));\\n int newNumber=(first+second)%10;\\n newString+=newNumber;\\n if(i>=(n-2)){\\n if(newString.length()==2){\\n break;\\n }else{\\n i=-1;\\n s=newString;\\n newString=\\\"\\\";\\n n=s.length();\\n }\\n }\\n }\\n //System.out.print(\\\"NewString: \\\"+newString);\\n if(newString.charAt(0)==newString.charAt(1)){\\n return true;\\n }\\n\\n return false;\\n \\n }\\n}\"]]"
},
"javascript": {
"code": "/**\n * @param {string} s\n * @return {boolean}\n */\nvar hasSameDigits = function(s) {\n while (s.length > 2) {\n let nextS = '';\n for (let i = 0; i < s.length - 1; i++) {\n const a = parseInt(s[i], 10);\n const b = parseInt(s[i + 1], 10);\n nextS += (a + b) % 10;\n }\n s = nextS;\n }\n return s[0] === s[1];\n};",
"memory": 5900,
"memoryDistribution": "[[5900, 89.212, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n while (s.length > 2) {\\n let nextS = '';\\n for (let i = 0; i < s.length - 1; i++) {\\n const a = parseInt(s[i], 10);\\n const b = parseInt(s[i + 1], 10);\\n nextS += (a + b) % 10;\\n }\\n s = nextS;\\n }\\n return s[0] === s[1];\\n};\"], [54200, 0.4149, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n const digits = Array.from(s, Number);\\n \\n while (digits.length !== 2) {\\n for (let i = 0; i < digits.length - 1; i++) {\\n digits[i] = (digits[i] + digits[i + 1]) % 10;\\n }\\n digits.pop();\\n }\\n \\n return digits[0] === digits[1];\\n};\"], [54700, 0.4149, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n // Solution 1\\n // let newStr = '';\\n\\n // while (s.length > 2) {\\n // for (let i = 0; i < s.length - 1; i++) {\\n // const firstDigit = Number(s[i]);\\n // const secondDigit = Number(s[i + 1]);\\n // const res = (firstDigit + secondDigit) % 10;\\n // newStr += res;\\n // }\\n\\n // s = newStr;\\n // newStr = '';\\n // }\\n\\n // return s[0] === s[1];\\n\\n // Solution 2\\n const digits = Array.from(s, Number);\\n\\n while (digits.length !== 2) {\\n for (let i = 0; i < digits.length - 1; i++) {\\n digits[i] = (digits[i] + digits[i + 1]) % 10;\\n }\\n\\n digits.pop();\\n }\\n\\n return digits[0] === digits[1];\\n};\"], [55100, 0.8299, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n\\n const digits = Array.from(s, Number);\\n \\n while (digits.length !== 2) {\\n for (let i = 0; i < digits.length - 1; i++) {\\n digits[i] = (digits[i] + digits[i + 1]) % 10;\\n }\\n digits.pop();\\n }\\n \\n return digits[0] === digits[1];\\n};\"], [55400, 0.4149, \"function hasSameDigits(s) {\\n const res = new Uint8Array(s.length);\\n for (let i = 0; i < s.length; i++) {\\n res[i] = Number(s[i]);\\n }\\n for (let tgt = s.length; tgt > 2; tgt--) {\\n for (let i = 1; i < tgt; i++) {\\n res[i - 1] = (res[i - 1] + res[i]) % 10;\\n }\\n if (tgt === 3) return res[0] === res[1]; // Early return when only two digits remain\\n }\\n return res[0] === res[1]; // Fallback (for cases where input length is exactly 2)\\n}\"], [55600, 0.8299, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let digitArr = Array.from(s, Number);\\n\\n while (digitArr.length !== 2) {\\n for (let i = 0; i < digitArr.length - 1; i++) {\\n digitArr[i] = (digitArr[i] + digitArr[i + 1]) % 10;\\n }\\n digitArr.pop();\\n }\\n\\n return digitArr[0] === digitArr[1]\\n};\"], [55700, 0.4149, \"function hasSameDigits(s) {\\n\\tconst a = s.split(\\\"\\\").map(Number);\\n\\tconst n = a.length;\\n\\tfor (let k = n - 1; k > 1; --k) {\\n\\t\\tfor (let i = 0; i < k; ++i) {\\n\\t\\t\\ta[i] = (a[i] + a[i + 1]) % 10;\\n\\t\\t}\\n\\t}\\n\\treturn a[0] === a[1];\\n}\\n\"], [55800, 0.8299, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n s = s.split('')\\n while (s.length != 2) {\\n let store = new Array(s.length - 1);\\n for (let y = 0; y < s.length - 1; y++) store[y] = (Number(s[y]) + Number(s[y+1])) % 10;\\n s = store;\\n }\\n return s[0] === s[1] ? true : false;\\n};\"], [55900, 0.4149, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n\\n const digits = Array.from(s, Number);\\n \\n while (digits.length !== 2) {\\n for (let i = 0; i < digits.length - 1; i++) {\\n digits[i] = (digits[i] + digits[i + 1]) % 10;\\n }\\n digits.pop();\\n }\\n \\n return digits[0] === digits[1];\\n};\"], [56400, 0.4149, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n arr = [...s]\\n\\n while (arr.length > 2) {\\n arr = newDigit(arr)\\n }\\n\\n return arr[0] == arr[1]\\n};\\n\\nfunction newDigit(ar) {\\n temp = []\\n\\n for (let i = 0; i < ar.length - 1; i++) {\\n temp.push((Number(ar[i]) + Number(ar[i+1])) % 10)\\n }\\n\\n return temp\\n}\"], [56900, 1.2448, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let digits = [];\\n for (let i=0; i<s.length; i++) digits.push(Number(s[i]));\\n while (digits.length > 2) {\\n const next = [];\\n for (let i=0; i<digits.length-1; i++) next.push((digits[i] + digits[i+1]) % 10);\\n digits = next;\\n }\\n return digits[0] === digits[1]\\n};\"], [57100, 0.4149, \"function hasSameDigits(s) {\\n const a = s.split('').map(Number);\\n const n = a.length;\\n for (let k = n - 1; k > 1; --k) {\\n for (let i = 0; i < k; ++i) {\\n a[i] = (a[i] + a[i + 1]) % 10;\\n }\\n }\\n return a[0] === a[1];\\n}\\n\"], [57500, 0.8299, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n const arr = s.split(\\\"\\\").map(Number)\\n\\n while (arr.length > 2) {\\n for (let i = 0; i < arr.length - 1; i++) {\\n arr[i] = (arr[i] + arr[i + 1]) % 10; // Sum adjacent elements\\n }\\n arr.pop(); // Remove the last element (since it's already merged)\\n }\\n return arr[0] === arr[1]\\n};\"], [57700, 0.4149, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let array = [...s];\\n let result = [];\\n\\n while (array.length > 2) {\\n let left = 0;\\n result = [];\\n\\n while (left < array.length - 1) {\\n let sum = (parseInt(array[left]) + parseInt(array[left + 1])) % 10; \\n result.push(sum.toString()); \\n left++;\\n }\\n\\n array = result;\\n }\\n\\n return array[0] === array[1];\\n};\\n\"], [57800, 0.4149, \"/**\\n * @param {number} n\\n * @returns {number[]} - The nth row of Pascal's Triangle modulo 10\\n */\\n\\nconst computePascalRowMod10 = (n) => {\\n let prevRow = [1];\\n let curRow = [];\\n\\n for (let row = 1; row <= n; row++) {\\n curRow = Array(row + 1).fill(1);\\n\\n for (let col = 1; col < row; col++) {\\n curRow[col] = (prevRow[col - 1] + prevRow[col]) % 10;\\n }\\n\\n prevRow = curRow;\\n }\\n return prevRow;\\n};\\n\\nvar hasSameDigits = function(s) {\\n if (s.length === 2) return s[0] === s[1];\\n\\n const N = s.length;\\n const n = N - 2;\\n const pascalRow = computePascalRowMod10(n);\\n\\n let firstDigit = 0;\\n let secondDigit = 0;\\n\\n for (let i = 0; i <= n; i++) {\\n const times = pascalRow[i];\\n firstDigit = (firstDigit + (Number(s[i]) * times) % 10) % 10;\\n secondDigit = (secondDigit + (Number(s[N - 1 - i]) * times) % 10) % 10;\\n }\\n return firstDigit === secondDigit;\\n};\\n\\n\\n/*\\n34789 for 3 -> 4(3), 7(3), 8(1)\\n 9 -> 8(3), 7(3), 4(1)\\n3+4\\n4+7\\n7+8\\n8+9\\n\\n3+4+4+7\\n4+7+7+8\\n7+8+8+9\\n\\n3+4+4+7+4+7+7+8\\n4+7+7+8+7+8+8+9\\n*/\\n\\n/*\\n3902, for 3 -> 9(2), 0(1)\\n for 2 -> 0(2), 9(1)\\n\\n3+9\\n9+0\\n0+2\\n\\n3+9+9+0\\n9+0+0+2\\n\\n*/\\n\\n/*\\n347895, for 3 -> 4(4), 7(6), 8(4), 9(1)\\n for 5 -> 9(4), 8(6), 7(4), 4(1) \\n3+4\\n4+7\\n7+8\\n8+9\\n9+5\\n\\n3+4+4+7\\n4+7+7+8\\n7+8+8+9\\n8+9+9+5\\n\\n3+4+4+7+4+7+7+8\\n4+7+7+8+7+8+8+9\\n7+8+8+9+8+9+9+5\\n\\n3+4+4+7+4+7+7+8+4+7+7+8+7+8+8+9\\n4+7+7+8+7+8+8+9+7+8+8+9+8+9+9+5\\n*/\\n\\n/*\\n292\\n1 1 n=3\\n1 2 1 n=4\\n1 3 3 1 n=5\\n1 4 6 4 1 n=6\\n\\n*/\"], [58000, 0.4149, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n s = s.split('')\\n while (s.length != 2) {\\n let store = [];\\n for (let y = 0; y < s.length - 1; y++) {\\n store.push((Number(s[y]) + Number(s[y+1])) % 10);\\n }\\n s = store;\\n }\\n return s[0] === s[1] ? true : false;\\n};\"], [58100, 0.4149, \"var hasSameDigits = function(a = []) {\\n a = a.split(\\\"\\\").map(v => parseInt(v));\\n if (a.length < 2) return false;\\n\\n // Reduce array size using an in-place transformation approach\\n while (a.length > 2) {\\n for (let i = 0; i < a.length - 1; i++) {\\n a[i] = (a[i] + a[i + 1]) % 10;\\n }\\n a.length--; // Effectively removes the last element (pop equivalent)\\n }\\n\\n return a[0] === a[1];\\n};\\n\"], [58300, 0.8299, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n arr = [...s]\\n\\n while (arr.length > 2) {\\n arr = newDigit(arr)\\n }\\n\\n return arr[0] == arr[1]\\n};\\n\\nfunction newDigit (s) {\\n temp = []\\n for (let i = 0; i < s.length - 1; i++) {\\n temp.push((~~s[i] + ~~s[i+1]) % 10)\\n }\\n return temp\\n}\"], [58500, 0.4149, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let arrS = s.split(\\\"\\\").map(Number);\\n while (arrS.length > 2) {\\n let newArr = [];\\n for (let i = 0; i < arrS.length - 1; i++) {\\n newArr.push((arrS[i] + arrS[i + 1]) % 10);\\n }\\n arrS = newArr;\\n }\\n return arrS[0] === arrS[1];\\n};\"], [58600, 0.4149, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n while (s.length > 2) {\\n let newS = ''\\n for (let i = 0; i < s.length - 1; i++) {\\n sum = (parseInt(s[i]) + parseInt(s[i + 1])) % 10\\n newS += sum.toString()\\n }\\n s = newS\\n }\\n\\n return s[0] === s[1]\\n};\"], [58800, 1.6598, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n //Initialize the array with the numbers\\n sArray = s.split('')\\n //We use a loop while that keeps looping till the digits are only 2\\n while (sArray.length !== 2) {\\n //Array for the new number created\\n arrayNewNumbers = []\\n //Go through the array to array, but we don\\u2019t reach the last number, cuz we cant compare the last number with another number\\n for (var i = 0; i < sArray.length - 1; i++) {\\n //Do the operation and then append it to the new array\\n oper = (parseInt(sArray[i]) + parseInt(sArray[i + 1])) % 10\\n arrayNewNumbers.push(oper)\\n }\\n //The new sArray are the digits calculated\\n sArray = [...arrayNewNumbers]\\n }\\n if (sArray[0] === sArray[1]) {\\n return true\\n }\\n else {\\n return false\\n }\\n\\n};\"], [58900, 0.8299, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n while (s.length !== 2) {\\n let newS = \\\"\\\";\\n for (let i = 0; i < s.length - 1; i++) {\\n newS += (+s[i] + +s[i + 1]) % 10;\\n }\\n s = newS;\\n }\\n return s[0] === s[1];\\n};\"], [59100, 3.3195, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let newStr = s.split('').map(Number)\\n let curr = []\\n while(curr.length != 2) {\\n for(let i = 1; i < newStr.length; i+=1) {\\n let sum = newStr[i- 1] + newStr[i]\\n curr.push(sum % 10)\\n }\\n newStr = [...curr]\\n if(curr.length == 2) {\\n break\\n }\\n curr = []\\n } \\n\\n return curr[0] == curr[1]\\n};\\n\"], [59200, 1.6598, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n\\n let res = s.split('').map(Number)\\n\\n while (res.length > 2) {\\n let res1 = []\\n for (let i = 0; i < res.length - 1; i++) {\\n res1.push((res[i] + res[i + 1]) % 10)\\n }\\n res = res1\\n }\\n\\n return res[0] === res[1]\\n\\n\\n};\"], [59300, 1.2448, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let newStr = s.split('').map(Number)\\n let curr = []\\n let flag = true\\n while(flag) {\\n for(let i = 1; i < newStr.length; i+=1) {\\n let sum = newStr[i- 1] + newStr[i]\\n curr.push(sum % 10)\\n }\\n newStr = [...curr]\\n if(curr.length == 2) {\\n flag = false\\n break\\n }\\n curr = []\\n } \\n\\n return curr[0] == curr[1]\\n};\\n\"], [59400, 2.9046, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n function check(str){\\n if(str.length==2) return str;\\n let val = ''\\n for(let i=0;i<str.length-1;i++){\\n val+=(Number(str[i])+Number(str[i+1]))%10;\\n }\\n return check(val)\\n }\\n let a = check(s)\\n if(a[0]==a[1]){\\n return true\\n }else{\\n return false;\\n }\\n \\n};\"], [59500, 1.2448, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let newStr = s.split('').map(Number)\\n let curr = []\\n let flag = true\\n while(flag) {\\n for(let i = 1; i < newStr.length; i+=1) {\\n let sum = newStr[i- 1] + newStr[i]\\n curr.push(sum % 10)\\n }\\n newStr = [...curr]\\n if(curr.length == 2) {\\n flag = false\\n break\\n }\\n curr = []\\n } \\n\\n return curr[0] == curr[1]\\n};\\n\"], [59600, 2.9046, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n while (s.length > 2) {\\n let newS = ''\\n for (let p1 = 0; p1 < s.length - 1; p1++) {\\n newS += (parseInt(s[p1]) + parseInt(s[p1 + 1])) % 10\\n }\\n s = newS\\n }\\n return s[0] === s[1]\\n};\"], [59700, 4.1494, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let newStr = s.split('').map(Number)\\n let curr = []\\n let flag = true\\n while(true) {\\n for(let i = 1; i < newStr.length; i+=1) {\\n let sum = newStr[i- 1] + newStr[i]\\n curr.push(sum % 10)\\n }\\n newStr = [...curr]\\n if(curr.length == 2) {\\n flag = false\\n break\\n }\\n curr = []\\n } \\n\\n return curr[0] == curr[1]\\n};\\n\"], [59800, 6.639, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n //Initialize the array with the numbers\\n sArray = s.split('')\\n //We use a loop while that keeps looping till the digits are only 2\\n while (sArray.length !== 2) {\\n //Array for the new number created\\n arrayNewNumbers = []\\n //Go through the array to array, but we don\\u2019t reach the last number, cuz we cant compare the last number with another number\\n for (var i = 0; i < sArray.length - 1; i++) {\\n //Do the operation and then append it to the new array\\n oper = (parseInt(sArray[i]) + parseInt(sArray[i + 1])) % 10\\n arrayNewNumbers.push(oper)\\n }\\n //The new sArray are the digits calculated\\n sArray = [...arrayNewNumbers]\\n }\\n if (sArray[0] === sArray[1]) {\\n return true\\n }\\n else {\\n return false\\n }\\n\\n};\"], [59900, 9.9585, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n /**\\n Implement recursion\\n Recursively call the function until the string has 2 digits\\n */\\n\\n let newStr = \\\"\\\"\\n\\n for (let i = 0; i < s.length - 1; i++) {\\n let sum = parseInt(s[i]) + parseInt(s[i + 1])\\n newStr += (sum % 10).toString()\\n }\\n\\n if (newStr.length === 2) {\\n return newStr[0] === newStr[1]\\n } else {\\n return hasSameDigits(newStr)\\n }\\n};\"], [60000, 8.7137, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let newStr = s.split('').map(Number)\\n let curr = []\\n while(true) {\\n for(let i = 1; i < newStr.length; i+=1) {\\n let sum = newStr[i- 1] + newStr[i]\\n curr.push(sum % 10)\\n }\\n newStr = [...curr]\\n if(curr.length == 2) {\\n break\\n }\\n curr = []\\n } \\n\\n return curr[0] == curr[1]\\n};\\n\"], [60100, 3.7344, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n if((s.length === 2) && (s[0] === s[1])){\\n return true\\n } \\n if((s.length === 2) && (s[0] !== s[1])) {\\n return false\\n }\\n let str = \\\"\\\";\\n for(let i = 0; i < s.length - 1; i++){\\n str += (+(s[i]) + +(s[i + 1])) % 10\\n }\\n return hasSameDigits(str)\\n};\"], [60200, 5.3942, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n\\n while (s.length > 2) {\\n let temp = ''\\n\\n for (let i = 0; i < s.length - 1; i++) {\\n temp += ((Number(s[i]) + Number(s[i + 1])) % 10)\\n }\\n \\n s = temp\\n }\\n\\n return s[0] === s[1]\\n};\"], [60300, 2.9046, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let newS = s;\\n\\n while (newS.length > 2) {\\n let tmpS = \\\"\\\";\\n for (let i = 0; i < newS.length - 1; i++) {\\n tmpS += (parseInt(newS[i]) + parseInt(newS[i + 1])) % 10;\\n }\\n newS = tmpS;\\n }\\n\\n return newS[0] === newS[1];\\n};\"], [60400, 2.4896, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n\\n do {\\n let t = \\\"\\\"\\n for(let i = 1; i < s.length; ++i) {\\n t += ((Number(s[i - 1]) + Number(s[i])) % 10).toString();\\n }\\n\\n s = t\\n } while(s.length > 2)\\n\\n return s[0] == s[1]\\n};\"], [60500, 2.0747, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n while (s.length > 2) {\\n let result = '';\\n for (let i = 0; i < s.length - 1; i++) {\\n let sum = (s[i] - '0') + (s[i + 1] - '0');\\n result += (sum % 10).toString();\\n }\\n s = result;\\n }\\n return s[0] === s[1];\\n};\"], [60600, 0.8299, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let newS = [];\\n\\n const combineDigits = (a, b) => {\\n return ((parseInt(a) + parseInt(b))%10);\\n }\\n\\n for (let i=0; i<s.length-1; i++) {\\n newS.push(combineDigits(s[i], s[i+1]));\\n }\\n\\n if (newS.length === 2) {\\n return newS[0] === newS[1]\\n }\\n while (newS.length > 2) {\\n return hasSameDigits(newS)\\n }\\n\\n};\"], [60700, 0.8299, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n function toDigit(ch) {\\n return ch.charCodeAt(0) - '0'.charCodeAt(0);\\n }\\n\\n while (s.length > 2) {\\n let newString = \\\"\\\";\\n let end = s.length - 1;\\n for (let i = 0; i < end; i++) {\\n let sum = (toDigit(s[i]) + toDigit(s[i + 1])) % 10;\\n newString = newString + sum.toString();\\n }\\n s = newString;\\n }\\n\\n if (s[0] === s[1]) {\\n return true;\\n }\\n return false;\\n};\\n\"], [60800, 0.8299, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let arr = s.split('').map(n => Number(n));\\n while (arr.length > 2) {\\n let newArr = [];\\n for (let i = 0; i < arr.length - 1; i++) {\\n let sum = (arr[i] + arr[i + 1]) % 10;\\n newArr.push(sum);\\n }\\n arr = newArr;\\n }\\n return arr[0] == arr[1];\\n};\"], [60900, 0.8299, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n while (s.length > 2) {\\n let result = '';\\n for (let i = 0; i < s.length - 1; i++) {\\n let sum = (s[i] - '0') + (s[i + 1] - '0');\\n result += (sum % 10).toString();\\n }\\n s = result;\\n }\\n return s[0] === s[1];\\n};\"], [61000, 1.2448, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n let newStr = '';\\n\\n while (s.length > 2) {\\n for (let i = 0; i < s.length - 1; i++) {\\n const firstDigit = Number(s[i]);\\n const secondDigit = Number(s[i + 1]);\\n const res = (firstDigit + secondDigit) % 10;\\n newStr += res;\\n }\\n\\n s = newStr;\\n newStr = '';\\n }\\n\\n return s[0] === s[1];\\n};\"], [61100, 0.4149, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n var i = 0;\\n var j = i + 1;\\n var res = \\\"\\\";\\n\\n do{\\n while(j < s.length){\\n let num1 = Number(s.charAt(i));\\n let num2 = Number(s.charAt(j));\\n res += (num1 + num2) % 10;\\n i++;\\n j++;\\n }\\n i=0;\\n j=i + 1;\\n s = res.toString();\\n res = \\\"\\\";\\n }while((s.length > 2));\\n return s.charAt(0) == s.charAt(1);\\n};\"], [61200, 1.2448, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let str = \\\"\\\";\\n if((s.length === 2) && (s[0] === s[1])) return true\\n if((s.length === 2) && (s[0] !== s[1])) return false\\n for(let i = 0; i < s.length - 1; i++){\\n str += (+(s[i]) + +(s[i + 1])) % 10\\n }\\n return hasSameDigits(str)\\n};\"], [61300, 2.9046, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n function hai(str) {\\n if (str.length !== 2) {\\n let sum = \\\"\\\"\\n for (let i = 0; i < str.length - 1; i++) {\\n sum += (Number(str[i]) + Number(str[i + 1])) % 10\\n }\\n return hai(sum)\\n }\\n return str\\n }\\n let result = hai(s)\\n return result[0] === result[1]\\n}\"], [61400, 3.3195, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let r = calc(s)\\n\\n while (r.length > 2) {\\n r = calc(r.join(''))\\n }\\n \\n return r[0] === r[1]\\n};\\n\\nconst calc = (s) => {\\n const r = Array.from(s)\\n const x = []\\n\\n for (let i = 0; i < r.length - 1; i++) {\\n x.push((parseInt(r[i]) + parseInt(r[i + 1])) % 10)\\n }\\n \\n return x\\n}\"], [61500, 1.6598, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n\\n while (s.length > 2) {\\n let temp = ''\\n\\n for (let i = 0; i < s.length - 1; i++) {\\n temp += ((Number(s[i]) + Number(s[i + 1])) % 10)\\n }\\n \\n s = temp\\n }\\n\\n return s[0] === s[1]\\n};\"], [61600, 1.6598, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n\\n while (s.length > 2) {\\n let temp = ''\\n\\n for (let i = 0; i < s.length - 1; i++) {\\n temp += ((Number(s[i]) + Number(s[i + 1])) % 10)\\n }\\n \\n s = temp\\n }\\n\\n return s[0] === s[1]\\n};\"], [61700, 0.4149, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n while(s.length > 2){\\n let substring=\\\"\\\";\\n for(let i=0; i<s.length - 1; i++){\\n let firststring = parseInt(s[i]);\\n let secondstring = parseInt(s[i + 1]);\\n let sum = (firststring+secondstring) % 10;\\n substring+=sum;\\n }\\n s=substring;\\n }\\n return s[0] === s[1];\\n};\"], [61800, 0.4149, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let result = [];\\n\\n while (result.length != 2) {\\n result = [];\\n for (let i = 0; i < s.length - 1; i++) {\\n let first = Number(s[i]);\\n let second = Number(s[i+1]);\\n\\n let val = (first + second) % 10;\\n result.push(val);\\n }\\n s = result.join('');\\n }\\n\\n if (result[0] == result[1]) {\\n return true;\\n } else {\\n return false;\\n }\\n};\"], [61900, 2.4896, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n let length = s.length;\\n\\n let curS = s;\\n let curLength = length;\\n let curNums = [];\\n while (curLength > 1) {\\n curNums = curS.split('').map(Number);\\n let curArr = [];\\n for (let i = 0; i < curNums.length - 1; i++) {\\n let calc = (curNums[i] + curNums[i + 1]) % 10;\\n curArr.push(calc);\\n }\\n curS = curArr.join('');\\n curLength = curS.length;\\n }\\n return curNums[0] === curNums[1]\\n};\"], [62000, 0.4149, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\n\\nconst getResultant = function (s) {\\n let res = ''\\n for (let i = 0; i < s.length - 1; i++) {\\n res += ((Number(s[i]) + Number(s[i + 1])) % 10)\\n }\\n return res\\n}\\n\\nvar hasSameDigits = function (s) {\\n while (s.length !== 2) {\\n s = getResultant(s)\\n }\\n return s[0] === s[1] ? true : false\\n};\"], [62100, 0.8299, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n while (s.length > 2) {\\n let newStr = \\\"\\\";\\n for (let i = 0; i < s.length - 1; i++) {\\n const a = Number(s[i]);\\n const b = Number(s[i + 1]);\\n const newChar = (a + b) % 10;\\n newStr = newStr.concat(newChar);\\n }\\n s = newStr;\\n }\\n\\n return s[0] === s[1];\\n};\"], [62200, 0.8299, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\n\\nfunction provideResult(s) {\\n let finalString=\\\"\\\";\\n for(let i=0;i<s.length-1;i++) {\\n finalString+= (Number(s[i]) + Number(s[i+1]))%10;\\n }\\n return finalString;\\n}\\nvar hasSameDigits = function(s) {\\n \\n while(s.length!=2) {\\n s = provideResult(s);\\n }\\n if(s[0]==s[1]) {\\n return true;\\n } else {\\n return false;\\n }\\n};\"], [62900, 0.4149, \"const perform = ([a, ...b]) => b.map((x) => ([a, x] = [x, a], (+x + +a) % 10));\\nconst hasSameDigits = f = s => s.length < 3 ? s[0] === s[1] : f(perform(s));\"], [63000, 0.4149, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\n// var hasSameDigits = function(s) {\\n const perform = ([a, ...b]) => b.map((x) => ([a, x] = [x, a], (+x + +a) % 10));\\nconst hasSameDigits = f = s => s.length < 3 ? s[0] === s[1] : f(perform(s));\\n// };\"]]",
"runtime": 10,
"runtimeDistribution": "[[0, 0.8299, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n const digits = Array.from(s, Number);\\n \\n while (digits.length !== 2) {\\n for (let i = 0; i < digits.length - 1; i++) {\\n digits[i] = (digits[i] + digits[i + 1]) % 10;\\n }\\n digits.pop();\\n }\\n \\n return digits[0] === digits[1];\\n};\"], [1, 0.8299, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n\\n const digits = Array.from(s, Number);\\n \\n while (digits.length !== 2) {\\n for (let i = 0; i < digits.length - 1; i++) {\\n digits[i] = (digits[i] + digits[i + 1]) % 10;\\n }\\n digits.pop();\\n }\\n \\n return digits[0] === digits[1];\\n};\"], [2, 1.2448, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let digitArr = Array.from(s, Number);\\n\\n while (digitArr.length !== 2) {\\n for (let i = 0; i < digitArr.length - 1; i++) {\\n digitArr[i] = (digitArr[i] + digitArr[i + 1]) % 10;\\n }\\n digitArr.pop();\\n }\\n\\n return digitArr[0] === digitArr[1]\\n};\"], [3, 0.8299, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n // Solution 1\\n // let newStr = '';\\n\\n // while (s.length > 2) {\\n // for (let i = 0; i < s.length - 1; i++) {\\n // const firstDigit = Number(s[i]);\\n // const secondDigit = Number(s[i + 1]);\\n // const res = (firstDigit + secondDigit) % 10;\\n // newStr += res;\\n // }\\n\\n // s = newStr;\\n // newStr = '';\\n // }\\n\\n // return s[0] === s[1];\\n\\n // Solution 2\\n const digits = Array.from(s, Number);\\n\\n while (digits.length !== 2) {\\n for (let i = 0; i < digits.length - 1; i++) {\\n digits[i] = (digits[i] + digits[i + 1]) % 10;\\n }\\n\\n digits.pop();\\n }\\n\\n return digits[0] === digits[1];\\n};\"], [4, 2.9046, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n\\n const digits = Array.from(s, Number);\\n \\n while (digits.length !== 2) {\\n for (let i = 0; i < digits.length - 1; i++) {\\n digits[i] = (digits[i] + digits[i + 1]) % 10;\\n }\\n digits.pop();\\n }\\n \\n return digits[0] === digits[1];\\n};\"], [5, 2.0747, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n s = s.split('')\\n while (s.length != 2) {\\n let store = new Array(s.length - 1);\\n for (let y = 0; y < s.length - 1; y++) {\\n store[y] = (Number(s[y]) + Number(s[y+1])) % 10;\\n }\\n s = store;\\n }\\n return s[0] === s[1] ? true : false;\\n};\"], [6, 3.3195, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let newStr = s.split('').map(Number)\\n let curr = []\\n while(true) {\\n for(let i = 1; i < newStr.length; i+=1) {\\n let sum = newStr[i- 1] + newStr[i]\\n curr.push(sum % 10)\\n }\\n newStr = [...curr]\\n if(curr.length == 2) {\\n break\\n }\\n curr = []\\n } \\n\\n return curr[0] == curr[1]\\n};\\n\"], [7, 4.5643, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let newStr = s.split('').map(Number)\\n let curr = []\\n while(curr.length != 2) {\\n for(let i = 1; i < newStr.length; i+=1) {\\n let sum = newStr[i- 1] + newStr[i]\\n curr.push(sum % 10)\\n }\\n newStr = [...curr]\\n if(curr.length == 2) {\\n break\\n }\\n curr = []\\n } \\n\\n return curr[0] == curr[1]\\n};\\n\"], [8, 7.4689, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let newStr = s.split('').map(Number)\\n let curr = []\\n let flag = true\\n while(true) {\\n for(let i = 1; i < newStr.length; i+=1) {\\n let sum = newStr[i- 1] + newStr[i]\\n curr.push(sum % 10)\\n }\\n newStr = [...curr]\\n if(curr.length == 2) {\\n flag = false\\n break\\n }\\n curr = []\\n } \\n\\n return curr[0] == curr[1]\\n};\\n\"], [9, 7.8838, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n var i = 0;\\n var j = i + 1;\\n var res = \\\"\\\";\\n\\n do{\\n while(j < s.length){\\n let num1 = Number(s.charAt(i));\\n let num2 = Number(s.charAt(j));\\n res += (num1 + num2) % 10;\\n i++;\\n j++;\\n }\\n i=0;\\n j=i + 1;\\n s = res.toString();\\n res = \\\"\\\";\\n }while((s.length > 2));\\n return s.charAt(0) == s.charAt(1);\\n};\"], [10, 9.1286, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let arrS = s.split(\\\"\\\").map(Number);\\n while (arrS.length > 2) {\\n let newArr = [];\\n for (let i = 0; i < arrS.length - 1; i++) {\\n newArr.push((arrS[i] + arrS[i + 1]) % 10);\\n }\\n arrS = newArr;\\n }\\n return arrS[0] === arrS[1];\\n};\"], [11, 9.9585, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n while (s.length > 2) {\\n let newS = ''\\n for (let p1 = 0; p1 < s.length - 1; p1++) {\\n newS += (parseInt(s[p1]) + parseInt(s[p1 + 1])) % 10\\n }\\n s = newS\\n }\\n return s[0] === s[1]\\n};\"], [12, 11.6183, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let newStr = s.split('').map(Number)\\n let curr = []\\n let flag = true\\n while(flag) {\\n for(let i = 1; i < newStr.length; i+=1) {\\n let sum = newStr[i- 1] + newStr[i]\\n curr.push(sum % 10)\\n }\\n newStr = [...curr]\\n if(curr.length == 2) {\\n flag = false\\n break\\n }\\n curr = []\\n } \\n\\n return curr[0] == curr[1]\\n};\\n\"], [13, 7.0539, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let newStr = s.split('').map(Number)\\n let curr = []\\n let flag = true\\n while(flag) {\\n for(let i = 1; i < newStr.length; i+=1) {\\n let sum = newStr[i- 1] + newStr[i]\\n curr.push(sum % 10)\\n }\\n newStr = [...curr]\\n if(curr.length == 2) {\\n flag = false\\n break\\n }\\n curr = []\\n } \\n\\n return curr[0] == curr[1]\\n};\\n\"], [14, 10.7884, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n \\nwhile(s.length>2){\\n let newstr=\\\"\\\";\\nfor(let i=0;i<s.length-1;i++){\\n let sum=(Number(s[i])+Number(s[i+1]))%10\\n newstr+=sum\\n}\\ns=newstr\\n}\\n\\nlet a=s.split(\\\"\\\").map(Number)\\nif([...new Set(a)].length==1){\\n return(true)\\n}return false\\n};\"], [15, 6.639, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n \\n while (s.length > 2) {\\n let result = '';\\n for (let i = 0; i < s.length - 1; i++) {\\n let sum = (s[i] - '0') + (s[i + 1] - '0');\\n result += (sum % 10).toString();\\n }\\n s = result;\\n }\\n return s[0] === s[1];\\n \\n};\"], [16, 1.6598, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n while (s.length > 2) {\\n let newStr = \\\"\\\";\\n for (let i = 0; i < s.length - 1; i++) {\\n const sum = (parseInt(s[i]) + parseInt(s[i + 1])) % 10;\\n newStr += sum.toString();\\n }\\n s = newStr;\\n }\\n return s[0] === s[1]\\n};\\n\\n\\n\"], [17, 1.6598, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let temp = s;\\n while(temp.length > 2){\\n let local = \\\"\\\";\\n for(let i=0; i<temp.length-1; i++){\\n local += (parseInt(temp[i]) + parseInt(temp[i+1])) % 10;\\n }\\n temp = local;\\n }\\n return temp[0] == temp[1];\\n};\"], [18, 0.8299, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n while (s.length > 2) {\\n let temp = \\\"\\\";\\n\\n for (let i = 0; i < s.length - 1; i++) {\\n const num = (Number(s[i]) + Number(s[i + 1])) % 10;\\n temp += String(num);\\n }\\n\\n s = temp;\\n }\\n\\n return s[0] === s[1];\\n};\"], [19, 0.4149, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\n// var hasSameDigits = function(s) {\\n const perform = ([a, ...b]) => b.map((x) => ([a, x] = [x, a], (+x + +a) % 10));\\nconst hasSameDigits = f = s => s.length < 3 ? s[0] === s[1] : f(perform(s));\\n// };\"], [20, 0.4149, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n if(s.length == 2){\\n if(s[0] == s[1]){\\n console.log(\\\"if\\\")\\n return true\\n }else{\\n console.log(\\\"else\\\")\\n return false\\n } \\n }\\n\\n let result = \\\"\\\";\\n for(let i = 0; i < s.length - 1; i++){\\n result += (parseInt(s[i]) + parseInt(s[i + 1])) % 10\\n }\\n return hasSameDigits(result)\\n};\"], [21, 0.8299, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n let length = s.length;\\n\\n let curS = s;\\n let curLength = length;\\n let curNums = [];\\n while (curLength > 1) {\\n curNums = curS.split('').map(Number);\\n let curArr = [];\\n for (let i = 0; i < curNums.length - 1; i++) {\\n let calc = (curNums[i] + curNums[i + 1]) % 10;\\n curArr.push(calc);\\n }\\n curS = curArr.join('');\\n curLength = curS.length;\\n }\\n return curNums[0] === curNums[1]\\n};\"], [22, 0.4149, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n let newStr = '';\\n\\n while (s.length > 2) {\\n for (let i = 0; i < s.length - 1; i++) {\\n const firstDigit = Number(s[i]);\\n const secondDigit = Number(s[i + 1]);\\n const res = (firstDigit + secondDigit) % 10;\\n newStr += res;\\n }\\n\\n s = newStr;\\n newStr = '';\\n }\\n\\n return s[0] === s[1];\\n};\"], [23, 0.4149, \"const perform = ([a, ...b]) => b.map((x) => ([a, x] = [x, a], (+x + +a) % 10));\\nconst hasSameDigits = f = s => s.length < 3 ? s[0] === s[1] : f(perform(s));\"], [41, 0.4149, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n const arr = s.split(\\\"\\\").map(Number)\\n console.log(arr)\\n\\n while (arr.length > 2) {\\n for (let i = 0; i < arr.length - 1; i++) {\\n arr[i] = (arr[i] + arr[i + 1]) % 10; // Sum adjacent elements\\n }\\n arr.pop(); // Remove the last element (since it's already merged)\\n }\\n return arr[0] === arr[1]\\n};\"], [63, 0.4149, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n let prev = s.split('').map((dig) => +dig), curr;\\n while(prev.length > 2){\\n // console.log(prev);\\n curr = prev.reduce((curr, num, i) => \\n i === prev.length - 1\\n ? curr\\n : curr.concat([(num + prev[i + 1]) % 10])\\n , []);\\n prev = curr;\\n }\\n\\n // console.log(prev);\\n return prev[0] === prev[1];\\n};\"]]"
},
"python3": {
"code": "class Solution:\n def hasSameDigits(self, s: str) -> bool:\n current = [int(c) for c in s]\n while len(current) > 2:\n new_current = []\n for i in range(len(current) - 1):\n new_current.append((current[i] + current[i + 1]) % 10)\n current = new_current\n return current[0] == current[1]",
"memory": 1800,
"memoryDistribution": "[[1800, 46.6115, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n current = [int(c) for c in s]\\n while len(current) > 2:\\n new_current = []\\n for i in range(len(current) - 1):\\n new_current.append((current[i] + current[i + 1]) % 10)\\n current = new_current\\n return current[0] == current[1]\"], [17400, 0.1378, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n lists = [int(c) for c in s]\\n while len(lists) != 2:\\n for i in range(len(lists) - 1):\\n lists[i] = (lists[i] + lists[i + 1]) % 10\\n lists.pop()\\n return lists[0] == lists[1]\\n \"], [17500, 0.5284, \"import random\\nrandom.seed(5256)\\nclass Solution:\\r\\n def hasSameDigits(self, s: str) -> bool:\\r\\n if random.random() < 0.001:\\n return 62629\\n res = s\\r\\n while len(res) > 2:\\r\\n res = self.compute(res)\\r\\n return res[0] == res[1]\\r\\n def compute(self, s: str) -> str:\\r\\n res = \\\"\\\"\\r\\n for i in range(len(s) - 1):\\r\\n digit = (int(s[i]) + int(s[i+1])) % 10\\r\\n res += str(digit)\\r\\n return res\"], [17600, 4.4337, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n temp_str = s\\n new_num_str = \\\"\\\"\\n while len(temp_str) != 2:\\n for i in range(1, len(temp_str)):\\n new_num_str += str((int(temp_str[i-1]) + int(temp_str[i])) % 10)\\n temp_str = new_num_str\\n new_num_str = \\\"\\\"\\n return True if temp_str[0] == temp_str[1] else False \\n\\n \"], [17700, 18.8376, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n temp_str = s\\n new_num_str = \\\"\\\"\\n while len(temp_str) != 2:\\n for i in range(1, len(temp_str)):\\n new_num_str += str((int(temp_str[i-1]) + int(temp_str[i])) % 10)\\n # print(temp_num)\\n temp_str = new_num_str\\n new_num_str = \\\"\\\"\\n # print(temp_str)\\n return True if temp_str[0] == temp_str[1] else False \\n\\n \"], [17800, 29.451, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n ghk=list(s)\\n while len(ghk)!=2:\\n e_list=[]\\n for i in range(len(ghk)-1):\\n ghk1=(int(ghk[i])+int(ghk[i+1]))%10\\n e_list.append(str(ghk1))\\n ghk=e_list\\n \\n \\n\\n if ghk[0]==ghk[1]:\\n return True\\n return False\\n\\n\\n \\n \"], [17900, 17.8038, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n \\n def calc(st: List[int])-> List[int]:\\n newS =[]\\n for i in range(0, len(st)-1):\\n newS.append(( st[i] + st[i+1] )%10)\\n\\n\\n return calc(newS) if len( newS ) > 2 else newS\\n\\n o = calc([int( c ) for c in s])\\n ss = set(o)\\n return len(ss) == 1\\n\\n\"], [18000, 23.0875, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n while len(s) > 2:\\n temp = \\\"\\\"\\n i = 0\\n while i < len(s)-1:\\n cur = (int(s[i]) + int(s[i+1]))%10\\n temp += str(cur)\\n i += 1\\n s = temp\\n return s[0] == s[1]\"]]",
"runtime": 22,
"runtimeDistribution": "[[0, 0.1149, \"\\\"\\\"\\\"\\nUse code from 3463\\n\\\"\\\"\\\"\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n first = second = 0\\n N, comb = len(s) - 2, 1\\n X = 1 + N // 2\\n combs = [0] * X\\n s = [*map(int, s)]\\n for r in range(X): \\n combs[r] = comb % 10\\n needed = combs[r]\\n first = (first + s[r] * needed) % 10\\n second = (second + s[r + 1] * needed) % 10\\n comb *= (N - r) or 1\\n comb //= (r + 1) or 1\\n\\n i = 2 - (N & 1)\\n for r in range(X, N + 1):\\n needed = combs[X - r - i]\\n first = (first + s[r] * needed) % 10\\n second = (second + s[r + 1] * needed) % 10\\n\\n return first == second\\n\"], [1, 0.1838, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s) - 2\\n d1 = 0\\n d2 = 0\\n for k in range(len(s)-1):\\n mult = math.comb(n,k)\\n d1 += mult*int(s[k])\\n d2 += mult*int(s[k+1])\\n return (d2%10) == (d1%10)\\n \\n \"], [3, 0.1378, \"\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n first = second = 0\\n N, comb = len(s) - 2, 1\\n X = 1 + N // 2\\n combs = [0] * X\\n s = [*map(int, s)]\\n for r in range(X): \\n combs[r] = comb % 10\\n needed = combs[r]\\n first = (first + s[r] * needed) % 10\\n second = (second + s[r + 1] * needed) % 10\\n comb *= (N - r) or 1\\n comb //= (r + 1) or 1\\n\\n i = 2 - (N & 1)\\n for r in range(X, N + 1):\\n needed = combs[X - r - i]\\n first = (first + s[r] * needed) % 10\\n second = (second + s[r + 1] * needed) % 10\\n\\n return first == second\"], [4, 0.0459, \"import math\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n # abcdefgh\\n # a+b, b+c, c+d, d+e, e+f, f+g, g+h\\n # a+2b+c, b+2c+d, c+2d+e, d+2e+f, e+2f+g, f+2g+h\\n # a+3b+3c+d, b+3c+3d+e, c+3d+3e+f, d+3e+3f+g, e+3f+3g+h\\n # a+4b+6c+4d+e, b+4c+6d+3e+f, c+4d+6e+4f+g, d+4e+6f+4g+h\\n # a+5b+10c+10d+5e+f, b+5c+10d+10e+5f+g, c+5d+10e+10f+5g+h\\n # a+6b+15c+20d+15e+6f+g, b+6c+15d+20e+15f+6g+h\\n # a+5b+9c+5d-5e-9f-5g-h\\n # 0, 1, 6, 15, 20, 15, 6, 1, 0\\n \\n n = len(s)\\n coeff = [0] + [math.comb(n-2, i) for i in range(n-1)] + [0]\\n \\n running_sum = 0\\n for i in range(n):\\n running_sum += (coeff[i+1]-coeff[i])*int(s[i])\\n\\n return running_sum % 10 == 0 \\n \"], [5, 0.1379, \"import math\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n coefs = [0] * (n-1)\\n for i in range(n-1):\\n coefs[i] = math.comb(n-2, i)\\n \\n d1 = sum([coefs[i]*int(s[i]) for i in range(n-1)]) % 10\\n d2 = sum([coefs[i]*int(s[i+1]) for i in range(n-1)]) % 10\\n return d1==d2\\n\\n \"], [6, 0.023, \"import math\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n coefs = [0] * (n-1)\\n for i in range(n-1):\\n coefs[i] = math.comb(n-2, i)\\n \\n d1 = sum([coefs[i]*int(s[i]) for i in range(n-1)]) % 10\\n d2 = sum([coefs[i]*int(s[i+1]) for i in range(n-1)]) % 10\\n print(d1,d2)\\n return d1==d2\\n\\n \"], [7, 0.0689, \"def fromInt(x):\\n q, r = 0, 0\\n while x % 2 == 0:\\n x //= 2\\n q += 1\\n while x % 5 == 0:\\n x //= 5\\n r += 1\\n return (x % 10, q, r)\\n\\nFROM_INT = [None] + [fromInt(n) for n in range(1, 10**5+1)]\\nINV_POW = [None] + [pow(u, -1, 10) if u % 2 != 0 and u % 5 != 0 else None for u in range(1, 10+1)]\\nFROM_INT_INV = [None] + [(INV_POW[p], -q, -r) for p, q, r in FROM_INT[1:]]\\n\\ndef multiply(a, b):\\n p, q, r = a\\n u, v, w = b\\n return (p * u % 10, q + v, r + w)\\n\\ndef lastDigit(pqr):\\n p, q, r = pqr\\n if q > 0:\\n p *= [2, 4, 8, 6][q%4-1]\\n if r > 0:\\n p *= 5\\n return p % 10\\n\\ndef combLastDigits(n):\\n result = []\\n cnk = fromInt(1)\\n result.append(lastDigit(cnk))\\n for k in range(0, n):\\n cnk = multiply(cnk, multiply(FROM_INT[n-k], FROM_INT_INV[k+1]))\\n result.append(lastDigit(cnk))\\n return result\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n # Based on my solution from problem 3463\\n s = [int(c) for c in s]\\n binom = combLastDigits(len(s)-2)\\n firstDigit = sum(binom[i] * s[i] for i in range(len(s)-1)) % 10\\n secondDigit = sum(binom[i] * s[i+1] for i in range(len(s)-1)) % 10\\n return firstDigit == secondDigit\"], [9, 0.023, \"import math\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n \\\"\\\"\\\"\\n Return True if, after repeatedly replacing s by the sequence of\\n (s[i]+s[i+1])%10 until length is 2, the final two digits are equal.\\n \\\"\\\"\\\"\\n n = len(s)\\n num1 = num2 = 0\\n # Compute the two final digits via binomial weights mod 10\\n for i in range(n - 1):\\n coef = self._nCk_mod10(n - 2, i)\\n d1, d2 = int(s[i]), int(s[i+1])\\n num1 = (num1 + coef * d1) % 10\\n num2 = (num2 + coef * d2) % 10\\n return num1 == num2\\n\\n def _nCk_mod10(self, n: int, k: int) -> int:\\n \\\"\\\"\\\"\\n Return C(n, k) % 10 by computing it mod 2 and mod 5 separately\\n (via Lucas) and combining:\\n C % 10 = lookup[ C(n,k)%2 ][ C(n,k)%5 ]\\n \\\"\\\"\\\"\\n # Compute C(n, k) mod 2 and mod 5\\n m2 = self._lucas(n, k, 2)\\n m5 = self._lucas(n, k, 5)\\n # Precomputed CRT table: for mod2 in {0,1}, mod5 in {0..4}\\n lookup = [\\n [0, 6, 2, 8, 4], # if C mod 2 == 0\\n [5, 1, 7, 3, 9], # if C mod 2 == 1\\n ]\\n return lookup[m2][m5]\\n\\n def _lucas(self, n: int, k: int, p: int) -> int:\\n \\\"\\\"\\\"\\n Lucas Theorem to compute C(n,k) % p for prime p (p=2 or 5).\\n Break n,k into base-p digits and multiply small binomials.\\n \\\"\\\"\\\"\\n res = 1\\n while n > 0 or k > 0:\\n ni, ki = n % p, k % p\\n if ki > ni:\\n return 0\\n # small binomial C(ni, ki) fits in Python int\\n res = (res * math.comb(ni, ki)) % p\\n n //= p\\n k //= p\\n return res\\n\"], [10, 0.023, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n s = list(map(int,s))\\n while len(s) > 2:\\n t = []\\n a = s[0]\\n for b in s[1:]:\\n t.append((a+b)%10)\\n a = b\\n s = t\\n return s[0] == s[1]\\n \"], [11, 0.023, \"class Solution:\\n\\n def hasSameDigits(self, s: str) -> bool:\\n digits = [int(c) for c in s]\\n\\n def helper(digits):\\n new_digits = []\\n for i in range(len(digits)-1):\\n new_digits.append((digits[i] + digits[i+1]) % 10)\\n return new_digits\\n\\n while len(digits) > 2:\\n digits = helper(digits)\\n \\n return digits[0] == digits[1]\\n \\n \"], [12, 0.0459, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n nums = [int(c) for c in s]\\n\\n for i in range(n - 1, 1, -1):\\n for j in range(i):\\n nums[j] = (nums[j] + nums[j + 1]) % 10\\n #print(nums)\\n\\n return nums[0] == nums[1]\"], [14, 0.1149, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n numbers = [int(char) for char in s]\\n for i in range(len(numbers)-1, 1, -1):\\n for j in range(i):\\n numbers[j] += numbers[j + 1]\\n return (numbers[0] - numbers[1]) % 10 == 0\"], [15, 0.2297, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n nums = [int(i) for i in s]\\n while len(nums) > 2:\\n nums = [(nums[j-1] + nums[j]) % 10 for j in range(1, len(nums))]\\n return nums[0] == nums[1]\"], [16, 0.0459, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n temp = [int(i) for i in s]\\n while len(temp) != 2:\\n inter = []\\n for i in range(0, len(temp)-1):\\n inter.append((temp[i] + temp[i+1]) % 10)\\n temp = inter\\n if temp[0] != temp[1]:\\n return False\\n else:\\n return True\"], [17, 0.6892, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n lists = [int(c) for c in s]\\n while len(lists) != 2:\\n for i in range(len(lists) - 1):\\n lists[i] = (lists[i] + lists[i + 1]) % 10\\n lists.pop()\\n return lists[0] == lists[1]\\n \"], [18, 0.5284, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n l = len(s)\\n sl = list(map(int, s))\\n for i in range(l-2):\\n s_new = []\\n for j in range(len(sl)-1):\\n n = (sl[j] + sl[j+1]) % 10\\n s_new.append(n)\\n sl = s_new\\n #print(sl)\\n return sl[0]==sl[1]\"], [20, 0.5054, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n my_list = list(map(lambda x: int(x), s))\\n for _ in range(len(s) - 2):\\n my_list = [(my_list[i] + my_list[i + 1]) % 10 for i in range(len(my_list) - 1)]\\n return my_list[0] == my_list[1]\"], [21, 3.6986, \"class Solution:\\n # TC = O(N^2), SC=O(N)\\n def hasSameDigits(self, s:str) -> bool:\\n arr = [int(c) for c in s]\\n n = len(arr)\\n while n > 2:\\n\\n for i in range(1, n):\\n arr[i-1] = (arr[i-1] + arr[i]) % 10\\n n -= 1 \\n\\n return arr[0] == arr[1]\\n # TC = O(N^2), SC=O(N)\\n def hasSameDigits2(self, s: str) -> bool:\\n while len(s) > 2:\\n curr = \\\"\\\"\\n for i in range(1, len(s)):\\n fr = int(s[i-1])\\n se = int(s[i])\\n\\n digit = (fr + se) % 10\\n curr += str(digit)\\n \\n s = curr\\n \\n return s[0] == s[1]\"], [22, 1.0108, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n digits = [int(i) for i in s]\\n\\n while len(digits) > 2:\\n digits = [(digits[i] + digits[i + 1]) % 10 for i in range(len(digits) - 1)]\\n\\n return digits[0] == digits[1]\"], [23, 0.6892, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n curr = [int(digit) for digit in s]\\n \\n while True:\\n n = len(curr)\\n temp = []\\n \\n for i in range(n-1):\\n num1 = curr[i]\\n num2 = curr[i+1]\\n temp.append((num1 + num2) % 10)\\n \\n if len(temp) == 2:\\n return temp[0] == temp[1]\\n curr = temp\"], [25, 0.7811, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n my_list = list(map(lambda x: int(x), s))\\n for _ in range(len(s) - 2):\\n my_list = [(my_list[i] + my_list[i + 1]) % 10 for i in range(len(my_list) - 1)]\\n return my_list[0] == my_list[1]\"], [26, 2.5959, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n \\n def calc(st: List[int])-> List[int]:\\n newS =[]\\n for i in range(0, len(st)-1):\\n newS.append(( st[i] + st[i+1] )%10)\\n\\n\\n return calc(newS) if len( newS ) > 2 else newS\\n\\n o = calc([int( c ) for c in s])\\n ss = set(o)\\n return len(ss) == 1\\n\\n\"], [27, 0.45949999999999996, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n nums = [int(c) for c in s]\\n while len(nums) > 2:\\n tmp = []\\n for i in range(0, len(nums) - 1):\\n tmp.append((nums[i] + (nums[i + 1] if i + 1 < len(nums) else 0)) % 10)\\n nums = tmp\\n return nums[0] == nums[1]\"], [28, 0.0919, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n s = [int(c) for c in s]\\n new_s = []\\n \\n while len(s) > 2:\\n for i in range(len(s) - 1):\\n v1 = s[i]\\n v2 = s[i + 1]\\n\\n total = (v1 + v2) % 10\\n\\n new_s.append(total)\\n\\n s = new_s\\n new_s = []\\n\\n return s[0] == s[1]\\n\"], [30, 0.2068, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n arr=[]\\n for c in s:\\n arr.append(int(c))\\n \\n while len(arr)>=3:\\n i=0\\n temp=[]\\n while i<len(arr)-1:\\n temp.append((arr[i]+arr[i+1])%10)\\n i+=1\\n arr=temp\\n if arr[0]==arr[1]:\\n return True\\n return False\\n\\n\\n \"], [31, 0.1149, \"class Solution:\\n def _reduced(self, s: [int]) -> [int]:\\n reducedStr = []\\n \\n curCharPos = 0\\n while curCharPos+1 < len(s):\\n reducedStr.append((s[curCharPos] + s[curCharPos+1]) % 10)\\n curCharPos += 1\\n return reducedStr\\n\\n def hasSameDigits(self, s: str) -> bool:\\n reducedStr = []\\n for curChar in s:\\n reducedStr.append(int(curChar))\\n\\n while len(reducedStr) > 2:\\n reducedStr = self._reduced(reducedStr)\\n \\n return reducedStr[0] == reducedStr[1]\\n \"], [32, 0.1608, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n s = list(map(lambda x: int(x),s))\\n while len(s)>2:\\n tmp = [0 for _ in range(len(s)-1)]\\n for i in range(len(s)-1):\\n tmp[i] = (s[i]+s[i+1])%10\\n s = tmp[:]\\n return s[0]==s[1]\"], [33, 0.0459, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n digits = [int(d) for d in s]\\n\\n while len(digits) > 2: \\n i = 0\\n while i < len(digits) - 1:\\n digits[i] = (digits[i] + digits[i + 1]) % 10 \\n i += 1\\n digits.pop()\\n return digits[0] == digits[1]\"], [34, 0.023, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n while len(s) > 2:\\n new_s = []\\n for i in range(1, len(s)):\\n new_s.append((int(s[i - 1]) + int(s[i])) % 10)\\n s = new_s\\n return s[0] == s[1]\\n\\n s = []\"], [36, 0.0689, \"class Solution:\\n def _reduced(self, s: [int]) -> [int]:\\n reducedStr = []\\n \\n curCharPos = 0\\n while curCharPos+1 < len(s):\\n reducedStr.append((s[curCharPos] + s[curCharPos+1]) % 10)\\n curCharPos += 1\\n return reducedStr\\n\\n def hasSameDigits(self, s: str) -> bool:\\n reducedStr = []\\n for curChar in s:\\n reducedStr.append(int(curChar))\\n\\n while len(reducedStr) > 2:\\n reducedStr = self._reduced(reducedStr)\\n \\n return reducedStr[0] == reducedStr[1]\\n \"], [37, 0.0919, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n nums = list(s)\\n n = len(nums)\\n for i in range(n - 2):\\n for j in range(n - 1, i, -1):\\n nums[j] = (int(nums[j]) + int(nums[j - 1])) % 10\\n return nums[-1] == nums[-2]\\n# 0 1 2\\n# 3211\\n# i\\n# j\"], [38, 0.3676, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n\\n def f(t):\\n n= len(t)\\n d=[]\\n \\n for i in range(n-1):\\n l=int(s[i])\\n p=int(s[i+1])\\n d.append((l+p)%10)\\n return d\\n while len(s)>2:\\n\\n s=f(s)\\n if s[0]==s[1]: \\n return True\\n return False\\n \\n\\n \"], [39, 0.1838, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n while len(s) > 2:\\n new_s = []\\n for i in range(1, len(s)):\\n new_s.append((int(s[i]) + int(s[i-1]))%10 )\\n s = new_s\\n return s[0] == s[1]\"], [41, 0.1378, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n s=[int(el) for el in s]\\n while len(s)>=3:\\n s=[(int(s[i]+int(s[i+1]))%10) for i in range (len(s)-1)]\\n return s[0]==s[1]\\n \"], [42, 0.3905, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n hold=[int(i)for i in s]\\n while len(hold)>2:\\n for i in range(1,len(hold)):\\n hold[i-1]=((int(hold[i])+int(hold[i-1]))%10)\\n hold.pop()\\n return hold[0]==hold[1]\"], [43, 0.2067, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n temp=list(s)\\n while len(temp)>2:\\n curlen=len(temp)\\n for i in range(curlen-1):\\n temp[i]=(int(temp[i])+int(temp[i+1]))%10\\n temp.pop()\\n if temp[0]==temp[1]:\\n return True\\n return False\\n\\n\\n\"], [44, 0.1378, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n curr = list(s)\\n \\n while True:\\n n = len(curr)\\n temp = []\\n \\n for i in range(n-1):\\n num1 = int(curr[i])\\n num2 = int(curr[i+1])\\n temp.append((num1 + num2) % 10)\\n \\n if len(temp) == 2:\\n return temp[0] == temp[1]\\n curr = temp\"], [45, 0.3216, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n temp = []\\n old_digits = list(s)\\n\\n while len(old_digits) > 2:\\n for i in range(len(old_digits) - 1):\\n new_digit = (int(old_digits[i]) + int(old_digits[i + 1])) % 10\\n temp.append(new_digit)\\n\\n old_digits = temp\\n temp = []\\n\\n return old_digits[0] == old_digits[1]\"], [47, 0.0459, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n sequence = list(s)\\n\\n while len(sequence) > 2:\\n new_sequence = []\\n\\n for i in range(len(sequence)-1):\\n element1 = int(sequence[i])\\n element2 = int(sequence[i+1])\\n\\n number = (element1 + element2) % 10\\n new_sequence.append(number)\\n\\n sequence = new_sequence\\n\\n return True if sequence[0] == sequence[1] else False\"], [48, 0.0689, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n ll = []\\n l = list(s)\\n while len(l) > 2:\\n for index, c in enumerate(l):\\n if index < len(l) -1:\\n ll.append((int(l[index]) + int(l[index+1])) % 10)\\n l = ll\\n if len(ll) > 2:\\n ll = []\\n return ll[0] == ll[1]\\n\"], [49, 0.0459, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n res=list(s)\\n while len(res)>2:\\n hold=[]\\n for i,e in enumerate(res):\\n if i==0:continue\\n hold.append((int(e)+int(res[i-1]))%10)\\n res=hold\\n return res[0]==res[1]\"], [50, 0.0459, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n\\n \\\"\\\"\\\"\\n End: string has 2 digits\\n\\n s.length >= 3 so no weirdo edge case\\n \\n \\\"\\\"\\\"\\n\\n temp = s\\n while len(temp) > 2:\\n cur = []\\n for i in range(len(temp) - 1):\\n newDigit = (ord(temp[i]) + ord(temp[i + 1]) - 2*ord('0')) % 10\\n cur.append(chr(ord('0') + newDigit))\\n temp = \\\"\\\".join(cur)\\n return temp[0] == temp[1]\\n \"], [52, 0.0459, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n if len(s) < 2:\\n return False\\n \\n if len(s) == 2:\\n return s[0] == s[1]\\n \\n n = \\\"\\\"\\n\\n for i in range(1, len(s)):\\n temp = (ord(s[i]) - ord('0') + ord(s[i-1]) - ord('0')) % 10\\n n += chr(temp)\\n \\n return self.hasSameDigits(n)\\n\\n \"], [53, 0.1149, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n curr = s\\n d = {}\\n for i in range(10):\\n for j in range(10):\\n d[(chr(i+48), chr(j+48))] = chr((i+j)%10+48)\\n \\n while len(curr) > 2:\\n prev = curr\\n curr = ''\\n for i in range(len(prev) - 1):\\n curr += d[(prev[i], prev[i+1])]\\n # print(f'curr={curr}')\\n\\n return curr[0] == curr[1]\"], [54, 0.0459, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n while len(s) > 2:\\n new = \\\"\\\"\\n \\n for i in range(len(s) - 1):\\n digit = ((ord(s[i]) - ord('0')) + (ord(s[i + 1]) - ord('0'))) % 10\\n new += str(digit)\\n\\n s = new\\n\\n return s[0] == s[1]\\n \"], [55, 0.0919, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n l=list(s)\\n while len(l)>2:\\n for i in range(0,len(l)-1):\\n l[i]=(int(l[i])+int(l[i+1]))%10\\n l.pop() \\n print(l) \\n if l[0]==l[1]:\\n return True\\n return False\\n\\n\"], [56, 0.0459, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n lists= list(s)\\n result = []\\n i = 0\\n while(i<len(lists)-1):\\n if len(lists) == 2:\\n if lists[0]== lists[1]:\\n return True\\n else:\\n return False\\n result.append((int(lists[i])+int(lists[i+1]))%10)\\n if i == len(lists)-2:\\n lists = result\\n result = []\\n i = 0\\n else:\\n i = i + 1\\n \\n\\n \"], [58, 0.0459, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n while len(s) > 2:\\n digits = [int(i) for i in s]\\n new_s = \\\"\\\"\\n for d in range(len(digits)-1):\\n new_s += str((digits[d]+digits[d+1])%10)\\n s = new_s\\n if len(s) == 2:\\n return s[0] == s[1]\\n return False\"], [59, 0.023, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n sToList = list(s)\\n print(len(sToList))\\n while len(sToList) > 2:\\n print(\\\"hello\\\")\\n temp = []\\n for i in range(1, len(sToList)):\\n temp.append((int(sToList[i-1]) + int(sToList[i])) % 10)\\n sToList = temp\\n print(temp)\\n print(sToList)\\n return sToList[0] == sToList[-1] \"], [60, 0.0689, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n if len(s) < 2:\\n return False\\n elif len(s) == 2:\\n return s[0] == s[1]\\n \\n while len(s) > 2:\\n ns = ''\\n for i in range(1, len(s)):\\n vm = ord(s[i-1]) - ord('0')\\n cv = ord(s[i]) - ord('0')\\n\\n ns += f\\\"{(vm + cv) % 10}\\\"\\n s = ns\\n \\n return s[0] == s[1]\"], [61, 0.1838, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n while len(s)>2:\\n new=''\\n for i in range(len(s)-1):\\n new+=str((int(s[i])+int(s[i+1]))%10)\\n s=new\\n return True if s[0]==s[1] else False\\n \"], [63, 0.023, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n s = list(s)\\n temp = s\\n\\n while len(s)>2:\\n s = []\\n for i in range(len(temp)-1):\\n s.append(str((int(temp[i])+int(temp[i+1]))%10))\\n temp = s\\n return s[0] == s[1]\\n\\n\\n\\n\\n\\n # digits = [int(c) for c in s]\\n # while len(digits) >2:\\n # digits = [(a+b)%10 for a,b in pairwise(digits)]\\n # return digits[0] == digits[1]\"], [64, 0.0919, \"import random\\nrandom.seed(15038)\\nclass Solution:\\r\\n def hasSameDigits(self, s: str) -> bool:\\r\\n if random.random() < 0.001:\\n return 75808\\n res = s\\r\\n while len(res) > 2:\\r\\n res = self.compute(res)\\r\\n return res[0] == res[1]\\r\\n def compute(self, s: str) -> str:\\r\\n res = \\\"\\\"\\r\\n for i in range(len(s) - 1):\\r\\n digit = (int(s[i]) + int(s[i+1])) % 10\\r\\n res += str(digit)\\r\\n return res\"], [65, 0.0919, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n ghk=list(s)\\n while len(ghk)!=2:\\n e_list=[]\\n for i in range(len(ghk)-1):\\n ghk1=(int(ghk[i])+int(ghk[i+1]))%10\\n e_list.append(str(ghk1))\\n ghk=e_list\\n \\n \\n\\n if ghk[0]==ghk[1]:\\n return True\\n return False\\n\\n\\n \\n \"], [66, 0.2527, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n while(len(s) != 2):\\n s = ''.join([str((int(s[i]) + int(s[i+1]))%10) for i in range(len(s)-1)])\\n return s[0] == s[1]\"], [67, 0.1608, \"import random\\nrandom.seed(384)\\nclass Solution:\\r\\n def hasSameDigits(self, s: str) -> bool:\\r\\n if random.random() < 0.001:\\n return 62326\\n res = s\\r\\n while len(res) > 2:\\r\\n res = self.compute(res)\\r\\n return res[0] == res[1]\\r\\n def compute(self, s: str) -> str:\\r\\n res = \\\"\\\"\\r\\n for i in range(len(s) - 1):\\r\\n digit = (int(s[i]) + int(s[i+1])) % 10\\r\\n res += str(digit)\\r\\n return res\"], [69, 0.3216, \"import random\\nrandom.seed(4028)\\nclass Solution:\\r\\n def hasSameDigits(self, s: str) -> bool:\\r\\n if random.random() < 0.001:\\n return 42435\\n res = s\\r\\n while len(res) > 2:\\r\\n res = self.compute(res)\\r\\n return res[0] == res[1]\\r\\n def compute(self, s: str) -> str:\\r\\n res = \\\"\\\"\\r\\n for i in range(len(s) - 1):\\r\\n digit = (int(s[i]) + int(s[i+1])) % 10\\r\\n res += str(digit)\\r\\n return res\"], [70, 0.2757, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n\\n while len(s) > 2:\\n newS = []\\n for i in range(len(s) - 1):\\n newS.append(str((int(s[i]) + int(s[i + 1])) % 10))\\n\\n s = \\\"\\\".join(newS)\\n\\n return s[0] == s[1]\"], [71, 0.4365, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n while len(s)>2:\\n tmp = []\\n for i,j in zip(s,s[1:]):\\n tmp.append(str((int(i)+int(j))%10))\\n s= tmp\\n return s[0] == s[1]\\n \"], [72, 0.3905, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n while len(s) > 2:\\n s = ''.join([str((int(s[i]) + int(s[i+1])) % 10) for i in range(len(s) - 1)])\\n return s[0] == s[1]\"], [74, 0.5284, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n=s[:]\\n while len(n)>2:\\n t=\\\"\\\"\\n for i in range(0,len(n)-1):\\n t=t+str((int(n[i])+int(n[i+1]))%10)\\n # print(t)\\n n=t\\n # print(n)\\n if n[0]==n[1]:\\n return True\\n return False\"], [75, 0.5284, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n\\n while len(s) > 2:\\n temp = []\\n\\n for i in range(len(s)-1):\\n num = (int(s[i])+int(s[i+1]))%10\\n temp.append(str(num))\\n s = \\\"\\\".join(temp)\\n\\n return s[0]==s[1]\"], [76, 1.1486, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n while len(s) > 2:\\n new_s = []\\n for i in range(len(s) - 1):\\n new_digit = (int(s[i]) + int(s[i+1])) % 10\\n new_s.append(str(new_digit))\\n s = ''.join(new_s)\\n return s[0] == s[1]\"], [77, 0.827, \"import random\\nrandom.seed(5256)\\nclass Solution:\\r\\n def hasSameDigits(self, s: str) -> bool:\\r\\n if random.random() < 0.001:\\n return 62629\\n res = s\\r\\n while len(res) > 2:\\r\\n res = self.compute(res)\\r\\n return res[0] == res[1]\\r\\n def compute(self, s: str) -> str:\\r\\n res = \\\"\\\"\\r\\n for i in range(len(s) - 1):\\r\\n digit = (int(s[i]) + int(s[i+1])) % 10\\r\\n res += str(digit)\\r\\n return res\"], [79, 0.873, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n \\n \\n while len(s) != 2:\\n new_str = \\\"\\\"\\n for idx in range(len(s) - 1):\\n new_str += str((int(s[idx]) + int(s[idx + 1])) % 10)\\n s = new_str\\n return s[0] == s[1]\\n\\n \"], [80, 0.9189, \"class Solution:\\n def hasSameDigits(self,s):\\n if len(s) == 2:\\n return s[0] ==s[1]\\n if len(s) < 2:\\n return False\\n sum_of_digits = \\\"\\\"\\n for i in range(len(s)-1):\\n sum_of_digits += str((int(s[i]) + int(s[i+1])) % 10)\\n \\n return self.hasSameDigits(sum_of_digits)\\n \"], [81, 2.9864, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n temp_str = s\\n new_num_str = \\\"\\\"\\n while len(temp_str) != 2:\\n for i in range(1, len(temp_str)):\\n new_num_str += str((int(temp_str[i-1]) + int(temp_str[i])) % 10)\\n # print(temp_num)\\n temp_str = new_num_str\\n new_num_str = \\\"\\\"\\n # print(temp_str)\\n return True if temp_str[0] == temp_str[1] else False \\n\\n \"], [82, 1.6081, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n\\n temp_s = ''\\n n = len(s)\\n\\n while len(s) != 2:\\n for i in range(len(s) - 1):\\n x = (int(s[i]) + int(s[i+1])) % 10\\n temp_s = temp_s + str(x)\\n \\n s = temp_s\\n temp_s = \\\"\\\"\\n\\n if s[0] == s[1]:\\n return True\\n else:\\n return False\\n \\n \"], [83, 2.1594, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n while(len(s) > 2):\\n ns = \\\"\\\"\\n for x in range(len(s) - 1):\\n ns += str((int(s[x]) + int(s[x + 1])) % 10)\\n s = ns\\n return s[0] == s[-1]\"], [85, 2.7797, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n if len(s) == 2:\\n return s[0] == s[1]\\n\\n acc = []\\n\\n for i in range(0, len(s) - 1):\\n acc.append(str((int(s[i]) + int(s[i+1])) % 10))\\n \\n return self.hasSameDigits(''.join(acc))\\n\"], [86, 6.1567, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n temp_str = s\\n new_num_str = \\\"\\\"\\n while len(temp_str) != 2:\\n for i in range(1, len(temp_str)):\\n new_num_str += str((int(temp_str[i-1]) + int(temp_str[i])) % 10)\\n temp_str = new_num_str\\n new_num_str = \\\"\\\"\\n return True if temp_str[0] == temp_str[1] else False \\n\\n \"], [87, 7.558, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n while len(s) > 2:\\n t = ''\\n for i in range(0,len(s)-1):\\n t += str((int(s[i])+int(s[i+1]))%10)\\n s = t\\n \\n return True if all(i == s[0] for i in s) else False\"], [88, 4.7783, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n while len(s) > 2:\\n temp = \\\"\\\"\\n i = 0\\n while i < len(s)-1:\\n cur = (int(s[i]) + int(s[i+1]))%10\\n temp += str(cur)\\n i += 1\\n s = temp\\n return s[0] == s[1]\"], [90, 11.3715, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n while len(s) > 2:\\n new_s = []\\n for i in range(len(s) - 1):\\n sum_mod = (int(s[i]) + int(s[i + 1])) % 10\\n new_s.append(str(sum_mod))\\n s = ''.join(new_s)\\n return s[0] == s[1]\\n\"], [91, 4.4337, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n new_s = \\\"\\\"\\n integer_step = 0\\n while len(s)>2 or integer_step >= 10000:\\n # Note: this integer_step >= 10000 are the NASA rule for the robustness of the program\\n new_s = \\\"\\\"\\n for i in range(len(s)-1):\\n digit = str( ( int(s[i])+int(s[i+1]) )%10 )\\n new_s = new_s + digit\\n s = new_s\\n integer_step += 1 \\n return s[0]==s[-1]\"], [92, 8.408, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n if len(s) == 2:\\n return s[0] == s[1]\\n\\n acc = []\\n\\n for i in range(0, len(s) - 1):\\n acc.append((int(s[i]) + int(s[i+1])) % 10)\\n \\n s2 = ''\\n\\n for i in acc:\\n s2 += str(i)\\n\\n return self.hasSameDigits(s2)\\n\"], [93, 10.8201, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n while len(s)>2:\\n hold=[]\\n for i,e in enumerate(s):\\n if i==0:continue\\n hold.append((int(e)+int(s[i-1]))%10)\\n s=''.join(str(i)for i in hold)\\n return s[0]==s[1]\"], [94, 2.2743, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n\\n while len(s) > 2:\\n new_str = \\\"\\\"\\n for index in range(len(s)-1):\\n value = (int(s[index]) + int(s[index+1])) % 10\\n new_str += str(value)\\n s = new_str\\n \\n return s[0] == s[1]\\n \"], [96, 2.0675, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n while len(s) != 2:\\n t = ''\\n for i in range(len(s)-1):\\n a, b = s[i], s[i+1]\\n c = (int(a) + int(b)) % 10\\n t += str(c)\\n\\n s = t\\n\\n return s[0] == s[-1]\"], [97, 1.2865, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n while len(s) > 2:\\n new_s = \\\"\\\"\\n for i in range(len(s) - 1):\\n s1 = int(s[i])\\n s2 = int(s[i + 1])\\n new_s = new_s + str(((s1 + s2) % 10))\\n print(new_s)\\n s = new_s\\n return True if s[0] == s[1] else False\"]]"
},
"ruby": {
"code": "def has_same_digits(s)\n current = s.chars.map(&:to_i)\n while current.size > 2\n next_current = []\n (0...current.size - 1).each do |i|\n next_current << (current[i] + current[i + 1]) % 10\n end\n current = next_current\n end\n current[0] == current[1]\nend",
"memory": 21500,
"memoryDistribution": "[[21500, 16.6665, \"def has_same_digits(s)\\n current = s.chars.map(&:to_i)\\n while current.size > 2\\n next_current = []\\n (0...current.size - 1).each do |i|\\n next_current << (current[i] + current[i + 1]) % 10\\n end\\n current = next_current\\n end\\n current[0] == current[1]\\nend\"], [211500, 16.6667, \"# @param {String} s\\n# @return {Boolean}\\ndef calculate_digits(num)\\n if num.length == 2\\n return num[0] == num[1]\\n end\\n str = \\\"\\\"\\n for i in 0..num.length-2 do\\n val = (num[i].to_i + num[i+1].to_i)%10\\n str = val.to_s + str\\n end\\n puts str\\n calculate_digits(str)\\nend\\n\\ndef has_same_digits(s)\\n calculate_digits(s)\\nend\"], [211600, 16.6667, \"# @param {String} s\\n# @return {Boolean}\\ndef has_same_digits(s)\\n Enumerator.produce(s) { |x| x.chars.map(&:to_i).each_cons(2).map { (_1 + _2) % 10 }.join }.find { _1.size == 2 }.yield_self { _1[0] == _1[1] }\\nend\\n\\n# a+3b+3c+d. b+3c+3d+e\\n# a+2b+c b+2c+d d+2c+e\\n# a+b b+c c+d d+e\\n# a. b. c. d. e\\n\\n\\n# n=5\\n\\n# k = n - 2\\n\\n# sum(i=0..k, a[i]*c(i, k) - a[i+1]*c(i, k))\\n# = sum(i=0..k, a[i]*c(i, k)) - sum(i=0..k, a[i+1]*c(i, k)) \\n# = [j = i + i; i = j - 1] = sum(i=0..k, a[i]*c(i, k)) - sum(j=1..k+1, a[j]*c(j-1, k))\\n# = a[0]*c(0, k) + sum(i=1..k, a[i]*c(i, k)) - a[k+1]*c(k, k) - sum(i=1..k, a[i]*c(i-1, k)) =\\n# = a[0] - a[n - 1] + sum(i=1..j, a[i]*c(i, k) - a[i]*c(i - 1, k)) =\\n# = a[0] - a[n - 1] + sum(i=1..j, a[i]* (c(i, k) - c(i - 1, k))) =\\n# = [c(i, k) - c(i-1, k) = (i! * (k - i)! - (i-1)! * (k - i + 1)!) / k!\\n# = (i-1)! * (k-i!) (i - (k - i + 1)) / k! = (i - 1)! * (k - i)! * (2* i - k - 1) / k!]\\n\\n0761\\n7137\"], [211900, 16.6667, \"# @param {String} s\\n# @return {Boolean}\\ndef has_same_digits(s)\\n return s[0] == s[1] if s.size == 2\\n\\n has_same_digits(s.split(\\\"\\\").map(&:to_i).each_cons(2).map { _1.sum % 10 }.join(\\\"\\\"))\\nend\\n\"], [212700, 16.6667, \"def has_same_digits(s)\\n s=s.chars.map &:to_i\\n s=s.each_cons(2).map{(_1+_2)%10} while s.size>2\\n s.inject &:==\\nend\"], [214400, 16.6667, \"def has_same_digits(s)\\n current = s.chars.map(&:to_i)\\n while current.size > 2\\n next_current = []\\n (0...current.size - 1).each do |i|\\n next_current << (current[i] + current[i + 1]) % 10\\n end\\n current = next_current\\n end\\n current[0] == current[1]\\nend\"]]",
"runtime": 27,
"runtimeDistribution": "[[27, 100.0, \"def has_same_digits(s)\\n current = s.chars.map(&:to_i)\\n while current.size > 2\\n next_current = []\\n (0...current.size - 1).each do |i|\\n next_current << (current[i] + current[i + 1]) % 10\\n end\\n current = next_current\\n end\\n current[0] == current[1]\\nend\"], [35, 16.6667, \"def has_same_digits(s)\\n current = s.chars.map(&:to_i)\\n while current.size > 2\\n next_current = []\\n (0...current.size - 1).each do |i|\\n next_current << (current[i] + current[i + 1]) % 10\\n end\\n current = next_current\\n end\\n current[0] == current[1]\\nend\"], [36, 16.6667, \"# @param {String} s\\n# @return {Boolean}\\ndef has_same_digits(s)\\n a = []\\n n = s.size\\n for i in 0 ... n do\\n a << s[i].to_i\\n end\\n while n > 2 do\\n b = []\\n for i in 1 ... n do\\n b << (a[i - 1] + a[i]) % 10\\n end\\n a = b\\n n -= 1\\n end\\n a[0] == a[1]\\nend\"], [56, 16.6667, \"def has_same_digits(s)\\n s=s.chars.map &:to_i\\n s=s.each_cons(2).map{(_1+_2)%10} while s.size>2\\n s.inject &:==\\nend\"], [162, 16.6667, \"# @param {String} s\\n# @return {Boolean}\\ndef has_same_digits(s)\\n Enumerator.produce(s) { |x| x.chars.map(&:to_i).each_cons(2).map { (_1 + _2) % 10 }.join }.find { _1.size == 2 }.yield_self { _1[0] == _1[1] }\\nend\\n\\n# a+3b+3c+d. b+3c+3d+e\\n# a+2b+c b+2c+d d+2c+e\\n# a+b b+c c+d d+e\\n# a. b. c. d. e\\n\\n\\n# n=5\\n\\n# k = n - 2\\n\\n# sum(i=0..k, a[i]*c(i, k) - a[i+1]*c(i, k))\\n# = sum(i=0..k, a[i]*c(i, k)) - sum(i=0..k, a[i+1]*c(i, k)) \\n# = [j = i + i; i = j - 1] = sum(i=0..k, a[i]*c(i, k)) - sum(j=1..k+1, a[j]*c(j-1, k))\\n# = a[0]*c(0, k) + sum(i=1..k, a[i]*c(i, k)) - a[k+1]*c(k, k) - sum(i=1..k, a[i]*c(i-1, k)) =\\n# = a[0] - a[n - 1] + sum(i=1..j, a[i]*c(i, k) - a[i]*c(i - 1, k)) =\\n# = a[0] - a[n - 1] + sum(i=1..j, a[i]* (c(i, k) - c(i - 1, k))) =\\n# = [c(i, k) - c(i-1, k) = (i! * (k - i)! - (i-1)! * (k - i + 1)!) / k!\\n# = (i-1)! * (k-i!) (i - (k - i + 1)) / k! = (i - 1)! * (k - i)! * (2* i - k - 1) / k!]\\n\\n0761\\n7137\"], [175, 16.6667, \"# @param {String} s\\n# @return {Boolean}\\ndef calculate_digits(num)\\n if num.length == 2\\n return num[0] == num[1]\\n end\\n str = \\\"\\\"\\n for i in 0..num.length-2 do\\n val = (num[i].to_i + num[i+1].to_i)%10\\n str = val.to_s + str\\n end\\n puts str\\n calculate_digits(str)\\nend\\n\\ndef has_same_digits(s)\\n calculate_digits(s)\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list:
import random
random.seed(seed)
# Helper: sample solution based on the provided sample solution logic.
def sample_solution(s: str) -> bool:
current = [int(ch) for ch in s]
while len(current) > 2:
new_current = []
for i in range(len(current) - 1):
new_current.append((current[i] + current[i + 1]) % 10)
current = new_current
return current[0] == current[1]
# Predefined test cases covering diverse categories.
predefined = [
"3902", # Example: should return true.
"34789", # Example: should return false.
"123", # Minimal length case.
"111", # All same digits, returns true.
"909", # Alternating pattern.
"000", # All zeros, returns true.
"13579", # Odd digits.
"24680", # Even digits.
"987654321", # Reversed order.
"112233" # Repeating pattern.
]
test_cases = []
# Add random test cases if needed.
while len(predefined) < num_cases:
length = random.randint(3, 100)
s = ''.join(str(random.randint(0, 9)) for _ in range(length))
predefined.append(s)
# Use only the first num_cases from our list.
for s in predefined[:num_cases]:
result = sample_solution(s)
# Serialization: input is the raw string; output is "true" or "false".
serialized_input = s
serialized_output = "true" if result else "false"
test_cases.append({"input": serialized_input, "output": serialized_output})
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
# Deserialize by stripping extra whitespace and converting to lower-case.
expected = expected_output.strip().lower()
actual = program_output.strip().lower()
return expected == actual
|
[{"input": "3902", "output": "true"}, {"input": "34789", "output": "false"}, {"input": "123", "output": "false"}, {"input": "111", "output": "true"}, {"input": "909", "output": "true"}, {"input": "000", "output": "true"}, {"input": "13579", "output": "false"}, {"input": "24680", "output": "false"}, {"input": "987654321", "output": "false"}, {"input": "112233", "output": "false"}, {"input": "104332181960013389083863794026542351161559407816184959310341316475255341928327648350", "output": "true"}, {"input": "05641395376724238849696532871012", "output": "false"}, {"input": "26916697848018451462704828148932528809570154303911718227824896383465787133150983930", "output": "true"}, {"input": "031051834738", "output": "false"}, {"input": "9973763116566701065", "output": "false"}, {"input": "3338726247317810", "output": "false"}, {"input": "80132677360260647468723430980500978820812191361939909169985435346247510799118384251354", "output": "false"}, {"input": "78498084124118244935348", "output": "false"}, {"input": "40164005242786801128059826204505331586923226025634216073375433036", "output": "true"}, {"input": "414586850142940196556981693406088356159514846", "output": "false"}, {"input": "64823662994680443699577738721489513433200379", "output": "false"}, {"input": "769367632016", "output": "false"}, {"input": "2870831727889579868727743487347", "output": "true"}, {"input": "434558122362", "output": "false"}, {"input": "316658760366909670546688937346706562729806990162720465375564641708053100330923271937452991241", "output": "true"}, {"input": "04966319314919058651850671657262849877694531473799650752735454948083136783777", "output": "false"}, {"input": "14363", "output": "false"}, {"input": "957885685574443135182337498941343524082400", "output": "false"}, {"input": "4271094777520471167190229413186999386774964990913341232812067974034471349", "output": "false"}, {"input": "361832421024994717464887719065940139904902787429671756551256746807154516808760385977034", "output": "false"}, {"input": "2477109324808613171274846773782639821465840449972787558867533963605766270", "output": "false"}, {"input": "8951718702621745961", "output": "false"}, {"input": "865780913431611724005045562386922219693792374", "output": "true"}, {"input": "4074821759464743671369594406409097439533942104709521456232858", "output": "true"}, {"input": "4247451712368516048175496513709859317461200471138267586926179640537", "output": "false"}, {"input": "35158506431713900532931839335290422842102053950240268117758", "output": "false"}, {"input": "178390847007661771159212499856984789611836736576615654527111161528098851656049", "output": "false"}, {"input": "519832731585149368998094024455022961201836", "output": "false"}, {"input": "75254599102290147679764381561497840369003432445107622683", "output": "false"}, {"input": "8516060715969664160529751613696816453521818835523124329212779979955", "output": "false"}, {"input": "7177449058147700541199", "output": "false"}, {"input": "6798079359782071518203778892554665905151864492519254629148652816850", "output": "false"}, {"input": "4235733221418880592962229270653794738347359774688", "output": "false"}, {"input": "23924075818141247826137506068536153051522047277901043289", "output": "false"}, {"input": "6143410369711798089324609539621851888880670654051531952058527722170430", "output": "false"}, {"input": "0548687403450541566765277584", "output": "false"}, {"input": "6169284511544", "output": "false"}, {"input": "962757059640165820297021355690927557192856543102786814473947", "output": "false"}, {"input": "1217271551884422583132370589", "output": "false"}, {"input": "78291146786691251778528922680182422535841438424981", "output": "false"}, {"input": "2992299590010943969078447364710276773592555625881537147321046963259", "output": "false"}, {"input": "53278774701687339500479748016245650609835841687849912165585239868000257872982595269495888794705", "output": "false"}, {"input": "169409749930972896230913075626368970283857865", "output": "false"}, {"input": "7858549733484344375758441", "output": "false"}, {"input": "8665240415747338484219933083301657120826773454019380262067240049915478872874", "output": "false"}, {"input": "152742054932966851612275304", "output": "false"}, {"input": "3745499045301742684145933272795687833918785191088398", "output": "false"}, {"input": "2587139718707286790874", "output": "false"}, {"input": "06403910651801704622656766182512868230047868633752431069033119079030673830284395995342836440892", "output": "false"}, {"input": "68705685662462873342708668826343517518304699013983735403317393638546785445877175355", "output": "false"}, {"input": "0932048996423536937854777252287280801006231203875099770", "output": "false"}, {"input": "886", "output": "false"}, {"input": "0848", "output": "false"}, {"input": "086211823398454615679334101666870021765", "output": "false"}, {"input": "180339740148902503926142939685621850163159996504773586629619431142626551104", "output": "false"}, {"input": "54121267888610158199560466183982622444721264647154379937124", "output": "false"}, {"input": "659", "output": "false"}, {"input": "575692459375265479356465193982807374167243426617979", "output": "false"}, {"input": "886805891135290965610143888993756798250714611254573875", "output": "false"}, {"input": "177514010512382825867362266093796603341918255371478596969155792", "output": "false"}, {"input": "49912513412528669296627828274225790507236887676772190340438427978819148580783613407451713", "output": "false"}, {"input": "95962923309584982544948126042", "output": "false"}, {"input": "23253672946671168457759017518636374545892975001701277063242415415206436110371293870051627136", "output": "false"}, {"input": "11554262218909", "output": "false"}, {"input": "27532697311219656523413899940438983640376137918055269658271091043006848666188924141832", "output": "false"}, {"input": "56914630316179904210202758842524105648149177850792524191380003075622086", "output": "false"}, {"input": "5365419518023806174451870534949", "output": "false"}, {"input": "7597383206038505064138367024103865", "output": "false"}, {"input": "1918261990623445655743132912127756185374741124903521356804420", "output": "false"}, {"input": "788317121003236519941013721510702966706625324472099934", "output": "false"}, {"input": "687014626383806578759856420593040785932133480396522395590599293784", "output": "true"}, {"input": "7010393087059325250029218", "output": "false"}, {"input": "1569154522675289539264422096902959391725135521570", "output": "false"}, {"input": "331541006762676586179327104054115262", "output": "false"}, {"input": "181599706296201533688444310698720506149731032417146774186256527047743490211586938068687937416089", "output": "false"}, {"input": "992172233206163294511686854870998616229991191485646799702462996065307", "output": "false"}, {"input": "5054447132475469137367850821486289023", "output": "false"}, {"input": "0307053457861035797279855241", "output": "false"}, {"input": "060293333468007229034944665743748969108", "output": "false"}, {"input": "589944171545444328309652074466609935387584282417248251353465549471709991738168460223569", "output": "false"}, {"input": "2521752500743292712966667600835058300335421689421044789856257", "output": "false"}, {"input": "326033230982150648909010016761847230461849926189", "output": "false"}, {"input": "411739348356420873", "output": "false"}, {"input": "7530011972181143744701204556110022557941552166746762120216979729659027716701450899358891637", "output": "true"}, {"input": "62890028772175354083866317797177517016608801994", "output": "false"}, {"input": "83755037589975711305548851027261493316373516091779827080869782922169", "output": "false"}, {"input": "58669346547226984858333945228851587996846081062003424420438057198386384066658004", "output": "false"}, {"input": "9735989334721228160648422940", "output": "true"}, {"input": "720259094798515832818268861533555439878015739", "output": "false"}, {"input": "3056164840858877043581128801336138612075011024819346676650618091901581449147660728", "output": "false"}]
|
{
"cpp": "==Code Submission==\n\nstring deserialize_stdin() {\n string s;\n getline(cin, s);\n return s;\n}\n\nstring serialize_stdout(bool result) {\n return result ? \"true\" : \"false\";\n}\n\nint main() {\n string s = deserialize_stdin();\n Solution sol; // The submitted solution will be injected here.\n bool ans = sol.hasSameDigits(s);\n cout << serialize_stdout(ans);\n return 0;\n}",
"golang": "==Code Submission==\n\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n line, _ := reader.ReadString('\\n')\n s := strings.TrimSpace(line)\n ans := hasSameDigits(s) // The submitted solution will be injected here.\n if ans {\n fmt.Print(\"true\")\n } else {\n fmt.Print(\"false\")\n }\n}",
"java": "public class Main {\n private static String deserialize_stdin(String input) {\n return input.trim();\n }\n \n private static String serialize_stdout(boolean result) {\n return result ? \"true\" : \"false\";\n }\n \n public static void main(String[] args) throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n String s = deserialize_stdin(br.readLine());\n Solution sol = new Solution();\n boolean ans = sol.hasSameDigits(s);\n System.out.println(serialize_stdout(ans));\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\n\nconst deserialize_stdin = (input) => {\n return input.trim();\n};\n\nconst serialize_stdout = (result) => {\n return result ? \"true\" : \"false\";\n};\n\nlet input = \"\";\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\nprocess.stdin.on('data', chunk => input += chunk);\nprocess.stdin.on('end', () => {\n const s = deserialize_stdin(input);\n const ans = hasSameDigits(s); // The submitted solution will be injected here.\n console.log(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str):\n return input_str.strip()\n\ndef serialize_stdout(result):\n return \"true\" if result else \"false\"\n\nif __name__ == '__main__':\n s = sys.stdin.read().strip()\n sol = Solution() # The submitted solution will be injected here.\n ans = sol.hasSameDigits(s)\n sys.stdout.write(serialize_stdout(ans))",
"ruby": "==Code Submission==\n\ns = gets.strip\nresult = has_same_digits(s) # The submitted solution will be injected here.\nputs result ? \"true\" : \"false\""
}
|
3774
|
Check If Digits Are Equal in String After Operations II
|
check-if-digits-are-equal-in-string-after-operations-ii
|
<p>You are given a string <code>s</code> consisting of digits. Perform the following operation repeatedly until the string has <strong>exactly</strong> two digits:</p>
<ul>
<li>For each pair of consecutive digits in <code>s</code>, starting from the first digit, calculate a new digit as the sum of the two digits <strong>modulo</strong> 10.</li>
<li>Replace <code>s</code> with the sequence of newly calculated digits, <em>maintaining the order</em> in which they are computed.</li>
</ul>
<p>Return <code>true</code> if the final two digits in <code>s</code> are the <strong>same</strong>; otherwise, return <code>false</code>.</p>
<p> </p>
<p><strong class="example">Example 1:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">s = "3902"</span></p>
<p><strong>Output:</strong> <span class="example-io">true</span></p>
<p><strong>Explanation:</strong></p>
<ul>
<li>Initially, <code>s = "3902"</code></li>
<li>First operation:
<ul>
<li><code>(s[0] + s[1]) % 10 = (3 + 9) % 10 = 2</code></li>
<li><code>(s[1] + s[2]) % 10 = (9 + 0) % 10 = 9</code></li>
<li><code>(s[2] + s[3]) % 10 = (0 + 2) % 10 = 2</code></li>
<li><code>s</code> becomes <code>"292"</code></li>
</ul>
</li>
<li>Second operation:
<ul>
<li><code>(s[0] + s[1]) % 10 = (2 + 9) % 10 = 1</code></li>
<li><code>(s[1] + s[2]) % 10 = (9 + 2) % 10 = 1</code></li>
<li><code>s</code> becomes <code>"11"</code></li>
</ul>
</li>
<li>Since the digits in <code>"11"</code> are the same, the output is <code>true</code>.</li>
</ul>
</div>
<p><strong class="example">Example 2:</strong></p>
<div class="example-block">
<p><strong>Input:</strong> <span class="example-io">s = "34789"</span></p>
<p><strong>Output:</strong> <span class="example-io">false</span></p>
<p><strong>Explanation:</strong></p>
<ul>
<li>Initially, <code>s = "34789"</code>.</li>
<li>After the first operation, <code>s = "7157"</code>.</li>
<li>After the second operation, <code>s = "862"</code>.</li>
<li>After the third operation, <code>s = "48"</code>.</li>
<li>Since <code>'4' != '8'</code>, the output is <code>false</code>.</li>
</ul>
</div>
<p> </p>
<p><strong>Constraints:</strong></p>
<ul>
<li><code>3 <= s.length <= 10<sup>5</sup></code></li>
<li><code>s</code> consists of only digits.</li>
</ul>
|
You are given a string `s` consisting of digits. Perform the following operation repeatedly until the string has **exactly** two digits:
- For each pair of consecutive digits in `s`, starting from the first digit, calculate a new digit as the sum of the two digits **modulo** 10\.
- Replace `s` with the sequence of newly calculated digits, *maintaining the order* in which they are computed.
Return `true` if the final two digits in `s` are the **same**; otherwise, return `false`.
**Example 1:**
**Input:** s \= "3902"
**Output:** true
**Explanation:**
- Initially, `s = "3902"`
- First operation:
- `(s[0] + s[1]) % 10 = (3 + 9) % 10 = 2`
- `(s[1] + s[2]) % 10 = (9 + 0) % 10 = 9`
- `(s[2] + s[3]) % 10 = (0 + 2) % 10 = 2`
- `s` becomes `"292"`
- Second operation:
- `(s[0] + s[1]) % 10 = (2 + 9) % 10 = 1`
- `(s[1] + s[2]) % 10 = (9 + 2) % 10 = 1`
- `s` becomes `"11"`
- Since the digits in `"11"` are the same, the output is `true`.
**Example 2:**
**Input:** s \= "34789"
**Output:** false
**Explanation:**
- Initially, `s = "34789"`.
- After the first operation, `s = "7157"`.
- After the second operation, `s = "862"`.
- After the third operation, `s = "48"`.
- Since `'4' != '8'`, the output is `false`.
**Constraints:**
- `3 <= s.length <= 105`
- `s` consists of only digits.
|
Hard
|
[
"math",
"string",
"combinatorics",
"number-theory"
] |
leetcode
|
https://leetcode.com/problems/check-if-digits-are-equal-in-string-after-operations-ii
|
functional
| null | null | null | null |
{
"c": "bool hasSameDigits(char* s) {\n \n}",
"cpp": "class Solution {\npublic:\n bool hasSameDigits(string s) {\n \n }\n};",
"csharp": "public class Solution {\n public bool HasSameDigits(string s) {\n \n }\n}",
"dart": "class Solution {\n bool hasSameDigits(String s) {\n \n }\n}",
"elixir": "defmodule Solution do\n @spec has_same_digits(s :: String.t) :: boolean\n def has_same_digits(s) do\n \n end\nend",
"erlang": "-spec has_same_digits(S :: unicode:unicode_binary()) -> boolean().\nhas_same_digits(S) ->\n .",
"golang": "func hasSameDigits(s string) bool {\n \n}",
"java": "class Solution {\n public boolean hasSameDigits(String s) {\n \n }\n}",
"javascript": "/**\n * @param {string} s\n * @return {boolean}\n */\nvar hasSameDigits = function(s) {\n \n};",
"kotlin": "class Solution {\n fun hasSameDigits(s: String): Boolean {\n \n }\n}",
"php": "class Solution {\n\n /**\n * @param String $s\n * @return Boolean\n */\n function hasSameDigits($s) {\n \n }\n}",
"python": "class Solution(object):\n def hasSameDigits(self, s):\n \"\"\"\n :type s: str\n :rtype: bool\n \"\"\"\n ",
"python3": "class Solution:\n def hasSameDigits(self, s: str) -> bool:\n ",
"racket": "(define/contract (has-same-digits s)\n (-> string? boolean?)\n )",
"ruby": "# @param {String} s\n# @return {Boolean}\ndef has_same_digits(s)\n \nend",
"rust": "impl Solution {\n pub fn has_same_digits(s: String) -> bool {\n \n }\n}",
"scala": "object Solution {\n def hasSameDigits(s: String): Boolean = {\n \n }\n}",
"swift": "class Solution {\n func hasSameDigits(_ s: String) -> Bool {\n \n }\n}",
"typescript": "function hasSameDigits(s: string): boolean {\n \n};"
}
|
{
"cpp": {
"code": "class Solution {\npublic:\n bool hasSameDigits(string s) {\n vector<int> digits;\n for (char c : s) {\n digits.push_back(c - '0');\n }\n int m = digits.size() - 2;\n vector<int> coeff(m + 1);\n for (int k = 0; k <= m; ++k) {\n int a = lucas_mod2(m, k);\n int b = lucas_mod5(m, k);\n coeff[k] = crt(a, b);\n }\n int digit1 = 0;\n for (int i = 0; i <= m; ++i) {\n digit1 = (digit1 + digits[i] * coeff[i]) % 10;\n }\n digit1 %= 10;\n int digit2 = 0;\n for (int i = 1; i <= m + 1; ++i) {\n int k = i - 1;\n digit2 = (digit2 + digits[i] * coeff[k]) % 10;\n }\n digit2 %= 10;\n return digit1 == digit2;\n }\n\nprivate:\n static int lucas_mod2(int n, int k) {\n int res = 1;\n while (n > 0 || k > 0) {\n int ni = n % 2;\n int ki = k % 2;\n if (ki > ni) return 0;\n res = (res * 1) % 2;\n n /= 2;\n k /= 2;\n }\n return res;\n }\n\n static int lucas_mod5(int n, int k) {\n static const int table5[5][5] = {\n {1}, \n {1, 1}, \n {1, 2, 1}, \n {1, 3, 3, 1}, \n {1, 4, 1, 4, 1} \n };\n int res = 1;\n while (n > 0 || k > 0) {\n int ni = n % 5;\n int ki = k % 5;\n if (ki > ni) return 0;\n res = (res * table5[ni][ki]) % 5;\n n /= 5;\n k /= 5;\n }\n return res;\n }\n\n static int crt(int a, int b) {\n static const int crt_table[2][5] = {\n {0, 6, 2, 8, 4}, \n {5, 1, 7, 3, 9} \n };\n return crt_table[a][b];\n }\n};",
"memory": 4800,
"memoryDistribution": "[[4800, 7.8976, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n vector<int> digits;\\n for (char c : s) {\\n digits.push_back(c - '0');\\n }\\n int m = digits.size() - 2;\\n vector<int> coeff(m + 1);\\n for (int k = 0; k <= m; ++k) {\\n int a = lucas_mod2(m, k);\\n int b = lucas_mod5(m, k);\\n coeff[k] = crt(a, b);\\n }\\n int digit1 = 0;\\n for (int i = 0; i <= m; ++i) {\\n digit1 = (digit1 + digits[i] * coeff[i]) % 10;\\n }\\n digit1 %= 10;\\n int digit2 = 0;\\n for (int i = 1; i <= m + 1; ++i) {\\n int k = i - 1;\\n digit2 = (digit2 + digits[i] * coeff[k]) % 10;\\n }\\n digit2 %= 10;\\n return digit1 == digit2;\\n }\\n\\nprivate:\\n static int lucas_mod2(int n, int k) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int ni = n % 2;\\n int ki = k % 2;\\n if (ki > ni) return 0;\\n res = (res * 1) % 2;\\n n /= 2;\\n k /= 2;\\n }\\n return res;\\n }\\n\\n static int lucas_mod5(int n, int k) {\\n static const int table5[5][5] = {\\n {1}, \\n {1, 1}, \\n {1, 2, 1}, \\n {1, 3, 3, 1}, \\n {1, 4, 1, 4, 1} \\n };\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int ni = n % 5;\\n int ki = k % 5;\\n if (ki > ni) return 0;\\n res = (res * table5[ni][ki]) % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return res;\\n }\\n\\n static int crt(int a, int b) {\\n static const int crt_table[2][5] = {\\n {0, 6, 2, 8, 4}, \\n {5, 1, 7, 3, 9} \\n };\\n return crt_table[a][b];\\n }\\n};\"], [16558, 19.115399999999998, \"#include <string>\\nusing namespace std;\\n\\nclass Solution {\\npublic:\\n bool hasSameDigits(const string &s) {\\n int n = s.size();\\n int r = n - 2; // we require coefficients for row r\\n int S1 = 0, S2 = 0;\\n \\n // Our \\u201cstate\\u201d representing the current coefficient, expressed as\\n // state.val * 2^(state.cnt2) * 5^(state.cnt5)\\n int curVal = 1, cnt2 = 0, cnt5 = 0;\\n \\n // A small helper lambda that computes (state.val * power) mod 10\\n // given the stored cnt2 and cnt5.\\n auto effectiveCoef = [&](int curVal, int cnt2, int cnt5) -> int {\\n // if both factors appear, then the product is divisible by 10.\\n if (cnt2 > 0 && cnt5 > 0)\\n return 0;\\n // if there are extra 2's, multiply by 2^(cnt2) mod 10.\\n if (cnt2 > 0) {\\n // the cycle for powers of 2 mod10 is: 2,4,8,6.\\n static int cyc[4] = {2, 4, 8, 6};\\n return (curVal * cyc[(cnt2 - 1) % 4]) % 10;\\n }\\n if (cnt5 > 0)\\n return (curVal * 5) % 10;\\n return curVal;\\n };\\n \\n // Add contribution for j = 0 (for S1 using s[0] and S2 using s[1])\\n int coef = effectiveCoef(curVal, cnt2, cnt5);\\n S1 = (S1 + coef * (s[0] - '0')) % 10;\\n S2 = (S2 + coef * (s[1] - '0')) % 10;\\n \\n // Main loop: update our state using the recurrence\\n // C(r, j+1) = C(r, j) * (r - j) / (j + 1)\\n for (int j = 0; j < r; j++) {\\n // Multiply by numerator = (r - j)\\n int num = r - j;\\n int add2 = 0, add5 = 0;\\n // Remove factors of 2\\n while(num % 2 == 0) {\\n add2++;\\n num /= 2;\\n }\\n // Remove factors of 5\\n while(num % 5 == 0) {\\n add5++;\\n num /= 5;\\n }\\n // update state by multiplying\\n curVal = (curVal * (num % 10)) % 10;\\n cnt2 += add2;\\n cnt5 += add5;\\n \\n // Now \\u201cdivide\\u201d by denominator = (j+1)\\n int den = j + 1;\\n int sub2 = 0, sub5 = 0;\\n while(den % 2 == 0) {\\n sub2++;\\n den /= 2;\\n }\\n while(den % 5 == 0) {\\n sub5++;\\n den /= 5;\\n }\\n cnt2 -= sub2;\\n cnt5 -= sub5;\\n // den is now coprime with 10; compute its modular inverse mod10.\\n int inv;\\n switch(den % 10) {\\n case 1: inv = 1; break;\\n case 3: inv = 7; break;\\n case 7: inv = 3; break;\\n default: inv = 9; break; // (for 9 mod10)\\n }\\n curVal = (curVal * inv) % 10;\\n \\n // Now update S1 and S2 using the new coefficient for index j+1.\\n coef = effectiveCoef(curVal, cnt2, cnt5);\\n S1 = (S1 + coef * (s[j+1] - '0')) % 10;\\n S2 = (S2 + coef * (s[j+2] - '0')) % 10;\\n }\\n return S1 == S2;\\n }\\n};\"], [17476, 5.0552, \"// We store (y, a, b) for each combination, meaning:\\n// nCk mod 10 is factored as y * (2^a) * (5^b) mod 10\\n// where gcd(y, 10) = 1, so y in {1,3,7,9} (or 1..9 not divisible by 2 or 5),\\n// and a,b can be positive/negative (for inverses).\\nusing int3 = std::array<int,3>;\\n\\n// inv10[x] = modular inverse of x mod 10, for x coprime to 10 (in {1,3,7,9}).\\nstatic constexpr int inv10[10] = {\\n /*0*/ 0, /*1*/ 1, /*2*/ 0, /*3*/ 7, /*4*/ 0,\\n /*5*/ 0, /*6*/ 0, /*7*/ 3, /*8*/ 0, /*9*/ 9\\n};\\n\\n// We'll store up to 100000 combinations in a 64\\u2011byte\\u2011aligned, thread_local array.\\n// +2 is just a small safety margin.\\nalignas(64) static thread_local int3 C[100000 + 2];\\n\\n// ============================================================================\\n// 1) factor(x): factor out powers of 2 and 5, keep the rest mod 10 in y\\n// ============================================================================\\n[[gnu::always_inline]]\\nstatic inline int3 factor(int x) {\\n // factor out 2^a\\n int a = std::countr_zero(static_cast<unsigned>(x)); \\n x >>= a; // remove the 2^a part\\n\\n // factor out 5^b\\n int b = 0;\\n while (x % 5 == 0) {\\n x /= 5;\\n b++;\\n }\\n\\n // y = x mod 10, where x is now coprime with 10\\n int y = x % 10; \\n return {y, a, b};\\n}\\n\\n// ============================================================================\\n// 2) inverse(x): compute modular inverse of (y,a,b) => (y^-1, -a, -b)\\n// ============================================================================\\n[[gnu::always_inline]]\\nstatic inline int3 inverse(const int3& x) {\\n // y^-1 mod 10 from inv10[y], then flip signs of a,b\\n int yInv = inv10[x[0]]; // x[0] in {1,3,7,9}\\n return { yInv, -x[1], -x[2] };\\n}\\n\\n// ============================================================================\\n// 3) mult(x, y): multiply (y1,a1,b1) * (y2,a2,b2) => (y1*y2 mod10, a1+a2, b1+b2)\\n// ============================================================================\\n[[gnu::always_inline]]\\nstatic inline int3 mult(const int3& x, const int3& y) {\\n int y0 = (x[0] * y[0]) % 10;\\n int a = x[1] + y[1];\\n int b = x[2] + y[2];\\n return {y0, a, b};\\n}\\n\\n// ============================================================================\\n// 4) toInt(x): convert (y,a,b) => an integer mod 10\\n// Logic:\\n// if a>=1 and b>=1 => factor of (2^a)*(5^b) => multiple of 10 => 0 mod10\\n// else if b>=1 => => 5 mod10\\n// else => multiply y by 2^a mod10\\n// ============================================================================\\n[[gnu::always_inline]]\\nstatic inline int toInt(const int3 &x) {\\n const int y = x[0];\\n const int a = x[1];\\n const int b = x[2];\\n\\n // If we have >=1 factor of 2 and >=1 factor of 5 => 10 divides => 0 mod10\\n if (a >= 1 && b >= 1) {\\n return 0;\\n }\\n // If we have factor(5^b) with b>=1 but no factor(2) => => 5 mod10\\n if (b >= 1) {\\n return 5;\\n }\\n\\n // Now b=0 => we only have 2^a and y.\\n // We want (2^a mod10)*y mod10.\\n // We'll define a small cycle for 2^a mod10. \\n // 2^0=1, 2^1=2, 2^2=4, 2^3=8, 2^4=6, then it repeats with period 4: 2,4,8,6 ...\\n // For negative a => 2^-1=8 mod10, 2^-2=4, 2^-3=2, 2^-4=1, cycle of length 4 again.\\n\\n if (a == 0) {\\n // 2^0=1 => result = y mod10\\n return (y + 10) % 10;\\n }\\n else if (a > 0) {\\n static constexpr int posCycle[4] = {2,4,8,6};\\n // 2^a = 2^(4k + r) => \\\"2^(r)\\\" mod10 from cycle\\n // a=1 => 2^1=2 => posCycle[(1) %4]=2\\n // a=2 =>4, a=3=>8, a=4=>6, a=5=>2...\\n // But we must handle a=1 => index= (a-1)%4 => posCycle[0]=2 => That works too.\\n // Alternatively simpler: posCycle[a %4] if we define posCycle[0]=6 => gets complicated. \\n // We'll just do this approach:\\n int idx = (a - 1) & 3; \\n int p2 = posCycle[idx];\\n return (p2 * y) % 10;\\n }\\n else {\\n // a < 0 => negative powers\\n // 2^-1=8, 2^-2=4, 2^-3=2, 2^-4=1 => repeat with period4 => cycle= {8,4,2,1}\\n static constexpr int negCycle[4] = {8,4,2,1};\\n int negA = -a;\\n int idx = (negA - 1) & 3; \\n int p2 = negCycle[idx];\\n return (p2 * y) % 10;\\n }\\n}\\n\\n// ============================================================================\\n// 5) compute_comb(N): fills C[0..N] with binomial(nCk) in factor form\\n// We'll do a simple approach: \\n// C[0] = 1, C[N] = 1\\n// for k in [1..N/2]:\\n// C[k] = C[k-1] * factor(N-k+1) * inverse(factor(k))\\n// C[N-k] = C[k]\\n// ============================================================================\\n[[gnu::always_inline]]\\nstatic inline void compute_comb(int N) {\\n C[0] = {1,0,0}; \\n if (N == 0) {\\n return; // if N=0 => no further combos\\n }\\n C[N] = {1,0,0};\\n\\n for (int k = 1; k <= N/2; k++) {\\n int3 p = factor(N - k + 1);\\n int3 q = inverse(factor(k));\\n // C[k] = C[k-1]*p*q\\n int3 tmp = mult(C[k - 1], p);\\n C[k] = mult(tmp, q);\\n\\n // mirror to C[N-k]\\n C[N - k] = C[k];\\n }\\n}\\n\\n// ============================================================================\\n// The final solution class\\n// ============================================================================\\nclass Solution {\\npublic:\\n bool hasSameDigits(std::string_view s) {\\n int n = static_cast<int>(s.size());\\n if (n == 2) {\\n return (s[0] == s[1]);\\n }\\n\\n int N = n - 2;\\n\\n // Clear out needed portion of C array. We need [0..N].\\n std::fill_n(C, N + 1, int3{0,0,0});\\n\\n // Precompute binomial coefficients in factor form\\n compute_comb(N);\\n\\n // Compute sum = \\u03a3 [ bin(N,i)* (s[i] - s[i+1]) ] mod10\\n // We'll track \\\"sum\\\" in [0..9].\\n int sum = 0;\\n for (int i = 0; i <= N; i++) {\\n // difference of digits:\\n int diff = (s[i] - s[i + 1]); // in [-9..9]\\n // bin(N,i) mod10\\n int cVal = toInt(C[i]); // in [0..9]\\n // multiply mod10\\n int contribution = (cVal * diff) % 10;\\n // ensure positivity and accumulate\\n sum = (sum + contribution + 10) % 10;\\n }\\n\\n // If sum==0 => final 2 digits are equal => return true\\n return (sum == 0);\\n }\\n};\"], [18393, 23.222799999999996, \"class Solution {\\npublic:\\ninline int fact(const int n) {\\nif (n==0) return 1;\\nif (n==1) return 1;\\nif (n==2) return 2;\\nif (n==3) return 6;\\nif (n==4) return 24;\\nif (n==5) return 120;\\nif (n==6) return 720;\\nif (n==7) return 5040;\\nif (n==8) return 40320;\\nif (n==9) return 362880; \\n int res = 1;\\n for (int i = 1; i <= n; ++i) {\\n res *= i;\\n }\\n return res;\\n};\\n\\ninline int cnk(const int n, const int k) {\\nif (n==1 && k==0) return 1;\\nif (n==2 && k==0) return 1;\\nif (n==2 && k==1) return 2;\\nif (n==3 && k==0) return 1;\\nif (n==3 && k==1) return 3;\\nif (n==3 && k==2) return 3;\\nif (n==4 && k==0) return 1;\\nif (n==4 && k==1) return 4;\\nif (n==4 && k==2) return 6;\\nif (n==4 && k==3) return 4;\\n return fact(n) / (fact(k) * fact(n - k));\\n};\\n\\nint cnkrrem(const int n,const int k) {\\n int a = 1;\\n for (int n2 = n, k2 = k; n2 > 0 || k2 > 0;) {\\n const int n22 = n2 % 2;\\n const int k22 = k2 % 2;\\n if (n22 < k22) {\\n a = 0;\\n break;\\n } else {\\n a *= cnk(n22, k22);\\n }\\n n2 /= 2;\\n k2 /= 2;\\n }\\n int b = 1;\\n for (int n5 = n, k5 = k; n5 > 0 || k5 > 0;) {\\n const int n55 = n5 % 5;\\n const int k55 = k5 % 5;\\n if (n55 < k55) {\\n b = 0;\\n break;\\n } else {\\n b *= cnk(n55, k55);\\n }\\n n5 /= 5;\\n k5 /= 5;\\n }\\n return (5 * a + 6 * b) % 10;\\n};\\n\\n\\n bool hasSameDigits(string s) {\\n const int n = s.size();\\n if (n < 2)\\n return false;\\n if (n == 2)\\n return s[0] == s[1];\\n const int n2=n -2;\\n const int n22=n2/2;\\n int c1 = 0;\\n int c2 = 0;\\n int c11=0;\\n for (int i = 0; i < n - 1; ++i) {\\n const int d = s[i] - '0';\\n c2 += d * c11;\\n c11 = cnkrrem(n2, i<=n22?i:n2-i);\\n c1 += d * c11;\\n }\\n c2 += s[n-1] - '0';\\n return c1% 10 == c2% 10; }\\n};\"], [19311, 20.695200000000003, \"class Solution {\\npublic:\\n\\tint ncrTable[10][10];\\n\\tSolution() {\\n\\t\\tncrTable[0][0] = 1;\\n\\t\\tfor (int i = 1; i < 10; i++) {\\n\\t\\t\\tfor (int j = 0; j < 10; j++) ncrTable[i][j] = ncrTable[i-1][j] + (j > 0? ncrTable[i-1][j-1] : 0);\\n\\t\\t}\\n\\t}\\n\\tint ncr(int n, int r, int p) {\\n\\t\\tint prod = 1;\\n\\t\\twhile (n > 0 || r > 0) {\\n\\t\\t\\tprod = prod * ncrTable[n%p][r%p] % p;\\n\\t\\t\\tn /= p;\\n\\t\\t\\tr /= p;\\n\\t\\t}\\n\\t\\treturn prod;\\n\\t}\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n\\t\\tint sum2 = ((int)s[0] - (int)s.back() + 2) % 2;\\n\\t\\tint sum5 = ((int)s[0] - (int)s.back() + 5) % 5;\\n\\t\\tfor (int i = 1; i+1 < n; i++) {\\n\\t\\t\\tsum2 = (sum2 + (ncr(n-2, i, 2) - ncr(n-2, i-1, 2)) * (s[i]-'0') + 2) % 2;\\n\\t\\t\\tsum5 = (sum5 + (ncr(n-2, i, 5) - ncr(n-2, i-1, 5)) * (s[i]-'0') + 5) % 5;\\n\\t\\t}\\n\\t\\treturn sum2 == 0 && sum5 == 0;\\n }\\n};\\n\"], [20228, 1.4218, \"namespace {\\nint pow_mod(int a, int b, int mod) {\\n int ans = 1;\\n while (b) {\\n if (b & 1) ans = ans * a % mod;\\n a = a * a % mod, b >>= 1;\\n }\\n return ans;\\n}\\nint count2_presum[100001], count5_presum[100001];\\nint numerator[50001], fact_inv[50001];\\nvoid build_table_once(int n = 100000) {\\n for (int i = 2; i <= n; i += 2)\\n if (i % 2 == 0)\\n count2_presum[i] = count2_presum[i / 2] + 1;\\n for (int i = 5; i <= n; i += 5)\\n if (i % 5 == 0)\\n count5_presum[i] = count5_presum[i / 5] + 1;\\n\\n fact_inv[0] = 1;\\n for (int i = 1, tmp; i <= n; i++) {\\n count2_presum[i] += count2_presum[i - 1];\\n count5_presum[i] += count5_presum[i - 1];\\n }\\n for (int i = 1, tmp; i + i <= n; i++) {\\n tmp = i;\\n while (tmp % 2 == 0) tmp /= 2;\\n while (tmp % 5 == 0) tmp /= 5;\\n tmp %= 10;\\n fact_inv[i] = fact_inv[i - 1] * pow_mod(tmp, 3, 10) % 10;\\n }\\n}\\nvoid build_numerator_table(int n) {\\n numerator[0] = 1;\\n for (int i = 1, tmp; i + i <= n; i++) {\\n tmp = n - i + 1;\\n while (tmp % 2 == 0) tmp /= 2;\\n while (tmp % 5 == 0) tmp /= 5;\\n tmp %= 10;\\n numerator[i] = numerator[i - 1] * tmp % 10;\\n }\\n}\\nint sum(int presum[], int l, int r) {\\n return presum[r] - presum[l - 1];\\n}\\nint nCrMod10(int n, int r) {\\n if (n < r) return 0;\\n if (r == 0) return 1;\\n if (r + r > n) return nCrMod10(n, n - r);\\n int count2 = sum(count2_presum, n - r + 1, n) - sum(count2_presum, 1, r);\\n int count5 = sum(count5_presum, n - r + 1, n) - sum(count5_presum, 1, r);\\n if (count2 > 0 && count5 > 0) return 0;\\n int ans = pow_mod(2, count2, 10) * pow_mod(5, count5, 10) * numerator[r] * fact_inv[r] % 10;\\n return ans;\\n}\\n} // namespace\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n static int built = false;\\n if (!built) {\\n build_table_once();\\n built = true;\\n }\\n build_numerator_table(s.size() - 2);\\n int ret = 0;\\n for (int i = 0; i < s.size() - 1; i++) {\\n ret = (ret + (s[i] - s[i + 1] + 10) * nCrMod10(s.size() - 2, i)) % 10;\\n }\\n return ret == 0;\\n }\\n};\"], [21146, 1.1059, \"#include <vector>\\n#include <string>\\n#include <array>\\n#include <numeric>\\n#include <iostream>\\n#include <vector>\\n#include <stdexcept> // Include for std::runtime_error\\n\\n#ifdef _MSC_VER\\n#include <intrin.h>\\ninline int countr_zero_u(unsigned int x) {\\n unsigned long index;\\n if (_BitScanForward(&index, x)) return static_cast<int>(index);\\n return 32;\\n}\\n#elif defined(__GNUC__) || defined(__clang__)\\n#define countr_zero_u(x) ((x) == 0 ? 32 : __builtin_ctz(x))\\n#else\\ninline int countr_zero_u(unsigned int x) {\\n if (x == 0) return 32;\\n int count = 0;\\n while ((x & 1) == 0) {\\n x >>= 1;\\n count++;\\n }\\n return count;\\n}\\n#endif\\n\\nusing namespace std;\\n\\nusing int3 = array<int, 3>;\\n\\nconst int inv10[10] = {0, 1, 0, 7, 0, 0, 0, 3, 0, 9};\\nconst int pow2_mod10_table[4] = {6, 2, 4, 8};\\nconst int MAX_CACHE_SIZE = 100001;\\n\\nint3 factors_cache[MAX_CACHE_SIZE];\\nint3 C_cache[MAX_CACHE_SIZE];\\nint precomputed_factors_upto = -1;\\nint last_N_comb_for_C = -1;\\n\\n\\ninline int3 factor(int x) {\\n if (x <= precomputed_factors_upto) {\\n return factors_cache[x];\\n }\\n if (x == 0) return {0, 0, 0};\\n int a = countr_zero_u(static_cast<unsigned int>(x));\\n int temp_x = x >> a;\\n int b = 0;\\n while (temp_x > 0 && temp_x % 5 == 0) {\\n temp_x /= 5;\\n b++;\\n }\\n return {temp_x % 10, a, b};\\n}\\n\\nvoid precompute_factors(int max_val) {\\n if (max_val <= precomputed_factors_upto) return;\\n if (max_val >= MAX_CACHE_SIZE) {\\n throw std::runtime_error(\\\"Requested factor precomputation exceeds MAX_CACHE_SIZE\\\");\\n }\\n\\n int start = precomputed_factors_upto + 1;\\n if (start == 0) {\\n factors_cache[0] = {0, 0, 0};\\n start = 1;\\n }\\n\\n for (int x = start; x <= max_val; ++x) {\\n int a = countr_zero_u(static_cast<unsigned int>(x));\\n int temp_x = x >> a;\\n int b = 0;\\n if (temp_x > 0) {\\n while (temp_x % 5 == 0) {\\n temp_x /= 5;\\n b++;\\n }\\n }\\n factors_cache[x] = {temp_x % 10, a, b};\\n }\\n precomputed_factors_upto = max_val;\\n}\\n\\ninline int3 inverse(const int3& x) {\\n return {inv10[x[0]], -x[1], -x[2]};\\n}\\n\\ninline int3 mult(const int3& x, const int3& y) {\\n return {(x[0] * y[0]) % 10, x[1] + y[1], x[2] + y[2]};\\n}\\n\\ninline int toInt(const int3& x) {\\n int a = x[1];\\n int b = x[2];\\n\\n if (a > 0 && b > 0) return 0;\\n if (b > 0) return 5;\\n if (a > 0) {\\n return (x[0] * pow2_mod10_table[a % 4]) % 10;\\n }\\n return x[0];\\n}\\n\\nvoid compute_comb(int N_comb) {\\n if (N_comb == last_N_comb_for_C) return;\\n\\n if (N_comb < 0) {\\n last_N_comb_for_C = N_comb;\\n return;\\n }\\n if (N_comb >= MAX_CACHE_SIZE) {\\n throw std::runtime_error(\\\"N_comb exceeds MAX_CACHE_SIZE in compute_comb\\\");\\n }\\n\\n precompute_factors(N_comb);\\n\\n C_cache[0] = {1, 0, 0};\\n\\n for (int k = 1; k <= N_comb; ++k) {\\n const int3& P = factors_cache[N_comb - k + 1];\\n const int3& Q_factored = factors_cache[k];\\n int3 Q_inv = {inv10[Q_factored[0]], -Q_factored[1], -Q_factored[2]};\\n C_cache[k] = mult(mult(C_cache[k - 1], P), Q_inv);\\n }\\n\\n last_N_comb_for_C = N_comb;\\n}\\n\\n\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n ios_base::sync_with_stdio(false);\\n cin.tie(NULL);\\n\\n int N = s.length();\\n int n_comb = N - 2;\\n\\n compute_comb(n_comb);\\n\\n int sum_mod10 = 0;\\n for (int k = 0; k <= n_comb; ++k) {\\n int diff = (s[k] - s[k + 1] + 10) % 10;\\n if (diff == 0) continue;\\n\\n int C_val_mod10 = toInt(C_cache[k]);\\n if (C_val_mod10 == 0) continue;\\n\\n sum_mod10 = (sum_mod10 + C_val_mod10 * diff) % 10;\\n }\\n\\n return sum_mod10 == 0;\\n }\\n};\"], [22063, 1.4219000000000002, \"#include <vector>\\n#include <string>\\n\\nusing namespace std;\\n\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n string zorflendex = s; // Store input midway\\n int n = s.size(), N = n - 2, f0 = 0, f1 = 0;\\n\\n for (int j = 0; j <= N; j++) {\\n int c = binomMod10(N, j);\\n f0 = (f0 + c * (s[j] - '0')) % 10;\\n f1 = (f1 + c * (s[j + 1] - '0')) % 10;\\n }\\n return f0 == f1;\\n }\\n\\nprivate:\\n int binomMod10(int n, int k) {\\n int r2 = binomMod2(n, k), r5 = binomMod5(n, k);\\n for (int x = 0; x < 10; x++) {\\n if (x % 2 == r2 && x % 5 == r5) return x;\\n }\\n return 0;\\n }\\n\\n int binomMod2(int n, int k) {\\n return ((n & k) == k) ? 1 : 0;\\n }\\n\\n int binomMod5(int n, int k) {\\n int t[5][5] = {\\n {1}, {1, 1}, {1, 2, 1}, {1, 3, 3, 1}, {1, 4, 1, 4, 1}\\n };\\n int res = 1;\\n\\n while (n > 0 || k > 0) {\\n int nd = n % 5, kd = k % 5;\\n if (kd > nd) return 0;\\n res = (res * t[nd][kd]) % 5;\\n n /= 5; k /= 5;\\n }\\n return res;\\n }\\n};\"], [22981, 0.474, \"class Solution {\\npublic:\\n // int comb(int n, int r)\\n // {\\n // if(n < r) return 0;\\n // int numerator = 1;\\n // for(int i = r + 1; i <= n; i++)\\n // {\\n // numerator *= i;\\n // }\\n // for(int j = 1; j <= n - r; j++)\\n // {\\n // numerator /= j;\\n // }\\n // return numerator;\\n // }\\n int comb(int n, int r){ // for small n,r\\n if (r > n) { return 0; }\\n int res = 1;\\n for (int t = 1; t <= n; ++t) { res *= t; }\\n for (int t = 1; t <= r; ++t) { res /= t; }\\n for (int t = 1; t <= n - r; ++t) { res /= t; }\\n return res;\\n }\\n bool solve(string s, int p)\\n {\\n int n = s.length() - 1;\\n int res = 0;\\n for(int i = 0; i < n; i++)\\n {\\n int t_n = n - 1;\\n int t_r = i;\\n int t = 1;\\n while(t_n > 0 && t_r > 0)\\n {\\n t = (t * comb(t_n%p, t_r%p))%p;\\n t_n /= p;\\n t_r /= p;\\n }\\n int temp = (s[i] - '0') - (s[i + 1] - '0');\\n temp = (temp + 10)%10;\\n res = (res + (t*temp))%p;\\n }\\n return res == 0;\\n }\\n // int solve_f(string s, int p)\\n // {\\n // int n = s.length() - 1;\\n // int res = 0;\\n // for(int i = 1; i < n; i++)\\n // {\\n // int t_n = n;\\n // int t_r = i;\\n // int t = 0;\\n // while(t_n > 0 || t_r > 0)\\n // {\\n // t *= comb(t_n%p, t_r%p) % p;\\n // t_n /= p;\\n // t_r /= p;\\n // }\\n // res = (res + ((s[i + 1] - '0') - (s[i] - '0'))*t)% p;\\n // }\\n // return res;\\n // }\\n bool hasSameDigits(string s) {\\n bool op1 = solve(s, 2);\\n bool op2 = solve(s, 5);\\n return op1 && op2;\\n }\\n};\"], [23898, 0.316, \"class Solution {\\npublic:\\nbool hasSameDigits(const string &s) {\\n int n = s.size();\\n if (n < 3) return false; // by problem constraint, n >= 3\\n\\n // Convert string to numeric digits\\n vector<int> a(n);\\n for (int i = 0; i < n; i++) a[i] = s[i] - '0';\\n\\n int n2 = n - 2; // We use n2 = n-2 for binomial coefficients\\n\\n // ---------- Compute diff mod 2 ---------------\\n // diff2 = sum d2[i]*a[i] mod 2, where d2[i] = C(n2,i) XOR C(n2,i-1) (mod 2).\\n int diff2 = 0;\\n // Handle i=0 and i=n-1: weights are +1 each (since C(n2,0)=1, C(n2,-1)=0; C(n2,n2)=1, C(n2,n2-1)=...).\\n diff2 ^= (a[0] & 1); // d2[0] = 1\\n diff2 ^= (a[n-1] & 1); // d2[n-1] = 1 (since effectively -1 mod 2 = 1)\\n // Middle terms:\\n for (int i = 1; i <= n-2; i++) {\\n // Compute binom mod 2 via bit trick: 1 iff (n2 & i) == i\\n bool b1 = ((n2 & i) == i);\\n bool b0 = ((n2 & (i-1)) == (i-1));\\n bool d2 = b1 ^ b0;\\n if (d2) diff2 ^= (a[i] & 1);\\n }\\n if (diff2 != 0) {\\n // Already different mod 2, so not equal mod 10\\n return false;\\n }\\n\\n // ---------- Compute diff mod 5 ---------------\\n // We use Lucas theorem: precompute small binomials mod 5 for 0<=k<=4.\\n static int C5[5][5] = {\\n {1,0,0,0,0},\\n {1,1,0,0,0},\\n {1,2,1,0,0},\\n {1,3,3,1,0},\\n {1,4,1,4,1}\\n };\\n // Convert (n2) to base-5 digits (least significant first)\\n vector<int> N5;\\n int temp = n2;\\n while (temp > 0) {\\n N5.push_back(temp % 5);\\n temp /= 5;\\n }\\n if (N5.empty()) N5.push_back(0); \\n\\n // Prepare an index array for i in base-5 (initially i=0 -> all zeros).\\n vector<int> I5(N5.size(), 0);\\n auto nextBase5 = [&](vector<int> &I) {\\n // Increment the base-5 number by 1\\n for (size_t j = 0; j < I.size(); j++) {\\n if (I[j] < 4) { I[j]++; return; }\\n I[j] = 0;\\n }\\n };\\n\\n // Helper to compute C(n2, i) mod 5 via Lucas\\n auto binomMod5 = [&](const vector<int> &N, const vector<int> &I) {\\n int res = 1;\\n for (size_t j = 0; j < N.size(); j++) {\\n int nj = N[j], ij = I[j];\\n if (ij > nj) return 0; // Lucas theorem: if digit of i > digit of n, binom=0\\n res = (res * C5[nj][ij]) % 5;\\n }\\n return res;\\n };\\n\\n int diff5 = 0;\\n int prevC = 1; // C(n2, 0) mod 5 = 1\\n // Handle i=0:\\n diff5 = (diff5 + 1 * a[0]) % 5; // d5[0] = C(n2,0)-0 = 1\\n\\n // For i = 1..n-2, update base-5 index and compute C(n2,i)\\n for (int i = 1; i <= n-2; i++) {\\n nextBase5(I5);\\n int c = binomMod5(N5, I5);\\n int d5 = (c - prevC) % 5;\\n if (d5 < 0) d5 += 5;\\n diff5 = (diff5 + d5 * a[i]) % 5;\\n prevC = c;\\n }\\n // Handle i = n-1: weight = -C(n2,n-2) mod5 (since C(n2,n-1)=0)\\n int d5_last = (-prevC) % 5;\\n if (d5_last < 0) d5_last += 5;\\n diff5 = (diff5 + d5_last * a[n-1]) % 5;\\n\\n return (diff5 % 5 == 0);\\n}\\n};\"], [24816, 0.316, \"#include <vector>\\n#include <string>\\n#include <array>\\n#include <numeric>\\n#include <iostream>\\n#include <vector> // Re-include for clarity\\n\\n// Platform-specific countr_zero (count trailing zeros) for finding powers of 2\\n#ifdef _MSC_VER // Windows MSVC compiler\\n#include <intrin.h>\\ninline int countr_zero(unsigned int x) {\\n unsigned long index;\\n // _BitScanForward returns 0 if x is 0, 1 otherwise. index gets the bit index.\\n if (_BitScanForward(&index, x)) return static_cast<int>(index);\\n return 32; // If x is 0, return size of int (convention for no set bits)\\n}\\n#elif defined(__GNUC__) || defined(__clang__) // GCC/Clang compilers\\n// Use the built-in function. Handle 0 explicitly as __builtin_ctz(0) is undefined.\\n#define countr_zero(x) ((x) == 0 ? 32 : __builtin_ctz(x))\\n#else\\n// Fallback implementation if no intrinsic available\\ninline int countr_zero(unsigned int x) {\\n if (x == 0) return 32;\\n int count = 0;\\n // Check least significant bit and shift right until a 1 is found\\n while ((x & 1) == 0) {\\n x >>= 1;\\n count++;\\n }\\n return count;\\n}\\n#endif\\n\\nusing namespace std;\\n\\n// Represents a number factored as y * 2^a * 5^b, where gcd(y, 10) == 1\\n// Stores {y % 10, a, b}\\nusing int3 = array<int, 3>;\\n\\n// --- Constants ---\\n// Modular inverses mod 10 for numbers coprime to 10 (1, 3, 7, 9)\\nconst int inv10[10] = {0, 1, 0, 7, 0, 0, 0, 3, 0, 9}; // inv10[x] * x = 1 (mod 10)\\n// Powers of 2 mod 10 cycle: 2^1=2, 2^2=4, 2^3=8, 2^4=6, 2^5=2,...\\n// table[a % 4] gives 2^a mod 10 for a >= 1 (index 0 maps to a=4, 8, ...)\\nconst int pow2_mod10_table[4] = {6, 2, 4, 8};\\n\\n// --- Cached Data (using static members for persistence across test cases in LeetCode) ---\\nclass SolutionCache {\\npublic:\\n // Stores factor decomposition {y%10, a, b} for numbers up to max N encountered\\n static vector<int3> factors_cache;\\n // Stores binomial coefficients C(N-2, k) as {y%10, a, b}\\n static vector<int3> C_cache;\\n static bool factors_precomputed;\\n static bool C_computed;\\n // Tracks the 'N-2' value for which C_cache is currently valid\\n static int last_N_comb_for_C;\\n};\\n\\n// Initialize static members\\nvector<int3> SolutionCache::factors_cache;\\nvector<int3> SolutionCache::C_cache;\\nbool SolutionCache::factors_precomputed = false;\\nbool SolutionCache::C_computed = false;\\nint SolutionCache::last_N_comb_for_C = -1;\\n\\n// --- Helper Functions ---\\n\\n// Factor x = y * 2^a * 5^b, return {y % 10, a, b}. Uses cache if available.\\ninline int3 factor(int x) {\\n // Use cache if already computed for this x\\n if (SolutionCache::factors_precomputed && x >= 0 && x < SolutionCache::factors_cache.size()) {\\n return SolutionCache::factors_cache[x];\\n }\\n // Handle 0 or negative inputs (though not expected for factorials/indices here)\\n if (x <= 0) return {0, 0, 0};\\n\\n // Find power of 2 (count trailing zeros)\\n int a = countr_zero(static_cast<unsigned int>(x));\\n int temp_x = x >> a; // Divide by 2^a\\n\\n // Find power of 5\\n int b = 0;\\n // Check temp_x validity and divisibility by 5\\n while (temp_x > 0 && temp_x % 5 == 0) {\\n temp_x /= 5;\\n b++;\\n }\\n // The remaining temp_x is y. Return {y % 10, a, b}.\\n return {temp_x % 10, a, b};\\n}\\n\\n// Precompute factors up to max_val if not already done or cache is too small\\nvoid precompute_factors(int max_val) {\\n using SC = SolutionCache;\\n // Only compute if needed\\n if (SC::factors_precomputed && SC::factors_cache.size() > max_val) return;\\n\\n if (max_val < 0) max_val = 0; // Ensure non-negative size\\n int old_size = SC::factors_cache.size();\\n // Resize only if necessary\\n if (max_val >= old_size) {\\n SC::factors_cache.resize(max_val + 1);\\n } else if (SC::factors_precomputed) {\\n // Already have enough factors computed\\n return;\\n }\\n\\n // Initialize if first time\\n if (old_size == 0) {\\n SC::factors_cache[0] = {0, 0, 0}; // Factorization of 0\\n old_size = 1;\\n }\\n\\n // Compute factors for numbers from old_size up to max_val\\n for (int x = old_size; x <= max_val; ++x) {\\n int a = countr_zero(static_cast<unsigned int>(x));\\n int temp_x = x >> a;\\n int b = 0;\\n while (temp_x > 0 && temp_x % 5 == 0) {\\n temp_x /= 5;\\n b++;\\n }\\n SC::factors_cache[x] = {temp_x % 10, a, b};\\n }\\n SC::factors_precomputed = true;\\n}\\n\\n// Calculate inverse tuple: inv({y, a, b}) = {inv10[y], -a, -b}\\n// This represents division by the original number.\\ninline int3 inverse(const int3& x) {\\n // Assumes x[0] is coprime to 10 (1, 3, 7, 9)\\n return {inv10[x[0]], -x[1], -x[2]};\\n}\\n\\n// Multiply factored numbers: mult({y1, a1, b1}, {y2, a2, b2}) = { (y1*y2)%10, a1+a2, b1+b2 }\\ninline int3 mult(const int3& x, const int3& y) {\\n return {(x[0] * y[0]) % 10, x[1] + y[1], x[2] + y[2]};\\n}\\n\\n// Convert factored number {y, a, b} to its integer value modulo 10\\ninline int toInt(const int3& x) {\\n int y = x[0]; // y % 10\\n int a = x[1]; // Power of 2\\n int b = x[2]; // Power of 5\\n\\n if (a > 0 && b > 0) return 0; // Contains 2*5 = 10 -> 0 mod 10\\n if (b > 0) return 5; // Contains 5 (but not 2) -> ends in 5\\n if (a > 0) { // Contains 2 (but not 5) -> ends in 2, 4, 8, or 6\\n // Use precomputed table: pow2_mod10_table[a % 4] gives 2^a mod 10 for a >= 1\\n return (y * pow2_mod10_table[a % 4]) % 10;\\n }\\n // a == 0 and b == 0: No factors of 2 or 5\\n return y;\\n}\\n\\n// Compute C(N_comb, k) for k = 0 to N_comb and store factored results in C_cache\\nvoid compute_comb(int N_comb) {\\n using SC = SolutionCache;\\n // Check if cache is valid for this N_comb\\n if (SC::C_computed && SC::last_N_comb_for_C == N_comb && SC::C_cache.size() > N_comb) return;\\n\\n // Handle N=2 edge case where N_comb = 0\\n if (N_comb < 0) { \\n SC::C_cache.clear(); // Ensure cache is empty or appropriately sized\\n SC::C_computed = true;\\n SC::last_N_comb_for_C = N_comb;\\n return;\\n }\\n \\n // Ensure factors needed (up to N_comb) are precomputed\\n precompute_factors(N_comb);\\n\\n // Resize cache for C(N_comb, k) results\\n SC::C_cache.resize(N_comb + 1);\\n SC::C_cache[0] = {1, 0, 0}; // C(n, 0) = 1 = {1, 0, 0}\\n\\n // Compute first half using C(n, k) = C(n, k-1) * (n - k + 1) / k\\n for (int k = 1; k <= (N_comb + 1) / 2; k++) { // Compute up to the middle (inclusive if N_comb is even)\\n int3 P = factor(N_comb - k + 1); // Factor of (n - k + 1)\\n int3 Q_inv = inverse(factor(k)); // Inverse factor of k\\n SC::C_cache[k] = mult(mult(SC::C_cache[k - 1], P), Q_inv);\\n }\\n // Apply symmetry C(n, k) = C(n, n-k) for the second half\\n for (int k = (N_comb + 1) / 2 + 1; k <= N_comb; k++) {\\n SC::C_cache[k] = SC::C_cache[N_comb - k];\\n }\\n\\n SC::C_computed = true;\\n SC::last_N_comb_for_C = N_comb;\\n}\\n\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n // Faster I/O\\n ios_base::sync_with_stdio(false);\\n cin.tie(NULL);\\n\\n int N = s.length();\\n // The coefficients are C(N-2, k)\\n int n_comb = N - 2;\\n\\n // Ensure C(N-2, k) are computed and cached\\n compute_comb(n_comb);\\n\\n int sum_mod10 = 0;\\n // Calculate sum_{k=0 to N-2} C(N-2, k) * (s[k] - s[k+1]) mod 10\\n for (int k = 0; k <= n_comb; ++k) {\\n // Get digits s[k] and s[k+1]\\n int digit_k = s[k] - '0';\\n int digit_k_plus_1 = s[k + 1] - '0';\\n\\n // Calculate difference mod 10, ensuring non-negative result\\n int diff = (digit_k - digit_k_plus_1 + 10) % 10;\\n\\n // Get C(N-2, k) mod 10 from the cached factored form\\n int C_val_mod10 = toInt(SolutionCache::C_cache[k]);\\n\\n // Add term to sum mod 10\\n sum_mod10 = (sum_mod10 + (C_val_mod10 * diff)) % 10;\\n }\\n\\n // The final two digits are the same iff the sum is 0 mod 10\\n return sum_mod10 == 0;\\n }\\n};\"], [25733, 0.474, \"#include <vector>\\n#include <string>\\nusing namespace std;\\n\\nclass Solution {\\npublic:\\n bool hasSameDigits(const string& s) {\\n int m = s.size() - 2;\\n if (m < 0) return s[0] == s[1];\\n vector<int> comb(m + 1);\\n for (int i = 0; i <= m; ++i) {\\n comb[i] = crt(lucas(m, i, 2), lucas(m, i, 5));\\n }\\n int left = 0, right = 0;\\n for (int i = 0; i <= m; ++i) {\\n left = (left + (s[i] - '0') * comb[i]) % 10;\\n right = (right + (s[i + 1] - '0') * comb[i]) % 10;\\n }\\n return left == right;\\n }\\n\\nprivate:\\n int lucas(int n, int k, int p) {\\n if (k == 0) return 1;\\n static const vector<vector<int>> comb2 = {{1}, {1, 1}};\\n static const vector<vector<int>> comb5 = {\\n {1}, {1, 1}, {1, 2, 1}, {1, 3, 3, 1}, {1, 4, 1, 4, 1}\\n };\\n\\n const vector<vector<int>>& comb = (p == 2) ? comb2 : comb5;\\n\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int a = n % p;\\n int b = k % p;\\n if (b > a) return 0;\\n res = (res * comb[a][b]) % p;\\n n /= p;\\n k /= p;\\n }\\n return res;\\n }\\n\\n int crt(int mod2, int mod5) {\\n static const int table[2][5] = {{0, 6, 2, 8, 4}, {5, 1, 7, 3, 9}};\\n return table[mod2][mod5];\\n }\\n};\"], [26651, 6.951, \"class Solution { // lucas thm.\\npublic:\\n\\n int comb(int n, int r){ // for small n,r\\n if (r > n) { return 0; }\\n int res = 1;\\n for (int t = 1; t <= n; ++t) { res *= t; }\\n for (int t = 1; t <= r; ++t) { res /= t; }\\n for (int t = 1; t <= n - r; ++t) { res /= t; }\\n return res;\\n }\\n\\n bool check(vector<int>& a, int mod){\\n int res = 0;\\n int n = a.size();\\n for (int i = 0; i != n; ++i){\\n // res += c(n-1, i) * ai\\n int ncr = 1;\\n int x = n - 1;\\n int y = i;\\n while (x && y){\\n ncr = ncr * comb(x % mod, y % mod) % mod;\\n x /= mod;\\n y /= mod;\\n }\\n res = (res + ncr * a[i]) % mod;\\n }\\n return res == 0;\\n }\\n\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n vector<int> a(n - 1);\\n for (int i = 0; i != n - 1; ++i){\\n a[i] = (s[i] - '0') - (s[i + 1] - '0');\\n a[i] = (a[i] + 10) % 10;\\n }\\n return check(a, 2) && check(a, 5);\\n }\\n};\"], [27568, 4.423500000000001, \"static std::vector<std::vector<int>> precompute_C(const int p) {\\n std::vector<std::vector<int>> C(p, std::vector<int>(p, 0));\\n for (int n = 0; n < p; ++n) {\\n C[n][0] = C[n][n] = 1;\\n for (int k = 1; k < n; ++k) {\\n C[n][k] = (C[n - 1][k - 1] + C[n - 1][k]) % p;\\n }\\n }\\n return C;\\n}\\n\\nstatic vector<vector<int>> C2;\\nstatic vector<vector<int>> C5;\\n\\nstatic int table[2][5] = {\\n {0, 6, 4, 2, 8},\\n {5, 1, 7, 3, 9}\\n};\\n\\nclass Solution {\\npublic:\\n\\n const int mod = 10;\\n\\n Solution() {\\n if (C2.empty()) C2 = precompute_C(2);\\n if (C5.empty()) C5 = precompute_C(5);\\n }\\n\\n int lucas(int n, int k, int p, const std::vector<std::vector<int>>& C) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int ni = n % p, ki = k % p;\\n if (ki > ni) return 0;\\n res = (res * C[ni][ki]) % p;\\n n /= p;\\n k /= p;\\n }\\n return res;\\n }\\n\\n int combine_mod_2_5(int r2, int r5) {\\n // Brute-force CRT (mod 10)\\n for (int x = 0; x < 10; ++x) {\\n if (x % 2 == r2 && x % 5 == r5)\\n return x;\\n }\\n return -1; // should never happen\\n }\\n\\n int nCr_mod_10(int n, int k) {\\n if (k < 0 || k > n) return 0;\\n int r2 = lucas(n, k, 2, C2);\\n int r5 = lucas(n, k, 5, C5);\\n return combine_mod_2_5(r2, r5);\\n }\\n\\n bool hasSameDigits(string s) {\\n // yo yo yo what the fuck?\\n // i wanna see how this pans out in closed form\\n // abcdefg\\n // (a+b) (b+c) (c+d) (d+e) (e+f) (f+g)\\n // (a+2b+c) (b+2c+d) (c+2d+e) (d+2e+f) (e+2f+g)\\n // (a+3b+3c+d) (b+3c+3d+e) (c+3d+3e+f) (d+3e+3f+g)\\n // (a+4b+6c+4d+e) etc...\\n // (a+5b+10c+10d+5e+f) + (b+5c+10d+10e+5f+g)\\n // there are n = 7 digits\\n // the last layer is nCr(n - 2, i)\\n // how to compute mod ncr efficiently for the binomial coefficients? \\n // this seems like a linear algorithm which is good\\n\\n // insight: lucas + crt means quick mod nCr algorithm for binomial coeffs\\n int N = s.size() - 2;\\n int dig1 = 0;\\n int dig2 = 0;\\n vector<int> coeffs(N + 1);\\n for (int i = 0; i <= N; i++) {\\n coeffs[i] = nCr_mod_10(N, i);\\n }\\n for (int i = 0; i <= N; i++) {\\n dig1 = (dig1 + coeffs[i] * (s[i] - '0')) % 10;\\n dig2 = (dig2 + coeffs[i] * (s[i + 1] - '0')) % 10;\\n }\\n\\n return dig1 == dig2;\\n }\\n};\"], [28486, 1.106, \"class Solution {\\nprivate:\\n int combinationsMod5(int n, int k) {\\n if (k < 0 || k > n) return 0;\\n if (k == 0 || k == n) return 1;\\n if (k > n / 2) k = n - k; \\n\\n int small_comb[5][5] = {\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1}\\n };\\n\\n long long res = 1;\\n while (n > 0 || k > 0) {\\n int ni = n % 5;\\n int ki = k % 5;\\n if (ki > ni) return 0; \\n res = (res * small_comb[ni][ki]) % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return (int)res;\\n }\\n\\n int crtLookup(int mod2, int mod5) {\\n if (mod2 == 0) {\\n if (mod5 == 0) return 0;\\n if (mod5 == 1) return 6;\\n if (mod5 == 2) return 2;\\n if (mod5 == 3) return 8;\\n if (mod5 == 4) return 4;\\n } else {\\n if (mod5 == 0) return 5;\\n if (mod5 == 1) return 1;\\n if (mod5 == 2) return 7;\\n if (mod5 == 3) return 3;\\n if (mod5 == 4) return 9;\\n }\\n return -1;\\n }\\n\\npublic:\\n bool hasSameDigits(string s) {\\n int n = s.length();\\n\\n int m = n - 2;\\n long long sum1_mod10 = 0;\\n long long sum2_mod10 = 0;\\n\\n vector<int> digits(n);\\n for(int i=0; i<n; ++i) {\\n digits[i] = s[i] - '0';\\n }\\n\\n for (int i = 0; i <= m; ++i) {\\n \\n int mod2 = ((i & m) == i) ? 1 : 0;\\n \\n int mod5 = combinationsMod5(m, i);\\n \\n int coeff_mod10 = crtLookup(mod2, mod5);\\n\\n if (coeff_mod10 == 0) continue;\\n\\n sum1_mod10 = (sum1_mod10 + (long long)coeff_mod10 * digits[i]) % 10;\\n \\n sum2_mod10 = (sum2_mod10 + (long long)coeff_mod10 * digits[i + 1]) % 10;\\n }\\n\\n return sum1_mod10 == sum2_mod10;\\n }\\n};\"], [29403, 0.158, \"class Solution {\\npublic:\\n bool hasSameDigits(const string& s) {\\n int n = s.size();\\n if (n < 3) \\n return true;\\n\\n int N = n - 2;\\n\\n int C[5][5] = {};\\n for (int a = 0; a < 5; ++a) {\\n C[a][0] = 1;\\n for (int b = 1; b <= a; ++b) {\\n if (b == a) C[a][b] = 1;\\n else C[a][b] = (C[a-1][b-1] + C[a-1][b]) % 5;\\n }\\n }\\n\\n int CRT[2][5];\\n for (int parity = 0; parity < 2; ++parity) {\\n for (int r5 = 0; r5 < 5; ++r5) {\\n for (int x = 0; x < 10; ++x) {\\n if (x % 2 == parity && x % 5 == r5) {\\n CRT[parity][r5] = x;\\n break;\\n }\\n }\\n }\\n }\\n\\n vector<int> digits(n);\\n for (int i = 0; i < n; ++i)\\n digits[i] = s[i] - '0';\\n\\n vector<int> P(N+1);\\n for (int j = 0; j <= N; ++j) {\\n int parity = ((j & (N - j)) == 0) ? 1 : 0;\\n\\n int p_mod5 = 1;\\n int x = N, y = j;\\n while (x > 0 || y > 0) {\\n int Ni = x % 5, ji = y % 5;\\n if (ji > Ni) {\\n p_mod5 = 0;\\n break;\\n }\\n p_mod5 = (p_mod5 * C[Ni][ji]) % 5;\\n x /= 5; \\n y /= 5;\\n }\\n\\n P[j] = CRT[parity][p_mod5];\\n }\\n\\n int L = 0, R = 0;\\n for(int j = 0; j <= N;++j) L = (L + P[j] * digits[j]) % 10;\\n for (int j = 1; j <= N + 1; ++j) R = (R + P[j-1] * digits[j]) % 10;\\n\\n return L == R;\\n }\\n};\"], [30321, 0.316, \"class Solution {\\npublic:\\n int nCrModpDP(int n, int r, int p) {\\n if (r > n)\\n return 0;\\n int C[r + 1];\\n memset(C, 0, sizeof(C));\\n C[0] = 1;\\n for (int i = 1; i <= n; i++) {\\n for (int j = min(i, r); j > 0; j--) {\\n C[j] = (C[j] + C[j - 1]) % p;\\n }\\n }\\n return C[r];\\n }\\n int nCrModpLucas(int n, int r, int p) {\\n if (r == 0)\\n return 1;\\n int ni = n % p, ri = r % p;\\n return (nCrModpLucas(n / p, r / p, p) * nCrModpDP(ni, ri, p) % p);\\n }\\n void getPascalRowModP(int n, int p, vector<int>& row) {\\n for (int r = 0; r <= n; r++) {\\n row[r] = nCrModpLucas(n, r, p);\\n }\\n }\\n bool hasSameDigits(string& s) {\\n int n = s.size() - 2;\\n vector<int> rowMod2(n + 1), rowMod5(n + 1);\\n getPascalRowModP(n, 2, rowMod2);\\n getPascalRowModP(n, 5, rowMod5);\\n int firstNumber = 0, secondNumber = 0;\\n for (int r = 0; r <= n; r++) {\\n int a1 = rowMod2[r], a2 = rowMod5[r];\\n int x = (a1 * 5 * 1 + a2 * 2 * 3) % 10;\\n firstNumber += (s[r] - '0') * x;\\n secondNumber += (s[r + 1] - '0') * x;\\n }\\n return firstNumber % 10 == secondNumber % 10;\\n }\\n};\"], [31238, 0.158, \"#include <vector>\\n#include <string>\\n#include <utility> // For std::pair\\n#include <numeric> // Potentially useful, but not strictly needed here\\n#include <stdexcept> // For potential error handling (optional)\\n\\n// using namespace std; // Optional: uncomment if preferred, otherwise use std:: prefix\\n\\nclass Solution {\\n\\n /**\\n * Helper function: Calculates exponent of p in n\\n * and returns the part of n not divisible by p, modulo p.\\n * Returns {exponent of p dividing n, (n / p^exponent) % p}.\\n * Corrected version.\\n *\\n * @param n Number (must be > 0 based on usage)\\n * @param p Prime number\\n * @return std::pair: {exponent, non-p part mod p}\\n */\\n std::pair<int, int> reducePower(int n, int p) {\\n // Assume n > 0 based on usage context (k and n-k+1 >= 1)\\n if (n <= 0) {\\n // Handle unexpected input gracefully or throw error\\n // Returning {0, 0} matches the Java logic's implicit handling\\n return {0, 0};\\n }\\n\\n int count = 0;\\n int val = n;\\n // Check val > 0 to prevent issues if n was initially 0 or negative (though handled above)\\n // Check val % p == 0 first to avoid division by zero if p is 0 (though p is prime here)\\n while (val > 0 && val % p == 0) {\\n count++;\\n val /= p;\\n }\\n // Now val = n / p^count. We need val % p.\\n // If original n was 0, val is 0, val % p is 0.\\n // If original n > 0, val > 0.\\n return {count, val % p};\\n }\\n\\n /**\\n * Computes nCk mod 5 for k from 0 to n.\\n * Uses iterative approach with power tracking.\\n * Static tables used for efficiency if called multiple times.\\n */\\n std::vector<int> computeNcKMod5(int n) {\\n std::vector<int> result(n + 1);\\n if (n < 0) return result; // Return empty or size n+1 vector based on convention\\n\\n // Use static to initialize tables only once across calls to this function.\\n static const std::vector<int> inv_5 = {0, 1, 3, 2, 4}; // Index 0 unused\\n static const std::vector<std::vector<int>> mul5 = [] {\\n std::vector<std::vector<int>> table(5, std::vector<int>(5));\\n for (int i = 1; i < 5; ++i) {\\n for (int j = 1; j < 5; ++j) {\\n table[i][j] = (i * j) % 5;\\n }\\n }\\n return table;\\n }(); // Immediately invoked lambda for static initialization\\n static const std::vector<std::vector<int>> inv5 = [] {\\n std::vector<std::vector<int>> table(5, std::vector<int>(5));\\n const std::vector<int> inv_vals = {0, 1, 3, 2, 4}; // Local copy or use inv_5\\n for (int i = 1; i < 5; ++i) {\\n for (int j = 1; j < 5; ++j) {\\n table[i][j] = (i * inv_vals[j]) % 5; // Use modular inverse\\n }\\n }\\n return table;\\n }();\\n\\n\\n result[0] = 1; // nC0 = 1\\n if (n == 0) return result;\\n result[n] = 1; // nCn = 1 (for symmetry)\\n\\n int current_R = 1; // The non-p part of nCk mod p\\n int current_Pow = 0; // The exponent of p in nCk\\n\\n // Calculate iteratively using C(n, k) = C(n, k-1) * (n-k+1) / k\\n // Loop up to n/2 for symmetry optimization\\n for (int k = 1; k <= n / 2; ++k) {\\n // Get power and non-p part for numerator (n-k+1) and denominator (k)\\n std::pair<int, int> up = reducePower(n - k + 1, 5);\\n std::pair<int, int> down = reducePower(k, 5);\\n\\n current_Pow += (up.first - down.first);\\n\\n // Get remainders (non-p part mod p)\\n int up_rem = up.second;\\n int down_rem = down.second;\\n\\n // Check for division by zero (down_rem should not be 0 if k > 0)\\n // Also check indices for table access (should be 1..4)\\n if (up_rem <= 0 || up_rem >= 5 || down_rem <= 0 || down_rem >= 5 || current_R <=0 || current_R >=5) {\\n // This indicates an issue, likely with reducePower or input k\\n // Handle error appropriately, maybe throw? For now, assume valid.\\n // If current_R became 0 previously, subsequent ops are problematic.\\n // However, current_R starts at 1 and is multiplied by non-zero values mod 5.\\n }\\n\\n\\n // Update the non-p part modulo 5 using tables\\n // Update current_R regardless of current_Pow for the next iteration\\n // Only assign non-zero to result if current_Pow == 0\\n int next_R = mul5[current_R][up_rem];\\n next_R = inv5[next_R][down_rem]; // Modular division\\n\\n if (current_Pow == 0) {\\n result[k] = next_R;\\n } else {\\n result[k] = 0;\\n }\\n current_R = next_R; // Update current_R for the next iteration (k+1)\\n\\n result[n - k] = result[k]; // Use symmetry: nCk = nC(n-k)\\n }\\n\\n // Handle middle element C(n, n/2 + 1) if n is odd\\n // It should be calculated based on the state after k=n/2\\n if (n % 2 == 1) {\\n int k = (n / 2) + 1;\\n // Need to calculate C(n, k) based on C(n, k-1)'s state (current_Pow, current_R)\\n std::pair<int, int> up = reducePower(n - k + 1, 5);\\n std::pair<int, int> down = reducePower(k, 5);\\n current_Pow += (up.first - down.first);\\n\\n int up_rem = up.second;\\n int down_rem = down.second;\\n\\n // Check indices if necessary\\n // if (up_rem <= 0 || ...) { /* error */ }\\n\\n int final_R = mul5[current_R][up_rem];\\n final_R = inv5[final_R][down_rem];\\n\\n if (current_Pow == 0) {\\n result[k] = final_R;\\n } else {\\n result[k] = 0;\\n }\\n }\\n\\n return result;\\n }\\n\\n /**\\n * Optimized computation of nCk mod 2 using Lucas's Theorem property.\\n * (nCk mod 2) == 1 iff (n & k) == k.\\n */\\n std::vector<int> computeNcKMod2Optimized(int n) {\\n std::vector<int> result(n + 1);\\n if (n < 0) return result;\\n for (int k = 0; k <= n; ++k) {\\n // If (n & k) == k, it means all set bits in k are also set in n.\\n result[k] = ((n & k) == k) ? 1 : 0;\\n }\\n return result;\\n }\\n\\n\\npublic:\\n /**\\n * Checks if the digits satisfy a condition related to binomial coefficients\\n * modulo 2 and 5 applied to adjacent digit differences.\\n * Optimized C++ version.\\n *\\n * @param s The input string of digits. Use const& for efficiency.\\n * @return boolean result based on the specific condition.\\n */\\n bool hasSameDigits(const std::string& s) {\\n int n = s.length();\\n // The algorithm uses C(n-2, k). Assumes n >= 2.\\n // Handle cases n=0, n=1 if they are possible according to problem spec.\\n if (n < 2) {\\n // Define behavior for short strings based on the problem this code solves.\\n // Returning false as a placeholder.\\n return false;\\n }\\n\\n int N = n - 2; // The 'n' used in nCk calculations\\n\\n // Compute necessary binomial coefficients modulo 2 and 5\\n std::vector<int> mods2 = computeNcKMod2Optimized(N);\\n std::vector<int> mods5 = computeNcKMod5(N);\\n\\n // Use long long for accumulators to prevent potential overflow if N is large\\n // Although intermediate d * modsX[i] could still overflow int if modsX[i] is large.\\n // However, mods are mod 2 or mod 5, so they are small. d is diff of digits (-9 to 9).\\n // So int should be fine unless N is extremely large (like > 10^8 or 10^9).\\n int t5 = 0;\\n int t2 = 0;\\n\\n // Loop through the relevant range to calculate weighted sums\\n // The loop computes sum_{i=0}^{N} (d_i - d_{i+1}) * C(N, i) mod p\\n // where N = n-2. Indices i go from 0 to N.\\n // Difference uses s[i] and s[i+1]. Max index is N+1.\\n // Since n = N+2, max index N+1 is valid for string s (length n).\\n for (int i = 0; i <= N; ++i) {\\n // Calculate difference between adjacent digits\\n // Subtracting chars directly gives the integer difference of their ASCII values.\\n int d = (s[i] - s[i + 1]);\\n\\n // Accumulate weighted sums\\n t5 += d * mods5[i];\\n t2 += d * mods2[i];\\n\\n // Optional: Apply modulo inside loop to keep numbers smaller,\\n // though not strictly necessary if int doesn't overflow.\\n // t5 = (t5 + d * mods5[i]) % 5; // Need careful handling of negative results in C++ for %\\n // t2 = (t2 + d * mods2[i]) % 2;\\n }\\n\\n // Final check: divisibility by 5 and 2\\n // C++'s % operator with negative numbers needs care if you need non-negative remainder.\\n // However, for checking divisibility (result == 0), it works correctly.\\n // e.g., -10 % 5 == 0, -11 % 5 == -1\\n return (t5 % 5 == 0) && (t2 % 2 == 0);\\n }\\n};\\n\\n/*\\n// --- Example Usage ---\\n#include <iostream>\\nint main() {\\n Solution sol;\\n std::cout << std::boolalpha; // Print bools as true/false\\n\\n std::cout << \\\"Input: 11 => Result: \\\" << sol.hasSameDigits(\\\"11\\\") << std::endl; // N=0, loop 0..0. d=(1-1)=0. t5=0*C(0,0)=0, t2=0*C(0,0)=0. True.\\n std::cout << \\\"Input: 12 => Result: \\\" << sol.hasSameDigits(\\\"12\\\") << std::endl; // N=0, loop 0..0. d=(1-2)=-1. t5=-1*C(0,0)=-1. False.\\n std::cout << \\\"Input: 123 => Result: \\\" << sol.hasSameDigits(\\\"123\\\") << std::endl; // N=1. loop 0..1.\\n // i=0: d=1-2=-1. t5+=-1*C(1,0)=-1. t2+=-1*C(1,0)=-1.\\n // i=1: d=2-3=-1. t5+=-1*C(1,1)=-1-1=-2. t2+=-1*C(1,1)=-1-1=-2.\\n // t5=-2%5 != 0. False.\\n std::cout << \\\"Input: 132 => Result: \\\" << sol.hasSameDigits(\\\"132\\\") << std::endl; // N=1. loop 0..1.\\n // i=0: d=1-3=-2. t5+=-2*C(1,0)=-2. t2+=-2*C(1,0)=-2.\\n // i=1: d=3-2=1. t5+ S=1*C(1,1)=-2+1=-1. t2+=1*C(1,1)=-2+1=-1.\\n // t5=-1%5 != 0. False.\\n std::cout << \\\"Input: 555 => Result: \\\" << sol.hasSameDigits(\\\"555\\\") << std::endl; // N=1. loop 0..1.\\n // i=0: d=5-5=0. t5=0, t2=0.\\n // i=1: d=5-5=0. t5=0, t2=0. True.\\n std::cout << \\\"Input: 2772 => Result: \\\" << sol.hasSameDigits(\\\"2772\\\") << std::endl; // N=2. loop 0..2. C(2,k)mod5: 1,2,1. C(2,k)mod2: 1,0,1.\\n // i=0: d=2-7=-5. t5+=-5*1=-5. t2+=-5*1=-5.\\n // i=1: d=7-7=0. t5+=0*2= -5. t2+=0*0= -5.\\n // i=2: d=7-2=5. t5+=5*1= -5+5=0. t2+=5*1= -5+5=0.\\n // t5=0%5==0. t2=0%2==0. True.\\n\\n\\n return 0;\\n}\\n*/\"], [32156, 0.158, \"typedef long long ll;\\nint get_mod_inv_10(int a){\\n for(int x=1;x<10;x++)\\n if(((x*a)%10)==1)\\n return x;\\n return -1;\\n};\\nint get_pow(int a, int p){\\n int res=0;\\n while((a%p)==0){\\n a/=p;\\n res++;\\n }\\n return res;\\n};\\nint remove_pow(int &a, int p){\\n int res=0;\\n while((a%p)==0){\\n a/=p;\\n res++;\\n }\\n return res;\\n};\\nint p_2[4]={2,4,8,6};\\nint power_2_mod_10(int p){\\n if(p==0)\\n return 1;\\n return p_2[(p-1)%4];\\n};\\nint power_5_mod_10(int p){\\n if(p==0)\\n return 1;\\n return 5;\\n};\\nclass Solution {\\n vector<ll> get_multiplier(int len){\\n if(len<3)\\n return vector<ll>(len,1);\\n vector<ll> res(len,1);\\n res[1]=len-1;\\n int prev=res[1];\\n int pow_2=remove_pow(prev,2);\\n int pow_5=remove_pow(prev,5);\\n res[1]%=10;\\n prev%=10;\\n int y=len-2;\\n for(int x=2;x<=(len-1)/2;x++){\\n int y_cpy=y;\\n int x_cpy=x;\\n pow_2+=(remove_pow(y_cpy,2)-remove_pow(x_cpy,2));\\n pow_5+=(remove_pow(y_cpy,5)-remove_pow(x_cpy,5));\\n prev=(prev*y_cpy*get_mod_inv_10(x_cpy))%10;\\n res[x]=(prev*power_2_mod_10(pow_2)*power_5_mod_10(pow_5))%10;\\n y--;\\n }\\n for(int x=len-1;x>(len-1)/2;x--){\\n res[x]=res[len-x-1];\\n }\\n return res;\\n };\\npublic:\\n bool hasSameDigits(string s) {\\n int len=s.size();\\n vector<ll> multiplier=get_multiplier(len-1);\\n // for(auto &a:multiplier)\\n // cout<<a<<\\\" \\\";\\n // cout<<endl;\\n int a=0,b=0;\\n for(int x=0;x<len-1;x++){\\n a=(a+(s[x]-'0')*multiplier[x])%10;\\n b=(b+(s[x+1]-'0')*multiplier[x])%10;\\n }\\n // cout<<a<<\\\" \\\"<<b;\\n return a==b;\\n }\\n};\"], [33073, 0.4739, \"template <int MOD> struct mint {\\n static const int mod = MOD;\\n int v;\\n explicit operator int() const {\\n return v;\\n } // explicit -> don't silently convert to int\\n mint() { v = 0; }\\n mint(int64_t _v) {\\n v = int((-MOD < _v && _v < MOD) ? _v : _v % MOD);\\n if (v < 0)\\n v += MOD;\\n }\\n friend bool operator==(const mint& a, const mint& b) { return a.v == b.v; }\\n friend bool operator!=(const mint& a, const mint& b) { return !(a == b); }\\n friend bool operator<(const mint& a, const mint& b) { return a.v < b.v; }\\n friend std::string to_string(mint a) { return std::to_string(a.v); }\\n\\n mint& operator+=(const mint& m) {\\n if ((v += m.v) >= MOD)\\n v -= MOD;\\n return *this;\\n }\\n mint& operator-=(const mint& m) {\\n if ((v -= m.v) < 0)\\n v += MOD;\\n return *this;\\n }\\n mint& operator*=(const mint& m) {\\n v = int((int64_t)v * m.v % MOD);\\n return *this;\\n }\\n mint& operator/=(const mint& m) { return (*this) *= inv(m); }\\n friend mint pow(mint a, int64_t p) {\\n mint ans = 1;\\n assert(p >= 0);\\n for (; p; p /= 2, a *= a)\\n if (p & 1)\\n ans *= a;\\n return ans;\\n }\\n friend mint inv(const mint& a) {\\n if (a.v == 0)\\n return 0;\\n assert(a.v != 0);\\n return pow(a, MOD - 2);\\n }\\n\\n mint operator-() const { return mint(-v); }\\n mint& operator++() { return *this += 1; }\\n mint& operator--() { return *this -= 1; }\\n friend mint operator+(mint a, const mint& b) { return a += b; }\\n friend mint operator-(mint a, const mint& b) { return a -= b; }\\n friend mint operator*(mint a, const mint& b) { return a *= b; }\\n friend mint operator/(mint a, const mint& b) { return a /= b; }\\n};\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n bool ans = 0;\\n int n = s.size();\\n std::vector<mint<2>> F2(n + 1);\\n std::vector<mint<5>> F5(n + 1);\\n F2[0] = 1;\\n F5[0] = 1;\\n for (int i = 1; i <= n; i++) {\\n F2[i] = F2[i - 1] * mint<2>(i);\\n F5[i] = F5[i - 1] * mint<5>(i);\\n }\\n auto C2 = [&](int k, int N) {\\n mint<2> v = 1;\\n while (k || N) {\\n mint<2> i = N;\\n mint<2> j = k;\\n if (i < j)\\n return mint<2>(0);\\n v *= (F2[i.v] / F2[j.v] / F2[i.v - j.v]);\\n k /= 2;\\n N /= 2;\\n }\\n return v;\\n };\\n auto C5 = [&](int k, int N) {\\n mint<5> v = 1;\\n while (k || N) {\\n mint<5> i = N;\\n mint<5> j = k;\\n if (i < j)\\n return mint<5>(0);\\n v *= (F5[i.v] / F5[j.v] / F5[i.v - j.v]);\\n k /= 5;\\n N /= 5;\\n }\\n return v;\\n };\\n mint<2> firstS2 = 0, secondS2 = 0;\\n mint<5> firstS5 = 0, secondS5 = 0;\\n for (int i = 0; i < n - 1; i++) {\\n firstS2 += (C2(i, n - 2) * mint<2>(s[i] - '0'));\\n firstS5 += (C5(i, n - 2) * mint<5>(s[i] - '0'));\\n }\\n for (int i = 1; i < n; i++) {\\n secondS2 += (C2(i - 1, n - 2) * mint<2>(s[i] - '0'));\\n secondS5 += (C5(i - 1, n - 2) * mint<5>(s[i] - '0'));\\n }\\n ans = (firstS2.v == secondS2.v) && (firstS5.v == secondS5.v);\\n std::cout << firstS5.v << \\\" \\\" << secondS5.v;\\n return ans;\\n }\\n};\"], [33991, 0.4739, \"#include <string>\\n#include <vector>\\n#include <numeric>\\n\\nusing namespace std;\\n\\n// Global cache for precomputed binomial coefficients C(n, k) mod 5 for n < 5.\\n// This avoids redundant computations within the same test run or across multiple test cases if the instance is reused.\\nint C5[5][5];\\nbool C5_precomputed = false; // Flag to check if the cache is initialized\\n\\n/**\\n * @brief Precomputes binomial coefficients C(n, k) modulo 5 for small n (0 to 4).\\n * Uses Pascal's identity: C(n, k) = C(n-1, k-1) + C(n-1, k).\\n * The results are stored in the global cache C5.\\n */\\nvoid precompute_C5() {\\n // If already computed, do nothing.\\n if (C5_precomputed) return; \\n \\n // Initialize the cache table with 0s.\\n for(int i=0; i<5; ++i) {\\n for(int j=0; j<5; ++j) {\\n C5[i][j] = 0;\\n }\\n }\\n\\n // Compute C(i, j) mod 5 using Pascal's identity.\\n for (int i = 0; i < 5; ++i) {\\n C5[i][0] = 1; // Base case: C(i, 0) = 1\\n for (int j = 1; j <= i; ++j) {\\n // Pascal's Identity: C(i, j) = (C(i-1, j-1) + C(i-1, j)) mod 5\\n C5[i][j] = (C5[i-1][j-1] + C5[i-1][j]) % 5;\\n }\\n }\\n C5_precomputed = true; // Set flag indicating cache is ready.\\n}\\n\\n/**\\n * @brief Computes N choose k modulo 2.\\n * Based on Lucas's Theorem for p=2, C(N, k) is odd (1 mod 2) if and only if\\n * whenever a bit is 1 in the binary representation of k, the corresponding bit is also 1 in N.\\n * This condition is equivalent to checking if k is a \\\"submask\\\" of N, i.e., (k & N) == k.\\n * @param N The total number of items.\\n * @param k The number of items to choose.\\n * @return C(N, k) mod 2. Returns 0 if k < 0 or k > N.\\n */\\nint ncr_mod2(long long N, long long k) {\\n // Check for invalid arguments k < 0 or k > N.\\n if (k < 0 || k > N) return 0;\\n // Check the submask condition using bitwise AND.\\n return ((k & N) == k) ? 1 : 0;\\n}\\n\\n/**\\n * @brief Computes N choose k modulo 5 using Lucas's Theorem.\\n * Lucas's Theorem allows computing C(N, k) mod p by using the base-p digits of N and k.\\n * C(N, k) = Product[ C(Ni, ki) ] mod p, where Ni, ki are base-p digits.\\n * Uses precomputed values C(n, k) mod 5 for n < 5 stored in C5 cache.\\n * Includes optimization C(N, k) = C(N, N-k).\\n * @param N The total number of items.\\n * @param k The number of items to choose.\\n * @return C(N, k) mod 5. Returns 0 if k < 0 or k > N.\\n */\\nint ncr_mod5(long long N, long long k) {\\n // Validity check\\n if (k < 0 || k > N) return 0; \\n\\n // Utilize symmetry property C(N, k) = C(N, N-k). Process the smaller k.\\n if (k > N / 2) k = N - k; \\n \\n // Base case: C(N, 0) = 1. Also handles C(N, N) due to the symmetry optimization.\\n if (k == 0) return 1; \\n \\n long long current_N = N;\\n long long current_k = k;\\n long long res = 1; // Accumulator for the product of C(Ni, ki) mod 5\\n \\n // Iterate through the digits of N and k in base 5\\n while (current_N > 0 || current_k > 0) {\\n long long Ni = current_N % 5; // Last base-5 digit of N\\n long long ki = current_k % 5; // Last base-5 digit of k\\n \\n // If k's digit > N's digit, C(Ni, ki) = 0, so C(N, k) mod 5 is 0.\\n if (ki > Ni) return 0; \\n \\n // Multiply result by C(Ni, ki) mod 5 using precomputed table C5.\\n // If ki = 0, C(Ni, 0) = 1, so multiplication is unnecessary.\\n if (ki > 0) {\\n // Access precomputed values from C5 table. Ni and ki are in [0, 4].\\n res = (res * C5[Ni][ki]) % 5;\\n // Optimization: If result becomes 0 at any step, the final result is 0.\\n if (res == 0) return 0; \\n }\\n\\n // Move to the next higher-order digits (equivalent to integer division by 5).\\n current_N /= 5;\\n current_k /= 5;\\n }\\n return res; // The final result modulo 5\\n}\\n\\n/**\\n * @brief Computes N choose k modulo 10 using the Chinese Remainder Theorem (CRT).\\n * Combines the results from ncr_mod2 and ncr_mod5.\\n * We need X such that X = C(N, k) mod 2 and X = C(N, k) mod 5.\\n * The CRT solution gives X = (6 * mod5 - 5 * mod2) mod 10.\\n * @param N The total number of items.\\n * @param k The number of items to choose.\\n * @return C(N, k) mod 10. Returns 0 if k < 0 or k > N.\\n */\\nint ncr_mod10(long long N, long long k) {\\n // Basic validity check\\n if (k < 0 || k > N) return 0;\\n\\n // Compute C(N, k) modulo 2 and modulo 5\\n int mod2 = ncr_mod2(N, k);\\n int mod5 = ncr_mod5(N, k);\\n \\n // If C(N, k) is divisible by both 2 and 5, it must be divisible by 10.\\n if (mod2 == 0 && mod5 == 0) return 0;\\n\\n // Apply the CRT formula: X = (6 * mod5 - 5 * mod2) mod 10\\n int result = (6 * mod5 - 5 * mod2);\\n \\n // Ensure the result is non-negative and within the range [0, 9].\\n // The C++ % operator can yield negative results for negative dividends.\\n return (result % 10 + 10) % 10; \\n}\\n\\n\\nclass Solution {\\npublic:\\n /**\\n * @brief Checks if the final two digits of the string after repeated operations are the same.\\n * The final two digits are determined by the formula derived from the process,\\n * which involves binomial coefficients C(n-2, j) mod 10.\\n * @param s The initial string of digits.\\n * @return True if the final two digits are identical, False otherwise.\\n */\\n bool hasSameDigits(std::string s) {\\n int n = s.length();\\n // The problem constraints state n >= 3.\\n\\n // Ensure the C5 cache for ncr_mod5 calculation is initialized.\\n precompute_C5(); \\n\\n // The number of operations to reach length 2 is n-2.\\n // The final digits depend on binomial coefficients C(N, j) where N = n-2.\\n long long N = n - 2; \\n \\n // Convert the input string digits into a vector of integers for easier processing.\\n std::vector<int> a(n);\\n for (int i = 0; i < n; ++i) {\\n a[i] = s[i] - '0';\\n }\\n \\n // Compute and store the binomial coefficients C(N, j) mod 10 for j from 0 to N.\\n // This avoids recomputing the same coefficients multiple times.\\n std::vector<int> C(N + 1);\\n for (long long j = 0; j <= N; ++j) {\\n C[j] = ncr_mod10(N, j);\\n }\\n\\n // Calculate the first of the final two digits (S0).\\n // S0 = (Sum_{j=0 to N} C(N, j) * a[j]) mod 10\\n int S0 = 0;\\n for (long long j = 0; j <= N; ++j) {\\n // Use explicit (long long) cast for product to guard against potential intermediate overflow,\\n // although C[j]*a[j] is at most 81 which fits in int. It's safer practice.\\n S0 = (S0 + (long long)C[j] * a[j]) % 10;\\n }\\n\\n // Calculate the second of the final two digits (S1).\\n // S1 = (Sum_{j=0 to N} C(N, j) * a[j+1]) mod 10\\n int S1 = 0;\\n for (long long j = 0; j <= N; ++j) {\\n // Index a[j+1] is valid. Since j ranges up to N = n-2, j+1 ranges up to n-1.\\n // The vector `a` has size `n`, indexed 0 to n-1.\\n S1 = (S1 + (long long)C[j] * a[j+1]) % 10;\\n }\\n \\n // The function should return true if the two final digits S0 and S1 are identical.\\n return S0 == S1;\\n }\\n};\"], [34908, 0.158, \"class Solution {\\npublic:\\n int binpow(int a, int b){\\n int res = 1;\\n for(int i = 0; i < b; i++) res = res * a % 5;\\n return res;\\n }\\n int c(int k, vector<int>& pw, vector<int>& fact, vector<vector<int>>& dp){\\n int n = fact.size() - 1;\\n int res = fact[n] * binpow(fact[k], 3) * binpow(fact[n - k], 3) % 5;\\n if(pw[k] + pw[n - k] < pw[n]) res = 0;\\n int mod2 = (n & k) == k;\\n return dp[mod2][res];\\n }\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n vector<int> pw(n - 1, 0), fact(n - 1, 1);\\n vector<vector<int>> dp(2, vector<int>(5));\\n for(int i = 0; i < 10; i++) dp[i & 1][i % 5] = i;\\n for(int i = 1; i + 1 < n; i++){\\n pw[i] += pw[i - 1];\\n int j = i;\\n while(j % 5 == 0){\\n j /= 5;\\n pw[i]++;\\n }\\n fact[i] = fact[i - 1] * j % 5;\\n }\\n int res = 0;\\n for(int i = 0; i + 1 < s.size(); i++) res = (res + c(i, pw, fact, dp) * (s[i] - '0')) % 10;\\n for(int i = 1; i < s.size(); i++) res = (1000 + res - c(i - 1, pw, fact, dp) * (s[i] - '0')) % 10;\\n return !res;\\n }\\n};\"], [35826, 0.158, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n unsigned int n = s.size();\\n vector<int> comb5(n-1);\\n vector<int> comb2(n-1);\\n comb5[0]=1;\\n comb2[0]=1;\\n comb5[1]=(n-2)%5;\\n comb2[1]=(n-2)%2;\\n function<int(int)> factorial = [&factorial](int n)\\n {\\n if (n==0)return 1;\\n return n*factorial(n-1);\\n };\\n auto smallNcK = [&factorial](int n,int k)\\n {\\n int num = factorial(n);\\n int den = factorial(n-k)*factorial(k);\\n return (num/den)%5;\\n };\\n function<int(int,int)> nCk = [&nCk,&smallNcK](int n, int k)\\n {\\n if (n==k) return 1;\\n int ni = n%5;\\n int ki = k%5;\\n if (ki>ni) return 0;\\n return (nCk(n/5,k/5)*smallNcK(ni,ki))%5;\\n };\\n int num2 = countr_zero(n-2);\\n unsigned int num = n-3;\\n for (unsigned int i=2;i<n-1;i++)\\n {\\n num2+=countr_zero(num)-countr_zero(i);\\n if (!num2)comb2[i]=1;\\n comb5[i]=nCk(n-2,i);\\n num--;\\n }\\n int comb[2][5];\\n comb[0][0]=0;\\n comb[1][1]=1;\\n comb[0][2]=2;\\n comb[1][3]=3;\\n comb[0][4]=4;\\n comb[1][0]=5;\\n comb[0][1]=6;\\n comb[1][2]=7;\\n comb[0][3]=8;\\n comb[1][4]=9;\\n\\n int first = 0;\\n int second = 0;\\n for (int i=0;i<n-1;i++)\\n {\\n first+=(comb[comb2[i]][comb5[i]]*(s[i]-'0'))%10;\\n first%=10;\\n second+=(comb[comb2[i]][comb5[i]]*(s[i+1]-'0'))%10;\\n second%=10;\\n }\\n return first==second;\\n }\\n};\"], [36743, 0.158, \"#pragma GCC optimize(\\\"O3\\\", \\\"unroll-loops\\\")\\n\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n unsigned int n = s.size();\\n vector<int> comb5(n-1);\\n vector<int> comb2(n-1);\\n comb5[0]=1;\\n comb2[0]=1;\\n comb5[1]=(n-2)%5;\\n comb2[1]=(n-2)%2;\\n function<int(int)> factorial = [&factorial](int n)\\n {\\n if (n==0)return 1;\\n return n*factorial(n-1);\\n };\\n auto smallNcK = [&factorial](int n,int k)\\n {\\n int num = factorial(n);\\n int den = factorial(n-k)*factorial(k);\\n return (num/den)%5;\\n };\\n function<int(int,int)> nCk = [&nCk,&smallNcK](int n, int k)\\n {\\n if (n==k) return 1;\\n int ni = n%5;\\n int ki = k%5;\\n if (ki>ni) return 0;\\n return (nCk(n/5,k/5)*smallNcK(ni,ki))%5;\\n };\\n int num2 = countr_zero(n-2);\\n unsigned int num = n-3;\\n for (unsigned int i=2;i<n-1;i++)\\n {\\n num2+=countr_zero(num)-countr_zero(i);\\n if (!num2)comb2[i]=1;\\n comb5[i]=nCk(n-2,i);\\n num--;\\n }\\n int comb[2][5];\\n comb[0][0]=0;\\n comb[1][1]=1;\\n comb[0][2]=2;\\n comb[1][3]=3;\\n comb[0][4]=4;\\n comb[1][0]=5;\\n comb[0][1]=6;\\n comb[1][2]=7;\\n comb[0][3]=8;\\n comb[1][4]=9;\\n\\n int first = 0;\\n int second = 0;\\n for (int i=0;i<n-1;i++)\\n {\\n first+=(comb[comb2[i]][comb5[i]]*(s[i]-'0'))%10;\\n first%=10;\\n second+=(comb[comb2[i]][comb5[i]]*(s[i+1]-'0'))%10;\\n second%=10;\\n }\\n return first==second;\\n }\\n};\"], [37661, 0.158, \"class Solution {\\npublic:\\nconst int mod=10;\\nint power(int a, int b, int m) {\\n int res = 1;\\n while (b) {\\n if (b & 1) res = (res * a) % m;\\n a = (a * a) % m;\\n b >>= 1;\\n }\\n return res;\\n}\\n\\nint modInverse(int a, int m) {\\n return power(a, m - 2, m);\\n}\\n\\nint factMod(int n, int p) {\\n int res = 1;\\n for (int i = 1; i <= n; i++)\\n if (i % p) res = (res * i) % p;\\n return res;\\n}\\n\\nint nCrModP(int n, int r, int p) {\\n if (r > n) return 0;\\n if (n == r || r == 0) return 1;\\n return (factMod(n, p) * modInverse(factMod(r, p), p) % p * modInverse(factMod(n - r, p), p) % p) % p;\\n}\\n\\nint lucas(int n, int r, int p) {\\n if (r == 0) return 1;\\n return (lucas(n / p, r / p, p) * nCrModP(n % p, r % p, p)) % p;\\n}\\n\\nint chinese_remainder(int a1, int m1, int a2, int m2) {\\n int inv1 = modInverse(m1, m2), inv2 = modInverse(m2, m1);\\n return (a1 * m2 % (m1 * m2) * inv2 + a2 * m1 % (m1 * m2) * inv1) % (m1 * m2);\\n}\\n\\nint nCrMod10(int n, int r) {\\n int nCr2 = lucas(n, r, 2);\\n int nCr5 = lucas(n, r, 5);\\n return chinese_remainder(nCr2, 2, nCr5, 5);\\n}\\n bool hasSameDigits(string s) {\\n int val1=0,val2=0;\\n int n=s.size();\\n vector<int>bins;\\n for(int r=0;r<=n-2;r++){\\n bins.push_back(nCrMod10(n-2,r));\\n }\\n for(int i=0;i<n-1;i++){\\n val1=(val1+((s[i]-'0')*bins[i])%mod)%mod;\\n val2=(val2+((s[i+1]-'0')*bins[i]%mod))%mod;\\n }\\n return val1==val2;\\n }\\n};\"], [38578, 0.158, \"class Solution {\\npublic:\\n \\n\\n vector<vector<int>> precomputeSmallBinomials(int m) {\\n vector<vector<int>> tab(m, vector<int>(m, 0));\\n for (int k = 0; k < m; ++k) tab[0][k] = (k == 0);\\n for (int n = 0; n < m; ++n) tab[n][0] = 1;\\n for (int n = 1; n < m; ++n) {\\n for (int k = 1; k < m; ++k) {\\n tab[n][k] = tab[n-1][k] + tab[n-1][k-1]; \\n }\\n }\\n return tab;\\n }\\n\\n vector<vector<int>> binomials = precomputeSmallBinomials(5);\\n\\n bool hasSameDigits(string s) {\\n\\n \\n\\n vector digits = extractDigits(s);\\n createDifference(digits);\\n return isZeroMod(digits, 2) && isZeroMod(digits, 5);\\n }\\n\\n bool isZeroMod(vector<int> & digits, int p) {\\n int result = 0;\\n int n = digits.size();\\n for (int k = 0; k < n; ++k) {\\n result = (result + digits[k]%p*binomial(n - 1, k,p))%p;\\n }\\n return result == 0;\\n }\\n\\n int binomial(int n, int k, int p) {\\n int r = 1;\\n while (n > 0) {\\n r = r * binomials[n%p][k%p]%p;\\n n/=p;\\n k/=p;\\n }\\n return r;\\n }\\n\\n vector<int> extractDigits(string &s) {\\n vector<int> digits;\\n for (char ch : s) {\\n digits.push_back(ch - '0');\\n }\\n return digits;\\n }\\n\\n void createDifference(vector<int> &digits) {\\n for (int i = 0; i < digits.size() - 1; ++i) {\\n digits[i] -= digits[i + 1];\\n } \\n digits.pop_back();\\n }\\n};\"], [39496, 0.474, \"class Solution {\\npublic:\\n\\n int nChooseR(int const n, int const r)\\n {\\n if (n < r) return 0;\\n int product = 1;\\n for (int i = r + 1; i <= n; ++i)\\n {\\n product *= i;\\n }\\n for (int i = 1; i <= n - r; ++i)\\n {\\n product /= i;\\n }\\n return product;\\n }\\n\\n std::vector<int> generatePascalRow(int const n, int const primeModulus)\\n { \\n std::vector<int> pascal;\\n pascal.reserve(n);\\n for (int i = 0; i < n; ++i) pascal.push_back(1);\\n int r;\\n for (r = 1; r < n - 1; ++r)\\n {\\n int modulusProduct = 1;\\n //(n C r) == product of (ni C ri) where ni and ri are the digits of and r under p\\n int tempN = n - 1;\\n int tempR = r;\\n while (tempN > 0 && tempR > 0)\\n {\\n modulusProduct *= nChooseR(tempN % primeModulus, tempR % primeModulus);\\n tempR /= primeModulus;\\n tempN /= primeModulus;\\n }\\n pascal[r] = modulusProduct % primeModulus;\\n }\\n return pascal;\\n }\\n\\n bool reductionEquivalentUnderPrimeModulus(std::vector<int> const & digits, int const primeModulus)\\n {\\n auto nthPascal = generatePascalRow(digits.size() - 1, primeModulus);\\n int leftDigit = 0;\\n int rightDigit = 0;\\n for (int i = 0; i < digits.size() - 1; ++i)\\n {\\n leftDigit = (leftDigit + digits[i] * nthPascal[i]) % primeModulus;\\n rightDigit = (rightDigit + digits[i + 1] * nthPascal[i]) % primeModulus;\\n }\\n return leftDigit == rightDigit;\\n }\\n\\n bool hasSameDigits(string s)\\n {\\n std::vector<int> digits;\\n digits.reserve(s.size());\\n for (char const c : s)\\n {\\n digits.push_back(c - '0');\\n }\\n return reductionEquivalentUnderPrimeModulus(digits, 2) && reductionEquivalentUnderPrimeModulus(digits, 5);\\n }\\n};\"], [40413, 1.1059, \"class Solution {\\n int binCoe(int n, int r) {\\n if (r > n) return 0;\\n int res = 1;\\n for (int f = 1; f <= n; f++) res *= f;\\n for (int f = 1; f <= r; f++) res /= f;\\n for (int f = 1; f <= n-r; f++) res /= f;\\n return res;\\n }\\n\\n bool resMod(vector<int> nums, int mod) {\\n int res = 0;\\n for (int i = 0; i < nums.size(); i++) {\\n int nCr = 1, n = nums.size()-1, r = i;\\n for (; r; n /= mod, r /= mod) {\\n nCr = nCr*binCoe(n%mod, r%mod);\\n }\\n res = (res+nCr*nums[i])%mod;\\n }\\n return res == 0;\\n }\\npublic:\\n bool hasSameDigits(string s) {\\n int len = s.length();\\n vector<int> diff(len-1);\\n for (int i = 0; i < len-1; i++) {\\n diff[i] = (s[i]-s[i+1]+10)%10;\\n } \\n return resMod(diff, 2) && resMod(diff, 5);\\n }\\n};\"], [41331, 0.316, \"class Solution {\\npublic:\\n bool hasSameDigits(const string &s) {\\n int n = s.size(), k = n - 2;\\n vector<int> cnt5(k+1), fact5(k+1), invFact5(k+1);\\n cnt5[0] = 0; fact5[0] = 1;\\n for (int i = 1; i <= k; ++i) {\\n int t = i, c = 0;\\n while (t % 5 == 0) { t /= 5; ++c; }\\n cnt5[i] = cnt5[i-1] + c;\\n fact5[i] = fact5[i-1] * (t % 5) % 5;\\n }\\n static int inv5[5] = {0,1,3,2,4};\\n invFact5[k] = inv5[fact5[k]];\\n for (int i = k; i >= 1; --i) {\\n int t = i;\\n while (t % 5 == 0) t /= 5;\\n invFact5[i-1] = invFact5[i] * (t % 5) % 5;\\n }\\n\\n int S2 = 0, S5 = 0;\\n int half = (n - 1) / 2;\\n for (int j = 0; j <= half; ++j) {\\n int a = s[j] - '0', b = s[n-1-j] - '0';\\n bool c2 = (j == 0)\\n ? true\\n : ( ((j & (k-j))==0) ^ (((j-1)&(k-(j-1)))==0) );\\n int diff2 = (((a&1)-(b&1)+2)&1);\\n S2 ^= (c2 && diff2);\\n\\n int e5 = cnt5[k] - cnt5[j] - cnt5[k-j];\\n int C5 = e5>0 ? 0 : (int)((long long)fact5[k]*invFact5[j]%5*invFact5[k-j]%5);\\n int ep5 = j>0 ? cnt5[k] - cnt5[j-1] - cnt5[k-j+1] : 0;\\n int P5 = (j>0 && ep5==0)\\n ? (int)((long long)fact5[k]*invFact5[j-1]%5*invFact5[k-j+1]%5)\\n : 0;\\n int d5 = (C5 - P5 + 5) % 5;\\n int diff5 = (a - b) % 5; if (diff5<0) diff5 += 5;\\n S5 = (S5 + d5 * diff5) % 5;\\n }\\n return S2==0 && S5==0;\\n }\\n};\"], [42248, 0.158, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n precalc(n);\\n int sum = 0;\\n for (int i = 0; i <= n - 2; ++i) {\\n sum += (s[i] - s[i + 1]) * C(n - 2, i);\\n sum %= 10;\\n }\\n return sum == 0;\\n }\\n\\nprivate:\\n\\n vector<int> rest;\\n vector<int> power2;\\n vector<int> power5;\\n\\n void precalc(int n) {\\n rest.resize(n);\\n power2.resize(n);\\n power5.resize(n);\\n rest[0] = 1;\\n for (int k = 1; k < n; ++k) {\\n int t = k;\\n power2[k] = power2[k - 1];\\n while (t % 2 == 0) {\\n ++power2[k];\\n t /= 2;\\n }\\n power5[k] = power5[k - 1];\\n while (t % 5 == 0) {\\n ++power5[k];\\n t /= 5;\\n }\\n rest[k] = rest[k - 1] * t % 10;\\n }\\n }\\n\\n int binpow(int x, int p) {\\n if (p == 0) {\\n return 1;\\n }\\n if (p & 1) {\\n return binpow(x, p - 1) * x % 10;\\n }\\n return binpow(x * x % 10, p / 2);\\n }\\n\\n int C(int n, int k) {\\n int ans = binpow(2, power2[n] - power2[n - k] - power2[k]);\\n if (power5[n] - power5[n - k] - power5[k] > 0) {\\n ans *= 5;\\n }\\n int phi = 4;\\n ans *= rest[n] * binpow(rest[n - k] * rest[k], phi - 1);\\n ans %= 10;\\n return ans;\\n }\\n};\"], [43166, 0.474, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n precalc(n);\\n int sum = 0;\\n for (int i = 0; i <= n - 2; ++i) {\\n sum += (s[i] - s[i + 1]) * C(n - 2, i);\\n sum %= 10;\\n }\\n return sum == 0;\\n }\\n\\nprivate:\\n\\n vector<int> rest;\\n vector<int> power2;\\n vector<int> power5;\\n\\n void precalc(int n) {\\n rest.resize(n);\\n power2.resize(n);\\n power5.resize(n);\\n rest[0] = 1;\\n for (int k = 1; k < n; ++k) {\\n int t = k;\\n power2[k] = power2[k - 1];\\n while (t % 2 == 0) {\\n ++power2[k];\\n t /= 2;\\n }\\n power5[k] = power5[k - 1];\\n while (t % 5 == 0) {\\n ++power5[k];\\n t /= 5;\\n }\\n rest[k] = rest[k - 1] * t % 10;\\n }\\n }\\n\\n int binpow(int x, int p) {\\n if (p == 0) {\\n return 1;\\n }\\n if (p & 1) {\\n return binpow(x, p - 1) * x % 10;\\n }\\n return binpow(x * x % 10, p / 2);\\n }\\n\\n int C(int n, int k) {\\n int ans = binpow(2, power2[n] - power2[n - k] - power2[k]);\\n ans *= binpow(5, power5[n] - power5[n - k] - power5[k]);\\n int phi = 4;\\n ans *= rest[n] * binpow(rest[n - k], phi - 1) * binpow(rest[k], phi - 1);\\n ans %= 10;\\n return ans;\\n }\\n};\"], [44083, 0.79, \"class Solution {\\npublic:\\n // Helper: count the number of times p divides x.\\n int countFactors(int x, int p) {\\n int cnt = 0;\\n while (x % p == 0) {\\n cnt++;\\n x /= p;\\n }\\n return cnt;\\n }\\n \\n // Since our \\\"reduced\\\" numbers will be among {1,3,7,9}, we can precompute modular inverses mod 10.\\n int modInverse(int a) {\\n // For a in {1,3,7,9}\\n if(a == 1) return 1;\\n if(a == 3) return 7; // 3*7=21\\u22611 mod10\\n if(a == 7) return 3;\\n if(a == 9) return 9; // 9*9=81\\u22611 mod10\\n return 1; // default, should not happen\\n }\\n \\n bool hasSameDigits(string s) {\\n int n = s.size();\\n int n2 = n - 2; // we will be computing binomials for row (n-2)\\n \\n // Precompute tot2 and tot5 for factorials 0! ... (n2)!\\n vector<int> tot2(n2 + 1, 0), tot5(n2 + 1, 0);\\n tot2[0] = tot5[0] = 0;\\n for (int i = 1; i <= n2; i++) {\\n tot2[i] = tot2[i-1] + countFactors(i, 2);\\n tot5[i] = tot5[i-1] + countFactors(i, 5);\\n }\\n \\n // Precompute reduced factorial F[x] = (x! with all factors 2 and 5 removed) mod 10.\\n vector<int> F(n2 + 1, 0);\\n F[0] = 1;\\n for (int i = 1; i <= n2; i++) {\\n int tmp = i;\\n while (tmp % 2 == 0) tmp /= 2;\\n while (tmp % 5 == 0) tmp /= 5;\\n F[i] = (F[i-1] * (tmp % 10)) % 10;\\n }\\n \\n // Now we compute the sum S = sum_{i=0}^{n2} (C(n2,i) * (s[i]-s[i+1])) mod 10.\\n int S = 0;\\n // i goes from 0 to n2 (n2 = n-2) so that s[i+1] is valid (last index is n-1).\\n for (int i = 0; i <= n2; i++) {\\n // Compute binom = C(n2, i) mod 10.\\n int exp2 = tot2[n2] - ((i <= n2 ? tot2[i] : 0)) - tot2[n2 - i];\\n int exp5 = tot5[n2] - ((i <= n2 ? tot5[i] : 0)) - tot5[n2 - i];\\n int coeff = 0;\\n if(exp2 >= 1 && exp5 >= 1) {\\n // At least one full factor of 10 divides the number.\\n coeff = 0;\\n } else {\\n int extra = 1;\\n if(exp2 > 0 && exp5 == 0) {\\n // Multiply by 2^(exp2) mod 10. (Cycle of 2,4,8,6)\\n int cycle[4] = {2,4,8,6};\\n extra = cycle[(exp2 - 1) % 4];\\n }\\n else if(exp5 > 0 && exp2 == 0) {\\n // For any positive exponent of 5, 5^x mod10 is 5.\\n extra = 5;\\n }\\n // non2_5 part computed from reduced factorial F.\\n // C(n2, i) = F[n2] / (F[i] * F[n2-i]) (all computed mod 10, numbers here are coprime with 10)\\n int non2_5 = F[n2];\\n non2_5 = (non2_5 * modInverse(F[i])) % 10;\\n non2_5 = (non2_5 * modInverse(F[n2 - i])) % 10;\\n coeff = (non2_5 * extra) % 10;\\n }\\n // Compute difference between two consecutive digits of s.\\n int d = ((s[i] - '0') - (s[i+1] - '0')) % 10;\\n if(d < 0) d += 10;\\n S = (S + (coeff * d)) % 10;\\n }\\n \\n return S % 10 == 0;\\n }\\n};\"], [45001, 0.158, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n vector<int> digits;\\n for (char c : s) {\\n digits.push_back(c - '0');\\n }\\n int m = digits.size() - 2;\\n vector<int> coeff(m + 1);\\n for (int k = 0; k <= m; ++k) {\\n int a = lucas_mod2(m, k);\\n int b = lucas_mod5(m, k);\\n coeff[k] = crt(a, b);\\n }\\n int digit1 = 0;\\n for (int i = 0; i <= m; ++i) {\\n digit1 = (digit1 + digits[i] * coeff[i]) % 10;\\n }\\n digit1 %= 10;\\n int digit2 = 0;\\n for (int i = 1; i <= m + 1; ++i) {\\n int k = i - 1;\\n digit2 = (digit2 + digits[i] * coeff[k]) % 10;\\n }\\n digit2 %= 10;\\n return digit1 == digit2;\\n }\\n\\nprivate:\\n static int lucas_mod2(int n, int k) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int ni = n % 2;\\n int ki = k % 2;\\n if (ki > ni) return 0;\\n res = (res * 1) % 2;\\n n /= 2;\\n k /= 2;\\n }\\n return res;\\n }\\n\\n static int lucas_mod5(int n, int k) {\\n static const int table5[5][5] = {\\n {1}, \\n {1, 1}, \\n {1, 2, 1}, \\n {1, 3, 3, 1}, \\n {1, 4, 1, 4, 1} \\n };\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int ni = n % 5;\\n int ki = k % 5;\\n if (ki > ni) return 0;\\n res = (res * table5[ni][ki]) % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return res;\\n }\\n\\n static int crt(int a, int b) {\\n static const int crt_table[2][5] = {\\n {0, 6, 2, 8, 4}, \\n {5, 1, 7, 3, 9} \\n };\\n return crt_table[a][b];\\n }\\n};\"], [45918, 0.158, \"class Solution {\\nprivate:\\n vector<vector<int>> dp;\\n\\n int nCrModDP(int n, int r, int mod) {\\n if (dp[n][r] != -1) return dp[n][r];\\n vector<int> C(r + 1, 0);\\n C[0] = 1;\\n for (int i = 1; i <= n; ++i) {\\n for (int j = min(i, r); j > 0; --j) {\\n C[j] = (C[j] + C[j - 1]) % mod;\\n }\\n }\\n dp[n][r] = C[r];\\n return dp[n][r];\\n }\\n\\n int nCr(int n, int r, int mod) {\\n if (r == 0) return 1;\\n int ni = n % mod;\\n int ri = r % mod;\\n return (nCr(n / mod, r / mod, mod) * nCrModDP(ni, ri, mod)) % mod;\\n }\\n\\n bool checkSameDigits(const string& s, int mod) {\\n int n = s.length();\\n vector<int> vals;\\n for (int i = 0; i < n - 1; ++i) {\\n vals.push_back(nCr(n - 2, i, mod));\\n }\\n vals.push_back(0);\\n\\n int leftVal = 0, rightVal = 0;\\n\\n for (int i = 0; i < n; ++i) {\\n int val = s[i] - '0';\\n leftVal = (leftVal + val * vals[i]) % mod;\\n }\\n\\n reverse(vals.begin(), vals.end());\\n for (int i = 0; i < n; ++i) {\\n int val = s[i] - '0';\\n rightVal = (rightVal + val * vals[i]) % mod;\\n }\\n\\n return leftVal == rightVal;\\n }\\n\\npublic:\\n Solution() : dp(5, vector<int>(5, -1)) {}\\n\\n bool hasSameDigits(const string& s) {\\n return checkSameDigits(s, 2) && checkSameDigits(s, 5);\\n }\\n};\"], [46836, 0.158, \"class Solution {\\npublic:\\n vector<int> f5, f2, c5, c2;\\n int ncr2(int n, int r)\\n {\\n int x = c2[n] - c2[r] - c2[n - r];\\n return x ? 0 : f2[n];\\n }\\n int ncr5(int n, int r)\\n {\\n int x = c5[n] - c5[r] - c5[n - r];\\n int d1 = (f5[r] * f5[r] * f5[r]) % 5, d2 = (f5[n - r] * f5[n - r] * f5[n - r]) % 5;\\n return x ? 0 : (f5[n] * d1 * d2) % 5;\\n }\\n int crt(int x, int y)\\n {\\n for(int i = 0 ; i < 10 ; i ++)\\n if(i % 5 == x && i % 2 == y) return i;\\n return 0;\\n }\\n bool hasSameDigits(string s) {\\n int n = s.size(), l = 0, r = 0;\\n f5.resize(n + 1); f2.resize(n + 1); f5[0] = f2[0] = 1;\\n c2.resize(n + 1, 0); c5.resize(n + 1, 0);\\n for(int i = 1 ; i <= n ; i ++)\\n {\\n int x = 1 , y = 1;\\n for(int j = 2 ; i % j == 0 ; j *= 2)\\n {\\n c2[i] ++;\\n x = j;\\n }\\n for(int j = 5 ; i % j == 0 ; j *= 5)\\n {\\n c5[i] ++;\\n y = j;\\n }\\n f5[i] = (f5[i - 1] * i / y) % 5; f2[i] = (f2[i - 1] * i / x) % 2 ;\\n c2[i] += c2[i - 1]; c5[i] += c5[i - 1];\\n }\\n for(int i = 0 ; i <= n - 2 ; i ++)\\n {\\n int x = crt(ncr5(n - 2, i),ncr2(n - 2, i));\\n l = (l + x * (s[i] - '0')) % 10;\\n r = (r + x * (s[n - 1 - i] - '0')) % 10;\\n }\\n return l == r;\\n }\\n};\"], [47753, 0.316, \"class Solution {\\npublic:\\n vector<int> f5, f2, c5, c2;\\n int ncr2(int n, int r)\\n {\\n int x = c2[n] - c2[r] - c2[n - r];\\n return x ? 0 : f2[n];\\n }\\n int ncr5(int n, int r)\\n {\\n int x = c5[n] - c5[r] - c5[n - r];\\n int d1 = (f5[r] * f5[r] * f5[r]) % 5, d2 = (f5[n - r] * f5[n - r] * f5[n - r]) % 5;\\n return x ? 0 : (f5[n] * d1 * d2) % 5;\\n }\\n int crt(int x, int y)\\n {\\n for(int i = 0 ; i < 10 ; i ++)\\n if(i % 5 == x && i % 2 == y) return i;\\n return 0;\\n }\\n bool hasSameDigits(string s) {\\n int n = s.size(), l = 0, r = 0;\\n f5.resize(n + 1); f2.resize(n + 1); f5[0] = f2[0] = 1;\\n c2.resize(n + 1, 0); c5.resize(n + 1, 0);\\n for(int i = 1 ; i <= n ; i ++)\\n {\\n int x = 1 , y = 1;\\n for(int j = 2 ; i % j == 0 ; j *= 2)\\n {\\n c2[i] ++;\\n x = j;\\n }\\n for(int j = 5 ; i % j == 0 ; j *= 5)\\n {\\n c5[i] ++;\\n y = j;\\n }\\n f5[i] = (f5[i - 1] * i / y) % 5; f2[i] = (f2[i - 1] * i / x) % 2 ;\\n c2[i] += c2[i - 1]; c5[i] += c5[i - 1];\\n }\\n for(int i = 0 ; i <= n - 2 ; i ++)\\n {\\n int x = crt(ncr5(n - 2, i), ncr2(n - 2, i));\\n l = (l + x * (s[i] - '0')) % 10;\\n r = (r + x * (s[n - 1 - i] - '0')) % 10;\\n }\\n return l == r;\\n }\\n};\"], [48671, 0.158, \"class Solution {\\npublic:\\n int dp[5][2];\\n vector<int> f5, f2, c5, c2;\\n int ncr2(int n, int r)\\n {\\n int x = c2[n] - c2[r] - c2[n - r];\\n return x ? 0 : f2[n];\\n }\\n int ncr5(int n, int r)\\n {\\n int x = c5[n] - c5[r] - c5[n - r];\\n int d1 = (f5[r] * f5[r] * f5[r]) % 5, d2 = (f5[n - r] * f5[n - r] * f5[n - r]) % 5;\\n return x ? 0 : (f5[n] * d1 * d2) % 5;\\n }\\n bool hasSameDigits(string s) {\\n dp[0][0] = 0; dp[0][1] = 5; dp[1][0] = 6;dp[1][1] = 1; dp[2][0] = 2;\\n dp[2][1] = 7; dp[3][0] = 8; dp[3][1] = 3;dp[4][0] = 4; dp[4][1] = 9;\\n int n = s.size(), l = 0, r = 0;\\n f5.resize(n + 1); f2.resize(n + 1); f5[0] = f2[0] = 1;\\n c2.resize(n + 1, 0); c5.resize(n + 1, 0);\\n for(int i = 1 ; i <= n ; i ++)\\n {\\n int x = 1 , y = 1;\\n for(int j = 2 ; i % j == 0 ; j *= 2)\\n {\\n c2[i] ++;\\n x = j;\\n }\\n for(int j = 5 ; i % j == 0 ; j *= 5)\\n {\\n c5[i] ++;\\n y = j;\\n }\\n f5[i] = (f5[i - 1] * i / y) % 5; f2[i] = (f2[i - 1] * i / x) % 2 ;\\n c2[i] += c2[i - 1]; c5[i] += c5[i - 1];\\n }\\n for(int i = 0 ; i <= n - 2 ; i ++)\\n {\\n int x = dp[ncr5(n - 2, i)][ncr2(n - 2, i)];\\n l = (l + x * (s[i] - '0')) % 10;\\n r = (r + x * (s[n - 1 - i] - '0')) % 10;\\n }\\n return l == r;\\n }\\n};\"], [49588, 0.316, \"#define eb emplace_back\\n#define vi vector<int>\\n#define vvi vector<vi>\\n#define vb vector<bool>\\n#define vvb vector<vb>\\n#define ll long long\\n#define vl vector<ll>\\n#define vvl vector<vl>\\n#define pb push_back\\n#define all(x) (x).begin(), (x).end()\\n#define PII pair<int, int>\\n#define PLI pair<ll, int>\\n#define VPII vector<PII>\\n#define VPLI vector<PLI>\\n#define T3I tuple<int, int, int>\\n#define VT3I vector<T3I>\\n#define x first \\n#define y second \\n#define foru(i, a, b) for(int(i)=(a); (i) < (b); (i) ++)\\n#define fori(a, b) foru(i, a, b)\\n#define forj(a, b) foru(j, a, b)\\n#define ford(i, a, b) for(int(i)=(a); (i) >= (b); (i) --)\\n#define fordi(a, b) ford(i, a, b)\\n#define fordj(a, b) ford(j, a, b)\\nconst int MOD = 10;\\n\\nclass Solution {\\n ll q_pow(ll a, int b)\\n {\\n ll res = 1;\\n while(b)\\n {\\n if(b & 1)\\n {\\n res = res * a % MOD;\\n }\\n a = a * a % MOD;\\n b >>= 1;\\n }\\n return res;\\n }\\n\\n\\npublic:\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n int op = n - 2;\\n // C(op, 0, op)\\n vi F(op + 1), INV_F(op + 1); // i!\\uff0c 1/i!\\n vi p2(op + 1), p5(op + 1);\\n F[0] = 1;\\n fori(1, op + 1)\\n {\\n // \\u53bb\\u6389\\u6240\\u67092\\u548c5\\u7684\\u8d28\\u56e0\\u6570\\n int x = i;\\n int e2 = countr_zero((unsigned) x);\\n x >>= e2;\\n int e5 = 0;\\n while(x % 5 == 0)\\n {\\n e5 ++;\\n x /= 5;\\n }\\n // MOD = 10, \\u4e00\\u5b9a\\u4e0d\\u4f1a\\u7206int\\n F[i] = F[i - 1] * x % MOD;\\n p2[i] = p2[i - 1] + e2;\\n p5[i] = p5[i - 1] + e5;\\n }\\n INV_F[op] = q_pow(F[op], 3); // fai(10) - 1 = 3 \\n fordi(op, 1)\\n {\\n int x = i;\\n x >>= countr_zero((unsigned) x);\\n while(x % 5 == 0)\\n x /= 5;\\n INV_F[i - 1] = INV_F[i] * x % MOD;\\n }\\n\\n auto get = [&](int a, int b)\\n {\\n // MOD = 10, \\u65e0\\u9700\\u4e2d\\u9014\\u53d6\\u6a21\\n ll res = F[a] * INV_F[b] * INV_F[a - b] * q_pow(2, p2[a] - p2[b] - p2[a - b]) * q_pow(5, p5[a] - p5[b] - p5[a - b]) % MOD;\\n // \\u53d6\\u7ec4\\u5408\\u6570\\u65f6\\u8981\\u52a0\\u4e0a\\u4e4b\\u524d\\u53bb\\u9664\\u76842\\u548c5\\u7684\\u8d28\\u56e0\\u5b50\\n return res;\\n };\\n\\n ll num0 = 0, num1 = 0;\\n fori(0, op + 1)\\n {\\n ll c = get(op, i);\\n num0 = (num0 + (c * (s[i] - '0') % MOD)) % MOD;\\n num1 = (num1 + (c * (s[i + 1] - '0') % MOD)) % MOD;\\n // cout << c << \\\" \\\" << num0 << \\\" \\\" << num1 << endl;\\n }\\n // cout << num0 << \\\" \\\" << num1 << endl;\\n // return (num0%10) == (num1%10);\\n return num0 == num1;\\n }\\n};\"], [50506, 0.316, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n vector<int> f(n), c2(n), c5(n);\\n f[0] = 1;\\n for (int i = 1; i < n; i++) {\\n c2[i] = c2[i - 1];\\n c5[i] = c5[i - 1];\\n int t = i;\\n while (t % 2 == 0) {\\n c2[i]++;\\n t /= 2;\\n }\\n while (t % 5 == 0) {\\n c5[i]++;\\n t /= 5;\\n }\\n f[i] = f[i - 1] * t % 10;\\n }\\n vector<int> inv(10, 1);\\n for (int i = 0; i < 10; i++) {\\n for (int j = 0; j < 3; j++) {\\n inv[i] = inv[i] * i % 10;\\n }\\n }\\n vector<int> p2(n), p5(n);\\n p2[0] = p5[0] = 1;\\n for (int i = 1; i < n; i++) {\\n p2[i] = p2[i - 1] * 2 % 10;\\n p5[i] = p5[i - 1] * 5 % 10;\\n }\\n auto get = [&](int l, int r) {\\n int ret = 0;\\n for (int i = l; i <= r; i++) {\\n ret = (ret + (s[i] - '0') * f[r - l] * inv[f[i - l]] * inv[f[r - i]] * p2[c2[r - l] - c2[i - l] - c2[r - i]] * p5[c5[r - l] - c5[i - l] - c5[r - i]]) % 10;\\n }\\n return ret;\\n };\\n return get(0, n - 2) == get(1, n - 1);\\n }\\n};\"], [51423, 0.158, \"typedef long long ll;\\n\\nclass Solution {\\npublic:\\n ll M = 10;\\n\\n ll expm(ll a, ll b) {\\n ll c = 1;\\n while(b){\\n if(b&1)c=c*a%M;\\n a=a*a%M;\\n b>>=1;\\n }\\n return c;\\n }\\n\\n ll gcdExtended(ll a, ll b, ll &x, ll &y) {\\n if (b == 0) {\\n x = 1, y = 0;\\n return a;\\n }\\n ll x1, y1;\\n ll gcd = gcdExtended(b, a % b, x1, y1);\\n x = y1;\\n y = x1 - (a / b) * y1;\\n return gcd;\\n }\\n\\n ll inverse(ll a) {\\n ll x, y;\\n ll g = gcdExtended(a, M, x, y);\\n if (g != 1) return -1;\\n return (x % M + M) % M;\\n }\\n\\n bool hasSameDigits(string s) {\\n ll n = s.size() - 1;\\n ll facts[n+1][2], twos[n+1][2], fives[n+1][2];\\n memset(facts, 0, sizeof(facts));\\n memset(twos, 0, sizeof(twos));\\n memset(fives, 0, sizeof(fives));\\n facts[0][0] = 1;\\n twos[0][0] = 0;\\n fives[0][0] = 0;\\n for(ll i = 1; i < n; i++) {\\n ll x = i;\\n twos[i][0]=twos[i-1][0];\\n fives[i][0]=fives[i-1][0];\\n while(x%2==0){\\n twos[i][0]++;\\n x /= 2;\\n }\\n while(x%5==0){\\n fives[i][0]++;\\n x /= 5;\\n }\\n facts[i][0] = facts[i-1][0] * x % M;\\n }\\n facts[n][1] = 1;\\n twos[n][1] = 0;\\n fives[n][1] = 0;\\n for(ll i = n - 1; i >= 1; i--){\\n ll x = i;\\n twos[i][1]=twos[i+1][1];\\n fives[i][1]=fives[i+1][1];\\n while(x%2==0){\\n twos[i][1]++;\\n x /= 2;\\n }\\n while(x%5==0){\\n fives[i][1]++;\\n x /= 5;\\n }\\n facts[i][1] = facts[i+1][1] * x % M;\\n }\\n // for(ll i = 0; i < n + 1; i++) cout << fives[i][0] << \\\", \\\";\\n // cout << \\\"\\\\n\\\";\\n // for(ll i = 0; i < n + 1; i++) cout << fives[i][1] << \\\", \\\";\\n // cout << \\\"\\\\n\\\";\\n vector<ll> dig; for(auto x : s) dig.push_back(x - '0');\\n ll x = 0, y = 0;\\n ll p1 = 0, p2 = 1;\\n for(ll i = 0; i < n; i++) {\\n ll comb = facts[n-i][1] * inverse(facts[i][0]) % M;\\n // cout << facts[n-i][1] << \\\" \\\" << facts[i][0] << \\\" inv: \\\" << inverse(facts[i][0]) << \\\"\\\\n\\\";\\n // cout << twos[n-i][1] << \\\" \\\" << twos[i][0] << \\\"\\\\n\\\";\\n // cout << fives[n-i][1] << \\\" \\\" << fives[i][0] << \\\"\\\\n\\\";\\n // cout << \\\"======\\\" << \\\"\\\\n\\\";\\n\\n assert(twos[n-i][1] >= twos[i][0]);\\n assert(fives[n-i][1] >= fives[i][0]);\\n ll two = twos[n-i][1] - twos[i][0];\\n ll five = fives[n-i][1] - fives[i][0];\\n comb = comb * expm(2, two) % M;\\n comb = comb * expm(5, five) % M;\\n // cout << comb << \\\"\\\\n\\\";\\n x += dig[p1++] * comb;\\n y += dig[p2++] * comb;\\n x %= M;\\n y %= M;\\n }\\n return x==y;\\n }\\n};\"], [52341, 0.316, \"#include <iostream>\\n#include <vector>\\nusing namespace std;\\n\\nint binmod2(int n, int k) {\\n while (k > 0) {\\n if ((k & 1) > (n & 1))\\n return 0;\\n n >>= 1;\\n k >>= 1;\\n }\\n return 1;\\n}\\nint binsmall(int n, int k) {\\n if (k > n)\\n return 0;\\n int fact[5] = {1, 1, 2, 1, 4};\\n int numerator = fact[n];\\n int denominator = (fact[k] * fact[n - k]) % 5;\\n int deninv = 0;\\n for (int i = 0; i < 5; i++) {\\n if ((denominator * i) % 5 == 1) {\\n deninv = i;\\n break;\\n }\\n }\\n return (numerator * deninv) % 5;\\n}\\n\\nint binmod5(int n, int k) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int nd = n % 5;\\n int kd = k % 5;\\n if (kd > nd)\\n return 0;\\n res = (res * binsmall(nd, kd)) % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return res;\\n}\\n\\n\\nint binmod10(int n, int k) {\\n int mod2 = binmod2(n, k);\\n int mod5 = binmod5(n, k);\\n for (int i = 0; i < 10; i++) {\\n if (i % 2 == mod2 && i % 5 == mod5)\\n return i;\\n }\\n return 0;\\n}\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n // obs: pascal's triangle's n-2th term\\n\\n int n = (int)s.size();\\n vector<long long> A;\\n for(auto &ch: s) \\n A.push_back(ch-'0');\\n\\n vector<long long> C((int)s.size()-1);\\n for(int i = 0; i < (int)C.size(); i++) {\\n // C[i] = //n-2Ci \\n // C[i] = nCr(n-2,i,mod);\\n C[i] = binmod10(n-2, i);\\n }\\n auto get = [&](int l, int r)->int {\\n long long ans = 0;\\n for(int i = 0; i < (int)C.size(); i++) {\\n ans += A[i+l] * C[i];\\n ans %= 10;\\n }\\n return ans%10;\\n };\\n int left = get(0,n-2);\\n int right = get(1,n-1);\\n return left == right;\\n }\\n};\"], [53258, 0.158, \"#include <bits/stdc++.h>\\nusing namespace std;\\ntypedef long long int ll;\\ntypedef long double ld;\\n#define pb push_back\\n#define pf push_front\\n#define mp make_pair\\n#define bns binary_search\\n#define Lb lower_bound\\n#define Ub upper_bound\\n#define inf LLONG_MAX\\n#define vll vector<ll>\\n#define vvll vector<vll>\\n#define vd vector<double>\\n#define pii pair<ll,ll>\\n#define fr first\\n#define sc second\\n#define ninf LLONG_MIN\\n#define all(v) v.begin(),v.end()\\n#define rall(v) v.rbegin(),v.rend()\\n#define scin(s) cin.ignore();getline(cin,s);\\n#define rep(i,a,b) for(ll i=a;i<=b;i++)\\n#define rrep(i,a,b) for(ll i=a;i>=b;i--)\\n#define SEIVE seive();\\n#define PI \\t3.14159265358979323846\\n#define sz(s) ll(s.size())\\n\\n\\nclass Solution {\\npublic:\\n ll maxn,c=0;\\n vll minprime,sei,v; \\n void seive(){\\n \\tfor(ll i=0;i<=maxn;i++)minprime[i]=i;\\n \\tsei[0]=sei[1]=0;\\n \\tfor(ll i=2;i*i<=maxn;i++){\\n \\t\\tif(sei[i]==1){c++;\\n \\t\\t\\tfor(ll j=i*i;j<=maxn;j+=i){\\n \\t\\t\\t\\tsei[j]=0;\\n \\t\\t\\t\\tminprime[j]=min(minprime[j],i);\\n \\t\\t\\t}\\n \\t\\t}\\n \\t}\\t\\n \\tll ans=1,c=0;\\n \\trep(i,1,maxn){\\n \\t\\tif(sei[i]){\\n \\t\\t\\tv.pb(i);\\t\\t\\t\\n \\t\\t}\\n \\t}\\t\\n }\\n ll expo(ll x,ll n) {\\n \\tll res=1;\\n \\twhile(n) {\\n \\t\\tif(n%2) {\\n \\t\\t\\tres = (res*x)%10;\\n \\t\\t}\\n \\t\\tx = (x*x)%10;\\n \\t\\tn/=2;\\n \\t}\\n \\treturn res;\\n }\\n vll calcC(ll x) {\\n unordered_map<ll,ll> num;\\n unordered_map<ll,vll> v;\\n v[1] = {1,1,1,1};\\n v[2] = {2,4,8,6};\\n v[3] = {3,9,7,1};\\n v[5] = {5,5,5,5};\\n v[7] = {7,9,3,1};\\n v[9] = {9,1,9,1};\\n vll c(x+1, 1);\\n \\n ll y = x;\\n rep(i,1,y-1) {\\n ll p = x;\\n while(x>1) {\\n // cout<<x<<endl;\\n num[minprime[x]%10]++;\\n x/=minprime[x];\\n }\\n x=p-1;\\n p = i;\\n while(p>1) {\\n // cout<<x<<endl;\\n num[minprime[p]%10]--;\\n if (num[minprime[p]%10] == 0) num.erase(minprime[p]%10);\\n p/=minprime[p];\\n }\\n ll res = 1;\\n for (auto &e: num) {\\n ll y = e.second;\\n res = (res*(v[e.first][(y-1)%4]))%10;\\n }\\n c[i]=res;\\n }\\n return c;\\n }\\n bool hasSameDigits(string s) {\\n ll n = s.size();\\n maxn=n;\\n minprime = vll(maxn+1, 1);\\n sei = vll(maxn+1, 1);\\n seive();\\n vll c = calcC(n-2);\\n ll i = 1, j = n-3;\\n ll a = (s[0] - '0' + s[n-2] - '0')%10;\\n ll x = 1;\\n while(i<=j) {\\n if (i!=j) a = (a + ((s[i]-'0')*(c[x])) + ((s[j]-'0')*(c[n-2-x])))%10;\\n else a = (a + ((s[i]-'0')*(c[x])))%10;\\n x++;\\n i++;\\n j--;\\n }\\n ll b = (s[1] - '0' + s[n-1] - '0')%10;\\n i = 2, j = n-2;\\n x = 1;\\n while(i<=j) {\\n if (i!=j) b = (b + ((s[i]-'0')*(c[x])) + ((s[j]-'0')*(c[n-2-x])))%10;\\n else b = (b + ((s[i]-'0')*(c[x])))%10;\\n x++;\\n i++;\\n j--;\\n }\\n\\n return a==b;\\n }\\n};\"], [54176, 0.158, \"#include <vector>\\n#include <string>\\n#include <tuple>\\n\\n// We store constants in static class members.\\nclass Solution {\\nprivate:\\n // Modular inverses for 1,3,7,9 under mod 10.\\n static const int INV[10];\\n // Powers of 2 cycle in last digit: 2, 4, 8, 6.\\n static const int TWOS[4];\\n // Powers of 5 cycle in last digit: 5 (only one here).\\n static const int FIVES[1];\\n\\n // Equivalent of Python's mult(a, b)\\n // (a0 + b0, a1 + b1, (a2 * b2) % 10)\\n static inline std::tuple<int, int, int> mult(\\n const std::tuple<int, int, int>& a,\\n const std::tuple<int, int, int>& b\\n ) {\\n return {\\n std::get<0>(a) + std::get<0>(b),\\n std::get<1>(a) + std::get<1>(b),\\n (std::get<2>(a) * std::get<2>(b)) % 10\\n };\\n }\\n\\n // Equivalent of Python's div(a, b)\\n // (a0 - b0, a1 - b1, (a2 * INV[b2]) % 10)\\n static inline std::tuple<int, int, int> divide(\\n const std::tuple<int, int, int>& a,\\n const std::tuple<int, int, int>& b\\n ) {\\n return {\\n std::get<0>(a) - std::get<0>(b),\\n std::get<1>(a) - std::get<1>(b),\\n (std::get<2>(a) * INV[ std::get<2>(b) ]) % 10\\n };\\n }\\n\\n // Equivalent of Python's simplify(tup)\\n // Applies powers of 2 and 5 to the leftover to get final mod-10 digit.\\n static inline int simplify(const std::tuple<int, int, int>& t) {\\n int twos = std::get<0>(t);\\n int fives = std::get<1>(t);\\n int res = std::get<2>(t);\\n\\n if (twos > 0) {\\n res = (res * TWOS[(twos - 1) % 4]) % 10;\\n }\\n if (fives > 0) {\\n res = (res * FIVES[(fives - 1) % 1]) % 10;\\n }\\n return res;\\n }\\n\\n // Equivalent of Python's red(it): sum((a*b) % 10) % 10 over paired items.\\n static inline int red(const std::vector<int>& digits, const std::vector<int>& pascal) {\\n int sum = 0;\\n for (size_t i = 0; i < digits.size(); i++) {\\n sum = (sum + ((digits[i] * pascal[i]) % 10)) % 10;\\n }\\n return sum;\\n }\\n\\npublic:\\n // hasSameDigits function translated from Python\\n bool hasSameDigits(const std::string& s) {\\n // n = len(s) - 2\\n int n = static_cast<int>(s.size()) - 2;\\n\\n // Build factorials in terms of (count_of_2s, count_of_5s, leftover_mod_10)\\n std::vector<std::tuple<int, int, int>> facts;\\n facts.reserve(n + 1);\\n facts.push_back({0, 0, 1}); // for factorial(0)\\n\\n // Generate factorial representation up to n in the same manner.\\n while (n >= static_cast<int>(facts.size())) {\\n int num = static_cast<int>(facts.size());\\n int twos = 0;\\n while (num > 0 && (num % 2 == 0)) {\\n num /= 2;\\n twos++;\\n }\\n int fives = 0;\\n while (num > 0 && (num % 5 == 0)) {\\n num /= 5;\\n fives++;\\n }\\n // Multiply last factorial by the new triple.\\n facts.push_back(mult(facts.back(), {twos, fives, num % 10}));\\n }\\n\\n // Build the \\\"Pascal row\\\" mod 10 for nCk, 0 <= k <= n\\n std::vector<int> pascal;\\n pascal.reserve(n + 1);\\n for (int k = 0; k <= n; k++) {\\n auto temp = divide(facts[n], facts[k]);\\n auto comb = divide(temp, facts[n - k]);\\n pascal.push_back(simplify(comb));\\n }\\n\\n // Convert string s to two integer arrays: full and shifted\\n std::vector<int> sDigits(s.size()), sDigitsShift(s.size() - 1);\\n for (size_t i = 0; i < s.size(); i++) {\\n sDigits[i] = (s[i] - '0');\\n }\\n for (size_t i = 1; i < s.size(); i++) {\\n sDigitsShift[i - 1] = (s[i] - '0');\\n }\\n\\n // Calculate the red() value for the first and second positions\\n // a = red(zip(map(int, s), pascal))\\n int aVal = red(\\n std::vector<int>(sDigits.begin(), sDigits.begin() + (n + 1)),\\n pascal\\n );\\n\\n // b = red(zip(map(int, s[1:]), pascal))\\n int bVal = red(\\n std::vector<int>(sDigitsShift.begin(), sDigitsShift.begin() + (n + 1)),\\n pascal\\n );\\n\\n // Return whether they match\\n return (aVal == bVal);\\n }\\n};\\n\\n// Static member definitions\\nconst int Solution::INV[10] = {\\n 0, // 0 not used\\n 1, // INV of 1 under mod 10 is 1\\n 0, // 2 not in the dictionary\\n 7, // INV of 3 under mod 10 is 7\\n 0, // 4 not in the dictionary\\n 0, // 5 not in the dictionary\\n 0, // 6 not in the dictionary\\n 3, // INV of 7 under mod 10 is 3\\n 0, // 8 not in the dictionary\\n 9 // INV of 9 under mod 10 is 9\\n};\\n\\nconst int Solution::TWOS[4] = {2, 4, 8, 6};\\nconst int Solution::FIVES[1] = {5};\"], [55093, 0.158, \"class Solution {\\nprivate:\\n vector<vector<int>> C = {{1, 0, 0, 0, 0, 0}, {1, 1, 0, 0, 0, 0},\\n {1, 2, 1, 0, 0, 0}, {1, 3, 3, 1, 0, 0},\\n {1, 4, 6, 4, 1, 0}, {1, 5, 10, 10, 5, 1}};\\n int cmod(int n, int k, int p) {\\n int ans = 1;\\n while (n > 0 || k > 0) {\\n if (ans == 0)\\n return 0;\\n int a = n % p;\\n int b = k % p;\\n n /= p;\\n k /= p;\\n ans *= (C[a][b] % p);\\n }\\n\\n return ans % p;\\n }\\n\\npublic:\\n bool hasSameDigits(string s) {\\n // 0: (d1)(d2)(d3)(d4)(d5)(d6)\\n // 1: (d1+d2)(d2+d3)(d3+d4)(d4+d5)(d5+d6) - C(1, ...)\\n // 2: (d1 + 2*d2 + d3)(d2 + 2*d3 + d4)(d3 + 2*d4 + d5)(d4 + 2*d5 + d6) -\\n // C(2, ...)\\n // 3: (d1 + 3*d2 + 3*d3 + d4)(d2 + 3*d3 + 3*d4 + d5)(d3 + 3*d4 +\\n // 3*d5 + d6) - C(3, ...)\\n // 4: (d1 + 4*d2 + 6*d3 + 4*d4 + d5)(d2 + 4*d3 + 6*d4 + 4*d5 + d6) - C(n -\\n // 2, 0..n-2)\\n\\n vector<int> cmod2;\\n vector<int> cmod5;\\n vector<int> cmod10;\\n\\n int n = s.size();\\n\\n for (int i = 0; i <= n - 2; i++) {\\n int mod2 = cmod(n - 2, i, 2);\\n int mod5 = cmod(n - 2, i, 5);\\n cmod2.push_back(mod2);\\n cmod5.push_back(mod5);\\n int mod10 = (5 * mod2 + 6 * mod5) % 10;\\n cmod10.push_back(mod10);\\n }\\n\\n int s1 = 0;\\n int s2 = 0;\\n for (int i = 0; i < n - 1; i++) {\\n s1 += (s[i] - '0') * cmod10[i];\\n s1 %= 10;\\n }\\n\\n for (int i = 1; i < n; i++) {\\n s2 += (s[i] - '0') * cmod10[i - 1];\\n s2 %= 10;\\n }\\n\\n return s1 == s2;\\n }\\n};\"], [56011, 0.158, \"class Solution {\\npublic:\\nint fact(int n) {\\nif (n==0) return 1;\\nif (n==1) return 1;\\nif (n==2) return 2;\\nif (n==3) return 6;\\nif (n==4) return 24;\\nif (n==5) return 120;\\nif (n==6) return 720;\\nif (n==7) return 5040;\\nif (n==8) return 40320;\\nif (n==9) return 362880; \\n int res = 1;\\n for (int i = 1; i <= n; ++i) {\\n res *= i;\\n }\\n return res;\\n};\\n\\nint cnk(int n, int k) {\\nif (n==1 && k==0) return 1;\\nif (n==2 && k==0) return 1;\\nif (n==2 && k==1) return 2;\\nif (n==3 && k==0) return 1;\\nif (n==3 && k==1) return 3;\\nif (n==3 && k==2) return 3;\\nif (n==4 && k==0) return 1;\\nif (n==4 && k==1) return 4;\\nif (n==4 && k==2) return 6;\\nif (n==4 && k==3) return 4;\\n int res = 1;\\n res = fact(n) / fact(k) / fact(n - k);\\n return res;\\n};\\n\\nint cnkrrem(int n, int k) {\\n int a = 1;\\n for (int n2 = n, k2 = k; n2 > 0 || k2 > 0;) {\\n const int n22 = n2 % 2;\\n const int k22 = k2 % 2;\\n if (n22 < k22) {\\n a = 0;\\n break;\\n } else {\\n a *= cnk(n22, k22);\\n }\\n n2 /= 2;\\n k2 /= 2;\\n }\\n int b = 1;\\n for (int n5 = n, k5 = k; n5 > 0 || k5 > 0;) {\\n const int n55 = n5 % 5;\\n const int k55 = k5 % 5;\\n if (n55 < k55) {\\n b = 0;\\n break;\\n } else {\\n b *= cnk(n55, k55);\\n }\\n n5 /= 5;\\n k5 /= 5;\\n }\\n return (5 * a + 6 * b) % 10;\\n};\\n\\n\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n if (n < 2)\\n return false;\\n if (n == 2)\\n return s[0] == s[1];\\n int c1 = 0;\\n int c2 = 0;\\n int c11=0;\\n int c22=0;\\n unordered_map<int, int> m = {};\\n const int n2=n -2;\\n const int n22=n2/2;\\n\\n for (int i = 0; i < n - 1; ++i) {\\n if (i<=n22) {\\n c11 = cnkrrem(n2, i);\\n m[i]=c11;\\n } else {\\n c11=m[n2-i];\\n }\\n const int d= s[i] - '0';\\n c1 += d * c11;\\n c2 += d * c22;\\n c22=c11;\\n }\\n c2 += s[n-1] - '0';\\n\\n c1 %= 10;\\n c2 %= 10;\\n\\n return c1 == c2;\\n }\\n};\"], [56928, 0.158, \"#include <vector>\\n#include <string>\\n#include <algorithm>\\n\\nclass Solution {\\nprivate:\\n // A small struct to store (count_of_2s, count_of_5s, last_digit_mod_10).\\n struct Triple {\\n int twos;\\n int fives;\\n int lastDigit;\\n };\\n\\n // Inverse values mod 10 for digits 1, 3, 7, 9:\\n // INV[1] = 1, INV[3] = 7, INV[7] = 3, INV[9] = 9.\\n // All other entries are 0 (unused).\\n int inv[10] = {0, 1, 0, 7, 0, 0, 0, 3, 0, 9};\\n\\n // Patterns for powers of 2 mod 10 and powers of 5 mod 10.\\n // (Powers of 2 cycle through 2,4,8,6; powers of 5 mod 10 are always 5.)\\n std::vector<int> TWOS = {2, 4, 8, 6};\\n std::vector<int> FIVES = {5};\\n\\n // Multiplication of two Triples: add twos, add fives, multiply last-digit mod 10.\\n Triple multTriple(const Triple &a, const Triple &b) {\\n Triple result;\\n result.twos = a.twos + b.twos;\\n result.fives = a.fives + b.fives;\\n result.lastDigit = (a.lastDigit * b.lastDigit) % 10;\\n return result;\\n }\\n\\n // \\\"Division\\\" of two Triples: subtract twos, subtract fives, multiply by modular inverse of last-digit.\\n Triple divTriple(const Triple &a, const Triple &b) {\\n Triple result;\\n result.twos = a.twos - b.twos;\\n result.fives = a.fives - b.fives;\\n result.lastDigit = (a.lastDigit * inv[b.lastDigit]) % 10;\\n return result;\\n }\\n\\n // Simplify a Triple by incorporating any powers of 2 or 5.\\n // This adjusts the lastDigit by multiplying by the correct cycle element.\\n int simplify(const Triple &t) {\\n int twosCount = t.twos;\\n int fivesCount = t.fives;\\n int res = t.lastDigit;\\n\\n // If there are twos, multiply the result by 2^(count) mod 10 using the 4-cycle.\\n if (twosCount > 0) {\\n res = (res * TWOS[(twosCount - 1) % TWOS.size()]) % 10;\\n }\\n // If there are fives, multiply by 5^(count) mod 10 (which is always 5 if count>0).\\n if (fivesCount > 0) {\\n res = (res * FIVES[(fivesCount - 1) % FIVES.size()]) % 10;\\n }\\n return res;\\n }\\n\\npublic:\\n // Translated function: checks if summing digits * \\\"pascal\\\" for s and s[1:] \\n // yields the same final mod-10 result.\\n bool hasSameDigits(const std::string &s) {\\n // n is (length_of_string - 2)\\n int n = static_cast<int>(s.size()) - 2;\\n\\n // Precompute \\\"factorials\\\" in terms of (twos, fives, lastDigit) up to n.\\n // facts[i] represents the decomposition of i! (mod 10) plus the count of 2s and 5s.\\n std::vector<Triple> facts;\\n facts.push_back({0, 0, 1}); // base case for 0! => (0 twos, 0 fives, 1 mod 10)\\n\\n // Build up to facts[n].\\n while (n >= static_cast<int>(facts.size())) {\\n int num = static_cast<int>(facts.size()); // \\\"num\\\" = len(facts) in Python\\n int twos = 0;\\n while (num % 2 == 0) {\\n num /= 2;\\n twos++;\\n }\\n int fives = 0;\\n while (num % 5 == 0) {\\n num /= 5;\\n fives++;\\n }\\n // Multiply the previous factorial Triple by current (twos, fives, num mod 10).\\n facts.push_back(multTriple(facts.back(), {twos, fives, num % 10}));\\n }\\n\\n // Build the \\\"pascal\\\" row for nCk (k=0..n) mod 10, factoring out 2s and 5s.\\n std::vector<int> pascal;\\n pascal.reserve(n + 1);\\n for (int k = 0; k <= n; k++) {\\n // combination(n, k) mod 10 is (facts[n] / facts[k] / facts[n-k]) simplified\\n Triple temp1 = divTriple(facts[n], facts[k]);\\n Triple temp2 = divTriple(temp1, facts[n - k]);\\n pascal.push_back(simplify(temp2));\\n }\\n\\n // \\\"a\\\" in Python: red(zip(map(int, s), pascal))\\n // That effectively pairs s[0..n] with pascal[0..n], ignoring the last character of s.\\n int aVal = 0;\\n for (int i = 0; i <= n; i++) {\\n int digit = (s[i] - '0');\\n aVal = (aVal + (digit * pascal[i]) % 10) % 10;\\n }\\n\\n // \\\"b\\\" in Python: red(zip(map(int, s[1:]), pascal))\\n // That pairs s[1..(n+1)] with pascal[0..n].\\n int bVal = 0;\\n for (int i = 1; i <= n + 1; i++) {\\n int digit = (s[i] - '0');\\n bVal = (bVal + (digit * pascal[i - 1]) % 10) % 10;\\n }\\n\\n // Return whether the two mod-10 sums match.\\n return (aVal == bVal);\\n }\\n};\"], [57846, 0.158, \"class Solution {\\npublic:\\nint fact(int n) {\\nif (n==0) return 1;\\nif (n==1) return 1;\\nif (n==2) return 2;\\nif (n==3) return 6;\\nif (n==4) return 24;\\nif (n==5) return 120;\\nif (n==6) return 720;\\nif (n==7) return 5040;\\nif (n==8) return 40320;\\nif (n==9) return 362880; \\n int res = 1;\\n for (int i = 1; i <= n; ++i) {\\n res *= i;\\n }\\n return res;\\n};\\n\\nint cnk(int n, int k) {\\nif (n==1 && k==0) return 1;\\nif (n==2 && k==0) return 1;\\nif (n==2 && k==1) return 2;\\nif (n==3 && k==0) return 1;\\nif (n==3 && k==1) return 3;\\nif (n==3 && k==2) return 3;\\nif (n==4 && k==0) return 1;\\nif (n==4 && k==1) return 4;\\nif (n==4 && k==2) return 6;\\nif (n==4 && k==3) return 4;\\n int res = 1;\\n res = fact(n) / fact(k) / fact(n - k);\\n return res;\\n};\\n\\nint cnkrrem(int n, int k) {\\n int a = 1;\\n for (int n2 = n, k2 = k; n2 > 0 || k2 > 0;) {\\n const int n22 = n2 % 2;\\n const int k22 = k2 % 2;\\n if (n22 < k22) {\\n a = 0;\\n break;\\n } else {\\n a *= cnk(n22, k22);\\n }\\n n2 /= 2;\\n k2 /= 2;\\n }\\n int b = 1;\\n for (int n5 = n, k5 = k; n5 > 0 || k5 > 0;) {\\n const int n55 = n5 % 5;\\n const int k55 = k5 % 5;\\n if (n55 < k55) {\\n b = 0;\\n break;\\n } else {\\n b *= cnk(n55, k55);\\n }\\n n5 /= 5;\\n k5 /= 5;\\n }\\n return (5 * a + 6 * b) % 10;\\n};\\n\\n\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n if (n < 2)\\n return false;\\n if (n == 2)\\n return s[0] == s[1];\\n int c1 = 0;\\n int c2 = 0;\\n int c11=0;\\n int c22=0;\\n map<int, int> m = {};\\n const int n2=n -2;\\n const int n22=n2/2;\\n\\n for (int i = 0; i < n - 1; ++i) {\\n if (i<=n22) {\\n c11 = cnkrrem(n2, i);\\n m[i]=c11;\\n } else {\\n c11=m[n2-i];\\n }\\n const int d= s[i] - '0';\\n c1 += d * c11;\\n c2 += d * c22;\\n c22=c11;\\n }\\n c2 += s[n-1] - '0';\\n\\n c1 %= 10;\\n c2 %= 10;\\n\\n return c1 == c2;\\n }\\n};\"]]",
"runtime": 74,
"runtimeDistribution": "[[7, 7.898899999999999, \"const auto _ = std::cin.tie(nullptr)->sync_with_stdio(false);\\n#define l33tc0de\\n#ifdef l33tc0de\\nconst auto __ = [](){\\n struct __ { static void _(){ std::ofstream(\\\"display_runtime.txt\\\") << 0 << '\\\\n'; } };\\n std::atexit(&__::_);\\n return 0;\\n}();\\n#endif\\n\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n int m = n - 2;\\n\\n int m_digits[10], m_size = 0;\\n int temp = m;\\n if (temp == 0) {\\n m_digits[m_size++] = 0;\\n } else {\\n while (temp > 0) {\\n m_digits[m_size++] = temp % 5;\\n temp /= 5;\\n }\\n }\\n\\n const int small[5][5] = {{1, 0, 0, 0, 0}, {1, 1, 0, 0, 0}, {1, 2, 1, 0, 0}, {1, 3, 3, 1, 0}, {1, 4, 1, 4, 1}};\\n \\n int diff = 0;\\n for (int j = 0; j <= m; j++) {\\n int res5 = 1;\\n int x = j;\\n for (int i = 0; i < m_size; i++) {\\n int d = x % 5;\\n x /= 5;\\n int a = m_digits[i];\\n if (d > a) { \\n res5 = 0;\\n break;\\n }\\n res5 = (res5 * small[a][d]) % 5;\\n }\\n int c2 = ((m & j) == j) ? 1 : 0;\\n int coeff = ((res5 & 1) == c2) ? res5 : res5 + 5;\\n int delta = (s[j] - '0') - (s[j + 1] - '0');\\n diff = (diff + coeff * delta) % 10;\\n if (diff < 0)\\n diff += 10;\\n }\\n return diff == 0;\\n }\\n};\"], [21, 15.481799999999998, \"namespace {\\nint pow_mod(int a, int b, int mod) {\\n int ans = 1;\\n while (b) {\\n if (b & 1) ans = ans * a % mod;\\n a = a * a % mod, b >>= 1;\\n }\\n return ans;\\n}\\nint count2_presum[100001], count5_presum[100001];\\nint numerator[50001], fact_inv[50001];\\nvoid build_table_once(int n = 100000) {\\n for (int i = 2; i <= n; i += 2)\\n if (i % 2 == 0)\\n count2_presum[i] = count2_presum[i / 2] + 1;\\n for (int i = 5; i <= n; i += 5)\\n if (i % 5 == 0)\\n count5_presum[i] = count5_presum[i / 5] + 1;\\n\\n fact_inv[0] = 1;\\n for (int i = 1, tmp; i <= n; i++) {\\n count2_presum[i] += count2_presum[i - 1];\\n count5_presum[i] += count5_presum[i - 1];\\n }\\n for (int i = 1, tmp; i + i <= n; i++) {\\n tmp = i;\\n while (tmp % 2 == 0) tmp /= 2;\\n while (tmp % 5 == 0) tmp /= 5;\\n tmp %= 10;\\n fact_inv[i] = fact_inv[i - 1] * pow_mod(tmp, 3, 10) % 10;\\n }\\n}\\nvoid build_numerator_table(int n) {\\n numerator[0] = 1;\\n for (int i = 1, tmp; i + i <= n; i++) {\\n tmp = n - i + 1;\\n while (tmp % 2 == 0) tmp /= 2;\\n while (tmp % 5 == 0) tmp /= 5;\\n tmp %= 10;\\n numerator[i] = numerator[i - 1] * tmp % 10;\\n }\\n}\\nint sum(int presum[], int l, int r) {\\n return presum[r] - presum[l - 1];\\n}\\nint nCrMod10(int n, int r) {\\n if (n < r) return 0;\\n if (r == 0) return 1;\\n if (r + r > n) return nCrMod10(n, n - r);\\n int count2 = sum(count2_presum, n - r + 1, n) - sum(count2_presum, 1, r);\\n int count5 = sum(count5_presum, n - r + 1, n) - sum(count5_presum, 1, r);\\n if (count2 > 0 && count5 > 0) return 0;\\n int ans = pow_mod(2, count2, 10) * pow_mod(5, count5, 10) * numerator[r] * fact_inv[r] % 10;\\n return ans;\\n}\\n} // namespace\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n static int built = false;\\n if (!built) {\\n build_table_once();\\n built = true;\\n }\\n build_numerator_table(s.size() - 2);\\n int ret = 0;\\n for (int i = 0; i < s.size() - 1; i++) {\\n ret = (ret + (s[i] - s[i + 1] + 10) * nCrMod10(s.size() - 2, i)) % 10;\\n }\\n return ret == 0;\\n }\\n};\"], [36, 11.3746, \"// Time: O(nlogn)\\n// Space: O(1)\\n\\n// fast exponentiation\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n const auto& pow = [](uint64_t a, int b, int m) { // O(logMOD) = O(1)\\n a %= m;\\n uint64_t result = 1;\\n while (b) {\\n if (b & 1) {\\n result = (result * a) % m;\\n }\\n a = (a * a) % m;\\n b >>= 1;\\n }\\n return result;\\n };\\n\\n const auto& check = [&](int mod) {\\n const auto& decompose = [](int x, int mod) { // x = a * mod^cnt\\n int cnt = 0;\\n while (x > 1 && x % mod == 0) {\\n x /= mod;\\n ++cnt;\\n }\\n return pair(x, cnt);\\n };\\n\\n int result = 0, cnt = 0;\\n int curr = 1;\\n for (int i = 0; i <= size(s) - 2; ++i) {\\n if (cnt == 0) {\\n result = (result + curr * (s[i] - s[i + 1])) % mod;\\n }\\n const auto& [x1, c1] = decompose(size(s) - 2 - i, mod);\\n curr = (curr * x1) % mod;\\n cnt += c1;\\n const auto& [x2, c2] = decompose(i + 1, mod);\\n curr = (curr * pow(x2, mod - 2, mod)) % mod;\\n cnt -= c2;\\n }\\n return result == 0;\\n };\\n\\n return check(2) && check(5);\\n }\\n};\\n\\n// Time: O(nlogn)\\n// Space: O(1)\\nvector<vector<int>> LOOKUP(5 + 1, vector<int>(5 + 1, -1));\\n\\n// lucas's theorem\\nclass Solution2 {\\npublic:\\n bool hasSameDigits(string s) {\\n const auto& nCr = [&](int n, int r) {\\n if (n - r < r) {\\n r = n - r;\\n }\\n if (LOOKUP[n][r] == -1) {\\n int c = 1;\\n for (int k = 1; k <= r; ++k) {\\n c *= n - k + 1;\\n c /= k;\\n }\\n LOOKUP[n][r] = c;\\n }\\n return LOOKUP[n][r];\\n };\\n\\n // https://en.wikipedia.org/wiki/Lucas%27s_theorem\\n const auto& nCr_mod = [&](int n, int r, int mod) {\\n int result = 1;\\n while (n > 0 || r > 0) {\\n const int ni = n % mod;\\n n /= mod;\\n const int ri = r % mod;\\n r /= mod;\\n if (ni < ri) {\\n return 0;\\n }\\n result = (result * nCr(ni, ri)) % mod;\\n }\\n return result;\\n };\\n\\n vector<vector<int>> lookup(2, vector<int>(5));\\n for (int i = 0; i < 10; ++i) {\\n lookup[i % 2][i % 5] = i;\\n }\\n const auto& nC10 = [&](int n, int k) {\\n return lookup[nCr_mod(n, k, 2)][nCr_mod(n, k, 5)];\\n };\\n\\n int total = 0;\\n for (int i = 0; i <= size(s) - 2; ++i) {\\n total = (total + nC10(size(s) - 2, i) * (((s[i] - s[i + 1]) % 10 + 10) % 10)) % 10;\\n }\\n return total == 0;\\n }\\n};\"], [50, 6.9511, \"#include <bits/stdc++.h>\\nusing namespace std;\\n\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n int K = n - 2; // number of reduction steps\\n // precomputed C(a,b) mod 5 for 0<=b<=a<5\\n static const int C5[5][5] = {\\n {1,0,0,0,0},\\n {1,1,0,0,0},\\n {1,2,1,0,0},\\n {1,3,3,1,0},\\n {1,4,1,4,1}\\n };\\n \\n vector<int> w(K+1);\\n // build w[i] = binom(K, i) mod 10\\n for (int i = 0; i <= K; ++i) {\\n // 1) mod 2 via bit\\u2010check\\n int c2 = ((i & (K - i)) == 0 ? 1 : 0);\\n // 2) mod 5 via Lucas\\n int c5 = 1;\\n int ki = K, ii = i;\\n while (ki > 0 || ii > 0) {\\n int kd = ki % 5, id = ii % 5;\\n if (id > kd) { c5 = 0; break; }\\n c5 = (c5 * C5[kd][id]) % 5;\\n ki /= 5; \\n ii /= 5;\\n }\\n // 3) combine by CRT into mod 10\\n int x = c5;\\n if ((x % 2) != c2) x = (x + 5) % 10;\\n w[i] = x;\\n }\\n \\n // compute the two final digits\\n int a = 0, b = 0;\\n for (int i = 0; i <= K; ++i) {\\n int d0 = s[i] - '0';\\n int d1 = s[i+1] - '0';\\n a = (a + w[i] * d0) % 10;\\n b = (b + w[i] * d1) % 10;\\n }\\n return a == b;\\n }\\n};\\n\"], [64, 5.3713, \"class Solution {\\npublic:\\nint lucas_mod5(int n, int k, const vector<vector<int>> &small_binom) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int n_digit = n % 5;\\n int k_digit = k % 5;\\n if (k_digit > n_digit)\\n return 0;\\n res = (res * small_binom[n_digit][k_digit]) % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return res;\\n}\\n \\n// Computes C(n, k) mod 10 by combining results modulo 2 and modulo 5.\\n// For modulo 2 we use: C(n, k) mod 2 = 1 if and only if ((n & k) == k).\\n// The lookup table 'crt_table' maps (r2, r5) to the unique residue modulo 10.\\nint binom_mod10(int n, int k, const vector<vector<int>> &small_binom, const int crt_table[2][5]) {\\n int mod2 = ((n & k) == k) ? 1 : 0;\\n int mod5 = lucas_mod5(n, k, small_binom);\\n return crt_table[mod2][mod5];\\n}\\n \\n// Efficient method using the closed\\u2010form (linear) relation.\\n// Given string s of digits, let m = s.size()\\n// The final two digits after m-2 operations are:\\n// F0 = \\u03a3 (i = 0 to m-2) [C(m-2, i) * digit[i]] mod 10\\n// F1 = \\u03a3 (i = 0 to m-2) [C(m-2, i) * digit[i+1]] mod 10\\n// Return true if F0 == F1, false otherwise.\\nbool finalDigitsSame(const string &s) {\\n int m = s.size();\\n int N = m - 2; // The number of iterations (and the index of Pascal's row to use)\\n \\n // Convert s into an array of digits.\\n vector<int> digits(m);\\n for (int i = 0; i < m; i++) {\\n digits[i] = s[i] - '0';\\n }\\n \\n // CRT lookup table.\\n int crt_table[2][5] = {\\n {0, 6, 2, 8, 4}, // For even residues mod 2 (r2 = 0)\\n {5, 1, 7, 3, 9} // For odd residues mod 2 (r2 = 1)\\n };\\n \\n // Precomputed small binomials modulo 5: rows for n = 0,1,2,3,4.\\n vector<vector<int>> small_binom = {\\n {1}, // n = 0: [1]\\n {1, 1}, // n = 1: [1, 1]\\n {1, 2, 1}, // n = 2: [1, 2, 1]\\n {1, 3, 3, 1}, // n = 3: [1, 3, 3, 1]\\n {1, 4, 1, 4, 1} // n = 4: [1, 4, 6 mod5 = 1, 4, 1]\\n };\\n \\n int F0 = 0, F1 = 0;\\n for (int i = 0; i <= N; i++) {\\n int coeff = binom_mod10(N, i, small_binom, crt_table);\\n F0 = (F0 + coeff * digits[i]) % 10;\\n F1 = (F1 + coeff * digits[i+1]) % 10;\\n }\\n return F0 == F1;\\n}\\n bool hasSameDigits(string s) {\\n if (finalDigitsSame(s))\\n {\\n return true;\\n }\\n else\\n {\\n return false;\\n }\\n }\\n};\"], [74, 52.9223, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n vector<int> digits;\\n for (char c : s) {\\n digits.push_back(c - '0');\\n }\\n int m = digits.size() - 2;\\n vector<int> coeff(m + 1);\\n for (int k = 0; k <= m; ++k) {\\n int a = lucas_mod2(m, k);\\n int b = lucas_mod5(m, k);\\n coeff[k] = crt(a, b);\\n }\\n int digit1 = 0;\\n for (int i = 0; i <= m; ++i) {\\n digit1 = (digit1 + digits[i] * coeff[i]) % 10;\\n }\\n digit1 %= 10;\\n int digit2 = 0;\\n for (int i = 1; i <= m + 1; ++i) {\\n int k = i - 1;\\n digit2 = (digit2 + digits[i] * coeff[k]) % 10;\\n }\\n digit2 %= 10;\\n return digit1 == digit2;\\n }\\n\\nprivate:\\n static int lucas_mod2(int n, int k) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int ni = n % 2;\\n int ki = k % 2;\\n if (ki > ni) return 0;\\n res = (res * 1) % 2;\\n n /= 2;\\n k /= 2;\\n }\\n return res;\\n }\\n\\n static int lucas_mod5(int n, int k) {\\n static const int table5[5][5] = {\\n {1}, \\n {1, 1}, \\n {1, 2, 1}, \\n {1, 3, 3, 1}, \\n {1, 4, 1, 4, 1} \\n };\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int ni = n % 5;\\n int ki = k % 5;\\n if (ki > ni) return 0;\\n res = (res * table5[ni][ki]) % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return res;\\n }\\n\\n static int crt(int a, int b) {\\n static const int crt_table[2][5] = {\\n {0, 6, 2, 8, 4}, \\n {5, 1, 7, 3, 9} \\n };\\n return crt_table[a][b];\\n }\\n};\"], [79, 2.3698999999999995, \"class Solution {\\npublic:\\n bool hasSameDigits(const string& s) {\\n int n = s.size();\\n int m = n - 2;\\n const int C5[5][5] = {\\n {1,0,0,0,0},\\n {1,1,0,0,0},\\n {1,2,1,0,0},\\n {1,3,3,1,0},\\n {1,4,1,4,1}\\n };\\n\\n auto C5_lucas = [&](int n, int k) -> int {\\n int res = 1;\\n while (n || k) {\\n int ni = n % 5, ki = k % 5;\\n if (ki > ni) return 0;\\n res = res * C5[ni][ki] % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return res;\\n };\\n\\n auto C2 = [&](int n, int k) -> int {\\n return ((k & (n - k)) == 0) ? 1 : 0;\\n };\\n\\n auto C10 = [&](int n, int k) -> int {\\n int a2 = C2(n, k);\\n int a5 = C5_lucas(n, k);\\n return ((a5 & 1) == a2) ? a5 : (a5 + 5);\\n };\\n\\n int sum0 = 0, sum1 = 0;\\n\\n for (int i = 0; i < n; ++i) {\\n int digit = s[i] - '0';\\n if (i <= m)\\n sum0 = (sum0 + digit * C10(m, i)) % 10;\\n if (i >= 1 && i - 1 <= m)\\n sum1 = (sum1 + digit * C10(m, i - 1)) % 10;\\n }\\n\\n return sum0 == sum1;\\n }\\n};\"], [93, 1.896, \"class Solution {\\n int fact[5] = {1,1,2,6,24};\\n int ncr(int n, int r){\\n return fact[n]/(fact[r]*fact[n-r]);\\n }\\n int ncrmod2(int n, int r){\\n while(n || r){\\n int x=n%2, y=r%2;\\n if(x<y) return 0;\\n n/=2; r/=2;\\n }\\n return 1;\\n }\\n int ncrmod5(int n, int r){\\n int ans=1;\\n while(n || r){\\n int x=n%5, y=r%5;\\n if(x<y) return 0;\\n ans = (ans * ncr(x,y))%5;\\n n/=5; r/=5;\\n }\\n return ans;\\n }\\npublic:\\n bool hasSameDigits(string s) {\\n int n=(int)s.size();\\n vector<int> mod(n-1);\\n for(int i=0; i<n-1; i++){\\n int m2 = ncrmod2(n-2,i);\\n int m5 = ncrmod5(n-2,i);\\n if(!m2) mod[i] = m5 + ((m5%2) ? 5 : 0);\\n else mod[i] = m5 + ((m5%2) ? 0 : 5);\\n }\\n int fir = (mod[0]*(s[0]-'0'))%10;\\n int sec = (mod[n-2]*(s[n-1]-'0'))%10;\\n for(int i=1; i<n-1; i++){\\n fir = (fir + (mod[i]*(s[i]-'0'))%10)%10;\\n sec = (sec + (mod[i-1]*(s[i]-'0'))%10)%10;\\n }\\n return fir==sec;\\n }\\n};\"], [108, 2.8439999999999994, \"class Solution {\\npublic:\\n\\n int mod = 10;\\n\\n // Precomputed binomial coefficients mod 2 and mod 5 (for digits)\\n vector<vector<int>> C2;\\n vector<vector<int>> C5;\\n\\n Solution() {\\n if (C2.empty()) C2 = precompute_C(2);\\n if (C5.empty()) C5 = precompute_C(5);\\n }\\n\\n std::vector<std::vector<int>> precompute_C(int p) {\\n std::vector<std::vector<int>> C(p, std::vector<int>(p, 0));\\n for (int n = 0; n < p; ++n) {\\n C[n][0] = C[n][n] = 1;\\n for (int k = 1; k < n; ++k) {\\n C[n][k] = (C[n - 1][k - 1] + C[n - 1][k]) % p;\\n }\\n }\\n return C;\\n }\\n\\n int lucas(int n, int k, int p, const std::vector<std::vector<int>>& C) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int ni = n % p, ki = k % p;\\n if (ki > ni) return 0;\\n res = (res * C[ni][ki]) % p;\\n n /= p;\\n k /= p;\\n }\\n return res;\\n }\\n\\n int combine_mod_2_5(int r2, int r5) {\\n // Brute-force CRT (mod 10)\\n for (int x = 0; x < 10; ++x) {\\n if (x % 2 == r2 && x % 5 == r5)\\n return x;\\n }\\n return -1; // should never happen\\n }\\n\\n int nCr_mod_10(int n, int k) {\\n if (k < 0 || k > n) return 0;\\n int r2 = lucas(n, k, 2, C2);\\n int r5 = lucas(n, k, 5, C5);\\n return combine_mod_2_5(r2, r5);\\n }\\n\\n bool hasSameDigits(string s) {\\n // yo yo yo what the fuck?\\n // i wanna see how this pans out in closed form\\n // abcdefg\\n // (a+b) (b+c) (c+d) (d+e) (e+f) (f+g)\\n // (a+2b+c) (b+2c+d) (c+2d+e) (d+2e+f) (e+2f+g)\\n // (a+3b+3c+d) (b+3c+3d+e) (c+3d+3e+f) (d+3e+3f+g)\\n // (a+4b+6c+4d+e) etc...\\n // (a+5b+10c+10d+5e+f) + (b+5c+10d+10e+5f+g)\\n // there are n = 7 digits\\n // the last layer is nCr(n - 2, i)\\n // how to compute mod ncr efficiently for the binomial coefficients? \\n // this seems like a linear algorithm which is good\\n\\n // insight: lucas + crt means quick mod nCr algorithm for binomial coeffs\\n int N = s.size() - 2;\\n int dig1 = 0;\\n int dig2 = 0;\\n vector<int> coeffs(N + 1);\\n for (int i = 0; i <= N; i++) {\\n coeffs[i] = nCr_mod_10(N, i);\\n }\\n for (int i = 0; i <= N; i++) {\\n dig1 = (dig1 + coeffs[i] * (int) (s[i] - '0')) % 10;\\n dig2 = (dig2 + coeffs[i] * (int) (s[i + 1] - '0')) % 10;\\n }\\n\\n return dig1 == dig2;\\n }\\n};\"], [122, 1.5799, \"#include <vector>\\n#include <string>\\n#include <numeric>\\n#include <iostream>\\n#include <set> // Include multiset\\n#include <cmath> // Include cmath for sqrt if needed, though not here\\n#include <limits> // Include limits for numeric_limits\\n\\nusing namespace std;\\n\\ntypedef long long ll;\\n\\n// Precompute small factorials and combinations modulo 5 for Lucas Theorem\\nint C_mod5[5][5];\\n\\nvoid precompute_C_mod5() {\\n for (int i = 0; i < 5; ++i) {\\n C_mod5[i][0] = 1;\\n for (int j = 1; j <= i; ++j) {\\n C_mod5[i][j] = (C_mod5[i - 1][j - 1] + C_mod5[i - 1][j]) % 5;\\n }\\n }\\n}\\n\\n// Calculate C(n, k) mod 5 using Lucas Theorem\\nint Lucas(ll n, ll k, int p) {\\n if (k < 0 || k > n) {\\n return 0;\\n }\\n if (k == 0 || k == n) {\\n return 1;\\n }\\n if (k > n / 2) {\\n k = n - k;\\n }\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int ni = n % p;\\n int ki = k % p;\\n if (ki > ni) {\\n return 0; // C(ni, ki) is 0 if ki > ni\\n }\\n // Use precomputed values for C(ni, ki) % 5\\n res = (res * C_mod5[ni][ki]) % p;\\n n /= p;\\n k /= p;\\n }\\n return res;\\n}\\n\\n// Function to combine results using Chinese Remainder Theorem for mod 10\\nint CRT(int mod2, int mod5) {\\n // Find x such that x % 2 == mod2 and x % 5 == mod5\\n for (int x = 0; x < 10; ++x) {\\n if (x % 2 == mod2 && x % 5 == mod5) {\\n return x;\\n }\\n }\\n return -1; // Should not happen\\n}\\n\\n\\nclass Solution {\\npublic:\\n // *** RENAMED FUNCTION HERE ***\\n bool hasSameDigits(string s) {\\n precompute_C_mod5(); // Precompute combinations mod 5\\n\\n int n = s.length();\\n if (n <= 2) {\\n return n < 2 || s[0] == s[1];\\n }\\n ll m = (ll)n - 2; // Use long long for m\\n\\n vector<int> d(n);\\n for (int i = 0; i < n; ++i) {\\n d[i] = s[i] - '0';\\n }\\n\\n // Calculate f0 = sum C(m, i) * d_i (mod 10)\\n int f0_mod2 = 0;\\n int f0_mod5 = 0;\\n for (ll i = 0; i <= m; ++i) {\\n // Modulo 2 check: C(m, i) % 2 == 1 iff i is bitwise subset of m\\n if ((i & m) == i) {\\n f0_mod2 = (f0_mod2 + d[i]) % 2;\\n }\\n\\n // Modulo 5 calculation using Lucas Theorem\\n int lucas_val = Lucas(m, i, 5);\\n f0_mod5 = (f0_mod5 + (lucas_val * d[i]) % 5) % 5;\\n if (f0_mod5 < 0) f0_mod5 += 5; // Ensure positive result\\n }\\n if (f0_mod2 < 0) f0_mod2 += 2; // Ensure positive result\\n\\n\\n // Calculate f1 = sum C(m, i) * d_{i+1} (mod 10)\\n int f1_mod2 = 0;\\n int f1_mod5 = 0;\\n for (ll i = 0; i <= m; ++i) {\\n int d_next = (i + 1 < n) ? d[i + 1] : 0; // Handle index out of bounds\\n\\n // Modulo 2 check\\n if ((i & m) == i) {\\n f1_mod2 = (f1_mod2 + d_next) % 2;\\n }\\n\\n // Modulo 5 calculation\\n int lucas_val = Lucas(m, i, 5);\\n f1_mod5 = (f1_mod5 + (lucas_val * d_next) % 5) % 5;\\n if (f1_mod5 < 0) f1_mod5 += 5; // Ensure positive result\\n }\\n if (f1_mod2 < 0) f1_mod2 += 2; // Ensure positive result\\n\\n\\n // Combine results using CRT\\n int f0_mod10 = CRT(f0_mod2, f0_mod5);\\n int f1_mod10 = CRT(f1_mod2, f1_mod5);\\n\\n return f0_mod10 == f1_mod10;\\n }\\n};\"], [137, 1.4219, \"class Solution {\\nprivate:\\n vector<int> fact;\\npublic:\\n int nCrModm(int n, int r, int p) {\\n long long res = 1ll;\\n while (n && res) {\\n int nDig = n % p;\\n int rDig = r % p;\\n n /= p;\\n r /= p;\\n if (nDig < rDig) {\\n res = 0;\\n }\\n else {\\n res *= fact[nDig] / fact[nDig - rDig] / fact[rDig];\\n res %= p;\\n }\\n }\\n if (r) res = 0;\\n return res;\\n }\\n void populateFactorials(int n) {\\n fact.resize(n+1);\\n fact[0] = 1;\\n for (int i = 1; i <= n; i++) fact[i] = i*fact[i-1];\\n }\\n int chinRem(int a, int b) {\\n for (int i = 0; i < 10; i++) {\\n if (i % 2 == a && i % 5 == b) return i;\\n }\\n return 0;\\n }\\n bool hasSameDigits(string s) {\\n int lsum = 0, rsum = 0;\\n const int n = s.size(), NCHOOSE = n - 2;\\n \\n if (fact.empty()) populateFactorials(5);\\n \\n for (int i = 1; i < n; i++) {\\n int mult2 = nCrModm(NCHOOSE, i-1, 2);\\n int mult5 = nCrModm(NCHOOSE, i-1, 5);\\n int mult10 = chinRem(mult2, mult5);\\n \\n lsum += (s[i-1] - '0') * mult10;\\n rsum += (s[i] - '0') * mult10;\\n\\n lsum %= 10;\\n rsum %= 10;\\n }\\n return lsum == rsum;\\n }\\n};\"], [151, 1.8959, \"class Solution {\\npublic:\\n int lucas_mod2(int n, int r) {\\n while (r > 0) {\\n if ((r & 1) > (n & 1)) {\\n return 0; // If any bit of r > n, return 0\\n }\\n r >>= 1;\\n n >>= 1;\\n }\\n return 1; // All bits of r <= n, return 1\\n }\\n\\n // Function to compute nCr mod 5 using Lucas Theorem\\n int lucas_mod5(int n, int r) {\\n int res = 1;\\n while (r > 0) {\\n int ni = n % 5;\\n int ri = r % 5;\\n if (ri > ni) {\\n return 0; // If any digit of r > n in base 5, return 0\\n }\\n // Compute combination(ni, ri) mod 5\\n int comb = 1;\\n for (int i = 1; i <= ri; ++i) {\\n comb = comb * (ni - ri + i) / i;\\n }\\n res = (res * comb) % 5;\\n n /= 5;\\n r /= 5;\\n }\\n return res;\\n }\\n\\n // Function to compute nCr mod 10 using CRT\\n int nCr(int n, int r) {\\n if (r > n) {\\n return 0;\\n }\\n if (r == 0 || r == n) {\\n return 1;\\n }\\n\\n int mod2 = lucas_mod2(n, r);\\n int mod5 = lucas_mod5(n, r);\\n\\n // Find x such that x \\u2261 mod2 (mod 2) and x \\u2261 mod5 (mod 5)\\n for (int x = 0; x < 10; ++x) {\\n if (x % 2 == mod2 && x % 5 == mod5) {\\n return x;\\n }\\n }\\n return 0; // Fallback (should not reach here for valid inputs)\\n }\\n\\n\\n int getDigit(string str, int level){\\n int ans =0; \\n for(int i = 0; i<=level; i++){\\n int dig = str[i] - '0';\\n int coeff = nCr(level, i);\\n dig%=10; \\n coeff%=10; \\n ans+= (dig*coeff)%10;\\n ans%=10;\\n }\\n return ans; \\n }\\n\\n bool hasSameDigits(string s) {\\n int sz = s.size();\\n int level = sz - 2; \\n if(s.size()==2){\\n return s[0] == s[1];\\n }\\n int d1 = getDigit(s.substr(0, sz-1), level);\\n int d2 = getDigit(s.substr(1, sz-1), level);\\n return d1==d2; \\n }\\n};\\n\\n\\n/*\\n 1 \\n 2\\n 1\\n\\n 3 + 18 + 0 = 1\\n 9 + 2 = 1\\n\\n\\n*/\"], [166, 0.9480000000000001, \"class Solution {\\npublic:\\n\\nvoid increment(vector<int>& number, int base)\\n{\\n int i = 0;\\n while(i < number.size())\\n {\\n number[i]++;\\n if (number[i] >= base)\\n {\\n number[i] = 0;\\n i++;\\n }\\n else break;\\n }\\n}\\n\\nbool hasSameDigits(string s) {\\n vector<vector<int>> nChooseK5 = { {1,0,0,0,0},\\n {1,1,0,0,0},\\n {1,2,1,0,0},\\n {1,3,3,1,0},\\n {1,4,6,4,1}};\\n\\n int n = s.size() - 2;\\n vector<int> nBase5 = {};\\n vector<int> nBase2 = {};\\n while(n)\\n {\\n nBase5.push_back(n % 5);\\n n /= 5;\\n }\\n n = s.size() - 2;\\n while(n)\\n {\\n nBase2.push_back(n % 2);\\n n /= 2;\\n }\\n\\n vector<int> kBase5 = vector<int>(nBase5.size());\\n vector<int> kBase2 = vector<int>(nBase2.size());\\n int sum1 = 0;\\n int sum2 = 0;\\n\\n for(int i = 0; i < s.size() - 1; i++)\\n {\\n int product5 = 1;\\n int product2 = 1;\\n\\n for(int j = 0; j < nBase5.size(); j++)\\n {\\n product5 *= nChooseK5[nBase5[j]][kBase5[j]];\\n product5 %= 5;\\n }\\n for(int j = 0; j < nBase2.size(); j++)\\n {\\n product2 *= not (not nBase2[j] and kBase2[j]);\\n }\\n\\n int mod10;\\n\\n if (product5 % 2 xor product2)\\n mod10 = product5 + 5;\\n else\\n mod10 = product5;\\n\\n sum1 += (s[i] - '0') * mod10;\\n sum1 %= 10;\\n sum2 += (s[i + 1] - '0') * mod10;\\n sum2 %= 10;\\n\\n increment(kBase5, 5);\\n increment(kBase2, 2);\\n }\\n\\n return sum1 == sum2;\\n\\n}\\n};\"], [180, 1.106, \"class NCRLucas{\\n\\n public:\\n vector<int>fact;\\n\\n NCRLucas(int n,int p){\\n fact.resize(n+1,1);\\n for(int i=2;i<=n;i++){\\n fact[i]=(fact[i-1]*i)%p;\\n }\\n }\\n\\n \\n\\n int ncrlucas(int n,int r,int p){\\n\\n int res=1;\\n\\n while(n>0 || r>0){\\n\\n int N=n%p;\\n int R=r%p;\\n if(N<R) return 0;\\n\\n res=(res*ncrFermate(N,R,p))%p;\\n n/=p;\\n r/=p;\\n }\\n\\n return res;\\n }\\n\\n int ncrFermate(int n,int r,int p){\\n if(n<r)return 0;\\n int num=fact[n];\\n int deno=(fact[r]*fact[n-r])%p;\\n int inv=0;\\n for(int i=0;i<p;i++){\\n if((deno*i)%p==1){\\n inv=i;\\n break;\\n }\\n }\\n\\n return (num*inv)%p;\\n }\\n\\n};\\n\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int n=s.size();\\n long long first=0,second=0;\\n NCRLucas comb2(n-1,2);\\n NCRLucas comb5(n-1,5);\\n\\n for(int i=0;i<=n-2;i++){\\n int N=n-2;\\n int R=i;\\n \\n int ncr2=comb2.ncrlucas(N,R,2);\\n int ncr5=comb5.ncrlucas(N,R,5);\\n int ncr10=0; // any value from [0,9]\\n for(int j=0;j<=9;j++){\\n if(j%2==ncr2 && j%5==ncr5){\\n ncr10=j;\\n break;\\n }\\n }\\n\\n // cout<<ncr10<<endl;\\n\\n\\n first=(first+(ncr10*(s[i]-'0'))%10)%10;\\n\\n second=(second+(ncr10*(s[i+1]-'0'))%10)%10;\\n }\\n\\n return first==second;\\n }\\n};\"], [194, 0.474, \"class Solution {\\n public:\\n int fact(int n){\\n if(n == 0) return 1;\\n if(n == 1) return 1;\\n return fact(n - 1) * n;\\n }\\n\\n int bin(int n, int m){\\n return fact(n) / (fact(m) * fact(n-m));\\n }\\n\\n int bin_p(int p, int n, int m){\\n int val = 1;\\n while(n > 0 || m > 0){\\n if(m % p > n % p) \\n return 0;\\n val *= bin(n % p, m % p);\\n val %= p;\\n n /= p;\\n m /= p; \\n }\\n return val;\\n }\\n\\n int bin_10(int n, int m){\\n int b2 = bin_p(2, n, m), b5 = bin_p(5, n, m);\\n\\n for(int i = 0; i < 10; i++)\\n if(i % 2 == b2 && i % 5 == b5)\\n return i;\\n return -1;\\n }\\n\\n void fill(std::vector<int> &T){\\n for(int i = 0; i < T.size(); i++)\\n T[i] = bin_10(T.size()-1, i);\\n }\\n\\n bool hasSameDigits(std::string s) {\\n std::vector<int> T(s.size() - 1);\\n\\n fill(T);\\n\\n int first_d = 0, second_d = 0;\\n\\n for(int i = 0; i < s.size() - 1; i++){\\n first_d += (s[i] - '0') * T[i];\\n second_d += (s[i+1] - '0') * T[i];\\n }\\n \\n return first_d % 10 == second_d % 10;\\n }\\n };\"], [209, 0.79, \"class Solution {\\npublic:\\n int binmod10(int n, int k) {\\n int mod2 = binmod2(n, k);\\n int mod5 = binmod5(n, k);\\n for (int i = 0; i < 10; i++) {\\n if (i % 2 == mod2 && i % 5 == mod5)\\n return i;\\n }\\n return 0;\\n }\\n\\n int binmod2(int n, int k) {\\n while (k > 0) {\\n if ((k & 1) > (n & 1))\\n return 0;\\n n >>= 1;\\n k >>= 1;\\n }\\n return 1;\\n }\\n\\n int binmod5(int n, int k) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int nd = n % 5;\\n int kd = k % 5;\\n if (kd > nd)\\n return 0;\\n res = (res * binsmall(nd, kd)) % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return res;\\n }\\n\\n int binsmall(int n, int k) {\\n if (k > n)\\n return 0;\\n int fact[5] = {1, 1, 2, 1, 4};\\n int numerator = fact[n];\\n int denominator = (fact[k] * fact[n - k]) % 5;\\n int deninv = 0;\\n for (int i = 0; i < 5; i++) {\\n if ((denominator * i) % 5 == 1) {\\n deninv = i;\\n break;\\n }\\n }\\n return (numerator * deninv) % 5;\\n }\\n\\n bool hasSameDigits(string s) {\\n int L = s.size();\\n int m = L - 2;\\n int s1 = 0, s2 = 0;\\n for (int i = 0; i <= m; i++) {\\n int val = binmod10(m, i);\\n int d1 = s[i] - '0';\\n int d2 = s[i + 1] - '0';\\n s1 = (s1 + val * d1) % 10;\\n s2 = (s2 + val * d2) % 10;\\n }\\n return s1 == s2;\\n }\\n};\"], [223, 8.2149, \"class Solution {\\npublic:\\n int binmod10(int n, int k) {\\n int mod2 = binmod2(n, k);\\n int mod5 = binmod5(n, k);\\n for (int i = 0; i < 10; i++) {\\n if (i % 2 == mod2 && i % 5 == mod5)\\n return i;\\n }\\n return 0;\\n }\\n\\n int binmod2(int n, int k) {\\n while (k > 0) {\\n if ((k & 1) > (n & 1))\\n return 0;\\n n >>= 1;\\n k >>= 1;\\n }\\n return 1;\\n }\\n\\n int binmod5(int n, int k) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int nd = n % 5;\\n int kd = k % 5;\\n if (kd > nd)\\n return 0;\\n res = (res * binsmall(nd, kd)) % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return res;\\n }\\n\\n int binsmall(int n, int k) {\\n if (k > n)\\n return 0;\\n int fact[5] = {1, 1, 2, 1, 4};\\n int numerator = fact[n];\\n int denominator = (fact[k] * fact[n - k]) % 5;\\n int deninv = 0;\\n for (int i = 0; i < 5; i++) {\\n if ((denominator * i) % 5 == 1) {\\n deninv = i;\\n break;\\n }\\n }\\n return (numerator * deninv) % 5;\\n }\\n\\n bool hasSameDigits(string s) {\\n int L = s.size();\\n int m = L - 2;\\n int s1 = 0, s2 = 0;\\n for (int i = 0; i <= m; i++) {\\n int val = binmod10(m, i);\\n int d1 = s[i] - '0';\\n int d2 = s[i + 1] - '0';\\n s1 = (s1 + val * d1) % 10;\\n s2 = (s2 + val * d2) % 10;\\n }\\n return s1 == s2;\\n }\\n};\"], [238, 5.687399999999999, \"class Solution {\\npublic:\\n int binmod10(int n, int k) {\\n int mod2 = binmod2(n, k);\\n int mod5 = binmod5(n, k);\\n for (int i = 0; i < 10; i++) {\\n if (i % 2 == mod2 && i % 5 == mod5)\\n return i;\\n }\\n return 0;\\n }\\n\\n int binmod2(int n, int k) {\\n while (k > 0) {\\n if ((k & 1) > (n & 1))\\n return 0;\\n n >>= 1;\\n k >>= 1;\\n }\\n return 1;\\n }\\n\\n int binmod5(int n, int k) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int nd = n % 5;\\n int kd = k % 5;\\n if (kd > nd)\\n return 0;\\n res = (res * binsmall(nd, kd)) % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return res;\\n }\\n\\n int binsmall(int n, int k) {\\n if (k > n)\\n return 0;\\n int fact[5] = {1, 1, 2, 1, 4};\\n int numerator = fact[n];\\n int denominator = (fact[k] * fact[n - k]) % 5;\\n int deninv = 0;\\n for (int i = 0; i < 5; i++) {\\n if ((denominator * i) % 5 == 1) {\\n deninv = i;\\n break;\\n }\\n }\\n return (numerator * deninv) % 5;\\n }\\n \\n bool hasSameDigits(string s) {\\n int n = s.size()-2;\\n vector<int> sequence;\\n long long binomial_coeff = 1;\\n sequence.push_back(binomial_coeff);\\n\\n for (int k = 1; k <= n; ++k) {\\n binomial_coeff = binmod10(n,k);\\n // binomial_coeff = binomial_coeff * (n - k + 1) / k;\\n sequence.push_back(binomial_coeff);\\n // cout<<binomial_coeff<<\\\" \\\";\\n }\\n long long sum1=0, sum2=0;\\n for(int i=0; i<sequence.size(); i++){\\n sum1 += sequence[i]*(s[i]-'0' );\\n sum2 += sequence[i]*(s[i+1]-'0');\\n // cout<<sequence[i]*(s[i]-'0' )<<\\\" \\\"<<sequence[i]*(s[i+1]-'0' )<<endl;\\n }\\n if(sum1%10 == sum2%10)\\n return true;\\n return false;\\n }\\n};\"], [252, 0.79, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n int length=s.size();\\n int n=length-2;\\n int sum1=0,sum2=0;\\n for(int i=0;i<=n;i++){\\n int coeff=nCkMod10(n,i);\\n int d1=s[i]-'0';\\n int d2=s[i+1]-'0';\\n sum1=(sum1+(d1*coeff))%10;\\n sum2=(sum2+(d2*coeff))%10;\\n }\\n return sum1==sum2;\\n }\\n int nCkMod10(int n,int k){\\n int mod2Val=nCkLucasMod2(n,k);\\n int mod5Val=nCkLucasMod5(n,k);\\n for(int candidate=0;candidate<10;candidate++){\\n if(candidate%2==mod2Val && candidate%5==mod5Val){\\n return candidate;\\n }\\n }\\n return 0;\\n }\\n int nCkLucasMod2(int n,int k){\\n int res=1;\\n while(n>0 || k>0){\\n int nDigit=n%2;\\n int kDigit=k%2;\\n if(kDigit>nDigit) return 0;\\n res=(res*nCkMod2(nDigit,kDigit))%2;\\n n/=2;\\n k/=2;\\n }\\n return res;\\n }\\n int nCkMod2(int n,int k){\\n if(k>n) return 0;\\n return 1;\\n }\\n int nCkLucasMod5(int n,int k){\\n int res=1;\\n while(n>0 || k>0){\\n int nDigit=n%5;\\n int kDigit=k%5;\\n if(kDigit>nDigit) return 0;\\n res=(res*nCkMod5(nDigit,kDigit))%5;\\n n/=5;\\n k/=5;\\n }\\n return res;\\n }\\n int nCkMod5(int n,int k){\\n if(k>n) return 0;\\n int factMod5[5]={1,1,2,1,4};\\n int numerator=factMod5[n];\\n int denominator=(factMod5[n-k]*factMod5[k])%5;\\n int denoInv=0;\\n for(int candidate=0;candidate<5;candidate++){\\n if((denominator*candidate)%5==1){\\n denoInv=candidate;\\n }\\n }\\n return (numerator*denoInv)%5;\\n }\\n\\n};\"], [267, 1.7379999999999998, \"#include <iostream>\\n#include <vector>\\nusing namespace std;\\n\\nint binmod2(int n, int k) {\\n while (k > 0) {\\n if ((k & 1) > (n & 1))\\n return 0;\\n n >>= 1;\\n k >>= 1;\\n }\\n return 1;\\n}\\nint binsmall(int n, int k) {\\n if (k > n)\\n return 0;\\n int fact[5] = {1, 1, 2, 1, 4};\\n int numerator = fact[n];\\n int denominator = (fact[k] * fact[n - k]) % 5;\\n int deninv = 0;\\n for (int i = 0; i < 5; i++) {\\n if ((denominator * i) % 5 == 1) {\\n deninv = i;\\n break;\\n }\\n }\\n return (numerator * deninv) % 5;\\n}\\n\\nint binmod5(int n, int k) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int nd = n % 5;\\n int kd = k % 5;\\n if (kd > nd)\\n return 0;\\n res = (res * binsmall(nd, kd)) % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return res;\\n}\\n\\n\\nint binmod10(int n, int k) {\\n int mod2 = binmod2(n, k);\\n int mod5 = binmod5(n, k);\\n for (int i = 0; i < 10; i++) {\\n if (i % 2 == mod2 && i % 5 == mod5)\\n return i;\\n }\\n return 0;\\n}\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n // obs: pascal's triangle's n-2th term\\n\\n int n = (int)s.size();\\n vector<long long> A;\\n for(auto &ch: s) \\n A.push_back(ch-'0');\\n\\n vector<long long> C((int)s.size()-1);\\n for(int i = 0; i < (int)C.size(); i++) {\\n // C[i] = //n-2Ci \\n // C[i] = nCr(n-2,i,mod);\\n C[i] = binmod10(n-2, i);\\n }\\n auto get = [&](int l, int r)->int {\\n long long ans = 0;\\n for(int i = 0; i < (int)C.size(); i++) {\\n ans += A[i+l] * C[i];\\n ans %= 10;\\n }\\n return ans%10;\\n };\\n int left = get(0,n-2);\\n int right = get(1,n-1);\\n return left == right;\\n }\\n};\"], [281, 1.422, \"#include <bits/stdc++.h>\\nusing namespace std;\\nclass Solution {\\npublic:\\n int mod5(int n, int k) {\\n int fact[5] = {1, 1, 2, 6, 24};\\n for (int i = 0; i < 5; i++)\\n fact[i] %= 5;\\n int inv[5];\\n for(int i = 0; i< 5; i++)\\n {\\n inv[i] = i;\\n }\\n int res = 1;\\n while (n || k) {\\n int m = n % 5, j = k % 5;\\n if (j > m)\\n return 0;\\n int num = fact[m], den = (fact[j] * fact[m - j]) % 5;\\n int invDen = 1;\\n for (int x = 1; x < 5; x++) {\\n if ((den * x) % 5 == 1) {\\n invDen = x;\\n break;\\n }\\n }\\n int cur = (num * invDen) % 5;\\n res = (res * cur) % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return res;\\n }\\n int mod10(int n, int k) {\\n int a = ((n & k) == k) ? 1 : 0;\\n int b = mod5(n, k);\\n for (int x = 0; x < 10; x++) {\\n if (x % 2 == a && x % 5 == b)\\n return x;\\n }\\n return 0;\\n }\\n bool hasSameDigits(string s) {\\n int n = s.size(), m = n - 2;\\n long long A = 0, B = 0;\\n for (int i = 0; i <= m; i++) {\\n int temp = mod10(m, i);\\n A = (A + 1LL * temp * (s[i] - '0')) % 10;\\n }\\n for (int i = 0; i <= m; i++) {\\n int temp1 = mod10(m, i);\\n B = (B + 1LL * temp1 * (s[i + 1] - '0')) % 10;\\n }\\n return A == B;\\n }\\n};\"], [295, 0.632, \"class Solution {\\npublic:\\n int findDigit(int mod2, int mod5) {\\n for (int i = 0; i < 10; ++i) {\\n if (i % 2 == mod2 && i % 5 == mod5) return i;\\n }\\n return 0;\\n }\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n vector<int> cnt2(n), cnt5(n);\\n for (int i = 2; i < n; ++i) {\\n cnt2[i] = cnt2[i - 1];\\n int tmp = i;\\n while (tmp % 2 == 0) {\\n cnt2[i]++;\\n tmp /= 2;\\n }\\n\\n cnt5[i] = cnt5[i - 1];\\n tmp = i;\\n while (tmp % 5 == 0) {\\n cnt5[i]++;\\n tmp /= 5;\\n }\\n }\\n\\n int mod5 = 1;\\n int rev[5] = {0, 1, 3, 2, 4};\\n int diff = s[0] - s[1];\\n for (int i = 1; i <= n - 2; ++i) {\\n vector<int> x{i, n - 1 - i};\\n for (auto &xx : x) {\\n while (xx % 5 == 0) xx /= 5;\\n }\\n mod5 *= rev[x[0] % 5] * x[1];\\n mod5 %= 5;\\n \\n int d = findDigit(cnt2[n - 2] - cnt2[i] - cnt2[n - 2 - i] == 0, cnt5[n - 2] - cnt5[i] - cnt5[n - 2 - i] > 0 ? 0 : mod5);\\n diff += d * (s[i] - s[i + 1]);\\n }\\n\\n return diff % 10 == 0;\\n }\\n};\"], [310, 0.316, \"\\nclass Lucas_nCrModp{\\n\\n vector<int> fact, invFact, inv;\\n \\n public:\\n\\n Lucas_nCrModp(int p){\\n \\n fact.resize(p);\\n invFact.resize(p);\\n inv.resize(p);\\n \\n fact[0] = fact[1] = 1;\\n invFact[0] = invFact[1] = 1;\\n inv[0] = 1;\\n inv[1] = 1;\\n \\n for(int i = 2; i < p; i++){\\n fact[i] = fact[i-1] * i % p;\\n inv[i] = (p - p / i) * inv[p % i] % p;\\n invFact[i] = invFact[i - 1] * inv[i] % p; \\n }\\n }\\n\\n int find(int n, int r, int p){\\n\\n if(r < 0 or r > n) return 0;\\n if(r == 0 or r == n) return 1;\\n\\n if(n < p) \\n return fact[n] * invFact[r] * invFact[n - r] % p; \\n \\n return find(n / p, r / p, p)\\n * find(n % p, r % p, p) % p;\\n }\\n};\\n\\n\\nclass Solution {\\npublic:\\n\\n int CRT(int x, int y){\\n if(x == 0){\\n if(y == 0) return 0;\\n if(y == 1) return 6;\\n if(y == 2) return 2;\\n if(y == 3) return 8;\\n if(y == 4) return 4;\\n }\\n if(x == 1){\\n if(y == 0) return 5;\\n if(y == 1) return 1;\\n if(y == 2) return 7;\\n if(y == 3) return 3;\\n if(y == 4) return 9;\\n }\\n return -1;\\n }\\n\\n Lucas_nCrModp *lucas_p2, *lucas_p5;\\n\\n // returns nCr mod 10\\n int findBinCoefMod10(int n, int r){\\n int coefMod2 = lucas_p2 -> find(n, r, 2);\\n int coefMod5 = lucas_p5 -> find(n, r, 5);\\n return CRT(coefMod2, coefMod5);\\n }\\n\\n bool hasSameDigits(string s) {\\n \\n int n = s.length();\\n int digit1 = 0, digit2 = 0;\\n \\n lucas_p2 = new Lucas_nCrModp(2);\\n lucas_p5 = new Lucas_nCrModp(5);\\n\\n for(int i = 0; i < n - 1; i++){\\n \\n int binCoef = findBinCoefMod10(n - 2, i);\\n (digit1 += binCoef * (s[i] - '0')) %= 10;\\n (digit2 += binCoef * (s[i + 1] - '0')) %= 10;\\n }\\n return digit1 == digit2;\\n }\\n};\"], [324, 1.5799999999999996, \"class Solution { \\npublic:\\n int comb(int n, int r){ \\n if (r > n) { return 0; }\\n int res = 1;\\n for (int t = 1; t <= n; ++t) { res *= t; }\\n for (int t = 1; t <= r; ++t) { res /= t; }\\n for (int t = 1; t <= n - r; ++t) { res /= t; }\\n return res;\\n }\\n\\n bool check(vector<int>& a, int mod){\\n int res = 0;\\n int n = a.size();\\n for (int i = 0; i != n; ++i){\\n int ncr = 1;\\n int x = n - 1;\\n int y = i;\\n while (x && y){\\n ncr = ncr * comb(x % mod, y % mod) % mod;\\n x /= mod;\\n y /= mod;\\n }\\n res = (res + ncr * a[i]) % mod;\\n }\\n return res == 0;\\n }\\n\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n vector<int> a(n - 1);\\n for (int i = 0; i != n - 1; ++i){\\n a[i] = (s[i] - '0') - (s[i + 1] - '0');\\n a[i] = (a[i] + 10) % 10;\\n }\\n return check(a, 2) && check(a, 5);\\n }\\n};\"], [339, 2.6858999999999997, \"class Solution { // lucas thm.\\npublic:\\n\\n int comb(int n, int r){ // for small n,r\\n if (r > n) { return 0; }\\n int res = 1;\\n for (int t = 1; t <= n; ++t) { res *= t; }\\n for (int t = 1; t <= r; ++t) { res /= t; }\\n for (int t = 1; t <= n - r; ++t) { res /= t; }\\n return res;\\n }\\n\\n bool check(vector<int>& a, int mod){\\n int res = 0;\\n int n = a.size();\\n for (int i = 0; i != n; ++i){\\n // res += c(n-1, i) * ai\\n int ncr = 1;\\n int x = n - 1;\\n int y = i;\\n while (x && y){\\n ncr = ncr * comb(x % mod, y % mod) % mod;\\n x /= mod;\\n y /= mod;\\n }\\n res = (res + ncr * a[i]) % mod;\\n }\\n return res == 0;\\n }\\n\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n vector<int> a(n - 1);\\n for (int i = 0; i != n - 1; ++i){\\n a[i] = (s[i] - '0') - (s[i + 1] - '0');\\n a[i] = (a[i] + 10) % 10;\\n }\\n return check(a, 2) && check(a, 5);\\n }\\n};\"], [353, 0.474, \"class Solution {\\npublic:\\n using ll = long long;\\n static const int _n = 1e5 + 10;\\n static const int finalmod = 10;\\n static const int m1 = 5;\\n static const int m2 = 2; // 10/5=2\\n int invm1 = 1; // inv 5 mod 2 = 1\\n int invm2 = 3; // inv 2 mod 5 = 3 // we can do this by powmod if this is hard to calculate\\n static const int mod1 = 2;\\n static const int mod2 = 5; // 2 * 5 = 10, use CRT\\n static const int finmod = 10;\\n int n;\\n int fac1[_n], inv1[_n];\\n int fac2[_n], inv2[_n];\\n int C1(int m, int n) {\\n if (m < n)\\n return 0;\\n if (m < mod1 and n < mod1)\\n return 1ll * fac1[m] * inv1[n] % mod1 * inv1[m - n] % mod1;\\n return 1ll * C1(m / mod1, n / mod1) * C1(m % mod1, n % mod1) % mod1;\\n }\\n int C2(int m, int n) {\\n if (m < n)\\n return 0;\\n if (m < mod2 and n < mod2)\\n return 1ll * fac2[m] * inv2[n] % mod2 * inv2[m - n] % mod2;\\n return 1ll * C2(m / mod2, n / mod2) * C2(m % mod2, n % mod2) % mod2;\\n }\\n ll powmod(ll a, ll b, int mod) {\\n ll res = 1;\\n a %= mod;\\n assert(b >= 0);\\n for (; b; b >>= 1) {\\n if (b & 1)\\n res = res * a % mod;\\n a = a * a % mod;\\n }\\n return res;\\n }\\n void genInv1() {\\n fac1[0] = 1;\\n int len = min(mod1-1, n);\\n for (int i = 1; i <= len; i++) {\\n fac1[i] = 1ll * fac1[i - 1] * i % mod1;\\n }\\n // \\u4ee5\\u4e0b\\u9019\\u662f\\u7528exgcd\\u7b97\\n // int tmp1,tmp2;rep(i,0,n+1)exgcd(fac[i],mod,tmp1,inv[i],tmp2);\\n // \\u4ee5\\u4e0b\\u662f\\u7528Fermat's Little Thm\\u7b97\\n inv1[len] = powmod(fac1[len], mod1 - 2, mod1);\\n for (int i = len - 1; i >= 0; i--) {\\n inv1[i] = 1ll * inv1[i + 1] * (i + 1) % mod1;\\n }\\n }\\n void genInv2() {\\n fac2[0] = 1;\\n int len = min(mod2-1, n);\\n for (int i = 1; i <= len; i++) {\\n fac2[i] = 1ll * fac2[i - 1] * i % mod2;\\n }\\n // \\u4ee5\\u4e0b\\u9019\\u662f\\u7528exgcd\\u7b97\\n // int tmp1,tmp2;rep(i,0,n+1)exgcd(fac[i],mod,tmp1,inv[i],tmp2);\\n // \\u4ee5\\u4e0b\\u662f\\u7528Fermat's Little Thm\\u7b97\\n inv2[len] = powmod(fac2[len], mod2 - 2, mod2);\\n for (int i = len - 1; i >= 0; i--) {\\n inv2[i] = 1ll * inv2[i + 1] * (i + 1) % mod2;\\n }\\n }\\n\\n bool hasSameDigits(string s) {\\n n = s.size();\\n genInv1();\\n genInv2();\\n vector<int> cnt(n - 1);\\n\\n invm1 = powmod(m1, mod1-2, mod1);\\n invm2 = powmod(m2, mod2-2, mod2);\\n\\n for (int i = 0; i < n - 1; i++) {\\n cnt[i] = (C1(n - 2, i) * m1 % finmod * invm1 +\\n C2(n - 2, i) * m2 % finmod * invm2) % finmod;\\n }\\n int sum1 = 0, sum2 = 0;\\n for (int i = 0; i < n - 1; i++) {\\n sum1 = (1ll * sum1 + 1ll * cnt[i] * (s[i] - '0')) % finmod;\\n }\\n for (int i = 1; i < n; i++) {\\n sum2 = (1ll * sum2 + 1ll * cnt[i - 1] * (s[i] - '0')) % finmod;\\n }\\n return sum1 == sum2;\\n }\\n};\"], [368, 0.474, \"class Solution {\\npublic:\\n vector<int> getpowers(int n)\\n {\\n vector<int> V(3,0);\\n while(n>1 && n%2==0)\\n {\\n V[0]++;\\n n=n/2;\\n }\\n while(n>1 && n%5==0)\\n {\\n V[1]++;\\n n=n/5;\\n }\\n V[2]=n%10;\\n return V;\\n }\\n vector<int> Comb(int n)\\n {\\n vector<int> V(n+1,0);\\n int i=0,j=n;\\n V[i]=1;\\n V[j]=1;\\n int cnt2=0;\\n int cnt5=0;\\n int unit=1,s;\\n vector<int> v1,v2;\\n for(i=1,j=n-1;i<=j;i++,j--)\\n {\\n v1=getpowers(j+1);\\n v2=getpowers(i);\\n cnt2=cnt2+v1[0]-v2[0];\\n cnt5=cnt5+v1[1]-v2[1];\\n unit=unit*v1[2];\\n if(v2[2]==3)\\n unit=unit*7;\\n else if(v2[2]==7)\\n unit=unit*3;\\n else if(v2[2]==9)\\n unit=unit*9;\\n unit=unit%10;\\n V[i]=unit;\\n if(cnt2>0)\\n {\\n s=cnt2%4;\\n if(s==1)\\n V[i]*=2;\\n else if(s==2)\\n V[i]*=4;\\n else if(s==3)\\n V[i]*=8;\\n else\\n V[i]*=6;\\n }\\n if(cnt5>0)\\n V[i]*=5;\\n V[i]=V[i]%10;\\n V[j]=V[i];\\n }\\n return V;\\n }\\n bool hasSameDigits(string s) {\\n int n=s.size();\\n vector<int> V=Comb(n-2);\\n int a=0,b=0;\\n for(int i=0,j=n-1;i<n-1;i++,j--)\\n {\\n a=(a+V[i]*(s[i]-'0'))%10;\\n b=(b+V[i]*(s[j]-'0'))%10;\\n }\\n return a==b;\\n }\\n};\"], [382, 1.2638999999999998, \"class Solution {\\npublic:\\n int comb(int n, int r)\\n {\\n if(n < r) return 0;\\n int numerator = 1;\\n for(int i = r + 1; i <= n; i++)\\n {\\n numerator *= i;\\n }\\n for(int j = 1; j <= n - r; j++)\\n {\\n numerator /= j;\\n }\\n return numerator;\\n }\\n // int comb(int n, int r){ // for small n,r\\n // if (r > n) { return 0; }\\n // int res = 1;\\n // for (int t = 1; t <= n; ++t) { res *= t; }\\n // for (int t = 1; t <= r; ++t) { res /= t; }\\n // for (int t = 1; t <= n - r; ++t) { res /= t; }\\n // return res;\\n // }\\n bool solve(string s, int p)\\n {\\n int n = s.length() - 1;\\n int res = 0;\\n for(int i = 0; i < n; i++)\\n {\\n int t_n = n - 1;\\n int t_r = i;\\n int t = 1;\\n while(t_n > 0 && t_r > 0)\\n {\\n t = (t * comb(t_n%p, t_r%p))%p;\\n t_n /= p;\\n t_r /= p;\\n }\\n int temp = (s[i] - '0') - (s[i + 1] - '0');\\n temp = (temp + 10)%10;\\n res = (res + (t*temp))%p;\\n }\\n return res == 0;\\n }\\n // int solve_f(string s, int p)\\n // {\\n // int n = s.length() - 1;\\n // int res = 0;\\n // for(int i = 1; i < n; i++)\\n // {\\n // int t_n = n;\\n // int t_r = i;\\n // int t = 0;\\n // while(t_n > 0 || t_r > 0)\\n // {\\n // t *= comb(t_n%p, t_r%p) % p;\\n // t_n /= p;\\n // t_r /= p;\\n // }\\n // res = (res + ((s[i + 1] - '0') - (s[i] - '0'))*t)% p;\\n // }\\n // return res;\\n // }\\n bool hasSameDigits(string s) {\\n bool op1 = solve(s, 2);\\n bool op2 = solve(s, 5);\\n return op1 && op2;\\n }\\n};\"], [397, 0.474, \"class Solution {\\n public:\\n // Same as 3461. Check If Digits Are Equal in String After Operations I\\n bool hasSameDigits(const string& s) {\\n const int n = s.length();\\n int num1 = 0;\\n int num2 = 0;\\n\\n for (int i = 0; i + 1 < n; ++i) {\\n const int coefficient = nCkMod10(n - 2, i);\\n num1 += (coefficient * (s[i] - '0')) % 10;\\n num1 %= 10;\\n num2 += (coefficient * (s[i + 1] - '0')) % 10;\\n num2 %= 10;\\n }\\n\\n return num1 == num2;\\n }\\n\\n private:\\n // Returns (n, k) % 10.\\n int nCkMod10(int n, int k) {\\n const int mod2 = lucasTheorem(n, k, 2);\\n const int mod5 = lucasTheorem(n, k, 5);\\n static constexpr int lookup[2][5] = {\\n {0, 6, 2, 8, 4}, // mod2 == 0\\n {5, 1, 7, 3, 9} // mod2 == 1\\n };\\n return lookup[mod2][mod5];\\n }\\n\\n // Returns (n, k) % prime.\\n int lucasTheorem(int n, int k, int prime) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n const int nMod = n % prime;\\n const int kMod = k % prime;\\n res *= nCk(nMod, kMod);\\n res %= prime;\\n n /= prime;\\n k /= prime;\\n }\\n return res;\\n }\\n\\n // Returns (n, k).\\n int nCk(int n, int k) {\\n int res = 1;\\n for (int i = 0; i < k; ++i) {\\n res *= (n - i);\\n res /= (i + 1);\\n }\\n return res;\\n }\\n};\"], [411, 1.106, \"class Solution {\\n public:\\n bool hasSameDigits(const string& s) {\\n const int n = s.length();\\n int num1 = 0;\\n int num2 = 0;\\n\\n for (int i = 0; i + 1 < n; ++i) {\\n const int coefficient = nCkMod10(n - 2, i);\\n num1 += (coefficient * (s[i] - '0')) % 10;\\n num1 %= 10;\\n num2 += (coefficient * (s[i + 1] - '0')) % 10;\\n num2 %= 10;\\n }\\n\\n return num1 == num2;\\n }\\n\\n private:\\n int nCkMod10(int n, int k) {\\n const int mod2 = lucasTheorem(n, k, 2);\\n const int mod5 = lucasTheorem(n, k, 5);\\n static constexpr int lookup[2][5] = {\\n {0, 6, 2, 8, 4},\\n {5, 1, 7, 3, 9}\\n };\\n return lookup[mod2][mod5];\\n }\\n\\n int lucasTheorem(int n, int k, int prime) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n const int nMod = n % prime;\\n const int kMod = k % prime;\\n res *= nCk(nMod, kMod);\\n res %= prime;\\n n /= prime;\\n k /= prime;\\n }\\n return res;\\n }\\n\\n int nCk(int n, int k) {\\n int res = 1;\\n for (int i = 0; i < k; ++i) {\\n res *= (n - i);\\n res /= (i + 1);\\n }\\n return res;\\n }\\n};\"], [425, 0.632, \"class Solution {\\npublic:\\nint fact(int n) {\\nif (n==0) return 1;\\nif (n==1) return 1;\\nif (n==2) return 2;\\nif (n==3) return 6;\\nif (n==4) return 24;\\nif (n==5) return 120;\\nif (n==6) return 720;\\nif (n==7) return 5040;\\nif (n==8) return 40320;\\nif (n==9) return 362880; \\n int res = 1;\\n for (int i = 1; i <= n; ++i) {\\n res *= i;\\n }\\n return res;\\n};\\n\\nint cnk(int n, int k) {\\nif (n==1 && k==0) return 1;\\nif (n==2 && k==0) return 1;\\nif (n==2 && k==1) return 2;\\nif (n==3 && k==0) return 1;\\nif (n==3 && k==1) return 3;\\nif (n==3 && k==2) return 3;\\nif (n==4 && k==0) return 1;\\nif (n==4 && k==1) return 4;\\nif (n==4 && k==2) return 6;\\nif (n==4 && k==3) return 4;\\n int res = 1;\\n res = fact(n) / fact(k) / fact(n - k);\\n return res;\\n};\\n\\nint cnkrrem(int n, int k) {\\n int a = 1;\\n for (int n2 = n, k2 = k; n2 > 0 || k2 > 0;) {\\n const int n22 = n2 % 2;\\n const int k22 = k2 % 2;\\n if (n22 < k22) {\\n a = 0;\\n break;\\n } else {\\n a *= cnk(n22, k22);\\n }\\n n2 /= 2;\\n k2 /= 2;\\n }\\n int b = 1;\\n for (int n5 = n, k5 = k; n5 > 0 || k5 > 0;) {\\n const int n55 = n5 % 5;\\n const int k55 = k5 % 5;\\n if (n55 < k55) {\\n b = 0;\\n break;\\n } else {\\n b *= cnk(n55, k55);\\n }\\n n5 /= 5;\\n k5 /= 5;\\n }\\n return (5 * a + 6 * b) % 10;\\n};\\n\\n\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n if (n < 2)\\n return false;\\n if (n == 2)\\n return s[0] == s[1];\\n int c1 = 0;\\n int c2 = 0;\\n int c11=0;\\n int c22=0;\\n map<int, int> m = {};\\n const int n2=n -2;\\n const int n22=n2/2;\\n\\n for (int i = 0; i < n - 1; ++i) {\\n if (i<=n22) {\\n c11 = cnkrrem(n2, i);\\n m[i]=c11;\\n } else {\\n c11=m[n2-i];\\n }\\n const int d= s[i] - '0';\\n c1 += d * c11;\\n c2 += d * c22;\\n c22=c11;\\n }\\n c2 += s[n-1] - '0';\\n\\n c1 %= 10;\\n c2 %= 10;\\n\\n return c1 == c2;\\n }\\n};\"], [440, 0.9480000000000001, \"class Solution {\\npublic:\\n int comb_mod_p(int n, int k, int p) {\\n if (k < 0 || k > n) return 0;\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int ni = n % p, ki = k % p;\\n if (ki > ni) return 0;\\n // Compute niCki mod p\\n int num = 1, den = 1;\\n for (int i = 0; i < ki; ++i) {\\n num = num * (ni - i) % p;\\n den = den * (i + 1) % p;\\n }\\n // Fermat's little theorem for modular inverse\\n int den_inv = 1, exp = p - 2;\\n int base = den;\\n while (exp) {\\n if (exp & 1) den_inv = den_inv * base % p;\\n base = base * base % p;\\n exp >>= 1;\\n }\\n res = res * num % p * den_inv % p;\\n n /= p;\\n k /= p;\\n }\\n return res;\\n}\\n\\n// Combine mod 2 and mod 5 results to mod 10 using CRT\\nint crt(int a2, int a5) {\\n // x \\u2261 a2 (mod 2), x \\u2261 a5 (mod 5)\\n // x = 5*a2 + 6*a5 mod 10\\n return (5 * a2 + 6 * a5) % 10;\\n}\\n\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n int k = n - 2;\\n if (k < 0) return false;\\n int sum1 = 0, sum2 = 0;\\n for (int i = 0; i < n; ++i) {\\n // For the first digit: C(k, i) mod 10\\n int coeff1 = 0;\\n if (i <= k) {\\n int mod2_1 = comb_mod_p(k, i, 2);\\n int mod5_1 = comb_mod_p(k, i, 5);\\n coeff1 = crt(mod2_1, mod5_1);\\n }\\n // For the second digit: C(k, i-1) mod 10\\n int coeff2 = 0;\\n int j = i - 1;\\n if (j >= 0 && j <= k) {\\n int mod2_2 = comb_mod_p(k, j, 2);\\n int mod5_2 = comb_mod_p(k, j, 5);\\n coeff2 = crt(mod2_2, mod5_2);\\n }\\n int digit = s[i] - '0';\\n sum1 = (sum1 + digit * coeff1) % 10;\\n sum2 = (sum2 + digit * coeff2) % 10;\\n }\\n return sum1 == sum2;\\n }\\n};\"], [454, 0.158, \"class Solution {\\npublic:\\n\\tint ncrTable[10][10];\\n\\tSolution() {\\n\\t\\tncrTable[0][0] = 1;\\n\\t\\tfor (int i = 1; i < 10; i++) {\\n\\t\\t\\tfor (int j = 0; j < 10; j++) ncrTable[i][j] = ncrTable[i-1][j] + (j > 0? ncrTable[i-1][j-1] : 0);\\n\\t\\t}\\n\\t}\\n\\tint ncr(int n, int r, int p) {\\n\\t\\tint prod = 1;\\n\\t\\twhile (n > 0 || r > 0) {\\n\\t\\t\\tprod = prod * ncrTable[n%p][r%p] % p;\\n\\t\\t\\tn /= p;\\n\\t\\t\\tr /= p;\\n\\t\\t}\\n\\t\\treturn prod;\\n\\t}\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n\\t\\tint sum2 = ((int)s[0] - (int)s.back() + 2) % 2;\\n\\t\\tint sum5 = ((int)s[0] - (int)s.back() + 5) % 5;\\n\\t\\tfor (int i = 1; i+1 < n; i++) {\\n\\t\\t\\tsum2 = (sum2 + (ncr(n-2, i, 2) - ncr(n-2, i-1, 2)) * (s[i]-'0') + 2) % 2;\\n\\t\\t\\tsum5 = (sum5 + (ncr(n-2, i, 5) - ncr(n-2, i-1, 5)) * (s[i]-'0') + 5) % 5;\\n\\t\\t}\\n\\t\\treturn sum2 == 0 && sum5 == 0;\\n }\\n};\\n\"], [469, 0.158, \"class Solution {\\npublic:\\n\\tint ncrTable[10][10];\\n\\tSolution() {\\n\\t\\tncrTable[0][0] = 1;\\n\\t\\tfor (int i = 1; i < 10; i++) {\\n\\t\\t\\tfor (int j = 0; j < 10; j++) ncrTable[i][j] = ncrTable[i-1][j] + (j > 0? ncrTable[i-1][j-1] : 0);\\n\\t\\t}\\n\\t}\\n\\tint ncr(int n, int r, int p) {\\n\\t\\tif (p == 10) {\\n\\t\\t\\tint m2 = ncr(n, r, 2);\\n\\t\\t\\tint m5 = ncr(n, r, 5);\\n\\t\\t\\tfor (int i = 0; i < 10; i++) if (i % 2 == m2 && i % 5 == m5) return i;\\n\\t\\t\\treturn 0; // SHOULD NOT HAPPEN\\n\\t\\t} else {\\n\\t\\t\\tint prod = 1;\\n\\t\\t\\twhile (n > 0 || r > 0) {\\n\\t\\t\\t\\tprod = prod * ncrTable[n%p][r%p] % p;\\n\\t\\t\\t\\tn /= p;\\n\\t\\t\\t\\tr /= p;\\n\\t\\t\\t}\\n\\t\\t\\treturn prod;\\n\\t\\t}\\n\\t}\\n bool hasSameDigits(string s) {\\n int sum = ((int)s[0] - (int)s.back() + 10) % 10, n = s.size();\\n\\t\\tfor (int i = 1; i+1 < n; i++) {\\n\\t\\t\\tsum = (sum + (ncr(n-2, i, 10) - ncr(n-2, i-1, 10)) * (s[i]-'0') + 10) % 10;\\n\\t\\t}\\n\\t\\treturn sum == 0;\\n }\\n};\\n\"], [483, 0.158, \"class Solution {\\npublic:\\n\\nbool hasSameDigits(string s) {\\n auto nCrModpDP = [&](int n, int r, int p)->int{ \\n int C[r+1]; \\n memset(C, 0, sizeof(C)); \\n C[0] = 1;\\n for (int i = 1; i <= n; i++) { \\n for (int j = min(i, r); j > 0; j--) \\n C[j] = (C[j] + C[j-1])%p; \\n } \\n return C[r]; \\n }; \\n auto cnk = [&](auto&& cnk,int n, int r, int p)->int{\\n if (r==0)\\n return 1; \\n int ni = n%p, ri = r%p; \\n return (cnk(cnk,n/p, r/p, p) * nCrModpDP(ni, ri, p)) % p; \\n };\\n int n = (int)s.size();\\n vector<int> a(n);\\n for(int i = 0; i < n; ++ i) a[i] = s[i] - '0';\\n \\n int g = n - 2,l = 0,r = 0;\\n for(int i = 0; i < n - 1; ++ i){\\n int t = ((g & i) == i);\\n int gg = cnk(cnk,g,i,5),tt = 0; \\n if(gg % 2 == t) tt = gg;\\n else tt = gg + 5;\\n l = (l + tt * a[i]) % 10;\\n r = (r + tt * a[i + 1]) % 10;\\n }\\n return (l == r);\\n}\\n\\n\\n};\"], [498, 0.474, \"class Solution {\\npublic:\\nconst int mod=10;\\nint power(int a, int b, int m) {\\n int res = 1;\\n while (b) {\\n if (b & 1) res = (res * a) % m;\\n a = (a * a) % m;\\n b >>= 1;\\n }\\n return res;\\n}\\n\\nint modInverse(int a, int m) {\\n return power(a, m - 2, m);\\n}\\n\\nint factMod(int n, int p) {\\n int res = 1;\\n for (int i = 1; i <= n; i++)\\n if (i % p) res = (res * i) % p;\\n return res;\\n}\\n\\nint nCrModP(int n, int r, int p) {\\n if (r > n) return 0;\\n if (n == r || r == 0) return 1;\\n return (factMod(n, p) * modInverse(factMod(r, p), p) % p * modInverse(factMod(n - r, p), p) % p) % p;\\n}\\n\\nint lucas(int n, int r, int p) {\\n if (r == 0) return 1;\\n return (lucas(n / p, r / p, p) * nCrModP(n % p, r % p, p)) % p;\\n}\\n\\nint chinese_remainder(int a1, int m1, int a2, int m2) {\\n int inv1 = modInverse(m1, m2), inv2 = modInverse(m2, m1);\\n return (a1 * m2 % (m1 * m2) * inv2 + a2 * m1 % (m1 * m2) * inv1) % (m1 * m2);\\n}\\n\\nint nCrMod10(int n, int r) {\\n int nCr2 = lucas(n, r, 2);\\n int nCr5 = lucas(n, r, 5);\\n return chinese_remainder(nCr2, 2, nCr5, 5);\\n}\\n bool hasSameDigits(string s) {\\n int val1=0,val2=0;\\n int n=s.size();\\n vector<int>bins;\\n for(int r=0;r<=n-2;r++){\\n bins.push_back(nCrMod10(n-2,r));\\n }\\n for(int i=0;i<n-1;i++){\\n val1=(val1+((s[i]-'0')*bins[i])%mod)%mod;\\n val2=(val2+((s[i+1]-'0')*bins[i]%mod))%mod;\\n }\\n return val1==val2;\\n }\\n};\"], [512, 0.316, \"class Solution {\\npublic:\\n #define ll long long\\n\\n ll nCr(ll n, ll r) {\\n if(r > n) return 0 ;\\n\\n int res=1;\\n for(int i=1 ; i<=r ; i++) {\\n res *= n-i+1 ;\\n res /= i ;\\n }\\n return res ;\\n }\\n\\n int nCr_mod_Lucas_Theorem(int n, int r, int mod) { \\n int res=1 ;\\n\\n while(n && r)\\n {\\n int n_rem = n%mod ;\\n int r_rem = r%mod ;\\n\\n res = (res * nCr(n_rem, r_rem))%mod ;\\n n /= mod ;\\n r /= mod ;\\n }\\n \\n return res ;\\n }\\n\\n\\n bool hasSameDigits(string s) {\\n ll n = s.length();\\n ll num1 = 0, num2 = 0;\\n\\n for (ll i = 0; i <= n - 2; i++) \\n {\\n ll res2 = nCr_mod_Lucas_Theorem(n - 2, i, 2) ;\\n ll res5 = nCr_mod_Lucas_Theorem(n - 2, i, 5) ;\\n\\n int num = 0;\\n for (int x = 0; x < 10; x++) \\n {\\n if (x % 2 == res2 && x % 5 == res5) \\n {\\n num = x;\\n break;\\n }\\n }\\n num1 = (num1 + num * (s[i] - '0')) % 10;\\n }\\n\\n \\n for(ll i = 1; i <= n - 1; i++) \\n {\\n ll res2 = nCr_mod_Lucas_Theorem(n - 2, i - 1, 2) ;\\n ll res5 = nCr_mod_Lucas_Theorem(n - 2, i - 1, 5) ;\\n\\n int num = 0;\\n for (int x = 0; x < 10; x++) \\n {\\n if (x % 2 == res2 && x % 5 == res5) \\n {\\n num = x ;\\n break;\\n }\\n }\\n num2 = (num2 + num * (s[i] - '0')) % 10;\\n }\\n\\n return num1 == num2;\\n }\\n};\"], [526, 0.158, \"class Solution {\\nprivate:\\n vector<vector<int>> dp;\\n\\n int nCrModDP(int n, int r, int mod) {\\n if (dp[n][r] != -1) return dp[n][r];\\n vector<int> C(r + 1, 0);\\n C[0] = 1;\\n for (int i = 1; i <= n; ++i) {\\n for (int j = min(i, r); j > 0; --j) {\\n C[j] = (C[j] + C[j - 1]) % mod;\\n }\\n }\\n dp[n][r] = C[r];\\n return dp[n][r];\\n }\\n\\n int nCr(int n, int r, int mod) {\\n if (r == 0) return 1;\\n int ni = n % mod;\\n int ri = r % mod;\\n return (nCr(n / mod, r / mod, mod) * nCrModDP(ni, ri, mod)) % mod;\\n }\\n\\n bool checkSameDigits(const string& s, int mod) {\\n int n = s.length();\\n vector<int> vals;\\n for (int i = 0; i < n - 1; ++i) {\\n vals.push_back(nCr(n - 2, i, mod));\\n }\\n vals.push_back(0);\\n\\n int leftVal = 0, rightVal = 0;\\n\\n for (int i = 0; i < n; ++i) {\\n int val = s[i] - '0';\\n leftVal = (leftVal + val * vals[i]) % mod;\\n }\\n\\n reverse(vals.begin(), vals.end());\\n for (int i = 0; i < n; ++i) {\\n int val = s[i] - '0';\\n rightVal = (rightVal + val * vals[i]) % mod;\\n }\\n\\n return leftVal == rightVal;\\n }\\n\\npublic:\\n Solution() : dp(5, vector<int>(5, -1)) {}\\n\\n bool hasSameDigits(const string& s) {\\n return checkSameDigits(s, 2) && checkSameDigits(s, 5);\\n }\\n};\"], [541, 0.158, \"class Solution {\\npublic:\\n\\n long long choose(int n, int k) {\\n if(k > n) {\\n return 0;\\n }\\n if(k > n/2) {\\n return choose(n, n-k);\\n }\\n long top = 1;\\n long bottom = 1;\\n for(int i = 1 ; i <= k; i++) {\\n top *= (n - i + 1);\\n bottom *= i;\\n }\\n return top/bottom;\\n }\\n\\n int betterChoose(int n, int k, int p) {\\n long long currentProd = 1;\\n while(n != 0 || k != 0) {\\n currentProd *= (choose(n % p, k % p));\\n n = n / p;\\n k = k / p;\\n currentProd = currentProd % p;\\n }\\n return currentProd;\\n }\\n\\n long long superChoose(int n, int k) \\n {\\n int a = betterChoose(n, k, 5);\\n int b = betterChoose(n, k , 2);\\n int otherA = (a + 5) % 10;\\n if(b == 0 && a % 2 == 0) {\\n return a;\\n }\\n if(b == 1 && a % 2 == 1) {\\n return a;\\n }\\n return otherA;\\n }\\n\\n\\n bool hasSameDigits(string s) {\\n int topDigit = 0;\\n for(size_t i = 0; i < s.size() - 1; i++ ) {\\n topDigit += (s[i] - 48) * superChoose(s.size() - 2, i);\\n topDigit = topDigit % 10;\\n }\\n int bottomDigit = 0;\\n for(size_t i = 1; i < s.size(); i++ ) {\\n bottomDigit += (s[i] - 48) * superChoose(s.size() - 2, i - 1);\\n bottomDigit = bottomDigit % 10;\\n }\\n return topDigit == bottomDigit;\\n\\n }\\n};\"], [555, 0.158, \"class Solution {\\npublic:\\n // H\\u00e0m t\\u00ednh giai th\\u1eeba mod p\\n int factorialMod(int n, int p) {\\n int res = 1;\\n for (int i = 1; i <= n; i++)\\n res = (res * i) % p;\\n return res;\\n }\\n\\n // H\\u00e0m t\\u00ednh s\\u1ed1 ngh\\u1ecbch \\u0111\\u1ea3o theo Fermat nh\\u1ecf\\n int powerMod(int x, int y, int p) {\\n int res = 1;\\n x = x % p;\\n while (y > 0) {\\n if (y & 1) res = (res * x) % p;\\n y = y >> 1;\\n x = (x * x) % p;\\n }\\n return res;\\n }\\n\\n // H\\u00e0m t\\u00ednh nCk mod p\\n int binomialMod(int n, int k, int p) {\\n if (k > n) return 0;\\n int num = factorialMod(n, p);\\n int den = (factorialMod(k, p) * factorialMod(n - k, p)) % p;\\n return (num * powerMod(den, p - 2, p)) % p;\\n }\\n\\n // H\\u00e0m s\\u1eed d\\u1ee5ng \\u0110\\u1ecbnh l\\u00fd Lucas\\n int nCkModP(int n, int k, int p) {\\n if (k == 0) return 1;\\n int ni = n % p, ki = k % p;\\n return (nCkModP(n / p, k / p, p) * binomialMod(ni, ki, p)) % p;\\n }\\n bool hasSameDigits(string s) {\\n int n = s.length();\\n int ans = 0;\\n int bns = 0;\\n for(int i = 0; i < n-1; i++) {\\n ans += ((s[i] - s[i+1]) * nCkModP(n-2,i,2)) % 2;\\n bns += ((s[i] - s[i+1]) * nCkModP(n-2,i,5)) % 5;\\n }\\n if (abs(ans) % 2 == 0 && abs(bns) % 5 == 0) return true;\\n return false;\\n }\\n};\"], [570, 0.158, \"class Solution {\\npublic:\\n // H\\u00e0m t\\u00ednh giai th\\u1eeba mod p\\n int factorialMod(int n, int p) {\\n int res = 1;\\n for (int i = 1; i <= n; i++)\\n res = (res * i) % p;\\n return res;\\n }\\n\\n // H\\u00e0m t\\u00ednh s\\u1ed1 ngh\\u1ecbch \\u0111\\u1ea3o theo Fermat nh\\u1ecf\\n int powerMod(int x, int y, int p) {\\n int res = 1;\\n x = x % p;\\n while (y > 0) {\\n if (y & 1) res = (res * x) % p;\\n y = y >> 1;\\n x = (x * x) % p;\\n }\\n return res;\\n }\\n\\n // H\\u00e0m t\\u00ednh nCk mod p\\n int binomialMod(int n, int k, int p) {\\n if (k > n) return 0;\\n int num = factorialMod(n, p);\\n int den = (factorialMod(k, p) * factorialMod(n - k, p)) % p;\\n return (num * powerMod(den, p - 2, p)) % p;\\n }\\n\\n // H\\u00e0m s\\u1eed d\\u1ee5ng \\u0110\\u1ecbnh l\\u00fd Lucas\\n int nCkModP(int n, int k, int p) {\\n if (k == 0) return 1;\\n int ni = n % p, ki = k % p;\\n return (nCkModP(n / p, k / p, p) * binomialMod(ni, ki, p)) % p;\\n }\\n bool hasSameDigits(string s) {\\n int n = s.length();\\n int ans = 0;\\n int bns = 0;\\n for(int i = 0; i < n-1; i++) {\\n ans = (ans + (s[i] - s[i+1]) * nCkModP(n-2,i,2)) % 2;\\n bns = (bns + (s[i] - s[i+1]) * nCkModP(n-2,i,5)) % 5;\\n }\\n if (abs(ans) % 2 == 0 && abs(bns) % 5 == 0) return true;\\n return false;\\n }\\n};\"], [584, 0.158, \"class Solution {\\npublic:\\n int getMod(int n, int r, int p){\\n vector<int> fact(6,1);\\n for(int i=2;i<6;i++) fact[i]=i*fact[i-1];\\n int ans=1;\\n while(n){\\n if(n%p < r%p) return 0;\\n ans*=(fact[n%p]/(fact[r%p]*fact[n%p-r%p]))%p;\\n n/=p;r/=p;\\n }\\n return ans;\\n }\\n int ncr(int n, int r){ \\n return (5*getMod(n,r,2)+6*getMod(n,r,5))%10;\\n }\\n int getSum(string& s){\\n int n=s.length()-1;\\n int sum=0;\\n for(int r=0;r<(n+1)/2;r++){\\n sum+=(((s[r]-'0')+(s[n-r]-'0'))*ncr(n,r))%10;\\n }\\n if(n%2==0) sum+=((s[n/2]-'0')*ncr(n,n/2))%10;\\n return sum%10;\\n }\\n bool hasSameDigits(string s) {\\n string s1=s.substr(0,s.length()-1);\\n string s2=s.substr(1,s.length()-1);\\n return getSum(s1)==getSum(s2);\\n }\\n};\"], [599, 0.158, \"class Solution {\\nprivate:\\n vector<int> factorize(int x) {\\n int count2 = 0, count5 = 0;\\n while (x % 2 == 0) {\\n count2 += 1;\\n x /= 2;\\n }\\n while (x % 5 == 0) {\\n count5 += 1;\\n x /= 5;\\n }\\n return {x % 10, count2, count5};\\n }\\n\\npublic:\\n bool hasSameDigits(string s) {\\n int n = s.length();\\n if (n <= 2) {\\n return s[0] == s[1];\\n }\\n\\n int pascal = n - 1;\\n int diff = (s[0] - s[n - 1]) % 10;\\n\\n int rem = 1, count2 = 0, count5 = 0;\\n\\n int inverse[] = {0, 1, 0, 7, 0, 0, 0, 3, 0, 9};\\n\\n for (int i = 1; i < pascal; i += 1) {\\n int num = pascal - i;\\n int den = i;\\n\\n vector<int> numResult = factorize(num);\\n vector<int> denResult = factorize(den);\\n\\n rem = (rem * numResult[0] * inverse[denResult[0]]) % 10;\\n count2 = count2 + numResult[1] - denResult[1];\\n count5 = count5 + numResult[2] - denResult[2];\\n\\n int c;\\n if (count2 > 0 && count5 > 0) {\\n c = 0;\\n } else if (count2 > 0) {\\n int power[] = {6, 2, 4, 8};\\n int twoMod = power[count2 % 4];\\n if(count2 % 4 == 0) twoMod = 6;\\n c = (rem * twoMod) % 10;\\n } else if (count5 > 0) {\\n c = (rem * 5) % 10;\\n } else {\\n c = rem;\\n }\\n\\n diff = (diff + (s[i] - s[n - 1 - i]) * c) % 10;\\n }\\n\\n return diff % 10 == 0;\\n }\\n};\"], [613, 0.158, \"class Solution\\n{\\npublic:\\n int mod2(int n, int k)\\n {\\n while (k > 0)\\n {\\n if ((k & 1) > (n & 1))\\n return 0;\\n k >>= 1;\\n n >>= 1;\\n }\\n return 1;\\n }\\n\\n int mod5(int n, int k)\\n {\\n int res = 1;\\n vector<int> fact = {1, 1, 2, 1, 4};\\n while (k > 0)\\n {\\n int n_i = n % 5;\\n int k_i = k % 5;\\n if (k_i > n_i)\\n return 0;\\n int num = fact[n_i];\\n int den = (fact[k_i] * fact[n_i - k_i] % 5);\\n int denInv;\\n for (int i = 0; i < 5; i++)\\n {\\n if ((den * i) % 5 == 1)\\n {\\n denInv = i;\\n break;\\n }\\n }\\n res = (res % 5 * num % 5 * denInv % 5) % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return res;\\n }\\n\\n int mod10(int n, int k)\\n {\\n int m2 = mod2(n, k);\\n int m5 = mod5(n, k);\\n for (int i = 0; i < 10; i++)\\n {\\n if (i % 2 == m2 && i % 5 == m5)\\n return i;\\n }\\n return 0;\\n }\\n bool hasSameDigits(string s)\\n {\\n int n = s.size() - 2;\\n int ans1 = 0, ans2 = 0;\\n for (int i = 0; i < s.size() - 1; i++)\\n {\\n ans1 = (ans1 + (mod10(n, i) * (s[i] - '0')) % 10) % 10;\\n ans2 = (ans2 + (mod10(n, i) * (s[i + 1] - '0')) % 10) % 10;\\n }\\n return ans1 == ans2;\\n }\\n};\"], [628, 0.158, \"class Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n unsigned int n = s.size();\\n vector<int> comb5(n-1);\\n vector<int> comb2(n-1);\\n comb5[0]=1;\\n comb2[0]=1;\\n comb5[1]=(n-2)%5;\\n comb2[1]=(n-2)%2;\\n function<int(int)> factorial = [&factorial](int n)\\n {\\n if (n==0)return 1;\\n return n*factorial(n-1);\\n };\\n auto smallNcK = [&factorial](int n,int k)\\n {\\n int num = factorial(n);\\n int den = factorial(n-k)*factorial(k);\\n return (num/den)%5;\\n };\\n function<int(int,int)> nCk = [&nCk,&smallNcK](int n, int k)\\n {\\n if (n==k) return 1;\\n int ni = n%5;\\n int ki = k%5;\\n if (ki>ni) return 0;\\n return (nCk(n/5,k/5)*smallNcK(ni,ki))%5;\\n };\\n int num2 = countr_zero(n-2);\\n unsigned int num = n-3;\\n for (unsigned int i=2;i<n-1;i++)\\n {\\n num2+=countr_zero(num)-countr_zero(i);\\n if (!num2)comb2[i]=1;\\n comb5[i]=nCk(n-2,i);\\n num--;\\n }\\n int comb[2][5];\\n comb[0][0]=0;\\n comb[1][1]=1;\\n comb[0][2]=2;\\n comb[1][3]=3;\\n comb[0][4]=4;\\n comb[1][0]=5;\\n comb[0][1]=6;\\n comb[1][2]=7;\\n comb[0][3]=8;\\n comb[1][4]=9;\\n\\n int first = 0;\\n int second = 0;\\n for (int i=0;i<n-1;i++)\\n {\\n first+=(comb[comb2[i]][comb5[i]]*(s[i]-'0'))%10;\\n first%=10;\\n second+=(comb[comb2[i]][comb5[i]]*(s[i+1]-'0'))%10;\\n second%=10;\\n }\\n return first==second;\\n }\\n};\"], [642, 0.158, \"#pragma GCC optimize(\\\"O3\\\", \\\"unroll-loops\\\")\\n\\nclass Solution {\\npublic:\\n bool hasSameDigits(string s) {\\n unsigned int n = s.size();\\n vector<int> comb5(n-1);\\n vector<int> comb2(n-1);\\n comb5[0]=1;\\n comb2[0]=1;\\n comb5[1]=(n-2)%5;\\n comb2[1]=(n-2)%2;\\n function<int(int)> factorial = [&factorial](int n)\\n {\\n if (n==0)return 1;\\n return n*factorial(n-1);\\n };\\n auto smallNcK = [&factorial](int n,int k)\\n {\\n int num = factorial(n);\\n int den = factorial(n-k)*factorial(k);\\n return (num/den)%5;\\n };\\n function<int(int,int)> nCk = [&nCk,&smallNcK](int n, int k)\\n {\\n if (n==k) return 1;\\n int ni = n%5;\\n int ki = k%5;\\n if (ki>ni) return 0;\\n return (nCk(n/5,k/5)*smallNcK(ni,ki))%5;\\n };\\n int num2 = countr_zero(n-2);\\n unsigned int num = n-3;\\n for (unsigned int i=2;i<n-1;i++)\\n {\\n num2+=countr_zero(num)-countr_zero(i);\\n if (!num2)comb2[i]=1;\\n comb5[i]=nCk(n-2,i);\\n num--;\\n }\\n int comb[2][5];\\n comb[0][0]=0;\\n comb[1][1]=1;\\n comb[0][2]=2;\\n comb[1][3]=3;\\n comb[0][4]=4;\\n comb[1][0]=5;\\n comb[0][1]=6;\\n comb[1][2]=7;\\n comb[0][3]=8;\\n comb[1][4]=9;\\n\\n int first = 0;\\n int second = 0;\\n for (int i=0;i<n-1;i++)\\n {\\n first+=(comb[comb2[i]][comb5[i]]*(s[i]-'0'))%10;\\n first%=10;\\n second+=(comb[comb2[i]][comb5[i]]*(s[i+1]-'0'))%10;\\n second%=10;\\n }\\n return first==second;\\n }\\n};\"], [656, 0.158, \"class Solution {\\npublic:\\n using ll = long long;\\n \\n // Binary Exponentiation: Compute x^y mod p\\n ll power(ll x, ll y, ll p) {\\n ll res = 1;\\n x = x % p; \\n while (y > 0) {\\n if (y & 1) \\n res = (res * x) % p;\\n y = y >> 1;\\n x = (x * x) % p;\\n }\\n return res;\\n }\\n \\n // Extended Euclidean Algorithm to compute Modular Inverse of a modulo m\\n ll modInverse(ll a, ll m) {\\n ll m0 = m, t, q;\\n ll x0 = 0, x1 = 1;\\n if (m == 1) return 0;\\n while (a > 1) {\\n q = a / m;\\n t = m;\\n m = a % m, a = t;\\n t = x0;\\n x0 = x1 - q * x0;\\n x1 = t;\\n }\\n return (x1 + m0) % m0;\\n }\\n \\n // Compute nCr mod p for n, r < p (p is prime)\\n ll binomialModP(ll n, ll r, ll p) {\\n if (r > n) return 0;\\n ll num = 1, den = 1;\\n for (ll i = 0; i < r; i++) {\\n num = (num * (n - i)) % p;\\n den = (den * (i + 1)) % p;\\n }\\n return (num * modInverse(den, p)) % p;\\n }\\n \\n // Lucas' Theorem: Computes nCr mod p (p prime)\\n ll lucas(ll n, ll r, ll p) {\\n if (r == 0) return 1;\\n return (lucas(n / p, r / p, p) * binomialModP(n % p, r % p, p)) % p;\\n }\\n \\n // Specialized function to compute nCr mod 10 using Lucas for mod 2 and mod 5 and combining via CRT.\\n int binom_mod10(ll n, ll r) {\\n int mod2 = lucas(n, r, 2);\\n int mod5 = lucas(n, r, 5);\\n // We want x such that:\\n // x \\u2261 mod2 (mod 2)\\n // x \\u2261 mod5 (mod 5)\\n // Write x = mod5 + 5 * k. Since 5 \\u2261 1 (mod 2), we need:\\n // (mod5 + k) mod 2 = mod2.\\n int k = ((mod2 - (mod5 % 2)) % 2 + 2) % 2; // k is 0 or 1.\\n int res = (mod5 + 5 * k) % 10;\\n return res;\\n }\\n \\n // Revised function using the optimized binom_mod10\\n bool hasSameDigits(string s) {\\n int n = s.size();\\n ll c1 = 0;\\n // c1 = sum_{i=0}^{n-2} [ C(n-2, i) mod 10 * (s[i]-'0') ] mod 10\\n for (int i = 0; i < n - 1; i++) {\\n int m = binom_mod10(n - 2, i);\\n c1 = (c1 + m * (s[i] - '0')) % 10;\\n }\\n ll c2 = 0;\\n // c2 = sum_{i=1}^{n-1} [ C(n-2, i-1) mod 10 * (s[i]-'0') ] mod 10\\n for (int i = 1; i < n; i++) {\\n int m = binom_mod10(n - 2, i - 1);\\n c2 = (c2 + m * (s[i] - '0')) % 10;\\n }\\n return c1 == c2;\\n }\\n};\\n\"], [671, 0.158, \"class Solution {\\npublic:\\n std::map<std::pair<int, int>, int> binomCache;\\n static constexpr int inverses[] = {0, 1, 3, 2, 4};\\n\\n void ComputeBinomRow(int a) {\\n binomCache[{a, 0}] = 1;\\n binomCache[{a, a}] = 1;\\n int res = 1;\\n int pAdicEval2 = 0;\\n int pAdicEval5 = 0;\\n\\n for (int b = 1; b <= a/2; ++b) {\\n int i;\\n \\n i = a-b+1;\\n while (i % 2 == 0) {\\n pAdicEval2 += 1;\\n i /= 2; \\n }\\n\\n i = a-b+1;\\n while (i % 5 == 0) {\\n pAdicEval5 += 1;\\n i /= 5; \\n }\\n\\n i = b;\\n while (i % 2 == 0) {\\n pAdicEval2 -= 1;\\n i /= 2;\\n }\\n\\n i = b;\\n while (i % 5 == 0) {\\n pAdicEval5 -= 1;\\n i /= 5;\\n }\\n\\n i = a-b+1;\\n while (i % 5 == 0)\\n i /= 5;\\n res = (res * i % 5) % 5;\\n \\n i = b;\\n while (i % 5 == 0)\\n i /= 5;\\n res = (res * inverses[i % 5]) % 5;\\n\\n bool isEven = (pAdicEval2 > 0);\\n int resToUse = (pAdicEval5 > 0) ? 0 : res;\\n if ((resToUse % 2 == 0) == isEven) {\\n binomCache[{a, b}] = resToUse;\\n binomCache[{a, a-b}] = resToUse;\\n }\\n else {\\n binomCache[{a, b}] = resToUse+5;\\n binomCache[{a, a-b}] = resToUse+5;\\n }\\n }\\n }\\n\\n int CharToInt(char c) { \\n return static_cast<int>(c - '0');\\n }\\n\\n bool hasSameDigits(string s) {\\n ComputeBinomRow(s.length() - 2);\\n\\n int firstDigit = 0;\\n for (int i = 0; i < s.length() - 1; ++i) {\\n firstDigit = (\\n firstDigit + binomCache[{s.length() - 2, i}] * CharToInt(s[i])\\n ) % 10;\\n }\\n \\n int secondDigit = 0;\\n for (int i = 1; i < s.length(); ++i) {\\n secondDigit = (\\n secondDigit + binomCache[{s.length() - 2, i-1}] * CharToInt(s[i])\\n ) % 10;\\n }\\n return firstDigit == secondDigit;\\n }\\n\\n};\\n\"], [685, 0.158, \"class CRT {\\npublic:\\n\\n int modInverse(int a, int m) {\\n int m0 = m, x0 = 0, x1 = 1;\\n if (m == 1)\\n return 0;\\n\\n while (a > 1) {\\n int q = a / m;\\n int t = m;\\n m = a % m;\\n a = t;\\n t = x0;\\n x0 = x1 - q * x0;\\n x1 = t;\\n }\\n\\n if (x1 < 0)\\n x1 += m0;\\n\\n return x1;\\n }\\n\\n int findMinX(vector<int> num, vector<int> rem) {\\n int prod = 1;\\n int k = num.size();\\n\\n for (int i = 0; i < k; i++)\\n prod *= num[i];\\n\\n int result = 0;\\n\\n for (int i = 0; i < k; i++) {\\n int pp = prod / num[i];\\n result += rem[i] * modInverse(pp, num[i]) * pp;\\n }\\n\\n return result % prod;\\n }\\n\\n int operator()(int x, int y) {\\n vector<int> num = {2, 5};\\n vector<int> rem = {x, y};\\n return findMinX(num, rem);\\n }\\n};\\n\\n\\nclass Lucas_nCrModp{\\n\\n vector<int> fact, invFact, inv;\\n \\n public:\\n\\n Lucas_nCrModp(int p){\\n \\n fact.resize(p);\\n invFact.resize(p);\\n inv.resize(p);\\n \\n fact[0] = fact[1] = 1;\\n invFact[0] = invFact[1] = 1;\\n inv[0] = 1;\\n inv[1] = 1;\\n \\n for(int i = 2; i < p; i++){\\n fact[i] = fact[i-1] * i % p;\\n inv[i] = (p - p / i) * inv[p % i] % p;\\n invFact[i] = invFact[i - 1] * inv[i] % p; \\n }\\n }\\n\\n int find(int n, int r, int p){\\n\\n if(r < 0 or r > n) return 0;\\n if(r == 0 or r == n) return 1;\\n\\n if(n < p) \\n return fact[n] * invFact[r] * invFact[n - r] % p; \\n \\n return find(n / p, r / p, p)\\n * find(n % p, r % p, p) % p;\\n }\\n};\\n\\n\\nclass Solution {\\npublic:\\n\\n Lucas_nCrModp *lucas_p2, *lucas_p5;\\n CRT crt;\\n\\n\\n // returns nCr mod 10\\n int findBinCoefMod10(int n, int r){\\n\\n int coefMod2 = lucas_p2 -> find(n, r, 2);\\n int coefMod5 = lucas_p5 -> find(n, r, 5);\\n return crt.findMinX({2, 5}, {coefMod2, coefMod5});\\n }\\n\\n bool hasSameDigits(string s) {\\n \\n int n = s.length();\\n int digit1 = 0, digit2 = 0;\\n \\n lucas_p2 = new Lucas_nCrModp(2);\\n lucas_p5 = new Lucas_nCrModp(5);\\n\\n for(int i = 0; i < n - 1; i++){\\n \\n int binCoef = findBinCoefMod10(n - 2, i);\\n (digit1 += binCoef * (s[i] - '0')) %= 10;\\n (digit2 += binCoef * (s[i + 1] - '0')) %= 10;\\n }\\n return digit1 == digit2;\\n }\\n};\"], [700, 0.158, \"class CRT {\\npublic:\\n\\n // finds a inverse mod m using extended euclidean algorithm\\n int modInverse(int a, int m) {\\n int m0 = m, x0 = 0, x1 = 1;\\n if (m == 1)\\n return 0;\\n\\n while (a > 1) {\\n int q = a / m;\\n int t = m;\\n m = a % m;\\n a = t;\\n t = x0;\\n x0 = x1 - q * x0;\\n x1 = t;\\n }\\n\\n if (x1 < 0)\\n x1 += m0;\\n\\n return x1;\\n }\\n\\n // finds minimum x such that\\n // x % num[i] = rem[i] \\n int findMinX(vector<int> num, vector<int> rem) {\\n \\n int prod = 1;\\n int k = num.size();\\n\\n for (int i = 0; i < k; i++)\\n prod *= num[i];\\n\\n int result = 0;\\n for (int i = 0; i < k; i++) {\\n int pp = prod / num[i];\\n result += rem[i] * modInverse(pp, num[i]) * pp;\\n }\\n\\n return result % prod;\\n }\\n};\\n\\nclass Lucas_nCrModp{\\n\\n vector<int> fact, invFact, inv;\\n \\n public:\\n\\n Lucas_nCrModp(int p){\\n \\n fact.resize(p);\\n invFact.resize(p);\\n inv.resize(p);\\n \\n fact[0] = fact[1] = 1;\\n invFact[0] = invFact[1] = 1;\\n inv[0] = 1;\\n inv[1] = 1;\\n \\n for(int i = 2; i < p; i++){\\n fact[i] = fact[i-1] * i % p;\\n inv[i] = (p - p / i) * inv[p % i] % p;\\n invFact[i] = invFact[i - 1] * inv[i] % p; \\n }\\n }\\n\\n int find(int n, int r, int p){\\n\\n if(r < 0 or r > n) return 0;\\n if(r == 0 or r == n) return 1;\\n\\n if(n < p) \\n return fact[n] * invFact[r] * invFact[n - r] % p; \\n \\n return find(n / p, r / p, p)\\n * find(n % p, r % p, p) % p;\\n }\\n};\\n\\n\\nclass Solution {\\npublic:\\n\\n Lucas_nCrModp lucas_p2{2}, lucas_p5{5};\\n CRT crt;\\n\\n // returns nCr mod 10\\n int findBinCoefMod10(int n, int r){\\n return crt.findMinX(\\n {2, 5}, \\n {\\n lucas_p2.find(n, r, 2), \\n lucas_p5.find(n, r, 5)\\n }\\n );\\n }\\n\\n bool hasSameDigits(string s) {\\n \\n int n = s.length();\\n int digit1 = 0, digit2 = 0;\\n \\n for(int i = 0; i < n - 1; i++){\\n \\n int binCoef = findBinCoefMod10(n - 2, i);\\n (digit1 += binCoef * (s[i] - '0')) %= 10;\\n (digit2 += binCoef * (s[i + 1] - '0')) %= 10;\\n }\\n return digit1 == digit2;\\n }\\n};\"], [714, 0.158, \"#pragma GCC optimize(\\\"O3\\\", \\\"unroll-loops\\\")\\n \\nconst auto _ = std::cin.tie(nullptr)->sync_with_stdio(false);\\n \\n#define LC_HACK\\n#ifdef LC_HACK\\nconst auto __ = []() {\\n struct ___ { static void _() { std::ofstream(\\\"display_runtime.txt\\\") << 1000 << '\\\\n'; } };\\n std::atexit(&___::_);\\n return 0;\\n}();\\n#endif\\n\\nclass Solution {\\n public:\\n static constexpr uint8_t n0[15]{1,\\n 1,1,\\n 1,2,1,\\n 1,3,3,1,\\n 1,4,6,4,1};\\n\\n inline uint8_t nCr(const uint8_t n, const uint8_t r) const {\\n return n0[(n * (n + 1) >> 1) + r];\\n }\\n\\n inline uint8_t nCrMod2(uint32_t n, uint16_t r) const {\\n return (n & r) == r;\\n }\\n\\n inline uint8_t nCrMod5(uint32_t n, uint16_t r) const {\\n uint8_t out = 1;\\n uint8_t n_mod5, r_mod5;\\n while (n && r) {\\n n_mod5 = n%5;\\n r_mod5 = r%5;\\n if (n_mod5 < r_mod5) return 0;\\n out = (out * nCr(n_mod5, r_mod5)) % 5;\\n n /= 5;\\n r /= 5;\\n }\\n return out;\\n }\\n\\n uint8_t nCrMod10(uint32_t n, uint16_t r) const {\\n if (r > n) return 0;\\n if (r == 0 || r == n) return 1;\\n // Chinese remainder theorem\\n return (6 * nCrMod5(n, r) + 5 * nCrMod2(n, r)) % 10;\\n }\\n \\n \\n bool hasSameDigits(string& s) {\\n int res = 0;\\n\\n int n = s.size() - 1;\\n uint64_t* c_array = reinterpret_cast<uint64_t*>(s.data());\\n // Subtract\\n for (uint16_t i = 0; i < (n >> 3); ++i) {\\n *(c_array + i) -= 0x3030303030303030LLU;\\n }\\n for (int i = n & 0xFFFFF8 ; i <= n; ++i) {\\n s[i] -= 0x30;\\n }\\n\\n for (int j = 0; j <= (n >> 9); ++j) {\\n for (int i = (j << 9); i < min((n >> 1), (j + 1) << 9); ++i) {\\n res += nCrMod10(n - 1, i) * ((s[i] + s[n - i - 1]) | ((s[i + 1] + s[n - i] ) << 16));\\n }\\n\\n res = (((res & 0xFFFF) % 10) | (((res >> 16) % 10) << 16));\\n }\\n\\n if (n & 1) {\\n uint8_t coeff = nCrMod10(n - 1, (n >> 1));\\n res += coeff * (s[(n >> 1)] | (s[(n >> 1) + 1] << 16));\\n }\\n \\n return ((res & 0xFFFF) % 10) == ((res >> 16) % 10);\\n }\\n };\"], [729, 0.158, \"class CRT {\\npublic:\\n\\n int modInverse(int a, int m) {\\n int m0 = m, x0 = 0, x1 = 1;\\n if (m == 1)\\n return 0;\\n\\n while (a > 1) {\\n int q = a / m;\\n int t = m;\\n m = a % m;\\n a = t;\\n t = x0;\\n x0 = x1 - q * x0;\\n x1 = t;\\n }\\n\\n if (x1 < 0)\\n x1 += m0;\\n\\n return x1;\\n }\\n\\n // finds minimum x such that\\n // x % num[i] = rem[i] \\n int findMinX(vector<int> num, vector<int> rem) {\\n \\n int prod = 1;\\n int k = num.size();\\n\\n for (int i = 0; i < k; i++)\\n prod *= num[i];\\n\\n int result = 0;\\n for (int i = 0; i < k; i++) {\\n int pp = prod / num[i];\\n result += rem[i] * modInverse(pp, num[i]) * pp;\\n }\\n\\n return result % prod;\\n }\\n};\\n\\nclass Lucas_nCrModp{\\n\\n vector<int> fact, invFact, inv;\\n \\n public:\\n\\n Lucas_nCrModp(int p){\\n \\n fact.resize(p);\\n invFact.resize(p);\\n inv.resize(p);\\n \\n fact[0] = fact[1] = 1;\\n invFact[0] = invFact[1] = 1;\\n inv[0] = 1;\\n inv[1] = 1;\\n \\n for(int i = 2; i < p; i++){\\n fact[i] = fact[i-1] * i % p;\\n inv[i] = (p - p / i) * inv[p % i] % p;\\n invFact[i] = invFact[i - 1] * inv[i] % p; \\n }\\n }\\n\\n int find(int n, int r, int p){\\n\\n if(r < 0 or r > n) return 0;\\n if(r == 0 or r == n) return 1;\\n\\n if(n < p) \\n return fact[n] * invFact[r] * invFact[n - r] % p; \\n \\n return find(n / p, r / p, p)\\n * find(n % p, r % p, p) % p;\\n }\\n};\\n\\n\\nclass Solution {\\npublic:\\n\\n Lucas_nCrModp *lucas_p2, *lucas_p5;\\n CRT crt;\\n\\n // returns nCr mod 10\\n int findBinCoefMod10(int n, int r){\\n\\n int coefMod2 = lucas_p2 -> find(n, r, 2);\\n int coefMod5 = lucas_p5 -> find(n, r, 5);\\n return crt.findMinX({2, 5}, {coefMod2, coefMod5});\\n }\\n\\n bool hasSameDigits(string s) {\\n \\n int n = s.length();\\n int digit1 = 0, digit2 = 0;\\n \\n lucas_p2 = new Lucas_nCrModp(2);\\n lucas_p5 = new Lucas_nCrModp(5);\\n\\n for(int i = 0; i < n - 1; i++){\\n \\n int binCoef = findBinCoefMod10(n - 2, i);\\n (digit1 += binCoef * (s[i] - '0')) %= 10;\\n (digit2 += binCoef * (s[i + 1] - '0')) %= 10;\\n }\\n return digit1 == digit2;\\n }\\n};\"], [743, 0.158, \"class Solution {\\npublic:\\n int factorial(const int &number){\\n if( number == 0 || number == 1 ){\\n return 1;\\n }else{\\n int val {1};\\n for(int i =2; i<=number; i++){\\n val *= i;\\n }\\n return val;\\n }\\n }\\n\\n int nCr(const int &k, const int &n){\\n if( k > n ){\\n return 0;\\n }else{\\n if( k == n || k == 0 ){\\n return 1;\\n }else{\\n return factorial(n)/(factorial(k)*factorial(n-k));\\n }\\n }\\n }\\n\\n int nCrmod2(const int &k, const int &n){\\n // We compute the nCr with mod 2\\n if( k == n || k == 0 ){\\n return 1;\\n }\\n\\n int qk {k}, qn {n}, rk {0}, rn {0};\\n\\n while( qk > 0 && qn > 0 ){\\n // Retrieve the remainder\\n rk = qk%2;\\n rn = qn%2;\\n // Actualise the quotients\\n qk /= 2;\\n qn /= 2;\\n if( rk > rn ){\\n return 0;\\n }\\n }\\n return 1;\\n }\\n int nCrmod5(const int &k, const int &n){\\n // We compute the nCr with mod 5\\n if( k == n || k == 0 ){\\n return 1;\\n }\\n\\n int qk {k}, qn {n}, rk {0}, rn {0}, i;\\n int sizeVecN {0}, sizeVecK {0};\\n unsigned int prod {1};\\n std::vector<int> vecrk, vecrn;\\n\\n while( qk > 0 || qn > 0 ){\\n // Retrieve the remainder\\n if( qk > 0 ){\\n // Actualize values for k if quotient superior strict to 0\\n rk = qk%5;\\n vecrk.push_back(rk);\\n qk /= 5;\\n }\\n // Actualize values for n\\n rn = qn%5;\\n vecrn.push_back(rn);\\n qn /= 5;\\n if( qk > 0 && rk > rn ){\\n return 0;\\n }\\n\\n sizeVecN++;\\n }\\n sizeVecK = vecrk.size();\\n\\n // First fill the value of vecrk\\n for( i=0; i <sizeVecN-sizeVecK; i++ ){\\n vecrk.push_back(0);\\n }\\n\\n // Now compute the value \\n for( i=0; i<sizeVecN; i++ ){\\n prod*= nCr(vecrk.at(i), vecrn.at(i));\\n }\\n\\n return prod%5;\\n }\\n\\n int nCrmod10(const int &k, const int &n){\\n int ncrmod2, ncrmod5;\\n\\n ncrmod2 = nCrmod2(k, n);\\n ncrmod5 = nCrmod5(k, n);\\n\\n if( ncrmod2 == 0 ){\\n // Even\\n if( ncrmod5%2 == 0 ){\\n return ncrmod5;\\n }else{\\n return ncrmod5+5;\\n }\\n }else{\\n if( ncrmod5%2 == 0 ){\\n return ncrmod5+5;\\n }else{\\n return ncrmod5;\\n }\\n }\\n }\\n\\n\\n bool hasSameDigits(std::string s) {\\n char *cptr {nullptr};\\n cptr = new char [2];\\n int number;\\n unsigned int S1 {0}, S2 {0};\\n int size = s.size(), middle;\\n\\n int i = 0;\\n\\n int *nCrmod10Tab = new int[size-1];\\n\\n // We are going to compute the nCr in advance to cut the execution time\\n if( size%2 == 0 ){\\n middle = (size-1)/2;\\n }else{\\n middle = (size-1)/2 - 1;\\n }\\n for( i=0; i<=middle; i++){\\n nCrmod10Tab[i] = nCrmod10(i, size-2);\\n nCrmod10Tab[size-2-i] = nCrmod10Tab[i];\\n }\\n i = 0;\\n\\n for(const char &c: s){\\n // We retrieve the number\\n cptr[0] = c;\\n number = std::atoi(cptr);\\n\\n // Add to the sum\\n if( i == 0 ){\\n // First sum only\\n S1 += number*nCrmod10Tab[i];\\n }else if( i == size-1 ){\\n // Last sum only\\n S2 += number*nCrmod10Tab[i-1];\\n }else{\\n // Both sums\\n S1 += number*nCrmod10Tab[i];\\n S2 += number*nCrmod10Tab[i-1];\\n }\\n i++;\\n }\\n\\n S1 %= 10;\\n S2 %= 10;\\n\\n // Delete the temporary character and vector\\n delete [] cptr;\\n delete [] nCrmod10Tab;\\n\\n if( S1 == S2 ){\\n return true;\\n }else{\\n return false;\\n }\\n }\\n};\"], [757, 0.158, \"class Solution {\\npublic:\\n int nCrModpDP(int n, int r, int p) {\\n if (r > n)\\n return 0;\\n int C[r + 1];\\n memset(C, 0, sizeof(C));\\n C[0] = 1;\\n for (int i = 1; i <= n; i++) {\\n for (int j = min(i, r); j > 0; j--) {\\n C[j] = (C[j] + C[j - 1]) % p;\\n }\\n }\\n return C[r];\\n }\\n int nCrModpLucas(int n, int r, int p) {\\n if (r == 0)\\n return 1;\\n int ni = n % p, ri = r % p;\\n return (nCrModpLucas(n / p, r / p, p) * nCrModpDP(ni, ri, p) % p);\\n }\\n void getPascalRowModP(int n, int p, vector<int>& row) {\\n for (int r = 0; r <= n; r++) {\\n row[r] = nCrModpLucas(n, r, p);\\n }\\n }\\n bool hasSameDigits(string& s) {\\n int n = s.size() - 2;\\n vector<int> rowMod2(n + 1), rowMod5(n + 1);\\n getPascalRowModP(n, 2, rowMod2);\\n getPascalRowModP(n, 5, rowMod5);\\n int firstNumber = 0, secondNumber = 0;\\n for (int r = 0; r <= n; r++) {\\n int a1 = rowMod2[r], a2 = rowMod5[r];\\n int x = (a1 * 5 * 1 + a2 * 2 * 3) % 10;\\n firstNumber += (s[r] - '0') * x;\\n secondNumber += (s[r + 1] - '0') * x;\\n }\\n return firstNumber % 10 == secondNumber % 10;\\n }\\n};\"], [772, 0.158, \"class Solution {\\npublic:\\n int nCrModpDP(int n, int r, int p) {\\n if (r > n)\\n return 0;\\n int C[r + 1];\\n memset(C, 0, sizeof(C));\\n C[0] = 1;\\n for (int i = 1; i <= n; i++) {\\n for (int j = min(i, r); j > 0; j--) {\\n C[j] = (C[j] + C[j - 1]) % p;\\n }\\n }\\n return C[r];\\n }\\n int nCrModpLucas(int n, int r, int p) {\\n if (r == 0)\\n return 1;\\n int ni = n % p, ri = r % p;\\n return (nCrModpLucas(n / p, r / p, p) * nCrModpDP(ni, ri, p) % p);\\n }\\n void getPascalRowModP(int n, int p, vector<int>& row) {\\n for (int r = 0; r <= n; r++) {\\n row[r] = nCrModpLucas(n, r, p);\\n }\\n }\\n bool hasSameDigits(string& s) {\\n int n = s.size() - 2;\\n vector<int> rowMod2(n + 1), rowMod5(n + 1);\\n getPascalRowModP(n, 2, rowMod2);\\n getPascalRowModP(n, 5, rowMod5);\\n int firstNumber = 0, secondNumber = 0;\\n for (int r = 0; r <= n; r++) {\\n int a1 = rowMod2[r], a2 = rowMod5[r];\\n int x = (a1 * 5 * 1 + a2 * 2 * 3) % 10;\\n firstNumber += (s[r] - '0') * x;\\n secondNumber += (s[r + 1] - '0') * x;\\n }\\n return firstNumber % 10 == secondNumber % 10;\\n }\\n};\"]]"
},
"golang": {
"code": "func lucasMod2(n, k int) int {\n for k > 0 {\n if n%2 < k%2 {\n return 0\n }\n n /= 2\n k /= 2\n }\n return 1\n}\n\nfunc lucasMod5(n, k int) int {\n res := 1\n for n > 0 || k > 0 {\n nd := n % 5\n kd := k % 5\n if kd > nd {\n return 0\n }\n comb := 1\n for i := 0; i < kd; i++ {\n comb *= (nd - i)\n comb /= (i + 1)\n }\n res = (res * comb) % 5\n n /= 5\n k /= 5\n }\n return res\n}\n\nfunc hasSameDigits(s string) bool {\n m := len(s) - 2\n if m < 0 {\n return false\n }\n sum1, sum2 := 0, 0\n for i := 0; i <= m; i++ {\n a := lucasMod2(m, i)\n b := lucasMod5(m, i)\n coeff := (5*a + 6*b) % 10\n sum1 += coeff * int(s[i]-'0')\n sum2 += coeff * int(s[i+1]-'0')\n }\n sum1 %= 10\n sum2 %= 10\n return sum1 == sum2\n}",
"memory": 800,
"memoryDistribution": "[[800, 93.0232, \"func lucasMod2(n, k int) int {\\n for k > 0 {\\n if n%2 < k%2 {\\n return 0\\n }\\n n /= 2\\n k /= 2\\n }\\n return 1\\n}\\n\\nfunc lucasMod5(n, k int) int {\\n res := 1\\n for n > 0 || k > 0 {\\n nd := n % 5\\n kd := k % 5\\n if kd > nd {\\n return 0\\n }\\n comb := 1\\n for i := 0; i < kd; i++ {\\n comb *= (nd - i)\\n comb /= (i + 1)\\n }\\n res = (res * comb) % 5\\n n /= 5\\n k /= 5\\n }\\n return res\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n m := len(s) - 2\\n if m < 0 {\\n return false\\n }\\n sum1, sum2 := 0, 0\\n for i := 0; i <= m; i++ {\\n a := lucasMod2(m, i)\\n b := lucasMod5(m, i)\\n coeff := (5*a + 6*b) % 10\\n sum1 += coeff * int(s[i]-'0')\\n sum2 += coeff * int(s[i+1]-'0')\\n }\\n sum1 %= 10\\n sum2 %= 10\\n return sum1 == sum2\\n}\"], [8300, 2.3256, \"package main\\n\\nimport \\\"fmt\\\"\\n\\nfunc hasSameDigits(s string) bool {\\n n := len(s)\\n m := n - 2\\n\\n mDigits := make([]int, 10)\\n mSize := 0\\n temp := m\\n if temp == 0 {\\n mDigits[mSize] = 0\\n mSize++\\n } else {\\n for temp > 0 {\\n mDigits[mSize] = temp % 5\\n mSize++\\n temp /= 5\\n }\\n }\\n\\n small := [5][5]int{\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1},\\n }\\n\\n diff := 0\\n\\n for j := 0; j <= m; j++ {\\n res5 := 1\\n x := j\\n for i := 0; i < mSize; i++ {\\n d := x % 5\\n x /= 5\\n a := mDigits[i]\\n if d > a {\\n res5 = 0\\n break\\n }\\n res5 = (res5 * small[a][d]) % 5\\n }\\n\\n c2 := 0\\n if (m & j) == j {\\n c2 = 1\\n }\\n\\n coeff := res5\\n if (res5&1) != c2 {\\n coeff += 5\\n }\\n\\n delta := int(s[j]-'0') - int(s[j+1]-'0')\\n diff = (diff + coeff*delta) % 10\\n if diff < 0 {\\n diff += 10\\n }\\n }\\n\\n return diff == 0\\n}\\n\"], [8400, 4.6512, \"var COBIN5 = [5][5]int {\\n // C(0, k)\\n {1, 0, 0, 0, 0},\\n // C(1, k)\\n {1, 1, 0, 0, 0},\\n // C(2, k)\\n {1, 2, 1, 0, 0},\\n // C(3, k)\\n {1, 3, 3, 1, 0},\\n // C(4, k)\\n {1, 4, 6, 4, 1},\\n}\\n\\nfunc cobin10(n, k int) int {\\n // Use Lucas's theorem on C(n, k) mod 2\\n mod2 := 1\\n // A binomial coefficient C(n, k) is divisible by a prime p if and only if at least one of the base p digits of n is greater than the corresponding digit of m.\\n if k &^ n != 0 {\\n mod2 = 0\\n }\\n // Use Lucas's theorem on C(n, k) mod 5\\n mod5 := 1\\n for k > 0 {\\n qn, rn := n/5, n%5\\n qk, rk := k/5, k%5\\n if c := COBIN5[rn][rk]; c > 0 {\\n mod5 *= c\\n } else {\\n mod5 = 0\\n break\\n }\\n n, k = qn, qk\\n }\\n mod5 %= 5\\n\\n // combine mod 2 and mod 5 into mod 10\\n if mod5 & 1 == mod2 {\\n return mod5\\n } else {\\n return mod5 + 5\\n }\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n N := len(s)\\n n := N - 2\\n diff := 0\\n for i, m0, m1 := 0, 0, 0; i < N; i++ {\\n m0, m1 = cobin10(n, i), m0\\n diff += (m0 - m1) * int(s[i] - '0')\\n }\\n return diff % 10 == 0\\n}\"], [8500, 10.4651, \"// bin5 holds Pascal\\u2019s triangle rows 0\\u20134 mod 5.\\nvar bin5 = [5][5]int{\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1},\\n}\\n\\n// hasSameDigits returns true if, after reducing s by pairwise sums mod 10\\n// repeatedly down to two digits, the final two are equal.\\nfunc hasSameDigits(s string) bool {\\n N := len(s) - 2 // number of reductions needed\\n var sum2 uint8 // accumulate difference mod 2\\n var sum5 int // accumulate difference mod 5\\n\\n // iterate i = 0..N inclusive, reading s[i] and s[i+1] on the fly\\n for i, c := range s[:N+1] {\\n di := int(c - '0')\\n dip1 := int(s[i+1] - '0')\\n\\n // \\u2014\\u2014 mod 2 check via Lucas: C(N,i)%2 == 1 iff (N&i)==i\\n if (N & i) == i {\\n if (di-dip1)&1 != 0 {\\n sum2 ^= 1\\n }\\n }\\n\\n // \\u2014\\u2014 mod 5 check via Lucas + small Pascal table\\n c5 := 1\\n NN, ii := N, i\\n for NN > 0 || ii > 0 {\\n ni, iiDigit := NN%5, ii%5\\n if iiDigit > ni {\\n c5 = 0\\n break\\n }\\n c5 = (c5 * bin5[ni][iiDigit]) % 5\\n NN /= 5\\n ii /= 5\\n }\\n if c5 != 0 {\\n v := di - dip1\\n // bring into [0,4]\\n v %= 5\\n if v < 0 {\\n v += 5\\n }\\n sum5 = (sum5 + c5*v) % 5\\n }\\n }\\n\\n // final difference \\u2261 0 (mod 2) && \\u2261 0 (mod 5) \\u21d2 \\u2261 0 (mod 10)\\n return sum2 == 0 && sum5 == 0\\n}\"], [8600, 4.6512, \"\\nimport (\\n\\t\\\"fmt\\\"\\n\\t\\\"math\\\"\\n)\\n\\n\\nfunc mod10from2and5(m2 int, m5 int) int {\\n return (6 * m5 - 5 * m2) % 10\\n}\\n\\nfunc fillDigits(digits [][]int, n int, basepascal [][]int, base int) {\\n for k:=0; n > 0; k++ {\\n digits[k] = basepascal[n % base]\\n n = n / base\\n }\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n n := len(s) - 2;\\n pascal5 := [][]int {\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1},\\n }\\n\\n n5pascal := make([][]int, int(math.Log(float64(n)) - math.Log(5.))+2);\\n fillDigits(n5pascal, n, pascal5, 5)\\n\\n //i5digits := make([]int, int(math.Log(float64(n)) - math.Log(5.))+2);\\n ans := 0;\\n for i:=0; i<=n; i++ {\\n cNiMod2 := 0;\\n if i &^ n == 0 { cNiMod2 = 1; }\\n\\n cNiMod5 := 1;\\n \\n j := i;\\n for k:=0; j > 0; k++ {\\n cNiMod5 *= n5pascal[k][j%5];\\n j = j / 5;\\n }\\n \\n cNiMod10 := mod10from2and5(cNiMod2, cNiMod5);\\n ans += cNiMod10 * (int(s[i+1]) - int(s[i]));\\n }\\n\\n return ans % 10 == 0;\\n}\"], [8700, 2.3256, \"func hasSameDigits(s string) bool {\\n n := len(s);\\n m := n - 2;\\n\\n mDigits := make([]int, 10);\\n mSize := 0;\\n temp := m;\\n if temp == 0 {\\n mDigits[mSize] = 0;\\n mSize++;\\n } else {\\n for temp > 0 {\\n mDigits[mSize] = temp % 5;\\n mSize++;\\n temp /= 5;\\n }\\n }\\n\\n small := [5][5]int{\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1},\\n };\\n diff := 0;\\n for j := 0; j <= m; j++ {\\n res5 := 1;\\n x := j;\\n for i := 0; i < mSize; i++ {\\n d := x % 5;\\n x /= 5;\\n a := mDigits[i];\\n if d > a {\\n res5 = 0;\\n break;\\n }\\n res5 = (res5 * small[a][d]) % 5;\\n }\\n\\n c2 := 0;\\n if (m & j) == j {\\n c2 = 1;\\n }\\n\\n coeff := res5;\\n if (res5&1) != c2 {\\n coeff += 5;\\n }\\n\\n delta := int(s[j] - '0') - int(s[j+1] - '0');\\n diff = (diff + coeff * delta) % 10;\\n if diff < 0 {\\n diff += 10;\\n }\\n }\\n\\n return diff == 0;\\n}\"], [8800, 4.6512, \"\\nimport (\\n\\t\\\"fmt\\\"\\n\\t\\\"math\\\"\\n)\\n\\nfunc fillDigits(digits []int, n int, base int) {\\n for k:=0; n > 0; k++ {\\n digits[k] = n % base\\n n = n / base\\n }\\n}\\n\\nvar pascal5 = [][]int {\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1},\\n};\\n\\nfunc hasSameDigits(s string) bool {\\n n := len(s) - 2;\\n\\n n5digits := make([]int, int(math.Log(float64(n)) - math.Log(5.))+2);\\n fillDigits(n5digits, n, 5)\\n\\n //i5digits := make([]int, int(math.Log(float64(n)) - math.Log(5.))+2);\\n ans := 0;\\n for i:=0; i<=n; i++ {\\n cNiMod10 := 6;\\n for k, j := 0, i; j > 0; k++ {\\n cNiMod10 *= pascal5[n5digits[k]][j%5];\\n j = j / 5;\\n }\\n \\n if i &^ n == 0 {\\n cNiMod10 -= 5;\\n }\\n ans += cNiMod10 * (int(s[i+1]) - int(s[i]));\\n }\\n\\n return ans % 10 == 0;\\n}\"], [8900, 5.814, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits = operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nfunc operationPentiple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-5; i++ {\\n\\t\\tdigits[i] = (digits[i] + 5*digits[i+1] + 5*digits[i+4] + digits[i+5]) % 10\\n\\t}\\n\\tdigits = digits[:n-5]\\n\\treturn digits\\n}\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5] + digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) *2+ (digits[i+630] + digits[i+650]) *2\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [9000, 4.6512, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 642 {\\n\\t\\t\\tdigits = operation20(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n \\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\n\\nvar coeffs = []int{1, 640, 0, 0, 0, 8, 0, 0, 0, 0, 8, 0, 0, 0, 0, 6, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 6, 0, 0, 0, 0, 8, 0, 0, 0, 0, 8, 0, 0, 0, 0, 1}\\nvar k = len(coeffs)\\n\\nfunc operation20(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+640] + (digits[i+1]+digits[i+639])*640 + (digits[i+5]+digits[i+635])*8 + (digits[i+10]+digits[i+630])*8 + (digits[i+15]+digits[i+625])*6 + (digits[i+128]+digits[i+512])*5\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [9100, 2.3256, \"package main\\n\\nvar (\\n\\tpascalMod5Global [][]int\\n\\tcrtTableGlobal [2][5]int\\n)\\n\\nfunc init() {\\n\\tpascalMod5Global = make([][]int, 5)\\n\\tfor i := 0; i < 5; i++ {\\n\\t\\tpascalMod5Global[i] = make([]int, i+1)\\n\\t\\tpascalMod5Global[i][0] = 1\\n\\t\\tif i > 0 {\\n\\t\\t\\tpascalMod5Global[i][i] = 1\\n\\t\\t}\\n\\t\\tfor j := 1; j < i; j++ {\\n\\t\\t\\tpascalMod5Global[i][j] = (pascalMod5Global[i-1][j-1] + pascalMod5Global[i-1][j]) % 5\\n\\t\\t}\\n\\t}\\n\\n\\tcrtTableGlobal[0][0] = 0\\n\\tcrtTableGlobal[0][1] = 6\\n\\tcrtTableGlobal[0][2] = 2\\n\\tcrtTableGlobal[0][3] = 8\\n\\tcrtTableGlobal[0][4] = 4\\n\\tcrtTableGlobal[1][0] = 5\\n\\tcrtTableGlobal[1][1] = 1\\n\\tcrtTableGlobal[1][2] = 7\\n\\tcrtTableGlobal[1][3] = 3\\n\\tcrtTableGlobal[1][4] = 9\\n}\\n\\nfunc getCSmallMod5(n, k int) int {\\n\\tif k < 0 || k > n {\\n\\t\\treturn 0\\n\\t}\\n\\treturn pascalMod5Global[n][k]\\n}\\n\\nfunc calculateCMod10(n, k int) int {\\n\\tif k < 0 || k > n {\\n\\t\\treturn 0\\n\\t}\\n\\tif k == 0 || k == n {\\n\\t\\treturn 1\\n\\t}\\n\\tif k > n/2 {\\n\\t\\tk = n - k\\n\\t}\\n\\n\\tcMod2 := 0\\n\\tif (n & k) == k {\\n\\t\\tcMod2 = 1\\n\\t}\\n\\n\\tcMod5 := 1\\n\\ttempN, tempK := n, k\\n\\tfor tempN > 0 || tempK > 0 {\\n\\t\\tni := tempN % 5\\n\\t\\tki := tempK % 5\\n\\n\\t\\tvalCSmall := getCSmallMod5(ni, ki)\\n\\t\\t\\n\\t\\tif valCSmall == 0 {\\n\\t\\t\\tcMod5 = 0\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t\\tcMod5 = (cMod5 * valCSmall) % 5\\n\\t\\t\\n\\t\\ttempN /= 5\\n\\t\\ttempK /= 5\\n\\t}\\n\\t\\n\\treturn crtTableGlobal[cMod2][cMod5]\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n\\tnumDigits := len(s)\\n\\tK_ops := numDigits - 2\\n\\n\\tdigits := make([]int, numDigits)\\n\\tfor i, charRune := range s {\\n\\t\\tdigits[i] = int(charRune - '0')\\n\\t}\\n\\n\\tfinalDigit1 := 0\\n\\tfinalDigit2 := 0\\n\\n\\tfor i := 0; i <= K_ops; i++ {\\n\\t\\tcoeffMod10 := calculateCMod10(K_ops, i)\\n\\t\\t\\n\\t\\tif coeffMod10 == 0 {\\n\\t\\t\\tcontinue\\n\\t\\t}\\n\\n\\t\\tfinalDigit1 = (finalDigit1 + coeffMod10*digits[i]) % 10\\n\\t\\tfinalDigit2 = (finalDigit2 + coeffMod10*digits[i+1]) % 10\\n\\t}\\n\\t\\n\\treturn finalDigit1 == finalDigit2\\n}\"], [9200, 2.3256, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits = operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nfunc operationPentiple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-5; i++ {\\n\\t\\tdigits[i] = (digits[i] + 5*digits[i+1] + 5*digits[i+4] + digits[i+5]) % 10\\n\\t}\\n\\tdigits = digits[:n-5]\\n\\treturn digits\\n}\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] +\\n\\t\\t\\t(digits[i+5]+digits[i+1275]+digits[i+25]+digits[i+1255]+digits[i+30]+digits[i+1250])*6 +\\n\\t\\t\\t(digits[i+256]+digits[i+1024])*5 +\\n\\t\\t\\tdigits[i+625] + digits[i+655] + digits[i+625] + digits[i+655] + digits[i+630] +\\n\\t\\t\\tdigits[i+650] + digits[i+630] + digits[i+650]\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [9300, 9.3023, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits = operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nfunc operationPentiple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-5; i++ {\\n\\t\\tdigits[i] = (digits[i] + 5*digits[i+1] + 5*digits[i+4] + digits[i+5]) % 10\\n\\t}\\n\\tdigits = digits[:n-5]\\n\\treturn digits\\n}\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5] + digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + digits[i+625] + digits[i+655] + digits[i+625] + digits[i+655] + digits[i+630] + digits[i+650] + digits[i+630] + digits[i+650]\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [9400, 4.6512, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits = operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nfunc operationPentiple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-5; i++ {\\n\\t\\tdigits[i] = (digits[i] + 5*digits[i+1] + 5*digits[i+4] + digits[i+5]) % 10\\n\\t}\\n\\tdigits = digits[:n-5]\\n\\treturn digits\\n}\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] +\\n\\t\\t\\t(digits[i+5]+digits[i+1275]+digits[i+25]+digits[i+1255]+digits[i+30]+digits[i+1250])*6 +\\n\\t\\t\\t(digits[i+256]+digits[i+1024])*5 +\\n\\t\\t\\tdigits[i+625] + digits[i+655] + digits[i+625] + digits[i+655] + digits[i+630] +\\n\\t\\t\\tdigits[i+650] + digits[i+630] + digits[i+650]\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [9500, 1.1628, \"func hasSameDigits(s string) bool {\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t\\n\\tfor {\\n\\t\\t if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits = operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\n\\n\\nfunc operation1282(digits []int) []int {\\n\\tfor i := 0; i < len(digits)-(1281-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5]+digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) + (digits[i+625] + digits[i+655]) + (digits[i+630] + digits[i+650]) + (digits[i+630] + digits[i+650])\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(1281-1)]\\n\\n\\treturn digits\\n}\"], [9600, 4.6512, \"func hasSameDigits(s string) bool {\\n n := len(s)\\n N := n - 2\\n // decode string to digits\\n d := make([]int, n)\\n for i := range s {\\n d[i] = int(s[i] - '0')\\n }\\n // --- check mod 2 ---\\n // binom(N,i) mod 2 == 1 iff (N & i) == i\\n sum2 := 0\\n for i := 0; i <= N; i++ {\\n if (N&i) == i {\\n // v = d[i] - d[i+1]; add v mod2\\n if (d[i]-d[i+1])&1 != 0 {\\n sum2 ^= 1\\n }\\n }\\n }\\n if sum2 != 0 {\\n return false\\n }\\n // --- check mod 5 via Lucas ---\\n // Pascal\\u2019s triangle mod 5 for rows 0..4\\n bin5 := [5][5]int{\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1},\\n }\\n sum5 := 0\\n for i := 0; i <= N; i++ {\\n // compute C(N,i) mod 5 using Lucas\\n c := 1\\n NN, ii := N, i\\n for NN > 0 || ii > 0 {\\n ni, iiDigit := NN%5, ii%5\\n if iiDigit > ni {\\n c = 0\\n break\\n }\\n c = c * bin5[ni][iiDigit] % 5\\n NN /= 5\\n ii /= 5\\n }\\n if c == 0 {\\n continue\\n }\\n // v mod 5\\n v := d[i] - d[i+1]\\n v %= 5\\n if v < 0 {\\n v += 5\\n }\\n sum5 = (sum5 + c*v) % 5\\n }\\n return sum5 == 0\\n}\"], [9700, 8.1395, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits=operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5]+digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) + (digits[i+625] + digits[i+655]) + (digits[i+630] + digits[i+650]) + (digits[i+630] + digits[i+650])\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [9800, 2.3256, \"func hasSameDigits(s string) bool {\\n\\tC := [][]int{\\n\\t\\t{1, 0, 0, 0, 0},\\n\\t\\t{1, 1, 0, 0, 0},\\n\\t\\t{1, 2, 1, 0, 0},\\n\\t\\t{1, 3, 3, 1, 0},\\n\\t\\t{1, 4, 6, 4, 1},\\n\\t} // C(n,k)\\n\\tinv := [][]int{\\n\\t\\t{0, 5},\\n\\t\\t{6, 1},\\n\\t\\t{2, 7},\\n\\t\\t{8, 3},\\n\\t\\t{4, 9},\\n\\t} // r5,r2\\n\\tn := len(s) - 2\\n\\tcList := make([]int, n+1)\\n\\tfor i := range cList {\\n\\t\\ta, b := i, n\\n\\t\\tmul := 1\\n\\t\\tfor a > 0 || b > 0 {\\n\\t\\t\\tmul *= C[b%5][a%5]\\n\\t\\t\\ta /= 5\\n\\t\\t\\tb /= 5\\n\\t\\t\\tmul %= 5\\n\\t\\t}\\n\\t\\tr5 := mul\\n\\t\\ta, b = i, n\\n\\t\\tmul = 1\\n\\t\\tfor a > 0 || b > 0 {\\n\\t\\t\\tmul *= C[b%2][a%2]\\n\\t\\t\\ta /= 2\\n\\t\\t\\tb /= 2\\n\\t\\t\\tmul %= 2\\n\\t\\t}\\n\\t\\tr2 := mul\\n\\t\\tcList[i] = inv[r5][r2]\\n\\t}\\n\\n\\td1, d2 := 0, 0\\n\\tfor i := 0; i <= n; i++ {\\n\\t\\td1 += int(s[i]-'0') * cList[i]\\n\\t\\td1 %= 10\\n\\t\\td2 += int(s[i+1]-'0') * cList[i]\\n\\t\\td2 %= 10\\n\\t}\\n\\n\\treturn d1 == d2\\n}\"], [9900, 3.4884, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits=operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5]+digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) + (digits[i+625] + digits[i+655]) + (digits[i+630] + digits[i+650]) + (digits[i+630] + digits[i+650])\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [10000, 2.3256, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits = operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nfunc operationPentiple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-5; i++ {\\n\\t\\tdigits[i] = (digits[i] + 5*digits[i+1] + 5*digits[i+4] + digits[i+5]) % 10\\n\\t}\\n\\tdigits = digits[:n-5]\\n\\treturn digits\\n}\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] += digits[i+1280] + (digits[i+5] + digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) *2+ (digits[i+630] + digits[i+650]) *2\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [10100, 3.4884, \"// Global C array to match C++ implementation\\nvar C [][3]int\\n\\nfunc init() {\\n C = make([][3]int, 100000)\\n}\\n// Inverse calculates the modular inverse\\nfunc inverse(x [3]int) [3]int {\\n x0, a, b := x[0], x[1], x[2]\\n // Modular inverse under mod 10 using Euler's theorem\\n x0Inv := (x0*x0*x0) % 10 // x0^3 is inverse mod 10\\n return [3]int{x0Inv, -a, -b}\\n}\\n\\n// Mult multiplies two factors\\nfunc mult(x, y [3]int) [3]int {\\n return [3]int{(x[0]*y[0])%10, x[1]+y[1], x[2]+y[2]}\\n}\\n\\n// ToInt converts the factorized form to an integer mod 10\\nfunc toInt(x [3]int) int {\\n if x[1] >= 1 && x[2] >= 1 {\\n return 0\\n }\\n if x[2] >= 1 {\\n return 5\\n }\\n \\n if x[1] == 0 {\\n return x[0]\\n }\\n \\n // 2^x(mod 10) cycle: 2, 4, 8, 6\\n b2 := 0\\n switch x[1] % 4 {\\n case 0:\\n b2 = 6\\n case 1:\\n b2 = 2\\n case 2:\\n b2 = 4\\n case 3:\\n b2 = 8\\n }\\n \\n return (x[0] * b2) % 10\\n}\\n\\n\\n// ComputeComb computes combinations efficiently\\nfunc computeComb(N int) {\\n C[0] = [3]int{1, 0, 0}\\n if N == 0 {\\n return // Prevent C[N] access if N=0\\n }\\n C[N] = [3]int{1, 0, 0}\\n \\n for k := 1; k <= N/2; k++ {\\n p := factor(N-k+1)\\n q := inverse(factor(k))\\n C[k] = mult(mult(C[k-1], p), q)\\n C[N-k] = C[k]\\n }\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n n := len(s)\\n \\n // Clear only the needed part of C array\\n for i := 0; i < n-2; i++ {\\n C[i] = [3]int{0, 0, 0}\\n }\\n \\n // Compute combinations\\n computeComb(n-2)\\n \\n sum := 0\\n for i := 0; i <= n-2; i++ {\\n cVal := (toInt(C[i]) * (int(s[i]) - int(s[i+1]))) % 10\\n sum = (sum + cVal + 10) % 10 // Ensure non-negative\\n }\\n \\n return sum == 0\\n}\\n\\n// Factor decomposes x into y * 2^a * 5^b\\nfunc factor(x int) [3]int {\\n // Find trailing zeros (equivalent to countr_zero)\\n a := 0\\n for x&1 == 0 && x != 0 {\\n x >>= 1\\n a++\\n }\\n \\n b := 0\\n for x%5 == 0 && x != 0 {\\n x /= 5\\n b++\\n }\\n \\n return [3]int{x % 10, a, b} // Only keep mod 10 for y\\n}\\n\"], [10200, 2.3256, \"// Global C array to match C++ implementation\\nvar C [][3]int\\n\\nfunc init() {\\n C = make([][3]int, 100000)\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n n := len(s)\\n \\n // Clear only the needed part of C array\\n for i := 0; i < n-2; i++ {\\n C[i] = [3]int{0, 0, 0}\\n }\\n \\n // Compute combinations\\n computeComb(n-2)\\n \\n sum := 0\\n for i := 0; i <= n-2; i++ {\\n cVal := (toInt(C[i]) * (int(s[i]) - int(s[i+1]))) % 10\\n sum = (sum + cVal + 10) % 10 // Ensure non-negative\\n }\\n \\n return sum == 0\\n}\\n\\n// Factor decomposes x into y * 2^a * 5^b\\nfunc factor(x int) [3]int {\\n // Find trailing zeros (equivalent to countr_zero)\\n a := 0\\n for x&1 == 0 && x != 0 {\\n x >>= 1\\n a++\\n }\\n \\n b := 0\\n for x%5 == 0 && x != 0 {\\n x /= 5\\n b++\\n }\\n \\n return [3]int{x % 10, a, b} // Only keep mod 10 for y\\n}\\n\\n// Inverse calculates the modular inverse\\nfunc inverse(x [3]int) [3]int {\\n x0, a, b := x[0], x[1], x[2]\\n // Modular inverse under mod 10 using Euler's theorem\\n x0Inv := (x0*x0*x0) % 10 // x0^3 is inverse mod 10\\n return [3]int{x0Inv, -a, -b}\\n}\\n\\n// Mult multiplies two factors\\nfunc mult(x, y [3]int) [3]int {\\n return [3]int{(x[0]*y[0])%10, x[1]+y[1], x[2]+y[2]}\\n}\\n\\n// ToInt converts the factorized form to an integer mod 10\\nfunc toInt(x [3]int) int {\\n if x[1] >= 1 && x[2] >= 1 {\\n return 0\\n }\\n if x[2] >= 1 {\\n return 5\\n }\\n \\n if x[1] == 0 {\\n return x[0]\\n }\\n \\n // 2^x(mod 10) cycle: 2, 4, 8, 6\\n b2 := 0\\n switch x[1] % 4 {\\n case 0:\\n b2 = 6\\n case 1:\\n b2 = 2\\n case 2:\\n b2 = 4\\n case 3:\\n b2 = 8\\n }\\n \\n return (x[0] * b2) % 10\\n}\\n\\n// ComputeComb computes combinations efficiently\\nfunc computeComb(N int) {\\n C[0] = [3]int{1, 0, 0}\\n if N == 0 {\\n return // Prevent C[N] access if N=0\\n }\\n C[N] = [3]int{1, 0, 0}\\n \\n for k := 1; k <= N/2; k++ {\\n p := factor(N-k+1)\\n q := inverse(factor(k))\\n C[k] = mult(mult(C[k-1], p), q)\\n C[N-k] = C[k]\\n }\\n}\"], [10300, 1.1628, \"\\n// Compute modular inverse using extended euclid's algorithm\\nfunc modularInverse(x, m int) (int, bool) {\\n t, newt := 0, 1\\n r, newr := m, x\\n for newr != 0 {\\n q := r / newr\\n t, newt = newt, t-q*newt\\n r, newr = newr, r-q*newr\\n }\\n\\n if r > 1 {\\n return 0, false\\n }\\n if t < 0 {\\n t += m\\n }\\n return t, true\\n}\\n\\n// Decompose n into a * m^b\\nfunc decomp(n, m int) (int, int) {\\n r := 0\\n if n == 0 || m == 0 {\\n return 0, 0\\n }\\n for n%m == 0 {\\n n /= m\\n r++\\n }\\n return n, r\\n}\\n\\n// Get the nth row of pascal's triangle mod m\\nfunc pascalRow(n, m int) []int {\\n row := make([]int, n+1)\\n multiples, rem := 0, 1\\n\\n for i := 0; i <= n; i++ {\\n if i > 0 {\\n num, numP := decomp(n+1-i, m)\\n denom, denomP := decomp(i, m)\\n multiples += numP - denomP\\n bottom, ok := modularInverse(denom%m, m)\\n if !ok {\\n panic(\\\"Modular inverse failed\\\")\\n }\\n rem = (rem * (num % m) * bottom) % m\\n }\\n if multiples > 0 {\\n row[i] = 0\\n } else {\\n row[i] = rem\\n }\\n }\\n return row\\n}\\n\\nfunc atoiByte(c byte) int {\\n return int(c - '0')\\n}\\n\\n// Return the digit that we'd get from the string s after applying the whole process, mod m (where m is prime)\\nfunc getFinalDigit(s string, m int) int {\\n row := pascalRow(len(s)-1, m)\\n result := 0\\n for i, digit := range s {\\n result = (result + atoiByte(byte(digit))*row[i]) % m\\n }\\n return result\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n mod2 := getFinalDigit(s[:len(s)-1], 2) == getFinalDigit(s[1:], 2)\\n mod5 := getFinalDigit(s[:len(s)-1], 5) == getFinalDigit(s[1:], 5)\\n return mod2 && mod5\\n}\\n\"], [10400, 2.3256, \"func hasSameDigits(s string) bool {\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits = operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5]+digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) + (digits[i+625] + digits[i+655]) + (digits[i+630] + digits[i+650]) + (digits[i+630] + digits[i+650])\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [11000, 1.1628, \"\\n// Compute modular inverse using extended euclid's algorithm\\nfunc modularInverse(x, m int) (int, bool) {\\n t, newt := 0, 1\\n r, newr := m, x\\n for newr != 0 {\\n q := r / newr\\n t, newt = newt, t-q*newt\\n r, newr = newr, r-q*newr\\n }\\n\\n if r > 1 {\\n return 0, false\\n }\\n if t < 0 {\\n t += m\\n }\\n return t, true\\n}\\n\\n// Decompose n into a * m^b\\nfunc decomp(n, m int) (int, int) {\\n r := 0\\n if n == 0 || m == 0 {\\n return 0, 0\\n }\\n for n%m == 0 {\\n n /= m\\n r++\\n }\\n return n, r\\n}\\n\\n// Get the nth row of pascal's triangle mod m (Optimized)\\nfunc pascalRow(n, m int) []int {\\n row := make([]int, n+1)\\n multiples, rem := 0, 1\\n row[0] = 1 // Initialize the first element\\n\\n for i := 1; i <= n; i++ {\\n num, numP := decomp(n+1-i, m)\\n denom, denomP := decomp(i, m)\\n multiples += numP - denomP\\n bottom, ok := modularInverse(denom%m, m)\\n if !ok {\\n panic(\\\"Modular inverse failed\\\")\\n }\\n rem = (rem * (num % m) * bottom) % m\\n if multiples > 0 {\\n row[i] = 0\\n } else {\\n row[i] = rem\\n }\\n }\\n return row\\n}\\n\\nfunc atoiByte(c byte) int {\\n return int(c - '0')\\n}\\n\\n// Return the digit that we'd get from the string s after applying the whole process, mod m (where m is prime)\\nfunc getFinalDigit(s string, m int) int {\\n row := pascalRow(len(s)-1, m)\\n result := 0\\n for i, digit := range s {\\n result = (result + atoiByte(byte(digit))*row[i]) % m\\n }\\n return result\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n mod2 := getFinalDigit(s[:len(s)-1], 2) == getFinalDigit(s[1:], 2)\\n mod5 := getFinalDigit(s[:len(s)-1], 5) == getFinalDigit(s[1:], 5)\\n return mod2 && mod5\\n}\"], [11100, 1.1628, \"package main\\n\\n\\nfunc hasSameDigits(s string) bool {\\n\\tn := len(s)\\n\\tif n == 2 {\\n\\t\\treturn s[0] == s[1]\\n\\t}\\n\\tm := n - 2\\n\\n\\t// \\u041f\\u0440\\u0435\\u043e\\u0431\\u0440\\u0430\\u0437\\u0443\\u0435\\u043c \\u0441\\u0442\\u0440\\u043e\\u043a\\u0443 \\u0432 \\u0441\\u0440\\u0435\\u0437 \\u0446\\u0438\\u0444\\u0440.\\n\\ta := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\ta[i] = int(s[i] - '0')\\n\\t}\\n\\n\\tS0, S1 := 0, 0\\n\\t// \\u0421\\u0443\\u043c\\u043c\\u0438\\u0440\\u0443\\u0435\\u043c \\u043f\\u043e j \\u043e\\u0442 0 \\u0434\\u043e m \\u0432\\u043a\\u043b\\u044e\\u0447\\u0438\\u0442\\u0435\\u043b\\u044c\\u043d\\u043e.\\n\\tfor j := 0; j <= m; j++ {\\n\\t\\tb := binomMod10(m, j) // \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u043c C(m, j) mod 10.\\n\\t\\tS0 = (S0 + b*a[j]) % 10\\n\\t\\tS1 = (S1 + b*a[j+1]) % 10\\n\\t}\\n\\n\\treturn S0 == S1\\n}\\n\\n// binomMod10 \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u0442 C(n, k) mod 10 \\u0447\\u0435\\u0440\\u0435\\u0437 \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u0435 \\u043f\\u043e \\u043c\\u043e\\u0434\\u0443\\u043b\\u044f\\u043c 2 \\u0438 5 \\u0438 CRT.\\nfunc binomMod10(n, k int) int {\\n\\tr2 := binom2(n, k)\\n\\tr5 := binom5(n, k)\\n\\tcandidate := r5 % 10\\n\\tif candidate%2 == r2 {\\n\\t\\treturn candidate\\n\\t}\\n\\treturn (candidate + 5) % 10\\n}\\n\\n// binom2 \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u0442 C(n, k) mod 2.\\n// \\u0418\\u0437\\u0432\\u0435\\u0441\\u0442\\u043d\\u043e, \\u0447\\u0442\\u043e C(n, k) mod 2 = 1, \\u0435\\u0441\\u043b\\u0438 \\u0432\\u0441\\u0435 \\u0435\\u0434\\u0438\\u043d\\u0438\\u0447\\u043d\\u044b\\u0435 \\u0431\\u0438\\u0442\\u044b k \\u0441\\u043e\\u0434\\u0435\\u0440\\u0436\\u0430\\u0442\\u0441\\u044f \\u0432 n, \\u0438\\u043d\\u0430\\u0447\\u0435 0.\\nfunc binom2(n, k int) int {\\n\\tif k < 0 || k > n {\\n\\t\\treturn 0\\n\\t}\\n\\tif (n & k) == k {\\n\\t\\treturn 1\\n\\t}\\n\\treturn 0\\n}\\n\\n// binom5 \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u0442 C(n, k) mod 5 \\u043f\\u043e \\u0442\\u0435\\u043e\\u0440\\u0435\\u043c\\u0435 \\u041b\\u0443\\u043a\\u0430\\u0441\\u0430.\\n// \\u041f\\u0440\\u0435\\u0434\\u0441\\u0442\\u0430\\u0432\\u043b\\u044f\\u0435\\u043c n \\u0438 k \\u0432 \\u0441\\u0438\\u0441\\u0442\\u0435\\u043c\\u0435 \\u0441 \\u043e\\u0441\\u043d\\u043e\\u0432\\u0430\\u043d\\u0438\\u0435\\u043c 5 \\u0438 \\u043f\\u0435\\u0440\\u0435\\u043c\\u043d\\u043e\\u0436\\u0430\\u0435\\u043c \\u043c\\u0430\\u043b\\u0435\\u043d\\u044c\\u043a\\u0438\\u0435 \\u0431\\u0438\\u043d\\u043e\\u043c\\u0438\\u0430\\u043b\\u044c\\u043d\\u044b\\u0435 \\u043a\\u043e\\u044d\\u0444\\u0444\\u0438\\u0446\\u0438\\u0435\\u043d\\u0442\\u044b.\\nfunc binom5(n, k int) int {\\n\\tif k < 0 || k > n {\\n\\t\\treturn 0\\n\\t}\\n\\t// \\u0422\\u0430\\u0431\\u043b\\u0438\\u0446\\u0430 \\u0434\\u043b\\u044f C(n, k) mod 5, \\u0434\\u043b\\u044f n, k \\u043e\\u0442 0 \\u0434\\u043e 4.\\n\\ttable := [5][5]int{\\n\\t\\t{1, 0, 0, 0, 0},\\n\\t\\t{1, 1, 0, 0, 0},\\n\\t\\t{1, 2, 1, 0, 0},\\n\\t\\t{1, 3, 3, 1, 0},\\n\\t\\t{1, 4, 1, 4, 1},\\n\\t}\\n\\n\\tres := 1\\n\\tfor n > 0 || k > 0 {\\n\\t\\tni := n % 5\\n\\t\\tki := k % 5\\n\\t\\tif ki > ni {\\n\\t\\t\\treturn 0\\n\\t\\t}\\n\\t\\tres = (res * table[ni][ki]) % 5\\n\\t\\tn /= 5\\n\\t\\tk /= 5\\n\\t}\\n\\treturn res\\n}\\n\"], [12700, 1.1628, \"package main\\n\\n// \\u0413\\u043b\\u043e\\u0431\\u0430\\u043b\\u044c\\u043d\\u044b\\u0435 \\u043f\\u0440\\u0435\\u0434\\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u043d\\u044b\\u0435 \\u0442\\u0430\\u0431\\u043b\\u0438\\u0446\\u044b \\u0438 \\u043c\\u0430\\u0441\\u0441\\u0438\\u0432\\u044b.\\nvar (\\n\\tpascalMod5Global [][]int // \\u0425\\u0440\\u0430\\u043d\\u0438\\u0442 C(n,k) % 5 \\u0434\\u043b\\u044f n, k < 5\\n\\tpowersOf5Global []int // \\u0425\\u0440\\u0430\\u043d\\u0438\\u0442 \\u0441\\u0442\\u0435\\u043f\\u0435\\u043d\\u0438 5: 5^0, 5^1, ...\\n)\\n\\n// \\u041c\\u0430\\u043a\\u0441\\u0438\\u043c\\u0430\\u043b\\u044c\\u043d\\u043e\\u0435 \\u043a\\u043e\\u043b\\u0438\\u0447\\u0435\\u0441\\u0442\\u0432\\u043e \\u0446\\u0438\\u0444\\u0440 \\u0432 \\u043f\\u044f\\u0442\\u0435\\u0440\\u0438\\u0447\\u043d\\u043e\\u0439 \\u0437\\u0430\\u043f\\u0438\\u0441\\u0438 K (\\u0434\\u043b\\u044f K < 10^5, \\u044d\\u0442\\u043e 8 \\u0446\\u0438\\u0444\\u0440: K_0...K_7)\\nconst maxKBase5Digits = 8 \\n\\nfunc init() {\\n\\t// \\u0418\\u043d\\u0438\\u0446\\u0438\\u0430\\u043b\\u0438\\u0437\\u0430\\u0446\\u0438\\u044f pascalMod5Global\\n\\tpascalMod5Global = make([][]int, 5)\\n\\tfor i := 0; i < 5; i++ {\\n\\t\\tpascalMod5Global[i] = make([]int, i+1)\\n\\t\\tpascalMod5Global[i][0] = 1 \\n\\t\\tif i > 0 {\\n\\t\\t\\tpascalMod5Global[i][i] = 1 \\n\\t\\t}\\n\\t\\tfor j := 1; j < i; j++ {\\n\\t\\t\\tpascalMod5Global[i][j] = (pascalMod5Global[i-1][j-1] + pascalMod5Global[i-1][j]) % 5\\n\\t\\t}\\n\\t}\\n\\n\\t// \\u0418\\u043d\\u0438\\u0446\\u0438\\u0430\\u043b\\u0438\\u0437\\u0430\\u0446\\u0438\\u044f powersOf5Global\\n\\tpowersOf5Global = make([]int, maxKBase5Digits)\\n\\tpowersOf5Global[0] = 1\\n\\tfor k := 1; k < maxKBase5Digits; k++ {\\n\\t\\tpowersOf5Global[k] = powersOf5Global[k-1] * 5\\n\\t}\\n}\\n\\n// \\u0421\\u0442\\u0440\\u0443\\u043a\\u0442\\u0443\\u0440\\u0430 \\u0434\\u043b\\u044f \\u0438\\u043d\\u043a\\u0430\\u043f\\u0441\\u0443\\u043b\\u044f\\u0446\\u0438\\u0438 \\u0441\\u043e\\u0441\\u0442\\u043e\\u044f\\u043d\\u0438\\u044f \\u043f\\u0440\\u0438 \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u0438 T5.\\ntype t5Calculator struct {\\n\\tK int // \\u0417\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 K = N-2\\n\\ty []int // \\u041c\\u0430\\u0441\\u0441\\u0438\\u0432 \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0439 y_i = d_i - d_{i+1}\\n\\tmaxDigitIndex int // \\u041c\\u0430\\u043a\\u0441\\u0438\\u043c\\u0430\\u043b\\u044c\\u043d\\u044b\\u0439 \\u0438\\u043d\\u0434\\u0435\\u043a\\u0441 \\u0446\\u0438\\u0444\\u0440\\u044b \\u0432 \\u043f\\u044f\\u0442\\u0435\\u0440\\u0438\\u0447\\u043d\\u043e\\u0439 \\u0437\\u0430\\u043f\\u0438\\u0441\\u0438 K (\\u043d\\u0430\\u043f\\u0440\\u0438\\u043c\\u0435\\u0440, \\u0434\\u043b\\u044f (K_m...K_0)_5, \\u044d\\u0442\\u043e m)\\n\\tT5 int // \\u0420\\u0435\\u0437\\u0443\\u043b\\u044c\\u0442\\u0430\\u0442 T5\\n}\\n\\n// \\u0420\\u0435\\u043a\\u0443\\u0440\\u0441\\u0438\\u0432\\u043d\\u0430\\u044f \\u0444\\u0443\\u043d\\u043a\\u0446\\u0438\\u044f \\u0434\\u043b\\u044f \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u044f T5.\\n// digit_idx: \\u0442\\u0435\\u043a\\u0443\\u0449\\u0438\\u0439 \\u043e\\u0431\\u0440\\u0430\\u0431\\u0430\\u0442\\u044b\\u0432\\u0430\\u0435\\u043c\\u044b\\u0439 \\u0438\\u043d\\u0434\\u0435\\u043a\\u0441 \\u0446\\u0438\\u0444\\u0440\\u044b K (\\u043e\\u0442 maxDigitIndex \\u0434\\u043e 0).\\n// C_Ki_mod5_val: \\u0442\\u0435\\u043a\\u0443\\u0449\\u0435\\u0435 \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 \\u043f\\u0440\\u043e\\u0438\\u0437\\u0432\\u0435\\u0434\\u0435\\u043d\\u0438\\u044f C(K_j, i_j) \\u0434\\u043b\\u044f \\u0441\\u0442\\u0430\\u0440\\u0448\\u0438\\u0445 \\u0440\\u0430\\u0437\\u0440\\u044f\\u0434\\u043e\\u0432.\\n// current_i_val: \\u0442\\u0435\\u043a\\u0443\\u0449\\u0435\\u0435 \\u0441\\u043e\\u0431\\u0438\\u0440\\u0430\\u0435\\u043c\\u043e\\u0435 \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 i.\\nfunc (c *t5Calculator) recurse(digitIdx int, C_Ki_mod5_val int, currentIVal int) {\\n\\tif digitIdx < 0 { // \\u0412\\u0441\\u0435 \\u0446\\u0438\\u0444\\u0440\\u044b \\u043e\\u0431\\u0440\\u0430\\u0431\\u043e\\u0442\\u0430\\u043d\\u044b, i \\u0441\\u0444\\u043e\\u0440\\u043c\\u0438\\u0440\\u043e\\u0432\\u0430\\u043d\\u043e\\n\\t\\ttermRaw := C_Ki_mod5_val * c.y[currentIVal]\\n\\t\\ttermMod5 := termRaw % 5\\n\\t\\tif termMod5 < 0 {\\n\\t\\t\\ttermMod5 += 5\\n\\t\\t}\\n\\t\\tc.T5 = (c.T5 + termMod5) % 5\\n\\t\\treturn\\n\\t}\\n\\n\\t// K_j - \\u044d\\u0442\\u043e digitIdx-\\u0430\\u044f \\u0446\\u0438\\u0444\\u0440\\u0430 \\u0447\\u0438\\u0441\\u043b\\u0430 K \\u0432 \\u043f\\u044f\\u0442\\u0435\\u0440\\u0438\\u0447\\u043d\\u043e\\u0439 \\u0441\\u0438\\u0441\\u0442\\u0435\\u043c\\u0435 (K_j * 5^digitIdx)\\n\\tK_j := (c.K / powersOf5Global[digitIdx]) % 5\\n\\t\\n\\tfor i_j := 0; i_j <= K_j; i_j++ { // i_j - digitIdx-\\u0430\\u044f \\u0446\\u0438\\u0444\\u0440\\u0430 \\u0447\\u0438\\u0441\\u043b\\u0430 i\\n\\t\\t// pascalMod5Global[K_j][i_j] \\u044d\\u0442\\u043e C(K_j, i_j) % 5. \\u042d\\u0442\\u043e \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 \\u043d\\u0435 \\u0440\\u0430\\u0432\\u043d\\u043e 0, \\u0442.\\u043a. i_j <= K_j < 5.\\n\\t\\tnew_C_Ki_mod5_val := (C_Ki_mod5_val * pascalMod5Global[K_j][i_j]) % 5\\n\\t\\tc.recurse(digitIdx-1, new_C_Ki_mod5_val, currentIVal+i_j*powersOf5Global[digitIdx])\\n\\t}\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n\\tN := len(s)\\n\\tK := N - 2 // K - \\u044d\\u0442\\u043e 'n' \\u0432 C(n,k) \\u0438 \\u043a\\u043e\\u043b\\u0438\\u0447\\u0435\\u0441\\u0442\\u0432\\u043e \\u043e\\u043f\\u0435\\u0440\\u0430\\u0446\\u0438\\u0439\\n\\n\\tdigits := make([]int, N)\\n\\tfor i, charRune := range s {\\n\\t\\tdigits[i] = int(charRune - '0')\\n\\t}\\n\\n\\t// y_i = d_i - d_{i+1}. \\u042d\\u0442\\u0438 \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u044f \\u043c\\u043e\\u0433\\u0443\\u0442 \\u0431\\u044b\\u0442\\u044c \\u043e\\u0442\\u0440\\u0438\\u0446\\u0430\\u0442\\u0435\\u043b\\u044c\\u043d\\u044b\\u043c\\u0438.\\n\\ty := make([]int, K+1) \\n\\tfor i := 0; i <= K; i++ {\\n\\t\\ty[i] = digits[i] - digits[i+1]\\n\\t}\\n\\n\\t// \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u0435 T2 = (Sum_{i s.t. (K&i)==i} y_i) mod 2\\n\\tT2 := 0\\n\\tfor i := 0; i <= K; i++ {\\n\\t\\tif (K & i) == i { // \\u041f\\u0440\\u043e\\u0432\\u0435\\u0440\\u043a\\u0430, \\u044f\\u0432\\u043b\\u044f\\u0435\\u0442\\u0441\\u044f \\u043b\\u0438 i \\\"\\u043f\\u043e\\u0434\\u043c\\u0430\\u0441\\u043a\\u043e\\u0439\\\" K\\n\\t\\t\\ttermMod2 := y[i] % 2\\n\\t\\t\\tif termMod2 < 0 {\\n\\t\\t\\t\\ttermMod2 += 2\\n\\t\\t\\t}\\n\\t\\t\\tT2 = (T2 + termMod2) % 2\\n\\t\\t}\\n\\t}\\n\\n\\tif T2 != 0 { // \\u0415\\u0441\\u043b\\u0438 S \\u043d\\u0435 \\u0434\\u0435\\u043b\\u0438\\u0442\\u0441\\u044f \\u043d\\u0430 2, \\u0442\\u043e \\u0438 \\u043d\\u0430 10 \\u043d\\u0435 \\u0434\\u0435\\u043b\\u0438\\u0442\\u0441\\u044f\\n\\t\\treturn false\\n\\t}\\n\\n\\t// \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u0435 T5 = (Sum_{i s.t. forall j, i_j <= K_j} (C(K,i)%5 * y_i) ) mod 5\\n\\t\\n\\t// \\u041e\\u043f\\u0440\\u0435\\u0434\\u0435\\u043b\\u0435\\u043d\\u0438\\u0435 \\u043c\\u0430\\u043a\\u0441\\u0438\\u043c\\u0430\\u043b\\u044c\\u043d\\u043e\\u0433\\u043e \\u0438\\u043d\\u0434\\u0435\\u043a\\u0441\\u0430 \\u0446\\u0438\\u0444\\u0440\\u044b K \\u0432 \\u043f\\u044f\\u0442\\u0435\\u0440\\u0438\\u0447\\u043d\\u043e\\u0439 \\u0441\\u0438\\u0441\\u0442\\u0435\\u043c\\u0435 (m)\\n\\tm := -1\\n\\tif K == 0 {\\n\\t\\tm = 0\\n\\t} else {\\n\\t\\ttempK := K\\n\\t\\tfor tempK > 0 {\\n\\t\\t\\ttempK /= 5\\n\\t\\t\\tm++\\n\\t\\t}\\n\\t}\\n\\n\\tcalc := t5Calculator{\\n\\t\\tK: K,\\n\\t\\ty: y,\\n\\t\\tmaxDigitIndex: m,\\n\\t\\tT5: 0,\\n\\t}\\n\\tcalc.recurse(m, 1, 0) // \\u041d\\u0430\\u0447\\u0430\\u043b\\u044c\\u043d\\u044b\\u0439 \\u0432\\u044b\\u0437\\u043e\\u0432: (max_\\u0438\\u043d\\u0434\\u0435\\u043a\\u0441_\\u0446\\u0438\\u0444\\u0440\\u044b, C_mod_5=1, \\u0442\\u0435\\u043a\\u0443\\u0449\\u0435\\u0435_i=0)\\n\\t\\n\\t// T5 \\u0434\\u043e\\u043b\\u0436\\u0435\\u043d \\u0431\\u044b\\u0442\\u044c \\u043d\\u0435\\u043e\\u0442\\u0440\\u0438\\u0446\\u0430\\u0442\\u0435\\u043b\\u044c\\u043d\\u044b\\u043c (\\u0445\\u043e\\u0442\\u044f \\u043f\\u0440\\u0438 \\u0442\\u0435\\u043a\\u0443\\u0449\\u0435\\u0439 \\u043b\\u043e\\u0433\\u0438\\u043a\\u0435 \\u043e\\u043d \\u0438 \\u0442\\u0430\\u043a \\u0431\\u0443\\u0434\\u0435\\u0442 \\u0432 [0,4])\\n\\t// if calc.T5 < 0 { calc.T5 += 5 } // \\u0418\\u0437\\u043b\\u0438\\u0448\\u043d\\u0435, \\u0435\\u0441\\u043b\\u0438 termMod5 \\u0432\\u0441\\u0435\\u0433\\u0434\\u0430 \\u043f\\u043e\\u043b\\u043e\\u0436\\u0438\\u0442\\u0435\\u043b\\u0435\\u043d.\\n\\n\\treturn calc.T5 == 0 // \\u0415\\u0441\\u043b\\u0438 S \\u0434\\u0435\\u043b\\u0438\\u0442\\u0441\\u044f \\u043d\\u0430 5 (\\u0438 \\u0440\\u0430\\u043d\\u0435\\u0435 \\u043f\\u0440\\u043e\\u0432\\u0435\\u0440\\u0438\\u043b\\u0438 \\u043d\\u0430 2), \\u0442\\u043e \\u0434\\u0435\\u043b\\u0438\\u0442\\u0441\\u044f \\u043d\\u0430 10\\n}\"], [13200, 1.1628, \"package main\\n\\n// \\u0413\\u043b\\u043e\\u0431\\u0430\\u043b\\u044c\\u043d\\u044b\\u0435 \\u043f\\u0440\\u0435\\u0434\\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u043d\\u044b\\u0435 \\u0442\\u0430\\u0431\\u043b\\u0438\\u0446\\u044b \\u0438 \\u043c\\u0430\\u0441\\u0441\\u0438\\u0432\\u044b.\\nvar (\\n\\tpascalMod5Global [][]int // \\u0425\\u0440\\u0430\\u043d\\u0438\\u0442 C(n,k) % 5 \\u0434\\u043b\\u044f n, k < 5\\n\\tpowersOf5Global []int // \\u0425\\u0440\\u0430\\u043d\\u0438\\u0442 \\u0441\\u0442\\u0435\\u043f\\u0435\\u043d\\u0438 5: 5^0, 5^1, ...\\n)\\n\\n// \\u041c\\u0430\\u043a\\u0441\\u0438\\u043c\\u0430\\u043b\\u044c\\u043d\\u043e\\u0435 \\u043a\\u043e\\u043b\\u0438\\u0447\\u0435\\u0441\\u0442\\u0432\\u043e \\u0446\\u0438\\u0444\\u0440 \\u0432 \\u043f\\u044f\\u0442\\u0435\\u0440\\u0438\\u0447\\u043d\\u043e\\u0439 \\u0437\\u0430\\u043f\\u0438\\u0441\\u0438 K (\\u0434\\u043b\\u044f K < 10^5, \\u044d\\u0442\\u043e 8 \\u0446\\u0438\\u0444\\u0440: K_0...K_7)\\nconst maxKBase5Digits = 8 \\n\\nfunc init() {\\n\\t// \\u0418\\u043d\\u0438\\u0446\\u0438\\u0430\\u043b\\u0438\\u0437\\u0430\\u0446\\u0438\\u044f pascalMod5Global\\n\\tpascalMod5Global = make([][]int, 5)\\n\\tfor i := 0; i < 5; i++ {\\n\\t\\tpascalMod5Global[i] = make([]int, i+1)\\n\\t\\tpascalMod5Global[i][0] = 1 \\n\\t\\tif i > 0 {\\n\\t\\t\\tpascalMod5Global[i][i] = 1 \\n\\t\\t}\\n\\t\\tfor j := 1; j < i; j++ {\\n\\t\\t\\tpascalMod5Global[i][j] = (pascalMod5Global[i-1][j-1] + pascalMod5Global[i-1][j]) % 5\\n\\t\\t}\\n\\t}\\n\\n\\t// \\u0418\\u043d\\u0438\\u0446\\u0438\\u0430\\u043b\\u0438\\u0437\\u0430\\u0446\\u0438\\u044f powersOf5Global\\n\\tpowersOf5Global = make([]int, maxKBase5Digits)\\n\\tpowersOf5Global[0] = 1\\n\\tfor k := 1; k < maxKBase5Digits; k++ {\\n\\t\\tpowersOf5Global[k] = powersOf5Global[k-1] * 5\\n\\t}\\n}\\n\\n// \\u0421\\u0442\\u0440\\u0443\\u043a\\u0442\\u0443\\u0440\\u0430 \\u0434\\u043b\\u044f \\u0438\\u043d\\u043a\\u0430\\u043f\\u0441\\u0443\\u043b\\u044f\\u0446\\u0438\\u0438 \\u0441\\u043e\\u0441\\u0442\\u043e\\u044f\\u043d\\u0438\\u044f \\u043f\\u0440\\u0438 \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u0438 T5.\\ntype t5Calculator struct {\\n\\tK int // \\u0417\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 K = N-2\\n\\ty []int // \\u041c\\u0430\\u0441\\u0441\\u0438\\u0432 \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0439 y_i = d_i - d_{i+1}\\n\\tmaxDigitIndex int // \\u041c\\u0430\\u043a\\u0441\\u0438\\u043c\\u0430\\u043b\\u044c\\u043d\\u044b\\u0439 \\u0438\\u043d\\u0434\\u0435\\u043a\\u0441 \\u0446\\u0438\\u0444\\u0440\\u044b \\u0432 \\u043f\\u044f\\u0442\\u0435\\u0440\\u0438\\u0447\\u043d\\u043e\\u0439 \\u0437\\u0430\\u043f\\u0438\\u0441\\u0438 K (\\u043d\\u0430\\u043f\\u0440\\u0438\\u043c\\u0435\\u0440, \\u0434\\u043b\\u044f (K_m...K_0)_5, \\u044d\\u0442\\u043e m)\\n\\tT5 int // \\u0420\\u0435\\u0437\\u0443\\u043b\\u044c\\u0442\\u0430\\u0442 T5\\n}\\n\\n// \\u0420\\u0435\\u043a\\u0443\\u0440\\u0441\\u0438\\u0432\\u043d\\u0430\\u044f \\u0444\\u0443\\u043d\\u043a\\u0446\\u0438\\u044f \\u0434\\u043b\\u044f \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u044f T5.\\n// digit_idx: \\u0442\\u0435\\u043a\\u0443\\u0449\\u0438\\u0439 \\u043e\\u0431\\u0440\\u0430\\u0431\\u0430\\u0442\\u044b\\u0432\\u0430\\u0435\\u043c\\u044b\\u0439 \\u0438\\u043d\\u0434\\u0435\\u043a\\u0441 \\u0446\\u0438\\u0444\\u0440\\u044b K (\\u043e\\u0442 maxDigitIndex \\u0434\\u043e 0).\\n// C_Ki_mod5_val: \\u0442\\u0435\\u043a\\u0443\\u0449\\u0435\\u0435 \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 \\u043f\\u0440\\u043e\\u0438\\u0437\\u0432\\u0435\\u0434\\u0435\\u043d\\u0438\\u044f C(K_j, i_j) \\u0434\\u043b\\u044f \\u0441\\u0442\\u0430\\u0440\\u0448\\u0438\\u0445 \\u0440\\u0430\\u0437\\u0440\\u044f\\u0434\\u043e\\u0432.\\n// current_i_val: \\u0442\\u0435\\u043a\\u0443\\u0449\\u0435\\u0435 \\u0441\\u043e\\u0431\\u0438\\u0440\\u0430\\u0435\\u043c\\u043e\\u0435 \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 i.\\nfunc (c *t5Calculator) recurse(digitIdx int, C_Ki_mod5_val int, currentIVal int) {\\n\\tif digitIdx < 0 { // \\u0412\\u0441\\u0435 \\u0446\\u0438\\u0444\\u0440\\u044b \\u043e\\u0431\\u0440\\u0430\\u0431\\u043e\\u0442\\u0430\\u043d\\u044b, i \\u0441\\u0444\\u043e\\u0440\\u043c\\u0438\\u0440\\u043e\\u0432\\u0430\\u043d\\u043e\\n\\t\\ttermRaw := C_Ki_mod5_val * c.y[currentIVal]\\n\\t\\ttermMod5 := termRaw % 5\\n\\t\\tif termMod5 < 0 {\\n\\t\\t\\ttermMod5 += 5\\n\\t\\t}\\n\\t\\tc.T5 = (c.T5 + termMod5) % 5\\n\\t\\treturn\\n\\t}\\n\\n\\t// K_j - \\u044d\\u0442\\u043e digitIdx-\\u0430\\u044f \\u0446\\u0438\\u0444\\u0440\\u0430 \\u0447\\u0438\\u0441\\u043b\\u0430 K \\u0432 \\u043f\\u044f\\u0442\\u0435\\u0440\\u0438\\u0447\\u043d\\u043e\\u0439 \\u0441\\u0438\\u0441\\u0442\\u0435\\u043c\\u0435 (K_j * 5^digitIdx)\\n\\tK_j := (c.K / powersOf5Global[digitIdx]) % 5\\n\\t\\n\\tfor i_j := 0; i_j <= K_j; i_j++ { // i_j - digitIdx-\\u0430\\u044f \\u0446\\u0438\\u0444\\u0440\\u0430 \\u0447\\u0438\\u0441\\u043b\\u0430 i\\n\\t\\t// pascalMod5Global[K_j][i_j] \\u044d\\u0442\\u043e C(K_j, i_j) % 5. \\u042d\\u0442\\u043e \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 \\u043d\\u0435 \\u0440\\u0430\\u0432\\u043d\\u043e 0, \\u0442.\\u043a. i_j <= K_j < 5.\\n\\t\\tnew_C_Ki_mod5_val := (C_Ki_mod5_val * pascalMod5Global[K_j][i_j]) % 5\\n\\t\\tc.recurse(digitIdx-1, new_C_Ki_mod5_val, currentIVal+i_j*powersOf5Global[digitIdx])\\n\\t}\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n\\tN := len(s)\\n\\tK := N - 2 // K - \\u044d\\u0442\\u043e 'n' \\u0432 C(n,k) \\u0438 \\u043a\\u043e\\u043b\\u0438\\u0447\\u0435\\u0441\\u0442\\u0432\\u043e \\u043e\\u043f\\u0435\\u0440\\u0430\\u0446\\u0438\\u0439\\n\\n\\tdigits := make([]int, N)\\n\\tfor i, charRune := range s {\\n\\t\\tdigits[i] = int(charRune - '0')\\n\\t}\\n\\n\\t// y_i = d_i - d_{i+1}. \\u042d\\u0442\\u0438 \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u044f \\u043c\\u043e\\u0433\\u0443\\u0442 \\u0431\\u044b\\u0442\\u044c \\u043e\\u0442\\u0440\\u0438\\u0446\\u0430\\u0442\\u0435\\u043b\\u044c\\u043d\\u044b\\u043c\\u0438.\\n\\ty := make([]int, K+1) \\n\\tfor i := 0; i <= K; i++ {\\n\\t\\ty[i] = digits[i] - digits[i+1]\\n\\t}\\n\\n\\t// \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u0435 T2 = (Sum_{i s.t. (K&i)==i} y_i) mod 2\\n\\tT2 := 0\\n\\tfor i := 0; i <= K; i++ {\\n\\t\\tif (K & i) == i { // \\u041f\\u0440\\u043e\\u0432\\u0435\\u0440\\u043a\\u0430, \\u044f\\u0432\\u043b\\u044f\\u0435\\u0442\\u0441\\u044f \\u043b\\u0438 i \\\"\\u043f\\u043e\\u0434\\u043c\\u0430\\u0441\\u043a\\u043e\\u0439\\\" K\\n\\t\\t\\ttermMod2 := y[i] % 2\\n\\t\\t\\tif termMod2 < 0 {\\n\\t\\t\\t\\ttermMod2 += 2\\n\\t\\t\\t}\\n\\t\\t\\tT2 = (T2 + termMod2) % 2\\n\\t\\t}\\n\\t}\\n\\n\\tif T2 != 0 { // \\u0415\\u0441\\u043b\\u0438 S \\u043d\\u0435 \\u0434\\u0435\\u043b\\u0438\\u0442\\u0441\\u044f \\u043d\\u0430 2, \\u0442\\u043e \\u0438 \\u043d\\u0430 10 \\u043d\\u0435 \\u0434\\u0435\\u043b\\u0438\\u0442\\u0441\\u044f\\n\\t\\treturn false\\n\\t}\\n\\n\\t// \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u0435 T5 = (Sum_{i s.t. forall j, i_j <= K_j} (C(K,i)%5 * y_i) ) mod 5\\n\\t\\n\\t// \\u041e\\u043f\\u0440\\u0435\\u0434\\u0435\\u043b\\u0435\\u043d\\u0438\\u0435 \\u043c\\u0430\\u043a\\u0441\\u0438\\u043c\\u0430\\u043b\\u044c\\u043d\\u043e\\u0433\\u043e \\u0438\\u043d\\u0434\\u0435\\u043a\\u0441\\u0430 \\u0446\\u0438\\u0444\\u0440\\u044b K \\u0432 \\u043f\\u044f\\u0442\\u0435\\u0440\\u0438\\u0447\\u043d\\u043e\\u0439 \\u0441\\u0438\\u0441\\u0442\\u0435\\u043c\\u0435 (m)\\n\\tm := -1\\n\\tif K == 0 {\\n\\t\\tm = 0\\n\\t} else {\\n\\t\\ttempK := K\\n\\t\\tfor tempK > 0 {\\n\\t\\t\\ttempK /= 5\\n\\t\\t\\tm++\\n\\t\\t}\\n\\t}\\n\\n\\tcalc := t5Calculator{\\n\\t\\tK: K,\\n\\t\\ty: y,\\n\\t\\tmaxDigitIndex: m,\\n\\t\\tT5: 0,\\n\\t}\\n\\tcalc.recurse(m, 1, 0) // \\u041d\\u0430\\u0447\\u0430\\u043b\\u044c\\u043d\\u044b\\u0439 \\u0432\\u044b\\u0437\\u043e\\u0432: (max_\\u0438\\u043d\\u0434\\u0435\\u043a\\u0441_\\u0446\\u0438\\u0444\\u0440\\u044b, C_mod_5=1, \\u0442\\u0435\\u043a\\u0443\\u0449\\u0435\\u0435_i=0)\\n\\t\\n\\t// T5 \\u0434\\u043e\\u043b\\u0436\\u0435\\u043d \\u0431\\u044b\\u0442\\u044c \\u043d\\u0435\\u043e\\u0442\\u0440\\u0438\\u0446\\u0430\\u0442\\u0435\\u043b\\u044c\\u043d\\u044b\\u043c (\\u0445\\u043e\\u0442\\u044f \\u043f\\u0440\\u0438 \\u0442\\u0435\\u043a\\u0443\\u0449\\u0435\\u0439 \\u043b\\u043e\\u0433\\u0438\\u043a\\u0435 \\u043e\\u043d \\u0438 \\u0442\\u0430\\u043a \\u0431\\u0443\\u0434\\u0435\\u0442 \\u0432 [0,4])\\n\\t// if calc.T5 < 0 { calc.T5 += 5 } // \\u0418\\u0437\\u043b\\u0438\\u0448\\u043d\\u0435, \\u0435\\u0441\\u043b\\u0438 termMod5 \\u0432\\u0441\\u0435\\u0433\\u0434\\u0430 \\u043f\\u043e\\u043b\\u043e\\u0436\\u0438\\u0442\\u0435\\u043b\\u0435\\u043d.\\n\\n\\treturn calc.T5 == 0 // \\u0415\\u0441\\u043b\\u0438 S \\u0434\\u0435\\u043b\\u0438\\u0442\\u0441\\u044f \\u043d\\u0430 5 (\\u0438 \\u0440\\u0430\\u043d\\u0435\\u0435 \\u043f\\u0440\\u043e\\u0432\\u0435\\u0440\\u0438\\u043b\\u0438 \\u043d\\u0430 2), \\u0442\\u043e \\u0434\\u0435\\u043b\\u0438\\u0442\\u0441\\u044f \\u043d\\u0430 10\\n}\"]]",
"runtime": 74,
"runtimeDistribution": "[[13, 1.1628, \"package main\\n\\n// \\u0413\\u043b\\u043e\\u0431\\u0430\\u043b\\u044c\\u043d\\u044b\\u0435 \\u043f\\u0440\\u0435\\u0434\\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u043d\\u044b\\u0435 \\u0442\\u0430\\u0431\\u043b\\u0438\\u0446\\u044b \\u0438 \\u043c\\u0430\\u0441\\u0441\\u0438\\u0432\\u044b.\\nvar (\\n\\tpascalMod5Global [][]int // \\u0425\\u0440\\u0430\\u043d\\u0438\\u0442 C(n,k) % 5 \\u0434\\u043b\\u044f n, k < 5\\n\\tpowersOf5Global []int // \\u0425\\u0440\\u0430\\u043d\\u0438\\u0442 \\u0441\\u0442\\u0435\\u043f\\u0435\\u043d\\u0438 5: 5^0, 5^1, ...\\n)\\n\\n// \\u041c\\u0430\\u043a\\u0441\\u0438\\u043c\\u0430\\u043b\\u044c\\u043d\\u043e\\u0435 \\u043a\\u043e\\u043b\\u0438\\u0447\\u0435\\u0441\\u0442\\u0432\\u043e \\u0446\\u0438\\u0444\\u0440 \\u0432 \\u043f\\u044f\\u0442\\u0435\\u0440\\u0438\\u0447\\u043d\\u043e\\u0439 \\u0437\\u0430\\u043f\\u0438\\u0441\\u0438 K (\\u0434\\u043b\\u044f K < 10^5, \\u044d\\u0442\\u043e 8 \\u0446\\u0438\\u0444\\u0440: K_0...K_7)\\nconst maxKBase5Digits = 8 \\n\\nfunc init() {\\n\\t// \\u0418\\u043d\\u0438\\u0446\\u0438\\u0430\\u043b\\u0438\\u0437\\u0430\\u0446\\u0438\\u044f pascalMod5Global\\n\\tpascalMod5Global = make([][]int, 5)\\n\\tfor i := 0; i < 5; i++ {\\n\\t\\tpascalMod5Global[i] = make([]int, i+1)\\n\\t\\tpascalMod5Global[i][0] = 1 \\n\\t\\tif i > 0 {\\n\\t\\t\\tpascalMod5Global[i][i] = 1 \\n\\t\\t}\\n\\t\\tfor j := 1; j < i; j++ {\\n\\t\\t\\tpascalMod5Global[i][j] = (pascalMod5Global[i-1][j-1] + pascalMod5Global[i-1][j]) % 5\\n\\t\\t}\\n\\t}\\n\\n\\t// \\u0418\\u043d\\u0438\\u0446\\u0438\\u0430\\u043b\\u0438\\u0437\\u0430\\u0446\\u0438\\u044f powersOf5Global\\n\\tpowersOf5Global = make([]int, maxKBase5Digits)\\n\\tpowersOf5Global[0] = 1\\n\\tfor k := 1; k < maxKBase5Digits; k++ {\\n\\t\\tpowersOf5Global[k] = powersOf5Global[k-1] * 5\\n\\t}\\n}\\n\\n// \\u0421\\u0442\\u0440\\u0443\\u043a\\u0442\\u0443\\u0440\\u0430 \\u0434\\u043b\\u044f \\u0438\\u043d\\u043a\\u0430\\u043f\\u0441\\u0443\\u043b\\u044f\\u0446\\u0438\\u0438 \\u0441\\u043e\\u0441\\u0442\\u043e\\u044f\\u043d\\u0438\\u044f \\u043f\\u0440\\u0438 \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u0438 T5.\\ntype t5Calculator struct {\\n\\tK int // \\u0417\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 K = N-2\\n\\ty []int // \\u041c\\u0430\\u0441\\u0441\\u0438\\u0432 \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0439 y_i = d_i - d_{i+1}\\n\\tmaxDigitIndex int // \\u041c\\u0430\\u043a\\u0441\\u0438\\u043c\\u0430\\u043b\\u044c\\u043d\\u044b\\u0439 \\u0438\\u043d\\u0434\\u0435\\u043a\\u0441 \\u0446\\u0438\\u0444\\u0440\\u044b \\u0432 \\u043f\\u044f\\u0442\\u0435\\u0440\\u0438\\u0447\\u043d\\u043e\\u0439 \\u0437\\u0430\\u043f\\u0438\\u0441\\u0438 K (\\u043d\\u0430\\u043f\\u0440\\u0438\\u043c\\u0435\\u0440, \\u0434\\u043b\\u044f (K_m...K_0)_5, \\u044d\\u0442\\u043e m)\\n\\tT5 int // \\u0420\\u0435\\u0437\\u0443\\u043b\\u044c\\u0442\\u0430\\u0442 T5\\n}\\n\\n// \\u0420\\u0435\\u043a\\u0443\\u0440\\u0441\\u0438\\u0432\\u043d\\u0430\\u044f \\u0444\\u0443\\u043d\\u043a\\u0446\\u0438\\u044f \\u0434\\u043b\\u044f \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u044f T5.\\n// digit_idx: \\u0442\\u0435\\u043a\\u0443\\u0449\\u0438\\u0439 \\u043e\\u0431\\u0440\\u0430\\u0431\\u0430\\u0442\\u044b\\u0432\\u0430\\u0435\\u043c\\u044b\\u0439 \\u0438\\u043d\\u0434\\u0435\\u043a\\u0441 \\u0446\\u0438\\u0444\\u0440\\u044b K (\\u043e\\u0442 maxDigitIndex \\u0434\\u043e 0).\\n// C_Ki_mod5_val: \\u0442\\u0435\\u043a\\u0443\\u0449\\u0435\\u0435 \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 \\u043f\\u0440\\u043e\\u0438\\u0437\\u0432\\u0435\\u0434\\u0435\\u043d\\u0438\\u044f C(K_j, i_j) \\u0434\\u043b\\u044f \\u0441\\u0442\\u0430\\u0440\\u0448\\u0438\\u0445 \\u0440\\u0430\\u0437\\u0440\\u044f\\u0434\\u043e\\u0432.\\n// current_i_val: \\u0442\\u0435\\u043a\\u0443\\u0449\\u0435\\u0435 \\u0441\\u043e\\u0431\\u0438\\u0440\\u0430\\u0435\\u043c\\u043e\\u0435 \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 i.\\nfunc (c *t5Calculator) recurse(digitIdx int, C_Ki_mod5_val int, currentIVal int) {\\n\\tif digitIdx < 0 { // \\u0412\\u0441\\u0435 \\u0446\\u0438\\u0444\\u0440\\u044b \\u043e\\u0431\\u0440\\u0430\\u0431\\u043e\\u0442\\u0430\\u043d\\u044b, i \\u0441\\u0444\\u043e\\u0440\\u043c\\u0438\\u0440\\u043e\\u0432\\u0430\\u043d\\u043e\\n\\t\\ttermRaw := C_Ki_mod5_val * c.y[currentIVal]\\n\\t\\ttermMod5 := termRaw % 5\\n\\t\\tif termMod5 < 0 {\\n\\t\\t\\ttermMod5 += 5\\n\\t\\t}\\n\\t\\tc.T5 = (c.T5 + termMod5) % 5\\n\\t\\treturn\\n\\t}\\n\\n\\t// K_j - \\u044d\\u0442\\u043e digitIdx-\\u0430\\u044f \\u0446\\u0438\\u0444\\u0440\\u0430 \\u0447\\u0438\\u0441\\u043b\\u0430 K \\u0432 \\u043f\\u044f\\u0442\\u0435\\u0440\\u0438\\u0447\\u043d\\u043e\\u0439 \\u0441\\u0438\\u0441\\u0442\\u0435\\u043c\\u0435 (K_j * 5^digitIdx)\\n\\tK_j := (c.K / powersOf5Global[digitIdx]) % 5\\n\\t\\n\\tfor i_j := 0; i_j <= K_j; i_j++ { // i_j - digitIdx-\\u0430\\u044f \\u0446\\u0438\\u0444\\u0440\\u0430 \\u0447\\u0438\\u0441\\u043b\\u0430 i\\n\\t\\t// pascalMod5Global[K_j][i_j] \\u044d\\u0442\\u043e C(K_j, i_j) % 5. \\u042d\\u0442\\u043e \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 \\u043d\\u0435 \\u0440\\u0430\\u0432\\u043d\\u043e 0, \\u0442.\\u043a. i_j <= K_j < 5.\\n\\t\\tnew_C_Ki_mod5_val := (C_Ki_mod5_val * pascalMod5Global[K_j][i_j]) % 5\\n\\t\\tc.recurse(digitIdx-1, new_C_Ki_mod5_val, currentIVal+i_j*powersOf5Global[digitIdx])\\n\\t}\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n\\tN := len(s)\\n\\tK := N - 2 // K - \\u044d\\u0442\\u043e 'n' \\u0432 C(n,k) \\u0438 \\u043a\\u043e\\u043b\\u0438\\u0447\\u0435\\u0441\\u0442\\u0432\\u043e \\u043e\\u043f\\u0435\\u0440\\u0430\\u0446\\u0438\\u0439\\n\\n\\tdigits := make([]int, N)\\n\\tfor i, charRune := range s {\\n\\t\\tdigits[i] = int(charRune - '0')\\n\\t}\\n\\n\\t// y_i = d_i - d_{i+1}. \\u042d\\u0442\\u0438 \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u044f \\u043c\\u043e\\u0433\\u0443\\u0442 \\u0431\\u044b\\u0442\\u044c \\u043e\\u0442\\u0440\\u0438\\u0446\\u0430\\u0442\\u0435\\u043b\\u044c\\u043d\\u044b\\u043c\\u0438.\\n\\ty := make([]int, K+1) \\n\\tfor i := 0; i <= K; i++ {\\n\\t\\ty[i] = digits[i] - digits[i+1]\\n\\t}\\n\\n\\t// \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u0435 T2 = (Sum_{i s.t. (K&i)==i} y_i) mod 2\\n\\tT2 := 0\\n\\tfor i := 0; i <= K; i++ {\\n\\t\\tif (K & i) == i { // \\u041f\\u0440\\u043e\\u0432\\u0435\\u0440\\u043a\\u0430, \\u044f\\u0432\\u043b\\u044f\\u0435\\u0442\\u0441\\u044f \\u043b\\u0438 i \\\"\\u043f\\u043e\\u0434\\u043c\\u0430\\u0441\\u043a\\u043e\\u0439\\\" K\\n\\t\\t\\ttermMod2 := y[i] % 2\\n\\t\\t\\tif termMod2 < 0 {\\n\\t\\t\\t\\ttermMod2 += 2\\n\\t\\t\\t}\\n\\t\\t\\tT2 = (T2 + termMod2) % 2\\n\\t\\t}\\n\\t}\\n\\n\\tif T2 != 0 { // \\u0415\\u0441\\u043b\\u0438 S \\u043d\\u0435 \\u0434\\u0435\\u043b\\u0438\\u0442\\u0441\\u044f \\u043d\\u0430 2, \\u0442\\u043e \\u0438 \\u043d\\u0430 10 \\u043d\\u0435 \\u0434\\u0435\\u043b\\u0438\\u0442\\u0441\\u044f\\n\\t\\treturn false\\n\\t}\\n\\n\\t// \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u0435 T5 = (Sum_{i s.t. forall j, i_j <= K_j} (C(K,i)%5 * y_i) ) mod 5\\n\\t\\n\\t// \\u041e\\u043f\\u0440\\u0435\\u0434\\u0435\\u043b\\u0435\\u043d\\u0438\\u0435 \\u043c\\u0430\\u043a\\u0441\\u0438\\u043c\\u0430\\u043b\\u044c\\u043d\\u043e\\u0433\\u043e \\u0438\\u043d\\u0434\\u0435\\u043a\\u0441\\u0430 \\u0446\\u0438\\u0444\\u0440\\u044b K \\u0432 \\u043f\\u044f\\u0442\\u0435\\u0440\\u0438\\u0447\\u043d\\u043e\\u0439 \\u0441\\u0438\\u0441\\u0442\\u0435\\u043c\\u0435 (m)\\n\\tm := -1\\n\\tif K == 0 {\\n\\t\\tm = 0\\n\\t} else {\\n\\t\\ttempK := K\\n\\t\\tfor tempK > 0 {\\n\\t\\t\\ttempK /= 5\\n\\t\\t\\tm++\\n\\t\\t}\\n\\t}\\n\\n\\tcalc := t5Calculator{\\n\\t\\tK: K,\\n\\t\\ty: y,\\n\\t\\tmaxDigitIndex: m,\\n\\t\\tT5: 0,\\n\\t}\\n\\tcalc.recurse(m, 1, 0) // \\u041d\\u0430\\u0447\\u0430\\u043b\\u044c\\u043d\\u044b\\u0439 \\u0432\\u044b\\u0437\\u043e\\u0432: (max_\\u0438\\u043d\\u0434\\u0435\\u043a\\u0441_\\u0446\\u0438\\u0444\\u0440\\u044b, C_mod_5=1, \\u0442\\u0435\\u043a\\u0443\\u0449\\u0435\\u0435_i=0)\\n\\t\\n\\t// T5 \\u0434\\u043e\\u043b\\u0436\\u0435\\u043d \\u0431\\u044b\\u0442\\u044c \\u043d\\u0435\\u043e\\u0442\\u0440\\u0438\\u0446\\u0430\\u0442\\u0435\\u043b\\u044c\\u043d\\u044b\\u043c (\\u0445\\u043e\\u0442\\u044f \\u043f\\u0440\\u0438 \\u0442\\u0435\\u043a\\u0443\\u0449\\u0435\\u0439 \\u043b\\u043e\\u0433\\u0438\\u043a\\u0435 \\u043e\\u043d \\u0438 \\u0442\\u0430\\u043a \\u0431\\u0443\\u0434\\u0435\\u0442 \\u0432 [0,4])\\n\\t// if calc.T5 < 0 { calc.T5 += 5 } // \\u0418\\u0437\\u043b\\u0438\\u0448\\u043d\\u0435, \\u0435\\u0441\\u043b\\u0438 termMod5 \\u0432\\u0441\\u0435\\u0433\\u0434\\u0430 \\u043f\\u043e\\u043b\\u043e\\u0436\\u0438\\u0442\\u0435\\u043b\\u0435\\u043d.\\n\\n\\treturn calc.T5 == 0 // \\u0415\\u0441\\u043b\\u0438 S \\u0434\\u0435\\u043b\\u0438\\u0442\\u0441\\u044f \\u043d\\u0430 5 (\\u0438 \\u0440\\u0430\\u043d\\u0435\\u0435 \\u043f\\u0440\\u043e\\u0432\\u0435\\u0440\\u0438\\u043b\\u0438 \\u043d\\u0430 2), \\u0442\\u043e \\u0434\\u0435\\u043b\\u0438\\u0442\\u0441\\u044f \\u043d\\u0430 10\\n}\"], [16, 2.3256, \"\\nimport (\\n\\t\\\"fmt\\\"\\n\\t\\\"math\\\"\\n)\\n\\nfunc fillDigits(digits []int, n int, base int) {\\n for k:=0; n > 0; k++ {\\n digits[k] = n % base\\n n = n / base\\n }\\n}\\n\\nvar pascal5 = [][]int {\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1},\\n};\\n\\nfunc hasSameDigits(s string) bool {\\n n := len(s) - 2;\\n\\n n5digits := make([]int, int(math.Log(float64(n)) - math.Log(5.))+2);\\n fillDigits(n5digits, n, 5)\\n\\n //i5digits := make([]int, int(math.Log(float64(n)) - math.Log(5.))+2);\\n ans := 0;\\n for i:=0; i<=n; i++ {\\n cNiMod10 := 6;\\n for k, j := 0, i; j > 0; k++ {\\n cNiMod10 *= pascal5[n5digits[k]][j%5];\\n j = j / 5;\\n }\\n \\n if i &^ n == 0 {\\n cNiMod10 -= 5;\\n }\\n ans += cNiMod10 * (int(s[i+1]) - int(s[i]));\\n }\\n\\n return ans % 10 == 0;\\n}\"], [17, 4.6512, \"\\nimport (\\n\\t\\\"fmt\\\"\\n\\t\\\"math\\\"\\n)\\n\\n\\nfunc mod10from2and5(m2 int, m5 int) int {\\n return (6 * m5 - 5 * m2) % 10\\n}\\n\\nfunc fillDigits(digits []int, n int, base int) {\\n for k:=0; n > 0; k++ {\\n digits[k] = n % base\\n n = n / base\\n }\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n n := len(s) - 2;\\n\\n n5digits := make([]int, int(math.Log(float64(n)) - math.Log(5.))+2);\\n fillDigits(n5digits, n, 5)\\n\\n pascal5 := [][]int {\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1},\\n }\\n fmt.Println(pascal5);\\n\\n //i5digits := make([]int, int(math.Log(float64(n)) - math.Log(5.))+2);\\n ans := 0;\\n for i:=0; i<=n; i++ {\\n cNiMod2 := 0;\\n if i &^ n == 0 { cNiMod2 = 1; }\\n\\n cNiMod5 := 1;\\n \\n j := i;\\n for k:=0; j > 0; k++ {\\n cNiMod5 *= pascal5[n5digits[k]][j%5];\\n j = j / 5;\\n }\\n \\n cNiMod10 := mod10from2and5(cNiMod2, cNiMod5);\\n ans += cNiMod10 * (int(s[i+1]) - int(s[i]));\\n }\\n\\n return ans % 10 == 0;\\n}\"], [18, 2.3256, \"package main\\n\\n// \\u0413\\u043b\\u043e\\u0431\\u0430\\u043b\\u044c\\u043d\\u044b\\u0435 \\u043f\\u0440\\u0435\\u0434\\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u043d\\u044b\\u0435 \\u0442\\u0430\\u0431\\u043b\\u0438\\u0446\\u044b \\u0438 \\u043c\\u0430\\u0441\\u0441\\u0438\\u0432\\u044b.\\nvar (\\n\\tpascalMod5Global [][]int // \\u0425\\u0440\\u0430\\u043d\\u0438\\u0442 C(n,k) % 5 \\u0434\\u043b\\u044f n, k < 5\\n\\tpowersOf5Global []int // \\u0425\\u0440\\u0430\\u043d\\u0438\\u0442 \\u0441\\u0442\\u0435\\u043f\\u0435\\u043d\\u0438 5: 5^0, 5^1, ...\\n)\\n\\n// \\u041c\\u0430\\u043a\\u0441\\u0438\\u043c\\u0430\\u043b\\u044c\\u043d\\u043e\\u0435 \\u043a\\u043e\\u043b\\u0438\\u0447\\u0435\\u0441\\u0442\\u0432\\u043e \\u0446\\u0438\\u0444\\u0440 \\u0432 \\u043f\\u044f\\u0442\\u0435\\u0440\\u0438\\u0447\\u043d\\u043e\\u0439 \\u0437\\u0430\\u043f\\u0438\\u0441\\u0438 K (\\u0434\\u043b\\u044f K < 10^5, \\u044d\\u0442\\u043e 8 \\u0446\\u0438\\u0444\\u0440: K_0...K_7)\\nconst maxKBase5Digits = 8 \\n\\nfunc init() {\\n\\t// \\u0418\\u043d\\u0438\\u0446\\u0438\\u0430\\u043b\\u0438\\u0437\\u0430\\u0446\\u0438\\u044f pascalMod5Global\\n\\tpascalMod5Global = make([][]int, 5)\\n\\tfor i := 0; i < 5; i++ {\\n\\t\\tpascalMod5Global[i] = make([]int, i+1)\\n\\t\\tpascalMod5Global[i][0] = 1 \\n\\t\\tif i > 0 {\\n\\t\\t\\tpascalMod5Global[i][i] = 1 \\n\\t\\t}\\n\\t\\tfor j := 1; j < i; j++ {\\n\\t\\t\\tpascalMod5Global[i][j] = (pascalMod5Global[i-1][j-1] + pascalMod5Global[i-1][j]) % 5\\n\\t\\t}\\n\\t}\\n\\n\\t// \\u0418\\u043d\\u0438\\u0446\\u0438\\u0430\\u043b\\u0438\\u0437\\u0430\\u0446\\u0438\\u044f powersOf5Global\\n\\tpowersOf5Global = make([]int, maxKBase5Digits)\\n\\tpowersOf5Global[0] = 1\\n\\tfor k := 1; k < maxKBase5Digits; k++ {\\n\\t\\tpowersOf5Global[k] = powersOf5Global[k-1] * 5\\n\\t}\\n}\\n\\n// \\u0421\\u0442\\u0440\\u0443\\u043a\\u0442\\u0443\\u0440\\u0430 \\u0434\\u043b\\u044f \\u0438\\u043d\\u043a\\u0430\\u043f\\u0441\\u0443\\u043b\\u044f\\u0446\\u0438\\u0438 \\u0441\\u043e\\u0441\\u0442\\u043e\\u044f\\u043d\\u0438\\u044f \\u043f\\u0440\\u0438 \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u0438 T5.\\ntype t5Calculator struct {\\n\\tK int // \\u0417\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 K = N-2\\n\\ty []int // \\u041c\\u0430\\u0441\\u0441\\u0438\\u0432 \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0439 y_i = d_i - d_{i+1}\\n\\tmaxDigitIndex int // \\u041c\\u0430\\u043a\\u0441\\u0438\\u043c\\u0430\\u043b\\u044c\\u043d\\u044b\\u0439 \\u0438\\u043d\\u0434\\u0435\\u043a\\u0441 \\u0446\\u0438\\u0444\\u0440\\u044b \\u0432 \\u043f\\u044f\\u0442\\u0435\\u0440\\u0438\\u0447\\u043d\\u043e\\u0439 \\u0437\\u0430\\u043f\\u0438\\u0441\\u0438 K (\\u043d\\u0430\\u043f\\u0440\\u0438\\u043c\\u0435\\u0440, \\u0434\\u043b\\u044f (K_m...K_0)_5, \\u044d\\u0442\\u043e m)\\n\\tT5 int // \\u0420\\u0435\\u0437\\u0443\\u043b\\u044c\\u0442\\u0430\\u0442 T5\\n}\\n\\n// \\u0420\\u0435\\u043a\\u0443\\u0440\\u0441\\u0438\\u0432\\u043d\\u0430\\u044f \\u0444\\u0443\\u043d\\u043a\\u0446\\u0438\\u044f \\u0434\\u043b\\u044f \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u044f T5.\\n// digit_idx: \\u0442\\u0435\\u043a\\u0443\\u0449\\u0438\\u0439 \\u043e\\u0431\\u0440\\u0430\\u0431\\u0430\\u0442\\u044b\\u0432\\u0430\\u0435\\u043c\\u044b\\u0439 \\u0438\\u043d\\u0434\\u0435\\u043a\\u0441 \\u0446\\u0438\\u0444\\u0440\\u044b K (\\u043e\\u0442 maxDigitIndex \\u0434\\u043e 0).\\n// C_Ki_mod5_val: \\u0442\\u0435\\u043a\\u0443\\u0449\\u0435\\u0435 \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 \\u043f\\u0440\\u043e\\u0438\\u0437\\u0432\\u0435\\u0434\\u0435\\u043d\\u0438\\u044f C(K_j, i_j) \\u0434\\u043b\\u044f \\u0441\\u0442\\u0430\\u0440\\u0448\\u0438\\u0445 \\u0440\\u0430\\u0437\\u0440\\u044f\\u0434\\u043e\\u0432.\\n// current_i_val: \\u0442\\u0435\\u043a\\u0443\\u0449\\u0435\\u0435 \\u0441\\u043e\\u0431\\u0438\\u0440\\u0430\\u0435\\u043c\\u043e\\u0435 \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 i.\\nfunc (c *t5Calculator) recurse(digitIdx int, C_Ki_mod5_val int, currentIVal int) {\\n\\tif digitIdx < 0 { // \\u0412\\u0441\\u0435 \\u0446\\u0438\\u0444\\u0440\\u044b \\u043e\\u0431\\u0440\\u0430\\u0431\\u043e\\u0442\\u0430\\u043d\\u044b, i \\u0441\\u0444\\u043e\\u0440\\u043c\\u0438\\u0440\\u043e\\u0432\\u0430\\u043d\\u043e\\n\\t\\ttermRaw := C_Ki_mod5_val * c.y[currentIVal]\\n\\t\\ttermMod5 := termRaw % 5\\n\\t\\tif termMod5 < 0 {\\n\\t\\t\\ttermMod5 += 5\\n\\t\\t}\\n\\t\\tc.T5 = (c.T5 + termMod5) % 5\\n\\t\\treturn\\n\\t}\\n\\n\\t// K_j - \\u044d\\u0442\\u043e digitIdx-\\u0430\\u044f \\u0446\\u0438\\u0444\\u0440\\u0430 \\u0447\\u0438\\u0441\\u043b\\u0430 K \\u0432 \\u043f\\u044f\\u0442\\u0435\\u0440\\u0438\\u0447\\u043d\\u043e\\u0439 \\u0441\\u0438\\u0441\\u0442\\u0435\\u043c\\u0435 (K_j * 5^digitIdx)\\n\\tK_j := (c.K / powersOf5Global[digitIdx]) % 5\\n\\t\\n\\tfor i_j := 0; i_j <= K_j; i_j++ { // i_j - digitIdx-\\u0430\\u044f \\u0446\\u0438\\u0444\\u0440\\u0430 \\u0447\\u0438\\u0441\\u043b\\u0430 i\\n\\t\\t// pascalMod5Global[K_j][i_j] \\u044d\\u0442\\u043e C(K_j, i_j) % 5. \\u042d\\u0442\\u043e \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 \\u043d\\u0435 \\u0440\\u0430\\u0432\\u043d\\u043e 0, \\u0442.\\u043a. i_j <= K_j < 5.\\n\\t\\tnew_C_Ki_mod5_val := (C_Ki_mod5_val * pascalMod5Global[K_j][i_j]) % 5\\n\\t\\tc.recurse(digitIdx-1, new_C_Ki_mod5_val, currentIVal+i_j*powersOf5Global[digitIdx])\\n\\t}\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n\\tN := len(s)\\n\\tK := N - 2 // K - \\u044d\\u0442\\u043e 'n' \\u0432 C(n,k) \\u0438 \\u043a\\u043e\\u043b\\u0438\\u0447\\u0435\\u0441\\u0442\\u0432\\u043e \\u043e\\u043f\\u0435\\u0440\\u0430\\u0446\\u0438\\u0439\\n\\n\\tdigits := make([]int, N)\\n\\tfor i, charRune := range s {\\n\\t\\tdigits[i] = int(charRune - '0')\\n\\t}\\n\\n\\t// y_i = d_i - d_{i+1}. \\u042d\\u0442\\u0438 \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u044f \\u043c\\u043e\\u0433\\u0443\\u0442 \\u0431\\u044b\\u0442\\u044c \\u043e\\u0442\\u0440\\u0438\\u0446\\u0430\\u0442\\u0435\\u043b\\u044c\\u043d\\u044b\\u043c\\u0438.\\n\\ty := make([]int, K+1) \\n\\tfor i := 0; i <= K; i++ {\\n\\t\\ty[i] = digits[i] - digits[i+1]\\n\\t}\\n\\n\\t// \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u0435 T2 = (Sum_{i s.t. (K&i)==i} y_i) mod 2\\n\\tT2 := 0\\n\\tfor i := 0; i <= K; i++ {\\n\\t\\tif (K & i) == i { // \\u041f\\u0440\\u043e\\u0432\\u0435\\u0440\\u043a\\u0430, \\u044f\\u0432\\u043b\\u044f\\u0435\\u0442\\u0441\\u044f \\u043b\\u0438 i \\\"\\u043f\\u043e\\u0434\\u043c\\u0430\\u0441\\u043a\\u043e\\u0439\\\" K\\n\\t\\t\\ttermMod2 := y[i] % 2\\n\\t\\t\\tif termMod2 < 0 {\\n\\t\\t\\t\\ttermMod2 += 2\\n\\t\\t\\t}\\n\\t\\t\\tT2 = (T2 + termMod2) % 2\\n\\t\\t}\\n\\t}\\n\\n\\tif T2 != 0 { // \\u0415\\u0441\\u043b\\u0438 S \\u043d\\u0435 \\u0434\\u0435\\u043b\\u0438\\u0442\\u0441\\u044f \\u043d\\u0430 2, \\u0442\\u043e \\u0438 \\u043d\\u0430 10 \\u043d\\u0435 \\u0434\\u0435\\u043b\\u0438\\u0442\\u0441\\u044f\\n\\t\\treturn false\\n\\t}\\n\\n\\t// \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u0435 T5 = (Sum_{i s.t. forall j, i_j <= K_j} (C(K,i)%5 * y_i) ) mod 5\\n\\t\\n\\t// \\u041e\\u043f\\u0440\\u0435\\u0434\\u0435\\u043b\\u0435\\u043d\\u0438\\u0435 \\u043c\\u0430\\u043a\\u0441\\u0438\\u043c\\u0430\\u043b\\u044c\\u043d\\u043e\\u0433\\u043e \\u0438\\u043d\\u0434\\u0435\\u043a\\u0441\\u0430 \\u0446\\u0438\\u0444\\u0440\\u044b K \\u0432 \\u043f\\u044f\\u0442\\u0435\\u0440\\u0438\\u0447\\u043d\\u043e\\u0439 \\u0441\\u0438\\u0441\\u0442\\u0435\\u043c\\u0435 (m)\\n\\tm := -1\\n\\tif K == 0 {\\n\\t\\tm = 0\\n\\t} else {\\n\\t\\ttempK := K\\n\\t\\tfor tempK > 0 {\\n\\t\\t\\ttempK /= 5\\n\\t\\t\\tm++\\n\\t\\t}\\n\\t}\\n\\n\\tcalc := t5Calculator{\\n\\t\\tK: K,\\n\\t\\ty: y,\\n\\t\\tmaxDigitIndex: m,\\n\\t\\tT5: 0,\\n\\t}\\n\\tcalc.recurse(m, 1, 0) // \\u041d\\u0430\\u0447\\u0430\\u043b\\u044c\\u043d\\u044b\\u0439 \\u0432\\u044b\\u0437\\u043e\\u0432: (max_\\u0438\\u043d\\u0434\\u0435\\u043a\\u0441_\\u0446\\u0438\\u0444\\u0440\\u044b, C_mod_5=1, \\u0442\\u0435\\u043a\\u0443\\u0449\\u0435\\u0435_i=0)\\n\\t\\n\\t// T5 \\u0434\\u043e\\u043b\\u0436\\u0435\\u043d \\u0431\\u044b\\u0442\\u044c \\u043d\\u0435\\u043e\\u0442\\u0440\\u0438\\u0446\\u0430\\u0442\\u0435\\u043b\\u044c\\u043d\\u044b\\u043c (\\u0445\\u043e\\u0442\\u044f \\u043f\\u0440\\u0438 \\u0442\\u0435\\u043a\\u0443\\u0449\\u0435\\u0439 \\u043b\\u043e\\u0433\\u0438\\u043a\\u0435 \\u043e\\u043d \\u0438 \\u0442\\u0430\\u043a \\u0431\\u0443\\u0434\\u0435\\u0442 \\u0432 [0,4])\\n\\t// if calc.T5 < 0 { calc.T5 += 5 } // \\u0418\\u0437\\u043b\\u0438\\u0448\\u043d\\u0435, \\u0435\\u0441\\u043b\\u0438 termMod5 \\u0432\\u0441\\u0435\\u0433\\u0434\\u0430 \\u043f\\u043e\\u043b\\u043e\\u0436\\u0438\\u0442\\u0435\\u043b\\u0435\\u043d.\\n\\n\\treturn calc.T5 == 0 // \\u0415\\u0441\\u043b\\u0438 S \\u0434\\u0435\\u043b\\u0438\\u0442\\u0441\\u044f \\u043d\\u0430 5 (\\u0438 \\u0440\\u0430\\u043d\\u0435\\u0435 \\u043f\\u0440\\u043e\\u0432\\u0435\\u0440\\u0438\\u043b\\u0438 \\u043d\\u0430 2), \\u0442\\u043e \\u0434\\u0435\\u043b\\u0438\\u0442\\u0441\\u044f \\u043d\\u0430 10\\n}\"], [19, 2.3256, \"func hasSameDigits(s string) bool {\\n n := len(s);\\n m := n - 2;\\n\\n mDigits := make([]int, 10);\\n mSize := 0;\\n temp := m;\\n if temp == 0 {\\n mDigits[mSize] = 0;\\n mSize++;\\n } else {\\n for temp > 0 {\\n mDigits[mSize] = temp % 5;\\n mSize++;\\n temp /= 5;\\n }\\n }\\n\\n small := [5][5]int{\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1},\\n };\\n diff := 0;\\n for j := 0; j <= m; j++ {\\n res5 := 1;\\n x := j;\\n for i := 0; i < mSize; i++ {\\n d := x % 5;\\n x /= 5;\\n a := mDigits[i];\\n if d > a {\\n res5 = 0;\\n break;\\n }\\n res5 = (res5 * small[a][d]) % 5;\\n }\\n\\n c2 := 0;\\n if (m & j) == j {\\n c2 = 1;\\n }\\n\\n coeff := res5;\\n if (res5&1) != c2 {\\n coeff += 5;\\n }\\n\\n delta := int(s[j] - '0') - int(s[j+1] - '0');\\n diff = (diff + coeff * delta) % 10;\\n if diff < 0 {\\n diff += 10;\\n }\\n }\\n\\n return diff == 0;\\n}\"], [21, 1.1628, \"// Global C array to match C++ implementation\\nvar C [][3]int\\n\\nfunc init() {\\n C = make([][3]int, 100000)\\n}\\n\\n\\n// Factor decomposes x into y * 2^a * 5^b\\nfunc factor(x int) [3]int {\\n // Find trailing zeros (equivalent to countr_zero)\\n a := 0\\n for x&1 == 0 && x != 0 {\\n x >>= 1\\n a++\\n }\\n \\n b := 0\\n for x%5 == 0 && x != 0 {\\n x /= 5\\n b++\\n }\\n \\n return [3]int{x % 10, a, b} // Only keep mod 10 for y\\n}\\n\\n// Inverse calculates the modular inverse\\nfunc inverse(x [3]int) [3]int {\\n x0, a, b := x[0], x[1], x[2]\\n // Modular inverse under mod 10 using Euler's theorem\\n x0Inv := (x0*x0*x0) % 10 // x0^3 is inverse mod 10\\n return [3]int{x0Inv, -a, -b}\\n}\\n\\n// Mult multiplies two factors\\nfunc mult(x, y [3]int) [3]int {\\n return [3]int{(x[0]*y[0])%10, x[1]+y[1], x[2]+y[2]}\\n}\\n\\n// ToInt converts the factorized form to an integer mod 10\\nfunc toInt(x [3]int) int {\\n if x[1] >= 1 && x[2] >= 1 {\\n return 0\\n }\\n if x[2] >= 1 {\\n return 5\\n }\\n \\n if x[1] == 0 {\\n return x[0]\\n }\\n \\n // 2^x(mod 10) cycle: 2, 4, 8, 6\\n b2 := 0\\n switch x[1] % 4 {\\n case 0:\\n b2 = 6\\n case 1:\\n b2 = 2\\n case 2:\\n b2 = 4\\n case 3:\\n b2 = 8\\n }\\n \\n return (x[0] * b2) % 10\\n}\\n\\n// ComputeComb computes combinations efficiently\\nfunc computeComb(N int) {\\n C[0] = [3]int{1, 0, 0}\\n if N == 0 {\\n return // Prevent C[N] access if N=0\\n }\\n C[N] = [3]int{1, 0, 0}\\n \\n for k := 1; k <= N/2; k++ {\\n p := factor(N-k+1)\\n q := inverse(factor(k))\\n C[k] = mult(mult(C[k-1], p), q)\\n C[N-k] = C[k]\\n }\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n n := len(s)\\n \\n // Clear only the needed part of C array\\n for i := 0; i < n-2; i++ {\\n C[i] = [3]int{0, 0, 0}\\n }\\n \\n // Compute combinations\\n computeComb(n-2)\\n \\n sum := 0\\n for i := 0; i <= n-2; i++ {\\n cVal := (toInt(C[i]) * (int(s[i]) - int(s[i+1]))) % 10\\n sum = (sum + cVal + 10) % 10 // Ensure non-negative\\n }\\n \\n return sum == 0\\n}\"], [23, 9.3023, \"func hasSameDigits(s string) bool {\\n n := len(s)\\n N := n - 2\\n // decode string to digits\\n d := make([]int, n)\\n for i := range s {\\n d[i] = int(s[i] - '0')\\n }\\n // --- check mod 2 ---\\n // binom(N,i) mod 2 == 1 iff (N & i) == i\\n sum2 := 0\\n for i := 0; i <= N; i++ {\\n if (N&i) == i {\\n // v = d[i] - d[i+1]; add v mod2\\n if (d[i]-d[i+1])&1 != 0 {\\n sum2 ^= 1\\n }\\n }\\n }\\n if sum2 != 0 {\\n return false\\n }\\n // --- check mod 5 via Lucas ---\\n // Pascal\\u2019s triangle mod 5 for rows 0..4\\n bin5 := [5][5]int{\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1},\\n }\\n sum5 := 0\\n for i := 0; i <= N; i++ {\\n // compute C(N,i) mod 5 using Lucas\\n c := 1\\n NN, ii := N, i\\n for NN > 0 || ii > 0 {\\n ni, iiDigit := NN%5, ii%5\\n if iiDigit > ni {\\n c = 0\\n break\\n }\\n c = c * bin5[ni][iiDigit] % 5\\n NN /= 5\\n ii /= 5\\n }\\n if c == 0 {\\n continue\\n }\\n // v mod 5\\n v := d[i] - d[i+1]\\n v %= 5\\n if v < 0 {\\n v += 5\\n }\\n sum5 = (sum5 + c*v) % 5\\n }\\n return sum5 == 0\\n}\"], [24, 2.3256, \"// Global C array to match C++ implementation\\nvar C [][3]int\\n\\nfunc init() {\\n C = make([][3]int, 100000)\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n n := len(s)\\n \\n // Clear only the needed part of C array\\n for i := 0; i < n-2; i++ {\\n C[i] = [3]int{0, 0, 0}\\n }\\n \\n // Compute combinations\\n computeComb(n-2)\\n \\n sum := 0\\n for i := 0; i <= n-2; i++ {\\n cVal := (toInt(C[i]) * (int(s[i]) - int(s[i+1]))) % 10\\n sum = (sum + cVal + 10) % 10 // Ensure non-negative\\n }\\n \\n return sum == 0\\n}\\n\\n// Factor decomposes x into y * 2^a * 5^b\\nfunc factor(x int) [3]int {\\n // Find trailing zeros (equivalent to countr_zero)\\n a := 0\\n for x&1 == 0 && x != 0 {\\n x >>= 1\\n a++\\n }\\n \\n b := 0\\n for x%5 == 0 && x != 0 {\\n x /= 5\\n b++\\n }\\n \\n return [3]int{x % 10, a, b} // Only keep mod 10 for y\\n}\\n\\n// Inverse calculates the modular inverse\\nfunc inverse(x [3]int) [3]int {\\n x0, a, b := x[0], x[1], x[2]\\n // Modular inverse under mod 10 using Euler's theorem\\n x0Inv := (x0*x0*x0) % 10 // x0^3 is inverse mod 10\\n return [3]int{x0Inv, -a, -b}\\n}\\n\\n// Mult multiplies two factors\\nfunc mult(x, y [3]int) [3]int {\\n return [3]int{(x[0]*y[0])%10, x[1]+y[1], x[2]+y[2]}\\n}\\n\\n// ToInt converts the factorized form to an integer mod 10\\nfunc toInt(x [3]int) int {\\n if x[1] >= 1 && x[2] >= 1 {\\n return 0\\n }\\n if x[2] >= 1 {\\n return 5\\n }\\n \\n if x[1] == 0 {\\n return x[0]\\n }\\n \\n // 2^x(mod 10) cycle: 2, 4, 8, 6\\n b2 := 0\\n switch x[1] % 4 {\\n case 0:\\n b2 = 6\\n case 1:\\n b2 = 2\\n case 2:\\n b2 = 4\\n case 3:\\n b2 = 8\\n }\\n \\n return (x[0] * b2) % 10\\n}\\n\\n// ComputeComb computes combinations efficiently\\nfunc computeComb(N int) {\\n C[0] = [3]int{1, 0, 0}\\n if N == 0 {\\n return // Prevent C[N] access if N=0\\n }\\n C[N] = [3]int{1, 0, 0}\\n \\n for k := 1; k <= N/2; k++ {\\n p := factor(N-k+1)\\n q := inverse(factor(k))\\n C[k] = mult(mult(C[k-1], p), q)\\n C[N-k] = C[k]\\n }\\n}\"], [25, 2.3256, \"package main\\n\\nimport \\\"fmt\\\"\\n\\nfunc hasSameDigits(s string) bool {\\n n := len(s)\\n m := n - 2\\n\\n mDigits := make([]int, 10)\\n mSize := 0\\n temp := m\\n if temp == 0 {\\n mDigits[mSize] = 0\\n mSize++\\n } else {\\n for temp > 0 {\\n mDigits[mSize] = temp % 5\\n mSize++\\n temp /= 5\\n }\\n }\\n\\n small := [5][5]int{\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1},\\n }\\n\\n diff := 0\\n\\n for j := 0; j <= m; j++ {\\n res5 := 1\\n x := j\\n for i := 0; i < mSize; i++ {\\n d := x % 5\\n x /= 5\\n a := mDigits[i]\\n if d > a {\\n res5 = 0\\n break\\n }\\n res5 = (res5 * small[a][d]) % 5\\n }\\n\\n c2 := 0\\n if (m & j) == j {\\n c2 = 1\\n }\\n\\n coeff := res5\\n if (res5&1) != c2 {\\n coeff += 5\\n }\\n\\n delta := int(s[j]-'0') - int(s[j+1]-'0')\\n diff = (diff + coeff*delta) % 10\\n if diff < 0 {\\n diff += 10\\n }\\n }\\n\\n return diff == 0\\n}\\n\"], [27, 2.3256, \"// Global C array to match C++ implementation\\nvar C [][3]int\\n\\nfunc init() {\\n C = make([][3]int, 100000)\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n n := len(s)\\n \\n // Clear only the needed part of C array\\n for i := 0; i < n-2; i++ {\\n C[i] = [3]int{0, 0, 0}\\n }\\n \\n // Compute combinations\\n computeComb(n-2)\\n \\n sum := 0\\n for i := 0; i <= n-2; i++ {\\n cVal := (toInt(C[i]) * (int(s[i]) - int(s[i+1]))) % 10\\n sum = (sum + cVal + 10) % 10 // Ensure non-negative\\n }\\n \\n return sum == 0\\n}\\n\\n// Factor decomposes x into y * 2^a * 5^b\\nfunc factor(x int) [3]int {\\n // Find trailing zeros (equivalent to countr_zero)\\n a := 0\\n for x&1 == 0 && x != 0 {\\n x >>= 1\\n a++\\n }\\n \\n b := 0\\n for x%5 == 0 && x != 0 {\\n x /= 5\\n b++\\n }\\n \\n return [3]int{x % 10, a, b} // Only keep mod 10 for y\\n}\\n\\n// Inverse calculates the modular inverse\\nfunc inverse(x [3]int) [3]int {\\n x0, a, b := x[0], x[1], x[2]\\n // Modular inverse under mod 10 using Euler's theorem\\n x0Inv := (x0*x0*x0) % 10 // x0^3 is inverse mod 10\\n return [3]int{x0Inv, -a, -b}\\n}\\n\\n// Mult multiplies two factors\\nfunc mult(x, y [3]int) [3]int {\\n return [3]int{(x[0]*y[0])%10, x[1]+y[1], x[2]+y[2]}\\n}\\n\\n// ToInt converts the factorized form to an integer mod 10\\nfunc toInt(x [3]int) int {\\n if x[1] >= 1 && x[2] >= 1 {\\n return 0\\n }\\n if x[2] >= 1 {\\n return 5\\n }\\n \\n if x[1] == 0 {\\n return x[0]\\n }\\n \\n // 2^x(mod 10) cycle: 2, 4, 8, 6\\n b2 := 0\\n switch x[1] % 4 {\\n case 0:\\n b2 = 6\\n case 1:\\n b2 = 2\\n case 2:\\n b2 = 4\\n case 3:\\n b2 = 8\\n }\\n \\n return (x[0] * b2) % 10\\n}\\n\\n// ComputeComb computes combinations efficiently\\nfunc computeComb(N int) {\\n C[0] = [3]int{1, 0, 0}\\n if N == 0 {\\n return // Prevent C[N] access if N=0\\n }\\n C[N] = [3]int{1, 0, 0}\\n \\n for k := 1; k <= N/2; k++ {\\n p := factor(N-k+1)\\n q := inverse(factor(k))\\n C[k] = mult(mult(C[k-1], p), q)\\n C[N-k] = C[k]\\n }\\n}\"], [28, 1.1628, \"func hasSameDigits(s string) bool {\\n n := len(s);\\n m := n - 2;\\n\\n mDigits := make([]int, 10);\\n mSize := 0;\\n temp := m;\\n if temp == 0 {\\n mDigits[mSize] = 0;\\n mSize++;\\n } else {\\n for temp > 0 {\\n mDigits[mSize] = temp % 5;\\n mSize++;\\n temp /= 5;\\n }\\n }\\n\\n small := [5][5]int{\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1},\\n };\\n diff := 0;\\n for j := 0; j <= m; j++ {\\n res5 := 1;\\n x := j;\\n for i := 0; i < mSize; i++ {\\n d := x % 5;\\n x /= 5;\\n a := mDigits[i];\\n if d > a {\\n res5 = 0;\\n break;\\n }\\n res5 = (res5 * small[a][d]) % 5;\\n }\\n\\n c2 := 0;\\n if (m & j) == j {\\n c2 = 1;\\n }\\n\\n coeff := res5;\\n if (res5&1) != c2 {\\n coeff += 5;\\n }\\n\\n delta := int(s[j] - '0') - int(s[j+1] - '0');\\n diff = (diff + coeff * delta) % 10;\\n if diff < 0 {\\n diff += 10;\\n }\\n }\\n\\n return diff == 0;\\n}\"], [29, 5.814, \"// Global C array to match C++ implementation\\nvar C [][3]int\\n\\nfunc hasSameDigits(s string) bool {\\n n := len(s)\\n \\n // Clear only the needed part of C array\\n for i := 0; i < n-2; i++ {\\n C[i] = [3]int{0, 0, 0}\\n }\\n \\n // Compute combinations\\n computeComb(n-2)\\n \\n sum := 0\\n for i := 0; i <= n-2; i++ {\\n cVal := (toInt(C[i]) * (int(s[i]) - int(s[i+1]))) % 10\\n sum = (sum + cVal + 10) % 10 // Ensure non-negative\\n }\\n \\n return sum == 0\\n}\\n\\nfunc init() {\\n C = make([][3]int, 100000)\\n}\\n\\n\\n// Factor decomposes x into y * 2^a * 5^b\\nfunc factor(x int) [3]int {\\n // Find trailing zeros (equivalent to countr_zero)\\n a := 0\\n for x&1 == 0 && x != 0 {\\n x >>= 1\\n a++\\n }\\n \\n b := 0\\n for x%5 == 0 && x != 0 {\\n x /= 5\\n b++\\n }\\n \\n return [3]int{x % 10, a, b} // Only keep mod 10 for y\\n}\\n\\n// Inverse calculates the modular inverse\\nfunc inverse(x [3]int) [3]int {\\n x0, a, b := x[0], x[1], x[2]\\n // Modular inverse under mod 10 using Euler's theorem\\n x0Inv := (x0*x0*x0) % 10 // x0^3 is inverse mod 10\\n return [3]int{x0Inv, -a, -b}\\n}\\n\\n// Mult multiplies two factors\\nfunc mult(x, y [3]int) [3]int {\\n return [3]int{(x[0]*y[0])%10, x[1]+y[1], x[2]+y[2]}\\n}\\n\\n// ToInt converts the factorized form to an integer mod 10\\nfunc toInt(x [3]int) int {\\n if x[1] >= 1 && x[2] >= 1 {\\n return 0\\n }\\n if x[2] >= 1 {\\n return 5\\n }\\n \\n if x[1] == 0 {\\n return x[0]\\n }\\n \\n // 2^x(mod 10) cycle: 2, 4, 8, 6\\n b2 := 0\\n switch x[1] % 4 {\\n case 0:\\n b2 = 6\\n case 1:\\n b2 = 2\\n case 2:\\n b2 = 4\\n case 3:\\n b2 = 8\\n }\\n \\n return (x[0] * b2) % 10\\n}\\n\\n// ComputeComb computes combinations efficiently\\nfunc computeComb(N int) {\\n C[0] = [3]int{1, 0, 0}\\n if N == 0 {\\n return // Prevent C[N] access if N=0\\n }\\n C[N] = [3]int{1, 0, 0}\\n \\n for k := 1; k <= N/2; k++ {\\n p := factor(N-k+1)\\n q := inverse(factor(k))\\n C[k] = mult(mult(C[k-1], p), q)\\n C[N-k] = C[k]\\n }\\n}\"], [30, 1.1628, \"// Global C array to match C++ implementation\\nvar C [][3]int\\n\\nfunc init() {\\n C = make([][3]int, 100000)\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n n := len(s)\\n \\n // Clear only the needed part of C array\\n for i := 0; i < n-2; i++ {\\n C[i] = [3]int{0, 0, 0}\\n }\\n \\n // Compute combinations\\n computeComb(n-2)\\n \\n sum := 0\\n for i := 0; i <= n-2; i++ {\\n cVal := (toInt(C[i]) * (int(s[i]) - int(s[i+1]))) % 10\\n sum = (sum + cVal + 10) % 10 // Ensure non-negative\\n }\\n \\n return sum == 0\\n}\\n\\n// Factor decomposes x into y * 2^a * 5^b\\nfunc factor(x int) [3]int {\\n // Find trailing zeros (equivalent to countr_zero)\\n a := 0\\n for x&1 == 0 && x != 0 {\\n x >>= 1\\n a++\\n }\\n \\n b := 0\\n for x%5 == 0 && x != 0 {\\n x /= 5\\n b++\\n }\\n \\n return [3]int{x % 10, a, b} // Only keep mod 10 for y\\n}\\n\\n// Inverse calculates the modular inverse\\nfunc inverse(x [3]int) [3]int {\\n x0, a, b := x[0], x[1], x[2]\\n // Modular inverse under mod 10 using Euler's theorem\\n x0Inv := (x0*x0*x0) % 10 // x0^3 is inverse mod 10\\n return [3]int{x0Inv, -a, -b}\\n}\\n\\n// Mult multiplies two factors\\nfunc mult(x, y [3]int) [3]int {\\n return [3]int{(x[0]*y[0])%10, x[1]+y[1], x[2]+y[2]}\\n}\\n\\n// ToInt converts the factorized form to an integer mod 10\\nfunc toInt(x [3]int) int {\\n if x[1] >= 1 && x[2] >= 1 {\\n return 0\\n }\\n if x[2] >= 1 {\\n return 5\\n }\\n \\n if x[1] == 0 {\\n return x[0]\\n }\\n \\n // 2^x(mod 10) cycle: 2, 4, 8, 6\\n b2 := 0\\n switch x[1] % 4 {\\n case 0:\\n b2 = 6\\n case 1:\\n b2 = 2\\n case 2:\\n b2 = 4\\n case 3:\\n b2 = 8\\n }\\n \\n return (x[0] * b2) % 10\\n}\\n\\n// ComputeComb computes combinations efficiently\\nfunc computeComb(N int) {\\n C[0] = [3]int{1, 0, 0}\\n if N == 0 {\\n return // Prevent C[N] access if N=0\\n }\\n C[N] = [3]int{1, 0, 0}\\n \\n for k := 1; k <= N/2; k++ {\\n p := factor(N-k+1)\\n q := inverse(factor(k))\\n C[k] = mult(mult(C[k-1], p), q)\\n C[N-k] = C[k]\\n }\\n}\"], [32, 2.3256, \"// Global C array to match C++ implementation\\nvar C [][3]int\\n\\nfunc init() {\\n C = make([][3]int, 100000)\\n}\\n// Inverse calculates the modular inverse\\nfunc inverse(x [3]int) [3]int {\\n x0, a, b := x[0], x[1], x[2]\\n // Modular inverse under mod 10 using Euler's theorem\\n x0Inv := (x0*x0*x0) % 10 // x0^3 is inverse mod 10\\n return [3]int{x0Inv, -a, -b}\\n}\\n\\n// Mult multiplies two factors\\nfunc mult(x, y [3]int) [3]int {\\n return [3]int{(x[0]*y[0])%10, x[1]+y[1], x[2]+y[2]}\\n}\\n\\n// ToInt converts the factorized form to an integer mod 10\\nfunc toInt(x [3]int) int {\\n if x[1] >= 1 && x[2] >= 1 {\\n return 0\\n }\\n if x[2] >= 1 {\\n return 5\\n }\\n \\n if x[1] == 0 {\\n return x[0]\\n }\\n \\n // 2^x(mod 10) cycle: 2, 4, 8, 6\\n b2 := 0\\n switch x[1] % 4 {\\n case 0:\\n b2 = 6\\n case 1:\\n b2 = 2\\n case 2:\\n b2 = 4\\n case 3:\\n b2 = 8\\n }\\n \\n return (x[0] * b2) % 10\\n}\\n\\n\\n// ComputeComb computes combinations efficiently\\nfunc computeComb(N int) {\\n C[0] = [3]int{1, 0, 0}\\n if N == 0 {\\n return // Prevent C[N] access if N=0\\n }\\n C[N] = [3]int{1, 0, 0}\\n \\n for k := 1; k <= N/2; k++ {\\n p := factor(N-k+1)\\n q := inverse(factor(k))\\n C[k] = mult(mult(C[k-1], p), q)\\n C[N-k] = C[k]\\n }\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n n := len(s)\\n \\n // Clear only the needed part of C array\\n for i := 0; i < n-2; i++ {\\n C[i] = [3]int{0, 0, 0}\\n }\\n \\n // Compute combinations\\n computeComb(n-2)\\n \\n sum := 0\\n for i := 0; i <= n-2; i++ {\\n cVal := (toInt(C[i]) * (int(s[i]) - int(s[i+1]))) % 10\\n sum = (sum + cVal + 10) % 10 // Ensure non-negative\\n }\\n \\n return sum == 0\\n}\\n\\n// Factor decomposes x into y * 2^a * 5^b\\nfunc factor(x int) [3]int {\\n // Find trailing zeros (equivalent to countr_zero)\\n a := 0\\n for x&1 == 0 && x != 0 {\\n x >>= 1\\n a++\\n }\\n \\n b := 0\\n for x%5 == 0 && x != 0 {\\n x /= 5\\n b++\\n }\\n \\n return [3]int{x % 10, a, b} // Only keep mod 10 for y\\n}\\n\"], [33, 2.3256, \"// Global precomputed table for C(n, k) mod 5 where 0 <= k <= n < 5.\\n// This is used by the nCr_mod5 function implementing Lucas's Theorem.\\n// Access using small_nCr_mod5[n][k].\\nvar small_nCr_mod5 = [5][5]int64{\\n\\t{1, 0, 0, 0, 0}, // n=0: C(0,0)=1\\n\\t{1, 1, 0, 0, 0}, // n=1: C(1,0)=1, C(1,1)=1\\n\\t{1, 2, 1, 0, 0}, // n=2: C(2,0)=1, C(2,1)=2, C(2,2)=1\\n\\t{1, 3, 3, 1, 0}, // n=3: C(3,0)=1, C(3,1)=3, C(3,2)=3, C(3,3)=1\\n\\t{1, 4, 1, 4, 1}, // n=4: C(4,0)=1, C(4,1)=4, C(4,2)=6=1, C(4,3)=4, C(4,4)=1\\n}\\n\\n// nCr_mod2 calculates the binomial coefficient C(n, r) modulo 2.\\n// It leverages the property that C(n, r) is odd (1 mod 2) if and only if\\n// the set bits in the binary representation of r are a subset of the set bits in n.\\n// This is equivalent to checking if (r & n) == r.\\n// Returns 0 or 1.\\nfunc nCr_mod2(n, r int64) int64 {\\n\\t// C(n, r) is 0 if r is outside the valid range [0, n].\\n\\tif r < 0 || r > n {\\n\\t\\treturn 0\\n\\t}\\n\\t// Check the bitwise condition.\\n\\tif (r & n) == r {\\n\\t\\treturn 1\\n\\t}\\n\\treturn 0\\n}\\n\\n// nCr_mod5 calculates the binomial coefficient C(n, r) modulo 5 using Lucas's Theorem.\\n// Lucas's Theorem states that C(n, r) = product(C(ni, ri)) mod p, where ni and ri\\n// are the digits of n and r in base p (here p=5).\\n// Returns the result [0, 4] or -1 if an internal error occurs (which shouldn't happen with valid inputs).\\nfunc nCr_mod5(n, r int64) int64 {\\n\\t// C(n, r) is 0 if r is outside the valid range [0, n].\\n\\tif r < 0 || r > n {\\n\\t\\treturn 0\\n\\t}\\n\\t// Handle base cases efficiently: C(n, 0) = 1, C(n, n) = 1.\\n\\tif r == 0 || r == n {\\n\\t\\treturn 1\\n\\t}\\n\\t// Optimization: C(n, r) = C(n, n-r). Calculate using the smaller of r and n-r.\\n\\tif r > n/2 {\\n\\t\\tr = n - r\\n\\t}\\n\\n\\tres := int64(1) // Initialize result\\n\\tnn, rr := n, r // Use copies to iterate through digits without modifying original n, r.\\n\\n\\t// Process digits of n and r in base 5 from least significant to most significant.\\n\\tfor rr > 0 {\\n\\t\\tni := nn % 5 // Get the last digit of n in base 5.\\n\\t\\tki := rr % 5 // Get the last digit of r in base 5.\\n\\n\\t\\t// According to Lucas's Theorem, if ki > ni for any digit pair, C(n, r) mod 5 is 0.\\n\\t\\tif ki > ni {\\n\\t\\t\\treturn 0\\n\\t\\t}\\n\\n\\t\\t// Safety check for array bounds, although ni and ki should be within [0, 4].\\n\\t\\t// Using int() conversion for array indexing.\\n\\t\\tif ni < 0 || ki < 0 || int(ni) >= len(small_nCr_mod5) || int(ki) >= len(small_nCr_mod5[0]) {\\n\\t\\t\\t// This block indicates an unexpected state, likely a bug or invalid input assumption.\\n\\t\\t\\t// fmt.Printf(\\\"Internal error in nCr_mod5: Invalid indices ni=%d, ki=%d\\\\n\\\", ni, ki)\\n\\t\\t\\treturn -1 // Return -1 to indicate an internal error.\\n\\t\\t}\\n\\n\\t\\t// Multiply the result by C(ni, ki) mod 5 using the precomputed table.\\n\\t\\tres = (res * small_nCr_mod5[ni][ki]) % 5\\n\\n\\t\\t// Move to the next digits by integer division by 5.\\n\\t\\tnn /= 5\\n\\t\\trr /= 5\\n\\t}\\n\\t// The loop terminates when rr becomes 0, meaning all base-5 digits of r have been processed.\\n\\treturn res\\n}\\n\\n// nCr_mod10 calculates the binomial coefficient C(n, r) modulo 10.\\n// It combines the results of C(n, r) mod 2 and C(n, r) mod 5 using the Chinese Remainder Theorem (CRT).\\n// Since 10 = 2 * 5 (coprime factors), a unique solution modulo 10 exists for any pair of residues mod 2 and mod 5.\\n// Returns the result [0, 9] or -1 if an internal error occurs.\\nfunc nCr_mod10(n, r int64) int64 {\\n\\t// C(n, r) is 0 if r is outside the valid range [0, n].\\n\\tif r < 0 || r > n {\\n\\t\\treturn 0\\n\\t}\\n\\n\\t// Calculate the residues modulo 2 and 5.\\n\\tmod2 := nCr_mod2(n, r)\\n\\tmod5 := nCr_mod5(n, r)\\n\\n\\t// Check if nCr_mod5 returned an error.\\n\\tif mod5 == -1 {\\n\\t\\t// Propagate the internal error indication.\\n\\t\\t// fmt.Println(\\\"Error propagated from nCr_mod5 in nCr_mod10\\\")\\n\\t\\treturn -1\\n\\t}\\n\\n\\t// Apply CRT logic to find x such that x = mod2 (mod 2) and x = mod5 (mod 5).\\n\\t// This is implemented using a switch based on the values of mod2 and mod5.\\n\\t// The mapping covers all possible combinations and returns the unique result mod 10.\\n\\tif mod2 == 0 {\\n\\t\\tswitch mod5 {\\n\\t\\tcase 0: return 0 // 0 mod 2, 0 mod 5 => 0 mod 10\\n\\t\\tcase 1: return 6 // 0 mod 2, 1 mod 5 => 6 mod 10\\n\\t\\tcase 2: return 2 // 0 mod 2, 2 mod 5 => 2 mod 10\\n\\t\\tcase 3: return 8 // 0 mod 2, 3 mod 5 => 8 mod 10\\n\\t\\tcase 4: return 4 // 0 mod 2, 4 mod 5 => 4 mod 10\\n\\t\\tdefault: // This case should not be reached if mod5 is in [0, 4].\\n\\t\\t\\t// fmt.Printf(\\\"Internal error in nCr_mod10: Invalid mod5 value %d with mod2=0\\\\n\\\", mod5)\\n\\t\\t\\treturn -1\\n\\t\\t}\\n\\t} else { // mod2 == 1\\n\\t\\tswitch mod5 {\\n\\t\\tcase 0: return 5 // 1 mod 2, 0 mod 5 => 5 mod 10\\n\\t\\tcase 1: return 1 // 1 mod 2, 1 mod 5 => 1 mod 10\\n\\t\\tcase 2: return 7 // 1 mod 2, 2 mod 5 => 7 mod 10\\n\\t\\tcase 3: return 3 // 1 mod 2, 3 mod 5 => 3 mod 10\\n\\t\\tcase 4: return 9 // 1 mod 2, 4 mod 5 => 9 mod 10\\n\\t\\tdefault: // This case should not be reached.\\n\\t\\t\\t// fmt.Printf(\\\"Internal error in nCr_mod10: Invalid mod5 value %d with mod2=1\\\\n\\\", mod5)\\n\\t\\t\\treturn -1\\n\\t\\t}\\n\\t}\\n}\\n\\n// hasSameDigits solves the problem by calculating the difference between the final two digits\\n// modulo 10, without explicitly simulating the operations.\\n// It leverages the observation that the final digits are linear combinations of the initial digits\\n// with coefficients involving binomial coefficients C(N-2, k).\\n// Returns true if the difference is 0 (meaning the final digits are the same), false otherwise.\\nfunc hasSameDigits(s string) bool {\\n\\tN := int64(len(s)) // Get the length of the input string.\\n\\t// Constraints: 3 <= N <= 10^5.\\n\\n\\t// n is the number of reduction operations needed to reach a length of 2.\\n\\t// n = N - 2. This is also the 'n' in the binomial coefficients C(n, k).\\n\\t// Since N >= 3, we have n >= 1.\\n\\tn := N - 2\\n\\n\\t// sum_diff accumulates the difference (final_digit_0 - final_digit_1) modulo 10.\\n\\t// If sum_diff is 0 at the end, the final digits are the same.\\n\\tsum_diff := int64(0)\\n\\n\\t// prev_cnk stores the value C(n, k-1) mod 10 calculated in the previous iteration (k-1).\\n\\t// This allows calculating the coefficient C(n, k) - C(n, k-1) efficiently.\\n\\tvar prev_cnk int64\\n\\n\\t// Iterate through each digit d_k of the initial string s (from k=0 to N-1).\\n\\tfor k := int64(0); k < N; k++ {\\n\\t\\tdigit := int64(s[k] - '0') // Convert the character digit to its integer value.\\n\\n\\t\\tvar coef_k int64 // This will store the coefficient for the current digit d_k.\\n\\t\\tvar current_cnk int64 // Temporary variable to store C(n, k) mod 10.\\n\\n\\t\\t// Determine the coefficient based on the index k.\\n\\t\\tif k == 0 {\\n\\t\\t\\t// For the first digit d_0 (k=0), the coefficient is C(n, 0) = 1.\\n\\t\\t\\tcoef_k = 1\\n\\t\\t\\t// Store C(n, 0) mod 10 (which is 1) in prev_cnk for the next iteration (k=1).\\n\\t\\t\\tprev_cnk = 1\\n\\n\\t\\t} else if k <= n { // For digits d_k where 1 <= k <= n (n = N-2).\\n\\t\\t\\t// The coefficient is C(n, k) - C(n, k-1) mod 10.\\n\\n\\t\\t\\t// Calculate C(n, k) mod 10.\\n\\t\\t\\tcurrent_cnk = nCr_mod10(n, k)\\n\\t\\t\\tif current_cnk == -1 { // Check if nCr_mod10 returned an error.\\n\\t\\t\\t\\t// fmt.Printf(\\\"Error calculating nCr_mod10(n=%d, k=%d)\\\\n\\\", n, k)\\n\\t\\t\\t\\treturn false // Indicate failure if an internal error occurred.\\n\\t\\t\\t}\\n\\n\\t\\t\\t// Calculate the coefficient: (C(n, k) - C(n, k-1)) mod 10.\\n\\t\\t\\t// prev_cnk holds C(n, k-1) mod 10 from the previous iteration.\\n\\t\\t\\t// Add 10 before taking modulo to ensure the result is non-negative.\\n\\t\\t\\tcoef_k = (current_cnk - prev_cnk + 10) % 10\\n\\n\\t\\t\\t// Update prev_cnk for the next iteration (k+1). It will store C(n, k) mod 10.\\n\\t\\t\\tprev_cnk = current_cnk\\n\\n\\t\\t} else { // For the last digit d_{N-1} (where k = n + 1 = N - 1).\\n\\t\\t\\t// The coefficient is -C(n, n) mod 10.\\n\\t\\t\\t// Since C(n, n) = 1 (for n >= 0, and here n >= 1), the coefficient is -1 mod 10.\\n\\t\\t\\tcoef_k = 9 // -1 mod 10 is equivalent to 9.\\n\\t\\t\\t// No need to calculate C(n, k) or update prev_cnk as this is the last iteration.\\n\\t\\t}\\n\\n\\t\\t// Calculate the contribution of the current digit d_k to the total difference sum.\\n\\t\\tterm := (coef_k * digit) % 10\\n\\t\\t// Add this term to the accumulator, keeping the sum modulo 10.\\n\\t\\tsum_diff = (sum_diff + term) % 10\\n\\t}\\n\\n\\t// After iterating through all digits, if sum_diff is 0, it means\\n\\t// final_digit_0 - final_digit_1 = 0 mod 10, so the final digits are the same.\\n\\treturn sum_diff == 0\\n}\"], [36, 1.1628, \"\\nimport (\\n\\t\\\"fmt\\\"\\n\\t\\\"math\\\"\\n)\\n\\n\\nfunc mod10from2and5(m2 int, m5 int) int {\\n return (6 * m5 - 5 * m2) % 10\\n}\\n\\nfunc fillDigits(digits []int, n int, base int) {\\n for k:=0; n > 0; k++ {\\n digits[k] = n % base\\n n = n / base\\n }\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n n := len(s) - 2;\\n\\n n5digits := make([]int, int(math.Log(float64(n)) - math.Log(5.))+2);\\n fillDigits(n5digits, n, 5)\\n\\n pascal5 := [][]int {\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1},\\n }\\n fmt.Println(pascal5);\\n\\n //i5digits := make([]int, int(math.Log(float64(n)) - math.Log(5.))+2);\\n ans := 0;\\n for i:=0; i<=n; i++ {\\n cNiMod2 := 0;\\n if i &^ n == 0 { cNiMod2 = 1; }\\n\\n cNiMod5 := 1;\\n \\n j := i;\\n for k:=0; j > 0; k++ {\\n cNiMod5 *= pascal5[n5digits[k]][j%5];\\n j = j / 5;\\n }\\n \\n cNiMod10 := mod10from2and5(cNiMod2, cNiMod5);\\n ans += cNiMod10 * (int(s[i+1]) - int(s[i]));\\n ans %= 10;\\n }\\n\\n return ans == 0;\\n}\"], [37, 1.1628, \"var (\\n\\tcombTable2 = [][]int{\\n\\t\\t{1},\\n\\t\\t{1, 1},\\n\\t}\\n\\tcombTable5 = [][]int{\\n\\t\\t{1},\\n\\t\\t{1, 1},\\n\\t\\t{1, 2, 1},\\n\\t\\t{1, 3, 3, 1},\\n\\t\\t{1, 4, 1, 4, 1},\\n\\t}\\n\\tmod10Table = [2][5]int{\\n\\t\\t{0, 6, 2, 8, 4},\\n\\t\\t{5, 1, 7, 3, 9},\\n\\t}\\n)\\n\\nfunc hasSameDigits(s string) bool {\\n\\tn := len(s)\\n\\tif n < 3 {\\n\\t\\treturn false\\n\\t}\\n\\tk := n - 2\\n\\n\\tsum := 0\\n\\tvar prevMod2, prevMod5 int\\n\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tcurrentMod2, currentMod5 := 0, 0\\n\\t\\tif i <= k {\\n\\t\\t\\tcurrentMod2 = lucasIterative(k, i, 2, combTable2)\\n\\t\\t\\tcurrentMod5 = lucasIterative(k, i, 5, combTable5)\\n\\t\\t}\\n\\n\\t\\tvar dMod2, dMod5 int\\n\\t\\tif i == 0 {\\n\\t\\t\\tdMod2 = currentMod2 % 2\\n\\t\\t\\tdMod5 = currentMod5 % 5\\n\\t\\t} else {\\n\\t\\t\\tdMod2 = (currentMod2 - prevMod2) % 2\\n\\t\\t\\tdMod5 = (currentMod5 - prevMod5) % 5\\n\\t\\t}\\n\\t\\tif dMod2 < 0 {\\n\\t\\t\\tdMod2 += 2\\n\\t\\t}\\n\\t\\tif dMod5 < 0 {\\n\\t\\t\\tdMod5 += 5\\n\\t\\t}\\n\\n\\t\\td := mod10Table[dMod2][dMod5]\\n\\t\\tdigit := int(s[i] - '0')\\n\\t\\tsum = (sum + d*digit) % 10\\n\\n\\t\\tprevMod2, prevMod5 = currentMod2, currentMod5\\n\\t}\\n\\n\\treturn sum%10 == 0\\n}\\n\\nfunc lucasIterative(n, k, p int, combTable [][]int) int {\\n\\tif k == 0 {\\n\\t\\treturn 1\\n\\t}\\n\\tif n < k {\\n\\t\\treturn 0\\n\\t}\\n\\tres := 1\\n\\tfor n > 0 && k > 0 {\\n\\t\\tni := n % p\\n\\t\\tki := k % p\\n\\t\\tif ki > ni {\\n\\t\\t\\treturn 0\\n\\t\\t}\\n\\t\\tres = (res * combTable[ni][ki]) % p\\n\\t\\tn /= p\\n\\t\\tk /= p\\n\\t}\\n\\tif k > 0 {\\n\\t\\treturn 0\\n\\t}\\n\\treturn res\\n}\"], [40, 1.1628, \"package main\\n\\n// Precomputed table for binom5\\nvar binom5Table = [5][5]int{\\n\\t{1, 0, 0, 0, 0},\\n\\t{1, 1, 0, 0, 0},\\n\\t{1, 2, 1, 0, 0},\\n\\t{1, 3, 3, 1, 0},\\n\\t{1, 4, 1, 4, 1},\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n\\tn := len(s)\\n\\t\\n\\t// Handle the simple case directly\\n\\tif n == 2 {\\n\\t\\treturn s[0] == s[1]\\n\\t}\\n\\t\\n\\tm := n - 2\\n\\t\\n\\t// Convert string to digit array\\n\\ta := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\ta[i] = int(s[i] - '0')\\n\\t}\\n\\t\\n\\tS0, S1 := 0, 0\\n\\tfor j := 0; j <= m; j++ {\\n\\t\\t// Calculate binomial coefficient C(m,j) mod 10\\n\\t\\tb := binomMod10(m, j)\\n\\t\\t\\n\\t\\t// Update sums\\n\\t\\tS0 = (S0 + b*a[j]) % 10\\n\\t\\tS1 = (S1 + b*a[j+1]) % 10\\n\\t}\\n\\t\\n\\treturn S0 == S1\\n}\\n\\n// binomMod10 computes C(n, k) mod 10 using Chinese Remainder Theorem\\nfunc binomMod10(n, k int) int {\\n\\t// Handle edge cases\\n\\tif k < 0 || k > n {\\n\\t\\treturn 0\\n\\t}\\n\\t\\n\\tr2 := binom2(n, k)\\n\\tr5 := binom5(n, k)\\n\\t\\n\\t// Apply Chinese Remainder Theorem\\n\\tcandidate := r5 % 10\\n\\tif candidate%2 == r2 {\\n\\t\\treturn candidate\\n\\t}\\n\\treturn (candidate + 5) % 10\\n}\\n\\n// binom2 computes C(n, k) mod 2\\n// C(n, k) mod 2 = 1 if all bits set in k are also set in n, otherwise 0\\nfunc binom2(n, k int) int {\\n\\tif k < 0 || k > n {\\n\\t\\treturn 0\\n\\t}\\n\\tif (n & k) == k {\\n\\t\\treturn 1\\n\\t}\\n\\treturn 0\\n}\\n\\n// binom5 computes C(n, k) mod 5 using Lucas' Theorem\\nfunc binom5(n, k int) int {\\n\\tif k < 0 || k > n {\\n\\t\\treturn 0\\n\\t}\\n\\t\\n\\tres := 1\\n\\tfor n > 0 || k > 0 {\\n\\t\\tni := n % 5\\n\\t\\tki := k % 5\\n\\t\\tif ki > ni {\\n\\t\\t\\treturn 0\\n\\t\\t}\\n\\t\\tres = (res * binom5Table[ni][ki]) % 5\\n\\t\\tn /= 5\\n\\t\\tk /= 5\\n\\t}\\n\\treturn res\\n} \"], [41, 1.1628, \"package main\\n\\n\\nfunc hasSameDigits(s string) bool {\\n\\tn := len(s)\\n\\tif n == 2 {\\n\\t\\treturn s[0] == s[1]\\n\\t}\\n\\tm := n - 2\\n\\n\\t// \\u041f\\u0440\\u0435\\u043e\\u0431\\u0440\\u0430\\u0437\\u0443\\u0435\\u043c \\u0441\\u0442\\u0440\\u043e\\u043a\\u0443 \\u0432 \\u0441\\u0440\\u0435\\u0437 \\u0446\\u0438\\u0444\\u0440.\\n\\ta := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\ta[i] = int(s[i] - '0')\\n\\t}\\n\\n\\tS0, S1 := 0, 0\\n\\t// \\u0421\\u0443\\u043c\\u043c\\u0438\\u0440\\u0443\\u0435\\u043c \\u043f\\u043e j \\u043e\\u0442 0 \\u0434\\u043e m \\u0432\\u043a\\u043b\\u044e\\u0447\\u0438\\u0442\\u0435\\u043b\\u044c\\u043d\\u043e.\\n\\tfor j := 0; j <= m; j++ {\\n\\t\\tb := binomMod10(m, j) // \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u043c C(m, j) mod 10.\\n\\t\\tS0 = (S0 + b*a[j]) % 10\\n\\t\\tS1 = (S1 + b*a[j+1]) % 10\\n\\t}\\n\\n\\treturn S0 == S1\\n}\\n\\n// binomMod10 \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u0442 C(n, k) mod 10 \\u0447\\u0435\\u0440\\u0435\\u0437 \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u0435 \\u043f\\u043e \\u043c\\u043e\\u0434\\u0443\\u043b\\u044f\\u043c 2 \\u0438 5 \\u0438 CRT.\\nfunc binomMod10(n, k int) int {\\n\\tr2 := binom2(n, k)\\n\\tr5 := binom5(n, k)\\n\\tcandidate := r5 % 10\\n\\tif candidate%2 == r2 {\\n\\t\\treturn candidate\\n\\t}\\n\\treturn (candidate + 5) % 10\\n}\\n\\n// binom2 \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u0442 C(n, k) mod 2.\\n// \\u0418\\u0437\\u0432\\u0435\\u0441\\u0442\\u043d\\u043e, \\u0447\\u0442\\u043e C(n, k) mod 2 = 1, \\u0435\\u0441\\u043b\\u0438 \\u0432\\u0441\\u0435 \\u0435\\u0434\\u0438\\u043d\\u0438\\u0447\\u043d\\u044b\\u0435 \\u0431\\u0438\\u0442\\u044b k \\u0441\\u043e\\u0434\\u0435\\u0440\\u0436\\u0430\\u0442\\u0441\\u044f \\u0432 n, \\u0438\\u043d\\u0430\\u0447\\u0435 0.\\nfunc binom2(n, k int) int {\\n\\tif k < 0 || k > n {\\n\\t\\treturn 0\\n\\t}\\n\\tif (n & k) == k {\\n\\t\\treturn 1\\n\\t}\\n\\treturn 0\\n}\\n\\n// binom5 \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u0442 C(n, k) mod 5 \\u043f\\u043e \\u0442\\u0435\\u043e\\u0440\\u0435\\u043c\\u0435 \\u041b\\u0443\\u043a\\u0430\\u0441\\u0430.\\n// \\u041f\\u0440\\u0435\\u0434\\u0441\\u0442\\u0430\\u0432\\u043b\\u044f\\u0435\\u043c n \\u0438 k \\u0432 \\u0441\\u0438\\u0441\\u0442\\u0435\\u043c\\u0435 \\u0441 \\u043e\\u0441\\u043d\\u043e\\u0432\\u0430\\u043d\\u0438\\u0435\\u043c 5 \\u0438 \\u043f\\u0435\\u0440\\u0435\\u043c\\u043d\\u043e\\u0436\\u0430\\u0435\\u043c \\u043c\\u0430\\u043b\\u0435\\u043d\\u044c\\u043a\\u0438\\u0435 \\u0431\\u0438\\u043d\\u043e\\u043c\\u0438\\u0430\\u043b\\u044c\\u043d\\u044b\\u0435 \\u043a\\u043e\\u044d\\u0444\\u0444\\u0438\\u0446\\u0438\\u0435\\u043d\\u0442\\u044b.\\nfunc binom5(n, k int) int {\\n\\tif k < 0 || k > n {\\n\\t\\treturn 0\\n\\t}\\n\\t// \\u0422\\u0430\\u0431\\u043b\\u0438\\u0446\\u0430 \\u0434\\u043b\\u044f C(n, k) mod 5, \\u0434\\u043b\\u044f n, k \\u043e\\u0442 0 \\u0434\\u043e 4.\\n\\ttable := [5][5]int{\\n\\t\\t{1, 0, 0, 0, 0},\\n\\t\\t{1, 1, 0, 0, 0},\\n\\t\\t{1, 2, 1, 0, 0},\\n\\t\\t{1, 3, 3, 1, 0},\\n\\t\\t{1, 4, 1, 4, 1},\\n\\t}\\n\\n\\tres := 1\\n\\tfor n > 0 || k > 0 {\\n\\t\\tni := n % 5\\n\\t\\tki := k % 5\\n\\t\\tif ki > ni {\\n\\t\\t\\treturn 0\\n\\t\\t}\\n\\t\\tres = (res * table[ni][ki]) % 5\\n\\t\\tn /= 5\\n\\t\\tk /= 5\\n\\t}\\n\\treturn res\\n}\\n\"], [45, 1.1628, \"var (\\n\\tcombTable2 = [][]int{\\n\\t\\t{1},\\n\\t\\t{1, 1},\\n\\t}\\n\\tcombTable5 = [][]int{\\n\\t\\t{1},\\n\\t\\t{1, 1},\\n\\t\\t{1, 2, 1},\\n\\t\\t{1, 3, 3, 1},\\n\\t\\t{1, 4, 1, 4, 1},\\n\\t}\\n\\tmod10Table = [2][5]int{\\n\\t\\t{0, 6, 2, 8, 4},\\n\\t\\t{5, 1, 7, 3, 9},\\n\\t}\\n)\\n\\nfunc hasSameDigits(s string) bool {\\n\\tn := len(s)\\n\\tif n < 3 {\\n\\t\\treturn false\\n\\t}\\n\\tk := n - 2\\n\\n\\tsum := 0\\n\\tvar prevMod2, prevMod5 int\\n\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tcurrentMod2, currentMod5 := 0, 0\\n\\t\\tif i <= k {\\n\\t\\t\\tcurrentMod2 = lucasIterative(k, i, 2, combTable2)\\n\\t\\t\\tcurrentMod5 = lucasIterative(k, i, 5, combTable5)\\n\\t\\t}\\n\\n\\t\\tvar dMod2, dMod5 int\\n\\t\\tif i == 0 {\\n\\t\\t\\tdMod2 = currentMod2 % 2\\n\\t\\t\\tdMod5 = currentMod5 % 5\\n\\t\\t} else {\\n\\t\\t\\tdMod2 = (currentMod2 - prevMod2) % 2\\n\\t\\t\\tdMod5 = (currentMod5 - prevMod5) % 5\\n\\t\\t}\\n\\t\\tif dMod2 < 0 {\\n\\t\\t\\tdMod2 += 2\\n\\t\\t}\\n\\t\\tif dMod5 < 0 {\\n\\t\\t\\tdMod5 += 5\\n\\t\\t}\\n\\n\\t\\td := mod10Table[dMod2][dMod5]\\n\\t\\tdigit := int(s[i] - '0')\\n\\t\\tsum = (sum + d*digit) % 10\\n\\n\\t\\tprevMod2, prevMod5 = currentMod2, currentMod5\\n\\t}\\n\\n\\treturn sum%10 == 0\\n}\\n\\nfunc lucasIterative(n, k, p int, combTable [][]int) int {\\n\\tif k == 0 {\\n\\t\\treturn 1\\n\\t}\\n\\tif n < k {\\n\\t\\treturn 0\\n\\t}\\n\\tres := 1\\n\\tfor n > 0 && k > 0 {\\n\\t\\tni := n % p\\n\\t\\tki := k % p\\n\\t\\tif ki > ni {\\n\\t\\t\\treturn 0\\n\\t\\t}\\n\\t\\tres = (res * combTable[ni][ki]) % p\\n\\t\\tn /= p\\n\\t\\tk /= p\\n\\t}\\n\\tif k > 0 {\\n\\t\\treturn 0\\n\\t}\\n\\treturn res\\n}\"], [46, 1.1628, \"\\nfunc hasSameDigits(s string) bool {\\n\\tn := len(s)\\n\\tx, y := 0, 0\\n\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tcoeff := binomialMod10(n-2, i)\\n\\t\\tx = (x + coeff*(int(s[i])-48)) % 10\\n\\t\\ty = (y + coeff*(int(s[i+1])-48)) % 10\\n\\t}\\n\\n\\treturn x == y\\n}\\n\\n// binomialMod10 calculates binomial coefficient modulo 10\\nfunc binomialMod10(n, k int) int {\\n\\tmod2 := binomialMod2(n, k)\\n\\tmod5 := binomialMod5(n, k)\\n\\n\\tfor x := 0; x < 10; x++ {\\n\\t\\tif x%2 == mod2 && x%5 == mod5 {\\n\\t\\t\\treturn x\\n\\t\\t}\\n\\t}\\n\\treturn 0\\n}\\n\\n// binomialMod2 calculates binomial coefficient modulo 2\\nfunc binomialMod2(n, k int) int {\\n\\tif (n & k) == k {\\n\\t\\treturn 1\\n\\t}\\n\\treturn 0\\n}\\n\\n// binomialMod5 calculates binomial coefficient modulo 5 using a lookup table\\nfunc binomialMod5(n, k int) int {\\n\\ttuples := [][]int{\\n\\t\\t{1},\\n\\t\\t{1, 1},\\n\\t\\t{1, 2, 1},\\n\\t\\t{1, 3, 3, 1},\\n\\t\\t{1, 4, 1, 4, 1},\\n\\t}\\n\\tresult := 1\\n\\n\\tfor n > 0 || k > 0 {\\n\\t\\tnthd := n % 5\\n\\t\\tkthd := k % 5\\n\\n\\t\\tif kthd > nthd {\\n\\t\\t\\treturn 0\\n\\t\\t}\\n\\n\\t\\tresult = (result * tuples[nthd][kthd]) % 5\\n\\t\\tn /= 5\\n\\t\\tk /= 5\\n\\t}\\n\\treturn result\\n}\"], [50, 3.4884, \"package main\\n\\nvar (\\n\\tpascalMod5Global [][]int\\n\\tcrtTableGlobal [2][5]int\\n)\\n\\nfunc init() {\\n\\tpascalMod5Global = make([][]int, 5)\\n\\tfor i := 0; i < 5; i++ {\\n\\t\\tpascalMod5Global[i] = make([]int, i+1)\\n\\t\\tpascalMod5Global[i][0] = 1\\n\\t\\tif i > 0 {\\n\\t\\t\\tpascalMod5Global[i][i] = 1\\n\\t\\t}\\n\\t\\tfor j := 1; j < i; j++ {\\n\\t\\t\\tpascalMod5Global[i][j] = (pascalMod5Global[i-1][j-1] + pascalMod5Global[i-1][j]) % 5\\n\\t\\t}\\n\\t}\\n\\n\\tcrtTableGlobal[0][0] = 0\\n\\tcrtTableGlobal[0][1] = 6\\n\\tcrtTableGlobal[0][2] = 2\\n\\tcrtTableGlobal[0][3] = 8\\n\\tcrtTableGlobal[0][4] = 4\\n\\tcrtTableGlobal[1][0] = 5\\n\\tcrtTableGlobal[1][1] = 1\\n\\tcrtTableGlobal[1][2] = 7\\n\\tcrtTableGlobal[1][3] = 3\\n\\tcrtTableGlobal[1][4] = 9\\n}\\n\\nfunc getCSmallMod5(n, k int) int {\\n\\tif k < 0 || k > n {\\n\\t\\treturn 0\\n\\t}\\n\\treturn pascalMod5Global[n][k]\\n}\\n\\nfunc calculateCMod10(n, k int) int {\\n\\tif k < 0 || k > n {\\n\\t\\treturn 0\\n\\t}\\n\\tif k == 0 || k == n {\\n\\t\\treturn 1\\n\\t}\\n\\tif k > n/2 {\\n\\t\\tk = n - k\\n\\t}\\n\\n\\tcMod2 := 0\\n\\tif (n & k) == k {\\n\\t\\tcMod2 = 1\\n\\t}\\n\\n\\tcMod5 := 1\\n\\ttempN, tempK := n, k\\n\\tfor tempN > 0 || tempK > 0 {\\n\\t\\tni := tempN % 5\\n\\t\\tki := tempK % 5\\n\\n\\t\\tvalCSmall := getCSmallMod5(ni, ki)\\n\\t\\t\\n\\t\\tif valCSmall == 0 {\\n\\t\\t\\tcMod5 = 0\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t\\tcMod5 = (cMod5 * valCSmall) % 5\\n\\t\\t\\n\\t\\ttempN /= 5\\n\\t\\ttempK /= 5\\n\\t}\\n\\t\\n\\treturn crtTableGlobal[cMod2][cMod5]\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n\\tnumDigits := len(s)\\n\\tK_ops := numDigits - 2\\n\\n\\tdigits := make([]int, numDigits)\\n\\tfor i, charRune := range s {\\n\\t\\tdigits[i] = int(charRune - '0')\\n\\t}\\n\\n\\tfinalDigit1 := 0\\n\\tfinalDigit2 := 0\\n\\n\\tfor i := 0; i <= K_ops; i++ {\\n\\t\\tcoeffMod10 := calculateCMod10(K_ops, i)\\n\\t\\t\\n\\t\\tif coeffMod10 == 0 {\\n\\t\\t\\tcontinue\\n\\t\\t}\\n\\n\\t\\tfinalDigit1 = (finalDigit1 + coeffMod10*digits[i]) % 10\\n\\t\\tfinalDigit2 = (finalDigit2 + coeffMod10*digits[i+1]) % 10\\n\\t}\\n\\t\\n\\treturn finalDigit1 == finalDigit2\\n}\"], [74, 1.1628, \"func lucasMod2(n, k int) int {\\n for k > 0 {\\n if n%2 < k%2 {\\n return 0\\n }\\n n /= 2\\n k /= 2\\n }\\n return 1\\n}\\n\\nfunc lucasMod5(n, k int) int {\\n res := 1\\n for n > 0 || k > 0 {\\n nd := n % 5\\n kd := k % 5\\n if kd > nd {\\n return 0\\n }\\n comb := 1\\n for i := 0; i < kd; i++ {\\n comb *= (nd - i)\\n comb /= (i + 1)\\n }\\n res = (res * comb) % 5\\n n /= 5\\n k /= 5\\n }\\n return res\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n m := len(s) - 2\\n if m < 0 {\\n return false\\n }\\n sum1, sum2 := 0, 0\\n for i := 0; i <= m; i++ {\\n a := lucasMod2(m, i)\\n b := lucasMod5(m, i)\\n coeff := (5*a + 6*b) % 10\\n sum1 += coeff * int(s[i]-'0')\\n sum2 += coeff * int(s[i+1]-'0')\\n }\\n sum1 %= 10\\n sum2 %= 10\\n return sum1 == sum2\\n}\"], [76, 1.1628, \"var (\\n\\tcombTable5 = [5][5]int{\\n\\t\\t{1, 0, 0, 0, 0},\\n\\t\\t{1, 1, 0, 0, 0},\\n\\t\\t{1, 2, 1, 0, 0},\\n\\t\\t{1, 3, 3, 1, 0},\\n\\t\\t{1, 4, 1, 4, 1},\\n\\t}\\n\\tmod10Table = [2][5]int{\\n\\t\\t{0, 6, 2, 8, 4},\\n\\t\\t{5, 1, 7, 3, 9},\\n\\t}\\n)\\nfunc hasSameDigits(s string) bool {\\n\\tn := len(s)\\n\\tif n < 3 {\\n\\t\\treturn false\\n\\t}\\n\\tk := n - 2\\n\\n\\tdigitsK := get5DigitsFast(k)\\n\\tsum := 0\\n\\tvar prevMod2, prevMod5 int\\n\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tvar currentMod2, currentMod5 int\\n\\t\\tif i > k {\\n\\t\\t\\tcurrentMod2, currentMod5 = 0, 0\\n\\t\\t} else {\\n\\t\\t\\tcurrentMod2 = 0\\n\\t\\t\\tif (i & k) == i {\\n\\t\\t\\t\\tcurrentMod2 = 1\\n\\t\\t\\t}\\n\\n\\t\\t\\tdigitsI := get5DigitsFast(i)\\n\\t\\t\\tcurrentMod5 = 1\\n\\t\\t\\tfor j := 0; j < len(digitsK); j++ {\\n\\t\\t\\t\\tcurrDigit := 0\\n\\t\\t\\t\\tif j < len(digitsI) {\\n\\t\\t\\t\\t\\tcurrDigit = digitsI[j]\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\tif currDigit > digitsK[j] {\\n\\t\\t\\t\\t\\tcurrentMod5 = 0\\n\\t\\t\\t\\t\\tbreak\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\tcurrentMod5 = (currentMod5 * combTable5[digitsK[j]][currDigit]) % 5\\n\\t\\t\\t}\\n\\t\\t}\\n\\n\\t\\tdMod2 := currentMod2 - prevMod2\\n\\t\\tif i > 0 {\\n\\t\\t\\tdMod2 %= 2\\n\\t\\t\\tif dMod2 < 0 {\\n\\t\\t\\t\\tdMod2 += 2\\n\\t\\t\\t}\\n\\t\\t}\\n\\n\\t\\tdMod5 := currentMod5 - prevMod5\\n\\t\\tif i > 0 {\\n\\t\\t\\tdMod5 %= 5\\n\\t\\t\\tif dMod5 < 0 {\\n\\t\\t\\t\\tdMod5 += 5\\n\\t\\t\\t}\\n\\t\\t}\\n\\n\\t\\td := mod10Table[dMod2][dMod5]\\n\\t\\tsum = (sum + d*int(s[i]-'0')) % 10\\n\\n\\t\\tprevMod2, prevMod5 = currentMod2, currentMod5\\n\\t}\\n\\n\\treturn sum%10 == 0\\n}\\n\\nfunc get5DigitsFast(x int) (digits [20]int) { // \\u0424\\u0438\\u043a\\u0441\\u0438\\u0440\\u043e\\u0432\\u0430\\u043d\\u043d\\u044b\\u0439 \\u0440\\u0430\\u0437\\u043c\\u0435\\u0440 20\\n\\tpos := 0\\n\\tfor x > 0 {\\n\\t\\tdigits[pos] = x % 5\\n\\t\\tx /= 5\\n\\t\\tpos++\\n\\t}\\n\\treturn\\n}\"], [95, 1.1628, \"var combMod5Table = [5][5]int{\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1},\\n}\\n\\nvar crtLookup = [2][5]int{\\n {0, 6, 2, 8, 4}, // mod2=0\\n {5, 1, 7, 3, 9}, // mod2=1\\n}\\n\\nfunc combMod5(a, b int) int {\\n if a < b {\\n return 0\\n }\\n return combMod5Table[a][b]\\n}\\n\\nfunc lucas(n, k int, p int) int {\\n res := 1\\n for k > 0 {\\n ni := n % p\\n ki := k % p\\n if ni < ki {\\n return 0\\n }\\n var comb int\\n if p == 2 {\\n if ni >= ki {\\n comb = 1\\n } else {\\n comb = 0\\n }\\n } else if p == 5 {\\n comb = combMod5(ni, ki)\\n } else {\\n comb = 0 // Not needed for this problem\\n }\\n res = (res * comb) % p\\n n /= p\\n k /= p\\n }\\n return res\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n n := len(s)\\n if n < 2 {\\n return false\\n }\\n if n == 2 {\\n return s[0] == s[1]\\n }\\n m := n - 2\\n\\n coefficients := make([]int, m+1)\\n for k := 0; k <= m; k++ {\\n mod2 := lucas(m, k, 2)\\n mod5 := lucas(m, k, 5)\\n coefficients[k] = crtLookup[mod2][mod5%5]\\n }\\n\\n sum1 := 0\\n for i := 0; i <= m; i++ {\\n digit := int(s[i] - '0')\\n sum1 = (sum1 + coefficients[i]*digit) % 10\\n }\\n\\n sum2 := 0\\n for i := 0; i <= m; i++ {\\n digit := int(s[i+1] - '0')\\n sum2 = (sum2 + coefficients[i]*digit) % 10\\n }\\n\\n return sum1 == sum2\\n}\"], [122, 1.1628, \"func hasSameDigits(s string) bool {\\n\\tC := [][]int{\\n\\t\\t{1, 0, 0, 0, 0},\\n\\t\\t{1, 1, 0, 0, 0},\\n\\t\\t{1, 2, 1, 0, 0},\\n\\t\\t{1, 3, 3, 1, 0},\\n\\t\\t{1, 4, 6, 4, 1},\\n\\t} // C(n,k)\\n\\tinv := [][]int{\\n\\t\\t{0, 5},\\n\\t\\t{6, 1},\\n\\t\\t{2, 7},\\n\\t\\t{8, 3},\\n\\t\\t{4, 9},\\n\\t} // r5,r2\\n\\tn := len(s) - 2\\n\\tcList := make([]int, n+1)\\n\\tfor i := range cList {\\n\\t\\ta, b := i, n\\n\\t\\tmul := 1\\n\\t\\tfor a > 0 || b > 0 {\\n\\t\\t\\tmul *= C[b%5][a%5]\\n\\t\\t\\ta /= 5\\n\\t\\t\\tb /= 5\\n\\t\\t\\tmul %= 5\\n\\t\\t}\\n\\t\\tr5 := mul\\n\\t\\ta, b = i, n\\n\\t\\tmul = 1\\n\\t\\tfor a > 0 || b > 0 {\\n\\t\\t\\tmul *= C[b%2][a%2]\\n\\t\\t\\ta /= 2\\n\\t\\t\\tb /= 2\\n\\t\\t\\tmul %= 2\\n\\t\\t}\\n\\t\\tr2 := mul\\n\\t\\tcList[i] = inv[r5][r2]\\n\\t}\\n\\n\\td1, d2 := 0, 0\\n\\tfor i := 0; i <= n; i++ {\\n\\t\\td1 += int(s[i]-'0') * cList[i]\\n\\t\\td1 %= 10\\n\\t\\td2 += int(s[i+1]-'0') * cList[i]\\n\\t\\td2 %= 10\\n\\t}\\n\\n\\treturn d1 == d2\\n}\"], [148, 1.1628, \"var (\\n\\tcombTable5 = [][]int{\\n\\t\\t{1},\\n\\t\\t{1, 1},\\n\\t\\t{1, 2, 1},\\n\\t\\t{1, 3, 3, 1},\\n\\t\\t{1, 4, 1, 4, 1},\\n\\t}\\n\\tmod10Table = [2][5]int{\\n\\t\\t{0, 6, 2, 8, 4},\\n\\t\\t{5, 1, 7, 3, 9},\\n\\t}\\n)\\nfunc hasSameDigits(s string) bool {\\n\\tn := len(s)\\n\\tif n < 3 {\\n\\t\\treturn false\\n\\t}\\n\\tkParam := n - 2\\n\\n\\tnDigits := get5Digits(kParam)\\n\\tprecompute5Digits := make([][]int, kParam+1)\\n\\tfor i := 0; i <= kParam; i++ {\\n\\t\\tprecompute5Digits[i] = get5Digits(i)\\n\\t}\\n\\n\\tsum := 0\\n\\tvar prevMod2, prevMod5 int\\n\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tvar currentMod2, currentMod5 int\\n\\t\\tif i > kParam {\\n\\t\\t\\tcurrentMod2, currentMod5 = 0, 0\\n\\t\\t} else {\\n\\t\\t\\tcurrentMod2 = 0\\n\\t\\t\\tif (i & kParam) == i {\\n\\t\\t\\t\\tcurrentMod2 = 1\\n\\t\\t\\t}\\n\\n\\t\\t\\tcurrentDigits := precompute5Digits[i]\\n\\t\\t\\tcurrentMod5 = 1\\n\\t\\t\\tfor j := 0; j < len(nDigits); j++ {\\n\\t\\t\\t\\tcurrDigit := 0\\n\\t\\t\\t\\tif j < len(currentDigits) {\\n\\t\\t\\t\\t\\tcurrDigit = currentDigits[j]\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\tif currDigit > nDigits[j] {\\n\\t\\t\\t\\t\\tcurrentMod5 = 0\\n\\t\\t\\t\\t\\tbreak\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\tcurrentMod5 = (currentMod5 * combTable5[nDigits[j]][currDigit]) % 5\\n\\t\\t\\t}\\n\\t\\t}\\n\\n\\t\\tvar dMod2, dMod5 int\\n\\t\\tif i == 0 {\\n\\t\\t\\tdMod2, dMod5 = currentMod2%2, currentMod5%5\\n\\t\\t} else {\\n\\t\\t\\tdMod2 = (currentMod2 - prevMod2) % 2\\n\\t\\t\\tif dMod2 < 0 {\\n\\t\\t\\t\\tdMod2 += 2\\n\\t\\t\\t}\\n\\t\\t\\tdMod5 = (currentMod5 - prevMod5) % 5\\n\\t\\t\\tif dMod5 < 0 {\\n\\t\\t\\t\\tdMod5 += 5\\n\\t\\t\\t}\\n\\t\\t}\\n\\n\\t\\td := mod10Table[dMod2][dMod5]\\n\\t\\tsum = (sum + d*int(s[i]-'0')) % 10\\n\\n\\t\\tprevMod2, prevMod5 = currentMod2, currentMod5\\n\\t}\\n\\n\\treturn sum%10 == 0\\n}\\n\\nfunc get5Digits(x int) []int {\\n\\tif x == 0 {\\n\\t\\treturn []int{0}\\n\\t}\\n\\tdigits := make([]int, 0, 7)\\n\\tfor x > 0 {\\n\\t\\tdigits = append(digits, x%5)\\n\\t\\tx /= 5\\n\\t}\\n\\treturn digits\\n}\"], [157, 1.1628, \"// comb computes n choose k for small n and k\\nfunc comb(n, k int) int {\\n\\tif k < 0 || k > n {\\n\\t\\treturn 0\\n\\t}\\n\\tif k == 0 || k == n {\\n\\t\\treturn 1\\n\\t}\\n\\tif k == 1 || k == n-1 {\\n\\t\\treturn n\\n\\t}\\n\\t// n is small enough (at most 5), brute force\\n\\treturn comb(n-1, k-1) + comb(n-1, k)\\n}\\n\\nfunc lucasTheorem(n, k, p int) int {\\n\\tproduct := 1\\n\\tfor n != 0 || k != 0 {\\n\\t\\tnDig := n % p\\n\\t\\tkDig := k % p\\n\\t\\tif kDig > nDig {\\n\\t\\t\\treturn 0\\n\\t\\t}\\n\\t\\tproduct *= comb(nDig, kDig)\\n\\t\\tproduct %= p\\n\\t\\tn /= p\\n\\t\\tk /= p\\n\\t}\\n\\treturn product\\n}\\n\\nfunc binom(n, k int) int {\\n\\tm2 := lucasTheorem(n, k, 2)\\n\\tm5 := lucasTheorem(n, k, 5)\\n\\n\\tif m2 == 0 {\\n\\t\\tswitch m5 {\\n\\t\\tcase 0:\\n\\t\\t\\treturn 0\\n\\t\\tcase 1:\\n\\t\\t\\treturn 6\\n\\t\\tcase 2:\\n\\t\\t\\treturn 2\\n\\t\\tcase 3:\\n\\t\\t\\treturn 8\\n\\t\\tcase 4:\\n\\t\\t\\treturn 4\\n\\t\\t}\\n\\t} else { // m2 == 1\\n\\t\\tswitch m5 {\\n\\t\\tcase 0:\\n\\t\\t\\treturn 5\\n\\t\\tcase 1:\\n\\t\\t\\treturn 1\\n\\t\\tcase 2:\\n\\t\\t\\treturn 7\\n\\t\\tcase 3:\\n\\t\\t\\treturn 3\\n\\t\\tcase 4:\\n\\t\\t\\treturn 9\\n\\t\\t}\\n\\t}\\n\\tpanic(\\\"How??\\\")\\n}\\n\\nfunc hasSameDigits(str string) bool {\\n\\tn1, n2 := 0, 0\\n\\tn := len(str)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tmultiple := binom(n-2, i)\\n\\t\\tdigit1 := int(str[i] - '0')\\n\\t\\tdigit2 := int(str[i+1] - '0')\\n\\t\\tn1 += multiple * digit1 % 10\\n\\t\\tn1 %= 10\\n\\t\\tn2 += multiple * digit2 % 10\\n\\t\\tn2 %= 10\\n\\t}\\n\\treturn n1 == n2\\n}\"], [161, 2.3256, \"var (\\n\\tcombTable5 = [][]int{\\n\\t\\t{1},\\n\\t\\t{1, 1},\\n\\t\\t{1, 2, 1},\\n\\t\\t{1, 3, 3, 1},\\n\\t\\t{1, 4, 1, 4, 1},\\n\\t}\\n\\tmod10Table = [2][5]int{\\n\\t\\t{0, 6, 2, 8, 4},\\n\\t\\t{5, 1, 7, 3, 9},\\n\\t}\\n)\\nfunc hasSameDigits(s string) bool {\\n\\tn := len(s)\\n\\tif n < 3 {\\n\\t\\treturn false\\n\\t}\\n\\tkParam := n - 2\\n\\n\\tnDigits := get5Digits(kParam)\\n\\tprecompute5Digits := make([][]int, kParam+1)\\n\\tfor i := 0; i <= kParam; i++ {\\n\\t\\tprecompute5Digits[i] = get5Digits(i)\\n\\t}\\n\\n\\tsum := 0\\n\\tvar prevMod2, prevMod5 int\\n\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tvar currentMod2, currentMod5 int\\n\\t\\tif i > kParam {\\n\\t\\t\\tcurrentMod2, currentMod5 = 0, 0\\n\\t\\t} else {\\n\\t\\t\\tcurrentMod2 = 0\\n\\t\\t\\tif (i & kParam) == i {\\n\\t\\t\\t\\tcurrentMod2 = 1\\n\\t\\t\\t}\\n\\n\\t\\t\\tcurrentDigits := precompute5Digits[i]\\n\\t\\t\\tcurrentMod5 = 1\\n\\t\\t\\tfor j := 0; j < len(nDigits); j++ {\\n\\t\\t\\t\\tcurrDigit := 0\\n\\t\\t\\t\\tif j < len(currentDigits) {\\n\\t\\t\\t\\t\\tcurrDigit = currentDigits[j]\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\tif currDigit > nDigits[j] {\\n\\t\\t\\t\\t\\tcurrentMod5 = 0\\n\\t\\t\\t\\t\\tbreak\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\tcurrentMod5 = (currentMod5 * combTable5[nDigits[j]][currDigit]) % 5\\n\\t\\t\\t}\\n\\t\\t}\\n\\n\\t\\tvar dMod2, dMod5 int\\n\\t\\tif i == 0 {\\n\\t\\t\\tdMod2, dMod5 = currentMod2%2, currentMod5%5\\n\\t\\t} else {\\n\\t\\t\\tdMod2 = (currentMod2 - prevMod2) % 2\\n\\t\\t\\tif dMod2 < 0 {\\n\\t\\t\\t\\tdMod2 += 2\\n\\t\\t\\t}\\n\\t\\t\\tdMod5 = (currentMod5 - prevMod5) % 5\\n\\t\\t\\tif dMod5 < 0 {\\n\\t\\t\\t\\tdMod5 += 5\\n\\t\\t\\t}\\n\\t\\t}\\n\\n\\t\\td := mod10Table[dMod2][dMod5]\\n\\t\\tsum = (sum + d*int(s[i]-'0')) % 10\\n\\n\\t\\tprevMod2, prevMod5 = currentMod2, currentMod5\\n\\t}\\n\\n\\treturn sum%10 == 0\\n}\\n\\nfunc get5Digits(x int) []int {\\n\\tif x == 0 {\\n\\t\\treturn []int{0}\\n\\t}\\n\\tdigits := make([]int, 0, 7)\\n\\tfor x > 0 {\\n\\t\\tdigits = append(digits, x%5)\\n\\t\\tx /= 5\\n\\t}\\n\\treturn digits\\n}\"], [163, 1.1628, \"\\n// Compute modular inverse using extended euclid's algorithm\\nfunc modularInverse(x, m int) (int, bool) {\\n t, newt := 0, 1\\n r, newr := m, x\\n for newr != 0 {\\n q := r / newr\\n t, newt = newt, t-q*newt\\n r, newr = newr, r-q*newr\\n }\\n\\n if r > 1 {\\n return 0, false\\n }\\n if t < 0 {\\n t += m\\n }\\n return t, true\\n}\\n\\n// Decompose n into a * m^b\\nfunc decomp(n, m int) (int, int) {\\n r := 0\\n if n == 0 || m == 0 {\\n return 0, 0\\n }\\n for n%m == 0 {\\n n /= m\\n r++\\n }\\n return n, r\\n}\\n\\n// Get the nth row of pascal's triangle mod m (Optimized)\\nfunc pascalRow(n, m int) []int {\\n row := make([]int, n+1)\\n multiples, rem := 0, 1\\n row[0] = 1 // Initialize the first element\\n\\n for i := 1; i <= n; i++ {\\n num, numP := decomp(n+1-i, m)\\n denom, denomP := decomp(i, m)\\n multiples += numP - denomP\\n bottom, ok := modularInverse(denom%m, m)\\n if !ok {\\n panic(\\\"Modular inverse failed\\\")\\n }\\n rem = (rem * (num % m) * bottom) % m\\n if multiples > 0 {\\n row[i] = 0\\n } else {\\n row[i] = rem\\n }\\n }\\n return row\\n}\\n\\nfunc atoiByte(c byte) int {\\n return int(c - '0')\\n}\\n\\n// Return the digit that we'd get from the string s after applying the whole process, mod m (where m is prime)\\nfunc getFinalDigit(s string, m int) int {\\n row := pascalRow(len(s)-1, m)\\n result := 0\\n for i, digit := range s {\\n result = (result + atoiByte(byte(digit))*row[i]) % m\\n }\\n return result\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n mod2 := getFinalDigit(s[:len(s)-1], 2) == getFinalDigit(s[1:], 2)\\n mod5 := getFinalDigit(s[:len(s)-1], 5) == getFinalDigit(s[1:], 5)\\n return mod2 && mod5\\n}\"], [164, 1.1628, \"func hasSameDigits(s string) bool {\\n n := len(s)\\n \\n // Define C slice to store combinations\\n C := make([][3]int, 100000)\\n \\n // Helper functions\\n factor := func(x int) [3]int {\\n a := 0\\n for x%2 == 0 {\\n x >>= 1\\n a++\\n }\\n \\n b := 0\\n for x%5 == 0 {\\n x /= 5\\n b++\\n }\\n \\n return [3]int{x % 10, a, b} // Only keep mod 10 for y\\n }\\n \\n inverse := func(x [3]int) [3]int {\\n x0, a, b := x[0], x[1], x[2]\\n // Modular inverse under mod 10 using Euler's theorem (Euler-phi(10)=4)\\n x0_inv := (x0*x0*x0) % 10 // x0^3 is inverse mod 10\\n return [3]int{x0_inv, -a, -b}\\n }\\n \\n mult := func(x, y [3]int) [3]int {\\n return [3]int{x[0]*y[0]%10, x[1]+y[1], x[2]+y[2]}\\n }\\n \\n toInt := func(x [3]int) int { // mod 10\\n if x[1] >= 1 && x[2] >= 1 {\\n return 0\\n }\\n if x[2] >= 1 {\\n return 5\\n }\\n B := [4]int{6, 2, 4, 8} // 2^x(mod 10) cycle\\n if x[1] == 0 {\\n return x[0]\\n }\\n B2 := B[x[1]%4]\\n return x[0] * B2 % 10\\n }\\n \\n compute_comb := func(N int) {\\n C[0] = [3]int{1, 0, 0}\\n if N == 0 {\\n return // Prevent C[N] access if N=0\\n }\\n C[N] = [3]int{1, 0, 0}\\n \\n for k := 1; k <= N/2; k++ {\\n P := factor(N-k+1)\\n Q := inverse(factor(k))\\n C[k] = mult(mult(C[k-1], P), Q)\\n C[N-k] = C[k]\\n }\\n }\\n \\n // Clear C slice\\n for i := 0; i < n-2; i++ {\\n C[i] = [3]int{0, 0, 0}\\n }\\n \\n compute_comb(n - 2)\\n \\n sum := 0\\n for i := 0; i <= n-2; i++ {\\n C_val := (toInt(C[i]) * (int(s[i]) - int(s[i+1]))) % 10\\n sum = (sum + C_val + 10) % 10 // Ensure non-negative\\n }\\n \\n return sum == 0\\n}\"], [167, 1.1628, \"var (\\n\\tcombTable5 = [][]int{\\n\\t\\t{1},\\n\\t\\t{1, 1},\\n\\t\\t{1, 2, 1},\\n\\t\\t{1, 3, 3, 1},\\n\\t\\t{1, 4, 1, 4, 1},\\n\\t}\\n\\tmod10Table = [2][5]int{\\n\\t\\t{0, 6, 2, 8, 4},\\n\\t\\t{5, 1, 7, 3, 9},\\n\\t}\\n)\\nfunc hasSameDigits(s string) bool {\\n\\tn := len(s)\\n\\tif n < 3 {\\n\\t\\treturn false\\n\\t}\\n\\tkParam := n - 2\\n\\n\\tnDigits := get5Digits(kParam)\\n\\tprecompute5Digits := make([][]int, kParam+1)\\n\\tfor i := 0; i <= kParam; i++ {\\n\\t\\tprecompute5Digits[i] = get5Digits(i)\\n\\t}\\n\\n\\tsum := 0\\n\\tvar prevMod2, prevMod5 int\\n\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tvar currentMod2, currentMod5 int\\n\\t\\tif i > kParam {\\n\\t\\t\\tcurrentMod2, currentMod5 = 0, 0\\n\\t\\t} else {\\n\\t\\t\\tcurrentMod2 = 0\\n\\t\\t\\tif (i & kParam) == i {\\n\\t\\t\\t\\tcurrentMod2 = 1\\n\\t\\t\\t}\\n\\n\\t\\t\\tcurrentDigits := precompute5Digits[i]\\n\\t\\t\\tcurrentMod5 = 1\\n\\t\\t\\tfor j := 0; j < len(nDigits); j++ {\\n\\t\\t\\t\\tcurrDigit := 0\\n\\t\\t\\t\\tif j < len(currentDigits) {\\n\\t\\t\\t\\t\\tcurrDigit = currentDigits[j]\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\tif currDigit > nDigits[j] {\\n\\t\\t\\t\\t\\tcurrentMod5 = 0\\n\\t\\t\\t\\t\\tbreak\\n\\t\\t\\t\\t}\\n\\t\\t\\t\\tcurrentMod5 = (currentMod5 * combTable5[nDigits[j]][currDigit]) % 5\\n\\t\\t\\t}\\n\\t\\t}\\n\\n\\t\\tvar dMod2, dMod5 int\\n\\t\\tif i == 0 {\\n\\t\\t\\tdMod2, dMod5 = currentMod2%2, currentMod5%5\\n\\t\\t} else {\\n\\t\\t\\tdMod2 = (currentMod2 - prevMod2) % 2\\n\\t\\t\\tif dMod2 < 0 {\\n\\t\\t\\t\\tdMod2 += 2\\n\\t\\t\\t}\\n\\t\\t\\tdMod5 = (currentMod5 - prevMod5) % 5\\n\\t\\t\\tif dMod5 < 0 {\\n\\t\\t\\t\\tdMod5 += 5\\n\\t\\t\\t}\\n\\t\\t}\\n\\n\\t\\td := mod10Table[dMod2][dMod5]\\n\\t\\tsum = (sum + d*int(s[i]-'0')) % 10\\n\\n\\t\\tprevMod2, prevMod5 = currentMod2, currentMod5\\n\\t}\\n\\n\\treturn sum%10 == 0\\n}\\n\\nfunc get5Digits(x int) []int {\\n\\tif x == 0 {\\n\\t\\treturn []int{0}\\n\\t}\\n\\tdigits := make([]int, 0, 7)\\n\\tfor x > 0 {\\n\\t\\tdigits = append(digits, x%5)\\n\\t\\tx /= 5\\n\\t}\\n\\treturn digits\\n}\"], [189, 1.1628, \"func hasSameDigits(s string) bool {\\n\\tn := len(s)\\n\\tif n < 3 {\\n\\t\\treturn false\\n\\t}\\n\\tk := n - 2\\n\\n\\tcombTable2 := [][]int{\\n\\t\\t{1},\\n\\t\\t{1, 1},\\n\\t}\\n\\n\\tcombTable5 := [][]int{\\n\\t\\t{1},\\n\\t\\t{1, 1},\\n\\t\\t{1, 2, 1},\\n\\t\\t{1, 3, 3, 1},\\n\\t\\t{1, 4, 1, 4, 1},\\n\\t}\\n\\n\\tmod10Table := [2][5]int{\\n\\t\\t{0, 6, 2, 8, 4},\\n\\t\\t{5, 1, 7, 3, 9},\\n\\t}\\n\\n\\tsum := 0\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tvar currentMod2, currentMod5 int\\n\\t\\tif i > k {\\n\\t\\t\\tcurrentMod2 = 0\\n\\t\\t\\tcurrentMod5 = 0\\n\\t\\t} else {\\n\\t\\t\\tcurrentMod2 = lucas(k, i, 2, combTable2)\\n\\t\\t\\tcurrentMod5 = lucas(k, i, 5, combTable5)\\n\\t\\t}\\n\\n\\t\\tvar prevMod2, prevMod5 int\\n\\t\\tif i == 0 {\\n\\t\\t\\tprevMod2, prevMod5 = 0, 0\\n\\t\\t} else {\\n\\t\\t\\tif i-1 > k {\\n\\t\\t\\t\\tprevMod2, prevMod5 = 0, 0\\n\\t\\t\\t} else {\\n\\t\\t\\t\\tprevMod2 = lucas(k, i-1, 2, combTable2)\\n\\t\\t\\t\\tprevMod5 = lucas(k, i-1, 5, combTable5)\\n\\t\\t\\t}\\n\\t\\t}\\n\\n\\t\\tdMod2 := (currentMod2 - prevMod2) % 2\\n\\t\\tif dMod2 < 0 {\\n\\t\\t\\tdMod2 += 2\\n\\t\\t}\\n\\t\\tdMod5 := (currentMod5 - prevMod5) % 5\\n\\t\\tif dMod5 < 0 {\\n\\t\\t\\tdMod5 += 5\\n\\t\\t}\\n\\n\\t\\td := mod10Table[dMod2][dMod5]\\n\\n\\t\\tdigit := int(s[i] - '0')\\n\\t\\tsum = (sum + d*digit) % 10\\n\\t}\\n\\n\\treturn sum%10 == 0\\n}\\n\\nfunc lucas(n, k, p int, combTable [][]int) int {\\n\\tif k == 0 {\\n\\t\\treturn 1\\n\\t}\\n\\tif n < k {\\n\\t\\treturn 0\\n\\t}\\n\\tni := n % p\\n\\tki := k % p\\n\\tif ki > ni {\\n\\t\\treturn 0\\n\\t}\\n\\treturn (lucas(n/p, k/p, p, combTable) * combTable[ni][ki]) % p\\n}\"], [192, 1.1628, \"\\nfunc remainder(a1, a2, n1, n2 int) int {\\n\\tN := n1 * n2\\n\\tfor x := 0; x < N; x++ {\\n\\t\\tif x%n1 == a1 && x%n2 == a2 {\\n\\t\\t\\treturn x\\n\\t\\t}\\n\\t}\\n\\treturn 0\\n}\\n\\nfunc b10(n, k int) int {\\n\\tres2 := lucas(n, k, 2)\\n\\tres5 := lucas(n, k, 5)\\n\\treturn remainder(res2, res5, 2, 5)\\n}\\n\\nfunc lucas(n, k, p int) int {\\n\\tres := 1\\n\\tfor n > 0 || k > 0 {\\n\\t\\tni := n % p\\n\\t\\tki := k % p\\n\\t\\tif ki > ni {\\n\\t\\t\\treturn 0\\n\\t\\t}\\n\\t\\tb := binom(ni, ki)\\n\\t\\tres = (res * b) % p\\n\\n\\t\\tn /= p\\n\\t\\tk /= p\\n\\t}\\n\\treturn res\\n}\\n\\nfunc binom(n, k int) int {\\n\\tret := factorial(n) / (factorial(k) * factorial(n-k))\\n\\treturn ret\\n}\\n\\nfunc factorial(n int) int {\\n\\tret := 1\\n\\tfor i := n; i > 0; i-- {\\n\\t\\tret *= i\\n\\t}\\n\\treturn ret\\n}\\n\\nfunc hasSameDigits(s string) bool {\\n\\trunes := []rune(s)\\n\\tn := len(runes)\\n\\tl := n - 2\\n\\ta := 0\\n\\tb := 0\\n\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tw := b10(l, i)\\n\\t\\tch1 := int(runes[i] - '0')\\n\\t\\tch2 := int(runes[i+1] - '0')\\n\\n\\t\\ta = (a + w*ch1) % 10\\n\\t\\tb = (b + w*ch2) % 10\\n\\t}\\n\\n\\treturn a == b\\n}\"], [194, 1.1628, \"func hasSameDigits(s string) bool {\\n // Global arrays to match the C++ implementation\\n C := make([][3]int, 100000)\\n \\n // Helper function to count trailing zeros (equivalent to countr_zero in C++)\\n countr_zero := func(x int) int {\\n if x == 0 {\\n return 0\\n }\\n count := 0\\n for x&1 == 0 {\\n x >>= 1\\n count++\\n }\\n return count\\n }\\n \\n // Direct port of factor function\\n factor := func(x int) [3]int {\\n a := countr_zero(x)\\n x >>= a\\n b := 0\\n for x%5 == 0 {\\n x /= 5\\n b++\\n }\\n return [3]int{x % 10, a, b} // Only keep mod 10 for y\\n }\\n \\n // Direct port of inverse function\\n inverse := func(x [3]int) [3]int {\\n x0, a, b := x[0], x[1], x[2]\\n // Modular inverse under mod 10 using Euler's theorem (Euler-phi(10)=4)\\n x0_inv := (x0*x0*x0) % 10 // x0^3 is inverse mod 10\\n return [3]int{x0_inv, -a, -b}\\n }\\n \\n // Direct port of mult function\\n mult := func(x, y [3]int) [3]int {\\n return [3]int{x[0]*y[0]%10, x[1]+y[1], x[2]+y[2]}\\n }\\n \\n // Direct port of toInt function\\n toInt := func(x [3]int) int { // mod 10\\n if x[1] >= 1 && x[2] >= 1 {\\n return 0\\n }\\n if x[2] >= 1 {\\n return 5\\n }\\n B := [4]int{6, 2, 4, 8} // 2^x(mod 10) cycle\\n if x[1] == 0 {\\n return x[0]\\n }\\n B2 := B[x[1]%4]\\n return x[0] * B2 % 10\\n }\\n \\n // Direct port of compute_comb function\\n compute_comb := func(N int) {\\n C[0] = [3]int{1, 0, 0}\\n if N == 0 {\\n return // Prevent C[N] access if N=0\\n }\\n C[N] = [3]int{1, 0, 0}\\n \\n for k := 1; k <= N/2; k++ {\\n P := factor(N-k+1)\\n Q := inverse(factor(k))\\n C[k] = mult(mult(C[k-1], P), Q)\\n C[N-k] = C[k]\\n }\\n }\\n \\n // Main function logic\\n n := len(s)\\n \\n // Clear C array (equivalent to fill in C++)\\n for i := 0; i < n-2; i++ {\\n C[i] = [3]int{0, 0, 0}\\n }\\n \\n compute_comb(n-2)\\n \\n sum := 0\\n for i := 0; i <= n-2; i++ {\\n C_val := (toInt(C[i]) * (int(s[i]) - int(s[i+1]))) % 10\\n sum = (sum + C_val + 10) % 10 // Ensure non-negative\\n }\\n \\n return sum == 0\\n}\"], [251, 1.1628, \"func hasSameDigits(s string) bool {\\n\\tn := len(s) - 2\\n\\n\\tvar a, b int\\n\\n\\tfor i := 0; i <= n; i++ {\\n\\t\\tco := nCkMod10(n, i)\\n\\t\\ta += (co * int(s[i] - '0')) % 10\\n\\t\\ta %= 10\\n\\t\\tb += (co * int(s[i+1] - '0')) % 10\\n\\t\\tb %= 10\\n\\t}\\n\\n\\treturn a == b\\n\\n}\\n\\nfunc nCkMod10(n, k int) int {\\n\\tlookup := [2][5]int{\\n\\t\\t{0, 6, 2, 8, 4},\\n\\t\\t{5, 1, 7, 3, 9},\\n\\t}\\n\\treturn lookup[lucasTheorem(n, k, 2)][lucasTheorem(n, k, 5)]\\n}\\n\\nfunc lucasTheorem(n, k, prime int) int {\\n\\tres := 1\\n\\tvar nMod, kMod int\\n\\tfor n > 0 || k > 0 {\\n\\t\\tnMod = n % prime\\n\\t\\tkMod = k % prime\\n\\t\\tres *= nCk(nMod, kMod)\\n\\t\\tres %= prime\\n\\t\\tn /= prime\\n\\t\\tk /= prime\\n\\t}\\n\\treturn res\\n}\\n\\nfunc nCk(n, k int) int {\\n\\tres := 1\\n\\tfor i := 0; i < k; i++ {\\n\\t\\tres *= (n - i)\\n\\t\\tres /= (i + 1)\\n\\t}\\n\\treturn res\\n}\"], [254, 1.1628, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits = operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nfunc operationPentiple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-5; i++ {\\n\\t\\tdigits[i] = (digits[i] + 5*digits[i+1] + 5*digits[i+4] + digits[i+5]) % 10\\n\\t}\\n\\tdigits = digits[:n-5]\\n\\treturn digits\\n}\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] += digits[i+1280] + (digits[i+5] + digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) *2+ (digits[i+630] + digits[i+650]) *2\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [256, 1.1628, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits = operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nfunc operationPentiple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-5; i++ {\\n\\t\\tdigits[i] = (digits[i] + 5*digits[i+1] + 5*digits[i+4] + digits[i+5]) % 10\\n\\t}\\n\\tdigits = digits[:n-5]\\n\\treturn digits\\n}\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5] + digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) + (digits[i+625] + digits[i+655]) + (digits[i+630] + digits[i+650]) + (digits[i+630] + digits[i+650])\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [260, 1.1628, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits = operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nfunc operationPentiple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-5; i++ {\\n\\t\\tdigits[i] = (digits[i] + 5*digits[i+1] + 5*digits[i+4] + digits[i+5]) % 10\\n\\t}\\n\\tdigits = digits[:n-5]\\n\\treturn digits\\n}\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5] + digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) + (digits[i+625] + digits[i+655]) + (digits[i+630] + digits[i+650]) + (digits[i+630] + digits[i+650])\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [263, 1.1628, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits=operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5]+digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) + (digits[i+625] + digits[i+655]) + (digits[i+630] + digits[i+650]) + (digits[i+630] + digits[i+650])\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [265, 2.3256, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits=operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5]+digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) + (digits[i+625] + digits[i+655]) + (digits[i+630] + digits[i+650]) + (digits[i+630] + digits[i+650])\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [266, 1.1628, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits = operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nfunc operationPentiple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-5; i++ {\\n\\t\\tdigits[i] = (digits[i] + 5*digits[i+1] + 5*digits[i+4] + digits[i+5]) % 10\\n\\t}\\n\\tdigits = digits[:n-5]\\n\\treturn digits\\n}\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5] + digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) *2+ (digits[i+630] + digits[i+650]) *2\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [268, 1.1628, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits=operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5]+digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) + (digits[i+625] + digits[i+655]) + (digits[i+630] + digits[i+650]) + (digits[i+630] + digits[i+650])\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [269, 1.1628, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n }else if len(digits) >=7{\\n digits= operationPentiple(digits)\\n } else if len(digits) >= 6 {\\n\\t\\t\\tdigits=operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nfunc operationPentiple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-5; i++ {\\n\\t\\tdigits[i] = (digits[i] + 5*digits[i+1] + 5*digits[i+4]+digits[i+5]) % 10\\n\\t}\\n\\tdigits = digits[:n-5]\\n\\treturn digits\\n}\\n\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5]+digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) + (digits[i+625] + digits[i+655]) + (digits[i+630] + digits[i+650]) + (digits[i+630] + digits[i+650])\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [271, 2.3256, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n } else if len(digits) >= 6 {\\n\\t\\t\\tdigits=operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nfunc operationPentiple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-5; i++ {\\n\\t\\tdigits[i] = (digits[i] + 5*digits[i+1] + 5*digits[i+4]+digits[i+5]) % 10\\n\\t}\\n\\tdigits = digits[:n-5]\\n\\treturn digits\\n}\\n\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5]+digits[i+1275])+ (digits[i+5]+digits[i+1275])+ (digits[i+5]+digits[i+1275])+ (digits[i+5]+digits[i+1275])+ (digits[i+5]+digits[i+1275])+ (digits[i+5]+digits[i+1275]) + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) + (digits[i+625] + digits[i+655]) + (digits[i+630] + digits[i+650]) + (digits[i+630] + digits[i+650])\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [275, 1.1628, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n } else if len(digits) >= 6 {\\n\\t\\t\\tdigits=operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nfunc operationPentiple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-5; i++ {\\n\\t\\tdigits[i] = (digits[i] + 5*digits[i+1] + 5*digits[i+4]+digits[i+5]) % 10\\n\\t}\\n\\tdigits = digits[:n-5]\\n\\treturn digits\\n}\\n\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5]+digits[i+1275])+ (digits[i+5]+digits[i+1275])+ (digits[i+5]+digits[i+1275])+ (digits[i+5]+digits[i+1275])+ (digits[i+5]+digits[i+1275])+ (digits[i+5]+digits[i+1275]) + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) + (digits[i+625] + digits[i+655]) + (digits[i+630] + digits[i+650]) + (digits[i+630] + digits[i+650])\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [276, 1.1628, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284{\\n\\t\\t\\tdigits = operation1282(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n \\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i]+digits[i+1280] + (digits[i+5]+digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625]+digits[i+655])+(digits[i+625]+digits[i+655]) + (digits[i+630]+digits[i+650])+(digits[i+630]+digits[i+650]) \\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [280, 3.4884, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits = operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nfunc operationPentiple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-5; i++ {\\n\\t\\tdigits[i] = (digits[i] + 5*digits[i+1] + 5*digits[i+4] + digits[i+5]) % 10\\n\\t}\\n\\tdigits = digits[:n-5]\\n\\treturn digits\\n}\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5] + digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) << 1+ (digits[i+630] + digits[i+650]) << 1\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [284, 1.1628, \"func hasSameDigits(s string) bool {\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t\\n\\tfor {\\n\\t\\t if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits = operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\n\\n\\nfunc operation1282(digits []int) []int {\\n\\tfor i := 0; i < len(digits)-(1281-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5]+digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + (digits[i+625] + digits[i+655]) + (digits[i+625] + digits[i+655]) + (digits[i+630] + digits[i+650]) + (digits[i+630] + digits[i+650])\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(1281-1)]\\n\\n\\treturn digits\\n}\"], [285, 1.1628, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits = operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nfunc operationPentiple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-5; i++ {\\n\\t\\tdigits[i] = (digits[i] + 5*digits[i+1] + 5*digits[i+4] + digits[i+5]) % 10\\n\\t}\\n\\tdigits = digits[:n-5]\\n\\treturn digits\\n}\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] +\\n\\t\\t\\t(digits[i+5]+digits[i+1275]+digits[i+25]+digits[i+1255]+digits[i+30]+digits[i+1250])*6 +\\n\\t\\t\\t(digits[i+256]+digits[i+1024])*5 +\\n\\t\\t\\tdigits[i+625] + digits[i+655] + digits[i+625] + digits[i+655] + digits[i+630] +\\n\\t\\t\\tdigits[i+650] + digits[i+630] + digits[i+650]\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"], [287, 2.3256, \"func hasSameDigits(s string) bool {\\n\\t//fmt.Println(s)\\n\\tn := len(s)\\n\\tdigits := make([]int, n)\\n\\tfor i := 0; i < n; i++ {\\n\\t\\tdigits[i], _ = strconv.Atoi(string(s[i]))\\n\\t}\\n\\t//fmt.Println(digits)\\n\\n\\t/*if len(digits)%2 == 1 {\\n\\t\\tdigits = operation(digits)\\n\\t}\\n\\tfmt.Println(digits)\\n\\n\\tdigits = operationAll(digits)\\n\\tfmt.Println(digits)*/\\n\\tfor {\\n\\t\\tif len(digits) == 3 {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t} else if len(digits) > 1284 {\\n\\t\\t\\tdigits = operation1282(digits)\\n\\t\\t} else if len(digits) >= 6 {\\n\\t\\t\\tdigits = operationQuadruple(digits)\\n\\t\\t} else if len(digits) >= 4 {\\n\\t\\t\\tdigits = operationDouble(digits)\\n\\t\\t} else {\\n\\t\\t\\tdigits = operation(digits)\\n\\t\\t}\\n\\n\\t\\t//fmt.Println(len(digits))\\n\\t\\tif len(digits) > 2 {\\n\\t\\t\\tcontinue\\n\\t\\t} else {\\n\\t\\t\\tbreak\\n\\t\\t}\\n\\t}\\n\\n\\tif digits[0] == digits[1] {\\n\\t\\treturn true\\n\\t}\\n\\t//fmt.Println(digits)\\n\\treturn false\\n}\\n\\nfunc operation(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-1; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1]) % 10\\n\\t}\\n\\tdigits = digits[:n-1]\\n\\treturn digits\\n}\\n\\nfunc operationDouble(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-2; i++ {\\n\\t\\tdigits[i] = (digits[i] + digits[i+1] + digits[i+1] + digits[i+2]) % 10\\n\\t}\\n\\tdigits = digits[:n-2]\\n\\treturn digits\\n}\\n\\nfunc operationQuadruple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-4; i++ {\\n\\t\\tdigits[i] = (digits[i] + 4*digits[i+1] + 6*digits[i+2] + 4*digits[i+3] + digits[i+4]) % 10\\n\\t}\\n\\tdigits = digits[:n-4]\\n\\treturn digits\\n}\\n\\nfunc operationPentiple(digits []int) []int {\\n\\tn := len(digits)\\n\\tfor i := 0; i < n-5; i++ {\\n\\t\\tdigits[i] = (digits[i] + 5*digits[i+1] + 5*digits[i+4] + digits[i+5]) % 10\\n\\t}\\n\\tdigits = digits[:n-5]\\n\\treturn digits\\n}\\n\\nvar k = 1281\\n\\nfunc operation1282(digits []int) []int {\\n\\t//fmt.Printf(\\\"Address of array = %p\\\\n\\\", &digits)\\n\\n\\tfor i := 0; i < len(digits)-(k-1); i++ {\\n\\t\\tdigits[i] = digits[i] + digits[i+1280] + (digits[i+5] + digits[i+1275])*6 + (digits[i+25]+digits[i+1255])*6 + (digits[i+30]+digits[i+1250])*6 + (digits[i+256]+digits[i+1024])*5 + digits[i+625] + digits[i+655] + digits[i+625] + digits[i+655] + digits[i+630] + digits[i+650] + digits[i+630] + digits[i+650]\\n\\n\\t\\tdigits[i] = digits[i] % 10\\n\\t}\\n\\n\\tdigits = digits[:len(digits)-(k-1)]\\n\\n\\treturn digits\\n}\"]]"
},
"java": {
"code": "class Solution {\n public boolean hasSameDigits(String s) {\n int n = s.length();\n int k = n - 2;\n if (k == 0) {\n return s.charAt(0) == s.charAt(1);\n }\n\n List<Integer> digitsK_p2 = getDigits(k, 2);\n List<Integer> digitsK_p5 = getDigits(k, 5);\n\n int[] coeff = new int[k + 1];\n for (int j = 0; j <= k; j++) {\n int a = lucasModWithDigits(j, 2, digitsK_p2);\n int b = lucasModWithDigits(j, 5, digitsK_p5);\n coeff[j] = (5 * a + 6 * b) % 10;\n }\n\n int sum0 = 0;\n int sum1 = 0;\n for (int j = 0; j <= k; j++) {\n int digit0 = s.charAt(j) - '0';\n sum0 = (sum0 + digit0 * coeff[j]) % 10;\n int digit1 = s.charAt(j + 1) - '0';\n sum1 = (sum1 + digit1 * coeff[j]) % 10;\n }\n return sum0 == sum1;\n }\n\n private List<Integer> getDigits(int n, int p) {\n List<Integer> digits = new ArrayList<>();\n while (n > 0) {\n digits.add(n % p);\n n /= p;\n }\n return digits;\n }\n\n private int lucasModWithDigits(int j, int p, List<Integer> digitsN) {\n if (j == 0) {\n return 1;\n }\n List<Integer> digitsK = new ArrayList<>();\n int jCopy = j;\n while (jCopy > 0) {\n digitsK.add(jCopy % p);\n jCopy /= p;\n }\n while (digitsK.size() < digitsN.size()) {\n digitsK.add(0);\n }\n int res = 1;\n for (int i = 0; i < digitsK.size(); i++) {\n int ni = (i < digitsN.size()) ? digitsN.get(i) : 0;\n int ki = digitsK.get(i);\n if (ki > ni) {\n return 0;\n }\n if (p == 2) {\n if (ni == 0) {\n if (ki != 0) return 0;\n res = (res * 1) % p;\n } else if (ni == 1) {\n if (ki == 0 || ki == 1) res = (res * 1) % p;\n else return 0;\n }\n } else if (p == 5) {\n int[][] table = {\n {1, 0, 0, 0, 0},\n {1, 1, 0, 0, 0},\n {1, 2, 1, 0, 0},\n {1, 3, 3, 1, 0},\n {1, 4, 1, 4, 1}\n };\n res = (res * table[ni][ki]) % 5;\n }\n }\n return res;\n }\n}",
"memory": 5500,
"memoryDistribution": "[[5500, 8.2121, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int k = n - 2;\\n if (k == 0) {\\n return s.charAt(0) == s.charAt(1);\\n }\\n\\n List<Integer> digitsK_p2 = getDigits(k, 2);\\n List<Integer> digitsK_p5 = getDigits(k, 5);\\n\\n int[] coeff = new int[k + 1];\\n for (int j = 0; j <= k; j++) {\\n int a = lucasModWithDigits(j, 2, digitsK_p2);\\n int b = lucasModWithDigits(j, 5, digitsK_p5);\\n coeff[j] = (5 * a + 6 * b) % 10;\\n }\\n\\n int sum0 = 0;\\n int sum1 = 0;\\n for (int j = 0; j <= k; j++) {\\n int digit0 = s.charAt(j) - '0';\\n sum0 = (sum0 + digit0 * coeff[j]) % 10;\\n int digit1 = s.charAt(j + 1) - '0';\\n sum1 = (sum1 + digit1 * coeff[j]) % 10;\\n }\\n return sum0 == sum1;\\n }\\n\\n private List<Integer> getDigits(int n, int p) {\\n List<Integer> digits = new ArrayList<>();\\n while (n > 0) {\\n digits.add(n % p);\\n n /= p;\\n }\\n return digits;\\n }\\n\\n private int lucasModWithDigits(int j, int p, List<Integer> digitsN) {\\n if (j == 0) {\\n return 1;\\n }\\n List<Integer> digitsK = new ArrayList<>();\\n int jCopy = j;\\n while (jCopy > 0) {\\n digitsK.add(jCopy % p);\\n jCopy /= p;\\n }\\n while (digitsK.size() < digitsN.size()) {\\n digitsK.add(0);\\n }\\n int res = 1;\\n for (int i = 0; i < digitsK.size(); i++) {\\n int ni = (i < digitsN.size()) ? digitsN.get(i) : 0;\\n int ki = digitsK.get(i);\\n if (ki > ni) {\\n return 0;\\n }\\n if (p == 2) {\\n if (ni == 0) {\\n if (ki != 0) return 0;\\n res = (res * 1) % p;\\n } else if (ni == 1) {\\n if (ki == 0 || ki == 1) res = (res * 1) % p;\\n else return 0;\\n }\\n } else if (p == 5) {\\n int[][] table = {\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1}\\n };\\n res = (res * table[ni][ki]) % 5;\\n }\\n }\\n return res;\\n }\\n}\"], [45100, 0.9662, \"class Solution {\\n public int lucasModP(int n, int r, int p) {\\n\\t int result = 1;\\n\\t while (n > 0 || r > 0) {\\n\\t int nI = n % p;\\n\\t int rI = r % p;\\n\\n\\t if (rI > nI) {\\n\\t return 0; \\n\\t }\\n\\t result = (result * binomialModP(nI, rI, p)) % p;\\n\\t n /= p;\\n\\t r /= p;\\n\\t }\\n\\t return result;\\n\\t}\\n\\n\\tprivate int binomialModP(int n, int r, int p) {\\n\\t if (r > n) return 0;\\n\\t int result = 1;\\n\\t for (int i = 0; i < r; i++) {\\n\\t result = (result * (n - i)) % p;\\n\\t result = (result * modInverse(i + 1, p)) % p;\\n\\t }\\n\\t return result;\\n\\t}\\n\\n\\tprivate int modInverse(int a, int p) {\\n\\t return power(a, p - 2, p);\\n\\t}\\n\\n\\tprivate int power(int base, int exp, int mod) {\\n\\t int result = 1;\\n\\t base = base % mod;\\n\\t while (exp > 0) {\\n\\t if (exp % 2 == 1) {\\n\\t result = (result * base) % mod;\\n\\t }\\n\\t exp = exp >> 1;\\n\\t base = (base * base) % mod;\\n\\t }\\n\\t return result;\\n\\t}\\n\\n\\n\\tpublic int nCr(int n, int r) {\\n\\t int mod2 = lucasModP(n, r, 2);\\n\\t int mod5 = lucasModP(n, r, 5);\\n\\t \\n\\t return chineseRemainderTheorem(mod2, mod5);\\n\\t}\\n\\n\\tprivate int chineseRemainderTheorem(int mod2, int mod5) {\\t \\n\\t int x = (mod5 - mod2) % 5;\\n\\t if (x < 0) x += 5;\\n\\t \\n\\t int inv2 = modInverse(2, 5);\\n\\t x = (mod2 + x * inv2 * 2) % 10;\\n\\t return x;\\n\\t}\\n\\n\\n\\tpublic boolean hasSameDigits(String s) {\\n\\t\\tint sz = s.length();\\n\\t\\tint newSz = sz - 2;\\n\\t\\tchar c1 = s.charAt(0), c2;\\n\\t\\tint left = 0, right = 0;\\n\\t\\tfor (int i = 0; i <= newSz; i++) {\\n\\t\\t\\tleft = (left + (nCr(newSz, i) * (c1 - '0'))) % 10;\\n\\t\\t\\tc2 = s.charAt(i + 1);\\n\\t\\t\\tright = (right + (nCr(newSz, i) * (c2 - '0'))) % 10;\\n\\t\\t\\tc1 = c2;\\n\\t\\t}\\n\\t\\treturn left == right;\\n }\\n}\"], [45200, 0.9662, \" class Solution {\\n static int[][] F = {\\n {1,0,0,0,0},\\n {1,1,0,0,0},\\n {1,2,1,0,0},\\n {1,3,3,1,0},\\n {1,4,6,4,1}\\n };\\n \\n int l5(int n, int k) {\\n int r = 1;\\n while(n > 0 || k > 0) {\\n int ni = n % 5, ki = k % 5;\\n if(ki > ni) return 0;\\n r = (r * F[ni][ki]) % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return r;\\n }\\n \\n int m2(int n, int k) {\\n return ((n & k) == k) ? 1 : 0;\\n }\\n \\n int cmb(int a, int b) {\\n for (int x = 0; x < 10; x++) {\\n if(x % 2 == a && x % 5 == b) return x;\\n }\\n return 0;\\n }\\n \\n int ff(int n, int k) {\\n int a = m2(n, k);\\n int b = l5(n, k);\\n return cmb(a, b);\\n }\\n \\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int L = n - 2;\\n int r0 = 0, r1 = 0;\\n for (int j = 0; j <= L; j++) {\\n int c = ff(L, j);\\n int d = s.charAt(j) - '0';\\n r0 = (r0 + c * d) % 10;\\n }\\n for (int j = 0; j <= L; j++) {\\n int c = ff(L, j);\\n int d = s.charAt(j + 1) - '0';\\n r1 = (r1 + c * d) % 10;\\n }\\n return r0 == r1;\\n }\\n}\"], [45300, 3.3816, \"class Solution {\\n // Small 5\\u00d75 table of C(n,k) mod 5 for 0 \\u2264 n,k \\u2264 4\\n private static final int[][] C5 = {\\n {1,0,0,0,0},\\n {1,1,0,0,0},\\n {1,2,1,0,0},\\n {1,3,3,1,0},\\n {1,4,6%5,4,1}\\n };\\n // Precomputed mapping from (mod5,mod2) \\u2192 unique x mod10\\n private static final int[][] CRT = new int[5][2];\\n static {\\n // Build CRT[a][b] = x in [0..9] with x%5==a and x%2==b\\n for(int a=0;a<5;a++){\\n for(int b=0;b<2;b++){\\n for(int x=0;x<10;x++){\\n if(x%5==a && x%2==b){\\n CRT[a][b] = x;\\n break;\\n }\\n }\\n }\\n }\\n }\\n\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n // Edge: if already length 2\\n if (n == 2) return s.charAt(0) == s.charAt(1);\\n\\n // We'll compute final two sums:\\n // X = \\u03a3_{i=0..n-2} [C(n-2,i) mod10] * digit(i)\\n // Y = \\u03a3_{i=1..n-1} [C(n-2,i-1) mod10] * digit(i)\\n // and check X%10 == Y%10.\\n\\n int mod = 10, \\n xSum = 0, \\n ySum = 0;\\n int m = n - 2;\\n\\n for (int i = 0; i <= m; i++) {\\n int d1 = s.charAt(i) - '0';\\n int d2 = s.charAt(i+1) - '0';\\n\\n // C_mod2 = 1 iff no carries in binary for (i, m-i)\\n int c2 = (((i) & (m - i)) == 0) ? 1 : 0;\\n // C_mod5 via Lucas: multiply digitwise in base-5\\n int c5 = 1;\\n int a = m, b = i;\\n while (a > 0 || b > 0) {\\n int ai = a % 5, bi = b % 5;\\n if (bi > ai) { c5 = 0; break; }\\n c5 = (c5 * C5[ai][bi]) % 5;\\n a /= 5; b /= 5;\\n }\\n // Combine to mod10\\n int coef = CRT[c5][c2];\\n\\n // Accumulate\\n xSum = (xSum + coef * d1) % mod;\\n ySum = (ySum + coef * d2) % mod;\\n }\\n\\n return xSum == ySum;\\n }\\n}\\n\"], [45400, 6.2802, \"class Solution {\\n // rename this to match the driver\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int[] d = new int[n];\\n for (int i = 0; i < n; i++) {\\n d[i] = s.charAt(i) - '0';\\n }\\n\\n int m = n - 2;\\n int final0 = 0, final1 = 0;\\n for (int j = 0; j <= m; j++) {\\n int w = combMod10(m, j);\\n final0 = (final0 + w * d[j]) % 10;\\n final1 = (final1 + w * d[j + 1]) % 10;\\n }\\n return final0 == final1;\\n }\\n\\n // compute C(n,k) mod 10 via CRT\\n private int combMod10(int n, int k) {\\n int r2 = ((k & (n - k)) == 0) ? 1 : 0; // mod 2\\n int r5 = combMod5(n, k); // mod 5\\n return ((r5 & 1) == r2) ? r5 : r5 + 5; // CRT\\n }\\n\\n // Lucas\\u2019s theorem in base-5 for C(n,k) mod 5\\n private static final int[][] C5 = {\\n {1},\\n {1,1},\\n {1,2,1},\\n {1,3,3,1},\\n {1,4,1,4,1}\\n };\\n private int combMod5(int n, int k) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int ni = n % 5, ki = k % 5;\\n if (ki > ni) return 0;\\n res = (res * C5[ni][ki]) % 5;\\n n /= 5; k /= 5;\\n }\\n return res;\\n }\\n}\\n\"], [45500, 6.7633, \"class Solution {\\n\\n public boolean hasSameDigits(String s) {\\n int X=s.length()-2, x=0, y=0;\\n for(int j=0;j<=X;j++){\\n int coeff=binomialMode10(X,j);\\n x=(x+coeff*(s.charAt(j)-'0'))%10;\\n y=(y+coeff*(s.charAt(j+1)-'0'))%10;\\n }\\n return x==y;\\n }\\n\\n private int binomialMode10(int n, int k){\\n int i=binomialMode2(n, k);\\n int j=binomialMode5(n, k);\\n for(int x=0;x<10;x++){\\n if(x%2==i && x%5==j) return x;\\n }\\n return 0;\\n }\\n\\n private int binomialMode2(int n, int k){\\n return ((n&k)==k)?1:0;\\n }\\n\\n private int binomialMode5(int n, int k){\\n int[][] tuples={{1},{1,1},{1,2,1},{1,3,3,1},{1,4,1,4,1}};\\n int result=1;\\n while(n>0||k>0){\\n int nthd=n%5;\\n int kthd=k%5;\\n if(kthd>nthd) return 0;\\n result=(result*tuples[nthd][kthd])%5;\\n n/=5;\\n k/=5;\\n }\\n return result;\\n }\\n \\n}\"], [45600, 7.7295, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n if (n <= 2) {\\n return s.charAt(0) == s.charAt(1);\\n }\\n\\n int pascal = n - 1;\\n int diff = (Character.getNumericValue(s.charAt(0)) - Character.getNumericValue(s.charAt(n - 1))) % 10;\\n\\n int rem = 1, count2 = 0, count5 = 0;\\n\\n int[] inverse = {0, 1, 0, 7, 0, 0, 0, 3, 0, 9};\\n\\n for (int i = 1; i < pascal; i += 1) {\\n int num = pascal - i;\\n int den = i;\\n\\n int[] numResult = factorize(num);\\n int[] denResult = factorize(den);\\n\\n rem = (rem * numResult[0] * inverse[denResult[0]]) % 10;\\n count2 = count2 + numResult[1] - denResult[1];\\n count5 = count5 + numResult[2] - denResult[2];\\n\\n int c;\\n if (count2 > 0 && count5 > 0) {\\n c = 0;\\n } else if (count2 > 0) {\\n int[] power = {6, 2, 4, 8};\\n int twoMod = power[count2 % 4];\\n if(count2 % 4 == 0) twoMod = 6;\\n c = (rem * twoMod) % 10;\\n } else if (count5 > 0) {\\n c = (rem * 5) % 10;\\n } else {\\n c = rem;\\n }\\n\\n diff = (diff + (Character.getNumericValue(s.charAt(i)) - Character.getNumericValue(s.charAt(n - 1 - i))) * c) % 10;\\n }\\n\\n return diff % 10 == 0;\\n }\\n\\n private int[] factorize(int x) {\\n int count2 = 0, count5 = 0;\\n while (x % 2 == 0) {\\n count2 += 1;\\n x /= 2;\\n }\\n while (x % 5 == 0) {\\n count5 += 1;\\n x /= 5;\\n }\\n return new int[]{x % 10, count2, count5};\\n }\\n}\"], [45700, 10.1449, \"class Solution {\\n public int mod10Inverse(int n) {\\n return switch(n) {\\n case 1 -> 1;\\n case 3 -> 7;\\n case 7 -> 3;\\n case 9 -> 9;\\n default -> 0;\\n };\\n }\\n public int[] nthRowOfPascalTriangle(int n) {\\n int[] row = new int[n+1];\\n int prev = 1;\\n row[0]=prev;\\n row[n]=prev;\\n int twos = 0;\\n int fives = 0;\\n for(int i=1;i<(n+2)/2;i++) {\\n int num = n-i+1;\\n int den = i;\\n while(num%2==0) {\\n num/=2;\\n twos++;\\n }\\n while(num%5==0) {\\n num/=5;\\n fives++;\\n }\\n while(den%2==0) {\\n den/=2;\\n twos--;\\n }\\n while(den%5==0) {\\n den/=5;\\n fives--;\\n }\\n prev = prev*num*mod10Inverse(den%10)%10;\\n if(twos>0 && fives>0) {\\n row[i]=0;\\n row[n-i]=0;\\n } else {\\n int res = (prev*(int)Math.pow(2,twos)*(int)Math.pow(5,fives))%10;\\n row[i]=res;\\n row[n-i]=res;\\n }\\n }\\n return row;\\n }\\n public boolean hasSameDigits(String s) {\\n int[] pascal = nthRowOfPascalTriangle(s.length()-2);\\n int first = 0;\\n int second = 0;\\n for(int i=0;i<s.length()-1;i++) {\\n first += pascal[i]*((int)s.charAt(i)-48);\\n second += pascal[i]*((int)s.charAt(i+1)-48);\\n }\\n first%=10;\\n second%=10;\\n return first==second;\\n }\\n}\"], [45800, 13.5266, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int N = n - 2;\\n int f0 = 0, f1 = 0;\\n\\n for (int j = 0; j <= N; j++) {\\n int c = binomMod10(N, j);\\n f0 = (f0 + c * (s.charAt(j) - '0')) % 10;\\n f1 = (f1 + c * (s.charAt(j + 1) - '0')) % 10;\\n }\\n return f0 == f1;\\n }\\n\\n private int binomMod10(int n, int k) {\\n int r2 = binomMod2(n, k);\\n int r5 = binomMod5(n, k);\\n for (int x = 0; x < 10; x++) {\\n if (x % 2 == r2 && x % 5 == r5) return x;\\n }\\n return 0;\\n }\\n\\n private int binomMod2(int n, int k) {\\n return ((n & k) == k) ? 1 : 0;\\n }\\n\\n private int binomMod5(int n, int k) {\\n int[][] t = {\\n {1}, {1, 1}, {1, 2, 1}, {1, 3, 3, 1}, {1, 4, 1, 4, 1}\\n };\\n int res = 1;\\n\\n while (n > 0 || k > 0) {\\n int nd = n % 5;\\n int kd = k % 5;\\n if (kd > nd) return 0;\\n res = (res * t[nd][kd]) % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return res;\\n }\\n}\"], [45900, 4.8309, \"/*\\nTook a bit to figure that: the two values are left with are\\nthe result of f3 modulo 10.\\n\\nWe need to use Lucas's Theorum to get the last digit of the binomial\\n*/\\n\\nclass Solution {\\n\\n int fact(int n) {\\n return switch(n) {\\n case 0 -> 1;\\n case 1-> 1;\\n case 2-> 2;\\n case 3-> 6;\\n case 4-> 24;\\n case 5-> 120;\\n default -> throw new IllegalArgumentException();\\n };\\n }\\n\\n int binomial(int n, int k) {\\n if (n < k) {\\n return 0;\\n }\\n int numerator = fact(n);\\n int denominator =(fact(k) * fact(n - k));\\n return numerator / denominator;\\n }\\n\\n int lookup_5_2_solution(int xMod5, int xMod2) {\\n return switch (xMod2) {\\n case 0 ->\\n switch (xMod5) {\\n case 0 -> 0;\\n case 1 -> 6;\\n case 2 -> 2;\\n case 3 -> 8;\\n case 4 -> 4;\\n default -> throw new IllegalArgumentException();\\n };\\n case 1 ->\\n switch (xMod5) {\\n case 0 -> 5;\\n case 1 -> 1;\\n case 2 -> 7;\\n case 3 -> 3;\\n case 4 -> 9;\\n default -> throw new IllegalArgumentException();\\n };\\n default -> throw new IllegalArgumentException();\\n };\\n }\\n\\n int binomialCoefficientLastDigit(int N, int K) {\\n int xMod5 = 1;\\n int xMod2 = 1;\\n\\n int n = N;\\n int k = K;\\n\\n while (n > 0) {\\n xMod5 *= binomial(n % 5, k % 5);\\n xMod5 %= 5;\\n n /= 5;\\n k /= 5;\\n }\\n\\n n = N;\\n k = K;\\n while (n > 0) {\\n xMod2 *= binomial(n % 2, k % 2);\\n xMod2 %= 2;\\n n /= 2;\\n k /= 2;\\n }\\n return lookup_5_2_solution(xMod5, xMod2);\\n }\\n\\n public boolean hasSameDigits(String s) {\\n int sumsLength = s.length() - 1;\\n int[] pascalRowLastDigits = IntStream.range(0, sumsLength)\\n .map(k -> binomialCoefficientLastDigit(sumsLength - 1, k))\\n .toArray();\\n int[] digits = s.chars().map(c -> c - '0').toArray();\\n int firstDigitsSum = 0;\\n int secondDigitsSum = 0;\\n\\n for (int i = 0; i < sumsLength; i++) {\\n firstDigitsSum += pascalRowLastDigits[i] * digits[i];\\n secondDigitsSum += pascalRowLastDigits[i] * digits[i+1];\\n }\\n\\n return (firstDigitsSum % 10) == (secondDigitsSum % 10);\\n }\\n // CLOJURE CODE BELOW\\n /*\\n(defn f1 [i]\\n(loop [s (->> i (map int) (map #(- % (int \\\\0))))]\\n (if (<= (count s) 2)\\n s #_(when (= (first s) (second s)) s)\\n (recur (map #(mod (+ %1 %2) 10) s (rest s))))))\\n\\n(defn f2 [i]\\n(loop [s (->> i (map int) (map #(- % (int \\\\0))))]\\n (if (<= (count s) 2)\\n s\\n (recur (map #(list %1 %2) s (rest s))))))\\n\\n(defn left-pad-with [desired-width padding padee]\\n(concat (repeat (- desired-width (count padee)) padding) padee))\\n\\n(defn fact [n] (apply * (range 1 (inc n))))\\n(defn binomial [n k]\\n(if (< n k) 0 (/ (fact n) (* (fact k) (fact (- n k))))))\\n(defn binomial-ld1 [n k] (mod (binomial n k) 10))\\n; using Lucas's Theorum\\n\\n(def lookup-5-2 {\\n[0 0] 0\\n[1 0] 6\\n[2 0] 2\\n[3 0] 8\\n[4 0] 4\\n[0 1] 5\\n[1 1] 1\\n[2 1] 7\\n[3 1] 3\\n[4 1] 9\\n})\\n\\n(defn binomial-ld2 [n k]\\n(let [\\nn-digits-2 (->> n (#(Integer/toString % 2)) (map char) (map int) (map #(- % (int \\\\0))))\\nn-digits-5 (->> n (#(Integer/toString % 5)) (map char) (map int) (map #(- % (int \\\\0))))\\nk-digits-2 (->> k (#(Integer/toString % 2)) (map char) (map int) (map #(- % (int \\\\0))) (left-pad-with (count n-digits-2) 0))\\nk-digits-5 (->> k (#(Integer/toString % 5)) (map char) (map int) (map #(- % (int \\\\0))) (left-pad-with (count n-digits-5) 0))\\nx-mod-2 (->> (map binomial n-digits-2 k-digits-2) (apply *) (#(mod % 2)))\\nx-mod-5 (->> (map binomial n-digits-5 k-digits-5) (apply *) (#(mod % 5)))\\n]\\n(lookup-5-2 [x-mod-5 x-mod-2])))\\n\\n(defn f3 [i]\\n(let [sums-len (dec (count i)),\\npascal-row-ld (->> (range sums-len)\\n #_(map #(binomial-ld1 (dec sums-len) %))\\n (map #(binomial-ld2 (dec sums-len) %))\\n )\\ndgts (->> i (map int) (map #(- % (int \\\\0))))\\n]\\n[\\n(->> dgts drop-last (map * pascal-row-ld))\\n(->> dgts (drop 1) (map * pascal-row-ld))\\n]\\n))\\n\\n(prn (map #(mod (* % 3) 10) (range 20)))\\n(prn (map #(mod (* % 13) 10) (range 20)))\\n\\n#_(->> (range 1000 2000)\\n (map (juxt #(->> % str (map char) f2) identity))\\n #_(filter first)\\n (map prn)\\n doall\\n #_(map second)\\n #_(reduce +)\\n #_prn)\\n\\n(def R [\\\\1 \\\\2 \\\\3 \\\\4 \\\\5 \\\\6 \\\\7 \\\\8])\\n(def R2 [\\\\7 \\\\9 \\\\5 \\\\2])\\n\\n (prn (f1 R))\\n #_(prn (f2 R))\\n #_(prn (count (f2 R)))\\n #_(prn (map flatten (f2 R)))\\n #_(prn (->> R f2 (map flatten) (map (partial apply +))))\\n #_(prn (->> R f2 (map flatten) (map sort)))\\n #_(prn (->> R f2 (map flatten) (map sort) (map frequencies)))\\n (prn (->> R f3))\\n (prn (->> R f3 (map (partial apply +))))\\n\\n (prn (->> R2 f1))\\n (prn (->> R2 f3 (map (partial apply +)) (map #(mod % 10))))\\n #_(prn (apply + (flatten (f2 R))))\\n\\n; vim: syntax=clojure\\n\\n */\\n}\"], [46000, 5.7971, \"class Solution {\\n private int nCr_mod_5(int n, int r) {\\n if (r < 0 || r > n) return 0;\\n if (r == 0 || r == n) return 1;\\n if (r > n / 2) r = n - r;\\n if (n < 5) {\\n if (n == 0) return 1;\\n if (n == 1) return 1;\\n if (n == 2) return (r == 1) ? 2 : 1;\\n if (n == 3) return (r == 1) ? 3 : 1;\\n if (n == 4) {\\n if (r == 0) return 1;\\n if (r == 1) return 4;\\n if (r == 2) return 1;\\n }\\n return 0;\\n }\\n int n_div_5 = n / 5;\\n int r_div_5 = r / 5;\\n int n_mod_5 = n % 5;\\n int r_mod_5 = r % 5;\\n return (nCr_mod_5(n_div_5, r_div_5) * nCr_mod_5(n_mod_5, r_mod_5)) % 5;\\n }\\n private int get_C_mod_10(int N, int i) {\\n if (i < 0 || i > N) return 0;\\n int mod2 = ((N & i) == i) ? 1 : 0;\\n int mod5 = nCr_mod_5(N, i);\\n return (5 * mod2 + 6 * mod5) % 10;\\n }\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int N = n - 2;\\n int final_digit_0 = 0;\\n for (int i = 0; i <= N; i++) {\\n int digit = s.charAt(i) - '0';\\n int coeff = get_C_mod_10(N, i);\\n final_digit_0 = (final_digit_0 + coeff * digit) % 10;\\n }\\n int final_digit_1 = 0;\\n for (int i = 0; i <= N; i++) {\\n int digit = s.charAt(i + 1) - '0';\\n int coeff = get_C_mod_10(N, i);\\n final_digit_1 = (final_digit_1 + coeff * digit) % 10;\\n }\\n return final_digit_0 == final_digit_1;\\n }\\n}\"], [46100, 2.8986, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int N = n - 2;\\n int f0 = 0, f1 = 0;\\n\\n for (int j = 0; j <= N; j++) {\\n int c = binomMod10(N, j);\\n f0 = (f0 + c * (s.charAt(j) - '0')) % 10;\\n f1 = (f1 + c * (s.charAt(j + 1) - '0')) % 10;\\n }\\n return f0 == f1;\\n }\\n\\n private int binomMod10(int n, int k) {\\n int r2 = binomMod2(n, k);\\n int r5 = binomMod5(n, k);\\n for (int x = 0; x < 10; x++) {\\n if (x % 2 == r2 && x % 5 == r5) return x;\\n }\\n return 0;\\n }\\n\\n private int binomMod2(int n, int k) {\\n return ((n & k) == k) ? 1 : 0;\\n }\\n\\n private int binomMod5(int n, int k) {\\n int[][] t = {\\n {1}, {1, 1}, {1, 2, 1}, {1, 3, 3, 1}, {1, 4, 1, 4, 1}\\n };\\n int res = 1;\\n\\n while (n > 0 || k > 0) {\\n int nd = n % 5;\\n int kd = k % 5;\\n if (kd > nd) return 0;\\n res = (res * t[nd][kd]) % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return res;\\n }\\n}\"], [46200, 0.9662, \"class Solution {\\n\\n int comb(int n, int r){ \\n if (r > n) { return 0; }\\n int res = 1;\\n for (int t = 1; t <= n; ++t) { res *= t; }\\n for (int t = 1; t <= r; ++t) { res /= t; }\\n for (int t = 1; t <= n - r; ++t) { res /= t; }\\n return res;\\n }\\n\\n boolean check(int[] a, int mod){\\n int res = 0;\\n int n = a.length;\\n for (int i = 0; i != n; ++i){\\n int ncr = 1;\\n int x = n - 1;\\n int y = i;\\n while (x > 0 && y > 0){\\n ncr = ncr * comb(x % mod, y % mod) % mod;\\n x /= mod;\\n y /= mod;\\n }\\n res = (res + ncr * a[i]) % mod;\\n }\\n return res == 0;\\n }\\n public boolean hasSameDigits(String str) {\\n char[] s = str.toCharArray();\\n int n = str.length();\\n int[] a = new int[n-1];\\n for (int i = 0; i != n - 1; ++i){\\n a[i] = (s[i] - '0') - (s[i + 1] - '0');\\n a[i] = (a[i] + 10) % 10;\\n }\\n return check(a, 2) && check(a, 5);\\n }\\n}\\n\"], [46300, 0.4831, \"class Solution {\\n\\n // Helper: compute nCk mod p for n, k < p.\\n private int binomModPrime(int n, int k, int p) {\\n if (k > n) return 0;\\n int[] fact = new int[p];\\n fact[0] = 1;\\n for (int i = 1; i < p; i++) {\\n fact[i] = (fact[i-1] * i) % p;\\n }\\n // In mod p (p is prime) every nonzero element has an inverse.\\n int invK = modInverse(fact[k], p);\\n int invNK = modInverse(fact[n - k], p);\\n return (int)(((long)fact[n] * invK % p) * invNK % p);\\n }\\n \\n // Helper: compute modular inverse of a mod p (p prime) using Fermat's little theorem.\\n private int modInverse(int a, int p) {\\n return modPow(a, p - 2, p);\\n }\\n \\n // Helper: fast exponentiation mod mod.\\n private int modPow(int base, int exp, int mod) {\\n int result = 1;\\n base %= mod;\\n while(exp > 0) {\\n if ((exp & 1) == 1)\\n result = (int)((long)result * base % mod);\\n base = (int)((long)base * base % mod);\\n exp >>= 1;\\n }\\n return result;\\n }\\n \\n // Lucas theorem: compute nCk mod p (for any nonnegative n, k)\\n private int lucas(int n, int k, int p) {\\n if (k == 0) return 1;\\n int n0 = n % p;\\n int k0 = k % p;\\n if (k0 > n0) return 0;\\n return (int)((long)binomModPrime(n0, k0, p) * lucas(n / p, k / p, p) % p);\\n }\\n \\n // Combine a result mod2 and mod5 into a result mod10.\\n // Solve: x \\u2261 mod2 (mod 2) and x \\u2261 mod5 (mod 5).\\n private int combineCRT(int mod2, int mod5) {\\n // The two candidates modulo 10 are: mod5 and mod5 + 5.\\n int cand = mod5;\\n if (cand % 2 != mod2) {\\n cand += 5;\\n }\\n return cand % 10;\\n }\\n \\n // Compute binom(n, k) mod 10 using CRT from Lucas mod2 and mod5.\\n private int binomMod10(int n, int k) {\\n int res2 = lucas(n, k, 2);\\n int res5 = lucas(n, k, 5);\\n return combineCRT(res2, res5);\\n }\\n \\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n // If the string is already two digits, just compare.\\n if(n == 2) {\\n return s.charAt(0) == s.charAt(1);\\n }\\n int m = n - 2; // number of operations\\n \\n // We want to compute:\\n // T = a0 + sum_{i=1}^{n-2} [binom(m, i) - binom(m, i-1)] * a_i - binom(m, n-2)*a_{n-1} (mod 10)\\n // where a_i are the digits.\\n int T = 0;\\n // a0 coefficient is 1.\\n T = (T + (s.charAt(0) - '0')) % 10;\\n \\n // For i = 1 to n-2.\\n for (int i = 1; i <= n - 2; i++) {\\n int b1 = binomMod10(m, i); // binom(m, i) mod 10\\n int b2 = binomMod10(m, i - 1); // binom(m, i-1) mod 10\\n int coeff = (b1 - b2) % 10;\\n if(coeff < 0) coeff += 10;\\n int digit = s.charAt(i) - '0';\\n T = (T + coeff * digit) % 10;\\n }\\n // For i = n-1, coefficient is - binom(m, n-2) mod 10.\\n int bLast = binomMod10(m, n - 2);\\n int coeffLast = (-bLast) % 10;\\n if(coeffLast < 0) coeffLast += 10;\\n int lastDigit = s.charAt(n - 1) - '0';\\n T = (T + coeffLast * lastDigit) % 10;\\n \\n // The final two digits are the same exactly when T \\u2261 0 (mod 10)\\n return T % 10 == 0;\\n }\\n}\\n\"], [46400, 0.4831, \"/*\\nRuntime 65 ms\\nBeats 100.00% of users with Java\\nMemory 46.5 MB\\nBeats 100.00% of users with Java\\n*/\\n\\nclass Solution {\\n static TreeMap<Integer, int[][]> BC_MOD_PRE = new TreeMap<>();\\n static {\\n int size = 5;\\n BC_MOD_PRE.put(size, new int[][] {{0,1},{1,5},{4,5},{5,1}});\\n\\n size = 20;\\n BC_MOD_PRE.put(size, new int[][] {{0,1},{4,5},{5,4},{10,6},{15,4},{16,5},{20,1}});\\n\\n size = 50;\\n BC_MOD_PRE.put(size, new int[][] {{0,1},{2,5},{16,5},{18,5},{25,2},{32,5},{34,5},{48,5},{50,1}});\\n\\n size = 130;\\n BC_MOD_PRE.put(size, new int[][] {{0,1},{2,5},{5,6},{125,6},{128,5},{130,1}});\\n\\n size = 260;\\n BC_MOD_PRE.put(size, new int[][] {{0,1},{4,5},{5,2},{10,6},{125,2},{130,4},{135,2},{250,6},{255,2},{256,5},{260,1}});\\n\\n size = 640;\\n BC_MOD_PRE.put(size, new int[][] {{0,1},{5,8},{10,8},{15,6},{128,5},{512,5},{625,6},{630,8},{635,8},{640,1}});\\n\\n size = 1280;\\n BC_MOD_PRE.put(size, new int[][] {{0,1},{5,6},{25,6},{30,6},{256,5},{625,2},{630,2},{650,2},{655,2},{1024,5},{1250,6},{1255,6},{1275,6},{1280,1}});\\n\\n size = 3200;\\n BC_MOD_PRE.put(size, new int[][] {{0,1},{25,8},{50,8},{75,6},{128,5},{1024,5},{1152,5},{2048,5},{2176,5},{3072,5},{3125,6},{3150,8},{3175,8},{3200,1}});\\n\\n size = 6400;\\n BC_MOD_PRE.put(size, new int[][] {{0,1},{25,6},{125,6},{150,6},{256,5},{2048,5},{2304,5},{3125,2},{3150,2},{3250,2},{3275,2},{4096,5},{4352,5},{6144,5},{6250,6},{6275,6},{6375,6},{6400,1}});\\n\\n size = 16400;\\n BC_MOD_PRE.put(size, new int[][] {{0,1},{16,5},{25,6},{125,6},{150,6},{625,6},{650,6},{750,6},{775,6},{15625,6},{15650,6},{15750,6},{15775,6},{16250,6},{16275,6},{16375,6},{16384,5},{16400,1}});\\n\\n size = 53250;\\n BC_MOD_PRE.put(size, new int[][] {{0,1},{2,5},{125,6},{3125,2},{3250,2},{4096,5},{4098,5},{6250,6},{6375,6},{15625,8},{15750,8},{16384,5},{16386,5},{18750,6},{18875,6},{20480,5},{20482,5},{21875,8},{22000,8},{31250,8},{31375,8},{32768,5},{32770,5},{34375,6},{34500,6},{36864,5},{36866,5},{37500,8},{37625,8},{46875,6},{47000,6},{49152,5},{49154,5},{50000,2},{50125,2},{53125,6},{53248,5},{53250,1}});\\n\\n size = 82000;\\n BC_MOD_PRE.put(size, new int[][] {{0,1},{16,5},{64,5},{80,5},{125,6},{625,6},{750,6},{3125,6},{3250,6},{3750,6},{3875,6},{16384,5},{16400,5},{16448,5},{16464,5},{65536,5},{65552,5},{65600,5},{65616,5},{78125,6},{78250,6},{78750,6},{78875,6},{81250,6},{81375,6},{81875,6},{81920,5},{81936,5},{81984,5},{82000,1}});\\n }\\n\\n public boolean hasSameDigits(String s) {\\n List<Integer> digits = new ArrayList<>();\\n for (char c : s.toCharArray()) {\\n digits.add(c - '0');\\n }\\n int n = digits.size() - 2;\\n Integer last = BC_MOD_PRE.floorKey(n);\\n while (last != null) {\\n List<Integer> next = new ArrayList<>();\\n for (int i = 0; i + last < digits.size(); i++) {\\n int result = 0;\\n for (int[] map : BC_MOD_PRE.get(last)) {\\n result += map[1] * digits.get(i + map[0]);\\n }\\n next.add(result % 10);\\n }\\n digits = next;\\n n = digits.size() - 2;\\n last = BC_MOD_PRE.floorKey(n);\\n }\\n if (digits.size() == 2) {\\n return digits.get(0) == digits.get(1);\\n }\\n return hasSameDigits(digits);\\n }\\n\\n private boolean hasSameDigits(List<Integer> digits) {\\n int n = digits.size() - 2;\\n\\n long b = 1;\\n\\n int[] bc = new int[n + 1];\\n bc[0] = 1;\\n for (int i = 1; i <= n / 2; i++) {\\n b = b * (n - i + 1) / i;\\n bc[i] = (int) (b % 10);\\n }\\n\\n int r1 = 0;\\n for (int i = 0; i < digits.size() - 1; i++) {\\n r1 += digits.get(i) * bc[Math.min(i, n - i)];\\n r1 %= 10;\\n }\\n int r2 = 0;\\n for (int i = 1; i < digits.size(); i++) {\\n r2 += digits.get(i) * bc[Math.min(i - 1, n - i + 1)];\\n r2 %= 10;\\n }\\n return r1 == r2;\\n }\\n}\"], [46700, 0.4831, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n\\n int[] mods5 = computeNcKMod5(n - 2);\\n int t5 = 0;\\n for (int i = 0; i < mods5.length; i++) {\\n int d = (s.charAt(i) - s.charAt(i + 1));\\n t5 += d * mods5[i];\\n }\\n if (t5%5 != 0) return false;\\n\\n int[] mods2 = computeNcKMod2(n - 2);\\n int t2 = 0;\\n for (int i = 0; i < mods2.length; i++) {\\n int d = (s.charAt(i) - s.charAt(i + 1));\\n t2 += d * mods2[i];\\n }\\n return t2 % 2 == 0;\\n }\\n\\n public int[] computeNcKMod5(int n) {\\n int[] result = new int[n + 1];\\n result[0] = 1; // nC0 = 1\\n result[n] = 1; // nC0 = 1\\n\\n int current = 1;\\n int currentPow = 0;\\n int[] inv_5 = new int[] { 1, 1, 3, 2, 4 };\\n int[][] mul5 = new int[5][5];\\n int[][] inv5 = new int[5][5];\\n for (int i = 1; i < 5; i++) {\\n for (int j = 1; j < 5; j++) {\\n mul5[i][j] = (i * j) % 5;\\n inv5[i][j] = (i * inv_5[j]) % 5;\\n }\\n }\\n for (int k = 1; k <= n; k++) {\\n int[] up = reducePower(n - k + 1, 5);\\n int[] down = reducePower(k, 5);\\n currentPow += (up[0] - down[0]);\\n current = mul5[current][up[1]];\\n current = inv5[current][down[1]];\\n\\n result[k] = currentPow == 0 ? current : 0;\\n result[n - k] = result[k];\\n if (n - k <= k)\\n break;\\n }\\n\\n return result;\\n }\\n\\n public int[] computeNcKMod2(int n) {\\n int[] result = new int[n + 1];\\n result[0] = 1; // nC0 = 1\\n result[n] = 1; // nC0 = 1\\n\\n int current = 1;\\n int currentPow = 0;\\n\\n for (int k = 1; k <= n; k++) {\\n int[] up = reducePower(n - k + 1, 2);\\n int[] down = reducePower(k, 2);\\n currentPow += (up[0] - down[0]);\\n result[k] = currentPow == 0 ? current : 0;\\n result[n - k] = result[k];\\n if (n - k <= k)\\n break;\\n }\\n\\n return result;\\n }\\n\\n int[] reducePower(int n, int p) {\\n int c = 0;\\n while (n % p == 0) {\\n c++;\\n n /= p;\\n }\\n return new int[] { c, n % p };\\n }\\n}\"], [47000, 0.4831, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n\\n int[] mods5 = computeNcKMod5(n - 2);\\n int t5 = 0;\\n for (int i = 0; i < mods5.length; i++) {\\n int d = (s.charAt(i) - s.charAt(i + 1));\\n t5 += d * mods5[i];\\n }\\n if (t5%5 != 0) return false;\\n\\n int[] mods2 = computeNcKMod2(n - 2);\\n int t2 = 0;\\n for (int i = 0; i < mods2.length; i++) {\\n int d = (s.charAt(i) - s.charAt(i + 1));\\n t2 += d * mods2[i];\\n }\\n return t2 % 2 == 0;\\n }\\n\\n public int[] computeNcKMod5(int n) {\\n int[] result = new int[n + 1];\\n result[0] = 1; // nC0 = 1\\n result[n] = 1; // nC0 = 1\\n\\n int current = 1;\\n int currentPow = 0;\\n int[] inv_5 = new int[] { 1, 1, 3, 2, 4 };\\n int[][] mul5 = new int[5][5];\\n int[][] inv5 = new int[5][5];\\n for (int i = 1; i < 5; i++) {\\n for (int j = 1; j < 5; j++) {\\n mul5[i][j] = (i * j) % 5;\\n inv5[i][j] = (i * inv_5[j]) % 5;\\n }\\n }\\n for (int k = 1; k <= n; k++) {\\n int[] up = reducePower(n - k + 1, 5);\\n int[] down = reducePower(k, 5);\\n currentPow += (up[0] - down[0]);\\n current = mul5[current][up[1]];\\n current = inv5[current][down[1]];\\n\\n result[k] = currentPow == 0 ? current : 0;\\n result[n - k] = result[k];\\n if (n - k <= k)\\n break;\\n }\\n\\n return result;\\n }\\n\\n public int[] computeNcKMod2(int n) {\\n int[] result = new int[n + 1];\\n result[0] = 1; // nC0 = 1\\n result[n] = 1; // nC0 = 1\\n\\n int current = 1;\\n int currentPow = 0;\\n\\n for (int k = 1; k <= n; k++) {\\n int[] up = reducePower(n - k + 1, 2);\\n int[] down = reducePower(k, 2);\\n currentPow += (up[0] - down[0]);\\n result[k] = currentPow == 0 ? current : 0;\\n result[n - k] = result[k];\\n if (n - k <= k)\\n break;\\n }\\n\\n return result;\\n }\\n\\n int[] reducePower(int n, int p) {\\n int c = 0;\\n while (n % p == 0) {\\n c++;\\n n /= p;\\n }\\n return new int[] { c, n % p };\\n }\\n}\"], [47200, 0.4831, \"class Solution {//\\u65b0\\u77e5\\u8bc6\\uff0c\\u4e0d\\u4f1a\\n private static final int MOD = 10;\\n private static final int MX = 100_000;\\n\\n private static final int[] f = new int[MX + 1];\\n private static final int[] invF = new int[MX + 1];\\n private static final int[] p2 = new int[MX + 1];\\n private static final int[] p5 = new int[MX + 1];\\n\\n static {\\n f[0] = 1;\\n for (int i = 1; i <= MX; i++) {\\n int x = i;\\n // \\u8ba1\\u7b97 2 \\u7684\\u5e42\\u6b21\\n int e2 = Integer.numberOfTrailingZeros(x);\\n x >>= e2;\\n // \\u8ba1\\u7b97 5 \\u7684\\u5e42\\u6b21\\n int e5 = 0;\\n while (x % 5 == 0) {\\n e5++;\\n x /= 5;\\n }\\n f[i] = f[i - 1] * x % MOD;\\n p2[i] = p2[i - 1] + e2;\\n p5[i] = p5[i - 1] + e5;\\n }\\n\\n invF[MX] = pow(f[MX], 3); // \\u6b27\\u62c9\\u5b9a\\u7406\\u6c42\\u9006\\u5143\\n for (int i = MX; i > 0; i--) {\\n int x = i;\\n x >>= Integer.numberOfTrailingZeros(x);\\n while (x % 5 == 0) {\\n x /= 5;\\n }\\n invF[i - 1] = invF[i] * x % MOD;\\n }\\n }\\n\\n private static int pow(int x, int n) {\\n int res = 1;\\n while (n > 0) {\\n if (n % 2 > 0) {\\n res = res * x % MOD;\\n }\\n x = x * x % MOD;\\n n /= 2;\\n }\\n return res;\\n }\\n\\n private int comb(int n, int k) {\\n // \\u7531\\u4e8e\\u6bcf\\u9879\\u90fd < 10\\uff0c\\u6240\\u4ee5\\u65e0\\u9700\\u4e2d\\u9014\\u53d6\\u6a21\\n return f[n] * invF[k] * invF[n - k] *\\n pow(2, p2[n] - p2[k] - p2[n - k]) *\\n pow(5, p5[n] - p5[k] - p5[n - k]) % MOD;\\n }\\n\\n public boolean hasSameDigits(String S) {\\n char[] s = S.toCharArray();\\n int diff = 0;\\n for (int i = 0; i < s.length - 1; i++) {\\n diff += comb(s.length - 2, i) * (s[i] - s[i + 1]);\\n }\\n return diff % MOD == 0;\\n }\\n}\\n\\n// \\u4f5c\\u8005\\uff1a\\u7075\\u8336\\u5c71\\u827e\\u5e9c\\n// \\u94fe\\u63a5\\uff1ahttps://leetcode.cn/problems/check-if-digits-are-equal-in-string-after-operations-ii/solutions/3086169/mo-shu-wei-he-shu-shi-de-zu-he-shu-by-en-8x7t/\\n// \\u6765\\u6e90\\uff1a\\u529b\\u6263\\uff08LeetCode\\uff09\\n// \\u8457\\u4f5c\\u6743\\u5f52\\u4f5c\\u8005\\u6240\\u6709\\u3002\\u5546\\u4e1a\\u8f6c\\u8f7d\\u8bf7\\u8054\\u7cfb\\u4f5c\\u8005\\u83b7\\u5f97\\u6388\\u6743\\uff0c\\u975e\\u5546\\u4e1a\\u8f6c\\u8f7d\\u8bf7\\u6ce8\\u660e\\u51fa\\u5904\\u3002\"], [47300, 0.4831, \"class Solution {//\\u65b0\\u77e5\\u8bc6\\uff0c\\u4e0d\\u4f1a\\n private static final int MOD = 10;\\n private static final int MX = 100_000;\\n\\n private static final int[] f = new int[MX + 1];\\n private static final int[] invF = new int[MX + 1];\\n private static final int[] p2 = new int[MX + 1];\\n private static final int[] p5 = new int[MX + 1];\\n\\n static {\\n f[0] = 1;\\n for (int i = 1; i <= MX; i++) {\\n int x = i;\\n // \\u8ba1\\u7b97 2 \\u7684\\u5e42\\u6b21\\n int e2 = Integer.numberOfTrailingZeros(x);\\n x >>= e2;\\n // \\u8ba1\\u7b97 5 \\u7684\\u5e42\\u6b21\\n int e5 = 0;\\n while (x % 5 == 0) {\\n e5++;\\n x /= 5;\\n }\\n f[i] = f[i - 1] * x % MOD;\\n p2[i] = p2[i - 1] + e2;\\n p5[i] = p5[i - 1] + e5;\\n }\\n\\n invF[MX] = pow(f[MX], 3); // \\u6b27\\u62c9\\u5b9a\\u7406\\u6c42\\u9006\\u5143\\n for (int i = MX; i > 0; i--) {\\n int x = i;\\n x >>= Integer.numberOfTrailingZeros(x);\\n while (x % 5 == 0) {\\n x /= 5;\\n }\\n invF[i - 1] = invF[i] * x % MOD;\\n }\\n }\\n\\n private static int pow(int x, int n) {\\n int res = 1;\\n while (n > 0) {\\n if (n % 2 > 0) {\\n res = res * x % MOD;\\n }\\n x = x * x % MOD;\\n n /= 2;\\n }\\n return res;\\n }\\n\\n private int comb(int n, int k) {\\n // \\u7531\\u4e8e\\u6bcf\\u9879\\u90fd < 10\\uff0c\\u6240\\u4ee5\\u65e0\\u9700\\u4e2d\\u9014\\u53d6\\u6a21\\n return f[n] * invF[k] * invF[n - k] *\\n pow(2, p2[n] - p2[k] - p2[n - k]) *\\n pow(5, p5[n] - p5[k] - p5[n - k]) % MOD;\\n }\\n\\n public boolean hasSameDigits(String S) {\\n char[] s = S.toCharArray();\\n int diff = 0;\\n for (int i = 0; i < s.length - 1; i++) {\\n diff += comb(s.length - 2, i) * (s[i] - s[i + 1]);\\n }\\n return diff % MOD == 0;\\n }\\n}\\n\\n// \\u4f5c\\u8005\\uff1a\\u7075\\u8336\\u5c71\\u827e\\u5e9c\\n// \\u94fe\\u63a5\\uff1ahttps://leetcode.cn/problems/check-if-digits-are-equal-in-string-after-operations-ii/solutions/3086169/mo-shu-wei-he-shu-shi-de-zu-he-shu-by-en-8x7t/\\n// \\u6765\\u6e90\\uff1a\\u529b\\u6263\\uff08LeetCode\\uff09\\n// \\u8457\\u4f5c\\u6743\\u5f52\\u4f5c\\u8005\\u6240\\u6709\\u3002\\u5546\\u4e1a\\u8f6c\\u8f7d\\u8bf7\\u8054\\u7cfb\\u4f5c\\u8005\\u83b7\\u5f97\\u6388\\u6743\\uff0c\\u975e\\u5546\\u4e1a\\u8f6c\\u8f7d\\u8bf7\\u6ce8\\u660e\\u51fa\\u5904\\u3002\"], [47500, 0.4831, \"class Solution {\\n // Precomputed C(a, b) mod 5 for a, b from 0 to 4\\n private static final int[][] c_table = {\\n {1, 0, 0, 0, 0}, // C(0, b)\\n {1, 1, 0, 0, 0}, // C(1, b)\\n {1, 2, 1, 0, 0}, // C(2, b)\\n {1, 3, 3, 1, 0}, // C(3, b)\\n {1, 4, 1, 4, 1} // C(4, b)\\n };\\n private static final int D = 8; // Max base 5 digits for m <= 10^5 (since 5^7 < 10^5 < 5^8)\\n\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int[] digits = new int[n];\\n for (int i = 0; i < n; i++) {\\n digits[i] = s.charAt(i) - '0';\\n }\\n\\n int m = n - 2;\\n int[] m_digits = getBase5Digits(m); // Base 5 digits of m\\n long sum1 = 0;\\n long sum2 = 0;\\n\\n for (int k = 0; k <= m; k++) {\\n int[] k_digits = getBase5Digits(k); // Base 5 digits of k\\n // Compute C(m, k) mod 5 using Lucas' Theorem\\n int c_mod_5 = computeCModP(m_digits, k_digits, 5);\\n // Compute C(m, k) mod 2 using binary property\\n int c_mod_2 = ((m & k) == k) ? 1 : 0;\\n // Find coeff such that coeff \\u2261 c_mod_2 (mod 2) and coeff \\u2261 c_mod_5 (mod 5)\\n int coeff = findCoeff(c_mod_2, c_mod_5);\\n // Update sums\\n sum1 = (sum1 + (long) coeff * digits[k]) % 10;\\n sum2 = (sum2 + (long) coeff * digits[k + 1]) % 10;\\n }\\n\\n return sum1 == sum2;\\n }\\n\\n // Convert number to base 5 digits (up to D digits)\\n private int[] getBase5Digits(int x) {\\n int[] digits = new int[D];\\n for (int i = 0; i < D && x > 0; i++) {\\n digits[i] = x % 5;\\n x /= 5;\\n }\\n return digits;\\n }\\n\\n // Compute C(m, k) mod p using precomputed table and base p digits\\n private int computeCModP(int[] m_digits, int[] k_digits, int p) {\\n int result = 1;\\n for (int i = 0; i < D; i++) {\\n int mi = m_digits[i];\\n int ki = k_digits[i];\\n if (ki > mi) return 0; // C(mi, ki) = 0 if ki > mi\\n result = (result * c_table[mi][ki]) % p;\\n }\\n return result;\\n }\\n\\n // Find x (0-9) such that x \\u2261 a (mod 2) and x \\u2261 b (mod 5)\\n private int findCoeff(int a, int b) {\\n for (int x = 0; x < 10; x++) {\\n if (x % 2 == a && x % 5 == b) return x;\\n }\\n return -1; // Should never occur due to CRT\\n }\\n}\"], [47600, 0.9662, \"import java.util.*;\\n\\nclass Solution {\\n private static final int MOD = 10;\\n private static final int MX = 100_000;\\n\\n private static final int[] f = new int[MX + 1];\\n private static final int[] invF = new int[MX + 1];\\n private static final int[] p2 = new int[MX + 1];\\n private static final int[] p5 = new int[MX + 1];\\n\\n static {\\n f[0] = 1;\\n for (int i = 1; i <= MX; i++) {\\n int x = i;\\n // \\u8ba1\\u7b97 2 \\u7684\\u5e42\\u6b21\\n int e2 = Integer.numberOfTrailingZeros(x);\\n x >>= e2;\\n // \\u8ba1\\u7b97 5 \\u7684\\u5e42\\u6b21\\n int e5 = 0;\\n while (x % 5 == 0) {\\n e5++;\\n x /= 5;\\n }\\n f[i] = f[i - 1] * x % MOD;\\n p2[i] = p2[i - 1] + e2;\\n p5[i] = p5[i - 1] + e5;\\n }\\n\\n invF[MX] = pow(f[MX], 3); // \\u6b27\\u62c9\\u5b9a\\u7406\\u6c42\\u9006\\u5143\\n for (int i = MX; i > 0; i--) {\\n int x = i;\\n x >>= Integer.numberOfTrailingZeros(x);\\n while (x % 5 == 0) {\\n x /= 5;\\n }\\n invF[i - 1] = invF[i] * x % MOD;\\n }\\n }\\n\\n private static int pow(int x, int n) {\\n int res = 1;\\n while (n > 0) {\\n if (n % 2 > 0) {\\n res = res * x % MOD;\\n }\\n x = x * x % MOD;\\n n /= 2;\\n }\\n return res;\\n }\\n\\n private int comb(int n, int k) {\\n // \\u7531\\u4e8e\\u6bcf\\u9879\\u90fd < 10\\uff0c\\u6240\\u4ee5\\u65e0\\u9700\\u4e2d\\u9014\\u53d6\\u6a21\\n return f[n] * invF[k] * invF[n - k] *\\n pow(2, p2[n] - p2[k] - p2[n - k]) *\\n pow(5, p5[n] - p5[k] - p5[n - k]) % MOD;\\n }\\n\\n public boolean hasSameDigits(String S) {\\n char[] s = S.toCharArray();\\n int diff = 0;\\n for (int i = 0; i < s.length - 1; i++) {\\n diff += comb(s.length - 2, i) * (s[i] - s[i + 1]);\\n }\\n return diff % MOD == 0;\\n }\\n\\n static void tr(Object... o) {\\n System.out.println(Arrays.deepToString(o));\\n }\\n\\n}\"], [47900, 0.4831, \"import java.lang.reflect.Array;\\nimport java.util.ArrayList;\\nimport java.util.Arrays;\\nimport java.util.Collection;\\nimport java.util.List;\\nimport java.util.function.IntFunction;\\nimport java.util.function.IntToLongFunction;\\nimport java.util.function.IntUnaryOperator;\\nimport java.util.function.Supplier;\\n\\nclass Solution {\\n public boolean hasSameDigits(String s) {\\n var n = s.length();\\n var modCombos5 = new LongOps.SmallPrimePowerModCombos(n - 2, 5);\\n var y02 = 0;\\n var y05 = 0;\\n var y12 = 0;\\n var y15 = 0;\\n for (int i = 0; i <= n - 2; i++) {\\n var c2 = nChooseKmod2(n - 2, i);\\n var c5 = modCombos5.nChooseK(n - 2, i);\\n\\n int d0 = s.charAt(n - 2 - i) - '0';\\n y02 += c2 * d0;\\n y05 += c5 * d0;\\n\\n int d1 = s.charAt(n - 1 - i) - '0';\\n y12 += c2 * d1;\\n y15 += c5 * d1;\\n }\\n\\n y02 %= 2;\\n y12 %= 2;\\n y05 %= 5;\\n y15 %= 5;\\n return y02 == y12 && y05 == y15;\\n }\\n\\n private static int nChooseKmod2(int n, int k) {\\n return (k & n) == k ? 1 : 0;\\n }\\n\\n static class LongOps {\\n public static final long FLOOR_OF_SQRT_LONG_MAX = 3037000499L;\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n public static long floorOfSqrt(long x) {\\n if (x < 0) throw new IllegalArgumentException(\\\"\\\" + x);\\n\\n var l = 0L;\\n var r = FLOOR_OF_SQRT_LONG_MAX;\\n\\n var res = -1L;\\n do {\\n var m = l + (r - l) / 2;\\n if (m * m <= x) {\\n res = m;\\n l = m + 1;\\n } else {\\n r = m - 1;\\n }\\n } while (l <= r);\\n\\n return res;\\n }\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n public static long modPow(long a, long b, long mod) {\\n if (b < 0) throw new IllegalArgumentException(\\\"b=\\\" + b);\\n checkMod(mod);\\n\\n a %= mod;\\n var res = 1L % mod;\\n while (b != 0) {\\n if ((b & 1) != 0) {\\n res = (res * a) % mod;\\n }\\n\\n a = (a * a) % mod;\\n b >>= 1;\\n }\\n\\n return res;\\n }\\n\\n public static long modInv(long a, long mod) {\\n if (mod <= 0) {\\n throw new IllegalArgumentException(\\\"mod=\\\" + mod);\\n }\\n\\n var eucl = extEuclid(a, mod);\\n if (eucl.gcd != 1) {\\n return 0;\\n }\\n\\n return eucl.x < 0 ? eucl.x + mod : eucl.x;\\n }\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n public static long[] primeModInvsTable(int n, long primeMod) {\\n if (n < 1 || primeMod <= n) {\\n throw new IllegalArgumentException(\\\"n=\\\" + n + \\\", primeMod=\\\" + primeMod);\\n }\\n\\n var table = new long[n + 1];\\n table[0] = 0;\\n table[1] = 1;\\n\\n for (int i = 2; i < table.length; i++) {\\n long ir = table[(int) (primeMod % i)];\\n table[i] = ir == 0 ? 0 : primeMod - (primeMod / i * ir) % primeMod;\\n }\\n return table;\\n }\\n\\n public static class GcdWithFactors {\\n private long gcd;\\n private long x;\\n private long y;\\n\\n private GcdWithFactors() {\\n\\n }\\n\\n public long gcd() {\\n return gcd;\\n }\\n\\n public long x() {\\n return x;\\n }\\n\\n public long y() {\\n return y;\\n }\\n }\\n\\n public static GcdWithFactors extEuclid(long a, long b) {\\n var res = new GcdWithFactors();\\n extEuclid0(a, b, res);\\n return res;\\n }\\n\\n private static void extEuclid0(long a, long b, GcdWithFactors res) {\\n if (b == 0) {\\n res.gcd = a;\\n res.x = 1;\\n res.y = 0;\\n } else {\\n extEuclid0(b, a % b, res);\\n var tmpX = res.x;\\n var tmpY = res.y;\\n\\n res.x = tmpY;\\n res.y = tmpX - tmpY * (a / b);\\n }\\n }\\n\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n private static void checkMod(long mod) {\\n if (mod < 1 || mod > FLOOR_OF_SQRT_LONG_MAX) {\\n throw new IllegalArgumentException(\\\"mod=\\\" + mod);\\n }\\n }\\n\\n /**\\n * Calculates binomial coefficients n over k modulo prime powers p^e even if p is smaller or equal to n.\\n */\\n public static class SmallPrimePowerModCombos {\\n final int e;\\n final int p;\\n final int mod;\\n final int[] pPowersInFactorials;\\n final int[] factorialsWithoutPowers;\\n\\n public SmallPrimePowerModCombos(int n, int p, int e) {\\n if (p <= 1 || e < 1) {\\n throw new IllegalArgumentException(\\\"n=\\\" + n + \\\", p=\\\" + p + \\\", e=\\\" + e);\\n }\\n\\n var mod = p;\\n for (int i = 1; i < e; i++) {\\n mod = Math.multiplyExact(mod, p);\\n }\\n\\n this.e = e;\\n this.p = p;\\n this.mod = mod;\\n\\n this.pPowersInFactorials = new int[n + 1];\\n this.factorialsWithoutPowers = new int[n + 1];\\n\\n factorialsWithoutPowers[0] = 1;\\n for (int i = 1, ip = 1; i <= n; i++, ip++) {\\n pPowersInFactorials[i] = pPowersInFactorials[i - 1];\\n\\n if (ip != p) {\\n factorialsWithoutPowers[i] = modMul(i, factorialsWithoutPowers[i - 1]);\\n } else {\\n var ii = i;\\n do {\\n pPowersInFactorials[i]++;\\n ii /= p;\\n } while (ii % p == 0);\\n\\n factorialsWithoutPowers[i] = modMul(ii, factorialsWithoutPowers[i - 1]);\\n ip = 0;\\n }\\n\\n }\\n }\\n\\n public SmallPrimePowerModCombos(int n, int p) {\\n this(n, p, 1);\\n }\\n\\n public int nChooseK(int n, int k) {\\n var powers = pPowersInFactorials[n] - pPowersInFactorials[k] - pPowersInFactorials[n - k];\\n if (powers >= e) return 0;\\n\\n var res = 1;\\n for (int i = 0; i < powers; i++) {\\n res *= p;\\n }\\n\\n res = modMul(res, factorialsWithoutPowers[n]);\\n res = modMul(res, modInv(factorialsWithoutPowers[k], mod));\\n res = modMul(res, modInv(factorialsWithoutPowers[n - k], mod));\\n return res;\\n }\\n\\n private int modMul(long a, long b) {\\n return (int) ((a * b) % mod);\\n }\\n }\\n\\n public record PrimeFactor(long p, int q) {}\\n\\n public static List<PrimeFactor> primeFactorsOf(long n) {\\n if (n <= 0) {\\n throw new IllegalArgumentException(\\\"n=\\\" + n);\\n }\\n\\n var res = new ArrayList<PrimeFactor>();\\n for (long p = 2; p * p <= n; p++) {\\n if (n % p == 0) {\\n var e = 0;\\n do {\\n n /= p;\\n e++;\\n } while (n % p == 0);\\n\\n res.add(new PrimeFactor(p, e));\\n }\\n }\\n\\n if (n > 1) {\\n res.add(new PrimeFactor(n, 1));\\n }\\n\\n return res;\\n }\\n }\\n\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int minOf(int... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Integer.MAX_VALUE;\\n for (int i : is) {\\n res = Math.min(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int maxOf(int... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Integer.MIN_VALUE;\\n for (int i : is) {\\n res = Math.max(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long minOf(long... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Long.MAX_VALUE;\\n for (long i : is) {\\n res = Math.min(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long maxOf(long... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Long.MIN_VALUE;\\n for (long i : is) {\\n res = Math.max(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> ExtendedArrayList<T> fillList(int n, Supplier<T> supplier) {\\n return fillList(n, ignore -> supplier.get());\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> ExtendedArrayList<T> fillList(int n, IntFunction<T> valueAt) {\\n var res = new ExtendedArrayList<T>(n);\\n for (int i = 0; i < n; i++) {\\n res.add(valueAt.apply(i));\\n }\\n\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> T[] fillArray(int n, Class<T> clazz, Supplier<T> supplier) {\\n return fillArray(n, clazz, ignore -> supplier.get());\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> T[] fillArray(int n, Class<T> clazz, IntFunction<T> valueAt) {\\n @SuppressWarnings(\\\"unchecked\\\") var res = (T[]) Array.newInstance(clazz, n);\\n\\n for (int i = 0; i < n; i++) {\\n res[i] = valueAt.apply(i);\\n }\\n\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\", \\\"SameParameterValue\\\"})\\n static <T> T[] fillArray(int n, T value) {\\n @SuppressWarnings(\\\"unchecked\\\") var res = (T[]) Array.newInstance(value.getClass(), n);\\n Arrays.fill(res, value);\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int[] fillIntArray(int n, IntUnaryOperator valueAt) {\\n var res = new int[n];\\n for (int i = 0; i < n; i++) {\\n res[i] = valueAt.applyAsInt(i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int[] fillIntArray(int n, int value) {\\n var res = new int[n];\\n Arrays.fill(res, value);\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long[] fillLongArray(int n, IntToLongFunction valueAt) {\\n var res = new long[n];\\n for (int i = 0; i < n; i++) {\\n res[i] = valueAt.applyAsLong(i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long[] fillLongArray(int n, long value) {\\n var res = new long[n];\\n Arrays.fill(res, value);\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long gcd(long a, long b) {\\n while (b != 0) {\\n var bb = a % b;\\n a = b;\\n b = bb;\\n }\\n\\n return a;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int gcd(int a, int b) {\\n while (b != 0) {\\n var bb = a % b;\\n a = b;\\n b = bb;\\n }\\n\\n return a;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\", \\\"UnusedReturnValue\\\"})\\n static class ExtendedArrayList<T> extends ArrayList<T> {\\n public ExtendedArrayList(int initialCapacity) {\\n super(initialCapacity);\\n }\\n\\n public ExtendedArrayList() {\\n\\n }\\n\\n public ExtendedArrayList(Collection<? extends T> c) {\\n super(c);\\n }\\n\\n T getFromEnd(int offset) {\\n return get(size() - offset - 1);\\n }\\n\\n T getFst() {\\n return get(0);\\n }\\n\\n T getLst() {\\n return getFromEnd(0);\\n }\\n\\n T removeLst() {\\n return remove(size() - 1);\\n }\\n }\\n}\"], [48000, 1.9324, \"import java.util.Arrays; // Required for Arrays.fill if used, though not strictly needed here\\n\\nclass Solution {\\n\\n /**\\n * Checks if the digits satisfy a condition related to binomial coefficients\\n * modulo 2 and 5 applied to adjacent digit differences.\\n * Optimized for speed.\\n *\\n * @param s The input string of digits.\\n * @return boolean result based on the specific condition.\\n */\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n // The algorithm uses C(n-2, k). Assumes n >= 2.\\n // Handle cases n=0, n=1 if they are possible according to problem spec.\\n if (n < 2) {\\n // Define behavior for short strings based on the problem this code solves.\\n // Returning false as a placeholder.\\n return false;\\n }\\n\\n int N = n - 2; // The 'n' used in nCk calculations\\n\\n // Optimization 1: Use faster computation for nCk mod 2\\n int[] mods2 = computeNcKMod2Optimized(N);\\n\\n // Use the original (but potentially corrected reducePower) for nCk mod 5\\n int[] mods5 = computeNcKMod5(N);\\n\\n int t5 = 0;\\n int t2 = 0;\\n\\n // Optimization 2: Use toCharArray() - potentially minor gain\\n char[] chars = s.toCharArray();\\n\\n // Optimization 3: Merge loops for t2 and t5 calculation\\n // The loop computes sum_{i=0}^{N} (d_i - d_{i+1}) * C(N, i) mod p\\n // where N = n-2. Indices i go from 0 to N.\\n // Difference uses chars[i] and chars[i+1]. Max index is N+1.\\n // Since n = N+2, max index N+1 is valid for chars array (length n).\\n for (int i = 0; i <= N; i++) {\\n // Calculate difference between adjacent digits\\n int d = (chars[i] - chars[i + 1]); // chars[i+1] is safe up to i=N\\n\\n // Accumulate weighted sums\\n // No need for intermediate modulo, standard ints should suffice unless N is huge\\n t5 += d * mods5[i];\\n t2 += d * mods2[i];\\n }\\n\\n // Final check: divisibility by 5 and 2\\n // Java's % operator handles negative numbers correctly for (t % p == 0) check\\n return (t5 % 5 == 0) && (t2 % 2 == 0);\\n }\\n\\n /**\\n * Computes nCk mod 5 for k from 0 to n.\\n * Uses iterative approach with power tracking.\\n * Depends on the corrected `reducePower`.\\n */\\n public int[] computeNcKMod5(int n) {\\n int[] result = new int[n + 1];\\n if (n < 0) return result; // Handle invalid input\\n\\n // Precompute tables for multiplication and modular inverse modulo 5\\n // Done only once per call to computeNcKMod5\\n int[] inv_5 = new int[] { 1, 1, 3, 2, 4 }; // inv_5[0] unused\\n int[][] mul5 = new int[5][5];\\n int[][] inv5 = new int[5][5];\\n for (int i = 1; i < 5; i++) {\\n for (int j = 1; j < 5; j++) {\\n mul5[i][j] = (i * j) % 5;\\n inv5[i][j] = (i * inv_5[j]) % 5;\\n }\\n }\\n\\n result[0] = 1; // nC0 = 1\\n if (n == 0) return result;\\n // nCn = 1. Will be set by symmetry later if using loop up to n/2.\\n // Explicitly setting result[n]=1 isn't strictly needed if loop handles symmetry right.\\n\\n int current_R = 1; // The non-p part of nCk mod p\\n int current_Pow = 0; // The exponent of p in nCk\\n\\n // Calculate iteratively using C(n, k) = C(n, k-1) * (n-k+1) / k\\n // Loop up to n, calculating each term. Symmetry can optimize this.\\n // Let's use symmetry optimization from original code: loop up to n/2\\n result[n] = 1; // Set nCn = 1 explicitly for symmetry to work\\n\\n for (int k = 1; k <= n / 2; k++) {\\n // Get power and non-p part for numerator (n-k+1) and denominator (k)\\n int[] up = reducePower(n - k + 1, 5); // {pow5, (n-k+1)/5^pow5 mod 5}\\n int[] down = reducePower(k, 5); // {pow5, k/5^pow5 mod 5}\\n\\n current_Pow += (up[0] - down[0]);\\n\\n // Update the non-p part modulo 5 using tables\\n // Need to handle case where up[1] or down[1] is 0?\\n // reducePower returns val % p. If val (the non-p part) is 0, result is 0.\\n // This should only happen if n-k+1=0 or k=0, which are excluded by loop/inputs.\\n // If up[1] or down[1] can be 0, tables need checks. Assume they are 1,2,3,4.\\n if (up[1] == 0 || down[1] == 0) {\\n // This case implies n-k+1 or k was a multiple of 5, but the non-p part became 0?\\n // This shouldn't happen with the corrected reducePower returning val % p.\\n // If val % p is 0, it means val itself was 0? Only if input n=0.\\n // Let's assume inputs to reducePower are > 0.\\n // However, val % p could be 0 if val is a multiple of p. Check reducePower.\\n // Corrected reducePower returns val % p. If n=10, p=5 -> val=2, val%p = 2. OK.\\n // If n=25, p=5 -> val=1, val%p = 1. OK.\\n // If n=125, p=5 -> val=1, val%p = 1. OK.\\n // So up[1] and down[1] should be in [1, 2, 3, 4].\\n // Need to handle current_R == 0? It starts at 1. Can it become 0?\\n // If C(n,k) is divisible by 5 (current_Pow > 0), result[k]=0.\\n // If current_R * up[1] becomes 0 mod 5, current_R will be 0.\\n // mul5[0][j] is not defined. inv5[0][j] is not defined.\\n // Let's assume current_R stays non-zero if current_Pow == 0.\\n // If current_Pow > 0, the value doesn't matter as result[k] is 0.\\n }\\n\\n if (current_Pow == 0) { // Only update current_R if result is non-zero mod 5\\n current_R = mul5[current_R][up[1]];\\n current_R = inv5[current_R][down[1]];\\n result[k] = current_R;\\n } else {\\n result[k] = 0;\\n // If we are calculating C(n,k) = 0 mod 5, we still need to track the\\n // 'potential' non-zero part current_R for the *next* iteration C(n, k+1).\\n // So, update current_R even if result[k] is 0.\\n int next_R = mul5[current_R][up[1]];\\n next_R = inv5[next_R][down[1]];\\n current_R = next_R;\\n }\\n\\n result[n - k] = result[k]; // Use symmetry: nCk = nC(n-k)\\n }\\n\\n // Handle middle element C(n, n/2 + 1) if n is odd\\n if (n % 2 == 1) {\\n int k = (n / 2) + 1;\\n // Calculate C(n,k) based on C(n, k-1) which was the last step in the loop\\n int[] up = reducePower(n - k + 1, 5);\\n int[] down = reducePower(k, 5);\\n current_Pow += (up[0] - down[0]);\\n\\n if (current_Pow == 0) {\\n current_R = mul5[current_R][up[1]];\\n current_R = inv5[current_R][down[1]];\\n result[k] = current_R;\\n } else {\\n result[k] = 0;\\n }\\n }\\n\\n return result;\\n }\\n\\n /**\\n * Optimized computation of nCk mod 2 using Lucas's Theorem property.\\n * (nCk mod 2) == 1 iff (n & k) == k.\\n */\\n public int[] computeNcKMod2Optimized(int n) {\\n int[] result = new int[n + 1];\\n if (n < 0) return result;\\n for (int k = 0; k <= n; k++) {\\n // If (n & k) == k, it means all set bits in k are also set in n.\\n result[k] = ((n & k) == k) ? 1 : 0;\\n }\\n return result;\\n }\\n\\n\\n /**\\n * Helper function: Calculates exponent of p in n! (Legendre's Formula related)\\n * and returns the non-p part of n modulo p.\\n * Returns {exponent of p dividing n, (n / p^exponent) % p}.\\n * Corrected version.\\n *\\n * @param n Number (must be > 0)\\n * @param p Prime number\\n * @return int array: {exponent, non-p part mod p}\\n */\\n int[] reducePower(int n, int p) {\\n // Assume n > 0 based on usage context (k and n-k+1 >= 1)\\n if (n <= 0) {\\n // Should not happen if n >= 2 initially.\\n // Return something indicative or throw error.\\n return new int[]{0, 0}; // Placeholder\\n }\\n\\n int count = 0;\\n int val = n;\\n while (val > 0 && val % p == 0) {\\n count++;\\n val /= p;\\n }\\n // Now val = n / p^count. We need val % p.\\n // If val is 0 (only if original n was 0), result is 0.\\n // Otherwise, val is the part not divisible by p.\\n return new int[] { count, val % p };\\n }\\n\\n // --- Original computeNcKMod2 for reference (Not used in optimized version) ---\\n /*\\n public int[] computeNcKMod2(int n) {\\n int[] result = new int[n + 1];\\n result[0] = 1; // nC0 = 1\\n if (n==0) return result;\\n result[n] = 1; // nCn = 1\\n\\n //int current = 1; // Always 1 mod 2\\n int currentPow = 0;\\n\\n for (int k = 1; k <= n/2; k++) { // Use symmetry\\n int[] up = reducePower(n - k + 1, 2);\\n int[] down = reducePower(k, 2);\\n currentPow += (up[0] - down[0]);\\n result[k] = currentPow == 0 ? 1 : 0; // nCk mod 2 is 1 iff power of 2 is 0\\n result[n - k] = result[k];\\n }\\n // Handle middle element for odd n\\n if (n % 2 == 1) {\\n int k = (n / 2) + 1;\\n int[] up = reducePower(n - k + 1, 2);\\n int[] down = reducePower(k, 2);\\n currentPow += (up[0] - down[0]);\\n result[k] = currentPow == 0 ? 1 : 0;\\n }\\n\\n return result;\\n }\\n */\\n}\"], [48100, 0.4831, \"class Solution {\\n \\n int mod = 10;\\n public boolean hasSameDigits(String s) {\\n char[] ch = s.toCharArray();\\n int n = ch.length, dep = n - 2;\\n long sum1 = 0, sum2 = 0;\\n int[] fact = new int[n + 1], infact = new int[n + 1];\\n int[] p2 = new int[n + 1], p5 = new int[n + 1];\\n\\n fact[0] = 1;\\n for(int i = 1; i <= n; i++) {\\n int e2 = 0, e5 = 0;\\n int x = i;\\n while(x % 2 == 0) { e2++; x /= 2; }\\n while(x % 5 == 0) { e5++; x /= 5; }\\n fact[i] = fact[i - 1] * x % mod;\\n p2[i] = p2[i - 1] + e2;\\n p5[i] = p5[i - 1] + e5;\\n }\\n\\n // infact[n] = pow(fact[n], 3); // \\u6b27\\u62c9\\u5b9a\\u7406\\u6c42\\u9006\\u5143\\n // for (int i = n; i > 0; i--) {\\n // int x = i;\\n // x >>= Integer.numberOfTrailingZeros(x);\\n // while (x % 5 == 0) {\\n // x /= 5;\\n // }\\n // infact[i - 1] = infact[i] * x % mod;\\n // }\\n infact[0] = 1;\\n // infact[1] = pow(fact[1], 3); // \\u6b27\\u62c9\\u5b9a\\u7406\\u6c42\\u9006\\u5143\\n for (int i = 1; i <= n; i++) {\\n // int x = i;\\n // x >>= Integer.numberOfTrailingZeros(x);\\n // while (x % 5 == 0) {\\n // x /= 5;\\n // }\\n infact[i] = pow(fact[i], 3) % mod;\\n }\\n\\n for(int i = 0; i <= n - 2; i++) {\\n int cost = ch[i] - '0';\\n sum1 += cost * fact[dep] * infact[i] * infact[dep - i] * pow(2, p2[dep] - p2[i] - p2[dep - i]) * pow(5, p5[dep] - p5[i] - p5[dep - i]) % mod;\\n sum1 %= mod;\\n }\\n for(int i = 1; i <= n - 1; i++) {\\n int cost = ch[i] - '0';\\n sum2 += cost * fact[dep] * infact[i - 1] * infact[dep - i + 1] * pow(2, p2[dep] - p2[i - 1] - p2[dep - i + 1]) * pow(5, p5[dep] - p5[i - 1] - p5[dep - i + 1]) % mod;\\n sum2 %= mod;\\n }\\n\\n return sum1 == sum2;\\n }\\n\\n int pow(int base, int pow) {\\n if(pow == 1) return base;\\n if(pow == 0) return 1;\\n\\n int half = pow(base, pow / 2);\\n if(pow % 2 == 0) return half * half % mod;\\n return half * half * base % mod;\\n }\\n\\n // int pow(int x, int n) {\\n // int res = 1;\\n // while (n > 0) {\\n // if (n % 2 > 0) {\\n // res = res * x % mod;\\n // }\\n // x = x * x % mod;\\n // n /= 2;\\n // }\\n // return res;\\n // }\\n}\"], [48200, 0.4831, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n String buffer = \\\"3272\\\";\\n boolean breaker = true;\\n if(s.length() >= buffer.length() && breaker){\\n for(int i = 0; i < buffer.length(); i++){\\n if(buffer.charAt(i) != s.charAt(i)){\\n breaker = false;\\n }\\n }\\n if(breaker){\\n return true;\\n } \\n }\\n buffer = \\\"25201\\\";\\n breaker = true;\\n if(s.length() >= buffer.length() && breaker){\\n for(int i = 0; i < buffer.length(); i++){\\n if(buffer.charAt(i) != s.charAt(i)){\\n breaker = false;\\n }\\n }\\n if(breaker){\\n return false;\\n } \\n }\\n buffer = \\\"8734\\\";\\n breaker = true;\\n if(s.length() >= buffer.length() && breaker){\\n for(int i = 0; i < buffer.length(); i++){\\n if(buffer.charAt(i) != s.charAt(i)){\\n breaker = false;\\n }\\n }\\n if(breaker){\\n return true;\\n } \\n }\\n buffer = \\\"60048\\\";\\n breaker = true;\\n if(s.length() >= buffer.length() && breaker){\\n for(int i = 0; i < buffer.length(); i++){\\n if(buffer.charAt(i) != s.charAt(i)){\\n breaker = false;\\n }\\n }\\n if(breaker){\\n return false;\\n } \\n }\\n buffer = \\\"17674\\\";\\n breaker = true;\\n if(s.length() >= buffer.length() && breaker){\\n for(int i = 0; i < buffer.length(); i++){\\n if(buffer.charAt(i) != s.charAt(i)){\\n breaker = false;\\n }\\n }\\n if(breaker){\\n return false;\\n } \\n }\\n buffer = \\\"94326\\\";\\n breaker = true;\\n if(s.length() >= buffer.length() && breaker){\\n for(int i = 0; i < buffer.length(); i++){\\n if(buffer.charAt(i) != s.charAt(i)){\\n breaker = false;\\n }\\n }\\n if(breaker){\\n return false;\\n } \\n }\\n buffer = \\\"1506063\\\";\\n breaker = true;\\n if(s.length() >= buffer.length() && breaker){\\n for(int i = 0; i < buffer.length(); i++){\\n if(buffer.charAt(i) != s.charAt(i)){\\n breaker = false;\\n }\\n }\\n if(breaker){\\n return false;\\n } \\n }\\n buffer = \\\"467645\\\";\\n breaker = true;\\n if(s.length() >= buffer.length() && breaker){\\n for(int i = 0; i < buffer.length(); i++){\\n if(buffer.charAt(i) != s.charAt(i)){\\n breaker = false;\\n }\\n }\\n if(breaker){\\n return false;\\n } \\n }\\n buffer = \\\"91605074038131562\\\";\\n breaker = true;\\n if(s.length() >= buffer.length() && breaker){\\n for(int i = 0; i < buffer.length(); i++){\\n if(buffer.charAt(i) != s.charAt(i)){\\n breaker = false;\\n }\\n }\\n if(breaker){\\n return false;\\n } \\n }\\n buffer = \\\"6935419\\\";\\n breaker = true;\\n if(s.length() >= buffer.length() && breaker){\\n for(int i = 0; i < buffer.length(); i++){\\n if(buffer.charAt(i) != s.charAt(i)){\\n breaker = false;\\n }\\n }\\n if(breaker){\\n return false;\\n } \\n }\\n buffer = \\\"6624456\\\";\\n breaker = true;\\n if(s.length() >= buffer.length() && breaker){\\n for(int i = 0; i < buffer.length(); i++){\\n if(buffer.charAt(i) != s.charAt(i)){\\n breaker = false;\\n }\\n }\\n if(breaker){\\n return false;\\n } \\n }\\n buffer = \\\"1683564\\\";\\n breaker = true;\\n if(s.length() >= buffer.length() && breaker){\\n for(int i = 0; i < buffer.length(); i++){\\n if(buffer.charAt(i) != s.charAt(i)){\\n breaker = false;\\n }\\n }\\n if(breaker){\\n return false;\\n } \\n }\\n buffer = \\\"695004095\\\";\\n breaker = true;\\n if(s.length() >= buffer.length() && breaker){\\n for(int i = 0; i < buffer.length(); i++){\\n if(buffer.charAt(i) != s.charAt(i)){\\n breaker = false;\\n }\\n }\\n if(breaker){\\n return false;\\n } \\n }\\n buffer = \\\"00000000000\\\";\\n breaker = true;\\n if(s.length() >= buffer.length() && breaker){\\n for(int i = 0; i < buffer.length(); i++){\\n if(buffer.charAt(i) != s.charAt(i)){\\n breaker = false;\\n }\\n }\\n if(breaker){\\n return true;\\n } \\n }\\n buffer = \\\"3999009990009\\\";\\n breaker = true;\\n if(s.length() >= buffer.length() && breaker){\\n for(int i = 0; i < buffer.length(); i++){\\n if(buffer.charAt(i) != s.charAt(i)){\\n breaker = false;\\n }\\n }\\n if(breaker){\\n return false;\\n } \\n }\\n char[] digits = new char[s.length()];\\n //char[] newDigits;\\n for(int i = 0; i < s.length(); i++){\\n digits[i] = s.charAt(i);\\n }\\n int length = s.length() - 1;\\n while(length > 1){\\n //newDigits = new char[digits.length - 1];\\n for(int i = 0; i < length; i++){\\n int digit = ((int)(digits[i] + digits[i + 1] - '0')) % 10;\\n digits[i] = (char)(digit + '0');\\n }\\n\\n length--;\\n }\\n s = \\\"\\\" + digits[0] + digits[1];\\n return(s.charAt(0) == s.charAt(1));\\n }\\n}\"], [48300, 0.4831, \"class Solution {\\n \\n int mod = 10;\\n public boolean hasSameDigits(String s) {\\n char[] ch = s.toCharArray();\\n int n = ch.length, dep = n - 2;\\n long sum1 = 0, sum2 = 0;\\n int[] fact = new int[n + 1], infact = new int[n + 1];\\n int[] p2 = new int[n + 1], p5 = new int[n + 1];\\n\\n fact[0] = 1;\\n for(int i = 1; i <= n; i++) {\\n int e2 = 0, e5 = 0;\\n int x = i;\\n while(x % 2 == 0) { e2++; x /= 2; }\\n while(x % 5 == 0) { e5++; x /= 5; }\\n fact[i] = fact[i - 1] * x % mod;\\n p2[i] = p2[i - 1] + e2;\\n p5[i] = p5[i - 1] + e5;\\n }\\n\\n infact[n] = pow(fact[n], 3); // \\u6b27\\u62c9\\u5b9a\\u7406\\u6c42\\u9006\\u5143\\n for (int i = n; i > 0; i--) {\\n int x = i;\\n x >>= Integer.numberOfTrailingZeros(x);\\n while (x % 5 == 0) {\\n x /= 5;\\n }\\n infact[i - 1] = infact[i] * x % mod;\\n }\\n\\n for(int i = 0; i <= n - 2; i++) {\\n int cost = ch[i] - '0';\\n sum1 += cost * fact[dep] * infact[i] * infact[dep - i] * pow(2, p2[dep] - p2[i] - p2[dep - i]) * pow(5, p5[dep] - p5[i] - p5[dep - i]) % mod;\\n sum1 %= mod;\\n }\\n for(int i = 1; i <= n - 1; i++) {\\n int cost = ch[i] - '0';\\n sum2 += cost * fact[dep] * infact[i - 1] * infact[dep - i + 1] * pow(2, p2[dep] - p2[i - 1] - p2[dep - i + 1]) * pow(5, p5[dep] - p5[i - 1] - p5[dep - i + 1]) % mod;\\n sum2 %= mod;\\n }\\n\\n return sum1 == sum2;\\n }\\n\\n int pow(int base, int pow) {\\n if(pow == 1) return base;\\n if(pow == 0) return 1;\\n\\n int half = pow(base, pow / 2);\\n if(pow % 2 == 0) return half * half % mod;\\n return half * half * base % mod;\\n }\\n\\n // int pow(int x, int n) {\\n // int res = 1;\\n // while (n > 0) {\\n // if (n % 2 > 0) {\\n // res = res * x % mod;\\n // }\\n // x = x * x % mod;\\n // n /= 2;\\n // }\\n // return res;\\n // }\\n}\"], [48700, 0.4831, \"import java.lang.reflect.Array;\\nimport java.util.ArrayList;\\nimport java.util.Arrays;\\nimport java.util.Collection;\\nimport java.util.List;\\nimport java.util.function.IntFunction;\\nimport java.util.function.IntToLongFunction;\\nimport java.util.function.IntUnaryOperator;\\nimport java.util.function.Supplier;\\n\\nclass Solution {\\n public boolean hasSameDigits(String s) {\\n var n = s.length();\\n var modCombos5 = new LongOps.SmallPrimePowerModCombos(n - 2, 5);\\n var y02 = 0;\\n var y05 = 0;\\n var y12 = 0;\\n var y15 = 0;\\n for (int i = 0; i <= n - 2; i++) {\\n var c2 = nChooseKmod2(n - 2, i);\\n var c5 = modCombos5.nChooseK(n - 2, i);\\n\\n int d0 = s.charAt(n - 2 - i) - '0';\\n y02 += c2 * d0;\\n y02 %= 2;\\n y05 += c5 * d0;\\n y05 %= 5;\\n\\n int d1 = s.charAt(n - 1 - i) - '0';\\n y12 += c2 * d1;\\n y12 %= 2;\\n y15 += c5 * d1;\\n y15 %= 5;\\n }\\n\\n return y02 == y12 && y05 == y15;\\n }\\n\\n private static int nChooseKmod2(int n, int k) {\\n return (k & n) == k ? 1 : 0;\\n }\\n\\n static class LongOps {\\n public static final long FLOOR_OF_SQRT_LONG_MAX = 3037000499L;\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n public static long floorOfSqrt(long x) {\\n if (x < 0) throw new IllegalArgumentException(\\\"\\\" + x);\\n\\n var l = 0L;\\n var r = FLOOR_OF_SQRT_LONG_MAX;\\n\\n var res = -1L;\\n do {\\n var m = l + (r - l) / 2;\\n if (m * m <= x) {\\n res = m;\\n l = m + 1;\\n } else {\\n r = m - 1;\\n }\\n } while (l <= r);\\n\\n return res;\\n }\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n public static long modPow(long a, long b, long mod) {\\n if (b < 0) throw new IllegalArgumentException(\\\"b=\\\" + b);\\n checkMod(mod);\\n\\n a %= mod;\\n var res = 1L % mod;\\n while (b != 0) {\\n if ((b & 1) != 0) {\\n res = (res * a) % mod;\\n }\\n\\n a = (a * a) % mod;\\n b >>= 1;\\n }\\n\\n return res;\\n }\\n\\n public static long modInv(long a, long mod) {\\n if (mod <= 0) {\\n throw new IllegalArgumentException(\\\"mod=\\\" + mod);\\n }\\n\\n var eucl = extEuclid(a, mod);\\n if (eucl.gcd != 1) {\\n return 0;\\n }\\n\\n return eucl.x < 0 ? eucl.x + mod : eucl.x;\\n }\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n public static long[] primeModInvsTable(int n, long primeMod) {\\n if (n < 1 || primeMod <= n) {\\n throw new IllegalArgumentException(\\\"n=\\\" + n + \\\", primeMod=\\\" + primeMod);\\n }\\n\\n var table = new long[n + 1];\\n table[0] = 0;\\n table[1] = 1;\\n\\n for (int i = 2; i < table.length; i++) {\\n long ir = table[(int) (primeMod % i)];\\n table[i] = ir == 0 ? 0 : primeMod - (primeMod / i * ir) % primeMod;\\n }\\n return table;\\n }\\n\\n public static class GcdWithFactors {\\n private long gcd;\\n private long x;\\n private long y;\\n\\n private GcdWithFactors() {\\n\\n }\\n\\n public long gcd() {\\n return gcd;\\n }\\n\\n public long x() {\\n return x;\\n }\\n\\n public long y() {\\n return y;\\n }\\n }\\n\\n public static GcdWithFactors extEuclid(long a, long b) {\\n var res = new GcdWithFactors();\\n extEuclid0(a, b, res);\\n return res;\\n }\\n\\n private static void extEuclid0(long a, long b, GcdWithFactors res) {\\n if (b == 0) {\\n res.gcd = a;\\n res.x = 1;\\n res.y = 0;\\n } else {\\n extEuclid0(b, a % b, res);\\n var tmpX = res.x;\\n var tmpY = res.y;\\n\\n res.x = tmpY;\\n res.y = tmpX - tmpY * (a / b);\\n }\\n }\\n\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n private static void checkMod(long mod) {\\n if (mod < 1 || mod > FLOOR_OF_SQRT_LONG_MAX) {\\n throw new IllegalArgumentException(\\\"mod=\\\" + mod);\\n }\\n }\\n\\n /**\\n * Calculates binomial coefficients n over k modulo prime powers p^e even if p is smaller or equal to n.\\n */\\n public static class SmallPrimePowerModCombos {\\n final int e;\\n final int p;\\n final int mod;\\n final int[] pPowersInFactorials;\\n final int[] factorialsWithoutPowers;\\n\\n public SmallPrimePowerModCombos(int n, int p, int e) {\\n if (p <= 1 || e < 1) {\\n throw new IllegalArgumentException(\\\"n=\\\" + n + \\\", p=\\\" + p + \\\", e=\\\" + e);\\n }\\n\\n var mod = p;\\n for (int i = 1; i < e; i++) {\\n mod = Math.multiplyExact(mod, p);\\n }\\n\\n this.e = e;\\n this.p = p;\\n this.mod = mod;\\n\\n this.pPowersInFactorials = new int[n + 1];\\n this.factorialsWithoutPowers = new int[n + 1];\\n\\n factorialsWithoutPowers[0] = 1;\\n for (int i = 1, ip = 1; i <= n; i++, ip++) {\\n pPowersInFactorials[i] = pPowersInFactorials[i - 1];\\n\\n if (ip != p) {\\n factorialsWithoutPowers[i] = modMul(i, factorialsWithoutPowers[i - 1]);\\n } else {\\n var ii = i;\\n do {\\n pPowersInFactorials[i]++;\\n ii /= p;\\n } while (ii % p == 0);\\n\\n factorialsWithoutPowers[i] = modMul(ii, factorialsWithoutPowers[i - 1]);\\n ip = 0;\\n }\\n\\n }\\n }\\n\\n public SmallPrimePowerModCombos(int n, int p) {\\n this(n, p, 1);\\n }\\n\\n public int nChooseK(int n, int k) {\\n var powers = pPowersInFactorials[n] - pPowersInFactorials[k] - pPowersInFactorials[n - k];\\n if (powers >= e) return 0;\\n\\n var res = 1;\\n for (int i = 0; i < powers; i++) {\\n res *= p;\\n }\\n\\n res = modMul(res, factorialsWithoutPowers[n]);\\n res = modMul(res, modInv(factorialsWithoutPowers[k], mod));\\n res = modMul(res, modInv(factorialsWithoutPowers[n - k], mod));\\n return res;\\n }\\n\\n private int modMul(long a, long b) {\\n return (int) ((a * b) % mod);\\n }\\n }\\n\\n public record PrimeFactor(long p, int q) {}\\n\\n public static List<PrimeFactor> primeFactorsOf(long n) {\\n if (n <= 0) {\\n throw new IllegalArgumentException(\\\"n=\\\" + n);\\n }\\n\\n var res = new ArrayList<PrimeFactor>();\\n for (long p = 2; p * p <= n; p++) {\\n if (n % p == 0) {\\n var e = 0;\\n do {\\n n /= p;\\n e++;\\n } while (n % p == 0);\\n\\n res.add(new PrimeFactor(p, e));\\n }\\n }\\n\\n if (n > 1) {\\n res.add(new PrimeFactor(n, 1));\\n }\\n\\n return res;\\n }\\n }\\n\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int minOf(int... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Integer.MAX_VALUE;\\n for (int i : is) {\\n res = Math.min(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int maxOf(int... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Integer.MIN_VALUE;\\n for (int i : is) {\\n res = Math.max(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long minOf(long... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Long.MAX_VALUE;\\n for (long i : is) {\\n res = Math.min(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long maxOf(long... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Long.MIN_VALUE;\\n for (long i : is) {\\n res = Math.max(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> ExtendedArrayList<T> fillList(int n, Supplier<T> supplier) {\\n return fillList(n, ignore -> supplier.get());\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> ExtendedArrayList<T> fillList(int n, IntFunction<T> valueAt) {\\n var res = new ExtendedArrayList<T>(n);\\n for (int i = 0; i < n; i++) {\\n res.add(valueAt.apply(i));\\n }\\n\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> T[] fillArray(int n, Class<T> clazz, Supplier<T> supplier) {\\n return fillArray(n, clazz, ignore -> supplier.get());\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> T[] fillArray(int n, Class<T> clazz, IntFunction<T> valueAt) {\\n @SuppressWarnings(\\\"unchecked\\\") var res = (T[]) Array.newInstance(clazz, n);\\n\\n for (int i = 0; i < n; i++) {\\n res[i] = valueAt.apply(i);\\n }\\n\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\", \\\"SameParameterValue\\\"})\\n static <T> T[] fillArray(int n, T value) {\\n @SuppressWarnings(\\\"unchecked\\\") var res = (T[]) Array.newInstance(value.getClass(), n);\\n Arrays.fill(res, value);\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int[] fillIntArray(int n, IntUnaryOperator valueAt) {\\n var res = new int[n];\\n for (int i = 0; i < n; i++) {\\n res[i] = valueAt.applyAsInt(i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int[] fillIntArray(int n, int value) {\\n var res = new int[n];\\n Arrays.fill(res, value);\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long[] fillLongArray(int n, IntToLongFunction valueAt) {\\n var res = new long[n];\\n for (int i = 0; i < n; i++) {\\n res[i] = valueAt.applyAsLong(i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long[] fillLongArray(int n, long value) {\\n var res = new long[n];\\n Arrays.fill(res, value);\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long gcd(long a, long b) {\\n while (b != 0) {\\n var bb = a % b;\\n a = b;\\n b = bb;\\n }\\n\\n return a;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int gcd(int a, int b) {\\n while (b != 0) {\\n var bb = a % b;\\n a = b;\\n b = bb;\\n }\\n\\n return a;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\", \\\"UnusedReturnValue\\\"})\\n static class ExtendedArrayList<T> extends ArrayList<T> {\\n public ExtendedArrayList(int initialCapacity) {\\n super(initialCapacity);\\n }\\n\\n public ExtendedArrayList() {\\n\\n }\\n\\n public ExtendedArrayList(Collection<? extends T> c) {\\n super(c);\\n }\\n\\n T getFromEnd(int offset) {\\n return get(size() - offset - 1);\\n }\\n\\n T getFst() {\\n return get(0);\\n }\\n\\n T getLst() {\\n return getFromEnd(0);\\n }\\n\\n T removeLst() {\\n return remove(size() - 1);\\n }\\n }\\n}\"], [49000, 0.4831, \"public class Solution {\\n private int powMod10(int a, int n) {\\n int x = 1;\\n while (n >= 1) {\\n if (n % 2 == 1) {x = (x * a) % 10;}\\n a = (a * a) % 10;\\n n /= 2;\\n }\\n return x;\\n }\\n private int[] f(int n) {\\n int[] ns = new int [n + 1];\\n int[] n2 = new int [n + 1];\\n int[] n5 = new int [n + 1];\\n ns[0] = 1;\\n for (int i = 1; i <= n; ++i) {\\n int m = i;\\n n2[i] = n2[i - 1];\\n n5[i] = n5[i - 1];\\n while (m % 2 == 0) { m /= 2; n2[i]++; }\\n while (m % 5 == 0) { m /= 5; n5[i]++; }\\n ns[i] = (ns[i - 1] * m) % 10;\\n }\\n int[] inv = new int [10];\\n for (int i = 1; i < 10; ++i) {\\n for (int j = 0; j < 10; ++j) {\\n if (i * j % 10 == 1) {inv[i] = j;}\\n }\\n }\\n int[] xs = new int [n + 1];\\n for (int k = 0; k <= n; ++k) {\\n int a = 0;\\n int s2 = n2[n] - n2[n - k] - n2[k];\\n int s5 = n5[n] - n5[n - k] - n5[k];\\n if (s2 == 0 || s5 == 0) {\\n a = (ns[n] * inv[ns[n - k]] * inv[ns[k]] * powMod10(2, s2) * powMod10(5, s5)) % 10;\\n }\\n xs[k] = a;\\n }\\n return xs;\\n }\\n\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int[] xs = f(n - 2); \\n int[] arr = new int[n];\\n for (int i = 0; i < n; i++) {\\n arr[i] = (int)(s.charAt(i) - '0');\\n } \\n int num1 = 0;\\n int num2 = 0;\\n for (int i = 0; i < n - 1; i++) {\\n num1 = (num1 + xs[i] * arr[i]) % 10;\\n num2 = (num2 + xs[i] * arr[i + 1]) % 10;\\n } \\n return num1 == num2;\\n }\\n}\\n\"], [49200, 0.4831, \"class Solution {\\n int mod = 10;\\n public boolean hasSameDigits(String s) {\\n char[] ch = s.toCharArray();\\n int n = ch.length, dep = n - 2;\\n int[] fac = new int[n + 1], facinv = new int[n + 1];\\n int[] p2 = new int[n + 1], p5 = new int[n + 1];\\n \\n fac[0] = facinv[0] = 1;\\n \\n for(int i = 1; i <= n; i++) {\\n int x = i, e2 = 0, e5 = 0;\\n while(x % 2 == 0) {e2++; x /= 2;};\\n while(x % 5 == 0) {e5++; x /= 5;};\\n p2[i] = p2[i - 1] + e2;\\n p5[i] = p5[i - 1] + e5;\\n fac[i] = fac[i - 1] * x % mod;\\n }\\n \\n // facinv[n] = pow(fac[n], 3);\\n // for(int i = n; i >= 1; i--) {\\n // int x = i;\\n // while(x % 2 == 0) {x /= 2;};\\n // while(x % 5 == 0) {x /= 5;};\\n // facinv[i - 1] = facinv[i] * x % mod;\\n // }\\n \\n for (int i = 1; i <= n; i++) {\\n facinv[i] = pow(fac[i], 3) % mod;\\n }\\n \\n long sum1 = 0, sum2 = 0;\\n for(int i = 0; i <= n - 2; i++) {\\n int cost = ch[i] - '0';\\n sum1 += cost * fac[dep] * facinv[i] * facinv[dep - i] * pow(2, p2[dep] - p2[i] - p2[dep - i]) * pow(5, p5[dep] - p5[i] - p5[dep - i]) % mod;\\n sum1 %= mod;\\n }\\n for(int i = 1; i <= n - 1; i++) {\\n int cost = ch[i] - '0';\\n sum2 += cost * fac[dep] * facinv[i - 1] * facinv[dep - i + 1] * pow(2, p2[dep] - p2[i - 1] - p2[dep - i + 1]) * pow(5, p5[dep] - p5[i - 1] - p5[dep - i + 1]) % mod;\\n sum2 %= mod;\\n }\\n\\n return sum1 == sum2;\\n }\\n \\n int pow(int base, int pow) {\\n if(pow == 1) return base;\\n if(pow == 0) return 1;\\n int half = pow(base, pow / 2);\\n if(pow % 2 == 0) return half * half % mod;\\n return half * half * base % mod;\\n }\\n}\"], [49300, 0.9662, \"class Solution {\\n int mod = 10;\\n public boolean hasSameDigits(String s) {\\n char[] ch = s.toCharArray();\\n int n = ch.length;\\n int[] fac = new int[n + 1], facinv = new int[n + 1];\\n int[] p2 = new int[n + 1], p5 = new int[n + 1];\\n fac[0] = facinv[0] = 1;\\n\\n for(int i = 1; i <= n; i++) {\\n int x = i, e2 = 0, e5 = 0;\\n while(x % 2 == 0) { e2++; x /= 2; };\\n while(x % 5 == 0) { e5++; x /= 5; };\\n fac[i] = fac[i - 1] * x % mod;\\n p2[i] = p2[i - 1] + e2;\\n p5[i] = p5[i - 1] + e5;\\n }\\n\\n // facinv[n] = pow(fac[n], 3);\\n // for(int i = n; i > 0; i--) {\\n // int x = i;\\n // while(x % 2 == 0) { x /= 2; };\\n // while(x % 5 == 0) { x /= 5; };\\n // facinv[i - 1] = facinv[i] * x % mod;\\n // }\\n\\n for (int i = 1; i <= n; i++) {\\n facinv[i] = pow(fac[i], 3) % mod;\\n }\\n\\n\\n long sum1 = 0, sum2 = 0;\\n int dep = n - 2;\\n for(int i = 0; i <= n - 2; i++) {\\n int cost = ch[i] - '0';\\n sum1 += cost * fac[dep] * facinv[i] * facinv[dep - i] * pow(2, p2[dep] - p2[i] - p2[dep - i]) * pow(5, p5[dep] - p5[i] - p5[dep - i]) % mod;\\n sum1 %= mod;\\n }\\n for(int i = 1; i <= n - 1; i++) {\\n int cost = ch[i] - '0';\\n sum2 += cost * fac[dep] * facinv[i - 1] * facinv[dep - i + 1] * pow(2, p2[dep] - p2[i - 1] - p2[dep - i + 1]) * pow(5, p5[dep] - p5[i - 1] - p5[dep - i + 1]) % mod;\\n sum2 %= mod;\\n }\\n\\n return sum1 == sum2;\\n\\n }\\n\\n int pow(int base, int pow) {\\n if(pow == 1) return base;\\n if(pow == 0) return 1;\\n int half = pow(base, pow / 2);\\n if(pow % 2 == 1) return half * half * base % mod;\\n return half * half % mod;\\n }\\n}\"], [50200, 0.4831, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int[] mods2 = computeNcKMod10(n-2, 2);\\n int[] mods = computeNcKMod10(n-2, 5);\\n \\n int t1 = 0;\\n int t2 = 0;\\n for (int i = 0; i < mods.length; i++) {\\n int d = (s.charAt(i)-s.charAt(i+1));\\n t1 += d * mods[i];\\n t2 += d * mods2[i];\\n }\\n return t1%5 == 0 && t2%2 == 0;\\n }\\n\\n public int[] computeNcKMod10(int n, int p) {\\n int[] result = new int[n + 1];\\n result[0] = 1; // nC0 = 1\\n result[n] = 1; // nC0 = 1\\n\\n int current = 1;\\n int currentPow = 0;\\n for (int k = 1; k <= n; k++) {\\n int[] up = reducePower(n-k+1, p);\\n int[] down = reducePower(k, p);\\n currentPow += (up[0] - down[0]);\\n current = (current * up[1]);\\n current = (current * modInverse(down[1], p)) % p;\\n result[k] = currentPow == 0? current : 0;\\n result[n-k] = result[k];\\n if (n-k <= k) break;\\n }\\n \\n return result;\\n }\\n\\n int[] reducePower(int n, int p) {\\n int c = 0;\\n while(n%p == 0) {\\n c++;\\n n/=p;\\n }\\n return new int[]{c, n};\\n }\\n\\n private int modInverse(int a, int mod) {\\n if (mod == 2) return 1;\\n for (int i = 1; i < mod; i++) {\\n if ((a * i) % mod == 1) {\\n return i;\\n }\\n }\\n return 1; // Should never reach here for valid inputs\\n }\\n}\"], [50600, 0.9662, \"class Solution {\\n\\n // Compute nCr mod p using Lucas's Theorem\\n private int nCrModP(int n, int r, int p) {\\n int result = 1;\\n while (n > 0 || r > 0) {\\n int ni = n % p;\\n int ri = r % p;\\n if (ri > ni) return 0;\\n result = (result * nCrModPSmall(ni, ri, p)) % p;\\n n /= p;\\n r /= p;\\n }\\n return result;\\n }\\n\\n // Compute nCr mod small p using Pascal's triangle\\n private int nCrModPSmall(int n, int r, int p) {\\n if (r == 0 || r == n) return 1;\\n int[] C = new int[r + 1];\\n C[0] = 1;\\n for (int i = 1; i <= n; i++) {\\n for (int j = Math.min(i, r); j > 0; j--) {\\n C[j] = (C[j] + C[j - 1]) % p;\\n }\\n }\\n return C[r];\\n }\\n\\n // Combine mod2 and mod5 to get mod10 using CRT\\n private int combineMod10(int mod2, int mod5) {\\n // mod2 \\u2208 {0,1}, mod5 \\u2208 {0..4}\\n for (int i = 0; i < 10; i++) {\\n if (i % 2 == mod2 && i % 5 == mod5) {\\n return i;\\n }\\n }\\n return 0; // shouldn't happen\\n }\\n\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int[] digits = new int[n];\\n for (int i = 0; i < n; i++) {\\n digits[i] = s.charAt(i) - '0';\\n }\\n\\n int left = 0, right = 0;\\n for (int i = 0; i < n - 1; i++) {\\n int coeffMod2 = nCrModP(n - 2, i, 2);\\n int coeffMod5 = nCrModP(n - 2, i, 5);\\n int coeff = combineMod10(coeffMod2, coeffMod5);\\n\\n left = (left + coeff * digits[i]) % 10;\\n right = (right + coeff * digits[i + 1]) % 10;\\n }\\n\\n return left == right;\\n }\\n}\\n\"], [50700, 0.9662, \"class Solution {\\n static int nCrMod10(int n, int r) {\\n int mod2 = nCrMod2(n, r);\\n int mod5 = nCrMod5(n, r);\\n return (5 * mod2 + 6 * mod5) % 10;\\n }\\n \\n static int nCrMod2(int n, int r) {\\n return ((n & r) == r) ? 1 : 0;\\n }\\n \\n static int nCrMod5(int n, int r) {\\n if (r > n) return 0;\\n int[] fact = {1, 1, 2, 1, 4};\\n int[] invFact = new int[5];\\n for (int i = 0; i < 5; i++) {\\n invFact[i] = modInverse5(fact[i]);\\n }\\n int anss = 1;\\n while (n > 0 || r > 0) {\\n int n_i = n % 5;\\n int r_i = r % 5;\\n n /= 5;\\n r /= 5;\\n if (r_i > n_i) return 0;\\n int term = fact[n_i];\\n term = (int) (((long) term * invFact[r_i]) % 5);\\n term = (int) (((long) term * invFact[n_i - r_i]) % 5);\\n anss = (anss * term) % 5;\\n }\\n return anss;\\n }\\n \\n static int modInverse5(int x) {\\n return power(x, 3, 5);\\n }\\n \\n static int power(int x, int y, int mod) {\\n int res = 1;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n res = (res * x) % mod;\\n x = (x * x) % mod;\\n y >>= 1;\\n }\\n return res;\\n }\\n \\n static boolean hasSameDigits(String s) {\\n char[] nums = s.toCharArray();\\n int n = nums.length;\\n int x = n - 2, y = 0;\\n int ans = 0;\\n for (int i = 0; i < n - 1; i++) {\\n int val = nCrMod10(x, y++);\\n ans = (ans + ((int)(nums[i] - '0') * val)) % 10;\\n }\\n int temo = ans;\\n y = 0;\\n int one = 0;\\n for (int i = 1; i < n; i++) {\\n int val = nCrMod10(x, y);\\n one = (one + ((int)(nums[i] - '0') * val)) % 10;\\n y++;\\n }\\n return temo == one;\\n }\\n}\"], [50800, 3.3816, \"class Solution {\\n static int nCrMod10(int n, int r) {\\n int mod2 = nCrMod2(n, r);\\n int mod5 = nCrMod5(n, r);\\n return (5 * mod2 + 6 * mod5) % 10;\\n }\\n \\n static int nCrMod2(int n, int r) {\\n return ((n & r) == r) ? 1 : 0;\\n }\\n \\n static int nCrMod5(int n, int r) {\\n if (r > n) return 0;\\n int[] fact = {1, 1, 2, 1, 4};\\n int[] invFact = new int[5];\\n for (int i = 0; i < 5; i++) {\\n invFact[i] = modInverse5(fact[i]);\\n }\\n int anss = 1;\\n while (n > 0 || r > 0) {\\n int n_i = n % 5;\\n int r_i = r % 5;\\n n /= 5;\\n r /= 5;\\n if (r_i > n_i) return 0;\\n int term = fact[n_i];\\n term = (int) (((long) term * invFact[r_i]) % 5);\\n term = (int) (((long) term * invFact[n_i - r_i]) % 5);\\n anss = (anss * term) % 5;\\n }\\n return anss;\\n }\\n \\n static int modInverse5(int x) {\\n return power(x, 3, 5);\\n }\\n \\n static int power(int x, int y, int mod) {\\n int res = 1;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n res = (res * x) % mod;\\n x = (x * x) % mod;\\n y >>= 1;\\n }\\n return res;\\n }\\n \\n static boolean hasSameDigits(String s) {\\n char[] nums = s.toCharArray();\\n int n = nums.length;\\n int x = n - 2, y = 0;\\n int ans = 0;\\n for (int i = 0; i < n - 1; i++) {\\n int val = nCrMod10(x, y++);\\n ans = (ans + ((int)(nums[i] - '0') * val)) % 10;\\n }\\n int temo = ans;\\n y = 0;\\n int one = 0;\\n for (int i = 1; i < n; i++) {\\n int val = nCrMod10(x, y);\\n one = (one + ((int)(nums[i] - '0') * val)) % 10;\\n y++;\\n }\\n return temo == one;\\n }\\n}\"], [50900, 0.4831, \"class Solution {\\n static int nCrMod10(int n, int r) {\\n int mod2 = nCrMod2(n, r);\\n int mod5 = nCrMod5(n, r);\\n return (5 * mod2 + 6 * mod5) % 10;\\n }\\n \\n static int nCrMod2(int n, int r) {\\n return ((n & r) == r) ? 1 : 0;\\n }\\n \\n static int nCrMod5(int n, int r) {\\n if (r > n) return 0;\\n int[] fact = {1, 1, 2, 1, 4};\\n int[] invFact = new int[5];\\n for (int i = 0; i < 5; i++) {\\n invFact[i] = modInverse5(fact[i]);\\n }\\n int anss = 1;\\n while (n > 0 || r > 0) {\\n int n_i = n % 5;\\n int r_i = r % 5;\\n n /= 5;\\n r /= 5;\\n if (r_i > n_i) return 0;\\n int term = fact[n_i];\\n term = (int) (((long) term * invFact[r_i]) % 5);\\n term = (int) (((long) term * invFact[n_i - r_i]) % 5);\\n anss = (anss * term) % 5;\\n }\\n return anss;\\n }\\n \\n static int modInverse5(int x) {\\n return power(x, 3, 5);\\n }\\n \\n static int power(int x, int y, int mod) {\\n int res = 1;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n res = (res * x) % mod;\\n x = (x * x) % mod;\\n y >>= 1;\\n }\\n return res;\\n }\\n \\n static boolean hasSameDigits(String s) {\\n char[] nums = s.toCharArray();\\n int n = nums.length;\\n int x = n - 2, y = 0;\\n int ans = 0;\\n for (int i = 0; i < n - 1; i++) {\\n int val = nCrMod10(x, y++);\\n ans = (ans + ((int)(nums[i] - '0') * val)) % 10;\\n }\\n int temo = ans;\\n y = 0;\\n int one = 0;\\n for (int i = 1; i < n; i++) {\\n int val = nCrMod10(x, y);\\n one = (one + ((int)(nums[i] - '0') * val)) % 10;\\n y++;\\n }\\n return temo == one;\\n }\\n}\"], [51000, 2.4155, \"class Solution {\\n static int nCrMod10(int n, int r) {\\n int mod2 = nCrMod2(n, r);\\n int mod5 = nCrMod5(n, r);\\n return (5 * mod2 + 6 * mod5) % 10;\\n }\\n \\n static int nCrMod2(int n, int r) {\\n return ((n & r) == r) ? 1 : 0;\\n }\\n \\n static int nCrMod5(int n, int r) {\\n if (r > n) return 0;\\n int[] fact = {1, 1, 2, 1, 4};\\n int[] invFact = new int[5];\\n for (int i = 0; i < 5; i++) {\\n invFact[i] = modInverse5(fact[i]);\\n }\\n int anss = 1;\\n while (n > 0 || r > 0) {\\n int n_i = n % 5;\\n int r_i = r % 5;\\n n /= 5;\\n r /= 5;\\n if (r_i > n_i) return 0;\\n int term = fact[n_i];\\n term = (int) (((long) term * invFact[r_i]) % 5);\\n term = (int) (((long) term * invFact[n_i - r_i]) % 5);\\n anss = (anss * term) % 5;\\n }\\n return anss;\\n }\\n \\n static int modInverse5(int x) {\\n return power(x, 3, 5);\\n }\\n \\n static int power(int x, int y, int mod) {\\n int res = 1;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n res = (res * x) % mod;\\n x = (x * x) % mod;\\n y >>= 1;\\n }\\n return res;\\n }\\n \\n static boolean hasSameDigits(String s) {\\n char[] nums = s.toCharArray();\\n int n = nums.length;\\n int x = n - 2, y = 0;\\n int ans = 0;\\n for (int i = 0; i < n - 1; i++) {\\n int val = nCrMod10(x, y++);\\n ans = (ans + ((int)(nums[i] - '0') * val)) % 10;\\n }\\n int temo = ans;\\n y = 0;\\n int one = 0;\\n for (int i = 1; i < n; i++) {\\n int val = nCrMod10(x, y);\\n one = (one + ((int)(nums[i] - '0') * val)) % 10;\\n y++;\\n }\\n return temo == one;\\n }\\n}\"], [51100, 0.4831, \"class Solution {\\n static int nCrMod10(int n, int r) {\\n int mod2 = nCrMod2(n, r);\\n int mod5 = nCrMod5(n, r);\\n return (5 * mod2 + 6 * mod5) % 10;\\n }\\n \\n static int nCrMod2(int n, int r) {\\n return ((n & r) == r) ? 1 : 0;\\n }\\n \\n static int nCrMod5(int n, int r) {\\n if (r > n) return 0;\\n int[] fact = {1, 1, 2, 1, 4};\\n int[] invFact = new int[5];\\n for (int i = 0; i < 5; i++) {\\n invFact[i] = modInverse5(fact[i]);\\n }\\n int anss = 1;\\n while (n > 0 || r > 0) {\\n int n_i = n % 5;\\n int r_i = r % 5;\\n n /= 5;\\n r /= 5;\\n if (r_i > n_i) return 0;\\n int term = fact[n_i];\\n term = (int) (((long) term * invFact[r_i]) % 5);\\n term = (int) (((long) term * invFact[n_i - r_i]) % 5);\\n anss = (anss * term) % 5;\\n }\\n return anss;\\n }\\n \\n static int modInverse5(int x) {\\n return power(x, 3, 5);\\n }\\n \\n static int power(int x, int y, int mod) {\\n int res = 1;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n res = (res * x) % mod;\\n x = (x * x) % mod;\\n y >>= 1;\\n }\\n return res;\\n }\\n \\n static boolean hasSameDigits(String s) {\\n char[] nums = s.toCharArray();\\n int n = nums.length;\\n int x = n - 2, y = 0;\\n int ans = 0;\\n for (int i = 0; i < n - 1; i++) {\\n int val = nCrMod10(x, y++);\\n ans = (ans + ((int)(nums[i] - '0') * val)) % 10;\\n }\\n int temo = ans;\\n y = 0;\\n int one = 0;\\n for (int i = 1; i < n; i++) {\\n int val = nCrMod10(x, y);\\n one = (one + ((int)(nums[i] - '0') * val)) % 10;\\n y++;\\n }\\n return temo == one;\\n }\\n}\"], [51300, 0.4831, \"class Solution {\\n static int nCrMod10(int n, int r) {\\n int mod2 = nCrMod2(n, r);\\n int mod5 = nCrMod5(n, r);\\n return (5 * mod2 + 6 * mod5) % 10;\\n }\\n \\n static int nCrMod2(int n, int r) {\\n return ((n & r) == r) ? 1 : 0;\\n }\\n \\n static int nCrMod5(int n, int r) {\\n if (r > n) return 0;\\n int[] fact = {1, 1, 2, 1, 4};\\n int[] invFact = new int[5];\\n for (int i = 0; i < 5; i++) {\\n invFact[i] = modInverse5(fact[i]);\\n }\\n int anss = 1;\\n while (n > 0 || r > 0) {\\n int n_i = n % 5;\\n int r_i = r % 5;\\n n /= 5;\\n r /= 5;\\n if (r_i > n_i) return 0;\\n int term = fact[n_i];\\n term = (int) (((long) term * invFact[r_i]) % 5);\\n term = (int) (((long) term * invFact[n_i - r_i]) % 5);\\n anss = (anss * term) % 5;\\n }\\n return anss;\\n }\\n \\n static int modInverse5(int x) {\\n return power(x, 3, 5);\\n }\\n \\n static int power(int x, int y, int mod) {\\n int res = 1;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n res = (res * x) % mod;\\n x = (x * x) % mod;\\n y >>= 1;\\n }\\n return res;\\n }\\n \\n static boolean hasSameDigits(String s) {\\n char[] nums = s.toCharArray();\\n int n = nums.length;\\n int x = n - 2, y = 0;\\n int ans = 0;\\n for (int i = 0; i < n - 1; i++) {\\n int val = nCrMod10(x, y++);\\n ans = (ans + ((int)(nums[i] - '0') * val)) % 10;\\n }\\n int temo = ans;\\n y = 0;\\n int one = 0;\\n for (int i = 1; i < n; i++) {\\n int val = nCrMod10(x, y);\\n one = (one + ((int)(nums[i] - '0') * val)) % 10;\\n y++;\\n }\\n return temo == one;\\n }\\n}\"], [51400, 0.4831, \"class Solution {\\n static int nCrMod10(int n, int r) {\\n int mod2 = nCrMod2(n, r);\\n int mod5 = nCrMod5(n, r);\\n return (5 * mod2 + 6 * mod5) % 10;\\n }\\n \\n static int nCrMod2(int n, int r) {\\n return ((n & r) == r) ? 1 : 0;\\n }\\n \\n static int nCrMod5(int n, int r) {\\n if (r > n) return 0;\\n int[] fact = {1, 1, 2, 1, 4};\\n int[] invFact = new int[5];\\n for (int i = 0; i < 5; i++) {\\n invFact[i] = modInverse5(fact[i]);\\n }\\n int anss = 1;\\n while (n > 0 || r > 0) {\\n int n_i = n % 5;\\n int r_i = r % 5;\\n n /= 5;\\n r /= 5;\\n if (r_i > n_i) return 0;\\n int term = fact[n_i];\\n term = (int) (((long) term * invFact[r_i]) % 5);\\n term = (int) (((long) term * invFact[n_i - r_i]) % 5);\\n anss = (anss * term) % 5;\\n }\\n return anss;\\n }\\n \\n static int modInverse5(int x) {\\n return power(x, 3, 5);\\n }\\n \\n static int power(int x, int y, int mod) {\\n int res = 1;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n res = (res * x) % mod;\\n x = (x * x) % mod;\\n y >>= 1;\\n }\\n return res;\\n }\\n \\n static boolean hasSameDigits(String s) {\\n char[] nums = s.toCharArray();\\n int n = nums.length;\\n int x = n - 2, y = 0;\\n int ans = 0;\\n for (int i = 0; i < n - 1; i++) {\\n int val = nCrMod10(x, y++);\\n ans = (ans + ((int)(nums[i] - '0') * val)) % 10;\\n }\\n int temo = ans;\\n y = 0;\\n int one = 0;\\n for (int i = 1; i < n; i++) {\\n int val = nCrMod10(x, y);\\n one = (one + ((int)(nums[i] - '0') * val)) % 10;\\n y++;\\n }\\n return temo == one;\\n }\\n}\"], [51500, 0.4831, \"class Solution {\\n static int nCrMod10(int n, int r) {\\n int mod2 = nCrMod2(n, r);\\n int mod5 = nCrMod5(n, r);\\n return (5 * mod2 + 6 * mod5) % 10;\\n }\\n \\n static int nCrMod2(int n, int r) {\\n return ((n & r) == r) ? 1 : 0;\\n }\\n \\n static int nCrMod5(int n, int r) {\\n if (r > n) return 0;\\n int[] fact = {1, 1, 2, 1, 4};\\n int[] invFact = new int[5];\\n for (int i = 0; i < 5; i++) {\\n invFact[i] = modInverse5(fact[i]);\\n }\\n int anss = 1;\\n while (n > 0 || r > 0) {\\n int n_i = n % 5;\\n int r_i = r % 5;\\n n /= 5;\\n r /= 5;\\n if (r_i > n_i) return 0;\\n int term = fact[n_i];\\n term = (int) (((long) term * invFact[r_i]) % 5);\\n term = (int) (((long) term * invFact[n_i - r_i]) % 5);\\n anss = (anss * term) % 5;\\n }\\n return anss;\\n }\\n \\n static int modInverse5(int x) {\\n return power(x, 3, 5);\\n }\\n \\n static int power(int x, int y, int mod) {\\n int res = 1;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n res = (res * x) % mod;\\n x = (x * x) % mod;\\n y >>= 1;\\n }\\n return res;\\n }\\n \\n static boolean hasSameDigits(String s) {\\n char[] nums = s.toCharArray();\\n int n = nums.length;\\n int x = n - 2, y = 0;\\n int ans = 0;\\n for (int i = 0; i < n - 1; i++) {\\n int val = nCrMod10(x, y++);\\n ans = (ans + ((int)(nums[i] - '0') * val)) % 10;\\n }\\n int temo = ans;\\n y = 0;\\n int one = 0;\\n for (int i = 1; i < n; i++) {\\n int val = nCrMod10(x, y);\\n one = (one + ((int)(nums[i] - '0') * val)) % 10;\\n y++;\\n }\\n return temo == one;\\n }\\n}\"], [51800, 0.4831, \"class Solution {\\n static int nCrMod10(int n, int r) {\\n int mod2 = nCrMod2(n, r);\\n int mod5 = nCrMod5(n, r);\\n return (5 * mod2 + 6 * mod5) % 10;\\n }\\n \\n static int nCrMod2(int n, int r) {\\n return ((n & r) == r) ? 1 : 0;\\n }\\n \\n static int nCrMod5(int n, int r) {\\n if (r > n) return 0;\\n int[] fact = {1, 1, 2, 1, 4};\\n int[] invFact = new int[5];\\n for (int i = 0; i < 5; i++) {\\n invFact[i] = modInverse5(fact[i]);\\n }\\n int anss = 1;\\n while (n > 0 || r > 0) {\\n int n_i = n % 5;\\n int r_i = r % 5;\\n n /= 5;\\n r /= 5;\\n if (r_i > n_i) return 0;\\n int term = fact[n_i];\\n term = (int) (((long) term * invFact[r_i]) % 5);\\n term = (int) (((long) term * invFact[n_i - r_i]) % 5);\\n anss = (anss * term) % 5;\\n }\\n return anss;\\n }\\n \\n static int modInverse5(int x) {\\n return power(x, 3, 5);\\n }\\n \\n static int power(int x, int y, int mod) {\\n int res = 1;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n res = (res * x) % mod;\\n x = (x * x) % mod;\\n y >>= 1;\\n }\\n return res;\\n }\\n \\n static boolean hasSameDigits(String s) {\\n char[] nums = s.toCharArray();\\n int n = nums.length;\\n int x = n - 2, y = 0;\\n int ans = 0;\\n for (int i = 0; i < n - 1; i++) {\\n int val = nCrMod10(x, y++);\\n ans = (ans + ((int)(nums[i] - '0') * val)) % 10;\\n }\\n int temo = ans;\\n y = 0;\\n int one = 0;\\n for (int i = 1; i < n; i++) {\\n int val = nCrMod10(x, y);\\n one = (one + ((int)(nums[i] - '0') * val)) % 10;\\n y++;\\n }\\n return temo == one;\\n }\\n}\"], [52900, 0.4831, \"class Solution {\\n static int binomialModuloPrime(int n, int r, int p) {\\n if (r > n)\\n return 0;\\n int result = 1;\\n\\n while (n > 0 || r > 0) {\\n int ni = n % p, ri = r % p;\\n if (ri > ni)\\n return 0;\\n result = (result * binomial(ni, ri, p)) % p;\\n n /= p;\\n r /= p;\\n }\\n return result;\\n }\\n\\n static int binomial(int n, int r, int p) {\\n if (r > n)\\n return 0;\\n if (r == 0 || r == n)\\n return 1;\\n\\n int[] fact = new int[n + 1];\\n fact[0] = 1;\\n for (int i = 1; i <= n; i++) {\\n fact[i] = (fact[i - 1] * i) % p;\\n }\\n\\n return (fact[n] * modInverse(fact[r], p) % p * modInverse(fact[n - r], p) % p) % p;\\n }\\n\\n static int modInverse(int a, int p) {\\n return power(a, p - 2, p);\\n }\\n\\n static int power(int x, int y, int p) {\\n int result = 1;\\n x %= p;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n result = (result * x) % p;\\n x = (x * x) % p;\\n y >>= 1;\\n }\\n return result;\\n }\\n\\n static int chineseRemainderTheorem(int a1, int m1, int a2, int m2) {\\n int M = m1 * m2;\\n int M1 = M / m1, M2 = M / m2;\\n int y1 = modInverse(M1, m1), y2 = modInverse(M2, m2);\\n return (a1 * M1 % M * y1 % M + a2 * M2 % M * y2 % M) % M;\\n }\\n\\n static List<Integer> getPascalRow(int n) {\\n List<Integer> row = new ArrayList<>();\\n for (int r = 0; r <= n; r++) {\\n int mod2 = binomialModuloPrime(n, r, 2);\\n int mod5 = binomialModuloPrime(n, r, 5);\\n int mod10 = chineseRemainderTheorem(mod2, 2, mod5, 5);\\n row.add(mod10);\\n }\\n return row;\\n }\\n\\n public boolean hasSameDigits(String s) {\\n int l = s.length();\\n List<Integer> list = getPascalRow(l - 2);\\n long first = 0;\\n long second = 0;\\n for (int i = 0; i < l - 1; i++) {\\n first = (first + (s.charAt(i) - '0') * list.get(i)) % 10;\\n second = (second + (s.charAt(i + 1) - '0') * list.get(i)) % 10;\\n }\\n return first == second;\\n }\\n}\"], [53100, 0.4831, \"import java.util.ArrayList;\\nimport java.util.List;\\n\\npublic class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int k = n - 2;\\n if (k < 0) {\\n return false; // As per problem constraints, n >= 3\\n }\\n\\n // Precompute comb_mod5 lookup table\\n int[][] combMod5 = {\\n {1, 0, 0, 0, 0}, // n=0\\n {1, 1, 0, 0, 0}, // n=1\\n {1, 2, 1, 0, 0}, // n=2\\n {1, 3, 3, 1, 0}, // n=3\\n {1, 4, 1, 4, 1} // n=4\\n };\\n\\n List<Integer> kDigits = getBase5Reversed(k);\\n int lenK = kDigits.size();\\n\\n // CRT table for mod2 and mod5 to mod10\\n int[][] crtTable = {\\n {0, 6, 2, 8, 4}, // mod2=0\\n {5, 1, 7, 3, 9} // mod2=1\\n };\\n\\n // Precompute mod10 for each i from 0 to k\\n int[] mod10 = new int[k + 1];\\n for (int i = 0; i <= k; i++) {\\n int mod2 = ((i & k) == i) ? 1 : 0;\\n\\n List<Integer> iDigits = getBase5Reversed(i);\\n boolean valid = true;\\n int product = 1;\\n for (int j = 0; j < lenK; j++) {\\n int idigit = (j < iDigits.size()) ? iDigits.get(j) : 0;\\n int kdigit = kDigits.get(j);\\n if (idigit > kdigit) {\\n valid = false;\\n break;\\n }\\n product = (product * combMod5[kdigit][idigit]) % 5;\\n }\\n int mod5 = valid ? product % 5 : 0;\\n\\n mod10[i] = crtTable[mod2][mod5];\\n }\\n\\n // Convert input string to digit array\\n char[] chars = s.toCharArray();\\n int[] digits = new int[chars.length];\\n for (int i = 0; i < chars.length; i++) {\\n digits[i] = chars[i] - '0';\\n }\\n\\n // Compute S1 and S2\\n int s1 = 0;\\n int s2 = 0;\\n for (int i = 0; i <= k; i++) {\\n s1 = (s1 + mod10[i] * digits[i]) % 10;\\n s2 = (s2 + mod10[i] * digits[i + 1]) % 10;\\n }\\n\\n return s1 == s2;\\n }\\n\\n private List<Integer> getBase5Reversed(int num) {\\n List<Integer> digits = new ArrayList<>();\\n if (num == 0) {\\n digits.add(0);\\n return digits;\\n }\\n while (num > 0) {\\n digits.add(num % 5);\\n num /= 5;\\n }\\n return digits;\\n }\\n}\"], [53200, 0.4831, \"public class Solution {\\n\\n private static final int[][] C_MOD_5 = {\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1}\\n };\\n\\n private int nCrMod5(long n, long k) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int ni = (int)(n % 5), ki = (int)(k % 5);\\n if (ki > ni) return 0;\\n res *= C_MOD_5[ni][ki];\\n res %= 5;\\n if (res == 0) return 0;\\n n /= 5;\\n k /= 5;\\n }\\n return res;\\n }\\n\\n private int nCrMod2(long n, long k) {\\n return ((n & k) == k) ? 1 : 0;\\n }\\n\\n private int combineCRT(int mod2, int mod5) {\\n // Precomputed lookup table (mod2, mod5) -> mod10\\n final int[][] CRT = {\\n {0, 6, 2, 8, 4}, // mod2 == 0\\n {5, 1, 7, 3, 9} // mod2 == 1\\n };\\n return CRT[mod2][mod5];\\n }\\n\\n private int nCrMod10(long n, long k) {\\n if (k < 0 || k > n) return 0;\\n if (k == 0 || k == n) return 1;\\n if (k > n / 2) k = n - k;\\n int mod2 = nCrMod2(n, k);\\n int mod5 = nCrMod5(n, k);\\n return combineCRT(mod2, mod5);\\n }\\n\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n if (n <= 1) return true;\\n if (n == 2) return s.charAt(0) == s.charAt(1);\\n\\n int[] d = new int[n];\\n for (int i = 0; i < n; i++) {\\n d[i] = s.charAt(i) - '0';\\n }\\n\\n long comb_n = n - 2;\\n int f0 = 0, f1 = 0;\\n for (int k = 0; k <= comb_n; k++) {\\n int coeff = nCrMod10(comb_n, k);\\n if (coeff == 0) continue;\\n f0 = (f0 + coeff * d[k]) % 10;\\n f1 = (f1 + coeff * d[k + 1]) % 10;\\n }\\n\\n return f0 == f1;\\n }\\n}\\n\"], [53800, 0.4831, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int r = n - 2; // We will use binomials with n-2 in the upper index.\\n int[] d = new int[n];\\n for (int i = 0; i < n; i++) {\\n d[i] = s.charAt(i) - '0';\\n }\\n \\n // S = sum_{i=0}^{n-2} C(n-2, i) * (d[i] - d[i+1]) mod 10.\\n int S = 0;\\n for (int i = 0; i <= r; i++) {\\n int coeffMod2 = binomMod2(r, i); // C(r, i) mod 2.\\n int coeffMod5 = lucas(r, i, 5); // C(r, i) mod 5.\\n int coeff = (5 * coeffMod2 + 6 * coeffMod5) % 10; // Combine via CRT.\\n int delta = d[i] - d[i + 1];\\n S = (S + coeff * delta) % 10;\\n if (S < 0) S += 10;\\n }\\n // If S is 0 modulo 10, then the two final digits are the same.\\n return S % 10 == 0;\\n }\\n \\n // Compute C(n, k) mod 2 using the property that it is 1 if and only if (n & k) == k.\\n private int binomMod2(int n, int k) {\\n return ((n & k) == k) ? 1 : 0;\\n }\\n \\n // Compute C(n, k) mod p using Lucas' theorem.\\n // Here p is a prime (we use p = 5).\\n private int lucas(int n, int k, int p) {\\n int result = 1;\\n while (n > 0 || k > 0) {\\n int n_i = n % p;\\n int k_i = k % p;\\n if (k_i > n_i) return 0;\\n result = (result * nCrSmall(n_i, k_i, p)) % p;\\n n /= p;\\n k /= p;\\n }\\n return result;\\n }\\n \\n // For p = 5, compute C(n, r) mod 5 when 0 <= n < 5.\\n // We use the precomputed factorials mod 5: fact[0]=1, fact[1]=1, fact[2]=2, fact[3]=6 mod 5 = 1, fact[4]=24 mod 5 = 4.\\n // And the inverses modulo 5 (recall: inverse of 2 is 3, inverse of 3 is 2, inverse of 4 is 4).\\n private int nCrSmall(int n, int r, int p) {\\n // Precomputed factorials mod 5 for n=0,...,4.\\n int[] fact = {1, 1, 2, 1, 4};\\n // Precomputed modular inverses mod 5 for 1,2,3,4.\\n // (We never need the inverse of 0.)\\n int[] inv = {0, 1, 3, 2, 4};\\n \\n int numerator = fact[n];\\n int denominator = (fact[r] * fact[n - r]) % p;\\n if (denominator == 0) return 0; // (Should not occur for 0 <= n < p.)\\n int invDenom = 0;\\n // Since denominator is one of 1,2,3,4 mod 5, we can use the precomputed inverses.\\n if (denominator == 1) invDenom = 1;\\n else if (denominator == 2) invDenom = 3;\\n else if (denominator == 3) invDenom = 2;\\n else if (denominator == 4) invDenom = 4;\\n return (numerator * invDenom) % p;\\n }\\n}\\n\"], [53900, 0.9662, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n // f[i]: factorial(i) with 2s and 5s removed, mod 10\\n int[] f = new int[n];\\n int[] c2 = new int[n];\\n int[] c5 = new int[n];\\n f[0] = 1;\\n\\n // Build f, c2, c5\\n for (int i = 1; i < n; i++) {\\n int t = i;\\n c2[i] = c2[i-1];\\n c5[i] = c5[i-1];\\n while (t % 2 == 0) {\\n c2[i]++; t /= 2;\\n }\\n while (t % 5 == 0) {\\n c5[i]++; t /= 5;\\n }\\n f[i] = (f[i-1] * t) % 10;\\n }\\n\\n // Inverses of f[i] mod 10 (\\u03c6(10)=4 \\u21d2 inverse = f[i]^(4-1) mod10)\\n int[] invF = new int[n];\\n for (int i = 0; i < n; i++) {\\n invF[i] = modPow(f[i], 3, 10);\\n }\\n\\n // Powers of 2 and 5 mod 10\\n int[] p2 = new int[n];\\n int[] p5 = new int[n];\\n p2[0] = p5[0] = 1;\\n for (int i = 1; i < n; i++) {\\n p2[i] = (p2[i-1] * 2) % 10;\\n p5[i] = (p5[i-1] * 5) % 10;\\n }\\n\\n // Compute the two weighted sums and compare\\n int sum0 = weightedSum(s, 0, n - 2, f, c2, c5, invF, p2, p5);\\n int sum1 = weightedSum(s, 1, n - 1, f, c2, c5, invF, p2, p5);\\n return sum0 == sum1;\\n }\\n\\n // Sum_{i=l..r} (digit * C(r-l, i-l) mod10)\\n private int weightedSum(String s, int l, int r,\\n int[] f, int[] c2, int[] c5,\\n int[] invF, int[] p2, int[] p5) {\\n int mod = 10;\\n int len = r - l;\\n int baseFact = f[len];\\n int e2 = c2[len];\\n int e5 = c5[len];\\n int total = 0;\\n\\n for (int i = l; i <= r; i++) {\\n int a = i - l, b = r - i;\\n int comb = baseFact;\\n comb = (comb * invF[a]) % mod;\\n comb = (comb * invF[b]) % mod;\\n comb = (comb * p2[e2 - c2[a] - c2[b]]) % mod;\\n comb = (comb * p5[e5 - c5[a] - c5[b]]) % mod;\\n\\n int digit = s.charAt(i) - '0';\\n total = (total + digit * comb) % mod;\\n }\\n return total;\\n }\\n\\n // Fast exponentiation x^e mod m\\n private int modPow(int x, int e, int m) {\\n int res = 1;\\n x %= m;\\n while (e > 0) {\\n if ((e & 1) == 1) res = (res * x) % m;\\n x = (x * x) % m;\\n e >>= 1;\\n }\\n return res;\\n }\\n}\\n\"], [54400, 1.4493, \"import java.lang.reflect.Array;\\nimport java.util.ArrayList;\\nimport java.util.Arrays;\\nimport java.util.Collection;\\nimport java.util.List;\\nimport java.util.function.IntFunction;\\nimport java.util.function.IntToLongFunction;\\nimport java.util.function.IntUnaryOperator;\\nimport java.util.function.Supplier;\\n\\nclass Solution {\\n public boolean hasSameDigits(String s) {\\n var n = s.length();\\n var modCombos2 = new LongOps.SmallPrimePowerModCombos(n - 2, 2);\\n var modCombos5 = new LongOps.SmallPrimePowerModCombos(n - 2, 5);\\n var gcdWithFactors = LongOps.extEuclid(2, 5);\\n var y0 = 0;\\n var y1 = 0;\\n var l2 = (int) gcdWithFactors.x();\\n var l5 = (int) gcdWithFactors.y();\\n for (int i = 0; i <= n - 2; i++) {\\n var c2 = modCombos2.nChooseK(n - 2, i);\\n var c5 = modCombos5.nChooseK(n - 2, i);\\n var c10 = (c2 * l5 * 5 + c5 * l2 * 2) % 10;\\n y0 += c10 * (s.charAt(n - 2 - i) - '0');\\n y0 %= 10;\\n y1 += c10 * (s.charAt(n - 1 - i) - '0');\\n y1 %= 10;\\n }\\n\\n if (y0 < 0) y0 += 10;\\n if (y1 < 0) y1 += 10;\\n return y0 == y1;\\n }\\n\\n static class LongOps {\\n public static final long FLOOR_OF_SQRT_LONG_MAX = 3037000499L;\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n public static long floorOfSqrt(long x) {\\n if (x < 0) throw new IllegalArgumentException(\\\"\\\" + x);\\n\\n var l = 0L;\\n var r = FLOOR_OF_SQRT_LONG_MAX;\\n\\n var res = -1L;\\n do {\\n var m = l + (r - l) / 2;\\n if (m * m <= x) {\\n res = m;\\n l = m + 1;\\n } else {\\n r = m - 1;\\n }\\n } while (l <= r);\\n\\n return res;\\n }\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n public static long modPow(long a, long b, long mod) {\\n if (b < 0) throw new IllegalArgumentException(\\\"b=\\\" + b);\\n checkMod(mod);\\n\\n a %= mod;\\n var res = 1L % mod;\\n while (b != 0) {\\n if ((b & 1) != 0) {\\n res = (res * a) % mod;\\n }\\n\\n a = (a * a) % mod;\\n b >>= 1;\\n }\\n\\n return res;\\n }\\n\\n public static long modInv(long a, long mod) {\\n if (mod <= 0) {\\n throw new IllegalArgumentException(\\\"mod=\\\" + mod);\\n }\\n\\n var eucl = extEuclid(a, mod);\\n if (eucl.gcd != 1) {\\n return 0;\\n }\\n\\n return eucl.x < 0 ? eucl.x + mod : eucl.x;\\n }\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n public static long[] primeModInvsTable(int n, long primeMod) {\\n if (n < 1 || primeMod <= n) {\\n throw new IllegalArgumentException(\\\"n=\\\" + n + \\\", primeMod=\\\" + primeMod);\\n }\\n\\n var table = new long[n + 1];\\n table[0] = 0;\\n table[1] = 1;\\n\\n for (int i = 2; i < table.length; i++) {\\n long ir = table[(int) (primeMod % i)];\\n table[i] = ir == 0 ? 0 : primeMod - (primeMod / i * ir) % primeMod;\\n }\\n return table;\\n }\\n\\n public static class GcdWithFactors {\\n private long gcd;\\n private long x;\\n private long y;\\n\\n private GcdWithFactors() {\\n\\n }\\n\\n public long gcd() {\\n return gcd;\\n }\\n\\n public long x() {\\n return x;\\n }\\n\\n public long y() {\\n return y;\\n }\\n }\\n\\n public static GcdWithFactors extEuclid(long a, long b) {\\n var res = new GcdWithFactors();\\n extEuclid0(a, b, res);\\n return res;\\n }\\n\\n private static void extEuclid0(long a, long b, GcdWithFactors res) {\\n if (b == 0) {\\n res.gcd = a;\\n res.x = 1;\\n res.y = 0;\\n } else {\\n extEuclid0(b, a % b, res);\\n var tmpX = res.x;\\n var tmpY = res.y;\\n\\n res.x = tmpY;\\n res.y = tmpX - tmpY * (a / b);\\n }\\n }\\n\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n private static void checkMod(long mod) {\\n if (mod < 1 || mod > FLOOR_OF_SQRT_LONG_MAX) {\\n throw new IllegalArgumentException(\\\"mod=\\\" + mod);\\n }\\n }\\n\\n /**\\n * Calculates binomial coefficients n over k modulo prime powers p^e even if p is smaller or equal to n.\\n */\\n public static class SmallPrimePowerModCombos {\\n final int e;\\n final int p;\\n final int mod;\\n final int[] pPowersInFactorials;\\n final int[] factorialsWithoutPowers;\\n\\n public SmallPrimePowerModCombos(int n, int p, int e) {\\n if (p <= 1 || e < 1) {\\n throw new IllegalArgumentException(\\\"n=\\\" + n + \\\", p=\\\" + p + \\\", e=\\\" + e);\\n }\\n\\n var mod = p;\\n for (int i = 1; i < e; i++) {\\n mod = Math.multiplyExact(mod, p);\\n }\\n\\n this.e = e;\\n this.p = p;\\n this.mod = mod;\\n\\n this.pPowersInFactorials = new int[n + 1];\\n this.factorialsWithoutPowers = new int[n + 1];\\n\\n factorialsWithoutPowers[0] = 1;\\n for (int i = 1, ip = 1; i <= n; i++, ip++) {\\n pPowersInFactorials[i] = pPowersInFactorials[i - 1];\\n\\n if (ip != p) {\\n factorialsWithoutPowers[i] = modMul(i, factorialsWithoutPowers[i - 1]);\\n } else {\\n var ii = i;\\n do {\\n pPowersInFactorials[i]++;\\n ii /= p;\\n } while (ii % p == 0);\\n\\n factorialsWithoutPowers[i] = modMul(ii, factorialsWithoutPowers[i - 1]);\\n ip = 0;\\n }\\n\\n }\\n }\\n\\n public SmallPrimePowerModCombos(int n, int p) {\\n this(n, p, 1);\\n }\\n\\n public int nChooseK(int n, int k) {\\n var powers = pPowersInFactorials[n] - pPowersInFactorials[k] - pPowersInFactorials[n - k];\\n if (powers >= e) return 0;\\n\\n var res = 1;\\n for (int i = 0; i < powers; i++) {\\n res *= p;\\n }\\n\\n res = modMul(res, factorialsWithoutPowers[n]);\\n res = modMul(res, modInv(factorialsWithoutPowers[k], mod));\\n res = modMul(res, modInv(factorialsWithoutPowers[n - k], mod));\\n return res;\\n }\\n\\n private int modMul(long a, long b) {\\n return (int) ((a * b) % mod);\\n }\\n }\\n\\n public record PrimeFactor(long p, int q) {}\\n\\n public static List<PrimeFactor> primeFactorsOf(long n) {\\n if (n <= 0) {\\n throw new IllegalArgumentException(\\\"n=\\\" + n);\\n }\\n\\n var res = new ArrayList<PrimeFactor>();\\n for (long p = 2; p * p <= n; p++) {\\n if (n % p == 0) {\\n var e = 0;\\n do {\\n n /= p;\\n e++;\\n } while (n % p == 0);\\n\\n res.add(new PrimeFactor(p, e));\\n }\\n }\\n\\n if (n > 1) {\\n res.add(new PrimeFactor(n, 1));\\n }\\n\\n return res;\\n }\\n }\\n\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int minOf(int... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Integer.MAX_VALUE;\\n for (int i : is) {\\n res = Math.min(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int maxOf(int... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Integer.MIN_VALUE;\\n for (int i : is) {\\n res = Math.max(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long minOf(long... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Long.MAX_VALUE;\\n for (long i : is) {\\n res = Math.min(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long maxOf(long... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Long.MIN_VALUE;\\n for (long i : is) {\\n res = Math.max(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> ExtendedArrayList<T> fillList(int n, Supplier<T> supplier) {\\n return fillList(n, ignore -> supplier.get());\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> ExtendedArrayList<T> fillList(int n, IntFunction<T> valueAt) {\\n var res = new ExtendedArrayList<T>(n);\\n for (int i = 0; i < n; i++) {\\n res.add(valueAt.apply(i));\\n }\\n\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> T[] fillArray(int n, Class<T> clazz, Supplier<T> supplier) {\\n return fillArray(n, clazz, ignore -> supplier.get());\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> T[] fillArray(int n, Class<T> clazz, IntFunction<T> valueAt) {\\n @SuppressWarnings(\\\"unchecked\\\") var res = (T[]) Array.newInstance(clazz, n);\\n\\n for (int i = 0; i < n; i++) {\\n res[i] = valueAt.apply(i);\\n }\\n\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\", \\\"SameParameterValue\\\"})\\n static <T> T[] fillArray(int n, T value) {\\n @SuppressWarnings(\\\"unchecked\\\") var res = (T[]) Array.newInstance(value.getClass(), n);\\n Arrays.fill(res, value);\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int[] fillIntArray(int n, IntUnaryOperator valueAt) {\\n var res = new int[n];\\n for (int i = 0; i < n; i++) {\\n res[i] = valueAt.applyAsInt(i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int[] fillIntArray(int n, int value) {\\n var res = new int[n];\\n Arrays.fill(res, value);\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long[] fillLongArray(int n, IntToLongFunction valueAt) {\\n var res = new long[n];\\n for (int i = 0; i < n; i++) {\\n res[i] = valueAt.applyAsLong(i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long[] fillLongArray(int n, long value) {\\n var res = new long[n];\\n Arrays.fill(res, value);\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long gcd(long a, long b) {\\n while (b != 0) {\\n var bb = a % b;\\n a = b;\\n b = bb;\\n }\\n\\n return a;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int gcd(int a, int b) {\\n while (b != 0) {\\n var bb = a % b;\\n a = b;\\n b = bb;\\n }\\n\\n return a;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\", \\\"UnusedReturnValue\\\"})\\n static class ExtendedArrayList<T> extends ArrayList<T> {\\n public ExtendedArrayList(int initialCapacity) {\\n super(initialCapacity);\\n }\\n\\n public ExtendedArrayList() {\\n\\n }\\n\\n public ExtendedArrayList(Collection<? extends T> c) {\\n super(c);\\n }\\n\\n T getFromEnd(int offset) {\\n return get(size() - offset - 1);\\n }\\n\\n T getFst() {\\n return get(0);\\n }\\n\\n T getLst() {\\n return getFromEnd(0);\\n }\\n\\n T removeLst() {\\n return remove(size() - 1);\\n }\\n }\\n}\"], [54500, 0.4831, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int k = n - 2;\\n if (k == 0) {\\n return s.charAt(0) == s.charAt(1);\\n }\\n\\n List<Integer> digitsK_p2 = getDigits(k, 2);\\n List<Integer> digitsK_p5 = getDigits(k, 5);\\n\\n int[] coeff = new int[k + 1];\\n for (int j = 0; j <= k; j++) {\\n int a = lucasModWithDigits(j, 2, digitsK_p2);\\n int b = lucasModWithDigits(j, 5, digitsK_p5);\\n coeff[j] = (5 * a + 6 * b) % 10;\\n }\\n\\n int sum0 = 0;\\n int sum1 = 0;\\n for (int j = 0; j <= k; j++) {\\n int digit0 = s.charAt(j) - '0';\\n sum0 = (sum0 + digit0 * coeff[j]) % 10;\\n int digit1 = s.charAt(j + 1) - '0';\\n sum1 = (sum1 + digit1 * coeff[j]) % 10;\\n }\\n return sum0 == sum1;\\n }\\n\\n private List<Integer> getDigits(int n, int p) {\\n List<Integer> digits = new ArrayList<>();\\n while (n > 0) {\\n digits.add(n % p);\\n n /= p;\\n }\\n return digits;\\n }\\n\\n private int lucasModWithDigits(int j, int p, List<Integer> digitsN) {\\n if (j == 0) {\\n return 1;\\n }\\n List<Integer> digitsK = new ArrayList<>();\\n int jCopy = j;\\n while (jCopy > 0) {\\n digitsK.add(jCopy % p);\\n jCopy /= p;\\n }\\n while (digitsK.size() < digitsN.size()) {\\n digitsK.add(0);\\n }\\n int res = 1;\\n for (int i = 0; i < digitsK.size(); i++) {\\n int ni = (i < digitsN.size()) ? digitsN.get(i) : 0;\\n int ki = digitsK.get(i);\\n if (ki > ni) {\\n return 0;\\n }\\n if (p == 2) {\\n if (ni == 0) {\\n if (ki != 0) return 0;\\n res = (res * 1) % p;\\n } else if (ni == 1) {\\n if (ki == 0 || ki == 1) res = (res * 1) % p;\\n else return 0;\\n }\\n } else if (p == 5) {\\n int[][] table = {\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1}\\n };\\n res = (res * table[ni][ki]) % 5;\\n }\\n }\\n return res;\\n }\\n}\"], [54600, 0.9662, \"import java.lang.reflect.Array;\\nimport java.util.ArrayList;\\nimport java.util.Arrays;\\nimport java.util.Collection;\\nimport java.util.List;\\nimport java.util.function.IntFunction;\\nimport java.util.function.IntToLongFunction;\\nimport java.util.function.IntUnaryOperator;\\nimport java.util.function.Supplier;\\n\\nclass Solution {\\n public boolean hasSameDigits(String s) {\\n var n = s.length();\\n var modCombos2 = new LongOps.SmallPrimePowerModCombos(n - 2, 2);\\n var modCombos5 = new LongOps.SmallPrimePowerModCombos(n - 2, 5);\\n var y02 = 0;\\n var y05 = 0;\\n var y12 = 0;\\n var y15 = 0;\\n for (int i = 0; i <= n - 2; i++) {\\n var c2 = modCombos2.nChooseK(n - 2, i);\\n var c5 = modCombos5.nChooseK(n - 2, i);\\n\\n int d0 = s.charAt(n - 2 - i) - '0';\\n y02 += c2 * d0;\\n y02 %= 2;\\n y05 += c5 * d0;\\n y05 %= 5;\\n\\n int d1 = s.charAt(n - 1 - i) - '0';\\n y12 += c2 * d1;\\n y12 %= 2;\\n y15 += c5 * d1;\\n y15 %= 5;\\n }\\n\\n return y02 == y12 && y05 == y15;\\n }\\n\\n static class LongOps {\\n public static final long FLOOR_OF_SQRT_LONG_MAX = 3037000499L;\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n public static long floorOfSqrt(long x) {\\n if (x < 0) throw new IllegalArgumentException(\\\"\\\" + x);\\n\\n var l = 0L;\\n var r = FLOOR_OF_SQRT_LONG_MAX;\\n\\n var res = -1L;\\n do {\\n var m = l + (r - l) / 2;\\n if (m * m <= x) {\\n res = m;\\n l = m + 1;\\n } else {\\n r = m - 1;\\n }\\n } while (l <= r);\\n\\n return res;\\n }\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n public static long modPow(long a, long b, long mod) {\\n if (b < 0) throw new IllegalArgumentException(\\\"b=\\\" + b);\\n checkMod(mod);\\n\\n a %= mod;\\n var res = 1L % mod;\\n while (b != 0) {\\n if ((b & 1) != 0) {\\n res = (res * a) % mod;\\n }\\n\\n a = (a * a) % mod;\\n b >>= 1;\\n }\\n\\n return res;\\n }\\n\\n public static long modInv(long a, long mod) {\\n if (mod <= 0) {\\n throw new IllegalArgumentException(\\\"mod=\\\" + mod);\\n }\\n\\n var eucl = extEuclid(a, mod);\\n if (eucl.gcd != 1) {\\n return 0;\\n }\\n\\n return eucl.x < 0 ? eucl.x + mod : eucl.x;\\n }\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n public static long[] primeModInvsTable(int n, long primeMod) {\\n if (n < 1 || primeMod <= n) {\\n throw new IllegalArgumentException(\\\"n=\\\" + n + \\\", primeMod=\\\" + primeMod);\\n }\\n\\n var table = new long[n + 1];\\n table[0] = 0;\\n table[1] = 1;\\n\\n for (int i = 2; i < table.length; i++) {\\n long ir = table[(int) (primeMod % i)];\\n table[i] = ir == 0 ? 0 : primeMod - (primeMod / i * ir) % primeMod;\\n }\\n return table;\\n }\\n\\n public static class GcdWithFactors {\\n private long gcd;\\n private long x;\\n private long y;\\n\\n private GcdWithFactors() {\\n\\n }\\n\\n public long gcd() {\\n return gcd;\\n }\\n\\n public long x() {\\n return x;\\n }\\n\\n public long y() {\\n return y;\\n }\\n }\\n\\n public static GcdWithFactors extEuclid(long a, long b) {\\n var res = new GcdWithFactors();\\n extEuclid0(a, b, res);\\n return res;\\n }\\n\\n private static void extEuclid0(long a, long b, GcdWithFactors res) {\\n if (b == 0) {\\n res.gcd = a;\\n res.x = 1;\\n res.y = 0;\\n } else {\\n extEuclid0(b, a % b, res);\\n var tmpX = res.x;\\n var tmpY = res.y;\\n\\n res.x = tmpY;\\n res.y = tmpX - tmpY * (a / b);\\n }\\n }\\n\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n private static void checkMod(long mod) {\\n if (mod < 1 || mod > FLOOR_OF_SQRT_LONG_MAX) {\\n throw new IllegalArgumentException(\\\"mod=\\\" + mod);\\n }\\n }\\n\\n /**\\n * Calculates binomial coefficients n over k modulo prime powers p^e even if p is smaller or equal to n.\\n */\\n public static class SmallPrimePowerModCombos {\\n final int e;\\n final int p;\\n final int mod;\\n final int[] pPowersInFactorials;\\n final int[] factorialsWithoutPowers;\\n\\n public SmallPrimePowerModCombos(int n, int p, int e) {\\n if (p <= 1 || e < 1) {\\n throw new IllegalArgumentException(\\\"n=\\\" + n + \\\", p=\\\" + p + \\\", e=\\\" + e);\\n }\\n\\n var mod = p;\\n for (int i = 1; i < e; i++) {\\n mod = Math.multiplyExact(mod, p);\\n }\\n\\n this.e = e;\\n this.p = p;\\n this.mod = mod;\\n\\n this.pPowersInFactorials = new int[n + 1];\\n this.factorialsWithoutPowers = new int[n + 1];\\n\\n factorialsWithoutPowers[0] = 1;\\n for (int i = 1, ip = 1; i <= n; i++, ip++) {\\n pPowersInFactorials[i] = pPowersInFactorials[i - 1];\\n\\n if (ip != p) {\\n factorialsWithoutPowers[i] = modMul(i, factorialsWithoutPowers[i - 1]);\\n } else {\\n var ii = i;\\n do {\\n pPowersInFactorials[i]++;\\n ii /= p;\\n } while (ii % p == 0);\\n\\n factorialsWithoutPowers[i] = modMul(ii, factorialsWithoutPowers[i - 1]);\\n ip = 0;\\n }\\n\\n }\\n }\\n\\n public SmallPrimePowerModCombos(int n, int p) {\\n this(n, p, 1);\\n }\\n\\n public int nChooseK(int n, int k) {\\n var powers = pPowersInFactorials[n] - pPowersInFactorials[k] - pPowersInFactorials[n - k];\\n if (powers >= e) return 0;\\n\\n var res = 1;\\n for (int i = 0; i < powers; i++) {\\n res *= p;\\n }\\n\\n res = modMul(res, factorialsWithoutPowers[n]);\\n res = modMul(res, modInv(factorialsWithoutPowers[k], mod));\\n res = modMul(res, modInv(factorialsWithoutPowers[n - k], mod));\\n return res;\\n }\\n\\n private int modMul(long a, long b) {\\n return (int) ((a * b) % mod);\\n }\\n }\\n\\n public record PrimeFactor(long p, int q) {}\\n\\n public static List<PrimeFactor> primeFactorsOf(long n) {\\n if (n <= 0) {\\n throw new IllegalArgumentException(\\\"n=\\\" + n);\\n }\\n\\n var res = new ArrayList<PrimeFactor>();\\n for (long p = 2; p * p <= n; p++) {\\n if (n % p == 0) {\\n var e = 0;\\n do {\\n n /= p;\\n e++;\\n } while (n % p == 0);\\n\\n res.add(new PrimeFactor(p, e));\\n }\\n }\\n\\n if (n > 1) {\\n res.add(new PrimeFactor(n, 1));\\n }\\n\\n return res;\\n }\\n }\\n\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int minOf(int... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Integer.MAX_VALUE;\\n for (int i : is) {\\n res = Math.min(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int maxOf(int... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Integer.MIN_VALUE;\\n for (int i : is) {\\n res = Math.max(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long minOf(long... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Long.MAX_VALUE;\\n for (long i : is) {\\n res = Math.min(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long maxOf(long... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Long.MIN_VALUE;\\n for (long i : is) {\\n res = Math.max(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> ExtendedArrayList<T> fillList(int n, Supplier<T> supplier) {\\n return fillList(n, ignore -> supplier.get());\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> ExtendedArrayList<T> fillList(int n, IntFunction<T> valueAt) {\\n var res = new ExtendedArrayList<T>(n);\\n for (int i = 0; i < n; i++) {\\n res.add(valueAt.apply(i));\\n }\\n\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> T[] fillArray(int n, Class<T> clazz, Supplier<T> supplier) {\\n return fillArray(n, clazz, ignore -> supplier.get());\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> T[] fillArray(int n, Class<T> clazz, IntFunction<T> valueAt) {\\n @SuppressWarnings(\\\"unchecked\\\") var res = (T[]) Array.newInstance(clazz, n);\\n\\n for (int i = 0; i < n; i++) {\\n res[i] = valueAt.apply(i);\\n }\\n\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\", \\\"SameParameterValue\\\"})\\n static <T> T[] fillArray(int n, T value) {\\n @SuppressWarnings(\\\"unchecked\\\") var res = (T[]) Array.newInstance(value.getClass(), n);\\n Arrays.fill(res, value);\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int[] fillIntArray(int n, IntUnaryOperator valueAt) {\\n var res = new int[n];\\n for (int i = 0; i < n; i++) {\\n res[i] = valueAt.applyAsInt(i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int[] fillIntArray(int n, int value) {\\n var res = new int[n];\\n Arrays.fill(res, value);\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long[] fillLongArray(int n, IntToLongFunction valueAt) {\\n var res = new long[n];\\n for (int i = 0; i < n; i++) {\\n res[i] = valueAt.applyAsLong(i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long[] fillLongArray(int n, long value) {\\n var res = new long[n];\\n Arrays.fill(res, value);\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long gcd(long a, long b) {\\n while (b != 0) {\\n var bb = a % b;\\n a = b;\\n b = bb;\\n }\\n\\n return a;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int gcd(int a, int b) {\\n while (b != 0) {\\n var bb = a % b;\\n a = b;\\n b = bb;\\n }\\n\\n return a;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\", \\\"UnusedReturnValue\\\"})\\n static class ExtendedArrayList<T> extends ArrayList<T> {\\n public ExtendedArrayList(int initialCapacity) {\\n super(initialCapacity);\\n }\\n\\n public ExtendedArrayList() {\\n\\n }\\n\\n public ExtendedArrayList(Collection<? extends T> c) {\\n super(c);\\n }\\n\\n T getFromEnd(int offset) {\\n return get(size() - offset - 1);\\n }\\n\\n T getFst() {\\n return get(0);\\n }\\n\\n T getLst() {\\n return getFromEnd(0);\\n }\\n\\n T removeLst() {\\n return remove(size() - 1);\\n }\\n }\\n}\"], [54800, 0.4831, \"/*\\nTook a bit to figure that: the two values are left with are\\nthe result of f3 modulo 10.\\n\\nWe need to use Lucas's Theorum to get the last digit of the binomial\\n*/\\n\\nclass Solution {\\n\\n int fact(int n) {\\n return switch(n) {\\n case 0 -> 1;\\n case 1-> 1;\\n case 2-> 2;\\n case 3-> 6;\\n case 4-> 24;\\n case 5-> 120;\\n default -> throw new IllegalArgumentException();\\n };\\n }\\n\\n int binomial(int n, int k) {\\n if (n < k) {\\n return 0;\\n }\\n int numerator = fact(n);\\n int denominator =(fact(k) * fact(n - k));\\n return numerator / denominator;\\n }\\n\\n int lookup_5_2_solution(int xMod5, int xMod2) {\\n return switch (xMod2) {\\n case 0 ->\\n switch (xMod5) {\\n case 0 -> 0;\\n case 1 -> 6;\\n case 2 -> 2;\\n case 3 -> 8;\\n case 4 -> 4;\\n default -> throw new IllegalArgumentException();\\n };\\n case 1 ->\\n switch (xMod5) {\\n case 0 -> 5;\\n case 1 -> 1;\\n case 2 -> 7;\\n case 3 -> 3;\\n case 4 -> 9;\\n default -> throw new IllegalArgumentException();\\n };\\n default -> throw new IllegalArgumentException();\\n };\\n }\\n\\n int binomialCoefficientLastDigit(int n, int k) {\\n String n2 = Integer.toString(n, 2);\\n String n5 = Integer.toString(n, 5);\\n String ik2 = Integer.toString(k, 2);\\n String ik5 = Integer.toString(k, 5);\\n String k2 = \\\"0\\\".repeat(n2.length() - ik2.length()) + ik2;\\n String k5 = \\\"0\\\".repeat(n5.length() - ik5.length()) + ik5;\\n int xMod5 = 1;\\n int xMod2 = 1;\\n for (int i = 0; i < k5.length(); i++) {\\n xMod5 *= binomial(n5.charAt(i) - '0', k5.charAt(i) - '0');\\n xMod5 %= 5;\\n }\\n for (int i = 0; i < k2.length(); i++) {\\n xMod2 *= binomial(n2.charAt(i) - '0', k2.charAt(i) - '0');\\n xMod2 %= 2;\\n }\\n\\nreturn lookup_5_2_solution(xMod5, xMod2);\\n\\n\\n }\\n\\n public boolean hasSameDigits(String s) {\\n int sumsLength = s.length() - 1;\\n int[] pascalRowLastDigits = IntStream.range(0, sumsLength)\\n .map(k -> binomialCoefficientLastDigit(sumsLength - 1, k))\\n .toArray();\\n int[] digits = s.chars().map(c -> c - '0').toArray();\\n int firstDigitsSum = 0;\\n int secondDigitsSum = 0;\\n\\n for (int i = 0; i < sumsLength; i++) {\\n firstDigitsSum += pascalRowLastDigits[i] * digits[i];\\n secondDigitsSum += pascalRowLastDigits[i] * digits[i+1];\\n }\\n\\n return (firstDigitsSum % 10) == (secondDigitsSum % 10);\\n }\\n // CLOJURE CODE BELOW\\n /*\\n(defn f1 [i]\\n(loop [s (->> i (map int) (map #(- % (int \\\\0))))]\\n (if (<= (count s) 2)\\n s #_(when (= (first s) (second s)) s)\\n (recur (map #(mod (+ %1 %2) 10) s (rest s))))))\\n\\n(defn f2 [i]\\n(loop [s (->> i (map int) (map #(- % (int \\\\0))))]\\n (if (<= (count s) 2)\\n s\\n (recur (map #(list %1 %2) s (rest s))))))\\n\\n(defn left-pad-with [desired-width padding padee]\\n(concat (repeat (- desired-width (count padee)) padding) padee))\\n\\n(defn fact [n] (apply * (range 1 (inc n))))\\n(defn binomial [n k]\\n(if (< n k) 0 (/ (fact n) (* (fact k) (fact (- n k))))))\\n(defn binomial-ld1 [n k] (mod (binomial n k) 10))\\n; using Lucas's Theorum\\n\\n(def lookup-5-2 {\\n[0 0] 0\\n[1 0] 6\\n[2 0] 2\\n[3 0] 8\\n[4 0] 4\\n[0 1] 5\\n[1 1] 1\\n[2 1] 7\\n[3 1] 3\\n[4 1] 9\\n})\\n\\n(defn binomial-ld2 [n k]\\n(let [\\nn-digits-2 (->> n (#(Integer/toString % 2)) (map char) (map int) (map #(- % (int \\\\0))))\\nn-digits-5 (->> n (#(Integer/toString % 5)) (map char) (map int) (map #(- % (int \\\\0))))\\nk-digits-2 (->> k (#(Integer/toString % 2)) (map char) (map int) (map #(- % (int \\\\0))) (left-pad-with (count n-digits-2) 0))\\nk-digits-5 (->> k (#(Integer/toString % 5)) (map char) (map int) (map #(- % (int \\\\0))) (left-pad-with (count n-digits-5) 0))\\nx-mod-2 (->> (map binomial n-digits-2 k-digits-2) (apply *) (#(mod % 2)))\\nx-mod-5 (->> (map binomial n-digits-5 k-digits-5) (apply *) (#(mod % 5)))\\n]\\n(lookup-5-2 [x-mod-5 x-mod-2])))\\n\\n(defn f3 [i]\\n(let [sums-len (dec (count i)),\\npascal-row-ld (->> (range sums-len)\\n #_(map #(binomial-ld1 (dec sums-len) %))\\n (map #(binomial-ld2 (dec sums-len) %))\\n )\\ndgts (->> i (map int) (map #(- % (int \\\\0))))\\n]\\n[\\n(->> dgts drop-last (map * pascal-row-ld))\\n(->> dgts (drop 1) (map * pascal-row-ld))\\n]\\n))\\n\\n(prn (map #(mod (* % 3) 10) (range 20)))\\n(prn (map #(mod (* % 13) 10) (range 20)))\\n\\n#_(->> (range 1000 2000)\\n (map (juxt #(->> % str (map char) f2) identity))\\n #_(filter first)\\n (map prn)\\n doall\\n #_(map second)\\n #_(reduce +)\\n #_prn)\\n\\n(def R [\\\\1 \\\\2 \\\\3 \\\\4 \\\\5 \\\\6 \\\\7 \\\\8])\\n(def R2 [\\\\7 \\\\9 \\\\5 \\\\2])\\n\\n (prn (f1 R))\\n #_(prn (f2 R))\\n #_(prn (count (f2 R)))\\n #_(prn (map flatten (f2 R)))\\n #_(prn (->> R f2 (map flatten) (map (partial apply +))))\\n #_(prn (->> R f2 (map flatten) (map sort)))\\n #_(prn (->> R f2 (map flatten) (map sort) (map frequencies)))\\n (prn (->> R f3))\\n (prn (->> R f3 (map (partial apply +))))\\n\\n (prn (->> R2 f1))\\n (prn (->> R2 f3 (map (partial apply +)) (map #(mod % 10))))\\n #_(prn (apply + (flatten (f2 R))))\\n\\n; vim: syntax=clojure\\n\\n */\\n}\"], [54900, 0.4831, \"/*\\nTook a bit to figure that: the two values are left with are\\nthe result of f3 modulo 10.\\n\\nWe need to use Lucas's Theorum to get the last digit of the binomial\\n*/\\n\\nclass Solution {\\n\\n int fact(int n) {\\n return switch(n) {\\n case 0 -> 1;\\n case 1-> 1;\\n case 2-> 2;\\n case 3-> 6;\\n case 4-> 24;\\n case 5-> 120;\\n default -> throw new IllegalArgumentException();\\n };\\n }\\n\\n int binomial(int n, int k) {\\n if (n < k) {\\n return 0;\\n }\\n int numerator = fact(n);\\n int denominator =(fact(k) * fact(n - k));\\n return numerator / denominator;\\n }\\n\\n int lookup_5_2_solution(int xMod5, int xMod2) {\\n return switch (xMod2) {\\n case 0 ->\\n switch (xMod5) {\\n case 0 -> 0;\\n case 1 -> 6;\\n case 2 -> 2;\\n case 3 -> 8;\\n case 4 -> 4;\\n default -> throw new IllegalArgumentException();\\n };\\n case 1 ->\\n switch (xMod5) {\\n case 0 -> 5;\\n case 1 -> 1;\\n case 2 -> 7;\\n case 3 -> 3;\\n case 4 -> 9;\\n default -> throw new IllegalArgumentException();\\n };\\n default -> throw new IllegalArgumentException();\\n };\\n }\\n\\n int binomialCoefficientLastDigit(int n, int k) {\\n String n2 = Integer.toString(n, 2);\\n String n5 = Integer.toString(n, 5);\\n String ik2 = Integer.toString(k, 2);\\n String ik5 = Integer.toString(k, 5);\\n String k2 = \\\"0\\\".repeat(n2.length() - ik2.length()) + ik2;\\n String k5 = \\\"0\\\".repeat(n5.length() - ik5.length()) + ik5;\\n int xMod5 = IntStream.range(0, k5.length()).map(i -> binomial(n5.charAt(i) - '0', k5.charAt(i) - '0')).reduce(1, Math::multiplyExact) % 5;\\n int xMod2 = IntStream.range(0, k2.length()).map(i -> binomial(n2.charAt(i) - '0', k2.charAt(i) - '0')).reduce(1, Math::multiplyExact) % 2;\\n\\nreturn lookup_5_2_solution(xMod5, xMod2);\\n\\n\\n }\\n\\n public boolean hasSameDigits(String s) {\\n int sumsLength = s.length() - 1;\\n int[] pascalRowLastDigits = IntStream.range(0, sumsLength)\\n .map(k -> binomialCoefficientLastDigit(sumsLength - 1, k))\\n .toArray();\\n int[] digits = s.chars().map(c -> c - '0').toArray();\\n int firstDigitsSum = IntStream.range(0, sumsLength).map(i -> pascalRowLastDigits[i] * digits[i]).reduce(0, Math::addExact);\\n int secondDigitsSum = IntStream.range(0, sumsLength).map(i -> pascalRowLastDigits[i] * digits[i+1]).reduce(0, Math::addExact);\\n\\n return (firstDigitsSum % 10) == (secondDigitsSum % 10);\\n }\\n // CLOJURE CODE BELOW\\n /*\\n(defn f1 [i]\\n(loop [s (->> i (map int) (map #(- % (int \\\\0))))]\\n (if (<= (count s) 2)\\n s #_(when (= (first s) (second s)) s)\\n (recur (map #(mod (+ %1 %2) 10) s (rest s))))))\\n\\n(defn f2 [i]\\n(loop [s (->> i (map int) (map #(- % (int \\\\0))))]\\n (if (<= (count s) 2)\\n s\\n (recur (map #(list %1 %2) s (rest s))))))\\n\\n(defn left-pad-with [desired-width padding padee]\\n(concat (repeat (- desired-width (count padee)) padding) padee))\\n\\n(defn fact [n] (apply * (range 1 (inc n))))\\n(defn binomial [n k]\\n(if (< n k) 0 (/ (fact n) (* (fact k) (fact (- n k))))))\\n(defn binomial-ld1 [n k] (mod (binomial n k) 10))\\n; using Lucas's Theorum\\n\\n(def lookup-5-2 {\\n[0 0] 0\\n[1 0] 6\\n[2 0] 2\\n[3 0] 8\\n[4 0] 4\\n[0 1] 5\\n[1 1] 1\\n[2 1] 7\\n[3 1] 3\\n[4 1] 9\\n})\\n\\n(defn binomial-ld2 [n k]\\n(let [\\nn-digits-2 (->> n (#(Integer/toString % 2)) (map char) (map int) (map #(- % (int \\\\0))))\\nn-digits-5 (->> n (#(Integer/toString % 5)) (map char) (map int) (map #(- % (int \\\\0))))\\nk-digits-2 (->> k (#(Integer/toString % 2)) (map char) (map int) (map #(- % (int \\\\0))) (left-pad-with (count n-digits-2) 0))\\nk-digits-5 (->> k (#(Integer/toString % 5)) (map char) (map int) (map #(- % (int \\\\0))) (left-pad-with (count n-digits-5) 0))\\nx-mod-2 (->> (map binomial n-digits-2 k-digits-2) (apply *) (#(mod % 2)))\\nx-mod-5 (->> (map binomial n-digits-5 k-digits-5) (apply *) (#(mod % 5)))\\n]\\n(lookup-5-2 [x-mod-5 x-mod-2])))\\n\\n(defn f3 [i]\\n(let [sums-len (dec (count i)),\\npascal-row-ld (->> (range sums-len)\\n #_(map #(binomial-ld1 (dec sums-len) %))\\n (map #(binomial-ld2 (dec sums-len) %))\\n )\\ndgts (->> i (map int) (map #(- % (int \\\\0))))\\n]\\n[\\n(->> dgts drop-last (map * pascal-row-ld))\\n(->> dgts (drop 1) (map * pascal-row-ld))\\n]\\n))\\n\\n(prn (map #(mod (* % 3) 10) (range 20)))\\n(prn (map #(mod (* % 13) 10) (range 20)))\\n\\n#_(->> (range 1000 2000)\\n (map (juxt #(->> % str (map char) f2) identity))\\n #_(filter first)\\n (map prn)\\n doall\\n #_(map second)\\n #_(reduce +)\\n #_prn)\\n\\n(def R [\\\\1 \\\\2 \\\\3 \\\\4 \\\\5 \\\\6 \\\\7 \\\\8])\\n(def R2 [\\\\7 \\\\9 \\\\5 \\\\2])\\n\\n (prn (f1 R))\\n #_(prn (f2 R))\\n #_(prn (count (f2 R)))\\n #_(prn (map flatten (f2 R)))\\n #_(prn (->> R f2 (map flatten) (map (partial apply +))))\\n #_(prn (->> R f2 (map flatten) (map sort)))\\n #_(prn (->> R f2 (map flatten) (map sort) (map frequencies)))\\n (prn (->> R f3))\\n (prn (->> R f3 (map (partial apply +))))\\n\\n (prn (->> R2 f1))\\n (prn (->> R2 f3 (map (partial apply +)) (map #(mod % 10))))\\n #_(prn (apply + (flatten (f2 R))))\\n\\n; vim: syntax=clojure\\n\\n */\\n}\"], [55000, 0.4831, \"/*\\nTook a bit to figure that: the two values are left with are\\nthe result of f3 modulo 10.\\n\\nWe need to use Lucas's Theorum to get the last digit of the binomial\\n*/\\n\\nclass Solution {\\n\\n int fact(int n) {\\n return switch(n) {\\n case 0 -> 1;\\n case 1-> 1;\\n case 2-> 2;\\n case 3-> 6;\\n case 4-> 24;\\n case 5-> 120;\\n default -> throw new IllegalArgumentException();\\n };\\n }\\n\\n int binomial(int n, int k) {\\n if (n < k) {\\n return 0;\\n }\\n int numerator = fact(n);\\n int denominator =(fact(k) * fact(n - k));\\n return numerator / denominator;\\n }\\n\\n int lookup_5_2_solution(int xMod5, int xMod2) {\\n return switch (xMod2) {\\n case 0 ->\\n switch (xMod5) {\\n case 0 -> 0;\\n case 1 -> 6;\\n case 2 -> 2;\\n case 3 -> 8;\\n case 4 -> 4;\\n default -> throw new IllegalArgumentException();\\n };\\n case 1 ->\\n switch (xMod5) {\\n case 0 -> 5;\\n case 1 -> 1;\\n case 2 -> 7;\\n case 3 -> 3;\\n case 4 -> 9;\\n default -> throw new IllegalArgumentException();\\n };\\n default -> throw new IllegalArgumentException();\\n };\\n }\\n\\n int binomialCoefficientLastDigit(int n, int k) {\\n String n2 = Integer.toString(n, 2);\\n String n5 = Integer.toString(n, 5);\\n String ik2 = Integer.toString(k, 2);\\n String ik5 = Integer.toString(k, 5);\\n String k2 = \\\"0\\\".repeat(n2.length() - ik2.length()) + ik2;\\n String k5 = \\\"0\\\".repeat(n5.length() - ik5.length()) + ik5;\\n int xMod5 = IntStream.range(0, k5.length()).map(i -> binomial(n5.charAt(i) - '0', k5.charAt(i) - '0')).reduce(1, Math::multiplyExact) % 5;\\n int xMod2 = IntStream.range(0, k2.length()).map(i -> binomial(n2.charAt(i) - '0', k2.charAt(i) - '0')).reduce(1, Math::multiplyExact) % 2;\\n\\nreturn lookup_5_2_solution(xMod5, xMod2);\\n\\n\\n }\\n\\n public boolean hasSameDigits(String s) {\\n int sumsLength = s.length() - 1;\\n int[] pascalRowLastDigits = IntStream.range(0, sumsLength)\\n .map(k -> binomialCoefficientLastDigit(sumsLength - 1, k))\\n .toArray();\\n List<Integer> digits = s.chars().map(c -> c - '0').boxed().toList();\\n int firstDigitsSum = IntStream.range(0, sumsLength).map(i -> pascalRowLastDigits[i] * digits.get(i)).reduce(0, Math::addExact);\\n int secondDigitsSum = IntStream.range(0, sumsLength).map(i -> pascalRowLastDigits[i] * digits.get(i + 1)).reduce(0, Math::addExact);\\n\\n return (firstDigitsSum % 10) == (secondDigitsSum % 10);\\n }\\n // CLOJURE CODE BELOW\\n /*\\n(defn f1 [i]\\n(loop [s (->> i (map int) (map #(- % (int \\\\0))))]\\n (if (<= (count s) 2)\\n s #_(when (= (first s) (second s)) s)\\n (recur (map #(mod (+ %1 %2) 10) s (rest s))))))\\n\\n(defn f2 [i]\\n(loop [s (->> i (map int) (map #(- % (int \\\\0))))]\\n (if (<= (count s) 2)\\n s\\n (recur (map #(list %1 %2) s (rest s))))))\\n\\n(defn left-pad-with [desired-width padding padee]\\n(concat (repeat (- desired-width (count padee)) padding) padee))\\n\\n(defn fact [n] (apply * (range 1 (inc n))))\\n(defn binomial [n k]\\n(if (< n k) 0 (/ (fact n) (* (fact k) (fact (- n k))))))\\n(defn binomial-ld1 [n k] (mod (binomial n k) 10))\\n; using Lucas's Theorum\\n\\n(def lookup-5-2 {\\n[0 0] 0\\n[1 0] 6\\n[2 0] 2\\n[3 0] 8\\n[4 0] 4\\n[0 1] 5\\n[1 1] 1\\n[2 1] 7\\n[3 1] 3\\n[4 1] 9\\n})\\n\\n(defn binomial-ld2 [n k]\\n(let [\\nn-digits-2 (->> n (#(Integer/toString % 2)) (map char) (map int) (map #(- % (int \\\\0))))\\nn-digits-5 (->> n (#(Integer/toString % 5)) (map char) (map int) (map #(- % (int \\\\0))))\\nk-digits-2 (->> k (#(Integer/toString % 2)) (map char) (map int) (map #(- % (int \\\\0))) (left-pad-with (count n-digits-2) 0))\\nk-digits-5 (->> k (#(Integer/toString % 5)) (map char) (map int) (map #(- % (int \\\\0))) (left-pad-with (count n-digits-5) 0))\\nx-mod-2 (->> (map binomial n-digits-2 k-digits-2) (apply *) (#(mod % 2)))\\nx-mod-5 (->> (map binomial n-digits-5 k-digits-5) (apply *) (#(mod % 5)))\\n]\\n(lookup-5-2 [x-mod-5 x-mod-2])))\\n\\n(defn f3 [i]\\n(let [sums-len (dec (count i)),\\npascal-row-ld (->> (range sums-len)\\n #_(map #(binomial-ld1 (dec sums-len) %))\\n (map #(binomial-ld2 (dec sums-len) %))\\n )\\ndgts (->> i (map int) (map #(- % (int \\\\0))))\\n]\\n[\\n(->> dgts drop-last (map * pascal-row-ld))\\n(->> dgts (drop 1) (map * pascal-row-ld))\\n]\\n))\\n\\n(prn (map #(mod (* % 3) 10) (range 20)))\\n(prn (map #(mod (* % 13) 10) (range 20)))\\n\\n#_(->> (range 1000 2000)\\n (map (juxt #(->> % str (map char) f2) identity))\\n #_(filter first)\\n (map prn)\\n doall\\n #_(map second)\\n #_(reduce +)\\n #_prn)\\n\\n(def R [\\\\1 \\\\2 \\\\3 \\\\4 \\\\5 \\\\6 \\\\7 \\\\8])\\n(def R2 [\\\\7 \\\\9 \\\\5 \\\\2])\\n\\n (prn (f1 R))\\n #_(prn (f2 R))\\n #_(prn (count (f2 R)))\\n #_(prn (map flatten (f2 R)))\\n #_(prn (->> R f2 (map flatten) (map (partial apply +))))\\n #_(prn (->> R f2 (map flatten) (map sort)))\\n #_(prn (->> R f2 (map flatten) (map sort) (map frequencies)))\\n (prn (->> R f3))\\n (prn (->> R f3 (map (partial apply +))))\\n\\n (prn (->> R2 f1))\\n (prn (->> R2 f3 (map (partial apply +)) (map #(mod % 10))))\\n #_(prn (apply + (flatten (f2 R))))\\n\\n; vim: syntax=clojure\\n\\n */\\n}\"], [55300, 0.9662, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n final int n = s.length();\\n int num1 = 0, num2 = 0;\\n\\n int[] digits = new int[n];\\n for (int i = 0; i < n; ++i)\\n digits[i] = s.charAt(i) - '0';\\n\\n int[] coeffs = new int[n - 1];\\n for (int i = 0; i < n - 1; ++i)\\n coeffs[i] = nCMOD10(n - 2, i);\\n\\n for (int i = 0; i + 1 < n; ++i) {\\n num1 = (num1 + coeffs[i] * digits[i]) % 10;\\n num2 = (num2 + coeffs[i] * digits[i + 1]) % 10;\\n }\\n\\n return num1 == num2;\\n }\\n\\n private int nCMOD10(int n, int k) {\\n final int mod2 = lucasTheorem(n, k, 2);\\n final int mod5 = lucasTheorem(n, k, 5);\\n int[][] lookup = {\\n {0, 6, 2, 8, 4},\\n {5, 1, 7, 3, 9}\\n };\\n return lookup[mod2][mod5];\\n }\\n\\n private int lucasTheorem(int n, int k, int prime) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int nMod = n % prime;\\n int kMod = k % prime;\\n res = (res * fastComb(nMod, kMod)) % prime;\\n n /= prime;\\n k /= prime;\\n }\\n return res;\\n }\\n\\n private int fastComb(int n, int k) {\\n if (k > n) return 0;\\n if (k == 0 || k == n) return 1;\\n if (k == 1) return n;\\n if (k == 2) return n * (n - 1) / 2;\\n if (k == 3) return n * (n - 1) * (n - 2) / 6;\\n if (k == 4) return n * (n - 1) * (n - 2) * (n - 3) / 24;\\n return 0; \\n }\\n}\\n\"], [55500, 0.4831, \"class Solution {\\n private int binomialMod10(int n, int k) \\n {\\n int i = binomialMod2(n, k);\\n int j = binomialMod5(n, k);\\n\\n for (int x = 0; x < 10; x++) \\n {\\n if (x % 2 == i && x % 5 == j) \\n {\\n return x;\\n }\\n }\\n return 0;\\n }\\n\\n // Step 5: Compute Binomial Coefficient Modulo 2\\n private int binomialMod2(int n, int k) \\n {\\n return ((n & k) == k) ? 1 : 0;\\n }\\n\\n // Step 6: Compute Binomial Coefficient Modulo 5 Using Lookup Table\\n private int binomialMod5(int n, int k) \\n {\\n int[][] tuples = {{1}, {1, 1}, {1, 2, 1}, {1, 3, 3, 1}, {1, 4, 1, 4, 1}};\\n int result = 1;\\n\\n while (n > 0 || k > 0) \\n {\\n int nthd = n % 5;\\n int kthd = k % 5;\\n\\n if (kthd > nthd) return 0;\\n\\n result = (result * tuples[nthd][kthd]) % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return result;\\n }\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n\\n long[] arr = new long[n-1];\\n // arr[0] = 1;\\n\\n // arr[n-2] = 1;\\n\\n // long curr = 1;\\n // long nmr = n - 2;\\n // long den = 1;\\n // for (int i = 1; i < n /2; i++) {\\n // long num = (curr * nmr) / den;\\n // if (num % 10 == 0) num = 10;\\n // else\\n // num = num % 10;\\n\\n // System.out.println(i + \\\" \\\" + num + \\\" \\\" + curr + \\\" \\\" + nmr + \\\" \\\"+den);\\n // nmr--;\\n // den++;\\n // curr = num;\\n // arr[i] = num;\\n // }\\n\\n // for (int i = n/2; i < n-1; i++) {\\n // int index = n-2 - i;\\n // arr[i] = arr[index];\\n // }\\n\\n for (int i = 0; i < n-1; i++) {\\n arr[i] = binomialMod10(n-2, i);\\n }\\n\\n long digit1 = 0;\\n long digit2 = 0;\\n\\n for (int i = 0; i < n-1; i++) {\\n // System.out.print(arr[i] + \\\" \\\");\\n long dig1 = s.charAt(i) - '0';\\n long dig2 = s.charAt(i+1) - '0';\\n \\n digit1 = (digit1 + arr[i] * dig1) % 10;\\n\\n digit2 = (digit2 + arr[i] * dig2) % 10;\\n }\\n\\n // System.out.println();\\n // System.out.println(digit1 + \\\" \\\" + digit2);\\n\\n return digit1 == digit2;\\n }\\n}\"]]",
"runtime": 572,
"runtimeDistribution": "[[25, 2.4154999999999998, \"import java.util.Arrays; // Required for Arrays.fill if used, though not strictly needed here\\n\\nclass Solution {\\n\\n /**\\n * Checks if the digits satisfy a condition related to binomial coefficients\\n * modulo 2 and 5 applied to adjacent digit differences.\\n * Optimized for speed.\\n *\\n * @param s The input string of digits.\\n * @return boolean result based on the specific condition.\\n */\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n // The algorithm uses C(n-2, k). Assumes n >= 2.\\n // Handle cases n=0, n=1 if they are possible according to problem spec.\\n if (n < 2) {\\n // Define behavior for short strings based on the problem this code solves.\\n // Returning false as a placeholder.\\n return false;\\n }\\n\\n int N = n - 2; // The 'n' used in nCk calculations\\n\\n // Optimization 1: Use faster computation for nCk mod 2\\n int[] mods2 = computeNcKMod2Optimized(N);\\n\\n // Use the original (but potentially corrected reducePower) for nCk mod 5\\n int[] mods5 = computeNcKMod5(N);\\n\\n int t5 = 0;\\n int t2 = 0;\\n\\n // Optimization 2: Use toCharArray() - potentially minor gain\\n char[] chars = s.toCharArray();\\n\\n // Optimization 3: Merge loops for t2 and t5 calculation\\n // The loop computes sum_{i=0}^{N} (d_i - d_{i+1}) * C(N, i) mod p\\n // where N = n-2. Indices i go from 0 to N.\\n // Difference uses chars[i] and chars[i+1]. Max index is N+1.\\n // Since n = N+2, max index N+1 is valid for chars array (length n).\\n for (int i = 0; i <= N; i++) {\\n // Calculate difference between adjacent digits\\n int d = (chars[i] - chars[i + 1]); // chars[i+1] is safe up to i=N\\n\\n // Accumulate weighted sums\\n // No need for intermediate modulo, standard ints should suffice unless N is huge\\n t5 += d * mods5[i];\\n t2 += d * mods2[i];\\n }\\n\\n // Final check: divisibility by 5 and 2\\n // Java's % operator handles negative numbers correctly for (t % p == 0) check\\n return (t5 % 5 == 0) && (t2 % 2 == 0);\\n }\\n\\n /**\\n * Computes nCk mod 5 for k from 0 to n.\\n * Uses iterative approach with power tracking.\\n * Depends on the corrected `reducePower`.\\n */\\n public int[] computeNcKMod5(int n) {\\n int[] result = new int[n + 1];\\n if (n < 0) return result; // Handle invalid input\\n\\n // Precompute tables for multiplication and modular inverse modulo 5\\n // Done only once per call to computeNcKMod5\\n int[] inv_5 = new int[] { 1, 1, 3, 2, 4 }; // inv_5[0] unused\\n int[][] mul5 = new int[5][5];\\n int[][] inv5 = new int[5][5];\\n for (int i = 1; i < 5; i++) {\\n for (int j = 1; j < 5; j++) {\\n mul5[i][j] = (i * j) % 5;\\n inv5[i][j] = (i * inv_5[j]) % 5;\\n }\\n }\\n\\n result[0] = 1; // nC0 = 1\\n if (n == 0) return result;\\n // nCn = 1. Will be set by symmetry later if using loop up to n/2.\\n // Explicitly setting result[n]=1 isn't strictly needed if loop handles symmetry right.\\n\\n int current_R = 1; // The non-p part of nCk mod p\\n int current_Pow = 0; // The exponent of p in nCk\\n\\n // Calculate iteratively using C(n, k) = C(n, k-1) * (n-k+1) / k\\n // Loop up to n, calculating each term. Symmetry can optimize this.\\n // Let's use symmetry optimization from original code: loop up to n/2\\n result[n] = 1; // Set nCn = 1 explicitly for symmetry to work\\n\\n for (int k = 1; k <= n / 2; k++) {\\n // Get power and non-p part for numerator (n-k+1) and denominator (k)\\n int[] up = reducePower(n - k + 1, 5); // {pow5, (n-k+1)/5^pow5 mod 5}\\n int[] down = reducePower(k, 5); // {pow5, k/5^pow5 mod 5}\\n\\n current_Pow += (up[0] - down[0]);\\n\\n // Update the non-p part modulo 5 using tables\\n // Need to handle case where up[1] or down[1] is 0?\\n // reducePower returns val % p. If val (the non-p part) is 0, result is 0.\\n // This should only happen if n-k+1=0 or k=0, which are excluded by loop/inputs.\\n // If up[1] or down[1] can be 0, tables need checks. Assume they are 1,2,3,4.\\n if (up[1] == 0 || down[1] == 0) {\\n // This case implies n-k+1 or k was a multiple of 5, but the non-p part became 0?\\n // This shouldn't happen with the corrected reducePower returning val % p.\\n // If val % p is 0, it means val itself was 0? Only if input n=0.\\n // Let's assume inputs to reducePower are > 0.\\n // However, val % p could be 0 if val is a multiple of p. Check reducePower.\\n // Corrected reducePower returns val % p. If n=10, p=5 -> val=2, val%p = 2. OK.\\n // If n=25, p=5 -> val=1, val%p = 1. OK.\\n // If n=125, p=5 -> val=1, val%p = 1. OK.\\n // So up[1] and down[1] should be in [1, 2, 3, 4].\\n // Need to handle current_R == 0? It starts at 1. Can it become 0?\\n // If C(n,k) is divisible by 5 (current_Pow > 0), result[k]=0.\\n // If current_R * up[1] becomes 0 mod 5, current_R will be 0.\\n // mul5[0][j] is not defined. inv5[0][j] is not defined.\\n // Let's assume current_R stays non-zero if current_Pow == 0.\\n // If current_Pow > 0, the value doesn't matter as result[k] is 0.\\n }\\n\\n if (current_Pow == 0) { // Only update current_R if result is non-zero mod 5\\n current_R = mul5[current_R][up[1]];\\n current_R = inv5[current_R][down[1]];\\n result[k] = current_R;\\n } else {\\n result[k] = 0;\\n // If we are calculating C(n,k) = 0 mod 5, we still need to track the\\n // 'potential' non-zero part current_R for the *next* iteration C(n, k+1).\\n // So, update current_R even if result[k] is 0.\\n int next_R = mul5[current_R][up[1]];\\n next_R = inv5[next_R][down[1]];\\n current_R = next_R;\\n }\\n\\n result[n - k] = result[k]; // Use symmetry: nCk = nC(n-k)\\n }\\n\\n // Handle middle element C(n, n/2 + 1) if n is odd\\n if (n % 2 == 1) {\\n int k = (n / 2) + 1;\\n // Calculate C(n,k) based on C(n, k-1) which was the last step in the loop\\n int[] up = reducePower(n - k + 1, 5);\\n int[] down = reducePower(k, 5);\\n current_Pow += (up[0] - down[0]);\\n\\n if (current_Pow == 0) {\\n current_R = mul5[current_R][up[1]];\\n current_R = inv5[current_R][down[1]];\\n result[k] = current_R;\\n } else {\\n result[k] = 0;\\n }\\n }\\n\\n return result;\\n }\\n\\n /**\\n * Optimized computation of nCk mod 2 using Lucas's Theorem property.\\n * (nCk mod 2) == 1 iff (n & k) == k.\\n */\\n public int[] computeNcKMod2Optimized(int n) {\\n int[] result = new int[n + 1];\\n if (n < 0) return result;\\n for (int k = 0; k <= n; k++) {\\n // If (n & k) == k, it means all set bits in k are also set in n.\\n result[k] = ((n & k) == k) ? 1 : 0;\\n }\\n return result;\\n }\\n\\n\\n /**\\n * Helper function: Calculates exponent of p in n! (Legendre's Formula related)\\n * and returns the non-p part of n modulo p.\\n * Returns {exponent of p dividing n, (n / p^exponent) % p}.\\n * Corrected version.\\n *\\n * @param n Number (must be > 0)\\n * @param p Prime number\\n * @return int array: {exponent, non-p part mod p}\\n */\\n int[] reducePower(int n, int p) {\\n // Assume n > 0 based on usage context (k and n-k+1 >= 1)\\n if (n <= 0) {\\n // Should not happen if n >= 2 initially.\\n // Return something indicative or throw error.\\n return new int[]{0, 0}; // Placeholder\\n }\\n\\n int count = 0;\\n int val = n;\\n while (val > 0 && val % p == 0) {\\n count++;\\n val /= p;\\n }\\n // Now val = n / p^count. We need val % p.\\n // If val is 0 (only if original n was 0), result is 0.\\n // Otherwise, val is the part not divisible by p.\\n return new int[] { count, val % p };\\n }\\n\\n // --- Original computeNcKMod2 for reference (Not used in optimized version) ---\\n /*\\n public int[] computeNcKMod2(int n) {\\n int[] result = new int[n + 1];\\n result[0] = 1; // nC0 = 1\\n if (n==0) return result;\\n result[n] = 1; // nCn = 1\\n\\n //int current = 1; // Always 1 mod 2\\n int currentPow = 0;\\n\\n for (int k = 1; k <= n/2; k++) { // Use symmetry\\n int[] up = reducePower(n - k + 1, 2);\\n int[] down = reducePower(k, 2);\\n currentPow += (up[0] - down[0]);\\n result[k] = currentPow == 0 ? 1 : 0; // nCk mod 2 is 1 iff power of 2 is 0\\n result[n - k] = result[k];\\n }\\n // Handle middle element for odd n\\n if (n % 2 == 1) {\\n int k = (n / 2) + 1;\\n int[] up = reducePower(n - k + 1, 2);\\n int[] down = reducePower(k, 2);\\n currentPow += (up[0] - down[0]);\\n result[k] = currentPow == 0 ? 1 : 0;\\n }\\n\\n return result;\\n }\\n */\\n}\"], [33, 1.4493, \"import java.io.BufferedReader;\\nimport java.io.InputStreamReader;\\nimport java.io.IOException;\\n\\npublic class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int m = n - 2;\\n\\n // --- \\u041f\\u043e\\u0434\\u0433\\u043e\\u0442\\u043e\\u0432\\u043a\\u0430 \\u0431\\u0438\\u043d\\u043e\\u043c\\u0438\\u0430\\u043b\\u0435\\u0439 \\u043c\\u043e\\u0434 5 \\u0434\\u043b\\u044f 0 <= N,K <= 4 ---\\n int[][] C5 = new int[5][5];\\n for (int i = 0; i < 5; i++) {\\n C5[i][0] = C5[i][i] = 1;\\n for (int j = 1; j < i; j++) {\\n C5[i][j] = (C5[i-1][j-1] + C5[i-1][j]) % 5;\\n }\\n }\\n\\n // \\u0420\\u0430\\u0437\\u043b\\u043e\\u0436\\u0435\\u043d\\u0438\\u0435 m \\u0432 base-5\\n int tmp = m;\\n int L = 0;\\n int[] n5 = new int[20]; // \\u0445\\u0432\\u0430\\u0442\\u0438\\u0442 \\u0434\\u043b\\u044f m <= 1e5, 5^10 ~ 1e7\\n if (tmp == 0) {\\n n5[L++] = 0;\\n } else {\\n while (tmp > 0) {\\n n5[L++] = tmp % 5;\\n tmp /= 5;\\n }\\n }\\n int[] i5 = new int[L]; // \\u0446\\u0438\\u0444\\u0440\\u044b \\u0442\\u0435\\u043a\\u0443\\u0449\\u0435\\u0433\\u043e i \\u0432 base-5, \\u0438\\u043d\\u0438\\u0446\\u0438\\u0430\\u043b\\u0438\\u0437\\u0438\\u0440\\u043e\\u0432\\u0430\\u043d\\u044b \\u043d\\u0443\\u043b\\u044f\\u043c\\u0438\\n\\n int F0 = 0, F1 = 0;\\n // \\u041e\\u0441\\u043d\\u043e\\u0432\\u043d\\u043e\\u0439 \\u0446\\u0438\\u043a\\u043b \\u043f\\u043e i = 0..m\\n for (int i = 0; i <= m; i++) {\\n // 1) \\u0431\\u0443\\u043b\\u0438\\u043d \\u041f\\u0440\\u043e\\u0432\\u0435\\u0440\\u043a\\u0430 \\u0431\\u0438\\u043d\\u043e\\u043c\\u0430 mod 2: 1 \\u0442\\u043e\\u0433\\u0434\\u0430 \\u0438 \\u0442\\u043e\\u043b\\u044c\\u043a\\u043e \\u0442\\u043e\\u0433\\u0434\\u0430, \\u043a\\u043e\\u0433\\u0434\\u0430 (i & ~m) == 0\\n int r2 = ((i & ~m) == 0) ? 1 : 0;\\n\\n // 2) \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u043c \\u0431\\u0438\\u043d\\u043e\\u043c\\u0438\\u0430\\u043b \\u043c\\u043e\\u0434 5 \\u0447\\u0435\\u0440\\u0435\\u0437 \\u0446\\u0438\\u0444\\u0440\\u044b base-5\\n int r5 = 1;\\n for (int d = 0; d < L; d++) {\\n int id = i5[d], nd = n5[d];\\n if (id > nd) {\\n r5 = 0;\\n break;\\n }\\n r5 = (r5 * C5[nd][id]) % 5;\\n }\\n\\n // 3) CRT \\u0438\\u0437 (mod2, mod5) \\u0432 mod10\\n int c10 = (r5 % 2 == r2 ? r5 : r5 + 5);\\n\\n // 4) \\u041d\\u0430\\u043a\\u043e\\u043f\\u043b\\u0435\\u043d\\u0438\\u0435 \\u0438\\u0442\\u043e\\u0433\\u043e\\u0432\\u044b\\u0445 \\u0434\\u0432\\u0443\\u0445 \\u0441\\u0443\\u043c\\u043c\\n F0 = (F0 + c10 * (s.charAt(i) - '0')) % 10;\\n F1 = (F1 + c10 * (s.charAt(i+1) - '0')) % 10;\\n\\n // \\u0418\\u043d\\u043a\\u0440\\u0435\\u043c\\u0435\\u043d\\u0442 i5 (base-5)\\n for (int pos = 0; pos < L; pos++) {\\n if (++i5[pos] < 5) break;\\n i5[pos] = 0;\\n }\\n }\\n\\n return (F0 == F1 ? true : false);\\n }\\n}\"], [41, 2.4154999999999998, \"import java.lang.reflect.Array;\\nimport java.util.ArrayList;\\nimport java.util.Arrays;\\nimport java.util.Collection;\\nimport java.util.List;\\nimport java.util.function.IntFunction;\\nimport java.util.function.IntToLongFunction;\\nimport java.util.function.IntUnaryOperator;\\nimport java.util.function.Supplier;\\n\\nclass Solution {\\n public boolean hasSameDigits(String s) {\\n var n = s.length();\\n var modCombos5 = new LongOps.SmallPrimePowerModCombos(n - 2, 5);\\n var y02 = 0;\\n var y05 = 0;\\n var y12 = 0;\\n var y15 = 0;\\n for (int i = 0; i <= n - 2; i++) {\\n var c2 = nChooseKmod2(n - 2, i);\\n var c5 = modCombos5.nChooseK(n - 2, i);\\n\\n int d0 = s.charAt(n - 2 - i) - '0';\\n y02 += c2 * d0;\\n y05 += c5 * d0;\\n\\n int d1 = s.charAt(n - 1 - i) - '0';\\n y12 += c2 * d1;\\n y15 += c5 * d1;\\n }\\n\\n y02 %= 2;\\n y12 %= 2;\\n y05 %= 5;\\n y15 %= 5;\\n return y02 == y12 && y05 == y15;\\n }\\n\\n private static int nChooseKmod2(int n, int k) {\\n return (k & n) == k ? 1 : 0;\\n }\\n\\n static class LongOps {\\n public static final long FLOOR_OF_SQRT_LONG_MAX = 3037000499L;\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n public static long floorOfSqrt(long x) {\\n if (x < 0) throw new IllegalArgumentException(\\\"\\\" + x);\\n\\n var l = 0L;\\n var r = FLOOR_OF_SQRT_LONG_MAX;\\n\\n var res = -1L;\\n do {\\n var m = l + (r - l) / 2;\\n if (m * m <= x) {\\n res = m;\\n l = m + 1;\\n } else {\\n r = m - 1;\\n }\\n } while (l <= r);\\n\\n return res;\\n }\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n public static long modPow(long a, long b, long mod) {\\n if (b < 0) throw new IllegalArgumentException(\\\"b=\\\" + b);\\n checkMod(mod);\\n\\n a %= mod;\\n var res = 1L % mod;\\n while (b != 0) {\\n if ((b & 1) != 0) {\\n res = (res * a) % mod;\\n }\\n\\n a = (a * a) % mod;\\n b >>= 1;\\n }\\n\\n return res;\\n }\\n\\n public static long modInv(long a, long mod) {\\n if (mod <= 0) {\\n throw new IllegalArgumentException(\\\"mod=\\\" + mod);\\n }\\n\\n var eucl = extEuclid(a, mod);\\n if (eucl.gcd != 1) {\\n return 0;\\n }\\n\\n return eucl.x < 0 ? eucl.x + mod : eucl.x;\\n }\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n public static long[] primeModInvsTable(int n, long primeMod) {\\n if (n < 1 || primeMod <= n) {\\n throw new IllegalArgumentException(\\\"n=\\\" + n + \\\", primeMod=\\\" + primeMod);\\n }\\n\\n var table = new long[n + 1];\\n table[0] = 0;\\n table[1] = 1;\\n\\n for (int i = 2; i < table.length; i++) {\\n long ir = table[(int) (primeMod % i)];\\n table[i] = ir == 0 ? 0 : primeMod - (primeMod / i * ir) % primeMod;\\n }\\n return table;\\n }\\n\\n public static class GcdWithFactors {\\n private long gcd;\\n private long x;\\n private long y;\\n\\n private GcdWithFactors() {\\n\\n }\\n\\n public long gcd() {\\n return gcd;\\n }\\n\\n public long x() {\\n return x;\\n }\\n\\n public long y() {\\n return y;\\n }\\n }\\n\\n public static GcdWithFactors extEuclid(long a, long b) {\\n var res = new GcdWithFactors();\\n extEuclid0(a, b, res);\\n return res;\\n }\\n\\n private static void extEuclid0(long a, long b, GcdWithFactors res) {\\n if (b == 0) {\\n res.gcd = a;\\n res.x = 1;\\n res.y = 0;\\n } else {\\n extEuclid0(b, a % b, res);\\n var tmpX = res.x;\\n var tmpY = res.y;\\n\\n res.x = tmpY;\\n res.y = tmpX - tmpY * (a / b);\\n }\\n }\\n\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n private static void checkMod(long mod) {\\n if (mod < 1 || mod > FLOOR_OF_SQRT_LONG_MAX) {\\n throw new IllegalArgumentException(\\\"mod=\\\" + mod);\\n }\\n }\\n\\n /**\\n * Calculates binomial coefficients n over k modulo prime powers p^e even if p is smaller or equal to n.\\n */\\n public static class SmallPrimePowerModCombos {\\n final int e;\\n final int p;\\n final int mod;\\n final int[] pPowersInFactorials;\\n final int[] factorialsWithoutPowers;\\n\\n public SmallPrimePowerModCombos(int n, int p, int e) {\\n if (p <= 1 || e < 1) {\\n throw new IllegalArgumentException(\\\"n=\\\" + n + \\\", p=\\\" + p + \\\", e=\\\" + e);\\n }\\n\\n var mod = p;\\n for (int i = 1; i < e; i++) {\\n mod = Math.multiplyExact(mod, p);\\n }\\n\\n this.e = e;\\n this.p = p;\\n this.mod = mod;\\n\\n this.pPowersInFactorials = new int[n + 1];\\n this.factorialsWithoutPowers = new int[n + 1];\\n\\n factorialsWithoutPowers[0] = 1;\\n for (int i = 1, ip = 1; i <= n; i++, ip++) {\\n pPowersInFactorials[i] = pPowersInFactorials[i - 1];\\n\\n if (ip != p) {\\n factorialsWithoutPowers[i] = modMul(i, factorialsWithoutPowers[i - 1]);\\n } else {\\n var ii = i;\\n do {\\n pPowersInFactorials[i]++;\\n ii /= p;\\n } while (ii % p == 0);\\n\\n factorialsWithoutPowers[i] = modMul(ii, factorialsWithoutPowers[i - 1]);\\n ip = 0;\\n }\\n\\n }\\n }\\n\\n public SmallPrimePowerModCombos(int n, int p) {\\n this(n, p, 1);\\n }\\n\\n public int nChooseK(int n, int k) {\\n var powers = pPowersInFactorials[n] - pPowersInFactorials[k] - pPowersInFactorials[n - k];\\n if (powers >= e) return 0;\\n\\n var res = 1;\\n for (int i = 0; i < powers; i++) {\\n res *= p;\\n }\\n\\n res = modMul(res, factorialsWithoutPowers[n]);\\n res = modMul(res, modInv(factorialsWithoutPowers[k], mod));\\n res = modMul(res, modInv(factorialsWithoutPowers[n - k], mod));\\n return res;\\n }\\n\\n private int modMul(long a, long b) {\\n return (int) ((a * b) % mod);\\n }\\n }\\n\\n public record PrimeFactor(long p, int q) {}\\n\\n public static List<PrimeFactor> primeFactorsOf(long n) {\\n if (n <= 0) {\\n throw new IllegalArgumentException(\\\"n=\\\" + n);\\n }\\n\\n var res = new ArrayList<PrimeFactor>();\\n for (long p = 2; p * p <= n; p++) {\\n if (n % p == 0) {\\n var e = 0;\\n do {\\n n /= p;\\n e++;\\n } while (n % p == 0);\\n\\n res.add(new PrimeFactor(p, e));\\n }\\n }\\n\\n if (n > 1) {\\n res.add(new PrimeFactor(n, 1));\\n }\\n\\n return res;\\n }\\n }\\n\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int minOf(int... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Integer.MAX_VALUE;\\n for (int i : is) {\\n res = Math.min(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int maxOf(int... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Integer.MIN_VALUE;\\n for (int i : is) {\\n res = Math.max(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long minOf(long... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Long.MAX_VALUE;\\n for (long i : is) {\\n res = Math.min(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long maxOf(long... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Long.MIN_VALUE;\\n for (long i : is) {\\n res = Math.max(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> ExtendedArrayList<T> fillList(int n, Supplier<T> supplier) {\\n return fillList(n, ignore -> supplier.get());\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> ExtendedArrayList<T> fillList(int n, IntFunction<T> valueAt) {\\n var res = new ExtendedArrayList<T>(n);\\n for (int i = 0; i < n; i++) {\\n res.add(valueAt.apply(i));\\n }\\n\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> T[] fillArray(int n, Class<T> clazz, Supplier<T> supplier) {\\n return fillArray(n, clazz, ignore -> supplier.get());\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> T[] fillArray(int n, Class<T> clazz, IntFunction<T> valueAt) {\\n @SuppressWarnings(\\\"unchecked\\\") var res = (T[]) Array.newInstance(clazz, n);\\n\\n for (int i = 0; i < n; i++) {\\n res[i] = valueAt.apply(i);\\n }\\n\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\", \\\"SameParameterValue\\\"})\\n static <T> T[] fillArray(int n, T value) {\\n @SuppressWarnings(\\\"unchecked\\\") var res = (T[]) Array.newInstance(value.getClass(), n);\\n Arrays.fill(res, value);\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int[] fillIntArray(int n, IntUnaryOperator valueAt) {\\n var res = new int[n];\\n for (int i = 0; i < n; i++) {\\n res[i] = valueAt.applyAsInt(i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int[] fillIntArray(int n, int value) {\\n var res = new int[n];\\n Arrays.fill(res, value);\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long[] fillLongArray(int n, IntToLongFunction valueAt) {\\n var res = new long[n];\\n for (int i = 0; i < n; i++) {\\n res[i] = valueAt.applyAsLong(i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long[] fillLongArray(int n, long value) {\\n var res = new long[n];\\n Arrays.fill(res, value);\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long gcd(long a, long b) {\\n while (b != 0) {\\n var bb = a % b;\\n a = b;\\n b = bb;\\n }\\n\\n return a;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int gcd(int a, int b) {\\n while (b != 0) {\\n var bb = a % b;\\n a = b;\\n b = bb;\\n }\\n\\n return a;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\", \\\"UnusedReturnValue\\\"})\\n static class ExtendedArrayList<T> extends ArrayList<T> {\\n public ExtendedArrayList(int initialCapacity) {\\n super(initialCapacity);\\n }\\n\\n public ExtendedArrayList() {\\n\\n }\\n\\n public ExtendedArrayList(Collection<? extends T> c) {\\n super(c);\\n }\\n\\n T getFromEnd(int offset) {\\n return get(size() - offset - 1);\\n }\\n\\n T getFst() {\\n return get(0);\\n }\\n\\n T getLst() {\\n return getFromEnd(0);\\n }\\n\\n T removeLst() {\\n return remove(size() - 1);\\n }\\n }\\n}\"], [49, 0.9662, \"import java.math.BigInteger;\\n\\nclass Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int[] mod5 = new int[n - 1]; // mod[i] = i choose (n - 1) mod 5\\n int[] fac2 = new int[n -1]; // counts 2 factors (we only need to check divisibility)\\n int[] fac5 = new int[n - 1]; // counts 5 factor\\n\\n int[] inverse5 = {0, 1, 3, 2, 4};\\n fac2[0] = 0;\\n fac2[n - 2] = 0;\\n\\n mod5[0] = 1;\\n mod5[n - 2] = 1;\\n\\n fac5[0] = 0;\\n fac5[n -2] = 0;\\n\\n for(int i = 1; i <= n - 3; i++){\\n // Track factors mod 2 \\n Pair a_2 = factors(i, 2); // divisor\\n Pair a_5 = factors(i,5); // divisor\\n\\n Pair b_2 = factors(n -i - 1, 2);\\n Pair b_5 = factors(n - i - 1, 5);\\n\\n fac2[i] = fac2[i - 1] + b_2.count - a_2.count;\\n fac5[i] = fac5[i - 1] + b_5.count - a_5.count;\\n\\n mod5[i] = mod5[i - 1]*b_5.modulo*inverse5[a_5.modulo] %5;\\n }\\n\\n int[] arr = new int[n - 1];\\n for(int i = 0; i < n - 1; i++){\\n int m5 = fac5[i] != 0 ? 0 : mod5[i];\\n int m2 = fac2[i] != 0 ? 0 : 1;\\n arr[i] = m5 % 2 == m2 ? m5 : m5 + 5;\\n \\n }\\n\\n\\n int a = 0;\\n int b = 0;\\n for(int i = 0; i < n -1; i++){\\n\\n a += (arr[i]*((int) s.charAt(i)))%10;\\n b += (arr[i]*((int) s.charAt(i+1)))%10;\\n }\\n\\n return (a%10) == (b%10);\\n }\\n\\n public Pair factors(int n, int div){\\n Pair res = new Pair(0,0);\\n while(n % div == 0){\\n n /= div;\\n res.count++;\\n }\\n res.modulo = n % div;\\n\\n return res;\\n }\\n\\n}\\n\\n\\nclass Pair {\\n int count;\\n int modulo;\\n\\n Pair(int cnt, int mod){\\n count = cnt;\\n modulo = mod;\\n }\\n}\"], [57, 1.4493, \"import java.lang.reflect.Array;\\nimport java.util.ArrayList;\\nimport java.util.Arrays;\\nimport java.util.Collection;\\nimport java.util.List;\\nimport java.util.function.IntFunction;\\nimport java.util.function.IntToLongFunction;\\nimport java.util.function.IntUnaryOperator;\\nimport java.util.function.Supplier;\\n\\nclass Solution {\\n public boolean hasSameDigits(String s) {\\n var n = s.length();\\n var modCombos2 = new LongOps.SmallPrimePowerModCombos(n - 2, 2);\\n var modCombos5 = new LongOps.SmallPrimePowerModCombos(n - 2, 5);\\n var gcdWithFactors = LongOps.extEuclid(2, 5);\\n var y0 = 0;\\n var y1 = 0;\\n var l2 = (int) gcdWithFactors.x();\\n var l5 = (int) gcdWithFactors.y();\\n for (int i = 0; i <= n - 2; i++) {\\n var c2 = modCombos2.nChooseK(n - 2, i);\\n var c5 = modCombos5.nChooseK(n - 2, i);\\n var c10 = (c2 * l5 * 5 + c5 * l2 * 2) % 10;\\n y0 += c10 * (s.charAt(n - 2 - i) - '0');\\n y0 %= 10;\\n y1 += c10 * (s.charAt(n - 1 - i) - '0');\\n y1 %= 10;\\n }\\n\\n if (y0 < 0) y0 += 10;\\n if (y1 < 0) y1 += 10;\\n return y0 == y1;\\n }\\n\\n static class LongOps {\\n public static final long FLOOR_OF_SQRT_LONG_MAX = 3037000499L;\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n public static long floorOfSqrt(long x) {\\n if (x < 0) throw new IllegalArgumentException(\\\"\\\" + x);\\n\\n var l = 0L;\\n var r = FLOOR_OF_SQRT_LONG_MAX;\\n\\n var res = -1L;\\n do {\\n var m = l + (r - l) / 2;\\n if (m * m <= x) {\\n res = m;\\n l = m + 1;\\n } else {\\n r = m - 1;\\n }\\n } while (l <= r);\\n\\n return res;\\n }\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n public static long modPow(long a, long b, long mod) {\\n if (b < 0) throw new IllegalArgumentException(\\\"b=\\\" + b);\\n checkMod(mod);\\n\\n a %= mod;\\n var res = 1L % mod;\\n while (b != 0) {\\n if ((b & 1) != 0) {\\n res = (res * a) % mod;\\n }\\n\\n a = (a * a) % mod;\\n b >>= 1;\\n }\\n\\n return res;\\n }\\n\\n public static long modInv(long a, long mod) {\\n if (mod <= 0) {\\n throw new IllegalArgumentException(\\\"mod=\\\" + mod);\\n }\\n\\n var eucl = extEuclid(a, mod);\\n if (eucl.gcd != 1) {\\n return 0;\\n }\\n\\n return eucl.x < 0 ? eucl.x + mod : eucl.x;\\n }\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n public static long[] primeModInvsTable(int n, long primeMod) {\\n if (n < 1 || primeMod <= n) {\\n throw new IllegalArgumentException(\\\"n=\\\" + n + \\\", primeMod=\\\" + primeMod);\\n }\\n\\n var table = new long[n + 1];\\n table[0] = 0;\\n table[1] = 1;\\n\\n for (int i = 2; i < table.length; i++) {\\n long ir = table[(int) (primeMod % i)];\\n table[i] = ir == 0 ? 0 : primeMod - (primeMod / i * ir) % primeMod;\\n }\\n return table;\\n }\\n\\n public static class GcdWithFactors {\\n private long gcd;\\n private long x;\\n private long y;\\n\\n private GcdWithFactors() {\\n\\n }\\n\\n public long gcd() {\\n return gcd;\\n }\\n\\n public long x() {\\n return x;\\n }\\n\\n public long y() {\\n return y;\\n }\\n }\\n\\n public static GcdWithFactors extEuclid(long a, long b) {\\n var res = new GcdWithFactors();\\n extEuclid0(a, b, res);\\n return res;\\n }\\n\\n private static void extEuclid0(long a, long b, GcdWithFactors res) {\\n if (b == 0) {\\n res.gcd = a;\\n res.x = 1;\\n res.y = 0;\\n } else {\\n extEuclid0(b, a % b, res);\\n var tmpX = res.x;\\n var tmpY = res.y;\\n\\n res.x = tmpY;\\n res.y = tmpX - tmpY * (a / b);\\n }\\n }\\n\\n\\n @SuppressWarnings(\\\"DuplicatedCode\\\")\\n private static void checkMod(long mod) {\\n if (mod < 1 || mod > FLOOR_OF_SQRT_LONG_MAX) {\\n throw new IllegalArgumentException(\\\"mod=\\\" + mod);\\n }\\n }\\n\\n /**\\n * Calculates binomial coefficients n over k modulo prime powers p^e even if p is smaller or equal to n.\\n */\\n public static class SmallPrimePowerModCombos {\\n final int e;\\n final int p;\\n final int mod;\\n final int[] pPowersInFactorials;\\n final int[] factorialsWithoutPowers;\\n\\n public SmallPrimePowerModCombos(int n, int p, int e) {\\n if (p <= 1 || e < 1) {\\n throw new IllegalArgumentException(\\\"n=\\\" + n + \\\", p=\\\" + p + \\\", e=\\\" + e);\\n }\\n\\n var mod = p;\\n for (int i = 1; i < e; i++) {\\n mod = Math.multiplyExact(mod, p);\\n }\\n\\n this.e = e;\\n this.p = p;\\n this.mod = mod;\\n\\n this.pPowersInFactorials = new int[n + 1];\\n this.factorialsWithoutPowers = new int[n + 1];\\n\\n factorialsWithoutPowers[0] = 1;\\n for (int i = 1, ip = 1; i <= n; i++, ip++) {\\n pPowersInFactorials[i] = pPowersInFactorials[i - 1];\\n\\n if (ip != p) {\\n factorialsWithoutPowers[i] = modMul(i, factorialsWithoutPowers[i - 1]);\\n } else {\\n var ii = i;\\n do {\\n pPowersInFactorials[i]++;\\n ii /= p;\\n } while (ii % p == 0);\\n\\n factorialsWithoutPowers[i] = modMul(ii, factorialsWithoutPowers[i - 1]);\\n ip = 0;\\n }\\n\\n }\\n }\\n\\n public SmallPrimePowerModCombos(int n, int p) {\\n this(n, p, 1);\\n }\\n\\n public int nChooseK(int n, int k) {\\n var powers = pPowersInFactorials[n] - pPowersInFactorials[k] - pPowersInFactorials[n - k];\\n if (powers >= e) return 0;\\n\\n var res = 1;\\n for (int i = 0; i < powers; i++) {\\n res *= p;\\n }\\n\\n res = modMul(res, factorialsWithoutPowers[n]);\\n res = modMul(res, modInv(factorialsWithoutPowers[k], mod));\\n res = modMul(res, modInv(factorialsWithoutPowers[n - k], mod));\\n return res;\\n }\\n\\n private int modMul(long a, long b) {\\n return (int) ((a * b) % mod);\\n }\\n }\\n\\n public record PrimeFactor(long p, int q) {}\\n\\n public static List<PrimeFactor> primeFactorsOf(long n) {\\n if (n <= 0) {\\n throw new IllegalArgumentException(\\\"n=\\\" + n);\\n }\\n\\n var res = new ArrayList<PrimeFactor>();\\n for (long p = 2; p * p <= n; p++) {\\n if (n % p == 0) {\\n var e = 0;\\n do {\\n n /= p;\\n e++;\\n } while (n % p == 0);\\n\\n res.add(new PrimeFactor(p, e));\\n }\\n }\\n\\n if (n > 1) {\\n res.add(new PrimeFactor(n, 1));\\n }\\n\\n return res;\\n }\\n }\\n\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int minOf(int... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Integer.MAX_VALUE;\\n for (int i : is) {\\n res = Math.min(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int maxOf(int... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Integer.MIN_VALUE;\\n for (int i : is) {\\n res = Math.max(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long minOf(long... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Long.MAX_VALUE;\\n for (long i : is) {\\n res = Math.min(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long maxOf(long... is) {\\n if (is.length == 0) {\\n throw new IllegalArgumentException();\\n }\\n\\n var res = Long.MIN_VALUE;\\n for (long i : is) {\\n res = Math.max(res, i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> ExtendedArrayList<T> fillList(int n, Supplier<T> supplier) {\\n return fillList(n, ignore -> supplier.get());\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> ExtendedArrayList<T> fillList(int n, IntFunction<T> valueAt) {\\n var res = new ExtendedArrayList<T>(n);\\n for (int i = 0; i < n; i++) {\\n res.add(valueAt.apply(i));\\n }\\n\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> T[] fillArray(int n, Class<T> clazz, Supplier<T> supplier) {\\n return fillArray(n, clazz, ignore -> supplier.get());\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static <T> T[] fillArray(int n, Class<T> clazz, IntFunction<T> valueAt) {\\n @SuppressWarnings(\\\"unchecked\\\") var res = (T[]) Array.newInstance(clazz, n);\\n\\n for (int i = 0; i < n; i++) {\\n res[i] = valueAt.apply(i);\\n }\\n\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\", \\\"SameParameterValue\\\"})\\n static <T> T[] fillArray(int n, T value) {\\n @SuppressWarnings(\\\"unchecked\\\") var res = (T[]) Array.newInstance(value.getClass(), n);\\n Arrays.fill(res, value);\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int[] fillIntArray(int n, IntUnaryOperator valueAt) {\\n var res = new int[n];\\n for (int i = 0; i < n; i++) {\\n res[i] = valueAt.applyAsInt(i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int[] fillIntArray(int n, int value) {\\n var res = new int[n];\\n Arrays.fill(res, value);\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long[] fillLongArray(int n, IntToLongFunction valueAt) {\\n var res = new long[n];\\n for (int i = 0; i < n; i++) {\\n res[i] = valueAt.applyAsLong(i);\\n }\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long[] fillLongArray(int n, long value) {\\n var res = new long[n];\\n Arrays.fill(res, value);\\n return res;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static long gcd(long a, long b) {\\n while (b != 0) {\\n var bb = a % b;\\n a = b;\\n b = bb;\\n }\\n\\n return a;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\"})\\n static int gcd(int a, int b) {\\n while (b != 0) {\\n var bb = a % b;\\n a = b;\\n b = bb;\\n }\\n\\n return a;\\n }\\n\\n @SuppressWarnings({\\\"DuplicatedCode\\\", \\\"unused\\\", \\\"UnusedReturnValue\\\"})\\n static class ExtendedArrayList<T> extends ArrayList<T> {\\n public ExtendedArrayList(int initialCapacity) {\\n super(initialCapacity);\\n }\\n\\n public ExtendedArrayList() {\\n\\n }\\n\\n public ExtendedArrayList(Collection<? extends T> c) {\\n super(c);\\n }\\n\\n T getFromEnd(int offset) {\\n return get(size() - offset - 1);\\n }\\n\\n T getFst() {\\n return get(0);\\n }\\n\\n T getLst() {\\n return getFromEnd(0);\\n }\\n\\n T removeLst() {\\n return remove(size() - 1);\\n }\\n }\\n}\"], [65, 3.3816999999999995, \"import java.math.BigInteger;\\n\\nclass Solution {\\n // public ArrayList<Integer> nthRowOfPascalTriangle(int n) {\\n // ArrayList<Integer> row = new ArrayList<>(n+1);\\n // BigInteger prev = BigInteger.ONE;\\n // row.add(1);\\n // for(int i=1;i<n+1;i++) {\\n // prev = prev.multiply(BigInteger.valueOf((long)(n-i+1))).divide(BigInteger.valueOf((long)i));\\n // row.add(prev.mod(BigInteger.TEN).intValue());\\n // }\\n // return row;\\n // }\\n public int mod10Inverse(int n) {\\n if(n%2==0) {\\n System.out.println(n+\\\" this shouldn't have happened\\\");\\n }\\n return switch(n) {\\n case 1 -> 1;\\n case 3 -> 7;\\n case 7 -> 3;\\n case 9 -> 9;\\n default -> 0;\\n };\\n }\\n public ArrayList<Integer> nthRowOfPascalTriangle(int n) {\\n ArrayList<Integer> row = new ArrayList<>(n+1);\\n int prev = 1;\\n row.add(prev);\\n int twos = 0;\\n int fives = 0;\\n for(int i=1;i<n+1;i++) {\\n int num = n-i+1;\\n int den = i;\\n while(num%2==0) {\\n num/=2;\\n twos++;\\n }\\n while(num%5==0) {\\n num/=5;\\n fives++;\\n }\\n while(den%2==0) {\\n den/=2;\\n twos--;\\n }\\n while(den%5==0) {\\n den/=5;\\n fives--;\\n }\\n prev = prev*num*mod10Inverse(den%10)%10;\\n if(twos>0 && fives>0) {\\n row.add(0);\\n } else {\\n row.add((prev*(int)Math.pow(2,twos)*(int)Math.pow(5,fives))%10);\\n }\\n }\\n return row;\\n }\\n public boolean hasSameDigits(String s) {\\n ArrayList<Integer> pascal = nthRowOfPascalTriangle(s.length()-2);\\n int first = 0;\\n int second = 0;\\n for(int i=0;i<s.length()-1;i++) {\\n first += pascal.get(i)*((int)s.charAt(i)-48);\\n second += pascal.get(i)*((int)s.charAt(i+1)-48);\\n }\\n first%=10;\\n second%=10;\\n return first==second;\\n }\\n}\"], [73, 4.3479, \"class Solution {\\n // Small 5\\u00d75 table of C(n,k) mod 5 for 0 \\u2264 n,k \\u2264 4\\n private static final int[][] C5 = {\\n {1,0,0,0,0},\\n {1,1,0,0,0},\\n {1,2,1,0,0},\\n {1,3,3,1,0},\\n {1,4,6%5,4,1}\\n };\\n // Precomputed mapping from (mod5,mod2) \\u2192 unique x mod10\\n private static final int[][] CRT = new int[5][2];\\n static {\\n // Build CRT[a][b] = x in [0..9] with x%5==a and x%2==b\\n for(int a=0;a<5;a++){\\n for(int b=0;b<2;b++){\\n for(int x=0;x<10;x++){\\n if(x%5==a && x%2==b){\\n CRT[a][b] = x;\\n break;\\n }\\n }\\n }\\n }\\n }\\n\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n // Edge: if already length 2\\n if (n == 2) return s.charAt(0) == s.charAt(1);\\n\\n // We'll compute final two sums:\\n // X = \\u03a3_{i=0..n-2} [C(n-2,i) mod10] * digit(i)\\n // Y = \\u03a3_{i=1..n-1} [C(n-2,i-1) mod10] * digit(i)\\n // and check X%10 == Y%10.\\n\\n int mod = 10, \\n xSum = 0, \\n ySum = 0;\\n int m = n - 2;\\n\\n for (int i = 0; i <= m; i++) {\\n int d1 = s.charAt(i) - '0';\\n int d2 = s.charAt(i+1) - '0';\\n\\n // C_mod2 = 1 iff no carries in binary for (i, m-i)\\n int c2 = (((i) & (m - i)) == 0) ? 1 : 0;\\n // C_mod5 via Lucas: multiply digitwise in base-5\\n int c5 = 1;\\n int a = m, b = i;\\n while (a > 0 || b > 0) {\\n int ai = a % 5, bi = b % 5;\\n if (bi > ai) { c5 = 0; break; }\\n c5 = (c5 * C5[ai][bi]) % 5;\\n a /= 5; b /= 5;\\n }\\n // Combine to mod10\\n int coef = CRT[c5][c2];\\n\\n // Accumulate\\n xSum = (xSum + coef * d1) % mod;\\n ySum = (ySum + coef * d2) % mod;\\n }\\n\\n return xSum == ySum;\\n }\\n}\\n\"], [81, 3.3817, \"import java.util.*;\\n\\nclass Solution {\\n // Precompute small (n choose k) mod 5 table. C_mod_5[n][k] = C(n, k) % 5.\\n // Valid for 0 <= k <= n <= 4.\\n private static final int[][] C_mod_5 = {\\n {1}, // n=0: C(0,0)=1\\n {1, 1}, // n=1: C(1,0)=1, C(1,1)=1\\n {1, 2, 1}, // n=2: C(2,0)=1, C(2,1)=2, C(2,2)=1\\n {1, 3, 3, 1}, // n=3: C(3,0)=1, C(3,1)=3, C(3,2)=3, C(3,3)=1\\n {1, 4, 1, 4, 1} // n=4: C(4,0)=1, C(4,1)=4, C(4,2)=6%5=1, C(4,3)=4, C(4,4)=1\\n };\\n\\n /**\\n * Calculates (n choose k) modulo p using Lucas's Theorem.\\n * This optimized version assumes k is already adjusted such that 0 <= k <= n/2\\n * (or k=0), and p is 2 or 5.\\n *\\n * @param n The total number of items.\\n * @param k The number of items to choose (0 <= k <= n/2).\\n * @param p The prime modulus (2 or 5).\\n * @return (n choose k) % p.\\n */\\n private int nCr_mod_p(int n, int k, int p) {\\n if (p == 2) {\\n // (n choose k) % 2 == 1 if and only if the bits of k are a subset of the bits of n.\\n // This is equivalent to (k & n) == k (using bitwise AND).\\n return ((k & n) == k) ? 1 : 0;\\n }\\n\\n // p must be 5\\n long result = 1;\\n long nl = n; // Use long to avoid overflow during division/modulo if n is large\\n long kl = k;\\n\\n // Apply Lucas's Theorem: C(n, k) % p = Product[ C(ni, ki) % p ]\\n // where ni and ki are the base-p digits of n and k.\\n // Loop while k still has non-zero digits in base 5.\\n while (kl > 0) {\\n int ni = (int)(nl % 5); // Get the last base-5 digit of n\\n int ki = (int)(kl % 5); // Get the last base-5 digit of k\\n\\n // If ki > ni, then C(ni, ki) = 0, making the whole product 0 mod 5.\\n if (ki > ni) {\\n return 0;\\n }\\n\\n // Look up C(ni, ki) % 5 from the precomputed table.\\n // ni and ki are guaranteed to be between 0 and 4.\\n result = (result * C_mod_5[ni][ki]) % 5;\\n\\n // Move to the next digits (equivalent to integer division by 5).\\n nl /= 5;\\n kl /= 5;\\n }\\n // Once kl becomes 0, all remaining ki are 0. C(ni, 0) = 1.\\n // So, the remaining digits of n don't affect the result % 5.\\n return (int)result;\\n }\\n\\n /**\\n * Calculates (n choose k) modulo 10.\\n * It uses Lucas's Theorem for modulo 2 and modulo 5, then combines\\n * the results using the Chinese Remainder Theorem (CRT).\\n *\\n * @param n The total number of items.\\n * @param k The number of items to choose.\\n * @return (n choose k) % 10.\\n */\\n private int nCr_mod_10(int n, int k) {\\n // Handle edge cases where C(n, k) is trivially 0 or 1.\\n if (k < 0 || k > n) {\\n return 0; // C(n, k) = 0 if k is out of range [0, n]\\n }\\n // Optimization: C(n, k) = C(n, n-k). Use the smaller value between k and n-k\\n // to potentially speed up the Lucas theorem calculation (especially for mod 5).\\n if (k > n / 2) {\\n k = n - k;\\n }\\n // Base case: C(n, 0) = 1 (this also covers C(n, n) due to the optimization).\\n if (k == 0) {\\n return 1;\\n }\\n\\n // Now we know 1 <= k <= n/2.\\n // Calculate C(n, k) mod 2\\n int mod2 = nCr_mod_p(n, k, 2);\\n // Calculate C(n, k) mod 5\\n int mod5 = nCr_mod_p(n, k, 5);\\n\\n // Combine results using CRT. We need z such that:\\n // z = mod2 (mod 2)\\n // z = mod5 (mod 5)\\n // The unique solution z in [0, 9] must be either mod5 or mod5 + 5.\\n int z = mod5; // Start with the value satisfying the mod 5 congruence.\\n // Check if it also satisfies the mod 2 congruence.\\n if (z % 2 != mod2) {\\n // If not, the other candidate (mod5 + 5) must satisfy both congruences.\\n z += 5;\\n }\\n // z is now the unique solution modulo 10.\\n return z;\\n }\\n\\n /**\\n * Performs the described operation repeatedly on a string of digits until\\n * it has exactly two digits, then checks if those two digits are the same.\\n * This implementation uses a mathematical shortcut based on binomial coefficients\\n * to avoid simulating the process step-by-step, achieving O(N log N) time complexity.\\n *\\n * @param s The initial string of digits.\\n * @return true if the final two digits are the same, false otherwise.\\n */\\n public boolean hasSameDigits(String s) {\\n int N = s.length();\\n\\n // Handle edge cases:\\n // If N <= 1, the process cannot result in exactly two digits.\\n if (N <= 1) {\\n return false;\\n }\\n // If N == 2, the process stops immediately. Check the initial digits.\\n if (N == 2) {\\n return s.charAt(0) == s.charAt(1);\\n }\\n\\n // If N > 2, the process takes N-2 steps. The final two digits F0 and F1 can be calculated directly:\\n // F0 = Sum_{i=0 to N-2} [ C(N-2, i) * s[i] ] % 10\\n // F1 = Sum_{i=0 to N-2} [ C(N-2, i) * s[i+1] ] % 10\\n // where C(n, k) is the binomial coefficient \\\"n choose k\\\".\\n\\n int n_coeff = N - 2; // The 'n' parameter for C(n, k) in the formula.\\n\\n int finalDigit0 = 0; // Accumulator for the first final digit (F0)\\n int finalDigit1 = 0; // Accumulator for the second final digit (F1)\\n\\n // Iterate i from 0 to N-2 to compute the sums.\\n for (int i = 0; i <= n_coeff; i++) {\\n // Calculate the coefficient C(N-2, i) modulo 10.\\n int coeff = nCr_mod_10(n_coeff, i);\\n\\n // Optimization: If the coefficient is 0 mod 10, this term contributes 0\\n // to both sums modulo 10, so we can skip it.\\n if (coeff == 0) {\\n continue;\\n }\\n\\n // Get the integer value of the digit s[i].\\n int d0 = s.charAt(i) - '0';\\n // Add the contribution to finalDigit0, keeping the sum modulo 10.\\n finalDigit0 = (finalDigit0 + coeff * d0) % 10;\\n\\n // Get the integer value of the digit s[i+1].\\n // The index i+1 is valid, ranging from 1 to N-1.\\n int d1 = s.charAt(i + 1) - '0';\\n // Add the contribution to finalDigit1, keeping the sum modulo 10.\\n finalDigit1 = (finalDigit1 + coeff * d1) % 10;\\n }\\n\\n // The modulo operator (%) in Java can return negative results if the dividend is negative.\\n // Adjust the results to be in the range [0, 9].\\n if (finalDigit0 < 0) {\\n finalDigit0 += 10;\\n }\\n if (finalDigit1 < 0) {\\n finalDigit1 += 10;\\n }\\n\\n // Return true if the calculated final two digits are identical.\\n return finalDigit0 == finalDigit1;\\n }\\n}\"], [89, 2.4154999999999998, \"/**\\n * Optimized solution using Binomial Coefficients and Lucas's Theorem.\\n * Time Complexity: O(N log N)\\n * Space Complexity: O(N)\\n */\\npublic class Solution {\\n\\n // Precompute C(a, b) % 5 for 0 <= b <= a <= 4\\n private static final int[][] C_MOD_5 = {\\n // k=0 k=1 k=2 k=3 k=4\\n { 1, 0, 0, 0, 0 }, // n=0\\n { 1, 1, 0, 0, 0 }, // n=1\\n { 1, 2, 1, 0, 0 }, // n=2\\n { 1, 3, 3, 1, 0 }, // n=3\\n { 1, 4, 1, 4, 1 } // n=4 (C(4,2)=6=1 mod 5)\\n };\\n\\n // Computes C(n, k) % 5 using Lucas's Theorem\\n private int nCrMod5(long n, long k) {\\n long n_rem = n;\\n long k_rem = k;\\n int result = 1;\\n while (n_rem > 0 || k_rem > 0) {\\n int ni = (int)(n_rem % 5);\\n int ki = (int)(k_rem % 5);\\n if (ki > ni) return 0; // C(ni, ki) = 0 if ki > ni\\n result = (result * C_MOD_5[ni][ki]) % 5;\\n if (result == 0) return 0; // Optimization\\n n_rem /= 5;\\n k_rem /= 5;\\n }\\n return result; // result is already in [0, 4]\\n }\\n\\n // Computes C(n, k) % 2 using bitwise property\\n private int nCrMod2(long n, long k) {\\n return ((n & k) == k) ? 1 : 0; // 1 if k is submask of n, 0 otherwise\\n }\\n\\n // Combines results mod 2 and mod 5 using CRT logic\\n private int combineCRT(int mod2, int mod5) {\\n // Find z in [0, 9] where z % 2 == mod2 and z % 5 == mod5\\n if (mod5 == 0) return (mod2 == 1) ? 5 : 0; // Ends in 0 or 5\\n if (mod5 == 1) return (mod2 == 1) ? 1 : 6; // Ends in 1 or 6\\n if (mod5 == 2) return (mod2 == 1) ? 7 : 2; // Ends in 2 or 7\\n if (mod5 == 3) return (mod2 == 1) ? 3 : 8; // Ends in 3 or 8\\n if (mod5 == 4) return (mod2 == 1) ? 9 : 4; // Ends in 4 or 9\\n return -1; // Should not happen\\n }\\n\\n // Computes C(n, k) % 10\\n private int nCrMod10(long n, long k) {\\n if (k < 0 || k > n) return 0;\\n if (k == 0 || k == n) return 1;\\n // Use symmetry C(n, k) = C(n, n-k) for potentially faster calculation\\n if (k > n / 2) k = n - k;\\n\\n int mod2 = nCrMod2(n, k);\\n int mod5 = nCrMod5(n, k);\\n return combineCRT(mod2, mod5);\\n }\\n\\n /**\\n * Main method using the O(N log N) approach.\\n */\\n public boolean hasSameDigits(String s) {\\n int N = s.length();\\n\\n // Handle edge cases N=0, 1, 2\\n if (N <= 1) return true; // No comparison possible/needed\\n if (N == 2) return s.charAt(0) == s.charAt(1);\\n\\n // Parse digits: O(N)\\n int[] d = new int[N];\\n for (int i = 0; i < N; i++) {\\n d[i] = s.charAt(i) - '0';\\n }\\n\\n // Set up parameters for binomial coefficients C(n, k)\\n long n_binomial = N - 2; // Use long in case N is large\\n\\n int f0 = 0; // Final digit 0: Sum C(n, k) * d[k]\\n int f1 = 0; // Final digit 1: Sum C(n, k) * d[k+1]\\n\\n // Calculate sums: O(N * log N)\\n for (int k = 0; k <= n_binomial; k++) {\\n // Calculate C(n, k) % 10\\n int coeff = nCrMod10(n_binomial, (long)k); // Cast k to long\\n\\n if (coeff == 0) continue; // Skip terms with zero coefficient\\n\\n // Accumulate modulo 10\\n f0 = (f0 + coeff * d[k]) % 10;\\n // k+1 is safe index: k <= N-2 => k+1 <= N-1\\n f1 = (f1 + coeff * d[k + 1]) % 10;\\n }\\n\\n // Compare the final results\\n return f0 == f1;\\n }\\n}\"], [97, 2.8986, \"public class Solution {\\n\\n private static final int[][] C_MOD_5 = {\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1}\\n };\\n\\n private int nCrMod5(long n, long k) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int ni = (int)(n % 5), ki = (int)(k % 5);\\n if (ki > ni) return 0;\\n res *= C_MOD_5[ni][ki];\\n res %= 5;\\n if (res == 0) return 0;\\n n /= 5;\\n k /= 5;\\n }\\n return res;\\n }\\n\\n private int nCrMod2(long n, long k) {\\n return ((n & k) == k) ? 1 : 0;\\n }\\n\\n private int combineCRT(int mod2, int mod5) {\\n // Precomputed lookup table (mod2, mod5) -> mod10\\n final int[][] CRT = {\\n {0, 6, 2, 8, 4}, // mod2 == 0\\n {5, 1, 7, 3, 9} // mod2 == 1\\n };\\n return CRT[mod2][mod5];\\n }\\n\\n private int nCrMod10(long n, long k) {\\n if (k < 0 || k > n) return 0;\\n if (k == 0 || k == n) return 1;\\n if (k > n / 2) k = n - k;\\n int mod2 = nCrMod2(n, k);\\n int mod5 = nCrMod5(n, k);\\n return combineCRT(mod2, mod5);\\n }\\n\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n if (n <= 1) return true;\\n if (n == 2) return s.charAt(0) == s.charAt(1);\\n\\n int[] d = new int[n];\\n for (int i = 0; i < n; i++) {\\n d[i] = s.charAt(i) - '0';\\n }\\n\\n long comb_n = n - 2;\\n int f0 = 0, f1 = 0;\\n for (int k = 0; k <= comb_n; k++) {\\n int coeff = nCrMod10(comb_n, k);\\n if (coeff == 0) continue;\\n f0 = (f0 + coeff * d[k]) % 10;\\n f1 = (f1 + coeff * d[k + 1]) % 10;\\n }\\n\\n return f0 == f1;\\n }\\n}\\n\"], [105, 26.57, \"class Solution {\\n\\n public boolean hasSameDigits(String s) {\\n int X=s.length()-2, x=0, y=0;\\n for(int j=0;j<=X;j++){\\n int coeff=binomialMode10(X,j);\\n x=(x+coeff*(s.charAt(j)-'0'))%10;\\n y=(y+coeff*(s.charAt(j+1)-'0'))%10;\\n }\\n return x==y;\\n }\\n\\n private int binomialMode10(int n, int k){\\n int i=binomialMode2(n, k);\\n int j=binomialMode5(n, k);\\n for(int x=0;x<10;x++){\\n if(x%2==i && x%5==j) return x;\\n }\\n return 0;\\n }\\n\\n private int binomialMode2(int n, int k){\\n return ((n&k)==k)?1:0;\\n }\\n\\n private int binomialMode5(int n, int k){\\n int[][] tuples={{1},{1,1},{1,2,1},{1,3,3,1},{1,4,1,4,1}};\\n int result=1;\\n while(n>0||k>0){\\n int nthd=n%5;\\n int kthd=k%5;\\n if(kthd>nthd) return 0;\\n result=(result*tuples[nthd][kthd])%5;\\n n/=5;\\n k/=5;\\n }\\n return result;\\n }\\n \\n}\"], [113, 1.4493, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n if (n < 3) return false; \\n \\n int N = n - 2;\\n int n0 = 0, n1 = 0;\\n \\n for (int j = 0; j <= N; j++) {\\n int c = bMod10(N, j);\\n n0 = (n0 + c * (s.charAt(j) - '0')) % 10;\\n n1 = (n1 + c * (s.charAt(j + 1) - '0')) % 10;\\n }\\n \\n return n0 == n1;\\n }\\n \\n private int bMod10(int n, int k) {\\n if (k < 0 || k > n) return 0;\\n if (k == 0 || k == n) return 1;\\n \\n \\n k = Math.min(k, n - k);\\n \\n \\n int r2 = bMod2(n, k);\\n int r5 = bMod5(n, k);\\n \\n \\n for (int x = 0; x < 10; x++) {\\n if (x % 2 == r2 && x % 5 == r5) return x;\\n }\\n return 0; \\n }\\n \\n private int bMod2(int n, int k) {\\n \\n return ((n & k) == k) ? 1 : 0;\\n }\\n \\n private int bMod5(int n, int k) {\\n \\n int[][] gird = {\\n {1, 0, 0, 0, 0}, \\n {1, 1, 0, 0, 0}, \\n {1, 2, 1, 0, 0}, \\n {1, 3, 3, 1, 0}, \\n {1, 4, 1, 4, 1} \\n };\\n \\n int ans = 1;\\n while (n > 0 || k > 0) {\\n int l = n % 5;\\n int m = k % 5;\\n if (m > l) return 0;\\n ans = (ans * gird[l][m]) % 5;\\n n /= 5;\\n k /= 5;\\n }\\n return ans;\\n }\\n}\\n\"], [121, 1.4493, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int r = n - 2; // We will use binomials with n-2 in the upper index.\\n int[] d = new int[n];\\n for (int i = 0; i < n; i++) {\\n d[i] = s.charAt(i) - '0';\\n }\\n \\n // S = sum_{i=0}^{n-2} C(n-2, i) * (d[i] - d[i+1]) mod 10.\\n int S = 0;\\n for (int i = 0; i <= r; i++) {\\n int coeffMod2 = binomMod2(r, i); // C(r, i) mod 2.\\n int coeffMod5 = lucas(r, i, 5); // C(r, i) mod 5.\\n int coeff = (5 * coeffMod2 + 6 * coeffMod5) % 10; // Combine via CRT.\\n int delta = d[i] - d[i + 1];\\n S = (S + coeff * delta) % 10;\\n if (S < 0) S += 10;\\n }\\n // If S is 0 modulo 10, then the two final digits are the same.\\n return S % 10 == 0;\\n }\\n \\n // Compute C(n, k) mod 2 using the property that it is 1 if and only if (n & k) == k.\\n private int binomMod2(int n, int k) {\\n return ((n & k) == k) ? 1 : 0;\\n }\\n \\n // Compute C(n, k) mod p using Lucas' theorem.\\n // Here p is a prime (we use p = 5).\\n private int lucas(int n, int k, int p) {\\n int result = 1;\\n while (n > 0 || k > 0) {\\n int n_i = n % p;\\n int k_i = k % p;\\n if (k_i > n_i) return 0;\\n result = (result * nCrSmall(n_i, k_i, p)) % p;\\n n /= p;\\n k /= p;\\n }\\n return result;\\n }\\n \\n // For p = 5, compute C(n, r) mod 5 when 0 <= n < 5.\\n // We use the precomputed factorials mod 5: fact[0]=1, fact[1]=1, fact[2]=2, fact[3]=6 mod 5 = 1, fact[4]=24 mod 5 = 4.\\n // And the inverses modulo 5 (recall: inverse of 2 is 3, inverse of 3 is 2, inverse of 4 is 4).\\n private int nCrSmall(int n, int r, int p) {\\n // Precomputed factorials mod 5 for n=0,...,4.\\n int[] fact = {1, 1, 2, 1, 4};\\n // Precomputed modular inverses mod 5 for 1,2,3,4.\\n // (We never need the inverse of 0.)\\n int[] inv = {0, 1, 3, 2, 4};\\n \\n int numerator = fact[n];\\n int denominator = (fact[r] * fact[n - r]) % p;\\n if (denominator == 0) return 0; // (Should not occur for 0 <= n < p.)\\n int invDenom = 0;\\n // Since denominator is one of 1,2,3,4 mod 5, we can use the precomputed inverses.\\n if (denominator == 1) invDenom = 1;\\n else if (denominator == 2) invDenom = 3;\\n else if (denominator == 3) invDenom = 2;\\n else if (denominator == 4) invDenom = 4;\\n return (numerator * invDenom) % p;\\n }\\n}\\n\"], [129, 2.8986, \"class Solution {\\n \\n int mod = 10;\\n public boolean hasSameDigits(String s) {\\n char[] ch = s.toCharArray();\\n int n = ch.length, dep = n - 2;\\n long sum1 = 0, sum2 = 0;\\n int[] fact = new int[n + 1], infact = new int[n + 1];\\n int[] p2 = new int[n + 1], p5 = new int[n + 1];\\n\\n fact[0] = 1;\\n for(int i = 1; i <= n; i++) {\\n int e2 = 0, e5 = 0;\\n int x = i;\\n while(x % 2 == 0) { e2++; x /= 2; }\\n while(x % 5 == 0) { e5++; x /= 5; }\\n fact[i] = fact[i - 1] * x % mod;\\n p2[i] = p2[i - 1] + e2;\\n p5[i] = p5[i - 1] + e5;\\n }\\n\\n infact[n] = pow(fact[n], 3); // \\u6b27\\u62c9\\u5b9a\\u7406\\u6c42\\u9006\\u5143\\n for (int i = n; i > 0; i--) {\\n int x = i;\\n x >>= Integer.numberOfTrailingZeros(x);\\n while (x % 5 == 0) {\\n x /= 5;\\n }\\n infact[i - 1] = infact[i] * x % mod;\\n }\\n\\n for(int i = 0; i <= n - 2; i++) {\\n int cost = ch[i] - '0';\\n sum1 += cost * fact[dep] * infact[i] * infact[dep - i] * pow(2, p2[dep] - p2[i] - p2[dep - i]) * pow(5, p5[dep] - p5[i] - p5[dep - i]) % mod;\\n sum1 %= mod;\\n }\\n for(int i = 1; i <= n - 1; i++) {\\n int cost = ch[i] - '0';\\n sum2 += cost * fact[dep] * infact[i - 1] * infact[dep - i + 1] * pow(2, p2[dep] - p2[i - 1] - p2[dep - i + 1]) * pow(5, p5[dep] - p5[i - 1] - p5[dep - i + 1]) % mod;\\n sum2 %= mod;\\n }\\n\\n return sum1 == sum2;\\n }\\n\\n int pow(int base, int pow) {\\n if(pow == 1) return base;\\n if(pow == 0) return 1;\\n\\n int half = pow(base, pow / 2);\\n if(pow % 2 == 0) return half * half % mod;\\n return half * half * base % mod;\\n }\\n\\n // int pow(int x, int n) {\\n // int res = 1;\\n // while (n > 0) {\\n // if (n % 2 > 0) {\\n // res = res * x % mod;\\n // }\\n // x = x * x % mod;\\n // n /= 2;\\n // }\\n // return res;\\n // }\\n}\"], [137, 3.3816999999999995, \"class Solution {\\n\\n /* --------- Pascal triangle for one base\\u20115 digit --------- */\\n private static final int[][] C5 = new int[5][5];\\n static {\\n for (int n = 0; n < 5; ++n) {\\n C5[n][0] = C5[n][n] = 1;\\n for (int k = 1; k < n; ++k)\\n C5[n][k] = (C5[n-1][k-1] + C5[n-1][k]) % 5;\\n }\\n }\\n\\n /** C(n,k) (mod\\u00a05) via Lucas theorem, k\\u00a0<=\\u00a0100\\u00a0000 -> \\u2264\\u00a06 digits in base\\u20115 */\\n private static int chooseMod5(int n, int k) {\\n if (k < 0 || k > n) return 0;\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int ni = n % 5, ki = k % 5;\\n if (ki > ni) return 0;\\n res = (res * C5[ni][ki]) % 5;\\n n /= 5; k /= 5;\\n }\\n return res;\\n }\\n\\n /** C(n,k) (mod\\u00a02) \\u2013\\u00a0odd\\u00a0iff (k & (n\\u2011k)) == 0 */\\n private static int chooseMod2(int n, int k) {\\n return (k >= 0 && k <= n && ((k & (n - k)) == 0)) ? 1 : 0;\\n }\\n\\n public boolean hasSameDigits(String s) {\\n final int n = s.length(), rounds = n - 2;\\n\\n int diff2 = 0; // \\u03a3 coeff\\u00b7digit (mod\\u00a02)\\n int diff5 = 0; // \\u03a3 coeff\\u00b7digit (mod\\u00a05)\\n\\n char[] ch = s.toCharArray();\\n\\n for (int i = 0; i < n; ++i) {\\n int digit = ch[i] - '0';\\n\\n /* ---- coefficient mod\\u00a02 ---- */\\n int c2 = chooseMod2(rounds, i);\\n int c2m1 = chooseMod2(rounds, i - 1);\\n int coef2 = c2 ^ c2m1; // (c2 - c2m1) mod\\u00a02\\n diff2 ^= (coef2 & (digit & 1)); // add mod\\u00a02\\n\\n /* ---- coefficient mod\\u00a05 ---- */\\n int c5 = chooseMod5(rounds, i);\\n int c5m1 = chooseMod5(rounds, i - 1);\\n int coef5 = c5 - c5m1;\\n if (coef5 < 0) coef5 += 5; // keep within 0..4\\n diff5 = (diff5 + coef5 * (digit % 5)) % 5;\\n }\\n\\n /* final two digits equal \\u21d4 sum == 0 (mod\\u00a02 and mod\\u00a05) */\\n return diff2 == 0 && diff5 == 0;\\n }\\n}\\n\"], [145, 1.4493, \"class Solution {//\\u65b0\\u77e5\\u8bc6\\uff0c\\u4e0d\\u4f1a\\n private static final int MOD = 10;\\n private static final int MX = 100_000;\\n\\n private static final int[] f = new int[MX + 1];\\n private static final int[] invF = new int[MX + 1];\\n private static final int[] p2 = new int[MX + 1];\\n private static final int[] p5 = new int[MX + 1];\\n\\n static {\\n f[0] = 1;\\n for (int i = 1; i <= MX; i++) {\\n int x = i;\\n // \\u8ba1\\u7b97 2 \\u7684\\u5e42\\u6b21\\n int e2 = Integer.numberOfTrailingZeros(x);\\n x >>= e2;\\n // \\u8ba1\\u7b97 5 \\u7684\\u5e42\\u6b21\\n int e5 = 0;\\n while (x % 5 == 0) {\\n e5++;\\n x /= 5;\\n }\\n f[i] = f[i - 1] * x % MOD;\\n p2[i] = p2[i - 1] + e2;\\n p5[i] = p5[i - 1] + e5;\\n }\\n\\n invF[MX] = pow(f[MX], 3); // \\u6b27\\u62c9\\u5b9a\\u7406\\u6c42\\u9006\\u5143\\n for (int i = MX; i > 0; i--) {\\n int x = i;\\n x >>= Integer.numberOfTrailingZeros(x);\\n while (x % 5 == 0) {\\n x /= 5;\\n }\\n invF[i - 1] = invF[i] * x % MOD;\\n }\\n }\\n\\n private static int pow(int x, int n) {\\n int res = 1;\\n while (n > 0) {\\n if (n % 2 > 0) {\\n res = res * x % MOD;\\n }\\n x = x * x % MOD;\\n n /= 2;\\n }\\n return res;\\n }\\n\\n private int comb(int n, int k) {\\n // \\u7531\\u4e8e\\u6bcf\\u9879\\u90fd < 10\\uff0c\\u6240\\u4ee5\\u65e0\\u9700\\u4e2d\\u9014\\u53d6\\u6a21\\n return f[n] * invF[k] * invF[n - k] *\\n pow(2, p2[n] - p2[k] - p2[n - k]) *\\n pow(5, p5[n] - p5[k] - p5[n - k]) % MOD;\\n }\\n\\n public boolean hasSameDigits(String S) {\\n char[] s = S.toCharArray();\\n int diff = 0;\\n for (int i = 0; i < s.length - 1; i++) {\\n diff += comb(s.length - 2, i) * (s[i] - s[i + 1]);\\n }\\n return diff % MOD == 0;\\n }\\n}\\n\\n// \\u4f5c\\u8005\\uff1a\\u7075\\u8336\\u5c71\\u827e\\u5e9c\\n// \\u94fe\\u63a5\\uff1ahttps://leetcode.cn/problems/check-if-digits-are-equal-in-string-after-operations-ii/solutions/3086169/mo-shu-wei-he-shu-shi-de-zu-he-shu-by-en-8x7t/\\n// \\u6765\\u6e90\\uff1a\\u529b\\u6263\\uff08LeetCode\\uff09\\n// \\u8457\\u4f5c\\u6743\\u5f52\\u4f5c\\u8005\\u6240\\u6709\\u3002\\u5546\\u4e1a\\u8f6c\\u8f7d\\u8bf7\\u8054\\u7cfb\\u4f5c\\u8005\\u83b7\\u5f97\\u6388\\u6743\\uff0c\\u975e\\u5546\\u4e1a\\u8f6c\\u8f7d\\u8bf7\\u6ce8\\u660e\\u51fa\\u5904\\u3002\"], [152, 1.4493, \"import java.util.ArrayList;\\nimport java.util.List;\\n\\npublic class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int k = n - 2;\\n if (k < 0) {\\n return false; // As per problem constraints, n >= 3\\n }\\n\\n // Precompute comb_mod5 lookup table\\n int[][] combMod5 = {\\n {1, 0, 0, 0, 0}, // n=0\\n {1, 1, 0, 0, 0}, // n=1\\n {1, 2, 1, 0, 0}, // n=2\\n {1, 3, 3, 1, 0}, // n=3\\n {1, 4, 1, 4, 1} // n=4\\n };\\n\\n List<Integer> kDigits = getBase5Reversed(k);\\n int lenK = kDigits.size();\\n\\n // CRT table for mod2 and mod5 to mod10\\n int[][] crtTable = {\\n {0, 6, 2, 8, 4}, // mod2=0\\n {5, 1, 7, 3, 9} // mod2=1\\n };\\n\\n // Precompute mod10 for each i from 0 to k\\n int[] mod10 = new int[k + 1];\\n for (int i = 0; i <= k; i++) {\\n int mod2 = ((i & k) == i) ? 1 : 0;\\n\\n List<Integer> iDigits = getBase5Reversed(i);\\n boolean valid = true;\\n int product = 1;\\n for (int j = 0; j < lenK; j++) {\\n int idigit = (j < iDigits.size()) ? iDigits.get(j) : 0;\\n int kdigit = kDigits.get(j);\\n if (idigit > kdigit) {\\n valid = false;\\n break;\\n }\\n product = (product * combMod5[kdigit][idigit]) % 5;\\n }\\n int mod5 = valid ? product % 5 : 0;\\n\\n mod10[i] = crtTable[mod2][mod5];\\n }\\n\\n // Convert input string to digit array\\n char[] chars = s.toCharArray();\\n int[] digits = new int[chars.length];\\n for (int i = 0; i < chars.length; i++) {\\n digits[i] = chars[i] - '0';\\n }\\n\\n // Compute S1 and S2\\n int s1 = 0;\\n int s2 = 0;\\n for (int i = 0; i <= k; i++) {\\n s1 = (s1 + mod10[i] * digits[i]) % 10;\\n s2 = (s2 + mod10[i] * digits[i + 1]) % 10;\\n }\\n\\n return s1 == s2;\\n }\\n\\n private List<Integer> getBase5Reversed(int num) {\\n List<Integer> digits = new ArrayList<>();\\n if (num == 0) {\\n digits.add(0);\\n return digits;\\n }\\n while (num > 0) {\\n digits.add(num % 5);\\n num /= 5;\\n }\\n return digits;\\n }\\n}\"], [160, 0.9662, \"import java.lang.StringBuilder; // Keep import in case needed elsewhere, not used in final logic\\n\\nclass Solution {\\n\\n // Precomputed table for C(n, k) mod 5, for n < 5.\\n // C[n][k] = C(n, k) % 5\\n // C(n,k) = n! / (k! * (n-k)!)\\n // C(0,0)=1\\n // C(1,0)=1, C(1,1)=1\\n // C(2,0)=1, C(2,1)=2, C(2,2)=1\\n // C(3,0)=1, C(3,1)=3, C(3,2)=3, C(3,3)=1\\n // C(4,0)=1, C(4,1)=4, C(4,2)=6%5=1, C(4,3)=4, C(4,4)=1\\n private static final int[][] C_SMALL_MOD5 = {\\n {1}, // n=0\\n {1, 1}, // n=1\\n {1, 2, 1}, // n=2\\n {1, 3, 3, 1}, // n=3\\n {1, 4, 1, 4, 1} // n=4\\n };\\n\\n /**\\n * Calculates C(n, k) mod p using Lucas's Theorem.\\n * Assumes p is prime and C_SMALL_MOD_P contains precomputed C(ni, ki) mod p for ni < p.\\n * Time Complexity: O(log_p N)\\n */\\n private long nCrModP(long n, long k, int p, int[][] C_SMALL_MOD_P) {\\n if (k < 0 || k > n) {\\n return 0;\\n }\\n // Optimization: C(n, k) = C(n, n-k). Use smaller k.\\n // Removed this optimization as Lucas theorem handles large k fine.\\n // It might be slightly faster but adds complexity. Keep it simple first.\\n // if (k > n / 2) {\\n // k = n - k;\\n // }\\n\\n long result = 1;\\n while (n > 0 || k > 0) {\\n long ni = n % p;\\n long ki = k % p;\\n\\n // If ki > ni, then C(ni, ki) = 0, so C(n, k) mod p = 0\\n if (ki > ni) {\\n return 0;\\n }\\n\\n // Multiply by C(ni, ki) mod p using the precomputed table.\\n // Indices are safe: 0 <= ki <= ni < p\\n result = (result * C_SMALL_MOD_P[(int)ni][(int)ki]) % p;\\n\\n n /= p;\\n k /= p;\\n }\\n return result;\\n }\\n\\n /**\\n * Calculates C(n, k) mod 10 using CRT (mod 2 and mod 5).\\n * Time Complexity: O(log N)\\n */\\n private int nCrMod10(long n, long k) {\\n if (k < 0 || k > n) {\\n return 0;\\n }\\n\\n // Calculate C(n, k) mod 2 using Kummer's theorem insight:\\n // C(n, k) is odd iff (n & k) == k\\n long cMod2 = ((n & k) == k) ? 1 : 0;\\n\\n // Calculate C(n, k) mod 5 using Lucas's theorem helper\\n long cMod5 = nCrModP(n, k, 5, C_SMALL_MOD5);\\n\\n // Combine using CRT: find x such that x = cMod2 (mod 2) and x = cMod5 (mod 5).\\n // Solution: x = (6 * cMod5 - 5 * cMod2) mod 10\\n // This formula comes from applying the extended Euclidean algorithm or by inspection.\\n // Check:\\n // If x = 6*c5 - 5*c2, then x % 5 = (6*c5 - 0) % 5 = c5 % 5 = c5.\\n // And x % 2 = (0 - 5*c2) % 2 = (-1*c2) % 2 = c2 % 2 = c2. (Since -1 mod 2 = 1)\\n long result = (6 * cMod5 - 5 * cMod2);\\n\\n // Ensure result is in [0, 9] because Java's % can be negative.\\n return (int) ((result % 10 + 10) % 10);\\n }\\n\\n /**\\n * Optimized solution using Binomial Coefficients and CRT.\\n * Time Complexity: O(N * log N)\\n * Space Complexity: O(1)\\n */\\n public boolean hasSameDigits(String s) {\\n int N = s.length();\\n // Constraint: 3 <= s.length <= 10^5\\n\\n // We need to compute sums involving C(N-2, k)\\n long M = N - 2;\\n\\n int finalDigit1 = 0;\\n // Calculate finalDigit1 = ( Sum_{k=0}^{M} [ C(M, k) * s[k] ] ) % 10\\n for (int k = 0; k <= M; k++) {\\n int coeff = nCrMod10(M, k);\\n if (coeff == 0) { // Optimization: skip if coefficient is 0 mod 10\\n continue;\\n }\\n // k is the index for C(M,k) and also the index for s\\n int digit = s.charAt(k) - '0';\\n finalDigit1 = (finalDigit1 + coeff * digit) % 10;\\n }\\n // Ensure non-negative result (although intermediate % should handle it)\\n finalDigit1 = (finalDigit1 + 10) % 10;\\n\\n\\n int finalDigit2 = 0;\\n // Calculate finalDigit2 = ( Sum_{k=0}^{M} [ C(M, k) * s[k+1] ] ) % 10\\n for (int k = 0; k <= M; k++) {\\n // The corresponding index in the original string s is k+1.\\n int s_index = k + 1;\\n\\n // Important: If s_index is out of bounds, this term doesn't exist.\\n // s has length N. Max valid index is N-1.\\n // We need k+1 <= N-1 => k <= N-2 => k <= M.\\n // The loop condition k <= M already ensures this, provided s has at least k+1 elements.\\n if (s_index >= N) {\\n // This shouldn't happen if loop goes correctly to M=N-2,\\n // because max k is N-2, so max s_index is N-1.\\n // However, as a safeguard or if logic changes, it's good practice.\\n break; // Or continue, but break is safer if indices are wrong\\n }\\n\\n int coeff = nCrMod10(M, k);\\n if (coeff == 0) { // Optimization\\n continue;\\n }\\n\\n int digit = s.charAt(s_index) - '0';\\n finalDigit2 = (finalDigit2 + coeff * digit) % 10;\\n }\\n // Ensure non-negative result\\n finalDigit2 = (finalDigit2 + 10) % 10;\\n\\n return finalDigit1 == finalDigit2;\\n }\\n}\"], [168, 0.4831, \"class Solution {\\n \\n int mod = 10;\\n public boolean hasSameDigits(String s) {\\n char[] ch = s.toCharArray();\\n int n = ch.length, dep = n - 2;\\n long sum1 = 0, sum2 = 0;\\n int[] fact = new int[n + 1], infact = new int[n + 1];\\n int[] p2 = new int[n + 1], p5 = new int[n + 1];\\n\\n fact[0] = 1;\\n for(int i = 1; i <= n; i++) {\\n int e2 = 0, e5 = 0;\\n int x = i;\\n while(x % 2 == 0) { e2++; x /= 2; }\\n while(x % 5 == 0) { e5++; x /= 5; }\\n fact[i] = fact[i - 1] * x % mod;\\n p2[i] = p2[i - 1] + e2;\\n p5[i] = p5[i - 1] + e5;\\n }\\n\\n infact[n] = pow(fact[n], 3); // \\u6b27\\u62c9\\u5b9a\\u7406\\u6c42\\u9006\\u5143\\n for (int i = n; i > 0; i--) {\\n int x = i;\\n x >>= Integer.numberOfTrailingZeros(x);\\n while (x % 5 == 0) {\\n x /= 5;\\n }\\n infact[i - 1] = infact[i] * x % mod;\\n }\\n\\n\\n for(int i = 0; i <= n - 2; i++) {\\n int cost = ch[i] - '0';\\n // System.out.println(\\\"cost: \\\" + cost);\\n sum1 += cost * fact[dep] * infact[i] * infact[dep - i] * pow(2, p2[dep] - p2[i] - p2[dep - i]) * pow(5, p5[dep] - p5[i] - p5[dep - i]) % mod;\\n sum1 %= mod;\\n }\\n // System.out.println(\\\"------\\\");\\n for(int i = 1; i <= n - 1; i++) {\\n int cost = ch[i] - '0';\\n // System.out.println(\\\"cost: \\\" + cost + \\\", i: \\\" + i + \\\", dep: \\\" + dep);\\n sum2 += cost * fact[dep] * infact[i - 1] * infact[dep - i + 1] * pow(2, p2[dep] - p2[i - 1] - p2[dep - i + 1]) * pow(5, p5[dep] - p5[i - 1] - p5[dep - i + 1]) % mod;\\n sum2 %= mod;\\n }\\n\\n // for(int i = 1; i < n - 1; i++) {\\n // int cost = ch[i] - '0';\\n // sum2 += cost * fact[dep] * infact[i] * infact[dep - i];\\n // }\\n System.out.println(\\\"sum1: \\\" + sum1 + \\\", sum2: \\\" + sum2);\\n return sum1 == sum2;\\n }\\n\\n int pow(int x, int n) {\\n int res = 1;\\n while (n > 0) {\\n if (n % 2 > 0) {\\n res = res * x % mod;\\n }\\n x = x * x % mod;\\n n /= 2;\\n }\\n return res;\\n }\\n}\"], [176, 0.4831, \"import java.lang.StringBuilder; // Not used in the optimized solution but kept if needed elsewhere\\n\\nclass Solution {\\n\\n // Precomputed table for C(n, k) mod 5, for n < 5.\\n // C(n,k) = n! / (k! * (n-k)!)\\n // Example: C(4,2) = 6. C(4,2) mod 5 = 1.\\n private static final int[][] C_SMALL_MOD5 = {\\n {1}, // n=0: C(0,0)=1\\n {1, 1}, // n=1: C(1,0)=1, C(1,1)=1\\n {1, 2, 1}, // n=2: C(2,0)=1, C(2,1)=2, C(2,2)=1\\n {1, 3, 3, 1}, // n=3: C(3,0)=1, C(3,1)=3, C(3,2)=3, C(3,3)=1\\n {1, 4, 1, 4, 1} // n=4: C(4,0)=1, C(4,1)=4, C(4,2)=1, C(4,3)=4, C(4,4)=1\\n };\\n\\n /**\\n * Calculates C(n, k) mod p using Lucas's Theorem.\\n * Assumes p is prime and C_SMALL_MOD_P contains precomputed C(ni, ki) mod p for ni < p.\\n * Time Complexity: O(log_p N)\\n *\\n * @param n The total number of items.\\n * @param k The number of items to choose.\\n * @param p The prime modulus.\\n * @param C_SMALL_MOD_P Precomputed table C[ni][ki] % p for ni < p.\\n * @return C(n, k) mod p.\\n */\\n private long nCrModP(long n, long k, int p, int[][] C_SMALL_MOD_P) {\\n // If k is outside the valid range [0, n], the combination is 0.\\n if (k < 0 || k > n) {\\n return 0;\\n }\\n // Optimization: Use symmetry C(n, k) = C(n, n-k). Calculate with the smaller k.\\n if (k > n / 2) {\\n k = n - k;\\n }\\n // Base case: C(n, 0) = 1.\\n if (k == 0) {\\n return 1;\\n }\\n\\n long result = 1;\\n // Apply Lucas's Theorem by processing digits of n and k in base p.\\n while (n > 0 || k > 0) {\\n long ni = n % p; // Last digit of n in base p\\n long ki = k % p; // Last digit of k in base p\\n\\n // If ki > ni, then C(ni, ki) = 0, making the whole product C(n, k) mod p equal to 0.\\n if (ki > ni) {\\n return 0;\\n }\\n\\n // Multiply the result by C(ni, ki) mod p using the precomputed table.\\n // Indices are safe because 0 <= ki <= ni < p.\\n result = (result * C_SMALL_MOD_P[(int)ni][(int)ki]) % p;\\n\\n // Move to the next digits by integer division.\\n n /= p;\\n k /= p;\\n }\\n return result;\\n }\\n\\n /**\\n * Calculates C(n, k) mod 10 using the Chinese Remainder Theorem (CRT).\\n * It combines the results of C(n, k) mod 2 and C(n, k) mod 5.\\n * Time Complexity: O(log N) due to nCrModP call.\\n *\\n * @param n The total number of items.\\n * @param k The number of items to choose.\\n * @return C(n, k) mod 10.\\n */\\n private int nCrMod10(long n, long k) {\\n // Handle cases where k is out of range [0, n].\\n if (k < 0 || k > n) {\\n return 0;\\n }\\n\\n // Calculate C(n, k) mod 2.\\n // Property derived from Lucas's theorem for p=2:\\n // C(n, k) is odd (1 mod 2) if and only if there are no carries when adding k and (n-k) in binary.\\n // This is equivalent to checking if the set bits of k are a subset of the set bits of n ((k & n) == k).\\n long cMod2 = ((k & n) == k) ? 1 : 0;\\n\\n // Calculate C(n, k) mod 5 using the helper function nCrModP.\\n long cMod5 = nCrModP(n, k, 5, C_SMALL_MOD5);\\n\\n // Combine mod 2 and mod 5 results using the CRT formula.\\n // We need x such that x = cMod2 (mod 2) and x = cMod5 (mod 5).\\n // The unique solution modulo 10 is given by x = (6 * cMod5 - 5 * cMod2) mod 10.\\n long result = (6 * cMod5 - 5 * cMod2);\\n\\n // Ensure the result is non-negative and within [0, 9].\\n // Java's % operator can return negative results (e.g., -5 % 10 = -5).\\n return (int) ((result % 10 + 10) % 10);\\n }\\n\\n /**\\n * Determines if the final two digits are the same after repeatedly applying the sum-modulo-10 operation.\\n * This optimized solution uses properties of binomial coefficients modulo 10.\\n * Time Complexity: O(N * log N), where N is the length of the input string s.\\n * Space Complexity: O(1) (excluding the input string storage).\\n *\\n * @param s The input string consisting of digits.\\n * @return true if the final two digits are the same, false otherwise.\\n */\\n public boolean hasSameDigits(String s) {\\n int N = s.length();\\n // Constraint: 3 <= s.length <= 10^5\\n\\n // After N-2 steps, the string length becomes 2.\\n // The final digits depend on the initial digits s[0]...s[N-1]\\n // and binomial coefficients C(N-2, k).\\n long n_comb = N - 2; // The 'n' parameter for C(n, k)\\n\\n // Calculate the first of the final two digits.\\n // Formula: finalDigit1 = ( Sum_{j=0}^{N-2} [ C(N-2, j) * s[j] ] ) mod 10\\n int finalDigit1 = 0;\\n for (int j = 0; j <= n_comb; j++) { // j corresponds to the index in C(n_comb, j) and s[j]\\n // Calculate the coefficient C(n_comb, j) mod 10\\n int coeff = nCrMod10(n_comb, j);\\n\\n // If the coefficient is 0 mod 10, this term doesn't contribute to the sum mod 10.\\n if (coeff == 0) {\\n continue;\\n }\\n\\n // Get the digit s[j] as an integer value.\\n int digit = s.charAt(j) - '0';\\n\\n // Add the weighted digit (coeff * digit) to the sum, taking modulo 10 at each step.\\n finalDigit1 = (finalDigit1 + coeff * digit) % 10;\\n }\\n // Ensure the final sum is non-negative (although it should be with non-negative inputs).\\n finalDigit1 = (finalDigit1 + 10) % 10;\\n\\n // Calculate the second of the final two digits.\\n // Formula: finalDigit2 = ( Sum_{k=0}^{N-2} [ C(N-2, k) * s[k+1] ] ) mod 10\\n int finalDigit2 = 0;\\n for (int k = 0; k <= n_comb; k++) { // k corresponds to the index in C(n_comb, k)\\n // The corresponding index in the original string s is k+1.\\n int s_index = k + 1;\\n\\n // If the string index goes out of bounds, we've processed all relevant terms.\\n if (s_index >= N) {\\n break;\\n }\\n\\n // Calculate the coefficient C(n_comb, k) mod 10\\n int coeff = nCrMod10(n_comb, k);\\n\\n // If the coefficient is 0 mod 10, skip this term.\\n if (coeff == 0) {\\n continue;\\n }\\n\\n // Get the digit s[k+1] as an integer value.\\n int digit = s.charAt(s_index) - '0';\\n\\n // Add the weighted digit to the sum, taking modulo 10.\\n finalDigit2 = (finalDigit2 + coeff * digit) % 10;\\n }\\n // Ensure the final sum is non-negative.\\n finalDigit2 = (finalDigit2 + 10) % 10;\\n\\n // Compare the two final digits.\\n return finalDigit1 == finalDigit2;\\n }\\n}\"], [184, 0.9662, \"import java.util.*;\\n\\npublic class Solution {\\n private static final Map<Integer, Integer> INV = new HashMap<>() {{\\n put(1, 1);\\n put(3, 7);\\n put(7, 3);\\n put(9, 9);\\n }};\\n\\n private static final int[] TWOS = {2, 4, 8, 6};\\n private static final int[] FIVES = {5};\\n\\n private static int[] mult(int[] a, int[] b) {\\n return new int[] {\\n a[0] + b[0],\\n a[1] + b[1],\\n (a[2] * b[2]) % 10\\n };\\n }\\n\\n private static int[] div(int[] a, int[] b) {\\n return new int[] {\\n a[0] - b[0],\\n a[1] - b[1],\\n (a[2] * INV.get(b[2])) % 10\\n };\\n }\\n\\n private static int simplify(int[] tup) {\\n int twos = tup[0];\\n int fives = tup[1];\\n int res = tup[2];\\n\\n if (twos > 0) {\\n res = (res * TWOS[(twos - 1) % TWOS.length]) % 10;\\n }\\n\\n if (fives > 0) {\\n res = (res * FIVES[(fives - 1) % FIVES.length]) % 10;\\n }\\n\\n return res;\\n }\\n\\n private static int red(List<int[]> items) {\\n int sum = 0;\\n for (int[] item : items) {\\n sum = (sum + (item[0] * item[1]) % 10) % 10;\\n }\\n return sum;\\n }\\n\\n public boolean hasSameDigits(String s) {\\n int n = s.length() - 2;\\n\\n List<int[]> facts = new ArrayList<>();\\n facts.add(new int[]{0, 0, 1});\\n\\n while (n >= facts.size()) {\\n int num = facts.size();\\n int twos = 0;\\n while (num % 2 == 0) {\\n num /= 2;\\n twos++;\\n }\\n\\n int fives = 0;\\n while (num % 5 == 0) {\\n num /= 5;\\n fives++;\\n }\\n\\n facts.add(mult(facts.get(facts.size() - 1), new int[]{twos, fives, num}));\\n }\\n\\n List<Integer> pascal = new ArrayList<>();\\n for (int k = 0; k <= n; k++) {\\n int[] div1 = div(facts.get(n), facts.get(k));\\n int[] div2 = div(div1, facts.get(n - k));\\n pascal.add(simplify(div2));\\n }\\n\\n List<int[]> aPairs = new ArrayList<>();\\n List<int[]> bPairs = new ArrayList<>();\\n\\n for (int i = 0; i < pascal.size(); i++) {\\n aPairs.add(new int[]{Character.getNumericValue(s.charAt(i)), pascal.get(i)});\\n }\\n\\n for (int i = 0; i < pascal.size(); i++) {\\n bPairs.add(new int[]{Character.getNumericValue(s.charAt(i + 1)), pascal.get(i)});\\n }\\n\\n return red(aPairs) == red(bPairs);\\n }\\n}\\n\"], [192, 0.4831, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int L=s.length();\\n int m=L-2;\\n int arr[]=new int[m+1];\\n for(int i=0;i<=m;i++)\\n {\\n arr[i]=binmod10(m,i);\\n }\\n int s1=0,s2=0;\\n for(int i=0;i<=m;i++)\\n {\\n s1=((s.charAt(i)-'0')*arr[i]+s1)%10;\\n s2=((s.charAt(i+1)-'0')*arr[i]+s2)%10;\\n }\\n System.out.println(s1);\\n System.out.println(s2);\\n return s1==s2;\\n \\n }\\n int binmod10(int n,int r)\\n {\\n int x=binmod(n,r,2);\\n int y=binmod(n,r,5);\\n for(int i=0;i<10;i++)\\n {\\n if(i%2==x && i%5==y)\\n return i;\\n }\\n return 0;\\n }\\n int binmod(int n, int r, int p) {\\n int res = 1;\\n while (n > 0 || r > 0) {\\n int x = n % p;\\n int y = r % p;\\n if (y > x) return 0; // If r > n at this position, return 0 as combination is not possible\\n res = (res * ncr(x, y)) % p; // Multiply and take modulo 10 to keep the number manageable\\n n = n / p; // Move to the next base p digit of n\\n r = r / p; // Move to the next base p digit of r\\n }\\n return res;\\n}\\n\\n int ncr(int n, int r) {\\n if (r > n) return 0; // If r > n, return 0 (invalid combination)\\n if (r == 0 || r == n) return 1; // nCr(n, 0) and nCr(n, n) are both 1\\n\\n // Optimizing: Use the smaller of r and n-r for efficiency\\n r = Math.min(r, n - r);\\n\\n int res = 1;\\n for (int i = 1; i <= r; i++) {\\n res = res * n / i; // Multiply first and then divide\\n n--;\\n }\\n return res;\\n}\\n\\n}\\n\"], [200, 0.4831, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length(), m = n - 2;\\n int F0 = 0, F1 = 0;\\n // For each i from 0 to m, the coefficient is C(m,i) mod 10.\\n // F0 = \\u03a3\\u208d\\u1d62\\u208c\\u2080\\u208e\\u1d50 [ C(m,i) * digit[i] ] mod 10\\n // F1 = \\u03a3\\u208d\\u1d62\\u208c\\u2080\\u208e\\u1d50 [ C(m,i) * digit[i+1] ] mod 10\\n for (int i = 0; i <= m; i++) {\\n int coeff = binomMod10(m, i); \\n F0 = (F0 + coeff * (s.charAt(i) - '0')) % 10;\\n F1 = (F1 + coeff * (s.charAt(i + 1) - '0')) % 10;\\n }\\n return F0 == F1;\\n }\\n \\n // Compute binom(n, k) mod 10 via Lucas theorem.\\n // Since 10 = 2 * 5 (non\\u2010prime), we compute mod2 and mod5 then combine.\\n private int binomMod10(int n, int k) {\\n int mod2 = lucas(n, k, 2);\\n int mod5 = lucas(n, k, 5);\\n return combineMod(mod2, mod5);\\n }\\n \\n // Lucas theorem: for prime p, binom(n,k) mod p = \\u220f binom(n_i, k_i) mod p\\n private int lucas(int n, int k, int p) {\\n int res = 1;\\n while(n > 0 || k > 0) {\\n int n_i = n % p, k_i = k % p;\\n if(k_i > n_i) return 0;\\n res = (res * smallBinom(n_i, k_i, p)) % p;\\n n /= p;\\n k /= p;\\n }\\n return res;\\n }\\n \\n // For n, k < p (with p prime), compute nCk exactly then mod p.\\n private int smallBinom(int n, int k, int p) {\\n if(k > n) return 0;\\n if(k == 0 || k == n) return 1;\\n int res = 1;\\n for (int i = 1; i <= k; i++) {\\n res = res * (n - i + 1) / i;\\n }\\n return res % p;\\n }\\n \\n // Given x \\u2261 a (mod 2) and x \\u2261 b (mod 5), find unique x in [0,9].\\n private int combineMod(int a, int b) {\\n for (int x = 0; x < 10; x++) {\\n if(x % 2 == a && x % 5 == b) return x;\\n }\\n return 0; // Should never happen.\\n }\\n}\"], [208, 0.4831, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n final int n = s.length();\\n // If already length 2, just compare directly\\n if (n == 2) {\\n return s.charAt(0) == s.charAt(1);\\n }\\n int sum1 = 0, sum2 = 0;\\n // After n\\u22122 rounds, the two digits are\\n // sum_{i=0..n-2} [C(n-2, i) * s[i]] mod10\\n // and sum_{i=0..n-2} [C(n-2, i) * s[i+1]] mod10\\n for (int i = 0; i + 1 < n; ++i) {\\n int coef = nCkMod10(n - 2, i);\\n sum1 = (sum1 + coef * (s.charAt(i) - '0')) % 10;\\n sum2 = (sum2 + coef * (s.charAt(i+1) - '0')) % 10;\\n }\\n return sum1 == sum2;\\n }\\n\\n // Return C(n, k) % 10 via Lucas (mod 2 and mod 5) + CRT lookup\\n private int nCkMod10(int n, int k) {\\n int r2 = lucas(n, k, 2);\\n int r5 = lucas(n, k, 5);\\n // lookup[r2][r5] gives C(n,k)%10 when\\n // \\u2261 r2 (mod 2) and \\u2261 r5 (mod 5)\\n int[][] lookup = {\\n {0, 6, 2, 8, 4}, // r2 == 0\\n {5, 1, 7, 3, 9} // r2 == 1\\n };\\n return lookup[r2][r5];\\n }\\n\\n // Standard Lucas\\u2019s theorem for prime p\\n private int lucas(int n, int k, int p) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int ni = n % p;\\n int ki = k % p;\\n if (ki > ni) return 0;\\n res = res * smallBinom(ni, ki) % p;\\n n /= p;\\n k /= p;\\n }\\n return res;\\n }\\n\\n // Compute C(n, k) directly for n, k < p\\n private int smallBinom(int n, int k) {\\n int r = 1;\\n for (int i = 1; i <= k; ++i) {\\n r = r * (n - i + 1) / i;\\n }\\n return r;\\n }\\n}\\n\"], [216, 1.9324, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length(), m = n - 2;\\n int F0 = 0, F1 = 0;\\n // For each i from 0 to m, the coefficient is C(m,i) mod 10.\\n // F0 = \\u03a3\\u208d\\u1d62\\u208c\\u2080\\u208e\\u1d50 [ C(m,i) * digit[i] ] mod 10\\n // F1 = \\u03a3\\u208d\\u1d62\\u208c\\u2080\\u208e\\u1d50 [ C(m,i) * digit[i+1] ] mod 10\\n for (int i = 0; i <= m; i++) {\\n int coeff = binomMod10(m, i); \\n F0 = (F0 + coeff * (s.charAt(i) - '0')) % 10;\\n F1 = (F1 + coeff * (s.charAt(i + 1) - '0')) % 10;\\n }\\n return F0 == F1;\\n }\\n \\n // Compute binom(n, k) mod 10 via Lucas theorem.\\n // Since 10 = 2 * 5 (non\\u2010prime), we compute mod2 and mod5 then combine.\\n private int binomMod10(int n, int k) {\\n int mod2 = lucas(n, k, 2);\\n int mod5 = lucas(n, k, 5);\\n return combineMod(mod2, mod5);\\n }\\n \\n // Lucas theorem: for prime p, binom(n,k) mod p = \\u220f binom(n_i, k_i) mod p\\n private int lucas(int n, int k, int p) {\\n int res = 1;\\n while(n > 0 || k > 0) {\\n int n_i = n % p, k_i = k % p;\\n if(k_i > n_i) return 0;\\n res = (res * smallBinom(n_i, k_i, p)) % p;\\n n /= p;\\n k /= p;\\n }\\n return res;\\n }\\n \\n // For n, k < p (with p prime), compute nCk exactly then mod p.\\n private int smallBinom(int n, int k, int p) {\\n if(k > n) return 0;\\n if(k == 0 || k == n) return 1;\\n int res = 1;\\n for (int i = 1; i <= k; i++) {\\n res = res * (n - i + 1) / i;\\n }\\n return res % p;\\n }\\n \\n // Given x \\u2261 a (mod 2) and x \\u2261 b (mod 5), find unique x in [0,9].\\n private int combineMod(int a, int b) {\\n for (int x = 0; x < 10; x++) {\\n if(x % 2 == a && x % 5 == b) return x;\\n }\\n return 0; // Should never happen.\\n }\\n}\"], [224, 1.4493, \"/**\\n * \\u0420\\u0435\\u0448\\u0435\\u043d\\u0438\\u0435 \\u0437\\u0430\\u0434\\u0430\\u0447\\u0438 \\u043f\\u0440\\u043e\\u0432\\u0435\\u0440\\u043a\\u0438 \\u0440\\u0430\\u0432\\u0435\\u043d\\u0441\\u0442\\u0432\\u0430 \\u043f\\u043e\\u0441\\u043b\\u0435\\u0434\\u043d\\u0438\\u0445 \\u0434\\u0432\\u0443\\u0445 \\u0446\\u0438\\u0444\\u0440 \\u043f\\u043e\\u0441\\u043b\\u0435 \\u0441\\u0435\\u0440\\u0438\\u0438 \\u043e\\u043f\\u0435\\u0440\\u0430\\u0446\\u0438\\u0439.\\n * \\n * \\u0417\\u0430\\u0434\\u0430\\u0447\\u0430: \\u0414\\u0430\\u043d\\u0430 \\u0441\\u0442\\u0440\\u043e\\u043a\\u0430 s, \\u0441\\u043e\\u0441\\u0442\\u043e\\u044f\\u0449\\u0430\\u044f \\u0438\\u0437 \\u0446\\u0438\\u0444\\u0440. \\u0412\\u044b\\u043f\\u043e\\u043b\\u043d\\u044f\\u0435\\u043c \\u0441\\u043b\\u0435\\u0434\\u0443\\u044e\\u0449\\u0443\\u044e \\u043e\\u043f\\u0435\\u0440\\u0430\\u0446\\u0438\\u044e \\u0434\\u043e \\u0442\\u0435\\u0445 \\u043f\\u043e\\u0440, \\n * \\u043f\\u043e\\u043a\\u0430 \\u0441\\u0442\\u0440\\u043e\\u043a\\u0430 \\u043d\\u0435 \\u0431\\u0443\\u0434\\u0435\\u0442 \\u0441\\u043e\\u0434\\u0435\\u0440\\u0436\\u0430\\u0442\\u044c \\u0440\\u043e\\u0432\\u043d\\u043e \\u0434\\u0432\\u0435 \\u0446\\u0438\\u0444\\u0440\\u044b:\\n * 1. \\u0414\\u043b\\u044f \\u043a\\u0430\\u0436\\u0434\\u043e\\u0439 \\u043f\\u0430\\u0440\\u044b \\u043f\\u043e\\u0441\\u043b\\u0435\\u0434\\u043e\\u0432\\u0430\\u0442\\u0435\\u043b\\u044c\\u043d\\u044b\\u0445 \\u0446\\u0438\\u0444\\u0440 \\u0432 s, \\u043d\\u0430\\u0447\\u0438\\u043d\\u0430\\u044f \\u0441 \\u043f\\u0435\\u0440\\u0432\\u043e\\u0439, \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u043c\\n * \\u043d\\u043e\\u0432\\u0443\\u044e \\u0446\\u0438\\u0444\\u0440\\u0443 \\u043a\\u0430\\u043a \\u0441\\u0443\\u043c\\u043c\\u0443 \\u0434\\u0432\\u0443\\u0445 \\u0446\\u0438\\u0444\\u0440 \\u043f\\u043e \\u043c\\u043e\\u0434\\u0443\\u043b\\u044e 10.\\n * 2. \\u0417\\u0430\\u043c\\u0435\\u043d\\u044f\\u0435\\u043c s \\u043f\\u043e\\u0441\\u043b\\u0435\\u0434\\u043e\\u0432\\u0430\\u0442\\u0435\\u043b\\u044c\\u043d\\u043e\\u0441\\u0442\\u044c\\u044e \\u0432\\u043d\\u043e\\u0432\\u044c \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u043d\\u044b\\u0445 \\u0446\\u0438\\u0444\\u0440 \\u0432 \\u043f\\u043e\\u0440\\u044f\\u0434\\u043a\\u0435 \\u0438\\u0445 \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u044f.\\n * \\n * \\u0412\\u0435\\u0440\\u043d\\u0443\\u0442\\u044c true, \\u0435\\u0441\\u043b\\u0438 \\u0434\\u0432\\u0435 \\u0444\\u0438\\u043d\\u0430\\u043b\\u044c\\u043d\\u044b\\u0435 \\u0446\\u0438\\u0444\\u0440\\u044b \\u0432 s \\u043e\\u0434\\u0438\\u043d\\u0430\\u043a\\u043e\\u0432\\u044b\\u0435, \\u0438\\u043d\\u0430\\u0447\\u0435 - false.\\n */\\nclass Solution {\\n /**\\n * \\u041f\\u0440\\u043e\\u0432\\u0435\\u0440\\u044f\\u0435\\u0442, \\u0431\\u0443\\u0434\\u0443\\u0442 \\u043b\\u0438 \\u043f\\u043e\\u0441\\u043b\\u0435\\u0434\\u043d\\u0438\\u0435 \\u0434\\u0432\\u0435 \\u0446\\u0438\\u0444\\u0440\\u044b \\u043e\\u0434\\u0438\\u043d\\u0430\\u043a\\u043e\\u0432\\u044b\\u043c\\u0438 \\u043f\\u043e\\u0441\\u043b\\u0435 \\u0432\\u044b\\u043f\\u043e\\u043b\\u043d\\u0435\\u043d\\u0438\\u044f \\u043e\\u043f\\u0435\\u0440\\u0430\\u0446\\u0438\\u0439.\\n *\\n * @param s \\u0441\\u0442\\u0440\\u043e\\u043a\\u0430 \\u0446\\u0438\\u0444\\u0440\\n * @return true, \\u0435\\u0441\\u043b\\u0438 \\u043f\\u043e\\u0441\\u043b\\u0435\\u0434\\u043d\\u0438\\u0435 \\u0434\\u0432\\u0435 \\u0446\\u0438\\u0444\\u0440\\u044b \\u043e\\u0434\\u0438\\u043d\\u0430\\u043a\\u043e\\u0432\\u044b, \\u0438\\u043d\\u0430\\u0447\\u0435 false\\n */\\n public boolean hasSameDigits(String s) {\\n // \\u0415\\u0441\\u043b\\u0438 \\u0432 \\u0441\\u0442\\u0440\\u043e\\u043a\\u0435 \\u043c\\u0435\\u043d\\u0435\\u0435 3 \\u0446\\u0438\\u0444\\u0440, \\u043f\\u0440\\u043e\\u0432\\u0435\\u0440\\u044f\\u0435\\u043c \\u043d\\u0430\\u043f\\u0440\\u044f\\u043c\\u0443\\u044e\\n if (s.length() <= 2) {\\n return s.length() == 2 && s.charAt(0) == s.charAt(1);\\n }\\n \\n // \\u0414\\u043b\\u044f \\u0441\\u0442\\u0440\\u043e\\u043a\\u0438 \\u0434\\u043b\\u0438\\u043d\\u043e\\u0439 n \\u0444\\u0438\\u043d\\u0430\\u043b\\u044c\\u043d\\u044b\\u0435 \\u0434\\u0432\\u0430 \\u0447\\u0438\\u0441\\u043b\\u0430 \\u0437\\u0430\\u0432\\u0438\\u0441\\u044f\\u0442 \\u043e\\u0442 \\u043a\\u043e\\u044d\\u0444\\u0444\\u0438\\u0446\\u0438\\u0435\\u043d\\u0442\\u043e\\u0432 \\u043f\\u0435\\u0440\\u0435\\u0434\\n // \\u043a\\u0430\\u0436\\u0434\\u043e\\u0439 \\u0446\\u0438\\u0444\\u0440\\u043e\\u0439 \\u0438\\u0441\\u0445\\u043e\\u0434\\u043d\\u043e\\u0439 \\u0441\\u0442\\u0440\\u043e\\u043a\\u0438.\\n // \\u0412\\u043c\\u0435\\u0441\\u0442\\u043e \\u043c\\u043e\\u0434\\u0435\\u043b\\u0438\\u0440\\u043e\\u0432\\u0430\\u043d\\u0438\\u044f \\u0432\\u0441\\u0435\\u0433\\u043e \\u043f\\u0440\\u043e\\u0446\\u0435\\u0441\\u0441\\u0430, \\u043c\\u044b \\u0441\\u0440\\u0430\\u0437\\u0443 \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u043c \\u0438\\u0442\\u043e\\u0433\\u043e\\u0432\\u044b\\u0435 \\u0446\\u0438\\u0444\\u0440\\u044b\\n int firstDigit = 0; // \\u041f\\u0435\\u0440\\u0432\\u0430\\u044f \\u0438\\u0437 \\u0434\\u0432\\u0443\\u0445 \\u0444\\u0438\\u043d\\u0430\\u043b\\u044c\\u043d\\u044b\\u0445 \\u0446\\u0438\\u0444\\u0440\\n int secondDigit = 0; // \\u0412\\u0442\\u043e\\u0440\\u0430\\u044f \\u0438\\u0437 \\u0434\\u0432\\u0443\\u0445 \\u0444\\u0438\\u043d\\u0430\\u043b\\u044c\\u043d\\u044b\\u0445 \\u0446\\u0438\\u0444\\u0440\\n \\n // \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u043c \\u043a\\u043e\\u044d\\u0444\\u0444\\u0438\\u0446\\u0438\\u0435\\u043d\\u0442\\u044b \\u0434\\u043b\\u044f \\u043a\\u0430\\u0436\\u0434\\u043e\\u0439 \\u043f\\u043e\\u0437\\u0438\\u0446\\u0438\\u0438 \\u0438 \\u0443\\u043c\\u043d\\u043e\\u0436\\u0430\\u0435\\u043c \\u043d\\u0430 \\u0441\\u043e\\u043e\\u0442\\u0432\\u0435\\u0442\\u0441\\u0442\\u0432\\u0443\\u044e\\u0449\\u0443\\u044e \\u0446\\u0438\\u0444\\u0440\\u0443\\n for (int i = 0; i < s.length() - 1; i++) {\\n // \\u041f\\u043e\\u043b\\u0443\\u0447\\u0430\\u0435\\u043c \\u0431\\u0438\\u043d\\u043e\\u043c\\u0438\\u0430\\u043b\\u044c\\u043d\\u044b\\u0439 \\u043a\\u043e\\u044d\\u0444\\u0444\\u0438\\u0446\\u0438\\u0435\\u043d\\u0442 C(n-2,i) \\u043f\\u043e \\u043c\\u043e\\u0434\\u0443\\u043b\\u044e 10\\n int coefficient = computeBinomialCoefficientMod10(s.length() - 2, i);\\n \\n // \\u041f\\u0440\\u0438\\u0431\\u0430\\u0432\\u043b\\u044f\\u0435\\u043c \\u043a \\u043f\\u0435\\u0440\\u0432\\u043e\\u0439 \\u0444\\u0438\\u043d\\u0430\\u043b\\u044c\\u043d\\u043e\\u0439 \\u0446\\u0438\\u0444\\u0440\\u0435\\n firstDigit = (firstDigit + coefficient * (s.charAt(i) - '0')) % 10;\\n \\n // \\u041f\\u0440\\u0438\\u0431\\u0430\\u0432\\u043b\\u044f\\u0435\\u043c \\u043a \\u0432\\u0442\\u043e\\u0440\\u043e\\u0439 \\u0444\\u0438\\u043d\\u0430\\u043b\\u044c\\u043d\\u043e\\u0439 \\u0446\\u0438\\u0444\\u0440\\u0435\\n secondDigit = (secondDigit + coefficient * (s.charAt(i + 1) - '0')) % 10;\\n }\\n \\n return firstDigit == secondDigit;\\n }\\n \\n /**\\n * \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u0442 \\u0431\\u0438\\u043d\\u043e\\u043c\\u0438\\u0430\\u043b\\u044c\\u043d\\u044b\\u0439 \\u043a\\u043e\\u044d\\u0444\\u0444\\u0438\\u0446\\u0438\\u0435\\u043d\\u0442 C(n,k) \\u043f\\u043e \\u043c\\u043e\\u0434\\u0443\\u043b\\u044e 10.\\n * \\u0418\\u0441\\u043f\\u043e\\u043b\\u044c\\u0437\\u0443\\u0435\\u0442 \\u043a\\u0438\\u0442\\u0430\\u0439\\u0441\\u043a\\u0443\\u044e \\u0442\\u0435\\u043e\\u0440\\u0435\\u043c\\u0443 \\u043e\\u0431 \\u043e\\u0441\\u0442\\u0430\\u0442\\u043a\\u0430\\u0445 \\u0438 \\u0442\\u0435\\u043e\\u0440\\u0435\\u043c\\u0443 \\u041b\\u0443\\u043a\\u0430\\u0441\\u0430 \\u0434\\u043b\\u044f \\u044d\\u0444\\u0444\\u0435\\u043a\\u0442\\u0438\\u0432\\u043d\\u043e\\u0433\\u043e \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u044f.\\n *\\n * @param n \\u0432\\u0435\\u0440\\u0445\\u043d\\u0438\\u0439 \\u043f\\u0430\\u0440\\u0430\\u043c\\u0435\\u0442\\u0440 \\u0434\\u043b\\u044f C(n,k)\\n * @param k \\u043d\\u0438\\u0436\\u043d\\u0438\\u0439 \\u043f\\u0430\\u0440\\u0430\\u043c\\u0435\\u0442\\u0440 \\u0434\\u043b\\u044f C(n,k)\\n * @return \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 C(n,k) % 10\\n */\\n private int computeBinomialCoefficientMod10(int n, int k) {\\n // \\u0415\\u0441\\u043b\\u0438 k \\u0432\\u044b\\u0445\\u043e\\u0434\\u0438\\u0442 \\u0437\\u0430 \\u0434\\u043e\\u043f\\u0443\\u0441\\u0442\\u0438\\u043c\\u044b\\u0439 \\u0434\\u0438\\u0430\\u043f\\u0430\\u0437\\u043e\\u043d, \\u0440\\u0435\\u0437\\u0443\\u043b\\u044c\\u0442\\u0430\\u0442 0\\n if (k < 0 || k > n) {\\n return 0;\\n }\\n \\n // \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u043c C(n,k) % 2 \\u0438 C(n,k) % 5 \\u0441 \\u043f\\u043e\\u043c\\u043e\\u0449\\u044c\\u044e \\u0442\\u0435\\u043e\\u0440\\u0435\\u043c\\u044b \\u041b\\u0443\\u043a\\u0430\\u0441\\u0430\\n int mod2 = computeLucasTheoremMod(n, k, 2);\\n int mod5 = computeLucasTheoremMod(n, k, 5);\\n \\n // \\u0418\\u0441\\u043f\\u043e\\u043b\\u044c\\u0437\\u0443\\u0435\\u043c \\u043f\\u0440\\u0435\\u0434\\u0432\\u0430\\u0440\\u0438\\u0442\\u0435\\u043b\\u044c\\u043d\\u043e \\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u043d\\u0443\\u044e \\u0442\\u0430\\u0431\\u043b\\u0438\\u0446\\u0443 \\u0434\\u043b\\u044f \\u0432\\u043e\\u0441\\u0441\\u0442\\u0430\\u043d\\u043e\\u0432\\u043b\\u0435\\u043d\\u0438\\u044f C(n,k) % 10\\n // \\u043d\\u0430 \\u043e\\u0441\\u043d\\u043e\\u0432\\u0435 \\u043a\\u0438\\u0442\\u0430\\u0439\\u0441\\u043a\\u043e\\u0439 \\u0442\\u0435\\u043e\\u0440\\u0435\\u043c\\u044b \\u043e\\u0431 \\u043e\\u0441\\u0442\\u0430\\u0442\\u043a\\u0430\\u0445\\n int[][] lookupTable = {\\n {0, 6, 2, 8, 4}, // \\u043a\\u043e\\u0433\\u0434\\u0430 mod2 == 0\\n {5, 1, 7, 3, 9} // \\u043a\\u043e\\u0433\\u0434\\u0430 mod2 == 1\\n };\\n \\n return lookupTable[mod2][mod5];\\n }\\n \\n /**\\n * \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u0442 \\u0431\\u0438\\u043d\\u043e\\u043c\\u0438\\u0430\\u043b\\u044c\\u043d\\u044b\\u0439 \\u043a\\u043e\\u044d\\u0444\\u0444\\u0438\\u0446\\u0438\\u0435\\u043d\\u0442 C(n,k) \\u043f\\u043e \\u043c\\u043e\\u0434\\u0443\\u043b\\u044e prime\\n * \\u0438\\u0441\\u043f\\u043e\\u043b\\u044c\\u0437\\u0443\\u044f \\u0442\\u0435\\u043e\\u0440\\u0435\\u043c\\u0443 \\u041b\\u0443\\u043a\\u0430\\u0441\\u0430: C(n,k) % p = \\u03a0 C(n_i,k_i) % p,\\n * \\u0433\\u0434\\u0435 n_i \\u0438 k_i - \\u0446\\u0438\\u0444\\u0440\\u044b \\u0432 base-p \\u043f\\u0440\\u0435\\u0434\\u0441\\u0442\\u0430\\u0432\\u043b\\u0435\\u043d\\u0438\\u0438 n \\u0438 k.\\n *\\n * @param n \\u0432\\u0435\\u0440\\u0445\\u043d\\u0438\\u0439 \\u043f\\u0430\\u0440\\u0430\\u043c\\u0435\\u0442\\u0440\\n * @param k \\u043d\\u0438\\u0436\\u043d\\u0438\\u0439 \\u043f\\u0430\\u0440\\u0430\\u043c\\u0435\\u0442\\u0440\\n * @param prime \\u043f\\u0440\\u043e\\u0441\\u0442\\u043e\\u0435 \\u0447\\u0438\\u0441\\u043b\\u043e (\\u043c\\u043e\\u0434\\u0443\\u043b\\u044c)\\n * @return \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 C(n,k) % prime\\n */\\n private int computeLucasTheoremMod(int n, int k, int prime) {\\n int result = 1;\\n \\n // \\u0420\\u0430\\u0437\\u043b\\u043e\\u0436\\u0435\\u043d\\u0438\\u0435 \\u043f\\u043e \\u043e\\u0441\\u043d\\u043e\\u0432\\u0430\\u043d\\u0438\\u044e prime\\n while (n > 0 || k > 0) {\\n int nMod = n % prime; // \\u043e\\u0441\\u0442\\u0430\\u0442\\u043e\\u043a n \\u043f\\u0440\\u0438 \\u0434\\u0435\\u043b\\u0435\\u043d\\u0438\\u0438 \\u043d\\u0430 prime\\n int kMod = k % prime; // \\u043e\\u0441\\u0442\\u0430\\u0442\\u043e\\u043a k \\u043f\\u0440\\u0438 \\u0434\\u0435\\u043b\\u0435\\u043d\\u0438\\u0438 \\u043d\\u0430 prime\\n \\n // \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u043c C(nMod,kMod) \\u0438 \\u0443\\u043c\\u043d\\u043e\\u0436\\u0430\\u0435\\u043c \\u043d\\u0430 \\u043d\\u0430\\u043a\\u043e\\u043f\\u043b\\u0435\\u043d\\u043d\\u044b\\u0439 \\u0440\\u0435\\u0437\\u0443\\u043b\\u044c\\u0442\\u0430\\u0442\\n if (kMod > nMod) {\\n return 0; // \\u0415\\u0441\\u043b\\u0438 kMod > nMod, \\u0442\\u043e C(nMod,kMod) = 0\\n }\\n \\n result = (result * computeSmallBinomialCoefficient(nMod, kMod)) % prime;\\n \\n // \\u041f\\u0435\\u0440\\u0435\\u0445\\u043e\\u0434\\u0438\\u043c \\u043a \\u0441\\u043b\\u0435\\u0434\\u0443\\u044e\\u0449\\u0438\\u043c \\u0446\\u0438\\u0444\\u0440\\u0430\\u043c\\n n /= prime;\\n k /= prime;\\n }\\n \\n return result;\\n }\\n \\n /**\\n * \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u0442 \\u0431\\u0438\\u043d\\u043e\\u043c\\u0438\\u0430\\u043b\\u044c\\u043d\\u044b\\u0439 \\u043a\\u043e\\u044d\\u0444\\u0444\\u0438\\u0446\\u0438\\u0435\\u043d\\u0442 C(n,k) \\u0434\\u043b\\u044f \\u043c\\u0430\\u043b\\u044b\\u0445 \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0439.\\n *\\n * @param n \\u0432\\u0435\\u0440\\u0445\\u043d\\u0438\\u0439 \\u043f\\u0430\\u0440\\u0430\\u043c\\u0435\\u0442\\u0440\\n * @param k \\u043d\\u0438\\u0436\\u043d\\u0438\\u0439 \\u043f\\u0430\\u0440\\u0430\\u043c\\u0435\\u0442\\u0440\\n * @return \\u0437\\u043d\\u0430\\u0447\\u0435\\u043d\\u0438\\u0435 C(n,k)\\n */\\n private int computeSmallBinomialCoefficient(int n, int k) {\\n // \\u041e\\u043f\\u0442\\u0438\\u043c\\u0438\\u0437\\u0430\\u0446\\u0438\\u044f \\u0434\\u043b\\u044f \\u043a\\u0440\\u0430\\u0439\\u043d\\u0438\\u0445 \\u0441\\u043b\\u0443\\u0447\\u0430\\u0435\\u0432\\n if (k == 0 || k == n) {\\n return 1;\\n }\\n if (k == 1 || k == n - 1) {\\n return n;\\n }\\n \\n // \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u043c \\u0434\\u043b\\u044f \\u043e\\u0441\\u0442\\u0430\\u043b\\u044c\\u043d\\u044b\\u0445 \\u0441\\u043b\\u0443\\u0447\\u0430\\u0435\\u0432\\n int result = 1;\\n for (int i = 0; i < k; i++) {\\n result *= (n - i);\\n result /= (i + 1);\\n }\\n return result;\\n }\\n}\"], [232, 0.4831, \"class Solution {\\n \\n int mod = 10;\\n public boolean hasSameDigits(String s) {\\n char[] ch = s.toCharArray();\\n int n = ch.length, dep = n - 2;\\n long sum1 = 0, sum2 = 0;\\n int[] fact = new int[n + 1], infact = new int[n + 1];\\n int[] p2 = new int[n + 1], p5 = new int[n + 1];\\n\\n fact[0] = 1;\\n for(int i = 1; i <= n; i++) {\\n int e2 = 0, e5 = 0;\\n int x = i;\\n while(x % 2 == 0) { e2++; x /= 2; }\\n while(x % 5 == 0) { e5++; x /= 5; }\\n fact[i] = fact[i - 1] * x % mod;\\n p2[i] = p2[i - 1] + e2;\\n p5[i] = p5[i - 1] + e5;\\n }\\n\\n // infact[n] = pow(fact[n], 3); // \\u6b27\\u62c9\\u5b9a\\u7406\\u6c42\\u9006\\u5143\\n // for (int i = n; i > 0; i--) {\\n // int x = i;\\n // x >>= Integer.numberOfTrailingZeros(x);\\n // while (x % 5 == 0) {\\n // x /= 5;\\n // }\\n // infact[i - 1] = infact[i] * x % mod;\\n // }\\n infact[0] = 1;\\n // infact[1] = pow(fact[1], 3); // \\u6b27\\u62c9\\u5b9a\\u7406\\u6c42\\u9006\\u5143\\n for (int i = 1; i <= n; i++) {\\n // int x = i;\\n // x >>= Integer.numberOfTrailingZeros(x);\\n // while (x % 5 == 0) {\\n // x /= 5;\\n // }\\n infact[i] = pow(fact[i], 3) % mod;\\n }\\n\\n System.out.println(Arrays.toString(fact));\\n System.out.println(Arrays.toString(infact));\\n\\n for(int i = 0; i <= n - 2; i++) {\\n int cost = ch[i] - '0';\\n sum1 += cost * fact[dep] * infact[i] * infact[dep - i] * pow(2, p2[dep] - p2[i] - p2[dep - i]) * pow(5, p5[dep] - p5[i] - p5[dep - i]) % mod;\\n sum1 %= mod;\\n }\\n for(int i = 1; i <= n - 1; i++) {\\n int cost = ch[i] - '0';\\n sum2 += cost * fact[dep] * infact[i - 1] * infact[dep - i + 1] * pow(2, p2[dep] - p2[i - 1] - p2[dep - i + 1]) * pow(5, p5[dep] - p5[i - 1] - p5[dep - i + 1]) % mod;\\n sum2 %= mod;\\n }\\n\\n return sum1 == sum2;\\n }\\n\\n int pow(int base, int pow) {\\n if(pow == 1) return base;\\n if(pow == 0) return 1;\\n\\n int half = pow(base, pow / 2);\\n if(pow % 2 == 0) return half * half % mod;\\n return half * half * base % mod;\\n }\\n\\n // int pow(int x, int n) {\\n // int res = 1;\\n // while (n > 0) {\\n // if (n % 2 > 0) {\\n // res = res * x % mod;\\n // }\\n // x = x * x % mod;\\n // n /= 2;\\n // }\\n // return res;\\n // }\\n}\"], [240, 0.4831, \"class Solution {\\n int[][] binom2;\\n int[][] binom5;\\n \\n public Solution() {\\n binom2 = new int[2][2];\\n binom2[0][0] = 1;\\n binom2[1][0] = 1;\\n binom2[1][1] = 1;\\n binom5 = new int[5][5];\\n for (int i = 0; i < 5; i++) {\\n for (int j = 0; j <= i; j++) {\\n if (j == 0 || j == i) \\n binom5[i][j] = 1;\\n else \\n binom5[i][j] = (binom5[i - 1][j - 1] + binom5[i - 1][j]) % 5;\\n }\\n }\\n }\\n \\n int lucas(int n, int k, int p) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int ni = n % p;\\n int ki = k % p;\\n if (ki > ni) return 0;\\n if (p == 2) \\n res = (res * binom2[ni][ki]) % 2;\\n else if (p == 5) \\n res = (res * binom5[ni][ki]) % 5;\\n n /= p;\\n k /= p;\\n }\\n return res;\\n }\\n \\n int binomMod10(int n, int k) {\\n int mod2 = lucas(n, k, 2);\\n int mod5 = lucas(n, k, 5);\\n for (int x = mod5; x < 10; x += 5) {\\n if (x % 2 == mod2) return x;\\n }\\n return 0;\\n }\\n \\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int m = n - 2;\\n int f0 = 0, f1 = 0;\\n for (int j = 0; j <= m; j++) {\\n int c = binomMod10(m, j);\\n int d = s.charAt(j) - '0';\\n f0 = (f0 + c * d) % 10;\\n }\\n for (int j = 0; j <= m; j++) {\\n int c = binomMod10(m, j);\\n int d = s.charAt(j + 1) - '0';\\n f1 = (f1 + c * d) % 10;\\n }\\n return f0 == f1;\\n }\\n}\"], [248, 0.4831, \"import java.util.Arrays;\\nclass Solution {\\n\\n private static final long[][] C_MOD5 = {\\n /*n=0*/ {1, 0, 0, 0, 0},\\n /*n=1*/ {1, 1, 0, 0, 0},\\n /*n=2*/ {1, 2, 1, 0, 0},\\n /*n=3*/ {1, 3, 3, 1, 0},\\n /*n=4*/ {1, 4, 1, 4, 1} // C(4,2)=6%5=1\\n };\\n\\n // C(n, k) % 2 \\u0434\\u043b\\u044f n < 2\\n private static final long[][] C_MOD2 = {\\n /*n=0*/ {1, 0},\\n /*n=1*/ {1, 1}\\n };\\n\\n // \\u0422\\u0430\\u0431\\u043b\\u0438\\u0446\\u0430 \\u043f\\u043e\\u0438\\u0441\\u043a\\u0430 \\u0434\\u043b\\u044f CRT: result = crt_lookup[mod2][mod5]\\n private static final int[][] CRT_LOOKUP_MOD10 = {\\n // mod5: 0 1 2 3 4\\n { 0, 6, 2, 8, 4 }, // mod2 = 0\\n { 5, 1, 7, 3, 9 } // mod2 = 1\\n };\\n\\n // --- \\u0412\\u0441\\u043f\\u043e\\u043c\\u043e\\u0433\\u0430\\u0442\\u0435\\u043b\\u044c\\u043d\\u044b\\u0435 \\u0444\\u0443\\u043d\\u043a\\u0446\\u0438\\u0438 ---\\n\\n /**\\n * \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u0442 C(n, k) mod p (p - \\u043f\\u0440\\u043e\\u0441\\u0442\\u043e\\u0435) \\u0438\\u0441\\u043f\\u043e\\u043b\\u044c\\u0437\\u0443\\u044f \\u0422\\u0435\\u043e\\u0440\\u0435\\u043c\\u0443 \\u041b\\u044e\\u043a\\u0430.\\n * C_small - \\u043f\\u0440\\u0435\\u0434\\u0432\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u043d\\u0430\\u044f \\u0442\\u0430\\u0431\\u043b\\u0438\\u0446\\u0430 C(a, b) % p \\u0434\\u043b\\u044f a, b < p.\\n */\\n private long nCrModP(long n, long r, int p, long[][] C_small) {\\n if (r < 0 || r > n) {\\n return 0;\\n }\\n long result = 1;\\n while (n > 0 || r > 0) {\\n long ni = n % p;\\n long ri = r % p;\\n if (ri > ni) {\\n return 0; // C(ni, ri) = 0 \\u0435\\u0441\\u043b\\u0438 ri > ni\\n }\\n result = (result * C_small[(int)ni][(int)ri]) % p;\\n n /= p;\\n r /= p;\\n }\\n return result;\\n }\\n\\n /**\\n * \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u044f\\u0435\\u0442 C(n, r) mod 10.\\n */\\n private long nCrMod10(long n, long r) {\\n // \\u041e\\u043f\\u0442\\u0438\\u043c\\u0438\\u0437\\u0430\\u0446\\u0438\\u044f: C(n, r) = C(n, n-r). \\u041c\\u043e\\u0436\\u0435\\u0442 \\u0443\\u0441\\u043a\\u043e\\u0440\\u0438\\u0442\\u044c Lucas, \\u0435\\u0441\\u043b\\u0438 r > n/2.\\n if (r > n / 2) {\\n r = n - r;\\n }\\n // \\u0411\\u0430\\u0437\\u043e\\u0432\\u044b\\u0435 \\u0441\\u043b\\u0443\\u0447\\u0430\\u0438 (\\u0445\\u043e\\u0442\\u044f Lucas \\u0438\\u0445 \\u0442\\u043e\\u0436\\u0435 \\u043e\\u0431\\u0440\\u0430\\u0431\\u0430\\u0442\\u044b\\u0432\\u0430\\u0435\\u0442)\\n if (r < 0 || r > n) return 0;\\n if (r == 0) return 1; // C(n, 0) = 1\\n\\n long mod2 = nCrModP(n, r, 2, C_MOD2);\\n long mod5 = nCrModP(n, r, 5, C_MOD5);\\n\\n return CRT_LOOKUP_MOD10[(int)mod2][(int)mod5];\\n }\\n\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n\\n // \\u0423\\u0441\\u043b\\u043e\\u0432\\u0438\\u0435: 3 <= s.length. \\u041e\\u0431\\u0440\\u0430\\u0431\\u043e\\u0442\\u0430\\u0435\\u043c n=2 \\u043d\\u0430 \\u0432\\u0441\\u044f\\u043a\\u0438\\u0439 \\u0441\\u043b\\u0443\\u0447\\u0430\\u0439.\\n if (n < 2) return false;\\n if (n == 2) return s.charAt(0) == s.charAt(1);\\n\\n // \\u041a\\u043e\\u043b\\u0438\\u0447\\u0435\\u0441\\u0442\\u0432\\u043e \\u0448\\u0430\\u0433\\u043e\\u0432 k = n - 2.\\n // \\u041d\\u0443\\u0436\\u043d\\u044b \\u043a\\u043e\\u044d\\u0444\\u0444\\u0438\\u0446\\u0438\\u0435\\u043d\\u0442\\u044b C(k, i) = C(n - 2, i).\\n long k_steps = n - 2;\\n\\n long finalDigit0 = 0; // \\u041f\\u0435\\u0440\\u0432\\u0430\\u044f \\u0438\\u0437 \\u0434\\u0432\\u0443\\u0445 \\u0444\\u0438\\u043d\\u0430\\u043b\\u044c\\u043d\\u044b\\u0445 \\u0446\\u0438\\u0444\\u0440\\n long finalDigit1 = 0; // \\u0412\\u0442\\u043e\\u0440\\u0430\\u044f \\u0438\\u0437 \\u0434\\u0432\\u0443\\u0445 \\u0444\\u0438\\u043d\\u0430\\u043b\\u044c\\u043d\\u044b\\u0445 \\u0446\\u0438\\u0444\\u0440\\n\\n // \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u0435 finalDigit0 = sum( C(k_steps, i) * d_i ) mod 10\\n // i \\u0438\\u0434\\u0435\\u0442 \\u043e\\u0442 0 \\u0434\\u043e k_steps\\n for (int i = 0; i <= k_steps; i++) {\\n int digit = s.charAt(i) - '0';\\n if (digit == 0) continue; // \\u041f\\u0440\\u043e\\u043f\\u0443\\u0441\\u043a \\u0434\\u043b\\u044f \\u0443\\u0441\\u043a\\u043e\\u0440\\u0435\\u043d\\u0438\\u044f\\n\\n long coefficient = nCrMod10(k_steps, i);\\n if (coefficient == 0) continue; // \\u041f\\u0440\\u043e\\u043f\\u0443\\u0441\\u043a \\u0434\\u043b\\u044f \\u0443\\u0441\\u043a\\u043e\\u0440\\u0435\\u043d\\u0438\\u044f\\n\\n finalDigit0 = (finalDigit0 + coefficient * digit) % 10;\\n }\\n\\n // \\u0412\\u044b\\u0447\\u0438\\u0441\\u043b\\u0435\\u043d\\u0438\\u0435 finalDigit1 = sum( C(k_steps, i) * d_{i+1} ) mod 10\\n // i \\u0438\\u0434\\u0435\\u0442 \\u043e\\u0442 0 \\u0434\\u043e k_steps\\n for (int i = 0; i <= k_steps; i++) {\\n // d_{i+1} \\u0441\\u043e\\u043e\\u0442\\u0432\\u0435\\u0442\\u0441\\u0442\\u0432\\u0443\\u0435\\u0442 s.charAt(i+1). \\u041c\\u0430\\u043a\\u0441. \\u0438\\u043d\\u0434\\u0435\\u043a\\u0441 = k_steps+1 = n-1.\\n int digit = s.charAt(i + 1) - '0';\\n if (digit == 0) continue;\\n\\n // \\u041a\\u043e\\u044d\\u0444\\u0444\\u0438\\u0446\\u0438\\u0435\\u043d\\u0442 C(k_steps, i) \\u0442\\u043e\\u0442 \\u0436\\u0435 \\u0441\\u0430\\u043c\\u044b\\u0439\\n long coefficient = nCrMod10(k_steps, i);\\n if (coefficient == 0) continue;\\n\\n finalDigit1 = (finalDigit1 + coefficient * digit) % 10;\\n }\\n\\n // \\u0412 Java (%) \\u043c\\u043e\\u0436\\u0435\\u0442 \\u0432\\u0435\\u0440\\u043d\\u0443\\u0442\\u044c \\u043e\\u0442\\u0440\\u0438\\u0446\\u0430\\u0442\\u0435\\u043b\\u044c\\u043d\\u044b\\u0439 \\u0440\\u0435\\u0437\\u0443\\u043b\\u044c\\u0442\\u0430\\u0442, \\u0435\\u0441\\u043b\\u0438 \\u0434\\u0435\\u043b\\u0438\\u043c\\u043e\\u0435 \\u043e\\u0442\\u0440\\u0438\\u0446\\u0430\\u0442\\u0435\\u043b\\u044c\\u043d\\u043e.\\n // \\u0412 \\u043d\\u0430\\u0448\\u0435\\u043c \\u0441\\u043b\\u0443\\u0447\\u0430\\u0435 digit \\u0438 coefficient \\u043d\\u0435\\u043e\\u0442\\u0440\\u0438\\u0446\\u0430\\u0442\\u0435\\u043b\\u044c\\u043d\\u044b, \\u043d\\u043e \\u0434\\u043b\\u044f \\u043f\\u043e\\u043b\\u043d\\u043e\\u0439 \\u0443\\u0432\\u0435\\u0440\\u0435\\u043d\\u043d\\u043e\\u0441\\u0442\\u0438:\\n // finalDigit0 = (finalDigit0 % 10 + 10) % 10;\\n // finalDigit1 = (finalDigit1 % 10 + 10) % 10;\\n // \\u041e\\u0434\\u043d\\u0430\\u043a\\u043e, \\u0442.\\u043a. \\u0432\\u0441\\u0435 \\u0441\\u043b\\u0430\\u0433\\u0430\\u0435\\u043c\\u044b\\u0435 >= 0, \\u0440\\u0435\\u0437\\u0443\\u043b\\u044c\\u0442\\u0430\\u0442 % 10 \\u0442\\u043e\\u0436\\u0435 \\u0431\\u0443\\u0434\\u0435\\u0442 >= 0.\\n\\n return finalDigit0 == finalDigit1;\\n }\\n}\"], [256, 0.4831, \"class Solution {\\n\\n // Compute nCr mod p using Lucas's Theorem\\n private int nCrModP(int n, int r, int p) {\\n int result = 1;\\n while (n > 0 || r > 0) {\\n int ni = n % p;\\n int ri = r % p;\\n if (ri > ni) return 0;\\n result = (result * nCrModPSmall(ni, ri, p)) % p;\\n n /= p;\\n r /= p;\\n }\\n return result;\\n }\\n\\n // Compute nCr mod small p using Pascal's triangle\\n private int nCrModPSmall(int n, int r, int p) {\\n if (r == 0 || r == n) return 1;\\n int[] C = new int[r + 1];\\n C[0] = 1;\\n for (int i = 1; i <= n; i++) {\\n for (int j = Math.min(i, r); j > 0; j--) {\\n C[j] = (C[j] + C[j - 1]) % p;\\n }\\n }\\n return C[r];\\n }\\n\\n // Combine mod2 and mod5 to get mod10 using CRT\\n private int combineMod10(int mod2, int mod5) {\\n // mod2 \\u2208 {0,1}, mod5 \\u2208 {0..4}\\n for (int i = 0; i < 10; i++) {\\n if (i % 2 == mod2 && i % 5 == mod5) {\\n return i;\\n }\\n }\\n return 0; // shouldn't happen\\n }\\n\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int[] digits = new int[n];\\n for (int i = 0; i < n; i++) {\\n digits[i] = s.charAt(i) - '0';\\n }\\n\\n int left = 0, right = 0;\\n for (int i = 0; i < n - 1; i++) {\\n int coeffMod2 = nCrModP(n - 2, i, 2);\\n int coeffMod5 = nCrModP(n - 2, i, 5);\\n int coeff = combineMod10(coeffMod2, coeffMod5);\\n\\n left = (left + coeff * digits[i]) % 10;\\n right = (right + coeff * digits[i + 1]) % 10;\\n }\\n\\n return left == right;\\n }\\n}\\n\"], [264, 0.4831, \"import java.util.*;\\n\\nclass Solution {\\n\\n // Main method: Given a string s of digits,\\n // perform (n-2) rounds of the \\\"add adjacent digits mod 10\\\" operation in one step.\\n // Return true if the final two digits are equal.\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n // When s has exactly 2 digits we can simply compare them.\\n if (n == 2) {\\n return s.charAt(0) == s.charAt(1);\\n }\\n \\n // Let R = n - 2.\\n int R = n - 2;\\n int final0 = 0, final1 = 0;\\n \\n // Loop over i from 0 to R (there are R+1 terms).\\n // The i-th coefficient is C(R, i) mod 10.\\n for (int i = 0; i <= R; i++) {\\n int comb = getBinomMod10(R, i);\\n \\n // Multiply coefficient with the corresponding digit.\\n // (s.charAt(i) - '0') converts the character to an integer.\\n final0 = (final0 + comb * (s.charAt(i) - '0')) % 10;\\n final1 = (final1 + comb * (s.charAt(i + 1) - '0')) % 10;\\n }\\n \\n return final0 == final1;\\n }\\n \\n // getBinomMod10 uses Lucas's theorem to compute C(n, k) modulo p\\n // for p = 2 and p = 5 separately and then uses the Chinese remainder theorem\\n // to combine them to a number modulo 10.\\n private int getBinomMod10(int n, int k) {\\n int mod2 = binomLucas(n, k, 2);\\n int mod5 = binomLucas(n, k, 5);\\n return combineCRT(mod2, mod5);\\n }\\n \\n // Computes C(n, k) mod p using Lucas\\u2019s theorem.\\n // p should be a small prime (in our case, 2 or 5).\\n private int binomLucas(int n, int k, int p) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int n_i = n % p;\\n int k_i = k % p;\\n if (k_i > n_i) {\\n return 0;\\n }\\n res = (res * binomSmall(n_i, k_i, p)) % p;\\n n /= p;\\n k /= p;\\n }\\n return res;\\n }\\n \\n // For numbers less than p (with p = 2 or 5), compute C(n, k) mod p.\\n private int binomSmall(int n, int k, int p) {\\n if (k > n) {\\n return 0;\\n }\\n // Precomputed factorials for p up to 5.\\n int[] fact;\\n int[] inv; // modular inverses modulo p.\\n if (p == 2) {\\n fact = new int[]{1, 1}; // fact[0]=1, fact[1]=1\\n inv = new int[]{0, 1}; // Only 1 has an inverse mod2.\\n } else if (p == 5) {\\n fact = new int[]{1, 1, 2, 1, 4}; // 0! = 1, 1! = 1, 2! = 2, 3! = 6 mod5 = 1, 4! = 24 mod5 = 4\\n // Inverses mod5: 1->1, 2->3 (since 2*3=6 mod5=1), 3->2, 4->4 (4*4=16 mod5 = 1)\\n inv = new int[]{0, 1, 3, 2, 4};\\n } else {\\n // Should never happen for our use case.\\n return 0;\\n }\\n \\n // Compute C(n, k) = fact[n] / (fact[k] * fact[n-k]) mod p.\\n int numerator = fact[n];\\n int denominator = (fact[k] * fact[n - k]) % p;\\n // Multiply by modular inverse of denominator modulo p.\\n // Since p is small, we can simply iterate to find the inverse.\\n int invDenom = modInverse(denominator, p);\\n return (numerator * invDenom) % p;\\n }\\n \\n // Computes the modular inverse of a modulo p.\\n // Here p is prime (either 2 or 5).\\n private int modInverse(int a, int p) {\\n // Since p is small, we can loop through possible inverses.\\n for (int x = 1; x < p; x++) {\\n if ((a * x) % p == 1) {\\n return x;\\n }\\n }\\n return 1; // Should not happen for valid a.\\n }\\n \\n // Given x mod2 and x mod5, find the unique x modulo 10.\\n // We simply test candidates 0 .. 9.\\n private int combineCRT(int mod2, int mod5) {\\n for (int candidate = 0; candidate < 10; candidate++) {\\n if (candidate % 2 == mod2 && candidate % 5 == mod5) {\\n return candidate;\\n }\\n }\\n return 0; // Fallback (should not occur).\\n }\\n \\n // --- Optional: A main() method for local testing ---\\n public static void main(String[] args) {\\n Solution sol = new Solution();\\n \\n // Example 1: s = \\\"3902\\\" should return true.\\n String s1 = \\\"3902\\\";\\n System.out.println(\\\"Input: \\\" + s1 + \\\" -> \\\" + sol.hasSameDigits(s1)); // Expected: true\\n \\n // Example 2: s = \\\"34789\\\" should return false.\\n String s2 = \\\"34789\\\";\\n System.out.println(\\\"Input: \\\" + s2 + \\\" -> \\\" + sol.hasSameDigits(s2)); // Expected: false\\n }\\n}\\n\"], [272, 0.4831, \"class Solution {\\n private int nCr_mod_5(int n, int r) {\\n if (r < 0 || r > n) return 0;\\n if (r == 0 || r == n) return 1;\\n if (r > n / 2) r = n - r;\\n if (n < 5) {\\n if (n == 0) return 1;\\n if (n == 1) return 1;\\n if (n == 2) return (r == 1) ? 2 : 1;\\n if (n == 3) return (r == 1) ? 3 : 1;\\n if (n == 4) {\\n if (r == 0) return 1;\\n if (r == 1) return 4;\\n if (r == 2) return 1;\\n }\\n return 0;\\n }\\n int n_div_5 = n / 5;\\n int r_div_5 = r / 5;\\n int n_mod_5 = n % 5;\\n int r_mod_5 = r % 5;\\n return (nCr_mod_5(n_div_5, r_div_5) * nCr_mod_5(n_mod_5, r_mod_5)) % 5;\\n }\\n private int get_C_mod_10(int N, int i) {\\n if (i < 0 || i > N) return 0;\\n int mod2 = ((N & i) == i) ? 1 : 0;\\n int mod5 = nCr_mod_5(N, i);\\n return (5 * mod2 + 6 * mod5) % 10;\\n }\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int N = n - 2;\\n int final_digit_0 = 0;\\n for (int i = 0; i <= N; i++) {\\n int digit = s.charAt(i) - '0';\\n int coeff = get_C_mod_10(N, i);\\n final_digit_0 = (final_digit_0 + coeff * digit) % 10;\\n }\\n int final_digit_1 = 0;\\n for (int i = 0; i <= N; i++) {\\n int digit = s.charAt(i + 1) - '0';\\n int coeff = get_C_mod_10(N, i);\\n final_digit_1 = (final_digit_1 + coeff * digit) % 10;\\n }\\n return final_digit_0 == final_digit_1;\\n }\\n}\"], [279, 0.4831, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int k = n - 2;\\n if (k <= 0) { // \\ubb38\\uc81c \\uc870\\uac74\\uc5d0 \\ub530\\ub77c k >=1 (n >=3)\\n return n == 2 ? s.charAt(0) == s.charAt(1) : false;\\n }\\n \\n int[][] mod10Table = {\\n {0, 6, 2, 8, 4},\\n {5, 1, 7, 3, 9}\\n };\\n \\n int leftSum = 0;\\n int rightSum = 0;\\n \\n for (int i = 0; i <= k; i++) {\\n int c = getCoeff(k, i, mod10Table);\\n int digitLeft = s.charAt(i) - '0';\\n leftSum = (leftSum + digitLeft * c) % 10;\\n \\n int digitRight = s.charAt(i + 1) - '0';\\n rightSum = (rightSum + digitRight * c) % 10;\\n }\\n \\n return leftSum == rightSum;\\n }\\n \\n private int getCoeff(int n, int k, int[][] mod10Table) {\\n int mod2 = combMod(n, k, 2);\\n int mod5 = combMod(n, k, 5);\\n return mod10Table[mod2][mod5 % 5];\\n }\\n \\n private int combMod(int n, int k, int p) {\\n if (k > n) return 0;\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int ni = n % p;\\n int ki = k % p;\\n if (ki > ni) return 0;\\n \\n int numer = 1;\\n int denom = 1;\\n for (int i = 0; i < ki; i++) {\\n numer = (numer * (ni - i)) % p;\\n denom = (denom * (i + 1)) % p;\\n }\\n \\n int denomInv = powMod(denom, p - 2, p);\\n res = (res * numer) % p;\\n res = (res * denomInv) % p;\\n \\n n /= p;\\n k /= p;\\n }\\n return res;\\n }\\n \\n private int powMod(int a, int b, int mod) {\\n int res = 1;\\n a %= mod;\\n while (b > 0) {\\n if ((b & 1) != 0) {\\n res = (res * a) % mod;\\n }\\n a = (a * a) % mod;\\n b >>= 1;\\n }\\n return res;\\n }\\n}\\n\"], [287, 0.4831, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int mod = 10;\\n int n = s.length();\\n int m = n - 2;\\n int[][] suf = new int[m + 1][3];\\n int m1 = m;\\n while (m1 % 2 == 0) {\\n suf[m][1]++;\\n m1 /= 2;\\n }\\n while (m1 % 5 == 0) {\\n suf[m][2]++;\\n m1 /= 5;\\n }\\n suf[m][0] = m1 % mod;\\n for (int i = m - 1; i >= 1; i--) {\\n m1 = i;\\n while (m1 % 2 == 0) {\\n suf[i][1]++;\\n m1 /= 2;\\n }\\n while (m1 % 5 == 0) {\\n suf[i][2]++;\\n m1 /= 5;\\n }\\n suf[i][0] = m1 * suf[i + 1][0] % mod;\\n suf[i][1] += suf[i + 1][1];\\n suf[i][2] += suf[i + 1][2];\\n }\\n int[][] pre = new int[m + 1][3];\\n pre[1][0] = 1;\\n for (int i = 2; i <= m; i++) {\\n m1 = i;\\n while (m1 % 2 == 0) {\\n pre[i][1]++;\\n m1 /= 2;\\n }\\n while (m1 % 5 == 0) {\\n pre[i][2]++;\\n m1 /= 5;\\n }\\n pre[i][0] = m1 * pre[i - 1][0] % mod;\\n pre[i][1] += pre[i - 1][1];\\n pre[i][2] += pre[i - 1][2];\\n }\\n int sum1 = 0;\\n for (int i = 0; i < n - 1; i++) {\\n // sum1 += combine(m, i, 10) * (s.charAt(i) - 48);\\n int num = s.charAt(i) - 48;\\n if (i == 0 || i == n - 2) {\\n sum1 += num;\\n } else {\\n // long a = Math.min(suf[i + 1][1], suf[i + 1][2]);\\n // long b = Math.min(pre[m - i][1], pre[m - i][2]);\\n // if (a == b || b == 0) {\\n // int c = (int) (pre[m - i][0] * power1(2, (int) (pre[m - i][1] - b), mod) % mod\\n // * power1(5, (int) (pre[m - i][2] - b), mod) % mod);\\n // int d = (int) (suf[i + 1][0] * power1(2, (int) (suf[i + 1][1] - a), mod) % mod\\n // * power1(5, (int) (suf[i + 1][2] - a), mod) % mod);\\n for (int j = 0; j < 10; j++) {\\n int x = 10 * j + suf[i + 1][0];\\n if (x % pre[m - i][0] == 0) {\\n sum1 += x / pre[m - i][0] * power1(2, suf[i + 1][1] - pre[m - i][1], mod)\\n * power1(5, suf[i + 1][2] - pre[m - i][2], mod) * num % 10;\\n break;\\n }\\n }\\n // }\\n }\\n sum1 %= 10;\\n }\\n int sum2 = 0;\\n for (int i = 1; i < n; i++) {\\n // sum2 += combine(m, i - 1, 10) * (s.charAt(i) - 48);\\n int num = s.charAt(i) - 48;\\n if (i == 1 || i == n - 1) {\\n sum2 += num;\\n } else {\\n // long a = Math.min(suf[i][1], suf[i][2]);\\n // long b = Math.min(pre[m - i + 1][1], pre[m - i + 1][2]);\\n // if (a == b || b == 0) {\\n // int c = (int) (pre[m - i + 1][0] * power1(2, (int) (pre[m - i + 1][1] - b), mod) % mod\\n // * power1(5, (int) (pre[m - i + 1][2] - b), mod) % mod);\\n // int d = (int) (suf[i][0] * power1(2, (int) (suf[i][1] - a), mod) % mod\\n // * power1(5, (int) (suf[i][2] - a), mod) % mod);\\n for (int j = 0; j < 10; j++) {\\n int x = 10 * j + suf[i][0];\\n if (x % pre[m - i + 1][0] == 0) {\\n sum2 += x / pre[m - i + 1][0] * power1(2, suf[i][1] - pre[m - i + 1][1], mod)\\n * power1(5, suf[i][2] - pre[m - i + 1][2], mod) * num % 10;\\n break;\\n }\\n }\\n // }\\n }\\n sum2 %= 10;\\n }\\n return sum1 == sum2;\\n }\\n\\n static int power1(int b, int n, int mod) {\\n if (n == 0) {\\n return 1;\\n }\\n if (n == 1) {\\n return b;\\n }\\n int pow = b;\\n int remain = 1;\\n while (n > 1) {\\n if (n % 2 != 0) {\\n remain *= pow;\\n remain %= mod;\\n }\\n pow *= pow;\\n pow %= mod;\\n n /= 2;\\n }\\n return pow * remain % mod;\\n }\\n}\"], [295, 0.4831, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int mod = 10;\\n int n = s.length();\\n int m = n - 2;\\n int[][] suf = new int[m + 1][3];\\n int m1 = m;\\n while (m1 % 2 == 0) {\\n suf[m][1]++;\\n m1 /= 2;\\n }\\n while (m1 % 5 == 0) {\\n suf[m][2]++;\\n m1 /= 5;\\n }\\n suf[m][0] = m1 % mod;\\n for (int i = m - 1; i >= 1; i--) {\\n m1 = i;\\n while (m1 % 2 == 0) {\\n suf[i][1]++;\\n m1 /= 2;\\n }\\n while (m1 % 5 == 0) {\\n suf[i][2]++;\\n m1 /= 5;\\n }\\n suf[i][0] = m1 * suf[i + 1][0] % mod;\\n suf[i][1] += suf[i + 1][1];\\n suf[i][2] += suf[i + 1][2];\\n }\\n int[][] pre = new int[m + 1][3];\\n pre[1][0] = 1;\\n for (int i = 2; i <= m; i++) {\\n m1 = i;\\n while (m1 % 2 == 0) {\\n pre[i][1]++;\\n m1 /= 2;\\n }\\n while (m1 % 5 == 0) {\\n pre[i][2]++;\\n m1 /= 5;\\n }\\n pre[i][0] = m1 * pre[i - 1][0] % mod;\\n pre[i][1] += pre[i - 1][1];\\n pre[i][2] += pre[i - 1][2];\\n }\\n int sum1 = 0;\\n for (int i = 0; i < n - 1; i++) {\\n // sum1 += combine(m, i, 10) * (s.charAt(i) - 48);\\n int num = s.charAt(i) - 48;\\n if (i == 0 || i == n - 2) {\\n sum1 += num;\\n } else {\\n // long a = Math.min(suf[i + 1][1], suf[i + 1][2]);\\n // long b = Math.min(pre[m - i][1], pre[m - i][2]);\\n // if (a == b || b == 0) {\\n // int c = (int) (pre[m - i][0] * power1(2, (int) (pre[m - i][1] - b), mod) % mod\\n // * power1(5, (int) (pre[m - i][2] - b), mod) % mod);\\n // int d = (int) (suf[i + 1][0] * power1(2, (int) (suf[i + 1][1] - a), mod) % mod\\n // * power1(5, (int) (suf[i + 1][2] - a), mod) % mod);\\n for (int j = 0; j < 10; j++) {\\n int x = 10 * j + suf[i + 1][0];\\n if (x % pre[m - i][0] == 0) {\\n sum1 += x / pre[m - i][0] * power1(2, (int) (suf[i + 1][1] - pre[m - i][1]), mod)\\n * power1(5, (int) (suf[i + 1][2] - pre[m - i][2]), mod) * num % 10;\\n break;\\n }\\n }\\n // }\\n }\\n sum1 %= 10;\\n }\\n int sum2 = 0;\\n for (int i = 1; i < n; i++) {\\n // sum2 += combine(m, i - 1, 10) * (s.charAt(i) - 48);\\n int num = s.charAt(i) - 48;\\n if (i == 1 || i == n - 1) {\\n sum2 += num;\\n } else {\\n // long a = Math.min(suf[i][1], suf[i][2]);\\n // long b = Math.min(pre[m - i + 1][1], pre[m - i + 1][2]);\\n // if (a == b || b == 0) {\\n // int c = (int) (pre[m - i + 1][0] * power1(2, (int) (pre[m - i + 1][1] - b), mod) % mod\\n // * power1(5, (int) (pre[m - i + 1][2] - b), mod) % mod);\\n // int d = (int) (suf[i][0] * power1(2, (int) (suf[i][1] - a), mod) % mod\\n // * power1(5, (int) (suf[i][2] - a), mod) % mod);\\n for (int j = 0; j < 10; j++) {\\n int x = 10 * j + suf[i][0];\\n if (x % pre[m - i + 1][0] == 0) {\\n sum2 += x / pre[m - i + 1][0] * power1(2, (int) (suf[i][1] - pre[m - i + 1][1]), mod)\\n * power1(5, (int) (suf[i][2] - pre[m - i + 1][2]), mod) * num % 10;\\n break;\\n }\\n }\\n // }\\n }\\n sum2 %= 10;\\n }\\n return sum1 == sum2;\\n }\\n\\n static long power1(int b, int n, int mod) {\\n if (n == 0) {\\n return 1;\\n }\\n if (n == 1) {\\n return b;\\n }\\n long pow = b;\\n long remain = 1;\\n while (n > 1) {\\n if (n % 2 != 0) {\\n remain *= pow;\\n remain %= mod;\\n }\\n pow *= pow;\\n pow %= mod;\\n n /= 2;\\n }\\n return pow * remain % mod;\\n }\\n}\"], [303, 0.9662, \"class Solution {\\n static int nCrMod10(int n, int r) {\\n int mod2 = nCrMod2(n, r);\\n int mod5 = nCrMod5(n, r);\\n return (5 * mod2 + 6 * mod5) % 10;\\n }\\n \\n static int nCrMod2(int n, int r) {\\n return ((n & r) == r) ? 1 : 0;\\n }\\n \\n static int nCrMod5(int n, int r) {\\n if (r > n) return 0;\\n int[] fact = {1, 1, 2, 1, 4};\\n int[] invFact = new int[5];\\n for (int i = 0; i < 5; i++) {\\n invFact[i] = modInverse5(fact[i]);\\n }\\n int anss = 1;\\n while (n > 0 || r > 0) {\\n int n_i = n % 5;\\n int r_i = r % 5;\\n n /= 5;\\n r /= 5;\\n if (r_i > n_i) return 0;\\n int term = fact[n_i];\\n term = (int) (((long) term * invFact[r_i]) % 5);\\n term = (int) (((long) term * invFact[n_i - r_i]) % 5);\\n anss = (anss * term) % 5;\\n }\\n return anss;\\n }\\n \\n static int modInverse5(int x) {\\n return power(x, 3, 5);\\n }\\n \\n static int power(int x, int y, int mod) {\\n int res = 1;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n res = (res * x) % mod;\\n x = (x * x) % mod;\\n y >>= 1;\\n }\\n return res;\\n }\\n \\n static boolean hasSameDigits(String s) {\\n char[] nums = s.toCharArray();\\n int n = nums.length;\\n int x = n - 2, y = 0;\\n int ans = 0;\\n for (int i = 0; i < n - 1; i++) {\\n int val = nCrMod10(x, y++);\\n ans = (ans + ((int)(nums[i] - '0') * val)) % 10;\\n }\\n int temo = ans;\\n y = 0;\\n int one = 0;\\n for (int i = 1; i < n; i++) {\\n int val = nCrMod10(x, y);\\n one = (one + ((int)(nums[i] - '0') * val)) % 10;\\n y++;\\n }\\n return temo == one;\\n }\\n}\"], [311, 1.4493, \"class Solution {\\n static int nCrMod10(int n, int r) {\\n int mod2 = nCrMod2(n, r);\\n int mod5 = nCrMod5(n, r);\\n return (5 * mod2 + 6 * mod5) % 10;\\n }\\n \\n static int nCrMod2(int n, int r) {\\n return ((n & r) == r) ? 1 : 0;\\n }\\n \\n static int nCrMod5(int n, int r) {\\n if (r > n) return 0;\\n int[] fact = {1, 1, 2, 1, 4};\\n int[] invFact = new int[5];\\n for (int i = 0; i < 5; i++) {\\n invFact[i] = modInverse5(fact[i]);\\n }\\n int anss = 1;\\n while (n > 0 || r > 0) {\\n int n_i = n % 5;\\n int r_i = r % 5;\\n n /= 5;\\n r /= 5;\\n if (r_i > n_i) return 0;\\n int term = fact[n_i];\\n term = (int) (((long) term * invFact[r_i]) % 5);\\n term = (int) (((long) term * invFact[n_i - r_i]) % 5);\\n anss = (anss * term) % 5;\\n }\\n return anss;\\n }\\n \\n static int modInverse5(int x) {\\n return power(x, 3, 5);\\n }\\n \\n static int power(int x, int y, int mod) {\\n int res = 1;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n res = (res * x) % mod;\\n x = (x * x) % mod;\\n y >>= 1;\\n }\\n return res;\\n }\\n \\n static boolean hasSameDigits(String s) {\\n char[] nums = s.toCharArray();\\n int n = nums.length;\\n int x = n - 2, y = 0;\\n int ans = 0;\\n for (int i = 0; i < n - 1; i++) {\\n int val = nCrMod10(x, y++);\\n ans = (ans + ((int)(nums[i] - '0') * val)) % 10;\\n }\\n int temo = ans;\\n y = 0;\\n int one = 0;\\n for (int i = 1; i < n; i++) {\\n int val = nCrMod10(x, y);\\n one = (one + ((int)(nums[i] - '0') * val)) % 10;\\n y++;\\n }\\n return temo == one;\\n }\\n}\"], [319, 0.9662, \"class Solution {\\n static int nCrMod10(int n, int r) {\\n int mod2 = nCrMod2(n, r);\\n int mod5 = nCrMod5(n, r);\\n return (5 * mod2 + 6 * mod5) % 10;\\n }\\n \\n static int nCrMod2(int n, int r) {\\n return ((n & r) == r) ? 1 : 0;\\n }\\n \\n static int nCrMod5(int n, int r) {\\n if (r > n) return 0;\\n int[] fact = {1, 1, 2, 1, 4};\\n int[] invFact = new int[5];\\n for (int i = 0; i < 5; i++) {\\n invFact[i] = modInverse5(fact[i]);\\n }\\n int anss = 1;\\n while (n > 0 || r > 0) {\\n int n_i = n % 5;\\n int r_i = r % 5;\\n n /= 5;\\n r /= 5;\\n if (r_i > n_i) return 0;\\n int term = fact[n_i];\\n term = (int) (((long) term * invFact[r_i]) % 5);\\n term = (int) (((long) term * invFact[n_i - r_i]) % 5);\\n anss = (anss * term) % 5;\\n }\\n return anss;\\n }\\n \\n static int modInverse5(int x) {\\n return power(x, 3, 5);\\n }\\n \\n static int power(int x, int y, int mod) {\\n int res = 1;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n res = (res * x) % mod;\\n x = (x * x) % mod;\\n y >>= 1;\\n }\\n return res;\\n }\\n \\n static boolean hasSameDigits(String s) {\\n char[] nums = s.toCharArray();\\n int n = nums.length;\\n int x = n - 2, y = 0;\\n int ans = 0;\\n for (int i = 0; i < n - 1; i++) {\\n int val = nCrMod10(x, y++);\\n ans = (ans + ((int)(nums[i] - '0') * val)) % 10;\\n }\\n int temo = ans;\\n y = 0;\\n int one = 0;\\n for (int i = 1; i < n; i++) {\\n int val = nCrMod10(x, y);\\n one = (one + ((int)(nums[i] - '0') * val)) % 10;\\n y++;\\n }\\n return temo == one;\\n }\\n}\"], [327, 0.9662, \"class Solution {\\n static int nCrMod10(int n, int r) {\\n int mod2 = nCrMod2(n, r);\\n int mod5 = nCrMod5(n, r);\\n return (5 * mod2 + 6 * mod5) % 10;\\n }\\n \\n static int nCrMod2(int n, int r) {\\n return ((n & r) == r) ? 1 : 0;\\n }\\n \\n static int nCrMod5(int n, int r) {\\n if (r > n) return 0;\\n int[] fact = {1, 1, 2, 1, 4};\\n int[] invFact = new int[5];\\n for (int i = 0; i < 5; i++) {\\n invFact[i] = modInverse5(fact[i]);\\n }\\n int anss = 1;\\n while (n > 0 || r > 0) {\\n int n_i = n % 5;\\n int r_i = r % 5;\\n n /= 5;\\n r /= 5;\\n if (r_i > n_i) return 0;\\n int term = fact[n_i];\\n term = (int) (((long) term * invFact[r_i]) % 5);\\n term = (int) (((long) term * invFact[n_i - r_i]) % 5);\\n anss = (anss * term) % 5;\\n }\\n return anss;\\n }\\n \\n static int modInverse5(int x) {\\n return power(x, 3, 5);\\n }\\n \\n static int power(int x, int y, int mod) {\\n int res = 1;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n res = (res * x) % mod;\\n x = (x * x) % mod;\\n y >>= 1;\\n }\\n return res;\\n }\\n \\n static boolean hasSameDigits(String s) {\\n char[] nums = s.toCharArray();\\n int n = nums.length;\\n int x = n - 2, y = 0;\\n int ans = 0;\\n for (int i = 0; i < n - 1; i++) {\\n int val = nCrMod10(x, y++);\\n ans = (ans + ((int)(nums[i] - '0') * val)) % 10;\\n }\\n int temo = ans;\\n y = 0;\\n int one = 0;\\n for (int i = 1; i < n; i++) {\\n int val = nCrMod10(x, y);\\n one = (one + ((int)(nums[i] - '0') * val)) % 10;\\n y++;\\n }\\n return temo == one;\\n }\\n}\"], [335, 0.4831, \"class Solution {\\n static int binomialModuloPrime(int n, int r, int p) {\\n if (r > n)\\n return 0;\\n int result = 1;\\n\\n while (n > 0 || r > 0) {\\n int ni = n % p, ri = r % p;\\n if (ri > ni)\\n return 0;\\n result = (result * binomial(ni, ri, p)) % p;\\n n /= p;\\n r /= p;\\n }\\n return result;\\n }\\n\\n static int binomial(int n, int r, int p) {\\n if (r > n)\\n return 0;\\n if (r == 0 || r == n)\\n return 1;\\n\\n int[] fact = new int[n + 1];\\n fact[0] = 1;\\n for (int i = 1; i <= n; i++) {\\n fact[i] = (fact[i - 1] * i) % p;\\n }\\n\\n return (fact[n] * modInverse(fact[r], p) % p * modInverse(fact[n - r], p) % p) % p;\\n }\\n\\n static int modInverse(int a, int p) {\\n return power(a, p - 2, p);\\n }\\n\\n static int power(int x, int y, int p) {\\n int result = 1;\\n x %= p;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n result = (result * x) % p;\\n x = (x * x) % p;\\n y >>= 1;\\n }\\n return result;\\n }\\n\\n static int chineseRemainderTheorem(int a1, int m1, int a2, int m2) {\\n int M = m1 * m2;\\n int M1 = M / m1, M2 = M / m2;\\n int y1 = modInverse(M1, m1), y2 = modInverse(M2, m2);\\n return (a1 * M1 % M * y1 % M + a2 * M2 % M * y2 % M) % M;\\n }\\n\\n static List<Integer> getPascalRow(int n) {\\n List<Integer> row = new ArrayList<>();\\n for (int r = 0; r <= n; r++) {\\n int mod2 = binomialModuloPrime(n, r, 2);\\n int mod5 = binomialModuloPrime(n, r, 5);\\n int mod10 = chineseRemainderTheorem(mod2, 2, mod5, 5);\\n row.add(mod10);\\n }\\n return row;\\n }\\n\\n public boolean hasSameDigits(String s) {\\n int l = s.length();\\n List<Integer> list = getPascalRow(l - 2);\\n long first = 0;\\n long second = 0;\\n for (int i = 0; i < l - 1; i++) {\\n first = (first + (s.charAt(i) - '0') * list.get(i)) % 10;\\n second = (second + (s.charAt(i + 1) - '0') * list.get(i)) % 10;\\n }\\n return first == second;\\n }\\n}\"], [343, 4.8309999999999995, \"class Solution {\\n static int nCrMod10(int n, int r) {\\n int mod2 = nCrMod2(n, r);\\n int mod5 = nCrMod5(n, r);\\n return (5 * mod2 + 6 * mod5) % 10;\\n }\\n \\n static int nCrMod2(int n, int r) {\\n return ((n & r) == r) ? 1 : 0;\\n }\\n \\n static int nCrMod5(int n, int r) {\\n if (r > n) return 0;\\n int[] fact = {1, 1, 2, 1, 4};\\n int[] invFact = new int[5];\\n for (int i = 0; i < 5; i++) {\\n invFact[i] = modInverse5(fact[i]);\\n }\\n int anss = 1;\\n while (n > 0 || r > 0) {\\n int n_i = n % 5;\\n int r_i = r % 5;\\n n /= 5;\\n r /= 5;\\n if (r_i > n_i) return 0;\\n int term = fact[n_i];\\n term = (int) (((long) term * invFact[r_i]) % 5);\\n term = (int) (((long) term * invFact[n_i - r_i]) % 5);\\n anss = (anss * term) % 5;\\n }\\n return anss;\\n }\\n \\n static int modInverse5(int x) {\\n return power(x, 3, 5);\\n }\\n \\n static int power(int x, int y, int mod) {\\n int res = 1;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n res = (res * x) % mod;\\n x = (x * x) % mod;\\n y >>= 1;\\n }\\n return res;\\n }\\n \\n static boolean hasSameDigits(String s) {\\n char[] nums = s.toCharArray();\\n int n = nums.length;\\n int x = n - 2, y = 0;\\n int ans = 0;\\n for (int i = 0; i < n - 1; i++) {\\n int val = nCrMod10(x, y++);\\n ans = (ans + ((int)(nums[i] - '0') * val)) % 10;\\n }\\n int temo = ans;\\n y = 0;\\n int one = 0;\\n for (int i = 1; i < n; i++) {\\n int val = nCrMod10(x, y);\\n one = (one + ((int)(nums[i] - '0') * val)) % 10;\\n y++;\\n }\\n return temo == one;\\n }\\n}\"], [351, 0.9662, \"class Solution {\\n static int nCrMod10(int n, int r) {\\n int mod2 = nCrMod2(n, r);\\n int mod5 = nCrMod5(n, r);\\n return (5 * mod2 + 6 * mod5) % 10;\\n }\\n \\n static int nCrMod2(int n, int r) {\\n return ((n & r) == r) ? 1 : 0;\\n }\\n \\n static int nCrMod5(int n, int r) {\\n if (r > n) return 0;\\n int[] fact = {1, 1, 2, 1, 4};\\n int[] invFact = new int[5];\\n for (int i = 0; i < 5; i++) {\\n invFact[i] = modInverse5(fact[i]);\\n }\\n int anss = 1;\\n while (n > 0 || r > 0) {\\n int n_i = n % 5;\\n int r_i = r % 5;\\n n /= 5;\\n r /= 5;\\n if (r_i > n_i) return 0;\\n int term = fact[n_i];\\n term = (int) (((long) term * invFact[r_i]) % 5);\\n term = (int) (((long) term * invFact[n_i - r_i]) % 5);\\n anss = (anss * term) % 5;\\n }\\n return anss;\\n }\\n \\n static int modInverse5(int x) {\\n return power(x, 3, 5);\\n }\\n \\n static int power(int x, int y, int mod) {\\n int res = 1;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n res = (res * x) % mod;\\n x = (x * x) % mod;\\n y >>= 1;\\n }\\n return res;\\n }\\n \\n static boolean hasSameDigits(String s) {\\n char[] nums = s.toCharArray();\\n int n = nums.length;\\n int x = n - 2, y = 0;\\n int ans = 0;\\n for (int i = 0; i < n - 1; i++) {\\n int val = nCrMod10(x, y++);\\n ans = (ans + ((int)(nums[i] - '0') * val)) % 10;\\n }\\n int temo = ans;\\n y = 0;\\n int one = 0;\\n for (int i = 1; i < n; i++) {\\n int val = nCrMod10(x, y);\\n one = (one + ((int)(nums[i] - '0') * val)) % 10;\\n y++;\\n }\\n return temo == one;\\n }\\n}\"], [359, 0.4831, \"class Solution {\\n\\n int comb(int n, int r){ \\n if (r > n) { return 0; }\\n int res = 1;\\n for (int t = 1; t <= n; ++t) { res *= t; }\\n for (int t = 1; t <= r; ++t) { res /= t; }\\n for (int t = 1; t <= n - r; ++t) { res /= t; }\\n return res;\\n }\\n\\n boolean check(int[] a, int mod){\\n int res = 0;\\n int n = a.length;\\n for (int i = 0; i != n; ++i){\\n int ncr = 1;\\n int x = n - 1;\\n int y = i;\\n while (x > 0 && y > 0){\\n ncr = ncr * comb(x % mod, y % mod) % mod;\\n x /= mod;\\n y /= mod;\\n }\\n res = (res + ncr * a[i]) % mod;\\n }\\n return res == 0;\\n }\\n public boolean hasSameDigits(String str) {\\n char[] s = str.toCharArray();\\n int n = str.length();\\n int[] a = new int[n-1];\\n for (int i = 0; i != n - 1; ++i){\\n a[i] = (s[i] - '0') - (s[i + 1] - '0');\\n a[i] = (a[i] + 10) % 10;\\n }\\n return check(a, 2) && check(a, 5);\\n }\\n}\\n\"], [367, 0.4831, \"class Solution {\\n\\n public int nCr(int n, int r) {\\n if(r>n) { return 0; }\\n int res = 1;\\n for(int i = 1; i<=n; ++i) { res *= i; }\\n for(int i = 1; i<=r; ++i) { res /= i; }\\n for(int i = 1; i<=n-r; ++i) { res/=i; }\\n return res;\\n }\\n public boolean check(int[] a, int p) {\\n int res = 0;\\n int n = a.length;\\n for (int i = 0; i<n; ++i) {\\n int ncr = 1;\\n int x = n-1;\\n int y = i;\\n while(x>0 && y>0) {\\n ncr = ncr * nCr(x%p, y%p)%p;\\n x/=p;\\n y/=p;\\n }\\n res = (res + ncr *a[i])%p;\\n }\\n return res == 0;\\n }\\n public boolean hasSameDigits(String s) {\\n int a[] = new int[s.length()-1];\\n for(int i = 0; i<s.length() -1;++i) {\\n a[i] = (s.charAt(i) - '0') - (s.charAt(i+1) - '0');\\n a[i] = (a[i]+10)%10;\\n }\\n return check(a, 2) && check(a, 5);\\n }\\n}\"], [375, 0.4831, \"class Solution {\\n static int[] f = new int[10];\\n\\n static {\\n f[0] = 1;\\n for (int i = 1; i < 10; i++)\\n f[i] = f[i - 1] * i;\\n }\\n\\n static int cnr(int n, int r, int p) {\\n if (n < r)\\n return 0;\\n return f[n] / f[n - r] / f[r] % p;\\n }\\n\\n public boolean hasSameDigits(String s) {\\n int[][] pmp = new int[10][10];\\n for (int i = 0; i < 10; i++)\\n pmp[i % 2][i % 5] = i;\\n int n = s.length();\\n\\n int t1 = 0;\\n int t2 = 0;\\n for (int i = 0; i < n - 1; i++) {\\n int cr2 = lucas(n - 2, i, 2);\\n int cr5 = lucas(n - 2, i, 5);\\n t1 += pmp[cr2][cr5] * (s.charAt(i) - '0');\\n t1 %= 10;\\n t2 += pmp[cr2][cr5] * (s.charAt(i + 1) - '0');\\n t2 %= 10;\\n }\\n\\n return t1 == t2;\\n }\\n\\n int lucas(int n, int r, int p) {\\n if (r == 0 || n == r)\\n return 1;\\n return lucas(n / p, r / p, p) * cnr(n % p, r % p, p)%p;\\n }\\n}\"], [383, 0.4831, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n final int n = s.length();\\n int num1 = 0, num2 = 0;\\n\\n int[] digits = new int[n];\\n for (int i = 0; i < n; ++i)\\n digits[i] = s.charAt(i) - '0';\\n\\n int[] coeffs = new int[n - 1];\\n for (int i = 0; i < n - 1; ++i)\\n coeffs[i] = nCMOD10(n - 2, i);\\n\\n for (int i = 0; i + 1 < n; ++i) {\\n num1 = (num1 + coeffs[i] * digits[i]) % 10;\\n num2 = (num2 + coeffs[i] * digits[i + 1]) % 10;\\n }\\n\\n return num1 == num2;\\n }\\n\\n private int nCMOD10(int n, int k) {\\n final int mod2 = lucasTheorem(n, k, 2);\\n final int mod5 = lucasTheorem(n, k, 5);\\n int[][] lookup = {\\n {0, 6, 2, 8, 4},\\n {5, 1, 7, 3, 9}\\n };\\n return lookup[mod2][mod5];\\n }\\n\\n private int lucasTheorem(int n, int k, int prime) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int nMod = n % prime;\\n int kMod = k % prime;\\n res = (res * fastComb(nMod, kMod)) % prime;\\n n /= prime;\\n k /= prime;\\n }\\n return res;\\n }\\n\\n private int fastComb(int n, int k) {\\n if (k > n) return 0;\\n if (k == 0 || k == n) return 1;\\n if (k == 1) return n;\\n if (k == 2) return n * (n - 1) / 2;\\n if (k == 3) return n * (n - 1) * (n - 2) / 6;\\n if (k == 4) return n * (n - 1) * (n - 2) * (n - 3) / 24;\\n return 0; \\n }\\n}\\n\"], [391, 0.4831, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n final int n = s.length();\\n int num1 = 0, num2 = 0;\\n\\n int[] digits = new int[n];\\n for (int i = 0; i < n; ++i)\\n digits[i] = s.charAt(i) - '0';\\n\\n int[] coeffs = new int[n - 1];\\n for (int i = 0; i < n - 1; ++i)\\n coeffs[i] = nCMOD10(n - 2, i);\\n\\n for (int i = 0; i + 1 < n; ++i) {\\n num1 = (num1 + coeffs[i] * digits[i]) % 10;\\n num2 = (num2 + coeffs[i] * digits[i + 1]) % 10;\\n }\\n\\n return num1 == num2;\\n }\\n\\n private int nCMOD10(int n, int k) {\\n final int mod2 = lucasTheorem(n, k, 2);\\n final int mod5 = lucasTheorem(n, k, 5);\\n int[][] lookup = {\\n {0, 6, 2, 8, 4},\\n {5, 1, 7, 3, 9}\\n };\\n return lookup[mod2][mod5];\\n }\\n\\n private int lucasTheorem(int n, int k, int prime) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n int nMod = n % prime;\\n int kMod = k % prime;\\n res = (res * fastComb(nMod, kMod)) % prime;\\n n /= prime;\\n k /= prime;\\n }\\n return res;\\n }\\n\\n private int fastComb(int n, int k) {\\n if (k > n) return 0;\\n if (k == 0 || k == n) return 1;\\n if (k == 1) return n;\\n if (k == 2) return n * (n - 1) / 2;\\n if (k == 3) return n * (n - 1) * (n - 2) / 6;\\n if (k == 4) return n * (n - 1) * (n - 2) * (n - 3) / 24;\\n return 0; \\n }\\n}\\n\"], [399, 0.4831, \"class Solution {\\n\\n public boolean hasSameDigits(String s) {\\n final int n = s.length();\\n final int[] digits = s.chars().map(numChar -> numChar - '0').toArray();\\n final int[][] lookup = {{0, 6, 2, 8, 4}, {5, 1, 7, 3, 9}};\\n int a = 0;\\n int b = 0;\\n int coeff;\\n for (int i = 0; i + 1 < n; ++i) {\\n coeff = lookup[nCkMod(n-2, i, 2)][nCkMod(n-2, i, 5)];\\n a = (a + (coeff * digits[i]) % 10) % 10;\\n b = (b + (coeff * digits[i + 1]) % 10) % 10;\\n }\\n return a == b;\\n }\\n\\n int nCkMod(int n, int k, final int mod) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n res = (res * nCk(n % mod, k % mod) % mod);\\n n /= mod;\\n k /= mod;\\n }\\n return res;\\n }\\n\\n int nCk(final int n, final int k) {\\n int res = 1;\\n for (int i = 0; i < k; res = (res * (n - i)) / ++i) ;\\n return res;\\n }\\n}\"], [406, 0.4831, \"class Solution {\\n // Same as 3461. Check If Digits Are Equal in String After Operations I\\n public boolean hasSameDigits(String s) {\\n final int n = s.length();\\n int num1 = 0;\\n int num2 = 0;\\n\\n for (int i = 0; i + 1 < n; ++i) {\\n final int coefficient = nCMOD10(n - 2, i);\\n num1 += (coefficient * (s.charAt(i) - '0')) % 10;\\n num1 %= 10;\\n num2 += (coefficient * (s.charAt(i + 1) - '0')) % 10;\\n num2 %= 10;\\n }\\n\\n return num1 == num2;\\n }\\n\\n // Returns (n, k) % 10.\\n private int nCMOD10(int n, int k) {\\n final int mod2 = lucasTheorem(n, k, 2);\\n final int mod5 = lucasTheorem(n, k, 5);\\n int[][] lookup = {\\n {0, 6, 2, 8, 4}, // mod2 == 0\\n {5, 1, 7, 3, 9} // mod2 == 1\\n };\\n return lookup[mod2][mod5];\\n }\\n\\n // Returns (n, k) % prime.\\n private int lucasTheorem(int n, int k, int prime) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n final int nMod = n % prime;\\n final int MOD = k % prime;\\n res *= nCk(nMod, MOD);\\n res %= prime;\\n n /= prime;\\n k /= prime;\\n }\\n return res;\\n }\\n\\n // Returns (n, k).\\n private int nCk(int n, int k) {\\n int res = 1;\\n for (int i = 0; i < k; ++i) {\\n res *= (n - i);\\n res /= (i + 1);\\n }\\n return res;\\n }\\n}\"], [414, 0.4831, \"class Solution {\\n // Same as 3461. Check If Digits Are Equal in String After Operations I\\n public boolean hasSameDigits(String s) {\\n final int n = s.length();\\n int num1 = 0;\\n int num2 = 0;\\n\\n for (int i = 0; i + 1 < n; ++i) {\\n final int coefficient = nCMOD10(n - 2, i);\\n num1 += (coefficient * (s.charAt(i) - '0')) % 10;\\n num1 %= 10;\\n num2 += (coefficient * (s.charAt(i + 1) - '0')) % 10;\\n num2 %= 10;\\n }\\n\\n return num1 == num2;\\n }\\n\\n // Returns (n, k) % 10.\\n private int nCMOD10(int n, int k) {\\n final int mod2 = lucasTheorem(n, k, 2);\\n final int mod5 = lucasTheorem(n, k, 5);\\n int[][] lookup = {\\n {0, 6, 2, 8, 4}, // mod2 == 0\\n {5, 1, 7, 3, 9} // mod2 == 1\\n };\\n return lookup[mod2][mod5];\\n }\\n\\n // Returns (n, k) % prime.\\n private int lucasTheorem(int n, int k, int prime) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n final int nMod = n % prime;\\n final int MOD = k % prime;\\n res *= nCk(nMod, MOD);\\n res %= prime;\\n n /= prime;\\n k /= prime;\\n }\\n return res;\\n }\\n\\n // Returns (n, k).\\n private int nCk(int n, int k) {\\n int res = 1;\\n for (int i = 0; i < k; ++i) {\\n res *= (n - i);\\n res /= (i + 1);\\n }\\n return res;\\n }\\n}\"], [422, 0.4831, \"class Solution {\\n // Same as 3461. Check If Digits Are Equal in String After Operations I\\n public boolean hasSameDigits(String s) {\\n final int n = s.length();\\n int num1 = 0;\\n int num2 = 0;\\n\\n for (int i = 0; i + 1 < n; ++i) {\\n final int coefficient = nCMOD10(n - 2, i);\\n num1 += (coefficient * (s.charAt(i) - '0')) % 10;\\n num1 %= 10;\\n num2 += (coefficient * (s.charAt(i + 1) - '0')) % 10;\\n num2 %= 10;\\n }\\n\\n return num1 == num2;\\n }\\n\\n // Returns (n, k) % 10.\\n private int nCMOD10(int n, int k) {\\n final int mod2 = lucasTheorem(n, k, 2);\\n final int mod5 = lucasTheorem(n, k, 5);\\n int[][] lookup = {\\n {0, 6, 2, 8, 4}, // mod2 == 0\\n {5, 1, 7, 3, 9} // mod2 == 1\\n };\\n return lookup[mod2][mod5];\\n }\\n\\n // Returns (n, k) % prime.\\n private int lucasTheorem(int n, int k, int prime) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n final int nMod = n % prime;\\n final int MOD = k % prime;\\n res *= nCk(nMod, MOD);\\n res %= prime;\\n n /= prime;\\n k /= prime;\\n }\\n return res;\\n }\\n\\n // Returns (n, k).\\n private int nCk(int n, int k) {\\n int res = 1;\\n for (int i = 0; i < k; ++i) {\\n res *= (n - i);\\n res /= (i + 1);\\n }\\n return res;\\n }\\n}\"], [430, 0.4831, \"class Solution {\\n // Same as 3461. Check If Digits Are Equal in String After Operations I\\n public boolean hasSameDigits(String s) {\\n final int n = s.length();\\n int num1 = 0;\\n int num2 = 0;\\n\\n for (int i = 0; i + 1 < n; ++i) {\\n final int coefficient = nCMOD10(n - 2, i);\\n num1 += (coefficient * (s.charAt(i) - '0')) % 10;\\n num1 %= 10;\\n num2 += (coefficient * (s.charAt(i + 1) - '0')) % 10;\\n num2 %= 10;\\n }\\n\\n return num1 == num2;\\n }\\n\\n // Returns (n, k) % 10.\\n private int nCMOD10(int n, int k) {\\n final int mod2 = lucasTheorem(n, k, 2);\\n final int mod5 = lucasTheorem(n, k, 5);\\n int[][] lookup = {\\n {0, 6, 2, 8, 4}, // mod2 == 0\\n {5, 1, 7, 3, 9} // mod2 == 1\\n };\\n return lookup[mod2][mod5];\\n }\\n\\n // Returns (n, k) % prime.\\n private int lucasTheorem(int n, int k, int prime) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n final int nMod = n % prime;\\n final int MOD = k % prime;\\n res *= nCk(nMod, MOD);\\n res %= prime;\\n n /= prime;\\n k /= prime;\\n }\\n return res;\\n }\\n\\n // Returns (n, k).\\n private int nCk(int n, int k) {\\n int res = 1;\\n for (int i = 0; i < k; ++i) {\\n res *= (n - i);\\n res /= (i + 1);\\n }\\n return res;\\n }\\n}\\n\\n\\n\"], [438, 0.9662, \"class Solution {\\n // Same as 3461. Check If Digits Are Equal in String After Operations I\\n public boolean hasSameDigits(String s) {\\n final int n = s.length();\\n int num1 = 0;\\n int num2 = 0;\\n\\n for (int i = 0; i + 1 < n; ++i) {\\n final int coefficient = nCMOD10(n - 2, i);\\n num1 += (coefficient * (s.charAt(i) - '0')) % 10;\\n num1 %= 10;\\n num2 += (coefficient * (s.charAt(i + 1) - '0')) % 10;\\n num2 %= 10;\\n }\\n\\n return num1 == num2;\\n }\\n\\n // Returns (n, k) % 10.\\n private int nCMOD10(int n, int k) {\\n final int mod2 = lucasTheorem(n, k, 2);\\n final int mod5 = lucasTheorem(n, k, 5);\\n int[][] lookup = {\\n {0, 6, 2, 8, 4}, // mod2 == 0\\n {5, 1, 7, 3, 9} // mod2 == 1\\n };\\n return lookup[mod2][mod5];\\n }\\n\\n // Returns (n, k) % prime.\\n private int lucasTheorem(int n, int k, int prime) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n final int nMod = n % prime;\\n final int MOD = k % prime;\\n res *= nCk(nMod, MOD);\\n res %= prime;\\n n /= prime;\\n k /= prime;\\n }\\n return res;\\n }\\n\\n // Returns (n, k).\\n private int nCk(int n, int k) {\\n int res = 1;\\n for (int i = 0; i < k; ++i) {\\n res *= (n - i);\\n res /= (i + 1);\\n }\\n return res;\\n }\\n}\"], [446, 0.4831, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n final int n = s.length();\\n int num1 = 0;\\n int num2 = 0;\\n for (int i = 0; i + 1 < n; ++i) {\\n final int coefficient = nCkMod10(n - 2, i);\\n num1 += (coefficient * (s.charAt(i) - '0')) % 10;\\n num1 %= 10;\\n num2 += (coefficient * (s.charAt(i + 1) - '0')) % 10;\\n num2 %= 10;\\n }\\n return num1 == num2;\\n }\\n\\n private int nCkMod10(int n, int k) {\\n final int mod2 = lucasTheorem(n, k, 2);\\n final int mod5 = lucasTheorem(n, k, 5);\\n int[][] lookup = {\\n { 0, 6, 2, 8, 4 },\\n { 5, 1, 7, 3, 9 }\\n };\\n return lookup[mod2][mod5];\\n }\\n\\n private int lucasTheorem(int n, int k, int prime) {\\n int res = 1;\\n while (n > 0 || k > 0) {\\n final int nMod = n % prime;\\n final int kMod = k % prime;\\n res *= nCk(nMod, kMod);\\n res %= prime;\\n n /= prime;\\n k /= prime;\\n }\\n return res;\\n }\\n\\n private int nCk(int n, int k) {\\n int res = 1;\\n for (int i = 0; i < k; ++i) {\\n res *= (n - i);\\n res /= (i + 1);\\n }\\n return res;\\n }\\n}\"], [454, 0.4831, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int k = n - 2;\\n if (k == 0) {\\n return s.charAt(0) == s.charAt(1);\\n }\\n\\n List<Integer> digitsK_p2 = getDigits(k, 2);\\n List<Integer> digitsK_p5 = getDigits(k, 5);\\n\\n int[] coeff = new int[k + 1];\\n for (int j = 0; j <= k; j++) {\\n int a = lucasModWithDigits(j, 2, digitsK_p2);\\n int b = lucasModWithDigits(j, 5, digitsK_p5);\\n coeff[j] = (5 * a + 6 * b) % 10;\\n }\\n\\n int sum0 = 0;\\n int sum1 = 0;\\n for (int j = 0; j <= k; j++) {\\n int digit0 = s.charAt(j) - '0';\\n sum0 = (sum0 + digit0 * coeff[j]) % 10;\\n int digit1 = s.charAt(j + 1) - '0';\\n sum1 = (sum1 + digit1 * coeff[j]) % 10;\\n }\\n return sum0 == sum1;\\n }\\n\\n private List<Integer> getDigits(int n, int p) {\\n List<Integer> digits = new ArrayList<>();\\n while (n > 0) {\\n digits.add(n % p);\\n n /= p;\\n }\\n return digits;\\n }\\n\\n private int lucasModWithDigits(int j, int p, List<Integer> digitsN) {\\n if (j == 0) {\\n return 1;\\n }\\n List<Integer> digitsK = new ArrayList<>();\\n int jCopy = j;\\n while (jCopy > 0) {\\n digitsK.add(jCopy % p);\\n jCopy /= p;\\n }\\n while (digitsK.size() < digitsN.size()) {\\n digitsK.add(0);\\n }\\n int res = 1;\\n for (int i = 0; i < digitsK.size(); i++) {\\n int ni = (i < digitsN.size()) ? digitsN.get(i) : 0;\\n int ki = digitsK.get(i);\\n if (ki > ni) {\\n return 0;\\n }\\n if (p == 2) {\\n if (ni == 0) {\\n if (ki != 0) return 0;\\n res = (res * 1) % p;\\n } else if (ni == 1) {\\n if (ki == 0 || ki == 1) res = (res * 1) % p;\\n else return 0;\\n }\\n } else if (p == 5) {\\n int[][] table = {\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1}\\n };\\n res = (res * table[ni][ki]) % 5;\\n }\\n }\\n return res;\\n }\\n}\"], [462, 0.4831, \"/*\\nTook a bit to figure that: the two values are left with are\\nthe result of f3 modulo 10.\\n\\nWe need to use Lucas's Theorum to get the last digit of the binomial\\n*/\\n\\nclass Solution {\\n\\n int fact(int n) {\\n return switch(n) {\\n case 0 -> 1;\\n case 1-> 1;\\n case 2-> 2;\\n case 3-> 6;\\n case 4-> 24;\\n case 5-> 120;\\n default -> throw new IllegalArgumentException();\\n };\\n }\\n\\n int binomial(int n, int k) {\\n if (n < k) {\\n return 0;\\n }\\n int numerator = fact(n);\\n int denominator =(fact(k) * fact(n - k));\\n return numerator / denominator;\\n }\\n\\n int lookup_5_2_solution(int xMod5, int xMod2) {\\n return switch (xMod2) {\\n case 0 ->\\n switch (xMod5) {\\n case 0 -> 0;\\n case 1 -> 6;\\n case 2 -> 2;\\n case 3 -> 8;\\n case 4 -> 4;\\n default -> throw new IllegalArgumentException();\\n };\\n case 1 ->\\n switch (xMod5) {\\n case 0 -> 5;\\n case 1 -> 1;\\n case 2 -> 7;\\n case 3 -> 3;\\n case 4 -> 9;\\n default -> throw new IllegalArgumentException();\\n };\\n default -> throw new IllegalArgumentException();\\n };\\n }\\n\\n int binomialCoefficientLastDigit(int N, int K) {\\n int xMod5 = 1;\\n int xMod2 = 1;\\n\\n int n = N;\\n int k = K;\\n\\n while (n > 0) {\\n xMod5 *= binomial(n % 5, k % 5);\\n xMod5 %= 5;\\n n /= 5;\\n k /= 5;\\n }\\n\\n n = N;\\n k = K;\\n while (n > 0) {\\n xMod2 *= binomial(n % 2, k % 2);\\n xMod2 %= 2;\\n n /= 2;\\n k /= 2;\\n }\\n return lookup_5_2_solution(xMod5, xMod2);\\n }\\n\\n public boolean hasSameDigits(String s) {\\n int sumsLength = s.length() - 1;\\n int[] pascalRowLastDigits = IntStream.range(0, sumsLength)\\n .map(k -> binomialCoefficientLastDigit(sumsLength - 1, k))\\n .toArray();\\n int[] digits = s.chars().map(c -> c - '0').toArray();\\n int firstDigitsSum = 0;\\n int secondDigitsSum = 0;\\n\\n for (int i = 0; i < sumsLength; i++) {\\n firstDigitsSum += pascalRowLastDigits[i] * digits[i];\\n secondDigitsSum += pascalRowLastDigits[i] * digits[i+1];\\n }\\n\\n return (firstDigitsSum % 10) == (secondDigitsSum % 10);\\n }\\n // CLOJURE CODE BELOW\\n /*\\n(defn f1 [i]\\n(loop [s (->> i (map int) (map #(- % (int \\\\0))))]\\n (if (<= (count s) 2)\\n s #_(when (= (first s) (second s)) s)\\n (recur (map #(mod (+ %1 %2) 10) s (rest s))))))\\n\\n(defn f2 [i]\\n(loop [s (->> i (map int) (map #(- % (int \\\\0))))]\\n (if (<= (count s) 2)\\n s\\n (recur (map #(list %1 %2) s (rest s))))))\\n\\n(defn left-pad-with [desired-width padding padee]\\n(concat (repeat (- desired-width (count padee)) padding) padee))\\n\\n(defn fact [n] (apply * (range 1 (inc n))))\\n(defn binomial [n k]\\n(if (< n k) 0 (/ (fact n) (* (fact k) (fact (- n k))))))\\n(defn binomial-ld1 [n k] (mod (binomial n k) 10))\\n; using Lucas's Theorum\\n\\n(def lookup-5-2 {\\n[0 0] 0\\n[1 0] 6\\n[2 0] 2\\n[3 0] 8\\n[4 0] 4\\n[0 1] 5\\n[1 1] 1\\n[2 1] 7\\n[3 1] 3\\n[4 1] 9\\n})\\n\\n(defn binomial-ld2 [n k]\\n(let [\\nn-digits-2 (->> n (#(Integer/toString % 2)) (map char) (map int) (map #(- % (int \\\\0))))\\nn-digits-5 (->> n (#(Integer/toString % 5)) (map char) (map int) (map #(- % (int \\\\0))))\\nk-digits-2 (->> k (#(Integer/toString % 2)) (map char) (map int) (map #(- % (int \\\\0))) (left-pad-with (count n-digits-2) 0))\\nk-digits-5 (->> k (#(Integer/toString % 5)) (map char) (map int) (map #(- % (int \\\\0))) (left-pad-with (count n-digits-5) 0))\\nx-mod-2 (->> (map binomial n-digits-2 k-digits-2) (apply *) (#(mod % 2)))\\nx-mod-5 (->> (map binomial n-digits-5 k-digits-5) (apply *) (#(mod % 5)))\\n]\\n(lookup-5-2 [x-mod-5 x-mod-2])))\\n\\n(defn f3 [i]\\n(let [sums-len (dec (count i)),\\npascal-row-ld (->> (range sums-len)\\n #_(map #(binomial-ld1 (dec sums-len) %))\\n (map #(binomial-ld2 (dec sums-len) %))\\n )\\ndgts (->> i (map int) (map #(- % (int \\\\0))))\\n]\\n[\\n(->> dgts drop-last (map * pascal-row-ld))\\n(->> dgts (drop 1) (map * pascal-row-ld))\\n]\\n))\\n\\n(prn (map #(mod (* % 3) 10) (range 20)))\\n(prn (map #(mod (* % 13) 10) (range 20)))\\n\\n#_(->> (range 1000 2000)\\n (map (juxt #(->> % str (map char) f2) identity))\\n #_(filter first)\\n (map prn)\\n doall\\n #_(map second)\\n #_(reduce +)\\n #_prn)\\n\\n(def R [\\\\1 \\\\2 \\\\3 \\\\4 \\\\5 \\\\6 \\\\7 \\\\8])\\n(def R2 [\\\\7 \\\\9 \\\\5 \\\\2])\\n\\n (prn (f1 R))\\n #_(prn (f2 R))\\n #_(prn (count (f2 R)))\\n #_(prn (map flatten (f2 R)))\\n #_(prn (->> R f2 (map flatten) (map (partial apply +))))\\n #_(prn (->> R f2 (map flatten) (map sort)))\\n #_(prn (->> R f2 (map flatten) (map sort) (map frequencies)))\\n (prn (->> R f3))\\n (prn (->> R f3 (map (partial apply +))))\\n\\n (prn (->> R2 f1))\\n (prn (->> R2 f3 (map (partial apply +)) (map #(mod % 10))))\\n #_(prn (apply + (flatten (f2 R))))\\n\\n; vim: syntax=clojure\\n\\n */\\n}\"], [470, 0.4831, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n=s.length();\\n int m=n-2;\\n int a=0;\\n int b=0;\\n for(int i=0;i<s.length()-1;i++){\\n int bc=f(m,i);\\n // System.out.println(bc);\\n a=(a+bc*(s.charAt(i)-'0'));\\n b=(b+bc*(s.charAt(i+1)-'0'));\\n }\\n return a%10==b%10;\\n }\\n public int f(int m,int j){\\n int a=l(m,j,5);\\n int b=l(m,j,2);\\n for(int i=0;i<=9;i++){\\n if((i%2==b)&&(i%5==a)){\\n return i;\\n }\\n }\\n return 0;\\n }\\n public int power(int x, int y, int p) {\\n int res = 1;\\n x = x % p;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n res = (res * x) % p;\\n y = y >> 1;\\n x = (x * x) % p;\\n }\\n return res;\\n }\\n\\n // Function to compute modular inverse of n under modulo p\\n // Using Fermat's Little Theorem: n^(p-2) % p is the inverse of n modulo p when p is prime\\n public int modInverse(int n, int p) {\\n return power(n, p - 2, p);\\n }\\n\\n // Function to compute nCr % p using factorials and modular inverses\\n public int nCrModP(int n, int r, int p) {\\n if (r > n)\\n return 0;\\n if (r == 0)\\n return 1;\\n\\n int[] fact = new int[(int)n + 1];\\n fact[0] = 1;\\n for (int i = 1; i <= n; i++) {\\n fact[i] = (fact[i - 1] * i) % p;\\n }\\n int result = fact[(int)n];\\n result = (result * modInverse(fact[(int)r], p)) % p;\\n result = (result * modInverse(fact[(int)(n - r)], p)) % p;\\n return result;\\n }\\n\\n // Lucas' Theorem implementation to compute C(n, r) % p\\n public int l(int n, int r, int p) {\\n if (r == 0)\\n return 1;\\n return (l(n / p, r / p, p) * nCrModP(n % p, r % p, p)) % p;\\n }\\n //39024\\n // 3 +9 9+0 0+2 2+4\\n // 3+9+9+0 9+0+0+2 0+2+2+4\\n //3+9+9+0+9+0+0+2 9+0+0+2+0+2+2+4\\n}\"], [478, 0.4831, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n=s.length();\\n int m=n-2;\\n int a=0;\\n int b=0;\\n for(int i=0;i<s.length()-1;i++){\\n int bc=f(m,i);\\n // System.out.println(bc);\\n a=(a+bc*(s.charAt(i)-'0'));\\n b=(b+bc*(s.charAt(i+1)-'0'));\\n }\\n return a%10==b%10;\\n }\\n public int f(int m,int j){\\n int a=l(m,j,5);\\n int b=l(m,j,2);\\n for(int i=0;i<=9;i++){\\n if((i%2==b)&&(i%5==a)){\\n return i;\\n }\\n }\\n return 0;\\n }\\n public int power(int x, int y, int p) {\\n int res = 1;\\n x = x % p;\\n while (y > 0) {\\n if ((y & 1) == 1)\\n res = (res * x) % p;\\n y = y >> 1;\\n x = (x * x) % p;\\n }\\n return res;\\n }\\n\\n // Function to compute modular inverse of n under modulo p\\n // Using Fermat's Little Theorem: n^(p-2) % p is the inverse of n modulo p when p is prime\\n public int modInverse(int n, int p) {\\n return power(n, p - 2, p);\\n }\\n\\n // Function to compute nCr % p using factorials and modular inverses\\n public int nCrModP(int n, int r, int p) {\\n if (r > n)\\n return 0;\\n if (r == 0)\\n return 1;\\n\\n int[] fact = new int[(int)n + 1];\\n fact[0] = 1;\\n for (int i = 1; i <= n; i++) {\\n fact[i] = (fact[i - 1] * i) % p;\\n }\\n int result = fact[(int)n];\\n result = (result * modInverse(fact[(int)r], p)) % p;\\n result = (result * modInverse(fact[(int)(n - r)], p)) % p;\\n return result;\\n }\\n\\n // Lucas' Theorem implementation to compute C(n, r) % p\\n public int l(int n, int r, int p) {\\n if (r == 0)\\n return 1;\\n return (l(n / p, r / p, p) * nCrModP(n % p, r % p, p)) % p;\\n }\\n //39024\\n // 3 +9 9+0 0+2 2+4\\n // 3+9+9+0 9+0+0+2 0+2+2+4\\n //3+9+9+0+9+0+0+2 9+0+0+2+0+2+2+4\\n}\"], [572, 7.2453, \"class Solution {\\n public boolean hasSameDigits(String s) {\\n int n = s.length();\\n int k = n - 2;\\n if (k == 0) {\\n return s.charAt(0) == s.charAt(1);\\n }\\n\\n List<Integer> digitsK_p2 = getDigits(k, 2);\\n List<Integer> digitsK_p5 = getDigits(k, 5);\\n\\n int[] coeff = new int[k + 1];\\n for (int j = 0; j <= k; j++) {\\n int a = lucasModWithDigits(j, 2, digitsK_p2);\\n int b = lucasModWithDigits(j, 5, digitsK_p5);\\n coeff[j] = (5 * a + 6 * b) % 10;\\n }\\n\\n int sum0 = 0;\\n int sum1 = 0;\\n for (int j = 0; j <= k; j++) {\\n int digit0 = s.charAt(j) - '0';\\n sum0 = (sum0 + digit0 * coeff[j]) % 10;\\n int digit1 = s.charAt(j + 1) - '0';\\n sum1 = (sum1 + digit1 * coeff[j]) % 10;\\n }\\n return sum0 == sum1;\\n }\\n\\n private List<Integer> getDigits(int n, int p) {\\n List<Integer> digits = new ArrayList<>();\\n while (n > 0) {\\n digits.add(n % p);\\n n /= p;\\n }\\n return digits;\\n }\\n\\n private int lucasModWithDigits(int j, int p, List<Integer> digitsN) {\\n if (j == 0) {\\n return 1;\\n }\\n List<Integer> digitsK = new ArrayList<>();\\n int jCopy = j;\\n while (jCopy > 0) {\\n digitsK.add(jCopy % p);\\n jCopy /= p;\\n }\\n while (digitsK.size() < digitsN.size()) {\\n digitsK.add(0);\\n }\\n int res = 1;\\n for (int i = 0; i < digitsK.size(); i++) {\\n int ni = (i < digitsN.size()) ? digitsN.get(i) : 0;\\n int ki = digitsK.get(i);\\n if (ki > ni) {\\n return 0;\\n }\\n if (p == 2) {\\n if (ni == 0) {\\n if (ki != 0) return 0;\\n res = (res * 1) % p;\\n } else if (ni == 1) {\\n if (ki == 0 || ki == 1) res = (res * 1) % p;\\n else return 0;\\n }\\n } else if (p == 5) {\\n int[][] table = {\\n {1, 0, 0, 0, 0},\\n {1, 1, 0, 0, 0},\\n {1, 2, 1, 0, 0},\\n {1, 3, 3, 1, 0},\\n {1, 4, 1, 4, 1}\\n };\\n res = (res * table[ni][ki]) % 5;\\n }\\n }\\n return res;\\n }\\n}\"]]"
},
"javascript": {
"code": "var hasSameDigits = function(s) {\n function lucas(n, k, p) {\n let res = 1;\n while (n > 0 || k > 0) {\n const a = n % p;\n const b = k % p;\n if (b > a) return 0;\n let comb = 1;\n for (let i = a - b + 1; i <= a; i++) {\n comb = (comb * i) % p;\n }\n let denom = 1;\n for (let i = 2; i <= b; i++) {\n denom = (denom * i) % p;\n }\n let invDenom = 1;\n let exponent = p - 2;\n let base = denom;\n while (exponent > 0) {\n if (exponent % 2 === 1) {\n invDenom = (invDenom * base) % p;\n }\n base = (base * base) % p;\n exponent = Math.floor(exponent / 2);\n }\n comb = (comb * invDenom) % p;\n res = (res * comb) % p;\n n = Math.floor(n / p);\n k = Math.floor(k / p);\n }\n return res;\n }\n\n const k = s.length - 2;\n if (k < 0) return false;\n\n let sum1 = 0, sum2 = 0;\n\n for (let i = 0; i <= k; i++) {\n const mod2 = lucas(k, i, 2);\n const mod5 = lucas(k, i, 5);\n\n const a = mod2;\n const b = mod5;\n\n let delta = (a - (b % 2)) % 2;\n if (delta < 0) delta += 2;\n\n const c = (delta * 5 + b) % 10;\n\n const d1 = parseInt(s[i], 10);\n sum1 = (sum1 + c * d1) % 10;\n\n const d2 = parseInt(s[i + 1], 10);\n sum2 = (sum2 + c * d2) % 10;\n }\n\n return sum1 === sum2;\n};",
"memory": 6200,
"memoryDistribution": "[[6200, 79.592, \"var hasSameDigits = function(s) {\\n function lucas(n, k, p) {\\n let res = 1;\\n while (n > 0 || k > 0) {\\n const a = n % p;\\n const b = k % p;\\n if (b > a) return 0;\\n let comb = 1;\\n for (let i = a - b + 1; i <= a; i++) {\\n comb = (comb * i) % p;\\n }\\n let denom = 1;\\n for (let i = 2; i <= b; i++) {\\n denom = (denom * i) % p;\\n }\\n let invDenom = 1;\\n let exponent = p - 2;\\n let base = denom;\\n while (exponent > 0) {\\n if (exponent % 2 === 1) {\\n invDenom = (invDenom * base) % p;\\n }\\n base = (base * base) % p;\\n exponent = Math.floor(exponent / 2);\\n }\\n comb = (comb * invDenom) % p;\\n res = (res * comb) % p;\\n n = Math.floor(n / p);\\n k = Math.floor(k / p);\\n }\\n return res;\\n }\\n\\n const k = s.length - 2;\\n if (k < 0) return false;\\n\\n let sum1 = 0, sum2 = 0;\\n\\n for (let i = 0; i <= k; i++) {\\n const mod2 = lucas(k, i, 2);\\n const mod5 = lucas(k, i, 5);\\n\\n const a = mod2;\\n const b = mod5;\\n\\n let delta = (a - (b % 2)) % 2;\\n if (delta < 0) delta += 2;\\n\\n const c = (delta * 5 + b) % 10;\\n\\n const d1 = parseInt(s[i], 10);\\n sum1 = (sum1 + c * d1) % 10;\\n\\n const d2 = parseInt(s[i + 1], 10);\\n sum2 = (sum2 + c * d2) % 10;\\n }\\n\\n return sum1 === sum2;\\n};\"], [59200, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n const n = s.length;\\n // Conforme enunciado, n >= 3\\n if(n < 3) return false;\\n \\n const N = n - 2; // Precisamos dos coeficientes da linha (n-2) do tri\\u00e2ngulo de Pascal.\\n \\n // Precompute small binomials mod 5 para x=0..4.\\n // smallBinom[x][y] = binom(x, y) mod 5.\\n const smallBinom = [\\n [1], // 0: binom(0,0)=1\\n [1, 1], // 1: 1,1\\n [1, 2, 1], // 2: 1,2,1\\n [1, 3, 3, 1], // 3: 1,3,3,1\\n [1, 4, 1, 4, 1] // 4: 1,4,6 mod5=1,4,1\\n ];\\n \\n // Fun\\u00e7\\u00e3o que computa binom(N, i) mod2, usando a propriedade de subm\\u00e1scara.\\n function binomMod2(N, i) {\\n return ((N & i) === i) ? 1 : 0;\\n }\\n \\n // Fun\\u00e7\\u00e3o que computa binom(N, i) mod5 via Lucas.\\n // Aqui N e i s\\u00e3o n\\u00fameros inteiros.\\n function binomMod5(N, i) {\\n let res = 1;\\n while (N > 0 || i > 0) {\\n const nDigit = N % 5;\\n const iDigit = i % 5;\\n if (iDigit > nDigit) return 0;\\n res = (res * smallBinom[nDigit][iDigit]) % 5;\\n N = Math.floor(N / 5);\\n i = Math.floor(i / 5);\\n }\\n return res;\\n }\\n \\n // Para cada i de 0 a N, computamos binom(N, i) mod 10 via CRT:\\n // Como 10 = 2 * 5 e os inversos s\\u00e3o:\\n // inv(5 mod 2) = 1 e inv(2 mod 5) = 3, a f\\u00f3rmula \\u00e9:\\n // result = (5 * binomMod2 + 6 * binomMod5) mod 10.\\n let sumMod = 0;\\n for (let i = 0; i <= N; i++) {\\n const a = binomMod2(N, i); // 0 ou 1\\n const b = binomMod5(N, i); // valor em {0,1,2,3,4}\\n const coef = (5 * a + 6 * b) % 10; // binom(N, i) mod 10.\\n // Diferen\\u00e7a entre d\\u00edgitos consecutivos: s[i] - s[i+1]\\n let diff = (s.charCodeAt(i) - 48) - (s.charCodeAt(i+1) - 48);\\n diff = ((diff % 10) + 10) % 10; // ajustar para [0,9]\\n sumMod = (sumMod + coef * diff) % 10;\\n }\\n \\n return sumMod === 0;\\n};\\n\"], [59400, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n const n = s.length;\\n const m = n - 2;\\n if (m < 0) {\\n return s[0] === s[1];\\n }\\n \\n let digit0 = 0;\\n let digit1 = 0;\\n \\n for (let i = 0; i <= m; i++) {\\n const a = lucasMod2(m, i);\\n const b = lucasMod5(m, i);\\n const c10 = (5 * a + 6 * b) % 10;\\n \\n digit0 = (digit0 + c10 * (s.charCodeAt(i) - 48)) % 10;\\n if (i + 1 < n) {\\n digit1 = (digit1 + c10 * (s.charCodeAt(i + 1) - 48)) % 10;\\n }\\n }\\n \\n return digit0 === digit1;\\n};\\n\\nfunction lucasMod2(n, k) {\\n if (k === 0) return 1;\\n while (k > 0) {\\n if (n === 0) return 0;\\n const ni = n % 2;\\n const ki = k % 2;\\n if (ki > ni) return 0;\\n n = Math.floor(n / 2);\\n k = Math.floor(k / 2);\\n }\\n return 1;\\n}\\n\\nfunction lucasMod5(n, k) {\\n if (k === 0) return 1;\\n let res = 1;\\n while (n > 0 || k > 0) {\\n const ni = n % 5;\\n const ki = k % 5;\\n if (ki > ni) return 0;\\n let comb = 1;\\n if (ki !== 0) {\\n for (let i = 0; i < ki; i++) {\\n comb = (comb * (ni - i)) % 5;\\n }\\n const invFact = [1, 1, 3, 1, 4][ki];\\n comb = (comb * invFact) % 5;\\n }\\n res = (res * comb) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return res;\\n}\"], [59700, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n const n = s.length;\\n const m = n - 2;\\n if (m < 0) {\\n return s[0] === s[1];\\n }\\n \\n let digit0 = 0;\\n let digit1 = 0;\\n \\n for (let i = 0; i <= m; i++) {\\n const a = lucasMod2(m, i);\\n const b = lucasMod5(m, i);\\n const c10 = (5 * a + 6 * b) % 10;\\n \\n digit0 = (digit0 + c10 * (s.charCodeAt(i) - 48)) % 10;\\n if (i + 1 < n) {\\n digit1 = (digit1 + c10 * (s.charCodeAt(i + 1) - 48)) % 10;\\n }\\n }\\n \\n return digit0 === digit1;\\n};\\n\\nfunction lucasMod2(n, k) {\\n if (k === 0) return 1;\\n while (k > 0) {\\n if (n === 0) return 0;\\n const ni = n % 2;\\n const ki = k % 2;\\n if (ki > ni) return 0;\\n n = Math.floor(n / 2);\\n k = Math.floor(k / 2);\\n }\\n return 1;\\n}\\n\\nfunction lucasMod5(n, k) {\\n if (k === 0) return 1;\\n let res = 1;\\n while (n > 0 || k > 0) {\\n const ni = n % 5;\\n const ki = k % 5;\\n if (ki > ni) return 0;\\n let comb = 1;\\n if (ki !== 0) {\\n for (let i = 0; i < ki; i++) {\\n comb = (comb * (ni - i)) % 5;\\n }\\n const invFact = [1, 1, 3, 1, 4][ki];\\n comb = (comb * invFact) % 5;\\n }\\n res = (res * comb) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return res;\\n}\"], [60200, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nconst hasSameDigits = areDigitsSame = function(s) {\\n const n = s.length;\\n \\n // Edge case\\n if (n <= 2) {\\n return s[0] === s[1];\\n }\\n \\n if(s.indexOf(\\\"32721547700\\\") == 0 || s.indexOf(\\\"07186657\\\") == 0 || s.indexOf(\\\"873431014\\\") == 0)\\n return true;\\n if(s.indexOf(\\\"66244565770\\\") == 0)\\n return false;\\n\\n // For extremely large inputs, use the fastest method\\n if (n >= 10000) {\\n // Mathematical shortcut: after all operations, the result depends\\n // on the parity of the original string length\\n \\n // When we analyze the pattern carefully, we find:\\n // - For even length strings: odd indices contribute to first digit, \\n // even indices to second digit\\n // - For odd length strings: even indices contribute to first digit,\\n // odd indices to second digit\\n \\n let a = 0, b = 0;\\n \\n if (n % 2 === 0) {\\n // Even length\\n for (let i = 0; i < n; i++) {\\n const digit = s.charCodeAt(i) - 48;\\n if (i % 2 === 0) {\\n a = (a + digit) % 10;\\n } else {\\n b = (b + digit) % 10;\\n }\\n }\\n } else {\\n // Odd length\\n for (let i = 0; i < n; i++) {\\n const digit = s.charCodeAt(i) - 48;\\n if (i % 2 === 0) {\\n b = (b + digit) % 10;\\n } else {\\n a = (a + digit) % 10;\\n }\\n }\\n }\\n \\n return a === b;\\n }\\n \\n // For smaller inputs, use the direct approach for accuracy\\n // This is the most reliable method that works for all inputs\\n let digits = new Uint8Array(n);\\n for (let i = 0; i < n; i++) {\\n digits[i] = s.charCodeAt(i) - 48;\\n }\\n \\n let len = n;\\n while (len > 2) {\\n for (let i = 0; i < len - 1; i++) {\\n digits[i] = (digits[i] + digits[i + 1]) % 10;\\n }\\n len--;\\n }\\n \\n return digits[0] === digits[1];\\n}\"], [60900, 4.0816, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n const N = s.length;\\n const n = N - 2;\\n // Precompute the small 5\\u00d75 binomial table mod 5\\n const C5 = [\\n [1],\\n [1,1],\\n [1,2,1],\\n [1,3,3,1],\\n [1,4,1,4,1] // note: 6 mod 5 = 1\\n ];\\n\\n // Turn string into digit array\\n const a = new Uint8Array(N);\\n for (let i = 0; i < N; i++) {\\n a[i] = s.charCodeAt(i) - 48;\\n }\\n\\n // 1) Check D mod 2 == 0\\n let sum2 = 0;\\n for (let i = 0; i <= n; i++) {\\n // binom(n,i) mod 2 is 1 iff no carry bits in i + (n-i)\\n if ((i & (n - i)) === 0) {\\n // (a[i] - a[i+1]) mod 2 === a[i] xor a[i+1]\\n sum2 ^= (a[i] ^ a[i+1]);\\n }\\n }\\n if ((sum2 & 1) !== 0) return false;\\n\\n // 2) Check D mod 5 == 0\\n let sum5 = 0;\\n for (let i = 0; i <= n; i++) {\\n // compute binom(n,i) mod 5 via Lucas\\n let x = n, y = i, coeff = 1;\\n while (x > 0 || y > 0) {\\n const nd = x % 5, id = y % 5;\\n if (id > nd) { coeff = 0; break; }\\n coeff = (coeff * C5[nd][id]) % 5;\\n x = Math.floor(x / 5);\\n y = Math.floor(y / 5);\\n }\\n if (coeff !== 0) {\\n // (a[i] - a[i+1]) mod 5, in [0..4]\\n const diff = (a[i] + 5 - a[i+1]) % 5;\\n sum5 = (sum5 + coeff * diff) % 5;\\n }\\n }\\n return sum5 === 0;\\n};\"], [61300, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n const n = s.length;\\n if (n === 2) {\\n return s[0] === s[1];\\n }\\n\\n const binom_table = [\\n [1], // 0: 1\\n [1, 1], // 1: 1,1\\n [1, 2, 1], // 2: 1,2,1\\n [1, 3, 3, 1], // 3: 1,3,3,1\\n [1, 4, 1, 4, 1] // 4: 1,4,6(=1),4,1\\n ];\\n\\n function binom_mod5(m, k) {\\n if (k < 0 || k > m) return 0;\\n let res = 1;\\n while (m > 0 || k > 0) {\\n const m_digit = m % 5;\\n const k_digit = k % 5;\\n if (k_digit > m_digit) return 0;\\n res = (res * binom_table[m_digit][k_digit]) % 5;\\n m = Math.floor(m / 5);\\n k = Math.floor(k / 5);\\n }\\n return res;\\n }\\n\\n let sum_mod2 = 0;\\n let sum_mod5 = 0;\\n let zorflendex = new Uint8Array(n);\\n for (let i = 0; i < n; i++) {\\n zorflendex[i] = s.charCodeAt(i) - 48;\\n let c_i_mod2, c_i_mod5;\\n if (i === 0) {\\n c_i_mod2 = 1;\\n c_i_mod5 = 1;\\n } else if (i === n - 1) {\\n c_i_mod2 = 1; // -1 \\u2261 1 mod 2\\n c_i_mod5 = 4; // -1 \\u2261 4 mod 5\\n } else {\\n const binom_i_mod2 = (i & (n - 2)) === i ? 1 : 0;\\n const binom_im1_mod2 = ((i - 1) & (n - 2)) === (i - 1) ? 1 : 0;\\n c_i_mod2 = (binom_i_mod2 + binom_im1_mod2) % 2;\\n\\n const binom_i_mod5 = binom_mod5(n - 2, i);\\n const binom_im1_mod5 = binom_mod5(n - 2, i - 1);\\n c_i_mod5 = (binom_i_mod5 - binom_im1_mod5 + 5) % 5;\\n }\\n const s_i = zorflendex[i];\\n sum_mod2 = (sum_mod2 + (c_i_mod2 * (s_i % 2))) % 2;\\n sum_mod5 = (sum_mod5 + (c_i_mod5 * (s_i % 5))) % 5;\\n }\\n return sum_mod2 === 0 && sum_mod5 === 0;\\n};\"], [61600, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n var length = s.length;\\n if(length == 3) {\\n return s[0] == s[2];\\n }\\n\\n if(length == 77066)\\n return false;\\n\\n if(length == 66288)\\n return true;\\n\\n if(length == 100000 || length == 98818) {\\n if(s[0] == \\\"1\\\" || s[0] == \\\"4\\\" || s[0] == \\\"3\\\")\\n return false;\\n if(s[0] == \\\"8\\\")\\n return true;\\n return parseInt(s[0]) < 5;\\n }\\n \\n //Do the first past while its a string\\n s = s.split('');\\n for(var i=0; i<s.length-1; i++) {\\n s[i] = (parseInt(s[i]) + parseInt(s[i+1])) % 10; \\n }\\n\\n //Do the remaining passes as an integer array\\n var numberDone = 1;\\n while(s.length - numberDone > 3) {\\n for(var i=0; i<s.length - 1 - numberDone; i++) {\\n s[i] = (s[i] + s[i+1]) % 10;\\n }\\n numberDone++;\\n }\\n\\n return s[0] == s[2];\\n};\"], [61800, 4.0816, \"var hasSameDigits = function(s) {\\n function lucas(n, k, p) {\\n let res = 1;\\n while (n > 0 || k > 0) {\\n const a = n % p;\\n const b = k % p;\\n if (b > a) return 0;\\n let comb = 1;\\n for (let i = a - b + 1; i <= a; i++) {\\n comb = (comb * i) % p;\\n }\\n let denom = 1;\\n for (let i = 2; i <= b; i++) {\\n denom = (denom * i) % p;\\n }\\n let invDenom = 1;\\n let exponent = p - 2;\\n let base = denom;\\n while (exponent > 0) {\\n if (exponent % 2 === 1) {\\n invDenom = (invDenom * base) % p;\\n }\\n base = (base * base) % p;\\n exponent = Math.floor(exponent / 2);\\n }\\n comb = (comb * invDenom) % p;\\n res = (res * comb) % p;\\n n = Math.floor(n / p);\\n k = Math.floor(k / p);\\n }\\n return res;\\n }\\n\\n const k = s.length - 2;\\n if (k < 0) return false;\\n\\n let sum1 = 0, sum2 = 0;\\n\\n for (let i = 0; i <= k; i++) {\\n const mod2 = lucas(k, i, 2);\\n const mod5 = lucas(k, i, 5);\\n\\n const a = mod2;\\n const b = mod5;\\n\\n let delta = (a - (b % 2)) % 2;\\n if (delta < 0) delta += 2;\\n\\n const c = (delta * 5 + b) % 10;\\n\\n const d1 = parseInt(s[i], 10);\\n sum1 = (sum1 + c * d1) % 10;\\n\\n const d2 = parseInt(s[i + 1], 10);\\n sum2 = (sum2 + c * d2) % 10;\\n }\\n\\n return sum1 === sum2;\\n};\"], [62300, 2.0408, \"function hasSameDigits(s) {\\n function cal(a, mod) {\\n let count = 0;\\n while (a > 0 && a % mod === 0) {\\n count++;\\n a = Math.floor(a / mod);\\n }\\n return [a % mod, count];\\n }\\n\\n function test(mod) {\\n let n = s.length;\\n let res = 0;\\n let r = 1;\\n let c = 0;\\n\\n for (let i = 0; i < n - 1; i++) {\\n if (c === 0) {\\n res += r * (parseInt(s[i]) - parseInt(s[i + 1]));\\n }\\n\\n let [rr, cc] = cal(n - 2 - i, mod);\\n r = (r * rr) % mod;\\n c += cc;\\n\\n [rr, cc] = cal(i + 1, mod);\\n r = (r * modInverse(rr, mod)) % mod;\\n c -= cc;\\n }\\n return res % mod === 0;\\n }\\n\\n function modInverse(x, mod) {\\n return powerMod(x, mod - 2, mod);\\n }\\n\\n function powerMod(x, y, mod) {\\n let result = 1;\\n while (y > 0) {\\n if (y % 2 === 1) {\\n result = (result * x) % mod;\\n }\\n x = (x * x) % mod;\\n y = Math.floor(y / 2);\\n }\\n return result;\\n }\\n\\n return test(2) && test(5);\\n}\"], [62600, 2.0408, \"var hasSameDigits = function(s) {\\n const n = s.length;\\n if (n <= 2) return true;\\n const N = n - 2; // we'll need binomials C(N, k) for k = 0..N\\n\\n // Precomputed factorials for mod2 and mod5 (for numbers 0..(p-1))\\n const fact2 = [1, 1]; // for mod2, only 0 and 1\\n const fact5 = [1, 1, 2, 1, 4]; // for mod5; (0!:1, 1!:1, 2!:2, 3!:6 mod5=1, 4!:24 mod5=4)\\n\\n // Fast exponentiation mod m\\n function modPow(a, b, m) {\\n let res = 1;\\n a = a % m;\\n while(b > 0) {\\n if (b & 1) res = (res * a) % m;\\n a = (a * a) % m;\\n b = b >> 1;\\n }\\n return res;\\n }\\n \\n // Modular inverse mod m (m is prime: 2 or 5)\\n function modInv(a, m) {\\n return modPow(a, m - 2, m);\\n }\\n \\n // Compute C(n, k) mod p for n, k < p using precomputed factorials 'fact'\\n function C_mod_p(n, k, p, fact) {\\n if (k < 0 || k > n) return 0;\\n // Since n, k < p (p = 2 or 5, very small), we can use:\\n return ((fact[n] * modInv(fact[k], p)) % p * modInv(fact[n - k], p)) % p;\\n }\\n \\n // Lucas theorem: compute C(n, k) mod p for arbitrary n, k.\\n function lucas(n, k, p, fact) {\\n if (k === 0) return 1;\\n let ni = n % p, ki = k % p;\\n if (ki > ni) return 0;\\n return (lucas(Math.floor(n / p), Math.floor(k / p), p, fact) * C_mod_p(ni, ki, p, fact)) % p;\\n }\\n \\n // Combine the results for mod 2 and mod 5 via CRT to get binom(n,k) mod 10.\\n // We want x \\u2261 a (mod 2) and x \\u2261 b (mod 5). A valid combination is:\\n // x = (a * 5 * inv5 + b * 2 * inv2) mod 10,\\n // where inv5 = (5\\u207b\\u00b9 mod 2) and inv2 = (2\\u207b\\u00b9 mod 5).\\n function binom_mod10(n, k) {\\n let a = lucas(n, k, 2, fact2); // mod 2 result\\n let b = lucas(n, k, 5, fact5); // mod 5 result\\n let inv5 = 1; // because 5 mod2 = 1 so its inverse is 1\\n let inv2 = 3; // 2\\u207b\\u00b9 mod5 is 3 (since 2*3 = 6 \\u2261 1 mod5)\\n return ( (a * 5 * inv5) + (b * 2 * inv2) ) % 10;\\n }\\n \\n // Using the closed\\u2010form: after (n-2) operations, the final two digits are:\\n // f0 = \\u03a3 (C(N, i) * s[i]) mod 10\\n // f1 = \\u03a3 (C(N, i-1) * s[i]) mod 10\\n // (Where we treat C(N, x)=0 if x<0 or x>N.)\\n let f0 = 0, f1 = 0;\\n for (let i = 0; i < n; i++) {\\n let c1 = (i < 0 || i > N) ? 0 : binom_mod10(N, i);\\n let c2 = ((i - 1) < 0 || (i - 1) > N) ? 0 : binom_mod10(N, i - 1);\\n let d = parseInt(s[i]);\\n f0 = (f0 + c1 * d) % 10;\\n f1 = (f1 + c2 * d) % 10;\\n }\\n return f0 === f1;\\n};\\n\"], [62700, 2.0408, \"var hasSameDigits = function(s) {\\n const n = s.length;\\n if (n <= 2) return true;\\n const N = n - 2; // we'll need binomials C(N, k) for k = 0..N\\n\\n // Precomputed factorials for mod2 and mod5 (for numbers 0..(p-1))\\n const fact2 = [1, 1]; // for mod2, only 0 and 1\\n const fact5 = [1, 1, 2, 1, 4]; // for mod5; (0!:1, 1!:1, 2!:2, 3!:6 mod5=1, 4!:24 mod5=4)\\n\\n // Fast exponentiation mod m\\n function modPow(a, b, m) {\\n let res = 1;\\n a = a % m;\\n while(b > 0) {\\n if (b & 1) res = (res * a) % m;\\n a = (a * a) % m;\\n b = b >> 1;\\n }\\n return res;\\n }\\n \\n // Modular inverse mod m (m is prime: 2 or 5)\\n function modInv(a, m) {\\n return modPow(a, m - 2, m);\\n }\\n \\n // Compute C(n, k) mod p for n, k < p using precomputed factorials 'fact'\\n function C_mod_p(n, k, p, fact) {\\n if (k < 0 || k > n) return 0;\\n // Since n, k < p (p = 2 or 5, very small), we can use:\\n return ((fact[n] * modInv(fact[k], p)) % p * modInv(fact[n - k], p)) % p;\\n }\\n \\n // Lucas theorem: compute C(n, k) mod p for arbitrary n, k.\\n function lucas(n, k, p, fact) {\\n if (k === 0) return 1;\\n let ni = n % p, ki = k % p;\\n if (ki > ni) return 0;\\n return (lucas(Math.floor(n / p), Math.floor(k / p), p, fact) * C_mod_p(ni, ki, p, fact)) % p;\\n }\\n \\n // Combine the results for mod 2 and mod 5 via CRT to get binom(n,k) mod 10.\\n // We want x \\u2261 a (mod 2) and x \\u2261 b (mod 5). A valid combination is:\\n // x = (a * 5 * inv5 + b * 2 * inv2) mod 10,\\n // where inv5 = (5\\u207b\\u00b9 mod 2) and inv2 = (2\\u207b\\u00b9 mod 5).\\n function binom_mod10(n, k) {\\n let a = lucas(n, k, 2, fact2); // mod 2 result\\n let b = lucas(n, k, 5, fact5); // mod 5 result\\n let inv5 = 1; // because 5 mod2 = 1 so its inverse is 1\\n let inv2 = 3; // 2\\u207b\\u00b9 mod5 is 3 (since 2*3 = 6 \\u2261 1 mod5)\\n return ( (a * 5 * inv5) + (b * 2 * inv2) ) % 10;\\n }\\n \\n // Using the closed\\u2010form: after (n-2) operations, the final two digits are:\\n // f0 = \\u03a3 (C(N, i) * s[i]) mod 10\\n // f1 = \\u03a3 (C(N, i-1) * s[i]) mod 10\\n // (Where we treat C(N, x)=0 if x<0 or x>N.)\\n let f0 = 0, f1 = 0;\\n for (let i = 0; i < n; i++) {\\n let c1 = (i < 0 || i > N) ? 0 : binom_mod10(N, i);\\n let c2 = ((i - 1) < 0 || (i - 1) > N) ? 0 : binom_mod10(N, i - 1);\\n let d = parseInt(s[i]);\\n f0 = (f0 + c1 * d) % 10;\\n f1 = (f1 + c2 * d) % 10;\\n }\\n return f0 === f1;\\n};\\n\"], [63200, 2.0408, \"var hasSameDigits = function(s) {\\n const n = s.length;\\n if (n <= 2) return true;\\n const N = n - 2; // we'll need binomials C(N, k) for k = 0..N\\n\\n // Precomputed factorials for mod2 and mod5 (for numbers 0..(p-1))\\n const fact2 = [1, 1]; // for mod2, only 0 and 1\\n const fact5 = [1, 1, 2, 1, 4]; // for mod5; (0!:1, 1!:1, 2!:2, 3!:6 mod5=1, 4!:24 mod5=4)\\n\\n // Fast exponentiation mod m\\n function modPow(a, b, m) {\\n let res = 1;\\n a = a % m;\\n while(b > 0) {\\n if (b & 1) res = (res * a) % m;\\n a = (a * a) % m;\\n b = b >> 1;\\n }\\n return res;\\n }\\n \\n // Modular inverse mod m (m is prime: 2 or 5)\\n function modInv(a, m) {\\n return modPow(a, m - 2, m);\\n }\\n \\n // Compute C(n, k) mod p for n, k < p using precomputed factorials 'fact'\\n function C_mod_p(n, k, p, fact) {\\n if (k < 0 || k > n) return 0;\\n // Since n, k < p (p = 2 or 5, very small), we can use:\\n return ((fact[n] * modInv(fact[k], p)) % p * modInv(fact[n - k], p)) % p;\\n }\\n \\n // Lucas theorem: compute C(n, k) mod p for arbitrary n, k.\\n function lucas(n, k, p, fact) {\\n if (k === 0) return 1;\\n let ni = n % p, ki = k % p;\\n if (ki > ni) return 0;\\n return (lucas(Math.floor(n / p), Math.floor(k / p), p, fact) * C_mod_p(ni, ki, p, fact)) % p;\\n }\\n \\n // Combine the results for mod 2 and mod 5 via CRT to get binom(n,k) mod 10.\\n // We want x \\u2261 a (mod 2) and x \\u2261 b (mod 5). A valid combination is:\\n // x = (a * 5 * inv5 + b * 2 * inv2) mod 10,\\n // where inv5 = (5\\u207b\\u00b9 mod 2) and inv2 = (2\\u207b\\u00b9 mod 5).\\n function binom_mod10(n, k) {\\n let a = lucas(n, k, 2, fact2); // mod 2 result\\n let b = lucas(n, k, 5, fact5); // mod 5 result\\n let inv5 = 1; // because 5 mod2 = 1 so its inverse is 1\\n let inv2 = 3; // 2\\u207b\\u00b9 mod5 is 3 (since 2*3 = 6 \\u2261 1 mod5)\\n return ( (a * 5 * inv5) + (b * 2 * inv2) ) % 10;\\n }\\n \\n // Using the closed\\u2010form: after (n-2) operations, the final two digits are:\\n // f0 = \\u03a3 (C(N, i) * s[i]) mod 10\\n // f1 = \\u03a3 (C(N, i-1) * s[i]) mod 10\\n // (Where we treat C(N, x)=0 if x<0 or x>N.)\\n let f0 = 0, f1 = 0;\\n for (let i = 0; i < n; i++) {\\n let c1 = (i < 0 || i > N) ? 0 : binom_mod10(N, i);\\n let c2 = ((i - 1) < 0 || (i - 1) > N) ? 0 : binom_mod10(N, i - 1);\\n let d = parseInt(s[i]);\\n f0 = (f0 + c1 * d) % 10;\\n f1 = (f1 + c2 * d) % 10;\\n }\\n return f0 === f1;\\n};\\n\"], [63600, 4.0816, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nconst hasSameDigits = s => {\\n let x = 0\\n let y = 0\\n const offset = '0'.charCodeAt(0)\\n for (let i = 0; i <= s.length - 2; i++) {\\n let coeff = binmodten(s.length - 2, i)\\n x = (x + coeff * (s.charCodeAt(i) - offset)) % 10\\n y = (y + coeff * (s.charCodeAt(i + 1) - offset)) % 10\\n }\\n return x === y\\n};\\nconst binmodten = (n, k) => {\\n let i = ((n & k) === k) ? 1 : 0\\n\\n const mfive = (n, k) => {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ]\\n let result = 1\\n\\n while (n > 0 || k > 0) {\\n let nf = n % 5\\n let kf = k % 5\\n\\n if (kf > nf) return 0\\n\\n result = (result * tuples[nf][kf]) % 5\\n n = Math.floor(n / 5)\\n k = Math.floor(k / 5)\\n }\\n return result;\\n };\\n let j = mfive(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x;\\n }\\n }\\n return 0;\\n};\"], [64599, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\n;\\nvar hasSameDigits = function (s) {\\n // Step 1: Initialize Variables\\n let size = s.length;\\n let X = size - 2;\\n let x = 0, y = 0;\\n\\n // Step 2: Compute Alternating Sum Using Binomial Coefficients\\n for (let j = 0; j <= X; j++) {\\n let coeff = binomialMod10(X, j);\\n x = (x + coeff * (s.charCodeAt(j) - '0'.charCodeAt(0))) % 10;\\n y = (y + coeff * (s.charCodeAt(j + 1) - '0'.charCodeAt(0))) % 10;\\n }\\n\\n // Step 3: Compare Alternating Sums\\n return x === y;\\n};\\n\\n// Step 4: Compute Binomial Coefficient Modulo 10\\nvar binomialMod10 = function (n, k) {\\n let i = ((n & k) === k) ? 1 : 0;\\n\\n var binomialMod5 = function (n, k) {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ];\\n let result = 1;\\n\\n while (n > 0 || k > 0) {\\n let nthd = n % 5;\\n let kthd = k % 5;\\n\\n if (kthd > nthd) return 0;\\n\\n result = (result * tuples[nthd][kthd]) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return result;\\n };\\n let j = binomialMod5(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x;\\n }\\n }\\n return 0;\\n};\"], [64700, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nconst hasSameDigits = s => {\\n let x = 0\\n let y = 0\\n const offset = '0'.charCodeAt(0)\\n for (let i = 0; i <= s.length - 2; i++) {\\n let coeff = binmodten(s.length - 2, i)\\n x = (x + coeff * (s.charCodeAt(i) - offset)) % 10\\n y = (y + coeff * (s.charCodeAt(i + 1) - offset)) % 10\\n }\\n return x === y\\n};\\nconst binmodten = (n, k) => {\\n const i = ((n & k) === k) ? 1 : 0\\n\\n const mfive = (n, k) => {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ]\\n let result = 1\\n\\n while (n > 0 || k > 0) {\\n let nf = n % 5\\n let kf = k % 5\\n\\n if (kf > nf) return 0\\n\\n result = (result * tuples[nf][kf]) % 5\\n n = Math.floor(n / 5)\\n k = Math.floor(k / 5)\\n }\\n return result;\\n };\\n let j = mfive(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x;\\n }\\n }\\n return 0;\\n};\"], [64800, 2.0408, \"var hasSameDigits = function (s) {\\n // Step 1: Initialize Variables\\n let size = s.length;\\n let X = size - 2;\\n let x = 0, y = 0;\\n\\n // Step 2: Compute Alternating Sum Using Binomial Coefficients\\n for (let j = 0; j <= X; j++) {\\n let coeff = binomialMod10(X, j);\\n x = (x + coeff * (s.charCodeAt(j) - '0'.charCodeAt(0))) % 10;\\n y = (y + coeff * (s.charCodeAt(j + 1) - '0'.charCodeAt(0))) % 10;\\n }\\n\\n // Step 3: Compare Alternating Sums\\n return x === y;\\n};\\n\\n// Step 4: Compute Binomial Coefficient Modulo 10\\nvar binomialMod10 = function (n, k) {\\n let i = binomialMod2(n, k);\\n let j = binomialMod5(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x;\\n }\\n }\\n return 0;\\n};\\n\\n// Step 5: Compute Binomial Coefficient Modulo 2\\nvar binomialMod2 = function (n, k) {\\n return ((n & k) === k) ? 1 : 0;\\n};\\n\\n// Step 6: Compute Binomial Coefficient Modulo 5 Using Lookup Table\\nvar binomialMod5 = function (n, k) {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ];\\n let result = 1;\\n\\n while (n > 0 || k > 0) {\\n let nthd = n % 5;\\n let kthd = k % 5;\\n\\n if (kthd > nthd) return 0;\\n\\n result = (result * tuples[nthd][kthd]) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return result;\\n};\"], [64900, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nconst hasSameDigits = s => {\\n const binomMod5 = (n, r) => {\\n const table = [\\n [1, 0, 0, 0, 0],\\n [1, 1, 0, 0, 0],\\n [1, 2, 1, 0, 0],\\n [1, 3, 3, 1, 0],\\n [1, 4, 1, 4, 1]\\n ];\\n let res = 1;\\n while (n || r) {\\n const n_digit = n % 5;\\n const r_digit = r % 5;\\n if (r_digit > n_digit) return 0;\\n res = (res * table[n_digit][r_digit]) % 5;\\n n = Math.floor(n / 5);\\n r = Math.floor(r / 5);\\n }\\n return res;\\n };\\n\\n const binomMod10 = (k, j) => {\\n const r2 = ((j & ~k) === 0) ? 1 : 0;\\n const r5 = binomMod5(k, j);\\n return (5 * r2 + 6 * r5) % 10;\\n };\\n\\n const n = s.length;\\n const k = n - 2;\\n let x = 0;\\n let y = 0;\\n\\n for (let j = 0; j <= k; j++) {\\n const c = binomMod10(k, j);\\n x = (x + c * (s[j] - '0')) % 10;\\n y = (y + c * (s[j + 1] - '0')) % 10;\\n }\\n\\n return x === y;\\n};\"], [65000, 6.1224, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nconst hasSameDigits = s => {\\n const binomMod5 = (n, r) => {\\n const table = [\\n [1, 0, 0, 0, 0],\\n [1, 1, 0, 0, 0],\\n [1, 2, 1, 0, 0],\\n [1, 3, 3, 1, 0],\\n [1, 4, 1, 4, 1]\\n ];\\n let res = 1;\\n while (n || r) {\\n const n_digit = n % 5;\\n const r_digit = r % 5;\\n if (r_digit > n_digit) return 0;\\n res = (res * table[n_digit][r_digit]) % 5;\\n n = Math.floor(n / 5);\\n r = Math.floor(r / 5);\\n }\\n return res;\\n };\\n\\n const binomMod10 = (k, j) => {\\n const r2 = ((j & ~k) === 0) ? 1 : 0;\\n const r5 = binomMod5(k, j);\\n return (5 * r2 + 6 * r5) % 10;\\n };\\n\\n const n = s.length;\\n const k = n - 2;\\n let x = 0;\\n let y = 0;\\n\\n for (let j = 0; j <= k; j++) {\\n const c = binomMod10(k, j);\\n x = (x + c * (s[j] - '0')) % 10;\\n y = (y + c * (s[j + 1] - '0')) % 10;\\n }\\n\\n return x === y;\\n};\"], [65099, 6.1224, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n // Step 1: Initialize Variables\\n let size = s.length;\\n let X = size - 2;\\n let x = 0, y = 0;\\n\\n // Step 2: Compute Alternating Sum Using Binomial Coefficients\\n for (let j = 0; j <= X; j++) {\\n let coeff = binomialMod10(X, j);\\n x = (x + coeff * (s.charCodeAt(j) - '0'.charCodeAt(0))) % 10;\\n y = (y + coeff * (s.charCodeAt(j + 1) - '0'.charCodeAt(0))) % 10;\\n }\\n\\n // Step 3: Compare Alternating Sums\\n return x === y;\\n};\\n\\n// Step 4: Compute Binomial Coefficient Modulo 10\\nvar binomialMod10 = function (n, k) {\\n let i = binomialMod2(n, k);\\n let j = binomialMod5(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x;\\n }\\n }\\n return 0;\\n};\\n\\n// Step 5: Compute Binomial Coefficient Modulo 2\\nvar binomialMod2 = function (n, k) {\\n return ((n & k) === k) ? 1 : 0;\\n};\\n\\n// Step 6: Compute Binomial Coefficient Modulo 5 Using Lookup Table\\nvar binomialMod5 = function (n, k) {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ];\\n let result = 1;\\n\\n while (n > 0 || k > 0) {\\n let nthd = n % 5;\\n let kthd = k % 5;\\n\\n if (kthd > nthd) return 0;\\n\\n result = (result * tuples[nthd][kthd]) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return result;\\n};\"], [65200, 4.0816, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nconst hasSameDigits = s => {\\n let x = 0\\n let y = 0\\n const offset = '0'.charCodeAt(0)\\n for (let i = 0; i <= s.length - 2; i++) {\\n let coeff = binmodten(s.length - 2, i)\\n x = (x + coeff * (s.charCodeAt(i) - offset)) % 10\\n y = (y + coeff * (s.charCodeAt(i + 1) - offset)) % 10\\n }\\n return x === y\\n};\\nconst binmodten = (n, k) => {\\n const i = ((n & k) === k) ? 1 : 0\\n\\n const mfive = (n, k) => {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ]\\n let result = 1\\n\\n while (n > 0 || k > 0) {\\n let nf = n % 5\\n let kf = k % 5\\n\\n if (kf > nf) return 0\\n\\n result = (result * tuples[nf][kf]) % 5\\n n = Math.floor(n / 5)\\n k = Math.floor(k / 5)\\n }\\n return result;\\n };\\n let j = mfive(n, k)\\n \\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x\\n }\\n }\\n return 0;\\n};\"], [65300, 12.2449, \"var hasSameDigits = function (s) {\\n // Step 1: Initialize Variables\\n let size = s.length;\\n let X = size - 2;\\n let x = 0, y = 0;\\n\\n // Step 2: Compute Alternating Sum Using Binomial Coefficients\\n for (let j = 0; j <= X; j++) {\\n let coeff = binomialMod10(X, j);\\n x = (x + coeff * (s.charCodeAt(j) - '0'.charCodeAt(0))) % 10;\\n y = (y + coeff * (s.charCodeAt(j + 1) - '0'.charCodeAt(0))) % 10;\\n }\\n\\n // Step 3: Compare Alternating Sums\\n return x === y;\\n};\\n\\n// Step 4: Compute Binomial Coefficient Modulo 10\\nvar binomialMod10 = function (n, k) {\\n let i = binomialMod2(n, k);\\n let j = binomialMod5(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x;\\n }\\n }\\n return 0;\\n};\\n\\n// Step 5: Compute Binomial Coefficient Modulo 2\\nvar binomialMod2 = function (n, k) {\\n return ((n & k) === k) ? 1 : 0;\\n};\\n\\n// Step 6: Compute Binomial Coefficient Modulo 5 Using Lookup Table\\nvar binomialMod5 = function (n, k) {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ];\\n let result = 1;\\n\\n while (n > 0 || k > 0) {\\n let nthd = n % 5;\\n let kthd = k % 5;\\n\\n if (kthd > nthd) return 0;\\n\\n result = (result * tuples[nthd][kthd]) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return result;\\n};\"], [65400, 12.2449, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nconst hasSameDigits = s => {\\n let x = 0\\n let y = 0\\n const offset = '0'.charCodeAt(0)\\n for (let i = 0; i <= s.length - 2; i++) {\\n let coeff = binmodten(s.length - 2, i)\\n x = (x + coeff * (s.charCodeAt(i) - offset)) % 10\\n y = (y + coeff * (s.charCodeAt(i + 1) - offset)) % 10\\n }\\n return x === y\\n}\\nconst binmodten = (n, k) => {\\n const i = ((n & k) === k) ? 1 : 0\\n\\n const mfive = (n, k) => {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ]\\n let result = 1\\n\\n while (n > 0 || k > 0) {\\n let nf = n % 5\\n let kf = k % 5\\n\\n if (kf > nf) return 0\\n\\n result = (result * tuples[nf][kf]) % 5\\n n = Math.floor(n / 5)\\n k = Math.floor(k / 5)\\n }\\n return result\\n }\\n let j = mfive(n, k)\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x\\n }\\n }\\n return 0;\\n}\"], [65500, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n\\n let n = s.length;\\n let x = 0, y = 0;\\n\\n // Compute alternating sums using binomial properties mod 10\\n for (let i = 0; i < n - 1; i++) {\\n let coeff = binomialMod10(n - 2, i);\\n x = (x + coeff * (s.charCodeAt(i) - 48)) % 10;\\n y = (y + coeff * (s.charCodeAt(i + 1) - 48)) % 10;\\n }\\n\\n return x === y;\\n};\\n\\n// Compute binomial coefficient modulo 10\\nvar binomialMod10 = function (n, k) {\\n let mod2 = binomialMod2(n, k);\\n let mod5 = binomialMod5(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === mod2 && x % 5 === mod5) {\\n return x;\\n }\\n }\\n return 0;\\n};\\n\\n// Compute binomial coefficient modulo 2\\nvar binomialMod2 = function (n, k) {\\n return ((n & k) === k) ? 1 : 0;\\n};\\n\\n// Compute binomial coefficient modulo 5 using lookup table\\nvar binomialMod5 = function (n, k) {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ];\\n let result = 1;\\n\\n while (n > 0 || k > 0) {\\n let nthd = n % 5;\\n let kthd = k % 5;\\n\\n if (kthd > nthd) return 0;\\n\\n result = (result * tuples[nthd][kthd]) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return result;\\n};\"], [65600, 6.1224, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n let x = 0, y = 0;\\n for (let j = 0; j <= s.length - 2; j++) {\\n let coeff = binmodten(s.length - 2, j);\\n x = (x + coeff * (s.charCodeAt(j) - '0'.charCodeAt(0))) % 10;\\n y = (y + coeff * (s.charCodeAt(j + 1) - '0'.charCodeAt(0))) % 10;\\n }\\n return x === y;\\n };\\nconst binmodten = function (n, k) {\\n let i = ((n & k) === k) ? 1 : 0;\\n\\n const mfive = function (n, k) {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ];\\n let result = 1;\\n\\n while (n > 0 || k > 0) {\\n let nthd = n % 5;\\n let kthd = k % 5;\\n\\n if (kthd > nthd) return 0;\\n\\n result = (result * tuples[nthd][kthd]) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return result;\\n };\\n let j = mfive(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x;\\n }\\n }\\n return 0;\\n};\"], [66300, 2.0408, \"const hasSameDigits = s => {\\n const binomMod5 = (n, r) => {\\n const table = [\\n [1, 0, 0, 0, 0],\\n [1, 1, 0, 0, 0],\\n [1, 2, 1, 0, 0],\\n [1, 3, 3, 1, 0],\\n [1, 4, 1, 4, 1]\\n ];\\n let res = 1;\\n while (n || r) {\\n const n_digit = n % 5;\\n const r_digit = r % 5;\\n if (r_digit > n_digit) return 0;\\n res = (res * table[n_digit][r_digit]) % 5;\\n n = Math.floor(n / 5);\\n r = Math.floor(r / 5);\\n }\\n return res;\\n };\\n\\n const binomMod10 = (k, j) => {\\n const r2 = ((j & ~k) === 0) ? 1 : 0;\\n const r5 = binomMod5(k, j);\\n return (5 * r2 + 6 * r5) % 10;\\n };\\n\\n const n = s.length;\\n const k = n - 2;\\n let x = 0;\\n let y = 0;\\n\\n for (let j = 0; j <= k; j++) {\\n const c = binomMod10(k, j);\\n x = (x + c * (s[j] - '0')) % 10;\\n y = (y + c * (s[j + 1] - '0')) % 10;\\n }\\n\\n return x === y;\\n};\"], [69900, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n const n = s.length;\\n const N = n - 2; \\n const invN = ~N; \\n\\n const a = Array(n);\\n for (let i = 0; i < n; i++) {\\n a[i] = s.charCodeAt(i) - 48;\\n }\\n\\n const d2 = new Uint8Array(N + 1);\\n const d5 = new Uint8Array(N + 1);\\n for (let i = 0; i <= N; i++) {\\n const diff = a[i] - a[i + 1];\\n d2[i] = ((diff % 2) + 2) & 1; \\n let m5 = diff % 5;\\n if (m5 < 0) m5 += 5;\\n d5[i] = m5; \\n }\\n\\n let s2 = 0;\\n for (let i = 0; i <= N; i++) {\\n if ((i & invN) === 0) {\\n s2 ^= d2[i];\\n }\\n }\\n if (s2 !== 0) return false;\\n\\n const N5 = [];\\n for (let t = N; t > 0; t = Math.floor(t / 5)) {\\n N5.push(t % 5);\\n }\\n const D = N5.length; \\n const comb5 = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1],\\n ];\\n\\n const digits5 = new Uint8Array(D);\\n let s5 = 0;\\n for (let i = 0; i <= N; i++) {\\n let c = 1;\\n for (let j = 0; j < D; j++) {\\n const ij = digits5[j], Nj = N5[j];\\n if (ij > Nj) { c = 0; break; }\\n c = (c * comb5[Nj][ij]) % 5;\\n }\\n s5 = (s5 + c * d5[i]) % 5;\\n\\n for (let j = 0; j < D; j++) {\\n digits5[j]++;\\n if (digits5[j] < 5) break;\\n digits5[j] = 0;\\n }\\n }\\n return s5 === 0;\\n};\"]]",
"runtime": 243,
"runtimeDistribution": "[[32, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n const N = s.length;\\n const n = N - 2;\\n // Precompute the small 5\\u00d75 binomial table mod 5\\n const C5 = [\\n [1],\\n [1,1],\\n [1,2,1],\\n [1,3,3,1],\\n [1,4,1,4,1] // note: 6 mod 5 = 1\\n ];\\n\\n // Turn string into digit array\\n const a = new Uint8Array(N);\\n for (let i = 0; i < N; i++) {\\n a[i] = s.charCodeAt(i) - 48;\\n }\\n\\n // 1) Check D mod 2 == 0\\n let sum2 = 0;\\n for (let i = 0; i <= n; i++) {\\n // binom(n,i) mod 2 is 1 iff no carry bits in i + (n-i)\\n if ((i & (n - i)) === 0) {\\n // (a[i] - a[i+1]) mod 2 === a[i] xor a[i+1]\\n sum2 ^= (a[i] ^ a[i+1]);\\n }\\n }\\n if ((sum2 & 1) !== 0) return false;\\n\\n // 2) Check D mod 5 == 0\\n let sum5 = 0;\\n for (let i = 0; i <= n; i++) {\\n // compute binom(n,i) mod 5 via Lucas\\n let x = n, y = i, coeff = 1;\\n while (x > 0 || y > 0) {\\n const nd = x % 5, id = y % 5;\\n if (id > nd) { coeff = 0; break; }\\n coeff = (coeff * C5[nd][id]) % 5;\\n x = Math.floor(x / 5);\\n y = Math.floor(y / 5);\\n }\\n if (coeff !== 0) {\\n // (a[i] - a[i+1]) mod 5, in [0..4]\\n const diff = (a[i] + 5 - a[i+1]) % 5;\\n sum5 = (sum5 + coeff * diff) % 5;\\n }\\n }\\n return sum5 === 0;\\n};\"], [47, 2.0408, \" \\n function choose2(n, k) {\\n return ((n - k) & k) === 0 ? 1 : 0;\\n} function quickChoose5(n, k) {\\n const K = k;\\n let j = n - k;\\n let acc = 1;\\n while (j || k) {\\n const jj = j % 5,\\n kk = k % 5;\\n if (jj + kk >= 5) {\\n return 0;\\n }\\n if (jj === 2 && kk === 2) {\\n } else {\\n acc *= 1 + jj * kk;\\n }\\n acc %= 5;\\n j = Math.floor(j / 5);\\n k = Math.floor(k / 5);\\n }\\n return acc;\\n} function hasSameDigits(s) {\\n const n = s.length - 2;\\n\\n // mod 2\\n let left = 0;\\n let right = 0;\\n for (let i = 0; i <= n; i++) {\\n const c = choose2(n, i);\\n left += c * s[i];\\n right += c * s[i + 1];\\n }\\n left %= 2;\\n right %= 2;\\n if (left !== right) {\\n return false;\\n }\\n // mod 5\\n left = 0;\\n right = 0;\\n for (let i = 0; i <= n; i++) {\\n const c = quickChoose5(n, i);\\n left += c * s[i];\\n right += c * s[i + 1];\\n left %= 5;\\n right %= 5;\\n }\\n return left === right;\\n} \"], [55, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n const n = s.length;\\n // Conforme enunciado, n >= 3\\n if(n < 3) return false;\\n \\n const N = n - 2; // Precisamos dos coeficientes da linha (n-2) do tri\\u00e2ngulo de Pascal.\\n \\n // Precompute small binomials mod 5 para x=0..4.\\n // smallBinom[x][y] = binom(x, y) mod 5.\\n const smallBinom = [\\n [1], // 0: binom(0,0)=1\\n [1, 1], // 1: 1,1\\n [1, 2, 1], // 2: 1,2,1\\n [1, 3, 3, 1], // 3: 1,3,3,1\\n [1, 4, 1, 4, 1] // 4: 1,4,6 mod5=1,4,1\\n ];\\n \\n // Fun\\u00e7\\u00e3o que computa binom(N, i) mod2, usando a propriedade de subm\\u00e1scara.\\n function binomMod2(N, i) {\\n return ((N & i) === i) ? 1 : 0;\\n }\\n \\n // Fun\\u00e7\\u00e3o que computa binom(N, i) mod5 via Lucas.\\n // Aqui N e i s\\u00e3o n\\u00fameros inteiros.\\n function binomMod5(N, i) {\\n let res = 1;\\n while (N > 0 || i > 0) {\\n const nDigit = N % 5;\\n const iDigit = i % 5;\\n if (iDigit > nDigit) return 0;\\n res = (res * smallBinom[nDigit][iDigit]) % 5;\\n N = Math.floor(N / 5);\\n i = Math.floor(i / 5);\\n }\\n return res;\\n }\\n \\n // Para cada i de 0 a N, computamos binom(N, i) mod 10 via CRT:\\n // Como 10 = 2 * 5 e os inversos s\\u00e3o:\\n // inv(5 mod 2) = 1 e inv(2 mod 5) = 3, a f\\u00f3rmula \\u00e9:\\n // result = (5 * binomMod2 + 6 * binomMod5) mod 10.\\n let sumMod = 0;\\n for (let i = 0; i <= N; i++) {\\n const a = binomMod2(N, i); // 0 ou 1\\n const b = binomMod5(N, i); // valor em {0,1,2,3,4}\\n const coef = (5 * a + 6 * b) % 10; // binom(N, i) mod 10.\\n // Diferen\\u00e7a entre d\\u00edgitos consecutivos: s[i] - s[i+1]\\n let diff = (s.charCodeAt(i) - 48) - (s.charCodeAt(i+1) - 48);\\n diff = ((diff % 10) + 10) % 10; // ajustar para [0,9]\\n sumMod = (sumMod + coef * diff) % 10;\\n }\\n \\n return sumMod === 0;\\n};\\n\"], [60, 2.0408, \"function hasSameDigits(s) {\\n function cal(a, mod) {\\n let count = 0;\\n while (a > 0 && a % mod === 0) {\\n count++;\\n a = Math.floor(a / mod);\\n }\\n return [a % mod, count];\\n }\\n\\n function test(mod) {\\n let n = s.length;\\n let res = 0;\\n let r = 1;\\n let c = 0;\\n\\n for (let i = 0; i < n - 1; i++) {\\n if (c === 0) {\\n res += r * (parseInt(s[i]) - parseInt(s[i + 1]));\\n }\\n\\n let [rr, cc] = cal(n - 2 - i, mod);\\n r = (r * rr) % mod;\\n c += cc;\\n\\n [rr, cc] = cal(i + 1, mod);\\n r = (r * modInverse(rr, mod)) % mod;\\n c -= cc;\\n }\\n return res % mod === 0;\\n }\\n\\n function modInverse(x, mod) {\\n return powerMod(x, mod - 2, mod);\\n }\\n\\n function powerMod(x, y, mod) {\\n let result = 1;\\n while (y > 0) {\\n if (y % 2 === 1) {\\n result = (result * x) % mod;\\n }\\n x = (x * x) % mod;\\n y = Math.floor(y / 2);\\n }\\n return result;\\n }\\n\\n return test(2) && test(5);\\n}\"], [62, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n\\n let n = s.length;\\n let x = 0, y = 0;\\n\\n // Compute alternating sums using binomial properties mod 10\\n for (let i = 0; i < n - 1; i++) {\\n let coeff = binomialMod10(n - 2, i);\\n x = (x + coeff * (s.charCodeAt(i) - 48)) % 10;\\n y = (y + coeff * (s.charCodeAt(i + 1) - 48)) % 10;\\n }\\n\\n return x === y;\\n};\\n\\n// Compute binomial coefficient modulo 10\\nvar binomialMod10 = function (n, k) {\\n let mod2 = binomialMod2(n, k);\\n let mod5 = binomialMod5(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === mod2 && x % 5 === mod5) {\\n return x;\\n }\\n }\\n return 0;\\n};\\n\\n// Compute binomial coefficient modulo 2\\nvar binomialMod2 = function (n, k) {\\n return ((n & k) === k) ? 1 : 0;\\n};\\n\\n// Compute binomial coefficient modulo 5 using lookup table\\nvar binomialMod5 = function (n, k) {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ];\\n let result = 1;\\n\\n while (n > 0 || k > 0) {\\n let nthd = n % 5;\\n let kthd = k % 5;\\n\\n if (kthd > nthd) return 0;\\n\\n result = (result * tuples[nthd][kthd]) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return result;\\n};\"], [66, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n function cal(a, mod) {\\n let count = 0;\\n while (a > 0 && a % mod === 0) {\\n count++;\\n a = Math.floor(a / mod);\\n }\\n return [a % mod, count];\\n }\\n\\n function test(mod) {\\n const n = s.length;\\n let res = 0;\\n let r = 1;\\n let c = 0;\\n\\n for (let i = 0; i < n - 1; i++) {\\n if (c === 0) {\\n \\n res += r * (parseInt(s[i]) - parseInt(s[i + 1]));\\n res %= mod;\\n }\\n\\n let [rr, cc] = cal(n - 2 - i, mod);\\n r = (r * rr) % mod;\\n c += cc;\\n\\n [rr, cc] = cal(i + 1, mod);\\n r = (r * modInverse(rr, mod)) % mod;\\n c -= cc;\\n }\\n\\n return res % mod === 0;\\n }\\n\\n function modInverse(x, mod) {\\n return powerMod(x, mod - 2, mod);\\n }\\n\\n function powerMod(x, y, mod) {\\n let result = 1;\\n x %= mod;\\n while (y > 0) {\\n if (y % 2 === 1) {\\n result = (result * x) % mod;\\n }\\n x = (x * x) % mod;\\n y = Math.floor(y / 2);\\n }\\n return result;\\n }\\n\\n return test(2) && test(5);\\n};\\n\"], [67, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n // Step 1: Initialize Variables\\n let size = s.length;\\n let X = size - 2;\\n let x = 0, y = 0;\\n\\n // Step 2: Compute Alternating Sum Using Binomial Coefficients\\n for (let j = 0; j <= X; j++) {\\n let coeff = binomialMod10(X, j);\\n x = (x + coeff * (s.charCodeAt(j) - '0'.charCodeAt(0))) % 10;\\n y = (y + coeff * (s.charCodeAt(j + 1) - '0'.charCodeAt(0))) % 10;\\n }\\n\\n // Step 3: Compare Alternating Sums\\n return x === y;\\n};\\n\\n// Step 4: Compute Binomial Coefficient Modulo 10\\nvar binomialMod10 = function (n, k) {\\n let i = binomialMod2(n, k);\\n let j = binomialMod5(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x;\\n }\\n }\\n return 0;\\n};\\n\\n// Step 5: Compute Binomial Coefficient Modulo 2\\nvar binomialMod2 = function (n, k) {\\n return ((n & k) === k) ? 1 : 0;\\n};\\n\\n// Step 6: Compute Binomial Coefficient Modulo 5 Using Lookup Table\\nvar binomialMod5 = function (n, k) {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ];\\n let result = 1;\\n\\n while (n > 0 || k > 0) {\\n let nthd = n % 5;\\n let kthd = k % 5;\\n\\n if (kthd > nthd) return 0;\\n\\n result = (result * tuples[nthd][kthd]) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return result;\\n};\"], [70, 4.0816, \"var hasSameDigits = function (s) {\\n // Step 1: Initialize Variables\\n let size = s.length;\\n let X = size - 2;\\n let x = 0, y = 0;\\n\\n // Step 2: Compute Alternating Sum Using Binomial Coefficients\\n for (let j = 0; j <= X; j++) {\\n let coeff = binomialMod10(X, j);\\n x = (x + coeff * (s.charCodeAt(j) - '0'.charCodeAt(0))) % 10;\\n y = (y + coeff * (s.charCodeAt(j + 1) - '0'.charCodeAt(0))) % 10;\\n }\\n\\n // Step 3: Compare Alternating Sums\\n return x === y;\\n};\\n\\n// Step 4: Compute Binomial Coefficient Modulo 10\\nvar binomialMod10 = function (n, k) {\\n let i = binomialMod2(n, k);\\n let j = binomialMod5(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x;\\n }\\n }\\n return 0;\\n};\\n\\n// Step 5: Compute Binomial Coefficient Modulo 2\\nvar binomialMod2 = function (n, k) {\\n return ((n & k) === k) ? 1 : 0;\\n};\\n\\n// Step 6: Compute Binomial Coefficient Modulo 5 Using Lookup Table\\nvar binomialMod5 = function (n, k) {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ];\\n let result = 1;\\n\\n while (n > 0 || k > 0) {\\n let nthd = n % 5;\\n let kthd = k % 5;\\n\\n if (kthd > nthd) return 0;\\n\\n result = (result * tuples[nthd][kthd]) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return result;\\n};\"], [72, 4.0816, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n // Step 1: Initialize Variables\\n let size = s.length;\\n let X = size - 2;\\n let x = 0, y = 0;\\n\\n // Step 2: Compute Alternating Sum Using Binomial Coefficients\\n for (let j = 0; j <= X; j++) {\\n let coeff = binomialMod10(X, j);\\n x = (x + coeff * (s.charCodeAt(j) - '0'.charCodeAt(0))) % 10;\\n y = (y + coeff * (s.charCodeAt(j + 1) - '0'.charCodeAt(0))) % 10;\\n }\\n\\n // Step 3: Compare Alternating Sums\\n return x === y;\\n};\\n\\n// Step 4: Compute Binomial Coefficient Modulo 10\\nvar binomialMod10 = function (n, k) {\\n let i = binomialMod2(n, k);\\n let j = binomialMod5(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x;\\n }\\n }\\n return 0;\\n};\\n\\n// Step 5: Compute Binomial Coefficient Modulo 2\\nvar binomialMod2 = function (n, k) {\\n return ((n & k) === k) ? 1 : 0;\\n};\\n\\n// Step 6: Compute Binomial Coefficient Modulo 5 Using Lookup Table\\nvar binomialMod5 = function (n, k) {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ];\\n let result = 1;\\n\\n while (n > 0 || k > 0) {\\n let nthd = n % 5;\\n let kthd = k % 5;\\n\\n if (kthd > nthd) return 0;\\n\\n result = (result * tuples[nthd][kthd]) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return result;\\n};\"], [73, 6.1224, \"var hasSameDigits = function (s) {\\n // Step 1: Initialize Variables\\n let size = s.length;\\n let X = size - 2;\\n let x = 0, y = 0;\\n\\n // Step 2: Compute Alternating Sum Using Binomial Coefficients\\n for (let j = 0; j <= X; j++) {\\n let coeff = binomialMod10(X, j);\\n x = (x + coeff * (s.charCodeAt(j) - '0'.charCodeAt(0))) % 10;\\n y = (y + coeff * (s.charCodeAt(j + 1) - '0'.charCodeAt(0))) % 10;\\n }\\n\\n // Step 3: Compare Alternating Sums\\n return x === y;\\n};\\n\\n// Step 4: Compute Binomial Coefficient Modulo 10\\nvar binomialMod10 = function (n, k) {\\n let i = binomialMod2(n, k);\\n let j = binomialMod5(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x;\\n }\\n }\\n return 0;\\n};\\n\\n// Step 5: Compute Binomial Coefficient Modulo 2\\nvar binomialMod2 = function (n, k) {\\n return ((n & k) === k) ? 1 : 0;\\n};\\n\\n// Step 6: Compute Binomial Coefficient Modulo 5 Using Lookup Table\\nvar binomialMod5 = function (n, k) {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ];\\n let result = 1;\\n\\n while (n > 0 || k > 0) {\\n let nthd = n % 5;\\n let kthd = k % 5;\\n\\n if (kthd > nthd) return 0;\\n\\n result = (result * tuples[nthd][kthd]) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return result;\\n};\"], [74, 8.1633, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nconst hasSameDigits = s => {\\n let x = 0\\n let y = 0\\n const offset = '0'.charCodeAt(0)\\n for (let i = 0; i <= s.length - 2; i++) {\\n let coeff = binmodten(s.length - 2, i)\\n x = (x + coeff * (s.charCodeAt(i) - offset)) % 10\\n y = (y + coeff * (s.charCodeAt(i + 1) - offset)) % 10\\n }\\n return x === y\\n}\\nconst binmodten = (n, k) => {\\n const i = ((n & k) === k) ? 1 : 0\\n\\n const mfive = (n, k) => {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ]\\n let result = 1\\n\\n while (n > 0 || k > 0) {\\n let nf = n % 5\\n let kf = k % 5\\n\\n if (kf > nf) return 0\\n\\n result = (result * tuples[nf][kf]) % 5\\n n = Math.floor(n / 5)\\n k = Math.floor(k / 5)\\n }\\n return result\\n }\\n let j = mfive(n, k)\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x\\n }\\n }\\n return 0;\\n}\"], [75, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\n;\\nvar hasSameDigits = function (s) {\\n // Step 1: Initialize Variables\\n let size = s.length;\\n let X = size - 2;\\n let x = 0, y = 0;\\n\\n // Step 2: Compute Alternating Sum Using Binomial Coefficients\\n for (let j = 0; j <= X; j++) {\\n let coeff = binomialMod10(X, j);\\n x = (x + coeff * (s.charCodeAt(j) - '0'.charCodeAt(0))) % 10;\\n y = (y + coeff * (s.charCodeAt(j + 1) - '0'.charCodeAt(0))) % 10;\\n }\\n\\n // Step 3: Compare Alternating Sums\\n return x === y;\\n};\\n\\n// Step 4: Compute Binomial Coefficient Modulo 10\\nvar binomialMod10 = function (n, k) {\\n let i = ((n & k) === k) ? 1 : 0;\\n\\nvar binomialMod5 = function (n, k) {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ];\\n let result = 1;\\n\\n while (n > 0 || k > 0) {\\n let nthd = n % 5;\\n let kthd = k % 5;\\n\\n if (kthd > nthd) return 0;\\n\\n result = (result * tuples[nthd][kthd]) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return result;\\n};\\n let j = binomialMod5(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x;\\n }\\n }\\n return 0;\\n};\"], [76, 6.1224, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\n;\\nvar hasSameDigits = function (s) {\\n // Step 1: Initialize Variables\\n let size = s.length;\\n let X = size - 2;\\n let x = 0, y = 0;\\n\\n // Step 2: Compute Alternating Sum Using Binomial Coefficients\\n for (let j = 0; j <= X; j++) {\\n let coeff = binomialMod10(X, j);\\n x = (x + coeff * (s.charCodeAt(j) - '0'.charCodeAt(0))) % 10;\\n y = (y + coeff * (s.charCodeAt(j + 1) - '0'.charCodeAt(0))) % 10;\\n }\\n\\n // Step 3: Compare Alternating Sums\\n return x === y;\\n};\\n\\n// Step 4: Compute Binomial Coefficient Modulo 10\\nvar binomialMod10 = function (n, k) {\\n let i = binomialMod2(n, k);\\n let j = binomialMod5(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x;\\n }\\n }\\n return 0;\\n};\\n\\n// Step 5: Compute Binomial Coefficient Modulo 2\\nvar binomialMod2 = function (n, k) {\\n return ((n & k) === k) ? 1 : 0;\\n};\\n\\nvar binomialMod5 = function (n, k) {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ];\\n let result = 1;\\n\\n while (n > 0 || k > 0) {\\n let nthd = n % 5;\\n let kthd = k % 5;\\n\\n if (kthd > nthd) return 0;\\n\\n result = (result * tuples[nthd][kthd]) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return result;\\n};\\n\"], [77, 8.1633, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n let x = 0, y = 0;\\n for (let j = 0; j <= s.length - 2; j++) {\\n let coeff = binmodten(s.length - 2, j);\\n x = (x + coeff * (s.charCodeAt(j) - '0'.charCodeAt(0))) % 10;\\n y = (y + coeff * (s.charCodeAt(j + 1) - '0'.charCodeAt(0))) % 10;\\n }\\n return x === y;\\n };\\nconst binmodten = function (n, k) {\\n let i = ((n & k) === k) ? 1 : 0;\\n\\n const mfive = function (n, k) {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ];\\n let result = 1;\\n\\n while (n > 0 || k > 0) {\\n let nthd = n % 5;\\n let kthd = k % 5;\\n\\n if (kthd > nthd) return 0;\\n\\n result = (result * tuples[nthd][kthd]) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return result;\\n };\\n let j = mfive(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x;\\n }\\n }\\n return 0;\\n};\"], [78, 4.0816, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function (s) {\\n // Step 1: Initialize Variables\\n let size = s.length;\\n let X = size - 2;\\n let x = 0, y = 0;\\n\\n // Step 2: Compute Alternating Sum Using Binomial Coefficients\\n for (let j = 0; j <= X; j++) {\\n let coeff = binomialMod10(X, j);\\n x = (x + coeff * (s.charCodeAt(j) - '0'.charCodeAt(0))) % 10;\\n y = (y + coeff * (s.charCodeAt(j + 1) - '0'.charCodeAt(0))) % 10;\\n }\\n\\n // Step 3: Compare Alternating Sums\\n return x === y;\\n};\\n\\n// Step 4: Compute Binomial Coefficient Modulo 10\\nvar binomialMod10 = function (n, k) {\\n let i = binomialMod2(n, k);\\n let j = binomialMod5(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x;\\n }\\n }\\n return 0;\\n};\\n\\n// Step 5: Compute Binomial Coefficient Modulo 2\\nvar binomialMod2 = function (n, k) {\\n return ((n & k) === k) ? 1 : 0;\\n};\\n\\n// Step 6: Compute Binomial Coefficient Modulo 5 Using Lookup Table\\nvar binomialMod5 = function (n, k) {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ];\\n let result = 1;\\n\\n while (n > 0 || k > 0) {\\n let nthd = n % 5;\\n let kthd = k % 5;\\n\\n if (kthd > nthd) return 0;\\n\\n result = (result * tuples[nthd][kthd]) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return result;\\n};\"], [80, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\n;\\nvar hasSameDigits = function (s) {\\n // Step 1: Initialize Variables\\n let size = s.length;\\n let X = size - 2;\\n let x = 0, y = 0;\\n\\n // Step 2: Compute Alternating Sum Using Binomial Coefficients\\n for (let j = 0; j <= X; j++) {\\n let coeff = binomialMod10(X, j);\\n x = (x + coeff * (s.charCodeAt(j) - '0'.charCodeAt(0))) % 10;\\n y = (y + coeff * (s.charCodeAt(j + 1) - '0'.charCodeAt(0))) % 10;\\n }\\n\\n // Step 3: Compare Alternating Sums\\n return x === y;\\n};\\n\\n// Step 4: Compute Binomial Coefficient Modulo 10\\nvar binomialMod10 = function (n, k) {\\n let i = ((n & k) === k) ? 1 : 0;\\n\\n var binomialMod5 = function (n, k) {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ];\\n let result = 1;\\n\\n while (n > 0 || k > 0) {\\n let nthd = n % 5;\\n let kthd = k % 5;\\n\\n if (kthd > nthd) return 0;\\n\\n result = (result * tuples[nthd][kthd]) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return result;\\n };\\n let j = binomialMod5(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x;\\n }\\n }\\n return 0;\\n};\"], [81, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nconst hasSameDigits = s => {\\n let x = 0\\n let y = 0\\n const offset = '0'.charCodeAt(0)\\n for (let i = 0; i <= s.length - 2; i++) {\\n let coeff = binmodten(s.length - 2, i)\\n x = (x + coeff * (s.charCodeAt(i) - offset)) % 10\\n y = (y + coeff * (s.charCodeAt(i + 1) - offset)) % 10\\n }\\n return x === y\\n};\\nconst binmodten = (n, k) => {\\n const i = ((n & k) === k) ? 1 : 0\\n\\n const mfive = (n, k) => {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ]\\n let result = 1\\n\\n while (n > 0 || k > 0) {\\n let nf = n % 5\\n let kf = k % 5\\n\\n if (kf > nf) return 0\\n\\n result = (result * tuples[nf][kf]) % 5\\n n = Math.floor(n / 5)\\n k = Math.floor(k / 5)\\n }\\n return result;\\n };\\n let j = mfive(n, k)\\n \\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x\\n }\\n }\\n return 0;\\n};\"], [82, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nconst hasSameDigits = s => {\\n let x = 0\\n let y = 0\\n const offset = '0'.charCodeAt(0)\\n for (let i = 0; i <= s.length - 2; i++) {\\n let coeff = binmodten(s.length - 2, i)\\n x = (x + coeff * (s.charCodeAt(i) - offset)) % 10\\n y = (y + coeff * (s.charCodeAt(i + 1) - offset)) % 10\\n }\\n return x === y\\n};\\nconst binmodten = (n, k) => {\\n const i = ((n & k) === k) ? 1 : 0\\n\\n const mfive = (n, k) => {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ]\\n let result = 1\\n\\n while (n > 0 || k > 0) {\\n let nf = n % 5\\n let kf = k % 5\\n\\n if (kf > nf) return 0\\n\\n result = (result * tuples[nf][kf]) % 5\\n n = Math.floor(n / 5)\\n k = Math.floor(k / 5)\\n }\\n return result;\\n };\\n let j = mfive(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x;\\n }\\n }\\n return 0;\\n};\"], [83, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nconst hasSameDigits = s => {\\n let x = 0\\n let y = 0\\n const offset = '0'.charCodeAt(0)\\n for (let i = 0; i <= s.length - 2; i++) {\\n let coeff = binmodten(s.length - 2, i)\\n x = (x + coeff * (s.charCodeAt(i) - offset)) % 10\\n y = (y + coeff * (s.charCodeAt(i + 1) - offset)) % 10\\n }\\n return x === y\\n};\\nconst binmodten = (n, k) => {\\n let i = ((n & k) === k) ? 1 : 0\\n\\n const mfive = (n, k) => {\\n const tuples = [\\n [1],\\n [1, 1],\\n [1, 2, 1],\\n [1, 3, 3, 1],\\n [1, 4, 1, 4, 1]\\n ]\\n let result = 1\\n\\n while (n > 0 || k > 0) {\\n let nf = n % 5\\n let kf = k % 5\\n\\n if (kf > nf) return 0\\n\\n result = (result * tuples[nf][kf]) % 5\\n n = Math.floor(n / 5)\\n k = Math.floor(k / 5)\\n }\\n return result;\\n };\\n let j = mfive(n, k);\\n\\n for (let x = 0; x < 10; x++) {\\n if (x % 2 === i && x % 5 === j) {\\n return x;\\n }\\n }\\n return 0;\\n};\"], [84, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n const n = s.length;\\n if (n < 2) return false;\\n if (n === 2) return s[0] === s[1];\\n\\n const a = new Array(n);\\n for (let i = 0; i < n; i++) {\\n a[i] = s.charCodeAt(i) - 48;\\n }\\n\\n const m = n - 2;\\n const mod2 = new Array(m + 1);\\n for (let i = 0; i <= m; i++) {\\n mod2[i] = ((i & (m - i)) === 0) ? 1 : 0;\\n }\\n const C5tbl = [\\n [1], \\n [1,1], \\n [1,2,1], \\n [1,3,3,1], \\n [1,4,1,4,1] \\n ];\\n const m5digits = [];\\n for (let x = m; x > 0; x = Math.floor(x/5)) {\\n m5digits.push(x % 5);\\n }\\n const L = m5digits.length;\\n const C10 = new Array(m + 1);\\n for (let i = 0; i <= m; i++) {\\n let c5 = 1, x = i;\\n for (let d = 0; d < L; d++) {\\n const id = x % 5,\\n nd = m5digits[d];\\n if (id > nd) { c5 = 0; break; }\\n c5 = (c5 * C5tbl[nd][id]) % 5;\\n x = Math.floor(x/5);\\n }\\n const c2 = mod2[i];\\n let c10 = c5;\\n if ((c10 & 1) !== c2) {\\n c10 = (c10 + 5) % 10;\\n }\\n C10[i] = c10;\\n }\\n let d0 = 0, d1 = 0;\\n for (let i = 0; i <= m; i++) {\\n d0 = (d0 + a[i] * C10[i]) % 10;\\n d1 = (d1 + a[i+1] * C10[i]) % 10;\\n }\\n\\n return d0 === d1;\\n};\\n\"], [85, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nconst hasSameDigits = s => {\\n const binomMod5 = (n, r) => {\\n const table = [\\n [1, 0, 0, 0, 0],\\n [1, 1, 0, 0, 0],\\n [1, 2, 1, 0, 0],\\n [1, 3, 3, 1, 0],\\n [1, 4, 1, 4, 1]\\n ];\\n let res = 1;\\n while (n || r) {\\n const n_digit = n % 5;\\n const r_digit = r % 5;\\n if (r_digit > n_digit) return 0;\\n res = (res * table[n_digit][r_digit]) % 5;\\n n = Math.floor(n / 5);\\n r = Math.floor(r / 5);\\n }\\n return res;\\n };\\n\\n const binomMod10 = (k, j) => {\\n const r2 = ((j & ~k) === 0) ? 1 : 0;\\n const r5 = binomMod5(k, j);\\n return (5 * r2 + 6 * r5) % 10;\\n };\\n\\n const n = s.length;\\n const k = n - 2;\\n let x = 0;\\n let y = 0;\\n\\n for (let j = 0; j <= k; j++) {\\n const c = binomMod10(k, j);\\n x = (x + c * (s[j] - '0')) % 10;\\n y = (y + c * (s[j + 1] - '0')) % 10;\\n }\\n\\n return x === y;\\n};\"], [86, 2.0408, \"const hasSameDigits = s => {\\n const binomMod5 = (n, r) => {\\n const table = [\\n [1, 0, 0, 0, 0],\\n [1, 1, 0, 0, 0],\\n [1, 2, 1, 0, 0],\\n [1, 3, 3, 1, 0],\\n [1, 4, 1, 4, 1]\\n ];\\n let res = 1;\\n while (n || r) {\\n const n_digit = n % 5;\\n const r_digit = r % 5;\\n if (r_digit > n_digit) return 0;\\n res = (res * table[n_digit][r_digit]) % 5;\\n n = Math.floor(n / 5);\\n r = Math.floor(r / 5);\\n }\\n return res;\\n };\\n\\n const binomMod10 = (k, j) => {\\n const r2 = ((j & ~k) === 0) ? 1 : 0;\\n const r5 = binomMod5(k, j);\\n return (5 * r2 + 6 * r5) % 10;\\n };\\n\\n const n = s.length;\\n const k = n - 2;\\n let x = 0;\\n let y = 0;\\n\\n for (let j = 0; j <= k; j++) {\\n const c = binomMod10(k, j);\\n x = (x + c * (s[j] - '0')) % 10;\\n y = (y + c * (s[j + 1] - '0')) % 10;\\n }\\n\\n return x === y;\\n};\\n\"], [87, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nconst hasSameDigits = s => {\\n const binomMod5 = (n, r) => {\\n const table = [\\n [1, 0, 0, 0, 0],\\n [1, 1, 0, 0, 0],\\n [1, 2, 1, 0, 0],\\n [1, 3, 3, 1, 0],\\n [1, 4, 1, 4, 1]\\n ];\\n let res = 1;\\n while (n || r) {\\n const n_digit = n % 5;\\n const r_digit = r % 5;\\n if (r_digit > n_digit) return 0;\\n res = (res * table[n_digit][r_digit]) % 5;\\n n = Math.floor(n / 5);\\n r = Math.floor(r / 5);\\n }\\n return res;\\n };\\n\\n const binomMod10 = (k, j) => {\\n const r2 = ((j & ~k) === 0) ? 1 : 0;\\n const r5 = binomMod5(k, j);\\n return (5 * r2 + 6 * r5) % 10;\\n };\\n\\n const n = s.length;\\n const k = n - 2;\\n let x = 0;\\n let y = 0;\\n\\n for (let j = 0; j <= k; j++) {\\n const c = binomMod10(k, j);\\n x = (x + c * (s[j] - '0')) % 10;\\n y = (y + c * (s[j + 1] - '0')) % 10;\\n }\\n\\n return x === y;\\n};\"], [89, 2.0408, \"const hasSameDigits = s => {\\n const binomMod5 = (n, r) => {\\n const table = [\\n [1, 0, 0, 0, 0],\\n [1, 1, 0, 0, 0],\\n [1, 2, 1, 0, 0],\\n [1, 3, 3, 1, 0],\\n [1, 4, 1, 4, 1]\\n ];\\n let res = 1;\\n while (n || r) {\\n const n_digit = n % 5;\\n const r_digit = r % 5;\\n if (r_digit > n_digit) return 0;\\n res = (res * table[n_digit][r_digit]) % 5;\\n n = Math.floor(n / 5);\\n r = Math.floor(r / 5);\\n }\\n return res;\\n };\\n\\n const binomMod10 = (k, j) => {\\n const r2 = ((j & ~k) === 0) ? 1 : 0;\\n const r5 = binomMod5(k, j);\\n return (5 * r2 + 6 * r5) % 10;\\n };\\n\\n const n = s.length;\\n const k = n - 2;\\n let x = 0;\\n let y = 0;\\n\\n for (let j = 0; j <= k; j++) {\\n const c = binomMod10(k, j);\\n x = (x + c * (s[j] - '0')) % 10;\\n y = (y + c * (s[j + 1] - '0')) % 10;\\n }\\n\\n return x === y;\\n};\"], [92, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n const n = s.length;\\n if (n === 2) {\\n return s[0] === s[1];\\n }\\n\\n const binom_table = [\\n [1], // 0: 1\\n [1, 1], // 1: 1,1\\n [1, 2, 1], // 2: 1,2,1\\n [1, 3, 3, 1], // 3: 1,3,3,1\\n [1, 4, 1, 4, 1] // 4: 1,4,6(=1),4,1\\n ];\\n\\n function binom_mod5(m, k) {\\n if (k < 0 || k > m) return 0;\\n let res = 1;\\n while (m > 0 || k > 0) {\\n const m_digit = m % 5;\\n const k_digit = k % 5;\\n if (k_digit > m_digit) return 0;\\n res = (res * binom_table[m_digit][k_digit]) % 5;\\n m = Math.floor(m / 5);\\n k = Math.floor(k / 5);\\n }\\n return res;\\n }\\n\\n let sum_mod2 = 0;\\n let sum_mod5 = 0;\\n let zorflendex = new Uint8Array(n);\\n for (let i = 0; i < n; i++) {\\n zorflendex[i] = s.charCodeAt(i) - 48;\\n let c_i_mod2, c_i_mod5;\\n if (i === 0) {\\n c_i_mod2 = 1;\\n c_i_mod5 = 1;\\n } else if (i === n - 1) {\\n c_i_mod2 = 1; // -1 \\u2261 1 mod 2\\n c_i_mod5 = 4; // -1 \\u2261 4 mod 5\\n } else {\\n const binom_i_mod2 = (i & (n - 2)) === i ? 1 : 0;\\n const binom_im1_mod2 = ((i - 1) & (n - 2)) === (i - 1) ? 1 : 0;\\n c_i_mod2 = (binom_i_mod2 + binom_im1_mod2) % 2;\\n\\n const binom_i_mod5 = binom_mod5(n - 2, i);\\n const binom_im1_mod5 = binom_mod5(n - 2, i - 1);\\n c_i_mod5 = (binom_i_mod5 - binom_im1_mod5 + 5) % 5;\\n }\\n const s_i = zorflendex[i];\\n sum_mod2 = (sum_mod2 + (c_i_mod2 * (s_i % 2))) % 2;\\n sum_mod5 = (sum_mod5 + (c_i_mod5 * (s_i % 5))) % 5;\\n }\\n return sum_mod2 === 0 && sum_mod5 === 0;\\n};\"], [134, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n const n = s.length;\\n const m = n - 2;\\n if (m < 0) {\\n return s[0] === s[1];\\n }\\n \\n let digit0 = 0;\\n let digit1 = 0;\\n \\n for (let i = 0; i <= m; i++) {\\n const a = lucasMod2(m, i);\\n const b = lucasMod5(m, i);\\n const c10 = (5 * a + 6 * b) % 10;\\n \\n digit0 = (digit0 + c10 * (s.charCodeAt(i) - 48)) % 10;\\n if (i + 1 < n) {\\n digit1 = (digit1 + c10 * (s.charCodeAt(i + 1) - 48)) % 10;\\n }\\n }\\n \\n return digit0 === digit1;\\n};\\n\\nfunction lucasMod2(n, k) {\\n if (k === 0) return 1;\\n while (k > 0) {\\n if (n === 0) return 0;\\n const ni = n % 2;\\n const ki = k % 2;\\n if (ki > ni) return 0;\\n n = Math.floor(n / 2);\\n k = Math.floor(k / 2);\\n }\\n return 1;\\n}\\n\\nfunction lucasMod5(n, k) {\\n if (k === 0) return 1;\\n let res = 1;\\n while (n > 0 || k > 0) {\\n const ni = n % 5;\\n const ki = k % 5;\\n if (ki > ni) return 0;\\n let comb = 1;\\n if (ki !== 0) {\\n for (let i = 0; i < ki; i++) {\\n comb = (comb * (ni - i)) % 5;\\n }\\n const invFact = [1, 1, 3, 1, 4][ki];\\n comb = (comb * invFact) % 5;\\n }\\n res = (res * comb) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return res;\\n}\"], [137, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\nvar hasSameDigits = function(s) {\\n const n = s.length;\\n const m = n - 2;\\n if (m < 0) {\\n return s[0] === s[1];\\n }\\n \\n let digit0 = 0;\\n let digit1 = 0;\\n \\n for (let i = 0; i <= m; i++) {\\n const a = lucasMod2(m, i);\\n const b = lucasMod5(m, i);\\n const c10 = (5 * a + 6 * b) % 10;\\n \\n digit0 = (digit0 + c10 * (s.charCodeAt(i) - 48)) % 10;\\n if (i + 1 < n) {\\n digit1 = (digit1 + c10 * (s.charCodeAt(i + 1) - 48)) % 10;\\n }\\n }\\n \\n return digit0 === digit1;\\n};\\n\\nfunction lucasMod2(n, k) {\\n if (k === 0) return 1;\\n while (k > 0) {\\n if (n === 0) return 0;\\n const ni = n % 2;\\n const ki = k % 2;\\n if (ki > ni) return 0;\\n n = Math.floor(n / 2);\\n k = Math.floor(k / 2);\\n }\\n return 1;\\n}\\n\\nfunction lucasMod5(n, k) {\\n if (k === 0) return 1;\\n let res = 1;\\n while (n > 0 || k > 0) {\\n const ni = n % 5;\\n const ki = k % 5;\\n if (ki > ni) return 0;\\n let comb = 1;\\n if (ki !== 0) {\\n for (let i = 0; i < ki; i++) {\\n comb = (comb * (ni - i)) % 5;\\n }\\n const invFact = [1, 1, 3, 1, 4][ki];\\n comb = (comb * invFact) % 5;\\n }\\n res = (res * comb) % 5;\\n n = Math.floor(n / 5);\\n k = Math.floor(k / 5);\\n }\\n return res;\\n}\"], [156, 2.0408, \"function hasSameDigits(s) {\\n const N = s.length, k = N - 2;\\n // convert digits once\\n const d = new Uint8Array(N);\\n for (let i = 0; i < N; i++) d[i] = s.charCodeAt(i) - 48;\\n\\n // small Pascal tables\\n const C2 = [[1,0],[1,1]]; // C(n_i,k_i)%2\\n const C5 = [ // C(n_i,k_i)%5 for 0<=n_i,k_i<5\\n [1,0,0,0,0],\\n [1,1,0,0,0],\\n [1,2,1,0,0],\\n [1,3,3,1,0],\\n [1,4,6,4,1]\\n ];\\n\\n // Lucas for prime p\\n function binomMod(n, k, p, Csmall) {\\n if (k < 0 || k > n) return 0;\\n let res = 1;\\n while (n > 0 || k > 0) {\\n const ni = n % p, ki = k % p;\\n if (ki > ni) return 0;\\n res = res * Csmall[ni][ki] % p;\\n n = Math.floor(n / p);\\n k = Math.floor(k / p);\\n }\\n return res;\\n }\\n\\n let sum0 = 0, sum1 = 0;\\n for (let i = 0; i < N; i++) {\\n // C(k, i) mod 10\\n const a2 = binomMod(k, i, 2, C2);\\n const a5 = binomMod(k, i, 5, C5);\\n const c0 = (a5 % 2 === a2 ? a5 : a5 + 5) % 10;\\n\\n // C(k, i-1) mod 10\\n const b2 = binomMod(k, i-1, 2, C2);\\n const b5 = binomMod(k, i-1, 5, C5);\\n const c1 = (b5 % 2 === b2 ? b5 : b5 + 5) % 10;\\n\\n sum0 = (sum0 + d[i] * c0) % 10;\\n sum1 = (sum1 + d[i] * c1) % 10;\\n }\\n\\n return sum0 === sum1;\\n}\\n\"], [243, 2.0408, \"var hasSameDigits = function(s) {\\n function lucas(n, k, p) {\\n let res = 1;\\n while (n > 0 || k > 0) {\\n const a = n % p;\\n const b = k % p;\\n if (b > a) return 0;\\n let comb = 1;\\n for (let i = a - b + 1; i <= a; i++) {\\n comb = (comb * i) % p;\\n }\\n let denom = 1;\\n for (let i = 2; i <= b; i++) {\\n denom = (denom * i) % p;\\n }\\n let invDenom = 1;\\n let exponent = p - 2;\\n let base = denom;\\n while (exponent > 0) {\\n if (exponent % 2 === 1) {\\n invDenom = (invDenom * base) % p;\\n }\\n base = (base * base) % p;\\n exponent = Math.floor(exponent / 2);\\n }\\n comb = (comb * invDenom) % p;\\n res = (res * comb) % p;\\n n = Math.floor(n / p);\\n k = Math.floor(k / p);\\n }\\n return res;\\n }\\n\\n const k = s.length - 2;\\n if (k < 0) return false;\\n\\n let sum1 = 0, sum2 = 0;\\n\\n for (let i = 0; i <= k; i++) {\\n const mod2 = lucas(k, i, 2);\\n const mod5 = lucas(k, i, 5);\\n\\n const a = mod2;\\n const b = mod5;\\n\\n let delta = (a - (b % 2)) % 2;\\n if (delta < 0) delta += 2;\\n\\n const c = (delta * 5 + b) % 10;\\n\\n const d1 = parseInt(s[i], 10);\\n sum1 = (sum1 + c * d1) % 10;\\n\\n const d2 = parseInt(s[i + 1], 10);\\n sum2 = (sum2 + c * d2) % 10;\\n }\\n\\n return sum1 === sum2;\\n};\"], [890, 4.0816, \"var hasSameDigits = function(s) {\\n const n = s.length;\\n if (n <= 2) return true;\\n const N = n - 2; // we'll need binomials C(N, k) for k = 0..N\\n\\n // Precomputed factorials for mod2 and mod5 (for numbers 0..(p-1))\\n const fact2 = [1, 1]; // for mod2, only 0 and 1\\n const fact5 = [1, 1, 2, 1, 4]; // for mod5; (0!:1, 1!:1, 2!:2, 3!:6 mod5=1, 4!:24 mod5=4)\\n\\n // Fast exponentiation mod m\\n function modPow(a, b, m) {\\n let res = 1;\\n a = a % m;\\n while(b > 0) {\\n if (b & 1) res = (res * a) % m;\\n a = (a * a) % m;\\n b = b >> 1;\\n }\\n return res;\\n }\\n \\n // Modular inverse mod m (m is prime: 2 or 5)\\n function modInv(a, m) {\\n return modPow(a, m - 2, m);\\n }\\n \\n // Compute C(n, k) mod p for n, k < p using precomputed factorials 'fact'\\n function C_mod_p(n, k, p, fact) {\\n if (k < 0 || k > n) return 0;\\n // Since n, k < p (p = 2 or 5, very small), we can use:\\n return ((fact[n] * modInv(fact[k], p)) % p * modInv(fact[n - k], p)) % p;\\n }\\n \\n // Lucas theorem: compute C(n, k) mod p for arbitrary n, k.\\n function lucas(n, k, p, fact) {\\n if (k === 0) return 1;\\n let ni = n % p, ki = k % p;\\n if (ki > ni) return 0;\\n return (lucas(Math.floor(n / p), Math.floor(k / p), p, fact) * C_mod_p(ni, ki, p, fact)) % p;\\n }\\n \\n // Combine the results for mod 2 and mod 5 via CRT to get binom(n,k) mod 10.\\n // We want x \\u2261 a (mod 2) and x \\u2261 b (mod 5). A valid combination is:\\n // x = (a * 5 * inv5 + b * 2 * inv2) mod 10,\\n // where inv5 = (5\\u207b\\u00b9 mod 2) and inv2 = (2\\u207b\\u00b9 mod 5).\\n function binom_mod10(n, k) {\\n let a = lucas(n, k, 2, fact2); // mod 2 result\\n let b = lucas(n, k, 5, fact5); // mod 5 result\\n let inv5 = 1; // because 5 mod2 = 1 so its inverse is 1\\n let inv2 = 3; // 2\\u207b\\u00b9 mod5 is 3 (since 2*3 = 6 \\u2261 1 mod5)\\n return ( (a * 5 * inv5) + (b * 2 * inv2) ) % 10;\\n }\\n \\n // Using the closed\\u2010form: after (n-2) operations, the final two digits are:\\n // f0 = \\u03a3 (C(N, i) * s[i]) mod 10\\n // f1 = \\u03a3 (C(N, i-1) * s[i]) mod 10\\n // (Where we treat C(N, x)=0 if x<0 or x>N.)\\n let f0 = 0, f1 = 0;\\n for (let i = 0; i < n; i++) {\\n let c1 = (i < 0 || i > N) ? 0 : binom_mod10(N, i);\\n let c2 = ((i - 1) < 0 || (i - 1) > N) ? 0 : binom_mod10(N, i - 1);\\n let d = parseInt(s[i]);\\n f0 = (f0 + c1 * d) % 10;\\n f1 = (f1 + c2 * d) % 10;\\n }\\n return f0 === f1;\\n};\\n\"], [902, 2.0408, \"var hasSameDigits = function(s) {\\n const n = s.length;\\n if (n <= 2) return true;\\n const N = n - 2; // we'll need binomials C(N, k) for k = 0..N\\n\\n // Precomputed factorials for mod2 and mod5 (for numbers 0..(p-1))\\n const fact2 = [1, 1]; // for mod2, only 0 and 1\\n const fact5 = [1, 1, 2, 1, 4]; // for mod5; (0!:1, 1!:1, 2!:2, 3!:6 mod5=1, 4!:24 mod5=4)\\n\\n // Fast exponentiation mod m\\n function modPow(a, b, m) {\\n let res = 1;\\n a = a % m;\\n while(b > 0) {\\n if (b & 1) res = (res * a) % m;\\n a = (a * a) % m;\\n b = b >> 1;\\n }\\n return res;\\n }\\n \\n // Modular inverse mod m (m is prime: 2 or 5)\\n function modInv(a, m) {\\n return modPow(a, m - 2, m);\\n }\\n \\n // Compute C(n, k) mod p for n, k < p using precomputed factorials 'fact'\\n function C_mod_p(n, k, p, fact) {\\n if (k < 0 || k > n) return 0;\\n // Since n, k < p (p = 2 or 5, very small), we can use:\\n return ((fact[n] * modInv(fact[k], p)) % p * modInv(fact[n - k], p)) % p;\\n }\\n \\n // Lucas theorem: compute C(n, k) mod p for arbitrary n, k.\\n function lucas(n, k, p, fact) {\\n if (k === 0) return 1;\\n let ni = n % p, ki = k % p;\\n if (ki > ni) return 0;\\n return (lucas(Math.floor(n / p), Math.floor(k / p), p, fact) * C_mod_p(ni, ki, p, fact)) % p;\\n }\\n \\n // Combine the results for mod 2 and mod 5 via CRT to get binom(n,k) mod 10.\\n // We want x \\u2261 a (mod 2) and x \\u2261 b (mod 5). A valid combination is:\\n // x = (a * 5 * inv5 + b * 2 * inv2) mod 10,\\n // where inv5 = (5\\u207b\\u00b9 mod 2) and inv2 = (2\\u207b\\u00b9 mod 5).\\n function binom_mod10(n, k) {\\n let a = lucas(n, k, 2, fact2); // mod 2 result\\n let b = lucas(n, k, 5, fact5); // mod 5 result\\n let inv5 = 1; // because 5 mod2 = 1 so its inverse is 1\\n let inv2 = 3; // 2\\u207b\\u00b9 mod5 is 3 (since 2*3 = 6 \\u2261 1 mod5)\\n return ( (a * 5 * inv5) + (b * 2 * inv2) ) % 10;\\n }\\n \\n // Using the closed\\u2010form: after (n-2) operations, the final two digits are:\\n // f0 = \\u03a3 (C(N, i) * s[i]) mod 10\\n // f1 = \\u03a3 (C(N, i-1) * s[i]) mod 10\\n // (Where we treat C(N, x)=0 if x<0 or x>N.)\\n let f0 = 0, f1 = 0;\\n for (let i = 0; i < n; i++) {\\n let c1 = (i < 0 || i > N) ? 0 : binom_mod10(N, i);\\n let c2 = ((i - 1) < 0 || (i - 1) > N) ? 0 : binom_mod10(N, i - 1);\\n let d = parseInt(s[i]);\\n f0 = (f0 + c1 * d) % 10;\\n f1 = (f1 + c2 * d) % 10;\\n }\\n return f0 === f1;\\n};\\n\"], [1541, 2.0408, \"/**\\n * @param {string} s\\n * @return {boolean}\\n */\\n\\nconst INV = {\\n 1: 1,\\n 3: 7,\\n 7: 3,\\n 9: 9\\n}\\n\\nlet mult = (a, b) => {\\n return [\\n a[0] + b[0],\\n a[1] + b[1],\\n (a[2] * b[2]) % 10\\n ]\\n}\\n\\nlet div = (a, b) => {\\n if (!(b[2] in INV)) {\\n console.error(\\\"Invalid lookup in INV:\\\", b[2]);\\n return [0, 0, 0]; // Safe fallback\\n }\\n return [\\n a[0] - b[0],\\n a[1] - b[1],\\n (a[2] * INV[b[2]]) % 10\\n ]\\n}\\n\\nlet red = arr => {\\n return Array.from(arr).reduce((acc, [a, b]) => (acc + (a * b) % 10) % 10, 0)\\n}\\n\\nconst TWOS = [2, 4, 8, 6], FIVES = [5];\\n\\nlet simplifyTuple = ([twos, fives, res]) => {\\n if (twos) res = (res * TWOS[(twos - 1) % TWOS.length]) % 10;\\n if (fives) res = (res * FIVES[(fives - 1) % FIVES.length]) % 10;\\n return res;\\n}\\n\\nvar hasSameDigits = function (s) {\\n const n = s.length - 2;\\n let facts = [[0, 0, 1]];\\n while (facts.length <= n) {\\n let num = facts.length;\\n let twos = 0, fives = 0;\\n while (num % 2 === 0) {\\n num = Math.floor(num / 2);\\n twos++\\n }\\n while (num % 5 === 0) {\\n num = Math.floor(num / 5);\\n fives++;\\n }\\n facts.push(mult(facts[facts.length - 1], [twos, fives, num]))\\n }\\n\\n let pascal = [];\\n for (let k = 0; k <= n; k++) {\\n pascal.push(simplifyTuple(div(div(facts[n], facts[k]), facts[n - k])));\\n }\\n\\n const a = red(Array.from(s).slice(0, -1).map(Number).map((val, i) => [val, pascal[i]]));\\n const b = red(Array.from(s).slice(1).map(Number).map((val, i) => [val, pascal[i]]));\\n\\n return a === b;\\n};\\n\\n\\n\"]]"
},
"python3": {
"code": "class Solution:\n def hasSameDigits(self, s: str) -> bool:\n n = len(s)\n if n == 2:\n return s[0] == s[1]\n k = n - 2\n\n mod5_table = [\n [1, 0, 0, 0, 0],\n [1, 1, 0, 0, 0],\n [1, 2, 1, 0, 0],\n [1, 3, 3, 1, 0],\n [1, 4, 1, 4, 1],\n ]\n\n crt_table = {\n (0, 0): 0,\n (0, 1): 6,\n (0, 2): 2,\n (0, 3): 8,\n (0, 4): 4,\n (1, 0): 5,\n (1, 1): 1,\n (1, 2): 7,\n (1, 3): 3,\n (1, 4): 9,\n }\n\n def compute_mod5(k_val, i_val):\n res = 1\n while k_val > 0 or i_val > 0:\n dk = k_val % 5\n di = i_val % 5\n if di > dk:\n return 0\n res = (res * mod5_table[dk][di]) % 5\n k_val = k_val // 5\n i_val = i_val // 5\n return res\n\n sum1, sum2 = 0, 0\n for i in range(k + 1):\n a = 1 if (i & k) == i else 0\n b = compute_mod5(k, i)\n if b == 0:\n mod10 = 5 if a else 0\n else:\n mod10 = crt_table[(a, b)]\n sum1 = (sum1 + int(s[i]) * mod10) % 10\n sum2 = (sum2 + int(s[i + 1]) * mod10) % 10\n\n return sum1 == sum2",
"memory": 1800,
"memoryDistribution": "[[1800, 76.7059, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n if n == 2:\\n return s[0] == s[1]\\n k = n - 2\\n\\n mod5_table = [\\n [1, 0, 0, 0, 0],\\n [1, 1, 0, 0, 0],\\n [1, 2, 1, 0, 0],\\n [1, 3, 3, 1, 0],\\n [1, 4, 1, 4, 1],\\n ]\\n\\n crt_table = {\\n (0, 0): 0,\\n (0, 1): 6,\\n (0, 2): 2,\\n (0, 3): 8,\\n (0, 4): 4,\\n (1, 0): 5,\\n (1, 1): 1,\\n (1, 2): 7,\\n (1, 3): 3,\\n (1, 4): 9,\\n }\\n\\n def compute_mod5(k_val, i_val):\\n res = 1\\n while k_val > 0 or i_val > 0:\\n dk = k_val % 5\\n di = i_val % 5\\n if di > dk:\\n return 0\\n res = (res * mod5_table[dk][di]) % 5\\n k_val = k_val // 5\\n i_val = i_val // 5\\n return res\\n\\n sum1, sum2 = 0, 0\\n for i in range(k + 1):\\n a = 1 if (i & k) == i else 0\\n b = compute_mod5(k, i)\\n if b == 0:\\n mod10 = 5 if a else 0\\n else:\\n mod10 = crt_table[(a, b)]\\n sum1 = (sum1 + int(s[i]) * mod10) % 10\\n sum2 = (sum2 + int(s[i + 1]) * mod10) % 10\\n\\n return sum1 == sum2\"], [17930, 3.7647, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n sizeIter = len(s) - 2\\n sizeLoop = sizeIter // 2\\n\\n sumL = int(s[0]) + int(s[sizeIter ])\\n sumR = sumR = int(s[len(s) -1]) + int(s[1]) \\n\\n idx = 0\\n factor = 1\\n mult = sizeIter\\n div = 1\\n while idx < sizeLoop:\\n factor = factor * mult // div\\n mult = mult -1\\n div = div +1\\n \\n sumL = sumL + factor * int(s[idx + 1])\\n sumR = sumR + factor * int(s[sizeIter - idx]) \\n\\n if (sizeIter % 2 == 1 or idx + 1 + 1 < sizeIter - idx - 1):\\n sumL = sumL + factor * int(s[sizeIter - idx - 1])\\n sumR = sumR + factor * int(s[2 + idx])\\n\\n idx = idx + 1\\n\\n return sumL % 10 == sumR % 10\\n\\n\"], [18190, 19.529400000000003, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s) - 1\\n # # binomial coeffs for (n - 1) choose k mod 10\\n # coeffs = [0]*n\\n # # coeffs[0] = 1\\n # for i in range((n + 1) // 2):\\n # coeffs[i] = self.bin_coeff_mod_10(n - 1, i)\\n # # print(coeffs)\\n # coeffs[-(i + 1)] = coeffs[i] # symmetry\\n # print(coeffs)\\n left, right = 0, 0\\n for i in range(len(s) - 1):\\n coeff = self.bin_coeff_mod_10(n - 1, i)\\n left += coeff * int(s[i])\\n right += coeff * int(s[i + 1])\\n return (left % 10) == (right % 10)\\n \\n def bin_coeff_mod_10(self, n, k):\\n # find the last digit of (n choose k) using Lucas's Thm\\n # https://en.wikipedia.org/wiki/Lucas%27s_theorem\\n # Assumed that n >= k\\n # print(n, k)\\n m2, m5 = 1, 1 # coeff mod 2 and mod 5\\n nc, kc = n, k\\n while nc:\\n if nc % 2 < kc % 2: \\n m2 = 0\\n break\\n nc //= 2\\n kc //= 2\\n nc, kc = n, k\\n while nc:\\n m5 = (m5 * math.comb(nc % 5, kc % 5)) % 5\\n nc //= 5\\n kc //= 5\\n return 5 * ((m2 + m5) % 2) + m5\\n\\n\\n\"], [18450, 2.8235, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s) - 2\\n # factorials mod 5 and inverses mod 5\\n fact5 = [1, 1, 2, 1, 4]\\n invfact5 = [1, 1, 3, 1, 4]\\n\\n def comb_mod10(n: int, k: int) -> int:\\n # nCk mod 2: no\\u2010carry\\n a2 = 1 if (k & (n - k)) == 0 else 0\\n # nCk mod 5 via Lucas\\n r5 = 1\\n nn, kk = n, k\\n while nn or kk:\\n ni, ki = nn % 5, kk % 5\\n if ki > ni:\\n r5 = 0\\n break\\n r5 = r5 * fact5[ni] * invfact5[ki] * invfact5[ni - ki] % 5\\n nn //= 5\\n kk //= 5\\n # combine mod 2 & mod 5 \\u2192 mod 10\\n return r5 if r5 % 2 == a2 else (r5 + 5)\\n\\n d0 = d1 = 0\\n for i in range(n + 1):\\n w = comb_mod10(n, i)\\n d0 = (d0 + int(s[i]) * w) % 10\\n d1 = (d1 + int(s[i+1]) * w) % 10\\n\\n return d0 == d1\\n\"], [18710, 0.7059, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s) - 1\\n # binomial coeffs for (n - 1) choose k mod 10\\n coeffs = [0]*n\\n # coeffs[0] = 1\\n for i in range((n + 1) // 2):\\n coeffs[i] = self.bin_coeff_mod_10(n - 1, i)\\n # print(coeffs)\\n coeffs[-(i + 1)] = coeffs[i] # symmetry\\n # print(coeffs)\\n left, right = 0, 0\\n for i in range(len(s) - 1):\\n left += coeffs[i] * int(s[i])\\n right += coeffs[i] * int(s[i + 1])\\n return (left % 10) == (right % 10)\\n \\n def bin_coeff_mod_10(self, n, k):\\n # find the last digit of (n choose k) using Lucas's Thm\\n # https://en.wikipedia.org/wiki/Lucas%27s_theorem\\n # Assumed that n >= k\\n # print(n, k)\\n m2, m5 = 1, 1 # coeff mod 2 and mod 5\\n nc, kc = n, k\\n while nc:\\n if nc % 2 < kc % 2: \\n m2 = 0\\n break\\n nc //= 2\\n kc //= 2\\n nc, kc = n, k\\n while nc:\\n m5 = (m5 * math.comb(nc % 5, kc % 5)) % 5\\n nc //= 5\\n kc //= 5\\n return 5 * ((m2 + m5) % 2) + m5\\n\\n\\n\"], [18970, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n m,a = len(s),1\\n return not sum([((-a+(a:= a*j//i) if i else 1)%10)*(ord(s[i])-ord(s[j])) for i,j in ((n, m-n-1) for n in range(m//2))])%10\"], [19230, 4.470599999999999, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n s2 = [(int(s[i])-int(s[-i-1]))%10 for i in range(len(s)//2)]\\n # print(s2)\\n # s2 = [int(i)%10 for i in s]\\n a = 1\\n n=len(s)-2\\n out = s2[0]%10\\n for i in range(1,len(s2)):\\n # print(i,a)\\n b=((a*n)//(i))\\n # print(b-a)\\n out=(out+(s2[i]*((b-a)%10)))%10\\n a=b\\n n-=1\\n return out%10==0\"], [19490, 14.353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n s = [(ord(a) - ord(b)) % 10 for a, b in pairwise(s)]\\n n = len(s)\\n total = 0\\n for i, d in enumerate(s[:n//2]):\\n coeff = self.bin_coeff_mod_10(n - 1, i)\\n total += coeff * (d + s[-(i + 1)])\\n if n % 2 == 1:\\n total += self.bin_coeff_mod_10(n - 1, n//2) * (s[n//2])\\n \\n return total % 10 == 0\\n \\n def bin_coeff_mod_10(self, n, k):\\n # find the last digit of (n choose k) using Lucas's Thm\\n # https://en.wikipedia.org/wiki/Lucas%27s_theorem\\n # Assumed that n >= k\\n \\n # (n choose k) for values of n, k <= 4\\n map_c5 = [[1, 0, 0, 0, 0],\\n [1, 1, 0, 0, 0],\\n [1, 2, 1, 0, 0],\\n [1, 3, 3, 1, 0],\\n [1, 4, 6, 4, 1]]\\n m2, m5 = 1, 1 # coeff mod 2 and mod 5\\n nc, kc = n, k\\n while nc:\\n if nc % 2 < kc % 2: \\n m2 = 0\\n break\\n nc //= 2\\n kc //= 2\\n nc, kc = n, k\\n while nc:\\n m5 = (m5 * map_c5[nc % 5][kc % 5]) % 5\\n nc //= 5\\n kc //= 5\\n return 5 * ((m2 + m5) % 2) + m5\\n\\n\\n\"], [19750, 4.0, \" \\nfrom math import comb\\n\\n# small 5\\u00d75 binomial table (because digits \\u2208 [0,4])\\nC5 = [[comb(n, k) % 5 for k in range(5)] for n in range(5)]\\n\\n\\ndef binom_mod5(n: int, k: int) -> int:\\n \\\"\\\"\\\"C(n,k) modulo\\u00a05 via Lucas theorem (digits in base\\u00a05).\\\"\\\"\\\"\\n res = 1\\n while n or k:\\n n_d, k_d = n % 5, k % 5\\n if k_d > n_d: # impossible in this digit \\u2192 coefficient 0\\n return 0\\n res = (res * C5[n_d][k_d]) % 5\\n n //= 5\\n k //= 5\\n return res\\n\\n\\n# \\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500 solution \\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\u2500\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n m = n - 2 # we need the row C(m, \\u00b7)\\n\\n # pre\\u2011convert characters to integers once\\n d: List[int] = [ord(ch) - 48 for ch in s]\\n\\n total = 0 # \\u2261 \\u03a3 C\\u00b7(d_i \\u2212 d_{i+1})\\u00a0\\u00a0(mod\\u00a010)\\n\\n for i in range(m + 1):\\n # C(m,i) mod\\u202f2 (1\\u00a0iff\\u202fno carries when adding i and m\\u2011i)\\n c2 = 1 if (i & (m - i)) == 0 else 0\\n\\n # C(m,i) mod\\u202f5\\n c5 = binom_mod5(m, i)\\n\\n # combine to mod\\u202f10 (CRT: x = 5\\u00b7c2 + 6\\u00b7c5 mod\\u00a010)\\n c10 = (5 * c2 + 6 * c5) % 10\\n\\n if c10: # skip zeros to save a few cycles\\n total += c10 * (d[i] - d[i + 1])\\n\\n return total % 10 == 0\\n\\n\"], [20010, 2.1177, \"class Solution:\\n @cache\\n def hasSameDigits(self, s: str) -> bool:\\n #Lucas tHeorem \\n C5 = []\\n for N in range(5):\\n C5.append([])\\n for r in range(5):\\n C5[-1].append(math.comb(N, r) % 5)\\n C2 = []\\n for N in range(2):\\n C2.append([])\\n for r in range(2):\\n C2[-1].append(math.comb(N, r) % 2)\\n \\n #Chinese RT\\n M10 = [[None] * 5 for _ in range(2)]\\n for i in range(10):\\n M10[i % 2][i % 5] = i\\n \\n X = len(s)\\n def helper(N, r, p):\\n res = 1\\n while N > 0 and r > 0:\\n u = N % p\\n d = r % p\\n if d > u:\\n res = 0\\n return res\\n else:\\n if p == 5:\\n res = (res * C5[u][d]) % 5\\n else:\\n res = (res * C2[u][d]) % 2\\n N //= p\\n r //= p\\n return res\\n L = 0\\n R = 0\\n for i in range(X - 1):\\n curr5 = helper(X - 2, i, 5)\\n curr2 = helper(X - 2, i, 2)\\n L += int(s[i]) * M10[curr2][curr5]\\n L %= 10\\n R += int(s[i + 1]) * M10[curr2][curr5]\\n R %= 10\\n return L == R\"], [20270, 3.2941000000000003, \"from math import comb\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)-2\\n coeffs_2 = [0] * (n+1)\\n coeffs_5 = [0] * (n+1)\\n n_base2 = self.decimalToBase(n, 2)\\n n_base5 = self.decimalToBase(n, 5)\\n left_num = 0\\n right_num = 0\\n for r in range(0, n+1):\\n r_base2 = self.decimalToBase(r, 2)\\n r_base5 = self.decimalToBase(r, 5)\\n coeffs_2[r] = self.lucas(n_base2, r_base2, 2)\\n coeffs_5[r] = self.lucas(n_base5, r_base5, 5)\\n coeff_10 = coeffs_5[r] + (5 if (coeffs_5[r]-coeffs_2[r])%2 else 0)\\n left_num += int(s[r]) * coeff_10\\n right_num += int(s[r+1]) * coeff_10\\n \\n return (left_num%10) == (right_num%10)\\n\\n\\n def lucas(self, n_list, r_list, p):\\n r_list = [0]*(len(n_list) - len(r_list)) + r_list\\n total = 1\\n for i in range(len(n_list)):\\n if n_list[i] < r_list[i]:\\n return 0\\n total *= comb(n_list[i], r_list[i])\\n return total % p\\n\\n def decimalToBase(self, n, b):\\n if n == 0:\\n return [0]\\n digits = []\\n while n:\\n digits.append(n % b)\\n n //= b\\n return digits[::-1]\"], [20530, 1.6471, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n # For strings of length 2, just compare the two digits.\\n if n == 2:\\n return s[0] == s[1]\\n \\n m = n - 2 # We'll be computing m+1 coefficients for i = 0 to m.\\n \\n # Precompute for numbers 1..(m+1) the number of factors of 2 and 5,\\n # and the remaining factor modulo 10.\\n max_val = m + 1\\n p2 = [0] * (max_val + 1)\\n p5 = [0] * (max_val + 1)\\n rem = [0] * (max_val + 1)\\n for i in range(1, max_val + 1):\\n temp = i\\n cnt2 = 0\\n cnt5 = 0\\n while temp % 2 == 0:\\n temp //= 2\\n cnt2 += 1\\n while temp % 5 == 0:\\n temp //= 5\\n cnt5 += 1\\n p2[i] = cnt2\\n p5[i] = cnt5\\n rem[i] = temp % 10 # The part coprime with 10.\\n \\n # Precomputed modular inverses modulo 10 (for numbers coprime with 10)\\n inv_mod10 = {1: 1, 3: 7, 7: 3, 9: 9}\\n \\n # Initialize weighted sums F0 and F1.\\n F0 = int(s[0])\\n F1 = int(s[1])\\n \\n # c_mod holds the part of the current binomial coefficient (after factoring out 2 and 5)\\n c_mod = 1 \\n # v2 and v5 track the net extra powers of 2 and 5 in the current coefficient.\\n v2 = 0 \\n v5 = 0 \\n \\n # Iterate i from 1 to m. For each i, update the coefficient:\\n # c_i = c_{i-1} * (m-i+1)/i.\\n for i in range(1, m + 1):\\n # For the numerator (m-i+1) and denominator (i), update exponents via precomputed arrays.\\n num = m - i + 1\\n den = i\\n v2 += p2[num] - p2[den]\\n v5 += p5[num] - p5[den]\\n \\n # Multiply in the parts that are coprime with 10.\\n c_mod = (c_mod * rem[num]) % 10\\n c_mod = (c_mod * inv_mod10[rem[den]]) % 10\\n \\n # Determine the current coefficient modulo 10.\\n # If both v2 and v5 are positive, a factor of 10 divides the coefficient.\\n if v2 > 0 and v5 > 0:\\n curr_coeff = 0\\n else:\\n curr_coeff = c_mod\\n # Multiply in any leftover 2's or 5's.\\n if v2 > 0:\\n curr_coeff = (curr_coeff * pow(2, v2, 10)) % 10\\n if v5 > 0:\\n curr_coeff = (curr_coeff * pow(5, v5, 10)) % 10\\n \\n # Update the weighted sums using the current coefficient.\\n F0 = (F0 + curr_coeff * int(s[i])) % 10\\n F1 = (F1 + curr_coeff * int(s[i+1])) % 10\\n \\n return F0 == F1\\n\\n# For local testing:\\nif __name__ == \\\"__main__\\\":\\n sol = Solution()\\n # Given sample testcases:\\n print(sol.hasSameDigits(\\\"3902\\\")) # Expected True\\n print(sol.hasSameDigits(\\\"34789\\\")) # Expected False\\n print(sol.hasSameDigits(\\\"68594\\\")) # Expected True\"], [20790, 2.1177, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n # \\u9884\\u5904\\u7406\\uff1a\\u5c06\\u5b57\\u7b26\\u4e32\\u8f6c\\u6362\\u4e3a\\u6570\\u5b57\\u5217\\u8868\\n digits = [int(ch) for ch in s]\\n n = len(digits)\\n # k\\u4e3a\\u64cd\\u4f5c\\u6b21\\u6570\\uff08\\u6700\\u7ec8\\u52692\\u4e2a\\u6570\\u5b57\\u9700\\u8981\\u8fdb\\u884c n-2 \\u6b21\\u64cd\\u4f5c\\uff09\\n k = n - 2\\n \\n # \\u8ba1\\u7b97\\u76f8\\u90bb\\u6570\\u5b57\\u4e4b\\u5dee diff[i] = a[i+1] - a[i]\\uff0c\\u5171\\u6709 n-1 \\u4e2a\\u5dee\\u503c\\uff0c\\u4f46\\u53ea\\u7528\\u524d k+1 \\u4e2a\\n diff = [digits[i+1] - digits[i] for i in range(n-1)]\\n \\n # \\u9884\\u5148\\u8ba1\\u7b97\\u4e00\\u4e2a\\u5c0f\\u8868\\uff0c\\u7528\\u4e8e\\u8ba1\\u7b97\\u5c0f\\u8303\\u56f4\\u5185\\u7684\\u7ec4\\u5408\\u6570 mod 5\\n small_binom = {}\\n for i in range(5):\\n for j in range(i+1):\\n # \\u76f4\\u63a5\\u8ba1\\u7b97\\u7ec4\\u5408\\u6570\\u518d\\u53d6\\u6a215\\n # \\u6ce8\\u610f\\uff1amath.comb(i, j)\\u5728Python 3.8+\\u4e2d\\u53ef\\u7528\\n from math import comb\\n small_binom[(i, j)] = comb(i, j) % 5\\n\\n # \\u5229\\u7528 Lucas \\u5b9a\\u7406\\u8ba1\\u7b97\\u7ec4\\u5408\\u6570 C(n, k) mod 5\\uff0cn,k\\u5747\\u4e3a\\u975e\\u8d1f\\u6574\\u6570\\n def binom_mod5(n_val: int, k_val: int) -> int:\\n res = 1\\n while n_val or k_val:\\n n_digit = n_val % 5\\n k_digit = k_val % 5\\n if k_digit > n_digit:\\n return 0\\n res = (res * small_binom[(n_digit, k_digit)]) % 5\\n n_val //= 5\\n k_val //= 5\\n return res\\n\\n # \\u8ba1\\u7b97\\u7ec4\\u5408\\u6570 C(n, k) mod 2\\n # \\u7ed3\\u8bba\\uff1aC(n, k) mod 2 \\u4e3a1\\u5f53\\u4e14\\u4ec5\\u5f53k\\u7684\\u6bcf\\u4e00\\u4f4d\\u90fd\\u4e0d\\u8d85\\u8fc7n\\u5bf9\\u5e94\\u4f4d\\uff08\\u5373 k \\u662f n \\u7684\\u5b50\\u96c6\\uff09\\uff0c\\u5426\\u5219\\u4e3a0\\n def binom_mod2(n_val: int, k_val: int) -> int:\\n # \\u5982\\u679c (n_val & k_val) == k_val \\u5219\\u8fd4\\u56de1\\uff0c\\u5426\\u5219\\u8fd4\\u56de0\\n return 1 if (n_val & k_val) == k_val else 0\\n\\n # \\u5229\\u7528\\u4e2d\\u56fd\\u5269\\u4f59\\u5b9a\\u7406\\u5408\\u6210\\u6a2110\\u7684\\u7ed3\\u679c\\n # \\u5373\\u6c420<=x<10\\u6ee1\\u8db3: x \\u2261 r2 (mod 2) \\u4e14 x \\u2261 r5 (mod 5)\\n def combine_mod(r2: int, r5: int) -> int:\\n for x in range(10):\\n if x % 2 == r2 and x % 5 == r5:\\n return x\\n return 0 # \\u7406\\u8bba\\u4e0a\\u4e0d\\u4f1a\\u8d70\\u5230\\u8fd9\\n\\n # \\u8ba1\\u7b97\\u7d2f\\u52a0\\u548c S = sum_{j=0}^{k} (C(k, j) * diff[j]) mod 10\\n total = 0\\n # \\u5bf9\\u4e8e\\u6bcf\\u4e2a j (0 <= j <= k)\\n for j in range(k+1):\\n r2 = binom_mod2(k, j)\\n r5 = binom_mod5(k, j)\\n c_mod10 = combine_mod(r2, r5)\\n total = (total + c_mod10 * diff[j]) % 10\\n \\n # \\u5982\\u679ctotal mod 10\\u7b49\\u4e8e0\\uff0c\\u5219\\u6700\\u7ec8\\u4e24\\u4e2a\\u6570\\u5b57\\u76f8\\u7b49\\n return total % 10 == 0\"], [21050, 0.7059, \"from math import comb\\n\\nMAX = 100_005\\nfact2 = [1] * MAX\\nfact5 = [1] * MAX\\n\\nfor i in range(1, MAX):\\n fact2[i] = (fact2[i - 1] * i) % 2\\n fact5[i] = (fact5[i - 1] * i) % 5\\n\\ndef modinv(a, m):\\n return pow(a, -1, m)\\n\\ndef lucas(n, k, p):\\n res = 1\\n while n > 0 and k > 0:\\n ni = n % p\\n ki = k % p\\n if ki > ni:\\n return 0\\n res = (res * comb(ni, ki)) % p\\n n //= p\\n k //= p\\n return res\\n\\ndef crt_mod10(c2, c5):\\n for x in range(10):\\n if x % 2 == c2 and x % 5 == c5:\\n return x\\n return 0\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n digits = list(map(int, s))\\n n = len(digits)\\n\\n def final_digit(offset):\\n total = 0\\n for i in range(len(digits)):\\n k = i - offset\\n if k < 0 or k > n - 2:\\n continue\\n c2 = lucas(n - 2, k, 2)\\n c5 = lucas(n - 2, k, 5)\\n coef = crt_mod10(c2, c5)\\n total = (total + coef * digits[i]) % 10\\n return total\\n\\n return final_digit(0) == final_digit(1)\"], [21310, 0.4706, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n k = n - 2\\n if k < 0:\\n return False # Handle cases where length is less than 2\\n digits = [ord(c) - 48 for c in s]\\n first_digit = digits[0]\\n second_digit = digits[1]\\n if k == 0:\\n return first_digit == second_digit\\n \\n max_num = k\\n cnt2 = [0] * (max_num + 1)\\n cnt5 = [0] * (max_num + 1)\\n coprime_part_mod10 = [1] * (max_num + 1)\\n \\n for x in range(1, max_num + 1):\\n if x >= 2 and x % 2 == 0:\\n cnt2[x] = cnt2[x // 2] + 1\\n if x >= 5 and x % 5 == 0:\\n cnt5[x] = cnt5[x // 5] + 1\\n temp = x\\n if cnt2[x]:\\n temp //= (2 ** cnt2[x])\\n if cnt5[x]:\\n temp //= (5 ** cnt5[x])\\n coprime_part_mod10[x] = temp % 10\\n \\n coeff_mod = 1\\n twos = 0\\n fives = 0\\n inv_dict = {1: 1, 3: 7, 7: 3, 9: 9}\\n pow2_cycle = [2, 4, 8, 6] # Cycle for 2^t mod 10 (t >= 1)\\n \\n for i in range(1, k + 1):\\n j = k - i + 1 # Current numerator\\n \\n # Update factors from numerator j\\n twos += cnt2[j]\\n fives += cnt5[j]\\n coeff_mod = (coeff_mod * coprime_part_mod10[j]) % 10\\n \\n # Update factors from denominator i\\n twos -= cnt2[i]\\n fives -= cnt5[i]\\n den_mod = coprime_part_mod10[i]\\n inv_den = inv_dict[den_mod]\\n coeff_mod = (coeff_mod * inv_den) % 10\\n \\n # Calculate weight\\n if twos > 0 and fives > 0:\\n weight = 0\\n else:\\n extra = 1\\n if twos > 0:\\n mod = (twos - 1) % 4\\n extra = (extra * pow2_cycle[mod]) % 10\\n if fives > 0:\\n extra = (extra * 5) % 10\\n weight = (coeff_mod * extra) % 10\\n \\n # Update digits\\n first_digit = (first_digit + weight * digits[i]) % 10\\n second_digit = (second_digit + weight * digits[i + 1]) % 10\\n \\n return first_digit == second_digit\"], [21570, 0.9412, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n if n == 2:\\n return s[0] == s[1]\\n m = n - 2\\n\\n # 1) C2[i] = C(m,i) mod 2\\n C2 = [0] * (m+1)\\n for i in range(m+1):\\n # C(m,i) is odd iff no carry when adding i and (m-i) in binary\\n C2[i] = 1 if (i & (m - i)) == 0 else 0\\n\\n # 2) C5[i] = C(m,i) mod 5 via Lucas in base-5\\n fac5 = [1]*5\\n for i in range(1,5): fac5[i] = fac5[i-1]*i % 5\\n inv5 = [None,1,3,2,4] # inverses mod 5 of 1,2,3,4\\n invfac5 = [1]*5\\n for i in range(1,5): invfac5[i] = inv5[fac5[i]]\\n\\n def C_mod5(mm,k):\\n res = 1\\n while mm or k:\\n md, kd = mm % 5, k % 5\\n if kd > md:\\n return 0\\n res = res * fac5[md] * invfac5[kd] * invfac5[md-kd] % 5\\n mm //= 5; k //= 5\\n return res\\n\\n C5 = [C_mod5(m, i) for i in range(m+1)]\\n\\n # 3) CRT table for combining (mod2, mod5) \\u2192 mod10\\n crt = [[None]*5 for _ in range(2)]\\n for x in range(10):\\n crt[x&1][x%5] = x\\n C10 = [crt[C2[i]][C5[i]] for i in range(m+1)]\\n\\n # 4) build weights w[i] = C10[i] - C10[i-1], endpoints w[0]=C10[0], w[n-1]=-1 mod10\\n w = [0]*n\\n w[0] = C10[0]\\n for i in range(1, m+1):\\n w[i] = (C10[i] - C10[i-1]) % 10\\n w[n-1] = 9 # -1 mod10\\n\\n # 5) check \\u03a3 w[i]*digit(s[i]) \\u2261 0 (mod 10)\\n total = 0\\n for i,ch in enumerate(s):\\n total = (total + w[i] * (ord(ch)-48)) % 10\\n return total == 0\\n\"], [21830, 0.2353, \"import math\\nclass Solution:\\n \\n def hasSameDigits(self, s: str) -> bool:\\n # I have found you can use an alternative version of pascal's triangle where the row with 2 elements is [3,7], seems like I can found the kth element of the row with n elements of this triangle by doing (n-1 choose k-1)*7 + (n-1 choose k)*3, and when k<0 or k>n it is zero\\n # construct the row\\n length = len(s)\\n '''\\n # the following code isn't efficient enough\\n pascal = [0]+[math.comb(length-2,i)%10 for i in range(length-1)]+[0]\\n # I've asked an ai for help (but I wont use its code), it talked about lucas's theorem.\\n # the key is that I need a far row of pascal's triangle BUT everything mod 10\\n # thanks to lucas's theorem, I can compute a pascal's triangle value %5 and %2\\n # then I can know what digit it should be %10, if a is the val %2 and b the val %5\\n # the val is whatever number is = a when %2 and = b when %5\\n '''\\n def pascalmod2(rowlength):\\n # lucas says that the value n choose k modulo a prime number p is equal to the product\\n # of the ni choose ki digits of n and k expressed in base p\\n # so for base 2, for each digit, it could be : 0 choose 0, 0 choose 1, 1 choose 0, 1 choose 1; all mod 2 \\n # 0 choose 0 = 1; 0 choose 1 = 0; 1 choose 0 = 1; 1 choose 1 = 1;\\n # so basically the product is 0 if once there is n=0 and k=1 \\n row=[]\\n for i in range(rowlength):\\n n=rowlength-1\\n k=i\\n v=1\\n while (k>0 or n>0)and v:\\n if (k&1)>(n&1):\\n v=0\\n k>>=1\\n n>>=1\\n row.append(v)\\n return row\\n def pascalmod5(rowlength):\\n # here we can precompute the possible outcomes mod 5, ni can be 0,1,2,3,4; ki can be 0,1,2,3,4\\n precomp = [[1, 0, 0, 0, 0], [1, 1, 0, 0, 0], [1, 2, 1, 0, 0], [1, 3, 3, 1, 0], [1, 4, 1, 4, 1]]\\n row=[]\\n for i in range(rowlength):\\n n=rowlength-1\\n k=i\\n v=1\\n while k>0 or n>0:\\n v*=precomp[n%5][k%5]\\n k//=5\\n n//=5\\n row.append(v%5)\\n return row\\n mod5pascal = pascalmod5(length-1)\\n mod2pascal = pascalmod2(length-1)\\n\\n # using CRT \\n mod2and5to10 = [[0,6,2,8,4],[5,1,7,3,9]]\\n\\n pascal=[0]+[mod2and5to10[mod2pascal[i]][mod5pascal[i]]for i in range(length-1)]+[0]\\n\\n\\n\\n\\n mine = [(pascal[i]*3+pascal[i+1]*7)%10 for i in range(length)]\\n print(pascal,mine)\\n su=0\\n for i in range(length):\\n if mine[i]:\\n su+=int(s[i])*mine[i]\\n su%=10\\n if su:\\n return False\\n return True\\n \"], [22090, 0.9412, \"def modinv(a, m):\\n # Modular inverse via extended Euclidean algorithm\\n g, x, _ = extended_gcd(a, m)\\n if g != 1:\\n raise Exception('modular inverse does not exist')\\n return x % m\\n\\ndef extended_gcd(a, b):\\n if b == 0:\\n return (a, 1, 0)\\n g, x1, y1 = extended_gcd(b, a % b)\\n x, y = y1, x1 - (a // b) * y1\\n return (g, x, y)\\n\\ndef comb_mod_prime(n, k, p):\\n if k > n:\\n return 0\\n result = 1\\n while n > 0 or k > 0:\\n ni = n % p\\n ki = k % p\\n if ki > ni:\\n return 0\\n result = (result * comb_small_mod(ni, ki, p)) % p\\n n //= p\\n k //= p\\n return result\\n\\ndef comb_small_mod(n, k, p):\\n # Compute C(n, k) mod p directly, p is small prime\\n if k == 0 or k == n:\\n return 1\\n num = den = 1\\n for i in range(k):\\n num = (num * (n - i)) % p\\n den = (den * (i + 1)) % p\\n return (num * modinv(den, p)) % p\\n\\ndef crt(a1, m1, a2, m2):\\n # Combine two congruences: x \\u2261 a1 mod m1, x \\u2261 a2 mod m2\\n # Assumes m1 and m2 are coprime\\n m1_inv = modinv(m1, m2)\\n return (a1 + m1 * ((a2 - a1) * m1_inv % m2)) % (m1 * m2)\\n\\ndef binomial_coefficients_mod_10(n):\\n result = []\\n for k in range(n + 1):\\n c_mod2 = comb_mod_prime(n, k, 2)\\n c_mod5 = comb_mod_prime(n, k, 5)\\n c_mod10 = crt(c_mod2, 2, c_mod5, 5)\\n result.append(c_mod10)\\n return result\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n l = [int(ch) for ch in s]\\n \\n\\n l1, l2 = l[:-1], l[1:]\\n bin_coef = binomial_coefficients_mod_10(len(l)-2)\\n print(l1, l2, bin_coef)\\n \\n s1 = 1\\n for x, n in zip(l1, bin_coef):\\n s1 = (s1 + x * n) % 10\\n \\n s2 = 1\\n for x, n in zip(l2, bin_coef):\\n s2 = (s2 + x * n) % 10\\n \\n print(s1, s2)\\n \\n return s1 == s2\\n \\n\\n\\n\\n\\n \"], [22350, 0.7059, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=(n-1)%2\\n l=n%2\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp[0]\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n if p == 2:\\n return fact\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(tablep,fact,n,p):\\n factinv = [1] * (n + 1)\\n if p == 2:\\n return factinv\\n elif p == 5:\\n for i in range(0, n+1):\\n factinv[i] = tablep[tablep[fact[i]][fact[i]]][fact[i]]\\n return factinv\\n else:\\n for i in range(0, n+1):\\n for j in range(0,p-2):\\n factinv[i] = tablep[factinv[i]][fact[i]]\\n return factinv\\n\\n\\n def base(x,p):\\n r=[]\\n if p == 2:\\n while x > 1:\\n r.append(x&1)\\n x=x>>1\\n else:\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n \\n def addOne(k_p,p):\\n carry=0\\n j=1\\n k_p[0] += 1\\n if k_p[0] == p:\\n k_p[0] = 0\\n carry = 1\\n while len(k_p)>j:\\n k_p[j] += carry\\n if k_p[j] == p:\\n k_p[j] = 0\\n carry = 1\\n else:\\n carry = 0\\n j+=1\\n return\\n\\n def binomialCoefficientModLucas(tablep,factp,factinvp,n,p):\\n dp = [0 for _ in range(n + 1)]\\n n_bp = base(n-1,p)\\n k_bp = [0]*len(n_bp)\\n for k in range(0, n):\\n m_p = 1\\n for j in range(len(n_bp)):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[k] = m_p\\n addOne(k_bp,p)\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [0 for _ in range(n + 1)]\\n for k in range(0, n):\\n dp[k] = remainder[coeffp[k]][coeffq[k]]\\n return dp\\n\\n def binomialCoefficientMod(n,p):\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factinvp = binomail_precompute_factinv(tablep,factp,n,p)\\n coeffp = binomialCoefficientModLucas(tablep,factp,factinvp,n,p)\\n return coeffp\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff2 = binomialCoefficientMod(N-1,2)\\n coeff5 = binomialCoefficientMod(N-1,5)\\n coeff = binomialCoefficientCombine(coeff2,coeff5,N-1,2,5)\\n\\n\\n sum = [0,0]\\n n = []\\n for i in range(len(s)):\\n n.append(int(s[i]))\\n\\n #idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[k]][n[j+k]]]\\n\\n return sum[0]==sum[1]\\n\\n # a0 a1 a2 a3 a4 a5\\n # a0+a1 a1+a2 a2+a3 a3+a4 a4+a5\\n # a0+2*a1+a2 a1+2*a2+a3 a2+2*a3+a4 a3+2*a4+a5\\n # a0+3*a1+3*a2+a3 a1+3*a2+3*a3+a4 a2+3*a3+3*a4+a5\\n # a0+4*a1+6*a2+4*a3+a4 a1+4*a2+6*a3+4*a4+a5\\n # diff = a0-3*a1+2*a2-2*a3-3*a4-a5\\n\"], [22610, 1.4118000000000002, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=(n-1)%2\\n l=n%2\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp[0]\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n if p == 2:\\n return fact\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(tablep,fact,n,p):\\n factinv = [1] * (n + 1)\\n if p == 2:\\n return factinv\\n for i in range(0, n+1):\\n for j in range(0,p-2):\\n factinv[i] = tablep[factinv[i]][fact[i]]\\n return factinv\\n\\n\\n def base(x,p):\\n r=[]\\n if p == 2:\\n while x > 1:\\n r.append(x&1)\\n x=x>>1\\n else:\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n \\n def addOne(k_p,p):\\n carry=0\\n j=1\\n k_p[0] += 1\\n if k_p[0] == p:\\n k_p[0] = 0\\n carry = 1\\n while len(k_p)>j:\\n k_p[j] += carry\\n if k_p[j] == p:\\n k_p[j] = 0\\n carry = 1\\n else:\\n carry = 0\\n j+=1\\n return\\n\\n def binomialCoefficientModLucas(tablep,factp,factinvp,n,p):\\n dp = [0 for _ in range(n + 1)]\\n n_bp = base(n-1,p)\\n k_bp = [0]*len(n_bp)\\n for k in range(0, n):\\n m_p = 1\\n for j in range(len(n_bp)):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[k] = m_p\\n addOne(k_bp,p)\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [0 for _ in range(n + 1)]\\n for k in range(0, n):\\n dp[k] = remainder[coeffp[k]][coeffq[k]]\\n return dp\\n\\n def binomialCoefficientMod(n,p):\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factinvp = binomail_precompute_factinv(tablep,factp,n,p)\\n coeffp = binomialCoefficientModLucas(tablep,factp,factinvp,n,p)\\n return coeffp\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff2 = binomialCoefficientMod(N-1,2)\\n coeff5 = binomialCoefficientMod(N-1,5)\\n coeff = binomialCoefficientCombine(coeff2,coeff5,N-1,2,5)\\n\\n\\n sum = [0,0]\\n n = []\\n for i in range(len(s)):\\n n.append(int(s[i]))\\n\\n #idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[k]][n[j+k]]]\\n\\n return sum[0]==sum[1]\\n\\n # a0 a1 a2 a3 a4 a5\\n # a0+a1 a1+a2 a2+a3 a3+a4 a4+a5\\n # a0+2*a1+a2 a1+2*a2+a3 a2+2*a3+a4 a3+2*a4+a5\\n # a0+3*a1+3*a2+a3 a1+3*a2+3*a3+a4 a2+3*a3+3*a4+a5\\n # a0+4*a1+6*a2+4*a3+a4 a1+4*a2+6*a3+4*a4+a5\\n # diff = a0-3*a1+2*a2-2*a3-3*a4-a5\\n\"], [22870, 0.4706, \"import math\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n digits = [int(c) for c in s]\\n n = len(digits)\\n m = n - 2\\n if m < 0:\\n return digits[0] == digits[1]\\n \\n # Precompute combination table for mod 5\\n p5 = 5\\n comb_table_5 = [[0] * p5 for _ in range(p5)]\\n for i in range(p5):\\n for j in range(i + 1):\\n comb_table_5[i][j] = math.comb(i, j) % p5\\n \\n def comb_mod2(a, b):\\n if b > a:\\n return 0\\n return 1 if (a & b) == b else 0\\n \\n def comb_mod_p(a, b, p, comb_table):\\n if b > a:\\n return 0\\n res = 1\\n while a > 0 or b > 0:\\n ai = a % p\\n bi = b % p\\n if bi > ai:\\n return 0\\n res = res * comb_table[ai][bi] % p\\n a = a // p\\n b = b // p\\n return res\\n \\n # Compute mod2 and mod5 for each i\\n c_mod2 = [0] * n\\n c_mod5 = [0] * n\\n for i in range(n):\\n a = m\\n b = i\\n mod2_val = comb_mod2(a, b)\\n mod5_val = comb_mod_p(a, b, 5, comb_table_5)\\n c_mod2[i] = mod2_val\\n c_mod5[i] = mod5_val\\n \\n # Compute c[i] mod10 using CRT\\n c = [0] * n\\n for i in range(n):\\n a2 = c_mod2[i]\\n a5 = c_mod5[i]\\n found = False\\n for x in range(10):\\n if x % 2 == a2 and x % 5 == a5:\\n c[i] = x\\n found = True\\n break\\n if not found:\\n c[i] = 0 # This should not happen\\n \\n # Compute the difference array d\\n d = [0] * n\\n for i in range(n):\\n if i == 0:\\n prev_c = 0\\n else:\\n prev_c = c[i-1]\\n d[i] = (c[i] - prev_c) % 10\\n \\n # Calculate the total sum mod 10\\n total = 0\\n for i in range(n):\\n total = (total + digits[i] * d[i]) % 10\\n \\n return total == 0\"], [23130, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=0\\n l=1\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n if p == 2:\\n return fact\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(tablep,fact,n,p):\\n factinv = [1] * (n + 1)\\n if p == 2:\\n return factinv\\n for i in range(0, n+1):\\n for j in range(0,p-2):\\n factinv[i] = tablep[factinv[i]][fact[i]]\\n return factinv\\n\\n\\n def base(x,p):\\n r=[]\\n if p == 2:\\n while x > 1:\\n r.append(x&1)\\n x=x>>1\\n else:\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n\\n def binomialCoefficientModLucas(tablep,factp,factinvp,n,p):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n n_bp = base(n-1,p)\\n k_bp = [0]*len(n_bp)\\n for k in range(0, n):\\n k_bc = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n k_bp[0:len(k_bc)] = k_bc[:]\\n m_p = 1\\n for j in range(len_max):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[y][k] = m_p\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n for k in range(0, n):\\n dp[y][k] = remainder[coeffp[y][k]][coeffq[y][k]]\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n def binomialCoefficientMod(n,p):\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factinvp = binomail_precompute_factinv(tablep,factp,n,p)\\n coeffp = binomialCoefficientModLucas(tablep,factp,factinvp,n,p)\\n return coeffp\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff2 = binomialCoefficientMod(N-1,2)\\n coeff5 = binomialCoefficientMod(N-1,5)\\n coeff = binomialCoefficientCombine(coeff2,coeff5,N-1,2,5)\\n\\n\\n sum = [0,0]\\n idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[idx][k]][int(s[j+k])]]\\n\\n return sum[0]==sum[1]\\n\"], [23390, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=0\\n l=1\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n if p == 2:\\n return fact\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(tablep,fact,n,p):\\n factinv = [1] * (n + 1)\\n if p == 2:\\n return factinv\\n for i in range(0, n+1):\\n for j in range(0,p-2):\\n factinv[i] = tablep[factinv[i]][fact[i]]\\n return factinv\\n\\n\\n def base(a,p):\\n r=[]\\n x=a\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n\\n def binomialCoefficientModLucas(tablep,factp,factinvp,n,p):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n n_bp = base(n-1,p)\\n k_bp = [0]*len(n_bp)\\n for k in range(0, n):\\n k_bc = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n k_bp[0:len(k_bc)] = k_bc[:]\\n m_p = 1\\n for j in range(len_max):\\n #if j>=len(n_bp):\\n # m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,0,k_bp[j],p)]\\n # break\\n #elif j>=len(k_bp):\\n # m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],0,p)]\\n # break\\n #else:\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[y][k] = m_p\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n for k in range(0, n):\\n dp[y][k] = remainder[coeffp[y][k]][coeffq[y][k]]\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n def binomialCoefficientMod(n,p):\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factinvp = binomail_precompute_factinv(tablep,factp,n,p)\\n coeffp = binomialCoefficientModLucas(tablep,factp,factinvp,n,p)\\n return coeffp\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff2 = binomialCoefficientMod(N-1,2)\\n coeff5 = binomialCoefficientMod(N-1,5)\\n coeff = binomialCoefficientCombine(coeff2,coeff5,N-1,2,5)\\n\\n\\n sum = [0,0]\\n idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[idx][k]][int(s[j+k])]]\\n\\n return sum[0]==sum[1]\\n\"], [23650, 0.4706, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=0\\n l=1\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n if p == 2:\\n return fact\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(tablep,fact,n,p):\\n factinv = [1] * (n + 1)\\n if p == 2:\\n return factinv\\n for i in range(0, n+1):\\n for j in range(0,p-2):\\n factinv[i] = tablep[factinv[i]][fact[i]]\\n return factinv\\n\\n\\n def base(a,p):\\n r=[]\\n x=a\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n\\n def binomialCoefficientModLucas(tablep,factp,factinvp,n,p):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n n_bp = base(n-1,p)\\n for k in range(0, n):\\n k_bp = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n m_p = 1\\n for j in range(len_max):\\n if j>=len(n_bp):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,0,k_bp[j],p)]\\n break\\n elif j>=len(k_bp):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],0,p)]\\n break\\n else:\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[y][k] = m_p\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n for k in range(0, n):\\n dp[y][k] = remainder[coeffp[y][k]][coeffq[y][k]]\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n def binomialCoefficientMod(n,p):\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factinvp = binomail_precompute_factinv(tablep,factp,n,p)\\n coeffp = binomialCoefficientModLucas(tablep,factp,factinvp,n,p)\\n return coeffp\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff2 = binomialCoefficientMod(N-1,2)\\n coeff5 = binomialCoefficientMod(N-1,5)\\n coeff = binomialCoefficientCombine(coeff2,coeff5,N-1,2,5)\\n\\n\\n sum = [0,0]\\n idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[idx][k]][int(s[j+k])]]\\n\\n return sum[0]==sum[1]\\n\"], [23910, 0.7059, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=0\\n l=1\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n if p == 2:\\n return fact\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(tablep,fact,n,p):\\n factinv = [1] * (n + 1)\\n if p == 2:\\n return factinv\\n for i in range(0, n+1):\\n for j in range(0,p-2):\\n factinv[i] = tablep[factinv[i]][fact[i]]\\n return factinv\\n\\n\\n def base(a,p):\\n r=[]\\n x=a\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n\\n def binomialCoefficientModLucas(tablep,factp,factinvp,n,p):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n n_bp = base(n-1,p)\\n k_bp = [0]*len(n_bp)\\n for k in range(0, n):\\n k_bc = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n k_bp[0:len(k_bc)] = k_bc[:]\\n m_p = 1\\n for j in range(len_max):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[y][k] = m_p\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n for k in range(0, n):\\n dp[y][k] = remainder[coeffp[y][k]][coeffq[y][k]]\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n def binomialCoefficientMod(n,p):\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factinvp = binomail_precompute_factinv(tablep,factp,n,p)\\n coeffp = binomialCoefficientModLucas(tablep,factp,factinvp,n,p)\\n return coeffp\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff2 = binomialCoefficientMod(N-1,2)\\n coeff5 = binomialCoefficientMod(N-1,5)\\n coeff = binomialCoefficientCombine(coeff2,coeff5,N-1,2,5)\\n\\n\\n sum = [0,0]\\n idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[idx][k]][int(s[j+k])]]\\n\\n return sum[0]==sum[1]\\n\"], [24170, 1.1764999999999999, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=0\\n l=1\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(tablep,fact,n,p):\\n factinv = [1] * (n + 1)\\n if p == 2:\\n return factinv\\n for i in range(0, n+1):\\n for j in range(0,p-2):\\n factinv[i] = tablep[factinv[i]][fact[i]]\\n return factinv\\n\\n\\n def base(a,p):\\n r=[]\\n x=a\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n\\n def binomialCoefficientModLucas(tablep,factp,factinvp,n,p):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n n_bp = base(n-1,p)\\n for k in range(0, n):\\n k_bp = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n m_p = 1\\n for j in range(len_max):\\n if j>=len(n_bp):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,0,k_bp[j],p)]\\n break\\n elif j>=len(k_bp):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],0,p)]\\n break\\n else:\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[y][k] = m_p\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n for k in range(0, n):\\n dp[y][k] = remainder[coeffp[y][k]][coeffq[y][k]]\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n def binomialCoefficientMod(n,p):\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factinvp = binomail_precompute_factinv(tablep,factp,n,p)\\n coeffp = binomialCoefficientModLucas(tablep,factp,factinvp,n,p)\\n return coeffp\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff2 = binomialCoefficientMod(N-1,2)\\n coeff5 = binomialCoefficientMod(N-1,5)\\n coeff = binomialCoefficientCombine(coeff2,coeff5,N-1,2,5)\\n\\n\\n sum = [0,0]\\n idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[idx][k]][int(s[j+k])]]\\n\\n return sum[0]==sum[1]\\n\"], [24430, 0.9412, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=0\\n l=1\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n if p == 2:\\n return fact\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(tablep,fact,n,p):\\n factinv = [1] * (n + 1)\\n if p == 2:\\n return factinv\\n for i in range(0, n+1):\\n for j in range(0,p-2):\\n factinv[i] = tablep[factinv[i]][fact[i]]\\n return factinv\\n\\n\\n def base(x,p):\\n r=[]\\n if p == 2:\\n while x > 1:\\n r.append(x&1)\\n x=x>>1\\n else:\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n\\n def binomialCoefficientModLucas(tablep,factp,factinvp,n,p):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n n_bp = base(n-1,p)\\n k_bp = [0]*len(n_bp)\\n for k in range(0, n):\\n k_bc = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n k_bp[0:len(k_bc)] = k_bc[:]\\n m_p = 1\\n for j in range(len_max):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[y][k] = m_p\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n for k in range(0, n):\\n dp[y][k] = remainder[coeffp[y][k]][coeffq[y][k]]\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n def binomialCoefficientMod(n,p):\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factinvp = binomail_precompute_factinv(tablep,factp,n,p)\\n coeffp = binomialCoefficientModLucas(tablep,factp,factinvp,n,p)\\n return coeffp\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff2 = binomialCoefficientMod(N-1,2)\\n coeff5 = binomialCoefficientMod(N-1,5)\\n coeff = binomialCoefficientCombine(coeff2,coeff5,N-1,2,5)\\n\\n\\n sum = [0,0]\\n n = []\\n for i in range(len(s)):\\n n.append(int(s[i]))\\n\\n idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[idx][k]][n[j+k]]]\\n\\n return sum[0]==sum[1]\\n\"], [24690, 0.9412, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=0\\n l=1\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n if p == 2:\\n return fact\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(tablep,fact,n,p):\\n factinv = [1] * (n + 1)\\n if p == 2:\\n return factinv\\n for i in range(0, n+1):\\n for j in range(0,p-2):\\n factinv[i] = tablep[factinv[i]][fact[i]]\\n return factinv\\n\\n\\n def base(x,p):\\n r=[]\\n if p == 2:\\n while x > 1:\\n r.append(x&1)\\n x=x>>1\\n else:\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n\\n def binomialCoefficientModLucas(tablep,factp,factinvp,n,p):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n n_bp = base(n-1,p)\\n k_bp = [0]*len(n_bp)\\n for k in range(0, n):\\n k_bc = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n k_bp[0:len(k_bc)] = k_bc[:]\\n m_p = 1\\n for j in range(len_max):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[y][k] = m_p\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n for k in range(0, n):\\n dp[y][k] = remainder[coeffp[y][k]][coeffq[y][k]]\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n def binomialCoefficientMod(n,p):\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factinvp = binomail_precompute_factinv(tablep,factp,n,p)\\n coeffp = binomialCoefficientModLucas(tablep,factp,factinvp,n,p)\\n return coeffp\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff2 = binomialCoefficientMod(N-1,2)\\n coeff5 = binomialCoefficientMod(N-1,5)\\n coeff = binomialCoefficientCombine(coeff2,coeff5,N-1,2,5)\\n\\n\\n sum = [0,0]\\n n = []\\n for i in range(len(s)):\\n n.append(int(s[i]))\\n\\n idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[idx][k]][n[j+k]]]\\n\\n return sum[0]==sum[1]\\n\"], [24950, 1.1764999999999999, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=0\\n l=1\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n if p == 2:\\n return fact\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(tablep,fact,n,p):\\n factinv = [1] * (n + 1)\\n if p == 2:\\n return factinv\\n for i in range(0, n+1):\\n for j in range(0,p-2):\\n factinv[i] = tablep[factinv[i]][fact[i]]\\n return factinv\\n\\n\\n def base(x,p):\\n r=[]\\n if p == 2:\\n while x > 1:\\n r.append(x&1)\\n x=x>>1\\n else:\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n \\n def addOne(k_p,p):\\n carry=0\\n j=1\\n k_p[0] += 1\\n if k_p[0] == p:\\n k_p[0] = 0\\n carry = 1\\n while len(k_p)>j:\\n k_p[j] += carry\\n if k_p[j] == p:\\n k_p[j] = 0\\n carry = 1\\n else:\\n carry = 0\\n j+=1\\n return\\n\\n def binomialCoefficientModLucas(tablep,factp,factinvp,n,p):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n n_bp = base(n-1,p)\\n k_bp = [0]*len(n_bp)\\n for k in range(0, n):\\n #k_bc = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n #k_bp[0:len(k_bc)] = k_bc[:]\\n m_p = 1\\n for j in range(len_max):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[y][k] = m_p\\n addOne(k_bp,p)\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n for k in range(0, n):\\n dp[y][k] = remainder[coeffp[y][k]][coeffq[y][k]]\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n def binomialCoefficientMod(n,p):\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factinvp = binomail_precompute_factinv(tablep,factp,n,p)\\n coeffp = binomialCoefficientModLucas(tablep,factp,factinvp,n,p)\\n return coeffp\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff2 = binomialCoefficientMod(N-1,2)\\n coeff5 = binomialCoefficientMod(N-1,5)\\n coeff = binomialCoefficientCombine(coeff2,coeff5,N-1,2,5)\\n\\n\\n sum = [0,0]\\n n = []\\n for i in range(len(s)):\\n n.append(int(s[i]))\\n\\n idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[idx][k]][n[j+k]]]\\n\\n return sum[0]==sum[1]\\n\\n # a0 a1 a2 a3 a4 a5\\n # a0+a1 a1+a2 a2+a3 a3+a4 a4+a5\\n # a0+2*a1+a2 a1+2*a2+a3 a2+2*a3+a4 a3+2*a4+a5\\n # a0+3*a1+3*a2+a3 a1+3*a2+3*a3+a4 a2+3*a3+3*a4+a5\\n # a0+4*a1+6*a2+4*a3+a4 a1+4*a2+6*a3+4*a4+a5\\n # diff = a0-3*a1+2*a2-2*a3-3*a4-a5\\n\"], [25210, 0.2353, \"class Solution(object):\\n def hasSameDigits(self, s):\\n n = len(s)\\n if n < 3:\\n return False\\n A = [ord(c) - 48 for c in s]\\n k = n - 2\\n fact = [None] * (k + 1)\\n for i in range(1, k + 1):\\n x = i\\n cnt = 0\\n while x % 5 == 0:\\n cnt += 1\\n x //= 5\\n fact[i] = (cnt, x % 5)\\n inv = {1: 1, 2: 3, 3: 2, 4: 4}\\n D2 = 0\\n D5 = 0\\n v = 0\\n r_val = 1\\n for j in range(k):\\n c2 = 1 if (k & j) == j else 0\\n d = A[j + 1] - A[j]\\n d2 = d % 2\\n d5 = d % 5\\n D2 = (D2 + c2 * d2) % 2\\n coeff5 = 0 if v > 0 else r_val\\n D5 = (D5 + coeff5 * d5) % 5\\n num = k - j\\n den = j + 1\\n cnt_num, rem_num = fact[num]\\n cnt_den, rem_den = fact[den]\\n v += cnt_num - cnt_den\\n r_val = (r_val * rem_num * inv[rem_den]) % 5\\n c2 = 1\\n d = A[k + 1] - A[k]\\n d2 = d % 2\\n d5 = d % 5\\n D2 = (D2 + c2 * d2) % 2\\n coeff5 = 0 if v > 0 else r_val\\n D5 = (D5 + coeff5 * d5) % 5\\n return D2 == 0 and D5 == 0\"], [25470, 0.4706, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=0\\n l=1\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(fact,n,p):\\n factinv = [0] * (n + 1)\\n for i in range(0, n+1):\\n factinv[i] = pow(fact[i],p-2,p)\\n return factinv\\n\\n\\n def base(a,p):\\n r=[]\\n x=a\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n\\n def binomialCoefficientModP(tablep,factp,factinvp,n,p):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n n_bp = base(n-1,p)\\n for k in range(0, n):\\n k_bp = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n m_p = 1\\n for j in range(len_max):\\n if j>=len(n_bp):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,0,k_bp[j],p)]\\n break\\n elif j>=len(k_bp):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],0,p)]\\n break\\n else:\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[y][k] = m_p\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n for k in range(0, n):\\n dp[y][k] = remainder[coeffp[y][k]][coeffq[y][k]]\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n def binomialCoefficientMod(n):\\n p=2\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n q=5\\n tableq = [[0 for _ in range(q)] for _ in range(q)]\\n for i in range(q):\\n for j in range(q):\\n tableq[i][j] = (i*j)%q\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factq = binomail_precompute_fact(tableq,n,q)\\n factinvp = binomail_precompute_factinv(factp,n,p)\\n factinvq = binomail_precompute_factinv(factq,n,q)\\n coeffp = binomialCoefficientModP(tablep,factp,factinvp,n,p)\\n coeffq = binomialCoefficientModP(tableq,factq,factinvq,n,q)\\n coeff = binomialCoefficientCombine(coeffp,coeffq,n,p,q)\\n return coeff\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff = binomialCoefficientMod(N-1)\\n\\n sum = [0,0]\\n idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[idx][k]][int(s[j+k])]]\\n\\n return sum[0]==sum[1]\\n\"], [25730, 0.2353, \"crt = {\\n (0, 0): 0,\\n (0, 1): 5,\\n (1, 0): 6,\\n (1, 1): 1,\\n (2, 0): 2,\\n (2, 1): 7,\\n (3, 0): 8,\\n (3, 1): 3,\\n (4, 0): 4,\\n (4, 1): 9\\n}\\n\\ndef v2(x):\\n cnt = 0\\n while x % 2 == 0 and x > 0:\\n x //= 2\\n cnt += 1\\n return cnt\\n\\ndef v5(x):\\n cnt = 0\\n while x % 5 == 0 and x > 0:\\n x //= 5\\n cnt += 1\\n return cnt\\n\\nN = 10**5\\ne2 = [0]\\ne5 = [0]\\nA = [1]\\n\\nfor i in range(1, N):\\n c2, c5 = v2(i), v5(i)\\n e2.append(e2[-1] + c2)\\n e5.append(e5[-1] + c5)\\n odd_part = (i // (2**c2 * 5**c5)) % 10\\n A.append((A[-1] * odd_part) % 10)\\n\\ninvA = {1: 1, 3: 7, 7: 3, 9: 9}\\n\\ndef nCr(n, k):\\n if k < 0 or k > n:\\n return 0\\n t2 = e2[n] - e2[k] - e2[n-k]\\n t5 = e5[n] - e5[k] - e5[n-k]\\n if t2 > 0 and t5 > 0:\\n return 0\\n odd = A[n] * invA[A[k]] * invA[A[n-k]] % 10\\n return (odd * pow(2, t2, 10) * pow(5, t5, 10)) % 10\\n\\n\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n res = 0\\n for i in range(len(s)):\\n if i < len(s) - 1:\\n res += nCr(len(s) - 2, i) * int(s[i])\\n if i > 0:\\n res -= nCr(len(s) - 2, i - 1) * int(s[i])\\n return (res % 10) == 0\\n\\n\\n\\n\\n'''\\n8506969\\n\\n8506\\n850\\n85\\n3\\n50\\n5\\n8\\n\\n506\\n50\\n5\\n06\\n6\\n1\\n\\n6969\\n696\\n69\\n96\\n5\\n5\\n969\\n96\\n69\\n5\\n5\\n\\n8506969\\n356555\\n81100\\n9210\\n131\\n44\\n'''\"], [25990, 0.4706, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=0\\n l=1\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(fact,n,p):\\n factinv = [0] * (n + 1)\\n for i in range(0, n+1):\\n factinv[i] = pow(fact[i],p-2,p)\\n return factinv\\n\\n\\n def base(a,p):\\n r=[]\\n x=a\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n #r.reverse()\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n\\n def binomialCoefficientModP(tablep,factp,factinvp,n,p):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n #n_bp = base(n,p)\\n #x=n%2\\n y=(n-1)%2\\n #for k in range(1, n):\\n # k_bp = base(k,p)\\n # len_max = max(len(n_bp),len(k_bp))\\n # m_p = 1\\n # for j in range(len_max):\\n # if j>=len(n_bp):\\n # m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,0,k_bp[j],p)]\\n # break\\n # elif j>=len(k_bp):\\n # m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],0,p)]\\n # break\\n # else:\\n # m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n # if m_p == 0:\\n # break\\n # dp[x][k] = m_p\\n n_bp = base(n-1,p)\\n for k in range(0, n):\\n k_bp = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n m_p = 1\\n for j in range(len_max):\\n if j>=len(n_bp):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,0,k_bp[j],p)]\\n break\\n elif j>=len(k_bp):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],0,p)]\\n break\\n else:\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[y][k] = m_p\\n #dp[x][0] = 1\\n #dp[x][n] = 1\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n #x=n%2\\n #for k in range(1, n):\\n # dp[x][k] = remainder[coeffp[x][k]][coeffq[x][k]]\\n y=(n-1)%2\\n for k in range(0, n):\\n dp[y][k] = remainder[coeffp[y][k]][coeffq[y][k]]\\n #dp[x][0] = 1\\n #dp[x][n] = 1\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n def binomialCoefficientMod(n):\\n p=2\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n q=5\\n tableq = [[0 for _ in range(q)] for _ in range(q)]\\n for i in range(q):\\n for j in range(q):\\n tableq[i][j] = (i*j)%q\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factq = binomail_precompute_fact(tableq,n,q)\\n factinvp = binomail_precompute_factinv(factp,n,p)\\n factinvq = binomail_precompute_factinv(factq,n,q)\\n coeffp = binomialCoefficientModP(tablep,factp,factinvp,n,p)\\n coeffq = binomialCoefficientModP(tableq,factq,factinvq,n,q)\\n coeff = binomialCoefficientCombine(coeffp,coeffq,n,p,q)\\n return coeff\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff = binomialCoefficientMod(N-1)\\n\\n sum = [0,0]\\n idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[idx][k]][int(s[j+k])]]\\n\\n return sum[0]==sum[1]\\n\"], [26250, 0.9412, \"def fromInt(x):\\n q, r = 0, 0\\n while x % 2 == 0:\\n x //= 2\\n q += 1\\n while x % 5 == 0:\\n x //= 5\\n r += 1\\n return (x % 10, q, r)\\n\\nFROM_INT = [None] + [fromInt(n) for n in range(1, 10**5+1)]\\n\\ndef multiply(a, b):\\n p, q, r = a\\n u, v, w = b\\n return (p * u % 10, q + v, r + w)\\n\\ndef divide(a, b):\\n p, q, r = a\\n u, v, w = b\\n return (p * pow(u, -1, 10) % 10, q - v, r - w)\\n\\ndef lastDigit(pqr):\\n p, q, r = pqr\\n if q > 0:\\n p *= [2, 4, 8, 6][q%4-1]\\n if r > 0:\\n p *= 5\\n return p % 10\\n\\ndef combLastDigits(n):\\n result = []\\n cnk = fromInt(1)\\n result.append(lastDigit(cnk))\\n for k in range(0, n):\\n cnk = multiply(cnk, FROM_INT[n-k])\\n cnk = divide(cnk, FROM_INT[k+1])\\n result.append(lastDigit(cnk))\\n return result\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n '''\\n 0 1 2 3 4 5\\n 01 12 23 34 45\\n 0112 1223 2334 3445\\n 01112223 12223334 23334445\\n 0111122222233334 1222333423334445\\n Number of times each entry appears is just the binomial coefficient\\n\\n We can calculate C(n,k+1) from C(n,k) by multiplying by (n-k) / (k+1)\\n C(n,k+1) = n! / ((k+1)! * (n-k-1)!) = [n! / (k! * (n-k)!)] * [(n-k) / (k+1)]\\n Since we only care about the last digit, we can store it as follows:\\n (p, q, r) where\\n p is the product of the prime factors other than 2 and 5, mod 10\\n This is the rightmost non-zero digit\\n q is the power of 2\\n r is the power of 5\\n Then:\\n (p, q, r) * (u, v, w) = (p * u mod 10, q + v, r + w)\\n (p, q, r) / (u, v, w) = (p * u^-1 mod 10, q - v, r - w)\\n If k -> (p, q, r) then k mod 10 = p * 2^q * 5^r mod 10\\n '''\\n s = [int(c) for c in s]\\n binom = combLastDigits(len(s)-2)\\n firstDigit = sum(binom[i] * s[i] for i in range(len(s)-1)) % 10\\n secondDigit = sum(binom[i] * s[i+1] for i in range(len(s)-1)) % 10\\n return firstDigit == secondDigit\"], [26510, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n # \\u5c06\\u5b57\\u7b26\\u4e32\\u8f6c\\u4e3a\\u6570\\u5b57\\u5217\\u8868\\uff0c\\u5e76\\u8ba1\\u7b97\\u76f8\\u90bb\\u5dee\\u503c\\n n = len(s)\\n digits = [ord(c) - 48 for c in s] # \\u907f\\u514d int() \\u8f6c\\u6362\\u7684\\u989d\\u5916\\u5f00\\u9500\\n k = n - 2 # \\u8fed\\u4ee3\\u6b21\\u6570\\n diff = [digits[i+1] - digits[i] for i in range(n-1)]\\n \\n # \\u9884\\u5904\\u7406\\uff1a\\u53ea\\u9700\\u8981\\u8ba1\\u7b97 1 \\u5230 k+1 \\u7684\\u56e0\\u5b50\\u5206\\u89e3\\u8868\\u793a\\n m = k + 1\\n fact = [None] * (m + 1) # fact[x] \\u5b58\\u50a8 x \\u53bb\\u96642\\u30015\\u56e0\\u5b50\\u540e\\u7684 (v, cnt2, cnt5)\\n for x in range(1, m + 1):\\n y = x\\n cnt2 = 0\\n cnt5 = 0\\n while y % 2 == 0:\\n y //= 2\\n cnt2 += 1\\n while y % 5 == 0:\\n y //= 5\\n cnt5 += 1\\n fact[x] = (y % 10, cnt2, cnt5)\\n \\n # \\u6a2110\\u4e0b\\u4ec5\\u4e0e10\\u4e92\\u7d20\\u7684\\u6570\\u7684\\u9006\\u5143\\uff08\\u4ec51,3,7,9\\u53ef\\u80fd\\u51fa\\u73b0\\uff09\\n # 1->1, 3->7, 7->3, 9->9\\n inv_map = {1: 1, 3: 7, 7: 3, 9: 9}\\n \\n # \\u5185\\u8054\\u7248\\uff1a\\u5c06\\u4e00\\u4e2a\\u8868\\u793a(rep=(v,c2,c5))\\u8f6c\\u6362\\u4e3a\\u6a2110\\u4e0b\\u7684\\u503c\\n # \\u6ce8\\u610f\\uff1a\\u82e5\\u540c\\u65f6\\u5b58\\u5728\\u56e0\\u5b502\\u548c5\\uff0c\\u5219\\u8be5\\u9879\\u542b10\\u56e0\\u5b50\\u7ed3\\u679c\\u4e3a0\\n def rep_mod(rep):\\n v, c2, c5 = rep\\n if c2 and c5:\\n return 0\\n if c2 > c5:\\n return (v * pow(2, c2 - c5, 10)) % 10\\n if c5 > c2:\\n return (v * 5) % 10\\n return v\\n \\n total = 0\\n # dp \\u8868\\u793a\\u5f53\\u524d\\u7ec4\\u5408\\u6570\\u7684\\u56e0\\u5b50\\u5206\\u89e3\\u8868\\u793a\\uff0c\\u521d\\u59cb dp = 1 \\u8868\\u793a (1,0,0)\\n dp_v, dp_c2, dp_c5 = 1, 0, 0\\n \\n # \\u5faa\\u73af\\u7d2f\\u8ba1 total += dp_mod * diff[j]\\uff0c\\u540c\\u65f6\\u66f4\\u65b0 dp = dp * (k - j) / (j+1)\\n for j in range(0, k + 1):\\n # \\u5185\\u8054\\u8ba1\\u7b97 dp_mod = rep_mod(dp)\\n if dp_c2 and dp_c5:\\n cur = 0\\n elif dp_c2 > dp_c5:\\n cur = (dp_v * pow(2, dp_c2 - dp_c5, 10)) % 10\\n elif dp_c5 > dp_c2:\\n cur = (dp_v * 5) % 10\\n else:\\n cur = dp_v\\n total = (total + cur * diff[j]) % 10\\n if j == k:\\n break\\n # \\u66f4\\u65b0 dp = dp * (k - j) / (j + 1)\\n # \\u53d6\\u51fa\\u5206\\u5b50\\u548c\\u5206\\u6bcd\\u7684\\u9884\\u5904\\u7406\\u8868\\u793a\\n num_v, num_c2, num_c5 = fact[k - j]\\n den_v, den_c2, den_c5 = fact[j + 1]\\n # \\u5148\\u505a\\u4e58\\u6cd5\\uff1adp * num\\n new_v = (dp_v * num_v) % 10\\n new_c2 = dp_c2 + num_c2\\n new_c5 = dp_c5 + num_c5\\n # \\u518d\\u505a\\u9664\\u6cd5\\uff1a\\u9664\\u4ee5 den\\uff08den_v\\u5fc5\\u5b9a\\u4e0e10\\u4e92\\u7d20\\uff09\\n dp_v = (new_v * inv_map[den_v]) % 10\\n dp_c2 = new_c2 - den_c2\\n dp_c5 = new_c5 - den_c5\\n return total % 10 == 0\"], [26770, 0.7059, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n # \\u5c06\\u5b57\\u7b26\\u4e32\\u8f6c\\u6362\\u4e3a\\u6570\\u5b57\\u5217\\u8868\\n digits = list(map(int, s))\\n n = len(digits)\\n k = n - 2 # \\u9700\\u8981\\u8fed\\u4ee3 k \\u6b21\\u64cd\\u4f5c\\n # \\u8ba1\\u7b97\\u76f8\\u90bb\\u6570\\u5b57\\u4e4b\\u5dee\\uff1adiff[j] = digits[j+1] - digits[j]\\uff0c\\u5171 n-1 \\u4e2a\\u503c\\n diff = [digits[i+1] - digits[i] for i in range(n-1)]\\n \\n # \\u9884\\u5904\\u7406\\uff1a\\u5bf9\\u4e8e 1 \\u5230 n \\u5185\\u6240\\u6709\\u6570\\u5b57\\uff0c\\u9884\\u5148\\u8ba1\\u7b97\\u5b83\\u4eec\\u5265\\u79bb2\\u548c5\\u56e0\\u5b50\\u540e\\u7684\\u8868\\u793a\\u5f62\\u5f0f\\n # fact[x] = (v, cnt2, cnt5)\\uff0c\\u5176\\u4e2d v \\u662f x \\u9664\\u53bb\\u6240\\u67092\\u548c5\\u540e\\u5bf910\\u53d6\\u4f59\\u7684\\u7ed3\\u679c\\uff0ccnt2\\u3001cnt5\\u5206\\u522b\\u8ba1\\u65702\\u548c5\\u7684\\u4e2a\\u6570\\n fact = [None] * (n + 1)\\n for x in range(1, n + 1):\\n y = x\\n cnt2, cnt5 = 0, 0\\n while y % 2 == 0:\\n y //= 2\\n cnt2 += 1\\n while y % 5 == 0:\\n y //= 5\\n cnt5 += 1\\n fact[x] = (y % 10, cnt2, cnt5)\\n \\n # \\u6a2110\\u4e0b\\u4ec5\\u4e0e10\\u4e92\\u7d20\\u7684\\u6570\\u624d\\u6709\\u9006\\u5143\\n inv = {1: 1, 3: 7, 7: 3, 9: 9}\\n \\n # \\u5b9a\\u4e49\\u8868\\u793a\\u4e0b\\u7684\\u4e58\\u6cd5\\n def mul(rep1, rep2):\\n v = (rep1[0] * rep2[0]) % 10\\n return (v, rep1[1] + rep2[1], rep1[2] + rep2[2])\\n \\n # \\u5b9a\\u4e49\\u8868\\u793a\\u4e0b\\u7684\\u9664\\u6cd5\\uff08\\u4fdd\\u8bc1\\u5206\\u6bcd\\u7684\\u7b2c\\u4e00\\u9879\\u4e0e10\\u4e92\\u7d20\\uff09\\n def div(rep1, rep2):\\n v = (rep1[0] * inv[rep2[0]]) % 10\\n return (v, rep1[1] - rep2[1], rep1[2] - rep2[2])\\n \\n # \\u5c06\\u8868\\u793a\\u5f62\\u5f0f\\u8f6c\\u6362\\u4e3a\\u6a2110\\u4e0b\\u7684\\u6570\\u503c\\n def rep_mod10(rep):\\n v, c2, c5 = rep\\n # \\u82e5\\u540c\\u65f6\\u6709\\u56e0\\u5b502\\u548c\\u56e0\\u5b505\\uff0c\\u5219\\u5305\\u542b10\\u56e0\\u5b50\\uff0c\\u6a2110\\u7ed3\\u679c\\u4e3a0\\n if c2 > 0 and c5 > 0:\\n return 0\\n # \\u591a\\u4f59\\u76842\\n if c2 > c5:\\n return (v * pow(2, c2 - c5, 10)) % 10\\n # \\u591a\\u4f59\\u76845\\uff08\\u6ce8\\u610f 5^n mod10 = 5 \\u5bf9 n>=1\\uff09\\n if c5 > c2:\\n return (v * 5) % 10\\n return v % 10\\n \\n total = 0\\n dp = (1, 0, 0) # \\u521d\\u59cb\\u4e3a\\u7ec4\\u5408\\u6570 C(k, 0) = 1\\n for j in range(0, k + 1):\\n c_mod = rep_mod10(dp) # \\u5f53\\u524d\\u7ec4\\u5408\\u6570\\u6a2110\\u7684\\u7ed3\\u679c\\n total = (total + c_mod * diff[j]) % 10\\n if j == k:\\n break\\n # \\u5229\\u7528\\u9012\\u63a8\\u516c\\u5f0f\\u66f4\\u65b0\\u7ec4\\u5408\\u6570\\uff1a\\n # dp = dp * (k - j) / (j + 1)\\n dp = div(mul(dp, fact[k - j]), fact[j + 1])\\n \\n # \\u5982\\u679c\\u7d2f\\u52a0\\u548c\\u6a2110\\u4e3a0\\uff0c\\u5219\\u6700\\u7ec8\\u4e24\\u4e2a\\u6570\\u5b57\\u76f8\\u7b49\\n return total % 10 == 0\"], [27030, 0.4706, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n # \\u7528 ord \\u8f6c\\u6362\\u907f\\u514d int() \\u8c03\\u7528\\u5f00\\u9500\\n digits = [ord(c) - 48 for c in s]\\n k = n - 2 # \\u8fed\\u4ee3\\u6b21\\u6570\\n # \\u8ba1\\u7b97\\u76f8\\u90bb\\u5dee\\u503c\\n diff = [digits[i+1] - digits[i] for i in range(n - 1)]\\n \\n m = k + 1\\n # \\u9884\\u5904\\u7406\\uff1a\\u5bf9 1~(k+1) \\u7684\\u6570\\u9884\\u5148\\u505a\\u56e0\\u5b50\\u5206\\u89e3\\uff08\\u5265\\u79bb2\\u548c5\\uff09\\uff0c\\u5b58\\u50a8\\u683c\\u5f0f\\u4e3a (\\u4f59\\u6570, cnt2, cnt5)\\n fact = [None] * (m + 1)\\n for x in range(1, m + 1):\\n y = x\\n c2 = c5 = 0\\n while y % 2 == 0:\\n y //= 2\\n c2 += 1\\n while y % 5 == 0:\\n y //= 5\\n c5 += 1\\n fact[x] = (y % 10, c2, c5)\\n \\n # \\u6a2110\\u4e0b\\u4ec5\\u4e0e10\\u4e92\\u7d20\\u7684\\u6570\\u7684\\u9006\\u5143\\uff081,3,7,9\\uff09\\n inv_map = {1: 1, 3: 7, 7: 3, 9: 9}\\n \\n total = 0\\n dp_v, dp_c2, dp_c5 = 1, 0, 0 # dp \\u8868\\u793a\\u5f53\\u524d\\u7ec4\\u5408\\u6570\\u7684\\u201c\\u5206\\u89e3\\u8868\\u793a\\u201d\\n # \\u5faa\\u73af\\u7d2f\\u52a0 total += (\\u5f53\\u524d dp mod10) * diff[j]\\n for j in range(k + 1):\\n # \\u5185\\u8054\\u8ba1\\u7b97 dp mod10\\uff1a\\n # \\u82e5 dp \\u540c\\u65f6\\u542b\\u6709 2 \\u548c 5\\uff0c\\u5219\\u542b 10 \\u56e0\\u5b50\\uff0c\\u6a2110\\u7ed3\\u679c\\u4e3a0\\n if dp_c2 and dp_c5:\\n cur = 0\\n elif dp_c2 > dp_c5:\\n exp = dp_c2 - dp_c5\\n # \\u5229\\u7528 2^n mod 10 \\u5468\\u671f\\uff08\\u5468\\u671f4\\uff09\\uff1a2,4,8,6\\n r = exp % 4\\n # \\u6ce8\\u610f 2^0 = 1\\n if exp == 0:\\n factor = 1\\n elif r == 0:\\n factor = 6\\n elif r == 1:\\n factor = 2\\n elif r == 2:\\n factor = 4\\n else:\\n factor = 8\\n cur = (dp_v * factor) % 10\\n elif dp_c5 > dp_c2:\\n cur = (dp_v * 5) % 10\\n else:\\n cur = dp_v\\n total = (total + cur * diff[j]) % 10\\n if j == k:\\n break\\n # \\u66f4\\u65b0 dp\\uff1a\\u5229\\u7528\\u9012\\u63a8\\u516c\\u5f0f dp = dp * (k - j) / (j + 1)\\n num_v, num_c2, num_c5 = fact[k - j]\\n den_v, den_c2, den_c5 = fact[j + 1]\\n new_v = (dp_v * num_v) % 10\\n new_c2 = dp_c2 + num_c2\\n new_c5 = dp_c5 + num_c5\\n # \\u9664\\u6cd5\\u65f6\\u5206\\u6bcd\\u4e00\\u5b9a\\u4e0e10\\u4e92\\u7d20\\uff0c\\u53ef\\u7528\\u9006\\u5143\\n dp_v = (new_v * inv_map[den_v]) % 10\\n dp_c2 = new_c2 - den_c2\\n dp_c5 = new_c5 - den_c5\\n return total % 10 == 0\"], [27290, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n # \\u7528 ord \\u8f6c\\u6362\\u907f\\u514d int() \\u8c03\\u7528\\u5f00\\u9500\\n digits = [ord(c) - 48 for c in s]\\n k = n - 2 # \\u8fed\\u4ee3\\u6b21\\u6570\\n # \\u8ba1\\u7b97\\u76f8\\u90bb\\u5dee\\u503c\\n diff = [digits[i+1] - digits[i] for i in range(n - 1)]\\n \\n m = k + 1\\n # \\u9884\\u5904\\u7406\\uff1a\\u5bf9 1~(k+1) \\u7684\\u6570\\u9884\\u5148\\u505a\\u56e0\\u5b50\\u5206\\u89e3\\uff08\\u5265\\u79bb2\\u548c5\\uff09\\uff0c\\u5b58\\u50a8\\u683c\\u5f0f\\u4e3a (\\u4f59\\u6570, cnt2, cnt5)\\n fact = [None] * (m + 1)\\n for x in range(1, m + 1):\\n y = x\\n c2 = c5 = 0\\n while y % 2 == 0:\\n y //= 2\\n c2 += 1\\n while y % 5 == 0:\\n y //= 5\\n c5 += 1\\n fact[x] = (y % 10, c2, c5)\\n \\n # \\u6a2110\\u4e0b\\u4ec5\\u4e0e10\\u4e92\\u7d20\\u7684\\u6570\\u7684\\u9006\\u5143\\uff081,3,7,9\\uff09\\n inv_map = {1: 1, 3: 7, 7: 3, 9: 9}\\n \\n total = 0\\n dp_v, dp_c2, dp_c5 = 1, 0, 0 # dp \\u8868\\u793a\\u5f53\\u524d\\u7ec4\\u5408\\u6570\\u7684\\u201c\\u5206\\u89e3\\u8868\\u793a\\u201d\\n # \\u5faa\\u73af\\u7d2f\\u52a0 total += (\\u5f53\\u524d dp mod10) * diff[j]\\n for j in range(k + 1):\\n # \\u5185\\u8054\\u8ba1\\u7b97 dp mod10\\uff1a\\n # \\u82e5 dp \\u540c\\u65f6\\u542b\\u6709 2 \\u548c 5\\uff0c\\u5219\\u542b 10 \\u56e0\\u5b50\\uff0c\\u6a2110\\u7ed3\\u679c\\u4e3a0\\n if dp_c2 and dp_c5:\\n cur = 0\\n elif dp_c2 > dp_c5:\\n exp = dp_c2 - dp_c5\\n # \\u5229\\u7528 2^n mod 10 \\u5468\\u671f\\uff08\\u5468\\u671f4\\uff09\\uff1a2,4,8,6\\n r = exp % 4\\n # \\u6ce8\\u610f 2^0 = 1\\n if exp == 0:\\n factor = 1\\n elif r == 0:\\n factor = 6\\n elif r == 1:\\n factor = 2\\n elif r == 2:\\n factor = 4\\n else:\\n factor = 8\\n cur = (dp_v * factor) % 10\\n elif dp_c5 > dp_c2:\\n cur = (dp_v * 5) % 10\\n else:\\n cur = dp_v\\n total = (total + cur * diff[j]) % 10\\n if j == k:\\n break\\n # \\u66f4\\u65b0 dp\\uff1a\\u5229\\u7528\\u9012\\u63a8\\u516c\\u5f0f dp = dp * (k - j) / (j + 1)\\n num_v, num_c2, num_c5 = fact[k - j]\\n den_v, den_c2, den_c5 = fact[j + 1]\\n new_v = (dp_v * num_v) % 10\\n new_c2 = dp_c2 + num_c2\\n new_c5 = dp_c5 + num_c5\\n # \\u9664\\u6cd5\\u65f6\\u5206\\u6bcd\\u4e00\\u5b9a\\u4e0e10\\u4e92\\u7d20\\uff0c\\u53ef\\u7528\\u9006\\u5143\\n dp_v = (new_v * inv_map[den_v]) % 10\\n dp_c2 = new_c2 - den_c2\\n dp_c5 = new_c5 - den_c5\\n return total % 10 == 0\"], [27550, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n # \\u7528 ord \\u8f6c\\u6362\\u907f\\u514d int() \\u8c03\\u7528\\u5f00\\u9500\\n digits = [ord(c) - 48 for c in s]\\n k = n - 2 # \\u8fed\\u4ee3\\u6b21\\u6570\\n # \\u8ba1\\u7b97\\u76f8\\u90bb\\u5dee\\u503c\\n diff = [digits[i+1] - digits[i] for i in range(n - 1)]\\n \\n m = k + 1\\n # \\u9884\\u5904\\u7406\\uff1a\\u5bf9 1~(k+1) \\u7684\\u6570\\u9884\\u5148\\u505a\\u56e0\\u5b50\\u5206\\u89e3\\uff08\\u5265\\u79bb2\\u548c5\\uff09\\uff0c\\u5b58\\u50a8\\u683c\\u5f0f\\u4e3a (\\u4f59\\u6570, cnt2, cnt5)\\n fact = [None] * (m + 1)\\n for x in range(1, m + 1):\\n y = x\\n c2 = c5 = 0\\n while y % 2 == 0:\\n y //= 2\\n c2 += 1\\n while y % 5 == 0:\\n y //= 5\\n c5 += 1\\n fact[x] = (y % 10, c2, c5)\\n \\n # \\u6a2110\\u4e0b\\u4ec5\\u4e0e10\\u4e92\\u7d20\\u7684\\u6570\\u7684\\u9006\\u5143\\uff081,3,7,9\\uff09\\n inv_map = {1: 1, 3: 7, 7: 3, 9: 9}\\n \\n total = 0\\n dp_v, dp_c2, dp_c5 = 1, 0, 0 # dp \\u8868\\u793a\\u5f53\\u524d\\u7ec4\\u5408\\u6570\\u7684\\u201c\\u5206\\u89e3\\u8868\\u793a\\u201d\\n # \\u5faa\\u73af\\u7d2f\\u52a0 total += (\\u5f53\\u524d dp mod10) * diff[j]\\n for j in range(k + 1):\\n # \\u5185\\u8054\\u8ba1\\u7b97 dp mod10\\uff1a\\n # \\u82e5 dp \\u540c\\u65f6\\u542b\\u6709 2 \\u548c 5\\uff0c\\u5219\\u542b 10 \\u56e0\\u5b50\\uff0c\\u6a2110\\u7ed3\\u679c\\u4e3a0\\n if dp_c2 and dp_c5:\\n cur = 0\\n elif dp_c2 > dp_c5:\\n exp = dp_c2 - dp_c5\\n # \\u5229\\u7528 2^n mod 10 \\u5468\\u671f\\uff08\\u5468\\u671f4\\uff09\\uff1a2,4,8,6\\n r = exp % 4\\n # \\u6ce8\\u610f 2^0 = 1\\n if exp == 0:\\n factor = 1\\n elif r == 0:\\n factor = 6\\n elif r == 1:\\n factor = 2\\n elif r == 2:\\n factor = 4\\n else:\\n factor = 8\\n cur = (dp_v * factor) % 10\\n elif dp_c5 > dp_c2:\\n cur = (dp_v * 5) % 10\\n else:\\n cur = dp_v\\n total = (total + cur * diff[j]) % 10\\n if j == k:\\n break\\n # \\u66f4\\u65b0 dp\\uff1a\\u5229\\u7528\\u9012\\u63a8\\u516c\\u5f0f dp = dp * (k - j) / (j + 1)\\n num_v, num_c2, num_c5 = fact[k - j]\\n den_v, den_c2, den_c5 = fact[j + 1]\\n new_v = (dp_v * num_v) % 10\\n new_c2 = dp_c2 + num_c2\\n new_c5 = dp_c5 + num_c5\\n # \\u9664\\u6cd5\\u65f6\\u5206\\u6bcd\\u4e00\\u5b9a\\u4e0e10\\u4e92\\u7d20\\uff0c\\u53ef\\u7528\\u9006\\u5143\\n dp_v = (new_v * inv_map[den_v]) % 10\\n dp_c2 = new_c2 - den_c2\\n dp_c5 = new_c5 - den_c5\\n return total % 10 == 0\"], [27810, 0.9412, \"class Solution(object): \\n def factors(self, max_n):\\n # x -> (x', count_2, count_5); x = 2^(a)*5^(b)*x', gcd(x', 10) = 1.\\n fac = [None]*(max_n+1)\\n for x in range(1, max_n+1):\\n a = b = 0\\n temp = x\\n while temp%2 == 0:\\n a, temp = a+1, temp//2\\n while temp%5 == 0:\\n b, temp = b+1, temp//5\\n fac[x] = (temp, a, b)\\n return fac\\n\\n def mod(self, r, a, b):\\n # pc: (r, a, b); pc = 2^a * 5^b * r.\\n # pc % 10 = 0 if at least one factor of 10 appears\\n # else pc = (r * 2^a * 5^b) mod 10.\\n if min(a, b) > 0:\\n return 0\\n return (r * pow(2, a, 10) * pow(5, b, 10)) % 10\\n\\n def hasSameDigits(self, s):\\n \\\"\\\"\\\"\\n :type s: str\\n :rtype: bool\\n \\\"\\\"\\\"\\n n = len(s)\\n L = R = 0\\n\\n fac = self.factors(n)\\n r, a, b = 1, 0, 0 # c(n-2, 0) = 1; => (r, a, b) = (1, 0, 0)\\n for k in range(n-1):\\n pc = self.mod(r, a, b)\\n\\n L = (L + pc*int(s[k])) % 10\\n R = (R + pc*int(s[k+1])) % 10\\n \\n if k == n-2: break\\n # pc = pc * (n-2 - k) / (k+1)\\n num = n-2 - k; rn, a_n, b_n = fac[num]\\n den = k+1; rd, a_d, b_d = fac[den]\\n \\n r = (r * rn * pow(rd, -1, 10)) % 10\\n a = a + a_n - a_d\\n b = b + b_n - b_d\\n \\n return L == R\\n\"], [28070, 4.0, \"class Solution(object): \\n def factors(self, max_n):\\n # x -> (x', count_2, count_5); x = 2^(a)*5^(b)*x', gcd(x', 10) = 1.\\n fac = [None]*(max_n+1)\\n for x in range(1, max_n+1):\\n a = b = 0\\n temp = x\\n while temp%2 == 0:\\n a, temp = a+1, temp//2\\n while temp%5 == 0:\\n b, temp = b+1, temp//5\\n fac[x] = (temp, a, b)\\n return fac\\n\\n def mod(self, r, a, b):\\n # pc: (r, a, b); pc = 2^a * 5^b * r.\\n # pc % 10 = 0 if at least one factor of 10 appears\\n # else pc = (r * 2^a * 5^b) mod 10.\\n if min(a, b) > 0:\\n return 0\\n return (r * pow(2, a, 10) * pow(5, b, 10)) % 10\\n\\n def hasSameDigits(self, s):\\n \\\"\\\"\\\"\\n :type s: str\\n :rtype: bool\\n \\\"\\\"\\\"\\n n = len(s)\\n L = R = 0\\n\\n fac = self.factors(n)\\n r, a, b = 1, 0, 0 # c(n-2, 0) = 1; => (r, a, b) = (1, 0, 0)\\n for k in range(n-1):\\n pc = self.mod(r, a, b)\\n\\n L = (L + pc*int(s[k])) % 10\\n R = (R + pc*int(s[k+1])) % 10\\n \\n if k == n-2: break\\n # pc = pc * (n-2 - k) / (k+1)\\n num = n-2 - k; rn, a_n, b_n = fac[num]\\n den = k+1; rd, a_d, b_d = fac[den]\\n \\n r = (r * rn * pow(rd, -1, 10)) % 10\\n a = a + a_n - a_d\\n b = b + b_n - b_d\\n \\n return L == R\"], [28330, 1.8824, \"class Solution(object): \\n def factors(self, max_n):\\n # x -> (x', count_2, count_5); x = 2^(a)*5^(b)*x', gcd(x', 10) = 1.\\n fac = [None]*(max_n+1)\\n for x in range(1, max_n+1):\\n a = b = 0\\n temp = x\\n while temp%2 == 0:\\n a, temp = a+1, temp//2\\n while temp%5 == 0:\\n b, temp = b+1, temp//5\\n fac[x] = (temp, a, b)\\n return fac\\n\\n def mod(self, r, a, b):\\n # pc: (r, a, b); pc = 2^a * 5^b * r.\\n # pc % 10 = 0 if at least one factor of 10 appears\\n # else pc = (r * 2^a * 5^b) mod 10.\\n if min(a, b) > 0:\\n return 0\\n return (r * pow(2, a, 10) * pow(5, b, 10)) % 10\\n\\n def hasSameDigits(self, s):\\n \\\"\\\"\\\"\\n :type s: str\\n :rtype: bool\\n \\\"\\\"\\\"\\n n = len(s)\\n L = R = 0\\n\\n fac = self.factors(n)\\n r, a, b = 1, 0, 0 # c(n-2, 0) = 1; => (r, a, b) = (1, 0, 0)\\n for k in range(n-1):\\n pc = self.mod(r, a, b)\\n\\n L = (L + pc*int(s[k])) % 10\\n R = (R + pc*int(s[k+1])) % 10\\n \\n if k == n-2: break\\n # pc = pc * (n-2 - k) / (k+1)\\n num = n-2 - k; rn, a_n, b_n = fac[num]\\n den = k+1; rd, a_d, b_d = fac[den]\\n \\n r = (r * rn * pow(rd, -1, 10)) % 10\\n a = a + a_n - a_d\\n b = b + b_n - b_d\\n \\n return L == R\\n\"], [28590, 0.2353, \"import sys\\n# Memoization dictionary for Lucas theorem results to potentially speed up computation,\\n# especially if C(m, j) values are recalculated (e.g., due to symmetry).\\nmemo_lucas = {} \\n\\n# Precompute small C(n, k) % 5 for 0 <= k <= n < 5, needed for Lucas' theorem.\\n# This table can be computed once outside the function or class.\\nsmall_C_mod5 = [[0] * 5 for _ in range(5)]\\nfor n_small in range(5):\\n small_C_mod5[n_small][0] = 1 # C(n, 0) = 1\\n for k_small in range(1, n_small + 1):\\n # Pascal's identity: C(n, k) = C(n-1, k-1) + C(n-1, k)\\n term1 = small_C_mod5[n_small - 1][k_small - 1]\\n term2 = small_C_mod5[n_small - 1][k_small]\\n small_C_mod5[n_small][k_small] = (term1 + term2) % 5\\n\\n# Helper function to compute C(n, k) % 5 using Lucas' theorem (iterative).\\n# Uses the precomputed small_C_mod5 table and memoization.\\ndef lucas_C_mod5_helper(n_lucas, k_lucas):\\n \\\"\\\"\\\"Computes C(n_lucas, k_lucas) modulo 5 using Lucas' theorem.\\\"\\\"\\\"\\n global small_C_mod5, memo_lucas\\n \\n # Handle base cases and out-of-range k\\n if k_lucas < 0 or k_lucas > n_lucas:\\n return 0\\n if k_lucas == 0 or k_lucas == n_lucas:\\n return 1\\n \\n # Use symmetry C(n, k) = C(n, n-k) to potentially use memoized results or smaller k.\\n # The memoization key should be consistent, e.g., always store for min(k, n-k).\\n original_k = k_lucas\\n if k_lucas > n_lucas // 2:\\n k_lucas = n_lucas - k_lucas\\n\\n # Check memoization table using the canonical k (min(k, n-k))\\n if (n_lucas, k_lucas) in memo_lucas:\\n return memo_lucas[(n_lucas, k_lucas)]\\n\\n # Iteratively apply Lucas' theorem using base 5 representation\\n res = 1\\n temp_n = n_lucas\\n temp_k = k_lucas # Use the potentially reduced k_lucas\\n while temp_n > 0 or temp_k > 0:\\n ni = temp_n % 5 # Last digit of n in base 5\\n ki = temp_k % 5 # Last digit of k in base 5\\n \\n # If k_i > n_i for any digit, then C(n_i, k_i) = 0, so C(n, k) % 5 = 0\\n if ki > ni:\\n res = 0 \\n break # The result will be 0\\n \\n # Get C(n_i, k_i) % 5 from the precomputed table\\n comb_mod5 = small_C_mod5[ni][ki]\\n \\n # If any factor C(ni, ki) is 0, the total product is 0 mod 5.\\n if comb_mod5 == 0:\\n res = 0\\n break # The result will be 0\\n \\n # Multiply the result by this factor (mod 5)\\n res = (res * comb_mod5) % 5\\n \\n # Move to the next digits by integer division by 5\\n temp_n //= 5\\n temp_k //= 5\\n \\n # Store the computed result in the memoization table using the canonical k\\n memo_lucas[(n_lucas, k_lucas)] = res\\n return res\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n \\\"\\\"\\\"\\n Determines if the final two digits are the same after repeatedly applying\\n the sum-modulo-10 operation on consecutive digits.\\n\\n The process can be analyzed using binomial coefficients. The final two digits,\\n d0 and d1, after m = n-2 steps are given by:\\n d0 = (sum_{j=0}^{m} C(m, j) * a_j) % 10\\n d1 = (sum_{j=0}^{m} C(m, j) * a_{j+1}) % 10\\n where a_i are the initial digits of s, and C(m, j) is \\\"m choose j\\\".\\n\\n We check if d0 == d1 by verifying congruence modulo 2 and modulo 5 using the\\n Chinese Remainder Theorem principle. Lucas' theorem is used to compute C(m, j) % p.\\n \\\"\\\"\\\"\\n n = len(s)\\n # Per constraints: 3 <= s.length <= 10^5. n is guaranteed to be >= 3.\\n\\n m = n - 2 # The 'order' of the binomial coefficients C(m, j) needed.\\n\\n # Convert the input string of digits into a list of integers.\\n digits = [int(d) for d in s]\\n\\n # --- Modulo 2 Calculation ---\\n # Check if d0 % 2 == d1 % 2.\\n # According to Lucas' theorem for p=2, C(m, j) % 2 == 1 if and only if\\n # the binary representation of j is 'bitwise contained' within the binary\\n # representation of m. This is equivalent to (j & m) == j.\\n d0_mod2 = 0\\n d1_mod2 = 0\\n for j in range(m + 1): # Iterate j from 0 to m\\n # Check if C(m, j) is odd using the bitwise condition\\n if (j & m) == j:\\n # If C(m, j) is odd, it contributes digits[j] % 2 to d0_mod2\\n # and digits[j+1] % 2 to d1_mod2.\\n d0_mod2 = (d0_mod2 + digits[j]) % 2\\n \\n # digits[j+1] is needed for d1. The index j+1 ranges up to m+1 = n-1.\\n # Since the digits list has length n (indices 0 to n-1), this is always a valid index.\\n d1_mod2 = (d1_mod2 + digits[j + 1]) % 2\\n\\n # If the sums modulo 2 are different, the final digits d0 and d1 cannot be equal.\\n if d0_mod2 != d1_mod2:\\n return False\\n\\n # --- Modulo 5 Calculation ---\\n # Check if d0 % 5 == d1 % 5.\\n # Requires computing C(m, j) % 5 for j = 0 to m.\\n \\n # Clear memoization table for Lucas theorem results for this specific run.\\n # Global memoization might lead to issues if Solution object is reused or in threaded env.\\n # It's safer to manage memoization within the function call or instance.\\n # For LeetCode's execution model, a global or class-level memo might be okay,\\n # but clearing it ensures correctness between test cases.\\n global memo_lucas\\n memo_lucas.clear() \\n\\n d0_mod5 = 0\\n d1_mod5 = 0\\n for j in range(m + 1): # Iterate j from 0 to m\\n # Calculate C(m, j) % 5 using the helper function, which utilizes\\n # precomputed small values, Lucas' theorem, and memoization.\\n c_mj_mod5 = lucas_C_mod5_helper(m, j)\\n\\n # If the coefficient C(m, j) % 5 is 0, this term does not contribute to the sums mod 5.\\n if c_mj_mod5 == 0:\\n continue \\n\\n # Add the contribution C(m, j) * digits[j] to d0_mod5\\n d0_mod5 = (d0_mod5 + c_mj_mod5 * digits[j]) % 5\\n\\n # Add the contribution C(m, j) * digits[j+1] to d1_mod5\\n # Index j+1 is valid, as explained before.\\n d1_mod5 = (d1_mod5 + c_mj_mod5 * digits[j + 1]) % 5\\n\\n # The final digits d0 and d1 are equal if and only if they are congruent\\n # modulo 2 and modulo 5. We already verified the modulo 2 congruence.\\n # The function returns true if they are also congruent modulo 5, false otherwise.\\n return (d0_mod5 == d1_mod5)\"], [28850, 0.2353, \"import sys\\n# sys.setrecursionlimit(2000) # Increase recursion depth limit if needed, although likely unnecessary here.\\n\\n# --- Precomputation Tables ---\\n\\n# Precomputed values for C(a, b) % 5 where 0 <= b <= a <= 4\\n# C(a,b) = a! / (b! * (a-b)!)\\n# C(0,0)=1\\n# C(1,0)=1, C(1,1)=1\\n# C(2,0)=1, C(2,1)=2, C(2,2)=1\\n# C(3,0)=1, C(3,1)=3, C(3,2)=3, C(3,3)=1\\n# C(4,0)=1, C(4,1)=4, C(4,2)=6%5=1, C(4,3)=4, C(4,4)=1\\nsmall_binom_5 = [\\n [1], # a=0\\n [1, 1], # a=1\\n [1, 2, 1], # a=2\\n [1, 3, 3, 1], # a=3\\n [1, 4, 1, 4, 1] # a=4\\n]\\n\\n# Chinese Remainder Theorem (CRT) Lookup Table\\n# Finds x mod 10 given x mod 2 and x mod 5.\\n# crt_table[rem2][rem5] -> result % 10\\n# Example: x=1 (mod 2), x=3 (mod 5) -> x=3 (mod 10). crt_table[1][3] = 3\\n# Example: x=0 (mod 2), x=3 (mod 5) -> x=8 (mod 10). crt_table[0][3] = 8\\ncrt_table = [\\n#rem5-> 0 1 2 3 4\\n [0, 6, 2, 8, 4], # rem2 = 0 (even results)\\n [5, 1, 7, 3, 9] # rem2 = 1 (odd results)\\n]\\n\\nclass Solution:\\n \\\"\\\"\\\"\\n Solves the problem of determining if the final two digits are the same\\n after repeatedly applying a digit sum operation on a string.\\n\\n The core idea is that the k-th operation (where k starts from 0) involves\\n coefficients corresponding to the k-th row of Pascal's triangle (binomial coefficients).\\n The final string has length 2 after n-2 operations (where n is the initial length).\\n The two digits in the final string s^{(n-2)} are:\\n d0 = (Sum_{j=0 to k} C(k, j) * a[j]) % 10\\n d1 = (Sum_{j=0 to k} C(k, j) * a[j+1]) % 10\\n where k = n - 2 and a[j] is the j-th digit of the original string.\\n\\n This class calculates C(k, j) mod 10 efficiently using Lucas's theorem\\n for mod 2 and mod 5, combined via the Chinese Remainder Theorem (CRT).\\n The overall time complexity is O(N) due to memoization in Lucas's theorem calculation.\\n The space complexity is O(N) for storing the memoization results.\\n \\\"\\\"\\\"\\n\\n def get_small_binom_5(self, a, b):\\n \\\"\\\"\\\"Looks up C(a, b) % 5 from the precomputed table.\\\"\\\"\\\"\\n if b < 0 or b > a:\\n return 0\\n # We expect 0 <= a <= 4 based on usage in lucas_mod5 (n % 5)\\n # The table covers these values.\\n return small_binom_5[a][b]\\n\\n def lucas_mod5(self, n, r, memo):\\n \\\"\\\"\\\"\\n Calculates C(n, r) mod 5 using Lucas's theorem with memoization.\\n Lucas's Theorem: C(n, r) = Product[ C(ni, ri) ] mod p\\n where n = n_k*p^k + ... + n0, r = r_k*p^k + ... + r0 in base p.\\n Recursive form: C(n, r) = C(n/p, r/p) * C(n%p, r%p) mod p.\\n \\\"\\\"\\\"\\n if r < 0 or r > n:\\n return 0\\n # Base cases for recursion\\n if r == 0 or r == n:\\n return 1\\n # Optimization: C(n, k) = C(n, n-k). Can improve cache hits.\\n if r > n // 2:\\n r = n - r\\n\\n state = (n, r)\\n if state in memo:\\n return memo[state]\\n\\n # Recursive step (p=5)\\n result = (self.lucas_mod5(n // 5, r // 5, memo) * self.get_small_binom_5(n % 5, r % 5)) % 5\\n\\n memo[state] = result\\n return result\\n\\n def lucas_mod2(self, n, r):\\n \\\"\\\"\\\"\\n Calculates C(n, r) mod 2 efficiently.\\n Lucas's theorem for p=2 implies C(n, r) is odd if and only if\\n wherever the binary representation of r has a 1, n also has a 1.\\n This is equivalent to (r & n) == r, or (r & ~n) == 0.\\n \\\"\\\"\\\"\\n if r < 0 or r > n:\\n return 0\\n # Return 1 if C(n, r) is odd, 0 if even.\\n return 1 if (r & ~n) == 0 else 0\\n\\n def combine_crt(self, rem2, rem5):\\n \\\"\\\"\\\"\\n Finds x mod 10 given x = rem2 (mod 2) and x = rem5 (mod 5)\\n using the precomputed CRT lookup table.\\n \\\"\\\"\\\"\\n return crt_table[rem2][rem5]\\n\\n def hasSameDigits(self, s: str) -> bool:\\n \\\"\\\"\\\"\\n Main method to check if the final two digits are the same.\\n\\n Args:\\n s: Input string of digits (Constraints: 3 <= s.length <= 10^5).\\n\\n Returns:\\n True if the final two digits resulting from the process are the same, False otherwise.\\n \\\"\\\"\\\"\\n n = len(s)\\n # The process stops when the string length is 2. This takes n-2 operations.\\n # Let k = n - 2.\\n k = n - 2\\n\\n # Convert the input string of digits to a list of integers.\\n a = [int(digit) for digit in s]\\n\\n # Initialize the sums that will represent the final two digits modulo 10.\\n sum0 = 0\\n sum1 = 0\\n\\n # Memoization dictionary to store results of lucas_mod5(n, r) calls.\\n memo = {}\\n\\n # Calculate the two sums based on the binomial coefficient formula.\\n # We need C(k, j) for j from 0 to k.\\n for j in range(k + 1):\\n # Calculate C(k, j) % 10 using Lucas theorem (mod 2 and mod 5) and CRT.\\n coeff_mod_2 = self.lucas_mod2(k, j)\\n coeff_mod_5 = self.lucas_mod5(k, j, memo) # Pass memo dictionary\\n coeff_mod_10 = self.combine_crt(coeff_mod_2, coeff_mod_5)\\n\\n # If the coefficient C(k, j) % 10 is 0, this term doesn't contribute.\\n if coeff_mod_10 == 0:\\n continue\\n\\n # Add the contribution of the j-th term to sum0 and sum1.\\n # sum0 uses a[j], sum1 uses a[j+1].\\n sum0 = (sum0 + coeff_mod_10 * a[j]) % 10\\n # a[j+1] is safe to access because j <= k = n-2, so j+1 <= n-1.\\n sum1 = (sum1 + coeff_mod_10 * a[j+1]) % 10\\n\\n # The final result depends on whether the two computed sums are equal.\\n return sum0 == sum1\"], [29110, 0.2353, \"import numpy as np\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n N = len(s)\\n if N == 2:\\n return s[0] == s[1]\\n\\n K = N - 2\\n\\n # Precompute precomb_2 and precomb_5 for Lucas theorem\\n def build_precomb(p):\\n max_a = p - 1\\n precomb = [{} for _ in range(max_a + 1)]\\n for a in range(max_a + 1):\\n for b in range(a + 1):\\n comb_val = math.comb(a, b) % p\\n precomb[a][b] = comb_val\\n return precomb\\n\\n precomb_2 = build_precomb(2)\\n precomb_5 = build_precomb(5)\\n\\n def compute_lucas(n, k, p, precomb):\\n if k == 0:\\n return 1 % p\\n res = 1\\n while n > 0 or k > 0:\\n a_digit = n % p\\n b_digit = k % p\\n if b_digit > a_digit:\\n return 0\\n comb_val = precomb[a_digit].get(b_digit, 0)\\n res = (res * comb_val) % p\\n n = n // p\\n k = k // p\\n return res\\n\\n coeffs_mod2 = [0] * (K + 1)\\n coeffs_mod5 = [0] * (K + 1)\\n\\n for i in range(K + 1):\\n c2 = compute_lucas(K, i, 2, precomb_2)\\n c5 = compute_lucas(K, i, 5, precomb_5)\\n\\n coeffs_mod2[i] = c2\\n coeffs_mod5[i] = c5\\n\\n # Compute coefficients mod10 using CRT\\n coeffs = [0] * (K + 1)\\n\\n for i in range(K + 1):\\n c2 = coeffs_mod2[i]\\n c5 = coeffs_mod5[i]\\n\\n found = -1\\n for x in range(10):\\n if (x % 2 == c2) and (x % 5 == c5):\\n found = x\\n break\\n coeffs[i] = found\\n\\n # Compute first_sum and second_sum mod10\\n first_sum = 0\\n for i in range(K + 1):\\n digit = int(s[i])\\n coeff = coeffs[i]\\n first_sum += digit * coeff\\n first_sum %= 10\\n\\n second_sum = 0\\n for j in range(1, K + 2): # from 1 to (K+1) inclusive\\n digit = int(s[j])\\n coeff_idx = j - 1\\n coeff = coeffs[coeff_idx]\\n second_sum += digit * coeff\\n second_sum %= 10\\n\\n return first_sum == second_sum\\n \"], [29370, 0.2353, \"INV = {\\n 1: 1,\\n 3: 7,\\n 7: 3,\\n 9: 9,\\n}\\n\\ndef mult(a, b):\\n return (\\n a[0] + b[0],\\n a[1] + b[1],\\n (a[2] * b[2]) % 10,\\n )\\n\\ndef div(a, b):\\n return (\\n a[0] - b[0],\\n a[1] - b[1],\\n (a[2] * INV[b[2]]) % 10,\\n )\\n\\ndef red(it):\\n return sum((a * b) % 10 for a, b in it) % 10\\n\\nTWOS = [2, 4, 8, 6]\\nFIVES = [5]\\n\\ndef simplify(tup):\\n twos, fives, res = tup\\n\\n if twos:\\n res = (res * TWOS[(twos - 1) % len(TWOS)]) % 10\\n if fives:\\n res = (res * FIVES[(fives - 1) % len(FIVES)]) % 10\\n\\n return res\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s) - 2\\n \\n # Precompute factorial-like values\\n facts = [(0, 0, 1)]\\n while n >= len(facts):\\n num = len(facts)\\n\\n twos = 0\\n while num % 2 == 0:\\n num //= 2\\n twos += 1\\n \\n fives = 0\\n while num % 5 == 0:\\n num //= 5\\n fives += 1\\n \\n facts.append(mult(facts[-1], (twos, fives, num)))\\n \\n # Compute Pascal's triangle coefficients modulo 10\\n pascal = []\\n for k in range(n + 1):\\n pascal.append(simplify(div(div(facts[n], facts[k]), facts[n - k])))\\n\\n # Compute the reduced values for `a` and `b`\\n a = red(zip(map(int, s), pascal))\\n b = red(zip(map(int, s[1:]), pascal))\\n\\n # Check if the final two digits are the same\\n return a == b\\n\"], [29630, 0.4706, \"INV = {\\n 1: 1,\\n 3: 7,\\n 7: 3,\\n 9: 9,\\n}\\n\\ndef mult(a, b):\\n return (\\n a[0] + b[0],\\n a[1] + b[1],\\n (a[2] * b[2]) % 10,\\n )\\n\\ndef div(a, b):\\n return (\\n a[0] - b[0],\\n a[1] - b[1],\\n (a[2] * INV[b[2]]) % 10,\\n )\\n\\ndef red(it):\\n return sum((a * b) % 10 for a, b in it) % 10\\n\\nTWOS = [2, 4, 8, 6]\\nFIVES = [5]\\ndef simplify(tup):\\n twos, fives, res = tup\\n\\n if twos:\\n res = (res * TWOS[(twos - 1) % len(TWOS)]) % 10\\n if fives:\\n res = (res * FIVES[(fives - 1) % len(FIVES)]) % 10\\n\\n return res\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s) - 2\\n \\n facts = [(0, 0, 1)]\\n while n >= len(facts):\\n num = len(facts)\\n\\n twos = 0\\n while num % 2 == 0:\\n num //= 2\\n twos += 1\\n \\n fives = 0\\n while num % 5 == 0:\\n num //= 5\\n fives += 1\\n \\n facts.append(mult(facts[-1], (twos, fives, num)))\\n \\n pascal = []\\n for k in range(n + 1):\\n pascal.append(simplify(div(div(facts[n], facts[k]), facts[n - k])))\\n\\n a = red(zip(map(int, s), pascal))\\n b = red(zip(map(int, s[1:]), pascal))\\n\\n return a == b\"], [29890, 2.3529, \"INV = {\\n 1: 1,\\n 3: 7,\\n 7: 3,\\n 9: 9,\\n}\\n\\ndef mult(a, b):\\n return (\\n a[0] + b[0],\\n a[1] + b[1],\\n (a[2] * b[2]) % 10,\\n )\\n\\ndef div(a, b):\\n return (\\n a[0] - b[0],\\n a[1] - b[1],\\n (a[2] * INV[b[2]]) % 10,\\n )\\n\\ndef red(it):\\n return sum((a * b) % 10 for a, b in it) % 10\\n\\nTWOS = [2, 4, 8, 6]\\nFIVES = [5]\\ndef simplify(tup):\\n twos, fives, res = tup\\n\\n if twos:\\n res = (res * TWOS[(twos - 1) % len(TWOS)]) % 10\\n if fives:\\n res = (res * FIVES[(fives - 1) % len(FIVES)]) % 10\\n\\n return res\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s) - 2\\n \\n facts = [(0, 0, 1)]\\n while n >= len(facts):\\n num = len(facts)\\n\\n twos = 0\\n while num % 2 == 0:\\n num //= 2\\n twos += 1\\n \\n fives = 0\\n while num % 5 == 0:\\n num //= 5\\n fives += 1\\n \\n facts.append(mult(facts[-1], (twos, fives, num)))\\n \\n pascal = []\\n for k in range(n + 1):\\n pascal.append(simplify(div(div(facts[n], facts[k]), facts[n - k])))\\n\\n a = red(zip(map(int, s), pascal))\\n b = red(zip(map(int, s[1:]), pascal))\\n\\n return a == b\"], [30150, 3.2941, \"INV = {\\n 1: 1,\\n 3: 7,\\n 7: 3,\\n 9: 9,\\n}\\n\\ndef mult(a, b):\\n return (\\n a[0] + b[0],\\n a[1] + b[1],\\n (a[2] * b[2]) % 10,\\n )\\n\\ndef div(a, b):\\n return (\\n a[0] - b[0],\\n a[1] - b[1],\\n (a[2] * INV[b[2]]) % 10,\\n )\\n\\ndef red(it):\\n return sum((a * b) % 10 for a, b in it) % 10\\n\\nTWOS = [2, 4, 8, 6]\\nFIVES = [5]\\ndef simplify(tup):\\n twos, fives, res = tup\\n\\n if twos:\\n res = (res * TWOS[(twos - 1) % len(TWOS)]) % 10\\n if fives:\\n res = (res * FIVES[(fives - 1) % len(FIVES)]) % 10\\n\\n return res\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s) - 2\\n \\n facts = [(0, 0, 1)]\\n while n >= len(facts):\\n num = len(facts)\\n\\n twos = 0\\n while num % 2 == 0:\\n num //= 2\\n twos += 1\\n \\n fives = 0\\n while num % 5 == 0:\\n num //= 5\\n fives += 1\\n \\n facts.append(mult(facts[-1], (twos, fives, num)))\\n \\n pascal = []\\n for k in range(n + 1):\\n pascal.append(simplify(div(div(facts[n], facts[k]), facts[n - k])))\\n\\n a = red(zip(map(int, s), pascal))\\n b = red(zip(map(int, s[1:]), pascal))\\n\\n return a == b\"], [30410, 1.8824, \"INV = {\\n 1: 1,\\n 3: 7,\\n 7: 3,\\n 9: 9,\\n}\\n\\ndef mult(a, b):\\n return (\\n a[0] + b[0],\\n a[1] + b[1],\\n (a[2] * b[2]) % 10,\\n )\\n\\ndef div(a, b):\\n return (\\n a[0] - b[0],\\n a[1] - b[1],\\n (a[2] * INV[b[2]]) % 10,\\n )\\n\\ndef red(it):\\n return sum((a * b) % 10 for a, b in it) % 10\\n\\nTWOS = [2, 4, 8, 6]\\nFIVES = [5]\\ndef simplify(tup):\\n twos, fives, res = tup\\n\\n if twos:\\n res = (res * TWOS[(twos - 1) % len(TWOS)]) % 10\\n if fives:\\n res = (res * FIVES[(fives - 1) % len(FIVES)]) % 10\\n\\n return res\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s) - 2\\n \\n facts = [(0, 0, 1)]\\n while n >= len(facts):\\n num = len(facts)\\n\\n twos = 0\\n while num % 2 == 0:\\n num //= 2\\n twos += 1\\n \\n fives = 0\\n while num % 5 == 0:\\n num //= 5\\n fives += 1\\n \\n facts.append(mult(facts[-1], (twos, fives, num)))\\n \\n pascal = []\\n for k in range(n + 1):\\n pascal.append(simplify(div(div(facts[n], facts[k]), facts[n - k])))\\n\\n a = red(zip(map(int, s), pascal))\\n b = red(zip(map(int, s[1:]), pascal))\\n\\n return a == b\"], [30670, 0.9412, \"INV = {\\n 1: 1,\\n 3: 7,\\n 7: 3,\\n 9: 9,\\n}\\n\\ndef mult(a, b):\\n return (\\n a[0] + b[0],\\n a[1] + b[1],\\n (a[2] * b[2]) % 10,\\n )\\n\\ndef div(a, b):\\n return (\\n a[0] - b[0],\\n a[1] - b[1],\\n (a[2] * INV[b[2]]) % 10,\\n )\\n\\ndef red(it):\\n return sum((a * b) % 10 for a, b in it) % 10\\n\\nTWOS = [2, 4, 8, 6]\\nFIVES = [5]\\ndef simplify(tup):\\n twos, fives, res = tup\\n\\n if twos:\\n res = (res * TWOS[(twos - 1) % len(TWOS)]) % 10\\n if fives:\\n res = (res * FIVES[(fives - 1) % len(FIVES)]) % 10\\n\\n return res\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s) - 2\\n \\n facts = [(0, 0, 1)]\\n while n >= len(facts):\\n num = len(facts)\\n\\n twos = 0\\n while num % 2 == 0:\\n num //= 2\\n twos += 1\\n \\n fives = 0\\n while num % 5 == 0:\\n num //= 5\\n fives += 1\\n \\n facts.append(mult(facts[-1], (twos, fives, num)))\\n \\n pascal = []\\n for k in range(n + 1):\\n pascal.append(simplify(div(div(facts[n], facts[k]), facts[n - k])))\\n\\n a = red(zip(map(int, s), pascal))\\n b = red(zip(map(int, s[1:]), pascal))\\n\\n return a == b\"], [30930, 0.4706, \"INV = {\\n 1: 1,\\n 3: 7,\\n 7: 3,\\n 9: 9,\\n}\\n\\ndef mult(a, b):\\n return (\\n a[0] + b[0],\\n a[1] + b[1],\\n (a[2] * b[2]) % 10,\\n )\\n\\ndef div(a, b):\\n return (\\n a[0] - b[0],\\n a[1] - b[1],\\n (a[2] * INV[b[2]]) % 10,\\n )\\n\\ndef red(it):\\n return sum((a * b) % 10 for a, b in it) % 10\\n\\nTWOS = [2, 4, 8, 6]\\nFIVES = [5]\\ndef simplify(tup):\\n twos, fives, res = tup\\n\\n if twos:\\n res = (res * TWOS[(twos - 1) % len(TWOS)]) % 10\\n if fives:\\n res = (res * FIVES[(fives - 1) % len(FIVES)]) % 10\\n\\n return res\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s) - 2\\n \\n facts = [(0, 0, 1)]\\n while n >= len(facts):\\n num = len(facts)\\n\\n twos = 0\\n while num % 2 == 0:\\n num //= 2\\n twos += 1\\n \\n fives = 0\\n while num % 5 == 0:\\n num //= 5\\n fives += 1\\n \\n facts.append(mult(facts[-1], (twos, fives, num)))\\n \\n pascal = []\\n for k in range(n + 1):\\n pascal.append(simplify(div(div(facts[n], facts[k]), facts[n - k])))\\n\\n a = red(zip(map(int, s), pascal))\\n b = red(zip(map(int, s[1:]), pascal))\\n\\n return a == b\"], [31190, 0.2353, \"def fromInt(x):\\n q, r = 0, 0\\n while x % 2 == 0:\\n x //= 2\\n q += 1\\n while x % 5 == 0:\\n x //= 5\\n r += 1\\n return (x % 10, q, r)\\n\\nFROM_INT = [None] + [fromInt(n) for n in range(1, 10**5+1)]\\nINV_POW = [None] + [pow(u, -1, 10) if u % 2 != 0 and u % 5 != 0 else None for u in range(1, 10+1)]\\nFROM_INT_INV = [None] + [(INV_POW[p], -q, -r) for p, q, r in FROM_INT[1:]]\\n\\ndef multiply(a, b):\\n p, q, r = a\\n u, v, w = b\\n return (p * u % 10, q + v, r + w)\\n\\ndef divide(a, b):\\n p, q, r = a\\n u, v, w = b\\n return (p * INV_POW[u] % 10, q - v, r - w)\\n\\ndef lastDigit(pqr):\\n p, q, r = pqr\\n if q > 0:\\n p *= [2, 4, 8, 6][q%4-1]\\n if r > 0:\\n p *= 5\\n return p % 10\\n\\ndef combLastDigits(n):\\n result = []\\n cnk = fromInt(1)\\n result.append(lastDigit(cnk))\\n for k in range(0, n):\\n cnk = multiply(cnk, multiply(FROM_INT[n-k], FROM_INT_INV[k+1]))\\n result.append(lastDigit(cnk))\\n return result\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n '''\\n 0 1 2 3 4 5\\n 01 12 23 34 45\\n 0112 1223 2334 3445\\n 01112223 12223334 23334445\\n 0111122222233334 1222333423334445\\n Number of times each entry appears is just the binomial coefficient\\n\\n We can calculate C(n,k+1) from C(n,k) by multiplying by (n-k) / (k+1)\\n C(n,k+1) = n! / ((k+1)! * (n-k-1)!) = [n! / (k! * (n-k)!)] * [(n-k) / (k+1)]\\n Since we only care about the last digit, we can store it as follows:\\n (p, q, r) where\\n p is the product of the prime factors other than 2 and 5, mod 10\\n This is the rightmost non-zero digit\\n q is the power of 2\\n r is the power of 5\\n Then:\\n (p, q, r) * (u, v, w) = (p * u mod 10, q + v, r + w)\\n (p, q, r) / (u, v, w) = (p * u^-1 mod 10, q - v, r - w)\\n If k -> (p, q, r) then k mod 10 = p * 2^q * 5^r mod 10\\n '''\\n s = [int(c) for c in s]\\n binom = combLastDigits(len(s)-2)\\n firstDigit = sum(binom[i] * s[i] for i in range(len(s)-1)) % 10\\n secondDigit = sum(binom[i] * s[i+1] for i in range(len(s)-1)) % 10\\n return firstDigit == secondDigit\"], [31450, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s) - 2\\n \\n # For small inputs, use the direct approach\\n if n <= 20:\\n digits = [int(d) for d in s]\\n while len(digits) > 2:\\n digits = [(digits[i] + digits[i+1]) % 10 for i in range(len(digits) - 1)]\\n return digits[0] == digits[1]\\n \\n # For larger inputs, use binomial coefficients\\n # Precompute factorial representations as (twos, fives, other)\\n facts = []\\n twos, fives, other = 0, 0, 1\\n for i in range(n + 1):\\n facts.append((twos, fives, other))\\n num = i + 1\\n \\n # Count factors of 2\\n temp_twos = 0\\n while num % 2 == 0:\\n num //= 2\\n temp_twos += 1\\n twos += temp_twos\\n \\n # Count factors of 5\\n temp_fives = 0\\n while num % 5 == 0:\\n num //= 5\\n temp_fives += 1\\n fives += temp_fives\\n \\n # Multiply by remaining factors\\n other = (other * (num % 10)) % 10\\n \\n # Multiplicative inverses mod 10\\n inv = {1: 1, 3: 7, 7: 3, 9: 9}\\n \\n # Compute binomial coefficients\\n coeffs = []\\n for k in range(n + 1):\\n n_fact = facts[n]\\n k_fact = facts[k]\\n nk_fact = facts[n-k]\\n \\n twos = n_fact[0] - k_fact[0] - nk_fact[0]\\n fives = n_fact[1] - k_fact[1] - nk_fact[1]\\n other = n_fact[2]\\n \\n # Division using modular multiplicative inverses\\n if k_fact[2] in inv and nk_fact[2] in inv:\\n other = (other * inv[k_fact[2]] % 10 * inv[nk_fact[2]]) % 10\\n else:\\n coeffs.append(0)\\n continue\\n \\n # Apply powers of 2\\n if twos > 0:\\n other = (other * [2, 4, 8, 6][(twos - 1) % 4]) % 10\\n \\n # Apply powers of 5\\n if fives > 0:\\n other = (other * 5) % 10\\n \\n coeffs.append(other)\\n \\n # Calculate final digits\\n digits = [int(d) for d in s]\\n first = sum((d * c) % 10 for d, c in zip(digits[:n+1], coeffs)) % 10\\n second = sum((d * c) % 10 for d, c in zip(digits[1:n+2], coeffs)) % 10\\n \\n return first == second\"], [31710, 0.2353, \"import numpy as np\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n k = n - 2 # \\u6211\\u4eec\\u9700\\u8981\\u8ba1\\u7b97\\u9636\\u4e58\\u76f4\\u5230 k = n-2\\n \\n # \\u5c06\\u5b57\\u7b26\\u4e32\\u8f6c\\u6362\\u4e3a numpy \\u6570\\u7ec4\\uff08uint8\\uff09\\u5b58\\u653e\\u5404\\u6570\\u5b57\\uff08\\u5229\\u7528 ascii \\u7f16\\u7801\\u52a0\\u901f\\uff09\\n # \\u6ce8\\u610f\\uff1as.encode('ascii') \\u5f97\\u5230 bytes\\uff0c\\u6bcf\\u4e2a\\u5b57\\u7b26\\u5bf9\\u5e94\\u5176 ascii \\u7801\\n digits = np.frombuffer(s.encode('ascii'), dtype=np.uint8) - 48\\n\\n # -----------------------------\\n # \\u9884\\u5904\\u7406\\uff1a\\u8ba1\\u7b97 0! \\u5230 (n-2)! \\u7684\\u201c\\u5206\\u89e3\\u8868\\u793a\\u201d\\n # \\u5206\\u522b\\u5b58\\uff1afact_v[i]\\uff1a\\u53bb\\u9664 2 \\u548c 5 \\u540e\\u7684\\u90e8\\u5206\\uff0c\\u6a2110\\uff08\\u4fdd\\u8bc1\\u4e0e10\\u4e92\\u7d20\\uff09\\n # fact_c2[i]\\uff1ai! \\u4e2d\\u56e0\\u5b502\\u7684\\u603b\\u4e2a\\u6570\\n # fact_c5[i]\\uff1ai! \\u4e2d\\u56e0\\u5b505\\u7684\\u603b\\u4e2a\\u6570\\n fact_v = np.empty(k+1, dtype=np.int64)\\n fact_c2 = np.empty(k+1, dtype=np.int64)\\n fact_c5 = np.empty(k+1, dtype=np.int64)\\n fact_v[0] = 1\\n fact_c2[0] = 0\\n fact_c5[0] = 0\\n for i in range(1, k+1):\\n x = i\\n cnt2 = 0\\n cnt5 = 0\\n # \\u63d0\\u53d6\\u56e0\\u5b502\\n while x % 2 == 0:\\n x //= 2\\n cnt2 += 1\\n # \\u63d0\\u53d6\\u56e0\\u5b505\\n while x % 5 == 0:\\n x //= 5\\n cnt5 += 1\\n # \\u4f59\\u6570\\u90e8\\u5206 mod 10\\n r = x % 10\\n fact_v[i] = (fact_v[i-1] * r) % 10\\n fact_c2[i] = fact_c2[i-1] + cnt2\\n fact_c5[i] = fact_c5[i-1] + cnt5\\n \\n # -----------------------------\\n # \\u6c42 binom[j] = C(n-2, j) mod 10, \\u5bf9 j = 0,..., k\\n binom = np.empty(k+1, dtype=np.int64)\\n # \\u9884\\u5148\\u5b9a\\u4e49\\u4ec5\\u53ef\\u80fd\\u51fa\\u73b0\\u7684\\u4e0e10\\u4e92\\u7d20\\u6570\\u7684\\u9006\\u5143\\n inv_map = {1:1, 3:7, 7:3, 9:9}\\n def modinv(x):\\n return inv_map[int(x)]\\n # \\u5468\\u671f\\u8868\\uff1a2^e mod10 \\u5bf9 e>=1 \\u7684\\u5468\\u671f\\u4e3a (2,4,8,6)\\n cycle = (2, 4, 8, 6)\\n for j in range(0, k+1):\\n # \\u7ec4\\u5408\\u6570\\u516c\\u5f0f\\uff1aC(k, j) = fact(k) / (fact(j)*fact(k-j))\\n # \\u5148\\u8ba1\\u7b97\\u57fa\\u7840\\u90e8\\u5206\\uff08\\u5747\\u5728\\u4e0e10\\u4e92\\u7d20\\u7684\\u90e8\\u5206\\u4e2d\\u8fdb\\u884c\\uff0c\\u6545\\u53ef\\u4ee5\\u53d6\\u9006\\u5143\\uff09\\n base = (fact_v[k] * modinv(fact_v[j]) * modinv(fact_v[k-j])) % 10\\n # \\u8ba1\\u7b97\\u6307\\u6570\\u5dee\\n e2 = fact_c2[k] - fact_c2[j] - fact_c2[k-j]\\n e5 = fact_c5[k] - fact_c5[j] - fact_c5[k-j]\\n # \\u5982\\u679c\\u540c\\u65f6\\u6709 2 \\u548c 5\\uff0c\\u5219\\u8be5\\u9879\\u542b 10 \\u56e0\\u5b50\\uff0c\\u6a2110\\u7ed3\\u679c\\u4e3a 0\\n if e2 > 0 and e5 > 0:\\n binom[j] = 0\\n elif e2 > e5:\\n diff = e2 - e5\\n # \\u82e5 diff>=1\\uff0c\\u7528\\u5468\\u671f\\u8868\\uff1a2^(diff) mod10 = cycle[(diff-1)%4]\\n binom[j] = (base * cycle[(diff-1) % 4]) % 10\\n elif e5 > e2:\\n binom[j] = (base * 5) % 10\\n else:\\n binom[j] = base % 10\\n \\n # -----------------------------\\n # \\u6839\\u636e\\u6570\\u5b66\\u63a8\\u5bfc\\uff0c\\u6700\\u7ec8 S = -a_0 + sum_{i=1}^{n-2} (binom[i-1] - binom[i])*a_i + a_{n-1} mod10\\n # \\u6784\\u9020\\u7cfb\\u6570\\u6570\\u7ec4 c\\uff1a\\u957f\\u5ea6 n\\uff0cc[0] = -1, c[n-1] = 1, \\u5bf9 1<=i<=n-2, c[i] = (binom[i-1] - binom[i]) mod10\\n c = np.empty(n, dtype=np.int64)\\n c[0] = -1\\n c[n-1] = 1\\n if n > 2:\\n c[1:n-1] = (binom[:n-2] - binom[1:n-1]) % 10\\n # \\u8ba1\\u7b97 S = sum(c[i]*digits[i]) mod10\\uff08\\u5229\\u7528 numpy \\u70b9\\u4e58\\uff0c\\u5185\\u90e8 C \\u5b9e\\u73b0\\u975e\\u5e38\\u5feb\\uff09\\n S = int(np.dot(c, digits) % 10)\\n return S == 0\"], [31970, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n \\\"\\\"\\\"\\n Performs the described digit sum modulo 10 operation repeatedly until \\n the string has two digits and checks if they are the same.\\n Uses a mathematical approach based on binomial coefficients modulo 10.\\n\\n Args:\\n s: The input string consisting of digits.\\n\\n Returns:\\n True if the final two digits are the same, False otherwise.\\n \\\"\\\"\\\"\\n \\n n = len(s)\\n # Constraints state 3 <= n <= 10^5, so n >= 3.\\n m = n - 2 # Number of operations needed to reach length 2\\n \\n digits = [int(d) for d in s]\\n\\n # --- Helper functions for C(n, k) mod 10 ---\\n\\n # Precomputed C(n', k') mod 5 for n' <= 4 (needed for Lucas Theorem base case)\\n C_mod5_small = [\\n [1], # n=0\\n [1, 1], # n=1\\n [1, 2, 1], # n=2\\n [1, 3, 3, 1], # n=3\\n [1, 4, 1, 4, 1] # n=4 (C(4,2)=6%5=1)\\n ]\\n \\n def combinations_small_mod_5(n_small, k_small):\\n # Gets C(n_small, k_small) mod 5 for 0 <= k_small <= n_small <= 4\\n if k_small < 0 or k_small > n_small: \\n return 0 \\n # Safety checks for list index bounds\\n if n_small >= len(C_mod5_small) or k_small >= len(C_mod5_small[n_small]):\\n return 0 # Should not happen with correct Lucas usage\\n return C_mod5_small[n_small][k_small]\\n\\n # Memoization for Lucas Theorem results (mod 5)\\n memo_lucas_mod5 = {}\\n def get_binom_mod_p(n_lucas, k_lucas, p, combinations_small_func):\\n # Lucas Theorem for C(n, k) mod p (p must be prime)\\n # Assumes k_lucas >= 0 and k_lucas <= n_lucas from caller\\n \\n state = (n_lucas, k_lucas)\\n if state in memo_lucas_mod5:\\n return memo_lucas_mod5[state]\\n\\n res = 1\\n temp_n, temp_k = n_lucas, k_lucas # Use temps for iteration\\n \\n while temp_n > 0: # Loop while there are digits in base p\\n ni = temp_n % p\\n ki = temp_k % p\\n \\n # Get C(ni, ki) mod p using the precomputed small combinations function\\n term = combinations_small_func(ni, ki)\\n \\n if term == 0: # Optimization: if any C(ni, ki) = 0 mod p, the result is 0\\n memo_lucas_mod5[state] = 0\\n return 0\\n \\n res = (res * term) % p\\n \\n temp_n //= p\\n temp_k //= p\\n \\n # If temp_k > 0 after temp_n is 0, means original k > n (handled by caller)\\n memo_lucas_mod5[state] = res\\n return res\\n\\n # Precomputed Chinese Remainder Theorem lookup for (mod 2, mod 5) -> mod 10\\n # Key: (result_mod_2, result_mod_5), Value: result_mod_10\\n CRT_lookup = {\\n (0, 0): 0, (0, 1): 6, (0, 2): 2, (0, 3): 8, (0, 4): 4,\\n (1, 0): 5, (1, 1): 1, (1, 2): 7, (1, 3): 3, (1, 4): 9\\n }\\n\\n # Memoization dictionary for C(m, k) mod 10\\n # Key: (n_binom, k_binom_sym) where k_binom_sym = min(k, n-k)\\n memo_binom_mod_10 = {} \\n\\n def get_binom_mod_10(n_binom, k_binom):\\n # Handle base/edge cases first\\n if k_binom < 0 or k_binom > n_binom:\\n return 0\\n if k_binom == 0 or k_binom == n_binom:\\n return 1\\n \\n # Use symmetry C(n, k) = C(n, n-k) for memoization key\\n if k_binom > n_binom // 2:\\n k_binom_sym = n_binom - k_binom\\n else:\\n k_binom_sym = k_binom\\n \\n # Check memoization using the symmetric k\\n memo_key = (n_binom, k_binom_sym)\\n if memo_key in memo_binom_mod_10:\\n return memo_binom_mod_10[memo_key]\\n\\n # --- Calculate C(n_binom, k_binom_sym) mod 10 ---\\n # Mod 2: C(n, k) is odd iff (n & k) == k\\n mod2 = 1 if (n_binom & k_binom_sym) == k_binom_sym else 0\\n\\n # Mod 5: Use Lucas Theorem for C(n_binom, k_binom_sym) mod 5\\n mod5 = get_binom_mod_p(n_binom, k_binom_sym, 5, combinations_small_mod_5)\\n\\n # Combine using CRT lookup\\n result = CRT_lookup[(mod2, mod5)] \\n \\n # Store in memo using the symmetric k key\\n memo_binom_mod_10[memo_key] = result\\n \\n return result\\n\\n # --- Calculate the two final digits ---\\n final_sum0 = 0\\n final_sum1 = 0\\n\\n for i in range(m + 1): # i from 0 to m (inclusive) which is 0 to n-2\\n # Calculate C(m, i) % 10\\n coeff_mod_10 = get_binom_mod_10(m, i)\\n \\n # Optimization: if coefficient is 0, it contributes nothing to the sum\\n if coeff_mod_10 == 0:\\n continue \\n\\n # Add contribution to the first final digit: coeff * digits[i]\\n final_sum0 = (final_sum0 + coeff_mod_10 * digits[i]) % 10\\n \\n # Add contribution to the second final digit: coeff * digits[i+1]\\n # Index i+1 goes from 1 to m+1 (which is n-1), valid for the digits list\\n final_sum1 = (final_sum1 + coeff_mod_10 * digits[i+1]) % 10\\n \\n # Check if the two final calculated digits are equal\\n return final_sum0 == final_sum1\"], [32230, 0.2353, \"class Solution:\\n # --- Precompute outside the main function for potential reuse ---\\n # Precomputed C(n', k') mod 5 for n' <= 4 (Lucas base case)\\n C_mod5_small = [\\n [1], # n=0\\n [1, 1], # n=1\\n [1, 2, 1], # n=2\\n [1, 3, 3, 1], # n=3\\n [1, 4, 1, 4, 1] # n=4 (C(4,2)=6%5=1)\\n ]\\n\\n # Precomputed Chinese Remainder Theorem lookup for (mod 2, mod 5) -> mod 10\\n CRT_lookup = {\\n (0, 0): 0, (0, 1): 6, (0, 2): 2, (0, 3): 8, (0, 4): 4,\\n (1, 0): 5, (1, 1): 1, (1, 2): 7, (1, 3): 3, (1, 4): 9\\n }\\n \\n # Memoization dictionaries (class level to persist across calls if needed, \\n # or could be inside hasSameDigits if instance-based)\\n memo_lucas_mod5 = {} \\n memo_binom_mod_10 = {} # Key: (n, k_symmetric)\\n\\n def combinations_small_mod_5(self, n_small, k_small):\\n # Gets C(n_small, k_small) mod 5 for 0 <= k_small <= n_small <= 4\\n if k_small < 0 or k_small > n_small or n_small >= len(self.C_mod5_small) or k_small >= len(self.C_mod5_small[n_small]): \\n return 0 \\n return self.C_mod5_small[n_small][k_small]\\n\\n def get_binom_mod_p_lucas(self, n_lucas, k_lucas, p):\\n # Lucas Theorem for C(n, k) mod p (p must be prime)\\n # Assumes k_lucas >= 0 and k_lucas <= n_lucas (checked by caller)\\n \\n state = (n_lucas, k_lucas, p)\\n if state in self.memo_lucas_mod5:\\n return self.memo_lucas_mod5[state]\\n\\n res = 1\\n temp_n, temp_k = n_lucas, k_lucas\\n \\n while temp_n > 0: # Loop while there are digits in base p\\n ni = temp_n % p\\n ki = temp_k % p\\n \\n # We only need C(ni, ki) mod 5, use the small precomputed table\\n term = self.combinations_small_mod_5(ni, ki)\\n \\n if term == 0: # Optimization: if any C(ni, ki) = 0 mod p, the result is 0\\n self.memo_lucas_mod5[state] = 0\\n return 0\\n \\n res = (res * term) % p\\n \\n temp_n //= p\\n temp_k //= p\\n \\n # If temp_k > 0 after temp_n is 0, implies original k > n, handled by caller check\\n self.memo_lucas_mod5[state] = res\\n return res\\n\\n def get_binom_mod_10(self, n_binom, k_binom):\\n # Calculates C(n_binom, k_binom) mod 10 using CRT and memoization\\n \\n # Handle base/edge cases first\\n if k_binom < 0 or k_binom > n_binom:\\n return 0\\n if k_binom == 0 or k_binom == n_binom:\\n return 1\\n \\n # Use symmetry C(n, k) = C(n, n-k) for memoization key\\n k_binom_sym = min(k_binom, n_binom - k_binom)\\n \\n # Check memoization using the symmetric k\\n memo_key = (n_binom, k_binom_sym)\\n if memo_key in self.memo_binom_mod_10:\\n return self.memo_binom_mod_10[memo_key]\\n\\n # --- Calculate C(n_binom, k_binom_sym) mod 10 ---\\n # Mod 2: C(n, k) is odd iff (n & k) == k\\n # Calculate with k_binom_sym as it gives the same parity result\\n mod2 = 1 if (n_binom & k_binom_sym) == k_binom_sym else 0\\n\\n # Mod 5: Use Lucas Theorem for C(n_binom, k_binom_sym) mod 5\\n mod5 = self.get_binom_mod_p_lucas(n_binom, k_binom_sym, 5)\\n\\n # Combine using CRT lookup\\n result = self.CRT_lookup[(mod2, mod5)] \\n \\n # Store in memo using the symmetric k key\\n self.memo_binom_mod_10[memo_key] = result\\n \\n return result\\n\\n def hasSameDigits(self, s: str) -> bool:\\n \\\"\\\"\\\"\\n Optimized mathematical approach using binomial coefficients mod 10.\\n \\\"\\\"\\\"\\n n = len(s)\\n m = n - 2 # Number of operations needed to reach length 2\\n \\n digits = [int(d) for d in s]\\n\\n # Clear memos if running multiple test cases within the same Solution object instance\\n # (LeetCode usually creates a new instance per test case, but good practice)\\n self.memo_lucas_mod5.clear()\\n self.memo_binom_mod_10.clear()\\n\\n final_sum0 = 0\\n final_sum1 = 0\\n\\n for i in range(m + 1): # i from 0 to m (inclusive) which is 0 to n-2\\n # Calculate C(m, i) % 10 efficiently using memoization\\n coeff_mod_10 = self.get_binom_mod_10(m, i)\\n \\n # Optimization: if coefficient is 0, it contributes nothing to the sum\\n if coeff_mod_10 == 0:\\n continue \\n\\n # Add contribution to the first final digit: coeff * digits[i]\\n final_sum0 = (final_sum0 + coeff_mod_10 * digits[i]) % 10\\n \\n # Add contribution to the second final digit: coeff * digits[i+1]\\n final_sum1 = (final_sum1 + coeff_mod_10 * digits[i+1]) % 10\\n \\n # Check if the two final calculated digits are equal\\n return final_sum0 == final_sum1\"], [32490, 0.4706, \"import numpy as np\\n\\ndef nCrModpDP(n, r, p): \\n\\n if n < r:\\n return 0\\n try:\\n C = [0] * (n + 1); \\n \\n C[0] = 1; \\n \\n for i in range(1, (n + 1)): \\n \\n j = min(i, r); \\n while(j > 0): \\n C[j] = (C[j] + C[j - 1]) % p; \\n j -= 1; \\n return C[r]; \\n except:\\n print(f\\\"n = {n}, r = {r}, p = {p}\\\")\\n \\n\\n\\n\\ndef nCrModpDP_cache(n, r, cache): \\n if n < r:\\n return 0\\n return cache[n, r]\\n\\ndef nCrModpLucas(n, r, p, cache): \\n # Base case \\n if (r == 0): \\n return 1; \\n \\n ni = int(n % p); \\n ri = int(r % p); \\n \\n return (nCrModpLucas(int(n / p), int(r / p), p, cache) * \\n nCrModpDP_cache(ni, ri, cache)) % p; # Remaining digits \\n\\ndef get_binomial_coef_mod(n, mod, cache):\\n\\n return np.array([nCrModpLucas(n, k, mod, cache) for k in range(n + 1)])\\n\\n\\n\\nclass Solution:\\n\\n def hasSameDigits(self, s: str) -> bool:\\n number_list = np.array([ int(x) for x in s])\\n cache_2 = np.zeros(shape=(2,2))\\n for i in range(2):\\n for j in range(2):\\n cache_2[i, j] = nCrModpDP(i, j, 2)\\n binomial_coef_2 = get_binomial_coef_mod(len(number_list)-2, 2, cache_2)\\n\\n if (binomial_coef_2.dot(number_list[:-1])%2 != binomial_coef_2.dot(number_list[1:] )%2):\\n return False\\n \\n cache_5 = np.zeros(shape=(5,5))\\n for i in range(5):\\n for j in range(5):\\n cache_5[i, j] = nCrModpDP(i, j, 5)\\n\\n binomial_coef_5 = get_binomial_coef_mod(len(number_list)-2, 5, cache_5)\\n if (binomial_coef_5.dot(number_list[:-1])%5 != binomial_coef_5.dot(number_list[1:] )%5):\\n return False\\n return True\"], [32750, 0.4706, \"class Solution:\\n # --- Precompute outside the main function for potential reuse ---\\n # Precomputed C(n', k') mod 5 for n' <= 4 (Lucas base case)\\n C_mod5_small = [\\n [1], # n=0\\n [1, 1], # n=1\\n [1, 2, 1], # n=2\\n [1, 3, 3, 1], # n=3\\n [1, 4, 1, 4, 1] # n=4 (C(4,2)=6%5=1)\\n ]\\n\\n # Precomputed Chinese Remainder Theorem lookup for (mod 2, mod 5) -> mod 10\\n CRT_lookup = {\\n (0, 0): 0, (0, 1): 6, (0, 2): 2, (0, 3): 8, (0, 4): 4,\\n (1, 0): 5, (1, 1): 1, (1, 2): 7, (1, 3): 3, (1, 4): 9\\n }\\n \\n # Memoization dictionaries (class level to persist across calls if needed, \\n # or could be inside hasSameDigits if instance-based)\\n memo_lucas_mod5 = {} \\n memo_binom_mod_10 = {} # Key: (n, k_symmetric)\\n\\n def combinations_small_mod_5(self, n_small, k_small):\\n # Gets C(n_small, k_small) mod 5 for 0 <= k_small <= n_small <= 4\\n if k_small < 0 or k_small > n_small or n_small >= len(self.C_mod5_small) or k_small >= len(self.C_mod5_small[n_small]): \\n return 0 \\n return self.C_mod5_small[n_small][k_small]\\n\\n def get_binom_mod_p_lucas(self, n_lucas, k_lucas, p):\\n # Lucas Theorem for C(n, k) mod p (p must be prime)\\n # Assumes k_lucas >= 0 and k_lucas <= n_lucas (checked by caller)\\n \\n state = (n_lucas, k_lucas, p)\\n if state in self.memo_lucas_mod5:\\n return self.memo_lucas_mod5[state]\\n\\n res = 1\\n temp_n, temp_k = n_lucas, k_lucas\\n \\n while temp_n > 0: # Loop while there are digits in base p\\n ni = temp_n % p\\n ki = temp_k % p\\n \\n # We only need C(ni, ki) mod 5, use the small precomputed table\\n term = self.combinations_small_mod_5(ni, ki)\\n \\n if term == 0: # Optimization: if any C(ni, ki) = 0 mod p, the result is 0\\n self.memo_lucas_mod5[state] = 0\\n return 0\\n \\n res = (res * term) % p\\n \\n temp_n //= p\\n temp_k //= p\\n \\n # If temp_k > 0 after temp_n is 0, implies original k > n, handled by caller check\\n self.memo_lucas_mod5[state] = res\\n return res\\n\\n def get_binom_mod_10(self, n_binom, k_binom):\\n # Calculates C(n_binom, k_binom) mod 10 using CRT and memoization\\n \\n # Handle base/edge cases first\\n if k_binom < 0 or k_binom > n_binom:\\n return 0\\n if k_binom == 0 or k_binom == n_binom:\\n return 1\\n \\n # Use symmetry C(n, k) = C(n, n-k) for memoization key\\n k_binom_sym = min(k_binom, n_binom - k_binom)\\n \\n # Check memoization using the symmetric k\\n memo_key = (n_binom, k_binom_sym)\\n if memo_key in self.memo_binom_mod_10:\\n return self.memo_binom_mod_10[memo_key]\\n\\n # --- Calculate C(n_binom, k_binom_sym) mod 10 ---\\n # Mod 2: C(n, k) is odd iff (n & k) == k\\n # Calculate with k_binom_sym as it gives the same parity result\\n mod2 = 1 if (n_binom & k_binom_sym) == k_binom_sym else 0\\n\\n # Mod 5: Use Lucas Theorem for C(n_binom, k_binom_sym) mod 5\\n mod5 = self.get_binom_mod_p_lucas(n_binom, k_binom_sym, 5)\\n\\n # Combine using CRT lookup\\n result = self.CRT_lookup[(mod2, mod5)] \\n \\n # Store in memo using the symmetric k key\\n self.memo_binom_mod_10[memo_key] = result\\n \\n return result\\n\\n def hasSameDigits(self, s: str) -> bool:\\n \\\"\\\"\\\"\\n Optimized mathematical approach using binomial coefficients mod 10.\\n \\\"\\\"\\\"\\n n = len(s)\\n m = n - 2 # Number of operations needed to reach length 2\\n \\n digits = [int(d) for d in s]\\n\\n # Clear memos if running multiple test cases within the same Solution object instance\\n # (LeetCode usually creates a new instance per test case, but good practice)\\n self.memo_lucas_mod5.clear()\\n self.memo_binom_mod_10.clear()\\n\\n final_sum0 = 0\\n final_sum1 = 0\\n\\n for i in range(m + 1): # i from 0 to m (inclusive) which is 0 to n-2\\n # Calculate C(m, i) % 10 efficiently using memoization\\n coeff_mod_10 = self.get_binom_mod_10(m, i)\\n \\n # Optimization: if coefficient is 0, it contributes nothing to the sum\\n if coeff_mod_10 == 0:\\n continue \\n\\n # Add contribution to the first final digit: coeff * digits[i]\\n final_sum0 = (final_sum0 + coeff_mod_10 * digits[i]) % 10\\n \\n # Add contribution to the second final digit: coeff * digits[i+1]\\n final_sum1 = (final_sum1 + coeff_mod_10 * digits[i+1]) % 10\\n \\n # Check if the two final calculated digits are equal\\n return final_sum0 == final_sum1\"], [33010, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n m = len(s)\\n if m < 3:\\n return True\\n\\n n = m - 2\\n\\n def precompute(p):\\n fact = [1] * p\\n invfact = [1] * p\\n for i in range(1, p):\\n fact[i] = (fact[i-1] * i) % p\\n for i in range(0, p):\\n invfact[i] = pow(fact[i], -1, p)\\n return fact, invfact\\n\\n fact2, invfact2 = precompute(2)\\n fact5, invfact5 = precompute(5)\\n\\n def comb_small(n_i, r_i, p, fact, invfact):\\n if r_i > n_i:\\n return 0\\n return (fact[n_i] * invfact[r_i] * invfact[n_i - r_i]) % p\\n\\n def lucas(n_val, r_val, p, fact, invfact):\\n res = 1\\n while n_val or r_val:\\n n_i = n_val % p\\n r_i = r_val % p\\n if r_i > n_i:\\n return 0\\n res = (res * comb_small(n_i, r_i, p, fact, invfact)) % p\\n n_val //= p\\n r_val //= p\\n return res\\n\\n lucas2_cache = {}\\n lucas5_cache = {}\\n def get_lucas(p, r, fact, invfact, cache):\\n if r in cache:\\n return cache[r]\\n res = lucas(n, r, p, fact, invfact)\\n cache[r] = res\\n return res\\n\\n def get_binom_mod10(r):\\n res2 = get_lucas(2, r, fact2, invfact2, lucas2_cache)\\n res5 = get_lucas(5, r, fact5, invfact5, lucas5_cache)\\n k = (3 * ((res5 - res2) % 5)) % 5 \\n return (res2 + 2 * k) % 10\\n\\n diff = 0\\n for i in range(n + 1):\\n d = int(s[i+1]) - int(s[i])\\n coeff = get_binom_mod10(i)\\n diff = (diff + coeff * d) % 10\\n\\n return diff % 10 == 0\\n\"], [33270, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n # We need to perform n-2 iterations, so set N = n - 2.\\n N = n - 2\\n # Convert the string digits to integers.\\n digits = list(map(int, s))\\n \\n # --- Precompute factorials modulo 5 for numbers 0..4 ---\\n fact5 = [1] * 5\\n for i in range(1, 5):\\n fact5[i] = (fact5[i - 1] * i) % 5\\n # Compute inverses modulo 5 using Fermat's little theorem (since 5 is prime).\\n invfact5 = [1] * 5\\n for i in range(1, 5):\\n invfact5[i] = pow(fact5[i], -1, 5)\\n \\n # --- Lucas theorem for modulo 5 ---\\n # This helper computes nCr mod 5 for small n (<5) using precomputed factorials.\\n def nCr_mod5(n_val: int, r_val: int) -> int:\\n if r_val > n_val:\\n return 0\\n return (fact5[n_val] * invfact5[r_val] * invfact5[n_val - r_val]) % 5\\n \\n from functools import lru_cache\\n \\n @lru_cache(maxsize=None)\\n def lucas_mod5(n_val: int, r_val: int) -> int:\\n res = 1\\n while n_val or r_val:\\n n_digit = n_val % 5\\n r_digit = r_val % 5\\n if r_digit > n_digit:\\n return 0\\n res = (res * nCr_mod5(n_digit, r_digit)) % 5\\n n_val //= 5\\n r_val //= 5\\n return res\\n \\n # --- Combine mod 2 and mod 5 results to compute nCr mod 10 ---\\n # For mod 2, there is a neat bit trick: binom(n, r) mod 2 is 1 if and only if every 1\\u2013bit in r is also a 1\\u2013bit in n.\\n def binom_mod_10(n_val: int, r_val: int) -> int:\\n # Compute nCr mod 2 using the bit property.\\n a2 = 1 if (r_val & ~n_val) == 0 else 0\\n # Compute nCr mod 5 via Lucas theorem.\\n a5 = lucas_mod5(n_val, r_val)\\n # Use the Chinese remainder theorem to combine mod 2 and mod 5 into mod 10.\\n # Solve for x \\u2261 a2 (mod 2) and x \\u2261 a5 (mod 5).\\n # Since 2's inverse mod 5 is 3 (because 2*3=6\\u22611 mod5), we can set:\\n k = (a5 - a2) % 5\\n x = (a2 + 2 * ((3 * k) % 5)) % 10\\n return x\\n \\n # --- Compute the two final digits as weighted sums ---\\n # After (n-2) iterations the two digits are:\\n # left_digit = sum_{j=0}^{N} binom(N, j) * digits[j] mod 10,\\n # right_digit = sum_{j=0}^{N} binom(N, j) * digits[j+1] mod 10.\\n S0 = 0\\n S1 = 0\\n for j in range(N + 1):\\n weight = binom_mod_10(N, j)\\n S0 = (S0 + weight * digits[j]) % 10\\n S1 = (S1 + weight * digits[j + 1]) % 10\\n return S0 == S1\\n\"]]",
"runtime": 1289,
"runtimeDistribution": "[[74, 1.4118000000000002, \"__import__(\\\"atexit\\\").register(lambda: open(\\\"display_runtime.txt\\\", \\\"w\\\").write(\\\"0\\\"))\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n m = n - 2\\n a0, a1 = 0, 0\\n\\n # Compute reduced values for a0 and a1\\n for i in range(m + 1):\\n coe = self.vikky1(m, i)\\n a0 = (a0 + coe * int(s[i])) % 10\\n a1 = (a1 + coe * int(s[i + 1])) % 10\\n\\n return a0 == a1\\n\\n def vikky1(self, n: int, k: int) -> int:\\n hemu2 = self.hemu(n, k)\\n cherry5 = self.cherry(n, k)\\n res = cherry5\\n\\n if res % 2 != hemu2:\\n res += 5\\n\\n return res % 10\\n\\n def cherry(self, n: int, k: int) -> int:\\n res = 1\\n p = 5\\n fact1 = [1, 1, 2, 1, 4]\\n fact2 = [1, 1, 3, 1, 4]\\n\\n # Compute Pascal's coefficients modulo p\\n while n > 0 or k > 0:\\n ndig = n % p\\n kdig = k % p\\n\\n if kdig > ndig:\\n return 0\\n\\n ans = fact1[ndig]\\n ans = (ans * fact2[kdig]) % p\\n ans = (ans * fact2[ndig - kdig]) % p\\n res = (res * ans) % p\\n\\n n //= p\\n k //= p\\n\\n return res\\n\\n def hemu(self, n: int, k: int) -> int:\\n # Check divisibility using bitwise operations\\n while n > 0 or k > 0:\\n nb = n & 1\\n kb = k & 1\\n\\n if kb > nb:\\n return 0\\n\\n n >>= 1\\n k >>= 1\\n\\n return 1\"], [222, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n s = [ord(a) - ord(b) for a,b in pairwise(s)]\\n n, res = len(s), 0\\n cnt2, cnt5, r5, j = 0, 0, 1, n-1\\n map10, map5 = [[0,5],[6,1],[2,7],[8,3],[4,9]], [\\n [-1,0,0,0,0],\\n [-1,1,3,2,4],\\n [-1,2,1,4,3],\\n [-1,3,4,1,2],\\n [-1,4,2,3,1]\\n ]\\n\\n for i, d in enumerate(s[:n//2], 1):\\n res += (d + s[-i]) * map10[r5 * (cnt5 == 0)][cnt2 == 0]\\n\\n \\n cnt2 += (j&-j).bit_length() - (i&-i).bit_length()\\n\\n jj, j = j, j-1\\n while not jj % 5:\\n jj //= 5\\n cnt5 += 1\\n r5 = r5 * jj % 5\\n \\n while not i % 5:\\n i //= 5\\n cnt5 -= 1\\n r5 = map5[r5][i%5]\\n \\n if n & 1:\\n res += s[n//2] * map10[r5 * (cnt5 == 0)][cnt2 == 0]\\n\\n return res % 10 == 0\"], [370, 0.4706, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n s = [ord(a) - ord(b) for a,b in pairwise(s)]\\n n, res = len(s), 0\\n cnt2, cnt5, r5, j = 0, 0, 1, n-1\\n map10, map5 = [[0,5],[6,1],[2,7],[8,3],[4,9]], [\\n [-1,0,0,0,0],\\n [-1,1,3,2,4],\\n [-1,2,1,4,3],\\n [-1,3,4,1,2],\\n [-1,4,2,3,1]\\n ]\\n\\n for i, d in enumerate(s[:n//2], 1):\\n res += (d + s[-i]) * map10[r5 * (cnt5 == 0)][cnt2 == 0]\\n\\n \\n cnt2 += (j&-j).bit_length() - (i&-i).bit_length()\\n\\n jj, j = j, j-1\\n while not jj % 5:\\n jj //= 5\\n cnt5 += 1\\n r5 = r5 * jj % 5\\n \\n while not i % 5:\\n i //= 5\\n cnt5 -= 1\\n r5 = map5[r5][i%5]\\n \\n if n & 1:\\n res += s[n//2] * map10[r5 * (cnt5 == 0)][cnt2 == 0]\\n\\n return res % 10 == 0\\n \"], [518, 0.2353, \"import sys\\n# input = sys.stdin.readline # Optional: Faster input reading\\n\\n# Precompute C(n, k) % 5 for n < 5\\n# Stays the same, define globally or pass as argument\\nC_small_mod5 = [\\n [1, 0, 0, 0, 0], # n=0\\n [1, 1, 0, 0, 0], # n=1\\n [1, 2, 1, 0, 0], # n=2\\n [1, 3, 3, 1, 0], # n=3\\n [1, 4, 1, 4, 1], # n=4 (C(4,2)=6%5=1)\\n]\\n\\n# Optimized nCr_mod5 using Lucas Theorem\\n# Pass table as argument to potentially reduce global lookup overhead slightly\\ndef nCr_mod5_opt(n, k, C_small_table):\\n # Base cases first\\n if k < 0 or k > n:\\n return 0\\n # Symmetry check - might not be faster, depends on implementation details\\n # if k > n // 2:\\n # k = n - k\\n # Lucas theorem core loop\\n res = 1\\n while k > 0: # Loop runs log_5(k) times approx\\n ni = n % 5\\n ki = k % 5\\n if ki > ni: # Essential check for correctness and speed\\n return 0\\n # Direct table lookup (passed as argument)\\n term = C_small_table[ni][ki]\\n # if term == 0: # This check is implicitly covered by ki > ni\\n # return 0\\n res = (res * term) % 5\\n # Integer division\\n n //= 5\\n k //= 5\\n # Only return 1 if k reached 0 successfully. If n became 0 while k > 0,\\n # it means original k > n, handled by initial check.\\n # The loop terminates when k becomes 0. If n also became 0 or positive, res holds the result.\\n return res\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n # Constraint n >= 3 removes need for n=2 edge case handling\\n\\n M = n - 2\\n # Convert digits to list - unavoidable O(N)\\n # Using tuple might be slightly faster for iteration later? Test needed.\\n digits = [int(d) for d in s]\\n # digits = tuple(int(d) for d in s) # Try tuple?\\n\\n # Use local variables for values used repeatedly in loops\\n local_M = M\\n local_digits = digits\\n\\n # --- Check Modulo 2 --- O(N)\\n # Sum directly, take modulo at the very end\\n sum0_mod2 = 0\\n sum1_mod2 = 0\\n for j in range(local_M + 1):\\n # Fast bitwise check for C(M, j) % 2\\n if (j & local_M) == j:\\n # Access digits list/tuple\\n sum0_mod2 += local_digits[j]\\n sum1_mod2 += local_digits[j+1]\\n\\n # Check parity only once after the loop\\n if (sum0_mod2 % 2) != (sum1_mod2 % 2):\\n return False\\n\\n # --- Check Modulo 5 --- O(N log N)\\n sum0_mod5 = 0\\n sum1_mod5 = 0\\n # Pass the small table directly to avoid potential global lookup overhead\\n C_table = C_small_mod5\\n for j in range(local_M + 1):\\n # Call the optimized nCr function\\n coeff_mod5 = nCr_mod5_opt(local_M, j, C_table) # O(log M)\\n \\n # Skip multiplication and addition if coefficient is zero\\n if coeff_mod5 != 0:\\n # Access digits list/tuple\\n sum0_mod5 += coeff_mod5 * local_digits[j]\\n sum1_mod5 += coeff_mod5 * local_digits[j+1]\\n\\n # Final modulo 5 check after the loop\\n # Overflow is not an issue here for N=10^5 and digits 0-9\\n return (sum0_mod5 % 5) == (sum1_mod5 % 5)\"], [666, 2.5883000000000003, \"import sys\\n# Memoization dictionary for Lucas theorem results to potentially speed up computation,\\n# especially if C(m, j) values are recalculated (e.g., due to symmetry).\\nmemo_lucas = {} \\n\\n# Precompute small C(n, k) % 5 for 0 <= k <= n < 5, needed for Lucas' theorem.\\n# This table can be computed once outside the function or class.\\nsmall_C_mod5 = [[0] * 5 for _ in range(5)]\\nfor n_small in range(5):\\n small_C_mod5[n_small][0] = 1 # C(n, 0) = 1\\n for k_small in range(1, n_small + 1):\\n # Pascal's identity: C(n, k) = C(n-1, k-1) + C(n-1, k)\\n term1 = small_C_mod5[n_small - 1][k_small - 1]\\n term2 = small_C_mod5[n_small - 1][k_small]\\n small_C_mod5[n_small][k_small] = (term1 + term2) % 5\\n\\n# Helper function to compute C(n, k) % 5 using Lucas' theorem (iterative).\\n# Uses the precomputed small_C_mod5 table and memoization.\\ndef lucas_C_mod5_helper(n_lucas, k_lucas):\\n \\\"\\\"\\\"Computes C(n_lucas, k_lucas) modulo 5 using Lucas' theorem.\\\"\\\"\\\"\\n global small_C_mod5, memo_lucas\\n \\n # Handle base cases and out-of-range k\\n if k_lucas < 0 or k_lucas > n_lucas:\\n return 0\\n if k_lucas == 0 or k_lucas == n_lucas:\\n return 1\\n \\n # Use symmetry C(n, k) = C(n, n-k) to potentially use memoized results or smaller k.\\n # The memoization key should be consistent, e.g., always store for min(k, n-k).\\n original_k = k_lucas\\n if k_lucas > n_lucas // 2:\\n k_lucas = n_lucas - k_lucas\\n\\n # Check memoization table using the canonical k (min(k, n-k))\\n if (n_lucas, k_lucas) in memo_lucas:\\n return memo_lucas[(n_lucas, k_lucas)]\\n\\n # Iteratively apply Lucas' theorem using base 5 representation\\n res = 1\\n temp_n = n_lucas\\n temp_k = k_lucas # Use the potentially reduced k_lucas\\n while temp_n > 0 or temp_k > 0:\\n ni = temp_n % 5 # Last digit of n in base 5\\n ki = temp_k % 5 # Last digit of k in base 5\\n \\n # If k_i > n_i for any digit, then C(n_i, k_i) = 0, so C(n, k) % 5 = 0\\n if ki > ni:\\n res = 0 \\n break # The result will be 0\\n \\n # Get C(n_i, k_i) % 5 from the precomputed table\\n comb_mod5 = small_C_mod5[ni][ki]\\n \\n # If any factor C(ni, ki) is 0, the total product is 0 mod 5.\\n if comb_mod5 == 0:\\n res = 0\\n break # The result will be 0\\n \\n # Multiply the result by this factor (mod 5)\\n res = (res * comb_mod5) % 5\\n \\n # Move to the next digits by integer division by 5\\n temp_n //= 5\\n temp_k //= 5\\n \\n # Store the computed result in the memoization table using the canonical k\\n memo_lucas[(n_lucas, k_lucas)] = res\\n return res\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n \\\"\\\"\\\"\\n Determines if the final two digits are the same after repeatedly applying\\n the sum-modulo-10 operation on consecutive digits.\\n\\n The process can be analyzed using binomial coefficients. The final two digits,\\n d0 and d1, after m = n-2 steps are given by:\\n d0 = (sum_{j=0}^{m} C(m, j) * a_j) % 10\\n d1 = (sum_{j=0}^{m} C(m, j) * a_{j+1}) % 10\\n where a_i are the initial digits of s, and C(m, j) is \\\"m choose j\\\".\\n\\n We check if d0 == d1 by verifying congruence modulo 2 and modulo 5 using the\\n Chinese Remainder Theorem principle. Lucas' theorem is used to compute C(m, j) % p.\\n \\\"\\\"\\\"\\n n = len(s)\\n # Per constraints: 3 <= s.length <= 10^5. n is guaranteed to be >= 3.\\n\\n m = n - 2 # The 'order' of the binomial coefficients C(m, j) needed.\\n\\n # Convert the input string of digits into a list of integers.\\n digits = [int(d) for d in s]\\n\\n # --- Modulo 2 Calculation ---\\n # Check if d0 % 2 == d1 % 2.\\n # According to Lucas' theorem for p=2, C(m, j) % 2 == 1 if and only if\\n # the binary representation of j is 'bitwise contained' within the binary\\n # representation of m. This is equivalent to (j & m) == j.\\n d0_mod2 = 0\\n d1_mod2 = 0\\n for j in range(m + 1): # Iterate j from 0 to m\\n # Check if C(m, j) is odd using the bitwise condition\\n if (j & m) == j:\\n # If C(m, j) is odd, it contributes digits[j] % 2 to d0_mod2\\n # and digits[j+1] % 2 to d1_mod2.\\n d0_mod2 = (d0_mod2 + digits[j]) % 2\\n \\n # digits[j+1] is needed for d1. The index j+1 ranges up to m+1 = n-1.\\n # Since the digits list has length n (indices 0 to n-1), this is always a valid index.\\n d1_mod2 = (d1_mod2 + digits[j + 1]) % 2\\n\\n # If the sums modulo 2 are different, the final digits d0 and d1 cannot be equal.\\n if d0_mod2 != d1_mod2:\\n return False\\n\\n # --- Modulo 5 Calculation ---\\n # Check if d0 % 5 == d1 % 5.\\n # Requires computing C(m, j) % 5 for j = 0 to m.\\n \\n # Clear memoization table for Lucas theorem results for this specific run.\\n # Global memoization might lead to issues if Solution object is reused or in threaded env.\\n # It's safer to manage memoization within the function call or instance.\\n # For LeetCode's execution model, a global or class-level memo might be okay,\\n # but clearing it ensures correctness between test cases.\\n global memo_lucas\\n memo_lucas.clear() \\n\\n d0_mod5 = 0\\n d1_mod5 = 0\\n for j in range(m + 1): # Iterate j from 0 to m\\n # Calculate C(m, j) % 5 using the helper function, which utilizes\\n # precomputed small values, Lucas' theorem, and memoization.\\n c_mj_mod5 = lucas_C_mod5_helper(m, j)\\n\\n # If the coefficient C(m, j) % 5 is 0, this term does not contribute to the sums mod 5.\\n if c_mj_mod5 == 0:\\n continue \\n\\n # Add the contribution C(m, j) * digits[j] to d0_mod5\\n d0_mod5 = (d0_mod5 + c_mj_mod5 * digits[j]) % 5\\n\\n # Add the contribution C(m, j) * digits[j+1] to d1_mod5\\n # Index j+1 is valid, as explained before.\\n d1_mod5 = (d1_mod5 + c_mj_mod5 * digits[j + 1]) % 5\\n\\n # The final digits d0 and d1 are equal if and only if they are congruent\\n # modulo 2 and modulo 5. We already verified the modulo 2 congruence.\\n # The function returns true if they are also congruent modulo 5, false otherwise.\\n return (d0_mod5 == d1_mod5)\"], [814, 2.5883000000000003, \"class Solution:\\n\\n def hasSameDigits(self, s: str) -> bool:\\n numbers = [int(c) for c in s]\\n\\n # for :\\n # comb_values_ratio[i][j] = iCj / iC(j-1) (mod 5) if 1<=i<=i<5\\n # = 1 else\\n\\n comb_values_ratio = [\\n [1, 1, 1, 1, 1, 1],\\n [1, 1, 1, 1, 1, 1],\\n [1, 2, 3, 1, 1, 1],\\n [1, 3, 1, 2, 1, 1],\\n [1, 4, 4, 4, 4, 1]]\\n\\n n = len(numbers)\\n expansion2 = list(reversed([int(digit) for digit in bin(n-2)[2:]]))\\n expansion5 = []\\n m = n-2\\n while m > 0:\\n m, r = divmod(m, 5)\\n expansion5.append(r)\\n\\n expansion2 += [0]\\n expansion5 += [0]\\n index_expansion2 = [0] * (1+len(expansion2))\\n index_expansion5 = [0] * (1+len(expansion5))\\n\\n count_5_above = 0\\n count_2_above = 0\\n\\n mod_2_value = 0\\n mod_5_value = 0\\n\\n comb_5_value = 1\\n\\n for num1, num2 in zip(numbers[:-1], numbers[1:]):\\n if count_5_above == 0:\\n mod_5_value += ((num1 - num2) * comb_5_value) % 5\\n if count_2_above == 0:\\n mod_2_value += (num1 - num2) % 2\\n\\n index_expansion5[0]+=1\\n comb_5_value *= comb_values_ratio[expansion5[0]][index_expansion5[0]]\\n if index_expansion5[0] == expansion5[0] + 1:\\n count_5_above += 1\\n pos = 0\\n while index_expansion5[pos] == 5:\\n index_expansion5[pos] = 0\\n count_5_above -= 1\\n pos += 1\\n index_expansion5[pos] += 1\\n comb_5_value *= comb_values_ratio[expansion5[pos]][index_expansion5[pos]]\\n if index_expansion5[pos] == expansion5[pos] + 1:\\n count_5_above += 1\\n comb_5_value %= 5\\n\\n index_expansion2[0]+=1\\n if index_expansion2[0] == expansion2[0] + 1:\\n count_2_above += 1\\n pos = 0\\n while index_expansion2[pos] == 2:\\n index_expansion2[pos] = 0\\n count_2_above -= 1\\n pos += 1\\n index_expansion2[pos] += 1\\n if index_expansion2[pos] == expansion2[pos] + 1:\\n count_2_above += 1\\n\\n return (mod_5_value % 5 == 0) and (mod_2_value % 2 == 0)\"], [962, 5.176599999999999, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n # \\u7528 ord \\u8f6c\\u6362\\u907f\\u514d int() \\u8c03\\u7528\\u5f00\\u9500\\n digits = [ord(c) - 48 for c in s]\\n k = n - 2 # \\u8fed\\u4ee3\\u6b21\\u6570\\n # \\u8ba1\\u7b97\\u76f8\\u90bb\\u5dee\\u503c\\n diff = [digits[i+1] - digits[i] for i in range(n - 1)]\\n \\n m = k + 1\\n # \\u9884\\u5904\\u7406\\uff1a\\u5bf9 1~(k+1) \\u7684\\u6570\\u9884\\u5148\\u505a\\u56e0\\u5b50\\u5206\\u89e3\\uff08\\u5265\\u79bb2\\u548c5\\uff09\\uff0c\\u5b58\\u50a8\\u683c\\u5f0f\\u4e3a (\\u4f59\\u6570, cnt2, cnt5)\\n fact = [None] * (m + 1)\\n for x in range(1, m + 1):\\n y = x\\n c2 = c5 = 0\\n while y % 2 == 0:\\n y //= 2\\n c2 += 1\\n while y % 5 == 0:\\n y //= 5\\n c5 += 1\\n fact[x] = (y % 10, c2, c5)\\n \\n # \\u6a2110\\u4e0b\\u4ec5\\u4e0e10\\u4e92\\u7d20\\u7684\\u6570\\u7684\\u9006\\u5143\\uff081,3,7,9\\uff09\\n inv_map = {1: 1, 3: 7, 7: 3, 9: 9}\\n \\n total = 0\\n dp_v, dp_c2, dp_c5 = 1, 0, 0 # dp \\u8868\\u793a\\u5f53\\u524d\\u7ec4\\u5408\\u6570\\u7684\\u201c\\u5206\\u89e3\\u8868\\u793a\\u201d\\n # \\u5faa\\u73af\\u7d2f\\u52a0 total += (\\u5f53\\u524d dp mod10) * diff[j]\\n for j in range(k + 1):\\n # \\u5185\\u8054\\u8ba1\\u7b97 dp mod10\\uff1a\\n # \\u82e5 dp \\u540c\\u65f6\\u542b\\u6709 2 \\u548c 5\\uff0c\\u5219\\u542b 10 \\u56e0\\u5b50\\uff0c\\u6a2110\\u7ed3\\u679c\\u4e3a0\\n if dp_c2 and dp_c5:\\n cur = 0\\n elif dp_c2 > dp_c5:\\n exp = dp_c2 - dp_c5\\n # \\u5229\\u7528 2^n mod 10 \\u5468\\u671f\\uff08\\u5468\\u671f4\\uff09\\uff1a2,4,8,6\\n r = exp % 4\\n # \\u6ce8\\u610f 2^0 = 1\\n if exp == 0:\\n factor = 1\\n elif r == 0:\\n factor = 6\\n elif r == 1:\\n factor = 2\\n elif r == 2:\\n factor = 4\\n else:\\n factor = 8\\n cur = (dp_v * factor) % 10\\n elif dp_c5 > dp_c2:\\n cur = (dp_v * 5) % 10\\n else:\\n cur = dp_v\\n total = (total + cur * diff[j]) % 10\\n if j == k:\\n break\\n # \\u66f4\\u65b0 dp\\uff1a\\u5229\\u7528\\u9012\\u63a8\\u516c\\u5f0f dp = dp * (k - j) / (j + 1)\\n num_v, num_c2, num_c5 = fact[k - j]\\n den_v, den_c2, den_c5 = fact[j + 1]\\n new_v = (dp_v * num_v) % 10\\n new_c2 = dp_c2 + num_c2\\n new_c5 = dp_c5 + num_c5\\n # \\u9664\\u6cd5\\u65f6\\u5206\\u6bcd\\u4e00\\u5b9a\\u4e0e10\\u4e92\\u7d20\\uff0c\\u53ef\\u7528\\u9006\\u5143\\n dp_v = (new_v * inv_map[den_v]) % 10\\n dp_c2 = new_c2 - den_c2\\n dp_c5 = new_c5 - den_c5\\n return total % 10 == 0\"], [1110, 8.706099999999998, \"class Solution:\\n _FACT = [1, 1, 2, 1, 4]\\n _FACT_INV = [1, 1, 3, 1, 4]\\n _MUL_MOD10 = [[i * j % 10 for j in range(10)] for i in range(10)]\\n\\n _MOD5_SMALL = [[0] * 5 for _ in range(5)]\\n for i in range(5):\\n for j in range(i + 1):\\n _MOD5_SMALL[i][j] = (_FACT[i] * _FACT_INV[j] * _FACT_INV[i - j]) % 5\\n\\n _COEF_CACHE = {}\\n for n in range(20):\\n for k in range(n + 1):\\n if k > n:\\n _COEF_CACHE[(n, k)] = 0\\n elif k == 0 or k == n:\\n _COEF_CACHE[(n, k)] = 1\\n elif k == 1 or k == n - 1:\\n _COEF_CACHE[(n, k)] = n % 10\\n else:\\n mod2 = int((k & n) == k)\\n if n < 5 and k < 5:\\n mod5 = _MOD5_SMALL[n][k]\\n else:\\n result = 1\\n n_temp, k_temp = n, k\\n while n_temp or k_temp:\\n n_i, k_i = n_temp % 5, k_temp % 5\\n if k_i > n_i:\\n result = 0\\n break\\n if n_i and k_i:\\n result = (result * _MOD5_SMALL[n_i][k_i]) % 5\\n n_temp, k_temp = n_temp // 5, k_temp // 5\\n mod5 = result\\n _COEF_CACHE[(n, k)] = (mod5 + (5 if (mod5 % 2) != mod2 else 0)) % 10\\n\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n if n <= 1:\\n return True\\n\\n m = n - 2\\n left = right = 0\\n mul_mod10 = self._MUL_MOD10\\n\\n digits = [ord(c) - 48 for c in s]\\n\\n coef = self._calc_coef_fast(m, 0)\\n left = (left + mul_mod10[digits[0]][coef]) % 10\\n right = (right + mul_mod10[digits[1]][coef]) % 10\\n\\n for i in range(1, m + 1):\\n coef = self._calc_coef_fast(m, i)\\n curr_d = digits[i]\\n next_d = digits[i + 1]\\n left = (left + mul_mod10[curr_d][coef]) % 10\\n right = (right + mul_mod10[next_d][coef]) % 10\\n\\n return left == right\\n\\n def _calc_coef_fast(self, n: int, k: int) -> int:\\n cached = self._COEF_CACHE.get((n, k))\\n if cached is not None:\\n return cached\\n\\n if k > n:\\n return 0\\n if k == 0 or k == n:\\n return 1\\n if k == 1 or k == n - 1:\\n return n % 10\\n\\n mod2 = int((k & n) == k)\\n if n < 5 and k < 5:\\n mod5 = self._MOD5_SMALL[n][k]\\n else:\\n result = 1\\n n_temp, k_temp = n, k\\n while n_temp or k_temp:\\n n_i, k_i = n_temp % 5, k_temp % 5\\n if k_i > n_i:\\n result = 0\\n break\\n if n_i and k_i:\\n result = (result * self._MOD5_SMALL[n_i][k_i]) % 5\\n n_temp, k_temp = n_temp // 5, k_temp // 5\\n mod5 = result\\n\\n coef = (mod5 + (5 if (mod5 % 2) != mod2 else 0)) % 10\\n self._COEF_CACHE[(n, k)] = coef\\n return coef\\n\"], [1258, 6.823699999999998, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n def cal(a, mod):\\n count = 0\\n while a > 0 and a % mod == 0:\\n count += 1\\n a //= mod\\n return a % mod, count\\n\\n def test(mod):\\n n = len(s)\\n res = 0\\n r = 1\\n c = 0\\n for i in range(n - 1):\\n if c == 0:\\n res += r * (int(s[i]) - int(s[i + 1]))\\n\\n rr, cc = cal(n - 2 - i, mod)\\n r = r * rr % mod\\n c += cc\\n\\n rr, cc = cal(i + 1, mod)\\n r = r * pow(rr, mod - 2, mod) % mod\\n c -= cc\\n return res % mod == 0\\n return test(2) and test(5)\\n \"], [1289, 73.1758, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n if n == 2:\\n return s[0] == s[1]\\n k = n - 2\\n\\n mod5_table = [\\n [1, 0, 0, 0, 0],\\n [1, 1, 0, 0, 0],\\n [1, 2, 1, 0, 0],\\n [1, 3, 3, 1, 0],\\n [1, 4, 1, 4, 1],\\n ]\\n\\n crt_table = {\\n (0, 0): 0,\\n (0, 1): 6,\\n (0, 2): 2,\\n (0, 3): 8,\\n (0, 4): 4,\\n (1, 0): 5,\\n (1, 1): 1,\\n (1, 2): 7,\\n (1, 3): 3,\\n (1, 4): 9,\\n }\\n\\n def compute_mod5(k_val, i_val):\\n res = 1\\n while k_val > 0 or i_val > 0:\\n dk = k_val % 5\\n di = i_val % 5\\n if di > dk:\\n return 0\\n res = (res * mod5_table[dk][di]) % 5\\n k_val = k_val // 5\\n i_val = i_val // 5\\n return res\\n\\n sum1, sum2 = 0, 0\\n for i in range(k + 1):\\n a = 1 if (i & k) == i else 0\\n b = compute_mod5(k, i)\\n if b == 0:\\n mod10 = 5 if a else 0\\n else:\\n mod10 = crt_table[(a, b)]\\n sum1 = (sum1 + int(s[i]) * mod10) % 10\\n sum2 = (sum2 + int(s[i + 1]) * mod10) % 10\\n\\n return sum1 == sum2\"], [1406, 4.9413, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s) - 2\\n \\n # For small inputs, use the direct approach\\n if n <= 20:\\n digits = [int(d) for d in s]\\n while len(digits) > 2:\\n digits = [(digits[i] + digits[i+1]) % 10 for i in range(len(digits) - 1)]\\n return digits[0] == digits[1]\\n \\n # For larger inputs, use binomial coefficients\\n # Precompute factorial representations as (twos, fives, other)\\n facts = []\\n twos, fives, other = 0, 0, 1\\n for i in range(n + 1):\\n facts.append((twos, fives, other))\\n num = i + 1\\n \\n # Count factors of 2\\n temp_twos = 0\\n while num % 2 == 0:\\n num //= 2\\n temp_twos += 1\\n twos += temp_twos\\n \\n # Count factors of 5\\n temp_fives = 0\\n while num % 5 == 0:\\n num //= 5\\n temp_fives += 1\\n fives += temp_fives\\n \\n # Multiply by remaining factors\\n other = (other * (num % 10)) % 10\\n \\n # Multiplicative inverses mod 10\\n inv = {1: 1, 3: 7, 7: 3, 9: 9}\\n \\n # Compute binomial coefficients\\n coeffs = []\\n for k in range(n + 1):\\n n_fact = facts[n]\\n k_fact = facts[k]\\n nk_fact = facts[n-k]\\n \\n twos = n_fact[0] - k_fact[0] - nk_fact[0]\\n fives = n_fact[1] - k_fact[1] - nk_fact[1]\\n other = n_fact[2]\\n \\n # Division using modular multiplicative inverses\\n if k_fact[2] in inv and nk_fact[2] in inv:\\n other = (other * inv[k_fact[2]] % 10 * inv[nk_fact[2]]) % 10\\n else:\\n coeffs.append(0)\\n continue\\n \\n # Apply powers of 2\\n if twos > 0:\\n other = (other * [2, 4, 8, 6][(twos - 1) % 4]) % 10\\n \\n # Apply powers of 5\\n if fives > 0:\\n other = (other * 5) % 10\\n \\n coeffs.append(other)\\n \\n # Calculate final digits\\n digits = [int(d) for d in s]\\n first = sum((d * c) % 10 for d, c in zip(digits[:n+1], coeffs)) % 10\\n second = sum((d * c) % 10 for d, c in zip(digits[1:n+2], coeffs)) % 10\\n \\n return first == second\"], [1555, 9.647300000000001, \"class Solution(object): \\n def factors(self, max_n):\\n # x -> (x', count_2, count_5); x = 2^(a)*5^(b)*x', gcd(x', 10) = 1.\\n fac = [None]*(max_n+1)\\n for x in range(1, max_n+1):\\n a = b = 0\\n temp = x\\n while temp%2 == 0:\\n a, temp = a+1, temp//2\\n while temp%5 == 0:\\n b, temp = b+1, temp//5\\n fac[x] = (temp, a, b)\\n return fac\\n\\n def mod(self, r, a, b):\\n # pc: (r, a, b); pc = 2^a * 5^b * r.\\n # pc % 10 = 0 if at least one factor of 10 appears\\n # else pc = (r * 2^a * 5^b) mod 10.\\n if min(a, b) > 0:\\n return 0\\n return (r * pow(2, a, 10) * pow(5, b, 10)) % 10\\n\\n def hasSameDigits(self, s):\\n \\\"\\\"\\\"\\n :type s: str\\n :rtype: bool\\n \\\"\\\"\\\"\\n n = len(s)\\n L = R = 0\\n\\n fac = self.factors(n)\\n r, a, b = 1, 0, 0 # c(n-2, 0) = 1; => (r, a, b) = (1, 0, 0)\\n for k in range(n-1):\\n pc = self.mod(r, a, b)\\n\\n L = (L + pc*int(s[k])) % 10\\n R = (R + pc*int(s[k+1])) % 10\\n \\n if k == n-2: break\\n # pc = pc * (n-2 - k) / (k+1)\\n num = n-2 - k; rn, a_n, b_n = fac[num]\\n den = k+1; rd, a_d, b_d = fac[den]\\n \\n r = (r * rn * pow(rd, -1, 10)) % 10\\n a = a + a_n - a_d\\n b = b + b_n - b_d\\n \\n return L == R\"], [1703, 4.470700000000001, \"import math\\nclass Solution:\\n \\n def hasSameDigits(self, s: str) -> bool:\\n # I have found you can use an alternative version of pascal's triangle where the row with 2 elements is [3,7], seems like I can found the kth element of the row with n elements of this triangle by doing (n-1 choose k-1)*7 + (n-1 choose k)*3, and when k<0 or k>n it is zero\\n # construct the row\\n length = len(s)\\n '''\\n # the following code isn't efficient enough\\n pascal = [0]+[math.comb(length-2,i)%10 for i in range(length-1)]+[0]\\n # I've asked an ai for help (but I wont use its code), it talked about lucas's theorem.\\n # the key is that I need a far row of pascal's triangle BUT everything mod 10\\n # thanks to lucas's theorem, I can compute a pascal's triangle value %5 and %2\\n # then I can know what digit it should be %10, if a is the val %2 and b the val %5\\n # the val is whatever number is = a when %2 and = b when %5\\n '''\\n def pascalmod2(rowlength):\\n # lucas says that the value n choose k modulo a prime number p is equal to the product\\n # of the ni choose ki digits of n and k expressed in base p\\n # so for base 2, for each digit, it could be : 0 choose 0, 0 choose 1, 1 choose 0, 1 choose 1; all mod 2 \\n # 0 choose 0 = 1; 0 choose 1 = 0; 1 choose 0 = 1; 1 choose 1 = 1;\\n # so basically the product is 0 if once there is n=0 and k=1 \\n for i in range(rowlength):\\n n=rowlength-1\\n k=i\\n v=1\\n while (k>0 or n>0)and v:\\n if (k&1)>(n&1):\\n v=0\\n k>>=1\\n n>>=1\\n yield v\\n #row += row[(-1-rowlength%2)::-1]\\n #return row\\n def pascalmod5(rowlength):\\n # here we can precompute the possible outcomes mod 5, ni can be 0,1,2,3,4; ki can be 0,1,2,3,4\\n precomp = [[1, 0, 0, 0, 0], [1, 1, 0, 0, 0], [1, 2, 1, 0, 0], [1, 3, 3, 1, 0], [1, 4, 1, 4, 1]]\\n for i in range(rowlength):\\n n=rowlength-1\\n k=i\\n v=1\\n while (k>0 or n>0)and v:\\n v*=precomp[n%5][k%5]\\n k//=5\\n n//=5\\n yield(v%5)\\n\\n mod5pascal = pascalmod5(length-1)\\n mod2pascal = pascalmod2(length-1)\\n\\n # using CRT \\n mod2and5to10 = [[0,6,2,8,4],[5,1,7,3,9]]\\n\\n pascal=[0]+[mod2and5to10[next(mod2pascal)][next(mod5pascal)]for i in range(length-1)]+[0]\\n\\n\\n\\n\\n mine = [(pascal[i]*3+pascal[i+1]*7)%10 for i in range(length)]\\n su=0\\n for i in range(length):\\n if mine[i]:\\n su+=int(s[i])*mine[i]\\n su%=10\\n if su:\\n return False\\n return True\\n \"], [1851, 12.000300000000001, \"INV = {\\n 1: 1,\\n 3: 7,\\n 7: 3,\\n 9: 9,\\n}\\n\\ndef mult(a, b):\\n return (\\n a[0] + b[0],\\n a[1] + b[1],\\n (a[2] * b[2]) % 10,\\n )\\n\\ndef div(a, b):\\n return (\\n a[0] - b[0],\\n a[1] - b[1],\\n (a[2] * INV[b[2]]) % 10,\\n )\\n\\ndef red(it):\\n return sum((a * b) % 10 for a, b in it) % 10\\n\\nTWOS = [2, 4, 8, 6]\\nFIVES = [5]\\ndef simplify(tup):\\n twos, fives, res = tup\\n\\n if twos:\\n res = (res * TWOS[(twos - 1) % len(TWOS)]) % 10\\n if fives:\\n res = (res * FIVES[(fives - 1) % len(FIVES)]) % 10\\n\\n return res\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s) - 2\\n \\n facts = [(0, 0, 1)]\\n while n >= len(facts):\\n num = len(facts)\\n\\n twos = 0\\n while num % 2 == 0:\\n num //= 2\\n twos += 1\\n \\n fives = 0\\n while num % 5 == 0:\\n num //= 5\\n fives += 1\\n \\n facts.append(mult(facts[-1], (twos, fives, num)))\\n \\n pascal = []\\n for k in range(n + 1):\\n pascal.append(simplify(div(div(facts[n], facts[k]), facts[n - k])))\\n\\n a = red(zip(map(int, s), pascal))\\n b = red(zip(map(int, s[1:]), pascal))\\n\\n return a == b\\n \"], [1999, 3.0589000000000004, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n inv = {1:1,3:7,7:3, 9:9}\\n twoRem = [2,4,8,6]\\n fiveRem = [5]\\n def mult(a, b):\\n return (a[0] + b[0], a[1] + b[1], (a[2] * b[2]) % 10 )\\n \\n def div(a, b):\\n return (a[0] - b[0], a[1] - b[1], (a[2] * inv[b[2]]) % 10 )\\n \\n def simplify(tup):\\n twos, fives, res = tup\\n if twos:\\n res = (res * (twoRem[(twos - 1)% 4] ) ) % 10\\n \\n if fives:\\n res = (res * 5) % 10\\n \\n return res\\n \\n n = len(s) - 2\\n facts = [(0,0,1)]\\n while n >= len(facts):\\n num = len(facts)\\n twos = fives = 0\\n while num % 2 == 0:\\n num //= 2\\n twos += 1\\n while num % 5 == 0:\\n num //= 5\\n fives += 1\\n \\n facts.append(mult(facts[-1], (twos, fives, num % 10)))\\n \\n pascal = []\\n for k in range(n + 1):\\n pascal.append(simplify(div(div(facts[n], facts[k]), facts[n - k])))\\n \\n def getNum(start):\\n res = 0\\n for index, num in enumerate(pascal):\\n res += ((pascal[index] * int(s[index + start])) % 10 )\\n res %= 10\\n \\n return res\\n \\n return getNum(0) == getNum(1)\"], [2147, 2.8236000000000003, \"import sys\\n# Setting recursion depth might be relevant if Lucas's theorem were implemented recursively,\\n# but an iterative approach is generally preferred for deep stacks.\\n# sys.setrecursionlimit(2000) \\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n \\\"\\\"\\\"\\n Calculates the final two digits using binomial coefficients modulo 10\\n and checks if they are the same. This avoids the O(N^2) simulation.\\n\\n Args:\\n s: A string consisting of digits (e.g., \\\"3902\\\"). \\n Constraints: 3 <= len(s) <= 10^5.\\n\\n Returns:\\n True if the final two digits are the same, False otherwise.\\n \\\"\\\"\\\"\\n try:\\n digits = [int(d) for d in s]\\n except ValueError:\\n raise ValueError(\\\"Input string must consist of only digits.\\\")\\n \\n N = len(digits)\\n\\n # Constraints state N >= 3. If N was 2, the process wouldn't run.\\n if N < 3:\\n # This case should not occur based on constraints.\\n # Handle appropriately if constraints could be different.\\n return False # Or raise an error\\n\\n n = N - 2 # Number of operation steps = exponent in binomial coefficients\\n\\n # --- Helper Functions for Calculating nCr mod 10 ---\\n\\n # Precomputed tables for nCr(ni, ji) mod 5 where ni, ji <= 4\\n # Factorials mod 5: 0!=1, 1!=1, 2!=2, 3!=6=1, 4!=24=4\\n fact_mod5 = [1, 1, 2, 1, 4]\\n # Inverse Factorials mod 5: inv(0!)=1, inv(1!)=1, inv(2!)=3, inv(3!)=1, inv(4!)=4\\n invfact_mod5 = [1, 1, 3, 1, 4] \\n\\n def nCr_small_mod5(ni, ji):\\n \\\"\\\"\\\" Calculates nCr(ni, ji) mod 5 for 0 <= ji <= ni <= 4 \\\"\\\"\\\"\\n if ji < 0 or ji > ni: return 0\\n if ji == 0 or ji == ni: return 1\\n # Use symmetry: nCr(n, k) = nCr(n, n-k)\\n if ji > ni // 2: ji = ni - ji \\n # Calculate using precomputed tables: ni! * inv(ji!) * inv((ni-ji)!) mod 5\\n num = fact_mod5[ni]\\n den = (invfact_mod5[ji] * invfact_mod5[ni - ji]) % 5\\n return (num * den) % 5\\n\\n def nCr_mod_5(n_arg, k_arg):\\n \\\"\\\"\\\" Calculates nCr(n_arg, k_arg) mod 5 using Lucas Theorem (iterative) \\\"\\\"\\\"\\n if k_arg < 0 or k_arg > n_arg: return 0\\n # Optimization using symmetry: nCr(n, k) = nCr(n, n-k)\\n if k_arg > n_arg // 2: k_arg = n_arg - k_arg\\n \\n # Make copies to modify within the loop\\n n_curr, k_curr = n_arg, k_arg \\n res = 1\\n while n_curr > 0 or k_curr > 0:\\n ni = n_curr % 5\\n ki = k_curr % 5\\n \\n # Calculate nCr for the base-5 digits\\n term = nCr_small_mod5(ni, ki)\\n \\n # If any term is 0, the entire product is 0 (mod 5)\\n if term == 0: \\n return 0 \\n \\n res = (res * term) % 5\\n \\n # Move to the next base-5 digit\\n n_curr //= 5\\n k_curr //= 5\\n return res\\n\\n def nCr_mod_2(n_arg, k_arg):\\n \\\"\\\"\\\" Calculates nCr(n_arg, k_arg) mod 2 (parity check) \\\"\\\"\\\"\\n if k_arg < 0 or k_arg > n_arg: return 0\\n # nCr is odd (1) if and only if the bits set in k are a subset of bits set in n\\n # This is checked using bitwise AND: (n & k) == k\\n return 1 if (n_arg & k_arg) == k_arg else 0\\n\\n def combine_crt(mod2, mod5):\\n \\\"\\\"\\\" \\n Combines result mod 2 (a) and mod 5 (b) to get result mod 10 \\n using the Chinese Remainder Theorem.\\n Solution x satisfies: x = a (mod 2), x = b (mod 5).\\n If b has the same parity as a (b % 2 == a), then x = b (mod 10).\\n If b has different parity from a (b % 2 != a), then x = b + 5 (mod 10).\\n \\\"\\\"\\\"\\n if (mod5 % 2) == mod2: \\n return mod5\\n else: \\n return (mod5 + 5) % 10\\n\\n # --- Main Calculation ---\\n D0 = 0 # Stores the sum for the first final digit\\n D1 = 0 # Stores the sum for the second final digit\\n\\n # Iterate through the terms of the summation (j from 0 to n)\\n for j in range(n + 1): \\n # Calculate the coefficient C(n, j) mod 10\\n coeff_mod_2 = nCr_mod_2(n, j)\\n coeff_mod_5 = nCr_mod_5(n, j)\\n\\n # Combine results using CRT\\n # Optimization: If both mod 2 and mod 5 results are 0, the coefficient mod 10 is 0.\\n if coeff_mod_2 == 0 and coeff_mod_5 == 0:\\n coeff_mod_10 = 0\\n else:\\n coeff_mod_10 = combine_crt(coeff_mod_2, coeff_mod_5)\\n\\n # If the coefficient is 0, this term doesn't contribute to the sums.\\n if coeff_mod_10 == 0:\\n continue\\n\\n # Add the contribution of this term to D0 and D1\\n # D0 term: coeff * d_j\\n # D1 term: coeff * d_{j+1}\\n \\n # Ensure index j is within bounds for digits (0 to N-1)\\n # j goes from 0 to n = N-2, so digits[j] is always valid.\\n D0 = (D0 + coeff_mod_10 * digits[j]) % 10\\n\\n # Ensure index j+1 is within bounds for digits (0 to N-1)\\n # j+1 goes from 1 to n+1 = N-1, so digits[j+1] is always valid.\\n D1 = (D1 + coeff_mod_10 * digits[j+1]) % 10\\n\\n # After the loop, D0 and D1 hold the final two digits modulo 10.\\n # Return whether they are the same.\\n return D0 == D1\"], [2295, 2.353, \"from functools import lru_cache\\n\\n\\n@lru_cache(maxsize=10000)\\ndef nCrModP(n, r, p):\\n \\\"\\\"\\\"\\n Cached nCrModP (dp implementation)\\n \\\"\\\"\\\"\\n if r == 0:\\n return 1\\n if r == 1:\\n return n % p\\n if r > n:\\n return 0\\n if n == r:\\n return 1\\n\\n if r > n - r:\\n r = n - r\\n\\n if p == 2:\\n return 1 if (n & r) == r else 0\\n\\n C = [0] * (r + 1)\\n C[0] = 1\\n for i in range(1, n + 1):\\n j = min(i, r)\\n while j > 0:\\n C[j] = (C[j] + C[j - 1]) % p\\n j -= 1\\n return C[r]\\n\\n\\n@lru_cache(maxsize=10000)\\ndef nCr_LT(n, r, p):\\n \\\"\\\"\\\"\\n Cached nCr_LT (Lucas's theorem)\\n \\\"\\\"\\\"\\n if r == 0:\\n return 1\\n if r == 1:\\n return n % p\\n if r > n:\\n return 0\\n if n == r:\\n return 1\\n\\n ni = n % p\\n ri = r % p\\n\\n fact1 = nCr_LT(n // p, r // p, p)\\n if fact1 == 0:\\n return 0\\n\\n fact2 = nCrModP(ni, ri, p)\\n if fact2 == 0:\\n return 0\\n\\n result = (fact1 * fact2) % p\\n return result\\n\\n\\n\\\"\\\"\\\"\\nLookup table\\n\\\"\\\"\\\"\\ncr_lookup = {\\n (0, 0): 0,\\n (0, 1): 6,\\n (0, 2): 2,\\n (0, 3): 8,\\n (0, 4): 4,\\n (1, 0): 5,\\n (1, 1): 1,\\n (1, 2): 7,\\n (1, 3): 3,\\n (1, 4): 9,\\n}\\n\\n\\nprecomputed_m2_values = {}\\nprecomputed_m5_values = {}\\nfor n in range(2, 101):\\n precomputed_m2_values[n] = [nCr_LT(n - 2, i, 2) for i in range(n - 1)]\\n precomputed_m5_values[n] = [nCr_LT(n - 2, i, 5) for i in range(n - 1)]\\n\\n\\nclass Solution:\\n def __init__(self):\\n \\\"\\\"\\\"\\n Applies a precomputation technique to improve the speed\\n of later calculations done using Lucas's theorem algo\\n \\\"\\\"\\\"\\n for n in range(1, 20):\\n for i in range(n):\\n nCr_LT(n - 2, i, 2)\\n nCr_LT(n - 2, i, 5)\\n\\n @staticmethod\\n def str_to_int(s: str) -> list[int]:\\n return [int(c) for c in s]\\n\\n def hasSameDigits(self, s: str) -> bool:\\n \\\"\\\"\\\"\\n Calculate the digit remaining 2 digits' symmetry\\n by applying nCr/ nCrModP\\n \\\"\\\"\\\"\\n n = len(s)\\n\\n if n <= 1:\\n return True\\n\\n if len(set(s)) == 1:\\n return True\\n\\n sn = self.str_to_int(s)\\n\\n if n in precomputed_m2_values and n in precomputed_m5_values:\\n m2_values = precomputed_m2_values[n]\\n m5_values = precomputed_m5_values[n]\\n else:\\n m2_values = [nCr_LT(n - 2, i, 2) for i in range(n - 1)]\\n m5_values = [nCr_LT(n - 2, i, 5) for i in range(n - 1)]\\n\\n x = 0\\n y = 0\\n\\n for i in range(n - 1):\\n m2 = m2_values[i]\\n m5 = m5_values[i]\\n\\n v = cr_lookup[(m2, m5)]\\n\\n x = (x + v * sn[i]) % 10\\n y = (y + v * sn[i + 1]) % 10\\n\\n return x == y\\n\\n\"], [2443, 2.1177, \"import math\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n \\\"\\\"\\\"\\n Return True if, after repeatedly replacing s by the sequence of\\n (s[i]+s[i+1])%10 until length is 2, the final two digits are equal.\\n \\\"\\\"\\\"\\n n = len(s)\\n num1 = num2 = 0\\n # Compute the two final digits via binomial weights mod 10\\n for i in range(n - 1):\\n coef = self._nCk_mod10(n - 2, i)\\n d1, d2 = int(s[i]), int(s[i+1])\\n num1 = (num1 + coef * d1) % 10\\n num2 = (num2 + coef * d2) % 10\\n return num1 == num2\\n\\n def _nCk_mod10(self, n: int, k: int) -> int:\\n \\\"\\\"\\\"\\n Return C(n, k) % 10 by computing it mod 2 and mod 5 separately\\n (via Lucas) and combining:\\n C % 10 = lookup[ C(n,k)%2 ][ C(n,k)%5 ]\\n \\\"\\\"\\\"\\n # Compute C(n, k) mod 2 and mod 5\\n m2 = self._lucas(n, k, 2)\\n m5 = self._lucas(n, k, 5)\\n # Precomputed CRT table: for mod2 in {0,1}, mod5 in {0..4}\\n lookup = [\\n [0, 6, 2, 8, 4], # if C mod 2 == 0\\n [5, 1, 7, 3, 9], # if C mod 2 == 1\\n ]\\n return lookup[m2][m5]\\n\\n def _lucas(self, n: int, k: int, p: int) -> int:\\n \\\"\\\"\\\"\\n Lucas Theorem to compute C(n,k) % p for prime p (p=2 or 5).\\n Break n,k into base-p digits and multiply small binomials.\\n \\\"\\\"\\\"\\n res = 1\\n while n > 0 or k > 0:\\n ni, ki = n % p, k % p\\n if ki > ni:\\n return 0\\n # small binomial C(ni, ki) fits in Python int\\n res = (res * math.comb(ni, ki)) % p\\n n //= p\\n k //= p\\n return res\"], [2591, 0.9412, \"import numpy as np\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n N = len(s)\\n if N == 2:\\n return s[0] == s[1]\\n\\n K = N - 2\\n\\n # Precompute precomb_2 and precomb_5 for Lucas theorem\\n def build_precomb(p):\\n max_a = p - 1\\n precomb = [{} for _ in range(max_a + 1)]\\n for a in range(max_a + 1):\\n for b in range(a + 1):\\n comb_val = math.comb(a, b) % p\\n precomb[a][b] = comb_val\\n return precomb\\n\\n precomb_2 = build_precomb(2)\\n precomb_5 = build_precomb(5)\\n\\n def compute_lucas(n, k, p, precomb):\\n if k == 0:\\n return 1 % p\\n res = 1\\n while n > 0 or k > 0:\\n a_digit = n % p\\n b_digit = k % p\\n if b_digit > a_digit:\\n return 0\\n comb_val = precomb[a_digit].get(b_digit, 0)\\n res = (res * comb_val) % p\\n n = n // p\\n k = k // p\\n return res\\n\\n coeffs_mod2 = [0] * (K + 1)\\n coeffs_mod5 = [0] * (K + 1)\\n\\n for i in range(K + 1):\\n c2 = compute_lucas(K, i, 2, precomb_2)\\n c5 = compute_lucas(K, i, 5, precomb_5)\\n\\n coeffs_mod2[i] = c2\\n coeffs_mod5[i] = c5\\n\\n # Compute coefficients mod10 using CRT\\n coeffs = [0] * (K + 1)\\n\\n for i in range(K + 1):\\n c2 = coeffs_mod2[i]\\n c5 = coeffs_mod5[i]\\n\\n found = -1\\n for x in range(10):\\n if (x % 2 == c2) and (x % 5 == c5):\\n found = x\\n break\\n coeffs[i] = found\\n\\n # Compute first_sum and second_sum mod10\\n first_sum = 0\\n for i in range(K + 1):\\n digit = int(s[i])\\n coeff = coeffs[i]\\n first_sum += digit * coeff\\n first_sum %= 10\\n\\n second_sum = 0\\n for j in range(1, K + 2): # from 1 to (K+1) inclusive\\n digit = int(s[j])\\n coeff_idx = j - 1\\n coeff = coeffs[coeff_idx]\\n second_sum += digit * coeff\\n second_sum %= 10\\n\\n return first_sum == second_sum\\n \"], [2739, 0.9412, \"class Solution:\\n def lucas(self,n, k):\\n res = 1\\n while n or k:\\n (n, n_i), (k, k_i) = divmod(n,5),divmod(k,5)\\n res = (res * (comb(n_i, k_i)%5)) % 5\\n return res\\n\\n def crt(self,n, k):\\n r2 = n & k == k\\n r5 = self.lucas(n, k) \\n \\n for c in range(10):\\n if c%2 == r2 and c%5 == r5:\\n return c\\n\\n def hasSameDigits(self, s: str) -> bool:\\n mods = [self.crt(len(s)-2,i) for i in range(len(s)-1)]\\n return sum(int(c)*mods[i] for i,c in enumerate(s[:-1]))%10 == sum(int(c)*mods[i] for i,c in enumerate(s[1:]))%10\"], [2887, 0.7059, \"def comb2(a,b):\\n res = 1\\n while a > 0 or b > 0:\\n a1 = a % 2\\n b1 = b % 2\\n if a1>=b1:\\n res *= comb(a1,b1) \\n else: return 0\\n a = a // 2\\n b = b // 2\\n res = res % 2\\n return res\\n@cache\\ndef comb5(a,b):\\n res = 1\\n while a > 0 or b > 0:\\n a1 = a % 5\\n b1 = b % 5\\n if a1>=b1:\\n res *= comb(a1,b1) \\n else: return 0\\n a = a // 5\\n b = b // 5\\n res = res % 5\\n return res\\n\\n\\n\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n N = len(s)\\n a2,b2,a5,b5 = 0,0,0,0\\n for i in range(N-1):\\n p = int(s[i])\\n q = int(s[i+1])\\n a2 = (a2 + p*comb2(N-2,i)) % 2\\n b2 = (b2 + q*comb2(N-2,i)) % 2\\n a5 = (a5 + p*comb5(N-2,i)) % 5\\n b5 = (b5 + q*comb5(N-2,i)) % 5\\n return a2==b2 and a5==b5\"], [3036, 0.9412, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n if n == 2:\\n return s[0] == s[1]\\n m = n - 2\\n s = [int(d) for d in s]\\n\\n # Modulo 2\\n a2 = 0\\n for k in range(m + 1):\\n if (k & m) == k:\\n a2 = (a2 + s[k] % 2) % 2\\n b2 = 0\\n for k in range(1, n):\\n j = k - 1\\n if (j & m) == j:\\n b2 = (b2 + s[k] % 2) % 2\\n\\n # Modulo 5 helper\\n def comb_mod5(a, b):\\n if b > a or b < 0:\\n return 0\\n if b == 0 or b == a:\\n return 1\\n if a == 1:\\n return 1\\n if a == 2:\\n if b == 1:\\n return 2\\n if a == 3:\\n if b == 1:\\n return 3\\n if b == 2:\\n return 3\\n if a == 4:\\n if b == 1:\\n return 4\\n if b == 2:\\n return 1 # C(4,2)=6%5=1\\n if b == 3:\\n return 4\\n return 0\\n\\n def lucas_comb(m, k, p):\\n if k > m or k < 0:\\n return 0\\n result = 1\\n while m > 0 or k > 0:\\n m_i = m % p\\n k_i = k % p\\n if k_i > m_i:\\n return 0\\n result = (result * comb_mod5(m_i, k_i)) % p\\n m //= p\\n k //= p\\n return result\\n\\n # Modulo 5\\n a5 = 0\\n for k in range(m + 1):\\n c = lucas_comb(m, k, 5)\\n a5 = (a5 + c * (s[k] % 5)) % 5\\n b5 = 0\\n for k in range(1, n):\\n j = k - 1\\n c = lucas_comb(m, j, 5)\\n b5 = (b5 + c * (s[k] % 5)) % 5\\n\\n return a2 == b2 and a5 == b5\"], [3184, 0.4706, \"import math\\n\\n# Precomputation outside the class for factorials and inverses mod 5\\n_fact_mod5 = [1] * 5\\n_invfact_mod5 = [1] * 5\\nfor i in range(1, 5):\\n _fact_mod5[i] = (_fact_mod5[i-1] * i) % 5\\n\\n# Calculate modular inverse using Fermat's Little Theorem (p=5)\\n# pow(a, p-2, p) is a^-1 mod p. We need inverse of _fact_mod5[4] = 4.\\n# pow(4, 5-2, 5) = pow(4, 3, 5) = 64 % 5 = 4.\\n_invfact_mod5[4] = pow(_fact_mod5[4], 5 - 2, 5)\\nfor i in range(3, -1, -1):\\n # invfact[i] = invfact[i+1] * (i+1) mod 5\\n _invfact_mod5[i] = (_invfact_mod5[i+1] * (i+1)) % 5\\n\\ndef _nCr_small_mod5(n, r):\\n \\\"\\\"\\\"Computes C(n, r) % 5 for 0 <= n < 5.\\\"\\\"\\\"\\n if r < 0 or r > n:\\n return 0\\n # Use precomputed values _fact_mod5, _invfact_mod5\\n # C(n, r) = n! / (r! * (n-r)!) mod 5\\n num = _fact_mod5[n]\\n # Denominator is (r! * (n-r)!) mod 5. We need its inverse.\\n # Inverse is (invfact[r] * invfact[n-r]) mod 5\\n den_inv = (_invfact_mod5[r] * _invfact_mod5[n-r]) % 5\\n return (num * den_inv) % 5\\n\\ndef _nCr_mod5(n, r):\\n \\\"\\\"\\\"Computes C(n, r) % 5 using Lucas's Theorem.\\\"\\\"\\\"\\n if r < 0 or r > n:\\n return 0\\n if r == 0 or r == n:\\n return 1\\n # Optimization: C(n, r) == C(n, n-r). Use smaller value for r.\\n if r > n // 2:\\n r = n - r\\n\\n res = 1\\n # Lucas's Theorem: C(n, r) = Prod[C(ni, ri)] mod p\\n # Iterate through digits of n and r in base 5\\n while r > 0: # Iterate while r > 0 is sufficient\\n ni = n % 5\\n ri = r % 5\\n # Compute C(ni, ri) mod 5 using precomputed values\\n term = _nCr_small_mod5(ni, ri)\\n if term == 0: # If any C(ni, ri) is 0, the whole product is 0\\n return 0\\n res = (res * term) % 5\\n n //= 5\\n r //= 5\\n # If r becomes 0, the remaining terms C(ni, 0) are 1, so the result is correct.\\n return res\\n\\ndef _nCr_mod2(n, r):\\n \\\"\\\"\\\"Computes C(n, r) % 2 using Lucas's Theorem property.\\\"\\\"\\\"\\n if r < 0 or r > n:\\n return 0\\n # Lucas's Theorem for p=2 implies C(n, r) is odd (1)\\n # if and only if for every bit set in r, the corresponding bit is also set in n.\\n # This is equivalent to (n & r) == r.\\n return 1 if (n & r) == r else 0\\n\\ndef _crt_mod10(a, b):\\n \\\"\\\"\\\"Combines results mod 2 (a) and mod 5 (b) to get result mod 10.\\\"\\\"\\\"\\n # We want to find x such that x = a (mod 2) and x = b (mod 5).\\n # From x = b (mod 5), x can be b, b+5.\\n # If x = b, then b = a (mod 2).\\n # If x = b+5, then b+5 = a (mod 2) => b+1 = a (mod 2).\\n # So, if a == b % 2, then x = b.\\n # If a != b % 2, then x = b + 5.\\n # This can be expressed as: x = b if (a - b) % 2 == 0 else b + 5\\n # A formula: x = ( (a - b + 2) % 2 * 5 + b ) % 10\\n diff_mod2 = (a - b + 2) % 2 # Ensures (a-b) mod 2 is 0 or 1\\n res = (diff_mod2 * 5 + b) % 10\\n return res\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n \\\"\\\"\\\"\\n Calculates the final two digits after repeated adjacent sum-mod-10 operations\\n using combinatorics (Pascal's triangle coefficients / binomial coefficients)\\n modulo 10, determined via modulo 2 and modulo 5 combined with CRT.\\n Returns True if the final two digits are the same, False otherwise.\\n \\\"\\\"\\\"\\n digits = [int(d) for d in s]\\n N = len(digits)\\n\\n # The number of operations is N - 2.\\n # The final two digits f0 and f1 are given by sums involving C(N-2, k).\\n n = N - 2 # This is the 'n' in C(n, k)\\n\\n f0_mod2 = 0\\n f1_mod2 = 0\\n f0_mod5 = 0\\n f1_mod5 = 0\\n\\n # Calculate f0 = sum_{i=0}^{n} C(n, i) * digits[i] (mod 2 and mod 5)\\n # The sum goes up to index n = N-2 for the digits array.\\n for i in range(n + 1):\\n digit_i = digits[i]\\n if digit_i == 0: # Optimization: skip if digit is 0\\n continue\\n\\n # Calculate C(n, i) mod 2 and mod 5\\n c_mod2 = _nCr_mod2(n, i)\\n c_mod5 = _nCr_mod5(n, i)\\n\\n # Update mod 2 sum: add 1 if C(n,i) is 1 and digit is 1 (mod 2)\\n # Equivalent to adding (c_mod2 * digit_i) mod 2\\n f0_mod2 = (f0_mod2 + c_mod2 * digit_i) % 2\\n\\n # Update mod 5 sum: add (C(n,i) * digit) mod 5\\n term_mod5 = (c_mod5 * digit_i) % 5\\n f0_mod5 = (f0_mod5 + term_mod5) % 5\\n\\n # Calculate f1 = sum_{i=1}^{n+1} C(n, i-1) * digits[i] (mod 2 and mod 5)\\n # The sum uses digits from index 1 to n+1 = N-1.\\n # The binomial coefficient index is k = i - 1, ranging from 0 to n.\\n for i in range(1, n + 2):\\n digit_i = digits[i]\\n if digit_i == 0: # Optimization\\n continue\\n\\n # Calculate C(n, i-1) mod 2 and mod 5\\n k = i - 1\\n c_mod2 = _nCr_mod2(n, k)\\n c_mod5 = _nCr_mod5(n, k)\\n\\n # Update mod 2 sum\\n f1_mod2 = (f1_mod2 + c_mod2 * digit_i) % 2\\n\\n # Update mod 5 sum\\n term_mod5 = (c_mod5 * digit_i) % 5\\n f1_mod5 = (f1_mod5 + term_mod5) % 5\\n\\n # Combine results using CRT to find f0 and f1 mod 10\\n f0 = _crt_mod10(f0_mod2, f0_mod5)\\n f1 = _crt_mod10(f1_mod2, f1_mod5)\\n\\n # Return true if the final two digits are the same\\n return f0 == f1\"], [3332, 0.7059, \"import numpy as np\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n k = n - 2 # \\u6211\\u4eec\\u9700\\u8981\\u8ba1\\u7b97\\u9636\\u4e58\\u76f4\\u5230 k = n-2\\n \\n # \\u5c06\\u5b57\\u7b26\\u4e32\\u8f6c\\u6362\\u4e3a numpy \\u6570\\u7ec4\\uff08uint8\\uff09\\u5b58\\u653e\\u5404\\u6570\\u5b57\\uff08\\u5229\\u7528 ascii \\u7f16\\u7801\\u52a0\\u901f\\uff09\\n # \\u6ce8\\u610f\\uff1as.encode('ascii') \\u5f97\\u5230 bytes\\uff0c\\u6bcf\\u4e2a\\u5b57\\u7b26\\u5bf9\\u5e94\\u5176 ascii \\u7801\\n digits = np.frombuffer(s.encode('ascii'), dtype=np.uint8) - 48\\n\\n # -----------------------------\\n # \\u9884\\u5904\\u7406\\uff1a\\u8ba1\\u7b97 0! \\u5230 (n-2)! \\u7684\\u201c\\u5206\\u89e3\\u8868\\u793a\\u201d\\n # \\u5206\\u522b\\u5b58\\uff1afact_v[i]\\uff1a\\u53bb\\u9664 2 \\u548c 5 \\u540e\\u7684\\u90e8\\u5206\\uff0c\\u6a2110\\uff08\\u4fdd\\u8bc1\\u4e0e10\\u4e92\\u7d20\\uff09\\n # fact_c2[i]\\uff1ai! \\u4e2d\\u56e0\\u5b502\\u7684\\u603b\\u4e2a\\u6570\\n # fact_c5[i]\\uff1ai! \\u4e2d\\u56e0\\u5b505\\u7684\\u603b\\u4e2a\\u6570\\n fact_v = np.empty(k+1, dtype=np.int64)\\n fact_c2 = np.empty(k+1, dtype=np.int64)\\n fact_c5 = np.empty(k+1, dtype=np.int64)\\n fact_v[0] = 1\\n fact_c2[0] = 0\\n fact_c5[0] = 0\\n for i in range(1, k+1):\\n x = i\\n cnt2 = 0\\n cnt5 = 0\\n # \\u63d0\\u53d6\\u56e0\\u5b502\\n while x % 2 == 0:\\n x //= 2\\n cnt2 += 1\\n # \\u63d0\\u53d6\\u56e0\\u5b505\\n while x % 5 == 0:\\n x //= 5\\n cnt5 += 1\\n # \\u4f59\\u6570\\u90e8\\u5206 mod 10\\n r = x % 10\\n fact_v[i] = (fact_v[i-1] * r) % 10\\n fact_c2[i] = fact_c2[i-1] + cnt2\\n fact_c5[i] = fact_c5[i-1] + cnt5\\n \\n # -----------------------------\\n # \\u6c42 binom[j] = C(n-2, j) mod 10, \\u5bf9 j = 0,..., k\\n binom = np.empty(k+1, dtype=np.int64)\\n # \\u9884\\u5148\\u5b9a\\u4e49\\u4ec5\\u53ef\\u80fd\\u51fa\\u73b0\\u7684\\u4e0e10\\u4e92\\u7d20\\u6570\\u7684\\u9006\\u5143\\n inv_map = {1:1, 3:7, 7:3, 9:9}\\n def modinv(x):\\n return inv_map[int(x)]\\n # \\u5468\\u671f\\u8868\\uff1a2^e mod10 \\u5bf9 e>=1 \\u7684\\u5468\\u671f\\u4e3a (2,4,8,6)\\n cycle = (2, 4, 8, 6)\\n for j in range(0, k+1):\\n # \\u7ec4\\u5408\\u6570\\u516c\\u5f0f\\uff1aC(k, j) = fact(k) / (fact(j)*fact(k-j))\\n # \\u5148\\u8ba1\\u7b97\\u57fa\\u7840\\u90e8\\u5206\\uff08\\u5747\\u5728\\u4e0e10\\u4e92\\u7d20\\u7684\\u90e8\\u5206\\u4e2d\\u8fdb\\u884c\\uff0c\\u6545\\u53ef\\u4ee5\\u53d6\\u9006\\u5143\\uff09\\n base = (fact_v[k] * modinv(fact_v[j]) * modinv(fact_v[k-j])) % 10\\n # \\u8ba1\\u7b97\\u6307\\u6570\\u5dee\\n e2 = fact_c2[k] - fact_c2[j] - fact_c2[k-j]\\n e5 = fact_c5[k] - fact_c5[j] - fact_c5[k-j]\\n # \\u5982\\u679c\\u540c\\u65f6\\u6709 2 \\u548c 5\\uff0c\\u5219\\u8be5\\u9879\\u542b 10 \\u56e0\\u5b50\\uff0c\\u6a2110\\u7ed3\\u679c\\u4e3a 0\\n if e2 > 0 and e5 > 0:\\n binom[j] = 0\\n elif e2 > e5:\\n diff = e2 - e5\\n # \\u82e5 diff>=1\\uff0c\\u7528\\u5468\\u671f\\u8868\\uff1a2^(diff) mod10 = cycle[(diff-1)%4]\\n binom[j] = (base * cycle[(diff-1) % 4]) % 10\\n elif e5 > e2:\\n binom[j] = (base * 5) % 10\\n else:\\n binom[j] = base % 10\\n \\n # -----------------------------\\n # \\u6839\\u636e\\u6570\\u5b66\\u63a8\\u5bfc\\uff0c\\u6700\\u7ec8 S = -a_0 + sum_{i=1}^{n-2} (binom[i-1] - binom[i])*a_i + a_{n-1} mod10\\n # \\u6784\\u9020\\u7cfb\\u6570\\u6570\\u7ec4 c\\uff1a\\u957f\\u5ea6 n\\uff0cc[0] = -1, c[n-1] = 1, \\u5bf9 1<=i<=n-2, c[i] = (binom[i-1] - binom[i]) mod10\\n c = np.empty(n, dtype=np.int64)\\n c[0] = -1\\n c[n-1] = 1\\n if n > 2:\\n c[1:n-1] = (binom[:n-2] - binom[1:n-1]) % 10\\n # \\u8ba1\\u7b97 S = sum(c[i]*digits[i]) mod10\\uff08\\u5229\\u7528 numpy \\u70b9\\u4e58\\uff0c\\u5185\\u90e8 C \\u5b9e\\u73b0\\u975e\\u5e38\\u5feb\\uff09\\n S = int(np.dot(c, digits) % 10)\\n return S == 0\"], [3480, 0.7059, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n m = len(s) - 2\\n \\n # Precompute combination tables for Lucas's theorem\\n # For p=2\\n comb_table_2 = [[0] * 2 for _ in range(2)]\\n comb_table_2[0][0] = 1\\n comb_table_2[1][0] = 1\\n comb_table_2[1][1] = 1\\n \\n # For p=5\\n comb_table_5 = [[0] * 5 for _ in range(5)]\\n for i in range(5):\\n comb_table_5[i][0] = 1\\n comb_table_5[i][i] = 1\\n for j in range(1, i):\\n comb_table_5[i][j] = (comb_table_5[i-1][j-1] + comb_table_5[i-1][j]) % 5\\n \\n def lucas(n, k, p, comb_table):\\n res = 1\\n while n > 0 or k > 0:\\n ni = n % p\\n ki = k % p\\n if ki > ni:\\n return 0\\n res = (res * comb_table[ni][ki]) % p\\n n = n // p\\n k = k // p\\n return res\\n \\n # Compute coefficients for the first final digit (C(m, i) mod 10 for i in 0..m)\\n coeff1 = []\\n for i in range(m + 1):\\n mod2 = lucas(m, i, 2, comb_table_2)\\n mod5 = lucas(m, i, 5, comb_table_5)\\n mod10 = (5 * mod2 + 6 * mod5) % 10\\n coeff1.append(mod10)\\n \\n # Compute coefficients for the second final digit (C(m, i-1) mod 10 for i in 1..m+1)\\n coeff2 = []\\n for j in range(m + 1):\\n mod2 = lucas(m, j, 2, comb_table_2)\\n mod5 = lucas(m, j, 5, comb_table_5)\\n mod10 = (5 * mod2 + 6 * mod5) % 10\\n coeff2.append(mod10)\\n \\n # Calculate sum1 and sum2\\n sum1 = 0\\n for i in range(m + 1):\\n sum1 += int(s[i]) * coeff1[i]\\n sum1 %= 10\\n \\n sum2 = 0\\n for idx in range(m + 1):\\n original_index = idx + 1\\n sum2 += int(s[original_index]) * coeff2[idx]\\n sum2 %= 10\\n \\n return sum1 == sum2\"], [3628, 0.7059, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n m = n - 2\\n if m < 0:\\n return False # according to constraints, n >= 3\\n \\n s_digits = list(map(int, s))\\n coeffs = [0] * (m + 1)\\n \\n for i in range(m + 1):\\n mod2 = self.lucas(m, i, 2)\\n mod5 = self.lucas(m, i, 5)\\n coeff = self.crt(mod2, mod5)\\n coeffs[i] = coeff\\n \\n digit1 = 0\\n digit2 = 0\\n for i in range(m + 1):\\n digit1 = (digit1 + coeffs[i] * s_digits[i]) % 10\\n digit2 = (digit2 + coeffs[i] * s_digits[i + 1]) % 10\\n \\n return digit1 == digit2\\n \\n def lucas(self, n, k, p):\\n res = 1\\n while n > 0 or k > 0:\\n ni = n % p\\n ki = k % p\\n if ki > ni:\\n return 0\\n res = res * self.comb(ni, ki, p) % p\\n n = n // p\\n k = k // p\\n return res\\n \\n def comb(self, n, k, p):\\n if k < 0 or k > n:\\n return 0\\n if k == 0 or k == n:\\n return 1 % p\\n k = min(k, n - k)\\n c = 1\\n for i in range(k):\\n c = c * (n - i) // (i + 1)\\n c %= p\\n return c % p\\n \\n def crt(self, a, b):\\n # Solve x \\u2261 a mod 2 and x \\u2261 b mod 5\\n # Find x mod 10\\n t = (a - (b % 2)) % 2\\n x = b + 5 * t\\n return x % 10\"], [3776, 0.2353, \"class Solution:\\n def sieve_of_eratosthenes_prime_digit_counts(self,n):\\n \\\"\\\"\\\"\\n Calculates the prime digit counts for numbers up to n using the Sieve of Eratosthenes.\\n\\n Args:\\n n: An integer.\\n\\n Returns:\\n A dictionary where keys are numbers from 2 to n, and values are dictionaries\\n representing the sum of the powers of prime factors with the same last digit.\\n The inner dictionary has last digits of prime factors as keys and the sum of\\n their powers as values.\\n \\\"\\\"\\\"\\n if n < 2:\\n return {}\\n\\n is_prime = [True] * (n + 1)\\n is_prime[0] = is_prime[1] = False\\n primes = []\\n for p in range(2, int(math.sqrt(n)) + 1):\\n if is_prime[p]:\\n for i in range(p * p, n + 1, p):\\n is_prime[i] = False\\n for p in range(2, n + 1):\\n if is_prime[p]:\\n primes.append(p)\\n\\n prime_digit_counts = {}\\n for num in range(2, n + 1):\\n digit_counts = {}\\n temp_num = num\\n for prime in primes:\\n if prime * prime > temp_num:\\n break\\n while temp_num % prime == 0:\\n last_digit = prime % 10\\n digit_counts[last_digit] = digit_counts.get(last_digit, 0) + 1\\n temp_num //= prime\\n if temp_num > 1: # Remaining factor is a prime number\\n last_digit = temp_num % 10\\n digit_counts[last_digit] = digit_counts.get(last_digit, 0) + 1\\n prime_digit_counts[num] = digit_counts\\n return prime_digit_counts\\n\\n def hasSameDigits(self, s: str) -> bool:\\n print (\\\"this many:\\\", len(s))\\n def generate_primes(N):\\n if N < 2:\\n return []\\n\\n primes = []\\n is_prime = [True] * (N + 1)\\n is_prime[0] = is_prime[1] = False\\n\\n for p in range(2, int(N**0.5) + 1):\\n if is_prime[p]:\\n for i in range(p * p, N + 1, p):\\n is_prime[i] = False\\n\\n for p in range(2, N + 1):\\n if is_prime[p]:\\n primes.append(p)\\n\\n return primes\\n\\n def to_digit(d):\\n return ord(d)-ord('0')\\n left = 0\\n right = 0\\n n = len(s)\\n print(n)\\n left = to_digit(s[0]) + to_digit(s[n-2])\\n right = to_digit(s[1]) + to_digit(s[n-1])\\n cache = {}\\n \\n X = 1 \\n primes = generate_primes(n)\\n boom = self.sieve_of_eratosthenes_prime_digit_counts(n)\\n boom[1] = {1:1}\\n ld_power = {\\n 1: {},\\n 2: {1:2, 2:4, 3:8, 4:6},\\n 3: {1:3, 2:9, 3:7, 4:1},\\n 5: {1:5},\\n 7: {1:7, 2:9, 3:3, 4:1},\\n 9: {1:9, 2:1},\\n }\\n ld_powermod = {2:4, 3:4, 5:1, 7:4, 9:2, 1:0}\\n powers = {1:0, 3:0, 5:0, 7:0, 9:0, 2:0} \\n def last_digit(x):\\n return x%10\\n x = 1\\n for i in range(1, (n-2)//2+1):\\n A = (n-i-1)\\n B = i \\n\\n for pd, pp in boom[A].items():\\n powers[pd]+=pp\\n for pd, pp in boom[B].items():\\n powers[pd]-=pp\\n \\n x = 1\\n for ld, power in powers.items():\\n if power !=0 and ld != 1: \\n multiplier = ld_power[ld][(power-1) % (ld_powermod[ld])+1]\\n #print (\\\"/ x=\\\", x ,\\\"*\\\", ld,\\\"^\\\", power, \\\"[\\\",multiplier, ld**power%10,\\\"]\\\") \\n x = x * multiplier\\n #print (\\\"\\\\ x=\\\", x) \\n x = x % 10\\n #X = (X * (n-i-1) / i)\\n #x2 = X %10 \\n #print (\\\"::\\\",x, x2, X)\\n \\n \\n left = (left+to_digit(s[i])*x) %10\\n #print (\\\"L1 \\\" , left)\\n if i != n-2-i:\\n left = (left+to_digit(s[n-2-i])*x) %10\\n #print (\\\"L2 \\\" , left)\\n right = (right + to_digit(s[i+1])*x) % 10\\n #print (\\\"R1 \\\" , right)\\n if i != n-2-i:\\n right = (right + to_digit(s[n-1-i])*x) % 10\\n #print (\\\"R2 \\\" , right)\\n #print (i, X, x, left, s[i], s[n-2-i], 'L ')\\n #print (i, X, x, right, s[i+1], s[n-1-i], ' R')\\n #print (\\\"==\\\",sum(powers))\\n print (left, right)\\n return left == right \\n\\n\"], [3924, 0.4706, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n def lucas(n, k, p):\\n if k < 0:\\n return 0\\n if p == 2:\\n res = 1\\n while n > 0 or k > 0:\\n ni = n % 2\\n ki = k % 2\\n if ki > ni:\\n return 0\\n res *= 1\\n n = n // 2\\n k = k // 2\\n return res % 2\\n elif p == 5:\\n comb_table = [\\n [1, 0, 0, 0, 0], # ni=0\\n [1, 1, 0, 0, 0], # ni=1\\n [1, 2, 1, 0, 0], # ni=2\\n [1, 3, 3, 1, 0], # ni=3\\n [1, 4, 1, 4, 1], # ni=4\\n ]\\n res = 1\\n while n > 0 or k > 0:\\n ni = n % 5\\n ki = k % 5\\n if ki > ni:\\n return 0\\n res = (res * comb_table[ni][ki]) % 5\\n n = n // 5\\n k = k // 5\\n return res % 5\\n else:\\n return 0\\n\\n n = len(s)\\n k = n - 2\\n left_sum2 = 0\\n left_sum5 = 0\\n right_sum2 = 0\\n right_sum5 = 0\\n\\n for i in range(n):\\n digit = int(s[i])\\n\\n # Contribution to left sum\\n if i <= k:\\n c_left2 = lucas(k, i, 2)\\n c_left5 = lucas(k, i, 5)\\n else:\\n c_left2 = 0\\n c_left5 = 0\\n left_sum2 += digit * c_left2\\n left_sum5 += digit * c_left5\\n\\n # Contribution to right sum\\n prev_i = i - 1\\n if 0 <= prev_i <= k:\\n c_right2 = lucas(k, prev_i, 2)\\n c_right5 = lucas(k, prev_i, 5)\\n else:\\n c_right2 = 0\\n c_right5 = 0\\n right_sum2 += digit * c_right2\\n right_sum5 += digit * c_right5\\n\\n # Modulo operations\\n left_sum2 %= 2\\n left_sum5 %= 5\\n right_sum2 %= 2\\n right_sum5 %= 5\\n\\n # Combine using Chinese Remainder Theorem\\n def combine(a, b):\\n return (5 * ((a - b) % 2) + b) % 10\\n\\n left_mod10 = combine(left_sum2, left_sum5)\\n right_mod10 = combine(right_sum2, right_sum5)\\n\\n return left_mod10 == right_mod10\\n \"], [4072, 0.2353, \"def modinv(a, m):\\n return pow(a, -1, m)\\n\\ndef comb_mod_prime(n, k, p):\\n if k > n:\\n return 0\\n result = 1\\n while n > 0 or k > 0:\\n ni = n % p\\n ki = k % p\\n if ki > ni:\\n return 0\\n result = (result * comb_small_mod(ni, ki, p)) % p\\n n //= p\\n k //= p\\n return result\\n\\ndef comb_small_mod(n, k, p):\\n # Compute C(n, k) mod p directly, p is small prime\\n if k == 0 or k == n:\\n return 1\\n num = den = 1\\n for i in range(k):\\n num = (num * (n - i)) % p\\n den = (den * (i + 1)) % p\\n return (num * modinv(den, p)) % p\\n\\ndef crt(a1, m1, a2, m2):\\n # Combine two congruences: x \\u2261 a1 mod m1, x \\u2261 a2 mod m2\\n # Assumes m1 and m2 are coprime\\n m1_inv = modinv(m1, m2)\\n return (a1 + m1 * ((a2 - a1) * m1_inv % m2)) % (m1 * m2)\\n\\ndef binomial_coefficients_mod_10(n):\\n result = []\\n for k in range(n + 1):\\n c_mod2 = comb_mod_prime(n, k, 2)\\n c_mod5 = comb_mod_prime(n, k, 5)\\n c_mod10 = crt(c_mod2, 2, c_mod5, 5)\\n result.append(c_mod10)\\n return result\\n\\ndef test(l: list[int]):\\n ...\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n l = [int(ch) for ch in s]\\n \\n\\n l1, l2 = l[:-1], l[1:]\\n bin_coef = binomial_coefficients_mod_10(len(l)-2)\\n \\n s1 = 1\\n for x, n in zip(l1, bin_coef):\\n s1 = (s1 + x * n) % 10\\n \\n s2 = 1\\n for x, n in zip(l2, bin_coef):\\n s2 = (s2 + x * n) % 10\\n\\n \\n return s1 == s2\\n \\n\\n\\n\\n\\n \"], [4220, 0.2353, \"from math import comb\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)-2\\n coeffs_2 = [0] * (n+1)\\n coeffs_5 = [0] * (n+1)\\n n_base2 = self.decimalToBase(n, 2)\\n n_base5 = self.decimalToBase(n, 5)\\n left_num = 0\\n right_num = 0\\n for r in range(0, n+1):\\n r_base2 = self.decimalToBase(r, 2)\\n r_base5 = self.decimalToBase(r, 5)\\n coeffs_2[r] = self.lucas(n_base2, r_base2, 2)\\n coeffs_5[r] = self.lucas(n_base5, r_base5, 5)\\n coeff_10 = coeffs_5[r] + (5 if (coeffs_5[r]-coeffs_2[r])%2 else 0)\\n left_num += int(s[r]) * coeff_10\\n right_num += int(s[r+1]) * coeff_10\\n \\n return (left_num%10) == (right_num%10)\\n\\n\\n\\n def lucas(self, n_list, r_list, p):\\n r_list = [0]*(len(n_list) - len(r_list)) + r_list\\n total = 1\\n for i in range(len(n_list)):\\n if n_list[i] < r_list[i]:\\n return 0\\n total *= comb(n_list[i], r_list[i])\\n return total % p\\n\\n def decimalToBase(self, n, b):\\n if n == 0:\\n return [0]\\n digits = []\\n while n:\\n digits.append(n % b)\\n n //= b\\n return digits[::-1]\"], [4368, 0.4706, \"def modinv(a, m):\\n return pow(a, -1, m)\\n # Modular inverse via extended Euclidean algorithm\\n g, x, _ = extended_gcd(a, m)\\n if g != 1:\\n raise Exception('modular inverse does not exist')\\n return x % m\\n\\ndef extended_gcd(a, b):\\n if b == 0:\\n return (a, 1, 0)\\n g, x1, y1 = extended_gcd(b, a % b)\\n x, y = y1, x1 - (a // b) * y1\\n return (g, x, y)\\n\\ndef comb_mod_prime(n, k, p):\\n if k > n:\\n return 0\\n result = 1\\n while n > 0 or k > 0:\\n ni = n % p\\n ki = k % p\\n if ki > ni:\\n return 0\\n result = (result * comb_small_mod(ni, ki, p)) % p\\n n //= p\\n k //= p\\n return result\\n\\ndef comb_small_mod(n, k, p):\\n # Compute C(n, k) mod p directly, p is small prime\\n if k == 0 or k == n:\\n return 1\\n num = den = 1\\n for i in range(k):\\n num = (num * (n - i)) % p\\n den = (den * (i + 1)) % p\\n return (num * modinv(den, p)) % p\\n\\ndef crt(a1, m1, a2, m2):\\n # Combine two congruences: x \\u2261 a1 mod m1, x \\u2261 a2 mod m2\\n # Assumes m1 and m2 are coprime\\n m1_inv = modinv(m1, m2)\\n return (a1 + m1 * ((a2 - a1) * m1_inv % m2)) % (m1 * m2)\\n\\ndef binomial_coefficients_mod_10(n):\\n result = []\\n for k in range(n + 1):\\n c_mod2 = comb_mod_prime(n, k, 2)\\n c_mod5 = comb_mod_prime(n, k, 5)\\n c_mod10 = crt(c_mod2, 2, c_mod5, 5)\\n result.append(c_mod10)\\n return result\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n l = [int(ch) for ch in s]\\n \\n\\n l1, l2 = l[:-1], l[1:]\\n bin_coef = binomial_coefficients_mod_10(len(l)-2)\\n print(l1, l2, bin_coef)\\n \\n s1 = 1\\n for x, n in zip(l1, bin_coef):\\n s1 = (s1 + x * n) % 10\\n \\n s2 = 1\\n for x, n in zip(l2, bin_coef):\\n s2 = (s2 + x * n) % 10\\n \\n print(s1, s2)\\n \\n return s1 == s2\\n \\n\\n\\n\\n\\n \"], [4517, 0.9412, \"from math import comb\\n\\nMAX = 100_005\\nfact2 = [1] * MAX\\nfact5 = [1] * MAX\\n\\nfor i in range(1, MAX):\\n fact2[i] = (fact2[i - 1] * i) % 2\\n fact5[i] = (fact5[i - 1] * i) % 5\\n\\ndef modinv(a, m):\\n return pow(a, -1, m)\\n\\ndef lucas(n, k, p):\\n res = 1\\n while n > 0 and k > 0:\\n ni = n % p\\n ki = k % p\\n if ki > ni:\\n return 0\\n res = (res * comb(ni, ki)) % p\\n n //= p\\n k //= p\\n return res\\n\\ndef crt_mod10(c2, c5):\\n for x in range(10):\\n if x % 2 == c2 and x % 5 == c5:\\n return x\\n return 0\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n digits = list(map(int, s))\\n n = len(digits)\\n\\n def final_digit(offset):\\n total = 0\\n for i in range(len(digits)):\\n k = i - offset\\n if k < 0 or k > n - 2:\\n continue\\n c2 = lucas(n - 2, k, 2)\\n c5 = lucas(n - 2, k, 5)\\n coef = crt_mod10(c2, c5)\\n total = (total + coef * digits[i]) % 10\\n return total\\n\\n return final_digit(0) == final_digit(1)\"], [4665, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n m = n - 2\\n \\n # Precomputed C(a, b) mod 5 for a, b <= 4\\n table5 = [\\n [1, 0, 0, 0, 0],\\n [1, 1, 0, 0, 0],\\n [1, 2, 1, 0, 0],\\n [1, 3, 3, 1, 0],\\n [1, 4, 1, 4, 1]\\n ]\\n \\n # Lookup for x \\u2261 a mod 2, x \\u2261 b mod 5\\n lookup = [\\n [0, 6, 2, 8, 4], # a=0\\n [5, 1, 7, 3, 9] # a=1\\n ]\\n \\n def get_digits(num, p):\\n if num == 0:\\n return [0]\\n digits = []\\n while num > 0:\\n digits.append(num % p)\\n num //= p\\n return digits\\n \\n def lucas_C(n, k, p, table):\\n if k > n or k < 0:\\n return 0\\n n_digits = get_digits(n, p)\\n k_digits = get_digits(k, p)\\n while len(k_digits) < len(n_digits):\\n k_digits.append(0)\\n prod = 1\\n for nj, kj in zip(n_digits, k_digits):\\n if kj > nj:\\n return 0\\n prod = (prod * table[nj][kj]) % p\\n return prod\\n \\n f_0_sum = f_1_sum = 0\\n for i in range(n):\\n # Compute f_0 coefficient\\n if i <= m:\\n a = 1 if (i & m) == i else 0\\n b = lucas_C(m, i, 5, table5)\\n x = lookup[a][b]\\n else:\\n x = 0\\n f_0_sum = (f_0_sum + x * int(s[i])) % 10\\n \\n # Compute f_1 coefficient\\n if i == 0:\\n y = 0\\n else:\\n a = 1 if ((i-1) & m) == (i-1) else 0\\n b = lucas_C(m, i-1, 5, table5)\\n y = lookup[a][b]\\n f_1_sum = (f_1_sum + y * int(s[i])) % 10\\n \\n return f_0_sum == f_1_sum\"], [4813, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n if n < 2:\\n return False\\n if n == 2:\\n return s[0] == s[1]\\n \\n original = [int(c) for c in s]\\n m = n - 2 # number of reduction steps needed to reach two digits\\n \\n sum0 = 0\\n sum1 = 0\\n \\n for i in range(m + 1):\\n # Compute C(m, i) mod 2 and mod 5\\n mod2 = self.binom_mod_prime(m, i, 2)\\n mod5 = self.binom_mod_prime(m, i, 5)\\n \\n # Combine using Chinese Remainder Theorem to get mod 10\\n # Solve x \\u2261 mod2 (mod 2) and x \\u2261 mod5 (mod 5)\\n t = ((mod5 - mod2) * 3) % 5 # 3 is inv of 2 mod 5\\n c_mod10 = mod2 + 2 * t\\n \\n # Update sums\\n sum0 += original[i] * c_mod10\\n sum1 += original[i + 1] * c_mod10\\n sum0 %= 10\\n sum1 %= 10\\n \\n return sum0 == sum1\\n \\n def binom_mod_prime(self, n: int, k: int, p: int) -> int:\\n result = 1\\n while n > 0 or k > 0:\\n ni = n % p\\n ki = k % p\\n if ki > ni:\\n return 0\\n # Calculate C(ni, ki) mod p\\n numer = 1\\n denom = 1\\n for i in range(ki):\\n numer = numer * (ni - i) % p\\n denom = denom * (i + 1) % p\\n denom_inv = pow(denom, p - 2, p)\\n res = (numer * denom_inv) % p\\n result = (result * res) % p\\n n //= p\\n k //= p\\n return result\"], [4961, 0.2353, \"def lucas_choose(n,m,p):\\n result = 1\\n while n != 0 and m != 0:\\n ni = n % p\\n mi = m % p\\n\\n result *= math.comb(ni,mi)\\n result %= p\\n \\n n //= p\\n m //= p\\n return result\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n digits = [int(x) for x in s]\\n n = len(digits)\\n N = n - 2\\n cNk = 1\\n a2,b2,a5,b5 = 0,0,0,0\\n for i in range(n - 1):\\n #print(n-2,i,cNk)\\n lc2 = lucas_choose(N,i,2)\\n lc5 = lucas_choose(N,i,5)\\n a2 = (a2 + lc2*digits[i]) % 2\\n b2 = (b2 + lc2*digits[i+1]) % 2\\n a5 = (a5 + lc5*digits[i]) % 5\\n b5 = (b5 + lc5*digits[i+1]) % 5\\n return a2 == b2 and a5 == b5\"], [5109, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n s = [int(x) for x in s]\\n\\n num = len(s) - 1\\n left = 0\\n right = 0\\n base_2_num = self.get_base_2(num - 1)\\n base_5_num = self.get_base_5(num - 1)\\n\\n for i in range(num):\\n base_2_i = self.get_base_2(i)\\n base_5_i = self.get_base_5(i)\\n base_2_coeff = self.lucas(base_2_num, base_2_i)\\n base_5_coeff = self.lucas(base_5_num, base_5_i)\\n curr_coeff = base_5_coeff if base_2_coeff == base_5_coeff % 2 else 5 + base_5_coeff\\n\\n left+=(s[i] * (curr_coeff))\\n right+=(s[i+1] * (curr_coeff))\\n\\n left %= 10\\n right %= 10\\n\\n return left == right\\n\\n def get_base_5(self, x: int) -> List[int]:\\n if x == 0: return [0]\\n\\n digits = []\\n while x > 0:\\n digits.append(x%5)\\n x //= 5\\n \\n return digits\\n\\n def get_base_2(self, x: int) -> List[int]:\\n if x==0: return [0]\\n\\n digits = []\\n while x > 0:\\n digits.append(x & 1)\\n x >>= 1\\n \\n return digits\\n\\n def lucas(self, m: List[int], n: List[int]) -> int:\\n if len(m) > len(n): n += [0] * (len(m) - len(n))\\n elif len(n) > len(m): m += [0] * (len(n) - len(m))\\n\\n prod = 1\\n for i in range(len(m)):\\n prod *= math.comb(m[i], n[i])\\n \\n return prod%5\"], [5257, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=(n-1)%2\\n l=n%2\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp[0]\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n if p == 2:\\n return fact\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(tablep,fact,n,p):\\n factinv = [1] * (n + 1)\\n if p == 2:\\n return factinv\\n elif p == 5:\\n for i in range(0, n+1):\\n factinv[i] = tablep[tablep[fact[i]][fact[i]]][fact[i]]\\n return factinv\\n else:\\n for i in range(0, n+1):\\n for j in range(0,p-2):\\n factinv[i] = tablep[factinv[i]][fact[i]]\\n return factinv\\n\\n\\n def base(x,p):\\n r=[]\\n if p == 2:\\n while x > 1:\\n r.append(x&1)\\n x=x>>1\\n else:\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n \\n def addOne(k_p,p):\\n carry=0\\n j=1\\n k_p[0] += 1\\n if k_p[0] == p:\\n k_p[0] = 0\\n carry = 1\\n while len(k_p)>j:\\n k_p[j] += carry\\n if k_p[j] == p:\\n k_p[j] = 0\\n carry = 1\\n else:\\n carry = 0\\n j+=1\\n return\\n\\n def binomialCoefficientModLucas(tablep,factp,factinvp,n,p):\\n dp = [0 for _ in range(n + 1)]\\n n_bp = base(n-1,p)\\n k_bp = [0]*len(n_bp)\\n for k in range(0, n):\\n m_p = 1\\n for j in range(len(n_bp)):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[k] = m_p\\n addOne(k_bp,p)\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [0 for _ in range(n + 1)]\\n for k in range(0, n):\\n dp[k] = remainder[coeffp[k]][coeffq[k]]\\n return dp\\n\\n def binomialCoefficientMod(n,p):\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factinvp = binomail_precompute_factinv(tablep,factp,n,p)\\n coeffp = binomialCoefficientModLucas(tablep,factp,factinvp,n,p)\\n return coeffp\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff2 = binomialCoefficientMod(N-1,2)\\n coeff5 = binomialCoefficientMod(N-1,5)\\n coeff = binomialCoefficientCombine(coeff2,coeff5,N-1,2,5)\\n\\n\\n sum = [0,0]\\n n = []\\n for i in range(len(s)):\\n n.append(int(s[i]))\\n\\n #idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[k]][n[j+k]]]\\n\\n return sum[0]==sum[1]\\n\\n # a0 a1 a2 a3 a4 a5\\n # a0+a1 a1+a2 a2+a3 a3+a4 a4+a5\\n # a0+2*a1+a2 a1+2*a2+a3 a2+2*a3+a4 a3+2*a4+a5\\n # a0+3*a1+3*a2+a3 a1+3*a2+3*a3+a4 a2+3*a3+3*a4+a5\\n # a0+4*a1+6*a2+4*a3+a4 a1+4*a2+6*a3+4*a4+a5\\n # diff = a0-3*a1+2*a2-2*a3-3*a4-a5\\n\"], [5405, 0.2353, \"def modinv(a, m):\\n # Modular inverse via extended Euclidean algorithm\\n g, x, _ = extended_gcd(a, m)\\n if g != 1:\\n raise Exception('modular inverse does not exist')\\n return x % m\\n\\ndef extended_gcd(a, b):\\n if b == 0:\\n return (a, 1, 0)\\n g, x1, y1 = extended_gcd(b, a % b)\\n x, y = y1, x1 - (a // b) * y1\\n return (g, x, y)\\n\\ndef comb_mod_prime(n, k, p):\\n if k > n:\\n return 0\\n result = 1\\n while n > 0 or k > 0:\\n ni = n % p\\n ki = k % p\\n if ki > ni:\\n return 0\\n result = (result * comb_small_mod(ni, ki, p)) % p\\n n //= p\\n k //= p\\n return result\\n\\ndef comb_small_mod(n, k, p):\\n # Compute C(n, k) mod p directly, p is small prime\\n if k == 0 or k == n:\\n return 1\\n num = den = 1\\n for i in range(k):\\n num = (num * (n - i)) % p\\n den = (den * (i + 1)) % p\\n return (num * modinv(den, p)) % p\\n\\ndef crt(a1, m1, a2, m2):\\n # Combine two congruences: x \\u2261 a1 mod m1, x \\u2261 a2 mod m2\\n # Assumes m1 and m2 are coprime\\n m1_inv = modinv(m1, m2)\\n return (a1 + m1 * ((a2 - a1) * m1_inv % m2)) % (m1 * m2)\\n\\ndef binomial_coefficients_mod_10(n):\\n result = []\\n for k in range(n + 1):\\n c_mod2 = comb_mod_prime(n, k, 2)\\n c_mod5 = comb_mod_prime(n, k, 5)\\n c_mod10 = crt(c_mod2, 2, c_mod5, 5)\\n result.append(c_mod10)\\n return result\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n l = [int(ch) for ch in s]\\n \\n\\n l1, l2 = l[:-1], l[1:]\\n bin_coef = binomial_coefficients_mod_10(len(l)-2)\\n print(l1, l2, bin_coef)\\n \\n s1 = 1\\n for x, n in zip(l1, bin_coef):\\n s1 = (s1 + x * n) % 10\\n \\n s2 = 1\\n for x, n in zip(l2, bin_coef):\\n s2 = (s2 + x * n) % 10\\n \\n print(s1, s2)\\n \\n return s1 == s2\\n \\n\\n\\n\\n\\n \"], [5553, 0.9412, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=0\\n l=1\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(fact,n,p):\\n if p == 2:\\n return [1]*(n+1)\\n factinv = [0] * (n + 1)\\n for i in range(0, n+1):\\n factinv[i] = pow(fact[i],p-2,p)\\n return factinv\\n\\n\\n def base(a,p):\\n r=[]\\n x=a\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n\\n def binomialCoefficientModP(tablep,factp,factinvp,n,p):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n n_bp = base(n-1,p)\\n for k in range(0, n):\\n k_bp = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n m_p = 1\\n for j in range(len_max):\\n if j>=len(n_bp):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,0,k_bp[j],p)]\\n break\\n elif j>=len(k_bp):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],0,p)]\\n break\\n else:\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[y][k] = m_p\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n for k in range(0, n):\\n dp[y][k] = remainder[coeffp[y][k]][coeffq[y][k]]\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n def binomialCoefficientMod(n):\\n p=2\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n q=5\\n tableq = [[0 for _ in range(q)] for _ in range(q)]\\n for i in range(q):\\n for j in range(q):\\n tableq[i][j] = (i*j)%q\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factq = binomail_precompute_fact(tableq,n,q)\\n factinvp = binomail_precompute_factinv(factp,n,p)\\n factinvq = binomail_precompute_factinv(factq,n,q)\\n coeffp = binomialCoefficientModP(tablep,factp,factinvp,n,p)\\n coeffq = binomialCoefficientModP(tableq,factq,factinvq,n,q)\\n coeff = binomialCoefficientCombine(coeffp,coeffq,n,p,q)\\n return coeff\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff = binomialCoefficientMod(N-1)\\n\\n sum = [0,0]\\n idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[idx][k]][int(s[j+k])]]\\n\\n return sum[0]==sum[1]\\n\"], [5701, 3.0589000000000004, \"class Solution:\\n # Same as 3461. Check If Digits Are Equal in String After Operations I\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n num1 = 0\\n num2 = 0\\n\\n for i in range(n - 1):\\n coefficient = self._nCkMod10(n - 2, i)\\n num1 += (coefficient * (int(s[i]) - 0)) % 10\\n num1 %= 10\\n num2 += (coefficient * (int(s[i + 1]) - 0)) % 10\\n num2 %= 10\\n\\n return num1 == num2\\n\\n def _nCkMod10(self, n: int, k: int) -> int:\\n \\\"\\\"\\\"Returns (n, k) % 10.\\\"\\\"\\\"\\n mod2 = self._lucasTheorem(n, k, 2)\\n mod5 = self._lucasTheorem(n, k, 5)\\n lookup = [\\n [0, 6, 2, 8, 4], # mod2 == 0\\n [5, 1, 7, 3, 9] # mod2 == 1\\n ]\\n return lookup[mod2][mod5]\\n\\n def _lucasTheorem(self, n: int, k: int, prime: int) -> int:\\n \\\"\\\"\\\"Returns (n, k) % prime.\\\"\\\"\\\"\\n res = 1\\n while n > 0 or k > 0:\\n nMod = n % prime\\n kMod = k % prime\\n res *= math.comb(nMod, kMod)\\n res %= prime\\n n //= prime\\n k //= prime\\n return res\"], [5849, 2.1177, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=0\\n l=1\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n if p == 2:\\n return fact\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(tablep,fact,n,p):\\n factinv = [1] * (n + 1)\\n if p == 2:\\n return factinv\\n for i in range(0, n+1):\\n for j in range(0,p-2):\\n factinv[i] = tablep[factinv[i]][fact[i]]\\n return factinv\\n\\n\\n def base(x,p):\\n r=[]\\n if p == 2:\\n while x > 1:\\n r.append(x&1)\\n x=x>>1\\n else:\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n\\n def binomialCoefficientModLucas(tablep,factp,factinvp,n,p):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n n_bp = base(n-1,p)\\n k_bp = [0]*len(n_bp)\\n for k in range(0, n):\\n k_bc = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n k_bp[0:len(k_bc)] = k_bc[:]\\n m_p = 1\\n for j in range(len_max):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[y][k] = m_p\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n for k in range(0, n):\\n dp[y][k] = remainder[coeffp[y][k]][coeffq[y][k]]\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n def binomialCoefficientMod(n,p):\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factinvp = binomail_precompute_factinv(tablep,factp,n,p)\\n coeffp = binomialCoefficientModLucas(tablep,factp,factinvp,n,p)\\n return coeffp\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff2 = binomialCoefficientMod(N-1,2)\\n coeff5 = binomialCoefficientMod(N-1,5)\\n coeff = binomialCoefficientCombine(coeff2,coeff5,N-1,2,5)\\n\\n\\n sum = [0,0]\\n n = []\\n for i in range(len(s)):\\n n.append(int(s[i]))\\n\\n idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[idx][k]][n[j+k]]]\\n\\n return sum[0]==sum[1]\\n\"], [5998, 1.4118000000000002, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=0\\n l=1\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n if p == 2:\\n return fact\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(tablep,fact,n,p):\\n factinv = [1] * (n + 1)\\n if p == 2:\\n return factinv\\n for i in range(0, n+1):\\n for j in range(0,p-2):\\n factinv[i] = tablep[factinv[i]][fact[i]]\\n return factinv\\n\\n\\n def base(x,p):\\n r=[]\\n if p == 2:\\n while x > 1:\\n r.append(x&1)\\n x=x>>1\\n else:\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n\\n def binomialCoefficientModLucas(tablep,factp,factinvp,n,p):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n n_bp = base(n-1,p)\\n k_bp = [0]*len(n_bp)\\n for k in range(0, n):\\n k_bc = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n k_bp[0:len(k_bc)] = k_bc[:]\\n m_p = 1\\n for j in range(len_max):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[y][k] = m_p\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n for k in range(0, n):\\n dp[y][k] = remainder[coeffp[y][k]][coeffq[y][k]]\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n def binomialCoefficientMod(n,p):\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factinvp = binomail_precompute_factinv(tablep,factp,n,p)\\n coeffp = binomialCoefficientModLucas(tablep,factp,factinvp,n,p)\\n return coeffp\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff2 = binomialCoefficientMod(N-1,2)\\n coeff5 = binomialCoefficientMod(N-1,5)\\n coeff = binomialCoefficientCombine(coeff2,coeff5,N-1,2,5)\\n\\n\\n sum = [0,0]\\n idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[idx][k]][int(s[j+k])]]\\n\\n return sum[0]==sum[1]\\n\"], [6146, 0.9412, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n def comb(n, k):\\n if k < 0 or k > n:\\n return 0\\n if k == 0 or k == n:\\n return 1\\n res = 1\\n for i in range(k):\\n res = res * (n - i) // (i + 1)\\n return res\\n \\n def lucas(n, k, p):\\n res = 1\\n while n > 0 or k > 0:\\n ni = n % p\\n ki = k % p\\n if ki > ni:\\n return 0\\n c = comb(ni, ki)\\n res = res * c % p\\n n = n // p\\n k = k // p\\n return res\\n \\n m = len(s)\\n k_val = m - 2\\n sum1 = 0\\n sum2 = 0\\n for i in range(m):\\n # Compute sum1\\n a = lucas(k_val, i, 2)\\n b = lucas(k_val, i, 5)\\n temp = (a - b) % 2\\n x = (5 * temp + b) % 10\\n sum1 = (sum1 + x * int(s[i])) % 10\\n \\n # Compute sum2\\n j = i - 1\\n if j < 0:\\n x2 = 0\\n else:\\n a2 = lucas(k_val, j, 2)\\n b2 = lucas(k_val, j, 5)\\n temp2 = (a2 - b2) % 2\\n x2 = (5 * temp2 + b2) % 10\\n sum2 = (sum2 + x2 * int(s[i])) % 10\\n \\n return sum1 == sum2\\n\"], [6294, 0.4706, \"from functools import lru_cache\\n\\n\\nclass Solution:\\n def __init__(self):\\n \\\"\\\"\\\"\\n Initialize with precomputed values\\n \\\"\\\"\\\"\\n self.cr_lookup = {\\n (0, 0): 0,\\n (0, 1): 6,\\n (0, 2): 2,\\n (0, 3): 8,\\n (0, 4): 4,\\n (1, 0): 5,\\n (1, 1): 1,\\n (1, 2): 7,\\n (1, 3): 3,\\n (1, 4): 9,\\n }\\n\\n self.setup_nCr_cache()\\n\\n self.precomputed_m2_values = {}\\n self.precomputed_m5_values = {}\\n for n in range(2, 101): # Use the original range from the reference\\n self.precomputed_m2_values[n] = [self.nCr_LT(n - 2, i, 2) for i in range(n - 1)]\\n self.precomputed_m5_values[n] = [self.nCr_LT(n - 2, i, 5) for i in range(n - 1)]\\n\\n for n in range(1, 20):\\n for i in range(n):\\n self.nCr_LT(n - 2, i, 2)\\n self.nCr_LT(n - 2, i, 5)\\n\\n def setup_nCr_cache(self):\\n \\\"\\\"\\\"\\n Setup caching for nCr functions\\n \\\"\\\"\\\"\\n self.nCrModP_cache = {}\\n self.nCr_LT_cache = {}\\n\\n @staticmethod\\n def str_to_int(s: str) -> list[int]:\\n \\\"\\\"\\\"Convert string digits to integers\\\"\\\"\\\"\\n return [ord(c) - ord('0') for c in s]\\n\\n def nCrModP(self, n, r, p):\\n \\\"\\\"\\\"\\n Calculate nCr mod p using dynamic programming approach\\n \\\"\\\"\\\"\\n key = (n, r, p)\\n if key in self.nCrModP_cache:\\n return self.nCrModP_cache[key]\\n\\n if r == 0:\\n return 1\\n if r == 1:\\n return n % p\\n if r > n:\\n return 0\\n if n == r:\\n return 1\\n\\n if r > n - r:\\n r = n - r\\n\\n if p == 2:\\n result = 1 if (n & r) == r else 0\\n self.nCrModP_cache[key] = result\\n return result\\n\\n C = [0] * (r + 1)\\n C[0] = 1\\n for i in range(1, n + 1):\\n j = min(i, r)\\n while j > 0:\\n C[j] = (C[j] + C[j - 1]) % p\\n j -= 1\\n\\n result = C[r]\\n self.nCrModP_cache[key] = result\\n return result\\n\\n def nCr_LT(self, n, r, p):\\n \\\"\\\"\\\"\\n Calculate nCr mod p using Lucas's Theorem\\n \\\"\\\"\\\"\\n key = (n, r, p)\\n if key in self.nCr_LT_cache:\\n return self.nCr_LT_cache[key]\\n\\n if r == 0:\\n return 1\\n if r == 1:\\n return n % p\\n if r > n:\\n return 0\\n if n == r:\\n return 1\\n\\n\\n ni = n % p\\n ri = r % p\\n\\n n_div = n // p\\n r_div = r // p\\n\\n fact1 = self.nCr_LT(n_div, r_div, p)\\n if fact1 == 0:\\n self.nCr_LT_cache[key] = 0\\n return 0\\n\\n fact2 = self.nCrModP(ni, ri, p)\\n if fact2 == 0:\\n self.nCr_LT_cache[key] = 0\\n return 0\\n\\n result = (fact1 * fact2) % p\\n self.nCr_LT_cache[key] = result\\n return result\\n\\n def hasSameDigits(self, s: str) -> bool:\\n \\\"\\\"\\\"\\n Calculate if the string has the same 2 final digits\\n by applying nCr/nCrModP\\n \\\"\\\"\\\"\\n n = len(s)\\n\\n if n <= 1:\\n return True\\n\\n if len(set(s)) == 1:\\n return True\\n\\n sn = self.str_to_int(s)\\n\\n # Use the exact algorithm from the reference solution\\n if n in self.precomputed_m2_values and n in self.precomputed_m5_values:\\n m2_values = self.precomputed_m2_values[n]\\n m5_values = self.precomputed_m5_values[n]\\n else:\\n m2_values = [self.nCr_LT(n - 2, i, 2) for i in range(n - 1)]\\n m5_values = [self.nCr_LT(n - 2, i, 5) for i in range(n - 1)]\\n\\n x = 0\\n y = 0\\n\\n for i in range(n - 1):\\n m2 = m2_values[i]\\n m5 = m5_values[i]\\n\\n v = self.cr_lookup[(m2, m5)]\\n\\n x = (x + v * sn[i]) % 10\\n y = (y + v * sn[i + 1]) % 10\\n\\n return x == y\\n\"], [6442, 0.7059, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=0\\n l=1\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n if p == 2:\\n return fact\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(tablep,fact,n,p):\\n factinv = [1] * (n + 1)\\n if p == 2:\\n return factinv\\n for i in range(0, n+1):\\n for j in range(0,p-2):\\n factinv[i] = tablep[factinv[i]][fact[i]]\\n return factinv\\n\\n\\n def base(x,p):\\n r=[]\\n if p == 2:\\n while x > 1:\\n r.append(x&1)\\n x=x>>1\\n else:\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n \\n def addOne(k_p,p):\\n carry=0\\n j=1\\n k_p[0] += 1\\n if k_p[0] == p:\\n k_p[0] = 0\\n carry = 1\\n while len(k_p)>j:\\n k_p[j] += carry\\n if k_p[j] == p:\\n k_p[j] = 0\\n carry = 1\\n else:\\n carry = 0\\n j+=1\\n return\\n\\n def binomialCoefficientModLucas(tablep,factp,factinvp,n,p):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n n_bp = base(n-1,p)\\n k_bp = [0]*len(n_bp)\\n for k in range(0, n):\\n #k_bc = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n #k_bp[0:len(k_bc)] = k_bc[:]\\n m_p = 1\\n for j in range(len_max):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[y][k] = m_p\\n addOne(k_bp,p)\\n #dp[y][0] = 1\\n #dp[y][n] = 0\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n for k in range(0, n):\\n dp[y][k] = remainder[coeffp[y][k]][coeffq[y][k]]\\n #dp[y][0] = 1\\n #dp[y][n] = 0\\n return dp\\n\\n def binomialCoefficientMod(n,p):\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factinvp = binomail_precompute_factinv(tablep,factp,n,p)\\n coeffp = binomialCoefficientModLucas(tablep,factp,factinvp,n,p)\\n return coeffp\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff2 = binomialCoefficientMod(N-1,2)\\n coeff5 = binomialCoefficientMod(N-1,5)\\n coeff = binomialCoefficientCombine(coeff2,coeff5,N-1,2,5)\\n\\n\\n sum = [0,0]\\n n = []\\n for i in range(len(s)):\\n n.append(int(s[i]))\\n\\n idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[idx][k]][n[j+k]]]\\n\\n return sum[0]==sum[1]\\n\\n # a0 a1 a2 a3 a4 a5\\n # a0+a1 a1+a2 a2+a3 a3+a4 a4+a5\\n # a0+2*a1+a2 a1+2*a2+a3 a2+2*a3+a4 a3+2*a4+a5\\n # a0+3*a1+3*a2+a3 a1+3*a2+3*a3+a4 a2+3*a3+3*a4+a5\\n # a0+4*a1+6*a2+4*a3+a4 a1+4*a2+6*a3+4*a4+a5\\n # diff = a0-3*a1+2*a2-2*a3-3*a4-a5\\n\"], [6590, 0.4706, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=0\\n l=1\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n if p == 2:\\n return fact\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(tablep,fact,n,p):\\n factinv = [1] * (n + 1)\\n if p == 2:\\n return factinv\\n for i in range(0, n+1):\\n for j in range(0,p-2):\\n factinv[i] = tablep[factinv[i]][fact[i]]\\n return factinv\\n\\n\\n def base(x,p):\\n r=[]\\n if p == 2:\\n while x > 1:\\n r.append(x&1)\\n x=x>>1\\n else:\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n \\n def addOne(k_p,p):\\n carry=0\\n j=1\\n k_p[0] += 1\\n if k_p[0] == p:\\n k_p[0] = 0\\n carry = 1\\n while len(k_p)>j:\\n k_p[j] += carry\\n if k_p[j] == p:\\n k_p[j] = 0\\n carry = 1\\n else:\\n carry = 0\\n j+=1\\n return\\n\\n def binomialCoefficientModLucas(tablep,factp,factinvp,n,p):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n n_bp = base(n-1,p)\\n k_bp = [0]*len(n_bp)\\n for k in range(0, n):\\n #k_bc = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n #k_bp[0:len(k_bc)] = k_bc[:]\\n m_p = 1\\n for j in range(len_max):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[y][k] = m_p\\n addOne(k_bp,p)\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n for k in range(0, n):\\n dp[y][k] = remainder[coeffp[y][k]][coeffq[y][k]]\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n def binomialCoefficientMod(n,p):\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factinvp = binomail_precompute_factinv(tablep,factp,n,p)\\n coeffp = binomialCoefficientModLucas(tablep,factp,factinvp,n,p)\\n return coeffp\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff2 = binomialCoefficientMod(N-1,2)\\n coeff5 = binomialCoefficientMod(N-1,5)\\n coeff = binomialCoefficientCombine(coeff2,coeff5,N-1,2,5)\\n\\n\\n sum = [0,0]\\n n = []\\n for i in range(len(s)):\\n n.append(int(s[i]))\\n\\n idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[idx][k]][n[j+k]]]\\n\\n return sum[0]==sum[1]\\n\\n # a0 a1 a2 a3 a4 a5\\n # a0+a1 a1+a2 a2+a3 a3+a4 a4+a5\\n # a0+2*a1+a2 a1+2*a2+a3 a2+2*a3+a4 a3+2*a4+a5\\n # a0+3*a1+3*a2+a3 a1+3*a2+3*a3+a4 a2+3*a3+3*a4+a5\\n # a0+4*a1+6*a2+4*a3+a4 a1+4*a2+6*a3+4*a4+a5\\n # diff = a0-3*a1+2*a2-2*a3-3*a4-a5\\n\"], [6738, 0.7059, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=0\\n l=1\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n if p == 2:\\n return fact\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(tablep,fact,n,p):\\n factinv = [1] * (n + 1)\\n if p == 2:\\n return factinv\\n for i in range(0, n+1):\\n for j in range(0,p-2):\\n factinv[i] = tablep[factinv[i]][fact[i]]\\n return factinv\\n\\n\\n def base(x,p):\\n r=[]\\n if p == 2:\\n while x > 1:\\n r.append(x&1)\\n x=x>>1\\n else:\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n \\n def addOne(k_p,p):\\n carry=0\\n j=1\\n k_p[0] += 1\\n if k_p[0] == p:\\n k_p[0] = 0\\n carry = 1\\n while len(k_p)>j:\\n k_p[j] += carry\\n if k_p[j] == p:\\n k_p[j] = 0\\n carry = 1\\n else:\\n carry = 0\\n j+=1\\n return\\n\\n def binomialCoefficientModLucas(tablep,factp,factinvp,n,p):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n n_bp = base(n-1,p)\\n k_bp = [0]*len(n_bp)\\n for k in range(0, n):\\n #k_bc = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n #k_bp[0:len(k_bc)] = k_bc[:]\\n m_p = 1\\n for j in range(len_max):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[y][k] = m_p\\n addOne(k_bp,p)\\n #dp[y][0] = 1\\n #dp[y][n] = 0\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n y=(n-1)%2\\n for k in range(0, n):\\n dp[y][k] = remainder[coeffp[y][k]][coeffq[y][k]]\\n #dp[y][0] = 1\\n #dp[y][n] = 0\\n return dp\\n\\n def binomialCoefficientMod(n,p):\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factinvp = binomail_precompute_factinv(tablep,factp,n,p)\\n coeffp = binomialCoefficientModLucas(tablep,factp,factinvp,n,p)\\n return coeffp\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff2 = binomialCoefficientMod(N-1,2)\\n coeff5 = binomialCoefficientMod(N-1,5)\\n coeff = binomialCoefficientCombine(coeff2,coeff5,N-1,2,5)\\n\\n\\n sum = [0,0]\\n n = []\\n for i in range(len(s)):\\n n.append(int(s[i]))\\n\\n idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[idx][k]][n[j+k]]]\\n\\n return sum[0]==sum[1]\\n\\n # a0 a1 a2 a3 a4 a5\\n # a0+a1 a1+a2 a2+a3 a3+a4 a4+a5\\n # a0+2*a1+a2 a1+2*a2+a3 a2+2*a3+a4 a3+2*a4+a5\\n # a0+3*a1+3*a2+a3 a1+3*a2+3*a3+a4 a2+3*a3+3*a4+a5\\n # a0+4*a1+6*a2+4*a3+a4 a1+4*a2+6*a3+4*a4+a5\\n # diff = a0-3*a1+2*a2-2*a3-3*a4-a5\\n\"], [6886, 0.7059, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n if n == 2:\\n return s[0] == s[1]\\n \\n digits = list(map(int, s))\\n N = n - 2 \\n mod = 10\\n F0, F1 = 0, 0\\n \\n for i in range(n - 1):\\n c2 = self.binom_mod2(N, i) \\n c5 = self.binom_mod5(N, i, 5) \\n r = (5 * c2 + 6 * c5) % mod\\n \\n F0 = (F0 + r * digits[i]) % mod\\n F1 = (F1 + r * digits[i+1]) % mod\\n \\n return F0 == F1\\n\\n def binom_mod2(self, n: int, k: int) -> int:\\n if k > n:\\n return 0\\n return 1 if (n & k) == k else 0\\n\\n def binom_mod5(self, n: int, k: int, p: int) -> int:\\n if k > n:\\n return 0\\n res = 1\\n while n or k:\\n n_i = n % p\\n k_i = k % p\\n if k_i > n_i:\\n return 0\\n res = (res * self.small_binom(n_i, k_i, p)) % p\\n n //= p\\n k //= p\\n return res\\n\\n def small_binom(self, n: int, k: int, p: int) -> int:\\n if k > n:\\n return 0\\n fact = [1] * p\\n for i in range(1, p):\\n fact[i] = (fact[i-1] * i) % p\\n inv_fact = [1] * p\\n inv_fact[p-1] = pow(fact[p-1], p-2, p)\\n for i in range(p-2, -1, -1):\\n inv_fact[i] = (inv_fact[i+1] * (i+1)) % p\\n return (fact[n] * inv_fact[k] * inv_fact[n-k]) % p\"], [7034, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s)\\n if n == 2:\\n return s[0] == s[1]\\n \\n digits = list(map(int, s))\\n N = n - 2 \\n mod = 10\\n F0, F1 = 0, 0\\n \\n for i in range(n - 1):\\n c2 = self.binom_mod2(N, i) \\n c5 = self.binom_mod5(N, i, 5) \\n r = (5 * c2 + 6 * c5) % mod\\n \\n F0 = (F0 + r * digits[i]) % mod\\n F1 = (F1 + r * digits[i+1]) % mod\\n \\n return F0 == F1\\n\\n def binom_mod2(self, n: int, k: int) -> int:\\n if k > n:\\n return 0\\n return 1 if (n & k) == k else 0\\n\\n def binom_mod5(self, n: int, k: int, p: int) -> int:\\n if k > n:\\n return 0\\n res = 1\\n while n or k:\\n n_i = n % p\\n k_i = k % p\\n if k_i > n_i:\\n return 0\\n res = (res * self.small_binom(n_i, k_i, p)) % p\\n n //= p\\n k //= p\\n return res\\n\\n def small_binom(self, n: int, k: int, p: int) -> int:\\n if k > n:\\n return 0\\n fact = [1] * p\\n for i in range(1, p):\\n fact[i] = (fact[i-1] * i) % p\\n inv_fact = [1] * p\\n inv_fact[p-1] = pow(fact[p-1], p-2, p)\\n for i in range(p-2, -1, -1):\\n inv_fact[i] = (inv_fact[i+1] * (i+1)) % p\\n return (fact[n] * inv_fact[k] * inv_fact[n-k]) % p\"], [7182, 0.2353, \"class Solution:\\n\\n p2_lookup = {\\n 0: {0: 1},\\n 1: {0: 1, 1: 1}\\n }\\n\\n p5_lookup = {\\n 0: {0: 1},\\n 1: {0: 1, 1: 1},\\n 2: {0: 1, 1: 2, 2: 1},\\n 3: {0: 1, 1: 3, 2: 3, 3: 1},\\n 4: {0: 1, 1: 4, 2: 1, 3: 4, 4: 1}\\n }\\n\\n def comb_mod(self, n, k, p):\\n if k == 0:\\n return 1\\n if n < k:\\n return 0\\n if p == 2:\\n lookup = self.p2_lookup\\n elif p == 5:\\n lookup = self.p5_lookup\\n else:\\n return 0\\n digits_n = []\\n while n > 0:\\n digits_n.append(n % p)\\n n = n // p\\n digits_k = []\\n while k > 0:\\n digits_k.append(k % p)\\n k = k // p\\n max_len = max(len(digits_n), len(digits_k))\\n digits_n += [0] * (max_len - len(digits_n))\\n digits_k += [0] * (max_len - len(digits_k))\\n res = 1\\n for dn, dk in zip(digits_n, digits_k):\\n if dk > dn:\\n return 0\\n res = (res * lookup[dn][dk]) % p\\n return res\\n\\n crt = {\\n (0, 0): 0,\\n (0, 1): 6,\\n (0, 2): 2,\\n (0, 3): 8,\\n (0, 4): 4,\\n (1, 0): 5,\\n (1, 1): 1,\\n (1, 2): 7,\\n (1, 3): 3,\\n (1, 4): 9,\\n }\\n\\n def hasSameDigits(self, s: str) -> bool:\\n L = len(s)\\n if L == 2:\\n return s[0] == s[1]\\n k = L - 2\\n sum1 = 0\\n sum2 = 0\\n for i in range(k + 1):\\n mod2 = self.comb_mod(k, i, 2)\\n mod5 = self.comb_mod(k, i, 5)\\n key = (mod2, mod5)\\n c = self.crt.get(key, 0)\\n sum1 += int(s[i]) * c\\n sum2 += int(s[i + 1]) * c\\n sum1 %= 10\\n sum2 %= 10\\n return sum1 == sum2\\n\"], [7330, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool: \\n n = len(s) - 1\\n fac = [1] * 6\\n for i in range(1, 6):\\n fac[i] = (fac[i - 1] * i) \\n\\n pascal = [0] * n\\n\\n def chinese_remainder(n, a):\\n sum = 0\\n prod = reduce(lambda x, y: x * y, n)\\n for n_i, a_i in zip(n, a):\\n p = prod // n_i\\n inv = pow(p, -1, n_i)\\n sum += a_i * inv * p\\n return sum % prod\\n \\n for k in range(n):\\n p5 = 1\\n n5, k5 = n - 1, k \\n while n5 or k5:\\n nd, kd = n5 % 5, k5 % 5\\n if nd < kd:\\n new = 0\\n else:\\n new = fac[nd] // (fac[kd] * fac[nd - kd]) \\n p5 = (p5 * new) % 5\\n n5 //= 5\\n k5 //= 5\\n n2, k2 = n - 1, k\\n p2 = 1\\n while n2 or k2:\\n nd, kd = n2 % 2, k2 % 2 \\n if nd < kd:\\n new = 0\\n else:\\n new = fac[nd] // (fac[kd] * fac[nd - kd])\\n p2 = (p2 * new) % 2\\n n2 //= 2\\n k2 //= 2\\n pascal[k] = chinese_remainder([2, 5], [p2, p5]) \\n \\n n1 = 0\\n for i in range(n):\\n n1 = (n1 + (int(s[i]) * pascal[i])) % 10\\n n2 = 0\\n for i in range(n):\\n n2 = (n2 + (int(s[i + 1]) * pascal[i])) % 10\\n return n1 == n2\\n \\n\\n\\n \\n\"], [7479, 0.7059, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n comb_table_2 = {\\n (0, 0): 1,\\n (1, 0): 1,\\n (1, 1): 1,\\n }\\n \\n comb_table_5 = {\\n (0, 0): 1,\\n (1, 0): 1,\\n (1, 1): 1,\\n (2, 0): 1,\\n (2, 1): 2,\\n (2, 2): 1,\\n (3, 0): 1,\\n (3, 1): 3,\\n (3, 2): 3,\\n (3, 3): 1,\\n (4, 0): 1,\\n (4, 1): 4,\\n (4, 2): 1,\\n (4, 3): 4,\\n (4, 4): 1,\\n }\\n\\n def comb(ni, ki, p):\\n if ki < 0 or ki > ni:\\n return 0\\n if p == 2:\\n return comb_table_2.get((ni, ki), 0)\\n elif p == 5:\\n return comb_table_5.get((ni, ki), 0)\\n else:\\n return 0\\n\\n def lucas(n, k, p):\\n if k == 0:\\n return 1\\n ni = n % p\\n ki = k % p\\n if ki > ni:\\n return 0\\n return (lucas(n // p, k // p, p) * comb(ni, ki, p)) % p\\n\\n def comb_mod(n, k):\\n if k < 0 or k > n:\\n return 0\\n mod2 = lucas(n, k, 2)\\n mod5 = lucas(n, k, 5)\\n for x in range(10):\\n if x % 2 == mod2 and x % 5 == mod5:\\n return x\\n return 0\\n\\n L = len(s)\\n if L == 2:\\n return s[0] == s[1]\\n \\n n = L - 2\\n sum1 = 0\\n sum2 = 0\\n \\n for i in range(L):\\n c1 = comb_mod(n, i) if i <= n else 0\\n prev_i = i - 1\\n c2 = comb_mod(n, prev_i) if 0 <= prev_i <= n else 0\\n sum1 = (sum1 + int(s[i]) * c1) % 10\\n sum2 = (sum2 + int(s[i]) * c2) % 10\\n \\n return sum1 == sum2\"], [7627, 0.2353, \"from copy import deepcopy\\nimport math\\nfrom functools import cache\\n\\nclass Solution:\\n debugging = False\\n LONGEST_LEN_STR = int(1e5)\\n binomial_coeff_table: List[List[int]] = []\\n\\n def get_num_base_digits(self, num: int, b: int) -> list[int]:\\n '''Return the digits of the base-10 num in the given base b.\\n Digit list is ordered from most to least significant'''\\n digits = []\\n while num > 0:\\n digits.append(num % b)\\n num //= b\\n return digits[::-1]\\n\\n def get_binomial_coeff_mod_prime(self, n: int, k: int, p: int) -> int:\\n '''Use Lucas's theorem to compute (n choose k) % p, where p is prime\\n Time complexity appears to be O(p**2 log(n))\\n O(log(n)) to get the base-p expansions of n, k\\n O(p**2) to compute the necessary binomial coefficients'''\\n n_base_p = self.get_num_base_digits(n, p)\\n k_base_p = self.get_num_base_digits(k, p)\\n k_base_p = [0]*(len(n_base_p) - len(k_base_p)) + k_base_p\\n reduced_coeffs = [\\n self.binomial_coeff_table[n_base_p[i]][k_base_p[i]]\\n for i in range(len(n_base_p))\\n ]\\n product_mod_p = 1\\n for coeff in reduced_coeffs:\\n product_mod_p *= coeff\\n product_mod_p %= p\\n return product_mod_p\\n\\n def chinese_remainder_theorem_solve(self, remainders: list[int], moduli: list[int]) -> int:\\n '''Assuming that the moduli are pairwise coprime, return the unique x\\n in [0, product(moduli)) such that x % moduli[i] == remainders[i]\\n for all 0 <= i < len(moduli)\\n \\n This can be done by replacing 2 of the systems with the ansatz based on\\n Bezout's identity. Continue replacing until only one congruence is left'''\\n final_answer = remainders[-1]\\n remainders = deepcopy(remainders)\\n moduli = deepcopy(moduli)\\n while len(remainders) >= 2:\\n r_1, r_2 = remainders[-2:]\\n m_1, m_2 = moduli[-2:]\\n # gcd, bezout_int_1, bezout_int_2 = self.extended_gcd(m_1, m_2)\\n gcd, bezout_int_1, bezout_int_2 = (1, -2, 1)\\n bezout_ansatz = r_1*bezout_int_2*m_2 + r_2*bezout_int_1*m_1\\n final_answer = bezout_ansatz\\n for _ in range(2):\\n remainders.pop()\\n moduli.pop()\\n remainders.append(bezout_ansatz)\\n moduli.append(m_1*m_2)\\n return final_answer % moduli[0]\\n\\n def get_binomial_coeff_mod(self, n: int, k: int, num: int) -> int:\\n '''Compute (n choose k) mod num. Num doesn't have to be prime\\n First, prime factorize num. Note that all prime factors need to have\\n multiplicity 1\\n Then, use Lucas's theorem to get (n choose k) mod each of these primes\\n Finally, finish with the Chinese remainder theorem to get (n choose k)\\n mod the original num'''\\n if num != 10:\\n raise ValueError(\\n 'This could easily be generalized, but I can save time here by '\\n 'hardcoding num = 10'\\n )\\n prime_factors = [2, 5]\\n coeff_mod_primes = [\\n self.get_binomial_coeff_mod_prime(n, k, p)\\n for p in prime_factors\\n ]\\n coeff_mod_original = self.chinese_remainder_theorem_solve(\\n remainders=coeff_mod_primes,\\n moduli=prime_factors\\n )\\n return coeff_mod_original\\n\\n def precompute_binomial_coeff_table(self) -> None:\\n '''To avoid getting a TLE, I may need to avoid relying on math.comb(). Instead,\\n precompute a table of binomial coefficients. Save it in a class variable so\\n that it only ever gets computed once'''\\n if len(self.binomial_coeff_table) > 0:\\n if self.debugging:\\n print(f'binomial coeff table already created')\\n return\\n self.binomial_coeff_table += [\\n [0 for _ in range(5+1)]\\n for _ in range(self.LONGEST_LEN_STR-1)\\n ]\\n for n in range(len(self.binomial_coeff_table)):\\n self.binomial_coeff_table[n][0] = 1\\n self.binomial_coeff_table[1][1] = 1\\n for n in range(2, len(self.binomial_coeff_table)):\\n for k in range(1, len(self.binomial_coeff_table[0])):\\n self.binomial_coeff_table[n][k] = (\\n self.binomial_coeff_table[n-1][k-1]\\n + self.binomial_coeff_table[n-1][k]\\n )\\n if self.debugging:\\n print(\\n 'self.binomial_coeff_table has shape '\\n f'{len(self.binomial_coeff_table), len(self.binomial_coeff_table[0])}'\\n )\\n\\n def lucas_theorem_approach(self, s: str) -> bool:\\n '''During the contest, I worked out binomial coeff expressions for the digits:\\n First digit = sum((n-2 choose i)d_i | 0 <= i <= n-2)\\n where n = len(s). Similarly for the second digit\\n However, I lacked the number theory knowledge to tractably compute these binomial\\n coeffs mod 10\\n \\n Following the hint, let's use Lucas's theorem to do so\\n This isn't the complete picture though. Lucas's theorem allows me to compute\\n the coeffs mod 2 and mod 5. Once I have these, I need the Chinese remainder\\n theorem to solve these congruence systems'''\\n first_digit = 0\\n second_digit = 0\\n s_digits = [int(ch) for ch in s]\\n coeffs_mod_10: List[int] = []\\n halfway_point = (len(s)-2) // 2\\n for i in range(len(s)-1):\\n if i <= halfway_point:\\n cur_coeff = self.get_binomial_coeff_mod(len(s)-2, i, 10)\\n else:\\n cur_coeff = coeffs_mod_10[len(s)-2-i]\\n coeffs_mod_10.append(cur_coeff)\\n first_digit = (first_digit + cur_coeff*s_digits[i]) % 10\\n second_digit = (second_digit + cur_coeff*s_digits[i+1]) % 10\\n if self.debugging:\\n print(f'final first half {coeffs_mod_10=}')\\n print(f'final {first_digit=}, {second_digit=}')\\n return (first_digit == second_digit)\\n\\n def hasSameDigits(self, s: str) -> bool:\\n self.precompute_binomial_coeff_table()\\n return self.lucas_theorem_approach(s)\\n \"], [7775, 0.2353, \"def maketable(p):\\n fact = [1] * (p)\\n for i in range(1, p):\\n fact[i] = (fact[i-1] * i) % p\\n # Fermat\\u306e\\u5c0f\\u5b9a\\u7406\\u306b\\u3088\\u308a\\u9006\\u5143\\u3092\\u8a08\\u7b97\\uff08p\\u306f\\u7d20\\u6570\\u306a\\u306e\\u3067\\uff09\\n inv_fact = [1] * (p)\\n inv_fact[p-1] = pow(fact[p-1], p-2, p)\\n for i in range(p-2, -1, -1):\\n inv_fact[i] = (inv_fact[i+1] * (i+1)) % p\\n return fact, inv_fact\\ntable = {2: maketable(2), 5: maketable(5)}\\n# \\u307e\\u305a\\u3001p < p \\u306b\\u3064\\u3044\\u3066\\u306e nCk mod p \\u3092\\u8a08\\u7b97\\u3059\\u308b\\u95a2\\u6570\\ndef nCk_mod_p(n, k, p):\\n if k < 0 or k > n:\\n return 0\\n fact, inv_fact = table[p]\\n return (fact[n] * inv_fact[k] % p) * inv_fact[n-k] % p\\n\\n# Lucas\\u306e\\u5b9a\\u7406\\u3092\\u7528\\u3044\\u3066\\u3001\\u4efb\\u610f\\u306e n, k \\u306b\\u5bfe\\u3057\\u3066 nCk mod p \\u3092\\u8a08\\u7b97\\u3059\\u308b\\u95a2\\u6570\\ndef lucas(n, k, p):\\n if k == 0:\\n return 1\\n ni = n % p\\n ki = k % p\\n return (lucas(n // p, k // p, p) * nCk_mod_p(ni, ki, p)) % p\\n\\n# \\u4e2d\\u56fd\\u5270\\u4f59\\u5b9a\\u7406\\u3092\\u7528\\u3044\\u3066\\u3001mod2 \\u3068 mod5 \\u304b\\u3089 mod10 \\u3092\\u5fa9\\u5143\\u3059\\u308b\\ndef crt(mod2, mod5):\\n # mod2 \\u306f x \\u2261 mod2 (mod 2), mod5 \\u306f x \\u2261 mod5 (mod 5)\\n # mod 10 \\u3067 x \\u306e\\u5019\\u88dc\\u3092 0\\uff5e9 \\u304b\\u3089\\u63a2\\u3059\\n for x in range(10):\\n if x % 2 == mod2 and x % 5 == mod5:\\n return x\\n return None # \\u901a\\u5e38\\u306f\\u5230\\u9054\\u3057\\u306a\\u3044\\n\\n# combination(n, m) mod 10 \\u3092\\u6c42\\u3081\\u308b\\u95a2\\u6570\\ndef combination_mod10(n, m):\\n mod2 = lucas(n, m, 2)\\n mod5 = lucas(n, m, 5)\\n return crt(mod2, mod5) \\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n cs = list(map(int, s))\\n n = len(cs)\\n #print(f'mod2={list(lucas(n - 2, i, 2) for i in range(n - 1))}')\\n #print(f'mod5={list(lucas(n - 2, i, 5) for i in range(n - 1))}')\\n pow_n_1_10 = [combination_mod10(n - 2, i) for i in range(n - 1)]\\n #print(f'cs={cs}, n={n}, pow_n_1_10={pow_n_1_10}')\\n l = sum(pow_n_1_10[i] * cs[i] for i in range(n - 1)) % 10\\n r = sum(pow_n_1_10[i] * cs[i + 1] for i in range(n - 1)) % 10\\n return l == r\"], [7923, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n \\\"\\\"\\\"\\n 1 4 6 4 1 N = 6, (N-2)cK\\n s t u v w 1 3 3 1 \\n a b c d 1 2 1\\n e f g 1 1\\n h i 1\\n\\n a = s+t, b = t+u, c= u+v\\n h = (s+t+t+u) + (t+u+u+v) %10\\n i = (b+c) + (c+d) %10\\n\\n length N\\n N-1 level\\n\\n Base Length = N-1\\n Pascal Triangle\\n 1 N-1, N-1C2... ... N-1, 1\\n\\n N! N! N-k+1\\n -------- = ------------- x -----\\n k!(N-k)! (k-1)!(N-k+1)! k\\n\\n nC0 = 1\\n nC1 = nC0 * n = n\\n nC2 = n * n-1/2...\\n \\\"\\\"\\\"\\n digits = [int(ch) for ch in s]\\n N = len(digits)\\n\\n seq = [1]\\n prev = 1\\n\\n def toDigits(n, b):\\n digits = []\\n while n:\\n digits.append(n % b)\\n n -= digits[-1]\\n n //= b\\n return digits\\n\\n def factorial(n): \\n ans = 1\\n while n:\\n ans *= n\\n n -= 1\\n return ans\\n\\n def nCkModb(n, k, b):\\n nds = toDigits(n, b)\\n kds = toDigits(k, b)\\n\\n ans = 1\\n for nd, kd in zip_longest(nds, kds, fillvalue=0):\\n if nd < kd:\\n return 0\\n \\n ans *= factorial(nd) // factorial(kd) // factorial(nd-kd)\\n return ans % b\\n\\n def nCkMod10(n, k):\\n b2 = nCkModb(n, k, 2)\\n b5 = nCkModb(n, k, 5)\\n\\n for i in range(10):\\n if i%2 == b2 and i%5==b5:\\n return i\\n\\n for k in range(1, N-1):\\n seq.append(nCkMod10(N-2, k))\\n \\n assert len(seq) == N-1\\n assert seq[-1] == 1, seq\\n\\n left = 0\\n for s, v in zip(seq, digits[:-1]):\\n left += (s*v)\\n left %= 10\\n\\n right = 0\\n for s, v in zip(seq, digits[1:]):\\n right += (s*v)\\n right %= 10\\n \\n return left == right\\n\\n\\n\\n\\n \\n\\n\\n\\n\"], [8071, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=0\\n l=1\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(fact,n,p):\\n factinv = [0] * (n + 1)\\n for i in range(0, n+1):\\n factinv[i] = pow(fact[i],p-2,p)\\n return factinv\\n\\n\\n def base(a,p):\\n r=[]\\n x=a\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n #r.reverse()\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n\\n def binomialCoefficientModP(tablep,factp,factinvp,n,p):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n n_bp = base(n,p)\\n x=n%2\\n y=(n-1)%2\\n for k in range(1, n):\\n k_bp = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n m_p = 1\\n for j in range(len_max):\\n if j>=len(n_bp):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,0,k_bp[j],p)]\\n break\\n elif j>=len(k_bp):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],0,p)]\\n break\\n else:\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[x][k] = m_p\\n n_bp = base(n-1,p)\\n for k in range(0, n):\\n k_bp = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n m_p = 1\\n for j in range(len_max):\\n if j>=len(n_bp):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,0,k_bp[j],p)]\\n break\\n elif j>=len(k_bp):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],0,p)]\\n break\\n else:\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[y][k] = m_p\\n dp[x][0] = 1\\n dp[x][n] = 1\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n #x=n%2\\n #for k in range(1, n):\\n # dp[x][k] = remainder[coeffp[x][k]][coeffq[x][k]]\\n y=(n-1)%2\\n for k in range(0, n):\\n dp[y][k] = remainder[coeffp[y][k]][coeffq[y][k]]\\n #dp[x][0] = 1\\n #dp[x][n] = 1\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n def binomialCoefficientMod(n):\\n p=2\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n q=5\\n tableq = [[0 for _ in range(q)] for _ in range(q)]\\n for i in range(q):\\n for j in range(q):\\n tableq[i][j] = (i*j)%q\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factq = binomail_precompute_fact(tableq,n,q)\\n factinvp = binomail_precompute_factinv(factp,n,p)\\n factinvq = binomail_precompute_factinv(factq,n,q)\\n coeffp = binomialCoefficientModP(tablep,factp,factinvp,n,p)\\n coeffq = binomialCoefficientModP(tableq,factq,factinvq,n,q)\\n coeff = binomialCoefficientCombine(coeffp,coeffq,n,p,q)\\n return coeff\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff = binomialCoefficientMod(N-1)\\n\\n sum = [0,0]\\n idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[idx][k]][int(s[j+k])]]\\n\\n return sum[0]==sum[1]\\n\"], [8219, 0.2353, \"#obv solution is too slow\\n#op^2(s)[0] = (s[0] + s[1]) + (s[1] + s[2]) mod 10\\n#op^3(s)[0] = op^2(s)[0] + op^2(s)[1] mod 10 = ((s[0] + s[1]) + (s[1] + s[2])) + ((s[1] + s[2]) + (s[2] + s[3])) mod 10\\n# coeffs 1, 3, 3, 1, idx 3 of pascal\\n# pascal's coeffs too big so compute mod 10\\n# use lucas' theorem and chinese remainder theorem\\n\\n\\n\\nclass Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n \\n def modinv(a, m):\\n # Modular inverse via Extended Euclidean Algorithm\\n g, x, y = extended_gcd(a, m)\\n if g != 1:\\n raise Exception(\\\"modular inverse does not exist\\\")\\n return x % m\\n\\n def extended_gcd(a, b):\\n if b == 0:\\n return a, 1, 0\\n g, x, y = extended_gcd(b, a % b)\\n return g, y, x - (a // b) * y\\n\\n def precompute(m):\\n # Precompute factorials and inverse factorials modulo m\\n fact = [1] * m\\n inv_fact = [1] * m\\n for i in range(1, m):\\n fact[i] = fact[i - 1] * i % m\\n for i in range(1, m):\\n inv_fact[i] = modinv(fact[i], m)\\n return fact, inv_fact\\n\\n def nCk_mod_p(n, k, p, fact, inv_fact):\\n if k > n:\\n return 0\\n return fact[n] * inv_fact[k] % p * inv_fact[n - k] % p\\n\\n def lucas(n, k, p):\\n fact, inv_fact = precompute(p)\\n res = 1\\n while n > 0 or k > 0:\\n ni, ki = n % p, k % p\\n if ki > ni:\\n return 0\\n res = res * nCk_mod_p(ni, ki, p, fact, inv_fact) % p\\n n //= p\\n k //= p\\n return res\\n\\n def crt(a1, m1, a2, m2):\\n # Combine a1 mod m1 and a2 mod m2 using CRT\\n # Solves x \\u2261 a1 (mod m1), x \\u2261 a2 (mod m2)\\n M = m1 * m2\\n m1_inv = modinv(m1, m2)\\n m2_inv = modinv(m2, m1)\\n x = (a1 * m2 * m2_inv + a2 * m1 * m1_inv) % M\\n return x\\n\\n def nCk_mod_10(n, k):\\n a1 = lucas(n, k, 2)\\n a2 = lucas(n, k, 5)\\n return crt(a1, 2, a2, 5)\\n \\n iterations = len(s) - 2\\n coeffs = [nCk_mod_10(iterations, k) for k in range(len(s)-1)]\\n s0, s1 = 0, 0\\n for i in range(len(s)-1):\\n s0 += coeffs[i] * int(s[i])\\n s1 += coeffs[i] * int(s[i+1])\\n s0 %= 10\\n s1 %= 10\\n return s0 == s1\\n\\n\\n\\n\\n\"], [8367, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n # SUM(0,n-2,n-2C_i * a_i) = SUM(0,n-2,N-2C_ia_i+1)\\n coeff, sum_ = 1, 0\\n digits = [int(d) for d in s]\\n n = len(digits)\\n for i in range(1, (n + 1) // 2):\\n sum_ += coeff * (digits[i] + digits[n-i] - digits[i-1] - digits[n-i-1])\\n coeff = (coeff * (n-1-i)) // i\\n \\n if n % 2 == 0:\\n sum_ += coeff * (digits[n // 2] - digits[n // 2 - 1])\\n return sum_ % 10 == 0\\n\"], [8515, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n # SUM(0,n-2,n-2C_i * a_i) = SUM(0,n-2,N-2C_ia_i+1)\\n coeff, sum_ = 1, 0\\n digits = [int(d) for d in s]\\n n = len(digits)\\n for i in range(1, (n + 1) // 2):\\n sum_ += coeff * (digits[i] + digits[n-i] - digits[i-1] - digits[n-i-1])\\n coeff = (coeff * (n-1-i)) // i\\n \\n if n % 2 == 0:\\n sum_ += coeff * (digits[n // 2] - digits[n // 2 - 1])\\n return sum_ % 10 == 0\\n\"], [8663, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n table=[0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8]\\n \\n table2=[[0 for _ in range(10)] for _ in range(10)]\\n for i in range(10):\\n for j in range(10):\\n table2[i][j] = (i*j)%10\\n\\n def binomialCoeff(n):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n k=0\\n l=1\\n for i in range(n + 1):\\n k^=1\\n l^=1\\n for j in range(min(i, n) + 1):\\n if j == 0 or j == i:\\n dp[l][j] = 1\\n else:\\n dp[l][j] = table[dp[k][j-1] + dp[k][j]]\\n return dp\\n \\n def binomail_precompute_fact(tablep,n,p):\\n fact = [1] * (n + 1)\\n for i in range(1, n + 1):\\n fact[i] = tablep[fact[i-1]][i%p]\\n return fact\\n\\n def binomail_precompute_factinv(fact,n,p):\\n factinv = [0] * (n + 1)\\n for i in range(0, n+1):\\n factinv[i] = pow(fact[i],p-2,p)\\n return factinv\\n\\n\\n def base(a,p):\\n r=[]\\n x=a\\n while x > 1:\\n r.append(x%p)\\n x//=p\\n r.append(x)\\n #r.reverse()\\n return r\\n\\n\\n def binomialCoefficient(tablep,fact,factinv,n,k,p):\\n if k>n:\\n return 0\\n return tablep[tablep[fact[n]][factinv[n-k]]][factinv[k]]\\n\\n def binomialCoefficientModP(tablep,factp,factinvp,n,p):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n n_bp = base(n,p)\\n x=n%2\\n y=(n-1)%2\\n for k in range(1, n):\\n k_bp = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n m_p = 1\\n for j in range(len_max):\\n if j>=len(n_bp):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,0,k_bp[j],p)]\\n break\\n elif j>=len(k_bp):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],0,p)]\\n break\\n else:\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[x][k] = m_p\\n n_bp = base(n-1,p)\\n for k in range(0, n):\\n k_bp = base(k,p)\\n len_max = max(len(n_bp),len(k_bp))\\n m_p = 1\\n for j in range(len_max):\\n if j>=len(n_bp):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,0,k_bp[j],p)]\\n break\\n elif j>=len(k_bp):\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],0,p)]\\n break\\n else:\\n m_p = tablep[m_p][binomialCoefficient(tablep,factp,factinvp,n_bp[j],k_bp[j],p)]\\n if m_p == 0:\\n break\\n dp[y][k] = m_p\\n dp[x][0] = 1\\n dp[x][n] = 1\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n\\n # chinese remainder theorem\\n # 0 1 2 3 4 5 6 7 8 9 mod 10\\n # 0 1 0 1 0 1 0 1 0 1 mod 2\\n # 0 1 2 3 4 0 1 2 3 4 mod 5\\n remainder = [[0,6,2,8,4],\\n [5,1,7,3,9]]\\n def binomialCoefficientCombine(coeffp,coeffq,n,p,q):\\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\\n x=n%2\\n for k in range(1, n):\\n dp[x][k] = remainder[coeffp[x][k]][coeffq[x][k]]\\n y=(n-1)%2\\n for k in range(0, n):\\n dp[y][k] = remainder[coeffp[y][k]][coeffq[y][k]]\\n dp[x][0] = 1\\n dp[x][n] = 1\\n dp[y][0] = 1\\n dp[y][n] = 0\\n return dp\\n\\n def binomialCoefficientMod(n):\\n p=2\\n tablep = [[0 for _ in range(p)] for _ in range(p)]\\n for i in range(p):\\n for j in range(p):\\n tablep[i][j] = (i*j)%p\\n q=5\\n tableq = [[0 for _ in range(q)] for _ in range(q)]\\n for i in range(q):\\n for j in range(q):\\n tableq[i][j] = (i*j)%q\\n\\n factp = binomail_precompute_fact(tablep,n,p)\\n factq = binomail_precompute_fact(tableq,n,q)\\n factinvp = binomail_precompute_factinv(factp,n,p)\\n factinvq = binomail_precompute_factinv(factq,n,q)\\n coeffp = binomialCoefficientModP(tablep,factp,factinvp,n,p)\\n coeffq = binomialCoefficientModP(tableq,factq,factinvq,n,q)\\n coeff = binomialCoefficientCombine(coeffp,coeffq,n,p,q)\\n return coeff\\n\\n\\n N = len(s)\\n #coeff = binomialCoeff(N-1)\\n coeff = binomialCoefficientMod(N-1)\\n\\n sum = [0,0]\\n idx=N%2\\n for j in range(0,2):\\n for k in range(N-1):\\n sum[j] = table[sum[j] + table2[coeff[idx][k]][int(s[j+k])]]\\n\\n return sum[0]==sum[1]\\n\"], [8811, 0.2353, \"class Solution:\\n def hasSameDigits(self, s: str) -> bool:\\n n = len(s) - 2\\n first, second = 0, 0\\n c = [1]\\n coeff = 1 \\n\\n for k in range(n + 1):\\n mod_coeff = coeff % 10\\n first = (first + mod_coeff * (ord(s[k]) - ord('0'))) % 10\\n second = (second + mod_coeff * (ord(s[k + 1]) - ord('0'))) % 10\\n\\n if k < n//2 :\\n if coeff % 10000000 == 0:\\n coeff = 0\\n else:\\n coeff = coeff * (n - k) // (k + 1) if k < n else 1 \\n c.append(coeff)\\n else:\\n coeff = c[n - 1 - k]\\n c.append(coeff)\\n\\n\\n # print(c[:15])\\n # print(c[-15:])\\n return first == second\"]]"
},
"ruby": {
"code": "def has_same_digits(s)\n m = s.length\n return s[0] == s[1] if m == 2\n\n k = m - 2\n digits = s.chars.map(&:to_i)\n\n mod5_table = [\n [1, 0, 0, 0, 0],\n [1, 1, 0, 0, 0],\n [1, 2, 1, 0, 0],\n [1, 3, 3, 1, 0],\n [1, 4, 1, 4, 1],\n ]\n\n crt_table = {\n [0, 0] => 0,\n [0, 1] => 6,\n [0, 2] => 2,\n [0, 3] => 8,\n [0, 4] => 4,\n [1, 0] => 5,\n [1, 1] => 1,\n [1, 2] => 7,\n [1, 3] => 3,\n [1, 4] => 9,\n }\n\n sum0 = 0\n sum1 = 0\n\n (0..k).each do |s_val|\n a = (k & s_val) == s_val ? 1 : 0\n\n n_temp = k\n k_temp = s_val\n res = 1\n loop do\n break if n_temp == 0 && k_temp == 0\n\n n_digit = n_temp % 5\n k_digit = k_temp % 5\n\n if k_digit > n_digit\n res = 0\n break\n end\n\n res = (res * mod5_table[n_digit][k_digit]) % 5\n\n n_temp /= 5\n k_temp /= 5\n end\n\n b = res % 5\n mod10 = crt_table[[a, b]]\n\n sum0 += mod10 * digits[s_val]\n sum1 += mod10 * digits[s_val + 1]\n end\n\n sum0 %= 10\n sum1 %= 10\n\n sum0 == sum1\nend",
"memory": 22200,
"memoryDistribution": "[[22200, 100.0, \"def has_same_digits(s)\\n m = s.length\\n return s[0] == s[1] if m == 2\\n\\n k = m - 2\\n digits = s.chars.map(&:to_i)\\n\\n mod5_table = [\\n [1, 0, 0, 0, 0],\\n [1, 1, 0, 0, 0],\\n [1, 2, 1, 0, 0],\\n [1, 3, 3, 1, 0],\\n [1, 4, 1, 4, 1],\\n ]\\n\\n crt_table = {\\n [0, 0] => 0,\\n [0, 1] => 6,\\n [0, 2] => 2,\\n [0, 3] => 8,\\n [0, 4] => 4,\\n [1, 0] => 5,\\n [1, 1] => 1,\\n [1, 2] => 7,\\n [1, 3] => 3,\\n [1, 4] => 9,\\n }\\n\\n sum0 = 0\\n sum1 = 0\\n\\n (0..k).each do |s_val|\\n a = (k & s_val) == s_val ? 1 : 0\\n\\n n_temp = k\\n k_temp = s_val\\n res = 1\\n loop do\\n break if n_temp == 0 && k_temp == 0\\n\\n n_digit = n_temp % 5\\n k_digit = k_temp % 5\\n\\n if k_digit > n_digit\\n res = 0\\n break\\n end\\n\\n res = (res * mod5_table[n_digit][k_digit]) % 5\\n\\n n_temp /= 5\\n k_temp /= 5\\n end\\n\\n b = res % 5\\n mod10 = crt_table[[a, b]]\\n\\n sum0 += mod10 * digits[s_val]\\n sum1 += mod10 * digits[s_val + 1]\\n end\\n\\n sum0 %= 10\\n sum1 %= 10\\n\\n sum0 == sum1\\nend\"], [221800, 50.0, \"def has_same_digits(s)\\n m = s.length\\n return s[0] == s[1] if m == 2\\n\\n k = m - 2\\n digits = s.chars.map(&:to_i)\\n\\n mod5_table = [\\n [1, 0, 0, 0, 0],\\n [1, 1, 0, 0, 0],\\n [1, 2, 1, 0, 0],\\n [1, 3, 3, 1, 0],\\n [1, 4, 1, 4, 1],\\n ]\\n\\n crt_table = {\\n [0, 0] => 0,\\n [0, 1] => 6,\\n [0, 2] => 2,\\n [0, 3] => 8,\\n [0, 4] => 4,\\n [1, 0] => 5,\\n [1, 1] => 1,\\n [1, 2] => 7,\\n [1, 3] => 3,\\n [1, 4] => 9,\\n }\\n\\n sum0 = 0\\n sum1 = 0\\n\\n (0..k).each do |s_val|\\n a = (k & s_val) == s_val ? 1 : 0\\n\\n n_temp = k\\n k_temp = s_val\\n res = 1\\n loop do\\n break if n_temp == 0 && k_temp == 0\\n\\n n_digit = n_temp % 5\\n k_digit = k_temp % 5\\n\\n if k_digit > n_digit\\n res = 0\\n break\\n end\\n\\n res = (res * mod5_table[n_digit][k_digit]) % 5\\n\\n n_temp /= 5\\n k_temp /= 5\\n end\\n\\n b = res % 5\\n mod10 = crt_table[[a, b]]\\n\\n sum0 += mod10 * digits[s_val]\\n sum1 += mod10 * digits[s_val + 1]\\n end\\n\\n sum0 %= 10\\n sum1 %= 10\\n\\n sum0 == sum1\\nend\"], [238200, 50.0, \"# @param {String} s\\n# @return {Boolean}\\ndef has_same_digits(s)\\n len = s.length()\\n med_l = s[0..len-3].chars\\n med_r = s[2..-1].chars\\n n = med_r.length-1\\n n5 = []\\n nsub = n\\n i = 0\\n \\n while(5**i <= n) do\\n n5.append(nsub % 5**(i+1) / 5**i)\\n nsub -= nsub % 5**(i+1)\\n i += 1\\n end\\n\\n s5_l = 0\\n s2_l = 0\\n s5_r = 0\\n s2_r = 0\\n cf = Array.new(5) { Array.new(5)}\\n\\n for o in 0..4\\n for u in 0..4\\n cf[o][u] = coeff(o,u)\\n end\\n end\\n\\n ki5 = [0]*n5.length\\n ki5[0] = -1\\n for k in 0..n\\n ki5[0] += 1\\n ret = ki5[0] / 5\\n ki5[0] = ki5[0] % 5\\n ind = 1\\n while ret > 0\\n ki5[ind] += 1\\n ret = ki5[ind] / 5\\n ki5[ind] = ki5[ind] % 5\\n ind += 1\\n end\\n\\n prod5 = 1\\n for l in 0..n5.length-1 \\n prod5 *= cf[n5[l]][ki5[l].to_i]\\n end\\n\\n s5_l += prod5*med_l[k].to_i\\n s5_r += prod5*med_r[k].to_i\\n\\n end\\n\\n s2_l = med_l.filter_map.with_index { |e,i| e.to_i if (i^n.to_i)&i == 0 }.reduce(:+)\\n s2_r = med_r.filter_map.with_index { |e,i| e.to_i if (i^n.to_i)&i == 0 }.reduce(:+)\\n \\n (s2_l % 2 == s2_r % 2) and (s5_l % 5 == s5_r % 5)\\nend\\n\\ndef coeff(n,k)\\n return 0 if k > n\\n fact(n)/(fact(k)*fact(n-k))\\nend\\n\\ndef fact(n)\\n return 1 if n==0\\n (1..n).reduce(:*)\\nend\"]]",
"runtime": 2459,
"runtimeDistribution": "[[2325, 50.0, \"# @param {String} s\\n# @return {Boolean}\\ndef has_same_digits(s)\\n len = s.length()\\n med_l = s[0..len-3].chars\\n med_r = s[2..-1].chars\\n n = med_r.length-1\\n n5 = []\\n nsub = n\\n i = 0\\n \\n while(5**i <= n) do\\n n5.append(nsub % 5**(i+1) / 5**i)\\n nsub -= nsub % 5**(i+1)\\n i += 1\\n end\\n\\n s5_l = 0\\n s2_l = 0\\n s5_r = 0\\n s2_r = 0\\n cf = Array.new(5) { Array.new(5)}\\n\\n for o in 0..4\\n for u in 0..4\\n cf[o][u] = coeff(o,u)\\n end\\n end\\n\\n ki5 = [0]*n5.length\\n ki5[0] = -1\\n for k in 0..n\\n ki5[0] += 1\\n ret = ki5[0] / 5\\n ki5[0] = ki5[0] % 5\\n ind = 1\\n while ret > 0\\n ki5[ind] += 1\\n ret = ki5[ind] / 5\\n ki5[ind] = ki5[ind] % 5\\n ind += 1\\n end\\n\\n prod5 = 1\\n for l in 0..n5.length-1 \\n prod5 *= cf[n5[l]][ki5[l].to_i]\\n end\\n\\n s5_l += prod5*med_l[k].to_i\\n s5_r += prod5*med_r[k].to_i\\n\\n end\\n\\n s2_l = med_l.filter_map.with_index { |e,i| e.to_i if (i^n.to_i)&i == 0 }.reduce(:+)\\n s2_r = med_r.filter_map.with_index { |e,i| e.to_i if (i^n.to_i)&i == 0 }.reduce(:+)\\n \\n (s2_l % 2 == s2_r % 2) and (s5_l % 5 == s5_r % 5)\\nend\\n\\ndef coeff(n,k)\\n return 0 if k > n\\n fact(n)/(fact(k)*fact(n-k))\\nend\\n\\ndef fact(n)\\n return 1 if n==0\\n (1..n).reduce(:*)\\nend\"], [2459, 50.0, \"def has_same_digits(s)\\n m = s.length\\n return s[0] == s[1] if m == 2\\n\\n k = m - 2\\n digits = s.chars.map(&:to_i)\\n\\n mod5_table = [\\n [1, 0, 0, 0, 0],\\n [1, 1, 0, 0, 0],\\n [1, 2, 1, 0, 0],\\n [1, 3, 3, 1, 0],\\n [1, 4, 1, 4, 1],\\n ]\\n\\n crt_table = {\\n [0, 0] => 0,\\n [0, 1] => 6,\\n [0, 2] => 2,\\n [0, 3] => 8,\\n [0, 4] => 4,\\n [1, 0] => 5,\\n [1, 1] => 1,\\n [1, 2] => 7,\\n [1, 3] => 3,\\n [1, 4] => 9,\\n }\\n\\n sum0 = 0\\n sum1 = 0\\n\\n (0..k).each do |s_val|\\n a = (k & s_val) == s_val ? 1 : 0\\n\\n n_temp = k\\n k_temp = s_val\\n res = 1\\n loop do\\n break if n_temp == 0 && k_temp == 0\\n\\n n_digit = n_temp % 5\\n k_digit = k_temp % 5\\n\\n if k_digit > n_digit\\n res = 0\\n break\\n end\\n\\n res = (res * mod5_table[n_digit][k_digit]) % 5\\n\\n n_temp /= 5\\n k_temp /= 5\\n end\\n\\n b = res % 5\\n mod10 = crt_table[[a, b]]\\n\\n sum0 += mod10 * digits[s_val]\\n sum1 += mod10 * digits[s_val + 1]\\n end\\n\\n sum0 %= 10\\n sum1 %= 10\\n\\n sum0 == sum1\\nend\"], [2462, 50.0, \"def has_same_digits(s)\\n m = s.length\\n return s[0] == s[1] if m == 2\\n\\n k = m - 2\\n digits = s.chars.map(&:to_i)\\n\\n mod5_table = [\\n [1, 0, 0, 0, 0],\\n [1, 1, 0, 0, 0],\\n [1, 2, 1, 0, 0],\\n [1, 3, 3, 1, 0],\\n [1, 4, 1, 4, 1],\\n ]\\n\\n crt_table = {\\n [0, 0] => 0,\\n [0, 1] => 6,\\n [0, 2] => 2,\\n [0, 3] => 8,\\n [0, 4] => 4,\\n [1, 0] => 5,\\n [1, 1] => 1,\\n [1, 2] => 7,\\n [1, 3] => 3,\\n [1, 4] => 9,\\n }\\n\\n sum0 = 0\\n sum1 = 0\\n\\n (0..k).each do |s_val|\\n a = (k & s_val) == s_val ? 1 : 0\\n\\n n_temp = k\\n k_temp = s_val\\n res = 1\\n loop do\\n break if n_temp == 0 && k_temp == 0\\n\\n n_digit = n_temp % 5\\n k_digit = k_temp % 5\\n\\n if k_digit > n_digit\\n res = 0\\n break\\n end\\n\\n res = (res * mod5_table[n_digit][k_digit]) % 5\\n\\n n_temp /= 5\\n k_temp /= 5\\n end\\n\\n b = res % 5\\n mod10 = crt_table[[a, b]]\\n\\n sum0 += mod10 * digits[s_val]\\n sum1 += mod10 * digits[s_val + 1]\\n end\\n\\n sum0 %= 10\\n sum1 %= 10\\n\\n sum0 == sum1\\nend\"]]"
}
}
|
def generate_test_cases(num_cases: int, seed: int = 42) -> list:
import random
random.seed(seed)
# Sample solution adapted from the provided sample solution.
def sample_solution(s: str) -> bool:
n = len(s)
if n == 2:
return s[0] == s[1]
k = n - 2
mod5_table = [
[1, 0, 0, 0, 0],
[1, 1, 0, 0, 0],
[1, 2, 1, 0, 0],
[1, 3, 3, 1, 0],
[1, 4, 1, 4, 1],
]
crt_table = {
(0, 0): 0,
(0, 1): 6,
(0, 2): 2,
(0, 3): 8,
(0, 4): 4,
(1, 0): 5,
(1, 1): 1,
(1, 2): 7,
(1, 3): 3,
(1, 4): 9,
}
def compute_mod5(k_val, i_val):
res = 1
while k_val > 0 or i_val > 0:
dk = k_val % 5
di = i_val % 5
if di > dk:
return 0
res = (res * mod5_table[dk][di]) % 5
k_val //= 5
i_val //= 5
return res
sum1, sum2 = 0, 0
for i in range(k + 1):
a = 1 if (i & k) == i else 0
b = compute_mod5(k, i)
if b == 0:
mod10 = 5 if a else 0
else:
mod10 = crt_table[(a, b)]
sum1 = (sum1 + int(s[i]) * mod10) % 10
sum2 = (sum2 + int(s[i + 1]) * mod10) % 10
return sum1 == sum2
test_cases = []
# Predefined test cases to cover different edge and core cases.
predefined = [
"3902", # Example: 3902 -> 292 -> 11 (true)
"34789", # Example: 34789 -> 7157 -> 862 -> 48 (false)
"123", # 123 -> 35 -> (3 != 5) false
"111", # 111 -> 22 -> true
"909", # 909 -> 99 -> true
"55555", # All same digits, eventually true
"123456", # Typical random case
"987654321", # Reversed digits
"31415926", # Random pattern
]
for s in predefined:
if len(test_cases) >= num_cases:
break
expected = "true" if sample_solution(s) else "false"
test_cases.append({"input": s, "output": expected})
# Generate additional random test cases if needed.
while len(test_cases) < num_cases:
length = random.randint(3, 20)
s = ''.join(random.choice("0123456789") for _ in range(length))
expected = "true" if sample_solution(s) else "false"
test_cases.append({"input": s, "output": expected})
return test_cases
|
def evaluate(expected_output: str, program_output: str) -> bool:
# Use the same simple deserialization: strip whitespace and lower-case.
expected = expected_output.strip().lower()
program = program_output.strip().lower()
return expected == program
|
[{"input": "3902", "output": "true"}, {"input": "34789", "output": "false"}, {"input": "123", "output": "false"}, {"input": "111", "output": "true"}, {"input": "909", "output": "true"}, {"input": "55555", "output": "true"}, {"input": "123456", "output": "false"}, {"input": "987654321", "output": "false"}, {"input": "31415926", "output": "false"}, {"input": "043321", "output": "false"}, {"input": "19600133890838637940", "output": "false"}, {"input": "65423511", "output": "false"}, {"input": "155940781618495", "output": "true"}, {"input": "103413164", "output": "false"}, {"input": "52553419283276483", "output": "true"}, {"input": "0305641395376", "output": "false"}, {"input": "24238849696532871", "output": "false"}, {"input": "1226", "output": "false"}, {"input": "66978", "output": "false"}, {"input": "80184514627", "output": "false"}, {"input": "482", "output": "false"}, {"input": "1489325288095701543", "output": "false"}, {"input": "3911", "output": "true"}, {"input": "182278248963834657", "output": "false"}, {"input": "7133150983930103105", "output": "false"}, {"input": "83473", "output": "false"}, {"input": "29973763116566701065", "output": "false"}, {"input": "333872", "output": "false"}, {"input": "2473178108013267", "output": "true"}, {"input": "360260647468723430", "output": "false"}, {"input": "05009788208121913619", "output": "false"}, {"input": "9909169985", "output": "false"}, {"input": "35346247510", "output": "false"}, {"input": "99118384251354278", "output": "false"}, {"input": "980841241182", "output": "false"}, {"input": "49353487401", "output": "false"}, {"input": "4005242786801128", "output": "false"}, {"input": "5982", "output": "false"}, {"input": "2045053315869232", "output": "false"}, {"input": "60256342", "output": "true"}, {"input": "607337", "output": "false"}, {"input": "43303654145868", "output": "false"}, {"input": "0142940196556", "output": "false"}, {"input": "1693406088356159514", "output": "false"}, {"input": "4656482366299468044", "output": "false"}, {"input": "699577738", "output": "false"}, {"input": "214895134332003791", "output": "false"}, {"input": "69367632016328708", "output": "false"}, {"input": "1727889579", "output": "false"}, {"input": "6872774348734714345", "output": "false"}, {"input": "8122362316658", "output": "true"}, {"input": "60366909670546688", "output": "false"}, {"input": "7346706562", "output": "false"}, {"input": "29806990162720465", "output": "false"}, {"input": "755646417", "output": "false"}, {"input": "805", "output": "false"}, {"input": "1003309232", "output": "false"}, {"input": "193745299124190496", "output": "false"}, {"input": "319314919058651", "output": "false"}, {"input": "5067165726284987769", "output": "false"}, {"input": "53147379965", "output": "true"}, {"input": "752", "output": "false"}, {"input": "354549480831367837", "output": "false"}, {"input": "701436349578856855", "output": "false"}, {"input": "44431351823374989", "output": "false"}, {"input": "134352408240", "output": "false"}, {"input": "8427", "output": "false"}, {"input": "094777", "output": "false"}, {"input": "2047116719022", "output": "false"}, {"input": "131869993867", "output": "false"}, {"input": "49649909133412328", "output": "false"}, {"input": "20679", "output": "false"}, {"input": "403447134936183242", "output": "false"}, {"input": "02499", "output": "false"}, {"input": "717464887719", "output": "false"}, {"input": "6594", "output": "false"}, {"input": "139", "output": "false"}, {"input": "490", "output": "false"}, {"input": "78742967", "output": "false"}, {"input": "75655", "output": "false"}, {"input": "256746", "output": "false"}, {"input": "07154516808760385977", "output": "false"}, {"input": "3482", "output": "false"}, {"input": "771093248086", "output": "false"}, {"input": "31712", "output": "false"}, {"input": "484677378263982146", "output": "false"}, {"input": "8404499727875", "output": "false"}, {"input": "8867533963605", "output": "false"}, {"input": "662702895171870262", "output": "true"}, {"input": "74596", "output": "false"}, {"input": "58657", "output": "false"}, {"input": "09134316117240050455", "output": "false"}, {"input": "2386922219693792", "output": "false"}, {"input": "7474074821", "output": "false"}, {"input": "59464743671369594", "output": "false"}, {"input": "064090974395", "output": "false"}, {"input": "3942104709", "output": "false"}, {"input": "21456232858842", "output": "false"}, {"input": "74517123685", "output": "false"}, {"input": "60481", "output": "false"}]
|
{
"cpp": "==Code Submission==\n\nstring deserialize_stdin(const string &input) {\n // For our problem, the entire input is the string itself.\n return input;\n}\n\nstring serialize_stdout(bool result) {\n return result ? \"true\" : \"false\";\n}\n\nint main(){\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n string line;\n getline(cin, line);\n string s = deserialize_stdin(line);\n Solution sol; // The submitted solution will be injected here.\n bool ans = sol.hasSameDigits(s);\n cout << serialize_stdout(ans);\n return 0;\n}",
"golang": "==Code Submission==\n\nfunc main() {\n reader := bufio.NewReader(os.Stdin)\n line, _ := reader.ReadString('\\n')\n line = strings.TrimSpace(line)\n s := line\n ans := hasSameDigits(s)\n if ans {\n fmt.Print(\"true\")\n } else {\n fmt.Print(\"false\")\n }\n}",
"java": "public class Main {\n private static String deserializeInput(String input) {\n // For our problem, the entire input is the string.\n return input.trim();\n }\n \n private static String serializeOutput(boolean result) {\n return result ? \"true\" : \"false\";\n }\n \n public static void main(String[] args) throws Exception {\n BufferedReader br = new BufferedReader(new InputStreamReader(System.in));\n String inputLine = br.readLine();\n String s = deserializeInput(inputLine);\n Solution sol = new Solution();\n boolean ans = sol.hasSameDigits(s);\n System.out.println(serializeOutput(ans));\n }\n}\n\n==Code Submission==",
"javascript": "==Code Submission==\n\nconst deserialize_stdin = (input) => {\n return input.trim();\n};\n\nconst serialize_stdout = (result) => {\n return result ? \"true\" : \"false\";\n};\n\nlet input = \"\";\nprocess.stdin.resume();\nprocess.stdin.setEncoding('utf8');\nprocess.stdin.on('data', chunk => { input += chunk; });\nprocess.stdin.on('end', () => {\n let s = deserialize_stdin(input);\n let ans = hasSameDigits(s); // The submitted solution will be injected here.\n console.log(serialize_stdout(ans));\n});",
"python3": "==Code Submission==\n\ndef deserialize_stdin(input_str):\n return input_str.strip()\n\ndef serialize_stdout(result):\n return \"true\" if result else \"false\"\n\ninput_str = sys.stdin.read().strip()\ns = deserialize_stdin(input_str)\nsol = Solution() # The submitted solution will be injected here.\nans = sol.hasSameDigits(s)\nsys.stdout.write(serialize_stdout(ans))",
"ruby": "==Code Submission==\n\ninput = gets.strip\ndef deserialize_stdin(input)\n input.strip\nend\n\ndef serialize_stdout(result)\n result ? \"true\" : \"false\"\nend\n\ns = deserialize_stdin(input)\nans = has_same_digits(s) # The submitted solution will be injected here.\nputs serialize_stdout(ans)"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.