problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let $a_{i j}, i=1,2, \ldots, m$ and $j=1,2, \ldots, n$, be positive real numbers. Prove that
$$
\sum_{i=1}^{m}\left(\sum_{j=1}^{n} \frac{1}{a_{i j}}\right)^{-1} \leq\left(\sum_{j=1}^{n}\left(\sum_{i=1}^{m} a_{i j}\right)^{-1}\right)^{-1} .
$$
When does the equality hold?
|
We will use the following
Lemma. If $a_{1}, a_{2}, \ldots, a_{n}, b_{1}, b_{2}, \ldots, b_{n}$ are positive real numbers then
$$
\frac{1}{\sum_{j=1}^{n} \frac{1}{a_{j}}}+\frac{1}{\sum_{j=1}^{n} \frac{1}{b_{j}}} \leq \frac{1}{\sum_{j=1}^{n} \frac{1}{a_{j}+b_{j}}}
$$
The equality holds when $\frac{a_{1}}{b_{1}}=\frac{a_{2}}{b_{2}}=\ldots=\frac{a_{n}}{b_{n}}$.
Proof. Set $x_{j}=\frac{1}{a_{j}}$ and $y_{j}=\frac{1}{b_{j}}$ for each $j=1,2, \ldots, n$. Then we have to prove that
$$
\frac{1}{\sum_{j=1}^{n} x_{j}}+\frac{1}{\sum_{j=1}^{n} y_{j}} \leq \frac{1}{\sum_{j=1}^{n} \frac{x_{j} y_{j}}{x_{j}+y_{j}}} \quad \text { or } \quad \sum_{j=1}^{n} \frac{x_{j} y_{j}}{x_{j}+y_{j}} \leq \frac{\left(\sum_{j=1}^{n} x_{j}\right)\left(\sum_{j=1}^{n} y_{j}\right)}{\sum_{j=1}^{n} x_{j}+\sum_{j=1}^{n} y_{j}}
$$
Subtract $\sum_{j=1}^{n} x_{j}$, and we have to prove that
$$
\sum_{j=1}^{n}\left(x_{j}-\frac{x_{j} y_{j}}{x_{j}+y_{j}}\right) \geq \sum_{j=1}^{n} x_{j}-\frac{\left(\sum_{j=1}^{n} x_{j}\right)\left(\sum_{j=1}^{n} y_{j}\right)}{\sum_{j=1}^{n} x_{j}+\sum_{j=1}^{n} y_{j}}
$$
or
$$
\sum_{j=1}^{n}\left(\frac{x_{j}^{2}}{x_{j}+y_{j}}\right) \geq \frac{\left(\sum_{j=1}^{n} x_{j}\right)^{2}}{\sum_{j=1}^{n} x_{j}+\sum_{j=1}^{n} y_{j}}
$$
The last one is a consequence of Cauchy-Schwarz inequality and thus the lemma is proved.
We will now prove that repeating the lemma we will get the desired inequality. For example, if $a_{1}, a_{2}, \ldots, a_{n}, b_{1}, b_{2}, \ldots, b_{n}, c_{1}, c_{2}, \ldots, c_{n}$ are positive reals then by repeating lemma two times we get
$$
\frac{1}{\sum_{j=1}^{n} \frac{1}{a_{j}}}+\frac{1}{\sum_{j=1}^{n} \frac{1}{b_{j}}}+\frac{1}{\sum_{j=1}^{n} \frac{1}{c_{j}}} \leq \frac{1}{\sum_{j=1}^{n} \frac{1}{a_{j}+b_{j}}}+\frac{1}{\sum_{j=1}^{n} \frac{1}{c_{j}}} \leq \frac{1}{\sum_{j=1}^{n} \frac{1}{\left(a_{j}+b_{j}\right)+c_{j}}}=\frac{1}{\sum_{j=1}^{n} \frac{1}{a_{j}+b_{j}+c_{j}}}
$$
Using similar reasoning we can prove by induction that
$$
\sum_{i=1}^{m}\left(\sum_{j=1}^{n} \frac{1}{a_{i j}}\right)^{-1}=\sum_{i=1}^{m} \frac{1}{\sum_{j=1}^{n} \frac{1}{a_{i j}}} \leq \frac{1}{\sum_{j=1}^{n} \frac{1}{\sum_{i=1}^{m} a_{i j}}}=\left(\sum_{j=1}^{n}\left(\sum_{i=1}^{m} a_{i j}\right)^{-1}\right)^{-1}
$$
which is the desired result.
The equality holds iff
$$
\frac{a_{i 1}}{a_{11}}=\frac{a_{i 2}}{a_{12}}=\ldots=\frac{a_{i n}}{a_{1 n}}
$$
for all $i=1,2, \ldots, m$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{i j}, i=1,2, \ldots, m$ and $j=1,2, \ldots, n$, be positive real numbers. Prove that
$$
\sum_{i=1}^{m}\left(\sum_{j=1}^{n} \frac{1}{a_{i j}}\right)^{-1} \leq\left(\sum_{j=1}^{n}\left(\sum_{i=1}^{m} a_{i j}\right)^{-1}\right)^{-1} .
$$
When does the equality hold?
|
We will use the following
Lemma. If $a_{1}, a_{2}, \ldots, a_{n}, b_{1}, b_{2}, \ldots, b_{n}$ are positive real numbers then
$$
\frac{1}{\sum_{j=1}^{n} \frac{1}{a_{j}}}+\frac{1}{\sum_{j=1}^{n} \frac{1}{b_{j}}} \leq \frac{1}{\sum_{j=1}^{n} \frac{1}{a_{j}+b_{j}}}
$$
The equality holds when $\frac{a_{1}}{b_{1}}=\frac{a_{2}}{b_{2}}=\ldots=\frac{a_{n}}{b_{n}}$.
Proof. Set $x_{j}=\frac{1}{a_{j}}$ and $y_{j}=\frac{1}{b_{j}}$ for each $j=1,2, \ldots, n$. Then we have to prove that
$$
\frac{1}{\sum_{j=1}^{n} x_{j}}+\frac{1}{\sum_{j=1}^{n} y_{j}} \leq \frac{1}{\sum_{j=1}^{n} \frac{x_{j} y_{j}}{x_{j}+y_{j}}} \quad \text { or } \quad \sum_{j=1}^{n} \frac{x_{j} y_{j}}{x_{j}+y_{j}} \leq \frac{\left(\sum_{j=1}^{n} x_{j}\right)\left(\sum_{j=1}^{n} y_{j}\right)}{\sum_{j=1}^{n} x_{j}+\sum_{j=1}^{n} y_{j}}
$$
Subtract $\sum_{j=1}^{n} x_{j}$, and we have to prove that
$$
\sum_{j=1}^{n}\left(x_{j}-\frac{x_{j} y_{j}}{x_{j}+y_{j}}\right) \geq \sum_{j=1}^{n} x_{j}-\frac{\left(\sum_{j=1}^{n} x_{j}\right)\left(\sum_{j=1}^{n} y_{j}\right)}{\sum_{j=1}^{n} x_{j}+\sum_{j=1}^{n} y_{j}}
$$
or
$$
\sum_{j=1}^{n}\left(\frac{x_{j}^{2}}{x_{j}+y_{j}}\right) \geq \frac{\left(\sum_{j=1}^{n} x_{j}\right)^{2}}{\sum_{j=1}^{n} x_{j}+\sum_{j=1}^{n} y_{j}}
$$
The last one is a consequence of Cauchy-Schwarz inequality and thus the lemma is proved.
We will now prove that repeating the lemma we will get the desired inequality. For example, if $a_{1}, a_{2}, \ldots, a_{n}, b_{1}, b_{2}, \ldots, b_{n}, c_{1}, c_{2}, \ldots, c_{n}$ are positive reals then by repeating lemma two times we get
$$
\frac{1}{\sum_{j=1}^{n} \frac{1}{a_{j}}}+\frac{1}{\sum_{j=1}^{n} \frac{1}{b_{j}}}+\frac{1}{\sum_{j=1}^{n} \frac{1}{c_{j}}} \leq \frac{1}{\sum_{j=1}^{n} \frac{1}{a_{j}+b_{j}}}+\frac{1}{\sum_{j=1}^{n} \frac{1}{c_{j}}} \leq \frac{1}{\sum_{j=1}^{n} \frac{1}{\left(a_{j}+b_{j}\right)+c_{j}}}=\frac{1}{\sum_{j=1}^{n} \frac{1}{a_{j}+b_{j}+c_{j}}}
$$
Using similar reasoning we can prove by induction that
$$
\sum_{i=1}^{m}\left(\sum_{j=1}^{n} \frac{1}{a_{i j}}\right)^{-1}=\sum_{i=1}^{m} \frac{1}{\sum_{j=1}^{n} \frac{1}{a_{i j}}} \leq \frac{1}{\sum_{j=1}^{n} \frac{1}{\sum_{i=1}^{m} a_{i j}}}=\left(\sum_{j=1}^{n}\left(\sum_{i=1}^{m} a_{i j}\right)^{-1}\right)^{-1}
$$
which is the desired result.
The equality holds iff
$$
\frac{a_{i 1}}{a_{11}}=\frac{a_{i 2}}{a_{12}}=\ldots=\frac{a_{i n}}{a_{1 n}}
$$
for all $i=1,2, \ldots, m$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2019_bmo_shortlist.jsonl",
"problem_match": "\nA4.",
"solution_match": "\nSolution."
}
|
e5eb2fdf-21b3-5fb2-ab76-e6bf0373514f
| 605,854
|
Let $a, b, c$ be positive real numbers, such that $(a b)^{2}+(b c)^{2}+(c a)^{2}=3$. Prove that
$$
\left(a^{2}-a+1\right)\left(b^{2}-b+1\right)\left(c^{2}-c+1\right) \geq 1 .
$$
|
The inequality is equivalent with
$$
\left(a^{2}-a+1\right)\left(b^{2}-b+1\right)\left(c^{2}-c+1\right) \geq 1 \Leftrightarrow\left(a^{3}+1\right)\left(b^{3}+1\right)\left(c^{3}+1\right) \geq(a+1)(b+1)(c+1) .
$$
Thus:
$$
\begin{gathered}
\prod_{c y c}\left(a^{3}+1\right)-\prod_{c y c}(a+1)=\sum_{c y c} a^{3}+\sum_{c y c}(a b)^{3}+(a b c)^{3}-\sum_{c y c} a-\sum_{c y c} a b-a b c= \\
\sum_{c y c}\left(a^{3}+a\right)+\sum_{c y c}\left(a^{3} b^{3}+a b\right)+\left[(a b c)^{3}+1+1\right]-2 \sum_{c y c} a-2 \sum_{c y c} a b-a b c-2^{A M \geq G M} \geq^{\sum_{c y c} a^{2} b^{2}=3} \\
2 \sum_{c y c} a^{2}+2 \sum_{c y c} a^{2} b^{2}+2 a b c-2 \sum_{c y c} a-2 \sum_{c y c} a b-2^{c y c}= \\
\sum_{c y c}\left(a^{2}-2 a+1\right)+\left(\sum_{c y c} a^{2}+2 a b c+1-2 \sum_{c y c} a b\right)= \\
\sum_{c y c}(a-1)^{2}+\left(\sum_{c y c} a^{2}+2 a b c+1-2 \sum_{c y c} a b\right) \geq\left(\sum_{c y c} a^{2}+2 a b c+1-2 \sum_{c y c} a b\right) .
\end{gathered}
$$
We will show that $\sum_{c y c} a^{2}+2 a b c+1-2 \sum_{c y c} a b \geq 0 \quad$ (1) for every $a, b, c \geq 0$.
Firstly, let us observe that
$$
(1+2 a b c)(a+b+c)=(1+a b c+a b c)(a+b+c) \geq 9 \sqrt[3]{a^{2} b^{2} c^{2} a b c}=9 a b c
$$
implying
$$
1+2 a b c \geq \frac{9 a b c}{a+b+c}
$$
Then, using Schur's Inequality, (i.e. $\sum_{c y c} a(a-b)(a-c) \geq 0$, for any $a, b, c \geq 0$ ) we obtain that
$$
\sum_{c y c} a^{2} \geq 2 \sum_{c y c} a b-\frac{9 a b c}{a+b+c}
$$
Returning to (1), we get:
$$
\begin{gathered}
\sum_{c y c} a^{2}+2 a b c+1-2 \sum_{c y c} a b \geq\left(2 \sum_{c y c} a b-\frac{9 a b c}{a+b+c}\right)+2 a b c+1-2 \sum_{c y c} a b= \\
(1+2 a b c)-\frac{9 a b c}{a+b+c} \geq 0
\end{gathered}
$$
which gives us $\prod_{\text {cyc }}\left(a^{3}+1\right)-\prod_{c y c}(a+1) \geq 0$ and, respectively, $\prod_{\text {cyc }}\left(a^{2}-a+1\right) \geq 1$.
## GEOMETRY
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers, such that $(a b)^{2}+(b c)^{2}+(c a)^{2}=3$. Prove that
$$
\left(a^{2}-a+1\right)\left(b^{2}-b+1\right)\left(c^{2}-c+1\right) \geq 1 .
$$
|
The inequality is equivalent with
$$
\left(a^{2}-a+1\right)\left(b^{2}-b+1\right)\left(c^{2}-c+1\right) \geq 1 \Leftrightarrow\left(a^{3}+1\right)\left(b^{3}+1\right)\left(c^{3}+1\right) \geq(a+1)(b+1)(c+1) .
$$
Thus:
$$
\begin{gathered}
\prod_{c y c}\left(a^{3}+1\right)-\prod_{c y c}(a+1)=\sum_{c y c} a^{3}+\sum_{c y c}(a b)^{3}+(a b c)^{3}-\sum_{c y c} a-\sum_{c y c} a b-a b c= \\
\sum_{c y c}\left(a^{3}+a\right)+\sum_{c y c}\left(a^{3} b^{3}+a b\right)+\left[(a b c)^{3}+1+1\right]-2 \sum_{c y c} a-2 \sum_{c y c} a b-a b c-2^{A M \geq G M} \geq^{\sum_{c y c} a^{2} b^{2}=3} \\
2 \sum_{c y c} a^{2}+2 \sum_{c y c} a^{2} b^{2}+2 a b c-2 \sum_{c y c} a-2 \sum_{c y c} a b-2^{c y c}= \\
\sum_{c y c}\left(a^{2}-2 a+1\right)+\left(\sum_{c y c} a^{2}+2 a b c+1-2 \sum_{c y c} a b\right)= \\
\sum_{c y c}(a-1)^{2}+\left(\sum_{c y c} a^{2}+2 a b c+1-2 \sum_{c y c} a b\right) \geq\left(\sum_{c y c} a^{2}+2 a b c+1-2 \sum_{c y c} a b\right) .
\end{gathered}
$$
We will show that $\sum_{c y c} a^{2}+2 a b c+1-2 \sum_{c y c} a b \geq 0 \quad$ (1) for every $a, b, c \geq 0$.
Firstly, let us observe that
$$
(1+2 a b c)(a+b+c)=(1+a b c+a b c)(a+b+c) \geq 9 \sqrt[3]{a^{2} b^{2} c^{2} a b c}=9 a b c
$$
implying
$$
1+2 a b c \geq \frac{9 a b c}{a+b+c}
$$
Then, using Schur's Inequality, (i.e. $\sum_{c y c} a(a-b)(a-c) \geq 0$, for any $a, b, c \geq 0$ ) we obtain that
$$
\sum_{c y c} a^{2} \geq 2 \sum_{c y c} a b-\frac{9 a b c}{a+b+c}
$$
Returning to (1), we get:
$$
\begin{gathered}
\sum_{c y c} a^{2}+2 a b c+1-2 \sum_{c y c} a b \geq\left(2 \sum_{c y c} a b-\frac{9 a b c}{a+b+c}\right)+2 a b c+1-2 \sum_{c y c} a b= \\
(1+2 a b c)-\frac{9 a b c}{a+b+c} \geq 0
\end{gathered}
$$
which gives us $\prod_{\text {cyc }}\left(a^{3}+1\right)-\prod_{c y c}(a+1) \geq 0$ and, respectively, $\prod_{\text {cyc }}\left(a^{2}-a+1\right) \geq 1$.
## GEOMETRY
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2019_bmo_shortlist.jsonl",
"problem_match": "\nA5.",
"solution_match": "\nSolution."
}
|
7ea726a6-17db-541e-9734-5667d9bb1015
| 605,868
|
Let $A B C D$ be a square of center $O$ and let $M$ be the symmetric of the point $B$ with respect to the point $A$. Let $E$ be the intersection of $C M$ and $B D$, and let $S$ be the intersection of $M O$ and $A E$. Show that $S O$ is the angle bisector of $\angle E S B$.
|
We have
$$
\left\{\begin{array}{l}
D C \equiv D A \\
\angle E D C \equiv \angle E D A \quad \Rightarrow \triangle D E C \equiv \triangle D E A \Rightarrow \angle D A E \equiv \angle D C E(*) . \\
D E \equiv D E
\end{array}\right.
$$
Let $C M \cap A D=\{P\}$, then follows $\triangle C D P \equiv \triangle B A P$ and $\angle P C D \equiv \angle P B A(* *)$.
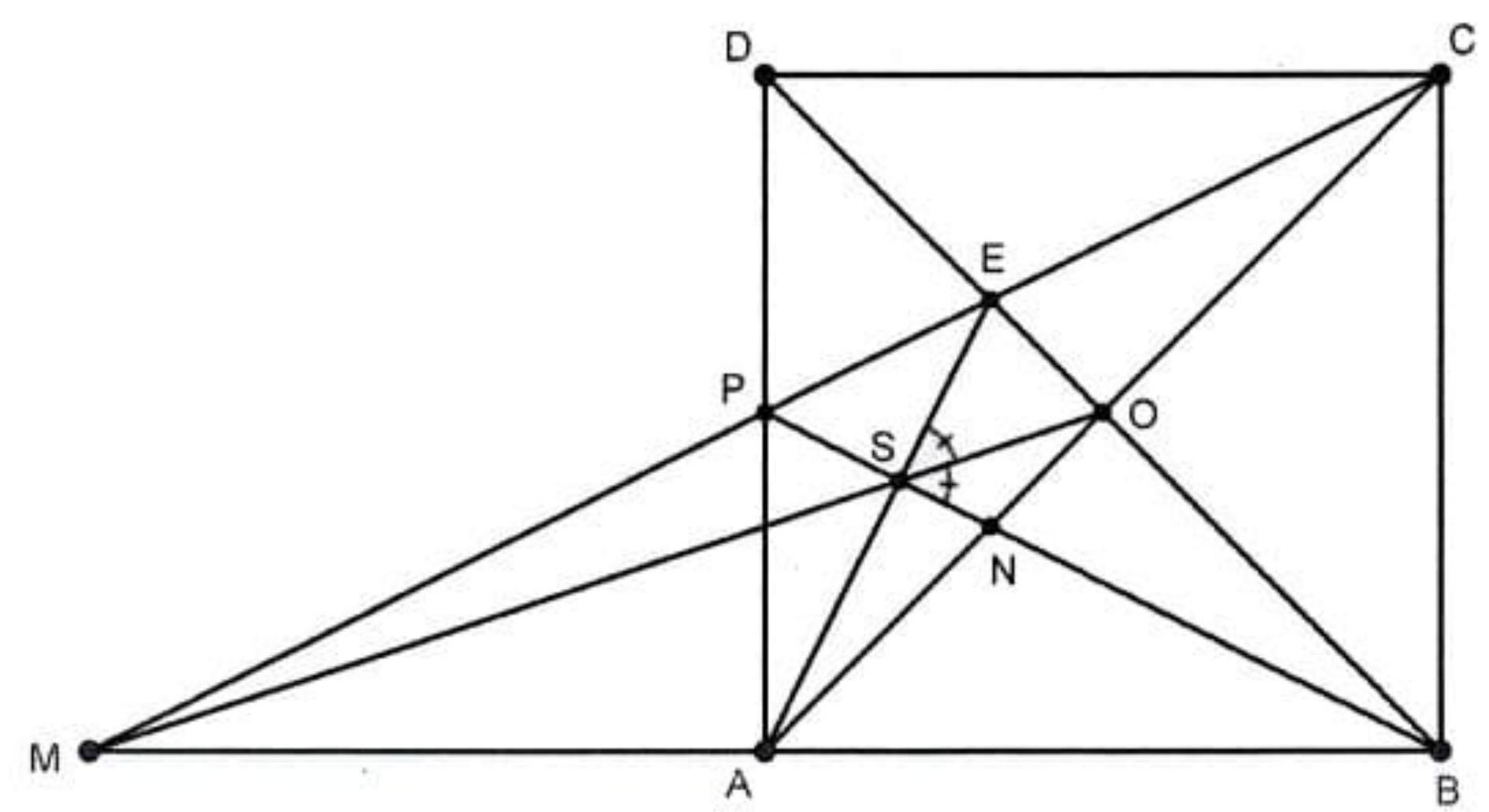
Figure 1: G1
From (*) and (**) follows $\angle D C P \equiv \angle D A E \equiv \angle P B A$.
Now, let $S^{\prime}=A E \cap P B$.
In the triangle $S^{\prime} A B$ we have
$$
m\left(\angle S^{\prime} A B\right)+m\left(\angle S^{\prime} B A\right)=m\left(\angle S^{\prime} A B\right)+m\left(\angle P A S^{\prime}\right)=m(\angle P A B)=90^{\circ},
$$
so $m\left(\angle B S^{\prime} A\right)=90^{\circ}$.
We show that $A E, B P$ and $M O$ are concurrent.
In the triangle $\triangle E M B$ we apply the Ceva theorem, so
$$
\frac{E P}{P M} \cdot \frac{M A}{A B} \cdot \frac{B O}{O E}=1 \Leftrightarrow \frac{E P}{P M}=\frac{O E}{B O}
$$
is true because $P O$ is a midsegment in the triangle $D A B(P O \| A B)$.
According to the Thales theorem in the triangle $E M B, \frac{E P}{P M}=\frac{E O}{O B}$ and $A E, B P$, $M O$ are concurrent in $S^{\prime}$, which is in fact $S$.
Let $P B \cap C A=\{N\}$. Because ESNO has $m(\angle E O N)+m(\angle E S N)=180^{\circ}$, it follows $E S N O$ cyclic and $m(\angle E S O)=m(\angle E N O)=m(\angle D A O)=45^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a square of center $O$ and let $M$ be the symmetric of the point $B$ with respect to the point $A$. Let $E$ be the intersection of $C M$ and $B D$, and let $S$ be the intersection of $M O$ and $A E$. Show that $S O$ is the angle bisector of $\angle E S B$.
|
We have
$$
\left\{\begin{array}{l}
D C \equiv D A \\
\angle E D C \equiv \angle E D A \quad \Rightarrow \triangle D E C \equiv \triangle D E A \Rightarrow \angle D A E \equiv \angle D C E(*) . \\
D E \equiv D E
\end{array}\right.
$$
Let $C M \cap A D=\{P\}$, then follows $\triangle C D P \equiv \triangle B A P$ and $\angle P C D \equiv \angle P B A(* *)$.

Figure 1: G1
From (*) and (**) follows $\angle D C P \equiv \angle D A E \equiv \angle P B A$.
Now, let $S^{\prime}=A E \cap P B$.
In the triangle $S^{\prime} A B$ we have
$$
m\left(\angle S^{\prime} A B\right)+m\left(\angle S^{\prime} B A\right)=m\left(\angle S^{\prime} A B\right)+m\left(\angle P A S^{\prime}\right)=m(\angle P A B)=90^{\circ},
$$
so $m\left(\angle B S^{\prime} A\right)=90^{\circ}$.
We show that $A E, B P$ and $M O$ are concurrent.
In the triangle $\triangle E M B$ we apply the Ceva theorem, so
$$
\frac{E P}{P M} \cdot \frac{M A}{A B} \cdot \frac{B O}{O E}=1 \Leftrightarrow \frac{E P}{P M}=\frac{O E}{B O}
$$
is true because $P O$ is a midsegment in the triangle $D A B(P O \| A B)$.
According to the Thales theorem in the triangle $E M B, \frac{E P}{P M}=\frac{E O}{O B}$ and $A E, B P$, $M O$ are concurrent in $S^{\prime}$, which is in fact $S$.
Let $P B \cap C A=\{N\}$. Because ESNO has $m(\angle E O N)+m(\angle E S N)=180^{\circ}$, it follows $E S N O$ cyclic and $m(\angle E S O)=m(\angle E N O)=m(\angle D A O)=45^{\circ}$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2019_bmo_shortlist.jsonl",
"problem_match": "\nG1.",
"solution_match": "\nSolution."
}
|
a6d394a0-ba81-5e3a-8718-66c53e035a8c
| 605,876
|
Let be a triangle $\triangle A B C$ with $m(\angle A B C)=75^{\circ}$ and $m(\angle A C B)=45^{\circ}$. The angle bisector of $\angle C A B$ intersects $C B$ at the point $D$. We consider the point $E \in(A B)$, such that $D E=D C$. Let $P$ be the intersection of the lines $A D$ and $C E$. Prove that $P$ is the midpoint of the segment $A D$.
|
Let $P^{\prime}$ be the midpoint of the segment $A D$. We will prove that $P^{\prime}=P$. Let $F \in A C$ such that $D F \perp A C$. The triangle $C D F$ is isosceles with $F D=F C$ and the triangle $D P^{\prime} F$ is equilateral as $m(\angle A D F)=60^{\circ}$. Thus, the triangle $F C P^{\prime}$ is isosceles $\left(F P^{\prime}=F C\right)$ and $m\left(\angle F C P^{\prime}\right)=m\left(\angle F P^{\prime} C\right)=15^{\circ}$.
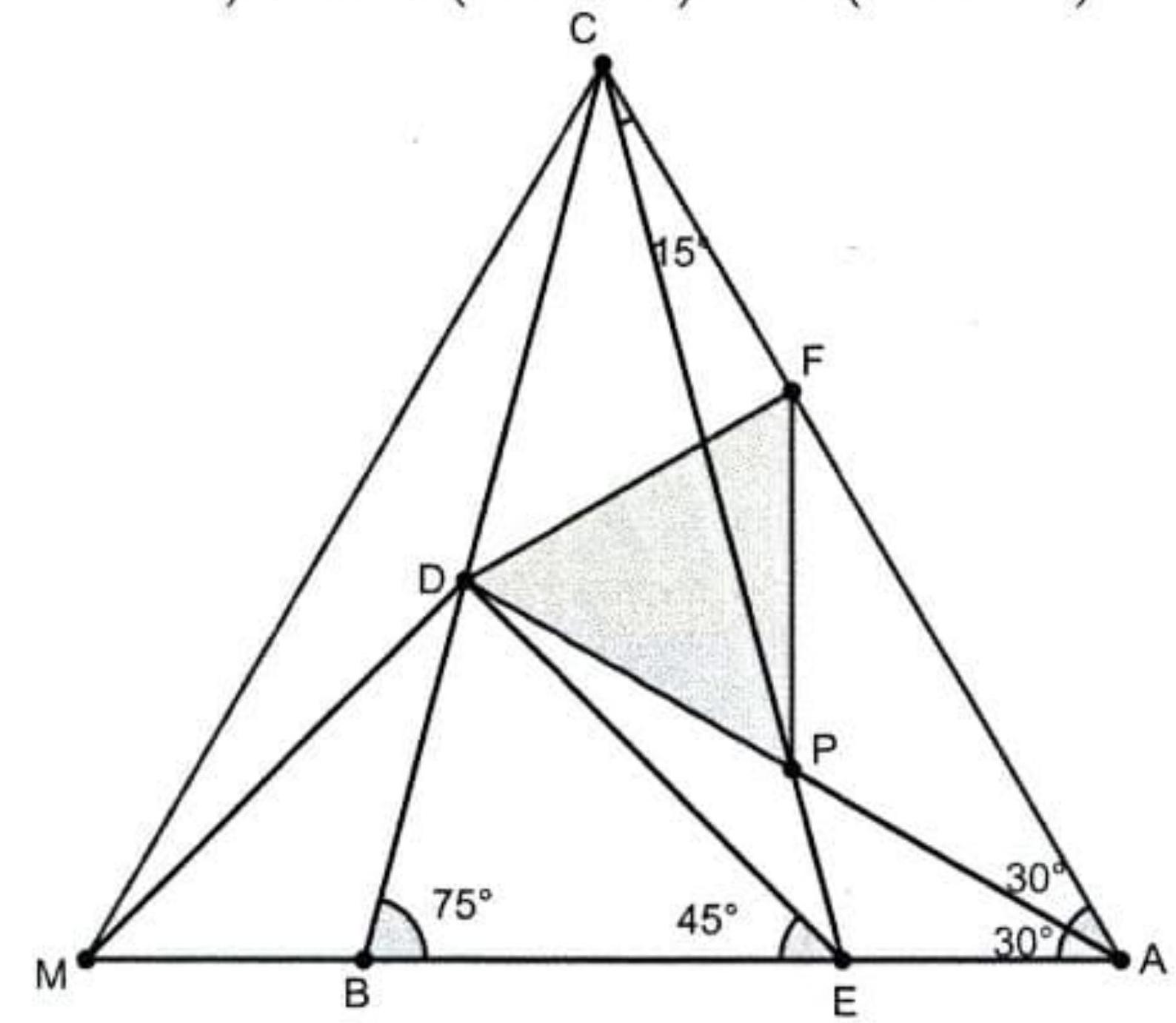
Figure 2: G2
We prove now that $m(\angle F C E)=15^{\circ}$.
Let $M$ be the point on $[A B$ such that the triangle $A C M$ is equilateral. As $\triangle A D C \equiv$ $\triangle A D M(S A S) \Rightarrow D C=D M(=D E)$ and $m(\angle A M D)=m(\angle A C D)=45^{\circ}$. It follows that the triangle $\triangle D M E$ is isosceles with $m(\angle D M E)=m(\angle D E M)=45^{\circ}$. In the triangle $\triangle B D E$ we have $m(\angle B D E)=60^{\circ}$ and thus $m(\angle C D E)=120^{\circ}$.As the triangle $D C E$ is isoscel with $m(\angle D C E)=m(\angle D E C)=30^{\circ}$. Finaly $m(\angle A C E)=m(\angle A C B)-$ $m(\angle B C E)=45^{\circ}-30^{\circ}=15^{\circ}$.
Thus $m\left(\angle F C P^{\prime}\right)=15^{\circ}=m(\angle F C E)$, and therefore $P^{\prime} \in C E$ and $P^{\prime}=P$, which means that $P$ is the midpoint of the segment $A D$.
Alternative solution: In the way as above we prove that $m(\angle B C E)=15^{\circ}$.
So the quadrilateral $A C D E$ is inscribed in a circle. Now, applying the sine rules to $\triangle D P E$ and $\triangle A P E$ we get
$$
\begin{gathered}
\frac{D P}{\sin 30^{\circ}}=\frac{P E}{\sin 15^{\circ}}, \quad \frac{A P}{\sin 105^{\circ}}=\frac{P E}{\sin 30^{\circ}} \Rightarrow \frac{D P}{\sin 30^{\circ}} \cdot \frac{\sin 105^{\circ}}{A P}=\frac{P E}{\sin 15^{\circ}} \cdot \frac{\sin 30^{\circ}}{P E}, \\
\frac{D P}{A P}=\frac{1}{\sin 30^{\circ}} 105^{\circ} \cdot \sin 15^{\circ} \\
=\frac{1}{4 \cdot \sin 105^{\circ} \cdot \sin 15^{\circ}}=\frac{1}{2 \cdot\left(\cos 90^{\circ}-\cos 120^{\circ}\right)}=\frac{1}{2 \cdot \frac{1}{2}}=1 .
\end{gathered}
$$
Thus, $Q P=A P$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let be a triangle $\triangle A B C$ with $m(\angle A B C)=75^{\circ}$ and $m(\angle A C B)=45^{\circ}$. The angle bisector of $\angle C A B$ intersects $C B$ at the point $D$. We consider the point $E \in(A B)$, such that $D E=D C$. Let $P$ be the intersection of the lines $A D$ and $C E$. Prove that $P$ is the midpoint of the segment $A D$.
|
Let $P^{\prime}$ be the midpoint of the segment $A D$. We will prove that $P^{\prime}=P$. Let $F \in A C$ such that $D F \perp A C$. The triangle $C D F$ is isosceles with $F D=F C$ and the triangle $D P^{\prime} F$ is equilateral as $m(\angle A D F)=60^{\circ}$. Thus, the triangle $F C P^{\prime}$ is isosceles $\left(F P^{\prime}=F C\right)$ and $m\left(\angle F C P^{\prime}\right)=m\left(\angle F P^{\prime} C\right)=15^{\circ}$.

Figure 2: G2
We prove now that $m(\angle F C E)=15^{\circ}$.
Let $M$ be the point on $[A B$ such that the triangle $A C M$ is equilateral. As $\triangle A D C \equiv$ $\triangle A D M(S A S) \Rightarrow D C=D M(=D E)$ and $m(\angle A M D)=m(\angle A C D)=45^{\circ}$. It follows that the triangle $\triangle D M E$ is isosceles with $m(\angle D M E)=m(\angle D E M)=45^{\circ}$. In the triangle $\triangle B D E$ we have $m(\angle B D E)=60^{\circ}$ and thus $m(\angle C D E)=120^{\circ}$.As the triangle $D C E$ is isoscel with $m(\angle D C E)=m(\angle D E C)=30^{\circ}$. Finaly $m(\angle A C E)=m(\angle A C B)-$ $m(\angle B C E)=45^{\circ}-30^{\circ}=15^{\circ}$.
Thus $m\left(\angle F C P^{\prime}\right)=15^{\circ}=m(\angle F C E)$, and therefore $P^{\prime} \in C E$ and $P^{\prime}=P$, which means that $P$ is the midpoint of the segment $A D$.
Alternative solution: In the way as above we prove that $m(\angle B C E)=15^{\circ}$.
So the quadrilateral $A C D E$ is inscribed in a circle. Now, applying the sine rules to $\triangle D P E$ and $\triangle A P E$ we get
$$
\begin{gathered}
\frac{D P}{\sin 30^{\circ}}=\frac{P E}{\sin 15^{\circ}}, \quad \frac{A P}{\sin 105^{\circ}}=\frac{P E}{\sin 30^{\circ}} \Rightarrow \frac{D P}{\sin 30^{\circ}} \cdot \frac{\sin 105^{\circ}}{A P}=\frac{P E}{\sin 15^{\circ}} \cdot \frac{\sin 30^{\circ}}{P E}, \\
\frac{D P}{A P}=\frac{1}{\sin 30^{\circ}} 105^{\circ} \cdot \sin 15^{\circ} \\
=\frac{1}{4 \cdot \sin 105^{\circ} \cdot \sin 15^{\circ}}=\frac{1}{2 \cdot\left(\cos 90^{\circ}-\cos 120^{\circ}\right)}=\frac{1}{2 \cdot \frac{1}{2}}=1 .
\end{gathered}
$$
Thus, $Q P=A P$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2019_bmo_shortlist.jsonl",
"problem_match": "\nG2.",
"solution_match": "\nSolution."
}
|
6d618284-fecc-50cd-b819-0863b5f55635
| 605,887
|
Let $A B C$ be a scalene and acute triangle, with circumcentre $O$. Let $\omega$ be the circle with centre $A$, tangent to $B C$ at $D$. Suppose there are two points $F$ and $G$ on $\omega$ such that $F G \perp A O, \angle B F D=\angle D G C$ and the couples of points $(B, F)$ and $(C, G)$ are in different halfplanes with respect to the line $A D$. Show that the tangents to $\omega$ at $F$ and $G$ meet on the circumcircle of $A B C$.
|
Consider any two points $F, G$ on $\omega$ such that $\angle B F D=\angle D G C$. Exploiting the isosceles triangles $\triangle A F G, \triangle A F D$, and $\triangle A D G$, we deduce (using directed angles throughout):
$$
\begin{gathered}
\angle D B F-\angle G C D=180^{\circ}-\angle B F D-\angle B D F-\left(180^{\circ}-\angle D G C-\angle C D G\right) \stackrel{(*)}{=} \\
\angle C D G-\angle F D B=\frac{1}{2} \cdot(\angle D A G-\angle D A F)=\frac{1}{2} \cdot\left[\left(180^{\circ}-2 \cdot \angle A D G\right)-\left(180^{\circ}-2 \cdot \angle A D F\right)\right]= \\
\angle A D F-\angle G D A=\angle D F A-\angle A G D=\angle D F G-\angle F G D \stackrel{(*)}{=} \angle B F G-\angle F G C,
\end{gathered}
$$
where we use $\angle B F D=\angle D G C$ at $\left(^{*}\right)$. Thus $B F G C$ is cyclic.
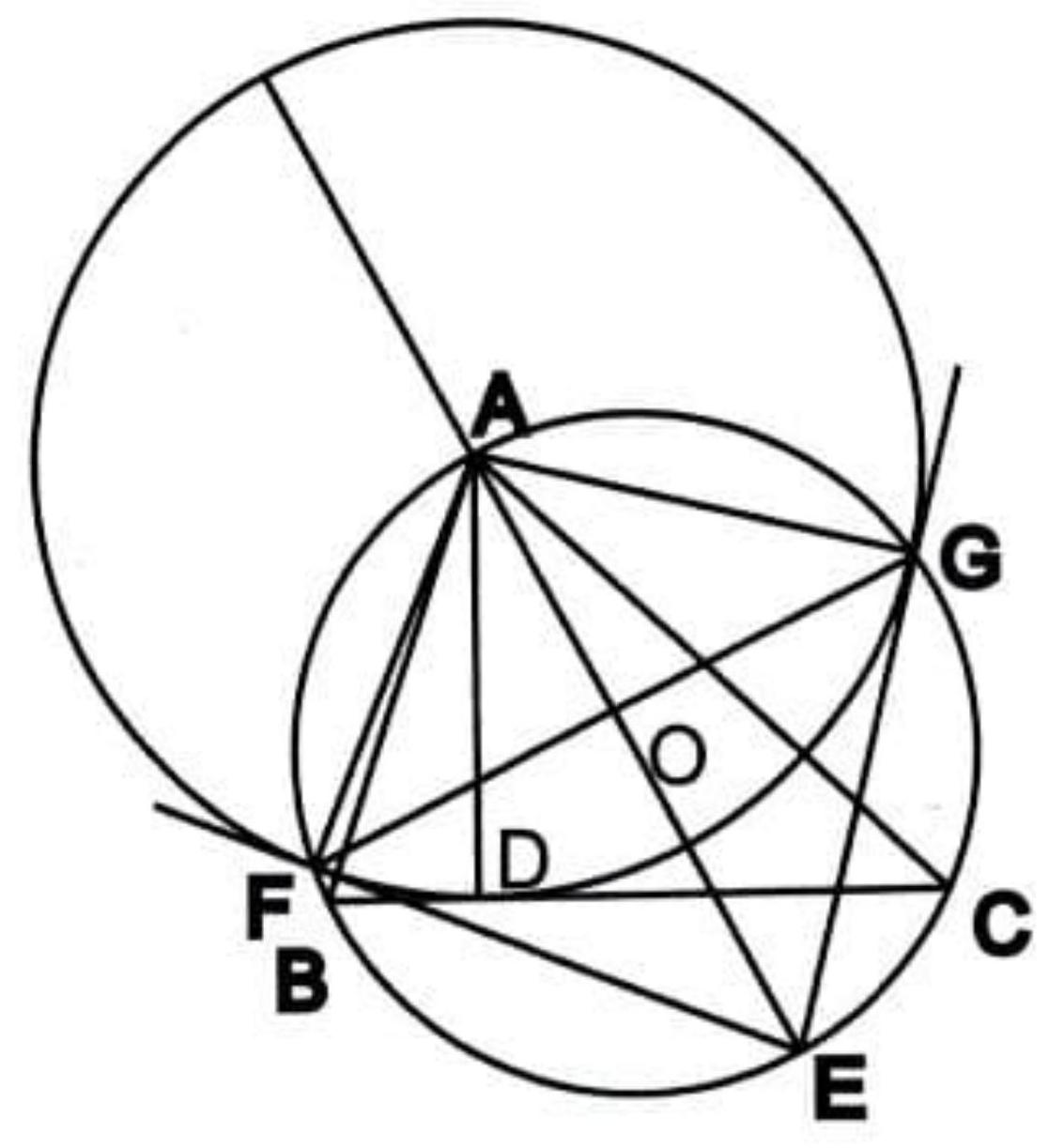
Figure 3: G3
Now, if in addition $F G \perp A O$, then since $A$ is the centre of $\omega$, in fact $A O$ is the perpendicular bisector of $F G$. But by definition, since $A B C$ is scalene, $A O$ meets the perpendicular bisector of $B C$ at $O$. Hence $O$ is the centre of $B F G C$, and thus in fact $B F A G C$ is cyclic. But then the lines perpendicular to $A F$ at $F$, and $A G$ at $G$ (the tangents to $\omega$ ) must intersect at $E$, the point antipodal to $A$ on $\odot B F A G C$.
Alternative solution: Let the circumcircle of $A B C$ be $\Gamma$. From the conditions, $G$ is the reflection of $F$ in the line $A O$. Let $B^{\prime}, D^{\prime}$ be the reflections of $B, D$ across this same line $A O$. Clearly $D^{\prime}$ also lies on $\omega$ and $B^{\prime}$ lies on $\Gamma$.
Then, using directed angles, $\angle C G D=\angle D F B=\angle B^{\prime} G D^{\prime}$ so
$$
\angle B^{\prime} G C=\angle B^{\prime} G D^{\prime}-\angle C G D^{\prime}=\angle C G D-\angle C G D^{\prime}=\angle D^{\prime} G D=\frac{1}{2} \angle D^{\prime} A D=\angle O A D .
$$
Then, exploiting the isogonality property that $\angle D A B=\angle C A O$, we have $\angle O A D=\angle C A B-2 \angle D A B=\angle A B C-\angle B C A=\angle A B C-\angle B^{\prime} B A=\angle B^{\prime} B C$.
So $G$ lies on $\Gamma$, and by the reflection property so does $F$.
But then, as in the previous solution, the tangents at $F$ and $G$ to $\omega$ must intersect at $E$, the point antipodal to $A$ on $\Gamma$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene and acute triangle, with circumcentre $O$. Let $\omega$ be the circle with centre $A$, tangent to $B C$ at $D$. Suppose there are two points $F$ and $G$ on $\omega$ such that $F G \perp A O, \angle B F D=\angle D G C$ and the couples of points $(B, F)$ and $(C, G)$ are in different halfplanes with respect to the line $A D$. Show that the tangents to $\omega$ at $F$ and $G$ meet on the circumcircle of $A B C$.
|
Consider any two points $F, G$ on $\omega$ such that $\angle B F D=\angle D G C$. Exploiting the isosceles triangles $\triangle A F G, \triangle A F D$, and $\triangle A D G$, we deduce (using directed angles throughout):
$$
\begin{gathered}
\angle D B F-\angle G C D=180^{\circ}-\angle B F D-\angle B D F-\left(180^{\circ}-\angle D G C-\angle C D G\right) \stackrel{(*)}{=} \\
\angle C D G-\angle F D B=\frac{1}{2} \cdot(\angle D A G-\angle D A F)=\frac{1}{2} \cdot\left[\left(180^{\circ}-2 \cdot \angle A D G\right)-\left(180^{\circ}-2 \cdot \angle A D F\right)\right]= \\
\angle A D F-\angle G D A=\angle D F A-\angle A G D=\angle D F G-\angle F G D \stackrel{(*)}{=} \angle B F G-\angle F G C,
\end{gathered}
$$
where we use $\angle B F D=\angle D G C$ at $\left(^{*}\right)$. Thus $B F G C$ is cyclic.

Figure 3: G3
Now, if in addition $F G \perp A O$, then since $A$ is the centre of $\omega$, in fact $A O$ is the perpendicular bisector of $F G$. But by definition, since $A B C$ is scalene, $A O$ meets the perpendicular bisector of $B C$ at $O$. Hence $O$ is the centre of $B F G C$, and thus in fact $B F A G C$ is cyclic. But then the lines perpendicular to $A F$ at $F$, and $A G$ at $G$ (the tangents to $\omega$ ) must intersect at $E$, the point antipodal to $A$ on $\odot B F A G C$.
Alternative solution: Let the circumcircle of $A B C$ be $\Gamma$. From the conditions, $G$ is the reflection of $F$ in the line $A O$. Let $B^{\prime}, D^{\prime}$ be the reflections of $B, D$ across this same line $A O$. Clearly $D^{\prime}$ also lies on $\omega$ and $B^{\prime}$ lies on $\Gamma$.
Then, using directed angles, $\angle C G D=\angle D F B=\angle B^{\prime} G D^{\prime}$ so
$$
\angle B^{\prime} G C=\angle B^{\prime} G D^{\prime}-\angle C G D^{\prime}=\angle C G D-\angle C G D^{\prime}=\angle D^{\prime} G D=\frac{1}{2} \angle D^{\prime} A D=\angle O A D .
$$
Then, exploiting the isogonality property that $\angle D A B=\angle C A O$, we have $\angle O A D=\angle C A B-2 \angle D A B=\angle A B C-\angle B C A=\angle A B C-\angle B^{\prime} B A=\angle B^{\prime} B C$.
So $G$ lies on $\Gamma$, and by the reflection property so does $F$.
But then, as in the previous solution, the tangents at $F$ and $G$ to $\omega$ must intersect at $E$, the point antipodal to $A$ on $\Gamma$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2019_bmo_shortlist.jsonl",
"problem_match": "\nG3.",
"solution_match": "\nSolution."
}
|
68066e38-8d2b-5f29-8406-e91fa64e18f0
| 605,899
|
Given an acute triangle $A B C$, let $M$ be the midpoint of $B C$ and $H$ the orthocentre. Let $\Gamma$ be the circle with diameter $H M$, and let $X, Y$ be distinct points on $\Gamma$ such that $A X, A Y$ are tangent to $\Gamma$. Prove that $B X Y C$ is cyclic.
|
Let $D$ be the foot of the altitude from $A$ to $B C$, which also lies on $\Gamma$. Let $O$ be the circumcentre of $\triangle A B C$. Since $\angle H D M=90^{\circ}$, note that rays $H D$ and $H M$ meet the circumcircle at points which are reflections in $O M$. Then, since $\angle B A D=\angle O A C$, we recover the well-known fact that ray $H M$ meets the circumcircle at $A^{\prime}$, the point antipodal to $A$. Therefore, the ray $M H$ meets the circumcircle at a point $T$ such that $\angle M T A=90^{\circ}$. Note that $T, D$ lie on the circle with diameter $A M$.
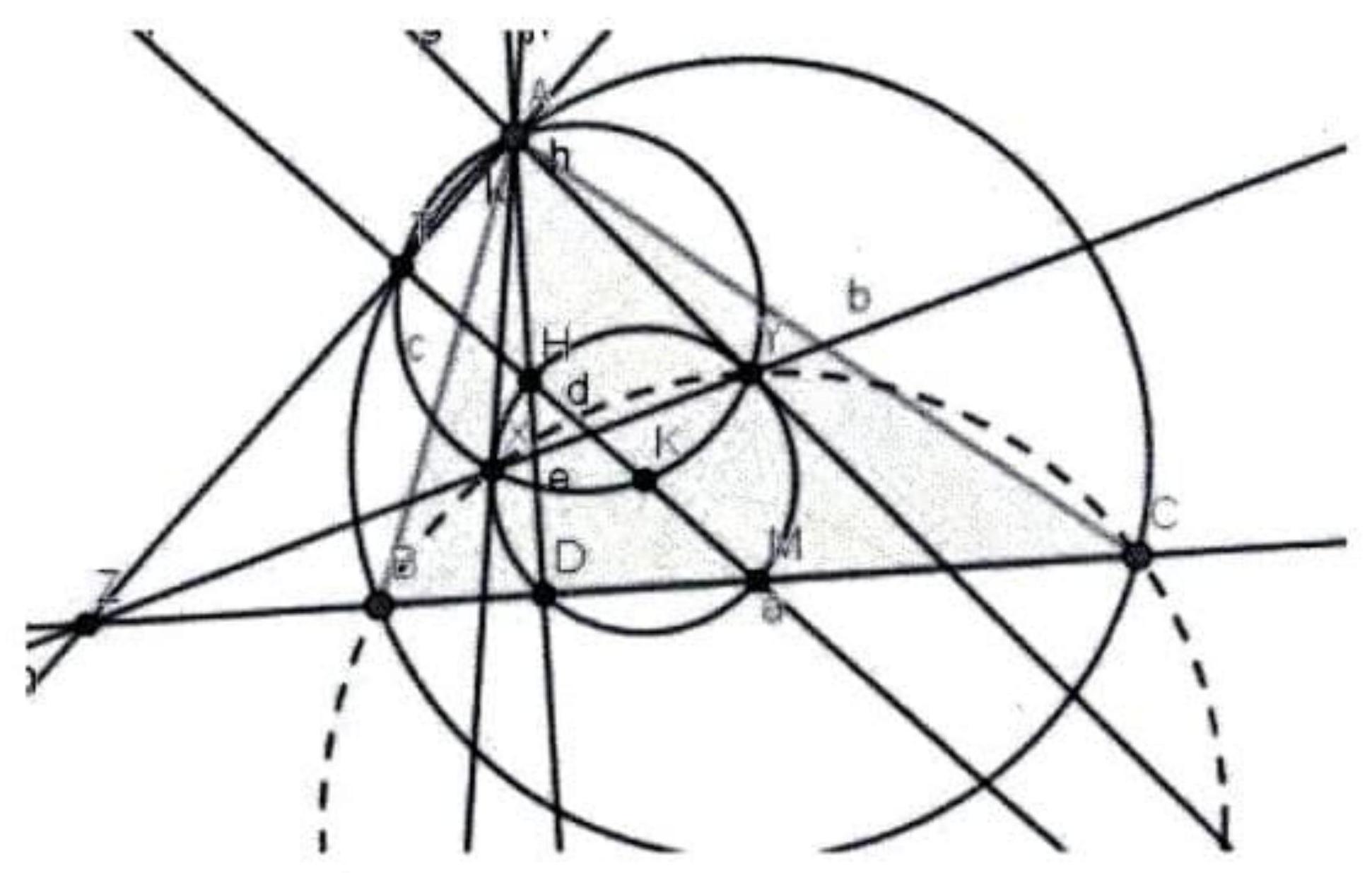
Figure 4: G4
Now, study $K$, the centre of $\Gamma$. Clearly $A X K Y$ is cyclic, with diameter $A K$, so $T$ also lies on this circle. We can now apply the radical axis theorem to the three circles $\odot A T X K Y, \odot A T D M, \odot H X D M Y$ to deduce that $A T, X Y, D M$ concur at a point, $Z$.
Then, by power of a point in $\odot A T X Y$, we have $Z X \cdot Z Y=Z T \cdot Z A$; but also by power of a point in the circumcircle, we have $Z A \cdot Z T=Z B \cdot Z C$. Therefore
$$
Z X \cdot Z Y=Z B \cdot Z C
$$
and the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given an acute triangle $A B C$, let $M$ be the midpoint of $B C$ and $H$ the orthocentre. Let $\Gamma$ be the circle with diameter $H M$, and let $X, Y$ be distinct points on $\Gamma$ such that $A X, A Y$ are tangent to $\Gamma$. Prove that $B X Y C$ is cyclic.
|
Let $D$ be the foot of the altitude from $A$ to $B C$, which also lies on $\Gamma$. Let $O$ be the circumcentre of $\triangle A B C$. Since $\angle H D M=90^{\circ}$, note that rays $H D$ and $H M$ meet the circumcircle at points which are reflections in $O M$. Then, since $\angle B A D=\angle O A C$, we recover the well-known fact that ray $H M$ meets the circumcircle at $A^{\prime}$, the point antipodal to $A$. Therefore, the ray $M H$ meets the circumcircle at a point $T$ such that $\angle M T A=90^{\circ}$. Note that $T, D$ lie on the circle with diameter $A M$.

Figure 4: G4
Now, study $K$, the centre of $\Gamma$. Clearly $A X K Y$ is cyclic, with diameter $A K$, so $T$ also lies on this circle. We can now apply the radical axis theorem to the three circles $\odot A T X K Y, \odot A T D M, \odot H X D M Y$ to deduce that $A T, X Y, D M$ concur at a point, $Z$.
Then, by power of a point in $\odot A T X Y$, we have $Z X \cdot Z Y=Z T \cdot Z A$; but also by power of a point in the circumcircle, we have $Z A \cdot Z T=Z B \cdot Z C$. Therefore
$$
Z X \cdot Z Y=Z B \cdot Z C
$$
and the result follows.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2019_bmo_shortlist.jsonl",
"problem_match": "\nG4.",
"solution_match": "\nSolution."
}
|
62b785c3-5b66-50d2-a3bf-92eb76756538
| 605,907
|
Let $A B C(B C>A C)$ be an acute triangle with circumcircle $k$ centered at $O$. The tangent to $k$ at $C$ intersects the line $A B$ at the point $D$. The circumcircles of triangles $B C D, O C D$ and $A O B$ intersect the ray $C A$ (beyond $A$ ) at the points $Q, P$ and $K$, respectively, such that $P \in(A K)$ and $K \in(P Q)$. The line $P D$ intersects the circumcircle of triangle $B K Q$ at the point $T$, so that $P$ and $T$ are in different halfplanes with respect to $B Q$. Prove that $T B=T Q$.
|
As $D C$ is tangent to $k$ at $C$ then $\angle O C D=90^{\circ}$. Denote by $X$ the midpoint of $A B$. Then $\angle O X A=90^{\circ}$ because of $O X$ is the perpendicular bisector of the side $A B$. The pentagon $P X O C D$ is inscribed in the circle with diameter $O D$, hence $\angle P X A=$ $\angle P X D=\angle P C D=\angle Q C D=\angle Q B A$ (the latter is due to $Q B C D$ being cyclic). We deduce that $P X \| Q B$ and that $P$ is the midpoint of $A Q$, so $A P=P Q$.
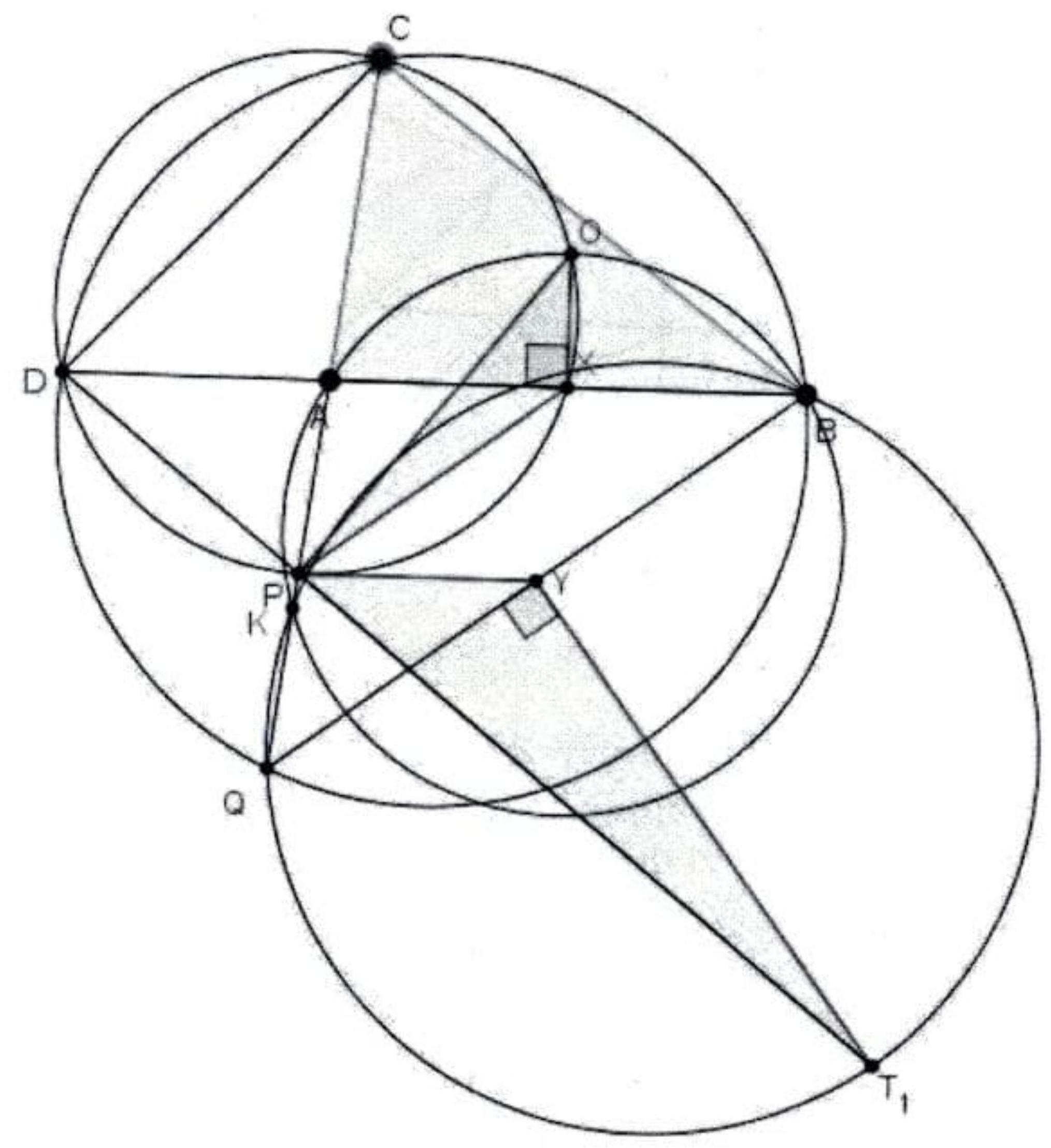
Figure 5: G5
Now let $T_{1}$ be the midpoint of the arc $B Q$, not containing $K$, from the circumcircle of $\triangle B K Q$, then $T_{1} B=T_{1} Q$. Due to $\angle D P O=90^{\circ}$, it suffices to show that $\angle O P T_{1}=90^{\circ}$ - indeed, $T \equiv T_{1}$ and $T B=T Q$ would follow.
Denote by $Y$ the midpoint of $B Q$. Then $\angle O X B=\angle T_{1} Y B=90^{\circ}$. The quadrilateral $Q K B T_{1}$ is inscribed in a circle, hence $\angle B T_{1} Q=180-\angle B K Q=\angle A K B$. Then $\angle X B O=$ $\frac{1}{2} \angle A K B=\frac{1}{2} \angle B T_{1} Q=\angle B T_{1} Y$ and thus $\triangle O X B \sim \triangle B Y T_{1}$. The quadrilaterals $P X B Y$
and $A X Y P$ are paralellograms, since $X Y$ and $P Y$ are middle lines of the triangle $A Q B$. Consequently,
$$
\frac{O X}{X P}=\frac{O X}{B Y}=\frac{X B}{T_{1} Y}=\frac{P Y}{T_{1} Y}
$$
which along with $\angle P X B=\angle P Y B$ and $\angle O X B=\angle T_{1} Y B$ gives $\angle O X P=\angle P Y T_{1}$ and $\triangle O X P \sim \triangle P Y T_{1}$. Thus $\angle X P O=\angle Y T_{1} P$ and $\angle P O X=\angle T_{1} P Y$.
In conclusion,
$$
\angle O P T_{1}=\angle X P Y+\angle X P O+\angle Y P T_{1}=\angle P X A+\angle X P O+\angle X O P=90^{\circ}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C(B C>A C)$ be an acute triangle with circumcircle $k$ centered at $O$. The tangent to $k$ at $C$ intersects the line $A B$ at the point $D$. The circumcircles of triangles $B C D, O C D$ and $A O B$ intersect the ray $C A$ (beyond $A$ ) at the points $Q, P$ and $K$, respectively, such that $P \in(A K)$ and $K \in(P Q)$. The line $P D$ intersects the circumcircle of triangle $B K Q$ at the point $T$, so that $P$ and $T$ are in different halfplanes with respect to $B Q$. Prove that $T B=T Q$.
|
As $D C$ is tangent to $k$ at $C$ then $\angle O C D=90^{\circ}$. Denote by $X$ the midpoint of $A B$. Then $\angle O X A=90^{\circ}$ because of $O X$ is the perpendicular bisector of the side $A B$. The pentagon $P X O C D$ is inscribed in the circle with diameter $O D$, hence $\angle P X A=$ $\angle P X D=\angle P C D=\angle Q C D=\angle Q B A$ (the latter is due to $Q B C D$ being cyclic). We deduce that $P X \| Q B$ and that $P$ is the midpoint of $A Q$, so $A P=P Q$.

Figure 5: G5
Now let $T_{1}$ be the midpoint of the arc $B Q$, not containing $K$, from the circumcircle of $\triangle B K Q$, then $T_{1} B=T_{1} Q$. Due to $\angle D P O=90^{\circ}$, it suffices to show that $\angle O P T_{1}=90^{\circ}$ - indeed, $T \equiv T_{1}$ and $T B=T Q$ would follow.
Denote by $Y$ the midpoint of $B Q$. Then $\angle O X B=\angle T_{1} Y B=90^{\circ}$. The quadrilateral $Q K B T_{1}$ is inscribed in a circle, hence $\angle B T_{1} Q=180-\angle B K Q=\angle A K B$. Then $\angle X B O=$ $\frac{1}{2} \angle A K B=\frac{1}{2} \angle B T_{1} Q=\angle B T_{1} Y$ and thus $\triangle O X B \sim \triangle B Y T_{1}$. The quadrilaterals $P X B Y$
and $A X Y P$ are paralellograms, since $X Y$ and $P Y$ are middle lines of the triangle $A Q B$. Consequently,
$$
\frac{O X}{X P}=\frac{O X}{B Y}=\frac{X B}{T_{1} Y}=\frac{P Y}{T_{1} Y}
$$
which along with $\angle P X B=\angle P Y B$ and $\angle O X B=\angle T_{1} Y B$ gives $\angle O X P=\angle P Y T_{1}$ and $\triangle O X P \sim \triangle P Y T_{1}$. Thus $\angle X P O=\angle Y T_{1} P$ and $\angle P O X=\angle T_{1} P Y$.
In conclusion,
$$
\angle O P T_{1}=\angle X P Y+\angle X P O+\angle Y P T_{1}=\angle P X A+\angle X P O+\angle X O P=90^{\circ}
$$
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2019_bmo_shortlist.jsonl",
"problem_match": "\nG5.",
"solution_match": "\nSolution."
}
|
1ec7dc96-a6ee-5c58-a087-06ff0d570c7a
| 605,918
|
Let $A B C$ be an acute triangle, and $A X, A Y$ two isogonal lines. Also, suppose that $K, S$ are the feet of perpendiculars from $B$ to $A X, A Y$, and $T, L$ are the feet of perpendiculars from $C$ to $A X, A Y$ respectively. Prove that $K L$ and $S T$ intersect on $B C$.
|
Denote $\phi=\widehat{X A B}=\widehat{Y A C}, \alpha=\widehat{C A X}=\widehat{B A Y}$. Then, because the quadrilaterals ABSK and ACTL are cyclic, we have
$$
\widehat{B S K}+\widehat{B A K}=180^{\circ}=\widehat{B S K}+\phi=\widehat{L A C}+\widehat{L T C}=\widehat{L T C}+\phi,
$$
so, due to the 90-degree angles formed, we have $\widehat{K S L}=\widehat{K T L}$. Thus, KLST is cyclic.
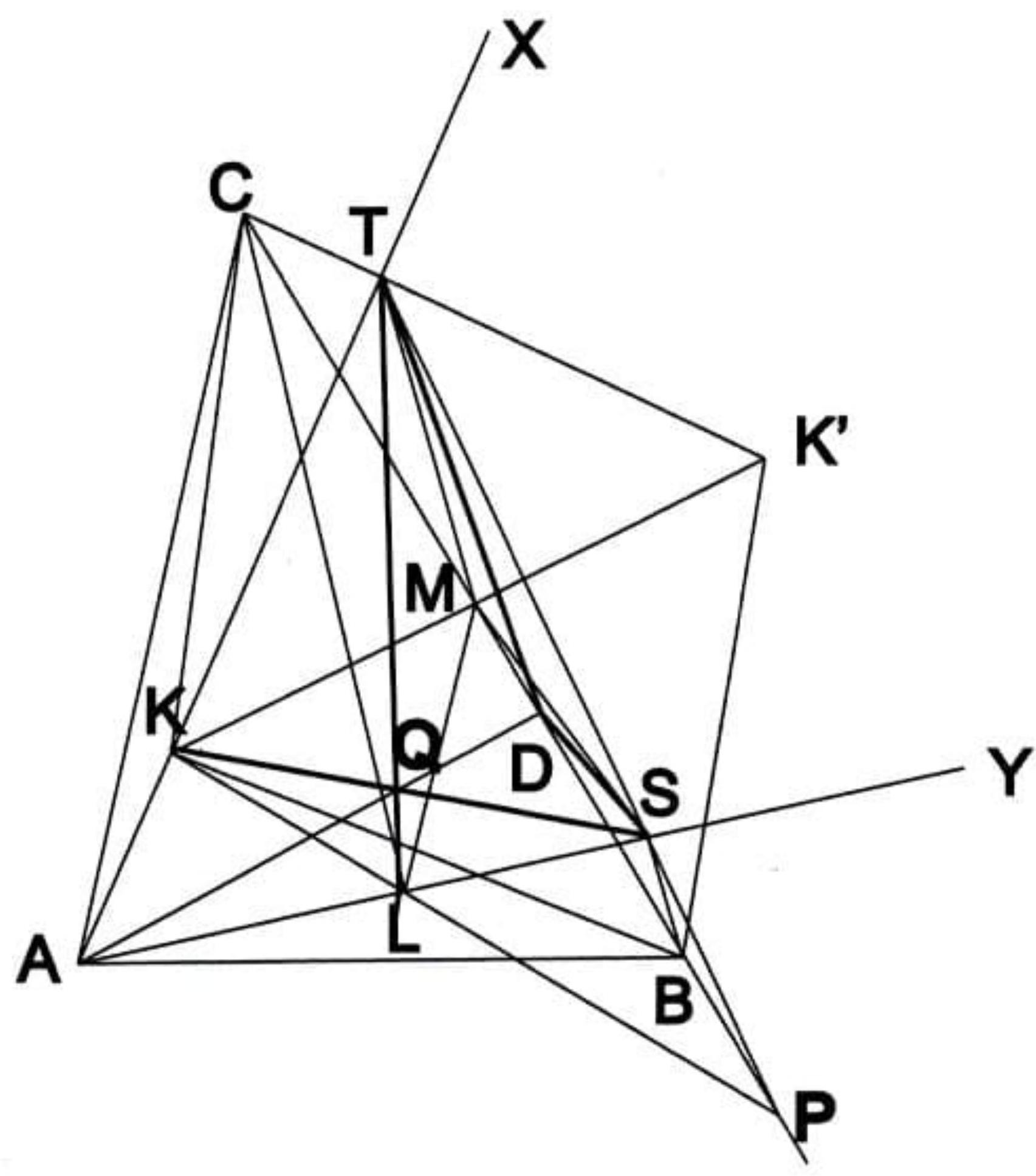
Figure 6: G6
Consider $M$ to be the midpoint of $B C$ and $K^{\prime}$ to be the symmetric point of $K$ with respect to $M$. Then, $B K C K^{\prime}$ is a parallelogram, and so $B K \| C K^{\prime}$. But $B K \| C T$, because they are both perpendicular to $A X$. So, $K^{\prime}$ lies on $C T$ and, as $\widehat{K T K^{\prime}}=90$ and $M$ is the midpoint of $K K^{\prime}, M K=M T$. In a similar way, we have that $M S=M L$. Thus, the center of $(K L S T)$ is $M$.
Consider $D$ to be the foot of altitude from $A$ to $B C$. Then, $D$ belongs in both $(A B K S)$ and ( $A C L T)$. So,
$$
\widehat{A D T}+\widehat{A C T}=180^{\circ}=\widehat{A B S}+\widehat{A D S}=\widehat{A D T}+90^{\circ}-\alpha=\widehat{A D S}+90^{\circ}-\alpha,
$$
and $A D$ is the bisector of $\widehat{S D T}$.
Because $D M$ is perpendicular to $A D, D M$ is the external bisector of this angle, and, as $M S=M T$, it follows that $D M S T$ is cyclic. In a similar way, we have that $D M L K$ is also cyclic.
So, we have that $S T, K L$ and $D M$ are the radical axes of these three circles, $(K L S T)$, $(D M S T),(D M K L)$. These lines are, therefore, concurrent, and we have proved the desired result.
Alternative solution. We continue after proving that $M$ is the center of $(K L S T)$. If $D$ is the foot of perpendicular from $A$ to $B C$, then $A S D K B$ is cyclic, as well as $A T D L C$. The radical axes of those two circles and ( $K L S T)$ are concurrent, thus $K S$ and $L T$ intersect on point $Q \in A D$. So, if $P$ is the intersection point of $K L$ and $T S$, due to Brokard's theorem, $A Q$ is perpendicular to $M P$. This is, of course, equivalent to proving that $P$ belongs on $B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle, and $A X, A Y$ two isogonal lines. Also, suppose that $K, S$ are the feet of perpendiculars from $B$ to $A X, A Y$, and $T, L$ are the feet of perpendiculars from $C$ to $A X, A Y$ respectively. Prove that $K L$ and $S T$ intersect on $B C$.
|
Denote $\phi=\widehat{X A B}=\widehat{Y A C}, \alpha=\widehat{C A X}=\widehat{B A Y}$. Then, because the quadrilaterals ABSK and ACTL are cyclic, we have
$$
\widehat{B S K}+\widehat{B A K}=180^{\circ}=\widehat{B S K}+\phi=\widehat{L A C}+\widehat{L T C}=\widehat{L T C}+\phi,
$$
so, due to the 90-degree angles formed, we have $\widehat{K S L}=\widehat{K T L}$. Thus, KLST is cyclic.

Figure 6: G6
Consider $M$ to be the midpoint of $B C$ and $K^{\prime}$ to be the symmetric point of $K$ with respect to $M$. Then, $B K C K^{\prime}$ is a parallelogram, and so $B K \| C K^{\prime}$. But $B K \| C T$, because they are both perpendicular to $A X$. So, $K^{\prime}$ lies on $C T$ and, as $\widehat{K T K^{\prime}}=90$ and $M$ is the midpoint of $K K^{\prime}, M K=M T$. In a similar way, we have that $M S=M L$. Thus, the center of $(K L S T)$ is $M$.
Consider $D$ to be the foot of altitude from $A$ to $B C$. Then, $D$ belongs in both $(A B K S)$ and ( $A C L T)$. So,
$$
\widehat{A D T}+\widehat{A C T}=180^{\circ}=\widehat{A B S}+\widehat{A D S}=\widehat{A D T}+90^{\circ}-\alpha=\widehat{A D S}+90^{\circ}-\alpha,
$$
and $A D$ is the bisector of $\widehat{S D T}$.
Because $D M$ is perpendicular to $A D, D M$ is the external bisector of this angle, and, as $M S=M T$, it follows that $D M S T$ is cyclic. In a similar way, we have that $D M L K$ is also cyclic.
So, we have that $S T, K L$ and $D M$ are the radical axes of these three circles, $(K L S T)$, $(D M S T),(D M K L)$. These lines are, therefore, concurrent, and we have proved the desired result.
Alternative solution. We continue after proving that $M$ is the center of $(K L S T)$. If $D$ is the foot of perpendicular from $A$ to $B C$, then $A S D K B$ is cyclic, as well as $A T D L C$. The radical axes of those two circles and ( $K L S T)$ are concurrent, thus $K S$ and $L T$ intersect on point $Q \in A D$. So, if $P$ is the intersection point of $K L$ and $T S$, due to Brokard's theorem, $A Q$ is perpendicular to $M P$. This is, of course, equivalent to proving that $P$ belongs on $B C$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2019_bmo_shortlist.jsonl",
"problem_match": "\nG6.",
"solution_match": "\nSolution."
}
|
06444c5c-1fd0-5295-8e41-660d3d201748
| 605,926
|
Let $A D, B E$, and $C F$ denote the altitudes of triangle $\triangle A B C$. Points $E^{\prime}$ and $F^{\prime}$ are the reflections of $E$ and $F$ over $A D$, respectively. The lines $B F^{\prime}$ and $C E^{\prime}$ intersect at $X$, while the lines $B E^{\prime}$ and $C F^{\prime}$ intersect at the point $Y$. Prove that if $H$ is the orthocenter of $\triangle A B C$, then the lines $A X, Y H$, and $B C$ are concurrent.
|
We will prove that the desired point of concurrency is the midpoint of $B C$. Assume that $\triangle A B C$ is acute. Let $(A B C)^{5}$ intersect $(A E F)$ at the point $Y^{\prime}$; we will prove that $Y=Y^{\prime}$.
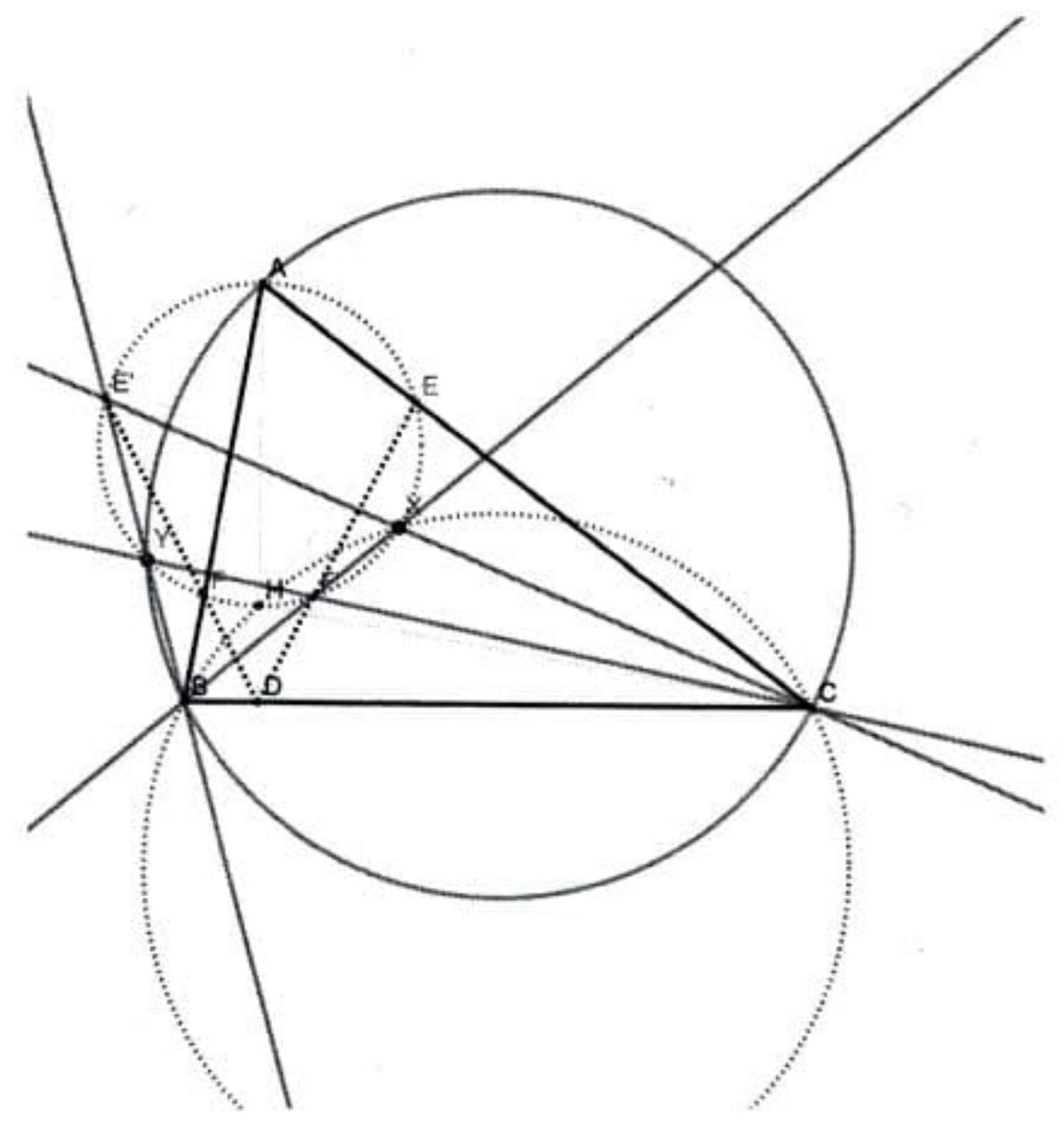
Figure 7: G7
Using the fact that $H$ is the incenter of $\triangle D E F$ we get that $D, E^{\prime}, F$ and $D, F^{\prime}, E$ are triples of collinear points. Furthermore,
$$
90^{\circ}=\angle{ }^{6} A E H=\angle A F^{\prime} H=\angle A E^{\prime} H=\angle A F H \Rightarrow F^{\prime}, E^{\prime}, H \in\left(A E F Y^{\prime}\right) .
$$
We will now prove that the points $Y^{\prime}, B, D, F^{\prime}$ are concyclic. Indeed,
$$
\angle Y^{\prime} B D=\angle Y^{\prime} B C=\angle Y^{\prime} A C=\angle Y^{\prime} A E=\angle Y^{\prime} F^{\prime} E \Rightarrow\left(Y^{\prime}, B, D, F^{\prime}\right) .
$$
Now, as
$$
\angle F^{\prime} Y^{\prime} B=\angle F^{\prime} D C=\angle E D C=\angle C A B=\angle C Y^{\prime} B,
$$
the points $C, F^{\prime}, Y^{\prime}$ are collinear. Similarly we get that $B, E^{\prime}, Y^{\prime}$ are collinear, which implies
$$
Y^{\prime}=Y=(A B C) \cap(A E F) .
$$
[^4]Since we proved this property using directed angles, we know that it is also true for obtuse triangles.
Notice that the points $A, B, C, H$ form an orthocentric system; in other words $H$ is the orthocenter of $\triangle A B C$ and $A$ is the orthocenter $\triangle H B C$. Furthermore, notice that $F^{\prime}$ is to $\triangle A B C$ as $E^{\prime}$ is to $\triangle H B C$ and that $E^{\prime}$ is to $\triangle A B C$ as $F^{\prime}$ is to $\triangle H B C$. This means that $X$ is to $\triangle H B C$ as $Y$ is to $\triangle A B C$ and, as we know the proven property is also true for obtuse triangles, we get
$$
X=(H B C) \cap(A E F) .
$$
By Reflecting the Orthocenter Lemma we know that in a triangle $A B C$, the reflection of its orthocenter over the midpoint of $B C$ is the antipode of $A$ w.r.t. ( $A B C$ ). Applying this Lemma on the triangles $A B C$ and $H B C$ we get that $Y H$ and $A X$ both go through the midpoint of $B C$, thus finishing the solution.
Remark 1: The crucial part of this solution is defining the points $X, Y$ as intersections of circles. This can also be achieved directly by using similar triangles or by using the Spiral Similarity Lemma on $\triangle H B C, \triangle H F^{\prime} E^{\prime}$ and $\triangle A B C, \triangle A E^{\prime} F^{\prime}$.
Remark 2: We can also invert around $A$ with radius $\sqrt{A H \cdot A D}$ or around $H$ with radius $\sqrt{H A \cdot H D}$ to prove that $X$ or $Y$ invert to the midpoint of $B C$ by using the existence of the nine-point circle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A D, B E$, and $C F$ denote the altitudes of triangle $\triangle A B C$. Points $E^{\prime}$ and $F^{\prime}$ are the reflections of $E$ and $F$ over $A D$, respectively. The lines $B F^{\prime}$ and $C E^{\prime}$ intersect at $X$, while the lines $B E^{\prime}$ and $C F^{\prime}$ intersect at the point $Y$. Prove that if $H$ is the orthocenter of $\triangle A B C$, then the lines $A X, Y H$, and $B C$ are concurrent.
|
We will prove that the desired point of concurrency is the midpoint of $B C$. Assume that $\triangle A B C$ is acute. Let $(A B C)^{5}$ intersect $(A E F)$ at the point $Y^{\prime}$; we will prove that $Y=Y^{\prime}$.

Figure 7: G7
Using the fact that $H$ is the incenter of $\triangle D E F$ we get that $D, E^{\prime}, F$ and $D, F^{\prime}, E$ are triples of collinear points. Furthermore,
$$
90^{\circ}=\angle{ }^{6} A E H=\angle A F^{\prime} H=\angle A E^{\prime} H=\angle A F H \Rightarrow F^{\prime}, E^{\prime}, H \in\left(A E F Y^{\prime}\right) .
$$
We will now prove that the points $Y^{\prime}, B, D, F^{\prime}$ are concyclic. Indeed,
$$
\angle Y^{\prime} B D=\angle Y^{\prime} B C=\angle Y^{\prime} A C=\angle Y^{\prime} A E=\angle Y^{\prime} F^{\prime} E \Rightarrow\left(Y^{\prime}, B, D, F^{\prime}\right) .
$$
Now, as
$$
\angle F^{\prime} Y^{\prime} B=\angle F^{\prime} D C=\angle E D C=\angle C A B=\angle C Y^{\prime} B,
$$
the points $C, F^{\prime}, Y^{\prime}$ are collinear. Similarly we get that $B, E^{\prime}, Y^{\prime}$ are collinear, which implies
$$
Y^{\prime}=Y=(A B C) \cap(A E F) .
$$
[^4]Since we proved this property using directed angles, we know that it is also true for obtuse triangles.
Notice that the points $A, B, C, H$ form an orthocentric system; in other words $H$ is the orthocenter of $\triangle A B C$ and $A$ is the orthocenter $\triangle H B C$. Furthermore, notice that $F^{\prime}$ is to $\triangle A B C$ as $E^{\prime}$ is to $\triangle H B C$ and that $E^{\prime}$ is to $\triangle A B C$ as $F^{\prime}$ is to $\triangle H B C$. This means that $X$ is to $\triangle H B C$ as $Y$ is to $\triangle A B C$ and, as we know the proven property is also true for obtuse triangles, we get
$$
X=(H B C) \cap(A E F) .
$$
By Reflecting the Orthocenter Lemma we know that in a triangle $A B C$, the reflection of its orthocenter over the midpoint of $B C$ is the antipode of $A$ w.r.t. ( $A B C$ ). Applying this Lemma on the triangles $A B C$ and $H B C$ we get that $Y H$ and $A X$ both go through the midpoint of $B C$, thus finishing the solution.
Remark 1: The crucial part of this solution is defining the points $X, Y$ as intersections of circles. This can also be achieved directly by using similar triangles or by using the Spiral Similarity Lemma on $\triangle H B C, \triangle H F^{\prime} E^{\prime}$ and $\triangle A B C, \triangle A E^{\prime} F^{\prime}$.
Remark 2: We can also invert around $A$ with radius $\sqrt{A H \cdot A D}$ or around $H$ with radius $\sqrt{H A \cdot H D}$ to prove that $X$ or $Y$ invert to the midpoint of $B C$ by using the existence of the nine-point circle.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2019_bmo_shortlist.jsonl",
"problem_match": "\nG7.",
"solution_match": "\nSolution."
}
|
7c062336-7226-594d-baa9-74a600ef2018
| 605,933
|
Given an acute triangle $A B C,(c)$ is circumcircle with center $O$ and $H$ the orthocenter of the triangle $A B C$. The line $A O$ intersects $(c)$ at the point $D$. Let $D_{1}, D_{2}$ and $H_{2}, H_{3}$ be the symmetrical points of the points $D$ and $H$ with respect to the lines $A B, A C$ respectively. Let $\left(c_{1}\right)$ be the circumcircle of the triangle $A D_{1} D_{2}$. Suppose that the line $A H$ intersects again $\left(c_{1}\right)$ at the point $U$, the line $H_{2} H_{3}$ intersects the segment $D_{1} D_{2}$ at the point $K_{1}$ and the line $D H_{3}$ intersects the segment $U D_{2}$ at the point $L_{1}$. Prove that one of the intersection points of the circumcircles of the triangles $D_{1} K_{1} H_{2}$ and $U D L_{1}$ lies on the line $K_{1} L_{1}$.
|
It is well known that the symmetrical points $H_{1}, H_{2}, H_{3}$ of $H$ with respect the sides $B C, A B, A C$ of the triangle $A B C$ respectively lie on the circle (c).
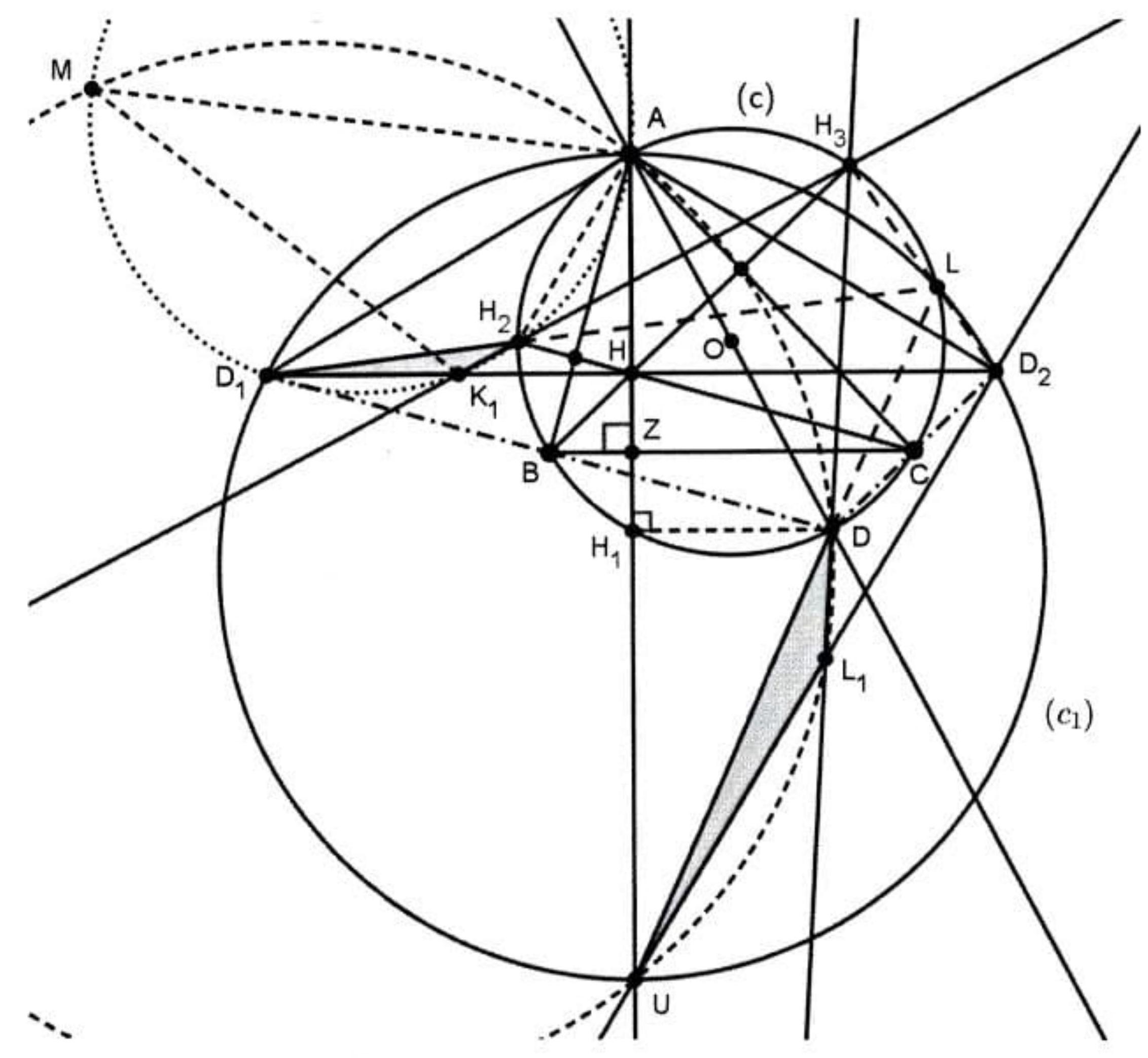
Figure 8: G8
Let $L$ be the second point of intersection of $(c)$ and $\left(c_{1}\right)$. First we will prove that the lines $D_{1} H_{2}, D_{2} H_{3}$ and $U D$ pass through the point $L$.
Suppose that the line $A H$ intersects the side $B C$ at the point $Z$. Since $H_{1} D\|B C\| D_{1} D_{2}$ and $B, C$ are the midpoints of the segments $D_{1} D, D_{2} D$ respectively, we get that $Z$ is the midpoint of the segment $H H_{1}$, so the point $H$ lies on $D_{1} D_{2}$. Therefore, $A H \perp D_{1} D_{2}$ and $A U$ is a diameter of $\left(c_{1}\right)$. Thus, $A L \perp U L$ and $A L \perp D L$. We have that the points $U, D, L$ are collinear. (1)
Now, $\angle A L D_{1}=\angle A D_{2} D_{1}, \angle A L H_{2}=\angle A C H_{2}$. Since $A H C D_{2}$ is cyclic we get
$\angle A C H_{2}=\angle A D_{2} D_{1}$. Therefore, $\angle A L H_{2}=\angle A L D_{1}$. So the points $D_{1}, H_{2}, L$ are collinear. (2)
Similarly,
$$
\angle D_{1} L D_{2}=\angle D_{1} A D_{2}=180^{\circ}-2\left(\angle A D_{1} H\right) .
$$
Since $A D_{1} B H$ is cyclic we have $\angle A D_{1} H=\angle A B H=\angle A B H_{3}$. Therefore, we get
$$
\angle D_{1} L D_{2}=180^{\circ}-2\left(\angle A B H_{3}\right)=180^{\circ}-2\left(\angle A D H_{3}\right)=180^{\circ}-\angle H_{2} D H_{3} .
$$
Thus,
$$
\angle D_{1} L D_{2}+\angle H_{2} D H_{3}=180^{\circ} \quad \text { or } \angle D_{1} L D_{2}+\angle H_{3} L H_{2}=180^{\circ} .
$$
So the points $H_{3}, L, D_{2}$ are collinear. (3)
From (1), (2), (3) we have that the lines $D_{1} H_{2}, D_{2} H_{3}$ and $U D$ are concurrent at the point $L$.
Also we have
$$
\angle H_{3} D A=\angle D_{2} D A-\angle C D H_{3}=\angle A D_{2} D-\angle C B H_{3}
$$
and because $B \mathrm{HD}_{2} \mathrm{C}$ is a parallelogram, we get $\angle C B H_{3}=\angle H D_{2} C$. So
$$
\angle H_{3} D A=\angle A D_{2} D-\angle H D_{2} C=\angle A D_{2} D_{1}=\angle A D_{1} D_{2}=\angle A U D_{2} .
$$
Therefore, the circumcircle of the triangle $U D L_{1}$ passes through the point $A$. Also, $\angle A D_{1} K_{1}=\angle D_{2} D_{1} A=\angle D_{2} U A$. But $A U L_{1} D$ is cyclic and we have $\angle D_{2} U A=\angle H_{3} D A=$ $\angle H_{3} B A=\angle H_{3} H_{2} A$. Therefore, $\angle A D_{1} K_{1}=\angle H_{3} H_{2} A$. Thus, the circumcircle of the triangle $D_{1} K_{1} H_{2}$ passes through the point $A$.
Because the points $H_{3}, L, D_{2}$ are collinear by the Desargues theorem, the lines $U D_{1}$, $L_{1} K_{1}, D H_{2}$ are concurrent, let say in the point $M$.
From the similarity of the triangles $U D L_{1}$ and $D_{1} K_{1} H_{2}$ we conclude that $M$ is the center of unique spiral similarity and because the circumcircles of the triangles $D_{1} K_{1} H_{2}$ and $U D L_{1}$ intersect at the point $A$, then the second point of intersection is $M$. Therefore, $M$ lies on the line $K_{1} L_{1}$.
Comment. We can prove the last part in a different way.
Let $M$ be the point of intersection of the circumcircles of the triangles $D_{1} K_{1} H_{2}$ and $U D L_{1}$. Now, we have
$$
\angle K_{1} M A=\angle H_{3} H_{2} A=\angle H_{3} B A=\angle A D H_{3}=\angle L_{1} U A=\angle L_{1} M A .
$$
Therefore, the points $L_{1}, K_{1}, M$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given an acute triangle $A B C,(c)$ is circumcircle with center $O$ and $H$ the orthocenter of the triangle $A B C$. The line $A O$ intersects $(c)$ at the point $D$. Let $D_{1}, D_{2}$ and $H_{2}, H_{3}$ be the symmetrical points of the points $D$ and $H$ with respect to the lines $A B, A C$ respectively. Let $\left(c_{1}\right)$ be the circumcircle of the triangle $A D_{1} D_{2}$. Suppose that the line $A H$ intersects again $\left(c_{1}\right)$ at the point $U$, the line $H_{2} H_{3}$ intersects the segment $D_{1} D_{2}$ at the point $K_{1}$ and the line $D H_{3}$ intersects the segment $U D_{2}$ at the point $L_{1}$. Prove that one of the intersection points of the circumcircles of the triangles $D_{1} K_{1} H_{2}$ and $U D L_{1}$ lies on the line $K_{1} L_{1}$.
|
It is well known that the symmetrical points $H_{1}, H_{2}, H_{3}$ of $H$ with respect the sides $B C, A B, A C$ of the triangle $A B C$ respectively lie on the circle (c).

Figure 8: G8
Let $L$ be the second point of intersection of $(c)$ and $\left(c_{1}\right)$. First we will prove that the lines $D_{1} H_{2}, D_{2} H_{3}$ and $U D$ pass through the point $L$.
Suppose that the line $A H$ intersects the side $B C$ at the point $Z$. Since $H_{1} D\|B C\| D_{1} D_{2}$ and $B, C$ are the midpoints of the segments $D_{1} D, D_{2} D$ respectively, we get that $Z$ is the midpoint of the segment $H H_{1}$, so the point $H$ lies on $D_{1} D_{2}$. Therefore, $A H \perp D_{1} D_{2}$ and $A U$ is a diameter of $\left(c_{1}\right)$. Thus, $A L \perp U L$ and $A L \perp D L$. We have that the points $U, D, L$ are collinear. (1)
Now, $\angle A L D_{1}=\angle A D_{2} D_{1}, \angle A L H_{2}=\angle A C H_{2}$. Since $A H C D_{2}$ is cyclic we get
$\angle A C H_{2}=\angle A D_{2} D_{1}$. Therefore, $\angle A L H_{2}=\angle A L D_{1}$. So the points $D_{1}, H_{2}, L$ are collinear. (2)
Similarly,
$$
\angle D_{1} L D_{2}=\angle D_{1} A D_{2}=180^{\circ}-2\left(\angle A D_{1} H\right) .
$$
Since $A D_{1} B H$ is cyclic we have $\angle A D_{1} H=\angle A B H=\angle A B H_{3}$. Therefore, we get
$$
\angle D_{1} L D_{2}=180^{\circ}-2\left(\angle A B H_{3}\right)=180^{\circ}-2\left(\angle A D H_{3}\right)=180^{\circ}-\angle H_{2} D H_{3} .
$$
Thus,
$$
\angle D_{1} L D_{2}+\angle H_{2} D H_{3}=180^{\circ} \quad \text { or } \angle D_{1} L D_{2}+\angle H_{3} L H_{2}=180^{\circ} .
$$
So the points $H_{3}, L, D_{2}$ are collinear. (3)
From (1), (2), (3) we have that the lines $D_{1} H_{2}, D_{2} H_{3}$ and $U D$ are concurrent at the point $L$.
Also we have
$$
\angle H_{3} D A=\angle D_{2} D A-\angle C D H_{3}=\angle A D_{2} D-\angle C B H_{3}
$$
and because $B \mathrm{HD}_{2} \mathrm{C}$ is a parallelogram, we get $\angle C B H_{3}=\angle H D_{2} C$. So
$$
\angle H_{3} D A=\angle A D_{2} D-\angle H D_{2} C=\angle A D_{2} D_{1}=\angle A D_{1} D_{2}=\angle A U D_{2} .
$$
Therefore, the circumcircle of the triangle $U D L_{1}$ passes through the point $A$. Also, $\angle A D_{1} K_{1}=\angle D_{2} D_{1} A=\angle D_{2} U A$. But $A U L_{1} D$ is cyclic and we have $\angle D_{2} U A=\angle H_{3} D A=$ $\angle H_{3} B A=\angle H_{3} H_{2} A$. Therefore, $\angle A D_{1} K_{1}=\angle H_{3} H_{2} A$. Thus, the circumcircle of the triangle $D_{1} K_{1} H_{2}$ passes through the point $A$.
Because the points $H_{3}, L, D_{2}$ are collinear by the Desargues theorem, the lines $U D_{1}$, $L_{1} K_{1}, D H_{2}$ are concurrent, let say in the point $M$.
From the similarity of the triangles $U D L_{1}$ and $D_{1} K_{1} H_{2}$ we conclude that $M$ is the center of unique spiral similarity and because the circumcircles of the triangles $D_{1} K_{1} H_{2}$ and $U D L_{1}$ intersect at the point $A$, then the second point of intersection is $M$. Therefore, $M$ lies on the line $K_{1} L_{1}$.
Comment. We can prove the last part in a different way.
Let $M$ be the point of intersection of the circumcircles of the triangles $D_{1} K_{1} H_{2}$ and $U D L_{1}$. Now, we have
$$
\angle K_{1} M A=\angle H_{3} H_{2} A=\angle H_{3} B A=\angle A D H_{3}=\angle L_{1} U A=\angle L_{1} M A .
$$
Therefore, the points $L_{1}, K_{1}, M$ are collinear.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2019_bmo_shortlist.jsonl",
"problem_match": "\nG8.",
"solution_match": "\nSolution."
}
|
63a076a4-353e-52de-8346-addf28d94bc9
| 605,942
|
Given semicircle (c) with diameter $A B$ and center $O$. On the (c) we take point $C$ such that the tangent at the $C$ intersects the line $A B$ at the point $E$. The perpendicular line from $C$ to $A B$ intersects the diameter $A B$ at the point $D$. On the (c) we get the points $H, Z$ such that $C D=C H=C Z$. The line $H Z$ intersects the lines $C O, C D, A B$ at the points $S, I, K$ respectively and the parallel line from $I$ to the line $A B$ intersects the lines $C O, C K$ at the points $L, M$ respectively. We consider the circumcircle $(k)$ of the triangle $L M D$, which intersects again the lines $A B, C K$ at the points $P, U$ respectively. Let $\left(e_{1}\right)$, $\left(e_{2}\right),\left(e_{3}\right)$ be the tangents of the $(k)$ at the points $L, M, P$ respectively and $R=\left(e_{1}\right) \cap\left(e_{2}\right)$, $X=\left(e_{2}\right) \cap\left(e_{3}\right), T=\left(e_{1}\right) \cap\left(e_{3}\right)$. Prove that if $Q$ is the center of $(k)$, the lines $R D, T U$, $X S$ pass through the same point, which lies in the line $I Q$.
|
Since $C H=C Z$ we have $O C \perp H Z$. So from the cyclic quadrilateral $S O D I$ we get
$$
C S \cdot C O=C I \cdot C D .
$$
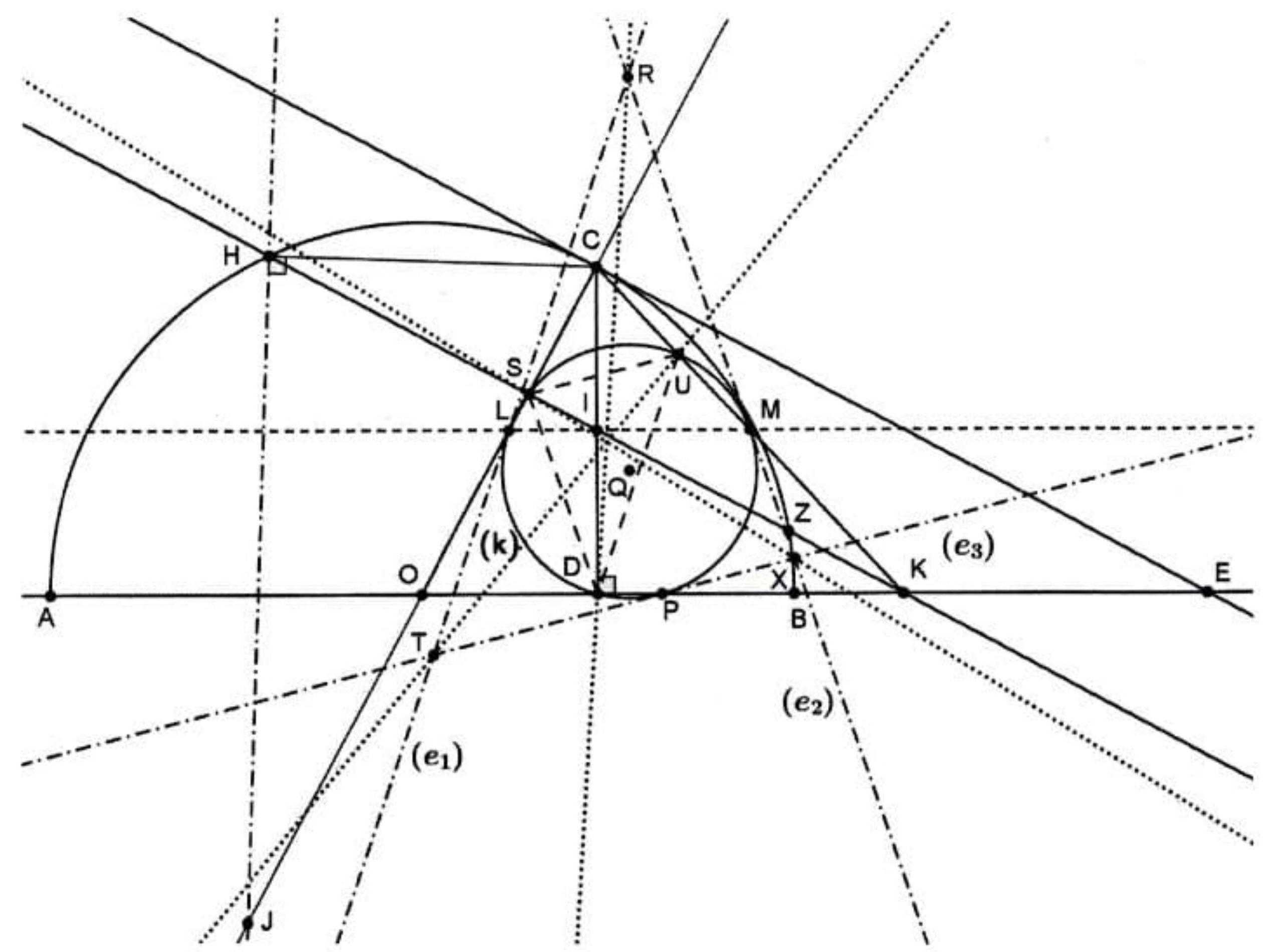
Figure 9: G9
We draw the perpendicular line $(v)$ to $H C$ at the point $H$. Let $J$ be the intersection point of lines $(v)$ and $C O$. Then $C J$ is diameter of the circle $(O, O A)$ and
$$
C J=2 C O
$$
From the right triangle $J H C$ we have
$$
H C^{2}=C S \cdot C J
$$
Therefore, from (1), (2) and (3) we get
$$
C S \cdot \frac{1}{2} C J=C I \cdot C D \quad \text { or } \quad H C^{2}=2 C I \cdot C D \text {. }
$$
However $H C=C D$ and thus $C D=2 C I$. Thus, $I$ is the midpoint of the segment $C D$. Nevertheless, $L M \| O K$, so the points $L, M$ are the midpoints of the sides $C O$ and $C K$ respectively. Therefore, the circumcircle $(k)$ of the triangle $L M D$ is the Euler circle of the $C O K$ and thus it passes through the point $S$.
We have $Q S=Q U$ and from the right triangles $O S K, O U K$ we get $P S=P U=\frac{O K}{2}$.
Therefore, the points $P, Q$ are located on the perpendicular bisector of the segment $S U$. Now, we conclude that $S U \| T X$, because $Q P \perp\left(e_{3}\right)$. Similarly, we prove that $D U \| R T$ and $S D \| R X$.
Since the triangles $S U D$ and $X T R$ are homothetic we get that the lines $R D, T U, X S$ are concurrent at the center $\mathcal{M}$ of homothety.
The points $I$ and $Q$ atre the incenters of homothetic triangles $S U D$ and $X T R$, respectively. Thus, the line $I Q$ passes through the point $\mathcal{M}$.
## NUMBER THEORY
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given semicircle (c) with diameter $A B$ and center $O$. On the (c) we take point $C$ such that the tangent at the $C$ intersects the line $A B$ at the point $E$. The perpendicular line from $C$ to $A B$ intersects the diameter $A B$ at the point $D$. On the (c) we get the points $H, Z$ such that $C D=C H=C Z$. The line $H Z$ intersects the lines $C O, C D, A B$ at the points $S, I, K$ respectively and the parallel line from $I$ to the line $A B$ intersects the lines $C O, C K$ at the points $L, M$ respectively. We consider the circumcircle $(k)$ of the triangle $L M D$, which intersects again the lines $A B, C K$ at the points $P, U$ respectively. Let $\left(e_{1}\right)$, $\left(e_{2}\right),\left(e_{3}\right)$ be the tangents of the $(k)$ at the points $L, M, P$ respectively and $R=\left(e_{1}\right) \cap\left(e_{2}\right)$, $X=\left(e_{2}\right) \cap\left(e_{3}\right), T=\left(e_{1}\right) \cap\left(e_{3}\right)$. Prove that if $Q$ is the center of $(k)$, the lines $R D, T U$, $X S$ pass through the same point, which lies in the line $I Q$.
|
Since $C H=C Z$ we have $O C \perp H Z$. So from the cyclic quadrilateral $S O D I$ we get
$$
C S \cdot C O=C I \cdot C D .
$$

Figure 9: G9
We draw the perpendicular line $(v)$ to $H C$ at the point $H$. Let $J$ be the intersection point of lines $(v)$ and $C O$. Then $C J$ is diameter of the circle $(O, O A)$ and
$$
C J=2 C O
$$
From the right triangle $J H C$ we have
$$
H C^{2}=C S \cdot C J
$$
Therefore, from (1), (2) and (3) we get
$$
C S \cdot \frac{1}{2} C J=C I \cdot C D \quad \text { or } \quad H C^{2}=2 C I \cdot C D \text {. }
$$
However $H C=C D$ and thus $C D=2 C I$. Thus, $I$ is the midpoint of the segment $C D$. Nevertheless, $L M \| O K$, so the points $L, M$ are the midpoints of the sides $C O$ and $C K$ respectively. Therefore, the circumcircle $(k)$ of the triangle $L M D$ is the Euler circle of the $C O K$ and thus it passes through the point $S$.
We have $Q S=Q U$ and from the right triangles $O S K, O U K$ we get $P S=P U=\frac{O K}{2}$.
Therefore, the points $P, Q$ are located on the perpendicular bisector of the segment $S U$. Now, we conclude that $S U \| T X$, because $Q P \perp\left(e_{3}\right)$. Similarly, we prove that $D U \| R T$ and $S D \| R X$.
Since the triangles $S U D$ and $X T R$ are homothetic we get that the lines $R D, T U, X S$ are concurrent at the center $\mathcal{M}$ of homothety.
The points $I$ and $Q$ atre the incenters of homothetic triangles $S U D$ and $X T R$, respectively. Thus, the line $I Q$ passes through the point $\mathcal{M}$.
## NUMBER THEORY
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2019_bmo_shortlist.jsonl",
"problem_match": "\nG9.",
"solution_match": "\nSolution."
}
|
cdb7cad7-0964-526d-b9e5-6a7590356336
| 605,951
|
Let $S \subset\{1, \ldots, n\}$ be a nonempty set, where $n$ is a positive integer. We denote by $s$ the greatest common divisor of the elements of the set $S$. We assume that $s \neq 1$ and let $d$ be its smallest divisor greater than 1 . Let $T \subset\{1, \ldots, n\}$ be a set such that $S \subset T$ and $|T| \geq 1+\left[\frac{n}{d}\right]$. Prove that the greatest common divisor of the elements in $T$ is 1 .
|
Let $t$ be the greatest common divisor of the elements in $T$. Due to the fact that $S \subset T$, we immediately get that $t / s$. Let us assume for the sake of contradiction that $t \neq 1$. From the previous observation we get that $t \geq d$.
By taking into account that $|T| \geq 1+\left[\frac{n}{d}\right]$, we infer that we can find at least $1+\left[\frac{n}{d}\right]$ elements in $T$. All of them will be divisible by $t$, and the largest of them, which we shall denote by $M$, will be at least $t \cdot\left(1+\left[\frac{n}{d}\right]\right)$. On the other hand, $t \geq d$, hence
$$
M \geq t \cdot\left(1+\left[\frac{n}{d}\right]\right) \geq d \cdot\left(1+\left[\frac{n}{d}\right]\right)>d \cdot \frac{n}{d}=n
$$
Therefore, $M>n$, which contradicts the fact that $M \in\{1, \ldots, n\}$.
In conclusion, $t=1$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $S \subset\{1, \ldots, n\}$ be a nonempty set, where $n$ is a positive integer. We denote by $s$ the greatest common divisor of the elements of the set $S$. We assume that $s \neq 1$ and let $d$ be its smallest divisor greater than 1 . Let $T \subset\{1, \ldots, n\}$ be a set such that $S \subset T$ and $|T| \geq 1+\left[\frac{n}{d}\right]$. Prove that the greatest common divisor of the elements in $T$ is 1 .
|
Let $t$ be the greatest common divisor of the elements in $T$. Due to the fact that $S \subset T$, we immediately get that $t / s$. Let us assume for the sake of contradiction that $t \neq 1$. From the previous observation we get that $t \geq d$.
By taking into account that $|T| \geq 1+\left[\frac{n}{d}\right]$, we infer that we can find at least $1+\left[\frac{n}{d}\right]$ elements in $T$. All of them will be divisible by $t$, and the largest of them, which we shall denote by $M$, will be at least $t \cdot\left(1+\left[\frac{n}{d}\right]\right)$. On the other hand, $t \geq d$, hence
$$
M \geq t \cdot\left(1+\left[\frac{n}{d}\right]\right) \geq d \cdot\left(1+\left[\frac{n}{d}\right]\right)>d \cdot \frac{n}{d}=n
$$
Therefore, $M>n$, which contradicts the fact that $M \in\{1, \ldots, n\}$.
In conclusion, $t=1$, as desired.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2019_bmo_shortlist.jsonl",
"problem_match": "\nTN2.",
"solution_match": "\nSolution."
}
|
53b6cdf9-32ee-5ff8-a1aa-b829b396fb2e
| 605,967
|
Let $f, g$ be functions from the positive integers to the integers. Vlad the impala is jumping around the integer grid. His initial position is $\mathbf{x}_{0}=(0,0)$, and for every $n \geqslant 1$, his jump is
$$
\mathbf{x}_{n}-\mathbf{x}_{n-1}=( \pm f(n), \pm g(n)) \text { or }( \pm g(n), \pm f(n))
$$
with eight possibilities in total. Is it always possible that Vlad can choose his jumps to return to his initial location $(0,0)$ infinitely many times when
(a) $f, g$ are polynomials with integer coefficients?
(b) $f, g$ are any pair of functions from the positive integers to the integers?
## Proposed by United Kingdom
|
1.
(a) Yes it is always possible. The key idea is the following: Let $b(n)$ be the number of 1 's in the binary expansion of $n=0,1,2, \ldots$.
Lemma: Given a polynomial $f$ with integer coefficients and degree at most $d$, then
$$
\sum_{k=0}^{2^{d+1}-1}(-1)^{b(k)} f(n+k)=f(n)-f(n+1)-f(n+2)+\cdots \pm f\left(n+\left(2^{d+1}-1\right)\right)=0
$$
Proof of Lemma: The result is clear for $d=0$. For $d \geqslant 1$, we have
$$
\sum_{k=0}^{2^{d+1}-1}(-1)^{b(k)} f(n+k)=\sum_{k=0}^{2^{d}-1}(-1)^{b(k)}\left[f(n+k)-f\left(n+k+2^{d}\right)\right] .
$$
So set $\tilde{f}(n)=f(n)-f\left(n+2^{d}\right)$, which is a polynomial of degree at most $d-1$. Then
$$
\sum_{k=0}^{2^{d+1}-1}(-1)^{b(k)} f(n+k)=\sum_{k=0}^{2^{d}-1} \tilde{f}(n+k)=0
$$
by induction, completing the proof of the lemma.
In particular, if we take
$$
\mathbf{x}_{n}-\mathbf{x}_{n-1}=\left((-1)^{b(n)} f(n),(-1)^{b(n)} g(n)\right),
$$
then $\mathbf{x}_{D}=\mathbf{0}$ whenever $D$ is a multiple of $2^{1+\max (\operatorname{deg}(f), \operatorname{deg}(g))}$.
(b) No, it is not always possible. Let $g$ be any suitable function. Then, we construct $f$ inductively. There are at most $8^{n-1}$ possibilities for $\mathbf{x}_{n-1}$, so choose $f(n)$ to be greater than the magnitude of all of them. Consequently $\mathbf{x}_{n}$ cannot be $\mathbf{0}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $f, g$ be functions from the positive integers to the integers. Vlad the impala is jumping around the integer grid. His initial position is $\mathbf{x}_{0}=(0,0)$, and for every $n \geqslant 1$, his jump is
$$
\mathbf{x}_{n}-\mathbf{x}_{n-1}=( \pm f(n), \pm g(n)) \text { or }( \pm g(n), \pm f(n))
$$
with eight possibilities in total. Is it always possible that Vlad can choose his jumps to return to his initial location $(0,0)$ infinitely many times when
(a) $f, g$ are polynomials with integer coefficients?
(b) $f, g$ are any pair of functions from the positive integers to the integers?
## Proposed by United Kingdom
|
1.
(a) Yes it is always possible. The key idea is the following: Let $b(n)$ be the number of 1 's in the binary expansion of $n=0,1,2, \ldots$.
Lemma: Given a polynomial $f$ with integer coefficients and degree at most $d$, then
$$
\sum_{k=0}^{2^{d+1}-1}(-1)^{b(k)} f(n+k)=f(n)-f(n+1)-f(n+2)+\cdots \pm f\left(n+\left(2^{d+1}-1\right)\right)=0
$$
Proof of Lemma: The result is clear for $d=0$. For $d \geqslant 1$, we have
$$
\sum_{k=0}^{2^{d+1}-1}(-1)^{b(k)} f(n+k)=\sum_{k=0}^{2^{d}-1}(-1)^{b(k)}\left[f(n+k)-f\left(n+k+2^{d}\right)\right] .
$$
So set $\tilde{f}(n)=f(n)-f\left(n+2^{d}\right)$, which is a polynomial of degree at most $d-1$. Then
$$
\sum_{k=0}^{2^{d+1}-1}(-1)^{b(k)} f(n+k)=\sum_{k=0}^{2^{d}-1} \tilde{f}(n+k)=0
$$
by induction, completing the proof of the lemma.
In particular, if we take
$$
\mathbf{x}_{n}-\mathbf{x}_{n-1}=\left((-1)^{b(n)} f(n),(-1)^{b(n)} g(n)\right),
$$
then $\mathbf{x}_{D}=\mathbf{0}$ whenever $D$ is a multiple of $2^{1+\max (\operatorname{deg}(f), \operatorname{deg}(g))}$.
(b) No, it is not always possible. Let $g$ be any suitable function. Then, we construct $f$ inductively. There are at most $8^{n-1}$ possibilities for $\mathbf{x}_{n-1}$, so choose $f(n)$ to be greater than the magnitude of all of them. Consequently $\mathbf{x}_{n}$ cannot be $\mathbf{0}$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nA4.",
"solution_match": "\n## Solution"
}
|
153677a8-db7b-513b-8cdb-7edfc6d686a1
| 606,050
|
Let $f, g$ be functions from the positive integers to the integers. Vlad the impala is jumping around the integer grid. His initial position is $\mathbf{x}_{0}=(0,0)$, and for every $n \geqslant 1$, his jump is
$$
\mathbf{x}_{n}-\mathbf{x}_{n-1}=( \pm f(n), \pm g(n)) \text { or }( \pm g(n), \pm f(n))
$$
with eight possibilities in total. Is it always possible that Vlad can choose his jumps to return to his initial location $(0,0)$ infinitely many times when
(a) $f, g$ are polynomials with integer coefficients?
(b) $f, g$ are any pair of functions from the positive integers to the integers?
## Proposed by United Kingdom
|
2.
(a) Given a polynomial $f$ of degree at most $d$ and integers $n, r$, we claim that
$$
\sum_{k=0}^{2^{d+1}-1} \varepsilon_{k} f\left(2^{d} n+r+k\right)=0
$$
for some choice of $\varepsilon_{0}, \varepsilon_{1}, \ldots, \varepsilon_{2^{d+1}-1} \in\{-1,1\}$. (Which are allowed to depend on $d$ and f.)
We proceed by induction on $d$, the case $d=0$ being immediate. For the inductive step we define the polynomial $g(n)=f(2 n+r+1)-f(2 n+r)$ which is a polynomial of degree at most $d-1$. Then
$$
\sum_{k=0}^{2^{d}-1} \varepsilon_{k} g\left(2^{d-1} n+k\right)=0
$$
for some choice of the $\varepsilon_{k}$ 's giving
$$
\sum_{k=0}^{2^{d+1}-1} \varepsilon_{k}^{\prime} f\left(2^{d} n+r+k\right)=0
$$
where $\varepsilon_{2 k}^{\prime}=-\varepsilon_{k}$ and $\varepsilon_{2 k+1}^{\prime}=\varepsilon_{k}$. This completes the proof of the claim.
Now the proof can be completed as in Solution 1.
(b) Apart from magnitude arguments, one could also use modulo arguments. For example, taking $f(0), g(0)$ to be odd and $f(n), g(n)$ to be even for every $n \geqslant 1$ works.
## Comments.
(1) We propose to omit part (b) as it is easy and furthermore it suggests that the answer to (a) is most likely affirmative.
(2) Giving a precise self-contained characterisation of $b(n)$ in Solution 1 is not necessary for the lemma. It could instead be phrased as:
There exists a sequence $\beta(k) \in\{-1,+1\}^{\mathbb{N}}$ such that $\sum \beta(k) f(n+k)=0$.
Then, one constructs $\beta(\cdot)$ inductively as part of the proof via $\beta\left(k+2^{d}\right)=-\beta(k)$ for $k<2^{d}$, which coincides with the original definition, ie $\beta(\cdot)=(-1)^{b(\cdot)}$.
(3) The sequence of signs in both solutions are essentially the same. (Either all signs exactly the same or all signs different.)
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $f, g$ be functions from the positive integers to the integers. Vlad the impala is jumping around the integer grid. His initial position is $\mathbf{x}_{0}=(0,0)$, and for every $n \geqslant 1$, his jump is
$$
\mathbf{x}_{n}-\mathbf{x}_{n-1}=( \pm f(n), \pm g(n)) \text { or }( \pm g(n), \pm f(n))
$$
with eight possibilities in total. Is it always possible that Vlad can choose his jumps to return to his initial location $(0,0)$ infinitely many times when
(a) $f, g$ are polynomials with integer coefficients?
(b) $f, g$ are any pair of functions from the positive integers to the integers?
## Proposed by United Kingdom
|
2.
(a) Given a polynomial $f$ of degree at most $d$ and integers $n, r$, we claim that
$$
\sum_{k=0}^{2^{d+1}-1} \varepsilon_{k} f\left(2^{d} n+r+k\right)=0
$$
for some choice of $\varepsilon_{0}, \varepsilon_{1}, \ldots, \varepsilon_{2^{d+1}-1} \in\{-1,1\}$. (Which are allowed to depend on $d$ and f.)
We proceed by induction on $d$, the case $d=0$ being immediate. For the inductive step we define the polynomial $g(n)=f(2 n+r+1)-f(2 n+r)$ which is a polynomial of degree at most $d-1$. Then
$$
\sum_{k=0}^{2^{d}-1} \varepsilon_{k} g\left(2^{d-1} n+k\right)=0
$$
for some choice of the $\varepsilon_{k}$ 's giving
$$
\sum_{k=0}^{2^{d+1}-1} \varepsilon_{k}^{\prime} f\left(2^{d} n+r+k\right)=0
$$
where $\varepsilon_{2 k}^{\prime}=-\varepsilon_{k}$ and $\varepsilon_{2 k+1}^{\prime}=\varepsilon_{k}$. This completes the proof of the claim.
Now the proof can be completed as in Solution 1.
(b) Apart from magnitude arguments, one could also use modulo arguments. For example, taking $f(0), g(0)$ to be odd and $f(n), g(n)$ to be even for every $n \geqslant 1$ works.
## Comments.
(1) We propose to omit part (b) as it is easy and furthermore it suggests that the answer to (a) is most likely affirmative.
(2) Giving a precise self-contained characterisation of $b(n)$ in Solution 1 is not necessary for the lemma. It could instead be phrased as:
There exists a sequence $\beta(k) \in\{-1,+1\}^{\mathbb{N}}$ such that $\sum \beta(k) f(n+k)=0$.
Then, one constructs $\beta(\cdot)$ inductively as part of the proof via $\beta\left(k+2^{d}\right)=-\beta(k)$ for $k<2^{d}$, which coincides with the original definition, ie $\beta(\cdot)=(-1)^{b(\cdot)}$.
(3) The sequence of signs in both solutions are essentially the same. (Either all signs exactly the same or all signs different.)
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nA4.",
"solution_match": "\n## Solution"
}
|
153677a8-db7b-513b-8cdb-7edfc6d686a1
| 606,050
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f(x y)=f(x) f(y)+f(f(x+y))
$$
holds for all $x, y \in \mathbb{R}$.
## Proposed by Romania
|
2 (Sketch). One can prove directly Claims 3 and 4 without the use of Claims 1 and 2. To prove Claim 3 we can make use of $P(x+1, y-1)$ which together with $P(x, y)$ and (1) gives
$$
f(x y+y-x)-c f(x y)=f(y)-c f(x) .
$$
Assuming $c=-1$, then (1) and (3) give that $f(x+2)=f(x)$ for every $x \in \mathbb{R}$. It follows that $f(x+2 n)=f(x)$ for every $x \in \mathbb{R}$ and every $n \in \mathbb{Z}$. Now with similar ideas as in the proof of Claim 1, it can be shown that for every $u, v \in \mathbb{R}$ there is $n \in \mathbb{N}$ large enough such that $u=x y+x-y+2 n$ and $v=x y+y-x$. Then using (3) we can get
$$
f(u)=f(x y+x-y+2 n)=f(x y+x-y)=f(x y+y-x)=f(v) .
$$
So $f$ is constant and it must be identically equal to $1 / 2$ which leads to a contradiction.
Now using (3) with $x=y$ and assuming $c \neq 1$ we get $f\left(x^{2}\right)=f(x)$. So $f$ is even. This eventually leads to $f(n)=1 /(1-c)=a=b$ for every integer $n$. Now $P(0,0)$ gives $a=a^{2}+f(a)$ and $P(a,-a)$ gives $f\left(-a^{2}\right)=f(a) f(-a)+f(a)$. Since $f$ is even we eventually get $f(a)=0$ which gives $a=0$ or $a=1$ both contraidicting the facts that $a \neq 0$ and $b \neq 1$.
So $c=1$ and using (1) and (3) one can eventually get $a=-1$. The solution can then finish in the same way as in Solution 1.
## COMBINATORICS
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f(x y)=f(x) f(y)+f(f(x+y))
$$
holds for all $x, y \in \mathbb{R}$.
## Proposed by Romania
|
2 (Sketch). One can prove directly Claims 3 and 4 without the use of Claims 1 and 2. To prove Claim 3 we can make use of $P(x+1, y-1)$ which together with $P(x, y)$ and (1) gives
$$
f(x y+y-x)-c f(x y)=f(y)-c f(x) .
$$
Assuming $c=-1$, then (1) and (3) give that $f(x+2)=f(x)$ for every $x \in \mathbb{R}$. It follows that $f(x+2 n)=f(x)$ for every $x \in \mathbb{R}$ and every $n \in \mathbb{Z}$. Now with similar ideas as in the proof of Claim 1, it can be shown that for every $u, v \in \mathbb{R}$ there is $n \in \mathbb{N}$ large enough such that $u=x y+x-y+2 n$ and $v=x y+y-x$. Then using (3) we can get
$$
f(u)=f(x y+x-y+2 n)=f(x y+x-y)=f(x y+y-x)=f(v) .
$$
So $f$ is constant and it must be identically equal to $1 / 2$ which leads to a contradiction.
Now using (3) with $x=y$ and assuming $c \neq 1$ we get $f\left(x^{2}\right)=f(x)$. So $f$ is even. This eventually leads to $f(n)=1 /(1-c)=a=b$ for every integer $n$. Now $P(0,0)$ gives $a=a^{2}+f(a)$ and $P(a,-a)$ gives $f\left(-a^{2}\right)=f(a) f(-a)+f(a)$. Since $f$ is even we eventually get $f(a)=0$ which gives $a=0$ or $a=1$ both contraidicting the facts that $a \neq 0$ and $b \neq 1$.
So $c=1$ and using (1) and (3) one can eventually get $a=-1$. The solution can then finish in the same way as in Solution 1.
## COMBINATORICS
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nA6.",
"solution_match": "\nSolution"
}
|
c20ca433-9f8e-5102-8f44-7c0071be6282
| 606,085
|
Let $\mathcal{A}_{n}$ be the set of $n$-tuples $x=\left(x_{1}, \ldots, x_{n}\right)$ with $x_{i} \in\{0,1,2\}$. A triple $x, y, z$ of distinct elements of $\mathcal{A}_{n}$ is called good if there is some $i$ such that $\left\{x_{i}, y_{i}, z_{i}\right\}=\{0,1,2\}$. A subset $A$ of $\mathcal{A}_{n}$ is called good if every three distinct elements of $A$ form a good triple.
Prove that every good subset of $\mathcal{A}_{n}$ has at most $2\left(\frac{3}{2}\right)^{n}$ elements.
## Proposed by Greece
|
1. We proceed by induction on $n$, the case $n=1$ being trivial. Let
$$
A_{0}=\left\{\left(x_{1}, \ldots, x_{n}\right) \in A: x_{n} \neq 0\right\}
$$
and define $A_{1}$ and $A_{2}$ similarly.
Since $A$ is good and $A_{0}$ is a subset of $A$, then $A_{0}$ is also good. Therefore, any three of its elements have a coordinate that differs. This coordinate cannot be the last one since 0 cannot appear as a last coordinate. This means that the set $A_{0}^{\prime}$ obtained from $A_{0}$ by deleting the last coordinate from each of its elements is a good subset of $\mathcal{A}_{n-1}$.
Moreover, if $\left|A_{0}\right| \geqslant 3$ then $\left|A_{0}^{\prime}\right|=\left|A_{0}\right|$. Indeed, if otherwise, then there is an element $a \in A_{0}^{\prime}$ such that $x, y \in A_{0}$, where $x$ and $y$ are obtained from $a$ by adding to it the digits 1 and 2 respectively as the $n$-th coordinate. But then if $z$ is any other element of $A_{0}$ then $x, y, z$ do not form a good triple, a contradiction. So by the inductive hypothesis
$$
\left|A_{0}\right| \leqslant \max \left\{2,\left|A_{0}^{\prime}\right|\right\} \leqslant 2\left(\frac{3}{2}\right)^{n-1}
$$
Similarly,
$$
\left|A_{2}\right|,\left|A_{3}\right| \leqslant 2\left(\frac{3}{2}\right)^{n-1}
$$
On the other hand, each element of $A$ appears in exactly two of $A_{0}, A_{1}, A_{2}$. As a result,
$$
|A|=\frac{1}{2}\left(\left|A_{0}\right|+\left|A_{1}\right|+\left|A_{2}\right|\right) \leqslant 2\left(\frac{3}{2}\right)^{n}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $\mathcal{A}_{n}$ be the set of $n$-tuples $x=\left(x_{1}, \ldots, x_{n}\right)$ with $x_{i} \in\{0,1,2\}$. A triple $x, y, z$ of distinct elements of $\mathcal{A}_{n}$ is called good if there is some $i$ such that $\left\{x_{i}, y_{i}, z_{i}\right\}=\{0,1,2\}$. A subset $A$ of $\mathcal{A}_{n}$ is called good if every three distinct elements of $A$ form a good triple.
Prove that every good subset of $\mathcal{A}_{n}$ has at most $2\left(\frac{3}{2}\right)^{n}$ elements.
## Proposed by Greece
|
1. We proceed by induction on $n$, the case $n=1$ being trivial. Let
$$
A_{0}=\left\{\left(x_{1}, \ldots, x_{n}\right) \in A: x_{n} \neq 0\right\}
$$
and define $A_{1}$ and $A_{2}$ similarly.
Since $A$ is good and $A_{0}$ is a subset of $A$, then $A_{0}$ is also good. Therefore, any three of its elements have a coordinate that differs. This coordinate cannot be the last one since 0 cannot appear as a last coordinate. This means that the set $A_{0}^{\prime}$ obtained from $A_{0}$ by deleting the last coordinate from each of its elements is a good subset of $\mathcal{A}_{n-1}$.
Moreover, if $\left|A_{0}\right| \geqslant 3$ then $\left|A_{0}^{\prime}\right|=\left|A_{0}\right|$. Indeed, if otherwise, then there is an element $a \in A_{0}^{\prime}$ such that $x, y \in A_{0}$, where $x$ and $y$ are obtained from $a$ by adding to it the digits 1 and 2 respectively as the $n$-th coordinate. But then if $z$ is any other element of $A_{0}$ then $x, y, z$ do not form a good triple, a contradiction. So by the inductive hypothesis
$$
\left|A_{0}\right| \leqslant \max \left\{2,\left|A_{0}^{\prime}\right|\right\} \leqslant 2\left(\frac{3}{2}\right)^{n-1}
$$
Similarly,
$$
\left|A_{2}\right|,\left|A_{3}\right| \leqslant 2\left(\frac{3}{2}\right)^{n-1}
$$
On the other hand, each element of $A$ appears in exactly two of $A_{0}, A_{1}, A_{2}$. As a result,
$$
|A|=\frac{1}{2}\left(\left|A_{0}\right|+\left|A_{1}\right|+\left|A_{2}\right|\right) \leqslant 2\left(\frac{3}{2}\right)^{n}
$$
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nC1.",
"solution_match": "\nSolution"
}
|
6f56bcec-c1bb-56cc-a295-9e98d418f65f
| 606,106
|
Let $\mathcal{A}_{n}$ be the set of $n$-tuples $x=\left(x_{1}, \ldots, x_{n}\right)$ with $x_{i} \in\{0,1,2\}$. A triple $x, y, z$ of distinct elements of $\mathcal{A}_{n}$ is called good if there is some $i$ such that $\left\{x_{i}, y_{i}, z_{i}\right\}=\{0,1,2\}$. A subset $A$ of $\mathcal{A}_{n}$ is called good if every three distinct elements of $A$ form a good triple.
Prove that every good subset of $\mathcal{A}_{n}$ has at most $2\left(\frac{3}{2}\right)^{n}$ elements.
## Proposed by Greece
|
2. Let
$$
B=\left\{x=\left(x_{1}, \ldots, x_{n}\right) \in \mathcal{A}_{n}: x_{i} \in\{0,1\}\right\}
$$
Let $A$ be a good subset of $\mathcal{A}_{n}$ and define $f: A \times B \rightarrow \mathcal{A}_{n}$ by $f(a, b)=a+b=\left(a_{1}+b_{1}, \ldots, a_{n}+b_{n}\right)$ where the addition is done modulo 3 .
We claim that if $(a, b),\left(a^{\prime}, b^{\prime}\right)$ and $\left(a^{\prime \prime}, b^{\prime \prime}\right)$ are distinct, then $f(a, b), f\left(a^{\prime}, b^{\prime}\right)$ and $f\left(a^{\prime \prime}, b^{\prime \prime}\right)$ cannot all be equal. Indeed assume $f(a, b)=f\left(a^{\prime}, b^{\prime}\right)=f\left(a^{\prime \prime}, b^{\prime \prime}\right)=\left(x_{1}, \ldots, x_{n}\right)$. So for each $i$ we have $a_{i}+b_{i}=a_{i}^{\prime}+b_{i}^{\prime}=a_{i}^{\prime \prime}+b_{i}^{\prime \prime}=x_{i}$. But then $a_{i}=x_{i}-b_{i} \in\left\{x_{i}, x_{i}-1\right\}$ and similarly $a_{i}^{\prime}, a_{i}^{\prime \prime} \in\left\{x_{i}, x_{i}-1\right\}$. So $\left\{a_{i}, a_{i}^{\prime}, a_{i}^{\prime \prime}\right\} \neq\{0,1,2\}$. Since this holds for each $i$ then $A$ cannot be a good set, contradiction.
Therefore $|A||B| \leqslant 2\left|\mathcal{A}_{n}\right|$ which gives $|A| \leqslant 2\left(\frac{3}{2}\right)^{n}$ as required.
Remark. Writing $f(n)$ for the maximal possible size of a good set, we proved that $f(n) \leqslant$ $2\left(\frac{3}{2}\right)^{n}$. We do not know the best possible asymptotic for $f(n)$ but we offer a corresponding lower bound which can increase the difficulty of the proposed problem.
We pick each element of $\mathcal{A}_{n}$ independently with probability $p$ to form a set $A$. For each bad triple $x, y, z$ of elements of $A$ we arbitrarily remove one of the elements to end up with a good set $B$. Note that there are at most $21^{n}$ bad triples $(x, y, z)$ since for coordinate $i$, out of the 27 triples of the form $\left(x_{i}, y_{i}, z_{i}\right)$, only 6 of them will make the triple $(x, y, z)$ a good triple. (Actually there are less than $21^{n}$ triples since this counts also triples where two or more of the $n$-tuples are the same.) So we get that
$$
\mathbb{E}|B| \geqslant p \cdot 3^{n}-p^{3} \cdot 21^{n} .
$$
Taking $p=\frac{1}{\sqrt{3 \cdot 7^{n}}}$ we get
$$
\mathbb{E}|B| \geqslant \frac{1}{\sqrt{3}}\left(\frac{9}{7}\right)^{n / 2}-\frac{1}{3 \sqrt{3}}\left(\frac{9}{7}\right)^{n / 2}=\frac{2}{3 \sqrt{3}}\left(\frac{9}{7}\right)^{n / 2}=C \alpha^{n}
$$
where $\alpha=1.13389 \ldots$ and $C=0.3849 \ldots$. It follows that there is a good set of size at least $C \alpha^{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $\mathcal{A}_{n}$ be the set of $n$-tuples $x=\left(x_{1}, \ldots, x_{n}\right)$ with $x_{i} \in\{0,1,2\}$. A triple $x, y, z$ of distinct elements of $\mathcal{A}_{n}$ is called good if there is some $i$ such that $\left\{x_{i}, y_{i}, z_{i}\right\}=\{0,1,2\}$. A subset $A$ of $\mathcal{A}_{n}$ is called good if every three distinct elements of $A$ form a good triple.
Prove that every good subset of $\mathcal{A}_{n}$ has at most $2\left(\frac{3}{2}\right)^{n}$ elements.
## Proposed by Greece
|
2. Let
$$
B=\left\{x=\left(x_{1}, \ldots, x_{n}\right) \in \mathcal{A}_{n}: x_{i} \in\{0,1\}\right\}
$$
Let $A$ be a good subset of $\mathcal{A}_{n}$ and define $f: A \times B \rightarrow \mathcal{A}_{n}$ by $f(a, b)=a+b=\left(a_{1}+b_{1}, \ldots, a_{n}+b_{n}\right)$ where the addition is done modulo 3 .
We claim that if $(a, b),\left(a^{\prime}, b^{\prime}\right)$ and $\left(a^{\prime \prime}, b^{\prime \prime}\right)$ are distinct, then $f(a, b), f\left(a^{\prime}, b^{\prime}\right)$ and $f\left(a^{\prime \prime}, b^{\prime \prime}\right)$ cannot all be equal. Indeed assume $f(a, b)=f\left(a^{\prime}, b^{\prime}\right)=f\left(a^{\prime \prime}, b^{\prime \prime}\right)=\left(x_{1}, \ldots, x_{n}\right)$. So for each $i$ we have $a_{i}+b_{i}=a_{i}^{\prime}+b_{i}^{\prime}=a_{i}^{\prime \prime}+b_{i}^{\prime \prime}=x_{i}$. But then $a_{i}=x_{i}-b_{i} \in\left\{x_{i}, x_{i}-1\right\}$ and similarly $a_{i}^{\prime}, a_{i}^{\prime \prime} \in\left\{x_{i}, x_{i}-1\right\}$. So $\left\{a_{i}, a_{i}^{\prime}, a_{i}^{\prime \prime}\right\} \neq\{0,1,2\}$. Since this holds for each $i$ then $A$ cannot be a good set, contradiction.
Therefore $|A||B| \leqslant 2\left|\mathcal{A}_{n}\right|$ which gives $|A| \leqslant 2\left(\frac{3}{2}\right)^{n}$ as required.
Remark. Writing $f(n)$ for the maximal possible size of a good set, we proved that $f(n) \leqslant$ $2\left(\frac{3}{2}\right)^{n}$. We do not know the best possible asymptotic for $f(n)$ but we offer a corresponding lower bound which can increase the difficulty of the proposed problem.
We pick each element of $\mathcal{A}_{n}$ independently with probability $p$ to form a set $A$. For each bad triple $x, y, z$ of elements of $A$ we arbitrarily remove one of the elements to end up with a good set $B$. Note that there are at most $21^{n}$ bad triples $(x, y, z)$ since for coordinate $i$, out of the 27 triples of the form $\left(x_{i}, y_{i}, z_{i}\right)$, only 6 of them will make the triple $(x, y, z)$ a good triple. (Actually there are less than $21^{n}$ triples since this counts also triples where two or more of the $n$-tuples are the same.) So we get that
$$
\mathbb{E}|B| \geqslant p \cdot 3^{n}-p^{3} \cdot 21^{n} .
$$
Taking $p=\frac{1}{\sqrt{3 \cdot 7^{n}}}$ we get
$$
\mathbb{E}|B| \geqslant \frac{1}{\sqrt{3}}\left(\frac{9}{7}\right)^{n / 2}-\frac{1}{3 \sqrt{3}}\left(\frac{9}{7}\right)^{n / 2}=\frac{2}{3 \sqrt{3}}\left(\frac{9}{7}\right)^{n / 2}=C \alpha^{n}
$$
where $\alpha=1.13389 \ldots$ and $C=0.3849 \ldots$. It follows that there is a good set of size at least $C \alpha^{n}$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nC1.",
"solution_match": "\nSolution"
}
|
6f56bcec-c1bb-56cc-a295-9e98d418f65f
| 606,106
|
There is a population $P$ of 10000 bacteria, some of which are friends (friendship is mutual), so that each bacterion has at least one friend and if we wish to assign to each bacterion a coloured membrane so that no two friends have the same colour, then there is a way to do it with 2021 colours, but not with 2020 or less.
Two friends $A$ and $B$ can decide to merge in which case they become a single bacterion whose friends are precisely the union of friends of $A$ and $B$. (Merging is not allowed if $A$ and $B$ are not friends.) It turns out that no matter how we perform one merge or two consecutive merges, in the resulting population it would be possible to assign 2020 colours or less so that no two friends have the same colour. Is it true that in any such population $P$ every bacterium has at least 2021 friends?
## Proposed by Bulgaria
|
1. The answer is affirmative.
We will use the terminology of graph theory. Here the vertices of our main graph $G$ are the bacteria and there is an edge between two precisely when they are friends. The degree $d(v)$ of a vertex $v$ of $G$ is the number of neighbours of $v$. The minimum degree $\delta(G)$ of $G$ is the smallest amongst all $d(v)$ for vertices $v$ of $G$. The chromatic number $\chi(G)$ of $G$ is the number of colours needed in order to colour the vertices such that neighbouring vertices get distinct colours.
It suffices to establish the following:
Claim. Let $k$ be a positive integer and let $G$ be a graph on $n>k$ vertices with $\delta(G) \geqslant 1$ and $\chi(G)=k$. Suppose that merging one pair or two pairs of vertices results in a graph $G^{\prime}$ with $\chi\left(G^{\prime}\right) \leqslant k-1$. Then $\delta(G) \geqslant k$.
We establish this in a series of claims.
Claim 1. $\delta(G) \geqslant k-1$.
Proof. Suppose for contradiction that we have a vertex $v$ of degree $r \leqslant k-2$ and denote its neighbours by $v_{1}, \ldots, v_{r}$. (Note that, by assumption, $v$ has at least one neighbour.)
Suppose we merge $v$ with $v_{i}$. We denote the new vertex by $v_{0}$, and we colour the obtained graph in $k-1$ colours. Note that at most $r \leqslant k-2$ colours can appear in the set $S_{1}=$ $\left\{v_{0}, v_{1}, \ldots, v_{i-1}, v_{i+1}, \ldots, v_{r}\right\}$. Therefore we can get a $(k-1)$-colouring of $G$ by assigning the colour of $v_{0}$ to $v_{i}$ and an unused colour (from the $k-1$ available) to $v$, thus contradicting the assumption that $\chi(G)=k$.
So from now on we may assume that there is a vertex $v$ of $G$ with $\operatorname{deg}(v)=k-1$, as otherwise the proof is complete. We denote its neighbours by $v_{1}, \ldots, v_{k-1}$.
Claim 2. The set of neighbours of $v$ induces a complete graph.
Proof of Claim 2. Suppose $v_{i} v_{j} \notin E(G)$. Merge $v$ with $v_{i}$, giving a next vertex $w$, and then merge $w$ with $v_{j}$, denoting the newest vertex by $v_{0}$. Then colour the resulting graph in $k-1$ colours. Note that at most $k-2$ colours can appear in the set $S_{2}=\left\{v_{0}, v_{1}, \ldots, v_{k-1}\right\} \backslash\left\{v_{i}, v_{j}\right\}$. So we can get a $(k-1)$-colouring of $G$ by assigning the colour of $v_{0}$ to $v_{i}$ and $v_{j}$ and an unused colour (from the $k-1$ available) to $v$, thus contradicting the assumption that $\chi(G)=k$.
Claim 3. For every edge $u w$, both $u$ and $w$ belong in the set $\left\{v, v_{1}, \ldots, v_{k-1}\right\}$.
Proof. Otherwise merge $u$ and $w$ and call the new vertex $z$. If $u, w \notin\left\{v, v_{1}, \ldots, v_{k-1}\right\}$ then by Claim 2 the resulting graph contains a complete graph on $\left\{v, v_{1}, \ldots, v_{k-1}\right\}$ and so its chromatic number is at least $k$, a contradiction. If one of $u, w$ belongs in the set $\left\{v, v_{1}, \ldots, v_{k-1}\right\}$, say
$u=v_{i}$, then the resulting graph contains a complete graph on $\left\{v, v_{1}, \ldots, v_{k-1}, z\right\} \backslash\left\{v_{i}\right\}$. This is again a contradiction.
From Claim 3 we see that $G$ consists of a complete set on $k$ vertices together with $n-k>0$ isolated vertices. This is a contradiction as $\delta(G) \geqslant 1$.
Remark. We do not know if the result is best possible or whether it can be improved to show $\delta(G) \geqslant 2022$.
## GEOMETRY
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There is a population $P$ of 10000 bacteria, some of which are friends (friendship is mutual), so that each bacterion has at least one friend and if we wish to assign to each bacterion a coloured membrane so that no two friends have the same colour, then there is a way to do it with 2021 colours, but not with 2020 or less.
Two friends $A$ and $B$ can decide to merge in which case they become a single bacterion whose friends are precisely the union of friends of $A$ and $B$. (Merging is not allowed if $A$ and $B$ are not friends.) It turns out that no matter how we perform one merge or two consecutive merges, in the resulting population it would be possible to assign 2020 colours or less so that no two friends have the same colour. Is it true that in any such population $P$ every bacterium has at least 2021 friends?
## Proposed by Bulgaria
|
1. The answer is affirmative.
We will use the terminology of graph theory. Here the vertices of our main graph $G$ are the bacteria and there is an edge between two precisely when they are friends. The degree $d(v)$ of a vertex $v$ of $G$ is the number of neighbours of $v$. The minimum degree $\delta(G)$ of $G$ is the smallest amongst all $d(v)$ for vertices $v$ of $G$. The chromatic number $\chi(G)$ of $G$ is the number of colours needed in order to colour the vertices such that neighbouring vertices get distinct colours.
It suffices to establish the following:
Claim. Let $k$ be a positive integer and let $G$ be a graph on $n>k$ vertices with $\delta(G) \geqslant 1$ and $\chi(G)=k$. Suppose that merging one pair or two pairs of vertices results in a graph $G^{\prime}$ with $\chi\left(G^{\prime}\right) \leqslant k-1$. Then $\delta(G) \geqslant k$.
We establish this in a series of claims.
Claim 1. $\delta(G) \geqslant k-1$.
Proof. Suppose for contradiction that we have a vertex $v$ of degree $r \leqslant k-2$ and denote its neighbours by $v_{1}, \ldots, v_{r}$. (Note that, by assumption, $v$ has at least one neighbour.)
Suppose we merge $v$ with $v_{i}$. We denote the new vertex by $v_{0}$, and we colour the obtained graph in $k-1$ colours. Note that at most $r \leqslant k-2$ colours can appear in the set $S_{1}=$ $\left\{v_{0}, v_{1}, \ldots, v_{i-1}, v_{i+1}, \ldots, v_{r}\right\}$. Therefore we can get a $(k-1)$-colouring of $G$ by assigning the colour of $v_{0}$ to $v_{i}$ and an unused colour (from the $k-1$ available) to $v$, thus contradicting the assumption that $\chi(G)=k$.
So from now on we may assume that there is a vertex $v$ of $G$ with $\operatorname{deg}(v)=k-1$, as otherwise the proof is complete. We denote its neighbours by $v_{1}, \ldots, v_{k-1}$.
Claim 2. The set of neighbours of $v$ induces a complete graph.
Proof of Claim 2. Suppose $v_{i} v_{j} \notin E(G)$. Merge $v$ with $v_{i}$, giving a next vertex $w$, and then merge $w$ with $v_{j}$, denoting the newest vertex by $v_{0}$. Then colour the resulting graph in $k-1$ colours. Note that at most $k-2$ colours can appear in the set $S_{2}=\left\{v_{0}, v_{1}, \ldots, v_{k-1}\right\} \backslash\left\{v_{i}, v_{j}\right\}$. So we can get a $(k-1)$-colouring of $G$ by assigning the colour of $v_{0}$ to $v_{i}$ and $v_{j}$ and an unused colour (from the $k-1$ available) to $v$, thus contradicting the assumption that $\chi(G)=k$.
Claim 3. For every edge $u w$, both $u$ and $w$ belong in the set $\left\{v, v_{1}, \ldots, v_{k-1}\right\}$.
Proof. Otherwise merge $u$ and $w$ and call the new vertex $z$. If $u, w \notin\left\{v, v_{1}, \ldots, v_{k-1}\right\}$ then by Claim 2 the resulting graph contains a complete graph on $\left\{v, v_{1}, \ldots, v_{k-1}\right\}$ and so its chromatic number is at least $k$, a contradiction. If one of $u, w$ belongs in the set $\left\{v, v_{1}, \ldots, v_{k-1}\right\}$, say
$u=v_{i}$, then the resulting graph contains a complete graph on $\left\{v, v_{1}, \ldots, v_{k-1}, z\right\} \backslash\left\{v_{i}\right\}$. This is again a contradiction.
From Claim 3 we see that $G$ consists of a complete set on $k$ vertices together with $n-k>0$ isolated vertices. This is a contradiction as $\delta(G) \geqslant 1$.
Remark. We do not know if the result is best possible or whether it can be improved to show $\delta(G) \geqslant 2022$.
## GEOMETRY
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nC6.",
"solution_match": "\nSolution"
}
|
44991854-8bef-5e74-b29d-1a4aef278b49
| 606,193
|
Let $A B C$ be a triangle with $A B<A C<B C$. On the side $B C$ we consider points $D$ and $E$ such that $B A=B D$ and $C E=C A$. Let $K$ be the circumcenter of triangle $A D E$ and let $F, G$ be the points of intersection of the lines $A D, K C$ and $A E, K B$ respectively. Let $\omega_{1}$ be the circumcircle of triangle $K D E, \omega_{2}$ the circle with center $F$ and radius $F E$, and $c_{3}$ the circle with center $G$ and radius $G D$.
Prove that $\omega_{1}, \omega_{2}$ and $\omega_{3}$ pass through the same point and that this point of intersection lies on the line $A K$.
Proposed by Greece
|
1. Since the triangles $B A D, K A D$ and $K D E$ are isosceles, then $\angle B A D=\angle B D A$ and $\angle K A D=\angle K D A$ and $\angle K D E=\angle K E D$. Therefore,
$$
\angle B A K=\angle B A D-\angle K A D=\angle B D A-\angle K D A=\angle K D E=\angle K E D=180^{\circ}-\angle B E K .
$$
So the points $B, E, K, A$ are concyclic. Similarly the points $C, D, K, A$ are also concyclic.
Let $M, N$ be the midpoints of $A D$ and $A E$ respectively. Since the triangle $A C E$ is isosceles, the perpendicular bisector of $A E$, say $\varepsilon_{1}$, passes through the points $C, K$ and $N$. Similarly, the perpendicular bisector of $A D$, say $\varepsilon_{2}$, passes through the points $B, K$ and $M$. Therefore the points $F, G$ lie on $\varepsilon_{1}$ and $\varepsilon_{2}$ respectively. Thus, using also the fact that $A K D C$ is a cyclic quadrilteral we get that
$$
\angle F D C=\angle A D C=\angle A K C=\angle E K C=\angle E K F .
$$
So the point $F$ lies on the circle $\omega_{1}$. Similarly $G$ also lies on $\omega_{1}$.
Let $I$ be the point of intersection of the line $A K$ with $\omega_{1}$. The triangles $A K F$ and $E K F$ are equal, so $\angle K A F=\angle K E F$. Since also $K, E, F, I$ all belong on $\omega_{1}$ then
$$
\angle K A F=\angle K E F=\angle F I K .
$$
It follows that $F I=F A=F E$. Therefore $I$ lies on $\omega_{2}$ as well. Similarly it also lies on $\omega_{3}$. So the circles $\omega_{1}, \omega_{2}, \omega_{3}$ all pass through $I$ which lies on line $A K$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B<A C<B C$. On the side $B C$ we consider points $D$ and $E$ such that $B A=B D$ and $C E=C A$. Let $K$ be the circumcenter of triangle $A D E$ and let $F, G$ be the points of intersection of the lines $A D, K C$ and $A E, K B$ respectively. Let $\omega_{1}$ be the circumcircle of triangle $K D E, \omega_{2}$ the circle with center $F$ and radius $F E$, and $c_{3}$ the circle with center $G$ and radius $G D$.
Prove that $\omega_{1}, \omega_{2}$ and $\omega_{3}$ pass through the same point and that this point of intersection lies on the line $A K$.
Proposed by Greece
|
1. Since the triangles $B A D, K A D$ and $K D E$ are isosceles, then $\angle B A D=\angle B D A$ and $\angle K A D=\angle K D A$ and $\angle K D E=\angle K E D$. Therefore,
$$
\angle B A K=\angle B A D-\angle K A D=\angle B D A-\angle K D A=\angle K D E=\angle K E D=180^{\circ}-\angle B E K .
$$
So the points $B, E, K, A$ are concyclic. Similarly the points $C, D, K, A$ are also concyclic.

Let $M, N$ be the midpoints of $A D$ and $A E$ respectively. Since the triangle $A C E$ is isosceles, the perpendicular bisector of $A E$, say $\varepsilon_{1}$, passes through the points $C, K$ and $N$. Similarly, the perpendicular bisector of $A D$, say $\varepsilon_{2}$, passes through the points $B, K$ and $M$. Therefore the points $F, G$ lie on $\varepsilon_{1}$ and $\varepsilon_{2}$ respectively. Thus, using also the fact that $A K D C$ is a cyclic quadrilteral we get that
$$
\angle F D C=\angle A D C=\angle A K C=\angle E K C=\angle E K F .
$$
So the point $F$ lies on the circle $\omega_{1}$. Similarly $G$ also lies on $\omega_{1}$.
Let $I$ be the point of intersection of the line $A K$ with $\omega_{1}$. The triangles $A K F$ and $E K F$ are equal, so $\angle K A F=\angle K E F$. Since also $K, E, F, I$ all belong on $\omega_{1}$ then
$$
\angle K A F=\angle K E F=\angle F I K .
$$
It follows that $F I=F A=F E$. Therefore $I$ lies on $\omega_{2}$ as well. Similarly it also lies on $\omega_{3}$. So the circles $\omega_{1}, \omega_{2}, \omega_{3}$ all pass through $I$ which lies on line $A K$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG1.",
"solution_match": "\nSolution"
}
|
54abb5db-fb59-538f-a6d5-28a0c7379e6d
| 606,206
|
Let $A B C$ be a triangle with $A B<A C<B C$. On the side $B C$ we consider points $D$ and $E$ such that $B A=B D$ and $C E=C A$. Let $K$ be the circumcenter of triangle $A D E$ and let $F, G$ be the points of intersection of the lines $A D, K C$ and $A E, K B$ respectively. Let $\omega_{1}$ be the circumcircle of triangle $K D E, \omega_{2}$ the circle with center $F$ and radius $F E$, and $c_{3}$ the circle with center $G$ and radius $G D$.
Prove that $\omega_{1}, \omega_{2}$ and $\omega_{3}$ pass through the same point and that this point of intersection lies on the line $A K$.
Proposed by Greece
|
2. Let $M$ the midpoint of $A D$. Then $B M$ is the perpendicular bisector of $A D$, because the triangle $A B D$ is isosceles. $K M$ is also the perpendicular bisector of $A D$, because the point $K$ is the circumcenter of the triangle $A E D$. So points $B, G, K, M$ are collinear and $G M$ is also the perpendicular bisector of $A D$. Therefore $G D=G A$ and so $A$ belongs on $\omega_{3}$. Similarly $A$ belongs on $\omega_{2}$.
Since $A D G$ is isosceles with $G A=G D$, it follows that $\angle E G D=2 \angle G A D=2 \angle E A D$. Since $A F E$ is isosceles with $F A=F E$, it follows that $\angle E F D=2 \angle F A E=2 \angle E A D$. We also have $E K D=2 \angle E A D$ as $K$ is the circumcenter of the triangle $E A D$. From the last three equalities it follows that $F, G$ belong on $\omega_{1}$.
Let $T \neq A$ be the second point of intersection of the circles $\omega_{2}, \omega_{3}$ and let $S=A T \cap F G$. Let $N$ be the midpoint of $A E$. Since $\angle A M K=\angle A N K=90^{\circ}$, then the points $A, M, K, N$ are concyclic and therefore $\angle N A K=\angle N M K$. Since $N M$ is parallel to $E D(M, N$ midpoints of $A D, A E)$ then $\angle N M K=\angle D B M=90^{\circ}-\angle M D B$. Since also $D, E, G, F$ are concyclic, then $\angle M D B=\angle F G N=90^{\circ}-\angle G A S$. From the above, it follows that $\angle N A K=\angle G A S$ and so $A, K, S$ are collinear. By definition of $S$, we get that $T$ also belongs on the same line.
Since $G F$ is the perpendicular bisector of $A T$ then $\angle G A K=\angle G A S=\angle G T S=\angle G T K$. But since $G K$ is the perpendiuclar bisector of $A D$ we also have $\angle G A K=\angle G D K$. Thus $\angle G T K=\angle G D K$ showing that $T$ belongs to $\omega_{1}$ as well.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B<A C<B C$. On the side $B C$ we consider points $D$ and $E$ such that $B A=B D$ and $C E=C A$. Let $K$ be the circumcenter of triangle $A D E$ and let $F, G$ be the points of intersection of the lines $A D, K C$ and $A E, K B$ respectively. Let $\omega_{1}$ be the circumcircle of triangle $K D E, \omega_{2}$ the circle with center $F$ and radius $F E$, and $c_{3}$ the circle with center $G$ and radius $G D$.
Prove that $\omega_{1}, \omega_{2}$ and $\omega_{3}$ pass through the same point and that this point of intersection lies on the line $A K$.
Proposed by Greece
|
2. Let $M$ the midpoint of $A D$. Then $B M$ is the perpendicular bisector of $A D$, because the triangle $A B D$ is isosceles. $K M$ is also the perpendicular bisector of $A D$, because the point $K$ is the circumcenter of the triangle $A E D$. So points $B, G, K, M$ are collinear and $G M$ is also the perpendicular bisector of $A D$. Therefore $G D=G A$ and so $A$ belongs on $\omega_{3}$. Similarly $A$ belongs on $\omega_{2}$.
Since $A D G$ is isosceles with $G A=G D$, it follows that $\angle E G D=2 \angle G A D=2 \angle E A D$. Since $A F E$ is isosceles with $F A=F E$, it follows that $\angle E F D=2 \angle F A E=2 \angle E A D$. We also have $E K D=2 \angle E A D$ as $K$ is the circumcenter of the triangle $E A D$. From the last three equalities it follows that $F, G$ belong on $\omega_{1}$.

Let $T \neq A$ be the second point of intersection of the circles $\omega_{2}, \omega_{3}$ and let $S=A T \cap F G$. Let $N$ be the midpoint of $A E$. Since $\angle A M K=\angle A N K=90^{\circ}$, then the points $A, M, K, N$ are concyclic and therefore $\angle N A K=\angle N M K$. Since $N M$ is parallel to $E D(M, N$ midpoints of $A D, A E)$ then $\angle N M K=\angle D B M=90^{\circ}-\angle M D B$. Since also $D, E, G, F$ are concyclic, then $\angle M D B=\angle F G N=90^{\circ}-\angle G A S$. From the above, it follows that $\angle N A K=\angle G A S$ and so $A, K, S$ are collinear. By definition of $S$, we get that $T$ also belongs on the same line.
Since $G F$ is the perpendicular bisector of $A T$ then $\angle G A K=\angle G A S=\angle G T S=\angle G T K$. But since $G K$ is the perpendiuclar bisector of $A D$ we also have $\angle G A K=\angle G D K$. Thus $\angle G T K=\angle G D K$ showing that $T$ belongs to $\omega_{1}$ as well.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG1.",
"solution_match": "\nSolution"
}
|
54abb5db-fb59-538f-a6d5-28a0c7379e6d
| 606,206
|
Let $A B C$ be a triangle with $A B<A C$. Let $\omega$ be a circle passing through $B, C$ and assume that $A$ is inside $\omega$. Suppose $X, Y$ lie on $\omega$ such that $\angle B X A=\angle A Y C$ and $X$ lies on the opposite side of $A B$ to $C$ while $Y$ lies on the opposite side of $A C$ to $B$.
Show that, as $X, Y$ vary on $\omega$, the line $X Y$ passes through a fixed point.
## Proposed by United Kingdom
|
1. Extend $X A$ and $Y A$ to meet $\omega$ again at $X^{\prime}$ and $Y^{\prime}$ respectively. We then have that:
$$
\angle Y^{\prime} Y C=\angle A Y C=\angle B X A=\angle B X X^{\prime} .
$$
so $B C X^{\prime} Y^{\prime}$ is an isosceles trapezium and hence $X^{\prime} Y^{\prime} \| B C$.
Let $\ell$ be the line through $A$ parallel to $B C$ and let $\ell$ intersect $\omega$ at $P, Q$ with $P$ on the opposite side of $A B$ to $C$. As $X^{\prime} Y^{\prime}\|B C\| P Q$ then
$$
\angle X A P=\angle X X^{\prime} Y^{\prime}=\angle X Y Y^{\prime}=\angle X Y A
$$
which shows that $\ell$ is tangent to the circumcircle of triangle $A X Y$. Let $X Y$ intersect $P Q$ at $Z$. By power of a point we have that
$$
Z A^{2}=Z X \cdot Z Y=Z P \cdot Z Q
$$
As $P, Q$ are independent of the positions of $X, Y$, this shows that $Z$ is fixed and hence $X Y$ passes through a fixed point.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B<A C$. Let $\omega$ be a circle passing through $B, C$ and assume that $A$ is inside $\omega$. Suppose $X, Y$ lie on $\omega$ such that $\angle B X A=\angle A Y C$ and $X$ lies on the opposite side of $A B$ to $C$ while $Y$ lies on the opposite side of $A C$ to $B$.
Show that, as $X, Y$ vary on $\omega$, the line $X Y$ passes through a fixed point.
## Proposed by United Kingdom
|
1. Extend $X A$ and $Y A$ to meet $\omega$ again at $X^{\prime}$ and $Y^{\prime}$ respectively. We then have that:
$$
\angle Y^{\prime} Y C=\angle A Y C=\angle B X A=\angle B X X^{\prime} .
$$
so $B C X^{\prime} Y^{\prime}$ is an isosceles trapezium and hence $X^{\prime} Y^{\prime} \| B C$.

Let $\ell$ be the line through $A$ parallel to $B C$ and let $\ell$ intersect $\omega$ at $P, Q$ with $P$ on the opposite side of $A B$ to $C$. As $X^{\prime} Y^{\prime}\|B C\| P Q$ then
$$
\angle X A P=\angle X X^{\prime} Y^{\prime}=\angle X Y Y^{\prime}=\angle X Y A
$$
which shows that $\ell$ is tangent to the circumcircle of triangle $A X Y$. Let $X Y$ intersect $P Q$ at $Z$. By power of a point we have that
$$
Z A^{2}=Z X \cdot Z Y=Z P \cdot Z Q
$$
As $P, Q$ are independent of the positions of $X, Y$, this shows that $Z$ is fixed and hence $X Y$ passes through a fixed point.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG3.",
"solution_match": "\nSolution"
}
|
6ce0d00a-c1dc-5d8b-9862-f0d02e9db389
| 606,236
|
Let $A B C$ be a triangle with $A B<A C$. Let $\omega$ be a circle passing through $B, C$ and assume that $A$ is inside $\omega$. Suppose $X, Y$ lie on $\omega$ such that $\angle B X A=\angle A Y C$ and $X$ lies on the opposite side of $A B$ to $C$ while $Y$ lies on the opposite side of $A C$ to $B$.
Show that, as $X, Y$ vary on $\omega$, the line $X Y$ passes through a fixed point.
## Proposed by United Kingdom
|
2. Let $B^{\prime}$ and $C^{\prime}$ be the points of intersection of the lines $A B$ and $A C$ with $\omega$ respectively and let $\omega_{1}$ be the circumcircle of the triangle $A B^{\prime} C^{\prime}$. Let $\varepsilon$ be the tangent to $\omega_{1}$ at the point $A$. Because $A B<A C$ the lines $B^{\prime} C^{\prime}$ and $\varepsilon$ intersects at a point $Z$ which is fixed and independent of $X$ and $Y$.
We have
$$
\angle Z A C^{\prime}=\angle C^{\prime} B^{\prime} A=\angle C^{\prime} B^{\prime} B=\angle C^{\prime} C B .
$$
Therefore, $\varepsilon \| B C$.
Let $X^{\prime}, Y^{\prime}$ be the points of intersection of the lines $X A, Y A$ with $\omega$ respecively. From the hypothesis we have $\angle B X X^{\prime}=\angle Y^{\prime} Y C$. Therefore
$$
\widehat{B X^{\prime}}=\widehat{Y^{\prime} C} \Longrightarrow \widehat{B C}+\widehat{C X^{\prime}}=\widehat{Y^{\prime} B}+\widehat{B C} \Longrightarrow \widehat{C X^{\prime}}=\widehat{Y^{\prime} B}
$$
and so $X^{\prime} Y^{\prime}\|B C\| \varepsilon$. Thus
$$
\angle X A Z=\angle X X^{\prime} Y^{\prime}=\angle X Y Y^{\prime}=\angle X Y A .
$$
From the last equality we have that $\varepsilon$ is also tangent to the circmucircle $\omega_{2}$ of the triangle $X A Y$. Consider now the radical centre of the circles $\omega, \omega_{1}, \omega_{2}$. This is the point of intersection of the radical axes $B^{\prime} C^{\prime}\left(\right.$ of $\omega$ and $\left.\omega_{1}\right), \varepsilon\left(\right.$ of $\omega_{1}$ and $\omega_{2}$ ) and $X Y$ (of $\omega$ and $\omega_{2}$ ).
This must be point $Z$ and therefore the variable line $X Y$ passes through the fixed point $Z$.
Remark: The condition that $A B<A C$ ensures that the point $Z$ exists (rather than being at infinity). If $X Y\|\ell\| B C$ then $A X=A Y$ and $X B=Y C$ so, as $\angle B X A=\angle A Y C$, we would have $\triangle A X B \cong \triangle A Y C$ and hence $A B=A C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B<A C$. Let $\omega$ be a circle passing through $B, C$ and assume that $A$ is inside $\omega$. Suppose $X, Y$ lie on $\omega$ such that $\angle B X A=\angle A Y C$ and $X$ lies on the opposite side of $A B$ to $C$ while $Y$ lies on the opposite side of $A C$ to $B$.
Show that, as $X, Y$ vary on $\omega$, the line $X Y$ passes through a fixed point.
## Proposed by United Kingdom
|
2. Let $B^{\prime}$ and $C^{\prime}$ be the points of intersection of the lines $A B$ and $A C$ with $\omega$ respectively and let $\omega_{1}$ be the circumcircle of the triangle $A B^{\prime} C^{\prime}$. Let $\varepsilon$ be the tangent to $\omega_{1}$ at the point $A$. Because $A B<A C$ the lines $B^{\prime} C^{\prime}$ and $\varepsilon$ intersects at a point $Z$ which is fixed and independent of $X$ and $Y$.

We have
$$
\angle Z A C^{\prime}=\angle C^{\prime} B^{\prime} A=\angle C^{\prime} B^{\prime} B=\angle C^{\prime} C B .
$$
Therefore, $\varepsilon \| B C$.
Let $X^{\prime}, Y^{\prime}$ be the points of intersection of the lines $X A, Y A$ with $\omega$ respecively. From the hypothesis we have $\angle B X X^{\prime}=\angle Y^{\prime} Y C$. Therefore
$$
\widehat{B X^{\prime}}=\widehat{Y^{\prime} C} \Longrightarrow \widehat{B C}+\widehat{C X^{\prime}}=\widehat{Y^{\prime} B}+\widehat{B C} \Longrightarrow \widehat{C X^{\prime}}=\widehat{Y^{\prime} B}
$$
and so $X^{\prime} Y^{\prime}\|B C\| \varepsilon$. Thus
$$
\angle X A Z=\angle X X^{\prime} Y^{\prime}=\angle X Y Y^{\prime}=\angle X Y A .
$$
From the last equality we have that $\varepsilon$ is also tangent to the circmucircle $\omega_{2}$ of the triangle $X A Y$. Consider now the radical centre of the circles $\omega, \omega_{1}, \omega_{2}$. This is the point of intersection of the radical axes $B^{\prime} C^{\prime}\left(\right.$ of $\omega$ and $\left.\omega_{1}\right), \varepsilon\left(\right.$ of $\omega_{1}$ and $\omega_{2}$ ) and $X Y$ (of $\omega$ and $\omega_{2}$ ).
This must be point $Z$ and therefore the variable line $X Y$ passes through the fixed point $Z$.
Remark: The condition that $A B<A C$ ensures that the point $Z$ exists (rather than being at infinity). If $X Y\|\ell\| B C$ then $A X=A Y$ and $X B=Y C$ so, as $\angle B X A=\angle A Y C$, we would have $\triangle A X B \cong \triangle A Y C$ and hence $A B=A C$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG3.",
"solution_match": "\nSolution"
}
|
6ce0d00a-c1dc-5d8b-9862-f0d02e9db389
| 606,236
|
Let $A B C$ be a right-angled triangle with $\angle B A C=90^{\circ}$. Let the height from $A$ cut its side $B C$ at $D$. Let $I, I_{B}, I_{C}$ be the incenters of triangles $A B C, A B D, A C D$ respectively. Let also $E_{B}, E_{C}$ be the excenters of $A B C$ with respect to vertices $B$ and $C$ respectively. If $K$ is the point of intersection of the circumcircles of $E_{C} I B_{I}$ and $E_{B} I C_{I}$, show that $K I$ passes through the midpoint $M$ of side $B C$.
## Proposed by Greece
|
Since $\angle E_{C} B I=90^{\circ}=I C E_{B}$, we conclude that $E_{C} B C E_{B}$ is cyclic. Moreover, we have that
$$
\angle B A I_{B}=\frac{1}{2} \angle B A D=\frac{1}{2} \widehat{C},
$$
so $A I_{B} \perp C I$. Similarly $A I_{C} \perp B I$. Therefore is the orthocenter of triangle $A I_{B} I_{C}$. It follows that
$$
\angle I I_{B} I_{C}=90^{\circ}-\angle A I_{C} I_{B}=\angle I A I_{C}=45^{\circ}-\angle I_{C} A C=45^{\circ}-\frac{1}{2} \widehat{B}=\frac{1}{2} \widehat{C}
$$
Therefore $I_{B} I_{C} C B$ is cyclic. Since $A E_{B} C I$ is also cyclic (on a circle of diameter $I E_{B}$ ) then
$$
\angle E_{C} E_{B} B=\angle A C I=\frac{1}{2} \widehat{C}=\angle I I_{B} I_{C},
$$
therefore $I_{B} I_{C} \| E_{B} E_{C}$.
From the inscribed quadrilaterals we get that
$$
\angle K I_{C} I=\angle K E_{B} I \quad \text { and } \quad K E_{C} I=\angle K I_{B} I,
$$
which implies that the triangles $K E_{C} I_{C}$ and $K I_{B} E_{B}$ are similar. So
$$
\frac{d\left(K, E_{C} I_{C}\right)}{d\left(K, E_{B} I_{B}\right)}=\frac{E_{C} I_{C}}{E_{B} I_{B}}
$$
But $I_{B} I_{C} \| E_{B} E_{C}$ and $I_{B} I_{C} C B$ is cyclic, therefore
$$
\frac{E_{C} I_{C}}{E_{B} I_{B}}=\frac{I I_{C}}{I I_{B}}=\frac{I B}{I C} .
$$
We deduce that
$$
\frac{d(K, I C)}{d(K, I B)}=\frac{I B}{I C},
$$
i.e. the distances of $K$ to the sides $I C$ and $I B$ are inversly analogous to the lenghts of these sides. So by a well known property of the median, $K$ lies on the median of the triangle IBC. (The last property of the median can be proved either by the law of sines, or by taking the distances of the distances of the median $M$ to the sides and prove by Thales theorem that $M, I, K$ are collinear.)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a right-angled triangle with $\angle B A C=90^{\circ}$. Let the height from $A$ cut its side $B C$ at $D$. Let $I, I_{B}, I_{C}$ be the incenters of triangles $A B C, A B D, A C D$ respectively. Let also $E_{B}, E_{C}$ be the excenters of $A B C$ with respect to vertices $B$ and $C$ respectively. If $K$ is the point of intersection of the circumcircles of $E_{C} I B_{I}$ and $E_{B} I C_{I}$, show that $K I$ passes through the midpoint $M$ of side $B C$.
## Proposed by Greece
|
Since $\angle E_{C} B I=90^{\circ}=I C E_{B}$, we conclude that $E_{C} B C E_{B}$ is cyclic. Moreover, we have that
$$
\angle B A I_{B}=\frac{1}{2} \angle B A D=\frac{1}{2} \widehat{C},
$$
so $A I_{B} \perp C I$. Similarly $A I_{C} \perp B I$. Therefore is the orthocenter of triangle $A I_{B} I_{C}$. It follows that
$$
\angle I I_{B} I_{C}=90^{\circ}-\angle A I_{C} I_{B}=\angle I A I_{C}=45^{\circ}-\angle I_{C} A C=45^{\circ}-\frac{1}{2} \widehat{B}=\frac{1}{2} \widehat{C}
$$
Therefore $I_{B} I_{C} C B$ is cyclic. Since $A E_{B} C I$ is also cyclic (on a circle of diameter $I E_{B}$ ) then

$$
\angle E_{C} E_{B} B=\angle A C I=\frac{1}{2} \widehat{C}=\angle I I_{B} I_{C},
$$
therefore $I_{B} I_{C} \| E_{B} E_{C}$.
From the inscribed quadrilaterals we get that
$$
\angle K I_{C} I=\angle K E_{B} I \quad \text { and } \quad K E_{C} I=\angle K I_{B} I,
$$
which implies that the triangles $K E_{C} I_{C}$ and $K I_{B} E_{B}$ are similar. So
$$
\frac{d\left(K, E_{C} I_{C}\right)}{d\left(K, E_{B} I_{B}\right)}=\frac{E_{C} I_{C}}{E_{B} I_{B}}
$$
But $I_{B} I_{C} \| E_{B} E_{C}$ and $I_{B} I_{C} C B$ is cyclic, therefore
$$
\frac{E_{C} I_{C}}{E_{B} I_{B}}=\frac{I I_{C}}{I I_{B}}=\frac{I B}{I C} .
$$
We deduce that
$$
\frac{d(K, I C)}{d(K, I B)}=\frac{I B}{I C},
$$
i.e. the distances of $K$ to the sides $I C$ and $I B$ are inversly analogous to the lenghts of these sides. So by a well known property of the median, $K$ lies on the median of the triangle IBC. (The last property of the median can be proved either by the law of sines, or by taking the distances of the distances of the median $M$ to the sides and prove by Thales theorem that $M, I, K$ are collinear.)
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG4.",
"solution_match": "\nSolution."
}
|
6372dcb0-b0ae-5645-a15d-1a0d6408a8ff
| 606,252
|
Let $A B C$ be an acute triangle with $A C>A B$ and circumcircle $\Gamma$. The tangent from $A$ to $\Gamma$ intersects $B C$ at $T$. Let $M$ be the midpoint of $B C$ and let $R$ be the reflection of $A$ in $B$. Let $S$ be a point so that $S A B T$ is a parallelogram and finally let $P$ be a point on line $S B$ such that $M P$ is parallel to $A B$.
Given that $P$ lies on $\Gamma$, prove that the circumcircle of $\triangle S T R$ is tangent to line $A C$.
## Proposed by United Kingdom
|
1. Let $N$ be the midpoint of $B S$ which, as $S A B T$ is a parallelogram, is also the midpoint of $T A$. Using $S T\|A B\| M P$ we get:
$$
\frac{N B}{B P}=\frac{1}{2} \cdot \frac{S B}{B P}=\frac{T B}{2 \cdot B M}=\frac{T B}{B C}
$$
which shows that $T A \| C P$.
Let $\Omega$ be the circle with diameter $O T$. As $\angle O M T=90^{\circ}=\angle T A O$ we have that $A, M$ lie on $\Omega$. We now show that $P$ lies on $\Omega$. As $T A \| C P$ and $T A$ is tangent to $\Gamma$ we have that $A P=A C$, so
$$
\angle T A P=\angle A C P=\angle C P A=\angle C B A=\angle T M P
$$
where in the last step we used the fact that $M P \| A B$. This shows that $P$ lies on $\Omega$. Furthermore, this shows that $\angle O P T=90^{\circ}$ and so $T P$ is also tangent to $\Gamma$.
Now we show that $R, S$ lie on $\Omega$ which would show that $\Omega$ is the circumcircle of triangle $S T R$. For $S$, using $S T \| A B$ and that $T A$ tangent to $\Gamma$ we have
$$
\angle T S P=\angle A B S=\angle A C P=\angle T A P .
$$
For $R$, the homothety with factor 2 centred at $A$ takes $B N$ to $R T$. So $B N \| R T$ and hence
$$
\angle A R T=\angle A B S=\angle T A P=\angle A P T,
$$
where the last step follows from $T A=T P$ as they are both tangents to $\Gamma$.
Finally, we observe that as $T A$ tangent to $\Gamma$ then
$$
\angle T A C=180^{\circ}-\angle C B A=\angle A B T=\angle T S A
$$
which, by the alternate segment theorem, means that line $A C$ is tangent to $\Omega$ as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with $A C>A B$ and circumcircle $\Gamma$. The tangent from $A$ to $\Gamma$ intersects $B C$ at $T$. Let $M$ be the midpoint of $B C$ and let $R$ be the reflection of $A$ in $B$. Let $S$ be a point so that $S A B T$ is a parallelogram and finally let $P$ be a point on line $S B$ such that $M P$ is parallel to $A B$.
Given that $P$ lies on $\Gamma$, prove that the circumcircle of $\triangle S T R$ is tangent to line $A C$.
## Proposed by United Kingdom
|
1. Let $N$ be the midpoint of $B S$ which, as $S A B T$ is a parallelogram, is also the midpoint of $T A$. Using $S T\|A B\| M P$ we get:
$$
\frac{N B}{B P}=\frac{1}{2} \cdot \frac{S B}{B P}=\frac{T B}{2 \cdot B M}=\frac{T B}{B C}
$$
which shows that $T A \| C P$.

Let $\Omega$ be the circle with diameter $O T$. As $\angle O M T=90^{\circ}=\angle T A O$ we have that $A, M$ lie on $\Omega$. We now show that $P$ lies on $\Omega$. As $T A \| C P$ and $T A$ is tangent to $\Gamma$ we have that $A P=A C$, so
$$
\angle T A P=\angle A C P=\angle C P A=\angle C B A=\angle T M P
$$
where in the last step we used the fact that $M P \| A B$. This shows that $P$ lies on $\Omega$. Furthermore, this shows that $\angle O P T=90^{\circ}$ and so $T P$ is also tangent to $\Gamma$.
Now we show that $R, S$ lie on $\Omega$ which would show that $\Omega$ is the circumcircle of triangle $S T R$. For $S$, using $S T \| A B$ and that $T A$ tangent to $\Gamma$ we have
$$
\angle T S P=\angle A B S=\angle A C P=\angle T A P .
$$
For $R$, the homothety with factor 2 centred at $A$ takes $B N$ to $R T$. So $B N \| R T$ and hence
$$
\angle A R T=\angle A B S=\angle T A P=\angle A P T,
$$
where the last step follows from $T A=T P$ as they are both tangents to $\Gamma$.
Finally, we observe that as $T A$ tangent to $\Gamma$ then
$$
\angle T A C=180^{\circ}-\angle C B A=\angle A B T=\angle T S A
$$
which, by the alternate segment theorem, means that line $A C$ is tangent to $\Omega$ as required.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG5.",
"solution_match": "\nSolution"
}
|
05dd8176-310b-5930-85db-da7b02287d20
| 604,158
|
Let $A B C$ be an acute triangle with $A C>A B$ and circumcircle $\Gamma$. The tangent from $A$ to $\Gamma$ intersects $B C$ at $T$. Let $M$ be the midpoint of $B C$ and let $R$ be the reflection of $A$ in $B$. Let $S$ be a point so that $S A B T$ is a parallelogram and finally let $P$ be a point on line $S B$ such that $M P$ is parallel to $A B$.
Given that $P$ lies on $\Gamma$, prove that the circumcircle of $\triangle S T R$ is tangent to line $A C$.
## Proposed by United Kingdom
|
2. We have
$$
\angle A P S=\angle A C B=\angle T A B=\angle A T S,
$$
so $S, A, P, T$ are concyclic on a circle $\Omega$. We also have
$$
\angle P A C=\angle P B C=\angle S B T=\angle P S A
$$
so $A C$ is tangent to $\Omega$. It remains to prove that $R$ belongs on $\Omega$.
As in Solution 1 we have that $T A \| C P$. Then
$$
\angle C P M=\angle A T S=\angle A P S .
$$
Since also $\angle B A P=\angle B C P$, then the triangles $A P B$ and $C P M$ are similar. But then the triangles $B P C$ and $R A P$ are also similar as $\angle R A P=\angle B C P$ and
$$
\frac{R A}{A P}=\frac{2 B A}{A P}=\frac{2 M C}{C P}=\frac{B C}{C P} .
$$
It now follows that
$$
\angle A R P=\angle P B C=\angle A S P
$$
and therefore $R$ belongs to $\Omega$ as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with $A C>A B$ and circumcircle $\Gamma$. The tangent from $A$ to $\Gamma$ intersects $B C$ at $T$. Let $M$ be the midpoint of $B C$ and let $R$ be the reflection of $A$ in $B$. Let $S$ be a point so that $S A B T$ is a parallelogram and finally let $P$ be a point on line $S B$ such that $M P$ is parallel to $A B$.
Given that $P$ lies on $\Gamma$, prove that the circumcircle of $\triangle S T R$ is tangent to line $A C$.
## Proposed by United Kingdom
|
2. We have
$$
\angle A P S=\angle A C B=\angle T A B=\angle A T S,
$$
so $S, A, P, T$ are concyclic on a circle $\Omega$. We also have
$$
\angle P A C=\angle P B C=\angle S B T=\angle P S A
$$
so $A C$ is tangent to $\Omega$. It remains to prove that $R$ belongs on $\Omega$.

As in Solution 1 we have that $T A \| C P$. Then
$$
\angle C P M=\angle A T S=\angle A P S .
$$
Since also $\angle B A P=\angle B C P$, then the triangles $A P B$ and $C P M$ are similar. But then the triangles $B P C$ and $R A P$ are also similar as $\angle R A P=\angle B C P$ and
$$
\frac{R A}{A P}=\frac{2 B A}{A P}=\frac{2 M C}{C P}=\frac{B C}{C P} .
$$
It now follows that
$$
\angle A R P=\angle P B C=\angle A S P
$$
and therefore $R$ belongs to $\Omega$ as required.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG5.",
"solution_match": "\nSolution"
}
|
05dd8176-310b-5930-85db-da7b02287d20
| 604,158
|
Let $A B C$ be an acute triangle such that $A B<A C$. Let $\omega$ be the circumcircle of $A B C$ and assume that the tangent to $\omega$ at $A$ intersects the line $B C$ at $D$. Let $\Omega$ be the circle with center $D$ and radius $A D$. Denote by $E$ the second intersection point of $\omega$ and $\Omega$. Let $M$ be the midpoint of $B C$. If the line $B E$ meets $\Omega$ again at $X$, and the line $C X$ meets $\Omega$ for the second time at $Y$, show that $A, Y$ and $M$ are collinear.
## Proposed by North Macedonia
|
1. Denote by $S$ the intersection point of $\Omega$ and the segment $B C$. Because $D A=D S$, we have $\angle D S A=\angle D A S$. Now using that $D A$ is tangent to $\omega$ we obtain:
$$
\angle B A S=\angle D A S-\angle D A B=\angle D S A-\angle D C A=\angle C A S .
$$
This means that the line $A S$ is the angle bisector of $\angle B A C$.
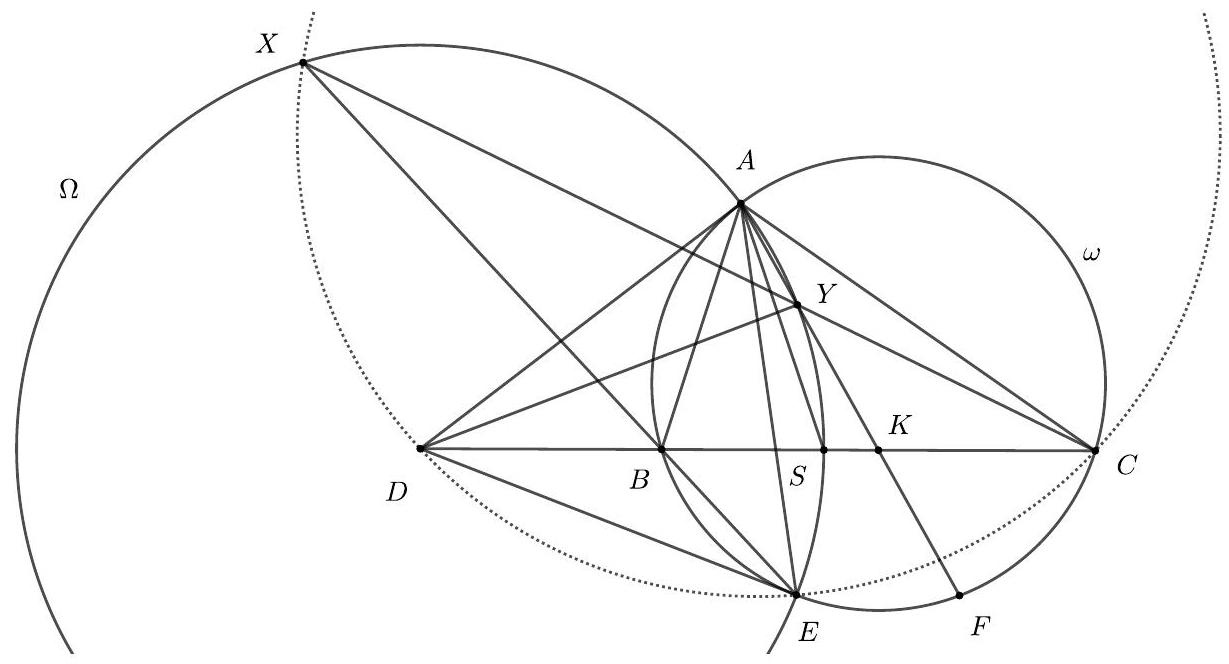
Notice that $D E$ is also tangent to $\omega$, because it is the second intersection point of $\omega$ and $\Omega$. From here, and from $D E=D X$, we see that
$$
\angle D C E=\angle B C E=\angle B E D=\angle D X E .
$$
It follows that $C E D X$ is a cyclic quadrilateral.
Since $D$ is the center of $\Omega$, then $\angle E D Y=2 \angle E X Y$. Since $C E D X$ is cyclic, we also have
$$
\angle S D E=\angle C D E=\angle C X E=\angle E X Y .
$$
Thus
$$
2 \angle S D E=2 \angle E X Y=\angle E D Y=\angle S D E+\angle S D Y
$$
and so $\angle S D E=\angle S D Y$. So we obtain
$$
\angle S A E=\frac{1}{2} \angle S D E=\frac{1}{2} \angle S D Y=\angle S A Y .
$$
Combining this with the fact that $A S$ is the angle bisector of $\angle B A C$, we see that the lines $A E$ and $A Y$ are symmetric with respect to the angle bisector of $\angle B A C$.
Now let $F$ be the second intersection point of the line $A Y$ and the circumcircle $\omega$. We have shown that $\angle B A E=\angle C A F$, which means that $B E=C F$ (two chords with the same corresponding central angle are equal). We similarly get $B F=C E$.
Since $D A$ is tangent to $\omega$, then $\angle B A D=\angle D C A$. Since also $\angle A D B=\angle C D A$ then the triangles $D A B$ and $D C A$ are similar. This gives.
$$
\frac{A B}{A C}=\frac{A D}{C D} .
$$
Similarly, the triangles $D E B$ and $D C E$ are similar, giving
$$
\frac{B E}{C E}=\frac{E D}{C D} .
$$
Combining these with $B E=C F$ and $B F=C E$ which we have shown above, and using that $D A=D E$ (tangents from the same point $D$ ), we get the relation
$$
\frac{C F}{B F}=\frac{B E}{C E}=\frac{E D}{C D}=\frac{A D}{C D}=\frac{A B}{A C} .
$$
Finally, let $K$ be the intersection point of the line $A Y$ with the segment $B C$. We have
$$
\frac{B K}{C K}=\frac{B K \sin (\angle B K A)}{B K \sin (\angle C K A)}=\frac{A B \sin (\angle B A K)}{A C \sin (\angle C A K)}=\frac{C F \sin (\angle B C F)}{B F \sin (\angle C B F)}=1 .
$$
Thus $K=M$ and $A, Y, M$ are collinear as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle such that $A B<A C$. Let $\omega$ be the circumcircle of $A B C$ and assume that the tangent to $\omega$ at $A$ intersects the line $B C$ at $D$. Let $\Omega$ be the circle with center $D$ and radius $A D$. Denote by $E$ the second intersection point of $\omega$ and $\Omega$. Let $M$ be the midpoint of $B C$. If the line $B E$ meets $\Omega$ again at $X$, and the line $C X$ meets $\Omega$ for the second time at $Y$, show that $A, Y$ and $M$ are collinear.
## Proposed by North Macedonia
|
1. Denote by $S$ the intersection point of $\Omega$ and the segment $B C$. Because $D A=D S$, we have $\angle D S A=\angle D A S$. Now using that $D A$ is tangent to $\omega$ we obtain:
$$
\angle B A S=\angle D A S-\angle D A B=\angle D S A-\angle D C A=\angle C A S .
$$
This means that the line $A S$ is the angle bisector of $\angle B A C$.

Notice that $D E$ is also tangent to $\omega$, because it is the second intersection point of $\omega$ and $\Omega$. From here, and from $D E=D X$, we see that
$$
\angle D C E=\angle B C E=\angle B E D=\angle D X E .
$$
It follows that $C E D X$ is a cyclic quadrilateral.
Since $D$ is the center of $\Omega$, then $\angle E D Y=2 \angle E X Y$. Since $C E D X$ is cyclic, we also have
$$
\angle S D E=\angle C D E=\angle C X E=\angle E X Y .
$$
Thus
$$
2 \angle S D E=2 \angle E X Y=\angle E D Y=\angle S D E+\angle S D Y
$$
and so $\angle S D E=\angle S D Y$. So we obtain
$$
\angle S A E=\frac{1}{2} \angle S D E=\frac{1}{2} \angle S D Y=\angle S A Y .
$$
Combining this with the fact that $A S$ is the angle bisector of $\angle B A C$, we see that the lines $A E$ and $A Y$ are symmetric with respect to the angle bisector of $\angle B A C$.
Now let $F$ be the second intersection point of the line $A Y$ and the circumcircle $\omega$. We have shown that $\angle B A E=\angle C A F$, which means that $B E=C F$ (two chords with the same corresponding central angle are equal). We similarly get $B F=C E$.
Since $D A$ is tangent to $\omega$, then $\angle B A D=\angle D C A$. Since also $\angle A D B=\angle C D A$ then the triangles $D A B$ and $D C A$ are similar. This gives.
$$
\frac{A B}{A C}=\frac{A D}{C D} .
$$
Similarly, the triangles $D E B$ and $D C E$ are similar, giving
$$
\frac{B E}{C E}=\frac{E D}{C D} .
$$
Combining these with $B E=C F$ and $B F=C E$ which we have shown above, and using that $D A=D E$ (tangents from the same point $D$ ), we get the relation
$$
\frac{C F}{B F}=\frac{B E}{C E}=\frac{E D}{C D}=\frac{A D}{C D}=\frac{A B}{A C} .
$$
Finally, let $K$ be the intersection point of the line $A Y$ with the segment $B C$. We have
$$
\frac{B K}{C K}=\frac{B K \sin (\angle B K A)}{B K \sin (\angle C K A)}=\frac{A B \sin (\angle B A K)}{A C \sin (\angle C A K)}=\frac{C F \sin (\angle B C F)}{B F \sin (\angle C B F)}=1 .
$$
Thus $K=M$ and $A, Y, M$ are collinear as required.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG6.",
"solution_match": "\nSolution"
}
|
7c76775d-c6fa-5405-b80d-9f53598d934d
| 604,185
|
Let $A B C$ be an acute triangle such that $A B<A C$. Let $\omega$ be the circumcircle of $A B C$ and assume that the tangent to $\omega$ at $A$ intersects the line $B C$ at $D$. Let $\Omega$ be the circle with center $D$ and radius $A D$. Denote by $E$ the second intersection point of $\omega$ and $\Omega$. Let $M$ be the midpoint of $B C$. If the line $B E$ meets $\Omega$ again at $X$, and the line $C X$ meets $\Omega$ for the second time at $Y$, show that $A, Y$ and $M$ are collinear.
## Proposed by North Macedonia
|
2. As in Solution 1, we let $S$ be the intersection of $\Omega$ with $B S$ and obtain that $A S$ is the angle bisector of $\angle B A C$ and that $A E$ and $A Y$ are symmetric with respect to $A S$.
Let $R=\sqrt{(A B)(A C)}$ and let $\Psi$ be the map obtained by first inverting on the circle centered at $A$ of radius $R$ and the reflecting on $A S$.
By construction of $\Psi$ we have $\Psi(B)=C$ and $\Psi(C)=B$. (After the inversion $B$ maps to a point $B^{\prime}$ on $A B$ such that $(A B)\left(A B^{\prime}\right)=R^{2}=(A B)(A C)$. So after the reflection $B^{\prime}$ maps to $C$.) Since the inversion of any line not passing through $A$ is a circle passing through $A$, then $\Psi(B C)$ is a circle passing through $A$. Since it also passes through $B$ and $C$ then $\Psi(B C)=\omega$.
Because $D A$ is tangent to $\omega$ at $A$, and $D$ is the center of $\Omega$, the circles $\omega$ and $\Omega$ are orthogonal. Both reflection and inversion preserve orthogonality and both are involutions. This means that $\Psi$ is an involution that preserves orthogonality. From here we conlude that the images $\Psi(\omega)=B C$ and $\Psi(\Omega)$ are orthogonal lines.
Since $\Psi(A S)=A S, \Phi(B C)=\omega$ and $S$ belongs on $B C$, then $\Psi(S)$ is the intersection of $A S$ with $\omega$. Since $A S$ is the angle bisector of triangle $A B C$, then $\Psi(S)=N$, the midpoint of the $\operatorname{arc} B C$ of $\omega$ not containing $A$.
Since $S$ belongs on $\Omega$ and $\Psi(\Omega)$ and $\Psi(\omega)$ are orthogonal lines, then $\Psi(\Omega)$ is the line perpendicular to $B C$ at $N$. It therefore contains the midpoint $M$ of $B C$.
The intersection point $E$ of $\omega$ and $\Omega$ maps to $\Psi(E)$, which is the intersection point of $\Psi(\omega)=B C$ and $\Psi(\Omega)=M N$, which must be equal to $M$, i.e. $\Psi(E)=M$. Because of this, we see that $A E$ and $A M$ are symmetric with respect to the angle bisector $A S$. Since also $A E$ and $A Y$ are symmetric with respect to $A S$, it follows that $A, M, Y$ are collinear as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle such that $A B<A C$. Let $\omega$ be the circumcircle of $A B C$ and assume that the tangent to $\omega$ at $A$ intersects the line $B C$ at $D$. Let $\Omega$ be the circle with center $D$ and radius $A D$. Denote by $E$ the second intersection point of $\omega$ and $\Omega$. Let $M$ be the midpoint of $B C$. If the line $B E$ meets $\Omega$ again at $X$, and the line $C X$ meets $\Omega$ for the second time at $Y$, show that $A, Y$ and $M$ are collinear.
## Proposed by North Macedonia
|
2. As in Solution 1, we let $S$ be the intersection of $\Omega$ with $B S$ and obtain that $A S$ is the angle bisector of $\angle B A C$ and that $A E$ and $A Y$ are symmetric with respect to $A S$.
Let $R=\sqrt{(A B)(A C)}$ and let $\Psi$ be the map obtained by first inverting on the circle centered at $A$ of radius $R$ and the reflecting on $A S$.
By construction of $\Psi$ we have $\Psi(B)=C$ and $\Psi(C)=B$. (After the inversion $B$ maps to a point $B^{\prime}$ on $A B$ such that $(A B)\left(A B^{\prime}\right)=R^{2}=(A B)(A C)$. So after the reflection $B^{\prime}$ maps to $C$.) Since the inversion of any line not passing through $A$ is a circle passing through $A$, then $\Psi(B C)$ is a circle passing through $A$. Since it also passes through $B$ and $C$ then $\Psi(B C)=\omega$.
Because $D A$ is tangent to $\omega$ at $A$, and $D$ is the center of $\Omega$, the circles $\omega$ and $\Omega$ are orthogonal. Both reflection and inversion preserve orthogonality and both are involutions. This means that $\Psi$ is an involution that preserves orthogonality. From here we conlude that the images $\Psi(\omega)=B C$ and $\Psi(\Omega)$ are orthogonal lines.
Since $\Psi(A S)=A S, \Phi(B C)=\omega$ and $S$ belongs on $B C$, then $\Psi(S)$ is the intersection of $A S$ with $\omega$. Since $A S$ is the angle bisector of triangle $A B C$, then $\Psi(S)=N$, the midpoint of the $\operatorname{arc} B C$ of $\omega$ not containing $A$.
Since $S$ belongs on $\Omega$ and $\Psi(\Omega)$ and $\Psi(\omega)$ are orthogonal lines, then $\Psi(\Omega)$ is the line perpendicular to $B C$ at $N$. It therefore contains the midpoint $M$ of $B C$.
The intersection point $E$ of $\omega$ and $\Omega$ maps to $\Psi(E)$, which is the intersection point of $\Psi(\omega)=B C$ and $\Psi(\Omega)=M N$, which must be equal to $M$, i.e. $\Psi(E)=M$. Because of this, we see that $A E$ and $A M$ are symmetric with respect to the angle bisector $A S$. Since also $A E$ and $A Y$ are symmetric with respect to $A S$, it follows that $A, M, Y$ are collinear as required.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG6.",
"solution_match": "\nSolution"
}
|
7c76775d-c6fa-5405-b80d-9f53598d934d
| 604,185
|
Let $A B C$ be an acute scalene triangle. Its $C$-excircle tangent to the segment $A B$ meets $A B$ at point $M$ and the extension of $B C$ beyond $B$ at point $N$. Analogously, its $B$-excircle tangent to the segment $A C$ meets $A C$ at point $P$ and the extension of $B C$ beyond $C$ at point $Q$. Denote by $A_{1}$ the intersection point of the lines $M N$ and $P Q$, and let $A_{2}$ be defined as the point, symmetric to $A$ with respect to $A_{1}$. Define the points $B_{2}$ and $C_{2}$, analogously. Prove that $\triangle A B C$ is similar to $\triangle A_{2} B_{2} C_{2}$.
## Proposed by Bulgaria
|
1. We shall use the standard notations for $A B C$, i.e. $\angle A B C=\beta, B C=a$ etc. We also write $s=\frac{a+b+c}{2}$ for the semiperimeter and $r$ for the inradius.
Let $M N$ intersect the altitude $A D(D$ lies on $B C)$ at the point $L$. We have that $\angle B A D=90^{\circ}-\beta$ and $\angle A M L=\angle B M N=\frac{\beta}{2}$. (Since $B M N$ is an isosceles triangle with $\angle M B N=180^{\circ}-\beta$.) It is known that $A M=s-b$ so by the Sine Law in the triangle $A M L$ we have
$$
\frac{A M}{\sin \angle A L M}=\frac{A L}{\sin \angle A M L} \Longrightarrow \frac{s-b}{\sin \left(90^{\circ}+\frac{\beta}{2}\right)}=\frac{A L}{\sin \frac{\beta}{2}} \Longrightarrow A L=(s-b) \tan \frac{\beta}{2}=r .
$$
Analogously we see that if $P Q$ intersects $A D$ at $L^{\prime}$, then $A L^{\prime}=r$. Therefore $L$ and $L^{\prime}$ coincide and since $A_{1}=M N \cap P Q$ by definition, we conclude that $L=L^{\prime}=A_{1}$. In particular, we can now view the point $A_{2}$ as the point on the $A$-altitude such that $A A_{2}=2 r$. Analogously $B_{2}$ and $C_{2}$ lie on the $B$-altitude and $C$-altitude, respectively, and $B B_{2}=C C_{2}=2 r$.
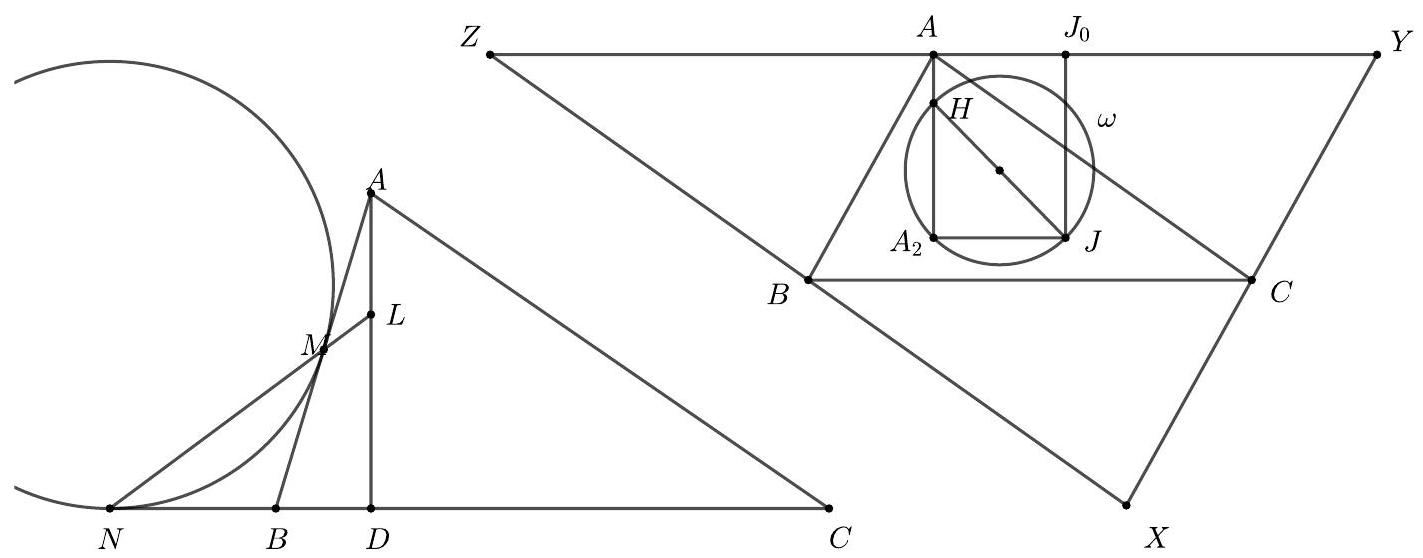
Now let $X$ be the reflection of $A$ on the midpoint of $B C$ and define $X Y Z$ analogously. So $X Y Z$ is the triangle whose midpoints of sides are $A, B$ and $C$. Let $J$ be the incenter of this triangle. As the triangles $X Y Z$ and $A B C$ are similar with ratio 2, the inradius of $X Y Z$ is equal to $2 r$. So if $J J_{0}$ is perpendicular to $Y Z$ (with $J_{0}$ on $Y Z$ ), then $A A_{2}$ and $J J_{0}$ are parallel (both perpendicular to $Y Z$ ) and equal, hence $A A_{2} J J_{0}$ is a rectangle and in particular $A_{2}$ is the foot of the perpendicular from $J$ to the $A$-altitude of $A B C$. It follows that $A_{2}, B_{2}$ and $C_{2}$ lie on the circle $\omega$ with diameter $J H$.
Now we finish with a simple angle chasing. The circle $k$ gives $\angle A_{2} B_{2} C_{2}=\angle A_{2} H C_{2}=$ $\angle 180^{\circ}-\angle A H C=\angle A B C$; similarly for the angles at $A_{2}$ and $C_{2}$. The desired similarity follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute scalene triangle. Its $C$-excircle tangent to the segment $A B$ meets $A B$ at point $M$ and the extension of $B C$ beyond $B$ at point $N$. Analogously, its $B$-excircle tangent to the segment $A C$ meets $A C$ at point $P$ and the extension of $B C$ beyond $C$ at point $Q$. Denote by $A_{1}$ the intersection point of the lines $M N$ and $P Q$, and let $A_{2}$ be defined as the point, symmetric to $A$ with respect to $A_{1}$. Define the points $B_{2}$ and $C_{2}$, analogously. Prove that $\triangle A B C$ is similar to $\triangle A_{2} B_{2} C_{2}$.
## Proposed by Bulgaria
|
1. We shall use the standard notations for $A B C$, i.e. $\angle A B C=\beta, B C=a$ etc. We also write $s=\frac{a+b+c}{2}$ for the semiperimeter and $r$ for the inradius.
Let $M N$ intersect the altitude $A D(D$ lies on $B C)$ at the point $L$. We have that $\angle B A D=90^{\circ}-\beta$ and $\angle A M L=\angle B M N=\frac{\beta}{2}$. (Since $B M N$ is an isosceles triangle with $\angle M B N=180^{\circ}-\beta$.) It is known that $A M=s-b$ so by the Sine Law in the triangle $A M L$ we have
$$
\frac{A M}{\sin \angle A L M}=\frac{A L}{\sin \angle A M L} \Longrightarrow \frac{s-b}{\sin \left(90^{\circ}+\frac{\beta}{2}\right)}=\frac{A L}{\sin \frac{\beta}{2}} \Longrightarrow A L=(s-b) \tan \frac{\beta}{2}=r .
$$
Analogously we see that if $P Q$ intersects $A D$ at $L^{\prime}$, then $A L^{\prime}=r$. Therefore $L$ and $L^{\prime}$ coincide and since $A_{1}=M N \cap P Q$ by definition, we conclude that $L=L^{\prime}=A_{1}$. In particular, we can now view the point $A_{2}$ as the point on the $A$-altitude such that $A A_{2}=2 r$. Analogously $B_{2}$ and $C_{2}$ lie on the $B$-altitude and $C$-altitude, respectively, and $B B_{2}=C C_{2}=2 r$.

Now let $X$ be the reflection of $A$ on the midpoint of $B C$ and define $X Y Z$ analogously. So $X Y Z$ is the triangle whose midpoints of sides are $A, B$ and $C$. Let $J$ be the incenter of this triangle. As the triangles $X Y Z$ and $A B C$ are similar with ratio 2, the inradius of $X Y Z$ is equal to $2 r$. So if $J J_{0}$ is perpendicular to $Y Z$ (with $J_{0}$ on $Y Z$ ), then $A A_{2}$ and $J J_{0}$ are parallel (both perpendicular to $Y Z$ ) and equal, hence $A A_{2} J J_{0}$ is a rectangle and in particular $A_{2}$ is the foot of the perpendicular from $J$ to the $A$-altitude of $A B C$. It follows that $A_{2}, B_{2}$ and $C_{2}$ lie on the circle $\omega$ with diameter $J H$.
Now we finish with a simple angle chasing. The circle $k$ gives $\angle A_{2} B_{2} C_{2}=\angle A_{2} H C_{2}=$ $\angle 180^{\circ}-\angle A H C=\angle A B C$; similarly for the angles at $A_{2}$ and $C_{2}$. The desired similarity follows.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG7.",
"solution_match": "\nSolution"
}
|
d91d1135-b8b9-598d-9c89-2c7e69ae59ea
| 604,216
|
Let $A B C$ be an acute scalene triangle. Its $C$-excircle tangent to the segment $A B$ meets $A B$ at point $M$ and the extension of $B C$ beyond $B$ at point $N$. Analogously, its $B$-excircle tangent to the segment $A C$ meets $A C$ at point $P$ and the extension of $B C$ beyond $C$ at point $Q$. Denote by $A_{1}$ the intersection point of the lines $M N$ and $P Q$, and let $A_{2}$ be defined as the point, symmetric to $A$ with respect to $A_{1}$. Define the points $B_{2}$ and $C_{2}$, analogously. Prove that $\triangle A B C$ is similar to $\triangle A_{2} B_{2} C_{2}$.
## Proposed by Bulgaria
|
2. As in Solution 1, we have that $A_{2}, B_{2}, C_{2}$ belong on the corresponding altitudes with $A A_{2}=B B_{2}=C C_{2}=2 r$. We present an approach with complex numbers (and minimal calculations) which can also complete the proof.
Set the incenter $I$ of the triangle $A B C$ to be the origin. We may assume that $r=1$. We write $a, b, c$ to denote $A^{\prime}, B^{\prime}, C^{\prime}$. Point $A$ is the intersection of the tangents to the unit circle (incircle) at $B^{\prime}$ and $C^{\prime}$ and is therefore represented by the complex number $2 b c /(b+c)$. Analogously the points $B$ and $C$ are represented by $2 a c /(a+c)$ and $2 a b /(a+b)$ respectively.
Since $A A_{2}=r=2$ and $A A_{2}$ is parallel to $I A^{\prime}$, we have that $A_{2}$ is represented by the complex number
$$
\frac{2 b c}{b+c}+2 a=\frac{2(a b+b c+c a)}{b+c}
$$
Now since $|c|=1$, then
$$
(A B)=\left|\frac{b c}{b+c}-\frac{a c}{a+c}\right|=\left|\frac{b-a}{(a+c)(b+c)}\right| .
$$
We also have
$$
\left(A_{2} B_{2}\right)=\left|\frac{2(a b+b c+c a)}{b+c}-\frac{2(a b+b c+c a)}{a+c}\right|=2|a b+b c+c a|\left(A_{2} B_{2}\right) .
$$
Analogously we get
$$
\frac{A_{2} B_{2}}{A B}=\frac{B_{2} C_{2}}{B C}=\frac{C_{2} A_{2}}{C A}=2|a b+b c+c a|
$$
So the triangle $A_{2} B_{2} C_{2}$ is similar to the triangle $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute scalene triangle. Its $C$-excircle tangent to the segment $A B$ meets $A B$ at point $M$ and the extension of $B C$ beyond $B$ at point $N$. Analogously, its $B$-excircle tangent to the segment $A C$ meets $A C$ at point $P$ and the extension of $B C$ beyond $C$ at point $Q$. Denote by $A_{1}$ the intersection point of the lines $M N$ and $P Q$, and let $A_{2}$ be defined as the point, symmetric to $A$ with respect to $A_{1}$. Define the points $B_{2}$ and $C_{2}$, analogously. Prove that $\triangle A B C$ is similar to $\triangle A_{2} B_{2} C_{2}$.
## Proposed by Bulgaria
|
2. As in Solution 1, we have that $A_{2}, B_{2}, C_{2}$ belong on the corresponding altitudes with $A A_{2}=B B_{2}=C C_{2}=2 r$. We present an approach with complex numbers (and minimal calculations) which can also complete the proof.
Set the incenter $I$ of the triangle $A B C$ to be the origin. We may assume that $r=1$. We write $a, b, c$ to denote $A^{\prime}, B^{\prime}, C^{\prime}$. Point $A$ is the intersection of the tangents to the unit circle (incircle) at $B^{\prime}$ and $C^{\prime}$ and is therefore represented by the complex number $2 b c /(b+c)$. Analogously the points $B$ and $C$ are represented by $2 a c /(a+c)$ and $2 a b /(a+b)$ respectively.
Since $A A_{2}=r=2$ and $A A_{2}$ is parallel to $I A^{\prime}$, we have that $A_{2}$ is represented by the complex number
$$
\frac{2 b c}{b+c}+2 a=\frac{2(a b+b c+c a)}{b+c}
$$
Now since $|c|=1$, then
$$
(A B)=\left|\frac{b c}{b+c}-\frac{a c}{a+c}\right|=\left|\frac{b-a}{(a+c)(b+c)}\right| .
$$
We also have
$$
\left(A_{2} B_{2}\right)=\left|\frac{2(a b+b c+c a)}{b+c}-\frac{2(a b+b c+c a)}{a+c}\right|=2|a b+b c+c a|\left(A_{2} B_{2}\right) .
$$
Analogously we get
$$
\frac{A_{2} B_{2}}{A B}=\frac{B_{2} C_{2}}{B C}=\frac{C_{2} A_{2}}{C A}=2|a b+b c+c a|
$$
So the triangle $A_{2} B_{2} C_{2}$ is similar to the triangle $A B C$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG7.",
"solution_match": "\nSolution"
}
|
d91d1135-b8b9-598d-9c89-2c7e69ae59ea
| 604,216
|
Can every positive rational number $q$ be written as
$$
\frac{a^{2021}+b^{2023}}{c^{2022}+d^{2024}}
$$
where $a, b, c, d$ are all positive integers?
Proposed by United Kingdom
|
The answer is yes. Set $a=x^{2023}, b=x^{2021}$ and $c=y^{2024}, d=y^{2022}$ for some integers $x, y$ and let $q=\frac{m}{n}$ in lowest terms. Then we could try to solve
$$
\frac{a^{2021}+b^{2023}}{c^{2022}+d^{2024}}=\frac{2 x^{2021 \times 2023}}{2 y^{2022 \times 2024}}=\frac{x^{2021 \times 2023}}{y^{2022 \times 2024}}=\frac{m}{n} .
$$
Consider setting $x=m^{x_{1}} n^{x_{2}}$ and $y=m^{y_{1}} n^{y_{2}}$. Then by considering powers of $m$ and powers of $n$ separately, it would be sufficient to solve the pair of equations
$$
2021 \times 2023 x_{1}-2022 \times 2024 y_{1}=1, \quad \text { and } \quad 2021 \times 2023 x_{2}-2022 \times 2024 y_{2}=-1
$$
We know that these equations have solutions in positive integers so long as $2021 \times 2023$ and $2022 \times 2024$ are coprime. Amongst integers which differ by at most three, the only possible common prime factors are 2 and 3. Clearly 2 is not a common prime factor of the products, nor is 3 , since only one of the four factors is divisible by 3 . So these two integers are coprime, and the equations have solutions.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Can every positive rational number $q$ be written as
$$
\frac{a^{2021}+b^{2023}}{c^{2022}+d^{2024}}
$$
where $a, b, c, d$ are all positive integers?
Proposed by United Kingdom
|
The answer is yes. Set $a=x^{2023}, b=x^{2021}$ and $c=y^{2024}, d=y^{2022}$ for some integers $x, y$ and let $q=\frac{m}{n}$ in lowest terms. Then we could try to solve
$$
\frac{a^{2021}+b^{2023}}{c^{2022}+d^{2024}}=\frac{2 x^{2021 \times 2023}}{2 y^{2022 \times 2024}}=\frac{x^{2021 \times 2023}}{y^{2022 \times 2024}}=\frac{m}{n} .
$$
Consider setting $x=m^{x_{1}} n^{x_{2}}$ and $y=m^{y_{1}} n^{y_{2}}$. Then by considering powers of $m$ and powers of $n$ separately, it would be sufficient to solve the pair of equations
$$
2021 \times 2023 x_{1}-2022 \times 2024 y_{1}=1, \quad \text { and } \quad 2021 \times 2023 x_{2}-2022 \times 2024 y_{2}=-1
$$
We know that these equations have solutions in positive integers so long as $2021 \times 2023$ and $2022 \times 2024$ are coprime. Amongst integers which differ by at most three, the only possible common prime factors are 2 and 3. Clearly 2 is not a common prime factor of the products, nor is 3 , since only one of the four factors is divisible by 3 . So these two integers are coprime, and the equations have solutions.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nN4.",
"solution_match": "\nSolution."
}
|
f7c15e13-0feb-5647-bd2a-61bda774ada7
| 604,289
|
Let $a, b$ and $c$ be positive integers satisfying the equation $(a, b)+[a, b]=2021^{c}$. If $|a-b|$ is a prime number, prove that the number $(a+b)^{2}+4$ is composite.
## Proposed by Serbia
|
We write $p=|a-b|$ and assume for contradiction that $q=(a+b)^{2}+4$ is a prime number.
Since $(a, b) \mid[a, b]$, we have that $(a, b) \mid 2021^{c}$. As $(a, b)$ also divides $p=|a-b|$, it follows that $(a, b) \in\{1,43,47\}$. We will consider all 3 cases separately:
(1) If $(a, b)=1$, then $1+a b=2021^{c}$, and therefore
$$
q=(a+b)^{2}+4=(a-b)^{2}+4(1+a b)=p^{2}+4 \cdot 2021^{c} .
$$
(a) Suppose $c$ is even. Since $q \equiv 1 \bmod 4$, it can be represented uniquely (up to order) as a sum of two (non-negative) squares. But (1) gives potentially two such representations so in order to have uniqueness we must have $p=2$. But then $4 \mid q$ a contradiction.
(b) If $c$ is odd then $a b=2021^{c}-1 \equiv 1 \bmod 3$. Thus $a \equiv b \bmod 3$ implying that $p=|a-b| \equiv 0 \bmod 3$. Therefore $p=3$. Without loss of generality $b=a+3$. Then $2021^{c}=a b+1=a^{2}+3 a+1$ and so
$$
(2 a+3)^{2}=4 a^{2}+12 a+9=4 \cdot 2021^{c}+5 .
$$
So 5 is a quadratic residue modulo 47 , a contradiction as
$$
\left(\frac{5}{47}\right)=\left(\frac{47}{5}\right)=\left(\frac{2}{5}\right)=-1 .
$$
(2) If $(a, b)=43$, then $p=|a-b|=43$ and we may assume that $a=43 k$ and $b=43(k+1)$, for some $k \in \mathbb{N}$. Then $2021^{c}=43+43 k(k+1)$ giving that
$$
(2 k+1)^{2}=4 k^{2}+4 k+4-3=4 \cdot 43^{c-1} \cdot 47-3 .
$$
So -3 is a quadratic residue modulo 47 , a contradiction as
$$
\left(\frac{-3}{47}\right)=\left(\frac{-1}{47}\right)\left(\frac{3}{47}\right)=\left(\frac{47}{3}\right)=\left(\frac{2}{3}\right)=-1 .
$$
(3) If $(a, b)=47$ then analogously there is a $k \in \mathbb{N}$ such that
$$
(2 k+1)^{2}=4 \cdot 43^{c} \cdot 47^{c-1}-3
$$
If $c>1$ then we get a contradiction in exactly the same way as in (2). If $c=1$ then $(2 k+1)^{2}=169$ giving $k=6$. This implies that $a+b=47 \cdot 6+47 \cdot 7=47 \cdot 13 \equiv 1 \bmod 5$. Thus $q=(a+b)^{2}+4 \equiv 0 \bmod 5$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a, b$ and $c$ be positive integers satisfying the equation $(a, b)+[a, b]=2021^{c}$. If $|a-b|$ is a prime number, prove that the number $(a+b)^{2}+4$ is composite.
## Proposed by Serbia
|
We write $p=|a-b|$ and assume for contradiction that $q=(a+b)^{2}+4$ is a prime number.
Since $(a, b) \mid[a, b]$, we have that $(a, b) \mid 2021^{c}$. As $(a, b)$ also divides $p=|a-b|$, it follows that $(a, b) \in\{1,43,47\}$. We will consider all 3 cases separately:
(1) If $(a, b)=1$, then $1+a b=2021^{c}$, and therefore
$$
q=(a+b)^{2}+4=(a-b)^{2}+4(1+a b)=p^{2}+4 \cdot 2021^{c} .
$$
(a) Suppose $c$ is even. Since $q \equiv 1 \bmod 4$, it can be represented uniquely (up to order) as a sum of two (non-negative) squares. But (1) gives potentially two such representations so in order to have uniqueness we must have $p=2$. But then $4 \mid q$ a contradiction.
(b) If $c$ is odd then $a b=2021^{c}-1 \equiv 1 \bmod 3$. Thus $a \equiv b \bmod 3$ implying that $p=|a-b| \equiv 0 \bmod 3$. Therefore $p=3$. Without loss of generality $b=a+3$. Then $2021^{c}=a b+1=a^{2}+3 a+1$ and so
$$
(2 a+3)^{2}=4 a^{2}+12 a+9=4 \cdot 2021^{c}+5 .
$$
So 5 is a quadratic residue modulo 47 , a contradiction as
$$
\left(\frac{5}{47}\right)=\left(\frac{47}{5}\right)=\left(\frac{2}{5}\right)=-1 .
$$
(2) If $(a, b)=43$, then $p=|a-b|=43$ and we may assume that $a=43 k$ and $b=43(k+1)$, for some $k \in \mathbb{N}$. Then $2021^{c}=43+43 k(k+1)$ giving that
$$
(2 k+1)^{2}=4 k^{2}+4 k+4-3=4 \cdot 43^{c-1} \cdot 47-3 .
$$
So -3 is a quadratic residue modulo 47 , a contradiction as
$$
\left(\frac{-3}{47}\right)=\left(\frac{-1}{47}\right)\left(\frac{3}{47}\right)=\left(\frac{47}{3}\right)=\left(\frac{2}{3}\right)=-1 .
$$
(3) If $(a, b)=47$ then analogously there is a $k \in \mathbb{N}$ such that
$$
(2 k+1)^{2}=4 \cdot 43^{c} \cdot 47^{c-1}-3
$$
If $c>1$ then we get a contradiction in exactly the same way as in (2). If $c=1$ then $(2 k+1)^{2}=169$ giving $k=6$. This implies that $a+b=47 \cdot 6+47 \cdot 7=47 \cdot 13 \equiv 1 \bmod 5$. Thus $q=(a+b)^{2}+4 \equiv 0 \bmod 5$, a contradiction.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nN6.",
"solution_match": "\nSolution."
}
|
6437f917-6b32-5520-8f50-32d856b8dc36
| 604,320
|
Let $K$ be a point inside the triangle $A B C$. Let $M$ and $N$ be points such that $M$ and $K$ are on opposite sides of the line $A B$, and $N$ and $K$ are on opposite sides of the line $B C$. Assume that
$$
\angle M A B=\angle M B A=\angle N B C=\angle N C B=\angle K A C=\angle K C A .
$$
Show that $M B N K$ is a parallelogram.
|
Denote $\angle M A B=\angle M B A=\cdots=\alpha$. Then
$$
\angle M A K=\alpha+(\angle B A C-\alpha)=\angle B A C,
$$
$\frac{|A M|}{|A B|}=\frac{1}{2 \cos \alpha}$ and $\frac{|A K|}{|A C|}=\frac{1}{2 \cos \alpha}$ (see Figure 1). Hence the triangles $M A K$ and $B A C$ are similar, implying $|M K|=\frac{|B C|}{2 \cos \alpha}$. Since $|B N|=\frac{|B C|}{2 \cos \alpha}$, we have $|M K|=|B N|$. Similarly we can show that $|B M|=|N K|$, and the result follows.
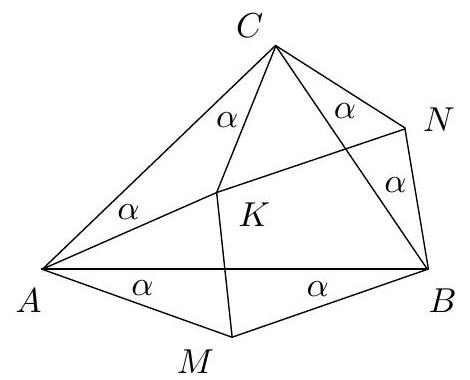
Figure 1
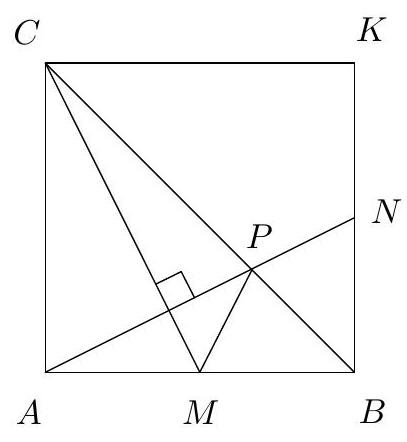
Figure 2
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $K$ be a point inside the triangle $A B C$. Let $M$ and $N$ be points such that $M$ and $K$ are on opposite sides of the line $A B$, and $N$ and $K$ are on opposite sides of the line $B C$. Assume that
$$
\angle M A B=\angle M B A=\angle N B C=\angle N C B=\angle K A C=\angle K C A .
$$
Show that $M B N K$ is a parallelogram.
|
Denote $\angle M A B=\angle M B A=\cdots=\alpha$. Then
$$
\angle M A K=\alpha+(\angle B A C-\alpha)=\angle B A C,
$$
$\frac{|A M|}{|A B|}=\frac{1}{2 \cos \alpha}$ and $\frac{|A K|}{|A C|}=\frac{1}{2 \cos \alpha}$ (see Figure 1). Hence the triangles $M A K$ and $B A C$ are similar, implying $|M K|=\frac{|B C|}{2 \cos \alpha}$. Since $|B N|=\frac{|B C|}{2 \cos \alpha}$, we have $|M K|=|B N|$. Similarly we can show that $|B M|=|N K|$, and the result follows.

Figure 1

Figure 2
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n1.",
"solution_match": "\n1."
}
|
fb639366-f078-5864-8494-c43ff23e77db
| 240,303
|
Given an isosceles triangle $A B C$ with $\angle A=90^{\circ}$. Let $M$ be the midpoint of $A B$. The line passing through $A$ and perpendicular to $C M$ intersects the side $B C$ at $P$. Prove that $\angle A M C=\angle B M P$.
|
Choose the point $K$ such that $A B K C$ is a square. Let $N$ be the point of intersection of $A P$ and $B K$ (see Figure 2). Since the lines $A N$ and $C M$ are perpendicular, $N$ is the midpoint of $B K$. Moreover, triangles $A M C$ and $B N A$ are congruent, which gives
$$
\angle A M C=\angle B N A
$$
Since $|B M|=|B N|$ and $\angle M B P=\angle N B P$, it follows that triangles $M B P$ and $N B P$ are congruent. This implies that
$$
\angle B M P=\angle B N P
$$
Combining (1) ja (2) yields the required equality.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given an isosceles triangle $A B C$ with $\angle A=90^{\circ}$. Let $M$ be the midpoint of $A B$. The line passing through $A$ and perpendicular to $C M$ intersects the side $B C$ at $P$. Prove that $\angle A M C=\angle B M P$.
|
Choose the point $K$ such that $A B K C$ is a square. Let $N$ be the point of intersection of $A P$ and $B K$ (see Figure 2). Since the lines $A N$ and $C M$ are perpendicular, $N$ is the midpoint of $B K$. Moreover, triangles $A M C$ and $B N A$ are congruent, which gives
$$
\angle A M C=\angle B N A
$$
Since $|B M|=|B N|$ and $\angle M B P=\angle N B P$, it follows that triangles $M B P$ and $N B P$ are congruent. This implies that
$$
\angle B M P=\angle B N P
$$
Combining (1) ja (2) yields the required equality.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n2.",
"solution_match": "\n2."
}
|
5d4ea946-e0b1-52f5-b41c-067d59fa6bc7
| 240,313
|
Given a triangle $A B C$ with $\angle A=90^{\circ}$ and $|A B| \neq|A C|$. The points $D, E, F$ lie on the sides $B C, C A, A B$, respectively, in such a way that $A F D E$ is a square. Prove that the line $B C$, the line $F E$ and the line tangent at the point $A$ to the circumcircle of the triangle $A B C$ intersect in one point.
|
Let $B C$ and $F E$ meet at $P$ (see Figure 3 ). It suffices to show that the line $A P$ is tangent to the circumcircle of the triangle $A B C$.
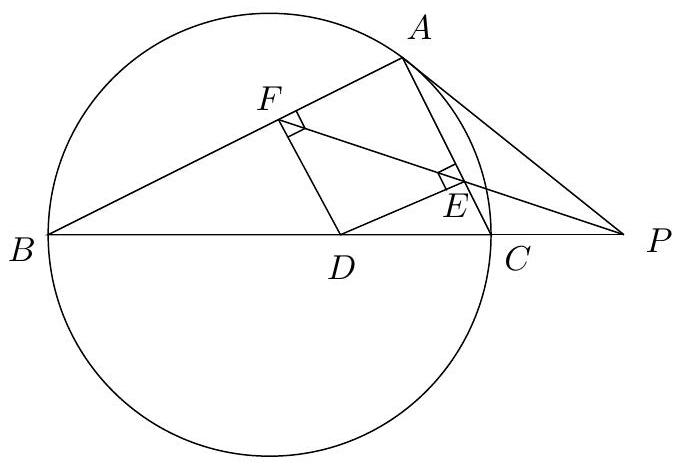
Figure 3
Since $F E$ is the axis of symmetry of the square $A F D E$, we have $\angle A P E=\angle B P F$. Moreover, $\angle A E P=135^{\circ}=\angle B F P$. Hence triangles $A P E$ and $B P F$ are similar, and $\angle C A P=\angle A B C$, i.e. the line $A P$ is tangent to the circumcircle of $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a triangle $A B C$ with $\angle A=90^{\circ}$ and $|A B| \neq|A C|$. The points $D, E, F$ lie on the sides $B C, C A, A B$, respectively, in such a way that $A F D E$ is a square. Prove that the line $B C$, the line $F E$ and the line tangent at the point $A$ to the circumcircle of the triangle $A B C$ intersect in one point.
|
Let $B C$ and $F E$ meet at $P$ (see Figure 3 ). It suffices to show that the line $A P$ is tangent to the circumcircle of the triangle $A B C$.

Figure 3
Since $F E$ is the axis of symmetry of the square $A F D E$, we have $\angle A P E=\angle B P F$. Moreover, $\angle A E P=135^{\circ}=\angle B F P$. Hence triangles $A P E$ and $B P F$ are similar, and $\angle C A P=\angle A B C$, i.e. the line $A P$ is tangent to the circumcircle of $A B C$.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n3.",
"solution_match": "\n3."
}
|
09e14b2b-a883-5c25-8ae3-30129ebcd1ca
| 240,322
|
Given a triangle $A B C$ with $\angle A=120^{\circ}$. The points $K$ and $L$ lie on the sides $A B$ and $A C$, respectively. Let $B K P$ and $C L Q$ be equilateral triangles constructed outside the triangle $A B C$. Prove that
$$
|P Q| \geqslant \frac{\sqrt{3}}{2} \cdot(|A B|+|A C|) .
$$
|
Since $\angle A B C+\angle A C B=60^{\circ}$, the lines $B P$ and $C Q$ are parallel. Let $X$ and $Y$ be the feet of perpendiculars from $A$ to $B P$ and $C Q$, respectively (see Figure 4). Then $|A X|=\frac{\sqrt{3}}{2}|A B|$ and $|A Y|=\frac{\sqrt{3}}{2}|A C|$. Since the points $X, A$ and $Y$ are collinear, we get
$$
|P Q| \geqslant|X Y|=\frac{\sqrt{3}}{2}(|A B|+|A C|)
$$
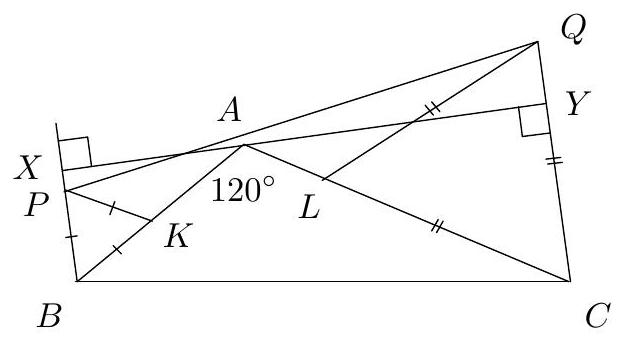
Figure 4
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a triangle $A B C$ with $\angle A=120^{\circ}$. The points $K$ and $L$ lie on the sides $A B$ and $A C$, respectively. Let $B K P$ and $C L Q$ be equilateral triangles constructed outside the triangle $A B C$. Prove that
$$
|P Q| \geqslant \frac{\sqrt{3}}{2} \cdot(|A B|+|A C|) .
$$
|
Since $\angle A B C+\angle A C B=60^{\circ}$, the lines $B P$ and $C Q$ are parallel. Let $X$ and $Y$ be the feet of perpendiculars from $A$ to $B P$ and $C Q$, respectively (see Figure 4). Then $|A X|=\frac{\sqrt{3}}{2}|A B|$ and $|A Y|=\frac{\sqrt{3}}{2}|A C|$. Since the points $X, A$ and $Y$ are collinear, we get
$$
|P Q| \geqslant|X Y|=\frac{\sqrt{3}}{2}(|A B|+|A C|)
$$

Figure 4
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n4.",
"solution_match": "\n4."
}
|
ea599d25-b072-5013-b7d4-8c50add62080
| 240,330
|
There is a frog jumping on a $2 k \times 2 k$ chessboard, composed of unit squares. The frog's jumps are of length $\sqrt{1+k^{2}}$ and they carry the frog from the center of a square to the center of another square. Some $m$ squares of the board are marked with an $x$, and all the squares into which the frog can jump from an $x$ 'd square (whether they carry an $x$ or not) are marked with an $\circ$. There are $n \circ$ 'd squares. Prove that $n \geqslant m$.
|
Label the squares by pairs of integers $(i, j)$ where $1 \leqslant i, j \leqslant 2 k$. Let $L$ be the set of all such pairs. Define a function $f: L \rightarrow L$ by
$$
f(i, j)= \begin{cases}(i+1, j+k) & \text { for } i \text { odd and } j \leqslant k \\ (i-1, j+k) & \text { for } i \text { even and } j \leqslant k, \\ (i+1, j-k) & \text { for } i \text { odd and } j>k, \\ (i-1, j-k) & \text { for } i \text { even and } j>k\end{cases}
$$
It is easy to see that $f$ is one-to-one. Let $X \subset L$ be the set of $\times^{\prime} \mathrm{d}$ squares and $O \subset L$ the set of o'd squares. Since the distance from $(i, j)$ to
$(i \pm 1, j \pm k)$ is $\sqrt{1+k^{2}}$, we have $f(i, j) \in O$ for every $(i, j) \in X$. Now, since $f$ is one-to-one, the number of elements in $f(S)$ is the same as the number of elements in $S$. As $f(X) \subset O$, the number of elements in $X$ is at most the number of elements in $O$, or $m \leqslant n$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There is a frog jumping on a $2 k \times 2 k$ chessboard, composed of unit squares. The frog's jumps are of length $\sqrt{1+k^{2}}$ and they carry the frog from the center of a square to the center of another square. Some $m$ squares of the board are marked with an $x$, and all the squares into which the frog can jump from an $x$ 'd square (whether they carry an $x$ or not) are marked with an $\circ$. There are $n \circ$ 'd squares. Prove that $n \geqslant m$.
|
Label the squares by pairs of integers $(i, j)$ where $1 \leqslant i, j \leqslant 2 k$. Let $L$ be the set of all such pairs. Define a function $f: L \rightarrow L$ by
$$
f(i, j)= \begin{cases}(i+1, j+k) & \text { for } i \text { odd and } j \leqslant k \\ (i-1, j+k) & \text { for } i \text { even and } j \leqslant k, \\ (i+1, j-k) & \text { for } i \text { odd and } j>k, \\ (i-1, j-k) & \text { for } i \text { even and } j>k\end{cases}
$$
It is easy to see that $f$ is one-to-one. Let $X \subset L$ be the set of $\times^{\prime} \mathrm{d}$ squares and $O \subset L$ the set of o'd squares. Since the distance from $(i, j)$ to
$(i \pm 1, j \pm k)$ is $\sqrt{1+k^{2}}$, we have $f(i, j) \in O$ for every $(i, j) \in X$. Now, since $f$ is one-to-one, the number of elements in $f(S)$ is the same as the number of elements in $S$. As $f(X) \subset O$, the number of elements in $X$ is at most the number of elements in $O$, or $m \leqslant n$.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n9.",
"solution_match": "\n9."
}
|
4955608d-da38-58ae-a230-b695c9124612
| 240,374
|
Let $x_{1}, x_{2}, \ldots, x_{n}$ be positive integers such that no one of them is an initial fragment of any other (for example, 12 is an initial fragment of $\underline{12}, \underline{12} 5$ and
12405). Prove that
$$
\frac{1}{x_{1}}+\frac{1}{x_{2}}+\cdots+\frac{1}{x_{n}}<3
$$
|
Let $\left\{y_{1}, \ldots, y_{k}\right\} \subset\left\{x_{1}, \ldots, x_{n}\right\}$ be a subset of numbers with the maximal number of digits, and differing from one another only by their last digits: $y_{1}=\overline{y \alpha_{1}}, y_{2}=\overline{y \alpha_{2}}, \ldots, y_{k}=\overline{y \alpha_{k}}$ (here $\overline{y \alpha_{i}}$ denotes the number consisting of $y$ as its initial fragment and $\alpha_{i}$ as its last digit). Then we have
$$
\frac{1}{y_{1}}+\ldots+\frac{1}{y_{k}} \leqslant \frac{1}{\overline{y 0}}+\ldots+\frac{1}{\overline{y 9}}<10 \cdot \frac{1}{\overline{y 0}}=\frac{1}{y}
$$
Let's replace all numbers $y_{1}, y_{2}, \ldots, y_{k}$ by a single $y$ in the set $\left\{x_{1}, \ldots, x_{n}\right\}$. Then the obtained set of numbers still has the property mentioned in the statement of the problem, and the sum of their reciprocals does not decrease. Continuing to reduce the given set of numbers in the same way, we finally obtain
$$
\frac{1}{x_{1}}+\frac{1}{x_{2}}+\cdots+\frac{1}{x_{n}} \leqslant \frac{1}{1}+\frac{1}{2}+\ldots+\frac{1}{9}<3
$$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $x_{1}, x_{2}, \ldots, x_{n}$ be positive integers such that no one of them is an initial fragment of any other (for example, 12 is an initial fragment of $\underline{12}, \underline{12} 5$ and
12405). Prove that
$$
\frac{1}{x_{1}}+\frac{1}{x_{2}}+\cdots+\frac{1}{x_{n}}<3
$$
|
Let $\left\{y_{1}, \ldots, y_{k}\right\} \subset\left\{x_{1}, \ldots, x_{n}\right\}$ be a subset of numbers with the maximal number of digits, and differing from one another only by their last digits: $y_{1}=\overline{y \alpha_{1}}, y_{2}=\overline{y \alpha_{2}}, \ldots, y_{k}=\overline{y \alpha_{k}}$ (here $\overline{y \alpha_{i}}$ denotes the number consisting of $y$ as its initial fragment and $\alpha_{i}$ as its last digit). Then we have
$$
\frac{1}{y_{1}}+\ldots+\frac{1}{y_{k}} \leqslant \frac{1}{\overline{y 0}}+\ldots+\frac{1}{\overline{y 9}}<10 \cdot \frac{1}{\overline{y 0}}=\frac{1}{y}
$$
Let's replace all numbers $y_{1}, y_{2}, \ldots, y_{k}$ by a single $y$ in the set $\left\{x_{1}, \ldots, x_{n}\right\}$. Then the obtained set of numbers still has the property mentioned in the statement of the problem, and the sum of their reciprocals does not decrease. Continuing to reduce the given set of numbers in the same way, we finally obtain
$$
\frac{1}{x_{1}}+\frac{1}{x_{2}}+\cdots+\frac{1}{x_{n}} \leqslant \frac{1}{1}+\frac{1}{2}+\ldots+\frac{1}{9}<3
$$
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n12.",
"solution_match": "\n12."
}
|
94656215-49a9-5c5e-aa32-1fb80ab992f9
| 240,401
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be an arithmetic progression of integers such that $i$ divides $a_{i}$ for $i=1,2, \ldots, n-1$ and $n$ does not divide $a_{n}$. Prove that $n$ is a power of a prime.
|
Assume $a_{i}=k+d i$ for $i=1,2, \ldots, n$. Then $k$ is a multiple of every $i \in\{1,2, \ldots, n-1\}$ but not a multiple of $n$. If $n=a b$ with $a, b>1$ and $\operatorname{gcd}(a, b)=1$, then $k$ is divisible by both $a$ and $b$, but not by $n$, which is a contradiction. Hence, $n$ has only one prime factor.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be an arithmetic progression of integers such that $i$ divides $a_{i}$ for $i=1,2, \ldots, n-1$ and $n$ does not divide $a_{n}$. Prove that $n$ is a power of a prime.
|
Assume $a_{i}=k+d i$ for $i=1,2, \ldots, n$. Then $k$ is a multiple of every $i \in\{1,2, \ldots, n-1\}$ but not a multiple of $n$. If $n=a b$ with $a, b>1$ and $\operatorname{gcd}(a, b)=1$, then $k$ is divisible by both $a$ and $b$, but not by $n$, which is a contradiction. Hence, $n$ has only one prime factor.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n13.",
"solution_match": "\n13."
}
|
fa0807f8-6260-5b0d-9597-6f0dd217d888
| 240,410
|
Let $n$ be a positive integer not divisible by 2 or 3 . Prove that for all integers $k$, the number $(k+1)^{n}-k^{n}-1$ is divisible by $k^{2}+k+1$.
|
Note that $n$ must be congruent to 1 or 5 modulo 6 , and proceed by induction on $\lfloor n / 6\rfloor$. It can easily be checked that the assertion holds for $n \in\{1,5\}$. Let $n>6$, and put $t=k^{2}+k+1$. The claim follows by:
$$
\begin{aligned}
(k+1)^{n}-k^{n}-1 & =(t+k)(k+1)^{n-2}-(t-(k+1)) k^{n-2}-1 \\
& \equiv k(k+1)^{n-2}+(k+1) k^{n-2}-1 \\
& \equiv(t-1)\left((k+1)^{n-3}+k^{n-3}\right)-1 \\
& \equiv-(k+1)^{n-3}-k^{n-3}-1 \\
& \equiv-(t+k)(k+1)^{n-5}-(t-(k+1)) k^{n-5}-1 \\
& \equiv-k(k+1)^{n-5}+(k+1) k^{n-5}-1 \\
& \equiv-(t-1)\left((k+1)^{n-6}-k^{n-6}\right)-1 \\
& \equiv(k+1)^{n-6}-k^{n-6}-1(\bmod t) .
\end{aligned}
$$
Alternative solution. Let $P(k)=(k+1)^{n}-k^{n}-1$, and let $\omega_{1}, \omega_{2}$ be the two roots of the quadratic polynomial $k^{2}+k+1$. The problem is then equivalent to showing that $P\left(\omega_{1}\right)=P\left(\omega_{2}\right)=0$ when $\operatorname{gcd}(n, 6)=1$, which is easy to check.
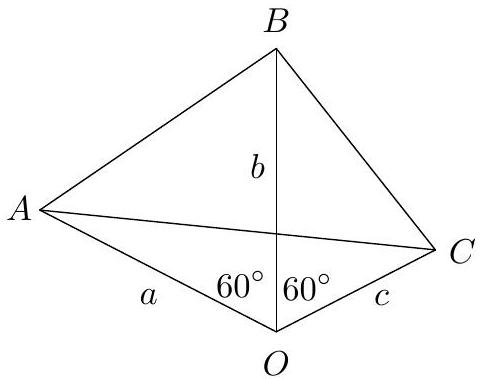
Figure 7
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer not divisible by 2 or 3 . Prove that for all integers $k$, the number $(k+1)^{n}-k^{n}-1$ is divisible by $k^{2}+k+1$.
|
Note that $n$ must be congruent to 1 or 5 modulo 6 , and proceed by induction on $\lfloor n / 6\rfloor$. It can easily be checked that the assertion holds for $n \in\{1,5\}$. Let $n>6$, and put $t=k^{2}+k+1$. The claim follows by:
$$
\begin{aligned}
(k+1)^{n}-k^{n}-1 & =(t+k)(k+1)^{n-2}-(t-(k+1)) k^{n-2}-1 \\
& \equiv k(k+1)^{n-2}+(k+1) k^{n-2}-1 \\
& \equiv(t-1)\left((k+1)^{n-3}+k^{n-3}\right)-1 \\
& \equiv-(k+1)^{n-3}-k^{n-3}-1 \\
& \equiv-(t+k)(k+1)^{n-5}-(t-(k+1)) k^{n-5}-1 \\
& \equiv-k(k+1)^{n-5}+(k+1) k^{n-5}-1 \\
& \equiv-(t-1)\left((k+1)^{n-6}-k^{n-6}\right)-1 \\
& \equiv(k+1)^{n-6}-k^{n-6}-1(\bmod t) .
\end{aligned}
$$
Alternative solution. Let $P(k)=(k+1)^{n}-k^{n}-1$, and let $\omega_{1}, \omega_{2}$ be the two roots of the quadratic polynomial $k^{2}+k+1$. The problem is then equivalent to showing that $P\left(\omega_{1}\right)=P\left(\omega_{2}\right)=0$ when $\operatorname{gcd}(n, 6)=1$, which is easy to check.

Figure 7
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n15.",
"solution_match": "\n15."
}
|
85e6ceaf-059a-56dc-97ed-b4bc827e0f2b
| 604,640
|
Prove that for all positive real numbers $a, b, c$ we have
$$
\sqrt{a^{2}-a b+b^{2}}+\sqrt{b^{2}-b c+c^{2}} \geqslant \sqrt{a^{2}+a c+c^{2}} .
$$
|
If $|O A|=a,|O B|=b,|O C|=c$ (see Figure 7), then the inequality follows from $|A C| \leqslant|A B|+|B C|$ by applying the cosine theorem to triangles $A O B$,
$B O C$ and $A O C$. The same argument holds if the quadrangle $O A B C$ is concave.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that for all positive real numbers $a, b, c$ we have
$$
\sqrt{a^{2}-a b+b^{2}}+\sqrt{b^{2}-b c+c^{2}} \geqslant \sqrt{a^{2}+a c+c^{2}} .
$$
|
If $|O A|=a,|O B|=b,|O C|=c$ (see Figure 7), then the inequality follows from $|A C| \leqslant|A B|+|B C|$ by applying the cosine theorem to triangles $A O B$,
$B O C$ and $A O C$. The same argument holds if the quadrangle $O A B C$ is concave.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n16.",
"solution_match": "\n16."
}
|
ad4f64c3-a692-5ffb-a3c4-1ddfedd843d1
| 604,655
|
Let $t \geqslant \frac{1}{2}$ be a real number and $n$ a positive integer. Prove that
$$
t^{2 n} \geqslant(t-1)^{2 n}+(2 t-1)^{n}
$$
|
Use induction. For $n=1$ the inequality reads $t^{2} \geqslant(t-1)^{2}+(2 t-1)$ which is obviously true. To prove the induction step it suffices to show that
$$
t^{2}(t-1)^{2 n}+t^{2}(2 t-1)^{n} \geqslant(t-1)^{2 n+2}+(2 t-1)^{n+1}
$$
This easily follows from $t^{2} \geqslant(t-1)^{2}$ (which is true for $t \geqslant \frac{1}{2}$ ) and $t^{2} \geqslant 2 t-1$ (which is true for any real $t$ ).
Alternative solution. Note that
$$
t^{2 n}=\left(t^{2}\right)^{n}=\left((t-1)^{2}+(2 t-1)\right)^{n} .
$$
Applying the binomial formula to the right-hand side we obtain a sum containing both summands of the right-hand side of the given equality and other summands each of which is clearly non-negative.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $t \geqslant \frac{1}{2}$ be a real number and $n$ a positive integer. Prove that
$$
t^{2 n} \geqslant(t-1)^{2 n}+(2 t-1)^{n}
$$
|
Use induction. For $n=1$ the inequality reads $t^{2} \geqslant(t-1)^{2}+(2 t-1)$ which is obviously true. To prove the induction step it suffices to show that
$$
t^{2}(t-1)^{2 n}+t^{2}(2 t-1)^{n} \geqslant(t-1)^{2 n+2}+(2 t-1)^{n+1}
$$
This easily follows from $t^{2} \geqslant(t-1)^{2}$ (which is true for $t \geqslant \frac{1}{2}$ ) and $t^{2} \geqslant 2 t-1$ (which is true for any real $t$ ).
Alternative solution. Note that
$$
t^{2 n}=\left(t^{2}\right)^{n}=\left((t-1)^{2}+(2 t-1)\right)^{n} .
$$
Applying the binomial formula to the right-hand side we obtain a sum containing both summands of the right-hand side of the given equality and other summands each of which is clearly non-negative.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n19.",
"solution_match": "\n19."
}
|
ba0bbc8c-5687-5407-8bed-c9787b197e66
| 240,469
|
For every positive integer $n$, let
$$
x_{n}=\frac{(2 n+1) \cdot(2 n+3) \cdots \cdots \cdot(4 n-1) \cdot(4 n+1)}{2 n \cdot(2 n+2) \cdots \cdots \cdot(4 n-2) \cdot 4 n}
$$
Prove that $\frac{1}{4 n}<x_{n}-\sqrt{2}<\frac{2}{n}$.
## Solutions
|
Squaring both sides of the given equality and applying $x(x+2) \leqslant(x+1)^{2}$ to the numerator of the obtained fraction and cancelling we have
$$
x_{n}^{2} \leqslant \frac{(2 n+1) \cdot(4 n+1)}{(2 n)^{2}}<2+\frac{2}{n} .
$$
Similarly (applying $x(x+2) \leqslant(x+1)^{2}$ to the denominator and cancelling) we get
$$
x_{n}^{2} \geqslant \frac{(4 n+1)^{2}}{2 n \cdot 4 n}>2+\frac{1}{n}
$$
Hence
$$
\frac{1}{n}<x_{n}^{2}-2<\frac{2}{n}
$$
and
$$
\frac{1}{n\left(x_{n}+\sqrt{2}\right)}<x_{n}-\sqrt{2}<\frac{2}{n\left(x_{n}+\sqrt{2}\right)} .
$$
From the first chain of inequalities we get $x_{n}>\sqrt{2}$ and $x_{n}<2$. The result then follows from the second chain of inequalities.
Comment. These inequalities can easily be improved. For example, the inequalities in the solution involving $x_{n}^{2}$ can immediately be replaced by $\frac{3}{2 n}<x_{n}^{2}-2<\frac{2}{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
For every positive integer $n$, let
$$
x_{n}=\frac{(2 n+1) \cdot(2 n+3) \cdots \cdots \cdot(4 n-1) \cdot(4 n+1)}{2 n \cdot(2 n+2) \cdots \cdots \cdot(4 n-2) \cdot 4 n}
$$
Prove that $\frac{1}{4 n}<x_{n}-\sqrt{2}<\frac{2}{n}$.
## Solutions
|
Squaring both sides of the given equality and applying $x(x+2) \leqslant(x+1)^{2}$ to the numerator of the obtained fraction and cancelling we have
$$
x_{n}^{2} \leqslant \frac{(2 n+1) \cdot(4 n+1)}{(2 n)^{2}}<2+\frac{2}{n} .
$$
Similarly (applying $x(x+2) \leqslant(x+1)^{2}$ to the denominator and cancelling) we get
$$
x_{n}^{2} \geqslant \frac{(4 n+1)^{2}}{2 n \cdot 4 n}>2+\frac{1}{n}
$$
Hence
$$
\frac{1}{n}<x_{n}^{2}-2<\frac{2}{n}
$$
and
$$
\frac{1}{n\left(x_{n}+\sqrt{2}\right)}<x_{n}-\sqrt{2}<\frac{2}{n\left(x_{n}+\sqrt{2}\right)} .
$$
From the first chain of inequalities we get $x_{n}>\sqrt{2}$ and $x_{n}<2$. The result then follows from the second chain of inequalities.
Comment. These inequalities can easily be improved. For example, the inequalities in the solution involving $x_{n}^{2}$ can immediately be replaced by $\frac{3}{2 n}<x_{n}^{2}-2<\frac{2}{n}$.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n20.",
"solution_match": "\n20."
}
|
06b9399f-8281-5e7e-bf32-2face87ec906
| 604,725
|
Let 2001 given points on a circle be colored either red or green. In one step all points are recolored simultaneously in the following way: If both direct neighbors of a point $P$ have the same color as $P$, then the color of $P$ remains unchanged, otherwise $P$ obtains the other color. Starting with the first coloring $F_{1}$, we obtain the colorings $F_{2}, F_{3}, \ldots$ after several recoloring steps. Prove that there is a number $n_{0} \leqslant 1000$ such that $F_{n_{0}}=F_{n_{0}+2}$. Is the assertion also true if 1000 is replaced by 999 ?
|
Answer: no.
Let the points be denoted by $1,2, \ldots, 2001$ such that $i, j$ are neighbors if $|i-j|=1$ or $\{i, j\}=\{1,2001\}$. We say that $k$ points form a monochromatic segment of length $k$ if the points are consecutive on the circle and if
they all have the same color. For a coloring $F$ let $d(F)$ be the maximum length of a monochromatic segment. Note that $d\left(F_{n}\right)>1$ for all $n$ since 2001 is odd. If $d\left(F_{1}\right)=2001$ then all points have the same color, hence $F_{1}=F_{2}=F_{3}=\ldots$ and we can choose $n_{0}=1$. Thus, let $1<d\left(F_{1}\right)<2001$. Below we shall prove the following implications:
If $3<d\left(F_{n}\right)<2001$, then $d\left(F_{n+1}\right)=d\left(F_{n}\right)-2 ;$
If $d\left(F_{n}\right)=3$, then $d\left(F_{n+1}\right)=2$;
If $d\left(F_{n}\right)=2$, then $d\left(F_{n+1}\right)=d\left(F_{n}\right)$ and $F_{n+2}=F_{n}$;
From (1) and (2) it follows that $d\left(F_{1000}\right) \leqslant 2$, hence by (3) we have $F_{1000}=F_{1002}$. Moreover, if $F_{1}$ is the coloring where 1 is colored red and all other points are colored green, then $d\left(F_{1}\right)=2000$ and thus $d\left(F_{1}\right)>d\left(F_{2}\right)>\ldots>d\left(F_{1000}\right)=2$ which shows that, for all $n<1000, F_{n} \neq F_{n+2}$ and thus 1000 cannot be replaced by 999 .
It remains to prove (1)-(3). Let $(i+1, \ldots, i+k)$ be a longest monochromatic segment for $F_{n}$ (considering the labels of the points modulo 2001). Then $(i+2, \ldots, i+k-1)$ is a monochromatic segment for $F_{n+1}$ and thus $d\left(F_{n+1}\right) \geqslant d\left(F_{n}\right)-2$. Moreover, if $(i+1, \ldots, i+k)$ is a longest monochromatic segment for $F_{n+1}$ where $k \geqslant 3$, then $(i, \ldots, i+k+1)$ is a monochromatic segment for $F_{n}$. From this and $F_{n+1}>1$ the implications (1) and (2) clearly follow. For proof of (3) note that if $d\left(F_{n}\right) \leqslant 2$ then $F_{n+1}$ is obtained from $F_{n}$ by changing the colour of all points.
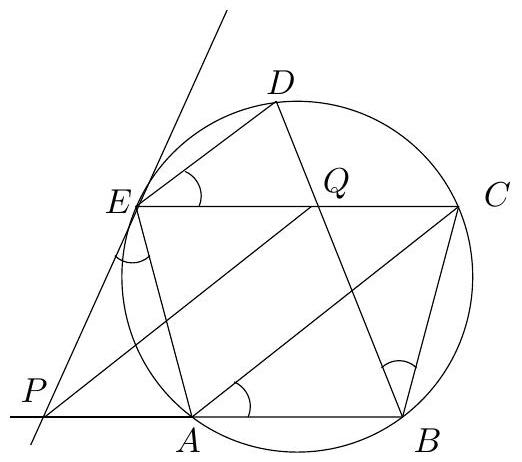
Figure 1
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let 2001 given points on a circle be colored either red or green. In one step all points are recolored simultaneously in the following way: If both direct neighbors of a point $P$ have the same color as $P$, then the color of $P$ remains unchanged, otherwise $P$ obtains the other color. Starting with the first coloring $F_{1}$, we obtain the colorings $F_{2}, F_{3}, \ldots$ after several recoloring steps. Prove that there is a number $n_{0} \leqslant 1000$ such that $F_{n_{0}}=F_{n_{0}+2}$. Is the assertion also true if 1000 is replaced by 999 ?
|
Answer: no.
Let the points be denoted by $1,2, \ldots, 2001$ such that $i, j$ are neighbors if $|i-j|=1$ or $\{i, j\}=\{1,2001\}$. We say that $k$ points form a monochromatic segment of length $k$ if the points are consecutive on the circle and if
they all have the same color. For a coloring $F$ let $d(F)$ be the maximum length of a monochromatic segment. Note that $d\left(F_{n}\right)>1$ for all $n$ since 2001 is odd. If $d\left(F_{1}\right)=2001$ then all points have the same color, hence $F_{1}=F_{2}=F_{3}=\ldots$ and we can choose $n_{0}=1$. Thus, let $1<d\left(F_{1}\right)<2001$. Below we shall prove the following implications:
If $3<d\left(F_{n}\right)<2001$, then $d\left(F_{n+1}\right)=d\left(F_{n}\right)-2 ;$
If $d\left(F_{n}\right)=3$, then $d\left(F_{n+1}\right)=2$;
If $d\left(F_{n}\right)=2$, then $d\left(F_{n+1}\right)=d\left(F_{n}\right)$ and $F_{n+2}=F_{n}$;
From (1) and (2) it follows that $d\left(F_{1000}\right) \leqslant 2$, hence by (3) we have $F_{1000}=F_{1002}$. Moreover, if $F_{1}$ is the coloring where 1 is colored red and all other points are colored green, then $d\left(F_{1}\right)=2000$ and thus $d\left(F_{1}\right)>d\left(F_{2}\right)>\ldots>d\left(F_{1000}\right)=2$ which shows that, for all $n<1000, F_{n} \neq F_{n+2}$ and thus 1000 cannot be replaced by 999 .
It remains to prove (1)-(3). Let $(i+1, \ldots, i+k)$ be a longest monochromatic segment for $F_{n}$ (considering the labels of the points modulo 2001). Then $(i+2, \ldots, i+k-1)$ is a monochromatic segment for $F_{n+1}$ and thus $d\left(F_{n+1}\right) \geqslant d\left(F_{n}\right)-2$. Moreover, if $(i+1, \ldots, i+k)$ is a longest monochromatic segment for $F_{n+1}$ where $k \geqslant 3$, then $(i, \ldots, i+k+1)$ is a monochromatic segment for $F_{n}$. From this and $F_{n+1}>1$ the implications (1) and (2) clearly follow. For proof of (3) note that if $d\left(F_{n}\right) \leqslant 2$ then $F_{n+1}$ is obtained from $F_{n}$ by changing the colour of all points.

Figure 1
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n5.",
"solution_match": "\n5."
}
|
7812cc1b-fd27-5495-9224-bcedfb25bad7
| 240,155
|
The points $A, B, C, D, E$ lie on the circle $c$ in this order and satisfy $A B \| E C$ and $A C \| E D$. The line tangent to the circle $c$ at $E$ meets the line $A B$ at $P$. The lines $B D$ and $E C$ meet at $Q$. Prove that $|A C|=|P Q|$.
|
The arcs $B C$ and $A E$ are of equal length (see Figure 1). Also, since
$A B \| E C$ and $E D \| A C$, we have $\angle C A B=\angle D E C$ and the $\operatorname{arcs} D C$ and $B C$ are of equal length. Since $P E$ is tangent to $c$ and $|A E|=|D C|$, then $\angle P E A=\angle D B C=\angle Q B C$. As $A B C D$ is inscribed in $c$, we have $\angle Q C B=180^{\circ}-\angle E A B=\angle P A E$. Also, $A B C D$ is an isosceles trapezium, whence $|A E|=|B C|$. So the triangles $A P E$ and $C Q B$ are congruent, and $|Q C|=|P A|$. Now $P A C Q$ is a quadrilateral with a pair of opposite sides equal and parallel. So $P A C Q$ is a parallelogram, and $|P Q|=|A C|$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The points $A, B, C, D, E$ lie on the circle $c$ in this order and satisfy $A B \| E C$ and $A C \| E D$. The line tangent to the circle $c$ at $E$ meets the line $A B$ at $P$. The lines $B D$ and $E C$ meet at $Q$. Prove that $|A C|=|P Q|$.
|
The arcs $B C$ and $A E$ are of equal length (see Figure 1). Also, since
$A B \| E C$ and $E D \| A C$, we have $\angle C A B=\angle D E C$ and the $\operatorname{arcs} D C$ and $B C$ are of equal length. Since $P E$ is tangent to $c$ and $|A E|=|D C|$, then $\angle P E A=\angle D B C=\angle Q B C$. As $A B C D$ is inscribed in $c$, we have $\angle Q C B=180^{\circ}-\angle E A B=\angle P A E$. Also, $A B C D$ is an isosceles trapezium, whence $|A E|=|B C|$. So the triangles $A P E$ and $C Q B$ are congruent, and $|Q C|=|P A|$. Now $P A C Q$ is a quadrilateral with a pair of opposite sides equal and parallel. So $P A C Q$ is a parallelogram, and $|P Q|=|A C|$.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n6.",
"solution_match": "\n6."
}
|
74b12f75-041c-58c1-b8f1-3bf455b08a5c
| 240,165
|
Given a parallelogram $A B C D$. A circle passing through $A$ meets the line segments $A B, A C$ and $A D$ at inner points $M, K, N$, respectively. Prove that
$$
|A B| \cdot|A M|+|A D| \cdot|A N|=|A K| \cdot|A C| .
$$
|
Let $X$ be the point on segment $A C$ such that $\angle A D X=\angle A K N$, then
$$
\angle A X D=\angle A N K=180^{\circ}-\angle A M K
$$
(see Figure 2). Triangles $N A K$ and $X A D$ are similar, having two pairs of equal angles, hence $|A X|=\frac{|A N| \cdot|A D|}{|A K|}$. Since triangles $M A K$ and $X C D$ are also similar, we have $|C X|=\frac{|A M| \cdot|C D|}{|A K|}=\frac{|A M| \cdot|A B|}{|A K|}$ and
$$
|A M| \cdot|A B|+|A N| \cdot|A D|=(|A X|+|C X|) \cdot|A K|=|A C| \cdot|A K| \text {. }
$$
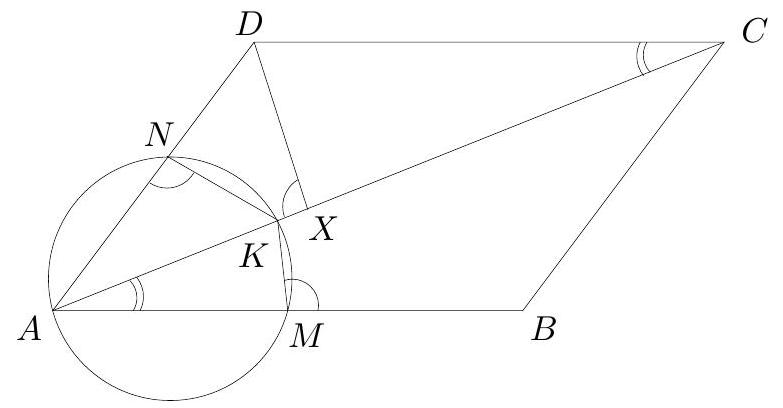
Figure 2
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a parallelogram $A B C D$. A circle passing through $A$ meets the line segments $A B, A C$ and $A D$ at inner points $M, K, N$, respectively. Prove that
$$
|A B| \cdot|A M|+|A D| \cdot|A N|=|A K| \cdot|A C| .
$$
|
Let $X$ be the point on segment $A C$ such that $\angle A D X=\angle A K N$, then
$$
\angle A X D=\angle A N K=180^{\circ}-\angle A M K
$$
(see Figure 2). Triangles $N A K$ and $X A D$ are similar, having two pairs of equal angles, hence $|A X|=\frac{|A N| \cdot|A D|}{|A K|}$. Since triangles $M A K$ and $X C D$ are also similar, we have $|C X|=\frac{|A M| \cdot|C D|}{|A K|}=\frac{|A M| \cdot|A B|}{|A K|}$ and
$$
|A M| \cdot|A B|+|A N| \cdot|A D|=(|A X|+|C X|) \cdot|A K|=|A C| \cdot|A K| \text {. }
$$

Figure 2
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n7.",
"solution_match": "\n7."
}
|
1373c768-91aa-5100-973f-41893999c926
| 240,174
|
Let $A B C D$ be a convex quadrilateral, and let $N$ be the midpoint of $B C$. Suppose further that $\angle A N D=135^{\circ}$. Prove that
$$
|A B|+|C D|+\frac{1}{\sqrt{2}} \cdot|B C| \geqslant|A D|
$$
|
Let $X$ be the point symmetric to $B$ with respect to $A N$, and let $Y$ be the point symmetric to $C$ with respect to $D N$ (see Figure 3 ). Then
$$
\angle X N Y=180^{\circ}-2 \cdot\left(180^{\circ}-135^{\circ}\right)=90^{\circ}
$$
and $|N X|=|N Y|=\frac{|B C|}{2}$. Therefore, $|X Y|=\frac{|B C|}{\sqrt{2}}$. Moreover, we have
$$
\begin{aligned}
& |A X|=|A B| \text { and }|D Y|=|D C| \text {. Consequently, } \\
& \qquad|A D| \leqslant|A X|+|X Y|+|Y D|=|A B|+\frac{|B C|}{\sqrt{2}}+|D C| .
\end{aligned}
$$
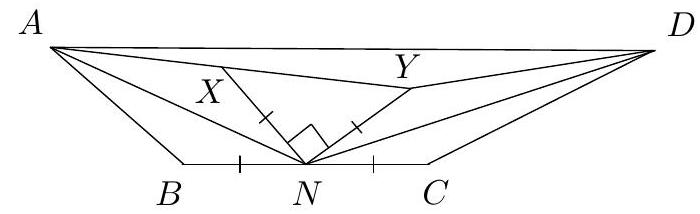
Figure 3
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $A B C D$ be a convex quadrilateral, and let $N$ be the midpoint of $B C$. Suppose further that $\angle A N D=135^{\circ}$. Prove that
$$
|A B|+|C D|+\frac{1}{\sqrt{2}} \cdot|B C| \geqslant|A D|
$$
|
Let $X$ be the point symmetric to $B$ with respect to $A N$, and let $Y$ be the point symmetric to $C$ with respect to $D N$ (see Figure 3 ). Then
$$
\angle X N Y=180^{\circ}-2 \cdot\left(180^{\circ}-135^{\circ}\right)=90^{\circ}
$$
and $|N X|=|N Y|=\frac{|B C|}{2}$. Therefore, $|X Y|=\frac{|B C|}{\sqrt{2}}$. Moreover, we have
$$
\begin{aligned}
& |A X|=|A B| \text { and }|D Y|=|D C| \text {. Consequently, } \\
& \qquad|A D| \leqslant|A X|+|X Y|+|Y D|=|A B|+\frac{|B C|}{\sqrt{2}}+|D C| .
\end{aligned}
$$

Figure 3
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n8.",
"solution_match": "\n8."
}
|
3727d9f6-f8eb-55ad-a10e-3b26dd3fd3d3
| 240,183
|
Let $a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of real numbers satisfying $a_{0}=1$ and $a_{n}=a_{\lfloor 7 n / 9\rfloor}+a_{\lfloor n / 9\rfloor}$ for $n=1,2, \ldots$ Prove that there exists a positive integer $k$ with $a_{k}<\frac{k}{2001 !}$.
(Here $\lfloor x\rfloor$ denotes the largest integer not greater than $x$.)
|
Consider the equation
$$
\left(\frac{7}{9}\right)^{x}+\left(\frac{1}{9}\right)^{x}=1 .
$$
It has a root $\frac{1}{2}<\alpha<1$, because $\sqrt{\frac{7}{9}}+\sqrt{\frac{1}{9}}=\frac{\sqrt{7}+1}{3}>1$ and $\frac{7}{9}+\frac{1}{9}<1$. We will prove that $a_{n} \leqslant M \cdot n^{\alpha}$ for some $M>0-$ since $\frac{n^{\alpha}}{n}$ will be arbitrarily small for large enough $n$, the claim follows from this immediately. We choose $M$ so that the inequality $a_{n} \leqslant M \cdot n^{\alpha}$ holds for $1 \leqslant n \leqslant 8$; since for $n \geqslant 9$ we have $1<[7 n / 9]<n$ and $1 \leqslant[n / 9]<n$, it follows by induction that
$$
\begin{aligned}
a_{n} & =a_{[7 n / 9]}+a_{[n / 9]} \leqslant M \cdot\left[\frac{7 n}{9}\right]^{\alpha}+M \cdot\left[\frac{n}{9}\right]^{\alpha} \leqslant \\
& \leqslant M \cdot\left(\frac{7 n}{9}\right)^{\alpha}+M \cdot\left(\frac{n}{9}\right)^{\alpha}=M \cdot n^{\alpha} \cdot\left(\left(\frac{7}{9}\right)^{\alpha}+\left(\frac{1}{9}\right)^{\alpha}\right)=M \cdot n^{\alpha} .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of real numbers satisfying $a_{0}=1$ and $a_{n}=a_{\lfloor 7 n / 9\rfloor}+a_{\lfloor n / 9\rfloor}$ for $n=1,2, \ldots$ Prove that there exists a positive integer $k$ with $a_{k}<\frac{k}{2001 !}$.
(Here $\lfloor x\rfloor$ denotes the largest integer not greater than $x$.)
|
Consider the equation
$$
\left(\frac{7}{9}\right)^{x}+\left(\frac{1}{9}\right)^{x}=1 .
$$
It has a root $\frac{1}{2}<\alpha<1$, because $\sqrt{\frac{7}{9}}+\sqrt{\frac{1}{9}}=\frac{\sqrt{7}+1}{3}>1$ and $\frac{7}{9}+\frac{1}{9}<1$. We will prove that $a_{n} \leqslant M \cdot n^{\alpha}$ for some $M>0-$ since $\frac{n^{\alpha}}{n}$ will be arbitrarily small for large enough $n$, the claim follows from this immediately. We choose $M$ so that the inequality $a_{n} \leqslant M \cdot n^{\alpha}$ holds for $1 \leqslant n \leqslant 8$; since for $n \geqslant 9$ we have $1<[7 n / 9]<n$ and $1 \leqslant[n / 9]<n$, it follows by induction that
$$
\begin{aligned}
a_{n} & =a_{[7 n / 9]}+a_{[n / 9]} \leqslant M \cdot\left[\frac{7 n}{9}\right]^{\alpha}+M \cdot\left[\frac{n}{9}\right]^{\alpha} \leqslant \\
& \leqslant M \cdot\left(\frac{7 n}{9}\right)^{\alpha}+M \cdot\left(\frac{n}{9}\right)^{\alpha}=M \cdot n^{\alpha} \cdot\left(\left(\frac{7}{9}\right)^{\alpha}+\left(\frac{1}{9}\right)^{\alpha}\right)=M \cdot n^{\alpha} .
\end{aligned}
$$
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n13.",
"solution_match": "\n13."
}
|
8056fe7e-4998-57fc-b0a2-431e6d47a783
| 240,230
|
There are $2 n$ cards. On each card some real number $x, 1 \leqslant x \leqslant 2$, is written (there can be different numbers on different cards). Prove that
the cards can be divided into two heaps with sums $s_{1}$ and $s_{2}$ so that $\frac{n}{n+1} \leqslant \frac{s_{1}}{s_{2}} \leqslant 1$.
|
Let the numbers be $x_{1} \leqslant x_{2} \leqslant \ldots \leqslant x_{2 n-1} \leqslant x_{2 n}$. We will show that the choice $s_{1}=x_{1}+x_{3}+x_{5}+\cdots+x_{2 n-1}$ and $s_{2}=x_{2}+x_{4}+\cdots+x_{2 n}$ solves the problem. Indeed, the inequality $\frac{s_{1}}{s_{2}} \leqslant 1$ is obvious and we have
$$
\begin{aligned}
\frac{s_{1}}{s_{2}} & =\frac{x_{1}+x_{3}+x_{5}+\ldots+x_{2 n-1}}{x_{2}+x_{4}+x_{6}+\ldots+x_{2 n}}=\frac{\left(x_{3}+x_{5}+\ldots+x_{2 n-1}\right)+x_{1}}{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+x_{2 n}} \geqslant \\
& \geqslant \frac{\left(x_{3}+x_{5}+\ldots+x_{2 n-1}\right)+1}{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+2} \geqslant \frac{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+1}{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+2}= \\
& =1-\frac{1}{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+2} \geqslant 1-\frac{1}{(n-1)+2}=\frac{n}{n+1} .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There are $2 n$ cards. On each card some real number $x, 1 \leqslant x \leqslant 2$, is written (there can be different numbers on different cards). Prove that
the cards can be divided into two heaps with sums $s_{1}$ and $s_{2}$ so that $\frac{n}{n+1} \leqslant \frac{s_{1}}{s_{2}} \leqslant 1$.
|
Let the numbers be $x_{1} \leqslant x_{2} \leqslant \ldots \leqslant x_{2 n-1} \leqslant x_{2 n}$. We will show that the choice $s_{1}=x_{1}+x_{3}+x_{5}+\cdots+x_{2 n-1}$ and $s_{2}=x_{2}+x_{4}+\cdots+x_{2 n}$ solves the problem. Indeed, the inequality $\frac{s_{1}}{s_{2}} \leqslant 1$ is obvious and we have
$$
\begin{aligned}
\frac{s_{1}}{s_{2}} & =\frac{x_{1}+x_{3}+x_{5}+\ldots+x_{2 n-1}}{x_{2}+x_{4}+x_{6}+\ldots+x_{2 n}}=\frac{\left(x_{3}+x_{5}+\ldots+x_{2 n-1}\right)+x_{1}}{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+x_{2 n}} \geqslant \\
& \geqslant \frac{\left(x_{3}+x_{5}+\ldots+x_{2 n-1}\right)+1}{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+2} \geqslant \frac{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+1}{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+2}= \\
& =1-\frac{1}{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+2} \geqslant 1-\frac{1}{(n-1)+2}=\frac{n}{n+1} .
\end{aligned}
$$
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n14.",
"solution_match": "\n14."
}
|
c0cdf51a-0bc8-58be-95b3-c7e189329c62
| 240,239
|
Let $a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of positive real numbers satisfying $i \cdot a_{i}^{2} \geqslant(i+1) \cdot a_{i-1} a_{i+1}$ for $i=1,2, \ldots$ Furthermore, let $x$ and $y$ be positive reals, and let $b_{i}=x a_{i}+y a_{i-1}$ for $i=1,2, \ldots$ Prove that the inequality $i \cdot b_{i}^{2}>(i+1) \cdot b_{i-1} b_{i+1}$ holds for all integers $i \geqslant 2$.
|
Let $i \geqslant 2$. We are given the inequalities
$$
(i-1) \cdot a_{i-1}^{2} \geqslant i \cdot a_{i} a_{i-2}
$$
and
$$
i \cdot a_{i}^{2} \geqslant(i+1) \cdot a_{i+1} a_{i-1} .
$$
Multiplying both sides of (6) by $x^{2}$, we obtain
$$
i \cdot x^{2} \cdot a_{i}^{2} \geqslant(i+1) \cdot x^{2} \cdot a_{i+1} a_{i-1}
$$
By (5),
$$
\frac{a_{i-1}^{2}}{a_{i} a_{i-2}} \geqslant \frac{i}{i-1}=1+\frac{1}{i-1}>1+\frac{1}{i}=\frac{i+1}{i}
$$
which implies
$$
i \cdot y^{2} \cdot a_{i-1}^{2}>(i+1) \cdot y^{2} \cdot a_{i} a_{i-2} .
$$
Multiplying (5) and (6), and dividing both sides of the resulting inequality by $i a_{i} a_{i-1}$, we get
$$
(i-1) \cdot a_{i} a_{i-1} \geqslant(i+1) \cdot a_{i+1} a_{i-2} .
$$
Adding $(i+1) a_{i} a_{i-1}$ to both sides of the last inequality and multiplying both sides of the resulting inequality by $x y$ gives
$$
i \cdot 2 x y \cdot a_{i} a_{i-1} \geqslant(i+1) \cdot x y \cdot\left(a_{i+1} a_{i-2}+a_{i} a_{i-1}\right) .
$$
Finally, adding up (7), (8) and (9) results in
$$
i \cdot\left(x a_{i}+y a_{i-1}\right)^{2}>(i+1) \cdot\left(x a_{i+1}+y a_{i}\right)\left(x a_{i-1}+y a_{i-2}\right)
$$
which is equivalent to the claim.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of positive real numbers satisfying $i \cdot a_{i}^{2} \geqslant(i+1) \cdot a_{i-1} a_{i+1}$ for $i=1,2, \ldots$ Furthermore, let $x$ and $y$ be positive reals, and let $b_{i}=x a_{i}+y a_{i-1}$ for $i=1,2, \ldots$ Prove that the inequality $i \cdot b_{i}^{2}>(i+1) \cdot b_{i-1} b_{i+1}$ holds for all integers $i \geqslant 2$.
|
Let $i \geqslant 2$. We are given the inequalities
$$
(i-1) \cdot a_{i-1}^{2} \geqslant i \cdot a_{i} a_{i-2}
$$
and
$$
i \cdot a_{i}^{2} \geqslant(i+1) \cdot a_{i+1} a_{i-1} .
$$
Multiplying both sides of (6) by $x^{2}$, we obtain
$$
i \cdot x^{2} \cdot a_{i}^{2} \geqslant(i+1) \cdot x^{2} \cdot a_{i+1} a_{i-1}
$$
By (5),
$$
\frac{a_{i-1}^{2}}{a_{i} a_{i-2}} \geqslant \frac{i}{i-1}=1+\frac{1}{i-1}>1+\frac{1}{i}=\frac{i+1}{i}
$$
which implies
$$
i \cdot y^{2} \cdot a_{i-1}^{2}>(i+1) \cdot y^{2} \cdot a_{i} a_{i-2} .
$$
Multiplying (5) and (6), and dividing both sides of the resulting inequality by $i a_{i} a_{i-1}$, we get
$$
(i-1) \cdot a_{i} a_{i-1} \geqslant(i+1) \cdot a_{i+1} a_{i-2} .
$$
Adding $(i+1) a_{i} a_{i-1}$ to both sides of the last inequality and multiplying both sides of the resulting inequality by $x y$ gives
$$
i \cdot 2 x y \cdot a_{i} a_{i-1} \geqslant(i+1) \cdot x y \cdot\left(a_{i+1} a_{i-2}+a_{i} a_{i-1}\right) .
$$
Finally, adding up (7), (8) and (9) results in
$$
i \cdot\left(x a_{i}+y a_{i-1}\right)^{2}>(i+1) \cdot\left(x a_{i+1}+y a_{i}\right)\left(x a_{i-1}+y a_{i-2}\right)
$$
which is equivalent to the claim.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n15.",
"solution_match": "\n15."
}
|
8821ba00-445e-59d8-9bdf-cd467ce57e3a
| 240,247
|
Let $n$ be a positive integer. Prove that at least $2^{n-1}+n$ numbers can be chosen from the set $\left\{1,2,3, \ldots, 2^{n}\right\}$ such that for any two different chosen numbers $x$ and $y, x+y$ is not a divisor of $x \cdot y$.
|
We choose the numbers $1,3,5, \ldots, 2^{n}-1$ and $2,4,8,16, \ldots, 2^{n}$, i.e. all odd numbers and all powers of 2 . Consider the three possible cases.
(1) If $x=2 a-1$ and $y=2 b-1$, then $x+y=(2 a-1)+(2 b-1)=2(a+b-1)$ is even and does not divide $x y=(2 a-1)(2 b-1)$ which is odd.
(2) If $x=2^{k}$ and $y=2^{m}$ where $k<m$, then $x+y=2^{k}\left(2^{m-k}+1\right)$ has an odd divisor greater than 1 and hence does not divide $x y=2^{a+b}$.
(3) If $x=2^{k}$ and $y=2 b-1$, then $x+y=2^{k}+(2 b-1)>(2 b-1)$ is odd and hence does not divide $x y=2^{k}(2 b-1)$ which has $2 b-1$ as its largest odd divisor.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer. Prove that at least $2^{n-1}+n$ numbers can be chosen from the set $\left\{1,2,3, \ldots, 2^{n}\right\}$ such that for any two different chosen numbers $x$ and $y, x+y$ is not a divisor of $x \cdot y$.
|
We choose the numbers $1,3,5, \ldots, 2^{n}-1$ and $2,4,8,16, \ldots, 2^{n}$, i.e. all odd numbers and all powers of 2 . Consider the three possible cases.
(1) If $x=2 a-1$ and $y=2 b-1$, then $x+y=(2 a-1)+(2 b-1)=2(a+b-1)$ is even and does not divide $x y=(2 a-1)(2 b-1)$ which is odd.
(2) If $x=2^{k}$ and $y=2^{m}$ where $k<m$, then $x+y=2^{k}\left(2^{m-k}+1\right)$ has an odd divisor greater than 1 and hence does not divide $x y=2^{a+b}$.
(3) If $x=2^{k}$ and $y=2 b-1$, then $x+y=2^{k}+(2 b-1)>(2 b-1)$ is odd and hence does not divide $x y=2^{k}(2 b-1)$ which has $2 b-1$ as its largest odd divisor.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n17.",
"solution_match": "\n17."
}
|
1eacab8c-c907-5293-9147-6f6e3a31c519
| 240,265
|
Let $a$ be an odd integer. Prove that $a^{2^{n}}+2^{2^{n}}$ and $a^{2^{m}}+2^{2^{m}}$ are relatively prime for all positive integers $n$ and $m$ with $n \neq m$.
|
Rewriting $a^{2^{n}}+2^{2^{n}}=a^{2^{n}}-2^{2^{n}}+2 \cdot 2^{2^{n}}$ and making repeated use of the identity
$$
a^{2^{n}}-2^{2^{n}}=\left(a^{2^{n-1}}-2^{2^{n-1}}\right) \cdot\left(a^{2^{n-1}}+2^{2^{n-1}}\right)
$$
we get
$$
\begin{gathered}
a^{2^{n}}+2^{2^{n}}=\left(a^{2^{n-1}}+2^{2^{n-1}}\right) \cdot\left(a^{2^{n-2}}+2^{2^{n-2}}\right) \cdot \ldots \cdot\left(a^{2^{m}}+2^{2^{m}}\right) \cdot \ldots \\
\ldots \cdot\left(a^{2}+2^{2}\right) \cdot(a+2) \cdot(a-2)+2 \cdot 2^{2^{n}}
\end{gathered}
$$
For $n>m$, assume that $a^{2^{n}}+2^{2^{n}}$ and $a^{2^{m}}+2^{2^{m}}$ have a common divisor $d>1$. Then an odd integer $d$ divides $2 \cdot 2^{2^{n}}$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a$ be an odd integer. Prove that $a^{2^{n}}+2^{2^{n}}$ and $a^{2^{m}}+2^{2^{m}}$ are relatively prime for all positive integers $n$ and $m$ with $n \neq m$.
|
Rewriting $a^{2^{n}}+2^{2^{n}}=a^{2^{n}}-2^{2^{n}}+2 \cdot 2^{2^{n}}$ and making repeated use of the identity
$$
a^{2^{n}}-2^{2^{n}}=\left(a^{2^{n-1}}-2^{2^{n-1}}\right) \cdot\left(a^{2^{n-1}}+2^{2^{n-1}}\right)
$$
we get
$$
\begin{gathered}
a^{2^{n}}+2^{2^{n}}=\left(a^{2^{n-1}}+2^{2^{n-1}}\right) \cdot\left(a^{2^{n-2}}+2^{2^{n-2}}\right) \cdot \ldots \cdot\left(a^{2^{m}}+2^{2^{m}}\right) \cdot \ldots \\
\ldots \cdot\left(a^{2}+2^{2}\right) \cdot(a+2) \cdot(a-2)+2 \cdot 2^{2^{n}}
\end{gathered}
$$
For $n>m$, assume that $a^{2^{n}}+2^{2^{n}}$ and $a^{2^{m}}+2^{2^{m}}$ have a common divisor $d>1$. Then an odd integer $d$ divides $2 \cdot 2^{2^{n}}$, a contradiction.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n18.",
"solution_match": "\n18."
}
|
a8e01fa4-2c0b-513a-afec-18d1951e6e13
| 240,276
|
Let $a, b, c, d$ be real numbers such that
$$
\begin{aligned}
a+b+c+d & =-2 \\
a b+a c+a d+b c+b d+c d & =0
\end{aligned}
$$
Prove that at least one of the numbers $a, b, c, d$ is not greater than -1 .
|
We can assume that $a$ is the least among $a, b, c, d$ (or one of the least, if some of them are equal), there are $n>0$ negative numbers among $a, b, c, d$, and the sum of the positive ones is $x$.
Then we obtain
$$
-2=a+b+c+d \geqslant n a+x .
$$
Squaring we get
$$
4=a^{2}+b^{2}+c^{2}+d^{2}
$$
which implies
$$
4 \leqslant n \cdot a^{2}+x^{2}
$$
as the square of the sum of positive numbers is not less than the sum of their squares.
Combining inequalities (1) and (2) we obtain
$$
\begin{aligned}
n a^{2}+(n a+2)^{2} & \geqslant 4, \\
n a^{2}+n^{2} a^{2}+4 n a & \geqslant 0, \\
a^{2}+n a^{2}+4 a & \geqslant 0 .
\end{aligned}
$$
As $n \leqslant 3$ (if all the numbers are negative, the second condition of the problem cannot be satisfied), we obtain from the last inequality that
$$
\begin{aligned}
& 4 a^{2}+4 a \geqslant 0, \\
& a(a+1) \geqslant 0 .
\end{aligned}
$$
As $a<0$ it follows that $a \leqslant-1$.
Alternative solution. Assume that $a, b, c, d>-1$. Denoting $A=a+1, B=b+1, C=c+1, D=d+1$ we have $A, B, C, D>0$. Then the first equation gives
$$
A+B+C+D=2 \text {. }
$$
We also have
$$
a b=(A-1)(B-1)=A B-A-B+1 .
$$
Adding 5 similar terms to the last one we get from the second equation
$$
A B+A C+A D+B C+B D+C D-3(A+B+C+D)+6=0 .
$$
In view of (3) this implies
$$
A B+A C+A D+B C+B D+C D=0,
$$
a contradiction as all the unknowns $A, B, C, D$ were supposed to be positive.
Another solution. Assume that the conditions of the problem hold:
$$
\begin{aligned}
a+b+c+d & =-2 \\
a b+a c+a d+b c+b d+c d & =0 .
\end{aligned}
$$
Suppose that
$$
a, b, c, d>-1 \text {. }
$$
If all of $a, b, c, d$ were negative, then (5) could not be satisfied, so at most three of them are negative. If two or less of them were negative, then (6) would imply that the sum of negative numbers, and hence also the sum $a+b+c+d$, is greater than $2 \cdot(-1)=-2$, which contradicts (4). So exactly three of $a, b, c, d$ are negative and one is nonnegative. Let $d$ be the nonnegative one. Then $d=-2-(a+b+c)<-2-(-1-1-1)=1$. Obviously $|a|,|b|,|c|,|d|<1$. Squaring (4) and subtracting 2 times (5), we get
$$
a^{2}+b^{2}+c^{2}+d^{2}=4,
$$
but
$$
a^{2}+b^{2}+c^{2}+d^{2}=|a|^{2}+|b|^{2}+|c|^{2}+|d|^{2}<4,
$$
a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $a, b, c, d$ be real numbers such that
$$
\begin{aligned}
a+b+c+d & =-2 \\
a b+a c+a d+b c+b d+c d & =0
\end{aligned}
$$
Prove that at least one of the numbers $a, b, c, d$ is not greater than -1 .
|
We can assume that $a$ is the least among $a, b, c, d$ (or one of the least, if some of them are equal), there are $n>0$ negative numbers among $a, b, c, d$, and the sum of the positive ones is $x$.
Then we obtain
$$
-2=a+b+c+d \geqslant n a+x .
$$
Squaring we get
$$
4=a^{2}+b^{2}+c^{2}+d^{2}
$$
which implies
$$
4 \leqslant n \cdot a^{2}+x^{2}
$$
as the square of the sum of positive numbers is not less than the sum of their squares.
Combining inequalities (1) and (2) we obtain
$$
\begin{aligned}
n a^{2}+(n a+2)^{2} & \geqslant 4, \\
n a^{2}+n^{2} a^{2}+4 n a & \geqslant 0, \\
a^{2}+n a^{2}+4 a & \geqslant 0 .
\end{aligned}
$$
As $n \leqslant 3$ (if all the numbers are negative, the second condition of the problem cannot be satisfied), we obtain from the last inequality that
$$
\begin{aligned}
& 4 a^{2}+4 a \geqslant 0, \\
& a(a+1) \geqslant 0 .
\end{aligned}
$$
As $a<0$ it follows that $a \leqslant-1$.
Alternative solution. Assume that $a, b, c, d>-1$. Denoting $A=a+1, B=b+1, C=c+1, D=d+1$ we have $A, B, C, D>0$. Then the first equation gives
$$
A+B+C+D=2 \text {. }
$$
We also have
$$
a b=(A-1)(B-1)=A B-A-B+1 .
$$
Adding 5 similar terms to the last one we get from the second equation
$$
A B+A C+A D+B C+B D+C D-3(A+B+C+D)+6=0 .
$$
In view of (3) this implies
$$
A B+A C+A D+B C+B D+C D=0,
$$
a contradiction as all the unknowns $A, B, C, D$ were supposed to be positive.
Another solution. Assume that the conditions of the problem hold:
$$
\begin{aligned}
a+b+c+d & =-2 \\
a b+a c+a d+b c+b d+c d & =0 .
\end{aligned}
$$
Suppose that
$$
a, b, c, d>-1 \text {. }
$$
If all of $a, b, c, d$ were negative, then (5) could not be satisfied, so at most three of them are negative. If two or less of them were negative, then (6) would imply that the sum of negative numbers, and hence also the sum $a+b+c+d$, is greater than $2 \cdot(-1)=-2$, which contradicts (4). So exactly three of $a, b, c, d$ are negative and one is nonnegative. Let $d$ be the nonnegative one. Then $d=-2-(a+b+c)<-2-(-1-1-1)=1$. Obviously $|a|,|b|,|c|,|d|<1$. Squaring (4) and subtracting 2 times (5), we get
$$
a^{2}+b^{2}+c^{2}+d^{2}=4,
$$
but
$$
a^{2}+b^{2}+c^{2}+d^{2}=|a|^{2}+|b|^{2}+|c|^{2}+|d|^{2}<4,
$$
a contradiction.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution."
}
|
60afcc44-95be-55cc-9a7b-22489ab96619
| 605,136
|
Let $n$ be a positive integer. Prove that
$$
\sum_{i=1}^{n} x_{i}\left(1-x_{i}\right)^{2} \leqslant\left(1-\frac{1}{n}\right)^{2}
$$
for all nonnegative real numbers $x_{1}, x_{2}, \ldots, x_{n}$ such that $x_{1}+x_{2}+\cdots+x_{n}=1$.
|
Expanding the expressions at both sides we obtain the equivalent inequality
$$
-\sum_{i} x_{i}^{3}+2 \sum_{i} x_{i}^{2}-\frac{2}{n}+\frac{1}{n^{2}} \geqslant 0
$$
It is easy to check that the left hand side is equal to
$$
\sum_{i}\left(2-\frac{2}{n}-x_{i}\right)\left(x_{i}-\frac{1}{n}\right)^{2}
$$
and hence is nonnegative.
Alternative solution. First note that for $n=1$ the required condition holds trivially, and for $n=2$ we have
$$
x(1-x)^{2}+(1-x) x^{2}=x(1-x) \leqslant\left(\frac{x+(1-x)}{2}\right)^{2}=\frac{1}{4}=\left(1-\frac{1}{2}\right)^{2} .
$$
So we may further consider the case $n \geqslant 3$.
Assume first that for each index $i$ the inequality $x_{i}<\frac{2}{3}$ holds. Let $f(x)=x(1-x)^{2}=x-2 x^{2}+x^{3}$, then $f^{\prime \prime}(x)=6 x-4$. Hence, the function $f$ is concave in the interval $\left[0, \frac{2}{3}\right]$. Thus, from Jensen's inequality we have
$$
\begin{aligned}
\sum_{i=1}^{n} x_{i}\left(1-x_{i}\right)^{2} & =\sum_{i=1}^{n} f\left(x_{i}\right) \leqslant n \cdot f\left(\frac{x_{1}+\ldots+x_{n}}{n}\right)=n \cdot f\left(\frac{1}{n}\right)= \\
& =n \cdot \frac{1}{n}\left(1-\frac{1}{n}\right)^{2}=\left(1-\frac{1}{n}\right)^{2} .
\end{aligned}
$$
If some $x_{i} \geqslant \frac{2}{3}$ then we have
$$
x_{i}\left(1-x_{i}\right)^{2} \leqslant 1 \cdot\left(1-\frac{2}{3}\right)^{2}=\frac{1}{9}
$$
For the rest of the terms we have
$$
\sum_{j \neq i} x_{j}\left(1-x_{j}\right)^{2} \leqslant \sum_{j \neq i} x_{j}=1-x_{i} \leqslant \frac{1}{3}
$$
Hence,
$$
\sum_{i=1}^{n} x_{i}\left(1-x_{i}\right)^{2} \leqslant \frac{1}{9}+\frac{1}{3}=\frac{4}{9} \leqslant\left(1-\frac{1}{n}\right)^{2}
$$
as $n \geqslant 3$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n$ be a positive integer. Prove that
$$
\sum_{i=1}^{n} x_{i}\left(1-x_{i}\right)^{2} \leqslant\left(1-\frac{1}{n}\right)^{2}
$$
for all nonnegative real numbers $x_{1}, x_{2}, \ldots, x_{n}$ such that $x_{1}+x_{2}+\cdots+x_{n}=1$.
|
Expanding the expressions at both sides we obtain the equivalent inequality
$$
-\sum_{i} x_{i}^{3}+2 \sum_{i} x_{i}^{2}-\frac{2}{n}+\frac{1}{n^{2}} \geqslant 0
$$
It is easy to check that the left hand side is equal to
$$
\sum_{i}\left(2-\frac{2}{n}-x_{i}\right)\left(x_{i}-\frac{1}{n}\right)^{2}
$$
and hence is nonnegative.
Alternative solution. First note that for $n=1$ the required condition holds trivially, and for $n=2$ we have
$$
x(1-x)^{2}+(1-x) x^{2}=x(1-x) \leqslant\left(\frac{x+(1-x)}{2}\right)^{2}=\frac{1}{4}=\left(1-\frac{1}{2}\right)^{2} .
$$
So we may further consider the case $n \geqslant 3$.
Assume first that for each index $i$ the inequality $x_{i}<\frac{2}{3}$ holds. Let $f(x)=x(1-x)^{2}=x-2 x^{2}+x^{3}$, then $f^{\prime \prime}(x)=6 x-4$. Hence, the function $f$ is concave in the interval $\left[0, \frac{2}{3}\right]$. Thus, from Jensen's inequality we have
$$
\begin{aligned}
\sum_{i=1}^{n} x_{i}\left(1-x_{i}\right)^{2} & =\sum_{i=1}^{n} f\left(x_{i}\right) \leqslant n \cdot f\left(\frac{x_{1}+\ldots+x_{n}}{n}\right)=n \cdot f\left(\frac{1}{n}\right)= \\
& =n \cdot \frac{1}{n}\left(1-\frac{1}{n}\right)^{2}=\left(1-\frac{1}{n}\right)^{2} .
\end{aligned}
$$
If some $x_{i} \geqslant \frac{2}{3}$ then we have
$$
x_{i}\left(1-x_{i}\right)^{2} \leqslant 1 \cdot\left(1-\frac{2}{3}\right)^{2}=\frac{1}{9}
$$
For the rest of the terms we have
$$
\sum_{j \neq i} x_{j}\left(1-x_{j}\right)^{2} \leqslant \sum_{j \neq i} x_{j}=1-x_{i} \leqslant \frac{1}{3}
$$
Hence,
$$
\sum_{i=1}^{n} x_{i}\left(1-x_{i}\right)^{2} \leqslant \frac{1}{9}+\frac{1}{3}=\frac{4}{9} \leqslant\left(1-\frac{1}{n}\right)^{2}
$$
as $n \geqslant 3$.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution."
}
|
7e81f685-983f-5182-b108-70c389480c17
| 605,166
|
Let $n$ be a positive integer. Consider $n$ points in the plane such that no three of them are collinear and no two of the distances between them are equal. One by one, we connect each point to the two points nearest to it by line segments (if there are already other line segments drawn to this point, we do not erase these). Prove that there is no point from which line segments will be drawn to more than 11 points.
|
Suppose there exists a point $A$ such that $A$ is connected to twelve points. Then there exist three points $B, C$ and $D$ such that $\angle B A C \leqslant 60^{\circ}, \angle B A D \leqslant 60^{\circ}$ and $\angle C A D \leqslant 60^{\circ}$.
We can assume that $|A D|>|A B|$ and $|A D|>|A C|$. By the cosine law we have
$$
\begin{aligned}
|B D|^{2} & =|A D|^{2}+|A B|^{2}-2|A D \| A B| \cos \angle B A D \\
& <|A D|^{2}+|A B|^{2}-2|A B|^{2} \cos \angle B A D \\
& =|A D|^{2}+|A B|^{2}(1-2 \cos \angle B A D) \\
& \leqslant|A D|^{2}
\end{aligned}
$$
since $1 \leqslant 2 \cos (\angle B A D)$. Hence $|B D|<|A D|$. Similarly we get $|C D|<|A D|$. Hence $A$ and $D$ should not be connected which is a contradiction.
Comment. It would be interesting to know whether 11 can be achieved or the actual bound is lower.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer. Consider $n$ points in the plane such that no three of them are collinear and no two of the distances between them are equal. One by one, we connect each point to the two points nearest to it by line segments (if there are already other line segments drawn to this point, we do not erase these). Prove that there is no point from which line segments will be drawn to more than 11 points.
|
Suppose there exists a point $A$ such that $A$ is connected to twelve points. Then there exist three points $B, C$ and $D$ such that $\angle B A C \leqslant 60^{\circ}, \angle B A D \leqslant 60^{\circ}$ and $\angle C A D \leqslant 60^{\circ}$.
We can assume that $|A D|>|A B|$ and $|A D|>|A C|$. By the cosine law we have
$$
\begin{aligned}
|B D|^{2} & =|A D|^{2}+|A B|^{2}-2|A D \| A B| \cos \angle B A D \\
& <|A D|^{2}+|A B|^{2}-2|A B|^{2} \cos \angle B A D \\
& =|A D|^{2}+|A B|^{2}(1-2 \cos \angle B A D) \\
& \leqslant|A D|^{2}
\end{aligned}
$$
since $1 \leqslant 2 \cos (\angle B A D)$. Hence $|B D|<|A D|$. Similarly we get $|C D|<|A D|$. Hence $A$ and $D$ should not be connected which is a contradiction.
Comment. It would be interesting to know whether 11 can be achieved or the actual bound is lower.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n11.",
"solution_match": "\nSolution."
}
|
055f4761-3661-5948-a320-8854ae5316a3
| 236,610
|
A set $S$ of four distinct points is given in the plane. It is known that for any point $X \in S$ the remaining points can be denoted by $Y, Z$ and $W$ so that
$$
|X Y|=|X Z|+|X W| .
$$
Prove that all the four points lie on a line.
|
Let $S=\{A, B, C, D\}$ and let $A B$ be the longest of the six segments formed by these four points (if there are several longest segments, choose any of them). If we choose $X=A$ then we must also choose $Y=B$. Indeed, if we would, for example, choose $Y=C$, we should have $|A C|=|A B|+|A D|$ contradicting the maximality of $A B$. Hence we get
$$
|A B|=|A C|+|A D| \text {. }
$$
Similarly, choosing $X=B$ we must choose $Y=A$ and we obtain
$$
|A B|=|B C|+|B D| \text {. }
$$
On the other hand, from the triangle inequality we know that
$$
\begin{aligned}
& |A B| \leqslant|A C|+|B C|, \\
& |A B| \leqslant|A D|+|B D|,
\end{aligned}
$$
where at least one of the inequalities is strict if all the four points are not on the same line. Hence, adding the two last inequalities we get
$$
2|A B|<|A C|+|B C|+|A D|+|B D| .
$$
On the other hand, adding (10) and (11) we get
$$
2|A B|=|A C|+|A D|+|B C|+|B D|,
$$
a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A set $S$ of four distinct points is given in the plane. It is known that for any point $X \in S$ the remaining points can be denoted by $Y, Z$ and $W$ so that
$$
|X Y|=|X Z|+|X W| .
$$
Prove that all the four points lie on a line.
|
Let $S=\{A, B, C, D\}$ and let $A B$ be the longest of the six segments formed by these four points (if there are several longest segments, choose any of them). If we choose $X=A$ then we must also choose $Y=B$. Indeed, if we would, for example, choose $Y=C$, we should have $|A C|=|A B|+|A D|$ contradicting the maximality of $A B$. Hence we get
$$
|A B|=|A C|+|A D| \text {. }
$$
Similarly, choosing $X=B$ we must choose $Y=A$ and we obtain
$$
|A B|=|B C|+|B D| \text {. }
$$
On the other hand, from the triangle inequality we know that
$$
\begin{aligned}
& |A B| \leqslant|A C|+|B C|, \\
& |A B| \leqslant|A D|+|B D|,
\end{aligned}
$$
where at least one of the inequalities is strict if all the four points are not on the same line. Hence, adding the two last inequalities we get
$$
2|A B|<|A C|+|B C|+|A D|+|B D| .
$$
On the other hand, adding (10) and (11) we get
$$
2|A B|=|A C|+|A D|+|B C|+|B D|,
$$
a contradiction.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n12.",
"solution_match": "\nSolution."
}
|
cf70de46-0caf-5644-86b2-39927420ea06
| 236,623
|
Let $A B C$ be an acute triangle with $\angle B A C>\angle B C A$, and let $D$ be a point on side $A C$ such that $|A B|=|B D|$. Furthermore, let $F$ be a point on the circumcircle of triangle $A B C$ such that line $F D$ is perpendicular to side $B C$ and points $F, B$ lie on different sides of line $A C$. Prove that line $F B$ is perpendicular to side $A C$.
|
Let $E$ be the other point on the circumcircle of triangle $A B C$ such that $|A B|=|E B|$. Let $D^{\prime}$ be the point of intersection of side $A C$ and the line perpendicular to side $B C$, passing through $E$. Then $\angle E C B=\angle B C A$ and the triangle $E C D^{\prime}$ is isosceles. As $E D^{\prime} \perp B C$, the triangle $B E D^{\prime}$ is also isosceles and $|B E|=\left|B D^{\prime}\right|$ implying $D=D^{\prime}$. Hence, the points $E, D, F$ lie on one line. We now have
$$
\angle E F B+\angle F D A=\angle B C A+\angle E D C=90^{\circ} .
$$
The required result now follows.
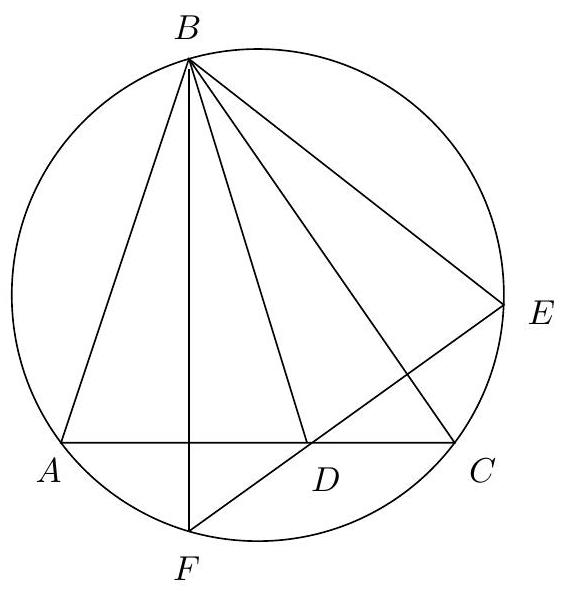
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with $\angle B A C>\angle B C A$, and let $D$ be a point on side $A C$ such that $|A B|=|B D|$. Furthermore, let $F$ be a point on the circumcircle of triangle $A B C$ such that line $F D$ is perpendicular to side $B C$ and points $F, B$ lie on different sides of line $A C$. Prove that line $F B$ is perpendicular to side $A C$.
|
Let $E$ be the other point on the circumcircle of triangle $A B C$ such that $|A B|=|E B|$. Let $D^{\prime}$ be the point of intersection of side $A C$ and the line perpendicular to side $B C$, passing through $E$. Then $\angle E C B=\angle B C A$ and the triangle $E C D^{\prime}$ is isosceles. As $E D^{\prime} \perp B C$, the triangle $B E D^{\prime}$ is also isosceles and $|B E|=\left|B D^{\prime}\right|$ implying $D=D^{\prime}$. Hence, the points $E, D, F$ lie on one line. We now have
$$
\angle E F B+\angle F D A=\angle B C A+\angle E D C=90^{\circ} .
$$
The required result now follows.

|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n13.",
"solution_match": "\nSolution."
}
|
16167e1c-4767-5152-a738-450299aef276
| 236,631
|
Let $L, M$ and $N$ be points on sides $A C, A B$ and $B C$ of triangle $A B C$, respectively, such that $B L$ is the bisector of angle $A B C$ and segments $A N, B L$ and $C M$ have a common point. Prove that if $\angle A L B=\angle M N B$ then $\angle L N M=90^{\circ}$.
|
Let $P$ be the intersection point of lines $M N$ and $A C$. Then $\angle P L B=\angle P N B$ and the quadrangle $P L N B$ is cyclic. Let $\omega$ be its circumcircle. It is sufficient to prove that $P L$ is a diameter of $\omega$.
Let $Q$ denote the second intersection point of the line $A B$ and $\omega$. Then $\angle P Q B=\angle P L B$ and
$$
\angle Q P L=\angle Q B L=\angle L B N=\angle L P N
$$
and the triangles $P A Q$ and $B A L$ are similar. Therefore,
$$
\frac{|P Q|}{|P A|}=\frac{|B L|}{|B A|}
$$
We see that the line $P L$ is a bisector of the inscribed angle $N P Q$. Now in order to prove that $P L$ is a diameter of $\omega$ it is sufficient to check that $|P N|=|P Q|$.
The triangles $N P C$ and $L B C$ are similar, hence
$$
\frac{|P N|}{|P C|}=\frac{|B L|}{|B C|}
$$
Note also that
$$
\frac{|A B|}{|B C|}=\frac{|A L|}{|C L|}
$$
by the properties of a bisector. Combining (12), (13) and (14) we have
$$
\frac{|P N|}{|P Q|}=\frac{|A L|}{|A P|} \cdot \frac{|C P|}{|C L|}
$$
We want to prove that the left hand side of this equality equals 1 . This follows from the fact that the quadruple of points $(P, A, L, C)$ is harmonic, as can be proven using standard methods (e.g. considering the quadrilateral $M B N S$, where $S=M C \cap A N$ ).
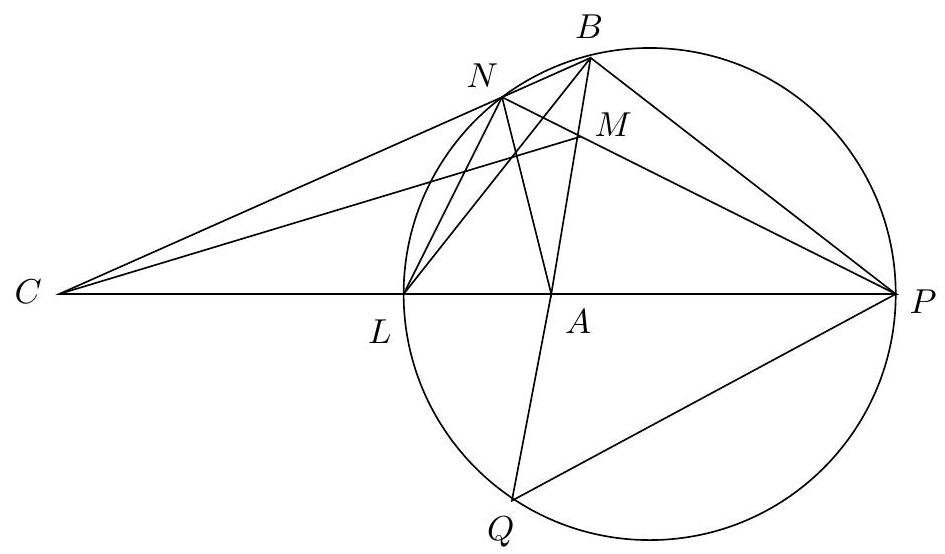
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $L, M$ and $N$ be points on sides $A C, A B$ and $B C$ of triangle $A B C$, respectively, such that $B L$ is the bisector of angle $A B C$ and segments $A N, B L$ and $C M$ have a common point. Prove that if $\angle A L B=\angle M N B$ then $\angle L N M=90^{\circ}$.
|
Let $P$ be the intersection point of lines $M N$ and $A C$. Then $\angle P L B=\angle P N B$ and the quadrangle $P L N B$ is cyclic. Let $\omega$ be its circumcircle. It is sufficient to prove that $P L$ is a diameter of $\omega$.
Let $Q$ denote the second intersection point of the line $A B$ and $\omega$. Then $\angle P Q B=\angle P L B$ and
$$
\angle Q P L=\angle Q B L=\angle L B N=\angle L P N
$$
and the triangles $P A Q$ and $B A L$ are similar. Therefore,
$$
\frac{|P Q|}{|P A|}=\frac{|B L|}{|B A|}
$$
We see that the line $P L$ is a bisector of the inscribed angle $N P Q$. Now in order to prove that $P L$ is a diameter of $\omega$ it is sufficient to check that $|P N|=|P Q|$.
The triangles $N P C$ and $L B C$ are similar, hence
$$
\frac{|P N|}{|P C|}=\frac{|B L|}{|B C|}
$$
Note also that
$$
\frac{|A B|}{|B C|}=\frac{|A L|}{|C L|}
$$
by the properties of a bisector. Combining (12), (13) and (14) we have
$$
\frac{|P N|}{|P Q|}=\frac{|A L|}{|A P|} \cdot \frac{|C P|}{|C L|}
$$
We want to prove that the left hand side of this equality equals 1 . This follows from the fact that the quadruple of points $(P, A, L, C)$ is harmonic, as can be proven using standard methods (e.g. considering the quadrilateral $M B N S$, where $S=M C \cap A N$ ).

|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n14.",
"solution_match": "\nSolution."
}
|
f246a15c-14fd-5b32-ae72-64e8a0b8b6b4
| 236,641
|
Show that the sequence
$$
\left(\begin{array}{l}
2002 \\
2002
\end{array}\right),\left(\begin{array}{c}
2003 \\
2002
\end{array}\right),\left(\begin{array}{l}
2004 \\
2002
\end{array}\right), \ldots
$$
considered modulo 2002, is periodic.
|
Define
$$
x_{n}^{k}=\left(\begin{array}{l}
n \\
k
\end{array}\right)
$$
and note that
$$
x_{n+1}^{k}-x_{n}^{k}=\left(\begin{array}{c}
n+1 \\
k
\end{array}\right)-\left(\begin{array}{l}
n \\
k
\end{array}\right)=\left(\begin{array}{c}
n \\
k-1
\end{array}\right)=x_{n}^{k-1}
$$
Let $m$ be any positive integer. We will prove by induction on $k$ that the sequence $\left\{x_{n}^{k}\right\}_{n=k}^{\infty}$ is periodic modulo $m$. For $k=1$ it is obvious that $x_{n}^{k}=n$ is periodic modulo $m$ with period $m$. Therefore it will suffice to show that the following is true: the sequence $\left\{x_{n}\right\}$ is periodic modulo $m$ if its difference sequence, $d_{n}=x_{n+1}-x_{n}$, is periodic modulo $m$.
Furthermore, if $t$ then the period of $\left\{x_{n}\right\}$ is equal to $h t$ where $h$ is the smallest positive integer such that $h\left(x_{t}-x_{0}\right) \equiv 0$ modulo $m$.
Indeed, let $t$ be the period of $\left\{d_{n}\right\}$ and $h$ be the smallest positive integer such that $h\left(x_{t}-x_{0}\right) \equiv 0$ modulo $m$. Then
$$
\begin{aligned}
x_{n+h t} & =x_{0}+\sum_{j=0}^{n+h t-1} d_{j}=x_{0}+\sum_{j=0}^{n-1} d_{j}+h\left(\sum_{j=0}^{t-1} d_{j}\right)= \\
& =x_{n}+h\left(x_{t}-x_{0}\right) \equiv x_{n}(\bmod m)
\end{aligned}
$$
for all $n$, so the sequence $\left\{x_{n}\right\}$ is in fact periodic modulo $m$ (with a period dividing $h t$ ).
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that the sequence
$$
\left(\begin{array}{l}
2002 \\
2002
\end{array}\right),\left(\begin{array}{c}
2003 \\
2002
\end{array}\right),\left(\begin{array}{l}
2004 \\
2002
\end{array}\right), \ldots
$$
considered modulo 2002, is periodic.
|
Define
$$
x_{n}^{k}=\left(\begin{array}{l}
n \\
k
\end{array}\right)
$$
and note that
$$
x_{n+1}^{k}-x_{n}^{k}=\left(\begin{array}{c}
n+1 \\
k
\end{array}\right)-\left(\begin{array}{l}
n \\
k
\end{array}\right)=\left(\begin{array}{c}
n \\
k-1
\end{array}\right)=x_{n}^{k-1}
$$
Let $m$ be any positive integer. We will prove by induction on $k$ that the sequence $\left\{x_{n}^{k}\right\}_{n=k}^{\infty}$ is periodic modulo $m$. For $k=1$ it is obvious that $x_{n}^{k}=n$ is periodic modulo $m$ with period $m$. Therefore it will suffice to show that the following is true: the sequence $\left\{x_{n}\right\}$ is periodic modulo $m$ if its difference sequence, $d_{n}=x_{n+1}-x_{n}$, is periodic modulo $m$.
Furthermore, if $t$ then the period of $\left\{x_{n}\right\}$ is equal to $h t$ where $h$ is the smallest positive integer such that $h\left(x_{t}-x_{0}\right) \equiv 0$ modulo $m$.
Indeed, let $t$ be the period of $\left\{d_{n}\right\}$ and $h$ be the smallest positive integer such that $h\left(x_{t}-x_{0}\right) \equiv 0$ modulo $m$. Then
$$
\begin{aligned}
x_{n+h t} & =x_{0}+\sum_{j=0}^{n+h t-1} d_{j}=x_{0}+\sum_{j=0}^{n-1} d_{j}+h\left(\sum_{j=0}^{t-1} d_{j}\right)= \\
& =x_{n}+h\left(x_{t}-x_{0}\right) \equiv x_{n}(\bmod m)
\end{aligned}
$$
for all $n$, so the sequence $\left\{x_{n}\right\}$ is in fact periodic modulo $m$ (with a period dividing $h t$ ).
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n17.",
"solution_match": "\nSolution."
}
|
f852e7b6-0bb4-56dd-9f1c-baebd24d6adf
| 236,669
|
Let $n$ be a positive integer. Prove that the equation
$$
x+y+\frac{1}{x}+\frac{1}{y}=3 n
$$
does not have solutions in positive rational numbers.
|
Suppose $x=\frac{p}{q}$ and $y=\frac{r}{s}$ satisfy the given equation, where $p, q, r, s$ are positive integers and $\operatorname{gcd}(p, q)=1, \operatorname{gcd}(r, s)=1$. We have
$$
\frac{p}{q}+\frac{r}{s}+\frac{q}{p}+\frac{s}{r}=3 n
$$
or
$$
\left(p^{2}+q^{2}\right) r s+\left(r^{2}+s^{2}\right) p q=3 n p q r s,
$$
so $r s \mid\left(r^{2}+s^{2}\right) p q$. Since $\operatorname{gcd}(r, s)=1$, we have $\operatorname{gcd}\left(r^{2}+s^{2}, r s\right)=1$ and $r s \mid p q$. Analogously $p q \mid r s$, so $r s=p q$ and hence there are either two or zero integers divisible by 3 among $p, q, r, s$. Now we have
$$
\begin{aligned}
\left(p^{2}+q^{2}\right) r s+\left(r^{2}+s^{2}\right) r s & =3 n(r s)^{2} \\
p^{2}+q^{2}+r^{2}+s^{2} & =3 n r s,
\end{aligned}
$$
but $3 n r s \equiv 0(\bmod 3)$ and $p^{2}+q^{2}+r^{2}+s^{2}$ is congruent to either 1 or 2 modulo 3 , a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer. Prove that the equation
$$
x+y+\frac{1}{x}+\frac{1}{y}=3 n
$$
does not have solutions in positive rational numbers.
|
Suppose $x=\frac{p}{q}$ and $y=\frac{r}{s}$ satisfy the given equation, where $p, q, r, s$ are positive integers and $\operatorname{gcd}(p, q)=1, \operatorname{gcd}(r, s)=1$. We have
$$
\frac{p}{q}+\frac{r}{s}+\frac{q}{p}+\frac{s}{r}=3 n
$$
or
$$
\left(p^{2}+q^{2}\right) r s+\left(r^{2}+s^{2}\right) p q=3 n p q r s,
$$
so $r s \mid\left(r^{2}+s^{2}\right) p q$. Since $\operatorname{gcd}(r, s)=1$, we have $\operatorname{gcd}\left(r^{2}+s^{2}, r s\right)=1$ and $r s \mid p q$. Analogously $p q \mid r s$, so $r s=p q$ and hence there are either two or zero integers divisible by 3 among $p, q, r, s$. Now we have
$$
\begin{aligned}
\left(p^{2}+q^{2}\right) r s+\left(r^{2}+s^{2}\right) r s & =3 n(r s)^{2} \\
p^{2}+q^{2}+r^{2}+s^{2} & =3 n r s,
\end{aligned}
$$
but $3 n r s \equiv 0(\bmod 3)$ and $p^{2}+q^{2}+r^{2}+s^{2}$ is congruent to either 1 or 2 modulo 3 , a contradiction.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n19.",
"solution_match": "\nSolution."
}
|
38425ca8-71e6-5970-a0fd-0c17305c1ef1
| 605,439
|
Does there exist an infinite non-constant arithmetic progression, each term of which is of the form $a^{b}$, where $a$ and $b$ are positive integers with $b \geqslant 2$ ?
Answer: no.
|
For an arithmetic progression $a_{1}, a_{2}, \ldots$ with difference $d$ the following holds:
$$
\begin{aligned}
S_{n} & =\frac{1}{a_{1}}+\frac{1}{a_{2}}+\ldots+\frac{1}{a_{n+1}}=\frac{1}{a_{1}}+\frac{1}{a_{1}+d}+\ldots+\frac{1}{a_{1}+n d} \geqslant \\
& \geqslant \frac{1}{m}\left(\frac{1}{1}+\frac{1}{2}+\ldots+\frac{1}{n+1}\right),
\end{aligned}
$$
where $m=\max \left(a_{1}, d\right)$. Therefore $S_{n}$ tends to infinity when $n$ increases.
On the other hand, the sum of reciprocals of the powers of a natural number $x \neq 1$ is
$$
\frac{1}{x^{2}}+\frac{1}{x^{3}}+\ldots=\frac{\frac{1}{x^{2}}}{1-\frac{1}{x}}=\frac{1}{x(x-1)}
$$
Hence, the sum of reciprocals of the terms of the progression required in the problem cannot exceed
$$
\frac{1}{1}+\frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\ldots=1+\left(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\ldots\right)=2
$$
a contradiction.
Alternative solution. Let $a_{k}=a_{0}+d k, k=0,1, \ldots$ Choose a prime number $p>d$ and set $k^{\prime} \equiv\left(p-a_{0}\right) d^{-1} \bmod p^{2}$. Then $a_{k^{\prime}}=a_{0}+k^{\prime} d \equiv p \bmod p^{2}$ and hence, $a_{k^{\prime}}$ can not be a power of a natural number.
Another solution. There can be at most $\lfloor\sqrt{n}\rfloor$ squares in the set $\{1,2, \ldots, n\}$, at most $\lfloor\sqrt[3]{n}\rfloor$ cubes in the same set, etc. The greatest power that can occur in the set $\{1,2, \ldots, n\}$ is $\left\lfloor\log _{2} n\right\rfloor$ and thus there are no more than
$$
\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor+\ldots+\left\lfloor\left\lfloor\log _{2} \sqrt[n]{n}\right\rfloor\right.
$$
powers among the numbers $1,2, \ldots, n$. Now we can estimate this sum above:
$$
\begin{aligned}
\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor+\ldots+\left\lfloor\left\lfloor\log _{2} \sqrt[n\rfloor\right]{n}\right\rfloor & \leqslant\lfloor\sqrt{n}\rfloor\left(\left\lfloor\log _{2} n\right\rfloor-1\right)< \\
& <\lfloor\sqrt{n}\rfloor \cdot\left\lfloor\log _{2} n\right\rfloor=o(n)
\end{aligned}
$$
This means that every arithmetic progression grows faster than the share of powers.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Does there exist an infinite non-constant arithmetic progression, each term of which is of the form $a^{b}$, where $a$ and $b$ are positive integers with $b \geqslant 2$ ?
Answer: no.
|
For an arithmetic progression $a_{1}, a_{2}, \ldots$ with difference $d$ the following holds:
$$
\begin{aligned}
S_{n} & =\frac{1}{a_{1}}+\frac{1}{a_{2}}+\ldots+\frac{1}{a_{n+1}}=\frac{1}{a_{1}}+\frac{1}{a_{1}+d}+\ldots+\frac{1}{a_{1}+n d} \geqslant \\
& \geqslant \frac{1}{m}\left(\frac{1}{1}+\frac{1}{2}+\ldots+\frac{1}{n+1}\right),
\end{aligned}
$$
where $m=\max \left(a_{1}, d\right)$. Therefore $S_{n}$ tends to infinity when $n$ increases.
On the other hand, the sum of reciprocals of the powers of a natural number $x \neq 1$ is
$$
\frac{1}{x^{2}}+\frac{1}{x^{3}}+\ldots=\frac{\frac{1}{x^{2}}}{1-\frac{1}{x}}=\frac{1}{x(x-1)}
$$
Hence, the sum of reciprocals of the terms of the progression required in the problem cannot exceed
$$
\frac{1}{1}+\frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\ldots=1+\left(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\ldots\right)=2
$$
a contradiction.
Alternative solution. Let $a_{k}=a_{0}+d k, k=0,1, \ldots$ Choose a prime number $p>d$ and set $k^{\prime} \equiv\left(p-a_{0}\right) d^{-1} \bmod p^{2}$. Then $a_{k^{\prime}}=a_{0}+k^{\prime} d \equiv p \bmod p^{2}$ and hence, $a_{k^{\prime}}$ can not be a power of a natural number.
Another solution. There can be at most $\lfloor\sqrt{n}\rfloor$ squares in the set $\{1,2, \ldots, n\}$, at most $\lfloor\sqrt[3]{n}\rfloor$ cubes in the same set, etc. The greatest power that can occur in the set $\{1,2, \ldots, n\}$ is $\left\lfloor\log _{2} n\right\rfloor$ and thus there are no more than
$$
\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor+\ldots+\left\lfloor\left\lfloor\log _{2} \sqrt[n]{n}\right\rfloor\right.
$$
powers among the numbers $1,2, \ldots, n$. Now we can estimate this sum above:
$$
\begin{aligned}
\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor+\ldots+\left\lfloor\left\lfloor\log _{2} \sqrt[n\rfloor\right]{n}\right\rfloor & \leqslant\lfloor\sqrt{n}\rfloor\left(\left\lfloor\log _{2} n\right\rfloor-1\right)< \\
& <\lfloor\sqrt{n}\rfloor \cdot\left\lfloor\log _{2} n\right\rfloor=o(n)
\end{aligned}
$$
This means that every arithmetic progression grows faster than the share of powers.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n20.",
"solution_match": "\nSolution."
}
|
41e10bd1-b8da-5339-9dda-f468f7533fab
| 605,446
|
Prove that any real solution of
$$
x^{3}+p x+q=0
$$
satisfies the inequality $4 q x \leq p^{2}$.
|
Let $x_{0}$ be a root of the qubic, then $x^{3}+p x+q=\left(x-x_{0}\right)\left(x^{2}+a x+b\right)=$ $x^{3}+\left(a-x_{0}\right) x^{2}+\left(b-a x_{0}\right) x-b x_{0}$. So $a=x_{0}, p=b-a x_{0}=b-x_{0}^{2},-q=b x_{0}$. Hence $p^{2}=b^{2}-2 b x_{0}^{2}+x_{0}^{4}$. Also $4 x_{0} q=-4 x_{0}^{2} b$. So $p^{2}-4 x_{0} q=b^{2}+2 b x_{0}^{2}+x_{0}^{4}=\left(b+x_{0}^{2}\right)^{2} \geq 0$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that any real solution of
$$
x^{3}+p x+q=0
$$
satisfies the inequality $4 q x \leq p^{2}$.
|
Let $x_{0}$ be a root of the qubic, then $x^{3}+p x+q=\left(x-x_{0}\right)\left(x^{2}+a x+b\right)=$ $x^{3}+\left(a-x_{0}\right) x^{2}+\left(b-a x_{0}\right) x-b x_{0}$. So $a=x_{0}, p=b-a x_{0}=b-x_{0}^{2},-q=b x_{0}$. Hence $p^{2}=b^{2}-2 b x_{0}^{2}+x_{0}^{4}$. Also $4 x_{0} q=-4 x_{0}^{2} b$. So $p^{2}-4 x_{0} q=b^{2}+2 b x_{0}^{2}+x_{0}^{4}=\left(b+x_{0}^{2}\right)^{2} \geq 0$.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution:"
}
|
0e5c5fc2-1b05-5f1f-bcc8-f57dac50d8e0
| 605,462
|
Let $x, y$ and $z$ be positive real numbers such that $x y z=1$. Prove that
$$
(1+x)(1+y)(1+z) \geq 2\left(1+\sqrt[3]{\frac{y}{x}}+\sqrt[3]{\frac{z}{y}}+\sqrt[3]{\frac{x}{z}}\right)
$$
|
Put $a=b x, b=c y$ and $c=a z$. The given inequality then takes the form
$$
\begin{aligned}
\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right) & \geq 2\left(1+\sqrt[3]{\frac{b^{2}}{a c}}+\sqrt[3]{\frac{c^{2}}{a b}}+\sqrt[3]{\frac{a^{2}}{b c}}\right) \\
& =2\left(1+\frac{a+b+c}{3 \sqrt[3]{a b c}}\right) .
\end{aligned}
$$
By the AM-GM inequality we have
$$
\begin{aligned}
\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right) & =\frac{a+b+c}{a}+\frac{a+b+c}{b}+\frac{a+b+c}{c}-1 \\
& \geq 3\left(\frac{a+b+c}{\sqrt[3]{a b c}}\right)-1 \geq 2 \frac{a+b+c}{\sqrt[3]{a b c}}+3-1=2\left(1+\frac{a+b+c}{\sqrt[3]{a b c}}\right) .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y$ and $z$ be positive real numbers such that $x y z=1$. Prove that
$$
(1+x)(1+y)(1+z) \geq 2\left(1+\sqrt[3]{\frac{y}{x}}+\sqrt[3]{\frac{z}{y}}+\sqrt[3]{\frac{x}{z}}\right)
$$
|
Put $a=b x, b=c y$ and $c=a z$. The given inequality then takes the form
$$
\begin{aligned}
\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right) & \geq 2\left(1+\sqrt[3]{\frac{b^{2}}{a c}}+\sqrt[3]{\frac{c^{2}}{a b}}+\sqrt[3]{\frac{a^{2}}{b c}}\right) \\
& =2\left(1+\frac{a+b+c}{3 \sqrt[3]{a b c}}\right) .
\end{aligned}
$$
By the AM-GM inequality we have
$$
\begin{aligned}
\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right) & =\frac{a+b+c}{a}+\frac{a+b+c}{b}+\frac{a+b+c}{c}-1 \\
& \geq 3\left(\frac{a+b+c}{\sqrt[3]{a b c}}\right)-1 \geq 2 \frac{a+b+c}{\sqrt[3]{a b c}}+3-1=2\left(1+\frac{a+b+c}{\sqrt[3]{a b c}}\right) .
\end{aligned}
$$
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution:"
}
|
0b386c5a-4a5f-5a5c-b242-a91743be5472
| 605,477
|
Let $x, y$ and $z$ be positive real numbers such that $x y z=1$. Prove that
$$
(1+x)(1+y)(1+z) \geq 2\left(1+\sqrt[3]{\frac{y}{x}}+\sqrt[3]{\frac{z}{y}}+\sqrt[3]{\frac{x}{z}}\right)
$$
|
Expanding the left side we obtain
$$
x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq 2\left(\sqrt[3]{\frac{y}{x}}+\sqrt[3]{\frac{z}{y}}+\sqrt[3]{\frac{x}{z}}\right)
$$
As $\sqrt[3]{\frac{y}{x}} \leq \frac{1}{3}\left(y+\frac{1}{x}+1\right)$ etc., it suffices to prove that
$$
x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq \frac{2}{3}\left(x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)+2
$$
which follows from $a+\frac{1}{a} \geq 2$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y$ and $z$ be positive real numbers such that $x y z=1$. Prove that
$$
(1+x)(1+y)(1+z) \geq 2\left(1+\sqrt[3]{\frac{y}{x}}+\sqrt[3]{\frac{z}{y}}+\sqrt[3]{\frac{x}{z}}\right)
$$
|
Expanding the left side we obtain
$$
x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq 2\left(\sqrt[3]{\frac{y}{x}}+\sqrt[3]{\frac{z}{y}}+\sqrt[3]{\frac{x}{z}}\right)
$$
As $\sqrt[3]{\frac{y}{x}} \leq \frac{1}{3}\left(y+\frac{1}{x}+1\right)$ etc., it suffices to prove that
$$
x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq \frac{2}{3}\left(x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)+2
$$
which follows from $a+\frac{1}{a} \geq 2$.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution 2:"
}
|
0b386c5a-4a5f-5a5c-b242-a91743be5472
| 605,477
|
Let $a, b, c$ be positive real numbers. Prove that
$$
\frac{2 a}{a^{2}+b c}+\frac{2 b}{b^{2}+c a}+\frac{2 c}{c^{2}+a b} \leq \frac{a}{b c}+\frac{b}{c a}+\frac{c}{a b} .
$$
|
First we prove that
$$
\frac{2 a}{a^{2}+b c} \leq \frac{1}{2}\left(\frac{1}{b}+\frac{1}{c}\right)
$$
which is equivalent to $0 \leq b(a-c)^{2}+c(a-b)^{2}$, and therefore holds true. Now we turn to the inequality
$$
\frac{1}{b}+\frac{1}{c} \leq \frac{1}{2}\left(\frac{2 a}{b c}+\frac{b}{c a}+\frac{c}{a b}\right),
$$
which by multiplying by $2 a b c$ is seen to be equivalent to $0 \leq(a-b)^{2}+(a-c)^{2}$. Hence we have proved that
Analogously we have
$$
\frac{2 a}{a^{2}+b c} \leq \frac{1}{4}\left(\frac{2 a}{b c}+\frac{b}{c a}+\frac{c}{a b}\right) .
$$
$$
\begin{aligned}
\frac{2 b}{b^{2}+c a} & \leq \frac{1}{4}\left(\frac{2 b}{c a}+\frac{c}{a b}+\frac{a}{b c}\right) \\
\frac{2 c}{c^{2}+a b} & \leq \frac{1}{4}\left(\frac{2 c}{a b}+\frac{a}{b c}+\frac{b}{c a}\right)
\end{aligned}
$$
and it suffices to sum the above three inequalities.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers. Prove that
$$
\frac{2 a}{a^{2}+b c}+\frac{2 b}{b^{2}+c a}+\frac{2 c}{c^{2}+a b} \leq \frac{a}{b c}+\frac{b}{c a}+\frac{c}{a b} .
$$
|
First we prove that
$$
\frac{2 a}{a^{2}+b c} \leq \frac{1}{2}\left(\frac{1}{b}+\frac{1}{c}\right)
$$
which is equivalent to $0 \leq b(a-c)^{2}+c(a-b)^{2}$, and therefore holds true. Now we turn to the inequality
$$
\frac{1}{b}+\frac{1}{c} \leq \frac{1}{2}\left(\frac{2 a}{b c}+\frac{b}{c a}+\frac{c}{a b}\right),
$$
which by multiplying by $2 a b c$ is seen to be equivalent to $0 \leq(a-b)^{2}+(a-c)^{2}$. Hence we have proved that
Analogously we have
$$
\frac{2 a}{a^{2}+b c} \leq \frac{1}{4}\left(\frac{2 a}{b c}+\frac{b}{c a}+\frac{c}{a b}\right) .
$$
$$
\begin{aligned}
\frac{2 b}{b^{2}+c a} & \leq \frac{1}{4}\left(\frac{2 b}{c a}+\frac{c}{a b}+\frac{a}{b c}\right) \\
\frac{2 c}{c^{2}+a b} & \leq \frac{1}{4}\left(\frac{2 c}{a b}+\frac{a}{b c}+\frac{b}{c a}\right)
\end{aligned}
$$
and it suffices to sum the above three inequalities.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution:"
}
|
24d1326e-4bbe-5f14-936f-c49ba46a510c
| 605,500
|
Let $a, b, c$ be positive real numbers. Prove that
$$
\frac{2 a}{a^{2}+b c}+\frac{2 b}{b^{2}+c a}+\frac{2 c}{c^{2}+a b} \leq \frac{a}{b c}+\frac{b}{c a}+\frac{c}{a b} .
$$
|
As $a^{2}+b c \geq 2 a \sqrt{b c}$ etc., it is sufficient to prove that
$$
\frac{1}{\sqrt{b c}}+\frac{1}{\sqrt{a c}}+\frac{1}{\sqrt{a b}} \leq \frac{a}{b c}+\frac{b}{c a}+\frac{c}{a b}
$$
which can be obtained by "inserting" $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$ between the left side and the right side.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers. Prove that
$$
\frac{2 a}{a^{2}+b c}+\frac{2 b}{b^{2}+c a}+\frac{2 c}{c^{2}+a b} \leq \frac{a}{b c}+\frac{b}{c a}+\frac{c}{a b} .
$$
|
As $a^{2}+b c \geq 2 a \sqrt{b c}$ etc., it is sufficient to prove that
$$
\frac{1}{\sqrt{b c}}+\frac{1}{\sqrt{a c}}+\frac{1}{\sqrt{a b}} \leq \frac{a}{b c}+\frac{b}{c a}+\frac{c}{a b}
$$
which can be obtained by "inserting" $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$ between the left side and the right side.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution 2:"
}
|
24d1326e-4bbe-5f14-936f-c49ba46a510c
| 605,500
|
A sequence $\left(a_{n}\right)$ is defined as follows: $a_{1}=\sqrt{2}, a_{2}=2$, and $a_{n+1}=a_{n} a_{n-1}^{2}$ for $n \geq 2$. Prove that for every $n \geq 1$ we have
$$
\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots\left(1+a_{n}\right)<(2+\sqrt{2}) a_{1} a_{2} \cdots a_{n} .
$$
|
First we prove inductively that for $n \geq 1, a_{n}=2^{2^{n-2}}$. We have $a_{1}=2^{2^{-1}}$, $a_{2}=2^{2^{0}}$ and
$$
a_{n+1}=2^{2^{n-2}} \cdot\left(2^{2^{n-3}}\right)^{2}=2^{2^{n-2}} \cdot 2^{2^{n-2}}=2^{2^{n-1}} .
$$
Since $1+a_{1}=1+\sqrt{2}$, we must prove, that
$$
\left(1+a_{2}\right)\left(1+a_{3}\right) \cdots\left(1+a_{n}\right)<2 a_{2} a_{3} \cdots a_{n} .
$$
The right-hand side is equal to
$$
2^{1+2^{0}+2^{1}+\cdots+2^{n-2}}=2^{2^{n-1}}
$$
and the left-hand side
$$
\begin{aligned}
\left(1+2^{2^{0}}\right) & \left(1+2^{2^{1}}\right) \cdots\left(1+2^{2^{n-2}}\right) \\
& =1+2^{2^{0}}+2^{2^{1}}+2^{2^{0}+2^{1}}+2^{2^{2}}+\cdots+2^{2^{0}+2^{1}+\cdots+2^{n-2}} \\
& =1+2+2^{2}+2^{3}+\cdots+2^{2^{n-1}-1} \\
& =2^{2^{n-1}}-1 .
\end{aligned}
$$
The proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
A sequence $\left(a_{n}\right)$ is defined as follows: $a_{1}=\sqrt{2}, a_{2}=2$, and $a_{n+1}=a_{n} a_{n-1}^{2}$ for $n \geq 2$. Prove that for every $n \geq 1$ we have
$$
\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots\left(1+a_{n}\right)<(2+\sqrt{2}) a_{1} a_{2} \cdots a_{n} .
$$
|
First we prove inductively that for $n \geq 1, a_{n}=2^{2^{n-2}}$. We have $a_{1}=2^{2^{-1}}$, $a_{2}=2^{2^{0}}$ and
$$
a_{n+1}=2^{2^{n-2}} \cdot\left(2^{2^{n-3}}\right)^{2}=2^{2^{n-2}} \cdot 2^{2^{n-2}}=2^{2^{n-1}} .
$$
Since $1+a_{1}=1+\sqrt{2}$, we must prove, that
$$
\left(1+a_{2}\right)\left(1+a_{3}\right) \cdots\left(1+a_{n}\right)<2 a_{2} a_{3} \cdots a_{n} .
$$
The right-hand side is equal to
$$
2^{1+2^{0}+2^{1}+\cdots+2^{n-2}}=2^{2^{n-1}}
$$
and the left-hand side
$$
\begin{aligned}
\left(1+2^{2^{0}}\right) & \left(1+2^{2^{1}}\right) \cdots\left(1+2^{2^{n-2}}\right) \\
& =1+2^{2^{0}}+2^{2^{1}}+2^{2^{0}+2^{1}}+2^{2^{2}}+\cdots+2^{2^{0}+2^{1}+\cdots+2^{n-2}} \\
& =1+2+2^{2}+2^{3}+\cdots+2^{2^{n-1}-1} \\
& =2^{2^{n-1}}-1 .
\end{aligned}
$$
The proof is complete.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution:"
}
|
9085e1fd-049f-5188-b002-20f2cce73610
| 236,767
|
Let $A B C D$ be a square. Let $M$ be an inner point on side $B C$ and $N$ be an inner point on side $C D$ with $\angle M A N=45^{\circ}$. Prove that the circumcentre of $A M N$ lies on $A C$.
|
Draw a circle $\omega$ through $M, C, N$; let it intersect $A C$ at $O$. We claim that $O$ is the circumcentre of $A M N$.
Clearly $\angle M O N=180^{\circ}-\angle M C N=90^{\circ}$. If the radius of $\omega$ is $R$, then $O M=$ $2 R \sin 45^{\circ}=R \sqrt{2}$; similarly $O N=R \sqrt{2}$. Hence we get that $O M=O N$. Then the circle with centre $O$ and radius $R \sqrt{2}$ will pass through $A$, since $\angle M A N=\frac{1}{2} \angle M O N$.
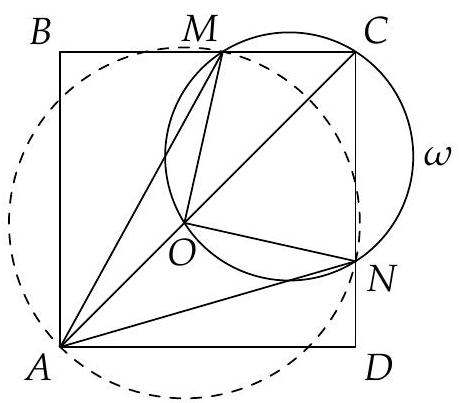
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a square. Let $M$ be an inner point on side $B C$ and $N$ be an inner point on side $C D$ with $\angle M A N=45^{\circ}$. Prove that the circumcentre of $A M N$ lies on $A C$.
|
Draw a circle $\omega$ through $M, C, N$; let it intersect $A C$ at $O$. We claim that $O$ is the circumcentre of $A M N$.
Clearly $\angle M O N=180^{\circ}-\angle M C N=90^{\circ}$. If the radius of $\omega$ is $R$, then $O M=$ $2 R \sin 45^{\circ}=R \sqrt{2}$; similarly $O N=R \sqrt{2}$. Hence we get that $O M=O N$. Then the circle with centre $O$ and radius $R \sqrt{2}$ will pass through $A$, since $\angle M A N=\frac{1}{2} \angle M O N$.

|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n12.",
"solution_match": "\nSolution:"
}
|
4ae661df-faa0-5bee-8197-961344b8c4af
| 236,837
|
Let $A B C D$ be a rectangle and $B C=2 \cdot A B$. Let $E$ be the midpoint of $B C$ and $P$ an arbitrary inner point of $A D$. Let $F$ and $G$ be the feet of perpendiculars drawn correspondingly from $A$ to $B P$ and from $D$ to $C P$. Prove that the points $E, F, P, G$ are concyclic.
|
From rectangular triangle $B A P$ we have $B P \cdot B F=A B^{2}=B E^{2}$. Therefore the circumference through $F$ and $P$ touching the line $B C$ between $B$ and $C$ touches it at $E$.
Analogously, the circumference through $P$ and $G$ touching the line $B C$ between $B$ and $C$ touches it at $E$. But there is only one circumference touching $B C$ at $E$ and passing through $P$.
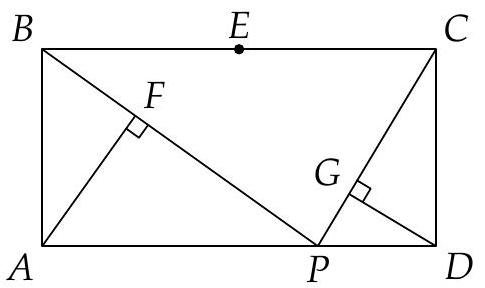
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a rectangle and $B C=2 \cdot A B$. Let $E$ be the midpoint of $B C$ and $P$ an arbitrary inner point of $A D$. Let $F$ and $G$ be the feet of perpendiculars drawn correspondingly from $A$ to $B P$ and from $D$ to $C P$. Prove that the points $E, F, P, G$ are concyclic.
|
From rectangular triangle $B A P$ we have $B P \cdot B F=A B^{2}=B E^{2}$. Therefore the circumference through $F$ and $P$ touching the line $B C$ between $B$ and $C$ touches it at $E$.
Analogously, the circumference through $P$ and $G$ touching the line $B C$ between $B$ and $C$ touches it at $E$. But there is only one circumference touching $B C$ at $E$ and passing through $P$.

|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n13.",
"solution_match": "\nSolution:"
}
|
619f35fb-87ac-5730-9921-f913e6120328
| 236,848
|
Let $A B C$ be an arbitrary triangle and $A M B, B N C, C K A$ regular triangles outward of $A B C$. Through the midpoint of $M N$ a perpendicular to $A C$ is constructed; similarly through the midpoints of $N K$ resp. KM perpendiculars to $A B$ resp. $B C$ are constructed. Prove that these three perpendiculars intersect at the same point.
|
Let $O$ be the midpoint of $M N$, and let $E$ and $F$ be the midpoints of $A B$ and $B C$, respectively. As triangle $M B C$ transforms into triangle $A B N$ when rotated $60^{\circ}$ around $B$ we get $M C=A N$ (it is also a well-known fact). Considering now the quadrangles $A M B N$ and $C M B N$ we get $O E=O F$ (from Eiler's formula $a^{2}+b^{2}+c^{2}+d^{2}=e^{2}+f^{2}+4 \cdot P Q^{2}$ or otherwise). As $E F \| A C$ we get from this that the perpendicular to $A C$ through $O$ passes through the circumcentre of $E F G$, as it is the perpendicular bisector of $E F$. The same holds for the other two perpendiculars.
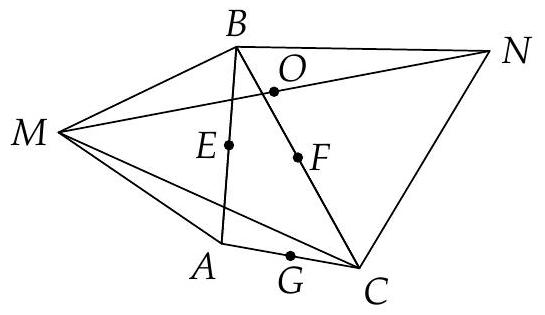
First solution
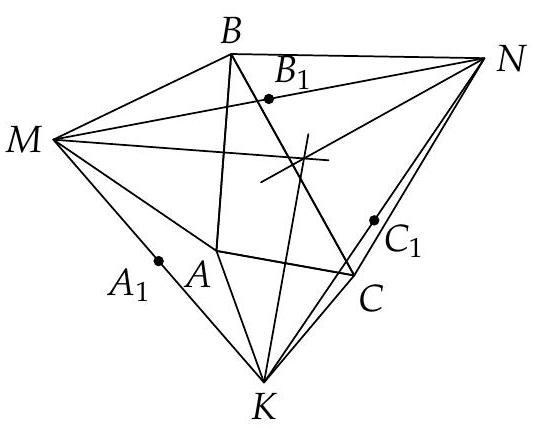
Second solution
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an arbitrary triangle and $A M B, B N C, C K A$ regular triangles outward of $A B C$. Through the midpoint of $M N$ a perpendicular to $A C$ is constructed; similarly through the midpoints of $N K$ resp. KM perpendiculars to $A B$ resp. $B C$ are constructed. Prove that these three perpendiculars intersect at the same point.
|
Let $O$ be the midpoint of $M N$, and let $E$ and $F$ be the midpoints of $A B$ and $B C$, respectively. As triangle $M B C$ transforms into triangle $A B N$ when rotated $60^{\circ}$ around $B$ we get $M C=A N$ (it is also a well-known fact). Considering now the quadrangles $A M B N$ and $C M B N$ we get $O E=O F$ (from Eiler's formula $a^{2}+b^{2}+c^{2}+d^{2}=e^{2}+f^{2}+4 \cdot P Q^{2}$ or otherwise). As $E F \| A C$ we get from this that the perpendicular to $A C$ through $O$ passes through the circumcentre of $E F G$, as it is the perpendicular bisector of $E F$. The same holds for the other two perpendiculars.

First solution

Second solution
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n14.",
"solution_match": "\nSolution:"
}
|
0a0ca09c-0909-5242-945c-736209c7b939
| 605,679
|
Let $A B C$ be an arbitrary triangle and $A M B, B N C, C K A$ regular triangles outward of $A B C$. Through the midpoint of $M N$ a perpendicular to $A C$ is constructed; similarly through the midpoints of $N K$ resp. KM perpendiculars to $A B$ resp. $B C$ are constructed. Prove that these three perpendiculars intersect at the same point.
|
Let us denote the midpoints of the segments $M N, N K, K M$ by $B_{1}, C_{1}, A_{1}$, respectively. It is easy to see that triangle $A_{1} B_{1} C_{1}$ is homothetic to triangle $N K M$ via the homothety centered at the intersection of the medians of triangle $N M K$ and dilation $-\frac{1}{2}$. The perpendiculars through $M, N, K$ to $A B, B C, C A$, respectively, are also the perpendicular bisectors of these sides, so they intersect in the circumcentre of triangle $A B C$. The desired result follows now from the homothety, and we find that that the common point of intersection is the circumcentre of the image of triangle $A B C$ under the homothety; that is, the circumcentre of the triangle with vertices the midpoints of the sides $A B, B C, C A$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an arbitrary triangle and $A M B, B N C, C K A$ regular triangles outward of $A B C$. Through the midpoint of $M N$ a perpendicular to $A C$ is constructed; similarly through the midpoints of $N K$ resp. KM perpendiculars to $A B$ resp. $B C$ are constructed. Prove that these three perpendiculars intersect at the same point.
|
Let us denote the midpoints of the segments $M N, N K, K M$ by $B_{1}, C_{1}, A_{1}$, respectively. It is easy to see that triangle $A_{1} B_{1} C_{1}$ is homothetic to triangle $N K M$ via the homothety centered at the intersection of the medians of triangle $N M K$ and dilation $-\frac{1}{2}$. The perpendiculars through $M, N, K$ to $A B, B C, C A$, respectively, are also the perpendicular bisectors of these sides, so they intersect in the circumcentre of triangle $A B C$. The desired result follows now from the homothety, and we find that that the common point of intersection is the circumcentre of the image of triangle $A B C$ under the homothety; that is, the circumcentre of the triangle with vertices the midpoints of the sides $A B, B C, C A$.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n14.",
"solution_match": "\nSolution 2:"
}
|
0a0ca09c-0909-5242-945c-736209c7b939
| 605,679
|
Let $P$ be the intersection point of the diagonals $A C$ and $B D$ in a cyclic quadrilateral. $A$ circle through $P$ touches the side $C D$ in the midpoint $M$ of this side and intersects the segments $B D$ and $A C$ in the points $Q$ and $R$, respectively. Let $S$ be a point on the segment $B D$ such that $B S=D Q$. The parallel to $A B$ through $S$ intersects $A C$ at $T$. Prove that $A T=R C$.
|
With reference to the figure below we have $C R \cdot C P=D Q \cdot D P=C M^{2}=D M^{2}$, which is equivalent to $R C=\frac{D Q \cdot D P}{C P}$. We also have $\frac{A T}{B S}=\frac{A P}{B P}=\frac{A T}{D Q}$, so $A T=\frac{A P \cdot D Q}{B P}$. Since $A B C D$ is cyclic the result now comes from the fact that $D P \cdot B P=A P \cdot C P$ (due to a well-known theorem).
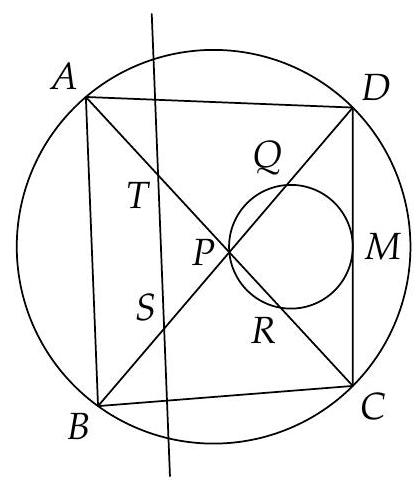
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be the intersection point of the diagonals $A C$ and $B D$ in a cyclic quadrilateral. $A$ circle through $P$ touches the side $C D$ in the midpoint $M$ of this side and intersects the segments $B D$ and $A C$ in the points $Q$ and $R$, respectively. Let $S$ be a point on the segment $B D$ such that $B S=D Q$. The parallel to $A B$ through $S$ intersects $A C$ at $T$. Prove that $A T=R C$.
|
With reference to the figure below we have $C R \cdot C P=D Q \cdot D P=C M^{2}=D M^{2}$, which is equivalent to $R C=\frac{D Q \cdot D P}{C P}$. We also have $\frac{A T}{B S}=\frac{A P}{B P}=\frac{A T}{D Q}$, so $A T=\frac{A P \cdot D Q}{B P}$. Since $A B C D$ is cyclic the result now comes from the fact that $D P \cdot B P=A P \cdot C P$ (due to a well-known theorem).

|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n15.",
"solution_match": "\nSolution:"
}
|
4d7f605b-1cca-56cc-948b-ef029667c2e9
| 236,876
|
All the positive divisors of a positive integer $n$ are stored into an array in increasing order. Mary has to write a program which decides for an arbitrarily chosen divisor $d>1$ whether it is a prime. Let $n$ have $k$ divisors not greater than $d$. Mary claims that it suffices to check divisibility of $d$ by the first $\lceil k / 2\rceil$ divisors of $n$ : If a divisor of $d$ greater than 1 is found among them, then $d$ is composite, otherwise d is prime. Is Mary right?
Answer: Yes, Mary is right.
|
Let $d>1$ be a divisor of $n$. Suppose Mary's program outputs "composite" for $d$. That means it has found a divisor of $d$ greater than 1 . Since $d>1$, the array contains at least 2 divisors of $d$, namely 1 and $d$. Thus Mary's program does not check divisibility of $d$ by $d$ (the first half gets complete before reaching $d$ ) which means that the divisor found lays strictly between 1 and $d$. Hence $d$ is composite indeed.
Suppose now $d$ being composite. Let $p$ be its smallest prime divisor; then $\frac{d}{p} \geq p$ or, equivalently, $d \geq p^{2}$. As $p$ is a divisor of $n$, it occurs in the array. Let $a_{1}, \ldots, a_{k}$ all divisors of $n$ smaller than $p$. Then $p a_{1}, \ldots, p a_{k}$ are less than $p^{2}$ and hence less than $d$.
As $a_{1}, \ldots, a_{k}$ are all relatively prime with $p$, all the numbers $p a_{1}, \ldots, p a_{k}$ divide $n$. The numbers $a_{1}, \ldots, a_{k}, p a_{1}, \ldots, p a_{k}$ are pairwise different by construction. Thus there are at least $2 k+1$ divisors of $n$ not greater than $d$. So Mary's program checks divisibility of $d$ by at least $k+1$ smallest divisors of $n$, among which it finds $p$, and outputs "composite".
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
All the positive divisors of a positive integer $n$ are stored into an array in increasing order. Mary has to write a program which decides for an arbitrarily chosen divisor $d>1$ whether it is a prime. Let $n$ have $k$ divisors not greater than $d$. Mary claims that it suffices to check divisibility of $d$ by the first $\lceil k / 2\rceil$ divisors of $n$ : If a divisor of $d$ greater than 1 is found among them, then $d$ is composite, otherwise d is prime. Is Mary right?
Answer: Yes, Mary is right.
|
Let $d>1$ be a divisor of $n$. Suppose Mary's program outputs "composite" for $d$. That means it has found a divisor of $d$ greater than 1 . Since $d>1$, the array contains at least 2 divisors of $d$, namely 1 and $d$. Thus Mary's program does not check divisibility of $d$ by $d$ (the first half gets complete before reaching $d$ ) which means that the divisor found lays strictly between 1 and $d$. Hence $d$ is composite indeed.
Suppose now $d$ being composite. Let $p$ be its smallest prime divisor; then $\frac{d}{p} \geq p$ or, equivalently, $d \geq p^{2}$. As $p$ is a divisor of $n$, it occurs in the array. Let $a_{1}, \ldots, a_{k}$ all divisors of $n$ smaller than $p$. Then $p a_{1}, \ldots, p a_{k}$ are less than $p^{2}$ and hence less than $d$.
As $a_{1}, \ldots, a_{k}$ are all relatively prime with $p$, all the numbers $p a_{1}, \ldots, p a_{k}$ divide $n$. The numbers $a_{1}, \ldots, a_{k}, p a_{1}, \ldots, p a_{k}$ are pairwise different by construction. Thus there are at least $2 k+1$ divisors of $n$ not greater than $d$. So Mary's program checks divisibility of $d$ by at least $k+1$ smallest divisors of $n$, among which it finds $p$, and outputs "composite".
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n17.",
"solution_match": "\nSolution:"
}
|
e28cea8f-c8cc-5dbd-a10e-d8f93a580cdb
| 605,730
|
Every integer is coloured with exactly one of the colours BLUE, GREEN, RED, YELLOW. Can this be done in such a way that if $a, b, c, d$ are not all 0 and have the same colour, then $3 a-2 b \neq 2 c-3 d$ ?
Answer: Yes.
|
A colouring with the required property can be defined as follows. For a non-zero integer $k$ let $k^{*}$ be the integer uniquely defined by $k=5^{m} \cdot k^{*}$, where $m$ is a nonnegative integer and $5 \nmid k^{*}$. We also define $0^{*}=0$. Two non-zero integers $k_{1}, k_{2}$ receive the same colour if and only if $k_{1}^{*} \equiv k_{2}^{*}(\bmod 5)$; we assign 0 any colour.
Assume $a, b, c, d$ has the same colour and that $3 a-2 b=2 c-3 d$, which we rewrite as $3 a-2 b-2 c+3 d=0$. Dividing both sides by the largest power of 5 which simultaneously divides $a, b, c, d$ (this makes sense since not all of $a, b, c, d$ are 0 ), we obtain
$$
3 \cdot 5^{A} \cdot a^{*}-2 \cdot 5^{B} \cdot b^{*}-2 \cdot 5^{C} \cdot c^{*}+3 \cdot 5^{D} \cdot d^{*}=0,
$$
where $A, B, C, D$ are nonnegative integers at least one of which is equal to 0 . The above equality implies
$$
3\left(5^{A} \cdot a^{*}+5^{B} \cdot b^{*}+5^{C} \cdot c^{*}+5^{D} \cdot d^{*}\right) \equiv 0 \quad(\bmod 5) .
$$
Assume $a, b, c, d$ are all non-zero. Then $a^{*} \equiv b^{*} \equiv c^{*} \equiv d^{*} \not \equiv 0(\bmod 5)$. This implies
$$
5^{A}+5^{B}+5^{C}+5^{D} \equiv 0 \quad(\bmod 5)
$$
which is impossible since at least one of the numbers $A, B, C, D$ is equal to 0 . If one or more of $a, b, c, d$ are 0 , we simply omit the corresponding terms from (1), and the same conclusion holds.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Every integer is coloured with exactly one of the colours BLUE, GREEN, RED, YELLOW. Can this be done in such a way that if $a, b, c, d$ are not all 0 and have the same colour, then $3 a-2 b \neq 2 c-3 d$ ?
Answer: Yes.
|
A colouring with the required property can be defined as follows. For a non-zero integer $k$ let $k^{*}$ be the integer uniquely defined by $k=5^{m} \cdot k^{*}$, where $m$ is a nonnegative integer and $5 \nmid k^{*}$. We also define $0^{*}=0$. Two non-zero integers $k_{1}, k_{2}$ receive the same colour if and only if $k_{1}^{*} \equiv k_{2}^{*}(\bmod 5)$; we assign 0 any colour.
Assume $a, b, c, d$ has the same colour and that $3 a-2 b=2 c-3 d$, which we rewrite as $3 a-2 b-2 c+3 d=0$. Dividing both sides by the largest power of 5 which simultaneously divides $a, b, c, d$ (this makes sense since not all of $a, b, c, d$ are 0 ), we obtain
$$
3 \cdot 5^{A} \cdot a^{*}-2 \cdot 5^{B} \cdot b^{*}-2 \cdot 5^{C} \cdot c^{*}+3 \cdot 5^{D} \cdot d^{*}=0,
$$
where $A, B, C, D$ are nonnegative integers at least one of which is equal to 0 . The above equality implies
$$
3\left(5^{A} \cdot a^{*}+5^{B} \cdot b^{*}+5^{C} \cdot c^{*}+5^{D} \cdot d^{*}\right) \equiv 0 \quad(\bmod 5) .
$$
Assume $a, b, c, d$ are all non-zero. Then $a^{*} \equiv b^{*} \equiv c^{*} \equiv d^{*} \not \equiv 0(\bmod 5)$. This implies
$$
5^{A}+5^{B}+5^{C}+5^{D} \equiv 0 \quad(\bmod 5)
$$
which is impossible since at least one of the numbers $A, B, C, D$ is equal to 0 . If one or more of $a, b, c, d$ are 0 , we simply omit the corresponding terms from (1), and the same conclusion holds.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n18.",
"solution_match": "\nSolution:"
}
|
bd17be0a-27aa-5441-a9c1-a6a7a253b54d
| 605,738
|
Let $a$ and $b$ be positive integers. Prove that if $a^{3}+b^{3}$ is the square of an integer, then $a+b$ is not a product of two different prime numbers.
|
Suppose $a+b=p q$, where $p \neq q$ are two prime numbers. We may assume that $p \neq 3$. Since
$$
a^{3}+b^{3}=(a+b)\left(a^{2}-a b+b^{2}\right)
$$
is a square, the number $a^{2}-a b+b^{2}=(a+b)^{2}-3 a b$ must be divisible by $p$ and $q$, whence $3 a b$ must be divisible by $p$ and $q$. But $p \neq 3$, so $p \mid a$ or $p \mid b$; but $p \mid a+b$, so $p \mid a$ and $p \mid b$. Write $a=p k, b=p \ell$ for some integers $k, \ell$. Notice that $q=3$, since otherwise, repeating the above argument, we would have $q|a, q| b$ and $a+b>p q)$. So we have
$$
3 p=a+b=p(k+\ell)
$$
and we conclude that $a=p, b=2 p$ or $a=2 p, b=p$. Then $a^{3}+b^{3}=9 p^{3}$ is obviously not a square, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a$ and $b$ be positive integers. Prove that if $a^{3}+b^{3}$ is the square of an integer, then $a+b$ is not a product of two different prime numbers.
|
Suppose $a+b=p q$, where $p \neq q$ are two prime numbers. We may assume that $p \neq 3$. Since
$$
a^{3}+b^{3}=(a+b)\left(a^{2}-a b+b^{2}\right)
$$
is a square, the number $a^{2}-a b+b^{2}=(a+b)^{2}-3 a b$ must be divisible by $p$ and $q$, whence $3 a b$ must be divisible by $p$ and $q$. But $p \neq 3$, so $p \mid a$ or $p \mid b$; but $p \mid a+b$, so $p \mid a$ and $p \mid b$. Write $a=p k, b=p \ell$ for some integers $k, \ell$. Notice that $q=3$, since otherwise, repeating the above argument, we would have $q|a, q| b$ and $a+b>p q)$. So we have
$$
3 p=a+b=p(k+\ell)
$$
and we conclude that $a=p, b=2 p$ or $a=2 p, b=p$. Then $a^{3}+b^{3}=9 p^{3}$ is obviously not a square, a contradiction.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n19.",
"solution_match": "\nSolution:"
}
|
e0aeead9-9fcd-5bed-9f5e-8368443b5b51
| 236,919
|
Let $n$ be a positive integer such that the sum of all the positive divisors of $n$ (except $n$ ) plus the number of these divisors is equal to $n$. Prove that $n=2 m^{2}$ for some integer $m$.
|
Let $t_{1}<t_{2}<\cdots<t_{s}$ be all positive odd divisors of $n$, and let $2^{k}$ be the maximal power of 2 that divides $n$. Then the full list of divisors of $n$ is the following:
$$
t_{1}, \ldots, t_{s}, 2 t_{1}, \ldots, 2 t_{s}, \ldots, 2^{k} t_{1}, \ldots, 2^{k} t_{s} .
$$
Hence,
$$
2 n=\left(2^{k+1}-1\right)\left(t_{1}+t_{2}+\cdots+t_{s}\right)+(k+1) s-1 .
$$
The right-hand side can be even only if both $k$ and $s$ are odd. In this case the number $n / 2^{k}$ has an odd number of divisors and therefore it is equal to a perfect square $r^{2}$. Writing $k=2 a+1$, we have $n=2^{k} r^{2}=2\left(2^{a} r\right)^{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer such that the sum of all the positive divisors of $n$ (except $n$ ) plus the number of these divisors is equal to $n$. Prove that $n=2 m^{2}$ for some integer $m$.
|
Let $t_{1}<t_{2}<\cdots<t_{s}$ be all positive odd divisors of $n$, and let $2^{k}$ be the maximal power of 2 that divides $n$. Then the full list of divisors of $n$ is the following:
$$
t_{1}, \ldots, t_{s}, 2 t_{1}, \ldots, 2 t_{s}, \ldots, 2^{k} t_{1}, \ldots, 2^{k} t_{s} .
$$
Hence,
$$
2 n=\left(2^{k+1}-1\right)\left(t_{1}+t_{2}+\cdots+t_{s}\right)+(k+1) s-1 .
$$
The right-hand side can be even only if both $k$ and $s$ are odd. In this case the number $n / 2^{k}$ has an odd number of divisors and therefore it is equal to a perfect square $r^{2}$. Writing $k=2 a+1$, we have $n=2^{k} r^{2}=2\left(2^{a} r\right)^{2}$.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n20.",
"solution_match": "\nSolution:"
}
|
a8a4d153-b02b-5cb8-a4ac-e1201402408f
| 605,764
|
Given a sequence $a_{1}, a_{2}, a_{3}, \ldots$ of non-negative real numbers satisfying the conditions
(1) $a_{n}+a_{2 n} \geq 3 n$
(2) $a_{n+1}+n \leq 2 \sqrt{a_{n} \cdot(n+1)}$
for all indices $n=1,2 \ldots$
(a) Prove that the inequality $a_{n} \geq n$ holds for every $n \in \mathbb{N}$.
(b) Give an example of such a sequence.
|
(a) Note that the inequality
$$
\frac{a_{n+1}+n}{2} \geq \sqrt{a_{n+1} \cdot n}
$$
holds, which together with the second condition of the problem gives
$$
\sqrt{a_{n+1} \cdot n} \leq \sqrt{a_{n} \cdot(n+1)}
$$
This inequality simplifies to
$$
\frac{a_{n+1}}{a_{n}} \leq \frac{n+1}{n}
$$
Now, using the last inequality for the index $n$ replaced by $n, n+1, \ldots, 2 n-1$ and multiplying the results, we obtain
$$
\frac{a_{2 n}}{a_{n}} \leq \frac{2 n}{n}=2
$$
or $2 a_{n} \geq a_{2 n}$. Taking into account the first condition of the problem, we have
$$
3 a_{n}=a_{n}+2 a_{n} \geq a_{n}+a_{2 n} \geq 3 n
$$
which implies $a_{n} \geq n$. (b) The sequence defined by $a_{n}=n+1$ satisfies all the conditions of the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Given a sequence $a_{1}, a_{2}, a_{3}, \ldots$ of non-negative real numbers satisfying the conditions
(1) $a_{n}+a_{2 n} \geq 3 n$
(2) $a_{n+1}+n \leq 2 \sqrt{a_{n} \cdot(n+1)}$
for all indices $n=1,2 \ldots$
(a) Prove that the inequality $a_{n} \geq n$ holds for every $n \in \mathbb{N}$.
(b) Give an example of such a sequence.
|
(a) Note that the inequality
$$
\frac{a_{n+1}+n}{2} \geq \sqrt{a_{n+1} \cdot n}
$$
holds, which together with the second condition of the problem gives
$$
\sqrt{a_{n+1} \cdot n} \leq \sqrt{a_{n} \cdot(n+1)}
$$
This inequality simplifies to
$$
\frac{a_{n+1}}{a_{n}} \leq \frac{n+1}{n}
$$
Now, using the last inequality for the index $n$ replaced by $n, n+1, \ldots, 2 n-1$ and multiplying the results, we obtain
$$
\frac{a_{2 n}}{a_{n}} \leq \frac{2 n}{n}=2
$$
or $2 a_{n} \geq a_{2 n}$. Taking into account the first condition of the problem, we have
$$
3 a_{n}=a_{n}+2 a_{n} \geq a_{n}+a_{2 n} \geq 3 n
$$
which implies $a_{n} \geq n$. (b) The sequence defined by $a_{n}=n+1$ satisfies all the conditions of the problem.
|
{
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution:"
}
|
2fc11caf-d590-57c2-bb99-60da48edbbfd
| 239,333
|
Let $P(x)$ be a polynomial with non-negative coefficients. Prove that if $P\left(\frac{1}{x}\right) P(x) \geq 1$ for $x=1$, then the same inequality holds for each positive $x$.
|
For $x>0$ we have $P(x)>0$ (because at least one coefficient is non-zero). From the given condition we have $(P(1))^{2} \geq 1$. Further, let's denote $P(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+$ $\cdots+a_{0}$. Then
$$
\begin{aligned}
P(x) P\left(\frac{1}{x}\right) & =\left(a_{n} x^{n}+\cdots+a_{0}\right)\left(a_{n} x^{-n}+\cdots+a_{0}\right) \\
& =\sum_{i=0}^{n} a_{i}^{2}+\sum_{i=1}^{n} \sum_{j=0}^{i-1}\left(a_{i-j} a_{j}\right)\left(x^{i}+x^{-i}\right) \\
& \geq \sum_{i=0}^{n} a_{i}^{2}+2 \sum_{i>j} a_{i} a_{j} \\
& =(P(1))^{2} \geq 1 .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $P(x)$ be a polynomial with non-negative coefficients. Prove that if $P\left(\frac{1}{x}\right) P(x) \geq 1$ for $x=1$, then the same inequality holds for each positive $x$.
|
For $x>0$ we have $P(x)>0$ (because at least one coefficient is non-zero). From the given condition we have $(P(1))^{2} \geq 1$. Further, let's denote $P(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+$ $\cdots+a_{0}$. Then
$$
\begin{aligned}
P(x) P\left(\frac{1}{x}\right) & =\left(a_{n} x^{n}+\cdots+a_{0}\right)\left(a_{n} x^{-n}+\cdots+a_{0}\right) \\
& =\sum_{i=0}^{n} a_{i}^{2}+\sum_{i=1}^{n} \sum_{j=0}^{i-1}\left(a_{i-j} a_{j}\right)\left(x^{i}+x^{-i}\right) \\
& \geq \sum_{i=0}^{n} a_{i}^{2}+2 \sum_{i>j} a_{i} a_{j} \\
& =(P(1))^{2} \geq 1 .
\end{aligned}
$$
|
{
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution:"
}
|
d95a1218-6fc8-5b6d-8983-6a2f62763207
| 239,340
|
Let $p, q, r$ be positive real numbers and $n \in \mathbb{N}$. Show that if $p q r=1$, then
$$
\frac{1}{p^{n}+q^{n}+1}+\frac{1}{q^{n}+r^{n}+1}+\frac{1}{r^{n}+p^{n}+1} \leq 1
$$
|
The key idea is to deal with the case $n=3$. Put $a=p^{n / 3}, b=q^{n / 3}$, and $c=r^{n / 3}$, so $a b c=(p q r)^{n / 3}=1$ and
$$
\frac{1}{p^{n}+q^{n}+1}+\frac{1}{q^{n}+r^{n}+1}+\frac{1}{r^{n}+p^{n}+1}=\frac{1}{a^{3}+b^{3}+1}+\frac{1}{b^{3}+c^{3}+1}+\frac{1}{c^{3}+a^{3}+1} .
$$
Now
$$
\frac{1}{a^{3}+b^{3}+1}=\frac{1}{(a+b)\left(a^{2}-a b+b^{2}\right)+1}=\frac{1}{(a+b)\left((a-b)^{2}+a b\right)+1} \leq \frac{1}{(a+b) a b+1} .
$$
Since $a b=c^{-1}$,
$$
\frac{1}{a^{3}+b^{3}+1} \leq \frac{1}{(a+b) a b+1}=\frac{c}{a+b+c}
$$
Similarly we obtain
$$
\frac{1}{b^{3}+c^{3}+1} \leq \frac{a}{a+b+c} \quad \text { and } \quad \frac{1}{c^{3}+a^{3}+1} \leq \frac{b}{a+b+c}
$$
Hence
$$
\frac{1}{a^{3}+b^{3}+1}+\frac{1}{b^{3}+c^{3}+1}+\frac{1}{c^{3}+a^{3}+1} \leq \frac{c}{a+b+c}+\frac{a}{a+b+c}+\frac{b}{a+b+c}=1,
$$
which was to be shown.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $p, q, r$ be positive real numbers and $n \in \mathbb{N}$. Show that if $p q r=1$, then
$$
\frac{1}{p^{n}+q^{n}+1}+\frac{1}{q^{n}+r^{n}+1}+\frac{1}{r^{n}+p^{n}+1} \leq 1
$$
|
The key idea is to deal with the case $n=3$. Put $a=p^{n / 3}, b=q^{n / 3}$, and $c=r^{n / 3}$, so $a b c=(p q r)^{n / 3}=1$ and
$$
\frac{1}{p^{n}+q^{n}+1}+\frac{1}{q^{n}+r^{n}+1}+\frac{1}{r^{n}+p^{n}+1}=\frac{1}{a^{3}+b^{3}+1}+\frac{1}{b^{3}+c^{3}+1}+\frac{1}{c^{3}+a^{3}+1} .
$$
Now
$$
\frac{1}{a^{3}+b^{3}+1}=\frac{1}{(a+b)\left(a^{2}-a b+b^{2}\right)+1}=\frac{1}{(a+b)\left((a-b)^{2}+a b\right)+1} \leq \frac{1}{(a+b) a b+1} .
$$
Since $a b=c^{-1}$,
$$
\frac{1}{a^{3}+b^{3}+1} \leq \frac{1}{(a+b) a b+1}=\frac{c}{a+b+c}
$$
Similarly we obtain
$$
\frac{1}{b^{3}+c^{3}+1} \leq \frac{a}{a+b+c} \quad \text { and } \quad \frac{1}{c^{3}+a^{3}+1} \leq \frac{b}{a+b+c}
$$
Hence
$$
\frac{1}{a^{3}+b^{3}+1}+\frac{1}{b^{3}+c^{3}+1}+\frac{1}{c^{3}+a^{3}+1} \leq \frac{c}{a+b+c}+\frac{a}{a+b+c}+\frac{b}{a+b+c}=1,
$$
which was to be shown.
|
{
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution:"
}
|
39bdbaef-4654-504c-8d97-06824497c772
| 239,347
|
Let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers with arithmetic mean $X$. Prove that there is a positive integer $K$ such that the arithmetic mean of each of the lists $\left\{x_{1}, x_{2}, \ldots, x_{K}\right\},\left\{x_{2}, x_{3}, \ldots, x_{K}\right\}$, $\ldots,\left\{x_{K-1}, x_{K}\right\},\left\{x_{K}\right\}$ is not greater than $X$.
|
Suppose the conclusion is false. This means that for every $K \in\{1,2, \ldots, n\}$, there exists a $k \leq K$ such that the arithmetic mean of $x_{k}, x_{k+1}, \ldots, x_{K}$ exceeds $X$. We now define a decreasing sequence $b_{1} \geq a_{1}>a_{1}-1=b_{2} \geq a_{2}>\cdots$ as follows: Put $b_{1}=n$, and for each $i$, let $a_{i}$ be the largest largest $k \leq b_{i}$ such that the arithmetic mean of $x_{a_{i}}, \ldots, x_{b_{i}}$ exceeds $X$; then put $b_{i+1}=a_{i}-1$ and repeat. Clearly for some $m, a_{m}=1$. Now, by construction, each of the sets $\left\{x_{a_{m}}, \ldots, x_{b_{m}}\right\},\left\{x_{a_{m-1}}, \ldots, x_{b_{m-1}}\right\}, \ldots,\left\{x_{a_{1}}, \ldots, x_{b_{1}}\right\}$ has arithmetic mean strictly greater than $X$, but then the union $\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$ of these sets has arithmetic mean strictly greater than $X$; a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers with arithmetic mean $X$. Prove that there is a positive integer $K$ such that the arithmetic mean of each of the lists $\left\{x_{1}, x_{2}, \ldots, x_{K}\right\},\left\{x_{2}, x_{3}, \ldots, x_{K}\right\}$, $\ldots,\left\{x_{K-1}, x_{K}\right\},\left\{x_{K}\right\}$ is not greater than $X$.
|
Suppose the conclusion is false. This means that for every $K \in\{1,2, \ldots, n\}$, there exists a $k \leq K$ such that the arithmetic mean of $x_{k}, x_{k+1}, \ldots, x_{K}$ exceeds $X$. We now define a decreasing sequence $b_{1} \geq a_{1}>a_{1}-1=b_{2} \geq a_{2}>\cdots$ as follows: Put $b_{1}=n$, and for each $i$, let $a_{i}$ be the largest largest $k \leq b_{i}$ such that the arithmetic mean of $x_{a_{i}}, \ldots, x_{b_{i}}$ exceeds $X$; then put $b_{i+1}=a_{i}-1$ and repeat. Clearly for some $m, a_{m}=1$. Now, by construction, each of the sets $\left\{x_{a_{m}}, \ldots, x_{b_{m}}\right\},\left\{x_{a_{m-1}}, \ldots, x_{b_{m-1}}\right\}, \ldots,\left\{x_{a_{1}}, \ldots, x_{b_{1}}\right\}$ has arithmetic mean strictly greater than $X$, but then the union $\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$ of these sets has arithmetic mean strictly greater than $X$; a contradiction.
|
{
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution:"
}
|
17a8904f-7c8d-5773-bf2b-a4f6141af2ea
| 239,355
|
Let $f$ be a non-constant polynomial with integer coefficients. Prove that there is an integer $n$ such that $f(n)$ has at least 2004 distinct prime factors.
|
Suppose the contrary. Choose an integer $n_{0}$ so that $f\left(n_{0}\right)$ has the highest number of prime factors. By translating the polynomial we may assume $n_{0}=0$. Setting $k=f(0)$, we have $f\left(w k^{2}\right) \equiv k\left(\bmod k^{2}\right)$, or $f\left(w k^{2}\right)=a k^{2}+k=(a k+1) k$. Since $\operatorname{gcd}(a k+1, k)=1$ and $k$ alone achieves the highest number of prime factors of $f$, we must have $a k+1= \pm 1$. This cannot happen for every $w$ since $f$ is non-constant, so we have a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $f$ be a non-constant polynomial with integer coefficients. Prove that there is an integer $n$ such that $f(n)$ has at least 2004 distinct prime factors.
|
Suppose the contrary. Choose an integer $n_{0}$ so that $f\left(n_{0}\right)$ has the highest number of prime factors. By translating the polynomial we may assume $n_{0}=0$. Setting $k=f(0)$, we have $f\left(w k^{2}\right) \equiv k\left(\bmod k^{2}\right)$, or $f\left(w k^{2}\right)=a k^{2}+k=(a k+1) k$. Since $\operatorname{gcd}(a k+1, k)=1$ and $k$ alone achieves the highest number of prime factors of $f$, we must have $a k+1= \pm 1$. This cannot happen for every $w$ since $f$ is non-constant, so we have a contradiction.
|
{
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"problem_match": "\n8.",
"solution_match": "\nSolution:"
}
|
dd3d175b-db3a-5a79-be26-39be2d79b091
| 239,391
|
$A$ set $S$ of $n-1$ natural numbers is given ( $n \geq 3$ ). There exists at least two elements in this set whose difference is not divisible by $n$. Prove that it is possible to choose a non-empty subset of $S$ so that the sum of its elements is divisible by $n$.
|
Suppose to the contrary that there exists a set $X=\left\{a_{1}, a_{2}, \ldots, a_{n-1}\right\}$ violating the statement of the problem, and let $a_{n-2} \not \equiv a_{n-1}(\bmod n)$. Denote $S_{i}=a_{1}+a_{2}+$ $\cdots+a_{i}, i=1, \ldots, n-1$. The conditions of the problem imply that all the numbers $S_{i}$ must give different remainders when divided by $n$. Indeed, if for some $j<k$ we had $S_{j} \equiv S_{k}(\bmod n)$, then $a_{j+1}+a_{j+2}+\cdots+a_{k}=S_{k}-S_{j} \equiv 0(\bmod n)$. Consider now the sum $S^{\prime}=S_{n-3}+a_{n-1}$. We see that $S^{\prime}$ can not be congruent to any of the sums $S_{i}$ (for $i \neq n-2$ the above argument works and for $i=n-2$ we use the assumption $a_{n-2} \not \equiv a_{n-1}$ $(\bmod n))$. Thus we have $n$ sums that give pairwise different remainders when divided by $n$, consequently one of them has to give the remainder 0 , a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
$A$ set $S$ of $n-1$ natural numbers is given ( $n \geq 3$ ). There exists at least two elements in this set whose difference is not divisible by $n$. Prove that it is possible to choose a non-empty subset of $S$ so that the sum of its elements is divisible by $n$.
|
Suppose to the contrary that there exists a set $X=\left\{a_{1}, a_{2}, \ldots, a_{n-1}\right\}$ violating the statement of the problem, and let $a_{n-2} \not \equiv a_{n-1}(\bmod n)$. Denote $S_{i}=a_{1}+a_{2}+$ $\cdots+a_{i}, i=1, \ldots, n-1$. The conditions of the problem imply that all the numbers $S_{i}$ must give different remainders when divided by $n$. Indeed, if for some $j<k$ we had $S_{j} \equiv S_{k}(\bmod n)$, then $a_{j+1}+a_{j+2}+\cdots+a_{k}=S_{k}-S_{j} \equiv 0(\bmod n)$. Consider now the sum $S^{\prime}=S_{n-3}+a_{n-1}$. We see that $S^{\prime}$ can not be congruent to any of the sums $S_{i}$ (for $i \neq n-2$ the above argument works and for $i=n-2$ we use the assumption $a_{n-2} \not \equiv a_{n-1}$ $(\bmod n))$. Thus we have $n$ sums that give pairwise different remainders when divided by $n$, consequently one of them has to give the remainder 0 , a contradiction.
|
{
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"problem_match": "\n9.",
"solution_match": "\nSolution:"
}
|
1504594c-992b-5342-8ac6-f9e59e5af724
| 239,399
|
Is there an infinite sequence of prime numbers $p_{1}, p_{2}, \ldots$ such that $\left|p_{n+1}-2 p_{n}\right|=1$ for each $n \in \mathbb{N}$ ?
Answer: No, there is no such sequence.
|
Suppose the contrary. Clearly $p_{3}>3$. There are two possibilities: If $p_{3} \equiv 1$ $(\bmod 3)$ then necessarily $p_{4}=2 p_{3}-1\left(\right.$ otherwise $\left.p_{4} \equiv 0(\bmod 3)\right)$, so $p_{4} \equiv 1(\bmod 3)$. Analogously $p_{5}=2 p_{4}-1, p_{6}=2 p_{5}-1$ etc. By an easy induction we have
$$
p_{n+1}-1=2^{n-2}\left(p_{3}-1\right), \quad n=3,4,5, \ldots
$$
If we set $n=p_{3}+1$ we have $p_{p_{3}+2}-1=2^{p_{3}-1}\left(p_{3}-1\right)$, from which
$$
p_{p_{3}+2} \equiv 1+1 \cdot\left(p_{3}-1\right)=p_{3} \equiv 0 \quad\left(\bmod p_{3}\right)
$$
a contradiction. The case $p_{3} \equiv 2(\bmod 3)$ is treated analogously.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Is there an infinite sequence of prime numbers $p_{1}, p_{2}, \ldots$ such that $\left|p_{n+1}-2 p_{n}\right|=1$ for each $n \in \mathbb{N}$ ?
Answer: No, there is no such sequence.
|
Suppose the contrary. Clearly $p_{3}>3$. There are two possibilities: If $p_{3} \equiv 1$ $(\bmod 3)$ then necessarily $p_{4}=2 p_{3}-1\left(\right.$ otherwise $\left.p_{4} \equiv 0(\bmod 3)\right)$, so $p_{4} \equiv 1(\bmod 3)$. Analogously $p_{5}=2 p_{4}-1, p_{6}=2 p_{5}-1$ etc. By an easy induction we have
$$
p_{n+1}-1=2^{n-2}\left(p_{3}-1\right), \quad n=3,4,5, \ldots
$$
If we set $n=p_{3}+1$ we have $p_{p_{3}+2}-1=2^{p_{3}-1}\left(p_{3}-1\right)$, from which
$$
p_{p_{3}+2} \equiv 1+1 \cdot\left(p_{3}-1\right)=p_{3} \equiv 0 \quad\left(\bmod p_{3}\right)
$$
a contradiction. The case $p_{3} \equiv 2(\bmod 3)$ is treated analogously.
|
{
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"problem_match": "\n10.",
"solution_match": "\nSolution:"
}
|
2fc854d5-3721-5eda-a778-c8e9a917df51
| 239,408
|
Through a point $P$ exterior to a given circle pass a secant and a tangent to the circle. The secant intersects the circle at $A$ and $B$, and the tangent touches the circle at $C$ on the same side of the diameter thorugh $P$ as $A$ and $B$. The projection of $C$ on the diameter is $Q$. Prove that $Q C$ bisects $\angle A Q B$.
|
Denoting the centre of the circle by $O$, we have $O Q \cdot O P=O A^{2}=O B^{2}$. Hence $\triangle O A Q \sim \triangle O P A$ and $\triangle O B Q \sim \triangle O P B$. Since $\triangle A O B$ is isosceles, we have
$\angle O A P+\angle O B P=180^{\circ}$, and therefore
$$
\begin{aligned}
\angle A Q P+\angle B Q P & =\angle A O P+\angle O A Q+\angle B O P+\angle O B Q \\
& =\angle A O P+\angle O P A+\angle B O P+\angle O P B \\
& =180^{\circ}-\angle O A P+180^{\circ}-\angle O B P \\
& =180^{\circ} .
\end{aligned}
$$
Thus $Q C$, being perpendicular to $Q P$, bisects $\angle A Q B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Through a point $P$ exterior to a given circle pass a secant and a tangent to the circle. The secant intersects the circle at $A$ and $B$, and the tangent touches the circle at $C$ on the same side of the diameter thorugh $P$ as $A$ and $B$. The projection of $C$ on the diameter is $Q$. Prove that $Q C$ bisects $\angle A Q B$.
|
Denoting the centre of the circle by $O$, we have $O Q \cdot O P=O A^{2}=O B^{2}$. Hence $\triangle O A Q \sim \triangle O P A$ and $\triangle O B Q \sim \triangle O P B$. Since $\triangle A O B$ is isosceles, we have
$\angle O A P+\angle O B P=180^{\circ}$, and therefore
$$
\begin{aligned}
\angle A Q P+\angle B Q P & =\angle A O P+\angle O A Q+\angle B O P+\angle O B Q \\
& =\angle A O P+\angle O P A+\angle B O P+\angle O P B \\
& =180^{\circ}-\angle O A P+180^{\circ}-\angle O B P \\
& =180^{\circ} .
\end{aligned}
$$
Thus $Q C$, being perpendicular to $Q P$, bisects $\angle A Q B$.
|
{
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"problem_match": "\n16.",
"solution_match": "\nSolution:"
}
|
3345a49a-dd82-5ff9-a36c-26822a77e155
| 606,022
|
A ray emanating from the vertex $A$ of the triangle $A B C$ intersects the side $B C$ at $X$ and the circumcircle of $A B C$ at $Y$. Prove that $\frac{1}{A X}+\frac{1}{X Y} \geq \frac{4}{B C}$.
|
From the GM-HM inequality we have
$$
\frac{1}{A X}+\frac{1}{X Y} \geq \frac{2}{\sqrt{A X \cdot X Y}}
$$
As $B C$ and $A Y$ are chords intersecting at $X$ we have $A X \cdot X Y=B X \cdot X C$. Therefore (1) transforms into
$$
\frac{1}{A X}+\frac{1}{X Y} \geq \frac{2}{\sqrt{B X \cdot X C}}
$$
We also have
$$
\sqrt{B X \cdot X C} \leq \frac{B X+X C}{2}=\frac{B C}{2}
$$
so from (2) the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
A ray emanating from the vertex $A$ of the triangle $A B C$ intersects the side $B C$ at $X$ and the circumcircle of $A B C$ at $Y$. Prove that $\frac{1}{A X}+\frac{1}{X Y} \geq \frac{4}{B C}$.
|
From the GM-HM inequality we have
$$
\frac{1}{A X}+\frac{1}{X Y} \geq \frac{2}{\sqrt{A X \cdot X Y}}
$$
As $B C$ and $A Y$ are chords intersecting at $X$ we have $A X \cdot X Y=B X \cdot X C$. Therefore (1) transforms into
$$
\frac{1}{A X}+\frac{1}{X Y} \geq \frac{2}{\sqrt{B X \cdot X C}}
$$
We also have
$$
\sqrt{B X \cdot X C} \leq \frac{B X+X C}{2}=\frac{B C}{2}
$$
so from (2) the result follows.
|
{
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"problem_match": "\n18.",
"solution_match": "\nSolution:"
}
|
55285261-a18b-5990-9a85-455cd306c779
| 239,474
|
$D$ is the midpoint of the side $B C$ of the given triangle $A B C . M$ is a point on the side $B C$ such that $\angle B A M=\angle D A C$. $L$ is the second intersection point of the circumcircle of the triangle $C A M$ with the side $A B . K$ is the second intersection point of the circumcircle of the triangle $B A M$ with the side $A C$. Prove that $K L \| B C$.
|
It is sufficient to prove that $C K: L B=A C: A B$.
The triangles $A B C$ and $M K C$ are similar beacuse they have common angle $C$ and $\angle C M K=180^{\circ}-\angle B M K=\angle K A B$ (the latter equality is due to the observation that $\angle B M K$ and $\angle K A B$ are the opposite angles in the insecribed quadrilateral $A K M B$ ).
By analogous reasoning the triangles $A B C$ and $M B L$ are similar. Therefore the triangles $M K C$ and $M B L$ are also similar and we have
$$
\frac{C K}{L B}=\frac{K M}{B M}=\frac{\frac{A M \sin K A M}{\sin A K M}}{\frac{A M \sin M A B}{\sin M B A}}=\frac{\sin K A M}{\sin M A B}=\frac{\sin D A B}{\sin D A C}=\frac{\frac{B D \sin B D A}{A B}}{\frac{C D \sin C D A}{A C}}=\frac{A C}{A B} .
$$
The second equality is due to the sinus theorem for triangles $A K M$ and $A B M$; the third is due to the equality $\angle A K M=180^{\circ}-\angle M B A$ in the inscribed quadrilateral $A K M B$; the fourth is due to the definition of the point $M$; and the fifth is due to the sinus theorem for triangles $A C D$ and $A B D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
$D$ is the midpoint of the side $B C$ of the given triangle $A B C . M$ is a point on the side $B C$ such that $\angle B A M=\angle D A C$. $L$ is the second intersection point of the circumcircle of the triangle $C A M$ with the side $A B . K$ is the second intersection point of the circumcircle of the triangle $B A M$ with the side $A C$. Prove that $K L \| B C$.
|
It is sufficient to prove that $C K: L B=A C: A B$.
The triangles $A B C$ and $M K C$ are similar beacuse they have common angle $C$ and $\angle C M K=180^{\circ}-\angle B M K=\angle K A B$ (the latter equality is due to the observation that $\angle B M K$ and $\angle K A B$ are the opposite angles in the insecribed quadrilateral $A K M B$ ).
By analogous reasoning the triangles $A B C$ and $M B L$ are similar. Therefore the triangles $M K C$ and $M B L$ are also similar and we have
$$
\frac{C K}{L B}=\frac{K M}{B M}=\frac{\frac{A M \sin K A M}{\sin A K M}}{\frac{A M \sin M A B}{\sin M B A}}=\frac{\sin K A M}{\sin M A B}=\frac{\sin D A B}{\sin D A C}=\frac{\frac{B D \sin B D A}{A B}}{\frac{C D \sin C D A}{A C}}=\frac{A C}{A B} .
$$
The second equality is due to the sinus theorem for triangles $A K M$ and $A B M$; the third is due to the equality $\angle A K M=180^{\circ}-\angle M B A$ in the inscribed quadrilateral $A K M B$; the fourth is due to the definition of the point $M$; and the fifth is due to the sinus theorem for triangles $A C D$ and $A B D$.
|
{
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"problem_match": "\n19.",
"solution_match": "\nSolution:"
}
|
e85dcbe2-2ce6-5302-9179-4afe4be8f70c
| 239,481
|
Three circular arcs $w_{1}, w_{2}, w_{3}$ with common endpoints $A$ and $B$ are on the same side of the line $A B ; w_{2}$ lies between $w_{1}$ and $w_{3}$. Two rays emanating from $B$ intersect these arcs at $M_{1}, M_{2}, M_{3}$ and $K_{1}, K_{2}, K_{3}$, respectively. Prove that $\frac{M_{1} M_{2}}{M_{2} M_{3}}=\frac{K_{1} K_{2}}{K_{2} K_{3}}$.
|
From inscribed angles we have $\angle A K_{1} B=\angle A M_{1} B$ and $\angle A K_{2} B=\angle A M_{2} B$. From this it follows that $\triangle A K_{1} K_{2} \sim \triangle A M_{1} M_{2}$, so
$$
\frac{K_{1} K_{2}}{M_{1} M_{2}}=\frac{A K_{2}}{A M_{2}}
$$
Similarly $\triangle A K_{2} K_{3} \sim \triangle A M_{2} M_{3}$, so
$$
\frac{K_{2} K_{3}}{M_{2} M_{3}}=\frac{A K_{2}}{A M_{2}}
$$
From these equations we get $\frac{K_{1} K_{2}}{M_{1} M_{2}}=\frac{K_{2} K_{3}}{M_{2} M_{3}}$, from which the desired property follows.
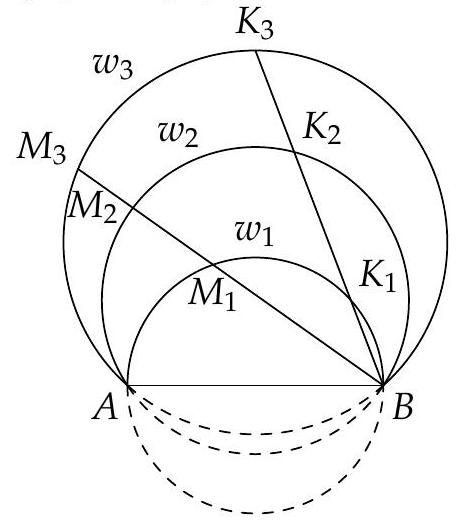
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Three circular arcs $w_{1}, w_{2}, w_{3}$ with common endpoints $A$ and $B$ are on the same side of the line $A B ; w_{2}$ lies between $w_{1}$ and $w_{3}$. Two rays emanating from $B$ intersect these arcs at $M_{1}, M_{2}, M_{3}$ and $K_{1}, K_{2}, K_{3}$, respectively. Prove that $\frac{M_{1} M_{2}}{M_{2} M_{3}}=\frac{K_{1} K_{2}}{K_{2} K_{3}}$.
|
From inscribed angles we have $\angle A K_{1} B=\angle A M_{1} B$ and $\angle A K_{2} B=\angle A M_{2} B$. From this it follows that $\triangle A K_{1} K_{2} \sim \triangle A M_{1} M_{2}$, so
$$
\frac{K_{1} K_{2}}{M_{1} M_{2}}=\frac{A K_{2}}{A M_{2}}
$$
Similarly $\triangle A K_{2} K_{3} \sim \triangle A M_{2} M_{3}$, so
$$
\frac{K_{2} K_{3}}{M_{2} M_{3}}=\frac{A K_{2}}{A M_{2}}
$$
From these equations we get $\frac{K_{1} K_{2}}{M_{1} M_{2}}=\frac{K_{2} K_{3}}{M_{2} M_{3}}$, from which the desired property follows.

|
{
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"problem_match": "\n20.",
"solution_match": "\nSolution:"
}
|
8d85c50e-913b-523f-a0a7-2f9fa1595235
| 239,491
|
Let $a_{0}$ be a positive integer. Define the sequence $a_{n}, n \geq 0$, as follows: If
$$
a_{n}=\sum_{i=0}^{j} c_{i} 10^{i}
$$
where $c_{i}$ are integers with $0 \leq c_{i} \leq 9$, then
$$
a_{n+1}=c_{0}^{2005}+c_{1}^{2005}+\cdots+c_{j}^{2005} .
$$
Is it possible to choose $a_{0}$ so that all the terms in the sequence are distinct?
Answer: No, the sequence must contain two equal terms.
|
It is clear that there exists a smallest positive integer $k$ such that
$$
10^{k}>(k+1) \cdot 9^{2005} .
$$
We will show that there exists a positive integer $N$ such that $a_{n}$ consists of less than $k+1$ decimal digits for all $n \geq N$. Let $a_{i}$ be a positive integer which consists of exactly $j+1$ digits, that is,
$$
10^{j} \leq a_{i}<10^{j+1} .
$$
We need to prove two statements:
- $a_{i+1}$ has less than $k+1$ digits if $j<k$; and
- $a_{i}>a_{i+1}$ if $j \geq k$.
To prove the first statement, notice that
$$
a_{i+1} \leq(j+1) \cdot 9^{2005}<(k+1) \cdot 9^{2005}<10^{k}
$$
and hence $a_{i+1}$ consists of less than $k+1$ digits. To prove the second statement, notice that $a_{i}$ consists of $j+1$ digits, none of which exceeds 9 . Hence $a_{i+1} \leq(j+1) \cdot 9^{2005}$ and because $j \geq k$, we get $a_{i} \geq 10^{j}>(j+1) \cdot 9^{2005} \geq a_{i+1}$, which proves the second statement. It is now easy to derive the result from this statement. Assume that $a_{0}$ consists of $k+1$ or more digits (otherwise we are done, because then it follows inductively that all terms of the sequence consist of less than $k+1$ digits, by the first statement). Then the sequence starts with a strictly decreasing segment $a_{0}>a_{1}>a_{2}>\cdots$ by the second statement, so for some index $N$ the number $a_{N}$ has less than $k+1$ digits. Then, by the first statement, each number $a_{n}$ with $n \geq N$ consists of at most $k$ digits. By the Pigeonhole Principle, there are two different indices $n, m \geq N$ such that $a_{n}=a_{m}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{0}$ be a positive integer. Define the sequence $a_{n}, n \geq 0$, as follows: If
$$
a_{n}=\sum_{i=0}^{j} c_{i} 10^{i}
$$
where $c_{i}$ are integers with $0 \leq c_{i} \leq 9$, then
$$
a_{n+1}=c_{0}^{2005}+c_{1}^{2005}+\cdots+c_{j}^{2005} .
$$
Is it possible to choose $a_{0}$ so that all the terms in the sequence are distinct?
Answer: No, the sequence must contain two equal terms.
|
It is clear that there exists a smallest positive integer $k$ such that
$$
10^{k}>(k+1) \cdot 9^{2005} .
$$
We will show that there exists a positive integer $N$ such that $a_{n}$ consists of less than $k+1$ decimal digits for all $n \geq N$. Let $a_{i}$ be a positive integer which consists of exactly $j+1$ digits, that is,
$$
10^{j} \leq a_{i}<10^{j+1} .
$$
We need to prove two statements:
- $a_{i+1}$ has less than $k+1$ digits if $j<k$; and
- $a_{i}>a_{i+1}$ if $j \geq k$.
To prove the first statement, notice that
$$
a_{i+1} \leq(j+1) \cdot 9^{2005}<(k+1) \cdot 9^{2005}<10^{k}
$$
and hence $a_{i+1}$ consists of less than $k+1$ digits. To prove the second statement, notice that $a_{i}$ consists of $j+1$ digits, none of which exceeds 9 . Hence $a_{i+1} \leq(j+1) \cdot 9^{2005}$ and because $j \geq k$, we get $a_{i} \geq 10^{j}>(j+1) \cdot 9^{2005} \geq a_{i+1}$, which proves the second statement. It is now easy to derive the result from this statement. Assume that $a_{0}$ consists of $k+1$ or more digits (otherwise we are done, because then it follows inductively that all terms of the sequence consist of less than $k+1$ digits, by the first statement). Then the sequence starts with a strictly decreasing segment $a_{0}>a_{1}>a_{2}>\cdots$ by the second statement, so for some index $N$ the number $a_{N}$ has less than $k+1$ digits. Then, by the first statement, each number $a_{n}$ with $n \geq N$ consists of at most $k$ digits. By the Pigeonhole Principle, there are two different indices $n, m \geq N$ such that $a_{n}=a_{m}$.
|
{
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution:"
}
|
bb8dfc87-d4ee-531a-8734-42a8cbb1540a
| 239,151
|
Let $\alpha, \beta$ and $\gamma$ be three angles with $0 \leq \alpha, \beta, \gamma<90^{\circ}$ and $\sin \alpha+\sin \beta+\sin \gamma=1$. Show that
$$
\tan ^{2} \alpha+\tan ^{2} \beta+\tan ^{2} \gamma \geq \frac{3}{8}
$$
|
Since $\tan ^{2} x=1 / \cos ^{2} x-1$, the inequality to be proved is equivalent to
$$
\frac{1}{\cos ^{2} \alpha}+\frac{1}{\cos ^{2} \beta}+\frac{1}{\cos ^{2} \gamma} \geq \frac{27}{8}
$$
The AM-HM inequality implies
$$
\begin{aligned}
\frac{3}{\frac{1}{\cos ^{2} \alpha}+\frac{1}{\cos ^{2} \beta}+\frac{1}{\cos ^{2} \gamma}} & \leq \frac{\cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma}{3} \\
& =\frac{3-\left(\sin ^{2} \alpha+\sin ^{2} \beta+\sin ^{2} \gamma\right)}{3} \\
& \leq 1-\left(\frac{\sin \alpha+\sin \beta+\sin \gamma}{3}\right)^{2} \\
& =\frac{8}{9}
\end{aligned}
$$
and the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $\alpha, \beta$ and $\gamma$ be three angles with $0 \leq \alpha, \beta, \gamma<90^{\circ}$ and $\sin \alpha+\sin \beta+\sin \gamma=1$. Show that
$$
\tan ^{2} \alpha+\tan ^{2} \beta+\tan ^{2} \gamma \geq \frac{3}{8}
$$
|
Since $\tan ^{2} x=1 / \cos ^{2} x-1$, the inequality to be proved is equivalent to
$$
\frac{1}{\cos ^{2} \alpha}+\frac{1}{\cos ^{2} \beta}+\frac{1}{\cos ^{2} \gamma} \geq \frac{27}{8}
$$
The AM-HM inequality implies
$$
\begin{aligned}
\frac{3}{\frac{1}{\cos ^{2} \alpha}+\frac{1}{\cos ^{2} \beta}+\frac{1}{\cos ^{2} \gamma}} & \leq \frac{\cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma}{3} \\
& =\frac{3-\left(\sin ^{2} \alpha+\sin ^{2} \beta+\sin ^{2} \gamma\right)}{3} \\
& \leq 1-\left(\frac{\sin \alpha+\sin \beta+\sin \gamma}{3}\right)^{2} \\
& =\frac{8}{9}
\end{aligned}
$$
and the result follows.
|
{
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution:"
}
|
8ae25e9c-1927-58cb-9613-639a12f7c2c8
| 239,161
|
Let $a, b, c$ be positive real numbers with $a b c=1$. Prove that
$$
\frac{a}{a^{2}+2}+\frac{b}{b^{2}+2}+\frac{c}{c^{2}+2} \leq 1
$$
|
For any positive real $x$ we have $x^{2}+1 \geq 2 x$. Hence
$$
\begin{aligned}
\frac{a}{a^{2}+2}+\frac{b}{b^{2}+2}+\frac{c}{c^{2}+2} & \leq \frac{a}{2 a+1}+\frac{b}{2 b+1}+\frac{c}{2 c+1} \\
& =\frac{1}{2+1 / a}+\frac{1}{2+1 / b}+\frac{1}{2+1 / c}=: R .
\end{aligned}
$$
$R \leq 1$ is equivalent to
$$
\left(2+\frac{1}{b}\right)\left(2+\frac{1}{c}\right)+\left(2+\frac{1}{a}\right)\left(2+\frac{1}{c}\right)+\left(2+\frac{1}{a}\right)\left(2+\frac{1}{b}\right) \leq\left(2+\frac{1}{a}\right)\left(2+\frac{1}{b}\right)\left(2+\frac{1}{c}\right)
$$
and to $4 \leq \frac{1}{a b}+\frac{1}{a c}+\frac{1}{b c}+\frac{1}{a b c}$. By $a b c=1$ and by the AM-GM inequality
$$
\frac{1}{a b}+\frac{1}{a c}+\frac{1}{b c} \geq 3 \sqrt[3]{\left(\frac{1}{a b c}\right)^{2}}=3
$$
the last inequality follows. Equality appears exactly when $a=b=c=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers with $a b c=1$. Prove that
$$
\frac{a}{a^{2}+2}+\frac{b}{b^{2}+2}+\frac{c}{c^{2}+2} \leq 1
$$
|
For any positive real $x$ we have $x^{2}+1 \geq 2 x$. Hence
$$
\begin{aligned}
\frac{a}{a^{2}+2}+\frac{b}{b^{2}+2}+\frac{c}{c^{2}+2} & \leq \frac{a}{2 a+1}+\frac{b}{2 b+1}+\frac{c}{2 c+1} \\
& =\frac{1}{2+1 / a}+\frac{1}{2+1 / b}+\frac{1}{2+1 / c}=: R .
\end{aligned}
$$
$R \leq 1$ is equivalent to
$$
\left(2+\frac{1}{b}\right)\left(2+\frac{1}{c}\right)+\left(2+\frac{1}{a}\right)\left(2+\frac{1}{c}\right)+\left(2+\frac{1}{a}\right)\left(2+\frac{1}{b}\right) \leq\left(2+\frac{1}{a}\right)\left(2+\frac{1}{b}\right)\left(2+\frac{1}{c}\right)
$$
and to $4 \leq \frac{1}{a b}+\frac{1}{a c}+\frac{1}{b c}+\frac{1}{a b c}$. By $a b c=1$ and by the AM-GM inequality
$$
\frac{1}{a b}+\frac{1}{a c}+\frac{1}{b c} \geq 3 \sqrt[3]{\left(\frac{1}{a b c}\right)^{2}}=3
$$
the last inequality follows. Equality appears exactly when $a=b=c=1$.
|
{
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution:"
}
|
88d0b1f8-7155-52e5-b2eb-51d1e93dbc3e
| 606,159
|
A rectangular array has $n$ rows and six columns, where $n>2$. In each cell there is written either 0 or 1 . All rows in the array are different from each other. For each pair of rows $\left(x_{1}, x_{2}, \ldots, x_{6}\right)$ and $\left(y_{1}, y_{2}, \ldots, y_{6}\right)$, the row $\left(x_{1} y_{1}, x_{2} y_{2}, \ldots, x_{6} y_{6}\right)$ can also be found in the array. Prove that there is a column in which at least half of the entries are zeroes.
|
Clearly there must be rows with some zeroes. Consider the case when there is a row with just one zero; we can assume it is $(0,1,1,1,1,1)$. Then for each row $\left(1, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}\right)$ there is also a row $\left(0, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}\right)$; the conclusion follows. Consider the case when there is a row with just two zeroes; we can assume it is $(0,0,1,1,1,1)$. Let $n_{i j}$ be the number of rows with first two elements $i, j$. As in the first case $n_{00} \geq n_{11}$. Let $n_{01} \geq n_{10}$; the other subcase is analogous. Now there are $n_{00}+n_{01}$ zeroes in the first column and $n_{10}+n_{11}$ ones in the first column; the conclusion follows. Consider now the case when each row contains at least three zeroes (except $(1,1,1,1,1,1$ ), if such a row exists). Let us prove that it is impossible that each such row contains exactly three zeroes. Assume the opposite. As $n>2$ there are at least two rows with zeroes; they are different, so their product contains at least four zeroes, a contradiction. So there are more then $3(n-1)$ zeroes in the array; so in some column there are more than $(n-1) / 2$ zeroes; so there are at least $n / 2$ zeroes.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A rectangular array has $n$ rows and six columns, where $n>2$. In each cell there is written either 0 or 1 . All rows in the array are different from each other. For each pair of rows $\left(x_{1}, x_{2}, \ldots, x_{6}\right)$ and $\left(y_{1}, y_{2}, \ldots, y_{6}\right)$, the row $\left(x_{1} y_{1}, x_{2} y_{2}, \ldots, x_{6} y_{6}\right)$ can also be found in the array. Prove that there is a column in which at least half of the entries are zeroes.
|
Clearly there must be rows with some zeroes. Consider the case when there is a row with just one zero; we can assume it is $(0,1,1,1,1,1)$. Then for each row $\left(1, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}\right)$ there is also a row $\left(0, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}\right)$; the conclusion follows. Consider the case when there is a row with just two zeroes; we can assume it is $(0,0,1,1,1,1)$. Let $n_{i j}$ be the number of rows with first two elements $i, j$. As in the first case $n_{00} \geq n_{11}$. Let $n_{01} \geq n_{10}$; the other subcase is analogous. Now there are $n_{00}+n_{01}$ zeroes in the first column and $n_{10}+n_{11}$ ones in the first column; the conclusion follows. Consider now the case when each row contains at least three zeroes (except $(1,1,1,1,1,1$ ), if such a row exists). Let us prove that it is impossible that each such row contains exactly three zeroes. Assume the opposite. As $n>2$ there are at least two rows with zeroes; they are different, so their product contains at least four zeroes, a contradiction. So there are more then $3(n-1)$ zeroes in the array; so in some column there are more than $(n-1) / 2$ zeroes; so there are at least $n / 2$ zeroes.
|
{
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"problem_match": "\n7.",
"solution_match": "\nSolution:"
}
|
66e708e9-f931-555c-9c7c-273ee22ea61e
| 606,189
|
Let the points $D$ and $E$ lie on the sides $B C$ and $A C$, respectively, of the triangle $A B C$, satisfying $B D=A E$. The line joining the circumcentres of the triangles $A D C$ and $B E C$ meets the lines $A C$ and $B C$ at $K$ and $L$, respectively. Prove that $K C=L C$.
|
Assume that the circumcircles of triangles $A D C$ and $B E C$ meet at $C$ and $P$. The problem is to show that the line $K L$ makes equal angles with the lines $A C$ and $B C$. Since the line joining the circumcentres of triangles $A D C$ and $B E C$ is perpendicular to the line $C P$, it suffices to show that $C P$ is the angle-bisector of $\angle A C B$.
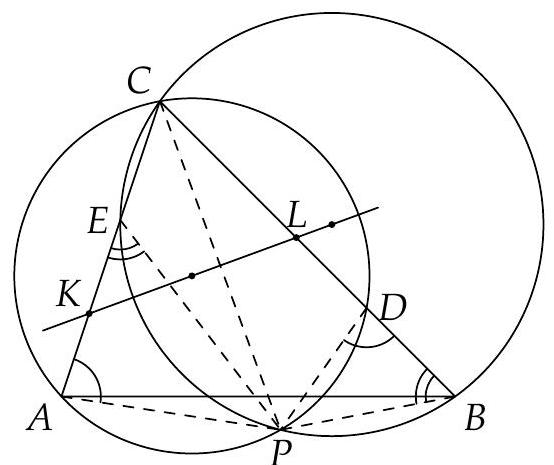
Since the points $A, P, D, C$ are concyclic, we obtain $\angle E A P=\angle B D P$. Analogously, we have $\angle A E P=\angle D B P$. These two equalities together with $A E=B D$ imply that triangles $A P E$ and $D P B$ are congruent. This means that the distance from $P$ to $A C$ is equal to the distance from $P$ to $B C$, and thus $C P$ is the angle-bisector of $\angle A C B$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let the points $D$ and $E$ lie on the sides $B C$ and $A C$, respectively, of the triangle $A B C$, satisfying $B D=A E$. The line joining the circumcentres of the triangles $A D C$ and $B E C$ meets the lines $A C$ and $B C$ at $K$ and $L$, respectively. Prove that $K C=L C$.
|
Assume that the circumcircles of triangles $A D C$ and $B E C$ meet at $C$ and $P$. The problem is to show that the line $K L$ makes equal angles with the lines $A C$ and $B C$. Since the line joining the circumcentres of triangles $A D C$ and $B E C$ is perpendicular to the line $C P$, it suffices to show that $C P$ is the angle-bisector of $\angle A C B$.

Since the points $A, P, D, C$ are concyclic, we obtain $\angle E A P=\angle B D P$. Analogously, we have $\angle A E P=\angle D B P$. These two equalities together with $A E=B D$ imply that triangles $A P E$ and $D P B$ are congruent. This means that the distance from $P$ to $A C$ is equal to the distance from $P$ to $B C$, and thus $C P$ is the angle-bisector of $\angle A C B$, as desired.
|
{
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"problem_match": "\n11.",
"solution_match": "\nSolution:"
}
|
34ac4dd2-3c4a-5c01-93a0-e3e9c33273ea
| 239,245
|
Let $A B C D$ be a convex quadrilateral such that $B C=A D$. Let $M$ and $N$ be the midpoints of $A B$ and $C D$, respectively. The lines $A D$ and $B C$ meet the line $M N$ at $P$ and $Q$, respectively. Prove that $C Q=D P$.
|
Let $A^{\prime}, B^{\prime}, C^{\prime}, D^{\prime}$ be the feet of the perpendiculars from $A, B, C, D$, respectively, onto the line $M N$. Then
$$
A A^{\prime}=B B^{\prime} \quad \text { and } \quad C C^{\prime}=D D^{\prime} \text {. }
$$
Denote by $X, Y$ the feet of the perpendiculars from $C, D$ onto the lines $B B^{\prime}, A A^{\prime}$, respectively. We infer from the above equalities that $A Y=B X$. Since also $B C=A D$, the right-angled triangles $B X C$ and $A Y D$ are congruent. This shows that
$$
\angle C^{\prime} C Q=\angle B^{\prime} B Q=\angle A^{\prime} A P=\angle D^{\prime} D P .
$$
Therefore, since $C C^{\prime}=D D^{\prime}$, the triangles $C C^{\prime} Q$ and $D D^{\prime} P$ are congruent. Thus $C Q=$ $D P$.
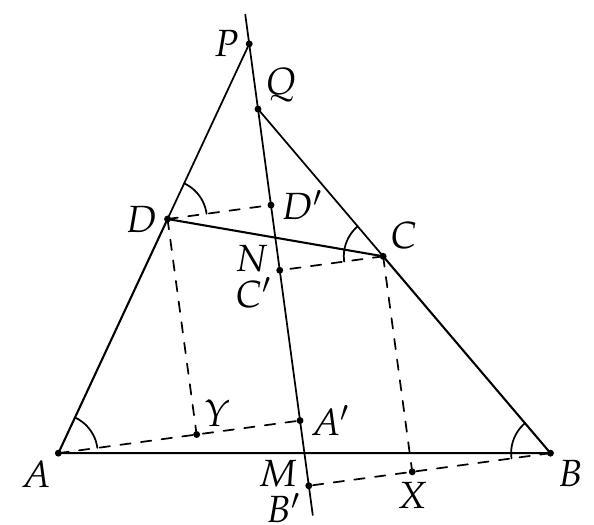
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral such that $B C=A D$. Let $M$ and $N$ be the midpoints of $A B$ and $C D$, respectively. The lines $A D$ and $B C$ meet the line $M N$ at $P$ and $Q$, respectively. Prove that $C Q=D P$.
|
Let $A^{\prime}, B^{\prime}, C^{\prime}, D^{\prime}$ be the feet of the perpendiculars from $A, B, C, D$, respectively, onto the line $M N$. Then
$$
A A^{\prime}=B B^{\prime} \quad \text { and } \quad C C^{\prime}=D D^{\prime} \text {. }
$$
Denote by $X, Y$ the feet of the perpendiculars from $C, D$ onto the lines $B B^{\prime}, A A^{\prime}$, respectively. We infer from the above equalities that $A Y=B X$. Since also $B C=A D$, the right-angled triangles $B X C$ and $A Y D$ are congruent. This shows that
$$
\angle C^{\prime} C Q=\angle B^{\prime} B Q=\angle A^{\prime} A P=\angle D^{\prime} D P .
$$
Therefore, since $C C^{\prime}=D D^{\prime}$, the triangles $C C^{\prime} Q$ and $D D^{\prime} P$ are congruent. Thus $C Q=$ $D P$.

|
{
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"problem_match": "\n12.",
"solution_match": "\nSolution:"
}
|
4ad28096-39c6-5d49-8c63-a71aa3409df1
| 239,254
|
Let the lines $e$ and $f$ be perpendicular and intersect each other at $O$. Let $A$ and $B$ lie on $e$ and $C$ and $D$ lie on $f$, such that all the five points $A, B, C, D$ and $O$ are distinct. Let the lines $b$ and $d$ pass through $B$ and $D$ respectively, perpendicularly to $A C$; let the lines $a$ and $c$ pass through $A$ and $C$ respectively, perpendicularly to $B D$. Let $a$ and $b$ intersect $a t X$ and $c$ and $d$ intersect at $Y$. Prove that $X Y$ passes through $O$.
|
Let $A_{1}$ be the intersection of $a$ with $B D, B_{1}$ the intersection of $b$ with $A C, C_{1}$ the intersection of $c$ with $B D$ and $D_{1}$ the intersection of $d$ with $A C$. It follows easily by the given right angles that the following three sets each are concyclic:
- $A, A_{1}, D, D_{1}, O$ lie on a circle $w_{1}$ with diameter $A D$.
- $B, B_{1}, C, C 1, O$ lie on a circle $w_{2}$ with diameter $B C$.
- $C, C_{1}, D, D_{1}$ lie on a circle $w_{3}$ with diameter $D C$.
We see that $O$ lies on the radical axis of $w_{1}$ and $w_{2}$. Also, $Y$ lies on the radical axis of $w_{1}$ and $w_{3}$, and on the radical axis of $w_{2}$ and $w_{3}$, so $Y$ is the radical centre of $w_{1}, w_{2}$ and $w_{3}$, so it lies on the radical axis of $w_{1}$ and $w_{2}$. Analogously we prove that $X$ lies on the radical axis of $w_{1}$ and $w_{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let the lines $e$ and $f$ be perpendicular and intersect each other at $O$. Let $A$ and $B$ lie on $e$ and $C$ and $D$ lie on $f$, such that all the five points $A, B, C, D$ and $O$ are distinct. Let the lines $b$ and $d$ pass through $B$ and $D$ respectively, perpendicularly to $A C$; let the lines $a$ and $c$ pass through $A$ and $C$ respectively, perpendicularly to $B D$. Let $a$ and $b$ intersect $a t X$ and $c$ and $d$ intersect at $Y$. Prove that $X Y$ passes through $O$.
|
Let $A_{1}$ be the intersection of $a$ with $B D, B_{1}$ the intersection of $b$ with $A C, C_{1}$ the intersection of $c$ with $B D$ and $D_{1}$ the intersection of $d$ with $A C$. It follows easily by the given right angles that the following three sets each are concyclic:
- $A, A_{1}, D, D_{1}, O$ lie on a circle $w_{1}$ with diameter $A D$.
- $B, B_{1}, C, C 1, O$ lie on a circle $w_{2}$ with diameter $B C$.
- $C, C_{1}, D, D_{1}$ lie on a circle $w_{3}$ with diameter $D C$.
We see that $O$ lies on the radical axis of $w_{1}$ and $w_{2}$. Also, $Y$ lies on the radical axis of $w_{1}$ and $w_{3}$, and on the radical axis of $w_{2}$ and $w_{3}$, so $Y$ is the radical centre of $w_{1}, w_{2}$ and $w_{3}$, so it lies on the radical axis of $w_{1}$ and $w_{2}$. Analogously we prove that $X$ lies on the radical axis of $w_{1}$ and $w_{2}$.

|
{
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"problem_match": "\n15.",
"solution_match": "\nSolution:"
}
|
cf50b6e2-764d-5f73-b858-6e25208ba778
| 606,293
|
Let $p$ be a prime number and let $n$ be a positive integer. Let $q$ be a positive divisor of $(n+1)^{p}-n^{p}$. Show that $q-1$ is divisible by $p$.
|
It is sufficient to show the statement for $q$ prime. We need to prove that
$$
(n+1)^{p} \equiv n^{p} \quad(\bmod q) \Longrightarrow q \equiv 1 \quad(\bmod p) .
$$
It is obvious that $\operatorname{gcd}(n, q)=\operatorname{gcd}(n+1, q)=1$ (as $n$ and $n+1$ cannot be divisible by $q$ simultaneously). Hence there exists a positive integer $m$ such that $m n \equiv 1(\bmod q)$. In fact, $m$ is just the multiplicative inverse of $n(\bmod q)$. Take $s=m(n+1)$. It is easy to see that
$$
s^{p} \equiv 1 \quad(\bmod q)
$$
Let $t$ be the smallest positive integer which satisfies $s^{t} \equiv 1(\bmod q)(t$ is the order of $s(\bmod q)$ ). One can easily prove that $t$ divides $p$. Indeed, write $p=a t+b$ where $0 \leq b<t$. Then
$$
1 \equiv s^{p} \equiv s^{a t+b} \equiv\left(s^{t}\right)^{a} \cdot s^{b} \equiv s^{b} \quad(\bmod q) .
$$
By the definition of $t$, we must have $b=0$. Hence $t$ divides $p$. This means that $t=1$ or $t=p$. However, $t=1$ is easily seen to give a contradiction since then we would have
$$
m(n+1) \equiv 1 \quad(\bmod q) \quad \text { or } \quad n+1 \equiv n \quad(\bmod q)
$$
Therefore $t=p$, and $p$ is the order of $s(\bmod q)$. By Fermat's little theorem,
$$
s^{q-1} \equiv 1 \quad(\bmod q)
$$
Since $p$ is the order of $s(\bmod q)$, we have that $p$ divides $q-1$, and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ be a prime number and let $n$ be a positive integer. Let $q$ be a positive divisor of $(n+1)^{p}-n^{p}$. Show that $q-1$ is divisible by $p$.
|
It is sufficient to show the statement for $q$ prime. We need to prove that
$$
(n+1)^{p} \equiv n^{p} \quad(\bmod q) \Longrightarrow q \equiv 1 \quad(\bmod p) .
$$
It is obvious that $\operatorname{gcd}(n, q)=\operatorname{gcd}(n+1, q)=1$ (as $n$ and $n+1$ cannot be divisible by $q$ simultaneously). Hence there exists a positive integer $m$ such that $m n \equiv 1(\bmod q)$. In fact, $m$ is just the multiplicative inverse of $n(\bmod q)$. Take $s=m(n+1)$. It is easy to see that
$$
s^{p} \equiv 1 \quad(\bmod q)
$$
Let $t$ be the smallest positive integer which satisfies $s^{t} \equiv 1(\bmod q)(t$ is the order of $s(\bmod q)$ ). One can easily prove that $t$ divides $p$. Indeed, write $p=a t+b$ where $0 \leq b<t$. Then
$$
1 \equiv s^{p} \equiv s^{a t+b} \equiv\left(s^{t}\right)^{a} \cdot s^{b} \equiv s^{b} \quad(\bmod q) .
$$
By the definition of $t$, we must have $b=0$. Hence $t$ divides $p$. This means that $t=1$ or $t=p$. However, $t=1$ is easily seen to give a contradiction since then we would have
$$
m(n+1) \equiv 1 \quad(\bmod q) \quad \text { or } \quad n+1 \equiv n \quad(\bmod q)
$$
Therefore $t=p$, and $p$ is the order of $s(\bmod q)$. By Fermat's little theorem,
$$
s^{q-1} \equiv 1 \quad(\bmod q)
$$
Since $p$ is the order of $s(\bmod q)$, we have that $p$ divides $q-1$, and we are done.
|
{
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"problem_match": "\n16.",
"solution_match": "\nSolution:"
}
|
aac08b0a-1dfe-54bd-9c2d-ea8b1846c2d2
| 239,291
|
Let $x$ and $y$ be positive integers and assume that $z=4 x y /(x+y)$ is an odd integer. Prove that at least one divisor of $z$ can be expressed in the form $4 n-1$ where $n$ is a positive integer.
|
Let $x=2^{s} x_{1}$ and $y=2^{t} y_{1}$ where $x_{1}$ and $y_{1}$ are odd integers. Without loss of generality we can assume that $s \geq t$. We have
$$
z=\frac{2^{s+t+2} x_{1} y_{1}}{2^{t}\left(2^{s-t} x_{1}+y_{1}\right)}=\frac{2^{s+2} x_{1} y_{1}}{2^{s-t} x_{1}+y_{1}}
$$
If $s \neq t$, then the denominator is odd and therefore $z$ is even. So we have $s=t$ and $z=2^{s+2} x_{1} y_{1} /\left(x_{1}+y_{1}\right)$. Let $x_{1}=d x_{2}, y_{1}=d y_{2}$ with $\operatorname{gcd}\left(x_{2}, y_{2}\right)=1$. So $z=$ $2^{s+2} d x_{2} y_{2} /\left(x_{2}+y_{2}\right)$. As $z$ is odd, it must be that $x_{2}+y_{2}$ is divisible by $2^{s+2} \geq 4$, so $x_{2}+y_{2}$ is divisible by 4 . As $x_{2}$ and $y_{2}$ are odd integers, one of them, say $x_{2}$ is congruent to 3 modulo 4. But $\operatorname{gcd}\left(x_{2}, x_{2}+y_{2}\right)=1$, so $x_{2}$ is a divisor of $z$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $x$ and $y$ be positive integers and assume that $z=4 x y /(x+y)$ is an odd integer. Prove that at least one divisor of $z$ can be expressed in the form $4 n-1$ where $n$ is a positive integer.
|
Let $x=2^{s} x_{1}$ and $y=2^{t} y_{1}$ where $x_{1}$ and $y_{1}$ are odd integers. Without loss of generality we can assume that $s \geq t$. We have
$$
z=\frac{2^{s+t+2} x_{1} y_{1}}{2^{t}\left(2^{s-t} x_{1}+y_{1}\right)}=\frac{2^{s+2} x_{1} y_{1}}{2^{s-t} x_{1}+y_{1}}
$$
If $s \neq t$, then the denominator is odd and therefore $z$ is even. So we have $s=t$ and $z=2^{s+2} x_{1} y_{1} /\left(x_{1}+y_{1}\right)$. Let $x_{1}=d x_{2}, y_{1}=d y_{2}$ with $\operatorname{gcd}\left(x_{2}, y_{2}\right)=1$. So $z=$ $2^{s+2} d x_{2} y_{2} /\left(x_{2}+y_{2}\right)$. As $z$ is odd, it must be that $x_{2}+y_{2}$ is divisible by $2^{s+2} \geq 4$, so $x_{2}+y_{2}$ is divisible by 4 . As $x_{2}$ and $y_{2}$ are odd integers, one of them, say $x_{2}$ is congruent to 3 modulo 4. But $\operatorname{gcd}\left(x_{2}, x_{2}+y_{2}\right)=1$, so $x_{2}$ is a divisor of $z$.
|
{
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"problem_match": "\n18.",
"solution_match": "\nSolution:"
}
|
40ed6a3f-2c4e-5779-976c-41b2b8f49301
| 606,313
|
Prove that for every polynomial $P(x)$ with real coefficients there exist a positive integer $m$ and polynomials $P_{1}(x), P_{2}(x), \ldots, P_{m}(x)$ with real coefficients such that
$$
P(x)=\left(P_{1}(x)\right)^{3}+\left(P_{2}(x)\right)^{3}+\cdots+\left(P_{m}(x)\right)^{3} .
$$
|
We will prove by induction on the degree of $P(x)$ that all polynomials can be represented as a sum of cubes. This is clear for constant polynomials. Now we proceed to the inductive step. It is sufficient to show that if $P(x)$ is a polynomial of degree $n$, then there exist polynomials $Q_{1}(x), Q_{2}(x), \ldots, Q_{r}(x)$ such that the polynomial
$$
P(x)-\left(Q_{1}(x)\right)^{3}-\left(Q_{2}(x)\right)^{3}-\cdots-\left(Q_{r}(x)\right)^{3}
$$
has degree at most $n-1$. Assume that the coefficient of $x^{n}$ in $P(x)$ is equal to $c$. We consider three cases: If $n=3 k$, we put $r=1, Q_{1}(x)=\sqrt[3]{c} x^{k}$; if $n=3 k+1$ we put $r=3$,
$$
Q_{1}(x)=\sqrt[3]{\frac{c}{6}} x^{k}(x-1), \quad Q_{2}(x)=\sqrt[3]{\frac{c}{6}} x^{k}(x+1), \quad Q_{3}(x)=-\sqrt[3]{\frac{c}{3}} x^{k+1}
$$
and if $n=3 k+2$ we put $r=2$ and
$$
Q_{1}(x)=\sqrt[3]{\frac{c}{3}} x^{k}(x+1), \quad Q_{2}(x)=-\sqrt[3]{\frac{c}{3}} x^{k+1}
$$
This completes the induction.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that for every polynomial $P(x)$ with real coefficients there exist a positive integer $m$ and polynomials $P_{1}(x), P_{2}(x), \ldots, P_{m}(x)$ with real coefficients such that
$$
P(x)=\left(P_{1}(x)\right)^{3}+\left(P_{2}(x)\right)^{3}+\cdots+\left(P_{m}(x)\right)^{3} .
$$
|
We will prove by induction on the degree of $P(x)$ that all polynomials can be represented as a sum of cubes. This is clear for constant polynomials. Now we proceed to the inductive step. It is sufficient to show that if $P(x)$ is a polynomial of degree $n$, then there exist polynomials $Q_{1}(x), Q_{2}(x), \ldots, Q_{r}(x)$ such that the polynomial
$$
P(x)-\left(Q_{1}(x)\right)^{3}-\left(Q_{2}(x)\right)^{3}-\cdots-\left(Q_{r}(x)\right)^{3}
$$
has degree at most $n-1$. Assume that the coefficient of $x^{n}$ in $P(x)$ is equal to $c$. We consider three cases: If $n=3 k$, we put $r=1, Q_{1}(x)=\sqrt[3]{c} x^{k}$; if $n=3 k+1$ we put $r=3$,
$$
Q_{1}(x)=\sqrt[3]{\frac{c}{6}} x^{k}(x-1), \quad Q_{2}(x)=\sqrt[3]{\frac{c}{6}} x^{k}(x+1), \quad Q_{3}(x)=-\sqrt[3]{\frac{c}{3}} x^{k+1}
$$
and if $n=3 k+2$ we put $r=2$ and
$$
Q_{1}(x)=\sqrt[3]{\frac{c}{3}} x^{k}(x+1), \quad Q_{2}(x)=-\sqrt[3]{\frac{c}{3}} x^{k+1}
$$
This completes the induction.
|
{
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution:"
}
|
b1ae1cbf-ddda-5495-bc37-ffb1c31fa200
| 241,700
|
An occasionally unreliable professor has devoted his last book to a certain binary operation $*$. When this operation is applied to any two integers, the result is again an integer. The operation is known to satisfy the following axioms:
(a) $x *(x * y)=y$ for all $x, y \in \mathbb{Z}$;
(b) $(x * y) * y=x$ for all $x, y \in \mathbb{Z}$.
The professor claims in his book that
(C1) the operation $*$ is commutative: $x * y=y * x$ for all $x, y \in \mathbb{Z}$.
(C2) the operation $*$ is associative: $(x * y) * z=x *(y * z)$ for all $x, y, z \in \mathbb{Z}$.
Which of these claims follow from the stated axioms?
Answer: (C1) is true; (C2) is false.
|
Write $(x, y, z)$ for $x * y=z$. So the axioms can be formulated as
$$
\begin{aligned}
& (x, y, z) \Longrightarrow(x, z, y) \\
& (x, y, z) \Longrightarrow(z, y, x) .
\end{aligned}
$$
(C1) is proved by the sequence $(x, y, z) \xrightarrow{(2)}(z, y, x) \xrightarrow{(1)}(z, x, y) \xrightarrow{(2)}(y, x, z)$.
A counterexample for (C2) is the operation $x * y=-(x+y)$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
An occasionally unreliable professor has devoted his last book to a certain binary operation $*$. When this operation is applied to any two integers, the result is again an integer. The operation is known to satisfy the following axioms:
(a) $x *(x * y)=y$ for all $x, y \in \mathbb{Z}$;
(b) $(x * y) * y=x$ for all $x, y \in \mathbb{Z}$.
The professor claims in his book that
(C1) the operation $*$ is commutative: $x * y=y * x$ for all $x, y \in \mathbb{Z}$.
(C2) the operation $*$ is associative: $(x * y) * z=x *(y * z)$ for all $x, y, z \in \mathbb{Z}$.
Which of these claims follow from the stated axioms?
Answer: (C1) is true; (C2) is false.
|
Write $(x, y, z)$ for $x * y=z$. So the axioms can be formulated as
$$
\begin{aligned}
& (x, y, z) \Longrightarrow(x, z, y) \\
& (x, y, z) \Longrightarrow(z, y, x) .
\end{aligned}
$$
(C1) is proved by the sequence $(x, y, z) \xrightarrow{(2)}(z, y, x) \xrightarrow{(1)}(z, x, y) \xrightarrow{(2)}(y, x, z)$.
A counterexample for (C2) is the operation $x * y=-(x+y)$.
|
{
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution:"
}
|
69286778-fec8-5655-8340-2fae8ea62ac1
| 241,720
|
The director has found out that six conspiracies have been set up in his department, each of them involving exactly three persons. Prove that the director can split the department in two laboratories so that none of the conspirative groups is entirely in the same laboratory.
|
Let the department consist of $n$ persons. Clearly $n>4$ (because $\left(\begin{array}{l}4 \\ 3\end{array}\right)<6$ ). If $n=5$, take three persons who do not make a conspiracy and put them in one laboratory, the other two in another. If $n=6$, note that $\left(\begin{array}{l}6 \\ 3\end{array}\right)=20$, so we can find a three-person set such that neither it nor its complement is a conspiracy; this set will form one laboratory. If $n \geq 7$, use induction. We have $\left(\begin{array}{l}n \\ 2\end{array}\right) \geq\left(\begin{array}{l}7 \\ 2\end{array}\right)=21>6 \cdot 3$, so there are two persons $A$ and $B$ who are not together in any conspiracy. Replace $A$ and $B$ by a new person $A B$ and use the inductive hypothesis; then replace $A B$ by initial persons $A$ and $B$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
The director has found out that six conspiracies have been set up in his department, each of them involving exactly three persons. Prove that the director can split the department in two laboratories so that none of the conspirative groups is entirely in the same laboratory.
|
Let the department consist of $n$ persons. Clearly $n>4$ (because $\left(\begin{array}{l}4 \\ 3\end{array}\right)<6$ ). If $n=5$, take three persons who do not make a conspiracy and put them in one laboratory, the other two in another. If $n=6$, note that $\left(\begin{array}{l}6 \\ 3\end{array}\right)=20$, so we can find a three-person set such that neither it nor its complement is a conspiracy; this set will form one laboratory. If $n \geq 7$, use induction. We have $\left(\begin{array}{l}n \\ 2\end{array}\right) \geq\left(\begin{array}{l}7 \\ 2\end{array}\right)=21>6 \cdot 3$, so there are two persons $A$ and $B$ who are not together in any conspiracy. Replace $A$ and $B$ by a new person $A B$ and use the inductive hypothesis; then replace $A B$ by initial persons $A$ and $B$.
|
{
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"problem_match": "\n8.",
"solution_match": "\nSolution:"
}
|
3c0a1e46-2cd3-5e1c-b14c-6410cb9671a4
| 241,750
|
In a triangle $A B C$, points $D, E$ lie on sides $A B, A C$ respectively. The lines $B E$ and $C D$ intersect at $F$. Prove that if
$$
B C^{2}=B D \cdot B A+C E \cdot C A,
$$
then the points $A, D, F, E$ lie on a circle.
|
Let $G$ be a point on the segment $B C$ determined by the condition $B G \cdot B C=$ $B D \cdot B A$. (Such a point exists because $B D \cdot B A<B C^{2}$.) Then the points $A, D, G, C$ lie on a circle. Moreover, we have
$$
C E \cdot C A=B C^{2}-B D \cdot B A=B C \cdot(B G+C G)-B C \cdot B G=C B \cdot C G,
$$
hence the points $A, B, G, E$ lie on a circle as well. Therefore
$$
\angle D A G=\angle D C G, \quad \angle E A G=\angle E B G,
$$
which implies that
$$
\begin{aligned}
\angle D A E+\angle D F E & =\angle D A G+\angle E A G+\angle B F C \\
& =\angle D C G+\angle E B G+\angle B F C .
\end{aligned}
$$
But the sum on the right side is the sum of angles in $\triangle B F C$. Thus $\angle D A E+\angle D F E=180^{\circ}$, and the desired result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In a triangle $A B C$, points $D, E$ lie on sides $A B, A C$ respectively. The lines $B E$ and $C D$ intersect at $F$. Prove that if
$$
B C^{2}=B D \cdot B A+C E \cdot C A,
$$
then the points $A, D, F, E$ lie on a circle.
|
Let $G$ be a point on the segment $B C$ determined by the condition $B G \cdot B C=$ $B D \cdot B A$. (Such a point exists because $B D \cdot B A<B C^{2}$.) Then the points $A, D, G, C$ lie on a circle. Moreover, we have
$$
C E \cdot C A=B C^{2}-B D \cdot B A=B C \cdot(B G+C G)-B C \cdot B G=C B \cdot C G,
$$
hence the points $A, B, G, E$ lie on a circle as well. Therefore
$$
\angle D A G=\angle D C G, \quad \angle E A G=\angle E B G,
$$
which implies that
$$
\begin{aligned}
\angle D A E+\angle D F E & =\angle D A G+\angle E A G+\angle B F C \\
& =\angle D C G+\angle E B G+\angle B F C .
\end{aligned}
$$
But the sum on the right side is the sum of angles in $\triangle B F C$. Thus $\angle D A E+\angle D F E=180^{\circ}$, and the desired result follows.
|
{
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"problem_match": "\n13.",
"solution_match": "\nSolution:"
}
|
efc09ad1-a68d-507c-a530-7127fba73de6
| 606,373
|
There are 2006 points marked on the surface of a sphere. Prove that the surface can be cut into 2006 congruent pieces so that each piece contains exactly one of these points inside it.
|
Choose a North Pole and a South Pole so that no two points are on the same parallel and no point coincides with either pole. Draw parallels through each point. Divide each of these parallels into 2006 equal arcs so that no point is the endpoint of any arc. In the sequel, "to connect two points" means to draw the smallest arc of the great circle passing through these points. Denote the points of division by $A_{i, j}$, where $i$ is the number of the parallel counting from North to South $(i=1,2, \ldots, 2006)$, and $A_{i, 1}, A_{i, 2}, \ldots, A_{i, 2006}$ are the points of division on the $i$ 'th parallel, where the numbering is chosen such that the marked point on the $i^{\prime}$ th parallel lies between $A_{i, i}$ and $A_{i, i+1}$.
Consider the lines connecting gradually
$$
\begin{gathered}
N-A_{1,1}-A_{2,1}-A_{3,1}-\cdots-A_{2006,1}-S \\
N-A_{1,2}-A_{2,2}-A_{3,2}-\cdots-A_{2006,2}-S \\
\vdots \\
N-A_{1,2006}-A_{2,2006}-A_{3,2006}-\cdots-A_{2006,2006}-S
\end{gathered}
$$
These lines divide the surface of the sphere into 2006 parts which are congruent by rotation; each part contains one of the given points.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
There are 2006 points marked on the surface of a sphere. Prove that the surface can be cut into 2006 congruent pieces so that each piece contains exactly one of these points inside it.
|
Choose a North Pole and a South Pole so that no two points are on the same parallel and no point coincides with either pole. Draw parallels through each point. Divide each of these parallels into 2006 equal arcs so that no point is the endpoint of any arc. In the sequel, "to connect two points" means to draw the smallest arc of the great circle passing through these points. Denote the points of division by $A_{i, j}$, where $i$ is the number of the parallel counting from North to South $(i=1,2, \ldots, 2006)$, and $A_{i, 1}, A_{i, 2}, \ldots, A_{i, 2006}$ are the points of division on the $i$ 'th parallel, where the numbering is chosen such that the marked point on the $i^{\prime}$ th parallel lies between $A_{i, i}$ and $A_{i, i+1}$.
Consider the lines connecting gradually
$$
\begin{gathered}
N-A_{1,1}-A_{2,1}-A_{3,1}-\cdots-A_{2006,1}-S \\
N-A_{1,2}-A_{2,2}-A_{3,2}-\cdots-A_{2006,2}-S \\
\vdots \\
N-A_{1,2006}-A_{2,2006}-A_{3,2006}-\cdots-A_{2006,2006}-S
\end{gathered}
$$
These lines divide the surface of the sphere into 2006 parts which are congruent by rotation; each part contains one of the given points.
|
{
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"problem_match": "\n14.",
"solution_match": "\nSolution:"
}
|
75687ba5-1dc1-573c-907f-2035cb9927b4
| 241,807
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.