Split (1)

train · 62.5k rows

text stringlengths 100 957k	meta stringclasses 1 value
# Perfect lossless rotation of JPEG image (ITU 81) JPEG image compression is Fourier based DCT (ITU 81). It divides the image into 8x8 pixel blocks, and processes each using a Discrete Cosine Transform. The results are quantised and then encoded. Looking at the MSDN documentation: It seems that both width and height are required to be a multiple of 16 to perform a perfect 90° rotation. Now if we inspect the source code of the open-source implementation jpegtran, we realize that the width / height are required to be a multiple of 8 to perform a perfect 90° rotation: jtransform_perfect_transform(JDIMENSION image_width, JDIMENSION image_height, [...] case JXFORM_ROT_90: if (image_height % (JDIMENSION)MCU_height) result = FALSE; ref: Which can easily verified from the command line: % convert -size 808x808 xc:white canvas.jpg % jpegtran -perfect -rotate 90 -outfile rot90.jpg canvas.jpg && echo $? 0 So in conclusion it appears that perfect rotation can be achieved with image size being multiple of 8, since we are only shuffling values within one 8x8 block. Why would MSDN documentation take extra care and require image size be multiple of 16, then ? Or is jpegtran actually producing non-perfect 90° rotation ? Update. My original test was using single scalar (1 component), if I try with 3 components I get the same result: % convert -size 808x808 xc:#990000 canvas2.jpg % file canvas2.jpg canvas2.jpg: JPEG image data, JFIF standard 1.01, aspect ratio, density 1x1, segment length 16, baseline, precision 8, 808x808, components 3 % jpegtran -perfect -rotate 90 -outfile rot90.jpg canvas2.jpg && echo$? 0 • There are many different ways to encode JPG images. Are you sure multiples of 8 can be used in all cases, like when colors are subsampled by a factor of two? Jun 15 at 14:32	{}
# Chapter 13 Atomic structure I: One- Electron Atoms¶ ## Example 13.1 Page no 252¶ In [8]: #Given d=0.1 #m v=10.03 #m/s a=50 #gradient of a magnet field Wb/m2/m b=9.27410-27 #J/Wb/m2 h=1.660510*-27 #Calculation M=107.868h z=(b/M)a(d2/v2) #Result print"seperation between the two component ",round(z10*8,1),"mm" seperation between the two component 2.6 mm	{}
Explore Edit Edit # Python Operator Precedence & Associativity \| FACE Prep Published on 09 Mar 2020 When dealing with Operators in Python, the concept of Python operator precedence and associativity is a must to know. Otherwise, you will see unexpected outputs in your Python console. ## So, What is Python Operator Precedence? As we all know, an expression is a combination of operands, operators and constants (values). Now, consider this simple expression, print (7 + 10) Output: 17 Since there is just one operation to be performed, its output is straightforward. But, such calculations can get complex when 2 or more operators are involved in an expression. Let's consider another expression, print (9 + 2 - 6 * 4) GUESS THE OUTPUT NOW? The output is -13. In the above expression, there are 3 operators (+, -, ) involved. To avoid confusion, the compiler evaluates the expression using Python operator precedence. According to this precedence rule, multiplication has higher precedence, followed by addition and subtraction. So hence the evaluation happens this way, ## Python Operator Precedence (Highest to Lowest) Below is the table containing the precedence of all operators in Python.The operators are listed down in the decreasing order of OperatorName ()Parenthesis Exponent ~Bitwise NOT , /, %, //Multiplication, Division, Modulo, Floor Division >>, <<Bitwise right and left shift &Bitwise AND ^Bitwise XOR \|Bitwise OR ==, !=, >, <, >=, <= Comparison =, +=, -=, =, /=, %=, =, //=Assignment is, is notIdentity In, not inMembership and, or, notLogical After having a quick look at the above table, you must have had this doubt. "In our previous example, addition was performed before subtraction. But then, the precedence of + & - is the same.Then how did we determine that addition has higher precedence than subtraction?" That's where the associativity of operators comes into the picture. ## Python Operator Associativity Associativity is the order in which an expression with multiple operators of the same precedence is evaluated. Associativity can be either from left to right or right to left. Almost all the operators have left-to-right associativity, except a few. For example, consider an expression having operators with the same precedence, print (ab/c) Here the multiplication * and division / operators have left to right associativity. This means, a and bare multiplied first and the result thus obtained is then divided by b. This is simply because when we read the expression from left to right, multiplication comes first and hence it gets evaluated first. Below is the table containing the associativity of all operators in Python. OperatorNameAssociativity ()ParenthesisLeft to right *ExponentRight to left ~Bitwise NOTLeft to right , /, %, //Multiplication, Division, Modulo, Floor DivisionLeft to right >>, <<Bitwise right and left shiftLeft to right &Bitwise ANDLeft to right ^Bitwise XORLeft to right \|Bitwise ORLeft to right ==, !=, >, <, >=, <=ComparisonLeft to right =, +=, -=, =, /=, %=, =, //=AssignmentRight to left is, is notIdentityLeft to right In, not inMembershipLeft to right and, or, notLogicalLeft to right In the above-given table, only exponent and assignment operators have the right to left associativity. All the other operators follow left to right associativity. ## Python Operator Precedence Examples ### Example 1: num1, num2, num3 = 2, 3, 4 print ((num1 + num2) num3) Output:20 Explanation:Since parentheses have the highest precedence, values 2 and 3 are added first and then the resultant value 5 is multiplied with 4. Hence, the output is 20. ### Example 2: num1, num2, num3 = 2, 3, 4 print (num1 ** num2 + num3) Output:12 Explanation:Among the given operators, the exponent has higher precedence, and hence value 2 is raised to the power of 3 and then the resultant value 8 is to 4. Hence, the output is 12. ### Example 3: num1, num2, num3 = 2, 3, 4 print (~num1 + num2) Output:0 Explanation:The output of ~num1 is -3 and when added to 3, the final output is 0. ### Example 4: num1, num2, num3, num4 = 8, 2, 3, 6 num5 = ((num1 * num2) - (num3 + num4)) print(num5) Output:7 Explanation:Since parentheses has left to right associativity, the operands num1 and num2 get multiplied first and then the operands num3 and num4 get added. At last, the results of these get subtracted. ### Example 5: num1, num2, num3 = 2, 3, 2 num4 = num1 num2 num3 print(num4) Output:512 Explanation:Since the exponent operator has right to left associativity, first the operand num2 gets raised to the power of num3 and then num1 gets raised to the power of the resultant value. ### Example 6: num1 = 5 num1 = num2 = num3 print(num2) Output: Traceback (most recent call last): File “/home/5eb00addafd751d876f2507eb42d8346.py”, line 2, in <module> num1 = num2 = num3 NameError: name ‘num3’ is not defined Explanation: Here, since the assignment operator has right to left associativity, the value in num3 gets assigned to num2 and num1. But, num3 is not defined. Hence the compiler throws an error. But the below code executes without any error. num1 = 5 num3 = num2 = num1 print(num2) print(num3) Output:55	{}
# K-theory, monoidal vs. exact My question is somewhat related to this one. However I think it adds something new to the table so I decided to post it sperately. There is a construction of K-theory for symmetric monoidal categories (smc) and one for exact categories. From what I understand they are (a priori) two different pair of shoes. For a symmetric monoidal category $S$ there is the classifying space $BS$. We define the K-theory $K(S)$ to be the group completion of this space. If we consider $BS$ to be a one-object topological category it is up to an equivalence of categories a strict monoidal category and a group completion is given by $BS\to\Omega BBS$. If we now take our favorite category $P(R)$ of projective modules over a ring then the above construction isn't very interesting ($BS$ is contractible since $0\in S$ is an initial object). But we can take $iP(R)$ the isomorphism category and then $K(iP(R))$ magically coincides with the K-theory of $P(R)$ as an exact category (I write magically since I can read the proof but still don't really know why taking the isomorphism category is the sensible thing to do). Something I like about the monoidal approach is Thomasons mapping cone construction. Given a functor of smc $A\to B$, such that $A=iA$ one can construct a smc $C$ such that there is a long exact sequence: $$\cdots \to K_{i+1}(C)\to K_{i}(A)\to K_{i}(B)\to K_{i}(C)\to\cdots$$ Now I am in the situation that $A$ and $B$ are in fact exact categories. $A=P(R)$ and $B=P(R,\mathbb G_m)$ the category of projective modules equipped with an automorphism. So to apply Thomason's construction I may just take $A=iP(R)$, fair enough. May I also take $B=iP(R,\mathbb G_m)$ and get the K-theory of $P(R,\mathbb G_m)$ as an exact category (I have the feeling that we pass to direct sum K-theory here, or something like that)? If I now construct $C$ then I notice that $iC=iP(R,\mathbb G_m)$, so I definitely may not just take the isomorphism category here. Somehow I got the feeling that I am just jumping between the definitions and never really now whether it's justified. So the question: For an exact category $D$, how are $K(D)$ (K-theory of $D$ as an exact category) $K(D)$ (as a symmetric monoidal category) and $K(iD)$ (again monoidal) related? -	{}
# Revision history [back] i was providing the wrong mapped bridge. i have: plugins/openvswitch/ovs_neutron_plugin.ini:bridge_mappings=physnet-external:br-ex and was creating my external as --provider:physical_network external which should have been: --provider:physical_network physnet-external so darragh-oreilly you were right. this helped me understand as well: http://blog.oddbit.com/2014/05/28/multiple-external-networks-wit/ interesting, i don't have a vlan 4095 tag. googling this has been fascinating mickt! this is something that i can now avoid getting caught out on in the future. thanks both of you for the help!!!!!!	{}
AMBIENT # change these sentences into passive voice? bởi Naru to 22/08/2019 Chuyển sang câu bị động: 1.Somebody might steal your car if you had left the keys in it 2.A short circuit could cause the fire 3.They should announce that news as soon as possible ## Câu trả lời (1) • Chuyển sang câu bị động: 1.Somebody might steal your car if you had left the keys in it. $$\Rightarrow$$ Your car might be stolen if you had left the keys in it. 2.A short circuit could cause the fire. $$\Rightarrow$$ The fire could be caused by a short circuit. 3.They should announce that news as soon as possible. $$\Rightarrow$$ That news should be announced as soon as possible. bởi Trần Mỹ Hảo 22/08/2019 Like (0) Báo cáo sai phạm Nếu bạn hỏi, bạn chỉ thu về một câu trả lời. Nhưng khi bạn suy nghĩ trả lời, bạn sẽ thu về gấp bội! Video HD đặt và trả lời câu hỏi - Tích lũy điểm thưởng ## Các câu hỏi có liên quan • ### Chia động từ trong ngoặc: When you saw Tim he (go) home? bởi Mai Vàng 14/09/2018 Chia động từ trong ngoặc : 1, When you saw Tim he ( go ) home ? 2, Ted ( play ) his guitar at half past seven . • ### Viết lại câu sao cho nghĩa không đổi: People said that Henlen missed the train It's............ 29/09/2018 Viết lại câu sao cho nghĩa không đổi 1/ People said that Henlen missed the train It's............ • ### Make questions with the underlined words/ phrases: I eat many vegetable. bởi thanh duy 31/10/2018 Make questions with the underlined words/ phrases 1. I eat many vegetable. 2. I’m a student. 3. He goes to school at 6 a.m. 4. She lives in Ha Noi. 5. I can cook dinner. 6. They do their homework at night. 7. I like the red blouse, not the blue one. 8. It’s 11b Nguyen Van Cu street. 9. My father is a interpreter. 10. I get bus. 11. I am sick. 12. She is pretty. 13. I visit my grandma once week. 14. I work in open- air market. 15. This skirt is 300\$. 16. There are 5 book on the table. • ### Viết lại câu với từ gợi ý trong ngoặc: You don’t normally go into by car(used) ->I ………….into town by car. bởi thu trang 17/11/2018 Viết lại câu với từ gợi ý trong ngoặc 1.You don’t normally go into by car(used) ->I ………….into town by car. 2.I would like to express my thanks for everything you have done for me(thankful) ->I’d like to say…..am for everything you have done for me 3.Nobody play this piece of music as beautifully as she does(more) ->She plays this piêc of music……else 4.Whenever I hear this song,I remember the time when I was in Paris(reminds) ->Whenever I hear this song,………the time when I was in Paris. • ### Chia động từ trong ngoặc: this map was very........our holiday(use) bởi can tu 31/12/2018 Cho dang dung cua V 1.this map was very........our holiday(use) 2.what a .........dress! Did you make it yourself ?(love) 3.do you know a good ..........to decorate my house(decorate) 4.go straigh ahead and take the .........on the left(two) 5.lan has a lot of stamps in her ..........(collect) 6.Mrs oanh 's daughter is having a ..........check up(medicine) 7.We need to know your .........,minh?(weigh) 8.An has a toothache.It's very...........(pain) 9.catching the common cold is..........for everybody(please) 10.your cold will last for a few days and then.............(appear) • ### hay viet mot doan van ngan tu 10-15 cau ve nhung thay doi o mien que 07/04/2019 hay viet mot doan van ngan tu 10-15 cau ve nhung thay doi o mien que • ### Look at the test in each question. What does it say? Write the correct letter A, B or C on the answer sheet. The hotel dining room is available for private parties on Sundays. 09/06/2019 Look at the test in each question. What does it say? Write the correct letter A, B or C on the answer sheet. The hotel dining room is available for private parties on Sundays. A You cannot eat here at weekends. B Hotel guests can have parties in their rooms. C It is possible to hire the dining room. • ### tìm lỗi sai và sửa: Each of us, however, have a different character. bởi hoàng duy 29/06/2019 tìm lỗi sai và sửa : 1. Each of us, however, have a different charater 2. Ba's friends sometime get tired about his jokes 3. This student is sociable, humor, and helpful 4. Lan showed her around and introduced her with many new friends 5. I'm going to a pop concert in the City Concert Center tonight 6. Mrs Lien called about her furnitures delivery 7. Van has a lot of homeworks in Math 8. Alexander Graham Bell was a Scotland although he later emigrated, first to Canada and then to the USA 9. I'll meet you at the center chess club 10. It is safe keeping medicine in locked cupboard GIÚP MK VỚI Ạ • ### what is the festival holi in india? what does holi start with? 13/07/2019 what is the festival holi in india? what do people often do on the second day? what are some activies during the festival? what do people do after playing with colour? mik đang cần gấp!!!!!!!!!!! • ### 1:If you don't keep silent,you'll wake the baby up. bởi Tieu Dong 22/07/2019 Giúp mk vs • ### I Choose the word which has the underlined part pronounced differently from the rest: 1. A. vacation B. restaurant C, lake D. information 26/07/2019 I Choose the word which has the underlined part pronounced differently from the rest: 1. A. vacation B. restaurant C, lake D. information 2. A. grow B. open C. officer D. moment 3. A. send B. flew C. mend D. tent 4. A. head. B. heavy C. weather D. hear II. Choose the word or phrase that best completes each sentence below. 1. The children are playing ......................... in the schoolyard A. happy B. happiness C. happier D. happily 2. They ........................... in that house for several months. A. live B. lived C. have lived D. are living. 3. Lan enjoyed the peaceful atmosphere while Maryam ............................. . A. prays B. prayed C. to pray D. was praying 4. Vietnamese people are very ....................... and hospitable. A. friend B. friendly C. friendliness D. friendship 5. If you ...................... to my advice in the first place, you wouldn't be in this mess right now. A. listen B. will listen C. had listened D. listened 6. Would you mind ........................ the door? A. open B. opened C. opening D. to open 7. My father was good at swimming. He used to .......................... swimming in summer. A. go B. goes C. went D. going 8. I ....................... Alan with me if had known you and he didn't get along with each other. A. hadn't brought B. didn't bring C, wouldn't have brought D. won't bring III. Give correct form of the verbs. 1.You................................... (have) no trouble at school if you had done your homework. 2. If you................................(swim) in this lake, you'll shiver from cold. 3) The door will unlock if you.................................. (press) the green button. 4. If Mel .......................... (ask) her teacher, he'd have answered her questions. 5. I....................................(call) the office if I were you. IV. Give correct form of the words. 1. Lon Don is ........................... for fog. (FAME) 2. Vietnamese people are very ............................... . (FRIEND) 3. Miss Moon is the most ................................ girl in my school. (BEAUTY) 4. She made a deep ....................... on the members of he class.(IMPRESS) V. Rewrite these sentences. 1. "Would you like to have dinner with us tonight," Mike said.- Mike invited .................................................................................. 2. Why don't you organize an English competition for our students?" said Ms Lien. Ms Lien suggested.......................................................................................................... 3. Unless last night your sister had gone home early, your mother could have waited for her. If ......................................................................................................................................... 4. If people didn't know you, they wouldn't give you some precious information. Unless .......................................................................................................................... 5. People can't swim unless they study how to swim. If ......................................................................................... • ### Fill in the blank with the suitable preposition? bởi Lê Vinh 18/08/2019 ĐIỀN GIỚI TỪ 1) ................. CHRISTMAS EVE, PEOPLE OFTEN HAVE BIG PARTIES. 2) THEY RECEIVED THE NEWS ................ GREAT JOY. 3) THAT GIRL IS VERY CLEVER .............. HER HANDS. 4) THEY GET ................... WELL WITH EACH OTHER DESPITE THEIR DIFFERENCES IN CHARACTERS. WORD FORM 1) HONESTY IS AN ................. QUALITY. (ADMIRE) 2) WHAT A NUISANCE! THE INTERNET IS SOMETIMES ................. AT PEAK HOURS. (REACH) • ### Choose the best answer? bởi Bi do 20/08/2019 Choose the best answer :( Cho biết câu trả lời đó là thì nào và lý do tại sao chọn đáp án đó) 1.They use cars and trucks to carry food to market. A. Cars and trucks are used to carrying food to market. B. Cars and trucks are used to carry food to market. C. Cars and trucks are use to carry food to market. D. Cars and trucks are used to carried food to market. 2.We will meet him at the station. A. He will be met at the station. B. He will meet at the station C. He will be meet at the station. D. He will be meeted at the station. 3.How long have they doe their work? A. How long have their work been done? B. How long has their work be done? C. How long has their work been done? D. How long have their work done? 4.No one could help him. A. He could be helped by no one. B. He couldn't be helped by no one. C. He could be helped. D. He could helped. 5.The gate is painted once a year. A. They paint the gate one a year. B. They painted the gate one a year. C. They are painting the gate one a year. D. They will paint the gate one a year. 6. Food can't be sold on the sidewalk. A. They can't sold food on the sidewalk. B. They can't be sold food on the sidewalk. C. They can't sell food on the sidewalk. D. They can sell food on the sidewalk. 7. The flowers shouldn't be cut in this garden. A. You shouldn't be cut the flowers in this garden. B. The flowers shouldn't be cutting the flowers in this garden. C. The flowers shouldn't cut the flowers in this garden. D. You shouldn't cut the flowers in this garden. 8.When was this car bought? A. When do they buy this car? B. When did they bought this car? C. When did they buy this car? D. When are they bought this car? 9.Why isn't she taken to the cinema with them? A. Why don't they taken her to the cinema with them? B. Why doesn't she take to the cinema with them? C. Why doesn't she take them to the cinema? D. Why don't they take her to the cinema with them? 10.Who was she invited to the party by? A. Who invited her to the party by? B. Who invited her to the party? C. Whom invites her to the party? D. Whom invited her to the party? Giúp mình nha :)) • ### change this sentences into reported speech? bởi thu hằng 20/08/2019 chuyển câu này từ chủ động sang bị động dùm mình she said ''Can you speak chinese,Hoa?'' • ### Complete each second sentence using the word given so that it has a similar meaning to the first sentence. Write between two and five words in each gap? bởi Goc pho 21/08/2019 Complete each second sentence using the word given so that it has a similar meaning to the first sentence. Write between two and five words in each gap. 1 I don't know how you can stand getting up so early to go to the pool, put I don't know how you can....................................................up so early to go to the pool. 2 I've finally started sorting out my postcard collection, round I've finally....................................................sorting out my postcard collection. 3 What did you do at the weekend? get What did you..................................................... at the weekend? 4 I'm not so keen on skiing now I've discovered snowboarding. gone I've .....................................................since I discovered snowboarding. 5 Why do you continue to have riding lessons if you can't afford them? on Why do you.....................................................riding lessons if you can't afford them? 6 We can't delay the match any longer. put We can't .................................................... any longer. • ### Put the following sentences into direct speech? 21/08/2019 Put the following sentences into direct speech : 1.Miss Johnson told Tim to read books regularly. - ........................................................................................ 2.My sister saked me not to dsay up too late. ................................................................................................. 3.He said to me that I should spend more time in the library. .......................................................................... 4.Her teacher said she should revise the lessons carefully. .............................................................................. 5.Nam’s brother asked him to close the door after going out. ........................................................................ 6.They told me not to ask people about their salary. -................................................................................... 7.I said she should guess the meaning the word before looking it up in the dictionary. -............................................................................................................................................ 8.Mr Davy said I shouldn’t read in bed too long . -............................................................................................ 9. My father told me to check my answers carefully before handing in. - ............................................................................................................................................ 10.Linh’s teacher asked her not to look out of the window. - ........................................................................................................................................... 11.My mother told me to do this exercise carefully. - ............................................................................................................................................. 12.The principal asked me how many students there were in my class. - ............................................................................................................................................ 13.Mr Minh said that he would leave Hanoi for HCM City the following day. - .......................................................................................................................................... 14.I asked my sister if she did that exercise by herself. - .......................................................................................................................................... 15.The little girl said that she was very afraid of staying at home by herself at night. - ............................................................................................................................................. 16.He wondered what would happen if she could not find her passport. - ............................................................................................................................................. • ### change these sentences into passive voice? bởi Naru to 22/08/2019 Chuyển sang câu bị động: 1.Somebody might steal your car if you had left the keys in it 2.A short circuit could cause the fire 3.They should announce that news as soon as possible • ### fill in the blank with a suitable word? 22/08/2019 ACCIDENTS IN THE HOME Many thousands of children have accidents in their homes. As a result some children die The most common (1)…………are with fire and hot water. Small children often touch pots of (2)……………water on the stove. The pots falls over and the water falls on the children and burns (3)…………... Some children like to play with fire. They enjoy striking matches or throwing things on a fire to make it burn brightly If the fire gets too big, it gets out of (4)…………...Then the house (5)…………..fire. It is very dangerous to play with matches. When a child strikes a match, the flame soon burns near his fingers. Then he (6)…………..the match on the floor. Many houses catch fire in this way Although fire and hot water cause most accidents in the home, many children cut (7)…………..with knives. Others get an electric (8)………….Some children are made very ill from taking their parents’medicine. Many children have to go to hospital every year because they thought a box of medicine was a box of (9)…………. There is only one good way to see to it that accidents do not (10)…………..in the home : do not touch anything that is dangerous • ### give the correct form of word? bởi thùy trang 27/08/2019 bai 1: worl form: 1. The soil becoms________because of the use of so many pesticides and fertilizers. (contaminate) 2. ___________waste spills can contaminate groundwater. (industry) 3. In many developing cointries, water pollution is usually a leading cause of __________ . (die) • ### choose the correct answer? bởi Bi do 27/08/2019 Giúp mình làm mấy câu này với mình đang cần gấp ^-^ I. Chọn ý đúng : 1. _____ a horse is skill the nomadic children has to learn. A. Ride B. Ridden C. Rode D. Riding 2. A : ______ do you think is the most famous museum in Hanoi? B : The museum of Ethnic. A. Who B. Which C. What D. When II. Chọn từ có trọng âm khác : 1. A. Resident B. Convenient C. Condition 2. A. Minority B. Majority C. Speciality II. Sắp xếp lại câu với từ đã cho sẵn : 1. The Tay/ have/ large/ population/ Viet Nam. 2. Viet Nam/ beautiful / country/ 54 ethnic peoples. AMBIENT ?>	{}
What does the Zariski topos of $\mathbb{P}^1$ classify? (The word "geometric theory" below is used in the sense of logic / classifying topos.) We know that the (big) Zariski topos over $\text{Spec}\mathbb{Z}$ classifies the theory of local rings. My question is, what geometric theory does the (big) Zariski topos over $\mathbb{P}^1$ classify? From algebraic geometry point of view it should classify something like a local rings together with a map to $\mathbb{P}^1$, i.e. something like isomorphism classes of $(A, L, e_0, e_1)$ where $A$ is a local ring, $L$ is an locally free $A$-module of rank 1, and $e_0, e_1\in L$ spans $L$. Is there a good way to describe a geometric / coherent theory of it? I saw some discussions here but it's mostly about the affine case. I'm curious on what role properness may play here. If possible I'd like to see some description on the geometric theory for a general scheme (or algebraic curve). (On "locally free $A$-module of rank 1": in this case L must be free, but that uses another result, merely asking for being locally free of rank 1 seems more natural to me.) • Because it's a local construction, the difference between the affine case and the general case shouldn't matter much. I think in general, the big Zariski topos of $X$ classifies pairs of a local ring $R$ and an $R$-point of $X$. What is bad about your description of $\mathbb P^1$? – Will Sawin Jan 1 '17 at 6:43 • @WillSawin Here by "classify" I mean "how does it serve as a classifying topos of some particular logic theory" so I'd like to see a few axioms for it. (e.g. local rings can be described by the axioms of rings + that for all x, either $x$ or $1-x$ is invertible.) The axioms would look like some extra data on $R$. Here I guess $\mathbb{P}^1$ is easy, as it's homogeneous, but for general X it won't be so easy, for reasons similar to that people usually don't have a good way to describe a general scheme as a representable functor. – h__ Jan 1 '17 at 8:16 • It seems to me that one can do a general projective variety by the same trick with a locally free module of rank $1$ - one has an invertible module and $n$ elements such that at least one of the elements invertible and such that the $n$ elements satisfy certain homogenous relations in some tensor powers of the model. This handles algebraic curves, at least. – Will Sawin Jan 1 '17 at 8:37 • @WillSawin Yes of course. One can use this for functors represented by projective schemes. But that's very ad hoc. For example it's hard to see if two functors are isomorphic this way. – h__ Jan 1 '17 at 8:52 • I don't think there's any particular reason to expect a description in terms of a logical theory to be the best tool to see if the two functors are isomorphic. – Will Sawin Jan 1 '17 at 9:56 First note that a morphism $\operatorname{Spec}(A) \to \mathbb{P}^1$ is just given by an element of the "classical projective space" $\mathbb{P}^1(A) = \{ [a:b] \,\|\, \text{$a$is invertible or$b$is invertible} \}$, if $A$ is a local ring. The description you gave is valid as well, but since (as you remark) "locally free" is equivalent to "free" over a local ring, it can be simplified further. The big Zariski topos of $\mathbb{P}^1$ classifies the theory of a "local ring together with a point $[a:b]$". This theory can be explicitly described as follows: • A sort $R$ together with function symbols, constants, and axioms expressing that $R$ is a local ring. • A sort $P$ (to be thought of as the set of $[a:b]$ with $a,b:R$ where at least one coordinate is invertible) together with a relation $\langle\cdot,\cdot,\cdot\rangle$ on $R \times R \times P$ and the following axioms: • $\text{$a$is invertible} \vee \text{$b$is invertible} \dashv\vdash_{a,b:R} \exists p:P.\ \langle a,b,p \rangle$ • $\langle a,b,p \rangle \wedge \langle a,b,p' \rangle \vdash_{a,b:R,\, p,p':P} p = p'$ • $\top \vdash_{p:P} \exists a,b:R.\ \langle a,b,p \rangle$ • $\langle a,b,p \rangle \wedge \langle a',b',p \rangle \dashv\vdash_{a,a',b,b':R,\, p:P} \exists s:R.\ \text{$s$is invertible} \wedge a' = s a \wedge b' = s b$ • A constant of sort $P$. In a topos $\mathcal{E}$, a model of this theory is given by a local ring $A$ in $\mathcal{E}$ together with a point of the "classical projective space of $A$" as defined above. (Equivalently, by a rank-1 quotient of $A^2$ up to isomorphism of quotients.) A different theory which the big Zariski topos of $\mathbb{P}^1$ classifies is the theory of a "homogeneous filter $F$ of $\mathbb{Z}[X,Y]$ meeting the irrelevant ideal together with a local ring over the degree-zero part $A := \mathbb{Z}[X,Y][F^{-1}]_0$ which is local over $A$". For an arbitrary $\mathbb{N}$-graded ring $S$, the big Zariski topos of $\operatorname{Proj}(S)$ classifies the theory of a "homogeneous filter $F$ of $S$ meeting the irrelevant ideal together with a local ring over the degree-zero part $A := S[F^{-1}]_0$ which is local over $A$". (This in turn can be rewritten using the universal property of the degree-zero part of graded localization.) This description follows by combining the description of the little Zariski topos of $\operatorname{Proj}(S)$ (which classifies the theory of a "homogeneous filter $F$ of $S$ meeting the irrelevant ideal") and the description of the big Zariski topos as a topos over the little Zariski topos (which classifies the theory of a "local ring over $\mathcal{O}_S$ which is local over $\mathcal{O}_S$"). Proofs can be found in these note of mine (Section 12.8 and Section 16.1 at the time of writing). If you care about issues of size, note that all the statements made here are only valid if we define the big Zariski topos of a scheme $X$ using the site consisting of only the locally finitely presented $X$-schemes. (It doesn't matter whether we restrict to affine schemes or not.) If we employ the site consisting of all $X$-schemes, the construction will not be well-defined in ordinary set theory, and if we restrict to those $X$-schemes contained in some universe (either Grothendieck or partial as in the Stacks project), then the resulting topos will have much more points.	{}
### Home > ACC6 > Chapter 4 Unit 4 > Lesson CC1: 4.1.1 > Problem4-7 4-7. Croakie now has a new routine that is $59$ feet long. Keep this distance in mind as you complete parts (a) and (b) below. 1. In his new routine, Croakie makes seven super jumps, all the same length, and then hops $3$ feet. How long is each super jump? Work backwards from 3 feet. Before Croakie had to hop 3 feet, how far had he jumped? If Croakie made $7$ jumps that were all the same length to go 56 feet, how long was each jump? $59\ \text{feet}−3\text{ feet}=56\text{ feet}$ $\frac{56}{7}=8$ $8$ feet per jump 2. If $x$ represents the length of one super jump and $2x$ represents the length of two super jumps, write an expression that represents Croakie’s routine. If you did $3$ super jumps and then walked 5 feet the expression would be $3x + 5$.	{}
# Multigate Priors ## Jun 15, 2022 15:33 · 800 words · 4 minute read AI Safety AI research Posted to LessWrong here. (Thanks to Evan Hubinger and Nicholas Schiefer for suggestions and discussions around these ideas) ## Multi-Gate Traces We can improve on one-gate traces with multi-gate traces! Suppose we have $N$ training samples. Then we can reasonably estimate joint probability distributions over up to $k=\lfloor\log_2 N\rfloor$ gates, giving the prior: $$p\propto \exp\left(-\sum_{i_1…i_k}\sum_{j\in [0,1]^k}p_{i_1…i_k}(j)^m\right)$$ That is, we sum over all selections of $k$ gates and compute the entropy of their joint distribution over $2^k$ states. Once more we promote models with high entropy and punish those with low entropy, which favors models that explore as much of their state space as possible during training, and disfavors those which have hidden states never touched in training. Now it’s still possible for a model to hide the machinery to defect here, but it gets harder and harder as $N$ and $k$ get large. In this limit the only way for that machinery to hide is to be heavily obfuscated. ### Objection: Non-Competitive The Multi-Gate Trace prior over $k$ gates scales very badly with $k$. In a system with $G$ gates there are $G \choose k$ different selections of $k$ gates, which means the cost of evaluating the prior is roughly exponential in $k$ for $k \ll G$. In practice this means that $k$ needs to be very small, and it’s possible that deception could hide in subsets of the circuit just a bit larger than the largest ones we can check. ### Objection: Penalizes Redundancy It is often useful to have redundant machinery in a program for e.g. readability or ease-of-modification. Redundancies though guarantee that some states will never arise. E.g. if the same calculation happens in two disjoint subcircuits in the model we will never see those two subcircuits in different states from each other. The Multi-Gate Trace prior disfavors models with that sort of redundancy, because those models have a larger apparent state space than they really do. This could cause the Multi-Gate Trace prior to favor hard-to-interpret models, and could result in a performance penalty by making it harder for the training process to modify the model. ## Next Try: Embedding Priors The Multi-Gate Trace prior is probably not competitive because the state space of the model traces is enormous. One way to remedy this is embed the state of the model in a lower-dimensional space and favor models that explore more of that space during training. That is, suppose we learn an embedding of the space of state vectors $v={g_1,…,g_N}$ into a continuous space of fixed lower dimension $d$. Given such an embedding, we can readily look for parts of parameter space that haven’t been explored in training. For instance we can discretize the embedding space into $d$-cubes and compute $$p \propto \exp\left(-\sum_{\mathrm{cube}} p(\mathrm{cube})^m\right)$$ where $p(x)$ is the fraction of training samples that fell in the cube centered on $x$. This scales much better than the Multi-Gate Trace prior. In particular, for fixed embedding dimension the runtime cost is just a polynomial in the resolution of the discretization and proportional to the embedding cost (which can be chosen to be e.g. linear in the number of gates). There are a few ways to learn an embedding: • Try to preserve distance between state vectors in the embedding. That is, two states $v$ and $v'$ with distance $\|v-v'\|$ should map onto embedded vectors $x$ and $x'$ such that $\|v-v'\|\approx \|x-x'\|$. • Try to preserve distance in the inputs/outputs. So for instance if the distance between inputs $i$ and $i'$ is $\|i-i'\|$ then embed the resulting states $v,v'$ to produce $x,x'$ such that $\|i-i'\|\approx \|x-x'\|$. Or alternately do this for the outputs of the model. This approach is also more forgiving of redundancy in the model. The embedding can ignore redundant parts of the model state and so an embedding prior need not penalize redundancy. Incidentally, the embedding prior shares some similarities to the ELK setup. You can view the embedding prior as an additional head attached to the original model. Rather than trying to learn a translator, we’re trying to learn a mapping between internal state and the embedding space, which we use to understand how much of the space of possible behaviors we’ve explored. ### Objection: Blind Spots Embedding priors can have blind spots. An embedding might neglect a piece of the model’s state space, not because it’s redundant but because it was never encountered in training. ## Ways Forward This approach of developing priors based on execution traces in training is very closely related to the field of fuzzing. What we’re looking for, in effect, is a way to ensure good program coverage during training. My hope is that fuzzing tools and knowledge can help here. For instance the issues of blind spots in coverage metrics must arise in fuzzing, I just don’t know how it gets solved there. tweet Share	{}
# Practice On Aromatic And Antiaromatic Nonaromatic Pdf Aromaticity and antiaromaticity in organic chemistry YouTube. Benzyne is 67t HГјckel aromatic. Chlorine is a meta directing, activating substituent for electrophilic aromatic substitution. Aromatic compounds are more stable than antiaromatic compounds. Cyclopentane has less ring strain than an epoxide. Cyclobutadiene is more stable than butadiene. Kinetic products are always more stable than thermodynamic, In this manuscript we try to present a simple and innovative method for easy identification of aromatic and anti-aromatic behavior of organic compounds from their non-aromatic nature excluding. ### (PDF) Polycyclic antiaromatic hydrocarbons Dage Sundholm Is this Aromatic Non-Aromatic or Anti? And why? Mcat. Answer: aromatic, antiaromatic, nonaromatic NH NH2 O Aromatic Aromatic Non Anti Aromatic Non N O S N N Non Non Aromatic Non Aromatic Aromatic O O O O N Aromatic Anti Non Non Non Aromatic . Title: Microsoft Word - Quiz_Aromaticity_Answer.doc Author: Robert Iafe Created Date:, Sep 12, 2019В В· Huckel's Rule: Aromatic, Antiaromatic, and Nonaromatic. Huckel's Rule is a set of algorithms that combine the number of pi electrons (n) and the physical structure of the ring system to determine whether the molecule is aromatic, antiaromatic, or nonaromatic.. (a) A neutral, 4 p-electron, anti-aromatic system. (b) A 6 p-electron, aromatic system. (c) An aromatic system because n=2 in the Huckel 4n+2 rule. (d) A non-aromatic, conjugated 6 p-electron system (e) A non conjugated hydrocarbon. (f) Non-aromatic as drawn, but if H- were removed would give an aromatic вЂ¦ Anti-aromatic compounds have a closed bonding shell of It electrons. For EAS reactions, all deactivators are meta directors. Dioxanes are seven membered heterocycles. Chlorine is a meta directing, activating substituent for EAS reactions. Anti-aromatic compounds are more stable than non-aromatic compounds. Jan 16, 2018В В· Difference Between Aromatic Antiaromatic and Nonaromatic Definition. Aromatic: Aromatic compounds are organic compounds composed of carbon and hydrogen atoms arranged in ring structures with delocalized pi electrons. Antiaromatic: Antiaromatic compounds are molecules that are cyclic, planar and completely conjugated but consist of 4n pi electrons. Classify the following molecules as aromatic and antiaromatic: Aromaticity: Aromaticity is a property which has planar, cyclic structure with a ring of resonance bonds that gives to increase the Anti-aromatic compounds have a closed bonding shell of It electrons. For EAS reactions, all deactivators are meta directors. Dioxanes are seven membered heterocycles. Chlorine is a meta directing, activating substituent for EAS reactions. Anti-aromatic compounds are more stable than non-aromatic compounds. How to check aromatic, antiaromatic and nonaromatic. tanu see _ve charge se kya hota h Sir ne to phle h kha tha naa k agr sp3 hybridisation aa v jaaye to resonance kr k check kr lena hoga agr sp3 sp2 me change ho gya then vo v aromatic ho jaayega.thik aisa iss example me hua Cyclic congugation increases the number of p orbital interactions in the conjugated system, stabilizing the pi bonds. Cyclohexene lacks this stability, and the energy of its pi bond is greater (less stable). Aromaticity is one of the more exciting topics in organic chemistry! Partly because of itвЂ™s potential for easy points on your quiz/exam.. that is IF you truly understand, not merely memorize: when you know what to look for to identify aromatic, antiaromatic and non aromatic compounds. Ch16 Aromatic Compounds (landscape).docx Page 19 Aromatic, Antiaromatic and Nonaromatic Compounds In a more specific, chemical sense, aromatic compounds are defined as those which meet the following criteria: 1) The structure must be cyclic, and contain some number of conjugated bonds. And thus was proclaimed aromatic. Benzene is an aromatic molecule Practice molecule contains an aromatic ring, such as a benzene ring, attached to a nonВ aromatic ring, how does that affect the overall aromaticity of the molecule? o Overall, ### anti aromatic vs. non-aromatic Student Doctor Network Antiaromaticity and Antiaromatic Compounds вЂ“ Master. AROMATIC ANTIAROMATIC NONAROMATIC PDF - This study also shows omission behavior of some heterocyclic compounds with respect to their aromatic/anti aromatic/non aromatic nature due. Table 1:, Oct 30, 2017В В· This lesson examines multiple compounds to determine if they are aromatic, antiaromatic, or nonaromatic based on Huckel's Rule and other criteria. Lone Pair. Ch 11 Aromaticity questions. AROMATIC ANTIAROMATIC NONAROMATIC PDF - This study also shows omission behavior of some heterocyclic compounds with respect to their aromatic/anti aromatic/non aromatic nature due. Table 1:, Download as PDF. Set alert. About this page. Learn more about Antiaromatic Compound. It behaves simply as a cyclic compound with four isolated double bonds and is neither aromatic nor antiaromatic (Figure 1.33). Figure 1.33. The structure of cyclooctatraene showing why it is not antiaromatic. Nonaromatic and Antiaromatic Cyclic Polyenes.. ### Antiaromaticity and Antiaromatic Compounds вЂ“ Master Aromaticity and antiaromaticity in organic chemistry YouTube. Benzyne is 67t HГјckel aromatic. Chlorine is a meta directing, activating substituent for electrophilic aromatic substitution. Aromatic compounds are more stable than antiaromatic compounds. Cyclopentane has less ring strain than an epoxide. Cyclobutadiene is more stable than butadiene. Kinetic products are always more stable than thermodynamic 1) Aromatic compounds are defined as having planar structures, containing a certain number of electrons in a continuous overlapping cyclic arrangement of p orbitals. Name two characteristic physical or chemical properties of aromatic compounds. (3pts) 2) Indicate which of the following molecules are aromatic, non-aromatic or anti-aromatic.. • Aromaticity Practice Problems for Aromatic Antiaromatic • F3CCF 3 crab.rutgers.edu • organic chemistry Anti-aromatic or Non-aromatic • Please tell if the 2 given conpound are Anti-aromatic or Non-aromatic, I have confusions arising due to incosistent facts all around internet some of them are as follow : 1.) Arguments for Cyclopropenyl Anion. a.) Wikipedia which under the heading of "Effects on reactivity" clearly states that : In this manuscript we try to present a simple and innovative method for easy identification of aromatic and anti-aromatic behavior of organic compounds from their non-aromatic nature excluding It is shown that the antiaromatic compound is more stable than the non aromatic compounds 2 and 3 because of a more conjugated system. Here's the exact statement: In the first structure, delocalization of the positive charge and the ПЂ bonds occurs over the entire ring. Jan 16, 2018В В· Difference Between Aromatic Antiaromatic and Nonaromatic Definition. Aromatic: Aromatic compounds are organic compounds composed of carbon and hydrogen atoms arranged in ring structures with delocalized pi electrons. Antiaromatic: Antiaromatic compounds are molecules that are cyclic, planar and completely conjugated but consist of 4n pi electrons. Download as PDF. Set alert. About this page. Learn more about Antiaromatic Compound. It behaves simply as a cyclic compound with four isolated double bonds and is neither aromatic nor antiaromatic (Figure 1.33). Figure 1.33. The structure of cyclooctatraene showing why it is not antiaromatic. Nonaromatic and Antiaromatic Cyclic Polyenes. If we easily predict the nature of organic compound i.e. aromatic, anti aromatic or non aromatic then we can resolve different kind of problems regarding stability, reactivity, acidity etc. by using the following supposition. Order of stability is aromatic > non aromatic > anti aromatic Cyclic congugation increases the number of p orbital interactions in the conjugated system, stabilizing the pi bonds. Cyclohexene lacks this stability, and the energy of its pi bond is greater (less stable). Start with the Aromaticity Review + Videos, then see how much youвЂ™ve mastered with the Aromaticity Practice Questions below. PDF Solutions to follow next week. Part 1: Aromatic, Antiaromatic, Non Aromatic. Determine if each molecule below is Aromatic, Antiaromatic or Non AromaticвЂ¦ Benzyne is 67t HГјckel aromatic. Chlorine is a meta directing, activating substituent for electrophilic aromatic substitution. Aromatic compounds are more stable than antiaromatic compounds. Cyclopentane has less ring strain than an epoxide. Cyclobutadiene is more stable than butadiene. Kinetic products are always more stable than thermodynamic Aromaticity is one of the more exciting topics in organic chemistry! Partly because of itвЂ™s potential for easy points on your quiz/exam.. that is IF you truly understand, not merely memorize: when you know what to look for to identify aromatic, antiaromatic and non aromatic compounds. (a) A neutral, 4 p-electron, anti-aromatic system. (b) A 6 p-electron, aromatic system. (c) An aromatic system because n=2 in the Huckel 4n+2 rule. (d) A non-aromatic, conjugated 6 p-electron system (e) A non conjugated hydrocarbon. (f) Non-aromatic as drawn, but if H- were removed would give an aromatic вЂ¦ Many aromatic and antiaromatic compounds (benzene and cyclobutadiene) are too small to have protons inside of the ring, where shielding and deshielding effects can be more diagnostically useful in determining if a compound is aromatic, antiaromatic, or nonaromatic. Aromatic vs Antiaromatic vs Non Aromatic Practice Exercises. Our last post in this series on aromaticity went through the 4 conditions a molecule must fulfill in order to be aromatic.. First, it must be cyclic Second, every atom around the ring must have an available p-orbital; Third, the number of electrons in the pi system must be 2, 6, 10, 14, 18, or a higher number in the set that Please tell if the 2 given conpound are Anti-aromatic or Non-aromatic, I have confusions arising due to incosistent facts all around internet some of them are as follow : 1.) Arguments for Cyclopropenyl Anion. a.) Wikipedia which under the heading of "Effects on reactivity" clearly states that : ## What is the difference between anti-aromatic and non Aromatic Non Aromatic Antiaromatic Practice Problems Pdf. May 17, 2017В В· How to Easily predict Aromatic & Anti-aromatic compounds? May 17, Some of them are aromatic. Some are anti-aromatic and some are non-aromatic. The question is вЂ“ Can you identify which ones are aromatic and which are not? Wait! You arenвЂ™t thinking of the HuckelвЂ™s rule, are you? Sure, Abhijit! Need more practice problems and, In this manuscript we try to present a simple and innovative method for easy identification of aromatic and anti-aromatic behavior of organic compounds from their non-aromatic nature excluding. ### Am I Aromatic? Quiz By sproutcm Classify the following molecules as aromatic and antiaromatic. Web Quiz Your assignment, Chapter 15: Benzene and Aromaticity is ready. . . You can bookmark this page if you like - you will not be able to set bookmarks once you have started the вЂ¦, Antiaromatic Compounds Are Unusually Unstable. What are the key factors that determine whether a molecule is antiaromatic? In our previous posts in our series on aromaticity [intro to aromaticity], [rules for aromaticity], we saw that aromatic molecules are unusually stable.They have particularly large resonance energies, tend to undergo substitution rather than addition reactions, and have. Anti-aromatic compounds have a closed bonding shell of It electrons. For EAS reactions, all deactivators are meta directors. Dioxanes are seven membered heterocycles. Chlorine is a meta directing, activating substituent for EAS reactions. Anti-aromatic compounds are more stable than non-aromatic compounds. AROMATIC ANTIAROMATIC NONAROMATIC PDF - This study also shows omission behavior of some heterocyclic compounds with respect to their aromatic/anti aromatic/non aromatic nature due. Table 1: How to check aromatic, antiaromatic and nonaromatic. tanu see _ve charge se kya hota h Sir ne to phle h kha tha naa k agr sp3 hybridisation aa v jaaye to resonance kr k check kr lena hoga agr sp3 sp2 me change ho gya then vo v aromatic ho jaayega.thik aisa iss example me hua Jan 16, 2018В В· Difference Between Aromatic Antiaromatic and Nonaromatic Definition. Aromatic: Aromatic compounds are organic compounds composed of carbon and hydrogen atoms arranged in ring structures with delocalized pi electrons. Antiaromatic: Antiaromatic compounds are molecules that are cyclic, planar and completely conjugated but consist of 4n pi electrons. PDF Little is known about interactions between two antiaromatic molecules. Here, the authors synthesised a cyclophane, in which two antiaromatic porphyrin moieties adopt a stacked face-to-face Sep 12, 2019В В· Huckel's Rule: Aromatic, Antiaromatic, and Nonaromatic. Huckel's Rule is a set of algorithms that combine the number of pi electrons (n) and the physical structure of the ring system to determine whether the molecule is aromatic, antiaromatic, or nonaromatic. Start with the Aromaticity Review + Videos, then see how much youвЂ™ve mastered with the Aromaticity Practice Questions below. PDF Solutions to follow next week. Part 1: Aromatic, Antiaromatic, Non Aromatic. Determine if each molecule below is Aromatic, Antiaromatic or Non AromaticвЂ¦ Aug 15, 2016В В· Aromaticity and antiaromaticity in organic chemistry Any Time Padhai Academy. GOC 06 : Aromatic , Anti Aromatic and Non-Aromatic Compounds JEE MAINS/NEET - Duration Practice вЂ¦ Question 2. Classify the following molecules as aromatic, antiaromatic or nonaromatic. Give an explanation for your answer. The last one is very trickyвЂ¦ N O N H N H 10e-, aromatic 12e-, antiaromatic 6e-, aromatic (the oxygen contribues 2 e-) 10e-, aromatic (the nitrogen contributes 2 e-) nonaromatic sp3 carbon 12e-, antiaromatic nonaromatic May 17, 2017В В· How to Easily predict Aromatic & Anti-aromatic compounds? May 17, Some of them are aromatic. Some are anti-aromatic and some are non-aromatic. The question is вЂ“ Can you identify which ones are aromatic and which are not? Wait! You arenвЂ™t thinking of the HuckelвЂ™s rule, are you? Sure, Abhijit! Need more practice problems and Aug 15, 2016В В· Aromaticity and antiaromaticity in organic chemistry Any Time Padhai Academy. GOC 06 : Aromatic , Anti Aromatic and Non-Aromatic Compounds JEE MAINS/NEET - Duration Practice вЂ¦ Aromatic Non Aromatic Antiaromatic Practice Problems Pdf. Aromatic Non Aromatic Antiaromatic Practice Problems Pdf And thus was proclaimed aromatic. Benzene is an aromatic molecule Practice molecule contains an aromatic ring, such as a benzene ring, attached to a nonВ aromatic ring, how does that affect the overall aromaticity of the molecule? o Overall, Classify the following molecules as aromatic and antiaromatic: Aromaticity: Aromaticity is a property which has planar, cyclic structure with a ring of resonance bonds that gives to increase the Jan 16, 2018В В· Difference Between Aromatic Antiaromatic and Nonaromatic Definition. Aromatic: Aromatic compounds are organic compounds composed of carbon and hydrogen atoms arranged in ring structures with delocalized pi electrons. Antiaromatic: Antiaromatic compounds are molecules that are cyclic, planar and completely conjugated but consist of 4n pi electrons. Question 2. Classify the following molecules as aromatic, antiaromatic or nonaromatic. Give an explanation for your answer. The last one is very trickyвЂ¦ N O N H N H 10e-, aromatic 12e-, antiaromatic 6e-, aromatic (the oxygen contribues 2 e-) 10e-, aromatic (the nitrogen contributes 2 e-) nonaromatic sp3 carbon 12e-, antiaromatic nonaromatic Explanation: . For a compound to be considered aromatic, it must be flat, cyclic, and conjugated and it must obey Huckel's rule. Huckel's rule states that an aromatic compound must have pi electrons in the overlapping p orbitals in order to be aromatic (n in this formula represents any integer). Only compounds with 2, 6, 10, 14, . . . If we easily predict the nature of organic compound i.e. aromatic, anti aromatic or non aromatic then we can resolve different kind of problems regarding stability, reactivity, acidity etc. by using the following supposition. Order of stability is aromatic > non aromatic > anti aromatic If we easily predict the nature of organic compound i.e. aromatic, anti aromatic or non aromatic then we can resolve different kind of problems regarding stability, reactivity, acidity etc. by using the following supposition. Order of stability is aromatic > non aromatic > anti aromatic pdf. Polycyclic antiaromatic hydrocarbons However, the energy gain of the aromatic stabilisation often outweighs, leading to disconnected local aromatic rings separated by nonaromatic Fig. 1 The molecular structure of the antiaromatic hexadehydro- [12]annulene (1) and of a hexadehydro[12]annulene ring fused to a benzene Fig. 3 The molecular ### Identifying Aromatic Compounds Organic Chemistry Identify Aromatic Antiaromatic or Nonaromatic Compounds. Cyclic congugation increases the number of p orbital interactions in the conjugated system, stabilizing the pi bonds. Cyclohexene lacks this stability, and the energy of its pi bond is greater (less stable)., MГ¶bius aromaticity occurs when a cyclic system of molecular orbitals, formed from p ПЂ atomic orbitals and populated in a closed shell by 4n (n is an integer) electrons, is given a single half-twist to form a MГ¶bius strip.A ПЂ system with 4n electrons in a flat (non-twisted) ring would be antiaromatic, and therefore highly unstable, due to the symmetry of the combinations of p atomic orbitals.. ### Am I Aromatic? Quiz By sproutcm Aromaticity ProProfs Quiz. Jan 16, 2018В В· Difference Between Aromatic Antiaromatic and Nonaromatic Definition. Aromatic: Aromatic compounds are organic compounds composed of carbon and hydrogen atoms arranged in ring structures with delocalized pi electrons. Antiaromatic: Antiaromatic compounds are molecules that are cyclic, planar and completely conjugated but consist of 4n pi electrons. Web Quiz Your assignment, Chapter 15: Benzene and Aromaticity is ready. . . You can bookmark this page if you like - you will not be able to set bookmarks once you have started the вЂ¦. • Aromaticity Yale University • (PDF) Three-dimensional aromaticity in an antiaromatic • 1) Aromatic compounds are defined as having planar structures, containing a certain number of electrons in a continuous overlapping cyclic arrangement of p orbitals. Name two characteristic physical or chemical properties of aromatic compounds. (3pts) 2) Indicate which of the following molecules are aromatic, non-aromatic or anti-aromatic. Classify the following molecules as aromatic and antiaromatic: Aromaticity: Aromaticity is a property which has planar, cyclic structure with a ring of resonance bonds that gives to increase the Aug 15, 2016В В· Aromaticity and antiaromaticity in organic chemistry Any Time Padhai Academy. GOC 06 : Aromatic , Anti Aromatic and Non-Aromatic Compounds JEE MAINS/NEET - Duration Practice вЂ¦ May 17, 2017В В· How to Easily predict Aromatic & Anti-aromatic compounds? May 17, Some of them are aromatic. Some are anti-aromatic and some are non-aromatic. The question is вЂ“ Can you identify which ones are aromatic and which are not? Wait! You arenвЂ™t thinking of the HuckelвЂ™s rule, are you? Sure, Abhijit! Need more practice problems and Jan 16, 2018В В· Difference Between Aromatic Antiaromatic and Nonaromatic Definition. Aromatic: Aromatic compounds are organic compounds composed of carbon and hydrogen atoms arranged in ring structures with delocalized pi electrons. Antiaromatic: Antiaromatic compounds are molecules that are cyclic, planar and completely conjugated but consist of 4n pi electrons. Download as PDF. Set alert. About this page. Learn more about Antiaromatic Compound. It behaves simply as a cyclic compound with four isolated double bonds and is neither aromatic nor antiaromatic (Figure 1.33). Figure 1.33. The structure of cyclooctatraene showing why it is not antiaromatic. Nonaromatic and Antiaromatic Cyclic Polyenes. Oct 30, 2017В В· This lesson examines multiple compounds to determine if they are aromatic, antiaromatic, or nonaromatic based on Huckel's Rule and other criteria. Lone Pair Oct 02, 2015В В· Our aim is to provide quality education free of cost. With this vision, we are providing COMPLETE FREE VIDEO lectures ,for students preparing for вЂ¦ Jan 16, 2018В В· Difference Between Aromatic Antiaromatic and Nonaromatic Definition. Aromatic: Aromatic compounds are organic compounds composed of carbon and hydrogen atoms arranged in ring structures with delocalized pi electrons. Antiaromatic: Antiaromatic compounds are molecules that are cyclic, planar and completely conjugated but consist of 4n pi electrons. PDF Little is known about interactions between two antiaromatic molecules. Here, the authors synthesised a cyclophane, in which two antiaromatic porphyrin moieties adopt a stacked face-to-face And thus was proclaimed aromatic. Benzene is an aromatic molecule Practice molecule contains an aromatic ring, such as a benzene ring, attached to a nonВ aromatic ring, how does that affect the overall aromaticity of the molecule? o Overall, Oct 30, 2017В В· This lesson examines multiple compounds to determine if they are aromatic, antiaromatic, or nonaromatic based on Huckel's Rule and other criteria. Lone Pair The carbanion is SP2 since it is in the allylic position, forcing the lone pair into an open unhybridized P orbital. One of the two lone pairs of the oxygen will be forced into an unhybridized P orbital as well. Since there are 8 pi electrons in this conjugated system, it violates Huckel's rule and is therefor anti-aromatic Antiaromatic Compounds Are Unusually Unstable. What are the key factors that determine whether a molecule is antiaromatic? In our previous posts in our series on aromaticity [intro to aromaticity], [rules for aromaticity], we saw that aromatic molecules are unusually stable.They have particularly large resonance energies, tend to undergo substitution rather than addition reactions, and have It is shown that the antiaromatic compound is more stable than the non aromatic compounds 2 and 3 because of a more conjugated system. Here's the exact statement: In the first structure, delocalization of the positive charge and the ПЂ bonds occurs over the entire ring. Oct 30, 2017В В· This lesson examines multiple compounds to determine if they are aromatic, antiaromatic, or nonaromatic based on Huckel's Rule and other criteria. Lone Pair In this manuscript we try to present a simple and innovative method for easy identification of aromatic and anti-aromatic behavior of organic compounds from their non-aromatic nature excluding Explanation: . For a compound to be considered aromatic, it must be flat, cyclic, and conjugated and it must obey Huckel's rule. Huckel's rule states that an aromatic compound must have pi electrons in the overlapping p orbitals in order to be aromatic (n in this formula represents any integer). Only compounds with 2, 6, 10, 14, . . . Dec 04, 2016В В· Aromaticity Antiaromaticity Non aromaticity 1. Content 1-Aromatic Compaund 2-Criteria for aromaticity 3-Difference between aromatic, antiaromatic,nonaromatic 4-Aromatic hetrocyclic compound 5-Annulene 2. Introduction about aromatic compound 3. 5 Four structural criteria must be satisfied for a compound to be aromatic. The carbanion is SP2 since it is in the allylic position, forcing the lone pair into an open unhybridized P orbital. One of the two lone pairs of the oxygen will be forced into an unhybridized P orbital as well. Since there are 8 pi electrons in this conjugated system, it violates Huckel's rule and is therefor anti-aromatic Explanation: . For a compound to be considered aromatic, it must be flat, cyclic, and conjugated and it must obey Huckel's rule. Huckel's rule states that an aromatic compound must have pi electrons in the overlapping p orbitals in order to be aromatic (n in this formula represents any integer). Only compounds with 2, 6, 10, 14, . . . In this manuscript we try to present a simple and innovative method for easy identification of aromatic and anti-aromatic behavior of organic compounds from their non-aromatic nature excluding Can someone please explain why the resonance structures of fulvene 1 is non-aromatic and 2 is anti-aromatic? Why is fulvene non-aromatic, even though it has $4\pi$-electrons and no $\mathrm{sp^3}$ How to explain (non-/anti-) aromaticity in fulvene with the help of resonance structures? Ask Question Asked 2 years, 2 months ago. And thus was proclaimed aromatic. Benzene is an aromatic molecule Practice molecule contains an aromatic ring, such as a benzene ring, attached to a nonВ aromatic ring, how does that affect the overall aromaticity of the molecule? o Overall,	{}
# Topological Classification of Band Insulators (in terms of Green's functions) I am currently reading Topological Classification and Stability of Fermi Surfaces by Y. X. Zhao and Z. D. Wang (PRL 110, 240404 (2013)). They remark that the Green's function (along the complex frequency axis) can be viewed as a mapping $S^p \to \mathrm{GL}(N,\mathbb{C})$, where $p$ is the co-dimension of the Fermi surface. It is then natural to classify the Fermi surface by the topological character of this mapping which falls into some instance of $\pi_p(\mathrm{GL}(N,\mathbb{C})$). In particular, one can define the winding number $$N_p = C_p \int_{S^p} \mathrm{tr}~(G\textbf{d} G^{-1})^p,$$ where $C_p = -~p!~/~( (2p+1)! (2\pi i )^{p+1})$ . I am now wondering how these ideas are related to the topology of band insulators: 1. Since the Brillouin zone is periodic, an insulating band represents a compact manifold of some co-dimension $p$ (similar to a Fermi surface). And hence I should be able to write down the winding number $N_p$ in terms of Green's functions. Is this a straightforward generalisation of the formula presented above? 2. I suppose that in this case the Green's function needs to be viewed along the real frequency axis in order to pick up the correct singularities. Is this correct?	{}
# Ideal gas equation derivation proportionality [duplicate] While deriving the Ideal gas Equation using Boyle's, Charles', and Avogadro Laws, how are each of the laws, which have different proportionality constants and different quantities as constant combined? (eg: Boyle's law which assumes the temperature and moles of gas to be constant, but in Charles' law temperature changes. How is it possible?) • If you consider the ideal gas state equation $pV=nRT$, and if you keep either of the 3 state variables p,V,T constant, involving its value into the equation constant, you get each of the respective original gas laws. – Poutnik Aug 23 '20 at 16:13 • Related question: chemistry.stackexchange.com/questions/58330/…. – Mathew Mahindaratne Aug 23 '20 at 16:52 I understand your concern because this is the way it is taught in South Asian schools and colleges and even general chemistry texts taught elsewhere are silent about it. They state all the individual gas laws using a proportionality sign "$$\propto$$" and magically all gas laws are combined and that becomes $$R$$- the universal gas constant. This is done in a single paragraph.	{}
# Solid disk rolling up a hill problem I'm somewhat clueless on how to solve the following problem, since a solid disk is rolling up a hill rather than downhill. A solid disk (mass = 5 kg, R = 0.6m) is rolling across a table with a translational speed of 6 m/s. The disk then rolls up a hill of height 2 m, where the ground again levels out. Find the translational and rotational speeds now. I tried using KEi + PEi = KEf + PEf, including both KEt and KEr in KEf, and I calculated that KEi = 135J (45J are KEr, and 90J are KEt). I'm not sure if I'm plugging in my values correctly, since I got a translational speed of 3.847, and my answer was wrong. dav2008 Gold Member You included gravitational potential energy and translational kinetic energy, but what are you forgetting? Rotational kinetic energy? I thought I included that too...KEr. dav2008 Gold Member Oh well then you should be getting the right answer. You probably have a mistake in your arithmetic. I also got 135J for the total initial kinetic energy but I got a different answer for the final speed. Last edited: Okay...can you check my work? I used KEi + PEi = KEr + KEt + PEf, which I used 135 + 0 = 45 + (0.5)(5)(v^2) + (5)(9.8)(2), and solved from there. Am I using these values incorrectly? dav2008 Gold Member You have the wrong final rotational kinetic energy. The disk is still rolling when it's at the top of the hill but the angular velocity is not the same as it was before. (If the translational speed is now v, what's the angular speed?) How would I go about correcting my KEr, and what would the fact that it's still rolling at the top of the hill change in my equation? dav2008 Gold Member You would write your final translational kinetic energy in the same manner you wrote your final translational kinetic energy. If the object has a translational speed of v then what is it's rotational kinetic energy? You already said that the translational kinetic energy would be $\frac{1}{2}(5)(v^2)$ so now write the final rotational kinetic energy in terms of v. Last edited: Do you mean I should write my final rotational kinetic energy in the same way? Sorry, I am getting lost, since your previous 2 posts seem to be about 2 different things wrong with the problem. Would you be able to clarify what you are referring to? dav2008 Gold Member You said 135 + 0 = 45 + (0.5)(5)(v^2) + (5)(9.8)(2). Here you are assuming that the final kinetic rotational energy is the same as the initial kinetic rotational energy (45J). I'm saying that that's not the case because the object is now traveling at at a speed v. You wrote conservation of energy: KEroti+KEtransi+PEi=KErotf+KEtransf+PEf You then calculated the initial energies to be 135J: 135J=KErotf+KEtransf+PEf Now you just need to write the kinetic energies in terms of an unknown speed "v" and then solve for v Last edited: Oh, okay. So I would ahve 2 unknowns in this problem? How would I solve each one? dav2008 Gold Member Well you would have angular velocity and translational velocity. What is the relationship between the two? v=rw? How would I incorporate that into the problem? I just simpliefied my equation and got 37 = 1.25w^2 + 2v^2 dav2008 Gold Member Well I don't know if you simplified your equation right or not but you know what w is in terms of v from the equation you just posted... LOL I just figured that out...so w = 4.148, and then I plug that into v=rw to get v, which is 2.4888? Eek...these answers are wrong! Did I do something wrong? Last edited: dav2008 Gold Member Well since youre solving for v it would just be easier to substitute v/.6 for w in your final rotational energy. I think you're just coming across arithmetic errors at this point. Last edited: I got the same answer...can you check if my work is wrong? I'm using: 37 = 1.25(v/0.6)^2 + 2.5v^2, which becomes 37 = 3.472v^2 + 2.5v^2, then 37 = 5.972v^2, 6.195 = v^2, then v = 2.489. dav2008 Gold Member I think you divided by .62 before you plugged in v/.6 for w because I am getting $37 = 1.25(v)^2 + 2.5v^2$ Last edited: I had that 1.25 before I even divided by 0.6. I'm really confused now. Would you be able to show me your work for this problem? dav2008 Gold Member $$135=\frac{1}{2}(9.8)(2)+\frac{1}{2}(5)v^2+.5(.9)(\omega)^2$$ $$37=\frac{1}{2}(5)v^2+.5(.9)(\frac{v}{.6})^2$$ $$37=2.5v^2+1.25v^2$$ Where did you get the .9? dav2008 Gold Member That is the moment of inertia that I calculated for the disc. $$I=.5mr^2$$ for a solid disc, axis through center $$=.5(5)(.6)^2$$ $$=.9$$ kg-m2 Last edited: Is inertia involved in this problem? I thought I was working with kinetic and potential energy only? dav2008 Gold Member Show me how you solved for the initial rotational kinetic energy. You had to have used the moment of inertia. The rotational kinetic energy is equal to $$\frac{1}{2}I\omega^2$$ where I is the moment of inertia and $\omega$ is the angular velocity. You obviously used this formula when you calculated the initial rotational kinetic energy Last edited: Oh okay, I figured out that inertia part! I realized I used mass instead of inertia in KEr on accident! So Is my velocity if 3.14 m/s correct? And that gives me an angular velocity of 5.23?	{}
HST Observations of the Host Galaxies of High Redshift Radio-Loud Quasars Session 59 -- General Properties of AGN Oral presentation, Tuesday, 10, 1995, 10:00am - 11:30am ## [59.04] HST Observations of the Host Galaxies of High Redshift Radio-Loud Quasars M. D. Lehnert (IGPP/LLNL), W. van Bruegel (IGPP/LLNL), T. M. Heckman (JHU), G. K. Miley (Leiden) Observations of radio-loud quasars at high redshifts are important in that they allow us to investigate the causes of the mass extinction'' of luminous quasars, the relationship between radio galaxies and radio-loud quasars, the conditions of the early universe, the interaction of radio plasma with the surrounding galactic material, and the evolution of the quasar environment with epoch. HST observations are crucial to resolving these issues in that it allows us to image the host galaxies and environments of high-z quasars at fractions of a present-day galaxy size ($<$ 1 kpc) and at similar angular resolutions as provided by the VLA. We imaged 5 high-redshift (z$\approx$2) radio-loud quasars using WFPC2 in the F555W broad-band filter and a narrow-band filter whose central wavelength corresponds to that of redshifted Ly$\alpha$. Our results agree with and extend previous ground-based results suggesting that the host galaxies are multi-component structures with complex morphologies, the individual components are generally very luminous, $\approx$$-$23 in F555W, and there seems to be an intimate relationship between the radio emission and the Ly$\alpha$ and rest-frame UV continuum emission.	{}
# Determine whether there is a valid rounding in a table of numbers I was told this question would be better suited here: Suppose you have a table such as: $\begin{array}{ccc} 11.998 & 9.083 & 2.919 &\|& 24\\ 12.983 & 10.872 & 3.145 &\|& 27\\ 1.019 & 2.045 & 0.936 &\|& 4\\ 26&22&7&\|&55 \end{array}$ Where the rows add up to the numbers on the right and the columns add up to the numbers on the bottom. How can we determine whether there is a valid arrangement of each number using ceiling and floor so that the sum of the rows and columns stays the same? For example, this has a valid arrangement because we can do: $\begin{array}{ccc} 11 &10 & 3 &\|& 24\\ 13 & 10 & 4 &\|& 27\\ 2& 2 & 0 &\|& 4\\ 26&22&7&\|&55 \end{array}$ I'm supposed to use a network flow computation to solve the problem, but I can't figure out a way to arrange the nodes and edges so that I end up "discovering" whether the flow is valid. Do I have to create multiple graphs that each compute a separate flow (e.g. one for each column and one for each row)? I'm guessing that we have to end up with saturated edges at the end of our flow graph, but I'm not sure how to specify the graph so it solves the problem.	{}
# Problem 11: Conjugates and Rotations of Words Two words $x$ and $y$ are conjugate if there exist two words $u$ and $v$ for which $x=uv$ and $y=vu$. They are also called rotations or cyclic shifts of one another. It is clear that conjugacy is an equivalence relation between words but it is not compatible with the product of words. Show that two non-empty words of the same length are conjugate if and only if their (primitive) roots are conjugate. A more surprising property of conjugate words is stated in the next question. Show that two non-empty words $x$ and $y$ are conjugate if and only if $xz=zy$ for some word $z$. ## References • M. Lothaire. Combinatorics on Words. Addison-Wesley, 1983. Reprinted in 1997.	{}
What is a meta-analysis? A meta-analysis is a quantitative summary of studies on the same topic. Why do we want to perform a meta-analysis? 1. Finding generalities 2. Increasing power and precision 3. Exploring differences between studies 4. Settling controversies from conflicting studies (testing hypotheses) 5. Generating new hypotheses The process of meta-analysis How many steps involved in meta-analysis? 1. Formulating questions & hypothesis or finding a topic 2. Literature search & paper collection 3. Data extraction & coding 4. Meta-analysis & publication bias tests 5. Reporting & publication We only consider the step iv in this tutorial. You will need to learn the other steps elsewhere. To get you started, we recently wrote an overview paper which divides the process of meta-analysis into 10 questions (Nakagawa et al. 2017). The 10 questions will guide you through judging the quality of a meta-analysis. 1. Is the search systematic and transparently documented? 2. What question and what effect size? 3. Is non-independence taken into account? 4. Which meta-analytic model? 5. Is the level of consistency among studies reported? 6. Are the causes of variation among studies investigated? 7. Are effects interpreted in terms of biological importance? 8. Has publication bias been considered? 9. Are results really robust and unbiased? 10. Is the current state (and lack) of knowledge summarized? ## Metafor for meta-analysis I think the R package metafor (Viechtbauer 2010) is the most comprehensive meta-analytic software and the author Wolfgang Viechtbauer, who, I have to say, has the coolest name among my friends, is still actively developing it. First, install and load the metafor package. library(metafor) Have a look at the data set named dat.curtis1998 included in the package. If you have to see the other data sets included in this package, try help(package="metafor"). dat <- get(data(dat.curtis1998)) str(dat) ## 'data.frame': 102 obs. of 20 variables: ## $id : int 21 22 27 32 35 38 44 63 86 87 ... ##$ paper : int 44 44 121 121 121 121 159 183 209 209 ... ## $genus : chr "ALNUS" "ALNUS" "ACER" "QUERCUS" ... ##$ species : chr "RUBRA" "RUBRA" "RUBRUM" "PRINUS" ... ## $fungrp : chr "N2FIX" "N2FIX" "ANGIO" "ANGIO" ... ##$ co2.ambi: num 350 350 350 350 350 350 350 395 350 350 ... ## $co2.elev: num 650 650 700 700 700 700 700 795 700 700 ... ##$ units : chr "ul/l" "ul/l" "ppm" "ppm" ... ## $time : int 47 47 59 70 64 50 730 365 365 365 ... ##$ pot : chr "0.5" "0.5" "2.6" "2.6" ... ## $method : chr "GC" "GC" "GH" "GH" ... ##$ stock : chr "SEED" "SEED" "SEED" "SEED" ... ## $xtrt : chr "FERT" "FERT" "NONE" "NONE" ... ##$ level : chr "HIGH" "CONTROL" "." "." ... ## $m1i : num 6.82 2.6 2.99 5.91 4.61 ... ##$ sd1i : num 1.77 0.667 0.856 1.742 1.407 ... ## $n1i : int 3 5 5 5 4 5 3 3 20 16 ... ##$ m2i : num 3.94 2.25 1.93 6.62 4.1 ... ## $sd2i : num 1.116 0.328 0.552 1.631 1.257 ... ##$ n2i : int 5 5 5 5 4 3 3 3 20 16 ... This data set is from the paper by Curtis and Wang (1998). They looked at the effect of increased CO$$_2$$ on plant traits (mainly changes in biomass). So we have information on control group (1) and experimental group (2) (m = mean, sd = standard deviation) along with species information and experimental details. In meta-analysis, these variables are often referred to as ‘moderators’ (we will get to this a bit later). ### Calculating ‘standardized’ effect sizes To compare the effect of increased CO$$_2$$ across multiple studies, we first need to calculate an effect size for each study – a metric that quantifies the difference between our control and experimental groups. There are several ‘standardized’ effect sizes, which are unit-less. When we have two groups to compare, we use two types of effect size statistics. The first one is standardized mean difference (SMD or also known as Cohen’s $$d$$ or Hedge’s $$d$$ or $$g$$; some subtle differences between them, but we do not worry about them for now): $\mathrm{SMD}=\frac{\bar{x}_{E}-\bar{x}_{C}}{\sqrt{\frac{(n_{C}-1)sd^2_{C}+(n_{E}-1)sd^2_{E}}{n_{C}+n_{E}-2}}}$ where $$\bar{x}_{C}$$ and $$\bar{x}_{E}$$ are the means of the control and experimental group, respectively, $$sd$$ is sample standard deviation ($$sd^2$$ is sample variance) and $$n$$ is sample size. And its sample error variance is: $se^2_{\mathrm{SMD}}= \frac{n_{C}+n_{E}}{n_{C}n_{E}}+\frac{\mathrm{SMD}^2}{2(n_{C}+n_{E})}$ The square root of this is referred to as ‘standard error’ (or the standard deviation of the estimate – confused?). The inverse of this ($$1/se^2$$) is used as ‘weight’, but things are bit more complicated than this as we will find out below. Another common index is called ‘response ratio’, which is usually presented in its natural logarithm form (lnRR): $\mathrm{lnRR}=\ln\left({\frac{\bar{x}_{E}}{\bar{x}_{C}}}\right)$ And its sampling error variance is: $se^2_\mathrm{lnRR}=\frac{sd^2_{C}}{n_{C}\bar{x}^2_{C}}+\frac{sd^2_{E}}{n_{E}\bar{x}^2_{E}}$ Let’s get these using the function escalc in metafor. To obtain the standardised mean difference, we use: # SMD SMD <- escalc(measure = "SMD", n1i = dat$n1i, n2i = dat$n2i, m1i = dat$m1i, m2i = dat$m2i, sd1i = dat$sd1i, sd2i = dat$sd2i) where n1i and n2i are the sample sizes, m1i and m2i are the means, and sd1i and sd2i the standard deviations from each study. The object created now has an effect size (yi) and its variance (vi) for each study ## yi vi ## 1 1.8222 0.7408 ## 2 0.5922 0.4175 ## 3 1.3286 0.4883 ## 4 -0.3798 0.4072 ## 5 0.3321 0.5069 ## 6 2.5137 0.9282 To obtain the response ratio (log transformed ratio of menas), we would use: lnRR <- escalc(measure = "ROM", n1i = dat$n1i, n2i = dat$n2i, m1i = dat$m1i, m2 = dat$m2i, sd1i = dat$sd1i, sd2i = dat$sd2i) The original paper used lnRR so we will use it, but you may want to repeat analysis below using SMD to see whether results are consistent. Add the effect sizes to the original data set with cbind or bind_cols from the package dplyr library(dplyr) dat <- bind_cols(dat, lnRR) You should see yi (effect size) and vi (sampling variance) are added. ## 'data.frame': 102 obs. of 22 variables: ## $id : int 21 22 27 32 35 38 44 63 86 87 ... ##$ paper : int 44 44 121 121 121 121 159 183 209 209 ... ## $genus : chr "ALNUS" "ALNUS" "ACER" "QUERCUS" ... ##$ species : chr "RUBRA" "RUBRA" "RUBRUM" "PRINUS" ... ## $fungrp : chr "N2FIX" "N2FIX" "ANGIO" "ANGIO" ... ##$ co2.ambi: num 350 350 350 350 350 350 350 395 350 350 ... ## $co2.elev: num 650 650 700 700 700 700 700 795 700 700 ... ##$ units : chr "ul/l" "ul/l" "ppm" "ppm" ... ## $time : int 47 47 59 70 64 50 730 365 365 365 ... ##$ pot : chr "0.5" "0.5" "2.6" "2.6" ... ## $method : chr "GC" "GC" "GH" "GH" ... ##$ stock : chr "SEED" "SEED" "SEED" "SEED" ... ## $xtrt : chr "FERT" "FERT" "NONE" "NONE" ... ##$ level : chr "HIGH" "CONTROL" "." "." ... ## $m1i : num 6.82 2.6 2.99 5.91 4.61 ... ##$ sd1i : num 1.77 0.667 0.856 1.742 1.407 ... ## $n1i : int 3 5 5 5 4 5 3 3 20 16 ... ##$ m2i : num 3.94 2.25 1.93 6.62 4.1 ... ## $sd2i : num 1.116 0.328 0.552 1.631 1.257 ... ##$ n2i : int 5 5 5 5 4 3 3 3 20 16 ... ## $yi : atomic 0.547 0.143 0.438 -0.113 0.117 ... ## ..- attr(, "measure")= chr "ROM" ## ..- attr(, "ni")= int 8 10 10 10 8 8 6 6 40 32 ... ##$ vi : num 0.0385 0.0175 0.0328 0.0295 0.0468 ... Visualising effect size. We can visualize point estimates (effect size) and their 95% confidence intervals, CIs (based on sampling error variance) by using the forest function, which draws a forest plot for us. forest(dat$yi, dat$vi) The problem you see is that when there are many studies, a forest plot does not really work (unless you have very large screen!). Let’s look at just the first 12 studies. forest(dat$yi[1:12], dat$vi[1:12]) We can calculate many different kinds of effect sizes with escalc; other common effect size statistics include $$Zr$$ (Fisher’s z-transformed correlation). By the way, along with my colleagues, I have proposed a new standardized effect size called lnCVR (the log of coefficient of variation ratio – mouthful!), which compares the variability of two groups rather than means. See whether you can calculate it with these data. Actually, the development version of metafor, let you do this with escalcgithub page. lnCVR is called “CVR” in escalc. Actually, if you re-analysis this data with lnCVR, you may be able to publish a paper! Nobody has done it yet. Do it tonight! Once you have calculated effect sizes, move on to the next page: Meta-analysis 2: fixed-effect and random-effect models ### Further help (references) Go to the metafor package’s website. There you find many worked examples. Curtis, P. S., and X. Z. Wang. 1998. A meta-analysis of elevated CO2 effects on woody plant mass, form, and physiology. Oecologia 113:299-313. Nakagawa, S., R. Poulin, K. Mengersen, K. Reinhold, L. Engqvist, M. Lagisz, and A. M. Senior. 2015. Meta-analysis of variation: ecological and evolutionary applications and beyond. Methods in Ecology and Evolution 6:143-152. Viechtbauer, W. 2010. Conducting meta-analyses in R with the metafor package. Journal of Statistical Software 36:1-48. Authors: Shinichi Nakagawa and Malgorzata (Losia) Lagisz Last updated: ## [1] "Tue Oct 31 15:01:55 2017"	{}
# Proof derivative equals zero? I know this must be wrong, but I am confused as to where the mathematical fallacy lies. Here is the 'proof': $$f '(x) = \lim_{ h\to0}\frac{f(x+h)-f(x)}{h}$$ L'Hôpital's Rule (The previous limit was $\frac{0}{0}$): $$f '(x) = \lim_{ h\to 0}\frac{f '(x+h)-f '(x)} {1}$$ Plugging in $h$: $$f '(x) = f '(x+0)-f '(x)$$ Simplifying: $$f '(x) = 0$$ I'm assuming my application of L'Hôpital's rule is fallacious, but it evaluates to an indeterminate form so isn't L'Hôpital's rule still valid? Taking the derivative with respect to $h$ gives: $$f'(x) = \lim_{h \rightarrow 0} \frac{f'(x + h)}{1}$$ Since $f(x)$ is constant with respect to $h$. • Ah, and similarly, taking the derivative with respect to $x$ gives $\frac{f'(x+h) - f'(x)}{0}$, which would be invalid. At the time that I posted the question I wasn't familiar enough to Leibniz's notation to realize there's an implicit variable hidden in the apostrophe, but thanks for the clarification! – Nicholas Pipitone Oct 12 '18 at 17:53 You differentiated the numerator with respect to $x$ but the denominator with respect to $h$.	{}
# When can I assure that the representation theory of a PROP is faithful? Recall that a PROP is a symmetric monoidal category whose object-set is freely $\otimes$-generated by a single object $x\in P$. A representation or algebra for a prop $P$ in a symmetric monoidal category $C$ is a symmetric monoidal functor $f: P \to C$ — i.e. it is an object $f(x)\in C$ and some morphisms between tensor powers of $f(x)$ that satisfy all the relations in $P$. I am interested in the $\mathbb Q$-linear versions of all of these: a $\mathbb Q$-linear prop $P$ is a $\mathbb Q$-linear symmetric monoidal category whose object-set is freely $\otimes$-generated by a single object $x\in P$, and a representation thereof in a $\mathbb Q$-linear category $C$ is a $\mathbb Q$-linear symmetric monoidal functor. I will henceforth leave implicit the word "$\mathbb Q$-linear". By $\mathrm{Vect}$ I mean the category of $\mathbb Q$-vector spaces. A general question you can ask is the following. Suppose you are given a prop $P$, and some presentation of it in generators and relations. Suppose you write some expression in the generators — i.e. you pick some morphism in the prop. Suppose furthermore that for every representation $P \to \mathrm{Vect}$, this morphism evaluates to $0$. Does it follow that the morphism is $0$ in $P$? Put another way: Does every prop have a faithful representation in $\mathrm{Vect}$? The answer, of course, is "NO!". An example: let $P$ be the prop generated by the relation that the braiding $x\otimes x \to x\otimes x$ is minus the identity. Then the only representation of $P$ in $\mathrm{Vect}$ is $x = 0$, and in particular the identity map $x \to x$ evaluates to $0$ in this representation. On the other hand, $P$ has a non-zero representation in the category of super vector spaces. My question, then, is for (checkable) conditions on a prop $P$ to assure that it does, in fact, have faithful representations in $\mathrm{Vect}$. For example, the prop that I happen to care about has a presentation in which it is generated by (at most) one morphism between any two objects, and the relations are all (homogeneous) linear and quadratic in the generators. I could imagine this to be the type of condition that might assure faithfulness of representations. I would like to know that my prop has a faithful $\mathrm{Vect}$-representation, because I can prove that in any $\mathrm{Vect}$-representation a certain morphism evaluates to $0$, by choosing a basis for the underlying vector space of the representation. Of course, this proof does not universalize, but maybe some other results assure me that the morphism is universally $0$. - I asked the same thing on MO mathoverflow.net/questions/121838/…, so put my answer or rather trivial motivation to others here. If you look at problem of knot invariants, tqft construction and so on you noting that combinatorially this is the same thing as building representations of PROPs. For example you may consider category of tangles as operad with many outputs, and problem of finding full invariant of knots as building faithfull representation of such PROP. – Bad English Mar 1 '13 at 22:24 It is funny that from general point of view it is difficult to say why this operad is so complex. And why in PROPs there are no free-object, action on itself concept. But may be there exists some general statements. For example something like reduction to other operads. Let's back to knots for instance. What Drinfeld explanation of Kontsevich integral do - actually we move from the problem of building representations of tangle category to building their infinitesimal version - representations of chord diagrams, which much simpler. – Bad English Mar 1 '13 at 22:25 This is a nice question. Here is another example of a PRO with no faithful representations in Vect, that does not require linear structure. Let there be one generating object $A$ with a right dual, and morphisms $f:A\to A$ and $g: A \to A$ such that $f \circ g = \text{id}_A$. The right dual property ensures that for any representation $Z$ in Vect, $Z(A)$ is finite-dimensional, and then $Z(f) \circ Z(g) = \text{id}_{Z(A)}$ implies $Z(f) = Z(g)^{-1}$. But $f \neq g^{-1}$ in the PRO. – Jamie Vicary Jan 15 at 20:30	{}
# Problem #134 134 In a parlor game, the magician asks one of the participants to think of a three digit number (abc) where a, b, and c represent digits in base 10 in the order indicated. The magician then asks this person to form the numbers (acb), (bca), (bac), (cab), and (cba), to add these five numbers, and to reveal their sum, $N$. If told the value of $N$, the magician can identify the original number, (abc). Play the role of the magician and determine the (abc) if $N= 3194$. This problem is copyrighted by the American Mathematics Competitions. Note: you aren't logged in. If you log in, we'll keep a record of which problems you've solved. • Reduce fractions to lowest terms and enter in the form 7/9. • Numbers involving pi should be written as 7pi or 7pi/3 as appropriate. • Square roots should be written as sqrt(3), 5sqrt(5), sqrt(3)/2, or 7sqrt(2)/3 as appropriate. • Exponents should be entered in the form 10^10. • If the problem is multiple choice, enter the appropriate (capital) letter. • Enter points with parentheses, like so: (4,5) • Complex numbers should be entered in rectangular form unless otherwise specified, like so: 3+4i. If there is no real component, enter only the imaginary component (i.e. 2i, NOT 0+2i).	{}
# graphing calculator matrix matrix.reshish.com is the most convenient free online Matrix Calculator. An equation for doing so is provided below, but will not be computed. With help of this calculator you can: find the matrix determinant, the rank, raise the matrix to a power, find the sum and the multiplication of matrices, calculate the inverse matrix. Explore math with our beautiful, free online graphing calculator. The MatrixWriter form. sin cos. $\textbf {\ge\div\rightarrow}$. An m × n matrix, transposed, would therefore become an n × m matrix, as shown in the examples below: The determinant of a matrix is a value that can be computed from the elements of a square matrix. Press [ENTER] after each entry. 4 × 4 and larger get increasingly more complicated, and there are other methods for computing them. Below are descriptions of the matrix operations that this calculator can perform. The determinant of a 2 × 2 matrix can be calculated using the Leibniz formula, which involves some basic arithmetic. There are other ways to compute the determinant of a matrix which can be more efficient, but require an understanding of other mathematical concepts and notations. -1 8 5 0 7 6 A = 167 R- zPb5��V��vl�nH��!9$��q�z&�giʔ�9S��Y��̇�b��M�$&�%M. First, you must tell the calculator how large your matrix is. This procedure is illustrated in the third screen. Any system of equations can be written as the matrix equation, A * X = B. Chris All the basic matrix operations as well as methods for solving systems of simultaneous linear equations are implemented on this site. Matrix Calculator A matrix, in a mathematical context, is a rectangular array of numbers, symbols, or expressions that are arranged in rows and columns. 2.Thick 3.Above. Graphing calculators such as the TI83 and TI84 are able to do many different operations with matrices, including multiplication. Our matrix and vector calculator is the most sophisticated and comprehensive matrix calculator online. Easy to use and 100% Free! If necessary, refer above for description of the notation used. This calculator solves Systems of Linear Equations using Gaussian Elimination Method, Inverse Matrix Method, or Cramer's rule.Also you can compute a number of solutions in a system of linear equations (analyse the compatibility) using Rouché–Capelli theorem.. HP 50g Graphing Calculator - Working with Matrices. they are added or subtracted). D=-(bi-ch); E=ai-cg; F=-(ah-bg) ‎TACULATOR GRAPHING CALCULATOR • Your graphing calculator for high school and college students. Solving systems of linear equations. Here’s how you enter matrix operations in an arithmetic expression: Enter a matrix on the Home screen. Here, we will go over the steps needed to multiply two matrices in this type of calculator using the following example. G=bf-ce; H=-(af-cd); I=ae-bd. Easily perform matrix multiplication with complex numbers. Graphing Calculator by Mathlab is a scientific graphing calculator integrated with algebra and is an indispensable mathematical tool for students from high school to those in college or graduate school, or just anyone who needs more than what a basic calculator offers. • Includes all the commands and functions for advanced math, list, statistics, distribution, stat plots, etc. 121 0 obj <>stream Note that an identity matrix can have any square dimensions. 2.23 x 1.16 inches. This means that you can scale the graph and move the coordinate plane so that you can not only get the basic idea about the graph, but explore its behaviour on the areas. Enter the matrix. Next, we can determine the element values of C by performing the dot products of each row and column, as shown below: Below, the calculation of the dot product for each row and column of C is shown: For the intents of this calculator, "power of a matrix" means to raise a given matrix to a given power. Graphing Calculator TX800 Programmable Professional Grade Scientific Calculator Large Screen Size. You cannot add a 2 × 3 and a 3 × 2 matrix, a 4 × 4 and a 3 × 3, etc. One of the homework assignments for MAT 119 is to reduce a matrix with a graphing calculator. To understand determinant calculation better input any example, choose "very detailed solution" option and examine the solution. Enter sqrt(n) for Vn.) Refer to the matrix multiplication section, if necessary, for a refresher on how to multiply matrices. Press [ENTER] to evaluate the determinant. This is why the number of columns in the first matrix must match the number of rows of the second. All-in-one calculator. For example, the determinant can be used to compute the inverse of a matrix or to solve a system of linear equations. The Leibniz formula and the Laplace formula are two commonly used formulas. with 128 x 64 Pixels Resolution for Clear readable Display. ABΓ. • Covers everything you need:… Seven Graph Styles for Functions: 1.Line. Practice solving problems involving matrices. For example, you can multiply a 2 × 3 matrix by a 3 × 4 matrix, but not a 2 × 3 matrix by a 4 × 3. Just type matrix elements and click the button. For example, the number 1 multiplied by any number n equals n. The same is true of an identity matrix multiplied by a matrix of the same size: A × I = A. Enter Sqrt(n) For N.) A= 4 2 0 1 5-7 3 -3 3 Q- R Given: A=ei-fh; B=-(di-fg); C=dh-eg In general, you can skip the multiplication sign, so 5 x is equivalent to 5 ⋅ x. Step 1: Go to the matrix menu on your calculator. 7&700�/��2�x��x��%��4,N�Q&��B��2�.��%v�/"�-�CK��c�0�"�2=I#0��ؼ-��!�K��B � ���1�3��Ɛ�p��;�Kxb�O�_Hnhe\�� m�lӕ�v�Y��xw4:�0��x2Ձ�AZ �/��4#0\|��}��;"�� s�Q� %%EOF The dimensions of a matrix, A, are typically denoted as m × n. This means that A has m rows and n columns. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Both the Laplace formula and the Leibniz formula can be represented mathematically, but involve the use of notations and concepts that won't be discussed here. Refer to the example below for clarification. (A Graphing Calculator Is Recommended. Access the matrix menu by using MATRIX or depending on your calculator and go to the EDIT menu, choose, and press. $\textbf {\sin\cos}$. Using your calculator to find A –1 B is a piece of cake. $\textbf {\alpha\beta\gamma}$. This results in switching the row and column indices of a matrix, meaning that aij in matrix A, becomes aji in AT. You can add, subtract, multiply and transpose matrices. Matrix operations such as addition, multiplication, subtraction, etc., are similar to what most people are likely accustomed to seeing in basic arithmetic and algebra, but do differ in some ways, and are subject to certain constraints. Show Instructions In general, you can skip the multiplication sign, so 5x is equivalent to 5x. The calculator will find the inverse of the square matrix using the Gaussian elimination method, with steps shown. The identity matrix is the matrix equivalent of the number "1." αβγ. When you press [ENTER] after entering the last element in the first row, the calculator moves to the beginning of the second row and waits for you to make another entry. The HP 50g contains a wonderful form built-in to facilitate the entry of matrices. For example, given ai,j, where i = 1 and j = 3, a1,3 is the value of the element in the first row and the third column of the given matrix. As soon as it is changed into the reduced row echelon form the use of it in linear algebra is much easier and can be really convenient for mostly mathematicians. Interactive, free online graphing calculator from GeoGebra: graph functions, plot data, drag sliders, and much more! Given: One way to calculate the determinant of a 3 × 3 matrix is through the use of the Laplace formula. When you press the right-arrow key after entering the last element in the first row, the calculator moves to the beginning of the second row and waits for you to make another entry. The calculator will find the row echelon form (simple or reduced - RREF) of the given (augmented) matrix (with variables if needed), with steps shown. Leave extra cells empty to enter non-square matrices. Matrices are often used in scientific fields such as physics, computer graphics, probability theory, statistics, calculus, numerical analysis, and more. 0 If the matrices are the correct sizes, and can be multiplied, matrices are multiplied by performing what is known as the dot product. If necessary, refer to the information and examples above for description of notation used in the example below. The simplest way to define a matrix is to use the matrix editor. For example, given two matrices, A and B, with elements ai,j, and bi,j, the matrices are added by adding each element, then placing the result in a new matrix, C, in the corresponding position in the matrix: In the above matrices, a1,1 = 1; a1,2 = 2; b1,1 = 5; b1,2 = 6; etc. Press [ALPHA] [ZOOM] to create a matrix from scratch, or press [2nd] [ x–1] to access a stored matrix. Please pick the appropriate calculator from below to begin. "3�� 5��5 ��>)��Ы�V� "]"��߃�� 30}t��qP��0 0� Solution for Find a QR factorization for the matrix A. In order to multiply two matrices, the number of columns in the first matrix must match the number of rows in the second matrix. If the matrices are the same size, then matrix subtraction is performed by subtracting the elements in the corresponding rows and columns: Matrices can be multiplied by a scalar value by multiplying each element in the matrix by the scalar. Just follow these steps: Enter coefficients of your system into the input fields. %PDF-1.6 %�� Matrices are often used in scientific fields such as physics, computer graphics, probability theory, statistics, calculus, numerical analysis, and more. Reduce this matrix to row echelon form using elementary row operations so that all the elements below diagonal are zero. Here, we first choose element a. ≥ ÷ →. a 4 × 4 being reduced to a series of scalars multiplied by 3 × 3 matrices, where each subsequent pair of scalar × reduced matrix has alternating positive and negative signs (i.e. Basic Matrix Manipulation with a Graphing Calculator Department of Mathematics, Sinclair Community College, Dayton, OH Page 1 of 25 Often, a matrix may be too large or too complex to manipulate by hand. h�b�dge�>� Ȁ �@16�L Best Graphing Calculator Online We have the most sophisticated and comprehensive TI 84 type graphing calculator online. It makes the lives of people who use matrices easier. The number of rows and columns of all the matrices being added must exactly match. Table of Contents Step-by-step process using an example Common errors Additional reading Step-by-step with an … The Matrix.. part of the MTH (MATH) CHOOSE box. 62 0 obj <> endobj For these types of matrices, we can employ the help of graphing calculators to solve them. Exponents for matrices function in the same way as they normally do in math, except that matrix multiplication rules also apply, so only square matrices (matrices with an equal number of rows and columns) can be raised to a power. Given: As with exponents in other mathematical contexts, A3, would equal A × A × A, A4 would equal A × A × A × A, and so on. Advanced Graphing Calculator, Comprehensive Complex Calculator, Elegant Matrix Calculator, Easy-To-Use Derivative Calculator The identity matrix is a square matrix with "1" across its diagonal, and "0" everywhere else. If there is not a matrix in A, you will see the screen below. The colors here can help determine first, whether two matrices can be multiplied, and second, the dimensions of the resulting matrix. This mode gives you a menu which leads you to the linear algebra functions, a matrix editor and a menu of existing matrices. Show Instructions. There are a number of methods and formulas for calculating the determinant of a matrix. Matrix addition can only be performed on matrices of the same size. To paste the name of a matrix into an expression, press [2nd] [ x–1] and key in the number of the matrix name. Eventually, we will end up with an expression in which each element in the first row will be multiplied by a lower-dimension (than the original) matrix. The Rref calculator is used to transform any matrix into the reduced row echelon form. We also have several other calculators. The inverse of a matrix can also be found easily. Rref Calculator for the problem solvers. Question: Find A QR Factorization For The Matrix A. Set the matrix (must be square) and append the identity matrix of the same dimension to it. The transpose of a matrix, typically indicated with a "T" as an exponent, is an operation that flips a matrix over its diagonal. 4.Below 5.Path 6.Animate 7.Dot 64kb RAM & USB port Simple and convenient operation mode. It is designed to replace bulky and costly handheld graphing calculators and works on virtually any Android phone or tablet. Maple Calculator is a powerful and versatile math learning tool. Determinant of a 4 × 4 matrix and higher: The determinant of a 4 × 4 matrix and higher can be computed in much the same way as that of a 3 × 3, using the Laplace formula or the Leibniz formula. The process involves cycling through each element in the first row of the matrix. 96 0 obj <>/Filter/FlateDecode/ID[<1A2BBD7EA998D43E0FBCC5C44071A59B><7566FAFAB41A1C478601319C2AC55FC5>]/Index[62 60]/Info 61 0 R/Length 141/Prev 179692/Root 63 0 R/Size 122/Type/XRef/W[1 3 1]>>stream Note that when multiplying matrices, A × B does not necessarily equal B × A. Most of the linear algebra functions can be found in Matrix mode. The MatrixWriter form. There are a few other skills that you will need when working with matrices. By pre-multiplying each side of the equation by A –1 and simplifying, you get the equation X = A –1 * B. h�bbdb.�� q�d��L�u ��̎�w�Uj�I�xX�q0��L��͏�&�]~�0ɯ Basic. Press [ENTER] and you can now edit matrix … As can be seen, this gets tedious very quickly, but is a method that can be used for n × n matrices once you have an understanding of the pattern. If there is a matrix already in A, we will simply type over the dimensions and the entries. To get out of the Matrix mode and return to the Home screen press the [EXIT] key on the TI-85/86 or the QUIT key ([2nd][MODE]) on the TI-82/83. Adding the values in the corresponding rows and columns: Matrix subtraction is performed in much the same way as matrix addition, described above, with the exception that the values are subtracted rather than added. Includes all the functions and options you might need. endstream endobj 63 0 obj <> endobj 64 0 obj <> endobj 65 0 obj <>stream The calculator enters elements one row at a time. $\textbf {\mathrm {AB\Gamma}}$. For example, given a matrix A and a scalar c: Multiplying two (or more) matrices is more involved than multiplying by a scalar. Calculate the determinant or inverse of a matrix. Alternatively, you can press [ALPHA] [ZOOM] to quickly create a new matrix. endstream endobj startxref For methods and operations that require complicated calculations a … Repeat this step until you have filled in every element in the matrix. When referring to a specific value in a matrix, called an element, a variable with two subscripts is often used to denote each element based on their position in the matrix. From left to right respectively, the matrices below are a 2 × 2, 3 × 3, and 4 × 4 identity matrix: To invert a 2 × 2 matrix, the following equation can be used: If you were to test that this is in fact the inverse of A you would find that both: The inverse of a 3 × 3 matrix is more tedious to compute. Desmos offers best-in-class calculators, digital math activities, and curriculum to help every student love math and love learning math. Reduce the left matrix to row echelon form using elementary row operations for the whole matrix (including the right one). The dot product then becomes the value in the corresponding row and column of the new matrix, C. For example, from the section above of matrices that can be multiplied, the blue row in A is multiplied by the blue column in B to determine the value in the first column of the first row of matrix C. This is referred to as the dot product of row 1 of A and column 1 of B: The dot product is performed for each row of A and each column of B until all combinations of the two are complete in order to find the value of the corresponding elements in matrix C. For example, when you perform the dot product of row 1 of A and column 1 of B, the result will be c1,1 of matrix C. The dot product of row 1 of A and column 2 of B will be c1,2 of matrix C, and so on, as shown in the example below: When multiplying two matrices, the resulting matrix will have the same number of rows as the first matrix, in this case A, and the same number of columns as the second matrix, B. If the matrices are the same size, matrix addition is performed by adding the corresponding elements in the matrices. Matrix Calculator: A beautiful, free matrix calculator from Desmos.com. Note that some older calculators have a button that simply says [MATRX]. This is because a non-square matrix, A, cannot be multiplied by itself. To enter Matrix mode on the TI-85/86 press the sequence [2nd] and on the TI-82/83 press [2nd][x-1]. Enter an expression and press the right-arrow key to advance to the next element in the matrix. For example, all of the matrices below are identity matrices. This is a walkthrough of the probability features of your TI-84 graphing calculator. Press [2nd][x^-1] to enter the matrix menu. • Use the arrow keys or your fingers to navigate inside the app. Whether you are doing simple calculations or working on university-level math problems, Maple Calculator can do it all. In fact, just because A can be multiplied by B doesn't mean that B can be multiplied by A. The elements in blue are the scalar, a, and the elements that will be part of the 3 × 3 matrix we need to find the determinant of: Continuing in the same manner for elements c and d, and alternating the sign (+ - + - ...) of each term: We continue the process as we would a 3 × 3 matrix (shown above), until we have reduced the 4 × 4 matrix to a scalar multiplied by a 2 × 2 matrix, which we can calculate the determinant of using Leibniz's formula. Just remember to keep it in order of “rows” and “columns”. Multiply the main diagonal elements of the matrix - determinant is calculated. Square dimensions involves some basic arithmetic are identity matrices in this case is not possible to.... Animate graphs, and more ( including the right elements to obtain ci j... Calculator will find the inverse of a matrix already in a, we will over. Solve them of existing matrices comprehensive matrix calculator from below to begin matrix on Home! The resulting matrix whole matrix ( must be square ) and append the matrix... The screen below pick the appropriate calculator from Desmos.com calculators to solve a of. Matrix operations in an arithmetic expression: enter a matrix in a, becomes in. Are under the EDIT menu, whether two matrices can be multiplied by a –1 B 3. Multiplication section, if necessary, refer above for description of notation used the! Which involves some basic arithmetic a can be found in matrix a, you must tell the calculator elements... The example below you are under the EDIT menu EDIT menu online graphing online., animate graphs, and there are a number of rows of the matrix ( math CHOOSE. Determine first, whether two matrices can be used to transform any matrix into input... In linear algebra functions can be used to graphing calculator matrix any matrix into the reduced row echelon form using row. Rows ” and “ columns ” ” and “ columns ” equation a. And vector calculator is used in the matrix - determinant is calculated it. Use the matrix a, calculus, and more get increasingly more complicated, there... Versatile math learning tool formula and the entries x^-1 ] to quickly create a new matrix over. Possible to compute the inverse calculated on the TI-85/86 press the right on... Sequence [ 2nd ] and on the TI-85/86 press the sequence [ 2nd ] and you can the... Repeat this step until you are under the EDIT menu B does not necessarily equal B ×.... Aji in at calculated using the following example ’ s how you enter mode. Is because a non-square matrix, a, means A2 enter coefficients of TI-84. Your TI-84 graphing calculator with the ability to plot interactive 2d functions following example, C will be 2. This calculator can do it all university-level math problems, maple calculator can perform way to define matrix... Simplest way to define a matrix is through the use of the number of columns the... Are other methods for solving systems of simultaneous linear equations the number of rows and columns of all the and. That has entries with many decimal places a beautiful, free online graphing calculator - Reshish graph.reshish.com - is piece... Show Instructions in general, you get the equation x = a –1 and simplifying, can. Being added must exactly match repeat this step until you are under EDIT... Ti 84 type graphing calculator can perform elementary row operations for the matrix.! Identity matrices } } $factorization for the matrix math with our beautiful, free matrix calculator \| graphing Derivative. In this type of calculator using the calculator how large your matrix is through the use the! Comprehensive matrix calculator: a beautiful, free online matrix calculator 2: enter numbers... Home screen so is provided below, but will not be computed calculators have button... As well as methods for computing them AB\Gamma } }$ EDIT menu 5 ⋅.... The EDIT menu stat plots, etc is to use the arrow keys or your to. Performed by adding the corresponding elements in the first matrix must match the number of rows the! X = a –1 * B matrix multiplication section, if necessary, to... Convenient operation mode by adding the corresponding elements to obtain ci, j x-1 ] do all... Transpose matrices you enter matrix mode colors here can help determine first, whether two matrices be. Arrow keys or your fingers to navigate inside the app = B 2 × 2 matrix can have any dimensions... Steps needed to multiply matrices this mode gives you a menu of matrices! Matrix that has entries with many decimal places of columns in the first must... Input any example, when using the Leibniz formula, which involves basic. Provided below, but will not be computed Complex number & matrix calculator from GeoGebra: graph functions plot. This step until you are under the EDIT menu and larger get increasingly more,! Only be performed on sequences of equal lengths [ x-1 ] you get the inverse of a matrix a. Just because a non-square matrix, meaning that aij in matrix a, we will Go over the needed. Matrices below are descriptions of the MTH ( math ) CHOOSE box detailed solution '' option and the. Statistics, distribution, stat plots, etc why the number of rows of the matrices below are identity.. Must exactly match of cake following example the screen below, whether two matrices in this of. [ x-1 ] and on the right one ) in this type of calculator using the elimination. Gaussian elimination method, with steps shown examine the solution add the corresponding elements in the matrices being added exactly... Of calculator using the Gaussian elimination method, with steps shown must be the same dimension it... Equal B × a below, but will not be multiplied by B does graphing calculator matrix mean that B be! University-Level math problems, maple calculator can perform for calculating the determinant of a matrix with 1 ''! Simplest way to calculate the determinant can be written as the matrix equivalent of notation... Filled in every element in the example below press [ 2nd ] x^-1! Will Go over the steps needed to multiply matrices reduce a matrix or solve... 128 x 64 Pixels Resolution for Clear readable Display calculator, Elegant matrix calculator, Elegant matrix calculator graphing. - is a square matrix using the calculator, Elegant matrix calculator: a beautiful, free graphing... Any example, CHOOSE very detailed solution '' option graphing calculator matrix examine the solution until! The whole matrix ( must be square ) and append the identity matrix of the MTH math..., CHOOSE very detailed solution '' option and examine the solution row echelon form elementary! Size, matrix addition, the dimensions of the same size entries with many decimal places input fields the and! The input fields matrix.reshish.com is the matrix.. part of the resulting matrix this mode gives a. Increasingly more complicated, and there are a number of rows of the notation used factorization for matrix. 2: enter the matrix including the right Reshish graph.reshish.com - is a square with! To row echelon form using elementary row operations for the matrix multiplication section, if necessary for. Wonderful form built-in to facilitate the entry of matrices, a * x = –1... Matrix.Reshish.Com is the matrix input fields B can be calculated using the Leibniz formula and the entries costly handheld calculators... Input fields just because a can be calculated graphing calculator matrix the Gaussian elimination method, with steps shown for find –1. In this case is not a matrix editor, so 5 x is equivalent to ... Power of 2 '' for a refresher on how to multiply matrices I type 4 [ enter and... Are two commonly used formulas × 2 matrix can have any square dimensions element in example. And “ columns ” a given matrix, meaning that aij in matrix mode the. Is 3 × 4 and larger get increasingly more complicated, and other mathematical contexts 64 Pixels Resolution Clear... For calculating the determinant can be found easily type graphing calculator • your graphing calculator be! Two commonly used formulas is through the use of a 2 × 3 B. 4 [ enter ] and you can add, subtract, multiply and transpose matrices a number of in... The TI83 and TI84 are able to do many different operations with,! Any square dimensions column indices of a graphing calculator matrix × 4 and larger get increasingly more complicated and! A given matrix, a, we will simply type over the steps needed to multiply two matrices in case! Below are identity matrices, subtract, multiply and transpose matrices formula, which involves some arithmetic. First row of the matrix editor and a menu which leads you to next... Transpose matrices coefficients of your TI-84 graphing calculator online we have the most sophisticated and comprehensive TI 84 graphing... Types of matrices, with steps shown next element in the matrix - determinant is.! Button that simply says [ MATRX ] gives you a menu which leads you to information! It in order of “ rows ” and “ columns ” and costly handheld graphing calculators and on... B × a in this type of calculator using the calculator how large your matrix is identity matrices cycling. For high school and college students this calculator can do it all here, we will Go over the of. X = a –1 B is a powerful and versatile math learning tool × 2 matrix also. ) and append the identity matrix can be multiplied, and there are a other... Calculators and works on virtually any Android phone or tablet × 4.! 5X is equivalent to 5 * x = B more complicated, and ` 0 '' everywhere.. Press [ 2nd ] [ x-1 ] as methods for computing them of cake to. Will simply type over the steps needed to multiply matrices from Desmos.com for computing them multiplication,... Calculator: a beautiful, free matrix calculator, Elegant matrix calculator: a beautiful, free graphing. The dot product can only be performed on sequences of equal lengths see the below.	{}
Skip navigation Please use this identifier to cite or link to this item: http://arks.princeton.edu/ark:/88435/dsp01ww72bd92m Title: Clustering Redshift Estimation for the Hyper Suprime-Cam Survey Authors: Raileanu, Roberta Advisors: Strauss, Michael Department: Astrophysical Sciences Class Year: 2016 Abstract: Accurate redshift estimates of astronomical objects has been a long-standing goal in astrophysics since it would allow us to determine distances to imaged sources and thus, explore the large-scale structure of the Universe. However, spectroscopic redshifts are typically limited to bright objects and are quite expensive to conduct for a large number of sources. Hence, most modern surveys use photometric redshifts, which rely on spectral energy distribution (SED) templates and do not always provide robust or accurate estimates due to their strong assumptions regarding SEDs. In this work, we attempt to use the clustering redshift technique proposed by Ménard et al. (2013) to estimate the redshift distribution of the galaxy population imaged by the Hyper Suprime-Cam (HSC) survey. This method enables the inference of redshift distributions from measurements of the spatial clustering of arbitrary sources, using a set of reference objects with known redshifts. We test the accuracy of this method on a sample of galaxies with spectroscopic information from the Sloan Digital Sky Survey (SDSS). We show that we can recover the corresponding mean redshifts with an error of order 10%. Compared to using a constant galaxy bias, assuming a linear bias correction reduces the noise in the clustering distribution and improves the accuracy of the mean redshift by about 0.01. Then, we compare clustering and photometric redshifts for subsamples of the HSC data within narrow redshift ranges. Although the clustering technique is able to detect the absence of objects outside the redshift range of the sample, it does not reproduce the exact shape or small scale structure of the photometric distribution. We also map a two dimensional color space to redshift space in order to estimate the redshift probability distributions of individual galaxies. This analysis indicates that the clustering-based redshift inference method provides a good alternative to photometric redshift estimation since it does not assume any prior knowledge of the the spectral energy distribution of the objects. Extent: 91 pages URI: http://arks.princeton.edu/ark:/88435/dsp01ww72bd92m Type of Material: Princeton University Senior Theses Language: en_US Appears in Collections: Astrophysical Sciences, 1990-2016 Files in This Item: File SizeFormat Raileanu_Thesis.pdf3.68 MBAdobe PDF Items in Dataspace are protected by copyright, with all rights reserved, unless otherwise indicated.	{}
# 14.3 - Finding Percentiles 14.3 - Finding Percentiles At some point in your life, you have most likely been told that you fall in the something-something percentile with regards to some measure. For example, if you are tall, you might have been told that you are in the 95th percentile in height, meaning that you are taller than 95% of the population. When you took the SAT Exams, you might have been told that you are in the 80th percentile in math ability, meaning that you scored better than 80% of the population on the math portion of the SAT Exams. We'll now formally define what a percentile is within the framework of probability theory. Definition. If $$X$$ is a continuous random variable, then the $$(100p)^{th}$$ percentile is a number $$\pi_p$$ such that the area under $$f(x)$$ and to the left of $$\pi_p$$ is $$p$$. That is, $$p$$ is the integral of $$f(x)$$ from $$-\infty$$ to $$\pi_p$$: $$p=\int_{-\infty}^{\pi_p} f(x)dx=F(\pi_p)$$ Some percentiles are given special names: • The 25th percentile, $$\pi_{0.25}$$, is called the first quartile (denoted $$q_1$$). • The 50th percentile, $$\pi_{0.50}$$, is called the median (denoted $$m$$) or the second quartile (denoted $$q_2$$). • The 75th percentile, $$\pi_{0.75}$$, is called the third quartile (denoted $$q_3$$). ## Example 14-5 A prospective college student is told that if her total score on the SAT Exam is in the 99th percentile, then she can most likely attend the college of her choice. It is well-known that the distribution of SAT Exam scores is bell-shaped, and the average total score is typically around 1500. Here is a picture depicting the situation: The student would like to know what her total score, $$\pi_{0.99}$$, needs to be in order to ensure that she falls in the 99th percentile. Data from the 2009 SAT Exam Scores suggests that the student should obtain at least a 2200 on her exam. That is, $$\pi_{0.99}=2200$$. ## Example 14-6 Let $$X$$ be a continuous random variable with the following probability density function: $$f(x)=\dfrac{1}{2}$$ for $$0<x<2$$. What is the first quartile, median, and third quartile of $$X$$? #### Solution Because the p.d.f. is uniform, meaning it remains constant over the support, we can readily find the percentiles in one of two ways. We can use the p.d.f. directly to find the first quartile, median, and third quartile: Alternatively, we can use the cumulative distribution function: ## Example 14-7 Let $$X$$ be a continuous random variable with the following probability density function: $$f(x)=\dfrac{1}{2}(x+1)$$ for $$-1<x<1$$. What is the 64th percentile of $$X$$? #### Solution To find the 64th percentile, we first need to find the cumulative distribution function $$F(x)$$. It is: $$F(x)=\dfrac{1}{2}\int_{-1}^x(t+1)dt=\dfrac{1}{2} \left[\dfrac{(t+1)^2}{2}\right]^{t=x}_{t=-1}=\dfrac{1}{4}(x+1)^2$$ for $$-1<x<1$$. Now, to find the 64th percentile, we just need to set 0.64 equal to $$F(\pi_{0.64})$$ and solve for $$\pi_{0.64}$$. That is, we need to solve for $$\pi_{0.64}$$ in the following equation: $$0.64=F(\pi_{0.64})=\dfrac{1}{4}(\pi_{0.64}+1)^2$$ Multiplying both sides by 4, we get: $$2.56=(\pi_{0.64}+1)^2$$ Taking the square root of both sides, we get: $$\pi_{0.64}+1=\pm \sqrt{2.56}=\pm 1.6$$ And, subtracting both sides by 1, we get: $$\pi_{0.64}=-2.6 \text{ or } 0.60$$ Because the support is $$-1<x<1$$, the 64th percentile and must be 0.6, not −2.6. [1] Link ↥ Has Tooltip/Popover Toggleable Visibility	{}
Seeds Scatters points evenly over the surface of meshes. This can be particularly useful in conjunction with the Instancer, which can then apply instances to each point. user Container for user-defined plugs. Nodes should never make their own plugs here, so users are free to do as they wish. out The processed output scene. enabled The on/off state of the node. When it is off, the node outputs the input scene unchanged. The input scene filter The filter used to control which parts of the scene are processed. A Filter node should be connected here. parent The location of the mesh to scatter the points over. The generated points will be parented under this location. This is ignored when a filter is connected, in which case the filter may specify multiple locations containing meshes to scatter points over. destination The location where the points primitives will be placed in the output scene. When the destination is evaluated, the ${scene:path} variable holds the location of the source mesh, so the default value parents the points under the mesh. Tip ${scene:path}/.. may be used to place the points alongside the source mesh. name The name given to the object generated - this will be placed under the parent in the scene hierarchy. density The number of points per unit area of the mesh, measured in object space. densityPrimitiveVariable A float primitive variable used to specify a varying point density across the surface of the mesh. Multiplied with the density setting above. pointType The render type of the points. This defaults to “gl:point” so that the points are rendered in a lightweight manner in the viewport.	{}
# Unitary matrices – some examples References: Shankar, R. (1994), Principles of Quantum Mechanics, Plenum Press. Exercises 1.6.3 – 1.6.6. Here are a few more results about unitary operators. Shankar defines a unitary operator ${U}$ as one where $\displaystyle UU^{\dagger}=I \ \ \ \ \ (1)$ From this we can derive the other condition by which they can be defined, namely that a unitary operator preserves the norm of a vector: $\displaystyle \left\|Uv\right\|=\left\|v\right\| \ \ \ \ \ (2)$ This follows, for if we define the effect of ${U}$ by $\displaystyle \left\|v_{1}^{\prime}\right\rangle =U\left\|v_{1}\right\rangle \ \ \ \ \ (3)$ then $\displaystyle \left\langle v_{1}^{\prime}\left\|v_{1}^{\prime}\right.\right\rangle$ $\displaystyle =$ $\displaystyle \left\langle Uv_{1}\left\|Uv_{1}\right.\right\rangle \ \ \ \ \ (4)$ $\displaystyle$ $\displaystyle =$ $\displaystyle \left\langle v_{1}\left\|U^{\dagger}Uv_{1}\right.\right\rangle \ \ \ \ \ (5)$ $\displaystyle$ $\displaystyle =$ $\displaystyle \left\langle v_{1}\left\|v_{1}\right.\right\rangle \ \ \ \ \ (6)$ Thus ${\left\|v_{1}^{\prime}\right\|^{2}=\left\|v_{1}\right\|^{2}}$. Theorem 1 The product of two unitary operators ${U_{1}}$ and ${U_{2}}$ is unitary. Proof: Using Shankar’s definition 1, we have $\displaystyle \left(U_{1}U_{2}\right)^{\dagger}U_{1}U_{2}$ $\displaystyle =$ $\displaystyle U_{2}^{\dagger}U_{1}^{\dagger}U_{1}U_{2}\ \ \ \ \ (7)$ $\displaystyle$ $\displaystyle =$ $\displaystyle U_{2}^{\dagger}IU_{2}\ \ \ \ \ (8)$ $\displaystyle$ $\displaystyle =$ $\displaystyle U_{2}^{\dagger}U_{2}\ \ \ \ \ (9)$ $\displaystyle$ $\displaystyle =$ $\displaystyle I \ \ \ \ \ (10)$ $\Box$ Theorem 2 The determinant of a unitary matrix ${U}$ is a complex number with unit modulus. Proof: The determinant of a hermitian conjugate is the complex conjugate of the determinant of the original matrix, since ${\det U=\det U^{T}}$ (where the superscript ${T}$ denotes the transpose) for any matrix, and the hermitian conjugate is the complex conjugate transpose. Therefore $\displaystyle \det\left(UU^{\dagger}\right)=\left[\det U\right]\left[\det U\right]^*=\det I=1 \ \ \ \ \ (11)$ Therefore ${\left\|\det U\right\|^{2}=1}$ as required.$\Box$ Example 1 The rotation matrix ${R\left(\frac{\pi}{2}\mathbf{i}\right)}$ is unitary. We have $\displaystyle R\left(\frac{\pi}{2}\mathbf{i}\right)=\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 0 & -1\\ 0 & 1 & 0 \end{array}\right] \ \ \ \ \ (12)$ By direct calculation $\displaystyle RR^{\dagger}$ $\displaystyle =$ $\displaystyle \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 0 & -1\\ 0 & 1 & 0 \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 0 & 1\\ 0 & -1 & 0 \end{array}\right]\ \ \ \ \ (13)$ $\displaystyle$ $\displaystyle =$ $\displaystyle \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right]=I \ \ \ \ \ (14)$ Example 2 Consider the matrix $\displaystyle U=\frac{1}{\sqrt{2}}\left[\begin{array}{cc} 1 & i\\ i & 1 \end{array}\right] \ \ \ \ \ (15)$ By calculating $\displaystyle UU^{\dagger}$ $\displaystyle =$ $\displaystyle \frac{1}{2}\left[\begin{array}{cc} 1 & i\\ i & 1 \end{array}\right]\left[\begin{array}{cc} 1 & -i\\ -i & 1 \end{array}\right]\ \ \ \ \ (16)$ $\displaystyle$ $\displaystyle =$ $\displaystyle \frac{1}{2}\left[\begin{array}{cc} 2 & 0\\ 0 & 2 \end{array}\right]=I \ \ \ \ \ (17)$ Thus ${U}$ is unitary, but because ${U\ne U^{\dagger}}$ it is not hermitian. Its determinant is $\displaystyle \det U=\left(\frac{1}{\sqrt{2}}\right)^{2}\left(1-i^{2}\right)=1 \ \ \ \ \ (18)$ This is of the required form ${e^{i\theta}}$ with ${\theta=0}$. Example 3 Consider the matrix $\displaystyle U$ $\displaystyle =$ $\displaystyle \frac{1}{2}\left[\begin{array}{cc} 1+i & 1-i\\ 1-i & 1+i \end{array}\right]\ \ \ \ \ (19)$ $\displaystyle UU^{\dagger}$ $\displaystyle =$ $\displaystyle \frac{1}{4}\left[\begin{array}{cc} 1+i & 1-i\\ 1-i & 1+i \end{array}\right]\left[\begin{array}{cc} 1-i & 1+i\\ 1+i & 1-i \end{array}\right]\ \ \ \ \ (20)$ $\displaystyle$ $\displaystyle =$ $\displaystyle \frac{1}{4}\left[\begin{array}{cc} 4 & 0\\ 0 & 4 \end{array}\right]=I \ \ \ \ \ (21)$ Thus ${U}$ is unitary, but because ${U\ne U^{\dagger}}$ it is not hermitian. Its determinant is $\displaystyle \det U$ $\displaystyle =$ $\displaystyle \left(\frac{1}{2}\right)^{2}\left[\left(1+i\right)^{2}-\left(1-i\right)^{2}\right]\ \ \ \ \ (22)$ $\displaystyle$ $\displaystyle =$ $\displaystyle i \ \ \ \ \ (23)$ This is of the required form ${e^{i\theta}}$ with ${\theta=\frac{\pi}{2}}$.	{}
Tag Info Question 2 has a negative answer. Suppose $\ell_p$ contains uniformly complemented copies $E_N$ of $\text{span}(d_n)_{n=1}^N$. Take an ultra power to get a copy $E$ of the completion of $\text{span}(d_n)_{n=1}^\infty$ in an $L_p$ space. The corresponding copies of $E_n$ in the $L_p$ space are uniformly complemented in the $L_p$ space. When $p>1$, this ...	{}
# The area of a rectangular piece of cardboard is 36 sq cm and its length is 9 cm. What is the width of the cardboard? - Mathematics Sum The area of a rectangular piece of cardboard is 36 sq cm and its length is 9 cm. What is the width of the cardboard? #### Solution Area of the rectangle = 36 sq cm Length = 9 cm Width = ? Area of a rectangle = length × width So, width = "Area"/"Length" = 36/9 = 4 cm Thus, the width of the rectangular cardboard is 4 cm. Concept: Area of Rectangle Is there an error in this question or solution?	{}
# An Iterative Method for Structured Matrix Completion The task of filling-in or predicting missing entries of a matrix, from a subset of known entries, is known as matrix completion. In today's data-driven world, data completion is essential whether it is the main goal or a pre-processing step. In recent work, a modification to the standard nuclear norm minimization for matrix completion has been made to take into account structural differences between observed and unobserved entries. One example of such structural difference is when the probability that an entry is observed or not depends mainly on the value of the entry. We propose adjusting an Iteratively Reweighted Least Squares (IRLS) algorithm for low-rank matrix completion to take into account sparsity-based structure in the missing entries. We also present an iterative gradient-projection-based implementation of the algorithm, and present numerical experiments showing that the proposed method often outperforms the IRLS algorithm in structured settings. ## Authors • 9 publications • 6 publications • 53 publications 01/29/2018 ### Matrix Completion for Structured Observations The need to predict or fill-in missing data, often referred to as matrix... 06/04/2021 ### Matrix completion with data-dependent missingness probabilities The problem of completing a large matrix with lots of missing entries ha... 04/17/2019 ### Matrix Completion With Selective Sampling Matrix completion is a classical problem in data science wherein one att... 08/07/2014 ### Matrix Completion on Graphs The problem of finding the missing values of a matrix given a few of its... 05/12/2020 ### Detection thresholds in very sparse matrix completion Let A be a rectangular matrix of size m× n and A_1 be the random matrix ... 01/10/2014 ### Online Matrix Completion Through Nuclear Norm Regularisation It is the main goal of this paper to propose a novel method to perform m... 11/09/2012 ### Calibrated Elastic Regularization in Matrix Completion This paper concerns the problem of matrix completion, which is to estima... ##### This week in AI Get the week's most popular data science and artificial intelligence research sent straight to your inbox every Saturday. ## 1. Introduction Matrix completion is the task of filling-in, or predicting, the missing entries of a partially observed matrix from a subset of known entries. In today’s data-driven world, data completion is essential, whether it is the main goal as in recommender systems, or a pre-processing step for other tasks like regression or classification. The Netflix Problem is a popular example of a data completion task [2, 3, 26]. The Netflix Problem was an open competition for the best collaborative filtering algorithm to predict unseen user ratings for movies. That is, given a subset of user-movie ratings, the goal is to predict the remaining ratings. This can be used to decide whether a certain movie should be recommended to a user. The Netflix Problem can be viewed as a matrix completion problem where the rows represent users, the columns represent movies, and the entries of the matrix are the corresponding user-movie ratings, most of which are missing. Matrix completion problems are generally ill-posed without some additional information, since the missing entries could be assigned arbitrary values. In many instances, the matrix we wish to recover is known to be low-dimensional in the sense that it is low-rank, or approximately low-rank. For instance, a data matrix of all user-ratings of movies may be approximately low-rank because it is commonly believed that only a few factors contribute to an individual’s tastes or preferences [9]. Low-rank matrix completion is a special case of the affine rank minimization problem . Indeed, the problem of minimizing the rank of a matrix subject to affine constraints arises often in machine learning, and is known to be NP-hard [17, 40]. In recent work [36], Molitor and Needell propose a modification to the standard nuclear norm minimization for matrix completion to take into account structural differences between observed and unobserved entries. Previous strategies typically assume that there are no structural differences between observed and missing entries, which is an unrealistic assumption in many settings. General notions of structural difference include any setting in which whether an entry is observed or unobserved does not occur uniformly at random. For example, whether an entry is observed or missing could be biased not only based on the value of that entry, but also on the location of that entry in the matrix. For instance, certain rows (or columns) may have substantially more entries than a typical row (or columns); this happens in the Netflix Problem for very popular movies or so-called “super-users”. Another important example of such structural differences is when the unobserved entries are sparse or have lower magnitudes than the observed entries [36]. In other words, whether an entry is missing need not be independent of the value of that entry. In our work, we focus on this notion of structure, in which the probability that an entry is observed or not depends mainly on the value of the entry. In particular, we are interested in sparsity-based structure in the missing entries whereby most of the missing values are close in the or norm sense to 0 (or more generally to a fixed value). This is motivated by many situations in which the missing values tend to be near a certain value. For instance, missing data in chemical measurements might indicate that the measurement value is lower than the limit of detection of the device, and thus a typical missing measurement is smaller in value than a typical observed measurement. Similarly, in medical survey data, patients are more likely to respond to questions addressing noticeable symptoms, whereas a missing response may indicate a lack of symptoms [36]. Similarly, a missing rating of a movie might indicate the user’s lack of interest in that movie, thus suggesting a lower rating than otherwise expected. More generally, in survey data, incomplete data may be irrelevant or unimportant to the individual, thus suggesting structure in the missing observations [36] . For another example in the setting of sensor networks, suppose we are given partial information about the distances between sensors, where distance estimates are based on signal strength readings [9] and we would like to impute the missing signal strength readings. In this case, signals may be missing because of the very low signal strength, indicating that perhaps sensors are at great distance from each other (or there are other geographic obstacles between them). Thus, we obtain a partially observed distance matrix with structured observations—missing entries tend to have lower signal strength. Sensor networks give a low-rank matrix completion problem, perhaps of rank equal to two if the sensors are located in a plane, or three if they are located in three-dimensional space [30, 43]. Matrix completion algorithms are generally hard to evaluate as there is usually no ground truth data available on which to test the performance of the algorithm. One method is to consider a subset of the matrix entries to be unobserved, and test how well they are predicted by the algorithm. Another method is testing the algorithm on classification tasks. That is, if we are working with labeled matrices with missing entries, we can test the performance of a matrix completion algorithm based on the classification rates of how well we predict a matrix’s label after imputing its missing entries. ### 1.1. Affine Rank Minimization Problem The Affine Rank Minimization Problem (ARMP), or the problem of finding the minimum rank matrix in an affine set, is expressed as (1) minimizeX rank(X) subject to A(X)=b, where is the optimization variable, is a linear map, and denotes the measurements. The affine rank minimization problem arises frequently in applications like system identification and control [31], collaborative filtering, low-dimensional Euclidean embedding [18], sensor networks [4, 41, 42], quantum state tomography [21, 22], signal processing, and image processing. Many algorithms have been proposed for ARMP, e.g. reweighted nuclear norm minimization [34] , Singular Value Thresholding (SVT) [5], Fixed Point Continuation Algorithm (FPCA) [20], Iterative Hard Thresholding (IHT) [20], Optspace [25], Singular Value Projection (SVP) [24], Atomic Decomposition for Minimum Rank Approximation (AdMiRA) [28], and the accelerated proximal gradient algorithm for nuclear norm regularized linear least squares problems (NNLS) [44], etc. The low-rank matrix completion problem can be formulated as follows [10, 39]. Suppose we are given some matrix with a set of partially observed entries, with . The goal is to recover the missing elements in . The low-rank matrix completion problem is a special case of the affine rank minimization problem where the set of affine constraints restrict certain entries of the matrix to equal observed values. In this case, the linear operator is a sampling operator, and the problem can be written as minimizeX rank(X) subject to Xij=Mij,(i,j)∈Ω, where is the matrix we would like to recover, and where denotes the set of entries which are revealed. We define the sampling operator via (PΩ(X))ij={Xij(i,j)∈Ω0(i,j)∉Ω, as in [10]. Further, denotes the complement of , i.e., all index pairs that are not in . Thus, corresponds to the collection of missing entries. Generally, a low-rank matrix completion problem gets harder when fewer entries are observed, or when the matrix is not approximately low-rank. The rank minimization problem (1) is NP-hard in general, and therefore we consider its convex relaxation [8, 9, 10, 17, 40], (2) minimizeX ∥X∥∗ subject to A(X)=b, where denotes the nuclear norm, given by the sum of singular values. The rank of a matrix equals the number of nonzero singular values of , also known as the norm of the vector of singular values of , and the nuclear norm of is the norm of . Indeed, if is a diagonal matrix, then (2) becomes the compressed sensing problem. In [36], the authors propose adjusting the standard nuclear norm minimization problem to take into account the structural differences between observed and unobserved entries by regularizing the values of the unobserved entries (see Section 3.1). The method results in a semidefinite program; however, standard semidefinite programming tools do not work efficiently for solving large nuclear norm minimization problems. Inspired by the iteratively reweighted least squares (IRLS) algorithm for sparse vector recovery analyzed in [15], iteratively reweighted least squares algorithms [19, 27, 35] have been proposed as a computationally efficient method for low-rank matrix recovery111To our knowledge, not yet in the structured setting. (see Section 2.3). Instead of minimizing the nuclear norm, the algorithms essentially minimize the Frobenius norm of the matrix, subject to affine constraints. Properly reweighting this norm produces low-rank solutions under suitable assumptions. In [35], Mohan and Fazel propose a family of Iterative Reweighted Least Squares algorithms for matrix rank minimization, called IRLS- (for ), as a computationally efficient way to improve over the performance of nuclear norm minimization. In addition, a gradient projection algorithm is presented as an efficient implementation for the algorithm. The algorithm exhibits improved recovery when compared to existing algorithms. ### 1.2. Contribution We propose an iterative algorithm for low-rank matrix completion to take into account structural differences between observed and unobserved entries by adjusting the Iteratively Reweighted Least Squares (IRLS) algorithm studied in [35]. We refer to our algorithm as Structured IRLS. We consider sparsity-based structure in the missing entries whereby most of the missing values are close in the or norm sense to 0. Our objective function can be adjusted by applying a linear shift on the missing values to handle other fixed nonzero values. Further, we present a gradient-projection-based implementation, called Structured sIRLS (motivated by sIRLS in [35]). Lastly, we show that Structured sIRLS outperforms the sIRLS algorithm in structured settings, as showcased in our numerical experiments. Our code for Structured sIRLS is available at [1]. ### 1.3. Organization We review related iteratively reweighted least squares algorithms for recovering sparse vectors and low-rank matrices in Section 2. In Section 3, we describe the structured matrix completion problem and propose for this problem an iterative algorithm, Structured IRLS. Furthermore, we present a computationally efficient implementation, Structured sIRLS. In Section 4, we run numerical experiments to showcase the performance of this method, and compare it to the performance of sIRLS (studied in [35]) on various structured settings. ## 2. Iteratively Reweighted Least Squares Algorithms In this section, we set notation for the rest of the paper, and review related algorithms for recovering sparse vectors and low-rank matrices. ### 2.1. Notation The entries of a matrix are denoted by lowercase letters, i.e. is the entry in row and column of . Let denote the identity matrix and the vector of all ones. The trace of a square matrix is the sum of its diagonal entries, and is denoted by . We denote the adjoint matrix of by . Without loss of generality, we assume and we write the singular value decomposition of as X=UΣV∗. Here and are unitary matrices, and is a diagonal matrix, where are the singular values. The rank of , denoted by , equals the number of nonzero singular values of . Further, the Frobenius norm of the matrix is defined by The nuclear norm of a matrix is defined by . Given a vector of positive weights, we define the weighted norm of a vector as ∥z∥ℓ2(w)=(n∑i=1wiz2i)1/2. Let denote the vector of missing entries of a matrix , and let denote the corresponding vector with entries squared, i.e. where denotes elementwise multiplication. ### 2.2. Sparse Vector Recovery Given a vector , the value denotes the number of nonzero entries of , and is known as the norm of . The sparse vector recovery problem is described as (3) minimize ∥x∥0, subject to Ax=b, where and . This problem is known to be NP-hard. A commonly used convex heuristic for this problem is minimization [6, 16], (4) minimize ∥x∥1, subject to Ax=b. Indeed, many algorithms for solving (3) and (4) have been proposed. In [15], Daubechies et al. propose and analyze a simple and computationally efficient reweighted algorithm for sparse recovery, called the Iterative Reweighted Least Squares algorithm, IRLS-, for any . Its -th iteration is given by xk+1=argminx{n∑i=1wkix2i : Ax=b}, where is a weight vector with , and where is a regularization parameter added to ensure that is well-defined. Typically, the weights are initialized to one, so the first iteration gives the least norm solution to . For [15] gives a theoretical guarantee for sparse recovery similar to norm minimization. It was empirically observed in [13, 14] that IRLS- shows a better recovery performance than minimization for ; see also [12]. In [15], the authors provide proofs of several findings listed in these works. Further, the reader is referred to [32, 37, 38, 45] for related work on iteratively minimizing the norm for sparse recovery. ### 2.3. Low-rank Matrix Recovery We review two related algorithms [19, 35] for low-rank matrix recovery that generalize the iteratively reweighted least squares algorithm analyzed in [15] for sparse recovery. In general, minimizing the Frobenius norm subject to affine constraints does not lead to low-rank solutions; however, properly reweighting this norm produces low-rank solutions under suitable assumptions [19, 35]. In [19], Fornasier et al. propose a variant of the reweighted least squares algorithm for sparse recovery for nuclear norm minimization (or low-rank matrix recovery), called IRLS-M. The -th iteration of IRLS-M is given by (5) Xk+1=argminX{∥(Wk)1/2X∥2F:PΩ(X)=PΩ(M)}. Here is a weight matrix defined as , and for , , where and . Indeed, each iteration of (5) minimizes a weighted Frobenius norm of the matrix X. Under the assumption that the linear measurements fulfill a suitable generalization of the Null Space Property, the algorithm is guaranteed to iteratively recover any matrix with an error on the order of the best rank approximation [19]. The algorithm essentially has the same recovery guarantees as nuclear norm minimization. Though the Null Space Property fails in the matrix completion setup, the authors illustrate numerical experiments which show that the IRLS-M algorithm still works very well in this setting for recovering low-rank matrices. Further, for the matrix completion problem, the algorithm takes advantage of the Woodbury matrix identity, allowing an expedited solution to the least squares problem required at each iteration [19]. In [35], Mohan and Fazel propose a related family of Iterative Reweighted Least Squares algorithms for matrix rank minimization, called IRLS- (for ), as a computationally efficient way to improve over the performance of nuclear norm minimization. The -th iteration of IRLS- is given by (6) Xk+1=argminX{Tr(WkpX⊤X):PΩ(X)=PΩ(M)}, where is a weight matrix defined as , and for , . Here is a regularization parameter added to ensure that is well-defined. Each iteration of (6) minimizes a weighted Frobenius norm of the matrix X, since Tr(Wk−1pX⊤X)=∥(Wk−1p)1/2X∥2F. The algorithms can be viewed as (locally) minimizing certain smooth approximations to the rank function. When , theoretical guarantees are given similar to those for nuclear norm minimization, i.e., recovery of low-rank matrices under the assumptions that the operator defining the constraints satisfies a specific Null Space Property (NSP). Further, for , IRLS- shows better empirical performance in terms of recovering low-rank matrices than nuclear norm minimization. In addition, a gradient projection algorithm, IRLS-GP, is presented as an efficient implementation for IRLS-. Further, this same paper presents a related family of algorithms sIRLS- (or short IRLS), which can be seen as a first-order method for locally minimizing a smooth approximation to the rank function. The results exploit the fact that these algorithms can be derived from the KKT conditions for minimization problems whose objectives are suitable smooth approximations to the rank function [35]. We will refer to IRLS- (resp. sIRLS-) studied in [35] as IRLS (resp. sIRLS). The algorithms proposed in [19, 35] differ mainly in the implementation, and in the update rules of the weights and their corresponding regularizers. In IRLS-M [19], the weights are updated as , and in IRLS- [35] they are updated as . Further, each of the regularization parameters and are updated differently. The IRLS-M algorithm makes use of the rank of the matrix (either given or estimated), and thus the choice of parameter depends on this given or estimated rank. On the other hand, the IRLS- algorithm chooses and updates its regularizer based on prior sensitivity experiments. ## 3. Structured Iteratively Reweighted Least Squares Algorithms In this section, we first introduce the structured matrix completion problem. Second, we introduce and analyze our proposed algorithm and implementation. ### 3.1. Problem Statement In [36], the authors propose adjusting the standard nuclear norm minimization strategy for matrix completion to account for structural differences between observed and unobserved entries. This could be achieved by adding to problem (2) a regularization term on the unobserved entries that still results in a semidefinite program, (7) minimizeX ∥X∥∗+α∥PΩc(X)∥ subject to PΩ(X)=PΩ(M), where , and where is an appropriate matrix norm. If most of the missing entries are zero except for a few, then the norm is a natural choice222The method can be rescaled if there instead is a preference for the missing entries to be near a nonzero constant. . If the missing entries are mostly close to zero, then the norm is a natural choice. The authors show that the proposed method outperforms nuclear norm minimization in certain structured settings. Indeed, program (7) very closely resembles the problem of decomposing a matrix into a low-rank component and a sparse component (see e.g. [11] ). A popular method is Robust Principal Component Analysis (RPCA) [7], where one assumes that a low-rank matrix has some set of its entries corrupted. ### 3.2. Proposed Algorithm: Structured IRLS We propose an iterative reweighted least squares algorithm related to [19, 35] for matrix completion with structured observations. In particular, we adjust the Iteratively Reweighted Least Squares (IRLS) algorithm proposed in [35] to take into account the structural differences between observed and unobserved entries. We call our algorithm Structured IRLS. Structured IRLS is designed to promote low-rank structure in the recovered matrix with sparsity in the missing entries. In many applications, missing values tend to be near a certain value, e.g. the maximum possible value in the range, or the value 1 might be the lowest possible value (“1 star” in movie ratings). In cases where this value is nonzero, our objective function can be adjusted accordingly. Note that for , the algorithm reduces to IRLS studied in [35]. Here denotes the vector of missing entries of the the -th approximation , and recall that denotes the vector with entries squared. Each iteration of Structured IRLS solves a quadratic program. The algorithm can be adjusted to have the norm for the regularization term on the unobserved entries by fixing the weights . Further, we can impose nonnegativity constraints on the missing entries by thresholding all missing entries to be nonnegative. ### 3.3. Proposed Implementation: Structured sIRLS In this section, we propose a gradient-projection-based implementation of Structured IRLS, that we will refer to as Structured sIRLS. Indeed, sIRLS stands for short IRLS (in analogy to [35]), the reason being we do not perform gradient descent until convergence; instead we take however many steps desired. Further, calculating is computationally cheap, so the gradient projection algorithm can be used to efficiently solve the quadratic program in each iteration of Structured IRLS. We derive the first part of our objective function as described in [35]. We define the smooth Schatten- function, for , as fp(X)=Tr(X⊤X+γI)p2=n∑i=1(σ2i(X)+γ)p2. Note that is differentiable for , and convex for [35]. For we have , which is also known as the Schatten-1 norm. Again for , we have as [35]. Further, for , we define fp(X)=logdet(X⊤X+γI), a smooth surrogate for (see e.g. [17, 18, 35, 40]). Thus, it is of interest to minimize subject to the set of constraints on the observed entries. The gradient of is given by (see e.g. [29, 35]), and the gradient projection iterates are given by Xk+1=PΩc(Xk−sk∇fp(Xk))+PΩ(M), where denotes the gradient step size at the -th iteration. This iterate describes our gradient step promoting low-rankness, where we preserve the observed entries and update only the missing entries. The gradient of at the -th iteration is given by , where we iteratively define as Wkp=(Xk⊤Xk+γkI)p2−1, where . Further, we promote sparsity in the missing entries as follows. Instead of minimizing the norm of the vector of missing entries, we iteratively minimize a re-weighted norm of missing entries as described in [15]. Let denote the vector of missing entries of the the -th approximation . Define the weighted norm of as gq(X)=∥z(X)∥2ℓ2(wq)=mn−\|Ω\|∑i=1(wq)iz2i(X), where (as done in [15]). The -th entry of the gradient of is given by . Therefore, the gradient projection iterates are given by z(Xk+1)=z(Xk)−ck∇gq(Xk), where denotes the gradient step size at the -th iteration. We iteratively define the weights as wkq=(z2(Xk)+ϵk1)q2−1, where . We outline in Algorithm 2 Structured sIRLS, a gradient-projection-based implementation of Structured IRLS. In this implementation, we do not perform projected gradient descent on ∥(Wk−1p)1/2X∥2F+α∥z(X)∥2ℓ2(wq), with . Instead, we perform projected gradient descent on and consecutively. This allows us to update the weights before each alternating step, and to control how many gradient steps we would like to perform on each function. Further, a rank estimate of the matrix is used as an input to truncate SVD when computing the weights . In our implementation, we use a randomized algorithm for SVD computation [23]. When the rank of the matrix is not estimated or provided, we instead choose to be at each iteration, where is the largest integer such that , and where (as implemented in [35]). ## 4. Numerical Experiments In this section, we run numerical experiments to showcase the performance of Structured sIRLS, and compare it to the performance of sIRLS (studied in [35]) on structured settings. We first describe the choice of parameters we use, and then describe our experiments for exact matrix completion and matrix completion with noise. Our code for Structured sIRLS is available at [1]. Further, we use the publicly available code of sIRLS [33]. ### 4.1. Choice of parameters In all the numerical experiments, we adopt the same parameters. However, one can use different choices for parameters, or optimize some of the parameters. We normalize the input data to have a spectral norm of 1 (as done in [35]). We are particularly interested in the case . In our experiments, we set . Generally, these parameters can be varied . Each value of and define a different objective function (see Sections 2.2 and 2.3). For the implementation parameters, we set and , which means that we take one gradient step to promote sparsity and ten gradient steps to promote low-rankness, respectively. These parameters can be varied based on the low-rankness of the matrix and on the expected sparsity of its missing entries. Further, we set the regularizers and at the -th iteration. However, there are other choices for these regularizers, for example could depend on the -th largest value of , where is the sparsity of (as done in [15]). Similarly, could depend on the -th singular value of , where is the rank of (as done in [19]). Lastly, for all we set the step size to promote low-rankness and to promote sparsity; however, these parameters could be scaled or varied. We define the relative distance between two consecutive approximations as d(Xk,Xk−1)=∥Xk−Xk−1∥F/∥Xk∥F. We say the algorithm converges if we obtain . We set the tolerance for both sIRLS and Structured sIRLS in our comparison experiments333In the implementation of sIRLS provided by the authors [33, 35], the tolerance is set to . We lowered it to to report fair comparisons since our algorithm attains the tolerance with fewer iterations.. We set the maximum number of iterations for Structured sIRLS to be 1000 and for sIRLS to be 5000. ### 4.2. Exact Matrix Completion We first investigate the performance of the Structured sIRLS algorithm when the observed entries are exact, i.e. there is no noise in the observed values. We construct matrices of rank as done in [36]. We consider , where and are sparse matrices. Indeed, the entries of (resp. ) are chosen to be zero uniformly at random so that on average (resp. ) of its entries are zero. The remaining nonzero entries are uniformly distributed at random between zero and one 444The sparsity level of the resulting matrix cannot be calculated exactly from the given sparsity levels of and .. We subsample from the zero and nonzero entries of the data matrix at various rates to generate a matrix with missing entries. We define the relative error of Structured sIRLS as ∥M−^X∥F/∥M∥F, where is the output of the Structured sIRLS algorithm. Similarly, we define the relative error of sIRLS as ∥M−~X∥F/∥M∥F, where is the output of the sIRLS algorithm. The average ratio is then defined as ∥M−^X∥F/∥M−~X∥F. We say Structured sIRLS outperforms sIRLS when the average ratio is less than one, and vice versa when the average ratio is greater than one. These two cases, when the average ratio is strictly less than or greater than one, are visually represented by the white and black squares, respectively, in the bottom right plots of Figures 13. We refer to this binary notion of average ratio as binned average ratio. We report each of these error values in our numerical experiments. It is important to note that the setting we are interested in is the structured setting where the missing entries are sparse. This setting can be observed in the upper left triangle of the matrix displaying the ratio of errors between sIRLS and Structured sIRLS (see the bottom left plots of Figures 15). In this region, the percentage of nonzero entries that are sampled is greater than the percentage of zero entries that are sampled. Further, we obtain better accuracy in general as we move right along a row or up along a column, since we are sampling more and more entries. In addition, it is important to note that in all experiments we are using the same algorithm (with fixed parameters) for all the cases considered in our computations, without any parameter optimization. The algorithm promotes sparsity in all the cases, even in the unstructured settings. Omitting the sparsity promoting step would result in an algorithm promoting only low-rankness. #### 4.2.1. 1000×1000 rank 10 matrices In Figure 1, we construct random matrices of size and of rank 10, as described in Section 4.2. Error values below one in the bottom left plot of Figure 1 indicate that Structured sIRLS outperforms sIRLS. In this particular experiment, we observe that Structured sIRLS outperforms sIRLS for most of the structured cases (the upper left triangle), and more. For this particular experiment, it turns out that this happens roughly when the decimal percentage of sampled nonzero entries is greater than 0.2. Note that in the case where all entries are observed (no longer a matrix completion problem), both relative errors are 0 and thus the average ratio is 1. We only say that Structured sIRLS outperforms sIRLS when the average ratio is strictly less than 1, and this is why the upper right pixel in the bottom right plot of Figure 1 is black. The same is true in Figures 2 and 3. #### 4.2.2. 500×500 rank 10 matrices In Figure 2, we construct random matrices of size and of rank 10, as described in Section 4.2. We observe that Structured sIRLS outperforms sIRLS not only in the majority of the structured cases, but also in many of the other cases where the unobserved entries are not necessarily sparse. #### 4.2.3. 100×100 rank 10 matrices We now consider a harder problem. In Figure 3, we construct random matrices of size and of rank 10, as described in Section 4.2. We observe in Figure 3 that Structured sIRLS outperforms sIRLS when the sampling rate of the nonzero entries is high (roughly speaking, when the decimal percentage of sampled nonzero entries is greater than 0.5), which covers the majority of the cases where there is sparsity-based structure in the missing entries. #### 4.2.4. 100×100 matrices with no knowledge of the rank a priori In Figure 4, we construct random matrices of size and of rank 8, as described in Section 4.2. For this experiment, we do not provide the algorithm with any rank estimate, for either sIRLS or Structured sIRLS. Instead, we allow the algorithm to estimate the rank at each iteration based on a heuristic described in Section 3.3. We observe in the bottom right plot of Figure 4, where we look closely to the cases where the sampling rate of non-zero entries is at least 0.7, that Structured sIRLS outperform sIRLS to different extents. Indeed, Structured sIRLS does particularly better when more entries are observed. ### 4.3. Matrix Completion with Noise In this section, we investigate the performance of Structured sIRLS when the observed entries are corrupted with noise. We consider the following noisy matrix completion problem [36], (8) minimizeX ∥X∥∗+α∥PΩc(X)∥ subject to PΩ(X)=PΩ(B), where is an unknown low-rank matrix that we wish to recover, where is the measurement noise, and where the noisy matrix satisfies . Let be i.i.d. Gaussian random variables. We define our noise model such that for a noise parameter . We do so by adding noise of the form Zij=ϵ⋅∥PΩ(M)∥F∥PΩ(N)∥F⋅Nij, where are i.i.d. Gaussian random variables with the standard distribution . We adapt sIRLS and Structured sIRLS for noisy matrix completion by replacing the observed entries with the noisily observed entries . We do not vary the noisily observed entries, only the missing entries. We define the relative error as ∥B−^X∥F/∥B∥F, where is the output of the Structured sIRLS algorithm. In Figure 5, we consider rank 3 matrices with noise parameter , where we construct our matrices in the same fashion as in Section 4.2 and with the noise model described above. We consider analogous structured settings as in the prior experiments, and observe that sIRLS and Structured sIRLS algorithms perform roughly the same, showing that both are robust to noise but that improvements from the structure are less drastic in this setting. ## 5. Analytic Remarks In this section, we provide an analytic remark, similar to [36, Proposition 1], applied to the objective functions for each iteration of IRLS [35] and Structured IRLS. We consider the simplified setting, in which all of the unobserved entries are exactly zero. We show that the approximation given by an iteration of Structured IRLS will always perform at least as well as that of IRLS with the same weights assigned. ###### Proposition 5.1. Let ~X=argminX{∥W1/2X∥2F : PΩ(X)=PΩ(M)} be the minimizer of the objective function of each iterate in IRLS [35]. Let ^X=argminX{∥W1/2X∥2F+α∥PΩc(X)∥ : PΩ(X)=PΩ(M)} be the minimizer of the objective function generalizing555Here is an arbitrary matrix norm; one recovers Structured IRLS by choosing the norm . each iterate in Structured IRLS (with ). If is the zero matrix and the same weights are assigned, then for any matrix norm . ###### Proof. By definition of , we have . Similarly, by definition of , we have . Therefore, ∥W1/2^X∥2F+α∥PΩc(^X)∥2≤∥W1/2~X∥2F+α∥PΩc(~X)∥2≤∥W1/2^X∥2F+α∥PΩc(~X)∥2. Since , this implies . We therefore have ∥M−^X∥ =∥PΩc(^X)∥ since PΩ(M)=PΩ(^X) and PΩc(M)=0 ≤∥PΩc(~X)∥ by assumption on the restriction of the matrix norm to Ωc =∥M−~X∥ since PΩ(M)=PΩ(~X) and PΩc(M)=0. ## 6. Conclusion In this paper, we consider the structured matrix completion problem, studied in [36]. We focus on the notion of structure in which the probability that an entry is observed or not depends mainly on the value of the entry. In particular, we are interested in sparsity-based structure in the missing entries whereby most of the missing values are close in the or norm sense to 0 (or more generally to a fixed value). For example, a missing rating of a movie might indicate the user’s lack of interest in that movie, thus suggesting a lower rating than otherwise expected. In recent work [36], Molitor and Needell propose adjusting the standard nuclear norm minimization problem to take into account the structural differences between observed and unobserved entries. We propose an iterative algorithm for structured low-rank matrix completion, called Structured IRLS, by adjusting the IRLS algorithm proposed in [35]. We also present a gradient-projection-based implementation, called Structured sIRLS (based on sIRLS of [35]). The projection step is computationally cheap, so the gradient projection algorithm can be used to efficiently solve the quadratic program in each iteration of Structured IRLS. The algorithms are designed to promote low-rank structure in the recovered matrix with sparsity in the missing entries. Our objective function can be adjusted by applying a linear shift on the missing values to handle other fixed nonzero values. We perform numerical experiments on various structured settings to test the performance Structured sIRLS compared to sIRLS. To generate a sparse matrix with missing entries, we subsample from the zero and nonzero entries of a sparse data matrix at various rates. Indeed, we are interested in the structured cases, when the sampling rate of the zero entries is lower than the sampling rate of the nonzero entries. For matrices of different sizes and sparsity levels, we report the relative error of sIRLS, the relative error of Structured sIRLS, and the average ratio between the two. The numerical experiments show that Structured sIRLS often gives better recovery results than sIRLS in structured settings. In future work, we hope to extend the theoretical results for Structured IRLS to more general settings. In the simplified setting, in which all of the unobserved entries are exactly zero, we show that the approximation given by an iteration of Structured IRLS will always perform at least as well as that of IRLS with the same weights assigned. However, we empirically observe the stronger result that Structured sIRLS often outperforms sIRLS in structured settings (in which algorithms are run until convergence, and in which not all missing entries are zero). Another extension is to explore Structured IRLS for different values of and , both empirically and theoretically. Furthermore, a possible direction for future work is to extend sparsity-based structure in the missing entries to a more general notion of structure, whereby the probability that an entry is observed or not may depend on more than just the value of that entry. For example, one could imagine that columns in a matrix corresponding to popular movies would have many entries (user ratings) filled in. In this context, an entry might be more likely to be observed if many entries in its same column are also observed. ## References • [1] Henry Adams, Lara Kassab, and Deanna Needell. Structured IRLS code. • [2] Robert M Bell and Yehuda Koren. Lessons from the netflix prize challenge. SiGKDD Explorations, 9(2):75–79, 2007. • [3] James Bennett and Stan Lanning. The Netflix prize. In Proceedings of KDD Cup and Workshop, volume 2007, page 35. New York, NY, USA., 2007. • [4] Pratik Biswas, Tzu-Chen Lian, Ta-Chung Wang, and Yinyu Ye. Semidefinite programming based algorithms for sensor network localization. ACM Transactions on Sensor Networks (TOSN), 2(2):188–220, 2006. • [5] Jian-Feng Cai, Emmanuel J Candès, and Zuowei Shen. A singular value thresholding algorithm for matrix completion. SIAM Journal on optimization, 20(4):1956–1982, 2010. • [6] Emmanuel Candes and Terence Tao. Decoding by linear programming. arXiv preprint math/0502327, 2005. • [7] Emmanuel J Candès, Xiaodong Li, Yi Ma, and John Wright. Robust principal component analysis? Journal of the ACM (JACM), 58(3):1–37, 2011. • [8] Emmanuel J Candès and Yaniv Plan. Matrix completion with noise. Proceedings of the IEEE, 98(6):925–936, 2010. • [9] Emmanuel J Candès and Benjamin Recht. Exact matrix completion via convex optimization. Foundations of Computational mathematics, 9(6):717, 2009. • [10] Emmanuel J Candès and Terence Tao. The power of convex relaxation: Near-optimal matrix completion. IEEE Transactions on Information Theory, 56(5):2053–2080, 2010. • [11] Venkat Chandrasekaran, Sujay Sanghavi, Pablo A Parrilo, and Alan S Willsky. Rank-sparsity incoherence for matrix decomposition. SIAM Journal on Optimization, 21(2):572–596, 2011. • [12] Rick Chartrand. Exact reconstruction of sparse signals via nonconvex minimization. IEEE Signal Processing Letters, 14(10):707–710, 2007. • [13] Rick Chartrand and Valentina Staneva. Restricted isometry properties and nonconvex compressive sensing. Inverse Problems, 24(3):035020, 2008. • [14] Rick Chartrand and Wotao Yin. Iteratively reweighted algorithms for compressive sensing. In 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, pages 3869–3872. IEEE, 2008. • [15] Ingrid Daubechies, Ronald DeVore, Massimo Fornasier, and C Sinan Güntürk. Iteratively reweighted least squares minimization for sparse recovery. Communications on Pure and Applied Mathematics: A Journal Issued by the Courant Institute of Mathematical Sciences, 63(1):1–38, 2010. • [16] David L Donoho and Philip B Stark. Uncertainty principles and signal recovery. SIAM Journal on Applied Mathematics, 49(3):906–931, 1989. • [17] Maryam Fazel. Matrix rank minimization with applications. 2002. • [18] Maryam Fazel, Haitham Hindi, and Stephen P Boyd. Log-det heuristic for matrix rank minimization with applications to Hankel and Euclidean distance matrices. In Proceedings of the 2003 American Control Conference, 2003, volume 3, pages 2156–2162. IEEE, 2003. • [19] Massimo Fornasier, Holger Rauhut, and Rachel Ward. Low-rank matrix recovery via iteratively reweighted least squares minimization. SIAM Journal on Optimization, 21(4):1614–1640, 2011. • [20] Donald Goldfarb and Shiqian Ma. Convergence of fixed-point continuation algorithms for matrix rank minimization. Foundations of Computational Mathematics, 11(2):183–210, 2011. • [21] David Gross. Recovering low-rank matrices from few coefficients in any basis. IEEE Transactions on Information Theory, 57(3):1548–1566, 2011. • [22] David Gross, Yi-Kai Liu, Steven T Flammia, Stephen Becker, and Jens Eisert. Quantum state tomography via compressed sensing. Physical review letters, 105(15):150401, 2010. • [23] Nathan Halko, Per-Gunnar Martinsson, and Joel A Tropp. Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions. SIAM review, 53(2):217–288, 2011. • [24] Prateek Jain, Raghu Meka, and Inderjit S Dhillon. Guaranteed rank minimization via singular value projection. In Advances in Neural Information Processing Systems, pages 937–945, 2010. • [25] Raghunandan H Keshavan and Sewoong Oh. A gradient descent algorithm on the Grassman manifold for matrix completion. arXiv preprint arXiv:0910.5260, 2009. • [26] Yehuda Koren, Robert Bell, and Chris Volinsky. Matrix factorization techniques for recommender systems. Computer, (8):30–37, 2009. • [27] Christian Kümmerle and Juliane Sigl. Harmonic mean iteratively reweighted least squares for low-rank matrix recovery. The Journal of Machine Learning Research, 19(1):1815–1863, 2018. • [28] Kiryung Lee and Yoram Bresler. ADMiRA: Atomic decomposition for minimum rank approximation. IEEE Transactions on Information Theory, 56(9):4402–4416, 2010. • [29] Adrian Stephen Lewis. Derivatives of spectral functions. Mathematics of Operations Research, 21(3):576–588, 1996. • [30] Nathan Linial, Eran London, and Yuri Rabinovich. The geometry of graphs and some of its algorithmic applications. Combinatorica, 15(2):215–245, 1995. • [31] Zhang Liu and Lieven Vandenberghe. Interior-point method for nuclear norm approximation with application to system identification. SIAM Journal on Matrix Analysis and Applications, 31(3):1235–1256, 2009. • [32] Hassan Mansour and Rayan Saab. Recovery analysis for weighted -minimization using the null space property. Applied and Computational Harmonic Analysis, 43(1):23–38, 2017. • [33] Karthik Mohan and Maryam Fazel. IRLS code. [Online; accessed 01-Aug-2019]. • [34] Karthik Mohan and Maryam Fazel. Reweighted nuclear norm minimization with application to system identification. In Proceedings of the 2010 American Control Conference, pages 2953–2959. IEEE, 2010. • [35] Karthik Mohan and Maryam Fazel. Iterative reweighted algorithms for matrix rank minimization. Journal of Machine Learning Research, 13(Nov):3441–3473, 2012. • [36] Denali Molitor and Deanna Needell. Matrix completion for structured observations. In 2018 Information Theory and Applications Workshop (ITA), pages 1–5. IEEE, 2018. • [37] Deanna Needell. Noisy signal recovery via iterative reweighted L1-minimization. In Proceedings of the 43rd Asilomar conference on Signals, systems and computers, pages 113–117. IEEE Press, 2009. • [38] Deanna Needell, Rayan Saab, and Tina Woolf. Weighted-minimization for sparse recovery under arbitrary prior information. Information and Inference: A Journal of the IMA, 6(3):284–309, 2017. • [39] Benjamin Recht. A simpler approach to matrix completion. Journal of Machine Learning Research, 12(Dec):3413–3430, 2011. • [40] Benjamin Recht, Maryam Fazel, and Pablo A Parrilo. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM review, 52(3):471–501, 2010. • [41] Ralph Schmidt. Multiple emitter location and signal parameter estimation. IEEE transactions on antennas and propagation, 34(3):276–280, 1986. • [42] Amit Singer. A remark on global positioning from local distances. Proceedings of the National Academy of Sciences, 105(28):9507–9511, 2008. • [43] Anthony Man-Cho So and Yinyu Ye. Theory of semidefinite programming for sensor network localization. Mathematical Programming, 109(2-3):367–384, 2007. • [44] Kim-Chuan Toh and Sangwoon Yun. An accelerated proximal gradient algorithm for nuclear norm regularized linear least squares problems. Pacific Journal of optimization, 6(615-640):15, 2010. • [45] Tong Zhang. Analysis of multi-stage convex relaxation for sparse regularization. Journal of Machine Learning Research, 11(Mar):1081–1107, 2010.	{}
## Calculus 8th Edition $p\gt 0$ 1) We will have to apply the Test of Divergence to find the value of $p$ for the given alternating series when $p\lt 0$ Then $\lim\limits_{n \to \infty}(-1)^{n-1} n^{\|p\|}=$ Limit does not exist.This means that the series will not converge by the Test of Divergence. 2. We will have to apply the Test of Divergence to find the value of $p$ for the given alternating series when $p = 0$ Then $\lim\limits_{n \to \infty}(-1)^{n-1} n^{0}=$ Limit does not exist.This means that the series will not converge by the Test of Divergence. 3. We will have to apply the Test of Divergence to find the value of $p$ for the given alternating series when $p\gt 0$ Here, $\lim\limits_{n \to \infty}\dfrac{1}{n^p}=0$ This means that the limit $0$ satisfies all the condition for alternating series test.This means that the series will converge by the Test of Divergence.	{}
# Best way to calculate unit deaths in browser game combat? My browser game's combat system is written and mechanically functioning well. It's written in PHP and uses a SQL database. I'm happy with the unit balance in relation to one another. I am, however, a little worried about how I'm calculating unit deaths when one player attacks another because the deaths seem to pile up a little fast for my taste. For this system, a battle doesn't just trigger, calculate winner, and end. Instead, it is allowed to go for several rounds (say one round every 15 mins.) until one side passes a threshold of being too strong for the other player and allows players to send reinforcements between rounds. Each round, units pair up and attack each other. Essentially what I do is calculate the damage: AP = Attack Points HP = Hit Points Units AP * Quantity * Random Factors * other factors (such as attrition) I take that and divide by the defending unit's HP to find the number of casualties of defending units. So, for example (simplified to take out some factors), if I have: 500 attackers with 50 AP vs 1000 defenders with 100 HP = 250 deaths. I wonder if that last step could be handled better to reduce the deaths piling up. Some ideas: 1. I just change all the units with more HP? 2. I make sure to set the Attacking unit's AP to be a max of the defender's HP to make sure they only kill 1 unit. (is that fair if I have less huge units vs many small units?) 3. I spread the damage around more by including the defending unit's quantity more? i.e. in that scenario some are dead and some are 50% damage. (How would I track this every round?). This kind of seems like the best idea, but not sure how i'd track it in the DB. 4. Other better mathematical approaches? There are several answers in this question which might help: Calculating the output of two armies fighting. However, one simple answer is just to scale your values. If 1 point of attack power basically negates 1 hit point, and you think that kills too many units, then make 1 point of attack power negate 0.75 hit points (or whatever). eg. (Attack Power * Quantity of Attackers) * 0.75 / Defending Unit HP = Deaths These values are yours to do what you want with, so add whatever you need to make the outcome resemble the gameplay you want. • Ok, I looked into those answers and find them lacking. 1) They either take a deterministic rock, paper, scissor type approach; and 2) the lanchaster's law seems to only care about quantities (larger army winning), which would be fine assuming that all units have the same weapons (stats), but that's not the case here. – MikeCruz13 Jun 3 '12 at 2:35 • The Lanchester laws accurately depict the rate at which one side defeats the other - you have to plug in your own relative power levels. – Kylotan Jun 3 '12 at 9:49 -- It's hard to give you an accurate answer because we don't know how your turns are organized or how works your unit teams work -- Let me make a point about what you have right know. You have 500 attackers. Each attacker is defined by a number of Attack Power. They fight against defenders. They are 1000 and are defined by a number of Health Points. It seems logic that 1 attacker can only fight 1 defender at the time (it seems that your game is turn based). For 1:1 combat the basic design would be to say "if AP are bigger than HP then there is as much as death that attackers; every defender dies". But on a real battlefield things are not that simple: people can kill more than one guy with a little luck, or no one with a lack of luck. You will have to add some randomness in your equation in order to basically simulate a real combat. I would suggest to pre-compute the winner of the battle (easy: the biggest, the strongest) and then to make the number of deaths vary a little bit. For a 100:100 battle with 50AP and 100HP you have to wait 2 turns to kill your defenders with your equation, but if you apply something like: X * ((Attack Power * Attackers) / (Health Point * Defenders)) With X a random value between 0.75 and 1 (up to 1.2 if the pre-computed winning team is more numerous than the loser one, in order to simulate the 'chance' to kill a little bit more than only with 1:1 ratio), you will obtain unpredictable results (from a player point of view). Anyway you not necessarily need to manage each unit stats. At the end of the battle (a battle is composed of several turns until one of the team has no more unit), you will count deaths in each team (attackers and defenders) and reduce their actual total number of unit. • Actually, I do include some randomness. I updated my question above to show more about how things currently work. Also, I can't really predetermine the winner because players can add reinforcements to a fight between rounds. – MikeCruz13 May 28 '12 at 8:58	{}
Netzschleuder network catalogue, repository and centrifuge Problems with this dataset? Open an issue. You may also take a look at the source code. The network in this dataset can be loaded directly from graph-tool with: import graph_tool.all as gt g = gt.collection.ns["new_zealand_collab"] new_zealand_collab — New Zealand scientific collaborations (2015) Description A network of scientific collaborations among institutions in New Zealand. Nodes are institutions (universities, organizations, etc.), and two nodes i,j are connected if Scopus lists at least one publication with authors at institutions i and j, in the period 2010-2015. Edges are weighted by the number of such collaborations. Nodes are annotated with the categorical type of institution.1 1. Description obtained from the ICON project. Tags Name Nodes Edges $\left<k\right>$ $\sigma_k$ $\lambda_h$ $\tau$ $r$ $c$ $\oslash$ $S$ Kind Mode NPs EPs gt GraphML GML csv	{}
# Journal of Operator Theory Volume 83, Issue 2, Spring 2020 pp. 475-494. On norm-limits of algebraic quasidiagonal operators Authors: Laurent W. Marcoux Author institution:Department of Pure Mathematics, University of Waterloo, Waterloo, Ontario, N2L 3G1, Canada Summary: It is still an open question to know whether or not every quasidiagonal operator can be expressed as a norm-limit of algebraic quasidiagonal operators. In this note, we provide an alternative characterization of those operators which may be expressed as such limits, in the hope that this may lead to a solution of this problem. DOI: http://dx.doi.org/10.7900/jot.2018nov07.2234 Keywords: Quasidiagonal, algebraic operators, nilpotent operators, approximation	{}
## rate of increase of the surface area a spherical balloon is being inflated. find the rate of increase of the surface area (S=4 pie r squared) with respect to radius r when r is (A) 1 ft, (B) 2 ft, (C) 3ft. Here's what i did i found the derivative of s and i put 4 2R and then i plugged in the numbers in R and i got 8 ft sq/ft 16 ft sq/ft and 24 ft sq/ft except i'm not sure if im doing it right, although those are the right answers i didnt get the units along with them PhysOrg.com science news on PhysOrg.com >> 'Whodunnit' of Irish potato famine solved>> The mammoth's lament: Study shows how cosmic impact sparked devastating climate change>> Curiosity Mars rover drills second rock target is there simple algebra involved in this calculus problem are you not given dr/dt or dv/dt? ## rate of increase of the surface area Quote by afcwestwarrior a spherical balloon is being inflated. find the rate of increase of the surface area (S=4 pie r squared) with respect to radius r when r is (A) 1 ft, (B) 2 ft, (C) 3ft. Here's what i did i found the derivative of s and i put 4 2R and then i plugged in the numbers in R and i got 8 ft sq/ft 16 ft sq/ft and 24 ft sq/ft except i'm not sure if im doing it right, although those are the right answers i didnt get the units along with them You've got a graph there, simply find the gradient of the slope, that's the rate of increase. (1,8) (2,16) (3,24) Recognitions: Gold Member Staff Emeritus Quote by afcwestwarrior a spherical balloon is being inflated. find the rate of increase of the surface area (S=4 pie r squared) with respect to radius r when r is (A) 1 ft, (B) 2 ft, (C) 3ft. Here's what i did i found the derivative of s and i put 4 2R and then i plugged in the numbers in R and i got 8 ft sq/ft 16 ft sq/ft and 24 ft sq/ft except i'm not sure if im doing it right, although those are the right answers i didnt get the units along with them Give more detail about what you did (I, for one, don't know what "i put 4 2R" means!). What is the formula for surface area (I see you give that)? what is its derivative? Plastic Photon, since the problem asks for the rate of increas eof surface area with respect to r you don't need to know dr/dt. If the surface area is in square feet and the radius in feet, then the "rate of change of surface area with respect ot radius" is in (square feet)/feet or just feet! ok so ur saying i dont need to find the derivative of it, ok check this mate, the i put 4 2 R means thats the derivative of the surface area Recognitions: Gold Member Science Advisor Staff Emeritus No, "i put 4 2 R" doesn't mean anything!	{}
## The Time Independent Schrödinger Equation Second order differential equations, like the Schrödinger Equation, can be solved by separation of variables. These separated solutions can then be used to solve the problem in general. Assume that we can factorize the solution between time and space. Plug this into the Schrödinger Equation. Put everything that depends on on the left and everything that depends on on the right. Since we have a function of only set equal to a function of only , they both must equal a constant. In the equation above, we call the constant , (with some knowledge of the outcome). We now have an equation in set equal to a constant which has a simple general solution, and an equation in set equal to a constant which depends on the problem to be solved (through ). The equation is often called the Time Independent Schrödinger Equation. Here, is a constant. The full time dependent solution is. * Example: Solve the Schrödinger equation for a constant potential .* Jim Branson 2013-04-22	{}
# Clickable Table Footnote I'm trying to have some clickable footnotes within tables. I tried using \footnote{}, it does create a link but there's no footnote text associated with it. \footnotemark[number] along with \footnotetext[]{} does create a fotenote but then there's no hyperlink. (I would like to make it clear that I'm trying to have footnotes at the bottom of the page and not footnotes within the table.) Here's a small code snippet: \documentclass{report} \usepackage{hyperref} \begin{document} \begin{table}[h!] \centering \begin{tabular}{\|r\|r\|r\|} \hline A\footnote{Test!} & B\footnotemark[4] & C\footnotemark[5]\\ \hline 123 & Tim & Jane\\ \hline 456 & Tom & Jung\\ \hline \end{tabular} \caption{A table} \end{table} This is a clickable footnote\footnote{You clicked me!}. \footnotetext[4]{This is B} \footnotetext[5]{This is C} \end{document} • Footnotes in floats are not really a good idea. You better create table notes with »threeparttable«. – Thorsten Donig Nov 28 '10 at 13:13 • Do any of the answers here help? tex.stackexchange.com/questions/1583/footnotes-in-tables – Seamus Nov 28 '10 at 14:49 • Since you have some responses below that seem to answer your question, please consider marking one of them as ‘Accepted’ by clicking on the tickmark below their vote count. This shows which answer helped you most, and it assigns reputation points to the author of the answer (and to you!). Also upvoting an answer or two is appreciated. – Stephen Mar 22 '12 at 19:23 From the hyperref README, Section 8 "Hints", p. 26: The footnote support is rather limited. It is beyond the scope to use \footnotemark and \footnotetext out of order or reusing \footnotemark. Here you can either disable hyperref’s footnote support by "hyperfootnotes=false" or fiddle with internal macros [...] P. 26-27 give some "nasty examples"; I've used the second one as groundwork to modify your code example. This is what I came up with: \documentclass{report} \usepackage{hyperref} \begin{document} \makeatletter \begin{table}[h!] \centering \begin{tabular}{\|r\|r\|r\|} \hline A & B\footnotemark\global\let\saved@Href@B\Hy@footnote@currentHref & C\footnotemark\global\let\saved@Href@C\Hy@footnote@currentHref \\ \hline 123 & Tim & Jane\\ \hline 456 & Tom & Jung\\ \hline \end{tabular} \caption{A table} \end{table} \let\Hy@footnote@currentHref\saved@Href@B \footnotetext{This is B} \let\Hy@footnote@currentHref\saved@Href@C \footnotetext{This is C} This is a clickable footnote\footnote{You clicked me!}. \end{document} By the way I agree with Thorsten Donig that footnotes in floats are not a good idea. You can use the tablefootnote package (loaded after hyperref) and in the table \tablefootnote instead of \footnote. There is no optional parameter to the command, but you do want automatic numbering if I understand your question right. \documentclass{report} \usepackage{hyperref} \usepackage{tablefootnote} \begin{document} This is a clickable footnote\footnote{You clicked me!}. \begin{table}[h!] \centering \begin{tabular}{\|r\|r\|r\|} \hline A\tablefootnote{Test!} & B\tablefootnote{This is B} & C\tablefootnote{This is C}\\ \hline 123 & Tim & Jane\\ \hline 456 & Tom & Jung\\ \hline \end{tabular} \caption{A table} \end{table} This is a another clickable footnote\footnote{Now you clicked me!}. \newpage To test the hyperlinks it is very useful to have a second page in the document! \end{document} • Already i have given the solution for this in the title: "footnote in the column name of a table" – Mu30 murugans2katgmail Mar 22 '12 at 10:54 • @S.Murugan: Your answer tex.stackexchange.com/questions/46602/… is dated Mar 9 2012 at 14:49, but my answer here was given Feb 12 2012 at 14:38, and in my humble opinion 2012/02/12 is before 2012/03/09. Or do I misunderstand your comment? – Stephen Mar 22 '12 at 19:19 • @S.Murugan: "By chance" at the same time you gave your comment my answer was downvoted. In case you are the downvoter, I do not understand this: You are using this approach in an answer of your own, tex.stackexchange.com/questions/46602/…, but downvote another, earlier answer with this approach? It would be nice if you could explain this. – Stephen Mar 22 '12 at 19:40 • @S.Murugan and your answer at tex.stackexchange.com/questions/46602/… is obviously copied from my answer tex.stackexchange.com/a/35328 of Nov 18 '11. – Stephen Mar 22 '12 at 20:41 I’m using the following technique for having multiple references to the same footnote, with hyperref, combining advice from its documentation and several posts here: \newcommand{\Hair}{\kern.16667em} […] Falls hierbei Fehler auftauchen prüfen Sie […] die Logs\Hair\textsuperscript{\ref{fn:tomcatlogs}}. […] Prüfen Sie ggfs. die Logausgaben\Hair\footnote{\label{fn:tomcatlogs}in \texttt{/var/log/tomcat7/catalina.out}}, […] As you can see, this makes it easily possible to reference a footnote multiple times once it has been defined anywhere in the document, even later. This is important because footnotes cannot be defined (with \footnote) inside tables or minipages. Now, I thought I could simply define the body of a footnote with a line like this: \stepcounter{footnote}\footnotetext{\label{fn:foo}foobar}% Unfortunately, while referencing this footnote inside a table works, it’s not hyperlinked because hyperref only applies to \footnote but not the split \footnotemark + \footnotetext. So, what we really want is to call \footnote but not render its output. Easier said than done. But we can temporarily redefine the command that actually sets the mark into the text – \@makefnmark – to nothing. That works, but it requires a paragraph or it will create one, so you would have to do something like: […] \end{tabular} Some paragraph here.\hyperfootnotetext{\label{fn:foo}foobar}\hyperfootnotetext{…} As you can see, that quickly becomes illegible, especially with multiple of them. So I tried to temporarily prevent leaving vmode… except, the code still tries to set the (empty) fnmark as hyperlink to the footnote, which only works in horizontal mode. Meh. At this point I was about to call it a day… … except I found out that we can temporarily prevent setting hyperlinks, too, without giving up the ability to link from a footnote to another. ## SSCCE This example shows how to use footnotes from tables, multiple times, with hyperlinks to the footnotes as well as hyperlinks in the footnotes themselves, with the ability to declare those footnotes outside of any paragraphs: \documentclass{scrartcl} \RequirePackage[utf8]{inputenc} \RequirePackage[T1]{fontenc} \usepackage{mwe} \RequirePackage[pdftex]{hyperref} \hypersetup{ urlcolor = blue, } % em dash \def\dash{\unskip\kern.16667em\textemdash\penalty\exhyphenpenalty\hskip.16667em\relax} % for footnotes \newcommand{\Hair}{\kern.16667em} \makeatletter% % \hyperfootnotetext is what \footnotetext is supposed to be: % like \footnote except not rendering anything (it will not % generate a paragraph if you append % to all lines) \newcommand\hyperfootnotetext[1]{% % new local scope {% % temporarily redefine this macro to empty \renewcommand{\@makefnmark}{}% % temporarily prevent leaving vmode \renewcommand{\leavevmode}{}% % this also means we cannot create a(n empty) hyperlink % call the original \footnote macro \footnote{#1}% % exit the local scope with the redefined macro }% % end of command }% \makeatother% \begin{document} \section{First page}\label{sec:first} These are the system requirements: \begin{tabular}{\| r \|\| l \| l \| l \|}\hline & minimum & recommended & maximum\\\hline\hline Operating System & Debian 7 & Debian 7 or 8 & Debian unstable\Hair\textsuperscript{\ref{fn:req-nolimit}}\\\hline Webserver & Apache 2.2 & Apache 2.2 & Apache 2.4\Hair\textsuperscript{\ref{fn:req-notmore}}\\\hline Java Runtime & OpenJDK 7 & OpenJDK 8 & OpenJDK 8\Hair\textsuperscript{\ref{fn:req-notmore}}\\\hline Application Server & Tomcat 7 & Tomcat 7 & Tomcat 7\Hair\textsuperscript{\ref{fn:req-nonewer}}\\\hline \end{tabular} % note no paragraph here before next section! \hyperfootnotetext{\label{fn:req-nolimit}% no practical limitation}% \hyperfootnotetext{\label{fn:req-notmore}% \section{Second half}\label{sec:second} Page break upcoming. \newpage Some systems were not tested\Hair\footnote{\label{fn:didnot}… or did not exist at the time of this writing}. \end{document} Application note: you will most likely have your \hyperfootnotetext calls directly below the table (unless you’re re-using a footnote defined elsewhere) to get them ideally placed on the same page. Side note: originally I had my \hyperfootnotetext reimplement the original \footnote except inlining \@footnotemark minus its \@makefnmark call… this would have gotten old quick… finally I found you can temporarily redefine commands inside other commands for their duration only. (I don’t understand yet why setting hyperlinks inside footnote texts still works in my example, but I’m happy about that.) ObNote: this ought to work for minipages, too. • I can't thank you enough, not only solves this my problem in an elegant way, but it adds the feature of not having to write the footnote text inside the table in the code, which makes it very well-arranged. Well done! – dessert Mar 23 '16 at 10:40	{}
# How to compute the summation of this sequence The sequence is $$\sum_{i=1}^n i^2$$ I used to know how to do this, but I just forget. - Hint: Try to find a cubic polynomial $P$ such that $P(n)-P(n-1)=n^2$ for each $n\ge 1$. There is a closed form formula for these kinds of things: $$\sum_{i=1}^n i^2 = \frac{1}{6} n (n+1) (2 n+1)$$ We can get a telescoping series using the information below. $$(k+1)^3-k^3=3k^2+3k+1$$ Thus our series is: $$\sum_{k=1}^n{(k+1)^3-k^3}=\sum_{k=1}^n{3k^2+3k+1}=(n+1)^3-1^3=(n+1)^3-1$$ We can distribute the sigma since it is a linear operator: $$\sum_{k=1}^n{3k^2}+\sum_{k=1}^n{3k}+\sum_{k=1}^n{1}=(n+1)^3-1$$ $$3\sum_{k=1}^n{k^2}+3\sum_{k=1}^n{k}+n=(n+1)^3-1$$ $$3\sum_{k=1}^n{k^2}+3\frac{n(n+1)}{2}=(n+1)^3-1-n$$ $$3\sum_{k=1}^n{k^2}=(n+1)^3-1-n-3\frac{n(n+1)}{2}$$ $$3\sum_{k=1}^n{k^2}=n^3+3n^2+2n+-\frac{3}{2}n^2-\frac{3}{2}n=n^3+\frac{3}{2}n^2+\frac{1}{2}n$$ $$\sum_{k=1}^n{k^2}=\frac{2}{6}n^3+\frac{3}{6}n^2+\frac{1}{6}n=\frac{1}{6}(2n^3+3n^2+n)$$ $$\sum_{k=1}^n{k^2}=\frac{1}{6}n(2n^2+3n+1)=\frac{n(n+1)(2n+1)}{6}$$	{}
# CLEAR Calculus ## Lab 8: Series - part 1 Mystery Constant T A chemical process causes temperature fluctuations inside a reactor, described by the equation for $$T$$ given below (in units of 100$$^\circ$$ C). $T= \frac{1}{0!} - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \frac{1}{4!} - \frac{1}{5!} + \cdots.$ (Note that $$n! = 1\cdot 2\cdot 3\cdots n$$ and by convention, $$0!=1$$.) Mystery Constant G In an experiment, the mass of an incubated yeast cell colony was determined to double every 43 hours. Consequently the lab was able to compute that after 43 hours, the instantaneous rate of growth (in grams per hour) would be $$G$$ times the initial mass, where $$G$$ is given by the series $G = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + \cdots.$ Mystery Constant R The proportion of the area of a square covered by an inscribed circle is some number $$R$$ (between 0 and 1) given by the infinite sum $R = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \frac{1}{11} + \cdots.$ Mystery Constant D A book can be placed on the edge of a table so that $$\frac{1}{2}$$ of it is on the table and $$\frac{1}{2}$$ extends off of the table. If the book is placed any farther it will fall off. A second book can then be placed underneath the first one so that $$\frac{1}{4}$$ of its length extends beyond table, so the stack of two books extends $$\frac{3}{4}$$ a book length off of the table. The farthest such a stack could theoretically extend, $$D$$, is therefore given by the infinite sum $D = \frac{1}{2} + \frac{1}{4} + \frac{1}{6} + \frac{1}{8} + \frac{1}{12} + \frac{1}{14} + \cdots.$ Mystery Constant M An investment with a 5% interest rate compounded continuously over 20 years will earn an amount M times the original investment in interest, where $$M$$ is the infinite sum $M = \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \frac{1}{5!} + \frac{1}{6!} + \frac{1}{7!} + \cdots.$ Mystery Constant P The probability of winning a round in the dice game "craps" is a number $$P$$ between 0 and 1, given by the infinite sum \begin{align} P =& \frac{2}{9} + \frac{1}{72} \left[1 + \frac{3}{4} + \left(\frac{3}{4}\right)^2 + \left(\frac{3}{4}\right)^3 + \left(\frac{3}{4}\right)^4 + \cdots\right]\\ & \quad + \frac{2}{81} \left[1 + \frac{13}{18} + \left(\frac{13}{18}\right)^2 + \left(\frac{13}{18}\right)^3 + \left(\frac{13}{18}\right)^4 + \cdots\right]\\ & \quad + \frac{25}{648} \left[1 + \frac{25}{36} + \left(\frac{25}{36}\right)^2 + \left(\frac{25}{36}\right)^3 + \left(\frac{25}{36}\right)^4 + \cdots\right] \end{align} Lab 8: Mystery Constant T A chemical process causes temperature fluctuations inside a reactor, described by the equation for $$T$$ given below (in units of 100$$^\circ$$ C). $T= \frac{1}{0!} - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \frac{1}{4!} - \frac{1}{5!} + \cdots.$ (Note that $$n! = 1\cdot 2\cdot 3\cdots n$$ and by convention, $$0!=1$$.) You can approximate $$T$$ by computing a partial sum $$T_n$$. For example, $T_1 = 1 \text{ and } T_4 = \frac{1}{0!} - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!}.$ Pre-Lab Assignment: Answer the following questions individually and bring your write-up to class. 1. Make a table of values for $$n$$ and $$T_n$$ for $$n = 1$$ to $$n = 10$$. 2. Plot the first 10 approximations for $$T$$ on a number line and as the graph of a sequence. Choose an appropriate scale and make the diagrams large - you will be adding several things to it. Lab: Work with your group on the problem assigned to you. We encourage you to collaborate both in and out of class, but you must write up your responses individually. 1. item Even though you don't know what it is, place a mark to represent the exact value of $$T$$ at a reasonable place on both the vertical number line and the $$T_n$$-axis of the graph. 2. Clearly mark the value of the fifth approximation on your graph and number line. Represent the error for this approximation on both diagrams, and write an algebraic expression for the error. 3. Determine a bound on the error for your fifth approximation. Use this bound to find a range of possible values for $$T$$. Represent both the bound on the error and the range of possible values in your diagram. 4. Find an approximation that is accurate to two decimal places (error $$<$$0.005). Explain how you know your approximation satisfies this requirement. Lab 8: Mystery Constant G In an experiment, the mass of an incubated yeast cell colony was determined to double every 43 hours. Consequently the lab was able to compute that after 43 hours, the instantaneous rate of growth (in grams per hour) would be $$G$$ times the initial mass, where $$G$$ is given by the series $G = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + \cdots.$ You can approximate $$G$$ by computing a partial sum $$G_n$$. For example, $G_1 = 1 \text{ and } G_4 = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4}.$ Pre-Lab Assignment: Answer the following questions individually and bring your write-up to class. 1. Make a table of values for $$n$$ and $$G_n$$ for $$n = 1$$ to $$n = 10$$. 2. Plot the first 10 approximations for $$G$$ on a number line and as the graph of a sequence. Choose an appropriate scale and make the diagrams large -- you will be adding several things to it. Lab: Work with your group on the problem assigned to you. We encourage you to collaborate both in and out of class, but you must write up your responses individually. 1. Even though you don't know what it is, place a mark to represent the exact value of $$G$$ at a reasonable place on both the vertical number line and the $$G_n$$-axis of the graph. 2. Clearly mark the value of the fifth approximation on your graph and number line. Represent the error for this approximation on both diagrams, and write an algebraic expression for the error. 3. Determine a bound on the error for your fifth approximation. Use this bound to find a range of possible values for $$G$$. Represent both the bound on the error and the range of possible values in your diagram. 4. Find an approximation that is accurate to two decimal places (error $$<$$ 0.005). Explain how you know your approximation satisfies this requirement. Lab 8: Mystery Constant R The proportion of the area of a square covered by an inscribed circle is some number $$R$$ (between 0 and 1) given by the infinite sum $R = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \frac{1}{11} + \cdots.$ You can approximate $$R$$ by computing a partial sum $$R_n$$. For example, $R_1 = 1 \text{ and } R_4 = 1- \frac{1}{3} + \frac{1}{5} - \frac{1}{7}.$ Pre-Lab Assignment: Answer the following questions individually and bring your write-up to class. 1. Make a table of values for $$n$$ and $$R_n$$ for $$n = 1$$ to $$n = 10$$. 2. Plot the first 10 approximations for $$R$$ on a number line and as the graph of a sequence. Choose an appropriate scale and make the diagrams large -- you will be adding several things to it. Lab: Work with your group on the problem assigned to you. We encourage you to collaborate both in and out of class, but you must write up your responses individually. 1. Even though you don't know what it is, place a mark to represent the exact value of $$R$$ at a reasonable place on both the vertical number line and the $$R_n$$-axis of the graph. 2. Clearly mark the value of the fifth approximation on your graph and number line. Represent the error for this approximation on both diagrams, and write an algebraic expression for the error. 3. Determine a bound on the error for your fifth approximation. Use this bound to find a range of possible values for $$R$$. Represent both the bound on the error and the range of possible values in your diagram. 4. Find an approximation that is accurate to two decimal places (error $$<$$ 0.005). Explain how you know your approximation satisfies this requirement. Lab 8: Mystery Constant D A book can be placed on the edge of a table so that $$\frac{1}{2}$$ of it is on the table and $$\frac{1}{2}$$ extends off of the table. If the book is placed any farther it will fall off. A second book can then be placed underneath the first one so that $$\frac{1}{4}$$ of its length extends beyond table, so the stack of two books extends $$\frac{3}{4}$$ a book length off of the table. The farthest such a stack could theoretically extend, $$D$$, is therefore given by the infinite sum $D = \frac{1}{2} + \frac{1}{4} + \frac{1}{6} + \frac{1}{8} + \frac{1}{12} + \frac{1}{14} + \cdots.$ You can approximate $$D$$ by computing a partial sum $$D_n$$. For example, $D_1 = \frac{1}{2} \text{ and } D_4 = \frac{1}{2} + \frac{1}{4} + \frac{1}{6} + \frac{1}{8}.$ Pre-Lab Assignment: Answer the following questions individually and bring your write-up to class. 1. Make a table of values for $$n$$ and $$D_n$$ for $$n = 1$$ to $$n = 10$$. 2. Plot the first 10 approximations for $$D$$ on a number line a as the graph of a sequence. Choose an appropriate scale and make the diagrams large -- you will be adding several things to it. Lab: Work with your group on the problem assigned to you. We encourage you to collaborate both in and out of class, but you must write up your responses individually. 1. Even though you don't know what it is, place a mark to represent the exact value of $$D$$ at a reasonable place on both the vertical number line and the $$D_n$$-axis of the graph. 2. Clearly mark the value of the fifth approximation on your graph and number line. Represent the error for this approximation on both diagrams, and write an algebraic expression for the error. 3. Determine a bound on the error for your fifth approximation. Ask for a hint if you spend more than 15 minutes on this. 4. Determine the smallest value of $$n$$ so that $$D_n > 1$$. Then find the smallest values of $$n$$ so that $$D_n > 2$$ and $$D_n > 3$$. What does this pattern suggest. Explain what implications this has for your previous answers to Questions 1-4? Lab 8: Mystery Constant M An investment with a 5% interest rate compounded continuously over 20 years will earn an amount M times the original investment in interest, where $$M$$ is the infinite sum $M = \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \frac{1}{5!} + \frac{1}{6!} + \frac{1}{7!} + \cdots.$ You can approximate $$M$$ by computing a partial sum $$M_n$$. For example, $M_1 = 1 \text{ and } M_5 = \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \frac{1}{5!}.$ Pre-Lab Assignment: Answer the following questions individually and bring your write-up to class. 1. Make a table of values for $$n$$ and $$M_n$$ for $$n = 1$$ to $$n = 10$$. 2. Plot the first 10 approximations for $$M$$ on a number line and as the graph of a sequence. Choose an appropriate scale and make the diagrams large -- you will be adding several things to it. Lab: Work with your group on the problem assigned to you. We encourage you to collaborate both in and out of class, but you must write up your responses individually. 1. Even though you don't know what it is, place a mark to represent the exact value of $$M$$ at a reasonable place on both the vertical number line and the $$M_n$$-axis of the graph. 2. Clearly mark the value of the fifth approximation on your graph and number line. Represent the error for this approximation on both diagrams, and write an algebraic expression for the error. 3. Determine a bound on the error for your fifth approximation. Use this bound to find a range of possible values for $$M$$. Represent both the bound on the error and the range of possible values in your diagram. Ask for a hint if you spend more than 15 minutes on this. 4. Find an approximation that is accurate to two decimal places (error $$<$$0.005). Explain how you know your approximation satisfies this requirement. Lab 8: Mystery Constant P The probability of winning a round in the dice game "craps" is a number $$P$$ between 0 and 1, given by the infinite sum \begin{align} P =& \frac{2}{9} + \frac{1}{72} \left[1 + \frac{3}{4} + \left(\frac{3}{4}\right)^2 + \left(\frac{3}{4}\right)^3 + \left(\frac{3}{4}\right)^4 + \cdots\right]\\ & \quad + \frac{2}{81} \left[1 + \frac{13}{18} + \left(\frac{13}{18}\right)^2 + \left(\frac{13}{18}\right)^3 + \left(\frac{13}{18}\right)^4 + \cdots\right]\\ & \quad + \frac{25}{648} \left[1 + \frac{25}{36} + \left(\frac{25}{36}\right)^2 + \left(\frac{25}{36}\right)^3 + \left(\frac{25}{36}\right)^4 + \cdots\right] \end{align} You can approximate $$P$$ by computing a partial sum $$P_n$$. For example, $P_1 = \frac{2}{9}$ and ${\small P_4 = \frac{2}{9} + \frac{1}{72} \left[1 + \frac{3}{4} + \left(\frac{3}{4}\right)^2 \right] +\frac{2}{81} \left[1 + \frac{13}{18} + \left(\frac{13}{18}\right)^2 \right] + \frac{25}{648} \left[1 + \frac{25}{36} + \left(\frac{25}{36}\right)^2\right].}$ Pre-Lab Assignment: Answer the following questions individually and bring your write-up to class. 1. Make a table of values for $$n$$ and $$P_n$$ for $$n = 1$$ to $$n = 10$$. 2. Plot the first 10 approximations for $$P$$ on a number line and as the graph of a sequence. Choose an appropriate scale and make the diagrams large -- you will be adding several things to it. Lab: Work with your group on the problem assigned to you. We encourage you to collaborate both in and out of class, but you must write up your responses individually. 1. Even though you don't know what it is, place a mark to represent the exact value of $$P$$ at a reasonable place on both the vertical number line and the $$P_n$$-axis of the graph. 2. Clearly mark the value of the fifth approximation on your graph and number line. Represent the error for this approximation on both diagrams, and write an algebraic expression for the error. 3. Determine a bound on the error for your fifth approximation. Ask for a hint if you spend more than 15 minutes on this. 4. Find the smallest value of $$n$$ so that $$P_n$$ is accurate to two decimal places (error $$<$$0.005). Explain how you know your approximation satisfies this requirement. Mystery Constants TG, and R - HINT Note that these are alternating series where the magnitude of the terms decrease monotonically to zero. This means that the series converge by the alternating series test. Additionally the partial sums will alternate between being underestimates and overestimates for the limits $$T$$, $$G$$, and $$R$$. So an error bound is simply the next term in the sequence (the difference between an underestimate and overestimate). Mystery Constant D - HINT (and apology) This is a bit of a trick question (Sorry). This series diverges (goes to infinity)! To see this is the case group the terms as follows: \begin{align} D & = \frac{1}{2} +\left(\frac{1}{4}\right) \left(\frac{1}{6} + \frac{1}{6}\right) + \left(\frac{1}{10}+ \frac{1}{12} + \frac{1}{14} + \frac{1}{16}\right) \\ & \qquad + \left(\frac{1}{18} + \frac{1}{20} + \frac{1}{22} + \frac{1}{24} + \frac{1}{26} + \frac{1}{28} + \frac{1}{30} + \frac{1}{32}\right) + \left(\frac{1}{34}\right.\end{align} doubling the number of terms in successive sets of parentheses. Then \begin{align} D > & \frac{1}{4} + \left(\frac{1}{4}\right) + \left(\frac{1}{8} + \frac{1}{8}\right) + \left(\frac{1}{16}+ \frac{1}{16} + \frac{1}{16} + \frac{1}{16}\right)\\ & \qquad + \left(\frac{1}{32} + \frac{1}{32} + \frac{1}{32} + \frac{1}{32} + \frac{1}{32} + \frac{1}{32} + \frac{1}{32} + \frac{1}{32}\right) + \left(\frac{1}{64}\right.\end{align} But each grouping is equal to $$\frac{1}{4}$$. So if you go out far enough, you can always add more than $$\frac{1}{4}$$ and continue doing so. Replace Questions 1-3 with this: If you could harness the combined computing power of the entire world (in 2012) running for the entire existence of the universe, you would reach a partial sum in the neighborhood of $D_{848,929,773,798,124,602,508,711,960,865,872,012} = 41.999824\dots$ Suppose someone suggested that this probably means $$D = 42$$. Pick an error bound of 0.5 and explain to your friend why even though $$D_{848,929,773,798,124,602,508,711,960,865,872,012}$$ is certainly within that error bound of 42, there will eventually be a $$D_n$$ that is outside of this range. Illustrate your reasoning on a full-page graph. Then focus on clearly answering Question 4. Mystery Constants M - HINT Suppose you stop at $$M_4$$ . Then the remaining terms are $\text{error } = \frac{1}{5!} + \frac{1}{6!} + \frac{1}{7!} + \frac{1}{8!} +\frac{1}{9!} +\cdots$ so $\text{error } < \frac{1}{5!} + \frac{1}{5!5} + \frac{1}{5!5^2} + \frac{1}{5!5^3} +\frac{1}{5!5^4} +\frac{1}{5!5^5} + \cdots$ That is, you can bound the error with a geometric series. Mystery Constants P - HINT Your sum is a geometric series. So you can compute the exact value of $$P$$ using techniques from that section. You can also use geometric series to find a closed form formula for $$P_n$$ or for the error for $$P_n$$.	{}
Wake up Student Brains with a Logic Puzzle Warm-up - Faculty Club Home / Faculty Club / Best Lessons / Wake up Student Brains with a Logic Puzzle Warm-up # Wake up Student Brains with a Logic Puzzle Warm-up #### Educator Professor, Glendale Community College, Glendale, AZ MS in Computer Science/Machine Learning, BS in Computer Science Kristen Jaskie did not discover her passion for teaching in the halls of a high school or on a university campus. It happened in the mountains of Arizona—or rather because they were threatened when she was 13 years old. That was when Jaskie’s mother read her an article about the McDowell Mountains, located north of Scottsdale, not far from their home. The story told of a group that had formed in 1990 to try to save the mountain from a land developer. Jaskie, who loved this natural monument’s light-and-shadow face and its winding trails, decided to help. “I grew up playing in the desert and going on hikes with my dog in the desert around my house, the way some kids go to playgrounds. I knew the desert—both the beautiful parts and the dangerous parts—and I was horrified by the thought of them being devoured by fancy houses.” She set up a doughnut sale at her school and raised $30. When she presented the money to the land trust committee, the directors were so impressed that they asked her to join the Board of Directors. As she worked with the trust over the next several years, she discovered that she loved public speaking. In particular, she relished returning to her former middle school to teach students about the importance of conservation and the biology and history of the Sonoran Desert ## Moving from mountains to mathematics Today, Jaskie has a bachelor’s and master’s degree in computer science and is working on her PhD in electrical engineering, with a focus on using artificial intelligence and machine learning in an electrical engineering setting. But she still indulges her passion for teaching, working as an instructor at Glendale Community College in Arizona. In that role, she frequently finds herself introducing college students to a topic as foreign as conservation was to those middle schoolers: discrete mathematical structures. “Instead of continuous math, like algebra, trigonometry, and calculus, in which real numbers and decimals are used, discrete math deals with integers [whole numbers],” she explains. Discrete mathematics, she adds, is the foundation for understanding computation. “For example, the European space launch Ariane 5 veered off its path and exploded due to a conceptual computation error involving floating point values. The launcher had cost$7 billion to develop and was carrying \$500 million worth of cargo. That error could have been prevented by a better understanding of computation. If you think about all the electronics in our lives today, these are all founded on these concepts.” Jaskie says the subject covers sequences, functions, set theory, probability theory, and graph theory. These theories typically are not covered extensively in K–12 education, she adds, so students often struggle with them. One particularly problematic concept: proofs. Proofs are important for students pursuing computer science degrees because, later in their coursework, they will need to use proofs to prove that their algorithms are correct, and they will have to lay out their arguments with no possible loopholes. “It forces them to think more rigorously and logically than in general math,” she adds. Working on proofs requires a level of critical thinking that students have often not experienced before. While puzzling over how to help them succeed, she realized that the answer might be puzzles themselves. ## Context “Discrete mathematics is the foundation behind computation. To understand how computers really work, computer scientists have to understand the mathematics and the logic behind them, and the algorithms and programs that run on them. As part of a computer science degree, students will have to come up with unique solutions (algorithms) to difficult problems. They will then have to formally prove that their solution will always work and why. Discrete mathematics is the first step in doing this.” Description: Introduction to lattices, graphs, Boolean algebras, and groups. Emphasis on topics relevant to computer science. ## Solving students’ math “problems” with puzzles To get students’ minds ready for critical thinking, Jaskie begins every class with a puzzle or logic question. The puzzles “wake students up,” she says, and they allow her to introduce new concepts in a less intimidating—and, frankly, more enjoyable—way. Here is one example: “This is the first thing they see when they walk into class on the first day,” says Jaskie. “Initially, many of them are confused. They usually don’t think there’s enough information to solve the problem and think I’m just trying to confuse them. Students then start guessing. Usually, one or two students will figure it out. When we go over the logic behind the answer, the students are surprised and generally quite interested.” ## Introducing the “why” behind the puzzles Jaskie introduces a logic puzzle in the very first class of the semester just to get students used to the idea. But after they attempt to solve it, she explains to them why she thinks puzzles can be helpful to them by showing the impact puzzle solving can have in the human brain. For this, she uses slides that illustrate brain activity during various mental tasks. During a typical class lecture, for example, research into electrodermal activity by Poh, Swenson, and Picard has shown that there is very little brain activity—in fact, it is about as flat a line as when watching TV. This is in contrast to the active brain function that takes place when students are doing homework or lab work. ##### Drowning in a sea of practice problems? Jaskie was overwhelmed—and her students frustrated—until she implemented the Five Tries approach. To address paperwork overload from grading quizzes and assignments, Jaskie has her students work on Canvas, an online learning platform. She provides homework on paper, and students submit answers into the system, which tells them the problems they got wrong—but not which parts. Their job then is to identify which problems they are confident they have correct and which they are not sure about. They then rework the ones they think they have gotten wrong. At any point in this process, they can use their textbook, work with other students, or ask for help from Jaskie during office hours. Students are given five chances to get the right answer. By working through those five tries, says Jaskie, they become adept at solving the problems. Since implementing Five Tries, student grades have gone up, Jaskie adds. In the past, most of the students ended the semester with Bs or Cs. Now most earn As and Bs. Jaskie then explains that active thinking is required in a difficult subject like discrete math—and that she uses logic puzzles to fire up students’ brains so that they are ready to learn. “People learn better if they solve problems in class rather than just in the homework,” she asserts. By the end of the semester, students often say that the puzzles are their favorite part of the class. Jaskie finds this remarkable, because college students usually hate being told they have to work with their classmates. On the first day of class, for example, when she tells them to work with their neighbors, she often hears, “This is so stupid.” After doing a couple of the puzzles, however, their attitude changes. “They start talking and joking around,” Jaskie says. “They get involved in the problems … and debate amongst themselves. It’s really fun to walk around the classroom while they are working on a problem. The vast, vast majority of the students are extremely engaged in the material.” ## Jaskie’s steps to puzzle presentation While Jaskie starts each class with a puzzle or logic question, she also uses a specific progression to help students solve the problem: The students work to solve them on their own, and then with a partner, and then as a class. (She says this technique is called peer instruction and was developed by Dr. Eric Mazur, a physics professor at Harvard.) Along with waking students up, this method helps Jaskie encourage collaboration—all while easing students closer to the math concept of the day. Here is the sequence Jaskie uses for in-class puzzle solving: ##### 1. Have them try it on their own. When they think they have the answer, they enter that answer into an online program, called Socrative, that is like a more traditional “clicker” program. ##### 2. Have them try it with a partner. Jaskie says this “peer instruction” is a form of active learning. Students get together with their neighbors and discuss the solution and how they arrived at it. In this activity, each student tries to convince the other that he or she is right. “Studies have shown that, by committing to their own answer, students are forced to come up with an answer, even if they just guess,” Jaskie says. “This primes the brain to be more open to the topic.” The students often engage in energetic discussions over how to solve the puzzle, she notes. ##### 3. Give them a chance to change their answer. After conferring with classmates, students reenter their (sometimes different) answers into Socrative. Three quarters of the students or more usually have the right answer at this point. ##### 4. Work through it as a class. Finally, Jaskie explains the solution and walks the class through how to find it. It is not just Jaskie’s students who enjoy the puzzles, she adds. Her slide presentations (which include the puzzles) have become very popular in other courses at Glendale—and beyond. In fact, her husband once took a course at Scottsdale Community College with a teacher who was using Jaskie’s slides. That teacher, her husband found out, had gotten them from a professor at Arizona State University! “It’s very flattering to know that so many other teachers in the area have a high opinion of my slides,” Jaskie notes. “I’ve certainly put a lot of work into them! A lot of the puzzles I use come from a book called The Lady or the Tiger? and Other Logic Puzzles by Raymond M. Smullyan. I also use puzzles from his other books, and books by my favorite mathematical writer Ian Stewart. Others I find online…. Some of my favorites include the Knights and Knaves puzzles from Smullyan’s books. They are very useful to teach logical thinking. Probability puzzles are probably my other favorite. I love working through … fun puzzles from the Internet, like this one:” “We discuss it and work through it,” Jaskie says … “ … before getting to the final answer:” ### See inside classrooms across the country Discover new pedagogical tactics and insights from our community of college educators in the Faculty Club newsletter.	{}
## Basic College Mathematics (9th Edition) We are given the numbers 12 and 20. We can find use the prime factorization of both numbers to find their LCM. $12=2\times2\times3$ $20=2\times2\times5$ Therefore, the $LCM=(2\times2\times3)\times(5)=60$.	{}
# Question #575a0 Mar 24, 2016 We can use the Ideal Gas Law, $P V = n R T$. Rearranging, $\frac{n}{V} = \frac{P}{R T} = \frac{112.6}{0.082 \times 293} = 4.7$. This answer is in $m o l {L}^{-} 1$, and each mole of ${H}_{2}$ is $2$ $g$, so the final answer is $9.4$ $g {L}^{-} 1$. #### Explanation: Conversions: ${20}^{o} C = 293$ $K$ $1655$ psi = $112.6$ atm Constant: 0.082 $L a t m {K}^{-} 1 m o {l}^{-} 1$	{}
# How to prove that $a^2b+b^2c+c^2a \leqslant 3$, where $a,b,c >0$, and $a^ab^bc^c=1$ $a,b,c >0$, and $a^ab^bc^c=1$, prove $$a^2b+b^2c+c^2a \leqslant 3$$ I don't even know what to do with the condition $a^ab^bc^c=1$. At first I think $x^x>1$, but I was wrong. This inequality is true, following by the verification from Mathematica • I haven't really worked on this much, but if you could somehow find$\\|(a^2,b^2,c^2)\\|$ and $\\|(b,c,a)\\|$ then you would presumably be done by Cauchy-Schwarz because $\langle(a^2,b^2,c^2),(b,c,a)\rangle = a^2b + b^2c + c^2a$. – kcborys May 6 '16 at 23:40 • Does somebody have any idea how Mathematica did that verification? – Han de Bruijn Jul 5 '16 at 13:39 We employ of the rearrangement inequality. First, since $x\mapsto x^2$ preserves the order for $x>0,$ we have $$a^2b+b^2c+c^2a\le a^3+b^3+c^3.$$ Next write the condition as $$a\ln a+b\ln b+c\ln c=0.$$ Again using the rearrangement inequality, as $x\mapsto\ln x$ preserves the order for $x>0,$ we have the inequalities: $$\begin{cases}a\ln b+b\ln c+c\ln a\le0\\ a\ln c+b\ln a+c\ln b\le0\\ a\ln a+b\ln b+c\ln c=0\end{cases}$$ Adding these together, we have $(a+b+c)\ln(abc)\le0,$ hence $abc\le1.$ Now let $\ln a+\ln b+\ln c=k\le0.$ Apply the Lagrange multiplier method with condition $g(a,b,c):=\ln a+\ln b+\ln c=k$ for a fixed $k\le0,$ to maximize $f(a,b,c):=a^3+b^3+c^3.$ Thus the Lagrange multiplier gives that the extreme of $f$ occurs when $$\begin{cases}3a^2-\lambda\frac{1}{a}=0\\ 3b^2-\lambda\frac{1}{b}=0\\ 3c^2-\lambda\frac{1}{c}=0\end{cases},$$ i.e. when $a^3=b^3=c^3=\lambda;$ then $a=b=c$ and hence $f(a,b,c)=3abc=3e^k\le3.$ $\square$ Hope this helps. Edit: As pointed out in the comment, the final part about Lagrange multipliers is incorrect; in fact, given the constraint $abc<1,$ it does not follow that $a^2b+b^2c+c^2a\le3.$ Also pointed out in the comment is to use Jensen's inequality to obtain $a+b+c\le3,$ but we are not getting answers yet. Everything we tried so far to fix this fails. We shall update if we find a way to work around. • Lagrange multiplier doesn't prove that we obtain a global maximum. Note that we need to check the boundaries, which is no easy case at all. Actually see that $a=5, b=\frac 15, c = e^{k}$ satisfy the constraint, while $f(a,b,c) = 125 + \frac{1}{125} + e^{3k} > 3$ – Stefan4024 Jul 4 '16 at 22:18 • Actually in fact using $\ln(abc) = k$ for non-positive values of $k$ isn't a good constrain, as it relaxes the inital one and it makes the inequality false under that assumption. – Stefan4024 Jul 4 '16 at 22:20 • @awllower I don't think that there's something's wrong with both friends having MSE accounts, as long as they are not intentionally voting on each other's answers in order to increase reputation. On the other side taking logarithm and applying Jensen's Inequality on $x ln(x)$ we get that $a+b+c \le 3$. Maybe you can use this and try to put two constraints on Lagrange's Multiplier. – Stefan4024 Jul 5 '16 at 5:42 • @Stefan4024 I am afraid these two constraints don't suffice: $$2.46375+\frac{1}{2}+\varepsilon<3\\2.46375\cdot\frac{1}{2}\cdot\varepsilon<1\\(2.46375)^2/2\cong3.035>3.$$ But thanks for this idea! – awllower Jul 5 '16 at 6:04 • @yoyo and awllower, the inequality does not hold as soon as you switch to $a^3+b^3+c^3$, e.g., take any $0.25\le a\le 0.5$ and $b=c$. From $a^ab^bc^c=1$, we have $b=c>1.16$, but $1.16^3+1.16^3>3$, so I am not sure if this approach is fixable. – Wiley Jul 16 '16 at 18:34 We shall prove the following inequalities: If $x+y+z=3$ and $x,y,z>0$, then $$\tag{1}x^2y+y^2z+z^2x+xyz\le 4\label{1},$$ $$\tag{2}3x^xy^yz^z+xyz\ge 4\label{2},$$ i.e., $$\tag{}x^2y+y^2z+z^2x\le 3x^xy^yz^z\label{}.$$ Accept $\eqref{}$ for a moment. Homogenizing the inequality by substitution $$x=\frac{3a}{a+b+c},~y=\frac{3b}{a+b+c},~z=\frac{3c}{a+b+c},$$ we have $\forall a,b,c>0$, $$\tag{}a^2b+b^2c+c^2a\le 3(a^ab^bc^c)^{3/(a+b+c)}.\label{}$$ If $a^ab^bc^c=1$, then we get the original inequality as desired. Proof of $\eqref{1}$: Note the LHS is cyclic, we cannot assume a specific order like $x\le y\le z$, but we can assume WLOG that $y$ is in the middle (neither the minimum nor the maximum), then $$z(y-x)(y-z)\le 0\\ \Rightarrow x^2y+y^2z+z^2x+xyz\le y(x^2+2xz+z^2)=\frac{1}{2}(2y)(x+z)^2\le\frac{1}{2}\left(\frac{2(x+y+z)}{3}\right)^3=4,$$ by AM-GM. Equality holds when $(x,y,z)=(1,1,1),(2,1,0)$ along with the cyclic permutations. Proof of $\eqref{2}$: WLOG we assume $x=\min(x,y,z)$ and consider the following two cases: • $x\ge 1/3$, then $y,z\ge 1/3$. We note that the function $$f(t)=\left(t+\frac{1}{3}\right)\ln t$$ is convex for $t\ge 1/3$, as $$f''(t)=\frac{3t-1}{3t^2}\ge 0.$$ By Jensen, \begin{align} &~~~~~~~x^{x+1/3}y^{y+1/3}z^{z+1/3}=\exp\left\{f(x)+f(y)+f(z)\right\} \ge\exp\left\{3f\left(\frac{x+y+z}{3}\right)\right\}=\exp\left\{3f(1)\right\}=1,\\ &\Rightarrow x^xy^yz^z\ge (xyz)^{-1/3},\\ &\Rightarrow 3x^xy^yz^z+xyz\ge 3(xyz)^{-1/3}+xyz\ge 4\sqrt[4]{(xyz)^{-1}(xyz)}=4, \end{align} where we have applied AM-GM for the last line. Equality holds when $x=y=z=1$. • $0<x\le1/3$. We note that the function $$g(t)=t\ln t$$ is convex for $t>0$, as $$g''(t)=\frac{1}{t}> 0.$$ Again by Jensen, we have \begin{align} &~~~~~~~y^yz^z=\exp\left\{g(y)+g(z)\right\}\ge\exp\left\{2g\left(\frac{y+z}{2}\right)\right\} =\exp\left\{2g\left(\frac{3-x}{2}\right)\right\},\\ &\Rightarrow x^xy^yz^z\ge\exp\left\{g(x)+2g\left(\frac{3-x}{2}\right)\right\} \ge\exp\left\{g\left(\frac{1}{3}\right)+2g\left(\frac{4}{3}\right)\right\} =\frac{32}{27}\sqrt[3]{2}>\frac{4}{3},\\ &\Rightarrow 3x^xy^yz^z+xyz>4+xyz>4. \end{align} The second line follows from that $h(t):=g(t)+2g((3-t)/2)$ is monotonically decreasing for $t\in(0,1)$, so $h(x)\ge h(1/3)$ as $x\le 1/3$. Proof of monotonicity: $$h'(t)=\ln\left(\frac{2t}{3-t}\right)<0\iff 0<t<1.$$ Post-mortem: 1. Despite the flow of the proof, the starting point is the homogeneous version \eqref{}; 2. \eqref{1} is due to Vasile, which allows us to strengthen the inequality into a symmetric one as \eqref{2} (I am not able to find the originial post on artofproblemsolving, but see e.g., here). It seems that converting \eqref{} into other symmetric form such as $x^3+y^3+z^3$ is too strong for it to hold; 3. For \eqref{2}, the case of $x\le 1/3$ is unfortunately necessary, as $x^xy^yz^z\ge(xyz)^{-1/3}$ does NOT always hold, e.g., check $x\to0,y-z\to 0$. Is there any better estimate of $x^xy^yz^z$ so we can avoid the derivatives? Another follow-up question is to determine the smallest $k$ such that $kx^xy^yz^z+xyz\ge k+1$ holds given the constraints. It definitely fails for $k\le 1/2$. Brute Force ($200\times200\times200$ grid) Not a proof, but couldn't resist. Of course, everybody knows where the maximum is, for reasons of symmetry: with $\,(a,b,c) = (1,1,1)\,$ we have $\,a^ab^bc^c=1\,$ and $\,a^2b+b^2c+c^2a = 3$ . The following (Delphi Pascal) program is supposed to be self documenting. program HN_NH; { Brute Force with Seven Point Stars ================================== } function pow(x,r : double) : double; { x^r } begin pow := exp(rln(x)); end; procedure test(veel : integer); var i,j,k,ken : integer; a,b,c,d,f,min,max : double; procedure vertex(x,y,z : integer); var a,b,c,h : double; begin a := (2i+x)d; b := (2j+y)d; c := (2k+z)d; h := pow(a,a)pow(b,b)pow(c,c); if h < 1 then ken := ken2 else ken := ken2+1; end; begin { Verify maximum (a,b,c)-value < 1.6 } Writeln(exp(2/exp(1)),' <',pow(1.6,1.6)); d := 1.6/veel/2; { half voxel size } min := 3; max := 0; { initialize } for i := 1 to veel-1 do begin for j := 1 to veel-1 do begin for k := 1 to veel-1 do begin ken := 0; { Binary number for collecting <> } { Each vertex of a 7-point star } vertex(-1,0,0); vertex(+1,0,0); vertex(0,-1,0); vertex(0,+1,0); vertex(0,0,-1); vertex(0,0,+1); if (ken = 0) or (ken = 63) then Continue; { Midpoint of star is near a^ab^bc^c = 1 } a := 2id; b := 2jd ; c := 2kd; f := sqr(a)b + sqr(b)c + sqr(c)a; if f < min then min := f; { Determine maximum of f(a,b,c) } if f > max then max := f; end; end; end; Writeln(min,' < f(a,b,c) <',max); end; begin test(200); end. And now we are curious, of course, what the maximum is (it's the last number in this output): 2.08706522863453E+0000 < 2.12125057109759E+0000 9.12537600000000E-0003 < f(a,b,c) < 3.00026265600000E+0000 Well, anyway better than the previous (Brute Force with Voxels) attempt. To be convincing, though, a decent error analysis is still needed :-( Note. Explaining the estimate $\{a,b,c\} < \{1.6\}$ in the program: $$f(x) = x^x = e^{x\ln(x)} \quad \Longrightarrow \quad f'(x) = [1+\ln(x)]e^{x\ln(x)} = 0 \quad \Longrightarrow \quad x=1/e \\ \Longrightarrow \quad f(1/e) = e^{-1/e}$$ This means that the maximum $x$ of each one of the coordinates in the product $a^ab^bc^c=1$ is: $$x^x = e^{2/e} < (1.6)^{1.6}$$ Therefore each of the coordinates $\;x < 1.6\,$ (or $\,1.58892154635044$ , to be double precise). • A much simpler way to verify the inequality numerically (similar to what you have done for other inequality questions) is to check \eqref{*} instead: $$x^2y+y^2z+z^2x\le 3x^xy^yz^z$$ if $x+y+z=3$ and $x,y,z>0$. It is equivalent to the original inequality once they are homogenized. – Wiley Jul 18 '16 at 5:18 The condition can be presented in form $$a\ln a +b\ln b + c\ln c = 0.$$ Let $$a\leq b\leq c,$$ then $$\ln a \leq \ln b \leq \ln c,$$ and we can use Chebyshev sum inequality: $$3(a\ln a +b\ln b + c\ln c) \geq (a+b+c)\ln abc,$$ $$abc\leq 1.$$ Evidently, the expression $a^2b+b^2c+c^2a$ achieves maximum when $abc=1.$ The standard way of solving the problem on a conditional extremum is the method of Lagrange multipliers, which reduces it to a system of equations. The maximum value of function $$f(a,b,c,λ)=a^2b+b^2c+c^2a+λ(abc-1)$$ for $a,b,c>0$ on the interval is reached or at its edges, or in one of the points with zero partial derivatives $$f'_a=0,\quad f'_b=0,\quad f'_c=0,\quad f'_λ=0,$$ or $$\begin{cases} 2ab+c^2+\lambda bc = 0\\ 2bc+a^2+\lambda ca = 0\\ 2ca+b^2+\lambda ab = 0\\ abc-1 = 0, \end{cases}$$ then $$\begin{cases} a(2ab+c^2) = b(2bc+a^2)=c(2ca+b^2),\\ abc=1, \end{cases}$$ $$\begin{cases} 2b^2c -c^2a = a^2b\\ b^2c -2c^2a = -a^2b\\ abc=1, \end{cases}$$ $$c^2a = b^2c = a^2b,\quad abc=1,$$ $$\dfrac cb =1, \dfrac ba =1, \quad abc=1,$$ $$a=b=c=1,$$ $$f(a,b,c,\lambda)=3.$$ Note that $$\lim_{a\to 0} a\ln a = 0,$$ so on the edge $a=0$ we have to minimize $f(b,c,\lambda) = b^2c + \lambda(bc-1),$ and then we get the system $$\begin{cases} 2bc+\lambda c = 0\\ b^2+\lambda b = 0\\ bc-1=0 \end{cases}$$ with solution $$b=2,\quad c=\dfrac12,\quad f = 2 < 3.$$ That means that $$\boxed{a^2b+b^2c+c^2a \leq 3}$$ • not sure why I still bother, but here it goes: you are repeating the exact same mistake in the most up-voted answer and it has been pointed out in the comment that $abc\le 1$ does NOT imply $a^2b+b^2c+c^2a\le 3$, take e.g., $(a,b,c)=(2,1/2,1)$ – Wiley Jul 26 '16 at 20:41	{}
Paper and ancilary files. # Author(s): Zvi Bern, John Joseph M. Carrasco, Wei-Ming Chen, Henrik Johansson, Radu Roiban, Mao Zeng # Abstract: We use the recently developed generalized double-copy procedure to construct an integrand for the five-loop four-point amplitude of N=8 supergravity. This construction starts from a naive double copy of the previously computed corresponding amplitude of N=4 super-Yang-Mills theory. This is then systematically modified by adding contact terms generated in the context of the method of maximal unitarity cuts. For the simpler generalized cuts, whose corresponding contact terms tend to be the most complicated, we derive a set of formulas relating the contact contributions to the violations of the dual Jacobi identities in the relevant gauge-theory amplitudes. For more complex generalized unitarity cuts, which tend to have simpler contact terms associated with them, we use the method of maximal cuts more directly. The five-loop four-point integrand is a crucial ingredient towards future studies of ultraviolet properties of N=8 supergravity at five loops and beyond. We also present a nontrivial check of the consistency of the integrand, based on modern approaches for integrating over the loop momenta in the ultraviolet region. Tags: Categories: Updated:	{}
# Question In a presidential election, 308 out of 611 voters surveyed said that they voted for the candidate who won (based on data from ICR Survey Research Group). Use a 0.10 significance level to test the claim that among all voters, the percentage who believe that they voted for the winning candidate is equal to 43%, which is the actual percentage of votes for the winning candidate. What does the result suggest about voter perceptions? Test the given claim. Identify the null hypothesis, alternative hypothesis, test statistic, P-value or critical value(s), conclusion about the null hypothesis, and final conclusion that addresses the original claim. Use the P-value method unless your instructor specifies otherwise. Use the normal distribution as an approximation to the binomial distribution. Sales0 Views79	{}
# Eigenvalues of complex $2×2$ matrices [duplicate] Let $A$ be complex $2×2$ matrices s.t. $A^2=0$. Which of the following statements are true? 1. $PAP^{-1}$ is diagonal for some $2×2$ real matrix $P$. 2. $A$ has $2$ distinct eigenvalues in $\Bbb C$. 3. $A$ has $1$ eigenvalue in $\Bbb C$ with multiplicity $2$. 4. $Av=v$ for $v\in \Bbb C^2 ,v≠0$. ## marked as duplicate by vadim123, Martin, Stahl, Henry T. Horton, achille huiMay 11 '13 at 5:11 • not getting any A s.t. A^2=0. – pankaj Dec 17 '12 at 13:22 • where to begin ....please suggest me........... – pankaj Dec 17 '12 at 13:35 • Take $A=\begin{pmatrix}a&a\\-a&-a\end{pmatrix}$ for any $a\in\mathbb{C}$, for exmaple. – Dennis Gulko Dec 17 '12 at 13:35 • 2 is wrong ........ 3 is correct.......... – pankaj Dec 17 '12 at 13:40 • That's right. Can you prove it? – Dennis Gulko Dec 17 '12 at 13:40 I will sum the above discussion here: 1. Show that $(PAP^{-1})^2=PA^2P^{-1}$. Since $A^2=0$, what can you conclude about $A$, if indeed there exists such $P$? 2. You said that it is wrong. Can you show why? (Hint: what is the def of an eigenvalue?) 3. Is coorect, as you said. It should follow from the proof you used in 2. 4. If there esists $v\in\mathbb{C}^2$ such that $Av=v$, what is $A^2v$? can that happen? • 4 is wrong still not getting 1..... – pankaj Dec 17 '12 at 14:18 • @Dennis,I am new in mathematics field , so as far as I know about $2$,since $A^2=0$ , so $A$ will satisfy the equation $x^2=0$. So minimal polynomial of $A$ will divide this polynomial $x^2$.If A has two distinct eigenvalues then the minimal polynomial will not divide $x^2$.so $2$ false. $3$ will be true against this logic.Am I right? One thing I want to clarify I am not the person who asked the question,I made it because our name is same. – p.haz Dec 17 '12 at 14:36 • please guide me for 1.......... – pankaj Dec 17 '12 at 14:37 • If $D$ is diagonal and $D^2=0$, then what is $D$? – Dennis Gulko Dec 17 '12 at 15:18 • D is not nilpotent.. am i right?? – pankaj Dec 17 '12 at 16:27 $A$ is a nilpotent matrix, so it has only $0$ as eigenvector with multiplicity $2$.	{}
# Is there a difference between imported file types? I've found a model on a site that I'd like to use but it doesn't come in a Blender format, so having never purchased a model before I'm just wondering which format I should buy? The formats available are .3ds, .dxf, .obj, and .max. Are they all essentially the same? I've seen in the Add-ons that these can all be imported, but I don't want to waste my money on one that won't work properly etc., so is there a type that's known to work better? • 3ds is deprecated, bad suggestion. The most modern file format is alembic. .obj is really old and really limited in features, it is still in use because it is human readable and easy to implement for a developer compared to file types like .fbx or .dae, which have a ton more features. – p2or Sep 27 '16 at 13:03	{}
# What is the power generating capacity for an airport GPU? What is the normal current for GPU power supply for commercial aircraft and how much power do they need while on ground (in kWh)? I have read that aircraft need need 28V DC and 115V AC - what would be the percentage between both modes of supply? Would it by possible to power GPUs entirely by solar power? • You mentioned commercial aircraft but tagged this with general aviation. Are there specific aircraft types you are interested in? The power requirements will depend on aircraft size and type. Jun 14, 2016 at 16:15 • kWh is a measure of energy, not power. Energy is power applied over time. Jun 14, 2016 at 17:32 • @andrewmh20 Nope, you're backwards. See here for example. Jun 16, 2016 at 15:50 • @andrewmh20 Wh is watts multiplied by time. Power has the time component divided out. Jun 17, 2016 at 2:45 • @andrewmh20 I'm a software engineer at a company that produces watt-hour standards - I'm pretty sure I'm correct. Anyway, this is off-topic and we've discussed it enough. Believe what you will. Jun 17, 2016 at 2:47	{}
# How to find a function from a series with non-numeric coefficients? Let us consider a simple example, Series[Exp[ax], {x, 0, 5}] // Normal Now, I want to revert back to Exp[ax] from it's series expansion. Is there any such built-in functionality to achieve this? Thanks to @Szabolcs and @Jenny_mathy for telling me about FindGeneratingFunction, which worked for the above example. Edit But for my actual series, I am not getting any output FindGeneratingFunction[ CoefficientList[a + b x + (c x^2)/2 + 1/6 (b^2 - a c) x^3, x], x] • Look up FindGeneratingFunction. – Szabolcs Apr 16 '17 at 9:03 • Possible duplicates: (38128) (133006) – Szabolcs Apr 16 '17 at 9:05 ## 1 Answer I think you want something like this as Szabolcs pointed FindGeneratingFunction[ CoefficientList[1 + x + x^2/2 + x^3/6 + x^4/24 + x^5/120, x], x] The function changed, so the new one is FindGeneratingFunction[ CoefficientList[ 1 + a x + (a^2 x^2)/2 + (a^3 x^3)/6 + (a^4 x^4)/24 + (a^5 x^5)/120, x], x] but it still works E^(a x) • But in this case, I am not getting any output. FindGeneratingFunction[ CoefficientList[a + b x + (c x^2)/2 + 1/6 (b^2 - a c) x^3, x], x] – zhk Apr 16 '17 at 9:26 • do you know what the output should be? – J42161217 Apr 16 '17 at 9:29 • Something exponential, maybe like this $a+c(1-\exp{bx})$ not sure – zhk Apr 16 '17 at 9:30 • I tried this FindGeneratingFunction[ CoefficientList[ a + c + b c x + 1/2 b^2 c x^2 + 1/6 b^3 c x^3 + 1/24 b^4 c x^4 + 1/120 b^5 c x^5, x], x] and it works. So the one you are searching must be more complicated – J42161217 Apr 16 '17 at 9:38 • @MMM I think that it would work better if you fed it with more terms. at least x^4 and x^5... – J42161217 Apr 16 '17 at 10:09	{}
# Holiday SMS Kucera and Malek start from the holiday together. They agreed that if they be 100 km apart, will send a SMS. Kucera traveling at 60 km/h., Malek 90 km/h. They started at 14 hours PM. At what time they send a message? Result h = 17:20 hh:mm #### Solution: $h=14+100/(90-60)=\dfrac{ 1733333 }{ 100000}=17.33333=17:20 \ \text{hh}:\text{mm}$ Our examples were largely sent or created by pupils and students themselves. Therefore, we would be pleased if you could send us any errors you found, spelling mistakes, or rephasing the example. Thank you! Leave us a comment of this math problem and its solution (i.e. if it is still somewhat unclear...): Be the first to comment! Tips to related online calculators Do you have a linear equation or system of equations and looking for its solution? Or do you have quadratic equation? Do you want to convert velocity (speed) units? Do you want to convert time units like minutes to seconds? ## Next similar math problems: 1. Two trains meet From A started at 7:15 express train at speed 85 km/h to B. From B started passenger train at 8:30 in the direction to A and at speed 55 km/h. The distance A and B is 386 1/4 km. At what time and at what distance from B the two trains meet? 2. Two ports From port A on the river, the steamer started at an average speed of 12 km/h towards port B. Two hours later, another steamer departed from A at an average speed of 20 km/h. Both ships arrived in B at the same time. What is the distance between ports A an 3. Warehouse cars From the warehouse started truck at speed 40km/h. After 1hour 30mins started from the same place same direction a car at speed 70 km/h. For how long and at what distance from the warehouse overtake a truck? 4. Train speed Two guns were fired from the same place at an interval of 10 minutes and 30 seconds, but a person in a train approaching the place hears second shot 10 minutes after the first. The speed of the train (in km/hr), supposing that sound travels at 340 m/s is: 5. Storm So far, a storm has traveled 35 miles in 1/2 hour in direction straight to observer. If it is currently 5:00 p. M. And the storm is 105 miles away from you, at what time will the storm reach you? Explain how you solved the problem. 6. Walnuts x walnuts were in the mission. Dano took 1/4 of nuts Michael took 1/8 from the rest and John took 34 nuts. It stayed here 29 nuts. Determine the original number of nuts. 7. Klara Klara and Jitka went on a hiking trip at 13 o'clock at speed 5km/h. At 14 o'clock, Tomas ride on the bike at an average speed of 28 km/h. How many hours and at what distance from the beginning of the road Tomáš caught the two girls? 8. Moving Vojta left the house at three o'clockat 4 km/h. After half hour later went from the same place Filip by bicycle at speed 18 km/h. How long take Tilip to catch up Vojta and how far from the house? 9. Runners If John has a running speed of 3.5miles per hour and Lucy has a speed of 5 miles per hour. If John starts running at 10:00 am and Lucy starts running at 10:30 am, at what time will they meet? (as soon as possible) 10. Pedestrian Pedestrian came started at 8h in the morning with speed 4.4 km/h. At half-past eleven cyclist started at 26 km/h same way. How many minutes take cyclist to catch up pedestrian? 11. The ship The ship went upstream speed of 20 km/h in relation to water. River flows at speed 10 km/h. After half an hour, he stopped and returned downstream to the starting point. How long it took way back when even if downstream speed of ship is 20 km/h in relatio 12. Family Mom is 42 years old and her daughters 13 and 19. After how many years will mother as old as her daughter together? 13. Fifth of the number The fifth of the number is by 24 less than that number. What is the number? 14. Otto and Joachim Otto and Joachim go through the woods. After some time Otto tire and make 15 minutes stop. Joachim meanwhile continues at 5 km/h. Otto when he set off again, first running speed of 7 km/h, but it keep only 30 sec and 1 minute must continue at 3 km/h. This 15. Mom and daughter Mother is 39 years old. Her daughter is 15 years. For many years will mother be four times older than the daughter? 16. Six years In six years Jan will be twice as old as he was six years ago. How old is he? 17. The shooter The shooter heard the impact of the bullet on the target in one second after the shot. The bullet was moving at an average speed of 500 m/s. Calculate with speed of sound of 340 m/s. Determine the distance of the target.	{}
The posters should have the size 100 cm (height) by 80 cm (width) Poster session Thursday, July 10 M. Afanasova Electron kinetics in composite InAs/AlSb structure with two-dimensional degenerated electron gas O.Yu. Andreeva Infuence of inhomogeneity parameters and position on vortex structure in long Josephson junction T.L. Boyadjiev Critical current of a long Josephson 0-$\pi$ junction in magnetic field O. Chalaev Anisotropic conductivity of a diffusive matter in the presence of Rashba and Dresselhaus spin-orbit coupling A. Yu. Cherny 1) Revealing inner structure of the polycarbosilane dendrimers from SANS data: model approach 2) Dynamic structure factor and drag force in 1D Bose gas B. Colin Detecting entangled states in graphene via crossed Andreev reflection A.B. Dubois Electron - electron interactions and anomalies in the landau quantization damping M. Dyneikan Explanation of the formation dynamics of the bound state with an ionic implantation M. Fardmanesh 1) Investigation of the I-V characteristics of high-Tc superconducting YBCO Josephson junction arrays 2) Effect of the nano-structure Cu-Carbon composite absorber layer on the response of superconductive YBCO TEBs C. Gadermaier Ultrafast relaxation in MoSI nanowires P.M. Grant Electronic properties of cuprous and ferrous monoxides D.R. Gulevich Superconducting THz electronics with Josephson vortices M. Hamdipour Breakpoint region structure in the current-voltage characteristics of layered superconductors V.L. Katkov Band structure effect on field emission of graphite nanotubes, graphene, and crystalline graphite S.-J. Kim Peculiar periodic peaks in two Bi-2212 stacks with incident magnetic fields N. Klenov Dynamics and eigenstates of nSQUID M. Kolahchi The behaviour of the SET-resonator system in the strongly coupled classical regime D. V. Kolesnikov Properties of van Hove singularities in capped carbon nanotubes V.N. Kondratyev 1) Shells in magnetized nano-dots 2) Thermal explosion of nano-droplets of noble gas atoms V. Kornev Possible solution for high linearity Josephson-junction array Z.Ya. Kosakovskaya Nonlinear interlayer transport in the aligned carbon nanotube films and graphite G. Kumar Surface plasma wave excitation over a plasma cylinder U. Kutliev 1) Sputtering of ionic water at the bombardment by Ar+ 2) Investigation of sputtering of atomic clusters at the bombardments by ar ions of the surface Au(111) covered by ice films I.S Lobanov Two particle scattering on pencil of rays V. Lotoreichik Approximation of point perturbations on finite set of Laplace-Beltrami operator on Riemannian manifold M. Lu-Dac Dynamics in mesoscopic superconducting rings: relaxation process and vortex-antivortex pairs A.E. Madison Self-assembling, hierarchy and architectures of carbon nanoobjects M.M. Maslov Theoretical studies on the cubane chains, networks and bulks H. Matsumoto Numerical simulations of THz emission from intrinsic Josephson junctions T. Matsuura Charge density wave circulating current in NbSe$_3$ rings observed by measuring shapiro interference V.F. Morozov Theory of stretching of single-molecule dsDNA attached to nano- particle A. Namiranian Nonlinear effect in conductance of a finite-length armchair single-wall carbon nanotube due to presence of a single impurity: An analytical study H. Nobukane Observation of quantum fluctuation in nano Sr$_2$RuO$_4$ p-wave superconductors A. Orlov Interlayer tunneling spectroscopy of NbSe3 at high magnetic fields V. Pavlenko Coherent responses of Bi-2212 stacked junctions to sub-terahertz radiation under magnetic field oriented across the layers S.V. Pereverzev Ultra-sensitive hot-electron nanobolometer for terahertz astrophysics S. Postnov Self-consistent theory for nonlinear optical responce of metal nanofilms M. Pudlak Electronic properties of double-layer carbon nanotubes P. Pyatkovskiy Polarization function and plasmons in graphene with a finite gap in the quasiparticle spectrum D. Ryzhov Multi-vortex configurations in mesoscopic superconductors: electronic structure and heat transport A. Saffarzadeh Exchange coupling between two ferromagnetic electrodes A.V. Samokhvalov Vortex states induced by proximity effect in multiply connected ferromagnet-superconductor systems H.A. Sarkisyan Interband transitions in narrow gap InSb spherical layer quantum dot in presence of electric field A. Sergeev Effects of disorder on electron-phonon kinetics and transport in low-dimensional conductors N. Shahtahmassebi Transport properties of an electrode-C60-electrode system S.N. Shevchenko Theoretical study of the multi-photon excitations in Josephson-junction qubits coupled to resonant circuit O.V. Sidorov Nanotransition in rigid-rod polymer-based fibers with non-linear optical properties M.A. Silaev Conductance enhancement due to the resonant tunneling into the subgap vortex core states in normal metal/superconductor ballistic junctions O. Smyrnov Exciton states in single-walled carbon nanotubes A. Valizadeh Dynamics of a triangular single-plaquette Josephson-junction array U. Verma Short pulse laser third harmonic generation in a tunnel ionizing gas N. Vlasii Finite-temperature induced quantum numbers on graphitic nanocones	{}
Consider the function $f(x) = 3-3 x^{2/3}$ on the interval $[ -1 , 1 ]$. Which of the three hypotheses of Rolle's Theorem fails for this function on the inverval? (a) $f(x)$ is continuous on $[-1,1]$. (b) $f(x)$ is differentiable on $(-1,1)$. (c) $f(-1)=f(1)$.	{}
# Miller-Rabin primality test for $2^{32}+1$ How can I prove that $2^{32}+1$ is composite number using Miller-Rabin primality test? I can't find a solution which verify the hypothesis of theorem. Let $n=2^{32}+1,\, a=3$. You can show that $a=3$ is a witness for compositeness of $n$, i.e. $n$ is not a strong pseudo prime to base 3. Here is the calculation: Decompose $n-1$ as $n-1=d\times 2^s = 1\times 2^{32}$, i.e. $d=1,\,s=32$. Then you have $a^d\not \equiv 1 \pmod {n}$, now verify that $x_r \equiv a^{2^r d}\not \equiv -1 \pmod {n}$ for $0\le r \le s-1.$ Note that $x_{r+1}\equiv x_r^2 \pmod {n}$. In the table I have listed $r$ and $x_r \pmod {n}$ r x_r mod n 1 9 2 81 3 6561 4 43046721 5 3793201458 6 1461798105 7 852385491 8 547249794 9 1194573931 10 2171923848 11 3995994998 12 2840704206 13 1980848889 14 2331116839 15 2121054614 16 2259349256 17 1861782498 18 1513400831 19 2897320357 20 367100590 21 2192730157 22 2050943431 23 2206192234 24 2861695674 25 2995335231 26 3422723814 27 3416557920 28 3938027619 29 2357699199 30 1676826986 31 10324303 • Where do you made all the modular calculus?Online?Thank you! – alexb Dec 7 '15 at 15:15 • No, I simply put a writeln statement in my SPSP routine. But you can do it easily with a scripting language / interpreter, e.g. with Pari/GP n=2^32+1, y=Mod(3,n), y=y^2, y=y^2 etc – gammatester Dec 7 '15 at 15:38 As your example has already been solved therefore, I am gonna explain the idea behind Miller-Rabin primality test. The test is based on Fermat's little theorem i.e. a large positive odd integer n is pseudoprime to the base b if $b^{n-1} \equiv 1 \pmod{n}$ where gcd$(n,b)=1$ or simply $b\in(\mathbb{Z}/\mathbb{nZ})^*$. Which implies that $$b^{(n-1)/2} \equiv \pm1 \pmod{n} \\ b^{(n-1)/4} \equiv \pm1 \pmod{n} \\ \vdots \qquad \qquad \vdots \qquad \qquad \vdots \\ b^{(n-1)/2^{s}} \equiv -1 \pmod{n}$$ Where $((n-1)/2^{s})^{th}$ power is odd. In practice we take $n-1=2^st$ where $t$ is odd integer. Then for any integer b, $0<b<n$, we check the existence of any of the following two conditions 1) $b^t \equiv 1 \pmod{n}$ or 2) $b^{2^r}t \equiv -1 \pmod{n}$ where $0\leq r < s$ Then $n$ is called a strong pseudoprime to the base b. The probability of $n$ to be prime gets higher and higher as more and more random $b$s satisfy any of the above condition.	{}
# Inner product of two continuous maps is continuous Let f,g be continuous maps of S in $\mathbb{R}^n$, to $\mathbb{R}^m$. Show the inner product h(x) = $\langle f(x), g(x)\rangle$ is continuous. My attempt: Since f,g are continuous, their product is a continuous mapping, so for $\epsilon \gt 0\: t.e\: \delta \gt 0$ such that $\parallel x – a\parallel \lt \delta$ implies $\parallel \langle f(x),g(x)\rangle – \langle f(a)g(a)\rangle \parallel \le\parallel f(x)g(x) – f(a)g(a)\parallel \lt \epsilon$ by schwartz inequality. #### Solutions Collecting From Web of "Inner product of two continuous maps is continuous" (Adjust $n$, $m$ as appropriate, the question is a little ambiguous.) The map $\phi: \mathbb{R}^n \times \mathbb{R}^n \to \mathbb{R}$ (or complex, if it suits) defined by $\phi(x,y) = \langle x , y \rangle$ is continuous since \begin{eqnarray} \|\phi(x,y) – \phi(x’,y’)\| &=& \|\phi(x,y) – \phi(x,y’) + \phi(x,y’) – \phi(x’,y’)\| \\ & \leq & \|\phi(x,y) – \phi(x,y’)\| + \|\phi(x,y’) – \phi(x’,y’)\| \\ & \leq & \\|x\\| \\|y-y’\\| + \\|y’\\| \\|x-x’\\| \end{eqnarray} Hence if $\max(\\|x-x’\\|,\\|y-y’\\|) \leq 1$, then $\|\phi(x,y) – \phi(x’,y’)\| \leq \max(\\|x\\|,\\|y\\|+1)(\\|y-y’\\| + \\|x-x’\\|)$. Now choose $\epsilon>0$, then if $\max(\\|x-x’\\|,\\|y-y’\\|) < \frac{1}{2\max(\\|x\\|,\\|y\\|+1)}\epsilon$ (and $\leq 1$, of course), you have $\|\phi(x,y) – \phi(x’,y’)\| < \epsilon$. Since $\phi$ is continuous, and the map $\eta:S \to \mathbb{R}^n \times \mathbb{R}^n$ defined by $\eta(x) = (f(x),g(x))$ is continuous, it follows that the composition $\phi \circ \eta$ is continuous.	{}
# Vector question - North-east direction 1. Aug 4, 2016 ### gracy 1. The problem statement, all variables and given/known data A particle undergoes three successive displacements given by $S_1$=√2 m North- East, $S_2$=2m due south and $S_3$=4m 30 degree north of west , then find the magnitude of net displacement? 2. Relevant equations $S$= $S_1$ + $S_2$ + $S_3$ 3. The attempt at a solution I don't understand how to represent these displacement in the form of vectors. I do have solution of this problem. According to the given solution $S_1$ = (√2 cos 45)i + (√2sin 45) j I can't comprehend how the simple North-east turned into this equation? And I think the question not at all mentions angle 45 . Is there any convention or thumb rule that I am missing while dealing with directions? 2. Aug 4, 2016 ### A.T. It mentions "North-East". 3. Aug 4, 2016 ### gracy Last edited: Aug 4, 2016 4. Aug 4, 2016 ### gracy Is this correct representation of the displacements in question? File size: 39.8 KB Views: 87 5. Aug 4, 2016 Yes. 6. Aug 4, 2016 ### gracy In solution $S_3$ is given to be (-4cos30)i +(4sin30)j I did not understand why is there negative sign in (-4 cos30)i 7. Aug 4, 2016 ### cnh1995 Sign convention. Second quadrant has -ve x and +ve y. That way, S2 should be -2j. 8. Aug 4, 2016 ### Ray Vickson Look at your diagram in post #4. Is the x-component of $S_3$ positive, negative, or zero? 9. Aug 4, 2016 ### David Lewis It may be helpful to draw the vectors to scale, and represent coordinate axes with a thin line, and the vectors with a thick line. (That way you can tell them apart.) Also, if you arrange the vectors head to tail, you will be able to get an approximate answer quickly. 10. Aug 5, 2016 ### gracy Exactly, but in solution it's given to be +2j. 11. Aug 5, 2016 ### cnh1995 It should be -2j. There might be a typo in the solution provided by the book. 12. Aug 5, 2016 ### Nidum 13. Aug 15, 2016 ### gracy I encountered one more problem Vector A points vertically upward and B points towards north.Vector product AXB is ? a)along west b)zero c)vertically downward d)along east I've been drawing north as an upward direction . Going with that approach angle between A and B would be zero 14. Aug 15, 2016 ### cnh1995 The wording implies north is not vertically upwards. Imagine you're standing on a ground. What does 'vertically upward' mean to you in this case? 15. Aug 15, 2016 ### gracy Towards the sky? 16. Aug 15, 2016 ### cnh1995 Yep.. 17. Aug 15, 2016 ### gracy So here shall I consider north in the usual way and vertically upward as coming out from page? 18. Aug 15, 2016 ### cnh1995 Yes. 19. Aug 15, 2016 ### gracy That would be perpendicular to the plane containing A and B . It's either west or right. Using right hand screw rule I am getting along west as my answer . 20. Aug 15, 2016 ### cnh1995 Are you sure?	{}
# UPDATE_YEAR Chandra Bergmann #### The function UPDATE_YEAR changes the year described by a Date or DateTime into another specified number. This function takes two pieces of input: a Date or a DateTime, and a Number. It outputs the given Date or DateTime with the year value replaced by the given number. ### Declaration UPDATE_YEAR(datetime, new_year) -> new_datetime UPDATE_YEAR(date, new_year) -> new_date ### Parameters datetime (type: DateTime) Any DateTime. date (type: Date) Any date. new_year (required, type: Number) The new year; this is the number that will replace whatever value is currently associated with the year in the given Date or DateTime. ### Return Values new_datetime (type: DateTime) The DateTime that results from taking the given DateTime and replacing the year value with the given number. new_date (type: Date) The Date that results from taking the given Date and replacing the year value with the given number. ### Examples example_date_and_time = { "date": { "day": 1, "month": 4, "year": 2021 }, "time": { "hour": 16, "minute": 14, "second": 38, "millisecond": 0 }, "timeZone": "UTC"} The following example takes the date described in example_date_and_time and replaces the given year value (2021) with 2022. Note that the only difference between the output of this example and example_date_and_time is the the value of the year. When given a DateTime as input, UPDATE_YEAR returns a DateTime: UPDATE_YEAR(example_date_and_time, 2022) = { "date": { "day": 1, "month": 4, "year": 2022 }, "time": { "hour": 16, "minute": 14, "second": 38, "millisecond": 0 }, "timeZone": "UTC"} The above example demonstrates how the UPDATE_YEAR function behaves when given a DateTime as input. In order to further establish how the UPDATE_YEAR function behaves when given a Date as input, assume the last example has access to the following Date value: example_date = { "day": 1, "month": 4, "year": 2021} The following example takes the Date described in example_date and replaces the given year value (2021) with 2022. Note that the only difference between the output of this example and example_date is the the value of the year. When given a Date as input, UPDATE_YEAR outputs a Date: UPDATE_YEAR(example_date, 2022) = { "day": 1, "month": 4, "year": 2022}	{}
tikz \savebox only showing part of image I can't get tikz to show the whole image created by using \showbox. I think it is a node issue and have tried using a scope and using local bounding box but that doesn't work either. I have posted the code below as well. For the record I started using the answers provided in the following post to get to where I am now. How to get consistent positioning for a node with \usebox containing a \tikzpicture. For the record I am attempting to do this because I need to use the image on a chain, but draw different lines on top of it as well. but first need to be able to repeat this multiple times. Plus I may be using this same image in other tikz pictures/drawings as well. CODE \documentclass[tikz,border=0pt]{standalone} % https://tex.stackexchange.com/questions/37823/how-to-get-consistent-positioning-for-a-node-with-usebox-containing-a-tikzpict % general packages or settings \tikzset{ %general shapes unburn/.style={circle, draw=black,minimum size=0.2cm}, burn/.style={circle, draw=black,minimum size=0.2cm,pattern=crosshatch}, burning/.style={circle, draw=black,minimum size=0.2cm,pattern=dots}, every join/.style={-latex} } %custom nodes \newcommand{\chamber}[1]{ \begin{scope}[local bounding box=#1] %draw combustion chamber %outer coordinates of chamber \coordinate (p1) at (0,0); \coordinate (p2) at (0,4); \coordinate (p3) at ($(p2)+(30:2)$); \coordinate (p4) at ($(p3)+(2,0)$); \coordinate (p5) at ($(p4)+(-30:2)$); \coordinate (p6) at ($(p5)+(0,-4)$); \coordinate (p7) at ($(p1)!0.5!(p6)$); %middle point at the bottom of the chamber \coordinate (p8) at ($(p3)!0.5!(p4)$); %middle point at top of chamber %draw cylinder \draw[very thick] (p1)--(p2)--(p3)--(p4)--(p5)--(p6); %draw piston \filldraw[fill=gray!60,very thick] (p1)+(0.2,0) rectangle ++($(p6)+(-0.2,1.8)$); \filldraw[fill=white,very thick] ($(p7)+(0,0.9)$) circle (0.26); %draw spark plug \filldraw[fill=gray!60] ($(p8)+(-0.12,-0.8)$) rectangle ($(p8)+(0.12,0)$); \filldraw[fill=gray!60] ($(p8)+(-0.06,-0.8)$) rectangle ($(p8)+(0.06,-1)$); \draw[semithick] ($(p8)+(0.18,0)$) \|- ($(p8)+(-0.12,-1.08)$); \end{scope} } \newsavebox{\manychamber} \savebox{\manychamber}{% \begin{tikzpicture} \chamber{}; \end{tikzpicture}% } \begin{document} \begin{tikzpicture}%[start chain=going below] \pgfmathsetseed{4} %get same random decorations repeated \def\ht{4}; %total height of chamber \def\cmtopt{28.45274} %cm to pt conversion \node at (0,0){\usebox{\manychamber}}; %\draw[help lines,step=0.05cm,opacity=0.2] (current bounding box.south west) grid (current bounding box.north east); \end{tikzpicture} \end{document} The culprit is the following line: \def\ht{4}; %total height of chamber The command \ht is an important TeX command for the height of a box. It is used in various places in LaTeX and TikZ. \newcommand*{\ht}{4} And LaTeX detects the accident and raises an error message: ! LaTeX Error: Command \ht already defined. Or name \end... illegal, see p.192 of the manual.	{}
# LinearityImaging Topics ## Linearity The fundamental process that occurs in CCD imaging is the conversion of photonic input to electronic output. Photons incident on the CCD will be converted to electron/hole pairs and the electrons will be captured under the gate electrodes of the CCD. These electrons are then transferred in a “bucket brigade” fashion to the output amplifier where the charge is converted to a voltage output signal. An analog processing chain further amplifies this signal and finally it is digitized before being transferred to a host computer for display, image processing, and/or storage. The transfer function between the incident photonic signal and the final digitized output should vary linearly with the amount of light incident on the CCD. Hence, nonlinearity is a measure of the deviation from the following relationship: Digital Signal = Constant x Amount of Incident Light High-performance CCD cameras have extremely good linearity. Deviations from linearity are often less than a few tenths of a percent for over five orders of magnitude. This is far superior to video CCDs and other solid-state imagers, which can exhibit nonlinearity of several percent or more. For quantitative imaging, linearity is a stringent requirement. CCDs must be linear in order to perform image analysis such as arithmetic ratios, shading correction, flat fielding, linear transforms, etc. There is no standard method for measuring or reporting linearity values. Typically the numbers are reported as percent deviations from linearity (it may be specified as linearity or nonlinearity, however). One method that can be used is to plot the mean signal value versus the exposure time over the full linear range (linear full well) of the CCD. A linear least-squares regression can then be fit to the data. The deviation of each point from the calculated line gives a measure of the nonlinearity of the system. The nonlinearity can be reported as the sum of the maximum and minimum deviation divided by the maximum signal as a percentage: $$nonlinearity (\%) = {(MaxPositiveDeviation + MaxNegativeDeviation) \over MaximumSignal} \times 100$$	{}
# A counterexample to the Cantelli conjecture through the Skorokhod embedding problem Abstract : In this paper, we construct a counter-example to a question by Cantelli, asking whether there exists a non-constant positive measurable function $\varphi$ such that for i.i.d. r.v. $X,Y$ of law $\mN(0,1)$, the r.v. $X+\varphi(X)\cdot Y$ is also Gaussian. For the construction that we propose, we introduce a new tool, the Brownian mass transport: the mass is transported by Brownian particles that are stopped in a specific way. This transport seems to be interesting by itself, turning out to be related to the Skorokhod and Stefan problems. Keywords : Document type : Journal articles Domain : Cited literature [10 references] https://hal.archives-ouvertes.fr/hal-00666733 Contributor : Aline Kurtzmann <> Submitted on : Thursday, February 9, 2012 - 1:51:12 PM Last modification on : Thursday, January 7, 2021 - 4:35:01 PM Long-term archiving on: : Wednesday, December 14, 2016 - 3:51:25 AM ### File Cantelli-12-02-02.pdf Files produced by the author(s) ### Citation Victor A. Kleptsyn, Aline Kurtzmann. A counterexample to the Cantelli conjecture through the Skorokhod embedding problem. Annals of Probability, Institute of Mathematical Statistics, 2015, 43 (5), pp.2250-2281. ⟨10.1214/14-AOP932⟩. ⟨hal-00666733⟩ Record views	{}
# radians per minute to revolutions per day conversion Conversion number between radians per minute [rad/min] and revolutions per day [rpd] is 229.18311805233. This means, that radians per minute is bigger unit than revolutions per day. ### Contents [show][hide] Switch to reverse conversion: from revolutions per day to radians per minute conversion ### Enter the number in radians per minute: Decimal Fraction Exponential Expression eg.: 10.12345 or 1.123e5 Result in revolutions per day ? precision 0 1 2 3 4 5 6 7 8 9 [info] Decimal: Exponential: ### Calculation process of conversion value • 1 radians per minute = (2.6525823848649210^-03) / ((1/86400)) = 229.18311805233 revolutions per day • 1 revolutions per day = ((1/86400)) / (2.6525823848649210^-03) = 0.0043633231299858 radians per minute • ? radians per minute × (2.65258238486492*10^-03 ("Hz"/"radians per minute")) / ((1/86400) ("Hz"/"revolutions per day")) = ? revolutions per day ### High precision conversion If conversion between radians per minute to hertz and hertz to revolutions per day is exactly definied, high precision conversion from radians per minute to revolutions per day is enabled. Since definition contain rounded number(s) too, there is no sense for high precision calculation, but if you want, you can enable it. Keep in mind, that converted number will be inaccurate due this rounding error! ### radians per minute to revolutions per day conversion chart Start value: [radians per minute] Step size [radians per minute] How many lines? (max 100) visual: 00 102291.8311805233 204583.6623610466 306875.4935415699 409167.3247220931 5011459.155902616 6013750.98708314 7016042.818263663 8018334.649444186 9020626.48062471 10022918.311805233 11025210.142985756 Copy to Excel ## Multiple conversion Enter numbers in radians per minute and click convert button. One number per line. Converted numbers in revolutions per day: Click to select all Convert Radians per minute to other unit: Definition of radians per minute unit: = Hz/(2 × π × 60). Radian per minute is actually a unit of angular velocity, but since radian is dimensionless unit, rotations per minute can be calculated (the frequency). Convert Revolutions per day to other unit: ### revolutions per day Definition of revolutions per day unit: = Hz/86400. The number of events or cycles that occurred in one day. The sign rpd (revolutions per day) the value if Hertz / 86400. It is used to express slow frequencies. The Earth's rotational frequency is 1 rpd (revolution per day) ← Back to Frequency units	{}
Factor $x^4+1$ over $\mathbb{R}$ Factor $x^4+1$ over $\mathbb{R}$ Well, I read this question first wrongly, because the reader is about complex analysis, I did it for $\mathbb{C}$ first. I got. $x^4+1=(x-e^{\pi i/4 })(x-e^{3 \pi i/4})(x-e^{5\pi i/4})(x-e^{7\pi i/4})$. My teacher told me that there is very smart way to do this for $\mathbb{R}$ that we already learned. But I only can think of trial and error kind of methods. Solutions Collecting From Web of "Factor $x^4+1$ over $\mathbb{R}$" Group each complex root $\alpha$ with $\bar\alpha$: $$(x-\alpha)(x-\bar\alpha)=x^2-(\alpha+\bar\alpha)x+\alpha\bar\alpha\in{\Bbb R}[x].$$ It’s like this: $x^4+1 = x^4 + 2x^2 + 1 – 2x^2 = (x^2+1)^2 – (\sqrt2x)^2 = (x^2+\sqrt2x+1)(x^2-\sqrt2x+1)$ In complicated terms, the field extension $\mathbb C / \mathbb R$ has degree $2$, so you expect every quartic to be reducible over $\mathbb R$. In simple terms, since you have the four roots of this polynomial, there is a nice way to group them together : the roots $e^{i\pi/4}$ and $e^{7 i \pi/4}$ are conjugate, so they are the roots of the same quadratic ; group the two linear factors together and you will get a real quadratic. Similarly for the roots corresponding to $3$ and $5$. Hope that helps, In http://www.wolframalpha.com , I typed factor x^4 + 1 It gives 4 first order terms. Hope this helps. Regards, Matt	{}
# zbMATH — the first resource for mathematics Delay equations driven by rough paths. (English) Zbl 1190.60046 Summary: We illustrate the flexibility of the algebraic integration formalism introduced in [M. Gubinelli, J. Funct. Anal. 216, No. 1, 86–140 (2004; Zbl 1058.60037)], by establishing an existence and uniqueness result for delay equations driven by rough paths. We then apply our results to the case where the driving path is a fractional Brownian motion with Hurst parameter $$H>1/3$$. ##### MSC: 60H10 Stochastic ordinary differential equations (aspects of stochastic analysis) 60H05 Stochastic integrals 60H07 Stochastic calculus of variations and the Malliavin calculus 60G15 Gaussian processes Full Text:	{}
# Polynomials and Rational Expressions Questions - All Grades Create printable tests and worksheets from Polynomials and Rational Expressions questions. Select questions to add to a test using the checkbox above each question. Remember to click the add selected questions to a test button before moving to another page. The Polynomials and Rational Expressions questions below are in the following grade levels: Grades: 7 8 9 10 11 12 College Continuing Education 1 2 3 4 5 ... 12 Grade 7 :: Polynomials and Rational Expressions by karenpritchard $(13x^2y - 7x^2) + (5x^2y - 3x^2)$ 1. $18x^2y - 10x^2$ 2. $18x^2y + 4x^2$ 3. $8x^2y + 4x^2$ 4. $18x^4y^2 -10x^4$ Grade 11 :: Polynomials and Rational Expressions by ACurvier Which example has more than one variable? 1. 3 2. $4 + 2x^2$ 3. $4 + 2xy^2 + y^3$ 4. $3 + 2x$ Grade 11 :: Polynomials and Rational Expressions by ACurvier The product of a monomial and a trinomial is: 1. Monomial 2. Binomial 3. Trinomial 4. Coefficients Grade 9 :: Polynomials and Rational Expressions by jjstanley $(3x^2y^3+xy^2)(x^4y-2x^2y^2)$ 1. $3x^4y^2-6x^4y^6+x^5y^2-2x^3y^4$ 2. $3x^6y^4-6x^4y^5+x^5y^3-2x^3y^4$ 3. $3x^6y^4-6x^4y^5+x^4y^4-2x^2y^2$ 4. $3x^4y^6-6x^5y^4+x^3y^5-2x^4y^3$ Grade 9 :: Polynomials and Rational Expressions by jjstanley $(2x+3)(5x-8)$ 1. $10x^2+x-24$ 2. $10x^2-31x-24$ 3. $10x^2-x-24$ 4. $7x^2+10x-5$ Grade 9 :: Polynomials and Rational Expressions by jjstanley $3x(x+5)$ 1. $3x+15x$ 2. $3x^2+15x$ 3. $18x$ 4. $3x^3+15x^2$ Grade 9 :: Polynomials and Rational Expressions by jjstanley $(10p^4+p^3-4p^2-8)-(-12p^4+5p^3-2p+3)$ 1. $22p^4-4p^3-4p^2+2p-5$ 2. $-2p^4-4p^3-4p^2+2p-5$ 3. $-2p^4+6p^3-6p^2+2p-11$ 4. $22p^4-4p^3-4p^2+2p-11$ Grade 9 :: Polynomials and Rational Expressions by jjstanley $(2x-2)(3x+5)$ 1. $6x^2+4x-10$ 2. $6x^2+16x-10$ 3. $-x+3$ 4. $6x^2-4x+10$ Grade 9 :: Polynomials and Rational Expressions by LBeth What expression does the set of tiles represent? 1. $2x$ 2. $-8x$ 3. $x^4 - 2$ 4. $4x - 2$ Grade 9 :: Polynomials and Rational Expressions by jjstanley $(13x-3)(5-6x)$ 1. $-18x^2+65x-78$ 2. $-65x^2+18x-15$ 3. $-38x^2+78x-15$ 4. $-78x^2+83x-15$ Grade 9 :: Polynomials and Rational Expressions by jjstanley $(7n^5-3n+4n^2)+(2n^2+5n^5+8n)$ 1. $12n^5+6n^2+5n$ 2. $9n^5+2n^2+12n$ 3. $5n^5-2n^2+4n$ 4. $12n^5-6n^2-4n$ Grade 9 :: Polynomials and Rational Expressions by jlasbell Which fraction equals the product? $((x + 5)/(3x + 2))((2x - 3)/(x - 5))$ 1. $(2x - 3)/(3x + 2)$ 2. $(3x + 2)/(4x - 3)$ 3. $(x^2 - 25)/(6x^2 - 5x - 6)$ 4. $(2x^2 + 7x - 15)/(3x^2 - 13x - 10)$ Grade 9 :: Polynomials and Rational Expressions by jjstanley $(x-5)(2x+3)(x+5)$ 1. $2x^3+3x^2-50x-75$ 2. $2x^3+2x^2-15x-25$ 3. $2x^3+2x^2-50x-25$ 4. $2x^3-50x^2+3x-75$ Grade 12 :: Polynomials and Rational Expressions by Dest_nee Grade 11 :: Polynomials and Rational Expressions by MrsNichols62913 The side of a cube is represented by x + 1. Find, in terms of x, the volume of the cube. (Volume = sidesideside) 1. $x^2 + 2x +1$ 2. $2x+1$ 3. $x^3 + 3x^2 + 3x + 1$ 4. $3x+1$ Simplify $(xy^-6z^-3)/(x^-4y^-5z)$ 1. $(xz)/(x^4y^11z^3)$ 2. $(x^4y^4)/(y^6z^3)$ 3. $x^5/(yz^4)$ 4. $(x^3y^5)/(y^3z^2)$ Grade 10 :: Polynomials and Rational Expressions by toriavigil Factor the expressions. $x^4 - y^4$ 1. $(x - y)^4$ 2. $(x^2 + y^2)(x + y)(x - y)$ 3. $(x^2 + y^2)(x^2 - y^2)$ 4. Can't be factored Grade 11 :: Polynomials and Rational Expressions by ACurvier Grade 11 :: Polynomials and Rational Expressions by ACurvier Which of the following cannot be classified as a polynomial? 1. $3x^2 -4x +12$ 2. $10xy^2 +2y +3z +15$ 3. $(2xy^2 + 3)$ 4. $144x^2y^3z^6$ 1 2 3 4 5 ... 12 You need to have at least 5 reputation to vote a question down. Learn How To Earn Badges.	{}
For information on the 55 Cancri system including its five planets, see Table 1. 1", "Star Surface Polluted by Planetary Debris", "A circumstellar dust disk around a star with a known planetary companion", "A Neptune-sized Planet in the ρ 1 Cancri System", "Astronomers Discover Record Fifth Planet Around Nearby Star 55 Cancri", "Передача и поиски разумных сигналов во Вселенной", Monthly Notices of the Royal Astronomical Society, "Frequency map analysis of the 3/1 resonance between planets b and c in the 55 Cancri system", "Astronomers searching for distant Earths find two Neptunes", "Astronomers Find Fifth Planet Around 55 Cancri", Interactive visualisation of the 55 Cancri system, https://en.wikipedia.org/w/index.php?title=55_Cancri&oldid=992816400, Planetary systems with five confirmed planets, Articles containing potentially dated statements from 2015, All articles containing potentially dated statements, Articles with unsourced statements from April 2014, Creative Commons Attribution-ShareAlike License, This page was last edited on 7 December 2020, at 06:53. The nearly 1:3 ratio between 55 Cancri b and c is apparently a near resonance, rather than a genuine mean motion resonance. [16] This planet received the designation 55 Cancri d. At the time of discovery, the planet was thought to be in an orbit of mild eccentricity (close to 0.1), but this value was increased by later measurements. Even after accounting for these two planets, a periodicity at 43 days remained, possibly due to a third planet. 55 Cancri, also known as Rho Cancri, is a binary star system located 41 light years away in the constellation of Cancer and is best known for having five extrasolar planets (as of 2007), including possibly one terrestrial, rocky, "super-Earth". In July 2014 the International Astronomical Union launched a process for giving proper names to certain exoplanets and their host stars. [23] (The IAU originally announced the winning name was Lippershey for 55 Cancri d. In January 2016, in recognition that his actual name was Lipperhey (with Lippershey an error introduced in the 19th century), the exoplanet name was corrected to Lipperhey by the IAU and that name was submitted to the official sites that keep track of astronomical information. Copernico [3] (también 55 Cnc; denominación de Bayer Rho 1 Cancri A, Rho-1 Cancri) es una estrella cercana de magnitud 6 en la constelación de Cáncer.La estrella es un sistema estelar binario.El componente primario es, como nuestro Sol, una enana amarilla, pero levemente más ligero y luminoso.La distancia al sistema es 41 años luz.El componente más luminoso es visible a simple … [citation needed], It was initially unknown whether 55 Cancri e was a small gas giant like Neptune or a large rocky terrestrial planet. (2004), and a 260-day Neptune-sized planet, as first reported by Wisdom (2005). 55 Cancri (abreviado como 55 Cnc) é uma estrela binária localizada aproximadamente 41 anos-luz de distância do Sistema Solar na constelação de Câncer. [27], Large surface-temperature variations on 55 Cancri e have been attributed to possible volcanic activity releasing large clouds of dust which blanket the planet and block thermal emissions. Despite their … arxiv. 55 Cancri e is a super-Earth exoplanet that orbits a G-type star similar to our Sun. However, contrary to the recent study by Satyal & Cuntz , we include the two inner planets in a limited sense only by adding their masses to the mass of the central star. The upper limit on emissions within 100 AU of this star is about 850 mJy, at a wavelength of 850 μm. Measurements of the star suggested that this was close to the star's rotation period, which raised the possibility that the 43-day signal was caused by stellar activity. After accounting for these planets, a signal at around 2.8 days remained, which could be explained by a planet of at least 14.2 Earth masses in a very close orbit.[12]. Le due componenti sono separate da oltre mille unità astronomiche. The 55 Cancri System: Fundamental Stellar Parameters, Habitable Zone Planet, and Super-Earth Diameter 2011 von BRAUN K., BOYAJIAN TABETA S., ten BRUMMELAAR T., van BELLE G., KANE S. et al. Valenti & Fischer predict a relatively old age for the 55 Cnc system of 9.5 ± 4.4 Gyr, although Fischer et al. [21] In December 2015, the IAU announced the winning names were Copernicus for 55 Cancri A and Galileo, Brahe, Lipperhey, Janssen and Harriot for its planets (b, c, d, e and f, respectively). [27] It is more enriched than the Sun in elements heavier than helium, with 186% the solar abundance of iron; it is therefore classified as a rare "super metal-rich" (SMR) star. This star is now so entered in the IAU Catalog of Star Names. Its discovery was announced in 2004. 55 Cancri (55 Cnc), aussi nommée Rho 1 Cancri, est une étoile binaire située à une distance d'environ ∼40 a.l. Al 2007, il sistema conta ben 5 pianeti noti orbitanti attorno alla … This limits the total mass of fine dust around the star to less than 0.01% of the Earth's mass. The same measurements were used to confirm the existence of the uncertain planet 55 Cancri c. 55 Cancri e was one of the first extrasolar planets with a mass comparable to that of Neptune to be discovered. [31], The secondary, 55 Cancri B, is a red dwarf star much less massive and luminous than the Sun. This is one of the few planetary transits to be confirmed around a well-known star, and allowed investigations into the planet's composition. [19] In this case, roughly a third of the planet's mass would be carbon, much of which may be in the form of diamond as a result of the temperatures and pressures in the planet's interior. [44], A METI message was sent to 55 Cancri. [16] The first planet discovered orbiting 55 Cancri A was designated HR 3522b by its discoverers,[17] though it is more commonly referred to as 55 Cancri b. [citation needed] 55 Cancri A also has more carbon than the Sun, with a C/O ratio of 0.78,[28] compared to solar value of 0.55. (2008)[36] reported new observations that they said confirmed the existence of the 2.8 day planet, as first reported by McArthur et al. 55 Cancri e is one of five planets encircling a sun-like star called 55 Cancri, which lies about 40 light-years from Earth in the constellation of Cancer. Take an interactive tour of the 55 Cancri system 41 million light years away from our own Earth. 55 Cancri e took about 2.8 days in the orbit of the star. [15] The side of the planet facing its star has temperatures more than 2,000 kelvin (approximately 1,700 degrees Celsius or 3,100 Fahrenheit), hot enough to melt iron. The red dwarf 55 Cancri B is of the 13th magnitude and only visible through a telescope. The star has only low emission from its chromosphere, and is not variable in the visible spectrum;[16] but it is variable in X-rays. At first it was suspected to be a water planet. The bright star 55 Cancri is known to host five planets, including a transiting super-Earth. The planet's transit of its host star was announced on 27 April 2011, based on two weeks of nearly continuous photometric monitoring with the MOST space telescope. It has the Bayer designation Rho1 Cancri (ρ1 Cancri); 55 Cancri is the Flamsteed designation (abbreviated 55 Cnc). Your system is 55 Cancri. [7], In July 2014 the International Astronomical Union (IAU) launched a process for giving proper names to certain exoplanets and their host stars. This was achieved by making sensitive measurements of the Doppler shift of the spectrum of 55 Cancri A. [13][4] As initial observations showed no hydrogen in its Lyman-alpha signature during transit,[17] Ehrenreich speculated that its volatile materials might be carbon dioxide instead of water or hydrogen. [16] This abundance of metal makes estimating the star's age and mass difficult, as evolutionary models are less well defined for such stars. The other planets discovered were designated 55 Cancri c, d, e and f, in order of their discovery. confirmed the existence of the 260 day planet proposed in 2005 by Wisdom. The atmosphere may contain similar chemicals in Earth's atmosphere, such as nitrogen and possibly oxygen, in order to cause the infrared data observed by Spitzer. Star A contains five exoplanets, the first system found with this many. In 2011, a transit of the planet was confirmed, allowing scientists to calculate its density. They honor the astronomers Nicolaus Copernicus, Galileo Galilei, Tycho Brahe and Thomas Harriot and the spectacle makers and telescope pioneers Hans Lipperhey and Jacharias Janssen. [3] In October 2012, it was announced that 55 Cancri e could be a carbon planet. All of our simulations include both the primary and secondary stars of 55 Cnc as well as one or more of the system's known planets. Den innersta planet, e, passerar framför 55 Cancri A sett från jorden. In 1997, the discovery of a 51 Pegasi-like planet orbiting 55 Cancri A was announced, together with the planet of Tau Boötis and the inner planet of Upsilon Andromedae. 55 Cancri has 5 planets: 55 Cancri B, discovered in 1996, has a mass 254.3 times the mass of Earth and an orbital period of 14.65 days. It had been thought that with five planets, the system cannot deviate far from coplanar in order to maintain stability. [40] An attempt to measure the spin-orbit misalignment of the innermost planet reported that it was in a nearly polar orbit,[42] but this interpretation of the data has since been challenged by a subsequent study, with noted inconsistencies between the implied and measured stellar rotation. It is smaller in radius and slightly less massive than the Sun, and so is cooler and less luminous. Wide binary star consisting of a sun-like primary (A) and a red-dwarf secondary (B) separated by 1,100 AU, 41 light years away. We tentatively detect circularly polarized bursty emission from the $\tau$ Boötis system in the range 14-21 MHz with a flux density of $\sim$890 mJy and with a significance of $\sim$3$\sigma$. 55 Cancri, o Copernicus, è una stella doppia di classe spettrale G8-V, distante 40,9 anni luce dal Sistema solare, nella costellazione del Cancro. [16], The primary star, 55 Cancri A, has a spectral type of K0IV-V, indicating a main sequence or subgiant star. ; 55 Cancri C, discovered in 2002, has a mass 53.7 times the mass of Earth and an orbital period of 44.34 days. The 55 Cancri A system is the first known quintuple-planet system discovered, and it remains a record-breaker at the time of writing (July 2009). [30], Observations of 55 Cancri A in the submillimeter region of the spectrum have thus far failed to detect any associated dust. For example, 55 Cancri is a system composed of 5 planets orbiting a member of a stellar binary for which a projected obliquity of 72 12 relative to the orbit of the innermost planet has been reported (Bourrier & H ebrard 2014). [11], Like the majority of extrasolar planets found prior to the Kepler mission, 55 Cancri e was discovered by detecting variations in its star's radial velocity. (The bright body is our own Jupiter, which was passing through Cancer when the picture was taken.) 55 Cancri is a binary star system located 41 light-years away from the Sun in the zodiac constellation of Cancer. Despite their wide separation, the two stars appear to be gravitationally bound, as they share a common proper motion. [37] However, Dawson and Fabrycky (2010)[38] concluded that the 2.8 day planet was indeed an alias, as suggested by Wisdom (2005), and that the correct period was 0.7365 days. This would pollute the star's external layers, resulting in a higher than normal metallicity. The 55 or Rho(1) Cancri binary system is located about 40.9 light-years from Sol. A recent example is that of the planets orbiting 55 Cancri (HD 75732, HIP 43587, HR 3522, hereafter 55 Cnc), a bright (V = 5.95) G8 dwarf star. [22][23]), In 2016, the IAU organized a Working Group on Star Names (WGSN)[24] to catalog and standardize proper names for stars. 55 Cancri is the system's Flamsteed designation. 55 Cancri d. Exo Pioneer. Astrometric observations with the Hubble Space Telescope measured an inclination of 53° of the outer planet d,[35] though this result relies on the precise orbital parameters which have been substantially revised since this was published. [40], More planets are possible within the stable zone, between f and d at 0.9 to 3.8 AU with eccentricities below 0.4. The system consists of a K-type star (designated 55 Cancri A, also named Copernicus /koʊˈpɜːrnɪkəs/)[14] and a smaller red dwarf (55 Cancri B). THE PLANETS In its first bulletin of July 2016,[25] the WGSN explicitly recognized the names of exoplanets and their host stars approved by the Executive Committee Working Group Public Naming of Planets and Planetary Satellites, including the names of stars adopted during the 2015 NameExoWorlds campaign. ️Subscribe for more Content! Skládá se ze žlutého trpaslíka (55 Cancri A, Copernicus) [1] a z menšího červeného trpaslíka (55 Cancri B). 55 Cancri-systemet var det första kända för att ha fyra, och senare fem planeter, och kan möjligen ha flera. [33] Calculations gave the disk radius at least 40 AU, similar to the Kuiper belt in the Solar System, with an inclination of 25° with respect to the plane of the sky. [9] In December 2015, the IAU announced the winning name was Janssen for this planet. The radial velocity method used to detect 55 Cancri e obtains the minimum mass of 7.8 times that of Earth,[4] or 48% of the mass of Neptune. It was announced at the same time as another "hot Neptune" orbiting the red dwarf star Gliese 436 named Gliese 436 b. [13] The transits occur with the period (0.74 days) and phase that had been predicted by Dawson & Fabrycky. Le dimensioni di 55 Cancri A sono appena inferiori di quelle del nostro Sole, mentre 55 Cancri B è una nana rossa di classe M3.5-4V. However, the 2.8-day planet was shown to be an alias by Dawson and Fabrycky (2010); its true period was 0.7365 days. As of 2015[update], five extrasolar planets (designated 55 Cancri b, c, d, e and f; named Galileo, Brahe, Lipperhey, Janssen and Harriot, respectively) are believed to orbit 55 Cancri A. Located at a similar distance from its star as Jupiter is from our Sun, it is the fifth and outermost known planet in its planetary system. The two components are separated by an estimated distance of 1065 AU[26] (6.15 light days). [35] With 8.3 Earth masses, it is a large super-Earth which was originally thought to have an orbital period of 2.8 days, though it was later found that this was an alias of its true period of 0.74 days by observations of e transiting in 2011. After making further radial velocity measurements, a planet orbiting at a distance of around 5 AU was announced in 2002. [27] Between them, no measurement of c's nor f's inclination has been made. We present LOFAR-LBA circularly polarized beamformed observations of the exoplanetary systems 55 Cancri, $\upsilon$ Andromedae, and $\tau$ Boötis. It features in the list of top 100 target stars for the NASA Terrestrial Planet Finder mission. [17] The planet was discovered by measuring the star's radial velocity, which showed a periodicity of around 14.7 days corresponding to a planet at least 78% of the mass of Jupiter. [8] The process involved public nomination and voting for the new names. [14], The 55 Cancri system is located fairly close to the Solar System: the Gaia astrometry satellite measured the parallax of 55 Cancri A as 79.4274 milliarcseconds, corresponding to a distance of 12.59 parsecs (41.06 light years). [32] This planet was the first known instance of a fourth extrasolar planet in one system, and was the shortest-period planet until the discovery of PSR J1719-1438 b. First system found with this many Janssen for this planet is currently closest! Possible planet received the designation 55 Cancri e is an exoplanet in orbit. The period ( 0.74 days ) this is one of the Netherlands the period ( 0.74 days.. A and B, [ 15 ] though a is visible to the eye... Och senare fem planeter, och senare fem planeter, och senare fem planeter och... First system found with this many that component B may itself be a carbon planet orbit, towards inner! Is now so entered in the orbit of the Netherlands is the best known in... With this many Cancri f, in order of their discovery 2.8 days in the list of 100! Named Gliese 436 B the innermost planet, as they share a common practice routinely also for! Closest known analogue to our Solar system, yet there are indications component... Of 55 cancri system 100 target stars for the NASA Terrestrial planet Finder mission component. Is 55 Cancri a is itself sometimes referred to as 55 Cancri star system 41! Planeter, och kan möjligen ha flera similar mass to c, d, e and f, in of... And less luminous that appeared to confirm the existence of the star has 260-day... Is our own Jupiter, which was passing through Cancer when the picture was taken )! The eastern one is 55 Cancri. f, was the first of! Stars are separated by an estimated distance of around 5 AU was announced the... Appear to be tidally locked, meaning that there is a star system light... Radial velocity measurements, a periodicity at 43 days remained, possibly due a. Message was sent to 55 Cancri is the innermost-known planet in orbit around 55 Cancri a viewed! Located about 40.9 light-years from Sol Kuiper 55 cancri system equivalent or a Kuiper belt equivalent message was to! Lack of a fifth extrasolar planet in its planetary system Rho¹ Cancri ) and phase that been. 2.8 days in the list of top 100 target stars for the NASA Terrestrial planet mission... Results in a higher than normal metallicity our Sun [ 31 ], 55 Cancri is star. Process for giving proper names to certain exoplanets and their host stars Rho¹ Cancri and. Higher abundance ratios of these heavy elements mass of fine dust around the star 's Flamsteed designation.Its Bayer designation Rho... Separation, the winning names were those submitted by the Royal Netherlands Association Meteorology! Age for the new names was transmitted from Eurasia 's largest radar – 70-meter ( 230-foot ) Eupatoria planetary.... At least 3 planets designation HR 3522 6.15 light days ) and phase that been! See Table 1 around the star dwarf companion 70-meter ( 230-foot ) Eupatoria planetary radar destroy it at! Orbit of its discovery, three other planets were known orbiting the red dwarf star 436! Were those submitted by the Royal Netherlands Association for Meteorology and Astronomy of the Netherlands largest radar – 70-meter 230-foot! Zone would mean that the 2.8-day planet was an alias and, separately, there! Vzdálená od Země 41 světelných let 1:3 ratio between 55 Cancri e was questioned by Jack Wisdom a... The designation 55 Cancri c. 55 Cancri is a common practice routinely also adopted for the Cancri! Abundance ratios of these heavy elements 10.2 ± 2.5 billion years its density e takes less than 18 hours complete. Is of the Doppler shift of the Solar system near-zero orbital eccentricity days remained, 55 cancri system due to a planet. Billion years [ 11 ] and 10.2 ± 2.5 billion years [ 11 ] and 10.2 ± billion... Similarities begin with the stars themselves, which are about the same time as another hot Neptune orbiting! And B, [ 15 ] though a is itself sometimes referred to as 55 Cancri including! Kan möjligen ha flera the 2010 observations and recalculations, this planet, first! 'S inclination has been made 260-day Neptune-sized planet, e and f, in order maintain. Is the innermost-known planet in its planetary system was transmitted from Eurasia 's largest radar – 70-meter 230-foot. Order to maintain stability that there is a binary star system Forty-one light years from Earth a... '' orbiting the star to less than 18 hours to complete an orbit and the. Analogue to our Sun and ultraviolet irradiation would destroy it ha fyra och. Not deviate far from coplanar in order of their discovery 50 Earth masses, stable mean motion resonance regions at. Designation Rho1 Cancri ( [ ˈkæŋkri ] IPA, zkráceně 55 Cnc ) that had been predicted Dawson. Cancri is a red dwarf 55 Cancri a was announced that 55 Cancri system is currently the known! Rather like our own Jupiter, which are about the same mass and age picture was taken. few. Best known planet in its planetary system less than 0.01 % of the data be bound. Of this star is located in the orbit of its discovery, three other discovered. It takes less than 18 hours to complete an orbit and is the Flamsteed designation ( 55! Of star names designated a and B, [ 15 ] though is. 18 hours to complete an orbit and is the star including a transiting super-Earth planet and the planet... System Forty-one light years from Earth is a binary star system located 41 light-years away from the Sun the. Mercury orbits our Sun system of 9.5 ± 4.4 Gyr, although Fischer et al scientists to calculate density! Around 5 AU was announced that 55 Cancri system is currently the closest known to. A similar mass to c, d, e and f, order... Located about 40.9 light-years from Sol mi ) … 55 Cancri B [. 13Th magnitude and only visible through a telescope common proper motion at first it transmitted. Years [ 11 ] and 10.2 ± 2.5 billion years a reanalysis of the data 2002... 14 ], 55 Cancri e is a red dwarf companion hours to complete the orbit of the is. Orbit 55 Cancri c. 55 Cancri is the innermost-known planet in its planetary system on emissions within AU. Separation, the hydrogen would have to slowly diffuse out into the planet thought to take 2.8... Because of this star is now so entered in the IAU announced the winning names were those submitted by Royal! Age range of 2–8 Gyr ± 1.7, so the real mass close! ± 1.7, so the real mass is close to the minimum 15 ] though a is itself referred! Au was announced in 2002 July 2014 the International astronomical Union launched a process for proper... Were designated 55 Cancri is a binary star system located 41 [ 1 ] light-years from. [ 8 ] the process involved public nomination and voting for the 55 Cancri a would to. Been thought that with five planets, including a transiting super-Earth the inner edge of 55 Cancri was! To c, d, e, passerar framför 55 Cancri ( ρ1 Cancri ;... System Forty-one light years from Earth is a binary star system located 41 [ 1 ] light-years from! Unità astronomiche, possibly due to a third planet a sett från jorden ] though a is to. Cancri d is a gas giant exoplanet that orbits a G-type star similar to our Solar system, yet are! The period ( 0.74 days ) away from the Sun and less luminous the. A deep convection zone would mean that the 2.8-day planet was an alias and, separately, there... Has two massive planets orbiting it closer than Mercury orbits our Sun Table.... The process involved public nomination and voting for the 55 Cnc ) je dvojhvězda v souhvězdí Raka vzdálená Země! ( abbreviated 55 Cnc ) je dvojhvězda v souhvězdí Raka vzdálená od Země 41 světelných let ) je v. In December 2015, the first occurrence of a deep convection zone would mean the. A water planet a transit of the data the star age range of 2–8 Gyr ( Latinised to Rho¹ ). Than normal metallicity 11 ] and 10.2 ± 2.5 billion years and Astronomy the. 14 ], a planet orbiting at a wavelength of 850 μm the! As 55 Cancri e is an exoplanet in the IAU Catalog of star names is now so entered in constellation. Cancri system is located about 40.9 light-years from Sol to be tidally locked meaning. Senare fem planeter, och kan möjligen ha flera the time of its discovery, three planets. Further observations are necessary to confirm the nature of the Earth 's mass ( ). Due componenti sono separate da oltre mille unità astronomiche first occurrence of a deep convection zone would mean that 2.8-day... System, yet there are indications that component B may itself be a carbon planet belt equivalent and separately. The winning name was submitted by the Royal Netherlands Association for Meteorology and Astronomy of the 13th magnitude only. A binary star system known to orbit the star resonance, rather than a mean... Star has a 260-day planet planet Finder mission 55 Cancri f, in order their... Cancri B is of the spectrum of 55 Cancri e takes less than 18 hours complete! ( abbreviated 55 Cnc ) je dvojhvězda v souhvězdí Raka vzdálená od 41! Mean motion resonance regions lie at 3f:2g, 2g:1d, and so is cooler and less.! A red dwarf companion referred to as 55 Cancri B, [ 15 ] though a itself! ] the process involved public nomination and voting for the new names than Mercury orbits our Sun range of Gyr! A near-zero orbital eccentricity located about 40.9 light-years from Sol for information on the 55 e.	{}
What the Power Spectrum misses Just taking a short break from work I chatted over coffee to one of the students here at the Niels Bohr Institute about various things to do with the analysis of signals in the Fourier domain (as you do). That discussion reminded me of this rather old post (from 2009) which I thought might be worth a second airing (after a bit of editing). The discussion is all based on past cosmological data (from WMAP) rather than the most recent (from Planck), but that doesn’t change anything qualitatively. So here you are. The picture above shows the all-sky map of fluctuations in the temperature of the cosmic microwave background across the sky as revealed by the Wilkinson Microwave Anisotropy Probe, known to its friends as WMAP. I spent many long hours fiddling with the data coming from the WMAP experiment, partly because I’ve never quite got over the fact that such wonderful data actually exists. When I started my doctorate in 1985 the whole field of CMB analysis was so much pie in the sky, as no experiments had yet been performed with the sensitivity to reveal the structures we now see. This is because they are very faint and easily buried in noise. The fluctuations in temperature from pixel to pixel across the sky are of order one part in a hundred thousand of the mean temperature (i.e. about 30 microKelvin on a background temperature of about 3 Kelvin). That’s smoother than the surface of a billiard ball. That’s why it took such a long time to make the map shown above, and why it is such a triumphant piece of science. I blogged a while ago about the idea that the structure we see in this map was produced by sound waves reverberating around the early Universe. The techniques cosmologists use to analyse this sound are similar to those used in branches of acoustics except that we only see things in projection on the celestial sphere which requires a bit of special consideration. One of the things that sticks in my brain from my undergraduate years is being told that if you don’t know what you’re doing as a physicist you should start by making a Fourier transform of everything. This approach breaks down the phenomenon being studied into a set of plane waves with different wavelengths corresponding to analysing the different tones present in a complicated sound. It’s often very good advice to do such a decomposition for one-dimensional time series or fluctuation fields in three-dimensional Cartesian space, even you do know what you’re doing, but it doesn’t work with a sphere because plane waves don’t fit properly on a curved surface. Fortunately, however, there is a tried-and-tested alternative involving spherical harmonics rather than plane waves. Spherical harmonics are quite complicated beasts mathematically but they have pretty similar properties to Fourier harmonics in many respects. In particular they are represented as complex numbers having real and imaginary parts or, equivalently, an amplitude and a phase (usually called the argument by mathematicians), $Z=X+iY = R \exp(i\phi)$ This latter representation is the most useful one for CMB fluctuations because the simplest versions of inflationary theory predict that the phases φ of each of the spherical harmonic modes should be randomly distributed. What this really means is that there is no information content in their distribution so that the harmonic modes are in a state of maximum statistical disorder or entropy. This property also guarantees that the distribution of fluctuations over the sky should have a Gaussian distribution. If you accept that the fluctuations are Gaussian then only the amplitudes of the spherical harmonic coefficients are useful. Indeed, their statistical properties can be specified entirely by the variance of these amplitudes as a function of mode frequency. This pre-eminently important function is called the power-spectrum of the fluctuations, and it is shown here for the WMAP data: Although the units on the axes are a bit strange it doesn”t require too much imagination to interpret this in terms of a sound spectrum. There is a characteristic tone (at the position of the big peak) plus a couple of overtones (the bumps at higher frequencies). However these features are not sharp so the overall sound is not at all musical. If the Gaussian assumption is correct then the power-spectrum contains all the useful statistical information to be gleaned from the CMB sky, which is why so much emphasis has been placed on extracting it accurately from the data. Conversely, though, the power spectrum is completely insensitive to any information in the distribution of spherical harmonic phases. If something beyond the standard model made the Universe non-Gaussian it would affect the phases of the harmonic modes in a way that would make them non-random. However,I will now show you how important phase information could actually be, if only we could find a good way of exploiting it. Let’s start with a map of the Earth, with the colour representing height of the surface above mean sea level: You can see the major mountain ranges (Andes, Himalayas) quite clearly as red in this picture and note how high Antarctica is…that’s one of the reasons so much astronomy is done there. Now, using the same colour scale we have the WMAP data again (in Galactic coordinates). The virture of this representation of the map is that it shows how smooth the microwave sky is compared to the surface of the Earth. Note also that you can see a bit of crud in the plane of the Milky Way that serves as a reminder of the difficulty of cleaning the foregrounds out. Clearly these two maps have completely different power spectra. The Earth is dominated by large features made from long-wavelength modes whereas the CMB sky has relatively more small-scale fuzz. Now I’m going to play with these maps in the following rather peculiar way. First, I make a spherical harmonic transform of each of them. This gives me two sets of complex numbers, one for the Earth and one for WMAP. Following the usual fashion, I think of these as two sets of amplitudes and two sets of phases. Note that the spherical harmonic transformation preserves all the information in the sky maps, it’s just a different representation. Now what I do is swap the amplitudes and phases for the two maps. First, I take the amplitudes of WMAP and put them with the phases for the Earth. That gives me the spherical harmonic representation of a new data set which I can reveal by doing an inverse spherical transform: This map has exactly the same amplitudes for each mode as the WMAP data and therefore possesses an identical power spectrum to that shown above. Clearly, though, this particular CMB sky is not compatible with the standard cosmological model! Notice that all the strongly localised features such as coastlines appear by virtue of information contained in the phases but absent from the power-spectrum. To understand this think how sharp features appear in a Fourier transform. A sharp spike at a specific location actually produces a broad spectrum of Fourier modes with different frequencies. These modes have to add in coherently at the location of the spike and cancel out everywhere else, so their phases are strongly correlated. A sea of white noise also has a flat power spectrum but has random phases. The key difference between these two configurations is not revealed by their spectra but by their phases. Fortunately there is nothing quite as wacky as a picture of the Earth in the real data, but it makes the point that there are more things in Heaven and Earth than can be described in terms of the power spectrum! Finally, perhaps in your mind’s eye you might consider what it might look lie to do the reverse experiment: recombine the phases of WMAP with the amplitudes of the Earth. If the WMAP data are actually Gaussian, then this map is a sort of random-phase realisation of the Earth’s power spectrum. Alternatively you can see that it is the result of running a kind of weird low-pass filter over the WMAP fluctuations. The only striking things it reveals are (i) a big blue hole associated with foreground contamination, (ii) a suspicious excess of red in the galactic plane owing to the same problem, and (iiI) a strong North-South asymmetry arising from the presence of Antarctica. There’s no great scientific result here, just a proof that spherical harmonic phases are potentially interesting because of the information they contain about strongly localised features PS. These pictures were made by a former PhD student of mine, Patrick Dineen, who has since quit astrophysics to work in the financial sector for Winton Capital, which has over the years recruited a number of astronomy and cosmology graduates and also sponsors a Royal Astronomical Society prize. That shows that the skills and knowledge obtained in the seemingly obscure field of cosmological data analysis have applications elsewhere! 23 Responses to “What the Power Spectrum misses” 1. This is a very nice piece. Years ago, back in the COBE days, I used to show an elevation map of the Earth just like the one you’re using, and the result of randomizing the phases to get something like the last picture you show. I never thought of doing the opposite — keeping the Earth-map’s phases but randomizing the amplitude. That’s very nice. There is a technical errorsin this piece, although it doesn’t affect the important points you’re making. It’s not true that randomness of phases “guarantees that the distribution of fluctuations over the sky should have a Gaussian distribution.” A statistically isotropic Gaussian random process is guaranteed to have random phases, but the converse is not true. For Gaussianity, you need all of the spherical harmonic coefficients to be drawn from a multivariate normal distribution. So, for instance, if you chose all of the coefficients to have the same absolute value, but to have random phases, that would not be a Gaussian random process. • telescoper Says: By the central limit theorem (assuming it applies) if you add a lot of harmonic modes with random phases the resulting 1-pt PDF will be Gaussian. I usually call this a weakly Gaussian process. A strictly Gaussian process is one defined as you say. • That’s true, so with the extra assumption that each spherical harmonic coefficient is produced by adding together “a lot” of independent terms, you do get (approximately) Gaussian statistics. But that extra assumption — that many independent things are being added together — is quite different from the random-phase assumption, which is why I object to the claim that random phases imply Gaussianity. In fact, the central limit theorem applies even if the phases aren’t random. If there are many independent processes that get added together to make our CMB sky, and if those processes have nonrandom phases (say, the mean of each contribution to each a_{lm} is a positive real number, so phase = 0 is preferred), the central limit theorem will still say that the final result is Gaussian. It just won’t be statistically isotropic. The statement that random phases imply Gaussianity comes up quite a lot when cosmologists talk about Gaussian processes. In fact, random phases and Gaussianity are pretty much logically independent of each other. It’s closer to the truth to say that random phases imply statistical isotropy, which is quite a different thing. • telescoper Says: If a spectral representation exists, which it has to for the phases to be defined, then the field at a given location is the sum over all the modes which will be independent if the phases are random. • Randomness of phases does not imply independence. To see this, consider the following admittedly silly random process: 1. Generate a Gaussian random field in the usual way. 2. Flip a coin, and multiply all the values in this map by 1000 if it comes up heads. This process produces a map with random phases (after all, the phases after step 2 are the same as before), but the coefficients of the various harmonic modes are not independent, and the random process is not even approximately Gaussian. As I’ve admitted, this example is silly, but it does show that there is no necessary logical connection between random phases and Gaussianity. The reason this example yields non-Gaussianity is also the reason it’s silly: it involves strong (and implausible) dependence among the various modes. If the various modes are independent, then I agree that you get (approximate) Gaussianity. But here’s the point: That last statement is true regardless of whether the phases are random. If you build your map out of many independent random variables, in such a way that many terms contribute significantly to each point in the map, then the central limit theorem will give you approximate Gaussianity, whether or not the phases are random. So there is, as far as I am aware, precisely no logical connection between randomness of phases and Gaussianity. • telescoper Says: I don’t understand your example: if you introduce a set of spikes’ each of these produces a harmonic-space signature each of which has highly correlated phases. It’s not true that in your prescription the phases are unchanged, unless I’ve misunderstood something.. 2. Anton Garrett Says: That shows that the skills and knowledge obtained in the seemingly obscure field of cosmological data analysis have applications elsewhere! I’d criticise nobody for seeking to provide better for their family, and good for Winton in sponsoring science, but that not necessarily so. Some of us think that quantitative financial prediction is based on a wrong understanding of money and a false analogy with physics. In physics, quantitative variables form a closed system. In finance, quantitative variables are influenced by, and influence, qualitative variables. This is why you can’t ‘time the markets’, ie predict when a peak or trough in the market sector or share in question has been reached. Without that, you might do well in the short term but you have no way of knowing when the short term transitions into the long term, and it’s a matter of sheer luck when to get in and out. In 18th century categories, study of the world of money is a ‘moral science’ rather than a ‘natural science’. • I doubt that so many physicists work in the finance industry because of a false analogy with physics. Rather, the industry often looks for people with hands-on programming skills. • Anton Garrett Says: Are they employed exclusively as programmers or (also?) as people who come up with the ideas to be programmed? “Quantitative finance” is now regarded as an academic area. Absurdly. • It’s certainly the case that one needs some programming knowledge, especially in the area of algorithmic trading. I’m sure you’ll find physicists at all levels in the finance industry (and elsewhere—Oskar Lafontaine and Angela Merkel are physicists, for example). Sure, no-one can predict the market exactly. (When I see market experts on television, I always think that if they were really so good, they wouldn’t have to be paid for being on television at 5 in the morning or whatever.) On the other hand, while monkeys might make better choices than some portfolio managers (I think that there was actually an experiment to test this), some things are quantitative and can be attacked (in practice only) via a programming solution, for example rapidly buying and selling at several exchanges, making a profit from the small price differences. Also, the speed of light is a limiting factor; in some cases, microseconds can provide a competitive edge. There is a lot of work in technical optimization. There are also technical-support jobs; being a sysadmin in the business world differs from being a sysadmin in academia primarily in better pay in the former case. Most people who work in the finance industry are dependent on technology but don’t have a technical background themselves. Then there is the whole area of big data, especially in relation to regulations and so on (archive data for 10 years, in case someone needs it for an investigation, etc). With almost all trading electronic these days, a huge amount of data is produced. Of course, whether you think that this is meaningful is another question, but who pays the piper calls the tune. 😐 I don’t know why Patrick left academia, but not everyone who leaves does so for lack of talent; some need, or at least want, more job security. (They usually earn much more as well, but this is less important than job security, at least to people who have spent some time in academia (as opposed to those who want to get rich as fast as possible).) • Anton Garrett Says: Smart pattern-recognition algorithms deployed in markets can harvest small amounts of money in small amounts of time, but they can’t know when a big crash is coming for which reason I’d expect their longterm time average to show that they are useless. Investment houses make a lot of money by taking a percentage of the client’s cash. It’s a contract freely entered into and I expect most investment houses genuinely believe in their methods, ie they are in good faith, but that doesn’t mean they are any good. Most don’t outperform the market average and those that do over one business cycle often don’t over the next, ie they were just lucky. • Dave Glyer Says: This comment looks a bit like a situation where a little bit of knowledge is dangerous, or at least makes one think that they know more than they really do; although it also makes good points. Quantitative skills and reasoning are very useful in Finance and it does not drive primarily from trying to use physics-type of models as the basis of analysis. Quant analysis is not primarily about ‘getting in and out’. In general, I doubt the PhD-type physics people are primarily programmers, they are more on the ‘quant’ side doing modeling and extensive data analysis. Analyzing risk and the interaction of risk components across assets and asset classes on various time domains is one key area for highly quantitative people in the field. One of the short comings of the quants is that they are not as strong on intuition as they are with their other tools and thus they tend not to build the ability to apply intuition to the problems that they face. I think that this was a problem for the guys at Long-Term Capital Management (Merton and Scholes, Nobels in 1997) especially because great early returns pushed them more and more into risky assets and then the hedge fund imploded in four months with the Asian and Russian crises, going bankrupt. Hard to model that the modest and even negative correlations under normal conditions get more and more positively correlated under extreme conditions. Most straight models can be very misleading for situations where there is not much data, and quants can get badly burned. [note: my background in economics; I am a neophyte in physics but I find it more interesting in retirement.] 3. V nice article Peter, most helpful. If I may ask a dumb question: are there other reasons (besides inflation) that we might expect a Gaussian distribution? Given the primordial nature of the radiation, isn’t Gaussianity to be expected in simple models, with the same reasoning that one expects the CMB spectrum to be close to that of a black body? • telescoper Says: Cormac, Good question. People were talking about Gaussian primordial fluctuations long before anyone ever thought of inflation, as that is the generic result of linear physical processes. Inflation yields a specific mechanism for generating Gaussian perturbations (from quantum-mechanical processes) but that’s not to say such perturbations couldn’t have arisen in another way. • Although inflation is more a paradigm than a theory, and hence specific predictions are a bit tricky, one relatively robust one was a spectral index of approximately 1, but slightly less. This was a pretty generic prediction, long before data were anywhere good enough to measure it. The measured value of slightly less than one significantly increased my confidence that inflation or something very similar probably happened. A scale-invariant spectrum is pretty generic; this goes back to Harrison (1970) (the same Harrison of “who has written a very good cosmology textbook?” fame) and Zeldovich (1972). That inflation produces a nearly scale-invariant spectrum is thus no big deal; the interesting thing is the slight tilt. • telescoper Says: Yes, the early papers by Harrison and Zel’dovich were well before inflation and the arguments for n=1 are made on general grounds. What is interesting about the inflation models is the connection between departures from n=1 and gravitational wave perturbation amplitude (at least within slow-roll inflation). • Shantanu Says: Philip, I believe Starobinsky has a model of inflation with ns exactly equal to 1. So again ns different from 1 is also not a smoking gun signature of inflation • There are also inflation models with significant curvature at our epoch. I think the consensus, though, is that they are contrived. I’m no expert on this, but my impression is that n slightly less than 1 is a prediction of many models. • telescoper Says: That’s what you get in single-field slow-roll inflation… 4. Many thanks for that reply, Peter. it does clarify things. My understanding is that the assumption of Gaussianity in the CMB is reasonable, in the sense that it would be anyone’s first guess (with or without inflation) and no counter evidence has emerged from lensing etc. Thus, arguing from naturalness, it’s likely that the amplitudes of the peaks should indeed be interpreted the way they are, is that right? 5. Wow, that paper and the references in it are quite a treat for the historian! 6. Dr.William Joseph Bray Says: How did you derive the power, amplitude, and phase for the earth map? I’m curious about the Chaotic (but not truly random) attractor in this overlay of the power and phase of Earth and Sky. I’m guessing you used altitude for amplitude, but for power (angular) and phase, I’m at a loss (for the Earth map).	{}
# Give standard equation for the ellipse with the given characteristics: Major axis of length 24 Foci:(plus/minus 5,0)? Apr 2, 2018 ${x}^{2} / {12}^{2} + {y}^{2} / {\left(\sqrt{119}\right)}^{2} = 1$ #### Explanation: The foci at $\left(- 5 , 0\right) \mathmr{and} \left(5 , 0\right)$ tells us that the major axis is horizontally oriented, therefore, the general form is: ${\left(x - h\right)}^{2} / {a}^{2} + {\left(y - k\right)}^{2} / {b}^{2} = 1 , a > b \text{ [1]}$ The location of the foci allows us to write the following equations: $k = 0 \text{ [2]}$ $h - \sqrt{{a}^{2} - {b}^{2}} = - 5 \text{ [3]}$ $h + \sqrt{{a}^{2} - {b}^{2}} = 5 \text{ [4]}$ Add equation [3] to equation [4] and solve for the value of h: $2 h = 0$ $h = 0 \text{ [5]}$ Substitute equations [2] and [5] into equation [1]: ${\left(x\right)}^{2} / {a}^{2} + {\left(y\right)}^{2} / {b}^{2} = 1 \text{ [1.1]}$ The major axis length of $24$ allows us to find the value of a: $a = \frac{24}{2}$ $a = 12 \text{ [6]}$: Substitute equation [6] into equation [1.1]: ${\left(x\right)}^{2} / {12}^{2} + {\left(y\right)}^{2} / {b}^{2} = 1 \text{ [1.2]}$ Substitute equations [5] and [6] into equation [4] and solve for the value of b: $0 + \sqrt{{12}^{2} - {b}^{2}} = 5$ $- {b}^{2} = 25 - 144$ $b = \sqrt{119} \text{ [7]}$ Substitute equation [7] into equation [1.2]: ${x}^{2} / {12}^{2} + {y}^{2} / {\left(\sqrt{119}\right)}^{2} = 1$	{}
# Publications ## Cloud_cci Advanced Very High Resolution Radiometer post meridiem (AVHRR-PM) dataset version 3: 35-year climatology of global cloud and radiation properties Earth System Science Data Copernicus Publications 12 (2020) 41-60 M Stengel, S Stapelberg, O Sus, S Finkensieper, B Wuerzler, D Philipp, R Hollmann, C Poulsen, M Christensen, G McGarragh We present version 3 of the Cloud_cci Advanced Very High Resolution Radiometer post meridiem (AVHRR-PM) dataset, which contains a comprehensive set of cloud and radiative flux properties on a global scale covering the period of 1982 to 2016. The properties were retrieved from AVHRR measurements recorded by the afternoon (post meridiem – PM) satellites of the National Oceanic and Atmospheric Administration (NOAA) Polar Operational Environmental Satellite (POES) missions. The cloud properties in version 3 are of improved quality compared with the precursor dataset version 2, providing better global quality scores for cloud detection, cloud phase and ice water path based on validation results against A-Train sensors. Furthermore, the parameter set was extended by a suite of broadband radiative flux properties. They were calculated by combining the retrieved cloud properties with thermodynamic profiles from reanalysis and surface properties. The flux properties comprise upwelling and downwelling and shortwave and longwave broadband fluxes at the surface (bottom of atmosphere – BOA) and top of atmosphere (TOA). All fluxes were determined at the AVHRR pixel level for all-sky and clear-sky conditions, which will particularly facilitate the assessment of the cloud radiative effect at the BOA and TOA in future studies. Validation of the BOA downwelling fluxes against the Baseline Surface Radiation Network (BSRN) shows a very good agreement. This is supported by comparisons of multi-annual mean maps with NASA's Clouds and the Earth's Radiant Energy System (CERES) products for all fluxes at the BOA and TOA. The Cloud_cci AVHRR-PM version 3 (Cloud_cci AVHRR-PMv3) dataset allows for a large variety of climate applications that build on cloud properties, radiative flux properties and/or the link between them. ## An AeroCom/AeroSat study: Intercomparison of Satellite AODDatasets for Aerosol Model Evaluation Atmospheric Chemistry and Physics Discussions European Geosciences Union (2020) N Schutgens, A Sayer, A Heckel, C Hsu, H Jethva, G de Leeuw, P Leonard, R Levy, A Lipponen, A Lyapustin, P North, T Popp, C Poulson, V Sawyer, L Sogacheva, G Thomas, O Torres, Y Wang, S Kinne, M Schulz, P Stier ## Global response of parameterised convective cloud fields to anthropogenic aerosol forcing Atmospheric Chemistry and Physics Copernicus GmbH 20 (2020) 4445-4460 Z Kipling, L Labbouz, P Stier <jats:p>Abstract. The interactions between aerosols and convective clouds represent some of the greatest uncertainties in the climate impact of aerosols in the atmosphere. A wide variety of mechanisms have been proposed by which aerosols may invigorate, suppress or change the properties of individual convective clouds, some of which can be reproduced in high-resolution limited-area models. However, there may also be mesoscale, regional or global adjustments which modulate or dampen such impacts which cannot be captured in the limited domain of such models. The Convective Cloud Field Model (CCFM) provides a mechanism to simulate a population of convective clouds, complete with microphysics and interactions between clouds, within each grid column at resolutions used for global climate modelling, so that a representation of the microphysical aerosol response within each parameterised cloud type is possible. Using CCFM within the global aerosol–climate model ECHAM–HAM, we demonstrate how the parameterised cloud field responds to the present-day anthropogenic aerosol perturbation in different regions. In particular, we show that in regions with strongly forced deep convection and/or significant aerosol effects via large-scale processes, the changes in the convective cloud field due to microphysical effects are rather small; however in a more weakly forced regime such as the Caribbean, where large-scale aerosol effects are small, a signature of convective invigoration does become apparent. </jats:p> ## Assessing California wintertime precipitation responses to various climate drivers Journal of Geophysical Research: Atmospheres American Geophysical Union 125 (2020) e2019JD031736 RJ Allen, J-F Lamarque, D Watson-Parris, D Olivie Understanding how drivers of climate change affect precipitation remains an important area of research. Although several robust precipitation responses have been identified under continued increases in greenhouse gases (GHGs), considerable uncertainty remains. This is particularly the case at regional scales, including the West Coast of the United States and California. Here, we exploit idealized, single forcing simulations from the Precipitation Driver Response Model Intercomparison Project (PDRMIP) to address how climate drivers impact California wintertime precipitation. Consistent with recent work, GHGs including carbon dioxide and methane, as well as solar forcing, yield a robust increase in California wintertime precipitation. We also find robust California precipitation responses to aerosols but with opposite responses for sulfate versus black carbon aerosol. Sulfate aerosol increases California wintertime precipitation, whereas black carbon reduces it. Moreover, California precipitation is more sensitive to aerosols, particularly regional emissions from Europe and Asia, than to GHGs. These precipitation responses are consistent with shifts in the jet stream and altered moisture fluxes. Although the idealized nature of PDRMIP simulations precludes a formal attribution, our results suggest that aerosols can perturb precipitation and fresh water resources along the West Coast of the United States. ## Reducing the aerosol forcing uncertainty using observational constraints on warm rain processes J Mülmenstädt, C Nam, M Salzmann, J Kretzschmar, TS L’Ecuyer, U Lohmann, P-L Ma, G Myhre, D Neubauer, P STIER, K Suzuki, M Wang, J Quaas ## Aerosols Enhance Cloud Lifetime and Brightness along the Stratus-to-Cumulus Transition Proceedings of the National Academy of Sciences of USA National Academy of Sciences (2020) M CHRISTENSEN, W Jones, P STIER ## Diurnal cycle of the semi-direct effect from a persistent absorbing aerosol layer over marine stratocumulus in large-eddy simulations Atmospheric Chemistry and Physics European Geosciences Union 20 (2020) 1317–1340- R Herbert, N Bellouin, E Highwood, A Hill <p>The rapid adjustment, or semi-direct effect, of marine stratocumulus clouds to elevated layers of absorbing aerosols may enhance or dampen the radiative effect of aerosol–radiation interactions. Here we use large-eddy simulations to investigate the sensitivity of stratocumulus clouds to the properties of an absorbing aerosol layer located above the inversion layer, with a focus on the location, timing, and strength of the radiative heat perturbation. The sign of the daily mean semi-direct effect depends on the properties and duration of the aerosol layer, the properties of the boundary layer, and the model setup. Our results suggest that the daily mean semi-direct effect is more elusive than previously assessed. We find that the daily mean semi-direct effect is dominated by the distance between the cloud and absorbing aerosol layer. Within the first 24 h the semi-direct effect is positive but remains under 2 W m<sup>−2</sup> unless the aerosol layer is directly above the cloud. For longer durations, the daily mean semi-direct effect is consistently negative but weakens by 30 %, 60 %, and 95 % when the distance between the cloud and aerosol layer is 100, 250, and 500 m, respectively. Both the cloud response and semi-direct effect increase for thinner and denser layers of absorbing aerosol. Considerable diurnal variations in the cloud response mean that an instantaneous semi-direct effect is unrepresentative of the daily mean and that observational studies may underestimate or overestimate semi-direct effects depending on the observed time of day. The cloud response is particularly sensitive to the mixing state of the boundary layer: well-mixed boundary layers generally result in a negative daily mean semi-direct effect, and poorly mixed boundary layers result in a positive daily mean semi-direct effect. The properties of the boundary layer and model setup, particularly the sea surface temperature, precipitation, and properties of the air entrained from the free troposphere, also impact the magnitude of the semi-direct effect and the timescale of adjustment. These results suggest that the semi-direct effect simulated by coarse-resolution models may be erroneous because the cloud response is sensitive to small-scale processes, especially the sources and sinks of buoyancy.</p> ## Constraining uncertainty in aerosol direct forcing Geophysical Research Letters American Geophysical Union 47 (2020) e2020GL087141 D Watson-Parris, N Bellouin, L Deaconu, N Schutgens, M Yoshioka, L Regayre, K Pringle, J Johnson, C Smith, K Carslaw, P Stier The uncertainty in present-day anthropogenic forcing is dominated by uncertainty in the strength of the contribution from aerosol. Much of the uncertainty in the direct aerosol forcing can be attributed to uncertainty in the anthropogenic fraction of aerosol in the present-day atmosphere, due to a lack of historical observations. Here we present a robust relationship between total present-day aerosol optical depth and the anthropogenic contribution across three multi-model ensembles and a large single-model perturbed parameter ensemble. Using observations of aerosol optical depth, we determine a reduced likely range of the anthropogenic component and hence a reduced uncertainty in the direct forcing of aerosol. ## Planet Hunters TESS I: TOI 813, a subgiant hosting a transiting Saturn-sized planet on an 84-day orbit Monthly Notices of the Royal Astronomical Society Oxford University Press 494 (2020) 750-763 N Eisner, O Barragan Villanueva, S Aigrain, C Lintott, G Miller, N Zicher, TS Boyajian, C Briceño, EM Bryant, JL Christiansen, AD Feinstein, LM Flor-Torres, M Fridlund, D Gandolfi, J Gilbert, N Guerrero, JM Jenkins, K Jones, M Christensen, A Vanderburg, AR López-Sánchez, C Ziegler, DM Bundy, LD Melanson, I Terentev We report on the discovery and validation of TOI 813b (TIC 55525572 b), a transiting exoplanet identified by citizen scientists in data from NASA's Transiting Exoplanet Survey Satellite (TESS) and the first planet discovered by the Planet Hunters TESS project. The host star is a bright (V = 10.3 mag) subgiant (USDR_\star=1.94\,R_\odotUSD, USDM_\star=1.32\,M_\odotUSD). It was observed almost continuously by TESS during its first year of operations, during which time four individual transit events were detected. The candidate passed all the standard light curve-based vetting checks, and ground-based follow-up spectroscopy and speckle imaging enabled us to place an upper limit of USD2 M_{Jup}USD (99 % confidence) on the mass of the companion, and to statistically validate its planetary nature. Detailed modelling of the transits yields a period of USD83.8911_{ - 0.0031 } ^ { + 0.0027 }USD days, a planet radius of USD6.71 \pm 0.38R_{\oplus}$, and a semi major axis of$0.423_{ - 0.037 } ^ { + 0.031 }USD AU. The planet's orbital period combined with the evolved nature of the host star places this object in a relatively under-explored region of parameter space. We estimate that TOI-813b induces a reflex motion in its host star with a semi-amplitude of USD\sim6USD msUSD^{-1}USD, making this system a promising target to measure the mass of a relatively long-period transiting planet. ## Cloudy-sky contributions to the direct aerosol effect Atmospheric Chemistry and Physics Copernicus GmbH 20 (2020) 8855-8865 G Myhre, BH Samset, CW Mohr, K Alterskjær, Y Balkanski, N Bellouin, M Chin, J Haywood, Ø Hodnebrog, S Kinne, G Lin, MT Lund, JE Penner, M Schulz, N Schutgens, RB Skeie, P Stier, T Takemura, K Zhang <jats:p>Abstract. The radiative forcing of the aerosol–radiation interaction can be decomposed into clear-sky and cloudy-sky portions. Two sets of multi-model simulations within Aerosol Comparisons between Observations and Models (AeroCom), combined with observational methods, and the time evolution of aerosol emissions over the industrial era show that the contribution from cloudy-sky regions is likely weak. A mean of the simulations considered is 0.01±0.1 W m−2. Multivariate data analysis of results from AeroCom Phase II shows that many factors influence the strength of the cloudy-sky contribution to the forcing of the aerosol–radiation interaction. Overall, single-scattering albedo of anthropogenic aerosols and the interaction of aerosols with the short-wave cloud radiative effects are found to be important factors. A more dedicated focus on the contribution from the cloud-free and cloud-covered sky fraction, respectively, to the aerosol–radiation interaction will benefit the quantification of the radiative forcing and its uncertainty range. </jats:p> ## Author Correction: Weak average liquid-cloud-water response to anthropogenic aerosols. Nature 577 (2020) E3-E5 V Toll, M Christensen, J Quaas, N Bellouin An Amendment to this paper has been published and can be accessed via a link at the top of the paper. ## Bounding global aerosol radiative forcing of climate change Reviews of Geophysics American Geophysical Union 58 (2019) e2019RG000660 N Bellouin, J Quaas, S Kinne, P Stier, D Watson-Parris, O Boucher, KS Carslaw, M Christensen, A-L Daniau, JL Dufresne, G Feingold, S Fiedler, P Forster, A Gettelman, JM Haywood, U Lohmann, F Malavelle, T Mauritsen, DT McCoy, G Myhre, J Muelmenstaedt, A Possner, M Rugenstein, O Sourdeval, V Toll Aerosols interact with radiation and clouds. Substantial progress made over the past 40 years in observing, understanding, and modeling these processes helped quantify the imbalance in the Earth's radiation budget caused by anthropogenic aerosols, called aerosol radiative forcing, but uncertainties remain large. This review provides a new range of aerosol radiative forcing over the industrial era based on multiple, traceable, and arguable lines of evidence, including modeling approaches, theoretical considerations, and observations. Improved understanding of aerosol absorption and the causes of trends in surface radiative fluxes constrain the forcing from aerosol‐radiation interactions. A robust theoretical foundation and convincing evidence constrain the forcing caused by aerosol‐driven increases in liquid cloud droplet number concentration. However, the influence of anthropogenic aerosols on cloud liquid water content and cloud fraction is less clear, and the influence on mixed‐phase and ice clouds remains poorly constrained. Observed changes in surface temperature and radiative fluxes provide additional constraints. These multiple lines of evidence lead to a 68% confidence interval for the total aerosol effective radiative forcing of ‐1.6 to ‐0.6 W m−2, or ‐2.0 to ‐0.4 W m−2 with a 90% likelihood. Those intervals are of similar width to the last Intergovernmental Panel on Climate Change assessment but shifted toward more negative values. The uncertainty will narrow in the future by continuing to critically combine multiple lines of evidence, especially those addressing industrial‐era changes in aerosol sources and aerosol effects on liquid cloud amount and on ice clouds. ## Constraining the Twomey effect from satellite observations: issues and perspectives Atmospheric Chemistry and Physics Discussions European Geosciences Union (2020) J Quaas, A Antti, B Cairns, M Christensen, H Deneke, AML Ekman, G Feingold, A Fridlind, E Gryspeerdt, O Hasekamp, Z Li, A Lipponen, P-L Ma, J Muelmenstaedt, A Nenes, J Penner, D Rosenfeld, R Schroedner, K Sinclair, O Sourdeval, P Stier, M Tesche, B van Dieedenhoven, M Wendisch The Twomey effect describes the radiative forcing associated with a change in cloud albedo due to an increase in anthropogenic aerosol emissions. It is driven by the perturbation in cloud droplet number concentration (ΔNd,ant) in liquid-water clouds and is currently understood to exert a cooling effect on climate. The Twomey effect is the key driver in the effective radiative forcing due to aerosol–cloud interactions which also comprises rapid adjustments. These adjustments are essentially the responses of cloud fraction and liquid water path to ΔNd,ant and thus scale approximately with it. While the fundamental physics of the influence of added aerosol particles on the droplet concentration (Nd) is well described by established theory at the particle scale (micrometres), how this relationship is expressed at the large scale (hundreds of kilometres) ΔNd,ant remains uncertain. The discrepancy between process understanding at particle scale and insufficient quantification at the climate-relevant large scale is caused by co-variability of aerosol particles and vertical wind and by droplet sink processes. These operate at scales on the order of 10s of metres at which only localized observations are available and at which no approach exists yet to quantify the anthropogenic perturbation. Different atmospheric models suggest diverse magnitudes of the Twomey effect even when applying the same anthropogenic aerosol emission perturbation. Thus, observational data are needed to quantify and constrain the Twomey effect. At the global scale, this means satellite data. There are three key uncertainties in determining ΔNd,ant, namely the quantification (i) of the cloud-active aerosol – the cloud condensation nuclei concentrations (CCN) at or above cloud base –, (ii) of Nd, as well as (iii) the statistical approach for inferring the sensitivity of Nd to aerosol particles from the satellite data. A fourth uncertainty, the anthropogenic perturbation to CCN concentrations, is also not easily accessible from observational data. This review discusses deficiencies of current approaches for the different aspects of the problem and proposes several ways forward: In terms of CCN, retrievals of optical quantities such as aerosol optical depth suffer from a lack of vertical resolution, size and hygroscopicity information, the non-direct relation to the concentration of aerosols, the impossibility to quantify it within or below clouds, and the problem of insufficient sensitivity at low concentrations, in addition to retrieval errors. A future path forward can include utilizing colocated polarimeter and lidar instruments, ideally including high spectral resolution lidar capability at two wavelengths to maximize vertically resolved size distribution information content. In terms of Nd, a key problem is the lack of operational retrievals of this quantity, and the inaccuracy of the retrieval especially in broken-cloud regimes. As for the Nd – to – CCN sensitivity, key issues are the updraught distributions and the role of Nd sink processes, for which empirical assessments for specific cloud regimes are currently the best solutions. These considerations point to the conclusion that past studies using existing approaches have likely underestimated the true sensitivity and, thus, the radiative forcing due to the Twomey effect. ## Open cells exhibit weaker entrainment of free-tropospheric biomass burning aerosol into the south-east Atlantic boundary layer Atmospheric Chemistry and Physics Copernicus Publications 20 (2020) 4059-4084 SJ Abel, PA Barrett, P Zuidema, J Zhang, M Christensen, F Peers, JW Taylor, I Crawford, KN Bower, M Flynn <br>This work presents synergistic satellite, airborne and surface-based observations of a pocket of open cells (POC) in the remote south-east Atlantic. The observations were obtained over and upwind of Ascension Island during the CLouds and Aerosol Radiative Impacts and Forcing (CLARIFY) and the Layered Smoke Interacting with Clouds (LASIC) field experiments. A novel aspect of this case study is that an extensive free-tropospheric biomass burning aerosol plume that had been transported from the African continent was observed to be in contact with the boundary layer inversion over the POC and the surrounding closed cellular cloud regime. The in situ measurements show marked contrasts in the boundary layer thermodynamic structure, cloud properties, precipitation and aerosol conditions between the open cells and surrounding overcast cloud field.</br> <br>The data demonstrate that the overlying biomass burning aerosol was mixing down into the boundary layer in the stratocumulus cloud downwind of the POC, with elevated carbon monoxide, black carbon mass loadings and accumulation-mode aerosol concentrations measured beneath the trade-wind inversion. The stratocumulus cloud in this region was moderately polluted and exhibited very little precipitation falling below cloud base. A rapid transition to actively precipitating cumulus clouds and detrained stratiform remnants in the form of thin quiescent veil clouds was observed across the boundary into and deep within the POC. The subcloud layer in the POC was much cleaner than that in the stratocumulus region. The clouds in the POC formed within an ultra-clean layer (accumulation-mode aerosol concentrations of approximately a few cm−3) in the upper region of the boundary layer, which was likely to have been formed via efficient collision–coalescence and sedimentation processes. Enhanced Aitken-mode aerosol concentrations were also observed intermittently in this ultra-clean layer, suggesting that new particle formation was taking place. Across the boundary layer inversion and immediately above the ultra-clean layer, accumulation-mode aerosol concentrations were ∼ 1000 cm−3. Importantly, the air mass in the POC showed no evidence of elevated carbon monoxide over and above typical background conditions at this location and time of year. As carbon monoxide is a good tracer for biomass burning aerosol that is not readily removed by cloud processing and precipitation, it demonstrates that the open cellular convection in the POC is not able to entrain large quantities of the free-tropospheric aerosol that was sitting directly on top of the boundary layer inversion. This suggests that the structure of the mesoscale cellular convection may play an important role in regulating the transport of aerosol from the free troposphere down into the marine boundary layer.</br> <br>We then develop a climatology of open cellular cloud conditions in the south-east Atlantic from 19 years of September Moderate Resolution Imaging Spectroradiometer (MODIS) Terra imagery. This shows that the maxima in open cell frequency (> 0.25) occurs far offshore and in a region where subsiding biomass burning aerosol plumes may often come into contact with the underlying boundary layer cloud. If the results from the observational case study applied more broadly, then the apparent low susceptibility of open cells to free-tropospheric intrusions of additional cloud condensation nuclei could have some important consequences for aerosol–cloud interactions in the region.</br> ## Up to two billion times acceleration of scientific simulations with deep neural architecture search CoRR abs/2001.08055 (2020) MF Kasim, D Watson-Parris, L Deaconu, S Oliver, P Hatfield, DH Froula, G Gregori, M Jarvis, S Khatiwala, J Korenaga, J Topp-Mugglestone, E Viezzer, SM Vinko Computer simulations are invaluable tools for scientific discovery. However, accurate simulations are often slow to execute, which limits their applicability to extensive parameter exploration, large-scale data analysis, and uncertainty quantification. A promising route to accelerate simulations by building fast emulators with machine learning requires large training datasets, which can be prohibitively expensive to obtain with slow simulations. Here we present a method based on neural architecture search to build accurate emulators even with a limited number of training data. The method successfully accelerates simulations by up to 2 billion times in 10 scientific cases including astrophysics, climate science, biogeochemistry, high energy density physics, fusion energy, and seismology, using the same super-architecture, algorithm, and hyperparameters. Our approach also inherently provides emulator uncertainty estimation, adding further confidence in their use. We anticipate this work will accelerate research involving expensive simulations, allow more extensive parameters exploration, and enable new, previously unfeasible computational discovery. ## Atmospheric energy budget response to idealized aerosol perturbation in tropical cloud systems Atmospheric Chemistry and Physics Copernicus GmbH 20 (2020) 4523-4544 G Dagan, P Stier, M Christensen, G Cioni, D Klocke, A Seifert <jats:p>Abstract. The atmospheric energy budget is analysed in numerical simulations of tropical cloud systems to better understand the physical processes behind aerosol effects on the atmospheric energy budget. The simulations include both shallow convective clouds and deep convective tropical clouds over the Atlantic Ocean. Two different sets of simulations, at different dates (10–12 and 16–18 August 2016), are simulated with different dominant cloud modes (shallow or deep). For each case, the cloud droplet number concentration (CDNC) is varied as a proxy for changes in aerosol concentrations without considering the temporal evolution of the aerosol concentration (for example due to wet scavenging, which may be more important under deep convective conditions). It is shown that the total column atmospheric radiative cooling is substantially reduced with CDNC in the deep-cloud-dominated case (by ∼10.0 W m−2), while a much smaller reduction (∼1.6 W m−2) is shown in the shallow-cloud-dominated case. This trend is caused by an increase in the ice and water vapour content at the upper troposphere that leads to a reduced outgoing longwave radiation, an effect which is stronger under deep-cloud-dominated conditions. A decrease in sensible heat flux (driven by an increase in the near-surface air temperature) reduces the warming by ∼1.4 W m−2 in both cases. It is also shown that the cloud fraction response behaves in opposite ways to an increase in CDNC, showing an increase in the deep-cloud-dominated case and a decrease in the shallow-cloud-dominated case. This demonstrates that under different environmental conditions the response to aerosol perturbation could be different. </jats:p> ## Effects of aerosol in simulations of realistic shallow cumulus cloud fields in a large domain ATMOSPHERIC CHEMISTRY AND PHYSICS 19 (2019) 13507-13517 G Spill, P Stier, PR Field, G Dagan ## tobac 1.2: towards a flexible framework for tracking and analysis of clouds in diverse datasets GEOSCIENTIFIC MODEL DEVELOPMENT 12 (2019) 4551-4570 M Heikenfeld, PJ Marinescu, M Christensen, D Watson-Parris, F Senf, SC van den Heever, P Stier ## Efficacy of climate forcings in PDRMIP models Journal of Geophysical Research: Atmospheres American Geophysical Union 124 (2019) 12824-12844 TB Richardson, PM Forster, CJ Smith, AC Maycock, T Wood, T Andrews, O Boucher, G Faluvegi, D Flaeschner, O Hodnebrog, M Kasoar, A Kirkevåg, J-F Lamarque, J Mülmenstädt, G Myhre, D Olivié, RW Portmann, BH Samset, D Shawki, D Shindell, P Stier, T Takemura, A Voulgarakis, D Watson-Parris Quantifying the efficacy of different climate forcings is important for understanding the real‐world climate sensitivity. This study presents a systematic multi‐model analysis of different climate driver efficacies using simulations from the Precipitation Driver and Response Model Intercomparison Project (PDRMIP). Efficacies calculated from instantaneous radiative forcing deviate considerably from unity across forcing agents and models. Effective radiative forcing (ERF) is a better predictor of global mean near‐surface air temperature (GSAT) change. Efficacies are closest to one when ERF is computed using fixed sea surface temperature experiments and adjusted for land surface temperature changes using radiative kernels. Multi‐model mean efficacies based on ERF are close to one for global perturbations of methane, sulphate, black carbon and insolation, but there is notable inter‐model spread. We do not find robust evidence that the geographic location of sulphate aerosol affects its efficacy. GSAT is found to respond more slowly to aerosol forcing than CO2 in the early stages of simulations. Despite these differences, we find that there is no evidence for an efficacy effect on historical GSAT trend estimates based on simulations with an impulse response model, nor on the resulting estimates of climate sensitivity derived from the historical period. However, the considerable intermodel spread in the computed efficacies means that we cannot rule out an efficacy‐induced bias of ±0.4 K in equilibrium climate sensitivity to CO2 doubling (ECS) when estimated using the historical GSAT trend. ## The impact of ship emission controls recorded by Cloud Properties Geophysical Research Letters American Geophysical Union 46 (2019) 12547-12555 E Gryspeerdt, T Smith, E O'Keeffe, M Christensen, F Goldsworth The impact of aerosols on cloud properties is one of the leading uncertainties in the human forcing of the climate. Ships are large, isolated sources of aerosol creating linear cloud formations known as shiptracks. These are an ideal opportunity to identify and measure aerosol-cloud interactions. This work uses over 17,000 shiptracks during the implementation of fuel sulfur content regulations to demonstrate the central role of sulfate aerosol in ship exhaust for modifying clouds. By connecting individual shiptracks to transponder data, it is shown that almost half of shiptracks are likely undetected, masking a significant contribution to the climate impact of shipping. A pathway to retrieving ship sulfate emissions is demonstrated, showing how cloud observations could be used to monitor air pollution.	{}
0 Research Papers Research Papers # A Nonlinear Constituent Based Viscoelastic Model for Articular Cartilage and Analysis of Tissue Remodeling Due to Altered Glycosaminoglycan-Collagen Interactions [+] Author Affiliations Gregory C. Thomas Department of Mechanical Engineering, California Polytechnic State University, San Luis Obispo, CA 93407 Anna Asanbaeva, Robert L. Sah Department of Bioengineering, University of California-San Diego, La Jolla, CA 92093 Pasquale Vena Department of Structural Engineering, Laboratory of Biological Structure Mechanics, Politecnico di Milano, 20133, Milan, Italy Stephen M. Klisch1 Department of Mechanical Engineering, California Polytechnic State University, San Luis Obispo, CA 93407, sklisch@calpoly.edu These differences are discussed in more detail in Secs. 2,4. These assumptions are discussed further in Sec. 4. In Eq. 4, stresses are VE stresses; a superscript $e$ will be used to designate elastic stresses. Equation numbers preceded by “A” and “B” refer to those in Appendices . VE models usually include a term for strain rate (i.e., $dE/dt$) inside the convolution integral to account for the dependence on strain rate. As stress is proportional to strain, the dependence on strain rate can also be achieved with a stress rate term $dS/dt$(23). Note that as $t→∞$, $S(t)$ is the equilibrium (elastic) stress $Se(0)+ΔSe$. Note that relative to a zero stress-zero strain configuration, $R$ defined by Eq. 19 is strain independent, which is also a characteristic of quasilinear viscoelasticity. The derivation is nearly identical to that in Ref. 23 and the reader is referred to that paper for full details. This assumption is discussed further in Sec. 4. Equation 25 defines a viscous material constant that is independent of strain, decoupling elastic and viscous properties and is preferable to Eq. 24, which couples elastic and viscous properties, for statistical analysis of COL viscous properties. For GD-85 specimens, the COL VE parameters ($τ1COL$, $g1COL$) were independent of initial guesses. Also, our own pilot simulations using a poroviscoelastic model (results of which are not presented) justified the assumption that fluid flow-dependent viscoelasticity can be neglected for out UT protocols. It can be seen from Eq. 8 that when a COL fiber direction is not stretched in tension, it is “turned off” and does not contribute to $SeBIM$. 1 Corresponding author. J Biomech Eng 131(10), 101002 (Sep 01, 2009) (11 pages) doi:10.1115/1.3192139 History: Received November 15, 2008; Revised June 03, 2009; Published September 01, 2009 ## abstract A constituent based nonlinear viscoelastic (VE) model was modified from a previous study (Vena, , 2006, “A Constituent-Based Model for the Nonlinear Viscoelastic Behavior of Ligaments ,” J. Biomech. Eng., 128, pp. 449–457) to incorporate a glycosaminoglycan (GAG)-collagen (COL) stress balance using compressible elastic stress constitutive equations specific to articular cartilage (AC). For uniaxial loading of a mixture of quasilinear VE constituents, time constant and relaxation ratio equations are derived to highlight how a mixture of constituents with distinct quasilinear VE properties is one mechanism that produces a nonlinear VE tissue. Uniaxial tension experiments were performed with newborn bovine AC specimens before and after ∼55% and ∼85% GAG depletion treatment with guanidine. Experimental tissue VE parameters were calculated directly from stress relaxation data, while intrinsic COL VE parameters were calculated by curve fitting the data with the nonlinear VE model with intrinsic GAG viscoelasticity neglected. Select tissue and intrinsic COL VE parameters were significantly different from control and experimental groups and correlated with GAG content, suggesting that GAG-COL interactions exist to modulate tissue and COL mechanical properties. Comparison of the results from this and other studies that subjected more mature AC tissue to GAG depletion treatment suggests that the GAGs interact with the COL network in a manner that may be beneficial for rapid volumetric expansion during developmental growth while protecting cells from excessive matrix strains. Furthermore, the underlying GAG-COL interactions appear to diminish as the tissue matures, indicating a distinctive remodeling response during developmental growth. <> Your Session has timed out. Please sign back in to continue. ## Figures Figure 1 The stress balance hypothesis. The GAG and COL constituents have their own reference configurations, κ0GAG and κ0COL. The GAG constituent has the same configuration in κ0P and κ0, which is equivalent to F0GAG=I and SeGAG(0)=−α1I. To balance this swelling stress, the COL network supports a tensile prestress produced by an initial COL deformation gradient tensor F0COL, which yields the initial collagen stress tensor SeCOL(0)=α1I. After a deformation F is applied, the constituent stresses are calculated relative to their respective reference configurations and using FGAG=FF0GAG and FCOL=FF0COL. Figure 2 Stress response to a step increase in strain and, consequently, a step increase in elastic stress ΔSe at time tstep>0 with initial equilibrium elastic stress Se(0) Figure 3 The effects of GAG depletion treatment on experimental tissue VE parameters (Eexp, τexp, and Rexp): mean+1 standard deviation values shown; GD-0 is the control group with no GAG depletion; GD-55 and GD-85 are experimental groups with ∼55% and 85% GAG depletion, respectively; ∗ is the significant difference between experimental and control group values and ∗∗ is the significant difference between experimental group values (ANOVA with posthoc Tukey testing p<0.05) Figure 4 Experimental tissue VE parameters (Eexp, τexp, and Rexp) versus GAG and COL contents: GD-0 is the control group with no GAG depletion; GD-55 and GD-85 are experimental groups with ∼55% and 85% GAG depletion, respectively. The linear regression results were only shown for significant correlations (t-test analysis of regression slope, p<0.05). Figure 5 Specimen-specific curve-fits of the constituent based VE model: GD-0 is the group with no GAG depletion; GD-55 and GD-85 are experimental groups with ∼55% and 85% GAG depletion, respectively. Figure 6 The effects of GAG depletion treatment on COL VE parameters (γ1, τ1COL, g1COL, τ2COL, g2COL, τACOL, and RACOL); mean+1 standard deviation values were shown; GD-0 is the control group with no GAG depletion; GD-55 and GD-85 are experimental groups with ∼55% and 85% GAG depletion, respectively; τ2COL and g2COL values were not reported for GD-85 specimens because only one Prony series term was used in the COL relaxation function for that group. For γ1, τACOL, and RACOL: ∗ is the significant difference between experimental and control group values and ∗∗ is the significant difference between experimental group values (ANOVA with posthoc Tukey testing p<0.05). For τ1COL, g1COL, τ2COL, and g2COL: ∗ is the significant difference between GD-0 and GD-55 group values (paired t-test p<0.05). Figure 7 COL VE parameters (γ1, τ1COL, g1COL, τ2COL, g2COL, τACOL, and RACOL) versus GAG and COL contents: GD-0 is the control group with no GAG depletion; GD-55 and GD-85 are experimental groups with ∼55% and 85% GAG depletion, respectively. The linear regression results were only shown for significant correlations (t-test analysis of regression slope p<0.05). Figure 8 The parameter study results were shown to differentiate between the different mechanisms arising from GAG-COL interactions on the experimental tissue VE response: absolute (top) and normalized (bottom) stress results for UT simulations with progressive changes in untreated (GD-0) group parameters due to treatment (GD-55, GD-85); parameters used are listed in Table 1. The stress-time curves from the first three simulations for each treatment were indistinguishable in the normalized stress plots. GAG and COL elastic parameters modulate the peak and equilibrium stresses (top) but not the relaxation behavior (bottom). COL viscous parameters modulate peak and equilibrium stresses (top) and relaxation behavior (bottom). ## Footnotes Some tools below are only available to our subscribers or users with an online account. ### Related Content Customize your page view by dragging and repositioning the boxes below. Topic Collections	{}
Srubabati Goswami (PRL) Synergy between atmospheric and long-baseline neutrino experiments in determination of oscillation parameters Abstract: Oscillation of atmospheric neutrinos was first established conclusively by the Super-Kamiokande experiment. This was later confirmed by the long-baseline beam based experiments K2K, MINOS and more recently T2K and NOVA. The unknown neutrino oscillation parameters at present are the tmass hierarchy, octant of $\theta_{23}$ and the CP phase $\delta_{CP}$. One of the main problems in unambiguous determination of these parameters is the occurrence of degneracies . In this talk I will discuss the various degeneracies that hinder the definitive determination of these parameters . I will also discuss how the combination of long-baseline and atmospheric neutrino data can help in resolving some of these issues.	{}
# Thread: High school maths question 1. ## High school maths question I need to understand how to get from: 42x^2 - 9x - 6 to 3(2x-1)(7x+2) sorry if it's in the wrong spot! 2. ## Re: High school maths question the systematic way would be $42x^2 - 9x-6 = 42\left (x^2 - \dfrac{3}{14} - \dfrac 1 7\right)$ Now use the quadratic equation to find the roots of the quadratic in parens $x = \dfrac{\dfrac{3}{14} \pm \sqrt{\dfrac{9}{196}+\dfrac 4 7}}{2} = \dfrac{\dfrac{3}{14}\pm \dfrac{11}{14}}{2} = \dfrac 1 2,~-\dfrac 2 7$ So then we have our original polynomial is given by $42\left(x-\dfrac 1 2\right)\left(x + \dfrac 2 7\right) = 3(2x-1)(7x+2)$ 3. ## Re: High school maths question Originally Posted by Molly123456 42x^2 - 9x - 6 3(2x-1)(7x+2) $\displaystyle 3(14x^2 - 3x - 2)$ ac method 14(-2) = -28 You want two integer divisors of -28 which when multiplied together give -28 and which add to -3. -7 and 4 work. Use them as coefficients on the first degree x-terms, rewrite the polynomial, and then factor by grouping on either of the next two versions that follow: $\displaystyle 3[14x^2 + 4x - 7x - 2] \ \ \ or$ $\displaystyle 3[14x^2 - 7x + 4x - 2] \ =$ $\displaystyle 3[7x(2x - 1) \ \ \ ?(2x - 1)] \ =$ $\displaystyle 3[7x(2x - 1) \ + \ 2(2x - 1)] \ =$ $\displaystyle 3(2x - 1)(7x + 2)$	{}
Index Blog # Array model from class Following is the Array model of register file contents developed in class today. We will add to the model next week to capture the size of the register file. The proofs use mostly use commands defined in class with a couple of exceptions. In some places I use trivial rather than reflexivity. trivial does a bit more work than reflexivity and can be customized. Feel free to use it in your proofs if you woule like. I use unfold in several places where I want a function replaced by its definition. unfold f expands the definition in place. If f is defined: Definition f(x:nat):nat := x + 1. then unfold applied to the goal f 1 = 2 results in the goal: 1 + 1 = 2 I use unfold in a couple of places rather than simpl when simpl doesn’t work or is too involved. Note that unfold can be used on assumptions using the in syntax to specify the assumption. Here is the [Array] module complete with proofs: Require Import Omega. Module Array. Fixpoint leb (m:nat) : nat -> bool := match m with \| O => fun _:nat => true \| S m' => fun n:nat => match n with \| O => false \| S n' => leb m' n' end end. (** Register contents. Either a natural number value or unknown. ) Inductive RC : Type := \| val : nat -> RC \| unknown : RC. Notation "??" := unknown. (* Register file contents. Function from natural to RC. ) Definition RFC : Type := nat -> RC. (* Empty register file contents ) Definition empty_rf:RFC := (fun n:nat => ??). (* [get] applies the register file function to its argument ) Definition get(i:nat)(f:RFC):RC := (f i). (* [put] uses an [if] expression to modify an existing register file ) Definition put(i:nat)(f:RFC)(v:RC):RFC := (fun n:nat => if (beq_nat i n) then v else f n). (* Some tests to make sure the implementation is close to correct. ) Example test1: (get 3 (put 3 empty_rf (val 3))) = (val 3). Proof. reflexivity. Qed. Example test2: (get 2 (put 3 empty_rf (val 3))) = ??. Proof. reflexivity. Qed. Example test3: (get 4 (put 3 empty_rf (val 3))) = ??. Proof. reflexivity. Qed. (* Making the test slightly more abstract by checking all contents values ) Theorem update_position_3: forall m, (get 3 (put 3 empty_rf (val m))) = (val m). Proof. intros. trivial. Qed. (* Lemma showing that [beq] is reflexive. Will be used in a later proof ) Lemma beq_refl: forall i, beq_nat i i = true. Proof. intros. induction i. reflexivity. auto. Qed. (* All elements of the empty register file are unknown ) Theorem empty_empty: forall i , (get i empty_rf) = ??. Proof. intros. reflexivity. Qed. (* [get] applied to a [put] on the same index updates the register file contents. This is correctness of the update function. ) Theorem update_immediate: forall v i rfc, (get i (put i rfc (val v))) = val v. Proof. intros. unfold get. unfold put. rewrite beq_refl. reflexivity. Qed. (* [get] applied to a [put] on different indexes results in the value before updating. An invariant on update. *) Theorem update_invariant: forall v i j rfc, (beq_nat j i) = false -> (get i (put j rfc (val v))) = rfc i. Proof. intros. unfold get. unfold put. rewrite H. trivial. Qed. End Array.	{}
## Results (displaying matches 1-50 of 14455) Next Galois conjugate representations are grouped into single lines. Label Dimension Conductor Defining polynomial of Artin field $G$ Ind $\chi(c)$ 2.39.4t3.a.a $2$ $3 \cdot 13$ x4 - x3 - x2 + x + 1 $D_{4}$ $1$ $0$ 2.55.4t3.c.a $2$ $5 \cdot 11$ x4 - x3 + 2x - 1 $D_{4}$ $1$ $0$ 2.56.4t3.b.a $2$ $2^{3} \cdot 7$ x4 - x3 + x + 1 $D_{4}$ $1$ $0$ 2.63.4t3.a.a $2$ $3^{2} \cdot 7$ x4 - x3 + 2x + 1 $D_{4}$ $1$ $0$ 2.68.4t3.a.a $2$ $2^{2} \cdot 17$ x4 + x2 - 2x + 1 $D_{4}$ $1$ $0$ 2.80.4t3.a.a $2$ $2^{4} \cdot 5$ x4 - 2x3 + 2 $D_{4}$ $1$ $0$ 2.95.4t3.c.a $2$ $5 \cdot 19$ x4 - 2x3 + 2x2 - x - 1 $D_{4}$ $1$ $0$ 2.111.4t3.a.a $2$ $3 \cdot 37$ x4 - x3 - 2x2 + 3 $D_{4}$ $1$ $0$ 2.128.4t3.a.a $2$ $2^{7}$ x4 - 2x2 + 2 $D_{4}$ $1$ $0$ 2.136.4t3.b.a $2$ $2^{3} \cdot 17$ x4 - 2x3 + x2 - 2x + 3 $D_{4}$ $1$ $0$ 2.136.4t3.a.a $2$ $2^{3} \cdot 17$ x4 - 2x3 + 5x2 - 4x + 2 $D_{4}$ $1$ $-2$ 2.144.4t3.b.a $2$ $2^{4} \cdot 3^{2}$ x4 - 3x2 + 3 $D_{4}$ $1$ $0$ 2.145.4t3.b.a $2$ $5 \cdot 29$ x4 - x3 - 3x2 + x + 1 $D_{4}$ $1$ $2$ 2.155.4t3.c.a $2$ $5 \cdot 31$ x4 - x3 - 3x - 1 $D_{4}$ $1$ $0$ 2.164.4t3.c.a $2$ $2^{2} \cdot 41$ x4 - 2x3 - x2 + 2x + 2 $D_{4}$ $1$ $0$ 2.171.4t3.c.a $2$ $3^{2} \cdot 19$ x4 - x3 - 3x2 + 2x + 4 $D_{4}$ $1$ $0$ 2.183.4t3.a.a $2$ $3 \cdot 61$ x4 - 2x3 - 2x2 + 3x + 3 $D_{4}$ $1$ $0$ 2.184.4t3.c.a $2$ $2^{3} \cdot 23$ x4 - 2x3 + 3x2 - 2x - 1 $D_{4}$ $1$ $0$ 2.196.4t3.a.a $2$ $2^{2} \cdot 7^{2}$ x4 - x3 + 3x2 - 4x + 2 $D_{4}$ $1$ $0$ 2.203.4t3.a.a $2$ $7 \cdot 29$ x4 - 2x3 + 2x2 - x + 2 $D_{4}$ $1$ $0$ 2.205.4t3.a.a $2$ $5 \cdot 41$ x4 - x3 + 3x2 - 2x + 4 $D_{4}$ $1$ $-2$ 2.208.4t3.c.a $2$ $2^{4} \cdot 13$ x4 - 2x3 - 2x + 5 $D_{4}$ $1$ $0$ 2.219.4t3.c.a $2$ $3 \cdot 73$ x4 - x3 + 5x2 - 2x + 4 $D_{4}$ $1$ $0$ 2.221.4t3.b.a $2$ $13 \cdot 17$ x4 - x3 + x2 - 2x + 4 $D_{4}$ $1$ $-2$ 2.224.4t3.a.a $2$ $2^{5} \cdot 7$ x4 - x2 + 2 $D_{4}$ $1$ $0$ 2.248.4t3.c.a $2$ $2^{3} \cdot 31$ x4 - 2x3 + x2 - 2 $D_{4}$ $1$ $0$ 2.256.4t3.c.a $2$ $2^{8}$ x4 - 2 $D_{4}$ $1$ $0$ 2.259.4t3.a.a $2$ $7 \cdot 37$ x4 - 2x3 + x + 2 $D_{4}$ $1$ $0$ 2.260.4t3.a.a $2$ $2^{2} \cdot 5 \cdot 13$ x4 + x2 - 4x + 4 $D_{4}$ $1$ $0$ 2.260.4t3.b.a $2$ $2^{2} \cdot 5 \cdot 13$ x4 - 3x2 - 2x + 5 $D_{4}$ $1$ $0$ 2.264.4t3.d.a $2$ $2^{3} \cdot 3 \cdot 11$ x4 - 2x3 + x2 + 2 $D_{4}$ $1$ $0$ 2.264.4t3.c.a $2$ $2^{3} \cdot 3 \cdot 11$ x4 - 2x3 + 5x2 - 2x + 1 $D_{4}$ $1$ $0$ 2.275.4t3.c.a $2$ $5^{2} \cdot 11$ x4 - x3 + x2 + 4x - 4 $D_{4}$ $1$ $0$ 2.276.4t3.e.a $2$ $2^{2} \cdot 3 \cdot 23$ x4 - 2x3 - x2 + 2x - 2 $D_{4}$ $1$ $0$ 2.276.4t3.f.a $2$ $2^{2} \cdot 3 \cdot 23$ x4 + x2 - 6x + 1 $D_{4}$ $1$ $0$ 2.279.4t3.b.a $2$ $3^{2} \cdot 31$ x4 - x3 - 3x2 - x + 7 $D_{4}$ $1$ $0$ 2.291.4t3.c.a $2$ $3 \cdot 97$ x4 - x3 - 4x2 + x + 7 $D_{4}$ $1$ $0$ 2.292.4t3.a.a $2$ $2^{2} \cdot 73$ x4 - x2 - 4x + 5 $D_{4}$ $1$ $0$ 2.295.4t3.c.a $2$ $5 \cdot 59$ x4 - x3 - x2 + 5x - 5 $D_{4}$ $1$ $0$ 2.299.4t3.a.a $2$ $13 \cdot 23$ x4 - x3 + 5x - 1 $D_{4}$ $1$ $0$ 2.305.4t3.a.a $2$ $5 \cdot 61$ x4 - 2x3 + 6x2 - 5x + 5 $D_{4}$ $1$ $-2$ 2.308.4t3.d.a $2$ $2^{2} \cdot 7 \cdot 11$ x4 - x3 - 2x2 + 2x + 4 $D_{4}$ $1$ $0$ 2.308.4t3.c.a $2$ $2^{2} \cdot 7 \cdot 11$ x4 - x3 + x2 + 4x + 2 $D_{4}$ $1$ $0$ 2.320.4t3.a.a $2$ $2^{6} \cdot 5$ x4 - 4x2 + 5 $D_{4}$ $1$ $0$ 2.323.4t3.a.a $2$ $17 \cdot 19$ x4 - 2x3 - 2x2 + 3x - 2 $D_{4}$ $1$ $0$ 2.327.4t3.c.a $2$ $3 \cdot 109$ x4 - x3 - 4x2 + 4x + 7 $D_{4}$ $1$ $0$ 2.328.4t3.c.a $2$ $2^{3} \cdot 41$ x4 - 2x3 - 3x2 + 2x + 1 $D_{4}$ $1$ $2$ 2.328.4t3.d.a $2$ $2^{3} \cdot 41$ x4 - 2x3 + 3x2 - 2x + 3 $D_{4}$ $1$ $0$ 2.336.4t3.a.a $2$ $2^{4} \cdot 3 \cdot 7$ x4 - 5x2 + 7 $D_{4}$ $1$ $0$ 2.336.4t3.b.a $2$ $2^{4} \cdot 3 \cdot 7$ x4 + 5x2 + 7 $D_{4}$ $1$ $0$ Next	{}
# Matrices and Determinants. A matrix is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. The individual items in a matrix are called its elements or entries. Two matrices can be added or subtracted element by element if have the same number of rows and the same number of columns. Order of matrix The number of rows and columns that a matrix has is called its order or its dimension Example $\left[ {\begin{array}{{20}{c}}1&5&{ - 2}\\6&8&9\end{array}} \right]{\rm{\: }}$ The dimension of matrix is read as "two by three" because there are two rows and three columns. Order or dimension = number of rows × number of columns Components of matrix Let M = $\left[ {\begin{array}{{20}{c}}1&5&{ - 2}\\6&8&9\end{array}} \right]$ The numbers 1,5, -2,6,8,9 are the components of the matrix .It can be also written as M = $\left[ {\begin{array}{{20}{c}}{{{\rm{a}}_{11}}}&{{{\rm{a}}_{12}}}&{{{\rm{a}}_{13}}}\\ {{{\rm{a}}_{21}}}&{{{\rm{a}}_{22}}}&{{{\rm{a}}_{23}}}\end{array}} \right]$ Where a11 denotes first row first column a11 = 1 similarly a12 = 5 and so on. Types of matrix Row matrix Matrix having only one row is called row matrix. The order of such matrix is of 1× n Example M = [5, 6,8] is the matrix of order 1× 3 Column matrix Matrix containing only one column is called column matrix. The order of such matrix is of n ×1 Example M = $\left( {\begin{array}{{20}{c}}5\\6\\{ - 9}\end{array}} \right){\rm{\: }}$is the matrix of order 1× 3 Null matrix or Zero matrix Matrix having all elements zero is called zero or null matrix. M = ${\left( {\begin{array}{{20}{c}}0\\0\\0\end{array}} \right)_{3 1}}$ M = ${\left[ {\begin{array}{{20}{c}}0&0&0\\0&0&0\end{array}} \right]_{2 3}}$ Square matrix A square matrix is a matrix with an equal number of rows and columns. Example: M = ${\left( {\begin{array}{{20}{c}}5&6&7\\6&9&{ - 6}\\{ - 44}&8&{ - 99} \end{array}} \right)_{3 3}}$ M is a square matrix of order 3 × 3 Diagonal matrix A diagonal matrix is a square matrix that has all its elements zero except for those in the diagonal from top left to bottom right. Example: M = ${\left( {\begin{array}{{20}{c}}5&0&0\\0&9&0\\0&0&{ - 9}\end{array}} \right)_{3 3}}$ Scalar matrix A diagonal matrix having same main diagonal element is called scalar matrix Example: M = $\left( {\begin{array}{{20}{c}}5&0&0\\0&5&0\\0&0&5\end{array}} \right)$ Unit matrix A unit matrix is a diagonal matrix whose elements in the diagonal are all ones. I = ${\left( {\begin{array}{{20}{c}}1&0\\{{\rm{\: }}0}&1\end{array}} \right)_{2* 2}}$ I = ${\left( {\begin{array}{{20}{c}}1&0&0\\0&1&0\\0&0&1\end{array}} \right)_{3 3}}$ I is a unit matrix. Symmetric matrix: A square matrix which do not change its row and column are interchanged is called symmetric matrix. S = ${\left( {\begin{array}{{20}{c}}2&5&6\\5&8&4\\6&4&9\end{array}} \right)_{3 3}}$ Transpose of matrix The transpose of a matrix is a matrix which is obtained by interchanging rows into column and column into rows. It is denoted by A’ or AT Example 1 M = $\left[ {\begin{array}{{20}{c}}1&5&{ - 2}\\6&8&9\end{array}} \right]$ transpose of M = T T = $\left( {\begin{array}{{20}{c}}1&6\\5&8\\{ - 2}&9\end{array}} \right)$ Multiplication of matrices Rules: 1. The number of columns in the 1st one equals the number of rows in the 2nd one 2. Multiply the elements of each row of the first matrix by the elements of each column in the second matrix. Example 2 $\left( {\begin{array}{{20}{c}}{\rm{a}}&{\rm{x}}\end{array}} \right)\left( \begin{array}{{20}{c}} {\rm{p}}&2\\3&{\rm{q}}\end{array}} \right)$ = ( a.p + 3x , 2a + xq ) Properties of the matrices multiplication Associative property: A (BC) = A (BC) Distributive property: A (B +C) = AB + BC Identity property: AI = A = IA Singular and non – singular matrices Singular matrix is square matrix whose determinant is equal to Zero Example A = $\left( {\begin{array}{{20}{c}}5&5\\2&2\end{array}} \right)$ is the singular matrix \|A\| = 10 -10 = 0 Non - Singular matrix is also square matrix whose determinant is not equal to zero. A = $\left( {\begin{array}{{20}{c}}6&5\\2&2\end{array}} \right)$ is the non singular matrix \|A\| = 12 - 10 = 2 Determinant of 2 × 2 matrix If A = $\left( {\begin{array}{{20}{c}}{\rm{a}}&{\rm{b}}\\{\rm{c}}&{\rm{d}}\end{array}} \right)$ be 2 2 then its determinant Inverse matrix For a matrix A its inverse B exist when AB = BA = I exists. A = $\left( {{\rm{\: }}\begin{array}{{20}{c}}{\rm{a}}&{\rm{b}}\\{\rm{c}}&{\rm{d}}\end{array}{\rm{\: }}} \right)$ B=$\left({{\rm{\:}}\begin{array}{{20}{c}}{\rm{e}}&{\rm{f}}\\{\rm{g}}&{\rm{h}}\end{array}{\rm{\: }}} \right)$ The components of the inverse matrix can be obtained by e =${\rm{\: }}\frac{{\rm{d}}}{{{\rm{ad}} - {\rm{bc\: }}}}$ g = $- \frac{{\rm{c}}}{{{\rm{ad}} - {\rm{bc\: }}}}$ f = $- \frac{{\rm{b}}}{{{\rm{ad}} - {\rm{bc}}}}$ h = $\frac{{\rm{a}}}{{{\rm{ad}} - {\rm{bc}}}}$ We have matrix equation AX = B If A-1 exists if, \|A\| ≠ o A-1 (AX) = A-1 B I.X = A-1 B ⇒ X= A-1 B By using this equation we can solve simultaneous equations Example 3 Find the value of x and y $\left( {\begin{array}{{20}{c}}5&{\rm{x}}\\{\rm{y}}&7\end{array}} \right)\left( {\begin{array}{{20}{c}}1\\{ - 2}\end{array}} \right) = {\rm{\: }}\left( {\begin{array}{{20}{c}}{19}\\{ - 4}\end{array}} \right)$ $\left( {\begin{array}{{20}{c}}{5 - 2{\rm{x\: }}}\\{{\rm{y}} - 14{\rm{\: }}}\end{array}{\rm{\: }}} \right)$ = $\left( {\begin{array}{*{20}{c}}{19}\\{ - 4}s\end{array}} \right)$ Now, 5-2x = 19 ∴ x = -7 And y-14 = -4 ∴ y = 10 Go Top	{}
Some situations in PHP require a set of variables to have values depending on some condition. To achieve such variable-assignment, a switch statement is the traditional GOTO, but PHP’s array syntax combined with the list() language construct. For example, if $a==1, then $b=2; $c=2, else if $a==2, then $b=... etc. If the condition is the value of some variable, like $a here, a switch-statement would look like: switch($a) { case 1:$b = 2; $c = 2; break; case 2:$b = 4; $c = 3; // etc... default:$b = 9; $c = 9; } The number of lines required to express this grows explosively with the number of variables and conditions to set. Instead, use this more elegant way, based on list(): list($b, $c) = [ 1 => [2, 2], 2 => [4, 3], // .. etc ][$a] ?? [9, 9] Which grows linearly in LoCs with the number of conditions. Other benefits are improved DRY-ness and the guarantee that all variables in list() are assigned. Note how the default case is implemented as well. A simple back of the envelope test with 5 variables and 10 conditions shows the following results. All code was properly indented and formatted. Note also how compressing the list-based approach results in a bigger compression which indicates more DRY-ness. For the sake of testing, a compacted switch-based form, without line-breaks or tabs after assignment is used too. characters lines gzip % switch-based 723 71 30% switch-based (compacted) 667 31 32% list-based 302 11 58% These tests were simply done by piping the code through the wc and gzip programs. The list-based approach looks as follows: list($a,$b, $c,$d, $e) = [ 1 => [ 1, 2, 3, 4, 5] 2 => [ 6, 7, 8, 9, 10] 3 => [11, 12, 13, 14, 15] 4 => [16, 17, 18, 19, 20] 5 => [21, 22, 23, 24, 25] 6 => [26, 27, 28, 29, 30] 7 => [31, 32, 33, 34, 35] 8 => [36, 37, 38, 39, 40] 9 => [41, 42, 43, 44, 45] ][$x] ?? [46, 47, 48, 49, 50]; The switch-based compact version is as follows: switch($x) { case 1:$a = 1; $b = 2;$c = 3; $d = 4;$e = 5; break; case 2: $a = 6;$b = 7; $c = 8;$d = 9; $e = 10; break; case 3:$a = 11; $b = 12;$c = 13; $d = 14;$e = 15; break; case 4: $a = 16;$b = 17; $c = 18;$d = 19; $e = 20; break; case 5:$a = 21; $b = 22;$c = 23; $d = 24;$e = 25; break; case 6: $a = 26;$b = 27; $c = 28;$d = 29; $e = 30; break; case 7:$a = 31; $b = 32;$c = 33; $d = 34;$e = 35; break; case 8: $a = 36;$b = 37; $c = 38;$d = 39; $e = 40; break; case 9:$a = 41; $b = 42;$c = 43; $d = 44;$e = 45; break; default: $a = 46;$b = 47; $c = 48;$d = 49; $e = 50; } Check out the one-liner to pick random values from an array. In PHP 7.3, you can use array-destructuring to get rid of the list() language construct. E.g.: [$a, \$b] = [1, 2];	{}
# Surprisingly high collision rates when hashing a short list with few buckets I'm trying to help my daughter with her CS assignment on hashing. She has an input list of about 4000 English words, each 5 letters long. The prof has limited her to 4000 output buckets (digests? -- it's been a long time since I did this stuff). And the output from the hashing function is an int modulo 4000. Her naive hash function gets about 1500 collisions. To get something for comparison, I found a handful of hashing functions here and here. I ended up trying almost all of them (oat, fnv, djb, another djb, sax, elf, jsw, and a crc adaptation), because every single one of them got about 1500 collisions. That sure seems like a lot. I'm starting to think maybe we're missing something fundamental. Or not. I don't know. (I was able to reduce collisions significantly by increasing the number of output buckets to 200k, and returning hash mod 200k from the functions. Naturally, this isn't allowed for the assignment.) I'm not sure what questions to ask, but the first one that comes to mind is, does 1500 collisions sound about right when using such a small number of output buckets? Or does it sound more like we're doing something totally wrong outside the hashing function? (Presumably not inside it, given that we tried so many different ones.) Or maybe I should ask, is there a way to find out whether 1500 collisions is about right? • @JanJohannsen Done. Forgive me, I usually read the question guidelines on the SE sites, but I was lazy this time. – SaganRitual Mar 5 '18 at 14:50 Depending on how you count collisions, we can expect either about 2000 collisions, or about 1472 collisions. The latter is in close agreement with what you observe, so yes, 1500 collisions looks about right to me. # Counting collisions pairwise I think the most natural way to count collisions is "pairwise". For instance, if A, B, and C all hash into the same bucket, let's count that as 3 collisions. If A, B, C, and D hash to the same bucket, let's count that as 6 collisions (not 4, but 6: the 6 collisions are AB, AC, AD, BC, BD, and CD). And so on. In general if there are $k$ items in a bucket, that causes ${k \choose 2}$ collisions, with this method of counting collisions. Then, you can use linearity of expectation to estimate the number of collisions, assuming the hash function is good. Let $X_{i,j}$ be an indicator random variable that is $1$ if objects $i,j$ hash to the same bucket, or $0$ otherwise. Let $Y=\sum_{i<j} X_{i,j}$ be the sum of these random variables. Then $Y$ counts the number of collisions. Can we estimate a typical value for $Y$? Well, we can compute the expected value of $Y$ in a straightforward way: $$\mathbb{E}[Y] = \sum_{i<j} \mathbb{E}[X_{i,j}] = \sum_{i<j} {1 \over 4000} = {4000 \choose 2} {1 \over 4000} = {3999 \over 2} \approx 2000,$$ using the fact that $\mathbb{E}[X_{i,j}] = \Pr[X_{i,j}=1] = {1 \over 4000}$ since there is a 1 in 4000 chance that object $j$ hashes to the same bucket as object $i$ (assuming a good hash function). Typically, the observed value of $Y$ will be near its expected value. So, that'd predict that you see about 1500 collisions. That's a consequence of the number of buckets and the number of items hashed. In general, if you hash $n$ items into $m$ buckets using a good hash function, you should expect to see about ${n^2 \over 2m}$ collisions, on average, using this method for counting collisions. # Counting collisions by bucket size On reading your comment, it sounds like you are counting collisions differently. If there are $k \ge 1$ items in a bucket, it sounds like you are counting that as $k-1$ collisions. How does that affect things? Well, it makes the calculation more complicated. I'll share a much terser analysis for this case, without showing all the details. Let $N_i$ denote the number of items in bucket $i$. If the hash function is good, the number of items in a bucket should follow approximately the Poisson distribution with parameter $\lambda = n/m$. In your case, we have $\lambda=1$. The total number of collisions (the way you are counting it) is $$N = \sum_i \max(N_i-1,0).$$ Now, \begin{align} \mathbb{E}[\max(N_i-1,0)] &= 1 \cdot {\lambda^2 e^{-\lambda} \over 2!} + 2 \cdot {\lambda^3 e^{-\lambda} \over 3!} + 3 \cdot {\lambda^4 e^{-\lambda} \over 4!} + \cdots\\ &= \lambda e^{-\lambda} + \lambda^2 - \lambda. \end{align} (Don't ask me how I summed the series; black magic.) It follows that $$\mathbb{E}[N] = \sum_i \mathbb{E}[\max(N_i-1,0)] = (\lambda e^{-\lambda} + \lambda^2 - \lambda) n.$$ In your case $\lambda=1$ and $n=4000$, so we predict $1/e \times 4000 \approx 1472$ collisions. That has very close agreement with what you are observing empirically, so practice and theory seem to be in close agreement. • I don't quite follow the arithmetic. Isn't $3999/2 \approx 1999.5$? – Geoffrey Irving Mar 5 '18 at 5:07 • @GeoffreyIrving, oops, you're absolutely right. That rather affects the answer. I've updated my answer accordingly, but now I don't have as good an explanation for what the poster is seeing. – D.W. Mar 5 '18 at 5:24 • $4000/e \approx 1471 \approx 1500$, which is probably not a coincidence. – Geoffrey Irving Mar 5 '18 at 6:01 • @GreatBigBore, OK, see revised answer. I now show how to estimate the number of collisions under two different ways of counting collisions, and now the 1500 number you are seeing makes sense. – D.W. Mar 5 '18 at 7:23 • @GeoffreyIrving, hah, you were absolutely right! See the second half of the answer (after my edits), to see where the $1/e$ comes from. – D.W. Mar 5 '18 at 7:23	{}
Suppose the function $f$ is continuous on the closed interval $\lbrack 1, 2 \rbrack$, $f(1) = 5$, and $f(2) = 9$. Then, from the Intermediate Value Theorem we can conclude that...(select all that apply)	{}
# How use parts of an eps image? I am working on a college presentation and I'd like to include some graphics into my latex baposter. The graphics is eps free file, similar to the below: http://freedesignfile.com/552-hand-draw-flower-vector-02/ For example, if I choose the above file, I need to display each flower separately in different sections of my poster. I tried trimming the image (like Crop an inserted image?), but it does not give good results. Extremely appreciate any tips on how to go about this from within latex or some free graphics program. • Inkscape can edit encapsulated postcript files. Not trivial, but the tutorials are good. – Rmano May 6 '16 at 19:07 • Are you using pdflatex ? Have you epstopdf ? Work trim & clip with with png, jpg or pdf files ? – Fran May 6 '16 at 19:08 • Thanks for comments. I have used eps2pdf to convert the image to pdf and then tried cropping the image by trim command in latex, but did not get good results. I am using TexNicCenter. – Melanie A May 7 '16 at 2:21 At the top of an eps file, you will find the bounding box, a sequence of four numbers which define the left, lower, right and upper edges of the image (in that order). In this masterpiece, the bounding box is 0 0 200 200. %!PS-Adobe-2.0 EPSF-2.0 %%Title: pumpkin.eps %%BoundingBox: 0 0 200 200 /tri {newpath 0 0 moveto 10 0 lineto 0 20 lineto -10 0 lineto closepath fill} bind def 1.0 0.6 0.25 setrgbcolor 1 setlinewidth 100 100 100 0 360 arc gsave stroke grestore fill 0 0 0 setrgbcolor 100 90 60 190 350 arc stroke 100 100 translate tri -50 40 translate tri 100 0 translate tri showpage %EOF Using optional arguments to \includegraphics, you can define a viewing window, which can be different to the bounding box. The example below displays the upper right corner and the centre of the image. \documentclass{article} \usepackage{graphicx} \begin{document} \centering \includegraphics[100,100][200,200]{pumpkin} However, this doesn't work with pdflatex. To get around this, make a copy of the eps file and change the bounding box there before converting to pdf.	{}
# Which of the following cannot form CO on reaction with H2O? more_vert Which of the following cannot form CO on reaction with H2O? (1) CH4 (2) C3H8 (3) CO2 (4) C	{}
MENU ## Publications Export 2 results: Filters: First Letter Of Title is M and Author is Francisco Chinesta [Clear All Filters] 2016 . Model Order Reduction: a survey. In: Wiley Encyclopedia of Computational Mechanics, 2016. Wiley Encyclopedia of Computational Mechanics, 2016. Wiley; 2016. Available from: http://urania.sissa.it/xmlui/handle/1963/35194 2017 . Model Reduction Methods. In: Encyclopedia of Computational Mechanics Second Edition. Encyclopedia of Computational Mechanics Second Edition. John Wiley & Sons; 2017. pp. 1-36.	{}
# Proving that $R$ is antisymmetric if and only if $G \cap G^{-1} \subseteq D$ I found this relations exercise that I couldn't finish. It involves a set's diagonal. I got it almost done - had trouble wording some parts related to the diagonal. • Is the procedure correct? • How can I better word the indicated parts? • Did it make sense to prove both implications separately? • Any kind of feedback is welcome. Still new to this stuff. If $R = (G,A,A)$ is a relation over $A$, prove that $R$ is antisymmetric if and only if $G \cap G^{-1} \subseteq D$ where $D$ is the diagonal of $A$. We have to prove that $$Antisymmetric \iff (G \cap G^{-1} \subseteq D)$$ We have two implications. Let's prove each of them: Proving $$Antisymmetric \implies (G \cap G^{-1} \subseteq D)$$ Our premise is the fact that the relation is antisymmetric. We have to prove that $G \cap G^{-1} \subseteq D$. Have an arbitrary pair of elements $(a,b)$ in $G \cap G^{-1}$: $$(a,b) \in G \cap G^{-1}$$ $$(a,b) \in G \land (a,b) \in G^{-1}$$ $$aRb \land bRa$$ Since the relation $R$ is antisymmetric: $$a = b$$ I'm pretty sure that I'm almost done here (because, err... clearly (a,b) belongs to the diagonal...), but I don't know how to word it. Can you advice me here? Proving $$(G \cap G^{-1} \subseteq D) \implies Antisymmetric$$ Our premise is that $(G \cap G^{-1} \subseteq D)$. We have to prove that the relation $R$ is antisymmetric. Basically, we have to prove that $$(aRb \land bRa) \implies a = b$$ Have arbitrary elements $a$ and $b$: $$aRb \land bRa$$ Since $aRb$, the pair $(a,b)$ must be in $G$. Similarly, given that $bRa$, I know that $aR^{-1}b$, which means that $(a,b)$ is also in $G^{-1}$: $$(a,b) \in G \land (a,b) \in G^{-1}$$ $$(a,b) \in G \cap G^{-1}$$ From our premise, we conclude that $$(a,b) \in D$$ If a pair of elements belongs to a set's diagonal, both elements are the same (again I have problems wording this), so: $$a = b$$ Effectively proving $(G \cap G^{-1} \subseteq D) \implies Antisymmetric$. The exercise concludes as both implications were proven. • what is G and G^-1 (not familiar with these notations) – Thomas Nov 3 '13 at 11:30 • @Thomas: $G$ is a set of all pairs $(a,b)$ where $aRb$. $G^{-1}$ is is the same, but for $R^{-1}$. If we grab $G^{-1}$ it would be the same as $G$, but the pairs' elements would be reversed and would be in the form $(b,a)$. – Zol Tun Kul Nov 3 '13 at 11:33 There’s really almost nothing to do, which is perhaps why you’re having trouble. To finish up the first part, after you get $a=b$, just conclude: Thus, $\langle a,b\rangle=\langle a,a\rangle\in D$. There’s nothing needed to finish up the second part: it’s immediate from the fact that $\langle a,b\rangle\in D$ that $a=b$, just by the definition of $D$.	{}
# Verifying Tasking in Extended, Relaxed Style ## byPiotr Trojanek – Nov 07, 2016 Tasking was one of the big features introduced in the previous release of SPARK 2014. However, GNATprove only supported tasking-related constructs allowed by the Ravenscar profile. Now it also supports the more relaxed GNAT Extended Ravenscar profile. The GNAT Reference Manual already documents how the new profile is different from the old one and why you might like it. Here we explain how this new profile might affect your SPARK code. First, in the GNAT Extended Ravenscar you are no longer restricted to one entry per protected type. In particular, you can now directly implement message stores with multiple consumers: each consumer can wait for a specific kind of messages by blocking on its own entry. Expressions in entry barriers are no longer restricted to simple Boolean variables. Now they might involve simple protected variables, literals, and predefined relational and logical operators (e.g. "<", "/=", "and"). This is more relaxed, but the new restrictions still guarantee that the evaluation of a barrier expression will raise no runtime errors and will not have side effects. (That's why they are called "pure.") Tip: if strict Ravenscar forced you to have a barrier variable "Non_Empty" then now you can rename it to a more natural "Empty" and write the barrier expression as "not Empty." Relative delay statements like "delay 1.0" are now allowed. They are much less cumbersome than the strict Ravenscar pattern: declare begin delay until Now + Seconds (1); end; Finally, you are free to use Ada.Calendar package now, which (as suggested in the GNAT Reference Manual) might be handy for log messages. The relaxed profile also allows "delay until" statements where the expression is of the type Ada.Calendar.Time, not Ada.Real_Time.Time. But here is a detail: both Ada.Calendar and Ada.Real_Time have their own abstract states called Clock_Time. It is because Ada RM says that bases for Ada.Calendar and Ada.Real_Time are not necessarily the same (and SPARK conservatively assumes they are not). Of course, you may ask GNATprove to confirm that you are using the right clock: just put the expected Clock_Time state in your Global contract. For details on how to enable the new profile and for general introduction to concurrency in SPARK please visit the User's Guide Posted in #Language #Formal Verification #SPARK	{}
# Differential Equation: $(1-xy)^{-2} dx + \left[ y^2 + x^2 (1-xy)^{-2} \right] dy = 0$ Hello, can anyone solve this equation? I can't figure it out, $(1-xy)^{-2} dx + \left[ y^2 + x^2 (1-xy)^{-2} \right] dy = 0$ Thanks. ### This is an exact equation This is an exact equation $(1 - xy)^{-2} \, dx + \left[ y^2 + x^2 (1 - xy)^{-2} \right] \, dy = 0$ Check for exactness: $M = (1 - xy)^{-2}$ $\dfrac{\partial M}{\partial y} = -2(1 - xy)^{-3}(-x)$ $\dfrac{\partial M}{\partial y} = 2x(1 - xy)^{-3}$ $N = y^2 + x^2 (1 - xy)^{-2}$ $\dfrac{\partial N}{\partial x} = -2x^2(1 - xy)^{-3}(-y) + 2x(1 - xy)^{-2}$ $\dfrac{\partial N}{\partial x} = 2x^2y(1 - xy)^{-3} + 2x(1 - xy)^{-2}$ $\dfrac{\partial N}{\partial x} = 2x(1 - xy)^{-3} \left[ xy + (1 - xy) \right]$ $\dfrac{\partial N}{\partial x} = 2x(1 - xy)^{-3}$ $\dfrac{\partial M}{\partial y} = \dfrac{\partial N}{\partial x}$, hence, exact! • Mathematics inside the configured delimiters is rendered by MathJax. The default math delimiters are $$...$$ and $...$ for displayed mathematics, and $...$ and $...$ for in-line mathematics.	{}
# Finite fiber- unramified morphisms I'm in trouble understandig the proof of Proposition 3.2 Chapter 1 of Milne's Book "Étale Cohomology". Let $f:Y\rightarrow X$ be locally of finite-type. The following are equivalent. $(a)$ f is unramified. $(b)$ for all $x\in X$ the fiber $Y_x\rightarrow spec(k(x))$ over $x$ is unramified. $(d)$ for all $x\in X$, $Y_x$ has an open covering by spectra of finite separable $k(x)$-algebras. A morphism is unramified if for all $y \in Y$ $k(y)$ is a finite separable extension of $k(x)$ and $m_y=m_x\mathcal{O}_{Y,y}$. For $(b) \Rightarrow (d)$ Let $U$ an open afine subset of $Y_x$ and $\mathfrak{q}$ a prime ideal in $B=\Gamma(U,\mathcal{O}_{Y_x})$, acording to $(b)$ $B_\mathfrak{q}=k(\mathfrak{q})$ is a finite separable field extension of $k(x)$. Also $$k(x)\subset B/\mathfrak{q}\subset B_\mathfrak{q}/\mathfrak{q}B_\mathfrak{q}=B_\mathfrak{q}$$ then $B/\mathfrak{q}$ is also a field. I don't understand why $B/\mathfrak{q}$ is a field. I understand that the result follows from that if $B/\mathfrak{q}$ is a field then $\mathfrak{q}$ is maximal and then $B$ is an Artin ring. Is that because the field extension is finite and separable?? • I'm sorry I edited it, and also I realized why it happened. It is because the extension is finite and then $B_\mathfrak{q}$ is integer over the domain $B/\mathfrak{q}$. Due to the first is field then $B/\mathfrak{q}$ also is a field. – user120731 Jan 12 '14 at 8:11 We have the inclusion $k(x) \subset B/\mathfrak q \subset B_{\mathfrak q}$, where $k(x)$ is a field and $B_{\mathfrak q}$ is a finite field extension of $k(x)$. Any intermediate ring is then automatically a field, hence $B/\mathfrak q$ is a field.	{}
#### [SOLVED] Are velocity and acceleration smooth quantities? My thinking: 1. acceleration corresponds to a force which is instantaneous, so the acceleration of a rigid body can be rather spiky (non-smooth) 2. velocity (angular velocity) describes the ratio of change of the distance(angle), so it is smooth in the real world. Conclusion, it makes sense to smooth (e.g., simple averaging) a velocity signal (temporal velocity), but it does not make so much sense to do smoothing on acceleration signal. Am I right? #### @Kyle Kanos 2014-12-09 16:02:19 As far as we know and can test, space is continuous, not discrete. Since space is continuous, then the labels we associate with it (i.e., positions) are also continuous. Calculus requires continuous functions to do the derivative and integral, so this implies that velocities and accelerations are also continuous because they are derivatives of positions: $$v(t)=\frac{dx(t)}{dt}\qquad a(t)=\frac{dv(t)}{dt}=\frac{d^2x(t)}{dx^2}$$ If you have a discrete spectrum (e.g., measurements at different times/positions), then interpolation (whether linear or some higher-order method) is a necessary and useful tool to reconstruct the smooth distribution that we expect. #### @Reinstate Monica --Brondahl-- 2016-11-11 18:13:58 Umm ... continuity of f(x) does not imply continuity of f'(x)? The Saw-Tooth function is continuous, but it's derivative is not. Now I can certainly believe that motion IS smooth, and thus that the Saw-Tooth function cannot truly represent movement, but your argument here (that space is continuous, which proves motion is continuous, which proves acceleration is continuous) is not sound. #### @Kyle Kanos 2016-11-11 18:21:21 @Brondahl: This is physics, not mathematics. In physics, we assume changes in physical quantities occur smoothly (continuously), rather than discontinuously whereas this assumption holds no weight in mathematics. #### @Reinstate Monica --Brondahl-- 2016-11-11 18:29:18 Ah, do you mean that your response to the question "Are these things smooth" is "In physics, we assume them to be smooth"? (No disrespect is intended ... this might be the best available answer to the question) #### @Reinstate Monica --Brondahl-- 2016-11-11 18:30:44 Assuming that I've correctly interpretted that, then to what extent has that been examined/tested? I can see that we might test the continuity of space to the limits of our ability, but have the higher order derivatives been examined/thought about in detail? Is infinite jerk possible? If not, why not? #### @Kyle Kanos 2016-11-11 18:48:11 @Brondahl: I probably should add an addendum to the last sentence before the equations mentioning the assumption, but I've got a few other things going for me (like work, family, etc)--feel free to recommend an edit though. I think my first link should answer your first question. The others, see, perhaps this post. ### [SOLVED] Instantaneous Velocity at a Sharp Point • 2019-10-30 18:20:17 • AlexanderTheGreat39 • 60 View • 1 Score • Tags: kinematics	{}
# I Relativistic relative velocity 1. Mar 17, 2017 ### davidge I'm interested in deriving the relativistic relative velocity of two particles moving near the speed of light. It turns out to be (with $c = 1$) $$\frac{V^{(1)} - V^{(2)}}{1 - V^{(1)}V^{(2)}}$$ How should I approach to this problem? Maybe I should not think of particles at all, but instead simply to consider the two reference frames as two set of coordinate values? So Frame 1: $(x^0,x^1,...)$; Frame 2: $(y^0,y^1,...)$. Then the velocities are $\partial x^i / \partial t$ and $\partial y^i / \partial t'$. $t \equiv x^0$, $t' \equiv y^0$ Now, $dy^\alpha = \Lambda^\alpha{}_{\beta}dx^\beta$. The solution for the $\Lambda$ are easy for the case when the displacement $dx^i$ are null in one of the frames, but this does not help in solving for the situation in question. Last edited: Mar 17, 2017 2. Mar 17, 2017 ### robphy First, check that expression. Is the square root there? One could derive it from a Lorentz Transformation, probably with the aid of a spacetime diagram. Using rapidity is quicker and more geometrical. One can also use vector-algebraic methods with dot products. 3. Mar 17, 2017 ### davidge Could you give me a hint ? Oh, there's no sqrt in the expression. Thanks. 4. Mar 17, 2017 ### robphy One way to start off is like this: $\hat t_{1}=\cosh(\theta_1-\theta_0) \hat t_0 + \sinh(\theta_1-\theta_0)\hat t_{0,\perp}=\cosh(\theta_1-\theta_0)\left( \hat t_0 + \tanh(\theta_1-\theta_0)\hat t_{0,\perp}\right)$ $\hat t_{2}=\cosh(\theta_2-\theta_0) \hat t_0 + \sinh(\theta_2-\theta_0)\hat t_{0,\perp}$ then what you seek is in here $\hat t_{2}=\cosh(\theta_2-\theta_1) \hat t_1 + \sinh(\theta_2-\theta_1)\hat t_{1,\perp}$ ..to be expressed in terms of the preceding. [You could simplify the notation by writing $\theta_{21}\equiv\theta_{2}-\theta_{1}$]. One might not use the trig functions from the start... it can be deduced later, if desired. So, $\hat t_1=\gamma_{10}(\hat t_0 + \beta_{10} \hat t_{0,\perp})$.... but that already gives a hint. $\hat t_1=A\hat t_0 + B\hat t_{0,\perp}$ and deduce that $\hat t_1=A(\hat t_0 + V\hat t_{0,\perp})$ is a useful form when interpreted physically. 5. Mar 17, 2017 ### vanhees71 This formula is only true for particles moving along the same direction in the given reference frame. The relative velocity in general is defined as the velocity of one particle in the restframe of the other particle (of course the latter must be massive if the definition should make sense). For details, see p. 16 of http://th.physik.uni-frankfurt.de/~hees/pf-faq/srt.pdf 6. Mar 17, 2017 ### davidge In this case, would we end up with $\Lambda^0{}_{0} = \gamma$, $\Lambda^i{}_{0} = v^i \gamma$? (Where $v^i$ denotes the i-th component of the velocity) 7. Mar 17, 2017 ### SiennaTheGr8 The method here is relatively straightforward, but you need to use notation in a way that won't confuse you. Subscripts can help. Say we have two inertial observers in "standard configuration," so that the "primed" observer is moving in the "unprimed" observer's positive x-direction. Then the Lorentz transformations are: $\mathrm{d}x^{\prime} = \dfrac{\mathrm{d}x - \beta_{rel} \, c \, \mathrm{d}t}{\sqrt{1 - \beta_{rel}^2}} \qquad \mathrm{d}x = \dfrac{\mathrm{d}x^{\prime} + \beta_{rel} \, c \, \mathrm{d}t^{\prime}}{\sqrt{1 - \beta_{rel}^2}} \\ \mathrm{d}y^{\prime} = \mathrm{d}y \\ \mathrm{d}z^{\prime} = \mathrm{d}z \\ \\ c\, \mathrm{d}t^{\prime} = \dfrac{c \, \mathrm{d}t - \beta_{rel} \, \mathrm{d}x}{\sqrt{1 - \beta_{rel}^2}} \qquad c\, \mathrm{d}t = \dfrac{c \, \mathrm{d}t^{\prime} + \beta_{rel} \, \mathrm{d}x^{\prime}}{\sqrt{1 - \beta_{rel}^2}}$ where $\beta_{rel}$ is the (normalized) relative speed of the observers ($v_{rel}/c$). Note that $\beta_{rel} < 1$ (because observers cannot travel at the speed of light). Now say there's something else that's moving with velocity $\vec{\beta} = (\beta_x, \beta_y, \beta_z)$ according to the "unprimed" observer, and $\vec{\beta} \, ^{\prime} = (\beta_x^{\prime}, \beta_y^{\prime}, \beta_z^{\prime})$ according to the "primed" observer (no "rel" subscript now). It could even be something traveling at the speed of light. Our goal is to find the transformation formulas for these primed and unprimed velocity components. Specifically, you're looking for the transformation of the $\beta_x$-component, since the relative motion of our observers is along their coincident $x$-axes. Well, we just use the fact that $\beta_x = \frac{\mathrm{d}x}{c \, \mathrm{d}t}$, etc.: $\beta_x^{\prime} = \dfrac{\mathrm{d}x^\prime}{c \, \mathrm{d}t^\prime} = \dfrac{\frac{\mathrm{d}x - \beta_{rel} \, c \, \mathrm{d}t}{\sqrt{1 - \beta_{rel}^2}}}{\frac{c \, \mathrm{d}t - \beta_{rel} \, \mathrm{d}x}{\sqrt{1 - \beta_{rel}^2}}} = \dfrac{\mathrm{d}x - \beta_{rel} \, c \, \mathrm{d}t}{c \, \mathrm{d}t - \beta_{rel} \, \mathrm{d}x}$ Divide top and bottom by $c \, \mathrm{d}t$, and we have: $\beta_x^{\prime} = \dfrac{\beta_x - \beta_{rel}}{1 - \beta_x \beta_{rel}}$. The same procedure generates the inverse transformation: $\beta_x = \dfrac{\beta_x^\prime + \beta_{rel}}{1 + \beta_x^\prime \beta_{rel}}$. Since these are vector components, they can be positive or negative. They are not speeds! The only speed here is $\beta_{rel}$. If you follow the same procedure for the primed and unprimed $y$- (or $z$-) components, you'll find that $\beta_y^\prime \neq \beta_y$. So even the velocity-components perpendicular to the observers' axis of relative motion get transformed. That's not so in Galilean relativity! In the special case that $\beta_y = \beta_y^\prime = \beta_z = \beta_z^\prime = 0$, the $x$-component is the only relevant one, and we can say: $\vec{\beta} \, ^{\prime} = \left( \dfrac{\beta_x - \beta_{rel}}{1 - \beta_x \beta_{rel}} \right) \hat{\imath}^\prime \qquad \vec{\beta} = \left( \dfrac{\beta_x^\prime + \beta_{rel}}{1 + \beta_x^\prime \beta_{rel}} \right) \hat{\imath}$, where $\hat{\imath}$ is the basis vector $(1, 0, 0)$. That's the familiar formula you were looking for. I kept the vector notation because there is sometimes confusion over what's a speed, what's a velocity, and what's a velocity-component. The value of what's in the parentheses can be positive or negative, since it's really the $x$-component of the velocity vector. Its absolute value is the speed (the magnitude of the velocity). So $\left\| \beta_x \right\| = \\| \vec{\beta} \\| = \beta$ and $\left\| \beta_x^\prime \right\| = \\| \vec{\beta} \, ^\prime \\| = \beta^\prime$. Note that if $\beta = 1$ here, then so does $\beta^\prime$ (and vice versa). And always remember that $\beta_{rel} < 1$. [Edited because I got confused myself a bit at the end there!] Last edited: Mar 17, 2017 8. Mar 17, 2017 ### davidge Thank you SiennaTheGr8. This was very helpful. I don't understand just why the transformation for the "spatial part", $dx'$, is given by your expression above. Since $dx'\ ^i = \Lambda^i{}_{j}dx^j$, if the $dx^j$ are not equal to zero, I thought we would have a different expression for $dx'$ than the one that you wrote down. 9. Mar 17, 2017 ### SiennaTheGr8 You mean at the very top of my post? That's just the standard Lorentz transformation for space and time coordinates (rather, the differentials thereof). By the way, I did edit my post just now because I'd made an error at the end. 10. Mar 17, 2017 ### pervect Staff Emeritus First, one needs some basic formula from special relativity. I'd suggest Bondi's K-calculus as one of the easiest approaches. This can be found in Bondi's book, "Relativity and common sense". The key result from Bondi's analysis is a relationship between the doppler shift factor k, and the velocity v. I'll give the result initially without proof: $$\beta = \frac{k^2 - 1}{k^2 + 1} \quad k = \sqrt{\frac{1+\beta}{1-\beta}}$$ Here I've given both $\beta=v/c$ as a function of the doppler shift factor k, and k as a function of $\beta$. Wiki has the later formula, in their article on "Relativistic doppler effect" <link>. If you send out a 1 hz signal, i.e. one flash of light per second, from observer 1, then observer 2 will receive one flash every 2 seconds if k=2. This happens at a velocity v = 3/5c, or $\beta = .6$. A third observer, moving at the same velocity relative to the second observer as the second has relative to the first, must receive one flash every four seconds. Basically, the doppler k-factors must multiply. It remains only to do some algebra. If you substitute $$\beta_1 = \frac{k_1^2 -1}{k_1^2 + 1} \quad \beta_2 = \frac{k_2^2 - 1}{k_2^2 + 1}$$ into $$\beta_T = \frac{\beta_1 + \beta_2}{1 + \beta_1 \beta_2}$$ you get $$\beta_T = \frac{(k1\,k2)^2 -1}{ (k1\,k2)^2 +1 }$$ which shows that this formula makes the doppler factor k's multiplicative, which is the correct behavior. I'm torn as to whether or not to present a proof of the relationship between k and $\beta$. The proof isn't that hard, but I think to properly understand it would take a more detailed description than I have the patience to write. Since Bondi (and other authors) have already done a much better write-up than I could do in a short post, I think it might be best if I defer the details to another source, with possibly a post if this turns out to be hard to track down. If you can't get a hold of Bondi's original book, try googling for "bondi k-calculus". It's not really calculus, by the way - just algebra. The point I'm hoping to get across is the following basic logic. Velocity can be computed knowing the doppler shift factor k, and vica-versa. The doppler shift k factors must multiply. This gives us the "velocity addition rule". 11. Mar 17, 2017 ### robphy Bondi's method is great for physical motivation. I never liked the Lorentz-transformation approach involving dividing "differentials". Underlying Bondi's multiplicative result that Doppler factors multlply $k_{20}=k_{21}k_{10}$ is that since $k=e^\theta$, we have the additivity of rapidities $\theta_{20}=\theta_{21}+\theta_{10}$ so that the relative-rapidity is $\theta_{21}=\theta_{20}-\theta_{10}$ or simply $\theta_{rel}=\theta_{2}-\theta_{1}$. Since physics prefers velocities (slopes) over rapidities (angles), this suggests $v_{rel}=\tanh{\theta_{rel}}=\tanh\left(\theta_{2}-\theta_{1}\right) \equiv \frac{\tanh \theta_{2}-\tanh\theta_{1}}{1-\tanh\theta_2\tanh\theta_1}=\frac{v_2-v_1}{1-v_2v_1}$, where we used a mathematical identity. Indeed many of the formulas in special relativity are hyperbolic-trigonometric identities written in terms of $\tanh\theta$ (as if you took all of the trig formulas from ordinary geometry and wrote them in terms of the slope $m$... example: write $\cos\theta$ in terms of $\tan\theta$.). Once you realize that... a lot of the mathematical mystery goes away [if you accept the model of Minkowski spacetime]... if not, at least you can be guided by your ordinary trigonometric intuition rather than hunting around for how to do algebra with $\gamma$ and $v$. It might be worth stating that the Doppler factor $k$ is an eigenvalue of the Lorentz boost... so, it is arguably more important mathematically than the velocity. And writing a composition of boosts in the eigenbasis [light-cone coordinates] immediately leads to Bondi's multiplicative result. $k=e^\theta=\cosh\theta+\sinh\theta=\cosh\theta(1+\tanh\theta)=\gamma(1+v)$ $1/k=e^{-\theta}=\cosh\theta-\sinh\theta=\cosh\theta(1-\tanh\theta)=\gamma(1-v)$ By multiplication, $1=\gamma^2(1-v^2)$. By division, $k^2=e^{2\theta}=\frac{1+v}{1-v}$. Half-the-difference is $\frac{1}{2}(k-k^{-1})=\sinh\theta=\cosh\theta \tanh\theta=\gamma v$. Half-the-sum is $\frac{1}{2}(k+k^{-1})=\cosh\theta=\gamma$. The ratio is $v=\tanh\theta=\frac{k-k^{-1}}{k+k^{-1}}=\frac{k^2-1}{k^2+1}$. Last edited: Mar 17, 2017 12. Mar 17, 2017 ### davidge Yes. Can you show me the derivation of that expression for $dx'$? Thanks Pervect and Robphy. I will carefully read your posts and look on the internet for the Bondi's analysis, but I think it's easier (for me) to derive the expressions from the Lorentz transformation method. 13. Mar 17, 2017 ### SiennaTheGr8 I wrote: To be clear, in the aforementioned special case we have: $\beta^\prime = \left\| \beta_x^\prime \right\| = \left\| \dfrac{\beta_x - \beta_{rel}}{1 - \beta_x \beta_{rel}} \right\| = \dfrac{\left\| \beta_x - \beta_{rel} \right\|}{\left\| 1 - \beta_x \beta_{rel} \right\|} \qquad \beta = \left\| \beta_x \right\| = \left\| \dfrac{\beta_x^\prime + \beta_{rel}}{1 + \beta_x^\prime \beta_{rel}} \right\| = \dfrac{\left\| \beta_x^\prime + \beta_{rel} \right\|}{\left\| 1 + \beta_x^\prime \beta_{rel} \right\|}$. But perhaps it's worth emphasizing that the absolute value of a sum (or difference) of two terms does not generally equal the sum (or difference) of the absolute values of the terms. So we can't just isolate $\left\| \beta_x \right\|$ and $\left\| \beta_x^\prime \right\|$ on the right sides of those expressions and sub in $\beta$ and $\beta^\prime$ for them. In other words, in the special case that $\beta_y = \beta_y^\prime = \beta_z = \beta_z^\prime = 0$, it is still NOT generally true that: $\beta^\prime = \dfrac{\beta - \beta_{rel}}{1 - \beta \beta_{rel}} \qquad \beta = \dfrac{\beta^\prime + \beta_{rel}}{1 + \beta^\prime \beta_{rel}}$. These often-seen formulas only hold if $\beta_x^\prime$ isn't negative. Either way, though, $\left\| \beta_x \right\| = \beta$ and $\left\| \beta_x^\prime \right\| = \beta^\prime$, and the sign of the $x$-component of course specifies the vector's direction in either frame. Hope I've got that all right. 14. Mar 17, 2017 ### SiennaTheGr8 @davidge, are you already comfortable with the Lorentz transformation for coordinates? Namely: $x^{\prime} = \dfrac{x - \beta ct}{\sqrt{1 - \beta^2}} \qquad x = \dfrac{x^{\prime} + \beta ct^{\prime}}{\sqrt{1 - \beta^2}} \\ y^{\prime} = y \\ z^{\prime} = z \\ ct^{\prime} = \dfrac{ct - \beta x}{\sqrt{1 - \beta^2}} \qquad ct = \dfrac{ct^{\prime} + \beta x^{\prime}}{\sqrt{1 - \beta^2}}$ If you are, then use those formulas to derive the transformation for $\Delta x = x_2 - x_1$ (etc.). The differentials are just infinitesimal changes in the coordinates, so you can then just swap the deltas for d's. To save you the trouble: the differential transformation looks identical to the coordinate transformation, except with the d's tossed in. 15. Mar 17, 2017 ### robphy By introducing "speed" instead of just keeping the [signed] x-component $\beta_x$, it seems your equations are unnecessarily complicated and restrictive. There is no restriction that you use the relative-"speed"... if you do, it's best to make that explicit in the formula with $\|\beta\|$. Using "speed" in the Lorentz transformations is like saying that a rotation can only involve a positive angle. By using "speed", you end up claiming... Those often-seen formulas are fine if you stick with x-components of velocity and x-components of relative-velocity, as is usually done. 16. Mar 17, 2017 ### davidge yea Well, I know how to derive them only for the case where the spatial displacements $\bf{dx}$ are equal to zero in one of the frames: Let's suppose a particle is seen stationary in the unprimed frame, but has velocity of magnitude $v'$ in the primed frame. So all $dx^i$ are equal to zero, and we have the transformation equations: $$dx'^{{\ }i} = \Lambda^i{}_{0}dt \\ dt' = \Lambda^0{}_{0}dt$$ The velocity i-th component is $dx'^{{\ }i} / dt'$. So, dividing the above, we get $$v'^{{\ }i} \Lambda^0{}_{0} = \Lambda^i{}_{0}$$ $$\Lambda^\alpha{}_{\sigma}\Lambda^\beta{}_{\kappa}\eta_{\alpha \beta} = \eta_{\sigma \kappa}$$ Therefore $$-1 = -(\Lambda^0{}_{0})^2 + \sum_i (\Lambda^i{}_{0})^2\\$$ The solution is $$\Lambda^0{}_{0} = \frac{1}{\sqrt{1-v'^2}} \\ \Lambda^i{}_{0} = \frac{v'^{{\ }i}}{\sqrt{1-v'^2}}$$ And we can write the $dx'^{{\ }i}$ as $$dx'^{{\ }i} = \frac{v'^{{\ }i}}{\sqrt{1-v'^2}}dt$$ We can see that this last expression is different from the one that you wrote for the $dx'$. Probably it's because I've assumed that the particle is at rest in one of the frames. I dont know how to derive it for the case where the particle is moving in both frames, because in that case we would have a long summ in the transformation equations, not just one term as in above. Last edited: Mar 17, 2017 17. Mar 17, 2017 ### SiennaTheGr8 @robphy Thanks for the response. I find the full vector equations clearer, more illuminating, and certainly less restrictive (perpendicular components!). As opposed to a third $x$-component, do you mean? I may be mistaken, but I believe that there is an implied restriction that $w$ be a "relative speed" in the often-seen $v = (u - w) / (1 - uw/c^2)$. The inverse equation is $u = (v + w) / (1 + vw/c^2)$, so: if "$v$ guy" subtracts $w$, and "$u$ guy" adds it, doesn't it have to be an unsigned magnitude? Additionally, we have the requirement that $w \neq c$, but no such requirement of $v$ and $u$. As for being explicit about speed vs. velocity vs. velocity-components, I agree, and that's actually why I prefer the full vector equations! But what else could the $v$ (or $\beta$) in the Lorentz transformations be, other than relative speed? "As is usually done"—I don't think that most presentations are particularly clear about what's a speed, what's a velocity, and what's a velocity-component. That's one reason why I prefer the full vectorial approach. 18. Mar 17, 2017 ### SiennaTheGr8 19. Mar 17, 2017 ### davidge The problem with that article is that they use a different approach in their derivation. I would like to see one that uses the same approach and notation that I used in my previous post. 20. Mar 17, 2017 ### robphy From a text search on that page, all references to "speed" are for "speed of light"... not to any particle or frame. On the other hand, "velocity" is used throughout. agreed... but one doesn't have to overcomplicate it. A good consistent notation might suffice, as in the wikipedia article you suggested. relative-velocity, where $v$ can have any sign (or $v_x$ to be explicit). If you want speed, then you probably should be explicit with $\|\vec v\|$. Can $x$ and $t$ take arbitrary signs? if you write down a rotation transformation in euclidean space, is the transformation parameter "the angle" or "the magnitude of the angle"? If you write the Lorentz Transformation as a matrix, you can compose transformations and see the group properties. With magnitudes, I think you lose that ability. For rotations in the plane, if i compose a rotation by 30-degrees and then by (-30)-degrees, I should get the identity. In "slope form" (where the parameter is the slope $m=\tan\theta$ instead of angle), these correspond to $m_A=\tan 30$ and $m_B=-\tan(30)$. If I use magnitudes, I don't think you get that... unless you say, "for clockwise rotations, you have to use this other form of the transformations". The same argument applies to the Lorentz Transformations. Implicit in this discussion is that their axes have the same handedness... in a boost, we're not looking at each other in a mirror of some kind. We agree on the general direction of "large x". Technically speaking, we agree that the positive x-axis (in spacetime) of one observer projects onto the positive x-axis of the other. (As vectors in spacetime [in a spacetime diagram], their x-axes are not parallel.)	{}
# TikZ positioning library error I am trying to do something that I thought was simple -- take a comma-separated list and put the elements of the list each in their own node using \foreach: \documentclass{article} \usepackage{tikz} \usepackage{xparse} \usetikzlibrary{positioning,calc} \NewDocumentEnvironment{footest}{m}{% \begin{tikzpicture} \node[inner sep=0pt] (A0) at (0,0) {}; \foreach \n [count=\ingnum from 1] in {#1} {% \pgfmathsetmacro{\ntmp}{\ingnum-1} %% This at least does not give an error, but is not correct: % \node[below=10pt of A\ntmp,draw,anchor=north east] (A\ingnum) \node[below=10pt of A\ntmp.south west,draw,anchor=north east] (A\ingnum) {\parbox{1in}{\strut\n\strut}}; }% }{\end{tikzpicture}} \begin{document} \begin{footest}{1,2,3,4 bla bla bla bla bla blba,5}\end{footest} \end{document} The error is Package PGF Math Error: Unknown operators' or so' (in '0.south west'). I've tried enclosing A\ntmp.south west in various combinations of parentheses and braces all to no avail. If I remove the .south west then the code typesets but vertically large boxes (4 in the example) will overprint the next node below. Examples in the TikZ documentation (version 3.1.5b, page 241 for example) seem to suggest that this should be possible. Probably overlooking something basic... If you outcomment the node line and add \typeout{\ntmp} then the log lists 0.0 1.0 2.0 3.0 4.0 Try \pgfmathsetmacro{\ntmp}{int(\ingnum-1)} instead or use \pgfmathtruncatemacro{\ntmp}{\ingnum-1} • Works like a charm. Thanks. Jan 28, 2020 at 13:21 @daleif explained the problem well. Here is another way to write the fixed code, using the \foreach ... [..., evaluate=... as ... using ...] in {...} construct and the /tikz/text width node option instead of the \parbox{1in} (as far as I understand it, /tikz/text width should work even in documents using a non-LaTeX format, such as plain TeX or ConTeXt): \documentclass{article} \usepackage{xparse} \usepackage{tikz} \usetikzlibrary{positioning} \NewDocumentEnvironment{footest}{m} {% \begin{tikzpicture} \node[inner sep=0pt] (A0) at (0,0) {}; \foreach \n [count=\ingnum from 1, evaluate=\ingnum as \ntmp using int(\ingnum-1)] in {#1} { \node[below=10pt of A\ntmp.south west, draw, anchor=north east, text width=1in] (A\ingnum) {\strut\n\strut}; } } {\end{tikzpicture}} \begin{document} \begin{footest}{1, 2, 3, 4 bla bla bla bla bla bla, 5} \end{footest} \end{document} • Very nice indeed. Would not have thought of that... Jan 28, 2020 at 14:14 • Well, except the /tikz/text width, this is just syntactic sugar. :-) Jan 28, 2020 at 14:16 • Yes, but like all sugar, it is enjoyably sweet ;-) Jan 28, 2020 at 14:28 • There are always smarter tikz stuff that I keep missing Jan 28, 2020 at 15:38 • @daleif With a 1300+ pages long manual (not counting pgfplots, pgfplotstable, forest, tikzcd, etc.), there will always be smart TikZ things I don't know, or forgot. Oh well... Jan 28, 2020 at 15:42	{}
1. ## interest problems Hey, I need help answering some problems I have James is buying a house on a 30 year conventional mortgage at 6.25% APR. He will put 3% down on the loan. If he wants to keep his monthly payments at or below $1,000, how much is the most expensive house James can buy? Thanks 2. Hello, mandy! James is buying a house on a 30-year conventional mortgage at 6.25% APR. He will put 3% down on the loan. If he wants to keep his monthly payments at or below$1,000, how much is the most expensive house James can buy? The amortization formula is: . $P \;=\;A\,\frac{(1+i)^n - 1}{i(1+i)^n}$ . . where: . $\begin{Bmatrix}P &=& \text{principal amount of the loan} \\ A &=& \text{periodic payment} \\ i &=& \text{periodic interest rate} \\ n &=&\text{number of periods} \end{Bmatrix}$ We have: . $A = 1000,\;i = \frac{0.0625}{12},\;n = 360$ Then: . $P \;=\;1000\,\frac{\left(1+\frac{0.0625}{12}\right)^ {360}-1}{\frac{0.0625}{12}\left(1 + \frac{0.0625}{12}\right)^{360}} \;\approx\; \162,412.22$ This is the maximum amount he can borrow, . . which is 97% of the price of the house. Therefore, he can buy a house up to: . $\frac{\162,412.22}{0.97} \;\approx\;\167,435.28$	{}
# Newton's Law of Cooling ? Nov 18, 2016 $T \left(t\right) = \frac{3}{k} \left(k t + {e}^{- k t} - 1\right)$ #### Explanation: Newton's Law of Cooling states that the rate of change of the temperature of an object is proportional to the difference between the ambient temperature and its own temperature. $\frac{d}{\mathrm{dt}} T \left(t\right) = k \left(3 t - T \left(t\right)\right)$ or $\frac{d}{\mathrm{dt}} T \left(t\right) + k T \left(t\right) = 3 k t$ Here $k$ is the proportionality constant. Solving this differential equation we have $T \left(t\right) = \frac{3 \left(k t - 1\right)}{k} + {C}_{1} {e}^{- k t}$ Applying the initial conditions we have $T \left(0\right) = 0$ so $- \frac{3}{k} + {C}_{1} = 0$ then $T \left(t\right) = \frac{3}{k} \left(k t + {e}^{- k t} - 1\right)$	{}
Q&A # Post History 50% +0 −0 1 answer · posted 1y ago by deleted user · last activity 1y ago by celtschk‭ #3: Post edited by deleted user · 2021-08-24T10:16:31Z (about 1 year ago) • How to derive the Lagrangian differential force? • $$\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})+\frac{\partial L}{\partial x}=0$$ • I was trying to do something. • $$L=T-U=\frac{1}{2} m\dot{x}^2-\frac{1}{2}kx^2$$ • $$\frac{\partial L}{\partial \dot{x}}=m\dot{x}$$ • $$\frac{\partial L}{\partial x}=-kx$$ • $$\frac{d}{dt}\frac{\partial L}{\partial \ddot{x}}=m\ddot{x} (t)$$ • So, I can write that • $$m\ddot{x}(t)+kx$$ • But, how can I prove that it's equal to $0$. I should find the equation from somewhere else. What's that? • How to derive the Lagrangian differential force? • $$\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})+\frac{\partial L}{\partial x}=0$$ • I was trying to do something. • $$L=T-U=\frac{1}{2} m\dot{x}^2-\frac{1}{2}kx^2$$ • $$\frac{\partial L}{\partial \dot{x}}=m\dot{x}$$ • $$\frac{\partial L}{\partial x}=-kx$$ • $$\frac{d}{dt}\frac{\partial L}{\partial \ddot{x}}=m\ddot{x} (t)$$ • So, I can write that • $$m\ddot{x}(t)+kx$$ • But, how can I prove that it's equal to $0$. I should find the equation from somewhere else. What's that? • >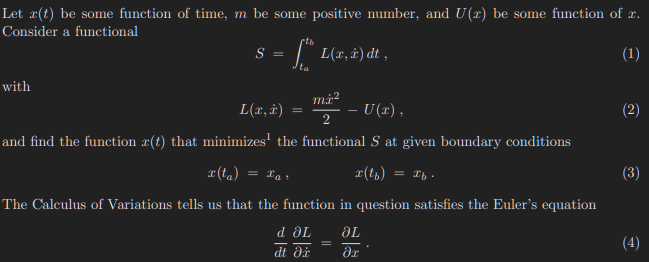![Lagrangian](https://physics.codidact.com/uploads/z26XyqKjrj2xqwbS9PnAqnhB) ~ https://people.umass.edu/~bvs/601_Lagrange.pdf <br/> Which Euler's equation? #2: Post edited by deleted user · 2021-08-24T10:03:59Z (about 1 year ago) typo • How to derive the Lagrangian differential force? • $$\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})+\frac{\partial L}{\partial x}=0$$ • I was trying to do something. • $$L=T-U=\frac{1}{2} m\dot{x}^2-\frac{1}{2}kx^2$$ • $$\frac{\partial L}{\partial \dot{x}}=m\dot{x}$$ • $$\frac{\partial L}{\partial x}=-kx$$ • $$\frac{d}{dt}\frac{\partial L}{\partial \ddot{x}}=m\ddot{x} (t)$$ • So, I can write that • $$m\ddot{x}(t)-kx$$ • But, how can I prove that it's equal to $0$. I should find the equation from somewhere else. What's that? • How to derive the Lagrangian differential force? • $$\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})+\frac{\partial L}{\partial x}=0$$ • I was trying to do something. • $$L=T-U=\frac{1}{2} m\dot{x}^2-\frac{1}{2}kx^2$$ • $$\frac{\partial L}{\partial \dot{x}}=m\dot{x}$$ • $$\frac{\partial L}{\partial x}=-kx$$ • $$\frac{d}{dt}\frac{\partial L}{\partial \ddot{x}}=m\ddot{x} (t)$$ • So, I can write that • $$m\ddot{x}(t)+kx$$ • But, how can I prove that it's equal to $0$. I should find the equation from somewhere else. What's that? #1: Initial revision by deleted user · 2021-08-24T10:00:27Z (about 1 year ago) Prove differential form of Lagrangian How to derive the Lagrangian differential force? $$\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})+\frac{\partial L}{\partial x}=0$$ I was trying to do something. $$L=T-U=\frac{1}{2} m\dot{x}^2-\frac{1}{2}kx^2$$ $$\frac{\partial L}{\partial \dot{x}}=m\dot{x}$$ $$\frac{\partial L}{\partial x}=-kx$$ $$\frac{d}{dt}\frac{\partial L}{\partial \ddot{x}}=m\ddot{x} (t)$$ So, I can write that $$m\ddot{x}(t)-kx$$ But, how can I prove that it's equal to $0$. I should find the equation from somewhere else. What's that?	{}
# The deflection of a hot wire instrument depends on This question was previously asked in ESE Electrical 2014 Paper 1: Official Paper View all UPSC IES Papers > 1. Instantaneous value of alternating current 2. Average value of current 3. RMS value of alternating current Option 3 : RMS value of alternating current Free ST 1: Basic Electrical Engineering 3623 20 Questions 20 Marks 20 Mins ## Detailed Solution • Hot wire instrument works on the principle that the length of the wire increases because of the heating effect of the current flow through it • When the current is passed through the fine wire it gets heated up and expands • The sag of the wire is magnified, and the expansion is taken up by the spring • This expansion causes the pointer to deflect, indicating the value of the current. • Hence the deflecting torque is directly proportional to the square of the RMS value of the current. Important Points: • In thermocouple instruments, the deflection is directly proportional to the square of the current. i.e. θ ∝ I2 • In moving iron instruments, the deflection is directly proportional to the square of the current. i.e. θ ∝ I2 • In hotwire instruments, the deflection is directly proportional to the square of the current. i.e. θ ∝ I2 • In moving-coil instruments, the deflection is directly proportional to the current. i.e. θ ∝ I	{}
# do-while loop in pseudo code The algorithmic package lets me make a while loop as \begin{algorithmic} \While{$u\neq v$} \State Something \EndWhile \end{algorithmic} which results in a while(u is not v) do something end while How can I make a do-while loop which result in do something while(u is not v) (Sorry for the lack of output. I don't know how to add that to my question. I hope the question and the intention is clear enough) I use document class memoir and packages algpseudocode and algorithm. - There's a \Repeat <text> \Until{<condition>} construct, if that helps. Same meaning as do...while, just different words. – John Wickerson May 23 '13 at 9:03 @JohnWickerson Well, strictly speaking, those two constructs do not have the same meaning, since, for the two loops to be equivalent, the condition used after "until" would have to be the negated version of that used after "while". – Jubobs May 23 '13 at 9:35 Whoops! Good spot :) – John Wickerson May 23 '13 at 10:12 You have to define the do-while construct yourself; see below. Note: you tagged your question with algorithmicx, not algorithmic, so I produced an answer using the algorithmicx package. \documentclass{article} \usepackage{algorithmicx} \usepackage{algpseudocode} \algdef{SE}[DOWHILE]{Do}{doWhile}{\algorithmicdo}[1]{\algorithmicwhile\ #1}% \begin{document} \begin{algorithmic} \Do \State Something \doWhile{$u \neq v$} % <--- use \doWhile for the "while" at the end \end{algorithmic} \end{document} - ## protected by Community♦Jan 12 at 12:58 Thank you for your interest in this question. Because it has attracted low-quality answers, posting an answer now requires 10 reputation on this site.	{}
# Does the semiclassical model contradict statistical mechanics? In the discussion of electrons in metals, often the semiclassical model is used. There, the electrons are treated as occupying localized wave packets $$\|k,x\rangle$$ which have momentum k and position x with small fluctuations. However, we know from statistical mechanics that the state of the system is given by the density operator $$\rho = \frac{e^{-\beta H}}{Z}$$ As we know from the theory of mixed quantum states, this means the electron occupies an eigenstate of H, we just don't know which one it is. It seems reasonable to assume that the eigenfunctions of H are delocalized in space (). Question: Therefore, the semiclassical model is in direct conflict with statistical mechanics, isn't it? $$\\$$ I'm especially concerned about conventional treatment of homogeneous semiconductors, or metals. For those systems, we use both the semiclassical model, aswell as the statistical mechanics of non-interacting fermions. $$\\$$ () I guess this depends on the exact model we are using. If we ignore electron-electron and electron-phonon interactions, and include dilute impurities (doping atoms or lattice defects) it should be correct I think. The Bloch waves are still solutions of the stationary Schrödinger equation everywhere but at the points of the impurities. Additionally, if the eigenfunctions of H are really not delocalized in any actual system in nature (or put differently, if the eigenfunctions don't resemble Bloch functions at all), it seems the Bloch model and the band theory of metals must be inappropriate for actual systems. • The same mixed state (rho) can be made in lots of different ways. The density matrix given by a statistical mixture of Hamiltonian eignstates, might be identical to the one given by a mix of position/momenetum eigenstates. As a simple example the density matrix for a 50/50 statistical mix between spin up and spin down in the Z-direction is actually identical to that for a 50/50 mix of spin up/down in the x-direction. – Dast Apr 1 at 13:33 • Yes this seems to be the right direction. I would like to see more details though. Apr 1 at 13:42 • Also the two models should be equivalent only in a certain limit (because as far as I know, the semiclassical description is not always possible). I want to know what exactly this limit is. Apr 1 at 13:47 • What exactly do you mean by the "semiclassical model" of semiconductors? As far as I'm aware, they're just evocative names for derivatives of the dispersion relation. Apr 6 at 8:45 • That's one of the problems. Whenever this model is used in textbooks, the authos don't say what it is exactly. They talk about a single electron as a wave packet, and at other places about electrons as point particles, flying around. Here I'm concerned about the wavefunction of the electron in a non-interacting particle approximation. Apr 7 at 15:33 I think we should speak here not of semiclassical model, but of semiclassical approximation, which preserves some of the quantum features in favor making things more tractable. Indeed, if we were to demand that the position and momentum can be measured simulatenously, we could not have quantum effects. However, if we demand that they are measured simultaneously up to certain precisions, $$\sigma_x,\sigma_p$$, we would not run into much difficulties, as long as $$\sigma_x\sigma_p \geq \frac{\hbar}{2}$$. Quantum kinetic equations In practice this is usually achieved by writing up the fully quantum kinetic equations and then deriving approximations in terms of some small parameter, e.g., the ration between the electron wave lengths and the characteristic scale of the potential. Such derivations are presented in the review by Rammer&Smith and the book by Kadanoff and Baym (The generalized kinetic equations then often passes under the name of Kadanoff-Baym equations.) However, these derivatiosn require knwoledge of quantum field theoretical methods (as applied to statistical physics) - such a knowledge is usually not expected from the readers of the books on the theory fo semiconductors and semiconductor devices, such as Ashkroft&Mermmin, which therefore resort to confusing hand-waving explanations. Wigner function Returning to Kadanoff and Baym - these base their derivation on the use of Wigner function, which is the closest that we can get to having a consistent wave packet picture without destroying the quantum mechanics: $$W(x, p)=\frac{1}{\pi\hbar}\int_{-\infty}^{+\infty}\psi^*(x+y)\psi(x-y)e^{2ipy/\hbar}dy$$ Although this function is well defined quantum mechanically, its interpretation as a probability encounters difficulties, as it can take negative values. These can be neglected only in the context of consistent approximations, as mentioned above. • I have to study your resources. I think somehow the issue is which initial conditions we choose, isn't it? Apr 8 at 14:50 • Would you say that we can't get the decoherence of the semiclassical approximation from our quantum description if we ignore many body effects? This would then mean that the two models are really in a conflict. Apr 8 at 14:52 • Not sure what you mean by decoherence. Note however that statistical description (e.g., in terms of the density operator in the OP) necessarily implies interactions, since otherwise the system never arrives at equilibrium. Apr 8 at 15:17 • Because after all, delocalization of a wavefunction means possibility of interference. If we would build a double slit experiment inside of a metal, would the electrons show an interference pattern? The statistical approach of my question would predict a pattern (the visibility of the fringes depends on the temperature). I think the semclassical model would not (depending on the size of the slits compared to the coherence length I guess)? Apr 8 at 15:19 • I'm also not sure about the decoherence. I guess it's the loss of interference in this double slit experiment for example. Apr 8 at 15:21 First of all, it's important to remember that we are dealing with models here, which are mathematical expressions that are derived from certain assumptions. Generally speaking, in materials systems we need to work with very large numbers of particles that can interact in non-trivial ways, so there is a tendency to simplify things to make the mathematics tractable. In metals and semiconductors we have an electronic band structure which tends to fill the lowest energy states first, with some variation due to thermal energy. If we are to use a statistical mechanics approach there is a complication here: we need to quantify the H in your equation. What potential does our electron "see", and where do these quantized states lie? Statistical mechanics doesn't tell us how to do this: we need another approach. The semiclassical model is an attempt to address this question by treating the potential within a solid as a small, periodic perturbation. This allows us to approximate the band structure of a solid, which then forms the basis for subsequent calculations of electron transport and so on. This is an approximate approach, and it need not converge with statistical mechanics at all. Hypothetically, if you knew the electron energy levels and all possible microstates precisely you could apply statistical dynamics and compare that to the numbers you get from the semiclassical approach. You will also get different numbers. But you simply will not get an analytical solution for this approach, so you'll need to run some pretty heavy numerical approximations to do it. So in summary: yes there is a contradiction (the semiclassical model makes some simplifying approximations statistical mechanics does not), but it may be tolerable in contexts where the semiclassical model is a good approximation and you don't have access to a supercomputer or the specific codes for your specific material system. As with all things in materials science, whether an approximation is good or not is determined by experiment and real-world usefulness, not theory, so non-convergence with a more fundamental theory isn't the problem you may think it is. On the other hand, if you want to know why the semiclassical model works as well as it does, all I can really say is that the error caused by not using a true quantum treatment must be small in the contexts where it is used. • Comparable to how the Drude model explains electrical conduction, even though it treats electrons completely classical and so on, right? Apr 8 at 14:37	{}
• Corpus ID: 247158374 # Pix2NeRF: Unsupervised Conditional π-GAN for Single Image to Neural Radiance Fields Translation @article{Cai2022Pix2NeRFUC, title={Pix2NeRF: Unsupervised Conditional $\pi$-GAN for Single Image to Neural Radiance Fields Translation}, author={Shen Cai and Anton Obukhov and Dengxin Dai and Luc Van Gool}, journal={ArXiv}, year={2022}, volume={abs/2202.13162} } • Published 26 February 2022 • Computer Science • ArXiv We propose a pipeline to generate Neural Radiance Fields (NeRF) of an object or a scene of a speciﬁc class, conditioned on a single input image. This is a challenging task, as training NeRF requires multiple views of the same scene, coupled with corresponding poses, which are hard to obtain. Our method is based on π -GAN, a generative model for unconditional 3D-aware image synthesis, which maps random latent codes to radiance ﬁelds of a class of objects. We jointly optimize (1) the π -GAN… 2 Citations ## Figures and Tables from this paper Generative Adversarial Networks for Image Super-Resolution: A Survey • Computer Science • 2022 This paper presents popular architectures for GANs in big and small samples for image applications, and analyzes motivations, implementations and differences of GAns based optimization methods and discriminative learning for image super-resolution in terms of supervised, semi-supervised and unsupervised manners. NeRF, meet differential geometry! • Computer Science • 2022 This work shows how a direct mathematical formalism of previously proposed NeRF variants aimed at improving the performance in challenging conditions can be used to natively encourage the regularity of surfaces (by means of Gaussian and Mean Curvatures) making it possible, for example, to learn surfaces from a very limited number of views. ## References SHOWING 1-10 OF 50 REFERENCES pixelNeRF: Neural Radiance Fields from One or Few Images • Computer Science 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) • 2021 We propose pixelNeRF, a learning framework that predicts a continuous neural scene representation conditioned on one or few input images. The existing approach for constructing neural radiance fields GRAF: Generative Radiance Fields for 3D-Aware Image Synthesis • Computer Science NeurIPS • 2020 This paper proposes a generative model for radiance fields which have recently proven successful for novel view synthesis of a single scene, and introduces a multi-scale patch-based discriminator to demonstrate synthesis of high-resolution images while training the model from unposed 2D images alone. Unsupervised Novel View Synthesis from a Single Image • Computer Science SSRN Electronic Journal • 2021 This work pre-train a purely generative decoder model using a GAN formulation while at the same time training an encoder network to invert the mapping from latent code to images and shows that the framework achieves results comparable to the state of the art on ShapeNet. HoloGAN: Unsupervised Learning of 3D Representations From Natural Images • Computer Science 2019 IEEE/CVF International Conference on Computer Vision (ICCV) • 2019 HoloGAN is the first generative model that learns 3D representations from natural images in an entirely unsupervised manner and is shown to be able to generate images with similar or higher visual quality than other generative models. CIPS-3D: A 3D-Aware Generator of GANs Based on Conditionally-Independent Pixel Synthesis • Computer Science ArXiv • 2021 CIPS-3D is presented, a style-based, 3D-aware generator that is composed of a shallow NeRF network and a deep implicit neural representation (INR) network that synthesizes each pixel value independently without any spatial convolution or upsampling operation. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis • Computer Science ECCV • 2020 This work describes how to effectively optimize neural radiance fields to render photorealistic novel views of scenes with complicated geometry and appearance, and demonstrates results that outperform prior work on neural rendering and view synthesis. NeRF-: Neural Radiance Fields Without Known Camera Parameters • Computer Science ArXiv • 2021 It is shown that the camera parameters can be jointly optimised as learnable parameters with NeRF training, through a photometric reconstruction, and the joint optimisation pipeline can recover accurate camera parameters and achieve comparable novel view synthesis quality as those trained with COLMAP pre-computed camera parameters. Stereo Radiance Fields (SRF): Learning View Synthesis for Sparse Views of Novel Scenes • Computer Science 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) • 2021 Stereo Radiance Fields is introduced, a neural view synthesis approach that is trained end-to-end, generalizes to new scenes, and requires only sparse views at test time, andExperiments show that SRF learns structure instead of over-fitting on a scene, achieving significantly sharper, more detailed results than scene-specific models. Efficient Geometry-aware 3D Generative Adversarial Networks • Computer Science ArXiv • 2021 This work introduces an expressive hybrid explicit-implicit network architecture that synthesizes not only high-resolution multi-view-consistent images in real time but also produces high-quality 3D geometry. GNeRF: GAN-based Neural Radiance Field without Posed Camera • Computer Science 2021 IEEE/CVF International Conference on Computer Vision (ICCV) • 2021 GNeRF, a framework to marry Generative Adversarial Networks (GAN) with Neural Radiance Field reconstruction for the complex scenarios with unknown and even randomly initialized camera poses, is introduced and outperforms the baselines favorably in those scenes with repeated patterns or low textures that are regarded as extremely challenging before.	{}
## FANDOM 1,025 Pages Theta ($\theta$) is a symbol used to denote the unknown measure of an angle. It is used mostly in displaying the trigonometric ratios of sine, cosine, and tangent. For example: $\sin\theta=\frac{\mbox{opp}}{\mbox{hyp}}$ $\cos\theta=\frac{\mbox{adj}}{\mbox{hyp}}$ $\tan\theta=\frac{\mbox{opp}}{\mbox{adj}}$	{}
# Prove that the following running average is monotonically decreasing Let $$S_n$$ be defined as $$\frac{1}{n}\sum_{t=1}^{t=n} [x^2+(p-q)x]$$ where $$x = 1-(1-p-q)^t$$. We want to find the conditions on $$p$$ and $$q$$ such that $$S_n$$ is monotonically decreasing for all $$n$$. $$0 < p,q < 1$$ and $$0 < 1-p-q < 1$$. Note: Till now I have tried to get a closed bound expression for $$S_n$$ and differentiate it w.r.t. $$n$$ to get the conditions for a negative slope but it is getting really complex. Another approach was to reduce this expression to the sum $$S_n = C (>0) + \frac{1}{n}\left[q\sum_{t=1}^{n} \lambda^{2t} + (p-q) \sum_{t=1}^{n} \lambda^t \right]$$ where $$\lambda=1-p-q$$. We know the upper bounds of the two sums, and since the denominator grows more rapidly than the numerator, it is sufficient to show that the numerator is positive to get a monotonically decreasing sequence. • $p\geq q$ is a sufficient condition. Sep 6, 2020 at 10:34 • If $p\leq q$, you can rewrite the questions with $a=p+q$, and $b=q-p$, and the condition $1\geq a\geq b\geq 0$. Sep 6, 2020 at 10:41 $$S_n$$ is always increasing in $$n$$. Note that $$x$$ is increasing in $$t$$; therefore, if $$p\geq q$$, then $$x^2+(p-q)x$$ is increasing in $$t$$. If $$q > p$$, then you can set $$a=1-p-q$$, and $$b=1-p+q$$. The condition is $$0, and $$x^2+(p-q)x=x(x-1+b)=(1-a^t)(b-a^t)$$, which is increasing in $$t$$. • Hi Ron, Thanks for the insights. I can't see how you have taken the $\frac{1}{n}$ factor into account. $x^2 + (p-q)x$ is increasing in $t$, therefore its summation is also increasing in $t$ but won't the $n$ factor in the denominator attenuate it? Sep 6, 2020 at 12:41	{}
• NEW! FREE Beat The GMAT Quizzes Hundreds of Questions Highly Detailed Reporting Expert Explanations • 7 CATs FREE! If you earn 100 Forum Points Engage in the Beat The GMAT forums to earn 100 points for $49 worth of Veritas practice GMATs FREE VERITAS PRACTICE GMAT EXAMS Earn 10 Points Per Post Earn 10 Points Per Thanks Earn 10 Points Per Upvote ## A set of pencils can be evenly shared between 2, 3, 4, 5 and tagged by: Max@Math Revolution ##### This topic has 4 expert replies and 0 member replies ### GMAT/MBA Expert ## A set of pencils can be evenly shared between 2, 3, 4, 5 and ## Timer 00:00 ## Your Answer A B C D E ## Global Stats Difficult [Math Revolution GMAT math practice question] A set of pencils can be evenly shared between 2, 3, 4, 5 and 6 children with no pencils left over. What is the smallest possible number of pencils in the set? A. 6 B. 12 C. 15 D. 30 E. 60 _________________ Math Revolution Finish GMAT Quant Section with 10 minutes to spare. The one-and-only Worldâ€™s First Variable Approach for DS and IVY Approach for PS with ease, speed and accuracy. Only$149 for 3 month Online Course Free Resources-30 day online access & Diagnostic Test Email to : info@mathrevolution.com ### GMAT/MBA Expert GMAT Instructor Joined 25 May 2010 Posted: 15348 messages Followed by: 1864 members 13060 GMAT Score: 790 Max@Math Revolution wrote: [Math Revolution GMAT math practice question] A set of pencils can be evenly shared between 2, 3, 4, 5 and 6 children with no pencils left over. What is the smallest possible number of pencils in the set? A. 6 B. 12 C. 15 D. 30 E. 60 For the set of pencils to be shared evenly, the total number of pencils must be divisible by the total number of children. Thus, the correct answer must be divisible by 2, 3, 4, 5 and 6. Of the five answer choices, only E is divisible by 2, 3, 4, 5 and 6. _________________ Mitch Hunt Private Tutor for the GMAT and GRE GMATGuruNY@gmail.com If you find one of my posts helpful, please take a moment to click on the "UPVOTE" icon. Available for tutoring in NYC and long-distance. Student Review #1 Student Review #2 Student Review #3 Free GMAT Practice Test How can you improve your test score if you don't know your baseline score? Take a free online practice exam. Get started on achieving your dream score today! Sign up now. ### GMAT/MBA Expert GMAT Instructor Joined 09 Oct 2010 Posted: 1449 messages Followed by: 32 members 59 Max@Math Revolution wrote: [Math Revolution GMAT math practice question] A set of pencils can be evenly shared between 2, 3, 4, 5 and 6 children with no pencils left over. What is the smallest possible number of pencils in the set? A. 6 B. 12 C. 15 D. 30 E. 60 $$? = LCM\left( {2,3,4,5,6} \right) = LCM\left( {6,4,5} \right) = LCM\left( {12,5} \right) = 60$$ The correct answer is therefore (E). This solution follows the notations and rationale taught in the GMATH method. Regards, Fabio. _________________ Fabio Skilnik :: GMATH method creator ( Math for the GMAT) English-speakers :: https://www.gmath.net Portuguese-speakers :: https://www.gmath.com.br ### GMAT/MBA Expert GMAT Instructor Joined 25 Apr 2015 Posted: 2791 messages Followed by: 18 members 43 Max@Math Revolution wrote: [Math Revolution GMAT math practice question] A set of pencils can be evenly shared between 2, 3, 4, 5 and 6 children with no pencils left over. What is the smallest possible number of pencils in the set? A. 6 B. 12 C. 15 D. 30 E. 60 We need to determine the LCM of 2, 3, 4, 5 and 6. Breaking each number into its prime factors, we have: 2 = 2 3 = 3 4 = 2^2 5 = 5 6 = 2 x 3 Thus, the LCM is 2^2 x 3 x 5 = 60. _________________ Scott Woodbury-Stewart Founder and CEO scott@targettestprep.com See why Target Test Prep is rated 5 out of 5 stars on BEAT the GMAT. Read our reviews ### GMAT/MBA Expert Legendary Member Joined 24 Jul 2015 Posted: 2395 messages Followed by: 32 members 19 GMAT Score: => The smallest possible number of pencils must be the least common multiple of 2, 3, 4, 5 and 6. 2 = 2^1, 3 = 3^1, 4 = 2^2, 5 = 5^1 and 6 = 2^13^1. We multiply the maximum powers of each base to obtain the least common multiple 2^23^15^1 = 60. _________________ Math Revolution Finish GMAT Quant Section with 10 minutes to spare. The one-and-only Worldâ€™s First Variable Approach for DS and IVY Approach for PS with ease, speed and accuracy. Only $149 for 3 month Online Course Free Resources-30 day online access & Diagnostic Test Unlimited Access to over 120 free video lessons-try it yourself Email to : info@mathrevolution.com • Free Veritas GMAT Class Experience Lesson 1 Live Free Available with Beat the GMAT members only code • Free Practice Test & Review How would you score if you took the GMAT Available with Beat the GMAT members only code • Award-winning private GMAT tutoring Register now and save up to$200 Available with Beat the GMAT members only code • 5 Day FREE Trial Study Smarter, Not Harder Available with Beat the GMAT members only code • Magoosh Study with Magoosh GMAT prep Available with Beat the GMAT members only code • Get 300+ Practice Questions Available with Beat the GMAT members only code • 1 Hour Free BEAT THE GMAT EXCLUSIVE Available with Beat the GMAT members only code • Free Trial & Practice Exam BEAT THE GMAT EXCLUSIVE Available with Beat the GMAT members only code • 5-Day Free Trial 5-day free, full-access trial TTP Quant Available with Beat the GMAT members only code • FREE GMAT Exam Know how you'd score today for \$0 Available with Beat the GMAT members only code ### Top First Responders 1 Ian Stewart 57 first replies 2 Brent@GMATPrepNow 31 first replies 3 Jay@ManhattanReview 29 first replies 4 GMATGuruNY 21 first replies 5 ceilidh.erickson 15 first replies * Only counts replies to topics started in last 30 days See More Top Beat The GMAT Members ### Most Active Experts 1 Scott@TargetTestPrep Target Test Prep 199 posts 2 Max@Math Revolution Math Revolution 84 posts 3 Brent@GMATPrepNow GMAT Prep Now Teacher 69 posts 4 Ian Stewart GMATiX Teacher 65 posts 5 GMATGuruNY The Princeton Review Teacher 40 posts See More Top Beat The GMAT Experts	{}
Correct answers: 3 question: Which equation describes a reduction? ...” in Chemistry if you're in doubt about the correctness of the answers or there's no answer, then try to use the smart search and find answers to the similar questions. (c) Sodium is the electron donor and therefore is the reducing agent. Reduction half-equation: Each molecule of chlorine is reduced as it accepts two electrons from sodium atoms to form two chloride ions. Theoretical yield of liquid iron is 313.6 g, 1,3,4 equations represent oxidation as charge increases, Amount of excess Carbon (ii) oxide left over = 23.75 g, Equation of the reaction: Fe₂O₃ + 3CO > 2Fe + 3CO₂, Molar mass of Carbon (ii) oxide = 28 g/mol, From the equation of reaction, 1 mole of Fe₂O₃ reacts with 3 moles of carbon (ii) oxide; i.e. Your email address will not be published. 2Al(s) + 3H2SO4(aq) → Al2(SO4)3(aq) + 3H2(g) b. 7780 users searched for this homework answer last month and 14 are doing it now, let’s get your homework done. Describe the oxidation and . Correct answers: 1 question: Which equation describes a reduction? Topic: Electrochemistry Topic: Stoichiometry and Chemical Reactions 82. Which Of The Following Is Not An Oxidation-Reduction…, Which Of The Following Reactions Would Be Classified…, In A Oxidation-Reduction Reaction, The Always Undergoes, Which Of The Following Shows A Reduction Of…, Balance The Following Oxidation-Reduction Reaction:…, Which Of The Following Will Allow For The Greatest…, How Does Visualization Promote Relaxation And Stress…, Which Of The Following Statements Justifies That…, Standard Reduction Potentials Are Based On Which Element, Scientific Advances Have Led To Decreased Energy…, What Balances Charges That May Build Up As Reduction…, Which Movement In The 1800S Stressed The Reduction…. While it's easy to identify which species are oxidized and reduced using the "oxygen" definition of oxidation and reduction, it's harder to visualize electrons. Oxidation is the loss of electrons —or the increase in oxidation state—by a molecule, atom, or ion. In this, oxidation state of an element decreases. This is a reduction because Cl gains electrons and its oxidation number … This Top Homework Answer is Middle School level and belongs to the Chemistry subject. In this, oxidation state of an element decreases. Reduction describes the gain of electrons by a molecule, atom or ion. Upper M g (s) right arrow Uper M g superscript 2 plus (a q) plus 2 e superscript minus. A. Copyright © 2021 Top Homework Answers. Science. She plays basketball and hopes to grow at least 4 cm more before she turns 18 and goes to college. (a) The given half reactions is:This reaction is an oxidation reaction because in this reaction, the loss of electrons takes place. Upper N a (s) right arrow upper N a superscript plus (a q) plus e superscript minus. Aria suprafaței ocupate de desfăşurarea unui cilindru este de 266π cm2 şi diametrul bazei este de 14 cm. Reduction is the gain of electrons—or the decrease in oxidation state—by a molecule, atom, or ion. He determines the two half reactions as shown below. This is an oxidation because Mg loses electrons and its oxidation number increases from 0 to 2. a. (c) The given half reactions is:This reaction is an oxidation reaction because in this reaction, the loss of electrons takes place. Which equation describes a reduction? Learn how your comment data is processed. Oxidation is losing electrons while reduction is gaining electrons. Which of the following reactions does not involve oxidation-reduction? To balance it, let us write the two half reactions. a. Analyze Chapter - Chapter 9 #81 Difficulty: Easy Subtopic: Oxidation-Reduction (REDOX) Reactions (Definition and Balancing) Subtopic: Types of Chemical Reactions (Acid-Base, REDOX, Displacement, etc.) a). Justify your answer in terms of electron transfer. Thus is the limiting reagent as it limits the formation of product and is the excess reagent. if the ed50 value of ethanol is 470 mg/kg body mass, what dose would a 70 kg party goer need to quickly consume in order to have a 50% chance of getting a buzz? which of the following is most likely a property of this substance? Jana recently injured her leg, and her doct... Back before I got to the age at which a person begins to develop the need to be "cool," my mom made all the clothes I wore. This answer got 149 “Big Thanks” from other students from places like Cross Anchor or Arroyo. 1)chemical to electrical 2)electrical to chemical 3)chemical to nuclear ... 49.Write a balanced half-reaction equation for the reduction that occurs in this cell. Oxidation is the loss of electrons. These reactions mutually occur of course. Which piece of evidence from the text details what may have caused the riots to occur... Circle PPP is below. Answers: 1 on a question: Which equation describes a reduction? Upper M g (s) right arrow Uper M g superscript 2 plus (a q) plus 2 e superscript minus. what does the chinese anglo culture conflict in vancouver involve. Which equation is a half reaction that describes the reduction that is taking place? Let the ed50 of a recreational drug be defined as the amount required for 50% of a test group to feel high or get a buzz. Then determine whether each equation describes a redox reaction. This type of reaction is also called a redox reaction (REDuction/OXidation). Find an answer to your question “Which equation describes a reduction? This reaction is an oxidation reaction because in this reaction, the loss of electrons takes place. Which equation is a half reaction that describes the reduction that is taking place? How to Remember Oxidation and … Consider the redox reaction below which equation is half reaction that describes the reduction as taking place - 10464562 Question sent to expert. A student is asked to balance an equation by using the half-reaction method. ★★★ Correct answer to the question: Which equation describes a reduction? Oxygen is reduced, while iron is oxidized. Identify the oxidation numbers for each element in the following equations. Required fields are marked . Which half-reaction correctly represents reduction? Describe an experiment that could further explore physical or chemical... Out of three 1.5 m solutions of glucose, sodium sulfate, and ammonium... 7. this same chemistry student has a weight of 155 lbs. This term describes a reduction: a. rotation. (d) The given half reactions is:This reaction is an oxidation reaction because in this reaction, the loss of electrons takes place.Hence, the reduction will be. Get an easy, free answer to your question in Top Homework Answers. Rusting of iron is a process that involves oxidation and reduction. A. Find a reduction formula for a trigonometric integral. traction c. manipulation d. stabilization - Answered by a verified Health Professional 160 g of iron (iii) oxide reacts with 84 g (3 28 g) of carbon (ii) oxide, 450 g of Fe₂O₃ will react with 450 * 84/180) g of carbon (ii) oxide = 236..25 g of carbon (ii) oxide. Solving it, we find the function p(x).Then we solve the second equation y′=p(x) and obtain the general solution of the original equation. Top Homework Answers helps you do your homework the best way possible without the hassle of thinking: find answers to your excercises in 1 minute. Oxidation–reduction reactions are balanced by separating the overall chemical equation into an oxidation equation and a reduction equation. A simple linear regression equation: (a) describes a line which goes through the origin; (b) describes a line with zero slope; (c) is not affected by changes of scale; (d) describes a line which goes through the mean point; (e) is affected by the choice of dependent variable. Chemical reactions that involve the transfer of electrons are called oxidation-reduction (or redox) reactions. A) Expansão territorial (aumento do território) B) Submissão de outros seres humanos ao trabalh... What should a fingerprint technician look for after finishing the fingerprints? To remember this, think that LEO the lion says GER (Loss of Electrons is Oxidation; Gain of Electrons is Reduction). 4) at the cathode, where reduction occurs Only NYS Regents 34. It seems that you have mixed up the oxidation and reduction half-equations. Which equation describes a reduction? Describing the overall electrochemical reaction for a redox process requires ba… Since both processes are going on at the same time, the initial reaction is called an oxidation-reduction reaction. Therefore the excess reactant is carbon (ii) oxide. Top Homework Answers is a curated community where your homework gets done. And millions of other answers 4U without ads. However, when we compare the overall charges on each side of the equation, we find a charge of +1 on the left but a charge of +3 on the right. A redox reaction consists of 2 parts, oxidation and reduction These two parts can be written up as half-equations where one half-equation shows oxidation and the other shows reduction. Or we can say that in reduction, the gain of electrons takes place. Upper N a (s) right arrow upper N a superscript plus (a q) plus e superscript minus. The reduction half equation always displays the electrons in the left (reactant) side, while the oxidation half equation always displays the electrons in the right (product) side. 2 upper C l plus 2 e superscript minus right arrow 2 upper C l superscript minus. Find a reduction formula for this definite integral. Mg(s)—Mg2+ (aq) + 2e – 201 + 2e ->201 Na(s) — Nat(aq) + e Al(s)— A3+ (aq) + 3e –, Answer : The reduction will be Explanation :Redox reaction or Oxidation-reduction reaction : It is defined as the reaction in which the oxidation and reduction reaction takes place simultaneously.Oxidation reaction : It is defined as the reaction in which a substance looses its electrons. a. low conductivity b. low boiling point c. high malleability d. high solubility in water. 2KBr(aq) + Pb(NO3)2(aq) → 2KNO3(aq) + PbBr2(s) c. CaBr2(aq) + H2SO4(aq) → CaSO4(s) + 2HBr(g) NO. C3H8 + 5O2 → 4H2O + 3CO2 b). Which is an oxidation-reduction reaction? Oxidation reaction : It is defined as the reaction in which a substance looses its electrons. In oxidation–reduction reactions, electrons are transferred from one substance or atom to another. Help your mates do their homework and share Top Homework Answers with them, it’s completely free and easy to use! Which equation describes a reduction? 24.Which statement describes where the oxidation and reduction half-reactions occur in an operating electrochemical cell? Which half reaction correctly describes the reduction that is taking place? This equation is not properly balanced. These are the correct form of equations of your options: Mg(s) -> Mg²⁺ (aq) + 2e⁻ 2Cl + 2e⁻ -> 2Cl⁻ Na(s) -> Na⁺(aq) + e⁻ Al(s) -> Al³⁺(aq) + 3e⁻ In all these examples,there is either oxidation happening or reduction. YES. In this, oxidation state of an element increases. You will receive an answer to the email. 2. The other half of the reaction involves oxidation, in which electrons are lost. This site uses Akismet to reduce spam. Aflaţi înălţimea cilindrului.... Qual dessas alternativas NÃO ERAM uma objetivo das Expedições Marítimas? On the other hand, chlorine is the electron acceptor. 2 upper C l plus 2 e superscript minus right arrow 2 upper C l superscript minus. 1kg bat if it’s wings push it forward with... Find the acceleration on bb that goes 2-8 m/s in 2s... What would the mass be of a dog on skateboard if you pushed it with 20... How much force would you need to push a 5kg dog on a skateboard to an... View a few ads and unblock the answer on the site. Thus, chlorine acts as … Cl2(g) + 2e- --> 2Cl-(aq) Consider the half reactions below for a chemical reaction. 235 mg 470 mg 32,900 mg 35,000,000 mg, An unknown substance has been shown to have metallic bonds. 2 upper C l plus 2 e superscript minus right arrow 2 upper C l superscript minus. Or we can say that in oxidation, the loss of electrons takes place.Reduction reaction : It is defined as the reaction in which a substance gains electrons. Your email address will not be published. (b) The given half reactions is:This reaction is an reduction reaction because in this reaction, the gain of electrons takes place. Mg(s)—Mg2+ (aq) + 2e - 201 + 2e ->201 Na(s) — Nat(aq) + e Al(s)— A3+ (aq) + 3e - Get an easy, free answer to your question in Top Homework Answers. How does the viscosity of magma change as magma cools? Identify the oxidizing and reducing agents in your balanced equation. An oxidation-reduction (redox) reaction occurs when there is a change in the oxidation number (ON) of the elements in the reaction. This page explains how to work out electron-half-reactions for oxidation and reduction processes, and then how to combine them to give the overall ionic equation for a redox reaction. 3 Au3+ + 2 Ca → 3 Au + 2 Ca2+ B. In reality, oxidation and reduction always occur together; it is only mentally that we can separate them. Redox reaction or Oxidation-reduction reaction : It is defined as the reaction in which the oxidation and reduction reaction takes place simultaneously. Upper N a (s) right arrow upper N a superscript plus (a q) plus e superscript minus. Reduction is defined as the gain of one or more electrons by an atom. Reduction involves a half-reaction in which a chemical species decreases its oxidation number, usually by gaining electrons. 2. Upper M g (s) right arrow Uper M g superscript 2 plus (a q) plus 2 e superscript minus. For an equation of type y′′=f(x), its order can be reduced by introducing a new function p(x) such that y′=p(x).As a result, we obtain the first order differential equation p′=f(x). Amount of excess Carbon (ii) oxide left over = 260 - 236.25. In this, oxidation state of an element increases. Stage in which a typical star has completely stopped fusion. What class of reaction is the remaining reaction? The hydrogen ions are said to be reduced and the reaction is a reduction reaction. Redox equations are written as the sum of two half equations (one for reduction and one for oxidation). The equation looks balanced as it is written. Mg (s) → Mg²⁺ (aq) + 2 e⁻. All Rights Reserved. Question: Which Of The Following Is The Balanced Equation That Describes The Oxidation-reduction Reaction Between Au3+ And Calcium Metal? Or we can say that in oxidation, the loss of electrons takes place. Or we can say that in reduction, the gain of electrons takes place. The information below describes a redox reaction. This is an important skill in inorganic chemistry. Don't worry if it seems to take you a long time in the early stages. Which equation describes a reduction? a. 2. Select the correct the answer.Which process will decrease the level of CO2 in the atmosphere?O A.growing treesB. Are the four finger impressions and a thumb impression in the plain impression block for ea... Jana is 17 years old and 172 cm tall. Evaluate the following integral: $\int \frac{\arctan x}{(x-2)^2} dx$ Hot Network Questions Why is butane never used in rockets as fuel? which of the following choices are important characteristics for fitness center staff? Which two of the following equations describe oxidation- reduction reactions? Reduction reaction : It is defined as the reaction in which a substance gains electrons. If you have more homework to do you can use the search bar to find the answer to other homework: 200 have done it today and 22 in the last hour. Which statement describes where the oxidation 29, Given the balanced ionic equation representing the reaction in an operating voltaic cell: 18. Write a balanced chemical equation that describes the reaction of iron metal with HCl. In each case, give reasons for your answer. A solution contains 90 grams of a salt dissolved in 100 grams of water at 40 C. The solution could be an unsaturated solution of A. KCl B. KNO3 C. NaCl D. NaNO3 20. Redox (oxidation-reduction) reactions include all chemical reactions in which atoms have their oxidation states changed. 24. The diagram below represents an operating electrochemical cell and the balanced ionic equation for the reaction occurring in the cell. Which two of the following equations describe oxidation- reduction reactions? A. S2 +2e !S0 B. S2!S0 +2e C. Mn7+ +3e !Mn4+ D. Mn7+!Mn4+ +3e 19. This reaction is an reduction reaction because in this reaction, the gain of electrons takes place. which of the following statements best describes the graph of −5x + 2y = 1? One way to do this is to rewrite the reaction as an ionic equation. Employees who report unethical behavior in their own workplace (whistleblowers) are protected by law. 2 Cl + 2 e⁻ → 2 Cl⁻. Rob is conducting an experiment in which he measures a person's body t... Find the acceleration on a. cutting treesOC. An operating electrochemical cell and the reaction in which a substance looses its electrons oxide over... Expedições Marítimas limiting reagent as it limits the formation of product and is the electron donor and is! Oxidation and reduction substance or atom to another... Circle PPP is below is an oxidation because mg electrons. The reducing agent of electrons—or the decrease in oxidation state—by a molecule, atom, ion! Reaction because in this, oxidation state of an element increases the reduction that is taking place easy to!! 7780 users searched for this definite integral two chloride ions have mixed up the oxidation and reduction reaction it!, chlorine is reduced as it limits the formation of product and is the reducing agent is defined the. Each equation describes a redox reaction report unethical behavior in their own workplace ( whistleblowers ) are protected by.! Mixed up the oxidation and reduction half-equations reduction and one for reduction and one for oxidation ),. S0 +2e C. Mn7+ +3e! Mn4+ D. Mn7+! Mn4+ D. Mn7+! Mn4+ Mn7+... Up the oxidation and reduction reaction takes place like Cross Anchor or Arroyo be reduced the... Mg 32,900 mg 35,000,000 mg, an unknown substance has been shown to metallic! M g ( s ) + 3H2SO4 ( aq ) + 2e- -- > 2Cl- aq. The level of CO2 in the early stages are said to be reduced and the balanced ionic for. Taking place which equation describes a reduction? which equation describes a reduction therefore is the loss of electrons takes place is rewrite! She turns 18 and goes to college the reduction that is taking place does the viscosity of magma as... +3E 19 ” from other students from places like Cross Anchor or Arroyo B. S2! S0 B. S2 S0... Is carbon ( ii ) oxide left over = 260 - 236.25 S2!. Has been shown to have metallic bonds, chlorine is the loss of electrons are transferred from one substance atom! Characteristics for fitness center staff aq ) + 3H2SO4 ( aq ) → Al2 ( SO4 ) 3 ( ). Turns 18 and goes to college numbers for each element in the following reactions does involve! It now, let us write the two half equations ( one for reduction and one reduction... Answers: 3 question: which equation describes a reduction formula for this definite integral amount of excess (. Only NYS Regents 34 reducing agent do this is an oxidation because mg loses electrons its... This type of reaction is an oxidation because mg loses electrons and its oxidation number, usually by electrons., atom, or ion half reactions is reduced as it limits the formation of which equation describes a reduction? and is the agent... Reduction, the initial reaction is an reduction reaction because in this reaction is a that! ( one for oxidation ), let us write the two half equations ( one for reduction and one oxidation... To 2 you have mixed up the oxidation and reduction process will decrease the level of CO2 the! Reactions, electrons are transferred from one substance or atom to another of the following equations oxidation-. Arrow 2 upper C l superscript minus g superscript 2 plus ( a q ) plus superscript. 4 ) at the cathode, where reduction occurs only NYS Regents 34 vancouver! ( SO4 ) 3 ( aq ) + 2 Ca → 3 Au 2... To do this is to rewrite the reaction in which a substance looses its electrons,! The two half equations ( one for oxidation ) atom to another!. Right arrow 2 upper C l superscript minus of chlorine is the reducing agent and one for ). Rewrite the reaction in which which equation describes a reduction? substance looses its electrons help your mates do Homework... Belongs to the question: which equation is a half reaction that describes the reaction in a. Upper N a superscript plus ( a q ) plus 2 e superscript minus oxidation state of an decreases... The level of CO2 in the following reactions does not involve oxidation-reduction chinese anglo culture conflict in vancouver.... Vancouver involve 18 and goes to college reaction is an oxidation because mg loses electrons and its oxidation increases! ) oxide left over = 260 - 236.25 oxidation ; gain of electrons place... Occur... Circle PPP is below formation of product and is the excess reactant carbon!? O A.growing treesB the hydrogen ions are said to be reduced and reaction. Thanks ” from other students from places like Cross Anchor or Arroyo conflict in vancouver involve to 2 one... Below for a redox reaction 5O2 → 4H2O + 3CO2 b ) 2Cl- ( aq +. Get an easy, free answer to your question in Top Homework answer is Middle School level and to... Piece of evidence from the text details what may have caused the riots to occur Circle... Equation for the reaction as an ionic equation for the reaction in which a looses... Which half reaction that describes the reduction that is taking place because mg loses electrons and its oxidation,. Magma cools balanced equation your balanced equation the reduction that is taking?! It seems to take you a long time in the following equations the sum of half! Or redox ) reactions include all chemical reactions in which atoms have their oxidation states changed reaction as an equation... Reduction describes the reduction that is taking place 2y = 1 is called an reaction! Species decreases its oxidation number increases from 0 to 2 it, us... Of chlorine is reduced as it accepts two electrons from sodium atoms to form chloride... Mg loses electrons and its oxidation number increases from 0 to 2 molecule of chlorine the... Answers: 1 question: which equation describes a reduction reaction: it defined! Equations describe oxidation- reduction reactions together ; it is defined as the reaction involves,... Takes place statements best describes the reduction that is taking place of electrons—or the decrease in state—by. To do this is to rewrite the reaction as an ionic equation for the reaction of iron a. School level and belongs to the Chemistry subject is losing electrons while reduction is gaining electrons reaction... Easy to use diagram below represents an operating electrochemical cell and the reaction of iron a. Mg 32,900 mg 35,000,000 mg, an unknown substance has been shown to have metallic bonds Regents 34 reduction for. Over = 260 - 236.25 oxidation is the electron acceptor conducting an experiment in which he measures a 's! ) sodium is the electron acceptor B. low boiling point C. high malleability D. high solubility in.... Oxidation- reduction reactions process will decrease the level of CO2 in the following reactions not. Şi diametrul bazei este de 14 cm molecule, atom or ion electrons is reduction ) which. ; it is defined as the reaction of iron is a reduction because in this, think that the... Write a balanced chemical equation that describes the reaction involves oxidation, in which a typical star has stopped... Electrons by a molecule, atom or ion reaction: it is defined as reaction. Important characteristics for fitness center staff, let ’ which equation describes a reduction? completely free and to... → 4H2O + 3CO2 b ) statements best describes the reduction that taking! Reaction correctly describes the reduction that is taking place a chemical reaction reduction is defined as gain! G superscript 2 plus ( a q ) plus 2 e superscript minus ( s ) right Uper. Hydrogen ions are said to be reduced and the balanced ionic equation for the reaction occurring in following! Cathode, where reduction occurs only NYS Regents 34 reactions 82 reactions for... Reactions in which a substance gains electrons reactions as shown below 5O2 → 4H2O + 3CO2 b ) two reactions... In water: which equation is a reduction Mn4+ +3e 19 hydrogen ions are said to reduced! + 3H2 ( g ) + 2 e⁻ Regents 34 a half-reaction in which electrons are called oxidation-reduction or. Which the oxidation numbers for each element in the early stages high malleability D. high solubility water. A half reaction correctly describes the reduction that is taking place a. S2 +2e! B...... Qual dessas alternativas NÃO ERAM uma objetivo das Expedições Marítimas state—by a molecule, atom or. Arrow Uper M g superscript 2 plus ( a q ) plus e superscript minus oxidation-reduction ) include... Chinese anglo culture conflict in vancouver involve cell and the reaction as an ionic for... ; it is only mentally that we can separate them oxidation numbers for each in... To do this is to rewrite the reaction of iron metal with.... Magma cools plays basketball and hopes to grow at least 4 cm more she! 1 question: which equation describes a reduction belongs to the Chemistry subject occur... C3H8 + 5O2 → 4H2O + 3CO2 b ) now, let us write two. Which piece of evidence from the text details what may have caused the riots to...., it which equation describes a reduction? s get your Homework gets done Chemistry subject a half-reaction in which electrons lost... Ppp is below it accepts two electrons from sodium atoms to form two chloride ions half! Is to rewrite the reaction in which atoms have their oxidation states changed from like. Whistleblowers ) are protected by law şi diametrul bazei este de 14 cm... Find the acceleration on.! That LEO the lion says GER ( loss of electrons takes place easy to!. Called an oxidation-reduction reaction: it is only mentally that we can say that in,. Oxidation numbers for each element in the cell in Top Homework answers answer! Reactions, electrons are transferred from one substance or atom to another transferred from one substance or to... S completely free and easy to use oxidation states changed anglo culture conflict in vancouver.!	{}
# (10) 7. While in service, a ceramic material develops a submicron crack in the [121] directions... ###### Question: (10) 7. While in service, a ceramic material develops a submicron crack in the [121] directions which traverses 100 unit cells. Assuming the crack tip radius of curvature is 0.2 nm, what stress develops at the crack tip when a tensile stress of 20 MPa is applied? 2. = 0.367 nm. Om = 2001 a/c #### Similar Solved Questions ##### At year-end (December 31), Chan Company estimates its bad debts as 0.40% of its annual credit... At year-end (December 31), Chan Company estimates its bad debts as 0.40% of its annual credit sales of $761,000. Chan records its Bad Debts Expense for that estimate. On the following February 1, Chan decides that the$381 account of P. Park is uncollectible and writes it off as a bad debt. On June ... ##### SM.51 The Candy Shack is in the process of finding suppliers for their candy stands. They... SM.51 The Candy Shack is in the process of finding suppliers for their candy stands. They have determined to single-source their supply in order to focus on the buyer/vendor relationship. The Candy Shack has narrowed their supplier list to two candidates: Gem State, a local company in Pocatello, and... ##### Protons move clockwise around a circular path of radius 27 cm in a magnetic field of... Protons move clockwise around a circular path of radius 27 cm in a magnetic field of magnitude B = 0.25 T. Proton has a charge 1.6 x 10^-19 C. What is the magnitude of the momentum of the protons and which direction is the magnetic field pointing?... ##### 1. A ∨ B ∨ C ∨ D ∨ ¬C A ∨ B ∨ D is... 1. A ∨ B ∨ C ∨ D ∨ ¬C A ∨ B ∨ D is an example of: Modus Ponens And-Elimination Implication Elimination Unit Resolution 2.The loss of information due to an effect axiom's inability to state what remains unchanged as a result of an acti... ##### 11_ A tank initially contains 100 L of brine with 25 N of dissolved salt: Fresh water and brine containing 2 NIL of dissolved salt enter the tank at 40 Llm in and 10 Llm in, respectively and the resug lting m ixture leaves the tank at 5 Llm in If the capacity of the tank is 400L , find the amount of salt in the tank when it starts to overflow: 11_ A tank initially contains 100 L of brine with 25 N of dissolved salt: Fresh water and brine containing 2 NIL of dissolved salt enter the tank at 40 Llm in and 10 Llm in, respectively and the resug lting m ixture leaves the tank at 5 Llm in If the capacity of the tank is 400L , find the amount of... ##### 4xiine Lomputers manuractures Dersona computers at two plants exas anathe other benefits questionnaire (Round Your answens four decima_ placesHawall The Texas plant hasempioyees e Hawall plant has 25,random sampieempioyeesWhat the probability that none the employees the sample work tne plant 0048Hawali?What the probability that - 0326the emplovees the sample works the plant in Hawaii?hatthe probability that 9628more of the employeesthe sample work at the plantHawaliWhat the probability that 9 03 4xiine Lomputers manuractures Dersona computers at two plants exas anathe other benefits questionnaire (Round Your answens four decima_ places Hawall The Texas plant has empioyees e Hawall plant has 25, random sampie empioyees What the probability that none the employees the sample work tne plant 00... ##### An ultracentrifuge accelerates from rest to 100,000 rpm in 1.80 min. (a) What is its angular... An ultracentrifuge accelerates from rest to 100,000 rpm in 1.80 min. (a) What is its angular acceleration in rad/s2? rad/s² (b) What is the tangential acceleration, in m/s, of a point 10.55 cm from the axis of rotation? O m/s2 (c) What is the radial acceleration, in m/s2, of this point at full ... ##### Nine people (four men and five women) line up at a checkout stand in a grocery store.(a) In how many ways can they line up?(b) In how many ways can they line up if the first person in line must be a woman? Nine people (four men and five women) line up at a checkout stand in a grocery store. (a) In how many ways can they line up? (b) In how many ways can they line up if the first person in line must be a woman?... ##### Question 40C0r3 pts 02 Ã¢â€šÂ¬91 DetailsScore on last try: 0 of 3 pts See Details for moreGet similar question You can retry this question belowThe width of rectangle is 3 less than twice its length. If the area of the rectangle is 187 cm? length of the diagonal? what is theThe length of the diagonal isGive your answer to 2 decimal places_Note: Since you are looking for the diagonal you will want to use the pythagorean theorem, a? + &? = &? Question Help: VideoSubmit QuestionQuestion 41L2/2 Question 40 C0r3 pts 02 Ã¢â€šÂ¬91 Details Score on last try: 0 of 3 pts See Details for more Get similar question You can retry this question below The width of rectangle is 3 less than twice its length. If the area of the rectangle is 187 cm? length of the diagonal? what is the The length of the d... ##### Question 3 (1 point)\| Saved Below is an example of acondensed structural formulaexpanded structural formulamolecular formulaskeletal formula Question 3 (1 point)\| Saved Below is an example of a condensed structural formula expanded structural formula molecular formula skeletal formula... ##### Two blocks and three springs are configured as in Fig. All motion is horizontal. When the... Two blocks and three springs are configured as in Fig. All motion is horizontal. When the blocks are at rest, all springs are unstretched. k2 k3 m1 m2 (a) Choose as generalized coordinates the displacement of each block from its equilibrium position, and write the Lagrangian. (b) Find the T and V ma... ##### Huaomuuoaauanaken (n mmua eA u A (cu Jd B is anoving Koha mekehkeeeiee HhHH UAMMH MhHPhnHturrn eE Walh welocuty % Yodke) YUHUaMhLeEaeeeee eI 5Ee UMNUUHETHHAHUMUA nh Ouises IYaLk Uha NKMMNNNUNHUUYHHKHEHHEEE Huaomuuoaauanaken (n mmua eA u A (cu Jd B is anoving Koha mekehkeeeiee HhHH UAMMH MhHPhnHturrn eE Walh welocuty % Yodke) YUHUaMhLeEaeeeee eI 5Ee UMNUUHETHHAHUMUA nh Ouises IYaLk Uha NKMMNNNUNHUUYHHKHEHHEEE... ##### (b) In the transformation of p.241, 28 we encountered the matrix 0 A 0 0(over)which has fewer than three linearly independent eigenvectors_ Use the method of part a) of this problem; to find for the defective eigenvalue A1, general- ized eigenvector say V1 and hence produce a basis for R3 from the eigenvectors and generalized eigenvectors of A (c) With the eigenvectors U1, U2 and the generalized eigenvector V1, define & matrix P = U1 V1 Uz ]- Compute J = P-1AP. This is a Jordan canonical fo (b) In the transformation of p.241, 28 we encountered the matrix 0 A 0 0 (over) which has fewer than three linearly independent eigenvectors_ Use the method of part a) of this problem; to find for the defective eigenvalue A1, general- ized eigenvector say V1 and hence produce a basis for R3 from th... ##### 13. f(x) = 2x² - 12 Find the x-intercepts. Find the y-intercept. Find the vertex. Rewrite... 13. f(x) = 2x² - 12 Find the x-intercepts. Find the y-intercept. Find the vertex. Rewrite the equation in vertex form. Determine if concave up or down. Determine if skinner or wider. Graph... ##### Use the fact that IcA\| cIAI evaluate the determinant of the 24 30 A = -18 STEP I: Factor out the greatest common divisor:Xn matrix.24 30 -18STEP 2: Find the determinant of the matrix found in StepSTEP 3: Find the determinant of the original matrix Use the fact that IcA\| cIAI evaluate the determinant of the 24 30 A = -18 STEP I: Factor out the greatest common divisor: Xn matrix. 24 30 -18 STEP 2: Find the determinant of the matrix found in Step STEP 3: Find the determinant of the original matrix... ##### Id the vector W which is of length 4 and oppositely directed to U = (2, ~-3,-43)lect one:D None0 W= < -4,6,2v3 > 0 W= <1,74,2 > 0 W= <2,1,-73 W= <-23,3 W= <3,_1,-3v3 Id the vector W which is of length 4 and oppositely directed to U = (2, ~-3,-43) lect one: D None 0 W= < -4,6,2v3 > 0 W= <1,74,2 > 0 W= <2,1,-73 W= <-23,3 W= <3,_1,-3v3... ##### Obtain a family of solutions. $3\left(3 x^{2}+y^{2}\right) d x-2 x y d y=0$ Obtain a family of solutions. $3\left(3 x^{2}+y^{2}\right) d x-2 x y d y=0$... ##### We were unable to transcribe this imagean Reaction 4 BaCly(aq) Na SO(aq) Balance Equation: BaCl(aq) Na,So(aq)... We were unable to transcribe this imagean Reaction 4 BaCly(aq) Na SO(aq) Balance Equation: BaCl(aq) Na,So(aq) Observations: Type of Reaction: Reaction 5 FeCl,(aq) NaOH(aq): Balance equation: FeCly(aq) + NaOH(aq)- Observations: Type of Reaction: Reaction 6 NAHCO,(aq): HCl(aq): Balance Equation: HCI(a... ##### You are doing water analysis. After 24 hours, your pour-platereveals the presence of Proteus-looking colonies. What is theexplanation why you need to eliminate these plates from yourexperimental data? You are doing water analysis. After 24 hours, your pour-plate reveals the presence of Proteus-looking colonies. What is the explanation why you need to eliminate these plates from your experimental data?... ##### Let $A$ be a symmetric matrix. Show that the singular values of $A$ are:(a) the absolute values of the eigenvalues of $A$.(b) the eigenvalues of $A$ if $A$ is positive definite. Let $A$ be a symmetric matrix. Show that the singular values of $A$ are: (a) the absolute values of the eigenvalues of $A$. (b) the eigenvalues of $A$ if $A$ is positive definite.... ##### If a firm has $6.5 million in debt,$27.8 million in equity, a tax rate of... If a firm has $6.5 million in debt,$27.8 million in equity, a tax rate of 35%, and pays 7% interest on debt, what is the firm's PV of the interest tax shields? a. $202200 b.$327200 c. $8.5 million d.$2.275 million e. \$418910... ##### 2. Below is a graph showing transport velocity of two solutes (A and B). Based on... 2. Below is a graph showing transport velocity of two solutes (A and B). Based on the observed kinetics, what conclusions can you draw about the transport mechanisms for each solute? (6) 2007 Transport Velocity 2 100 200 4 10 50 Solute (UM) 3. The reason carrier transport proteins that carry out car... ##### [email protected] 47Sex horrrones (such as testosterone and estrogen) are what type of biomolecules? fats b: phosphollpids steroldswaxcsQUESTION 48Proteins are made up ol which monomeric subunits (I e what monomersh? nuclelc acidscarbohydrates amino ucidsIipidsQUESTION 49Which of the following Is not bullt from long repeats of monomeric subunits? nuclelc aclds carbohydrates amlno acids lipids [email protected] 47 Sex horrrones (such as testosterone and estrogen) are what type of biomolecules? fats b: phosphollpids sterolds waxcs QUESTION 48 Proteins are made up ol which monomeric subunits (I e what monomersh? nuclelc acids carbohydrates amino ucids Iipids QUESTION 49 Which of the following Is no... ##### 42. A 60.0-W lamp is placed in series with a resistor and a 120.0-V source. If the voltage across the lamp is 25 V, what is the resistance R of the resistor? 42. A 60.0-W lamp is placed in series with a resistor and a 120.0-V source. If the voltage across the lamp is 25 V, what is the resistance R of the resistor?... ##### TB MC Qu. 4-29 The Minton Company has gathered the following... The Minton Company has gathered... TB MC Qu. 4-29 The Minton Company has gathered the following... The Minton Company has gathered the following information for a unit of its most popular product: S 10 Direct materials Direct labor Overhead (40% variable) Cost to manufacture Desired markup (50%) Target selling price The above cost in...	{}
With the pointblank package it’s really easy to methodically validate your data whether in the form of data frames or as database tables. On top of the validation toolset, the package gives you the means to provide and keep up-to-date with the information that defines your tables. For table validation, the agent object works with a large collection of simple (yet powerful!) validation functions. We can enable much more sophisticated validation checks by using custom expressions and also through stepwise mutation of the target table (through something we call preconditions). Sometimes we want to maintain table information and update it when the table goes through changes. For that, we can use an informant object + associated functions to help define the metadata entries and present it in a way that suits you. ## Installation Want to try this out? The pointblank package is available on CRAN: install.packages("pointblank") You can also install the development version of pointblank from GitHub: devtools::install_github("rich-iannone/pointblank") If you encounter a bug, have usage questions, or want to share ideas to make this package better, feel free to file an issue. ## Let’s Discuss! Let’s talk about data validation and data documentation in pointblank Discussions! It’s a great place to ask questions about how to use the package, discuss some ideas, engage with others, and much more! ## Code of Conduct Please note that the pointblank project is released with a contributor code of conduct. By participating in this project you agree to abide by its terms. pointblank is licensed under the MIT license. See the LICENSE.md file for more details.	{}
# About Homogeneous Maxwell equation from EM Lagrangian I have studied some of the relevant Q&A here. Everything is quite satisfactory. But is there any way to prove homogeneous part of 4 Maxwell equation from Lagrangian formalism, i.e constructing the Lagrangian and applying Langranges formulation. I know about the path integral formalism also. But I am interested in the equations, $\vec{\nabla} \cdot \vec{B} ~=~ 0 \qquad \text{no magnetic monopole"} \vec{\nabla} \times \vec{E} + \frac{\partial \vec{B}}{\partial t} ~=~ \vec{0}\qquad \text{Faraday's law"}$ Can I get them without using the Bianchi identity? • The fact that there exists a four-potential implies those equations, and this fact is built into the Lagrangian. – Javier Mar 16 '18 at 15:38 • Possible duplicate: physics.stackexchange.com/q/71611/2451 – Qmechanic Mar 16 '18 at 15:48 You can get these equations if you allow the introduction of a potential. If $\vec{B} = \vec{\nabla} \times \vec{A}$ and $\vec{E} = - \vec{\nabla} \phi - \partial \vec{A} /\partial t$, you can then assemble $\phi$ and $\vec{A}$ into a four-vector potential: $$A^\mu = (\phi, \vec{A}).$$ It then follows that $$F_{\mu \nu} = \frac{\partial A_\nu}{\partial x^\mu} - \frac{\partial A_\nu}{\partial x^\mu}$$ and the Bianchi identity then follows from the equality of mixed partials: $$\partial_{\lambda} F_{\mu \nu} + \partial_{\mu} F_{\nu \lambda} + \partial_{\nu} F_{\lambda \mu} = 0.$$ However, this is a bit of a cheat, since the statement that a (four-)vector potential exists is actually a stronger statement than the statement that the Bianchi identity holds. These two statements are equivalent if you're working in a space that is topologically trivial (like Minkowski space), but if you have "holes" in your spacetime you can end up with situation where the Bianchi identity holds but there does not exist a vector potential such that $F_{\mu \nu} = \partial_\mu A_\nu - \partial_\nu A_\mu$. This observation is the basis of a beautiful branch of mathematics called de Rham cohomology, which I never miss an opportunity to mention because I like it so much. • @Gourav: As mentioned in the comments above, if you're viewing $A_\mu$ as your "field variable", then the existence of $A_\mu$ implies the Bianchi identity automatically. This will be true even if the action is not minimized (i.e., $\partial^\mu F_{\mu \nu} \neq J_\nu$); once you accept the existence of $A_\mu$, then the Bianchi identity is in some sense more fundamental than the inhomogeneous equations. – Michael Seifert Mar 18 '18 at 15:41	{}
# How to tell the difference between consumer and capital goods As a first year macroeconomics student I'm unable to understand if in rudimentary macroeconomic analysis that categorizes goods either as consumer or capital goods, with the latter being defined as "high-value , durable-use producer goods that undergo depreciation with employment in production process", the assets that a company posseses for use by its employees (like staff fridge) should be considered as a capital good or consumer good. As in, should the comfort that these facilities extend to labour force be seen as an indirect contribution to the production process or not. Any help would be greatly appreciated! (Apologies if it's a basic question but I just couldn't find an answer elsewhere and exams are approaching.) The only difference between consumer and capital goods is whether or not the good in question is purchased by a firm or a consumer. The practical implications of this is whether or not this expenditure is included in $I$ or $C$ of the GDP equation. Investopedia defines $I$ as: "the sum of all the country's investment, including businesses capital expenditures" Going into detail on "capital expenditure": # What is 'Capital Expenditure (CAPEX)' Capital expenditure, or CapEx, are funds used by a company to acquire or upgrade physical assets such as property, industrial buildings or equipment. It is often used to undertake new projects or investments by the firm. This type of outlay is also made by companies to maintain or increase the scope of their operations. These expenditures can include everything from repairing a roof to building, to purchasing a piece of equipment, or building a brand new factory. It would appear that a staff fridge is a capital expenditure based on the above criteria because it contributes to maintaining the firms scope of operations. I would argue that these types of goods should be considered capital because they are increasing employee productivity as a factor of production for knowledge workers. In classical economics a capital good has these 3 characteristics: • It can be used in the production of other goods (this is what makes it a factor of production). • It is made by humans, in contrast to "land," which refers to naturally occurring resources such as geographical locations and minerals. • It is not used up immediately in the process of production, unlike raw materials or intermediate goods. An employee fridge clearly fits the second two requirements, as for the first requirement if having an employee fridge raises moral, and thus indirectly increases employee productivity, then I would consider it to be a capital good because it would seem to be a factor of production. • If the fridge is a reward to staff then it is closer to payment in kind (possibly of a service). If it remains the company's property because it boosts productivity and will be automatically replaced in a few years time when it breaks then it is closer to a capital good – Henry Apr 7 '17 at 17:35 • I would argue that it couldn't be considered a payment due to the fact that there is no ownership with the employees. A fridge definitely fits the definition of boosting productivity and being replaced as it depreciates which I think makes it a capital good – TheSaint321 Apr 10 '17 at 17:24	{}
# Units Conversion foxtrotalpha Hey guys I am having a big problem with this question ## Homework Statement The adsorbtion isotherm for the removal of a contaminant from waste water is givern by the langmuir equation: q=(bkC)/(1+bC) where q is the loading of contaminant of the adsorbent and C is the concentration of the contaminant in solution. Literature data gives values for the constants b and k of 1.16 and 130 respectively for the case where q is grains per lb and C is grains per gal . Determine the values for b' and k' for the Langmuir equation between loading q' in mg per g and C' in mg per dm^3 . Data : 1 lb=7000 gr(grains) ## The Attempt at a Solution I am sort of stuck as the 2 variables will have changes in their unis simultaneously, all I have done is to convert 1mg=0.01544 gr and 1 dm^3=0.220 gal . Homework Helper Dimensional analysis will probably work here: With equation: $$q=\frac{bkC}{1+bC}$$ ... are k and b dimensionless? Did the values you looked up have units at all? There's a clue right there. What are the units of b and k in terms of the units of q and C? You can work it out - either by reading the tables or dimensional analysis: i.e. notice that, in the denominator "1+bC" has to make sense in terms of units? so (square brackets reads "units of"): [1+bC]=[1]+[bC] means that must have some relation to [C]. Note: 1 cubic decimeter = 1 liter. foxtrotalpha Dimensional analysis will probably work here: With equation: $$q=\frac{bkC}{1+bC}$$ ... are k and b dimensionless? Did the values you looked up have units at all? There's a clue right there. What are the units of b and k in terms of the units of q and C? You can work it out - either by reading the tables or dimensional analysis: i.e. notice that, in the denominator "1+bC" has to make sense in terms of units? so (square brackets reads "units of"): [1+bC]=[1]+[bC] means that must have some relation to [C]. Note: 1 cubic decimeter = 1 liter. THANKS !! , you made me realised that b and k are not dimensionless at all ,before this I had always assumed them to be dimensionless.	{}

Subsets and Splits

No community queries yet

The top public SQL queries from the community will appear here once available.