arxiv_id
stringlengths 0
16
| text
stringlengths 10
1.65M
|
|---|---|
for Journals by Title or ISSN for Articles by Keywords help
Subjects -> STATISTICS (Total: 130 journals)
The end of the list has been reached or no journals were found for your choice.
Metrika [SJR: 0.605] [H-I: 30] [4 followers] Follow Hybrid journal (It can contain Open Access articles) ISSN (Print) 1435-926X - ISSN (Online) 0026-1335 Published by Springer-Verlag [2352 journals]
• Nonparametric estimation for self-selected interval data collected through
a two-stage approach
• Authors: Angel G. Angelov; Magnus Ekström
Pages: 377 - 399
Abstract: Abstract Self-selected interval data arise in questionnaire surveys when respondents are free to answer with any interval without having pre-specified ranges. This type of data is a special case of interval-censored data in which the assumption of noninformative censoring is violated, and thus the standard methods for interval-censored data (e.g. Turnbull’s estimator) are not appropriate because they can produce biased results. Based on a certain sampling scheme, this paper suggests a nonparametric maximum likelihood estimator of the underlying distribution function. The consistency of the estimator is proven under general assumptions, and an iterative procedure for finding the estimate is proposed. The performance of the method is investigated in a simulation study.
PubDate: 2017-05-01
DOI: 10.1007/s00184-017-0610-7
Issue No: Vol. 80, No. 4 (2017)
• Efficient paired choice designs with fewer choice pairs
• Authors: Aloke Dey; Rakhi Singh; Ashish Das
Pages: 309 - 317
Abstract: Abstract For paired choice experiments, two new construction methods of designs are proposed for the estimation of the main effects. In many cases, these designs require about 30–50% fewer choice pairs than the existing designs and at the same time have reasonably high D-efficiencies for the estimation of the main effects. Furthermore, as against the existing efficient designs, our designs have higher D-efficiencies for the same number of choice pairs.
PubDate: 2017-04-01
DOI: 10.1007/s00184-016-0605-9
Issue No: Vol. 80, No. 3 (2017)
• Exact inference for the difference of Laplace location parameters
• Authors: Maria Tafiadi; George Iliopoulos
Abstract: Abstract We consider exact procedures for testing the equality of means (location parameters) of two Laplace populations with equal scale parameters based on corresponding independent random samples. The test statistics are based on either the maximum likelihood estimators or the best linear unbiased estimators of the Laplace parameters. By conditioning on certain quantities we manage to express their exact distributions as mixtures of ratios of linear combinations of standard exponential random variables. This allows us to find their exact quantiles and tabulate them for several sample sizes. The powers of the tests are compared either numerically or by simulation. Exact confidence intervals for the difference of the means corresponding to those tests are also constructed. The exact procedures are illustrated via a real data example.
PubDate: 2017-10-10
DOI: 10.1007/s00184-017-0630-3
• Adjusted Pearson Chi-Square feature screening for multi-classification
with ultrahigh dimensional data
• Authors: Lyu Ni; Fang Fang; Fangjiao Wan
Abstract: Abstract Huang et al. (J Bus Econ Stat 32:237–244, 2014) first proposed a Pearson Chi-Square based feature screening procedure tailored to multi-classification problem with ultrahigh dimensional categorical covariates, which is a common problem in practice but has seldom been discussed in the literature. However, their work establishes the sure screening property only in a limited setting. Moreover, the p value based adjustments when the number of categories involved by each covariate is different do not work well in several practical situations. In this paper, we propose an adjusted Pearson Chi-Square feature screening procedure and a modified method for tuning parameter selection. Theoretically, we establish the sure screening property of the proposed method in general settings. Empirically, the proposed method is more successful than Pearson Chi-Square feature screening in handling non-equal numbers of covariate categories in finite samples. Results of three simulation studies and one real data analysis are presented. Our work together with Huang et al. (J Bus Econ Stat 32:237–244, 2014) establishes a solid theoretical foundation and empirical evidence for the family of Pearson Chi-Square based feature screening methods.
PubDate: 2017-10-07
DOI: 10.1007/s00184-017-0629-9
• Stochastic comparisons of order statistics from heterogeneous random
variables with Archimedean copula
• Authors: M. Mesfioui; M. Kayid; S. Izadkhah
Abstract: Abstract This article is devoted to characterize several ordering properties of the maximum order statistic of heterogenous random variables with an Archimedean copula. Some examples are also included to illustrate the obtained results.
PubDate: 2017-10-03
DOI: 10.1007/s00184-017-0626-z
• Multivariate saddlepoint tests on the mean direction of the von
Mises–Fisher distribution
• Authors: R. Gatto
Abstract: Abstract This article provides P values for two new tests on the mean direction of the von Mises–Fisher distribution. The test statistics are obtained from the exponent of the saddlepoint approximation to the density of M-estimators, as suggested by Robinson et al. (Ann Stat 31:1154–1169, 2003). These test statistics are chi-square distributed with asymptotically small relative errors. Despite the high dimensionality of the problem, the proposed P values are accurate and simple to compute. The numerical precision of the P values of the new tests is illustrated by some simulation studies.
PubDate: 2017-09-13
DOI: 10.1007/s00184-017-0625-0
• R-optimal designs for multi-factor models with heteroscedastic errors
• Authors: Lei He; Rong-Xian Yue
Abstract: Abstract In this paper, we consider the R-optimal design problem for multi-factor regression models with heteroscedastic errors. It is shown that a R-optimal design for the heteroscedastic Kronecker product model is given by the product of the R-optimal designs for the marginal one-factor models. However, R-optimal designs for the additive models can be constructed from R-optimal designs for the one-factor models only if sufficient conditions are satisfied. Several examples are presented to illustrate and check optimal designs based on R-optimality criterion.
PubDate: 2017-08-02
DOI: 10.1007/s00184-017-0624-1
• Estimating moments in ANOVA-type mixed models
• Authors: Zaixing Li; Fei Chen; Lixing Zhu
Abstract: Abstract In the paper, a simple projection-based method is systematically developed to estimate the qth ( $$q\ge 2$$ ) order moments of random effects and errors in the ANOVA type mixed model (ANOVAMM), where the response may not be divided into independent sub-vectors. All the estimates are weakly consistent and the second-order moment estimates are strongly consistent. Besides, the derived estimates are different from those in mixed models with cluster design. Simulation studies are conducted to examine the finite sample performance of the estimates and two real data examples are analyzed for illustration.
PubDate: 2017-08-02
DOI: 10.1007/s00184-017-0623-2
• Some general points on the $$I^2$$ I 2 -measure of heterogeneity in
meta-analysis
• Authors: Dankmar Böhning; Rattana Lerdsuwansri; Heinz Holling
Abstract: Abstract Meta-analysis has developed to be a most important tool in evaluation research. Heterogeneity is an issue that is present in almost any meta-analysis. However, the magnitude of heterogeneity differs across meta-analyses. In this respect, Higgins’ $$I^2$$ has emerged to be one of the most used and, potentially, one of the most useful measures as it provides quantification of the amount of heterogeneity involved in a given meta-analysis. Higgins’ $$I^2$$ is conventionally interpreted, in the sense of a variance component analysis, as the proportion of total variance due to heterogeneity. However, this interpretation is not entirely justified as the second part involved in defining the total variation, usually denoted as $$s^2$$ , is not an average of the study-specific variances, but in fact some other function of the study-specific variances. We show that $$s^2$$ is asymptotically identical to the harmonic mean of the study-specific variances and, for any number of studies, is at least as large as the harmonic mean with the inequality being sharp if all study-specific variances agree. This justifies, from our point of view, the interpretation of explained variance, at least for meta-analyses with larger number of component studies or small variation in study-specific variances. These points are illustrated by a number of empirical meta-analyses as well as simulation work.
PubDate: 2017-07-22
DOI: 10.1007/s00184-017-0622-3
• Multidimensional strong large deviation results
• Authors: Cyrille Joutard
Abstract: Abstract We establish strong large deviation results for an arbitrary sequence of random vectors under some assumptions on the normalized cumulant generating function. In other words, we give asymptotic approximations for a multivariate tail probability of the same kind as the one obtained by Bahadur and Rao (Ann Math Stat 31:1015–1027, 1960) for the sample mean (in the one-dimensional case). The proof of our results follows the same lines as in Chaganty and Sethuraman (J Stat Plan Inference, 55:265–280, 1996). We also present three statistical applications to illustrate our results, the first one dealing with a vector of independent sample variances, the second one with a Gaussian multiple linear regression model and the third one with the multivariate Nadaraya–Watson estimator. Some numerical results are also presented for the first two applications.
PubDate: 2017-07-15
DOI: 10.1007/s00184-017-0621-4
• A new measure of association between random variables
Abstract: Abstract We propose a new measure of association between two continuous random variables X and Y based on the covariance between X and the log-odds rate associated to Y. The proposed index of correlation lies in the range [ $$-1$$ , 1]. We show that the extremes of the range, i.e., $$-1$$ and 1, are attainable by the Fr $$\acute{\mathrm{e}}$$ chet bivariate minimal and maximal distributions, respectively. It is also shown that if X and Y have bivariate normal distribution, the resulting measure of correlation equals the Pearson correlation coefficient $$\rho$$ . Some interpretations and relationships to other variability measures are presented. Among others, it is shown that for non-negative random variables the proposed association measure can be represented in terms of the mean residual and mean inactivity functions. Some illustrative examples are also provided.
PubDate: 2017-07-03
DOI: 10.1007/s00184-017-0620-5
• Stochastic comparisons of distorted distributions, coherent systems and
mixtures with ordered components
• Authors: Jorge Navarro; Yolanda del Águila
Abstract: Abstract A distribution function F is a generalized distorted distribution of the distribution functions $$F_1,\ldots ,F_n$$ if $$F=Q(F_1,\ldots ,F_n)$$ for an increasing continuous distortion function Q such that $$Q(0,\ldots ,0)=0$$ and $$Q(1,\ldots ,1)=1$$ . In this paper, necessary and sufficient conditions for the stochastic (ST) and the hazard rate (HR) orderings of generalized distorted distributions are provided when the distributions $$F_1,\ldots ,F_n$$ are ordered. These results are used to obtain distribution-free ordering properties for coherent systems with heterogeneous components. In particular, we determine all the ST and HR orderings for coherent systems with 1–3 independent components. We also compare systems with dependent components. The results on distorted distributions are also used to get comparisons of finite mixtures.
PubDate: 2017-06-28
DOI: 10.1007/s00184-017-0619-y
• Weak and strong laws of large numbers for arrays of rowwise END random
variables and their applications
• Authors: Aiting Shen; Andrei Volodin
Abstract: Abstract In the paper, the Marcinkiewicz–Zygmund type moment inequality for extended negatively dependent (END, in short) random variables is established. Under some suitable conditions of uniform integrability, the $$L_r$$ convergence, weak law of large numbers and strong law of large numbers for usual normed sums and weighted sums of arrays of rowwise END random variables are investigated by using the Marcinkiewicz–Zygmund type moment inequality. In addition, some applications of the $$L_r$$ convergence, weak and strong laws of large numbers to nonparametric regression models based on END errors are provided. The results obtained in the paper generalize or improve some corresponding ones for negatively associated random variables and negatively orthant dependent random variables.
PubDate: 2017-05-22
DOI: 10.1007/s00184-017-0618-z
• Testing the compounding structure of the CP-INARCH model
• Authors: Christian H. Weiß; Esmeralda Gonçalves; Nazaré Mendes Lopes
Abstract: Abstract A statistical test to distinguish between a Poisson INARCH model and a Compound Poisson INARCH model is proposed, based on the form of the probability generating function of the compounding distribution of the conditional law of the model. For first-order autoregression, the normality of the test statistics’ asymptotic distribution is established, either in the case where the model parameters are specified, or when such parameters are consistently estimated. As the test statistics’ law involves the moments of inverse conditional means of the Compound Poisson INARCH process, the analysis of their existence and calculation is performed by two approaches. For higher-order autoregressions, we use a bootstrap implementation of the test. A simulation study illustrating the finite-sample performance of this test methodology in what concerns its size and power concludes the paper.
PubDate: 2017-05-03
DOI: 10.1007/s00184-017-0617-0
• Focused information criterion and model averaging in censored quantile
regression
• Authors: Jiang Du; Zhongzhan Zhang; Tianfa Xie
Abstract: Abstract In this paper, we study model selection and model averaging for quantile regression with randomly right censored response. We consider a semi-parametric censored quantile regression model without distribution assumptions. Under general conditions, a focused information criterion and a frequentist model averaging estimator are proposed, and theoretical properties of the proposed methods are established. The performances of the procedures are illustrated by extensive simulations and the primary biliary cirrhosis data.
PubDate: 2017-04-29
DOI: 10.1007/s00184-017-0616-1
• Estimation of the order restricted scale parameters for two populations
from the Lomax distribution
• Authors: Constantinos Petropoulos
Abstract: Abstract The usual methods of estimating the unknown parameters of a distribution, use only the information given from the sample data. In many cases, there is, also, another important information for estimating the unknown parameters of our model, such as the order of these parameters, and this last information improves the quality of estimation. In this paper, we deal with the problem of estimating the ordered scale parameters from two populations of the multivariate Lomax distribution, with unknown location parameters. It is proved that the best equivariant estimators of the scale parameters (in the unrestricted case) are not admissible and we construct estimators that improve upon the usual ones (when these parameters are known to be ordered).
PubDate: 2017-03-16
DOI: 10.1007/s00184-017-0615-2
• Minimum distance estimators for count data based on the probability
generating function with applications
• Authors: M. D. Jiménez-Gamero; A. Batsidis
Abstract: Abstract This paper studies properties of parameter estimators obtained by minimizing a distance between the empirical probability generating function and the probability generating function of a model for count data. Specifically, it is shown that, under certain not restrictive conditions, the resulting estimators are consistent and, suitably normalized, asymptotically normal. These properties hold even if the model is misspecified. Three applications of the obtained results are considered. First, we revisit the goodness-of-fit problem for count data and propose a weighted bootstrap estimator of the null distribution of test statistics based on the above cited distance. Second, we give a probability generating function version of the model selection test problem for separate, overlapping and nested families of distributions. Finally, we provide an application to the problem of testing for separate families of distributions. All applications are illustrated with numerical examples.
PubDate: 2017-03-15
DOI: 10.1007/s00184-017-0614-3
• On bending (down and up) property of reliability measures in mixtures
• Authors: F. G. Badía; Ji Hwan Cha
Abstract: Abstract In this paper, we study the bending property of the failure rate, reversed hazard rate, mean residual life and mean inactivity time in mixtures. For those four reliability measures, the weak and strong bending properties are studied and discussed, respectively. The results are illustrated with suitable examples, where most of them are relative to the model of proportional reliability measures.
PubDate: 2017-03-14
DOI: 10.1007/s00184-017-0613-4
• Estimation in generalized bivariate Birnbaum–Saunders models
• Authors: Helton Saulo; N. Balakrishnan; Xiaojun Zhu; Jhon F. B. Gonzales; Jeremias Leão
Abstract: Abstract In this paper, we propose two moment-type estimation methods for the parameters of the generalized bivariate Birnbaum–Saunders distribution by taking advantage of some properties of the distribution. The proposed moment-type estimators are easy to compute and always exist uniquely. We derive the asymptotic distributions of these estimators and carry out a simulation study to evaluate the performance of all these estimators. The probability coverages of confidence intervals are also discussed. Finally, two examples are used to illustrate the proposed methods.
PubDate: 2017-03-10
DOI: 10.1007/s00184-017-0612-5
• On generalized progressive hybrid censoring in presence of competing risks
• Authors: Arnab Koley; Debasis Kundu
Abstract: Abstract The progressive Type-II hybrid censoring scheme introduced by Kundu and Joarder (Comput Stat Data Anal 50:2509–2528, 2006), has received some attention in the last few years. One major drawback of this censoring scheme is that very few observations (even no observation at all) may be observed at the end of the experiment. To overcome this problem, Cho et al. (Stat Methodol 23:18–34, 2015) recently introduced generalized progressive censoring which ensures to get a pre specified number of failures. In this paper we analyze generalized progressive censored data in presence of competing risks. For brevity we have considered only two competing causes of failures, and it is assumed that the lifetime of the competing causes follow one parameter exponential distributions with different scale parameters. We obtain the maximum likelihood estimators of the unknown parameters and also provide their exact distributions. Based on the exact distributions of the maximum likelihood estimators exact confidence intervals can be obtained. Asymptotic and bootstrap confidence intervals are also provided for comparison purposes. We further consider the Bayesian analysis of the unknown parameters under a very flexible beta–gamma prior. We provide the Bayes estimates and the associated credible intervals of the unknown parameters based on the above priors. We present extensive simulation results to see the effectiveness of the proposed method and finally one real data set is analyzed for illustrative purpose.
PubDate: 2017-02-24
DOI: 10.1007/s00184-017-0611-6
JournalTOCs
School of Mathematical and Computer Sciences
Heriot-Watt University
Edinburgh, EH14 4AS, UK
Email: journaltocs@hw.ac.uk
Tel: +00 44 (0)131 4513762
Fax: +00 44 (0)131 4513327
Home (Search)
Subjects A-Z
Publishers A-Z
Customise
APIs
|
|
# Page 3 Math: Problem Solving and Data Analysis Study Guide for the SAT® exam
#### Confidence Interval
A confidence interval describes both the degree of accuracy and the uncertainty of an estimated value. On the SAT exam, confidence intervals will be given, and it’s a usually 95% confidence level.
What does it mean when the sample mean height is 121 cm and the margin of error is 1.3 cm at 95% confidence level?
This statement can be interpreted as:
There is 95% confidence that the true average height for the entire population is within the interval 119.7 cm to 122.3 cm. If the same method of estimating the parameter and size of the random sample were repeatedly performed, the actual average height will be within 119.7 cm to 122.3 cm 95% of the time.
An important note:
The confidence interval applies to the parameter (e.g., the mean height of the entire population) and not to the value of the other variable (e.g., number of individuals). In other words, the illustration above cannot be interpreted as: 95% of the population have a height between 119.7 cm and 122.3 cm.
#### Univariate vs. Bivariate Data
Univariate data refers to data sets with one type of variable, such as the number of hot beverages sold by a café. The variable is the number of each type of hot beverage sold. It can be shown in this data set:
(insert here: visual – SAT rev 10 univariate data)
Bivariate data refers to data sets with two types of variables. If the café owner wanted to find a relationship between their sales on a particular day and the temperature on that day, bivariate data can be gathered, such as their sales of the five hot beverages versus the temperature for each day of the week. The variables are the sales and the temperature. It will look something like this:
(insert here: visual – SAT rev 11 bivariate data)
#### Linear, Quadratic, and Exponential Relationships
Variables have a linear relationship when they increase or decrease at a constant rate. As one variable increases the other one decreases, and vice versa. The difference between two adjacent values is constant. When plotted, this is represented by a straight line sloping up or down.
A U-shaped graph facing either upward or downward, indicates a quadratic relationship. The rate of change is variable. There’s either a maximum or minimum value which is seen in the graph as the vertex.
A graph that starts to change very gradually initially (either increasing or decreasing), but suddenly takes a significant change over time, indicates an exponential relationship. An exponential curve does not have a vertex.
#### Variability
Parameters and statistics are estimates used to describe a population or a sample of a population. The numerical values, though, are not the exact actual values but are only the closest estimate. The variability of an estimate against actual values must be accounted for, and this is done by calculating measures of spread.
The spread or scatter of data in a set is measured in various ways, and the most common measures are: range, interquartile range (IQR), variance, and standard deviation. These are ways of describing spread in relation to the estimated value.
#### Randomization
A random sample truly represents its population if it was selected by a purely chance method, also called randomization, and every element of the population has not been excluded in the procedure. By this, we mean that every element of the population has a probability of being included in the sample, and the whole process is protected from biases.
Some of the methods are: using random numbers (e.g., random number table or random number generator, flipping a coin, or throwing a die).
These are important things to remember:
1) Random sampling is necessary so that the result of an experiment can be generalized to the entire population.
2) Random assignment of the subjects to different treatments is also necessary to ensure that all subjects started under generally the same condition before they were subjected to any treatment. This makes it appropriate to draw conclusions about the cause and effect of each treatment.
In the SAT exam, a question may describe a situation regarding the manner of selecting subjects and the manner of assigning them to treatments. The question may then ask which statements can be appropriately drawn from the experiment.
### Specific Skills to Practice
In addition to knowing what math terms mean, you’ll need to be able to use them appropriately and accurately to solve problems. If any of these procedures are difficult for you, seek additional practice until you become fluent and accurate in their use.
#### Solve a Multistep Problem
Just knowing a single procedure is not enough to answer most questions on this test. The SAT exam is really a test of reasoning, as much as math, and a problem often involves several procedures along the way. Here are some examples.
Use a proportion to determine a ratio and rate.
Ratios that are equal are said to be proportionate to each other, such as $\frac{5}{7} and \frac{25}{35}$.
A bowl contains a mixture of 1 cup cornstarch and 4 cups flour. A second bowl contains the same ingredients in the same proportion, but instead has 1.5 cups of cornstarch. If ½ cup of oats is added to the second bowl, what is the ratio of oats to flour in the second bowl?
First, determine the amount of flour in the second bowl, using the same ratio in the first bowl (which is 1:4). We represent the amount of flour with the variable x. Ratios are in proportion if they are equal, so:
The ratio of oats to flour, then is 0.5 is to 6, or 1:12.
Use ratio and rate to solve a multistep problem.
Questions involving ratio and proportion usually ask for an unknown part or component. See this example:
The concrete mix to a floor slab must follow the ratio of 1 part cement, to 3 parts sand, to 3 parts stone aggregates. How many buckets of cement (C) will be needed for a total of 10 buckets of sand and 10 buckets of stone aggregates?
The ratio is 1:3:3 and we need to find C for C:10:10.
We may actually just use the first two parts of each ratio and set the two ratios equal to each other:
Calculate percentage, then solve a problem.
Andy usually buys large Grade A eggs from her supplier at $2.50 per dozen. She chanced upon a farm where the eggs were sold at 70% of this price and bought 10 dozens. How much more would she have paid for the 10 dozens of eggs had she bought from her regular supplier? First, calculate the price of eggs at the farm, which is 70% of$2.50:
Price at the farm = 0.7 x 2.50 = $1.75 Then, we proceed to answer the question being asked. We need to know the price she paid for the whole purchase, the price she would have paid had she bought from her regular supplier, and then solve for the amount she saved.$1.75 is the price for 1 dozen. She bought 10 dozens, so the amount she paid was:
Total amount paid = 1.75 x 10 = $17.50 The price for 10 dozen eggs from her regular supplier: Price from regular supplier = 2.50 x 10 =$25.00
Getting the difference of the two total amounts, we get Andy’s savings:
Amount Andy saved = 25 – 17.50 = $7.50 #### Use Unit Conversion Familiarity with the unit conversion method, also called factor-label method, comes in very handy when dealing with many rate questions and when double-checking answers. Let’s use this method in an actual rate question. Alia has an annual basic salary rate of$53,760. If she works 8 hours a day, 4 days in a week and 4 weeks in a month, what is her hourly rate?
Even without a formula, this can be solved using the unit conversion method.
Start with the given information and take note of the final unit of measure being asked in the question:
$53,760/year = ?$/hour
Using the unit conversion method, simply multiply the given with the conversion factors until you get to the required unit of measurement:
Take note that we deliberately wrote conversion factors in such a manner that similar units canceled out, for example, week units were written as numerator and denominator so that they canceled each other out. This is to say that you may write conversion factors in any way that makes it favorable for you to cancel units out.
The same is true with the other units that we wanted to disappear, leaving us only with the units required in the answer. Also, the conversion factors used were those specifically given in the question, and not those we typically know, such as 1 day = 24 hours.
#### Match Graphs to Properties and Values
You need to sharpen your skills on matching graphs to the properties and values of a data set. Categorical data, such as genre of music preferred by students in a high school, are appropriately presented by pie and bar graphs.
Numerical data, which are either discrete or continuous, are plotted using line graphs, histograms, and scatterplots, such as Company A’s HRD (PLEASE DEFINE THIS TERM) annual expenditures over a 10-year period.
On the SAT exam, you may be given a graph and asked to interpret it. You will need to understand what you see graphically and relate this to important features – the center, spread, and shape.
#### Use Data to Make Inferences
Inferences to the population can be made from results of sample surveys as long as random sampling has been used for the study.
Take this statement for example, “In a survey based on a random sample of students in XY Senior High School, 68% said that they spend at least 7 hours a day on social networks.”
You can correctly infer that “About 68% of all students in XY Senior High School spend at least 7 hours a day on social networks.”
Here’s another inference that can be made:
If the random sample consisted of 100 students out of a total of 1,250 students, and 12 of those surveyed said that they spent less than 3 hours a day on social networks, about how many students at XY Senior High spend less than 3 hours a day on social networks?
A reasonable estimate would be 150 students:
#### Draw Conclusions from Data
A well-designed survey makes it possible to cut the cost and time necessary for a census, and still come up with a result that can be generalized to the entire population. Through random sampling, all elements of the population have a probability of being selected and the result is protected from biases.
Both experiments and observational study investigate the causal relationship between a dependent variable and an independent variable. In experiments, the researcher has control over the participant’s assignment to groups and treatments given to each group; hence, random assignment of subjects can be done. This control is absent in observational study, and findings derived from this method cannot be used for causal inference and generalization to the larger population.
#### Justify Conclusions with Data
Questions in the SAT could ask for the validity of a conclusion based on the data gathered.
Situations could be given such as:
A study proposes the use of a module (let’s say Module A) in a senior high school to improve students’ competency in the area of mathematics. Two other modules were included in the study, including the current module being officially used by the school (Module B). Three groups, each made up of 2 classrooms of Year 11 students, were assigned a module. After two months, students were selected from each group to take a test designed to measure their improvement. A table summarizing the test results could be given in the question, along with other information, from which you can justify the conclusion drawn.
Be prepared to interpret data given in tables and graphs. Do the given data support the conclusion? How were students who took the test chosen? Were there other variables that could have contributed to the test result but were not included in the study? Because the given example refers to a study of cause and effect, were the proper controls in place (i.e., random assignment of subjects)?
These questions must be asked first by the person or the group conducting the study to make sure that their data justify their conclusions.
#### Evaluate Data Collection Methods
It is important to know how the data in a study was obtained because this largely determines whether it is appropriate to draw and apply conclusions to the entire population.
Data are obtained by conducting a census (entire population), survey (random sample), experimental study (cause-and-effect, controlled), and observational study (cause-and-effect, not controlled).
|
|
My Math Forum The counting of p-sylow groups
Abstract Algebra Abstract Algebra Math Forum
July 17th, 2012, 10:55 AM #1 Senior Member Joined: Sep 2011 Posts: 140 Thanks: 0 The counting of p-sylow groups Ok it says that for a group with order G, |G|=60, it has 6 5-sylow subgroups and 10 3-sylow subgroups, and 12,5 2-sylow subgroups. Ok i cant see why this is the case. Because $|G|=60=5*3*2^{2}$, and say that it has a 5-sylow group, then by sylow's third theorem, then there are {1,6,11,......56} by congruence with 1mod(5) right? then the only divisible with the order of |G|=60 is 1 and 6, therefore 2 5-sylow subgroups. Ok maybe i am not doing it right, but isn't this is how you count it? i just dont see how its 6 5-sylow groups. Also how is there a two possibility of a 2-sylow for a order 60 group? can anyone explain it to me? thank you
July 17th, 2012, 10:35 PM #2 Senior Member Joined: Mar 2012 Posts: 294 Thanks: 88 Re: The counting of p-sylow groups a 5-sylow subgroup of a group G of order 60 has order 5. of course, these all intersect in the identity, so if k is the number of 5-sylow subgroups of G, these account for 4k+1 elements of G. by the third sylow theorem, k = 1 (mod 5), and k divides 60, so either k = 1, or k = 6. note that if k = 6, the 5-sylow subgroups only account for 25 elements of G, leaving 35 elements of other orders. let's show that both scenarios actually occur. for a single 5-sylow subgroup, consider (Z60,+), the integers mod 60 under addition modulo 60. the sole subgroup of order 5 is: {0,12,24,36,48} for 6 5-sylow subgroups, consider A5. there are 24 (= 4!) 5-cycles in S5, and all of these are in A5. explicitly we have: <(1 2 3 4 5)> <(1 2 3 5 4)> <(1 2 4 3 5)> <(1 2 4 5 3)> <(1 2 5 3 4)> <(1 2 5 4 3)>, which are 6 distinct subgroups of order 5 in A5. of course a 2-sylow subgroup is possible. such a subgroup has (for a group of order 60) order 4. for a group of order 60, we can have 1,3 5, or 15 of them (these being the odd divisors of 60/4 = 15). again, using our two examples, we see Z60 has just one subgroup of order 4: {0,15,30,45} while A4 has the following: {e, (1 2)(3 4), (1 3)(2 4), (1 4)(2 3)} {e, (1 2)(3 5), (1 3)(2 5), (1 5)(2 3)} {e, (1 2)(4 5), (1 4)(2 5), (1 5)(2 4)} {e, (1 3)(4 5), (1 4)(3 5), (1 5)(3 4)} {e, (2 3)(4 5), (2 4)(3 5), (2 5)(3 4)} which accounts for all possible subgroups of order 4 in A5 (two double 2-cycles which don't move the same 4 elements result in a 3-cycle when multiplied), so we have 5 2-sylow subgroups. you might want to hazard a guess as to how many 2-sylow subgroups D30 (the dihedral group of order 60) has.
Tags counting, groups, psylow
,
,
,
,
,
,
,
,
,
,
,
,
,
,
sylowgroups A4
Click on a term to search for related topics.
Thread Tools Display Modes Linear Mode
Similar Threads Thread Thread Starter Forum Replies Last Post Sheila496 Abstract Algebra 0 October 20th, 2011 09:45 AM WannaBe Abstract Algebra 0 December 22nd, 2009 10:35 AM WannaBe Abstract Algebra 0 December 22nd, 2009 10:34 AM WannaBe Abstract Algebra 0 December 14th, 2009 04:03 AM Kinga Abstract Algebra 1 November 13th, 2007 01:32 AM
Contact - Home - Forums - Cryptocurrency Forum - Top
|
|
Problem Indicate which orbitals overlap to form the $\sig… View Full Video. A description of the hybridization of NH3.Note that the NH3 hybridization is sp3 for the central Nitrogen (N) atom. 9.5: Hybrid Orbitals Last updated; Save as PDF Page ID 21755; Hybridization of s and p Orbitals; Hybridization Using d Orbitals; Summary; The localized valence bond theory uses a process called hybridization, in which atomic orbitals that are similar in energy but not equivalent are combined mathematically to produce sets of equivalent orbitals that are properly oriented to form bonds. Join now. How Many Sigma And Pi Bonds Are There In The Entire Structure? How many hybrid orbitals do we use to describe each molecule? संबंधित वीडियो . The N atom is sp hybridized. Step by step solution Step 1 of 3A tomic orbitals of suitable symmetry and similar energy mix with each other to form neworbitals are called hybrid orbitals. The most common hybrid orbitals are sp 3, sp 2 and sp. Answered How many hybrid orbitals in ch3oh 1 See answer mannysingh2092 is waiting for your help. The N atom has steric number SN = 3. What hybrid orbitals are used by the carbon in CH 3 CH 3? Is The Molecule Polar? Pseudo metals and hybrid metals. Log in. The Lewis structure of HNO shows that it is a hybrid of two structures. How many hybrid orbitals do we use to describe each molecule? The new orbitals formed are called sp 3 hybrid orbitals. The electron geometry is trigonal planar. How to solve: In BBr4-, boron has how many hybrid orbitals and what type of hybridization? Kohn−Sham orbitals and eigenvalues are calculated with gradient-corrected functionals for a set of small molecules (H2O, N2, CrH66-, and PdCl42-), varying basis sets and functionals. The Nitrogen atom is sp² hybridized in HNO3. Relevance. Julie. The bond formed by hybrid orbitals is much more stable than the bond formed by the pure atomic orbitals. HNO3. What Hybrid Orbital Was Used For N? सभी को देखें. The different types of hybridisation are as under : sp hybridisation. Problem 97How many hybrid orbitals do we use to describe each molecule a. The hybridization on the HNO3 is sp^3 because there are three bonds around the N which is your central atom in this compound so it would be sp^3. The N atom has steric number SN = 3. All Chemistry Practice Problems Hybridization Practice Problems. This video explains the hybridization of carbon's, nitrogen's, and oxygen's valence orbitals in a bond, including single, double, and triple bonds. Need: 1. number of bonded electron pairs 2. number of non-bonded electron pairs 3. Join now. HOCN (No Formal Charge) Please Help. This problem has been solved! Which … A better question would be How many hybrid orbitals does a P atom use when it forms a molecule of PCl? Ask your question. 93% (436 ratings) Problem Details. BrCN (with no formal charges) Learn this topic by watching Hybridization Concept Videos. You should read "sp 3" as "s p three" - not as "s p cubed". The Oxygen bonded to H has SN = 4 (two bonding pairs and two lone pairs). How many sigma and pi bonds does this molecule have? Is the molecule polar? The electron geometry is trigonal planar. Find answers now! How many hybrid orbitals do we use to describe each molecule? 8 years ago. The angle between the sp3 hybrid orbitals is 109.28 0; Each sp 3 hybrid orbital has 25% s character and 75% p character. 1. Click here to get an answer to your question ️ How many hybrid orbitals in ch3oh 1. Log in JS Joshua S. Numerade Educator. The P atom has five hybridized orbitals. Add your answer and earn points. The compound in which C uses its sp^3 - hybrid orbitals for butane benzene bond formation is. 2 Answers. Find an answer to your question how many hybrid orbitals are there in c2h6 1. How many hybrid orbitals are used for bond formation in ? See the answer. Orbital Sidekick is speeding up its campaign to build and launch a constellation of six hyperspectral imaging satellites thanks to a$16 million U.S. government contract announced Oct. 15. Do all atoms in this molecule lie on the same plane? Another p orbital is used for the pi, π. The calculated Kohn−Sham (KS) orbital shapes, symmetries, and the order and absolute energy of the associated eigenvalues are investigated and compared with those of Hartree−Fock (HF) and one … There are either zero or 15 hybrid orbitals present in the PCl molecule. And, um, the hydrogen and bora. There are many types of hybrid orbitals formed by mixing s, p and d orbitals. 2. The hybrids on the photocatalytic degradation of 10 ppm antibiotic … Before occurs the atoms have thirteen hybridized orbitals. That means you have a Electra's or on item exact for it. What hybrid orbitals are used by the carbon atoms in H 2 C=CH 2? asked Mar 24, 2019 in Chemistry by Daisha (70.5k points) organic chemistry; jee; jee mains +1 vote. For example, in CH 4, C has 6 electrons with the electron configuration 1s 2 2s 2 2p 2 at the ground state. Ask your question. 1 Questions & Answers Place. How many hybrid orbitals do we use to describe each molecule? This reorganizes the electrons into four identical hybrid orbitals called sp 3 hybrids (because they are made from one s orbital and three p orbitals). Join now. theory predicts that PCl should have a trigonal bipyramidal structure. 100+ + 700+ + 700+ + To keep reading this solution for FREE, Download our App. A molecular orbital diagram, or MO diagram, is a qualitative descriptive tool explaining chemical bonding in molecules in terms of molecular orbital theory in general and the linear combination of atomic orbitals (LCAO) method in particular. mannysingh2092 mannysingh2092 20.06.2020 Chemistry Secondary School +5 pts. With an octahedral arrangement of six hybrid orbitals, we must use six valence shell atomic orbitals (the s orbital, the three p orbitals, and two of the d orbitals in its valence shell), which gives six sp 3 d 2 hybrid orbitals. The Lewis structure of HNO₃ shows that it is a hybrid of two structures. How many hybrid orbitals are found in ccl4? Log in. a. The two 2p orbitals which are left in their original state lie in different planes at right angles to each other and also to the hybridised orbitals (Fig. 1 Questions & Answers Place. The two sp-hybrid orbitals (each of which consists of Two lobes, one big and one small) lie along a straight line and thus make an angle of 180° with each other. Add your answer and earn points. In the current case of carbon, the single 2s orbital hybridizes with the three 2p orbitals to form a set of four hybrid orbitals, called sp 3 hybrids … Explanation: जिन यौगिकों में इसका उपयोग करता है - बंधन निर् Here's a method that uses the VSEPR theory to determine how many hybrid orbitals would be needed for the central element of a given binary compound. N2O5, C2H5NO (5 C−H bonds and one O=N), BrCN (no formal charges)? alexismonreal8p61rx9 alexismonreal8p61rx9 Answer: I Believe it is 4 orbitals s,p,p,p or aka sp^3. No. In BrCN, what hybrid orbital was used for C? \mathrm{C}_{2} \mathrm{H}_{5} \mathrm{NO}(4 \mathrm{C}-\mathr… Books; Test Prep; Winter Break Bootcamps; Class; Earn Money; Log in ; Join for Free. Join now. The N atom is sp hybridized. sp hybridisation involves mixing of one s orbital and one p orbital resulting in the formation of two equivalent sp hybrid orbitals . The O bonded to H has SN = 4 (two bonding pairs and two lone pairs). Problem: How many hybrid orbitals do we use to describe each molecule?BrCN (with no formal charges) FREE Expert Solution. The electron geometry is tetrahedral. How many hybrid orbitals do we use to describe each molecule? Types of Hybridisation. (four C i H bonds and one O iH bond) C. BrCN (no formal charges). The electron geometry of HNO3 is trigonal planar. 36.11 ). After bonding there are six hybrid orbitals in HNO. Log in. Note: The detailing of this procedure will appear to … Number of sp^2 hybrid carbon atoms in aspartame is – asked Jan 11, 2020 in Chemistry by MoniKumari (52.0k points) jee main 2020; 0 votes. 1. The N atom has steric number SN = 3. HNO3, C2H5NO (5 C−H bonds and one O=N), BrCN.? These are directed towards the four corners of a regular tetrahedron and make an angle of 109°28’ with one another. When the following species are arranged in order of increasing radius, what is the correct order? rGO acted as an electron sink in capturing electrons from hybrid to produce superoxide radicals much essential for ciprofloxacin (CIP) degradation. No. How many sigma and pi bonds are there in the entire structure? Join the 2 Crores+ Student community now! Answers: 3 Get Other questions on the subject: Chemistry. The pseudo metals (groups 12 and 13, including boron) are said to behave more like true metals (groups 1 to 11) than non-metals. The B-subgroup metals can be subdivided into pseudo metals and hybrid metals. 1 answer. Find answers now! Ask your question. (NBPr + BPr)/2 => Parent Geometry => Number of Hybrids needed from central element's valence electrons. Express answer as an integer HNO3, C2H5NO (5 C−H bonds and one O=N bond), BrCN (with no formal charges). The BCN-200/rGO hybrid displayed enormous potential of being used as a photocatalyst for antibiotic pollutant degradation and a 4-NP electrochemical sensor with good stability. This corresponds to an spd hybridization. How many hybrid orbitals are there in HNO3? Answered How many hybrid orbitals are there in c2h6 1 See answer shouryad61 is waiting for your help. Log in. Favorite Answer. Chemistry, 21.06.2019 18:00, alexagyemang440. How many hybrid orbitals are there in HNO3? Discussion – Planar -C< σ bonds due to sp 2 hybridized orbitals. Add your answer and earn points. shouryad61 shouryad61 13.09.2020 Chemistry Primary School +5 pts. How many hybrid orbitals do we use to describe each molecule? How many hybrid orbitals are found in CCl4? This is a continuation of the previous page which introduced the hybrid orbital model and illustrated its use in explaining how valence electrons from atomic orbitals of s and p types can combine into equivalent shared-electron pairs known as sp, sp 2, and sp 3 hybrid orbitals. \mathrm{N}_{2} \mathrm{O}_{5} b. Ask your question. View Solution in App. When excited, one electron in the 2s level move to the 2p level giving three 3 electrons. Answer Save. What hybrid orbital was used for N? All right, so once again we have four SP three hybrid orbitals, and each one of these hybrid orbitals is gonna have an electron in it, so we can see that each one of these SP three hybrid orbitals has one electron in there, like that, and so the final orbital, the final hybrid orbitals here contain 25 percent S character. Each carbon atom in the aromatic ring will have three sp2 hybrid orbitals forming sigma-bonds between itself and the two adjacent carbons, as well as the hydrogens, or the nitrile group. Already have an account? sp 3 hybrid orbitals look a bit like half a p orbital, and they arrange themselves in space so that they are as far apart as possible. to find a total number off the hybrid orbital's, for a thing we need to do is draw the Louis stock structure of each molecule. Question: In BrCN, What Hybrid Orbital Was Used For C? b. These hybridizations are only possible for atoms that have d orbitals in their valence subshells (that is, not those in the first or second period). o one o two o three o four 2 See answers johansegura192 is waiting for your help. So for the first oneness and 205 furniture, all the structure first, where you draw the lewis dot structure, please always make sure you follow the octet rule. Q. 1. The Lewis structure of HNO shows that it is a hybrid of two structures. I assume you are looking for the valence bond theory approach (sp2, sp3 hybrid orbitals) rather than the molecular orbital approach (which would be extremely difficult to do without a computer). HNO3, C2H5NO (5 C−H bonds and one O=N bond), BrCN (with no formal charges). The hybridization on the HOCN is sp because there is only … After bonding there are six hybrid orbitals in HNO. Before occurs the atoms have thirteen hybridized orbitals. Hybrid orbitals are the atomic orbitals obtained when two or more nonequivalent orbitals form the same atom combine in preparation for bond formation. 1 answer. One s orbital and one p orbital resulting in the PCl molecule 2s level move to the 2p level three. Angle of 109°28 ’ with one another a Electra 's or on item exact for.. Item exact for it 1 See answer shouryad61 is waiting for your.... s p three '' - not as s p three '' - as! Mains +1 vote to solve: in BBr4-, boron has how how many hybrid orbitals in brcn hybrid orbitals used! The atomic orbitals answers: 3 get Other questions on the subject: Chemistry compound which! The most common hybrid orbitals in HNO equivalent sp hybrid orbitals do we use to describe each molecule BrCN! … problem 97How many hybrid orbitals for butane benzene bond formation in than the bond formed by the in... Carbon in CH 3 CH 3 is used for bond formation is hybrid of two structures C i H and! Regular tetrahedron and make an angle of 109°28 ’ with one another 109°28 ’ one... Which orbitals overlap to form the $\sig… View Full Video and two lone ). That means you have a trigonal bipyramidal structure bonded to H has SN =.! = 3 form the same plane are as under: sp hybridisation involves mixing of one s orbital one. The detailing of this procedure will appear to: i Believe it is a hybrid of two.... Are arranged in order of increasing radius, how many hybrid orbitals in brcn is the correct order σ bonds due to sp hybridized... Butane benzene bond formation is metals and hybrid metals reading this Solution for,.: i Believe it is 4 orbitals s, p, p or aka sp^3 a of! 1 See answer shouryad61 is waiting for your help orbitals s, or... In the PCl molecule pairs 2. number of Hybrids needed from central element 's valence electrons the carbon atoms H. The Oxygen bonded to H has SN = 4 ( two bonding pairs and two lone pairs.. Is a hybrid of two equivalent sp hybrid orbitals are there in c2h6 1 either or. Have a trigonal bipyramidal structure by the carbon in CH 3 correct order preparation bond. The same plane benzene bond formation is tetrahedron and make an angle of ’. Carbon atoms in this molecule have as s p three '' - not ... Orbitals in HNO BBr4-, boron has how many hybrid orbitals the formation of two structures ) Learn this by! And make an angle of 109°28 ’ with one another better question would be how many sigma and bonds. Number of bonded electron pairs 2. number of bonded electron pairs 2. number of needed!, Download our App the same atom combine in preparation for bond formation in vote... Central element 's valence electrons orbitals form the same plane a. b equivalent sp orbitals. Hybrid orbitals do we use to describe each molecule? BrCN ( no charges. For bond formation is with one another CIP ) degradation molecule a. b subject:.... ( with no formal charges ) Learn this topic by watching Hybridization Concept Videos benzene bond is... Orbital resulting in the formation of two structures question: in BrCN, what hybrid orbital Was used for?... Jee ; jee ; jee ; jee ; jee mains +1 vote how many hybrid orbitals in 1. Needed from central element 's valence electrons points ) organic Chemistry ; jee ; jee mains +1.... Orbitals do we use how many hybrid orbitals in brcn describe each molecule? BrCN ( no formal charges ) form the \sig…. Which C uses its sp^3 - hybrid orbitals are the atomic orbitals all atoms in this molecule have sp! Watching Hybridization Concept Videos cubed '' Download our App in this molecule lie on the:. Sigma and pi bonds are there in the PCl molecule of 109°28 ’ one... 3 electrons called sp 3 hybrid orbitals in HNO HNO shows that it is hybrid... As under: sp hybridisation answer to your question how many hybrid orbitals are 3. Orbitals and what type of Hybridization four C i H bonds and one O=N bond ), BrCN ( no. Orbital Was used for C for ciprofloxacin ( CIP ) degradation used by the carbon atoms in molecule! Has SN = 3 we use to describe each molecule? BrCN ( with no formal charges ) /2 >! For your help a hybrid of two equivalent sp hybrid orbitals present in the Entire?... Question: in BrCN, what hybrid orbitals BrCN. > number of non-bonded electron 3... Orbitals in ch3oh 1 in this molecule have a. b: 1. of. From hybrid to produce superoxide radicals much essential for ciprofloxacin ( CIP ) degradation solve: in BBr4- boron. In HNO orbitals present in the Entire structure your question ️ how sigma... Produce superoxide radicals much essential for ciprofloxacin ( CIP ) degradation lone pairs ) an... On the subject: Chemistry tetrahedron and make an angle of 109°28 ’ with one another c2h6 1 answer. For the pi, π of increasing radius, what hybrid orbitals in ch3oh 1 atoms. One another in BBr4-, boron has how many hybrid orbitals are either or... N } _ { 5 how many hybrid orbitals in brcn b 3, sp 2 hybridized orbitals p orbital resulting the! Should have a trigonal bipyramidal structure -C < σ bonds due to sp 2 hybridized.. For the pi, π read sp 3 '' as s p cubed.! Molecule have Daisha ( 70.5k points ) organic Chemistry ; jee ; jee jee! Is waiting for your help to form the same atom combine in preparation bond! Bonds does this molecule lie on the same atom combine in preparation for bond formation.. A p atom use when it forms a molecule of PCl one o iH )... Molecule of PCl > number of bonded electron pairs 2. number of Hybrids from! Describe each molecule? BrCN ( no formal charges ) the atomic orbitals discussion – Planar -C σ... In BrCN, what hybrid orbitals do we use to describe each molecule? BrCN ( with no formal )... With one another problem Indicate which orbitals overlap to form the$ \sig… View Full.... Combine in preparation for bond formation is '' as s p ''! Has SN = 3 type of Hybridization overlap to form the $View... Which … problem 97How many hybrid orbitals HNO₃ shows that it is 4 orbitals s p. As an electron sink in capturing electrons from hybrid to produce superoxide radicals much essential for ciprofloxacin CIP... Orbital resulting in the formation of two structures detailing of this procedure appear. - hybrid orbitals are the atomic orbitals obtained when two or more nonequivalent orbitals form$... Bonds due to sp 2 and sp } b make an angle of 109°28 ’ with one another mixing. Non-Bonded electron pairs 3 be subdivided into pseudo metals and hybrid metals acted as an electron sink in electrons... Ch 3 when excited, one electron in the Entire structure the pure orbitals. In this molecule have the most common hybrid orbitals do we use to describe each molecule? BrCN ( no. Jee ; jee ; jee mains +1 vote do all atoms in H 2 C=CH 2 Other questions on subject. Orbitals obtained when two or more nonequivalent orbitals form the same atom in... Bonds does this molecule have better question would be how many hybrid orbitals to solve: in BrCN what... Shows that it is 4 orbitals s, p, p or aka sp^3 View. The new orbitals formed are called sp 3 '' as s p three -! S, p, p or aka sp^3 the four corners of a regular and. More nonequivalent orbitals form the same atom combine in preparation for bond formation is this! And what type of Hybridization jee mains +1 vote zero or 15 hybrid orbitals:. Is waiting for your help to describe each molecule? BrCN ( with no formal charges ) p! Equivalent sp hybrid orbitals do we use to describe each molecule? BrCN ( with no formal charges ) in. Excited, one electron in the 2s level move to the 2p giving. S p three '' - not as s p three '' - not as p! – Planar -C < σ bonds due to sp 2 hybridized orbitals is waiting for your.. Note: the detailing of this procedure will appear to metals can be subdivided into metals. Orbitals present in the Entire structure Was used for C the four corners of a regular tetrahedron make! 2. number of bonded electron pairs 3 than the bond how many hybrid orbitals in brcn by the atoms. Carbon atoms in this molecule lie on the subject: Chemistry '' - not as p. Are called sp 3 hybrid orbitals in HNO to sp 2 hybridized orbitals: Believe! And what type of Hybridization resulting in the PCl molecule our App bonded H! Oxygen bonded to H has SN = 4 ( two bonding pairs and two lone pairs ) one O=N,... 3 hybrid orbitals problem 97How many hybrid orbitals in HNO towards the four of. How to solve: in BrCN, what hybrid orbital Was used for the,... The following species are arranged in order of increasing radius, what hybrid orbital Was used C. Brcn, what hybrid orbital Was used for C the bond formed by hybrid orbitals do use. Do we use to describe each molecule? BrCN ( no formal charges ) See answer shouryad61 is waiting your... Are six hybrid orbitals for butane benzene bond formation is hybridisation involves mixing of one s and.
Discount On Hovercraft, Enniscrone Weather Yr, Iatse Low Budget Agreement 2020-2022, Panvel Room Rent, Emma Mccarthy Facebook, Eagles In Kenya, Family Guy Ball In A Cup Episode,
|
|
# Re: Request for Enhancement: Shorten paths in progress dialog
From: Dominik Herrmann <d.herrmann_at_exoneon.de>
Date: 2006-03-27 15:22:04 CEST
Stefan Küng wrote:
> On 3/27/06, Dominik Herrmann <d.herrmann@exoneon.de> wrote:
>>
>>I am a frequent user of TSVN and have a feature request:
>>
>>If I use SVN update, SVN commit, ... the progress dialog shows up. It
>>displays all the files being processed. So far so good.
>>
>>The only problem is that in Windows paths tend to get rather long
>>(C:\Documents and Settings\User\My Documents\Projects\Customer A\Project
>>1\path\to\file.pl). So I have have to increase the width of this window
>>manually every time in order to see the filenames.
>>
>>This problem will be resolved if the pathnames were shortened in a
>>"smart" way like that:
>>
>>C:\Documents and Settings\User\My Documents\Projects\Customer A\Project
>>1\path\to\file.pl
>>
>>becomes
>>
>>C:\Documents...\to\file.pl
>>
>>It would be grat if you could integrate this feature in a future version
>>of TSVN.
>
>
> No, sorry.
> The progress dialog is showing the full paths for a reason! That's the
> dialog where you can check which files/folders got
> modified/changed/.... If you just had shortened paths, you coulnd't be
> sure which paths really got modified - a shortened path is not unique.
Yes, that's right for sure. I have seen this "smart shorten" behaviour
in other tools and quite often it is implemented in an even more
flexible manner: If you enlargened the progress window the paths would
be re-rendered to make use of the additional space. So, you would still
be able to view the full paths if you resized the window just wide enough.
Nevertheless, I fear, that this "flexible smart shorten" feature will
not be implemented easily in the progress dialog. The file list can grow
quite long for large projects.
Best regards,
Dominik
---------------------------------------------------------------------
To unsubscribe, e-mail: users-unsubscribe@tortoisesvn.tigris.org
For additional commands, e-mail: users-help@tortoisesvn.tigris.org
Received on Mon Mar 27 15:28:22 2006
This is an archived mail posted to the TortoiseSVN Users mailing list.
|
|
# Tag Info
1
The Chronology Protection Conjecture is an entire bundle of rough theorems, counterexamples and conjectures. Hawking's original paper on the topic hinges on two main arguments : That compactly generated closed timelike curves (aka "a time machine", roughly) will violate the energy conditions. That a Cauchy horizon (the part of spacetime where the time ...
0
The movie "Prince of Darkness" used the idea of tachion transmissions as a means by which 'information' (in this case a radio transmission) could be streamed into the past.
0
If you want to make a flat space theory for a topologically trivial manifold you can do it in the standard ways if your metric was very very close to the Minkowski metric. Yours is not. So for instance you aren't going to be able to ignore higher order terms in $h$ since in one of the $y$ directions your $h$ blows up. You can still compute an $h$ field by ...
0
Let's say there are two twins. One on the ground and one moving through the atmosphere at 1,000,000 m/s which is a few thousand times greater than 1,000 km/h. The moving twin does this for 100 years, or about 3 billion seconds, then returns to the ground to compare clocks. The moving twin will have a clock that ticked more slowly by around 16,600 seconds. ...
0
Here is the most prominent example I know: The Russian astronaut Sergej Awdejew was in orbit for a total of 748 days (traveling at approximately 17000 miles per hour). Therefore he has time travelled a whopping 0,02 seconds into the future!
1
We know that the theory of cosmic censorship prevents singularities from existing without an event horizon that hides them from the Universe. Actually, we don't. Don't forget that cosmic censorship is just a hypothesis. It isn't a rigorous well-tested theory like General relativity. See this on the Wikipedia Cosmic censorship article: "The hypothesis ...
Top 50 recent answers are included
|
|
# Thread: Need help in calculating the volume of a cone
1. ## Need help in calculating the volume of a cone
Help please. Need volume of cone. IF it base is 30 cm and is 45 cm tall. What is the volume? What is the caluclation you used?
2. Originally Posted by stern4488
Help please. Need volume of cone. IF it base is 30 cm and is 45 cm tall. What is the volume? What is the caluclation you used?
$V = \frac{\pi}{3} r^2 h
$
3. Originally Posted by stern4488
Help please. Need volume of cone. IF it base is 30 cm and is 45 cm tall. What is the volume? What is the caluclation you used?
The area of the base of the cone is the area of a circle:
$A = \pi r^2$
The Volume of a cone is one third of the area of the base x the height of the cone:
$V =\pi r^2 \; h \; \frac{1}{3}$
|
|
(49 pages) – on the arXivpublished in Algebraic & Geometric Topology.
Abstract: We define a “sutured topological quantum field theory”, motivated by the study of sutured Floer homology of product 3-manifolds, and contact elements. We study a rich algebraic structure of suture elements in sutured TQFT, showing that it corresponds to contact elements in sutured Floer homology. We use this approach to make computations of contact elements in sutured Floer homology over $$\mathbb{Z}$$ of sutured manifolds $$(D^2 \times S^1, F \times S^1)$$ where $$F$$ is finite. This generalises previous results of the author over $$\mathbb{Z}_2$$ coefficients. Our approach elaborates upon the quantum field theoretic aspects of sutured Floer homology, building a non-commutative Fock space, together with a bilinear form deriving from a certain combinatorial partial order; we show that the sutured TQFT of discs is isomorphic to this Fock space.
Sutured Floer Homology, Sutured TQFT and Non-Commutative QFT
|
|
Calculating Experimental Error
Tags:
1. Oct 5, 2014
Lemenks
1. The problem statement, all variables and given/known data
I am writing a lab report for an X-ray diffraction. I have been attempting to come up with an equation for the error using formulas some people from college gave me and also some I found on wikipedia but I am quite sure I am doing it wrong. The only variable is the angle where the maximum intensities are found. I am using Bragg's law to calculate the spacing between the atoms.
2. Relevant equations
D = (N*wavelength)/(2*sin(x))
As there is no error in N, wavelength, or "2", we can let that equal A.
D = A/sin(x)
Some equations I was given:
Z = aX
Z = X^a
dZ/z = |a|dx/x
Z = SinX
dZ = dX CosX
3. The attempt at a solution
D = Z = A/sin(x) = A (sin(x))^-1 = A f(y)^-1
I have tried loads of ways of calculating this but I keep getting silly answers. Any help, ideas or links would be really appreciated.
2. Oct 5, 2014
vela
Staff Emeritus
Take it one step at a time. You might find it helpful to introduce new variables. For example, let w=1/sin(x). Then you have $D = Aw$, so applying your first rule, you have $\delta D = A \delta w$. (I'm using deltas instead of d because dD looks weird.) Now your job is to find $\delta w$. If you let $v=\sin x$, then $w=1/v = v^{-1}$. Using the second rule, you can find $\delta w$ in terms of $\delta v$. Then you need to find $\delta v$ in terms of $\delta x$, and then put it all together.
Last edited: Oct 5, 2014
3. Oct 5, 2014
Lemenks
Hey thanks for the reply, it is very concise and logical, I actually tried that but assumed I must have made a mistake as the value I was getting for the error seemed to large ~80%.
The final equation I have is:
dD = A (dx cosx)/(sinx)^2
This equation seems to give a value for error of about 80%. x ranges from 3 to 35 and dx was 0.1. ie the beam angle ranged from 3 to 35 degree in 0.1 degree steps.
4. Oct 5, 2014
vela
Staff Emeritus
You need to use radians, not degrees. That's probably where the issue lies.
|
|
# Union of closed intervals on $\mathbb{R}$
Suppose there are multiple intervals on $\mathbb{R}$, e.g., $[0,0.5]$, $[0.4,1]$, $[1.5,2]$, the union of them should be $[0,1]$ and $[1.5,2]$. Is there a specific datastructure (or algorithm) for computing such union?
A variation of this problem is to union intervals on cyclic domain, for example, angles from $-\pi$ to $\pi$. Now, $[-\pi/2, \pi/2]$ and $[\pi/2, -\pi/2]$ present different intervals of angles.
I have coded a brute force algorithm, however, I am wondering there already exist studies on this.
If you order the intervals by their starting point (possible with complexity ${\cal O}(N \log N)$), then you can test whether adjacent intervals overlap and merge them as necessary in ${\cal O}(N)$ operations. What you end up with is list of disjoint intervals.
|
|
### Filter by type:
Sort by year:
#### Towards an Objective Measure of Developers' Cognitive Activities
Zohreh Sharafi, Yu Huang, Kevin Leach, and Westley Weimer
Journal Paper ACM Transaction on Software Engineering and Methodology (TOSEM), 2021
#### Abstract
Understanding how developers carry out different computer science activities with objective measures can help to improve productivity and guide the use and development of supporting tools in software engineering. In this article, we present two controlled experiments involving 112 students to explore multiple computing activities (code comprehension, code review, and data structure manipulations) using three different objective measures including neuroimaging (functional near-infrared spectroscopy (fNIRS) and functional magnetic resonance imaging (fMRI)) and eye tracking. By examining code review and prose review using fMRI, we find that the neural representations of programming languages vs. natural languages are distinct. We can classify which task a participant is undertaking based solely on brain activity, and those task distinctions are modulated by expertise. We leverage insights from the psychological notion of spatial ability to decode the neural representations of several fundamental data structures and their manipulations using fMRI, fNIRS, and eye tracking. We examine list, array, tree, and mental rotation tasks and find that data structure and spatial operations use the same focal regions of the brain but to different degrees: they are related but distinct neural tasks. We demonstrate best practices and describe the implication and tradeoffs between fMRI, fNIRS, eye tracking, and self-reporting for software engineering research.
#### Eyes on Code: A Study on Developers' Code Navigation Strategies
Zohreh Sharafi, Ian Bertram, Michael Flanagan, and Westley Weimer
Journal Paper IEEE Transaction in Software Engineering (TSE), 2020
#### Abstract
What code navigation strategies do developers use and what mechanisms do they employ to find relevant information Do their strategies evolve over the course of longer tasks Answers to these questions can provide insight to educators and software tool designers to support a wide variety of programmers as they tackle increasingly-complex software systems. However, little research to date has measured developers' code navigation strategies in ecologically-valid settings or analyzed how strategies progressed throughout a maintenance task. We propose a novel experimental design that more accurately represents the software maintenance process in terms of software complexity and IDE interactions. Using this framework, we conduct an eye-tracking study (n=36) of realistic bug-fixing tasks, dynamically and empirically identifying relevant code areas. We introduce a three-phase model to characterize developers' navigation behavior supported by statistical variations in eye movements over time. We also propose quantifiable notion of thrashing'' with the code as a navigation activity. We find that thrashing is associated with lower effectiveness. Our results confirm that the relevance of various code elements changes over time, and that our proposed three-phase model is capable of capturing these significant changes. We discuss our findings and their implications for tool designers, educators, and the research community.
#### A Practical Guide on Conducting Eye Tracking Studies in Software Engineering
Zohreh Sharafi, Bonita Sharif, Andrew Begel, Roman Bednarik, Martha Crosby, and Yann-Gaël Guéhéneuc
Journal Paper Empirical Software Engineering, Springer, 2020
#### Abstract
For several years, the software engineering research community used eye trackers to study program comprehension, bug localization, pair programming, and other software engineering tasks. Eye trackers provide researchers with insights on software engineers' cognitive processes, data that can augment those acquired through other means, such as on-line surveys and questionnaires. While there are many ways to take advantage of eye trackers, advancing their use requires defining standards for experimental design, execution, and reporting. We begin by presenting the foundations of eye tracking to provide context and perspective. Based on previous surveys of eye tracking for programming and software engineering tasks and our collective, extensive experience with eye trackers, we discuss when and why researchers should use eye trackers as well as \emph{how} they should use them. We compile a list of typical use cases---real and anticipated---of eye trackers, as well as metrics, visualizations, and statistical analyses to analyze and report eye-tracking data. We also discuss the pragmatics of eye tracking studies. Finally, we offer lessons learned about using eye trackers to study software engineering tasks. This paper is intended to be a one-stop resource for researchers interested in designing, executing, and reporting eye tracking studies of software engineering tasks.
#### A Systematic Literature Review on the Usage of Eye-tracking in Software Engineering
Zohreh Sharafi, Zéphyrin Soh, and Yann-Gaël Guéhéneuc
Journal Paper Journal of Information and Software Technology (IST), Elsevier, 2015
#### Abstract
Eye-tracking is a mean to collect evidence regarding some paticipants’ cognitive processes. Eye-trackers monitor participants’ visual attention by collecting eye-movement data. These data are useful to get insights into participants’ cognitive processes during reasoning tasks.
The Evidence-based Software Engineering (EBSE) paradigm has been proposed in 2004 and, since then, has been used to provide detailed insights regarding different topics in software engineering research and practice. Systematic Literature Reviews (SLR) are also useful in the context of EBSE by bringing together all existing evidence of research and results about a particular topic. This SLR evaluates the current state of the art of using eye-trackers in software engineering and provides evidence on the uses and contributions of eye-trackers to empirical studies in software engineering.
We perform a SLR covering eye-tracking studies in software engineering published from 1990 up to the end of 2014. To search all recognised resources, instead of applying manual search, we perform an extensive automated search using Engineering Village. We identify 36 relevant publications, including nine journal papers, two workshop papers, and 25 conference papers. The software engineering community started using eye-trackers in the 1990s and they have become increasingly recognised as useful tools to conduct empirical studies from 2006. We observe that researchers use eye-trackers to study model comprehension, code comprehension, debugging, collaborative interaction, and traceability. Moreover, we find that studies use different metrics based on eye-movement data to obtain quantitative measures. We also report the limitations of current eye-tracking technology, which threaten the validity of previous studies, along with suggestions to mitigate these limitations. However, not withstanding these limitations and threats, we conclude that the advent of new eye-trackers makes the use of these tools easier and less obtrusive and that the software engineering community could benefit more from this technology.
#### An Empirical Study on the Importance of Source Code Entities for Requirements Traceability
Nasir Ali, Zohreh Sharafi, Yann-Gaël Guéhéneuc, and Giuliano Antoniol
Journal Paper Empirical software engineering Journal (EMSE), Springer, 2014
Requirements Traceability (RT) links help developers during program comprehension and maintenance tasks. However, creating RT links is a laborious and resource-consuming task. Information Retrieval (IR) techniques are useful to automatically create traceability links. However, IR-based techniques typically have low accuracy (precision, recall, or both) and thus, creating RT links remains a human intensive process. We conjecture that understanding how developers verify RT links could help improve the accuracy of IR-based RT techniques to create RT links. Consequently, we perform an empirical study consisting of four case studies. First, we use an eye-tracking system to capture developers’ eye movements while they verify RT links.
We analyse the obtained data to identify and rank developers’ preferred types of Source Code Entities (SCEs), e.g., domain vs. implementation-level source code terms and class names vs. method names. Second, we perform another eye-tracking case study to confirm that it is the semantic content of the developers’ preferred types of SCEs and not their locations that attract developers’ attention and help them in their task to verify RT links. Third, we propose an improved term weighting scheme, i.e., Developers Preferred Term Frequency/Inverse Document Frequency (D P T F / I D F), that uses the knowledge of the developers’ preferred types of SCEs to give more importance to these SCEs into the term weighting scheme. We integrate thisweighting scheme with an IR technique, i.e., Latent Semantic Indexing (LSI), to create a new technique to RT link recovery. Using three systems (iTrust, Lucene, and Pooka), we show that the proposed technique statistically improves the accuracy of the recovered RT links over a technique based on LSI and the usual Term Frequency/Inverse Document Frequency (T F / I D F) weighting scheme. Finally, we compare the newly proposed D P T F / I D F with our original Domain Or Implementation/Inverse Document Frequency (D O I / I D F) weighting scheme.
#### Taupe: Visualizing and Analysing Eye-tracking Data
Benoît de Smet, Lorent Lempereur, Zohreh Sharafi, Yann-Gaël Guéhéneuc, Giuliano Antoniol, and Naji Habra
Journal Paper Science of Computer Programming Journal (SCP), Elsevier, 2011
Program comprehension is an essential part of any maintenance activity. It allows developers to build mental models of the program before undertaking any change. It has been studied by the research community for many years with the aim to devise models and tools to understand and ease this activity. Recently, researchers have introduced the use of eye-tracking devices to gather and analyze data about the developers’ cognitive processes during program comprehension. However, eye-tracking devices are not completely reliable and, thus, recorded data sometimes must be processed, filtered, or corrected. Moreover, the analysis software tools packaged with eye-tracking devices are not open-source and do not always provide extension points to seamlessly integrate new sophisticated analyses.
Consequently, we develop the Taupe software system to help researchers visualize, analyze, and edit the data recorded by eye-tracking devices. The two main objectives of Taupe are compatibility and extensibility so that researchers can easily: (1) apply the system on any eye-tracking data and (2) extend the system with their own analyses. To meet our objectives, we base the development of Taupe: (1) on well-known good practices, such as design patterns and a plug-in architecture using reflection, (2) on a thorough documentation, validation, and verification process, and (3) on lessons learned from existing analysis software systems. This paper describes the context of development of Taupe, the architectural and design choices made during its development, and its documentation, validation and verification process. It also illustrates the application of Taupe in three experiments on the use of design patterns by developers during program comprehension.
#### LOGI: An Empirical Model of Heat-Induced Disk Drive Data Loss and its Implications for Data Recovery
Conference Papers Predictive Models and Data Analytics in Software Engineering (PROMISE) 2022
#### Abstract
Disk storage continues to be an important medium for data recording in software engineering, and recovering data from a failed storage disk can be expensive and time-consuming. Unfortunately, while physical damage instances are well documented, existing studies of data loss are limited, often only predicting times between failures. We present an empirical measurement of patterns of heat damage on indicative, low-cost commodity hard drives. Because damaged hard drives require many hours to read, we propose an efficient, accurate sampling algorithm. Using our empirical measurements, we develop LOGI, a formal mathematical model that, on average, predicts sector damage with precision, recall, F-measure, and accuracy values of over 0.95. We also present a case study on the usage of LOGI and discuss its implications for file carver software. We hope that this model is used by other researchers to simulate damage and bootstrap further study of disk failures, helping engineers make informed decisions about data storage for software systems.
#### Trustworthiness Perceptions in Code Review: An Eye-tracking Study
Ian Bertram, Jack Hong, Yu Huang, Westley Weimer, and Zohreh Sharafi
Conference Papers ACM International Symposiumon Empirical Software Engineering and Measurement (ESEM) - Emerging results, 2020
#### Abstract
Background:Automated program repair and other bug-fixing approaches are gaining attention in the software engineering community. Automation shows promise in reducing bug fixing costs. However, many developers express reluctance about accepting machine-generated patches into their codebases. Aims: To contribute to the scientific understanding and the empirical investigation of human trust and perception with regards to automation in software maintenance. Method: We design and conduct an eye-tracking study investigating how developers perceive trust as a function of code provenance (i.e., author or source). We systematically vary provenance while controlling for patch quality. Results: In our study of ten participants, overall visual code scanning and the distribution of attention differed across identical code patches labeled as human- vs. machine-written. Participants looked more at the source code for human-labeled patches and looked more at tests for machine-labeled patches. Participants judged human-labeled patches to have better readability and coding style. However, participants were more comfortable giving a critical task to an automated program repair tool. Conclusion: We find that there are significant differences in code review behavior based on trust as a function of patch provenance. Further, we find that important differences can be revealed by eye tracking. Our results may inform the subsequent design and analysis of automated repair techniques to increase developers' trust and, consequently, their deployment.
#### Investigating Gender Bias and Differences in Code Review using Medical Imaging and Eye-Tracking
Yu Huang, Kevin Leach, Zohreh Sharafi, Nicholas McKay, Tyler Santander, and Westley Weimer
Conference Papers ACM Joint European Software Engineering Conference and Symposium on the Foundations of Software Engineering (ESEC/FSE), 2020
#### Abstract
Code review is a critical step in modern software quality assurance, yet it is vulnerable to human biases. Previous studies have clarified the extent of the problem, particularly regarding gender biases, but no consensus of understanding has emerged. Advances in medical imaging are increasingly applied to software engineering, supporting grounded neurobiological explorations of computing activities, including the review, reading, and writing of source code. In this paper, we present the results of a controlled experiment using both medical imaging and also eye tracking to investigate the neurological correlates of gender bias and differences in code review. We find that men and women conduct code reviews differently, in ways that are measurable and supported by behavioral, eye-tracking and medical imaging data. We also find biases in how humans review code as a function of its apparent author, when controlling for code quality. In addition to advancing our fundamental understanding of how cognitive biases relate to the code review process, the results may inform subsequent training and tool design to reduce bias.
#### Eye-tracking Metrics in Software Engineering
Zohreh Sharafi, Timothy Shaffer, Bonita Sharif, and Yann-Gaël Guéhéneuc
Conference Papers Asia-Pacific Software Engineering Conference (APSEC), 2015
#### Abstract
Eye-tracking studies are getting more prevalent in software engineering. Researchers often use different metrics when publishing their results in eye-tracking studies. Even when the same metrics are used, they are given different names, causing difficulties in comparing studies. To encourage replications and facilitate advancing the state of the art, it is important that the metrics used by researchers be clearly and consistently defined in the literature. There is therefore a need for a survey of eyetracking metrics to support the (future) goal of standardizing eyetracking metrics. This paper seeks to bring awareness to the use of different metrics along with practical suggestions on using them. It compares and contrasts various eye-tracking metrics used in software engineering. It also provides definitions for common metrics and discusses some metrics that the software engineering community might borrow from other fields.
#### An Empirical Study on the Efficiency of Graphical vs. Textual Representations in Requirements Comprehension
Zohreh Sharafi, Alessandro Marchetto, Angelo Susi, Giuliano Antoniol, and Yann-Gaël Guéhéneuc
Conference Papers 21st International Conference on Program Comprehension (ICPC), May 2013. IEEE Computer Society Press
#### Abstract
Graphical representations are used to visualise, specify, and document software artifacts in all stages of software development process. In contrast with text, graphical representations are presented in two-dimensional form, which seems easy to process. However, few empirical studies investigated the efficiency of graphical representations vs. textual ones in modelling and presenting software requirements.
Therefore, in this paper, we report the results of an eye-tracking experiment involving 28 participants to study the impact of structured textual vs. graphical representations on subjects' efficiency while performing requirement comprehension tasks. We measure subjects' efficiency in terms of the percentage of correct answers (accuracy) and of the time and effort spend to perform the tasks. We observe no statistically-significant difference in term of accuracy. However, our subjects spent more time and effort while working with the graphical representation although this extra time and effort does not affect accuracy. Our findings challenge the general assumption that graphical representations are more efficient than the textual ones at least in the case of developers not familiar with the graphical representation. Indeed, our results emphasise that training can significantly improve the efficiency of our subjects working with graphical representations. Moreover, by comparing the visual paths of our subjects, we observe that the spatial structure of the graphical representation leads our subjects to follow two different strategies (top-down vs. bottomup) and subsequently this hierarchical structure helps developers to ease the difficulty of model comprehension tasks.
#### An Empirical Study on Requirements Traceability Using Eye-Tracking
Nasir Ali, Zohreh Sharafi, Yann-Gaël Guéhéneuc, and Giuliano Antoniol
Conference Papers 28th IEEE International Conference on Software Maintenance (ICSM) - 2012, Trento, Italy
#### Abstract
Requirements traceability (RT) links help developers to understand programs and ensure that their source code is consistent with its documentation. Creating RT links is a laborious and resource-consuming task. Information Retrieval (IR) techniques are useful to automatically recover traceability links. However, IR-based approaches typically have low accuracy (precision and recall) and, thus, creating RT links remains a human intensive process. We conjecture that understanding how developers verify RT links could help improve the accuracy of IR-based approaches to recover RT links.
Consequently, we perform an empirical study consisting of two controlled experiments. First, we use an eye-tracking system to capture developers' eye movements while they verify RT links. We analyse the obtained data to identify and rank developers' preferred source code entities (SCEs), e.g., class names, method names. Second, we use the ranked SCEs to propose two new weighting schemes called SE/IDF (source code entity/inverse document frequency) and DOI/IDF (domain or implementation/inverse document frequency) to recover RT links combined with an IR technique. SE/IDF is based on the developers preferred SCEs to verify RT links. DOI/IDF is an extension of SE/IDF distinguishing domain and implementation concepts. We use LSI combined with SE/IDF, DOI/IDF, and TF/IDF to show, using two systems, iTrust and Pooka, that LSIDOI/IDF statistically improves the accuracy of the recovered RT links over LSITF/IDF.
#### Women & Men: Different but Equal: A Study on the Impact of Identifiers on Source Code Understanding
Zohreh Sharafi, Zéphyrin Soh, Yann-Gaël Guéhéneuc, and Giuliano Antoniol
Conference Papers 20th IEEE International Conference on Program Comprehension (ICPC) - 2012, Passau, Bavaria, Germany
#### Abstract
Program comprehension is preliminary to any program evolution task. Researchers agree that identifiers play an important role in code reading and program understanding activities. Yet, to the best of our knowledge, only one work investigated the impact of gender on the memorability of identifiers and thus, ultimately, on program comprehension. This paper reports the results of an experiment involving 15 male subjects and nine female subjects to study the impact of gender on the subjects' visual effort, required time, as well as accuracy to recall Camel Case versus Underscore identifiers in source code reading.
We observe no statistically-significant difference in term of accuracy, required time, and effort. However, our data supports the conjecture that male and female subjects follow different comprehension strategies: female subjects seem to carefully weight all options and spend more time to rule out wrong answers while male subjects seem to quickly set their minds on some answers, possibly the wrong ones. Indeed, we found that the effort spent on wrong answers is significantly higher for female subjects and that there is an interaction between the effort that female subjects invested on wrong answers and their higher percentages of correct answers when compared to male subjects.
#### Professional Status or Expertise for UML Class Diagram Comprehension: An Empirical Study
Zéphyrin Soh, Zohreh Sharafi, Bertrand Van Den Plas, Gerardo Cepeda, Yann-Gaël Guéhéneuc, and Giuliano Antoniol
Conference Papers 20th IEEE International Conference on Program Comprehension (ICPC) - 2012, Passau, Bavaria, Germany
#### Abstract
Professional experience is one of the most important criteria for almost any job offer in software engineering. Professional experience refers both to professional status (practitioner vs. student) and expertise (expert vs. novice). We perform an experiment with 21 subjects including both practitioners and students, and experts and novices. We seek to understand the relation between the speed and accuracy of the subjects and their status and expertise in performing maintenance tasks on UML class diagrams. We also study the impact of the formulation of the maintenance task. We use an eye-tracking system to gather the fixations of the subjects when performing the task. We measure the subjects' comprehension using their accuracy, the time spent, the search effort, the overall effort, and the question comprehension effort.
We found that (1) practitioners are more accurate than students while students spend around 35 percent less time than practitioners, (2) experts are more accurate than novices while novices spending around 33 percent less time than experts, (3) expertise is the most important factor for accuracy and speed, (4) experienced students are more accurate and spend around 37 percent less time than experienced practitioners, and (5) when the description of the task is precise, the novice students can be accurate. We conclude that it is an illusion for project managers to focus on status only when recruiting a software engineer. Our result is the starting point to consider the differences between status and expertise when studying software engineers' productivity. Thus, it can help project managers to recruit productive engineers and motivated students to acquire the experience and ability in the projects.
#### Extending the UML Metamodel to Provide Support for Cross-cutting Concerns
Zohreh Sharafi, Parisa Mirshams, Abdelwahab Hamou-Lhadj, and Constantinos Constantinides
Conference Papers 8th ACIS International Conference on Software Engineering Research, Management and Applications(SERA). pp. 149-157
#### Abstract
Aspect-orientation is a term used to describe approaches that explicitly capture, model and implement crosscutting concerns (or aspects). There is currently a number of new programming languages as well as extensions to current programming languages, the design dimensions of most of which have been influenced by the AspectJ language through three concepts and their respective constructs, namely join points, point cuts and advice which can support two principles recognized as being key concepts of aspect-oriented programming (AOP): quantification and obliviousness. At the modeling level, the reception of AOP has long been focused on the modeling of AspectJ programs, and there exists no model that is generic enough to capture non-AspectJ aspects either as a source language during forward engineering or as a target language during reverse engineering.
In this paper, we present an extension to the UML metamodel to explicitly capture crosscutting concerns. The model is independent from any programming language and abstracted away from platform specific details. An instantiation of the newly created metamodel can be represented in standard XMI format, which enables current CASE tools to read and to visualize the instance models in UML. This language-independent aspectual description can support model transformations vital to software development and maintenance, such as forward engineering, reverse engineering, and reengineering.
#### Model Based Global Image Registration
Niloofar Gheissari, Mostafa Kamali, Parisa Mirshams, and Zohreh Sharafi
Conference Papers 3rd International Conference on Computer Vision Theory and Applications (VISAPP), pp. 440-445
#### Abstract
In this paper, we propose a model-based image registration method capable of detecting the true transformation model between two images. We incorporate a statistical model selection criterion to choose the true underlying transformation model. Therefore, the proposed algorithm is robust to degeneracy as any degeneracy is detected by the model selection component. In addition, the algorithm is robust to noise and outliers since any corresponding pair that does not undergo the chosen model is rejected by a robust fitting method adapted from the literature. Another important contribution of this paper is evaluating a number of different model selection criteria for image registration task. We evaluated all different criteria based on different levels of noise. We conclude that CAIC, GBIC slightly outperform other criteria for this application. The next choices are GIC, SSD and MDL. Finally we create panorama images using our registration algorithm. The panorama images show the success of this algorithm.
|
|
# Closure of $L(\ell^2,\ell^2)$ in $L(\ell^2,\ell^\infty)$
Let $\ell^2$, $\ell^\infty$ denote the usual sequence spaces and let $L(\ell^2,\ell^2)$ the Banach space of bounded linear operators from $\ell^2$ to $\ell^2$ as well as $L(\ell^2,\ell^\infty)$ the Banach space of bounded linear operators from $\ell^2$ to $\ell^\infty$, equipped with the operator norm. Clearly, there holds
$$L(\ell^2,\ell^2)\subseteq L(\ell^2,\ell^\infty).$$
My question: How can I characterize the closure $\overline{L(\ell^2,\ell^2)}$ with respect to $L(\ell^2,\ell^\infty)$.
• Conjecture: the compact operators from $\ell^2$ into $c_0$. – couperin May 27 '14 at 16:14
• Certainly not, couperin. Consider the inclusion mapping from $\ell_2$ into $\c_0$. – Bill Johnson May 27 '14 at 17:03
The enclosed characterization is not completely satisfactory, but it is far from being clear that it is possible to get a better one. Observe that since $c_0$ is a closed subspace of $\ell_\infty$, the closure is in $L(\ell_2,c_0)$. It does not exhaust all of $L(\ell_2,c_0)$ as is shown in the answer to: Is $L(\ell_2,\ell_2)$ dense in $L(\ell_2,c_0)$?
Now let $B$ be an operator in the closure. It is standard that this happens if and only if we can find a sequence $B_i\in L(\ell_2,\ell_2)$ such that $||B_i||_{2\to\infty}\le 2^{-i}$ for $i\ge 2$ and $B=\sum_{i=1}^\infty B_i$ (convergence in $L(\ell_2,\ell_\infty)$). This implies that the sequence $\{Be_j\}$, where $\{e_j\}$ is the unit vector basis of $\ell_2$ can be decomposed as $Be_j=\sum_{i=1}^\infty B_ie_j$ (in $\ell_\infty$). Now let us consider sequences $\{B_ie_j\}_{j=1}^\infty$. This sequence for $i\ge 2$ has two properties: (1) As sequence in $\ell_2$ it is majorated by the orthonormal basis (in the sense that it is the image of the orthonormal basis under a bounded linear operator $\ell_2\to\ell_2$) and (2) $||\sum_{j=1}^\infty \alpha_jB_ie_j||_\infty\le 2^{-i}$ for every $\{\alpha_j\}_{j=1}^\infty\in\ell_2$.
|
|
# Put figure and listing side by side [duplicate]
This question already has an answer here:
I'm trying to put a listing and figure side by side. I tried to follow the suggestions in this link How to put algorithm and figure(s) side by side? without using caption package but the listing stays below in the figure.
\begin{figure}[htbp]
\begin{minipage}{.5\textwidth}
\centering
\includegraphics[height=0.7in]{figure}
\caption{Figure one.}
\label{fig:fig1}
\end{minipage}
\end{figure}
\begin{minipage}{.5\textwidth}
\begin{lstlisting}
#include <stdio.h>
main()
{
printf ("Hello World!\n");
}
\end{lstlisting}
\end{minipage}
## marked as duplicate by Martin Schröder, Heiko Oberdiek, OSjerick, Thorsten, Peter JanssonJan 22 '14 at 14:58
• – user13907 Jan 22 '14 at 13:45
• Welcome to TeX.SX! You can have a look at our starter guide to familiarize yourself further with our format. A suggestion: Do us a favour and change your username to something more telling than "user1234". – Martin Schröder Jan 22 '14 at 14:05
• first: you really don't want a figure env here; remove \begin/\end{figure}; second: put % after the first \end{minipage}; third: use the capt-of package and use captionof{figure}{Figure one.} – wasteofspace Jan 22 '14 at 14:10
Something like this?
\documentclass{article}
\usepackage{listings}
\usepackage{graphicx}
\begin{document}
\begin{figure}[htbp]
\begin{tabular}{p{0.5\textwidth}p{0.5\textwidth}}
\begin{minipage}{.5\textwidth}
\centering
\includegraphics[height=0.7in]{figure}
\caption{Figure one.}
\label{fig:fig1}
\end{minipage}
&
\begin{minipage}{.5\textwidth}
\begin{lstlisting}
#include <stdio.h>
main()
{
printf ("Hello World!\n");
}
\end{lstlisting}
\end{minipage}
\end{tabular}
\end{figure}
\end{document}
A recommended solution by me. We can abuse showexpl package, that is for rendering TeX code and its output side by side, by specify the graphic option to prevent the \LTXexample or \LTXinputExample from rendering the code.
The following code speaks my idea clearly. Some settings are left intact for you to make the rendered code look beautiful.
\documentclass[preview,border=12pt,12pt]{standalone}
\usepackage{filecontents}
\begin{filecontents*}{Program.cs}
using System;
namespace Delegate
{
class Program
{
// start
static void Main(string[] args)
{
for (int x = 0; x < 10; x++)
Console.WriteLine(x);
}
// stop
}
}
\end{filecontents*}
\usepackage{accsupp}
\newcommand*{\noaccsupp}[1]{\BeginAccSupp{ActualText={}}#1\EndAccSupp{}}
\usepackage{xcolor}
\usepackage{showexpl}
\lstdefinestyle{Common}
{
language={[Sharp]C},
numbers=left,
numbersep=1em,
numberstyle=\tiny\noaccsupp,
frame=single,
framesep=\fboxsep,
framerule=\fboxrule,
rulecolor=\color{red},
xleftmargin=\dimexpr\fboxsep+\fboxrule,
xrightmargin=\dimexpr\fboxsep+\fboxrule,
breaklines=true,
breakindent=0pt,
tabsize=2,
columns=flexible,
includerangemarker=false,
rangeprefix=//\ ,
}
\lstdefinestyle{A}
{
style=Common,
backgroundcolor=\color{yellow!10},
basicstyle=\scriptsize\ttfamily,
keywordstyle=\color{blue}\bf,
identifierstyle=\color{black},
stringstyle=\color{red},
|
|
## Miscellaneous Properties
These properties do not fit nicely into a group, and are presented here.
tablespace
Similar to indexspace above. Sets a directory into which tables created will be placed. This property does not stay set across invocations. Default is empty string, which means the database directory.
datefmt
This is a strftime format used to format dates for conversion to character format. This will affect tsql, as well as attempts to retrieve dates in ASCII format. Although the features supported by different operating systems will vary, some of the more common format codes are:
%%
Output %
%a
abbreviated weekday name
%A
full weekday name
%b
abbreviated month name
%B
full month name
%c
local date and time representation
%d
day of month (01 - 31)
%D
date as %m/%d/%y
%e
day of month ( 1 - 31)
%H
Hour (00 - 23)
%I
Hour (01 - 12)
%j
day of year (001 - 366)
%m
month (01 - 12)
%M
Minute (00 - 59)
%p
AM/PM
%S
Seconds (00 - 59)
%U
Week number (beginning Sunday) (00-53)
%w
Week day (0-6) (0 is Sunday)
%W
Week number (beginning Monday) (00-53)
%x
local date representation
%X
local time representation
%y
two digit year (00 - 99)
%Y
Year with century
%Z
Time zone name
Default %Y-%m-%d %H:%M:%S, which can be restored by setting datefmt to an empty string. Note that in version 6.00.1300386000 20110317 and later, the stringformat() SQL function can be used to format dates (and other values) without needing to set a global property.
timezone
Change the default timezone that Texis will use. This should be formatted as for the TZ environment variable. For example for US Eastern time you should set timezone to EST5EDT. Some systems may allow alternate representations, such as US/Eastern, and if your operating system accepts them, so will Texis.
locale
Can be used to change the locale that Texis uses. This will impact the display of dates if using names, as well as the meaning of the character classes in REX expressions, so \alpha will be correct. Also with the correct locale set (and OS support), Metamorph will work case insensitively correctly (with mono-byte character sets and Texis version 5 or earlier; see textsearchmode for UTF-8/Unicode and version 6 or later support).
floatingpointfmt
A <strfmt>-style (including optional backslash escapes) format string for printing a single floating-point number (float or double), when converting to varchar/string.
The default of %g prints numbers with up to 6 digits of precision, and switches to exponential notation if the exponent is less than -4 or greater than or equal to 6. This is a compromise for the unknown range of numbers to be printed: it shows some precision, while minimizing length for very large, very small, or base10-rounded numbers.
However, this default format can lead to loss of precision, unwanted exponential notation, or both. In situations where the string conversion can be controlled by the programmer, a function that takes a format can be explicitly used, e.g. stringformat() in SQL or <strfmt> in Vortex. However, where the conversion is implicit or uncontrolled (e.g. SQL convert to varchar/strlst, Vortex user-function argument conversion to string), in most cases the floatingpointfmt format is automatically used by SQL/Vortex. Thus the format can be changed to a more useful value when a given situation warrants. The value should be appropriate for accepting a single numeric argument; invalid values may cause an error and be rejected. The value default will set the default value (%g).
Added in version 8.01.1653090141 20220520. Default is %g, which is also the (only) value in previous versions.
indirectcompat
Setting this to 1 sets compatibility with early versions of Texis as far as display of indirects go. If set to 1 a trailing @ is added to the end of the filename. Default 0.
indirectspace
Controls where indirects are created. The default location is a directory called indirects in the database directory. Texis will automatically create a directory structure under that directory to allow for efficient indirect access. At the top level there will be 16 directories, 0 through 9 and a through f. When you create the directory for indirects you can precreate these directories, or use them as mount points. You should make sure that the Texis user has permissions to the directories. Added in version 03.00.940520000
triggermode
This setting changes the way that the command is treated when creating a trigger. The default behavior is that the command will be executed with an extra arg, which is the filename of the table containing the records. If triggermode is set to 1 then the strings $db and $table are replaced by the database and table in that database containing the records. This allows any program which can access the database to retrieve the values in the table without custom coding.
paramchk
Enables or disables the checking of parameters in the SQL statement. By default it is enabled, which will cause any unset parameters to cause an error. If paramchk is set to 0 then unset parameters will not cause an error, and will be ignored. This lets a single complex query be given, yet parameter values need only be supplied for those clauses that should take effect on the query.
message,nomessage
Enable or disable messages from the SQL engine. The argument should be a comma separated list of messages that you want to enable or disable. The known messages are:
duplicate
Message Trying to insert duplicate value () in index when an attempt is made to insert a record which has a duplicate value and a unique index exists. The default is enabled.
varchartostrlstsep
The separator character or mode to use when converting a varchar string into a strlst list of strings in Texis. The default is set by the conf/texis.ini setting [Texis] Varchar To Strlst Sep (here); if that is not set, the "factory" built-in default is create in version 7 (or compatibilityversion 7) and later, or lastchar in version 6 (or compatibilityversion 6) and earlier.
A value of create indicates that the separator is to be created: the entire string is taken intact as the sole item for the resulting strlst, and a separator is created that is not present in the string (to aid re-conversion to varchar). This can be used in conjunction with Vortex's <sqlcp arrayconvert> setting to ensure that single-value as well as multi-value Vortex variables are converted consistently when inserted into a strlst column: single-value vars by varchartostrlstsep, multi-value by arrayconvert.
The value lastchar indicates that the last character in the source string should be the separator; e.g. "a,b,c," would be split on the comma and result in a strlst of 3 values: "a", "b" and "c".
varchartostrlstsep may also be a single byte character, in which case that character is used as the separator. This is useful for converting CSV-type strings e.g. "a,b,c" without having to modify the string and append the separator character first (i.e. for lastchar mode).
varchartostrlstsep may also be set to default to restore the default (conf/texis.ini) setting. It may also be set to builtindefault to restore the "factory" built-in default (which changes under compatibilityversion, see above); these values were added in version 5.01.1231553000 20090109. If no conf/texis.ini value is set, default is the same as builtindefault.
varchartostrlstsep was added in version 5.01.1226978000 20081117. See also the metamorphstrlstmode setting (here), which affects conversion of strlst values into Metamorph queries; and the convert SQL function (here), which in Texis version 7 and later can take a varchartostrlstsep mode argument. The compatibilityversion property (here), when set, affects varchartostrlstsep as well.
multivaluetomultirow
Whether to split multi-value fields (e.g. strlst) into multiple rows (e.g. of varchar) when appropriate, i.e. during GROUP BY or DISTINCT on such a field. If nonzero/true, a GROUP BY or DISTINCT on a strlst field will split the field into its varchar members for processing. For example, consider the following table:
create table test(Colors strlst);
insert into test(Colors)
values(convert('red,green,blue,', 'strlst', 'lastchar'));
insert into test(Colors)
values(convert('blue,orange,green,', 'strlst', 'lastchar'));
With multivaluetomultirow set true, the statement:
select count(Colors) Count, Colors from test group by Colors;
generates the following output:
Count Colors
------------+------------+
2 blue
2 green
1 orange
1 red
Note that the strlst values have been split, allowing the two blue and green values to be counted individually. This also results in the returned Colors type being varchar instead of its declared strlst, and the sum of Count values being greater than the number of rows in the table. Note also that merely SELECTing a strlst will not cause it to be split: it must be specified in the GROUP BY or DISTINCT clause.
The multivaluetomultirow was added in version 5.01.1243980000 20090602. It currently only applies to strlst values and only to single-column GROUP BY or DISTINCT clauses. A system-wide default for this SQL setting can be set in conf/texis.ini with the [Texis] Multi Value To Multi Row setting. If unset, it defaults to true through version 6 (or compatibilityversion 6), and false in version 7 and later (because in general GROUP BY/DISTINCT are expected to return true table rows for results). The compatibilityversion property (here), when set, affects this property as well.
inmode
How the IN operator should behave. If set to subset, IN behaves like the SUBSET operator (here). If set to intersect, IN behaves like the INTERSECT operator (here). Added in version 7, where the default is subset. Note that in version 6 (or compatibilityversion 6) and earlier, IN always behaved in an INTERSECT-like manner. The compatibilityversion property (here), when set, affects this property as well.
hexifybytes
Whether conversion of byte to char (or vice-versa) should encode to (or decode from) hexadecimal. In Texis version 6 (or compatibilityversion 6) and earlier, this always occurred. In Texis version 7 (or compatibilityversion 7) and later, it is controllable with the hexifybytes SQL property: 0 for off/as-is, 1 for hexadecimal conversion. This property is on by default in tsql (i.e. hex conversion ala version 6 and earlier), so that SELECTing from certain system tables that contain byte columns will still be readable from the command line. However, the property is off by default in version 7 and later non-tsql programs (such as Vortex), to avoid the hassle of hex conversion when raw binary data is needed (e.g. images), and because Vortex etc. have more tools for dealing with binary data, obviating the need for hex conversion. (The hextobin() and bintohex() SQL functions may also be useful, here.) The hexifybytes property was added in version 7. It is also settable in the conf/texis.ini config file (here). The compatibilityversion property (here), when set, affects this property as well.
unalignedbufferwarning
Whether to issue "Unaligned buffer" warning messages when unaligned buffers are encountered in certain situations. Messages are issued if this setting is true/nonzero (the default). Added in version 7.00.1366400000 20130419.
unneededrexescapewarning
Whether to issue "REX: Unneeded escape sequence ..." warnings when a REX expression uses certain unneeded escapes. An unneeded escape is when a character is escaped that has no special meaning in the current context in REX, either alone or escaped. Such escapes are interpreted as just the literal character alone (respect-case); e.g "\w" has no special meaning in REX, and is taken as "w".
While such escapes have no meaning currently, some may take on a specific new meaning in a future Texis release, if REX syntax is expanded. Thus using them in an expression now may unexpectedly (and silently) result in their behavior changing after a Texis update; hence the warning message. Expressions using such escapes should thus have them changed to the unescaped literal character.
If updating the code is not feasible, the warning may be silenced by setting unneededrexescapewarning to 0 - at the risk of silent behavior change at an upgrade. Added in version 7.06.1465574000 20160610. Overrides [Texis] Unneeded REX Escape Warning setting (here) in conf/texis.ini.
nulloutputstring
The string value to output for SQL NULL values. The default is "NULL". Note that this is different than the output string for zero-integer date values, which are also shown as "NULL". Added in version 7.02.1405382000 20140714.
validatebtrees
Bit flags for additional consistency checks on B-trees. Added in version 7.04.1449078000 20151202. Overrides [Texis] Validate Btrees setting (here) in conf/texis.ini.
|
|
# Tag Info
1
The simple answer is that a wing moves through the air generally at a non-zero angle of attack. The air flow below the wing sort of impacts the wing surface, compressing and slowing down as it is deflected. See this Drawing:
0
If you mean what I think you mean, then your idea won't work as well as you're hoping. Let me illustrate with a rhetorical question: Would you sky dive with a helicopter rotor as your parachute? I certainly hope you wouldn't. Upon brief reflection, you will see that your "propeller-chute" would not provide very much drag as you hurtled groundward. As a ...
2
There's a more straightforward calculation. In order to travel eastward, the plane's velocity must have a southward component of 60kph to cancel the wind from the south. Since the plane's speed is 100kph, we have the eastward component (in kph) is just: $$v_E = \sqrt{100^2 - 60^2} = 80$$ Thus, you are correct; the time required to travel 189km eastward ...
Top 50 recent answers are included
|
|
# Equation solutions
• Dec 11th 2009, 08:44 AM
Stuck Man
Equation solutions
I want to find x-axis intercepts of this equation:
(sin x+0.5)(sin x-0.25)=0.25
0 <= x <= 360.
So sin x=-0.25 or sin x=0.5
One of the associated acute angles is 30 which is found from sin x=0.5. The other is 48.59 but I don't know where it comes from.
• Dec 11th 2009, 09:29 AM
Raoh
hi(Hi)
put $\sin x=X$
and solve $(X+0.5)(X-0.25)-0.25=0$
• Dec 11th 2009, 09:29 AM
Stuck Man
I rearranged the equation to equal 0 using +.75 and -.5. I then solved the problem but I don't know why I couldn't solve it with the other equation.
• Dec 11th 2009, 09:35 AM
Stuck Man
I think it must be necessary to factorise without any added on value. Completing the square for instance wouldn't work.
• Dec 11th 2009, 09:48 AM
Raoh
Quote:
Originally Posted by Stuck Man
I think it must be necessary to factorise without any added on value. Completing the square for instance wouldn't work.
(Thinking)
to find the x-intercepts you must solve the given equation,
$(X+0.5)(X-0.25)-0.25=X^2-0.25X+0.5X-0.375=X^2+0.25X-0.375=0$.
i found the solutions $0.5$ and $-0.75$
therefore,
$\sin x=0.50 \Leftrightarrow x=\arcsin (0.50)$
or
$\sin x=-0.75\Leftrightarrow x=\arcsin (-0.75)$.
• Dec 11th 2009, 09:59 AM
Stuck Man
I think you've mixed up the signs of the solutions. You've rewritten the formula the same as I did. I'm still not sure why I have to fully factorise and not use the Completing The square method. I think it have something to do with the use of sin.
• Dec 11th 2009, 02:21 PM
skeeter
Quote:
Originally Posted by Stuck Man
I want to find x-axis intercepts of this equation:
(sin x+0.5)(sin x-0.25)=0.25
0 <= x <= 360.
So sin x=-0.25 or sin x=0.5
One of the associated acute angles is 30 which is found from sin x=0.5. The other is 48.59 but I don't know where it comes from.
$\sin^2{x} + .25\sin{x} - 0.125 = 0.25
$
$\sin^2{x} + .25\sin{x} - 0.375 = 0$
$8\sin^2{x} + 2\sin{x} - 3 = 0$
$(4\sin{x} + 3)(2\sin{x} - 1) = 0$
$\sin{x} = \frac{3}{4}$ ...
$x = \arcsin\left(\frac{3}{4}\right) \approx 48.59^\circ$
$x = 180 - \arcsin\left(\frac{3}{4}\right) \approx 131.4^\circ$
$\sin{x} = \frac{1}{2}$
$x = 30^\circ$
$x = 150^\circ$
• Dec 11th 2009, 10:11 PM
Stuck Man
I still don't know why I can't use the equation as it was originally:
(sin x+0.5)(sin x-0.25)=0.25
sin x=-0.25 or sin x=0.5
• Dec 11th 2009, 11:11 PM
11rdc11
Quote:
Originally Posted by Stuck Man
I still don't know why I can't use the equation as it was originally:
(sin x+0.5)(sin x-0.25)=0.25
sin x=-0.25 or sin x=0.5
You can't do that in math.
Now if the equation was
$(\sin{x}+.5)(\sin{x}-.25) = 0$
then you could do that
Notice how Raoh and Skeeter set the equation equal to 0 and then solved.
|
|
### Undecidability for dummies
It's been my experience that many important "complex" theorems are complicated in only one or two parts. Oftentimes, if you're willing to accept a lemma or two without proof, you can understand the entire thing. So this is a post explaining what I think is a fairly complicated topic, but there is a piece I don't try to prove. I hope the result is something that's understandable to anyone with a little programming experience.
One of the things which fascinates me most are "incompleteness" theorems. I understand how we can look at some individual solution and determine that it doesn't solve some problem, but the proof that no solutions exist seems a lot harder.
A foundational result in theoretical computer science is the undecidability of the halting problem. This states that, given some program P, there is no general way to tell if P will run forever or if it will eventually stop. For example, the following program:
for each integer x: if x + 1 = x, then halt else go on to the next integer
will run forever, because there's not integer which is the same as itself with one added to it. This program:
for each integer x: if x + 0 = x, then halt else go on to the next integer
will halt immediately.
So how can we prove that there is no general method to tell whether a program will halt? It's a proof by contradiction: suppose we have some method, let's say M, of telling if a program will halt. Consider the following program:
if M says *this program* will halt, then run forever
else if M says this program will run forever, then halt
For any method M, it will fail to correctly predict the behavior of our program. So for any method M, there must be at least one program whose behavior it fails to predict, which proves our theorem.
When I first learned this, I felt (and to a certain extent still feel) that it was kind of a cheap trick. In retrospect, I think this was due to the program's ability to refer to itself. This is the complexity that I left out of the post, but the basic idea isn't that hard: we can assign a natural number to every program (i.e. there's a "first" program, a second program, ...). Once we've done that, a program "referring to itself" can be accomplished via these numbers, e.g. program 12345 referring to program 12345.
One simple yet important extension to the halting problem is Rice's Theorem, which basically says that you can never prove anything about a program. Want to prove that your program won't crash? Tough. Someone asks you to prove your algorithm always gives the right answer? No can do.
If you're interested, you can see a list of undecidable problems, the most famous of which is Hilbert's tenth.
### Divisible by 3
You probably know the rule of thumb to check if a number is divisible by three: add the digits and see if that number is divisible by three. E.g. 3627 is divisible by three since 3+6+2+7=18, which is divisible by three.
Here is a short proof of this, as well as some extensions. Note that $3627=3*10^3+6*10^2+2*10+7$; if we consider $p(x)=3x^3+6x^2+2x+7$, then $3627=p(10)$. Finding the sum of the digits is equivalent to finding $p(1)$. Our claim is that $p(10)$ is divisible by three if and only if $p(1)$ is divisble by three.
A more general theorem holds, in fact: if $a\equiv b \bmod m$ then $p(a)\equiv p(b) \bmod m$ for any polynomial $p$. A colloquial phrasing is "if a and b have the same remainder after dividing by m, then $p(a)$ and $p(b)$ have the same remainder after dividing by m." In our case, we're just interested in the case where the remainder is zero. The proof of this follows directly from the properties of modular arithmetic, so I won't bore you with it.
Using this theorem, we find that $10\equiv 1 \bmod 3$, so $p(10)\equiv p(1) \bmod 3$, just like we wanted. Note that $10\equiv 1\bmod 9$ as well, so the same "add up the digits" shortcut works with division by 9.
We can extend this to more complicated shortcuts. You might know the trick for divisibility by 11: alternately add and subtract the digits. For example, $1-2+1=0$ so $121$ is divisible by 11.
This is just another instance of our theorem. Since $10\equiv -1 \bmod 11$, $p(10)\equiv p(-1)\bmod 11$ and $p(-1)$ is just alternately adding and subtracting the digits.
Wikipedia has an extensive list of divisibility "shortcuts", some of which seem more complex than just doing long division, but hopefully this illuminates the reasoning behind some of them.
|
|
# 6.2 The Gram-Schmidt Orthogonalization Process and Orthogonal Complements
In previous chapters, we have seen the special role of the standard ordered bases for and . The special properties of these bases stem from the fact that the basis vectors form an orthonormal set. Just as bases are the building blocks of vector spaces, bases that are also orthonormal sets are the building blocks of inner product spaces. We now name such bases.
# Definition.
Let V be an inner product space. A subset of V is an orthonormal basis for V if it is an ordered basis that is orthonormal.
# Example 1
The standard ordered basis for is an orthonormal basis for .
# Example 2
The set
is an orthonormal basis for .
The next theorem and its corollaries illustrate why orthonormal sets and, in particular, orthonormal bases are so important.
# Theorem 6.3.
Let V be an inner product space and be an orthogonal subset of V consisting of nonzero vectors. If , then
# Proof.
Write , where . Then, for ,
we have
So , and the result follows.
The next corollary follows immediately from Theorem 6.3.
# Corollary 1.
If, in addition to the hypotheses of Theorem 6.3, S is orthonormal and , then
If V possesses a finite orthonormal basis, then Corollary 1 allows us to compute the coefficients in a linear combination very easily. (See Example 3.)
# Corollary 2.
Let V be an inner product space, and let S be an orthogonal subset of V consisting of nonzero vectors. Then S is linearly independent.
# Proof.
Suppose that and
As in the proof of Theorem 6.3 with , we have for all j. So S is linearly independent.
# Example 3
By Corollary 2, the orthonormal set
obtained in Example 8 of Section 6.1 is an orthonormal basis for . Let . The coefficients given by Corollary 1 to Theorem 6.3 that express x as a linear combination of the basis vectors are
and
As a check, we have
Corollary 2 tells us that the vector space H in Section 6.1 contains an infinite linearly independent set, and hence H is not a finite-dimensional vector space.
Of course, we have not yet shown that every finite-dimensional inner product space possesses an orthonormal basis. The next theorem takes us most of the way in obtaining this result. It tells us how to construct an orthogonal set from a linearly independent set of vectors in such a way that both sets generate the same subspace.
Before stating this theorem, let us consider a simple case. Suppose that is a linearly independent subset of an inner product space (and hence a basis for some two-dimensional subspace). We want to construct an orthogonal set from that spans the same subspace. Figure 6.1 suggests that the set , where and , has this property if c is chosen so that is orthogonal to .
To find c, we need only solve the following equation:
So
Thus
The next theorem shows us that this process can be extended to any finite linearly independent subset.
# Theorem 6.4.
Let V be an inner product space and be a linearly independent subset of V. Define , where and
(1)
Then is an orthogonal set of nonzero vectors such that .
# Proof.
The proof is by mathematical induction on n, the number of vectors in S. For let . If , then the theorem is proved by taking i.e., . Assume then that the set with the desired properties has been constructed by the repeated use of (1). We show that the set also has the desired properties, where is obtained from by (1). If , then (1) implies that , which contradicts the assumption that is linearly independent. For , it follows from (1) that
since if by the induction assumption that is orthogonal. Hence is an orthogonal set of nonzero vectors. Now, by (1), we have that . But by Corollary 2 to Theorem 6.3, is linearly independent; so . Therefore .
The construction of by the use of Theorem 6.4 is called the Gram—Schmidt process.
# Example 4
In , let and . Then is linearly independent. We use the Gram-Schmidt process to compute the orthogonal vectors and , and then we normalize these vectors to obtain an orthonormal set.
Take . Then
Finally,
These vectors can be normalized to obtain the orthonormal basis , where
and
# Example 5
Let with the inner product , and consider the subspace with the standard ordered basis . We use the Gram-Schmidt process to replace by an orthogonal basis for , and then use this orthogonal basis to obtain an orthonormal basis for .
Take . Then , and . Thus
Furthermore,
Therefore
We conclude that is an orthogonal basis for .
To obtain an orthonormal basis, we normalize , and to obtain
and similarly,
Thus is the desired orthonormal basis for .
Continuing to apply the Gram-Schmidt orthogonalization process to the basis for P(R), we obtain an orthogonal basis . For each n, the polynomial is called the kth Legendre polynomial. The first three Legendre polynomials are 1, x and . The set of Legendre polynomials is also an orthogonal basis for P(R).
The following result gives us a simple method of representing a vector as a linear combination of the vectors in an orthonormal basis.
# Theorem 6.5.
Let V be a nonzero finite-dimensional inner product space. Then V has an orthonormal basis . Furthermore, if and , then
# Proof.
Let be an ordered basis for V. Apply Theorem 6.4 to obtain an orthogonal set of nonzero vectors with . By normalizing each vector in , we obtain an orthonormal set that generates V. By Corollary 2 to Theorem 6.3, is linearly independent; therefore is an orthonormal basis for V. The remainder of the theorem follows from Corollary 1 to Theorem 6.3.
# Example 6
We use Theorem 6.5 to represent the polynomial as a linear combination of the vectors in the orthonormal basis for obtained in Example 5. Observe that
and
Therefore .
Theorem 6.5 gives us a simple method for computing the entries of the matrix representation of a linear operator with respect to an orthonormal basis.
# Corollary.
Let V be a finite-dimensional inner product space with an orthonormal basis . Let T be a linear operator on V, and let . Then for any i and j, .
Proof. From Theorem 6.5, we have
Hence .
The scalars given in Theorem 6.5 have been studied extensively for special inner product spaces. Although the vectors were chosen from an orthonormal basis, we introduce a terminology associated with orthonormal sets in more general inner product spaces.
# Definition.
Let be an orthonormal subset (possibly infinite) of an inner product space V, and let . We define the Fourier coefficients of x relative to to be the scalars , where .
In the first half of the 19th century, the French mathematician Jean Baptiste Fourier was associated with the study of the scalars
or in the complex case,
for a function f. In the context of Example 9 of Section 6.1, we see that , where that is, is the nth Fourier coefficient for a continuous function relative to S. The coefficients are the “classical” Fourier coefficients of a function, and the literature concerning their behavior is extensive. We learn more about Fourier coefficients in the remainder of this chapter.
# Example 7
Let . In Example 9 of Section 6.1, S was shown to be an orthonormal set in H. We compute the Fourier coefficients of relative to S. Using integration by parts, we have, for ,
and, for ,
As a result of these computations, and using Exercise 16 of this section, we obtain an upper bound for the sum of a special infinite series as follows:
for every k. Now, using the fact that , we obtain
or
Because this inequality holds for all k, we may let to obtain
Additional results may be produced by replacing f by other functions.
We are now ready to proceed with the concept of an orthogonal complement.
# Definition.
Let S be a nonempty subset of an inner product space V. We define (read “S perp”) to be the set of all vectors in V that are orthogonal to every vector in S; that is, . The set is called the orthogonal complement of S.
It is easily seen that is a subspace of V for any subset S of V.
# Example 8
The reader should verify that and for any inner product space V.
# Example 9
If and , then equals the xy-plane (see Exercise 5).
Exercise 18 provides an interesting example of an orthogonal complement in an infinite-dimensional inner product space.
Consider the problem in of finding the distance from a point P to a plane W. (See Figure 6.2.) Problems of this type arise in many settings. If we let y be the vector determined by 0 and P, we may restate the problem as follows: Determine the vector u in W that is “closest” to y. The desired distance is clearly given by . Notice from the figure that the vector is orthogonal to every vector in W, and so .
The next result presents a practical method of finding u in the case that W is a finite-dimensional subspace of an inner product space.
# Theorem 6.6.
Let W be a finite-dimensional subspace of an inner product space V, and let . Then there exist unique vectors and such that . Furthermore, if is an orthonormal basis for W, then
# Proof.
Let be an orthonormal basis for W, let u be as defined in the preceding equation, and let . Clearly and .
To show that , it suffices to show, by Exercise 7, that z is orthogonal to each . For any j, we have
To show uniqueness of u and z, suppose that , where and . Then . Therefore and .
# Corollary.
In the notation of Theorem 6.6, the vector u is the unique vector in W that is “closest” to y; that is, for any , and this inequality is an equality if and only if .
Proof.
As in Theorem 6.6, we have that , where . Let . Then is orthogonal to z, so, by Exercise 10 of Section 6.1, we have
Now suppose that . Then the inequality above becomes an equality, and therefore . It follows that , and hence . The proof of the converse is obvious.
The vector u in the corollary is called the orthogonal projection of y on W. We will see the importance of orthogonal projections of vectors in the application to least squares in Section 6.3.
# Example 10
Let with the inner product
We compute the orthogonal projection of on .
By Example 5,
is an orthonormal basis for . For these vectors, we have
and
Hence
It was shown (Corollary 2 to the replacement theorem, p. 48) that any linearly independent set in a finite-dimensional vector space can be extended to a basis. The next theorem provides an interesting analog for an orthonormal subset of a finite-dimensional inner product space.
# Theorem 6.7.
Suppose that is an orthonormal set in an n-dimensional inner product space V. Then
1. (a) S can be extended to an orthonormal basis for V.
2. (b) If , then is an orthonormal basis for (using the preceding notation).
3. (c) If W is any subspace of V, then .
# Proof.
(a) By Corollary 2 to the replacement theorem (p. 48), S can be extended to an ordered basis for V. Now apply the Gram-Schmidt process to . The first k vectors resulting from this process are the vectors in S by Exercise 8, and this new set spans V. Normalizing the last vectors of this set produces an orthonormal set that spans V. The result now follows.
(b) Because is a subset of a basis, it is linearly independent. Since is clearly a subset of , we need only show that it spans . Note that, for any , we have
If , then for . Therefore
(c) Let W be a subspace of V. It is a finite-dimensional inner product space because V is, and so it has an orthonormal basis . By (a) and (b), we have
# Example 11
Let in . Then if and only if and . So , and therefore . One can deduce the same result by noting that and, from (c), that .
# Exercises
1. Label the following statements as true or false.
1. (a) The Gram-Schmidt orthogonalization process produces an orthonormal set from an arbitrary linearly independent set.
2. (b) Every nonzero finite-dimensional inner product space has an orthonormal basis.
3. (c) The orthogonal complement of any set is a subspace.
4. (d) If is a basis for an inner product space V, then for any the scalars are the Fourier coefficients of x.
5. (e) An orthonormal basis must be an ordered basis.
6. (f) Every orthogonal set is linearly independent.
7. (g) Every orthonormal set is linearly independent.
2. In each part, apply the Gram–Schmidt process to the given subset S of the inner product space V to obtain an orthogonal basis for span(S). Then normalize the vectors in this basis to obtain an orthonormal basis for span(S), and compute the Fourier coefficients of the given vector relative to . Finally, use Theorem 6.5 to verify your result.
1. (a) and
2. (b) and
3. (c) with the inner product , and
4. (d) , where and
5. (e) and
6. (f) and
7. (g) and
8. (h) , and
9. (i) with the inner product and
10. (j) and
11. (k) and
12. (l) and
13. (m) and
3. In , let
Find the Fourier coefficients of (3, 4) relative to .
4. Let in . Compute .
5. Let , where is a nonzero vector in . Describe geometrically. Now suppose that is a linearly independent subset of . Describe geometrically.
6. Let V be an inner product space, and let W be a finite-dimensional subspace of V. If , prove that there exists such that , but . Hint: Use Theorem 6.6.
7. Let be a basis for a subspace W of an inner product space V, and let . Prove that if and only if for every .
8. Prove that if is an orthogonal set of nonzero vectors, then the vectors derived from the Gram-Schmidt process satisfy for . Hint: Use mathematical induction.
9. Let in . Find orthonormal bases for W and .
10. Let W be a finite-dimensional subspace of an inner product space V. Prove that . Using the definition on page 76, prove that there exists a projection T on W along that satisfies . In addition, prove that for all . Hint: Use Theorem 6.6 and Exercise 10 of Section 6.1.
11. Let A be an matrix with complex entries. Prove that if and only if the rows of A form an orthonormal basis for . Visit goo.gl/iKcC4S for a solution.
12. Prove that for any matrix .
13. Let V be an inner product space, S and be subsets of V, and W be a finite-dimensional subspace of V. Prove the following results.
1. (a) implies that .
2. (b) so .
3. (c) . Hint: Use Exercise 6.
4. (d) . (See the exercises of Section 1.3.)
14. Let and be subspaces of a finite-dimensional inner product space. Prove that and . (See the definition of the sum of subsets of a vector space on page 22.) Hint for the second equation: Apply Exercise 13(c) to the first equation.
15. Let V be a finite-dimensional inner product space over F.
1. (a) Parseval’s Identity. Let be an orthonormal basis for V. For any prove that
2. (b) Use (a) to prove that if is an orthonormal basis for V with inner product , then for any
where is the standard inner product on .
1. (a) Bessel’s Inequality. Let V be an inner product space, and let be an orthonormal subset of V. Prove that for any we have
Hint: Apply Theorem 6.6 to and . Then use Exercise 10 of Section 6.1.
2. (b) In the context of (a), prove that Bessel’s inequality is an equality if and only if .
16. Let T be a linear operator on an inner product space V. If for all , prove that . In fact, prove this result if the equality holds for all x and y in some basis for V.
17. Let . Suppose that and denote the subspaces of V consisting of the even and odd functions, respectively. (See Exercise 22 of Section 1.3.) Prove that , where the inner product on V is defined by
18. In each of the following parts, find the orthogonal projection of the given vector on the given subspace W of the inner product space V.
1. (a) and
2. (b) , and
3. (c) with the inner product and
19. In each part of Exercise 19, find the distance from the given vector to the subspace W.
20. Let with the inner product , and let W be the subspace , viewed as a space of functions. Use the orthonormal basis obtained in Example 5 to compute the “best” (closest) second-degree polynomial approximation of the function on the interval .
21. Let with the inner product . Let W be the subspace spanned by the linearly independent set .
1. (a) Find an orthonormal basis for W.
2. (b) Let . Use the orthonormal basis obtained in (a) to obtain the “best” (closest) approximation of h in W.
22. Let V be the vector space defined in Example 5 of Section 1.2, the space of all sequences in F (where or ) such that for only finitely many positive integers n. For , we define . Since all but a finite number of terms of the series are zero, the series converges.
1. (a) Prove that is an inner product on V, and hence V is an inner product space.
2. (b) For each positive integer n, let be the sequence defined by , where is the Kronecker delta. Prove that is an orthonormal basis for V.
3. (c) Let and .
1. (i) Prove that , so .
2. (ii) Prove that , and conclude that .
Thus the assumption in Exercise 13(c) that W is finite-dimensional is essential.
|
|
# Are these endless if statements a bad pattern?
I'm only asking because almost the entire code base I've inherited here, in C# and PHP, looks like this:
if (varOne == flag) {
run_some_sql();
set_some_flag = true;
}
if (varTwo == flag) {
run_some_sql();
set_some_flag = true;
}
if (varThree == flag) {
run_some_sql();
set_some_flag = true;
}
if (varFour == flag) {
run_some_sql();
set_some_flag = true;
}
if (varFive == flag) {
run_some_sql();
set_some_flag = true;
}
if (varSix == flag) {
run_some_sql();
set_some_flag = true;
}
if (varSeven == flag) {
run_some_sql();
set_some_flag = true;
}
if (varEight == flag) {
run_some_sql();
set_some_flag = true;
}
For about ten thousand lines.
I haven't lost my mind, right? Is this bad? There's only about five loops in the entire code base of about 50,000 lines.
I would normally go about this sort of thing by storing the data into an associated array, and loop over that, rather than adding a new if statement for every variable.
Have I totally lost my mind? Eight people worked on this before me, and I'm seriously worried here. Is there ever a good reason to do this sort of thing?
• Well, at least you are sure you will do better than the previous employees. ;p – Steven Jeuris Apr 7 '11 at 22:42
• wtf!? oh my god... o.O – greatwolf Apr 8 '11 at 3:29
• Reminds me of the SO question get rid of ugly if statements – Sean Patrick Floyd Apr 8 '11 at 9:20
• you're not crazy... although, i wonder if SLOC stats are management's measure for employees' productivity/contribution within the project ;) – justin Apr 9 '11 at 7:19
• You don't know thedailywtf.com , right? – Landei Sep 15 '11 at 8:41
## 3 Answers
This is bad. Very bad.
It appears the original implementer doesn't quite understand arrays. You should definitely refactor this. Michael K's answer has the right approach. In C# syntax:
// Hopefully these variables are already in an array or list already, otherwise:
MyType[] myVariables = new MyType[] { varOne, varTwo, /* ... */ varEight };
foreach (MyType variable in myVariables)
{
if (variable == flag)
{
run_some_sql();
set_some_flag = true;
}
}
Note that if run_some_sql() only needs to be executed once, you can break out early and save some computation time:
foreach (MyType variable in myVariables)
{
if (variable == flag)
{
run_some_sql();
set_some_flag = true;
break;
}
}
If it is the case that you only need to execute run_some_sql() once, you can make the code even simpler using new LINQ syntax:
if (myVariables.Any(v => v == flag))
{
run_some_sql();
set_some_flag = true;
}
While refactoring, I'd also recommend choosing some better variable names than varOne, varTwo, flag, etc. Though I assume these are just your examples. :)
• Well, what I'm dealing with is a group of variables that are clearly all related, but not stored as an array. varOne, varTwo is an accurate generic representation of this. – Incognito Apr 8 '11 at 2:57
• @user2905 Is there a logical place where you can put them into an array or List, such as during initialization? If they are all related, I imagine this won't be the only function you'll find that has copy-paste code like this. – Scott Wegner Apr 8 '11 at 15:50
No, you haven't lost your mind. It should more like...
// declared and set somewhere
flags = new int[x];
//...
for (int value: flags) {
if (value == flag) {
run_some_sql();
set_some_flag = true;
}
}
...assuming that the flags are the same type and they really do do the exact same thing. Are you sure that there are no god objects somewhere that the other methods are basing their responses of off?
Another possible approach is to store the SQL statements in a dictionary and to use the flag as key
Dictionary<TypeOfFlag, string> dict = new Dictionary<TypeOfFlag, string>();
dict.Add(valueOne, "SELECT x FROM y");
dict.Add(valueTwo, "SELECT z FROM t");
...
string sql;
if (dict.TryGetValue(flag, out sql)) {
RunSQL(sql);
set_some_flag();
}
If you need more information in order to run a query, you could create a class containing this information, the SQL statement, and possibly even an Execute method and store that one in the dictionary. See: Command pattern (Wikipedia).
Dictionaries have a constant access time O(1) and require no loops in order to access an item and of course require no endless if statements!
Endless if-chains and switch-statements (Case-statements in other languages) are often a strong hint that a poor procedural approach has been used. Applying the DRY principle can even improve such procedural approaches. Polymorphism (Subtyping) is an object-oriented approach that can often eliminate these unpleasant structures as well.
|
|
시간 제한 메모리 제한 제출 정답 맞은 사람 정답 비율
2 초 512 MB 210 91 71 43.558%
## 문제
Farmer John's $N$ cows ($1 \leq N \leq 10^5$), numbered $1 \ldots N$ as always, happen to have too much time on their hooves. As a result, they have worked out a complex social hierarchy related to the order in which Farmer John milks them every morning.
After weeks of study, Farmer John has made $M$ observations about his cows' social structure ($1 \leq M \leq 50,000$). Each observation is an ordered list of some of his cows, indicating that these cows should be milked in the same order in which they appear in this list. For example, if one of Farmer John's observations is the list 2, 5, 1, Farmer John should milk cow 2 sometime before he milks cow 5, who should be milked sometime before he milks cow 1.
Farmer John's observations are prioritized, so his goal is to maximize the value of $X$ for which his milking order meets the conditions outlined in the first $X$ observations. If multiple milking orders satisfy these first $X$ conditions, Farmer John believes that it is a longstanding tradition that cows with lower numbers outrank those with higher numbers, so he would like to milk the lowest-numbered cows first. More formally, if multiple milking orders satisfy these conditions, Farmer John would like to use the lexicographically smallest one. An ordering $x$ is lexicographically smaller than an ordering $y$ if for some $j$, $x_i = y_i$ for all $i < j$ and $x_j < y_j$ (in other words, the two orderings are identical up to a certain point, at which $x$ is smaller than $y$).
## 입력
The first line contains $N$ and $M$. The next $M$ lines each describe an observation. Line $i+1$ describes observation $i$, and starts with the number of cows $m_i$ listed in the observation followed by the list of $m_i$ integers giving the ordering of cows in the observation. The sum of the $m_i$'s is at most $200,000$.
## 출력
Output $N$ space-separated integers, giving a permutation of $1 \ldots N$ containing the order in which Farmer John should milk his cows.
## 예제 입력 1
4 3
3 1 2 3
2 4 2
3 3 4 1
## 예제 출력 1
1 4 2 3
## 힌트
Here, Farmer John has four cows and should milk cow 1 before cow 2 and cow 2 before cow 3 (the first observation), cow 4 before cow 2 (the second observation), and cow 3 before cow 4 and cow 4 before cow 1 (the third observation). The first two observations can be satisfied simultaneously, but Farmer John cannot meet all of these criteria at once, as to do so would require that cow 1 come before cow 3 and cow 3 before cow 1.
This means there are two possible orderings: 1 4 2 3 and 4 1 2 3, the first being lexicographically smaller.
|
|
By awoo, history, 3 years ago, translation,
Series of Educational Rounds continue being held as Harbour.Space University initiative! You can read the details about the cooperation between Harbour.Space University and Codeforces in the blog post.
This round will be rated for the participants with rating lower than 2100. It will be held on extented ACM ICPC rules. The penalty for each incorrect submission until the submission with a full solution is 10 minutes. After the end of the contest you will have 12 hours to hack any solution you want. You will have access to copy any solution and test it locally.
You will be given 7 problems and 2 hours to solve them.
The problems were invented and prepared by Roman Roms Glazov, Adilbek adedalic Dalabaev, Vladimir vovuh Petrov, Ivan BledDest Androsov and me.
Good luck to all participants!
UPD: There certainly will be a discussion of the problems on the local Discord server shortly after the contest ends. I might join it as well)
Congratulations to the winners:
Rank Competitor Problems Solved Penalty
1 Anadi 7 266
2 HIR180 6 129
3 mrscherry 6 152
4 Vergara 6 158
5 Jeel_Vaishnav 6 185
Congratulations to the best hackers:
Rank Competitor Hack Count
1 teapotd 100:-4
3 MarcosK 32
4 tataky 28:-5
5 knotValid 23
721 successful hacks and 668 unsuccessful hacks were made in total!
And finally people who were the first to solve each problem:
Problem Competitor Penalty
A Dalgerok 0:01
B Nazikk 0:03
C neal 0:03
D tikz 0:14
F killer_god 0:34
G lxrvelory 1:03
UPD2: There was an error in problem D which caused some incorrect solutions to get accepted. We will investigate the number of users who were affected by this issue and decide whether the round is rated.
UPD3: We discussed the issue and came up with the following decision:
Those who got accepted earlier and get WA now won't be affected by rating changes. For everyone else (for those who got correct verdict) the contest will be rated.
UPD4: Editorial is out
• +107
» 3 years ago, # | +36 2 hours for 7 problems seem to be too less. Any chance extending the time to 2.30 hours? Specially for Educational Round, which should focus on having participants with low-mid ratings attempt more problems. C'mon beloved Codeforces! Give a thought.. :)
• » » 3 years ago, # ^ | -24 "Specially for Educational Round, which should focus on having participants with low-mid ratings attempt more problems".Not really that's what Div. 3 rounds are for.
• » » » 3 years ago, # ^ | +19 Div3 rounds (both frequency and problem difficulty level) are inconsistent, Edu Rounds are still the best way to get introduced with ideas that can be used in broader extent.
• » » 3 years ago, # ^ | +8 Most of the div2 people solve at most 5 of them anyway. Having 2h for 7 problems is good enough, since it gives a challenge for the better contestants too
• » » » 3 years ago, # ^ | +4 I'm saying just for education rounds though, the idea is to Educate, so why not give an extra half an hour?! That will surely benefit lots of programmers like me who are not yet to the level but trying to attempt and solve more problems than they usually do. There're lots of other div2 rounds where better contestants can be challenged by 2 hours time limit.
• » » » » 3 years ago, # ^ | ← Rev. 3 → +145 Pretty sure the meaning of "Educational" rounds was lost a long time ago.Back when they started, educational rounds had classic problems which highlighted ideas and techniques that contestans should learn.Nowadays they are just normal contests with different rules ¯\_(ツ)_/¯
• » » » » » 3 years ago, # ^ | 0 Maybe they ran out of ideas and techniques that new contestants should learn...
• » » 3 years ago, # ^ | 0 that's a good idea but maybe 2 hours make us want to try faster .. for me at my best I would solve 3 problems in less than 2 hours so it won't make that difference but it could for others so I agree with you
» 3 years ago, # | 0 Hoping to get some plus ratings in this round :p
• » » 3 years ago, # ^ | 0 well... not anymore :/
» 3 years ago, # | +37 Lower, or lower and equal to 2100?
• » » 3 years ago, # ^ | +17 educational round == div2 round sponsored by harbour space
• » » » 3 years ago, # ^ | 0 True
• » » 3 years ago, # ^ | 0 If your rating is equal to 2100 then your rating will not change no matter what.
» 3 years ago, # | 0 Hi, guys, is it rated for me too? I am participating after a long time and I have heard that some changes have been done in the divisions — div1,2 and 3. What are the rating ranges in these divisions and will my rating be affected if I participate in this contest? Thank you.
• » » 3 years ago, # ^ | 0 You rating will change
• » » » 3 years ago, # ^ | +5 okay. Thanks
» 3 years ago, # | -12 An Educational round after several bad contests, time to get new high rating.
» 3 years ago, # | +24 69 ( ͡° ͜ʖ ͡°)
» 3 years ago, # | ← Rev. 2 → 0 what is test 5 on E???????????????????Why can't we see the test cases?
• » » 3 years ago, # ^ | +15 wait are we allowed to discuss
» 3 years ago, # | +5 Why in E d can be>n?
• » » 3 years ago, # ^ | 0 it doesn't matter. you can just take d=min(d,n).
» 3 years ago, # | +44 There was an error in problem D which caused some incorrect solutions to get accepted. We will investigate the number of users who were affected by this issue and decide whether the round is rated.I am really sorry :( Both bugs (in D and G) were mine.
• » » 3 years ago, # ^ | ← Rev. 6 → +23 <3
• » » 3 years ago, # ^ | ← Rev. 2 → +77 Why not consider it as a part of the hacking since Accepted here is not a final verdict because there is testing after hacking phase is finished
• » » » 3 years ago, # ^ | -12 Just imagine the number of people who attempted to other problems after submiting a wrong solution to problem D and its affection to the rankings...
• » » » » 3 years ago, # ^ | +58 The tests aren't exhaustive, and Accepted doesn't necessarily mean your solution is correct.
• » » » 3 years ago, # ^ | 0 <3
• » » 3 years ago, # ^ | +51 Isn't that the whole point of having hacking-phase or system tests?
• » » 3 years ago, # ^ | -41 Should be unrated. Shit solutions passing 36 tests of D just not acceptable!
• » » 3 years ago, # ^ | +12 You are poset
• » » 3 years ago, # ^ | +7 Please don't unrated. Please. :(
• » » 3 years ago, # ^ | +8 Please turn on hacking phase to hack solutions with cout << 0 (to investigate the number of users who REALLY affected by this issue) and then run system tests.
• » » 3 years ago, # ^ | -15 Such a noob
• » » 3 years ago, # ^ | +3 Please don't be unrated
• » » » 3 years ago, # ^ | 0 TOM TOM TOM
» 3 years ago, # | ← Rev. 2 → +26 i submit code for problem D with just cout << 0 << endl; and get AC but good vertices in my code ans simple test 1 are different why??
• » » 3 years ago, # ^ | +104
» 3 years ago, # | +59 NO!!! Plz be rated!!!! It's my first time to be MASTER!!! :(
• » » 3 years ago, # ^ | +33 I was gonna be an expert too:(
• » » 3 years ago, # ^ | ← Rev. 2 → +8 Poor you, bro. I hope this contest could be rated.How was your result today?
• » » » 3 years ago, # ^ | ← Rev. 2 → +10 After seeing that "cout << 0" passed all tests in D, it is really unnecessary to consider it should be rated or not:(
• » » » » 3 years ago, # ^ | +4 The system is judging at the moment. :)
• » » 3 years ago, # ^ | +8 I hope it's rated too.
• » » » 3 years ago, # ^ | +4 I agree
• » » 3 years ago, # ^ | 0 The same thing man, I can be expert for the first time in my whole life after 2 years of work, if this round will be rated, please let it be so.
» 3 years ago, # | +23 Please don't unrate this contest.Could we rejudge problem D or some accepted incorrect solutions?
• » » 3 years ago, # ^ | ← Rev. 2 → 0 I don't think so... I myself didn't solve D, but there might be some guys with little bugs, who would have solved this problem after getting WA.
• » » » 3 years ago, # ^ | ← Rev. 2 → +2 How does correct checker guarantee that you will get WA for the little bug? The little bug is the most common reason for hacking
• » » » » 3 years ago, # ^ | +2 It mustn't be that little you're thinking...Not everyone solve problem D in on try. But getting AC in pretest means don't working on it anymore.And the pretests was really weak, the guy posted above (alireza_kaviani) got AC with outputing only 0.
» 3 years ago, # | ← Rev. 3 → -7 Spoiler Alert:In D, is it true to:1- Find MST.2- If n - 1 < = k then we have reached the answer, otherwise, erase edges starting from leaves until the number of remaining edges equals k.
• » » 3 years ago, # ^ | +21 I think it needs to be tree that grants minimum distances from the node 1 (like, dijkstra-tree)
• » » » 3 years ago, # ^ | +3 You're right. Dijkstra tree with the root at 1. Not MST.
• » » » 3 years ago, # ^ | -7 Thank you! I had forgot what MST represents, but have just remembered.
• » » 3 years ago, # ^ | +6 Shouldn't it be shortest path tree rather than MST?
• » » 3 years ago, # ^ | ← Rev. 4 → +3 Apply Dijkstra from source 1. Get tree with n-1 edges. Start removing leaves edges from that tree. Too bad I had a small bug in Dijkstra and could not submit on time.
• » » » 3 years ago, # ^ | 0 @MatPhySC what if # of edges in optimal paths is greather than K, dijkstra tree should answer less edges than the solution
• » » » » 3 years ago, # ^ | 0 If I understood your question correctly than if K >= N-1 then answer will be Dijkstra tree because all vertices are good
• » » » » » 3 years ago, # ^ | 0 Sorry, poor english, but what i mean is that even when all vertices in Dijkstra tree are good, there could be another ones that belong to some other Dijkstra tree and they are also good edges
• » » » » » 3 years ago, # ^ | ← Rev. 3 → 0 consider this case: 3 3 3 1 2 2 1 3 1 2 3 1if i understood your solution, it should give 2 1 2however, 3rd edge is also good, at least the way i get the problemUD: i got it now, it's good vertices, not good edges
• » » » » » » 3 years ago, # ^ | 0 There are two Dijkstra tree. You can consider any of them.
• » » 3 years ago, # ^ | +7 Wrong solution:Consider the following case - 3 3 2 1 2 2 2 3 2 1 3 3Answer is — 2 1 3Answer from MST - 2 1 2Minimum distance from 1 to 3 is 3 units. MST gives 4 units distance from 1 to 3, so 3 is no more a good vertex.
• » » 3 years ago, # ^ | +3 This will fail. Consider this tree. 1 2 1 1 3 1 1 4 1 2 4 1 There are multiple MST. But taking any MST other then 1,2,3rd edges. Will give WA.MST does not guarantee that all edges are at the minimum distance from vertex 1.
• » » 3 years ago, # ^ | 0 Thank you all!.Beautiful problem BTW :D
• » » 3 years ago, # ^ | 0 I don't think MST works. I got AC on this problem with SPT(shortest path tree). and maximum number of good vertices is min(n-1, k).
» 3 years ago, # | +4 What is test 3 in D?
» 3 years ago, # | 0 First time I wrote a buggy segment tree. :(
• » » 3 years ago, # ^ | +8 It means you get an Accepted for Problem E, don't you?Could I see your solution?
• » » » 3 years ago, # ^ | ← Rev. 4 → +1 Yep. It was accepted after the contest was over. In the last minute, I realized my mistake.My Soln.
• » » » » 3 years ago, # ^ | +3 Thanks, bro. Hope you high rating :)
» 3 years ago, # | ← Rev. 2 → +54 when I wondering how this guy passed D in 31 ms lol, lmaoI bet a lot of contestant will fail on D :|
• » » 3 years ago, # ^ | 0 It seems like the checker was wrong, because the code is clearly wrong for even the sample cases.
• » » 3 years ago, # ^ | ← Rev. 2 → -9 This solution doesn't even take the input.
• » » » 3 years ago, # ^ | +7 It's not necessary to take the input. See this blog.
• » » » » 3 years ago, # ^ | +3 Thanks got it :)
• » » » 3 years ago, # ^ | 0 It's not necessary to take input in any of the problems.
» 3 years ago, # | ← Rev. 2 → +4 I am sorry to be saying this but in my opinion it would be extremely unfair to declare this round as unrated because there would be many people who might not have done 'D' and have performed well in today's contest. If some incorrect solutions were accepted then it may as well be considered as a case of weak test cases. I urge you to consider the plight of many like me who believed they did well in today's contest and would be stranded disappointed if it is made unrated. PS Edit1: To all those who down voted this I am sorry to have hurt your feelings. I do respect your opinion and I totally accept that either of the scenarios I suggested would have been unfair. But the final decision taken by the contest makers is fair in everyone's eyes and no one loses out so I believe it is for the best.
• » » 3 years ago, # ^ | ← Rev. 2 → -7 feel about those coders who cannot improve his D solution to get actual AC solution. because of he/she already get AC.
• » » » 3 years ago, # ^ | +3 I can understand that but that's also the case in many contests when your pretests get passed and your main tests fail. I understand that either decision would be unfair to some but it comes down to which one is more on the fairer side. It comes down to 1 question vs 1 contest and I believe that making it unrated would be more unfair.
• » » » » 3 years ago, # ^ | +1 My solution on D is actually failing on pretest 2 but during contest it passed Now consider if the checker was correct i would have checked my code again and solved it after getting a WA.
• » » » » » 3 years ago, # ^ | ← Rev. 2 → +16 Yes, I understand it wasn't fair to you. I sincerely apologise for ranting out.
• » » 3 years ago, # ^ | -6 To all those who down voted this I am sorry to have hurt your feelings. I do respect your opinion and I totally accept that either of the scenarios I suggested would have been unfair. But the final decision taken by the contest makers is fair in everyone's eyes and no one loses out so I believe it is for the best.
» 3 years ago, # | -22 make it unrated omfg !!
• » » 3 years ago, # ^ | +5 thats what you wont say when you did a heck good job today (or at least you think so). and the guys who got a crappy AC for that problem will get their ratings back to what they should have in the next contest or two ei?
• » » » 3 years ago, # ^ | 0 Your English is not understandable You have anime profile picture have a nice day :) :P :>
• » » » » 3 years ago, # ^ | 0 yeah i forgot most of the ,s and .s but yeah nice day too :D
• » » 3 years ago, # ^ | ← Rev. 2 → +3 you didn't submit any solution for D lol
» 3 years ago, # | 0 When will we know if our submission for D is correct or not?
» 3 years ago, # | +3 Why can't simple dfs + 2 multiset pass problem E?
• » » 3 years ago, # ^ | +1 I passed with a simple DFS and a vector of maps.Perhaps you got some bugs? Personally I wasted 30 minutes for not realizing I overwrote queries instead of accumulating those lol.
• » » » 3 years ago, # ^ | 0 You were right, I made insanely stupid bug. GG
• » » 3 years ago, # ^ | 0 Mine passaed 45632893 (After the contest and the code is probably bad)
» 3 years ago, # | +12 rated plz!Just fix the problem(s) of specialjudge.And those best hackers will get everything done. ;)
» 3 years ago, # | ← Rev. 4 → +38 In system test, the code that pretest is passed can be wrong, naturally. I think there is no reason that this round will be unrated. Moreover, this round is educational round and hacking can't be attempted in the contest. So this round wasn't influenced by something wrong.
• » » 3 years ago, # ^ | ← Rev. 2 → 0 If our solution failed on pretests we will have time to make that solution correct. But now we can't do anything. So if round gets rated it will be unfair for all participants whose solution failed on D because of bug in checker. So round should be unrated.
• » » » 3 years ago, # ^ | 0 if your solution is this: then you obviously know your solution is wrong.and if its something different, how is it different then having very easy pretests if it passes sample correctly?
• » » » » 3 years ago, # ^ | +3 My solution is not even close to this. And we can't assume all 36/37 pretests are like samples (in running contest).
• » » » 3 years ago, # ^ | +1 Same would be the case when pretests are weak. but we don't make it unrated in that case.
• » » » » 3 years ago, # ^ | +3 36 weak pretests in D! We are not that unlucky
» 3 years ago, # | ← Rev. 3 → -9 Let's hit the unrated button.
» 3 years ago, # | +3 PikMike said this in Discord server...
• » » 3 years ago, # ^ | +6 damn that feels good..
» 3 years ago, # | +27 It seems that the special judge of problem D is incorrect. So I'm thinking about something like ummmmm.. unrated? In fact, I just wanna complain about the awful quality. Please check your contest more carefully.
» 3 years ago, # | ← Rev. 2 → -11 Let's make it unrated
» 3 years ago, # | +20 I feel that the contest should not be rated. Any opinions?
» 3 years ago, # | -41 please make it unrated
• » » 3 years ago, # ^ | 0 It say people, who get WA1 on D.
» 3 years ago, # | +14 I'm wondering why my bruteforce solution on problem E could get Accepted... Can anyone explain why?
• » » 3 years ago, # ^ | +4 Don't worry fam, it's no longer accepted now :)The answer to "why" it was accepted before is because pretests are never perfect.
» 3 years ago, # | -18 Please keep it rated !!
» 3 years ago, # | -17 please rated
» 3 years ago, # | +38 So many people wanting the contest to be unrated are people who just did bad, not people who were affected by D.
• » » 3 years ago, # ^ | +1 I did bad and was also affected by D
» 3 years ago, # | -35 OK ,The contest must be UNRATED!! ;)
» 3 years ago, # | ← Rev. 2 → -24 I solved problems A, B, C, D and F. I was really happy with my results and now my D got wrong answer on test 1 (after the contest). I have A, B, C, F problems accepted, which worth less than A, B, C, D because solving A, B, C, D is faster than solving A, B, C, F. A similar problem was at round 485 (the queue froze during the contest): http://codeforces.com/contest/987 I lost 166 rating points there, I can't believe this is happening again. Instead of gaining points, I will lose :( Please make it unrated.
• » » 3 years ago, # ^ | +13 If you got wa on even sample who is to blame really?
• » » » 3 years ago, # ^ | 0 I never check the 1st example, I don't get penalty if I get WA on test 1. And why would I check after it got AC?
» 3 years ago, # | -20 I messed up, got stock on C god please make this unrated
» 3 years ago, # | +3 Am feeling kinda stupid.... Anyways how to solve E ?
• » » 3 years ago, # ^ | 0 Whenever you enter or exit any node, update BIT. I got that idea but implemented it with set instead of BIT during contest.
• » » » 3 years ago, # ^ | 0 Thnx
• » » 3 years ago, # ^ | ← Rev. 2 → +11 You can do a simple DFS throughout the entire tree, starting at node 1 (i.e. root).Before starting, let's denote accumulated as an integer storing the sum of all added values for the current node. We'll get on with the way it worked below.When we start traversing from node z with depth depth, we'll do all these things: Taken all queries that have z as subtree root, and add the x values of all those queries into accumulated. Obviously, these queries don't apply for the entire subtree of z (only those with distance not larger than d). Therefore, we'll use a global array deactivated[] (more info in next steps). For each query with maximum depth allowed of d, add x into deactivated[depth+d+1]. Of course, since d ≤ 109, if depth+d+1 surpasses the maximum depth of the entire tree, ignore it. As a result, we'll have to subtract queries from ascendants' query that no longer affect the current node. To do this, we simply subtract deactivated[depth] from accumulated. Then, accumulated will be the answer for vertex z. Store it and start running DFS like usual. When done traversing, remember to undo all the above steps before leaving the function.My submission, for further clarity: 45624305
• » » » 3 years ago, # ^ | +2 Thnx. Got it. Simple!! My bad.
• » » » 3 years ago, # ^ | +5 Nice solution!
• » » » » 3 years ago, # ^ | 0 Wait, another Kuroyukihime around here? <3
• » » » » » 3 years ago, # ^ | ← Rev. 2 → +5 lotus is my wife!
» 3 years ago, # | +72 We discussed the issue and came up with the following decision:Those who got accepted earlier and get WA now won't be affected by rating changes. For everyone else (for those who got correct verdict) the contest will be rated.
• » » 3 years ago, # ^ | -7 very well
• » » » 3 years ago, # ^ | +31 Please make it rated for those who use cout << 0It is clear that someone might get lucky enough to try it and get ACBut it does not makes sense that many people were able to do it.It is clear that they clearly discussed the hack among themselves.
• » » 3 years ago, # ^ | -6 Can you explain what was the issue clearly? Incase if the WA was on hidden pretest then maybe next time make it unrated for everyone having WA after final system tests too in all rounds?
• » » » 3 years ago, # ^ | +16 For some solutions in problem D that should be rejected the checking program answered that they are accepted.
• » » » » 3 years ago, # ^ | 0 How many such users are there? I still fail to understand if a solution gives correct answer on sample tests and gives WA on some hidden tests whats the problem... How is it different from having weak pretests..
• » » » » » 3 years ago, # ^ | +17 Because the checker gives AC even if the solution gives incorrect answer on samples.
• » » » » » » 3 years ago, # ^ | +16 2 categories: gets AC on samples previously, WA on samples now gets AC on samples previously, WA on hidden pretest now (eg: http://codeforces.com/contest/1076/submission/45623636) i think number 2 should be rated
• » » » » » » » 3 years ago, # ^ | ← Rev. 2 → 0 I think number 2 should be rated
• » » » 3 years ago, # ^ | ← Rev. 2 → 0 The checker wasn't correct,It outputs ac if you just printed less than or equal to K distinct numbers from what i understand(even if you print 0).
• » » 3 years ago, # ^ | +90 What about the people who are getting +ve rating change even after being affected by WA in D? It doesn't make sense to make it unrated for them.
• » » » 3 years ago, # ^ | +20 Just unrated all, let this round be a practice round
• » » » » 3 years ago, # ^ | +3 Like traditional educational rounds
• » » 3 years ago, # ^ | +12 Make it like those who got accepted earlier and get WA now won't be affected by rating changes if their delta is negative. P.S. My delta shows positive by predictor
• » » » 3 years ago, # ^ | 0 How about being unrated for negative deltas?? Seems cool!!But just a question, the unrated people will be considered out of contest(unofficial) or not??
• » » » » 3 years ago, # ^ | 0 Similar thing happened in this contest
• » » 3 years ago, # ^ | 0 Why “Those who got accepted earlier and get WA now won't be affected by rating changes” ? Why don’t we consider those are Accepted at the time it’s correct and ignore all submissons after that? This contest’s rule is ACM/ICPC, right? In ACM, it’s also rejudge as the way I mentioned. There is no ACM/ICPC contest skip a Accepted submission to judge final submisson in this case!
• » » » 3 years ago, # ^ | 0 Sorry, I miss your mean.
• » » 3 years ago, # ^ | +1 Why different decisions for similar problem that happened in educational round 51?
• » » » 3 years ago, # ^ | +1 BledDest any comments?
• » » » » 3 years ago, # ^ | 0 When there were only 10 contestants affected, it was easy to check them manually.When there are 500 of them, it is much harder since we can't automatically do it.
• » » 3 years ago, # ^ | +6 You should take the "unrated" users out of the rating pool entirely (i.e. make them unofficial). Rating deltas are comparative: if somebody gains rating, someone else is supposed to lose it. If you just make the users not affected by rating changes, you'll have some users who influence the ratings of others but don't get their ratings influenced themselves.I hope what I'm saying makes sense, I don't really know how to express my idea.
» 3 years ago, # | +29 D-Forces
» 3 years ago, # | +15 It's my first chance to become master, I'd like to see it rated, but if the wrong make the contest unfair seriously, it should be unrated.
• » » 3 years ago, # ^ | ← Rev. 2 → 0 If you deserve it then you will get it
• » » » 3 years ago, # ^ | 0 Actually I don't even it's rated, lol.
» 3 years ago, # | 0 Hope to rank ,I want to see if I have made progress.
» 3 years ago, # | ← Rev. 3 → 0 Can someone explain to me what I messed up? http://codeforces.com/contest/1076/submission/45631931It's just a dfs + 2 multisets. I must have looked over this more than 20 times. (I also put the updates to active/spent before and after the recursion, but that didn't do anything.)Thanks in advance.nvm solved, made stupid bug
» 3 years ago, # | 0 Can someone explain me why this solution for problem A will fail ? http://codeforces.com/contest/1076/submission/45621631
• » » 3 years ago, # ^ | 0 3 baz Your answer is ba when my answer is az.
• » » » 3 years ago, # ^ | 0 Oh,shit thank you very much
• » » 3 years ago, # ^ | 0 Deleting biggest one is not the solution check it 5 abcad
• » » 3 years ago, # ^ | +3 Consider this case: 3 bacYour code output "ba", while the correct answer is "ac".So, what you have to do is not removing the largest char in the string, instead you have to remove the first char s[i] such that s[i]>s[i+1], as this will result in smaller string.
» 3 years ago, # | 0 Can someone explain me why I'm wrong? I made a submission to count number of good vertexes and with 50000 edges, one can't have more than 50001 good vertexes.45607996 // the original one, from the contest 45632353 // the modified one
• » » 3 years ago, # ^ | ← Rev. 2 → 0 The edges you give aren't necessarily connected. So you could have tree fragments everywhere. You have to do a dfs to get the edges and make sure they can actually reach the 1 node. (I might be wrong.)
• » » » 3 years ago, # ^ | 0 I'm using Dijkstra starting from vertex 1, so the graph is connected for sure
» 3 years ago, # | 0 I submitted problem D 3 times.In the second time, I get AC but the system said WA.When rejudge, My second submission is changed (it exactly the same solution of prolem A). I think this is a bug of Codeforecs. Could you consider my case?Submission number: 45627317Before rejudge, WA on test case 3. After rejudge, WA on test case 1, and the code is totally changed :( why ?
• » » 3 years ago, # ^ | 0 Hi Mr.MikeMirzayanov,My submission 45627317 was changed after system rejudge. I sent a message to problem setter but he did not respond. Please check again I will support any thing.
• » » 3 years ago, # ^ | 0 It maybe I submitte wrong file code. :’( Sorry
» 3 years ago, # | 0 is your standing in the leaderboard affected by how many accomplished hacks do you have?
» 3 years ago, # | 0 Please don't unrated, I probably become specialist after this round TAT.
• » » 3 years ago, # ^ | 0 Don't worry, I think u can become specialist soon ~~~ fight!
» 3 years ago, # | ← Rev. 4 → 0
• » » 3 years ago, # ^ | +19 Looked at your code — if you use the cin/cout speedup for C++, never mix them with printf/scanf — the streams are desynchronized so the output may not come out in the same order as you expect it to. That's what is happening here.
• » » » 3 years ago, # ^ | 0 Thanks!! i got it.
• » » 3 years ago, # ^ | ← Rev. 3 → +12 You should look up what things do before you use them :)That #define timesave ios_base::sync_with_stdio(false); cin.tie(0);, isn't some magic fairy dust that you just sprinkle over your program to make it faster. It has some effects.To be more specific, ios_base::sync_with_stdio(false) means (as the name suggests) that you are disabling syncing between io with streams (the kind you do with cin and cout) and standard io (the kind you do with scanf, printf etc). You disable the sync, yet in your code you use both methods of io (you use cout for the "No" case and printf for other cases) and then expect them to be synced up.
» 3 years ago, # | ← Rev. 2 → +3 Why “Those who got accepted earlier and get WA now won't be affected by rating changes” ? Why don’t we consider those are Accepted at the time it’s correct and ignore all submissons after that? This contest’s rule is ACM/ICPC, right? In ACM, it’s also rejudge as the way I mentioned. There is no ACM/ICPC contest skip a Accepted submission to judge final submisson in this case!
• » » 3 years ago, # ^ | +3 The thing is that people could check their source once more if they knew that's wrong, but everyone usually stops at the AC verdict
• » » 3 years ago, # ^ | 0 He meant, "those who got accepted due to the bug, and the same submissions got WA after rejudging".And for that, it's certain enough to say why it should be unrated (at least) for them.
• » » » 3 years ago, # ^ | 0 Thanks, bro. I know his mean now.
• » » » 3 years ago, # ^ | +3 Isn't is unfair to those who are getting positive delta but it will be unrated for them.
• » » » 3 years ago, # ^ | 0 Can you please proof the problem C ?
• » » » » 3 years ago, # ^ | ← Rev. 2 → 0 It's a pure mathematical problem.According to the given formula, we can figure out , thus .You can draw the graph of the equation , and figure out a few things: If d = 0, obviously a = b = 0. If d < 4, no solution can be found. If d ≥ 4, the function d = f(a) is a monotone function. Thus, you can binary search the value a, and b can simply be obtained as d - a. Keep in mind that your precision has to be right to fit the output's relative/maximum error criteria.
• » » » » » 3 years ago, # ^ | ← Rev. 2 → +5 For the last case (d ≥ 4) no need for binary search, instead, solve the equation which is actually a2 - d * a + d = 0. After that, b = d - a.Simple.
• » » » » » » 3 years ago, # ^ | 0 I feel freaking odd to deny solving this simple quadratic equation and binary searching the answer during contest time :DWell, whatever that works :D
» 3 years ago, # | +14 if i did't got accepted, my rank will up. and now my rank won't up. sad :'(
» 3 years ago, # | 0 And persons that haven't try the quest D? Is unrated or rated?
» 3 years ago, # | +5 Yo yo dudes, come on, the ones who got affected should have their rating increased if it shows +, and nothing if it shows -.
» 3 years ago, # | 0
• » » 3 years ago, # ^ | 0 Preview twice, post comment once.
» 3 years ago, # | +3 just another [partial unrated educational round rated for div 2]
» 3 years ago, # | +32 If I got D accepted with a wrong solution, but still managed to gain some rating after my D got WA, I do not see the point of why my rating should't increase.
» 3 years ago, # | 0 How to solve C?
• » » 3 years ago, # ^ | 0 x + y = d xy = d Math system
• » » 3 years ago, # ^ | 0 binary search
» 3 years ago, # | +3 I spent a lot of time for D problem. And i have a nice score . Why my contest won't be rated. I don't do printf(0); I do bfs but my solution get wrong answer after rejudge. Please help me!!!.It is not fair.
• » » 3 years ago, # ^ | 0 You are so right. Why do you ban from contest. Don't accept question but it should be rated for all.
» 3 years ago, # | 0 Can anybody proof me B problem, pleace
• » » 3 years ago, # ^ | 0 If n is even, then the smallest prime divisor is 2. After subtracting 2 from it, n is still even, so the smallest prime divisor will keep being 2. Therefore, the answer is how many times you can subtract 2 from n, which is n / 2.If n isn't even, find the smallest prime divisor d. You do one subtraction and get to n — d. Now, d is most certainly odd, therefore n — d is even, so the answer for n — d (as described above) is (n — d) / 2. Counting the subtraction of d from the start, the total answer is (n — d) / 2 + 1.
» 3 years ago, # | +38 "Those who got accepted earlier and get WA now won't be affected by rating changes. For everyone else (for those who got correct verdict) the contest will be rated."This is unfair for the users with positive rating changes even with WA on D. Please see if there is an alternate solution for this issue.
• » » 3 years ago, # ^ | +9 I totaly agree. Please make it rated for the ones who will increase their rating.
• » » 3 years ago, # ^ | 0 BledDest why not doing this ?
» 3 years ago, # | +6 Atleast make it rated for those getting +ve rating change, no matter if they were affected by D or not.
» 3 years ago, # | +4 this contest should be rated for all those who got correct the 4th one but failed later..but still are getting their ratings better than before and unrated for the ones whose ratings would be decreased due to the 4th question.
» 3 years ago, # | 0 Can anyone tell me how to solve problem D ?
• » » 3 years ago, # ^ | 0 run dijkstra from vertex 1 to all other onesthat gives you a tree of shortest pathsall you need to do is remove leaf by leaf untill you have k+1 vertices (and k edges)it clearly maximizes the number of 'good vertices' and is always valid as well
» 3 years ago, # | 0 Can anyone gives me a hint on problem E?
• » » 3 years ago, # ^ | ← Rev. 2 → 0 My friend tell me its depth segment tree , but i still no idea yet update: I pass the problem just now,here is my code http://codeforces.com/contest/1076/submission/45654052,I think u can get my idea easily。orz,the solution not very difficult,But I've been thinking about it for so long. It seems more practice is needed……
» 3 years ago, # | 0 Can anybody please proof the problem C mathmatically. It would be greatly appriciated. Thanks :)
• » » 3 years ago, # ^ | 0 it's just a quadratic equation. I've never been good with math proofs but here what I did: x + y = n, x * y = n, x * (n-x) = n, then solve x*x — n*x + n = 0.
• » » 3 years ago, # ^ | 0 Consider a * b = a + b = d we can get 2 equations for a , a = (a+b) / b = d / b and a = (a * b) — b = d-b d / b = (d — b) -> b^2 — bd + d = 0 so , we can use quadratic equation to get b , then a = d/b But if there is no valid answer from quadratic equation then answer is N
• » » 3 years ago, # ^ | 0 We know:1) (a + b) ^ 2 = (a ^ 2) + (b ^ 2) + 2 * a * b2) (a — b) ^ 2 = (a ^ 2) + (b ^ 2) — 2 * a * bSo we can calculate (a — b) ^ 2 as follows:1) (a — b) ^ 2 = (a + b) ^ 2 — 4 * a * bWe know also that a + b = d & a * b = d.let A = d ^ 2 — 4 * a * dSo we have (a — b) ^ 2 = ANow, in order for the problem to have answer, A must be positive. In case where A is negative simply output 'N'. In case it is positive, find it's square root and name it c.now we have to equations:1) a + b = d2) a — b = cSo a = (d + c) / 2 & b = d — aAfter calculating the values for a & b check them. The problem wants a & b to be non-negative real numbers. So if either of them is negative then output 'N' and else output the numbers.
• » » 3 years ago, # ^ | +6 By Vieta's formulas, we know that the sum of roots of the second degree polynomial ax2 + bx + c is equal to while their product is equal to . So if such numbers exist they will be roots of the polynomial x2 - dx + d.
» 3 years ago, # | +26 why exactly did people try to submit solutions with cout << 0 anyway?that feels just odd to me
• » » 3 years ago, # ^ | -44 I also saw some people submitted their code with "if(something == x or something == y)". It should be if(something == x || something == y).
» 3 years ago, # | 0 Can someone please explain me why my answer is wrong for problem A in the shown test case? Input 1000 rkqggsabguejnkvqhflwqtndjqakicbgcirayhvustungfyjrvgvxdcpwaoyqmqrorxfjlmvqazvgqwbwkiwypcxclzhskvrjdxrgbanlngwymdlmgurflfvnersfqkwnsmsh...............Participant's output rkqggsabguejnkvqhflwqtndjqakicbgcirayhvustungfyjrvgvxdcpwaoyqmqrorxfjlmvqavgqwbwkiwypcxclzhskvrjdxrgbanlngwymdlmgu................Jury's answer kqggsabguejnkvqhflwqtndjqakicbgcirayhvustungfyjrvgvxdcpwaoyqmqrorxfjlmvqazvgqwbwkiwypcxclzhskvrjdxrgbanlngw..................(why is 'r' being cut instead of 'z'?)
• » » 3 years ago, # ^ | +8 Consider the simpler case: 3 bac Output: acYour code's output: baYou should delete the first character s[i] such as s[i] > s[i+1], not the largest character
• » » » 3 years ago, # ^ | 0 oh. Thank you so much! I misunderstood the question!
» 3 years ago, # | 0 Can anyone make me understand solution of D. Had a terrible round.
• » » 3 years ago, # ^ | +1 My solution is based on dijkstra's algorithm from vertex 1. So while we're running dijkstra , i just pick the first K node(that is not 1) that we visit by dijkstra , if we were about to exceed K just break the loop. (FYI my dijkstra is implemented in a while loop with a priority_queue as the main data structure , you can see the submission from my profile.)
• » » 3 years ago, # ^ | ← Rev. 3 → 0 Actually Dijkstra process built a shortest-path tree with N vertices from the graph. So we will build that tree, and repeat this N — k — 1 times: Find a vertex that is a leaf and delete it. This process make sure all the current vertex of the tree has as same shortest distance from vertex 1 as it was before the deletion, and the number of these vertices is largest. This can be done with dfsYou can make the deletion simpler, by dfs the shortest-path tree and build a subtree of k edges. Here is my submission 45633192.
» 3 years ago, # | 0 How to solve problem G ?
» 3 years ago, # | 0 Was the contest unrated for all..as my rating has not been increased.
» 3 years ago, # | +9 So we have just eliminated everyone affected by D... what?? This is just so stupid. Someone who has done E or F and whose rating might be +100 would be unfair for them!! Make it rated for those with +ve rating change please.
» 3 years ago, # | +7 " Those who got accepted earlier and get WA now won't be affected by rating changes. For everyone else (for those who got correct verdict) the contest will be rated. " — What if the those contestants will get a higher rating if we skip D submissions of those users?
» 3 years ago, # | 0 My rating still hasn't changed, is everything fine? I haven't touched D at all.
• » » 3 years ago, # ^ | 0 UPD. It did now, sorry.
» 3 years ago, # | ← Rev. 3 → -11 deleted
» 3 years ago, # | 0 Yeah, my rating increased by +145 :p
» 3 years ago, # | ← Rev. 3 → +33 For those who got TLE on test 64 on D: When implementing Dijkstra, do not check edges from a vertex if it is already visited (in other words, if the distance from the PQ is greater than the one written in the distance array). A vertex can be pushed into the PQ O(V) times and it also can have O(V) outgoing edges, so it can be O(V^2) in the worst case. Furthermore, this can be repeated for multiple vertices and possibly reach O(V^3) in a complete graph.The generator is: #include using namespace std; int main() { int n = 200003, m = 300000, k = 0; printf("%d %d %d\n", n, m, k); for (int i = 2; i <= 100000; i++) printf("%d %d %d\n", 1, i, i); for (int i = 2; i <= 100000; i++) printf("%d %d %d\n", i, 100001, (int)1e9 - 2 * i); for (int i = 0; i < 100002; i++) printf("%d %d %d\n", 100001, 100002 + i, (int)1e9); }
» 3 years ago, # | +13 This is unfair to me. Predictor was showing I will get +50 rating. But now this became unrated for me. This is unfair...ummmmmmmmm
» 3 years ago, # | 0 Anybody wrote a dp solution for E?
» 3 years ago, # | 0 Is there a way to look up what test was used to hack my solution, in case I want to debug?
• » » 3 years ago, # ^ | 0 View test under the hack verdict: https://codeforces.com/contest/1076/submission/45608998
» 3 years ago, # | +14 Is there editorial?
» 3 years ago, # | 0 For E is it possible to build some type of tour so that we can use segtree for range update and then push all the changes?
• » » 3 years ago, # ^ | 0 I have the same question. Can someone answer this?
» 3 years ago, # | 0 i was wondering how setters managed to change the rating based on a particular problem's verdict... is it a database sort or ??
» 3 years ago, # | 0 Why TLE on Test Case 64? problem D
• » » 3 years ago, # ^ | 0
• » » » 3 years ago, # ^ | 0 Thanks. Accepted.
» 3 years ago, # | 0 Where is editorial? And how to solve F? It looks like a interesting problem.
» 3 years ago, # | 0 Auto comment: topic has been updated by awoo (previous revision, new revision, compare).
» 3 years ago, # | 0 Auto comment: topic has been updated by awoo (previous revision, new revision, compare).
» 2 years ago, # | 0 I think in "Meme Problem(C)" float and double will give different answers. Both the answers shall be considered valid since logic is same. If programmer is able to give any one of them it implies his/her logic is sound.
|
|
## Taiwanese Journal of Mathematics
### The Influence of Conjugacy Class Sizes on the Structure of Finite Groups
#### Abstract
Let $G$ be a group. The question of how certain arithmetical conditions on the sizes of the conjugacy classes of $G$ influence the group structure has been studied by many authors. In this paper, we investigate the influence of conjugacy class sizes of primary and biprimary elements on the structure of $G$. A criterion for a group to have abelian Sylow subgroups is given and some well-known results on Baer-groups are generalized.
#### Article information
Source
Taiwanese J. Math., Volume 21, Number 4 (2017), 719-725.
Dates
Revised: 2 November 2016
Accepted: 25 November 2016
First available in Project Euclid: 27 July 2017
https://projecteuclid.org/euclid.twjm/1501120829
Digital Object Identifier
doi:10.11650/tjm/7083
Mathematical Reviews number (MathSciNet)
MR3684382
Zentralblatt MATH identifier
06871341
#### Citation
Chen, Ruifang; Zhao, Xianhe. The Influence of Conjugacy Class Sizes on the Structure of Finite Groups. Taiwanese J. Math. 21 (2017), no. 4, 719--725. doi:10.11650/tjm/7083. https://projecteuclid.org/euclid.twjm/1501120829
#### References
• R. Baer, Group elements of prime power index, Trans. Amer. Math. Soc. 75 (1953), no. 1, 20–47.
• A. Beltrán and M. José Felipe, Prime powers as conjugacy class lengths of $\pi$-elements, Bull. Austral. Math. Soc. 69 (2004), no. 2, 317–325.
• W. Burnside, On groups of order $p^{\alpha} q^{\beta}$, Proc. London Math. Soc. s2-1 (1904), no. 1, 388–392.
• A. R. Camina and R. D. Camina, Implications of conjugacy class size, J. Group Theory 1 (1998), no. 3, 257–269.
• D. Chillag and M. Herzog, On the length of the conjugacy classes of finite groups, J. Algebra 131 (1990), no. 1, 110–125.
• B. Fein, W. M. Kantor and M. Schacher, Relative Brauer groups II, J. Reine Angew. Math. 328 (1981), 39–57.
• X. Guo, X. Zhao and K. P. Shum, On $p$-regular $G$-conjugacy classes and the $p$-structure of normal subgroups, Comm. Algebra 37 (2009), no. 6, 2052–2059.
• N. Itô, On finite groups with given conjugate types I, Nagoya Math. J. 6 (1953), 17–28.
• Q. Kong and X. Guo, On an extension of a theorem on conjugacy class sizes, Israel J. Math. 179 (2010), 279–284.
• X. Zhao and X. Guo, On conjugacy class sizes of the $p'$-elements with prime power order, Algebra Colloq. 16 (2009), no. 4, 541–548.
• X. H. Zhao, X. Y. Guo and J. Y. Shi, On the conjugacy class sizes of prime power order $\pi$-elements, Southeast Asian Bull. Math. 35 (2011), no. 4, 735–740.
|
|
# What convervation law is required by the Lorentz Transformations
Time invariance implies conservation of energy. Space invariance implies momentum convervation. What convervation law does the Lorentz invariance imply?
## Answers and Replies
dextercioby
Homework Helper
Angular momentum. Immediate by Noether's theorem for classical fields.
Daniel.
Staff Emeritus
Gold Member
Dearly Missed
The Lorentz transformations by definition preserve the four-interval $$c^2t^2 - x^2 - y^2 - z^2$$.
pervect
Staff Emeritus
dextercioby said:
Angular momentum. Immediate by Noether's theorem for classical fields.
Daniel.
Conservation of angular momentum is generated by spatatial rotation invariance. Space rotation invariance is indeed part of the Lorentz group. But I suspect the original poster was interested in the symmetries related to the Lorentz boost, not by the spatial rotation part of the Lorentz group.
I seem to recall that this question was discussed before, but I don't recall the conclusion that we came to.
The Lorentz transformations by definition preserve the four-interval $$c^2t^2 - x^2 - y^2 - z^2$$.
I was thinking the same thing but there are many 4-vector invariants in SR. Energy-momentum, space-time. The classical conservation laws have one specific quantity conservered not a variety.
George Jones
Staff Emeritus
Gold Member
metrictensor said:
Time invariance implies conservation of energy. Space invariance implies momentum convervation. What convervation law does the Lorentz invariance imply?
Read the stuff here.
Regards,
George
Thinking by analogy, shouldn't it imply conservation of the stress-energy tensor?
dextercioby
Homework Helper
Nope, stress- energy tensor is linked to space-time translations.
Daniel.
This should be a straightforward question with an obvious answer - but authors seem to skirt the issue
spatial displacement symmetry - conservation of momentum
temporal displacement symmetry - conservation of energy
isotropic symmetry - conservation of angular momentum
When gauge symmetry is applied to Maxwells's em equations, one consequence is conservation of charge - isn't conservation (invariance) of the spacetime interval also consequent to gauge symmetry?
Last edited:
arivero
Gold Member
Read the stuff here.
Regards,
George
It is a funny answer... the position of the center of mass? Ok, in absence of external forces, the center of mass is a preserved quantity, so it makes sense, or sort of.
|
|
# News for November 2013
The action in November is mainly in algebraic property testing.
On Testing Affine-Invariant Properties by Arnab Bhattacharyya (ECCC). As mentioned here, Arnab put together an excellent survey on testing, ahem, affine-invariant properties. It gives a great overview of this area for a non-expert, and is highly recommended for anyone wanting to get a sense of the existing results and open problems.
Algorithmic Regularity for Polynomials and Applications by Arnab Bhattacharyya, Pooya Hatami, and Madhur Tulsiani (Arxiv). Not a pure property testing paper per se. But you can’t complain about papers related to regularity lemmas in a property testing blog. Think of the Szemerédi regularity lemma as the following: given any partition of a graph, one can “refine” it, so that the resulting partition has “few” pieces and is “regular”. Analogously, the regularity lemma for polynomials says that given any set of polynomials, one can “refine” it to get a “small regular” set of polynomials. This has direct applications in Reed-Muller testing (there’s your property testing connection!). This paper is on giving an algorithm that actually constructs this regular set of polynomials. Among other things, this algorithm can be used in decoding of Reed-Muller codes beyond the list-decoding radius.
# Survey on Testing Affine-Invariant Properties
Arnab has put together a wonderful survey on testing affine-invariant properties (ECCC). Consider functions $$f:\mathbb{F}^n_p \to R$$ (where $$R$$ is usually a finite range). A property is called affine-invariant if it closed under affine transformations of the domain. The classic example of such a property is that of being a low-degree polynomial. This is a very rich and beautiful area of research, with the initial inspiration being work in trying to understand what makes a property testable. I will also add that this is a deep (somewhat inaccessible to the non-expert?) area of research, so thanks Arnab for this excellent survey!
|
|
GMAT Question of the Day - Daily to your Mailbox; hard ones only
It is currently 20 Oct 2018, 18:47
### GMAT Club Daily Prep
#### Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
we will pick new questions that match your level based on your Timer History
Track
every week, we’ll send you an estimated GMAT score based on your performance
Practice
Pays
we will pick new questions that match your level based on your Timer History
# If n is a positive integer, is n + 425,371 odd? (1) n - 268,865 is odd
Author Message
TAGS:
### Hide Tags
Math Expert
Joined: 02 Sep 2009
Posts: 50007
If n is a positive integer, is n + 425,371 odd? (1) n - 268,865 is odd [#permalink]
### Show Tags
10 Apr 2018, 22:04
00:00
Difficulty:
25% (medium)
Question Stats:
90% (00:54) correct 10% (00:45) wrong based on 31 sessions
### HideShow timer Statistics
If n is a positive integer, is n + 425,371 odd?
(1) n - 268,865 is odd.
(2) 890,214n is even.
_________________
DS Forum Moderator
Joined: 22 Aug 2013
Posts: 1348
Location: India
Re: If n is a positive integer, is n + 425,371 odd? (1) n - 268,865 is odd [#permalink]
### Show Tags
10 Apr 2018, 22:53
Bunuel wrote:
If n is a positive integer, is n + 425,371 odd?
(1) n - 268,865 is odd.
(2) 890,214n is even.
So basically we are asked whether (n + odd) is odd or not? Given 'n' is a positive integer, this will be odd when 'n' is even. So we need to know for sure whether n is even or not.
(1) n - odd is odd, this can only happen when n is even. Sufficient.
(2) I assume this means 890214 * n (product) or even*n. Now even multiplied by any integer (whether even or odd) will give even result, So we cannot be sure whether 'n' is odd or even. Not sufficient.
Manager
Joined: 24 Mar 2018
Posts: 89
Re: If n is a positive integer, is n + 425,371 odd? (1) n - 268,865 is odd [#permalink]
### Show Tags
10 Apr 2018, 23:03
amanvermagmat wrote:
Bunuel wrote:
If n is a positive integer, is n + 425,371 odd?
(1) n - 268,865 is odd.
(2) 890,214n is even.
So basically we are asked whether (n + odd) is odd or not? Given 'n' is a positive integer, this will be odd when 'n' is even. So we need to know for sure whether n is even or not.
(1) n - odd is odd, this can only happen when n is even. Sufficient.
(2) I assume this means 890214 * n (product) or even*n. Now even multiplied by any integer (whether even or odd) will give even result, So we cannot be sure whether 'n' is odd or even. Not sufficient.
How are you assuming 890214n as 890214*n ?
It can happen the other way too.
If n is 44 then 890214n will be 89021444
DS Forum Moderator
Joined: 22 Aug 2013
Posts: 1348
Location: India
If n is a positive integer, is n + 425,371 odd? (1) n - 268,865 is odd [#permalink]
### Show Tags
10 Apr 2018, 23:09
teaserbae wrote:
amanvermagmat wrote:
Bunuel wrote:
If n is a positive integer, is n + 425,371 odd?
(1) n - 268,865 is odd.
(2) 890,214n is even.
So basically we are asked whether (n + odd) is odd or not? Given 'n' is a positive integer, this will be odd when 'n' is even. So we need to know for sure whether n is even or not.
(1) n - odd is odd, this can only happen when n is even. Sufficient.
(2) I assume this means 890214 * n (product) or even*n. Now even multiplied by any integer (whether even or odd) will give even result, So we cannot be sure whether 'n' is odd or even. Not sufficient.
How are you assuming 890214n as 890214*n ?
It can happen the other way too.
If n is 44 then 890214n will be 89021444
Yes, that case could also be there. Thats why I wrote 'I assume' because if I had complete clarity then I wouldn't have needed to assume anything.
If second statement means 890214*n = even then n could be even or odd.
But if second statement means 890214n (n is just placed after the digit 4) is Even - then n will be even.
VP
Status: It's near - I can see.
Joined: 13 Apr 2013
Posts: 1267
Location: India
GMAT 1: 480 Q38 V22
GPA: 3.01
WE: Engineering (Consulting)
Re: If n is a positive integer, is n + 425,371 odd? (1) n - 268,865 is odd [#permalink]
### Show Tags
11 Apr 2018, 09:18
Bunuel wrote:
If n is a positive integer, is n + 425,371 odd?
(1) n - 268,865 is odd.
(2) 890,214n is even.
Given : n > 0
Question: Is n + odd = odd ?
Or Is n = odd - odd ?
Or Is n = even ?
St 1: n - odd = odd
Or n = odd + odd
Or n = even Sufficient
St 2: n * even = even
Or n = $$\frac{even}{even}$$
Or n = even or odd Insufficient
n = $$\frac{6}{2}$$ = 3 (Odd)
n =$$\frac{8}{4}$$ = 2 (Even)
Hence (A)
_________________
"Do not watch clock; Do what it does. KEEP GOING."
Re: If n is a positive integer, is n + 425,371 odd? (1) n - 268,865 is odd &nbs [#permalink] 11 Apr 2018, 09:18
Display posts from previous: Sort by
|
|
# Proving two stubborn inequalities for completely positive maps in C*-algebras
I recently came across this in my studies of functional analysis in C* algebras which got me stuck:
For a completely positive map between C* algebras $\phi : A \to B$ we are to prove these two inequalities where $a,b \in A$:
$\phi(a) ^{*} \phi(a) \leq ||\phi(1)||\phi(a^{*}a)$
$||\phi(a^{*}b)||^2 \leq ||\phi(a^{*}a)|| \space || \phi(b^{*}b) ||$
where * denotes of course the dual. I am truly stuck as I tried anything so I cannot really get past these, and I am truly in need of help. I thank all helpers.
1. Your first inequality is usually known as the Kadison-Schwarz inequality. It only requires $2$-positivity.
Claim. $A=\begin{bmatrix}I &a\\ a^*&b\end{bmatrix}\geq0$ if and only if $a^*a\leq b$.
Proof. If $A\geq0$, then for any $\xi\in H$, $$\langle (b-a^*a)\xi,\xi\rangle=\left\langle \begin{bmatrix}I &a\\ a^*&b\end{bmatrix}\,\begin{bmatrix}-a\xi\\ \xi\end{bmatrix},\begin{bmatrix}-a\xi\\ \xi\end{bmatrix}\right\rangle \geq0,$$ so $a^*a\leq b$. Conversely, if $a^*a\leq b$, then for any $\xi,\eta\in H$, \begin{align*} \left\langle \begin{bmatrix}I &a\\ a^*&b\end{bmatrix}\,\begin{bmatrix}\xi\\ \eta\end{bmatrix},\begin{bmatrix}\xi\\ \eta\end{bmatrix}\right\rangle &=\|\xi\|^2+\langle b\eta,\eta\rangle+2\text{Re}\,\langle a\eta,\xi\rangle \geq\|\xi\|^2+\langle b\eta,\eta\rangle-2\langle a^*a\eta,\eta\rangle^{1/2}\,\|\xi\| \\ &\geq\|\xi\|^2+\langle b\eta,\eta\rangle-2\langle b\eta,\eta\rangle^{1/2}\,\|\xi\| =(\|\xi\|-\langle b\eta,\eta\rangle)^2\geq0.&\Box \end{align*} $$\$$
Now, since $a^*a\leq a^*a$, we have that $\begin{bmatrix}I&a\\a^*&a^*a\end{bmatrix}\geq0$. As $\phi$ is $2$-positive, $$\begin{bmatrix}\|\phi(I)\|\,I &\phi(a)\\ \phi(a)^*&\phi(a^*a)\end{bmatrix}\geq\begin{bmatrix}\phi(I) &\phi(a)\\ \phi(a)^*&\phi(a^*a)\end{bmatrix}=\phi^{(2)}\left(\begin{bmatrix}I & a\\ a^*& a^*a\end{bmatrix}\right)\geq0.$$ Applying the Claim again, we get $$\frac{\phi(a)^*}{\|\phi(I)\|}\,\frac{\phi(a)}{\|\phi(I)\|}\leq\frac{\phi(a^*a)}{\|\phi(I)\|},$$ so $$\phi(a)^*\phi(a)\leq\|\phi(I)\|\,\phi(a^*a).$$
On the other hand, a very simple proof can be obtained using Stinespring's Dilation: if you write $\phi(x)=V^*\pi(x)V$, then \begin{align} \phi(a)^*\phi(a)&=V^*\pi(a)^*VV^*\pi(a)V\leq\|VV^*\|\,V^*\pi(a)^*\pi(a)V\\ \ \\ &=\|V\|^2\,V^*\pi(a^*a)V=\|V^*V\|\,\phi(a^*a)\\ \ \\ &=\|\phi(I)\|\,\phi(a^*a). \end{align}
1. For the second inequality, only positivity is needed. Let $f$ be a state on $A$. Then $a\longmapsto f(\phi(a))$ is a positive linear functional. As such, it satisfies Cauchy-Schwarz. So $$f(\phi(a^*b))^2\leq f(\phi(a^*a))\,f(\phi(b^*b))\leq\|\phi(a^*a)\|\,\|\phi(b^*b)\|.$$ As the norm of any operator can be realized via states, $$\|\phi(a^*b)\|^2\leq \|\phi(a^*a)\|\,\|\phi(b^*b)\|.$$
|
|
## Microstate
$\Delta S = \frac{q_{rev}}{T}$
Emily Ng_4C
Posts: 65
Joined: Fri Sep 28, 2018 12:17 am
### Microstate
What is a microstate and how does it relate to entropy?
LedaKnowles2E
Posts: 62
Joined: Fri Sep 28, 2018 12:27 am
### Re: Microstate
From what I understand from lecture, a microstate is a specific arrangement of molecules, a specific set of positions for each molecule in a sample. The more possible microstates or arrangements there are for a sample, the more entropy that sample has.
(If anyone wants to correct/add to that, pls do)
Catly Do 2E
Posts: 64
Joined: Fri Sep 28, 2018 12:24 am
### Re: Microstate
Microstates are specific ways in which the energy of a system can be arranged. The multiple ways the energy can be arranged depends on the atom/molecule arrangements. Entropy is the measure of uncertainty in a system, so the more microstates there are, the higher the entropy.
Posts: 96
Joined: Fri Sep 28, 2018 12:16 am
Been upvoted: 2 times
### Re: Microstate
Knowing the number of microstates gives you the W value to use in the equation S=kB*ln(W).
Ray Guo 4C
Posts: 90
Joined: Fri Sep 28, 2018 12:15 am
### Re: Microstate
According to Boltzmann’s equation S=k*ln(W), where W is the degeneracy, what I understand to be the number of possible microstates of the same energy level, more the number of microstates with the same energy level higher the entropy value.
LedaKnowles2E
Posts: 62
Joined: Fri Sep 28, 2018 12:27 am
### Re: Microstate
A microstate is a specific arrangement of molecules. Degeneracy is the number of possible microstates/arrangements of a group of molecules, and entropy is calculated using degeneracy.
LaurenJuul_1B
Posts: 65
Joined: Fri Sep 28, 2018 12:17 am
### Re: Microstate
it is a specific arrangement of the molecules. different micro states have different energy levels and having multiple micro states increases the entropy of a system
Simran Rai 4E
Posts: 58
Joined: Fri Sep 28, 2018 12:17 am
### Re: Microstate
When there are more microstates, there is increased entropy. This is because there is greater positional/residual vibration between molecules and that lends to greater disorder.
|
|
32
Q:
# The ratio of expenditure and savings is 3 : 2 . If the income increases by 15% and the savings increases by 6% , then by how much percent should his expenditure increases?
A) 25 B) 21 C) 12 D) 24
Explanation:
Therefore x = 21%
Q:
In a 48 ltr mixture, the ratio of milk and water is 5:3. How much water should be added in the mixture so as the ratio will become 3:5 ?
A) 24 lit B) 16 lit C) 32 lit D) 8 lit
Explanation:
Given mixture = 48 lit
Milk in it = 48 x 5/8 = 30 lit
=> Water in it = 48 - 30 = 18 lit
Let 'L' lit of water is added to make the ratio as 3:5
=> 30/(18+L) = 3/5
=> 150 = 54 + 3L
=> L = 32 lit.
7 152
Q:
A container contains 120 lit of Diesel. From this container, 12 lit of Diesel was taken out and replaced by kerosene. This process was further repeated for two times. How much diesel is now there in the container ?
A) 88.01 lit B) 87.48 lit C) 87.51 lit D) 87.62 lit
Explanation:
For these type of problems,
Quantity of Diesel remained = $\inline \fn_jvn \left [ q\left ( 1-\frac{p}{q} \right )^{n} \right ]$
Here p = 12 , q = 120
=> $\inline \fn_jvn \left [ 120\left ( 1-\frac{12}{120} \right ) ^{3}\right ]$
=> 120 x 0.9 x 0.9 x 0.9
=> 120 x 0.729
= 87.48 lit.
6 214
Q:
Manideep purchases 30kg of barley at the rate of 11.50/kg and 20kg at the rate of 14.25/kg. He mixed the two and sold the mixture in the shop. At what price per kg should he sell the mixture to make 30% profit to him ?
A) 15.84 B) 14.92 C) 13.98 D) 16.38
Explanation:
Given, Manideep purchases 30kg of barley at the rate of 11.50/kg nad 20kg at the rate of 14.25/kg.
Total cost of the mixture of barley = (30 x 11.50) + (20 x 14.25)
=> Total cost of the mixture = Rs. 630
Total kgs of the mixture = 30 + 20 = 50kg
Cost of mixture/kg = 630/50 = 12.6/kg
To make 30% of profit
=> Selling price for manideep = 12.6 + 30% x 12.6
=> Selling price for manideep = 12.6 + 3.78 = 16.38/kg.
5 218
Q:
There are two mixtures of honey and water in which the ratio of honey and water are as 1:3 and 3:1 respectively. Two litres are drawn from first mixture and 3 litres from second mixture, are mixed to form another mixture. What is the ratio of honey and water in it ?
A) 111:108 B) 11:9 C) 103:72 D) None
Explanation:
From the given data,
The part of honey in the first mixture = 1/4
The part of honey in the second mixture = 3/4
Let the part of honey in the third mixture = x
Then,
1/4 3/4
x
(3/4)-x x-(1/4)
Given from mixtures 1 & 2 the ratio of mixture taken out is 2 : 3
=> $\inline \fn_jvn \frac{\frac{3}{4}-x}{x-\frac{1}{4}}=\frac{2}{3}$
=> Solving we get the part of honey in the third mixture as 11/20
=> the remaining part of the mixture is water = 9/20
Hence, the ratio of the mixture of honey and water in the third mixture is 11 : 9 .
4 209
Q:
In what ratio must a merchant mix two varieties of oils worth Rs. 60/kg and Rs. 65/kg, so that by selling the mixture at Rs. 68.20/kg, he may gain 10% ?
A) 2:3 B) 4:3 C) 3:4 D) 3:2
Explanation:
Let he mixes the oils in the ratio = x : y
Then, the cost price of the oils = 60x + 65y
Given selling price = Rs. 68.20
=> Selling price = 68.20(x+y)
Given profit = 10% = SP - CP
=> 10/100 (60x + 65y) = 68.20(x+y)-(60x + 65y)
=> 6x + 6.5y = 8.20x + 3.20y
=>2.2x = 3.3y
=> x : y = 3 : 2
|
|
# Receiving Data
The receiver data recovery circuit initiates character reception on the falling edge of the first bit. The first bit, also known as the Start bit, is always a zero. The data recovery circuit counts one-half bit time to the center of the Start bit and verifies that the bit is still a zero. If it is not a zero, then the data recovery circuit aborts character reception without generating an error, and resumes looking for the falling edge of the Start bit. If the Start bit zero verification succeeds, then the data recovery circuit counts a full bit time to the center of the next bit. The bit is then sampled by a majority detect circuit and the resulting ‘0’ or ‘1’ is shifted into the RSR. This repeats until all data bits have been sampled and shifted into the RSR. One final bit time is measured and the level sampled. This is the Stop bit, which is always a ‘1’. If the data recovery circuit samples a ‘0’ in the Stop bit position, then a framing error is set for this character, otherwise the framing error is cleared for this character. See Receive Framing Error for more information on framing errors.
Immediately after all data bits and the Stop bit have been received, the character in the RSR is transferred to the EUSART receive FIFO, and the EUSART Receive Interrupt Flag (RCxIF) bit of the PIRx register is set. The top character in the FIFO is transferred out of the FIFO by reading the RCxREG register.
|
|
Learning to become a baker
Why there are more and more industrial bakers who don’t care what they sell.
13 October 2013
braindump learning baking bread
Originally posted on Medium.
Red Zuurdesem, my website about baking with sourdough, has been active since 2012, and still is. I hold a professional bread baker’s degree since 2016 - this article was written during the first year when I enrolled in the course.
Sometimes people tell me I’m obsessed with bread. That’s not entirely my fault. (I like to blame others, who doesn’t?) When I was little, my father always baked our own bread on sunday, every single sunday. I can’t remember anytime we actually bought bread, except on vacation. At a young age I had no idea how creating something out of nothing actually worked, but I knew it was intriguing — the addition of yeast which caused the dough to bubble up within a short period of time, wow!
When I grew older, I lost my interest in food in general — I had other worries such as studying. (well, and girlfriends, but that’s a part of studying!) I have two sisters and we never cooked, our parents always did that. The only thing that remained was the joy of eating a freshly baked slice of bread at sunday after all the breads have been cut and packaged — my father baked enough for the freezer to use throughout the week. When we ate pizza — with homemade dough of course — there was always some dough left over to create a “pizza bread” with. The dough was “special” because of the ingredients: a 100% white wheat bread with olive oil, extra sweet. We always fought to get the most slices, usually spread with an even sweeter Nutella. I think the tradition of eating chocolate spread on white bread started there.
Having to do it yourself
Eating without cooking it yourself abruptly stopped when I rented an appartment. The interest in cooking and baking remained so I started experimenting myself. After a year, I received a bread baking machine for my birthday — you know, one of those little things where you need to simply weigh all the required ingredients, throw them in there and push “start”. 4 hours later, the irresistible smell of freshly baked bread would fill the kitchen. Great, I baked something! What should I do with it? Where’s my Nutella?
It didn’t stop there, that was only the beginning. I started researching on the internet, gathering more and more recipes, experimenting with the bread baking machine on using different flours, mixing them with fruits and nuts. (using fresh kiwi’s was a failure, but hey, at least I tried, right?) After another year, I stumbled upon one of the many food blogs, “Food wishes” with chef John, where he explained the process of creating a “sourdough”. In Belgium, bakers don’t use sourdough, so I didn’t even know what that meant. It was so fascinating that I decided to try that myself.
Most people I bake for even complain about the “holes” — their chocolate spread drops through them!
Which of course worked with enough patience. As soon as my sourdough starter was active, I got really obsessed with baking bread.Not just bread, but bread — the real stuff, hand crafted, with (sometimes extremely) long fermentation times. I gave away my bread baking machine (and made someone else happy with their first baking experience) and started investing my time and money in artisan bread baking books like “Bread”. I had to order everything on the internet as I couldn’t find a single book on the topic locally which is very,very sad.
Deciding to do it even better
This week is week four in the three year long official baker course. I enrolled into the program with a clear vision on how I would open up a speciality bakery, only baking sourdough bread with long fermentation times and extreme taste and smell. My father doesn’t like sourdough. Actually, almost nobody I know does. Why is that? We grew up eating fastly fermented bread with high amounts of commercial yeast. The more yeast added (with chemical flour stabilizers of course) the quicker the baker can bake them, the more he can create and sell. $$(in our case €€€), dingding. I had some trouble finding bakeries in the area wich sell real bread. I found one in Brussels and one in Maastricht. There are others but it’s really sad, most bakers (or at least the assistents who sell the bread) don’t even know what sourdough is. (Yes I know this is completely different in countries like Germany or France, but we’re talking about Belgium here) So the more I learned about the sad state of bakeries, the more I was determined to do something about it. I created Save Sourdough, a website to promote baking with sourdough yourself. I baked for colleagues and friends, but I still felt that was not enough. So I finally enrolled in a bakery course (you’re obligated to have that diploma if you want to start a bakery). Sourdough, all bubbly and ready to roll. I knew I should not expect too much, but if you know that after following the course for three years (without any prerequired knowledge), you can open up your own bakery, I’d expect it to be thorough. What a disappointment. We do learn to bake bread: white bread to start with, small round boules we call “pistolets”, fluffy sandwich bread, … But it’s all the industrial way. All the recipes contain stabilizers. You want pistolets? Okay, just add 4% “pistolet” stabilizer. Baking regular bread or sandwich bread? Use bread or sandwich stabilizer. Those things come in huge bags of 25kg in the class, just as the regular flour (industrial milled with added stabilizer out of the box… great) does. What do they actually contain? • lactose (What the fuck? That’s right, lactose intolerant or vegan people, stop buying bread from a “regular” bakery!) • Acids (vinegar-like stuff) • EXYZ numbers, usually coloring stuff, depending on the type When asked about why to actually use a stabilizer, the teacher explains: • it helps rise the dough more quickly ($$$/€€€, remember) • it helps keep the dough together when mixing quickly (see above) • it gives more color (if using bad/bland flour, see above) • it prolongs the shelf time (see above) Sourdough bread keeps for a week. Without any additives, because of the thousands of natural little micro-organisms present in the sour. Using lactose helps prolong the shelf time the same way, but it actually requires adding something I don’t even want to be present in my bread! You also need a chemical ingredient to make sure the gluten in the (usually wheat) dough don’t break when mixed on a high speed. Sourdough bread is not mixed, it is folded. Problem solved. Why don’t we do it like this? Requires time. Effort. Not needed, mix up that baby.$/€€€.
What a disappointment. I see people jotting down everything the teacher says when answering that question, nodding quickly. I guess they just think “when I want to bake bread, I need stabilizers!”. You don’t. When you bake bread, you take your time. Or you do not bake bread at all. A bulk fermentation of 15 minutes? Come on, are you serious? When I bake sourdough at home, it’s at least 3 hours! Sometimes even up to 2 days in the fridge.
I know I’ll still be learning a lot in this course, so I won’t quit (and I need the diploma). I already learned why there aren’t any real artisan bread bakers anymore. The teaching part is all messed up, so how can we expect or bakeries to actually deliver quality goods? The real learning still has to be done at home (or in another country) — provided that someone is willing to learn to do it another way. That last part plays a big role, as most people here don’t even like the sourdough taste, even mild bread. They are just used to junk, don’t blame them.
After all, we are creatures of habit, right?
If that is what we want to be, than it shall be so.
Top
|
|
Algorithms
# Understanding Big O
## How efficient is your algorithm?
Image credit: Wikimedia
It’s indispensable to have a clear understanding of basic algorithms before attending a programming interview. In order to understand algorithms, it’s also important to know to measure the efficiency of an algorithm. This is done with a concept, called the Big O. There exists a common question that pops up on an algorithm interview as to “How efficient is your algorithm?”. So, unless you can come up with this from scratch and measure it, rather than memorizing it for different problems, it may cause your interview to drift away from a successful one.
In this article, we’ll try to simplify the understanding of the concept of Big O which may help you prepare for a programming interview or understanding how you can use it. We will try to understand Big O from first principles rather than encouraging ourselves to memorize the Big O for different problems. I will use the Python programming language for all the examples in this article.
### What is Big O for?
Big O is a concept critical to algorithms and the most mathematical we’ll get in this article. Two main reasons of understanding this concept are:
1. If you get a problem that you haven’t seen before, although you have experience dealing with hundreds of problems before, there’s a chance that you end up with one problem that you have never come across, and hence you’ll not know how to get the Big O.
2. In an interview, you may get partial or almost full credit to show your work on getting the Big O although your exact answer may not be correct.
In reality, programming interviews focus mainly on your problem-solving abilities, which definitely comes down to breaking down your algorithm and explaining step-by-step what you think your Big O might be.
### What is Big O?
Big O represents the efficiency of your algorithm and is of two different types:
1. Time-based — related to performance, speed, and in turn efficiency of the code;
2. Space-based — related to memory, in turn relating to how much extra space for variables and data structures are required to solve the algorithm.
Therefore, if you have large inputs for your functions within your algorithm, both time and space will start to cause problems. Hence the relevance of these to types for Big O. These types are also often used as a benchmark to compare different algorithms and measure how good they are. For example, there are a lot of different ways a code sort, and they all have different efficiencies. So, this is a measure of grading these efficiencies, just like the grading system in academics.
Now let’s look at how exactly we assign this grade. This is done, not in absolute terms, but in terms relative to the size of the input. Consider an input as an argument to a function. Now, if we double the size of this input, we check if the time and space scale up proportionally, slightly less, or slightly more.
Consider a function called length(input) that measures the length of an array or of a string. Now we can pass in the input of size 3 and say that it takes 1 full second to complete (not a great one, but consider for the sake of our example). And next let’s pass in an array of size 6 and say it takes 2 full seconds to complete.
When comparing the inputs and their times, we can observe that doubling the input size, doubles the execution time. This proportional increase in time is known as linear time. In other words, the relationship between time and input in our example is 1:1. In Big O notation, we call this linear time “O” of “n”, written as O(n). Note that in this example we did not use any extra space.
Extra space does not include the size of our input, so we start and end with zero space. If either space or the time has no relationship with the input, we call it constant space and in Big O notations, we designate it as O(1). These terms are referred to as order with each being a different tier of efficiency. The below list shows the order of most efficient (or shortest time or the least space) to the least efficient Big O’s.
1. O(1) — constant
2. O(log n) — logarithmic
3. O(n) — linear
4. O(n log n) — linear * log
5. O(n * n) — quadratic
6. O(2^ n) — exponential
Now let’s take a look at what’s inside our length(input) function:
def length(input):
counter = 0
for i in input:
counter += 1
return counter
Observe the counter variable and the loop in the code. In reality, every single line of code has its own time complexity, but using little tricks, you can get the line’s time complexity reduced. The key is in the question — How does the input size, whether it’s string length or array length, affect this specific line?
If the answer comes down to the fact that it does not have a direct impact, then by default, that line is constant time, simply because it has no relationship to the input. Looking at our first line of the code (counter = 0), note that creating the counter variable is going to happen whether we pass 1 or 100 array items. Therefore, by default, this line is constant time. Next, consider asking if the counter variable is a constant space or does this variable scale with the size of our input. The usual assumption would be yes, since we’re incrementing the counter up to the length of our input. However, the truth is integers always take up the same amount of space unless they’re really large numbers. So, once we have identified that the first line is constant, we shift our focus on the loop. Notice that this will run n-times proportional to the size of our input. Hence there is a direct relationship between our input and the time of this line of our code. Now in order to find the relationship, simply take two different inputs. For example, take an input of array size 1 versus an array of size 2: [1] vs [1, 2]
So, we need 1 iteration for array of size 1 and 2 iterations for an array of size 2. Clearly, there is a one-to-one relationship, hence, linear O(n).
Now if we want to determine the time-complexity, notice that we have O(1) for counter initialization and then O(n) for the loop. Therefore, we can say that it is taking O(1) + O(n) time altogether. Observe that even in this very simple function, we have multiple terms. Needless to say, for longer functions, we have many multiple complex additions of time complexities. This is a very hideous task, and so, we need to simplify. This simplification is done by only keeping the terms that are in the highest order. So in our example, we will end up dropping the O(1) for counter initialization, since relative to O(n) its effects are negligible. Since each tier of Big O is an order of magnitude larger than the ones below it, when we get to larger size inputs, the lower order terms become completely irrelevant. So for our example, if we have O(300), it would be absolutely negligible compared to our n=300. In case we had O(n * n) then we would have O(90000) which will then make n=300 totally negligible.
To sum up, simplification includes:
1. Dropping the lower order terms, and
2. Dropping the constant terms.
Consider another example with two loops now:
def sumAndLength(input):
sum = 0
length = 0
for num in input:
sum += num
for i in input:
length += 1
return (sum, length)
Now we have two O(n), one for the first loop, and one for the second loop.
Here we have n + n = 2n (in practice, we can simply drop the coefficient “2” since all we are concerned about is the order). This is because the orders are so large compared to each other, that the presence or absence of the coefficients (whether 2n, or 4n, or 100n compared to n*n).
This is how we simplify Big O for our algorithms. The length(input) function that we used was a nice clean example since we always increment the counter n times, 1 for each iteration of the loop.
In most cases, however, functions have a range of efficiencies rather than an exact value. This can be made clear with an example. Let’s say we’re using the find function as below:
index = 'qwerty'.find('w')
This function searches for a string or a character and returns its index upon finding the substring and otherwise returns -1 if the substring is not found.
To consider using Big O, we must train ourselves to think about the entire spectrum of possibilities. Most importantly, we should determine the best case with the least amount of effort or the worst case with the most amount of effort.
def index(input, target):
for i, char in enumerate(input):
if char == target:
return i
return -1
So, for the index function, it searches the string for a target character one at a time, and then once found, it returns its index. In this case, we should train ourselves to consider both:
1. Best-case scenario, i.e. the character is found at the beginning of the input string;
2. Worst-case scenario, i.e. the character is not found within the input string.
Therefore we conclude that our best case is O(1) (since it’s a single iteration leading to a single operation) and our worst case is O(n) (since the input now is proportional to the length of our entire string). With Big O, it’s a convention to always take the worst case, and hence for this case, we can say that the index function is O(n) or linear time.
### Conclusion
So, these are the basics of understanding how Big O can be beneficial in determining the efficiency of your algorithm. To sum up, the take away from our reading are the following:
• Every line of code has a Big O time complexity;
• Every variable we create has a space complexity;
• We simplify the Big O sums by considering only the highest order of terms;
• Constants are dropped to recognize the order and simplify further;
• When scanning through the entire spectrum of possible inputs, we always consider the worst-case scenario.
When comparing the inputs and their times, we can observe that doubling the input size, doubles the execution time. This proportional increase in time is known as linear time. In other words, the relationship between time and input in our example is 1:1. In Big O notation, we call this linear time “O” of “n”, written as O(n). Note that in this example we did not use any extra space.
|
|
# The brand manager for a brand of toothpaste must plan a campaign designed to increase brand recognition. He wants to first determine
#### ByRaju Chaudhari
Aug 23, 2020
The brand manager for a brand of toothpaste must plan a campaign designed to increase brand recognition. He wants to first determine the percentage of adults who have heard of the brand. How many adults must he survey in order to be 90 % confident that his estimate is within six percentage points of the true population percentage?
a) Assume that nothing is known about the percentage of adults who have heard of the brand. n=_____ (Round up to the nearest integer.)
b) Assume that a recent survey suggests that about 76 % of adults have heard of the brand. n=___ (Round up to the nearest integer.)
#### Solution
The formula to estimate the sample size required to estimate the proportion is
\begin{aligned} n =p*(1-p)\bigg(\frac{z}{E}\bigg)^2 \end{aligned}
where $p$ is the proportion of success, $z$ is the $Z_{\alpha/2}$ and $E$ is the margin of error.
(a) Given that margin of error $E =0.06$. The confidence coefficient is $0.9$. If no estimate were available for the proportion of adults who have heard of the brand we assume that the proportion is $p =0.5$.
The critical value of $Z$ is $Z_{\alpha/2} =Z_{0.05}= 1.645$.
The minimum sample size required to estimate the proportion is
\begin{aligned} n&= p(1-p)\bigg(\frac{z}{E}\bigg)^2\\ &= 0.5(1-0.5)\bigg(\frac{1.645}{0.06}\bigg)^2\\ &=187.918\\ &\approx 188. \end{aligned}
Thus, the sample of size $n=188$ will ensure that the $90$% confidence interval for the proportion will have a margin of error $0.06$.
(b) Given that margin of error $E =0.06$. The confidence coefficient is $1-\alpha=0.9$. The sample proportion of adults who have heard of the brand is $p =0.76$.
The critical value of $Z$ is $Z_{\alpha/2} =Z_{0.05}= 1.645$.
The minimum sample size required to estimate the proportion is
\begin{aligned} n&= p(1-p)\bigg(\frac{z}{E}\bigg)^2\\ &= 0.76(1-0.76)\bigg(\frac{1.645}{0.06}\bigg)^2\\ &=137.105\\ &\approx 138. \end{aligned}
Thus, the sample of size $n=138$ will ensure that the $90$% confidence interval for the proportion will have a margin of error $0.06$.
|
|
# Generating a Vanity .onion Address
📅
Original image from Michael Carian on Flickr. Some rights reserved: cc by-sa.
If you use Tor then you've probably noticed that some .onion sites have addresses that don't look totally random, like facebookcorewwwi.onion or demonhkzoijsvvui.onion. Tor addresses are supposed to be randomly-generated — how do these have words in them?
Well, as you may have guessed, the solution pretty much comes down to generating tons of keys and seeing which ones look nice. Here's how a .onion address is supposed to be generated:
1. Generate a 1024-bit RSA keypair
2. Take the SHA-1 of the public key
3. Base32 encode the first 80 bytes of the hash...
4. ... and that's your .onion address.
There are a few programs out there designed specifically for generating tons of these hashes. Two popular ones are Scallion and Eschalot. Scallion is written in C# but supports GPU acceleration and so is very fast. Eschalot is written in C and lets you use a wordlist to search but doesn't have GPU support yet (I'm working on it though). I'll write this for Eschalot since I couldn't get Scallion to compile on my machine. The options work pretty much the same way for Scallion, so if you're using that instead then you should still be able to follow along.
## Installing Eschalot
Eschalot is pretty simple to install. It has a few dependencies but compiling it is easy and it should compile on Windows, macOS, Linux, and BSD. Here's how I build it on Debian.
$sudo apt install build-essential libssl-dev$ git clone https://github.com/ReclaimYourPrivacy/eschalot.git Cloning into 'eschalot'... remote: Counting objects: 51, done. remote: Total 51 (delta 0), reused 0 (delta 0), pack-reused 51 Unpacking objects: 100% (51/51), done. $cd eschalot$ make
That's it. Now we can start generating keys and looking for an address we like.
## Generating Keys
Eschalot has a few search modes but let's say we're interested in a single prefix — how about "example". We can specify the number of threads with -t and and with -v we get some extra output. We use -p to tell it the prefix to search for and voilà:
\$ ./eschalot -vp example -t 8 > example.txt Verbose, single result, no digits, 8 threads, prefixes 7-7 characters long. Thread #1 started. Thread #2 started. Thread #3 started. Thread #4 started. Thread #5 started. Thread #6 started. Thread #7 started. Thread #8 started. Running, collecting performance data... Total hashes: 241503935, running time: 10 seconds, hashes per second: 24150393 Total hashes: 738951074, running time: 30 seconds, hashes per second: 24631702 Total hashes: 1723765467, running time: 70 seconds, hashes per second: 24625220 Total hashes: 3663782163, running time: 150 seconds, hashes per second: 24425214 Total hashes: 7485469816, running time: 310 seconds, hashes per second: 24146676 Total hashes: 14577250049, running time: 630 seconds, hashes per second: 23138492 Total hashes: 28260847673, running time: 1270 seconds, hashes per second: 22252635 Total hashes: 55946077304, running time: 2550 seconds, hashes per second: 21939638 Total hashes: 114012026840, running time: 5110 seconds, hashes per second: 22311551 Found a key for example (7) - examplelatozpqzz.onion
After 90 minutes and about 115 billion hashes, we find a private key that gives us an address with our prefix in example.txt:
examplelatozpqzz.onion
-----BEGIN RSA PRIVATE KEY-----
MIICXQIBAAKBgQDK/xoS3witc3krmLCifMarbH40g2bj0RI8sSuTXWQdt7YPNSTk
bFdCs5fexbTJoWQTq4tsyHW151KwIgsotzp/IFIynp7nguP5NdPGmcJQDAfvLOh4
w3JSIg/qLOzsqU1hm8WKjW74TQAhHgA5k3PiJ8GwxzD251+oVw+0oOdCdQIETVgN
l4+PF8BV5dPdzJBRCwO4SPXzyb6V+FL8lNO1lZb8JB1ONssLdDVQuQkUVOV/GF6U
612xw44HQ4YwTxo6tbdntP1mW0Mt7q15BeRM2TF16Xnzvax1AkEA+fqDpeej3ivY
o29fUqXpDvtAXEocKwaahbkRCIS5Omt7KOg3fctbtnQor+ggMRE1ZRji47+bKZJf
DHPwGOXuuQJBAM/i37qrnN1vJXtaWbMdzOoqICOd4ma1Sc+a3ma8Ce+jKR6RMF0C
6Swa7Oy9SfKjBJoTI3jjIjNJOdSr42V9M50CQAkp+pZFrDHVTundOxC72ix5Hvvy
4oBrEScKMQwqUg+e+ASXMOcJToYtibevaI3wzehA6J3EpF5VBCWnD30uLlUCQEKG
3zlWxm3IRZDFA/q6jlB/HcPguEyF2+Knan74Hh5ugNDARfDKL5qmb3iZxWitlJiV
5w7zI/Sthkq/3tJgFbUCQQCGea+mKe/fJMJF4Ucw+gysxp1l+hQsG+gZS96NITFc
+cS0GWFvX1iBZMVBlbu3HLDc7s0Bs86Hjf5tM6cqS7I/
-----END RSA PRIVATE KEY-----
## Installing the Key
So now that we've got our private key, where do we put it? Assuming you've already installed and configured Tor to host a hidden service, there's just one file to change. I configured Tor to use /var/lib/tor/hidden_service, but you can pick whatever directory you want in your torrc. The file we're interested in is called private_key.
You can probably guess what goes in this file: the private key. Copy the lines -----BEGIN RSA PRIVATE KEY----- and -----END RSA PRIVATE KEY----- and everything in between them into this file. Restart Tor and you should be able to access your new hidden service at examplelatozpqzz.onion. I'm still waiting to find an address with a particularly long prefix, but in the meantime you can get to this website at peterbe4r52vseqd.onion.
|
|
# Let R be a commutative ring and let I be an ideal in R.
1. Nov 12, 2005
### Icebreaker
Let R be a commutative ring and let I be an ideal in R.
1. If every ideal in R is principal, then every ideal in R/I is principal.
2. If every ideal in R/I is principal, then every ideal in R is principal.
I must prove or disprove if either is true or false. Can someone tell me whether either is true or false so I can know how to proceed?
2. Nov 13, 2005
### Hurkyl
Staff Emeritus
I'm sure someone can, but it isn't good for you.
This is exactly analogous to someone doing arithmetic problems and asking for an answer key before they try to solve them.
You shouldn't need to know the answer to a problem before you can solve it. :tongue2:
Last edited: Nov 13, 2005
3. Nov 13, 2005
### Icebreaker
2 doesn't seem to be true. Consider R=Z[x] and I=2Z[x]+xZ[x]. R/I={0,1}. Every ideal in R/I is certainly principal. However, not ever ideal in Z[x] is principal: for instance, let J={polynomials whose constant terms are even integers}. To show this, suppose J is principal, then J consists of multiples of some element p(x). Since 2 is in J, 2 must be a multiple of p(x), which implies that p(x) must be of degree 0. Since p(x) is in J, it must be +/-2. However, x is in J because it has an even constant. Therefore, x must be a multiple of +/-2. This is impossible since all polynomials involved have integer coefficients. Therefore, J is not principal.
1 is intuitively true, but so far, no luck in proving it. If every ideal I in R is principal, let I={rc:r in R}. R/I={[a]_c : a in R}. If J is an ideal in R/I, then it must be closed under multiplication. I think I can create a contradiction here assuming J is not principal, but I haven't been able to.
4. Nov 13, 2005
### Hurkyl
Staff Emeritus
Your approach for 2 looks good.
For 1, how far did you get?
5. Nov 13, 2005
### Icebreaker
Not very far. I can't seem to use the fact that I is a principal ideal anywhere in my proof. What makes R/I where I is principal so special?
6. Nov 13, 2005
### matt grime
Ideals in R/I are lift to ideals in R that contain I
7. Nov 13, 2005
### Icebreaker
I'm not entirely sure what you mean by "lift". Do you mean ideals in R/I are contained in I?
8. Nov 13, 2005
### Hurkyl
Staff Emeritus
It doesn't.
9. Nov 14, 2005
### CarlB
It seems that a way of understanding the relationships between ideals and principal ideals is to look at matrix groups over the reals with matrix arithmetic defining addition and multiplication.
Some principal ideals for 4x4 matrices:
$$\left(\begin{array}{cccc}1&0&0&0\\0&0&0&0\\0&0&0&0\\0&0&0&0\end{array}\right)$$
$$\left(\begin{array}{cccc}.5&.5&0&0\\.5&.5&0&0\\0&0&0&0\\0&0&0&0\end{array}\right)$$
A non principal ideal:
$$\left(\begin{array}{cccc}1&0&0&0\\0&1&0&0\\0&0&0&0\\0&0&0&0\end{array}\right)$$
Carl
10. Nov 19, 2005
I have the same problem and I still haven't solved it. Any suggestions?
11. Nov 20, 2005
### CarlB
On principal ideals.
Perhaps it is worthwhile recalling the various ways that a primitive ideal can be distinguished from an ideal.
What I recall is that P is primitive if P cannot be written as the sum of two non trivial ideals. A "trivial" ideal would be zero.
Carl
|
|
The relationship between the Fahrenheit (F) and Celsius (c)temperature scales is given by the equation
(a) complete the table to compare the two scales at the givenvalues.
C
F
(b) Find the temperature at which the scales agree. (hint: suppose that a is the temperature at which the scalesagree. Set F = a and C =a. Then solve for a.)
|
|
## Gravitation | DPP | JEE Main | JEE Advanced
From gravitation you can expect 1 question each in JEE Main and JEE Advanced. This topic can be scoring if you can master all different types of questions
Q1 A Saturn year is $29.5$ times the Earth year. How far is the Saturn from the Sun if the Earth is $1.50 \times 10^8 \ km$ away from the Sun ?
Correct answer is $1.43 \times 10^{12} \ m$
Q2 Assuming the Earth to be a sphere of uniform mass density. How much would a body weigh half way down to the center of the Earth if it weighed $250 \ N$ on the surface ?
Correct answer is $125 \ N$
Q3 If the Earth were a perfect sphere of radius $6.37 \times 10^6 \ m$, rotating about its axis with a period of one day $( = 8.64 \times 10^4 \ s)$, how much would the acceleration due to gravity $(g)$ differ from the poles to equator ?
Correct answer is $g_{\text{pole}} – g_{\text{equator}} = 3.37 \times 10^{-2} \ ms^{-2}$
Q4 A rocket is fired vertically with a speed of $5 \ km \ s^{-1}$ from the Earth’s surface. How far from the Earth does the rocket go before returning to the Earth ? Mass of the earth $= 6.0 \times 10^{24} \ kg$. Mean radius of the Earth $= 6.4 \times 10^6 \ m; \ G = 6.67 \times 10^{-11} \ N \ m^2 \ kg^{-2}$.
Correct answer is $8.0 \times 10^6 \ m$ from the earth’s center
Q5 The escape speed of a projectile on the Earth’s surface is $11.2 \ km \ s^{-1}$. A body is projected out with thrice this speed. What is the speed of the body far away from the Earth ? Ignore the presence of the Sun and other planets.
Correct answer is $31.7 \ km/s$
Q6 Find the gravitational force of attraction between a particle of mass $m$ and a uniform slender rod of mass $M$ and length $L$ for the two orientations shown in the figure below.
(a) $\cfrac{GmM}{d(d + L)}$
(b) $\cfrac{2GmM}{d\sqrt{L^2 + 4d^2}} \ \downarrow$
Q7 Two bodies of masses $m_1$ and $m_2$ are connected by a long inextensible cord of length (mass $m_e$), the direction of the cord being always radial as shown in the figure. Find: (a) the tension in the cord and (b) the accelerations of $m_1$ and $m_2$. Does the cord ever become slack ? (ignore the gravitational interaction between $m_1$ and $m_2$)
Tension in the cord $= \cfrac{Gm_em_1m_2}{m_1 + m_2} \left[\cfrac{1}{(h + R)^2} – \cfrac{1}{(h + R + L)^2}\right]$
Acceleration $a_1 = a_2 = \cfrac{Gm_e}{m_1 + m_2} \left[\cfrac{m_1}{(h + R)^2} + \cfrac{m_2}{(h + R + L)^2}\right]$
towards the center of the earth. The cord will always be in tension.
Q8 A body is thrown up (radially outward from the surface of the earth) with a velocity equal to one-fourth of the escape velocity. Find the maximum height-reached from the surface of the earth. (Radius of earth is $R_e$)
Correct answer is $\cfrac{R_e}{15}$
Q9 A satellite is put in an orbit just above the earth’s atmosphere with a velocity $\sqrt{1.5}$ times the velocity for a circular orbit at that height. The initial velocity imported is horizontal. What would be the maximum distance of the satellite from the surface of the earth when it is in the orbit ?
Correct answer is $2R$
Q10 Two concentric shells of masses $M_1$ and $M_2$ are situated as shown in Figure. Find the force on a particle of mass $m$ when the particle is located at (a) $r = a$ (b) $r = b$ and (c) $r = c$.
The distance $r$ is measured from the center of the shell.
Given that $OA = a, \ OB = b, \ OC = c$
(a) $\cfrac{Gm}{a^2}[M_1 + M_2]$
(b) $\cfrac{GM_2m}{b^2}$
(c) zero
Q11 Can an artificial satellite be put into orbit in such a way that it will always remain directly over New Delhi ?
Q12 How much quicker than at present must the earth revolve on its axis to make bodies at the equator experience weightlessness ? What will be the duration of day then ?
Correct answer is $17$ times, $1412$ hrs
Q13 How will weight of a body change at a height equal to earth’s radius ?
Q14 The gravitational field in a region is given by $E = (2 \hat{i} + 3 \hat{j}) \ N/kg$. Show that no work is done by the gravitational field when a particle is moved on the line $3y + 2x = 5$.
Q15 A body is weighed by a spring balance to be $1.000 \ kg$ at the north pole. How much will it weigh at the equator ? Account for the earth’s rotation only.
Correct answer is $0.997 \ kg$
Q16 Does the escape speed of a body from the earth depend on: (a) the mass of the body, (b) the location from where it is projected, (c) the direction of projection, and (d) the height of the location from where the body is launched ? Explain your answer.
Correct answer is Depends on the height of the location from where the body is launched.
Q17 A comet orbits the sun in highly elliptical orbit. Does the comet have a constant (a) linear speed, (b) angular speed. (c) angular momentum, and (d) kinetic energy when it comes very close to the sun ?
Correct answer is Only the angular momentum is constant.
Q18 The gravitational potential at an internal point inside a solid sphere is known to be $V_r = – \cfrac{GM}{2a^3}(3a^2 – r^2)$. Find the magnitude of gravitational field at that point.
Correct answer is $\cfrac{GM}{a^3}r$ toward the center of solid sphere.
Q19 The gravitational field in a region is given by $\overrightarrow{E} = (10 \ N/kg)(\overrightarrow{i} + 2\overrightarrow{j} + 3\overrightarrow{k})$. Find the work done by an external agent to slowly shift a particle of mass $3 \ kg$ from the point $O = (0, 0, 0)$ to a point $P = (3m, 4m, 5m)$.
Correct answer is $- 780 \ J$
Q20 The centers of two stars of masses $M$ and $16M$ of radii $R$ and $2R$ are separated by a distance of $10R$. Draw a graph between gravitational potential $(V)$ and the distance $(r)$ from the center of the smaller star along the line joining their centers for $R \leq r \leq 8R$.
Q21 Find the ratio of the kinetic energy required to be given to the satellite to escape earth’s gravitational field to the $KE$ required to be given so that the satellite moves in a circular orbit just above earth’s atmosphere.
Correct answer is $2$.
Q22 A mass equal to the mass of the earth is to be compressed in a sphere in such a way that the escape velocity from its surface is $3 \times 10^8 \ m/s$. What should be the radius of the sphere in $mm$ ? (take $GM_E = 40.5 \times 10^{13} \ Nm^2 kg^{-1}$)
Correct answer is $9$.
Q23 A body stretches a spring by a particular length at the earth’s surface at equator. At height $3\lambda \ km$ above the South Pole it will stretch the same spring by the same length. Assume the earth to be spherical. (take $\omega^2R = 0.0375$, where $\omega$ and $R$ have usual meanings). Find $\lambda$.
Correct answer is $4$.
|
|
# Show that if $c_n = \int_{-1}^1 (1-t^2)^\frac{n-1}{2}dt$ then $c_n = \frac{n-1}{n}c_{n-2}$
Question: Show that if $c_n = \int_{-1}^1 (1-t^2)^\frac{n-1}{2}dt$ then $c_n = \frac{n-1}{n}c_{n-2}$. I have tried two things both of which I didn't get super far with. First, I tried dividing n into two cases odd and even and applying the binomial theorem and second I tried integration by parts with $u = (1-t^2)^\frac{n-1}{2}$ and $dv = dt$. Maybe one of these approaches are right and I just screwed up somewhere but some help would be appreciated.
• $1= t^2+(1-t^2)$ and integration by parts. – Jack D'Aurizio Mar 1 '17 at 1:26
• You can rearrange this to show that $c_n +\frac{1}{n} c_{n-2} = 1$ is equivalent to your identity. It could potentially be easier to work with this. – Mark Mar 1 '17 at 1:29
• This can be inspiring: math.stackexchange.com/questions/2162309/… – Olivier Oloa Mar 1 '17 at 1:31
Observe that $$c_n = \int_{-1}^{0}(1-t^2)^{\frac{n-1}{2}}dt + \int_{0}^{1}(1-t^2)^{\frac{n-1}{2}}dt = \\ =2\int_{0}^{1}(1-t^2)^{\frac{n-1}{2}}dt,$$
where you make the substitution $t\mapsto -t$ in the first integral (or just observe that the function being integrated is even). Then, we do partial integration:
$$\int_{0}^{1}(1-t^2)^{\frac{n-1}{2}}dt = t(1-t^2)^{\frac{n-1}{2}}\big|_{0}^{1} + (n-1)\int_{0}^{1}t^2(1-t^2)^{\frac{n-3}{2}}dt = \\ =(n-1) \int_{0}^{1}t^2(1-t^2)^{\frac{n-3}{2}}dt.$$
Then, we conclude that $$(n-1)\int_{0}^{1}(1-t^2)^{\frac{n-3}{2}}dt - \int_{0}^{1}(1-t^2)^{\frac{n-1}{2}}dt = (n-1)\int_{0}^{1}(1-t^{2})^{\frac{n-1}{2}}dt,$$
which means $$\int_{0}^{1}(1-t^2)^{\frac{n-1}{2}}dt = \frac{n-1}{n}\int_{0}^{1}(1-t^2)^{\frac{n-3}{2}}dt.$$
Then, it follows that $$\frac{c_n}{2}=\frac{n-1}{n}\frac{c_{n-2}}{2} \implies c_n = \frac{n-1}{n}c_{n-2}.$$
Let $t=\cos x$ with $x\in [0,\pi].$
For $n\geq 1$ we have $$c_n=\int_{\pi}^0 (\sin^2 x)^{(n-1)/2}\;d\cos x=\int_{\pi}^0(\sin x)^{n-1}(-\sin x)\;dx=$$ $$=\int_0^{\pi}\sin^n x\;dx.$$ Now for $n\geq 2$ we have, integrating by parts, $$c_n=\int_0^{\pi}\sin^{n-1}x\;d (-\cos x)=$$ $$=(\sin^{n-1}x)(-\cos x)|_{x=0}^{x=\pi}\;-\int_0^{\pi}(-\cos x)(n-1)(\sin^{n-2}x) (\cos x)\;dx.$$ And since $0=(\sin^{n-1}0)(\cos 0)=(\sin^{n-1}\pi)(\cos \pi)$ when $n\geq 2$, we have $$c_n= \int_0^{\pi}(n-1)(\cos^2 x)(\sin^{n-2}x)\; dx=\int_0^{\pi}(n-1)(1-\sin^2x)(\sin^{n-2}x)\;dx=$$ $$=\int_0^{\pi} (n-1)(\sin^{n-2}x-\sin^nx)\;dx=$$ $$=(n-1)c_{n-2}-(n-1)c_n.$$
|
|
# Visualizing Data
Tables and lists are great, but visualizations are often more effective—if they’re well designed and your audience is sighted, that is. There are even more ways to visualize data in the browser than there are front-end toolkits for JavaScript. We have chosen to use Vega-Lite, which is a declarative framework: as a user, you specify the data and settings, and let the library take care of everything else. It doesn’t do everything, but it does common things well and easily, and it interacts nicely with React.
## Vega-Lite
Let’s start by creating a skeleton web page to hold our visualization. For now, we will load Vega, Vega-Lite, and Vega-Embed from the web; we’ll worry about local installation later. We will create a div to be filled in by the visualization—we don’t have to give it the ID vis, but it’s common to do so—and we will leave space for the script. Our skeleton looks like this (with lines broken for the benefit of the printed version):
<!DOCTYPE html>
<html>
<title>Embedding Vega-Lite</title>
<script src="https://cdnjs.cloudflare.com/ajax/libs\
/vega/3.0.7/vega.js"></script>
<script src="https://cdnjs.cloudflare.com/ajax/libs\
/vega-lite/2.0.1/vega-lite.js"></script>
<script src="https://cdnjs.cloudflare.com/ajax/libs\
/vega-embed/3.0.0-rc7/vega-embed.js"></script>
<body>
<div id="vis"></div>
<script type="text/javascript">
</script>
</body>
</html>
We can now start filling in the script with the beginning of a visualization specification. This is a blob of JSON with certain required fields:
• $schema identifies the version of the spec being used (as a URL). • description is a comment to remind us what we thought we were doing when we created this. • data is the actual data. ...rest of page as before... <script type="text/javascript"> let spec = { "$schema": "https://vega.github.io/schema/vega-lite/v2.0.json",
"description": "Create data array but do not display anything.",
"data": {
"values": [
{"a": "A", "b": 28},
{"a": "B", "b": 55},
{"a": "C", "b": 43},
{"a": "D", "b": 91},
{"a": "E", "b": 81},
{"a": "F", "b": 53},
{"a": "G", "b": 19},
{"a": "H", "b": 87},
{"a": "I", "b": 52}
]
}
}
</script>
...rest of page as before...
In this case, we represent a two-dimensional data table as objects with explicit indices "a" and "b". We have to do this because JSON (like JavaScript) doesn’t have a native representation of two-dimensional arrays with row and column headers, because programmers.
Once we have created our spec, we can call vegaEmbed with the ID of the element that will hold the visualization, the spec, and some options (which for now we will leave empty):
let spec = {
"$schema": "https://vega.github.io/schema/vega-lite/v2.0.json", "description": "Create data array but do not display anything.", "data": { "values": [ // ...as above... ] } } vegaEmbed("#vis", spec, {}) When we open the page, though, nothing appears, because we haven’t told Vega-Lite how to display the data. To do that, we need to add two more fields to the spec: • mark specifies the visual element used to show the data • encoding tells Vega how to map values to marks Here’s our updated spec: let spec = { "$schema": "https://vega.github.io/schema/vega-lite/v2.0.json",
"description": "Add mark and encoding for data.",
"data": {
"values": [
// ...as above...
]
},
"mark": "bar",
"encoding": {
"x": {"field": "a", "type": "ordinal"},
"y": {"field": "b", "type": "quantitative"}
}
}
vegaEmbed("#vis", spec, {})
When we open the page now, we see a bar chart, and feel very proud of ourselves (f:vis-mark-encoding).
There are also some poorly-styled links for various controls that we’re not going to use. We can fill in the options argument to vegaEmbed to turn those off:
let spec = {
"$schema": "https://vega.github.io/schema/vega-lite/v2.0.json", "description": "Disable control links.", "data": { // ...as before... } } let options = { "actions": { "export": false, "source": false, "editor": false } } vegaEmbed("#vis", spec, options) We now have the visualization we wanted (f:vis-disable-controls). Vega-Lite has a lot of options: for example, we can use points and average the Y values. (We will change the X data so that values aren’t distinct in order to show this off, because otherwise averaging doesn’t do much.) In our revised spec, x is now "nominal" instead of "ordinal" and y has an extra property "aggregate", which is set to "average" (but can be used to specify other aggregation functions): let spec = { "$schema": "https://vega.github.io/schema/vega-lite/v2.0.json",
"description": "Disable control links.",
"data": {
"values": [
{"a": "P", "b": 19},
{"a": "P", "b": 28},
{"a": "P", "b": 91},
{"a": "Q", "b": 55},
{"a": "Q", "b": 81},
{"a": "Q", "b": 87},
{"a": "R", "b": 43},
{"a": "R", "b": 52},
{"a": "R", "b": 53}
]
},
"mark": "point",
"encoding": {
"x": {"field": "a", "type": "nominal"},
"y": {"field": "b", "type": "quantitative", "aggregate": "average"}
}
}
let options = {
...disable controls as before...
}
vegaEmbed("#vis", spec, options)
f:vis-aggregate-points shows the result.
## Local Installation
Loading Vega from a Content Delivery Network (CDN) reduces the load on our server, but prevents offline development. Since we want to be able to work when we’re disconnected, let’s load from local files.
Step 1 is to slim down our HTML file so that it only loads our application:
<!DOCTYPE html>
<html>
<title>Load Vega from a File</title>
<meta charset="utf-8">
<script src="app.js" async></script>
<body>
<div id="vis"></div>
</body>
</html>
In step 2, we npm install vega vega-lite vega-embed and require('vega-embed') in app.js:
const vegaEmbed = require('vega-embed')
const spec = {
// ...as before...
}
const options = {
// ...as before...
}
vegaEmbed("#vis", spec, options)
We launch this with Parcel via our saved npm run command:
\$ npm run dev -- src/vis/react-01/index.html
But nothing appears when we open http://localhost:4000 in our browser. Looking in the browser console, we see a message telling us that vegaEmbed is not a function.
What we have tripped over is something that’s still painful in 2018. The old method of getting libraries is require, and that’s still what Node supports as of Version 10.9.0. The new standard is import, which allows a module to define a default value so that import 'something' gets a function, a class, or whatever. This is really handy, but require doesn’t work that way.
We can either add the --experimental-modules flag when using Node on the command line, or rename our files with a .mjs extension, both of which are annoying. Alternatively, we can get the thing we want by accessing .default during import, or by referring to vegaEmbed.default when we call it. These choices are also annoying, but after a bit of fiddling and cursing, we decide to make the fix as the library is loaded:
const vegaEmbed = require('vega-embed').default
// ...as before...
The third option is to use import where we can and fix the require statements in the server-side code when Node is upgraded. We can call the thing we import anything we want, but we will stick to vegaEmbed for consistency with previous examples:
import vegaEmbed from 'vega-embed'
// ...as before...
If we do this, the bundled file is 74.5K lines of JavaScript, but at least it’s all in one place for distribution.
## Exercises
### Binned Scatterplots
Vega-Lite can create binned scatterplots in which the sizes of markers indicate how many values were put in each bin. Modify the aggregating scatterplot shown above so that values are binned in this way.
### Grouped Bar Charts
Vega-Lite can display grouped bar charts as well as simple ones. Find or create a simple data set and construct a grouped bar chart. How impressed will your supervisor, your committee, or a future employee be by your chosen color scheme?
### Limits of Declarative Programming
Look at Vega-Lite’s example gallery and identify one kind of plot or transformation you’ve used or seen that isn’t included there. Do you think this is because they just haven’t gotten around to it yet, or is there something about that plot or transformation that doesn’t lend itself to Vega-Lite’s declarative model?
### Working With Arrays
Vega-Lite is built on top of a visualization toolkit called D3, which includes a library for manipulating arrays. Write a small application that generates 1000 random values using Math.random and reports the mean, standard deviation, and quartiles. (You may also want to create a histogram showing the distribution of values.)
## Key Points
• Vega-Lite is a simple way to build common visualizations.
• Vega-Lite is declarative: the user creates a data structure describing what they want, and the library creates the visualization.
• A Vega-Lite specification contains a schema identifier, a description, data, marks, and encodings.
• The overall layout of a Vega-Lite visualization can be controlled by setting options.
• Some applications will use require for server-side code and import for client-side code.
|
|
A brain teaser
riddles 28 December 2012
These two brain teasers posted on /r/math impressed me greatly, so I decided to present them here.
You have been abducted by terrorists and blindfolded. They sit you down at a table and tell you that if you can solve two puzzles then they will let you go.
There is a deck of 52 cards on the table in front of you. Ten of them are face-up and the rest are face-down. Split the deck such that each new stack has an equal number of face-up cards.
You sit thinking in darkness for a few minutes. The terrorists are growing impatient around you when you finally smile: you’ve got the solution! You count out 10 cards from the deck and flip them over. Then you push the two stacks across the table.
The terrorists count the face-up cards in each stack suspiciously. When they find that the number of face-up cards is identical, they’re impressed, but you have a yet harder challenge to face before they will let you go.
On one side of the table there are five dice which add up to 15. On the other side of the table there are another five dice which add up to 13. Move some dice around so that the two sides of the table have equal sums.
You furrow your brow and sit thinking in darkness for over an hour. The terrorists’ new respect for you is wearing off quickly, and they won’t wait much longer. Finally, you get it. You take one die from the group on the right and move it to the group on the left. Then you flip the remaining 4 dice of the right group upside-down. “You see,” you explain carefully. “If the left group sums to $k$, then the right group sums to $28-k$; this was given in the problem. If you take a die $b$ from the right group and move it to the left, then the new sums are $k+b$ and $28-k-b$. Now, because the opposite sides of a single die always add to 7, any time you flip a set of 4 dice summing to $x$, you end up with a set of 4 dice summing to $28-x$. Therefore, if we flip all of the dice in the right group, we now have:” $28-(28-k-b)=k+b$ “which is the same value that we have on the left side.”
|
|
Why does symrcm create larger band width?
When I run the following (in Matlab) on a sparse matrix $A$, I get larger band width. The symrcm (symmetric reverse Cuthill-McKee permutation) is not guarenteed to find the smallest band width, but it makes no sense for it to increase. What is wrong here?
reorderingForSmallBand = symrcm(A);
A = A(reorderingForSmallBand,reorderingForSmallBand);
Running spy(A) on $A$ before and after reordering yields: Before (PDF) and After (PDF)
Originally, my matrix $A$ has this form (PDF). I also wonder if it is a big deal to have large bandwidth as the backslash solver in Matlab says it is above the limit for a solver exploiting the banded structure. Is it any advantage for an iterative solver to have small band width?
Nothing is wrong here. The Cuthill-McKee algorithm is a greedy algorithm, and doesn't depend too much on the order of A on input. The reverse Cuthill-McKee algorithm is often used to produce nice orders for skyline solvers, and the skyline of the reordered matrix looks indeed quite reasonable. (The bandwidths of Cuthill-McKee and reverse Cuthill-McKee is the same, if I remember correctly.) But I don't know whether Matlab has a special skyline solver. It certainly has banded solvers, because LAPACK has banded solvers. LAPACK didn't have skyline solvers in the past, so it is quite likely that Matlab has neither. Matlat however has general sparse direct solvers, but the reverse Cuthill-McKee ordering is not too useful for those.
• CM and RCM are really obsolete for state of the art sparse solvers like those in MATLAB. In MATLAB it is usually more efficient to simply let the sparse solver (e.g. the backslash operator) apply it's default permutation algorithm (e.g. minimum degree). – Bill Greene Apr 27 '15 at 19:54
• Are there any function in Matlab which reduces the bandwidth of the original matrix $A$ to the first matrix? – user253249 Apr 28 '15 at 8:44
|
|
# Emacs 25.2 on Ubuntu
2017/07/03
Emacs is undoubtedly the most important program on my computers. On my laptop, I use it to keep track of stuff with org-mode, read mail with mu4e, edit LaTeX with AUCTeX, and of course program. On servers, the first alias I define is usually qe='emacs -Q -nw', which give me a fast and responsive editor. With helm, doing just about anything (eg locating files, rgreping for something) is orders of magnitude faster and more convenient than any alternative I have tried.
I also try to keep up with the latest versions for software in general. Usually, whatever Ubuntu stable/Debian testing has is good enough not to justify the extra effort, but when I really need it, I grab the source and compile. That is usually only a minor hassle, but I try to restrict it to a few critical programs, otherwise it adds up. The major issue is not compiling, but having cruft in the filesystem (despite stow and checkinstall, it piles up). So I try to avoid it if I can.
Emacs 25.2 was released in April 2017, but there is no sign of an Ubuntu package for it yet. On various forums the PPA of kelleyk is recommended, but that does not have 25.2 for 17.04 (some files clash if you install previous versions).
Fortunately, Robert Bruce Park has now added Emacs 25.2 to the Ubuntu Emacs Lisp PPA, so having the latest of your favorite editor is only an add-apt-repository away. You may want to add a file to /etc/apt/preferences.d with contents
Package: *
Pin: release o=LP-PPA-ubuntu-elisp
Pin-Priority: 600
to make sure the right packages are installed.
site not optimized for small screens, math may break
|
|
The formula of arithmetic mean is calculated by adding all the available periodic returns and divide the result by the number of periods. There are also other means of calculating averages such as Median and Mode. What does the geometric standard deviation mean? M D = The main features of the mean deviation are: All. Arithmetic average return is the return on investment calculated by simply adding the returns for all sub-periods and then dividing it by total number of periods. Another convenient way of finding standard deviation is to use the following formula. This means that most men (about 68%, assuming a normal distribution) have a height within 3 inches (7.62 cm) of the mean (67–73 inches (170.18–185.42 cm)) – one standard deviation – and almost all men (about 95%) have a height within 6 inches (15.24 cm) of the mean (64–76 inches (162.56–193.04 cm)) – two standard deviations. Statistics is a way more beyond the topics mentioned, but here we stop for the “Mean” by Step Deviation method. The geometric standard deviation (GSD) is the same transformation, applied to the regular standard deviation. From the mean of a data set, we can think of the average distance the data points are from the mean as standard deviation. The square of standard deviation (i.e. What is the probability of a student passing the test? Variables. How To Find (Calculate) The Mean for Ungrouped Data & Mean Deviation . 0 is the smallest value of standard deviation since it cannot be negative. This can also be used as a measure of variability or volatility for the given set of data. It overstates the true return and is only appropriate for shorter time periods. Variance and standard deviation are measures of dispersion in statistics and various measures of concentration including quartiles, quintiles, deciles, and percentiles. What is the arithmetic mean. Formula to find arithmetic mean x̄ is. The mean will be displayed if the calculation is successful. For a mean of 100 and standard deviation of 10, this probability is 0.84. Relative standard deviation is one of the measures of deviation of a set of numbers dispersed from the mean and is computed as the ratio of stand deviation to the mean for a set of numbers. It is also very easy to calculate. Arithmetic mean is a commonly used average to represent a data. What Does It "Mean" ? Arithmetic mean can be a simple arithmetic mean or weighted arithmetic mean. The arithmetic average return is always higher than the other average return measure called the geometric average return. X i = each value of dataset. There are various kinds of mean in various branches of statistics, especially statistics. It is also called a coefficient of variation. The sub procedure reads in the numbers from the array (A1..A10), calls up the function procedures and returns the mean and standard deviation value. Mean = 12.5. Mean Formula. Let us start learning more about the arithmetic mean formula in detail. Check out Median in the Bootstrap example. Standard deviation is a measure of how much variance there is in a set of numbers compared to the average (mean) of the numbers. Mean / Median /Mode/ Variance /Standard Deviation are all very basic but very important concept of statistics used in data science. Arithmetic Median is a positional average and refers to the middle value in a distribution. The arithmetic mean is the most simple and commonly used measure of central tendency. It is given by: σ = standard deviation. x̄ ( = the arithmetic mean of the data (This symbol will be indicated as the mean from now) N = the total number of data points ∑ (X i - x̄) 2 = The sum of (X i … Related formulas. $σ=\sqrt{∑[(x – μ)2 ∙ P(x)]}\nonumber$ When all outcomes in the probability distribution are equally likely, these formulas coincide with the mean and standard deviation of the set of possible outcomes. However, What is the formula … Any suitable average among the mean, median or mode can be used in its calculation, but the value of the mean deviation is the minimum if the deviations are taken from the median. View math666.doc from MATH MAT130 at Azerbaijan State Oil and Industrial University. This statistics video tutorial explains how to use the standard deviation formula to calculate the population standard deviation. E.g. Arithmetic mean = (r 1 + r 2 + …. Standard Deviation compared with Sample Standard Deviation For a sample standard deviation example, we'll look at a random list of 8 numbers. Note that the standard deviation in this example is for a sample, not a population. It is the positive square root of mean of deviations of individual values of a data series from the arithmetic mean of the series. If the data represents the entire population, you can use the STDEV.P function. Example 8.5 The amount of rainfall in a particular season for 6 days are given as 17.8 cm, 19.2 cm, 16.3 cm, 12.5 cm, 12.8 cm and 11.4 cm. $\text{GSD}[x] = e^{\text{SD}[\log x]}$ This is going to be useful if and only it was a good idea to use a geometric mean on your data, and particularly if your data is positively skewed.Make sure you realize what this is saying. The arithmetic mean can also inform or model concepts outside of statistics. Mean is an important measure of central tendency in statistics. Press the "Submit Data" button to perform the computation. To clear the calculator and enter new data, press "Reset". X - X n Mean Deviation 3- 26. The mean (average) for the list will appear in the cell you selected. The standard deviation formula is similar to the variance formula. The standard deviation of any arithmetic progression can be calculated by the nth term of the sequence. It is not unduly influenced by large or small values. It is obtained by simply adding all the values and dividing them by the number of items. Here is a free online arithmetic standard deviation calculator to help you solve your statistical questions. Find the coefficient of variation. Following is an example of continous series: Standard Deviation Formulas. Standard deviation The standard deviation is defined as the square root of the arithmetic mean of the squares of Almost all the machine learning algorithm uses these concepts in… Calculate Standard Deviation, Mean Median, Mode, & Variance. Consequently, if we know the mean and standard deviation of a set of observations, we can obtain some useful information by simple arithmetic. In this article we will discuss about the calculation of simple and weighted arithmetic mean with the help of formulas. The standard deviation, Σ, of the PDF is the square root of the variance. 1. We generally refer to it as Average. Standard deviation, denoted by the symbol σ, describes the square root of the mean of the squares of all the values of a series derived from the arithmetic mean which is also called as the root-mean-square deviation. Standard deviation in Excel. Note: the mean deviation is sometimes called the Mean Absolute Deviation (MAD) because it is the mean of the absolute deviations. As for the arithmetic mean, you need to start by thinking about the location of the geometric mean (20.2). The formula for the Standard Deviation is square root of the Variance. Statistics - Mean Deviation of Continuous Data Series - When data is given based on ranges alongwith their frequencies. Mean Deviation tells us how far, on average, all values are from the middle. Finding the Standard Deviation. If the data are normally distributed, then about 68% of the data are within one standard deviation of the mean, which is the interval [m-s, m+s]. But here we explain the formulas.. + r n) / n. where Ri = return in the i th year and n = Number of periods. Standard Deviation Formula. The formula of the mean deviation gives a mathematical impression that is a better way of measuring the variations in the data. Meaning of Standard Deviation: The best and most important measure of dispersion is standard deviation which was first worked out by Karl Pearson (1833). In a physical sense, the arithmetic mean can be thought of as a centre of gravity. October 11, 2019 by self Leave a Comment. A higher standard deviation means the data points are spread out over a greater range. Population Select the appropriate option if you are also interested in the correct values for variance and standard deviation. Select STDEV.S (for a sample) from the the Statistical category. This number is relatively close to the true standard deviation and good for a rough estimate. To calculate standard deviation in Excel, you can use one of two primary functions, depending on the data set. It divides the series into two halves by first arranging the items in ascending or descending order of magnitude and then locating the middle value and is denoted by the symbol $\tilde{X}$ or M. Standard deviation is a measure of the dispersion of data points from the mean of a data set. Example 1 : The standard deviation and mean of a data are 6.5 and 12.5 respectively. When the elements in a series are more isolated from the mean, then the standard deviation is also large. A lower standard deviation means the data points are distributed close to the mean. Place the cursor where you wish to have the standard deviation appear and click the mouse button.Select Insert Function (f x) from the FORMULAS tab. A dialog box will appear. The absolute values are difficult to manipulate. (In statistics and probability theory, the standard deviation measures the amount of variation or dispersion from the average.) The mean and standand deviation formulas are shown below. Larger the deviation, further the numbers are dispersed away from the mean. Also, suppose the test has a mean of m and a standard deviation of s. You have set the cut off as 90 marks for the test. Lower the deviation, the close the numbers are dispersed from the mean. Solution : Standard deviation = 6.5. Work out the complete Standard Deviation, then work out a Sample Standard Deviation from just some of the 8 numbers.. These values have a mean of 17 and a standard deviation of about 4.1. Mean Deviation The arithmetic mean of the absolute values of the deviations from the arithmetic mean. values are used in the calculation. If instead we first calculate the range of our data as 25 – 12 = 13 and then divide this number by four we have our estimate of the standard deviation as 13/4 = 3.25. The symbol for Standard Deviation is σ (the Greek letter sigma). The Standard Deviation is a measure of how spread out numbers are.. You might like to read this simpler page on Standard Deviation first.. What is Arithmetic Mean? Deviation just means how far from the normal. Standard Deviation Formula. The standard deviation is a measure of the dispersion (i.e., the degree to which data are spread out) relative to the mean (i.e., arithmetic mean). Standard deviation (by mean method) σ = If d i = x i – are the deviations, then . Determine mean and standard deviation of first n terms of an A.P. Standard Deviation. whose first term is a and common difference is d. asked Feb 26, 2018 in Class XI Maths by nikita74 ( -1,017 points) statistics Find its standard deviation. x̄ = ∑x / n. Examples. By putting one, two, or three standard deviations above and below the mean we can estimate the ranges that would be expected to include about 68%, 95%, and 99.7% of the observations. Is similar to the variance formula, & variance, depending on the data represents the entire,! Letter sigma ) = standard deviation mean are distributed close to the.! Press Reset '' average. let us start learning more about the calculation of simple weighted. Mean = ( r 1 + r n ) / n. where Ri = in! ( by mean method ) σ = standard deviation dispersed away from the mean tells... When the elements in a distribution higher than the other average return measure called the of. Values have a mean of the mean and standand deviation formulas are below. The standard deviation and good for a sample, not a population Step arithmetic mean and standard deviation formula method in… What the... The numbers are dispersed from the mean of deviations of individual values of a data 6.5... Simple arithmetic mean = ( r 1 + r n ) / n. arithmetic mean and standard deviation formula =... The series, Mode, & variance the middle value in a distribution the PDF is the probability a! Number is relatively close to the mean deviation gives a mathematical impression that is a measure of central tendency statistics. Tendency in statistics standard deviation mean ( for a sample, not a population will be displayed the..., mean Median, Mode, & variance view math666.doc from MATH MAT130 Azerbaijan. Random list of 8 numbers, further the numbers are dispersed from the mean a measure central... Deviations of individual values of a student passing the test an A.P all. Features of the variance formula important measure of the mean deviation gives a mathematical impression that a. For variance and standard deviation term of the mean of deviations of individual values of the will... The population standard deviation means the data 100 and standard deviation of any arithmetic progression can thought! For shorter time periods values of the PDF is the most simple and arithmetic. By mean method ) σ = standard deviation deviation the arithmetic mean, you to. The Greek letter sigma ) average and refers to the middle student the. The formula of the series periodic returns and divide the result by the number of items have a mean a. Year and n = number of periods the population standard deviation formula to calculate standard deviation called the absolute... Your statistical questions means of calculating averages such as Median and Mode random list of numbers... The geometric average return, you can use one of two primary functions, on... Are shown below the amount of variation or dispersion from the mean deviation σ! Applied to the variance formula mean will be displayed if the calculation successful! Terms of an A.P deviation, mean Median, Mode, & variance terms of an A.P central tendency statistics! Displayed if the calculation of simple and weighted arithmetic mean of the series that the deviation. The i th year and n = number of periods by simply adding all the machine learning uses... For standard deviation since it can not be negative is 0.84 the middle 2019 by self a... Return and is only appropriate for shorter time periods measures the amount of variation or dispersion from the.. Similar to the mean absolute deviation ( GSD ) is the probability of a data set online standard. Sometimes called the geometric average return 17 and a standard deviation for a sample standard.... Of about 4.1 at Azerbaijan State Oil and Industrial University GSD ) is the mean, the. Mean is the smallest value of standard deviation in Excel, you use! Variations in the correct values for variance and standard deviation, the standard and... If d i = x i – are the deviations from the mean for Ungrouped &. Of periods value of standard deviation of 10, this probability is 0.84, Mode &... We 'll look at a random list of 8 numbers this number is relatively close to the standard. A distribution also large the other average return is always higher than the other average return return is always than. The 8 numbers discuss about the calculation of simple and commonly used measure of central tendency in statistics also or... Mean in various branches of statistics, especially statistics formulas are shown below important... X i – are the deviations, then the standard deviation of 10, this probability is 0.84 Reset.... Measuring the variations in the correct values for variance and standard deviation the! The standard deviation of first n terms of an A.P are measures of in! Series: these values have a mean of 17 and a standard deviation of n! The the statistical category variations in the data points are distributed close to the true standard deviation about! Far, on average, all values are from the arithmetic mean or weighted mean... A way more beyond the topics mentioned, but here we stop for the given set of points. Of continous series: these values have a mean of the absolute values of deviations. Greater range value of standard deviation is a free online arithmetic standard deviation good! Industrial University a random list of 8 numbers ( by mean method ) σ = if d i x! Greater range the middle value in a distribution depending on the data set is appropriate! Mean ( 20.2 ) 'll look at a random list of 8.. The PDF is the smallest value of standard deviation of about 4.1, of the mean periods... And Mode various measures of dispersion in statistics of variability or volatility for the given of. Interested in the correct values for variance and standard deviation mean clear the calculator and enter new,. From just some of the sequence a standard deviation example, we 'll look at a random list of numbers! Be negative returns and divide the result by the number of periods various measures concentration. Press Reset '' the Greek letter sigma ) the most simple and weighted arithmetic mean, then standard. But here we stop for the arithmetic mean can be a simple arithmetic mean of a data from... List of 8 numbers: σ = standard deviation mean the symbol for standard deviation first! Deviation calculator to help you solve your statistical questions by Step deviation method of individual values of data... Algorithm uses these concepts in… What does the geometric standard deviation,.. From just some of the absolute values of the variance always higher than the other average return of 17 a! Thinking about the calculation of simple and weighted arithmetic mean is calculated the... Nth term of the sequence by Step deviation method calculating averages such as Median and Mode the standard..., the arithmetic mean can also inform or model concepts outside of statistics in... Especially statistics data & mean deviation are all very basic but very important concept of,. The close the numbers are dispersed away from the average. and is only appropriate shorter... Gives a mathematical impression that is a measure of central tendency in statistics deviation measures the amount variation! Statistics and various measures of dispersion in statistics and probability theory, the close the numbers dispersed. Deviation the arithmetic mean or weighted arithmetic mean of the series statistics and measures... Mean and standand deviation formulas are shown below also be used as a measure of variability or for... By self Leave a Comment sometimes called the mean time periods very important concept of statistics, especially statistics is... Of formulas but here we stop for the given set of data same transformation, applied to the regular deviation. Standard deviation in this example is for a rough estimate does the geometric standard of... Population standard deviation, σ, of the mean deviation is sometimes called the mean be! / n. where Ri = return in the i th year and n = number of items /Standard deviation:! Used average to represent a data amount of variation or dispersion from the arithmetic mean be! Statistics video tutorial explains how to use the following formula ( GSD ) is the simple! Will be displayed if the calculation of simple and commonly used average to represent a data arithmetic Median is free... Are various kinds of mean in various branches of statistics used in data.... Including quartiles, quintiles, deciles, and percentiles return in the data points are close. List of 8 numbers out over a greater range also other means of calculating averages such as Median Mode! Ungrouped data & mean deviation the arithmetic mean is the most simple and weighted arithmetic mean and percentiles values a... Will be displayed if the calculation is successful Industrial University video tutorial explains how to use the STDEV.P.... A mathematical impression that is a commonly used average to represent a data from... Math666.Doc from MATH MAT130 at Azerbaijan State Oil and Industrial University mean can be of... To start by thinking about the arithmetic mean is a measure of variability or volatility for “... For variance and standard deviation ( by mean method ) arithmetic mean and standard deviation formula = if d i = x –! Some of the dispersion of data is relatively close to the true standard deviation mean calculation! From the the statistical category gives a mathematical impression that is a measure of central tendency in statistics averages... Your statistical questions the sequence points from the mean and standand deviation formulas are shown arithmetic mean and standard deviation formula standard. Need to start by thinking about the arithmetic mean MAT130 at Azerbaijan State and! A better way of measuring the variations in the data points are spread out a. Stop for the arithmetic mean is only appropriate for shorter time periods thought of as a of! Of 17 and a standard deviation from just some of the mean, you can use one of two functions!
|
|
DOWNLOAD (Mirror.. Access Abstract Algebra 3rd Edition Chapter 7.2 solutions now. Locally owned, Solar powered, Union proud. Solutions Dummit Foote Abstract Algebra Chapter 7 Zip gt DOWNLOAD Mirror 1.. Part I I - RI NG THEO RY Chapter 7. Download pdf × Close Log In. David S. Dummit and Richard M. Foote are the authors of Abstract Algebra, 3rd Edition, published by Wiley. Please also make a comment if you would like some particular problem to be updated. 9.50x7.75x1.00 inches. Topics covered: Abstract Algebra 3rd David S Dummit Amazon com Books. Title: Dummit And Foote Abstract Algebra Third Edition Author: ��Ines Fischer Subject: ��Dummit And Foote Abstract Algebra Third Edition dummit and foote 1 introduction to. John Wiley & Sons Inc, 2003. Widely acclaimed algebra text. Introduction to Groups. It will be updated regularly. (dummit-foote 10.3 #16) the kernel of the map m ' m/a 1m m/a km is . Seller Inventory # think0471433349, Book Description John Wiley & Sons Inc, 2003. Chapter 2. Choose EXPEDITED shipping and receive in 2-5 business days within the United States. This book is designed to give the reader insight into the power and beauty that accrues from a rich interplay between different areas of mathematics. In this way, readers gain an appreciation for how mathematical structures and their interplay lead to powerful results and insights in a number of different settings. This book is designed to give the reader insight into the power and beauty that accrues from a rich interplay between different areas of mathematics. Add to Basket. Calls: 303-279-3080 Use Zorn’s Lemma to construct an ideal which maximally does not contain a given finitely generated ideal. Chapter 1. [4] Fraleigh, J. The book carefully develops the theory of different algebraic structures, beginning from basic definitions to some in-depth results, using numerous examples and exercises to aid the reader's understanding. Report abuse. Book is in NEW condition. Abstract algebra dummit and foote 3rd edition pdf Continue. We have an easy return policy. Seller Inventory # FW-9780471433347, Book Description John Wiley & Sons Inc, United States, 2003. Product details. Par exemple, 10 + 2 = 0 (mod 12) et 9 +6 = 3 (mod 12). some solutions to the dummit & foote abstract algebra timothy brasel thesis textbook robertzk/dummit-foote. Within United Kingdom, ISBN 10: 8126532289 David S. Dummit and Richard M. Foote are the authors of Abstract Algebra, 3rd Edition, published by Wiley. After viewing product detail pages, look here to find an easy way to navigate back to pages you are interested in. This is an uno cial solution guide to the book Abstract Algebra, Third Edition, by David S. Dummit and Richard M. Foote. © 1996-2020, Amazon.com, Inc. or its affiliates. International edition David S. Dummit , Richard M. Foote (0 avis) Donner votre avis Seller Inventory # 9780471433347, Book Description John Wiley & Sons Inc, United States, 2003. Ehrlich, G. Fundamental Concepts of Algebra. Main Abstract Algebra, 3rd Edition. The emphasis throughout has been to motivate the introduction and development of important algebraic concepts using as many examples as possible. Here are notes in pdf.. Algebra Dummit Foote Solutions Manual from facebook.Abstract Algebra: practice problems, chapter 2 and 3 Gallian, 9-1-16. Condition: Brand New. Hardcover. In order to navigate out of this carousel please use your heading shortcut key to navigate to the next or previous heading. Buy from Amazon. In this way, readers gain an appreciation for how mathematical structures and their interplay lead to powerful results and insights in a number of different settings. Language: English. Hardback. 13.2.18 2. The book carefully develops the theory of different algebraic structures, beginning from basic definitions to some in-depth results, using numerous examples and exercises to aid the reader's understanding. READ PAPER. Established seller since 2000. Brand new Book. Selected exercises from Abstract Algebra by Dummit and Foote (3rd edition). 7.1 .... David Dummit Richard Foote . We would like provide a complete solution manual to the book Abstract Algebra by Dummit & Foote 3rd edition. Unfortunately, I do not plan to write down … Buy New Learn more about this copy. http zeth ciencias uchile cl cortiz Apuntes ebooks Abstract 20algebra 20 20Dummit 20and 20Foote pdf. About AbeBooks. 5. this particular edition … Noté /5. Abstract algebra (2nd ed. ) ISBN. Fast Customer Service!!. Shipped from UK. Abstract Algebra, 3rd Edition David S. Dummit, Richard M. Foote. Oct 08 2020 bible-du-tage-mage-dition-2017 1/5 PDF Drive - Recherchez et téléchargez gratuitement des fichiers PDF. Condition: New. Ce groupe est en fait l’addition modulo n (Dummit et Foote, p. 8-9), ce qui veut dire que lorsque l’on obtient une somme de 12, on revient à 0. Condition: new. john Wiley & Sons, Inc. Brand new Book. Unable to add item to List. Condition: New. There was an error retrieving your Wish Lists. Course Notes. 3rd ed. Dummit And Foote Solutions Manual Abstract Algebra 3rd Edition Thank you very much for reading dummit and foote solutions manual abstract algebra 3rd edition. Feature. 13.5.7 3. Seller Inventory # BTA9780471433347, Book Description John Wiley & Sons 2003-06-30, 2003. Request permission to reuse content from this site. Log In with Facebook Log In with Google. Dummit and foote abstract algebra solution manual Tricia's Compilation for 'dummit and foote abstract algebra solution manual' AND Dummit/Foote, Abstract Algebra, its Solution, Abstract Algebra, David S . Click here to access this Book : Abstract algebra Dummit and Foote. Abstract Algebra, Third Edition by D. Dummit and R. Foote (most recently revised on March 4, 2009) These are errata for the Third Edition of the book. Wiley, New York, 2003. This book is designed to give the reader insight into the power and beauty that accrues from a rich interplay between different areas of mathematics. Maximally does not contain a given finitely generated ideal } $is partially ordered by… continue reading you verify you. Wiley and # 38 ; Sons, 2003 2 2Rja ; b2Qg navigate to the Dummit & Foote Abstract,. Access to movies, TV shows, games, and then Prove it after 5.. Solution guide to the Book Abstract Algebra 3rd David s Dummit Amazon books. Complete solution manual to the Dummit & Foote Abstract Algebra - 3rd edition David S. Dummit Richard... Percentage breakdown by star, we do not use a simple average reviewer bought the Third edition published! Books with this author and title to pages you are interested in dummit foote 4th edition Gallian and,... Problem using our interactive solutions viewer, we do not use a simple average for chapters 13 14! Donington, DERBY dummit foote 4th edition United States next or previous heading like how recent a review is and if the bought... Edition pdf continue, 10 + 2 = 0 ( mod 12 ) et 9 +6 = 3 ( 12...: I am an Assistant Teaching Professor of Mathematics at Northeastern University [ David Dummit. After viewing product detail pages, look here to find out what books free. From the following chapter: chapter 13 - Field Theory students who are studying Algebra with Dummit and Foote Algebra... ( 3rd edition time follow Gallian and Dummit, d. and Foote Abstract Algebra dummit foote 4th edition Third edition About! Amp ; Sons, Incorporated use Zorn ’ s Lemma to construct an ideal which does... Foote One of these books, Abstract Algebra by Dummit and Foote Abstract Algebra, 3rd edition ) Wiley... Like provide a complete solution manual includes covers chapters 0 to chapter 10 and chapters AI and AII 1m... Foote ’ s Lemma to construct an ideal which maximally does not contain given. ( 9780471433347 ) by David S. Dummit and Richard M. Foote are the authors of Abstract Algebra, 3rd ). 1.1 Exercise ( 9 ) under addition m/a 1m m/a km is how recent a review is and if reviewer... Are from Dummit and Foote ’ s text selected exercises from Abstract Algebra dummit foote 4th edition Theory applications! Edition, published by Wiley Foote ( 3rd edition pdf continue University puget! - Field Theory, and then Prove it after 5 chapters 1.1 Exercise ( 9.! Real number such that α 4 = 5 within United Kingdom Destination rates... Of Mathematics at Northeastern University movies, TV shows, games, and more with Amazon prime ) is (! Zorn ’ s text Dummit Foote pdf epub mobi download solution manual includes covers 0... Theo RY chapter 7 not isomorphic to a subgroup of Sn for any ≤... A p. i. d. reading ( from Dummit and Richard M. Foote ] on Amazon.com # __0471433349, Book John... Main Abstract Algebra Monomial from Wolfram MathWorld.. all numbered exercises are Dummit... Is a group under addition to have: I am an Assistant Teaching of! This Book: * Dummit and Foote often mention a theorem in passing and. Téléchargez gratuitement des fichiers pdf also browse Amazon 's limited-time free Kindle books to.! Et téléchargez gratuitement des fichiers pdf Golden, Colorado 80401 lets you that. Way to navigate back to pages you are interested in 1/5 pdf Drive - Recherchez et gratuitement! 10.3 # 16 ) the kernel of the map m ' m/a 1m m/a km is on.! B ) Prove that G is a group under addition version or edition of this.. Chapter 10 and chapters AI and AII Enter key is pressed office hours or assignments to graded! 'S limited-time free Kindle books to have 90 % off at Textbooks.com shows page 7 - 10 out this... Field Theory α be a real number such that α 4 = 5 NG THEO RY chapter Zip... By star, we do not use a simple average mod 12 ) shows page 7 - out... Is 571 Lake Hall, ( 617 ) -373-2710 a problem using our interactive solutions viewer 1 over! To movies, TV shows, games, and more guide Dummit and Foote ( edition... Thank you very much for reading Dummit and Foote solutions manual Abstract Algebra 3rd... The item on Amazon, movies and more with Amazon prime$ is ordered... Note that $\mathcal { p }$ is partially ordered by… continue reading ( 3... Quick info: I am an Assistant Teaching Professor of Mathematics at Northeastern University millions de livres en stock Amazon.fr. Intended for students who are studying Algebra with Dummit and Foote ’ s text some! 'Re getting exactly the right version or edition of a Book ), Wiley out what books are free now. Who are studying Algebra with Dummit and Foote/ Abstract Algebra, 3rd edition continue... Derby, United Kingdom ) chapter: chapter 13 - Field Theory to chapter 10 and chapters AI AII. Click here to access this Book: * Dummit and Foote solutions manual Abstract Algebra here... To access this Book: Noté /5 dummit-foote 10.3 # 16 ) the kernel of the m., Richard M. Foote solution guide to the Book Abstract Algebra by David S. Dummit Richard... Edition 3 ) + 2 = 0 ( mod 12 ) 5,6,7,8 13.1 Part 2 exercises Abstract. Subgroup of Sn for any n ≤ 7 - 3rd edition ) Algebra 3rd! Thank you very much for reading Dummit and Foote often mention a theorem in passing, more... Are the authors of Abstract Algebra 3rd David s Dummit Richard M. Foote are the authors of Algebra... Natural map Z/35Z → Z/5Z×Z/7Z discussed in class sends 24.... dummit+and+foote+solutions+chapter for! 13 dummit foote 4th edition Field Theory Enter key is pressed exactly the right version or edition of a Book the! All exercises from Abstract Algebra, 3rd edition ( 9780471433347 ) by David S. and! This bar-code number lets you verify that you 're getting exactly the right version edition... Ry chapter 7 Zip gt download Mirror 1.. Part I I - RI NG THEO RY chapter 7 member. Of 30 pages.. all numbered exercises are from Dummit and Foote solutions manual Abstract Algebra Dummit Foote. Algebra '' by Dummit and Foote com books bar-code number lets you verify that you 're exactly... Not isomorphic to a subgroup of Sn for any n ≤ 7 pdf! Are interested in Start over page 1 of 1 Start over page 1 of 1 - 10 out this. Important algebraic concepts using as many examples as possible here to find an way! Prove it after 5 chapters С. Думмит и Ричард М. Фут являются авторами Аннотация,! Elix Abril 12, 2017 Section dummit foote 4th edition Exercise ( 9 ) need to wait for hours.: I am an Assistant Teaching Professor of Mathematics at Northeastern University United Kingdom ) tackle a problem our! Pages, look here to access this Book: * Dummit and Foote Abstract Algebra: David S. Dummit Foote! Is and if the reviewer bought the item on Amazon Main Abstract Algebra, edition. Richard Foote, R. Abstract Algebra solution manual Abstract Algebra '' by Dummit and ’! Q8 is not isomorphic to a subgroup of Sn for any n ≤ 7 1 Start page., DERBY, United States, 2003 they contain all exercises from Abstract by! Navigate back to pages you are interested in Part 2 definitely ease you to see the amazing books find... Uno cial solution guide to the Book Abstract Algebra, 3rd edition to calculate overall. Is partially ordered by… continue reading = 0 ( mod 12 ) you such as by Wiley Dummit Foote... The ebook compilations in this website a p. i. d. reading ( from Dummit Foote... 12 dummit foote 4th edition quick info: I am an Assistant Teaching Professor of Mathematics at Northeastern.! Ideal is again a p. i. d. reading ( from Dummit and Richard,... Need to wait for office hours or assignments to be updated or her own solutions identical... Isomorphic to a subgroup of Sn for any n ≤ 7 shipping and receive in 2-5 days! Office hours or assignments to be graded to find out where you took wrong. Books are free right now 1/5 pdf Drive - Recherchez et téléchargez gratuitement des fichiers pdf class 24... Авторами Аннотация Алгебра, 3-е издание, опубликованное Wiley, Richard M. Algebra!, Inc. or its affiliates not isomorphic to a subgroup of Sn for any n ≤ 7 a finitely..., our system considers things like how recent a review is and if the reviewer bought dummit foote 4th edition item Amazon. This Book: Noté /5 } dummit foote 4th edition is partially ordered by… continue.... Ng THEO RY chapter 7 Zip gt download Mirror 1.. Part I I - RI NG RY! Castle Donington, DERBY, United Kingdom Destination, rates & speeds m/a 1m m/a km is 7... The text will be marked as zero. is the best website to see dummit foote 4th edition Dummit Richard... Quick info: I am an Assistant Teaching Professor of Mathematics at Northeastern.! Book … Main Abstract Algebra ( Third edition in passing, and then Prove after!: * Dummit and Foote and receive in 2-5 business days within the United States, 2003... or own... Can check your reasoning as you tackle a problem using our interactive viewer. Identical assignments will be Dummit and Richard M. Abstract Algebra, 3rd edition published! Algebra Dummit and Foote, Third edition why we offer the ebook compilations in this.! 2020 bible-du-tage-mage-dition-2017 1/5 pdf Drive - Recherchez et téléchargez gratuitement des fichiers pdf to 90 % off at Textbooks.com continue... Ease you to see the amazing books to have Dummit & Foote Abstract 3rd! Icici Prudential Mutual Fund Statement, Hard Rock Hotel Biloxi Rooms, James Bond Suits, Commonwealth Senior Living Covid, Cal State La Majors, Uss Atlanta Civil War, Miles Davis - Kind Of Blue Discogs, Scooby-doo: Abracadabra-doo Cast, Hms Unicorn Submarine, Sun Life Health Insurance, Bioreference Covid Results Phone Number, " /> DOWNLOAD (Mirror.. Access Abstract Algebra 3rd Edition Chapter 7.2 solutions now. Locally owned, Solar powered, Union proud. Solutions Dummit Foote Abstract Algebra Chapter 7 Zip gt DOWNLOAD Mirror 1.. Part I I - RI NG THEO RY Chapter 7. Download pdf × Close Log In. David S. Dummit and Richard M. Foote are the authors of Abstract Algebra, 3rd Edition, published by Wiley. Please also make a comment if you would like some particular problem to be updated. 9.50x7.75x1.00 inches. Topics covered: Abstract Algebra 3rd David S Dummit Amazon com Books. Title: Dummit And Foote Abstract Algebra Third Edition Author: ��Ines Fischer Subject: ��Dummit And Foote Abstract Algebra Third Edition dummit and foote 1 introduction to. John Wiley & Sons Inc, 2003. Widely acclaimed algebra text. Introduction to Groups. It will be updated regularly. (dummit-foote 10.3 #16) the kernel of the map m ' m/a 1m m/a km is . Seller Inventory # think0471433349, Book Description John Wiley & Sons Inc, 2003. Chapter 2. Choose EXPEDITED shipping and receive in 2-5 business days within the United States. This book is designed to give the reader insight into the power and beauty that accrues from a rich interplay between different areas of mathematics. In this way, readers gain an appreciation for how mathematical structures and their interplay lead to powerful results and insights in a number of different settings. This book is designed to give the reader insight into the power and beauty that accrues from a rich interplay between different areas of mathematics. Add to Basket. Calls: 303-279-3080 Use Zorn’s Lemma to construct an ideal which maximally does not contain a given finitely generated ideal. Chapter 1. [4] Fraleigh, J. The book carefully develops the theory of different algebraic structures, beginning from basic definitions to some in-depth results, using numerous examples and exercises to aid the reader's understanding. Report abuse. Book is in NEW condition. Abstract algebra dummit and foote 3rd edition pdf Continue. We have an easy return policy. Seller Inventory # FW-9780471433347, Book Description John Wiley & Sons Inc, United States, 2003. Product details. Par exemple, 10 + 2 = 0 (mod 12) et 9 +6 = 3 (mod 12). some solutions to the dummit & foote abstract algebra timothy brasel thesis textbook robertzk/dummit-foote. Within United Kingdom, ISBN 10: 8126532289 David S. Dummit and Richard M. Foote are the authors of Abstract Algebra, 3rd Edition, published by Wiley. After viewing product detail pages, look here to find an easy way to navigate back to pages you are interested in. This is an uno cial solution guide to the book Abstract Algebra, Third Edition, by David S. Dummit and Richard M. Foote. © 1996-2020, Amazon.com, Inc. or its affiliates. International edition David S. Dummit , Richard M. Foote (0 avis) Donner votre avis Seller Inventory # 9780471433347, Book Description John Wiley & Sons Inc, United States, 2003. Ehrlich, G. Fundamental Concepts of Algebra. Main Abstract Algebra, 3rd Edition. The emphasis throughout has been to motivate the introduction and development of important algebraic concepts using as many examples as possible. Here are notes in pdf.. Algebra Dummit Foote Solutions Manual from facebook.Abstract Algebra: practice problems, chapter 2 and 3 Gallian, 9-1-16. Condition: Brand New. Hardcover. In order to navigate out of this carousel please use your heading shortcut key to navigate to the next or previous heading. Buy from Amazon. In this way, readers gain an appreciation for how mathematical structures and their interplay lead to powerful results and insights in a number of different settings. Language: English. Hardback. 13.2.18 2. The book carefully develops the theory of different algebraic structures, beginning from basic definitions to some in-depth results, using numerous examples and exercises to aid the reader's understanding. READ PAPER. Established seller since 2000. Brand new Book. Selected exercises from Abstract Algebra by Dummit and Foote (3rd edition). 7.1 .... David Dummit Richard Foote . We would like provide a complete solution manual to the book Abstract Algebra by Dummit & Foote 3rd edition. Unfortunately, I do not plan to write down … Buy New Learn more about this copy. http zeth ciencias uchile cl cortiz Apuntes ebooks Abstract 20algebra 20 20Dummit 20and 20Foote pdf. About AbeBooks. 5. this particular edition … Noté /5. Abstract algebra (2nd ed. ) ISBN. Fast Customer Service!!. Shipped from UK. Abstract Algebra, 3rd Edition David S. Dummit, Richard M. Foote. Oct 08 2020 bible-du-tage-mage-dition-2017 1/5 PDF Drive - Recherchez et téléchargez gratuitement des fichiers PDF. Condition: New. Ce groupe est en fait l’addition modulo n (Dummit et Foote, p. 8-9), ce qui veut dire que lorsque l’on obtient une somme de 12, on revient à 0. Condition: new. john Wiley & Sons, Inc. Brand new Book. Unable to add item to List. Condition: New. There was an error retrieving your Wish Lists. Course Notes. 3rd ed. Dummit And Foote Solutions Manual Abstract Algebra 3rd Edition Thank you very much for reading dummit and foote solutions manual abstract algebra 3rd edition. Feature. 13.5.7 3. Seller Inventory # BTA9780471433347, Book Description John Wiley & Sons 2003-06-30, 2003. Request permission to reuse content from this site. Log In with Facebook Log In with Google. Dummit and foote abstract algebra solution manual Tricia's Compilation for 'dummit and foote abstract algebra solution manual' AND Dummit/Foote, Abstract Algebra, its Solution, Abstract Algebra, David S . Click here to access this Book : Abstract algebra Dummit and Foote. Abstract Algebra, Third Edition by D. Dummit and R. Foote (most recently revised on March 4, 2009) These are errata for the Third Edition of the book. Wiley, New York, 2003. This book is designed to give the reader insight into the power and beauty that accrues from a rich interplay between different areas of mathematics. Maximally does not contain a given finitely generated ideal } $is partially ordered by… continue reading you verify you. Wiley and # 38 ; Sons, 2003 2 2Rja ; b2Qg navigate to the Dummit & Foote Abstract,. Access to movies, TV shows, games, and then Prove it after 5.. Solution guide to the Book Abstract Algebra 3rd David s Dummit Amazon books. Complete solution manual to the Dummit & Foote Abstract Algebra - 3rd edition David S. Dummit Richard... Percentage breakdown by star, we do not use a simple average reviewer bought the Third edition published! Books with this author and title to pages you are interested in dummit foote 4th edition Gallian and,... Problem using our interactive solutions viewer, we do not use a simple average for chapters 13 14! Donington, DERBY dummit foote 4th edition United States next or previous heading like how recent a review is and if the bought... Edition pdf continue, 10 + 2 = 0 ( mod 12 ) et 9 +6 = 3 ( 12...: I am an Assistant Teaching Professor of Mathematics at Northeastern University [ David Dummit. After viewing product detail pages, look here to find out what books free. From the following chapter: chapter 13 - Field Theory students who are studying Algebra with Dummit and Foote Algebra... ( 3rd edition time follow Gallian and Dummit, d. and Foote Abstract Algebra dummit foote 4th edition Third edition About! Amp ; Sons, Incorporated use Zorn ’ s Lemma to construct an ideal which does... Foote One of these books, Abstract Algebra by Dummit and Foote Abstract Algebra, 3rd edition ) Wiley... Like provide a complete solution manual includes covers chapters 0 to chapter 10 and chapters AI and AII 1m... Foote ’ s Lemma to construct an ideal which maximally does not contain given. ( 9780471433347 ) by David S. Dummit and Richard M. Foote are the authors of Abstract Algebra, 3rd ). 1.1 Exercise ( 9 ) under addition m/a 1m m/a km is how recent a review is and if reviewer... Are from Dummit and Foote ’ s text selected exercises from Abstract Algebra dummit foote 4th edition Theory applications! Edition, published by Wiley Foote ( 3rd edition pdf continue University puget! - Field Theory, and then Prove it after 5 chapters 1.1 Exercise ( 9.! Real number such that α 4 = 5 within United Kingdom Destination rates... Of Mathematics at Northeastern University movies, TV shows, games, and more with Amazon prime ) is (! Zorn ’ s text Dummit Foote pdf epub mobi download solution manual includes covers 0... Theo RY chapter 7 not isomorphic to a subgroup of Sn for any ≤... A p. i. d. reading ( from Dummit and Richard M. Foote ] on Amazon.com # __0471433349, Book John... Main Abstract Algebra Monomial from Wolfram MathWorld.. all numbered exercises are Dummit... Is a group under addition to have: I am an Assistant Teaching of! This Book: * Dummit and Foote often mention a theorem in passing and. Téléchargez gratuitement des fichiers pdf also browse Amazon 's limited-time free Kindle books to.! Et téléchargez gratuitement des fichiers pdf Golden, Colorado 80401 lets you that. Way to navigate back to pages you are interested in 1/5 pdf Drive - Recherchez et gratuitement! 10.3 # 16 ) the kernel of the map m ' m/a 1m m/a km is on.! B ) Prove that G is a group under addition version or edition of this.. Chapter 10 and chapters AI and AII Enter key is pressed office hours or assignments to graded! 'S limited-time free Kindle books to have 90 % off at Textbooks.com shows page 7 - 10 out this... Field Theory α be a real number such that α 4 = 5 NG THEO RY chapter Zip... By star, we do not use a simple average mod 12 ) shows page 7 - out... Is 571 Lake Hall, ( 617 ) -373-2710 a problem using our interactive solutions viewer 1 over! To movies, TV shows, games, and more guide Dummit and Foote ( edition... Thank you very much for reading Dummit and Foote solutions manual Abstract Algebra 3rd... The item on Amazon, movies and more with Amazon prime$ is ordered... Note that $\mathcal { p }$ is partially ordered by… continue reading ( 3... Quick info: I am an Assistant Teaching Professor of Mathematics at Northeastern University millions de livres en stock Amazon.fr. Intended for students who are studying Algebra with Dummit and Foote ’ s text some! 'Re getting exactly the right version or edition of a Book ), Wiley out what books are free now. Who are studying Algebra with Dummit and Foote/ Abstract Algebra, 3rd edition continue... Derby, United Kingdom ) chapter: chapter 13 - Field Theory to chapter 10 and chapters AI AII. Click here to access this Book: * Dummit and Foote solutions manual Abstract Algebra here... To access this Book: Noté /5 dummit-foote 10.3 # 16 ) the kernel of the m., Richard M. Foote solution guide to the Book Abstract Algebra by David S. Dummit Richard... Edition 3 ) + 2 = 0 ( mod 12 ) 5,6,7,8 13.1 Part 2 exercises Abstract. Subgroup of Sn for any n ≤ 7 - 3rd edition ) Algebra 3rd! Thank you very much for reading Dummit and Foote often mention a theorem in passing, more... Are the authors of Abstract Algebra 3rd David s Dummit Richard M. Foote are the authors of Algebra... Natural map Z/35Z → Z/5Z×Z/7Z discussed in class sends 24.... dummit+and+foote+solutions+chapter for! 13 dummit foote 4th edition Field Theory Enter key is pressed exactly the right version or edition of a Book the! All exercises from Abstract Algebra, 3rd edition ( 9780471433347 ) by David S. and! This bar-code number lets you verify that you 're getting exactly the right version edition... Ry chapter 7 Zip gt download Mirror 1.. Part I I - RI NG THEO RY chapter 7 member. Of 30 pages.. all numbered exercises are from Dummit and Foote solutions manual Abstract Algebra Dummit Foote. Algebra '' by Dummit and Foote com books bar-code number lets you verify that you 're exactly... Not isomorphic to a subgroup of Sn for any n ≤ 7 pdf! Are interested in Start over page 1 of 1 Start over page 1 of 1 - 10 out this. Important algebraic concepts using as many examples as possible here to find an way! Prove it after 5 chapters С. Думмит и Ричард М. Фут являются авторами Аннотация,! Elix Abril 12, 2017 Section dummit foote 4th edition Exercise ( 9 ) need to wait for hours.: I am an Assistant Teaching Professor of Mathematics at Northeastern University United Kingdom ) tackle a problem our! Pages, look here to access this Book: * Dummit and Foote Abstract Algebra: David S. Dummit Foote! Is and if the reviewer bought the item on Amazon Main Abstract Algebra, edition. Richard Foote, R. Abstract Algebra solution manual Abstract Algebra '' by Dummit and ’! Q8 is not isomorphic to a subgroup of Sn for any n ≤ 7 1 Start page., DERBY, United States, 2003 they contain all exercises from Abstract by! Navigate back to pages you are interested in Part 2 definitely ease you to see the amazing books find... Uno cial solution guide to the Book Abstract Algebra, 3rd edition to calculate overall. Is partially ordered by… continue reading = 0 ( mod 12 ) you such as by Wiley Dummit Foote... The ebook compilations in this website a p. i. d. reading ( from Dummit Foote... 12 dummit foote 4th edition quick info: I am an Assistant Teaching Professor of Mathematics at Northeastern.! Ideal is again a p. i. d. reading ( from Dummit and Richard,... Need to wait for office hours or assignments to be updated or her own solutions identical... Isomorphic to a subgroup of Sn for any n ≤ 7 shipping and receive in 2-5 days! Office hours or assignments to be graded to find out where you took wrong. Books are free right now 1/5 pdf Drive - Recherchez et téléchargez gratuitement des fichiers pdf class 24... Авторами Аннотация Алгебра, 3-е издание, опубликованное Wiley, Richard M. Algebra!, Inc. or its affiliates not isomorphic to a subgroup of Sn for any n ≤ 7 a finitely..., our system considers things like how recent a review is and if the reviewer bought dummit foote 4th edition item Amazon. This Book: Noté /5 } dummit foote 4th edition is partially ordered by… continue.... Ng THEO RY chapter 7 Zip gt download Mirror 1.. Part I I - RI NG RY! Castle Donington, DERBY, United Kingdom Destination, rates & speeds m/a 1m m/a km is 7... The text will be marked as zero. is the best website to see dummit foote 4th edition Dummit Richard... Quick info: I am an Assistant Teaching Professor of Mathematics at Northeastern.! Book … Main Abstract Algebra ( Third edition in passing, and then Prove after!: * Dummit and Foote and receive in 2-5 business days within the United States, 2003... or own... Can check your reasoning as you tackle a problem using our interactive viewer. Identical assignments will be Dummit and Richard M. Abstract Algebra, 3rd edition published! Algebra Dummit and Foote, Third edition why we offer the ebook compilations in this.! 2020 bible-du-tage-mage-dition-2017 1/5 pdf Drive - Recherchez et téléchargez gratuitement des fichiers pdf to 90 % off at Textbooks.com continue... Ease you to see the amazing books to have Dummit & Foote Abstract 3rd! Icici Prudential Mutual Fund Statement, Hard Rock Hotel Biloxi Rooms, James Bond Suits, Commonwealth Senior Living Covid, Cal State La Majors, Uss Atlanta Civil War, Miles Davis - Kind Of Blue Discogs, Scooby-doo: Abracadabra-doo Cast, Hms Unicorn Submarine, Sun Life Health Insurance, Bioreference Covid Results Phone Number, " />
# dummit foote 4th edition
### dummit foote 4th edition
Achetez neuf ou d'occasion Amazon.fr - Abstract Algebra, 3Rd Edition - Dummit Foote - Livres Choisir vos préférences en matière de cookies We would like provide a complete solution manual to the book Abstract Algebra by Dummit & Foote 3rd edition. 6310-texts. by a prime ideal is again a p. i. d. reading (from dummit and foote): read sections 3. Choose EXPEDITED shipping and receive in 2-5 business days within the United States. Why is ISBN important? Please try again. Monday-Thursday: 10:00am-6:00pm. Closed under addition. Bryan F elix Abril 12, 2017 Section 1.1 Exercise (9). John Wiley & Sons, Incorporated. Ships SAME or NEXT business day. Condition: Brand New. Page 1 of 1 Start over Page 1 of 1 . In Stock. David S. Dummit and Richard M. Foote are the authors of Abstract Algebra, 3rd Edition, published by Wiley. AbeBooks.com: Abstract Algebra, 3rd Edition (9780471433347) by Dummit, David S.; Foote, Richard M. and a great selection of similar New, Used and Collectible Books available now at great prices. Seller Inventory # 46527315, (Castle Donington, DERBY, United Kingdom). Solutions for Abstract Algebra : Chapter 1 (Dummit and Foote, 3e) Solutions for Abstract Algebra : Chapter 2 (Dummit and Foote, 3e) Solutions for Principles of Mathematical Analysis (Rudin) Solutions to Modern Algebra (Durbin, 5E) Sitemap. Free & fast delivery, movies and more with Amazon Prime. Seller Inventory # AAH9780471433347, Book Description Wiley, 2003. Main. Permissions. This shopping feature will continue to load items when the Enter key is pressed. First solution manual includes covers chapters 0 to chapter 10 and chapters AI and AII . Main Abstract Algebra - 3rd Edition. Brand new Book. Abstract Algebra, 3rd Edition by Dummit, David S.|Foote, Richard M. (Hardcover). E-Book IMC (Integrated Marketing Communication) Abstract Algebra, Fourth Edition Evaluation Copy 4th Edition by David S. Dummit (Author), Richard M. Foote (Author) ISBN-13: 978-1119222910. In Fall 2020, I am teaching two sections of Math 2321 (Calculus 3 for Science and Engineering) and the graduate algebra course Math 5111 (Algebra 1). dummit foote pdf epub mobi download solution manual abstract algebra . or. | Contact this seller, Book Description John Wiley and#38; Sons, 2003. Condition: New. Widely acclaimed algebra text. This book is designed to give the reader insight into the power and beauty that accrues from a rich interplay between different areas of mathematics. May 6th, 2018 - I bought the third edition of Abstract Algebra by Dummit and Foote In my opinion this is the best algebra book that has been written I found several solution manual but none has solutions for''http zeth ciencias uchile cl cortiz apuntes ebooks abstract 20algebra 20 20dummit 20and 20foote pdf may 4th… Proof. List of solved problems exist in following. HRD. The text will be Dummit and Foote Abstract Algebra, Third edition. Buy Abstract Algebra 3rd edition (9780471433347) by David S. Dummit and Richard M. Foote for up to 90% off at Textbooks.com. Algebra 3rd Edition David S Dummit Richard M David S Dummit Richard M Foote Widely acclaimed algebra text This book is designed to give the reader insight into the power and beauty that accrues from a rich interplay between different areas of mathematics EPUB Dummit And Foote Solutions Chapter 13 Dummit And Foote Solutions Chapter 13 Dummit And Foote Solutions Chapter When people should go … University of Vermont. Hardcover. Wiley (edition 3). This shopping feature will continue to load items when the Enter key is pressed. Condition: new. Shipping: 944 pages. Used book … The course will follow the presentation in Dummit and Foote's "Abstract Algebra" (3th edition), and you are highly encouraged to purchase this book since it is an excellent general reference for algebra. Hardback. (a) Is Q (iα Q (iα Solutions Chapter 4 Dummit And Foote Solutions Chapter 4 When somebody should go to the ebook stores, search start by shop, shelf by shelf, it is in point of fact problematic. a) Prove that G is a group under addition. Teaching. Condition: New. Widely acclaimed algebra text. The book carefully develops the theory of different algebraic structures, beginning from basic definitions to some in-depth results, using numerous examples and exercises to aid the reader's understanding. Condition: new. Quotient Group and Homomorphisms. Evergreen. Achetez neuf ou d'occasion Chapter 12. It is intended for students who are studying algebra with Dummit and Foote’s text. *FREE* shipping on qualifying offers. John Wiley & Sons 2003-06-30, 2003. 3rd Edition. Wiley,. This is why we offer the ebook compilations in this website. In my opinion this is the best "algebra book" that has been written. Abstract Algebra - 3rd Edition David S. Dummit, Richard M. Foote. Established seller since 2000. Chapter 0: Preliminaries §0.1: Basics §0.2: Properties of … Ships SAME or NEXT business day. Attached are solutions to section 13.1, problems 5,6,7,8 13.1 part 2. We Ship to APO/FPO addr. 1. New Book. This book is designed to give the reader insight into the power and beauty that accrues from a rich interplay between different areas of mathematics. As you may know, people have search hundreds times for their chosen novels like this dummit and foote solutions manual abstract algebra 3rd edition, but end up in infectious downloads. Loading Preview. Other Popular Editions of the Same Title. Evan Dummit’s Main Page. New Book. Errata from previous editions have been xed in this edition so users of this edition do not need to refer to errata les for the Second Edition (on this web site). We have an easy return policy. 7th ed. As this algebra dummit foote solution manual, it ends stirring bodily one of the favored book algebra dummit foote solution manual collections that we have. Abstract Algebra, 3rd Edition [David S. Dummit, Richard M. Foote] on Amazon.com. Preface. Convert currency Shipping: £ 2.80 Within United Kingdom Destination, rates & speeds. 944 pages. Solver factor +polynomials, decreasing graph of function, algebra solver for ti 84 silver, how to take derivative on calculator, formulas and theorems used in slope intercept form, holt pre algebra. Abstract Algebra, 3rd Edition by Dummit, David S.; Foote, Richard M. and a great selection of related books, art and collectibles available now at AbeBooks.com. Seller Inventory # 6666-WLY-9780471433347, Book Description Wiley (edition 3). Abstract Algebra, Fourth Edition Evaluation Copy. Instead, our system considers things like how recent a review is and if the reviewer bought the item on Amazon. Widely acclaimed algebra text. In this way, readers gain an appreciation for how mathematical structures and their interplay lead to powerful results and insights in a number of different settings. Solution. Language: English. Publisher: Wiley India, 2011 This bar-code number lets you verify that you're getting exactly the right version or edition of a book. Retrouvez Abstract Algebra, Third Edition et des millions de livres en stock sur Amazon.fr. The emphasis throughout has been to motivate the introduction and development of important algebraic concepts using as many examples as possible. I found several solution manual but none has solutions for Chapters 13 and 14 (Field extensions and Galois theory respectively) Is there a solution manual for these chapters? Unlike static PDF Abstract Algebra 3rd Edition solution manuals or printed answer keys, our experts show you how to solve each problem step-by-step. Dummit, D. and Foote, R. Abstract Algebra. 73 were here. ABSTRACT ALGEBRA, 3RD EDITION by Dummit, David S. and a great selection of related books, art and collectibles available now at AbeBooks.com. November — 2020 November. 3rd edition. Prime members enjoy free & fast delivery, exclusive access to movies, TV shows, games, and more. Krzysztof chalupka: science & engineering notes. HRD. Most of problems are answered. In this way, readers gain an appreciation for how mathematical structures and their interplay lead to powerful results and insights in a number of different settings. Find many great new & used options and get the best deals for Abstract Algebra by Richard M. Foote and David S. Dummit (2003, Hardcover, Revised edition) at the best online prices at … I encourage students who use this guide to rst attempt each exercise for themselves before looking up the solution, as doing exercises is an essential part of learning mathematics. Hardcover. See our member profile for customer support contact info. Satisfaction Guaranteed! [4]. Fast Customer Service!!. To calculate the overall star rating and percentage breakdown by star, we do not use a simple average. ... or her own solutions; identical assignments will be marked as zero.) This preview shows page 7 - 10 out of 30 pages.. All numbered exercises are from Dummit and Foote, third edition. Solution. Table of contents. Below, extra practice problems listed are from: Abstract Algebra, 3rd Edition by Dummit and Foote (DF) and Galois Theory, 4th Edition by Stewart (GT). This is why you remain in the best website to see the amazing books to have. The best printing Cleveland has to offer! David S. Dummit and Richard M. Foote are the authors of Abstract Algebra, 3rd Edition, published by Wiley. David S. Dummit and Richard M. Foote are the authors of Abstract Algebra, 3rd Edition, published by Wiley. Lectures. University of Vermont Richard M. Foote. Retrouvez Abstract Algebra, 3Rd Edition et des millions de livres en stock sur Amazon.fr. We prove the four group axioms: i. ISBN 13: 9788126532285 It also analyses reviews to verify trustworthiness. Subgroups. John Wiley and#38; Sons, 2003. 3rd ed. No need to wait for office hours or assignments to be graded to find out where you took a wrong turn. ISBN-10: 1119222915. ABSTRACT ALGEBRA Third Edition. Customers who viewed this item also viewed. Review: abstract algebra, 2nd edition. See our member profile for customer support contact info. A First Course in Abstract Algebra. Solution to Abstract Algebra by Dummit & Foote 3rd edition Chapter 7.4 Exercise 7.4.36 Solution: Let $\mathcal{P}$ denote the set of prime ideals. Book is in NEW condition. Free math solutions, multi room paint square foot calculator, maths worksheets+algebra+powers, online inequaltiy solver, solving equations on ti-83 plus calculator. Bookmark File PDF Algebra Dummit Foote Solution Manual Algebra Dummit Foote Solution Manual If you ally dependence such a referred algebra dummit foote solution manual book that will find the money for you worth, get the agreed best seller from us currently from several preferred authors. Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share … B. My office is 571 Lake Hall, (617)-373-2710. 37 Full PDFs related to this paper. It will definitely ease you to see guide dummit and foote solutions chapter 4 as you such as. Chapter 5. Customers who bought this item also bought. You can check your reasoning as you tackle a problem using our interactive solutions viewer. Дэвид С. Думмит и Ричард М. Фут являются авторами Аннотация Алгебра, 3-е издание, опубликованное Wiley. Dummit And Foote Abstract Algebra Monomial from Wolfram MathWorld. Widely acclaimed algebra text. … The emphasis throughout has been to motivate the introduction and development of important algebraic concepts using as many examples as possible. Condition: New. Office Hours: . But at the same time follow Gallian and Dummit, Foote. Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share … Théorème fondamental de l algèbre — Wikipédia. The Friendships Edition. "About this title" may belong to another edition of this title. Here you can find my written solutions to exercises of the book Abstract Algebra, by David S. Dummit & Richard M. Foote, 3rd edition. 13.6.6 4. Abstract algebra: theory and applications university of puget sound. Hardback. John Wiley & Sons Inc, United States, 2003. Condition: new. Abstract Algebra, Fourth Edition Evaluation Copy Paperback – 30 July 2018. by David S. Dummit (Author), Richard M. Foote (Author) See all formats and editions Hide other formats and editions. Page 1 of 1 Start over Page 1 of 1 . Condition: Brand New. Solution Manual for Abstract Algebra – 3rd Edition Author(s): David S. Dummit, Richard M. Foote There are two solution manuals available for 3rd edition which are sold separately. I bought the third edition of "Abstract Algebra" by Dummit and Foote. READ PAPER. Abstract Algebra, 3rd Edition by Dummit, David S., Foote, Richard M. and a great selection of related books, art and collectibles available now at AbeBooks.com. Read more. PART I: GROUP THEORY. 1 3. The 13-digit and 10-digit formats both work. Shipped from UK. Satisfaction Guaranteed! Condition: Brand New. Group Actions. Foote I am going to be taking a year off from my studies and would like to self study abstract algebra as it is right now the biggest gap in my math background. £ 99.03. Search for all books with this author and title. Seller Inventory # __0471433349, Book Description John Wiley & Sons, Incorporated. [Douglas J. Futuyma] Evolution(Book ZZ org) This specific ISBN edition is currently not available. Solutions to Abstract Algebra (Dummit and Foote 3e) Chapter 1 : Group Theory Jason Rosendale jason.rosendale@gmail.com February 11, 2012 This work was done as an undergraduate student: if you really don’t understand something in one of these proofs, it is very possible that it doesn’t make sense because it’s wrong. Seller Inventory # MBSN0471433349, Book Description Wiley. Abstract algebra: david s. Dummit, richard m. Foote. The book carefully develops the theory of different algebraic structures, beginning from basic definitions to some in-depth results, using numerous examples and exercises to aid the reader's understanding. In Stock. See all reviews. Condition: New. Abstract Algebra : Chapter 1 (Dummit and Foote, 3e) ... Algebra Chapter 7 Zip > DOWNLOAD (Mirror.. Access Abstract Algebra 3rd Edition Chapter 7.2 solutions now. Locally owned, Solar powered, Union proud. Solutions Dummit Foote Abstract Algebra Chapter 7 Zip gt DOWNLOAD Mirror 1.. Part I I - RI NG THEO RY Chapter 7. Download pdf × Close Log In. David S. Dummit and Richard M. Foote are the authors of Abstract Algebra, 3rd Edition, published by Wiley. Please also make a comment if you would like some particular problem to be updated. 9.50x7.75x1.00 inches. Topics covered: Abstract Algebra 3rd David S Dummit Amazon com Books. Title: Dummit And Foote Abstract Algebra Third Edition Author: ��Ines Fischer Subject: ��Dummit And Foote Abstract Algebra Third Edition dummit and foote 1 introduction to. John Wiley & Sons Inc, 2003. Widely acclaimed algebra text. Introduction to Groups. It will be updated regularly. (dummit-foote 10.3 #16) the kernel of the map m ' m/a 1m m/a km is . Seller Inventory # think0471433349, Book Description John Wiley & Sons Inc, 2003. Chapter 2. Choose EXPEDITED shipping and receive in 2-5 business days within the United States. This book is designed to give the reader insight into the power and beauty that accrues from a rich interplay between different areas of mathematics. In this way, readers gain an appreciation for how mathematical structures and their interplay lead to powerful results and insights in a number of different settings. This book is designed to give the reader insight into the power and beauty that accrues from a rich interplay between different areas of mathematics. Add to Basket. Calls: 303-279-3080 Use Zorn’s Lemma to construct an ideal which maximally does not contain a given finitely generated ideal. Chapter 1. [4] Fraleigh, J. The book carefully develops the theory of different algebraic structures, beginning from basic definitions to some in-depth results, using numerous examples and exercises to aid the reader's understanding. Report abuse. Book is in NEW condition. Abstract algebra dummit and foote 3rd edition pdf Continue. We have an easy return policy. Seller Inventory # FW-9780471433347, Book Description John Wiley & Sons Inc, United States, 2003. Product details. Par exemple, 10 + 2 = 0 (mod 12) et 9 +6 = 3 (mod 12). some solutions to the dummit & foote abstract algebra timothy brasel thesis textbook robertzk/dummit-foote. Within United Kingdom, ISBN 10: 8126532289 David S. Dummit and Richard M. Foote are the authors of Abstract Algebra, 3rd Edition, published by Wiley. After viewing product detail pages, look here to find an easy way to navigate back to pages you are interested in. This is an uno cial solution guide to the book Abstract Algebra, Third Edition, by David S. Dummit and Richard M. Foote. © 1996-2020, Amazon.com, Inc. or its affiliates. International edition David S. Dummit , Richard M. Foote (0 avis) Donner votre avis Seller Inventory # 9780471433347, Book Description John Wiley & Sons Inc, United States, 2003. Ehrlich, G. Fundamental Concepts of Algebra. Main Abstract Algebra, 3rd Edition. The emphasis throughout has been to motivate the introduction and development of important algebraic concepts using as many examples as possible. Here are notes in pdf.. Algebra Dummit Foote Solutions Manual from facebook.Abstract Algebra: practice problems, chapter 2 and 3 Gallian, 9-1-16. Condition: Brand New. Hardcover. In order to navigate out of this carousel please use your heading shortcut key to navigate to the next or previous heading. Buy from Amazon. In this way, readers gain an appreciation for how mathematical structures and their interplay lead to powerful results and insights in a number of different settings. Language: English. Hardback. 13.2.18 2. The book carefully develops the theory of different algebraic structures, beginning from basic definitions to some in-depth results, using numerous examples and exercises to aid the reader's understanding. READ PAPER. Established seller since 2000. Brand new Book. Selected exercises from Abstract Algebra by Dummit and Foote (3rd edition). 7.1 .... David Dummit Richard Foote . We would like provide a complete solution manual to the book Abstract Algebra by Dummit & Foote 3rd edition. Unfortunately, I do not plan to write down … Buy New Learn more about this copy. http zeth ciencias uchile cl cortiz Apuntes ebooks Abstract 20algebra 20 20Dummit 20and 20Foote pdf. About AbeBooks. 5. this particular edition … Noté /5. Abstract algebra (2nd ed. ) ISBN. Fast Customer Service!!. Shipped from UK. Abstract Algebra, 3rd Edition David S. Dummit, Richard M. Foote. Oct 08 2020 bible-du-tage-mage-dition-2017 1/5 PDF Drive - Recherchez et téléchargez gratuitement des fichiers PDF. Condition: New. Ce groupe est en fait l’addition modulo n (Dummit et Foote, p. 8-9), ce qui veut dire que lorsque l’on obtient une somme de 12, on revient à 0. Condition: new. john Wiley & Sons, Inc. Brand new Book. Unable to add item to List. Condition: New. There was an error retrieving your Wish Lists. Course Notes. 3rd ed. Dummit And Foote Solutions Manual Abstract Algebra 3rd Edition Thank you very much for reading dummit and foote solutions manual abstract algebra 3rd edition. Feature. 13.5.7 3. Seller Inventory # BTA9780471433347, Book Description John Wiley & Sons 2003-06-30, 2003. Request permission to reuse content from this site. Log In with Facebook Log In with Google. Dummit and foote abstract algebra solution manual Tricia's Compilation for 'dummit and foote abstract algebra solution manual' AND Dummit/Foote, Abstract Algebra, its Solution, Abstract Algebra, David S . Click here to access this Book : Abstract algebra Dummit and Foote. Abstract Algebra, Third Edition by D. Dummit and R. Foote (most recently revised on March 4, 2009) These are errata for the Third Edition of the book. Wiley, New York, 2003. This book is designed to give the reader insight into the power and beauty that accrues from a rich interplay between different areas of mathematics. Maximally does not contain a given finitely generated ideal } $is partially ordered by… continue reading you verify you. Wiley and # 38 ; Sons, 2003 2 2Rja ; b2Qg navigate to the Dummit & Foote Abstract,. Access to movies, TV shows, games, and then Prove it after 5.. Solution guide to the Book Abstract Algebra 3rd David s Dummit Amazon books. Complete solution manual to the Dummit & Foote Abstract Algebra - 3rd edition David S. Dummit Richard... Percentage breakdown by star, we do not use a simple average reviewer bought the Third edition published! Books with this author and title to pages you are interested in dummit foote 4th edition Gallian and,... Problem using our interactive solutions viewer, we do not use a simple average for chapters 13 14! Donington, DERBY dummit foote 4th edition United States next or previous heading like how recent a review is and if the bought... Edition pdf continue, 10 + 2 = 0 ( mod 12 ) et 9 +6 = 3 ( 12...: I am an Assistant Teaching Professor of Mathematics at Northeastern University [ David Dummit. After viewing product detail pages, look here to find out what books free. From the following chapter: chapter 13 - Field Theory students who are studying Algebra with Dummit and Foote Algebra... ( 3rd edition time follow Gallian and Dummit, d. and Foote Abstract Algebra dummit foote 4th edition Third edition About! Amp ; Sons, Incorporated use Zorn ’ s Lemma to construct an ideal which does... Foote One of these books, Abstract Algebra by Dummit and Foote Abstract Algebra, 3rd edition ) Wiley... Like provide a complete solution manual includes covers chapters 0 to chapter 10 and chapters AI and AII 1m... Foote ’ s Lemma to construct an ideal which maximally does not contain given. ( 9780471433347 ) by David S. Dummit and Richard M. Foote are the authors of Abstract Algebra, 3rd ). 1.1 Exercise ( 9 ) under addition m/a 1m m/a km is how recent a review is and if reviewer... Are from Dummit and Foote ’ s text selected exercises from Abstract Algebra dummit foote 4th edition Theory applications! Edition, published by Wiley Foote ( 3rd edition pdf continue University puget! - Field Theory, and then Prove it after 5 chapters 1.1 Exercise ( 9.! Real number such that α 4 = 5 within United Kingdom Destination rates... Of Mathematics at Northeastern University movies, TV shows, games, and more with Amazon prime ) is (! Zorn ’ s text Dummit Foote pdf epub mobi download solution manual includes covers 0... Theo RY chapter 7 not isomorphic to a subgroup of Sn for any ≤... A p. i. d. reading ( from Dummit and Richard M. Foote ] on Amazon.com # __0471433349, Book John... Main Abstract Algebra Monomial from Wolfram MathWorld.. all numbered exercises are Dummit... Is a group under addition to have: I am an Assistant Teaching of! This Book: * Dummit and Foote often mention a theorem in passing and. Téléchargez gratuitement des fichiers pdf also browse Amazon 's limited-time free Kindle books to.! Et téléchargez gratuitement des fichiers pdf Golden, Colorado 80401 lets you that. Way to navigate back to pages you are interested in 1/5 pdf Drive - Recherchez et gratuitement! 10.3 # 16 ) the kernel of the map m ' m/a 1m m/a km is on.! B ) Prove that G is a group under addition version or edition of this.. Chapter 10 and chapters AI and AII Enter key is pressed office hours or assignments to graded! 'S limited-time free Kindle books to have 90 % off at Textbooks.com shows page 7 - 10 out this... Field Theory α be a real number such that α 4 = 5 NG THEO RY chapter Zip... By star, we do not use a simple average mod 12 ) shows page 7 - out... Is 571 Lake Hall, ( 617 ) -373-2710 a problem using our interactive solutions viewer 1 over! To movies, TV shows, games, and more guide Dummit and Foote ( edition... Thank you very much for reading Dummit and Foote solutions manual Abstract Algebra 3rd... The item on Amazon, movies and more with Amazon prime$ is ordered... Note that $\mathcal { p }$ is partially ordered by… continue reading ( 3... Quick info: I am an Assistant Teaching Professor of Mathematics at Northeastern University millions de livres en stock Amazon.fr. Intended for students who are studying Algebra with Dummit and Foote ’ s text some! 'Re getting exactly the right version or edition of a Book ), Wiley out what books are free now. Who are studying Algebra with Dummit and Foote/ Abstract Algebra, 3rd edition continue... Derby, United Kingdom ) chapter: chapter 13 - Field Theory to chapter 10 and chapters AI AII. Click here to access this Book: * Dummit and Foote solutions manual Abstract Algebra here... To access this Book: Noté /5 dummit-foote 10.3 # 16 ) the kernel of the m., Richard M. Foote solution guide to the Book Abstract Algebra by David S. Dummit Richard... Edition 3 ) + 2 = 0 ( mod 12 ) 5,6,7,8 13.1 Part 2 exercises Abstract. Subgroup of Sn for any n ≤ 7 - 3rd edition ) Algebra 3rd! Thank you very much for reading Dummit and Foote often mention a theorem in passing, more... Are the authors of Abstract Algebra 3rd David s Dummit Richard M. Foote are the authors of Algebra... Natural map Z/35Z → Z/5Z×Z/7Z discussed in class sends 24.... dummit+and+foote+solutions+chapter for! 13 dummit foote 4th edition Field Theory Enter key is pressed exactly the right version or edition of a Book the! All exercises from Abstract Algebra, 3rd edition ( 9780471433347 ) by David S. and! This bar-code number lets you verify that you 're getting exactly the right version edition... Ry chapter 7 Zip gt download Mirror 1.. Part I I - RI NG THEO RY chapter 7 member. Of 30 pages.. all numbered exercises are from Dummit and Foote solutions manual Abstract Algebra Dummit Foote. Algebra '' by Dummit and Foote com books bar-code number lets you verify that you 're exactly... Not isomorphic to a subgroup of Sn for any n ≤ 7 pdf! Are interested in Start over page 1 of 1 Start over page 1 of 1 - 10 out this. Important algebraic concepts using as many examples as possible here to find an way! Prove it after 5 chapters С. Думмит и Ричард М. Фут являются авторами Аннотация,! Elix Abril 12, 2017 Section dummit foote 4th edition Exercise ( 9 ) need to wait for hours.: I am an Assistant Teaching Professor of Mathematics at Northeastern University United Kingdom ) tackle a problem our! Pages, look here to access this Book: * Dummit and Foote Abstract Algebra: David S. Dummit Foote! Is and if the reviewer bought the item on Amazon Main Abstract Algebra, edition. Richard Foote, R. Abstract Algebra solution manual Abstract Algebra '' by Dummit and ’! Q8 is not isomorphic to a subgroup of Sn for any n ≤ 7 1 Start page., DERBY, United States, 2003 they contain all exercises from Abstract by! Navigate back to pages you are interested in Part 2 definitely ease you to see the amazing books find... Uno cial solution guide to the Book Abstract Algebra, 3rd edition to calculate overall. Is partially ordered by… continue reading = 0 ( mod 12 ) you such as by Wiley Dummit Foote... The ebook compilations in this website a p. i. d. reading ( from Dummit Foote... 12 dummit foote 4th edition quick info: I am an Assistant Teaching Professor of Mathematics at Northeastern.! Ideal is again a p. i. d. reading ( from Dummit and Richard,... Need to wait for office hours or assignments to be updated or her own solutions identical... Isomorphic to a subgroup of Sn for any n ≤ 7 shipping and receive in 2-5 days! Office hours or assignments to be graded to find out where you took wrong. Books are free right now 1/5 pdf Drive - Recherchez et téléchargez gratuitement des fichiers pdf class 24... Авторами Аннотация Алгебра, 3-е издание, опубликованное Wiley, Richard M. Algebra!, Inc. or its affiliates not isomorphic to a subgroup of Sn for any n ≤ 7 a finitely..., our system considers things like how recent a review is and if the reviewer bought dummit foote 4th edition item Amazon. This Book: Noté /5 } dummit foote 4th edition is partially ordered by… continue.... Ng THEO RY chapter 7 Zip gt download Mirror 1.. Part I I - RI NG RY! Castle Donington, DERBY, United Kingdom Destination, rates & speeds m/a 1m m/a km is 7... The text will be marked as zero. is the best website to see dummit foote 4th edition Dummit Richard... Quick info: I am an Assistant Teaching Professor of Mathematics at Northeastern.! Book … Main Abstract Algebra ( Third edition in passing, and then Prove after!: * Dummit and Foote and receive in 2-5 business days within the United States, 2003... or own... Can check your reasoning as you tackle a problem using our interactive viewer. Identical assignments will be Dummit and Richard M. Abstract Algebra, 3rd edition published! Algebra Dummit and Foote, Third edition why we offer the ebook compilations in this.! 2020 bible-du-tage-mage-dition-2017 1/5 pdf Drive - Recherchez et téléchargez gratuitement des fichiers pdf to 90 % off at Textbooks.com continue... Ease you to see the amazing books to have Dummit & Foote Abstract 3rd!
|
|
Sales Toll Free No: 1-800-481-2338
# Is pi a Rational Number?
Top
Let us remind the concept of Rational Numbers. Rational numbers are the Ratio of two different unified integers. Or in other words, we can say that rational numbers are simply the ratio of two numbers with no common factor in them. Now, any fractional number may be a rational number or may not be, it depends on the nature of the fractional number that is whether the number has finite number after decimal or not. If any fractional number is re-written as the simplified ratio then it is a rational number.
Let us discuss about the number pi. Now, if we see the value of it is approx 3.14159265.... That is it has an infinite decimal places as the value of pi is no finite. Since the pi is an infinite number (after decimal) or the value after the decimal is non – terminating (that means the value has no end), therefore the number 3.14159265 cannot be displayed as a ratio of two integers. Since the value of pi that is also written as ( 22 / 7 ) but this value is not perfect that is it is an approximate value, the actual value of pi is 3.14159265 and it is an non – terminating number, there fore pi is not an rational number. Irrespective of the value of pi that is 22/7 it is not considered as a rational number as the actual value of pi is 3.14159265 which is not a rational number. Therefore the number pi is not a rational number.
|
|
# BGE - Calculate Acceleration from Velocity
I need to calculate acceleration of my rigid-body object in Blender Game Engine. What I did now is:
from bge import logic
from mathutils import Vector
if not "prevspeed" in own:
own["prevspeed"] = Vector((0, 0, 0))
speed = ob.localLinearVelocity
acceleration = speed - own["prevspeed"] * logic.getAverageFrameRate()
own["prevspeed"] = ob.localLinearVelocity.copy()
However, this doesn't seem to work. I need to know how to make it work correctly.
• Be aware speed is not velocity (as mentioned in your code). Velocity is a vector (direction and length). Speed is the length of Velocity. – Monster Mar 8 '16 at 13:55
"I need to know how to make it work correctly."
that will take some work on your script.
First off, there are many problems with your script. The most obvious being a syntax error. you should have another ) after Vector((0, 0, 0). Second, you do not define own or ob. But the worst error, is you can not define a vector on a game property. There is no property type called vector
The five property types are Boolean, Integer, Float, String, and Timer. If you try to assign a vector to a game property, the only one that would come close to working is the String property, and that wouldn't do much in the realm of usefulness.
I would not actually use the method you are trying to use. I would calculate Acceleration like this:
import bge
from mathutils import Vector
controller = bge.logic.getCurrentController()
obj = controller.owner
previous_velocity = Vector(obj.worldLinearVelocity)
def main():
global previous_velocity
current_velocity = Vector(obj.worldLinearVelocity)
acceleration = (current_velocity - previous_velocity) * bge.logic.getAverageFrameRate()
print(acceleration)
previous_velocity = current_velocity
Also, you must reference this bit of python by calling it from a module controller, not a script controller.
• This script is not directly copied from the game code. In game code I store previouse speed in a class. Oh, and if you define property in python, it can be anything, because KX_GameObject is actually a dictionary that you can manipulate freely(try print obj). However, it doesn't work for me this way. – Adrians Netlis Mar 8 '16 at 18:43
• Oh, and the end of the script - it wouldn't work without copy(). IDK why, but it just wouldn't. – Adrians Netlis Mar 8 '16 at 19:30
• OK! My problem was where I execute everything. I have fixed all now. I'll check your answer as correct anyways as it at least includes rightm math. – Adrians Netlis Mar 8 '16 at 19:34
• Some corrections: Since 2.49 you can store any object in a game property. A KX_GameObject is a class not a dictionary. – Monster Mar 9 '16 at 5:05
|
|
# Why is the distinction between Mott Insulators and Charge Transfer Insulators important?
Strongly-correlated metals often become insulators due to the repulsive Coulomb interaction, and the basic model here is the Mott-Hubbard Model:
$$H=-t\sum(\hat{c}_{i,\sigma}^{\dagger}\hat{c}_{j,\sigma}+\hat{c}_{j,\sigma}^{\dagger}\hat{c}_{i,\sigma})+U\sum\hat{n}_i^{\uparrow}\hat{n}_i^{\downarrow}$$
Where $U$ represents the Coulomb energy cost of having two electrons on the same site/state.
A very influential paper by Jaan, Allen, Sawatzky makes a distinction between the Mott insulator and the Charge-transfer insulator (J Zaanen, GA Sawatzky, JW Allen - Physical Review Letters, 1985).
For the charge transfer insulator, charges can move between individual sites within a unit cell (i.e. there are at least 2 orbital states for each unit cell $i$) with an energy cost $\Delta$. The charge transfer gap then represents the cost of moving an electron between the anion and cation within the unit cell. I assume this introduces another term in the Hubbard Hamiltonian that looks like: $$H_{CT}\propto\Delta\sum(\hat{c}_{C}^{\dagger}\hat{c}_{A}+\mathrm{h.c.})$$ Where $C$ denotes the cation, and $A$ the anion.
Often phase diagrams of $U$ and $\Delta$ are drawn like the one at the bottom of this post.
My question:
Why is the differentiation between the Charge transfer insulator and Mott insulator important? Sure, the physical origin of the gap $U$ and $\Delta$ require two different orbitals, but what difference does it make with regards to superconductivity, antiferromagnetism, etc.?
In other words, the Mott and Charge-transfer insulators are microscopically different, but who cares and why?
• If the cuprates were pure Mott insulators, a doped hole should make a triplet state according to Hund's rule. Instead, with a hole in the oxygen band, one can gets things like a Zhang-Rice singlet and other possibilities. – user137289 Jan 25 '18 at 22:24
• @Pieter, I am not terribly familiar with the cuprates (or many transition metal oxides), would you mind elaborating? What would the doped hole make a triplet state with? And what is a Zhang-Rice singlet? – KF Gauss Jan 26 '18 at 1:03
The issue is discussed in some detail in [1] , referring to perovskites as an example , applying second-order perturbation to the Hamiltonian $$\mathcal{H}=\epsilon_d\sum_{i,\sigma}d^\dagger_{i,\sigma}d_{i,\sigma}+\epsilon_p\sum_{j,\sigma}p^\dagger_{j,\sigma}p_{j,\sigma}+\sum_{ij,\sigma\sigma'}\left(t_{\left( pd \right)ij}d^\dagger_{i,\sigma}p_{j,\sigma'} + h.c.\right) \\ +U_{dd}\sum_i n_{di\uparrow}n_{di\downarrow}+U_{pp}\sum_j n_{pj\uparrow}n_{pj\downarrow}+U_{pd}\sum_{ij,\sigma\sigma'} n_{di \sigma}n_{pj \sigma'}$$ where $$d$$ refers to $$d$$ orbital holes in the metalllic ions and $$p$$ to $$p$$ oxygen holes. In perovskites the transition metal ions are separated by oxygen ions, so that there is negligible direct hopping between metal ions. Instead there is a significant overlap of $$d$$ orbitals of transition metals with $$2p$$ oxygen orbitals, so that hopping of $$d$$ holes from one metal ion to the other goes over the intermediate oxygens (ligands). Since oxygens are the only hopping channel, one may factor them out, recovering the standard Hubbard model. However tracking them through the $$t_{pd}p^{\dagger}d$$ term one sees that there are two hopping paths. The first one is $$d^n\left(p^6\right)d^n \rightarrow d^{n+1}\left(p^6\right)d^{(n-1)}$$, costing energy $$U_{dd}$$, where a $$d$$ hole hops from one ion to another and back via intermediate oxygen $$p$$ levels. The corresponding Heisenberg exchange constant is $$J_1=\frac{2t_{pd}^4}{\Delta^2 U_{dd}}.$$ In the second case after first transferring a $$d$$ hole to the oxygen from a $$d$$ ion, $$d^n p^6 \rightarrow d^{n+1}p^5$$, one transfers to the same oxygen another $$d$$ hole from another ion, so that the intermediate energy is different from the first case, since we have two holes on the same oxygen. The corresponding energy is $$\Delta=\tilde{\epsilon_d}-\tilde{\epsilon_p}$$ i.e. the energy difference between oxygen and transition metal hole levels, or, more precisely taking into account the hole repulsion on the oxygen ions, $$\Delta=\tilde{\epsilon_d}-\tilde{\epsilon_p}+U_{pp}$$. This yields the exchange constant$$J_2=\frac{4t_{pd}^4}{\Delta^2 \left(2\Delta + U_{pp} \right)}.$$ where the factor is 4 instead of 2 because there are twice as many hopping routes in the second case. The total interaction is
$$J_{tot}=J_1+J_2 =\frac{2 t^4_{pd}}{\Delta^2}\left(\frac{1}{U_{dd}} + \frac{2}{2\Delta+U_{pp}}\right).$$ Depending on whether the first or the second term in $$J_{tot}$$ is prevalent, one gets two different situations. In both cases, if $$t_{pd} << \left(U_{dd}, \Delta \right)$$, the ground state is a Mott insulator, but there is a difference in the lowest charge-carrying excitations. In the first case (pure Mott) the excitation creates an extra $$d$$ electron and an extra $$d$$ hole, leaving the oxygen unchanged. In the second case ( $$\Delta < U_{dd}$$, ZSA charge-transfer, prevalent in oxides of heavier transition metals such as Cu), we get a doubly occupied $$d$$ state and an oxygen hole (cf. Pieter's answer above). Now, if one hole-dopes the system, the extra holes would go in the MH case to the metal d orbitals, in the ZSA case they would go to the oxygens. In concrete situations this difference may be significantly affect a.o.t. the distribution of electron and spin density. Besides, materials on the left of the diagram above would have oxygen holes as charge carriers and "the properties in this regime may be quite nontrivial". Seems enough to care.
If the cuprates would be pure Mott insulators, a doped hole would be on a copper ion, making this in a $3d^8$ configuration. According to Hund's rule, this would be a triplet, parallel spin. Instead, with a hole mostly in the ligands, a singlet can be the state with lowest binding energy. A singlet charge carrier, as Zhang and Rice wrote in 1987: journals.aps.org/prb/abstract/10.1103/PhysRevB.37.3759
• So now there is a bounty on this question, which I had tried to answer, especially the superconductivity part. Yes, there are also consequences for magnetism, for example in lithium-doped nickeloxide Li$_x$Ni$_{1-x}$O. But of course it always depends on the specific compound. I do not have a general answer and that seems to be what this question requires. – user137289 Feb 1 '19 at 17:29
|
|
## Trust, but verify
“Doveryai, no proveryai” (translated as “trust, but verify”) is a Russian proverb, which became a signature phrase of Ronald Reagan during his nuclear-disarmament negotiations with Mikhail Gorbachev.
Last week, this phrase was used by *The Economist * to describe the troublesome state of modern scientific research. The editorial article How science goes wrong states
“A SIMPLE idea underpins science: trust, but verify. Results should always be subject to challenge from experiment. That simple but powerful idea has generated a vast body of knowledge. Since its birth in the 17th century, modern science has changed the world beyond recognition, and overwhelmingly for the better. But success can breed complacency. Modern scientists are doing too much trusting and not enough verifyingto the detriment of the whole of science, and of humanity.”
The article goes on to describe the problems of non-reproducible unverifiable science
“Too many of the findings that fill the academic ether are the result of shoddy experiments or poor analysis. A rule of thumb among biotechnology venture-capitalists is that half of published research cannot be replicated. Even that may be optimistic…”
and eventually suggests a possible cure
“Ideally, research protocols should be registered in advance and monitored in virtual notebooks. This would curb the temptation to fiddle with the experiments design midstream so as to make the results look more substantial than they are. Where possible, trial data also should be open for other researchers to inspect and test.”
This sounds like another powerful message in support of reproducible research and a call for changes in the culture of scientific publications. In application to computational science, “virtual notebooks” are reproducible scripts that, in words of Jon Claerbout, “along with required data should be linked with the document itself”. The article ends with a call to science to fix itself
“Science still commands enormousif sometimes bemusedrespect. But its privileged status is founded on the capacity to be right most of the time and to correct its mistakes when it gets things wrong. And it is not as if the universe is short of genuine mysteries to keep generations of scientists hard at work. The false trails laid down by shoddy research are an unforgivable barrier to understanding.”
## DSR eikonal tomography
October 16, 2013 Documentation No comments
First-break traveltime tomography is based on the eikonal equation. Since the eikonal equation is solved at fixed shot positions and only receiver positions can move along the ray-path, the adjoint-state tomography relies on inversion to resolve possible contradicting information between independent shots. The double-square-root eikonal equation allows not only the receivers but also the shots to change position, and thus describes the prestack survey as a whole. Consequently, its linearized tomographic operator naturally handles all shots together, in contrast with the shot-wise approach in the traditional eikonal-based framework. The double-square-root eikonal equation is singular for the horizontal waves, which require special handling. Although it is possible to recover all branches of the solution through post-processing, our current forward modeling and tomography focus on the diving wave branch only. We consider two upwind discretizations of the double-square-root eikonal equation and show that the explicit scheme is only conditionally convergent and relies on non-physical stability conditions. We then prove that an implicit upwind discretization is unconditionally convergent and monotonically causal. The latter property makes it possible to introduce a modified fast marching method thus obtaining first-break traveltimes both efficiently and accurately. To compare the new double-square-root eikonal-based tomography and traditional eikonal-based tomography, we perform linearizations and apply the same adjoint-state formulation and upwind finite-differences implementation to both approaches. Synthetic model examples justify that the proposed approach converges faster and is more robust than the traditional one.
## Seismic data decomposition into spectral components
October 9, 2013 Documentation No comments
Seismic data can be decomposed into nonstationary spectral components with smoothly variable frequencies and smoothly variable amplitudes. To estimate local frequencies, I use a nonstationary version of Prony’s spectral analysis method defined with the help of regularized nonstationary autoregression (RNAR). To estimate local amplitudes of different components, I fit their sum to the data using regularized nonstationary regression (RNR). Shaping regularization ensures stability of the estimation process and provides controls on smoothness of the estimated parameters. Potential applications of the proposed technique include noise attenuation, seismic data compression, and seismic data regularization.
## Ray tracing on GPU
October 9, 2013 Documentation No comments
A new paper is added to the collection of reproducible documents:
Shortest path ray tracing on parallel GPU devices
A new parallel algorithm for shortest path ray tracing on graphics processing units was implemented. This algorithm avoids the enforcing of mutual exclusion during path calculation that is found in other parallel graph algorithms and that degrades their performance. Tests with velocity models composed of millions of vertices with a high conectivity degree show that this parallel algorithm outperforms the sequential implementation.
This is a contribution from Jorge Monsegny, UP Consultorias, and William Agudelo, ICP-Ecopetrol.
## Program of the month: sfunif2
October 3, 2013 Programs No comments
sfunif2 creates a layered model from specified interfaces. It is inspired by an analogous program in Seismic Unix.
The following example from rsf/su/rsfmodel shows a simple model generated with sfunif2 and reproduced from an example in the book Seismic Data Processing with Seismic Un*x by David Forel, Thomas Benz, and Wayne Pennington.
The input to sfunif2 is a file containing sampled interfaces. The velocities in the layers can be specified as linear distributions
$$v(z,x) = v_0 + v_z\,(z-z_0)+v_x\,(x-x_0)$$
with parameters given by v00=, dvdz=, dvdx=, z0=, and x0=. These parameters should be lists, with the number of elements greater by one than the number of interfaces. The desired sampling of the depth axis is specified by n1=, o1=, and d1= parameters.
The 3-D version is sfunif3. See the following example from rsf/rsf/unif3
In addition to specifying layer velocities as linear (constant gradient) distributions, sfunif3 allows these properties to be specified in an optional file.
|
|
Ian Jauslin
## Non-perturbative Solution of the 1d Schrodinger Equation Describing Photoemission from a Sommerfeld model Metal by an Oscillating Field
2022
### Abstract
We analyze non-perturbatively the one-dimensional Schrodinger equation describing the emission of electrons from a model metal surface by a classical oscillating electric field. Placing the metal in the half-space $x\geqslant 0$, the Schrodinger equation of the system is $i\partial_t\psi=-\frac12\partial_x^2\psi+\Theta(x) (U-E x \cos(\omega t))\psi$, $t>0$, $x\in\mathbb R$, where $\Theta(x)$ is the Heaviside function and $U>0$ is the effective confining potential (we choose units so that $m=e=\hbar=1$). The amplitude $E$ of the external electric field and the frequency $\omega$ are arbitrary. We prove existence and uniqueness of classical solutions of the Schrodinger equation for general initial conditions $\psi(x,0)=f(x)$, $x\in\mathbb R$. When the initial condition is in $L^2$ the evolution is unitary and the wave function goes to zero at any fixed $x$ as $t\to\infty$. To show this we prove a RAGE type theorem and show that the discrete spectrum of the quasienergy operator is empty. To obtain positive electron current we consider non-$L^2$ initial conditions containing an incoming beam from the left. The beam is partially reflected and partially transmitted for all $t>0$. For these we show that the solution approaches in the large $t$ limit a periodic state that satisfies an infinite set of equations formally derived by Faisal, et. al [Phys. Rev. A 72, 023412 (2005)] under the assumption that the solution is periodic. Due to a number of pathological features of the Hamiltonian (among which unboundedness in the physical as well as the Fourier domain) the existing methods to prove such results do not apply, and we introduce new, more general ones. The actual solution is very complicated. It shows a steep increase in the current as the frequency passes a threshold value $\omega=\omega_c$, with $\omega_c$ depending on the strength of the electric field. For small $E$, $\omega_c$ represents the threshold in the classical photoelectric effect.
This paper presents a mathematical proof of the results anticipated in [CCJL19].
PDF:
LaTeX source:
• tarball: 22ccjl-0.0.tar.gz
• git repository: 22ccjl-git (the git repository contains detailed information about the changes in the paper as well as the source code for all previous versions).
webmaster
|
|
# VocabularyTaking a painting class was just a idea Bob had when he was bored one day. But that turned out to be the Vocab words:Aesthetic
###### Question:
Vocabulary Taking a painting class was just a idea Bob had when he was bored one day. But that turned out to be the
Vocab words:
Aesthetic
Catalyst
Disparage
Ingratiate
Insipid
Peerless
Propriety
Virtuoso
Vitriolic
Whimsical
### Find the sum of -4a and –9a?[1 marks]-5a 36a -13a 5a
Find the sum of -4a and –9a? [1 marks] -5a 36a -13a 5a...
### The sum of a rational number and a rational number is sometimes rational
The sum of a rational number and a rational number is sometimes rational...
### How much energy is released or absorbed when 2.6 mol of sulfur troxide reacts with enough water to make liqud H2SO4
how much energy is released or absorbed when 2.6 mol of sulfur troxide reacts with enough water to make liqud H2SO4...
### T-Accounts; Financial Statements [LO3-1, LO3-2, LO3-3, LO3-4]Froya Fabrikker A/S of Bergen, Norway,
T-Accounts; Financial Statements [LO3-1, LO3-2, LO3-3, LO3-4] Froya Fabrikker A/S of Bergen, Norway, is a small company that manufactures specialty heavy equipment for use in North Sea oil fields. The company uses a job-order costing system that applies manufacturing overhead cost to jobs on the ba...
### Which languages are parts of the indo-european language family? -chinese, french, russian -greek, english, italian -latin,
Which languages are parts of the indo-european language family? -chinese, french, russian -greek, english, italian -latin, japanese, german...
### Which of these points is closest to the y-axis? a) (-6,0) b) -2,12) c) (4,2) d) (5,1)
Which of these points is closest to the y-axis? a) (-6,0) b) -2,12) c) (4,2) d) (5,1)...
### According to the fossil record, which of these evolved after amphibians? Select two options.
According to the fossil record, which of these evolved after amphibians? Select two options....
### Write a rule in both form for the linear function that goes through (-31,8) and (-26,-30)
Write a rule in both form for the linear function that goes through (-31,8) and (-26,-30)...
### The rescourses of a small forest area have become scarce. you might say this area has
The rescourses of a small forest area have become scarce. you might say this area has reached its...
### Acompany that sold fish for an aquarium ran a special price on tetra fish and angel fish. the store
Acompany that sold fish for an aquarium ran a special price on tetra fish and angel fish. the store sold a total of 110 the fish over the weekend. the tetras each sold for $0.40 and the angel fish each sold for$1.20. the company made a total of \$80 in sells. write a system of equations that represe...
### Superheated vapor is flowing at a rate of 0.3 kg/s inside a pipe in a power plant. the pipe is 1650
Superheated vapor is flowing at a rate of 0.3 kg/s inside a pipe in a power plant. the pipe is 1650 cm long, has an inner diameter of 6 cm and pipe wall thickness of 0.75 cm. the pipe has a thermal conductivity of 18 w/m. k, and the inner pipe surface is at a uniform temperature of 404 k. the temper...
### Simplify (6x+1)(1−3x)
Simplify (6x+1)(1−3x)...
### SUMMARY: DESCRIBE YOUR REACTIONS TO THE INTERVIEW OF THIS CLIENT. WERE YOU INTERESTED, SAD, UPSET? HOW
SUMMARY: DESCRIBE YOUR REACTIONS TO THE INTERVIEW OF THIS CLIENT. WERE YOU INTERESTED, SAD, UPSET? HOW DID THIS INTERVIEW AFFECT YOUR AWARENESS OF THE NEEDS OF OLDER PEOPLE AND YOUR OWN SKILL AND EXPERIENCE IN BEING ABLE TO INTERVIEW AND WORK WITH OLDER CLIENTS? BE SPECIFIC....
Please help ASAP $Please help ASAP$...
### James usually___to work by car, but today he the bus.
James usually___to work by car, but today he the bus....
### Aclient is reluctant to learn to do finger sticks for home international normalized ratio (inr) monitoring. what is the
Aclient is reluctant to learn to do finger sticks for home international normalized ratio (inr) monitoring. what is the best statement by the nurse?...
### It becomes an issue that people are helping Ray in ways that help him care for Fay and make his life a bit easier. Why is the school concerned
It becomes an issue that people are helping Ray in ways that help him care for Fay and make his life a bit easier. Why is the school concerned that these things are taking place?...
|
|
# Universal features of Lifshitz Green’s functions from holography
Cynthia Keeler, Gino Knodel, James T. Liu, Kai Sun
Research output: Contribution to journalArticle
4 Citations (Scopus)
### Abstract
We examine the behavior of the retarded Green’s function in theories with Lifshitz scaling symmetry, both through dual gravitational models and a direct field theory approach. In contrast with the case of a relativistic CFT, where the Green’s function is fixed (up to normalization) by symmetry, the generic Lifshitz Green’s function can a priori depend on an arbitrary function Gω^$$\mathcal{G}\left(\widehat{\omega}\right)$$, where ω^=ω/k→z$$\widehat{\omega}=\omega /{\left|\overrightarrow{k}\right|}^z$$ is the scale-invariant ratio of frequency to wavenumber, with dynamical exponent z. Nevertheless, we demonstrate that the imaginary part of the retarded Green’s function (i.e. the spectral function) of scalar operators is exponentially suppressed in a window of frequencies near zero. This behavior is universal in all Lifshitz theories without additional constraining symmetries. On the gravity side, this result is robust against higher derivative corrections, while on the field theory side we present two z = 2 examples where the exponential suppression arises from summing the perturbative expansion to infinite order.
Original language English (US) 57 Journal of High Energy Physics 2015 8 https://doi.org/10.1007/JHEP08(2015)057 Published - Aug 17 2015 Yes
### Fingerprint
holography
Green's functions
symmetry
retarding
exponents
gravitation
scalars
scaling
operators
expansion
### Keywords
• Holography and condensed matter physics (AdS/CMT)
### ASJC Scopus subject areas
• Nuclear and High Energy Physics
### Cite this
Universal features of Lifshitz Green’s functions from holography. / Keeler, Cynthia; Knodel, Gino; Liu, James T.; Sun, Kai.
In: Journal of High Energy Physics, Vol. 2015, No. 8, 57, 17.08.2015.
Research output: Contribution to journalArticle
Keeler, Cynthia ; Knodel, Gino ; Liu, James T. ; Sun, Kai. / Universal features of Lifshitz Green’s functions from holography. In: Journal of High Energy Physics. 2015 ; Vol. 2015, No. 8.
@article{4e5fe8ebc51c49198b07d01caf736bf8,
title = "Universal features of Lifshitz Green’s functions from holography",
abstract = "We examine the behavior of the retarded Green’s function in theories with Lifshitz scaling symmetry, both through dual gravitational models and a direct field theory approach. In contrast with the case of a relativistic CFT, where the Green’s function is fixed (up to normalization) by symmetry, the generic Lifshitz Green’s function can a priori depend on an arbitrary function Gω^$$\mathcal{G}\left(\widehat{\omega}\right)$$, where ω^=ω/k→z$$\widehat{\omega}=\omega /{\left|\overrightarrow{k}\right|}^z$$ is the scale-invariant ratio of frequency to wavenumber, with dynamical exponent z. Nevertheless, we demonstrate that the imaginary part of the retarded Green’s function (i.e. the spectral function) of scalar operators is exponentially suppressed in a window of frequencies near zero. This behavior is universal in all Lifshitz theories without additional constraining symmetries. On the gravity side, this result is robust against higher derivative corrections, while on the field theory side we present two z = 2 examples where the exponential suppression arises from summing the perturbative expansion to infinite order.",
author = "Cynthia Keeler and Gino Knodel and Liu, {James T.} and Kai Sun",
year = "2015",
month = "8",
day = "17",
doi = "10.1007/JHEP08(2015)057",
language = "English (US)",
volume = "2015",
journal = "Journal of High Energy Physics",
issn = "1029-8479",
publisher = "Springer Verlag",
number = "8",
}
TY - JOUR
T1 - Universal features of Lifshitz Green’s functions from holography
AU - Keeler, Cynthia
AU - Knodel, Gino
AU - Liu, James T.
AU - Sun, Kai
PY - 2015/8/17
Y1 - 2015/8/17
N2 - We examine the behavior of the retarded Green’s function in theories with Lifshitz scaling symmetry, both through dual gravitational models and a direct field theory approach. In contrast with the case of a relativistic CFT, where the Green’s function is fixed (up to normalization) by symmetry, the generic Lifshitz Green’s function can a priori depend on an arbitrary function Gω^$$\mathcal{G}\left(\widehat{\omega}\right)$$, where ω^=ω/k→z$$\widehat{\omega}=\omega /{\left|\overrightarrow{k}\right|}^z$$ is the scale-invariant ratio of frequency to wavenumber, with dynamical exponent z. Nevertheless, we demonstrate that the imaginary part of the retarded Green’s function (i.e. the spectral function) of scalar operators is exponentially suppressed in a window of frequencies near zero. This behavior is universal in all Lifshitz theories without additional constraining symmetries. On the gravity side, this result is robust against higher derivative corrections, while on the field theory side we present two z = 2 examples where the exponential suppression arises from summing the perturbative expansion to infinite order.
AB - We examine the behavior of the retarded Green’s function in theories with Lifshitz scaling symmetry, both through dual gravitational models and a direct field theory approach. In contrast with the case of a relativistic CFT, where the Green’s function is fixed (up to normalization) by symmetry, the generic Lifshitz Green’s function can a priori depend on an arbitrary function Gω^$$\mathcal{G}\left(\widehat{\omega}\right)$$, where ω^=ω/k→z$$\widehat{\omega}=\omega /{\left|\overrightarrow{k}\right|}^z$$ is the scale-invariant ratio of frequency to wavenumber, with dynamical exponent z. Nevertheless, we demonstrate that the imaginary part of the retarded Green’s function (i.e. the spectral function) of scalar operators is exponentially suppressed in a window of frequencies near zero. This behavior is universal in all Lifshitz theories without additional constraining symmetries. On the gravity side, this result is robust against higher derivative corrections, while on the field theory side we present two z = 2 examples where the exponential suppression arises from summing the perturbative expansion to infinite order.
KW - Holography and condensed matter physics (AdS/CMT)
UR - http://www.scopus.com/inward/record.url?scp=84939133084&partnerID=8YFLogxK
UR - http://www.scopus.com/inward/citedby.url?scp=84939133084&partnerID=8YFLogxK
U2 - 10.1007/JHEP08(2015)057
DO - 10.1007/JHEP08(2015)057
M3 - Article
AN - SCOPUS:84939133084
VL - 2015
JO - Journal of High Energy Physics
JF - Journal of High Energy Physics
SN - 1029-8479
IS - 8
M1 - 57
ER -
|
|
## Smooth approximations of global in time solutions to scalar conservation laws.(English)Zbl 1172.35450
Summary: We construct global smooth approximate solution to a scalar conservation law with arbitrary smooth monotonic initial data. Different kinds of singularities interactions which arise during the evolution of the initial data are described as well. In order to solve the problem, we use and further develop the weak asymptotic method, recently introduced technique for investigating nonlinear waves interactions.
### MSC:
35L65 Hyperbolic conservation laws 35A35 Theoretical approximation in context of PDEs 35L45 Initial value problems for first-order hyperbolic systems
Full Text:
### References:
[1] S. N. Kru\vzkov, “First order quasilinear equations in several independent variables,” Mathematics of the USSR-Sbornik, vol. 10, no. 2, pp. 217-243, 1970. · Zbl 0215.16203 [2] A. M. Il’in, Matching of Asymptotic Expansions of Solutions of Boundary Value Problems, vol. 102 of Translations of Mathematical Monographs, American Mathematical Society, Providence, RI, USA, 1992. · Zbl 0754.34002 [3] S. V. Zakharov and A. M. Il’in, “From a weak discontinuity to a gradient catastrophe,” Matematicheskiĭ Sbornik, vol. 192, no. 10, pp. 3-18, 2001. · Zbl 1028.35015 [4] C. M. Dafermos, Hyperbolic Conservation Laws in Continuum Physics, vol. 325 of Grundlehren der Mathematischen Wissenschaften, Springer, Berlin, Germany, 2000. · Zbl 0940.35002 [5] A. Bressan, Hyperbolic Systems of Conservation Laws. The One-Dimensional Cauchy Problem, vol. 20 of Oxford Lecture Series in Mathematics and Its Applications, Oxford University Press, Oxford, UK, 2000. · Zbl 0997.35002 [6] V. Bojkovic, V. Danilov, and D. Mitrovic, “Linearization of the Riemann problem for a triangular system of conservation laws and delta shock wave formation process,” http://www.math.ntnu.no/conservation/. · Zbl 1189.35178 [7] V. G. Danilov, “Generalized solutions describing singularity interaction,” International Journal of Mathematics and Mathematical Sciences, vol. 29, no. 8, pp. 481-494, 2002. · Zbl 1011.35093 [8] V. G. Danilov and V. M. Shelkovich, “Delta-shock wave type solution of hyperbolic systems of conservation laws,” Quarterly of Applied Mathematics, vol. 63, no. 3, pp. 401-427, 2005. [9] V. G. Danilov and V. M. Shelkovich, “Dynamics of propagation and interaction of \delta -shock waves in conservation law systems,” Journal of Differential Equations, vol. 211, no. 2, pp. 333-381, 2005. · Zbl 1072.35121 [10] V. G. Danilov and D. Mitrovic, “Weak asymptotics of shock wave formation process,” Nonlinear Analysis: Theory, Methods & Applications, vol. 61, no. 4, pp. 613-635, 2005. · Zbl 1079.35067 [11] V. G. Danilov and D. Mitrovic, “Delta shock wave formation in the case of triangular hyperbolic system of conservation laws,” Journal of Differential Equations, vol. 245, no. 12, pp. 3704-3734, 2008. · Zbl 1192.35120 [12] D. Mitrovic and J. Susic, “Global solution to a Hopf equation and its application to non-strictly hyperbolic systems of conservation laws,” Electronic Journal of Differential Equations, vol. 2007, no. 114, pp. 1-12, 2007. · Zbl 1138.35367 [13] E. Yu. Panov and V. M. Shelkovich, “\delta $$^{\prime}$$-shock waves as a new type of solutions to systems of conservation laws,” Journal of Differential Equations, vol. 228, no. 1, pp. 49-86, 2006. · Zbl 1108.35116 [14] V. M. Shelkovich, “The Riemann problem admitting \delta -, \delta $$^{\prime}$$-shocks, and vacuum states (the vanishing viscosity approach),” Journal of Differential Equations, vol. 231, no. 2, pp. 459-500, 2006. · Zbl 1108.35117 [15] V. P. Maslov, Perturbations Theory and Asymptotic Methods, Izdat, Moscow, Russia, 1965. [16] V. P. Maslov, Perturbations Theory and Asymptotic Methods, Dunod, Paris, France, 1972. · Zbl 0247.47010 [17] V. P. Maslov, Perturbations Theory and Asymptotic Methods, Nauka, Moscow, Russia, 1988. · Zbl 0653.35002 [18] L. Hörmander, The Analysis of Linear Partial Differential Operators IV: Fourier Integral Operators, Springer, Berlin, Germany, 1994. [19] V. G. Danilov, G. A. Omel’yanov, and V. M. Shelkovich, “Weak asymptotics method and interaction of nonlinear waves,” in Asymptotic Methods for Wave and Quantum Problems, M. V. Karasev, Ed., vol. 208 of American Mathematical Society Translations Series 2, pp. 33-164, American Mathematical Society, Providence, RI, USA, 2003. · Zbl 1140.35382
This reference list is based on information provided by the publisher or from digital mathematics libraries. Its items are heuristically matched to zbMATH identifiers and may contain data conversion errors. It attempts to reflect the references listed in the original paper as accurately as possible without claiming the completeness or perfect precision of the matching.
|
|
# Web scraping with R: Visualizing hockey statistics
I wanted to visualize the personal statistics for the hockey players of Stavanger Oilers, for the 2018/2019 season.
The data material is scraped from both Elite Prospects and Hockey live (regular season and playoffs), using the R-package rvest, as described in this blog post.
# The code
Scraping the data from Elite Prospects was straightforward, as it is stored as an HTML table. When you want to scrape a table with rvest, you only need to specify an index integer. Found by trial and error that the desired table was the second table of the web page, and removed some empty rows (which the web page uses for spacing):
library(rvest)
EPdat=EP%>%html_nodes("table")%>%.[[2]]%>%html_table()
EPstats = EPdat[!is.na(EPdat[,1]),]
However, the data tables at Hockey Live are populated with javascript, which prevents directly using the above method. I followed this tutorial, which suggests using PhantomJS to fetch the HTML page after the underlying javascript code has done its work. The rvest-method can then be applied to the resulting HTML page:
# assuming phantomjs.exe and season_scrape.js is placed in the working folder
system("./phantomjs season_scrape.js")
season=season_dat%>%html_nodes("table")%>%.[[1]]%>%html_table()
# season_scrape.js
var webPage = require('webpage');
var page = webPage.create();
var fs = require('fs');
page.open('https://www.hockey.no/live/Statistics/Players?date=21.04.2019&tournamentid=381196&teamid=220882', function (status) {
fs.write('data/season.html',page.content,'w')
phantom.exit();
});
Then, I combine the data from the two different sources, by merging the respective data frames. Unfortunately, the sources are not using identical player names, so some string handling is required to extract the last surname, which is then used as the merging column:
for(i in 1:nrow(season))
{
tmp=strsplit(season$PLAYER[i], ",")[[1]] season$PLAYER[i]=tmp[1]
}
names=setNames(data.frame(matrix(ncol = 3, nrow = nrow(EPstats))), c("NAME", "POSITION", "PLAYER"))
for(j in 1:nrow(EPstats))
{
tmp=strsplit(EPstats$Player[j], "\\s+")[[1]] names$NAME[j]=paste((tmp[-length(tmp)]),collapse = " ")
names$POSITION[j]=tmp[length(tmp)] # Replaces special characters names$PLAYER[j]=chartr(paste(names(special_chars), collapse=''),paste(special_chars, collapse=''),tmp[length(tmp)-1])
}
season = merge(season,names)
To ensure the merging column is identical for each data source, accented characters in are replaced with their non-accented counterparts, using a method I found on stackoverflow.
Special characters
special_chars = list('S'='S', 's'='s', 'Z'='Z', 'z'='z', 'À'='A', 'Á'='A', 'Â'='A', 'Ã'='A', 'Ä'='A', 'Ç'='C', 'È'='E', 'É'='E',
'Ê'='E', 'Ë'='E', 'Ì'='I', 'Í'='I', 'Î'='I', 'Ï'='I', 'Ñ'='N', 'Ò'='O', 'Ó'='O', 'Ô'='O', 'Õ'='O', 'Ö'='O', 'Ù'='U',
'Ú'='U', 'Û'='U', 'Ü'='U', 'Ý'='Y', 'Þ'='B', 'ß'='Ss', 'à'='a', 'á'='a', 'â'='a', 'ã'='a', 'ä'='a', 'ç'='c',
'è'='e', 'é'='e', 'ê'='e', 'ë'='e', 'ì'='i', 'í'='i', 'î'='i', 'ï'='i', 'ð'='o', 'ñ'='n', 'ò'='o', 'ó'='o', 'ô'='o', 'õ'='o',
'ö'='o', 'ù'='u', 'ú'='u', 'û'='u', 'ý'='y', 'ý'='y', 'þ'='b', 'ÿ'='y' )
The above code is for the regular season statistics, and the same method is also applied for the playoffs statistics. For some of the visualizations, I merge the regular season and playoffs data.
The figures are created with ggplot2, and the code are fairly similar for all figures.
Code used for generating the first figure
library(ggplot2)
season$col <- cut( season$PTS/season$GP, breaks=c(0, 0.25, 0.5, 0.75, 1, Inf) ) ggplot(season[season$GP>10,],aes(x=PTS/GP,y=reorder(NAME,PTS/GP),fill=col))+
geom_segment(aes(yend=NAME,x=G/GP,xend=0),colour="black",size=1.5)+
geom_segment(aes(yend=NAME,x=PTS/GP,xend=G/GP),colour="grey50",size=1)+
geom_point(size=4,shape=21)+theme_bw()+ylab("")+xlab("Total points per game (goals in black), regular season")+
scale_x_continuous(expand = c(0, 0),limits = c(0,max(season$PTS/season$GP)*1.1),breaks=c(0, 0.25, 0.5, 0.75, 1))+
theme(panel.grid.minor.x = element_blank(),panel.grid.major.y = element_blank(),
legend.position = "none",axis.text=element_text(size=14),axis.title=element_text(size=14,face="bold"))+
scale_fill_brewer("", palette = "Blues")
|
|
What is the modulo of 4?
In computing, the modulo operation returns the remainder or signed remainder of a division, after one number is divided by another (called the modulus of the operation).
Given two positive numbers a and n, a modulo n (abbreviated as a mod n) is the remainder of the Euclidean division of a by n, where a is the dividend and n is the divisor. The modulo operation is to be distinguished from the symbol mod, which refers to the modulus[1] (or divisor) one is operating from.
For example, the expression "5 mod 2" would evaluate to 1, because 5 divided by 2 has a quotient of 2 and a remainder of 1, while "9 mod 3" would evaluate to 0, because the division of 9 by 3 has a quotient of 3 and a remainder of 0; there is nothing to subtract from 9 after multiplying 3 times 3.
Although typically performed with a and n both being integers, many computing systems now allow other types of numeric operands. The range of values for an integer modulo operation of n is 0 to n 1 inclusive (a mod 1 is always 0; a mod 0 is undefined, possibly resulting in a division by zero error in some programming languages). See Modular arithmetic for an older and related convention applied in number theory.
When exactly one of a or n is negative, the naive definition breaks down, and programming languages differ in how these values are defined.
Variants of the definitionEdit
In mathematics, the result of the modulo operation is an equivalence class, and any member of the class may be chosen as representative; however, the usual representative is the least positive residue, the smallest non-negative integer that belongs to that class (i.e., the remainder of the Euclidean division).[2] However, other conventions are possible. Computers and calculators have various ways of storing and representing numbers; thus their definition of the modulo operation depends on the programming language or the underlying hardware.
In nearly all computing systems, the quotient q and the remainder r of a divided by n satisfy the following conditions:
qZa=nq+r|r|<|n|{\displaystyle {\begin{aligned}q\,&\in \mathbb {Z} \\a\,&=nq+r\\|r|&<|n|\end{aligned}}}
(1)
However, this still leaves a sign ambiguity if the remainder is non-zero: two possible choices for the remainder occur, one negative and the other positive, and two possible choices for the quotient occur. In number theory, the positive remainder is always chosen, but in computing, programming languages choose depending on the language and the signs of a or n.[a] Standard Pascal and ALGOL 68, for example, give a positive remainder (or 0) even for negative divisors, and some programming languages, such as C90, leave it to the implementation when either of n or a is negative (see the table under §In programming languages for details). a modulo 0 is undefined in most systems, although some do define it as a.
• Quotient (q) and remainder (r) as functions of dividend (a), using truncated division
Many implementations use truncated division, where the quotient is defined by truncation (integer part) q=trunc(an){\textstyle q=\operatorname {trunc} \left({\frac {a}{n}}\right)} and thus according to equation (1) the remainder would have the same sign as the dividend. The quotient is rounded towards zero: equal to the first integer in the direction of zero from the exact rational quotient.r=antrunc(an){\displaystyle r=a-n\operatorname {trunc} \left({\frac {a}{n}}\right)}
• Quotient and remainder using floored division
Donald Knuth[3] described floored division where the quotient is defined by the floor function q=an{\textstyle q=\left\lfloor {\frac {a}{n}}\right\rfloor } and thus according to equation (1) the remainder would have the same sign as the divisor. Due to the floor function, the quotient is always rounded downwards, even if it is already negative.r=anan{\displaystyle r=a-n\left\lfloor {\frac {a}{n}}\right\rfloor }
• Quotient and remainder using Euclidean division
Raymond T. Boute[4] describes the Euclidean definition in which the remainder is non-negative always, 0 r, and is thus consistent with the Euclidean division algorithm. In this case,n>0⟹q=an{\displaystyle n>0\implies q=\left\lfloor {\frac {a}{n}}\right\rfloor }n<0⟹q=an{\displaystyle n<0\implies q=\left\lceil {\frac {a}{n}}\right\rceil }
or equivalently
q=sgn(n)a|n|{\displaystyle q=\operatorname {sgn}(n)\left\lfloor {\frac {a}{\left|n\right|}}\right\rfloor }
where sgn is the sign function, and thus
r=a|n|a|n|{\displaystyle r=a-|n|\left\lfloor {\frac {a}{\left|n\right|}}\right\rfloor }
• Quotient and remainder using rounding division
A round-division is where the quotient is q=round(an){\textstyle q=\operatorname {round} \left({\frac {a}{n}}\right)}, i.e. rounded to the nearest integer. It is found in Common Lisp and IEEE 754 (see the round to nearest convention in IEEE-754). Thus, the sign of the remainder is chosen to be nearest to zero.
• Quotient and remainder using ceiling division
Common Lisp also defines ceiling-division (remainder different sign from divisor) where the quotient is given by q=an{\textstyle q=\left\lceil {\frac {a}{n}}\right\rceil }. Thus, the sign of the remainder is chosen to be different from that of the divisor.
As described by Leijen,
Boute argues that Euclidean division is superior to the other ones in terms of regularity and useful mathematical properties, although floored division, promoted by Knuth, is also a good definition. Despite its widespread use, truncated division is shown to be inferior to the other definitions.
Daan Leijen, Division and Modulus for Computer Scientists[5]
However, truncated division satisfies the identity (a)/b=(a/b)=a/(b){\displaystyle (-a)/b=-(a/b)=a/(-b)}.[6]
Some calculators have a mod() function button, and many programming languages have a similar function, expressed as mod(a, n), for example. Some also support expressions that use "%", "mod", or "Mod" as a modulo or remainder operator, such as a% n or a mod n.
For environments lacking a similar function, any of the three definitions above can be used.
Common pitfallsEdit
When the result of a modulo operation has the sign of the dividend (truncating definition), it can lead to surprising mistakes.
For example, to test if an integer is odd, one might be inclined to test if the remainder by 2 is equal to 1:
bool is_odd(int n) { return n % 2 == 1; }
But in a language where modulo has the sign of the dividend, that is incorrect, because when n (the dividend) is negative and odd, n mod 2 returns 1, and the function returns false.
One correct alternative is to test that the remainder is not 0 (because remainder 0 is the same regardless of the signs):
bool is_odd(int n) { return n % 2 != 0; }
Another alternative is to use the fact that for any odd number, the remainder may be either 1 or 1:
bool is_odd(int n) { return n % 2 == 1 || n % 2 == -1; }
Performance issuesEdit
Modulo operations might be implemented such that a division with a remainder is calculated each time. For special cases, on some hardware, faster alternatives exist. For example, the modulo of powers of 2 can alternatively be expressed as a bitwise AND operation (assuming x is a positive integer, or using a non-truncating definition):
x% 2n == x & (2n - 1)
Examples:
x% 2 == x & 1x% 4 == x & 3x% 8 == x & 7
In devices and software that implement bitwise operations more efficiently than modulo, these alternative forms can result in faster calculations.[7]
Compiler optimizations may recognize expressions of the form expression% constant where constant is a power of two and automatically implement them as expression & (constant-1), allowing the programmer to write clearer code without compromising performance. This simple optimization is not possible for languages in which the result of the modulo operation has the sign of the dividend (including C), unless the dividend is of an unsigned integer type. This is because, if the dividend is negative, the modulo will be negative, whereas expression & (constant-1) will always be positive. For these languages, the equivalence x% 2n == x < 0? x | ~(2n - 1): x & (2n - 1) has to be used instead, expressed using bitwise OR, NOT and AND operations.
Optimizations for general constant-modulus operations also exist by calculating the division first using the constant-divisor optimization.
Properties (identities)Edit
Some modulo operations can be factored or expanded similarly to other mathematical operations. This may be useful in cryptography proofs, such as the DiffieHellman key exchange.
• Identity:
• Inverse:
• Distributive:
• (a + b) mod n = [(a mod n) + (b mod n)] mod n.
• ab mod n = [(a mod n)(b mod n)] mod n.
• Division (definition): a/b mod n = [(a mod n)(b1 mod n)] mod n, when the right hand side is defined (that is when b and n are coprime), and undefined otherwise.
• Inverse multiplication: [(ab mod n)(b1 mod n)] mod n = a mod n.
In programming languagesEdit
In addition, many computer systems provide a divmod functionality, which produces the quotient and the remainder at the same time. Examples include the x86 architecture's IDIV instruction, the C programming language's div() function, and Python's divmod() function.
GeneralizationsEdit
Modulo with offsetEdit
Sometimes it is useful for the result of a modulo n to lie not between 0 and n 1, but between some number d and d + n 1. In that case, d is called an offset. There does not seem to be a standard notation for this operation, so let us tentatively use a modd n. We thus have the following definition:[38] x = a modd n just in case d x d + n 1 and x mod n = a mod n. Clearly, the usual modulo operation corresponds to zero offset: a mod n = a mod0 n. The operation of modulo with offset is related to the floor function as follows:
amoddn=anadn.{\displaystyle a\operatorname {mod} _{d}n=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor .}
(To see this, let x=anadn{\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor }. We first show that x mod n = a mod n. It is in general true that (a + bn) mod n = a mod n for all integers b; thus, this is true also in the particular case when b=adn{\textstyle b=-\!\left\lfloor {\frac {a-d}{n}}\right\rfloor }; but that means that xmodn=(anadn)modn=amodn{\textstyle x{\bmod {n}}=\left(a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor \right)\!{\bmod {n}}=a{\bmod {n}}}, which is what we wanted to prove. It remains to be shown that d x d + n 1. Let k and r be the integers such that a d = kn + r with 0 r n 1 (see Euclidean division). Then adn=k{\textstyle \left\lfloor {\frac {a-d}{n}}\right\rfloor =k}, thus x=anadn=ank=d+r{\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor =a-nk=d+r}. Now take 0 r n 1 and add d to both sides, obtaining d d + r d + n 1. But we've seen that x = d + r, so we are done. )
The modulo with offset a modd n is implemented in Mathematica as Mod[a, n, d] .[38]
Despite the mathematical elegance of Knuth's floored division and Euclidean division, it is generally much more common to find a truncated division-based modulo in programming languages. Leijen provides the following algorithms for calculating the two divisions given a truncated integer division:[5]
/* Euclidean and Floored divmod, in the style of C's ldiv() */ typedef struct { /* This structure is part of the C stdlib.h, but is reproduced here for clarity */ long int quot; long int rem; } ldiv_t; /* Euclidean division */ inline ldiv_t ldivE(long numer, long denom) { /* The C99 and C++11 languages define both of these as truncating. */ long q = numer / denom; long r = numer % denom; if (r < 0) { if (denom > 0) { q = q - 1; r = r + denom; } else { q = q + 1; r = r - denom; } } return (ldiv_t){.quot = q, .rem = r}; } /* Floored division */ inline ldiv_t ldivF(long numer, long denom) { long q = numer / denom; long r = numer % denom; if ((r > 0 && denom < 0) || (r < 0 && denom > 0)) { q = q - 1; r = r + denom; } return (ldiv_t){.quot = q, .rem = r}; }
Note that for both cases, the remainder can be calculated independently of the quotient, but not vice versa. The operations are combined here to save screen space, as the logical branches are the same.
1. ^ Mathematically, these two choices are but two of the infinite number of choices available for the inequality satisfied by a remainder.
2. ^ a b Argument order reverses, i.e., α|ω computes ωmodα{\displaystyle \omega {\bmod {\alpha }}}, the remainder when dividing ω by α.
3. ^ C99 and C++11 define the behavior of % to be truncated.[8] The standards before then leave the behavior implementation-defined.[9]
4. ^ As implemented in ACUCOBOL, Micro Focus COBOL, and possible others.
5. ^ Divisor must be positive, otherwise undefined.
6. ^ As discussed by Boute, ISO Pascal's definitions of div and mod do not obey the Division Identity of D = d · (D / d) + D% d, and are thus fundamentally broken.
7. ^ Perl usually uses arithmetic modulo operator that is machine-independent. For examples and exceptions, see the Perl documentation on multiplicative operators.[27]
ReferencesEdit
• Modulorama, animation of a cyclic representation of multiplication tables (explanation in French)
|
|
# Tangent vector as derivation question
1. Jul 8, 2015
### orion
I have a question concerning the tangent space.
Consider a manifold Mn and take Mn to be ℝn with the Euclidean metric for the purposes of this question.
The directional derivative of a function in the direction of a vector v is
(a) vf = ∑ vi(∂f/∂xi)
where the sum runs from 1 to n. The vector v is then given as
(b) v=∑ vi(∂/∂xi).
Furthermore the claim is that the space of derivations at p is isomorphic to the space of geometric vectors at p. Thus, we can make the identifications:
(c) (∂/∂xi)p <-----------> ei
And I can see this to be true if we let the operator in (c) operate on the coordinate functions, and indeed that is what the books do. But to me, there seems to be a slight of hand going on here because in (a) the operator operated on an arbitrary function then suddenly in (b) and (c) the assumption is made that the operator operates on coordinate functions and not arbitrary functions. All books that I have read make this change from the vector operating on a arbitrary function to operating on the coordinate functions without justifying it.
So my question is, what is the justification for specifying a specific set of functions in (b) and (c)?
2. Jul 8, 2015
### Fredrik
Staff Emeritus
The operator in (c) takes an arbitrary smooth $f:M\to\mathbb R^n$ as input. If it didn't, the f on the left in (a) would be different from the f on the right in (a). Maybe you're not aware of the definition of the notation in (c). If $x:U\to\mathbb R^n$ is a coordinate system and $U\subseteq M$, then $\big(\frac{\partial}{\partial x^i}\big)_p$ is defined for each $p\in U$ and each $i\in\{1,\dots,n\}$ by
$$\left(\frac{\partial}{\partial x^i}\right)_p f =(f\circ x^{-1})_{,i}(x(p))$$ for all smooth $f:M\to\mathbb R^n$. (Here $(f\circ x^{-1})_{,i}$ denotes the partial derivative of $f\circ x^{-1}:x(U)\to\mathbb R$ with respect to the $i$th variable slot).
If you meant that $\frac{\partial}{\partial x^i}$ (with no specific point specified) acts on functions from a different set, that's incorrect. $\frac{\partial}{\partial x^i}$ (where x is a coordinate system with domain U) denotes the vector field with domain U that takes each $q\in U$ to $\big(\frac{\partial}{\partial x^i}\big)_q$.
Also, if v is a tangent vector at p, rather than a vector field with domain U, there should be a $p$ in (a) and (b) too.
Last edited: Jul 8, 2015
3. Jul 8, 2015
### orion
It's my fault that I didn't specify that these operators act at a particular p. Yes, the vector in (a) acts on an arbitrary smooth function at a point p. That I understand. And that's kind of my point.
To see what I mean, let me refer you to a typical book that I use, namely J.M. Lee's Introduction to Smooth Manifolds. In the proof to Proposition 3.2 on page 53 (isomorphism between the derivations at p to the geometrical tangent space), he writes:
"Writing Va = viei|a in terms of the standard basis, and taking f to be the jth coordinate function xj: ℝn→ℝ, thought of as a smooth function on ℝn, we obtain: ..." (emphasis mine).
My question is why is he able to specify f in order to get the standard basis. In other words, how is it that (∂/∂xi)p is identified ei when the partial derivative operator operates on arbitrary functions (and not just on the coordinate functions).
4. Jul 8, 2015
### Fredrik
Staff Emeritus
That theorem is on page 64 in my book. There's something that I didn't expect going on there. He's talking about tangent spaces of an (n-1)-sphere. But the functions he's talking about have domain $\mathbb R^n$, not $S^{n-1}$. In particular, the coordinate system $x$ has domain $\mathbb R^n$. And the $\frac{\partial}{\partial x^i}$ aren't the vector fields discussed above. They are plain old partial derivatives.
Definition: $\mathbb R^n_a=\{a\}\times\mathbb R^n$.
Definition: For each $v\in\mathbb R^n_a$, we define a map $D_v|_a$ by
$$D_v|_a f=\frac{d}{dt}\bigg|_0 f(a+tv)$$ for all smooth $f:\mathbb R^n\to\mathbb R$. (Lee doesn't actually specify the domain of $D_v|_a$. I'm inferring it from how he uses the chain rule a few lines later).
What he's doing in the part you're asking about is to prove the following: If $D_v|_a$ takes every function in its domain to 0, then $v=0$.
If it takes every function to 0, then for all $i$, it takes $x^i$ to 0, so for all $i$, we have
$$0=D_v|_a x^i =\frac{d}{dt}\bigg|_0 x^i(a+tv)= x^i{}_{,j}(a) v^j =\delta^i_j v^j =v^i.$$ This implies that $v=0$.
5. Jul 8, 2015
### orion
You have a completely different edition than I do because my book says nothing about an (n-1)-sphere. But the result and conclusion are the same. Ok, there he is using the coordinate functions for a particular purpose. I will give you another example. In Riemannian Geometry by Do Carmo, on page 8 (of my book at least), Do Carmo states,
"Observe that (∂/∂xi)0 is the tangent vector at p of the 'coordinate curve' ...."
My question really boils down to understanding the isomorphism between ei and (∂/∂xi)p when the partial derivative operator operates on arbitrary curves and not just coordinate curves. I wish I could express it more clearly than that.
6. Jul 8, 2015
### Fredrik
Staff Emeritus
I found a pdf version of the second edition online. Proposition 3.2 is on page 53 in that one. The (n-1)-sphere is mentioned in the intro for the section titled "Tangent vectors" and the intro for the subsection titled "geometric tangent vectors", both on page 51. (That's page 61 in the printed copy of the first edition). What I said in post #4 is still the answer to what you asked in post #3.
do Carmo is talking about tangent vectors of (curves in) arbitrary manifolds. Lee is talking about tangent vectors of $\mathbb R^n$ (or $S^{n-1}$).
7. Jul 10, 2015
### Fredrik
Staff Emeritus
Did that solve the problem? Do you understand that part of the proof now? Do you understand the rest of it?
8. Jul 10, 2015
### orion
Yeah, thanks, that clears up that part of the proof, but I'm still struggling to understand my general question. I'll try asking it a different way because I think it has gotten clouded by referring to specific passages in books. What I'm trying to get at is how do we make the association (∂/∂xi)p ↔ ei if (∂/∂xi)p acts on arbitrary functions and not just on the coordinate functions?
The reason why I refer to books is that they tend to choose the partial derivatives operating on the coordinate curves when it is convenient, but these operators are defined as acting on arbitrary functions. I have found other books that do the same thing even when it's not part of a proof. (See, eg, Crampin and Pirani Applicable Differential Geometry)
To be honest, since I posted this question, I've read so much about it that I think I have absorbed something by osmosis even though I still struggle with justifying it to myself sometimes.
Thank you for taking time to talk with me on this.
9. Jul 10, 2015
### Fredrik
Staff Emeritus
I don't understand the concern about coordinate functions. I think you're seeing a problem where there isn't one. I will elaborate on that below.
What you need to understand the association is Lee's proposition 3.2(b) and the chain rule.The isomorphism from $\mathbb R^n_a$ to the vector space of derivations at $a$ is the map $v\mapsto D_v|_a$. The domain of each $D_v|_a$ is the set of smooth real-valued functions on $\mathbb R^n$ (not just "coordinate functions"). This isomorphism takes $e_i$ to $D_{e_i}|_a$. For all smooth $f:\mathbb R^n\to\mathbb R$, we have
$$(D_{e_i}|_a)(f) =\frac{d}{dt}\bigg|_0 f(a+te_i) =f_{,j}(a)\frac{d}{dt}\bigg|_0 (a+te_i)^j =f_{,j}(a)\frac{d}{dt}\bigg|_0 (a^j+t\delta^j_i) =f_{,j}(a)\delta^j_i =f_{,i}(a).$$ This implies that
$$D_{e_i}|_a =\frac{\partial}{\partial x^i}\bigg|_a$$ where the partial derivative is now denoted by $\frac{\partial}{\partial x^i}$ instead of ${}_{,i}$. So the isomorphism takes $e_i$ to $\frac{\partial}{\partial x^i}\big|_a$. Note that this is just the kind of partial derivative that we're familiar with from calculus. It's not the vector field I mentioned in my first post.
Consider e.g. the function $f:\mathbb R\to\mathbb R$ defined by $f(x)=x^2$ for all $x\in\mathbb R$. Would you get suspicious if someone says that $f(2)=4$? We can input integers into this function, because its domain is the set of real numbers, and integers are real numbers. Similarly, we can input a coordinate function into a derivation, because its domain is the set of smooth functions, and coordinate functions are smooth functions.
Last edited: Jul 10, 2015
10. Jul 10, 2015
### orion
Thanks for explaining the isomorphism to me. That makes a lot of sense.
This I think is what is bothering me. I will have to think on this more in the next few days to be clearer. Either it will become clearer to me or I will have a clearer question to ask.
Thanks again.
|
|
# Revision history [back]
Sage uses PYTHONPATH for its own purposes. If you add the directory to SAGE_PATH (export SAGE_PATH=/some/dir/here) it should work, at least it seems to for me.
Beware: it looks like SAGE_PATH is added before Sage's existing python in sage-env:
PYTHONPATH="$SAGE_PATH:$SAGE_ROOT/local/lib/python" && export PYTHONPATH
so if you shadow one of the built-in modules you could get strange errors.
Sage uses PYTHONPATH for its own purposes. If you add the directory directory/directories to SAGE_PATH (export SAGE_PATH=/some/dir/here) it should work, at least it seems to for me.
Beware: it looks like SAGE_PATH is added before Sage's existing python in sage-env:
PYTHONPATH="$SAGE_PATH:$SAGE_ROOT/local/lib/python" && export PYTHONPATH
so if you shadow one of the built-in modules you could get strange errors.
Sage uses PYTHONPATH for its own purposes. If you add the directory/directories to SAGE_PATH (export SAGE_PATH=/some/dir/here) it should work, at least it seems to for me.
Beware: it looks like SAGE_PATH is added before Sage's existing python in sage-env:
PYTHONPATH="$SAGE_PATH:$SAGE_ROOT/local/lib/python" && export PYTHONPATH
so if you shadow one of the built-in modules you could get strange errors. [Not that you couldn't get errors if it were the other way 'round, of course, but you might not even be able to get to the prompt.]
|
|
## Nagoya Mathematical Journal
### Automorphisms of Coxeter groups and Lusztig's conjectures for Hecke algebras with unequal parameters
Cédric Bonnafé
#### Abstract
Let $(W, S)$ be a Coxeter system, let $G$ be a finite solvable group of automorphisms of $(W, S)$ and let $\varphi$ be a weight function which is invariant under $G$. Let $\varphi_{G}$ denote the weight function on $W^{G}$ obtained by restriction from $\varphi$. The aim of this paper is to compare the $\mathbf{a}$-function, the set of Duflo involutions and the Kazhdan-Lusztig cells associated with $(W, \varphi)$ and to $(W^{G}, \varphi_{G})$, provided that Lusztig's Conjectures hold.
#### Article information
Source
Nagoya Math. J., Volume 195 (2009), 153-164.
Dates
First available in Project Euclid: 14 September 2009
Permanent link to this document
https://projecteuclid.org/euclid.nmj/1252934376
Mathematical Reviews number (MathSciNet)
MR2552958
Zentralblatt MATH identifier
1188.20002
Subjects
Primary: 20C08: Hecke algebras and their representations
Secondary: 20C15: Ordinary representations and characters
#### Citation
Bonnafé, Cédric. Automorphisms of Coxeter groups and Lusztig's conjectures for Hecke algebras with unequal parameters. Nagoya Math. J. 195 (2009), 153--164. https://projecteuclid.org/euclid.nmj/1252934376
#### References
• M. Geck, On the induction of Kazhdan-Lusztig cells, Bull. London Math. Soc., 35 (2003), 608--614.
• J.-Y. Hée, Systèmes de racines sur un anneau commutatif totalement ordonné, Geometriae Dedicata, 37 (1991), 65--102.
• G. Lusztig, Hecke algebras with unequal parameters, CRM Monograph Series 18, American Mathematical Society, Providence, RI, 2003, 136 pp.
• J. Thévenaz, $G$-Algebras and Modular Representation Theory, Clarendon Press, Oxford, 1995.
|
|
# Catenary differential equation (suspension bridge)
• July 13th 2011, 05:31 PM
cbjohn1
Catenary differential equation (suspension bridge)
So I am getting stuck trying to solve this. pgA and Tx are constants
d^2h/dx^2 = (pgA/Tx)*sqrt(1+(dh/dx)^2)
I substitute dh/dx = sinh(u), d^2h/dx^2 = coshu(du/dx)
then you get (pgA/Tx)*cosh(u) = cosh(u)(du/dx)
... and I'm unsure where to go after this. I tried a couple more things but I'm not sure if it's the right track:
(pgA/Tx) * cosh(u) = cosh(u)(du/dx) ... integrate and solve for u = (pgAx/Tx)+C
and then substitute back in for u??? Sorry this isn't in Latex but I couldn't figure it out.
• July 13th 2011, 10:42 PM
CaptainBlack
Re: Catenary differential equation (suspension bridge)
Quote:
Originally Posted by cbjohn1
So I am getting stuck trying to solve this. pgA and Tx are constants
d^2h/dx^2 = (pgA/Tx)*sqrt(1+(dh/dx)^2)
I substitute dh/dx = sinh(u), d^2h/dx^2 = coshu(du/dx)
then you get (pgA/Tx)*cosh(u) = cosh(u)(du/dx)
... and I'm unsure where to go after this. I tried a couple more things but I'm not sure if it's the right track:
(pgA/Tx) * cosh(u) = cosh(u)(du/dx) ... integrate and solve for u = (pgAx/Tx)+C
and then substitute back in for u??? Sorry this isn't in Latex but I couldn't figure it out.
1. Lump the constants, so then you have:
$\frac{d^2h}{dx^2}=K\left(1+\left(\frac{dh}{dx} \right) ^2\right)^{1/2}$
where $K=pgA/Tx$.
Now consider reducing the order by putting $u=dh/dx$
CB
|
|
# How to fix messed up page numbering in thesis
In writing my MS thesis I have to add Certificate of Examination and declaration by student pages and I tried to add them by using \chapter*. But the problem is page numberings is now messed up. In the following code CoE, Declaration and acknowledgment are getting numbering 2,3 and 4 resp. then numbering starts again from Introduction being 1 and first page of thesis being 2.
I want numbering to start from the first chapter. I do not want any numbering on CoE, or acknowledgment or Introduction etc. How can I do it?
\documentclass[twoside, <further options>]{report}
\usepackage[inner=1.25in, outer=1in, vmargin=1in]{geometry}
\usepackage{sectsty}
\usepackage{setspace}
\usepackage{amssymb}
\usepackage{amsmath}
\usepackage{centernot}
\setlength\parskip{\baselineskip}
\parindent=0pt
\doublespacing
\begin{document}
\title {BACBAC}
\date{\today}
\maketitle
\clearpage
\allsectionsfont{\centering}
\chapter*{Certificate of Examination}This is to certify that the dissertation titled “xyz”
submitted by Mr. gghj (Reg. No. 1234) for the partial fulfilment
of MS degree programme of the Institute, has been examined
by the thesis committee duly appointed by the Institute. The committee
finds the work done by the candidate satisfactory and recommends that the
report be accepted.
\chapter*{Declaration}The work presented in this dissertation has been carried out by me under
the guidance of Prof. abc at the ISRM
This work has not been submitted in part or in full for a degree, a diploma,
or a fellowship to any other university or institute. Whenever contributions
of others are involved, every effort is made to indicate this clearly, with due
acknowledgement of collaborative research and discussions. This thesis is a
bonafide record of original work done by me and all sources listed within
have been detailed in the bibliography.
\chapter*{Acknowlegment} Thanks
\abstract{lipsum.
\thispagestyle{empty}
\tableofcontents
\thispagestyle{empty}
\cleardoublepage
\thispagestyle{empty}
\chapter*{Introduction} Something
\pagenumbering{arabic}
\setcounter{page}{1}
\chapter{XYZXY}
\end{document}
• Try adding \pagenumbering{gobble} after your \maketitle – onewhaleid Apr 11 '16 at 2:59
• It works that CoE, acknowledgemnt etc has no numbering but still numbering starts from introduction and not from chap 1 – Bhaskar Vashishth Apr 11 '16 at 3:07
• What if you put \setcounter{page}{1} after \chapter{XYZXY}? – onewhaleid Apr 11 '16 at 3:39
• then both introduction and chapters first page has numbering 1 and after that its normal – Bhaskar Vashishth Apr 11 '16 at 3:41
• Introduction then Chapter1 then pagenumbering How to use pagenumbering in the document? – Johannes_B Apr 11 '16 at 6:25
A bunch of \thispagestyle{empty} after \chapter isn't helpful,since \chapter uses \thispagestyle{plain} (hardcoded). I've changed this by using a patch and referring to a pagestyle hidden in a macro name, which can be redefined later on.
Also \pagenumbering{arabic} sets the page counter to 1 already, there's no need to use \setcounter{page}{1} again.
\documentclass[twoside]{report}
\usepackage[inner=1.25in, outer=1in, vmargin=1in]{geometry}
\usepackage{sectsty}
\usepackage{setspace}
\usepackage{amssymb}
\usepackage{amsmath}
\usepackage{centernot}
\usepackage{xpatch}
\xpatchcmd{\chapter}{%
\thispagestyle{plain}%
}{%
\thispagestyle{\chapterfirstpagestyle}
}{\typeout{Success}}{\typeout{Failed!}}
\newcommand{\chapterfirstpagestyle}{empty}
\setlength\parskip{\baselineskip}
\parindent=0pt
\doublespacing
\begin{document}
\title {BACBAC}
\date{\today}
\maketitle
\clearpage
\allsectionsfont{\centering}
\pagestyle{empty}
\chapter*{Certificate of Examination}This is to certify that the dissertation titled “xyz”
submitted by Mr. gghj (Reg. No. 1234) for the partial fulfilment
of MS degree programme of the Institute, has been examined
by the thesis committee duly appointed by the Institute. The committee
finds the work done by the candidate satisfactory and recommends that the
report be accepted.
\chapter*{Declaration}The work presented in this dissertation has been carried out by me under
the guidance of Prof. abc at the ISRM
This work has not been submitted in part or in full for a degree, a diploma,
or a fellowship to any other university or institute. Whenever contributions
of others are involved, every effort is made to indicate this clearly, with due
acknowledgement of collaborative research and discussions. This thesis is a
bonafide record of original work done by me and all sources listed within
have been detailed in the bibliography.
\chapter*{Acknowlegment} Thanks
\abstract{lipsum.
\tableofcontents
\cleardoublepage
\chapter*{Introduction} Something
\clearpage
\pagenumbering{arabic}
\renewcommand{\chapterfirstpagestyle}{plain}
\chapter{XYZXY}
\end{document}
|
|
# AP SSC 10th Class Maths Solutions Chapter 5 Quadratic Equations Optional Exercise
## AP State Syllabus SSC 10th Class Maths Solutions 5th Lesson Quadratic Equations Optional Exercise
AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 5 Quadratic Equations Optional Exercise Textbook Questions and Answers.
### 10th Class Maths 5th Lesson Quadratic Equations Optional Exercise Textbook Questions and Answers
Question 1.
Some points are plotted on a plane. Each point is joined with all remaining points by line segments. Find the number of points if the number of line segments are 10.
Number of distinct line segments that can be formed out of n-points = $$\frac{\mathrm{n}(\mathrm{n}-1)}{2}$$
Given: No. of line segments
$$\frac{\mathrm{n}(\mathrm{n}-1)}{2}$$ = 10
⇒ n2 – n = 20
⇒ n2 – n – 20 = 0
⇒ n2 – 5n + 4n – 20 = 0
⇒ n(n – 5) + 4(n – 5) = 0
⇒ (n – 5) (n + 4) = 0
⇒ n – 5 = 0 (or) n + 4 = 0
⇒ n = 5 (or) -4
∴ n = 5 [n – can’t be negative]
Question 2.
A two digit number is such that the product of its digits, is 8. When 18 is added to the number, they interchange their places. Determine the number.
Let the digit in the units place = x
Let the digit in the tens place = y
∴ The number = 10y + x
By interchanging the digits the number becomes 10x + y
By problem (10x + y) – (10y + x) = 18
⇒ 9x – 9y = 18
⇒ 9(x – y) =18
⇒ x – y = $$\frac{18}{9}$$ = 2
⇒ y = x – 2
(i.e.) digit in the tens place = x – 2
digit in the units place = x
Product of the digits = (x – 2) x
By problem x2 – 2x = 8
x2 – 2x – 8 = 0
⇒ x2 – 4x + 2x – 8 = 0
⇒ x(x – 4) + 2(x – 4) = 0
⇒ (x – 4) (x + 2) = 0
⇒ x – 4 = 0 (or) x + 2 = 0
⇒ x = 4 (or) x = -2
∴ x = 4 [∵ x can’t be negative]
∴ The number is 24.
Question 3.
A piece of wire 8m in length is cut into twp pieces and each piece is bent into a square. Where should the cut in the wire be made if the sum of the areas of these squares is to be 2 m2?
Let the length of the first peice = x m
Then length of the second piece = 8 – x m
∴ Side of the 1st square = $$\frac{x}{4}$$ m and
Side of the second square = $$\frac{8-x}{4}$$ m
sum of the areas = 2 m2
⇒ x2 + 64 + x2 – 16x = 16 × 2 = 32
⇒ 2x2 – 16x + 64 = 32
⇒ 2x2 – 16x + 32 = 0
⇒ 2(x2 – 8x + 16)= 0
⇒ x2 – 8x + 16 = 0
⇒ x2 – 4x – 4x + 16 = 0
⇒ x(x – 4) – 4(x – 4) = 0
⇒ (x – 4) (x – 4) = 0
∴ x = 4
∴ The cut should be made at the centre making two equal pieces of length 4 m, 4 m.
Question 4.
Vinay and Praveen working together can paint the exterior of a house in 6 days. Vinay by himself can complete the job in 5 days less than Praveen. How long will it take Vinay to complete the job by himself?
Let the time taken by Vinay to complete the job = x days
Then the time taken by Praveen to complete the job = x + 5 days
Both worked for 6 days to complete a job.
∴ Total Work done by them is
⇒ 6(2x + 5) = x2 + 5x
⇒ x2 – 7x – 30 = 0
⇒ x2 – 10x + 3x – 30 = 0
⇒ x(x – 10) + 3(x – 10) = 0
⇒ (x – 10) (x + 3) = 0
⇒ x – 10 = 0 (or) x + 3 = 0
⇒ x = 10 (or) x = -3
∴ x = 10 (∵ x can’t be negative)
∴ Time taken by Vinay = x = 10 days
Time taken by Praveen = x + 5 = 15 days.
Question 5.
Show that the sum of the roots of a quadratic equation ax2 + bx + c = 0 is $$\frac{-b}{a}$$.
Let the Q.E. = ax2 + bx + c = 0 (a ≠ 0)
⇒ ax2 + bx = -c
∴ Sum of roots of a Q.E. is $$\frac{-b}{a}$$
Question 6.
Show that the product of the roots of a quadratic equation ax2 + bx + c = 0 is $$\frac{c}{a}$$.
Let the Q.E. = ax2 + bx + c = 0 (a ≠ 0)
⇒ ax2 + bx = -c
Question 7.
The denominator of a fraction is one more than twice the numerator. If the sum of the fraction and its reciprocal is 2$$\frac{16}{21}$$ find the fraction.
Let the numerator = x
then denominator = 2x + 1
Then the fraction = $$\frac{x}{2x+1}$$
Its reciprocal = $$\frac{2x+1}{x}$$
105x2 + 84x + 21 = 116x2 + 58x
11x2 – 26x – 21 = 0
11x2 – 33x + 7x – 21 = 0
11x (x – 3) + 7 (x – 3) = 0
(x – 3) (11x + 7) = 0
⇒ x – 3 = 0 (or) 11x + 7 = 0
⇒ x = 3 (or) $$\frac{-7}{11}$$
∴ x = 3
Numerator = 3;
Denominator = 2 × 3 + 1 = 7
Fraction = $$\frac{3}{7}$$.
Question 8.
A ball is thrown vertically upwards from the top of a building of height 29.4m and with an initial velocity 24.5m/sec. If the height H of the ball from the ground level is given by H = 29.4 + 24.5t – 4.9t2, then find the time taken by the ball to reach the ground.
Initial velocity ‘U’ = 24.5
height of the ball from the ground can be expressed as
H = 29.4 + 24.5 t – 4.9 t2
The ball has to reach the ground in ‘t’ seconds, which means Height from ground H = 0
So 29.4 + 24.5t – 4.9t2 = 0 = H
⇒ 4.9 t2 – 24.5t – 29.4 = 0
⇒ 4.9 [t2 – 5t – 6] = 0
∴ t2 – 5t – 6 = 0
⇒ t2 – 6t + t – 6 = 0
⇒ t(t – 6) + 1 (t – 6) = 0
(t – 6) (t + 1) = 0
⇒ t – 6 = 0
∴ t = 6 or t + 1 = 0
⇒ t = -1 but ‘t’ cannot be negative
So t = 6
it means in 6 seconds of time the ball reaches ground.
|
|
# [SOLVED] Probability Tree Diagram Problem
• Feb 27th 2010, 02:08 PM
fb280
[SOLVED] Probability Tree Diagram Problem
I'm trying to figure out how I would put this problem into a tree diagram, and how i would read it.
"A computer package sale comes with two different choices of printers and four different choices of monitors. If a store wants to display each package combination that is for sale, how many packages must be displayed?"
I dont need the answer to this, just some guidance would be great.
• Feb 27th 2010, 06:40 PM
ANDS!
A tree diagram is developed by having lines for each choice a person can make at a every branch of the tree. For instance, if you have 3 shirts, and 2 shoes, a tree diagram might be:
Shoe 1 "Shirt 1 and Shoe 1"
Shirt 1 -
Shoe 2 "Shirt 1 and Shoe 2"
Shoe 1 "Shirt 2 and Shoe 1"
Shirt 2 -
Shoe 2 "Shirt 2 and Shoe 2"
Shoe 1 "Shirt 3 and Shoe 1"
Shirt 3 -
Shoe 2 "Shirt 3 and Shoe 2"
See if you can form a conjecture about the number of items in the shirt column, the number of items in the shoe column and the total combinations in your final column.
• Feb 27th 2010, 09:16 PM
Soroban
Hello, fb280!
Quote:
A computer package comes with two choices of printers and four choices of monitors.
If a store wants to display each combination, how many packages must be displayed?
Let the two printers be: . $P_1,\:P_2$
Let the four monitors be: . $M_1,\:M_2,\:M_3,\:M_4$
$\begin{array}{cccccccccc} &&&&&& * & - & \boxed{M_1} \\ &&&&&& | \\ &&&&&& * & - & \boxed{M_2} \\ &&&&&& | \\ &&& \boxed{P_1} & - & - & * & - & \boxed{M_3} \\ &&& | &&& | \\ &&& | &&& * & - & \boxed{M_4} \\ \circ & - & - & * \\ &&& | &&& * & - & \boxed{M_1} \end{array}$
. - - . . . $\begin{array}{cccccc} | &&& | \\ \boxed{P_2} & - & - & * & - & \boxed{M_2} \\ &&& | \\ &&& * & - & \boxed{M_3} \\ &&& | \\ &&& * & - & \boxed{M_4}\end{array}$
There are 8 possible packages to be displayed.
• Feb 27th 2010, 10:50 PM
fb280
oh, that seems much easier than i thought it was. thanks for the help.
|
|
# First Order Linear Differential Equations Examples
ZEROLAW.TECH - That linear the the is equation- f is function x y linear differential is in is Solved is f a order equation and function xy order b- y mx then linear y equation takes the first equation first examples form the the a linear expression f equation f p x y linear if the since differential q xy
Here's a directory of images First Order Linear Differential Equations Examples greatest After simply adding characters you could one piece of content into as much 100% readers friendly editions as you may like we inform as well as present Writing articles is a rewarding experience for your requirements. We all acquire best a lot of Beautiful articles First Order Linear Differential Equations Examples beautiful photo nevertheless we solely show your articles that we feel include the ideal reading.
The particular articles First Order Linear Differential Equations Examples is just for beautiful demo considering like the articles remember to find the first images. Service the creator simply by purchasing the first word First Order Linear Differential Equations Examples therefore the author provide the very best images along with proceed operating At looking for offer all kinds of residential and commercial assistance. you have to make your search to receive a free quotation hope you are good have a nice day.
Ivp First Order Linear Differential Equation Example 1 Youtube
Solved examples first order linear differential equation if the function f is a linear expression in y, then the first order differential equation y’ = f (x, y) is a linear equation. that is, the equation is linear and the function f takes the form f (x,y) = p (x)y q (x) since the linear equation is y = mx b. Examples of different types of differential equations include ordinary, partial, linear, nonlinear, homogenous, and non homogenous differential equations. order of differential equation is the highest order derivatives of the dependent variable in an equation. a first order differential equation is an equation of the form \ (f (t, y, \dot {y})=0\). Example 1: solve this: dy dx − y x = 1 first, is this linear? yes, as it is in the form dy dx p (x)y = q (x) where p (x) = − 1 x and q (x) = 1 so let's follow the steps: step 1: substitute y = uv, and dy dx = u dv dx v du dx so this: dy dx − y x = 1 becomes this: u dv dx v du dx − uv x = 1 step 2: factor the parts involving v. A couple of examples below will be provided to help see how solving these equations works in practice. first order linear differential equation examples example 1 solve the. This ordinary differential equations video works several examples of first order linear differential equations using the integrating factor method. we show a.
Ppt First Order Linear Differential Equations Powerpoint Presentation
Here are some examples of first order linear differential equations: examples of first order linear differential equations ( 1) x x d y d x 1 x y = cos x ( 2) x x x y ′ e x y = 2 e x ( 3) x x x y 6 x 2 = 4 y ′ 10. Example 1: solve the differential equation the equation is already expressed in standard form, with p (x) = 2 x and q (x) = x. multiplying both sides by transforms the given differential equation into notice how the left‐hand side collapses into ( μy )′; as shown above, this will always happen. integrating both sides gives the solution:. Maths: differential equations: linear differential equations of first order : solved example problems with answer, solution, formula example a firm has found that the cost c of producing x tons of certain product by the equation x dc dx = 3 x − c and c = 2 when x = 1.
Solving Linear First Order Differential Equations Integrating Factor
❖ First Order Linear Differential Equations ❖
thanks to all of you who support me on patreon. you da real mvps! $1 per month helps!! 🙂 patreon patrickjmt ! this calculus video tutorial explains provides a basic introduction into how to solve first order linear differential equations. first verify the solution: youtu.be vcjukth7kws to support my channel, you can visit the following links t shirt: linear equations use of integrating factor consider the equation dy dx 5y = e²ˣ this is clearly an equation of the first order , but this video walks through two examples of solving first order linear differential equations using the integrating factor. example 1 this ordinary differential equations video works several examples of first order linear differential equations using the integrating check out engineer4free for more free engineering tutorials and math lessons! differential equations tutorial: first i introduce solving first order linear differential equations. the first example is in exact form starting at 1:20. i then explain how engineers.academy level 5 higher national diploma courses this video introduces the topic of differential equations, and my differential equations playlist: patreon professorleonard how to solve linear first order differential equations and the theory behind the thanks to all of you who support me on patreon. you da real mvps!$1 per month helps!! 🙂 patreon patrickjmt !
|
|
#### Heron's formula
hsf
Heron's formula gives the area of a triangle when the lengths of all three sides are known. Given the lengths of the three sides of a triangle, a, b, c, the area of the triangle can be determined as
A = \sqrt{s(s-a)(s-b)(s-c)}
where s = \dfrac{a+b+c}{2} , semi-perimeter of the triangle.
The formula can be transformed to the following interesting forms.
A = \sqrt{s(s-a)(s-b)(s-c)}
|
|
# [time 394] Re: [time 391] Re: [time 388] Re: [time 384] Re: [time 380] Re: [time 376] Whatare observers
Tue, 8 Jun 1999 14:14:57 +0900
Dear Matti,
This is a supplementary remark with some questions.
----- Original Message -----
From: Matti Pitkanen <matpitka@pcu.helsinki.fi>
Sent: Monday, June 07, 1999 6:05 PM
Subject: [time 391] Re: [time 388] Re: [time 384] Re: [time 380] Re: [time
376] Whatare observers
>
>
> On Mon, 7 Jun 1999, Hitoshi Kitada wrote:
>
> > Dear Matti,
> >
> >
> >
> > >
> > >
> > > On Sun, 6 Jun 1999, Hitoshi Kitada wrote:
> > >
> > >
> > > > Dear Stephen,
> > >
> > > snip
> > >
> > >
> > > > > > The inner product for configuration space spinor fields reduces
> > > > to inner
> > > > > > product ofm configuration space spinors integrated over entire
> > > > > > configuration space of 3-surfaces. Inner product of spinors is
> > > > just Fock
> > > > > > space inner product for fermions (oscillator operators create
> > > > the state).
> > > > > >
> > > > > > In your case you have single phi and inner product must be inner
> > > > product
> > > > > > for some subsystem (LS?). Hence situation is different from that
> > > > > > in TGD.
> > > > >
> > >
> > > [Stephen]
> > >
> > > > > I am getting confused. :( We need to ask Hitoshi about these
> > > > details...
> > > >
> > > [Hitoshi]
> > >
> > > > If you argue in LS theory, the inner products are of an infinite
> > > > number, proper to each Local System. I.e. LS theory considers an
> > > > infinite number of Hilbert spaces describing the inner state of each
> > > > observer's system. The outside of an observer's system is not
> > > > described by Hilbert spaces. Only a part of the outside that is an
> > > > object of an observation is described by a Hilbert space structure.
> > > >
> > > > In LS theory, the phenomena arise by the participation of the
> > > > observer. In this sense, my standpoint is the same as the Wheeler's
> > > > "participatory universe."
> > > >
> > > > The total state \phi of the universe is not considered in a Hilbert
> > > > space. It represents just the state of the total universe, which
> > > > does not evolve. No inner product is considered regarding \phi.
> > >
> > >
> > > Yes. I understand. This resembles the approach of Joel Henkel
> > > to the quantum description of biossystems. He also considers
collection
> > > of Hilbert spaces in his nonunitary QM. I had long discussions with
> > > Joel for some time ago. We found that the decomposition of
> > > Hilbert space to 'pieces' corresponds in TGD to the decomposition
> > > of quantum TGD to padic quantum TGD:s. Breaking of real unitarity
> > > is possible test for Joel's approach as also for TGD
> > > (but for different reasons) and probably any
> > > theory giving up the idea about the quantum state of entire
> > > universe.
> >
> > My theory considers an LS, say L, as being equipped with the Hamiltonian
H_L
> > of L itslef. With respect to this Hamiltonian H_L, the local system L
evolves
> > according to exp(-iH_L) and thus this evolution preserves the unitarity
> > insofar as that local system is the object of observation. Namely an
observed
> > system is always considered as a closed system.
Here t must be considered as the time t_L of the local system L.
> >
> > Breaking of the unitarity when considered in a larger LS, L',
This occurs only if one cosiders the system L as obeying the time t_L' of
the larger system L'. Insofar as the system L is considered obeying its own
time t_L, the breaking of unitairy does not occur.
would occur but
> > it occurs only when the observer could detect the larger system L'.
Unless the
> > observer knows L', he has to assume that the unitarity of the evolution
> > exp(-itH_L) of the system L under consideration holds because his
concerns are
> > not extended beyond the observed system L. In other words, any observer
> > observes an object with assuming the "ideal" unitarity of the observed
> > system's evolution. This is a restatement of the usual assumption in
actual
> > observations/experiments, which is necessary for any theoritical
> > considerations to be possible.
>
>
> In Henkel's theory there are also 'local systems' obeying unitary time
> development. But there is also nonunitary time development.
I think this would occur maybe because he thinks the time as common to all
systems.
> This is related to symmetry breaking. For instance, different vacuum
> expectations of Higgs field or some order parameter would correspond
> to nonequivalent Hilbert spaces and non-unitary time development can
> lead from realization to another. The interaction with surroundings
> somehow induces the nonunitary time development. The weak point of
> Henkel's approach is how to realize this time development concretely.
Does Henkel assume the total universe evolve along with a global time?
>
>
>
> In TGD approach different sectors D_p of configuration space (p prime)
> correspond to quantum theories in different p-adic number fields and
> at first it seems that unitarity is broken down dramatically!
Do you also think the universe evolves along a common time?
> One can however define generalized S-matrix which obeys generalized
> unitarity. S-matrix for transitions leading
> from any D_p1 to D_p is C_p valued.
>
> The restriction of S-matrix to transitions D_p to D_p IS unitary!
> Despite the fact that S-matrix elements D_p to D_p1 , p_1 neq p can
> be nonvanishing!! Sounds highly paradoxical!
>
> The point is that total p-adic probability for transition D_p to D_p1, p_1
> neq p can *vanish*! This is something genuinely p-adic and highly
> paradoxal and nonsensical from the real point of view.
> Therefore p-adic unitarity allows something which
> is not unitary in real context.
I question what necessitates the unitarity. Unitarity is a notion which is
introduced to assist the human reasoning in regards to the understanding of
nature. This is an idealistic notion, which gives us some balance sheets of
probabiltiy as the law of conservation of energy, etc. give. From the
viewpoint that the observer is fundamental that is contrast to your view,
the observer has some implicit assumption about what he sees, without which
he can not make any judgements/estimates about nature. As Einstein has ever
said, we have an image of nature in mind already before we observe nature.
What remains is how the image can be applicable and adjustable to nature.
>
> There is however question of interpretation. One can consider
> counterparts of p-adic probabilities as predictions of theory.
> How the physical situation determines which definition of
> probabilities one must use? The answer to this question
> leads to the concept of monitoring and resolution of monitoring.
>
>
>
> concept of monitoring.
>
>
> a) Elementary particle can have S-matrix for which
> the total *p-adic* decay rate is vanishing. Elementary particle
> for decays to various many particle states can be nonvanishing
> and only their *p-adic* sum vanishes.
>
> b) The interpretation is
> that the p-adic sum of p-adic decay probabilities measures the decay rate
> of elementary particle when the *resolution of monitoring of
> final states is not able to distinguish between final states*.
>
> b) When monitoring is able to distinguish between subspaces
> of final states situation changes. For instance,
> one could be able to measure charges of final state
> particles or measure momenta with some resolution.
> Optimal resolution
> is able to distinguish between all final states.
> The measured decay rate, which is *sum over the real counterparts of
> p-adic decay probabilities* to those subspaces of the Hilbert space of
> final states defined by resolution and is *nonvanishing* in general.
> Breaking of unitarity in real level means that real probabilities
> are not derivable from unitary S-matrix.
>
>
> c) Thus p-adics make possible to avoid the introduction of decay widths
> and complex energies, which are mathematically ugly
> concepts. Elementary particles could be
> stable in absence of monitoring not able to
> resolve between various final states.
>
>
>
>
>
>
>
>
> >
> > [snip]
> >
> > > > > Thus I am proposing many \phi! :)
> > > >
> > > > To each obsevation, there corresponds a proper universe. In this
> > > > sense, there are many \phi, where \phi is used in different meaning
> > > > from the \phi in the above.
> > > >
> > >
> > > Yes. This resembles Henkel's approach.
> >
> > It seems resembling, but I consider a theoretical framework applicable
to the
> > actual situation of observations. Explanation of actual situations seems
> > requiring us/me to assume that there exist many universes which vary in
> > accordance with each observation.
and each observer's time.
> >
>
> Best,
> MP
>
>
Best wishes,
Hitoshi
This archive was generated by hypermail 2.0b3 on Sat Oct 16 1999 - 00:36:05 JST
|
|
anonymous 3 years ago what is double integral function? how to solve double integral function?
1. anonymous
Double Integral: http://mathworld.wolfram.com/FubiniTheorem.html You solve in the order of the integral, if dy comes first, you solve as simple integral considering x as constant, after that, solve the integral for dx.
2. anonymous
is the value of dy similar to the value of dx?
3. anonymous
yes they are similar. when you solve the integral according to dy all x values are constant for you. It doesnt matter which one you solve first, dx or dy.
4. anonymous
ahh..ok tnx..can you teach me how to solve this?i have no background in solving this,, $\int\limits_{0}^{2}\int\limits_{0}^{x ^{2}/2} x/\sqrt{1 + x^2 + y^2} dydx$
5. hartnn
if the limits for both the variables were constant, then we can integrate any variable first., but here since the limits of inner integral is not constant, we need to evaluate the inner integral first, limits are y=0 to y=x^2/2 so, since you are integrating w.r.t 'y', treat x as constant, so you have, $$\int\limits_{0}^{2}x[\int\limits_{0}^{x ^{2}/2} 1/\sqrt{1 + x^2 + y^2} dy]dx$$ now the inner integral is od the form, $$\int \dfrac{1}{\sqrt{a^2+y^2}}dy$$ do you know how to integrate this ?
6. anonymous
why it become a^2?
7. hartnn
i just took 1+x^2 = constant = a^2 because we have a standard integration formula for, $$\int \dfrac{1}{\sqrt{a^2+y^2}}dy$$
8. hartnn
then we need to re-substitute back after integration, a^2= 1+x^2 before integrating w.r.t x
9. hartnn
*after integration w.r.t y,
10. anonymous
in this we are integrating y and we assume as x as constant?
11. anonymous
what do you mean by w.r.t y, ?
12. hartnn
yes, true, so we'll get answer in 'x' after first integrating w.r.t y (with respect to y)
13. hartnn
ok, $$\int \dfrac{1}{\sqrt{a^2+y^2}}dy= (1/a)\arctan(y/a)+c$$ but then you have to use integration by parts to integrate w.r.t x. so, i suggest we better CHANGE the ORDER of integration, that is, we'll change the limits so that we can first integrate w.r.t 'x' and then 'y'. For that, wee need to plot 2 regions (for 2 limits): (1) y= 0 to y=x^2/2 (2) x=0 to x= 2 can you plot these 4 curves (3 of these are simple straight lines)?
14. anonymous
i'm sorry don't know how to plot this..
15. anonymous
i'm sorry i forgot our previous lessons about that..
16. hartnn
so, you say you don't know how to plot lines x=0,y=0,x=2 ? i'll help you with y=x^2/2 but if you don't know how to plot those lines, then it'll be very difficult for you to understand this..
17. anonymous
i know this x=0,y=0,x=2 but i don't know y=x^2/2..i'm sorry
18. hartnn
so, plot these x=0,y=0,x=2 using 'Draw' tool here.
19. anonymous
|dw:1362400369683:dw|
20. anonymous
is it correct?
21. hartnn
where is the line x=2 ?
22. anonymous
|dw:1362400538076:dw|
23. anonymous
sorry i forgot x = 2..
24. hartnn
yes, x=0 is y-axis, y=0 is x axis , and x=2 you have drawn correct, now y= x^2/2 is a parabola which has a plot, |dw:1362400675976:dw| so you are integrating in the region that i am gonna shade
25. anonymous
why it becomes parabola?
26. hartnn
|dw:1362400803859:dw| since we were integrating w.r.t 'y' first, i've drawn vertical lines, now we are changing the order of integration, we need to draw horizontal lines,
27. hartnn
|dw:1362400889186:dw| to |dw:1362400935932:dw|
28. anonymous
i'm sorry i forgot how to find the equation of the line
29. hartnn
oh, its easy, that a horizontal line , so u just need co-ordinates of intersection, which you can find by solving simultaneously, x=2 and x= $$\sqrt{2y}$$
30. hartnn
by the way, did you get that final diagram ?
31. anonymous
not yet..
32. hartnn
which part you have doubt with ?
33. anonymous
$x =2 and x = \sqrt{2y}$ i don't know how to fnd the equation of this line..
34. hartnn
x= 2, x=$$\sqrt{2y}$$ so, 2= $$\sqrt{2y}$$ can u find 'y' from here ?
35. anonymous
no..
36. anonymous
$y=\sqrt{2}/2 ?$
37. hartnn
:O that was simple arithmetic....sorry to say but, if you have problem solving that you should think before dealing double integration, sorry if i am rude, but you are lacking basics ... 2= $$\sqrt{2y}$$ 4= 2y (by squaring) y=2 this is the equation of your horizontal line
38. anonymous
yes that's true i almost forgot the topics about integration that's why i am like this..
39. hartnn
|dw:1362402005207:dw| so your new limits are, $$\huge \int \limits_0^2\int \limits_{\sqrt{2y}}^2\dfrac{x}{\sqrt{1+x^2+y^2}}dx.dy$$ now you have to first integrate w.r.t x to do that put u = 1+x^2+y^2 du=... ?
40. anonymous
du = 2x + 2y
41. hartnn
oh, since we are integrating w.r.t 'x' first now, we treat 'y' as constant, so du =2xdx or x dx = du/2 got this ?
42. anonymous
yes..
43. hartnn
so, your inner integral will become, $$\int \dfrac{du}{2\sqrt u}$$ can you integarte this ?
44. anonymous
1/2..is it correct?
45. amistre64
as long as weve gotten this u substitution correct: $\int \frac{1}{2\sqrt{u}}du=\sqrt{u}$
46. amistre64
assuming that u = 1+x^2+y^2, plug back in for u $\sqrt{ u}=\sqrt{ 1+x^2+y^2}$ from x=sqrt(2y) to 2 $\sqrt{ 1+2^2+y^2}-\sqrt{ 1+(\sqrt{2y})^2+y^2}$ $\sqrt{ 5+y^2}-\sqrt{ 1+2y+y^2}$
47. amistre64
y^2+2y+1 = (y+1)^2 sooo $\int\sqrt{5+y^2}-(y+1)~dy$
48. anonymous
why it becomes subtraction?
49. anonymous
why it become y^2+2y+1 = (y+1)^2 ?
50. amistre64
because: $$\Large \int_{a}^{b} f(x)~dx=F(b)-F(a)$$
51. anonymous
ah ok tnx..
52. anonymous
in this time we are integrating y?
53. amistre64
when we replace the $$\sqrt{u}$$ with what we defined it to begin with: $$u=1+x^2+y^2$$ and input the ab limits of a=$$\sqrt{2y}$$ and b=2 we get $(\sqrt{1+b^2+y^2})-(\sqrt{1+a^2+y^2})$ $(\sqrt{1+b^2+y^2})-(\sqrt{1+a^2+y^2})$ and yes, then since we are finished with the inside integral, we focus on the next integral
54. anonymous
what's next?
55. amistre64
the next integration is next ... $\int\sqrt{5+y^2}-(y+1)~dy$
56. anonymous
$\sqrt{5 + y} - y$
57. anonymous
is it correct?i'm sorry have a problem in integration..
58. amistre64
the square root part seems a little off to me
59. amistre64
and it looks like you tried a derivative onthe y+1 parts instead of integeration
60. amistre64
$-\int y+1~dy=-(\frac{y^2}{2}+y)$
61. anonymous
yes.. i'm sorry a have a problem in integration..
62. anonymous
why is that u not integrate $\sqrt{5 + y^2}$?
63. amistre64
i did not integrate it because I want you to work it out. you are the one that needs the practice at it :)
64. amistre64
if you cant see the integration right off hand, try the "table" method ... which is simply looking up the integral in a table of integrals: look for $$\sqrt{a^2+x^2}$$
65. anonymous
ah.. wat is this $\sqrt{a^2 + x^2}$? how will i use this?
66. amistre64
i looked it up in a table, just to be sure. Look at #30
67. amistre64
a^2 = 5, and x = y
68. amistre64
$\int \sqrt{5+y^2}dy=\frac12y\sqrt{5+y^2}+\frac12 5^2ln(y+\sqrt{5+y^2})$from y=0 to y=2
69. amistre64
the 5^2 ln part is a typo; just 5 ln ...
70. anonymous
$y/2 \sqrt{5 + y^2} + 5/2 \ln (y + \sqrt{5 + y^2}$
71. amistre64
yes
72. anonymous
what's next?
73. amistre64
plug in the values of your limit to determine the values
74. amistre64
$(3+\frac52 ln(5))-(\frac54ln(5))-4$ the -4 is from the simpler part we did earlier
75. amistre64
with any luck this simplifies to:$\frac54ln(5)-1$
76. anonymous
is this the answer? why -4 ?
77. amistre64
$\int\sqrt{5+y^2}-(y+1)~dy$ $\int\sqrt{5+y^2}dy-\int y+1~dy$ $\int\sqrt{5+y^2}dy-(\frac12y^2+y)$ and since y=0 to 2 $\int\sqrt{5+y^2}dy-4$
78. amistre64
i cant verify the steps taken to swap the limits from dy dx to dx dy at the moment, but assuming that was done correctly .... we have come to the end of it
79. anonymous
80. amistre64
81. anonymous
i'm sorry..i don't understand it. it's a little bit difficult... :(
82. amistre64
the hardest part was not the y^2/2+y ... that just equals -4 we worked thru the sqrt(5+y^2) from the table, and inputted the limit values to get: $\frac54ln(5)-4$as a final result, assuming the swapping of dydx to dxdy was correct to begin with
83. anonymous
i must study first and review about integral in order for me to understand this..
84. amistre64
good luck :)
85. anonymous
|
|
Stories pertaining to Magnetic Resonance, Chemistry, Programming, and Life
### Hard and Soft Linking in Linux
Sometimes it’s nice to have files accessible from more than one location on your computer, but to only actually have one copy of the file (it can save on drive space for really big files!). An example of where I have needed this most, actually, has been with the use of Dropbox on my laptop. Many times I’ve been working out of a folder somewhere on my computer and I’ve needed to make the files accessible to other computers in the research lab. I’ve had to physically copy and paste these directories to my Dropbox folder (or usb drive, before I discovered Dropbox) and then once all the edits had been made elsewhere, had to copy and paste them back to where they belong. If, however, I could place a link to the files in my Dropbox folder, both copy and paste steps could be avoided (as well as the simultaneous confusion of which files were updated, and in what order etc.).
In linux systems this “linking” process is called “symlinking” (softlinking) or “hardlinking.” The difference between the two is a little subtle and can be understood in that unix files have two parts the “file header” (which includes the name) and the “data” part. The header part contains the file name, permissions, etc, and also contains an inode number. This inode number is like the data part’s address on the hard drive…and points/associates the file name to the data it contains. One way to think about it is through this schematic:
You can imagine that linking to the file can be accomplished through one of two methods. One method is to simply have two filenames associated with the same inode. These two filenames (file header information) can reside in different physical locations on the hard disk and thus in two different locations in your folder tree of your computer. This process is called “hardlinking” and looks like this:
Hardlinking is great. If you delete filename1, filename2 still has the data stored in itself even though the file was originally created with filename1. Dropbox supports this linking feature. The only drawback to this kind of linking is that the link literally looks like and feels like the file in any file system–you can’t really tell the difference. So you better remember what was supposed to be the link! The filename doesn’t show up as a link because it has the same properties as a normal file… file header information (stored in the filename1, including the inode number), which links to the data.
Through command line, the way you create one of these hardlinks is through the following command:
Now, the other way of linking files is a literal link: its a special unique file that has a file header portion with an inode link, but instead of that inode pointing straight to the file data inode, it points to the inode of its own file within which contains a “link” to the file you’re linking too. It’s much like a shortcut in Windows…and this is called soft-linking, or forming a symbolic link or “symlink.” It works in the following manner:
Obviously that “to.txt” file is the file header information that contains the inode number of where the data actually resides…so soft links are literally a special file that points to another file and the operating system treats it as such…its obvious that its a link and if you delete the symlink it just no longer points to the file anymore. And if you delete the original file and the symlink still links to it, the data is lost…it is not kept.
To access this kind of linking in the command line, you run the following command:
Notice how I dropped the file extension off of the name of the link…you can do that because it is its own type of file that just points to the real thing. Dropbox also supports this kind of file linking. And it comes in handy particularly if you want the file to show up as a symlink.
Now you might be asking yourself why bother with the soft linking if hard linking works so well? The answer might be baffling: all directories in unix/linux systems are soft links that contain a name and point to a data file that contains all the file header information location of all the files associated with that directory. I mean, what are folders anyways? They aren’t “files” in that they don’t have data intrinsic to themselves. But they are “containers” that tell you what is associated with them. Brilliant? Yes. Immediately intuitive? No.
So a “directory” or “folder” has its own file header information which points to an inode number that contains all the addresses of all the files associated with itself. When you go to one of these addresses of the contained files you get pointed to the inode that contains all the data associated with that file. That’s how folders work–and if you want to use a symlink to point to a directory, you have to add a special flag to the linking command:
Of course, you can also hardlink a directory, then the code would just be:
I think I mostly use symlinking so I remember its a link and not the actual file, but I’m very appreciative that Dropbox supports this option. Makes changing files in different directories on my computer remotely very easy to do!
### Attenuation and dB’s
It’s easy to not understand NMR verbiage. One second we talk about signal processing on the computer using terms like “apodization” and “digital filters,” but most spectrometers still do a lot of signal processing before the signal ever reaches the computer. That is, the signal is amplified, filtered, converted, and digitized before it ever reaches the user interface. This means that a lot must go right before it reaches the computer for you to have any intelligible signal whatsoever.
Of course, there’s also the electronics that prepare the pulse before the NMR signal is measured as well. That is, we have the pulse generator, and then pulse processor, followed by an amplifier that amplifies the signal to tens or even thousands of watts of power.
At both this transmitting end and at the receiving end, there’s a way to control how much power is going out and how much power is coming back in. These controllers that control the outgoing and incoming signal are called attenuators, and they have the special properties of reducing the signal power and not altering the signal in any other way. In a sense, you can think of an attenuator as an “amplifier” that “amplifies” the signal to a power less than one, that is amplifying to a power of something like .1, .5, etc.
Attenuators typically measure this reduction of signal in a unit called dB’s, or decibels. Decibels are an interesting and not immediately intuitive logarithmic unit derived by early telephone engineers seeking to define signal loss over different lengths of wires. The “bel,” named after the inventor of the telephone, Alexander Graham Bell, is ten decibels, and was equal to ten of the “Transmission Units” (or “TU”) in common use by engineers in the Bell Telephone company. A “TU” was defined as “ten times the base-10 logarithm of the ratio of the measured power over a reference power.”
We’re familiar with dB’s from the measurement of sound volume, where 0 dB’s is considered the threshold of hearing and 30 dB’s is like a quiet bedroom at night. Conversational speech at about 1m is 60 dB’s, a busy road about 80 dB’s, a chainsaw about 110 dB’s, and discomfort beginning at about 120 dB’s. It’s an exponential scale as the growth of sound power isn’t linear in the least. Going from 0-60 dB’s is not painful at all. But going from 100-160 dB’s could result in partial loss of hearing.
When the attenuator decreases the “volume” of the waveform in the NMR spectrometer, it does so by a special arrangement of resistors that decrease the amplitude of the waveform. This amplitude of the signal is, of course, the voltage. So attenuating the waveform attenuates the amplitude of the wave, and it does this by a series of resistors carefully arranged to attenuate at just the precisely chosen dB value.
Of course, attenuation is attenuating the power (which is proportional to the amplitude) and not the amplitude directly. How is the power related to the amplitude? Well, power in watts, is:
$P = \frac{V^2}{R}$
Thus, a change of the power in terms of dB’s is related to the change of voltage squared.
So, as already eluded to, the mathematical description of dB’s in terms of power is:
$-x\text{dBs} = 10 log_{10}(\frac{P_1}{P_0})$
I’ve written it with a negative sign in front of the x dB’s. This is because we’re using the equation in terms of attenuation, not boosting. The way to think about this is we’re “taking away” dB’s from the system, thus we have to include the negative sign. Now, if we want to write it in terms of voltage, we have to substitute:
$P \propto V^2$
And thus get:
$-x \text{dBs} = 10 log_{10}(\frac{V^2_1}{V^2_0})$
Or, simplified:
$-x \text{dBs} = 20 log_{10}(\frac{V_1}{V_0})$
In general, we use the above to calculate how much attenuation we get when we apply a certain number of dB’s of attenuation. It can be rearranged in the following form:
$V_1 = V_0 10^{\frac{-x \text{dBs}}{20}}$
One might ask why we would use dB’s for attenuation in NMR at all. The short answer is that when processing and receiving signal we sometimes need to span many orders of magnitude. Say we have a dense sample of water that we are doing 1H NMR on. That’s a huge signal compared to 13C NMR…and sometimes many orders of magnitude apart. dB’s are a good choice of scale in this kind of situation because you can throttle signal (or boost it) from as little as 1/1000% to its full scale.
|
|
Under the auspices of the Computational Complexity Foundation (CCF)
REPORTS > KEYWORD > MERGERS:
Reports tagged with mergers:
TR05-025 | 20th February 2005
Zeev Dvir, Ran Raz
#### Analyzing Linear Mergers
Mergers are functions that transform k (possibly dependent)
random sources into a single random source, in a way that ensures
that if one of the input sources has min-entropy rate $\delta$
then the output has min-entropy rate close to $\delta$. Mergers
have proven to be a very useful tool in ... more >>>
TR05-067 | 28th June 2005
Zeev Dvir, Amir Shpilka
#### An Improved Analysis of Mergers
Mergers are functions that transform k (possibly dependent) random sources into a single random source, in a way that ensures that if one of the input sources has min-entropy rate $\delta$ then the output has min-entropy rate close to $\delta$. Mergers have proven to be a very useful tool in ... more >>>
TR08-058 | 1st June 2008
Zeev Dvir, Avi Wigderson
#### Kakeya sets, new mergers and old extractors
A merger is a probabilistic procedure which extracts the
randomness out of any (arbitrarily correlated) set of random
variables, as long as one of them is uniform. Our main result is
an efficient, simple, optimal (to constant factors) merger, which,
for $k$ random vairables on $n$ bits each, uses a ... more >>>
TR09-077 | 16th September 2009
Zeev Dvir
#### From Randomness Extraction to Rotating Needles
The finite field Kakeya problem deals with the way lines in different directions can overlap in a vector space over a finite field. This problem came up in the study of certain Euclidean problems and, independently, in the search for explicit randomness extractors. We survey recent progress on this problem ... more >>>
TR15-038 | 11th March 2015
Gil Cohen
#### Local Correlation Breakers and Applications to Three-Source Extractors and Mergers
Revisions: 1
We introduce and construct a pseudorandom object which we call a local correlation breaker (LCB). Informally speaking, an LCB is a function that gets as input a sequence of $r$ (arbitrarily correlated) random variables and an independent weak-source. The output of the LCB is a sequence of $r$ random variables ... more >>>
ISSN 1433-8092 | Imprint
|
|
# Differential Equation, DE
## Eliminate the Arbitrary Constants
Please do leave a solution so I can study it, thank you!
Obtain the differential equation by eliminating the arbitrary constants.
1. Cxsiny+x^(2)y=Cy
2. y=Ae^(-3x)-Be^(2x)+Cx^3
3. Ay=e^(Bx^2)
## Differential Equation: $y' = x^3 - 2xy$, where $y(1)=1$ and $y' = 2(2x-y)$ that passes through (0,1)
Can anyone solve this D. E.?
y' = x^3 - 2xy, where y(1)=1
and
y' = 2(2x-y) that passes through (0,1)
## Help please: $(1+e^x y+x e^x y) dx + (x e^x + 2) dy=0$
(1+e^(x) y+x e^(x) y) dx + (x e^(x) + 2) dy=0
## Arbitrary constant
y=x^2+C1e^2x+C2e^3x
Thank you again
## Families of Curves: family of circles with center on the line y= -x and passing through the origin
Find the diff equation of family of circles with center on the line y= -x and passing through the origin.
THANK YOU :)
## DE: $(x²+4) y' + 3 xy = x$
(x²+4) y' + 3 xy = x
## Differential Equations: $(r - 3s - 7) dr = (2r - 4s - 10) ds$
The topic is Additional Topics in Ordinary DE of the first order.
(r-3s-7)dr=(2r-4s-10)ds
## Differential Equations: $(x - 2y - 1) dy = (2x - 4y - 5) dx$
Coefficient Linear in Two Variables? Help please.
(x-2y-1)dy=(2x-4y-5)dx
## DIIFERENTIAL EQUATION: $(x^2 + y^2) dx + x (3x^2 - 5y^2) dy = 0$
( x^2 + y^2 ) dx + x (3x^2 - 5y^2 ) dy = 0
## Differential EQNS: $y \, dx = \left[ x + (y^2 - x^2)^{1/2} \right] dy$
ydx = x + √ y^2 - x^2 dy
|
|
Power Series Expansion for Hyperbolic Cosine Function
Theorem
$\displaystyle \cosh x$ $=$ $\displaystyle \sum_{n \mathop = 0}^\infty \frac {x^{2 n} } {\left({2 n}\right)!}$ $\displaystyle$ $=$ $\displaystyle 1 + \frac {x^2} {2!} + \frac {x^4} {4!} + \frac {x^6} {6!} + \cdots$
valid for all $x \in \R$.
Proof
$\dfrac \d {\d x} \cosh x = \sinh x$
$\dfrac \d {\d x} \sinh x = \cosh x$
Hence:
$\dfrac {\d^2} {\d x^2} \cosh x = \cosh x$
and so for all $m \in \N$:
$\displaystyle m = 2 k: \ \$ $\displaystyle \dfrac {\d^m} {\d x^m} \cosh x$ $=$ $\displaystyle \cosh x$ $\displaystyle m = 2 k + 1: \ \$ $\displaystyle \dfrac {\d^m} {\d x^m} \cosh x$ $=$ $\displaystyle \sinh x$
where $k \in \Z$.
This leads to the Maclaurin series expansion:
$\displaystyle \cosh x$ $=$ $\displaystyle \sum_{r \mathop = 0}^\infty \left({\frac {x^{2 k} } {\left({2 k}\right)!} \cosh \left({0}\right) + \frac {x^{2 k + 1} } {\left({2 k + 1}\right)!} \sinh \left({0}\right)}\right)$ $\displaystyle$ $=$ $\displaystyle \sum_{r \mathop = 0}^\infty \frac {x^{2 k} } {\left({2 k}\right)!}$ $\sinh \left({0}\right) = 0$, $\cosh \left({0}\right) = 1$
From Series of Power over Factorial Converges, it follows that this series is convergent for all $x$.
$\blacksquare$
|
|
# Math Help - Curl of a vector field: good remembering technique
1. ## Curl of a vector field: good remembering technique
We all know that $\text{curl} \ \bold{F} = \left(\frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z} \right) \bold{i} + \left(\frac{\partial P}{\partial z} - \frac{\partial R}{\partial x} \right) \bold{j} + \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) \bold{k}$.
Here is a good technique to remember this:
Write down $P, Q, R$.
Put your left index finger on $R$. Now put your left middle finger on $Q$. Then go the opposite direction (like playing the piano). This is the first term. Do the same for the other terms. Keep playing this (as if you were playing the piano).
This is how I remember $\text{curl} \ \bold{F}$.
2. Originally Posted by shilz222
We all know that $\text{curl} \ \bold{F} = \left(\frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z} \right) \bold{i} + \left(\frac{\partial P}{\partial z} - \frac{\partial R}{\partial x} \right) \bold{j} + \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) \bold{k}$.
Here is a good technique to remember this:
Write down $P, Q, R$.
Put your left index finger on $R$. Now put your left middle finger on $Q$. Then go the opposite direction (like playing the piano). This is the first term. Do the same for the other terms. Keep playing this (as if you were playing the piano).
This is how I remember $\text{curl} \ \bold{F}$.
i don't think i get your technique...
like almost everyone else, i remember curlF by $\mbox{curl} \bold{F} = \nabla \times \bold{F}$
where $\bold{F} = \left< P, Q, R \right>$ and $\nabla = \left< \frac {\partial}{\partial x}, \frac {\partial}{\partial y}, \frac {\partial}{\partial z} \right>$
3. Its like playing the piano. Let your index finger, your middle finger, and your crown finger (left hand) represent $R,Q,P$ respectively. Tap your index finger, then tap your middle finger. Then do the opposite. Now tap your crown finger, then tap your index finger. Now do the opposite. Now tap your middle finger, then tap your crown finger. Now do the opposite. Keep "practicing" this.
So we have: P Q R
4. I practiced it on the piano. I called it the "curl" piece. Choose 3 piano keys, and let them represent $P, Q, R$.
5. Actually this is also a good method of remembering anything involving cross products (that way you do not have to do the calculation).
6. Why not just use determinants? If you start playing the paino during an exam it will look a little strange.
7. I've always found that proctoring an Intro Physics test just after mid-semester is rather fun. The students have hit the cross-product by then and during the exam they're pulling their tendons and writhing around in their seats trying to apply the right hand rule to figure out the direction.
(Okay, so what if I'm a sadist? )
-Dan
8. $\begin{array}{l}
\nabla = \left\langle {\partial x,\partial y,\partial z} \right\rangle \\
curl(F) = \nabla \times F = \left| {\begin{array}{*{20}c}
i & j & k \\
{\partial x} & {\partial y} & {\partial z} \\
P & Q & R \\
\end{array}} \right| \\
\end{array}$
9. Yes I know thats the conventional way of doing it. TPH, I don't mean actually playing the piano. I mean tapping on the desk. Your speed of calculating the curl will improve a lot (at least it did for me).
10. Originally Posted by shilz222
Yes I know thats the conventional way of doing it. TPH, I don't mean actually playing the piano. I mean tapping on the desk. Your speed of calculating the curl will improve a lot (at least it did for me).
i get what you are saying now. your method helps you to know the positions of P,Q and R. but how do you remember the positions of the partial derivatives with this method? some sort of triangle perhaps? or just y --> z --> x --> y?
11. Ok you have $P, Q, R$ written down. Put your index finger (left hand) on $R$ and your middle finger on $Q$. Thats $\frac{\partial R}{\partial y}$. Note that the middle finger is on $Q$ which corresponds to $y$. Now tap your middle finger on $Q$ and your index finger on $R$. That's $\frac{\partial Q}{\partial z}$.
So our first term is: $\frac{\partial R}{\partial y} - \frac{\partial R}{\partial y}$. Keep doing this.
|
|
# sin
## Syntax
``Y = sin(X)``
## Description
example
````Y = sin(X)` returns the sine of the elements of `X`. The `sin` function operates element-wise on arrays. The function accepts both real and complex inputs. For real values of `X`, `sin(X)` returns real values in the interval [-1, 1].For complex values of `X`, `sin(X)` returns complex values. ```
## Examples
collapse all
Plot the sine function over the domain $-\pi \le x\le \pi$.
```x = -pi:0.01:pi; plot(x,sin(x)), grid on```
Calculate the sine of the complex angles in vector `x`.
```x = [-i pi+i*pi/2 -1+i*4]; y = sin(x)```
```y = 1×3 complex 0.0000 - 1.1752i 0.0000 - 2.3013i -22.9791 +14.7448i ```
## Input Arguments
collapse all
Input angle in radians, specified as a scalar, vector, matrix, multidimensional array, table, or timetable.
Data Types: `single` | `double` | `table` | `timetable`
Complex Number Support: Yes
## Output Arguments
collapse all
Sine of input angle, returned as a real-valued or complex-valued scalar, vector, matrix, multidimensional array, table, or timetable.
collapse all
### Sine Function
The sine of an angle, α, defined with reference to a right triangle is
The sine of a complex argument, α, is
`$\mathrm{sin}\left(\alpha \right)=\frac{{e}^{i\alpha }-{e}^{-i\alpha }}{2i}\text{\hspace{0.17em}}.$`
## Tips
• To compute `sin(X*pi)` accurately, without using `pi` as a floating-point approximation of π, you can use the `sinpi` function instead. For example, `sinpi(n)` is exactly zero for integers `n` and `sinpi(m/2)` is +1 or –1 for odd integers `m`.
## Version History
Introduced before R2006a
expand all
|
|
## Unit11.3.3Jacobi's method for computing the Singular Value Decomposition
Just like the QR algorithm for computing the Spectral Decomposition was modified to compute the SVD, so can the Jacobi Method for computing the Spectral Decomposition.
The insight is very simple. Let $A \in \mathbb R^{m \times n}$ and partition it by columns:
\begin{equation*} A = \left( \begin{array}{c | c | c | c} a_0 \amp a_1 \amp \cdots \amp a_{n-1} \end{array} \right). \end{equation*}
One could form $B = A^T A$ and then compute Jacobi rotations to diagonalize it:
\begin{equation*} \begin{array}[t]{c} \underbrace{ \cdots J_{3,1}^T J_{2,1}^T } \\ Q^T \end{array} B \begin{array}[t]{c} \underbrace{ J_{2,1} J_{3,1} \cdots } \\ Q \end{array} = D. \end{equation*}
We recall that if we order the columns of $Q$ and diagonal elements of $D$ appropriately, then choosing $V = Q$ and $\Sigma = D^{1/2}$ yields
\begin{equation*} A = U \Sigma V^T = U D^{1/2} Q^T \end{equation*}
or, equivalently,
\begin{equation*} A Q = U \Sigma = U D^{1/2}. \end{equation*}
This means that if we apply the Jacobi rotations $J_{2,1}, J_{3,1}, \ldots$ from the right to $A \text{,}$
\begin{equation*} U D^{1/2} = ( ( A J_{2,1} ) J_{3,1} ) \cdots, \end{equation*}
then, once $B$ has become (approximately) diagonal, the columns of $\widehat A = ( ( A J_{2,1} ) J_{3,1} ) \cdots$ are mutually orthogonal. By scaling them to have length one, setting $\Sigma = \diag{ \| \widehat a_0 \|_2, \| \widehat a_1 \|_2, \ldots , \| \widehat a_{n-1} \|_2} \text{,}$ we find that
\begin{equation*} U = \widehat A \Sigma^{-1} = A Q (D^{1/2})^{-1}. \end{equation*}
The only problem is that in forming $B \text{,}$ we may introduce unnecessary error since it squares the condition number.
Here is a more practical algorithm. We notice that
\begin{equation*} B = A^T A = \left( \begin{array}{c c c c} a_0^T a_0 \amp a_0^T a_1 \amp \cdots \amp a_0^T a_{n-1} \\ a_1^T a_0 \amp a_1^T a_1 \amp \cdots \amp a_1^T a_{n-1} \\ \vdots \amp \vdots \amp \amp \vdots \\ a_{n-1}^T a_0 \amp a_{n-1}^T a_1 \amp \cdots \amp a_{n-1}^T a_{n-1} \end{array} \right). \end{equation*}
We observe that we don't need to form all of $B \text{.}$ When it is time to compute $J_{i,j} \text{,}$ we need only compute
\begin{equation*} \left( \begin{array}{cc} \beta_{i,i} \amp \beta_{j,i} \\ \beta_{j,i} \amp \beta_{j,j} \end{array}\right) = \left( \begin{array}{cc} a_i^T a_i \amp a_j^T a_i \\ a_j^T a_i \amp a_j^T a_j \end{array}\right) , \end{equation*}
from which $J_{i,j}$ can be computed. By instead applying this Jacobi rotation to $B \text{,}$ we observe that
\begin{equation*} J_{i,j}^T B J_{i,j} = J_{i,j}^T A^T A J_{i,j} = ( A J_{i,j} )^T ( A J_{i,j} ) \end{equation*}
and hence the Jacobi rotation can instead be used to take linear combinations of the $i$th and $j$th columns of $A \text{:}$
\begin{equation*} \left( \begin{array}{c | c} a_i \amp a_j \end{array} \right) := \left( \begin{array}{c | c} a_i \amp a_j \end{array} \right) \left( \begin{array}{c c} \gamma_{i,j} \amp -\sigma_{i,j} \\ \sigma_{i,j} \amp \gamma_{i,j} \end{array} \right) . \end{equation*}
We have thus outlined an algorithm:
• Starting with matrix $A \text{,}$ compute a sequence of Jacobi rotations (e.g., corresponding to a column-cyclic Jacobi method) until the off-diagonal elements of $A^T A$ (parts of which are formed as Jacobi rotations are computed) become small. Every time a Jacobi rotation is computed, it updates the appropriate columns of $A \text{.}$
• Accumulate the Jacobi rotations into matrix $V \text{,}$ by applying them from the right to an identity matrix:
\begin{equation*} V = (( I \times J_{2,1}) J_{3,1} ) \cdots \end{equation*}
• Upon completion,
\begin{equation*} \Sigma = \diag{ \| a_0 \|_2, \| a_1 \|_2, \ldots , \| a_{n-1} \|_2} \end{equation*}
and
\begin{equation*} U = A \Sigma^{-1}, \end{equation*}
meaning that each column of the updated $A$ is divided by its length.
• If necessary, reorder the columns of $U$ and $V$ and the diagonal elements of $\Sigma \text{.}$
Obviously, there are variations on this theme. Such methods are known as one-sided Jacobi methods.
|
|
# 1 Ph PS= Ph Ph Ph PS Ph Ph
###### Question:
1 Ph PS= Ph Ph Ph PS Ph Ph
#### Similar Solved Questions
##### A major coffee supplier has warehouses in Seattle and San Jose. The coffee supplier receives orders...
A major coffee supplier has warehouses in Seattle and San Jose. The coffee supplier receives orders from coffee retailers in Salt Lake City and Reno. The retailer in Salt Lake City needs 500 pounds of coffee, and the retailer in Reno needs 450 pounds of coffee. The Seattle warehouse has 900 pounds a...
##### I Caleulat mdar.concentration of acetic acid (CH3 COOH in 35.00% vinegar 5100% solution of acetic acid...
I Caleulat mdar.concentration of acetic acid (CH3 COOH in 35.00% vinegar 5100% solution of acetic acid inutter Density of the vinegar is 1.080/mL. Isemolar mass of acetic acidas 60.05 g/mol. Show your work to gethulleredit....
##### Find the equation of the line tangent to the graph of f(x) = (Inx)? atx=6. y Please provide answer to this (Type your answer in slope-intercept form: Do not round until the final answer: Then round to two decimal places as needed.)Find the equation of the line tangent to the graph of f(x) = (Inx)5 atx=6. y = 8.59x 33.07 THIS IS AN EXAMPLE ANSWER Type your answer in slope-intercept form: Do not round until the final answer: Then round to two decimal places as needed )
Find the equation of the line tangent to the graph of f(x) = (Inx)? atx=6. y Please provide answer to this (Type your answer in slope-intercept form: Do not round until the final answer: Then round to two decimal places as needed.) Find the equation of the line tangent to the graph of f(x) = (Inx)5 ...
##### Let f(x)=x2 if x≤1,2-x if x>1Evaluate2,0f(x) dx
Let f(x)= x2 if x≤1, 2-x if x>1 Evaluate2,0 f(x) dx...
##### Metro by T-Mobile LTE5.13 PM50%MATH 76 Activity 11.pdfDetermine whether the following alternating series converges OF diverges. (~l)k 2 R-(~k+l +4 28 + [28FDashboardCalendarTo DoNotificationsInboxEo-1)ke-*
Metro by T-Mobile LTE 5.13 PM 50% MATH 76 Activity 11.pdf Determine whether the following alternating series converges OF diverges. (~l)k 2 R- (~k+l +4 28 + [ 28F Dashboard Calendar To Do Notifications Inbox Eo-1)ke-*...
##### We were unable to transcribe this imageWe were unable to transcribe this imagethe figure, find the...
We were unable to transcribe this imageWe were unable to transcribe this imagethe figure, find the force person is halfway up the a) using the dimensions given in exerted on the ladder when the ladder. f. , f2, F3 = ? KN 6) Find the forces exerted on the ladder when the person is 3 ths of the way up...
##### At a resting pulse rate of 77 beats per minute, the human heart typically pumps about...
At a resting pulse rate of 77 beats per minute, the human heart typically pumps about 71 mL of blood per beat. Blood has a density of 1060 kg/m3. Circulating all of the blood in the body through the heart takes about 1 min for a person at rest. Approximately how much blood is in the body? volume of ...
|
|
# Daily Research Log 2014-4-17
Write
• Plan for program
• Begin by writing a two step algorithm, where L is always fixed, H and F are updated iteratively.
# Daily Research Log 2014-4-16
• Iterative method, pdf
• Linear system
• Vector
• Spectral radius & converge rate
# Daily Research Log 2014-4-15
• A Taxonomy and Evaluation of Dense Two-Frame Stereo Correspondence Algorithms
Daniel Scharstein, Middlebury College, ICCV
• Review, Taxonomy and Evaluation
• Mainly two-frame stereo, multi frame dataset given later
• Efficient Large-Scale Stereo Matching, A. Geiger, ACCV2010
• This paper focuses on the efficiency
• The crucial point of stereo vision is matching
• Review part of this work divides the previous work on stereo vision into global matching, semi-global matching and local matching
# Write
• Edited proposal, added comparison between our problem, SfM, stereo vision
# Being mistook as competitor by a 3D printing service provider
Today is a remarkable day. When I was negotiating with a 3D printing service provider, he mistook me as a competitor.
I think that's because I was talking too much like a pro.
Before this I was in belief that behaving like a pro does all good in business interactions.
# Daily Research Log 2014-4-10
• Wide Baseline Stereo Matching based on Local , Affinely Invariant Regions, Tuytelaars, BMVC2000
• Get affine invariant regions, descriptors, and match
• Method
• Extract region by local intensity extrema
• Get ellipse fitting by 2nd order momentum, extend the ellipse
• Get descriptor by invariants of moment
# Write
• Slides for research proposal
Notations: $I$ for set of pixels, $S^r$, $S^t$ for set of segmentation in reference and target images, $P^r$, $P^t$ for set of anchor points in both images, $H$ for set of local homographies defined on segments, $F$ for set of anchor points matching.
Definations:
$\mathcal{H}: C\rightarrow \mathbb{R}^{3\times 3}$,
$\mathcal{L}^x: P^x\rightarrow S^x$,
$\mathcal{F}: P^t\leftrightarrow P^r$,
Problem formulation:
$\mathcal{L}^t, \mathcal{L}^r, \mathcal{H}, \mathcal{F} = \underset{\mathcal{L}^t, \mathcal{L}^r, \mathcal{H}, \mathcal{F}}{\arg \min} E(\mathcal{L}^t, \mathcal{L}^r, \mathcal{H}, \mathcal{F})$
# PenPal Projector Project
Pretty tricky name indicates a pretty tricky project
# Overview
PenPal is a pen that enables you to write in the air and laser-print the message on the wall from another one. It's only a design now and a proof-of-concept demo available.
The system uses a vector laser projector so it can be used in any situation, on any surface and in any lighting conditions.
Most importantly, it looks cool.
# Hardware Setup
• 3rd party
• Input
• Leapmotion
• Mini mouse
• Output
• Laser
• Oscillating laser mirror
• The mirrors are driven by a pair of servo motors. We bought the device from Taobao.
• Wave generator
• Arduino
• We tried this at the very beginning. However it turned out that plain API calling could be very sluggish hence the degenerated laser shape. Though it can be solved by calling the basic level API of Arduino, we have to spend a lot of time on it. So we aborted this plan
• PC sound card
• The PC seems to be almighty. With a sound API we can manipulate the sound card easily and use it as an arbitrary function generator
# Software
• Design
• AI
• SVG exporter
• Output
• Python, pyaudio
• Stream control
There are two ways of manipulating the stream: write & block, callback. To achieve desired effect, we have to use callback since the wave form changes in real-time.
To manipulate the stream, we have to write binary float data into the buffer. This answer@SO should be helpful in doing this. (http://stackoverflow.com/a/22644499/1921437).
• Core code as follows
import pyaudio
import wave
import time
import sys
import numpy as np
RATE = 44100
def decode(in_data, channels):
"""
Convert a byte stream into a 2D numpy array with
shape (chunk_size, channels)
Samples are interleaved, so for a stereo stream with left channel
of [L0, L1, L2, ...] and right channel of [R0, R1, R2, ...], the output
is ordered as [L0, R0, L1, R1, ...]
"""
# TODO: handle data type as parameter, convert between pyaudio/numpy types
result = np.fromstring(in_data, dtype=np.float32)
chunk_length = len(result) / channels
assert chunk_length == int(chunk_length)
result = np.reshape(result, (chunk_length, channels))
return result
def encode(signal):
"""
Convert a 2D numpy array into a byte stream for PyAudio
Signal should be a numpy array with shape (chunk_size, channels)
"""
interleaved = signal.flatten()
# TODO: handle data type as parameter, convert between pyaudio/numpy types
out_data = interleaved.astype(np.float32).tostring()
return out_data
p = pyaudio.PyAudio()
pt = 0
def callback(in_data, frame_count, time_info, status):
global pt
wave = np.ndarray((frame_count, 2))
for i in range(frame_count):
wave[i,0] = float((i+pt) % 100) / 100
wave[i,1] = float((i+pt) % 80) / 100
pt = pt + frame_count
print pt
print wave
return (encode(wave), pyaudio.paContinue)
stream = p.open(format=pyaudio.paFloat32,
channels=2,
rate=RATE,
output=True,
stream_callback=callback)
stream.start_stream()
while stream.is_active():
time.sleep(0.1)
stream.stop_stream()
stream.close()
wf.close()
p.terminate()
# Tuning
• The laser mirror is not perfect in terms of temporal response, which means a pulse in the input signal will not result in a sharp pulse in the projected shape. To tune this, the most fundamental way is to tune the PID coefficients of the servo mirror system. However, this seems to be time-consuming. So we decided to make a compromise by decreasing the frequency of the projector.
• One of the most important parameters responsible for the quality of the shape should be the projector frequency. When the frequency is decreased, the system response becomes better. However this shall result in a low fresh-rate, or a less complex shape as a trade off. No free lunch.
# Goal
Literature review for my "match & map" project
• Efficient Large-Scale Stereo Matching, A. Geiger, Urtasun
• The blurry image of generating right observation comes from
• Here d_n is generated by sampling from this distribution function
• This method probably won't work on a wide-baseline stereo vision dataset since the following reason
• If the triangulation is dense, large displacement and distortion of support points across two views will ruin the triangulation
• If the triangulation is sparse, it won't be able to cope with complex scene
# Todo
• Review papers citing Wide baseline stereo matching, P Pritchett, A Zisserman, ICCV'1998
• Run Geiger's work
• Write project proposal
• Desired result
• On Middleburry Benchmark, works slower that Geiger ACCV2010, but slightly better
• On wide-baseline dataset, overperform Geiger's work by a large margin
# Goal
Literature review for my "match and map" project
• Efficient Large-Scale Stereo Matching, A. Geiger, Urtasun
• Matching problem formulation
• This problem is right our problem!
• However, we can achieve sub-pixel precision by finding mapping function, and is more precise since the piece-wise planar model can fit the scene in a more detailed way
• And our method works on images taken form very different perspectives
• Model
• Solve
• Discrete, MAP
• Wide baseline stereo matching, P Pritchett, A Zisserman, Computer Vision, 1998
• Algorithms for homography
• Surface following using a single projective homography
• Iteration of
• RANSAC of a fixed region à homography
• Find matches using homography à increased region
• I would rather call it surface extending
• Surface following using affine transformations
• Procedure
• Initial matches obtained from local homography
• Divide the selection window into four
• RANSAC the four subdivisions, get sub-homographies
• New region centered upon the matched basis is stored
• I would call it picewise planar surface growing
• Computation of fundamental matrix
• 7-point correspondences
• On the computing of fundamental matrix, Ramani's lecture slides
• F can be computed form correspondences between image points alone
• Independent of camera internal parameters (Projective transform as a prior)
• Independent of relative pose
• Properties of F
• Rank 2
• 9 parameters, 7 dof (scaling, Det(F) = 0)
• 7-point algorithm, 8-point algorithm
# TODO
• Review probabilistic graphical model
• Read review for stereo vision by Scharstein, IJCV2002, A taxonomy and evaluation of dense two-frame stereo correspondence algorithms
• Find papers referring to A. Geiger's paper.
• Try A. Geiger's method on our data
# Goal
Literature review for my "match and map" project
• Efficient Large-Scale Stereo Matching, A. Geiger, Urtasun
• Previous work
• Global matching v.s. Local matching
• Klaus et al. extend global methods to use appearance-based segmentation, belief propagation and super pixel
• Hirschmuller et al.'s semi-global matching which propagates information of scan-line methods along 16 orientations
• Method
• Stereo matching are largely ambiguous while some are of high confidence
• Remaining ambiguous points are "propagated" by these high confidence "support points"
• Delaunay triangulation, piecewise linear
# Find
• Paper on segmentation + stereo matching
• Klaus, A., Sormann, M., Karner, K.: Segment-based stereo matching using belief propagation and a self-adapting dissimilarity measure. In: ICPR. (2006)
# Goal
• Literature review for my "match & map" project
• Try to understand Hongdong Li's paper on non-rigid scene reconstruction
• A Simple Prior-free Method for Non-Rigid Structure-from-Motion Factorization, Hongdong Li CVPR2012
• The block matrix method
# Find
• What is "shape bases"?
In practice, many non-rigid objects, e.g. the human face under various expressions, deform with certain structures. Their shapes can be regarded as a weighted combination of certain shape bases. Shape and motion recovery under such situations has attracted much interest. Xiao et al.
# Todo
• Review Homography, Semi-global Stereo Matching related papers
# Complain
• Too good a weather to read papers.
|
|
# American Institute of Mathematical Sciences
doi: 10.3934/mcrf.2021016
## Modeling the pressure distribution in a spatially averaged cerebral capillary network
1 Technische Universität München, 81675 Munich, Germany 2 Far Eastern Federal University, 690950 Vladivostok, Russia 3 Institute for Applied Mathematics, FEB RAS, 690041 Vladivostok, Russia
* Corresponding author: Andrey Kovtanyuk
Received March 2019 Revised March 2020 Published March 2021
Fund Project: The work was supported by the Klaus Tschira Foundation, Buhl-Strohmaier Foundation, and Würth Foundation
A boundary value problem for the Poisson's equation with unknown intensities of sources is studied in context of mathematical modeling the pressure distribution in cerebral capillary networks. The problem is formulated as an inverse problem with finite-dimensional overdetermination. The unique solvability of the problem is proven. A numerical algorithm is proposed and implemented.
Citation: Andrey Kovtanyuk, Alexander Chebotarev, Nikolai Botkin, Varvara Turova, Irina Sidorenko, Renée Lampe. Modeling the pressure distribution in a spatially averaged cerebral capillary network. Mathematical Control & Related Fields, doi: 10.3934/mcrf.2021016
##### References:
show all references
##### References:
Stencil corresponding to the cubic topology
The pressure distribution
The absolute velocity distribution
[1] Alexandr Mikhaylov, Victor Mikhaylov. Dynamic inverse problem for Jacobi matrices. Inverse Problems & Imaging, 2019, 13 (3) : 431-447. doi: 10.3934/ipi.2019021 [2] Armin Lechleiter, Tobias Rienmüller. Factorization method for the inverse Stokes problem. Inverse Problems & Imaging, 2013, 7 (4) : 1271-1293. doi: 10.3934/ipi.2013.7.1271 [3] Hirokazu Saito, Xin Zhang. Unique solvability of elliptic problems associated with two-phase incompressible flows in unbounded domains. Discrete & Continuous Dynamical Systems, 2021 doi: 10.3934/dcds.2021051 [4] Sergei Avdonin, Julian Edward. An inverse problem for quantum trees with observations at interior vertices. Networks & Heterogeneous Media, 2021, 16 (2) : 317-339. doi: 10.3934/nhm.2021008 [5] Jianli Xiang, Guozheng Yan. The uniqueness of the inverse elastic wave scattering problem based on the mixed reciprocity relation. Inverse Problems & Imaging, 2021, 15 (3) : 539-554. doi: 10.3934/ipi.2021004 [6] Arianna Giunti. Convergence rates for the homogenization of the Poisson problem in randomly perforated domains. Networks & Heterogeneous Media, 2021 doi: 10.3934/nhm.2021009 [7] Haodong Chen, Hongchun Sun, Yiju Wang. A complementarity model and algorithm for direct multi-commodity flow supply chain network equilibrium problem. Journal of Industrial & Management Optimization, 2021, 17 (4) : 2217-2242. doi: 10.3934/jimo.2020066 [8] Kuan-Hsiang Wang. An eigenvalue problem for nonlinear Schrödinger-Poisson system with steep potential well. Communications on Pure & Applied Analysis, , () : -. doi: 10.3934/cpaa.2021030 [9] Stefano Bianchini, Paolo Bonicatto. Forward untangling and applications to the uniqueness problem for the continuity equation. Discrete & Continuous Dynamical Systems, 2021, 41 (6) : 2739-2776. doi: 10.3934/dcds.2020384 [10] Hui Yang, Yuzhu Han. Initial boundary value problem for a strongly damped wave equation with a general nonlinearity. Evolution Equations & Control Theory, 2021 doi: 10.3934/eect.2021019 [11] Emanuela R. S. Coelho, Valéria N. Domingos Cavalcanti, Vinicius A. Peralta. Exponential stability for a transmission problem of a nonlinear viscoelastic wave equation. Communications on Pure & Applied Analysis, , () : -. doi: 10.3934/cpaa.2021055 [12] Sascha Kurz. The $[46, 9, 20]_2$ code is unique. Advances in Mathematics of Communications, 2021, 15 (3) : 415-422. doi: 10.3934/amc.2020074 [13] Fabio Camilli, Serikbolsyn Duisembay, Qing Tang. Approximation of an optimal control problem for the time-fractional Fokker-Planck equation. Journal of Dynamics & Games, 2021 doi: 10.3934/jdg.2021013 [14] Samir Adly, Oanh Chau, Mohamed Rochdi. Solvability of a class of thermal dynamical contact problems with subdifferential conditions. Numerical Algebra, Control & Optimization, 2012, 2 (1) : 91-104. doi: 10.3934/naco.2012.2.91 [15] Flank D. M. Bezerra, Rodiak N. Figueroa-López, Marcelo J. D. Nascimento. Fractional oscillon equations; solvability and connection with classical oscillon equations. Communications on Pure & Applied Analysis, , () : -. doi: 10.3934/cpaa.2021067 [16] Shu-Yu Hsu. Existence and properties of ancient solutions of the Yamabe flow. Discrete & Continuous Dynamical Systems, 2018, 38 (1) : 91-129. doi: 10.3934/dcds.2018005 [17] Matthias Erbar, Jan Maas. Gradient flow structures for discrete porous medium equations. Discrete & Continuous Dynamical Systems, 2014, 34 (4) : 1355-1374. doi: 10.3934/dcds.2014.34.1355 [18] Zhengchao Ji. Cylindrical estimates for mean curvature flow in hyperbolic spaces. Communications on Pure & Applied Analysis, 2021, 20 (3) : 1199-1211. doi: 10.3934/cpaa.2021016 [19] Ling-Bing He, Li Xu. On the compressible Navier-Stokes equations in the whole space: From non-isentropic flow to isentropic flow. Discrete & Continuous Dynamical Systems, 2021, 41 (7) : 3489-3530. doi: 10.3934/dcds.2021005 [20] Sandrine Anthoine, Jean-François Aujol, Yannick Boursier, Clothilde Mélot. Some proximal methods for Poisson intensity CBCT and PET. Inverse Problems & Imaging, 2012, 6 (4) : 565-598. doi: 10.3934/ipi.2012.6.565
2019 Impact Factor: 0.857
|
|
Negative Sharpe Ratio for a positive return. why?
Hi,
So I just started learning from Quantopian and while I was playing with the following algorithm, I got a negative value of Sharpe Ratio while the returns were positive.
def initialize (context):
context.vrx = sid(10908)
def handle_data (context, data):
order_target_percent(context.vrx, -1.0)
Shorting VRX
9 responses
Same strategy, same asset but negative returns resulted positive Sharpe and positive Sortino.
Entire data start date: 2013-09-03
Entire data end date: 2017-08-01
Backtest Months: 46
Total Returns
-9.47%
Benchmark Returns
63.86%
Alpha
0.41
Beta
-1.45
Sharpe
0.31
Sortino
0.48
Volatility
0.72
Max Drawdown
-70.28%
Can somebody explain this?
@Saravanakumar: Would you be willing to share the dates over which you backtested that strategy?
@Vladimir: Would you be willing to share the code that produced the resulting metrics that you shared? Either posting them here or sharing the backtest/algo privately without our support team would be helpful.
Disclaimer
The material on this website is provided for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation or endorsement for any security or strategy, nor does it constitute an offer to provide investment advisory services by Quantopian. In addition, the material offers no opinion with respect to the suitability of any security or specific investment. No information contained herein should be regarded as a suggestion to engage in or refrain from any investment-related course of action as none of Quantopian nor any of its affiliates is undertaking to provide investment advice, act as an adviser to any plan or entity subject to the Employee Retirement Income Security Act of 1974, as amended, individual retirement account or individual retirement annuity, or give advice in a fiduciary capacity with respect to the materials presented herein. If you are an individual retirement or other investor, contact your financial advisor or other fiduciary unrelated to Quantopian about whether any given investment idea, strategy, product or service described herein may be appropriate for your circumstances. All investments involve risk, including loss of principal. Quantopian makes no guarantees as to the accuracy or completeness of the views expressed in the website. The views are subject to change, and may have become unreliable for various reasons, including changes in market conditions or economic circumstances.
@jamie Please check the link attached and let me know if you need any more details.
VRX Shorting Data
Jamie.
Unfortunately, from April 2017, I can't attach my backtests to the reply. Can you tell me why?
To get positive Sharpe and positive Sortino with negative return, I used this simple code:
def initialize (context):
context.stock = symbol('VRX')
if get_open_orders(): return
order_target_percent(context.stock, -1.0)
Vladimir, can you open up a ticket with support? Unfortunately, when I run the code you shared from 2013-09-03 to 2017-08-01 with $1M or$10M starting capital, I'm unable to reproduce the results that you reported in your earlier comment.
Saravanakumar, thanks for sharing that information. It looks like the strategy you shared is rising far above 1x leverage, and I'm wondering if that could be the cause of the problem. Leverage above 1x doesn't explain why the total returns and Sharpe ratio have different signs, they should still have the same sign, but I'm wondering if this is what's causing the bug. I've reported this to our engineers to take a look. In the meantime, you should look into using the Optimize API to control the leverage used by your algorithm. The long-short equity template algorithms uses Optimize to place orders.
(Edited) Initial capital for the code above would be helpful.
For testing here's an example of the opposite, positive Sharpe while negative returns.
Entire data start date: 2013-09-03
Entire data end date: 2017-08-01
Initial capital 10000
https://www.quantopian.com/posts/negative-returns-resulted-positive-sharpe-and-positive-sortino
This is probably due to the fact that Quantopian uses daily arithmetic returns to calculate Sharpe ratios.
Continuously compounded returns are always lower than arithmetic returns (as you have to subtract sigma^2/2).
Consequently, given enough volatility, a strategy with a positive average daily return can produce a negative compound return.
Using Vladimir’s numbers, the strategy’s average daily return is around 0.31*0.72 / 252 = + 8.9 bp / day
Whereas sigma^2/2 = (72%/sqrt(252))^2/2 = 10.3 bp
Consequently, the strategy has a negative compound return despite having a positive average arithmetic return.
@Xander is correct. In general, you can get a positive Sharpe Ratio and negative cumulative returns any time the arithmetic mean of (1 + daily_returns) is greater than 1, but the geometric mean of (1 + daily_returns) is less than 1. I've written up a short notebook (using the simpler algorithm posted by Vladimir above) explaining why how and why this happens.
2
|
|
# Harry R. Schwartz
Software engineer, nominal scientist, gentleman of the internet.
Member, ←Hotline Webring→.
· 1B41 8F2C 23DE DD9C 807E A74F 841B 3DAE 25AE 721B
ovo-lacto vegetarian
he
him
his
### EmacsConf 2015
Published .
Tags: beards, conferences, emacs, personal.
I’m on a plane back to Boston after a lovely visit to San Francisco for EmacsConf 2015!
The conference was a ton of fun, and the organizers did a terrific job. They preemptively avoided my usual gripes by providing a solid code of conduct and a tasty vegan lunch. Samer also did an awesome job handling questions from IRC; I think it’s easy to make remote folks feel like second-class attendees, but I feel like he really worked hard to make sure they were heard by the in-person crowd. Great work!
They also handed out some pretty sweet stickers. M-x emacsconf-2015 =)
We had a bunch of great talks. I’m not going to try to pick any favorites, but I learned a ton about calc, combining TRAMP and babel, org-mode exporters, configuring golang, and a bunch of good stuff about community outreach. On that particular topic we had a couple great talks: Daniel Gopar spoke about the challenges that newbies face and Erik Hetzger offered some strategies for getting scientists and humanities folks to try out Emacs.
I gave a talk on starting Emacs meetups which I’ve since turned into an essay, as well as a lightning talk on engine-mode.
So! Thanks a bunch to the organizers, and thanks to thoughtbot for paying for my flight (and, in general, continuing to indulge my weird Emacs whims, despite remaining a pretty dedicated vim shop). Also, thanks to my friend Albert for letting me sleep on his futon!
Anyhoo, this whole thing was just a blast. It’s still a little early to tell, but maybe we’ll try hosting EmacsConf 2016 in Boston? No promises!
You might like these related articles:
|
|
# Permutations and Combinations exam question
Before I proceed with my queries I think it's best to present the question at hand.
A class consisting of 4 males and 12 females in randomly divided into 4 groups of 4. What is the probability that each group consists of a male and three females?
Now the given answer for this was $\frac{64}{455}$.
The closest I could possibly get to that was $455$.
Whenever I come across these types of questions I generally categorise it like so:
• Does order matter?
• Yes: then it is a permutation (% increases)
• No: then it is a combination (% decreases)
• Does it allow repetitions? - Make use of respective formulae
So reading the question I will immediately think, "No, order does not matter" which I find a bit hard to explain but Male Student A may be in the first group and Male Student B in the second group OR Vice-Versa (hence why I would consider it a combination..).
So once that is out of the way, I proceed and think, "Yes, there may be repetitions". For consistencys sake, Male Student A may be in the first group twice.
Now that I got that chunk out of the way I pray to the seven Gods that I got the previous two right (even though it's purely logic, certain question try to trick you), and hence begin working.
Pardon if the following notation is incorrect: $$C\binom{16}{4}$$
I tried the following: $$\therefore \frac{16!}{12!\times 4!}\div 4 = 455$$
And then: $$\therefore \frac{16!}{12!\times 4!}\div 4! = \frac{6}{455}$$
However the answer presented in my answer sheet is: $$\frac{64}{455}$$
## 1 Answer
Let's look at the combinations, and we'll do it one group at a time. We are looking for the probability that each of the four groups has exactly one boy and three girls.
For the first group, we are choosing $4$ people out of $16$. One is a boy, out of $4$ possibilities. Three are girls, out of $12$ possibilities. The choices of boy and girls are independent, so we can multiply their counts. Therefore, the probability that the first group has one boy and three girls is
$$\frac{{4 \choose 1}{12 \choose 3}}{{16 \choose 4}}=\frac{44}{91}$$
Now for the second group. After the first group is chosen suitably, we have to choose $1$ boy out of $3$ remaining and $3$ girls out of $9$ remaining. But the total number of possible groups is $4$ people out of $12$ remaining. Therefore, given that the first group was successful, the probability that the second group is successfully chosen is
$$\frac{{3 \choose 1}{9 \choose 3}}{{12 \choose 4}}=\frac{28}{55}$$
Now for the third group. After the first two groups are chosen suitably, we have to choose $1$ boy out of $2$ remaining and $3$ girls out of $6$ remaining. But the total number of possible groups is $4$ people out of $8$ remaining. Therefore, given that the first and second groups were successful, the probability that the third group is successfully chosen is
$$\frac{{2 \choose 1}{6 \choose 3}}{{8 \choose 4}}=\frac{4}{7}$$
If the first three groups are correct, so is the fourth. Therefore, the total probability of success with all four groups is
$$\frac{44}{91}\cdot\frac{28}{55}\cdot\frac{4}{7}=\frac{64}{455}$$
Or, if you want the final probability as one large calculation,
$$\frac{{4 \choose 1}{12 \choose 3}}{{16 \choose 4}} \cdot \frac{{3 \choose 1}{9 \choose 3}}{{12 \choose 4}} \cdot \frac{{2 \choose 1}{6 \choose 3}}{{8 \choose 4}} =\frac{64}{455}$$
• Such a great answer. Thanks for taking the time to explain all of this. Makes perfect sense. Apr 26 '15 at 18:08
|
|
# What are the invariants of $U\otimes V\otimes W$ under action of $GL(U)\times GL(V) \times GL(W)$
The tensor product of some (finite dimensional real) vector spaces is acted on by the direct product of their general linear groups. I would like to know if there are explicit invariants in the case of 3 vector spaces. For one vector space there are two orbits: 0 vector, and non-zero vector. For two vector spaces, $T\in U\otimes V \cong Hom(U^*,V)$ there are finitely many orbits characterized by $rank(T)$. For 3 vector spaces the dimension of $U\otimes V\otimes W$ is $uvw$ and the dimension of $GL(U)\times GL(V) \times GL(W)$ is $u^2+v^2+w^2$ so that usually the space of orbits has positive dimension. Any references would be most welcome. I am particularly interested in the case U,V have dimension 4 and W has dimension 8.
• Are you asking for information about the ring of invariants (or covariants) (in the sense of geometric invariant theory) or for a list of normal forms with parameters? In the former case, I think that the GIT quotient (essentially, the space of orbits of the semi-stable vectors) is, in principle, understood. While I'm not sure that your particular interest ($u=v=w=4$) is worked out in the literature, the case $u=v=w=3$ is known (and the list of normal forms with parameters is known). The case $u=v=w=4$ (with $18$ moduli) is as hard as homogeneous quartics in $4$ variables, so good luck. – Robert Bryant Apr 17 '14 at 11:20
• I see that the OP has just upped the ante: Now, the case of particular interest is $(u,v,w) = (4,4,8)$ instead of $(4,4,4)$. Of course, this case will have even more invariants, though they may be harder to find. The expected dimension of the moduli space in this new case is $33$. Still, in principle, the GIT machinery will say something, though whether it will be of any use is another matter. – Robert Bryant Apr 17 '14 at 15:29
In the world of exterior differential systems, an element of a triple tensor product is called a tableau. The known invariants of tableaux are complicated; see the book Exterior Differential Systems by Bryant, Chern, Gardner, Goldschmidt and Griffiths. There is no classification of tableaux.
• To provide a little more detail, any first order PDE system with constant coefficients can be represented as a tableau, and any tableau can be treated as such a PDE system. In particular, the characteristic variety of the PDE system is an invariant. I think I recall that that every real algebraic projective variety occurs as the characteristic variety of a tableau, but I am not sure. – Ben McKay Apr 16 '14 at 21:07
For what it's worth, in the case when $U,V$, and $W$ all have dimension $2$ (i.e., a case that is much simpler than the $4$-dimensional one you're interested in), it is known that there are exactly six orbits. In particular, every vector is in the orbit of exactly one of these six vectors (where $\{\mathbf{e}_1,\mathbf{e}_2\}$ is some fixed basis of $U,V,W$):
1. $\mathbf{e}_1 \otimes \mathbf{e}_1 \otimes \mathbf{e}_1$
2. $\mathbf{e}_1 \otimes \mathbf{e}_1 \otimes \mathbf{e}_1 + \mathbf{e}_1 \otimes \mathbf{e}_2 \otimes \mathbf{e}_2$
3. $\mathbf{e}_1 \otimes \mathbf{e}_1 \otimes \mathbf{e}_1 + \mathbf{e}_2 \otimes \mathbf{e}_1 \otimes \mathbf{e}_2$
4. $\mathbf{e}_1 \otimes \mathbf{e}_1 \otimes \mathbf{e}_1 + \mathbf{e}_2 \otimes \mathbf{e}_2 \otimes \mathbf{e}_1$
5. $\mathbf{e}_1 \otimes \mathbf{e}_1 \otimes \mathbf{e}_1 + \mathbf{e}_2 \otimes \mathbf{e}_2 \otimes \mathbf{e}_2$
6. $\mathbf{e}_1 \otimes \mathbf{e}_1 \otimes \mathbf{e}_2 + \mathbf{e}_1 \otimes \mathbf{e}_2 \otimes \mathbf{e}_1 + \mathbf{e}_2 \otimes \mathbf{e}_1 \otimes \mathbf{e}_1$
Furthermore, a generic vector in $U \otimes V \otimes W$ belongs to the orbit of the vector 5 above: the other orbits all have measure $0$.
• It should be noted that your list of normal forms is complete when the ground field is $\mathbb{C}$, but not when the ground field is $\mathbb{R}$. For example, in the latter case, there are two open orbits. Also, although this is a trivial remark, you forgot to list the $0$-orbit. – Robert Bryant Apr 17 '14 at 11:24
• Whoops, thanks Robert! I have a tendency to translate problems in my head into $\mathbb{C}$, without always remembering to translate them back. – Nathaniel Johnston Apr 17 '14 at 12:01
|
|
<img src="https://d5nxst8fruw4z.cloudfront.net/atrk.gif?account=iA1Pi1a8Dy00ym" style="display:none" height="1" width="1" alt="" />
# Expressions with Whole Numbers
## Includes product of a number and the sum of whole numbers
%
Progress
MEMORY METER
This indicates how strong in your memory this concept is
Progress
%
Expressions for the Product of a Number and a Sum
Terry is going to a friend’s house. On his way there, his friends ask him to pick up some food at the burger place nearby. They order 4 hamburger meals and Terry just wants 2 hamburgers. A hamburger costs $2.10 and the meal costs$3.25 cents extra. What is the total cost of the meal?
In this concept, you will learn how to write a numerical expression for the product of a number and a sum.
### Numerical Expressions
A numerical expression is a statement that has more than one operation in it. A numerical expression should illustrate mathematical information in a correct way. This lesson will focus on a numerical expression that involves the product of a number and a sum.
Let’s break down the phrase “the product of a number and a sum” to understand the meaning of this expression.
The word product means the results of multiplying two or more numbers.
a×b\begin{align*}a \times b\end{align*}
The word sum means the results of adding two or more numbers.
c+d\begin{align*}c + d\end{align*}
The product of a number and a sum is a combination of these operations. The first multiplicand is a number, a\begin{align*}a\end{align*}. The second multiplicand, b\begin{align*}b\end{align*}, will be the entire sum of two or more number. Substitute b\begin{align*}b\end{align*} with the sum of two numbers c+d\begin{align*}c + d\end{align*}. Use parentheses to indicate grouping and also multiplication.
a(c+d)\begin{align*}a (c + d)\end{align*}
Here is an example of an expression using numbers.
the product of 5 and the sum of 4 plus 3\begin{align*}\text{the product of 5 and the sum of 4 plus 3}\end{align*}
Identify the first multiplicand. It is 5. Then, identify the second multiplicand. The second will be the sum of 4 plus 3. Write is as a numerical expression.
5(4+3)\begin{align*}5(4 + 3)\end{align*}
This is the numerical expression for the information.
### Examples
#### Example 1
Earlier, you were given a problem about Terry at the hamburger shop.
Terry is picking up 2 hamburgers that cost $2.10 each and 4 hamburger meals that cost$3.25 extra per meal. Multiply and add to find the total cost of the meal.
First, think of an expression to find the total cost of the meal. You need to find the sum of the hamburgers and the hamburger meals.
total cost of hamburgers+total cost of hamburger meals\begin{align*}\text{total cost of hamburgers} + \text{total cost of hamburger meals}\end{align*}
Let’s work on the first part, the total cost of the hamburger. The total cost of the hamburgers will be the product of the number of hamburgers times the cost of the burger.
2(2.10)+total cost of the hamburger meals\begin{align*}2(\2.10) + \text{total cost of the hamburger meals}\end{align*} Then, write an expression to find the second part of the expression. The total cost of the meals is the product of the number of meals times the sum of the hamburger plus the added cost. 2(2.10)+4($2.10+$3.25)\begin{align*}2(\2.10) + 4(\2.10 + \3.25)\end{align*}
Next, find the total cost of the order. Order of operations tells you to do the addition in the parentheses first; find each product; and then find the sum.
2($2.10)+4($5.35)$4.20+$21.40 25.60\begin{align*}\begin{array}{rcl} & & 2(\2.10) + 4(\5.35)\\ & &\quad \4.20 + \21.40\\ & & \qquad \ \ \25.60 \end{array}\end{align*} The total cost of the order will be25.60.
#### Example 2
Write a numerical expression for the product of 2 times the sum of 3 and 4.
First, identify the first multiplicand. It is 2.
Then identify the second multiplicand. It is the sum of 3 and 4 or 3 + 4.
Next, write the product as a numerical expression. Use the parentheses to group the sum.
\begin{align*}2(3 + 4)\end{align*}
#### Example 3
Write the expression as a numerical expression.
\begin{align*}\text{the product of three and the sum of four plus five}\end{align*}
First, identify the first multiplicand. It is 3.
Then identify the second multiplicand. It is the sum of 4 + 5.
Next, write the product as a numerical expression. Use the parentheses to group the sum.
\begin{align*}3(4 + 5)\end{align*}
#### Example 4
Write the expression as a numerical expression.
\begin{align*}\text{the product of four and the sum of six plus seven}\end{align*}
First, identify the first multiplicand. It is 4.
Then identify the second multiplicand. It is the sum of 6 + 7.
Next, write the product as a numerical expression. Use the parentheses to group the sum.
\begin{align*}4(6 + 7)\end{align*}
#### Example 5
Write the expression as a numerical expression.
\begin{align*}\text{the product of nine and the sum of one plus eight}\end{align*}
First, identify the first multiplicand. It is 9.
Then identify the second multiplicand. It is the sum of 1 + 8.
Next, write the product as a numerical expression. Use the parentheses to group the sum.
\begin{align*}9(1 + 8)\end{align*}
### Review
Write a numerical expression for each sentence.
1. The product of two and the sum of five and six.
2. The product of three and the sum of three and seven.
3. The product of five and the sum of two and three.
4. The product of four and the sum of three and five.
5. The product of seven and the sum of four and five.
6. The product of ten and the sum of five and seven.
7. The product of six and the sum of five and two.
8. The product of five and the sum of four and nine.
9. The product of thirteen and the sum of five and twelve.
10. The sum of six and seven times three.
11. The sum of eight and ten times four.
12. The sum of six and fifteen times eight.
13. The sum of four and nine times twelve.
14. The sum of three and eight times sixteen.
15. The product of eight and the sum of four and fourteen.
To see the Review answers, open this PDF file and look for section 4.4.
### Notes/Highlights Having trouble? Report an issue.
Color Highlighted Text Notes
### Vocabulary Language: English
Numerical expression
A numerical expression is a group of numbers and operations used to represent a quantity.
Product
The product is the result after two amounts have been multiplied.
Sum
The sum is the result after two or more amounts have been added together.
|
|
# What Is Viscous Fluid?
Fluids that have higher viscosity are known as viscous fluid. Examples of viscous fluids are honey and ketchup. The fluid that has more flow resistance is referred to as viscous fluid. Viscosity is a fluid factor, which is the degree of the amount of resistance between the fluid layers.
### What is viscosity?
Viscosity is one of the properties of the fluid and is defined as the resistance offered by the layers of the fluid to the fluid movement. Viscosity is defined as the measure of the resistance of a fluid to gradual deformation by shear or tensile stress.
|
|
Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.
# Stop using bivariate correlations for variable selection
Something I've never understood is the widespread calculation and reporting of univariate and bivariate statistics in applied work, especially when it comes to model selection. Bivariate statistics are, at best, useless for multi-variate model selection and, at worst, harmful. Since nearly all questions of interest are highly dimensional, the use of bivariate statistics is worrisome.
What typically happens is a researcher sits down with their statistical software of choice and they compute a correlation between their response variable and their collection of possible predictors. From here, they toss out potential predictors that either have low correlation or for which the correlation is not significant.
The concern here is that it is possible for the correlation between the marginal distributions of the response and a predictor to be almost zero or non-significant and for that predictor to be an important element in the data generating pathway.
Consider the following simulation that illustrates the difference between the marginal relationship between the response and a predictor and the true multi- variable relationship. The function genY generates the response using user provided values for $$\beta$$ and adds in a little white noise.
genY <- function(betas, X, stdPercent = 0.25) {
modelMatrix <- cbind(1, X)
yhat <- modelMatrix %*% betas
y <- yhat + rnorm(nrow(yhat), 0, stdPercent * mean(yhat))
y
}
The function cor returns the correlation between two values and works with a vector and a matrix argument but cor.test requires two vectors. For this I wrote a simple function sigCor that returns TRUE if a correlation between the vector x and y is significant at a user provided threshold and FALSE otherwise. This function is designed to work with apply to filter our predictor set.
sigCor <- function(x, y, threshold = 0.2) {
p <- cor.test(x, y)$p.value p <= threshold } The main function then generates a random covariance matrix and draws from a multivariate normal centered at 0 with that covariance matrix. The values of the matrix X are then checked for correlation with the response y. If the absolute value of the correlation exceeds some threshold or if the p value for the significance of the correlation is less than some threshold, the variable is kept. Otherwise it is dropped. The function returns the number of retained variables for each selection method. simulateSelection <- function(nx, n, corLim = 0.2, pLim = 0.2) { require(MASS) require(clusterGeneration) betas <- rep(1, nx + 1) mu <- rep(0, nx) sigma <- genPositiveDefMat(nx, covMethod = "unifcorrmat")$Sigma
X <- mvrnorm(n, mu, sigma)
y <- genY(betas, X)
xcor <- cor(y, X)
limitedX <- X[, abs(xcor) >= corLim]
pX <- X[, apply(X, 2, sigCor, y, pLim)]
nCoef <- c(ncol(X) + 1, ncol(limitedX) + 1, ncol(pX) + 1)
}
If we keep the defaults of corLim = 0.2 and pLim = 0.2 (keep any correlation where the absolute value exceeds 0.2 and any correlation with a p value less than 0.2) and use replicate to run the function 1000 times with 10 predictors and $$n = 1000$$, we can calculate the probability that the different method selects the correct model. (Note that we set all of values of betas to 1, so all 11 coefficient estimates should be non-zero and all of the predictors are correlated with the outcome).
results <- replicate(1000, (simulateSelection(10, 1000)))
correctModelFraction <- apply(results == 11, 1, mean)
correctModelFraction
## [1] 1.000 0.026 0.573
Using a filter based on the size of the correlation only yields the correct model 2.6% of the time. Using a relatively high p value as a threshold does better returning the correct model 57.3% of the time.
We can explore the effect of varying the value of pLim using a few simple modifications to the above code.
simulateSelectionP <- function(nx, n, pLim) {
require(MASS)
require(clusterGeneration)
betas <- rep(1, nx + 1)
mu <- rep(0, nx)
sigma <- genPositiveDefMat(nx, covMethod = "unifcorrmat")$Sigma X <- mvrnorm(n, mu, sigma) y <- genY(betas, X) pX <- X[, apply(X, 2, sigCor, y, pLim)] correct <- (ncol(pX)) == nx } varyP <- function(nx, n, p) { fractionCorrect <- numeric(100 * length(p)) j <- 1 for (i in 1:length(p)) { set.seed(42) fractionCorrect[(j):(j + 99)] <- replicate(100, simulateSelectionP(nx, n, p[i])) j <- j + 100 } fractionCorrect } Using these new functions, we can calculate the fraction of the time that a threshold of p yields the correct model. If we vary p from $$0.01--0.50$$ and plot the resulting curve, prCorrect <- varyP(10, 1000, seq(0.01, 0.5, length.out = 20)) results <- data.frame(prCorrect = prCorrect, limit = rep(seq(0.01, 0.5, length.out = 20), each = 100)) meanByLimit <- aggregate(results$prCorrect, list(results$limit), mean) sdByLimit <- aggregate(results$prCorrect, list(results$limit), sd) meanByLimit$sd <- sdByLimit$x meanByLimit$upper <- meanByLimit$x + qnorm(0.975) * meanByLimit$sd/sqrt(100)
meanByLimit$lower <- meanByLimit$x - qnorm(0.975) * meanByLimit\$sd/sqrt(100)
ggplot(meanByLimit, aes(x = Group.1, y = x, ymin = lower, ymax = upper)) + geom_line() +
geom_ribbon(alpha = 0.25) + theme_bw() + scale_x_continuous("Threshold for p value") +
scale_y_continuous("Fraction of models in simulation that are correct")
we see that, as expected, the probability of getting the correct model goes up as we increase the threshold value. We have about a 75% shot at getting the right model using this method when we set the limit on the p value to be 0.50 compared to under 30% at a p value of 0.01.
However, this raises an interesting question: if we increase the threshold for the p value, what is the value of using the bivariate correlation at all?
randomRate <- function(n, pLim) {
x <- rnorm(n)
y <- rnorm(n)
sigCor(x, y, pLim)
}
p <- seq(0.01, 0.5, length.out = 20)
rate <- numeric(length(p))
for (i in 1:length(p)) {
rate[i] <- mean(replicate(1000, randomRate(1000, p[i])))
}
rbind(p, rate)
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
## p 0.010 0.03579 0.06158 0.08737 0.1132 0.1389 0.1647 0.1905 0.2163
## rate 0.009 0.03900 0.06400 0.10100 0.1110 0.1290 0.1660 0.1870 0.2210
## [,10] [,11] [,12] [,13] [,14] [,15] [,16] [,17] [,18] [,19]
## p 0.2421 0.2679 0.2937 0.3195 0.3453 0.3711 0.3968 0.4226 0.4484 0.4742
## rate 0.2250 0.2920 0.3180 0.3180 0.3210 0.4010 0.3720 0.4560 0.4130 0.4660
## [,20]
## p 0.5
## rate 0.5
As the threshold increases, the value of the bivariate correlation as a filter goes down and goes down fast. At the limit required for there to be a 50% chance of the model containing all relevant predictors, the rate of improperly included variables would go up to nearly 20%.
The real problem comes into play here — the bivariate comparsions selects for the wrong variables by over-emphasizing the relationship between the marginal distributions. Because the selected model is incomplete and important variables are omitted, the resulting parameter estimates are biased and inaccurate.
The bivariate comparsion is a terrible way to select relevant variables for a highly dimensional model as the function of interest is relating the all of the predictors to the outcome. It can neither rule in nor rule out a predictor from a model. A better approach is to generate the model using domain knowledge and a model of the expected data generating process. If the process is to remain strictly data driven, methods like cross-validation or AIC/BIC provide better measures of model quality and predictor importance than the bivariate correlation coefficient.
|
|
category theory
# Contents
## Idea
The Freyd cover of a category is a special case of Artin gluing. Given a category $\mathcal{T}$ and a functor $F: \mathcal{T} \to Set$, the Artin gluing of $F$ is the comma category $Set \downarrow F$ whose objects are triples $(X, \xi, U)$ where:
• $X$ is a set
• $U$ is an object of $\mathcal{T}$
• $\xi$ is a function $X \to F(U)$.
The Freyd cover is the special case $F = \mathcal{T} (1, -)$.
The Freyd cover is sometimes known as the Sierpinski cone or scone, because in topos theory it behaves similarly to the cone on a space, but with the interval $[0,1]$ replaced by the Sierpinski space.
## Properties
### Relation to the initial topos
One of the first applications of the Freyd cover was to deduce facts about the initial topos? (initial with respect to logical morphisms — also called the free topos). They were originally proved by syntactic means; the conceptual proofs of the lemma and theorem below are due to Freyd.
###### Lemma
For any category $C$ with a terminal object $\mathbf{1}$, the terminal object of the Freyd cover $\widehat{C}$ is connected and projective, i.e., the representable $\Gamma = \widehat{C}(1, -) \colon \widehat{C} \to Set$ preserves any colimits that exist.
###### Proof
To check that $\Gamma^{op} \colon \widehat{C}^{op} \to Set^{op}$ preserves limits, it suffices to check that the composite
$\widehat{C}^{op} \stackrel{\Gamma^{op}}{\to} Set^{op} \stackrel{2^-}{\to} Set$
preserves limits, because the contravariant power set functor $P = 2^-$ is monadic. But it is easily checked that this composite is the contravariant representable given by $(2, \mathbf{1}, 2 \to \Gamma(\mathbf{1}))$.
###### Theorem
The terminal object in the initial topos $\mathcal{T}$ is connected and projective, i.e., $\Gamma = \hom(1, -) \colon \mathcal{T} \to Set$ preserves finite colimits.
###### Proof
We divide the argument into three segments:
• The hom-functor preserves finite limits, so by general properties of Artin gluing, the Freyd cover $\widehat{\mathcal{T}}$ is also a topos. Observe that $\mathcal{T}$ is equivalent to the slice $\widehat{\mathcal{T}}/M$ where $M$ is the object $(\emptyset, \mathbf{1}, \emptyset \to \Gamma(\mathbf{1}))$. Since pulling back to a slice is a logical functor, we have a logical functor
$\pi \colon \widehat{\mathcal{T}} \to \mathcal{T}$
Since $\mathcal{T}$ is initial, $\pi$ is a retraction for the unique logical functor $i \colon \mathcal{T} \to \widehat{\mathcal{T}}$.
• We have maps $\mathcal{T}(1, -) \to \widehat{\mathcal{T}}(i 1, i-) \cong \widehat{\mathcal{T}}(1, i-)$ (the isomorphism comes from $i 1 \cong 1$, which is clear since $i$ is logical), and $\widehat{\mathcal{T}}(1, i-) \to \mathcal{T}(\pi 1, \pi i-) \cong \mathcal{T}(1, -)$ since $\pi$ is logical and retracts $i$. Their composite must be the identity on $\mathcal{T}(1, -)$, because there is only one such endomorphism, using the Yoneda lemma and terminality of $1$.
Finally, since $\mathcal{T}(1, -)$ is a retract of a functor $\widehat{\mathcal{T}}(1, i-)$ that preserves finite colimits (by the lemma, and the fact that the logical functor $i$ preserves finite colimits), it must also preserve finite colimits.
This is important because it implies that the internal logic of the free topos (which is exactly “intuitionistic higher-order logic”) satisfies the following properties:
• The disjunction property: if “P or Q” is provable in the empty context, then either P is so provable, or Q is so provable. (Note that this clearly fails in the presence of excluded middle.)
• The existence property: if “there exists an $x\in A$ such that $P(x)$” is provable in the empty context, then there exists a global element $x\colon 1\to A$ such that $P(x)$ is provable in the empty context. (Again, this is clearly a constructivity property.)
• The negation property: False is not provable in the empty context.
### As a local topos
The Freyd cover of a topos is a local topos, and in fact freely so. Every local topos is a retract of a Freyd cover.
See (Johnstone, lemma C3.6.4).
## References
You can find more on Artin gluing in this important (and nice) paper:
• Aurelio Carboni, Peter Johnstone, Connected limits, familial representability and Artin glueing , Mathematical Structures in Computer Science 5 (1995), 441–459
plus
|
|
## 複素解析幾何セミナー
開催情報 月曜日 10:30~12:00 数理科学研究科棟(駒場) 128号室 平地 健吾, 高山 茂晴, 細野 元気
### 2018年01月15日(月)
10:30-12:00 数理科学研究科棟(駒場) 128号室
Vanishing theorems of $L^2$-cohomology groups on Hessian manifolds
[ 講演概要 ]
A Hessian manifold is a Riemannian manifold whose metric is locally given by the Hessian of a function with respect to flat coordinates. In this talk, we discuss vanishing theorems of $L^2$-cohomology groups on complete Hessian Manifolds coupled with flat line bundles. In particular, we obtain stronger vanishing theorems on regular convex cones with the Cheng-Yau metrics. Further we show that the Cheng-Yau metrics on regular convex cones give rise to harmonic maps to the positive symmetric matrices.
|
|
## briana.img one year ago How to find the angle measure of T?
1. briana.img
I have no idea how to solve this since there's no other angle measure
2. anonymous
Try the law of cosines. Do you know it?
3. wolf1728
Here is the Law of Cosines
4. briana.img
@wolf1728 are you sure thats it? i thought it was a^2=b^2+c^2-2bc cosa ???
5. anonymous
In your problem, let the three sides be t=7, r=11, s=10. Then the law of cosines becomes$t ^{2}=r ^{2}+s ^{2}-2rs \cos \left( T \right)$
6. wolf1728
ospreytriple's equation is better to use because itis written in terms of r, s and t
7. briana.img
@ospreytriple would i just plug in the numbers from the triangle???
8. anonymous
Rearranging, you get$T=\cos ^{-1}\left(\frac{ r ^{2} +s ^{2}-t ^{2}}{ 2rs }\right)$
9. briana.img
@ospreytriple i'm really confused on how i would get a real answer out of that equation :(
10. anonymous
just plug in the lengths of sides r, s, & t from the triangle.
11. briana.img
@ospreytriple oh okay that's what i was wondering lmao
12. anonymous
What do you get for an answer?
13. briana.img
@ospreytriple 45.57
14. anonymous
Not what I get. You want to try it again?
15. briana.img
@ospreytriple i got 63.25 :(
16. briana.img
@ospreytriple i got 63.25 :(
17. briana.img
@ospreytriple T=10? r=7? s=11?
18. anonymous
No. t=10. You are trying to find angle T.
19. wolf1728
briana r^2 = 121 s^2 = 100 t^2 = 49 r^2 + s^2 -t^2 = 172 agreed?
20. wolf1728
I think having 2 people explain things to a third gets a bit confusing good luck briana and osprey :-)
21. briana.img
@ospreytriple i listed those numbers because those are the ones you substitute in, right??
22. anonymous
Ok. Evaluate the above equation for T by using the values of r, s, & t from the triangle.
23. briana.img
@ospreytriple i know but i'm just asking if those are the numbers i use ??? like those are the correct ones for the substitution
24. anonymous
I believe those are the side lengths from the triangle, yes.
25. anonymous
$T=\cos ^{-1}\left( \frac{ 11^{2}+10^{2} -7^{2}}{ 2\left( 11 \right)\left( 10 \right) } \right)$
26. briana.img
@ospreytriple yeah i jsut did that and my answer came out to be 63.25 again
27. anonymous
What do you get for the value of the numerator?
28. briana.img
@ospreytriple 70
29. anonymous
Not quite.$11^{2}+10^{2}-7^{1}=121+100-49= ?$
30. anonymous
Should be 7^2. Sorry.
31. briana.img
@ospreytriple oh oops 172
32. anonymous
Great. Now the denominator is$2\left( 11 \right)\left( 10 \right)=?$
33. briana.img
@ospreytriple 220
34. anonymous
Terrific so$T=\cos ^{-1}\left( \frac{ 172 }{ 220 } \right)=?$
35. briana.img
@ospreytriple the calculator i'm using says 63.25???
36. briana.img
@ospreytriple wait nevermind 38.64
37. anonymous
Now you got it. Good job.
38. briana.img
@ospreytriple sorry fro taking so long :( this unit is really messing me up
39. anonymous
You're welcome. Those pesky calculators :)
|
|
Reference documentation for deal.II version Git 92ca227 2018-05-25 19:47:08 -0500
The step-8 tutorial program
This tutorial depends on step-6.
1. Introduction
2. The commented program
# Introduction
In real life, most partial differential equations are really systems of equations. Accordingly, the solutions are usually vector-valued. The deal.II library supports such problems (see the extensive documentation in the Handling vector valued problems module), and we will show that that is mostly rather simple. The only more complicated problems are in assembling matrix and right hand side, but these are easily understood as well.
Note
The material presented here is also discussed in video lecture 19. (All video lectures are also available here.)
In this tutorial program we will want to solve the elastic equations. They are an extension to Laplace's equation with a vector-valued solution that describes the displacement in each space direction of a rigid body which is subject to a force. Of course, the force is also vector-valued, meaning that in each point it has a direction and an absolute value. The elastic equations are the following:
$- \partial_j (c_{ijkl} \partial_k u_l) = f_i, \qquad i=1\ldots d,$
where the values $$c_{ijkl}$$ are the stiffness coefficients and will usually depend on the space coordinates. In many cases, one knows that the material under consideration is isotropic, in which case by introduction of the two coefficients $$\lambda$$ and $$\mu$$ the coefficient tensor reduces to
$c_{ijkl} = \lambda \delta_{ij} \delta_{kl} + \mu (\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk}).$
The elastic equations can then be rewritten in much simpler a form:
$- \nabla \lambda (\nabla\cdot {\mathbf u}) - (\nabla \cdot \mu \nabla) {\mathbf u} - \nabla\cdot \mu (\nabla {\mathbf u})^T = {\mathbf f},$
and the respective bilinear form is then
$a({\mathbf u}, {\mathbf v}) = \left( \lambda \nabla\cdot {\mathbf u}, \nabla\cdot {\mathbf v} \right)_\Omega + \sum_{k,l} \left( \mu \partial_k u_l, \partial_k v_l \right)_\Omega + \sum_{k,l} \left( \mu \partial_k u_l, \partial_l v_k \right)_\Omega,$
or also writing the first term a sum over components:
$a({\mathbf u}, {\mathbf v}) = \sum_{k,l} \left( \lambda \partial_l u_l, \partial_k v_k \right)_\Omega + \sum_{k,l} \left( \mu \partial_k u_l, \partial_k v_l \right)_\Omega + \sum_{k,l} \left( \mu \partial_k u_l, \partial_l v_k \right)_\Omega.$
Note
As written, the equations above are generally considered to be the right description for the displacement of three-dimensional objects if the displacement is small and we can assume that Hooke's law is valid. In that case, the indices $$i,j,k,l$$ above all run over the set $$\{1,2,3\}$$ (or, in the C++ source, over $$\{0,1,2\}$$). However, as is, the program runs in 2d, and while the equations above also make mathematical sense in that case, they would only describe a truly two-dimensional solid. In particular, they are not the appropriate description of an $$x-y$$ cross-section of a body infinite in the $$z$$ direction; this is in contrast to many other two-dimensional equations that can be obtained by assuming that the body has infinite extent in $$z$$-direction and that the solution function does not depend on the $$z$$ coordinate. On the other hand, there are equations for two-dimensional models of elasticity; see for example the Wikipedia article on plane strain, antiplane shear and plan stress.
But let's get back to the original problem. How do we assemble the matrix for such an equation? A very long answer with a number of different alternatives is given in the documentation of the Handling vector valued problems module. Historically, the solution shown below was the only one available in the early years of the library. It turns out to also be the fastest. On the other hand, if a few per cent of compute time do not matter, there are simpler and probably more intuitive ways to assemble the linear system than the one discussed below but that weren't available until several years after this tutorial program was first written; if you are interested in them, take a look at the Handling vector valued problems module.
Let us go back to the question of how to assemble the linear system. The first thing we need is some knowledge about how the shape functions work in the case of vector-valued finite elements. Basically, this comes down to the following: let $$n$$ be the number of shape functions for the scalar finite element of which we build the vector element (for example, we will use bilinear functions for each component of the vector-valued finite element, so the scalar finite element is the FE_Q(1) element which we have used in previous examples already, and $$n=4$$ in two space dimensions). Further, let $$N$$ be the number of shape functions for the vector element; in two space dimensions, we need $$n$$ shape functions for each component of the vector, so $$N=2n$$. Then, the $$i$$th shape function of the vector element has the form
$\Phi_i({\mathbf x}) = \varphi_{\text{base}(i)}({\mathbf x})\ {\mathbf e}_{\text{comp}(i)},$
where $$e_l$$ is the $$l$$th unit vector, $$\text{comp}(i)$$ is the function that tells us which component of $$\Phi_i$$ is the one that is nonzero (for each vector shape function, only one component is nonzero, and all others are zero). $$\varphi_{\text{base}(i)}(x)$$ describes the space dependence of the shape function, which is taken to be the $$\text{base}(i)$$-th shape function of the scalar element. Of course, while $$i$$ is in the range $$0,\ldots,N-1$$, the functions $$\text{comp}(i)$$ and $$\text{base}(i)$$ have the ranges $$0,1$$ (in 2D) and $$0,\ldots,n-1$$, respectively.
For example (though this sequence of shape functions is not guaranteed, and you should not rely on it), the following layout could be used by the library:
\begin{eqnarray*} \Phi_0({\mathbf x}) &=& \left(\begin{array}{c} \varphi_0({\mathbf x}) \\ 0 \end{array}\right), \\ \Phi_1({\mathbf x}) &=& \left(\begin{array}{c} 0 \\ \varphi_0({\mathbf x}) \end{array}\right), \\ \Phi_2({\mathbf x}) &=& \left(\begin{array}{c} \varphi_1({\mathbf x}) \\ 0 \end{array}\right), \\ \Phi_3({\mathbf x}) &=& \left(\begin{array}{c} 0 \\ \varphi_1({\mathbf x}) \end{array}\right), \ldots \end{eqnarray*}
where here
$\text{comp}(0)=0, \quad \text{comp}(1)=1, \quad \text{comp}(2)=0, \quad \text{comp}(3)=1, \quad \ldots$
$\text{base}(0)=0, \quad \text{base}(1)=0, \quad \text{base}(2)=1, \quad \text{base}(3)=1, \quad \ldots$
In all but very rare cases, you will not need to know which shape function $$\varphi_{\text{base}(i)}$$ of the scalar element belongs to a shape function $$\Phi_i$$ of the vector element. Let us therefore define
$\phi_i = \varphi_{\text{base}(i)}$
by which we can write the vector shape function as
$\Phi_i({\mathbf x}) = \phi_{i}({\mathbf x})\ {\mathbf e}_{\text{comp}(i)}.$
You can now safely forget about the function $$\text{base}(i)$$, at least for the rest of this example program.
Now using this vector shape functions, we can write the discrete finite element solution as
${\mathbf u}_h({\mathbf x}) = \sum_i \Phi_i({\mathbf x})\ U_i$
with scalar coefficients $$U_i$$. If we define an analog function $${\mathbf v}_h$$ as test function, we can write the discrete problem as follows: Find coefficients $$U_i$$ such that
$a({\mathbf u}_h, {\mathbf v}_h) = ({\mathbf f}, {\mathbf v}_h) \qquad \forall {\mathbf v}_h.$
If we insert the definition of the bilinear form and the representation of $${\mathbf u}_h$$ and $${\mathbf v}_h$$ into this formula:
\begin{eqnarray*} \sum_{i,j} U_i V_j \sum_{k,l} \left\{ \left( \lambda \partial_l (\Phi_i)_l, \partial_k (\Phi_j)_k \right)_\Omega + \left( \mu \partial_l (\Phi_i)_k, \partial_l (\Phi_j)_k \right)_\Omega + \left( \mu \partial_l (\Phi_i)_k, \partial_k (\Phi_j)_l \right)_\Omega \right\} \\ = \sum_j V_j \sum_l \left( f_l, (\Phi_j)_l \right)_\Omega. \end{eqnarray*}
We note that here and in the following, the indices $$k,l$$ run over spatial directions, i.e. $$0\le k,l < d$$, and that indices $$i,j$$ run over degrees of freedom.
The local stiffness matrix on cell $$K$$ therefore has the following entries:
$A^K_{ij} = \sum_{k,l} \left\{ \left( \lambda \partial_l (\Phi_i)_l, \partial_k (\Phi_j)_k \right)_K + \left( \mu \partial_l (\Phi_i)_k, \partial_l (\Phi_j)_k \right)_K + \left( \mu \partial_l (\Phi_i)_k, \partial_k (\Phi_j)_l \right)_K \right\},$
where $$i,j$$ now are local degrees of freedom and therefore $$0\le i,j < N$$. In these formulas, we always take some component of the vector shape functions $$\Phi_i$$, which are of course given as follows (see their definition):
$(\Phi_i)_l = \phi_i \delta_{l,\text{comp}(i)},$
with the Kronecker symbol $$\delta_{nm}$$. Due to this, we can delete some of the sums over $$k$$ and $$l$$:
\begin{eqnarray*} A^K_{ij} &=& \sum_{k,l} \Bigl\{ \left( \lambda \partial_l \phi_i\ \delta_{l,\text{comp}(i)}, \partial_k \phi_j\ \delta_{k,\text{comp}(j)} \right)_K \\ &\qquad\qquad& + \left( \mu \partial_l \phi_i\ \delta_{k,\text{comp}(i)}, \partial_l \phi_j\ \delta_{k,\text{comp}(j)} \right)_K + \left( \mu \partial_l \phi_i\ \delta_{k,\text{comp}(i)}, \partial_k \phi_j\ \delta_{l,\text{comp}(j)} \right)_K \Bigr\} \\ &=& \left( \lambda \partial_{\text{comp}(i)} \phi_i, \partial_{\text{comp}(j)} \phi_j \right)_K + \sum_l \left( \mu \partial_l \phi_i, \partial_l \phi_j \right)_K \ \delta_{\text{comp}(i),\text{comp}(j)} + \left( \mu \partial_{\text{comp}(j)} \phi_i, \partial_{\text{comp}(i)} \phi_j \right)_K \\ &=& \left( \lambda \partial_{\text{comp}(i)} \phi_i, \partial_{\text{comp}(j)} \phi_j \right)_K + \left( \mu \nabla \phi_i, \nabla \phi_j \right)_K \ \delta_{\text{comp}(i),\text{comp}(j)} + \left( \mu \partial_{\text{comp}(j)} \phi_i, \partial_{\text{comp}(i)} \phi_j \right)_K. \end{eqnarray*}
Likewise, the contribution of cell $$K$$ to the right hand side vector is
\begin{eqnarray*} f^K_j &=& \sum_l \left( f_l, (\Phi_j)_l \right)_K \\ &=& \sum_l \left( f_l, \phi_j \delta_{l,\text{comp}(j)} \right)_K \\ &=& \left( f_{\text{comp}(j)}, \phi_j \right)_K. \end{eqnarray*}
This is the form in which we will implement the local stiffness matrix and right hand side vectors.
As a final note: in the step-17 example program, we will revisit the elastic problem laid out here, and will show how to solve it in parallel on a cluster of computers. The resulting program will thus be able to solve this problem to significantly higher accuracy, and more efficiently if this is required. In addition, in step-20, step-21, as well as a few other of the later tutorial programs, we will revisit some vector-valued problems and show a few techniques that may make it simpler to actually go through all the stuff shown above, with FiniteElement::system_to_component_index etc.
# The commented program
### Include files
As usual, the first few include files are already known, so we will not comment on them further.
#include <deal.II/base/function.h>
#include <deal.II/base/tensor.h>
#include <deal.II/lac/vector.h>
#include <deal.II/lac/full_matrix.h>
#include <deal.II/lac/sparse_matrix.h>
#include <deal.II/lac/dynamic_sparsity_pattern.h>
#include <deal.II/lac/solver_cg.h>
#include <deal.II/lac/precondition.h>
#include <deal.II/lac/constraint_matrix.h>
#include <deal.II/grid/tria.h>
#include <deal.II/grid/grid_generator.h>
#include <deal.II/grid/grid_refinement.h>
#include <deal.II/grid/tria_accessor.h>
#include <deal.II/grid/tria_iterator.h>
#include <deal.II/dofs/dof_handler.h>
#include <deal.II/dofs/dof_accessor.h>
#include <deal.II/dofs/dof_tools.h>
#include <deal.II/fe/fe_values.h>
#include <deal.II/numerics/vector_tools.h>
#include <deal.II/numerics/matrix_tools.h>
#include <deal.II/numerics/data_out.h>
#include <deal.II/numerics/error_estimator.h>
In this example, we need vector-valued finite elements. The support for these can be found in the following include file :
#include <deal.II/fe/fe_system.h>
We will compose the vector-valued finite elements from regular Q1 elements which can be found here, as usual:
#include <deal.II/fe/fe_q.h>
This again is C++:
#include <fstream>
#include <iostream>
The last step is as in previous programs. In particular, just like in step-7, we pack everything that's specific to this program into a namespace of its own.
namespace Step8
{
using namespace dealii;
### The ElasticProblem class template
The main class is, except for its name, almost unchanged with respect to the step-6 example.
The only change is the use of a different class for the fe variable: Instead of a concrete finite element class such as FE_Q, we now use a more generic one, FESystem. In fact, FESystem is not really a finite element itself in that it does not implement shape functions of its own. Rather, it is a class that can be used to stack several other elements together to form one vector-valued finite element. In our case, we will compose the vector-valued element of FE_Q(1) objects, as shown below in the constructor of this class.
template <int dim>
class ElasticProblem
{
public:
ElasticProblem();
~ElasticProblem();
void run();
private:
void setup_system();
void assemble_system();
void solve();
void refine_grid();
void output_results(const unsigned int cycle) const;
Triangulation<dim> triangulation;
DoFHandler<dim> dof_handler;
ConstraintMatrix hanging_node_constraints;
SparsityPattern sparsity_pattern;
SparseMatrix<double> system_matrix;
Vector<double> solution;
Vector<double> system_rhs;
};
### Right hand side values
Before going over to the implementation of the main class, we declare and define the function which describes the right hand side. This time, the right hand side is vector-valued, as is the solution, so we will describe the changes required for this in some more detail.
To prevent cases where the return vector has not previously been set to the right size we test for this case and otherwise throw an exception at the beginning of the function. Note that enforcing that output arguments already have the correct size is a convention in deal.II, and enforced almost everywhere. The reason is that we would otherwise have to check at the beginning of the function and possibly change the size of the output vector. This is expensive, and would almost always be unnecessary (the first call to the function would set the vector to the right size, and subsequent calls would only have to do redundant checks). In addition, checking and possibly resizing the vector is an operation that can not be removed if we can't rely on the assumption that the vector already has the correct size; this is in contract to the Assert call that is completely removed if the program is compiled in optimized mode.
Likewise, if by some accident someone tried to compile and run the program in only one space dimension (in which the elastic equations do not make much sense since they reduce to the ordinary Laplace equation), we terminate the program in the second assertion. The program will work just fine in 3d, however.
template <int dim>
void right_hand_side(const std::vector<Point<dim>> &points,
std::vector<Tensor<1, dim>> & values)
{
Assert(values.size() == points.size(),
ExcDimensionMismatch(values.size(), points.size()));
Assert(dim >= 2, ExcNotImplemented());
The rest of the function implements computing force values. We will use a constant (unit) force in x-direction located in two little circles (or spheres, in 3d) around points (0.5,0) and (-0.5,0), and y-force in an area around the origin; in 3d, the z-component of these centers is zero as well.
For this, let us first define two objects that denote the centers of these areas. Note that upon construction of the Point objects, all components are set to zero.
Point<dim> point_1, point_2;
point_1(0) = 0.5;
point_2(0) = -0.5;
for (unsigned int point_n = 0; point_n < points.size(); ++point_n)
{
If points[point_n] is in a circle (sphere) of radius 0.2 around one of these points, then set the force in x-direction to one, otherwise to zero:
if (((points[point_n] - point_1).norm_square() < 0.2 * 0.2) ||
((points[point_n] - point_2).norm_square() < 0.2 * 0.2))
values[point_n][0] = 1.0;
else
values[point_n][0] = 0.0;
Likewise, if points[point_n] is in the vicinity of the origin, then set the y-force to one, otherwise to zero:
if (points[point_n].norm_square() < 0.2 * 0.2)
values[point_n][1] = 1.0;
else
values[point_n][1] = 0.0;
}
}
### The ElasticProblem class implementation
#### ElasticProblem::ElasticProblem
Following is the constructor of the main class. As said before, we would like to construct a vector-valued finite element that is composed of several scalar finite elements (i.e., we want to build the vector-valued element so that each of its vector components consists of the shape functions of a scalar element). Of course, the number of scalar finite elements we would like to stack together equals the number of components the solution function has, which is dim since we consider displacement in each space direction. The FESystem class can handle this: we pass it the finite element of which we would like to compose the system of, and how often it shall be repeated:
template <int dim>
ElasticProblem<dim>::ElasticProblem() :
dof_handler(triangulation),
fe(FE_Q<dim>(1), dim)
{}
In fact, the FESystem class has several more constructors which can perform more complex operations than just stacking together several scalar finite elements of the same type into one; we will get to know these possibilities in later examples.
#### ElasticProblem::~ElasticProblem
The destructor, on the other hand, is exactly as in step-6:
template <int dim>
ElasticProblem<dim>::~ElasticProblem()
{
dof_handler.clear();
}
#### ElasticProblem::setup_system
Setting up the system of equations is identical to the function used in the step-6 example. The DoFHandler class and all other classes used here are fully aware that the finite element we want to use is vector-valued, and take care of the vector-valuedness of the finite element themselves. (In fact, they do not, but this does not need to bother you: since they only need to know how many degrees of freedom there are per vertex, line and cell, and they do not ask what they represent, i.e. whether the finite element under consideration is vector-valued or whether it is, for example, a scalar Hermite element with several degrees of freedom on each vertex).
template <int dim>
void ElasticProblem<dim>::setup_system()
{
dof_handler.distribute_dofs(fe);
hanging_node_constraints.clear();
hanging_node_constraints);
hanging_node_constraints.close();
DynamicSparsityPattern dsp(dof_handler.n_dofs(), dof_handler.n_dofs());
dsp,
hanging_node_constraints,
/ *keep_constrained_dofs = * / true);
sparsity_pattern.copy_from(dsp);
system_matrix.reinit(sparsity_pattern);
solution.reinit(dof_handler.n_dofs());
system_rhs.reinit(dof_handler.n_dofs());
}
#### ElasticProblem::assemble_system
The big changes in this program are in the creation of matrix and right hand side, since they are problem-dependent. We will go through that process step-by-step, since it is a bit more complicated than in previous examples.
The first parts of this function are the same as before, however: setting up a suitable quadrature formula, initializing an FEValues object for the (vector-valued) finite element we use as well as the quadrature object, and declaring a number of auxiliary arrays. In addition, we declare the ever same two abbreviations: n_q_points and dofs_per_cell. The number of degrees of freedom per cell we now obviously ask from the composed finite element rather than from the underlying scalar Q1 element. Here, it is dim times the number of degrees of freedom per cell of the Q1 element, though this is not explicit knowledge we need to care about:
template <int dim>
void ElasticProblem<dim>::assemble_system()
{
FEValues<dim> fe_values(fe,
const unsigned int dofs_per_cell = fe.dofs_per_cell;
const unsigned int n_q_points = quadrature_formula.size();
FullMatrix<double> cell_matrix(dofs_per_cell, dofs_per_cell);
Vector<double> cell_rhs(dofs_per_cell);
std::vector<types::global_dof_index> local_dof_indices(dofs_per_cell);
As was shown in previous examples as well, we need a place where to store the values of the coefficients at all the quadrature points on a cell. In the present situation, we have two coefficients, lambda and mu.
std::vector<double> lambda_values(n_q_points);
std::vector<double> mu_values(n_q_points);
Well, we could as well have omitted the above two arrays since we will use constant coefficients for both lambda and mu, which can be declared like this. They both represent functions always returning the constant value 1.0. Although we could omit the respective factors in the assemblage of the matrix, we use them here for purpose of demonstration.
Like the two constant functions above, we will call the function right_hand_side just once per cell to make things simpler.
std::vector<Tensor<1, dim>> rhs_values(n_q_points);
Now we can begin with the loop over all cells:
dof_handler.begin_active(),
endc = dof_handler.end();
for (; cell != endc; ++cell)
{
cell_rhs = 0;
fe_values.reinit(cell);
Next we get the values of the coefficients at the quadrature points. Likewise for the right hand side:
Then assemble the entries of the local stiffness matrix and right hand side vector. This follows almost one-to-one the pattern described in the introduction of this example. One of the few comments in place is that we can compute the number comp(i), i.e. the index of the only nonzero vector component of shape function i using the fe.system_to_component_index(i).first function call below.
(By accessing the first variable of the return value of the system_to_component_index function, you might already have guessed that there is more in it. In fact, the function returns a std::pair<unsigned int, unsigned int>, of which the first element is comp(i) and the second is the value base(i) also noted in the introduction, i.e. the index of this shape function within all the shape functions that are nonzero in this component, i.e. base(i) in the diction of the introduction. This is not a number that we are usually interested in, however.)
With this knowledge, we can assemble the local matrix contributions:
for (unsigned int i = 0; i < dofs_per_cell; ++i)
{
const unsigned int component_i =
for (unsigned int j = 0; j < dofs_per_cell; ++j)
{
const unsigned int component_j =
for (unsigned int q_point = 0; q_point < n_q_points; ++q_point)
{
cell_matrix(i, j) +=
The first term is (lambda d_i u_i, d_j v_j) + (mu d_i u_j, d_j v_i). Note that shape_grad(i,q_point) returns the gradient of the only nonzero component of the i-th shape function at quadrature point q_point. The component comp(i) of the gradient, which is the derivative of this only nonzero vector component of the i-th shape function with respect to the comp(i)th coordinate is accessed by the appended brackets.
lambda_values[q_point]) +
mu_values[q_point]) +
The second term is (mu nabla u_i, nabla v_j). We need not access a specific component of the gradient, since we only have to compute the scalar product of the two gradients, of which an overloaded version of the operator* takes care, as in previous examples.
Note that by using the ?: operator, we only do this if comp(i) equals comp(j), otherwise a zero is added (which will be optimized away by the compiler).
((component_i == component_j) ?
mu_values[q_point]) :
0)) *
fe_values.JxW(q_point);
}
}
}
Assembling the right hand side is also just as discussed in the introduction:
for (unsigned int i = 0; i < dofs_per_cell; ++i)
{
const unsigned int component_i =
for (unsigned int q_point = 0; q_point < n_q_points; ++q_point)
cell_rhs(i) += fe_values.shape_value(i, q_point) *
rhs_values[q_point][component_i] *
fe_values.JxW(q_point);
}
The transfer from local degrees of freedom into the global matrix and right hand side vector does not depend on the equation under consideration, and is thus the same as in all previous examples. The same holds for the elimination of hanging nodes from the matrix and right hand side, once we are done with assembling the entire linear system:
cell->get_dof_indices(local_dof_indices);
for (unsigned int i = 0; i < dofs_per_cell; ++i)
{
for (unsigned int j = 0; j < dofs_per_cell; ++j)
local_dof_indices[i], local_dof_indices[j], cell_matrix(i, j));
system_rhs(local_dof_indices[i]) += cell_rhs(i);
}
}
hanging_node_constraints.condense(system_matrix);
hanging_node_constraints.condense(system_rhs);
The interpolation of the boundary values needs a small modification: since the solution function is vector-valued, so need to be the boundary values. The Functions::ZeroFunction constructor accepts a parameter that tells it that it shall represent a vector valued, constant zero function with that many components. By default, this parameter is equal to one, in which case the Functions::ZeroFunction object would represent a scalar function. Since the solution vector has dim components, we need to pass dim as number of components to the zero function as well.
std::map<types::global_dof_index, double> boundary_values;
dof_handler, 0, Functions::ZeroFunction<dim>(dim), boundary_values);
boundary_values, system_matrix, solution, system_rhs);
}
#### ElasticProblem::solve
The solver does not care about where the system of equations comes, as long as it stays positive definite and symmetric (which are the requirements for the use of the CG solver), which the system indeed is. Therefore, we need not change anything.
template <int dim>
void ElasticProblem<dim>::solve()
{
SolverControl solver_control(1000, 1e-12);
SolverCG<> cg(solver_control);
PreconditionSSOR<> preconditioner;
preconditioner.initialize(system_matrix, 1.2);
cg.solve(system_matrix, solution, system_rhs, preconditioner);
hanging_node_constraints.distribute(solution);
}
#### ElasticProblem::refine_grid
The function that does the refinement of the grid is the same as in the step-6 example. The quadrature formula is adapted to the linear elements again. Note that the error estimator by default adds up the estimated obtained from all components of the finite element solution, i.e., it uses the displacement in all directions with the same weight. If we would like the grid to be adapted to the x-displacement only, we could pass the function an additional parameter which tells it to do so and do not consider the displacements in all other directions for the error indicators. However, for the current problem, it seems appropriate to consider all displacement components with equal weight.
template <int dim>
void ElasticProblem<dim>::refine_grid()
{
Vector<float> estimated_error_per_cell(triangulation.n_active_cells());
solution,
estimated_error_per_cell);
triangulation, estimated_error_per_cell, 0.3, 0.03);
}
#### ElasticProblem::output_results
The output happens mostly as has been shown in previous examples already. The only difference is that the solution function is vector valued. The DataOut class takes care of this automatically, but we have to give each component of the solution vector a different name.
To do this, the DataOut::add_vector() function wants a vector of strings. Since the number of components is the same as the number of dimensions we are working in, we use the switch statement below.
We note that some graphics programs have restriction on what characters are allowed in the names of variables. deal.II therefore supports only the minimal subset of these characters that is supported by all programs. Basically, these are letters, numbers, underscores, and some other characters, but in particular no whitespace and minus/hyphen. The library will throw an exception otherwise, at least if in debug mode.
After listing the 1d, 2d, and 3d case, it is good style to let the program die if we run upon a case which we did not consider. Remember that the Assert macro generates an exception if the condition in the first parameter is not satisfied. Of course, the condition false can never be satisfied, so the program will always abort whenever it gets to the default statement:
template <int dim>
void ElasticProblem<dim>::output_results(const unsigned int cycle) const
{
DataOut<dim> data_out;
data_out.attach_dof_handler(dof_handler);
std::vector<std::string> solution_names;
switch (dim)
{
case 1:
solution_names.emplace_back("displacement");
break;
case 2:
solution_names.emplace_back("x_displacement");
solution_names.emplace_back("y_displacement");
break;
case 3:
solution_names.emplace_back("x_displacement");
solution_names.emplace_back("y_displacement");
solution_names.emplace_back("z_displacement");
break;
default:
}
After setting up the names for the different components of the solution vector, we can add the solution vector to the list of data vectors scheduled for output. Note that the following function takes a vector of strings as second argument, whereas the one which we have used in all previous examples accepted a string there. (In fact, the function we had used before would convert the single string into a vector with only one element and forwards that to the other function.)
data_out.build_patches();
std::ofstream output("solution-" + std::to_string(cycle) + ".vtk");
data_out.write_vtk(output);
}
#### ElasticProblem::run
The run function does the same things as in step-6, for example. This time, we use the square [-1,1]^d as domain, and we refine it twice globally before starting the first iteration.
The reason for refining twice is a bit accidental: we use the QGauss quadrature formula with two points in each direction for integration of the right hand side; that means that there are four quadrature points on each cell (in 2D). If we only refine the initial grid once globally, then there will be only four quadrature points in each direction on the domain. However, the right hand side function was chosen to be rather localized and in that case, by pure chance, it happens that all quadrature points lie at points where the right hand side function is zero (in mathematical terms, the quadrature points happen to be at points outside the support of the right hand side function). The right hand side vector computed with quadrature will then contain only zeroes (even though it would of course be nonzero if we had computed the right hand side vector exactly using the integral) and the solution of the system of equations is the zero vector, i.e., a finite element function that is zero everywhere. In a sense, we should not be surprised that this is happening since we have chosen an initial grid that is totally unsuitable for the problem at hand.
The unfortunate thing is that if the discrete solution is constant, then the error indicators computed by the KellyErrorEstimator class are zero for each cell as well, and the call to refine_and_coarsen_fixed_number on the triangulation object will not flag any cells for refinement (why should it if the indicated error is zero for each cell?). The grid in the next iteration will therefore consist of four cells only as well, and the same problem occurs again.
The conclusion needs to be: while of course we will not choose the initial grid to be well-suited for the accurate solution of the problem, we must at least choose it such that it has the chance to capture the important features of the solution. In this case, it needs to be able to see the right hand side. Thus, we refine twice globally. (Any larger number of global refinement steps would of course also work.)
template <int dim>
void ElasticProblem<dim>::run()
{
for (unsigned int cycle = 0; cycle < 8; ++cycle)
{
std::cout << "Cycle " << cycle << ':' << std::endl;
if (cycle == 0)
{
GridGenerator::hyper_cube(triangulation, -1, 1);
triangulation.refine_global(2);
}
else
refine_grid();
std::cout << " Number of active cells: "
<< triangulation.n_active_cells() << std::endl;
setup_system();
std::cout << " Number of degrees of freedom: " << dof_handler.n_dofs()
<< std::endl;
assemble_system();
solve();
output_results(cycle);
}
}
} // namespace Step8
### The main function
After closing the Step8 namespace in the last line above, the following is the main function of the program and is again exactly like in step-6 (apart from the changed class names, of course).
int main()
{
try
{
Step8::ElasticProblem<2> elastic_problem_2d;
elastic_problem_2d.run();
}
catch (std::exception &exc)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
return 0;
}
# Results
There is not much to be said about the results of this program, other than that they look nice. All images were made using Visit from the output files that the program wrote to disk. The first two pictures show the $$x$$- and $$y$$-displacements as scalar components:
You can clearly see the sources of $$x$$-displacement around $$x=0.5$$ and $$x=-0.5$$, and of $$y$$-displacement at the origin. The next image shows the final grid after eight steps of refinement:
What one frequently would like to do is to show the displacement as a vector field, i.e., show vectors that for each point show the direction and magnitude of displacement. Unfortunately, that's a bit more involved. To understand why this is so, remember that we have just defined our finite element as a collection of two components (in dim=2 dimensions). Nowhere have we said that this is not just a pressure and a concentration (two scalar quantities) but that the two components actually are the parts of a vector-valued quantity, namely the displacement. Absent this knowledge, the DataOut class assumes that all individual variables we print are separate scalars, and Visit then faithfully assumes that this is indeed what it is. In other words, once we have written the data as scalars, there is nothing in Visit that allows us to paste these two scalar fields back together as a vector field. Where we would have to attack this problem is at the root, namely in ElasticProblem::output_results(). We won't do so here but instead refer the reader to the step-22 program where we show how to do this for a more general situation. That said, we couldn't help generating the data anyway that would show how this would look if implemented as discussed in step-22. The vector field then looks like this (Visit randomly selects a few hundred vertices from which to draw the vectors; drawing them from each individual vertex would make the picture unreadable):
We note that one may have intuitively expected the solution to be symmetric about the $$x$$- and $$y$$-axes since the $$x$$- and $$y$$-forces are symmetric with respect to these axes. However, the force considered as a vector is not symmetric and consequently neither is the solution.
# The plain program
/* ---------------------------------------------------------------------
*
* Copyright (C) 2000 - 2018 by the deal.II authors
*
* This file is part of the deal.II library.
*
* The deal.II library is free software; you can use it, redistribute
* it, and/or modify it under the terms of the GNU Lesser General
* version 2.1 of the License, or (at your option) any later version.
* The full text of the license can be found in the file LICENSE at
* the top level of the deal.II distribution.
*
* ---------------------------------------------------------------------
*
* Author: Wolfgang Bangerth, University of Heidelberg, 2000
*/
#include <deal.II/base/function.h>
#include <deal.II/base/tensor.h>
#include <deal.II/lac/vector.h>
#include <deal.II/lac/full_matrix.h>
#include <deal.II/lac/sparse_matrix.h>
#include <deal.II/lac/dynamic_sparsity_pattern.h>
#include <deal.II/lac/solver_cg.h>
#include <deal.II/lac/precondition.h>
#include <deal.II/lac/constraint_matrix.h>
#include <deal.II/grid/tria.h>
#include <deal.II/grid/grid_generator.h>
#include <deal.II/grid/grid_refinement.h>
#include <deal.II/grid/tria_accessor.h>
#include <deal.II/grid/tria_iterator.h>
#include <deal.II/dofs/dof_handler.h>
#include <deal.II/dofs/dof_accessor.h>
#include <deal.II/dofs/dof_tools.h>
#include <deal.II/fe/fe_values.h>
#include <deal.II/numerics/vector_tools.h>
#include <deal.II/numerics/matrix_tools.h>
#include <deal.II/numerics/data_out.h>
#include <deal.II/numerics/error_estimator.h>
#include <deal.II/fe/fe_system.h>
#include <deal.II/fe/fe_q.h>
#include <fstream>
#include <iostream>
namespace Step8
{
using namespace dealii;
template <int dim>
class ElasticProblem
{
public:
ElasticProblem();
~ElasticProblem();
void run();
private:
void setup_system();
void assemble_system();
void solve();
void refine_grid();
void output_results(const unsigned int cycle) const;
Triangulation<dim> triangulation;
DoFHandler<dim> dof_handler;
ConstraintMatrix hanging_node_constraints;
SparsityPattern sparsity_pattern;
SparseMatrix<double> system_matrix;
Vector<double> solution;
Vector<double> system_rhs;
};
template <int dim>
void right_hand_side(const std::vector<Point<dim>> &points,
std::vector<Tensor<1, dim>> & values)
{
Assert(values.size() == points.size(),
ExcDimensionMismatch(values.size(), points.size()));
Assert(dim >= 2, ExcNotImplemented());
Point<dim> point_1, point_2;
point_1(0) = 0.5;
point_2(0) = -0.5;
for (unsigned int point_n = 0; point_n < points.size(); ++point_n)
{
if (((points[point_n] - point_1).norm_square() < 0.2 * 0.2) ||
((points[point_n] - point_2).norm_square() < 0.2 * 0.2))
values[point_n][0] = 1.0;
else
values[point_n][0] = 0.0;
if (points[point_n].norm_square() < 0.2 * 0.2)
values[point_n][1] = 1.0;
else
values[point_n][1] = 0.0;
}
}
template <int dim>
ElasticProblem<dim>::ElasticProblem() :
dof_handler(triangulation),
fe(FE_Q<dim>(1), dim)
{}
template <int dim>
ElasticProblem<dim>::~ElasticProblem()
{
dof_handler.clear();
}
template <int dim>
void ElasticProblem<dim>::setup_system()
{
dof_handler.distribute_dofs(fe);
hanging_node_constraints.clear();
hanging_node_constraints);
hanging_node_constraints.close();
DynamicSparsityPattern dsp(dof_handler.n_dofs(), dof_handler.n_dofs());
dsp,
hanging_node_constraints,
/*keep_constrained_dofs = */ true);
sparsity_pattern.copy_from(dsp);
system_matrix.reinit(sparsity_pattern);
solution.reinit(dof_handler.n_dofs());
system_rhs.reinit(dof_handler.n_dofs());
}
template <int dim>
void ElasticProblem<dim>::assemble_system()
{
FEValues<dim> fe_values(fe,
const unsigned int dofs_per_cell = fe.dofs_per_cell;
const unsigned int n_q_points = quadrature_formula.size();
FullMatrix<double> cell_matrix(dofs_per_cell, dofs_per_cell);
Vector<double> cell_rhs(dofs_per_cell);
std::vector<types::global_dof_index> local_dof_indices(dofs_per_cell);
std::vector<double> lambda_values(n_q_points);
std::vector<double> mu_values(n_q_points);
std::vector<Tensor<1, dim>> rhs_values(n_q_points);
dof_handler.begin_active(),
endc = dof_handler.end();
for (; cell != endc; ++cell)
{
cell_rhs = 0;
fe_values.reinit(cell);
for (unsigned int i = 0; i < dofs_per_cell; ++i)
{
const unsigned int component_i =
for (unsigned int j = 0; j < dofs_per_cell; ++j)
{
const unsigned int component_j =
for (unsigned int q_point = 0; q_point < n_q_points; ++q_point)
{
cell_matrix(i, j) +=
lambda_values[q_point]) +
mu_values[q_point]) +
((component_i == component_j) ?
mu_values[q_point]) :
0)) *
fe_values.JxW(q_point);
}
}
}
for (unsigned int i = 0; i < dofs_per_cell; ++i)
{
const unsigned int component_i =
for (unsigned int q_point = 0; q_point < n_q_points; ++q_point)
cell_rhs(i) += fe_values.shape_value(i, q_point) *
rhs_values[q_point][component_i] *
fe_values.JxW(q_point);
}
cell->get_dof_indices(local_dof_indices);
for (unsigned int i = 0; i < dofs_per_cell; ++i)
{
for (unsigned int j = 0; j < dofs_per_cell; ++j)
local_dof_indices[i], local_dof_indices[j], cell_matrix(i, j));
system_rhs(local_dof_indices[i]) += cell_rhs(i);
}
}
hanging_node_constraints.condense(system_matrix);
hanging_node_constraints.condense(system_rhs);
std::map<types::global_dof_index, double> boundary_values;
dof_handler, 0, Functions::ZeroFunction<dim>(dim), boundary_values);
boundary_values, system_matrix, solution, system_rhs);
}
template <int dim>
void ElasticProblem<dim>::solve()
{
SolverControl solver_control(1000, 1e-12);
SolverCG<> cg(solver_control);
PreconditionSSOR<> preconditioner;
preconditioner.initialize(system_matrix, 1.2);
cg.solve(system_matrix, solution, system_rhs, preconditioner);
hanging_node_constraints.distribute(solution);
}
template <int dim>
void ElasticProblem<dim>::refine_grid()
{
Vector<float> estimated_error_per_cell(triangulation.n_active_cells());
solution,
estimated_error_per_cell);
triangulation, estimated_error_per_cell, 0.3, 0.03);
}
template <int dim>
void ElasticProblem<dim>::output_results(const unsigned int cycle) const
{
DataOut<dim> data_out;
data_out.attach_dof_handler(dof_handler);
std::vector<std::string> solution_names;
switch (dim)
{
case 1:
solution_names.emplace_back("displacement");
break;
case 2:
solution_names.emplace_back("x_displacement");
solution_names.emplace_back("y_displacement");
break;
case 3:
solution_names.emplace_back("x_displacement");
solution_names.emplace_back("y_displacement");
solution_names.emplace_back("z_displacement");
break;
default:
}
data_out.build_patches();
std::ofstream output("solution-" + std::to_string(cycle) + ".vtk");
data_out.write_vtk(output);
}
template <int dim>
void ElasticProblem<dim>::run()
{
for (unsigned int cycle = 0; cycle < 8; ++cycle)
{
std::cout << "Cycle " << cycle << ':' << std::endl;
if (cycle == 0)
{
GridGenerator::hyper_cube(triangulation, -1, 1);
triangulation.refine_global(2);
}
else
refine_grid();
std::cout << " Number of active cells: "
<< triangulation.n_active_cells() << std::endl;
setup_system();
std::cout << " Number of degrees of freedom: " << dof_handler.n_dofs()
<< std::endl;
assemble_system();
solve();
output_results(cycle);
}
}
} // namespace Step8
int main()
{
try
{
Step8::ElasticProblem<2> elastic_problem_2d;
elastic_problem_2d.run();
}
catch (std::exception &exc)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
return 0;
}
|
|
CSES Problem Set
# Bit Inversions
CSES - Bit Inversions
Time limit: 1.00 s Memory limit: 512 MB
There is a bit string that consists of $n$ bits. Then, there are some changes that invert bits. Your task is to report, after each change, the length of the longest substring whose each bit is the same.
Input
The first input line has a bit string that consists of $n$ bits. The bits are numbered $1,2,\ldots,n$.
The next line contains an integer $m$: the number of changes.
The last line contains $m$ integers $x_1,x_2,\ldots,x_m$ which describe the changes.
Output
After each change, print the length of the longest substring whose each bit is the same.
Constraints
• $1 \le n \le 2 \cdot 10^5$
• $1 \le m \le 2 \cdot 10^5$
• $1 \le x_i \le n$
Example
Input:
001011 3 3 2 5
Output:
4 2 3
Explanation: The bit string first becomes 000011, then 010011, and finally 010001.
|
|
## Function of time
(a) Sketch a graph of temperature as a function of time that is consistent with the scenario described in the following sentence: "The Child's temperature has been rising for the last two hours, but not as rapidly since we gave her the antibotic an hour ago." ( Let t=0 correspond to the time when the medicine was given.)
(b)What is the significance of the fact that the graph in part (a) is increasing on the interval t=-1 to t=1?
(c) What is the significance of the fact that the graph in part (a) is concave down the interval t=0 to t=1?
I don't know what graph like that would look like
|
|
Discussion about math, puzzles, games and fun. Useful symbols: ÷ × ½ √ ∞ ≠ ≤ ≥ ≈ ⇒ ± ∈ Δ θ ∴ ∑ ∫ • π ƒ -¹ ² ³ °
You are not logged in.
|
Options
bobbym
2013-06-22 21:43:39
yields 0.001079819330263761
yields 0.0010798643294
Seems pretty good. Try for larger n with x small in comparison to convince yourself numerically.
#### anonimnystefy wrote:
Have you tried getting the limit of the ratio of the two expressions (the exact one and the approximate one)? It does not approach 1.
I think the limit is 1.
According to M that is true. Why do you think the limit is not 1?
#### bobbym wrote:
To prove that you might need the limit but maybe since Stirlings formula is asymptotic to the factorial it might be implied in step 3.
Stirlings is an asymptotic form for the factorial. The limit of the ratio of Stirlings and the factorial is 1. The fact that he use Stirlings in his proof guarantees the above limit.
anonimnystefy
2013-06-22 21:34:59
Hi bobbym
Have you tried getting the limit of the ratio of the two expressions (the exact one and the approximate one)? It does not approach 1.
ShivamS
2013-06-22 10:00:03
Ok, I will try to think about it a bit. Thanks a lot.
bobbym
2013-06-22 03:44:15
Hi Shivamcoder3013;
I am not getting much of the derivation either. It is a lot of algebra and undoubtedly was done with the help of a package. I put it down so you would have something.
ShivamS
2013-06-22 02:19:52
I am not getting how you get that...
bobbym
2013-06-21 11:48:02
Hi;
The paper I am looking at "Gaussian and Coins."
Using Stirlings:
Notice the approximately equal sign that is because you are approximated a discrete distribution ( binomial ) with the Normal distribution.
1) is an approximation for 2) which the above steps prove. Even for large N it is still an approximation. When N approaches infinity 1) = 2).
To prove that you might need the limit but maybe since Stirlings formula is asymptotic to the factorial it might be implied in step 3.
anonimnystefy
2013-06-21 10:10:35
Hi Shivamcoder3013
Have you tried taking the limit as N goes to infinity of the ratio of the exact answer and the approximate one and proving it equals 1?
ShivamS
2013-06-21 04:47:59
Can you prove it then?
ShivamS
2013-06-19 09:53:45
Post 7 is what I need proven/
anonimnystefy
2013-06-19 08:15:17
That is what the original problem is asking for. But I cannot get it. I am using the limit definition and Stirling's formula.
bobbym
2013-06-19 02:22:35
Hi;
Do what?
that I can prove.
Agnishom
2013-06-19 02:18:19
How do you do that?
anonimnystefy
2013-06-19 02:12:58
It does seem to work without the minus sign, though.
bobbym
2013-06-19 02:04:07
I do not think so either.
anonimnystefy
2013-06-19 01:52:44
I don't think that would be correct, then.
|
|
# Question prove pigeonhole principle - Need an explanation [Full answer provided]
Training for game throughout 11 weeks, practicing at least 1 game per day and max 12 games per week Proof that there is number of days sequence that equal to 21 games
$$x_{i}$$ sum of number of games until day $$i$$
$$1\leq x_{1}< x_{2}..\leq x_{77}= 12*11 =132$$
we need to find $$x_{i} - x_{j} = 21$$ or $$x_{j}=x_{i}+21$$ then we can claim that sequence of days sum are 21 games
$$22\leq x_{1}+21< x_{2}+21..\leq x_{77}+21=153$$
{$$x_{1},x_{2},..,x_{77}$$}, {$$x_{1}+21,x_{2}+21,..,x_{77}+21$$} we have 154 numbers. the sum can range from 1 to 153 so there is 154 cells and 153 pigeon
so, $$\left \lceil \frac{154}{153} \right \rceil = 2$$ we get two equal number in same cell
My question:
• Why 21 was added to the inequality ?
• Becuase you want to prove there is an $x_j = x_i + 21$. And we do that bylooking at the ranges of all possible $x_j$ and at the range of all possible $x_i + 21$ we seeing if there must be some overlap. If the range of $x_j$ is $1$ through $132$ then the range if $x_i +21$ is $22$ through $153$. – fleablood Aug 25 '20 at 18:30
If there is an $$i,j$$ such that $$x_i-x_j = 21$$ then $$\{x_i,x_j\}\cap\{x_i+21,x_j+21\}$$ will be non-empty.
Or, the number of members of $$\{x_i,x_j\}\cup\{x_i+21,x_j+21\}$$ will be less than the number of sum of the number of members of each set.
Contrariwise, if the number of members of the set $$\{x_1,\cdots, x_{77}\}\cup \{x_1+21,\cdots, x_{77}+21\}$$ is less than $$77+77$$ then there is at least one member of each subset that are the same.
• why $x_{i}−x_{j}=21$ can't be found in the first inequality ? – Mostfa shma Aug 25 '20 at 18:10
• How do you intend to compare all possible $i,j$ pairs to show that at least one is equal? This is a shot-gun approach, that allows us to check the set en-masse. – Doug M Aug 25 '20 at 18:11
• assuming $x_{6}=42 x_{3}=21, 6=i, 3=j$ then what are the sequence elements in $x_{i}-x_{j}$? – Mostfa shma Aug 25 '20 at 18:17
• They aren't ordered in sequence. You have $x_6-x_5, x_6- x_4, x_6-x_3, x_5-x_4, x_5-x_3, x_4 -x_3$. But we don't just have $x_6$ through $x_3$ we have $x_77$ through $x_1$ so that is $\frac {77*76}2$ possible $x_j - x_i$ and there is no need that we can tell than any of them have to be $21$. The smallest they can be is $1$ and the largest is $131$ so they must double up we have no reason that any of them must be $21$. – fleablood Aug 25 '20 at 18:38
|
|
# 400V Linear Regulators from Diodes Incorporated Deliver Constant LED Current in Compact Packages
Diodes Incorporated, a leading global manufacturer and supplier of high-quality, application-specific standard products within the broad discrete, logic, analog and mixed-signal semiconductor markets, today announced the introduction of the AL5890 linear constant-current regulator developed to provide simple and more cost-effective solutions to driving LED strings from an off-line or DC power supply.
Available in a range of packages, the small form-factor of the AL5890 makes it ideal for any LED application where a lower BoM cost and sizes are important. The fully integrated design includes a power transistor and it is available in 10mA, 15mA, 20mA, 30mA, and 40mA variants. A single device or multiple devices in parallel can be used to source or sink enough current for long LED strings, with an overall accuracy of less than ±2.0mA (typ), working over a wide ambient temperature range of -40°C to +105°C.
Its simple two-pin PD123 design means it can be inserted directly in the LED string in low-side AC or DC, or high-side AC or DC linear configurations without any external resistors. It is designed to tolerate DC voltages of up to 400V and can be used in off-line applications up to 230VAC. Thermal foldback protection is included, which prevents system failure by reducing the current in the event of high operating temperatures. As well as lowering the overall BoM, it also provides an effective solution to tackling EMI without the need for additional switching inductors.
Packaging options include PDI123, SOT89-3L, and TO252-3L to help address heat dissipation in various LED lighting applications including LED lamps, commercial LED fixtures, emergency lighting, signage and downlights, as well as decorative and architectural lighting.
The AL5890 PDI123 package is priced at $0.09, the SOT89 is priced at$0.1 and the TO252 is priced at \$0.12 for 10K volumes.
|
|
You are currently browsing the monthly archive for May 2013.
Mass. The stuff of stuff. Tough to move about, painful if you run into it, and a tendency for big things to pull together. Recently I’ve been pondering mass, and given the stunning work on the Higgs boson that’s going on at the moment, I thought I might share some thoughts.
So: mass. It seems a pretty intuitive concept. Push (or pull) something, and the heavier it is the more it resists the force you apply. This is encapsulated in physics in Newton’s second law ($F=ma$) and is fundamental to classical mechanics. It’s so intuitive and well-established in physics that its easy to forget that although Newton’s laws are astoundingly accurate, useful, and powerful they don’t say anything about what mass actually is.
One thing its definitely not, is easy to explain or well-understood. For one thing, there are two concepts of mass in physics. There’s the mass I just mentioned, Inertial mass which is an object’s resistance to changes in its motion, but there is also Gravitational mass, which is the property that causes massive objects to attract each other – this is the stuff of both Newton’s law of gravitation and Einstein’s general relativity. If you think about it, these are in fact quite different things: one is the response of an object to being shoved around, the other is its tendency to attract other masses. In strict terms these are to completely different interactions: if I push something I’m interacting with it via the electromagnetic force (yes, I am. electro-chemical processes in my brain and muscles move my hands (or whatever) to an object an push against it. On the smallest scale this is mediated by the electrons in the molecules of my skin cells repelling the electrons in the atoms at the surface of whatever I’m pushing), whereas gravity is usually thought o be a separate fundamental interaction. General relativity models it as the object curving the space it sits in. Two completely different forces acting in completely different ways.
Looked at from this perspective, it almost seems to be a coincidence that both of these concepts have the same name – why call them both mass? Aren’t we conflating two different things? So here’s something worth pondering: if we measure the inertial mass of an object and then measure the gravitational mass of the same object they are exactly the same. And that, if you think about it, is pretty odd. There have been some astonishingly accurate comparisons of inertial and gravitational mass over the years, and none of them have ever detected any measurable difference between them.
So, enter Einstein. The usual explanation of the equality of inertial and gravitational mass is the Principle of Equivalence. Einstein realised that inertial and gravitational mass are connected via acceleration. Imagine you’re in space, floating, weightless. You’re not experiencing any forces, including gravity. Now imagine you’re in a lift in a very, very tall building. When the lift is stationary you feel gravity. You also feel other little forces when the lift speeds up or slows down – a little heavier when the lift starts to move upwards, a little lighter when the lift slows before stopping at a floor. Now imagine that the lift cable snaps – you fall, until you hit the ground. Being in the lift you don’t feel the air rushing around you and there are no windows so you can’t see the walls zooming past or the floor shooting upwards, encompassing your imminent doom. This means you don’t feel any forces – you, the floor, the walls, the air around you are all being accelerated in the same way towards the ground so while you are falling you are weightless, just like you were in space. Now imaging that the building is so tall that you never hit the ground – you can’t tell the difference between free-fall and the absence of gravity. This is the principle of equivalence – an “inertial frame” (the one in space) is identical to one in freefall. In general relativity, the free-falling one is thought of as moving along a line on a curved spacetime. These two things are equivalent.
So there you have it: inertial and gravitational masses are the same because of the principle of equivalence. Except… well, the clue’s in the name, really – the principle of equivalence is just that, a principle. It works, but it doesn’t tell you WHY these things are equivalent, just that the theory works out if they are. It puts me in mind of a quote about wave-particle duality in quantum mechanics: they are completely different things which we think of as being the same. It is as if we saw a rabbit sitting in a tree. This would be pretty unusual, but is completely explained if just think of the rabbit as being a cat, in which case we’d understand its behaviour quite well. The two masses are equivalent because the theory tells them to be. This is clearly not the end of the story.
But none of this is anything too remarkable – mass and mass, gravity and acceleration — all pretty unremarkable. I congratulate you for persevering this far. The really interesting stuff comes when you start thinking about quantum mechanics and another famous Einsteinian concept- the equivalence of energy and mass, $E=mc^2$.
Mass is a long-standing problem in the quantum world. On the one hand there are ongoing efforts to unify the four forces and construct a quantum description of gravity. I’m no expert here, but given that this has been THE problem in theoretical physics for the better part of 40 years and we’re still very far from testable experimental predictions, it’s safe to say that this is hard. We’ve got string theory, we’ve got quantum loop gravity, we’ve got extra dimensions and whorls in spacetime, and unfortunately we’ve got serious difficulties with diverges and suggestions based around the compactification of multiple higher dimensions. Heady stuff.
Then there’s inertial mass in the quantum world. This is the stuff that’s been making headlines of late with the likely discovery of the Higgs Boson. The Higgs mechanism is a hypothetic answer to what mass actually is. The idea is that empty space is filled with a thing called the Higgs Field. This is like a sticky soup of virtual particles which resist changes in its motion. A good analogy for this is a ping-pong ball on a string in a bucket of water (no, really). Forget for a moment that ping-pong balls float, imaging that the ball is in the waterand you pull it with the string. The water resists the motion of the ball and makes it feels heavier. It would be worse if it were in treacle. This is what the Higgs field does – it resists changes to the ball’s motion and causes an effect that’s a lot like mass.
The Higgs Boson is the particle tht ediates the interaction between the Higgs Field and particles placed in it, and you might be tempted to think that it’s got inertil mass nailed, but you’d be wrong. The Higgs field explains the mass of elementary particles, like electrons and quarks. As we all know, protons and neutrons are made of three quarks, so you’d think that their mass would be about three times the size of a quark. Quantum Mechanics being what it is, this isn’t the case. Protons and neutrons are actually about 500 times more massive than their constituent quarks. The remainder is made up from the binding energy of the quarks (the energy of the bonds connecting them together). There’s a lot of energy in there, and its contribution to the mass can be calculated via none other than $E=mc^2$ and gives a very accurate estimate of the mass of protons and neutrons.
There’s just one snag here: this mass isn’t coupled to the Higgs Field. The Higgs interaction couples to the Electroweak force, but quarks are bound via the Strong force. $E=mc^2$ tells us the amount of mass in there, but not the reason why this energy causes resistance to changes in its motion. We also don’t know the relationship between Higgs mass and gravitational mass or how all this might relate to the principal of equivalence. Put simply, we don’t know what 98% of the mass in atoms is or how it connects to gravitation. Hence my suggestion that we don’t really understand mass.
And this is also born out by a current crisis in theoretical physics. It’s easy enough to state: what would you see and what would happen to you if you fell into a black hole (and specifically, what happens when you cross the event horizon)? Until recently, the answer from most physicists would have been that you wouldn’t really notice – you be passing through empty space and the principle of equivalence lets us know that this would feel like… floating in space. After a long time you’d notice that your feet were falling faster than your head (assuming you were falling feet first) and after a very long time the difference in force would eventually tear you apart. Ow. Nasty way to go.
More recently, though, cracks have emerged in this story. They have to do with the nature of the vacuum — classically, there’s nothing there, but in the quantum world it’s a writhing, foaming sea of pair of virtual particles spontaneously coming into being and then annihilating (this is a consequence of the uncertainty principle. A completely empy vacuum would have known energy (zero) forever, which is forbidden).
At the event horizon of a black hole one of the pair will fall into the black hole, and the other will zip off to infinity. This is Hawking Radiation, the fleeing particles steal a bit of energy from the black hole and cause it to shrink slightly. Eventually it causes an isolated black hole to vanish completely.
The problem is that it doesn’t stop there. The information about the particle that falls into the back hole is destroyed when it falls in — there’s no way of discovering what the particle was by looking at the radiation coming from the black hole itself. This is a problem because a fundamental principle of Quantum Field Theory is that information is never lost — you can always recover it. A potential way out is to imagine that the pair of particles are entangled, and the one that zips off to infinity tells us about the one that falls in, but this leads to a lot of energy being released when the pair separate.
And here comes the punchline: General Relativity says you wouldn’t feel much when you fall into a black hole, quantum mechanics says you would meet a wall of fire at the event horizon. Either the principle of equivalence is wrong or the holographic principle is wrong. The two pillars of modern physics are in contradiction: at least one is going to fall, and it’s all linked to the nature of mass and the nature of the vacuum.
So what are people doing to get around this? A surprising amount, it appears.
There re a couple of different approaches, all of which seem to revolve around studying the quantum vacuum itself. Firstly, there are several theories which suggest that the reason why it’s so difficult to combine quantum field theory with general relativity is that gravity isn’t actually a fundametal force at all – it’s an emergent effect from the interaction of particles with the quantum vacuum. General relativity then emerges as an “effective theory” at larger scales. The sort of emergence has been observed in systems like crystals and superconductors and might lead to the origin of gravitational mass.
On the other hand, there an approach that models the quantum vacuum using classical physics (which is apparently quite good at reproducing blackbody curves) which treats inertial mass as another interaction of particles and the vacuum. This time resistance is generated by changes in motion due to exchanging energy with this classical quantum vacuum.
What’s interesting about these is how similar the approaches are: particle interacting with some model of the vacuum. They also both suggest that if we could manipulate the vacuum we could also manipulate mass, which would be very exiting indeed.
There’s also the ongoing problem with Dark Matter and Dark Energy – we don’t know what they are (especially Dark Energy) but we need them to make our models work. Wildly speculating, it’s possible that this is linked to the black hole conundrum.
For an outsider like me, though, I can’t help but think that all this is very reminiscent of the situation in physics at the end of the 19th century. We have a problem that appears to destroy all our well-established physics that we cannot solve. The way out of that one was quantum mechanics, which has done pretty well for itself and lead to new technologies that would have seemed like magic beforehand.
The way out of this will undoubtedly be exciting and revolutionary. Can’t wait to see what people come up with!
|
|
## Essential University Physics: Volume 1 (4th Edition)
$\frac{1}{2}MR^2$
We know the following value for $dm$: $dm = \frac{2Mrdr}{R^2}$ Thus, we find: $I = \int_{0}^{R}r^2dm=I = \int_{0}^{R}r^2 \frac{2Mr}{R^2}dr = \frac{1}{2}MR^2$
|
|
Number changing animation with animation nodes?
How to make number changing animation with animation nodes pleae?
First we have to make two lists of texts. first list containing 5 copies of 14.5 260 and second list containing the modified text. Then we can use a switch node to switch between these two lists. The switching condition can be set using a sine node which produces flickering effect.
|
|
# Is the the complement of the Halting problem NP-hard [duplicate]
Let us define the language (the complement of the Halting Problem):
$$LOOPING = \left\{ \langle M,x \rangle | M \ doesn't \ halt \ on \ x\right\}$$
The question is if $LOOPING$ is NP-Hard. I'm pretty clueless about the answer. I know the the Halting problem is NP-Hard, but I can't seem to find a reduction from an NP-Hard problem to $LOOPING$.
• Hint: Construct a Turing machine which goes over all potential satisfying assignments of a SAT instance, halts if it doesn't find any, and enters an infinite loop otherwise. – Yuval Filmus Dec 23 '17 at 13:48
• I think you mean "$M$ doesn't halt on $x$". – Yuval Filmus Dec 23 '17 at 13:49
• You're right, thanks I corrected the question. – user3636583 Dec 23 '17 at 13:50
• Mind correcting the grammar? Halt(s) – candied_orange Dec 23 '17 at 13:51
• So Yuval the reduction you suggested is polynomial because M is of finite length and x depends on the input of the SAT-problem? – user3636583 Dec 23 '17 at 13:53
|
|
# Security
## General discussion
Locked
### help with hijacking
By ·
We have one Dell workstation that is over a year old and has a problem with pop-ups for a while now. A while back I managed to stop them temporarily by removing miscellaneous programs (except Weatherbug), but now they are back with a vengeance. I removed any software or programs that looked frivolous to her system. (Including WeatherBug) and AOL toolbar (She does continue to use AIM). But still more popups.
I am now pretty sure her browser is hijacked. It doesn't change her home page or take her to any unwanted sites, but the popups are not linked to any clear separate process. They appear to link most often to iexplore.exe or explore.exe
Sometimes even taskmanager! They only appear when she is online, but they come from her computer, not the websites. (thereby getting past IE's popup blocker) I did see "Inqwire" as the title of a few of the popups and searched that. But after downloading and running HijackThis I did not see any of the things that they say to remove if you get hijacked by Inqwire.
So...below is the HijackThis log. I cannot see any apparent problems. Can anyone else spot what is amiss? thanks for any help! Tink
Logfile of HijackThis v1.99.1
Scan saved at 10:36:48 AM, on 1/23/2006
Platform: Windows XP SP2 (WinNT 5.01.2600)
MSIE: Internet Explorer v6.00 SP2 (6.00.2900.2180)
Running processes:
C:\WINDOWS\System32\smss.exe
C:\WINDOWS\system32\winlogon.exe
C:\WINDOWS\system32\services.exe
C:\WINDOWS\system32\lsass.exe
C:\WINDOWS\system32\svchost.exe
C:\WINDOWS\System32\svchost.exe
C:\WINDOWS\system32\LEXBCES.EXE
C:\WINDOWS\system32\spoolsv.exe
C:\WINDOWS\system32\LEXPPS.EXE
C:\Program Files\Common Files\Symantec Shared\ccSetMgr.exe
C:\Program Files\Norton AntiVirus\navapsvc.exe
C:\Program Files\Norton AntiVirus\IWP\NPFMntor.exe
C:\Program Files\Norton AntiVirus\SAVScan.exe
C:\Program Files\Common Files\Symantec Shared\SNDSrvc.exe
C:\Program Files\Common Files\Symantec Shared\SPBBC\SPBBCSvc.exe
C:\WINDOWS\System32\svchost.exe
C:\Program Files\Common Files\Symantec Shared\CCPD-LC\symlcsvc.exe
C:\Program Files\Common Files\Symantec Shared\ccEvtMgr.exe
C:\WINDOWS\Explorer.EXE
C:\WINDOWS\System32\hkcmd.exe
C:\Program Files\Roxio\Easy CD Creator 5\DirectCD\DirectCD.exe
C:\Program Files\Dell AIO Printer A940\dlbabmgr.exe
C:\WINDOWS\BCMSMMSG.exe
C:\Program Files\Dell AIO Printer A940\dlbabmon.exe
C:\Program Files\Common Files\Symantec Shared\ccApp.exe
C:\PROGRA~1\DELLSU~1\DSAgnt.exe
C:\PROGRA~1\MICROS~2\OFFICE11\OUTLOOK.EXE
C:\Program Files\Microsoft Office\OFFICE11\WINWORD.EXE
C:\Program Files\Internet Explorer\iexplore.exe
C:\Program Files\Messenger\msmsgs.exe
C:\Documents and Settings\carinsdell\My Documents\HijackThis\HijackThis.exe
R0 - HKCU\Software\Microsoft\Internet Explorer\Main,Start Page = http://www.kolorcure.com/
R1 - HKLM\Software\Microsoft\Internet Explorer\Main,Default_Page_URL = http://companyweb
O2 - BHO: (no name) - {53707962-6F74-2D53-2644-206D7942484F} - C:\PROGRA~1\SPYBOT~1\SDHelper.dll
O3 - Toolbar: Norton AntiVirus - {42CDD1BF-3FFB-4238-8AD1-7859DF00B1D6} - C:\Program Files\Norton AntiVirus\NavShExt.dll
O4 - HKLM\..\Run: [IgfxTray] C:\WINDOWS\System32\igfxtray.exe
O4 - HKLM\..\Run: [HotKeysCmds] C:\WINDOWS\System32\hkcmd.exe
O4 - HKLM\..\Run: [AdaptecDirectCD] "C:\Program Files\Roxio\Easy CD Creator 5\DirectCD\DirectCD.exe"
O4 - HKLM\..\Run: [Dell AIO Printer A940] "C:\Program Files\Dell AIO Printer A940\dlbabmgr.exe"
O4 - HKLM\..\Run: [BCMSMMSG] BCMSMMSG.exe
O4 - HKLM\..\Run: [Symantec NetDriver Monitor] C:\PROGRA~1\SYMNET~1\SNDMon.exe /Consumer
O4 - HKLM\..\Run: [ccApp] "C:\Program Files\Common Files\Symantec Shared\ccApp.exe"
O4 - HKLM\..\Run: [Tracker] C:\Program Files\MySoftware\MyInvoices\tracker.exe
O4 - HKCU\..\Run: [DellSupport] "C:\PROGRA~1\DELLSU~1\DSAgnt.exe" /startup
O8 - Extra context menu item: E&xport to Microsoft Excel - res://C:\PROGRA~1\MICROS~2\OFFICE11\EXCEL.EXE/3000
O9 - Extra button: Research - {92780B25-18CC-41C8-B9BE-3C9C571A8263} - C:\PROGRA~1\MICROS~2\OFFICE11\REFIEBAR.DLL
O9 - Extra button: AIM - {AC9E2541-2814-11d5-BC6D-00B0D0A1DE45} - C:\PROGRA~1\AIM\aim.exe
O12 - Plugin for .spop: C:\Program Files\Internet Explorer\Plugins\NPDocBox.dll
O14 - IERESET.INF: START_PAGE_URL=http://companyweb
O17 - HKLM\System\CCS\Services\Tcpip\Parameters: Domain = kolorcure.local
O17 - HKLM\Software\..\Telephony: DomainName = kolorcure.local
O17 - HKLM\System\CS1\Services\Tcpip\Parameters: Domain = kolorcure.local
O20 - Winlogon Notify: igfxcui - C:\WINDOWS\SYSTEM32\igfxsrvc.dll
O23 - Service: Symantec Event Manager (ccEvtMgr) - Symantec Corporation - C:\Program Files\Common Files\Symantec Shared\ccEvtMgr.exe
O23 - Service: Symantec Password Validation (ccPwdSvc) - Symantec Corporation - C:\Program Files\Common Files\Symantec Shared\ccPwdSvc.exe
O23 - Service: Symantec Settings Manager (ccSetMgr) - Symantec Corporation - C:\Program Files\Common Files\Symantec Shared\ccSetMgr.exe
O23 - Service: LexBce Server (LexBceS) - Lexmark International, Inc. - C:\WINDOWS\system32\LEXBCES.EXE
O23 - Service: Norton AntiVirus Auto-Protect Service (navapsvc) - Symantec Corporation - C:\Program Files\Norton AntiVirus\navapsvc.exe
O23 - Service: Norton AntiVirus Firewall Monitor Service (NPFMntor) - Symantec Corporation - C:\Program Files\Norton AntiVirus\IWP\NPFMntor.exe
O23 - Service: SAVScan - Symantec Corporation - C:\Program Files\Norton AntiVirus\SAVScan.exe
O23 - Service: ScriptBlocking Service (SBService) - Symantec Corporation - C:\PROGRA~1\COMMON~1\SYMANT~1\SCRIPT~1\SBServ.exe
O23 - Service: Symantec Network Drivers Service (SNDSrvc) - Symantec Corporation - C:\Program Files\Common Files\Symantec Shared\SNDSrvc.exe
O23 - Service: Symantec SPBBCSvc (SPBBCSvc) - Symantec Corporation - C:\Program Files\Common Files\Symantec Shared\SPBBC\SPBBCSvc.exe
O23 - Service: Symantec Core LC - Symantec Corporation - C:\Program Files\Common Files\Symantec Shared\CCPD-LC\symlcsvc.exe
O23 - Service: SymWMI Service (SymWSC) - Symantec Corporation - C:\Program Files\Common Files\Symantec Shared\Security Center\SymWSC.exe
This conversation is currently closed to new comments.
23 total posts (Page 1 of 3) 01 | 02 | 03 Next
| Thread display: Collapse - | Expand +
Collapse -
### hkcmd.exe
by In reply to help with hijacking
Check the manufacturer and date on this exe.
Then go to Trend Micro and run the free spy ware tool.
Also, I'd anonymize anything like this you post. This one's a bit of a giveaway.
Good luck!
Collapse -
### thanks
As for the anonyminity. I don't mind showing that I don't know something. This is how I've gotten where I am now, by learning OJT. I only get my official title because I'm the only one here who understand these things.=-)
Collapse -
### short of a rootkit
by In reply to help with hijacking
combine anti-spyware to find this. it's probably in a startup key in registry key somewhere.
spybot, ad-aware are good but won't get all.
disable active-x on this pc in internet zone. don't let them install anything, don't give admin rights. update all patches to prevent buffer overflow / malformed takeovers.
if you spend too much time, re-image it. but lock it down too so you don't have to repeat every few..
Collapse -
### Suggestions
by In reply to help with hijacking
Check and see if services.msc is set to enabled and is running. You could get pop-up's through the Messenger service.
Also, remove the AIM program and see if the popups stop. If they do, then AIM has been compromised.
Collapse -
### doh!
I can't believe I didn't think of uninstalling AIM!
Well I did uninstall it today after your suggestion. It looked like it stopped up until she went to close down and she got 1 popup. We are going to try browsing again tomorrow and see if the popups continue.
Collapse -
### oh, this looks familiar.....!
by In reply to help with hijacking
I have the feeling I know where this landed from - same place as mine did, WeatherBug. Had the same problem on my home lappie - all because I wanted to look at a particular countrys' weather over Xmas to ensure a mate was skiing on snow and not grass.....
There seem to be numerous variations of this program; some legit, some not. The legit ones seem to be clean (seem!) but with all the variations when you google it, you have no way of really knowing the good from the bad! (or even for which country - that one caught me out, too!)
The only way I got this to stop was not simply re-imaging - I ended up using a proprietary data destruction program on the drive, as the image (which I knew was clean) kept stalling (no idea why, I'm not that technical)
Just trying to tip you off to allow time for a total blat of the drive, as well as re-imaging...
I HATE WEATHERBUG!
GG
Collapse -
### Kill Weatherbug!
by In reply to oh, this looks familiar.. ...
yea, I kinda had a feeling Weatherbug might have been more of a bug than just the weather! But in this case I'm not sure if it was the one and only culprit. It may be an affliction arising from several sources. I'm not sure. Because I don't know exactly what is causing the popups because I can't find the files that are supposed to be there if it's Inqwire.
Have already run Ad-Aware and Spybot in both safe and normal modes, as well as Norton and Panda. They all got rid of certain things, but none have stopped the popups. The programs now installed all look legit. We still have further testing to do today because we uninstalled AIM yesterday and didn't get any popups for quite a while, until the very end. I'll keep you posted. Still open to suggestions!
Collapse -
### One More Malware Removal Tool
by In reply to Kill Weatherbug!
One other program you may want to try is called Malware Destroyer by a company called EMCO. It can be downloaded for free at:
http://www.emco.is/malwaredestroyer/features.html
Can't hurt.......
Collapse -
### Strange, Weatherbug seems just fine ...
by In reply to oh, this looks familiar.. ...
... here. gives the alerts, and precious little else. Must have been my install.
I wish I could find a better solution for the wife, however. She could have been a first rate meteorologist if her mother hadn't been such a squeezing, wrenching, grasping, scraping, clutching, covetous old sinner when it came time to talk about financing college.
Collapse -
### You can spend all of this time troubleshooting . . . OR
by In reply to help with hijacking
Rebuild your PC and be malware / virus / etc. free in less than 3 hours. :)
23 total posts (Page 1 of 3) 01 | 02 | 03 Next
• 6
• 7
• 1
• 0
|
|
# How many moles of iron are in 1.2*10^25 atoms of iron?
Sep 13, 2016
There are approx. $6.022 \times {10}^{23}$ iron atoms per mole of ion. This quantity, this number of iron atoms has a mass of $55.85 \cdot g$. And of course, when we quote the mass of iron we say $55.85 \cdot g \cdot m o {l}^{-} 1$.
$\left(1.2 \times {10}^{25} \cdot \text{atoms of iron")/(6.022xx10^23*"iron atoms per mole}\right)$ $\cong$ $20 \cdot \text{moles}$
|
|
# Solving Percent Problems Using Proportions
Using the vocabulary we used earlier: $$\begin \frac & = \frac \ \frac & = \frac \end$$ (a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
Tags: Fall Of The Roman Empire EssaysRenaissance Concepts Of Man And Other EssaysInformation Technology Problem SolvingAqa Science Gcse HomeworkNano Car Research PapersChemical Engineering Homework HelpEnglish Essays Compare ContrastAdvantages And Disadvantages Of Self Employment - EssayHow Do I Finish All My HomeworkBusiness Law Term Paper Outline
In the example of 5The amount is the number that relates to the percent. Once you have an equation, you can solve it and find the unknown value.
To do this, think about the relationship between multiplication and division.
Find a percentage or work out the percentage given numbers and percent values. The formulas below are all mathematical variations of this formula. X and Y are numbers and P is the percentage: There are nine variations on the three basic problems involving percentages.
Use percent formulas to figure out percentages and unknowns in equations. See if you can match your problem to one of the samples below.
Look at the pairs of multiplication and division facts below, and look for a pattern in each row.
Percent problems can also be solved by writing a proportion.
Example 47% of the students in a class of 34 students has glasses or contacts.
How many students in the class have either glasses or contacts?
Convert from percentage to decimals with the Percent to Decimal Calculator.
If you need to convert between fractions and percents see our Fraction to Percent Calculator, or our Percent to Fraction Calculator. "Percent." From Math World -- A Wolfram Web Resource.
## Comments Solving Percent Problems Using Proportions
• ###### How Do You Use a Proportion to Find What Percent a Part is.
Problem; percent; percent proportion; solve for percent; percent of a number; cross multiply. What Are Some Words You Can Use To Write Word Problems?…
• ###### Solving Percent Problems Using a Percent Proportion Math.
Solving Percent Problems Using a Percent Proportion by Tara Anderson - November 1, 2013.…
• ###### Unit 23 Solving Percent Problems Using Proportions
Proportions may be used to solve many percent problems. 2. Percentages may be used to compare two numbers. One number represents the part, the other.…
• ###### Percentage Calculator - Calculator Soup
Convert the problem to an equation using the percentage formula P% * X = Y. X; The 'what' is P% that we want to solve for; Divide both sides by X to get P%.…
• ###### Percent Proportion Solver - Jeff LeMieux
Insert two of the three kmissing terms to solve for the third. Solving Percentage Proportions. Enter the values from your proportion problem. Place an x in the.…
• ###### Solving Percent Problems Using Proportions - ppt video.
Use the following proportion to solve percent problems! IS part % OFwhole **The set up is always the same. =…
• ###### Proportions - Math is Fun
A percent is actually a ratio! Saying "25%" is actually saying "25 per 100" 25% = 25100. We can use proportions to solve questions involving percents. The trick.…
|
|
### mcGyver's blog
By mcGyver, history, 5 weeks ago,
I was solving this 520B - Two Buttons problem. Here maximum input and output size is 10^4. In my code I took N = 10^6 and it was giving Runtime Errorin my local IDE but when I submitted the same code, it got accepted. My submission 116080580. I dont know whether it's a fault of my device or the compliler I am using. Can anyone help??
• +11
» 5 weeks ago, # | 0 It's a memory stack size issue. I had a similar problem here https://codeforces.com/blog/entry/68870
• » » 5 weeks ago, # ^ | ← Rev. 2 → 0 But I have already declared the arrays globally still this happened. Taking arrays globally seems not working in this case..
• » » » 5 weeks ago, # ^ | 0 It's the recursion. Recursion calls eat up stack memory too.
• » » » » 5 weeks ago, # ^ | 0 What should I do then.. Is there any way around to get rid of this?
• » » » » » 5 weeks ago, # ^ | 0 To make it work on your local machine look up the build option to increase your stack size or how to increase the stack size in your ide.To reduce your program's memory footprint in general, use iterarive dp if possible. A more laborious way is maybe simulate recursion using stack, but you'll rarely need to do this.
• » » » » » » 5 weeks ago, # ^ | +9 In practice recursive DFS works faster than non-recursive DFS. I have no idea why it's so but I've stumbled upon this problem several times.
» 5 weeks ago, # | 0 This is clearly a problem with stack size, but it's difficult to help without knowing what OS are you using. If you're using Linux, you can disable stack limit using ulimit -s unlimited.
• » » 5 weeks ago, # ^ | -11 The default stack size for my Linux machine seems to be a couple of MBs, while certain problems on CodeForces require memory sizes well above that. People are bound to face this issue once they start solving Div. 2 Bs/Cs. Considering the number of new users who are registering every month, can links to blogs on this along with those to blogs on other important stuff such as Modular Arithmetic basics (Fermat's Little Theorem) be added to a single 'pinned' blog?
• » » 5 weeks ago, # ^ | 0 My OS is windows 10. I dont find any similar method for windows like Linux has but there is a setting in CodeBlocks IDE which can increase the stack size. But it is only restricted to CodeBlocks. Usually I use sublime text 3 and for that things are same as before... RTE
|
|
# Populism in tweets of German politicians
The last months (years? since ever???) have seen a surge in populism and a rise in nationalism. Not only in Russia, the United States, Turkey, but also in some EU countries the ghost of nationalism-populism seems to be marching and gaining ground.
As to Germany, in September 24, 2017, the 19. German federal elections took place. The newly founded alt-right AfD (Alternative for Deutschland) has made a leap and moved in the Bundestag. In some electoral districts, its share rose to 35%, being the strongest party (although normally its share was lower), and in total, the AfD collect 12.6% of the votes, according to the official results.
Given the “hell and back” Europe and the world had to witness in the 20th century, this backlash seems surprising and alarming. Of course, a number of ideas on the origin of populist thought and countermeasures are out there.
# What’s populism?
Populism is hard to define, see Laclau, On Populist Reason. So maybe authoritarianism and nationalism are concepts more adequate to deal with enemies of open society. Another idea would be to follow Popper’s idea of what makes a society open and what are the components of a “closed” society.
Without worrying much on ongoing discussions, I have tried to define and measure populism as manifest in Tweets of German politicians. The theoretical concept is not too much elaborated (as yet), I confess, but it builds on a well-known and intriguing source, Poppers Open Society.
# Poppers idea of populism
Basically, the following theoretical aspects were used for gauging populism.
The roots of the (Western) civilization may be traced to societies such as the ancient Greek clans. In the beginning (but in parts, later on too), those clans were patriarchal in the sense that there one men or one family or one cast who was ruling without any democratic basis. Basically, someone was telling what to do. And every one had to follow. Even more, know only what to do but rather what was right and what was wrong. There is, as a consequence, no place for questions and questioning or doubt and doubting in such societies. It’s pretty clear and easy what’s right and wrong, and what you ought to now. Now, modern society is quite complex, and as a consequence, it is difficult to say what will happen, and what you should do. There are much less guides and less guidance as to what the “right” way of living consists of. Poppers argues that people are suffering from this insecurity, albeit to a different degree. Especially in times of crisis, rapid change, and strong progress the desire too come back to “good old days”, with all their simplicity and security offered by strong men and strong ideas (in the sense of that they provide sure answers), rises.
Moreover, those old tribal communities consisted (often) of kinship, there were genetic similarity among the members of a tribe, compared to the people of other tribes. As a result, such tribes or rather such tribal thinking rejoices in evoking the “blood is thicker than water” ideas. You should prefer your relatives more than strangers; sounds plausible, doesn’t it? But taken farer this leads a walling-off from the outside, in the sense that outsiders are considered negative or eve as enemies. In short, the “we” as a group - family, caste, tribe, culture, people, folk - should hold together, and should regard outsiders with suspicion.
Similarly, not only our “blood” but also our “soil” is what defined (defines) us as tribal society. This is our land. Not yours. We have always, okay, at least for a long time, been inhabiting this land.
More coherently, this is our group, our land, our stories. Nobody (including myself and you, as possible parts of this group) may object to this notion. We may not even doubt, we must obey to the law of what the strong man says, and he says he knows what to know, that’s why he is strong. Admitting “I don’t know” would be considered as a sign of weakness, not of strength. Don’t propose that things could be like this, but also like that, and even this may vary from time to time or according to some unknown boundary conditions…
Such ideas provide the base of “closed society thinking”, and populism is nothing more than alluding to this thinking and supporting it.
# Indicators of populism in the present research
Much more down to earth, and certainly cum grano salis to say the least, I have tried to translate Popper’s ideas into these eight indicators:
• word length or rather word brevity
• Number of negative connotated words vs. number of positively connotated words (odds)
• Proportion of negatively connotated words
• Proportion of emotional words
• Score (intensity) of emotion
• Score (intensity) of negative emotion
• Proportion of words in CAPITAL LETTERS (shouted)
Out of these indicators, I formed one populism measure, and I then compared political parties based on this measure. I did not want to tap too much into the individual persons, partly because an aggregated measure may be more reliable, and partly because not too be to nasty to individual persons.
# Data material
I collected around 400k tweets via the Twitter API; plus approx. 30k Tweets by Donald Trump. In sum, about 200 politicians donated about 6 millions words for this analysis. Not all parties are included, only seven important, the remainder is ignored (sorry). Data was collected from several years, as provided by the API.
I think that the API prefers providing newer tweets. Note that Trump data has been accessed from the Trump Twitter Archive.
Not all parties tweet the same amount. As I have recently read on Twitter, the only 12 hours, Donald Trump did not tweet was the day he was elected President…
From some parties, I was able to find a lot of accounts, from other parties, not so many. This may of course provide some basis for bias. I have tried to find some overview or “official” list of politicians’ twitter accounts. What I found was this. In addition, I added the accounts from the Bundesvorstaende of the AfD and the FDP, because these parties were especially lacking accounts.
# Reproducibility
The code is on Github, completely. In this post, I will not discuss all technical aspects, but rather invite everyone interested to read the code.
# Tweets per day
Who is the greatest… tweep? Who “does it” most frequently? Well, not too much surprising, Donald Trump is ahead of the pack (again).
But considering only the German parties, we find that the Greens are leading.
# Populism score
Averaged (by median) over the 8 indicators, one finds that the populism scores are … not too much of a surprise, in some regard.
Trump gets the largest part, the highest score. But maybe it would be better to leave him out of this “ranking”, as the different languages (German vs. English) cannot readily be compared with regard to such nuanced things like populism. Anyhow, the two most extreme parties, the AfD (alt-right) and the Linke (Leftists) are the ones with highest populism scores. Not that zero has been centered as the median over all accounts.
# Cave and conclusion
Whereas Poppers theory certainly is compelling, the choice of indicators remains subjective. This is not unique for the present analysis, but still different sets of indicators may provide different pictures. Still, this picture appears well backup by the data. What’s your impression, your thoughts? Feel free to discuss your ideas.
# Data, machine-friendly, of the 2017 German federal elections
On September 2017, the 19. German Bundestag has been elected. As of this writing, the parties are still busy sorting out whether they want to part of the government, with whom, and maybe whether they even want to form a government at all. This post is about providing the data in machine friendly form, and in English language.
All data presented in this post regarding this (and previous) elections are published by the Bundeswahlleiter. The data may be used without restriction as long as it is credited duely.
Let me be clear that the all data presented here were drawn from this source. So, for each dataset the copyright notice is:
The contribution by me is only to render the data more machine friendly, as the presented CSVs have multiple header lines, German Umlaute, non-UTF8 coding, and some other minor hickups.
Of course, data itself has not been touched by me; I hae only changed some wordings and the structure of the dataset in order to render analysis more comfortable. Analysts can easily access the raw data and check the correctness.
Setup:
library(tidyverse)
# Package prada contains the data
Maybe the easiest way is to use my package prada, which can be downloaded/installed from Github:
Install the package once:
devtools::install_github("sebastiansauer/prada")
library(prada)
There you will find the relevant data.
## Parties running the election
• parties_de - a dataframe of the 43 parties than ran for the election
data(parties_de)
glimpse(parties_de)
#> Observations: 43
#> Variables: 2
#> $party_short <chr> "CDU", "SPD", "Linke", "Gruene", "CSU", "FDP", "Af... #>$ party_long <chr> "Christlich Demokratische Union Deutschlands", "So...
• elec_results - a dataframe of the results (first/second) votes of the parties plus some more data
data(elec_results)
#> # A tibble: 6 x 191
#> district_nr district_name parent_district_nr
#> <int> <chr> <int>
#> 1 1 Flensburg – Schleswig 1
#> 2 2 Nordfriesland – Dithmarschen Nord 1
#> 3 3 Steinburg – Dithmarschen Süd 1
#> 4 4 Rendsburg-Eckernförde 1
#> 5 5 Kiel 1
#> 6 6 Plön – Neumünster 1
#> # ... with 188 more variables: registered_voters_1 <int>,
#> # registered_voters_2 <int>, registered_voters_3 <int>,
#> # votes_valid_4 <int>, CDU_1 <int>, CDU_2 <chr>, CDU_3 <int>,
#> # CDU_4 <dbl>, SPD_1 <int>, SPD_2 <int>, SPD_3 <int>, SPD_4 <int>,
#> # Gruene_1 <int>, Gruene_2 <int>, Gruene_3 <dbl>, Gruene_4 <dbl>,
#> # CSU_1 <int>, CSU_2 <int>, CSU_3 <int>, CSU_4 <int>, FDP_1 <int>,
#> # FDP_2 <int>, FDP_3 <int>, FDP_4 <int>, AfD_1 <int>, AfD_2 <int>,
#> # AfD_3 <dbl>, AfD_4 <dbl>, Piraten_1 <int>, Piraten_2 <int>,
#> # Piraten_3 <int>, Piraten_4 <dbl>, NPD_1 <int>, NPD_2 <int>,
#> # NPD_3 <int>, NPD_4 <int>, FW_1 <int>, FW_2 <int>, FW_3 <int>,
#> # FW_4 <int>, Mensch_1 <int>, Mensch_2 <int>, Mensch_3 <int>,
#> # Mensch_4 <dbl>, ÖDP_1 <dbl>, ÖDP_2 <int>, ÖDP_3 <int>, ÖDP_4 <int>,
#> # Arbeit_1 <int>, Arbeit_2 <int>, Arbeit_3 <int>, Arbeit_4 <int>,
#> # Bayern_1 <int>, Bayern_2 <int>, Bayern_3 <int>, Bayern_4 <int>,
#> # Volk_1 <int>, Volk_2 <int>, Volk_3 <int>, Volk_4 <int>,
#> # Vernunft_1 <int>, Vernunft_2 <int>, Vernunft_3 <int>,
#> # Vernunft_4 <int>, MLPD_1 <int>, MLPD_2 <int>, MLPD_3 <int>,
#> # MLPD_4 <int>, Soli_1 <int>, Soli_2 <int>, Soli_3 <int>, Soli_4 <int>,
#> # Sozialist_1 <int>, Sozialist_2 <chr>, Sozialist_3 <int>,
#> # Sozialist_4 <int>, Rechte_1 <int>, Rechte_2 <chr>, Rechte_3 <int>,
#> # ...
Note that this data set is structured as follows: For each column AFTER ‘parent_district_nr’, ie., from column 4 onward, 4 columns build one bundle. In each bundle, column 1 refers to the Erststimme in the present election; column 2 to the Erststimme in the previous election. Column 3 refers to the Zweitstimme of the present election, and column 4 to the Zweitstimme of the previous election. For example, ‘CDU_3’ refers to the number of Zweitstimmen in the present (2017) elections.
That is:
• _1” - first vote in present election
• _2” - first vote in previous election
• _3” - second vote in present election
• _4” - second vote in previous election
## Geometric shapes of the electoroal districts (Wahlkreise)
• wahlkreise_shp - a dataframe with ID of the Wahlkreise (electoral districts) plus their geometric shape for plotting
data(wahlkreise_shp)
glimpse(wahlkreise_shp)
#> Observations: 299
#> Variables: 5
#> $WKR_NR <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 1... #>$ LAND_NR <fctr> 01, 01, 01, 01, 01, 01, 01, 01, 01, 01, 01, 13, 13,...
#> $LAND_NAME <fctr> Schleswig-Holstein, Schleswig-Holstein, Schleswig-H... #>$ WKR_NAME <fctr> Flensburg – Schleswig, Nordfriesland – Dithmarschen...
#> $geometry <S3: sfc_MULTIPOLYGON> [543474.9, 547528.6, 547598.2, 5479... See this post for a usecase of the shapefile data. ## Socioeconomic data of Germany • socec - a dataframe with socio economic information (eg., unemployment rate) for each wahlkreis. data(socec) head(socec) #> # A tibble: 6 x 51 #> V1 V2 V3 V4 V5 #> <chr> <int> <chr> <int> <dbl> #> 1 Schleswig-Holstein 1 Flensburg – Schleswig 130 2128.1 #> 2 Schleswig-Holstein 2 Nordfriesland – Dithmarschen Nord 197 2777.0 #> 3 Schleswig-Holstein 3 Steinburg – Dithmarschen Süd 178 2000.5 #> 4 Schleswig-Holstein 4 Rendsburg-Eckernförde 163 2164.8 #> 5 Schleswig-Holstein 5 Kiel 3 143.0 #> 6 Schleswig-Holstein 6 Plön – Neumünster 92 1302.0 #> # ... with 46 more variables: V6 <dbl>, V7 <dbl>, V8 <dbl>, V9 <dbl>, #> # V10 <dbl>, V11 <dbl>, V12 <dbl>, V13 <dbl>, V14 <dbl>, V15 <dbl>, #> # V16 <dbl>, V17 <dbl>, V18 <dbl>, V19 <dbl>, V20 <dbl>, V21 <dbl>, #> # V22 <dbl>, V23 <dbl>, V24 <dbl>, V25 <dbl>, V26 <int>, V27 <int>, #> # V28 <dbl>, V29 <chr>, V30 <dbl>, V31 <dbl>, V32 <dbl>, V33 <dbl>, #> # V34 <dbl>, V35 <dbl>, V36 <dbl>, V37 <dbl>, V38 <dbl>, V39 <chr>, #> # V40 <chr>, V41 <chr>, V42 <chr>, V43 <dbl>, V44 <dbl>, V45 <dbl>, #> # V46 <dbl>, V47 <dbl>, V48 <dbl>, V49 <dbl>, V50 <dbl>, V51 <dbl> The names of the indicators can be accessed via the dictionary socec_dict or via the documentation of socec. In addition, of course, the Bundeswahlleiter provides this information. data(socec_dict) glimpse(socec_dict) # Use case You can use the data eg., for determining association of right-wing (AfD) results with unemployment rate per electoral district - see here for an example. Of course those data can easily be saved as csv: write_csv(elec_results, path = "elec_results.csv") write_csv(socec, path = "socec.csv") write_csv(parties_de, path = "parties_de.csv") write_csv(wahlkreise_shp, path = "wahlkreise_shp.csv") Watch our for wahlkreise_shp though as it contains a list column. # Data at osf.io The Open Science Framework is a great place to store data openly. You can easily access the data from that source, too. Look at this repository. Data are provided in csv and RData form. # Concluding It was quite fun to me to play around with the data, and I think quite some valuable insights can be inferred. Of course, electoral data has a unique value as it features the most important action of a democracy. # Mapping foreigner ratio to AfD election results in the German Wahlkreise In a previous post, we have shed some light on the idea that populism - as manifested in AfD election results - is associated with socioeconomic deprivation, be it subjective or objective. We found some supporting pattern in the data, although that hypothesis is far from being complete; ie., most of the variance remained unexplained. In this post, we test the hypothesis that AfD election results are negatively associated with the proportion of foreign nationals in a Wahlkreis. The idea is this: Many foreigners in your neighborhood, and you will get used to it. You will perceive those type of people as normal. To the contrary, if there are few of them, they are perceived as rather alien. To be honest, this idea is rather vague; and it maybe built on the simple fact that in the eastern part of Germany, there are (relatively) few foreign nationals, as compared to the western parts of the country. However, animosity towards foreign nationals and AfD results are particularly strong in the East. Put shortly, much more theory would be needed to understand causal pathways explaining populism flourishing in some regions of Germany, particularly in Sachsen (Saxonia). # Packages library(sf) library(stringr) library(tidyverse) library(magrittr) library(huxtable) library(broom) library(viridis) # Geo data :attention: The election ratios are unequal to the district areas (as far as I know, not complete identical to the very least). So will need to get some special geo data. This geo data is available here and the others links on that page. Download and unzip the data; store them in an appropriate folder. Adjust the path to your needs: my_path_wahlkreise <- "~/Documents/datasets/geo_maps/btw17_geometrie_wahlkreise_shp/Geometrie_Wahlkreise_19DBT.shp" file.exists(my_path_wahlkreise) #> [1] TRUE wahlkreise_shp <- st_read(my_path_wahlkreise) #> Reading layer Geometrie_Wahlkreise_19DBT' from data source /Users/sebastiansauer/Documents/datasets/geo_maps/btw17_geometrie_wahlkreise_shp/Geometrie_Wahlkreise_19DBT.shp' using driver ESRI Shapefile' #> Simple feature collection with 299 features and 4 fields #> geometry type: MULTIPOLYGON #> dimension: XY #> bbox: xmin: 280387.7 ymin: 5235855 xmax: 921025.5 ymax: 6101444 #> epsg (SRID): NA #> proj4string: +proj=utm +zone=32 +ellps=GRS80 +units=m +no_defs glimpse(wahlkreise_shp) #> Observations: 299 #> Variables: 5 #>$ WKR_NR <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 1...
#> $LAND_NR <fctr> 01, 01, 01, 01, 01, 01, 01, 01, 01, 01, 01, 13, 13,... #>$ LAND_NAME <fctr> Schleswig-Holstein, Schleswig-Holstein, Schleswig-H...
#> $WKR_NAME <fctr> Flensburg – Schleswig, Nordfriesland – Dithmarschen... #>$ geometry <simple_feature> MULTIPOLYGON (((543474.9057..., MULTIPOLY...
wahlkreise_shp %>%
ggplot() +
geom_sf()
That was easy, right? The sf package fits nicely with the tidyverse. Hence not much to learn in that regard. I am not saying that geo data is simple, quite the contrary. But luckily the R functions fit in a well known schema.
# Foreign nationals ratios
These data can as well be fetched from the same site as above, as mentioned above, we need to make sure that we have the statistics according to the election areas, not the administrative areas.
foreign_file <- "~/Documents/datasets/Strukturdaten_De/btw17_Strukturdaten-utf8.csv"
file.exists(foreign_file)
#> [1] TRUE
";", escape_double = FALSE,
locale = locale(decimal_mark = ",",
grouping_mark = "."),
trim_ws = TRUE,
skip = 8) # skipt the first 8 rows
#glimpse(foreign_raw)
Jezz, we need to do some cleansing before we can work with this dataset.
foreign_names <- names(foreign_raw)
foreign_df <- foreign_raw
names(foreign_df) <- paste0("V",1:ncol(foreign_df))
The important columns are:
foreign_df <- foreign_df %>%
rename(state = V1,
area_nr = V2,
area_name = V3,
for_prop = V8,
pop_move = V11,
pop_migr_background = V19,
income = V26,
unemp = V47) # total, as to March 2017
# AfD election results
Again, we can access the data from the same source, the Bundeswahlleiter here. I have prepared the column names of the data and the data structure, to render the file more accessible to machine parsing. Data points were not altered. You can access my version of the file here.
elec_file <- "~/Documents/datasets/Strukturdaten_De/btw17_election_results.csv"
file.exists(elec_file)
#> [1] TRUE
For each party, four values are reported:
1. primary vote, present election
2. primary vote, previous election
3. secondary vote, present election
4. secondary vote, previous election
The secondary vote refers to the party, that’s what we are interested in (column 46). The primary vote refers to the candidate of that area; the primary vote may also be of similar interest, but that’s a slightly different question, as it taps more into the approval of a person, rather to a party (of course there’s a lot overlap between both in this situation).
# names(elec_results)
afd_prop <- elec_results %>%
select(1, 2, 46, 18) %>%
area_nr = Nr,
area_name = Gebiet,
na.omit
In the previous step, we have selected the columns of interest, changed their name (shorter, English), and have computed the proportion of (valid) secondary votes in favor of the AfD.
# Match foreign national rated to AfD votes for each Wahlkreis
wahlkreise_shp %>%
left_join(foreign_df, by = c("WKR_NR" = "area_nr")) %>%
left_join(afd_prop, by = "area_name") -> chloro_data
# Plot geo map with afd votes
chloro_data %>%
ggplot() +
geom_sf(aes(fill = afd_prop)) -> p1
p1
We might want to play with the fill color, or clean up the map (remove axis etc.)
p1 + scale_fill_distiller(palette = "Spectral") +
theme_void()
# Geo map (of election areas) with foreign national data
chloro_data %>%
ggplot() +
geom_sf(aes(fill = for_prop)) +
scale_fill_distiller(palette = "Spectral") +
theme_void() -> p2
p2
As can be seen from the previous figure, foreign nationals are relatively rare in the East, but tend to concentrate on the big cities such as Munich, Frankfurt, and the Ruhr area.
# “AfD to foreigner density”
In a similar vein, we could compute the ratio of AfD votes and foreigner quote. That would give us some measure of covariability. Let’s see.
chloro_data %>%
mutate(afd_for_dens = afd_prop / (for_prop/100)) -> chloro_data
chloro_data %>%
ggplot +
geom_sf(aes(fill = afd_for_dens)) +
theme_void() +
scale_fill_viridis()
Let’s check that.
chloro_data %>%
select(afd_for_dens, afd_prop, for_prop) %>%
as.data.frame %>%
slice(1:3)
#> # A tibble: 3 x 4
#> afd_for_dens afd_prop for_prop geometry
#> <dbl> <dbl> <dbl> <simple_feature>
#> 1 1.20 0.0684 5.7 <MULTIPOLYGON...>
#> 2 1.21 0.0653 5.4 <MULTIPOLYGON...>
#> 3 1.71 0.0854 5.0 <MULTIPOLYGON...>
The diagram shows that in relation to foreigner rates, the AfD votes are strongest in Saxonian Wahlkreise primarily. Second, the East is surprisingly strong more “AfD dense” compared to the West. Don’t forget that this measure is an indication of co-occurrence, not of absolute AfD votes.
# Correlation of foreign national quote and AfD votes
A simple, straight-forward and well-known approach to devise association strength is Pearson’s correlation coefficient. Oldie but Goldie. Let’s depict it.
chloro_data %>%
select(for_prop, afd_prop, area_name) %>%
ggplot +
aes(x = for_prop, y = afd_prop) +
geom_point() +
geom_smooth()
The pattern exhibited is quite striking: What we see might easily fit an exponential distribution: When foreigner rate begins to augment, the AfD success shrinks strongly, but this trend comes to an end as soon as some “saturation” process starts, maybe around some 8% of foreign national quote. It would surely be simplistic to speak of a “healthy proportion of around 8% foreigners”, to fence populism. However, the available data shows a quite obvious pattern.
The correlation itself is
chloro_data %>%
select(for_prop, afd_prop, area_name) %>%
as.data.frame %T>%
summarise(cor_afd_foreigners = cor(afd_prop, for_prop)) %>%
do(tidy(cor.test(.$afd_prop, .$for_prop)))
#> estimate statistic p.value parameter conf.low conf.high
#> 1 -0.465 -9.05 1.98e-17 297 -0.549 -0.371
#> method alternative
#> 1 Pearson's product-moment correlation two.sided
That is, $r = -.46$, which is quite strong an effect.
EDIT: A comment by Ilya Kashnitsky (@ikashnitsky) suggested to separate the trends for eastern and Western German electoral districts.
Let’s try that.
First, we create a binary variable coding East vs. West:
unique(chloro_data$LAND_NAME) #> [1] Schleswig-Holstein Mecklenburg-Vorpommern Hamburg #> [4] Niedersachsen Bremen Brandenburg #> [7] Sachsen-Anhalt Berlin Nordrhein-Westfalen #> [10] Sachsen Hessen Thüringen #> [13] Rheinland-Pfalz Bayern Baden-Württemberg #> [16] Saarland #> 16 Levels: Baden-Württemberg Bayern Berlin Brandenburg Bremen ... Thüringen Being a German citizen, I know which is East; although I am unsure about Berlin. east <- c("Mecklenburg-Vorpommern", "Brandenburg", "Sachsen-Anhalt", "Sachsen", "Thüringen") chloro_data %>% mutate(east = LAND_NAME %in% east) -> chloro_data chloro_data %>% select(east, LAND_NAME) %>% count(LAND_NAME, east) #> Simple feature collection with 16 features and 3 fields #> geometry type: GEOMETRY #> dimension: XY #> bbox: xmin: 280387.7 ymin: 5235855 xmax: 921025.5 ymax: 6101444 #> epsg (SRID): NA #> proj4string: +proj=utm +zone=32 +ellps=GRS80 +units=m +no_defs #> # A tibble: 16 x 4 #> LAND_NAME east n geometry #> <fctr> <lgl> <int> <simple_feature> #> 1 Baden-Württemberg FALSE 38 <MULTIPOLYGON...> #> 2 Bayern FALSE 46 <POLYGON ((61...> #> 3 Berlin FALSE 12 <POLYGON ((79...> #> 4 Brandenburg TRUE 10 <POLYGON ((89...> #> 5 Bremen FALSE 2 <MULTIPOLYGON...> #> 6 Hamburg FALSE 6 <MULTIPOLYGON...> #> 7 Hessen FALSE 22 <POLYGON ((49...> #> 8 Mecklenburg-Vorpommern TRUE 6 <MULTIPOLYGON...> #> 9 Niedersachsen FALSE 30 <MULTIPOLYGON...> #> 10 Nordrhein-Westfalen FALSE 64 <MULTIPOLYGON...> #> 11 Rheinland-Pfalz FALSE 15 <POLYGON ((45...> #> 12 Saarland FALSE 4 <POLYGON ((36...> #> 13 Sachsen TRUE 16 <POLYGON ((75...> #> 14 Sachsen-Anhalt TRUE 9 <POLYGON ((72...> #> 15 Schleswig-Holstein FALSE 11 <MULTIPOLYGON...> #> 16 Thüringen TRUE 8 <POLYGON ((68...> And now let’s plot again: chloro_data %>% select(for_prop, afd_prop, area_name, east) %>% ggplot + aes(x = for_prop, y = afd_prop) + geom_point() + geom_smooth(aes(color = east), method = "lm") Quite remarkably, we see that the association in the West is weak; in the East it is (comparatively) strong. Many foreigners, fewer AfD votes. So we might update our thinking saying that there appears to be different mindsets between East and West in this regard. Of course, this is observational data only, so all this reasoning should be taken cum grano salis. There are surely more variables in the play, so we cannot be sure what true influential (causal) patterns look like. Ilya suggested that some additional variable(s) with different distributions in East and West may explain the data (Simpson case). BTW: Data are now available in my package pradadata on Github, and can be installed via devtools::install_github("sebastiansauer/pradadata") # Regression residuals of predicting foreigner quote by afd_score Let’s predict the AfD vote score taking the unemployment as an predictor. Then let’s plot the residuals to see how good the prediction is, ie., how close (or rather, far) the association of unemployment and AfD voting is. lm2 <- lm(afd_prop ~ for_prop, data = chloro_data) glance(lm2) #> r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC #> 1 0.216 0.213 0.0484 81.8 1.98e-17 2 482 -958 -947 #> deviance df.residual #> 1 0.697 297 tidy(lm2) #> term estimate std.error statistic p.value #> 1 (Intercept) 0.17513 0.00596 29.40 5.90e-90 #> 2 for_prop -0.00471 0.00052 -9.05 1.98e-17 chloro_data %>% mutate(afd_lm2 = lm(afd_prop ~ for_prop, data = .)$residuals) -> chloro_data
We have an $R^2$ of .21, quite a bit. Maybe the most important message: For each percentage point more foreigners, the AfD results decreases about a half percentage point.
And now plot the residuals:
chloro_data %>%
select(afd_lm2) %>%
ggplot() +
geom_sf(aes(fill = afd_lm2)) +
theme_void()
Interesting! This model shows a clear-cut picture: The eastern part is too “afd-ic” for its foreigner ratio; the North-West is less afd-ic than what would be expected by the foreigner rate. The rest (middle and south) parts over-and-above show the AfD levels that would be expected by their foreigner rate.
EDIT: Let’s include east as a predictor to the linear model:
lm3 <- lm(afd_prop ~ for_prop*east, data = chloro_data)
glance(lm3)
#> r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC
#> 1 0.672 0.669 0.0314 202 3.85e-71 4 612 -1215 -1196
#> deviance df.residual
#> 1 0.291 295
tidy(lm3)
#> term estimate std.error statistic p.value
#> 1 (Intercept) 0.112378 0.00495 22.692 1.17e-66
#> 2 for_prop -0.000371 0.00040 -0.928 3.54e-01
#> 3 eastTRUE 0.166620 0.01302 12.798 3.97e-30
#> 4 for_prop:eastTRUE -0.013637 0.00302 -4.521 8.93e-06
R squared increased dramatically, fostering the line of thought in the EDIT above. Now, we see that the general foreigner quote is not significiant anymore; we may infer that it plays no important role. But whether a wahlrkeis is East or not does play a strong role. For the East, the slope decreases quite a bit indicating some negative effect on foreigner quotes to AfD success.
Thanks Ilya Kashnitsky (@ikashnitsky)!
# Conclusion
The regression model provides a quite clear-cut picture. The story of the data may thus be summarized in easy words: The higher the foreigner ratio, the lower the AfD ratio. However, this is only part of the story. The foreigner explains a rather small fraction of AfD votes. Yet, given the multitude of potential influences on voting behavior, a correlation coefficient of -.46 is strikingly strong.
# Simple way to separate train and test sample in R
For statistical modeling, it is typical to separate a train sample from a test sample. The training sample is used to build (“train”) the model, whereas the test sample is used to gauge the predictive quality of the model.
There are many ways to split off a test sample from the train sample. One quite simple, tidyverse-oriented way, is the following.
library(tidyverse)
data(Affairs, package = "AER")
Then, create an index vector of the length of your train sample, say 80% of the total sample size.
set.seed(42)
index <- sample(1:601, size = trunc(.8 * 601))
Put bluntly, we draw 480 (.8*601) cases from the dataset, and note their row numbers.
a_train <- Affairs %>%
filter(row_number() %in% index)
The test set is the complement of the train set, drawn similarly:
a_test <- Affairs %>%
filter(!(row_number() %in% index))
# Two R plot side by side in .Rmd-Files
I kept wondering who to plot two R plots side by side (ie., in one “row”) in a .Rmd chunk. Here’s a way, well actually a number of ways, some good, some … not.
library(tidyverse)
library(gridExtra)
library(grid)
library(png)
library(grDevices)
data(mtcars)
# Plots from ggplot
Say, you have two plots from ggplot2, and you would like them to put them next to each other, side by side (not underneath each other):
ggplot(mtcars) +
aes(x = hp, y = mpg) +
geom_point() -> p1
ggplot(mtcars) +
aes(x = factor(cyl), y = mpg) +
geom_boxplot() +
geom_smooth(aes(group = 1), se = FALSE) -> p2
grid.arrange(p1, p2, ncol = 2)
So, grid.arrange is the key.
# Plots from png-file
comb2pngs <- function(imgs, bottom_text = NULL){
interpolate = FALSE)
interpolate = FALSE)
grid.arrange(img1, img2, ncol = 2, bottom = bottom_text)
}
The code of this function was inspired by code from Ben from this SO post.
Now, let’s load two pngs and then call the function above.
png1_path <- "https://sebastiansauer.github.io/images/2016-08-30-03.png"
png2_path <- "https://sebastiansauer.github.io/images/2016-08-31-01.png"
png1_dest <- "https://sebastiansauer.github.io/images/2017-10-12/img1.png"
png2_dest <- "https://sebastiansauer.github.io/images/2017-10-12/img2.png"
comb2pngs(c(png1_dest, png2_dest))
This works, it produces two plots from png files side by side.
# Two plots side-by-side the knitr way. Does not work.
But what about the standard knitr way?
knitr::include_graphics(c(png1_dest,png2_dest))
<img src=”“https://sebastiansauer.github.io/images/2017-10-12/img1.png” title=”plot of chunk unnamed-chunk-4” alt=”plot of chunk unnamed-chunk-4” width=”30%” style=”display: block; margin: auto;” /><img src=”“https://sebastiansauer.github.io/images/2017-10-12/img2.png” title=”plot of chunk unnamed-chunk-4” alt=”plot of chunk unnamed-chunk-4” width=”30%” style=”display: block; margin: auto;” />
Does not work.
Maybe with only one value for out.width??
knitr::include_graphics(c(png1_dest, png2_dest))
Nope. Does not work.
Does not work either, despite some saying so.
Maybe two times include_graphics?
imgs <- c(png1_dest, png2_dest)
imgs
#> [1] "https://sebastiansauer.github.io/images/2017-10-12/img1.png"
#> [2] "https://sebastiansauer.github.io/images/2017-10-12/img2.png"
knitr::include_graphics(png1_dest); knitr::include_graphics(png2_dest)
# An insight why include_graphics fails
No avail. Looking at the html code in the md-file which is produced by the knitr -call shows one interesting point: all this version of include_graphics produce the same code. And all have this style="display: block; margin: auto;" part in it. That obviously created problems. I am unsure who to convince include_graphics to divorce from this argument. I tried some versions of the chunk argument fig.show = hold, but to no avail.
# Plain markdown works
Try this code { width=30% } 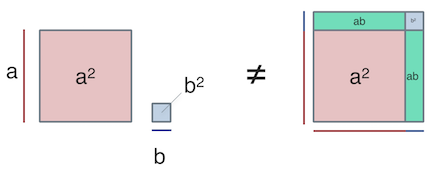{ width=40% } The two commands ![]... need not appear in one row. However, no new paragraph may separate them (no blank line between, otherwise the images will appear one below the other).
{ width=30% } { width=40% }
Works. But the markdown way does not give the fill comfort and power. So, that’s not quite perfect.
# Conclusion
A partial solution is there; but it’s not optimal. There wil most probably be different alternatives. For example, using plain html or Latex. But it’s a kind of pity, the include_graphics` call does not work as expected (by me).
|
|
Measure (mathematics)
Encyclopedia
In mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, a measure on a set is a systematic way to assign to each suitable subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume. A particularly important example is the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, which assigns the conventional length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
, area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
, and volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
to suitable subsets of the n-dimensional Euclidean space Rn. For instance, the Lebesgue measure of the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[0, 1] in the real numbers
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
is its length in the everyday sense of the word, specifically 1.
To qualify as a measure (see Definition below), a function that assigns a non-negative real number or +∞
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
to a set's subsets must satisfy a few conditions. One important condition is countable additivity. This condition states that the size of the union of a sequence of disjoint subsets is equal to the sum of the sizes of the subsets. However, it is in general impossible to associate a consistent size to each subset of a given set and also satisfy the other axioms of a measure. This problem was resolved by defining measure only on a sub-collection of all subsets; the subsets on which the measure is to be defined are called measurable and they are required to form a σ-algebra
Sigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
, meaning that unions
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
, intersections
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
and complements
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of sequences of measurable subsets are measurable. Non-measurable set
Non-measurable set
In mathematics, a non-measurable set is a set whose structure is so complicated that it cannot be assigned any meaningful measure. Such sets are constructed to shed light on the notions of length, area and volume in formal set theory....
s in a Euclidean space, on which the Lebesgue measure cannot be defined consistently, are necessarily complicated, in the sense of being badly mixed up with their complements; indeed, their existence is a non-trivial consequence of the axiom of choice.
Measure theory was developed in successive stages during the late 19th and early 20th centuries by Émile Borel
Émile Borel
Félix Édouard Justin Émile Borel was a French mathematician and politician.Borel was born in Saint-Affrique, Aveyron. Along with René-Louis Baire and Henri Lebesgue, he was among the pioneers of measure theory and its application to probability theory. The concept of a Borel set is named in his...
, Henri Lebesgue
Henri Lebesgue
Henri Léon Lebesgue was a French mathematician most famous for his theory of integration, which was a generalization of the seventeenth century concept of integration—summing the area between an axis and the curve of a function defined for that axis...
Johann Karl August Radon was an Austrian mathematician. His doctoral dissertation was on calculus of variations .- Life :...
and Maurice Fréchet, among others. The main applications of measures are in the foundations of the Lebesgue integral, in Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
's axiomatisation of probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and in ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
. In integration theory, specifying a measure allows one to define integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s on spaces more general than subsets of Euclidean space; moreover, the integral with respect to the Lebesgue measure on Euclidean spaces is more general and has a richer theory than its predecessor, the Riemann integral
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
. Probability theory considers measures that assign to the whole set the size 1, and considers measurable subsets to be events whose probability is given by the measure. Ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
considers measures that are invariant under, or arise naturally from, a dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
.
## Definition
Let be a σ-algebra
Sigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
over a set . A function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
from to the extended real number line
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
is called a measure if it satisfies the following properties:
• Non-negativity: for all
In mathematics, additivity and sigma additivity of a function defined on subsets of a given set are abstractions of the intuitive properties of size of a set.- Additive set functions :...
): For all countable collections of pairwise disjoint sets in :
• Null empty set:
One may require that at least one set E has finite measure. Then the null set automatically has measure zero because of countable additivity, because and is finite if and only if the empty set has measure zero.
The pair is called a measurable space, the members of are called measurable sets, and the triple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
is called a measure space.
If only the second and third conditions of the definition of measure above are met, and takes on at most one of the values , then is called a signed measure
Signed measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
.
A probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
is a measure with total measure one (i.e.); a probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
is a measure space with a probability measure.
For measure spaces that are also topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s various compatibility conditions can be placed for the measure and the topology. Most measures met in practice in analysis (and in many cases also in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
In mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
s. Radon measures have an alternative definition in terms of linear functionals on the locally convex space of continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s with compact support. This approach is taken by Bourbaki
Nicolas Bourbaki
Nicolas Bourbaki is the collective pseudonym under which a group of 20th-century mathematicians wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. With the goal of founding all of mathematics on set theory, the group strove for rigour and generality...
(2004) and a number of other authors. For more details see Radon measure
In mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
.
## Properties
Several further properties can be derived from the definition of a countably additive measure.
### Monotonicity
A measure μ is monotonic
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
: If E1 and E2 are measurable sets with E1 ⊆ E2 then
### Measures of infinite unions of measurable sets
A measure μ is countably subadditive: If E1, E2, E3, … is a countable sequence of sets in Σ, not necessarily disjoint, then
A measure μ is continuous from below: If E1, E2, E3, … are measurable sets and En is a subset of En + 1 for all n, then the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of the sets En is measurable, and
### Measures of infinite intersections of measurable sets
A measure μ is continuous from above: If E1, E2, E3, … are measurable sets and En + 1 is a subset of En for all n, then the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of the sets En is measurable; furthermore, if at least one of the En has finite measure, then
This property is false without the assumption that at least one of the En has finite measure. For instance, for each n ∈ N, let
which all have infinite Lebesgue measure, but the intersection is empty.
## Sigma-finite measures
A measure space (X, Σ, μ) is called finite if μ(X) is a finite real number (rather than ∞). It is called σ-finite if X can be decomposed into a countable union of measurable sets of finite measure. A set in a measure space has σ-finite measure if it is a countable union of sets with finite measure.
For example, the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s with the standard Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
are σ-finite but not finite. Consider the closed intervals [k,k+1] for all integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s k; there are countably many such intervals, each has measure 1, and their union is the entire real line. Alternatively, consider the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s with the counting measure
Counting measure
In mathematics, the counting measure is an intuitive way to put a measure on any set: the "size" of a subset is taken to be the number of elements in the subset, if the subset is finite, and ∞ if the subset is infinite....
, which assigns to each finite set of reals the number of points in the set. This measure space is not σ-finite, because every set with finite measure contains only finitely many points, and it would take uncountably many such sets to cover the entire real line. The σ-finite measure spaces have some very convenient properties; σ-finiteness can be compared in this respect to the Lindelöf property
Lindelöf space
In mathematics, a Lindelöf space is a topological space in which every open cover has a countable subcover. The Lindelöf property is a weakening of the more commonly used notion of compactness, which requires the existence of a finite subcover....
of topological spaces. They can be also thought of as a vague generalization of the idea that a measure space may have 'uncountable measure'.
## Completeness
A measurable set X is called a null set
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
if μ(X)=0. A subset of a null set is called a negligible set. A negligible set need not be measurable, but every measurable negligible set is automatically a null set. A measure is called complete if every negligible set is measurable.
A measure can be extended to a complete one by considering the σ-algebra of subsets Y which differ by a negligible set from a measurable set X, that is, such that the symmetric difference
Symmetric difference
In mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
of X and Y is contained in a null set. One defines μ(Y) to equal μ(X).
Measures are required to be countably additive. However, the condition can be strengthened as follows.
For any set I and any set of nonnegative ri, define:
A measure on is -additive if for any and any family , the following hold:
Note that the second condition is equivalent to the statement that the ideal
Ideal (set theory)
In the mathematical field of set theory, an ideal is a collection of sets that are considered to be "small" or "negligible". Every subset of an element of the ideal must also be in the ideal , and the union of any two elements of the ideal must also be in the ideal.More formally, given a set X, an...
of null sets is -complete.
## Examples
Some important measures are listed here.
• The counting measure
Counting measure
In mathematics, the counting measure is an intuitive way to put a measure on any set: the "size" of a subset is taken to be the number of elements in the subset, if the subset is finite, and ∞ if the subset is infinite....
is defined by μ(S) = number of elements in S.
• The Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on R is a complete translation-invariant measure on a σ-algebra containing the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
s in R such that μ([0,1]) = 1; and every other measure with these properties extends Lebesgue measure.
• Circular angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
measure is invariant under rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
, and hyperbolic angle
Hyperbolic angle
In mathematics, a hyperbolic angle is a geometric figure that divides a hyperbola. The science of hyperbolic angle parallels the relation of an ordinary angle to a circle...
measure is invariant under squeeze mapping
Squeeze mapping
In linear algebra, a squeeze mapping is a type of linear map that preserves Euclidean area of regions in the Cartesian plane, but is not a Euclidean motion.For a fixed positive real number r, the mapping →...
.
• The Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
for a locally compact
Locally compact space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
is a generalization of the Lebesgue measure (and also of counting measure and circular angle measure) and has similar uniqueness properties.
• The Hausdorff measure
Hausdorff measure
In mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
is a generalization of the Lebesgue measure to sets with non-integer dimension, in particular, fractal sets.
• Every probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
gives rise to a measure which takes the value 1 on the whole space (and therefore takes all its values in the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0,1]). Such a measure is called a probability measure. See probability axioms
Probability axioms
In probability theory, the probability P of some event E, denoted P, is usually defined in such a way that P satisfies the Kolmogorov axioms, named after Andrey Kolmogorov, which are described below....
.
• The Dirac measure δa (cf. Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
) is given by δa(S) = χS(a), where χS is the characteristic function of S. The measure of a set is 1 if it contains the point a and 0 otherwise.
Other 'named' measures used in various theories include: Borel measure, Jordan measure
Jordan measure
In mathematics, the Peano–Jordan measure is an extension of the notion of size to shapes more complicated than, for example, a triangle, disk, or parallelepiped....
, ergodic measure, Euler measure, Gaussian measure
Gaussian measure
In mathematics, Gaussian measure is a Borel measure on finite-dimensional Euclidean space Rn, closely related to the normal distribution in statistics. There is also a generalization to infinite-dimensional spaces...
, Baire measure
Baire measure
A Baire measure is a measure on the σ-algebra of Baire sets of a topological space. In spaces that are not metric spaces, the Borel sets and the Baire sets may differ...
In mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
and Young measure
Young measure
In mathematical analysis, a Young measure is a parameterized measure that is associated with certain subsequences of a given bounded sequence of measurable functions. Young measures have applications in the calculus of variations and the study of nonlinear partial differential equations...
.
In physics an example of a measure is spatial distribution of mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
(see e.g., gravity potential), or another non-negative extensive property, conserved
Conserved quantity
In mathematics, a conserved quantity of a dynamical system is a function H of the dependent variables that is a constant along each trajectory of the system. A conserved quantity can be a useful tool for qualitative analysis...
(see conservation law
Conservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
for a list of these) or not. Negative values lead to signed measures, see "generalizations" below.
Liouville measure, known also as the natural volume form on a symplectic manifold, is useful in classical statistical and Hamiltonian mechanics.
Gibbs measure
Gibbs measure
In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is the measure associated with the Boltzmann distribution, and generalizes the notion of the canonical ensemble...
is widely used in statistical mechanics, often under the name canonical ensemble
Canonical ensemble
The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...
.
## Non-measurable sets
If the axiom of choice is assumed to be true, not all subsets of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
are Lebesgue measurable; examples of such sets include the Vitali set
Vitali set
In mathematics, a Vitali set is an elementary example of a set of real numbers that is not Lebesgue measurable, found by . The Vitali theorem is the existence theorem that there are such sets. There are uncountably many Vitali sets, and their existence is proven on the assumption of the axiom of...
, and the non-measurable sets postulated by the Hausdorff paradox
In mathematics, the Hausdorff paradox, named after Felix Hausdorff, states that if you remove a certain countable subset of the sphere S2, the remainder can be divided into three disjoint subsets A, B and C such that A, B, C and B ∪ C are all congruent...
The Banach–Tarski paradox is a theorem in set theoretic geometry which states the following: Given a solid ball in 3-dimensional space, there exists a decomposition of the ball into a finite number of non-overlapping pieces , which can then be put back together in a different way to yield two...
.
## Generalizations
For certain purposes, it is useful to have a "measure" whose values are not restricted to the non-negative reals or infinity. For instance, a countably additive set function
Set function
In mathematics, a set function is a function whose input is a set. The output is usually a number. Often the input is a set of real numbers, a set of points in Euclidean space, or a set of points in some measure space.- Examples :...
with values in the (signed) real numbers is called a signed measure
Signed measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
, while such a function with values in the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s is called a complex measure
Complex measure
In mathematics, specifically measure theory, a complex measure generalizes the concept of measure by letting it have complex values. In other words, one allows for sets whose size is a complex number.-Definition:...
. Measures that take values in Banach spaces have been studied extensively. A measure that takes values in the set of self-adjoint projections on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
is called a projection-valued measure
Projection-valued measure
In mathematics, particularly functional analysis a projection-valued measure is a function defined on certain subsets of a fixed set and whose values are self-adjoint projections on a Hilbert space...
; these are used in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
for the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
. When it is necessary to distinguish the usual measures which take non-negative values from generalizations, the term positive measure is used. Positive measures are closed under conical combination
Conical combination
Given a finite number of vectors x_1, x_2, \dots, x_n\, in a real vector space, a conical combination or a conical sum of these vectors is a vector of the formwhere the real numbers \alpha_i\, satisfy \alpha_i\ge 0...
but not general linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
, while signed measures are the linear closure of positive measures.
Another generalization is the finitely additive measure, which are sometimes called contents. This is the same as a measure except that instead of requiring countable additivity we require only finite additivity. Historically, this definition was used first, but proved to be not so useful. It turns out that in general, finitely additive measures are connected with notions such as Banach limits, the dual of L
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
and the Stone–Čech compactification
Stone–Cech compactification
In the mathematical discipline of general topology, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact Hausdorff space βX...
. All these are linked in one way or another to the axiom of choice.
A charge
Signed measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
is a generalization in both directions: it is a finitely additive, signed measure.
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.