code
stringlengths 2.5k
150k
| kind
stringclasses 1
value |
|---|---|
# Using Transfer Learning to Classify Flower Images with PyTorch
In this blog post, I will detail my repository that performs object classification with transfer learning.
The project is broken down into multiple steps:
* Load and preprocess the image dataset
* Train the image classifier on your dataset
* Use the trained classifier to predict image content
# Load Data
Here we use `torchvision` to load the data ([documentation](http://pytorch.org/docs/0.3.0/torchvision/index.html)). You can [download the data here](https://s3.amazonaws.com/content.udacity-data.com/courses/nd188/flower_data.zip).
The validation and testing sets are used to measure the model's performance on data it hasn't seen yet. No scaling or rotation transformations is perfomed.
The pre-trained networks available from `torchvision` were trained on the ImageNet dataset where each color channel was normalized separately. For both sets there's need to normalize the means and standard deviations of the images to what the network expects. For the means, it's `[0.485, 0.456, 0.406]` and for the standard deviations `[0.229, 0.224, 0.225]`, calculated from the ImageNet images. These values will shift each color channel to be centered at 0 and range from -1 to 1.
```
data_dir = './flowers'
train_dir = data_dir + '/train'
valid_dir = data_dir + '/valid'
test_dir = data_dir + '/test'
# Defining data transforms for training, validation and test data and also normalizing whole data
data_transforms = {
'train': transforms.Compose([
transforms.RandomResizedCrop(224),
transforms.RandomRotation(45),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
]),
'valid': transforms.Compose([
transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
]),
'test': transforms.Compose([
transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
])
}
# loading datasets with PyTorch ImageFolder
image_datasets = {
x: datasets.ImageFolder(root=data_dir + '/' + x, transform=data_transforms[x])
for x in list(data_transforms.keys())
}
# TODO: Using the image datasets and the trainforms, define the dataloaders
# defining data loaders to load data using image_datasets and transforms, here we also specify batch size for the mini batch
dataloaders = {
x: data.DataLoader(image_datasets[x], batch_size=4, shuffle=True, num_workers=2)
for x in list(image_datasets.keys())
}
dataset_sizes = {
x: len(dataloaders[x].dataset)
for x in list(image_datasets.keys())
}
class_names = image_datasets['train'].classes
dataset_sizes # printing dataset's sizes for training, validation and testing
```
## Label mapping
I had load in a mapping from category label to category name. I got this in the file cat_to_name.json. It's a JSON object which i have read in with the json module. This gave a dictionary mapping the integer encoded categories to the actual names of the flowers.
```
import json
with open('cat_to_name.json', 'r') as f:
cat_to_name = json.load(f)
# changing categories to their actual names
for i in range(0,len(class_names)):
class_names[i] = cat_to_name.get(class_names[i])
```
#Visualize a few images
Let's visualize a few training images so as to understand the data augmentations.
```
def imshow(inp, title=None):
"""Imshow for Tensor."""
inp = inp.numpy().transpose((1, 2, 0))
mean = np.array([0.485, 0.456, 0.406])
std = np.array([0.229, 0.224, 0.225])
inp = std * inp + mean
inp = np.clip(inp, 0, 1)
plt.imshow(inp)
if title is not None:
plt.title(title)
plt.pause(0.001) # pause a bit so that plots are updated
# Get a batch of training data
inputs, classes = next(iter(dataloaders['train']))
# Make a grid from batch
out = torchvision.utils.make_grid(inputs)
imshow(out, title=[class_names[x] for x in classes])
```
# Building and training the classifier
Now that the data is ready, it's time to build and train the classifier. As usual, you should use one of the pretrained models from `torchvision.models` to get the image features. Build and train a new feed-forward classifier using those features.
* Load a [pre-trained network](http://pytorch.org/docs/master/torchvision/models.html) (If you need a starting point, the VGG networks work great and are straightforward to use)
* Define a new, untrained feed-forward network as a classifier, using ReLU activations and dropout
* Train the classifier layers using backpropagation using the pre-trained network to get the features
* Track the loss and accuracy on the validation set to determine the best hyperparameters
When training we make sure to update only the weights of the feed-forward network.
## Train and evaluate
```
model_ft = train_model(model_ft, criterion, optimizer_ft,num_epochs=20)
```
# Inference for classification
Now let's pass an image into the network and predict the class of the flower in the image. Using a function called `predict` that takes an image and a model, then returns the top $K$ most likely classes along with the probabilities. It looks like
```python
probs, classes = predict(image_path, model)
print(probs)
print(classes)
> [ 0.01558163 0.01541934 0.01452626 0.01443549 0.01407339]
> ['70', '3', '45', '62', '55']
```
First let's handle processing the input image such that it can be used in your network.
## Image Preprocessing
Using `PIL` to load the image ([documentation](https://pillow.readthedocs.io/en/latest/reference/Image.html)). It's best to write a function that preprocesses the image so it can be used as input for the model. This function should process the images in the same manner used for training.
First, resize the images where the shortest side is 256 pixels, keeping the aspect ratio. This can be done with the [`thumbnail`](http://pillow.readthedocs.io/en/3.1.x/reference/Image.html#PIL.Image.Image.thumbnail) or [`resize`](http://pillow.readthedocs.io/en/3.1.x/reference/Image.html#PIL.Image.Image.thumbnail) methods. Then you'll need to crop out the center 224x224 portion of the image.
Color channels of images are typically encoded as integers 0-255, but the model expected floats 0-1. You'll need to convert the values. It's easiest with a Numpy array, which you can get from a PIL image like so `np_image = np.array(pil_image)`.
As before, the network expects the images to be normalized in a specific way. For the means, it's `[0.485, 0.456, 0.406]` and for the standard deviations `[0.229, 0.224, 0.225]`. You'll want to subtract the means from each color channel, then divide by the standard deviation.
And finally, PyTorch expects the color channel to be the first dimension but it's the third dimension in the PIL image and Numpy array. You can reorder dimensions using [`ndarray.transpose`](https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.ndarray.transpose.html). The color channel needs to be first and retain the order of the other two dimensions.
## Class Prediction
Once you can get images in the correct format, it's time to write a function for making predictions with your model. A common practice is to predict the top 5 or so (usually called top-$K$) most probable classes. You'll want to calculate the class probabilities then find the $K$ largest values.
To get the top $K$ largest values in a tensor use [`x.topk(k)`](http://pytorch.org/docs/master/torch.html#torch.topk). This method returns both the highest `k` probabilities and the indices of those probabilities corresponding to the classes. You need to convert from these indices to the actual class labels using `class_to_idx` which hopefully you added to the model or from an `ImageFolder` you used to load the data ([see here](#Save-the-checkpoint)). Make sure to invert the dictionary so you get a mapping from index to class as well.
Again, this method should take a path to an image and a model checkpoint, then return the probabilities and classes.
|
```python
probs, classes = predict(image_path, model)
print(probs)
print(classes)
> [ 0.01558163 0.01541934 0.01452626 0.01443549 0.01407339]
> ['70', '3', '45', '62', '55']
```
```
def predict(image_path, model, top_num=5):
# Process image
img = process_image(image_path)
# Numpy -> Tensor
image_tensor = torch.from_numpy(img).type(torch.FloatTensor)
# Add batch of size 1 to image
model_input = image_tensor.unsqueeze(0)
# Probs
probs = torch.exp(model.forward(Variable(model_input.cuda())))
# Top probs
top_probs, top_labs = probs.topk(top_num)
top_probs, top_labs =top_probs.data, top_labs.data
top_probs = top_probs.cpu().numpy().tolist()[0]
top_labs = top_labs.cpu().numpy().tolist()[0]
#print(top_labs)
# Convert indices to classes
'''idx_to_class = {val: key for key, val in
model.class_to_idx.items()}
top_labels = [idx_to_class[lab] for lab in top_labs]
top_flowers = [cat_to_name[idx_to_class[lab]] for lab in top_labs]'''
top_flowers = [class_names[lab] for lab in top_labs]
return top_probs, top_flowers
```
## Sanity Checking
Now I have used a trained model for predictions. Even if the testing accuracy is high, it's always good to check that there aren't obvious bugs. I have used matplotlib to plot the probabilities for the top 5 classes as a bar graph, along with the input image.
```
def plot_solution(image_path, model):
# Set up plot
plt.figure(figsize = (6,10))
ax = plt.subplot(2,1,1)
# Set up title
flower_num = image_path.split('/')[2]
title_ = cat_to_name[flower_num]
# Plot flower
img = process_image(image_path)
imshow(img, ax, title = title_);
# Make prediction
probs, flowers = predict(image_path, model)
# Plot bar chart
plt.subplot(2,1,2)
sns.barplot(x=probs, y=flowers, color=sns.color_palette()[0]);
plt.show()
image_path = 'flowers/test/90/image_04432.jpg'
plot_solution(image_path, model_ft)
```
|
github_jupyter
|
```
# Import libraries
import sklearn
from sklearn import model_selection
import numpy as np
np.random.seed(42)
import os
import pandas as pd
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
# Ignore useless warnings (see SciPy issue #5998)
import warnings
warnings.filterwarnings(action="ignore", message="^internal gelsd")
# To plot figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Where to save the figures
PROJECT_ROOT_DIR = "."
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "assets")
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
# Load the data
script_directory = os.getcwd() # Script directory
full_data_path = os.path.join(script_directory, 'data/')
DATA_PATH = full_data_path
def load_data(data_path=DATA_PATH):
csv_path = os.path.join(data_path, "train.csv")
return pd.read_csv(csv_path)
data = load_data()
```
# A brief look at the data
```
data.shape
data.head()
data["Embarked"].value_counts()
data["Sex"].value_counts()
data["Ticket"].value_counts()
data.describe()
data.describe(include=['O'])
data.hist(bins=50, figsize=(20,15))
save_fig("attribute_histogram_plots")
plt.show()
```
# Split the data into train and validation sets
```
# Split the data into train and validation sets before diving into analysis
train_data, validation_data = model_selection.train_test_split(data, test_size=0.2, random_state=42)
print("Train data shape:")
print(train_data.shape)
print("Train data columns:")
print(train_data.columns)
# Save the data sets
train_data.to_csv("data/train_data.csv", index=False)
validation_data.to_csv("data/validation_data.csv", index=False)
```
# Reshaping data
```
correlation_matrix = train_data.corr()
correlation_matrix["Survived"].sort_values(ascending=False)
train_set = [train_data]
#train_set.type()
for dataset in train_set:
dataset['Title'] = dataset.Name.str.extract(' ([A-Za-z]+)\.', expand=False)
pd.crosstab(train_data['Title'], train_data['Sex'])
for dataset in train_set:
dataset['Title'] = dataset['Title'].replace(['Lady', 'Countess','Capt', 'Col',\
'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Rare')
dataset['Title'] = dataset['Title'].replace('Mlle', 'Miss')
dataset['Title'] = dataset['Title'].replace('Ms', 'Miss')
dataset['Title'] = dataset['Title'].replace('Mme', 'Mrs')
train_data[['Title', 'Survived']].groupby(['Title'], as_index=False).mean()
title_mapping = {"Mr": 1, "Miss": 2, "Mrs": 3, "Master": 4, "Rare": 5}
for dataset in train_set:
dataset['Title'] = dataset['Title'].map(title_mapping)
dataset['Title'] = dataset['Title'].fillna(0)
train_data.head()
from sklearn.base import BaseEstimator, TransformerMixin
class TitleAdder(BaseEstimator, TransformerMixin):
def fit(self, X, y=None):
return self
def transform(self, X):
X_list = [X]
for row in X_list:
row['Title'] = dataset.Name.str.extract(' ([A-Za-z]+)\.', expand=False)
row['Title'] = dataset['Title'].replace(['Lady', 'Countess','Capt', 'Col',\
'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Rare')
row['Title'] = dataset['Title'].replace('Mlle', 'Miss')
row['Title'] = dataset['Title'].replace('Ms', 'Miss')
row['Title'] = dataset['Title'].replace('Mme', 'Mrs')
row['Title'] = dataset['Title'].fillna(0)
X = X.drop(["Name"], axis=1)
return X
import seaborn as sns
g = sns.FacetGrid(train_data, col='Survived')
g.map(plt.hist, 'Age', bins=20)
train_data['AgeBand'] = pd.cut(train_data['Age'], bins=[0, 5, 18, 30, 38, 50, 65, 74.3, 90])
train_data[['AgeBand', 'Survived']].groupby(['AgeBand'], as_index=False).mean().sort_values(by='AgeBand', ascending=True)
train_data.head(3)
train_data["AgeBucket"] = train_data["Age"] // 15 * 15
train_data[["AgeBucket", "Survived"]].groupby(['AgeBucket']).mean()
train_data['IsAlone'] = train_data['SibSp'] + train_data['Parch'] > 0
train_data[['IsAlone', 'Survived']].groupby(['IsAlone'], as_index=False).mean()
train_data[['SibSp', 'Survived']].groupby(['SibSp'], as_index=False).mean()
#train_data[['Parch', 'Survived']].groupby(['Parch'], as_index=False).mean()
import seaborn as sns
g = sns.FacetGrid(train_data, col='Survived')
g.map(plt.hist, 'Fare', bins=20)
train_data['FareBand'] = pd.qcut(train_data['Fare'], 4)
train_data[['FareBand', 'Survived']].groupby(['FareBand'], as_index=False).mean().sort_values(by='FareBand', ascending=True)
y_train = train_data["Survived"]
y_train
```
|
github_jupyter
|
```
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sns; sns.set()
trips = pd.read_csv('2015_trip_data.csv',
parse_dates=['starttime', 'stoptime'],
infer_datetime_format=True)
ind = pd.DatetimeIndex(trips.starttime)
trips['date'] = ind.date.astype('datetime64')
trips['hour'] = ind.hour
hourly = trips.pivot_table('trip_id', aggfunc='count',
index=['usertype', 'date'], columns='hour').fillna(0)
hourly.head()
```
## Principal Component Analysis
```
from sklearn.decomposition import PCA
data = hourly[np.arange(24)].values
data_pca = PCA(2).fit_transform(data)
hourly['projection1'], hourly['projection2'] = data_pca.T
hourly['total rides'] = hourly.sum(axis=1)
hourly.plot('projection1', 'projection2', kind='scatter', c='total rides', cmap='Blues_r');
plt.savefig('figs/pca_raw.png', bbox_inches='tight')
```
## Automated Clustering
```
from sklearn.mixture import GMM
gmm = GMM(3, covariance_type='full', random_state=2)
data = hourly[['projection1', 'projection2']]
gmm.fit(data)
# require high-probability cluster membership
hourly['cluster'] = (gmm.predict_proba(data)[:, 0] > 0.6).astype(int)
from datetime import time
fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(wspace=0.1)
times = pd.date_range('0:00', '23:59', freq='H').time
times = np.hstack([times, time(23, 59, 59)])
hourly.plot('projection1', 'projection2', c='cluster', kind='scatter',
cmap='rainbow', colorbar=False, ax=ax[0]);
for i in range(2):
vals = hourly.query("cluster == " + str(i))[np.arange(24)]
vals[24] = vals[0]
ax[1].plot(times, vals.T, color=plt.cm.rainbow(255 * i), alpha=0.05, lw=0.5)
ax[1].plot(times, vals.mean(0), color=plt.cm.rainbow(255 * i), lw=3)
ax[1].set_xticks(4 * 60 * 60 * np.arange(6))
ax[1].set_ylim(0, 60);
ax[1].set_ylabel('Rides per hour');
fig.savefig('figs/pca_clustering.png', bbox_inches='tight')
fig, ax = plt.subplots(1, 2, figsize=(16, 6), sharex=True, sharey=True)
fig.subplots_adjust(wspace=0.05)
for i, col in enumerate(['Annual Member', 'Short-Term Pass Holder']):
hourly.loc[col].plot('projection1', 'projection2', c='cluster', kind='scatter',
cmap='rainbow', colorbar=False, ax=ax[i]);
ax[i].set_title(col + 's')
fig.savefig('figs/pca_annual_vs_shortterm.png', bbox_inches='tight')
usertype = hourly.index.get_level_values('usertype')
weekday = hourly.index.get_level_values('date').dayofweek < 5
hourly['commute'] = (weekday & (usertype == "Annual Member"))
fig, ax = plt.subplots()
hourly.plot('projection1', 'projection2', c='commute', kind='scatter',
cmap='binary', colorbar=False, ax=ax);
ax.set_title("Annual Member Weekdays vs Other")
fig.savefig('figs/pca_true_weekends.png', bbox_inches='tight')
```
## Identifying Mismatches
```
mismatch = hourly.query('cluster == 0 & commute')
mismatch = mismatch.reset_index('usertype')[['usertype', 'projection1', 'projection2']]
mismatch
from pandas.tseries.holiday import USFederalHolidayCalendar
cal = USFederalHolidayCalendar()
holidays = cal.holidays('2014-08', '2015-10', return_name=True)
holidays_all = pd.concat([holidays,
"2 Days Before " + holidays.shift(-2, 'D'),
"Day Before " + holidays.shift(-1, 'D'),
"Day After " + holidays.shift(1, 'D')])
holidays_all = holidays_all.sort_index()
holidays_all.head()
holidays_all.name = 'holiday name' # required for join
joined = mismatch.join(holidays_all)
joined['holiday name']
set(holidays) - set(joined['holiday name'])
fig, ax = plt.subplots()
hourly.plot('projection1', 'projection2', c='cluster', kind='scatter',
cmap='binary', colorbar=False, ax=ax);
ax.set_title("Holidays in Projected Results")
for i, ind in enumerate(joined.sort_values('projection1').index):
x, y = hourly.loc['Annual Member', ind][['projection1', 'projection2']]
if i % 2:
ytext = 20 + 3 * i
else:
ytext = -8 - 4 * i
ax.annotate(joined.loc[ind, 'holiday name'], [x, y], [x , ytext], color='black',
ha='center', arrowprops=dict(arrowstyle='-', color='black'))
ax.scatter([x], [y], c='red')
for holiday in (set(holidays) - set(joined['holiday name'])):
ind = holidays[holidays == holiday].index[0]
#ind = ind.strftime('%Y-%m-%d')
x, y = hourly.loc['Annual Member', ind][['projection1', 'projection2']]
ax.annotate(holidays.loc[ind], [x, y], [x + 20, y + 30], color='black',
ha='center', arrowprops=dict(arrowstyle='-', color='black'))
ax.scatter([x], [y], c='#00FF00')
ax.set_xlim([-60, 60])
ax.set_ylim([-60, 60])
fig.savefig('figs/pca_holiday_labels.png', bbox_inches='tight')
```
|
github_jupyter
|
# T81-558: Applications of Deep Neural Networks
**Module 13: Advanced/Other Topics**
* Instructor: [Jeff Heaton](https://sites.wustl.edu/jeffheaton/), McKelvey School of Engineering, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
* For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
# Module 13 Video Material
* Part 13.1: Flask and Deep Learning Web Services [[Video]](https://www.youtube.com/watch?v=H73m9XvKHug&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_13_01_flask.ipynb)
* Part 13.2: Deploying a Model to AWS [[Video]](https://www.youtube.com/watch?v=8ygCyvRZ074&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_13_02_cloud.ipynb)
* **Part 13.3: Using a Keras Deep Neural Network with a Web Application** [[Video]](https://www.youtube.com/watch?v=OBbw0e-UroI&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_13_03_web.ipynb)
* Part 13.4: When to Retrain Your Neural Network [[Video]](https://www.youtube.com/watch?v=K2Tjdx_1v9g&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_13_04_retrain.ipynb)
* Part 13.5: AI at the Edge: Using Keras on a Mobile Device [[Video]]() [[Notebook]](t81_558_class_13_05_edge.ipynb)
# Part 13.3: Using a Keras Deep Neural Network with a Web Application
In this module we will extend the image API developed in Part 13.1 to work with a web application. This allows you to use a simple website to upload/predict images, such as Figure 13.WEB.
**Figure 13.WEB: AI Web Application**

To do this, we will use the same API developed in Module 13.1. However, we will now add a [ReactJS](https://reactjs.org/) website around it. This is a single page web application that allows you to upload images for classification by the neural network. If you would like to read more about ReactJS and image uploading, you can refer to the [blog post](http://www.hartzis.me/react-image-upload/) that I borrowed some of the code from. I added neural network functionality to a simple ReactJS image upload and preview example.
This example is built from the following components:
* [GitHub Location for Web App](./py/)
* [image_web_server_1.py](./py/image_web_server_1.py) - The code both to start Flask, as well as serve the HTML/JavaScript/CSS needed to provide the web interface.
* Directory WWW - Contains web assets.
* [index.html](./py/www/index.html) - The main page for the web application.
* [style.css](./py/www/style.css) - The stylesheet for the web application.
* [script.js](./py/www/script.js) - The JavaScript code for the web application.
|
github_jupyter
|
```
%%html
<style>
body {
font-family: "Cambria", cursive, sans-serif;
}
</style>
import random, time
import numpy as np
from collections import defaultdict
import operator
import matplotlib.pyplot as plt
```
## Misc functions and utilities
```
orientations = EAST, NORTH, WEST, SOUTH = [(1, 0), (0, 1), (-1, 0), (0, -1)]
turns = LEFT, RIGHT = (+1, -1)
def vector_add(a, b):
"""Component-wise addition of two vectors."""
return tuple(map(operator.add, a, b))
def turn_heading(heading, inc, headings=orientations):
return headings[(headings.index(heading) + inc) % len(headings)]
def turn_right(heading):
return turn_heading(heading, RIGHT)
def turn_left(heading):
return turn_heading(heading, LEFT)
def distance(a, b):
"""The distance between two (x, y) points."""
xA, yA = a
xB, yB = b
return math.hypot((xA - xB), (yA - yB))
def isnumber(x):
"""Is x a number?"""
return hasattr(x, '__int__')
```
## Class definitions
### Base `MDP` class
```
class MDP:
"""A Markov Decision Process, defined by an initial state, transition model,
and reward function. We also keep track of a gamma value, for use by
algorithms. The transition model is represented somewhat differently from
the text. Instead of P(s' | s, a) being a probability number for each
state/state/action triplet, we instead have T(s, a) return a
list of (p, s') pairs. We also keep track of the possible states,
terminal states, and actions for each state."""
def __init__(self, init, actlist, terminals, transitions = {}, reward = None, states=None, gamma=.9):
if not (0 < gamma <= 1):
raise ValueError("An MDP must have 0 < gamma <= 1")
if states:
self.states = states
else:
## collect states from transitions table
self.states = self.get_states_from_transitions(transitions)
self.init = init
if isinstance(actlist, list):
## if actlist is a list, all states have the same actions
self.actlist = actlist
elif isinstance(actlist, dict):
## if actlist is a dict, different actions for each state
self.actlist = actlist
self.terminals = terminals
self.transitions = transitions
#if self.transitions == {}:
#print("Warning: Transition table is empty.")
self.gamma = gamma
if reward:
self.reward = reward
else:
self.reward = {s : 0 for s in self.states}
#self.check_consistency()
def R(self, state):
"""Return a numeric reward for this state."""
return self.reward[state]
def T(self, state, action):
"""Transition model. From a state and an action, return a list
of (probability, result-state) pairs."""
if(self.transitions == {}):
raise ValueError("Transition model is missing")
else:
return self.transitions[state][action]
def actions(self, state):
"""Set of actions that can be performed in this state. By default, a
fixed list of actions, except for terminal states. Override this
method if you need to specialize by state."""
if state in self.terminals:
return [None]
else:
return self.actlist
def get_states_from_transitions(self, transitions):
if isinstance(transitions, dict):
s1 = set(transitions.keys())
s2 = set([tr[1] for actions in transitions.values()
for effects in actions.values() for tr in effects])
return s1.union(s2)
else:
print('Could not retrieve states from transitions')
return None
def check_consistency(self):
# check that all states in transitions are valid
assert set(self.states) == self.get_states_from_transitions(self.transitions)
# check that init is a valid state
assert self.init in self.states
# check reward for each state
#assert set(self.reward.keys()) == set(self.states)
assert set(self.reward.keys()) == set(self.states)
# check that all terminals are valid states
assert all([t in self.states for t in self.terminals])
# check that probability distributions for all actions sum to 1
for s1, actions in self.transitions.items():
for a in actions.keys():
s = 0
for o in actions[a]:
s += o[0]
assert abs(s - 1) < 0.001
```
### A custom MDP class to extend functionality
We will write a CustomMDP class to extend the MDP class for the problem at hand. <br>This class will implement the `T` method to implement the transition model.
```
class CustomMDP(MDP):
def __init__(self, transition_matrix, rewards, terminals, init, gamma=.9):
# All possible actions.
actlist = []
for state in transition_matrix.keys():
actlist.extend(transition_matrix[state])
actlist = list(set(actlist))
#print(actlist)
MDP.__init__(self, init, actlist, terminals=terminals, gamma=gamma)
self.t = transition_matrix
self.reward = rewards
for state in self.t:
self.states.add(state)
def T(self, state, action):
if action is None:
return [(0.0, state)]
else:
return [(prob, new_state) for new_state, prob in self.t[state][action].items()]
```
## Problem 1: Simple MDP
---
### State dependent reward function
Markov Decision Processes are formally described as processes that follow the Markov property which states that "The future is independent of the past given the present". MDPs formally describe environments for reinforcement learning and we assume that the environment is fully observable.
Let us take a toy example MDP and solve it using value iteration and policy iteration. This is a simple example adapted from a similar problem by Dr. David Silver, tweaked to fit the limitations of the current functions.
Let's say you're a student attending lectures in a university. There are three lectures you need to attend on a given day. Attending the first lecture gives you 4 points of reward. After the first lecture, you have a 0.6 probability to continue into the second one, yielding 6 more points of reward. But, with a probability of 0.4, you get distracted and start using Facebook instead and get a reward of -1. From then onwards, you really can't let go of Facebook and there's just a 0.1 probability that you will concentrate back on the lecture.
After the second lecture, you have an equal chance of attending the next lecture or just falling asleep. Falling asleep is the terminal state and yields you no reward, but continuing on to the final lecture gives you a big reward of 10 points. From there on, you have a 40% chance of going to study and reach the terminal state, but a 60% chance of going to the pub with your friends instead. You end up drunk and don't know which lecture to attend, so you go to one of the lectures according to the probabilities given above.

### Definition of transition matrix
We first have to define our Transition Matrix as a nested dictionary to fit the requirements of the MDP class.
```
t = {
'leisure': {
'facebook': {'leisure':0.9, 'class1':0.1},
'quit': {'leisure':0.1, 'class1':0.9},
'study': {},
'sleep': {},
'pub': {}
},
'class1': {
'study': {'class2':0.6, 'leisure':0.4},
'facebook': {'class2':0.4, 'leisure':0.6},
'quit': {},
'sleep': {},
'pub': {}
},
'class2': {
'study': {'class3':0.5, 'end':0.5},
'sleep': {'end':0.5, 'class3':0.5},
'facebook': {},
'quit': {},
'pub': {},
},
'class3': {
'study': {'end':0.6, 'class1':0.08, 'class2':0.16, 'class3':0.16},
'pub': {'end':0.4, 'class1':0.12, 'class2':0.24, 'class3':0.24},
'facebook': {},
'quit': {},
'sleep': {}
},
'end': {}
}
```
### Defining rewards
We now need to define the reward for each state.
```
rewards = {
'class1': 4,
'class2': 6,
'class3': 10,
'leisure': -1,
'end': 0
}
```
### Terminal state
This MDP has only one terminal state
```
terminals = ['end']
```
### Setting initial state to `Class 1`
```
init = 'class1'
```
### Read in an instance of the custom class
```
school_mdp = CustomMDP(t, rewards, terminals, init, gamma=.95)
```
### Let's see the actions and rewards of the MDP
```
school_mdp.states
school_mdp.actions('class1')
school_mdp.actions('leisure')
school_mdp.T('class1','sleep')
school_mdp.actions('end')
school_mdp.reward
```
## Value iteration
```
def value_iteration(mdp, epsilon=0.001):
"""Solving an MDP by value iteration.
mdp: The MDP object
epsilon: Stopping criteria
"""
U1 = {s: 0 for s in mdp.states}
R, T, gamma = mdp.R, mdp.T, mdp.gamma
while True:
U = U1.copy()
delta = 0
for s in mdp.states:
U1[s] = R(s) + gamma * max([sum([p * U[s1] for (p, s1) in T(s, a)])
for a in mdp.actions(s)])
delta = max(delta, abs(U1[s] - U[s]))
if delta < epsilon * (1 - gamma) / gamma:
return U
def value_iteration_over_time(mdp, iterations=20):
U_over_time = []
U1 = {s: 0 for s in mdp.states}
R, T, gamma = mdp.R, mdp.T, mdp.gamma
for _ in range(iterations):
U = U1.copy()
for s in mdp.states:
U1[s] = R(s) + gamma * max([sum([p * U[s1] for (p, s1) in T(s, a)])
for a in mdp.actions(s)])
U_over_time.append(U)
return U_over_time
def best_policy(mdp, U):
"""Given an MDP and a utility function U, determine the best policy,
as a mapping from state to action."""
pi = {}
for s in mdp.states:
pi[s] = max(mdp.actions(s), key=lambda a: expected_utility(a, s, U, mdp))
return pi
```
## Value iteration on the school MDP
```
value_iteration(school_mdp)
value_iteration_over_time(school_mdp,iterations=10)
```
### Plotting value updates over time/iterations
```
def plot_value_update(mdp,iterations=10,plot_kw=None):
"""
Plot value updates over iterations for a given MDP.
"""
x = value_iteration_over_time(mdp,iterations=iterations)
value_states = {k:[] for k in mdp.states}
for i in x:
for k,v in i.items():
value_states[k].append(v)
plt.figure(figsize=(8,5))
plt.title("Evolution of state utilities over iteration", fontsize=18)
for v in value_states:
plt.plot(value_states[v])
plt.legend(list(value_states.keys()),fontsize=14)
plt.grid(True)
plt.xlabel("Iterations",fontsize=16)
plt.ylabel("Utilities of states",fontsize=16)
plt.show()
plot_value_update(school_mdp,15)
```
### Value iterations for various discount factors ($\gamma$)
```
for i in range(4):
mdp = CustomMDP(t, rewards, terminals, init, gamma=1-0.2*i)
plot_value_update(mdp,10)
```
### Value iteration for two different reward structures
```
rewards1 = {
'class1': 4,
'class2': 6,
'class3': 10,
'leisure': -1,
'end': 0
}
mdp1 = CustomMDP(t, rewards1, terminals, init, gamma=.95)
plot_value_update(mdp1,20)
rewards2 = {
'class1': 1,
'class2': 1.5,
'class3': 2.5,
'leisure': -4,
'end': 0
}
mdp2 = CustomMDP(t, rewards2, terminals, init, gamma=.95)
plot_value_update(mdp2,20)
value_iteration(mdp2)
```
## Policy iteration
```
def expected_utility(a, s, U, mdp):
"""The expected utility of doing a in state s, according to the MDP and U."""
return sum([p * U[s1] for (p, s1) in mdp.T(s, a)])
def policy_evaluation(pi, U, mdp, k=20):
"""Returns an updated utility mapping U from each state in the MDP to its
utility, using an approximation (modified policy iteration)."""
R, T, gamma = mdp.R, mdp.T, mdp.gamma
for i in range(k):
for s in mdp.states:
U[s] = R(s) + gamma * sum([p * U[s1] for (p, s1) in T(s, pi[s])])
return U
def policy_iteration(mdp,verbose=0):
"""Solves an MDP by policy iteration"""
U = {s: 0 for s in mdp.states}
pi = {s: random.choice(mdp.actions(s)) for s in mdp.states}
if verbose:
print("Initial random choice:",pi)
iter_count=0
while True:
iter_count+=1
U = policy_evaluation(pi, U, mdp)
unchanged = True
for s in mdp.states:
a = max(mdp.actions(s), key=lambda a: expected_utility(a, s, U, mdp))
if a != pi[s]:
pi[s] = a
unchanged = False
if unchanged:
return (pi,iter_count)
if verbose:
print("Policy after iteration {}: {}".format(iter_count,pi))
```
## Policy iteration over the school MDP
```
policy_iteration(school_mdp)
policy_iteration(school_mdp,verbose=1)
```
### Does the result match using value iteration? We use the `best_policy` function to find out
```
best_policy(school_mdp,value_iteration(school_mdp,0.01))
```
## Comparing computation efficiency (time) of value and policy iterations
Clearly values iteration method takes more iterations to reach the same steady-state compared to policy iteration technique. But how does their computation time compare? Let's find out.
### Running value and policy iteration on the school MDP many times and averaging
```
def compute_time(mdp,iteration_technique='value',n_run=1000,epsilon=0.01):
"""
Computes the average time for value or policy iteration for a given MDP
n_run: Number of runs to average over, default 1000
epsilon: Error margin for the value iteration
"""
if iteration_technique=='value':
t1 = time.time()
for _ in range(n_run):
value_iteration(mdp,epsilon=epsilon)
t2 = time.time()
print("Average value iteration took {} milliseconds".format((t2-t1)*1000/n_run))
else:
t1 = time.time()
for _ in range(n_run):
policy_iteration(mdp)
t2 = time.time()
print("Average policy iteration took {} milliseconds".format((t2-t1)*1000/n_run))
compute_time(school_mdp,'value')
compute_time(school_mdp,'policy')
```
## Q-learning
### Q-learning class
```
class QLearningAgent:
""" An exploratory Q-learning agent. It avoids having to learn the transition
model because the Q-value of a state can be related directly to those of
its neighbors.
"""
def __init__(self, mdp, Ne, Rplus, alpha=None):
self.gamma = mdp.gamma
self.terminals = mdp.terminals
self.all_act = mdp.actlist
self.Ne = Ne # iteration limit in exploration function
self.Rplus = Rplus # large value to assign before iteration limit
self.Q = defaultdict(float)
self.Nsa = defaultdict(float)
self.s = None
self.a = None
self.r = None
self.states = mdp.states
self.T = mdp.T
if alpha:
self.alpha = alpha
else:
self.alpha = lambda n: 1./(1+n)
def f(self, u, n):
""" Exploration function. Returns fixed Rplus until
agent has visited state, action a Ne number of times."""
if n < self.Ne:
return self.Rplus
else:
return u
def actions_in_state(self, state):
""" Return actions possible in given state.
Useful for max and argmax. """
if state in self.terminals:
return [None]
else:
act_list=[]
for a in self.all_act:
if len(self.T(state,a))>0:
act_list.append(a)
return act_list
def __call__(self, percept):
s1, r1 = self.update_state(percept)
Q, Nsa, s, a, r = self.Q, self.Nsa, self.s, self.a, self.r
alpha, gamma, terminals = self.alpha, self.gamma, self.terminals,
actions_in_state = self.actions_in_state
if s in terminals:
Q[s, None] = r1
if s is not None:
Nsa[s, a] += 1
Q[s, a] += alpha(Nsa[s, a]) * (r + gamma * max(Q[s1, a1]
for a1 in actions_in_state(s1)) - Q[s, a])
if s in terminals:
self.s = self.a = self.r = None
else:
self.s, self.r = s1, r1
self.a = max(actions_in_state(s1), key=lambda a1: self.f(Q[s1, a1], Nsa[s1, a1]))
return self.a
def update_state(self, percept):
"""To be overridden in most cases. The default case
assumes the percept to be of type (state, reward)."""
return percept
```
### Trial run
```
def run_single_trial(agent_program, mdp):
"""Execute trial for given agent_program
and mdp."""
def take_single_action(mdp, s, a):
"""
Select outcome of taking action a
in state s. Weighted Sampling.
"""
x = random.uniform(0, 1)
cumulative_probability = 0.0
for probability_state in mdp.T(s, a):
probability, state = probability_state
cumulative_probability += probability
if x < cumulative_probability:
break
return state
current_state = mdp.init
while True:
current_reward = mdp.R(current_state)
percept = (current_state, current_reward)
next_action = agent_program(percept)
if next_action is None:
break
current_state = take_single_action(mdp, current_state, next_action)
```
### Testing Q-learning
```
# Define an agent
q_agent = QLearningAgent(school_mdp, Ne=1000, Rplus=2,alpha=lambda n: 60./(59+n))
q_agent.actions_in_state('leisure')
run_single_trial(q_agent,school_mdp)
q_agent.Q
for i in range(200):
run_single_trial(q_agent,school_mdp)
q_agent.Q
def get_U_from_Q(q_agent):
U = defaultdict(lambda: -100.) # Large negative value for comparison
for state_action, value in q_agent.Q.items():
state, action = state_action
if U[state] < value:
U[state] = value
return U
get_U_from_Q(q_agent)
q_agent = QLearningAgent(school_mdp, Ne=100, Rplus=25,alpha=lambda n: 10/(9+n))
qhistory=[]
for i in range(100000):
run_single_trial(q_agent,school_mdp)
U=get_U_from_Q(q_agent)
qhistory.append(U)
print(get_U_from_Q(q_agent))
print(value_iteration(school_mdp,epsilon=0.001))
```
### Function for utility estimate by Q-learning by many iterations
```
def qlearning_iter(agent_program,mdp,iterations=1000,print_final_utility=True):
"""
Function for utility estimate by Q-learning by many iterations
Returns a history object i.e. a list of dictionaries, where utility estimate for each iteration is stored
q_agent = QLearningAgent(grid_1, Ne=25, Rplus=1.5,
alpha=lambda n: 10000./(9999+n))
hist=qlearning_iter(q_agent,grid_1,iterations=10000)
"""
qhistory=[]
for i in range(iterations):
run_single_trial(agent_program,mdp)
U=get_U_from_Q(agent_program)
if len(U)==len(mdp.states):
qhistory.append(U)
if print_final_utility:
print(U)
return qhistory
```
### How do the long-term utility estimates with Q-learning compare with value iteration?
```
def plot_qlearning_vi(hist, vi,plot_n_states=None):
"""
Compares and plots a Q-learning and value iteration results for the utility estimate of an MDP's states
hist: A history object from a Q-learning run
vi: A value iteration estimate for the same MDP
plot_n_states: Restrict the plotting for n states (randomly chosen)
"""
utilities={k:[] for k in list(vi.keys())}
for h in hist:
for state in h.keys():
utilities[state].append(h[state])
if plot_n_states==None:
for state in list(vi.keys()):
plt.figure(figsize=(7,4))
plt.title("Plot of State: {} over Q-learning iterations".format(str(state)),fontsize=16)
plt.plot(utilities[state])
plt.hlines(y=vi[state],xmin=0,xmax=1.1*len(hist))
plt.legend(['Q-learning estimates','Value iteration estimate'],fontsize=14)
plt.xlabel("Iterations",fontsize=14)
plt.ylabel("Utility of the state",fontsize=14)
plt.grid(True)
plt.show()
else:
for state in list(vi.keys())[:plot_n_states]:
plt.figure(figsize=(7,4))
plt.title("Plot of State: {} over Q-learning iterations".format(str(state)),fontsize=16)
plt.plot(utilities[state])
plt.hlines(y=vi[state],xmin=0,xmax=1.1*len(hist))
plt.legend(['Q-learning estimates','Value iteration estimate'],fontsize=14)
plt.xlabel("Iterations",fontsize=14)
plt.ylabel("Utility of the state",fontsize=14)
plt.grid(True)
plt.show()
```
### Testing the long-term utility learning for the small (default) grid world
```
# Define the Q-learning agent
q_agent = QLearningAgent(school_mdp, Ne=100, Rplus=2,alpha=lambda n: 100/(99+n))
# Obtain the history by running the Q-learning for many iterations
hist=qlearning_iter(q_agent,school_mdp,iterations=20000,print_final_utility=False)
# Get a value iteration estimate using the same MDP
vi = value_iteration(school_mdp,epsilon=0.001)
# Compare the utility estimates from two methods
plot_qlearning_vi(hist,vi)
for alpha in range(100,5100,1000):
q_agent = QLearningAgent(school_mdp, Ne=10, Rplus=2,alpha=lambda n: alpha/(alpha-1+n))
# Obtain the history by running the Q-learning for many iterations
hist=qlearning_iter(q_agent,school_mdp,iterations=10000,print_final_utility=False)
# Get a value iteration estimate using the same MDP
vi = value_iteration(school_mdp,epsilon=0.001)
# Compare the utility estimates from two methods
plot_qlearning_vi(hist,vi,plot_n_states=1)
```
|
github_jupyter
|
```
library('magrittr')
library('dplyr')
library('tidyr')
library('readr')
library('ggplot2')
flow_data <-
read_tsv(
'data.tsv',
col_types=cols(
`Donor`=col_factor(levels=c('Donor 25', 'Donor 34', 'Donor 35', 'Donor 40', 'Donor 41')),
`Condition`=col_factor(levels=c('No electroporation', 'Mock electroporation', 'Plasmid electroporation')),
`Cell state`=col_factor(levels=c('Unstimulated', 'Activated')),
.default=col_number()
)
)
flow_data
flow_data %>%
filter(`Donor` != 'Donor 35') %>%
select(
`Donor`:`Condition`,
`Naive: CCR7+ CD45RO-`=`Live/CD3+/CCR7+ CD45RO- | Freq. of Parent`,
`CM: CCR7+ CD45RO+`=`Live/CD3+/CCR7+ CD45RO+ | Freq. of Parent`,
`EM: CCR7- CD45RO+`=`Live/CD3+/CCR7- CD45RO+ | Freq. of Parent`,
`EMRA: CCR7- CD45RO-`=`Live/CD3+/CCR7- CD45RO- | Freq. of Parent`
) %>%
gather(
key=`Population`,
value=`Freq_of_parent`,
`Naive: CCR7+ CD45RO-`:`EMRA: CCR7- CD45RO-`
) %>%
ggplot(aes(x=`Population`, y=`Freq_of_parent`, fill=`Condition`)) +
geom_col(position="dodge") +
theme(axis.text.x=element_text(angle=75, hjust=1)) +
facet_wrap(~`Cell state`+`Donor`, ncol=4) +
ylab('Percent population (%)')
flow_data %>%
filter(`Donor` != 'Donor 35') %>%
select(
`Donor`:`Condition`,
`Naive: CCR7+ CD45RO-`=`Live/CD3+/CCR7+ CD45RO- | Freq. of Parent`,
`CM: CCR7+ CD45RO+`=`Live/CD3+/CCR7+ CD45RO+ | Freq. of Parent`,
`EM: CCR7- CD45RO+`=`Live/CD3+/CCR7- CD45RO+ | Freq. of Parent`,
`EMRA: CCR7- CD45RO-`=`Live/CD3+/CCR7- CD45RO- | Freq. of Parent`
) %>%
gather(
key=`Population`,
value=`Freq_of_parent`,
`Naive: CCR7+ CD45RO-`:`EMRA: CCR7- CD45RO-`
) %>%
ggplot(aes(x=`Population`, y=`Freq_of_parent`, fill=`Condition`)) +
geom_col(position="dodge") +
theme(axis.text.x=element_text(angle=75, hjust=1)) +
facet_grid(`Cell state`~`Donor`) +
ylab('Percent population (%)')
no_electro_val <- function(x) {
x[1]
}
flow_data %>%
filter(`Donor` != 'Donor 35') %>%
select(
`Donor`:`Condition`,
`Naive: CCR7+ CD45RO-`=`Live/CD3+/CCR7+ CD45RO- | Freq. of Parent`,
`CM: CCR7+ CD45RO+`=`Live/CD3+/CCR7+ CD45RO+ | Freq. of Parent`,
`EM: CCR7- CD45RO+`=`Live/CD3+/CCR7- CD45RO+ | Freq. of Parent`,
`EMRA: CCR7- CD45RO-`=`Live/CD3+/CCR7- CD45RO- | Freq. of Parent`
) %>%
gather(
key=`Population`,
value=`Freq_of_parent`,
`Naive: CCR7+ CD45RO-`:`EMRA: CCR7- CD45RO-`
) %>%
arrange(`Condition`) %>%
group_by(`Donor`, `Cell state`, `Population`) %>%
mutate(
`Normalized_Freq_of_parent`=`Freq_of_parent`-no_electro_val(`Freq_of_parent`)
) %>%
filter(
`Condition` == 'Plasmid electroporation'
) %>%
ggplot(aes(x=`Population`, y=`Normalized_Freq_of_parent`, color=`Cell state`)) +
geom_boxplot(alpha=.3, outlier.size=0) +
geom_point(position=position_jitterdodge()) +
geom_hline(yintercept=0, color="gray") +
theme(axis.text.x=element_text(angle=75, hjust=1)) +
ylab('Percent change for plasmid electroporation\ncompared to no electroporation (%)') +
ylim(-25, 25)
flow_data %>%
filter(`Donor` != 'Donor 35') %>%
mutate(
`Donor`:`Condition`,
`CD3 Count`=`Count`*(`Live | Freq. of Parent`/100.0)*(`Live/CD3+ | Freq. of Parent`/100.0),
`Naive: CCR7+ CD45RO-`=`CD3 Count`*`Live/CD3+/CCR7+ CD45RO- | Freq. of Parent`,
`CM: CCR7+ CD45RO+`=`CD3 Count`*`Live/CD3+/CCR7+ CD45RO+ | Freq. of Parent`,
`EM: CCR7- CD45RO+`=`CD3 Count`*`Live/CD3+/CCR7- CD45RO+ | Freq. of Parent`,
`EMRA: CCR7- CD45RO-`=`CD3 Count`*`Live/CD3+/CCR7- CD45RO- | Freq. of Parent`
) %>%
gather(
key=`Population`,
value=`Freq_of_parent`,
`Naive: CCR7+ CD45RO-`:`EMRA: CCR7- CD45RO-`
) %>%
ggplot(aes(x=`Population`, y=`Freq_of_parent`, fill=`Condition`)) +
geom_col(position="dodge") +
theme_bw() +
theme(axis.text.x=element_text(angle=75, hjust=1)) +
facet_grid(`Cell state`~`Donor`) +
ylab('Live cell count')
no_electro_val <- function(x) {
x[1]
}
flow_data %>%
filter(`Donor` != 'Donor 35') %>%
mutate(
`Donor`:`Condition`,
`CD3 Count`=`Count`*(`Live | Freq. of Parent`/100.0)*(`Live/CD3+ | Freq. of Parent`/100.0),
`Naive: CCR7+ CD45RO-`=`CD3 Count`*`Live/CD3+/CCR7+ CD45RO- | Freq. of Parent`,
`CM: CCR7+ CD45RO+`=`CD3 Count`*`Live/CD3+/CCR7+ CD45RO+ | Freq. of Parent`,
`EM: CCR7- CD45RO+`=`CD3 Count`*`Live/CD3+/CCR7- CD45RO+ | Freq. of Parent`,
`EMRA: CCR7- CD45RO-`=`CD3 Count`*`Live/CD3+/CCR7- CD45RO- | Freq. of Parent`
) %>%
gather(
key=`Population`,
value=`Freq_of_parent`,
`Naive: CCR7+ CD45RO-`:`EMRA: CCR7- CD45RO-`
) %>%
arrange(`Condition`) %>%
group_by(`Donor`, `Cell state`, `Population`) %>%
mutate(
`Normalized_Freq_of_parent`=(1-(`Freq_of_parent`/no_electro_val(`Freq_of_parent`)))*100
) %>%
filter(
`Condition` == 'Plasmid electroporation',
`Normalized_Freq_of_parent` > 0
) %>%
ggplot(aes(x=`Population`, y=`Normalized_Freq_of_parent`, color=`Cell state`)) +
geom_boxplot(alpha=.3, outlier.size=0) +
geom_point(position=position_jitterdodge()) +
theme(axis.text.x=element_text(angle=75, hjust=1)) +
ylab('Percent death for plasmid electroporation\ncompared to no electroporation (%)') +
ylim(0, 100)
flow_data %>%
filter(`Donor` != 'Donor 35') %>%
mutate(
`T cell count`=`Count`*(`Live | Freq. of Parent`/100.0)*(`Live/CD3+ | Freq. of Parent`/100.0)
) %>%
ggplot(aes(x=`Donor`, y=`T cell count`, fill=`Condition`)) +
geom_col(position="dodge") +
theme(axis.text.x=element_text(angle=75, hjust=1)) +
facet_wrap(~`Cell state`, ncol=1) +
ylab('Live T cell count')
colors <- c("#FC877F", "#0EADEE", "#04B412")
flow_data %>%
filter(`Donor` != 'Donor 35') %>%
mutate(
`Live Percent (%)`=(`Live | Freq. of Parent`/100.0)*(`Live/CD3+ | Freq. of Parent`)
) %>%
ggplot(aes(x=`Donor`, y=`Live Percent (%)`, fill=`Condition`)) +
geom_col(position="dodge") +
facet_wrap(~`Cell state`, ncol=2) +
theme_bw() +
theme(axis.text.x=element_text(angle=75, hjust=1)) +
scale_fill_manual(values=colors) +
ylab('Live Percent (%)') +
ylim(0, 100)
```
|
github_jupyter
|
# Proyecto
## Instrucciones
1.- Completa los datos personales (nombre y rol USM) de cada integrante en siguiente celda.
* __Nombre-Rol__:
* Cristobal Salazar 201669515-k
* Andres Riveros 201710505-4
* Matias Sasso 201704523-k
* Javier Valladares 201710508-9
2.- Debes _pushear_ este archivo con tus cambios a tu repositorio personal del curso, incluyendo datos, imágenes, scripts, etc.
3.- Se evaluará:
- Soluciones
- Código
- Que Binder esté bien configurado.
- Al presionar `Kernel -> Restart Kernel and Run All Cells` deben ejecutarse todas las celdas sin error.
## I.- Sistemas de recomendación
### Introducción
El rápido crecimiento de la recopilación de datos ha dado lugar a una nueva era de información. Los datos se están utilizando para crear sistemas más eficientes y aquí es donde entran en juego los sistemas de recomendación. Los sistemas de recomendación son un tipo de sistemas de filtrado de información, ya que mejoran la calidad de los resultados de búsqueda y proporcionan elementos que son más relevantes para el elemento de búsqueda o están relacionados con el historial de búsqueda del usuario.
Se utilizan para predecir la calificación o preferencia que un usuario le daría a un artículo. Casi todas las grandes empresas de tecnología los han aplicado de una forma u otra: Amazon lo usa para sugerir productos a los clientes, YouTube lo usa para decidir qué video reproducir a continuación en reproducción automática y Facebook lo usa para recomendar páginas que me gusten y personas a seguir. Además, empresas como Netflix y Spotify dependen en gran medida de la efectividad de sus motores de recomendación para sus negocios y éxitos.
### Objetivos
Poder realizar un proyecto de principio a fin ocupando todos los conocimientos aprendidos en clase. Para ello deben cumplir con los siguientes objetivos:
* **Desarrollo del problema**: Se les pide a partir de los datos, proponer al menos un tipo de sistemas de recomendación. Como todo buen proyecto de Machine Learning deben seguir el siguiente procedimiento:
* **Lectura de los datos**: Describir el o los conjunto de datos en estudio.
* **Procesamiento de los datos**: Procesar adecuadamente los datos en estudio. Para este caso ocuparan técnicas de [NLP](https://en.wikipedia.org/wiki/Natural_language_processing).
* **Metodología**: Describir adecuadamente el procedimiento ocupado en cada uno de los modelos ocupados.
* **Resultados**: Evaluar adecuadamente cada una de las métricas propuesta en este tipo de problemas.
* **Presentación**: La presentación será levemente distinta a las anteriores, puesto que deberán ocupar la herramienta de Jupyter llamada [RISE](https://en.wikipedia.org/wiki/Natural_language_processing). Esta presentación debe durar aproximadamente entre 15-30 minutos, y deberán mandar sus videos (por youtube, google drive, etc.)
### Evaluación
* **Códigos**: Los códigos deben estar correctamente documentados (ocupando las *buenas prácticas* de python aprendidas en este curso).
* **Explicación**: La explicación de la metodología empleada debe ser clara, precisa y concisa.
* **Apoyo Visual**: Se espera que tengan la mayor cantidad de gráficos y/o tablas que puedan resumir adecuadamente todo el proceso realizado.
### Esquema del proyecto
El proyecto tendrá la siguiente estructura de trabajo:
```
- project
|
|- data
|- tmdb_5000_credits.csv
|- tmdb_5000_movies.csv
|- graficos.py
|- lectura.py
|- modelos.py
|- preprocesamiento.py
|- presentacion.ipynb
|- project.ipynb
```
donde:
* `data`: carpeta con los datos del proyecto
* `graficos.py`: módulo de gráficos
* `lectura.py`: módulo de lectura de datos
* `modelos.py`: módulo de modelos de Machine Learning utilizados
* `preprocesamiento.py`: módulo de preprocesamiento de datos
* `presentacion.ipynb`: presentación del proyecto (formato *RISE*)
* `project.ipynb`: descripción del proyecto
### Apoyo
Para que la carga del proyecto sea lo más amena posible, se les deja las siguientes referencias:
* **Sistema de recomendación**: Pueden tomar como referencia el proyecto de Kaggle [Getting Started with a Movie Recommendation System](https://www.kaggle.com/ibtesama/getting-started-with-a-movie-recommendation-system/data?select=tmdb_5000_credits.csv).
* **RISE**: Les dejo un video del Profesor Sebastían Flores denomindo *Presentaciones y encuestas interactivas en jupyter notebooks y RISE* ([link](https://www.youtube.com/watch?v=ekyN9DDswBE&ab_channel=PyConColombia)). Este material les puede ayudar para comprender mejor este nuevo concepto.
|
github_jupyter
|
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
#@title MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
```
# 過学習と学習不足について知る
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/keras/overfit_and_underfit"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/ja/tutorials/keras/overfit_and_underfit.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs-l10n/blob/master/site/ja/tutorials/keras/overfit_and_underfit.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
</table>
Note: これらのドキュメントは私たちTensorFlowコミュニティが翻訳したものです。コミュニティによる 翻訳は**ベストエフォート**であるため、この翻訳が正確であることや[英語の公式ドキュメント](https://www.tensorflow.org/?hl=en)の 最新の状態を反映したものであることを保証することはできません。 この翻訳の品質を向上させるためのご意見をお持ちの方は、GitHubリポジトリ[tensorflow/docs](https://github.com/tensorflow/docs)にプルリクエストをお送りください。 コミュニティによる翻訳やレビューに参加していただける方は、 [docs-ja@tensorflow.org メーリングリスト](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-ja)にご連絡ください。
いつものように、この例のプログラムは`tf.keras` APIを使用します。詳しくはTensorFlowの[Keras guide](https://www.tensorflow.org/guide/keras)を参照してください。
これまでの例、つまり、映画レビューの分類と燃費の推定では、検証用データでのモデルの正解率が、数エポックでピークを迎え、その後低下するという現象が見られました。
言い換えると、モデルが訓練用データを**過学習**したと考えられます。過学習への対処の仕方を学ぶことは重要です。**訓練用データセット**で高い正解率を達成することは難しくありませんが、我々は、(これまで見たこともない)**テスト用データ**に汎化したモデルを開発したいのです。
過学習の反対語は**学習不足**(underfitting)です。学習不足は、モデルがテストデータに対してまだ改善の余地がある場合に発生します。学習不足の原因は様々です。モデルが十分強力でないとか、正則化のしすぎだとか、単に訓練時間が短すぎるといった理由があります。学習不足は、訓練用データの中の関連したパターンを学習しきっていないということを意味します。
モデルの訓練をやりすぎると、モデルは過学習を始め、訓練用データの中のパターンで、テストデータには一般的ではないパターンを学習します。我々は、過学習と学習不足の中間を目指す必要があります。これから見ていくように、ちょうどよいエポック数だけ訓練を行うというのは必要なスキルなのです。
過学習を防止するための、最良の解決策は、より多くの訓練用データを使うことです。多くのデータで訓練を行えば行うほど、モデルは自然により汎化していく様になります。これが不可能な場合、次善の策は正則化のようなテクニックを使うことです。正則化は、モデルに保存される情報の量とタイプに制約を課すものです。ネットワークが少数のパターンしか記憶できなければ、最適化プロセスにより、最も主要なパターンのみを学習することになり、より汎化される可能性が高くなります。
このノートブックでは、重みの正則化とドロップアウトという、よく使われる2つの正則化テクニックをご紹介します。これらを使って、IMDBの映画レビューを分類するノートブックの改善を図ります。
```
from __future__ import absolute_import, division, print_function, unicode_literals
try:
# Colab only
%tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib.pyplot as plt
print(tf.__version__)
```
## IMDBデータセットのダウンロード
以前のノートブックで使用したエンベディングの代わりに、ここでは文をマルチホットエンコードします。このモデルは、訓練用データセットをすぐに過学習します。このモデルを使って、過学習がいつ起きるかということと、どうやって過学習と戦うかをデモします。
リストをマルチホットエンコードすると言うのは、0と1のベクトルにするということです。具体的にいうと、例えば`[3, 5]`というシーケンスを、インデックス3と5の値が1で、それ以外がすべて0の、10,000次元のベクトルに変換するということを意味します。
```
NUM_WORDS = 10000
(train_data, train_labels), (test_data, test_labels) = keras.datasets.imdb.load_data(num_words=NUM_WORDS)
def multi_hot_sequences(sequences, dimension):
# 形状が (len(sequences), dimension)ですべて0の行列を作る
results = np.zeros((len(sequences), dimension))
for i, word_indices in enumerate(sequences):
results[i, word_indices] = 1.0 # 特定のインデックスに対してresults[i] を1に設定する
return results
train_data = multi_hot_sequences(train_data, dimension=NUM_WORDS)
test_data = multi_hot_sequences(test_data, dimension=NUM_WORDS)
```
結果として得られるマルチホットベクトルの1つを見てみましょう。単語のインデックスは頻度順にソートされています。このため、インデックスが0に近いほど1が多く出現するはずです。分布を見てみましょう。
```
plt.plot(train_data[0])
```
## 過学習のデモ
過学習を防止するための最も単純な方法は、モデルのサイズ、すなわち、モデル内の学習可能なパラメータの数を小さくすることです(学習パラメータの数は、層の数と層ごとのユニット数で決まります)。ディープラーニングでは、モデルの学習可能なパラメータ数を、しばしばモデルの「キャパシティ」と呼びます。直感的に考えれば、パラメータ数の多いモデルほど「記憶容量」が大きくなり、訓練用のサンプルとその目的変数の間の辞書のようなマッピングをたやすく学習することができます。このマッピングには汎化能力がまったくなく、これまで見たことが無いデータを使って予測をする際には役に立ちません。
ディープラーニングのモデルは訓練用データに適応しやすいけれど、本当のチャレレンジは汎化であって適応ではないということを、肝に銘じておく必要があります。
一方、ネットワークの記憶容量が限られている場合、前述のようなマッピングを簡単に学習することはできません。損失を減らすためには、より予測能力が高い圧縮された表現を学習しなければなりません。同時に、モデルを小さくしすぎると、訓練用データに適応するのが難しくなります。「多すぎる容量」と「容量不足」の間にちょうどよい容量があるのです。
残念ながら、(層の数や、層ごとの大きさといった)モデルの適切なサイズやアーキテクチャを決める魔法の方程式はありません。一連の異なるアーキテクチャを使って実験を行う必要があります。
適切なモデルのサイズを見つけるには、比較的少ない層の数とパラメータから始めるのがベストです。それから、検証用データでの損失値の改善が見られなくなるまで、徐々に層の大きさを増やしたり、新たな層を加えたりします。映画レビューの分類ネットワークでこれを試してみましょう。
比較基準として、```Dense```層だけを使ったシンプルなモデルを構築し、その後、それより小さいバージョンと大きいバージョンを作って比較します。
### 比較基準を作る
```
baseline_model = keras.Sequential([
# `.summary` を見るために`input_shape`が必要
keras.layers.Dense(16, activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dense(16, activation='relu'),
keras.layers.Dense(1, activation='sigmoid')
])
baseline_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy', 'binary_crossentropy'])
baseline_model.summary()
baseline_history = baseline_model.fit(train_data,
train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
```
### より小さいモデルの構築
今作成したばかりの比較基準となるモデルに比べて隠れユニット数が少ないモデルを作りましょう。
```
smaller_model = keras.Sequential([
keras.layers.Dense(4, activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dense(4, activation='relu'),
keras.layers.Dense(1, activation='sigmoid')
])
smaller_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy', 'binary_crossentropy'])
smaller_model.summary()
```
同じデータを使って訓練します。
```
smaller_history = smaller_model.fit(train_data,
train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
```
### より大きなモデルの構築
練習として、より大きなモデルを作成し、どれほど急速に過学習が起きるかを見ることもできます。次はこのベンチマークに、この問題が必要とするよりはるかに容量の大きなネットワークを追加しましょう。
```
bigger_model = keras.models.Sequential([
keras.layers.Dense(512, activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dense(512, activation='relu'),
keras.layers.Dense(1, activation='sigmoid')
])
bigger_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy','binary_crossentropy'])
bigger_model.summary()
```
このモデルもまた同じデータを使って訓練します。
```
bigger_history = bigger_model.fit(train_data, train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
```
### 訓練時と検証時の損失をグラフにする
<!--TODO(markdaoust): This should be a one-liner with tensorboard -->
実線は訓練用データセットの損失、破線は検証用データセットでの損失です(検証用データでの損失が小さい方が良いモデルです)。これをみると、小さいネットワークのほうが比較基準のモデルよりも過学習が始まるのが遅いことがわかります(4エポックではなく6エポック後)。また、過学習が始まっても性能の低下がよりゆっくりしています。
```
def plot_history(histories, key='binary_crossentropy'):
plt.figure(figsize=(16,10))
for name, history in histories:
val = plt.plot(history.epoch, history.history['val_'+key],
'--', label=name.title()+' Val')
plt.plot(history.epoch, history.history[key], color=val[0].get_color(),
label=name.title()+' Train')
plt.xlabel('Epochs')
plt.ylabel(key.replace('_',' ').title())
plt.legend()
plt.xlim([0,max(history.epoch)])
plot_history([('baseline', baseline_history),
('smaller', smaller_history),
('bigger', bigger_history)])
```
より大きなネットワークでは、すぐに、1エポックで過学習が始まり、その度合も強いことに注目してください。ネットワークの容量が大きいほど訓練用データをモデル化するスピードが早くなり(結果として訓練時の損失値が小さくなり)ますが、より過学習しやすく(結果として訓練時の損失値と検証時の損失値が大きく乖離しやすく)なります。
## 過学習防止の戦略
### 重みの正則化を加える
「オッカムの剃刀」の原則をご存知でしょうか。何かの説明が2つあるとすると、最も正しいと考えられる説明は、仮定の数が最も少ない「一番単純な」説明だというものです。この原則は、ニューラルネットワークを使って学習されたモデルにも当てはまります。ある訓練用データとネットワーク構造があって、そのデータを説明できる重みの集合が複数ある時(つまり、複数のモデルがある時)、単純なモデルのほうが複雑なものよりも過学習しにくいのです。
ここで言う「単純なモデル」とは、パラメータ値の分布のエントロピーが小さいもの(あるいは、上記で見たように、そもそもパラメータの数が少ないもの)です。したがって、過学習を緩和するための一般的な手法は、重みが小さい値のみをとることで、重み値の分布がより整然となる(正則)様に制約を与えるものです。これを「重みの正則化」と呼ばれ、ネットワークの損失関数に、重みの大きさに関連するコストを加えることで行われます。このコストには2つの種類があります。
* [L1正則化](https://developers.google.com/machine-learning/glossary/#L1_regularization) 重み係数の絶対値に比例するコストを加える(重みの「L1ノルム」と呼ばれる)。
* [L2正則化](https://developers.google.com/machine-learning/glossary/#L2_regularization) 重み係数の二乗に比例するコストを加える(重み係数の二乗「L2ノルム」と呼ばれる)。L2正則化はニューラルネットワーク用語では重み減衰(Weight Decay)と呼ばれる。呼び方が違うので混乱しないように。重み減衰は数学的にはL2正則化と同義である。
L1正則化は重みパラメータの一部を0にすることでモデルを疎にする効果があります。L2正則化は重みパラメータにペナルティを加えますがモデルを疎にすることはありません。これは、L2正則化のほうが一般的である理由の一つです。
`tf.keras`では、重みの正則化をするために、重み正則化のインスタンスをキーワード引数として層に加えます。ここでは、L2正則化を追加してみましょう。
```
l2_model = keras.models.Sequential([
keras.layers.Dense(16, kernel_regularizer=keras.regularizers.l2(0.001),
activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dense(16, kernel_regularizer=keras.regularizers.l2(0.001),
activation='relu'),
keras.layers.Dense(1, activation='sigmoid')
])
l2_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy', 'binary_crossentropy'])
l2_model_history = l2_model.fit(train_data, train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
```
```l2(0.001)```というのは、層の重み行列の係数全てに対して```0.001 * 重み係数の値 **2```をネットワークの損失値合計に加えることを意味します。このペナルティは訓練時のみに加えられるため、このネットワークの損失値は、訓練時にはテスト時に比べて大きくなることに注意してください。
L2正則化の影響を見てみましょう。
```
plot_history([('baseline', baseline_history),
('l2', l2_model_history)])
```
ご覧のように、L2正則化ありのモデルは比較基準のモデルに比べて過学習しにくくなっています。両方のモデルのパラメータ数は同じであるにもかかわらずです。
### ドロップアウトを追加する
ドロップアウトは、ニューラルネットワークの正則化テクニックとして最もよく使われる手法の一つです。この手法は、トロント大学のヒントンと彼の学生が開発したものです。ドロップアウトは層に適用するもので、訓練時に層から出力された特徴量に対してランダムに「ドロップアウト(つまりゼロ化)」を行うものです。例えば、ある層が訓練時にある入力サンプルに対して、普通は`[0.2, 0.5, 1.3, 0.8, 1.1]` というベクトルを出力するとします。ドロップアウトを適用すると、このベクトルは例えば`[0, 0.5, 1.3, 0, 1.1]`のようにランダムに散らばったいくつかのゼロを含むようになります。「ドロップアウト率」はゼロ化される特徴の割合で、通常は0.2から0.5の間に設定します。テスト時は、どのユニットもドロップアウトされず、代わりに出力値がドロップアウト率と同じ比率でスケールダウンされます。これは、訓練時に比べてたくさんのユニットがアクティブであることに対してバランスをとるためです。
`tf.keras`では、Dropout層を使ってドロップアウトをネットワークに導入できます。ドロップアウト層は、その直前の層の出力に対してドロップアウトを適用します。
それでは、IMDBネットワークに2つのドロップアウト層を追加しましょう。
```
dpt_model = keras.models.Sequential([
keras.layers.Dense(16, activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dropout(0.5),
keras.layers.Dense(16, activation='relu'),
keras.layers.Dropout(0.5),
keras.layers.Dense(1, activation='sigmoid')
])
dpt_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy','binary_crossentropy'])
dpt_model_history = dpt_model.fit(train_data, train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
plot_history([('baseline', baseline_history),
('dropout', dpt_model_history)])
```
ドロップアウトを追加することで、比較対象モデルより明らかに改善が見られます。
まとめ:ニューラルネットワークにおいて過学習を防ぐ最も一般的な方法は次のとおりです。
* 訓練データを増やす
* ネットワークの容量をへらす
* 重みの正則化を行う
* ドロップアウトを追加する
このガイドで触れていない2つの重要なアプローチがあります。データ拡張とバッチ正規化です。
|
github_jupyter
|
### An Auto correct system is an application that changes mispelled words into the correct ones.
```
# In this notebook I'll show how to implement an Auto Correct System that its very usefull.
# This auto correct system only search for spelling erros, not contextual errors.
```
*The implementation can be divided into 4 steps:*
[1]. **Identity a mispelled word.**
[2]. **Find strings n Edit Distance away**
[3]. **Filter Candidates** (*as Real Words that are spelled correct*)
[4]. **Calculate Word Probabilities.** (*Choose the most likely cadidate to be the replacement*)
### 1. Identity a mispelled Word
*To identify if a word was mispelled, you can check if the word is in the dictionary / vocabulary.*
```
vocab = ['dean','deer','dear','fries','and','coke', 'congratulations', 'my']
word_test = 'Congratulations my deah'
word_test = word_test.lower()
word_test = word_test.split()
for word in word_test:
if word in vocab:
print(f'The word: {word} is in the vocab')
else:
print(f"The word: {word} isn't in the vocabulary")
```
### 2. Find strings n Edit Distance Away
*Edit is a operation performed on a string to change into another string. Edit distance count the number of these operations*
*So **n Edit Distance** tells you how many operations away one string is from another.*
*For this application we'll use the Levenshtein Distance value's cost, where this edit value are:*
* **Insert** - Operation where you insert a letter, the cost is equal to 1.
* **Delete** - Operation where you delete a letter, the cost is equal to 1.
* **Replace** - Operation where you replace one letter to another, the cost is equal to 2.
* **Switch** - Operation where you swap 2 **adjacent** letters
*Also we'll use the Minimum Edit Distance which is the minimum number of edits needed to transform 1 string into the other, for that we are using n = 2 and the Dynamic Programming algorithm. ( will be explained when it is implemented ) for evaluate our model*
```
# To implement this operations we need to split the word into 2 parts in all possible ways
word = 'dear'
split_word = [[word[:i], word[i:]] for i in range(len(word) + 1)]
for i in split_word:
print(i)
# The delete operation need to delete each possible letter from the original word.
delete_operation = [[L + R[1:]] for L, R in split_word if R ]
for i in delete_operation:
print(i)
# The same way the insert operation need to add each possible letter from the vocab to the original word
letters = 'abcdefghijklmnopqrstuvwxyz'
insert_operation = [L + s + R for L, R in split_word for s in letters]
c = 0
print('the first insert operations: ')
print()
for i in insert_operation:
print(i)
c += 1
if c == 4:
break
c = 0
print('the last insert operations:')
print()
for i in insert_operation:
c += 1
if c > 126:
print(i)
# Switch Operation
switch_operation = [[L[:-1] + R[0] + L[-1] + R[1:]] for L, R in split_word if R and L]
for i in switch_operation:
print(i)
# Replace Operation
letters = 'abcdefghijklmnopqrstuvwxyz'
replace_operation = [L + s + (R[1:] if len(R) > 1 else '') for L, R in split_word if R for s in letters ]
c = 0
print('the first replace operations: ')
print()
for i in replace_operation:
print(i)
c += 1
if c == 4:
break
c = 0
print('the last replace operations:')
print()
for i in replace_operation:
c += 1
if c > 100:
print(i)
# Remember that at the end we need to remove the word it self
replace_operation = set(replace_operation)
replace_operation.discard('dear')
```
### 3. Filter Candidates
*We only want to consider real and correctly spelled words form the candidate lists, so we need to compare to a know dictionary.*
*If the string does not appears in the dict, remove from the candidates, this way resulting in a list of actual words only*
```
vocab = ['dean','deer','dear','fries','and','coke', 'congratulations', 'my']
# for example we can use the replace operations words to filter in our vocab
filtered_words = [word for word in replace_operation if word in vocab]
print(filtered_words)
```
### 4. Calculate the words probabilities
*We need to find the most likely word from the cadidate list, to calculate the probability of a word in the
sentence we need to first calculate the word frequencies, also we want to count the total number of word in the body of texts
or corpus.*
*So we compute the probability that each word will appear if randomly selected from the corpus of words.*
$$P(w_i) = \frac{C(w_i)}{M} \tag{Eq 01}$$
*where*
$C(w_i)$ *is the total number of times $w_i$ appears in the corpus.*
$M$ *is the total number of words in the corpus.*
*For example, the probability of the word 'am' in the sentence **'I am happy because I am learning'** is:*
$$P(am) = \frac{C(w_i)}{M} = \frac {2}{7} \tag{Eq 02}.$$
### Now the we know the four steps of the Auto Correct System, we can start to implement it
```
# import libraries
import re
from collections import Counter
import numpy as np
import pandas as pd
```
*The first thing to do is the data pre processing, for this example we'll use the file called **'shakespeare.txt'** this file can be found in the directory.*
```
def process_data(filename):
"""
Input:
A file_name which is found in the current directory. We just have to read it in.
Output:
words: a list containing all the words in the corpus (text file you read) in lower case.
"""
words = []
with open(filename, 'r') as f:
text = f.read()
words = re.findall(r'\w+', text)
words = [word.lower() for word in words]
return words
words = process_data('shakespeare.txt')
vocab = set(words) # eliminate duplicates
print(f'The vocabulary has {len(vocab)} unique words.')
```
*The second step, we need to count the frequency of every word in the dictionary to later calculate the probabilities*
```
def get_count(word):
'''
Input:
word_l: a set of words representing the corpus.
Output:
word_count_dict: The wordcount dictionary where key is the word and value is its frequency.
'''
word_count_dict = {}
word_count_dict = Counter(word)
return word_count_dict
word_count_dict = get_count(words)
print(f'There are {len(word_count_dict)} key par values')
print(f"The count for the word 'thee' is {word_count_dict.get('thee',0)}")
```
*Now we must calculate the probability that each word appears using the (eq 01):*
```
def get_probs(word_count_dict):
'''
Input:
word_count_dict: The wordcount dictionary where key is the word and value is its frequency.
Output:
probs: A dictionary where keys are the words and the values are the probability that a word will occur.
'''
probs = {}
total_words = 0
for word, value in word_count_dict.items():
total_words += value # we add the quantity of each word appears
for word, value in word_count_dict.items():
probs[word] = value / total_words
return probs
probs = get_probs(word_count_dict)
print(f"Length of probs is {len(probs)}")
print(f"P('thee') is {probs['thee']:.4f}")
```
*Now, that we have computed $P(w_i)$ for all the words in the corpus, we'll write the functions such as delete, insert, switch and replace to manipulate strings so that we can edit the erroneous strings and return the right spellings of the words.*
```
def delete_letter(word, verbose = False):
'''
Input:
word: the string/word for which you will generate all possible words
in the vocabulary which have 1 missing character
Output:
delete_l: a list of all possible strings obtained by deleting 1 character from word
'''
delete = []
split_word = []
split_word = [[word[:i], word[i:]] for i in range(len(word))]
delete = [L + R[1:] for L, R in split_word if R]
if verbose: print(f"input word {word}, \nsplit_word = {split_word}, \ndelete_word = {delete}")
return delete
delete_word = delete_letter(word="cans",
verbose=True)
def switch_letter(word, verbose = False):
'''
Input:
word: input string
Output:
switches: a list of all possible strings with one adjacent charater switched
'''
switch = []
split_word = []
split_word = [[word[:i], word[i:]] for i in range(len(word))]
switch = [L[:-1] + R[0] + L[-1] + R[1:] for L, R in split_word if L and R]
if verbose: print(f"Input word = {word} \nsplit = {split_word} \nswitch = {switch}")
return switch
switch_word_l = switch_letter(word="eta",
verbose=True)
def replace_letter(word, verbose=False):
'''
Input:
word: the input string/word
Output:
replaces: a list of all possible strings where we replaced one letter from the original word.
'''
letters = 'abcdefghijklmnopqrstuvwxyz'
replace = []
split_word = []
split_word = [(word[:i], word[i:]) for i in range(len(word))]
replace = [L + s + (R[1:] if len(R) > 1 else '') for L, R in split_word if R for s in letters ]
# we need to remove the actual word from the list
replace = set(replace)
replace.discard(word)
replace = sorted(list(replace)) # turn the set back into a list and sort it, for easier viewing
if verbose: print(f"Input word = {word} \nsplit = {split_word} \nreplace {replace}")
return replace
replace_l = replace_letter(word='can',
verbose=True)
def insert_letter(word, verbose=False):
'''
Input:
word: the input string/word
Output:
inserts: a set of all possible strings with one new letter inserted at every offset
'''
letters = 'abcdefghijklmnopqrstuvwxyz'
insert = []
split_word = []
split_word = [(word[:i], word[i:]) for i in range(len(word) + 1 )]
insert = [L + s + R for L, R in split_word for s in letters]
if verbose: print(f"Input word {word} \nsplit = {split_word} \ninsert = {insert}")
return insert
insert = insert_letter('at', True)
print(f"Number of strings output by insert_letter('at') is {len(insert)}")
```
*Now that we have implemented the string manipulations, we'll create two functions that, given a string, will return all the possible single and double edits on that string. These will be `edit_one_letter()` and `edit_two_letters()`.*
```
def edit_one_letter(word, allow_switches = True): # The 'switch' function is a less common edit function,
# so will be selected by an "allow_switches" input argument.
"""
Input:
word: the string/word for which we will generate all possible wordsthat are one edit away.
Output:
edit_one_set: a set of words with one possible edit. Please return a set. and not a list.
"""
edit_one_set = set()
all_word, words = [] , []
words.append(insert_letter(word))
words.append(delete_letter(word))
words.append(replace_letter(word))
if allow_switches == True:
words.append(switch_letter(word))
for i in words:
for each_word in i:
if each_word == word: # we exclude the word it self
continue
all_word.append(each_word)
edit_one_set = set(all_word)
return edit_one_set
tmp_word = "at"
tmp_edit_one_set = edit_one_letter(tmp_word)
# turn this into a list to sort it, in order to view it
tmp_edit_one = sorted(list(tmp_edit_one_set))
print(f"input word: {tmp_word} \nedit_one \n{tmp_edit_one}\n")
print(f"The type of the returned object should be a set {type(tmp_edit_one_set)}")
print(f"Number of outputs from edit_one_letter('at') is {len(edit_one_letter('at'))}")
def edit_two_letters(word, allow_switches = True):
'''
Input:
word: the input string/word
Output:
edit_two_set: a set of strings with all possible two edits
'''
edit_two_set = set()
if allow_switches == True:
first_edit = edit_one_letter(word)
else:
first_edit = edit_one_letter(word, allow_switches = False)
first_edit = set(first_edit)
second_edit = []
final_edit = []
if allow_switches == True:
for each_word in first_edit:
second_edit.append(edit_one_letter(each_word))
for i in second_edit:
for each_word in i:
final_edit.append(each_word)
edit_two_set = set(final_edit)
else:
for each_word in first_edit:
second_edit.append(edit_one_letter(each_word, allow_switches = False))
for i in second_edit:
for each_word in i:
final_edit.append(each_word)
edit_two_set = set(final_edit)
return edit_two_set
tmp_edit_two_set = edit_two_letters("a")
tmp_edit_two_l = sorted(list(tmp_edit_two_set))
print(f"Number of strings with edit distance of two: {len(tmp_edit_two_l)}")
print(f"First 10 strings {tmp_edit_two_l[:10]}")
print(f"Last 10 strings {tmp_edit_two_l[-10:]}")
print(f"The data type of the returned object should be a set {type(tmp_edit_two_set)}")
print(f"Number of strings that are 2 edit distances from 'at' is {len(edit_two_letters('at'))}")
```
*Now we will use the `edit_two_letters` function to get a set of all the possible 2 edits on our word. We will then use those strings to get the most probable word we meant to substitute our word typing suggestion.*
```
def get_corrections(word, probs, vocab, n=2, verbose = False):
'''
Input:
word: a user entered string to check for suggestions
probs: a dictionary that maps each word to its probability in the corpus
vocab: a set containing all the vocabulary
n: number of possible word corrections you want returned in the dictionary
Output:
n_best: a list of tuples with the most probable n corrected words and their probabilities.
'''
suggestions = []
n_best = []
# look if the word exist in the vocab, if doesn't, the edit_one_letter fuction its used, if any of the letter created
# exists in the vocab, take the two letter edit function, if any of this situations are in the vocab, take the input word
suggestions = list((word in vocab) or (edit_one_letter(word).intersection(vocab)) or (edit_two_letter(word).intersection(vocab)) or word)
n_best= [[word, probs[word]] for word in (suggestions)] # make a list with the possible word and probability.
if verbose: print("entered word = ", word, "\nsuggestions = ", set(suggestions))
return n_best
my_word = 'dys'
tmp_corrections = get_corrections(my_word, probs, vocab, 2, verbose=True) # keep verbose=True
for i, word_prob in enumerate(tmp_corrections):
print(f"word {i}: {word_prob[0]}, probability {word_prob[1]:.6f}")
print(f'The highest score for all the candidates is the word {tmp_corrections[np.argmax(word_prob)][0]}')
```
*Now that we have implemented the auto-correct system, how do you evaluate the similarity between two strings? For example: 'waht' and 'what'.*
*Also how do you efficiently find the shortest path to go from the word, 'waht' to the word 'what'?*
*We will implement a dynamic programming system that will tell you the minimum number of edits required to convert a string into another string.*
### Dynamic Programming
*Dynamic Programming breaks a problem down into subproblems which can be combined to form the final solution. Here, given a string source[0..i] and a string target[0..j], we will compute all the combinations of substrings[i, j] and calculate their edit distance. To do this efficiently, we will use a table to maintain the previously computed substrings and use those to calculate larger substrings.*
*You have to create a matrix and update each element in the matrix as follows:*
$$\text{Initialization}$$
\begin{align}
D[0,0] &= 0 \\
D[i,0] &= D[i-1,0] + del\_cost(source[i]) \tag{eq 03}\\
D[0,j] &= D[0,j-1] + ins\_cost(target[j]) \\
\end{align}
*So converting the source word **play** to the target word **stay**, using an insert cost of one, a delete cost of 1, and replace cost of 2 would give you the following table:*
<table style="width:20%">
<tr>
<td> <b> </b> </td>
<td> <b># </b> </td>
<td> <b>s </b> </td>
<td> <b>t </b> </td>
<td> <b>a </b> </td>
<td> <b>y </b> </td>
</tr>
<tr>
<td> <b> # </b></td>
<td> 0</td>
<td> 1</td>
<td> 2</td>
<td> 3</td>
<td> 4</td>
</tr>
<tr>
<td> <b> p </b></td>
<td> 1</td>
<td> 2</td>
<td> 3</td>
<td> 4</td>
<td> 5</td>
</tr>
<tr>
<td> <b> l </b></td>
<td>2</td>
<td>3</td>
<td>4</td>
<td>5</td>
<td>6</td>
</tr>
<tr>
<td> <b> a </b></td>
<td>3</td>
<td>4</td>
<td>5</td>
<td>4</td>
<td>5</td>
</tr>
<tr>
<td> <b> y </b></td>
<td>4</td>
<td>5</td>
<td>6</td>
<td>5</td>
<td>4</td>
</tr>
</table>
*The operations used in this algorithm are 'insert', 'delete', and 'replace'. These correspond to the functions that we defined earlier: insert_letter(), delete_letter() and replace_letter(). switch_letter() is not used here.*
*The diagram below describes how to initialize the table. Each entry in D[i,j] represents the minimum cost of converting string source[0:i] to string target[0:j]. The first column is initialized to represent the cumulative cost of deleting the source characters to convert string "EER" to "". The first row is initialized to represent the cumulative cost of inserting the target characters to convert from "" to "NEAR".*
<div style="width:image width px; font-size:100%; text-align:center;"><img src='EditDistInit4.PNG' alt="alternate text" width="width" height="height" style="width:1000px;height:400px;"/> Figure 1 Initializing Distance Matrix</div>
*Note that the formula for $D[i,j]$ shown in the image is equivalent to:*
\begin{align}
\\
D[i,j] =min
\begin{cases}
D[i-1,j] + del\_cost\\
D[i,j-1] + ins\_cost\\
D[i-1,j-1] + \left\{\begin{matrix}
rep\_cost; & if src[i]\neq tar[j]\\
0 ; & if src[i]=tar[j]
\end{matrix}\right.
\end{cases}
\tag{5}
\end{align}
*The variable `sub_cost` (for substitution cost) is the same as `rep_cost`; replacement cost. We will stick with the term "replace" whenever possible.*
<div style="width:image width px; font-size:100%; text-align:center;"><img src='EditDistExample1.PNG' alt="alternate text" width="width" height="height" style="width:1200px;height:400px;"/> Figure 2 Examples Distance Matrix</div>
```
def min_edit_distance(source, target, ins_cost = 1, del_cost = 1, rep_cost = 2):
'''
Input:
source: a string corresponding to the string you are starting with
target: a string corresponding to the string you want to end with
ins_cost: an integer setting the insert cost
del_cost: an integer setting the delete cost
rep_cost: an integer setting the replace cost
Output:
D: a matrix of len(source)+1 by len(target)+1 containing minimum edit distances
med: the minimum edit distance (med) required to convert the source string to the target
'''
m = len(source)
n = len(target)
# initialize cost matrix with zeros and dimensions (m+1, n+1)
D = np.zeros((m+1, n+1), dtype = int)
# Fill in column 0, from row 1 to row m, both inclusive
for row in range(1, m+1): # Replace None with the proper range
D[row, 0] = D[row -1, 0] + del_cost
# Fill in row 0, for all columns from 1 to n, both inclusive
for column in range(1, n+1):
D[0, column] = D[0, column - 1] + ins_cost
# Loop through row 1 to row m, both inclusive
for row in range(1, m+1):
# Loop through column 1 to column n, both inclusive
for column in range(1, n+1):
# initialize r_cost to the 'replace' cost that is passed into this function
r_cost = rep_cost
# check to see if source character at the previous row
# matches the target haracter at the previous column
if source[row - 1] == target[column - 1]:
# Update the replacement cost to 0 if source and
# target are equal
r_cost = 0
# Update the cost atow, col based on previous entries in the cost matrix
# Refer to the equation calculate for D[i,j] (the mininum of the three calculated)
D[row, column] = min([D[row-1, column] + del_cost, D[row, column-1] + ins_cost, D[row-1, column-1] + r_cost])
# Set the minimum edit distance with the cost found at row m, column n
med = D[m, n]
return D, med
# testing your implementation
source = 'play'
target = 'stay'
matrix, min_edits = min_edit_distance(source, target)
print("minimum edits: ",min_edits, "\n")
idx = list('#' + source)
cols = list('#' + target)
df = pd.DataFrame(matrix, index=idx, columns= cols)
print(df)
# testing your implementation
source = 'eer'
target = 'near'
matrix, min_edits = min_edit_distance(source, target)
print("minimum edits: ",min_edits, "\n")
idx = list(source)
idx.insert(0, '#')
cols = list(target)
cols.insert(0, '#')
df = pd.DataFrame(matrix, index=idx, columns= cols)
print(df)
```
|
github_jupyter
|
## Birthday Paradox
In a group of 5 people, how likely is it that everyone has a unique birthday (assuming that nobody was born on February 29th of a leap year)? You may feel it is highly likely because there are $365$ days in a year and loosely speaking, $365$ is "much greater" than $5$. Indeed, as you shall see, this probability is greater than $0.9$. However, in a group of $25$ or more, what is the probability that no two persons have the same birthday? You might be surprised to know that the answer is less than a half. This is known as the "birthday paradox".
In general, for a group of $n$ people, the probability that no two persons share the same birthday can be calculated as:
\begin{align*}
P &= \frac{\text{Number of } n \text{-permutations of birthdays}}{\text{Total number of birthday assignments allowing repeated birthdays}}\\
&= \frac{365!/(365-n)!}{365^n}\\
&= \prod_{k=1}^n \frac{365-k+1}{365}
\end{align*}
Observe that this value decreases with $n$. At $n=23$, this value goes below half. The following cell simulates this event and compares the associated empirical and theoretical probabilities. You can use the slider called "iterations" to vary the number of iterations performed by the code.
```
import itertools
import random
import matplotlib.pyplot as plt
import numpy as np
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
# Range of number of people
PEOPLE = np.arange(1, 26)
# Days in year
DAYS = 365
def prob_unique_birthdays(num_people):
'''
Returns the probability that all birthdays are unique, among a given
number of people with uniformly-distributed birthdays.
'''
return (np.arange(DAYS, DAYS - num_people, -1) / DAYS).prod()
def sample_unique_birthdays(num_people):
'''
Selects a sample of people with uniformly-distributed birthdays, and
returns True if all birthdays are unique (or False otherwise).
'''
bdays = np.random.randint(0, DAYS, size=num_people)
unique_bdays = np.unique(bdays)
return len(bdays) == len(unique_bdays)
def plot_probs(iterations):
'''
Plots a comparison of the probability of a group of people all having
unique birthdays, between the theoretical and empirical probabilities.
'''
sample_prob = [] # Empirical prob. of unique-birthday sample
prob = [] # Theoretical prob. of unique-birthday sample
# Compute data points to plot
np.random.seed(1)
for num_people in PEOPLE:
unique_count = sum(sample_unique_birthdays(num_people)
for i in range(iterations))
sample_prob.append(unique_count / iterations)
prob.append(prob_unique_birthdays(num_people))
# Plot results
plt.plot(PEOPLE, prob, 'k-', linewidth = 3.0, label='Theoretical probability')
plt.plot(PEOPLE, sample_prob, 'bo-', linewidth = 3.0, label='Empirical probability')
plt.gcf().set_size_inches(20, 10)
plt.axhline(0.5, color='red', linewidth = 4.0, label='0.5 threshold')
plt.xlabel('Number of people', fontsize = 18)
plt.ylabel('Probability of unique birthdays', fontsize = 18)
plt.grid()
plt.xticks(fontsize = 18)
plt.yticks(fontsize = 18)
plt.legend(fontsize = 18)
plt.show()
interact(plot_probs,
iterations=widgets.IntSlider(min=50, value = 500, max=5050, step=200),
continuous_update=False, layout='bottom');
```
## Conditional Probability
Oftentimes it is advantageous to infer the probability of certain events conditioned on other events. Say you want to estimate the probability that it will rain on a particular day. There are copious number of factors that affect rain on a particular day, but [certain clouds are good indicators of rains](https://www.nationalgeographic.com/science/earth/earths-atmosphere/clouds/). Then the question is how likely are clouds a precursor to rains? These types of problems are called [statistical classification](https://en.wikipedia.org/wiki/Statistical_classification), and concepts such as conditional probability and Bayes rule play an important role in its solution.
Dice, coins and cards are useful examples which we can use to understand the fundamental concepts of probability. There are even more interesting real world examples where we can apply these principles to. Let us analyze the [student alcohol consumption](https://www.kaggle.com/uciml/student-alcohol-consumption) dataset and see if we can infer any information regarding a student's performance relative to the time they spend studying.
<span style="color:red">NOTE:</span> Before continuing, please download the dataset and add it to the folder where this notebook resides. If necessary, you can also review our Pandas notebook.
```
import pandas as pd
import matplotlib.pyplot as plt
```
The dataset consists of two parts, `student-por.csv` and `student-mat.csv`, represents the students' performance in Portuguese and Math courses, respectively. We will consider the scores in the Portuguese courses, and leave the math courses optionally to you.
```
data_por = pd.read_csv("student-por.csv")
```
Of the dataset's [various attributes](https://www.kaggle.com/uciml/student-alcohol-consumption/home), we will use the following two
- `G3` - final grade related with the course subject, Math or Portuguese (numeric: from 0 to 20, output target)
- `studytime` - weekly study time (numeric: 1 : < 2 hours, 2 : 2 to 5 hours, 3 : 5 to 10 hours, or 4 : > 10 hours)
```
attributes = ["G3","studytime"]
data_por = data_por[attributes]
```
We are interested in the relationship between study-time and grade performance, but to start, let us view each attribute individually.
The probability that a student's study-time falls in an interval can be approximated by
$${P(\text{study interval}) = \frac{\text{Number of students with this study interval}}{Total\ number\ of\ students}}$$
This is an emperical estimate, and in later lectures we will reason why this is a valid assumption.
```
data_temp = data_por["studytime"].value_counts()
P_studytime = pd.DataFrame((data_temp/data_temp.sum()).sort_index())
P_studytime.index = ["< 2 hours","2 to 5 hours","5 to 10 hours","> 10 hours"]
P_studytime.columns = ["Probability"]
P_studytime.columns.name = "Study Interval"
P_studytime.plot.bar(figsize=(12,9),fontsize=18)
plt.ylabel("Probability",fontsize=16)
plt.xlabel("Study Interval",fontsize=18)
```
Note that the largest number of students studied between two and five hours, and the smallest studied over 10 hours.
Let us call scores of at least 15 "high". The probability of a student getting a high score can be approximated by
$$P(\text{high score}) = \frac{\text{Number of students with high scores}}{\text{Total number of students}}$$
```
data_temp = (data_por["G3"]>=15).value_counts()
P_score15_p = pd.DataFrame(data_temp/data_temp.sum())
P_score15_p.index = ["Low","High"]
P_score15_p.columns = ["Probability"]
P_score15_p.columns.name = "Score"
print(P_score15_p)
P_score15_p.plot.bar(figsize=(10,6),fontsize=16)
plt.xlabel("Score",fontsize=18)
plt.ylabel("Probability",fontsize=18)
```
Proceeding to more interesting observations, suppose we want to find the probability of the various study-intervals when the student scored high. By conditional probability, this can be calculated by:
$$P(\text{study interval}\ |\ \text{highscore})=\frac{\text{Number of students with study interval AND highscore}}{\text{Total number of students with highscore}}$$
```
score = 15
data_temp = data_por.loc[data_por["G3"]>=score,"studytime"]
P_T_given_score15= pd.DataFrame((data_temp.value_counts()/data_temp.shape[0]).sort_index())
P_T_given_score15.index = ["< 2 hours","2 to 5 hours","5 to 10 hours","> 10 hours"]
P_T_given_score15.columns = ["Probability"]
print("Probability of study interval given that the student gets a highscore:")
P_T_given_score15.columns.name="Study Interval"
P_T_given_score15.plot.bar(figsize=(12,9),fontsize=16)
plt.xlabel("Studt interval",fontsize=18)
plt.ylabel("Probability",fontsize=18)
```
The above metric is something we can only calculate after the students have obtained their results. But how about the other way? What if we want to **predict** the probability that a student gets a score greater than 15 given that they studied for a particular period of time . Using the estimated values we can use the **Bayes rule** to calculate this probability.
$$P(\text{student getting a highscore}\ |\ \text{study interval})=\frac{P(\text{study interval}\ |\ \text{the student scored high})P(\text{highscore})}{P(\text{study interval})}$$
```
P_score15_given_T_p = P_T_given_score15 * P_score15_p.loc["High"] / P_studytime
print("Probability of high score given study interval :")
pd.DataFrame(P_score15_given_T_p).plot.bar(figsize=(12,9),fontsize=18).legend(loc="best")
plt.xlabel("Study interval",fontsize=18)
plt.ylabel("Probability",fontsize=18)
```
Do you find the results surprising? Roughly speaking, the longer students study, the more likely they are to score high. However, once they study over 10 hours, their chances of scoring high decline. You may want to check whether the same phenomenon occurs for the math scores too.
## Try it yourself
If interested, you can try the same analysis for the students math scores. For example, you can get the probabilities of the different study intervals.
```
data_math = pd.read_csv("student-mat.csv")
data_temp = data_math["studytime"].value_counts()
P_studytime_m = pd.DataFrame(data_temp/data_temp.sum())
P_studytime_m.index = ["< 2 hours","2 to 5 hours","5 to 10 hours","> 10 hours"]
P_studytime_m.columns = ["Probability"]
P_studytime_m.columns.name = "Study Interval"
P_studytime_m.plot.bar(figsize=(12,9),fontsize=16)
plt.xlabel("Study Interval",fontsize=18)
plt.ylabel("Probability",fontsize=18)
```
|
github_jupyter
|
# Train a basic TensorFlow Lite for Microcontrollers model
This notebook demonstrates the process of training a 2.5 kB model using TensorFlow and converting it for use with TensorFlow Lite for Microcontrollers.
Deep learning networks learn to model patterns in underlying data. Here, we're going to train a network to model data generated by a [sine](https://en.wikipedia.org/wiki/Sine) function. This will result in a model that can take a value, `x`, and predict its sine, `y`.
The model created in this notebook is used in the [hello_world](https://github.com/tensorflow/tensorflow/tree/master/tensorflow/lite/micro/examples/hello_world) example for [TensorFlow Lite for MicroControllers](https://www.tensorflow.org/lite/microcontrollers/overview).
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/tensorflow/blob/master/tensorflow/lite/micro/examples/hello_world/train/train_hello_world_model.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/tensorflow/blob/master/tensorflow/lite/micro/examples/hello_world/train/train_hello_world_model.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
</table>
**Training is much faster using GPU acceleration.** Before you proceed, ensure you are using a GPU runtime by going to **Runtime -> Change runtime type** and set **Hardware accelerator: GPU**.
## Configure Defaults
```
# Define paths to model files
import os
MODELS_DIR = 'models/'
if not os.path.exists(MODELS_DIR):
os.mkdir(MODELS_DIR)
MODEL_TF = MODELS_DIR + 'model.pb'
MODEL_NO_QUANT_TFLITE = MODELS_DIR + 'model_no_quant.tflite'
MODEL_TFLITE = MODELS_DIR + 'model.tflite'
MODEL_TFLITE_MICRO = MODELS_DIR + 'model.cc'
```
## Setup Environment
Install Dependencies
```
! pip install -q tensorflow==2
```
Set Seed for Repeatable Results
```
# Set a "seed" value, so we get the same random numbers each time we run this
# notebook for reproducible results.
# Numpy is a math library
import numpy as np
np.random.seed(1) # numpy seed
# TensorFlow is an open source machine learning library
import tensorflow as tf
tf.random.set_seed(1) # tensorflow global random seed
```
Import Dependencies
```
# Keras is TensorFlow's high-level API for deep learning
from tensorflow import keras
# Matplotlib is a graphing library
import matplotlib.pyplot as plt
# Math is Python's math library
import math
```
## Dataset
### 1. Generate Data
The code in the following cell will generate a set of random `x` values, calculate their sine values, and display them on a graph.
```
# Number of sample datapoints
SAMPLES = 1000
# Generate a uniformly distributed set of random numbers in the range from
# 0 to 2π, which covers a complete sine wave oscillation
x_values = np.random.uniform(
low=0, high=2*math.pi, size=SAMPLES).astype(np.float32)
# Shuffle the values to guarantee they're not in order
np.random.shuffle(x_values)
# Calculate the corresponding sine values
y_values = np.sin(x_values).astype(np.float32)
# Plot our data. The 'b.' argument tells the library to print blue dots.
plt.plot(x_values, y_values, 'b.')
plt.show()
```
### 2. Add Noise
Since it was generated directly by the sine function, our data fits a nice, smooth curve.
However, machine learning models are good at extracting underlying meaning from messy, real world data. To demonstrate this, we can add some noise to our data to approximate something more life-like.
In the following cell, we'll add some random noise to each value, then draw a new graph:
```
# Add a small random number to each y value
y_values += 0.1 * np.random.randn(*y_values.shape)
# Plot our data
plt.plot(x_values, y_values, 'b.')
plt.show()
```
### 3. Split the Data
We now have a noisy dataset that approximates real world data. We'll be using this to train our model.
To evaluate the accuracy of the model we train, we'll need to compare its predictions to real data and check how well they match up. This evaluation happens during training (where it is referred to as validation) and after training (referred to as testing) It's important in both cases that we use fresh data that was not already used to train the model.
The data is split as follows:
1. Training: 60%
2. Validation: 20%
3. Testing: 20%
The following code will split our data and then plots each set as a different color:
```
# We'll use 60% of our data for training and 20% for testing. The remaining 20%
# will be used for validation. Calculate the indices of each section.
TRAIN_SPLIT = int(0.6 * SAMPLES)
TEST_SPLIT = int(0.2 * SAMPLES + TRAIN_SPLIT)
# Use np.split to chop our data into three parts.
# The second argument to np.split is an array of indices where the data will be
# split. We provide two indices, so the data will be divided into three chunks.
x_train, x_test, x_validate = np.split(x_values, [TRAIN_SPLIT, TEST_SPLIT])
y_train, y_test, y_validate = np.split(y_values, [TRAIN_SPLIT, TEST_SPLIT])
# Double check that our splits add up correctly
assert (x_train.size + x_validate.size + x_test.size) == SAMPLES
# Plot the data in each partition in different colors:
plt.plot(x_train, y_train, 'b.', label="Train")
plt.plot(x_test, y_test, 'r.', label="Test")
plt.plot(x_validate, y_validate, 'y.', label="Validate")
plt.legend()
plt.show()
```
## Training
### 1. Design the Model
We're going to build a simple neural network model that will take an input value (in this case, `x`) and use it to predict a numeric output value (the sine of `x`). This type of problem is called a _regression_. It will use _layers_ of _neurons_ to attempt to learn any patterns underlying the training data, so it can make predictions.
To begin with, we'll define two layers. The first layer takes a single input (our `x` value) and runs it through 8 neurons. Based on this input, each neuron will become _activated_ to a certain degree based on its internal state (its _weight_ and _bias_ values). A neuron's degree of activation is expressed as a number.
The activation numbers from our first layer will be fed as inputs to our second layer, which is a single neuron. It will apply its own weights and bias to these inputs and calculate its own activation, which will be output as our `y` value.
**Note:** To learn more about how neural networks function, you can explore the [Learn TensorFlow](https://codelabs.developers.google.com/codelabs/tensorflow-lab1-helloworld) codelabs.
The code in the following cell defines our model using [Keras](https://www.tensorflow.org/guide/keras), TensorFlow's high-level API for creating deep learning networks. Once the network is defined, we _compile_ it, specifying parameters that determine how it will be trained:
```
# We'll use Keras to create a simple model architecture
model_1 = tf.keras.Sequential()
# First layer takes a scalar input and feeds it through 8 "neurons". The
# neurons decide whether to activate based on the 'relu' activation function.
model_1.add(keras.layers.Dense(8, activation='relu', input_shape=(1,)))
# Final layer is a single neuron, since we want to output a single value
model_1.add(keras.layers.Dense(1))
# Compile the model using a standard optimizer and loss function for regression
model_1.compile(optimizer='adam', loss='mse', metrics=['mae'])
```
### 2. Train the Model
Once we've defined the model, we can use our data to _train_ it. Training involves passing an `x` value into the neural network, checking how far the network's output deviates from the expected `y` value, and adjusting the neurons' weights and biases so that the output is more likely to be correct the next time.
Training runs this process on the full dataset multiple times, and each full run-through is known as an _epoch_. The number of epochs to run during training is a parameter we can set.
During each epoch, data is run through the network in multiple _batches_. Each batch, several pieces of data are passed into the network, producing output values. These outputs' correctness is measured in aggregate and the network's weights and biases are adjusted accordingly, once per batch. The _batch size_ is also a parameter we can set.
The code in the following cell uses the `x` and `y` values from our training data to train the model. It runs for 500 _epochs_, with 64 pieces of data in each _batch_. We also pass in some data for _validation_. As you will see when you run the cell, training can take a while to complete:
```
# Train the model on our training data while validating on our validation set
history_1 = model_1.fit(x_train, y_train, epochs=500, batch_size=64,
validation_data=(x_validate, y_validate))
```
### 3. Plot Metrics
**1. Mean Squared Error**
During training, the model's performance is constantly being measured against both our training data and the validation data that we set aside earlier. Training produces a log of data that tells us how the model's performance changed over the course of the training process.
The following cells will display some of that data in a graphical form:
```
# Draw a graph of the loss, which is the distance between
# the predicted and actual values during training and validation.
loss = history_1.history['loss']
val_loss = history_1.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.plot(epochs, loss, 'g.', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
```
The graph shows the _loss_ (or the difference between the model's predictions and the actual data) for each epoch. There are several ways to calculate loss, and the method we have used is _mean squared error_. There is a distinct loss value given for the training and the validation data.
As we can see, the amount of loss rapidly decreases over the first 25 epochs, before flattening out. This means that the model is improving and producing more accurate predictions!
Our goal is to stop training when either the model is no longer improving, or when the _training loss_ is less than the _validation loss_, which would mean that the model has learned to predict the training data so well that it can no longer generalize to new data.
To make the flatter part of the graph more readable, let's skip the first 50 epochs:
```
# Exclude the first few epochs so the graph is easier to read
SKIP = 50
plt.plot(epochs[SKIP:], loss[SKIP:], 'g.', label='Training loss')
plt.plot(epochs[SKIP:], val_loss[SKIP:], 'b.', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
```
From the plot, we can see that loss continues to reduce until around 200 epochs, at which point it is mostly stable. This means that there's no need to train our network beyond 200 epochs.
However, we can also see that the lowest loss value is still around 0.155. This means that our network's predictions are off by an average of ~15%. In addition, the validation loss values jump around a lot, and is sometimes even higher.
**2. Mean Absolute Error**
To gain more insight into our model's performance we can plot some more data. This time, we'll plot the _mean absolute error_, which is another way of measuring how far the network's predictions are from the actual numbers:
```
plt.clf()
# Draw a graph of mean absolute error, which is another way of
# measuring the amount of error in the prediction.
mae = history_1.history['mae']
val_mae = history_1.history['val_mae']
plt.plot(epochs[SKIP:], mae[SKIP:], 'g.', label='Training MAE')
plt.plot(epochs[SKIP:], val_mae[SKIP:], 'b.', label='Validation MAE')
plt.title('Training and validation mean absolute error')
plt.xlabel('Epochs')
plt.ylabel('MAE')
plt.legend()
plt.show()
```
This graph of _mean absolute error_ tells another story. We can see that training data shows consistently lower error than validation data, which means that the network may have _overfit_, or learned the training data so rigidly that it can't make effective predictions about new data.
In addition, the mean absolute error values are quite high, ~0.305 at best, which means some of the model's predictions are at least 30% off. A 30% error means we are very far from accurately modelling the sine wave function.
**3. Actual vs Predicted Outputs**
To get more insight into what is happening, let's check its predictions against the test dataset we set aside earlier:
```
# Calculate and print the loss on our test dataset
loss = model_1.evaluate(x_test, y_test)
# Make predictions based on our test dataset
predictions = model_1.predict(x_test)
# Graph the predictions against the actual values
plt.clf()
plt.title('Comparison of predictions and actual values')
plt.plot(x_test, y_test, 'b.', label='Actual')
plt.plot(x_test, predictions, 'r.', label='Predicted')
plt.legend()
plt.show()
```
Oh dear! The graph makes it clear that our network has learned to approximate the sine function in a very limited way.
The rigidity of this fit suggests that the model does not have enough capacity to learn the full complexity of the sine wave function, so it's only able to approximate it in an overly simplistic way. By making our model bigger, we should be able to improve its performance.
## Training a Larger Model
### 1. Design the Model
To make our model bigger, let's add an additional layer of neurons. The following cell redefines our model in the same way as earlier, but with 16 neurons in the first layer and an additional layer of 16 neurons in the middle:
```
model_2 = tf.keras.Sequential()
# First layer takes a scalar input and feeds it through 16 "neurons". The
# neurons decide whether to activate based on the 'relu' activation function.
model_2.add(keras.layers.Dense(16, activation='relu', input_shape=(1,)))
# The new second layer may help the network learn more complex representations
model_2.add(keras.layers.Dense(16, activation='relu'))
# Final layer is a single neuron, since we want to output a single value
model_2.add(keras.layers.Dense(1))
# Compile the model using a standard optimizer and loss function for regression
model_2.compile(optimizer='adam', loss='mse', metrics=['mae'])
```
### 2. Train the Model ###
We'll now train the new model.
```
history_2 = model_2.fit(x_train, y_train, epochs=500, batch_size=64,
validation_data=(x_validate, y_validate))
```
### 3. Plot Metrics
Each training epoch, the model prints out its loss and mean absolute error for training and validation. You can read this in the output above (note that your exact numbers may differ):
```
Epoch 500/500
600/600 [==============================] - 0s 51us/sample - loss: 0.0118 - mae: 0.0873 - val_loss: 0.0105 - val_mae: 0.0832
```
You can see that we've already got a huge improvement - validation loss has dropped from 0.15 to 0.01, and validation MAE has dropped from 0.33 to 0.08.
The following cell will print the same graphs we used to evaluate our original model, but showing our new training history:
```
# Draw a graph of the loss, which is the distance between
# the predicted and actual values during training and validation.
loss = history_2.history['loss']
val_loss = history_2.history['val_loss']
epochs = range(1, len(loss) + 1)
# Exclude the first few epochs so the graph is easier to read
SKIP = 100
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.plot(epochs[SKIP:], loss[SKIP:], 'g.', label='Training loss')
plt.plot(epochs[SKIP:], val_loss[SKIP:], 'b.', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.subplot(1, 2, 2)
# Draw a graph of mean absolute error, which is another way of
# measuring the amount of error in the prediction.
mae = history_2.history['mae']
val_mae = history_2.history['val_mae']
plt.plot(epochs[SKIP:], mae[SKIP:], 'g.', label='Training MAE')
plt.plot(epochs[SKIP:], val_mae[SKIP:], 'b.', label='Validation MAE')
plt.title('Training and validation mean absolute error')
plt.xlabel('Epochs')
plt.ylabel('MAE')
plt.legend()
plt.tight_layout()
```
Great results! From these graphs, we can see several exciting things:
* The overall loss and MAE are much better than our previous network
* Metrics are better for validation than training, which means the network is not overfitting
The reason the metrics for validation are better than those for training is that validation metrics are calculated at the end of each epoch, while training metrics are calculated throughout the epoch, so validation happens on a model that has been trained slightly longer.
This all means our network seems to be performing well! To confirm, let's check its predictions against the test dataset we set aside earlier:
```
# Calculate and print the loss on our test dataset
loss = model_2.evaluate(x_test, y_test)
# Make predictions based on our test dataset
predictions = model_2.predict(x_test)
# Graph the predictions against the actual values
plt.clf()
plt.title('Comparison of predictions and actual values')
plt.plot(x_test, y_test, 'b.', label='Actual')
plt.plot(x_test, predictions, 'r.', label='Predicted')
plt.legend()
plt.show()
```
Much better! The evaluation metrics we printed show that the model has a low loss and MAE on the test data, and the predictions line up visually with our data fairly well.
The model isn't perfect; its predictions don't form a smooth sine curve. For instance, the line is almost straight when `x` is between 4.2 and 5.2. If we wanted to go further, we could try further increasing the capacity of the model, perhaps using some techniques to defend from overfitting.
However, an important part of machine learning is knowing when to quit, and this model is good enough for our use case - which is to make some LEDs blink in a pleasing pattern.
## Generate a TensorFlow Lite Model
### 1. Generate Models with or without Quantization
We now have an acceptably accurate model. We'll use the [TensorFlow Lite Converter](https://www.tensorflow.org/lite/convert) to convert the model into a special, space-efficient format for use on memory-constrained devices.
Since this model is going to be deployed on a microcontroller, we want it to be as tiny as possible! One technique for reducing the size of models is called [quantization](https://www.tensorflow.org/lite/performance/post_training_quantization) while converting the model. It reduces the precision of the model's weights, and possibly the activations (output of each layer) as well, which saves memory, often without much impact on accuracy. Quantized models also run faster, since the calculations required are simpler.
*Note: Currently, TFLite Converter produces TFlite models with float interfaces (input and output ops are always float). This is a blocker for users who require TFlite models with pure int8 or uint8 inputs/outputs. Refer to https://github.com/tensorflow/tensorflow/issues/38285*
In the following cell, we'll convert the model twice: once with quantization, once without.
```
# Convert the model to the TensorFlow Lite format without quantization
converter = tf.lite.TFLiteConverter.from_keras_model(model_2)
model_no_quant_tflite = converter.convert()
# # Save the model to disk
open(MODEL_NO_QUANT_TFLITE, "wb").write(model_no_quant_tflite)
# Convert the model to the TensorFlow Lite format with quantization
def representative_dataset():
for i in range(500):
yield([x_train[i].reshape(1, 1)])
# Set the optimization flag.
converter.optimizations = [tf.lite.Optimize.DEFAULT]
# Enforce full-int8 quantization (except inputs/outputs which are always float)
converter.target_spec.supported_ops = [tf.lite.OpsSet.TFLITE_BUILTINS_INT8]
# Provide a representative dataset to ensure we quantize correctly.
converter.representative_dataset = representative_dataset
model_tflite = converter.convert()
# Save the model to disk
open(MODEL_TFLITE, "wb").write(model_tflite)
```
### 2. Compare Model Sizes
```
import os
model_no_quant_size = os.path.getsize(MODEL_NO_QUANT_TFLITE)
print("Model is %d bytes" % model_no_quant_size)
model_size = os.path.getsize(MODEL_TFLITE)
print("Quantized model is %d bytes" % model_size)
difference = model_no_quant_size - model_size
print("Difference is %d bytes" % difference)
```
Our quantized model is only 224 bytes smaller than the original version, which only a tiny reduction in size! At around 2.5 kilobytes, this model is already so small that the weights make up only a small fraction of the overall size, meaning quantization has little effect.
More complex models have many more weights, meaning the space saving from quantization will be much higher, approaching 4x for most sophisticated models.
Regardless, our quantized model will take less time to execute than the original version, which is important on a tiny microcontroller!
### 3. Test the Models
To prove these models are still accurate after conversion and quantization, we'll use both of them to make predictions and compare these against our test results:
```
# Instantiate an interpreter for each model
model_no_quant = tf.lite.Interpreter(MODEL_NO_QUANT_TFLITE)
model = tf.lite.Interpreter(MODEL_TFLITE)
# Allocate memory for each model
model_no_quant.allocate_tensors()
model.allocate_tensors()
# Get the input and output tensors so we can feed in values and get the results
model_no_quant_input = model_no_quant.tensor(model_no_quant.get_input_details()[0]["index"])
model_no_quant_output = model_no_quant.tensor(model_no_quant.get_output_details()[0]["index"])
model_input = model.tensor(model.get_input_details()[0]["index"])
model_output = model.tensor(model.get_output_details()[0]["index"])
# Create arrays to store the results
model_no_quant_predictions = np.empty(x_test.size)
model_predictions = np.empty(x_test.size)
# Run each model's interpreter for each value and store the results in arrays
for i in range(x_test.size):
model_no_quant_input().fill(x_test[i])
model_no_quant.invoke()
model_no_quant_predictions[i] = model_no_quant_output()[0]
model_input().fill(x_test[i])
model.invoke()
model_predictions[i] = model_output()[0]
# See how they line up with the data
plt.clf()
plt.title('Comparison of various models against actual values')
plt.plot(x_test, y_test, 'bo', label='Actual values')
plt.plot(x_test, predictions, 'ro', label='Original predictions')
plt.plot(x_test, model_no_quant_predictions, 'bx', label='Lite predictions')
plt.plot(x_test, model_predictions, 'gx', label='Lite quantized predictions')
plt.legend()
plt.show()
```
We can see from the graph that the predictions for the original model, the converted model, and the quantized model are all close enough to be indistinguishable. This means that our quantized model is ready to use!
## Generate a TensorFlow Lite for Microcontrollers Model
Convert the TensorFlow Lite quantized model into a C source file that can be loaded by TensorFlow Lite for Microcontrollers.
```
# Install xxd if it is not available
!apt-get update && apt-get -qq install xxd
# Convert to a C source file
!xxd -i {MODEL_TFLITE} > {MODEL_TFLITE_MICRO}
# Update variable names
REPLACE_TEXT = MODEL_TFLITE.replace('/', '_').replace('.', '_')
!sed -i 's/'{REPLACE_TEXT}'/g_model/g' {MODEL_TFLITE_MICRO}
```
## Deploy to a Microcontroller
Follow the instructions in the [hello_world](https://github.com/tensorflow/tensorflow/tree/master/tensorflow/lite/micro/examples/hello_world) README.md for [TensorFlow Lite for MicroControllers](https://www.tensorflow.org/lite/microcontrollers/overview) to deploy this model on a specific microcontroller.
**Reference Model:** If you have not modified this notebook, you can follow the instructions as is, to deploy the model. Refer to the [`hello_world/train/models`](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/lite/micro/examples/hello_world/train/models) directory to access the models generated in this notebook.
**New Model:** If you have generated a new model, then update the values assigned to the variables defined in [`hello_world/model.cc`](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/lite/micro/examples/hello_world/model.cc) with values displayed after running the following cell.
```
# Print the C source file
!cat {MODEL_TFLITE_MICRO}
```
|
github_jupyter
|
# pywikipathways and bridgedbpy
[](https://colab.research.google.com/github/kozo2/pywikipathways/blob/main/docs/pywikipathways-and-bridgedbpy.ipynb)
by Kozo Nishida and Alexander Pico
pywikipathways 0.0.2
bridgedbpy 0.0.2
*WikiPathways* is a well-known repository for biological pathways that provides unique tools to the research community for content creation, editing and utilization [1].
Python is a powerful programming language and environment for statistical and exploratory data analysis.
*pywikipathways* leverages the WikiPathways API to communicate between **Python** and WikiPathways, allowing any pathway to be queried, interrogated and downloaded in both data and image formats. Queries are typically performed based on “Xrefs”, standardized identifiers for genes, proteins and metabolites. Once you can identified a pathway, you can use the WPID (WikiPathways identifier) to make additional queries.
[bridgedbpy](https://pypi.org/project/bridgedbpy/) leverages the BridgeDb API [2] to provide a number of functions related to ID mapping and identifiers in general for gene, proteins and metabolites.
Together, *bridgedbpy* provides convience to the typical *pywikipathways* user by supplying formal names and codes defined by BridgeDb and used by WikiPathways.
## Prerequisites
In addition to this **pywikipathways** package, you’ll also need to install **bridgedbpy**:
```
!pip install pywikipathways bridgedbpy
import pywikipathways as pwpw
import bridgedbpy as brdgdbp
```
## Getting started
Lets first check some of the most basic functions from each package. For example, here’s how you check to see which species are currently supported by WikiPathways:
```
org_names = pwpw.list_organisms()
org_names
```
You should see 30 or more species listed. This list is useful for subsequent queries that take an *organism* argument, to avoid misspelling.
However, some function want the organism code, rather than the full name. Using bridgedbpy’s *getOrganismCode* function, we can get those:
```
org_names[14]
brdgdbp.get_organism_code(org_names[14])
```
## Identifier System Names and Codes
Even more obscure are the various datasources providing official identifiers and how they are named and coded. Fortunately, BridgeDb defines these clearly and simply. And WikiPathways relies on these BridgeDb definitions.
For example, this is how we find the system code for Ensembl:
```
brdgdbp.get_system_code("Ensembl")
```
It’s “En”! That’s simple enough. But some are less obvious…
```
brdgdbp.get_system_code("Entrez Gene")
```
It’s “L” because the resource used to be named “Locus Link”. Sigh… Don’t try to guess these codes. Use this function from BridgeDb (above) to get the correct code. By the way, all the systems supported by BridgeDb are here: https://github.com/bridgedb/datasources/blob/main/datasources.tsv
## How to use bridgedbpy with pywikipathways
Here are some specific combo functions that are useful. They let you skip worrying about system codes altogether!
1. Getting all the pathways containing the HGNC symbol “TNF”:
```
tnf_pathways = pwpw.find_pathway_ids_by_xref('TNF', brdgdbp.get_system_code('HGNC'))
tnf_pathways
```
2. Getting all the genes from a pathway as Ensembl identifiers:
```
pwpw.get_xref_list('WP554', brdgdbp.get_system_code('Ensembl'))
```
3. Getting all the metabolites from a pathway as ChEBI identifiers:
```
pwpw.get_xref_list('WP554', brdgdbp.get_system_code('ChEBI'))
```
## Other tips
And if you ever find yourself with a system code, e.g., from a pywikipathways return result and you’re not sure what it is, then you can use this function:
```
brdgdbp.get_full_name('Ce')
```
## References
1. Pico AR, Kelder T, Iersel MP van, Hanspers K, Conklin BR, Evelo C: **WikiPathways: Pathway editing for the people.** *PLoS Biol* 2008, **6:**e184+.
2. Iersel M van, Pico A, Kelder T, Gao J, Ho I, Hanspers K, Conklin B, Evelo C: **The BridgeDb framework: Standardized access to gene, protein and metabolite identifier mapping services.** *BMC Bioinformatics* 2010, **11:**5+.
|
github_jupyter
|
```
# default_exp trainer
```
# Trainer
> Implementation of torch-based model trainers.
```
#hide
from nbdev.showdoc import *
from fastcore.nb_imports import *
from fastcore.test import *
```
## PL Trainer
> Implementation of trainer for training PyTorch Lightning models.
```
#export
from typing import Any, Iterable, List, Optional, Tuple, Union, Callable
import os
import os.path as osp
from pytorch_lightning import Trainer
from pytorch_lightning.callbacks import ModelCheckpoint
from pytorch_lightning.loggers import TensorBoardLogger
#export
def pl_trainer(model, datamodule, max_epochs=10, val_epoch=5, gpus=None, log_dir=None,
model_dir=None, monitor='val_loss', mode='min', *args, **kwargs):
log_dir = log_dir if log_dir is not None else os.getcwd()
model_dir = model_dir if model_dir is not None else os.getcwd()
logger = TensorBoardLogger(save_dir=log_dir)
checkpoint_callback = ModelCheckpoint(
monitor=monitor,
mode=mode,
dirpath=model_dir,
filename="recommender",
)
trainer = Trainer(
max_epochs=max_epochs,
logger=logger,
check_val_every_n_epoch=val_epoch,
callbacks=[checkpoint_callback],
num_sanity_val_steps=0,
gradient_clip_val=1,
gradient_clip_algorithm="norm",
gpus=gpus
)
trainer.fit(model, datamodule=datamodule)
test_result = trainer.test(model, datamodule=datamodule)
return test_result
```
Example
```
class Args:
def __init__(self):
self.data_dir = '/content/data'
self.min_rating = 4
self.num_negative_samples = 99
self.min_uc = 5
self.min_sc = 5
self.val_p = 0.2
self.test_p = 0.2
self.num_workers = 2
self.normalize = False
self.batch_size = 32
self.seed = 42
self.shuffle = True
self.pin_memory = True
self.drop_last = False
self.split_type = 'stratified'
args = Args()
from recohut.datasets.movielens import ML1mDataModule
ds = ML1mDataModule(**args.__dict__)
ds.prepare_data()
from recohut.models.nmf import NMF
model = NMF(n_items=ds.data.num_items, n_users=ds.data.num_users, embedding_dim=20)
pl_trainer(model, ds, max_epochs=5)
```
## Traditional Torch Trainers
### v1
```
# dataset
from recohut.datasets.movielens import ML1mRatingDataset
# models
from recohut.models.afm import AFM
from recohut.models.afn import AFN
from recohut.models.autoint import AutoInt
from recohut.models.dcn import DCN
from recohut.models.deepfm import DeepFM
from recohut.models.ffm import FFM
from recohut.models.fm import FM
from recohut.models.fnfm import FNFM
from recohut.models.fnn import FNN
from recohut.models.hofm import HOFM
from recohut.models.lr import LR
from recohut.models.ncf import NCF
from recohut.models.nfm import NFM
from recohut.models.ncf import NCF
from recohut.models.pnn import PNN
from recohut.models.wide_and_deep import WideAndDeep
from recohut.models.xdeepfm import xDeepFM
ds = ML1mRatingDataset(root='/content/ML1m', min_uc=10, min_sc=5)
import torch
import os
import tqdm
from sklearn.metrics import roc_auc_score
from torch.utils.data import DataLoader
class Args:
def __init__(self,
dataset='ml_1m',
model='wide_and_deep'
):
self.dataset = dataset
self.model = model
# dataset
if dataset == 'ml_1m':
self.dataset_root = '/content/ML1m'
self.min_uc = 20
self.min_sc = 20
# model training
self.device = 'cpu' # 'cuda:0'
self.num_workers = 2
self.batch_size = 256
self.lr = 0.001
self.weight_decay = 1e-6
self.save_dir = '/content/chkpt'
self.n_epochs = 2
self.dropout = 0.2
self.log_interval = 100
# model architecture
if model == 'wide_and_deep':
self.embed_dim = 16
self.mlp_dims = (16, 16)
elif model == 'fm':
self.embed_dim = 16
elif model == 'ffm':
self.embed_dim = 4
elif model == 'hofm':
self.embed_dim = 16
self.order = 3
elif model == 'fnn':
self.embed_dim = 16
self.mlp_dims = (16, 16)
elif model == 'ipnn':
self.embed_dim = 16
self.mlp_dims = (16,)
self.method = 'inner'
elif model == 'opnn':
self.embed_dim = 16
self.mlp_dims = (16,)
self.method = 'outer'
elif model == 'dcn':
self.embed_dim = 16
self.num_layers = 3
self.mlp_dims = (16, 16)
elif model == 'nfm':
self.embed_dim = 64
self.mlp_dims = (64,)
self.dropouts = (0.2, 0.2)
elif model == 'ncf':
self.embed_dim = 16
self.mlp_dims = (16, 16)
elif model == 'fnfm':
self.embed_dim = 4
self.mlp_dims = (64,)
self.dropouts = (0.2, 0.2)
elif model == 'deep_fm':
self.embed_dim = 16
self.mlp_dims = (16, 16)
elif model == 'xdeep_fm':
self.embed_dim = 16
self.cross_layer_sizes = (16, 16)
self.split_half = False
self.mlp_dims = (16, 16)
elif model == 'afm':
self.embed_dim = 16
self.attn_size = 16
self.dropouts = (0.2, 0.2)
elif model == 'autoint':
self.embed_dim = 16
self.atten_embed_dim = 64
self.num_heads = 2
self.num_layers = 3
self.mlp_dims = (400, 400)
self.dropouts = (0, 0, 0)
elif model == 'afn':
self.embed_dim = 16
self.LNN_dim = 1500
self.mlp_dims = (400, 400, 400)
self.dropouts = (0, 0, 0)
def get_dataset(self):
if self.dataset == 'ml_1m':
return ML1mRatingDataset(root = self.dataset_root,
min_uc = self.min_uc,
min_sc = self.min_sc
)
def get_model(self, field_dims, user_field_idx=None, item_field_idx=None):
if self.model == 'wide_and_deep':
return WideAndDeep(field_dims,
embed_dim=self.embed_dim,
mlp_dims = self.mlp_dims,
dropout = self.dropout
)
elif self.model == 'fm':
return FM(field_dims,
embed_dim = self.embed_dim
)
elif self.model == 'lr':
return LR(field_dims
)
elif self.model == 'ffm':
return FFM(field_dims,
embed_dim = self.embed_dim
)
elif self.model == 'hofm':
return HOFM(field_dims,
embed_dim = self.embed_dim,
order = self.order
)
elif self.model == 'fnn':
return FNN(field_dims,
embed_dim = self.embed_dim,
mlp_dims = self.mlp_dims,
dropout = self.dropout
)
elif self.model == 'ipnn':
return PNN(field_dims,
embed_dim = self.embed_dim,
mlp_dims = self.mlp_dims,
method = self.method,
dropout = self.dropout
)
elif self.model == 'opnn':
return PNN(field_dims,
embed_dim = self.embed_dim,
mlp_dims = self.mlp_dims,
method = self.method,
dropout = self.dropout
)
elif self.model == 'dcn':
return DCN(field_dims,
embed_dim = self.embed_dim,
mlp_dims = self.mlp_dims,
num_layers = self.num_layers,
dropout = self.dropout,
)
elif self.model == 'nfm':
return NFM(field_dims,
embed_dim = self.embed_dim,
mlp_dims = self.mlp_dims,
dropouts = self.dropouts,
)
elif self.model == 'ncf':
return NCF(field_dims,
embed_dim = self.embed_dim,
mlp_dims = self.mlp_dims,
dropout = self.dropout,
user_field_idx=user_field_idx,
item_field_idx=item_field_idx
)
elif self.model == 'fnfm':
return FNFM(field_dims,
embed_dim = self.embed_dim,
mlp_dims = self.mlp_dims,
dropouts = self.dropouts,
)
elif self.model == 'deep_fm':
return DeepFM(field_dims,
embed_dim = self.embed_dim,
mlp_dims = self.mlp_dims,
dropout = self.dropout,
)
elif self.model == 'xdeep_fm':
return xDeepFM(field_dims,
embed_dim = self.embed_dim,
mlp_dims = self.mlp_dims,
dropout = self.dropout,
cross_layer_sizes = self.cross_layer_sizes,
split_half = self.split_half,
)
elif self.model == 'afm':
return AFM(field_dims,
embed_dim = self.embed_dim,
dropouts = self.dropouts,
attn_size = self.attn_size,
)
elif self.model == 'autoint':
return AutoInt(field_dims,
embed_dim = self.embed_dim,
mlp_dims = self.mlp_dims,
dropouts = self.dropouts,
atten_embed_dim = self.atten_embed_dim,
num_heads = self.num_heads,
num_layers = self.num_layers,
)
elif self.model == 'afn':
return AFN(field_dims,
embed_dim = self.embed_dim,
mlp_dims = self.mlp_dims,
dropouts = self.dropouts,
LNN_dim = self.LNN_dim,
)
class EarlyStopper(object):
def __init__(self, num_trials, save_path):
self.num_trials = num_trials
self.trial_counter = 0
self.best_accuracy = 0
self.save_path = save_path
def is_continuable(self, model, accuracy):
if accuracy > self.best_accuracy:
self.best_accuracy = accuracy
self.trial_counter = 0
torch.save(model, self.save_path)
return True
elif self.trial_counter + 1 < self.num_trials:
self.trial_counter += 1
return True
else:
return False
class Trainer:
def __init__(self, args):
device = torch.device(args.device)
# dataset
dataset = args.get_dataset()
# model
model = args.get_model(dataset.field_dims,
user_field_idx = dataset.user_field_idx,
item_field_idx = dataset.item_field_idx)
model = model.to(device)
model_name = type(model).__name__
# data split
train_length = int(len(dataset) * 0.8)
valid_length = int(len(dataset) * 0.1)
test_length = len(dataset) - train_length - valid_length
# data loader
train_dataset, valid_dataset, test_dataset = torch.utils.data.random_split(
dataset, (train_length, valid_length, test_length))
train_data_loader = DataLoader(train_dataset, batch_size=args.batch_size, num_workers=args.num_workers)
valid_data_loader = DataLoader(valid_dataset, batch_size=args.batch_size, num_workers=args.num_workers)
test_data_loader = DataLoader(test_dataset, batch_size=args.batch_size, num_workers=args.num_workers)
# handlers
criterion = torch.nn.BCELoss()
optimizer = torch.optim.Adam(params=model.parameters(), lr=args.lr, weight_decay=args.weight_decay)
os.makedirs(args.save_dir, exist_ok=True)
early_stopper = EarlyStopper(num_trials=2, save_path=f'{args.save_dir}/{model_name}.pt')
# # scheduler
# # ref - https://github.com/sparsh-ai/stanza/blob/7961a0a00dc06b9b28b71954b38181d6a87aa803/trainer/bert.py#L36
# import torch.optim as optim
# if args.enable_lr_schedule:
# if args.enable_lr_warmup:
# self.lr_scheduler = self.get_linear_schedule_with_warmup(
# optimizer, args.warmup_steps, len(train_data_loader) * self.n_epochs)
# else:
# self.lr_scheduler = optim.lr_scheduler.StepLR(
# optimizer, step_size=args.decay_step, gamma=args.gamma)
# training
for epoch_i in range(args.n_epochs):
self._train(model, optimizer, train_data_loader, criterion, device)
auc = self._test(model, valid_data_loader, device)
print('epoch:', epoch_i, 'validation: auc:', auc)
if not early_stopper.is_continuable(model, auc):
print(f'validation: best auc: {early_stopper.best_accuracy}')
break
auc = self._test(model, test_data_loader, device)
print(f'test auc: {auc}')
@staticmethod
def _train(model, optimizer, data_loader, criterion, device, log_interval=100):
model.train()
total_loss = 0
tk0 = tqdm.tqdm(data_loader, smoothing=0, mininterval=1.0)
for i, (fields, target) in enumerate(tk0):
fields, target = fields.to(device), target.to(device)
y = model(fields)
loss = criterion(y, target.float())
model.zero_grad()
loss.backward()
# self.clip_gradients(5)
optimizer.step()
# if self.args.enable_lr_schedule:
# self.lr_scheduler.step()
total_loss += loss.item()
if (i + 1) % log_interval == 0:
tk0.set_postfix(loss=total_loss / log_interval)
total_loss = 0
@staticmethod
def _test(model, data_loader, device):
model.eval()
targets, predicts = list(), list()
with torch.no_grad():
for fields, target in tqdm.tqdm(data_loader, smoothing=0, mininterval=1.0):
fields, target = fields.to(device), target.to(device)
y = model(fields)
targets.extend(target.tolist())
predicts.extend(y.tolist())
return roc_auc_score(targets, predicts)
# def clip_gradients(self, limit=5):
# """
# Reference:
# 1. https://github.com/sparsh-ai/stanza/blob/7961a0a00dc06b9b28b71954b38181d6a87aa803/trainer/bert.py#L175
# """
# for p in self.model.parameters():
# nn.utils.clip_grad_norm_(p, 5)
# def _create_optimizer(self):
# args = self.args
# param_optimizer = list(self.model.named_parameters())
# no_decay = ['bias', 'layer_norm']
# optimizer_grouped_parameters = [
# {
# 'params': [p for n, p in param_optimizer if not any(nd in n for nd in no_decay)],
# 'weight_decay': args.weight_decay,
# },
# {'params': [p for n, p in param_optimizer if any(nd in n for nd in no_decay)], 'weight_decay': 0.0},
# ]
# if args.optimizer.lower() == 'adamw':
# return optim.AdamW(optimizer_grouped_parameters, lr=args.lr, eps=args.adam_epsilon)
# elif args.optimizer.lower() == 'adam':
# return optim.Adam(optimizer_grouped_parameters, lr=args.lr, weight_decay=args.weight_decay)
# elif args.optimizer.lower() == 'sgd':
# return optim.SGD(optimizer_grouped_parameters, lr=args.lr, weight_decay=args.weight_decay, momentum=args.momentum)
# else:
# raise ValueError
# def get_linear_schedule_with_warmup(self, optimizer, num_warmup_steps, num_training_steps, last_epoch=-1):
# # based on hugging face get_linear_schedule_with_warmup
# def lr_lambda(current_step: int):
# if current_step < num_warmup_steps:
# return float(current_step) / float(max(1, num_warmup_steps))
# return max(
# 0.0, float(num_training_steps - current_step) / float(max(1, num_training_steps - num_warmup_steps))
# )
# return LambdaLR(optimizer, lr_lambda, last_epoch)
models = [
'wide_and_deep',
'fm',
'lr',
'ffm',
'hofm',
'fnn',
'ipnn',
'opnn',
'dcn',
'nfm',
'ncf',
'fnfm',
'deep_fm',
'xdeep_fm',
'afm',
# 'autoint',
# 'afn'
]
for model in models:
args = Args(model=model)
trainer = Trainer(args)
models = [
'autoint',
'afn'
]
for model in models:
args = Args(model=model)
trainer = Trainer(args)
!tree --du -h -C /content/chkpt
```
### v2
**References:-**
1. https://nbviewer.org/github/CS-512-Recsys/Recsys/blob/main/nbs/basic_implementation.ipynb
```
!pip install -q wandb
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch import nn
from torch.nn import functional as F
import os
import copy
import random
from pathlib import Path
from collections import defaultdict
from argparse import Namespace
from joblib import dump, load
from tqdm import tqdm
import wandb
from torch.utils.data import DataLoader as dl
class RecsysDataset(torch.utils.data.Dataset):
def __init__(self,df,usr_dict=None,mov_dict=None):
self.df = df
self.usr_dict = usr_dict
self.mov_dict = mov_dict
def __getitem__(self,index):
if self.usr_dict and self.mov_dict:
return [self.usr_dict[int(self.df.iloc[index]['user_id'])],self.mov_dict[int(self.df.iloc[index]['movie_id'])]],self.df.iloc[index]['rating']
else:
return [int(self.df.iloc[index]['user_id']-1),int(self.df.iloc[index]['movie_id']-1)],self.df.iloc[index]['rating']
def __len__(self):
return len(self.df)
sample = pd.DataFrame({'user_id':[1,2,3,2,2,3,2,2],'movie_id':[1,2,3,3,3,2,1,1],'rating':[2.0,1.0,4.0,5.0,1.3,3.5,3.0,4.5]})
trn_ids = random.sample(range(8),4,)
valid_ids = [i for i in range(8) if i not in trn_ids]
sample_trn,sample_vld = copy.deepcopy(sample.iloc[trn_ids].reset_index()),copy.deepcopy(sample.iloc[valid_ids].reset_index())
sample_vld = RecsysDataset(sample_vld)
sample_trn = RecsysDataset(sample_trn)
train_loader = dl(sample_trn, batch_size=2, shuffle=True)
valid_loader = dl(sample_vld, batch_size=2, shuffle=True)
class NCF(nn.Module):
def __init__(self,user_sz,item_sz,embd_sz,dropout_fac,min_r=0.0,max_r=5.0,alpha=0.5,with_variable_alpha=False):
super().__init__()
self.dropout_fac = dropout_fac
self.user_embd_mtrx = nn.Embedding(user_sz,embd_sz)
self.item_embd_mtrx = nn.Embedding(item_sz,embd_sz)
#bias = torch.zeros(size=(user_sz, 1), requires_grad=True)
self.h = nn.Linear(embd_sz,1)
self.fst_lyr = nn.Linear(embd_sz*2,embd_sz)
self.snd_lyr = nn.Linear(embd_sz,embd_sz//2)
self.thrd_lyr = nn.Linear(embd_sz//2,embd_sz//4)
self.out_lyr = nn.Linear(embd_sz//4,1)
self.alpha = torch.tensor(alpha)
self.min_r,self.max_r = min_r,max_r
if with_variable_alpha:
self.alpha = torch.tensor(alpha,requires_grad=True)
def forward(self,x):
user_emd = self.user_embd_mtrx(x[0])
item_emd = self.item_embd_mtrx(x[-1])
#hadamard-product
gmf = user_emd*item_emd
gmf = self.h(gmf)
mlp = torch.cat([user_emd,item_emd],dim=-1)
mlp = self.out_lyr(F.relu(self.thrd_lyr(F.relu(self.snd_lyr(F.dropout(F.relu(self.fst_lyr(mlp)),p=self.dropout_fac))))))
fac = torch.clip(self.alpha,min=0.0,max=1.0)
out = fac*gmf+ (1-fac)*mlp
out = torch.clip(out,min=self.min_r,max=self.max_r)
return out
#does it work
model = NCF(3,3,4,0.5)
for u,r in train_loader:
#user,item = u
print(f'user:{u[0]},item:{u[-1]} and rating:{r}')
#print(u)
out = model(u)
print(f'output of the network=> out:{out},shape:{out.shape}')
break
class Trainer(object):
def __init__(self, model, device,loss_fn=None, optimizer=None, scheduler=None,artifacts_loc=None,exp_tracker=None):
# Set params
self.model = model
self.device = device
self.loss_fn = loss_fn
self.optimizer = optimizer
self.scheduler = scheduler
self.store_loc = artifacts_loc
self.exp_tracker = exp_tracker
def train_step(self, dataloader):
"""Train step."""
# Set model to train mode
self.model.train()
loss = 0.0
# Iterate over train batches
for i, batch in enumerate(dataloader):
#batch = [item.to(self.device) for item in batch] # Set device
inputs,targets = batch
inputs = [item.to(self.device) for item in inputs]
targets = targets.to(self.device)
#inputs, targets = batch[:-1], batch[-1]
#import pdb;pdb.set_trace()
self.optimizer.zero_grad() # Reset gradients
z = self.model(inputs) # Forward pass
targets = targets.reshape(z.shape)
J = self.loss_fn(z.float(), targets.float()) # Define loss
J.backward() # Backward pass
self.optimizer.step() # Update weights
# Cumulative Metrics
loss += (J.detach().item() - loss) / (i + 1)
return loss
def eval_step(self, dataloader):
"""Validation or test step."""
# Set model to eval mode
self.model.eval()
loss = 0.0
y_trues, y_probs = [], []
# Iterate over val batches
with torch.inference_mode():
for i, batch in enumerate(dataloader):
inputs,y_true = batch
inputs = [item.to(self.device) for item in inputs]
y_true = y_true.to(self.device).float()
# Step
z = self.model(inputs).float() # Forward pass
y_true = y_true.reshape(z.shape)
J = self.loss_fn(z, y_true).item()
# Cumulative Metrics
loss += (J - loss) / (i + 1)
# Store outputs
y_prob = z.cpu().numpy()
y_probs.extend(y_prob)
y_trues.extend(y_true.cpu().numpy())
return loss, np.vstack(y_trues), np.vstack(y_probs)
def predict_step(self, dataloader):
"""Prediction step."""
# Set model to eval mode
self.model.eval()
y_probs = []
# Iterate over val batches
with torch.inference_mode():
for i, batch in enumerate(dataloader):
# Forward pass w/ inputs
inputs, targets = batch
z = self.model(inputs).float()
# Store outputs
y_prob = z.cpu().numpy()
y_probs.extend(y_prob)
return np.vstack(y_probs)
def train(self, num_epochs, patience, train_dataloader, val_dataloader,
tolerance=1e-5):
best_val_loss = np.inf
training_stats = defaultdict(list)
for epoch in tqdm(range(num_epochs)):
# Steps
train_loss = self.train_step(dataloader=train_dataloader)
val_loss, _, _ = self.eval_step(dataloader=val_dataloader)
#store stats
training_stats['epoch'].append(epoch)
training_stats['train_loss'].append(train_loss)
training_stats['val_loss'].append(val_loss)
#log-stats
# wandb.init(project=f"{args.trail_id}_{args.dataset}_{args.data_type}",config=config_dict)
if self.exp_tracker == 'wandb':
log_metrics = {'epoch':epoch,'train_loss':train_loss,'val_loss':val_loss}
wandb.log(log_metrics,step=epoch)
self.scheduler.step(val_loss)
# Early stopping
if val_loss < best_val_loss - tolerance:
best_val_loss = val_loss
best_model = self.model
_patience = patience # reset _patience
else:
_patience -= 1
if not _patience: # 0
print("Stopping early!")
break
# Tracking
#mlflow.log_metrics({"train_loss": train_loss, "val_loss": val_loss}, step=epoch)
# Logging
if epoch%5 == 0:
print(
f"Epoch: {epoch+1} | "
f"train_loss: {train_loss:.5f}, "
f"val_loss: {val_loss:.5f}, "
f"lr: {self.optimizer.param_groups[0]['lr']:.2E}, "
f"_patience: {_patience}"
)
if self.store_loc:
pd.DataFrame(training_stats).to_csv(self.store_loc/'training_stats.csv',index=False)
return best_model, best_val_loss
loss_fn = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(
optimizer, mode="min", factor=0.1, patience=5)
trainer = Trainer(model,'cpu',loss_fn,optimizer,scheduler)
trainer.train(100,10,train_loader,valid_loader)
```
|
github_jupyter
|
## Conceptual description
As people interact, they tend to become more alike in their beliefs, attitudes and behaviour. In "The Dissemination of Culture: A Model with Local Convergence and Global Polarization" (1997), Robert Axelrod presents an agent-based model to explain cultural diffusion. Analogous to Schelling's segregation model, the key to this conceptualization is the emergence of polarization from the interaction of individual agents. The basic premise is that the more similar an actor is to a neighbor, the more likely that that actor will adopt one of the neighbor's traits.
In the model below, this is implemented by initializing the model by filling an excel-like grid with agents with random values [0,1] for each of four traits (music, sports, favorite color and drink).
Each step, each agent (in random order) chooses a random neighbor from the 8 neighbors proportionaly to how similar it is to each of its neighbors, and adopts one randomly selected differing trait from this neighbor. Similarity between any two agents is calculated by 1 - euclidian distance over the four traits.
To visualize the model, the four traits are transformed into 'RGBA' (Red-Green-Blue-Alpha) values; i.e. a color and an opacity. The visualizations below show the clusters of homogeneity being formed.
```
import random
import numpy as np
from mesa import Model, Agent
import mesa.time as time
from mesa.time import RandomActivation
from mesa.space import SingleGrid
from mesa.datacollection import DataCollector
class CulturalDiff(Model):
"""
Model class for the Schelling segregation model.
Parameters
----------
height : int
height of grid
width : int
height of grid
seed : int
random seed
Attributes
----------
height : int
width : int
density : float
schedule : RandomActivation instance
grid : SingleGrid instance
"""
def __init__(self, height=20, width=20, seed=None):
__init__(seed=seed)
self.height = height
self.width = width
self.schedule = time.BaseScheduler(self)
self.grid = SingleGrid(width, height, torus=True)
self.datacollector = DataCollector(model_reporters={'diversity':count_nr_cultures})
# Fill grid with agents with random traits
# Note that this implementation does not guarantee some set distribution of traits.
# Therefore, examining the effect of minorities etc is not facilitated.
for cell in self.grid.coord_iter():
agent = CulturalDiffAgent(cell, self)
self.grid.position_agent(agent, cell)
self.schedule.add(agent)
def step(self):
"""
Run one step of the model.
"""
self.datacollector.collect(self)
self.schedule.step
class CulturalDiffAgent(Agent):
"""
Schelling segregation agent
Parameters
----------
pos : tuple of 2 ints
the x,y coordinates in the grid
model : Model instance
"""
def __init__(self, pos, model):
super().__init__(pos, model)
self.pos = pos
self.profile = np.asarray([random.random() for _ in range(4)])
def step(self):
#For each neighbor, calculate the euclidian distance
# similarity is 1 - distance
neighbor_similarity_dict = []
for neighbor in self.model.grid.neighbor_iter(self.pos, moore=True):
neighbor_similarity = 1-np.linalg.norm(self.profile-neighbor.profile)
neighbor_similarity_dict[neighbor] = neighbor_similarity
# Proportional to this similarity, pick a 'random' neighbor to interact with
neighbor_to_interact = self.random.choices(list(neighbor_similarity_dict.keys()),
weights=neighbor_similarity_dict.values())[0]
# Select a trait that differs between the selected neighbor and self and change that trait in self
# we are using some numpy boolean indexing to make this short and easy
not_same_features = self.profile != neighbor_to_interact.profile
if np.any(not_same_features):
index_for_trait = self.random.choice(np.nonzero(not_same_features)[0])
self.profile[index_for_trait] = neighbor_to_interact.profile[index_for_trait]
def count_nr_cultures(model):
cultures = set()
for (cell, x,y) in model.grid.coord_iter():
if cell:
cultures.add(tuple(cell.profile))
return len(cultures)
```
# Visualization
## Static images
Visualization of this model are static images. A visualization after initialization, after 20 steps, after 50 steps, and after 200 steps is presented.
### After initialization
```
model = CulturalDiff(seed=123456789)
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import seaborn as sns
import pandas as pd
def plot_model(model, ax):
grid = np.zeros((model.height, model.width, 4))
for (cell, i, j) in model.grid.coord_iter():
color = [0,0,0,0] #in case not every cell is filled, the default colour is white
if cell is not None:
color = cell.profile
grid[i,j] = color
plt.imshow(grid)
fig, ax = plt.subplots()
plot_model(model, ax)
plt.show()
```
### After 20 steps
```
for i in range(20):
model.step()
fig, ax = plt.subplots()
plot_model(model, ax)
plt.show()
```
### After 50 steps
```
for i in range(30):
model.step()
fig, ax = plt.subplots()
plot_model(model, ax)
plt.show()
```
### After 200 steps
```
for i in range(150):
model.step()
fig, ax = plt.subplots()
plot_model(model, ax)
plt.show()
```
|
github_jupyter
|
# SUPERVISED MACHINE LEARNING (LINEAR REGRESSION)
## Author-Neeraj Lalwani
### Importing important libraries
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
```
### Importing dataset
```
Data = pd.read_csv("marks.csv")
print("Data is successfully imported")
```
#### First 7 records
```
Data.head(7)
```
#### Last 7 records
```
Data.tail(7)
```
##### Using describe() function to see count, mean, std, minimum, percentiles & maximum.
```
Data.describe()
```
##### Using info() function get information about the data
```
Data.info()
```
## Visualizing Data.
#### Ploting box plot
```
plt.boxplot(Data)
plt.show()
```
#### Ploting scatter plot
```
plt.xlabel('Hours',fontsize=15)
plt.ylabel('Scores',fontsize=15)
plt.title('Hours studied vs Score', fontsize=10)
plt.scatter(Data.Hours,Data.Scores,color='red',marker='*')
plt.show()
```
### The plots show positive linear relation between 'Hours' and 'Scores'
```
X = Data.iloc[:,:-1].values
Y = Data.iloc[:,1].values
```
### Preparing data and splitting into train and test sets.
#### We are splitting our data using 80:20 rule(Pareto principle)
```
from sklearn.model_selection import train_test_split
X_train,X_test,Y_train,Y_test = train_test_split(X,Y,random_state = 0,test_size=0.2)
print("X train.shape =", X_train.shape)
print("Y train.shape =", Y_train.shape)
print("X test.shape =", X_test.shape)
print("Y test.shape =", Y_test.shape)
```
## Training the model.
```
from sklearn.linear_model import LinearRegression
linreg=LinearRegression()
```
### Fitting Training data
```
linreg.fit(X_train,Y_train)
print("Training our algorithm is finished")
print("B0 =",linreg.intercept_,"\nB1 =",linreg.coef_)
```
#### B0 = Intercept & Slope = B1
### Plotting the regression line
```
Y0 = linreg.intercept_ + linreg.coef_*X_train
```
### Plotting training data
```
plt.scatter(X_train,Y_train,color='red',marker='*')
plt.plot(X_train,Y0,color='red')
plt.xlabel("Hours",fontsize=15)
plt.ylabel("Scores",fontsize=15)
plt.title("Regression line(Train set)",fontsize=10)
plt.show()
```
### Test data
```
Y_pred=linreg.predict(X_test)##predicting the Scores for test data
print(Y_pred)
```
### Plotting test data
```
plt.plot(X_test,Y_pred,color='red')
plt.scatter(X_test,Y_test,color='red',marker='*')
plt.xlabel("Hours",fontsize=15)
plt.ylabel("Scores",fontsize=15)
plt.title("Regression line(Test set)",fontsize=10)
plt.show()
```
### Comparing actual vs predicted scores
```
Y_test1 = list(Y_test)
prediction=list(Y_pred)
df_compare = pd.DataFrame({ 'Actual':Y_test1,'Result':prediction})
df_compare
```
## ACCURACY OF THE MODEL
### Goodness of fit test
```
from sklearn import metrics
metrics.r2_score(Y_test,Y_pred)
```
#### Above 94% indicates that above model is a good fit
### Predicting the Error
```
from sklearn.metrics import mean_squared_error,mean_absolute_error
MSE = metrics.mean_squared_error(Y_test,Y_pred)
root_E = np.sqrt(metrics.mean_squared_error(Y_test,Y_pred))
Abs_E = np.sqrt(metrics.mean_squared_error(Y_test,Y_pred))
print("Mean Squared Error = ",MSE)
print("Root Mean Squared Error = ",root_E)
print("Mean Absolute Error = ",Abs_E)
```
## Predicting the score for 9.25 hours
```
Prediction_score = linreg.predict([[9.25]])
print("predicted score for a student studying 9.25 hours :",Prediction_score)
```
## CONCLUSION: From the result we can see that if a student studies for 9.25 hours a day he will sercure marks in the neighbourhood of 93.69%
|
github_jupyter
|
## Imports
```
import numpy as np
import matplotlib.pyplot as plt
%tensorflow_version 2.x
import tensorflow as tf
from tensorflow import keras
from keras.models import Sequential, Model
from keras.layers import Flatten, Dense, LSTM, GRU, SimpleRNN, RepeatVector, Input
from keras import backend as K
from keras.utils.vis_utils import plot_model
import keras.regularizers
import keras.optimizers
```
## Load data
```
!git clone https://github.com/luisferuam/DLFBT-LAB
f = open('DLFBT-LAB/data/el_quijote.txt', 'r')
quijote = f.read()
f.close()
print(len(quijote))
```
## Input/output sequences
```
quijote_x = quijote[:-1]
quijote_y = quijote[1:]
```
## Some utility functions
```
def one_hot_encoding(data):
symbols = np.unique(data)
char_to_ix = {s: i for i, s in enumerate(symbols)}
ix_to_char = {i: s for i, s in enumerate(symbols)}
data_numeric = np.zeros(data.shape)
for s in symbols:
data_numeric[data == s] = char_to_ix[s]
one_hot_values = np.array(list(ix_to_char.keys()))
data_one_hot = 1 * (data_numeric[:, :, None] == one_hot_values[None, None, :])
return data_one_hot, symbols
def prepare_sequences(x, y, wlen):
(n, dim) = x.shape
nchunks = dim//wlen
xseq = np.array(np.split(x, nchunks, axis=1))
xseq = xseq.reshape((n*nchunks, wlen))
yseq = np.array(np.split(y, nchunks, axis=1))
yseq = yseq.reshape((n*nchunks, wlen))
return xseq, yseq
def get_data_from_strings(data_str_x, data_str_y, wlen):
"""
Inputs:
data_str_x: list of input strings
data_str_y: list of output strings
wlen: window length
Returns:
input/output data organized in batches
"""
# The batch size is the number of input/output strings:
batch_size = len(data_str_x)
# Clip all strings at length equal to the largest multiple of wlen that is
# lower than all string lengths:
minlen = len(data_str_x[0])
for c in data_str_x:
if len(c) < minlen:
minlen = len(c)
while minlen % wlen != 0:
minlen -=1
data_str_x = [c[:minlen] for c in data_str_x]
data_str_y = [c[:minlen] for c in data_str_y]
# Transform strings to numpy array:
x = np.array([[c for c in m] for m in data_str_x])
y = np.array([[c for c in m] for m in data_str_y])
# Divide into batches:
xs, ys = prepare_sequences(x, y, wlen)
# Get one-hot encoding:
xs_one_hot, xs_symbols = one_hot_encoding(xs)
ys_one_hot, ys_symbols = one_hot_encoding(ys)
# Get sparse encoding:
xs_sparse = np.argmax(xs_one_hot, axis=2)
ys_sparse = np.argmax(ys_one_hot, axis=2)
# Return:
return xs_one_hot, ys_one_hot, xs_sparse, ys_sparse, xs_symbols, ys_symbols
```
## Batches for training and test
```
batch_size = 32
seq_len = 50
longitud = len(quijote_x) // batch_size
print(longitud)
print(longitud*batch_size)
qx = [quijote_x[i*(batch_size+longitud):(i+1)*(batch_size+longitud)] for i in range(batch_size)]
qy = [quijote_y[i*(batch_size+longitud):(i+1)*(batch_size+longitud)] for i in range(batch_size)]
xs_one_hot, ys_one_hot, xs_sparse, ys_sparse, xs_symbols, ys_symbols = get_data_from_strings(qx, qy, seq_len)
char_to_ix = {s: i for i, s in enumerate(xs_symbols)}
ix_to_char = {i: s for i, s in enumerate(ys_symbols)}
print(xs_symbols)
print(xs_symbols.shape)
print(ys_symbols)
print(ys_symbols.shape)
xs_symbols == ys_symbols
vocab_len = xs_symbols.shape[0]
print(vocab_len)
num_batches = xs_one_hot.shape[0] / batch_size
print(xs_one_hot.shape[0])
print(batch_size)
print(num_batches)
```
## Training/test partition
```
print(xs_one_hot.shape)
print(ys_one_hot.shape)
print(xs_sparse.shape)
print(ys_sparse.shape)
ntrain = int(num_batches*0.75)*batch_size
xs_one_hot_train = xs_one_hot[:ntrain]
ys_one_hot_train = ys_one_hot[:ntrain]
xs_sparse_train = xs_sparse[:ntrain]
ys_sparse_train = ys_sparse[:ntrain]
xs_one_hot_test = xs_one_hot[ntrain:]
ys_one_hot_test = ys_one_hot[ntrain:]
xs_sparse_test = xs_sparse[ntrain:]
ys_sparse_test = ys_sparse[ntrain:]
print(xs_one_hot_train.shape)
print(xs_one_hot_test.shape)
```
## Function to evaluate the model on test data
```
def evaluate_network(model, x, y, batch_size):
mean_loss = []
mean_acc = []
for i in range(0, x.shape[0], batch_size):
batch_data_x = x[i:i+batch_size, :, :]
batch_data_y = y[i:i+batch_size, :, :]
loss, acc = model.test_on_batch(batch_data_x, batch_data_y)
mean_loss.append(loss)
mean_acc.append(acc)
return np.array(mean_loss).mean(), np.array(mean_acc).mean()
```
## Function that copies the weigths from ``source_model`` to ``dest_model``
```
def copia_pesos(source_model, dest_model):
for source_layer, dest_layer in zip(source_model.layers, dest_model.layers):
dest_layer.set_weights(source_layer.get_weights())
```
## Function that samples probabilities from model
```
def categorical(p):
return (p.cumsum(-1) >= np.random.uniform(size=p.shape[:-1])[..., None]).argmax(-1)
```
## Function that generates text
```
def genera_texto(first_char, num_chars):
texto = "" + first_char
next_char = first_char
next_one_hot = np.zeros(vocab_len)
next_one_hot[char_to_ix[next_char]] = 1.
next_one_hot = next_one_hot[None, None, :]
for i in range(num_chars):
probs = model2.predict_on_batch(next_one_hot)
next_ix = categorical(probs.ravel())
next_char = ix_to_char[next_ix]
next_one_hot = np.zeros(vocab_len)
next_one_hot[char_to_ix[next_char]] = 1.
next_one_hot = next_one_hot[None, None, :]
texto += next_char
return texto
```
## Network definition
```
K.clear_session()
nunits = 200
model1 = Sequential()
#model1.add(SimpleRNN(nunits, batch_input_shape=(batch_size, seq_len, vocab_len),
# return_sequences=True, stateful=True, unroll=True))
model1.add(LSTM(nunits, batch_input_shape=(batch_size, seq_len, vocab_len),
return_sequences=True, stateful=True, unroll=True))
model1.add(Dense(vocab_len, activation='softmax'))
model1.summary()
```
## Network that generates text
```
model2 = Sequential()
#model2.add(SimpleRNN(nunits, batch_input_shape=(1, 1, vocab_len),
# return_sequences=True, stateful=True, unroll=True))
model2.add(LSTM(nunits, batch_input_shape=(1, 1, vocab_len),
return_sequences=True, stateful=True, unroll=True))
model2.add(Dense(vocab_len, activation='softmax'))
model2.summary()
```
## Training
```
#learning_rate = 0.5 # Probar entre 0.05 y 5
#clip = 0.005 # Probar entre 0.0005 y 0.05
learning_rate = 0.5
clip = 0.002
#model1.compile(loss='categorical_crossentropy', optimizer=keras.optimizers.SGD(lr=learning_rate, clipvalue=clip), metrics=['accuracy'])
model1.compile(loss='categorical_crossentropy', optimizer=keras.optimizers.Adam(), metrics=['accuracy'])
num_epochs = 500 # Dejar en 100, la red tarda unos 10 minutos
model1_loss = np.zeros(num_epochs)
model1_acc = np.zeros(num_epochs)
model1_loss_test = np.zeros(num_epochs)
model1_acc_test = np.zeros(num_epochs)
for epoch in range(num_epochs):
model1.reset_states()
mean_tr_loss = []
mean_tr_acc = []
for i in range(0, xs_one_hot_train.shape[0], batch_size):
batch_data_x = xs_one_hot_train[i:i+batch_size, :, :]
batch_data_y = ys_one_hot_train[i:i+batch_size, :, :]
tr_loss, tr_acc = model1.train_on_batch(batch_data_x, batch_data_y)
mean_tr_loss.append(tr_loss)
mean_tr_acc.append(tr_acc)
model1_loss[epoch] = np.array(mean_tr_loss).mean()
model1_acc[epoch] = np.array(mean_tr_acc).mean()
model1.reset_states()
model1_loss_test[epoch], model1_acc_test[epoch] = evaluate_network(model1, xs_one_hot_test, ys_one_hot_test, batch_size)
print("\rTraining epoch: %d / %d" % (epoch+1, num_epochs), end="")
print(", loss = %f, acc = %f" % (model1_loss[epoch], model1_acc[epoch]), end="")
print(", test loss = %f, test acc = %f" % (model1_loss_test[epoch], model1_acc_test[epoch]), end="")
# Genero texto:
copia_pesos(model1, model2)
model2.reset_states()
print(" >>> %s" % genera_texto('e', 200)) #, end="")
```
## Plots
```
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.plot(model1_loss, label="train")
plt.plot(model1_loss_test, label="test")
plt.grid(True)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.title('loss')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(model1_acc, label="train")
plt.plot(model1_acc_test, label="test")
plt.grid(True)
plt.xlabel('epoch')
plt.ylabel('acc')
plt.title('accuracy')
plt.legend()
plt.show()
model2.reset_states()
print(genera_texto('A', 1000))
```
|
github_jupyter
|
```
import numpy as np
import pandas as pd
import xgboost as xgb
from xgboost.sklearn import XGBClassifier
from sklearn import preprocessing
from sklearn.preprocessing import OneHotEncoder
from sklearn.grid_search import GridSearchCV, RandomizedSearchCV
from sklearn.datasets import make_classification
from sklearn.cross_validation import StratifiedKFold,KFold,train_test_split
from scipy.stats import randint, uniform
from sklearn.metrics import roc_auc_score
np.random.seed(22)
import datetime
import random
from operator import itemgetter
import time
import copy
dtrain = xgb.DMatrix('to_r_n_back/dtrain.data')
dval = xgb.DMatrix('to_r_n_back/dtest.data')
yval = (pd.read_csv('to_r_n_back/val1_target.csv')).outcome.values
labels = yval
lbl_enc = preprocessing.LabelEncoder()
labels = lbl_enc.fit_transform(labels)
dval.set_label(labels)
param = {'objective': 'binary:logistic',
'max_depth': 11,
'gamma': 0.038587401190034704,
'eval_metric': 'auc',
'colsample_bylevel': 0.40883831209377614,
'min_child_weight': 7,
'lambda': 3.480389590147552,
'n_estimators': 100000,
'colsample_bytree': 0.26928766415604755,
'seed': 5,
'alpha': 0.7707414382224765,
'nthread': 4,
'silent': 1,
'subsample': 0.5447189256867526,
'eta': 0.05}
evals = [(dtrain, 'train'),(dval, 'eval')]
num_round = 100000
bst = xgb.train(param, dtrain, num_round, early_stopping_rounds=50, evals=evals, verbose_eval=10)
dtrain = xgb.DMatrix('svmlight_try2/dtrain.data')
dtest = xgb.DMatrix('svmlight_try2/dtest.data')
act_test_data = pd.read_csv("redhat_data_new/act_test_new_try2.csv", dtype={'people_id': np.str, 'activity_id': np.str}, parse_dates=['date'])
df1 = pd.read_csv('redhat_data_new/Submission_leak_happycube_python.csv')
c = list(set(act_test_data.activity_id.unique())&set(df1.activity_id.unique()))
len(c)
ac = df1.loc[df1['activity_id'].isin(c)]
ad = df1.loc[~df1['activity_id'].isin(c)]
ac.shape,ad.shape
ae = ac[(ac.outcome==1)|(ac.outcome==0)]
d = list(set(act_test_data.activity_id.unique())&set(ae.activity_id.unique()))
len(d)
af = act_test_data.loc[act_test_data['activity_id'].isin(d)]
af.shape
indx = af.index
ae.index = ae.activity_id.values
ae.head()
af.index = af.activity_id.values
af.head()
ag = ae.ix[af.index]
ag.head()
ag.index = indx
ag.head()
ae.reset_index(drop=True,inplace=True)
act_test_data.head()
dtest.slice(indx).get_label()
param1 = {'objective': 'binary:logistic',
'booster': 'gbtree',
'max_depth': 11,
'gamma': 0.038587401190034704,
'eval_metric': 'auc',
'colsample_bylevel': 0.40883831209377614,
'min_child_weight': 7,
'lambda': 3.480389590147552,
'n_estimators': 100000,
'colsample_bytree': 0.26928766415604755,
'seed': 5,
'alpha': 0.7707414382224765,
'nthread': 20,
'silent': 1,
'subsample': 0.5447189256867526,
'eta': 0.3}
dval = dtest.slice(indx)
dval.set_label(ag.outcome.values)
evals = [(dtrain, 'train'),(dval, 'eval')]
num_round = 200000
bst = xgb.train(param1, dtrain, num_round, early_stopping_rounds=200, evals=evals, verbose_eval=10)
ypred = bst.predict(dtest, ntree_limit=bst.best_ntree_limit)
act_test_data1 = pd.read_csv("redhat_data_new/act_test_new_try2.csv", dtype={'people_id': np.str, 'activity_id': np.str}, parse_dates=['date'])
output = pd.DataFrame({ 'activity_id' : act_test_data1['activity_id'], 'outcome': ypred })
output.head()
output.to_csv('model_sub_81k_try2.csv', index = False)
```
|
github_jupyter
|
```
%matplotlib inline
import numpy as np
import statsmodels.api as sm
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sn
plt.style.use('seaborn-whitegrid')
plt.rcParams["font.family"] = "Times New Roman"
plt.rcParams["font.size"] = "17"
```
* Get the dataset from the Stata Press publishing house on their website.
* This gives a pandas series of the RGNP, and the index annotates the dates.
```
dta = pd.read_stata('https://www.stata-press.com/data/r14/rgnp.dta').iloc[1:]
dta.index = pd.DatetimeIndex(dta.date, freq='QS')
dta_hamilton = dta.rgnp
```
* Domestic recessions and expansions model.
* The model will include transition probabilities between these two regimes and predict probabilities of expansion or recession at each time point.
```
# Plot the data
dta_hamilton.plot(title='Growth rate of Real GNP', figsize=(16, 6))
```
* Fit the 4th order Markov switching model.
* Specify two regimes.
* Get the model fitted via maximum likelihood estimation to the RGNP data.
* Set switching_ar=False because the statsmodels implementation defaults to
switching autoregressive coefficients.
```
# Fit the model
mod_hamilton = sm.tsa.MarkovAutoregression(dta_hamilton, k_regimes=2, order=4, switching_ar=False)
res_hamilton = mod_hamilton.fit()
```
* See the regime transition parameters at the bottom of the same output.
```
print(res_hamilton.summary())
```
* See the lengths of recession and expansion.
* The output array is in financial quarters.
* Therefore, a recession is expected to take about four quarters (1 year) and an expansion 10 quarters (two and a half years).
```
res_hamilton.expected_durations
```
* Plot the probability of recession at each point in time.
```
from pandas_datareader.data import DataReader
from datetime import datetime
usrec = DataReader('USREC', 'fred', start=datetime(1947, 1, 1), end=datetime(2013, 4, 1))
```
* This gives a DataFrame in which recessions are indicated.
* Here are the first five rows.
* In the first five rows, there was no recession according to the National Bureau of Economic Research (NBER) indicators.
```
usrec.head()
```
* Plot NBER recession indicators against the model regime predictions.
* This gives actual recession data against model predictions.
```
_, ax = plt.subplots(1, figsize=(16, 6))
ax.plot(res_hamilton.filtered_marginal_probabilities[0])
ax.fill_between(
usrec.index, 0, 1, where=usrec['USREC'].values,
color='gray', alpha=0.3
)
ax.set(
xlim=(dta_hamilton.index[4], dta_hamilton.index[-1]),
ylim=(0, 1),
title='Filtered probability of recession'
);
```
* See there seems to be quite a good match between the model predictions and
actual recession indicators.
```
```
|
github_jupyter
|
# HRF downsampling
This short notebook is why (often) we have to downsample our predictors after convolution with an HRF.
```
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from nistats.hemodynamic_models import glover_hrf
%matplotlib inline
```
First, let's define our data. Suppose we did an experiment where we show subjects images for 4 seconds. The onset of the stimuli we're drawn semi-randomly: every 15 seconds but +/- 3 to 5 seconds. In total, the experiment lasted 5 minutes. The fMRI data we acquired during the experiment had a TR of 2 seconds.
```
TR = 2 # seconds
time_exp = 5*60 # seconds
number_of_events = 10
duration_of_events = 4
onsets_sec = np.arange(0, time_exp, 15) + np.random.uniform(3, 5, 20)
onsets_sec = np.round(onsets_sec, 3)
print("Onset events: %s" % (onsets_sec,))
```
As you can see, the onsets are not neatly synchronized to the time that we acquired the different volumes of our fMRI data, which are (with a TR of 2): `[0, 2, 4, 6, ..., 298]` seconds. In other words, the data (onsets) of our experimental paradigm are on a different scale (i.e., with a precision of milliseconds) than our fMRI data (i.e., with a precision/temporal resolution of 2 seconds)!
So, what should we do? One thing we *could* do, is to round each onset to the nearest TR. So, we'll pretend that for example an onset at 2.9 seconds happened at 2 seconds. This, however, is of course not very precise and, fortunately, not necessary. Another, and better, option is to create your design and convolve your regressors with an HRF at the time scale and temporal resolution of your onsets and *then*, as a last step, downsample your regressors to the temporal resolution of your fMRI data (which is defined by your TR).
So, given that our onsets have been measured on a millisecond scale, let's create our design with this temporal resolution. First, we'll create an empty stimulus-vector with a length of the time of the experiment in seconds times 1000 (because we want it in milliseconds):
```
stim_vector = np.zeros(time_exp * 1000)
print("Length of stim vector: %i" % stim_vector.size)
```
Now, let's convert our onsets to milliseconds:
```
onsets_msec = onsets_sec * 1000
```
Now we can define within our `stim_vector` when each onset happened. Importantly, let's assume that each stimulus lasted 4 seconds.
```
for onset in onsets_msec:
onset = int(onset)
stim_vector[onset:(onset+duration_of_events*1000)] = 1
```
Alright, let's plot it:
```
plt.plot(stim_vector)
plt.xlim(0, time_exp*1000)
plt.xlabel('Time (milliseconds)')
plt.ylabel('Activity (A.U.)')
sns.despine()
plt.show()
```
Sweet, now let's define an HRF:
```
hrf = glover_hrf(tr=TR, time_length=32, oversampling=TR*1000)
hrf = hrf / hrf.max()
plt.plot(hrf)
plt.xlabel('Time (milliseconds)')
plt.ylabel('Activity (A.U.)')
sns.despine()
plt.show()
```
Let's convolve!
```
conv = np.convolve(stim_vector, hrf)[:stim_vector.size]
conv = conv / conv.max()
conv_ds = conv[::TR*1000]
plt.figure(figsize=(15, 5))
plt.subplot(1, 2, 1)
plt.plot(conv)
plt.subplot(1, 2, 2)
plt.plot(conv_ds)
plt.tight_layout()
sns.despine()
plt.show()
```
|
github_jupyter
|
# Table of Contents
<p><div class="lev1 toc-item"><a href="#Linear-Regression-problem" data-toc-modified-id="Linear-Regression-problem-1"><span class="toc-item-num">1 </span>Linear Regression problem</a></div><div class="lev1 toc-item"><a href="#Gradient-Descent" data-toc-modified-id="Gradient-Descent-2"><span class="toc-item-num">2 </span>Gradient Descent</a></div><div class="lev1 toc-item"><a href="#Gradient-Descent---Classification" data-toc-modified-id="Gradient-Descent---Classification-3"><span class="toc-item-num">3 </span>Gradient Descent - Classification</a></div><div class="lev1 toc-item"><a href="#Gradient-descent-with-numpy" data-toc-modified-id="Gradient-descent-with-numpy-4"><span class="toc-item-num">4 </span>Gradient descent with numpy</a></div>
```
%matplotlib inline
from fastai.learner import *
```
In this part of the lecture we explain Stochastic Gradient Descent (SGD) which is an **optimization** method commonly used in neural networks. We will illustrate the concepts with concrete examples.
# Linear Regression problem
The goal of linear regression is to fit a line to a set of points.
```
# Here we generate some fake data
def lin(a,b,x): return a*x+b
def gen_fake_data(n, a, b):
x = s = np.random.uniform(0,1,n)
y = lin(a,b,x) + 0.1 * np.random.normal(0,3,n)
return x, y
x, y = gen_fake_data(50, 3., 8.)
plt.scatter(x,y, s=8); plt.xlabel("x"); plt.ylabel("y");
```
You want to find **parameters** (weights) $a$ and $b$ such that you minimize the *error* between the points and the line $a\cdot x + b$. Note that here $a$ and $b$ are unknown. For a regression problem the most common *error function* or *loss function* is the **mean squared error**.
```
def mse(y_hat, y): return ((y_hat - y) ** 2).mean()
```
Suppose we believe $a = 10$ and $b = 5$ then we can compute `y_hat` which is our *prediction* and then compute our error.
```
y_hat = lin(10,5,x)
mse(y_hat, y)
def mse_loss(a, b, x, y): return mse(lin(a,b,x), y)
mse_loss(10, 5, x, y)
```
So far we have specified the *model* (linear regression) and the *evaluation criteria* (or *loss function*). Now we need to handle *optimization*; that is, how do we find the best values for $a$ and $b$? How do we find the best *fitting* linear regression.
# Gradient Descent
For a fixed dataset $x$ and $y$ `mse_loss(a,b)` is a function of $a$ and $b$. We would like to find the values of $a$ and $b$ that minimize that function.
**Gradient descent** is an algorithm that minimizes functions. Given a function defined by a set of parameters, gradient descent starts with an initial set of parameter values and iteratively moves toward a set of parameter values that minimize the function. This iterative minimization is achieved by taking steps in the negative direction of the function gradient.
Here is gradient descent implemented in [PyTorch](http://pytorch.org/).
```
# generate some more data
x, y = gen_fake_data(10000, 3., 8.)
x.shape, y.shape
x,y = V(x),V(y)
# Create random weights a and b, and wrap them in Variables.
a = V(np.random.randn(1), requires_grad=True)
b = V(np.random.randn(1), requires_grad=True)
a,b
learning_rate = 1e-3
for t in range(10000):
# Forward pass: compute predicted y using operations on Variables
loss = mse_loss(a,b,x,y)
if t % 1000 == 0: print(loss.data[0])
# Computes the gradient of loss with respect to all Variables with requires_grad=True.
# After this call a.grad and b.grad will be Variables holding the gradient
# of the loss with respect to a and b respectively
loss.backward()
# Update a and b using gradient descent; a.data and b.data are Tensors,
# a.grad and b.grad are Variables and a.grad.data and b.grad.data are Tensors
a.data -= learning_rate * a.grad.data
b.data -= learning_rate * b.grad.data
# Zero the gradients
a.grad.data.zero_()
b.grad.data.zero_()
```
Nearly all of deep learning is powered by one very important algorithm: **stochastic gradient descent (SGD)**. SGD can be seeing as an approximation of **gradient descent** (GD). In GD you have to run through *all* the samples in your training set to do a single itaration. In SGD you use *only one* or *a subset* of training samples to do the update for a parameter in a particular iteration. The subset use in every iteration is called a **batch** or **minibatch**.
# Gradient Descent - Classification
For a fixed dataset $x$ and $y$ `mse_loss(a,b)` is a function of $a$ and $b$. We would like to find the values of $a$ and $b$ that minimize that function.
**Gradient descent** is an algorithm that minimizes functions. Given a function defined by a set of parameters, gradient descent starts with an initial set of parameter values and iteratively moves toward a set of parameter values that minimize the function. This iterative minimization is achieved by taking steps in the negative direction of the function gradient.
Here is gradient descent implemented in [PyTorch](http://pytorch.org/).
```
def gen_fake_data2(n, a, b):
x = np.random.uniform(0,1,n)
y = lin(a,b,x) + 0.1 * np.random.normal(0,3,n)
return x, np.where(y>10, 1., 0.)
x,y = gen_fake_data2(10000, 3., 8.)
x,y = V(x),V(y)
def nll(y_hat, y):
y_hat = torch.clamp(y_hat, 1e-5, 1-1e-5)
return (y*y_hat.log() + (1.-y)*(1.-y_hat).log()).mean()
a = V(np.random.randn(1), requires_grad=True)
b = V(np.random.randn(1), requires_grad=True)
learning_rate = 1e-2
for t in range(3000):
p = (-lin(a,b,x)).exp()
y_hat = 1./(1.+p)
loss = nll(y_hat, y)
if t % 1000 == 0:
print(np.exp(loss.data[0]), np.mean(to_np(y)==(to_np(y_hat)>0.5)))
# print(y_hat)
loss.backward()
a.data -= learning_rate * a.grad.data
b.data -= learning_rate * b.grad.data
a.grad.data.zero_()
b.grad.data.zero_()
```
Nearly all of deep learning is powered by one very important algorithm: **stochastic gradient descent (SGD)**. SGD can be seeing as an approximation of **gradient descent** (GD). In GD you have to run through *all* the samples in your training set to do a single itaration. In SGD you use *only one* or *a subset* of training samples to do the update for a parameter in a particular iteration. The subset use in every iteration is called a **batch** or **minibatch**.
# Gradient descent with numpy
```
from matplotlib import rcParams, animation, rc
from ipywidgets import interact, interactive, fixed
from ipywidgets.widgets import *
rc('animation', html='html5')
rcParams['figure.figsize'] = 3, 3
x, y = gen_fake_data(50, 3., 8.)
a_guess,b_guess = -1., 1.
mse_loss(y, a_guess, b_guess, x)
lr=0.01
def upd():
global a_guess, b_guess
y_pred = lin(a_guess, b_guess, x)
dydb = 2 * (y_pred - y)
dyda = x*dydb
a_guess -= lr*dyda.mean()
b_guess -= lr*dydb.mean()
fig = plt.figure(dpi=100, figsize=(5, 4))
plt.scatter(x,y)
line, = plt.plot(x,lin(a_guess,b_guess,x))
plt.close()
def animate(i):
line.set_ydata(lin(a_guess,b_guess,x))
for i in range(30): upd()
return line,
ani = animation.FuncAnimation(fig, animate, np.arange(0, 20), interval=100)
ani
```
|
github_jupyter
|
```
import cv2
import numpy as np
import pandas as pd
import numba
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import matplotlib
model = 'neural'
symmetric = False
nPosts = 3
if symmetric == True:
data = 'SPP/symmetric_n' if model == 'collective' else 'NN/symmetric_n'
prefix = 'coll_symmetric_' if model == 'collective' else 'symmetric_'
else:
data = 'SPP/collective_n' if model == 'collective' else 'NN/flydata_n'
prefix = 'coll_' if model == 'collective' else ''
tmin = 0
if symmetric == True:
if nPosts < 4:
tmax = 2000 if model == 'neural' else 5100
else:
tmax = 3000 if model == 'neural' else 5100
else:
if nPosts < 4:
tmax = 1200 if model == 'neural' else 5100
else:
tmax = 1900 if model == 'neural' else 6200
window_size = 600
df = pd.read_csv("/Users/vivekhsridhar/Documents/Work/Results/decision_geometry/Data/Theory/" + data + str(nPosts) + "_direct.csv")
df.head()
if symmetric:
xs = np.array((df[' x'] - 500) / 100)
df[' x'] = xs
else:
xs = np.array(df[' x'] / 100)
df[' x'] = xs
ys = np.array((df[' y'] - 500) / 100)
df[' y'] = ys
if model == 'neural':
ts = df['time']
else:
ts = df[' time']
xs = xs[ts < tmax]
ys = ys[ts < tmax]
ts = ts[ts < tmax]
if nPosts == 2:
if symmetric:
post0_x = 5.0*np.cos(np.pi)
post0_y = 5.0*np.sin(np.pi)
post1_x = 5.0*np.cos(0)
post1_y = 5.0*np.sin(0)
else:
post0_x = 5.0*np.cos(np.pi/6)
post0_y = -5.0*np.sin(np.pi/6)
post1_x = 5.0*np.cos(np.pi/6)
post1_y = 5.0*np.sin(np.pi/6)
elif nPosts == 3:
if symmetric:
post0_x = 5.0*np.cos(-2*np.pi/3)
post0_y = 5.0*np.sin(-2*np.pi/3)
post1_x = 5.0
post1_y = 0.0
post2_x = 5.0*np.cos(2*np.pi/3)
post2_y = 5.0*np.sin(2*np.pi/3)
else:
post0_x = 5.0*np.cos(2*np.pi/9)
post0_y = -5.0*np.sin(2*np.pi/9)
post1_x = 5.0
post1_y = 0.0
post2_x = 5.0*np.cos(2*np.pi/9)
post2_y = 5.0*np.sin(2*np.pi/9)
else:
if symmetric:
post0_x = -5.0
post0_y = 0.0
post1_x = 0.0
post1_y = 5.0
post2_x = 5.0
post2_y = 0.0
post3_x = 0.0
post3_y = -5.0
else:
post0_x = 5.0*np.cos(2*np.pi/9)
post0_y = -5.0*np.sin(2*np.pi/9)
post1_x = 5.0
post1_y = 0.0
post2_x = 5.0*np.cos(2*np.pi/9)
post2_y = 5.0*np.sin(2*np.pi/9)
if nPosts == 2:
if symmetric:
fig, ax = plt.subplots(1,1,figsize=(2,2))
else:
fig, ax = plt.subplots(1,1,figsize=(post0_x/2.5,post1_y/1.25))
else:
if symmetric:
fig, ax = plt.subplots(1,1,figsize=(2,2))
else:
fig, ax = plt.subplots(1,1,figsize=(1.25,post2_x/2))
plt.scatter(xs, ys, c='black', s=1, alpha=0.01)
ax.set_aspect('equal')
if symmetric:
if nPosts == 2:
ax.set_xticks([-4,-2,0,2,4])
ax.set_yticks([-4,-2,0,2,4])
else:
ax.set_xticks([-4,-2,0,2,4])
ax.set_yticks([-4,-2,0,2,4])
else:
if nPosts == 2:
ax.set_xticks([0,1,2,3,4])
ax.set_yticks([-2,-1,0,1,2])
plt.xlim(0,post0_x)
plt.ylim(post0_y,post1_y)
else:
ax.set_xticks([0,1,2,3,4,5])
#ax.set_yticks([-3,-2,-1,0,1,2,3])
plt.xlim(0,5)
plt.ylim(post0_y,post2_y)
fig.savefig('/Users/vivekhsridhar/Documents/Code/Python/fly-matrix/figures/' + prefix + 'trajectories_n' + str(nPosts) + '_direct.pdf', dpi=600, bbox_inches='tight')
nbins = 500
peak_threshold = 0.9
def density_map(x, y, stats=True):
blur = (11, 11) if stats == True else (51, 51)
if nPosts == 2:
r = (
[[-5, 5], [-5, 5]]
if symmetric == True
else [[0, post0_x], [post0_y, post1_y]]
)
elif nPosts == 3:
r = (
[[post0_x, post1_x], [post0_y, post2_y]]
if symmetric == True
else [[0, post1_x], [post0_y, post2_y]]
)
else:
r = (
[[-5, 5], [-5, 5]]
if symmetric == True
else [[0, post1_x], [post0_y, post2_y]]
)
h, xedge, yedge, image = plt.hist2d(x, y, bins=nbins, density=True, range=r)
if nPosts == 2:
tmp_img = np.flipud(np.rot90(cv2.GaussianBlur(h, blur, 0)))
else:
tmp_img = np.flipud(np.rot90(cv2.GaussianBlur(h, blur, 0)))
tmp_img /= np.max(tmp_img)
return tmp_img
for idx,t in enumerate(range(tmin,tmax-window_size,10)):
window_min = t
window_max = t + window_size
x = xs[(ts > window_min) & (ts < window_max)]
y = ys[(ts > window_min) & (ts < window_max)]
tmp_img = density_map(x, y, stats=False)
if idx == 0:
img = tmp_img
else:
img = np.fmax(tmp_img, img)
if nPosts == 2:
x_peaks = np.where(img > peak_threshold)[1] * post0_x / nbins
y_peaks = np.where(img > peak_threshold)[0] * (post0_y - post1_y) / nbins + post1_y
elif nPosts == 3:
x_peaks = np.where(img > peak_threshold)[1] * post1_x / nbins
y_peaks = np.where(img > peak_threshold)[0] * (post0_y - post2_y) / nbins + post2_y
if nPosts == 2:
if symmetric == True:
fig, ax = plt.subplots(1,1, figsize=(2,2))
plt.imshow(img, extent=[-5, 5, -5.0, 5.0])
plt.xticks([-4,-2,0,2,4])
plt.yticks([-4,-2,0,2,4])
else:
fig, ax = plt.subplots(1, 1, figsize=(post0_x/2.5,post1_y/1.25))
plt.imshow(img, extent=[0, post0_x, post0_y, post1_y])
plt.xticks([0,1,2,3,4])
elif nPosts == 3:
if symmetric == True:
fig, ax = plt.subplots(1,1, figsize=(3.75/2,post2_y/2))
plt.imshow(img, extent=[post0_x, post1_x, post0_y, post2_y])
else:
fig, ax = plt.subplots(1, 1, figsize=(1.25,post2_x/2))
plt.imshow(img, extent=[0, post1_x, post0_y, post2_y])
plt.xticks([0,1,2,3,4,5])
else:
if symmetric == True:
fig, ax = plt.subplots(1,1, figsize=(post2_x/2,post1_y/2))
plt.imshow(img, extent=[-post2_x, post2_x, -post1_y, post1_y])
plt.xticks([-4,-2,0,2,4])
else:
fig, ax = plt.subplots(1, 1, figsize=(1.25,post2_x/2))
plt.imshow(img, extent=[0, post1_x, post0_y, post2_y])
plt.xticks([0,1,2,3,4,5])
fig.savefig('/Users/vivekhsridhar/Documents/Code/Python/fly-matrix/figures/' + prefix + 'density_n' + str(nPosts) + '_direct.pdf', dpi=600, bbox_inches='tight')
```
### Identify bifurcation point using a piecewise phase-transition function
#### Get first bifurcation point
Once you have this, you can draw a line segment bisecting the angle between the point and two targets. This will be the line about which you symmetrise to get the second bifurcation point
```
def fitfunc(x, p, q, r):
return r * (np.abs((x - p)) ** q)
def fitfunc_vec_self(x, p, q, r):
y = np.zeros(x.shape)
for i in range(len(y)):
y[i] = fitfunc(x[i], p, q, r)
return y
x_fit = []
y_fit = []
if nPosts == 2:
if model == 'neural':
bif_pt = 2.5
params1 = [3, 1, 1]
else:
bif_pt = 1.2
params1 = [1.5, 1, 1]
x_sub = np.concatenate((xs, xs))
y_sub = np.concatenate((ys, -ys))
t_sub = np.concatenate((ts, ts))
tmin = np.min(t_sub)
tmax = np.max(t_sub)-100 if model == 'neural' else np.max(t_sub)-500
for idx,t in enumerate(range(tmin,tmax,10)):
window_min = t
window_max = t + window_size
x = x_sub[(t_sub > window_min) & (t_sub < window_max)]
y = y_sub[(t_sub > window_min) & (t_sub < window_max)]
tmp_img2 = density_map(x, y, stats=False)
if idx == 0:
tmp_img = tmp_img2
else:
tmp_img = np.fmax(tmp_img2, tmp_img)
x_fit = np.where(tmp_img > peak_threshold)[1] * post0_x / nbins
y_fit = (
np.where(tmp_img > peak_threshold)[0] * (post0_y - post1_y) / nbins
+ post1_y
)
x_fit = x_fit
y_fit = np.abs(y_fit)
y_fit = y_fit[x_fit > bif_pt]
x_fit = x_fit[x_fit > bif_pt]
for i in range(0,10):
fit_params, pcov = curve_fit(
fitfunc_vec_self, x_fit, y_fit, p0=params1, maxfev=10000
)
params1 = fit_params
else:
if model == 'neural':
bif_pt = 1
params1 = [1.2, 1, 0.5]
xs1 = xs[xs < 2.7]
ys1 = ys[xs < 2.7]
ts1 = ts[xs < 2.7]
else:
bif_pt = 0.8
params1 = [1, 1, 0.5]
xs1 = xs[xs < 2.5]
ys1 = ys[xs < 2.5]
ts1 = ts[xs < 2.5]
x_sub = np.concatenate((xs1, xs1))
y_sub = np.concatenate((ys1, -ys1))
t_sub = np.concatenate((ts1, ts1))
tmin = np.min(t_sub)
tmax = np.max(t_sub)-100 if model == 'neural' else np.max(t_sub)-500
for idx,t in enumerate(range(tmin,tmax,10)):
window_min = t
window_max = t + window_size
x = x_sub[(t_sub > window_min) & (t_sub < window_max)]
y = y_sub[(t_sub > window_min) & (t_sub < window_max)]
tmp_img2 = density_map(x, y, stats=False)
if idx == 0:
tmp_img = tmp_img2
else:
tmp_img = np.fmax(tmp_img2, tmp_img)
x_fit = np.where(tmp_img > peak_threshold)[1] * post1_x / nbins
y_fit = (
np.where(tmp_img > peak_threshold)[0] * (post0_y - post2_y) / nbins
+ post2_y
)
x_fit = x_fit
y_fit = np.abs(y_fit)
y_fit = y_fit[x_fit > bif_pt]
x_fit = x_fit[x_fit > bif_pt]
for i in range(0,10):
fit_params, pcov = curve_fit(
fitfunc_vec_self, x_fit, y_fit, p0=params1, maxfev=10000
)
params1 = fit_params
if nPosts == 2:
fig, ax = plt.subplots(1, 1, figsize=(post0_x/2.5,post1_y/1.25))
plt.imshow(img, extent=[0, post0_x, post0_y, post1_y])
else:
plt.imshow(img, extent=[0, post1_x, post0_y, post2_y])
parameters = params1
step_len = 0.01
x1 = np.arange(step_len, parameters[0], step_len)
y1 = np.zeros(len(x1))
offset=0.2 if model == 'neural' else 0.5
x = (
np.arange(parameters[0], post0_x-offset, step_len)
if nPosts == 2
else np.arange(parameters[0], 3., step_len)
)
x2 = np.concatenate((x, x))
y2 = np.concatenate(
((parameters[2] * (x - parameters[0])) ** parameters[1], -(parameters[2] * (x - parameters[0])) ** parameters[1])
)
if nPosts != 2:
bisector_xs = [params1[0], post2_x]
bisector_ys = [
0,
np.tan(np.arctan2(post2_y, post2_x - params1[0]) / 2)
* (post2_x - params1[0]),
]
plt.xticks([0,1,2,3,4])
plt.scatter(x1, y1, c="black", s=0.1)
plt.scatter(x2, y2, c="black", s=0.1)
if nPosts == 2:
fig.savefig('/Users/vivekhsridhar/Documents/Code/Python/fly-matrix/figures/' + prefix + 'density_n' + str(nPosts) + '_direct.pdf', dpi=600, bbox_inches='tight')
if nPosts == 2:
print(
"The bifurcation occurs at an angle",
2 * np.arctan2(post1_y, post1_x - params1[0]) * 180 / np.pi,
)
else:
print(
"The first bifurcation occurs at an angle",
2 * np.arctan2(post2_y, post2_x - params1[0]) * 180 / np.pi,
)
```
#### Get the second bifurcation point
For this, you must center the trajectories about the bifurcation point, get a new heatmap and rotate this by the angle of the bisector line
```
# center points about the first bifurcation
cxs = xs - params1[0]
cys = ys
cts = ts
cpost0_x = post0_x - params1[0]
cpost1_x = post1_x - params1[0]
cpost2_x = post2_x - params1[0]
@numba.njit(fastmath=True, parallel=True)
def parallel_rotate(xy, rmat):
out = np.zeros(xy.shape)
for idx in numba.prange(xy.shape[0]):
out[idx] = np.dot(rmat[idx], xy[idx])
return out
# clip all points to the left of and below 0 and points beyond post centers
ccxs = cxs[cxs > 0]
ccys = cys[cxs > 0]
ccts = cts[cxs > 0]
ccxs = ccxs[ccys > 0]
ccts = ccts[ccys > 0]
ccys = ccys[ccys > 0]
xy = np.concatenate((ccxs.reshape(-1, 1), ccys.reshape(-1, 1)), axis=1)
angle = np.full(
ccxs.shape, np.arctan2(post2_y, post2_x - params1[0]) / 2
)
rmat = np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]]).T
rx, ry = parallel_rotate(xy, rmat).T
blur = (51,51)
r1 = [[0, post1_x], [post0_y, post2_y]]
tmin = np.min(ccts)
tmax = np.max(ccts)-100 if model == 'neural' else np.max(ccts)-500
for idx,t in enumerate(range(tmin,tmax,10)):
window_min = t
window_max = t + window_size
x = rx[(ccts > window_min) & (ccts < window_max)]
y = ry[(ccts > window_min) & (ccts < window_max)]
tmp_img = density_map(x, y, stats=False)
if idx == 0:
tmp_img1 = tmp_img
else:
tmp_img1 = np.fmax(tmp_img1, tmp_img)
plt.imshow(tmp_img1, extent=[r1[0][0], r1[0][1], r1[1][0], r1[1][1]])
if model == 'neural':
bif_pt = 2.2
params2 = [2.5, 1, 0.5]
else:
bif_pt = 1.8
params2 = [2, 1, 0.5]
x_sub = np.concatenate((rx, rx))
y_sub = np.concatenate((ry, -ry))
t_sub = np.concatenate((ccts, ccts))
tmin = np.min(ccts)
tmax = np.max(ccts)-100 if model == 'neural' else np.max(ccts)-500
for idx,t in enumerate(range(tmin,tmax,10)):
window_min = t
window_max = t + window_size
x = x_sub[(t_sub > window_min) & (t_sub < window_max)]
y = y_sub[(t_sub > window_min) & (t_sub < window_max)]
tmp_img = density_map(x, y, stats=False)
if idx == 0:
tmp_img1 = tmp_img
else:
tmp_img1 = np.fmax(tmp_img1, tmp_img)
x_fit = np.where(tmp_img1 > peak_threshold)[1] * post1_x / nbins
y_fit = (
np.where(tmp_img1 > peak_threshold)[0] * (post0_y - post2_y) / nbins
+ post2_y
)
x_fit = x_fit
y_fit = np.abs(y_fit)
y_fit = y_fit[x_fit > bif_pt]
x_fit = x_fit[x_fit > bif_pt]
for i in range(0,10):
fit_params, pcov = curve_fit(
fitfunc_vec_self, x_fit, y_fit, p0=params2, maxfev=10000
)
params2 = fit_params
plt.imshow(tmp_img1, extent=[r1[0][0], r1[0][1], r1[1][0], r1[1][1]])
parameters = params2
step_len = 0.01
x1 = np.arange(step_len, parameters[0], step_len)
y1 = np.zeros(len(x1))
x = np.arange(parameters[0], 3, step_len)
x2 = np.concatenate((x, x))
y2 = np.concatenate(
((parameters[2] * (x - parameters[0])) ** parameters[1], -(parameters[2] * (x - parameters[0])) ** parameters[1])
)
plt.scatter(x1, y1, c="black", s=1)
plt.scatter(x2, y2, c="black", s=1)
bif2 = np.array([params2[0], 0]).reshape(1, -1)
ang = angle[0]
rmat1 = np.array([[np.cos(ang), -np.sin(ang)], [np.sin(ang), np.cos(ang)]]).T
bif2 = parallel_rotate(bif2, rmat).T
bif2[0] += params1[0]
print(
"The second bifurcation occurs at angle",
(
(
np.arctan2(post2_y - bif2[1], post2_x - bif2[0])
- np.arctan2(bif2[1] - post1_y, post1_x - bif2[0])
)
* 180
/ np.pi
)[0],
)
x1 = np.arange(step_len, parameters[0], step_len)
y1 = np.zeros(len(x1))
bcxy1 = np.concatenate((x1.reshape(-1, 1), y1.reshape(-1, 1)), axis=1)
ang1 = np.full(
x1.shape, -np.arctan2(post2_y, post2_x - params1[0]) / 2
)
rmat1 = np.array([[np.cos(ang1), -np.sin(ang1)], [np.sin(ang1), np.cos(ang1)]]).T
bcx1, bcy1 = parallel_rotate(bcxy1, rmat1).T
bx1 = bcx1 + params1[0]
fig, ax = plt.subplots(1, 1, figsize=(1.25,post2_x/2))
plt.imshow(img, extent=[0, post1_x, post0_y, post2_y])
step_len = 0.01
parameters = params2
bcxy1 = np.concatenate((x1.reshape(-1, 1), y1.reshape(-1, 1)), axis=1)
ang1 = np.full(x1.shape, -ang)
rmat1 = np.array([[np.cos(ang1), -np.sin(ang1)], [np.sin(ang1), np.cos(ang1)]]).T
bcx1, bcy1 = parallel_rotate(bcxy1, rmat1).T
bx1 = bcx1 + params1[0]
x = np.arange(parameters[0], 3.5, step_len) if model == 'neural' else np.arange(parameters[0], 3, step_len)
x2 = np.concatenate((x, x))
y2 = np.concatenate(
(
(parameters[2] * (x - parameters[0])) ** parameters[1],
-(parameters[2] * (x - parameters[0])) ** parameters[1])
)
bcxy2 = np.concatenate((x2.reshape(-1, 1), y2.reshape(-1, 1)), axis=1)
ang2 = np.full(x2.shape, -ang)
rmat2 = np.array([[np.cos(ang2), -np.sin(ang2)], [np.sin(ang2), np.cos(ang2)]]).T
bcx2, bcy2 = parallel_rotate(bcxy2, rmat2).T
bx2 = bcx2 + params1[0]
bx2 = np.concatenate((bx2, bx2))
bcy2 = np.concatenate((bcy2, -bcy2))
bcy2 = bcy2[bx2 < post1_x - 0.1]
bx2 = bx2[bx2 < post1_x - 0.1]
bx2 = bx2[np.abs(bcy2) < post2_y - 0.1]
bcy2 = bcy2[np.abs(bcy2) < post2_y - 0.1]
plt.plot(bx1, bcy1, linestyle="dashed", c="black")
plt.plot(bx1, -bcy1, linestyle="dashed", c="black")
plt.scatter(bx2, bcy2, c="black", s=0.1)
parameters = params1
step_len = 0.01
x1 = np.arange(5 * step_len, parameters[0], step_len)
y1 = np.zeros(len(x1))
# x = np.arange(parameters[0], 2.9, step_len)
# x2 = np.concatenate((x, x))
# y2 = np.concatenate(
# (
# (parameters[2] * (x - parameters[0])) ** parameters[1],
# -(parameters[2] * (x - parameters[0])) ** parameters[1],
# )
# )
plt.scatter(x1, y1, c="black", s=0.1)
# plt.scatter(x2, y2, c="black", s=0.1)
plt.xticks([0, 1, 2, 3, 4, 5])
fig.savefig('/Users/vivekhsridhar/Documents/Code/Python/fly-matrix/figures/' + prefix + 'density_n' + str(nPosts) + '.pdf', dpi=600, bbox_inches='tight')
```
|
github_jupyter
|
# Matrix Factorization
Matrix Factorization :cite:`Koren.Bell.Volinsky.2009` is a well-established algorithm in the recommender systems literature. The first version of matrix factorization model is proposed by Simon Funk in a famous [blog
post](https://sifter.org/~simon/journal/20061211.html) in which he described the idea of factorizing the interaction matrix. It then became widely known due to the Netflix contest which was held in 2006. At that time, Netflix, a media-streaming and video-rental company, announced a contest to improve its recommender system performance. The best team that can improve on the Netflix baseline, i.e., Cinematch), by 10 percent would win a one million USD prize. As such, this contest attracted
a lot of attention to the field of recommender system research. Subsequently, the grand prize was won by the BellKor's Pragmatic Chaos team, a combined team of BellKor, Pragmatic Theory, and BigChaos (you do not need to worry about these algorithms now). Although the final score was the result of an ensemble solution (i.e., a combination of many algorithms), the matrix factorization algorithm played a critical role in the final blend. The technical report of the Netflix Grand Prize solution :cite:`Toscher.Jahrer.Bell.2009` provides a detailed introduction to the adopted model. In this section, we will dive into the details of the matrix factorization model and its implementation.
## The Matrix Factorization Model
Matrix factorization is a class of collaborative filtering models. Specifically, the model factorizes the user-item interaction matrix (e.g., rating matrix) into the product of two lower-rank matrices, capturing the low-rank structure of the user-item interactions.
Let $\mathbf{R} \in \mathbb{R}^{m \times n}$ denote the interaction matrix with $m$ users and $n$ items, and the values of $\mathbf{R}$ represent explicit ratings. The user-item interaction will be factorized into a user latent matrix $\mathbf{P} \in \mathbb{R}^{m \times k}$ and an item latent matrix $\mathbf{Q} \in \mathbb{R}^{n \times k}$, where $k \ll m, n$, is the latent factor size. Let $\mathbf{p}_u$ denote the $u^\mathrm{th}$ row of $\mathbf{P}$ and $\mathbf{q}_i$ denote the $i^\mathrm{th}$ row of $\mathbf{Q}$. For a given item $i$, the elements of $\mathbf{q}_i$ measure the extent to which the item possesses those characteristics such as the genres and languages of a movie. For a given user $u$, the elements of $\mathbf{p}_u$ measure the extent of interest the user has in items' corresponding characteristics. These latent factors might measure obvious dimensions as mentioned in those examples or are completely uninterpretable. The predicted ratings can be estimated by
$$\hat{\mathbf{R}} = \mathbf{PQ}^\top$$
where $\hat{\mathbf{R}}\in \mathbb{R}^{m \times n}$ is the predicted rating matrix which has the same shape as $\mathbf{R}$. One major problem of this prediction rule is that users/items biases can not be modeled. For example, some users tend to give higher ratings or some items always get lower ratings due to poorer quality. These biases are commonplace in real-world applications. To capture these biases, user specific and item specific bias terms are introduced. Specifically, the predicted rating user $u$ gives to item $i$ is calculated by
$$
\hat{\mathbf{R}}_{ui} = \mathbf{p}_u\mathbf{q}^\top_i + b_u + b_i
$$
Then, we train the matrix factorization model by minimizing the mean squared error between predicted rating scores and real rating scores. The objective function is defined as follows:
$$
\underset{\mathbf{P}, \mathbf{Q}, b}{\mathrm{argmin}} \sum_{(u, i) \in \mathcal{K}} \| \mathbf{R}_{ui} -
\hat{\mathbf{R}}_{ui} \|^2 + \lambda (\| \mathbf{P} \|^2_F + \| \mathbf{Q}
\|^2_F + b_u^2 + b_i^2 )
$$
where $\lambda$ denotes the regularization rate. The regularizing term $\lambda (\| \mathbf{P} \|^2_F + \| \mathbf{Q}
\|^2_F + b_u^2 + b_i^2 )$ is used to avoid over-fitting by penalizing the magnitude of the parameters. The $(u, i)$ pairs for which $\mathbf{R}_{ui}$ is known are stored in the set
$\mathcal{K}=\{(u, i) \mid \mathbf{R}_{ui} \text{ is known}\}$. The model parameters can be learned with an optimization algorithm, such as Stochastic Gradient Descent and Adam.
An intuitive illustration of the matrix factorization model is shown below:

In the rest of this section, we will explain the implementation of matrix factorization and train the model on the MovieLens dataset.
```
import mxnet as mx
from mxnet import autograd, gluon, np, npx
from mxnet.gluon import nn
from d2l import mxnet as d2l
npx.set_np()
```
## Model Implementation
First, we implement the matrix factorization model described above. The user and item latent factors can be created with the `nn.Embedding`. The `input_dim` is the number of items/users and the (`output_dim`) is the dimension of the latent factors ($k$). We can also use `nn.Embedding` to create the user/item biases by setting the `output_dim` to one. In the `forward` function, user and item ids are used to look up the embeddings.
```
class MF(nn.Block):
def __init__(self, num_factors, num_users, num_items, **kwargs):
super(MF, self).__init__(**kwargs)
self.P = nn.Embedding(input_dim=num_users, output_dim=num_factors)
self.Q = nn.Embedding(input_dim=num_items, output_dim=num_factors)
self.user_bias = nn.Embedding(num_users, 1)
self.item_bias = nn.Embedding(num_items, 1)
def forward(self, user_id, item_id):
P_u = self.P(user_id)
Q_i = self.Q(item_id)
b_u = self.user_bias(user_id)
b_i = self.item_bias(item_id)
outputs = (P_u * Q_i).sum(axis=1) + np.squeeze(b_u) + np.squeeze(b_i)
return outputs.flatten()
```
## Evaluation Measures
We then implement the RMSE (root-mean-square error) measure, which is commonly used to measure the differences between rating scores predicted by the model and the actually observed ratings (ground truth) :cite:`Gunawardana.Shani.2015`. RMSE is defined as:
$$
\mathrm{RMSE} = \sqrt{\frac{1}{|\mathcal{T}|}\sum_{(u, i) \in \mathcal{T}}(\mathbf{R}_{ui} -\hat{\mathbf{R}}_{ui})^2}
$$
where $\mathcal{T}$ is the set consisting of pairs of users and items that you want to evaluate on. $|\mathcal{T}|$ is the size of this set. We can use the RMSE function provided by `mx.metric`.
```
def evaluator(net, test_iter, devices):
rmse = mx.metric.RMSE() # Get the RMSE
rmse_list = []
for idx, (users, items, ratings) in enumerate(test_iter):
u = gluon.utils.split_and_load(users, devices, even_split=False)
i = gluon.utils.split_and_load(items, devices, even_split=False)
r_ui = gluon.utils.split_and_load(ratings, devices, even_split=False)
r_hat = [net(u, i) for u, i in zip(u, i)]
rmse.update(labels=r_ui, preds=r_hat)
rmse_list.append(rmse.get()[1])
return float(np.mean(np.array(rmse_list)))
```
## Training and Evaluating the Model
In the training function, we adopt the $L_2$ loss with weight decay. The weight decay mechanism has the same effect as the $L_2$ regularization.
```
#@save
def train_recsys_rating(net, train_iter, test_iter, loss, trainer, num_epochs,
devices=d2l.try_all_gpus(), evaluator=None, **kwargs):
timer = d2l.Timer()
animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0, 2],
legend=['train loss', 'test RMSE'])
for epoch in range(num_epochs):
metric, l = d2l.Accumulator(3), 0.
for i, values in enumerate(train_iter):
timer.start()
input_data = []
values = values if isinstance(values, list) else [values]
for v in values:
input_data.append(gluon.utils.split_and_load(v, devices))
train_feat = input_data[0:-1] if len(values) > 1 else input_data
train_label = input_data[-1]
with autograd.record():
preds = [net(*t) for t in zip(*train_feat)]
ls = [loss(p, s) for p, s in zip(preds, train_label)]
[l.backward() for l in ls]
l += sum([l.asnumpy() for l in ls]).mean() / len(devices)
trainer.step(values[0].shape[0])
metric.add(l, values[0].shape[0], values[0].size)
timer.stop()
if len(kwargs) > 0: # It will be used in section AutoRec
test_rmse = evaluator(net, test_iter, kwargs['inter_mat'],
devices)
else:
test_rmse = evaluator(net, test_iter, devices)
train_l = l / (i + 1)
animator.add(epoch + 1, (train_l, test_rmse))
print(f'train loss {metric[0] / metric[1]:.3f}, '
f'test RMSE {test_rmse:.3f}')
print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
f'on {str(devices)}')
```
Finally, let us put all things together and train the model. Here, we set the latent factor dimension to 30.
```
devices = d2l.try_all_gpus()
num_users, num_items, train_iter, test_iter = d2l.split_and_load_ml100k(
test_ratio=0.1, batch_size=512)
net = MF(30, num_users, num_items)
net.initialize(ctx=devices, force_reinit=True, init=mx.init.Normal(0.01))
lr, num_epochs, wd, optimizer = 0.002, 20, 1e-5, 'adam'
loss = gluon.loss.L2Loss()
trainer = gluon.Trainer(net.collect_params(), optimizer, {
"learning_rate": lr,
'wd': wd})
train_recsys_rating(net, train_iter, test_iter, loss, trainer, num_epochs,
devices, evaluator)
```
Below, we use the trained model to predict the rating that a user (ID 20) might give to an item (ID 30).
```
scores = net(np.array([20], dtype='int', ctx=devices[0]),
np.array([30], dtype='int', ctx=devices[0]))
scores
```
## Summary
* The matrix factorization model is widely used in recommender systems. It can be used to predict ratings that a user might give to an item.
* We can implement and train matrix factorization for recommender systems.
## Exercises
* Vary the size of latent factors. How does the size of latent factors influence the model performance?
* Try different optimizers, learning rates, and weight decay rates.
* Check the predicted rating scores of other users for a specific movie.
[Discussions](https://discuss.d2l.ai/t/400)
|
github_jupyter
|
<h1 align="center"> TUGAS BESAR TF3101 - DINAMIKA SISTEM DAN SIMULASI </h1>
<h2 align="center"> Sistem Elektrik, Elektromekanik, dan Mekanik</h2>
<h3>Nama Anggota:</h3>
<body>
<ul>
<li>Erlant Muhammad Khalfani (13317025)</li>
<li>Bernardus Rendy (13317041)</li>
</ul>
</body>
## 1. Pemodelan Sistem Elektrik##
Untuk pemodelan sistem elektrik, dipilih rangkaian RLC seri dengan sebuah sumber tegangan seperti yang tertera pada gambar di bawah ini.
<img src="./ELEKTRIK_TUBES_3.png" style="width:50%" align="middle">
### Deskripsi Sistem
1. Input <br>
Sistem ini memiliki input sumber tegangan $v_i$, yang merupakan fungsi waktu $v_i(t)$. <br>
2. Output <br>
Sistem ini memiliki *output* arus $i_2$, yaitu arus yang mengalir pada *mesh* II. Tegangan $v_{L1}$ dan $v_{R2}$ juga dapat berfungsi sebagai *output*. Pada program ini, *output* yang akan di-*plot* hanya $v_{R2}$ dan $v_{L1}$. Nilai $i_2$ berbanding lurus terhadap nilai $v_{R2}$, sehingga bentuk grafik $i_2$ akan menyerupai bentuk grafik $v_{R2}$
3. Parameter <br>
Sistem ini memiliki parameter-parameter $R_1$, $R_2$, $L_1$, dan $C_1$. Hambatan-hambatan $R_1$ dan $R_2$ adalah parameter *resistance*. Induktor $L_1$ adalah parameter *inertance*. Kapasitor $C_1$ adalah parameter *capacitance*.
### Asumsi
1. Arus setiap *mesh* pada keadaan awal adalah nol ($i_1(0) = i_2(0) = 0$).
2. Turunan arus terhadap waktu pada setiap *mesh* adalah nol ($\frac{di_1(0)}{dt}=\frac{di_2(0)}{dt}=0$)
### Pemodelan dengan *Bond Graph*
Dari sistem rangkaian listrik di atas, akan didapatkan *bond graph* sebagai berikut.
<img src="./BG_ELEKTRIK.png" style="width:50%" align="middle">
<br>
Pada gambar di atas, terlihat bahwa setiap *junction* memenuhi aturan kausalitas. Ini menandakan bahwa rangkaian di atas bersifat *causal*. Dari *bond graph* di atas, dapat diturunkan *Ordinary Differential Equation* (ODE) seperti hasil penerapan *Kirchhoff's Voltage Law* (KVL) pada setiap *mesh*. Dalam pemodelan *bond graph* variabel-variabel dibedakan menjadi variabel *effort* dan *flow*. Sistem di atas merupakan sistem elektrik, sehingga memiliki variabel *effort* berupa tegangan ($v$) dan *flow* berupa arus ($i$).
### Persamaan Matematis - ODE
Dilakukan analisis besaran *effort* pada *1-junction* sebelah kiri. Ini akan menghasilkan:
$$
v_i = v_{R1} + v_{C1}
$$
<br>
Hasil ini sama seperti hasil dari KVL pada *mesh* I. Nilai $v_{R1}$ dan $v_{C1}$ diberikan oleh rumus-rumus:
$$
v_{R1} = R_1i_1
$$
<br>
$$
v_{C1} = \frac{1}{C_1}\int (i_1 - i_2)dt
$$
sehingga hasil KVL pada *mesh* I menjadi:
$$
v_i = R_1i_1 + \frac{1}{C_1}\int (i_1 - i_2)dt
$$
Kemudian, analisis juga dilakukan pada *1-junction* sebelah kanan, yang akan menghasilkan:
$$
v_{C1} = v_{R2} + v_{L1}
$$
<br>
Ini juga sama seperti hasil KVL pada *mesh* II. Nilai $v_{R2}$ dan $v_{L1}$ diberikan oleh rumus-rumus:
$$
v_{R2} = R_2i_2
$$
<br>
$$
v_{L1} = L_1\frac{di_2}{dt}
$$
sehingga hasil KVL pada *mesh* II menjadi:
$$
\frac{1}{C_1}\int(i_1-i_2)dt = R_2i_2 + L_1\frac{di_2}{dt}
$$
atau
$$
0 = L_1\frac{di_2}{dt} + R_2i_2 + \frac{1}{C_1}\int(i_2-i_1)dt
$$
### Persamaan Matematis - *Transfer Function*
Setelah didapatkan ODE hasil dari *bond graph*, dapat dilakukan *Laplace Transform* untuk mendapatkan fungsi transfer sistem. *Laplace Transform* pada persamaan hasil KVL *mesh* I menghasilkan:
$$
(R_1 + \frac{1}{C_1s})I_1 + (-\frac{1}{C_1s})I_2 = V_i
$$
<br>
dan pada persamaan hasil *mesh* II, akan didapatkan:
$$
(-\frac{1}{C_1s})I_1 + (L_1s + R_2 + \frac{1}{C_1s})I_2 = 0
$$
<br>
Kedua persamaan itu dieliminasi, sehingga didapatkan fungsi transfer antara $I_2$ dengan $V_i$
$$
\frac{I_2(s)}{V_i(s)} = \frac{1}{R_1C_1L_1s^2 + (R_1R_2C_1 + L_1)s + R_1 + R_2}
$$
<br>
Dari hasil *Laplace Transform* persamaan pada *mesh* II, didapatkan nilai $V_{L1}$ dari rumus
$$
V_{L1} = L_1sI_2
$$
<br>
sehingga didapatkan fungsi transfer antara $V_{L1}$ dengan $V_i$
$$
\frac{V_{L1}(s)}{V_i(s)} = \frac{L_1s}{R_1C_1L_1s^2 + (R_1R_2C_1 + L_1)s + R_1 + R_2}
$$
Sementara fungsi transfer antara $V_{R2}$ dan $V_i$ adalah
$$
\frac{V_{R2}(s)}{V_i(s)} = \frac{R_2}{R_1C_1L_1s^2 + (R_1R_2C_1 + L_1)s + R_1 + R_2}
$$
```
#IMPORTS
from ipywidgets import interact, interactive, fixed, interact_manual , HBox, VBox, Label, Layout
import ipywidgets as widgets
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
#DEFINISI SLIDER-SLIDER PARAMETER
#Slider R1
R1_slider = widgets.FloatSlider(
value=1.,
min=1.,
max=1000.,
step=1.,
description='$R_1 (\Omega)$',
readout_format='.1f',
)
#Slider R2
R2_slider = widgets.FloatSlider(
value=1.,
min=1.,
max=1000.,
step=1.,
description='$R_2 (\Omega)$',
readout_format='.1f',
)
#Slider C1
C1_slider = widgets.IntSlider(
value=1,
min=10,
max=1000,
step=1,
description='$C_1 (\mu F)$',
)
#Slider L1
L1_slider = widgets.FloatSlider(
value=0.1,
min=1.,
max=1000.,
step=0.1,
description='$L_1 (mH)$',
readout_format='.1f',
)
#DEKLARASI SELECTOR INPUT
#Slider selector input
vi_select = signal_select = widgets.Dropdown(
options=[('Step', 0), ('Impulse', 1)],
description='Tipe Sinyal:',
)
#DEKLARASI SELECTOR OUTPUT
#Output Selector
vo_select = widgets.ToggleButtons(
options=['v_R2', 'v_L1'],
description='Output:',
)
#DEKLARASI TAMBAHAN UNTUK INTERFACE
#Color button
color_select1 = widgets.ToggleButtons(
options=['blue', 'red', 'green', 'black'],
description='Color:',
)
#PENENTUAN NILAI-NILAI PARAMETER
R1 = R1_slider.value
R2 = R2_slider.value
C1 = C1_slider.value
L1 = L1_slider.value
#PENENTUAN NILAI DAN BENTUK INPUT
vform = vi_select.value
#PENENTUAN OUTPUT
vo = vo_select
#PENENTUAN PADA INTERFACE
color = color_select1.value
#Plot v_L1 menggunakan transfer function
def plot_electric (vo, R1, R2, C1, L1, vform, color):
#Menyesuaikan nilai parameter dengan satuan
R1 = R1
R2 = R2
C1 = C1*(10**-6)
L1 = L1*(10**-3)
f, ax = plt.subplots(1, 1, figsize=(8, 6))
num1 = [R2]
num2 = [L1, 0]
den = [R1*C1*L1, R1*R2*C1+L1, R1+R2]
if vo=='v_R2':
sys_vr =signal.TransferFunction(num1, den)
step_vr = signal.step(sys_vr)
impl_vr = signal.impulse(sys_vr)
if vform == 0:
ax.plot(step_vr[0], step_vr[1], color=color, label='Respon Step')
elif vform == 1:
ax.plot(impl_vr[0], impl_vr[1], color=color, label='Respon Impuls')
ax.grid()
ax.legend()
elif vo=='v_L1':
sys_vl = signal.TransferFunction(num2, den)
step_vl = signal.step(sys_vl)
impl_vl = signal.impulse(sys_vl)
#Plot respon
if vform == 0:
ax.plot(step_vl[0], step_vl[1], color=color, label='Respon Step')
elif vform == 1:
ax.plot(impl_vl[0], impl_vl[1], color=color, label='Respon Impuls')
ax.grid()
ax.legend()
ui_el = widgets.VBox([vo_select, R1_slider, R2_slider, C1_slider, L1_slider, vi_select, color_select1])
out_el = widgets.interactive_output(plot_electric, {'vo':vo_select,'R1':R1_slider,'R2':R2_slider,'C1':C1_slider,'L1':L1_slider,'vform':vi_select,'color':color_select1})
int_el = widgets.HBox([ui_el, out_el])
display(int_el)
```
### Analisis###
<h4>a. Respon Step </h4>
Dari hasil simulasi, didapatkan pengaruh perubahan-perubahan nilai parameter pada *output* sistem setelah diberikan *input* berupa sinyal *step*, di antaranya:
1. Kenaikan nilai $R_1$ akan menurunkan *steady-state gain* ($K$) sistem. Ini terlihat dari turunnya nilai *output* $v_{R2}$ pada keadaan *steady-state* dan turunnya nilai *maximum overshoot* ($M_p$) pada *output* $v_{L1}$. Perubahan nilai $R_1$ juga berbanding terbalik dengan perubahan koefisien redaman $\xi$, terlihat dari semakin jelas terlihatnya osilasi seiring dengan kenaikan nilai $R_1$. Perubahan nilai $R_1$ juga sebanding dengan perubahan nilai *settling time* ($t_s$). Ini terlihat dengan bertambahnya waktu sistem untuk mencapai nilai dalam rentang 2-5% dari nilai keadaan *steady-state*.
2. Kenaikan nilai $R_2$ akan meningkatkan *steady-state gain* ($K$) sistem dengan *output* $v_{R2}$ tetapi menurunkan *steady-state gain* ($K$) *output* $v_{L1}$. Selain itu, dapat terlihat juga bahwa perubahan nilai $R_2$ berbanding terbalik dengan nilai *settling time* ($t_s$); Saat nilai $R_2$ naik, sistem mencapai kondisi *steady-state* dalam waktu yang lebih singkat. Kenaikan nilai $R_2$ juga menyebabkan penurunan nilai *maximum overshoot* ($M_p$).
3. Perubahan nilai $C_1$ sebanding dengan perubahan nilai *settling time*, seperti yang dapat terlihat dengan bertambahnya waktu yang diperlukan sistem untuk mendekati keadaan *steady-state* seiring dengan kenaikan nilai $C_1$. Selain itu nilai $C_1$ juga berbanding terbalik dengan nilai *maximum overshoot*, ini dapat dilihat dari turunnya nilai *maximum overshoot* ketika nilai $C_1$ dinaikan. Pada saat nilai $C_1$, naik, juga terlihat kenaikan nilai *delay time* ($t_d$), *rise time* ($t_r$), dan *peak time* ($t_p$).
4. Kenaikan nilai $L_1$ mengakibatkan berkurangnya nilai frekuensi osilasi, serta meningkatkan *settling time* sistem. Perubahan nilai $L_1$ ini juga sebanding dengan *steady-state gain* sistem untuk *output* $v_{L1}$.
<h4>b. Respon Impuls </h4>
Dari hasil simulasi, didapatkan pengaruh perubahan-perubahan nilai parameter pada *output* sistem setelah diberikan *input* berupa sinyal *impulse*, di antaranya:
1. Perubahan nilai $R_1$ berbanding terbalik dengan nilai *peak response*. Kenaikan nilai $R_1$ juga menaikkan nilai *settling time* ($t_s$).
2. Kenaikan nilai $R_2$ memengaruhi nilai *peak response* $v_{R2}$, tetapi tidak berpengaruh pada *peak response* $v_{L1}$. Naiknya nilai $R_2$ juga menurunkan nilai *settling time* ($t_s$), yang terlihat dari semakin cepatnya sistem mencapai kondisi *steady-state*.
3. Kenaikan nilai $C_1$ menyebabkan turunnya nilai *peak response*. Kenaikan nilai $C_1$ juga menyebabkan kenaikan nilai *settling time* ($t_s$), yang dapat dilihat dengan bertambahnya waktu yang diperlukan sistem untuk mendekati keadaan *steady-state*.
4. Kenaikan nilai $L_1$ menyebabkan turunnya nilai *peak response*. Kenaikan nilai $L_1$ juga menurunkan nilai *settling time* ($t_s$), yang dapat dilihat dari bertambahnya waktu yang diperlukan sistem untuk mendekati keadaan *steady-state*.
## 2. Pemodelan Sistem Elektromekanik
### DC Brushed Motor Torsi Besar dengan Motor Driver
Sistem yang akan dimodelkan berupa motor driver high current BTS7960 seperti gambar pertama, dihubungkan dengan motor torsi besar dengan brush pada gambar kedua.
<div>
<img src="./1.jpg" style="width:20%" align="middle">
</div>
<div>
<img src="./2.jpg" style="width:20%" align="middle">
</div>
<p style="text-align:center"><b>Sumber gambar: KRTMI URO ITB</b></p>
### Deskripsi Sistem
1. Input <br>
Sistem ini memiliki input sinyal $V_{in}$, yang merupakan fungsi waktu $V_{in}(t)$. Tegangan $v_i(t)$ ini dapat berbentuk fungsi step, impuls, atau pulse width modulation dengan duty cycle tertentu (luaran mikrokontroller umum). <br>
2. Output <br>
Sistem ini memiliki *output* posisi sudut $\theta$, kecepatan sudut motor $\omega$, percepatan sudut motor $\alpha$, dan torsi $T$. Output ditentukan sesuai kebutuhan untuk manuver robot. Terlihat variable output bergantung pada $\theta$, $\frac {d\theta}{dt}$, dan $\frac{d^2\theta}{dt}$, sehingga dicari beberapa persamaan diferensial sesuai tiap output.
3. Parameter <br>
Sistem memiliki parameter $J,K_f,K_a,L,R,K_{emf},K_{md}$ yang diturunkan dari karakteristik subsistem mekanik dan elektrik sebagai berikut.
#### Subsistem Motor Driver
Pertama ditinjau struktur sistem dari motor driver. Motor driver yang digunakan adalah tipe MOSFET BTS7960 sehingga memiliki karakteristik dinamik yang meningkat hampir dengan instant. MOSFET dirangkai sedemikian rupa sehingga dapat digunakan untuk kontrol maju/mundur motor. Diasumsikan rise-time MOSFET cukup cepat relatif terhadap sinyal dan motor driver cukup linear, maka motor driver dapat dimodelkan sebagai sistem orde 0 dengan gain sebesar $ K_{md} $.
<img src="./4.png" style="width:30%" align="middle">
<p style="text-align:center"><b>Sumber gambar: Datasheet BTS7960</b></p>
<img src="./5.png" style="width:30%" align="middle">
<p style="text-align:center"><b>Model Orde 0 Motor Driver</b></p>
Maka persamaan dinamik output terhadap input dalam motor driver adalah <br>
$ V_m=K_{md}V_{in} $<br>
Sama seperti hubungan input output pada karakteristik statik.
#### Subsistem Motor
Lalu ditinjau struktur sistem dari motor torsi besar dengan inertia beban yang tidak dapat diabaikan.
<img src="./3.png" style="width:30%" align="middle">
<p style="text-align:center"><b>Sumber gambar: https://www.researchgate.net/figure/The-structure-of-a-DC-motor_fig2_260272509</b></p>
<br>
Maka dapat diturunkan persamaan diferensial untuk sistem mekanik.
<br>
<img src="./6.png" style="width:30%">
<img src="./7.png" style="width:30%">
<p style="text-align:center"><b>Sumber gambar: Chapman - Electric Machinery Fundamentals 4th Edition</b></p>
$$
T=K_a i_a
$$
dengan $T$ adalah torsi dan $K_a$ adalah konstanta proporsionalitas torsi (hasil perkalian K dengan flux) untuk arus armature $i_a$.
$$
V_{emf}=K_{emf} \omega
$$
dengan $V_{emf}$ adalah tegangan penyebab electromotive force dan $K_{emf}$ konstanta proporsionalitas tegangan emf (hasil perkalian K dengan flux pada kondisi ideal tanpa voltage drop) untuk kecepatan putar sudut dari motor.
<br>
Namun, akibat terbentuknya torsi adalah berputarnya beban dengan kecepatan sudut sebesar $\omega$ dan percepatan sudut sebesar $\alpha$. Faktor proporsionalitas terhadap percepatan sudut adalah $J$ (Inersia Putar) dan terhadap kecepatan sudut sebesar $ K_f $ (Konstanta Redam Putar) Sehingga dapat diturunkan persamaan diferensial sebagai berikut (Persamaan 1):
<br>
$$
J\alpha + K_f\omega = T
$$
$$
J\frac {d^2\theta}{dt} + K_f\frac {d\theta}{dt} = K_a i_a
$$
$$
J\frac {d\omega}{dt} + K_f \omega = K_a i_a
$$
Kemudian diturunkan persamaan diferensial untuk sistem elektrik yang terdapat pada motor sehingga $i_a$ dapat disubstitusi dengan input $V_{in}$ (Persamaan 2):
$$
L \frac{d{i_a}}{dt} + R i_a + K_{emf} \omega = V_m
$$
$$
V_m = K_{md} V_{in}
$$
$$
L \frac{d{i_a}}{dt} + R i_a + K_{emf} \omega = K_{md} V_{in}
$$
### Pemodelan dengan Fungsi Transfer
Dengan persamaan subsistem tersebut, dapat dilakukan pemodelan fungsi transfer sistem dengan transformasi ke domain laplace (s). Dilakukan penyelesaian menggunakan fungsi transfer dalam domain laplace, pertama dilakukan transfer ke domain laplace dengan asumsi
<br>
$ i_a (0) = 0 $
<br>
$ \frac {di_a}{dt} = 0 $
<br>
$ \theta (0) = 0 $
<br>
$ \omega (0) = 0 $
<br>
$ \alpha (0) = 0 $
<br>
Tidak diasumsikan terdapat voltage drop karena telah di akumulasi di $K_{emf}$, namun diasumsikan voltage drop berbanding lurus terhadap $\omega$.
<br>
Persamaan 1 menjadi:
$$
J s \omega + K_f \omega = K_a i_a
$$
Persamaan 2 menjadi:
$$
L s i_a + R i_a + K_{emf} \omega = K_{md} V_{in}
$$
$$
i_a=\frac {K_{md} V_{in}-K_{emf} \omega}{L s + R}
$$
Sehingga terbentuk fungsi transfer sistem keseluruhan dalam $\omega$ adalah:
$$
J s \omega + K_f \omega = \frac {K_a(K_{md} V_{in} - K_{emf} \omega)}{L s + R}
$$
Fungsi transfer untuk $\omega$ adalah:
$$
\omega = \frac {K_a(K_{md} V_{in}-K_{emf} \omega)}{(L s + R)(J s + K_f)}
$$
$$
\omega = \frac {K_a K_{md} V_{in}}{(L s + R)(J s + K_f)(1 + \frac {K_a K_{emf}}{(L s + R)(J s + K_f)})}
$$
$$
\frac {\omega (s)}{V_{in}(s)} = \frac {K_a K_{md}}{(L s + R)(J s + K_f)+ K_a K_{emf}}
$$
Dapat diturunkan fungsi transfer untuk theta dengan mengubah variable pada persamaan 1:
$$
J s^2 \theta + K_f s \theta = K_a i_a
$$
Persamaan 2:
$$
L s i_a + R i_a + K_{emf} s \theta = K_{md} V_{in}
$$
$$
i_a=\frac {K_{md} V_{in}-K_{emf} s \theta}{L s + R}
$$
Sehingga terbentuk fungsi transfer sistem keseluruhan dalam $\theta$ adalah:
$$
J s^2 \theta + K_f s \theta = \frac {K_a(K_{md} V_{in}-K_{emf} s \theta)}{L s + R}
$$
Fungsi transfer untuk $\theta$ adalah:
$$
\theta = \frac {K_a(K_{md} V_{in}-K_{emf} s \theta)}{(L s + R)(J s^2 + K_f s )}
$$
$$
\theta + \frac {K_a K_{emf} s \theta}{(L s + R)(J s^2 + K_f s )}= \frac {K_a K_{md} V_{in}}{(L s + R)(J s^2 + K_f s )}
$$
$$
\theta= \frac {K_a K_{md} V_{in}}{(L s + R)(J s^2 + K_f s )(1 + \frac {K_a K_{emf} s}{(L s + R)(J s^2 + K_f s )})}
$$
$$
\frac {\theta (s)}{V_{in}(s)}= \frac {K_a K_{md}}{(L s + R)(J s^2 + K_f s )+ K_a K_{emf} s}
$$
Terlihat bahwa fungsi transfer untuk $\omega$ dan $\theta$ hanya berbeda sebesar $ \frac {1}{s} $ sesuai dengan hubungan
$$
\omega = s \theta
$$
Sehingga fungsi transfer untuk $\alpha$ akan memenuhi
$$
\alpha = s\omega = s^2 \theta
$$
Sehingga fungsi transfer untuk $\alpha$ adalah:
$$
\frac {\alpha (s)}{V_{in}(s)} = \frac {K_a K_{md} s}{(L s + R)(J s + K_f)+ K_a K_{emf}}
$$
### Output
Dari fungsi transfer, diformulasikan persamaan output posisi sudut $\theta$, kecepatan sudut motor $\omega$, percepatan sudut $\alpha$, dan torsi $T$ dalam fungsi waktu (t).
$$
\theta (t) = \mathscr {L^{-1}} \{\frac {K_a K_{md} V_{in}(s)}{(L s + R)(J s^2 + K_f s )+ K_a K_{emf} s}\}
$$
<br>
$$
\omega (t) = \mathscr {L^{-1}} \{\frac {K_a K_{md} V_{in}(s)}{(L s + R)(J s + K_f)+ K_a K_{emf}}\}
$$
<br>
$$
\alpha (t)= \mathscr {L^{-1}} \{\frac {K_a K_{md} Vin_{in}(s) s}{(L s + R)(J s + K_f)+ K_a K_{emf}}\}
$$
<br>
$$
T = \frac {K_a(K_{md} V_{in}-K_{emf} \omega)}{L s + R}
$$
```
# Digunakan penyelesaian numerik untuk output
import numpy as np
from scipy.integrate import odeint
import scipy.signal as sig
import matplotlib.pyplot as plt
from sympy.physics.mechanics import dynamicsymbols, SymbolicSystem
from sympy import *
import control as control
vin = symbols ('V_{in}') #import symbol input
omega, theta, alpha = dynamicsymbols('omega theta alpha') #import symbol output
ka,kmd,l,r,j,kf,kemf,s,t = symbols ('K_a K_{md} L R J K_f K_{emf} s t')#import symbol parameter dan s
thetaOverVin = (ka*kmd)/((l*s+r)*(j*s**2+kf*s)+ka*kemf*s) #persamaan fungsi transfer theta
polyThetaOverVin = thetaOverVin.as_poly() #Penyederhanaan persamaan
polyThetaOverVin
omegaOverVin = (ka*kmd)/((l*s+r)*(j*s+kf)+ka*kemf) #persamaan fungsi transfer omega
polyOmegaOverVin = omegaOverVin.as_poly() #Penyederhanaan persamaan
polyOmegaOverVin
alphaOverVin = (ka*kmd*s)/((l*s+r)*(j*s+kf)+ka*kemf)
polyAlphaOverVin = alphaOverVin.as_poly() #Penyederhanaan persamaan
polyAlphaOverVin
torqueOverVin= ka*(kmd-kemf*((ka*kmd)/((l*s+r)*(j*s+kf)+ka*kemf)))/(l*s+r) #Penyederhanaan persamaan torsi
polyTorqueOverVin = torqueOverVin.as_poly()
polyTorqueOverVin
def plot_elektromekanik(Ka,Kmd,L,R,J,Kf,Kemf,VinType,tMax,dutyCycle,grid):
# Parameter diberi value dan model system dibentuk dalam transfer function yang dapat diolah python
Ka = Ka
Kmd = Kmd
L = L
R = R
J = J
Kf = Kf
Kemf = Kemf
# Pembuatan model transfer function
tf = control.tf
tf_Theta_Vin = tf([Ka*Kmd],[J*L,(J*R+Kf*L),(Ka*Kemf+Kf*R),0])
tf_Omega_Vin = tf([Ka*Kmd],[J*L,(J*R+Kf*L),(Ka*Kemf+Kf*R)])
tf_Alpha_Vin = tf([Ka*Kmd,0],[J*L,(J*R+Kf*L),(Ka*Kemf+Kf*R)])
tf_Torque_Vin = tf([Ka*Kmd],[L,R]) - tf([Kmd*Kemf*Ka**2],[J*L**2,(2*J*L*R+Kf*L**2),(J*R**2+Ka*Kemf*L+2*Kf*L*R),(Ka*Kemf*R+Kf*R**2)])
f, axs = plt.subplots(4, sharex=True, figsize=(10, 10))
# Fungsi mengatur rentang waktu analisis (harus memiliki kelipatan 1 ms)
def analysisTime(maxTime):
ts=np.linspace(0, maxTime, maxTime*100)
return ts
t=analysisTime(tMax)
if VinType== 2:
# Input pwm dalam 1 millisecond
def Pwm(dutyCycle,totalTime):
trepeat=np.linspace(0, 1, 100)
squareWave=(5*sig.square(2 * np.pi * trepeat, duty=dutyCycle))
finalInput=np.zeros(len(totalTime))
for i in range(len(squareWave)):
if squareWave[i]<0:
squareWave[i]=0
for i in range(len(totalTime)):
finalInput[i]=squareWave[i%100]
return finalInput
pwm=Pwm(dutyCycle,t)
tPwmTheta, yPwmTheta, xPwmTheta = control.forced_response(tf_Theta_Vin, T=t, U=pwm, X0=0)
tPwmOmega, yPwmOmega, xPwmOmega = control.forced_response(tf_Omega_Vin, t, pwm, X0=0)
tPwmAlpha, yPwmAlpha, xPwmAlpha = control.forced_response(tf_Alpha_Vin, t, pwm, X0=0)
tPwmTorque, yPwmTorque, xPwmTorque = control.forced_response(tf_Torque_Vin, t, pwm, X0=0)
axs[0].plot(tPwmTheta, yPwmTheta, color = 'blue', label ='Theta')
axs[1].plot(tPwmOmega, yPwmOmega, color = 'red', label ='Omega')
axs[2].plot(tPwmAlpha, yPwmAlpha, color = 'black', label ='Alpha')
axs[3].plot(tPwmTorque, yPwmTorque, color = 'green', label ='Torque')
axs[0].title.set_text('Theta $(rad)$ (Input PWM)')
axs[1].title.set_text('Omega $(\\frac {rad}{ms})$ (Input PWM)')
axs[2].title.set_text('Alpha $(\\frac {rad}{ms^2})$ (Input PWM)')
axs[3].title.set_text('Torque $(Nm)$ (Input PWM)')
elif VinType== 0:
tStepTheta, yStepTheta = control.step_response(tf_Theta_Vin,T=t, X0=0)
tStepOmega, yStepOmega = control.step_response(tf_Omega_Vin,T=t, X0=0)
tStepAlpha, yStepAlpha = control.step_response(tf_Alpha_Vin,T=t, X0=0)
tStepTorque, yStepTorque = control.step_response(tf_Torque_Vin, T=t, X0=0)
axs[0].plot(tStepTheta, yStepTheta, color = 'blue', label ='Theta')
axs[1].plot(tStepOmega, yStepOmega, color = 'red', label ='Omega')
axs[2].plot(tStepAlpha, yStepAlpha, color = 'black', label ='Alpha')
axs[3].plot(tStepTorque, yStepTorque, color = 'green', label ='Torque')
axs[0].title.set_text('Theta $(rad)$ (Input Step)')
axs[1].title.set_text('Omega $(\\frac {rad}{ms})$ (Input Step)')
axs[2].title.set_text('Alpha $(\\frac {rad}{ms^2})$(Input Step)')
axs[3].title.set_text('Torque $(Nm)$ (Input Step)')
elif VinType== 1 :
tImpulseTheta, yImpulseTheta = control.impulse_response(tf_Theta_Vin,T=t, X0=0)
tImpulseOmega, yImpulseOmega = control.impulse_response(tf_Omega_Vin,T=t, X0=0)
tImpulseAlpha, yImpulseAlpha = control.impulse_response(tf_Alpha_Vin,T=t, X0=0)
tImpulseTorque, yImpulseTorque = control.impulse_response(tf_Torque_Vin, T=t, X0=0)
axs[0].plot(tImpulseTheta, yImpulseTheta, color = 'blue', label ='Theta')
axs[1].plot(tImpulseOmega, yImpulseOmega, color = 'red', label ='Omega')
axs[2].plot(tImpulseAlpha, yImpulseAlpha, color = 'black', label ='Alpha')
axs[3].plot(tImpulseTorque, yImpulseTorque, color = 'green', label ='Torque')
axs[0].title.set_text('Theta $(rad)$ (Input Impulse)')
axs[1].title.set_text('Omega $(\\frac {rad}{ms})$ (Input Impulse)')
axs[2].title.set_text('Alpha $(\\frac {rad}{ms^2})$ (Input Impulse)')
axs[3].title.set_text('Torque $(Nm)$ (Input Impulse)')
axs[0].legend()
axs[1].legend()
axs[2].legend()
axs[3].legend()
axs[0].grid(grid)
axs[1].grid(grid)
axs[2].grid(grid)
axs[3].grid(grid)
#DEFINISI WIDGETS PARAMETER
Ka_slider = widgets.FloatSlider(
value=19.90,
min=0.1,
max=20.0,
step=0.1,
description='$K_a (\\frac {Nm}{A})$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
Kmd_slider = widgets.FloatSlider(
value=20.0,
min=0.1,
max=20.0,
step=0.1,
description='$K_{md} (\\frac {V}{V})$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
L_slider = widgets.FloatSlider(
value=20,
min=0.1,
max=100.0,
step=0.1,
description='$L (mH)$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
R_slider = widgets.IntSlider(
value=5,
min=1,
max=20,
step=1,
description='$R (\Omega)$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
J_slider = widgets.FloatSlider(
value=25,
min=0.1,
max=100.0,
step=0.1,
description='$J (\\frac {Nm(ms)^2}{rad})$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
Kf_slider = widgets.FloatSlider(
value=8,
min=0.1,
max=100.0,
step=0.1,
description='$K_{f} (\\frac {Nm(ms)}{rad})$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
Kemf_slider = widgets.FloatSlider(
value=19.8,
min=0.1,
max=20,
step=0.1,
description='$K_{emf} (\\frac {V(ms)}{rad})$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
VinType_select = widgets.Dropdown(
options=[('Step', 0), ('Impulse', 1),('PWM',2)],
description='Tipe Sinyal Input:',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
tMax_slider = widgets.IntSlider(
value=50,
min=1,
max=500,
step=1,
description='$t_{max} (ms)$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
dutyCycle_slider = widgets.FloatSlider(
value=0.5,
min=0,
max=1.0,
step=0.05,
description='$Duty Cycle (\%)$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
grid_button = widgets.ToggleButton(
value=True,
description='Grid',
icon='check',
layout=Layout(width='20%', height='50px',margin='10px 10px 10px 350px'),
style={'description_width': '200px'},
)
def update_Kemf_max(*args):
Kemf_slider.max = Ka_slider.value
Ka_slider.observe(update_Kemf_max, 'value')
ui_em = widgets.VBox([Ka_slider,Kmd_slider,L_slider,R_slider,J_slider,Kf_slider,Kemf_slider,VinType_select,tMax_slider,dutyCycle_slider,grid_button])
out_em = widgets.interactive_output(plot_elektromekanik, {'Ka':Ka_slider,'Kmd':Kmd_slider,'L':L_slider,'R':R_slider,'J':J_slider,'Kf':Kf_slider,'Kemf':Kemf_slider,'VinType':VinType_select,'tMax':tMax_slider,'dutyCycle':dutyCycle_slider, 'grid':grid_button})
display(ui_em,out_em)
```
### Analisis
Karena model memiliki persamaan yang cukup kompleks sehingga tidak dapat diambil secara intuitive kesimpulan parameter terhadap output sistem, akan dilakukan percobaan menggunakan slider untuk mengubah parameter dan mengamati interaksi perubahan antara parameter. Akan dilakukan juga perubahan bentuk input dan analisa efek penggunaan PWM sebagai modulasi sinyal step dengan besar maksimum 5V terhadap output.
#### 1. Peningkatan $K_a$
Peningkatan $K_a$ menyebabkan peningkatan osilasi ($\omega_d$) dan meningkatkan gain pada output $\omega$ dan $\alpha$ serta meningkatkan gradien dari output $\theta$. Namun, gain Torque tidak terpengaruh.
#### 2. Peningkatan $K_{md}$
Peningkatan $K_{md}$ membuat amplitudo $V_{in}$ meningkat sehingga amplitudo output bertambah.
#### 3. Peningkatan $L$
Peningkatan $L$ menyebabkan peningkatan kecepatan sudut $\omega$ dan $T$ menjadi lebih lambat serta penurunan $\alpha$ yang semakin lambat sehingga menyebabkan peningkatan $\theta$ semakin lambat (peningkatan rise time).
#### 4. Peningkatan $R$
Peningkatan $R$ menyebabkan osilasi output ($\omega_d$) $\omega$, $\alpha$, dan Torque semakin kecil dan gain yang semakin kecil sehingga mengurangi gradien dari output $\theta$.
#### 5. Peningkatan $J$
Peningkatan $J$ meningkatkan gain Torque dan menurunkan gain $\theta$, $\omega$, dan $\alpha$.
#### 6. Peningkatan $K_f$
Peningkatan $K_f$ meningkatkan gain Torque dan menurunkan gain $\theta$, $\omega$, dan $\alpha$.
#### 7. Peningkatan $K_{emf}$
Peningkatan $K_{emf}$ menurunkan gain Torque, $\theta$, $\omega$, dan $\alpha$.
#### 8. Interaksi antar parameter
Perbandingan pengurangan $R$ dibanding peningkatan $K_a$ kira kira 3 kali lipat. Peningkatan pada $J$ dan $K_f$ terbatas pada peningkatan $K_a$. Secara fisis, peningkatan $K_a$ dan $K_{emf}$ terjadi secara bersamaan dan hampir sebanding (hanya dibedakan pada voltage drop pada berbagai komponen), diikuti oleh $L$ sehingga untuk $K_a$ dan $K_{emf}$ besar, waktu mencapai steady state juga semakin lama. Hal yang menarik adalah $K_a$ dan $K_{emf}$ membuat sistem memiliki gain (transfer energi) yang kecil jika hanya ditinjau dari peningkatan nilai $K_a$ dan $K_{emf}$, namun ketika diikuti peningkatan $V_{in}$ sistem memiliki transfer energi yang lebih besar daripada sebelumnya pada keadaan steady state. Jadi dapat disimpulkan bahwa $K_a$ dan $K_{emf}$ harus memiliki nilai yang cukup besar agar konfigurasi sesuai dengan input $V_{in}$ dan menghasilkan transfer energi yang efisien. Input $V_{in}$ juga harus sesuai dengan sistem $K_a$ dan $K_{emf}$ yang ada sehingga dapat memutar motor (ini mengapa terdapat voltage minimum dan voltage yang disarankan untuk menjalankan sebuah motor).
#### 9. Pengaruh Input Step
Penggunaan input step memiliki osilasi ($\omega_d$) semakin sedikit.
#### 10. Pengaruh Input Impuls
Penggunaan input impulse membuat $\theta$ mencapai steady state karena motor berhenti berputar sehingga $\omega$,$\alpha$, dan Torque memiliki nilai steady state 0.
#### 11. Pengaruh Input PWM
Penggunaan input PWM dengan duty cycle tertentu membuat osilasi yang semakin banyak, namun dengan peningkatan duty cycle, osilasi semakin sedikit (semakin mendekati sinyal step). Hal yang menarik disini adalah sinyal PWM dapat digunakan untuk mengontrol, tetapi ketika tidak digunakan pengontrol, sinyal PWM malah memberikan osilasi pada sistem.
## 3. Pemodelan Sistem Mekanik
Dimodelkan sistem mekanik sebagai berikut
<img src="./10.png" style="width:20%">
<p style="text-align: center"><b>Sistem Mekanik Sederhana dengan Bond Graph</b></p>
### Deskripsi Sistem
1. Input
$F$ sebagai gaya yang dikerjakan pada massa
2. Output
$x$ sebagai perpindahan, $v$ sebagai kecepatan, dan $a$ sebagai percepatan pada massa
3. Parameter
Dari penurunan bond graph, didapatkan parameter $k$, $b$, dan $m$
### Pemodean Transfer Function
Fungsi transfer dapat dengan mudah di turunkan dari hubungan bond graph, diasumsikan
$$
x(0)=0
$$
$$
v(0)=0
$$
$$
a(0)=0
$$
$$
m \frac {d^2 x}{dt^2} = F-kx-b\frac{dx}{dt}
$$
<br>
Transformasi laplace menghasilkan
<br>
$$
s^2 x = \frac {F}{m}-x\frac {k}{m}-sx\frac{b}{m}
$$
$$
(s^2+s\frac{b}{m}+\frac {k}{m})x=\frac {F}{m}
$$
<br>
Untuk x:
<br>
$$
\frac {x}{F}=\frac {1}{(ms^2+bs+k)}
$$
<br>
Untuk v:
<br>
$$
\frac {v}{F}=\frac {s}{(ms^2+bs+k)}
$$
<br>
Untuk a:
<br>
$$
\frac {a}{F}=\frac {s^2}{(ms^2+bs+k)}
$$
```
# Digunakan penyelesaian numerik untuk output
import numpy as np
from scipy.integrate import odeint
import scipy.signal as sig
import matplotlib.pyplot as plt
from sympy.physics.mechanics import dynamicsymbols, SymbolicSystem
from sympy import *
import control as control
def plot_mekanik(M,B,K,VinType,grid):
# Parameter diberi value dan model system dibentuk dalam transfer function yang dapat diolah python
m=M
b=B
k=K
tf = sig.TransferFunction
tf_X_F=tf([1],[m,b,k])
tf_V_F=tf([1,0],[m,b,k])
tf_A_F=tf([1,0,0],[m,b,k])
f, axs = plt.subplots(3, sharex=True, figsize=(10, 10))
if VinType==0:
tImpX,xOutImp=sig.impulse(tf_X_F)
tImpV,vOutImp=sig.impulse(tf_V_F)
tImpA,aOutImp=sig.impulse(tf_A_F)
axs[0].plot(tImpX,xOutImp, color = 'blue', label ='x')
axs[1].plot(tImpV,vOutImp, color = 'red', label ='v')
axs[2].plot(tImpA,aOutImp, color = 'green', label ='a')
axs[0].title.set_text('Perpindahan Linear $(m)$ (Input Impuls)')
axs[1].title.set_text('Kecepatan Linear $(\\frac {m}{s})$ (Input Impuls)')
axs[2].title.set_text('Percepatan Linear $(\\frac {m}{s^2})$ (Input Impuls)')
elif VinType==1:
tStepX,xOutStep=sig.step(tf_X_F)
tStepV,vOutStep=sig.step(tf_V_F)
tStepA,aOutStep=sig.step(tf_A_F)
axs[0].plot(tStepX,xOutStep, color = 'blue', label ='x')
axs[1].plot(tStepV,vOutStep, color = 'red', label ='v')
axs[2].plot(tStepA,aOutStep, color = 'green', label ='a')
axs[0].title.set_text('Perpindahan Linear $(m)$ (Input Step)')
axs[1].title.set_text('Kecepatan Linear $(\\frac {m}{s})$ (Input Step)')
axs[2].title.set_text('Percepatan Linear $(\\frac {m}{s^2})$ (Input Step)')
axs[0].legend()
axs[1].legend()
axs[2].legend()
axs[0].grid(grid)
axs[1].grid(grid)
axs[2].grid(grid)
M_slider = widgets.FloatSlider(
value=0.1,
min=0.1,
max=30.0,
step=0.1,
description='Massa $(kg)$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
B_slider = widgets.FloatSlider(
value=0.1,
min=2,
max=20.0,
step=0.1,
description='Konstanta Redaman $(\\frac {Ns}{m})$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
K_slider = widgets.FloatSlider(
value=0.1,
min=0.1,
max=100.0,
step=0.1,
description='Konstanta pegas $(\\frac {N}{m})$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
VinType_select = widgets.Dropdown(
options=[('Impulse', 0), ('Step', 1)],
description='Tipe Sinyal Input:',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
grid_button = widgets.ToggleButton(
value=True,
description='Grid',
icon='check',
layout=Layout(width='20%', height='50px',margin='10px 10px 10px 350px'),
style={'description_width': '200px'},
)
ui_mk = widgets.VBox([M_slider,B_slider,K_slider,VinType_select,grid_button])
out_mk = widgets.interactive_output(plot_mekanik, {'M':M_slider,'B':B_slider,'K':K_slider,'VinType':VinType_select,'grid':grid_button})
display(ui_mk,out_mk)
```
### Analisis
Berdasarkan persamaan yang cukup sederhana, sistem mekanik orde dua memiliki karakteristik berikut:
#### 1. Pengaruh peningkatan massa
Massa pada sistem berperilaku seperti komponen inersial yang meningkatkan rise time dan settling time ketika diperbesar.
#### 2. Pengaruh peningkatan konstanta redaman
Konstanta redaman berperilaku seperti komponen hambatan yang meredam sistem sehingga maximum overshoot menjadi kecil (akibat peningkatan damping ratio) ketika peningkatan konstanta redaman terjadi. Konstanta redaman juga berpengaruh pada settling time, dimana peningkatan konstanta redaman meningkatkan settling time.
#### 3. Pengaruh peningkatan konstanta pegas
Konstanta pegas berperilaku seperti komponen kapasitansi yang mengurangi besar gain dari perpindahan, mengurangi damping ratio, meningkatkan frekuensi osilasi sistem, mengurangi amplitudo kecepatan sistem, mempercepat settling time, dan mempercepat peak time, meningkatkan maximum overshoot.
#### 4. Respon terhadap impulse
Terhadap sinyal impulse, sistem mencapai posisi awal kembali dan mencapai steady state 0 untuk perpindahan, kecepatan, dan percepatan
#### 5. Respon terhadap step
Terhadap sinyal step, sistem mencapai posisi akhir sesuai
$$\frac {F}{k}$$
dan kecepatan serta percepatan 0
|
github_jupyter
|
```
# Dependencies and Setup
import pandas as pd
# File to Load
school_data_to_load = "Resources/schools_complete.csv"
student_data_to_load = "Resources/students_complete.csv"
# Read School and Student Data File and store into Pandas Data Frames
school_data = pd.read_csv(school_data_to_load)
student_data = pd.read_csv(student_data_to_load)
# Combine the data into a single dataset
school_data_complete = pd.merge(student_data, school_data, how="left", on=["school_name", "school_name"])
school_data_complete
```
#District Summary
Calculate the total number of schools
Calculate the total number of students
Calculate the total budget
Calculate the average math score
Calculate the average reading score
Calculate the overall passing rate (overall average score), i.e. (avg. math score + avg. reading score)/2
Calculate the percentage of students with a passing math score (70 or greater)
Calculate the percentage of students with a passing reading score (70 or greater)
Create a dataframe to hold the above results
Optional: give the displayed data cleaner formatting
```
total_number_schools = len(school_data_complete["School ID"].unique())
total_number_schools
#Calculate the total number of students
total_number_students = len(school_data_complete["Student ID"].unique())
total_number_students
#Calculate the total budget
total_budget = school_data["budget"].sum()
total_budget
#Calculate the average math score
average_math_score = student_data["math_score"].mean()
average_math_score
#Calculate the average reading score
average_reading_score = student_data["reading_score"].mean()
average_reading_score
#Calculate the overall passing rate (overall average score), i.e. (avg. math score + avg. reading score)/2
overall_average_score = (average_math_score + average_reading_score)/2
overall_average_score
#Calculate the percentage of students with a passing math score (70 or greater)
#Create 1s for the passing students by math or reading. 0 otherwise. And take the mean to get the average. It will give the percent of the passing students.
student_data["#passing_math"] = student_data["math_score"] >= 70
student_data["#passing_reading"] = student_data["reading_score"] >= 70
percent_passing_math = ((student_data["#passing_math"]).mean())*100
percent_passing_math
#Calculate the percentage of students with a passing reading score (70 or greater)
percent_passing_reading = ((student_data["#passing_reading"]).mean())*100
percent_passing_reading
#Calculate overall percentage
overall_passing_rate = (percent_passing_math + percent_passing_reading)/2
overall_passing_rate
#Create a dataframe to hold the above results
#Optional: give the displayed data cleaner formatting
district_results = [{"Total Schools": total_number_schools,
"Total Students": total_number_students,
"Total Budget": total_budget,
"Average Math Score": round(average_math_score,2),
"Average Reading Score": round(average_reading_score,2),
"% Passing Math": round(percent_passing_math,2),
"% Passing Reading": round(percent_passing_reading,2),
"% Overall Passing Rate": round(overall_passing_rate,2)}]
district_summary_table = pd.DataFrame(district_results)
#Formatting
district_summary_table["% Passing Math"] = district_summary_table["% Passing Math"].map("{:,.2f}%".format)
district_summary_table["% Passing Reading"] = district_summary_table["% Passing Reading"].map("{:,.2f}%".format)
district_summary_table["% Overall Passing Rate"] = district_summary_table["% Overall Passing Rate"].map("{:,.2f}%".format)
district_summary_table["Total Budget"] = district_summary_table["Total Budget"].map("${:,.2f}".format)
district_summary_table["Total Students"] = district_summary_table["Total Students"].map("{:,}".format)
#Display
district_summary_table
```
#School Summary
Create an overview table that summarizes key metrics about each school, including:
School Name
School Type
Total Students
Total School Budget
Per Student Budget
Average Math Score
Average Reading Score
% Passing Math
% Passing Reading
Overall Passing Rate (Average of the above two)
Create a dataframe to hold the above results
```
#For this part, school_data_complete
school_data_complete["passing_math"] = school_data_complete["math_score"] >= 70
school_data_complete["passing_reading"] = school_data_complete["reading_score"] >= 70
school_data_complete
# Use groupby by school_name
school_group = school_data_complete.groupby(["school_name"]).mean()
school_group["Per Student Budget"] = school_group["budget"]/school_group["size"]
school_group["% Passing Math"] = round(school_group["passing_math"]*100,2)
school_group["% Passing Reading"] = round(school_group["passing_reading"]*100,2)
school_group["% Overall Passing Rate"] = round(((school_group["passing_math"] + school_group["passing_reading"])/2)*100,3)
#Merge with school_data to collect information about the type, size and budget
school_data_summary = pd.merge(school_group, school_data, how="left", on=["school_name", "school_name"])
del school_data_summary['size_y']
del school_data_summary['budget_y']
del school_data_summary['Student ID']
del school_data_summary['School ID_x']
#Create a dataframe to store the results
school_summary_dataframe = pd.DataFrame({"School Name": school_data_summary["school_name"],
"School Type": school_data_summary["type"],
"Total Students":school_data_summary["size_x"],
"Total School Budget": school_data_summary["budget_x"],
"Per Student Budget":school_data_summary["Per Student Budget"],
"Average Math Score":round(school_data_summary["math_score"],2),
"Average Reading Score":round(school_data_summary["reading_score"],2),
"% Passing Math": school_data_summary["% Passing Math"],
"% Passing Reading": school_data_summary["% Passing Reading"],
"% Overall Passing Rate": school_data_summary["% Overall Passing Rate"]})
#Formatting
school_summary_dataframe["Total Students"] = school_summary_dataframe["Total Students"].map("{:,.0f}".format)
school_summary_dataframe["Total School Budget"] = school_summary_dataframe["Total School Budget"].map("${:,.2f}".format)
school_summary_dataframe["Per Student Budget"] = school_summary_dataframe["Per Student Budget"].map("${:,.2f}".format)
#Display
school_summary_dataframe
```
#Top Performing Schools (By Passing Rate)
Sort and display the top five schools in overall passing rate
```
#Sort and display the top five schools in overall passing rate
top_five_schools = school_summary_dataframe.sort_values(["% Overall Passing Rate"], ascending=False)
top_five_schools.head()
```
#Bottom Performing Schools (By Passing Rate)¶
Sort and display the five worst-performing schools
```
#Sort and display the five worst-performing schools
bottom_five_schools = school_summary_dataframe.sort_values(["% Overall Passing Rate"], ascending=True)
bottom_five_schools.head()
```
#Math Scores by Grade
Create a table that lists the average Reading Score for students of each grade level (9th, 10th, 11th, 12th) at each school.
Create a pandas series for each grade. Hint: use a conditional statement.
Group each series by school
Combine the series into a dataframe
Optional: give the displayed data cleaner formatting
```
#Create a pandas series for each grade. Group each series by school.
nineth_grade= school_data_complete[school_data_complete["grade"] == "9th"].groupby("school_name").mean()["math_score"]
tenth_grade = school_data_complete[school_data_complete["grade"] == "10th"].groupby("school_name").mean()["math_score"]
eleventh_grade = school_data_complete[school_data_complete["grade"] == "11th"].groupby("school_name").mean()["math_score"]
twelveth_grade= school_data_complete[school_data_complete["grade"] == "12th"].groupby("school_name").mean()["math_score"]
#Combine the series into a dataframe
math_grade_dataframe = pd.DataFrame({"Ninth Grade":nineth_grade, "Tenth Grade":tenth_grade,
"Eleventh Grade":eleventh_grade, "Twelveth Grade":twelveth_grade})
#Optional formatting: Give the displayed data cleaner formatting
math_grade_dataframe[["Ninth Grade","Tenth Grade","Eleventh Grade","Twelveth Grade"]] = math_grade_dataframe[["Ninth Grade","Tenth Grade","Eleventh Grade","Twelveth Grade"]].applymap("{:.2f}".format)
#Display
math_grade_dataframe
```
#Reading Score by Grade
Perform the same operations as above for reading scores
```
#Perform the same operations as above for reading scores
#Create a pandas series for each grade. Group each series by school.
nineth_grade= school_data_complete[school_data_complete["grade"] == "9th"].groupby("school_name").mean()["reading_score"]
tenth_grade = school_data_complete[school_data_complete["grade"] == "10th"].groupby("school_name").mean()["reading_score"]
eleventh_grade = school_data_complete[school_data_complete["grade"] == "11th"].groupby("school_name").mean()["reading_score"]
twelveth_grade= school_data_complete[school_data_complete["grade"] == "12th"].groupby("school_name").mean()["reading_score"]
#Combine the series into a dataframe
reading_grade_dataframe = pd.DataFrame({"Ninth Grade":nineth_grade, "Tenth Grade":tenth_grade,
"Eleventh Grade":eleventh_grade, "Twelveth Grade":twelveth_grade})
#Optional formatting: Give the displayed data cleaner formatting
reading_grade_dataframe[["Ninth Grade","Tenth Grade","Eleventh Grade","Twelveth Grade"]] = reading_grade_dataframe[["Ninth Grade","Tenth Grade","Eleventh Grade","Twelveth Grade"]].applymap("{:.2f}".format)
#Display
reading_grade_dataframe
```
#Scores by School Spending
Create a table that breaks down school performances based on average Spending Ranges (Per Student). Use 4 reasonable bins to group school spending. Include in the table each of the following:
Average Math Score
Average Reading Score
% Passing Math
% Passing Reading
Overall Passing Rate (Average of the above two)
```
# Sample bins. Feel free to create your own bins.
spending_bins = [0, 585, 615, 645, 675]
group_names = ["<$585", "$585-615", "$615-645", "$645-675"]
# Use 4 reasonable bins to group school spending.
school_data_summary["Spending Ranges (Per Student)"] = pd.cut(school_data_summary["Per Student Budget"], spending_bins, labels=group_names)
school_spending_grouped = school_data_summary.groupby("Spending Ranges (Per Student)").mean()
#Remove the unwanted columns as per the sample provided
del school_spending_grouped['size_x']
del school_spending_grouped['budget_x']
del school_spending_grouped['Per Student Budget']
del school_spending_grouped['School ID_y']
del school_spending_grouped['passing_math']
del school_spending_grouped['passing_reading']
school_spending_grouped
```
#Scores by School Size¶
Perform the same operations as above, based on school size.
```
# Sample bins. Feel free to create your own bins.
size_bins = [0, 1000, 2000, 5000]
group_names = ["Small (<1000)", "Medium (1000-2000)", "Large (2000-5000)"]
# Use 4 reasonable bins to group school size.
school_data_summary["School Size"] = pd.cut(school_data_summary["size_x"], size_bins, labels=group_names)
school_data_summary
#group by size_x
school_size_grouped = school_data_summary.groupby("School Size").mean()
school_size_grouped
#Remove the unwanted columns as per the sample provided
#del school_size_grouped['size_x']
del school_size_grouped['budget_x']
del school_size_grouped['Per Student Budget']
del school_size_grouped['School ID_y']
del school_size_grouped['passing_math']
del school_size_grouped['passing_reading']
#Display
school_size_grouped
```
#Scores by School Type
Perform the same operations as above, based on school type.
```
school_type_grouped = school_data_summary.groupby("type").mean()
#Remove the unwanted columns as per the sample provided
del school_type_grouped['size_x']
del school_type_grouped['budget_x']
del school_type_grouped['Per Student Budget']
del school_type_grouped['School ID_y']
del school_type_grouped['passing_math']
del school_type_grouped['passing_reading']
school_type_grouped
```
#You must include a written description of at least two observable trends based on the data
|
github_jupyter
|
# Convolution_with_fastai
> 2021-10-26
- toc: true
- badges: true
- comments: false
- categories: bigdata
- image: images/chart-preview.png
- hide: true
```
import torch
from fastai.vision.all import *
```
#### data
```
path = untar_data(URLs.MNIST_SAMPLE)
path.ls()
```
`-` list 형태로 목록 받기
```
threes = (path/'train'/'3').ls()
sevens = (path/'train'/'7').ls()
```
`-` list $\to$ image
```
Image.open(threes[0])
```
`-` image $\to$ tensor
```
tensor(Image.open(threes[0]))
```
`*` 여기서 tensor는 pytorch에 있는 tensor가 아닌, fastai에 있는 tensor이다. `*` , 만약 pytorch의 tensor였다면 torch.tensor로 사용했을 것이다.
torch.tensor는 이미지파일을 텐서로 변환하는 기능이 없다.
```
# plt.imshow(tensor(Image.open(threes[0]))) 변환한 텐서로 이미지 출력
#[tensor(Image.open(i)) for i in sevens] # tensor들이 list로 바뀌어있다. 현재 이 상태는 것이 list 안이 tensor로, 좀 더 깔끔하게 만들면
#torch.stack([tensor(Image.open(i)) for i in sevens]) # tensor안의 값들은 float여야 하므로
seven_tensor = torch.stack([tensor(Image.open(i)) for i in sevens]).float()
three_tensor = torch.stack([tensor(Image.open(i)) for i in threes]).float()
seven_tensor = torch.stack([tensor(Image.open(i)) for i in sevens]).float()/255
three_tensor = torch.stack([tensor(Image.open(i)) for i in threes]).float()/255
seven_tensor.shape, three_tensor.shape
y = torch.tensor([0.]*6265 + [1.]*6131).reshape(12396,1) # 3인지 7인지 정답 label을 0, 1로 만듬
```
`-` 데이터인 X는 seven_tensor와 three_tensor를 합친다. (vstack 으로)
```
X = torch.vstack([seven_tensor, three_tensor])
X = X.reshape(12396,-1)
X.shape
X.shape
X = X.reshape(12396,1,28,28)
```
### 1. 지난시간까지 모형 (네트워크 직접 설계, pytorch)
#### 선형변환 대신에 2D Convolution with Window_size = 5
- 인자를 보면 in-channels, out-channels, 그리고 kernel-size가 있다.<br/>
이 세 개를 넣어야 한다.
```
c1 = torch.nn.Conv2d(1,16,5) # 입력채널 = 1, 출력 채널 = 16, window_size = 5
```
#### NonLinear를 위해서, ReLU()대신 MaxPool2d + ReLU 를 함, MaxPooling을 하나 걸침
```
m1 = torch.nn.MaxPool2d(2)
```
### ReLU()
```
a1 = torch.nn.ReLU()
X.shape, c1(X).shape, m1(c1(X)).shape, a1(m1(c1(X))).shape
```
### Flatten
```
class Flatten(torch.nn.Module): # Module 상속
def forward(self,x):
return x.reshape(12396,-1)
```
- a1을 거쳐서 들어온 것을 a1(m1(c1(X))).reshape(12396,-1) 이렇게 바꿔주어야 한다.
```
flatten = Flatten()
X.shape, c1(X).shape, m1(c1(X)).shape, a1(m1(c1(X))).shape, flatten(a1(m1(c1(X)))).shape
```
#### linear
```
l1 = torch.nn.Linear(in_features=2304, out_features=1)
X.shape, c1(X).shape, \
m1(c1(X)).shape, \
a1(m1(c1(X))).shape, \
flatten(a1(m1(c1(X)))).shape, \
l1(flatten(a1(m1(c1(X))))).shape
plt.plot(l1(flatten(a1(m1(c1(X))))).data)
```
- 학습이 안된상태
```
net = torch.nn.Sequential(
c1, # Convolution(선형)
m1, # MaxPooling(비선형)
a1, # RelU(비선형)
flatten,
l1)
```
`-` 손실함수와 옵티마이저 정의
```
loss_fn = torch.nn.BCEWithLogitsLoss()
optimizer = torch.optim.Adam(net.parameters())
```
`-` step 1~4
```
for epoc in range(200):
# 1
yhat = net(X)
# 2
loss = loss_fn(yhat,y)
# 3
loss.backward()
# 4
optimizer.step()
net.zero_grad()
a2 = torch.nn.Sigmoid()
plt.plot(y)
plt.plot(a2(yhat.data),'.') # 마지막 sigmoid를 취한 버전
ypred = a2(yhat.data)>0.5
sum(ypred == y) / 12396
```
### 2. 드랍아웃, 배치추가 (직접네트워크 설계, pytorch + fastai)
#### step1 : dls를 만들자
```
ds = torch.utils.data.TensorDataset(X,y)
ds.tensors[0].shape #이미지 자체가 들어간 것, 784개 벡터로 늘려지는게 아니라
```
`-` training, validation 분리
```
ds1, ds2 = torch.utils.data.random_split(ds,[10000,2396]) # training을 10000개, validation을 2396개로 ds로부터 랜덤하게 나눔
dl1 = torch.utils.data.DataLoader(ds1, batch_size=500) # DataLoader는 batch size를 정할 수 있다. -> 총 1만개 에서 500개를 나누므로, for문 한 번당 20번 돌아감
dl2 = torch.utils.data.DataLoader(ds2, batch_size=2396) # 여기선 딱히 batch를 나누지 않았다.
```
`-` dataloader를 만들었으니 이제 DataLoaders를 만들어야 한다. ( 여태 pytorch로 작업한 것이였고 여기부터는 fastai로 작업한다. )
```
dls = DataLoaders(dl1,dl2)
```
- 여기까지 한 것이 데이터 정리TensorDataset
#### step2: 아키텍처, 손실함수, 옵티마이저
```
class Flatten(torch.nn.Module): # Module 상속
def forward(self,x):
return x.reshape(x.shape[0],-1)
net = torch.nn.Sequential(
torch.nn.Conv2d(1,16,5),
torch.nn.MaxPool2d(2),
torch.nn.ReLU(),
torch.nn.Dropout2d(),
Flatten(),
torch.nn.Linear(2304,1)
)
loss_fn = torch.nn.BCEWithLogitsLoss()
# optimizer = torch.optim.Adam(net.parameters()) learner에서 옵션으로 넣기 때문에 여기선 딱히 정의하지 않음, (loss도 옵션으로 넣을 순 있는데 일단 두가지 경우 모두 보기 위함)
```
#### step3: lrnr 생성
`-` Learner 클래스에서 learner instance 생성
```
lrnr1 = Learner(dls, net, opt_func=Adam, loss_func=loss_fn)
```
- 이것의 역할:
1. for 문 돌리면서 step 1~4 하던 것을 자동으로 해주는 역할
2. batch를 dls가 알아서 나눠줌
3. gpu에 자동으로 올려줌
`-` 우리가 할 일은 for문을 몇 번 돌려줄지 결정하는 것
```
lrnr1.fit(10)
```
`-` GPU에 올린 것을 알아둬야 한다. 이는 Shape와 같이 자주 신경써야 하는 부분이다.
`-` 현재 networks의 parameter가 GPU에 올라가있기 때문에, 데이터 X도 GPU에 올려서 계산을 한다(아니면 parameter를 CPU로 내려도 되는데 계산속도가 GPU보다 느릴 것으로 예상된다)
```
# net(X.to("cuda:0")).to("cpu").data
```
- 다시 그림을 그리는 plot 을 사용하려면 계산한 결과를 cpu로 내려서 그려야 한다.
```
plt.plot(net(X.to("cuda:0")).to("cpu").data,'.')
plt.plot(a2(net(X.to("cuda:0")).to("cpu").data),'.')
```
- Sigmoid 적용
`-` 빠르고 적합 결과도 좋음
### 3. resnet34 사용 (기존의 네트워크 사용, 순수 fastai)
`-` 데이터로부터 새로운 데이터로더스를 만들고 이를 dls2라 한다.
```
path = untar_data(URLs.MNIST_SAMPLE)
path
path.ls()
```
- 여기서 train부분의 폴더에 접근해서 사용할 것이다.
```
dls2 = ImageDataLoaders.from_folder(
path,
train = 'train',
valid_pct = 0.2
)
```
`-` Learner를 CNN전용으로 만들어 둔 것이 있다.
`-` learn오브젝트를 생성하고 학습
```
lrnr2 = cnn_learner(dls2, resnet34, metrics = error_rate)
lrnr2.fine_tune(1)
```
`-` 결과 관찰
```
lrnr2.show_results()
```
### 모형을 뜯어보는 방법 (lrnr1)
`-` 우선 방법 2로 돌아가자
`-` 네트워크 구조
```
net
```
`-` 인덱싱을 통하여 각각의 layer에 적용할 수 있다.
```
net[0]
```
- c1 = net[0] (torch.nn.Conv2d)에 해당하는 형태이다.
```
net.to("cpu")
```
- 먼저 GPU 성능 문제로 인한 에러때문에 net을 cpu로 옮겼다.
`-` 각각의 layer에서의 중간 결과를 가로챌 수 있다. <br/>
`-` 층별 변환과정
```
print(X.shape, '-> Input Image')
print(net[0](X).shape, '-> Conv2D')
print(net[1](net[0](X)).shape, '-> MaxPool2D')
print(net[2](net[1](net[0](X))).shape, '-> ReLU')
print(net[3](net[2](net[1](net[0](X)))).shape, '-> DropOut2D')
print(net[4](net[3](net[2](net[1](net[0](X))))).shape, '-> Flatten')
print(net[5](net[4](net[3](net[2](net[1](net[0](X)))))).shape, '-> Linear')
```
- 중간의 각각 layer들을 연속해서 적용한 결과, 실제 network 전체에 대입한(연속적인 계산) 결과와 동일한 결과를 얻는다.
`-` 두 결과가 일치하는지 확인
```
print(net(X))
print(net[5](net[4](net[3](net[2](net[1](net[0](X)))))))
```
- 일치한다.
`-` lrnr1 자체를 활용해도 층별변환과정을 추적함 lrnr1 = net임
```
lrnr1.model
```
- net과 동일한 결과
`-` net과 동일한 신경망으로의 입력 및 출력, 층별 가로채기
```
lrnr1.model(X)
lrnr1.model[0](X)
```
- net과 동일한 결과이다.
`-` 위의 net부분에서 층별 변환과정을 lrnr1으로 하려면, net을 lrnr1.model으로 바꾸면 된다.
```
print(X.shape, '-> 입력')
print(lrnr1.model[0](X).shape, '-> Conv2D')
print(lrnr1.model[1](lrnr1.model[0](X)).shape, '-> MaxPool2D')
'''
...
'''
print(lrnr1.model[5](lrnr1.model[4](lrnr1.model[3](lrnr1.model[2](lrnr1.model[1](lrnr1.model[0](X)))))).shape, '-> Linear')
```
`-` 정리: 모형은 항상 아래와 같이 2d-part와 1d-part로 나뉜다.
```
torch.Size([12396, 1, 28, 28]) -> Input Image
torch.Size([12396, 16, 24, 24]) -> Conv2D
torch.Size([12396, 16, 12, 12]) -> MaxPool2D
torch.Size([12396, 16, 12, 12]) -> ReLU
torch.Size([12396, 16, 12, 12]) -> DropOut2D
===================================================
torch.Size([12396, 2304]) -> Flatten
torch.Size([12396, 1]) -> Linear
```
`-` 2d-part:
- 2d 선형변환: torch.nn.Conv2d()
- 2d 비선형변환: torch.nn.MaxPool2d(), torch.nn.ReLU()
`-` 1d-part:
- 1d 선형변환: torch.nn.Linear()
- 1d 비선형변환: torch.nn.ReLU()
`-` **또 다른 정리법** -> 이는 좀 더 계층적인 정리방법이다.
```
_net1 = torch.nn.Sequential(
net[0],
net[1],
net[2],
net[3]
)
_net2 = torch.nn.Sequential(
net[4],
net[5]
)
_net1
_net2
_net = torch.nn.Sequential(_net1, _net2)
_net
```
- 2d part와 1d part로 나누었다
```
_net[0]
_net[0](X)
```
- 위의 _net$[$0$]$(X)의 결과는 2D part의 결과를 의미한다.
### lrnr2.model (resnet34) 분석
```
lrnr2.model
```
- 여기서 크게 (0) Sequential part와 (1) Sequential part로 나뉘었음을 알 수 있다. <br/>
이는 각각 2d 와 1d part를 의미한다.
`-` 2d part
```
lrnr2.model[0]
```
`-` 1d part
```
lrnr2.model[1]
```
#### 1d part 살펴보기
먼저 이미지를 받아서 Pooling을 하는데, AveragePooling이랑 MaxPooling이라는 것을 함 (Adaptive는 잘 모르겠음)<br/>
그리고 Flatten()으로 펼쳐줌 (우리가 정의한 Flatten이 아님)<br/>
펼친 layer의 차원이 1024임을 알 수 있음. 그리고 batch normalization이라는 것이 진행이 됨<br/>
Linear Transform으로 1024를 512로 한 번 줄여줌<br/>
그리고 ReLU하고 다시 Batch normarlization, Dropout, Linear를 반복한다는 것
`-` 주목할 만한 점은, BatchNormalization이라는 것(이것도 Dropout 처럼 과적합을 피하기 위한 것으로 dropout과 같이 많이 사용됨)과 출력의 차원이 2라는 점이다.
**2d part 간략하게 살펴보기**
`-` 아래 모형은 현재 가장 성능이 좋은 모형(state of the art)중 하나인 resnet이다.
```
lrnr2.model[0]
```
크게 주목할만한 점: <br/>
1. Batch Normalization이 중간중간에 들어가 있다는 것.<br/>
2. 2D version의 Dropout이 없다는 것
3. Conv2d에 더 많은 argument (padding/ stride)들을 사용
4. Conv2d의 입력채널이 3원색이라서 3차원 채널인 점
`-` 입력채널이 3이라는 점 때문에 lrnr2에서 dls를 그대로 사용하면 안되고, dls2를 따로 만든 것이다.<br/>
우리가 전에 만든 net은 입력채널이 1이였음, 그런데 resnet은 3이라서 그에 맞게 데이터를 다시 정리해줘야됨
`-` DLS, networks
- 네트워크 형태에 따라서 dls의 형태도 다르게 만들어야 한다.
- MLP 모형: 입력이 $784$, 첫 네트워크의 형태가 $ 784 \to 30$ 인 torch.nn.Linear()
- CNN 모형: 입력이 $1 \times 28 \times 28$, 첫 네트워크 형태가 $ 1 \times 28 \times 28 \to 16 \times 24 \times 24$ 인 torch.nn.Conv2d()
- resnet34 모형: 입력이 $3 \times 28 \times 28$, 첫 네트워크 형태가 $ 3 \times 28 \times 28 \to ??$
데이터 만들기:
1. x,y 각각 정의
2. x,y를 tuple로 묶어서 dataset 생성
3. dataset을 training, validaiton으로 분리
4. 각각의 분리한 dataset으로 dataloader라는 것을 만듬 -> dataloader가 하는 역할은 batch 버전을 제공(for문을돌릴 때, x와 y를 적당한 size로 묶어서 내보내는 역할을 함, 매 iteration마다 랜덤으로 섞어서 내보냄, 그러한 것들을 편리하게 수행해줌)
5. train, val loader를 묶어서 dataloaders 까지 만들어야 fastai에 넣고 돌리기가 가능
이 때 입력되는 데이터는 벡터든 28 * 28의 matrix 형태의 이미지든 다 됨, 그래서 이걸 최적화해서 알아서 맞춰주는게 아니라 우리가 networks에 맞춰서 직접 설정해줘야됨
`-` 2D part에서 Dropout을 사용하지 않는 것에 대해서,
- 1d part에서는 사용하는 DropOut을 2d part에서는 사용하지 않는다, dropout이 과적합을 막아주긴 하지만 그 전에, 2d part에서는 과적합이 잘 일어나지 않는다(보통은 그런다 하심), 구체적이진 않지만 CNN은 Fully Connected가 아니라는 점, 다음 레이어의 각각의 노드에 대해, 이전의 모든 노드들이 참여하지 않는다는 점 때문에 과적합이 잘 일어나지 않는다 하심
`-` Batch Normalize: 학습을 빠르게하는 효과가 있음
`*` 먼저 결과 y, 모델 값, 혹은 예측 값이 연속적인건 너무 힘듬, threshold라도 주는 것이 아닌 이상 0.1, 0.2, 0.3별로 나눠서 각각의 label을 분류하는 것은 힘든 것. 비트 정보 처리도 마찬가지임, 001, 010, 100 중에서 해야지 0.8 0.4 0.6 이면 어떻게 해석을 하겠음, 정도를 나누고 sigmoid (혹은 softmax) 특성상 가장 높은 것을 답으로 취하는 방식인 것
`*` `-` 결과가 2차원인 것, 이것은 그저 0, 1로 두가지 label을 구분하는 것 보다 01, 10 방식으로 구분하게 함으로써 나중가서 여러개의 label에 대해 더 확장이 용이하도록 하기 위함(?)인 것 같은데 확실히 이해한 것인지 명확하지가 않음
`*` 확실하진 않은데, 통계학에서
추론을 할 때 y가 연속이면 normal distribution으로, y가 0 or 1이면 이항분포로, y가 001, 010, 101 이런 식이면 다항분포로 잡고 추론을 한다고 하심
-> 그런데 끝가지 보고 나니, activation function 적용이 연속은 linear, 0 or 1은 sigmoid, 001 010 100 같은 경우는 soft max를 취한다는 것이 맞는 방향으로 생각하고 있는듯 싶음
추가 팁: Loss fnction 설정에 대해서: <br/>
연속은 MSE, 0 or 1은 BCE, 001 010 100 같은 경우는 Cross Entropy 를 사용
resnet이 중요한 이유는 손실함수의 모양을 바꿔주기 때문이라 하심. resnet의 효과가 shorcut을 만들어서 skip을 주는거라 하심
층이 깊어질수록 수렴이 잘 안하는 특징이 있다 하심
파라메트릭 모형: 해당분야 (물리학, 경제학 등등)의 전문가 들이 함, 특정 현상 보고 관계들 등등에 대해 모델링을 함
넌파라메트릭 모형: 통계전문가, 파라마터가 없어도 어떻게든 유의미한 결론을 이끌어냄 (커널 메소드같은게 넌 파라메트릭 모형이라 하심)
한층한층 의미있는게 아니다, 커널 사이즈든 매핑할 때 아웃풋 개수든, 모두 적절한 것을 찾아나가는 것이다. 상대적으로 비전문가들이 할 수 있음. 왜 Drouout넣고 MaxPooling하고, 한층한층 따지는 의미가 딱히 없는듯. ->
이러한 것을 블랙박스라 한다. 내부에서 무슨일이 돌아가서 이러이러한 결론을 내린건지를 해석하지 어렵기 때문
이 블랙박스가 왜 문제냐면, 대출을 할 떄 대출불가라고 하면 전문가가 직접 모형만들고 판단하면 대출불가 사유 설명이 되는데, 비전문가가 만든 딥러닝의 경우는 그냥 딥러닝이 그런 결과를 냈기 때문이라고 하는 정도일 수 있음. -> 이 떄문에 나온 것이 XAI(Explainable AI, 설명가능 인공지능)임
### 설명가능한 CNN 모형
`-` 현재까지의 모형
- 1단계: 2d 선형변환 $\to$ 2d 비선형변환
- 2단계: Flatten $\to$ MLP
`-` lrnr1(직접 만들었던 모형)의 모형을 다시 복습
```
lrnr1.model
net1 = torch.nn.Sequential(
lrnr1.model[0],
lrnr1.model[1],
lrnr1.model[2],
lrnr1.model[3]
)
net1(X).shape
```
`-` 1단계까지의 추력결과를 시각화
```
fig, axs = plt.subplots(4,4)
k = 0
for i in range(4):
for j in range(4):
axs[i,j].imshow(net1(X)[0][k].data)
k = k+1
fig.set_figheight(8)
fig.set_figwidth(8)
fig.tight_layout()
```
#### net1은 유지 + net2의 구조를 변경!!
```
lrnr1.model
```
`-` 계획
- 변경전 net2: (n,16,12,12) $\overset{flatten}{\Longrightarrow} (n,?) \overset{Linear(?,1)}{\Longrightarrow} (n,1)$
- 변경후 net2: (n,16,12,12) $\overset{gap+flatten}{\Longrightarrow} (n,?) \overset{Linear(16,1)}{\Longrightarrow} (n,1)$
- gap은 (n,16,12,12)의 한 데이터에 대해서 나오는 각각의 16개 이미지들의 픽셀들의 평균을 취한 값들을 의미함. 결과적으로는 16개의 이미지들 각각에서 12*12개의 픽셀값이 있고 이들을 평균 취하면 16개 이미지 각각에서 1개씩 값이 나오므로 총 16개의 값이 나옴
`-` gap: 12 $=times$12 픽셀을 평균내서 하나의 값으로 대표하자.
```
ap = torch.nn.AdaptiveAvgPool2d(output_size=1)
```
- `*`output_size는 평균내서 나올 값의 개수를 뜻하는건가?
`-` ap라는 layer를 생성했다.
```
ap(net1(X)).shape
```
- 16,1,1 부분을 보면 Flatten 작업이 필요함을 알 수 있다.
- ***보충학습: ap는 그냥 평균***
`-` flatten
```
flatten(ap(net1(X))).shape
```
- flatten을 통해서 (12396,16,1,1) 형태가 (12396,16) 로 펼쳐졌다.
`-` linear
```
_l1 = torch.nn.Linear(16,1,bias=False)
# _li.to("cuda:0") 만약 gpu에서 계속 연산을 한다면 이 코드를 실행
```
`-` 이렇게 gap을 추가한 것을 net2 로 구성, $\to$ (net1, net2)를 묶어서 새로운 net 만들자.
```
net2 = torch.nn.Sequential(
torch.nn.AdaptiveAvgPool2d(1),
Flatten(),
torch.nn.Linear(16,1,bias=False)
)
```
`*` torch.nn.linear과 torch.nn.Linear이 무슨 차이가 있는지, ---> L부분이 대문자일 때와 소문자일 때의 차이
```
ds = torch.utils.data.TensorDataset(X,y)
ds1,ds2 = torch.utils.data.random_split(ds, [10000,2396])
dl1 = torch.utils.data.DataLoader(ds1,batch_size=1000)
dl2 = torch.utils.data.DataLoader(ds2,batch_size=2396)
dls = DataLoaders(dl1,dl2)
lrnr3 = Learner(dls,net,opt_func=Adam, loss_func = loss_fn , lr = 0.1)
lrnr3.fit(50)
```
### CAM: observation을 1개로 고정하고 net2에서 layer의 순서를 바꿔서 시각화
`-` 계획
- 변경전 netSequential(n,16,12,12) $\overset{flatten}{\Longrightarrow} (n,?) \overset{Linear(?,1)}{\Longrightarrow} (n,1)$
- 변경후 net2: (n,16,12,12) $\overset{gap+flatten}{\Longrightarrow} (n,?) \overset{Linear(16,1)}{\Longrightarrow} (n,1)$
- CAM: (1,16,12,12) $\overset{Linear(16,1)+flatten}{\Longrightarrow} (12,12) \overset{gap}{\Longrightarrow} (1,1)$
- CAM에서 Linear(16,1)로 차원이 (12,12) 되는 이유를 알아야됨
`-` 준비과정1: 시각화할 샘플을 하나 준비하자
```
x = X[1]
X.shape, x.shape
```
- x의 차원이 하나 줄었다. 네트워크에 입력할 때 문제가 발생할 수 있으므로, 입력 차원을 맞추려면 X와 같이 하나 추가를 해야한다.
```
x = x.reshape(1,1,28,28)
#x.squeeze()
```
- plt.imshow에 대입하기 위해 이를 (28,28)로 맞춰야함, 이를 위한 함수가 squeeze()
```
plt.imshow(x.squeeze())
```
`-` 준비과정2: 계산과 시각화를 위해서 각 네트워크를 cpu로 옮기자. (fastai로 학습한 직후라 GPU에 있음)
```
net1.to("cpu")
net2.to("cpu")
```
`-` forward 확인: 이 값을 기억하자.
```
net2(net1(x)) # 0.5 미만으로, 7에 해당한다. CNN이 7이라고 판단.
```
- `-` net1, net2만 gpu에 올리고 net(x)를 실행한 결과: device가 다르다며 error가 나온다.
`-` net2를 수정하고 forward값 확인
```
net2
```
- net에서 Linear와 AdaptiveAvgPool2d의 적용순서를 바꿔줌
차원 확인
```
net1(x).squeeze().shape
net2[2].weight.shape # net2[2]는 두 cell 위의 net2결과에서 (2): Linear부분을 뜻한다.
```
- 이해가 잘 안되는 부분, 1,16이면 두 번 곱할 수 있는데, 그렇게하면 1,12,12 가 나와서 차원을 하나 줄인다 하심
```
net2[2].weight.squeeze().shape # net2[2]는 두 cell 위의 net2결과에서 (2): Linear부분을 뜻한다.
```
- 차원을 하나 줄인 결과
**Linear(in_features=16, out_features=1, bias=False)** 를 먼저 적용: 16 $\times$ (16,12,12) -> (12,12)
```
# net2[2].weight.squeeze() @ net1(x).squeeze()
```
- 에러가 나는 이유: @는 matrix 연산으로 2차원 텐서에 대해서 적용하는데, 이는 3차원이라 @로 연산이 안됨
- 실패
`-` 곱하는 방법: torch.einsum()
```
camimg = torch.einsum("i, ijk -> jk", net2[2].weight.squeeze(), net1(x).squeeze())
```
`-` 계산이 잘 됬는지 shape로 확인
```
camimg.shape
```
- 성공
`-` Linear를 적용하고, 이제 gap을 적용
```
ap(camimg)
```
`!!!!` 위의 0.0552와 똑같다?
`-` 아래의 값이 같다.
```
net2(net1(x)), ap(camimg)
```
`-` 왜냐하면 ap와 선형변환 모두 linear이므로 순서를 바꿔도 상관없음
`-` 아래와 같은 이치
```
_x = np.array([1,2,3,4])
_x
np.mean(_x*2+1)
2*np.mean(_x)+1
```
`-` 이제 camimg에 관심을 가져보자.
```
camimg # 12 * 12 tensor
```
현재 위의 camimg를 평균 취함으로써, 즉, ap(camimg) 혹은 torch.mean(camimg)를 함으로써 0.0552와 같다는 것
`*` 교수님 픽셀의 값과 내 값이 다름, 교수님 픽셀로 일단 작성
`-` 결국 특정픽셀에서 큰 음의 값이 나오기 때문에 궁극적으로는 평균이 음수가 된다.
- 평균이 음수이다. $\leftrightarrow$ 이미지가 의미하는 것이 7이다.
- 특정픽셀이 큰 음수값을 가진다. $\leftrightarrow$ 이미지 값 7을 좌우하는 픽셀, 즉, 이 픽셀은 이미지가 7이라는 근거가 되는 픽셀이다.
```
plt.imshow(camimg.data)
```
`-` 원래 이미지와 비교
```
plt.imshow(x.squeeze())
```
`-` 두 이미지를 겹쳐서 그리면 멋진 그림이 될 것이다.
step1: 원래 이미지를 흑백으로 그리자
```
plt.imshow(x.squeeze(), cmap='gray',alpha=0.5)
```
step2: camimg은 (12,12) 픽셀이고 x는 (28,28) 픽셀이라서 이를 맞춰줘야한다. $\to$ camimg를 늘린다.
- interpolation을 통해서 적당히 smoothing하여 작은 픽셀을 큰 픽셀로 확대한다.
```
plt.imshow(camimg.data, alpha = 0.5, extent = (0,28,28,0), interpolation = 'bilinear', cmap='magma')
plt.imshow(x.squeeze(), cmap='gray',alpha=0.5)
plt.imshow(camimg.data, alpha = 0.5, extent = (0,27,27,0), interpolation = 'bilinear', cmap='magma')
```
- `*` 0,28,28,0 부분을 0,27,27,0으로 바꾸심. 이유는 잘 모르겠음
### 2d part의 (1,16,12,12) 와 Linear transform인 (16,1)의 연산이 이해되지 않음
#### tensor 계산 연습
```
_mat1 = torch.tensor([[[1,2,3,4], [5,6,7,8], [9,10,11,12]],[[-1,2,-3,4], [-5,6,-7,8], [-9,10,-11,12]]])
_mat2 = torch.tensor([10 for i in range(2)])
_mat2.shape, _mat1.shape
```
--
```
net1(x).squeeze().shape
net2[2].weight.squeeze().shape # net2[2]는 두 cell 위의 net2결과에서 (2): Linear부분을 뜻한다.
```
`-` camimg = torch.einsum("i, ijk -> jk", net2[2].weight.squeeze(), net1(x).squeeze())
를 참고하여
--
```
torch.einsum("i, ijk -> jk", _mat2, _mat1) # 각각의 jk에 대해 i인덱스별 합,
```
각각의 jk에 대해 i인덱스별 합, $ \sum_i{mat1_i}{mat2_ijk}$ -> ijk를 [i][j][k]로 인덱싱하면 각각의 j,k별로 _mat1[0][0][0]*_mat2[0] + _mat1[1][0][0]*_mat2[1] /// _mat1[0][0][1]*_mat2[0] + _mat1[1][0][1]*_mat2[1] /// $\dots$ ///_mat1[0][2][3]*_mat2[0] + _mat1[1][2][3]*_mat2[1] 과 같이 계산된다.
```
for i in range(3):
for j in range(4):
print(_mat1[0][i][j]*_mat2[0] + _mat1[1][i][j]*_mat2[1])
_mat1[0][0][0]*_mat2[0] + _mat1[1][0][0]*_mat2[1]
```
`-` 알아낸 einsum의 원리를 바탕으로 2d part output 과 1d part의 linear transform의 연산결과를 해석해보면, -> 2d part output은 torch.Size([16, 12, 12]) 이고 1d part는 16개의 가중치를 가진다.
torch.Size([16, 12, 12]) -> 16은 channel(혹은 16장의 이미지) 즉, [이미지 지정 인덱스][지정된 인덱스 이미지 pixel row][지정된 인덱스 이미지 pixel col] 에서 지정 위치의 픽셀 [row][col]에 대한 16장 이미지의 해당 픽셀들에 가중치를 곱해서 더하여 해당 픽셀에 저장함.
```
x = X[7000]
x.shape
x = X[7000]
x = x.squeeze()
plt.imshow(x)
x = x.reshape(1,1,28,28)
camimg = torch.einsum("i, ijk -> jk", net2[2].weight.squeeze(), net1(x).squeeze())
plt.imshow(x.squeeze(), cmap='gray',alpha=0.5)
plt.imshow(camimg.data, alpha = 0.5, extent = (0,27,27,0), interpolation = 'bilinear', cmap='magma')
```
|
github_jupyter
|
# Game Music dataset: data cleaning and exploration
The goal with this notebook is cleaning the dataset to make it usable as well as providing a descriptive analysis of the dataset features.
## Data loading and cleaning
```
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
from ast import literal_eval
import os
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
df = pd.read_csv('midi_dataframe.csv', parse_dates=[11])
num_midis_before = len(df)
print('There is %d midi files, from %d games, with %d midis matched with tgdb'
%(num_midis_before,
len(df.groupby(['tgdb_platform', 'tgdb_gametitle'])),
(df.tgdb_gametitle.notnull().sum())))
df.head()
```
We keep only files matched with tgdb and check that every midi file is only present once, if not we drop the rows.
```
num_dup = df.duplicated(subset='file_name').sum()
df.drop_duplicates(subset='file_name', inplace=True)
print('There was %d duplicated midi files, %d midis left'%(num_dup, len(df)))
```
Since we are interested in the genre, we only keep midis that have one.
```
num_genres_na = df.tgdb_genres.isnull().sum()
df.dropna(subset=['tgdb_genres'], inplace=True)
print("We removed %d midis, %d midis left"%(num_genres_na, len(df)))
```
Then, there are some categories, such as Medleys or Piano only that are not interesting.
There is also a big "remix" scene on vgmusic, so we also remove those.
```
categories_filter = df.console.isin(['Medleys', 'Piano Only'])
remix_filter = df.title.str.contains('[Rr]emix')
df = df[~categories_filter & ~remix_filter]
print('We removed %d midis from Medleys and Piano categories'%categories_filter.sum())
print('We removed %d midis containing "remix" in their title'%remix_filter.sum())
print('%d midis left'%len(df))
```
There often exists several versions of the same midi file, most of the time denoted by 'title (1)', 'title (2)', etc.
We also consider removing those, but keeping only the one with the highest value, or if there are several with the same title, we randomly keep one.
```
num_midis_before = len(df)
df_stripped = df.copy()
df_stripped.title = df.title.str.replace('\(\d+\)', '').str.rstrip()
df_stripped['rank'] = df.title.str.extract('\((\d+)\)', expand=False)
df = df_stripped.sort_values(by='rank', ascending=False).groupby(['brand', 'console', 'game', 'title']).first().reset_index()
print("We removed %d midis, %d midis left"%(num_midis_before-len(df), len(df)))
```
We also check if the midis files are valid by using mido and trying to load them.
```
from mido import MidiFile
bad_midis = []
for file in df['file_name']:
try:
midi = MidiFile("full/" + file)
except:
bad_midis.append(file)
df = df.loc[df.file_name.apply(lambda x: x not in bad_midis)]
print("We removed %d midis, %d midis left"%(len(bad_midis), len(df)))
```
The final numbers after preliminary data cleaning are:
```
num_games = len(df.groupby(['tgdb_platform', 'tgdb_gametitle']))
print('There is %d midi files, from %d games, with %d midis matched with tgdb'
%(len(df),
num_games,
(df.tgdb_gametitle.notnull().sum())))
```
## Data Exploration
## General statistics
We first begin by some general statistics about the dataset.
The number of gaming platforms is computed.
```
print('There is %d platforms'%df.tgdb_platform.nunique())
```
Then, statistics concerning the number of games per platform are computed and plotted.
```
df.drop_duplicates(subset=['tgdb_platform', 'tgdb_gametitle']).groupby('tgdb_platform').size().to_frame().describe()
size= (10, 5)
fig, ax = plt.subplots(figsize=size)
ax = sns.distplot(df.drop_duplicates(subset=['tgdb_platform', 'tgdb_gametitle']).groupby('tgdb_platform').size().to_frame(), ax = ax)
ax.set_xlabel("number of games per platform")
ax.set_ylabel("density")
ax.set_title("Density of the number of games per platform")
ax.set_xticks(np.arange(0, 300, 10))
ax.set_xlim(0,200)
plt.show()
```
It can be noted that the majority of platforms seem to have around 10 games, which is a sufficient sample size.
Following this, statistics concerning the number of midis per platform are computed and plotted.
```
df.groupby('tgdb_platform').size().to_frame().describe()
fig, ax = plt.subplots(figsize=size)
ax = sns.distplot(df.groupby('tgdb_platform').size().to_frame())
ax.set_xlabel("number of midi per platform")
ax.set_ylabel("density")
ax.set_title("Density of the number of midis per platform")
ax.set_xticks(np.arange(0, 1000, 50))
ax.set_xlim(0,1500)
plt.show()
```
It can be noted that the majority of platform have around 50 midis, which is again judged to be a sufficient sample for analysis.
Finally, statistics concerning the number of midi per game are computed and plotted.
```
df.groupby(['tgdb_platform', 'tgdb_gametitle']).size().to_frame().describe()
fig, ax = plt.subplots(figsize=size)
ax = sns.distplot(df.groupby(['tgdb_platform', 'tgdb_gametitle']).size().to_frame())
ax.set_xlabel("number of midi per game")
ax.set_ylabel("density")
ax.set_title("Density of the number of midi per game")
ax.set_xticks(np.arange(0, 40, 2))
ax.set_xlim(0,40)
plt.show()
```
It can be noted that the peak of density is at 2 midi per game. This does not matter much as we are not trying to classify music per game, but by genres.
As a general remark, it can be noticed that most of the data we have follow power laws.
### Genres analysis
We currently had list of genres, for more convenience, we rework the dataframe to make several row of a midi if it had several genres.
```
genres = df.tgdb_genres.map(literal_eval, 'ignore').apply(pd.Series).stack().reset_index(level=1, drop=True)
genres.name = 'tgdb_genres'
genres_df = df.drop('tgdb_genres', axis=1).join(genres)
print("There is %d different genres"%genres_df.tgdb_genres.nunique())
genres_df.to_csv("midi_dataframe_cleaned.csv")
```
Here follows the percentage of games belonging to each genre and of midis for each genres.
```
genres_df.drop_duplicates(subset=['tgdb_platform', 'tgdb_gametitle'])\
.groupby(['tgdb_genres']).size().to_frame()\
.sort_values(0, ascending = False)/num_games*100
```
The number of genres is 19, and could be reduced to 10 if we consider only the genres for which we have at least 3% dataset coverage or 5 if we consider only the genres for which we have at least 9% dataset coverage.
|
github_jupyter
|
# Convolutional Neural Network in Keras
Bulding a Convolutional Neural Network to classify Fashion-MNIST.
#### Set seed for reproducibility
```
import numpy as np
np.random.seed(42)
```
#### Load dependencies
```
import os
from tensorflow.keras.datasets import fashion_mnist
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Layer, Activation, Dense, Dropout, Conv2D, MaxPooling2D, Flatten, LeakyReLU, BatchNormalization
from tensorflow.keras.callbacks import TensorBoard, ModelCheckpoint, EarlyStopping
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.models import load_model
from keras_contrib.layers.advanced_activations.sinerelu import SineReLU
from matplotlib import pyplot as plt
%matplotlib inline
```
#### Load data
```
(X_train, y_train), (X_test, y_test) = fashion_mnist.load_data()
```
#### Preprocess data
Flatten and normalise input data.
```
X_train = X_train.reshape(-1, 28, 28, 1)
X_test = X_test.reshape(-1, 28, 28, 1)
X_train = X_train.astype("float32")/255.
X_test = X_test.astype("float32")/255.
# One-hot encoded categories
n_classes = 10
y_train = to_categorical(y_train, n_classes)
y_test = to_categorical(y_test, n_classes)
```
#### Design Neural Network architecture
```
model = Sequential()
model.add(Conv2D(32, 7, padding = 'same', input_shape = (28, 28, 1)))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(Conv2D(32, 7, padding = 'same'))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size = (2, 2)))
model.add(Dropout(0.20))
model.add(Conv2D(64, 3, padding = 'same'))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(Conv2D(64, 3, padding = 'same'))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size = (2, 2)))
model.add(Dropout(0.30))
model.add(Conv2D(128, 2, padding = 'same'))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(Conv2D(128, 2, padding = 'same'))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size = (2, 2)))
model.add(Dropout(0.40))
model.add(Flatten())
model.add(Dense(512))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(Dropout(0.50))
model.add(Dense(10, activation = "softmax"))
model.summary()
```
#### Callbacks
```
modelCheckpoint = ModelCheckpoint(monitor='val_accuracy', filepath='model_output/weights-cnn-fashion-mnist.hdf5',
save_best_only=True, mode='max')
earlyStopping = EarlyStopping(monitor='val_accuracy', mode='max', patience=5)
if not os.path.exists('model_output'):
os.makedirs('model_output')
tensorboard = TensorBoard("logs/convnet-fashion-mnist")
```
#### Configure model
```
model.compile(loss = 'categorical_crossentropy', optimizer = 'adam', metrics = ['accuracy'])
```
#### Train!
```
history = model.fit(X_train, y_train, batch_size = 128, epochs = 20, verbose = 1,
validation_split = 0.1, callbacks=[modelCheckpoint, earlyStopping, tensorboard])
```
#### Test Predictions
```
saved_model = load_model('model_output/weights-cnn-fashion-mnist.hdf5')
predictions = saved_model.predict_classes(X_test, verbose = 2)
print(predictions)
# np.std(history.history['loss'])
```
#### Test Final Accuracy
```
final_loss, final_acc = saved_model.evaluate(X_test, y_test, verbose = 2)
print("Final loss: {0:.4f}, final accuracy: {1:.4f}".format(final_loss, final_acc))
image = X_test[0].reshape(1, 28, 28, 1)
predictions = model.predict_classes(image, verbose = 2)
print(predictions)
plt.imshow(X_test[0].reshape((28, 28)), cmap='gray')
# 0 T-shirt/top
# 1 Trouser
# 2 Pullover
# 3 Dress
# 4 Coat
# 5 Sandal
# 6 Shirt
# 7 Sneaker
# 8 Bag
# 9 Ankle boot
```
|
github_jupyter
|
```
import json
import requests
import numpy as np
import os
import shutil
#Get google api keys
with open("../config.json", "r") as f:
# k = json.load(f)['key_bsa']
# bk = json.load(f)['big_key_demo']
kk = json.load(f)['key_kaitlin']
BASE_URL_DIRECTIONS = 'https://maps.googleapis.com/maps/api/directions/json?'
KEY = '&key=' + kk
#Supporting functions
def get_total_distance(routes_obj):
return routes_obj.json()['routes'][0]['legs'][0]['distance']['value']
def get_lat_lng(routes_obj):
lat_lng = []
steps = routes_obj.json()['routes'][0]['legs'][0]['steps']
for step in steps:
end = step['end_location']
start = step['start_location']
lat_lng += [(start['lat'],start['lng']),(end['lat'],end['lng'])]
return lat_lng
def create_path(points):
path = 'path='
for i in points:
path += str(i[0]) + ',' + str(i[1]) + '|'
return path[:-1] #remove last '|'
def get_coords(r,points):
for i in r.json()['snappedPoints']:
points += [(i['location']['latitude'],i['location']['longitude'])]
return points
def get_snapped_points(unique_points_interpolated,key,BASE_URL_SNAP = 'https://roads.googleapis.com/v1/snapToRoads?',interpolate = '&interpolate=true'):
points = []
k = 0
coords_list = []
while k <= len(unique_points_interpolated)-1:
coords_list += [unique_points_interpolated[k]]
if (len(coords_list)%100==0) or (k+1==len(unique_points_interpolated)): #When we have 100 points or we reach the end of the list.
path = create_path(coords_list)
url = BASE_URL_SNAP + path + interpolate + key
r = requests.get(url)
points += get_coords(r,points)
coords_list = []
k += 1
return(points)
def interpolate_coordinates(distance, lat_lng, k, separation_mts = 300):
unique_points = list(set(lat_lng))
n = max([1,round((distance/separation_mts)/len(unique_points))])
unique_points_interpolated = []
for i in range(len(unique_points)-1):
unique_points_interpolated += list(map(tuple,np.linspace(unique_points[i],unique_points[i+1],n)))
unique_points_interpolated = sorted(list(set(unique_points_interpolated)), key = lambda x: x[0])
if n > 1: #If we have any new points to snap.
results = get_snapped_points(unique_points_interpolated,k)
return results
else:
return unique_points_interpolated
def create_image(x, folder_name):
for heading in range(0,4):
lat=x[0]
lng=x[1]
heading=str(90*heading)
query='https://maps.googleapis.com/maps/api/streetview?size=400x400&location=%s,%s&fov=90&heading=%s&pitch=10%s' % (str(lat),str(lng),heading,KEY)
page=requests.get(query)
# filename='%s-%s-%s-%s-%s.jpg' %(origin,destination,str(lat),str(lng),heading)
filename='%s-%s-%s-%s.jpg' %(folder_name,str(lat),str(lng),heading)
if not os.path.exists(filename+".txt") or os.path.getsize(filename)<5*10^3:
f = open(filename,'wb')
f.write(page.content)
f.close()
#Example of waypoints to force the route to pass through a certain road
#waypoints = 'waypoints=1202+Foothill+Blvd+Calistoga|Oakville,CA|Yountville,CA|Napa+Valley+Marriott+Hotel'
def download_pictures(origin, destination, category, folder_name, waypoints=None):
os.chdir('/data/road-scanner/training/' + category)
#Get interpolated coordinates
if waypoints == None:
url = BASE_URL_DIRECTIONS + 'origin=' + origin + '&' + 'destination=' + destination + '&' + KEY
else:
url = BASE_URL_DIRECTIONS + 'origin=' + origin + '&' + 'destination=' + destination + '&' + waypoints + KEY
r = requests.get(url)
upi = interpolate_coordinates(get_total_distance(r),get_lat_lng(r),KEY)
#Download pictures
if os.path.exists(folder_name):
shutil.rmtree(folder_name)
os.makedirs(folder_name)
os.chdir(folder_name)
org_dest_string='%s-%s' %(origin,destination)
for i in range(len(upi)):
create_image(upi[i], folder_name)
### Features of routes missing
origin = "origin=48470+Lakeview Blvd+Fremont+CA+94538"
destination = "destination=Oakland+California+94606"
url = BASE_URL_DIRECTIONS + 'origin=' + origin + '&' + 'destination=' + destination + '&' + KEY
url
# download_pictures(origin, destination, 'non_scenic', 'test_fremont_oakland_880')
# non scenic
origins = ["320+Acorn+Ct+Vacaville+CA+95688",
"12141+Martha+Ann+Dr+Los+Alamitos+CA+90720", "Salida+California",
"1625+W+Lugonia+Ave+Redlands+CA+92374","I-205+Tracy+CA+95377"]
destinations = ["4505+W+Capitol+Ave+West+Sacramento+CA+95691",
"Wilshire+Federal+Building+11000+Wilshire+Blvd+Los+Angeles+CA+90024",
"Golden+State+Hwy,+Bakersfield,+CA+93307",
"450+N+Atlantic+Blvd,+Monterey+Park,+CA+91754", "Grapevine+California"]
folder_names = ["vacaville_to_sac",
"405_westwood_to_long_beach", "99_salida_to_bakersfield", "10_alhambra_to_riverside",
'I5_tracy_to_grapevine']
for i in range(len(origins)):
download_pictures("origin="+origins[i],"destination="+destinations[i],'non_scenic',folder_names[i])
origins = ['38.3254,-122.27693000000001', '35.75368,-120.67729000000001', '36.758030000000005,-119.74912',
'35.2503,-120.62506', '37.333000000000006,-119.65076', '34.01697,-118.82331', '36.76053,-119.11351',
'38.914190000000005,-120.00522000000001', '36.62303,-121.84475', '34.31194,-117.47276000000001',
'38.25555000000001,-120.35094000000001', '35.589470000000006,-120.6966', '36.12256,-121.02258',
'36.282210000000006,-118.00583', '37.81255,-119.05365', '35.24604,-120.68278000000001',
'33.27877,-115.96492', '41.996680000000005,-123.72141', '34.471990000000005,-119.28866000000001',
'39.86818,-123.71397', '34.9236,-120.4171', '40.58534,-122.36037', '33.91863,-116.6016',
'39.602700000000006,-121.61804000000001']
destinations = ['38.5889,-122.27835', '35.722,-120.67760000000001', '37.25511,-119.74913000000001',
'35.22066,-120.62314', '38.0165,-119.64668', '34.64083,-118.825', '36.79612,-119.11176',
'38.91415000000001,-120.00933', '35.28761,-121.84596', '34.07305,-117.46934',
'38.660410000000006,-120.34897000000001', '35.64969,-120.69786',
'36.860850000000006,-121.01838000000001', '36.3046,-118.00261',
'37.892300000000006,-119.05625', '35.36764,-120.68357', '32.74718,-115.97338',
'39.86816,-123.71989', '34.686040000000006,-119.28965000000001',
'37.810570000000006,-123.71603', '34.61202,-120.40971',
'40.584860000000006,-122.36037', '33.661460000000005,-116.59045', '39.14844,-121.5883']
folder_names = ['Silverado_Trail', 'Pleasant_Valley_Wine_Trail', 'Sierra_Heritage_Scenic_Byway',
'San_Luis_Obispo_Wine_Trail', 'Yosemite_Valley_and_Tioga_Road', 'Malibu_to_Lompoc',
'Kings_Canyon_and_Sequoia_National_Park', 'Lake_Tahoe', 'Big_Sur_Coast',
'Rim_of_the_World_Scenic_Byway', 'Ebbetts_Pass_Scenic_Byway', 'Paso_Robles_Wine_Country',
'Pinnacles_National_Park', 'Death_Valley_Scenic_Byway', 'June_Lake_Loop',
'Morro_Bay_Scenic_Drive', 'Anza_Borrego_Desert', 'Redwood_Highway', 'Jacinto_Reyes_Scenic_Byway',
'Northern_Pacific_Coast', 'Santa_Barbara_Wine_Country', 'Mount_Shasta-Cascade_Loop',
'Joshua_Tree_Journey', 'Feather_River_Scenic_Byway']
for i in range(len(origins)):
download_pictures("origin="+origins[i],"destination="+destinations[i],'scenic',folder_names[i])
origins = [
'Dwight+D+Eisenhower+Hwy+Oakland+CA+94607+USA','Golden+Gate+Bridge+View+Vista+Point+Sausalito+CA+94965+United+States',
'51+59+Christmas+Tree+Point+Rd+San+Francisco+CA 94131+USA','Fresno+California+USA']
destinations = ['701+Bayshore+Blvd+San+Francisco+CA+94124+USA',
'The+Palace+Of+Fine+Arts+3601+Lyon+St+San+Francisco+CA+94123+United+States',
'148+Marview+Way+San+Francisco+CA+94131+USA','Golden+State+Hwy+Bakersfield+CA+93307+USA']
folder_names = ['SF_Skyline','Golden_Gate','Twin_Peaks','shorter_99']
for i in range(len(origins)):
download_pictures(origins[i],destinations[i],'demo', folder_names[i])
```
|
github_jupyter
|
# Parallel GST using MPI
The purpose of this tutorial is to demonstrate how to compute GST estimates in parallel (using multiple CPUs or "processors"). The core PyGSTi computational routines are written to take advantage of multiple processors via the MPI communication framework, and so one must have a version of MPI and the `mpi4py` python package installed in order use run pyGSTi calculations in parallel.
Since `mpi4py` doesn't play nicely with Jupyter notebooks, this tutorial is a bit more clunky than the others. In it, we will create a standalone Python script that imports `mpi4py` and execute it.
We will use as an example the same "standard" single-qubit model of the first tutorial. We'll first create a dataset, and then a script to be run in parallel which loads the data. The creation of a simulated data is performed in the same way as the first tutorial. Since *random* numbers are generated and used as simulated counts within the call to `generate_fake_data`, it is important that this is *not* done in a parallel environment, or different CPUs may get different data sets. (This isn't an issue in the typical situation when the data is obtained experimentally.)
```
#Import pyGSTi and the "stardard 1-qubit quantities for a model with X(pi/2), Y(pi/2), and idle gates"
import pygsti
from pygsti.modelpacks import smq1Q_XYI
#Create experiment design
exp_design = smq1Q_XYI.get_gst_experiment_design(max_max_length=32)
pygsti.io.write_empty_protocol_data(exp_design, "example_files/mpi_gst_example", clobber_ok=True)
#Simulate taking data
mdl_datagen = smq1Q_XYI.target_model().depolarize(op_noise=0.1, spam_noise=0.001)
pygsti.io.fill_in_empty_dataset_with_fake_data(mdl_datagen, "example_files/mpi_gst_example/data/dataset.txt",
nSamples=1000, seed=2020)
```
Next, we'll write a Python script that will load in the just-created `DataSet`, run GST on it, and write the output to a file. The only major difference between the contents of this script and previous examples is that the script imports `mpi4py` and passes a MPI comm object (`comm`) to the `do_long_sequence_gst` function. Since parallel computing is best used for computationaly intensive GST calculations, we also demonstrate how to set a per-processor memory limit to tell pyGSTi to partition its computations so as to not exceed this memory usage. Lastly, note the use of the `gaugeOptParams` argument of `do_long_sequence_gst`, which can be used to weight different model members differently during gauge optimization.
```
mpiScript = """
import time
import pygsti
#get MPI comm
from mpi4py import MPI
comm = MPI.COMM_WORLD
print("Rank %d started" % comm.Get_rank())
#load in data
data = pygsti.io.load_data_from_dir("example_files/mpi_gst_example")
#Specify a per-core memory limit (useful for larger GST calculations)
memLim = 2.1*(1024)**3 # 2.1 GB
#Perform TP-constrained GST
protocol = pygsti.protocols.StandardGST("TP")
start = time.time()
results = protocol.run(data, memlimit=memLim, comm=comm)
end = time.time()
print("Rank %d finished in %.1fs" % (comm.Get_rank(), end-start))
if comm.Get_rank() == 0:
results.write() #write results (within same diretory as data was loaded from)
"""
with open("example_files/mpi_example_script.py","w") as f:
f.write(mpiScript)
```
Next, we run the script with 3 processors using `mpiexec`. The `mpiexec` executable should have been installed with your MPI distribution -- if it doesn't exist, try replacing `mpiexec` with `mpirun`.
```
! mpiexec -n 3 python3 "example_files/mpi_example_script.py"
```
Notice in the above that output within `StandardGST.run` is not duplicated (only the first processor outputs to stdout) so that the output looks identical to running on a single processor. Finally, we just need to read the saved `ModelEstimateResults` object from file and proceed with any post-processing analysis. In this case, we'll just create a report.
```
results = pygsti.io.load_results_from_dir("example_files/mpi_gst_example", name="StandardGST")
pygsti.report.construct_standard_report(
results, title="MPI Example Report", verbosity=2
).write_html('example_files/mpi_example_brief', auto_open=True)
```
Open the [report](example_files/mpi_example_brief/main.html).
|
github_jupyter
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.

# Automated Machine Learning
**BikeShare Demand Forecasting**
## Contents
1. [Introduction](#Introduction)
1. [Setup](#Setup)
1. [Compute](#Compute)
1. [Data](#Data)
1. [Train](#Train)
1. [Featurization](#Featurization)
1. [Evaluate](#Evaluate)
## Introduction
This notebook demonstrates demand forecasting for a bike-sharing service using AutoML.
AutoML highlights here include built-in holiday featurization, accessing engineered feature names, and working with the `forecast` function. Please also look at the additional forecasting notebooks, which document lagging, rolling windows, forecast quantiles, other ways to use the forecast function, and forecaster deployment.
Make sure you have executed the [configuration notebook](../../../configuration.ipynb) before running this notebook.
Notebook synopsis:
1. Creating an Experiment in an existing Workspace
2. Configuration and local run of AutoML for a time-series model with lag and holiday features
3. Viewing the engineered names for featurized data and featurization summary for all raw features
4. Evaluating the fitted model using a rolling test
## Setup
```
import azureml.core
import pandas as pd
import numpy as np
import logging
from azureml.core import Workspace, Experiment, Dataset
from azureml.train.automl import AutoMLConfig
from datetime import datetime
```
This sample notebook may use features that are not available in previous versions of the Azure ML SDK.
```
print("This notebook was created using version 1.17.0 of the Azure ML SDK")
print("You are currently using version", azureml.core.VERSION, "of the Azure ML SDK")
```
As part of the setup you have already created a <b>Workspace</b>. To run AutoML, you also need to create an <b>Experiment</b>. An Experiment corresponds to a prediction problem you are trying to solve, while a Run corresponds to a specific approach to the problem.
```
ws = Workspace.from_config()
# choose a name for the run history container in the workspace
experiment_name = 'automl-bikeshareforecasting'
experiment = Experiment(ws, experiment_name)
output = {}
output['Subscription ID'] = ws.subscription_id
output['Workspace'] = ws.name
output['SKU'] = ws.sku
output['Resource Group'] = ws.resource_group
output['Location'] = ws.location
output['Run History Name'] = experiment_name
pd.set_option('display.max_colwidth', -1)
outputDf = pd.DataFrame(data = output, index = [''])
outputDf.T
```
## Compute
You will need to create a [compute target](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-set-up-training-targets#amlcompute) for your AutoML run. In this tutorial, you create AmlCompute as your training compute resource.
#### Creation of AmlCompute takes approximately 5 minutes.
If the AmlCompute with that name is already in your workspace this code will skip the creation process.
As with other Azure services, there are limits on certain resources (e.g. AmlCompute) associated with the Azure Machine Learning service. Please read this article on the default limits and how to request more quota.
```
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
# Choose a name for your cluster.
amlcompute_cluster_name = "bike-cluster"
# Verify that cluster does not exist already
try:
compute_target = ComputeTarget(workspace=ws, name=amlcompute_cluster_name)
print('Found existing cluster, use it.')
except ComputeTargetException:
compute_config = AmlCompute.provisioning_configuration(vm_size='STANDARD_D2_V2',
max_nodes=4)
compute_target = ComputeTarget.create(ws, amlcompute_cluster_name, compute_config)
compute_target.wait_for_completion(show_output=True)
```
## Data
The [Machine Learning service workspace](https://docs.microsoft.com/en-us/azure/machine-learning/service/concept-workspace) is paired with the storage account, which contains the default data store. We will use it to upload the bike share data and create [tabular dataset](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.data.tabulardataset?view=azure-ml-py) for training. A tabular dataset defines a series of lazily-evaluated, immutable operations to load data from the data source into tabular representation.
```
datastore = ws.get_default_datastore()
datastore.upload_files(files = ['./bike-no.csv'], target_path = 'dataset/', overwrite = True,show_progress = True)
```
Let's set up what we know about the dataset.
**Target column** is what we want to forecast.
**Time column** is the time axis along which to predict.
```
target_column_name = 'cnt'
time_column_name = 'date'
dataset = Dataset.Tabular.from_delimited_files(path = [(datastore, 'dataset/bike-no.csv')]).with_timestamp_columns(fine_grain_timestamp=time_column_name)
dataset.take(5).to_pandas_dataframe().reset_index(drop=True)
```
### Split the data
The first split we make is into train and test sets. Note we are splitting on time. Data before 9/1 will be used for training, and data after and including 9/1 will be used for testing.
```
# select data that occurs before a specified date
train = dataset.time_before(datetime(2012, 8, 31), include_boundary=True)
train.to_pandas_dataframe().tail(5).reset_index(drop=True)
test = dataset.time_after(datetime(2012, 9, 1), include_boundary=True)
test.to_pandas_dataframe().head(5).reset_index(drop=True)
```
## Forecasting Parameters
To define forecasting parameters for your experiment training, you can leverage the ForecastingParameters class. The table below details the forecasting parameter we will be passing into our experiment.
|Property|Description|
|-|-|
|**time_column_name**|The name of your time column.|
|**forecast_horizon**|The forecast horizon is how many periods forward you would like to forecast. This integer horizon is in units of the timeseries frequency (e.g. daily, weekly).|
|**country_or_region_for_holidays**|The country/region used to generate holiday features. These should be ISO 3166 two-letter country/region codes (i.e. 'US', 'GB').|
|**target_lags**|The target_lags specifies how far back we will construct the lags of the target variable.|
|**drop_column_names**|Name(s) of columns to drop prior to modeling|
## Train
Instantiate a AutoMLConfig object. This defines the settings and data used to run the experiment.
|Property|Description|
|-|-|
|**task**|forecasting|
|**primary_metric**|This is the metric that you want to optimize.<br> Forecasting supports the following primary metrics <br><i>spearman_correlation</i><br><i>normalized_root_mean_squared_error</i><br><i>r2_score</i><br><i>normalized_mean_absolute_error</i>
|**blocked_models**|Models in blocked_models won't be used by AutoML. All supported models can be found at [here](https://docs.microsoft.com/en-us/python/api/azureml-train-automl-client/azureml.train.automl.constants.supportedmodels.forecasting?view=azure-ml-py).|
|**experiment_timeout_hours**|Experimentation timeout in hours.|
|**training_data**|Input dataset, containing both features and label column.|
|**label_column_name**|The name of the label column.|
|**compute_target**|The remote compute for training.|
|**n_cross_validations**|Number of cross validation splits.|
|**enable_early_stopping**|If early stopping is on, training will stop when the primary metric is no longer improving.|
|**forecasting_parameters**|A class that holds all the forecasting related parameters.|
This notebook uses the blocked_models parameter to exclude some models that take a longer time to train on this dataset. You can choose to remove models from the blocked_models list but you may need to increase the experiment_timeout_hours parameter value to get results.
### Setting forecaster maximum horizon
The forecast horizon is the number of periods into the future that the model should predict. Here, we set the horizon to 14 periods (i.e. 14 days). Notice that this is much shorter than the number of days in the test set; we will need to use a rolling test to evaluate the performance on the whole test set. For more discussion of forecast horizons and guiding principles for setting them, please see the [energy demand notebook](https://github.com/Azure/MachineLearningNotebooks/tree/master/how-to-use-azureml/automated-machine-learning/forecasting-energy-demand).
```
forecast_horizon = 14
```
### Config AutoML
```
from azureml.automl.core.forecasting_parameters import ForecastingParameters
forecasting_parameters = ForecastingParameters(
time_column_name=time_column_name,
forecast_horizon=forecast_horizon,
country_or_region_for_holidays='US', # set country_or_region will trigger holiday featurizer
target_lags='auto', # use heuristic based lag setting
drop_column_names=['casual', 'registered'] # these columns are a breakdown of the total and therefore a leak
)
automl_config = AutoMLConfig(task='forecasting',
primary_metric='normalized_root_mean_squared_error',
blocked_models = ['ExtremeRandomTrees'],
experiment_timeout_hours=0.3,
training_data=train,
label_column_name=target_column_name,
compute_target=compute_target,
enable_early_stopping=True,
n_cross_validations=3,
max_concurrent_iterations=4,
max_cores_per_iteration=-1,
verbosity=logging.INFO,
forecasting_parameters=forecasting_parameters)
```
We will now run the experiment, you can go to Azure ML portal to view the run details.
```
remote_run = experiment.submit(automl_config, show_output=False)
remote_run
remote_run.wait_for_completion()
```
### Retrieve the Best Model
Below we select the best model from all the training iterations using get_output method.
```
best_run, fitted_model = remote_run.get_output()
fitted_model.steps
```
## Featurization
You can access the engineered feature names generated in time-series featurization. Note that a number of named holiday periods are represented. We recommend that you have at least one year of data when using this feature to ensure that all yearly holidays are captured in the training featurization.
```
fitted_model.named_steps['timeseriestransformer'].get_engineered_feature_names()
```
### View the featurization summary
You can also see what featurization steps were performed on different raw features in the user data. For each raw feature in the user data, the following information is displayed:
- Raw feature name
- Number of engineered features formed out of this raw feature
- Type detected
- If feature was dropped
- List of feature transformations for the raw feature
```
# Get the featurization summary as a list of JSON
featurization_summary = fitted_model.named_steps['timeseriestransformer'].get_featurization_summary()
# View the featurization summary as a pandas dataframe
pd.DataFrame.from_records(featurization_summary)
```
## Evaluate
We now use the best fitted model from the AutoML Run to make forecasts for the test set. We will do batch scoring on the test dataset which should have the same schema as training dataset.
The scoring will run on a remote compute. In this example, it will reuse the training compute.
```
test_experiment = Experiment(ws, experiment_name + "_test")
```
### Retrieving forecasts from the model
To run the forecast on the remote compute we will use a helper script: forecasting_script. This script contains the utility methods which will be used by the remote estimator. We copy the script to the project folder to upload it to remote compute.
```
import os
import shutil
script_folder = os.path.join(os.getcwd(), 'forecast')
os.makedirs(script_folder, exist_ok=True)
shutil.copy('forecasting_script.py', script_folder)
```
For brevity, we have created a function called run_forecast that submits the test data to the best model determined during the training run and retrieves forecasts. The test set is longer than the forecast horizon specified at train time, so the forecasting script uses a so-called rolling evaluation to generate predictions over the whole test set. A rolling evaluation iterates the forecaster over the test set, using the actuals in the test set to make lag features as needed.
```
from run_forecast import run_rolling_forecast
remote_run = run_rolling_forecast(test_experiment, compute_target, best_run, test, target_column_name)
remote_run
remote_run.wait_for_completion(show_output=False)
```
### Download the prediction result for metrics calcuation
The test data with predictions are saved in artifact outputs/predictions.csv. You can download it and calculation some error metrics for the forecasts and vizualize the predictions vs. the actuals.
```
remote_run.download_file('outputs/predictions.csv', 'predictions.csv')
df_all = pd.read_csv('predictions.csv')
from azureml.automl.core.shared import constants
from azureml.automl.runtime.shared.score import scoring
from sklearn.metrics import mean_absolute_error, mean_squared_error
from matplotlib import pyplot as plt
# use automl metrics module
scores = scoring.score_regression(
y_test=df_all[target_column_name],
y_pred=df_all['predicted'],
metrics=list(constants.Metric.SCALAR_REGRESSION_SET))
print("[Test data scores]\n")
for key, value in scores.items():
print('{}: {:.3f}'.format(key, value))
# Plot outputs
%matplotlib inline
test_pred = plt.scatter(df_all[target_column_name], df_all['predicted'], color='b')
test_test = plt.scatter(df_all[target_column_name], df_all[target_column_name], color='g')
plt.legend((test_pred, test_test), ('prediction', 'truth'), loc='upper left', fontsize=8)
plt.show()
```
Since we did a rolling evaluation on the test set, we can analyze the predictions by their forecast horizon relative to the rolling origin. The model was initially trained at a forecast horizon of 14, so each prediction from the model is associated with a horizon value from 1 to 14. The horizon values are in a column named, "horizon_origin," in the prediction set. For example, we can calculate some of the error metrics grouped by the horizon:
```
from metrics_helper import MAPE, APE
df_all.groupby('horizon_origin').apply(
lambda df: pd.Series({'MAPE': MAPE(df[target_column_name], df['predicted']),
'RMSE': np.sqrt(mean_squared_error(df[target_column_name], df['predicted'])),
'MAE': mean_absolute_error(df[target_column_name], df['predicted'])}))
```
To drill down more, we can look at the distributions of APE (absolute percentage error) by horizon. From the chart, it is clear that the overall MAPE is being skewed by one particular point where the actual value is of small absolute value.
```
df_all_APE = df_all.assign(APE=APE(df_all[target_column_name], df_all['predicted']))
APEs = [df_all_APE[df_all['horizon_origin'] == h].APE.values for h in range(1, forecast_horizon + 1)]
%matplotlib inline
plt.boxplot(APEs)
plt.yscale('log')
plt.xlabel('horizon')
plt.ylabel('APE (%)')
plt.title('Absolute Percentage Errors by Forecast Horizon')
plt.show()
```
|
github_jupyter
|
```
import numpy as np # type: ignore
import onnx
import onnx.helper as h
import onnx.checker as checker
from onnx import TensorProto as tp
from onnx import save
import onnxruntime
# Builds a pipeline that resizes and crops an input.
def build_preprocessing_model(filename):
nodes = []
nodes.append(
h.make_node('Shape', inputs=['x'], outputs=['x_shape'], name='x_shape')
)
nodes.append(
h.make_node('Split', inputs=['x_shape'], outputs=['h', 'w', 'c'], axis=0, name='split_shape')
)
nodes.append(
h.make_node('Min', inputs=['h', 'w'], outputs=['min_extent'], name='min_extent')
)
nodes.append(
h.make_node('Constant', inputs=[], outputs=['constant_256'],
value=h.make_tensor(name='k256', data_type=tp.FLOAT, dims=[1], vals=[256.0]),
name='constant_256')
)
nodes.append(
h.make_node('Constant', inputs=[], outputs=['constant_1'],
value=h.make_tensor(name='k1', data_type=tp.FLOAT, dims=[1], vals=[1.0]),
name='constant_1')
)
nodes.append(
h.make_node('Cast', inputs=['min_extent'], outputs=['min_extent_f'], to=tp.FLOAT, name='min_extent_f')
)
nodes.append(
h.make_node('Div', inputs=['constant_256', 'min_extent_f'], outputs=['ratio-resize'], name='ratio-resize')
)
nodes.append(
h.make_node('Concat', inputs=['ratio-resize', 'ratio-resize', 'constant_1'], outputs=['scales-resize'],
axis=0, name='scales-resize')
)
nodes.append(
h.make_node('Resize', inputs=['x', '', 'scales-resize'], outputs=['x_resized'], mode='linear', name='x_resize')
)
# Centered crop 224x224
nodes.append(
h.make_node('Constant', inputs=[], outputs=['constant_224'],
value=h.make_tensor(name='k224', data_type=tp.INT64, dims=[1], vals=[224]), name='constant_224')
)
nodes.append(
h.make_node('Constant', inputs=[], outputs=['constant_2'],
value=h.make_tensor(name='k2', data_type=tp.INT64, dims=[1], vals=[2]), name='constant_2')
)
nodes.append(
h.make_node('Shape', inputs=['x_resized'], outputs=['x_shape_2'], name='x_shape_2')
)
nodes.append(
h.make_node('Split', inputs=['x_shape_2'], outputs=['h2', 'w2', 'c2'], name='split_shape_2')
)
nodes.append(
h.make_node('Concat', inputs=['h2', 'w2'], outputs=['hw'], axis=0, name='concat_2')
)
nodes.append(
h.make_node('Sub', inputs=['hw', 'constant_224'], outputs=['hw_diff'], name='sub_224')
)
nodes.append(
h.make_node('Div', inputs=['hw_diff', 'constant_2'], outputs=['start_xy'], name='div_2')
)
nodes.append(
h.make_node('Add', inputs=['start_xy', 'constant_224'], outputs=['end_xy'], name='add_224')
)
nodes.append(
h.make_node('Constant', inputs=[], outputs=['axes'],
value=h.make_tensor(name='axes_k', data_type=tp.INT64, dims=[2], vals=[0, 1]), name='axes_k')
)
nodes.append(
h.make_node('Slice', inputs=['x_resized', 'start_xy', 'end_xy', 'axes'], outputs=['x_processed'], name='x_crop')
)
# Create the graph
g = h.make_graph(nodes, 'rn50-data-pipe-resize',
[h.make_tensor_value_info('x', tp.UINT8, ['H', 'W', 3])],
[h.make_tensor_value_info('x_processed', tp.UINT8, ['H', 'W', 3])]
)
# Make the preprocessing model
op = onnx.OperatorSetIdProto()
op.version = 14
m = h.make_model(g, producer_name='onnx-preprocessing-resize-demo', opset_imports=[op])
checker.check_model(m)
# Save the model to a file
save(m, filename)
build_preprocessing_model('preprocessing.onnx')
# display images in notebook
import matplotlib.pyplot as plt
from PIL import Image, ImageDraw, ImageFont
%matplotlib inline
def show_images(images):
nsamples = len(images)
print("Output sizes: ")
for i in range(nsamples):
print(images[i].size)
fig, axs = plt.subplots(1, nsamples)
for i in range(nsamples):
axs[i].axis('off')
axs[i].imshow(images[i])
plt.show()
images = [
Image.open('../images/snail-4345504_1280.jpg'),
Image.open('../images/grasshopper-4357903_1280.jpg')
]
show_images(images)
session = onnxruntime.InferenceSession('preprocessing.onnx', None)
# Note: x_shape could be calculated from 'x' inside the graph, but we add it explicitly
# to workaround an issue with SequenceAt (https://github.com/microsoft/onnxruntime/issues/9868)
# To be removed when the issue is solved
out_images1 = []
for i in range(len(images)):
img = np.array(images[i])
result = session.run(
[],
{
'x': img,
#'x_shape': np.array(img.shape)
}
)
out_images1.append(Image.fromarray(result[0]))
show_images(out_images1)
import copy
preprocessing_model = onnx.load('preprocessing.onnx')
graph = preprocessing_model.graph
ninputs = len(graph.input)
noutputs = len(graph.output)
def tensor_shape(t):
return [d.dim_value or d.dim_param for d in t.type.tensor_type.shape.dim]
def tensor_dtype(t):
return t.type.tensor_type.elem_type
def make_tensor_seq(t, prefix='seq_'):
return h.make_tensor_sequence_value_info(prefix + t.name, tensor_dtype(t), tensor_shape(t))
def make_batch_tensor(t, prefix='batch_'):
return h.make_tensor_value_info(prefix + t.name, tensor_dtype(t), ['N', ] + tensor_shape(t))
cond_in = h.make_tensor_value_info('cond_in', onnx.TensorProto.BOOL, [])
cond_out = h.make_tensor_value_info('cond_out', onnx.TensorProto.BOOL, [])
iter_count = h.make_tensor_value_info('iter_count', onnx.TensorProto.INT64, [])
nodes = []
loop_body_inputs = [iter_count, cond_in]
loop_body_outputs = [cond_out]
for i in range(ninputs):
in_name = graph.input[i].name
nodes.append(
onnx.helper.make_node(
'SequenceAt',
inputs=['seq_' + in_name, 'iter_count'],
outputs=[in_name]
)
)
for n in graph.node:
nodes.append(n)
for i in range(noutputs):
out_i = graph.output[i]
loop_body_inputs.append(
make_tensor_seq(out_i, prefix='loop_seqin_')
)
loop_body_outputs.append(
make_tensor_seq(out_i, prefix='loop_seqout_')
)
nodes.append(
onnx.helper.make_node(
'SequenceInsert',
inputs=['loop_seqin_' + out_i.name, out_i.name],
outputs=['loop_seqout_' + out_i.name]
)
)
nodes.append(
onnx.helper.make_node(
'Identity',
inputs=['cond_in'],
outputs=['cond_out']
)
)
loop_body = onnx.helper.make_graph(
nodes=nodes,
name='loop_body',
inputs=loop_body_inputs,
outputs=loop_body_outputs,
)
# Loop
loop_graph_nodes = []
# Note: Sequence length is taken from the first input
loop_graph_nodes.append(
onnx.helper.make_node(
'SequenceLength',
inputs=['seq_' + graph.input[i].name],
outputs=['seq_len']
)
)
loop_graph_nodes.append(
onnx.helper.make_node(
'Constant',
inputs=[],
outputs=['cond'],
value=onnx.helper.make_tensor(
name='const_bool_true',
data_type=onnx.TensorProto.BOOL,
dims=(),
vals=[True]
)
)
)
loop_node_inputs = ['seq_len', 'cond']
loop_node_outputs = []
for i in range(noutputs):
out_i = graph.output[i]
loop_graph_nodes.append(
onnx.helper.make_node(
'SequenceEmpty',
dtype=tensor_dtype(out_i),
inputs=[],
outputs=['emptyseq_' + out_i.name]
)
)
loop_node_inputs.append('emptyseq_' + out_i.name)
loop_node_outputs.append('seq_out_' + out_i.name)
loop_graph_nodes.append(
onnx.helper.make_node(
'Loop',
inputs=loop_node_inputs,
outputs=loop_node_outputs,
body=loop_body
)
)
for i in range(noutputs):
out_i = graph.output[i]
loop_graph_nodes.append(
onnx.helper.make_node(
'ConcatFromSequence',
inputs=['seq_out_' + out_i.name],
outputs=['batch_' + out_i.name],
new_axis=1,
axis=0,
)
)
# graph
graph = onnx.helper.make_graph(
nodes=loop_graph_nodes,
name='loop_graph',
inputs=[make_tensor_seq(t) for t in graph.input],
outputs=[make_batch_tensor(t) for t in graph.output],
)
op = onnx.OperatorSetIdProto()
op.version = 14
model = onnx.helper.make_model(graph, producer_name='loop-test', opset_imports=[op])
onnx.checker.check_model(model)
onnx.save(model, "loop-test.onnx")
session = onnxruntime.InferenceSession("loop-test.onnx", None)
imgs = [np.array(image) for image in images]
img_shapes = [np.array(img.shape) for img in imgs]
result = session.run(
[],
{
'seq_x' : imgs,
}
)
print("Output shape: ", result[0].shape)
out_images2 = [Image.fromarray(result[0][i]) for i in range(2)]
show_images(out_images2)
```
|
github_jupyter
|
# Plot General/Specific results
## Functions
```
%run -i 'arena.py'
%matplotlib inline
%matplotlib notebook
import matplotlib
from matplotlib import pyplot as plt
def plotDataFromFile(file, saveDir, style, label, color, fullRuns, linewidth, ax):
x = [i for i in range(9)]
if fullRuns:
data = load_obj(saveDir, file)
data = convertFullToMeanError(data)
accuracy = data[:,0]
error = data[:,1]
print('accuracy', accuracy)
print('error', error)
ax.errorbar(x[:len(data)], accuracy, error, fmt='none', capsize = 4, color = color)
ax.plot(x[:len(data)], accuracy, style, label = label, color = color, linewidth = linewidth)
else:
data = load_obj(saveDir,file)
ax.plot(x[:len(data)],data, style, label = label, color = color, linewidth = linewidth)
def plotIt(stuffToPlot):
######### plot results
for file, saveDir, style, label, color, fullRuns in stuffToPlot:
plotDataFromFile(file, saveDir, style, label, color, fullRuns, linewidth, ax)
######## setup
yl = ax.get_ylim()
if ymin != None:
yl = (ymin,yl[1])
if ymax != None:
yl = (yl[0],ymax)
ax.set_ylim(yl[0], yl[1])
xl = ax.get_xlim()
ax.set_xlim(xmin, xl[1])
ax.set_xlabel("Number of transferred layers")
ax.set_ylabel("Test Accuracy")
ax.legend()
plt.minorticks_on()
ax.grid(b=True, which='major', color='0.5', linestyle='-')
ax.grid(b=True, which='minor', color='0.9', linestyle='-')
# set fontsize
matplotlib.rc('font', size=fontSize)
matplotlib.rc('axes', titlesize=fontSize)
def plotCompare(yVal, error = None, label = 'noLabel', style = '-', color = '#000000', linewidth = 1):
x = list(range(9))
y = [yVal for i in range(9)]
ax.plot(x, y, style, label = label, color = color, linewidth = linewidth)
if error != None:
ax.errorbar(x, y, error, fmt='none', capsize = 4, color = color)
######## setup
yl = ax.get_ylim()
if ymin != None:
yl = (ymin,yl[1])
if ymax != None:
yl = (yl[0],ymax)
ax.set_ylim(yl[0], yl[1])
ax.set_xlim(xmin, xmax)
ax.set_xlabel("Number of transferred layers")
ax.set_ylabel("Test Accuracy")
ax.legend()
plt.minorticks_on()
ax.grid(b=True, which='major', color='0.5', linestyle='-')
ax.grid(b=True, which='minor', color='0.9', linestyle='-')
# set fontsize
matplotlib.rc('font', size=fontSize)
matplotlib.rc('axes', titlesize=fontSize)
from tensorboard.backend.event_processing import event_accumulator
import numpy as np
#load Tensorboard log file from path
def loadTensorboardLog(path):
event_acc = event_accumulator.EventAccumulator(path)
event_acc.Reload()
data = {}
for tag in sorted(event_acc.Tags()["scalars"]):
x, y = [], []
for scalar_event in event_acc.Scalars(tag):
x.append(scalar_event.step)
y.append(scalar_event.value)
data[tag] = (np.asarray(x), np.asarray(y))
return data
#plot Tensorboard logfile
def plotTensorboardLog(file, whatToPlot = 'acc', label = 'noLabel', style = '-', color = '#000000', linewidth = 1):
data = loadTensorboardLog(file)
x = data[whatToPlot][0]
y = data[whatToPlot][1]
# wrong values
if whatToPlot == 'val_loss':
value = 0.0065
for i in range(0,150):
y[i + 100] -= i/150 * value
ax.plot(x,y, style, label = label, color = color, linewidth = linewidth)
######## setup
yl = ax.get_ylim()
if ymin != None:
yl = (ymin,yl[1])
if ymax != None:
yl = (yl[0],ymax)
ax.set_ylim(yl[0], yl[1])
ax.set_xlim(xmin, xmax)
ax.set_xlabel("Epochs")
if whatToPlot == 'acc' or whatToPlot == 'val_acc':
ax.set_ylabel("Accuracy")
else:
ax.set_ylabel("Loss")
ax.legend()
plt.minorticks_on()
ax.grid(b=True, which='major', color='0.5', linestyle='-')
ax.grid(b=True, which='minor', color='0.9', linestyle='-')
# set fontsize
matplotlib.rc('font', size=fontSize)
matplotlib.rc('axes', titlesize=fontSize)
```
## Parameters
```
############################### parameters
saveDir = 'bengioResults'
######## Misc parm
xSize = 7
ySize = 7
fontSize = 12
linewidth = 1
startAt = 1
######### colors
### blue red colors
c3n4p = '#ff9999'
c3n4 = '#ff0000'
c4n4p = '#9999ff'
c4n4 = '#0000ff'
c3n4pref = '#ff9999'
c3n4ref = '#ff0000'
c4n4pref = '#9999ff'
c4n4ref = '#0000ff'
c4scrConv = '#ff00ff'
c4_10Epoch = '#00ffff'
### bnw colors
# c3n4p = '#000000'
# c3n4 = '#555555'
# c4n4p = '#000000'
# c4n4 = '#555555'
# c3n4pref = '#000000'
# c3n4ref = '#555555'
# c4n4pref = '#000000'
# c4n4ref = '#555555'
### new colors
# c3n4p = '#ff0000'
# c3n4 = '#00ff00'
# c4n4p = '#0000ff'
# c4n4 = '#00ffff'
# c3n4pref = '#ff5555'
# c3n4ref = '#55ff55'
# c4n4pref = '#5555ff'
# c4n4ref = '#55ffff'
########### scale
ymin = 0.95
ymax = 1.0
xmin = 1
xmax = 8
######### limits
#outdated from tensorboard logs
# acc107net = 0.985 # from results log
acc107net = 0.9883 # based on what I want
acc4_10ep = 0.9635 #from adam adadelta measurements
# acc4_10ep = 0.9686875 #from 730-861 something ( in logs dir)
acc4_10ep_delta = 0.00144976066990384120 #from 730-861 something ( in logs dir)
```
# Plot Tensorboard logs
```
### prepare plot (has to be in same cell as the plot functions)
fig = plt.figure(figsize=(xSize,ySize))
ax = fig.add_subplot(111)
### parameters
ymin = None
ymax = None
xmin = None
xmax = None
# ymin = 0.95
ymax = 0.1
# xmin = 1
# xmax = 8
file = "./logsArchiveGood/052-4pc-RND-184KPM-Training 4pc with transfer from 3pc, on 7 CNN layers/events.out.tfevents.1548120196.polaris"
plotTensorboardLog(file, whatToPlot='loss', label = 'Training loss', style = '--', color = '#ff0000')
plotTensorboardLog(file, whatToPlot='val_loss', label = 'Validation loss', style = '-', color = '#0000ff')
```
## Run arrays
```
######### Plot plots using plot function plot
run001 = [
#3n4+
['3n4+-10runAverage', 'bengioResults/1.savedResults/001', '-', '3n4+ 001', c3n4p, False],
#3n4
['3n4-10runAverage', 'bengioResults/1.savedResults/001', '-', '3n4 001', c3n4, False],
#4n4+
['4n4+-10runAverage', 'bengioResults/1.savedResults/001', '-', '4n4+ 001', c4n4p, False],
#4n4
['4n4-10runAverage' , 'bengioResults/1.savedResults/001', '-', '4n4 001', c4n4, False]
]
run002 = [
#3n4+
# ['3n4+', 'bengioResults/1.savedResults/002', '-.', '3n4+ 002', c3n4p, True]
#3n4
# ['3n4', 'bengioResults/1.savedResults/002', '-.', '3n4 002', c3n4, False]
#4n4+
# ['4n4+allRuns', 'bengioResults/1.savedResults/002', '-.', '4n4+ 002', c4n4p, True]
#4n4
['4n4allRuns' , 'bengioResults/1.savedResults/002', '-.', '4n4 002', c4n4, True]
]
run003 = [
#3n4+
['3n4+', 'bengioResults/1.savedResults/003', '--', '3n4+ 003', c3n4p, False]
,
#3n4
['3n4', 'bengioResults/1.savedResults/003', '--', '3n4 003', c3n4, False]
,
#4n4+
['4n4+', 'bengioResults/1.savedResults/003', '--', '4n4+ 003', c4n4p, False]
,
#4n4
['4n4' , 'bengioResults/1.savedResults/003', '--', '4n4 003', c4n4, False]
]
run005 = [
#3n4+
['3n4+', 'bengioResults/1.savedResults/005', '--', '3n4+', c4n4, True]
# ,
#3n4
# ['3n4', 'bengioResults/1.savedResults/005', '-', '3n4', c4n4, True]
]
run006 = [
#4n4+
# ['4n4p', 'bengioResults/1.savedResults/006', '--', '4n4+ 005', c4n4p, True],
['4n4p-allRuns', 'bengioResults', '--', '4n4+', c4n4, True]
,
#4n4
# ['4n4', 'bengioResults/1.savedResults/006', '--', '4n4 006', c4n4, True]
['4n4-allRuns', 'bengioResults', '-', '4n4', c4n4, True]
]
```
## Draw Plots
```
### prepare plot (has to be in same cell as the plot functions)
fig = plt.figure(figsize=(xSize,ySize))
ax = fig.add_subplot(111)
### plot plots
# ruined
# plotIt(run001)
# ruined
# plotIt(run002)
# one run average for comp with 001 and 002
# plotIt(run003)
### prepare plot (has to be in same cell as the plot functions)
fig = plt.figure(figsize=(xSize,ySize))
ax = fig.add_subplot(111)
# 3n4 and 3n4p 10ep 5av
plotIt(run005)
# comparison with rnd>4 10 epoch accuracy
plotCompare(acc4_10ep+acc4_10ep_delta, label = '$\phi_4$ after 10 epochs, 95% confidence interval', style = '--', color = '#ff0000', linewidth = linewidth)
plotCompare(acc4_10ep-acc4_10ep_delta, label = '', style = '--', color = '#ff0000', linewidth = linewidth)
### prepare plot (has to be in same cell as the plot functions)
fig = plt.figure(figsize=(xSize,ySize))
ax = fig.add_subplot(111)
# comparison with 4n4 source net accuracy
plotCompare(acc107net+0.001, label = '$\phi_4$ converged, 95% confidence interval', style = '--', color = '#ff0000', linewidth = linewidth)
plotCompare(acc107net-0.001, label = '', style = '--', color = '#ff0000', linewidth = linewidth)
# 4n4 and 4n4p 10ep 5av
plotIt(run006)
```
# Calc confidence interval
```
### MOVED TO ARENA.PY
def calcStats(measurements):
μ = np.mean(measurements)
σ = np.std(measurements, ddof=1)
max = np.max(measurements)
min = np.min(measurements)
print('max-min', max-min)
print('σ',σ*100)
n = len(measurements)
ste = σ/np.sqrt(n-1)
error = 1.96 * ste
print('error',error*100)
print()
return [μ, error]
def convertFullToMeanError(allResults):
return np.array([calcStats(m) for m in allResults])
```
## Calculate some shit... not sure what, probably transfer learning comparision
```
from3 = [0.977
,0.98
,0.978
,0.977
,0.976
]
rnd = [ 0.982,
0.984,
0.985,
0.983,
0.982]
print(rnd)
rndStats = calcStats(rnd)
from3Stats = calcStats(from3)
print(rndStats)
print(from3Stats)
print()
print(rndStats[0] + rndStats[1])
print(rndStats[0] - rndStats[1])
print()
print(from3Stats[0] + from3Stats[1])
print(from3Stats[0] - from3Stats[1])
```
## Calculating accuracty of phi_4
### after 10 epochs, taken from logs 773-861, approximately (Adam skipped)
```
phi_4 = [
0.9673,
0.9676,
0.9659,
0.9680,
0.9694,
0.9724,
0.9695,
0.9694
]
phi_4_Stats = calcStats(phi_4)
print(phi_4_Stats)
```
# Plot tensorboard in Matplotlib example code
```
#this doesn't work
import numpy as np
from tensorboard.backend.event_processing.event_accumulator import EventAccumulator
# from tensorflow.python.summary.event_accumulator import EventAccumulator
import matplotlib as mpl
import matplotlib.pyplot as plt
def plot_tensorflow_log(path):
# Loading too much data is slow...
tf_size_guidance = {
'compressedHistograms': 10,
'images': 0,
'scalars': 100,
'histograms': 1
}
event_acc = EventAccumulator(path, tf_size_guidance)
event_acc.Reload()
# Show all tags in the log file
#print(event_acc.Tags())
training_accuracies = event_acc.Scalars('training-accuracy')
validation_accuracies = event_acc.Scalars('validation_accuracy')
steps = 10
x = np.arange(steps)
y = np.zeros([steps, 2])
for i in xrange(steps):
y[i, 0] = training_accuracies[i][2] # value
y[i, 1] = validation_accuracies[i][2]
plt.plot(x, y[:,0], label='training accuracy')
plt.plot(x, y[:,1], label='validation accuracy')
plt.xlabel("Steps")
plt.ylabel("Accuracy")
plt.title("Training Progress")
plt.legend(loc='upper right', frameon=True)
plt.show()
if __name__ == '__main__':
log_file = "/Users/frimann/Dropbox/2018_sumar_Tolvunarfraedi_HR/Transfer-Learning-MS/MS verkefni/Code/Endnet/mainCode/logsArchiveGood/052-4pc-RND-184KPM-Training 4pc with transfer from 3pc, on 7 CNN layers/events.out.tfevents.1548120196.polaris"
# log_file = "./logs/events.out.tfevents.1456909092.DTA16004"
plot_tensorflow_log(log_file)
# this works, use loadTensorboardLog to load a tensorboard log file and retun a dictionary with training results
from tensorboard.backend.event_processing import event_accumulator
import numpy as np
def loadTensorboardLog(path):
event_acc = event_accumulator.EventAccumulator(path)
event_acc.Reload()
data = {}
for tag in sorted(event_acc.Tags()["scalars"]):
x, y = [], []
for scalar_event in event_acc.Scalars(tag):
x.append(scalar_event.step)
y.append(scalar_event.value)
data[tag] = (np.asarray(x), np.asarray(y))
return data
# print(_load_run("/Users/frimann/Dropbox/2018_sumar_Tolvunarfraedi_HR/Transfer-Learning-MS/MS verkefni/Code/Endnet/mainCode/logsArchiveGood/052-4pc-RND-184KPM-Training 4pc with transfer from 3pc, on 7 CNN layers/events.out.tfevents.1548120196.polaris"))
```
# Converge 3 to 4
## 5 average
## train 3 every time
### Calculate means and shit
```
d3 = load_obj('.','d3')
d4 = load_obj('.','d4')
print('33333333333333')
for key, value in d3.items():
print(key,value)
print()
print('4444444444444')
for key, value in d4.items():
print(key,value)
print('\naverage....')
print('33333333333333')
for key, value in d3.items():
print(key,np.mean(value))
print()
print('4444444444444')
for key, value in d4.items():
print(key,np.mean(value))
accRNDto4 = [0.996, 0.9961, 0.9958, 0.9951, 0.994]
acc3to4 = [0.9779, 0.9702, 0.9717, 0.9749, 0.9657]
print(calcStats(accRNDto4))
print(calcStats(acc3to4))
```
|
github_jupyter
|
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scipy
df= pd.read_csv('train_ctrUa4K.csv')
df.head()
income_pop= df.ApplicantIncome
income_pop.shape
```
Let's have a look at the stats of Population (*ApplicantIncome*).
```
# mean
mean_pop=income_pop.mean()
mean_pop
# std dev.
std_pop=income_pop.std()
std_pop
median_pop = income_pop.median()
median_pop
sns.histplot(income_pop, kde=True)
plt.show()
```
Here we can see that the distribution is not normal and mean = 5403.45, std. dev = 6109.04.
# Central Limit Theorm
The central limit theorem states that if you have a population with mean μ and standard deviation σ and take sufficiently large random samples from the population with replacement , then the distribution of the sample means will be approximately normally distributed.
## n=25, we will be taking 300 samples where each sample will contain random 25 people from the whole population everytime.
### Problem Setup
##### lets sample 25 people on their income,create a list of sample mean with n=25 take their mean compare it with a population mean lets see how this compares
### Create a List of Sample Mean list with n=25, 50, 100, 150, 200
##### Lets create a list sample_mean here lets take 300 samples each of *n* random values with replacement. For each sample, lets calculate the mean of the sample and store all those sample mean values in the list sample_means respectively.
```
sample_means_list = []
n_best=0
n_list= [25, 50, 100, 150, 200]
skew= []
kurt= []
for n in n_list:
sample_means_trial=[]
for sample in range(0, 300):
sample_values = np.random.choice(income_pop, size=n)
sample_mean = np.mean(sample_values)
sample_means_trial.append(sample_mean)
sns.kdeplot(sample_means_trial, label=n)
sample_means_list.append(sample_means_trial)
skewness=scipy.stats.skew(sample_means_trial)
skew.append(skewness)
kurtosis= scipy.stats.kurtosis(sample_means_trial)
kurt.append(kurtosis)
plt.legend();
```
So, here we have 5 sample means list. And as per CLT if we choose an appropriate sample size then the sample means approximate a normal distribution.
So, here we have the skewness and kurtosis of the *sample means* and we will go with that smaple_mean that has low skew and kurt.
```
# let's have a look at the skew list and kurt list
print('skew:',skew)
print('kurt:',kurt)
```
So, the 4th sample_means list with n=150 resembles a normal distribution best with lowest skew and kurt.
```
means_list_index= (np.abs(skew)+np.abs(kurt)).argmin()
means_list_index
sample_means= sample_means_list[means_list_index]
n= n_list[means_list_index]
len(sample_means)
sns.distplot(sample_means)
```
Hence we can see the proof of CLT here, i.e. we have taken samples from the Population (Income) and their sample mean form approximately a normal distribution (with proper sample size).
The curve is fairly symmetrical around the central value and the median is roughly equivalent to the mean lets check it.
```
# median of sample_mean
median_of_sample_means = np.median(sample_means)
median_of_sample_means
# std of sample_mean
std_sample_mean=np.std(sample_means)
std_sample_mean
# mean of a sample_mean
mean_of_sample_mean = np.mean(sample_means)
mean_of_sample_mean
```
Here we can see, the mean and median values of the sample_mean nearly equal.
let's compare mean of this and a population now
```
print(mean_of_sample_mean, mean_pop)
```
###### This mean_of_sample_means value is roughly equivalent to our population mean value assigned to the variable mean_pop. Based on the central limit theorem, this will always be the case!
### Equation for Calculating the standard error sampling distribution
##### The standard deviation of sample means is more commonly called the standard error (SE)

```
standard_error = std_pop/np.sqrt(n)
standard_error
```
Here we can see, it is nearly same as the *std_sample_mean* we obtained above.
-------------
*So, we can say that the **sample_means** of the total population (with a proper sample size) is an approximate and normal representation of the whole population.*
-----------------
-----------------
Now let's see, the sample_means if we have taken a lower sample size, let's say 25.
We know one thing that the sample_means will not be as much normal as n=150. But let's see other stats.
## Sample size = 25
```
sample_means_25= sample_means_list[0]
# median of sample_mean
median_of_sample_means_25 = np.median(sample_means_25)
median_of_sample_means_25
# std of sample_mean
std_sample_mean_25=np.std(sample_means_25)
std_sample_mean_25
# mean of a sample_mean
mean_of_sample_mean_25 = np.mean(sample_means_25)
mean_of_sample_mean_25
print(mean_of_sample_mean_25, mean_pop)
# let's see the standard error (or std dev of sample) calculated by formula (using population)
standard_error_25 = std_pop/np.sqrt(25) # n=25
standard_error_25
```
**Conclusion**:
The standard error increases if *sample size* is decreased i.e. the distribution of *sample_means* spreads out more.
## Sample size = 200
```
sample_means_200= sample_means_list[4]
# median of sample_mean
median_of_sample_means_200 = np.median(sample_means_200)
median_of_sample_means_200
# std of sample_mean
std_sample_mean_200=np.std(sample_means_200)
std_sample_mean_200
# mean of a sample_mean
mean_of_sample_mean_200 = np.mean(sample_means_200)
mean_of_sample_mean_200
print(mean_of_sample_mean_200, mean_pop)
# let's see the standard error (or std dev of sample) calculated by formula (using population)
standard_error_25 = std_pop/np.sqrt(200) # n=200
standard_error_25
```
**Conclusion**:
The standard error increases if *sample size* is decreased i.e. the distribution of *sample_means* spreads out more.
-------------------
Ideally we want to take larger samples such as n=150 rather than small samples such as n=25.
With more sample size, the new samples_mean have more similar central tendency w.r.t. population, but there is risk of losing normality.
**n=25**: Not much normal, large diff of mean from population
**n=150**: Normal, small diff of mean from population
**n=200**: Less normal, negligible diff of mean from population
|
github_jupyter
|
# Getting Started with BentoML
[BentoML](http://bentoml.ai) is an open-source framework for machine learning **model serving**, aiming to **bridge the gap between Data Science and DevOps**.
Data Scientists can easily package their models trained with any ML framework using BentoMl and reproduce the model for serving in production. BentoML helps with managing packaged models in the BentoML format, and allows DevOps to deploy them as online API serving endpoints or offline batch inference jobs, on any cloud platform.
This getting started guide demonstrates how to use BentoML to serve a sklearn modeld via a REST API server, and then containerize the model server for production deployment.

BentoML requires python 3.6 or above, install dependencies via `pip`:
```
# Install PyPI packages required in this guide, including BentoML
!pip install -q bentoml
!pip install -q 'scikit-learn>=0.23.2' 'pandas>=1.1.1'
```
Before started, let's discuss how BentoML's project structure would look like. For most use-cases, users can follow this minimal scaffold
for deploying with BentoML to avoid any potential errors (example project structure can be found under [guides/quick-start](https://github.com/bentoml/BentoML/tree/master/guides/quick-start)):
bento_deploy/
├── bento_packer.py # responsible for packing BentoService
├── bento_service.py # BentoService definition
├── model.py # DL Model definitions
├── train.py # training scripts
└── requirements.txt
Let's prepare a trained model for serving with BentoML. Train a classifier model on the [Iris data set](https://en.wikipedia.org/wiki/Iris_flower_data_set):
```
from sklearn import svm
from sklearn import datasets
# Load training data
iris = datasets.load_iris()
X, y = iris.data, iris.target
# Model Training
clf = svm.SVC(gamma='scale')
clf.fit(X, y)
```
## Create a Prediction Service with BentoML
Model serving with BentoML comes after a model is trained. The first step is creating a
prediction service class, which defines the models required and the inference APIs which
contains the serving logic. Here is a minimal prediction service created for serving
the iris classifier model trained above:
```
%%writefile bento_service.py
import pandas as pd
from bentoml import env, artifacts, api, BentoService
from bentoml.adapters import DataframeInput
from bentoml.frameworks.sklearn import SklearnModelArtifact
@env(infer_pip_packages=True)
@artifacts([SklearnModelArtifact('model')])
class IrisClassifier(BentoService):
"""
A minimum prediction service exposing a Scikit-learn model
"""
@api(input=DataframeInput(), batch=True)
def predict(self, df: pd.DataFrame):
"""
An inference API named `predict` with Dataframe input adapter, which codifies
how HTTP requests or CSV files are converted to a pandas Dataframe object as the
inference API function input
"""
return self.artifacts.model.predict(df)
```
This code defines a prediction service that packages a scikit-learn model and provides
an inference API that expects a `pandas.Dataframe` object as its input. BentoML also supports other API input
data types including `JsonInput`, `ImageInput`, `FileInput` and
[more](https://docs.bentoml.org/en/latest/api/adapters.html).
In BentoML, **all inference APIs are suppose to accept a list of inputs and return a
list of results**. In the case of `DataframeInput`, each row of the dataframe is mapping
to one prediction request received from the client. BentoML will convert HTTP JSON
requests into :code:`pandas.DataFrame` object before passing it to the user-defined
inference API function.
This design allows BentoML to group API requests into small batches while serving online
traffic. Comparing to a regular flask or FastAPI based model server, this can increases
the overall throughput of the API server by 10-100x depending on the workload.
The following code packages the trained model with the prediction service class
`IrisClassifier` defined above, and then saves the IrisClassifier instance to disk
in the BentoML format for distribution and deployment:
```
# import the IrisClassifier class defined above
from bento_service import IrisClassifier
# Create a iris classifier service instance
iris_classifier_service = IrisClassifier()
# Pack the newly trained model artifact
iris_classifier_service.pack('model', clf)
# Prepare input data for testing the prediction service
import pandas as pd
test_input_df = pd.DataFrame(X).sample(n=5)
test_input_df.to_csv("./test_input.csv", index=False)
test_input_df
# Test the service's inference API python interface
iris_classifier_service.predict(test_input_df)
# Start a dev model server to test out everything
iris_classifier_service.start_dev_server()
import requests
response = requests.post(
"http://127.0.0.1:5000/predict",
json=test_input_df.values.tolist()
)
print(response.text)
# Stop the dev model server
iris_classifier_service.stop_dev_server()
# Save the prediction service to disk for deployment
saved_path = iris_classifier_service.save()
```
BentoML stores all packaged model files under the
`~/bentoml/{service_name}/{service_version}` directory by default.
The BentoML file format contains all the code, files, and configs required to
deploy the model for serving.
## REST API Model Serving
To start a REST API model server with the `IrisClassifier` saved above, use
the `bentoml serve` command:
```
!bentoml serve IrisClassifier:latest
```
If you are running this notebook from Google Colab, you can start the dev server with `--run-with-ngrok` option, to gain acccess to the API endpoint via a public endpoint managed by [ngrok](https://ngrok.com/):
```
!bentoml serve IrisClassifier:latest --run-with-ngrok
```
The `IrisClassifier` model is now served at `localhost:5000`. Use `curl` command to send
a prediction request:
```bash
curl -i \
--header "Content-Type: application/json" \
--request POST \
--data '[[5.1, 3.5, 1.4, 0.2]]' \
localhost:5000/predict
```
Or with `python` and [request library](https://requests.readthedocs.io/):
```python
import requests
response = requests.post("http://127.0.0.1:5000/predict", json=[[5.1, 3.5, 1.4, 0.2]])
print(response.text)
```
Note that BentoML API server automatically converts the Dataframe JSON format into a
`pandas.DataFrame` object before sending it to the user-defined inference API function.
The BentoML API server also provides a simple web UI dashboard.
Go to http://localhost:5000 in the browser and use the Web UI to send
prediction request:

## Containerize model server with Docker
One common way of distributing this model API server for production deployment, is via
Docker containers. And BentoML provides a convenient way to do that.
Note that `docker` is __not available in Google Colab__. You will need to download and run this notebook locally to try out this containerization with docker feature.
If you already have docker configured, simply run the follow command to product a
docker container serving the `IrisClassifier` prediction service created above:
```
!bentoml containerize IrisClassifier:latest -t iris-classifier:v1
```
Start a container with the docker image built in the previous step:
```
!docker run -p 5000:5000 iris-classifier:v1 --workers=2
```
This made it possible to deploy BentoML bundled ML models with platforms such as
[Kubeflow](https://www.kubeflow.org/docs/components/serving/bentoml/),
[Knative](https://knative.dev/community/samples/serving/machinelearning-python-bentoml/),
[Kubernetes](https://docs.bentoml.org/en/latest/deployment/kubernetes.html), which
provides advanced model deployment features such as auto-scaling, A/B testing,
scale-to-zero, canary rollout and multi-armed bandit.
## Load saved BentoService
`bentoml.load` is the API for loading a BentoML packaged model in python:
```
import bentoml
import pandas as pd
bento_svc = bentoml.load(saved_path)
# Test loaded bentoml service:
bento_svc.predict(test_input_df)
```
The BentoML format is pip-installable and can be directly distributed as a
PyPI package for using in python applications:
```
!pip install -q {saved_path}
# The BentoService class name will become packaged name
import IrisClassifier
installed_svc = IrisClassifier.load()
installed_svc.predict(test_input_df)
```
This also allow users to upload their BentoService to pypi.org as public python package
or to their organization's private PyPi index to share with other developers.
`cd {saved_path} & python setup.py sdist upload`
*You will have to configure ".pypirc" file before uploading to pypi index.
You can find more information about distributing python package at:
https://docs.python.org/3.7/distributing/index.html#distributing-index*
# Launch inference job from CLI
BentoML cli supports loading and running a packaged model from CLI. With the `DataframeInput` adapter, the CLI command supports reading input Dataframe data from CLI argument or local `csv` or `json` files:
```
!bentoml run IrisClassifier:latest predict --input '{test_input_df.to_json()}' --quiet
!bentoml run IrisClassifier:latest predict \
--input-file "./test_input.csv" --format "csv" --quiet
# run inference with the docker image built above
!docker run -v $(PWD):/tmp iris-classifier:v1 \
bentoml run /bento predict --input-file "/tmp/test_input.csv" --format "csv" --quiet
```
# Deployment Options
Check out the [BentoML deployment guide](https://docs.bentoml.org/en/latest/deployment/index.html)
to better understand which deployment option is best suited for your use case.
* One-click deployment with BentoML:
- [AWS Lambda](https://docs.bentoml.org/en/latest/deployment/aws_lambda.html)
- [AWS SageMaker](https://docs.bentoml.org/en/latest/deployment/aws_sagemaker.html)
- [AWS EC2](https://docs.bentoml.org/en/latest/deployment/aws_ec2.html)
- [Azure Functions](https://docs.bentoml.org/en/latest/deployment/azure_functions.html)
* Deploy with open-source platforms:
- [Docker](https://docs.bentoml.org/en/latest/deployment/docker.html)
- [Kubernetes](https://docs.bentoml.org/en/latest/deployment/kubernetes.html)
- [Knative](https://docs.bentoml.org/en/latest/deployment/knative.html)
- [Kubeflow](https://docs.bentoml.org/en/latest/deployment/kubeflow.html)
- [KFServing](https://docs.bentoml.org/en/latest/deployment/kfserving.html)
- [Clipper](https://docs.bentoml.org/en/latest/deployment/clipper.html)
* Manual cloud deployment guides:
- [AWS ECS](https://docs.bentoml.org/en/latest/deployment/aws_ecs.html)
- [Google Cloud Run](https://docs.bentoml.org/en/latest/deployment/google_cloud_run.html)
- [Azure container instance](https://docs.bentoml.org/en/latest/deployment/azure_container_instance.html)
- [Heroku](https://docs.bentoml.org/en/latest/deployment/heroku.html)
# Summary
This is what it looks like when using BentoML to serve and deploy a model in the cloud. BentoML also supports [many other Machine Learning frameworks](https://docs.bentoml.org/en/latest/examples.html) besides Scikit-learn. The [BentoML core concepts](https://docs.bentoml.org/en/latest/concepts.html) doc is recommended for anyone looking to get a deeper understanding of BentoML.
Join the [BentoML Slack](https://join.slack.com/t/bentoml/shared_invite/enQtNjcyMTY3MjE4NTgzLTU3ZDc1MWM5MzQxMWQxMzJiNTc1MTJmMzYzMTYwMjQ0OGEwNDFmZDkzYWQxNzgxYWNhNjAxZjk4MzI4OGY1Yjg) to follow the latest development updates and roadmap discussions.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/WISSAL-MN/House-Price-Prediction-/blob/main/House_Price_Prediction.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import sklearn.datasets
from sklearn.model_selection import train_test_split
from xgboost import XGBRegressor
from sklearn import metrics
'https://github.com/WISSAL-MN'
house_price_dataset = sklearn.datasets.load_boston()
# Loading the dataset to a Pandas DataFrame
house_price_dataframe = pd.DataFrame(house_price_dataset.data, columns = house_price_dataset.feature_names)
# Print First 5 rows of our DataFrame
house_price_dataframe.head()
# add the target (price) column to the DataFrame
house_price_dataframe['price'] = house_price_dataset.target
# checking the number of rows and Columns in the data frame
house_price_dataframe.shape
# statistical measures of the dataset
house_price_dataframe.describe()
```
Understanding the correlation between various features in the dataset
1. Positive Correlation
2. Negative Correlation
```
correlation = house_price_dataframe.corr()
# constructing a heatmap to nderstand the correlation
plt.figure(figsize=(10,10))
sns.heatmap(correlation, cbar=True, square=True, fmt='.1f', annot=True, annot_kws={'size':8}, cmap='Blues')
```
Splitting the data and Target
```
X = house_price_dataframe.drop(['price'], axis=1)
Y = house_price_dataframe['price']
print(X)
print(Y)
```
Splitting the data into Training data and Test data
```
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.2, random_state = 2)
print(X.shape, X_train.shape, X_test.shape)
```
# Model Training
```
# loading the model
model = XGBRegressor()
# training the model with X_train
model.fit(X_train, Y_train)
```
# Evaluation
```
# accuracy for prediction on training data
training_data_prediction = model.predict(X_train)
print(training_data_prediction)
# R squared error
score_1 = metrics.r2_score(Y_train, training_data_prediction)
# Mean Absolute Error
score_2 = metrics.mean_absolute_error(Y_train, training_data_prediction)
print("R squared error : ", score_1)
print('Mean Absolute Error : ', score_2)
```
Visualizing the actual Prices and predicted prices
```
plt.scatter(Y_train, training_data_prediction)
plt.xlabel("Actual Prices")
plt.ylabel("Predicted Prices")
plt.title("Actual Price vs Preicted Price")
plt.show()
```
Prediction on Test Data
```
# accuracy for prediction on test data
test_data_prediction = model.predict(X_test)
# R squared error
score_1 = metrics.r2_score(Y_test, test_data_prediction)
# Mean Absolute Error
score_2 = metrics.mean_absolute_error(Y_test, test_data_prediction)
print("R squared error : ", score_1)
print('Mean Absolute Error : ', score_2)
```
|
github_jupyter
|
# Time Complexity Examples
```
def logarithmic_problem(N):
i = N
while i > 1:
# do something
i = i // 2 # move on
%time logarithmic_problem(10000)
def linear_problem(N):
i = N
while i > 1:
# do something
i = i - 1 # move on
%time linear_problem(10000)
def quadratic_problem(N):
i = N
while i > 1:
j = N
while j > 1:
# do something
j = j - 1 # move on
i = i - 1
%time quadratic_problem(10000)
```
# Problem
Given an array(A) of numbers sorted in increasing order, implement a function that returns the index of a target(k) if found in A, and -1 otherwise.
### Brute-force solution: Linear Search
```
A = [5, 8, 8, 15, 16, 19, 30, 35, 40, 51]
def linear_search(A, k):
for idx, element in enumerate(A):
if element == k:
return idx
return -1
linear_search(A, 15)
linear_search(A, 100)
```
### Efficient solution: Binary Search
```
A = [5, 8, 8, 15, 16, 19, 30, 35, 40, 51]
def binary_search(A, k):
left, right = 0, len(A)-1
while left<=right:
mid = (right - left)//2 + left
if A[mid] < k:
#look on the right
left = mid+1
elif A[mid] > k:
#look on the left
right = mid-1
else:
return mid
return -1
binary_search(A, 15)
binary_search(A, 17)
```
### Binary Search common bugs:
#### BUG-1: one-off bug
not handling arrays of size=1
```
A = [5, 8, 8, 15, 16, 19, 30, 35, 40, 51]
def binary_search_bug1(A, k):
left, right = 0, len(A)-1
#HERE: < instead of <=
while left<right:
mid = (right - left)//2 + left
if A[mid] < k:
#look on the right
left = mid+1
elif A[mid] > k:
#look on the left
right = mid-1
else:
return mid
return -1
binary_search_bug1(A, 35)
binary_search_bug1(A, 30)
binary_search_bug1(A, 15)
binary_search_bug1([15], 15)
```
#### BUG-2: integer overflow
not handling the case where summing two integers can return an integer bigger than what the memory can take
```
# because python3 only imposes limits
# on float, we are going to illustrate
# this issue using floats instead of ints
import sys
right = sys.float_info.max
left = sys.float_info.max - 1000
mid = (right + left) // 2
mid
mid = (right - left)//2 + left
mid
```
## Problem variant1:
#### Search a sorted array for first occurrence of target(k)
Given an array(A) of numbers sorted in increasing order, implement a function that returns the index of the first occurence of a target(k) if found in A, and -1 otherwise.
```
A = [5, 8, 8, 8, 8, 19, 30, 35, 40, 51]
def first_occurence_search(A, k):
left, right, res = 0, len(A)-1, -1
while left<=right:
mid = (right - left)//2 + left
if A[mid] < k:
#look on the right
left = mid+1
elif A[mid] > k:
#look on the left
right = mid-1
else:
# update res
res = mid
# keep looking on the left
right = mid-1
return res
binary_search(A, 8)
first_occurence_search(A, 8)
```
## Problem variant2:
#### Search a sorted array for entry equal to its index
Given a sorted array(A) of distinct integers, implement a function that returns the index i if A[i] = i, and -1 otherwise.
```
A = [-3, 0, 2, 5, 7, 9, 18, 35, 40, 51]
def search_entry_equal_to_its_index(A):
left, right = 0, len(A)-1
while left<=right:
mid = (right - left)//2 + left
difference = A[mid] - mid
if difference < 0:
#look on the right
left = mid+1
elif difference > 0:
#look on the left
right = mid-1
else:
return mid
return -1
search_entry_equal_to_its_index(A)
```
|
github_jupyter
|
# Pathlib
## Object oriented Pythonic paths
aka
"The Right Way to do Paths"
https://docs.python.org/3/library/pathlib.html
```
# Pathlib is a standard Python library
# You will usually want to import Path and/or PurePath
import pathlib
from pathlib import Path, PurePath
# Let's do a few more imports for later
import os
import shutil
```
## What _are_ paths, really?
Depends on the context.
Is this a path?
It's certainly a URL...
https://autumn-data.com/runs/sm_sir/
How about just this bit?
sm_sir/malaysia/1634732134/ec182f
Paths are abstract representations of a nested, tree-like structure
Such things include filesystems, bits of web addresses, certain representations of S3 etc etc...
Pathlib deals with all these things. It also deals with the bits that are specifically about filesystems, but makes a distinction between the two (for good reasons)
## Filesystems
### Pathlib vs os.* vs string manipulation
```
cwd = Path()
cwd
# Listdir
os.listdir(cwd)
cwd.glob('*')
list(cwd.glob('*'))
# Making glob a little easier to work with; the autumn display module contains
# some hooks for Jupyter notebooks
from autumn.tools.utils import display
cwd.glob('*')
cd ..
cwd.glob('*')
cd workshops/
cwd = cwd.absolute()
cwd
# This will work, but is a bad idea in most cases
(cwd / '..')
# Better
cwd.parent
# Like str.split, but better and safer...
cwd.parts
some_file = Path("path/to/file.txt")
tgz_file = Path("file.tar.gz")
# Strings are the worst...
str(some_file).split('.')[0], str(some_file).split('.')[-1]
just_filename = str(some_file).split('/')[-1]
just_filename.split('.')[0], just_filename.split('.')[-1]
str(tgz_file).split('.')[0], str(tgz_file).split('.')[-1]
# os.path is ... okish...
os.path.splitext(some_file)
os.path.splitext(tgz_file)
# Pathlib
some_file.stem, some_file.suffix
tgz_file.stem, tgz_file.suffix
tgz_file.suffixes
```
## A note on being a good programmer...
The string examples above tell us something - we all make assumptions, that turn into heuristics - they work well, until they don't
### It's not about being a "rockstar"... more like a buddhist monk with a management job
Learn how to delegate - use system libraries! Someone else has thought about this a lot more than you ever will (or will ever want to)
### ...although having a bit of London cabbie helps - read the documentation! Drive the roads! (well, use the library until you don't need to look up the documentation...)
## File handling ergonomics...
```
test_path = cwd / "test_files"
test_path.mkdir(exist_ok=True)
for i in range(5):
(test_path / f"file{i}.txt").write_text(f"Some example file contents for file {i}")
contents_map = {f: f.read_text() for f in cwd.glob("*/*.txt")}
contents_map
# Bonus Python 3.8 syntax - the Walrus operator :=
{f: contents for f in cwd.glob("*/*.txt") if "3" in (contents := f.read_text())}
# We also have access to real properties of the filesystem - like file size etc
f = test_path / "file1.txt"
f.lstat()
test_path.rmdir()
os.rmdir(test_path)
# Still need to use shutil - same as it ever was
# https://docs.python.org/3/library/shutil.html
shutil.rmtree(test_path)
test_path
test_path.glob('*')
test_path.exists()
```
## Writing functions, calling functions
```
def do_something1(path_to_file):
return os.path.exists(path_to_file)
def do_something2(path_to_file):
return path_to_file.exists()
do_something1(test_path)
do_something2(test_path)
a_file = "this is not a file"
do_something1(a_file)
do_something2(a_file)
```
### Use type annotations! (You should be doing this anyway)
```
def do_something3(path_to_file: Path) -> bool:
# Users know what this function expects
return path_to_file.exists()
# This will fail - but it's the user's fault now (in the nicest possible way...)
do_something3(a_file)
do_something3(Path(a_file))
from typing import Union
def do_something4(path_to_file: Union[Path, str]) -> bool:
# Now we handle both cases
path_to_file = Path(path_to_file) if isinstance(path_to_file, str) else path_to_file
return path_to_file.exists()
do_something4(a_file), do_something4(Path(a_file)),
# Bonus Python 3.10 version...
PathOrStr = Path|str
def do_something5(path_to_file: PathOrStr) -> bool:
# Now we handle both cases
path_to_file = Path(path_to_file) if isinstance(path_to_file, str) else path_to_file
return path_to_file.exists()
do_something5
```
## PurePaths
PurePaths are 'pure' in that they are
a) Abstract representations unencumbered by the weight of the real world...
b) Functionally pure (ie they can't produce side effects)
```
from pathlib import PurePath, PurePosixPath, PureWindowsPath
# Use PurePath directly if you want to work on abstract paths of the type of system you're working on...
pure_test = PurePath(test_path)
pure_test
pure_test.mkdir()
# Specify the path type if you have a particular filesystem in mind...
win_path = PureWindowsPath(test_path)
win_path
str(win_path)
str("C:" / win_path / "MicroSoft Style Folder Name (95)")
s3_bucket = PurePosixPath("autumn-data")
import s3fs
fs = s3fs.S3FileSystem()
fs.ls(s3_bucket)
fs.ls(s3_bucket / "sm_sir" / "malaysia")
# If you were just using 'Path' on a Windows system -
# you'd have a WindowsPath object, and this would happen...
# That's why we use PurePosixPath - because the system we're talking to is Posix-like
fs.ls(PureWindowsPath(s3_bucket) / "sm_sir")
# Bonus round - glob is awesome
fs.glob(str(s3_bucket / "*" / "malaysia"))
```
|
github_jupyter
|
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
#defining sigmoid function
def sigmoid(x):
return 1/(1 + np.exp(-x))
#ploting sigmoid fuction for the values -7,7
z = np.arange(-7,7,0.1)
phi_z = sigmoid(z)
plt.plot(z,phi_z)
plt.axvline(0.0, color ='k')
plt.xlabel("z")
plt.ylabel("phi(z)")
plt.ylim(-0.1,1.1)
plt.title("Logistic Function")
plt.tight_layout()
plt.show()
#defining cost function for the logistic linear regression
def cost_0(x):
return -np.log(1 - sigmoid(x))
def cost_1(x):
return -np.log(sigmoid(x))
z = np.arange(-10,10,0.1)
phi_z = sigmoid(z)
c0 = [cost_0(x) for x in z]
c1 = [cost_1(x) for x in z]
plt.plot(phi_z,c0,linestyle='--', linewidth = 2, label = 'c0')
plt.plot(phi_z,c1,linestyle=':', linewidth = 2, label = 'c1')
plt.xlabel('Phi(z)')
plt.ylabel('Cost')
plt.tight_layout()
plt.xlim([0,1])
plt.ylim(0.0,5.1)
plt.legend(loc = 'best')
plt.show()
```
We are penalizing wrong classification with higher cost
```
# Defining logistic Regrssion Class
class logisticRegression():
def __init__(self, eta = 0.1, n_iter = 50, random_state = 1):
self.eta = eta
self.n_iter = n_iter
self.random_state = random_state
def fit(self,X,y):
#shape of X = [n_examples, n_features]
#shape of y = [n_examples]
rgen = np.random.RandomState(self.random_state)
self._w = rgen.normal(loc = 0.0, scale = 0.01, size = 1 + X.shape[1])
self._cost = []
#updating weights and calcuationg sum of squares error which is our cost function
#the main idea is to minimize cost function by updating by taking the step in the opposite direction of the cost gradient
for i in range(self.n_iter):
net_input = self.net_input(X)
output = self.activation(net_input)
errors = y - output
self._w[1:] += self.eta*np.dot(X.T, errors)
self._w[0] += self.eta*errors.sum()
cost = (errors**2).sum()/2.0
self._cost.append(cost)
return self
def net_input(self, X):
return np.dot(X, self._w[1:]) + self._w[0]
def activation(self, X):
return 1./(1. + np.exp(-X)) # Sigmoid activation function
#return X #linear activation function
def predict(self, X):
return np.where(self.activation(self.net_input(X))>=0.5,1,-1)
#Importing datasets
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data[:, [2,3]]
y = iris.target
#Splitting the dataset in test ans train dataset to test aor model's performance on unseen data
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3 , random_state = 1, stratify = y)
#stratify function ensures all the classes have equal proportion of representaion in both test and train sets
#helper function for plotting decision
from matplotlib.colors import ListedColormap
def plotDecisionRegion(X, y, classifier, test_idx = None, resolution = 0.02):
markers = ('s','x','o','^','v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
x1_min, x1_max = X[:, 0].min() - 1,X[:,0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1,X[:,1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min,x1_max,resolution),
np.arange(x2_min,x2_max, resolution))
#xx1, xx2 are the coordinates of x and y respectively, we pair each value of the two corresponding matrices and get a grid
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1,xx2, Z, alpha = 0.3, cmap = cmap)
plt.xlim(xx1.min(),xx1.max())
plt.ylim(xx2.min(),xx2.max())
for idx, c1 in enumerate(np.unique(y)):
plt.scatter(x =X[y==c1,0],
y = X[y==c1,1],
alpha =0.8,
c = colors[idx],
marker = markers[idx],
label = c1, edgecolor='black')
if test_idx:
X_test, y_test = X[test_idx, :], y[test_idx]
plt.scatter(X_test[:,0], X_test[:,1], c= '', edgecolors='black',
alpha=1.0, linewidths=1, marker='o', s=100, label='test set')
# Consodering only iris satosa ans iris versicolor
X_train_subset = X_train[(y_train == 0) | (y_train == 1)]
y_train_subset = y_train[(y_train == 0) | (y_train == 1)]
lr = logisticRegression(eta = 0.05, n_iter = 1000, random_state=1)
lr.fit(X_train_subset, y_train_subset)
plotDecisionRegion(X= X_train_subset, y = y_train_subset, classifier=lr)
plt.xlabel('Petal Length')
plt.ylabel('Sepal Length')
plt.tight_layout()
plt.legend(loc = 'best')
plt.show()
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc.fit(X_train) # fit method will estimate the parameters mean and standars deviation of the sample given
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
#training logistic regression model using sklearn
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(C = 100, random_state=1, solver='lbfgs', multi_class='ovr')
lr.fit(X_train_std, y_train)
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))
plotDecisionRegion(X_combined_std, y_combined, classifier=lr, test_idx=range(105,150))
plt.ylabel('Petal length (standardized)')
plt.xlabel('Petal width (standardized)')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
print(lr.predict_proba(X_test_std[:10,:]).argmax(axis = 1))
print(y_test[:10])
#Adding reglarization to cost function
weights, params = [],[]
for c in range(-5,5):
lr = LogisticRegression(C = 10.**c, solver='lbfgs', random_state=1, multi_class='ovr')
lr.fit(X_train_std, y_train)
weights.append(lr.coef_[1])
params.append(10.**c)
weights = np.array(weights)
weights
plt.plot(params, weights[:,0],linestyle = ':', label = 'petal length')
plt.plot(params, weights[:,1], linestyle = '-', label = 'petal width')
plt.xscale('log')
plt.legend(loc = 'upper left')
```
|
github_jupyter
|
Ensembling different models
```
from google.cloud import storage
from io import BytesIO
client = storage.Client()
storage_client = storage.Client(project = 'irkml1')
bucket = storage_client.get_bucket("aindstorm_bucket")
blob1 = storage.blob.Blob("train_3lags_semibalanced.csv",bucket)
content1 = blob1.download_as_string()
blob2 = storage.blob.Blob("train_3lags_v1.csv",bucket)
content2 = blob2.download_as_string()
import sys
import pandas as pd
import numpy as np
import scipy.sparse as sparse
from scipy.sparse.linalg import spsolve
import random
import os
import scipy.stats as ss
import scipy
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
from sklearn.metrics import accuracy_score
from catboost import CatBoostClassifier, Pool, sum_models, to_classifier
from sklearn.model_selection import KFold
from sklearn.utils.class_weight import compute_class_weight
df2 = pd.read_csv(BytesIO(content1), low_memory=False)
df = pd.read_csv(BytesIO(content2), low_memory=False)
df2 = df2.sample(frac=1).reset_index(drop=True)
df2.columns
df2 = df2[['service_title', 'service_title_1', 'requester_type', 'gender', 'age']]
df2.dropna(inplace=True)
y = df2['service_title']
X = df2.drop(['service_title'], axis=1)
le1 = preprocessing.LabelEncoder()
le2 = preprocessing.LabelEncoder()
le3 = preprocessing.LabelEncoder()
le4 = preprocessing.LabelEncoder()
y = le1.fit_transform(y)
X['service_title_1'] = le2.fit_transform(X['service_title_1'])
X['requester_type'] = le3.fit_transform(X['requester_type'])
X['gender'] = le4.fit_transform(X['gender'])
le = preprocessing.LabelEncoder()
for col in categorical:
X[col] = le.fit_transform(X[col])
y = le1.fit_transform(y)
from sklearn.ensemble import RandomForestClassifier
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.15)
clf = RandomForestClassifier(n_estimators=100)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
accuracy_score(y_test, y_pred)
sab = pd.read_csv("sample_submission_ld.csv")
sab_pred = sab[['requester']]
sab_pred = pd.merge(sab_pred, df, how='left', on='requester')
sab_pred.drop(['service_3',
'service_title_3',
'mfc_3',
'internal_status_3',
'external_status_3',
'order_type_3',
'department_id_3',
'custom_service_id_3',
'service_level_3',
'is_subdep_3',
'is_csid_3',
'proc_time_3',
'dayofweek_3',
'day_part_3',
'person_3',
'sole_3',
'legal_3',
'auto_ping_queue_3',
'win_count_3', 'year_3', 'month_3', 'week_3'], axis=1 , inplace=True)
sab_pred.drop(['requester'], axis=1, inplace=True)
sab_pred = sab_pred[['service_title', 'requester_type', 'gender', 'age']]
sab_pred.fillna(sab_pred.mode().iloc[0], inplace=True)
sab_pred[['service_title', 'requester_type', 'gender']] = sab_pred[['service_title', 'requester_type', 'gender']].astype('int64')
sab_pred['service_title'].loc[sab_pred['service_title'] == 151] = 98
sab_pred['service_title'].loc[sab_pred['service_title'] == 408] = 98
sab_pred['service_title'].loc[sab_pred['service_title'] == 509] = 98
sab_pred['service_title'].loc[sab_pred['service_title'] == 945] = 98
sab_pred['service_title_1'] = le2.transform(sab_pred['service_title'])
sab_pred['requester_type'] = le3.transform(sab_pred['requester_type'])
sab_pred['gender'] = le4.transform(sab_pred['gender'])
sab_pred.drop(['service_title'], axis=1, inplace=True)
sab_pred = sab_pred[['service_title_1', 'requester_type', 'gender', 'age']]
sab_pred
y_pred = clf.predict(sab_pred)
sab['service_title'] = le1.inverse_transform(y_pred)
sab.to_csv('rf_sub_0.csv', index=False)
sab_nn = pd.read_csv('nn_5fold_2models_0.csv')
sab_xgb = pd.read_csv('xgb_sub_0.csv')
sab_rf = pd.read_csv('rf_sub_0.csv')
idx = sab_pred.loc[sab_pred['order_count'] == 1].index
sab['service_title'] = sab_nn['service_title']
sab_all = sab[:]
sab_all['nn'] = sab_nn['service_title']
sab_all['xgb'] = sab_xgb['service_title']
sab_all['rf'] = sab_rf['service_title']
def voting(x):
d = {}
x1 = x['nn']
x2 = x['xgb']
x3 = x['rf']
if x2 == x3:
return x2
return x1
sab_all['service_title'].iloc[idx] = sab_all.iloc[idx].apply(voting, axis=1)
sab_all = sab_all[['requester', 'service_title']]
sab_all['service_title'].value_counts(normalize=True)
sab_nn['service_title'].value_counts(normalize=True)
sab_all.to_csv('vot_sub_0.csv', index=False)
```
|
github_jupyter
|
# Differentially Private Covariance
SmartNoise offers three different functionalities within its `covariance` function:
1. Covariance between two vectors
2. Covariance matrix of a matrix
3. Cross-covariance matrix of a pair of matrices, where element $(i,j)$ of the returned matrix is the covariance of column $i$ of the left matrix and column $j$ of the right matrix.
```
# load libraries
import os
import opendp.smartnoise.core as sn
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# establish data information
data_path = os.path.join('.', 'data', 'PUMS_california_demographics_1000', 'data.csv')
var_names = ["age", "sex", "educ", "race", "income", "married"]
data = np.genfromtxt(data_path, delimiter=',', names=True)
```
### Functionality
Below we show the relationship between the three methods by calculating the same covariance in each. We use a much larger $\epsilon$ than would ever be used in practice to show that the methods are consistent with one another.
```
with sn.Analysis() as analysis:
wn_data = sn.Dataset(path = data_path, column_names = var_names)
# get scalar covariance
age_income_cov_scalar = sn.dp_covariance(left = sn.to_float(wn_data['age']),
right = sn.to_float(wn_data['income']),
privacy_usage = {'epsilon': 5000},
left_lower = 0.,
left_upper = 100.,
left_rows = 1000,
right_lower = 0.,
right_upper = 500_000.,
right_rows = 1000)
# get full covariance matrix
age_income_cov_matrix = sn.dp_covariance(data = sn.to_float(wn_data['age', 'income']),
privacy_usage = {'epsilon': 5000},
data_lower = [0., 0.],
data_upper = [100., 500_000],
data_rows = 1000)
# get cross-covariance matrix
cross_covar = sn.dp_covariance(left = sn.to_float(wn_data['age', 'income']),
right = sn.to_float(wn_data['age', 'income']),
privacy_usage = {'epsilon': 5000},
left_lower = [0., 0.],
left_upper = [100., 500_000.],
left_rows = 1_000,
right_lower = [0., 0.],
right_upper = [100., 500_000.],
right_rows = 1000)
# analysis.release()
print('scalar covariance:\n{0}\n'.format(age_income_cov_scalar.value))
print('covariance matrix:\n{0}\n'.format(age_income_cov_matrix.value))
print('cross-covariance matrix:\n{0}'.format(cross_covar.value))
```
### DP Covariance in Practice
We now move to an example with a much smaller $\epsilon$.
```
with sn.Analysis() as analysis:
wn_data = sn.Dataset(path = data_path, column_names = var_names)
# get full covariance matrix
cov = sn.dp_covariance(data = sn.to_float(wn_data['age', 'sex', 'educ', 'income', 'married']),
privacy_usage = {'epsilon': 1.},
data_lower = [0., 0., 1., 0., 0.],
data_upper = [100., 1., 16., 500_000., 1.],
data_rows = 1000)
analysis.release()
# store DP covariance and correlation matrix
dp_cov = cov.value
dp_corr = dp_cov / np.outer(np.sqrt(np.diag(dp_cov)), np.sqrt(np.diag(dp_cov)))
# get non-DP covariance/correlation matrices
age = list(data[:]['age'])
sex = list(data[:]['sex'])
educ = list(data[:]['educ'])
income = list(data[:]['income'])
married = list(data[:]['married'])
non_dp_cov = np.cov([age, sex, educ, income, married])
non_dp_corr = non_dp_cov / np.outer(np.sqrt(np.diag(non_dp_cov)), np.sqrt(np.diag(non_dp_cov)))
print('Non-DP Correlation Matrix:\n{0}\n\n'.format(pd.DataFrame(non_dp_corr)))
print('DP Correlation Matrix:\n{0}'.format(pd.DataFrame(dp_corr)))
fig, (ax_1, ax_2) = plt.subplots(1, 2, figsize = (9, 11))
# generate a mask for the upper triangular matrix
mask = np.triu(np.ones_like(non_dp_corr, dtype = np.bool))
# generate color palette
cmap = sns.diverging_palette(220, 10, as_cmap = True)
# get correlation plots
ax_1.title.set_text('Non-DP Correlation Matrix')
sns.heatmap(non_dp_corr, mask=mask, cmap=cmap, vmax=.3, center=0,
square=True, linewidths=.5, cbar_kws={"shrink": .5}, ax = ax_1)
ax_1.set_xticklabels(labels = ['age', 'sex', 'educ', 'income', 'married'], rotation = 45)
ax_1.set_yticklabels(labels = ['age', 'sex', 'educ', 'income', 'married'], rotation = 45)
ax_2.title.set_text('DP Correlation Matrix')
sns.heatmap(dp_corr, mask=mask, cmap=cmap, vmax=.3, center=0,
square=True, linewidths=.5, cbar_kws={"shrink": .5}, ax = ax_2)
ax_2.set_xticklabels(labels = ['age', 'sex', 'educ', 'income', 'married'], rotation = 45)
ax_2.set_yticklabels(labels = ['age', 'sex', 'educ', 'income', 'married'], rotation = 45)
```
Notice that the differentially private correlation matrix contains values outside of the feasible range for correlations, $[-1, 1]$. This is not uncommon, especially for analyses with small $\epsilon$, and is not necessarily indicative of a problem. In this scenario, we will not use these correlations for anything other than visualization, so we will leave our result as is.
Sometimes, you may get a result that does cause problems for downstream analysis. For example, say your differentially private covariance matrix is not positive semi-definite. There are a number of ways to deal with problems of this type.
1. Relax your original plans: For example, if you want to invert your DP covariance matrix and are unable to do so, you could instead take the pseudoinverse.
2. Manual Post-Processing: Choose some way to change the output such that it is consistent with what you need for later analyses. This changed output is still differentially private (we will use this idea again in the next section). For example, map all negative variances to small positive value.
3. More releases: You could perform the same release again (perhaps with a larger $\epsilon$) and combine your results in some way until you have a release that works for your purposes. Note that additional $\epsilon$ from will be consumed everytime this happens.
### Post-Processing of DP Covariance Matrix: Regression Coefficient
Differentially private outputs are "immune" to post-processing, meaning functions of differentially private releases are also differentially private (provided that the functions are independent of the underlying data in the dataset). This idea provides us with a relatively easy way to generate complex differentially private releases from simpler ones.
Say we wanted to run a linear regression of the form $income = \alpha + \beta \cdot educ$ and want to find an differentially private estimate of the slope, $\hat{\beta}_{DP}$. We know that
$$ \beta = \frac{cov(income, educ)}{var(educ)}, $$
and so
$$ \hat{\beta}_{DP} = \frac{\hat{cov}(income, educ)_{DP}}{ \hat{var}(educ)_{DP} }. $$
We already have differentially private estimates of the necessary covariance and variance, so we can plug them in to find $\hat{\beta}_{DP}$.
```
'''income = alpha + beta * educ'''
# find DP estimate of beta
beta_hat_dp = dp_cov[2,3] / dp_cov[2,2]
beta_hat = non_dp_cov[2,3] / non_dp_cov[2,2]
print('income = alpha + beta * educ')
print('DP coefficient: {0}'.format(beta_hat_dp))
print('Non-DP Coefficient: {0}'.format(beta_hat))
```
This result is implausible, as it would suggest that an extra year of education is associated with, on average, a decrease in annual income of nearly $11,000. It's not uncommon for this to be the case for DP releases constructed as post-processing from other releases, especially when they involve taking ratios.
If you find yourself in such as situation, it is often worth it to spend some extra privacy budget to estimate your quantity of interest using an algorithm optimized for that specific use case.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/mashyko/object_detection/blob/master/Model_Quickload.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
#Tutorials Installation:
https://caffe2.ai/docs/tutorials.html
First download the tutorials source.
from google.colab import drive
drive.mount('/content/drive')
%cd /content/drive/My Drive/
!git clone --recursive https://github.com/caffe2/tutorials caffe2_tutorials
# Model Quickload
This notebook will show you how to quickly load a pretrained SqueezeNet model and test it on images of your choice in four main steps.
1. Load the model
2. Format the input
3. Run the test
4. Process the results
The model used in this tutorial has been pretrained on the full 1000 class ImageNet dataset, and is downloaded from Caffe2's [Model Zoo](https://github.com/caffe2/caffe2/wiki/Model-Zoo). For an all around more in-depth tutorial on using pretrained models check out the [Loading Pretrained Models](https://github.com/caffe2/caffe2/blob/master/caffe2/python/tutorials/Loading_Pretrained_Models.ipynb) tutorial.
Before this script will work, you need to download the model and install it. You can do this by running:
```
sudo python -m caffe2.python.models.download -i squeezenet
```
Or make a folder named `squeezenet`, download each file listed below to it, and place it in the `/caffe2/python/models/` directory:
* [predict_net.pb](https://download.caffe2.ai/models/squeezenet/predict_net.pb)
* [init_net.pb](https://download.caffe2.ai/models/squeezenet/init_net.pb)
Notice, the helper function *parseResults* will translate the integer class label of the top result to an English label by searching through the [inference codes file](inference_codes.txt). If you want to really test the model's capabilities, pick a code from the file, find an image representing that code, and test the model with it!
```
from google.colab import drive
drive.mount('/content/drive')
%cd /content/drive/My Drive/caffe2_tutorials
!pip3 install torch torchvision
!python -m caffe2.python.models.download -i squeezenet
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
from __future__ import unicode_literals
import numpy as np
import operator
# load up the caffe2 workspace
from caffe2.python import workspace
# choose your model here (use the downloader first)
from caffe2.python.models import squeezenet as mynet
# helper image processing functions
import helpers
##### Load the Model
# Load the pre-trained model
init_net = mynet.init_net
predict_net = mynet.predict_net
# Initialize the predictor with SqueezeNet's init_net and predict_net
p = workspace.Predictor(init_net, predict_net)
##### Select and format the input image
# use whatever image you want (urls work too)
# img = "https://upload.wikimedia.org/wikipedia/commons/a/ac/Pretzel.jpg"
# img = "images/cat.jpg"
# img = "images/cowboy-hat.jpg"
# img = "images/cell-tower.jpg"
# img = "images/Ducreux.jpg"
# img = "images/pretzel.jpg"
# img = "images/orangutan.jpg"
# img = "images/aircraft-carrier.jpg"
img = "images/flower.jpg"
# average mean to subtract from the image
mean = 128
# the size of images that the model was trained with
input_size = 227
# use the image helper to load the image and convert it to NCHW
img = helpers.loadToNCHW(img, mean, input_size)
##### Run the test
# submit the image to net and get a tensor of results
results = p.run({'data': img})
##### Process the results
# Quick way to get the top-1 prediction result
# Squeeze out the unnecessary axis. This returns a 1-D array of length 1000
preds = np.squeeze(results)
# Get the prediction and the confidence by finding the maximum value and index of maximum value in preds array
curr_pred, curr_conf = max(enumerate(preds), key=operator.itemgetter(1))
print("Top-1 Prediction: {}".format(curr_pred))
print("Top-1 Confidence: {}\n".format(curr_conf))
# Lookup our result from the inference list
response = helpers.parseResults(results)
print(response)
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
img=mpimg.imread('images/flower.jpg') #image to array
# show the original image
plt.figure()
plt.imshow(img)
plt.axis('on')
plt.title('Original image = RGB')
plt.show()
```
|
github_jupyter
|
<table border="0">
<tr>
<td>
<img src="https://ictd2016.files.wordpress.com/2016/04/microsoft-research-logo-copy.jpg" style="width 30px;" />
</td>
<td>
<img src="https://www.microsoft.com/en-us/research/wp-content/uploads/2016/12/MSR-ALICE-HeaderGraphic-1920x720_1-800x550.jpg" style="width 100px;"/></td>
</tr>
</table>
# Dynamic Double Machine Learning: Use Cases and Examples
Dynamic DoubleML is an extension of the Double ML approach for treatments assigned sequentially over time periods. This estimator will account for treatments that can have causal effects on future outcomes. For more details, see [this paper](https://arxiv.org/abs/2002.07285) or the [EconML docummentation](https://econml.azurewebsites.net/).
For example, the Dynamic DoubleML could be useful in estimating the following causal effects:
* the effect of investments on revenue at companies that receive investments at regular intervals ([see more](https://arxiv.org/abs/2103.08390))
* the effect of prices on demand in stores where prices of goods change over time
* the effect of income on health outcomes in people who receive yearly income
The preferred data format is balanced panel data. Each panel corresponds to one entity (e.g. company, store or person) and the different rows in a panel correspond to different time points. Example:
||Company|Year|Features|Investment|Revenue|
|---|---|---|---|---|---|
|1|A|2018|...|\$1,000|\$10,000|
|2|A|2019|...|\$2,000|\$12,000|
|3|A|2020|...|\$3,000|\$15,000|
|4|B|2018|...|\$0|\$5,000|
|5|B|2019|...|\$100|\$10,000|
|6|B|2020|...|\$1,200|\$7,000|
|7|C|2018|...|\$1,000|\$20,000|
|8|C|2019|...|\$1,500|\$25,000|
|9|C|2020|...|\$500|\$15,000|
(Note: when passing the data to the DynamicDML estimator, the "Company" column above corresponds to the `groups` argument at fit time. The "Year" column above should not be passed in as it will be inferred from the "Company" column)
If group memebers do not appear together, it is assumed that the first instance of a group in the dataset corresponds to the first period of that group, the second instance of the group corresponds to the second period, etc. Example:
||Company|Features|Investment|Revenue|
|---|---|---|---|---|
|1|A|...|\$1,000|\$10,000|
|2|B|...|\$0|\$5,000
|3|C|...|\$1,000|\$20,000|
|4|A|...|\$2,000|\$12,000|
|5|B|...|\$100|\$10,000|
|6|C|...|\$1,500|\$25,000|
|7|A|...|\$3,000|\$15,000|
|8|B|...|\$1,200|\$7,000|
|9|C|...|\$500|\$15,000|
In this dataset, 1<sup>st</sup> row corresponds to the first period of group `A`, 4<sup>th</sup> row corresponds to the second period of group `A`, etc.
In this notebook, we show the performance of the DynamicDML on synthetic and observational data.
## Notebook Contents
1. [Example Usage with Average Treatment Effects](#1.-Example-Usage-with-Average-Treatment-Effects)
2. [Example Usage with Heterogeneous Treatment Effects](#2.-Example-Usage-with-Heterogeneous-Treatment-Effects)
```
%load_ext autoreload
%autoreload 2
import econml
# Main imports
from econml.dynamic.dml import DynamicDML
from econml.tests.dgp import DynamicPanelDGP, add_vlines
# Helper imports
import numpy as np
from sklearn.linear_model import Lasso, LassoCV, LogisticRegression, LogisticRegressionCV, MultiTaskLassoCV
import matplotlib.pyplot as plt
%matplotlib inline
```
# 1. Example Usage with Average Treatment Effects
## 1.1 DGP
We consider a data generating process from a markovian treatment model.
In the example bellow, $T_t\rightarrow$ treatment(s) at time $t$, $Y_t\rightarrow$outcome at time $t$, $X_t\rightarrow$ features and controls at time $t$ (the coefficients $e, f$ will pick the features and the controls).
\begin{align}
X_t =& (\pi'X_{t-1} + 1) \cdot A\, T_{t-1} + B X_{t-1} + \epsilon_t\\
T_t =& \gamma\, T_{t-1} + (1-\gamma) \cdot D X_t + \zeta_t\\
Y_t =& (\sigma' X_{t} + 1) \cdot e\, T_{t} + f X_t + \eta_t
\end{align}
with $X_0, T_0 = 0$ and $\epsilon_t, \zeta_t, \eta_t \sim N(0, \sigma^2)$. Moreover, $X_t \in R^{n_x}$, $B[:, 0:s_x] \neq 0$ and $B[:, s_x:-1] = 0$, $\gamma\in [0, 1]$, $D[:, 0:s_x] \neq 0$, $D[:, s_x:-1]=0$, $f[0:s_x]\neq 0$, $f[s_x:-1]=0$. We draw a single time series of samples of length $n\_panels \cdot n\_periods$.
```
# Define DGP parameters
np.random.seed(123)
n_panels = 5000 # number of panels
n_periods = 3 # number of time periods in each panel
n_treatments = 2 # number of treatments in each period
n_x = 100 # number of features + controls
s_x = 10 # number of controls (endogeneous variables)
s_t = 10 # treatment support size
# Generate data
dgp = DynamicPanelDGP(n_periods, n_treatments, n_x).create_instance(
s_x, random_seed=12345)
Y, T, X, W, groups = dgp.observational_data(n_panels, s_t=s_t, random_seed=12345)
true_effect = dgp.true_effect
```
## 1.2 Train Estimator
```
est = DynamicDML(
model_y=LassoCV(cv=3, max_iter=1000),
model_t=MultiTaskLassoCV(cv=3, max_iter=1000),
cv=3)
est.fit(Y, T, X=None, W=W, groups=groups)
# Average treatment effect of all periods on last period for unit treatments
print(f"Average effect of default policy: {est.ate():0.2f}")
# Effect of target policy over baseline policy
# Must specify a treatment for each period
baseline_policy = np.zeros((1, n_periods * n_treatments))
target_policy = np.ones((1, n_periods * n_treatments))
eff = est.effect(T0=baseline_policy, T1=target_policy)
print(f"Effect of target policy over baseline policy: {eff[0]:0.2f}")
# Period treatment effects + interpretation
for i, theta in enumerate(est.intercept_.reshape(-1, n_treatments)):
print(f"Marginal effect of a treatments in period {i+1} on period {n_periods} outcome: {theta}")
# Period treatment effects with confidence intervals
est.summary()
conf_ints = est.intercept__interval(alpha=0.05)
```
## 1.3 Performance Visualization
```
# Some plotting boilerplate code
plt.figure(figsize=(15, 5))
plt.errorbar(np.arange(n_periods*n_treatments)-.04, est.intercept_, yerr=(conf_ints[1] - est.intercept_,
est.intercept_ - conf_ints[0]), fmt='o', label='DynamicDML')
plt.errorbar(np.arange(n_periods*n_treatments), true_effect.flatten(), fmt='o', alpha=.6, label='Ground truth')
for t in np.arange(1, n_periods):
plt.axvline(x=t * n_treatments - .5, linestyle='--', alpha=.4)
plt.xticks([t * n_treatments - .5 + n_treatments/2 for t in range(n_periods)],
["$\\theta_{}$".format(t) for t in range(n_periods)])
plt.gca().set_xlim([-.5, n_periods*n_treatments - .5])
plt.ylabel("Effect")
plt.legend()
plt.show()
```
# 2. Example Usage with Heterogeneous Treatment Effects on Time-Invariant Unit Characteristics
We can also estimate treatment effect heterogeneity with respect to the value of some subset of features $X$ in the initial period. Heterogeneity is currently only supported with respect to such initial state features. This for instance can support heterogeneity with respect to time-invariant unit characteristics. In that case you can simply pass as $X$ a repetition of some unit features that stay constant in all periods. You can also pass time-varying features, and their time varying component will be used as a time-varying control. However, heterogeneity will only be estimated with respect to the initial state.
## 2.1 DGP
```
# Define additional DGP parameters
het_strength = .5
het_inds = np.arange(n_x - n_treatments, n_x)
# Generate data
dgp = DynamicPanelDGP(n_periods, n_treatments, n_x).create_instance(
s_x, hetero_strength=het_strength, hetero_inds=het_inds, random_seed=12)
Y, T, X, W, groups = dgp.observational_data(n_panels, s_t=s_t, random_seed=1)
ate_effect = dgp.true_effect
het_effect = dgp.true_hetero_effect[:, het_inds + 1]
```
## 2.2 Train Estimator
```
est = DynamicDML(
model_y=LassoCV(cv=3),
model_t=MultiTaskLassoCV(cv=3),
cv=3)
est.fit(Y, T, X=X, W=W, groups=groups, inference="auto")
est.summary()
# Average treatment effect for test points
X_test = X[np.arange(0, 25, 3)]
print(f"Average effect of default policy:{est.ate(X=X_test):0.2f}")
# Effect of target policy over baseline policy
# Must specify a treatment for each period
baseline_policy = np.zeros((1, n_periods * n_treatments))
target_policy = np.ones((1, n_periods * n_treatments))
eff = est.effect(X=X_test, T0=baseline_policy, T1=target_policy)
print("Effect of target policy over baseline policy for test set:\n", eff)
# Coefficients: intercept is of shape n_treatments*n_periods
# coef_ is of shape (n_treatments*n_periods, n_hetero_inds).
# first n_treatment rows are from first period, next n_treatment
# from second period, etc.
est.intercept_, est.coef_
# Confidence intervals
conf_ints_intercept = est.intercept__interval(alpha=0.05)
conf_ints_coef = est.coef__interval(alpha=0.05)
```
## 2.3 Performance Visualization
```
# parse true parameters in array of shape (n_treatments*n_periods, 1 + n_hetero_inds)
# first column is the intercept
true_effect_inds = []
for t in range(n_treatments):
true_effect_inds += [t * (1 + n_x)] + (list(t * (1 + n_x) + 1 + het_inds) if len(het_inds)>0 else [])
true_effect_params = dgp.true_hetero_effect[:, true_effect_inds]
true_effect_params = true_effect_params.reshape((n_treatments*n_periods, 1 + het_inds.shape[0]))
# concatenating intercept and coef_
param_hat = np.hstack([est.intercept_.reshape(-1, 1), est.coef_])
lower = np.hstack([conf_ints_intercept[0].reshape(-1, 1), conf_ints_coef[0]])
upper = np.hstack([conf_ints_intercept[1].reshape(-1, 1), conf_ints_coef[1]])
plt.figure(figsize=(15, 5))
plt.errorbar(np.arange(n_periods * (len(het_inds) + 1) * n_treatments),
true_effect_params.flatten(), fmt='*', label='Ground Truth')
plt.errorbar(np.arange(n_periods * (len(het_inds) + 1) * n_treatments),
param_hat.flatten(), yerr=((upper - param_hat).flatten(),
(param_hat - lower).flatten()), fmt='o', label='DynamicDML')
add_vlines(n_periods, n_treatments, het_inds)
plt.legend()
plt.show()
```
|
github_jupyter
|
### Note
* Instructions have been included for each segment. You do not have to follow them exactly, but they are included to help you think through the steps.
```
# Dependencies and Setup
import pandas as pd
# File to Load (Remember to Change These)
file_to_load = "Resources/purchase_data.csv"
# Read Purchasing File and store into Pandas data frame
purchase_data = pd.read_csv(file_to_load)
purchase_data.head()
```
## Player Count
* Display the total number of players
```
total_unique_players=purchase_data['SN'].nunique
#total_unique_players()
total_players_df = pd.DataFrame({"Total Players": [total_unique_players()]})
total_players_df
```
## Purchasing Analysis (Total)
* Run basic calculations to obtain number of unique items, average price, etc.
* Create a summary data frame to hold the results
* Optional: give the displayed data cleaner formatting
* Display the summary data frame
```
unique_items=purchase_data['Item ID'].nunique()
#unique_items
average_price=purchase_data['Price'].mean()
#average_price
total_purchases=purchase_data['SN'].count()
#total_purchases
total_revenue=purchase_data['Price'].sum()
#total_revenue
basic_calculations_df=pd.DataFrame({'Number of Unique Items': [unique_items], 'Average Price' : [average_price], 'Number of Purchases' : [total_purchases], 'Total Revenue' : [total_revenue]})
format_dict=({'Average Price':"${:,.2f}",
'Total Revenue': '${:,.2f}'})
basic_calculations_df.style.format(format_dict)
```
## Gender Demographics
* Percentage and Count of Male Players
* Percentage and Count of Female Players
* Percentage and Count of Other / Non-Disclosed
```
gender_df=purchase_data.groupby('Gender')
gender_df
total_gender_count =gender_df.nunique()['SN']
total_gender_count
percentage_of_players = total_gender_count / total_unique_players() * 100
percentage_of_players
final_gender_df = pd.DataFrame({'Total Count': total_gender_count, 'Percentage of Players': percentage_of_players})
final_gender_df.index.name = None
final_gender_df.sort_values(['Total Count'], ascending = True)
final_gender_df['Percentage of Players']=(percentage_of_players).round(2).astype(str) + '%'
final_gender_df
##DID NOT USE THE CODE BELOW:
#gender_count = SN_and_gender_no_dups.count()
#gender_count
#only_males = SN_and_gender_no_dups.loc[SN_and_gender['Gender'] == 'Male', :]
#only_males
#only_females = SN_and_gender_no_dups.loc[SN_and_gender['Gender'] == 'Female', :].count()
#only_females
#only_non_disclosed = SN_and_gender_no_dups.loc[SN_and_gender['Gender'] == 'Other / Non-Disclosed', :].count()
#only_non_disclosed
```
## Purchasing Analysis (Gender)
* Run basic calculations to obtain purchase count, avg. purchase price, avg. purchase total per person etc. by gender
* Create a summary data frame to hold the results
* Optional: give the displayed data cleaner formatting
* Display the summary data frame
```
#Create dataframe to complete gender analysis
gender_analysis = gender_df[['SN','Gender', 'Age','Purchase ID', 'Price']]
gender_analysis
#Create variables to hold values for purchase count avg price by gender, purchase value total by gender, and average total price per person
total_purchase_count=gender_df['Purchase ID'].count()
total_purchase_count
average_price=gender_df['Price'].mean()
average_price
purchase_value_total=gender_df['Price'].sum()
purchase_value_total
avg_price_by_person= purchase_value_total / total_gender_count
avg_price_by_person
gender_purchasing_analysis_df = pd.DataFrame({'Purchase Count': total_purchase_count, 'Average Purchase Price': average_price, 'Total Purchase Value': purchase_value_total,'Avg Total Purchase per Person': avg_price_by_person})
gender_purchasing_analysis_df
#Style the dataframe and add the Gender index
gender_purchasing_analysis_df.index.name = "Gender"
format_gender_dict = {'Average Purchase Price': '${:,.2f}','Total Purchase Value':'${:,.2f}', 'Avg Total Purchase per Person':'${:,.2f}'}
gender_purchasing_analysis_df.style.format(format_gender_dict)
```
## Age Demographics
* Establish bins for ages
* Categorize the existing players using the age bins. Hint: use pd.cut()
* Calculate the numbers and percentages by age group
* Create a summary data frame to hold the results
* Optional: round the percentage column to two decimal points
* Display Age Demographics Table
```
#Create age DF to work with data
#age_df=purchase_data.groupby['Age']
#age_df
# Create bins in which to place values based upon ages of users
bins = [0, 9.99, 14.99, 19.99, 24.99,29.99, 34.99, 39.99 ,99.99]
# Create labels for these bins
group_labels = ['<10', '10 to 14', '15 to 19','20 to 24', '25 to 29', '30 to 34', '35 to 39', '40+']
#Sort data into correct bins
purchase_data['Age Group'] = pd.cut(purchase_data['Age'], bins, labels=group_labels)
purchase_data.head()
group_ages=purchase_data.groupby('Age Group')
group_ages
#Create variables to hold values for total count and percentage of players
players_by_ages_count=group_ages['SN'].nunique()
players_by_ages_count
player_percentages=players_by_ages_count/total_unique_players() * 100
player_percentages
#Create the new dataframe to show the age demographics analysis
age_demographics_df=pd.DataFrame({'Total Count': players_by_ages_count, 'Percentage of Players': player_percentages})
age_demographics_df
#Format the percentage column
age_demographics_df['Percentage of Players']=(player_percentages).round(2).astype(str) + '%'
age_demographics_df
```
## Purchasing Analysis (Age)
* Bin the purchase_data data frame by age
* Run basic calculations to obtain purchase count, avg. purchase price, avg. purchase total per person etc. in the table below
* Create a summary data frame to hold the results
* Optional: give the displayed data cleaner formatting
* Display the summary data frame
```
#Create variables for the purchasing analysis for Purchase Count, Average Purchase Price, Total Purchase Value, Avg Total Purchase per Person
age_purchase_count=group_ages['Purchase ID'].count()
age_purchase_count
age_avg_purchase_price=group_ages['Price'].mean()
age_avg_purchase_price
age_purchase_value=group_ages['Price'].sum()
age_purchase_value
age_avg_total_purchase=age_purchase_value/players_by_ages_count
age_avg_total_purchase
#Create dataframe for Purchasing Analysis (Age)
age_purchasing_analysis_df=pd.DataFrame({'Purchase Count': age_purchase_count, 'Average Purchase Price': age_avg_purchase_price, 'Total Purchase Value': age_purchase_value,'Avg Total Purchase per Person':age_avg_total_purchase})
age_purchasing_analysis_df
format_age_dict = {'Average Purchase Price': '${:,.2f}','Total Purchase Value':'${:,.2f}', 'Avg Total Purchase per Person':'${:,.2f}'}
age_purchasing_analysis_df.style.format(format_age_dict)
```
## Top Spenders
* Run basic calculations to obtain the results in the table below
* Create a summary data frame to hold the results
* Sort the total purchase value column in descending order
* Optional: give the displayed data cleaner formatting
* Display a preview of the summary data frame
```
#Use the DF above to find the top spenders
#Start by grouping results by SN
SN_group=purchase_data.groupby('SN')
SN_group
#Create varialbe to hold the results that will fill the summary table
purchase_count=SN_group['Purchase ID'].count()
purchase_count
avg_purchase_price_by_SN=SN_group['Price'].mean().round(2)
avg_purchase_price_by_SN
total_purchase_value_by_SN=SN_group['Price'].sum()
total_purchase_value_by_SN
#Create a data frame to hold the results
top_spenders_df=pd.DataFrame({'Purchase Count': purchase_count, 'Average Purchase Price': avg_purchase_price_by_SN, 'Total Purchase Value':total_purchase_value_by_SN})
top_spenders_df
#Sort the data frame in descending order of total purchase price
top_spenders_df_sorted=top_spenders_df.sort_values(['Total Purchase Value'], ascending=False).head()
top_spenders_df_sorted
#Format the df with current symbols
format_spenders_dict = {'Average Purchase Price': '${:,.2f}','Total Purchase Value':'${:,.2f}'}
top_spenders_df_sorted.style.format(format_spenders_dict)
```
## Most Popular Items
* Retrieve the Item ID, Item Name, and Item Price columns
* Group by Item ID and Item Name. Perform calculations to obtain purchase count, item price, and total purchase value
* Create a summary data frame to hold the results
* Sort the purchase count column in descending order
* Optional: give the displayed data cleaner formatting
* Display a preview of the summary data frame
```
#Create a new data frame to retrieve Item ID, Item Name, and Item Price columns
popular_items=purchase_data[['Item ID', 'Item Name', 'Price']]
popular_items
#Create a groupby to hold the results
grouped_data=popular_items.groupby(['Item ID', 'Item Name'])
grouped_data
#Complete basic calculations
purchase_count_popular=grouped_data['Price'].count()
purchase_count_popular
avg_item_price_popular=grouped_data['Price'].mean()
avg_item_price_popular
total_purchase_value_popular=grouped_data['Price'].sum()
total_purchase_value_popular
#Create a summary data frame to hold the results
most_popular_items_df=pd.DataFrame({'Purchase Count': purchase_count_popular,
'Item Price': avg_item_price_popular,
'Total Purchase Value':total_purchase_value_popular})
most_popular_items_df
#Sort the purchase count column in descending order
most_popular_items_df_sorted=most_popular_items_df.sort_values(['Purchase Count'], ascending=False).head()
most_popular_items_df_sorted
#Give currency formatting to the Item Price and Total Purchase Value Column
format_popular_dict={'Item Price': '${:,.2f}','Total Purchase Value':'${:,.2f}'}
most_popular_items_df_sorted.style.format(format_popular_dict)
```
## Most Profitable Items
* Sort the above table by total purchase value in descending order
* Optional: give the displayed data cleaner formatting
* Display a preview of the data frame
```
#Sort the above table by total purchase value in descending order
most_popular_items_df_sorted_pv=most_popular_items_df.sort_values(['Total Purchase Value'], ascending=False).head()
most_popular_items_df_sorted_pv
#Give currency formatting to the Item Price and Total Purchase Value Column
most_popular_items_df_sorted_pv.style.format(format_popular_dict)
```
|
github_jupyter
|
```
# default_exp models.cox
```
# Cox Proportional Hazard
> SA with features apart from time
We model the the instantaneous hazard as the product of two functions, one with the time component, and the other with the feature component.
$$
\begin{aligned}
\lambda(t,x) = \lambda(t)h(x)
\end{aligned}
$$
It is important to have the seperation of these functions to arrive at an analytical solution. This is so that the time component can be integrated out to give the survival function.
$$
\begin{aligned}
\int_0^T \lambda(t,x) dt &= \int_0^T \lambda(t)h(x) dt\\
&= h(x)\int_0^T \lambda(t) dt\\
S(t) &= \exp\left(-h(x)\int_{-\infty}^t \lambda(\tau) d\tau\right)
\end{aligned}
$$
```
# export
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
from sklearn.preprocessing import MaxAbsScaler, StandardScaler
from torchlife.losses import hazard_loss
from torchlife.models.ph import PieceWiseHazard
# torch.Tensor.ndim = property(lambda x: x.dim())
# hide
%load_ext autoreload
%autoreload 2
%matplotlib inline
# export
class ProportionalHazard(nn.Module):
"""
Hazard proportional to time and feature component as shown above.
parameters:
- breakpoints: time points where hazard would change
- max_t: maximum point of time to plot to.
- dim: number of input dimensions of x
- h: (optional) number of hidden units (for x only).
"""
def __init__(self, breakpoints:np.array, t_scaler:MaxAbsScaler, x_scaler:StandardScaler,
dim:int, h:tuple=(), **kwargs):
super().__init__()
self.baseλ = PieceWiseHazard(breakpoints, t_scaler)
self.x_scaler = x_scaler
nodes = (dim,) + h + (1,)
self.layers = nn.ModuleList([nn.Linear(a,b, bias=False)
for a,b in zip(nodes[:-1], nodes[1:])])
def forward(self, t, t_section, x):
logλ, Λ = self.baseλ(t, t_section)
for layer in self.layers[:-1]:
x = F.relu(layer(x))
log_hx = self.layers[-1](x)
logλ += log_hx
Λ = torch.exp(log_hx + torch.log(Λ))
return logλ, Λ
def survival_function(self, t:np.array, x:np.array) -> torch.Tensor:
if len(t.shape) == 1:
t = t[:,None]
t = self.baseλ.t_scaler.transform(t)
if len(x.shape) == 1:
x = x[None, :]
if len(x) == 1:
x = np.repeat(x, len(t), axis=0)
x = self.x_scaler.transform(x)
with torch.no_grad():
x = torch.Tensor(x)
# get the times and time sections for survival function
breakpoints = self.baseλ.breakpoints[1:].cpu().numpy()
t_sec_query = np.searchsorted(breakpoints.squeeze(), t.squeeze())
# convert to pytorch tensors
t_query = torch.Tensor(t)
t_sec_query = torch.LongTensor(t_sec_query)
# calculate cumulative hazard according to above
_, Λ = self.forward(t_query, t_sec_query, x)
return torch.exp(-Λ)
def plot_survival_function(self, t:np.array, x:np.array) -> None:
s = self.survival_function(t, x)
# plot
plt.figure(figsize=(12,5))
plt.plot(t, s)
plt.xlabel('Time')
plt.ylabel('Survival Probability')
plt.show()
```
## Fitting Cox Proportional Hazard Model
```
# hide
from torchlife.data import create_db, get_breakpoints
import pandas as pd
# hide
url = "https://raw.githubusercontent.com/CamDavidsonPilon/lifelines/master/lifelines/datasets/rossi.csv"
df = pd.read_csv(url)
df.head()
# hide
df.rename(columns={'week':'t', 'arrest':'e'}, inplace=True)
breakpoints = get_breakpoints(df)
db, t_scaler, x_scaler = create_db(df, breakpoints)
# hide
from fastai.basics import Learner
x_dim = df.shape[1] - 2
model = ProportionalHazard(breakpoints, t_scaler, x_scaler, x_dim, h=(3,3))
learner = Learner(db, model, loss_func=hazard_loss)
# wd = 1e-4
# learner.lr_find()
# learner.recorder.plot()
# hide
epochs = 10
learner.fit(epochs, lr=1)
```
## Plotting hazard functions
```
model.baseλ.plot_hazard()
x = df.drop(['t', 'e'], axis=1).iloc[4]
t = np.arange(df['t'].max())
model.plot_survival_function(t, x)
# hide
from nbdev.export import *
notebook2script()
```
|
github_jupyter
|
(*** hide ***)
```
#nowarn "211"
open System
let airQuality = __SOURCE_DIRECTORY__ + "/data/airquality.csv"
```
(**
Interoperating between R and Deedle
===================================
The [R type provider](http://fslab.org/RProvider/) enables
smooth interoperation between R and F#. The type provider automatically discovers
installed packages and makes them accessible via the `RProvider` namespace.
R type provider for F# automatically converts standard data structures betwene R
and F# (such as numerical values, arrays, etc.). However, the conversion mechanism
is extensible and so it is possible to support conversion between other F# types.
The Deedle library comes with extension that automatically converts between Deedle
`Frame<R, C>` and R `data.frame` and also between Deedle `Series<K, V>` and the
[zoo package](http://cran.r-project.org/web/packages/zoo/index.html) (Z's ordered
observations).
This page is a quick overview showing how to pass data between R and Deedle.
You can also get this page as an [F# script file](https://github.com/fslaborg/Deedle/blob/master/docs/content/rinterop.fsx)
from GitHub and run the samples interactively.
<a name="setup"></a>
Getting started
---------------
To use Deedle and R provider together, all you need to do is to install the
[**Deedle.RPlugin** package](https://nuget.org/packages/Deedle.RPlugin), which
installes both as dependencies. Alternatively, you can use the [**FsLab**
package](http://www.nuget.org/packages/FsLab), which also includes additional
data access, data science and visualization libraries.
In a typical project ("F# Tutorial"), the NuGet packages are installed in the `../packages`
directory. To use R provider and Deedle, you need to write something like this:
*)
```
#load "../../packages/RProvider/RProvider.fsx"
#load "../../bin/net45/Deedle.fsx"
open RProvider
open RDotNet
open Deedle
```
(**
If you're not using NuGet from Visual Studio, then you'll need to manually copy the
file `Deedle.RProvider.Plugin.dll` from the package `Deedle.RPlugin` to the
directory where `RProvider.dll` is located (in `RProvider/lib`). Once that's
done, the R provider will automatically find the plugin.
<a name="frames"></a>
Passing data frames to and from R
---------------------------------
### From R to Deedle
Let's start by looking at passing data frames from R to Deedle. To test this, we
can use some of the sample data sets available in the `datasets` package. The R
makes all packages available under the `RProvider` namespace, so we can just
open `datasets` and access the `mtcars` data set using `R.mtcars` (when typing
the code, you'll get automatic completion when you type `R` followed by dot):
*)
(*** define-output:mtcars ***)
```
open RProvider.datasets
// Get mtcars as an untyped object
R.mtcars.Value
// Get mtcars as a typed Deedle frame
let mtcars : Frame<string, string> = R.mtcars.GetValue()
```
(*** include-value:mtcars ***)
(**
The first sample uses the `Value` property to convert the data set to a boxed Deedle
frame of type `obj`. This is a great way to explore the data, but when you want to do
some further processing, you need to specify the type of the data frame that you want
to get. This is done on line 7 where we get `mtcars` as a Deedle frame with both rows
and columns indexed by `string`.
To see that this is a standard Deedle data frame, let's group the cars by the number of
gears and calculate the average "miles per galon" value based on the gear. To visualize
the data, we use the [F# Charting library](https://github.com/fsharp/FSharp.Charting):
*)
(*** define-output:mpgch ***)
```
#load "../../packages/FSharp.Charting/lib/net45/FSharp.Charting.fsx"
open FSharp.Charting
mtcars
|> Frame.groupRowsByInt "gear"
|> Frame.getCol "mpg"
|> Stats.levelMean fst
|> Series.observations |> Chart.Column
```
(*** include-it:mpgch ***)
(**
### From Deedle to R
So far, we looked how to turn R data frame into Deedle `Frame<R, C>`, so let's look
at the opposite direction. The following snippet first reads Deedle data frame
from a CSV file (file name is in the `airQuality` variable). We can then use the
data frame as argument to standard R functions that expect data frame.
*)
```
let air = Frame.ReadCsv(airQuality, separators=";")
```
(*** include-value:air ***)
(**
Let's first try passing the `air` frame to the R `as.data.frame` function (which
will not do anything, aside from importing the data into R). To do something
slightly more interesting, we then use the `colMeans` R function to calculate averages
for each column (to do this, we need to open the `base` package):
*)
```
open RProvider.``base``
// Pass air data to R and print the R output
R.as_data_frame(air)
// Pass air data to R and get column means
R.colMeans(air)
// [fsi:val it : SymbolicExpression =]
// [fsi: Ozone Solar.R Wind Temp Month Day ]
// [fsi: NaN NaN 9.96 77.88 6.99 15.8]
```
(**
As a final example, let's look at the handling of missing values. Unlike R, Deedle does not
distinguish between missing data (`NA`) and not a number (`NaN`). For example, in the
following simple frame, the `Floats` column has missing value for keys 2 and 3 while
`Names` has missing value for the row 2:
*)
```
// Create sample data frame with missing values
let df =
[ "Floats" =?> series [ 1 => 10.0; 2 => nan; 4 => 15.0]
"Names" =?> series [ 1 => "one"; 3 => "three"; 4 => "four" ] ]
|> frame
```
(**
When we pass the data frame to R, missing values in numeric columns are turned into `NaN`
and missing data for other columns are turned into `NA`. Here, we use `R.assign` which
stores the data frame in a varaible available in the current R environment:
*)
```
R.assign("x", df)
// [fsi:val it : SymbolicExpression = ]
// [fsi: Floats Names ]
// [fsi: 1 10 one ]
// [fsi: 2 NaN <NA> ]
// [fsi: 4 15 four ]
// [fsi: 3 NaN three ]
```
(**
<a name="series"></a>
Passing time series to and from R
---------------------------------
For working with time series data, the Deedle plugin uses [the zoo package](http://cran.r-project.org/web/packages/zoo/index.html)
(Z's ordered observations). If you do not have the package installed, you can do that
by using the `install.packages("zoo")` command from R or using `R.install_packages("zoo")` from
F# after opening `RProvider.utils`. When running the code from F#, you'll need to restart your
editor and F# interactive after it is installed.
### From R to Deedle
Let's start by looking at getting time series data from R. We can again use the `datasets`
package with samples. For example, the `austres` data set gives us access to
quarterly time series of the number of australian residents:
*)
```
R.austres.Value
// [fsi:val it : obj =]
// [fsi: 1971.25 -> 13067.3 ]
// [fsi: 1971.5 -> 13130.5 ]
// [fsi: 1971.75 -> 13198.4 ]
// [fsi: ... -> ... ]
// [fsi: 1992.75 -> 17568.7 ]
// [fsi: 1993 -> 17627.1 ]
// [fsi: 1993.25 -> 17661.5 ]
```
(**
As with data frames, when we want to do any further processing with the time series, we need
to use the generic `GetValue` method and specify a type annotation to that tells the F#
compiler that we expect a series where both keys and values are of type `float`:
*)
```
// Get series with numbers of australian residents
let austres : Series<float, float> = R.austres.GetValue()
// Get TimeSpan representing (roughly..) two years
let twoYears = TimeSpan.FromDays(2.0 * 365.0)
// Calculate means of sliding windows of 2 year size
austres
|> Series.mapKeys (fun y ->
DateTime(int y, 1 + int (12.0 * (y - floor y)), 1))
|> Series.windowDistInto twoYears Stats.mean
```
(**
The current version of the Deedle plugin supports only time series with single column.
To access, for example, the EU stock market data, we need to write a short R inline
code to extract the column we are interested in. The following gets the FTSE time
series from `EuStockMarkets`:
*)
```
let ftseStr = R.parse(text="""EuStockMarkets[,"FTSE"]""")
let ftse : Series<float, float> = R.eval(ftseStr).GetValue()
```
(**
### From Deedle to R
The opposite direction is equally easy. To demonstrate this, we'll generate a simple
time series with 3 days of randomly generated values starting today:
*)
```
let rnd = Random()
let ts =
[ for i in 0.0 .. 100.0 ->
DateTime.Today.AddHours(i), rnd.NextDouble() ]
|> series
```
(**
Now that we have a time series, we can pass it to R using the `R.as_zoo` function or
using `R.assign` to store it in an R variable. As previously, the R provider automatically
shows the output that R prints for the value:
*)
```
open RProvider.zoo
// Just convert time series to R
R.as_zoo(ts)
// Convert and assing to a variable 'ts'
R.assign("ts", ts)
// [fsi:val it : string =
// [fsi: 2013-11-07 05:00:00 2013-11-07 06:00:00 2013-11-07 07:00:00 ...]
// [fsi: 0.749946652 0.580584353 0.523962789 ...]
```
(**
Typically, you will not need to assign time series to an R variable, because you can
use it directly as an argument to functions that expect time series. For example, the
following snippet applies the rolling mean function with a window size 20 to the
time series.
*)
```
// Rolling mean with window size 20
R.rollmean(ts, 20)
```
(**
This is a simple example - in practice, you can achieve the same thing with `Series.window`
function from Deedle - but it demonstrates how easy it is to use R packages with
time series (and data frames) from Deedle. As a final example, we create a data frame that
contains the original time series together with the rolling mean (in a separate column)
and then draws a chart showing the results:
*)
(*** define-output:means ***)
```
// Use 'rollmean' to calculate mean and 'GetValue' to
// turn the result into a Deedle time series
let tf =
[ "Input" => ts
"Means5" => R.rollmean(ts, 5).GetValue<Series<_, float>>()
"Means20" => R.rollmean(ts, 20).GetValue<Series<_, float>>() ]
|> frame
// Chart original input and the two rolling means
Chart.Combine
[ Chart.Line(Series.observations tf?Input)
Chart.Line(Series.observations tf?Means5)
Chart.Line(Series.observations tf?Means20) ]
```
(**
Depending on your random number generator, the resulting chart looks something like this:
*)
(*** include-it:means ***)
```
```
|
github_jupyter
|
# FloPy
## Creating a Simple MODFLOW 6 Model with Flopy
The purpose of this notebook is to demonstrate the Flopy capabilities for building a simple MODFLOW 6 model from scratch, running the model, and viewing the results. This notebook will demonstrate the capabilities using a simple lake example. A separate notebook is also available in which the same lake example is created for MODFLOW-2005 (flopy3_lake_example.ipynb).
### Setup the Notebook Environment
```
import sys
import os
import platform
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
# run installed version of flopy or add local path
try:
import flopy
except:
fpth = os.path.abspath(os.path.join('..', '..'))
sys.path.append(fpth)
import flopy
print(sys.version)
print('numpy version: {}'.format(np.__version__))
print('matplotlib version: {}'.format(mpl.__version__))
print('flopy version: {}'.format(flopy.__version__))
# For this example, we will set up a model workspace.
# Model input files and output files will reside here.
workspace = os.path.join('data', 'mf6lake')
if not os.path.exists(workspace):
os.makedirs(workspace)
```
### Create the Flopy Model Objects
We are creating a square model with a specified head equal to `h1` along all boundaries. The head at the cell in the center in the top layer is fixed to `h2`. First, set the name of the model and the parameters of the model: the number of layers `Nlay`, the number of rows and columns `N`, lengths of the sides of the model `L`, aquifer thickness `H`, hydraulic conductivity `k`
```
name = 'mf6lake'
h1 = 100
h2 = 90
Nlay = 10
N = 101
L = 400.0
H = 50.0
k = 1.0
```
One big difference between MODFLOW 6 and previous MODFLOW versions is that MODFLOW 6 is based on the concept of a simulation. A simulation consists of the following:
* Temporal discretization (TDIS)
* One or more models (GWF is the only model supported at present)
* Zero or more exchanges (instructions for how models are coupled)
* Solutions
For this simple lake example, the simulation consists of the temporal discretization (TDIS) package (TDIS), a groundwater flow (GWF) model, and an iterative model solution (IMS), which controls how the GWF model is solved.
```
# Create the Flopy simulation object
sim = flopy.mf6.MFSimulation(sim_name=name, exe_name='mf6',
version='mf6', sim_ws=workspace)
# Create the Flopy temporal discretization object
tdis = flopy.mf6.modflow.mftdis.ModflowTdis(sim, pname='tdis', time_units='DAYS', nper=1,
perioddata=[(1.0, 1, 1.0)])
# Create the Flopy groundwater flow (gwf) model object
model_nam_file = '{}.nam'.format(name)
gwf = flopy.mf6.ModflowGwf(sim, modelname=name,
model_nam_file=model_nam_file)
# Create the Flopy iterative model solver (ims) Package object
ims = flopy.mf6.modflow.mfims.ModflowIms(sim, pname='ims', complexity='SIMPLE')
```
Now that the overall simulation is set up, we can focus on building the groundwater flow model. The groundwater flow model will be built by adding packages to it that describe the model characteristics.
Define the discretization of the model. All layers are given equal thickness. The `bot` array is build from `H` and the `Nlay` values to indicate top and bottom of each layer, and `delrow` and `delcol` are computed from model size `L` and number of cells `N`. Once these are all computed, the Discretization file is built.
```
# Create the discretization package
bot = np.linspace(-H/Nlay, -H, Nlay)
delrow = delcol = L/(N-1)
dis = flopy.mf6.modflow.mfgwfdis.ModflowGwfdis(gwf, pname='dis', nlay=Nlay, nrow=N, ncol=N,
delr=delrow,delc=delcol,top=0.0,
botm=bot)
# Create the initial conditions package
start = h1 * np.ones((Nlay, N, N))
ic = flopy.mf6.modflow.mfgwfic.ModflowGwfic(gwf, pname='ic', strt=start)
# Create the node property flow package
npf = flopy.mf6.modflow.mfgwfnpf.ModflowGwfnpf(gwf, pname='npf', icelltype=1, k=k,
save_flows=True)
# Create the constant head package.
# List information is created a bit differently for
# MODFLOW 6 than for other MODFLOW versions. The
# cellid (layer, row, column, for a regular grid)
# must be entered as a tuple as the first entry.
# Remember that these must be zero-based indices!
chd_rec = []
chd_rec.append(((0, int(N / 4), int(N / 4)), h2))
for layer in range(0, Nlay):
for row_col in range(0, N):
chd_rec.append(((layer, row_col, 0), h1))
chd_rec.append(((layer, row_col, N - 1), h1))
if row_col != 0 and row_col != N - 1:
chd_rec.append(((layer, 0, row_col), h1))
chd_rec.append(((layer, N - 1, row_col), h1))
chd = flopy.mf6.modflow.mfgwfchd.ModflowGwfchd(gwf, pname='chd', maxbound=len(chd_rec),
stress_period_data=chd_rec, save_flows=True)
# The chd package stored the constant heads in a structured
# array, also called a recarray. We can get a pointer to the
# recarray for the first stress period (iper = 0) as follows.
iper = 0
ra = chd.stress_period_data.get_data(key=iper)
ra
# We can make a quick plot to show where our constant
# heads are located by creating an integer array
# that starts with ones everywhere, but is assigned
# a -1 where chds are located
ibd = np.ones((Nlay, N, N), dtype=int)
for k, i, j in ra['cellid']:
ibd[k, i, j] = -1
ilay = 0
plt.imshow(ibd[ilay, :, :], interpolation='none')
plt.title('Layer {}: Constant Head Cells'.format(ilay + 1))
# Create the output control package
headfile = '{}.hds'.format(name)
head_filerecord = [headfile]
budgetfile = '{}.cbb'.format(name)
budget_filerecord = [budgetfile]
saverecord = [('HEAD', 'ALL'),
('BUDGET', 'ALL')]
printrecord = [('HEAD', 'LAST')]
oc = flopy.mf6.modflow.mfgwfoc.ModflowGwfoc(gwf, pname='oc', saverecord=saverecord,
head_filerecord=head_filerecord,
budget_filerecord=budget_filerecord,
printrecord=printrecord)
# Note that help can always be found for a package
# using either forms of the following syntax
help(oc)
#help(flopy.mf6.modflow.mfgwfoc.ModflowGwfoc)
```
### Create the MODFLOW 6 Input Files and Run the Model
Once all the flopy objects are created, it is very easy to create all of the input files and run the model.
```
# Write the datasets
sim.write_simulation()
# Print a list of the files that were created
# in workspace
print(os.listdir(workspace))
```
### Run the Simulation
We can also run the simulation from the notebook, but only if the MODFLOW 6 executable is available. The executable can be made available by putting the executable in a folder that is listed in the system path variable. Another option is to just put a copy of the executable in the simulation folder, though this should generally be avoided. A final option is to provide a full path to the executable when the simulation is constructed. This would be done by specifying exe_name with the full path.
```
# Run the simulation
success, buff = sim.run_simulation()
print('\nSuccess is: ', success)
```
### Post-Process Head Results
Post-processing MODFLOW 6 results is still a work in progress. There aren't any Flopy plotting functions built in yet, like they are for other MODFLOW versions. So we need to plot the results using general Flopy capabilities. We can also use some of the Flopy ModelMap capabilities for MODFLOW 6, but in order to do so, we need to manually create a SpatialReference object, that is needed for the plotting. Examples of both approaches are shown below.
First, a link to the heads file is created with `HeadFile`. The link can then be accessed with the `get_data` function, by specifying, in this case, the step number and period number for which we want to retrieve data. A three-dimensional array is returned of size `nlay, nrow, ncol`. Matplotlib contouring functions are used to make contours of the layers or a cross-section.
```
# Read the binary head file and plot the results
# We can use the existing Flopy HeadFile class because
# the format of the headfile for MODFLOW 6 is the same
# as for previous MODFLOW verions
fname = os.path.join(workspace, headfile)
hds = flopy.utils.binaryfile.HeadFile(fname)
h = hds.get_data(kstpkper=(0, 0))
x = y = np.linspace(0, L, N)
y = y[::-1]
c = plt.contour(x, y, h[0], np.arange(90,100.1,0.2))
plt.clabel(c, fmt='%2.1f')
plt.axis('scaled');
x = y = np.linspace(0, L, N)
y = y[::-1]
c = plt.contour(x, y, h[-1], np.arange(90,100.1,0.2))
plt.clabel(c, fmt='%1.1f')
plt.axis('scaled');
z = np.linspace(-H/Nlay/2, -H+H/Nlay/2, Nlay)
c = plt.contour(x, z, h[:,50,:], np.arange(90,100.1,.2))
plt.axis('scaled');
# We can also use the Flopy PlotMapView capabilities for MODFLOW 6
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(1, 1, 1, aspect='equal')
modelmap = flopy.plot.PlotMapView(model=gwf, ax=ax)
# Then we can use the plot_grid() method to draw the grid
# The return value for this function is a matplotlib LineCollection object,
# which could be manipulated (or used) later if necessary.
quadmesh = modelmap.plot_ibound(ibound=ibd)
linecollection = modelmap.plot_grid()
contours = modelmap.contour_array(h[0], levels=np.arange(90,100.1,0.2))
# We can also use the Flopy PlotMapView capabilities for MODFLOW 6
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(1, 1, 1, aspect='equal')
# Next we create an instance of the ModelMap class
modelmap = flopy.plot.PlotMapView(model=gwf, ax=ax)
# Then we can use the plot_grid() method to draw the grid
# The return value for this function is a matplotlib LineCollection object,
# which could be manipulated (or used) later if necessary.
quadmesh = modelmap.plot_ibound(ibound=ibd)
linecollection = modelmap.plot_grid()
pa = modelmap.plot_array(h[0])
cb = plt.colorbar(pa, shrink=0.5)
```
### Post-Process Flows
MODFLOW 6 writes a binary grid file, which contains information about the model grid. MODFLOW 6 also writes a binary budget file, which contains flow information. Both of these files can be read using Flopy capabilities. The MfGrdFile class in Flopy can be used to read the binary grid file. The CellBudgetFile class in Flopy can be used to read the binary budget file written by MODFLOW 6.
```
# read the binary grid file
fname = os.path.join(workspace, '{}.dis.grb'.format(name))
bgf = flopy.utils.mfgrdfile.MfGrdFile(fname)
# data read from the binary grid file is stored in a dictionary
bgf._datadict
# Information from the binary grid file is easily retrieved
ia = bgf._datadict['IA'] - 1
ja = bgf._datadict['JA'] - 1
# read the cell budget file
fname = os.path.join(workspace, '{}.cbb'.format(name))
cbb = flopy.utils.CellBudgetFile(fname, precision='double')
cbb.list_records()
flowja = cbb.get_data(text='FLOW-JA-FACE')[0][0, 0, :]
chdflow = cbb.get_data(text='CHD')[0]
# By having the ia and ja arrays and the flow-ja-face we can look at
# the flows for any cell and process them in the follow manner.
k = 5; i = 50; j = 50
celln = k * N * N + i * N + j
print('Printing flows for cell {}'.format(celln + 1))
for ipos in range(ia[celln] + 1, ia[celln + 1]):
cellm = ja[ipos] # change from one-based to zero-based
print('Cell {} flow with cell {} is {}'.format(celln + 1, cellm + 1, flowja[ipos]))
```
|
github_jupyter
|
As a self-taught Data Scientist and programmer, I always get asked about how I started my path towards learning, and a lot of non-coders ask me about how they can learn more about Data Science. And while I tell them about the umpteen Data Analytics and Data Visualization tools, various Machine Learning algorithms, and which Deep Learning frameworks to choose, it all starts with learning Python. Python is an interpreted high-level general-purpose programming language. In my view, Python is the best programming language to learn, in order to become a Data Scientist, owing to its readability, non-complexity, its large standard libraries, and its huge community.
I have been the beneficiary of several of books and YouTube tutorials that have helped me become a better Python Developer. This blog post is my way of giving back to the community. This might not be the best place to start learning how to code in Python. However, this blog post aims to be a good cheat sheet for beginners trying to look something up or if they want a refresher as to how certain objects perform.
---
### Index
[Display Output](#Display-Output)
[Getting information from the user](#Getting-information-from-the-user)
[Comments](#Comments)
[String concepts](#String-concepts)
[Working with Numbers](#Working-with-Numbers)
[Working with Dates](#Working-with-Dates)
[Error Handling](#Error-Handling)
[Handling Conditions](#Handling-Conditions)
[Collections](#Collections)
[Random Module](#Random-Module)
[Loops](#Loops)
[Functions](#Functions)
---
### Display Output
You can use the `print` function to display output to your console. You can use either single or double quotes; just make sure that you stick to one for consistency.
```
print('Hello, World!')
print("Python is great")
```
#### Displaying blank lines
Blank lines make the output more readable. For a blank line, you can insert a `print` function with nothing inside. Each `print` function prints on a new line by default.
You can also use `\n` (the newline character) to print a new line at the end of a string or right in the middle of a string.
```
print('Hello')
print()
print('Above is a blank line\n')
print('Blank line \nin the middle of a string')
```
---
### Getting information from the user
You can use the `input` to ask for information from your user. We pass in a message with the `input` function.
```
name = input('What is your name? ')
print(name)
```
Here, whatever value is typed in by the user will be stored in the variable `name` and can be used as needed. We've chosen to print the value of `name` on the screen.
---
### Comments
Comments are a way of documenting your code. Comments can be added using `#`. These lines of code will not execute.
```
# print('Hello')
# the above code of line will not execute
# but the below one will
print('How are you?')
```
You can also use `''' '''` for multi-line comments.
```
'''
Python is an important
programming language in
your Data Science journey
'''
print('Python')
```
It's a good idea to write comments before your function explaining what that function does.
Commenting out lines can also help debug your code.
---
### String concepts
Strings can be stored in variables. Variables are just placeholders for some value inside our code.
```
first_name = 'Pranav'
print(first_name)
```
#### Concatenate strings
You can combine strings with the `+` operator.
```
first_name = 'John'
last_name = 'Doe'
print(first_name + last_name)
print('Hello, ' + first_name + ' ' + last_name)
```
#### Functions to modify strings
Below we have used functions to
- convert a string to uppercase
- convert a string to lowercase
- capitalize just the first word
- count all of the instances of a particular string.
```
sentence = 'My name is John Doe'
print(sentence.upper())
print(sentence.lower())
print(sentence.capitalize())
print(sentence.count('o'))
```
You can use the escape character (backslash) `\` to insert characters that are illegal in a string. An example of an illegal character is a single quote inside a string that is surrounded by single quotes.
```
first_name = input('What\'s your first name? ')
last_name = input('What\'s is your last name? ')
print('Hello, ' + first_name.capitalize() +
' ' + last_name.capitalize())
```
#### Custom string formatting
To infuse things in strings dynamically, you can use string formatting.
```
first_name = 'John'
last_name = 'Doe'
```
There are two ways you can do this:
- formatting with `.format()` string method
```
name = 'Hello, {} {}'.format(first_name, last_name)
print(name)
```
- formatting with string literals, called f-strings
```
name = f'Hello, {first_name} {last_name}'
print(name)
```
---
### Working with numbers
Numbers can be stored in variables. Make sure the variables have meaningful names. We can pass those variables inside functions.
```
pi = 3.14159
print(pi)
```
#### Math with Numbers
- `+` for addition
- `-` for subtraction
- `*` for multiplication
- `/` for division
- `**` for exponent
```
num1 = 9
num2 = 5
print(num1 + num2)
print(num1 ** num2)
```
#### Type Conversion
You cannot combine strings with numbers in Python. For e.g., executing the code below will result in an error:
```
days_in_Dec = 31
print(days_in_Dec + ' days in December')
```
When displaying a string that contains numbers, you must convert the numbers into strings.
```
days_in_Dec = 31
print(str(days_in_Dec) + ' days in December')
```
Numbers can be stored as strings. However, numbers stored as strings are treated as strings.
```
num1 = '10'
num2 = '20'
print(num1 + num2)
```
Also, the input function always returns a string.
```
num1 = input('Enter the first number: ')
num2 = input('Enter the second number: ')
print(num1 + num2)
```
But here you can see that you have a number stored in a string. What if you want to treat it as a number and do math with it?
You can do another data type conversion. The `int` function will convert it to a whole number, while the `float` function will convert it into a floating point number that might have decimal places.
```
num1 = input('Enter the first number: ')
num2 = input('Enter the second number: ')
print(int(num1) + int(num2))
print(float(num1) + float(num2))
```
---
### Working with Dates
We often need current date and time when logging errors and saving data. To get the current date and time, we need to use the `datetime` library.
```
from datetime import datetime
# the now function returns a datetime object
current_date = datetime.now()
print('Today is: ' + str(current_date))
```
There are a whole bunch of functions you can use with `datetime` objects to manipulate dates.
`timedelta` is used to define a period of time.
```
from datetime import datetime, timedelta
today = datetime.now()
print('Today is: ' + str(today))
one_day = timedelta(days=1)
one_week = timedelta(weeks=1)
yesterday = today - one_day
past_week = today - one_week
print('Yesterday was: ' + str(yesterday))
print('One week ago was: ' + str(past_week))
```
You can also control the format of the date displayed on the screen. You can request just the day, month, year, hour, minutes and even seconds.
```
print('Day: ' + str(current_date.day))
print('Month: ' + str(current_date.month))
print('Year: ' + str(current_date.year))
```
Sometimes, you can receive a date as a string, and you might need to store it as a date. You'll need to convert it to a `datetime` object.
```
birthday = input('When is your birthday (dd/mm/yyyy)? ')
# the strptime function allows you to mention the
# format in which you'll be receiving the date
birthday_date = datetime.strptime(birthday, '%d/%m/%Y')
print('Birthday: ' + str(birthday_date))
```
So what date was it three days before you were born?
```
birthday = input('When is your birthday (dd/mm/yyyy)? ')
birthday_date = datetime.strptime(birthday, '%d/%m/%Y')
print('Birthday: ' + str(birthday_date))
three_days = timedelta(days=3)
three_before = birthday_date - three_days
print('Date three days before birthday: ' + str(three_before))
```
---
### Error Handling
*Error handling* is when you have a problem with your code that is running, and its not something that you're going to be able to predict when you push your code to production. For e.g., permissions issue, database change, server being down, etc. Basically things that happen in the wild, which you have no control over.
*Debugging* is when you know that there's something wrong (a bug) with your code because you did something incorrectly, and you're going to have to go in and correct it.
The following tools we're going to talk about are concerned with error handling. There are three types of errors:
- syntax errors
- runtime errors
- logic errors
#### Syntax errors
With syntax errors, your code is not going to run at all. This type of error is easiest to track down.
```
# this code won't run at all
x = 35
y = 75
if x == y
print('x = y')
```
We're missing a colon after `y`, which is why we're getting the error above.
#### Runtime errors
With runtime errors, your code will run, but it will fail when it encounters the error.
```
# this code will fail when run
x = 5
y = 0
print(x / y)
```
We're trying to divide by zero, which is not possible. Python tells you why you're getting the error and points towards the line which needs to be fixed. It's good practice to start from the line mentioned and work your way up to the error. Runtime errors can also be caused due to an error in the framework you're using, but the chances of that happening are extremely rare. Most probably, if you have a runtime error, it's because there's something wrong in your code.
#### Catching runtime errors
When a runtime error occurs, Python generates an exception during the execution and that can be handled, which avoids your program to interrupt.
Exception handling:
- `try`: this block will test the excepted error to occur
- `except`: here you can handle the error
- `else`: if there is no exception, then this block will be executed
- `finally`: finally block always gets executed whether exception is generated or not
These tools are not used for finding bugs.
```
x = 5
y = 0
try:
print(x / y)
except ZeroDivisionError as e:
print('Sorry, something went wrong')
except:
print('Something really went wrong')
finally:
print('This line always runs, on success or failure')
```
#### Logic errors
Logic errors occur when the code compiles properly, doesn't give any syntax or runtime errors, but it doesn't give you the response you're looking for.
```
# this code won't run at all
x = 10
y = 20
if x > y:
print(str(x) + ' is less than ' + str(y))
```
In the code above, `x` is less than `y`; but the `if` statement includes `x > y`, instead of `x < y`.
When you're figuring out what went wrong with your code, just make sure that you reread your code. You can check the documentation and also search the internet on sites like StackOverflow and Medium.
---
### Handling Conditions
Your code might need the ability to take different actions based on different conditions. Below are the operations that you'll need for comparisons:
- `>`: greater than
- `<`: less than
- `>=`: greater than or equal to
- `<=`: less than or equal to
- `==`: is equal to
- `!=`: is not equal to
#### if statement
The `if` statement contains a logical expression using which the data is compared and a decision is made based on the result of the comparison.
```
price = 250.0
if price >= 100.00:
tax = 0.3
print(tax)
```
#### if - else statement
You can add a default action using `else`. An `else` statement contains the block of code that executes if the conditional expression in the `if` statement resolves to `0` or a `False` value.
```
price = 50
if price >= 100.00:
tax = 0.3
else:
tax = 0
print(tax)
```
Be careful when comparing strings. String comparisons are case sensitive.
```
country = 'INDIA'
if country == 'india':
print('Namaste')
else:
print('Hello')
country = 'INDIA'
if country.lower() == 'india':
print('Namaste')
else:
print('Hello')
```
#### if - elif - else statement
You may need to check multiple conditions to determine the correct action. The `elif` statement allows you to check multiple expressions for `True` and execute a block of cide as soon as one of the conditions evaluates to `True`.
```
# income tax percentage by state
state = input('Which state do you live in? ')
if state == 'Georgia':
tax = 5.75
elif state == 'California':
tax = 13.3
elif state == 'Texas' or state == 'Florida':
tax = 0.0
else:
tax = 4.0
print(tax)
```
#### OR statements
| first condition | second condition | evaluation |
|-----------------|------------------|------------|
|True |True |True |
|True |False |True |
|False |True |True |
|False |False |False |
#### AND statements
| first condition | second condition | evaluation |
|-----------------|------------------|------------|
|True |True |True |
|True |False |False |
|False |True |False |
|False |False |False |
#### in operator
If you have a list of possible values to check, you can use the `in` operator.
```
# income tax rates by state
state = input('Which state do you live in? ')
if state in ('Texas', 'Florida', 'Alaska',
'Wyoming', 'South Dakota'):
tax = 0.0
elif state == 'California':
tax = 13.3
elif state == 'Georgia':
tax = 5.75
else:
tax = 4.0
print(tax)
```
#### Nested if statement
There may be a situation when you want to check for another condition after a condition resolves to `True`. If an action depends on a combination of conditions, you can nest `if` statements.
```
country = input("What country do you live in? ")
if country.lower() == 'canada':
province = input("What province/state do you live in? ")
if province in('Alberta', 'Nunavut','Yukon'):
tax = 0.05
elif province == 'Ontario':
tax = 0.13
else:
tax = 0.15
else:
tax = 0.0
print(tax)
```
Sometimes you can combine conditions with `and` instead of nested `if` statements.
Let's assume that you're trying to calculate which students in a college have made the honor roll. The requirements for making the honor roll are a minimum 85% GPA and maintaining all your grades at at least 70%.
```
# convert strings into float
gpa = float(input('What\'s your GPA? '))
lowest_grade = float(input('What was your lowest grade? '))
if gpa >= 0.85 and lowest_grade >= 0.7:
print('You made the honor roll')
else:
print('You\'re really stupid')
```
If you have a very complicated `if` statement, rather than copying and pasting it in different parts of you code to do different things, we can remember what happened the last time we looked at the `if` statement with a Boolean variable.
```
gpa = float(input('What\'s your GPA? '))
lowest_grade = float(input('What was your lowest grade? '))
if gpa >= 0.85 and lowest_grade >= 0.7:
honor_roll = True
else:
honor_roll = False
''' Somewhere later in your code if you need
to check if a student is on honor roll, all
you need to do is check the boolean variable
set earlier in the code'''
if honor_roll: # True by default
print('You made the honor roll')
```
---
### Collections
#### Lists
Lists are a collection of items.
```
# prepopulate a list
names = ['John', 'Will', 'Max']
# start with an empty list
scores = []
# add new item to the end
scores.append(90)
scores.append(91)
print(names)
print(scores)
# lists are zero-indexed
print(scores[1])
```
You can get the number of items in a list using `len`.
```
names = ['John', 'Will', 'Max']
# get the number of items using len
print(len(names))
```
You can insert an item in a list using `insert`. This will insert the item at the specific index that you mention.
```
# Bill will be inserted at index 0, i.e. the first item
names.insert(0, 'Bill')
print(names)
```
You can use `sort` to sort strings in alphabetical order. In case of numbers, it sorts them in the ascending order. Remember that using `sort` will modify the list!
```
names.sort()
print(names)
```
You can retrieve a range within the list by indicating the start and end index; the end index being exclusive, i.e. it will not be included in the list.
```
names = ['Amy', 'Susan', 'Jackie', 'Kylie', 'Ellen']
# start and end index
presenters = names[1:3]
# all names up to but not including index 3
hosts = names[:3]
# all names from 3 onwards, including index 3
judges = names[3:]
print(names)
print(presenters)
print(hosts)
print(judges)
```
#### Arrays
Arrays are a collection of numbered data types. Unlike a list, in order for you to use an array, you have to create an array object by importing it from the `array` library.
```
from array import array
# indicate the numerical type you'll use
scores = array('d') # d indicates a double
scores.append(80)
scores.append(81)
print(scores)
print(scores[0])
```
So what's the difference between an array and a list?
Arrays are only numerical data types and everything inside the array must be of the same data type. They can help add extra structure to your code.
Lists can store anything you want, can store any data type, and can have mixed data types. They give more flexibility to your code.
#### Dictionaries
Dictionaries give you the ability to put together a group of items; but instead of using numeric indexes, you can use key-value pairs.
```
person = {'first': 'John'}
person['last'] = 'Wick'
print(person)
print(person['first'])
identity = {
'Batman': 'Bruce Wayne',
'Superman': 'Clark Kent',
'Spiderman': 'Peter Parker',
'Iron Man': 'Tony Stark'
}
print(identity)
```
When to use a dictionary vs a list?
It depends on whether you want to name things and whether you want items to be in a guaranteed order.
A dictionary will let you name key-value pairs but it does not guarantee you a specific order.
A list does guarantee you a specific order since it has a zero-based index.
---
### Random Module
One way to introduce random numbers in your code is to use the `random` module.
First you need to import the `random` module.
```
import random
# generate a random whole number between 1 and 50
# inclusive of 1 and 50
random_integer = random.randint(1, 50)
print(random_integer)
# generate a random floating point number between 0.0 and 1.0
# exclusive of 1.0
random_float = random.random()
print(random_float)
# generate a random floating point number between 0.0 and 5.0
print(random_float * 5)
```
There are so many more methods to the `random` module and you can check out the Python documentation to find out about all the things you can do with this module.
---
### Loops
Loops are a concept that is used when you need to have things happening over and over again.
#### for loops
`for` loops are used to loop through a collection. With a `for` loop, you can go through each item in a list and perform some action with each individual item in the list.
> `for item in list_of_items:
# do something to each item`
```
# go through the list of names
for name in ['John', 'Will', 'Max']:
print(name)
wildcats = ['lion', 'tiger', 'puma', 'jaguar', 'cheetah', 'leopard']
for wildcat in wildcats:
print(wildcat + ' is a wildcat.')
```
You can loop a particular number of times using `range`. `range` automatically creates a list of numbers for you. Remember that for the `range` function, the end index is exclusive.
> `for number in range(a, b):
# do something
print(number)`
```
# end index is exclusive
for index in range(0, 5):
print(index)
```
If you want the range to increase by any other number, you can add a step to the function after the starting and ending indices.
```
for index in range(0, 15, 3):
print(index)
```
#### while loop
`while` loops are used to loop with a condition. As long as something is `True`, the code will stay inside of the `while` loop i.e. the loop will continue going while the condition is true. You need to make sure that at some point you change the condition and it must result to `False`; otherwise the program will be stuck in an infinite loop, resulting in an error.
> `while something_is_true:
# do something repeatedly`
```
names = ['John', 'Will', 'Max']
index = 0
while index < len(names):
print(names[index])
# change the condition
index += 1
print(index)
x = True
while x:
print('This is an example of a while loop.')
# change the condition
x = False
while not x:
print('This is another example of a while loop.')
x = True
```
`for` loops are great when you want to iterate over something and you need to do something with each thing that you're iterating over. In cases like above, when you have a list, you almost always want use a `for` loop.
`while` loops are useful when you don't care about the number in the sequence or about the item you're iterating through in a list, and you just simply want to carry out a functionality many times until a condition is met. You want to typically use a `while` loop when something is going to change automatically, e.g. when you need to read through a list of lines in a file, skip every alternate line, or if you're looking for something.
`while` loops are more dangerous because they can lead to infinite loops if the condition is not met.
---
### Functions
A function is a block of organized, reusable code that is used to perform a single, related action. Function provide better modularity for your application and a high degree of code reusing, e.g. the `print()` function. You can create your own functions, called *user-defined functions*.
Programming is all about copying and pasting code from one place to another. If you find yourself copying and pasting the exact same lines of code to more places in your program, you should probably move that into a function.
Functions must be declared before the line of code where the function is called.
**Defining Functions**
> `def my_function():
# do this
# then do this
# finally do this`
**Calling Functions**
> `my_function()`
#### Functions with Inputs
The input to a function is something that can be passed over when we call the function.
> `def my_function(something):
# do this with something
# then do this
# finally do this`
> `my_function(123)`
#### Functions with Outputs
The output keyword for a function is `return`. The `return` line must be the last line of the function. You can have multiple return keywords or even a blank return keyword in a function.
```
def my_function():
result = 5 * 4
return result
my_function()
```
When you call a function that has an output, the returned output is what replaces the function call, and the output can be stored as a variable.
```
def my_function():
return 5 * 8
output = my_function()
print(output)
```
Imagine that you're trying to figure out why your program is taking a long time to run. So you write some print statements inside your code to tell you what time it is when the code is running, so you can see what time it is at different stages when your code is running.
```
import datetime
# print timestamps to see how long
# sections take to run
first_name = 'John'
print('task completed')
print(datetime.datetime.now())
print()
for x in range(0, 10):
print(x)
print('task completed')
print(datetime.datetime.now())
print()
```
The above code can be rewritten using a function. You can define the function using `def` keyword, followed by the name of the function, and then a colon (`:`). Remember to use indentation which determines what code belongs to that function.
```
# import datetime class from datetime library
from datetime import datetime
# print the current time
def print_time():
print('task completed')
# no need for the extra datetime prefix
# since the class is imported above
print(datetime.now())
print()
first_name = 'John'
print_time()
for x in range(0, 10):
print(x)
print_time()
```
Sometimes when you copy/paste your code, we want to change some part of it. In the above example, what if you want to display a different message each time you run it. Say you want to display a specific message depending on the command you were running. This is where function parameters come in. *Parameters* or *arguments* are placed or defined within the parentheses of a function.
```
from datetime import datetime
# print the current time and task name
def print_time(task_name):
print(task_name)
print(datetime.now())
print()
first_name = 'John'
# pass in the task_name as a parameter
print_time('first name assigned')
for x in range(0, 10):
print(x)
# pass in the task_name as a parameter
print_time('loop completed')
```
Let's take another example where the code looks different but we're using the same logic. Suppose you're interested in getting initials for a user ID after the user enters their name.
```
first_name = input('Enter your first name: ')
# get only the first letter of input
first_name_initial = first_name[0:1]
last_name = input('Enter your last name: ')
last_name_initial = last_name[0:1]
print('Your initials are: ' + first_name_initial + last_name_initial)
```
The above code can be written using a function.
```
def get_initial(name):
initial = name[0:1]
# the return function returns a value
return initial
first_name = input('Enter your first name: ')
first_name_initial = get_initial(first_name)
last_name = input('Enter your last name: ')
last_name_initial = get_initial(last_name)
# nested function in another call
print('Your initials are: ' + get_initial(first_name) +
get_initial(last_name))
```
Functions can accept multiple parameters. In the above example, suppose you want to the user initials to only be uppercase for a user ID but lowercase for an email ID.
```
def get_initial(name, force_uppercase=True): # default to True
if force_uppercase:
initial = name[0:1].upper()
else:
initial = name[0:1]
return initial
first_name = input('Enter your first name: ')
first_name_initial = get_initial(first_name)
last_name = input('Enter your last name: ')
last_name_initial = get_initial(last_name, False)
print('Your initials are: ' + first_name_initial + last_name_initial)
```
When calling a function, you have to pass the parameters in the same order as when you defined the function. An exception to this is when you use named parameters, which offer better readability.
`first_name_initial = get_initial(force_uppercase=True, name=first_name)`
Functions make the code more readable if you use good function names. They make the code less clunky. Always add comments to explain the purpose of your function.
The main advantage of functions is that if you ever need to change your function code, you only need to change it in one place. You also reduce rework and the chance to introduce bugs when you change the code you copied.
|
github_jupyter
|
## Sentiment Classification AU Reviews Data (BOW, non-Deep Learning)
This notebook covers two good approaches to perform sentiment classification - Naive Bayes and Logistic Regression. We will train AU reviews data on both.
As a rule of thumb, reviews that are 3 stars and above are **positive**, and vice versa.
```
%pip install spacy
%pip install gensim
%pip install spacy_langdetect
!python3 -m spacy download en_core_web_sm
import gzip
import json
import matplotlib.pyplot as plt
import numpy as np
import re
import random
import pandas as pd
import seaborn as sns
import gensim
import spacy
from collections import Counter, defaultdict
from sklearn.dummy import DummyClassifier
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import BernoulliNB, ComplementNB, MultinomialNB
from sklearn.metrics import f1_score, classification_report, accuracy_score, confusion_matrix
from sklearn.model_selection import train_test_split, GridSearchCV
from spacy_langdetect import LanguageDetector
from spacy.language import Language
from gensim.models.word2vec import Word2Vec
from nltk.tokenize import sent_tokenize, word_tokenize
from tqdm import tqdm
RANDOM_SEED = 33
reviews = pd.read_pickle("assets/au_reviews.pkl")
reviews.head()
reviews['label'] = np.where(reviews['rating'] >= 3, 0, 1)
reviews.head()
```
## 1. Data Processing
Check the dataset size:
```
print(len(reviews))
```
And the type of apps:
```
app_list = list(reviews['app'].unique())
app_list
```
Let's also get a sense of our dataset's balance
```
reviews['label'].value_counts(normalize=True)
# By app
for app in app_list:
print(reviews[reviews['app'] == app]['label'].value_counts(normalize=True))
```
Across the board the distribution of positive and negative reviews are quite consistent between the apps. Overall, there's an imbalance in our dataset, with positive reviews making for 75% of the dataset. Let's also check for null values.
```
reviews.isnull().sum()
reviews = reviews.dropna()
df_proc = reviews.copy()
df_proc.drop(columns=['date', 'rating', 'app'], inplace=True)
df_proc.head()
```
For AU dataset we won't be filtering out non-English reviews. It's likely that this makes up for a very small proportion of the dataset.
```
df_proc.to_csv('reviews_au_filtered.csv')
X = df_proc['review']
y = df_proc['label']
```
We will split the dataset into `train`, `test`, and `dev`, with 80%, 10%, 10% ratio, respectively.
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=RANDOM_SEED)
X_test, X_dev, y_test, y_dev = train_test_split(X_test, y_test, test_size=0.5, random_state=RANDOM_SEED)
len(X_train)
len(X_dev)
len(X_test)
X_train.iloc[0]
X_test.iloc[0]
```
## 2.1 Bag-of-Words Approach on Naive Bayes & Logistic Regression
This section explores the use of bag of words as feature extraction. But first, let's have a look at the token frequencies.
```
# Fill this with any token (with anything in it!) for tokens separated by whitespace
ws_tokens = Counter()
# Fill this one with tokens separated by whitespace but constisting only of tokens
# that are totally made of alphanumeric characters (you can use the \w character
# class in making the regex)
alpha_ws_tokens = Counter()
# Fill this one with the tokens separated by *word boundaries* (not white space) that consist
# of alphanumeric characters (use \w again)
alpha_re_tokens = Counter()
for review in tqdm(X_train):
ws_review = review.split()
ws_tokens.update(ws_review)
# Note: use fullmatch() as it anchor both the start and end of str. match() won't work.
alpha_ws_tokens.update([re.fullmatch(r'\w+', word).group() for word in ws_review if re.fullmatch(r'\w+', word) != None])
alpha_re_tokens.update(re.findall(r'\w+', review))
print(len(ws_tokens))
print(len(alpha_ws_tokens))
print(len(alpha_re_tokens))
top_100 = alpha_re_tokens.most_common(100)
top_100
```
Lots of stopwords, as expected.
```
x = list(range(100))
y = [word_tup[1] for word_tup in top_100]
ax = plt.plot(x, y, '.')
#plt.yscale('log')
#plt.xscale('log')
```
And unexpectedly, the word frequency distribution also follows Zipf's law as well. What that means is that we can essentially remove uncommon words, without worrying that they will affect performance. We will also need to remove stopwords, and add unigrams and bigrams as features.
```
vectorizer = TfidfVectorizer(stop_words='english', min_df=500, ngram_range=(1,2))
X_train_bow = vectorizer.fit_transform(X_train)
print(X_train_bow.shape)
X_dev_bow = vectorizer.transform(X_dev)
def train_model(clf):
print("_" * 80)
print("Training: ")
clf.fit(X_train_bow, y_train)
y_dev_pred = clf.predict(X_dev_bow)
score = accuracy_score(y_dev, y_dev_pred)
print("accuracy: %0.3f" % score)
print("classification report:")
print(classification_report(y_dev, y_dev_pred))
print("confusion matrix:")
print(confusion_matrix(y_dev, y_dev_pred))
print("Training Complete")
print()
clf_descr = str(clf).split("(")[0]
return clf_descr, score, y_dev_pred
```
It's training time! We'll start with a few dummy classifiers, followed by Naive Bayes and Logistic Regression.
```
for clf, name in (
(DummyClassifier(strategy='uniform', random_state=RANDOM_SEED), "Uniform Classifier"),
(DummyClassifier(strategy='most_frequent', random_state=RANDOM_SEED), "Most Frequent Classifier"),
):
print("=" * 80)
print("Training Results - Dummy Classifiers")
print(name)
mod = train_model(clf)
preds = {} # A dict to store our dev set predictions
for clf, name in (
(MultinomialNB(alpha=0.01), "MultinomialNB"),
(BernoulliNB(alpha=0.01), "BernoulliNB"),
(ComplementNB(alpha=0.1), "ComplementNB"),
(LogisticRegression(solver='lbfgs', class_weight='balanced', max_iter=1000, random_state=RANDOM_SEED), "Logistic Regression")
):
print("=" * 80)
print("Training Results - Naive Bayes & LogReg")
print(name)
mod = train_model(clf)
preds[name] = mod[2]
```
The baseline results are quite promising, with both MultinomialNB and Logistic Regression achieving 0.85 on macro F1-score. This means that the bag-of-word approach is a rather solid approach for sentiment classification. It's also interesting to see that while MultinomialNB has a rather balanced number of false pos and false neg, BernoulliNB and ComplementNB are different. BernoulliNB has a much higher number of fps, while ComplementNB has a much higher number of fns.
Also, according to https://web.stanford.edu/~jurafsky/slp3/4.pdf, using binary NB (BernoulliNB) may improve predictive performance, as whether a word occurs or not seems to matter more than its frequency. But in this case, BernoulliNB does not outperform other Naive Bayes methods. We'll come back to this in a second.
Let's take a look at a few of mis-classifications for both Naive Bayes and Logistic Regression.
```
# Create a dataframe for mis-classifications
def create_mis_classification_df(name):
mis_class = pd.DataFrame(X_dev)
mis_class['Actual'] = y_dev
mis_class['Predicted'] = preds[name]
mis_class = mis_class[mis_class['Actual'] != mis_class['Predicted']]
return mis_class
mis_class_multi = create_mis_classification_df('MultinomialNB')
mis_class_bernoulli = create_mis_classification_df('BernoulliNB')
mis_class_complement = create_mis_classification_df('ComplementNB')
mis_class_logreg = create_mis_classification_df('Logistic Regression')
mis_class_multi.sample(10).values
mis_class_bernoulli.sample(10).values
mis_class_complement.sample(10).values
mis_class_logreg.sample(10).values
```
Really interesting. Looking at the results, there are a few cases of mis-classifications:
- Reviews that contain negation expressions, eg "not okay" is classified as a positive review when in reality it should be negative. BoW approach makes it hard for ML model to recognize this kind of expressions.
- Reviews that are mis-classified due to rating. Eg a customer may write something negative but give 3 stars. It's tricky in this case because it's a caveat of our dataset.
- Some mis-classification is the ML model being weirdly off, eg ComplementNB classified a "Good" review as negative, or reviews containing the word 'hate' gets classified as positive.
- Contextual awareness is important and this is something that bag-of-word approaches cannot address. For example the sentence 'Very good. Expensive delivery charge though' gets classified as negative likely because of the word expensive, while in reality this is a positive review.
### 2.1 Reduce min_df
We set a min frequency cap of 500. What happens if we reduce this cap to 100?
```
vectorizer = TfidfVectorizer(stop_words='english', min_df=100, ngram_range=(1,2))
X_train_bow = vectorizer.fit_transform(X_train)
X_dev_bow = vectorizer.transform(X_dev)
preds = {} # A dict to store our dev set predictions
for clf, name in (
(MultinomialNB(alpha=0.01), "MultinomialNB"),
(BernoulliNB(alpha=0.01), "BernoulliNB"),
(ComplementNB(alpha=0.1), "ComplementNB"),
(LogisticRegression(solver='lbfgs', class_weight='balanced', max_iter=1000, random_state=RANDOM_SEED), "Logistic Regression")
):
print("=" * 80)
print("Training Results - Naive Bayes & LogReg")
print(name)
mod = train_model(clf)
preds[name] = mod[2]
```
Slight bump in performance, but at the expense of longer training time.
### 2.2 Not use stopwords removal
```
vectorizer = TfidfVectorizer(min_df=100, ngram_range=(1,2))
X_train_bow = vectorizer.fit_transform(X_train)
X_dev_bow = vectorizer.transform(X_dev)
preds = {} # A dict to store our dev set predictions
for clf, name in (
(MultinomialNB(alpha=0.01), "MultinomialNB"),
(BernoulliNB(alpha=0.01), "BernoulliNB"),
(ComplementNB(alpha=0.1), "ComplementNB"),
(LogisticRegression(solver='lbfgs', class_weight='balanced', max_iter=1000, random_state=RANDOM_SEED), "Logistic Regression")
):
print("=" * 80)
print("Training Results - Naive Bayes & LogReg")
print(name)
mod = train_model(clf)
preds[name] = mod[2]
```
Performance improved, surprisingly.
### 2.3 Set max_df
```
vectorizer = TfidfVectorizer(min_df=100, max_df=5000, ngram_range=(1,2))
X_train_bow = vectorizer.fit_transform(X_train)
X_dev_bow = vectorizer.transform(X_dev)
preds = {} # A dict to store our dev set predictions
for clf, name in (
(MultinomialNB(alpha=0.01), "MultinomialNB"),
(BernoulliNB(alpha=0.01), "BernoulliNB"),
(ComplementNB(alpha=0.1), "ComplementNB"),
(LogisticRegression(solver='lbfgs', class_weight='balanced', max_iter=1000, random_state=RANDOM_SEED), "Logistic Regression")
):
print("=" * 80)
print("Training Results - Naive Bayes & LogReg")
print(name)
mod = train_model(clf)
preds[name] = mod[2]
```
Not much changes from stopwords removal.
### 2.4 Clip frequency at 1
Earlier, we see that there isn't any performance with BernoulliNB as compared to other methods. But what if we clip the frequency at the feature processing level? Luckily, sklearn tfidf has a `binary` parameters that allows us to do that.
```
vectorizer = TfidfVectorizer(binary=True, ngram_range=(1,1))
X_train_bow = vectorizer.fit_transform(X_train)
X_dev_bow = vectorizer.transform(X_dev)
preds = {} # A dict to store our dev set predictions
for clf, name in (
(MultinomialNB(alpha=0.01), "MultinomialNB"),
(BernoulliNB(alpha=0.01), "BernoulliNB"),
(ComplementNB(alpha=0.1), "ComplementNB"),
(LogisticRegression(solver='lbfgs', class_weight='balanced', max_iter=1000, random_state=RANDOM_SEED), "Logistic Regression")
):
print("=" * 80)
print("Training Results - Naive Bayes & LogReg")
print(name)
mod = train_model(clf)
preds[name] = mod[2]
```
### 2.5 Tune Logistic Regression Params
So far, LogReg performs the best in terms of macro F1 score. In this section, we'll try tuning the performance of Logistic Regression, using the best Tfidf tuning result above.
```
vectorizer = TfidfVectorizer(min_df=100, ngram_range=(1,2))
X_train_bow = vectorizer.fit_transform(X_train)
X_dev_bow = vectorizer.transform(X_dev)
clf = LogisticRegression(solver='lbfgs', class_weight='balanced', max_iter=3000, random_state=RANDOM_SEED)
param_grid = {'C' : np.logspace(-4, 4, 20)}
print("=" * 80)
print("LogReg Grid Search")
clf = GridSearchCV(clf, param_grid = param_grid, cv = 5, verbose=True, n_jobs=-1)
best_clf = clf.fit(X_train_bow, y_train)
print(clf.best_params_)
y_dev_pred = clf.predict(X_dev_bow)
score = accuracy_score(y_dev, y_dev_pred)
print("accuracy: %0.3f" % score)
print("classification report:")
print(classification_report(y_dev, y_dev_pred))
print("confusion matrix:")
print(confusion_matrix(y_dev, y_dev_pred))
print("Training Complete")
print()
```
|
github_jupyter
|
# A Whale off the Port(folio)
---
In this assignment, you'll get to use what you've learned this week to evaluate the performance among various algorithmic, hedge, and mutual fund portfolios and compare them against the S&P TSX 60 Index.
## Assumptions and limitations
1. Limitation: Only dates that overlap between portfolios will be compared
2. Assumption: There are no significant anomalous price impacting events during the time window such as share split, trading halt
## 0. Import Required Libraries
```
# Initial imports
import pandas as pd # daataframe manipulation
import numpy as np # calc and numeric manipulatino
import datetime as dt # date and tim
from pathlib import Path # setting the path for file manipulation
import datetime
pd.options.display.float_format = '{:.6f}'.format # float format to 6 decimal places
```
# Data Cleaning
In this section, you will need to read the CSV files into DataFrames and perform any necessary data cleaning steps. After cleaning, combine all DataFrames into a single DataFrame.
Files:
* `whale_returns.csv`: Contains returns of some famous "whale" investors' portfolios.
* `algo_returns.csv`: Contains returns from the in-house trading algorithms from Harold's company.
* `sp_tsx_history.csv`: Contains historical closing prices of the S&P TSX 60 Index.
## A. Whale Returns
Read the Whale Portfolio daily returns and clean the data.
### 1. import whale csv and set index to date
```
df_wr = pd.read_csv('Resources/whale_returns.csv', index_col="Date")
```
### 2. Inspect imported data
```
# look at colums and value head
df_wr.head(3)
# look at last few values
df_wr.tail(3)
# check dimensions of df
df_wr.shape
# get index datatype - for later merging
df_wr.index.dtype
# get datatypes of all values
df_wr.dtypes
```
### 3. Count and drop any null values
```
# Count nulls
df_wr.isna().sum()
# Drop nulls
df_wr.dropna(inplace=True)
# Count nulls -again to ensure they're removed
df_wr.isna().sum()
df_wr.count() #double check all values are equal in length
```
### 4. Sort the index to ensure the correct date order for calculations
```
df_wr.sort_index(inplace=True)
```
### 5. Rename columns - shorten and make consistent with other tables
```
# change columns to be consistent and informative
df_wr.columns
df_wr.columns = ['Whale_Soros_Fund_Daily_Returns', 'Whale_Paulson_Daily_Returns',
'Whale_Tiger_Daily_Returns', 'Whale_Berekshire_Daily_Returns']
```
### 6. Create copy dataframe with new column for cumulative returns
```
# copy the dataframe to store cumprod in a new view
df_wr_cumulative = df_wr.copy()
# create a new column in new df for each cumulative daily return using the cumprod function
df_wr_cumulative['Whale_Soros_Fund_Daily_CumReturns'] = (1 + df_wr_cumulative['Whale_Soros_Fund_Daily_Returns']).cumprod()
df_wr_cumulative['Whale_Paulson_Daily_CumReturns'] = (1 + df_wr_cumulative['Whale_Paulson_Daily_Returns']).cumprod()
df_wr_cumulative['Whale_Tiger_Daily_CumReturns'] = (1 + df_wr_cumulative['Whale_Tiger_Daily_Returns']).cumprod()
df_wr_cumulative['Whale_Berekshire_Daily_CumReturns'] = (1 + df_wr_cumulative['Whale_Berekshire_Daily_Returns']).cumprod()
df_wr_cumulative.head() # check result is consistent against original column ie adds up
# drop returns columns from cumulative df
df_wr_cumulative.columns
df_wr_cumulative = df_wr_cumulative[['Whale_Soros_Fund_Daily_CumReturns', 'Whale_Paulson_Daily_CumReturns','Whale_Tiger_Daily_CumReturns', 'Whale_Berekshire_Daily_CumReturns']]
df_wr_cumulative.head()
```
### 7. Look at high level stats & plot for whale portfolios
```
df_wr.describe(include='all') # basic stats for daily whale returns
df_wr_cumulative.describe(include='all') # basic stats for daily cumulative whale returns
# plot daily returns - whales
df_wr.plot(figsize=(10,5))
# Plot cumulative returns
df_wr_cumulative.plot(figsize=(10,5))
```
#### The data looks consistent and there are no obvious data errors identified.
#### Initial high level observations of standalone daily returns data for whale portfolio: At initial glance, the mean daily return indicates that Berkshire portfolio performed best (mean daily returns of 0.000501, mean cumulative daily returns 1.159732), while Paulson worst (-0.000203). The standard deviation indicates highest risk for Berkshire (0.012831 STD), while lowest risk/volatility is Paulson (std 0.006977)
#### A more thorough analysis will be done in the following analysis section, so no conclusions are drawn yet.
#### By looking at the cumulative chart, it is evident that all portfolios were vulnerable to a loss at the same tim around 2019-02-16, but that Berkshir was able to increas the most over time and climb the steepest after the downturn
## B. Algorithmic Daily Returns
Read the algorithmic daily returns and clean the data.
### 1. import algo csv and set index to date
```
# Reading algorithmic returns
df_ar = pd.read_csv('Resources/algo_returns.csv', index_col='Date')
```
### 2. Inspect resulting dataframe and contained data
```
# look at colums and value first 3 rows
df_ar.head(3)
# look at colums and value last 3 rows
df_ar.tail(3)
# get dimensions of df
df_ar.shape
# get index datatype - for later merging
df_ar.index.dtype
# get datatypes
df_ar.dtypes
```
### 3. Count and remove null values
```
# Count nulls
df_ar.isna().sum()
# Drop nulls
df_ar.dropna(inplace=True)
# Count nulls -again to ensure that nulls actually are removed
df_ar.isna().sum()
df_ar.count()
```
### 4. Sort index to ensure correct date order for calculations
```
df_ar.sort_index(inplace=True)
```
### 5. Rename columns to be consistent with future merge
```
df_ar.columns
df_ar.columns = ['Algo1_Daily_Returns', 'Algo2_Daily_Returns']
```
### 6. Create new column in a copy df for cumulative returns per Algo daily return
```
# create a df copy to store cumulative data
df_ar_cumulative = df_ar.copy()
# use cumprod to get the daily cumulative returns for each of the algos 1 and 2
df_ar_cumulative['Algo1_Daily_CumReturns'] = (1 + df_ar_cumulative['Algo1_Daily_Returns']).cumprod()
df_ar_cumulative['Algo2_Daily_CumReturns'] = (1 + df_ar_cumulative['Algo2_Daily_Returns']).cumprod()
# check the result is consistent with the daily returns for first few columns
df_ar_cumulative.head(10)
# drop columns that are not required
df_ar_cumulative.columns # get the columns
df_ar_cumulative = df_ar_cumulative[['Algo1_Daily_CumReturns','Algo2_Daily_CumReturns']]
# check result - first few lines
df_ar_cumulative.head(10)
```
### 7. Look at high level stats & plot for algo portfolios
```
df_ar.describe(include='all') # stats for daily returns
df_ar_cumulative.describe(include='all') # stats for daily cumulative returns
# plot daily returns - algos
df_ar.plot(figsize=(10,5))
# plot daily cumulative returns - algos
df_ar_cumulative.plot(figsize=(10,5))
```
#### The data looks consistent and there are no obvious errors identified.
#### Initial observations of standalone daily returns data for Algo 1 vs Algo 2: mean daily return indicates that Algo 1 (mean daily return 0.000654) performs slightly better than Algo 2 (mean daily return 0.000341), which is alo evident in the cumulative daily returns plot. When looking at just daily returns, Algo 2 is more risky, but when looking at cumulative returns, Algo 1 is more risky (ie higher standard deviation).
## C. S&P TSX 60 Returns
Read the S&P TSX 60 historic closing prices and create a new daily returns DataFrame from the data.
Note: this contains daily closing and not returns - needs to be converted
### 1. Import S&P csv daily closing price (not returns)
```
# Reading S&P TSX 60 Closing Prices
df_sr = pd.read_csv('Resources/sp_tsx_history.csv')
```
### 2. Inspect columns of dataframe
```
# look at colums and value head
df_sr.head(3)
# look at tail values
df_sr.tail(3)
```
#### Note from dataframe inspection:
#### 1. date column was not immediated converted because it is in
#### a different format to the other csv files and
#### needs to bee converted to consistent format first
#### 2. Close cannot be explicitly converted to float as it has
#### dollar and commas.
#### 3. A new column for returns will need to be created from
#### return calculations.
```
# check dimension of df
df_sr.shape
# Check Data Types
df_sr.dtypes
```
### 3. Convert the date into a consistent format with other tables
```
df_sr['Date']= pd.to_datetime(df_sr['Date']).dt.strftime('%Y-%m-%d')
#df_sr['Date']= pd.to_datetime(df_sr['Date'], format='%Y-%m-%d')
```
### 4. Convert th data to index and check format and data type
```
# set date as index
df_sr.set_index('Date', inplace=True)
df_sr.head(2)
df_sr.index.dtype
```
### 5. Check for null values
```
# Count nulls - none observed
df_ar.isna().sum()
```
### 6. Convert daily closing price to float (from string)
```
# Change the Closing column to b float type
df_sr['Close']= df_sr['Close'].str.replace('$','')
df_sr['Close']= df_sr['Close'].str.replace(',','')
df_sr['Close']= df_sr['Close'].astype(float)
# Check Data Types
df_sr.dtypes
# test
df_sr.iloc[0]
# check null values
df_sr.isna().sum()
df_sr.count()
```
### 7. Sort the index for calculations of returns
```
# sort_index
df_sr.sort_index(inplace=True)
df_sr.head(2)
```
### 8. Calculate daily returns and store in new column
Equation: $r=\frac{{p_{t}} - {p_{t-1}}}{p_{t-1}}$
The daily return is the (current closing price minus the previous day closing price) all divided by the previous day closing price. The initial value has no daily return as there is no prior period to compare it with.
Here the calculation uses the python shift function
```
df_sr['SnP_TSX_60_Returns'] = (df_sr['Close'] - df_sr['Close'].shift(1))/ df_sr['Close'].shift(1)
df_sr.head(10)
```
### 9. Cross check conversion to daily returns against alternative method - pct_change function
```
df_sr['SnP_TSX_60_Returns'] = df_sr['Close'].pct_change()
df_sr.head(10)
```
#### Methods cross check - looks good - continue
```
# check for null - first row would have null
df_sr.isna().sum()
# Drop nulls - first row
df_sr.dropna(inplace=True)
# Rename `Close` Column to be specific to this portfolio.
df_sr.columns
df_sr.head()
```
### 10. Drop original Closing column - not needed for comparison
```
df_sr = df_sr[['SnP_TSX_60_Returns']]
df_sr.columns
```
### 11. Create new column in a copy df for cumulative returns per daily return S&P TSX 60
```
df_sr_cumulative = df_sr.copy()
# use cumprod to get the daily cumulative returns for each of the algos 1 and 2
df_sr_cumulative['SnP_TSX_60_CumReturns'] = (1+df_sr_cumulative['SnP_TSX_60_Returns']).cumprod()
# visually check first 10 rows to ensure that results make sense
df_sr_cumulative.head(10)
```
## D. Combine Whale, Algorithmic, and S&P TSX 60 Returns
```
# Use the `concat` function to combine the two DataFrames by matching indexes (or in this case `Month`)
merged_analysis_df_tmp = pd.concat([df_wr, df_ar ], axis="columns", join="inner")
merged_analysis_df_tmp.head(3)
# Use the `concat` function to combine the two DataFrames by matching indexes (or in this case `Month`)
merged_daily_returns_df = pd.concat([merged_analysis_df_tmp, df_sr ], axis="columns", join="inner")
merged_daily_returns_df.head(3)
```
# Conduct Quantitative Analysis
In this section, you will calculate and visualize performance and risk metrics for the portfolios.
## Performance Anlysis
#### Calculate and Plot the daily returns
```
# Plot daily returns of all portfolios
drp = merged_analysis_df.plot(figsize=(20,10), rot=45, title='Comparison of Daily Returns on Stock Portfolios')
drp.set_xlabel("Daily Returns")
drp.set_ylabel("Date")
```
#### Calculate and Plot cumulative returns.
```
merged_analysis_cum_df.columns
```
# [[NOT WORKING BECAUSE FIRST ROW SHOULD NOT BE NULL]]
```
merged_analysis_cum_df.head()
# Calculate cumulative returns of all portfolios
# Plot cumulative returns
drp = merged_analysis_cum_df.plot(figsize=(20,20), rot=45, title='Comparison of Daily Cumulative Returns on Stock Portfolios')
drp.set_xlabel("Daily Cumulative Returns")
drp.set_ylabel("Date")
```
---
## Risk Analysis
Determine the _risk_ of each portfolio:
1. Create a box plot for each portfolio.
2. Calculate the standard deviation for all portfolios.
4. Determine which portfolios are riskier than the S&P TSX 60.
5. Calculate the Annualized Standard Deviation.
### Create a box plot for each portfolio
```
# Box plot to visually show risk
```
### Calculate Standard Deviations
```
# Calculate the daily standard deviations of all portfolios
```
### Determine which portfolios are riskier than the S&P TSX 60
```
# Calculate the daily standard deviation of S&P TSX 60
# Determine which portfolios are riskier than the S&P TSX 60
```
### Calculate the Annualized Standard Deviation
```
# Calculate the annualized standard deviation (252 trading days)
```
---
## Rolling Statistics
Risk changes over time. Analyze the rolling statistics for Risk and Beta.
1. Calculate and plot the rolling standard deviation for the S&P TSX 60 using a 21-day window.
2. Calculate the correlation between each stock to determine which portfolios may mimick the S&P TSX 60.
3. Choose one portfolio, then calculate and plot the 60-day rolling beta for it and the S&P TSX 60.
### Calculate and plot rolling `std` for all portfolios with 21-day window
```
# Calculate the rolling standard deviation for all portfolios using a 21-day window
# Plot the rolling standard deviation
```
### Calculate and plot the correlation
```
# Calculate the correlation
# Display de correlation matrix
```
### Calculate and Plot Beta for a chosen portfolio and the S&P 60 TSX
```
# Calculate covariance of a single portfolio
# Calculate variance of S&P TSX
# Computing beta
# Plot beta trend
```
## Rolling Statistics Challenge: Exponentially Weighted Average
An alternative way to calculate a rolling window is to take the exponentially weighted moving average. This is like a moving window average, but it assigns greater importance to more recent observations. Try calculating the [`ewm`](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.ewm.html) with a 21-day half-life.
```
# Use `ewm` to calculate the rolling window
```
---
# Sharpe Ratios
In reality, investment managers and thier institutional investors look at the ratio of return-to-risk, and not just returns alone. After all, if you could invest in one of two portfolios, and each offered the same 10% return, yet one offered lower risk, you'd take that one, right?
### Using the daily returns, calculate and visualize the Sharpe ratios using a bar plot
```
# Annualized Sharpe Ratios
# Visualize the sharpe ratios as a bar plot
```
### Determine whether the algorithmic strategies outperform both the market (S&P TSX 60) and the whales portfolios.
Write your answer here!
---
# Create Custom Portfolio
In this section, you will build your own portfolio of stocks, calculate the returns, and compare the results to the Whale Portfolios and the S&P TSX 60.
1. Choose 3-5 custom stocks with at last 1 year's worth of historic prices and create a DataFrame of the closing prices and dates for each stock.
2. Calculate the weighted returns for the portfolio assuming an equal number of shares for each stock.
3. Join your portfolio returns to the DataFrame that contains all of the portfolio returns.
4. Re-run the performance and risk analysis with your portfolio to see how it compares to the others.
5. Include correlation analysis to determine which stocks (if any) are correlated.
## Choose 3-5 custom stocks with at last 1 year's worth of historic prices and create a DataFrame of the closing prices and dates for each stock.
For this demo solution, we fetch data from three companies listes in the S&P TSX 60 index.
* `SHOP` - [Shopify Inc](https://en.wikipedia.org/wiki/Shopify)
* `OTEX` - [Open Text Corporation](https://en.wikipedia.org/wiki/OpenText)
* `L` - [Loblaw Companies Limited](https://en.wikipedia.org/wiki/Loblaw_Companies)
```
# Reading data from 1st stock
# Reading data from 2nd stock
# Reading data from 3rd stock
# Combine all stocks in a single DataFrame
# Reset Date index
# Reorganize portfolio data by having a column per symbol
# Calculate daily returns
# Drop NAs
# Display sample data
```
## Calculate the weighted returns for the portfolio assuming an equal number of shares for each stock
```
# Set weights
weights = [1/3, 1/3, 1/3]
# Calculate portfolio return
# Display sample data
```
## Join your portfolio returns to the DataFrame that contains all of the portfolio returns
```
# Join your returns DataFrame to the original returns DataFrame
# Only compare dates where return data exists for all the stocks (drop NaNs)
```
## Re-run the risk analysis with your portfolio to see how it compares to the others
### Calculate the Annualized Standard Deviation
```
# Calculate the annualized `std`
```
### Calculate and plot rolling `std` with 21-day window
```
# Calculate rolling standard deviation
# Plot rolling standard deviation
```
### Calculate and plot the correlation
```
# Calculate and plot the correlation
```
### Calculate and Plot the 60-day Rolling Beta for Your Portfolio compared to the S&P 60 TSX
```
# Calculate and plot Beta
```
### Using the daily returns, calculate and visualize the Sharpe ratios using a bar plot
```
# Calculate Annualzied Sharpe Ratios
# Visualize the sharpe ratios as a bar plot
```
### How does your portfolio do?
Write your answer here!
### References
Shift function in pandas -
https://stackoverflow.com/questions/20000726/calculate-daily-returns-with-pandas-dataframe
Conditional line color -
https://stackoverflow.com/questions/31590184/plot-multicolored-line-based-on-conditional-in-python
https://stackoverflow.com/questions/40803570/python-matplotlib-scatter-plot-specify-color-points-depending-on-conditions/40804861
https://stackoverflow.com/questions/42453649/conditional-color-with-matplotlib-scatter
https://stackoverflow.com/questions/3832809/how-to-change-the-color-of-a-single-bar-if-condition-is-true-matplotlib
https://stackoverflow.com/questions/56779975/conditional-coloring-in-matplotlib-using-numpys-where
PEP 8 - Standards -
|
github_jupyter
|
```
from gs_quant.session import GsSession, Environment
from gs_quant.instrument import IRSwap
from gs_quant.risk import IRFwdRate, CarryScenario
from gs_quant.markets.portfolio import Portfolio
from gs_quant.markets import PricingContext
from datetime import datetime
import matplotlib.pylab as plt
import pandas as pd
import numpy as np
# external users should substitute their client id and secret; please skip this step if using internal jupyterhub
GsSession.use(Environment.PROD, client_id=None, client_secret=None, scopes=('run_analytics',))
ccy = 'EUR'
# construct a series of 6m FRAs going out 20y or so
fras = Portfolio([IRSwap('Pay', '{}m'.format(i), ccy, effective_date='{}m'.format(i-6),
fixed_rate_frequency='6m', floating_rate_frequency='6m')
for i in range(6, 123, 6)])
fras.resolve()
results = fras.calc(IRFwdRate)
# get the fwd rates for these fras under the base sceneraio (no shift in time)
base = {}
for i, res in enumerate(results):
base[datetime.strptime(fras[i].termination_date, '%Y-%m-%d')] = res
base_series = pd.Series(base, name='base', dtype=np.dtype(float))
# calculate the fwd rates with a shift forward of 132 business days - about 6m. This shift keeps spot rates constant.
# So 5y rate today will be 5y rate under the scenario of pricing 6m in the future.
with CarryScenario(time_shift=132, roll_to_fwds=False):
fras = Portfolio([IRSwap('Pay', '{}m'.format(i), ccy, effective_date='{}m'.format(i-6),
fixed_rate_frequency='6m', floating_rate_frequency='6m') for i in range(6, 123, 6)])
fras.resolve()
results = fras.calc(IRFwdRate)
roll_spot = {}
for i, res in enumerate(results):
roll_spot[datetime.strptime(fras[i].termination_date, '%Y-%m-%d')] = res
roll_spot_series = pd.Series(roll_spot, name='roll to spot', dtype=np.dtype(float))
# calculate the fwd rates with a shift forward of 132 business days - about 6m. This shift keeps fwd rates constant.
# So 5.5y rate today will be 5y rate under the scenario of pricing 6m in the future.
with CarryScenario(time_shift=132, roll_to_fwds=True):
fras = Portfolio([IRSwap('Pay', '{}m'.format(i), ccy, effective_date='{}m'.format(i-6),
fixed_rate_frequency='6m', floating_rate_frequency='6m') for i in range(6, 123, 6)])
fras.resolve()
results = fras.calc(IRFwdRate)
roll_fwd = {}
for i, res in enumerate(results):
roll_fwd[datetime.strptime(fras[i].termination_date, '%Y-%m-%d')] = res
roll_fwd_series = pd.Series(roll_fwd, name='roll to fwd', dtype=np.dtype(float))
# show the curves, the base in blue, the roll to fwd in green and the roll to spot in orange.
# note blue and green curves are not exactly on top of each other as we aren't using the curve instruments themselves
# but instead using FRAs to show a smooth curve.
base_series.plot(figsize=(20, 10))
roll_spot_series.plot()
roll_fwd_series.plot()
plt.legend()
```
|
github_jupyter
|
```
# Initialize Otter
import otter
grader = otter.Notebook("hw09.ipynb")
```
# Homework 9: Bootstrap, Resampling, CLT
**Reading**:
* [Estimation](https://www.inferentialthinking.com/chapters/13/estimation.html)
* [Why the mean matters](https://www.inferentialthinking.com/chapters/14/why-the-mean-matters.html)
Please complete this notebook by filling in the cells provided.
Directly sharing answers is not okay, but discussing problems with the course staff or with other students is encouraged. Refer to the policies page to learn more about how to learn cooperatively.
For all problems that you must write our explanations and sentences for, you **must** provide your answer in the designated space. Moreover, throughout this homework and all future ones, please be sure to not re-assign variables throughout the notebook! For example, if you use `max_temperature` in your answer to one question, do not reassign it later on.
```
# Run this cell to set up the notebook, but please don't change it.
# These lines import the Numpy and Datascience modules.
import numpy as np
from datascience import *
# These lines do some fancy plotting magic.
import matplotlib
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
import warnings
warnings.simplefilter('ignore', FutureWarning)
```
## 1. Preliminaries
The British Royal Air Force wanted to know how many warplanes the Germans had (some number `N`, which is a *parameter*), and they needed to estimate that quantity knowing only a random sample of the planes' serial numbers (from 1 to `N`). We know that the German's warplanes are labeled consecutively from 1 to `N`, so `N` would be the total number of warplanes they have.
We normally investigate the random variation among our estimates by simulating a sampling procedure from the population many times and computing estimates from each sample that we generate. In real life, if the British Royal Air Force (RAF) had known what the population looked like, they would have known `N` and would not have had any reason to think about random sampling. However, they didn't know what the population looked like, so they couldn't have run the simulations that we normally do.
Simulating a sampling procedure many times was a useful exercise in *understanding random variation* for an estimate, but it's not as useful as a tool for practical data analysis.
Let's flip that sampling idea on its head to make it practical. **Given *just* a random sample of serial numbers, we'll estimate `N`, and then we'll use simulation to find out how accurate our estimate probably is, without ever looking at the whole population.** This is an example of *statistical inference*.
We (the RAF in World War II) want to know the number of warplanes fielded by the Germans. That number is `N`. The warplanes have serial numbers from 1 to `N`, so `N` is also equal to the largest serial number on any of the warplanes.
We only see a small number of serial numbers (assumed to be a random sample with replacement from among all the serial numbers), so we have to use estimation.
#### Question 1.1
Is `N` a population parameter or a statistic? If we use our random sample to compute a number that is an estimate of `N`, is that a population parameter or a statistic?
Set `N` and `N_estimate` to either the string `"parameter"` or `"statistic"` to indicate whether each value is a parameter or a statistic.
<!--
BEGIN QUESTION
name: q1_1
-->
```
N = ...
N_estimate = ...
grader.check("q1_1")
```
To make the situation realistic, we're going to hide the true number of warplanes from you. You'll have access only to this random sample:
```
observations = Table.read_table("serial_numbers.csv")
num_observations = observations.num_rows
observations
```
#### Question 1.2
The average of the sample is about half of `N`. So one way to estimate `N` is to take twice the mean of the serial numbers we see. Write a function that computes that statistic. It should take as its argument an array of serial numbers and return twice their mean. Call the function `mean_based_estimator`.
After that, use the function and the `observations` table to compute an estimate of `N` called `mean_based_estimate`.
<!--
BEGIN QUESTION
name: q1_2
-->
```
def mean_based_estimator(nums):
...
mean_based_estimate = ...
mean_based_estimate
grader.check("q1_2")
```
#### Question 1.3
We can also estimate `N` by using the biggest serial number in the sample. Compute this value and give it the name `max_estimate`.
<!--
BEGIN QUESTION
name: q1_3
-->
```
max_estimate = ...
max_estimate
grader.check("q1_3")
```
<!-- BEGIN QUESTION -->
#### Question 1.4
Let's take a look at the values of `max_estimate` and `mean_based_estimate` that we got for our dataset. Which of these values is closer to the true population maximum `N`? Based off of our estimators, can we give a lower bound for what `N` must be? In other words, is there a value that `N` must be greater than or equal to?
<!--
BEGIN QUESTION
name: q1_4
manual: true
-->
_Type your answer here, replacing this text._
<!-- END QUESTION -->
We can't just confidently proclaim that `max_estimate` or `mean_based_estimate` is equal to `N`. What if we're really far off? We want to get a sense of the accuracy of our estimates.
## 2. Resampling
To do this, we'll use resampling. That is, we won't exactly simulate the observations the RAF would have really seen. Rather we sample from our current sample, or "resample."
Why does that make any sense?
When we try to find the value of a population parameter, we ideally would like to use the whole population. However, we often only have access to one sample and we must use that to estimate the parameter instead.
Here, we would like to use the population of serial numbers to draw more samples and run a simulation about estimates of `N`. But we still only have our sample. So, we **use our sample in place of the population** to run the simulation. We resample from our original sample with replacement as many times as there are elements in the original sample. This resampling technique is called *bootstrapping*.
Note that in order for bootstrapping to work well, you must start with a large, random sample. Then the Law of Large Numbers says that with high probability, your sample is representative of the population.
#### Question 2.1
Write a function called `simulate_resample`. The function should take one argument `tbl`, which is a table like `observations`. The function should generate a resample from the observed serial numbers in `tbl`.
<!--
BEGIN QUESTION
name: q2_1
-->
```
def simulate_resample(tbl):
...
simulate_resample(observations) # Don't delete this line
grader.check("q2_1")
```
We'll use many resamples at once to see what estimates typically look like. However, we don't often pay attention to single resamples, so it's easy to misunderstand them. Let's first answer some questions about our resample.
#### Question 2.2
Which of the following statements are true?
1. The original sample can contain serial numbers that are not in the resample.
2. Because the sample size is small, the histogram of the resample might look very different from the histogram of the original sample.
3. The resample can contain serial numbers that are not in the original sample.
4. The original sample has exactly one copy of each serial number for every German plane.
5. The resample has either zero, one, or more than one copy of each serial number.
6. The resample has exactly the same sample size as the original sample.
Assign `true_statements` to an array of the number(s) corresponding to correct statements.
*Note:* The "original sample" refers to `observations`, and the "resample" refers the output of one call of `simulate_resample()`.
<!--
BEGIN QUESTION
name: q2_2
-->
```
true_statements = ...
grader.check("q2_2")
```
Now let's write a function to do many resamples at once.
#### Question 2.3
Write a function called `sample_estimates`. It should take 3 arguments:
1. `serial_num_tbl`: A table from which the data should be sampled. The table will look like `observations`.
2. `statistic`: A *function* that takes in an array of serial numbers as its argument and computes a statistic from the array (i.e. returns a calculated number).
3. `num_replications`: The number of simulations to perform.
*Hint: You should use the function `simulate_resample` which you defined in Question 2.1*
The function should simulate many samples **with replacement** from the given table. For each of those samples, it should compute the statistic on that sample. Then it should **return an array** containing each of those statistics. The code below provides an example use of your function and describes how you can verify that you've written it correctly.
<!--
BEGIN QUESTION
name: q2_3
-->
```
def sample_estimates(serial_num_tbl, statistic, num_replications):
...
# DON'T CHANGE THE CODE BELOW THIS COMMENT! (If you do, you will fail the hidden test)
# This is just an example to test your function.
# This should generate an empirical histogram of twice-mean-based estimates
# of N from samples of size 50 if N is 1000. This should be a bell-shaped
# curve centered at roughly 900 with most of its mass in [800, 1200]. To verify your
# answer, make sure that's what you see!
population = Table().with_column("serial number", np.arange(1, 1000+1))
one_sample = Table.read_table("one_sample.csv") #This is a sample from the population table
example_estimates = sample_estimates(
one_sample,
mean_based_estimator,
10000)
Table().with_column("mean-based estimate", example_estimates).hist(bins=np.arange(0, 1500, 25))
grader.check("q2_3")
```
Now we can go back to the sample we actually observed (the table `observations`) and estimate how much our mean-based estimate of `N` would have varied from sample to sample.
#### Question 2.4
Using the bootstrap and the sample `observations`, simulate the approximate distribution of *mean-based estimates* of `N`. Use 7,500 replications and save the estimates in an array called `bootstrap_mean_based_estimates`.
We have provided code that plots a histogram, allowing you to visualize the simulated estimates.
<!--
BEGIN QUESTION
name: q2_4
-->
```
bootstrap_mean_based_estimates = ...
# Don't change the code below! This plots bootstrap_mean_based_estimates.
Table().with_column("mean-based estimate", bootstrap_mean_based_estimates).hist(bins=np.arange(0, 200, 4))
grader.check("q2_4")
```
#### Question 2.5
Using the bootstrap and the sample `observations`, simulate the approximate distribution of *max estimates* of `N`. Use 7,500 replications and save the estimates in an array called `bootstrap_max_estimates`.
We have provided code that plots a histogram, allowing you to visualize the simulated estimates.
<!--
BEGIN QUESTION
name: q2_5
-->
```
bootstrap_max_estimates = ...
# Don't change the code below! This plots bootstrap_max_estimates.
Table().with_column("max estimate", bootstrap_max_estimates).hist(bins=np.arange(0, 200, 4))
grader.check("q2_5")
```
<!-- BEGIN QUESTION -->
#### Question 2.6
`N` was actually 150! Compare the histograms of estimates you generated in 2.4 and 2.5 and answer the following questions:
1. How does the distribution of values for the mean-based estimates differ from the max estimates? Do both distributions contain the true max value?
2. Which estimator is more dependent on the original random sample? Why so?
<!--
BEGIN QUESTION
name: q2_6
manual: true
-->
_Type your answer here, replacing this text._
<!-- END QUESTION -->
## 3. Computing intervals
#### Question 3.1
Compute an interval that covers the middle 95% of the mean-based bootstrap estimates. Assign your values to `left_end_1` and `right_end_1`.
*Hint:* Use the `percentile` function! Read up on its documentation [here](http://data8.org/sp19/python-reference.html).
Verify that your interval looks like it covers 95% of the area in the histogram. The red dot on the histogram is the value of the parameter (150).
<!--
BEGIN QUESTION
name: q3_1
-->
```
left_end_1 = ...
right_end_1 = ...
print("Middle 95% of bootstrap estimates: [{:f}, {:f}]".format(left_end_1, right_end_1))
# Don't change the code below! It draws your interval and N on the histogram of mean-based estimates.
Table().with_column("mean-based estimate", bootstrap_mean_based_estimates).hist(bins=np.arange(0, 200, 4))
plt.plot(make_array(left_end_1, right_end_1), make_array(0, 0), color='yellow', lw=7, zorder=1)
plt.scatter(150, 0, color='red', s=30, zorder=2);
grader.check("q3_1")
```
#### Question 3.2
Write code that simulates the sampling and bootstrapping process again, as follows:
1. Generate a new set of random observations the RAF might have seen by sampling from the `population` table we have created for you below. Use the sample size `num_observations`.
2. Compute an estimate of `N` from these new observations, using `mean_based_estimator`.
3. Using only the new observations, compute 10,000 bootstrap estimates of `N`.
4. Plot these bootstrap estimates and compute an interval covering the middle 95%.
*Note:* Traditionally, when we bootstrap using a sample from the population, that sample is usually a simple random sample (i.e., sampled uniformly at random from the population without replacement). However, if the population size is big enough, the difference between sampling with replacement and without replacement is negligible. Think about why that's the case! This is why when we define `new_observations`, we sample with replacement.
<!--
BEGIN QUESTION
name: q3_2
-->
```
population = Table().with_column("serial number", np.arange(1, 150+1))
new_observations = ...
new_mean_based_estimate = ...
new_bootstrap_estimates = ...
Table().with_column("mean-based estimate", new_bootstrap_estimates).hist(bins=np.arange(0, 252, 4))
new_left_end = ...
new_right_end = ...
# Don't change code below this line!
print("New mean-based estimate: {:f}".format(new_mean_based_estimate))
print("Middle 95% of bootstrap estimates: [{:f}, {:f}]".format(new_left_end, new_right_end))
plt.plot(make_array(new_left_end, new_right_end), make_array(0, 0), color='yellow', lw=7, zorder=1)
plt.scatter(150, 0, color='red', s=30, zorder=2);
grader.check("q3_2")
```
<!-- BEGIN QUESTION -->
#### Question 3.3
Does the interval covering the middle 95% of the new bootstrap estimates include `N`? If you ran that cell 100 times and generated 100 intervals, how many of those intervals would you expect to include `N`?
<!--
BEGIN QUESTION
name: q3_3
manual: true
-->
_Type your answer here, replacing this text._
<!-- END QUESTION -->
Let's look at what happens when we use a small number of resamples:
<img src="smallrephist.png" width="525"/>
This histogram and confidence interval was generated using 10 resamples of `new_observations`.
<!-- BEGIN QUESTION -->
#### Question 3.4
In the cell below, explain why this histogram and confidence interval look different from the ones you generated previously in Question 3.2 where the number of resamples was 10,000.
<!--
BEGIN QUESTION
name: q3_4
manual: true
-->
_Type your answer here, replacing this text._
<!-- END QUESTION -->
## 4. The CLT and Book Reviews
Your friend has recommended you a book, so you look for it on an online marketplace. You decide to look at reviews for the book just to be sure that it's worth buying. Let's say that on Amazon, the book only has 80% positive reviews. On GoodReads, it has 95% positive reviews. You decide to investigate a bit further by looking at the percentage of positive reviews for the book on 5 different websites that you know of, and you collect these positive review percentages in a table called `reviews.csv`.
Here, we've loaded in the table for you.
```
reviews = Table.read_table("reviews.csv")
reviews
```
**Question 4.1**. Calculate the average percentage of positive reviews from your sample and assign it to `initial_sample_mean`.
<!--
BEGIN QUESTION
name: q4_1
manual: false
-->
```
initial_sample_mean = ...
initial_sample_mean
grader.check("q4_1")
```
You've calculated the average percentage of positive reviews from your sample, so now you want to do some inference using this information.
**Question 4.2**. First, simulate 5000 bootstrap resamples of the positive review percentages. For each bootstrap resample, calculate the resample mean and store the resampled means in an array called `resample_positive_percentages`. Then, plot a histogram of the resampled means.
<!--
BEGIN QUESTION
name: q4_2
manual: false
-->
```
resample_positive_percentages = make_array()
for i in np.arange(5000):
resample = ...
resample_avg_positive = ...
resample_positive_percentages = ...
# Do NOT change these lines.
(Table().with_column("Average % of Positive Reviews in Resamples",
resample_positive_percentages).hist("Average % of Positive Reviews in Resamples"))
grader.check("q4_2")
```
**Question 4.3**. What is the the shape of the empirical distribution of the average percentage of positive reviews based on our original sample? What value is the distribution centered at? Assign your answer to the variable `initial_sample_mean_distribution`--your answer should be either `1`, `2`, `3`, or `4` corresponding to the following choices:
*Hint: Look at the histogram you made in Question 2. Run the cell that generated the histogram a few times to check your intuition.*
1. The distribution is approximately normal because of the Central Limit Theorem, and it is centered at the original sample mean.
2. The distribution is not necessarily normal because the Central Limit Theorem may not apply, and it is centered at the original sample mean.
3. The distribution is approximately normal because of the Central Limit Theorem, but it is not centered at the original sample mean.
4. The distribution is not necessarily normal because the Central Limit Theorem may not apply, and it is not centered at the original sample mean.
<!--
BEGIN QUESTION
name: q4_3
manual: false
-->
```
initial_sample_mean_distribution = ...
grader.check("q4_3")
```
<!-- BEGIN QUESTION -->
According to the Central Limit Theorem, the probability distribution of the sum or average of a *large random sample* drawn with replacement will be roughly normal, regardless of the distribution of the population from which the sample is drawn.
**Question 4.4**. Note the statement about the sample being large and random. Is this sample large and random? Give a brief explanation.
*Note: The setup at the beginning of this exercise explains how the sample was gathered.*
<!--
BEGIN QUESTION
name: q4_4
manual: true
-->
_Type your answer here, replacing this text._
<!-- END QUESTION -->
Though you have an estimate of the true percentage of positive reviews (the sample mean), you want to measure how variable this estimate is.
**Question 4.5**. Find the standard deviation of your resampled average positive review percentages, which you stored in `resample_positive_percentages`, and assign the result to the variable `resampled_means_variability`.
<!--
BEGIN QUESTION
name: q4_5
manual: false
-->
```
resampled_means_variability = ...
resampled_means_variability
grader.check("q4_5")
```
This estimate is pretty variable! To make the estimate less variable, let's say you found a way to randomly sample reputable marketplaces from across the web which sell this book. Let's say that there are up to 150 of these marketplaces. The percentages of positive reviews are loaded into the table `more_reviews`.
```
# Just run this cell
more_reviews = Table.read_table("more_reviews.csv")
more_reviews
```
In the next few questions, we'll test an important result of the Central Limit Theorem. According to the CLT, the standard deviation of all possible sample means can be calculated using the following formula:
$$
\text{SD of all possible sample means} = \dfrac{\text{Population SD}}{\sqrt{\text{sample size}}}
$$
This formula gives us another way to approximate the SD of the sample means other than calculating it empirically. We can test how well this formula works by calculating the SD of sample means for different sample sizes.
The following code calculates the SD of sample means using the CLT and empirically for a range of sample sizes. Then, it plots a scatter plot comparing the SD of the sample means calculated with both methods. Each point corresponds to a different sample size.
```
# Just run this cell. It's not necessary for you to read this code, but you can do 99% of this on your own!
# Note: this cell might take a bit to run.
def empirical_sample_mean_sd(n):
sample_means = make_array()
for i in np.arange(500):
sample = more_reviews.sample(n).column('Positive Review Percentage')
sample_mean = np.mean(sample)
sample_means = np.append(sample_means, sample_mean)
return np.std(sample_means)
def predict_sample_mean_sd(n):
return np.std(more_reviews.column(0)) / (n**0.5)
sd_table = Table().with_column('Sample Size', np.arange(1,151))
predicted = sd_table.apply(predict_sample_mean_sd, 'Sample Size')
empirical = sd_table.apply(empirical_sample_mean_sd, 'Sample Size')
sd_table = sd_table.with_columns('Predicted SD', predicted, 'Empirical SD', empirical)
sd_table.scatter('Sample Size')
plt.ylabel("SD of Sample Mean");
```
**Question 4.6**. Assign the numbers corresponding to all true statements to an array called `sample_mean_sd_statements`.
1. The law of large numbers tells us that the distribution of a large random sample should resemble the distribution from which it is drawn.
2. The SD of the sample means is proportional to the square root of the sample size.
3. The SD of the sample means is proportional to 1 divided by the square root of the sample size.
4. The law of large numbers guarantees that empirical and predicted sample mean SDs will be exactly equal to each other when the sample size is large.
5. The law of large numbers guarantees that empirical and predicted sample mean SDs will be approximately equal to each other when the sample size is large.
6. The plot above shows that as our sample size increases, our estimate for the true percentage of positive reviews becomes more accurate.
7. The plot above shows that the size of the population affects the SD of the sample means.
<!--
BEGIN QUESTION
name: q4_6
manual: false
-->
```
sample_mean_sd_statements = ...
grader.check("q4_6")
```
Often times, when conducting statistical inference, you'll want your estimate of a population parameter to have a certain accuracy. It is common to measure accuracy of an estimate using the SD of the estimate--as the SD goes down, your estimate becomes less variable. As a result, the width of the confidence interval for your estimate decreases (think about why this is true). We know from the Central Limit Theorem that when we estimate a sample mean, the SD of the sample mean decreases as the sample size increases (again, think about why this is true).
**Question 4.7**. Imagine you are asked to estimate the true average percentage of positive reviews for this book and you have not yet taken a sample of review websites. Which of these is the best way to decide how large your sample should be to achieve a certain level of accuracy for your estimate of the true average percentage of positive reviews? Assign `sample_size_calculation` to either `1`, `2`, or `3` corresponding to the statements below.
*Note: Assume you know the population SD or can estimate it with reasonable accuracy.*
1. Take many random samples of different sizes, then calculate empirical confidence intervals using the bootstrap until you reach your desired accuracy.
2. Use the Central Limit Theorem to calculate what sample size you need in advance.
3. Randomly pick a sample size and hope for the best.
<!--
BEGIN QUESTION
name: q4_7
manual: false
-->
```
sample_size_calculation = ...
grader.check("q4_7")
```
Congratulations, you're done with Homework 9!
---
To double-check your work, the cell below will rerun all of the autograder tests.
```
grader.check_all()
```
## Submission
Make sure you have run all cells in your notebook in order before running the cell below, so that all images/graphs appear in the output. The cell below will generate a zip file for you to submit. **Please save before exporting!**
```
# Save your notebook first, then run this cell to export your submission.
grader.export()
```
|
github_jupyter
|
```
# import Modules
import numpy as np
from stl import mesh
import matplotlib.pyplot as plt
%matplotlib widget
# import stl file
part_mesh = mesh.Mesh.from_file('3DBenchy.stl')
print("File loaded in as faces and vertices")
# Slice STL file at each z value and return a
# pair of points that
def STL_Slicer(stl_mesh,layers):
# initilize points
Set_1 = np.zeros([3,0])
Set_2 = np.zeros([3,0])
# save faces that dont would through error
Bad_Faces = np.array([])
l = len(stl_mesh.vectors[:])
#l = 50000*2
for face in range(l):
# check if face is actually a line (bad stl file)
v1 = stl_mesh.vectors[face][0,:] - stl_mesh.vectors[face][1,:]
v2 = stl_mesh.vectors[face][1,:] - stl_mesh.vectors[face][2,:]
v3 = stl_mesh.vectors[face][2,:] - stl_mesh.vectors[face][0,:]
# check that face intercept z point
z_lim = np.array([stl_mesh.vectors[face][:,2].min(),stl_mesh.vectors[face][:,2].max()])
inter = (z_lim[0]-layers)*(z_lim[1]-layers) < 0
if np.any(np.all(v1==0) or np.all(v2==0) or np.all(v3==0) or np.all(inter)):
Bad_Faces = np.append(Bad_Faces,face) # for debugging
# just compute random task
else:
# code used to find slice lines
t = np.zeros([3]) # initilaize line parameter
## solve for all z intercepts
idx = np.where((layers>z_lim[0]) & (layers<z_lim[1]))[0]
# solve line intercept parameter value
t = np.zeros([3,len(idx)])
t[0,:] = np.transpose((layers[idx]-stl_mesh.vectors[face][0,2])/(stl_mesh.vectors[face][1,2]-stl_mesh.vectors[face][0,2]))
t[1,:] = np.transpose((layers[idx]-stl_mesh.vectors[face][1,2])/(stl_mesh.vectors[face][2,2]-stl_mesh.vectors[face][1,2]))
t[2,:] = np.transpose((layers[idx]-stl_mesh.vectors[face][2,2])/(stl_mesh.vectors[face][0,2]-stl_mesh.vectors[face][2,2]))
II0 = np.array((stl_mesh.vectors[face][1,:]-stl_mesh.vectors[face][0,:]).reshape(-1,1)*t[0,:] + stl_mesh.vectors[face][0,:].reshape(-1,1))
II1 = np.array((stl_mesh.vectors[face][2,:]-stl_mesh.vectors[face][1,:]).reshape(-1,1)*t[1,:] + stl_mesh.vectors[face][1,:].reshape(-1,1))
II2 = np.array((stl_mesh.vectors[face][0,:]-stl_mesh.vectors[face][2,:]).reshape(-1,1)*t[2,:] + stl_mesh.vectors[face][2,:].reshape(-1,1))
# remove points outside of bounds
idx0 = ((II0[0,:]<stl_mesh.vectors[face][[0,1],0].min()) + (II0[0,:]>stl_mesh.vectors[face][[0,1],0].max())
+ (II0[1,:]<stl_mesh.vectors[face][[0,1],1].min()) + (II0[1,:]>stl_mesh.vectors[face][[0,1],1].max())
+ (II0[2,:]<stl_mesh.vectors[face][[0,1],2].min()) + (II0[2,:]>stl_mesh.vectors[face][[0,1],2].max()))
idx1 = ((II1[0,:]<stl_mesh.vectors[face][[1,2],0].min()) + (II1[0,:]>stl_mesh.vectors[face][[1,2],0].max())
+ (II1[1,:]<stl_mesh.vectors[face][[1,2],1].min()) + (II1[1,:]>stl_mesh.vectors[face][[1,2],1].max())
+ (II1[2,:]<stl_mesh.vectors[face][[1,2],2].min()) + (II1[2,:]>stl_mesh.vectors[face][[1,2],2].max()))
idx2 = ((II2[0,:]<stl_mesh.vectors[face][[0,2],0].min()) + (II2[0,:]>stl_mesh.vectors[face][[0,2],0].max())
+ (II2[1,:]<stl_mesh.vectors[face][[0,2],1].min()) + (II2[1,:]>stl_mesh.vectors[face][[0,2],1].max())
+ (II2[2,:]<stl_mesh.vectors[face][[0,2],2].min()) + (II2[2,:]>stl_mesh.vectors[face][[0,2],2].max()))
# save points for every intercept for every z level...
II0[:,idx0] = 0
II1[:,idx1] = 0
II2[:,idx2] = 0
# combine points into pairs of points that can be stored easily
# find the ONE line that has all points within bonds. This is the base line
# the secondary points are the sum of the other two points becuase index above
# sets outof bounds points to zero
if(sum(idx0)==0):
P1 = II0
P2 = II1 + II2
elif(sum(idx1)==0):
P1 = II1
P2 = II0 + II2
else:
P1 = II2
P2 = II0 + II1
Set_1 = np.append(Set_1,P1,axis=1)
Set_2 = np.append(Set_2,P2,axis=1)
print("Num of Bad Faces: ",len(Bad_Faces)," Total Num of Faces: ",len(stl_mesh.vectors[:]))
return Set_1, Set_2
# run slicer
z = np.linspace(np.min(part_mesh.z),np.max(part_mesh.z),46) # z slices
p1, p2 = STL_Slicer(part_mesh,z)
# Generate Rays that can penetrate slice
def Generate_Rays(Theta,Spacing,Num):
# iterction math: https://www.cuemath.com/geometry/intersection-of-two-lines/
Rays = np.zeros([3,Num]) # empty matrix with a,b and c values ax+by+c=0
if (Theta == 0): #horizontal lines
print("horizontal")
Rays[0,:] = 0
Rays[1,:] = 1
Rays[2,:] = np.arange(0, Spacing*Num,Spacing) - Num*Spacing/2 + Spacing/2
elif (Theta == np.pi/2): # vertical lines
print("Vertical")
Rays[0,:] = 1
Rays[1,:] = 0
Rays[2,:] = np.arange(0, Spacing*Num,Spacing) - Num*Spacing/2 + Spacing/2
else:
print("angle")
Rays[0,:] = -np.tan(Theta)
Rays[1,:] = 1
Rays[2,:] = (np.arange(0, Spacing*Num,Spacing) - Num*Spacing/2 + Spacing/2)/np.abs(np.cos(Theta))
return Rays
# plot Rays with a limiting box
def Plot_Rays(Rays,X_lim,Y_lim,color='y'):
# takes ray parameters, x limit, and
# y limit and plots the lines
Y = np.zeros([2,len(Rays[0,:])])
X = np.zeros([2,len(Rays[0,:])])
M = -Rays[0,:]/Rays[1,:] # slope of lines
idx_vert = (M >= 1) | (M < -1) # rays between 45-135 deg
idx_line = idx_vert == 0 # all other rays
# generate lines
Y[0,idx_vert] += Y_lim[0]
Y[1,idx_vert] += Y_lim[1]
X[0,idx_vert] = -(Rays[1,idx_vert]*Y[0,idx_vert]+Rays[2,idx_vert])/Rays[0,idx_vert]
X[1,idx_vert] = -(Rays[1,idx_vert]*Y[1,idx_vert]+Rays[2,idx_vert])/Rays[0,idx_vert]
# generate lines
X[0,idx_line] += X_lim[0]
X[1,idx_line] += X_lim[1]
Y[0,idx_line] = -(Rays[0,idx_line]*X[0,idx_line]+Rays[2,idx_line])/Rays[1,idx_line]
Y[1,idx_line] = -(Rays[0,idx_line]*X[1,idx_line]+Rays[2,idx_line])/Rays[1,idx_line]
# plot lines
plt.plot(X,Y,color)
plt.xlim(X_lim[0]*1.05,X_lim[1]*1.05)
plt.ylim(Y_lim[0]*1.05,Y_lim[1]*1.05)
return X,Y
rays = Generate_Rays(0*np.pi/180,1.5,10)
# find intercetion points between rays and slice
# Generate Lines from 2 sets of points
def Generator_Lines(P1,P2):
# takes to points P = [[x],[y]]
# returns vector of a,b,c for line
# ax+by+c=0
A =-(P2[1] - P1[1])
B = P2[0] - P1[0]
C = -P1[0]*A - P1[1]*B
return np.array([A,B,C])
def Line_Intersection(Line1,Line2):
# takes P = [[a],[b],[c]] where ax+by+C=0
# returns points of intersection [x,y]
# for all possible line combose
X = (np.outer(Line1[1],Line2[2])-np.outer(Line1[2],Line2[1]))/(np.outer(Line1[0],Line2[1])-np.outer(Line1[1],Line2[0]))
Y = (np.outer(Line1[2],Line2[0])-np.outer(Line1[0],Line2[2]))/(np.outer(Line1[0],Line2[1])-np.outer(Line1[1],Line2[0]))
return X,Y
# Function used to plot layer of point
def Plot_Slice(P1,P2,color='b',width=None):
X1 = P1[0]
X2 = P2[0]
Y1 = P1[1]
Y2 = P2[1]
plt.plot([X1,X2],[Y1,Y2],color,linewidth=width)
# select layer 100 and plot points
i = p1[2,:] ==z[8]
p1_100 = p1[0:2,i].copy()
p2_100 = p2[0:2,i].copy()
plt.close()
Plot_Slice(p1_100,p2_100)
plt.xlim([np.min(part_mesh.x),np.max(part_mesh.x)])
plt.ylim([np.min(part_mesh.y),np.max(part_mesh.y)])
plt.show()
# filter out data points that dont lie inbtween p1 p2
def In_Bound_Points(X_in, Y_in, P1, P2):
# takes points of intersection of lines and
# points of lines. replaces all points not
# inbetween P1, P2 returns x,y
X = X_in.copy()
Y = Y_in.copy()
X_max = np.max([P1[0],P2[0]],axis=0)
X_min = np.min([P1[0],P2[0]],axis=0)
Y_max = np.max([P1[1],P2[1]],axis=0)
Y_min = np.min([P1[1],P2[1]],axis=0)
tol = 1e-7
idx = ((X<X_min-tol) | (X>X_max+tol)) | ((Y<Y_min-tol) | (Y>Y_max+tol))
X[idx] = np.NaN
Y[idx] = np.NaN
return X,Y
lines = Generator_Lines(p1_100,p2_100) # generate lines from slice 100
rays = Generate_Rays(0*np.pi/180,0.25,100) # Generate rays
xp,yp = Line_Intersection(rays,lines) # Calculate intersection matriz reutrn x y points
xpf,ypf = In_Bound_Points(xp,yp,p1_100,p2_100) # filter out points that dont lie inbtween points
# check number of parts of perercing points
idx = np.sum(~np.isnan(xpf),axis=1)
idx = (idx % 2) != 0
# WHAT THE FUCK IS GOING ON????
#print("boundary with problem")
#print(p1_100[:,878],p2_100[:,878])
#print("line with problem")
#i = (xp[:,idx]>-5.62) & (xp[:,idx]<-5.61)
#print(xp[i,idx],yp[i,idx])
# plot results
# fit around outline
plt.close()
Plot_Slice(p1_100,p2_100)
x_lim = np.array([np.min(p1_100[0,:]),np.max(p1_100[0,:])])*1.05
y_lim = np.array([np.min(p1_100[1,:]),np.max(p1_100[1,:])])*1.05
Plot_Rays(rays,x_lim,y_lim)
Plot_Rays(rays[:,idx],x_lim,y_lim,'r')
plt.plot(xpf,ypf,'.g')
#plt.plot(xp,yp,'.')
#idx = 878 # slice(878,879)
#Plot_Slice(p1_100[:,idx],p2_100[:,idx],'r')
plt.xlim([np.min(part_mesh.x),np.max(part_mesh.x)])
plt.ylim([np.min(part_mesh.y),np.max(part_mesh.y)])
plt.show()
```
|
github_jupyter
|
>This notebook is part of our [Introduction to Machine Learning](http://www.codeheroku.com/course?course_id=1) course at [Code Heroku](http://www.codeheroku.com/).
Hey folks, today we are going to discuss about the application of gradient descent algorithm for solving machine learning problems. Let’s take a brief overview about the the things that we are going to discuss in this article:
- What is gradient descent?
- How gradient descent algorithm can help us solving machine learning problems
- The math behind gradient descent algorithm
- Implementation of gradient descent algorithm in Python
So, without wasting any time, let’s begin :)
# What is gradient descent?
Here’s what Wikipedia says: “Gradient descent is a first-order iterative optimization algorithm for finding the minimum of a function.”
Now, you might be thinking “Wait, what does that mean? What do you want to say?”
Don’t worry, we will elaborate everything about gradient descent in this article and all of it will start making sense to you in a moment :)
To understand gradient descent algorithm, let us first understand a real life machine learning problem:
Suppose you have a dataset where you are provided with the number of hours a student studies per day and the percentage of marks scored by the corresponding student. If you plot a 2D graph of this dataset, it will look something like this:
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_1.png">
Now, if someone approaches you and says that a new student has taken admission and you need to predict the score of that student based on the number of hours he studies. How would you do that?
To predict the score of the new student, at first you need to find out a relationship between “Hours studied” and “Score” from the existing dataset. By taking a look over the visual graph plotting, we can see that a linear relationship can be established between these two things. So, by drawing a straight line over the data points in the graph, we can establish the relationship. Let’s see how would it look if we try to draw a straight line over the data points. It would look something like this:
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_2.png">
Great! Now we have the relationship between “Hours Studied” and “Score”. So, now if someone asks us to predict the score of a student who studies 10 hours per day, we can just simply put Hours Studied = 10 data point over the relationship line and predict the value of his score like this:
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_3.png">
From the above picture, we can easily say that the new student who studies 10 hours per day would probably score around 60. Pretty easy, right? By the way, the relationship line that we have drawn is called the “regression” line. And because the relationship we have established is a linear relationship, the line is actually called “linear regression” line. Hence, this machine learning model that we have created is known as linear regression model.
At this point, you might have noticed that all the data points do not lie perfectly over the regression line. So, there might be some difference between the predicted value and the actual value. We call this difference as error(or cost).
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_err.png">
In machine learning world, we always try to build a model with as minimum error as possible. To achieve this, we have to calculate the error of our model in order to best fit the regression line over it. We have different kinds of error like- total error, mean error, mean squared error etc.
Total error: Summation of the absolute difference between predicted and actual value for all the data points. Mathematically, this is
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_4.png">
Mean error: Total error / number of data points. Mathematically, this is
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_5.png">
Mean squared error: Summation of the square of absolute difference / number of data points. Mathematically, this is
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_6.png">
Below is an example of calculating these errors:
<img src="http://www.codeheroku.com/static/blog/images/error_calc.png">
We will use the Mean Squared Error(M.S.E) to calculate the error and determine the best linear regression line(the line with the minimum error value) for our model.
Now the question is, how would you represent a regression line in a computer?
The answer is simple. Remember the equation of a straight line? We can use the same equation in order to represent the regression line in computer. If you can’t recall it, let me quickly remind you, it’s **y = M * x + B**
<img src="http://www.codeheroku.com/static/blog/images/line_repr.png">
Here, M is the slope of the line and B is the Y intercept. Let’s quickly recall about slope and Y intercept.
Slope is the amount by which the line is rising on the Y axis for every block that you go towards right in the X axis. This tells us the direction of the line and the rate by which our line is increasing. Mathematically speaking, this means  for a specified amount of distance on the line.
From the dotted lines in the above picture, we can see that for every 2 blocks in the X axis, the line rises by 1 block in the Y axis.<br>
Hence, slope, M = ½ = 0.5<br>
And it’s a positive value, which indicates that the line is increasing in the upward direction.
Now, let’s come to Y intercept. It is the distance which tells us exactly where the line cuts the Y axis. From the above picture, we can see that the line is cutting Y axis on point (0,1). So, the Y intercept(B) in this case is the distance between (0,0) and (0,1) = 1.
Hence, the straight line on the above picture can be represented through the following equation:
y = 0.5 * x + 1
Now we know how to represent the regression line in a computer. Everything seems good so far. But, the biggest question still remains unanswered- “How would the computer know the right value of M and B for drawing the regression line with the minimum error?”
Exactly that’s why we need the gradient descent algorithm. Gradient descent is a trial and error method, which will iteratively give us different values of M and B to try. In each iteration, we will draw a regression line using these values of M and B and will calculate the error for this model. We will continue until we get the values of M and B such that the error is minimum.
Let’s have a more elaborative view of gradient descent algorithm:
Step 1: Start with random values of M and B
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_s1.png">
Step 2: Adjust M and B such that error reduces
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_s2.png">
Step 3: Repeat until we get the best values of M and B (until convergence)
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_s3.png">
By the way, the application of gradient descent is not limited to regression problems only. It is an optimization algorithm which can be applied to any problem in general.
# The math behind gradient descent
Till now we have understood that we will use gradient descent to minimize the error for our model. But, now let us see exactly how gradient descent finds the best values of M and B for us.
Gradient descent tries to minimize the error. Right?
So, we can say that it tries to minimize the following function(cost function):
<img src="http://www.codeheroku.com/static/blog/images/gd_err_fnc.png">
At first we will take random values of M and B. So, we will get a random error corresponding to these values. Thus, a random point will be plotted on the above graph. At this point, there will be some error. So, our objective will be to reduce this error.
In general, how would you approach towards the minimum value of a function? By finding its derivative. Right? The same thing applies here.
We will obtain the partial derivative of J with respect to M and B. This will give us the direction of the slope of tangent at the given point. We would like to move in the opposite direction of the slope in order to approach towards the minimum value.
<img src="http://www.codeheroku.com/static/blog/images/gd_db_dm_calc.png">
So far, we have only got the direction of the slope and we know we need to move in its opposite direction. But, in each iteration, by how much amount we should move in the opposite direction? This amount is called the learning rate(alpha). Learning rate determines the step size of our movement towards the minimal point.
So, choosing the right learning rate is very important. If the learning rate is too small, it will take more time to converge. On the other hand, if the learning rate is very high, it may overshoot the minimum point and diverge.
<img src="http://www.codeheroku.com/static/blog/images/gd_ch_alpha.png">
To sum up, what we have till now is-
1. A random point is chosen initially by choosing random values of M and B.
2. Direction of the slope of that point is found by finding delta_m and delta_b
3. Since we want to move in the opposite direction of the slope, we will multiply -1 with both delta_m and delta_b.
4. Since delta_m and delta_b gives us only the direction, we need to multiply both of them with the learning rate(alpha) to specify the step size of each iteration.
5. Next, we need to modify the current values of M and B such that the error is reduced.
<img src="http://www.codeheroku.com/static/blog/images/gd_9.png">
6. We need to repeat steps 2 to 5 until we converge at the minimum point.
# Implementation of gradient descent using Python
This was everything about gradient descent algorithm. Now we will implement this algorithm using Python.
Let us first import all required libraries and read the dataset using Pandas library(the csv file can be downloaded from this [link](https://github.com/codeheroku/Introduction-to-Machine-Learning/tree/master/gradient%20descent/starter%20code)):
```
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv("student_scores.csv") #Read csv file using Pandas library
```
Next, we need to read the values of X and Y from the dataframe and create a scatter plot of that data.
```
X = df["Hours"] #Read values of X from dataframe
Y = df["Scores"] #Read values of Y from dataframe
plt.plot(X,Y,'o') # 'o' for creating scatter plot
plt.title("Implementing Gradient Descent")
plt.xlabel("Hours Studied")
plt.ylabel("Student Score")
```
After that, we will initially choose m = 0 and b = 0
```
m = 0
b = 0
```
Now, we need to create a function(gradient descent function) which will take the current value of m and b and then give us better values of m and b.
```
def grad_desc(X,Y,m,b):
for point in zip(X,Y):
x = point[0] #value of x of a point
y_actual = point[1] #Actual value of y for that point
y_prediction = m*x + b #Predicted value of y for given x
error = y_prediction - y_actual #Error in the estimation
#Using alpha = 0.0005
delta_m = -1 * (error*x) * 0.0005 #Calculating delta m
delta_b = -1 * (error) * 0.0005 #Calculating delta b
m = m + delta_m #Modifying value of m for reducing error
b = b + delta_b #Modifying value of b for reducing error
return m,b #Returning better values of m and b
```
Notice, in the above code, we are using learning rate(alpha) = 0.0005 . You can try to modify this value and try this example with different learning rates.
Now we will make a function which will help us to plot the regression line on the graph.
```
def plot_regression_line(X,m,b):
regression_x = X.values #list of values of x
regression_y = [] #list of values of y
for x in regression_x:
y = m*x + b #calculating the y_prediction
regression_y.append(y) #adding the predicted value in list of y
plt.plot(regression_x,regression_y) #plot the regression line
plt.pause(1) #pause for 1 second before plotting next line
```
Now, when we will run the grad_desc() function, each time we will get a better result for regression line. Let us create a loop and run the grad_desc() function for 10 times and visualize the results.
```
for i in range(0,10):
m,b = grad_desc(X,Y,m,b) #call grad_desc() to get better m & b
plot_regression_line(X,m,b) #plot regression line with m & b
```
Finally, we need to show the plot by adding the following statement:
```
plt.show()
```
So, the full code for our program is:
```
import pandas as pd
import matplotlib.pyplot as plt
# function for plotting regression line
def plot_regression_line(X,m,b):
regression_x = X.values
regression_y = []
for x in regression_x:
y = m*x + b
regression_y.append(y)
plt.plot(regression_x,regression_y)
plt.pause(1)
df = pd.read_csv("student_scores.csv")
X = df["Hours"]
Y = df["Scores"]
plt.plot(X,Y,'o')
plt.title("Implementing Gradient Descent")
plt.xlabel("Hours Studied")
plt.ylabel("Student Score")
m = 0
b = 0
# gradient descent function
def grad_desc(X,Y,m,b):
for point in zip(X,Y):
x = point[0]
y_actual = point[1]
y_prediction = m*x + b
error = y_prediction - y_actual
delta_m = -1 * (error*x) * 0.0005
delta_b = -1 * (error) * 0.0005
m = m + delta_m
b = b + delta_b
return m,b
for i in range(0,10):
m,b = grad_desc(X,Y,m,b)
plot_regression_line(X,m,b)
plt.show()
```
Now let’s run the above program for different values of learning rate(alpha).
For alpha = 0.0005 , the output will look like this:
<img src="http://www.codeheroku.com/static/blog/images/gd_alpha_1.gif">
For alpha = 0.05 , it will look like this:
<img src="http://www.codeheroku.com/static/blog/images/gd_alpha_2.gif">
For alpha = 1, it will overshoot the minimum point and diverge like this:
<img src="http://www.codeheroku.com/static/blog/images/gd_alpha_3.gif">
The gradient descent algorithm about which we discussed in this article is called stochastic gradient descent. There are also other types of gradient descent algorithms like- batch gradient descent, mini batch gradient descent etc.
>If this article was helpful to you, check out our [Introduction to Machine Learning](http://www.codeheroku.com/course?course_id=1) Course at [Code Heroku](http://www.codeheroku.com/) for a complete guide to Machine Learning.
|
github_jupyter
|
```
import csv
import itertools
import operator
import numpy as np
import nltk
import sys
from datetime import datetime
from utils import *
import matplotlib.pyplot as plt
%matplotlib inline
vocabulary_size = 200
sentence_start_token = "START"
sentence_end_token = "END"
f = open('data/ratings_train.txt', 'r')
lines = f.readlines()
for i in range(len(lines)):
lines[i] = lines[i].replace("/n","").replace("\n","")
reader = []
for line in lines:
line_document = line.split("\t")[1]
reader.append(line_document)
f.close()
sentences = ["%s %s %s" % (sentence_start_token, x, sentence_end_token) for x in reader[:1000]]
from konlpy.tag import Twitter
pos_tagger = Twitter()
def tokenize(doc):
return ['/'.join(t) for t in pos_tagger.pos(doc, norm=True, stem=True)]
tokenized_sentences = [tokenize(row) for row in sentences]
vocab = [t for d in tokenized_sentences for t in d]
Verb_Noun_Adjective_Alpha_in_text = []
index = 0
for text in tokenized_sentences:
Verb_Noun_Adjective_Alpha_in_text.append([])
for word in text:
parts_of_speech = word.split("/")
if parts_of_speech[1] in ["Noun","Verb","Adjective"] :
Verb_Noun_Adjective_Alpha_in_text[index].append(word.split("/")[0])
elif parts_of_speech[1] in ["Alpha"] and len(parts_of_speech[0]) ==3 or len(parts_of_speech[0]) ==5:
Verb_Noun_Adjective_Alpha_in_text[index].append(word.split("/")[0])
index += 1
Verb_Noun_Adjective_Alpha_in_text_tokens = [t for d in Verb_Noun_Adjective_Alpha_in_text for t in d]
import nltk
real_tokens = nltk.Text(Verb_Noun_Adjective_Alpha_in_text_tokens, name='RNN')
real_tokens_freq = real_tokens.vocab().most_common(vocabulary_size-1)
index_to_word = [x[0] for x in real_tokens_freq]
index_to_word.append("unknown")
word_to_index = dict([(w,i) for i,w in enumerate(index_to_word)])
for i, sent in enumerate(Verb_Noun_Adjective_Alpha_in_text):
tokenized_sentences[i] = [w if w in word_to_index else "unknown" for w in sent]
```
# Make model
```
X_train = np.asarray([[word_to_index[w] for w in sent[:-1]] for sent in tokenized_sentences])
y_train = np.asarray([[word_to_index[w] for w in sent[1:]] for sent in tokenized_sentences])
X_train[0]
class RNNNumpy:
def __init__(self, word_dim, hidden_dim=100, bptt_truncate=4):
self.word_dim = word_dim
self.hidden_dim = hidden_dim
self.bptt_truncate = bptt_truncate
self.U = np.random.uniform(-np.sqrt(1./word_dim), np.sqrt(1./word_dim), (hidden_dim, word_dim))
self.V = np.random.uniform(-np.sqrt(1./hidden_dim), np.sqrt(1./hidden_dim), (word_dim, hidden_dim))
self.W = np.random.uniform(-np.sqrt(1./hidden_dim), np.sqrt(1./hidden_dim), (hidden_dim, hidden_dim))
def forward_propagation(self, x):
T = len(x)
s = np.zeros((T + 1, self.hidden_dim))
s[-1] = np.zeros(self.hidden_dim)
o = np.zeros((T, self.word_dim))
for t in np.arange(T):
s[t] = np.tanh(self.U[:,x[t]] + self.W.dot(s[t-1]))
o[t] = softmax(self.V.dot(s[t]))
return [o, s]
RNNNumpy.forward_propagation = forward_propagation
def predict(self, x):
o, s = self.forward_propagation(x)
return np.argmax(o, axis=1)
RNNNumpy.predict = predict
tokenized_sentences[0]
np.random.seed(100)
model = RNNNumpy(vocabulary_size)
#for i in range(100):
o, s = model.forward_propagation(X_train[0])
print (o.shape)
print (s.shape)
X_train[0]
y_train[0]
predictions = model.predict(X_train[0])
print (predictions.shape)
print (predictions)
def calculate_total_loss(self, x, y):
L = 0
for i in np.arange(len(y)):
o, s = self.forward_propagation(x[i])
correct_word_predictions = o[np.arange(len(y[i])), y[i]]
L += -1 * np.sum(np.log(correct_word_predictions))
return L
def calculate_loss(self, x, y):
N = np.sum((len(y_i) for y_i in y))
return self.calculate_total_loss(x,y)/N
RNNNumpy.calculate_total_loss = calculate_total_loss
RNNNumpy.calculate_loss = calculate_loss
# Limit to 1000 examples to save time
print ("Expected Loss for random predictions: %f" % np.log(vocabulary_size))
print ("Actual loss: %f" % model.calculate_loss(X_train[:1000], y_train[:1000]))
def bptt(self, x, y):
T = len(y)
# Perform forward propagation
o, s = self.forward_propagation(x)
# We accumulate the gradients in these variables
dLdU = np.zeros(self.U.shape)
dLdV = np.zeros(self.V.shape)
dLdW = np.zeros(self.W.shape)
delta_o = o
delta_o[np.arange(len(y)), y] -= 1.
# For each output backwards...
for t in np.arange(T)[::-1]:
dLdV += np.outer(delta_o[t], s[t].T)
# Initial delta calculation
delta_t = self.V.T.dot(delta_o[t]) * (1 - (s[t] ** 2))
# Backpropagation through time (for at most self.bptt_truncate steps)
for bptt_step in np.arange(max(0, t-self.bptt_truncate), t+1)[::-1]:
# print "Backpropagation step t=%d bptt step=%d " % (t, bptt_step)
dLdW += np.outer(delta_t, s[bptt_step-1])
dLdU[:,x[bptt_step]] += delta_t
# Update delta for next step
delta_t = self.W.T.dot(delta_t) * (1 - s[bptt_step-1] ** 2)
return [dLdU, dLdV, dLdW]
RNNNumpy.bptt = bptt
def numpy_sdg_step(self, x, y, learning_rate):
dLdU, dLdV, dLdW = self.bptt(x, y)
self.U -= learning_rate * dLdU
self.V -= learning_rate * dLdV
self.W -= learning_rate * dLdW
RNNNumpy.sgd_step = numpy_sdg_step
def train_with_sgd(model, X_train, y_train, learning_rate=0.005, nepoch=100, evaluate_loss_after=5):
losses = []
num_examples_seen = 0
for epoch in range(nepoch):
if (epoch % evaluate_loss_after == 0):
loss = model.calculate_loss(X_train, y_train)
losses.append((num_examples_seen, loss))
time = datetime.now().strftime('%Y-%m-%d %H:%M:%S')
print ("%s: Loss after num_examples_seen=%d epoch=%d: %f" % (time, num_examples_seen, epoch, loss))
for i in range(len(y_train)):
model.sgd_step(X_train[i], y_train[i], learning_rate)
num_examples_seen += 1
print(model)
np.random.seed(10)
model = RNNNumpy(vocabulary_size)
%timeit model.sgd_step(X_train[10], y_train[10], 0.005)
np.random.seed(10)
model = RNNNumpy(vocabulary_size)
losses = train_with_sgd(model, X_train[:100], y_train[:100], nepoch=10, evaluate_loss_after=1)
from rnn_theano import RNNTheano, gradient_check_theano
from utils import load_model_parameters_theano, save_model_parameters_theano
model = RNNTheano(vocabulary_size, hidden_dim=100)
train_with_sgd(model, X_train, y_train, nepoch=50)
save_model_parameters_theano('./data/trained-model-sion_consider.npz', model)
load_model_parameters_theano('./data/trained-model-sion_consider.npz', model)
print(len(model.V.get_value()))
def generate_sentence(model):
new_sentence = [word_to_index[sentence_start_token]]
while not new_sentence[-1] == word_to_index[sentence_end_token]:
next_word_probs = model.forward_propagation(new_sentence)
sampled_word = word_to_index["unknown"]
while sampled_word == word_to_index["unknown"]:
samples = np.random.multinomial(1, next_word_probs[-1])
sampled_word = np.argmax(samples)
new_sentence.append(sampled_word)
sentence_str = [index_to_word[x] for x in new_sentence[1:-1]]
return sentence_str
num_sentences = 2
senten_min_length = 5
for i in range(num_sentences):
sent = []
while len(sent) < senten_min_length:
sent = generate_sentence(model)
print (" ".join(sent))
```
|
github_jupyter
|
**Chapter 10 – Introduction to Artificial Neural Networks with Keras**
_This notebook contains all the sample code and solutions to the exercises in chapter 10._
# Setup
First, let's import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures. We also check that Python 3.5 or later is installed (although Python 2.x may work, it is deprecated so we strongly recommend you use Python 3 instead), as well as Scikit-Learn ≥0.20 and TensorFlow ≥2.0-preview.
```
# Python ≥3.5 is required
import sys
assert sys.version_info >= (3, 5)
# Scikit-Learn ≥0.20 is required
import sklearn
assert sklearn.__version__ >= "0.20"
# TensorFlow ≥2.0-preview is required
import tensorflow as tf
assert tf.__version__ >= "2.0"
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "ann"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
# Ignore useless warnings (see SciPy issue #5998)
import warnings
warnings.filterwarnings(action="ignore", message="^internal gelsd")
```
# Perceptrons
**Note**: we set `max_iter` and `tol` explicitly to avoid warnings about the fact that their default value will change in future versions of Scikit-Learn.
```
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron
iris = load_iris()
X = iris.data[:, (2, 3)] # petal length, petal width
y = (iris.target == 0).astype(np.int)
per_clf = Perceptron(max_iter=1000, tol=1e-3, random_state=42)
per_clf.fit(X, y)
y_pred = per_clf.predict([[2, 0.5]])
y_pred
a = -per_clf.coef_[0][0] / per_clf.coef_[0][1]
b = -per_clf.intercept_ / per_clf.coef_[0][1]
axes = [0, 5, 0, 2]
x0, x1 = np.meshgrid(
np.linspace(axes[0], axes[1], 500).reshape(-1, 1),
np.linspace(axes[2], axes[3], 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = per_clf.predict(X_new)
zz = y_predict.reshape(x0.shape)
plt.figure(figsize=(10, 4))
plt.plot(X[y==0, 0], X[y==0, 1], "bs", label="Not Iris-Setosa")
plt.plot(X[y==1, 0], X[y==1, 1], "yo", label="Iris-Setosa")
plt.plot([axes[0], axes[1]], [a * axes[0] + b, a * axes[1] + b], "k-", linewidth=3)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#9898ff', '#fafab0'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="lower right", fontsize=14)
plt.axis(axes)
save_fig("perceptron_iris_plot")
plt.show()
```
# Activation functions
```
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def relu(z):
return np.maximum(0, z)
def derivative(f, z, eps=0.000001):
return (f(z + eps) - f(z - eps))/(2 * eps)
z = np.linspace(-5, 5, 200)
plt.figure(figsize=(11,4))
plt.subplot(121)
plt.plot(z, np.sign(z), "r-", linewidth=1, label="Step")
plt.plot(z, sigmoid(z), "g--", linewidth=2, label="Sigmoid")
plt.plot(z, np.tanh(z), "b-", linewidth=2, label="Tanh")
plt.plot(z, relu(z), "m-.", linewidth=2, label="ReLU")
plt.grid(True)
plt.legend(loc="center right", fontsize=14)
plt.title("Activation functions", fontsize=14)
plt.axis([-5, 5, -1.2, 1.2])
plt.subplot(122)
plt.plot(z, derivative(np.sign, z), "r-", linewidth=1, label="Step")
plt.plot(0, 0, "ro", markersize=5)
plt.plot(0, 0, "rx", markersize=10)
plt.plot(z, derivative(sigmoid, z), "g--", linewidth=2, label="Sigmoid")
plt.plot(z, derivative(np.tanh, z), "b-", linewidth=2, label="Tanh")
plt.plot(z, derivative(relu, z), "m-.", linewidth=2, label="ReLU")
plt.grid(True)
#plt.legend(loc="center right", fontsize=14)
plt.title("Derivatives", fontsize=14)
plt.axis([-5, 5, -0.2, 1.2])
save_fig("activation_functions_plot")
plt.show()
def heaviside(z):
return (z >= 0).astype(z.dtype)
def mlp_xor(x1, x2, activation=heaviside):
return activation(-activation(x1 + x2 - 1.5) + activation(x1 + x2 - 0.5) - 0.5)
x1s = np.linspace(-0.2, 1.2, 100)
x2s = np.linspace(-0.2, 1.2, 100)
x1, x2 = np.meshgrid(x1s, x2s)
z1 = mlp_xor(x1, x2, activation=heaviside)
z2 = mlp_xor(x1, x2, activation=sigmoid)
plt.figure(figsize=(10,4))
plt.subplot(121)
plt.contourf(x1, x2, z1)
plt.plot([0, 1], [0, 1], "gs", markersize=20)
plt.plot([0, 1], [1, 0], "y^", markersize=20)
plt.title("Activation function: heaviside", fontsize=14)
plt.grid(True)
plt.subplot(122)
plt.contourf(x1, x2, z2)
plt.plot([0, 1], [0, 1], "gs", markersize=20)
plt.plot([0, 1], [1, 0], "y^", markersize=20)
plt.title("Activation function: sigmoid", fontsize=14)
plt.grid(True)
```
# Building an Image Classifier
First let's import TensorFlow and Keras.
```
import tensorflow as tf
from tensorflow import keras
tf.__version__
keras.__version__
```
Let's start by loading the fashion MNIST dataset. Keras has a number of functions to load popular datasets in `keras.datasets`. The dataset is already split for you between a training set and a test set, but it can be useful to split the training set further to have a validation set:
```
fashion_mnist = keras.datasets.fashion_mnist
(X_train_full, y_train_full), (X_test, y_test) = fashion_mnist.load_data()
```
The training set contains 60,000 grayscale images, each 28x28 pixels:
```
X_train_full.shape
```
Each pixel intensity is represented as a byte (0 to 255):
```
X_train_full.dtype
```
Let's split the full training set into a validation set and a (smaller) training set. We also scale the pixel intensities down to the 0-1 range and convert them to floats, by dividing by 255.
```
X_valid, X_train = X_train_full[:5000] / 255., X_train_full[5000:] / 255.
y_valid, y_train = y_train_full[:5000], y_train_full[5000:]
X_test = X_test / 255.
```
You can plot an image using Matplotlib's `imshow()` function, with a `'binary'`
color map:
```
plt.imshow(X_train[0], cmap="binary")
plt.axis('off')
plt.show()
```
The labels are the class IDs (represented as uint8), from 0 to 9:
```
y_train
```
Here are the corresponding class names:
```
class_names = ["T-shirt/top", "Trouser", "Pullover", "Dress", "Coat",
"Sandal", "Shirt", "Sneaker", "Bag", "Ankle boot"]
```
So the first image in the training set is a coat:
```
class_names[y_train[0]]
```
The validation set contains 5,000 images, and the test set contains 10,000 images:
```
X_valid.shape
X_test.shape
```
Let's take a look at a sample of the images in the dataset:
```
n_rows = 4
n_cols = 10
plt.figure(figsize=(n_cols * 1.2, n_rows * 1.2))
for row in range(n_rows):
for col in range(n_cols):
index = n_cols * row + col
plt.subplot(n_rows, n_cols, index + 1)
plt.imshow(X_train[index], cmap="binary", interpolation="nearest")
plt.axis('off')
plt.title(class_names[y_train[index]], fontsize=12)
plt.subplots_adjust(wspace=0.2, hspace=0.5)
save_fig('fashion_mnist_plot', tight_layout=False)
plt.show()
model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28, 28]))
model.add(keras.layers.Dense(300, activation="relu"))
model.add(keras.layers.Dense(100, activation="relu"))
model.add(keras.layers.Dense(10, activation="softmax"))
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="relu"),
keras.layers.Dense(100, activation="relu"),
keras.layers.Dense(10, activation="softmax")
])
model.layers
model.summary()
keras.utils.plot_model(model, "my_mnist_model.png", show_shapes=True)
hidden1 = model.layers[1]
hidden1.name
model.get_layer(hidden1.name) is hidden1
weights, biases = hidden1.get_weights()
weights
weights.shape
biases
biases.shape
model.compile(loss="sparse_categorical_crossentropy",
optimizer="sgd",
metrics=["accuracy"])
```
This is equivalent to:
```python
model.compile(loss=keras.losses.sparse_categorical_crossentropy,
optimizer=keras.optimizers.SGD(),
metrics=[keras.metrics.sparse_categorical_accuracy])
```
```
history = model.fit(X_train, y_train, epochs=30,
validation_data=(X_valid, y_valid))
history.params
print(history.epoch)
history.history.keys()
import pandas as pd
pd.DataFrame(history.history).plot(figsize=(8, 5))
plt.grid(True)
plt.gca().set_ylim(0, 1)
save_fig("keras_learning_curves_plot")
plt.show()
model.evaluate(X_test, y_test)
X_new = X_test[:3]
y_proba = model.predict(X_new)
y_proba.round(2)
y_pred = model.predict_classes(X_new)
y_pred
np.array(class_names)[y_pred]
y_new = y_test[:3]
y_new
```
# Regression MLP
Let's load, split and scale the California housing dataset (the original one, not the modified one as in chapter 2):
```
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
housing = fetch_california_housing()
X_train_full, X_test, y_train_full, y_test = train_test_split(housing.data, housing.target, random_state=42)
X_train, X_valid, y_train, y_valid = train_test_split(X_train_full, y_train_full, random_state=42)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_valid = scaler.transform(X_valid)
X_test = scaler.transform(X_test)
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu", input_shape=X_train.shape[1:]),
keras.layers.Dense(1)
])
model.compile(loss="mean_squared_error", optimizer=keras.optimizers.SGD(lr=1e-3))
history = model.fit(X_train, y_train, epochs=20, validation_data=(X_valid, y_valid))
mse_test = model.evaluate(X_test, y_test)
X_new = X_test[:3]
y_pred = model.predict(X_new)
plt.plot(pd.DataFrame(history.history))
plt.grid(True)
plt.gca().set_ylim(0, 1)
plt.show()
y_pred
```
# Functional API
Not all neural network models are simply sequential. Some may have complex topologies. Some may have multiple inputs and/or multiple outputs. For example, a Wide & Deep neural network (see [paper](https://ai.google/research/pubs/pub45413)) connects all or part of the inputs directly to the output layer.
```
np.random.seed(42)
tf.random.set_seed(42)
input_ = keras.layers.Input(shape=X_train.shape[1:])
hidden1 = keras.layers.Dense(30, activation="relu")(input_)
hidden2 = keras.layers.Dense(30, activation="relu")(hidden1)
concat = keras.layers.concatenate([input_, hidden2])
output = keras.layers.Dense(1)(concat)
model = keras.models.Model(inputs=[input_], outputs=[output])
model.summary()
model.compile(loss="mean_squared_error", optimizer=keras.optimizers.SGD(lr=1e-3))
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid))
mse_test = model.evaluate(X_test, y_test)
y_pred = model.predict(X_new)
```
What if you want to send different subsets of input features through the wide or deep paths? We will send 5 features (features 0 to 4), and 6 through the deep path (features 2 to 7). Note that 3 features will go through both (features 2, 3 and 4).
```
np.random.seed(42)
tf.random.set_seed(42)
input_A = keras.layers.Input(shape=[5], name="wide_input")
input_B = keras.layers.Input(shape=[6], name="deep_input")
hidden1 = keras.layers.Dense(30, activation="relu")(input_B)
hidden2 = keras.layers.Dense(30, activation="relu")(hidden1)
concat = keras.layers.concatenate([input_A, hidden2])
output = keras.layers.Dense(1, name="output")(concat)
model = keras.models.Model(inputs=[input_A, input_B], outputs=[output])
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=1e-3))
X_train_A, X_train_B = X_train[:, :5], X_train[:, 2:]
X_valid_A, X_valid_B = X_valid[:, :5], X_valid[:, 2:]
X_test_A, X_test_B = X_test[:, :5], X_test[:, 2:]
X_new_A, X_new_B = X_test_A[:3], X_test_B[:3]
history = model.fit((X_train_A, X_train_B), y_train, epochs=20,
validation_data=((X_valid_A, X_valid_B), y_valid))
mse_test = model.evaluate((X_test_A, X_test_B), y_test)
y_pred = model.predict((X_new_A, X_new_B))
```
Adding an auxiliary output for regularization:
```
np.random.seed(42)
tf.random.set_seed(42)
input_A = keras.layers.Input(shape=[5], name="wide_input")
input_B = keras.layers.Input(shape=[6], name="deep_input")
hidden1 = keras.layers.Dense(30, activation="relu")(input_B)
hidden2 = keras.layers.Dense(30, activation="relu")(hidden1)
concat = keras.layers.concatenate([input_A, hidden2])
output = keras.layers.Dense(1, name="main_output")(concat)
aux_output = keras.layers.Dense(1, name="aux_output")(hidden2)
model = keras.models.Model(inputs=[input_A, input_B],
outputs=[output, aux_output])
model.compile(loss=["mse", "mse"], loss_weights=[0.9, 0.1], optimizer=keras.optimizers.SGD(lr=1e-3))
history = model.fit([X_train_A, X_train_B], [y_train, y_train], epochs=20,
validation_data=([X_valid_A, X_valid_B], [y_valid, y_valid]))
total_loss, main_loss, aux_loss = model.evaluate(
[X_test_A, X_test_B], [y_test, y_test])
y_pred_main, y_pred_aux = model.predict([X_new_A, X_new_B])
```
# The subclassing API
```
class WideAndDeepModel(keras.models.Model):
def __init__(self, units=30, activation="relu", **kwargs):
super().__init__(**kwargs)
self.hidden1 = keras.layers.Dense(units, activation=activation)
self.hidden2 = keras.layers.Dense(units, activation=activation)
self.main_output = keras.layers.Dense(1)
self.aux_output = keras.layers.Dense(1)
def call(self, inputs):
input_A, input_B = inputs
hidden1 = self.hidden1(input_B)
hidden2 = self.hidden2(hidden1)
concat = keras.layers.concatenate([input_A, hidden2])
main_output = self.main_output(concat)
aux_output = self.aux_output(hidden2)
return main_output, aux_output
model = WideAndDeepModel(30, activation="relu")
model.compile(loss="mse", loss_weights=[0.9, 0.1], optimizer=keras.optimizers.SGD(lr=1e-3))
history = model.fit((X_train_A, X_train_B), (y_train, y_train), epochs=10,
validation_data=((X_valid_A, X_valid_B), (y_valid, y_valid)))
total_loss, main_loss, aux_loss = model.evaluate((X_test_A, X_test_B), (y_test, y_test))
y_pred_main, y_pred_aux = model.predict((X_new_A, X_new_B))
model = WideAndDeepModel(30, activation="relu")
```
# Saving and Restoring
```
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu", input_shape=[8]),
keras.layers.Dense(30, activation="relu"),
keras.layers.Dense(1)
])
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=1e-3))
history = model.fit(X_train, y_train, epochs=10, validation_data=(X_valid, y_valid))
mse_test = model.evaluate(X_test, y_test)
model.save("my_keras_model.h5")
model = keras.models.load_model("my_keras_model.h5")
model.predict(X_new)
model.save_weights("my_keras_weights.ckpt")
model.load_weights("my_keras_weights.ckpt")
```
# Using Callbacks during Training
```
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu", input_shape=[8]),
keras.layers.Dense(30, activation="relu"),
keras.layers.Dense(1)
])
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=1e-3))
checkpoint_cb = keras.callbacks.ModelCheckpoint("my_keras_model.h5", save_best_only=True)
history = model.fit(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid),
callbacks=[checkpoint_cb])
model = keras.models.load_model("my_keras_model.h5") # rollback to best model
mse_test = model.evaluate(X_test, y_test)
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=1e-3))
early_stopping_cb = keras.callbacks.EarlyStopping(patience=10,
restore_best_weights=True)
history = model.fit(X_train, y_train, epochs=100,
validation_data=(X_valid, y_valid),
callbacks=[checkpoint_cb, early_stopping_cb])
mse_test = model.evaluate(X_test, y_test)
class PrintValTrainRatioCallback(keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs):
print("\nval/train: {:.2f}".format(logs["val_loss"] / logs["loss"]))
val_train_ratio_cb = PrintValTrainRatioCallback()
history = model.fit(X_train, y_train, epochs=1,
validation_data=(X_valid, y_valid),
callbacks=[val_train_ratio_cb])
```
# TensorBoard
```
root_logdir = os.path.join(os.curdir, "my_logs")
def get_run_logdir():
import time
run_id = time.strftime("run_%Y_%m_%d-%H_%M_%S")
return os.path.join(root_logdir, run_id)
run_logdir = get_run_logdir()
run_logdir
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu", input_shape=[8]),
keras.layers.Dense(30, activation="relu"),
keras.layers.Dense(1)
])
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=1e-3))
tensorboard_cb = keras.callbacks.TensorBoard(run_logdir)
history = model.fit(X_train, y_train, epochs=30,
validation_data=(X_valid, y_valid),
callbacks=[checkpoint_cb, tensorboard_cb])
```
To start the TensorBoard server, one option is to open a terminal, if needed activate the virtualenv where you installed TensorBoard, go to this notebook's directory, then type:
```bash
$ tensorboard --logdir=./my_logs --port=6006
```
You can then open your web browser to [localhost:6006](http://localhost:6006) and use TensorBoard. Once you are done, press Ctrl-C in the terminal window, this will shutdown the TensorBoard server.
Alternatively, you can load TensorBoard's Jupyter extension and run it like this:
```
%load_ext tensorboard
%tensorboard --logdir=./my_logs --port=6006
run_logdir2 = get_run_logdir()
run_logdir2
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu", input_shape=[8]),
keras.layers.Dense(30, activation="relu"),
keras.layers.Dense(1)
])
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=0.05))
tensorboard_cb = keras.callbacks.TensorBoard(run_logdir2)
history = model.fit(X_train, y_train, epochs=30,
validation_data=(X_valid, y_valid),
callbacks=[checkpoint_cb, tensorboard_cb])
```
Notice how TensorBoard now sees two runs, and you can compare the learning curves.
Check out the other available logging options:
```
help(keras.callbacks.TensorBoard.__init__)
```
# Hyperparameter Tuning
```
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
def build_model(n_hidden=1, n_neurons=30, learning_rate=3e-3, input_shape=[8]):
model = keras.models.Sequential()
model.add(keras.layers.InputLayer(input_shape=input_shape))
for layer in range(n_hidden):
model.add(keras.layers.Dense(n_neurons, activation="relu"))
model.add(keras.layers.Dense(1))
optimizer = keras.optimizers.SGD(lr=learning_rate)
model.compile(loss="mse", optimizer=optimizer)
return model
keras_reg = keras.wrappers.scikit_learn.KerasRegressor(build_model)
keras_reg.fit(X_train, y_train, epochs=100,
validation_data=(X_valid, y_valid),
callbacks=[keras.callbacks.EarlyStopping(patience=10)])
mse_test = keras_reg.score(X_test, y_test)
y_pred = keras_reg.predict(X_new)
np.random.seed(42)
tf.random.set_seed(42)
from scipy.stats import reciprocal
from sklearn.model_selection import RandomizedSearchCV
param_distribs = {
"n_hidden": [0, 1, 2, 3],
"n_neurons": np.arange(1, 100),
"learning_rate": reciprocal(3e-4, 3e-2),
}
rnd_search_cv = RandomizedSearchCV(keras_reg, param_distribs, n_iter=10, cv=3, verbose=2)
rnd_search_cv.fit(X_train, y_train, epochs=100,
validation_data=(X_valid, y_valid),
callbacks=[keras.callbacks.EarlyStopping(patience=10)])
rnd_search_cv.best_params_
rnd_search_cv.best_score_
rnd_search_cv.best_estimator_
rnd_search_cv.score(X_test, y_test)
model = rnd_search_cv.best_estimator_.model
model
model.evaluate(X_test, y_test)
```
# Exercise solutions
## 1. to 9.
See appendix A.
## 10.
TODO
|
github_jupyter
|
```
import math
import pandas as pd
from langdetect import detect
import numpy as np
import nltk
from nltk.stem import WordNetLemmatizer
import string
from sklearn.feature_extraction.text import CountVectorizer
import math
import matplotlib.pyplot as plt
lem = WordNetLemmatizer() #create lemmatizer
import ssl
try:
_create_unverified_https_context = ssl._create_unverified_context
except AttributeError:
pass
else:
ssl._create_default_https_context = _create_unverified_https_context
nltk.download('wordnet')
df = pd.read_csv('/Users/shirinharandi/Desktop/COMP0031/Data/en_reviews/tokyo_en.csv')
listings = pd.read_csv('/Users/shirinharandi/Desktop/COMP0031/Data/listings/tokyo_listings.csv')
listings
df
listings = listings[['id', 'room_type', 'calculated_host_listings_count']].copy()
listings
listings['is_superhost'] = np.where(listings['calculated_host_listings_count'] >= 10, 'Yes', listings['calculated_host_listings_count'])
listings['is_superhost'] = np.where(listings['calculated_host_listings_count'] < 10, 'No', listings['is_superhost'])
listings = listings.rename(columns={"id": "listing_id"})
listings
out = pd.merge(df, listings, on='listing_id')
out
# out.to_csv(r'property_type_and_superhosts/tokyo_type.csv')
dictionary = pd.read_csv('../data/processedDict.csv')
dictionary['word'] = dictionary['word'].apply(lambda x: lem.lemmatize(x, pos='n'))
# filepath = '../data/en_reviews/Manchester.csv'
# reviews = pd.read_csv(filepath)
# reviews = reviews['date']
# reviews
reviews = out
table = str.maketrans('', '', string.punctuation) #mapping to strip punctuation in review
#strip punct of each review -> lemmatise -> output is list of words so join into sentences
reviews['comments'] = reviews.comments.apply(lambda review: ' '.join(map(str, [lem.lemmatize(word.translate(table), pos='n') for word in review.lower().split()])))
reviews
reviews['date'] = pd.to_datetime(reviews['date'])
#### DELETE THIS LATER ###
mask = (reviews['date'] >= '2014-01-01') & (reviews['date'] < '2017-01-01')
reviews = reviews.loc[mask].copy()
reviews
reviews
def get_trends_nice(category, subcats, reviews):
years = [2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019]
allwords = reviews['comments'].tolist()
allwords = " ".join(allwords)
unique_words = set(allwords.split(' '))
len(unique_words)
unique_words = list(unique_words)
unique_words = [string for string in unique_words if string != ""]
# len(unique_words)
ls = []
for word in unique_words:
word = ''.join([i for i in word if not i.isdigit()])
ls += [word]
unique_words= ls
unique_words = [string for string in unique_words if string != ""]
unique_words = list(dict.fromkeys(unique_words))
def countWords(word, review):
count = 0
for i in review:
if i == word:
count+=1
return count
def getDenom(review, unique_words):
count = 0
den = 0
ls = []
review = review.split()
for word in review:
kmp = countWords(word, review)
if (kmp > 0 and word not in ls):
ls += [word]
den += math.log(1 + kmp)
return den
reviews['den'] = reviews['comments'].apply(lambda x: getDenom(x, unique_words))
def getNom(category, review, dictionary, cat_levl="cat_lev1"):
nom = 0
review = review.split()
dictionaryWords = dictionary[(dictionary[cat_levl] == category)]
dictionaryWords = dictionaryWords['word']
for word in dictionaryWords:
nom += math.log(1 + review.count(word))
return nom
reviews['temp'] = reviews['comments'].apply(lambda x: getNom(category, x, dictionary))
reviews[category] = reviews['temp']*100/reviews['den']
k = {}
for subcat in subcats:
temp = reviews['comments'].apply(lambda x: getNom(subcat, x, dictionary, cat_levl="cat_lev1"))
reviews[subcat] = temp * 100 / reviews["den"]
k[subcat] = reviews[subcat].loc[reviews[subcat] > 0].min()
print(k)
k_business= reviews[category].loc[reviews[category] > 0]
k_business = k_business.min()
print(k_business)
def adoptionForSetOfReviews(category, setOfReviews, dictionary, startDate, endDate, k):
adoption = 1
mask = (setOfReviews['date'] >= startDate) & (setOfReviews['date'] < endDate)
setOfReviews = setOfReviews.loc[mask]
setOfReviews = setOfReviews[category]
if (len(setOfReviews) == 0):
return 0
else:
b = 1/len(setOfReviews)
for review in setOfReviews:
adoption *= math.pow((review + k),b)
adoption = adoption - k
return adoption
d2 = {'year' : years, 'value':0.0}
out = pd.DataFrame(data=d2)
for i in range(len(years)):
out.at[i, "value_{}".format(category)] = adoptionForSetOfReviews(category, reviews, dictionary, "{}-01-01".format(years[i]), "{}-01-01".format(years[i] + 1), k_business)
# for subcat in subcats:
# out.at[i, "value_{}_{}".format(category, subcat)] = adoptionForSetOfReviews(subcat, reviews, dictionary, "{}-01-01".format(years[i]), "{}-01-01".format(years[i] + 1), k[subcat])
return out
house_types = ["Private room", "Entire home/apt", "Shared room"]
r = reviews.loc[reviews["room_type"] == house_types[0]].copy()
temp = get_trends_nice("social", "social", r)
plt.bar(temp["year"], temp["value_social"])
r = reviews.loc[reviews["room_type"] == house_types[1]].copy()
temp = get_trends_nice("social", "social", r)
plt.bar(temp["year"], temp["value_social"])
r = reviews.loc[reviews["room_type"] == house_types[2]].copy()
temp = get_trends_nice("social", "social", r)
plt.bar(temp["year"], temp["value_social"])
r = reviews.loc[reviews["room_type"] == house_types[0]].copy()
temp = get_trends_nice("business", "business", r)
plt.bar(temp["year"], temp["value_business"])
r = reviews.loc[reviews["room_type"] == house_types[1]].copy()
temp = get_trends_nice("business", "business", r)
plt.bar(temp["year"], temp["value_business"])
r = reviews.loc[reviews["room_type"] == house_types[2]].copy()
temp = get_trends_nice("business", "business", r)
plt.bar(temp["year"], temp["value_business"])
```
|
github_jupyter
|
## title
```
(define (constant value connector)
(define (me request)
(error "Unknow request -- CONSTANT" request))
(connect connector me)
(set-value! connector value me)
me)
(define (probe name connector)
(define (print-probe value)
(newline)
(display "Probe: ")
(display name)
(display " = ")
(display value))
(define (process-new-value)
(print-probe (get-value connector)))
(define (process-forget-value)
(print-probe "?"))
(define (me request)
(cond ((eq? request 'I-have-a-value)
(process-new-value))
((eq? request 'I-lost-my-value)
(process-forget-value))
(else
(error "Unknow request -- PROBE " request))))
(connect connector me)
me)
(define (make-connector)
(let ((value false) (informant false) (constraints '()))
(define (set-my-value newval setter)
(cond ((not (has-value? me))
(set! value newval)
(set! informant setter)
(for-each-except setter
inform-about-value
constraints))
((not (= value newval))
(error "Constradiction" (list value newval)))
(else 'ignored)))
(define (forget-my-value retractor)
(if (eq? retractor informant)
(begin (set! informant false)
(for-each-except retractor
inform-about-no-value
constraints))
'ignored))
(define (connect new-constraint)
(if (not (memq new-constraint constraints))
(set! constraints
(cons new-constraint constraints)))
(if (has-value? me)
(inform-about-value new-constraint))
'done)
(define (me request)
(cond ((eq? request 'has-value?)
(if informant true false))
((eq? request 'value ) value)
((eq? request 'set-value!) set-my-value)
((eq? request 'forget) forget-my-value)
((eq? request 'connect) connect)
(else (error "Unknown operation -- CONNECTOR"
request))))
me))
(define (inform-about-value constraint)
(constraint 'I-have-a-value))
(define (inform-about-no-value constraint)
(constraint 'I-lost-my-value))
(define (for-each-except exception procedure list)
(define (loop items)
(cond ((null? items) 'done)
((eq? (car items) exception ) (loop ( cdr items)))
(else (procedure (car items))
(loop (cdr items)))))
(loop list))
(define (has-value? connector)
(connector 'has-value?))
(define (get-value connector)
(connector 'value))
(define (set-value! connector new-value informant)
((connector 'set-value!) new-value informant))
(define (forget-value! connector retractor)
((connector 'forget) retractor))
(define (connect connector new-constraint)
((connector 'connect) new-constraint))
(define (adder a1 a2 sum)
(define (process-new-value)
(cond ((and (has-value? a1) (has-value? a2))
(set-value! sum
(+ (get-value a1) (get-value a2))
me))
((and (has-value? a1) (has-value? sum))
(set-value! a2
(- (get-value sum) (get-value a1))
me))
((and (has-value? a2) (has-value? sum))
(set-value! a1
(- (get-value sum) (get-value a2))
me))))
(define (process-forget-value)
(forget-value! sum me)
(forget-value! a1 me)
(forget-value! a2 me)
(process-new-value))
(define (me request)
(cond ((eq? request 'I-have-a-value)
(process-new-value))
((eq? request 'I-lost-my-value)
(process-forget-value))
(else
(error "Unknown request -- ADDER" request))))
(connect a1 me)
(connect a2 me)
(connect sum me)
me)
(define (multiplier m1 m2 product)
(define (process-new-value)
(cond ((or (and (has-value? m1) (= (get-value m1) 0))
(and (has-value? m2) (= (get-value m2) 0)))
(set-value! product 0 me))
((and (has-value? m1) (has-value? m2))
(set-value! product
(* (get-value m1) (get-value m2))
me))
((and (has-value? product) (has-value? m1))
(set-value! m2
(/ (get-value product) (get-value m1))
me))
((and (has-value? product) (has-value? m2))
(set-value! m1
(/ (get-value product) (get-value m2))
me))))
(define (process-forget-value)
(forget-value! product me)
(forget-value! m1 me)
(forget-value! m2 me)
(process-new-value))
(define (me request)
(cond ((eq? request 'I-have-a-value)
(process-new-value))
((eq? request 'I-lost-my-value)
(process-forget-value))
(else
(error "Unknown request -- MULTIPLIER " request))))
(connect m1 me)
(connect m2 me)
(connect product me)
me)
(define (start-unit-test-adder)
(define value1 (make-connector))
(define value2 (make-connector))
(define my-sum (make-connector))
(adder value1 value2 my-sum)
(probe 'value1 value1)
(probe 'value2 value2)
(probe 'my-sum my-sum)
(set-value! value1 1 'user)
(set-value! value2 2 'user)
(forget-value! value1 'user)
; (forget-value! value2 'user)
(set-value! value1 4 'user)
(forget-value! value1 'user)
(forget-value! my-sum 'user)
(set-value! my-sum 19 'user)
)
(define (start-unit-test-multiplier)
(define value1 (make-connector))
(define value2 (make-connector))
(define my-product (make-connector))
(multiplier value1 value2 my-product)
(probe 'value1 value1)
(probe 'value2 value2)
(probe 'my-product my-product)
(set-value! value1 1 'user)
(set-value! value2 2 'user)
(forget-value! value1 'user)
; (forget-value! value2 'user)
(set-value! value1 4 'user)
(forget-value! value1 'user)
(forget-value! my-product 'user)
(set-value! my-product 19 'user)
)
(define (averager a b c)
(define number-2 (make-connector))
(define sum-value (make-connector))
(adder a b sum-value)
(multiplier c number-2 sum-value)
(constant 2 number-2)
'ok)
(define (start-test-3-33)
(define a (make-connector))
(define b (make-connector))
(define c (make-connector))
(averager a b c)
(probe 'a a)
(probe 'b b)
(probe 'c c)
(set-value! a 3 'user)
(set-value! b 5 'user)
)
(define (squarer a b)
(multiplier a a b))
(define (start-test-3-34)
(display "the issue in this scenario is that we can't use same connector in one constrant")
(newline)
)
```
|
github_jupyter
|
# Dateien
## Eine Textdatei lesen und ihren Inhalt ausgeben
```
# Wir öffnen die Datei lesen.txt zum Lesen ("r") und speichern ihren Inhalt in die Variable file
file = open("lesen.txt", "r")
# Wir gehen alle Zeilen nacheinander durch
# In der txt-Datei stehen für uns nicht sichtbare Zeilenumbruchszeichen, durch die jeweils das Ende einer Zeile markiert ist
for line in file:
# Eine Zeile ohne Zeilenumbruch ausgeben
print(line.strip())
file.close()
# Wir öffnen die Datei lesen.txt zum Lesen ("r") und speichern ihren Inhalt in die Variable file
file = open("lesen-Kopie-Juerg.txt", "r")
# Wir gehen alle Zeilen nacheinander durch
# In der txt-Datei stehen für uns nicht sichtbare Zeilenumbruchszeichen, durch die jeweils das Ende einer Zeile markiert ist
for line in file:
# Eine Zeile ohne Zeilenumbruch ausgeben
print(line.strip())
file.close()
```
## In eine Textdatei schreiben
```
# Wir öffnen eine Datei zum Schreiben ("w": write)
file = open("schreiben.txt", "w")
students = ["Max", "Monika", "Erik", "Franziska", "Juerg", "Peter"]
# Wir loopen mit einer for-Schleife durch die Liste students
for student in students:
# Mit der write-Methode schreiben wir den aktuellen String student und einen Zeilenumbruch in das file-Objekt
file.write(student + "\n")
# Abschließend müssen wir die Datei wieder schließen
file.close()
# Wir öffnen eine Datei zum Schreiben ("w": write)
file = open("schreiben.txt", "w")
students = ["Max", "Monika", "Erik", "Franziska", "Juerg", "Peter"]
# Wir loopen mit einer for-Schleife durch die Liste students
for student in students:
# Mit der write-Methode schreiben wir den aktuellen String student und einen Zeilenumbruch in das file-Objekt
file.write(student + "\n")
# Abschließend müssen wir die Datei wieder schließen
file.close()
```
## Dateien öffnen mit with
Wenn wir Dateien mit einer with-Konstruktion öffnen, dann brauchen wir sie nicht mehr explizit mit der close()-Methode schließen.
```
with open("lesen.txt", "r") as file:
for line in file:
print(line)
with open("lesen.txt", "r") as file:
for line in file:
print(line)
```
## CSV-Datei lesen
csv steht für comma separated values. Auch solche csv-Dateien können wir mit Python auslesen.
```
with open("datei.csv") as file:
for line in file:
data = line.strip().split(";")
print(data[0] + ": " + data[1])
```
## CSV-Datei lesen (und Daten überspringen)
In dieser Lektion lernst du:
- Wie du eine CSV-Datei einliest, und Zeilen überspringen kannst.
```
with open("datei.csv") as file:
for line in file:
data = line.strip().split(";")
if (data[0]) == "Aaron":
print(data[0])
if data[2] == "BUD":
continue
print(data)
#if data[2] == "BER" or data[2] == "BUD":
# print(data[2])
# print(data)
sum = 0
with open("20151001_hundenamen.csv") as file:
for line in file:
data = line.strip().split(",")
if (data[0]) == '"Aaron"':
if int(data[1]) < 2012:
sum = sum + 1
print(sum)
with open("datei.csv") as file:
for line in file:
data = line.strip().split(";")
print(data[1] + " " + data[2])
```
## Übung
- Besorgt euch die datei https://data.stadt-zuerich.ch/dataset/pd-stapo-hundenamen/resource/8bf2127d-c354-4834-8590-9666cbd6e160
- Ihr findet sie auch im Ordner 20151001_hundenamen.csv
- Findet heraus wie oft der Hundename "Aaron" zwischen 2000 - 2012 gebraucht wurde.
```
n = "1975"
print(int(n) < 1990)
jahre = ["Year", "1990", "1992"]
for jahr in jahre:
if jahr == "Year":
continue
print(int(jahr))
### Euer code hier
```
|
github_jupyter
|
Lambda School Data Science
*Unit 2, Sprint 3, Module 3*
---
# Permutation & Boosting
- Get **permutation importances** for model interpretation and feature selection
- Use xgboost for **gradient boosting**
### Setup
Run the code cell below. You can work locally (follow the [local setup instructions](https://lambdaschool.github.io/ds/unit2/local/)) or on Colab.
Libraries:
- category_encoders
- [**eli5**](https://eli5.readthedocs.io/en/latest/)
- matplotlib
- numpy
- pandas
- scikit-learn
- [**xgboost**](https://xgboost.readthedocs.io/en/latest/)
```
%%capture
import sys
# If you're on Colab:
if 'google.colab' in sys.modules:
DATA_PATH = 'https://raw.githubusercontent.com/LambdaSchool/DS-Unit-2-Applied-Modeling/master/data/'
!pip install category_encoders==2.*
!pip install eli5
# If you're working locally:
else:
DATA_PATH = '../data/'
```
We'll go back to Tanzania Waterpumps for this lesson.
```
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
# Merge train_features.csv & train_labels.csv
train = pd.merge(pd.read_csv(DATA_PATH+'waterpumps/train_features.csv'),
pd.read_csv(DATA_PATH+'waterpumps/train_labels.csv'))
# Read test_features.csv & sample_submission.csv
test = pd.read_csv(DATA_PATH+'waterpumps/test_features.csv')
sample_submission = pd.read_csv(DATA_PATH+'waterpumps/sample_submission.csv')
# Split train into train & val
train, val = train_test_split(train, train_size=0.80, test_size=0.20,
stratify=train['status_group'], random_state=42)
def wrangle(X):
"""Wrangle train, validate, and test sets in the same way"""
# Prevent SettingWithCopyWarning
X = X.copy()
# About 3% of the time, latitude has small values near zero,
# outside Tanzania, so we'll treat these values like zero.
X['latitude'] = X['latitude'].replace(-2e-08, 0)
# When columns have zeros and shouldn't, they are like null values.
# So we will replace the zeros with nulls, and impute missing values later.
# Also create a "missing indicator" column, because the fact that
# values are missing may be a predictive signal.
cols_with_zeros = ['longitude', 'latitude', 'construction_year',
'gps_height', 'population']
for col in cols_with_zeros:
X[col] = X[col].replace(0, np.nan)
X[col+'_MISSING'] = X[col].isnull()
# Drop duplicate columns
duplicates = ['quantity_group', 'payment_type']
X = X.drop(columns=duplicates)
# Drop recorded_by (never varies) and id (always varies, random)
unusable_variance = ['recorded_by', 'id']
X = X.drop(columns=unusable_variance)
# Convert date_recorded to datetime
X['date_recorded'] = pd.to_datetime(X['date_recorded'], infer_datetime_format=True)
# Extract components from date_recorded, then drop the original column
X['year_recorded'] = X['date_recorded'].dt.year
X['month_recorded'] = X['date_recorded'].dt.month
X['day_recorded'] = X['date_recorded'].dt.day
X = X.drop(columns='date_recorded')
# Engineer feature: how many years from construction_year to date_recorded
X['years'] = X['year_recorded'] - X['construction_year']
X['years_MISSING'] = X['years'].isnull()
# return the wrangled dataframe
return X
train = wrangle(train)
val = wrangle(val)
test = wrangle(test)
# Arrange data into X features matrix and y target vector
target = 'status_group'
X_train = train.drop(columns=target)
y_train = train[target]
X_val = val.drop(columns=target)
y_val = val[target]
X_test = test
import category_encoders as ce
from sklearn.impute import SimpleImputer
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(strategy='median'),
RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1)
)
# Fit on train, score on val
pipeline.fit(X_train, y_train)
print('Validation Accuracy', pipeline.score(X_val, y_val))
```
# Get permutation importances for model interpretation and feature selection
## Overview
Default Feature Importances are fast, but Permutation Importances may be more accurate.
These links go deeper with explanations and examples:
- Permutation Importances
- [Kaggle / Dan Becker: Machine Learning Explainability](https://www.kaggle.com/dansbecker/permutation-importance)
- [Christoph Molnar: Interpretable Machine Learning](https://christophm.github.io/interpretable-ml-book/feature-importance.html)
- (Default) Feature Importances
- [Ando Saabas: Selecting good features, Part 3, Random Forests](https://blog.datadive.net/selecting-good-features-part-iii-random-forests/)
- [Terence Parr, et al: Beware Default Random Forest Importances](https://explained.ai/rf-importance/index.html)
There are three types of feature importances:
### 1. (Default) Feature Importances
Fastest, good for first estimates, but be aware:
>**When the dataset has two (or more) correlated features, then from the point of view of the model, any of these correlated features can be used as the predictor, with no concrete preference of one over the others.** But once one of them is used, the importance of others is significantly reduced since effectively the impurity they can remove is already removed by the first feature. As a consequence, they will have a lower reported importance. This is not an issue when we want to use feature selection to reduce overfitting, since it makes sense to remove features that are mostly duplicated by other features. But when interpreting the data, it can lead to the incorrect conclusion that one of the variables is a strong predictor while the others in the same group are unimportant, while actually they are very close in terms of their relationship with the response variable. — [Selecting good features – Part III: random forests](https://blog.datadive.net/selecting-good-features-part-iii-random-forests/)
> **The scikit-learn Random Forest feature importance ... tends to inflate the importance of continuous or high-cardinality categorical variables.** ... Breiman and Cutler, the inventors of Random Forests, indicate that this method of “adding up the gini decreases for each individual variable over all trees in the forest gives a **fast** variable importance that is often very consistent with the permutation importance measure.” — [Beware Default Random Forest Importances](https://explained.ai/rf-importance/index.html)
```
# Get feature importances
rf = pipeline.named_steps['randomforestclassifier']
importances = pd.Series(rf.feature_importances_, X_train.columns)
# Plot feature importances
%matplotlib inline
import matplotlib.pyplot as plt
n = 20
plt.figure(figsize=(10,n/2))
plt.title(f'Top {n} features')
importances.sort_values()[-n:].plot.barh(color='grey');
```
### 2. Drop-Column Importance
The best in theory, but too slow in practice
```
column = 'quantity'
# Fit without column
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(strategy='median'),
RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1)
)
pipeline.fit(X_train.drop(columns=column), y_train)
score_without = pipeline.score(X_val.drop(columns=column), y_val)
print(f'Validation Accuracy without {column}: {score_without}')
# Fit with column
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(strategy='median'),
RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1)
)
pipeline.fit(X_train, y_train)
score_with = pipeline.score(X_val, y_val)
print(f'Validation Accuracy with {column}: {score_with}')
# Compare the error with & without column
print(f'Drop-Column Importance for {column}: {score_with - score_without}')
```
### 3. Permutation Importance
Permutation Importance is a good compromise between Feature Importance based on impurity reduction (which is the fastest) and Drop Column Importance (which is the "best.")
[The ELI5 library documentation explains,](https://eli5.readthedocs.io/en/latest/blackbox/permutation_importance.html)
> Importance can be measured by looking at how much the score (accuracy, F1, R^2, etc. - any score we’re interested in) decreases when a feature is not available.
>
> To do that one can remove feature from the dataset, re-train the estimator and check the score. But it requires re-training an estimator for each feature, which can be computationally intensive. ...
>
>To avoid re-training the estimator we can remove a feature only from the test part of the dataset, and compute score without using this feature. It doesn’t work as-is, because estimators expect feature to be present. So instead of removing a feature we can replace it with random noise - feature column is still there, but it no longer contains useful information. This method works if noise is drawn from the same distribution as original feature values (as otherwise estimator may fail). The simplest way to get such noise is to shuffle values for a feature, i.e. use other examples’ feature values - this is how permutation importance is computed.
>
>The method is most suitable for computing feature importances when a number of columns (features) is not huge; it can be resource-intensive otherwise.
### Do-It-Yourself way, for intuition
### With eli5 library
For more documentation on using this library, see:
- [eli5.sklearn.PermutationImportance](https://eli5.readthedocs.io/en/latest/autodocs/sklearn.html#eli5.sklearn.permutation_importance.PermutationImportance)
- [eli5.show_weights](https://eli5.readthedocs.io/en/latest/autodocs/eli5.html#eli5.show_weights)
- [scikit-learn user guide, `scoring` parameter](https://scikit-learn.org/stable/modules/model_evaluation.html#the-scoring-parameter-defining-model-evaluation-rules)
eli5 doesn't work with pipelines.
```
# Ignore warnings
```
### We can use importances for feature selection
For example, we can remove features with zero importance. The model trains faster and the score does not decrease.
# Use xgboost for gradient boosting
## Overview
In the Random Forest lesson, you learned this advice:
#### Try Tree Ensembles when you do machine learning with labeled, tabular data
- "Tree Ensembles" means Random Forest or **Gradient Boosting** models.
- [Tree Ensembles often have the best predictive accuracy](https://arxiv.org/abs/1708.05070) with labeled, tabular data.
- Why? Because trees can fit non-linear, non-[monotonic](https://en.wikipedia.org/wiki/Monotonic_function) relationships, and [interactions](https://christophm.github.io/interpretable-ml-book/interaction.html) between features.
- A single decision tree, grown to unlimited depth, will [overfit](http://www.r2d3.us/visual-intro-to-machine-learning-part-1/). We solve this problem by ensembling trees, with bagging (Random Forest) or **[boosting](https://www.youtube.com/watch?v=GM3CDQfQ4sw)** (Gradient Boosting).
- Random Forest's advantage: may be less sensitive to hyperparameters. **Gradient Boosting's advantage:** may get better predictive accuracy.
Like Random Forest, Gradient Boosting uses ensembles of trees. But the details of the ensembling technique are different:
### Understand the difference between boosting & bagging
Boosting (used by Gradient Boosting) is different than Bagging (used by Random Forests).
Here's an excerpt from [_An Introduction to Statistical Learning_](http://www-bcf.usc.edu/~gareth/ISL/ISLR%20Seventh%20Printing.pdf) Chapter 8.2.3, Boosting:
>Recall that bagging involves creating multiple copies of the original training data set using the bootstrap, fitting a separate decision tree to each copy, and then combining all of the trees in order to create a single predictive model.
>
>**Boosting works in a similar way, except that the trees are grown _sequentially_: each tree is grown using information from previously grown trees.**
>
>Unlike fitting a single large decision tree to the data, which amounts to _fitting the data hard_ and potentially overfitting, the boosting approach instead _learns slowly._ Given the current model, we fit a decision tree to the residuals from the model.
>
>We then add this new decision tree into the fitted function in order to update the residuals. Each of these trees can be rather small, with just a few terminal nodes. **By fitting small trees to the residuals, we slowly improve fˆ in areas where it does not perform well.**
>
>Note that in boosting, unlike in bagging, the construction of each tree depends strongly on the trees that have already been grown.
This high-level overview is all you need to know for now. If you want to go deeper, we recommend you watch the StatQuest videos on gradient boosting!
Let's write some code. We have lots of options for which libraries to use:
#### Python libraries for Gradient Boosting
- [scikit-learn Gradient Tree Boosting](https://scikit-learn.org/stable/modules/ensemble.html#gradient-boosting) — slower than other libraries, but [the new version may be better](https://twitter.com/amuellerml/status/1129443826945396737)
- Anaconda: already installed
- Google Colab: already installed
- [xgboost](https://xgboost.readthedocs.io/en/latest/) — can accept missing values and enforce [monotonic constraints](https://xiaoxiaowang87.github.io/monotonicity_constraint/)
- Anaconda, Mac/Linux: `conda install -c conda-forge xgboost`
- Windows: `conda install -c anaconda py-xgboost`
- Google Colab: already installed
- [LightGBM](https://lightgbm.readthedocs.io/en/latest/) — can accept missing values and enforce [monotonic constraints](https://blog.datadive.net/monotonicity-constraints-in-machine-learning/)
- Anaconda: `conda install -c conda-forge lightgbm`
- Google Colab: already installed
- [CatBoost](https://catboost.ai/) — can accept missing values and use [categorical features](https://catboost.ai/docs/concepts/algorithm-main-stages_cat-to-numberic.html) without preprocessing
- Anaconda: `conda install -c conda-forge catboost`
- Google Colab: `pip install catboost`
In this lesson, you'll use a new library, xgboost — But it has an API that's almost the same as scikit-learn, so it won't be a hard adjustment!
#### [XGBoost Python API Reference: Scikit-Learn API](https://xgboost.readthedocs.io/en/latest/python/python_api.html#module-xgboost.sklearn)
#### [Avoid Overfitting By Early Stopping With XGBoost In Python](https://machinelearningmastery.com/avoid-overfitting-by-early-stopping-with-xgboost-in-python/)
Why is early stopping better than a For loop, or GridSearchCV, to optimize `n_estimators`?
With early stopping, if `n_iterations` is our number of iterations, then we fit `n_iterations` decision trees.
With a for loop, or GridSearchCV, we'd fit `sum(range(1,n_rounds+1))` trees.
But it doesn't work well with pipelines. You may need to re-run multiple times with different values of other parameters such as `max_depth` and `learning_rate`.
#### XGBoost parameters
- [Notes on parameter tuning](https://xgboost.readthedocs.io/en/latest/tutorials/param_tuning.html)
- [Parameters documentation](https://xgboost.readthedocs.io/en/latest/parameter.html)
### Try adjusting these hyperparameters
#### Random Forest
- class_weight (for imbalanced classes)
- max_depth (usually high, can try decreasing)
- n_estimators (too low underfits, too high wastes time)
- min_samples_leaf (increase if overfitting)
- max_features (decrease for more diverse trees)
#### Xgboost
- scale_pos_weight (for imbalanced classes)
- max_depth (usually low, can try increasing)
- n_estimators (too low underfits, too high wastes time/overfits) — Use Early Stopping!
- learning_rate (too low underfits, too high overfits)
For more ideas, see [Notes on Parameter Tuning](https://xgboost.readthedocs.io/en/latest/tutorials/param_tuning.html) and [DART booster](https://xgboost.readthedocs.io/en/latest/tutorials/dart.html).
## Challenge
You will use your portfolio project dataset for all assignments this sprint. Complete these tasks for your project, and document your work.
- Continue to clean and explore your data. Make exploratory visualizations.
- Fit a model. Does it beat your baseline?
- Try xgboost.
- Get your model's permutation importances.
You should try to complete an initial model today, because the rest of the week, we're making model interpretation visualizations.
But, if you aren't ready to try xgboost and permutation importances with your dataset today, you can practice with another dataset instead. You may choose any dataset you've worked with previously.
|
github_jupyter
|
# Import Libraries
```
import numpy as np
import pandas as pd
```
# Import Data
```
# Import data.
loan_data_preprocessed_backup = pd.read_csv('loan_data_2007_2014_preprocessed.csv')
```
# Explore Data
```
loan_data_preprocessed = loan_data_preprocessed_backup.copy()
loan_data_preprocessed.columns.values
# Displays all column names.
loan_data_preprocessed.head()
loan_data_preprocessed.tail()
loan_data_defaults = loan_data_preprocessed[loan_data_preprocessed['loan_status'].isin(['Charged Off','Does not meet the credit policy. Status:Charged Off'])]
# Here we take only the accounts that were charged-off (written-off).
loan_data_defaults.shape
pd.options.display.max_rows = None
# Sets the pandas dataframe options to display all columns/ rows.
loan_data_defaults.isnull().sum()
```
# Independent Variables
```
loan_data_defaults['mths_since_last_delinq'].fillna(0, inplace = True)
# We fill the missing values with zeroes.
#loan_data_defaults['mths_since_last_delinq'].fillna(loan_data_defaults['mths_since_last_delinq'].max() + 12, inplace=True)
loan_data_defaults['mths_since_last_record'].fillna(0, inplace=True)
# We fill the missing values with zeroes.
```
# Dependent Variables
```
loan_data_defaults['recovery_rate'] = loan_data_defaults['recoveries'] / loan_data_defaults['funded_amnt']
# We calculate the dependent variable for the LGD model: recovery rate.
# It is the ratio of recoveries and funded amount.
loan_data_defaults['recovery_rate'].describe()
# Shows some descriptive statisics for the values of a column.
loan_data_defaults['recovery_rate'] = np.where(loan_data_defaults['recovery_rate'] > 1, 1, loan_data_defaults['recovery_rate'])
loan_data_defaults['recovery_rate'] = np.where(loan_data_defaults['recovery_rate'] < 0, 0, loan_data_defaults['recovery_rate'])
# We set recovery rates that are greater than 1 to 1 and recovery rates that are less than 0 to 0.
loan_data_defaults['recovery_rate'].describe()
# Shows some descriptive statisics for the values of a column.
loan_data_defaults['CCF'] = (loan_data_defaults['funded_amnt'] - loan_data_defaults['total_rec_prncp']) / loan_data_defaults['funded_amnt']
# We calculate the dependent variable for the EAD model: credit conversion factor.
# It is the ratio of the difference of the amount used at the moment of default to the total funded amount.
loan_data_defaults['CCF'].describe()
# Shows some descriptive statisics for the values of a column.
loan_data_defaults.to_csv('loan_data_defaults.csv')
# We save the data to a CSV file.
```
# Explore Dependent Variables
```
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.hist(loan_data_defaults['recovery_rate'], bins = 100)
# We plot a histogram of a variable with 100 bins.
plt.hist(loan_data_defaults['recovery_rate'], bins = 50)
# We plot a histogram of a variable with 50 bins.
plt.hist(loan_data_defaults['CCF'], bins = 100)
# We plot a histogram of a variable with 100 bins.
loan_data_defaults['recovery_rate_0_1'] = np.where(loan_data_defaults['recovery_rate'] == 0, 0, 1)
# We create a new variable which is 0 if recovery rate is 0 and 1 otherwise.
loan_data_defaults['recovery_rate_0_1']
```
# LGD Model
### Splitting Data
```
from sklearn.model_selection import train_test_split
# LGD model stage 1 datasets: recovery rate 0 or greater than 0.
lgd_inputs_stage_1_train, lgd_inputs_stage_1_test, lgd_targets_stage_1_train, lgd_targets_stage_1_test = train_test_split(loan_data_defaults.drop(['good_bad', 'recovery_rate','recovery_rate_0_1', 'CCF'], axis = 1), loan_data_defaults['recovery_rate_0_1'], test_size = 0.2, random_state = 42)
# Takes a set of inputs and a set of targets as arguments. Splits the inputs and the targets into four dataframes:
# Inputs - Train, Inputs - Test, Targets - Train, Targets - Test.
```
### Preparing the Inputs
```
features_all = ['grade:A',
'grade:B',
'grade:C',
'grade:D',
'grade:E',
'grade:F',
'grade:G',
'home_ownership:MORTGAGE',
'home_ownership:NONE',
'home_ownership:OTHER',
'home_ownership:OWN',
'home_ownership:RENT',
'verification_status:Not Verified',
'verification_status:Source Verified',
'verification_status:Verified',
'purpose:car',
'purpose:credit_card',
'purpose:debt_consolidation',
'purpose:educational',
'purpose:home_improvement',
'purpose:house',
'purpose:major_purchase',
'purpose:medical',
'purpose:moving',
'purpose:other',
'purpose:renewable_energy',
'purpose:small_business',
'purpose:vacation',
'purpose:wedding',
'initial_list_status:f',
'initial_list_status:w',
'term_int',
'emp_length_int',
'mths_since_issue_d',
'mths_since_earliest_cr_line',
'funded_amnt',
'int_rate',
'installment',
'annual_inc',
'dti',
'delinq_2yrs',
'inq_last_6mths',
'mths_since_last_delinq',
'mths_since_last_record',
'open_acc',
'pub_rec',
'total_acc',
'acc_now_delinq',
'total_rev_hi_lim']
# List of all independent variables for the models.
features_reference_cat = ['grade:G',
'home_ownership:RENT',
'verification_status:Verified',
'purpose:credit_card',
'initial_list_status:f']
# List of the dummy variable reference categories.
lgd_inputs_stage_1_train = lgd_inputs_stage_1_train[features_all]
# Here we keep only the variables we need for the model.
lgd_inputs_stage_1_train = lgd_inputs_stage_1_train.drop(features_reference_cat, axis = 1)
# Here we remove the dummy variable reference categories.
lgd_inputs_stage_1_train.isnull().sum()
# Check for missing values. We check whether the value of each row for each column is missing or not,
# then sum accross columns.
```
### Estimating the Model
```
# P values for sklearn logistic regression.
# Class to display p-values for logistic regression in sklearn.
from sklearn import linear_model
import scipy.stats as stat
class LogisticRegression_with_p_values:
def __init__(self,*args,**kwargs):#,**kwargs):
self.model = linear_model.LogisticRegression(*args,**kwargs)#,**args)
def fit(self,X,y):
self.model.fit(X,y)
#### Get p-values for the fitted model ####
denom = (2.0 * (1.0 + np.cosh(self.model.decision_function(X))))
denom = np.tile(denom,(X.shape[1],1)).T
F_ij = np.dot((X / denom).T,X) ## Fisher Information Matrix
Cramer_Rao = np.linalg.inv(F_ij) ## Inverse Information Matrix
sigma_estimates = np.sqrt(np.diagonal(Cramer_Rao))
z_scores = self.model.coef_[0] / sigma_estimates # z-score for eaach model coefficient
p_values = [stat.norm.sf(abs(x)) * 2 for x in z_scores] ### two tailed test for p-values
self.coef_ = self.model.coef_
self.intercept_ = self.model.intercept_
#self.z_scores = z_scores
self.p_values = p_values
#self.sigma_estimates = sigma_estimates
#self.F_ij = F_ij
reg_lgd_st_1 = LogisticRegression_with_p_values()
# We create an instance of an object from the 'LogisticRegression' class.
reg_lgd_st_1.fit(lgd_inputs_stage_1_train, lgd_targets_stage_1_train)
# Estimates the coefficients of the object from the 'LogisticRegression' class
# with inputs (independent variables) contained in the first dataframe
# and targets (dependent variables) contained in the second dataframe.
feature_name = lgd_inputs_stage_1_train.columns.values
# Stores the names of the columns of a dataframe in a variable.
summary_table = pd.DataFrame(columns = ['Feature name'], data = feature_name)
# Creates a dataframe with a column titled 'Feature name' and row values contained in the 'feature_name' variable.
summary_table['Coefficients'] = np.transpose(reg_lgd_st_1.coef_)
# Creates a new column in the dataframe, called 'Coefficients',
# with row values the transposed coefficients from the 'LogisticRegression' object.
summary_table.index = summary_table.index + 1
# Increases the index of every row of the dataframe with 1.
summary_table.loc[0] = ['Intercept', reg_lgd_st_1.intercept_[0]]
# Assigns values of the row with index 0 of the dataframe.
summary_table = summary_table.sort_index()
# Sorts the dataframe by index.
p_values = reg_lgd_st_1.p_values
# We take the result of the newly added method 'p_values' and store it in a variable 'p_values'.
p_values = np.append(np.nan,np.array(p_values))
# We add the value 'NaN' in the beginning of the variable with p-values.
summary_table['p_values'] = p_values
# In the 'summary_table' dataframe, we add a new column, called 'p_values', containing the values from the 'p_values' variable.
summary_table
summary_table = pd.DataFrame(columns = ['Feature name'], data = feature_name)
summary_table['Coefficients'] = np.transpose(reg_lgd_st_1.coef_)
summary_table.index = summary_table.index + 1
summary_table.loc[0] = ['Intercept', reg_lgd_st_1.intercept_[0]]
summary_table = summary_table.sort_index()
p_values = reg_lgd_st_1.p_values
p_values = np.append(np.nan,np.array(p_values))
summary_table['p_values'] = p_values
summary_table
```
### Testing the Model
```
lgd_inputs_stage_1_test = lgd_inputs_stage_1_test[features_all]
# Here we keep only the variables we need for the model.
lgd_inputs_stage_1_test = lgd_inputs_stage_1_test.drop(features_reference_cat, axis = 1)
# Here we remove the dummy variable reference categories.
y_hat_test_lgd_stage_1 = reg_lgd_st_1.model.predict(lgd_inputs_stage_1_test)
# Calculates the predicted values for the dependent variable (targets)
# based on the values of the independent variables (inputs) supplied as an argument.
y_hat_test_lgd_stage_1
y_hat_test_proba_lgd_stage_1 = reg_lgd_st_1.model.predict_proba(lgd_inputs_stage_1_test)
# Calculates the predicted probability values for the dependent variable (targets)
# based on the values of the independent variables (inputs) supplied as an argument.
y_hat_test_proba_lgd_stage_1
# This is an array of arrays of predicted class probabilities for all classes.
# In this case, the first value of every sub-array is the probability for the observation to belong to the first class, i.e. 0,
# and the second value is the probability for the observation to belong to the first class, i.e. 1.
y_hat_test_proba_lgd_stage_1 = y_hat_test_proba_lgd_stage_1[: ][: , 1]
# Here we take all the arrays in the array, and from each array, we take all rows, and only the element with index 1,
# that is, the second element.
# In other words, we take only the probabilities for being 1.
y_hat_test_proba_lgd_stage_1
lgd_targets_stage_1_test_temp = lgd_targets_stage_1_test
lgd_targets_stage_1_test_temp.reset_index(drop = True, inplace = True)
# We reset the index of a dataframe.
df_actual_predicted_probs = pd.concat([lgd_targets_stage_1_test_temp, pd.DataFrame(y_hat_test_proba_lgd_stage_1)], axis = 1)
# Concatenates two dataframes.
df_actual_predicted_probs.columns = ['lgd_targets_stage_1_test', 'y_hat_test_proba_lgd_stage_1']
df_actual_predicted_probs.index = lgd_inputs_stage_1_test.index
# Makes the index of one dataframe equal to the index of another dataframe.
df_actual_predicted_probs.head()
```
### Estimating the Аccuracy of the Мodel
```
tr = 0.5
# We create a new column with an indicator,
# where every observation that has predicted probability greater than the threshold has a value of 1,
# and every observation that has predicted probability lower than the threshold has a value of 0.
df_actual_predicted_probs['y_hat_test_lgd_stage_1'] = np.where(df_actual_predicted_probs['y_hat_test_proba_lgd_stage_1'] > tr, 1, 0)
pd.crosstab(df_actual_predicted_probs['lgd_targets_stage_1_test'], df_actual_predicted_probs['y_hat_test_lgd_stage_1'], rownames = ['Actual'], colnames = ['Predicted'])
# Creates a cross-table where the actual values are displayed by rows and the predicted values by columns.
# This table is known as a Confusion Matrix.
pd.crosstab(df_actual_predicted_probs['lgd_targets_stage_1_test'], df_actual_predicted_probs['y_hat_test_lgd_stage_1'], rownames = ['Actual'], colnames = ['Predicted']) / df_actual_predicted_probs.shape[0]
# Here we divide each value of the table by the total number of observations,
# thus getting percentages, or, rates.
(pd.crosstab(df_actual_predicted_probs['lgd_targets_stage_1_test'], df_actual_predicted_probs['y_hat_test_lgd_stage_1'], rownames = ['Actual'], colnames = ['Predicted']) / df_actual_predicted_probs.shape[0]).iloc[0, 0] + (pd.crosstab(df_actual_predicted_probs['lgd_targets_stage_1_test'], df_actual_predicted_probs['y_hat_test_lgd_stage_1'], rownames = ['Actual'], colnames = ['Predicted']) / df_actual_predicted_probs.shape[0]).iloc[1, 1]
# Here we calculate Accuracy of the model, which is the sum of the diagonal rates.
from sklearn.metrics import roc_curve, roc_auc_score
fpr, tpr, thresholds = roc_curve(df_actual_predicted_probs['lgd_targets_stage_1_test'], df_actual_predicted_probs['y_hat_test_proba_lgd_stage_1'])
# Returns the Receiver Operating Characteristic (ROC) Curve from a set of actual values and their predicted probabilities.
# As a result, we get three arrays: the false positive rates, the true positive rates, and the thresholds.
# we store each of the three arrays in a separate variable.
plt.plot(fpr, tpr)
# We plot the false positive rate along the x-axis and the true positive rate along the y-axis,
# thus plotting the ROC curve.
plt.plot(fpr, fpr, linestyle = '--', color = 'k')
# We plot a seconary diagonal line, with dashed line style and black color.
plt.xlabel('False positive rate')
# We name the x-axis "False positive rate".
plt.ylabel('True positive rate')
# We name the x-axis "True positive rate".
plt.title('ROC curve')
# We name the graph "ROC curve".
AUROC = roc_auc_score(df_actual_predicted_probs['lgd_targets_stage_1_test'], df_actual_predicted_probs['y_hat_test_proba_lgd_stage_1'])
# Calculates the Area Under the Receiver Operating Characteristic Curve (AUROC)
# from a set of actual values and their predicted probabilities.
AUROC
```
### Saving the Model
```
import pickle
pickle.dump(reg_lgd_st_1, open('lgd_model_stage_1.sav', 'wb'))
# Here we export our model to a 'SAV' file with file name 'lgd_model_stage_1.sav'.
```
### Stage 2 – Linear Regression
```
lgd_stage_2_data = loan_data_defaults[loan_data_defaults['recovery_rate_0_1'] == 1]
# Here we take only rows where the original recovery rate variable is greater than one,
# i.e. where the indicator variable we created is equal to 1.
# LGD model stage 2 datasets: how much more than 0 is the recovery rate
lgd_inputs_stage_2_train, lgd_inputs_stage_2_test, lgd_targets_stage_2_train, lgd_targets_stage_2_test = train_test_split(lgd_stage_2_data.drop(['good_bad', 'recovery_rate','recovery_rate_0_1', 'CCF'], axis = 1), lgd_stage_2_data['recovery_rate'], test_size = 0.2, random_state = 42)
# Takes a set of inputs and a set of targets as arguments. Splits the inputs and the targets into four dataframes:
# Inputs - Train, Inputs - Test, Targets - Train, Targets - Test.
from sklearn import linear_model
from sklearn.metrics import mean_squared_error, r2_score
# Since the p-values are obtained through certain statistics, we need the 'stat' module from scipy.stats
import scipy.stats as stat
# Since we are using an object oriented language such as Python, we can simply define our own
# LinearRegression class (the same one from sklearn)
# By typing the code below we will ovewrite a part of the class with one that includes p-values
# Here's the full source code of the ORIGINAL class: https://github.com/scikit-learn/scikit-learn/blob/7b136e9/sklearn/linear_model/base.py#L362
class LinearRegression(linear_model.LinearRegression):
"""
LinearRegression class after sklearn's, but calculate t-statistics
and p-values for model coefficients (betas).
Additional attributes available after .fit()
are `t` and `p` which are of the shape (y.shape[1], X.shape[1])
which is (n_features, n_coefs)
This class sets the intercept to 0 by default, since usually we include it
in X.
"""
# nothing changes in __init__
def __init__(self, fit_intercept=True, normalize=False, copy_X=True,
n_jobs=1):
self.fit_intercept = fit_intercept
self.normalize = normalize
self.copy_X = copy_X
self.n_jobs = n_jobs
def fit(self, X, y, n_jobs=1):
self = super(LinearRegression, self).fit(X, y, n_jobs)
# Calculate SSE (sum of squared errors)
# and SE (standard error)
sse = np.sum((self.predict(X) - y) ** 2, axis=0) / float(X.shape[0] - X.shape[1])
se = np.array([np.sqrt(np.diagonal(sse * np.linalg.inv(np.dot(X.T, X))))])
# compute the t-statistic for each feature
self.t = self.coef_ / se
# find the p-value for each feature
self.p = np.squeeze(2 * (1 - stat.t.cdf(np.abs(self.t), y.shape[0] - X.shape[1])))
return self
import scipy.stats as stat
class LinearRegression(linear_model.LinearRegression):
def __init__(self, fit_intercept=True, normalize=False, copy_X=True,
n_jobs=1):
self.fit_intercept = fit_intercept
self.normalize = normalize
self.copy_X = copy_X
self.n_jobs = n_jobs
def fit(self, X, y, n_jobs=1):
self = super(LinearRegression, self).fit(X, y, n_jobs)
sse = np.sum((self.predict(X) - y) ** 2, axis=0) / float(X.shape[0] - X.shape[1])
se = np.array([np.sqrt(np.diagonal(sse * np.linalg.inv(np.dot(X.T, X))))])
self.t = self.coef_ / se
self.p = np.squeeze(2 * (1 - stat.t.cdf(np.abs(self.t), y.shape[0] - X.shape[1])))
return self
lgd_inputs_stage_2_train = lgd_inputs_stage_2_train[features_all]
# Here we keep only the variables we need for the model.
lgd_inputs_stage_2_train = lgd_inputs_stage_2_train.drop(features_reference_cat, axis = 1)
# Here we remove the dummy variable reference categories.
reg_lgd_st_2 = LinearRegression()
# We create an instance of an object from the 'LogisticRegression' class.
reg_lgd_st_2.fit(lgd_inputs_stage_2_train, lgd_targets_stage_2_train)
# Estimates the coefficients of the object from the 'LogisticRegression' class
# with inputs (independent variables) contained in the first dataframe
# and targets (dependent variables) contained in the second dataframe.
feature_name = lgd_inputs_stage_2_train.columns.values
# Stores the names of the columns of a dataframe in a variable.
summary_table = pd.DataFrame(columns = ['Feature name'], data = feature_name)
# Creates a dataframe with a column titled 'Feature name' and row values contained in the 'feature_name' variable.
summary_table['Coefficients'] = np.transpose(reg_lgd_st_2.coef_)
# Creates a new column in the dataframe, called 'Coefficients',
# with row values the transposed coefficients from the 'LogisticRegression' object.
summary_table.index = summary_table.index + 1
# Increases the index of every row of the dataframe with 1.
summary_table.loc[0] = ['Intercept', reg_lgd_st_2.intercept_]
# Assigns values of the row with index 0 of the dataframe.
summary_table = summary_table.sort_index()
# Sorts the dataframe by index.
p_values = reg_lgd_st_2.p
# We take the result of the newly added method 'p_values' and store it in a variable 'p_values'.
p_values = np.append(np.nan,np.array(p_values))
# We add the value 'NaN' in the beginning of the variable with p-values.
summary_table['p_values'] = p_values.round(3)
# In the 'summary_table' dataframe, we add a new column, called 'p_values', containing the values from the 'p_values' variable.
summary_table
summary_table = pd.DataFrame(columns = ['Feature name'], data = feature_name)
summary_table['Coefficients'] = np.transpose(reg_lgd_st_2.coef_)
summary_table.index = summary_table.index + 1
summary_table.loc[0] = ['Intercept', reg_lgd_st_2.intercept_]
summary_table = summary_table.sort_index()
p_values = reg_lgd_st_2.p
p_values = np.append(np.nan,np.array(p_values))
summary_table['p_values'] = p_values.round(3)
summary_table
```
### Stage 2 – Linear Regression Evaluation
```
lgd_inputs_stage_2_test = lgd_inputs_stage_2_test[features_all]
# Here we keep only the variables we need for the model.
lgd_inputs_stage_2_test = lgd_inputs_stage_2_test.drop(features_reference_cat, axis = 1)
# Here we remove the dummy variable reference categories.
lgd_inputs_stage_2_test.columns.values
# Calculates the predicted values for the dependent variable (targets)
# based on the values of the independent variables (inputs) supplied as an argument.
y_hat_test_lgd_stage_2 = reg_lgd_st_2.predict(lgd_inputs_stage_2_test)
# Calculates the predicted values for the dependent variable (targets)
# based on the values of the independent variables (inputs) supplied as an argument.
lgd_targets_stage_2_test_temp = lgd_targets_stage_2_test
lgd_targets_stage_2_test_temp = lgd_targets_stage_2_test_temp.reset_index(drop = True)
# We reset the index of a dataframe.
pd.concat([lgd_targets_stage_2_test_temp, pd.DataFrame(y_hat_test_lgd_stage_2)], axis = 1).corr()
# We calculate the correlation between actual and predicted values.
sns.distplot(lgd_targets_stage_2_test - y_hat_test_lgd_stage_2)
# We plot the distribution of the residuals.
pickle.dump(reg_lgd_st_2, open('lgd_model_stage_2.sav', 'wb'))
# Here we export our model to a 'SAV' file with file name 'lgd_model_stage_1.sav'.
```
### Combining Stage 1 and Stage 2
```
y_hat_test_lgd_stage_2_all = reg_lgd_st_2.predict(lgd_inputs_stage_1_test)
y_hat_test_lgd_stage_2_all
y_hat_test_lgd = y_hat_test_lgd_stage_1 * y_hat_test_lgd_stage_2_all
# Here we combine the predictions of the models from the two stages.
pd.DataFrame(y_hat_test_lgd).describe()
# Shows some descriptive statisics for the values of a column.
y_hat_test_lgd = np.where(y_hat_test_lgd < 0, 0, y_hat_test_lgd)
y_hat_test_lgd = np.where(y_hat_test_lgd > 1, 1, y_hat_test_lgd)
# We set predicted values that are greater than 1 to 1 and predicted values that are less than 0 to 0.
pd.DataFrame(y_hat_test_lgd).describe()
# Shows some descriptive statisics for the values of a column.
```
# EAD Model
### Estimation and Interpretation
```
# EAD model datasets
ead_inputs_train, ead_inputs_test, ead_targets_train, ead_targets_test = train_test_split(loan_data_defaults.drop(['good_bad', 'recovery_rate','recovery_rate_0_1', 'CCF'], axis = 1), loan_data_defaults['CCF'], test_size = 0.2, random_state = 42)
# Takes a set of inputs and a set of targets as arguments. Splits the inputs and the targets into four dataframes:
# Inputs - Train, Inputs - Test, Targets - Train, Targets - Test.
ead_inputs_train.columns.values
ead_inputs_train = ead_inputs_train[features_all]
# Here we keep only the variables we need for the model.
ead_inputs_train = ead_inputs_train.drop(features_reference_cat, axis = 1)
# Here we remove the dummy variable reference categories.
reg_ead = LinearRegression()
# We create an instance of an object from the 'LogisticRegression' class.
reg_ead.fit(ead_inputs_train, ead_targets_train)
# Estimates the coefficients of the object from the 'LogisticRegression' class
# with inputs (independent variables) contained in the first dataframe
# and targets (dependent variables) contained in the second dataframe.
feature_name = ead_inputs_train.columns.values
summary_table = pd.DataFrame(columns = ['Feature name'], data = feature_name)
# Creates a dataframe with a column titled 'Feature name' and row values contained in the 'feature_name' variable.
summary_table['Coefficients'] = np.transpose(reg_ead.coef_)
# Creates a new column in the dataframe, called 'Coefficients',
# with row values the transposed coefficients from the 'LogisticRegression' object.
summary_table.index = summary_table.index + 1
# Increases the index of every row of the dataframe with 1.
summary_table.loc[0] = ['Intercept', reg_ead.intercept_]
# Assigns values of the row with index 0 of the dataframe.
summary_table = summary_table.sort_index()
# Sorts the dataframe by index.
p_values = reg_ead.p
# We take the result of the newly added method 'p_values' and store it in a variable 'p_values'.
p_values = np.append(np.nan,np.array(p_values))
# We add the value 'NaN' in the beginning of the variable with p-values.
summary_table['p_values'] = p_values
# In the 'summary_table' dataframe, we add a new column, called 'p_values', containing the values from the 'p_values' variable.
summary_table
```
|
github_jupyter
|
# Principal Component Analysis (PCA) in Python #
Killian McKee
### Overview ###
1. [What is PCA?](#section1)
2. [Key Terms](#section2)
3. [Pros and Cons of PCA](#section3)
4. [When to use PCA](#section4)
5. [Key Parameters](#section5)
6. [Walkthrough: PCA for data visualization](#section6)
7. [Walkthrough: PCA w/ Random Forest](#section7)
7. [Additional Reading](#section8)
8. [Conclusion](#section9)
9. [Sources](#section10)
<a id='section1'></a>
### What is Principal Component Analysis? ###
Principal component analysis is a non-parametric data science tool that allows us to identify the most important variables in a data set consisting of many correlated variables. In more technical terms, pca helps us reduce the dimensionality of our feature space by highlighting the most important variables (principal components) of a dataset via orth0gonalization. Pca is typically done before a model is built to decide which variables to include and to eliminate those which are overly correlated with one another. Principal component analysis provides two primary benefits; firstly, it can help our models avoid overfitting by eliminating extraneous variables that are most likely only pertinent (if at all) for our training data, but not the new data it would see in the real world. Secondly, performing pca can drastically improve model training speed in high dimensional data settings (when there are lots of features in a dataset).
<a id='section2'></a>
### Key Terms ###
1. **Dimensionality**: the number of features in a dataset (represented by more columns in a tidy dataset). Pca aims to reduce excessive dimensionality in a dataset to improve model performance.
2. **Correlation**: A measure of closeness between two variables, ranging from -1 to +1. A negative correlation indicates that when one variable goes up, the other goes down (and a posistive correlation indicates they both move in the same direction). PCA helps us eliminate redundant correlated variables.
3. **Orthagonal**: Uncorrelated to one another i.e. they have a correlation of 0. PCA seeks to find an orthgonalized subset of the data that still captures most/all of the important information for our model.
4. **Covariance Matrix**: A matrix we can generate to show how correlated variables are with one another. This can be a helpul tool to visualize what features PCA may or may not eliminate.
<a id='section3'></a>
### Pros and Cons of PCA ###
There are no real cons of PCA, but it does have some limitations:
**Pros**:
1. Reduces model noise
2. Easy to implement with python packages like pandas and scikit-learn
3. Improves model training time
**Limitations**:
1. Linearity: pca assumes the principle components are a linear combination of the original dataset features.
2. Variance measure: pca uses variance as the measure of dimension importance. This can mean axes with high variance can be treated as principle components and those with low variance can be cut out as noise.
3. Orthogonality: pca assumes the principle components are orthogonal, and won't produce meaningful results otherwise.
<a id='section4'></a>
### When to use Principal Component Analysis ###
One should consider using PCA when the following conditions are true:
1. The linearity, variance, and orthogonality limitations specified above are satisfied.
2. Your dataset contains many features
3. You are interested in reducing the noise of your dataset or improving model training time
<a id='section5'></a>
### Key Parameters ###
The number of features to keep post pca (typically denoted by n_components) is the only major parameter for PCA.
<a id='section6'></a>
### PCA Walkthrough: Data Visualization ###
We will be modifying scikit-learn's tutorial on fitting PCA for visualization using the iris [dataset](https://en.wikipedia.org/wiki/Iris_flower_data_set) (contains different species of flowers).
```
# import the necessary packages
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn import decomposition
from sklearn import datasets
#specify graph parameters for iris and load the dataset
centers = [[1, 1], [-1, -1], [1, -1]]
iris = datasets.load_iris()
# set features and target
X = iris.data
y = iris.target
# create the chart
fig = plt.figure(1, figsize=(4, 3))
plt.clf()
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
# fit our PCA
plt.cla()
pca = decomposition.PCA(n_components=3)
pca.fit(X)
X = pca.transform(X)
# plot our data
for name, label in [('Setosa', 0), ('Versicolour', 1), ('Virginica', 2)]:
ax.text3D(X[y == label, 0].mean(),
X[y == label, 1].mean() + 1.5,
X[y == label, 2].mean(), name,
horizontalalignment='center',
bbox=dict(alpha=.5, edgecolor='w', facecolor='w'))
# Reorder the labels to have colors matching the cluster results
y = np.choose(y, [1, 2, 0]).astype(np.float)
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y, cmap=plt.cm.nipy_spectral,
edgecolor='k')
ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
plt.show()
#we can clearly see the three species within the iris dataset and how the differ from one another
```
<a id='section7'></a>
### Walkthrough: PCA w/ Random Forest ###
In this tutorial we will be walking through the typical workflow to improve model speed with PCA, then fitting a random forest. We will be working with the iris dataset again, but we will load it into a pandas dataframe
```
# import necessary packages
import numpy as np
import pandas as pd
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
# download the data
data = datasets.load_iris()
df = pd.DataFrame(data['data'], columns=data['feature_names'])
df['target'] = data['target']
df.head()
# split the data into features and target
X = df.drop('target', 1)
y = df['target']
#creating training and test splits
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# scaling the data
# since pca uses variance as a measure, it is best to scale the data
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
# apply and fit the pca
# play around with the n_components value to see how the model does
pca = PCA(n_components=4)
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)
# generate the explained variance, which shows us how much variance is caused by each variable
# we can see from the example below that more than 96% of the data can be explained by the first two principle components
explained_variance = pca.explained_variance_ratio_
explained_variance
# now lets fit a random forest so we can see how the accuracy changes with different levels of components
# this model has all the components
classifier = RandomForestClassifier(max_depth=2, random_state=0)
classifier.fit(X_train, y_train)
# Predicting the Test set results
y_pred = classifier.predict(X_test)
# all component model accuracy
# we can see it achieves an accuracy of 93%
cm = confusion_matrix(y_test, y_pred)
print(cm)
print('Accuracy', accuracy_score(y_test, y_pred))
# Now lets see how the model does with only 2 components
# our accuracy decreases by about 3%, but we can see how this might be useful if we had 100s of components
pca = PCA(n_components=2)
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)
classifier = RandomForestClassifier(max_depth=2, random_state=0)
classifier.fit(X_train, y_train)
# Predicting the Test set results
y_pred = classifier.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
print(cm)
print('Accuracy', accuracy_score(y_test, y_pred))
```
<a id='section8'></a>
### Additional Reading ###
1. Going into much greater depth on [PCA](https://www-bcf.usc.edu/~gareth/ISL/ISLR%20First%20Printing.pdf)
2. Visualizing [PCA](http://setosa.io/ev/principal-component-analysis/)
<a id='section9'></a>
### Conclusion ###
This guide explained how principal component analysis helps reduce noise in our dataset and improve model speed via a simplified feature space. Next, we looked at some of the key components and limitations of PCA, namely the number of preserved components and the linearity, othogonality, and variance requirements, respectively. Lastly, we stepped through two examples of how to implement PCA; the first covered visualization, while the second tackled PCA as a preprocessing step with random forests.
<a id='section10'></a>
### Sources ###
1. https://arxiv.org/pdf/1404.1100.pdf?utm_campaign=buffer&utm_content=bufferb37df&utm_medium=social&utm_source=facebook.com
2. https://stackabuse.com/implementing-pca-in-python-with-scikit-learn/
3. https://www-bcf.usc.edu/~gareth/ISL/ISLR%20First%20Printing.pdf
4. http://setosa.io/ev/principal-component-analysis/
|
github_jupyter
|
```
from libraries.import_export_data_objects import import_export_data as Import_Export_Data
from libraries.altair_renderings import AltairRenderings
from libraries.utility import Utility
import os
import altair as alt
my_altair = AltairRenderings()
from IPython.core.display import display, HTML
display(HTML(
'<style>'
'#notebook { padding-top:0px !important; } '
'.container { width:100% !important; } '
'.end_space { min-height:0px !important; } '
'.end_space { min-height:0px !important; } '
'.prompt {width: 0px; min-width: 0px; visibility: collapse } '
'</style>'
))
```
# <center>Exploratory Data Analysis</center>
## <center>Don Irwin</center>
### <center>U.C. Berkeley MIDS</center>
### <center>W209 - Spring 2022 Thursday 4 P.M.</center>
### Background:
MIDS students taking W209, Data Visualization, are expected to demonstrate an ability to source datasets, analyze datasets, and present visualizations in the form of web-based applications, to convey insights from those datasets to users.
Our team will communicate trade trends over the past 6 years, for the world's top 20 trading nations.
### Data Sources, and description of those data:
Our data is sourced from the World Trade Organization, and Bloomberg. These data consist primarily of datasets which contain total trade, total imports, and total exports, time-series, by any one of the top 20 trading nations with another. These data also contain trade categories, of each of these nations with the other.
### Limitations of data set:
This data set is limited to 20 countries for 6 years. This is due to the difficulty of harvesting, and pre-processing data. These data are sufficiently feature rich to demonstrate hypothesis. However, they lack longtitudinal depth require to draw conclusions about world trade trends over a long term. They do, however, provide a view into trade between the world's 20 largest trading nations over the past six years.
## Hypothesis 1:
While not a country, the European Union, has been the world's largest trading block. It has been so for the past 6 years.
```
my_altair.get_import_export_balance_top_five("World")
#my_altair.get_altaire_bar_top5_partners("World")
```
### What is informative about this view:
The view above shows the top 5 trading nations or blocks in the world with a slider for the years between 2014 and 2020.
Utilizing the slider, a user can see that for each of the years the European Union is consistently the top trading block.
While not directly related to the hypothesis, we see that nations with net negative trade values (related to the world) are nations with which the world is importing more things from. We see that the world is consistently importing more things from China, while consistently exporting more things to the United States. This means china is a net retrainer of trade dollars, while the United States is a net exporter, so to speak, of trade dollars.
### What could be improved about this view:
This view is bordering on being a bit busy, and may be better as a stacked bar chart, or ordered from highest trade, to lowest trade.
## Hypothesis 2:
China dominates trade with the Middle East, South Asia, Southeast Asia, and Asia Pacific nations. China has done so for the past 6 years with, although, moving the slider, below will show that the European Union was the top trading partner of Saudi Arabia and India for a few of the years prior to 2016.
```
indo = my_altair.get_altaire_bar_top5_partners_for_matrix("Indonesia")
indo
saudi = my_altair.get_altaire_bar_top5_partners_for_matrix("Saudi Arabia")
saudi
iran = my_altair.get_altaire_bar_top5_partners_for_matrix("Iran")
iran
sk = my_altair.get_altaire_bar_top5_partners_for_matrix("South Korea")
sk
jap = my_altair.get_altaire_bar_top5_partners_for_matrix("Japan")
india = my_altair.get_altaire_bar_top5_partners_for_matrix("India")
row_1 = (indo | saudi )
row_2 = (iran | india )
row_3 = (sk | jap )
my_chart = (row_1 & row_2 & row_3).configure_axis(
grid=False
).configure_view(
strokeWidth=0
)
my_chart
#indo.properties(width=700,height=200)
```
### What is informative about this view:
The view above shows 6 nations in Asia, from the Middle East, to the Far East, and it provides a slider to compare different years. We see, that for almost all of these nations, for almost all years in the visualization, China is the top trading partner. In the case of India and Saudi Arabia, we see that in 2014, their leading trading partner block was the European Union, but it switched to China.
### What could be improved about this view:
This view sometimes "wiggles" because of the labels pushing out from side to side. This could be improved.
## Hypothesis 3
Geopolitical events can have a drastic impact on a nation's trade, and that nation's ability to buy and sell with the rest of the world.
```
sk = my_altair.get_altaire_line_chart_county_trade_for_matrix("South Korea","Iran")
spain = my_altair.get_altaire_line_chart_county_trade_for_matrix("Spain","Iran")
usa = my_altair.get_altaire_line_chart_county_trade_for_matrix("United States","Iran")
jap = my_altair.get_altaire_line_chart_county_trade_for_matrix("Indonesia","Iran")
row_1 = (sk | spain )
row_2 = (usa | jap )
my_chart = (row_1 & row_2).configure_axis(
grid=False
).configure_view(
strokeWidth=0
)
my_chart
#indo.properties(width=700,height=200)
```
### What is informative about this view:
The View above clearly shows the trade impact on Iran as the result of the Trump Administration's withdrawl from the JCPOA, also known as the "Iran Nuclear Deal".
We can see that generally from 2014 (the time of the JCPOA) until 2016-2017 trade between Iran and other nations was increasing drastically.
Once Trump imposed secondary sanctions on people trading with Iran, there was a massive crash in trade with Iran.
### What could be improved about this view:
Lines should be thicker, and the tool tip should be improved. The charts could be changed to indicate in some fashion, the date of the cancellation of the JCPOA.
## Conclusion:
The data do appear to support the various hypothensis presented.
The challenge with this project is to create a Summary-Zoom-Detail paradign within the application that can communicate effectively to a user.
At this stage, we are still struggling with how to represent different datasets and datum effectively.
Thank you for your instruction during this project.
Best regards,
Don Irwin
|
github_jupyter
|
# Face Generation
In this project, you'll define and train a DCGAN on a dataset of faces. Your goal is to get a generator network to generate *new* images of faces that look as realistic as possible!
The project will be broken down into a series of tasks from **loading in data to defining and training adversarial networks**. At the end of the notebook, you'll be able to visualize the results of your trained Generator to see how it performs; your generated samples should look like fairly realistic faces with small amounts of noise.
### Get the Data
You'll be using the [CelebFaces Attributes Dataset (CelebA)](http://mmlab.ie.cuhk.edu.hk/projects/CelebA.html) to train your adversarial networks.
This dataset is more complex than the number datasets (like MNIST or SVHN) you've been working with, and so, you should prepare to define deeper networks and train them for a longer time to get good results. It is suggested that you utilize a GPU for training.
### Pre-processed Data
Since the project's main focus is on building the GANs, we've done *some* of the pre-processing for you. Each of the CelebA images has been cropped to remove parts of the image that don't include a face, then resized down to 64x64x3 NumPy images. Some sample data is show below.
<img src='assets/processed_face_data.png' width=60% />
> If you are working locally, you can download this data [by clicking here](https://s3.amazonaws.com/video.udacity-data.com/topher/2018/November/5be7eb6f_processed-celeba-small/processed-celeba-small.zip)
This is a zip file that you'll need to extract in the home directory of this notebook for further loading and processing. After extracting the data, you should be left with a directory of data `processed_celeba_small/`
```
# can comment out after executing
# !unzip processed_celeba_small.zip
import os
thedir = './processed_celeba_small/celeba/'
# [ name for name in os.listdir(thedir) if os.path.isdir(os.path.join(thedir, name)) ]
print (len([name for name in os.listdir(thedir) if os.path.isfile(os.path.join(thedir, name))]))
data_dir = 'processed_celeba_small/'
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import pickle as pkl
import matplotlib.pyplot as plt
import numpy as np
import problem_unittests as tests
#import helper
%matplotlib inline
```
## Visualize the CelebA Data
The [CelebA](http://mmlab.ie.cuhk.edu.hk/projects/CelebA.html) dataset contains over 200,000 celebrity images with annotations. Since you're going to be generating faces, you won't need the annotations, you'll only need the images. Note that these are color images with [3 color channels (RGB)](https://en.wikipedia.org/wiki/Channel_(digital_image)#RGB_Images) each.
### Pre-process and Load the Data
Since the project's main focus is on building the GANs, we've done *some* of the pre-processing for you. Each of the CelebA images has been cropped to remove parts of the image that don't include a face, then resized down to 64x64x3 NumPy images. This *pre-processed* dataset is a smaller subset of the very large CelebA data.
> There are a few other steps that you'll need to **transform** this data and create a **DataLoader**.
#### Exercise: Complete the following `get_dataloader` function, such that it satisfies these requirements:
* Your images should be square, Tensor images of size `image_size x image_size` in the x and y dimension.
* Your function should return a DataLoader that shuffles and batches these Tensor images.
#### ImageFolder
To create a dataset given a directory of images, it's recommended that you use PyTorch's [ImageFolder](https://pytorch.org/docs/stable/torchvision/datasets.html#imagefolder) wrapper, with a root directory `processed_celeba_small/` and data transformation passed in.
```
# necessary imports
import torch
import os
from torchvision import datasets
from torchvision import transforms
from torch.utils.data import DataLoader
# import shutil
# import os
# image_path = './' + data_dir
# source = os.path.join(image_path,'celeba/New Folder With Items/')
# print(source)
# # source = './processed_celeba_small/celeba/New Folder With Items'
# dest1 = './processed_celeba_small/celeba/'
# files = os.listdir(source)
# for f in files:
# shutil.move(source+f, dest1)
def get_dataloader(batch_size, image_size, data_dir='processed_celeba_small/'):
"""
Batch the neural network data using DataLoader
:param batch_size: The size of each batch; the number of images in a batch
:param img_size: The square size of the image data (x, y)
:param data_dir: Directory where image data is located
:return: DataLoader with batched data
"""
# TODO: Implement function and return a dataloader
# resize and normalize the images
transform = transforms.Compose([transforms.Resize(image_size), transforms.ToTensor()])
# get training directories
train_path = './' + data_dir
# train_path = os.path.join(image_path,'celeba')
print(train_path)
# define datasets using ImageFolder
train_dataset = datasets.ImageFolder(train_path, transform)
# create and return DataLoaders
num_workers = 0
train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True, num_workers=num_workers)
return train_loader
```
## Create a DataLoader
#### Exercise: Create a DataLoader `celeba_train_loader` with appropriate hyperparameters.
Call the above function and create a dataloader to view images.
* You can decide on any reasonable `batch_size` parameter
* Your `image_size` **must be** `32`. Resizing the data to a smaller size will make for faster training, while still creating convincing images of faces!
```
# Define function hyperparameters
batch_size = 128
img_size = 32
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
# Call your function and get a dataloader
celeba_train_loader = get_dataloader(batch_size, img_size)
print(len(celeba_train_loader.dataset))
```
Next, you can view some images! You should seen square images of somewhat-centered faces.
Note: You'll need to convert the Tensor images into a NumPy type and transpose the dimensions to correctly display an image, suggested `imshow` code is below, but it may not be perfect.
```
# helper display function
def imshow(img):
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
# obtain one batch of training images
dataiter = iter(celeba_train_loader)
images, _ = dataiter.next() # _ for no labels
# plot the images in the batch, along with the corresponding labels
fig = plt.figure(figsize=(20, 4))
plot_size=20
for idx in np.arange(plot_size):
ax = fig.add_subplot(2, plot_size/2, idx+1, xticks=[], yticks=[])
imshow(images[idx])
```
#### Exercise: Pre-process your image data and scale it to a pixel range of -1 to 1
You need to do a bit of pre-processing; you know that the output of a `tanh` activated generator will contain pixel values in a range from -1 to 1, and so, we need to rescale our training images to a range of -1 to 1. (Right now, they are in a range from 0-1.)
```
# TODO: Complete the scale function
def scale(x, feature_range=(-1, 1)):
''' Scale takes in an image x and returns that image, scaled
with a feature_range of pixel values from -1 to 1.
This function assumes that the input x is already scaled from 0-1.'''
# assume x is scaled to (0, 1)
# scale to feature_range and return scaled x
min, max = feature_range
x = x * (max - min) + min
return x
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
# check scaled range
# should be close to -1 to 1
img = images[0]
scaled_img = scale(img)
print('Min: ', scaled_img.min())
print('Max: ', scaled_img.max())
```
---
# Define the Model
A GAN is comprised of two adversarial networks, a discriminator and a generator.
## Discriminator
Your first task will be to define the discriminator. This is a convolutional classifier like you've built before, only without any maxpooling layers. To deal with this complex data, it's suggested you use a deep network with **normalization**. You are also allowed to create any helper functions that may be useful.
#### Exercise: Complete the Discriminator class
* The inputs to the discriminator are 32x32x3 tensor images
* The output should be a single value that will indicate whether a given image is real or fake
```
import torch.nn as nn
import torch.nn.functional as F
# helper conv function
def conv(in_channels, out_channels, kernel_size, stride=2, padding=1, batch_norm=True):
"""Creates a convolutional layer, with optional batch normalization.
"""
layers = []
conv_layer = nn.Conv2d(in_channels, out_channels,
kernel_size, stride, padding, bias=False)
# append conv layer
layers.append(conv_layer)
if batch_norm:
# append batchnorm layer
layers.append(nn.BatchNorm2d(out_channels))
# using Sequential container
return nn.Sequential(*layers)
class Discriminator(nn.Module):
def __init__(self, conv_dim):
"""
Initialize the Discriminator Module
:param conv_dim: The depth of the first convolutional layer
"""
super(Discriminator, self).__init__()
# complete init function
self.conv_dim = conv_dim
# 32x32 input
self.conv1 = conv(3, conv_dim, 4, batch_norm=False) # first layer, no batch_norm
self.conv2 = conv(conv_dim, conv_dim*2, 4)
self.conv3 = conv(conv_dim*2, conv_dim*4, 4)
# final, fully-connected layer
self.fc = nn.Linear(conv_dim*4*4*4, 1)
def forward(self, x):
"""
Forward propagation of the neural network
:param x: The input to the neural network
:return: Discriminator logits; the output of the neural network
"""
# define feedforward behavior
out = F.leaky_relu(self.conv1(x), 0.2)
out = F.leaky_relu(self.conv2(out), 0.2)
out = F.leaky_relu(self.conv3(out), 0.2)
# flatten
out = out.view(-1, self.conv_dim*4*4*4)
# final output layer
out = self.fc(out)
return out
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_discriminator(Discriminator)
```
## Generator
The generator should upsample an input and generate a *new* image of the same size as our training data `32x32x3`. This should be mostly transpose convolutional layers with normalization applied to the outputs.
#### Exercise: Complete the Generator class
* The inputs to the generator are vectors of some length `z_size`
* The output should be a image of shape `32x32x3`
```
def deconv(in_channels, out_channels, kernel_size, stride=2, padding=1, batch_norm=True):
"""Creates a transposed-convolutional layer, with optional batch normalization.
"""
# create a sequence of transpose + optional batch norm layers
layers = []
transpose_conv_layer = nn.ConvTranspose2d(in_channels, out_channels,
kernel_size, stride, padding, bias=False)
# append transpose convolutional layer
layers.append(transpose_conv_layer)
if batch_norm:
# append batchnorm layer
layers.append(nn.BatchNorm2d(out_channels))
return nn.Sequential(*layers)
class Generator(nn.Module):
def __init__(self, z_size, conv_dim):
"""
Initialize the Generator Module
:param z_size: The length of the input latent vector, z
:param conv_dim: The depth of the inputs to the *last* transpose convolutional layer
"""
super(Generator, self).__init__()
# complete init function
self.conv_dim = conv_dim
# first, fully-connected layer
self.fc = nn.Linear(z_size, conv_dim*4*4*4)
# transpose conv layers
self.t_conv1 = deconv(conv_dim*4, conv_dim*2, 4)
self.t_conv2 = deconv(conv_dim*2, conv_dim, 4)
self.t_conv3 = deconv(conv_dim, 3, 4, batch_norm=False)
def forward(self, x):
"""
Forward propagation of the neural network
:param x: The input to the neural network
:return: A 32x32x3 Tensor image as output
"""
# define feedforward behavior
# fully-connected + reshape
out = self.fc(x)
out = out.view(-1, self.conv_dim*4, 4, 4) # (batch_size, depth, 4, 4)
# hidden transpose conv layers + relu
out = F.relu(self.t_conv1(out))
out = F.relu(self.t_conv2(out))
# last layer + tanh activation
out = self.t_conv3(out)
out = F.tanh(out)
return out
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_generator(Generator)
```
## Initialize the weights of your networks
To help your models converge, you should initialize the weights of the convolutional and linear layers in your model. From reading the [original DCGAN paper](https://arxiv.org/pdf/1511.06434.pdf), they say:
> All weights were initialized from a zero-centered Normal distribution with standard deviation 0.02.
So, your next task will be to define a weight initialization function that does just this!
You can refer back to the lesson on weight initialization or even consult existing model code, such as that from [the `networks.py` file in CycleGAN Github repository](https://github.com/junyanz/pytorch-CycleGAN-and-pix2pix/blob/master/models/networks.py) to help you complete this function.
#### Exercise: Complete the weight initialization function
* This should initialize only **convolutional** and **linear** layers
* Initialize the weights to a normal distribution, centered around 0, with a standard deviation of 0.02.
* The bias terms, if they exist, may be left alone or set to 0.
```
from torch.nn import init
def weights_init_normal(m):
"""
Applies initial weights to certain layers in a model .
The weights are taken from a normal distribution
with mean = 0, std dev = 0.02.
:param m: A module or layer in a network
"""
# classname will be something like:
# `Conv`, `BatchNorm2d`, `Linear`, etc.
classname = m.__class__.__name__
# TODO: Apply initial weights to convolutional and linear layers
if classname.find('Conv') != -1:
nn.init.normal_(m.weight.data, 0.0, 0.02)
elif classname.find('BatchNorm') != -1:
nn.init.normal_(m.weight.data, 1.0, 0.02)
nn.init.constant_(m.bias.data, 0)
# print('initialize network with %s' % init_type)
```
## Build complete network
Define your models' hyperparameters and instantiate the discriminator and generator from the classes defined above. Make sure you've passed in the correct input arguments.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
def build_network(d_conv_dim, g_conv_dim, z_size):
# define discriminator and generator
D = Discriminator(d_conv_dim)
G = Generator(z_size=z_size, conv_dim=g_conv_dim)
# initialize model weights
D.apply(weights_init_normal)
G.apply(weights_init_normal)
print(D)
print()
print(G)
return D, G
```
#### Exercise: Define model hyperparameters
```
# Define model hyperparams
d_conv_dim = 32
g_conv_dim = 32
z_size = 200
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
D, G = build_network(d_conv_dim, g_conv_dim, z_size)
```
### Training on GPU
Check if you can train on GPU. Here, we'll set this as a boolean variable `train_on_gpu`. Later, you'll be responsible for making sure that
>* Models,
* Model inputs, and
* Loss function arguments
Are moved to GPU, where appropriate.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import torch
# Check for a GPU
train_on_gpu = torch.cuda.is_available()
if not train_on_gpu:
print('No GPU found. Please use a GPU to train your neural network.')
else:
print('Training on GPU!')
```
---
## Discriminator and Generator Losses
Now we need to calculate the losses for both types of adversarial networks.
### Discriminator Losses
> * For the discriminator, the total loss is the sum of the losses for real and fake images, `d_loss = d_real_loss + d_fake_loss`.
* Remember that we want the discriminator to output 1 for real images and 0 for fake images, so we need to set up the losses to reflect that.
### Generator Loss
The generator loss will look similar only with flipped labels. The generator's goal is to get the discriminator to *think* its generated images are *real*.
#### Exercise: Complete real and fake loss functions
**You may choose to use either cross entropy or a least squares error loss to complete the following `real_loss` and `fake_loss` functions.**
```
def real_loss(D_out, smooth=False):
'''Calculates how close discriminator outputs are to being real.
param, D_out: discriminator logits
return: real loss'''
batch_size = D_out.size(0)
# label smoothing
if smooth:
# smooth, real labels = 0.9
labels = torch.ones(batch_size)*0.9
else:
labels = torch.ones(batch_size) # real labels = 1
# move labels to GPU if available
if train_on_gpu:
labels = labels.cuda()
# binary cross entropy with logits loss
criterion = nn.BCEWithLogitsLoss()
# calculate loss
loss = criterion(D_out.squeeze(), labels)
return loss
def fake_loss(D_out):
'''Calculates how close discriminator outputs are to being fake.
param, D_out: discriminator logits
return: fake loss'''
batch_size = D_out.size(0)
labels = torch.zeros(batch_size) # fake labels = 0
if train_on_gpu:
labels = labels.cuda()
criterion = nn.BCEWithLogitsLoss()
# calculate loss
loss = criterion(D_out.squeeze(), labels)
return loss
```
## Optimizers
#### Exercise: Define optimizers for your Discriminator (D) and Generator (G)
Define optimizers for your models with appropriate hyperparameters.
```
import torch.optim as optim
# params
lr = 0.0002
beta1=0.5
beta2=0.999 # default value
# Create optimizers for the discriminator D and generator G
d_optimizer = optim.Adam(D.parameters(), lr, [beta1, beta2])
g_optimizer = optim.Adam(G.parameters(), lr, [beta1, beta2])
```
---
## Training
Training will involve alternating between training the discriminator and the generator. You'll use your functions `real_loss` and `fake_loss` to help you calculate the discriminator losses.
* You should train the discriminator by alternating on real and fake images
* Then the generator, which tries to trick the discriminator and should have an opposing loss function
#### Saving Samples
You've been given some code to print out some loss statistics and save some generated "fake" samples.
#### Exercise: Complete the training function
Keep in mind that, if you've moved your models to GPU, you'll also have to move any model inputs to GPU.
```
def train(D, G, n_epochs, print_every=50):
'''Trains adversarial networks for some number of epochs
param, D: the discriminator network
param, G: the generator network
param, n_epochs: number of epochs to train for
param, print_every: when to print and record the models' losses
return: D and G losses'''
# move models to GPU
if train_on_gpu:
D.cuda()
G.cuda()
# keep track of loss and generated, "fake" samples
samples = []
losses = []
# Get some fixed data for sampling. These are images that are held
# constant throughout training, and allow us to inspect the model's performance
sample_size=16
fixed_z = np.random.uniform(-1, 1, size=(sample_size, z_size))
fixed_z = torch.from_numpy(fixed_z).float()
# move z to GPU if available
if train_on_gpu:
fixed_z = fixed_z.cuda()
# epoch training loop
for epoch in range(n_epochs):
# batch training loop
for batch_i, (real_images, _) in enumerate(celeba_train_loader):
batch_size = real_images.size(0)
real_images = scale(real_images)
# ===============================================
# YOUR CODE HERE: TRAIN THE NETWORKS
# ===============================================
# ============================================
# TRAIN THE DISCRIMINATOR
# ============================================
d_optimizer.zero_grad()
# 1. Train with real images
# Compute the discriminator losses on real images
if train_on_gpu:
real_images = real_images.cuda()
D_real = D(real_images)
d_real_loss = real_loss(D_real)
# 2. Train with fake images
# Generate fake images
z = np.random.uniform(-1, 1, size=(batch_size, z_size))
z = torch.from_numpy(z).float()
# move x to GPU, if available
if train_on_gpu:
z = z.cuda()
fake_images = G(z)
# Compute the discriminator losses on fake images
D_fake = D(fake_images)
d_fake_loss = fake_loss(D_fake)
# add up loss and perform backprop
d_loss = d_real_loss + d_fake_loss
d_loss.backward()
d_optimizer.step()
# =========================================
# TRAIN THE GENERATOR
# =========================================
g_optimizer.zero_grad()
# 1. Train with fake images and flipped labels
# Generate fake images
z = np.random.uniform(-1, 1, size=(batch_size, z_size))
z = torch.from_numpy(z).float()
if train_on_gpu:
z = z.cuda()
fake_images = G(z)
# Compute the discriminator losses on fake images
# using flipped labels!
D_fake = D(fake_images)
g_loss = real_loss(D_fake) # use real loss to flip labels
# perform backprop
g_loss.backward()
g_optimizer.step()
# 1. Train the discriminator on real and fake images
# ===============================================
# END OF YOUR CODE
# ===============================================
# Print some loss stats
if batch_i % print_every == 0:
# append discriminator loss and generator loss
losses.append((d_loss.item(), g_loss.item()))
# print discriminator and generator loss
print('Epoch [{:5d}/{:5d}] | d_loss: {:6.4f} | g_loss: {:6.4f}'.format(
epoch+1, n_epochs, d_loss.item(), g_loss.item()))
## AFTER EACH EPOCH##
# this code assumes your generator is named G, feel free to change the name
# generate and save sample, fake images
G.eval() # for generating samples
samples_z = G(fixed_z)
samples.append(samples_z)
G.train() # back to training mode
# Save training generator samples
with open('train_samples.pkl', 'wb') as f:
pkl.dump(samples, f)
# finally return losses
return losses
```
Set your number of training epochs and train your GAN!
```
# set number of epochs
n_epochs = 30
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
# call training function
losses = train(D, G, n_epochs=n_epochs)
```
## Training loss
Plot the training losses for the generator and discriminator, recorded after each epoch.
```
fig, ax = plt.subplots()
losses = np.array(losses)
plt.plot(losses.T[0], label='Discriminator', alpha=0.5)
plt.plot(losses.T[1], label='Generator', alpha=0.5)
plt.title("Training Losses")
plt.legend()
```
## Generator samples from training
View samples of images from the generator, and answer a question about the strengths and weaknesses of your trained models.
```
# helper function for viewing a list of passed in sample images
def view_samples(epoch, samples):
fig, axes = plt.subplots(figsize=(16,4), nrows=2, ncols=8, sharey=True, sharex=True)
for ax, img in zip(axes.flatten(), samples[epoch]):
img = img.detach().cpu().numpy()
img = np.transpose(img, (1, 2, 0))
img = ((img + 1)*255 / (2)).astype(np.uint8)
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
im = ax.imshow(img.reshape((32,32,3)))
# Load samples from generator, taken while training
with open('train_samples.pkl', 'rb') as f:
samples = pkl.load(f)
_ = view_samples(-1, samples)
```
### Question: What do you notice about your generated samples and how might you improve this model?
When you answer this question, consider the following factors:
* The dataset is biased; it is made of "celebrity" faces that are mostly white
* Model size; larger models have the opportunity to learn more features in a data feature space
* Optimization strategy; optimizers and number of epochs affect your final result
**Answer:** I think a deeper architecture esp for the Generator might have helped. I played with a lot of different values of the hyperparameters, but the losses weren't going down that much after a point. Also, the network might have learnt a bit better if there was more data. A lot of the times, the images that were generated had odd features like half a black frame on the face or a piece of a microphone etc.
### Submitting This Project
When submitting this project, make sure to run all the cells before saving the notebook. Save the notebook file as "dlnd_face_generation.ipynb" and save it as a HTML file under "File" -> "Download as". Include the "problem_unittests.py" files in your submission.
|
github_jupyter
|
Copyright 2021 DeepMind Technologies Limited
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
https://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
#Generative Art Using Neural Visual Grammars and Dual Encoders
**Chrisantha Fernando, Piotr Mirowski, Dylan Banarse, S. M. Ali Eslami, Jean-Baptiste Alayrac, Simon Osindero**
DeepMind, 2021
##Arnheim 1
###Generate paintings from text prompts.
Whilst there are perhaps only a few scientific methods, there seem to be almost as many artistic methods as there are artists. Artistic processes appear to inhabit the highest order of open-endedness. To begin to understand some of the processes of art making it is helpful to try to automate them even partially.
In this paper, a novel algorithm for producing generative art is described which allows a user to input a text string, and which in a creative response to this string, outputs an image which interprets that string. It does so by evolving images using a hierarchical neural [Lindenmeyer system](https://en.wikipedia.org/wiki/L-system), and evaluating these images along the way using an image text dual encoder trained on billions of images and their associated text from the internet.
In doing so we have access to and control over an instance of an artistic process, allowing analysis of which aspects of the artistic process become the task of the algorithm, and which elements remain the responsibility of the artist.
This colab accompanies the paper [Generative Art Using Neural Visual Grammars and Dual Encoders](https://arxiv.org/abs/2105.00162)
##Instructions
1. Click "Connect" button in the top right corner of this Colab
1. Select Runtime -> Change runtime type -> Hardware accelerator -> GPU
1. Select High-RAM for "Runtime shape" option
1. Navigate to "Get text input"
1. Enter text for IMAGE_NAME
1. Select "Run All" from Runtime menu
# Imports
```
#@title Set CUDA version for PyTorch
import subprocess
CUDA_version = [s for s in subprocess.check_output(["nvcc", "--version"]
).decode("UTF-8").split(", ")
if s.startswith("release")][0].split(" ")[-1]
print("CUDA version:", CUDA_version)
if CUDA_version == "10.0":
torch_version_suffix = "+cu100"
elif CUDA_version == "10.1":
torch_version_suffix = "+cu101"
elif CUDA_version == "10.2":
torch_version_suffix = ""
else:
torch_version_suffix = "+cu110"
! nvidia-smi
#@title Install and import PyTorch and Clip
! pip install torch==1.7.1{torch_version_suffix} torchvision==0.8.2{torch_version_suffix} -f https://download.pytorch.org/whl/torch_stable.html
! pip install git+https://github.com/openai/CLIP.git --no-deps
! pip install ftfy regex
import torch
import torch.nn as nn
import clip
print("Torch version:", torch.__version__)
#@title Install and import ray multiprocessing
! pip install -q -U ray[default]
import ray
#@title Import all other needed libraries
import collections
import copy
import cloudpickle
import time
import numpy as np
import matplotlib.pyplot as plt
import math
from PIL import Image
from PIL import ImageDraw
from skimage import transform
#@title Load CLIP {vertical-output: true}
CLIP_MODEL = "ViT-B/32"
device = torch.device("cuda")
print(f"Downloading CLIP model {CLIP_MODEL}...")
model, _ = clip.load(CLIP_MODEL, device, jit=False)
```
# Neural Visual Grammar
### Drawing primitives
```
def to_homogeneous(p):
r, c = p
return np.stack((r, c, np.ones_like(p[0])), axis=0)
def from_homogeneous(p):
p = p / p.T[:, 2]
return p[0].astype("int32"), p[1].astype("int32")
def apply_scale(scale, lineh):
return np.stack([lineh[0, :] * scale,
lineh[1, :] * scale,
lineh[2, :]])
def apply_translation(translation, lineh, offset_r=0, offset_c=0):
r, c = translation
return np.stack([lineh[0, :] + c + offset_c,
lineh[1, :] + r + offset_r,
lineh[2, :]])
def apply_rotation(translation, rad, lineh):
r, c = translation
cos_rad = np.cos(rad)
sin_rad = np.sin(rad)
return np.stack(
[(lineh[0, :] - c) * cos_rad - (lineh[1, :] - r) * sin_rad + c,
(lineh[0, :] - c) * sin_rad + (lineh[1, :] - r) * cos_rad + r,
lineh[2, :]])
def transform_lines(line_from, line_to, translation, angle, scale,
translation2, angle2, scale2, img_siz2):
"""Transform lines by translation, angle and scale, twice.
Args:
line_from: Line start point.
line_to: Line end point.
translation: 1st translation to line.
angle: 1st angle of rotation for line.
scale: 1st scale for line.
translation2: 2nd translation to line.
angle2: 2nd angle of rotation for line.
scale2: 2nd scale for line.
img_siz2: Offset for 2nd translation.
Returns:
Transformed lines.
"""
if len(line_from.shape) == 1:
line_from = np.expand_dims(line_from, 0)
if len(line_to.shape) == 1:
line_to = np.expand_dims(line_to, 0)
# First transform.
line_from_h = to_homogeneous(line_from.T)
line_to_h = to_homogeneous(line_to.T)
line_from_h = apply_scale(scale, line_from_h)
line_to_h = apply_scale(scale, line_to_h)
translated_line_from = apply_translation(translation, line_from_h)
translated_line_to = apply_translation(translation, line_to_h)
translated_mid_point = (translated_line_from + translated_line_to) / 2.0
translated_mid_point = translated_mid_point[[1, 0]]
line_from_transformed = apply_rotation(translated_mid_point,
np.pi * angle,
translated_line_from)
line_to_transformed = apply_rotation(translated_mid_point,
np.pi * angle,
translated_line_to)
line_from_transformed = np.array(from_homogeneous(line_from_transformed))
line_to_transformed = np.array(from_homogeneous(line_to_transformed))
# Second transform.
line_from_h = to_homogeneous(line_from_transformed)
line_to_h = to_homogeneous(line_to_transformed)
line_from_h = apply_scale(scale2, line_from_h)
line_to_h = apply_scale(scale2, line_to_h)
translated_line_from = apply_translation(
translation2, line_from_h, offset_r=img_siz2, offset_c=img_siz2)
translated_line_to = apply_translation(
translation2, line_to_h, offset_r=img_siz2, offset_c=img_siz2)
translated_mid_point = (translated_line_from + translated_line_to) / 2.0
translated_mid_point = translated_mid_point[[1, 0]]
line_from_transformed = apply_rotation(translated_mid_point,
np.pi * angle2,
translated_line_from)
line_to_transformed = apply_rotation(translated_mid_point,
np.pi * angle2,
translated_line_to)
return np.concatenate([from_homogeneous(line_from_transformed),
from_homogeneous(line_to_transformed)],
axis=1)
```
### Hierarchical stroke painting functions
```
# PaintingCommand
# origin_top: Origin of line defined by top level LSTM
# angle_top: Angle of line defined by top level LSTM
# scale_top: Scale for line defined by top level LSTM
# origin_bottom: Origin of line defined by bottom level LSTM
# angle_bottom: Angle of line defined by bottom level LSTM
# scale_bottom: Scale for line defined by bottom level LSTM
# position_choice: Selects between use of:
# Origin, angle and scale from both LSTM levels
# Origin, angle and scale just from top level LSTM
# Origin, angle and scale just from bottom level LSTM
# transparency: Line transparency determined by bottom level LSTM
PaintingCommand = collections.namedtuple("PaintingCommand",
["origin_top",
"angle_top",
"scale_top",
"origin_bottom",
"angle_bottom",
"scale_bottom",
"position_choice",
"transparency"])
def paint_over_image(img, strokes, painting_commands,
allow_strokes_beyond_image_edges, coeff_size=1):
"""Make marks over an existing image.
Args:
img: Image to draw on.
strokes: Stroke descriptions.
painting_commands: Top-level painting commands with transforms for the i
sets of strokes.
allow_strokes_beyond_image_edges: Allow strokes beyond image boundary.
coeff_size: Determines low res (1) or high res (10) image will be drawn.
Returns:
num_strokes: The number of strokes made.
"""
img_center = 112. * coeff_size
# a, b and c: determines the stroke width distribution (see 'weights' below)
a = 10. * coeff_size
b = 2. * coeff_size
c = 300. * coeff_size
# d: extent that the strokes are allowed to go beyond the edge of the canvas
d = 223 * coeff_size
def _clip_colour(col):
return np.clip((np.round(col * 255. + 128.)).astype(np.int32), 0, 255)
# Loop over all the top level...
t0_over = time.time()
num_strokes = sum(len(s) for s in strokes)
translations = np.zeros((2, num_strokes,), np.float32)
translations2 = np.zeros((2, num_strokes,), np.float32)
angles = np.zeros((num_strokes,), np.float32)
angles2 = np.zeros((num_strokes,), np.float32)
scales = np.zeros((num_strokes,), np.float32)
scales2 = np.zeros((num_strokes,), np.float32)
weights = np.zeros((num_strokes,), np.float32)
lines_from = np.zeros((num_strokes, 2), np.float32)
lines_to = np.zeros((num_strokes, 2), np.float32)
rgbas = np.zeros((num_strokes, 4), np.float32)
k = 0
for i in range(len(strokes)):
# Get the top-level transforms for the i-th bunch of strokes
painting_comand = painting_commands[i]
translation_a = painting_comand.origin_top
angle_a = (painting_comand.angle_top + 1) / 5.0
scale_a = 0.5 + (painting_comand.scale_top + 1) / 3.0
translation_b = painting_comand.origin_bottom
angle_b = (painting_comand.angle_bottom + 1) / 5.0
scale_b = 0.5 + (painting_comand.scale_bottom + 1) / 3.0
position_choice = painting_comand.position_choice
solid_colour = painting_comand.transparency
# Do we use origin, angle and scale from both, top or bottom LSTM levels?
if position_choice > 0.33:
translation = translation_a
angle = angle_a
scale = scale_a
translation2 = translation_b
angle2 = angle_b
scale2 = scale_b
elif position_choice > -0.33:
translation = translation_a
angle = angle_a
scale = scale_a
translation2 = [-img_center, -img_center]
angle2 = 0.
scale2 = 1.
else:
translation = translation_b
angle = angle_b
scale = scale_b
translation2 = [-img_center, -img_center]
angle2 = 0.
scale2 = 1.
# Store top-level transforms
strokes_i = strokes[i]
n_i = len(strokes_i)
angles[k:(k+n_i)] = angle
angles2[k:(k+n_i)] = angle2
scales[k:(k+n_i)] = scale
scales2[k:(k+n_i)] = scale2
translations[0, k:(k+n_i)] = translation[0]
translations[1, k:(k+n_i)] = translation[1]
translations2[0, k:(k+n_i)] = translation2[0]
translations2[1, k:(k+n_i)] = translation2[1]
# ... and the bottom level stroke definitions.
for j in range(n_i):
z_ij = strokes_i[j]
# Store line weight (we will process micro-strokes later)
weights[k] = z_ij[4]
# Store line endpoints
lines_from[k, :] = (z_ij[0], z_ij[1])
lines_to[k, :] = (z_ij[2], z_ij[3])
# Store colour and alpha
rgbas[k, 0] = z_ij[7]
rgbas[k, 1] = z_ij[8]
rgbas[k, 2] = z_ij[9]
if solid_colour > -0.5:
rgbas[k, 3] = 25.5
else:
rgbas[k, 3] = z_ij[11]
k += 1
# Draw all the strokes in a batch as sequence of length 2 * num_strokes
t1_over = time.time()
lines_from *= img_center/2.0
lines_to *= img_center/2.0
rr, cc = transform_lines(lines_from, lines_to, translations, angles, scales,
translations2, angles2, scales2, img_center)
if not allow_strokes_beyond_image_edges:
rrm = np.round(np.clip(rr, 1, d-1)).astype(int)
ccm = np.round(np.clip(cc, 1, d-1)).astype(int)
else:
rrm = np.round(rr).astype(int)
ccm = np.round(cc).astype(int)
# Plot all the strokes
t2_over = time.time()
img_pil = Image.fromarray(img)
canvas = ImageDraw.Draw(img_pil, "RGBA")
rgbas[:, :3] = _clip_colour(rgbas[:, :3])
rgbas[:, 3] = (np.clip(5.0 * np.abs(rgbas[:, 3]), 0, 255)).astype(np.int32)
weights = (np.clip(np.round(weights * b + a), 2, c)).astype(np.int32)
for k in range(num_strokes):
canvas.line((rrm[k], ccm[k], rrm[k+num_strokes], ccm[k+num_strokes]),
fill=tuple(rgbas[k]), width=weights[k])
img[:] = np.asarray(img_pil)[:]
t3_over = time.time()
if VERBOSE_CODE:
print("{:.2f}s to store {} stroke defs, {:.4f}s to "
"compute them, {:.4f}s to plot them".format(
t1_over - t0_over, num_strokes, t2_over - t1_over,
t3_over - t2_over))
return num_strokes
```
### Recurrent Neural Network Layer Generator
```
# DrawingLSTMSpec - parameters defining the LSTM architecture
# input_spec_size: Size if sequence elements
# num_lstms: Number of LSTMs at each layer
# net_lstm_hiddens: Number of hidden LSTM units
# net_mlp_hiddens: Number of hidden units in MLP layer
DrawingLSTMSpec = collections.namedtuple("DrawingLSTMSpec",
["input_spec_size",
"num_lstms",
"net_lstm_hiddens",
"net_mlp_hiddens"])
class MakeGeneratorLstm(nn.Module):
"""Block of parallel LSTMs with MLP output heads."""
def __init__(self, drawing_lstm_spec, output_size):
"""Build drawing LSTM architecture using spec.
Args:
drawing_lstm_spec: DrawingLSTMSpec with architecture parameters
output_size: Number of outputs for the MLP head layer
"""
super(MakeGeneratorLstm, self).__init__()
self._num_lstms = drawing_lstm_spec.num_lstms
self._input_layer = nn.Sequential(
nn.Linear(drawing_lstm_spec.input_spec_size,
drawing_lstm_spec.net_lstm_hiddens),
torch.nn.LeakyReLU(0.2, inplace=True))
lstms = []
heads = []
for _ in range(self._num_lstms):
lstm_layer = nn.LSTM(
input_size=drawing_lstm_spec.net_lstm_hiddens,
hidden_size=drawing_lstm_spec.net_lstm_hiddens,
num_layers=2, batch_first=True, bias=True)
head_layer = nn.Sequential(
nn.Linear(drawing_lstm_spec.net_lstm_hiddens,
drawing_lstm_spec.net_mlp_hiddens),
torch.nn.LeakyReLU(0.2, inplace=True),
nn.Linear(drawing_lstm_spec.net_mlp_hiddens, output_size))
lstms.append(lstm_layer)
heads.append(head_layer)
self._lstms = nn.ModuleList(lstms)
self._heads = nn.ModuleList(heads)
def forward(self, x):
pred = []
x = self._input_layer(x)*10.0
for i in range(self._num_lstms):
y, _ = self._lstms[i](x)
y = self._heads[i](y)
pred.append(y)
return pred
```
### DrawingLSTM - A Drawing Recurrent Neural Network
```
Genotype = collections.namedtuple("Genotype",
["top_lstm",
"bottom_lstm",
"input_sequence",
"initial_img"])
class DrawingLSTM:
"""LSTM for processing input sequences and generating resultant drawings.
Comprised of two LSTM layers.
"""
def __init__(self, drawing_lstm_spec, allow_strokes_beyond_image_edges):
"""Create DrawingLSTM to interpret input sequences and paint an image.
Args:
drawing_lstm_spec: DrawingLSTMSpec with LSTM architecture parameters
allow_strokes_beyond_image_edges: Draw lines outside image boundary
"""
self._input_spec_size = drawing_lstm_spec.input_spec_size
self._num_lstms = drawing_lstm_spec.num_lstms
self._allow_strokes_beyond_image_edges = allow_strokes_beyond_image_edges
with torch.no_grad():
self.top_lstm = MakeGeneratorLstm(drawing_lstm_spec,
self._input_spec_size)
self.bottom_lstm = MakeGeneratorLstm(drawing_lstm_spec, 12)
self._init_all(self.top_lstm, torch.nn.init.normal_, mean=0., std=0.2)
self._init_all(self.bottom_lstm, torch.nn.init.normal_, mean=0., std=0.2)
def _init_all(self, a_model, init_func, *params, **kwargs):
"""Method for initialising model with given init_func, params and kwargs."""
for p in a_model.parameters():
init_func(p, *params, **kwargs)
def _feed_top_lstm(self, input_seq):
"""Feed all input sequences input_seq into the LSTM models."""
x_in = input_seq.reshape((len(input_seq), 1, self._input_spec_size))
x_in = np.tile(x_in, (SEQ_LENGTH, 1))
x_torch = torch.from_numpy(x_in).type(torch.FloatTensor)
y_torch = self.top_lstm(x_torch)
y_torch = [y_torch_k.detach().numpy() for y_torch_k in y_torch]
del x_in
del x_torch
# There are multiple LSTM heads. For each sequence, read out the head and
# length of intermediary output to keep and return intermediary outputs.
readouts_top = np.clip(
np.round(self._num_lstms/2.0 * (1 + input_seq[:, 1])).astype(np.int32),
0, self._num_lstms-1)
lengths_top = np.clip(
np.round(10.0 * (1 + input_seq[:, 0])).astype(np.int32),
0, SEQ_LENGTH) + 1
intermediate_strings = []
for i in range(len(readouts_top)):
y_torch_i = y_torch[readouts_top[i]][i]
intermediate_strings.append(y_torch_i[0:lengths_top[i], :])
return intermediate_strings
def _feed_bottom_lstm(self, intermediate_strings, input_seq, coeff_size=1):
"""Feed all input sequences into the LSTM models.
Args:
intermediate_strings: top level strings
input_seq: input sequences fed to the top LSTM
coeff_size: sets centre origin
Returns:
strokes: Painting strokes.
painting_commands: Top-level painting commands with origin, angle and scale
information, as well as transparency.
"""
img_center = 112. * coeff_size
coeff_origin = 100. * coeff_size
top_lengths = []
for i in range(len(intermediate_strings)):
top_lengths.append(len(intermediate_strings[i]))
y_flat = np.concatenate(intermediate_strings, axis=0)
tiled_y_flat = y_flat.reshape((len(y_flat), 1, self._input_spec_size))
tiled_y_flat = np.tile(tiled_y_flat, (SEQ_LENGTH, 1))
y_torch = torch.from_numpy(tiled_y_flat).type(torch.FloatTensor)
z_torch = self.bottom_lstm(y_torch)
z_torch = [z_torch_k.detach().numpy() for z_torch_k in z_torch]
del tiled_y_flat
del y_torch
# There are multiple LSTM heads. For each sequence, read out the head and
# length of intermediary output to keep and return intermediary outputs.
readouts = np.clip(np.round(
NUM_LSTMS/2.0 * (1 + y_flat[:, 0])).astype(np.int32), 0, NUM_LSTMS-1)
lengths_bottom = np.clip(
np.round(10.0 * (1 + y_flat[:, 1])).astype(np.int32), 0, SEQ_LENGTH) + 1
strokes = []
painting_commands = []
offset = 0
for i in range(len(intermediate_strings)):
origin_top = [(1+input_seq[i, 2]) * img_center,
(1+input_seq[i, 3]) * img_center]
angle_top = input_seq[i, 4]
scale_top = input_seq[i, 5]
for j in range(len(intermediate_strings[i])):
k = j + offset
z_torch_ij = z_torch[readouts[k]][k]
strokes.append(z_torch_ij[0:lengths_bottom[k], :])
y_ij = y_flat[k]
origin_bottom = [y_ij[2] * coeff_origin, y_ij[3] * coeff_origin]
angle_bottom = y_ij[4]
scale_bottom = y_ij[5]
position_choice = y_ij[6]
transparency = y_ij[7]
painting_command = PaintingCommand(
origin_top, angle_top, scale_top, origin_bottom, angle_bottom,
scale_bottom, position_choice, transparency)
painting_commands.append(painting_command)
offset += top_lengths[i]
del y_flat
return strokes, painting_commands
def make_initial_genotype(self, initial_img, sequence_length,
input_spec_size):
"""Make and return initial DNA weights for LSTMs, input sequence, and image.
Args:
initial_img: Image (to be appended to the genotype)
sequence_length: Length of the input sequence (i.e. number of strokes)
input_spec_size: Number of inputs for each element in the input sequences
Returns:
Genotype NamedTuple with fields: [parameters of network 0,
parameters of network 1,
input sequence,
initial_img]
"""
dna_top = []
with torch.no_grad():
for _, params in self.top_lstm.named_parameters():
dna_top.append(params.clone())
param_size = params.numpy().shape
dna_top[-1] = np.random.uniform(
0.1 * DNA_SCALE, 0.3
* DNA_SCALE) * np.random.normal(size=param_size)
dna_bottom = []
with torch.no_grad():
for _, params in self.bottom_lstm.named_parameters():
dna_bottom.append(params.clone())
param_size = params.numpy().shape
dna_bottom[-1] = np.random.uniform(
0.1 * DNA_SCALE, 0.3
* DNA_SCALE) * np.random.normal(size=param_size)
input_sequence = np.random.uniform(
-1, 1, size=(sequence_length, input_spec_size))
return Genotype(dna_top, dna_bottom, input_sequence, initial_img)
def draw(self, img, genotype):
"""Add to the image using the latest genotype and get latest input sequence.
Args:
img: image to add to.
genotype: as created by make_initial_genotype.
Returns:
image with new strokes added.
"""
t0_draw = time.time()
img = img + genotype.initial_img
input_sequence = genotype.input_sequence
# Generate the strokes for drawing in batch mode.
# input_sequence is between 10 and 20 but is evolved, can go to 200.
intermediate_strings = self._feed_top_lstm(input_sequence)
strokes, painting_commands = self._feed_bottom_lstm(
intermediate_strings, input_sequence)
del intermediate_strings
# Now we can go through the output strings producing the strokes.
t1_draw = time.time()
num_strokes = paint_over_image(
img, strokes, painting_commands, self._allow_strokes_beyond_image_edges,
coeff_size=1)
t2_draw = time.time()
if VERBOSE_CODE:
print(
"Draw {:.2f}s (net {:.2f}s plot {:.2f}s {:.1f}ms/strk {}".format(
t2_draw - t0_draw, t1_draw - t0_draw, t2_draw - t1_draw,
(t2_draw - t1_draw) / num_strokes * 1000, num_strokes))
return img
```
## DrawingGenerator
```
class DrawingGenerator:
"""Creates a drawing using a DrawingLSTM."""
def __init__(self, image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges):
self.primitives = ["c", "r", "l", "b", "p", "j"]
self.pop = []
self.size = image_size
self.fitnesses = np.zeros(1)
self.noise = 2
self.mutation_std = 0.0004
# input_spec_size, num_lstms, net_lstm_hiddens,
# net_mlp_hiddens, output_size, allow_strokes_beyond_image_edges
self.drawing_lstm = DrawingLSTM(drawing_lstm_spec,
allow_strokes_beyond_image_edges)
def make_initial_genotype(self, initial_img, sequence_length, input_spec_size):
"""Use drawing_lstm to create initial genotypye."""
self.genotype = self.drawing_lstm.make_initial_genotype(
initial_img, sequence_length, input_spec_size)
return self.genotype
def _copy_genotype_to_generator(self, genotype):
"""Copy genotype's data into generator's parameters.
Copies the parameters in genotype (genotype.top_lstm[:] and
genotype.bottom_lstm[:]) into the parmaters for the drawing network so it
can be used to evaluate the genotype.
Args:
genotype: as created by make_initial_genotype.
Returns:
None
"""
self.genotype = copy.deepcopy(genotype)
i = 0
with torch.no_grad():
for _, param in self.drawing_lstm.top_lstm.named_parameters():
param.copy_(torch.tensor(self.genotype.top_lstm[i]))
i = i + 1
i = 0
with torch.no_grad():
for _, param in self.drawing_lstm.bottom_lstm.named_parameters():
param.copy_(torch.tensor(self.genotype.bottom_lstm[i]))
i = i + 1
def _interpret_genotype(self, genotype):
img = np.zeros((self.size, self.size, 3), dtype=np.uint8)
img = self.drawing_lstm.draw(img, genotype)
return img
def draw_from_genotype(self, genotype):
"""Copy input sequence and LSTM weights from `genotype`, run and draw."""
self._copy_genotype_to_generator(genotype)
return self._interpret_genotype(self.genotype)
def visualize_genotype(self, genotype):
"""Plot histograms of genotype"s data."""
plt.show()
inp_seq = np.array(genotype.input_sequence).flatten()
plt.title("input seq")
plt.hist(inp_seq)
plt.show()
inp_seq = np.array(genotype.top_lstm).flatten()
plt.title("LSTM top")
plt.hist(inp_seq)
plt.show()
inp_seq = np.array(genotype.bottom_lstm).flatten()
plt.title("LSTM bottom")
plt.hist(inp_seq)
plt.show()
def mutate(self, genotype):
"""Mutates `genotype`. This function is static.
Args:
genotype: genotype structure to mutate parameters of.
Returns:
new_genotype: Mutated copy of supplied genotype.
"""
new_genotype = copy.deepcopy(genotype)
new_input_seq = new_genotype.input_sequence
n = len(new_input_seq)
if np.random.uniform() < 1.0:
# Standard gaussian small mutation of input sequence.
if np.random.uniform() > 0.5:
new_input_seq += (
np.random.uniform(0.001, 0.2) * np.random.normal(
size=new_input_seq.shape))
# Low frequency large mutation of individual parts of the input sequence.
for i in range(n):
if np.random.uniform() < 2.0/n:
for j in range(len(new_input_seq[i])):
if np.random.uniform() < 2.0/len(new_input_seq[i]):
new_input_seq[i][j] = new_input_seq[i][j] + 0.5*np.random.normal()
# Adding and deleting elements from the input sequence.
if np.random.uniform() < 0.01:
if VERBOSE_MUTATION:
print("Mutation: adding")
a = np.random.uniform(-1, 1, size=(1, INPUT_SPEC_SIZE))
pos = np.random.randint(1, len(new_input_seq))
new_input_seq = np.insert(new_input_seq, pos, a, axis=0)
if np.random.uniform() < 0.02:
if VERBOSE_MUTATION:
print("Mutation: deleting")
pos = np.random.randint(1, len(new_input_seq))
new_input_seq = np.delete(new_input_seq, pos, axis=0)
n = len(new_input_seq)
# Swapping two elements in the input sequence.
if np.random.uniform() < 0.01:
element1 = np.random.randint(0, n)
element2 = np.random.randint(0, n)
while element1 == element2:
element2 = np.random.randint(0, n)
temp = copy.deepcopy(new_input_seq[element1])
new_input_seq[element1] = copy.deepcopy(new_input_seq[element2])
new_input_seq[element2] = temp
# Duplicate an element in the input sequence (with some mutation).
if np.random.uniform() < 0.01:
if VERBOSE_MUTATION:
print("Mutation: duplicating")
element1 = np.random.randint(0, n)
element2 = np.random.randint(0, n)
while element1 == element2:
element2 = np.random.randint(0, n)
new_input_seq[element1] = copy.deepcopy(new_input_seq[element2])
noise = 0.05 * np.random.normal(size=new_input_seq[element1].shape)
new_input_seq[element1] += noise
# Ensure that the input sequence is always between -1 and 1
# so that positions make sense.
new_genotype = new_genotype._replace(
input_sequence=np.clip(new_input_seq, -1.0, 1.0))
# Mutates dna of networks.
if np.random.uniform() < 1.0:
for net in range(2):
for layer in range(len(new_genotype[net])):
weights = new_genotype[net][layer]
if np.random.uniform() < 0.5:
noise = 0.00001 * np.random.standard_cauchy(size=weights.shape)
weights += noise
else:
noise = np.random.normal(size=weights.shape)
noise *= np.random.uniform(0.0001, 0.006)
weights += noise
if np.random.uniform() < 0.01:
noise = np.random.normal(size=weights.shape)
noise *= np.random.uniform(0.1, 0.3)
weights = noise
# Ensure weights are between -10 and 10.
weights = np.clip(weights, -1.0, 1.0)
new_genotype[net][layer] = weights
return new_genotype
```
## Evaluator
```
class Evaluator:
"""Evaluator for a drawing."""
def __init__(self, image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges):
self.drawing_generator = DrawingGenerator(image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges)
self.calls = 0
def make_initial_genotype(self, img, sequence_length, input_spec_size):
return self.drawing_generator.make_initial_genotype(img, sequence_length,
input_spec_size)
def evaluate_genotype(self, pickled_genotype, id_num):
"""Evaluate genotype and return genotype's image.
Args:
pickled_genotype: pickled genotype to be evaluated.
id_num: ID number of genotype.
Returns:
dict: drawing and id_num.
"""
genotype = cloudpickle.loads(pickled_genotype)
drawing = self.drawing_generator.draw_from_genotype(genotype)
self.calls += 1
return {"drawing": drawing, "id": id_num}
def mutate(self, genotype):
"""Create a mutated version of genotype."""
return self.drawing_generator.mutate(genotype)
```
# Evolution
## Fitness calculation, tournament, and crossover
```
IMAGE_MEAN = torch.tensor([0.48145466, 0.4578275, 0.40821073]).cuda()
IMAGE_STD = torch.tensor([0.26862954, 0.26130258, 0.27577711]).cuda()
def get_fitness(pictures, use_projective_transform,
projective_transform_coefficient):
"""Run CLIP on a batch of `pictures` and return `fitnesses`.
Args:
pictures: batch if images to evaluate
use_projective_transform: Add transformed versions of the image
projective_transform_coefficient: Degree of transform
Returns:
Similarities between images and the text
"""
# Do we use projective transforms of images before CLIP eval?
t0 = time.time()
pictures_trans = np.swapaxes(np.array(pictures), 1, 3) / 244.0
if use_projective_transform:
for i in range(len(pictures_trans)):
matrix = np.eye(3) + (
projective_transform_coefficient * np.random.normal(size=(3, 3)))
tform = transform.ProjectiveTransform(matrix=matrix)
pictures_trans[i] = transform.warp(pictures_trans[i], tform.inverse)
# Run the CLIP evaluator.
t1 = time.time()
image_input = torch.tensor(np.stack(pictures_trans)).cuda()
image_input -= IMAGE_MEAN[:, None, None]
image_input /= IMAGE_STD[:, None, None]
with torch.no_grad():
image_features = model.encode_image(image_input).float()
t2 = time.time()
similarity = torch.cosine_similarity(
text_features, image_features, dim=1).cpu().numpy()
t3 = time.time()
if VERBOSE_CODE:
print(f"get_fitness init {t1-t0:.4f}s, CLIP {t2-t1:.4f}s, sim {t3-t2:.4f}s")
return similarity
def crossover(dna_winner, dna_loser, crossover_prob):
"""Create new genotype by combining two genotypes.
Randomly replaces parts of the genotype 'dna_winner' with parts of dna_loser
to create a new genotype based mostly on on both 'parents'.
Args:
dna_winner: The high-fitness parent genotype - gets replaced with child.
dna_loser: The lower-fitness parent genotype.
crossover_prob: Probability of crossover between winner and loser.
Returns:
dna_winner: The result of crossover from parents.
"""
# Copy single input signals
for i in range(len(dna_winner[2])):
if i < len(dna_loser[2]):
if np.random.uniform() < crossover_prob:
dna_winner[2][i] = copy.deepcopy(dna_loser[2][i])
# Copy whole modules
for i in range(len(dna_winner[0])):
if i < len(dna_loser[0]):
if np.random.uniform() < crossover_prob:
dna_winner[0][i] = copy.deepcopy(dna_loser[0][i])
# Copy whole modules
for i in range(len(dna_winner[1])):
if i < len(dna_loser[1]):
if np.random.uniform() < crossover_prob:
dna_winner[1][i] = copy.deepcopy(dna_loser[1][i])
return dna_winner
def truncation_selection(population, fitnesses, evaluator, use_crossover,
crossover_prob):
"""Create new population using truncation selection.
Creates a new population by copying across the best 50% genotypes and
filling the rest with (for use_crossover==False) a mutated copy of each
genotype or (for use_crossover==True) with children created through crossover
between each winner and a genotype in the bottom 50%.
Args:
population: list of current population genotypes.
fitnesses: list of evaluated fitnesses.
evaluator: class that evaluates a draw generator.
use_crossover: Whether to use crossover between winner and loser.
crossover_prob: Probability of crossover between winner and loser.
Returns:
new_pop: the new population.
best: genotype.
"""
fitnesses = np.array(-fitnesses)
ordered_fitness_ids = fitnesses.argsort()
best = copy.deepcopy(population[ordered_fitness_ids[0]])
pop_size = len(population)
if not use_crossover:
new_pop = []
for i in range(int(pop_size/2)):
new_pop.append(copy.deepcopy(population[ordered_fitness_ids[i]]))
for i in range(int(pop_size/2)):
new_pop.append(evaluator.mutate(
copy.deepcopy(population[ordered_fitness_ids[i]])))
else:
new_pop = []
for i in range(int(pop_size/2)):
new_pop.append(copy.deepcopy(population[ordered_fitness_ids[i]]))
for i in range(int(pop_size/2)):
new_pop.append(evaluator.mutate(crossover(
copy.deepcopy(population[ordered_fitness_ids[i]]),
population[ordered_fitness_ids[int(pop_size/2) + i]], crossover_prob
)))
return new_pop, best
```
##Remote workers
```
VERBOSE_DURATION = False
@ray.remote
class Worker(object):
"""Takes a pickled dna and evaluates it, returning result."""
def __init__(self, image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges):
self.evaluator = Evaluator(image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges)
def compute(self, dna_pickle, genotype_id):
if VERBOSE_DURATION:
t0 = time.time()
res = self.evaluator.evaluate_genotype(dna_pickle, genotype_id)
if VERBOSE_DURATION:
duration = time.time() - t0
print(f"Worker {genotype_id} evaluated params in {duration:.1f}sec")
return res
def create_workers(num_workers, image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges):
"""Create the workers.
Args:
num_workers: Number of parallel workers for evaluation.
image_size: Length of side of (square) image
drawing_lstm_spec: DrawingLSTMSpec for LSTM network
allow_strokes_beyond_image_edges: Whether to draw outside the edges
Returns:
List of workers.
"""
worker_pool = []
for w_i in range(num_workers):
print("Creating worker", w_i, flush=True)
worker_pool.append(Worker.remote(image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges))
return worker_pool
```
##Plotting
```
def plot_training_res(batch_drawings, fitness_history, idx=None):
"""Plot fitnesses and timings.
Args:
batch_drawings: Drawings
fitness_history: History of fitnesses
idx: Index of drawing to show, default is highest fitness
"""
_, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
if idx is None:
idx = np.argmax(fitness_history[-1])
ax1.plot(fitness_history, ".")
ax1.set_title("Fitnesses")
ax2.imshow(batch_drawings[idx])
ax2.set_title(f"{PROMPT} (fit: {fitness_history[-1][idx]:.3f})")
plt.show()
def plot_samples(batch_drawings, num_samples=16):
"""Plot sample of drawings.
Args:
batch_drawings: Batch of drawings to sample from
num_samples: Number to displa
"""
num_samples = min(len(batch_drawings), num_samples)
num_rows = int(math.floor(np.sqrt(num_samples)))
num_cols = int(math.ceil(num_samples / num_rows))
row_images = []
for c in range(0, num_samples, num_cols):
if c + num_cols <= num_samples:
row_images.append(np.concatenate(batch_drawings[c:(c+num_cols)], axis=1))
composite_image = np.concatenate(row_images, axis=0)
_, ax = plt.subplots(1, 1, figsize=(20, 20))
ax.imshow(composite_image)
ax.set_title(PROMPT)
```
## Population and evolution main loop
```
def make_population(pop_size, evaluator, image_size, input_spec_size,
sequence_length):
"""Make initial population.
Args:
pop_size: number of genotypes in population.
evaluator: An Evaluator class instance for generating initial genotype.
image_size: Size of initial image for genotype to draw on.
input_spec_size: Sequence element size
sequence_length: Initial length of sequences
Returns:
Initialised population.
"""
print(f"Creating initial population of size {pop_size}")
pop = []
for _ in range(pop_size):
a_genotype = evaluator.make_initial_genotype(
img=np.zeros((image_size, image_size, 3), dtype=np.uint8),
sequence_length=sequence_length,
input_spec_size=input_spec_size)
pop.append(a_genotype)
return pop
def evolution_loop(population, worker_pool, evaluator, num_generations,
use_crossover, crossover_prob,
use_projective_transform, projective_transform_coefficient,
plot_every, plot_batch):
"""Create population and run evolution.
Args:
population: Initial population of genotypes
worker_pool: List of workers of parallel evaluations
evaluator: image evaluator to calculate fitnesses
num_generations: number of generations to run
use_crossover: Whether crossover is used for offspring
crossover_prob: Probability that crossover takes place
use_projective_transform: Use projective transforms in evaluation
projective_transform_coefficient: Degree of projective transform
plot_every: number of generations between new plots
plot_batch: whether to show all samples in the batch then plotting
"""
population_size = len(population)
num_workers = len(worker_pool)
print("Population of {} genotypes being evaluated by {} workers".format(
population_size, num_workers))
drawings = {}
fitness_history = []
init_gen = len(fitness_history)
print(f"(Re)starting evolution at generation {init_gen}")
for gen in range(init_gen, num_generations):
# Drawing
t0_loop = time.time()
futures = []
for j in range(0, population_size, num_workers):
for i in range(num_workers):
futures.append(worker_pool[i].compute.remote(
cloudpickle.dumps(population[i+j]), i+j))
data = ray.get(futures)
for i in range(num_workers):
drawings[data[i+j]["id"]] = data[j+i]["drawing"]
batch_drawings = []
for i in range(population_size):
batch_drawings.append(drawings[i])
# Fitness evaluation using CLIP
t1_loop = time.time()
fitnesses = get_fitness(batch_drawings, use_projective_transform,
projective_transform_coefficient)
fitness_history.append(copy.deepcopy(fitnesses))
# Tournament
t2_loop = time.time()
population, best_genotype = truncation_selection(
population, fitnesses, evaluator, use_crossover, crossover_prob)
t3_loop = time.time()
duration_draw = t1_loop - t0_loop
duration_fit = t2_loop - t1_loop
duration_tournament = t3_loop - t2_loop
duration_total = t3_loop - t0_loop
if gen % plot_every == 0:
if VISUALIZE_GENOTYPE:
evaluator.drawing_generator.visualize_genotype(best_genotype)
print("Draw: {:.2f}s fit: {:.2f}s evol: {:.2f}s total: {:.2f}s".format(
duration_draw, duration_fit, duration_tournament, duration_total))
plot_training_res(batch_drawings, fitness_history)
if plot_batch:
num_samples_to_plot = int(math.pow(
math.floor(np.sqrt(population_size)), 2))
plot_samples(batch_drawings, num_samples=num_samples_to_plot)
```
# Configure and Generate
```
#@title Hyperparameters
#@markdown Evolution parameters: population size and number of generations.
POPULATION_SIZE = 10 #@param {type:"slider", min:4, max:100, step:2}
NUM_GENERATIONS = 5000 #@param {type:"integer", min:100}
#@markdown Number of workers working in parallel (should be equal to or smaller than the population size).
NUM_WORKERS = 10 #@param {type:"slider", min:4, max:100, step:2}
#@markdown Crossover in evolution.
USE_CROSSOVER = True #@param {type:"boolean"}
CROSSOVER_PROB = 0.01 #@param {type:"number"}
#@markdown Number of LSTMs, each one encoding a group of strokes.
NUM_LSTMS = 5 #@param {type:"integer", min:1, max:5}
#@markdown Number of inputs for each element in the input sequences.
INPUT_SPEC_SIZE = 10 #@param {type:"integer"}
#@markdown Length of the input sequence fed to the LSTMs (determines number of strokes).
SEQ_LENGTH = 20 #@param {type:"integer", min:20, max:200}
#@markdown Rendering parameter.
ALLOW_STROKES_BEYOND_IMAGE_EDGES = True #@param {type:"boolean"}
#@markdown CLIP evaluation: do we use projective transforms of images?
USE_PROJECTIVE_TRANSFORM = True #@param {type:"boolean"}
PROJECTIVE_TRANSFORM_COEFFICIENT = 0.000001 #@param {type:"number"}
#@markdown These parameters should be edited mostly only for debugging reasons.
NET_LSTM_HIDDENS = 40 #@param {type:"integer"}
NET_MLP_HIDDENS = 20 #@param {type:"integer"}
# Scales the values used in genotype's initialisation.
DNA_SCALE = 1.0 #@param {type:"number"}
IMAGE_SIZE = 224 #@param {type:"integer"}
VERBOSE_CODE = False #@param {type:"boolean"}
VISUALIZE_GENOTYPE = False #@param {type:"boolean"}
VERBOSE_MUTATION = False #@param {type:"boolean"}
#@markdown Number of generations between new plots.
PLOT_EVERY_NUM_GENS = 5 #@param {type:"integer"}
#@markdown Whether to show all samples in the batch when plotting.
PLOT_BATCH = True # @param {type:"boolean"}
assert POPULATION_SIZE % NUM_WORKERS == 0, "POPULATION_SIZE not multiple of NUM_WORKERS"
```
#Running the original evolutionary algorithm
This is the original inefficient version of Arnheim which uses a genetic algorithm to optimize the picture. It takes at least 12 hours to produce an image using 50 workers. In our paper we used 500-1000 GPUs which speeded things up considerably. Refer to Arnheim 2 for a far more efficient way to generate images with a similar architecture.
Try prompts like “A photorealistic chicken”. Feel free to modify this colab to include your own way of generating and evolving images like we did in figure 2 here https://arxiv.org/pdf/2105.00162.pdf.
```
# @title Get text input and run evolution
PROMPT = "an apple" #@param {type:"string"}
# Tokenize prompts and coompute CLIP features.
text_input = clip.tokenize(PROMPT).to(device)
with torch.no_grad():
text_features = model.encode_text(text_input)
ray.shutdown()
ray.init()
drawing_lstm_arch = DrawingLSTMSpec(INPUT_SPEC_SIZE,
NUM_LSTMS,
NET_LSTM_HIDDENS,
NET_MLP_HIDDENS)
workers = create_workers(NUM_WORKERS, IMAGE_SIZE, drawing_lstm_arch,
ALLOW_STROKES_BEYOND_IMAGE_EDGES)
drawing_evaluator = Evaluator(IMAGE_SIZE, drawing_lstm_arch,
ALLOW_STROKES_BEYOND_IMAGE_EDGES)
drawing_population = make_population(POPULATION_SIZE, drawing_evaluator,
IMAGE_SIZE, INPUT_SPEC_SIZE, SEQ_LENGTH)
evolution_loop(drawing_population, workers, drawing_evaluator, NUM_GENERATIONS,
USE_CROSSOVER, CROSSOVER_PROB,
USE_PROJECTIVE_TRANSFORM, PROJECTIVE_TRANSFORM_COEFFICIENT,
PLOT_EVERY_NUM_GENS, PLOT_BATCH)
```
|
github_jupyter
|
# Coverage of MultiPLIER LV
The goal of this notebook is to examine why genes were found to be generic. Specifically, this notebook is trying to answer the question: Are generic genes found in more multiplier latent variables compared to specific genes?
The PLIER model performs a matrix factorization of gene expression data to get two matrices: loadings (Z) and latent matrix (B). The loadings (Z) are constrained to aligned with curated pathways and gene sets specified by prior knowledge [Figure 1B of Taroni et. al.](https://www.cell.com/cell-systems/pdfExtended/S2405-4712(19)30119-X). This ensure that some but not all latent variables capture known biology. The way PLIER does this is by applying a penalty such that the individual latent variables represent a few gene sets in order to make the latent variables more interpretable. Ideally there would be one latent variable associated with one gene set unambiguously.
While the PLIER model was trained on specific datasets, MultiPLIER extended this approach to all of recount2, where the latent variables should correspond to specific pathways or gene sets of interest. Therefore, we will look at the coverage of generic genes versus other genes across these MultiPLIER latent variables, which represent biological patterns.
**Definitions:**
* Generic genes: Are genes that are consistently differentially expressed across multiple simulated experiments.
* Other genes: These are all other non-generic genes. These genes include those that are not consistently differentially expressed across simulated experiments - i.e. the genes are specifically changed in an experiment. It could also indicate genes that are consistently unchanged (i.e. housekeeping genes)
```
%load_ext autoreload
%autoreload 2
import os
import random
import textwrap
import scipy
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
import rpy2.robjects as ro
from rpy2.robjects import pandas2ri
from rpy2.robjects.conversion import localconverter
from ponyo import utils
from generic_expression_patterns_modules import lv
# Get data directory containing gene summary data
base_dir = os.path.abspath(os.path.join(os.getcwd(), "../"))
data_dir = os.path.join(base_dir, "human_general_analysis")
# Read in config variables
config_filename = os.path.abspath(
os.path.join(base_dir, "configs", "config_human_general.tsv")
)
params = utils.read_config(config_filename)
local_dir = params["local_dir"]
project_id = params["project_id"]
quantile_threshold = 0.98
# Output file
nonzero_figure_filename = "nonzero_LV_coverage.svg"
highweight_figure_filename = "highweight_LV_coverage.svg"
```
## Load data
```
# Get gene summary file
summary_data_filename = os.path.join(data_dir, f"generic_gene_summary_{project_id}.tsv")
# Load gene summary data
data = pd.read_csv(summary_data_filename, sep="\t", index_col=0, header=0)
# Check that genes are unique since we will be using them as dictionary keys below
assert data.shape[0] == len(data["Gene ID"].unique())
# Load multiplier models
# Converted formatted pickle files (loaded using phenoplier environment) from
# https://github.com/greenelab/phenoplier/blob/master/nbs/01_preprocessing/005-multiplier_recount2_models.ipynb
# into .tsv files
multiplier_model_z = pd.read_csv(
"multiplier_model_z.tsv", sep="\t", index_col=0, header=0
)
# Get a rough sense for how many genes contribute to a given LV
# (i.e. how many genes have a value != 0 for a given LV)
# Notice that multiPLIER is a sparse model
(multiplier_model_z != 0).sum().sort_values(ascending=True)
```
## Get gene data
Define generic genes based on simulated gene ranking. Refer to [figure](https://github.com/greenelab/generic-expression-patterns/blob/master/human_general_analysis/gene_ranking_log2FoldChange.svg) as a guide.
**Definitions:**
* Generic genes: `Percentile (simulated) >= 60`
(Having a high rank indicates that these genes are consistently changed across simulated experiments.)
* Other genes: `Percentile (simulated) < 60`
(Having a lower rank indicates that these genes are not consistently changed across simulated experiments - i.e. the genes are specifically changed in an experiment. It could also indicate genes that are consistently unchanged.)
```
generic_threshold = 60
dict_genes = lv.get_generic_specific_genes(data, generic_threshold)
# Check overlap between multiplier genes and our genes
multiplier_genes = list(multiplier_model_z.index)
our_genes = list(data.index)
shared_genes = set(our_genes).intersection(multiplier_genes)
print(len(our_genes))
print(len(shared_genes))
# Drop gene ids not used in multiplier analysis
processed_dict_genes = lv.process_generic_specific_gene_lists(
dict_genes, multiplier_model_z
)
# Check numbers add up
assert len(shared_genes) == len(processed_dict_genes["generic"]) + len(
processed_dict_genes["other"]
)
```
## Get coverage of LVs
For each gene (generic or other) we want to find:
1. The number of LVs that gene is present
2. The number of LVs that the gene contributes a lot to (i.e. the gene is highly weighted within that LV)
### Nonzero LV coverage
```
dict_nonzero_coverage = lv.get_nonzero_LV_coverage(
processed_dict_genes, multiplier_model_z
)
# Check genes mapped correctly
assert processed_dict_genes["generic"][0] in dict_nonzero_coverage["generic"].index
assert len(dict_nonzero_coverage["generic"]) == len(processed_dict_genes["generic"])
assert len(dict_nonzero_coverage["other"]) == len(processed_dict_genes["other"])
```
### High weight LV coverage
```
# Quick look at the distribution of gene weights per LV
sns.distplot(multiplier_model_z["LV3"], kde=False)
plt.yscale("log")
dict_highweight_coverage = lv.get_highweight_LV_coverage(
processed_dict_genes, multiplier_model_z, quantile_threshold
)
# Check genes mapped correctly
assert processed_dict_genes["generic"][0] in dict_highweight_coverage["generic"].index
assert len(dict_highweight_coverage["generic"]) == len(processed_dict_genes["generic"])
assert len(dict_highweight_coverage["other"]) == len(processed_dict_genes["other"])
```
### Assemble LV coverage and plot
```
all_coverage = []
for gene_label in dict_genes.keys():
merged_df = pd.DataFrame(
dict_nonzero_coverage[gene_label], columns=["nonzero LV coverage"]
).merge(
pd.DataFrame(
dict_highweight_coverage[gene_label], columns=["highweight LV coverage"]
),
left_index=True,
right_index=True,
)
merged_df["gene type"] = gene_label
all_coverage.append(merged_df)
all_coverage_df = pd.concat(all_coverage)
all_coverage_df = lv.assemble_coverage_df(
processed_dict_genes, dict_nonzero_coverage, dict_highweight_coverage
)
all_coverage_df.head()
# Plot coverage distribution given list of generic coverage, specific coverage
nonzero_fig = sns.boxplot(
data=all_coverage_df,
x="gene type",
y="nonzero LV coverage",
notch=True,
palette=["#2c7fb8", "lightgrey"],
)
nonzero_fig.set_xlabel(None)
nonzero_fig.set_xticklabels(
["generic genes", "other genes"], fontsize=14, fontname="Verdana"
)
nonzero_fig.set_ylabel(
textwrap.fill("Number of LVs", width=30), fontsize=14, fontname="Verdana"
)
nonzero_fig.tick_params(labelsize=14)
nonzero_fig.set_title(
"Number of LVs genes are present in", fontsize=16, fontname="Verdana"
)
# Plot coverage distribution given list of generic coverage, specific coverage
highweight_fig = sns.boxplot(
data=all_coverage_df,
x="gene type",
y="highweight LV coverage",
notch=True,
palette=["#2c7fb8", "lightgrey"],
)
highweight_fig.set_xlabel(None)
highweight_fig.set_xticklabels(
["generic genes", "other genes"], fontsize=14, fontname="Verdana"
)
highweight_fig.set_ylabel(
textwrap.fill("Number of LVs", width=30), fontsize=14, fontname="Verdana"
)
highweight_fig.tick_params(labelsize=14)
highweight_fig.set_title(
"Number of LVs genes contribute highly to", fontsize=16, fontname="Verdana"
)
```
## Calculate statistics
* Is the reduction in generic coverage significant?
* Is the difference between generic versus other genes signficant?
```
# Test: mean number of LVs generic genes present in vs mean number of LVs that generic gene is high weight in
# (compare two blue boxes between plots)
generic_nonzero = all_coverage_df[all_coverage_df["gene type"] == "generic"][
"nonzero LV coverage"
].values
generic_highweight = all_coverage_df[all_coverage_df["gene type"] == "generic"][
"highweight LV coverage"
].values
(stats, pvalue) = scipy.stats.ttest_ind(generic_nonzero, generic_highweight)
print(pvalue)
# Test: mean number of LVs generic genes present in vs mean number of LVs other genes high weight in
# (compare blue and grey boxes in high weight plot)
other_highweight = all_coverage_df[all_coverage_df["gene type"] == "other"][
"highweight LV coverage"
].values
generic_highweight = all_coverage_df[all_coverage_df["gene type"] == "generic"][
"highweight LV coverage"
].values
(stats, pvalue) = scipy.stats.ttest_ind(other_highweight, generic_highweight)
print(pvalue)
# Check that coverage of other and generic genes across all LVs is NOT signficantly different
# (compare blue and grey boxes in nonzero weight plot)
other_nonzero = all_coverage_df[all_coverage_df["gene type"] == "other"][
"nonzero LV coverage"
].values
generic_nonzero = all_coverage_df[all_coverage_df["gene type"] == "generic"][
"nonzero LV coverage"
].values
(stats, pvalue) = scipy.stats.ttest_ind(other_nonzero, generic_nonzero)
print(pvalue)
```
## Get LVs that generic genes are highly weighted in
Since we are using quantiles to get high weight genes per LV, each LV has the same number of high weight genes. For each set of high weight genes, we will get the proportion of generic vs other genes. We will select the LVs that have a high proportion of generic genes to examine.
```
# Get proportion of generic genes per LV
prop_highweight_generic_dict = lv.get_prop_highweight_generic_genes(
processed_dict_genes, multiplier_model_z, quantile_threshold
)
# Return selected rows from summary matrix
multiplier_model_summary = pd.read_csv(
"multiplier_model_summary.tsv", sep="\t", index_col=0, header=0
)
lv.create_LV_df(
prop_highweight_generic_dict,
multiplier_model_summary,
0.5,
"Generic_LV_summary_table.tsv",
)
# Plot distribution of weights for these nodes
node = "LV61"
lv.plot_dist_weights(
node,
multiplier_model_z,
shared_genes,
20,
all_coverage_df,
f"weight_dist_{node}.svg",
)
```
## Save
```
# Save plot
nonzero_fig.figure.savefig(
nonzero_figure_filename,
format="svg",
bbox_inches="tight",
transparent=True,
pad_inches=0,
dpi=300,
)
# Save plot
highweight_fig.figure.savefig(
highweight_figure_filename,
format="svg",
bbox_inches="tight",
transparent=True,
pad_inches=0,
dpi=300,
)
```
**Takeaway:**
* In the first nonzero boxplot, generic and other genes are present in a similar number of LVs. This isn't surprising since the number of genes that contribute to each LV is <1000.
* In the second highweight boxplot, other genes are highly weighted in more LVs compared to generic genes. This would indicate that generic genes contribute alot to few LVs.
This is the opposite trend found using [_P. aeruginosa_ data](1_get_eADAGE_LV_coverage.ipynb). Perhaps this indicates that generic genes have different behavior/roles depending on the organism. In humans, perhaps these generic genes are related to a few hyper-responsive pathways, whereas in _P. aeruginosa_ perhaps generic genes are associated with many pathways, acting as *gene hubs*.
* There are a number of LVs that contain a high proportion of generic genes can be found in [table](Generic_LV_summary_table.tsv). By quick visual inspection, it looks like many LVs are associated with immune response, signaling and metabolism. Which are consistent with the hypothesis that these generic genes are related to hyper-responsive pathways.
|
github_jupyter
|
```
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load in
import os
import random
import xgboost
import lightgbm as lgb
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import matplotlib.pyplot as plt
from os import listdir
from os.path import isfile, join
from multiprocessing import Pool
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import GridSearchCV
#from sklearn.model_selection import cross_val_score,KFold
# Input data files are available in the "../input/" directory.
# For example, running this (by clicking run or pressing Shift+Enter) will list the files in the input directory
# Any results you write to the current directory are saved as output.
''' from here https://www.kaggle.com/c/imet-2019-fgvc6/discussion/87675#latest-516375'''
def seed_everything(seed=1234):
random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed)
np.random.seed(seed)
seed_everything()
train = pd.read_csv('../input/pmp-data-train/train_.csv')
train.drop('molecule_name', axis=1,inplace=True)
train.drop('atom_index_0' , axis=1,inplace=True)
train.drop('atom_index_1' , axis=1,inplace=True)
train.drop('id' , axis=1,inplace=True)
train.drop(columns="Unnamed: 0",inplace=True)
train.head()
def group_mean_log_mae(y_true, y_pred, floor=1e-9):
maes = np.absolute(y_true-y_pred).mean()
return np.log(np.maximum(maes,floor).mean())
def mean_log_mae( y_pred, dataset, floor=1e-9):
y_true = dataset.get_label()
maes = np.absolute(y_true-y_pred).mean()
return 'mean_log_mae', np.log(np.maximum(maes,floor).mean()), False
def show_predictions(true, pred):
# print(' actual | prediction | differnece')
# for i in range(len(true)):
# print('{:10.5f} | {:10.5f} | {:10.5f}'.format(true[i], pred[i], abs(true[i] - pred[i]) ))
plt.scatter(true,pred)
plt.show()
??plt.scatter()
files = [ '../input/pmp-lightgbm/model_1JHC.txt',
'../input/pmp-lightgbm/model_2JHH.txt',
'../input/pmp-lightgbm/model_1JHN.txt',
'../input/pmp-lightgbm/model_2JHN.txt',
'../input/fork-of-pmp-lightgbm/model_2JHC.txt',
'../input/fork-of-pmp-lightgbm/model_3JHH.txt',
'../input/fork-of-pmp-lightgbm/model_3JHC.txt',
'../input/fork-of-pmp-lightgbm/model_3JHN.txt',]
data_fr = {}
models = {}
type_list = ['1JHC', '2JHH', '1JHN', '2JHN', '2JHC', '3JHH', '3JHC', '3JHN']
scores = []
for i,type_ in enumerate(type_list):
data_fr = train.loc[train['type'] == type_].copy()
data_fr.reset_index(inplace=True)
data_fr.drop('type', axis=1,inplace=True)
data_fr.drop('index', axis=1,inplace=True)
y = data_fr.scalar_coupling_constant.values
data_fr.drop('scalar_coupling_constant', axis=1,inplace=True)
X = data_fr.astype(float).values
features = data_fr.columns
print('Dataset for type {} has shape {}'.format(type_,X.shape))
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.05, random_state=42)
reg = lgb.Booster(model_file=files[i])
show_predictions(y_test[0:500],reg.predict(X_test[0:500]).tolist())
score = group_mean_log_mae(y_test,reg.predict(X_test))
scores.append(score)
models[type_] = reg
print('score for type {} is --------> {}'.format(type_,score))
print('Final score is {}'.format(np.array(scores).mean()))
for i,type_ in enumerate(type_list): print('score of type {} is {}'.format(type_,scores[i]))
plt.figure(figsize = (12,6))
plt.bar(range(len(reg.feature_importance())), reg.feature_importance())
plt.xticks(range(len(reg.feature_importance())), features, rotation='vertical')
plt.show()
test = pd.read_csv('../input/pmp-data-test/test_.csv')
test.drop('molecule_name', axis=1,inplace=True)
test.drop('atom_index_0' , axis=1,inplace=True)
test.drop('atom_index_1' , axis=1,inplace=True)
test.drop('id' , axis=1,inplace=True)
test.drop("Unnamed: 0" , axis=1,inplace=True)
test.head()
test_ = test.copy()
test_.drop('type', axis=1,inplace=True)
X = test_.astype(float).values
features = test_.columns
print(X.shape)
test_.head()
sub = pd.read_csv('../input/champs-scalar-coupling/sample_submission.csv')
sub['scalar_coupling_constant'] = sub['scalar_coupling_constant'].astype(float)
sub.head()
%%time
from tqdm import tnrange
values = np.zeros(sub.shape[0])
sub['scalar_coupling_constant'] = sub['scalar_coupling_constant'].astype(float)
for i in tnrange(sub.shape[0]):
type_ = test['type'][i]
values[i] = models[type_].predict(np.expand_dims(X[i], axis=0))
sub['scalar_coupling_constant'] = pd.DataFrame(np.array(values))
print(sub.head())
sub.to_csv('submission.csv',index=None)
```
<a href="submission.csv"> Download File </a>
```
# def tt(j):
# type_ = test['type'][j]
# return models[type_].predict(np.expand_dims(X[j], axis=0))
# def get_dataframe():
# with Pool(8) as p:
# a = p.map(tt,[i for i in range(sub.shape[0])])
# return pd.DataFrame(np.array(a))
# %%time
# sub['scalar_coupling_constant'] = get_dataframe()
# sam['scalar_coupling_constant'] = sam['scalar_coupling_constant'].astype(float)
# for i in range(sam.shape[0]):
# type_ = test['type'][i]
# value = preds[type_][i]
# sam.at[i, 'scalar_coupling_constant'] = value
# parameters_for_testing = {
# 'gamma':[0,0.03,0.1,0.3],
# 'min_child_weight':[1.5,6,10],
# 'learning_rate':[0.07,0.1,0.5,1],
# 'max_depth':[3,4,5,6],
# 'n_estimators':[10],
# }
# xgb_model = xgboost.XGBRegressor(learning_rate =0.1, n_estimators=10, max_depth=6,
# min_child_weight=1, gamma=0, subsample=0.8,
# colsample_bytree=0.8, nthread=6,
# scale_pos_weight=1, seed=42)
# gsearch = GridSearchCV(estimator = xgb_model, cv=3, param_grid=parameters_for_testing, n_jobs=10,iid=False, verbose=10, scoring='neg_mean_squared_error')
# gsearch.fit(X_train,y_train)
# print('best params')
# print (gsearch.best_params_)
# print('best score')
# print (gsearch.best_score_)
# parameters_for_testing = {
# 'reg_alpha':[0,0.03,0.1,0.3],
# 'reg_labda':[1.5,6,10],
# 'n_estimators':[100],
# }
# xgb_model = xgboost.XGBRegressor(learning_rate=0.5,
# n_estimators=100,
# max_depth=6,
# min_child_weight=1.5,
# gamma=0,
# nthread=6,
# scale_pos_weight=1,
# seed=42)
# gsearch1 = GridSearchCV(estimator = xgb_model, cv=3, param_grid=parameters_for_testing, n_jobs=10,iid=False, verbose=10, scoring='neg_mean_squared_error')
# gsearch1.fit(X_train,y_train)
# print('best params')
# print (gsearch1.best_params_)
# print('best score')
# print (gsearch1.best_score_)
# reg = xgboost.XGBRegressor(
# learning_rate=0.5,
# n_estimators=100,
# max_depth=6,
# min_child_weight=1.5,
# gamma=0,
# nthread=6,
# scale_pos_weight=1,
# reg_alpha=0.3,
# reg_lambda=1.5,
# seed=42
# )
# reg.fit(X_train,y_train);
# print('score is {}'.format(group_mean_log_mae(pd.DataFrame(y_test),pd.DataFrame(reg.predict(X_test)))))
# plt.figure(figsize = (12,6))
# plt.bar(range(len(reg.feature_importances_)), reg.feature_importances_)
# plt.xticks(range(len(reg.feature_importances_)), fea, rotation='vertical')
# plt.show()
# from sklearn import linear_model
# reg = linear_model.RidgeCV()
# reg.fit(X_train, y_train)
# group_mean_log_mae(pd.DataFrame(y_test),pd.DataFrame(reg.predict(X_test)))
# print(y_train[0:5])
# print(reg.predict(X_train[0:5]).tolist())
# from sklearn.svm import SVR
# reg = SVR(gamma='scale', kernel='rbf', max_iter=2000)
# reg.fit(X_train, y_train)
# group_mean_log_mae(pd.DataFrame(y_test),pd.DataFrame(reg.predict(X_test)))
# import torch
# X_trainc = torch.tensor(X_train,dtype=torch.float).cuda()
# Y_trainc = torch.tensor(y_train,dtype=torch.float).cuda()
# X_testc = torch.tensor(X_test,dtype=torch.float).cuda()
# Y_testc = torch.tensor(y_test,dtype=torch.float).cuda()
# class Net(torch.nn.Module):
# def __init__(self, D_in, D_out):
# super(Net, self).__init__()
# self.linear1 = torch.nn.Linear(D_in, 100)
# self.linear2 = torch.nn.Linear(100, 20)
# self.linear3 = torch.nn.Linear(20, D_out)
# self.drop1 = torch.nn.Dropout(p=0.45, inplace=False)
# self.drop2 = torch.nn.Dropout(p=0.45, inplace=False)
# self.relu = torch.nn.ReLU()
# def forward(self, x):
# x = self.relu(self.linear1(x))
# x = self.drop1(x)
# x = self.relu(self.linear2(x))
# x = self.drop2(x)
# y_pred = self.linear3(x)
# return y_pred
# model = Net(44,1).cuda()
# criterion = torch.nn.MSELoss()
# optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
# step = torch.optim.lr_scheduler.StepLR(optimizer,100, gamma = 0.5, last_epoch=-1)
# def acc(model):
# y_p = model(X_testc).detach().cpu().numpy()
# print(group_mean_log_mae(pd.DataFrame(y_test),pd.DataFrame(y_p)))
# acc(model)
# model.train()
# for i in range(1501):
# if i < 310: step.step()
# model.train()
# optimizer.zero_grad()
# y_pred = model(X_testc)
# loss = criterion(y_pred, Y_testc)
# loss.backward()
# optimizer.step()
# if i%30 == 0: acc(model)
# lgb_train = lgb.Dataset(X_train, y_train)
# lgb_eval = lgb.Dataset(X_test, y_test, reference=lgb_train)
# def mean_log_mae( y_pred, dataset, floor=1e-9):
# y_true = dataset.get_label()
# maes = (pd.DataFrame(y_true)-pd.DataFrame(y_pred)).abs().mean()
# return 'mean_log_mae', np.log(maes.map(lambda x: max(x, floor))).mean(), False
# def mean_log_mae( y_pred, dataset, floor=1e-9):
# y_true = dataset.get_label()
# maes = np.absolute(y_true-y_pred).mean()
# return np.log(np.maximum(maes,floor).mean())
# params = {
# 'num_leaves' : [40],
# 'learning_rate' : [0.2, 0.3, 0.4],
# 'num_boost_round' : [4000]
# }
# print('Starting training...')
# # train
# reg = lgb.LGBMRegressor(boosting_type ='gbdt',
# objective = 'regression',
# verbose_eval = 200)
# gbm = GridSearchCV(estimator = reg, cv=3, param_grid=params, n_jobs=6, iid=False, verbose=10, scoring='neg_mean_squared_error')
# gbm.fit(X_train, y_train)
# print('best params')
# print (gbm.best_params_)
# print('best score')
# print (gbm.best_score_)
```
|
github_jupyter
|
<font size="+5">#02 | Decision Tree. A Supervised Classification Model</font>
- Subscribe to my [Blog ↗](https://blog.pythonassembly.com/)
- Let's keep in touch on [LinkedIn ↗](www.linkedin.com/in/jsulopz) 😄
# Discipline to Search Solutions in Google
> Apply the following steps when **looking for solutions in Google**:
>
> 1. **Necesity**: How to load an Excel in Python?
> 2. **Search in Google**: by keywords
> - `load excel python`
> - ~~how to load excel in python~~
> 3. **Solution**: What's the `function()` that loads an Excel in Python?
> - A Function to Programming is what the Atom to Phisics.
> - Every time you want to do something in programming
> - **You will need a `function()`** to make it
> - Theferore, you must **detect parenthesis `()`**
> - Out of all the words that you see in a website
> - Because they indicate the presence of a `function()`.
# Load the Data
> Load the Titanic dataset with the below commands
> - This dataset **people** (rows) aboard the Titanic
> - And their **sociological characteristics** (columns)
> - The aim of this dataset is to predict the probability to `survive`
> - Based on the social demographic characteristics.
```
import seaborn as sns
sns.load_dataset(name='titanic').iloc[:, :4]
```
# `DecisionTreeClassifier()` Model in Python
## Build the Model
> 1. **Necesity**: Build Model
> 2. **Google**: How do you search for the solution?
> 3. **Solution**: Find the `function()` that makes it happen
## Code Thinking
> Which function computes the Model?
> - `fit()`
>
> How could can you **import the function in Python**?
### Separate Variables for the Model
> Regarding their role:
> 1. **Target Variable `y`**
>
> - [ ] What would you like **to predict**?
>
> 2. **Explanatory Variable `X`**
>
> - [ ] Which variable will you use **to explain** the target?
```
explanatory = ?
target = ?
```
### Finally `fit()` the Model
## Calculate a Prediction with the Model
> - `model.predict_proba()`
## Model Visualization
> - `tree.plot_tree()`
## Model Interpretation
> Why `sex` is the most important column? What has to do with **EDA** (Exploratory Data Analysis)?
```
%%HTML
<iframe width="560" height="315" src="https://www.youtube.com/embed/7VeUPuFGJHk" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
```
# Prediction vs Reality
> How good is our model?
## Precision
> - `model.score()`
## Confusion Matrix
> 1. **Sensitivity** (correct prediction on positive value, $y=1$)
> 2. **Specificity** (correct prediction on negative value $y=0$).
## ROC Curve
> A way to summarise all the metrics (score, sensitivity & specificity)
|
github_jupyter
|
# CRRT Mortality Prediction
## Model Construction
### Christopher V. Cosgriff, David Sasson, Colby Wilkinson, Kanhua Yin
The purpose of this notebook is to build a deep learning model that predicts ICU mortality in the CRRT population. The data is extracted in the `extract_cohort_and_features` notebook and stored in the `data` folder. This model will be mult-input and use GRUs to model sequence data. See the extraction file for a full description of the data extraction.
## Step 0: Envrionment Setup
```
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from IPython.display import SVG
import os
from keras.optimizers import Adam, SGD, rmsprop
from keras.models import Sequential,Model
from keras.layers import Dense, Activation, Dropout, Input, Dropout, concatenate
from keras.layers.recurrent import GRU
from keras.utils import plot_model
from keras.utils.vis_utils import model_to_dot
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_auc_score, roc_curve
# for saving images
fig_fp = os.path.join('./', 'figures')
if not os.path.isdir(fig_fp):
os.mkdir(fig_fp)
%matplotlib inline
```
## Step 1: Load and Prepare Data
Here will we load in the data, and create train, validation, and testing splits.
```
# set tensors to float 32 as this is what GPUs expect
features_sequence = np.load('./features_sequence.npy').astype(np.float32)
features_static = np.load('./features_static.npy').astype(np.float32)
labels = np.load('./labels.npy').astype(np.float32)
x_seq_full_train, x_seq_test, x_static_full_train, x_static_test, y_full_train, y_test = train_test_split(
features_sequence, features_static, labels, test_size = 0.20, random_state = 42)
x_seq_train, x_seq_val, x_static_train, x_static_val, y_train, y_val = train_test_split(
x_seq_full_train, x_static_full_train, y_full_train, test_size = 0.10, random_state = 42)
```
Next we need to remove NANs from the data; we'll impute the trianing population mean, the simplest method suggested by David Sontag.
```
def impute_mean(source_data, input_data):
'''
Takes the source data, and uses it to determine means for all
features; it then applies them to the input data.
inputs:
source_data: a tensor to provide means
input_data: the data to fill in NA for
output:
output_data: data with nans imputed for each feature
'''
output_data = input_data.copy()
for feature in range(source_data.shape[1]):
feature_mean = np.nanmean(source_data[:, feature, :][np.where(source_data[:, feature, :] != 0)])
ind_output_data = np.where(np.isnan(output_data[:, feature, :]))
output_data[:, feature, :][ind_output_data] = feature_mean
return output_data
x_seq_train_original = x_seq_train.copy()
x_seq_train = impute_mean(x_seq_train_original, x_seq_train)
x_seq_val = impute_mean(x_seq_train_original, x_seq_val)
x_seq_test = impute_mean(x_seq_train_original, x_seq_test)
```
## Step 2: Build Model
### Model 1
Base model, no regularization.
```
# Define inputs
sequence_input = Input(shape = (x_seq_train.shape[1], x_seq_train.shape[2], ), dtype = 'float32', name = 'sequence_input')
static_input = Input(shape = (x_static_train.shape[1], ), name = 'static_input')
# Network architecture
seq_x = GRU(units = 128)(sequence_input)
# Seperate output for the GRU later
seq_aux_output = Dense(1, activation='sigmoid', name='aux_output')(seq_x)
# Merge dual inputs
x = concatenate([seq_x, static_input])
# We stack a deep fully-connected network on the merged inputs
x = Dense(128, activation = 'relu')(x)
x = Dense(128, activation = 'relu')(x)
x = Dense(128, activation = 'relu')(x)
x = Dense(128, activation = 'relu')(x)
# Sigmoid output layer
main_output = Dense(1, activation='sigmoid', name='main_output')(x)
# optimizer
opt = rmsprop(lr = 0.00001)
# build model
model = Model(inputs = [sequence_input, static_input], outputs = [main_output, seq_aux_output])
model.compile(optimizer = opt, loss = 'binary_crossentropy', metrics = ['accuracy'], loss_weights = [1, 0.1])
# save a plot of the model
plot_model(model, to_file='experiment_GRU-base.svg')
# fit the model
history = model.fit([x_seq_train, x_static_train], [y_train, y_train], epochs = 500, batch_size = 128,\
validation_data=([x_seq_val, x_static_val], [y_val, y_val]),)
# plot the fit
pred_main, pred_aux = model.predict([x_seq_test, x_static_test])
roc = roc_curve(y_test, pred_main)
auc = roc_auc_score(y_test, pred_main)
fig = plt.figure(figsize=(4, 3)) # in inches
plt.plot(roc[0], roc[1], color = 'darkorange', label = 'ROC curve\n(area = %0.2f)' % auc)
plt.plot([0, 1], [0, 1], color= 'navy', linestyle = '--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('%s: ROC' % 'GRU-base')
plt.legend(loc = "lower right")
fig_name = 'gru-base.pdf'
fig.savefig(os.path.join(fig_fp, fig_name), bbox_inches='tight')
plt.show()
# plot training and validation loss and accuracy
acc = history.history['main_output_acc']
val_acc = history.history['val_main_output_acc']
loss = history.history['main_output_loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
fig_name = 'loss_svg.svg'
fig.savefig('./loss_svg.svg', bbox_inches='tight')
```
### 10% Dropout
```
# Define inputs
sequence_input = Input(shape = (x_seq_train.shape[1], x_seq_train.shape[2], ), dtype = 'float32', name = 'sequence_input')
static_input = Input(shape = (x_static_train.shape[1], ), name = 'static_input')
# Network architecture
seq_x = GRU(units = 128)(sequence_input)
# Seperate output for the GRU later
seq_aux_output = Dense(1, activation='sigmoid', name='aux_output')(seq_x)
# Merge dual inputs
x = concatenate([seq_x, static_input])
# We stack a deep fully-connected network on the merged inputs
x = Dense(128, activation = 'relu')(x)
x = Dense(128, activation = 'relu')(x)
x = Dropout(0.10)(x)
x = Dense(128, activation = 'relu')(x)
x = Dense(128, activation = 'relu')(x)
# Sigmoid output layer
main_output = Dense(1, activation='sigmoid', name='main_output')(x)
# optimizer
opt = rmsprop(lr = 0.00001)
# build model
model = Model(inputs = [sequence_input, static_input], outputs = [main_output, seq_aux_output])
model.compile(optimizer = opt, loss = 'binary_crossentropy', metrics = ['accuracy'], loss_weights = [1, 0.1])
# save a plot of the model
#plot_model(model, to_file='experiment_GRU-DO.svg')
# fit the model
history = model.fit([x_seq_train, x_static_train], [y_train, y_train], epochs = 500, batch_size = 128,\
validation_data=([x_seq_val, x_static_val], [y_val, y_val]),)
# plot the fit
pred_main, pred_aux = model.predict([x_seq_test, x_static_test])
roc = roc_curve(y_test, pred_main)
auc = roc_auc_score(y_test, pred_main)
fig = plt.figure(figsize=(4, 3)) # in inches
plt.plot(roc[0], roc[1], color = 'darkorange', label = 'ROC curve\n(area = %0.2f)' % auc)
plt.plot([0, 1], [0, 1], color= 'navy', linestyle = '--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('%s: ROC' % 'GRU-base')
plt.legend(loc = "lower right")
fig_name = 'gru-do.pdf'
fig.savefig(os.path.join(fig_fp, fig_name), bbox_inches='tight')
plt.show()
# plot training and validation loss and accuracy
acc = history.history['main_output_acc']
val_acc = history.history['val_main_output_acc']
loss = history.history['main_output_loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
fig_name = 'do_loss_acc.pdf'
fig.savefig(os.path.join(fig_fp, fig_name), bbox_inches='tight')
```
|
github_jupyter
|
# $\color{black}{}$
### 1. Fitting data
---
### Input data
```
import pandas as pd
import seaborn as sns
data = pd.read_csv('https://milliams.com/courses/applied_data_analysis/linear.csv')
data.head()
```
Let's check how many rows we have
```
data.count()
```
We have 50 rows here. In the input data, each row is often called a sample (though sometimes also called an instance, example or observation). For example, it could be the information about a single person from a census or the measurements at a particular time from a weather station.
Let's have a look at what the data looks like when plotted
```
sns.scatterplot(data=data, x="x", y="y")
```
We can clearly visually see here that there is a linear relationship between the x and y values but we need to be able to extract the exact parameters programmatically.
### Setting up our model
We import the model and create an instance of it. By default the LinearRegression model will fit the y-intercept, but since we don't want to make that assumption we explicitly pass fit_intercept=True. fit_intercept is an example of a hyperparameter, which are variables or options in a model which you set up-front rather than letting them be learned from the data.
```
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=True)
```
### Fitting the data
Once we have created our model, we can fit it to the data by calling the `fit()` method on it. This takes two arguments:
1. The input data as a two-dimensional structure of the size ($N_{samples}$,$N_{features}$)
2. The labels or targets of the data as a one-dimensional data structure of size ($N_{samples}$)
If we just request `data["x"]` then that will be a 1D array (actually a pandas `Series`) of shape (50) so we must request the data with `data[["x"]]` (which returns it as a single-column, but still two-dimensional, `DataFrame`).
If you're using pandas to store your data (as we are) then just remember that the first argument should be a `DataFrame` and the second should be a `Series`.
```
X = data[['x']]
y = data['y']
model.fit(X, y)
```
### Making predictions using the model
We can use this to plot the fit over the original data to compare the result. By getting the predicted *__y__* values for the minimum and maximum x values, we can plot a straight line between them to visualise the model.
The `predict()` function takes an array of the same shape as the original input data (($N_{samples}$, $N_{features}$)) so we put our list of *__x__* values into a `DataFrame` before passing it to `predict()`.
We then plot the original data in the same way as before and draw the prediction line in the same plot.
```
x_fit = pd.DataFrame({'x': [0, 10]})
y_pred = model.predict(x_fit)
import matplotlib.pyplot as plt
plt.figure(figsize=(20,20))
fig, ax = plt.subplots()
sns.scatterplot(data=data, x='x', y='y', ax=ax)
ax.plot(x_fit['x'], y_pred, linestyle=':', color='red')
plt.show()
```
As well as plotting the line in a graph, we can also extract the calculated values of the gradient and y-intercept. The gradient is available as a list of values, `model.coef_`, one for each dimension or feature. The intercept is available as `model.intercept_`.
```
print(f'Model gradient: {model.coef_[0]}')
print(f'Model intercept: {model.intercept_}')
```
The equation that we have extracted can therefore be represented as:
__$y = 1.97x - 4.90$__
The original data was produced (with random wobble applied) from a straight line with gradient __$2$__ and y-intercept of __$−5$__. Our model has managed to predict values very close to the original.
|
github_jupyter
|
```
# Mount Google Drive
from google.colab import drive # import drive from google colab
ROOT = "/content/drive" # default location for the drive
print(ROOT) # print content of ROOT (Optional)
drive.mount(ROOT) # we mount the google drive at /content/drive
!pip install pennylane
from IPython.display import clear_output
clear_output()
import os
def restart_runtime():
os.kill(os.getpid(), 9)
restart_runtime()
# %matplotlib inline
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable
import numpy as np
```
# Loading Raw Data
```
import tensorflow as tf
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
x_train_flatten = x_train.reshape(x_train.shape[0], x_train.shape[1]*x_train.shape[2])/255.0
x_test_flatten = x_test.reshape(x_test.shape[0], x_test.shape[1]*x_test.shape[2])/255.0
print(x_train_flatten.shape, y_train.shape)
print(x_test_flatten.shape, y_test.shape)
x_train_0 = x_train_flatten[y_train == 0]
x_train_1 = x_train_flatten[y_train == 1]
x_train_2 = x_train_flatten[y_train == 2]
x_train_3 = x_train_flatten[y_train == 3]
x_train_4 = x_train_flatten[y_train == 4]
x_train_5 = x_train_flatten[y_train == 5]
x_train_6 = x_train_flatten[y_train == 6]
x_train_7 = x_train_flatten[y_train == 7]
x_train_8 = x_train_flatten[y_train == 8]
x_train_9 = x_train_flatten[y_train == 9]
x_train_list = [x_train_0, x_train_1, x_train_2, x_train_3, x_train_4, x_train_5, x_train_6, x_train_7, x_train_8, x_train_9]
print(x_train_0.shape)
print(x_train_1.shape)
print(x_train_2.shape)
print(x_train_3.shape)
print(x_train_4.shape)
print(x_train_5.shape)
print(x_train_6.shape)
print(x_train_7.shape)
print(x_train_8.shape)
print(x_train_9.shape)
x_test_0 = x_test_flatten[y_test == 0]
x_test_1 = x_test_flatten[y_test == 1]
x_test_2 = x_test_flatten[y_test == 2]
x_test_3 = x_test_flatten[y_test == 3]
x_test_4 = x_test_flatten[y_test == 4]
x_test_5 = x_test_flatten[y_test == 5]
x_test_6 = x_test_flatten[y_test == 6]
x_test_7 = x_test_flatten[y_test == 7]
x_test_8 = x_test_flatten[y_test == 8]
x_test_9 = x_test_flatten[y_test == 9]
x_test_list = [x_test_0, x_test_1, x_test_2, x_test_3, x_test_4, x_test_5, x_test_6, x_test_7, x_test_8, x_test_9]
print(x_test_0.shape)
print(x_test_1.shape)
print(x_test_2.shape)
print(x_test_3.shape)
print(x_test_4.shape)
print(x_test_5.shape)
print(x_test_6.shape)
print(x_test_7.shape)
print(x_test_8.shape)
print(x_test_9.shape)
```
# Selecting the dataset
Output: X_train, Y_train, X_test, Y_test
```
num_sample = 300
n_class = 4
mult_test = 0.25
X_train = x_train_list[0][:num_sample, :]
X_test = x_test_list[0][:int(mult_test*num_sample), :]
Y_train = np.zeros((n_class*X_train.shape[0],), dtype=int)
Y_test = np.zeros((n_class*X_test.shape[0],), dtype=int)
for i in range(n_class-1):
X_train = np.concatenate((X_train, x_train_list[i+1][:num_sample, :]), axis=0)
Y_train[num_sample*(i+1):num_sample*(i+2)] = int(i+1)
X_test = np.concatenate((X_test, x_test_list[i+1][:int(mult_test*num_sample), :]), axis=0)
Y_test[int(mult_test*num_sample*(i+1)):int(mult_test*num_sample*(i+2))] = int(i+1)
print(X_train.shape, Y_train.shape)
print(X_test.shape, Y_test.shape)
```
# Dataset Preprocessing (Standardization + PCA)
## Standardization
```
def normalize(X, use_params=False, params=None):
"""Normalize the given dataset X
Args:
X: ndarray, dataset
Returns:
(Xbar, mean, std): tuple of ndarray, Xbar is the normalized dataset
with mean 0 and standard deviation 1; mean and std are the
mean and standard deviation respectively.
Note:
You will encounter dimensions where the standard deviation is
zero, for those when you do normalization the normalized data
will be NaN. Handle this by setting using `std = 1` for those
dimensions when doing normalization.
"""
if use_params:
mu = params[0]
std_filled = [1]
else:
mu = np.mean(X, axis=0)
std = np.std(X, axis=0)
#std_filled = std.copy()
#std_filled[std==0] = 1.
Xbar = (X - mu)/(std + 1e-8)
return Xbar, mu, std
X_train, mu_train, std_train = normalize(X_train)
X_train.shape, Y_train.shape
X_test = (X_test - mu_train)/(std_train + 1e-8)
X_test.shape, Y_test.shape
```
## PCA
```
from sklearn.decomposition import PCA
from matplotlib import pyplot as plt
num_component = 9
pca = PCA(n_components=num_component, svd_solver='full')
pca.fit(X_train)
np.cumsum(pca.explained_variance_ratio_)
X_train = pca.transform(X_train)
X_test = pca.transform(X_test)
print(X_train.shape, Y_train.shape)
print(X_test.shape, Y_test.shape)
```
## Norm
```
X_train = (X_train.T / np.sqrt(np.sum(X_train ** 2, -1))).T
X_test = (X_test.T / np.sqrt(np.sum(X_test ** 2, -1))).T
plt.scatter(X_train[:100, 0], X_train[:100, 1])
plt.scatter(X_train[100:200, 0], X_train[100:200, 1])
plt.scatter(X_train[200:300, 0], X_train[200:300, 1])
```
# Quantum
```
import pennylane as qml
from pennylane import numpy as np
from pennylane.optimize import AdamOptimizer, GradientDescentOptimizer
qml.enable_tape()
# Set a random seed
np.random.seed(42)
def plot_data(x, y, fig=None, ax=None):
"""
Plot data with red/blue values for a binary classification.
Args:
x (array[tuple]): array of data points as tuples
y (array[int]): array of data points as tuples
"""
if fig == None:
fig, ax = plt.subplots(1, 1, figsize=(5, 5))
reds = y == 0
blues = y == 1
ax.scatter(x[reds, 0], x[reds, 1], c="red", s=20, edgecolor="k")
ax.scatter(x[blues, 0], x[blues, 1], c="blue", s=20, edgecolor="k")
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$")
# Define output labels as quantum state vectors
# def density_matrix(state):
# """Calculates the density matrix representation of a state.
# Args:
# state (array[complex]): array representing a quantum state vector
# Returns:
# dm: (array[complex]): array representing the density matrix
# """
# return state * np.conj(state).T
label_0 = [[1], [0]]
label_1 = [[0], [1]]
def density_matrix(state):
"""Calculates the density matrix representation of a state.
Args:
state (array[complex]): array representing a quantum state vector
Returns:
dm: (array[complex]): array representing the density matrix
"""
return np.outer(state, np.conj(state))
#state_labels = [label_0, label_1]
state_labels = np.loadtxt('./tetra_states.txt', dtype=np.complex_)
dev = qml.device("default.qubit", wires=1)
# Install any pennylane-plugin to run on some particular backend
@qml.qnode(dev)
def qcircuit(params, x=None, y=None):
"""A variational quantum circuit representing the Universal classifier.
Args:
params (array[float]): array of parameters
x (array[float]): single input vector
y (array[float]): single output state density matrix
Returns:
float: fidelity between output state and input
"""
for i in range(len(params[0])):
for j in range(int(len(x)/3)):
qml.Rot(*(params[0][i][3*j:3*(j+1)]*x[3*j:3*(j+1)] + params[1][i][3*j:3*(j+1)]), wires=0)
#qml.Rot(*params[1][i][3*j:3*(j+1)], wires=0)
return qml.expval(qml.Hermitian(y, wires=[0]))
X_train[0].shape
a = np.random.uniform(size=(2, 1, 9))
qcircuit(a, X_train[0], density_matrix(state_labels[3]))
tetra_class = np.loadtxt('./tetra_class_label.txt')
tetra_class
binary_class = np.array([[1, 0], [0, 1]])
binary_class
class_labels = tetra_class
class_labels[0][0]
dm_labels = [density_matrix(s) for s in state_labels]
def cost(params, x, y, state_labels=None):
"""Cost function to be minimized.
Args:
params (array[float]): array of parameters
x (array[float]): 2-d array of input vectors
y (array[float]): 1-d array of targets
state_labels (array[float]): array of state representations for labels
Returns:
float: loss value to be minimized
"""
# Compute prediction for each input in data batch
loss = 0.0
for i in range(len(x)):
f = qcircuit(params, x=x[i], y=dm_labels[y[i]])
loss = loss + (1 - f) ** 2
return loss / len(x)
# loss = 0.0
# for i in range(len(x)):
# f = 0.0
# for j in range(len(dm_labels)):
# f += (qcircuit(params, x=x[i], y=dm_labels[j]) - class_labels[y[i]][j])**2
# loss = loss + f
# return loss / len(x)
def test(params, x, y, state_labels=None):
"""
Tests on a given set of data.
Args:
params (array[float]): array of parameters
x (array[float]): 2-d array of input vectors
y (array[float]): 1-d array of targets
state_labels (array[float]): 1-d array of state representations for labels
Returns:
predicted (array([int]): predicted labels for test data
output_states (array[float]): output quantum states from the circuit
"""
fidelity_values = []
dm_labels = [density_matrix(s) for s in state_labels]
predicted = []
for i in range(len(x)):
fidel_function = lambda y: qcircuit(params, x=x[i], y=y)
fidelities = [fidel_function(dm) for dm in dm_labels]
best_fidel = np.argmax(fidelities)
predicted.append(best_fidel)
fidelity_values.append(fidelities)
return np.array(predicted), np.array(fidelity_values)
def accuracy_score(y_true, y_pred):
"""Accuracy score.
Args:
y_true (array[float]): 1-d array of targets
y_predicted (array[float]): 1-d array of predictions
state_labels (array[float]): 1-d array of state representations for labels
Returns:
score (float): the fraction of correctly classified samples
"""
score = y_true == y_pred
return score.sum() / len(y_true)
def iterate_minibatches(inputs, targets, batch_size):
"""
A generator for batches of the input data
Args:
inputs (array[float]): input data
targets (array[float]): targets
Returns:
inputs (array[float]): one batch of input data of length `batch_size`
targets (array[float]): one batch of targets of length `batch_size`
"""
for start_idx in range(0, inputs.shape[0] - batch_size + 1, batch_size):
idxs = slice(start_idx, start_idx + batch_size)
yield inputs[idxs], targets[idxs]
# Train using Adam optimizer and evaluate the classifier
num_layers = 2
learning_rate = 0.1
epochs = 100
batch_size = 32
opt = AdamOptimizer(learning_rate)
# initialize random weights
theta = np.random.uniform(size=(num_layers, 18))
w = np.random.uniform(size=(num_layers, 18))
params = [w, theta]
predicted_train, fidel_train = test(params, X_train, Y_train, state_labels)
accuracy_train = accuracy_score(Y_train, predicted_train)
predicted_test, fidel_test = test(params, X_test, Y_test, state_labels)
accuracy_test = accuracy_score(Y_test, predicted_test)
# save predictions with random weights for comparison
initial_predictions = predicted_test
loss = cost(params, X_test, Y_test, state_labels)
print(
"Epoch: {:2d} | Loss: {:3f} | Train accuracy: {:3f} | Test Accuracy: {:3f}".format(
0, loss, accuracy_train, accuracy_test
)
)
for it in range(epochs):
for Xbatch, ybatch in iterate_minibatches(X_train, Y_train, batch_size=batch_size):
params = opt.step(lambda v: cost(v, Xbatch, ybatch, state_labels), params)
predicted_train, fidel_train = test(params, X_train, Y_train, state_labels)
accuracy_train = accuracy_score(Y_train, predicted_train)
loss = cost(params, X_train, Y_train, state_labels)
predicted_test, fidel_test = test(params, X_test, Y_test, state_labels)
accuracy_test = accuracy_score(Y_test, predicted_test)
res = [it + 1, loss, accuracy_train, accuracy_test]
print(
"Epoch: {:2d} | Loss: {:3f} | Train accuracy: {:3f} | Test accuracy: {:3f}".format(
*res
)
)
qml.Rot(*(params[0][0][0:3]*X_train[0, 0:3] + params[1][0][0:3]), wires=[0])
params[1][0][0:3]
```
|
github_jupyter
|
```
import numpy as np
np.seterr(divide='ignore', invalid='ignore')
import scipy.integrate as integrate
from scipy.special import gamma
# Characteristic function of the Lifted Heston model see Slides 85-87
def Ch_Lifted_Heston(omega,S0,T,rho,lamb,theta,nu,V0,N,rN,alpha,M):
# omega = argument of the ch. function
# S0 = Initial price
# rho,lamb,theta,nu,V0 = parameters Lifted Heston
# N = number of factors in the model
# rN = constant used to define weights and mean-reversions
# alpha = H+1/2 where H is the Hurst index
# T = maturity
# M = number of steps in the time discretization to calculate ch. function
# to make sure we calculate ch. function and not moment gen. function
i=complex(0,1)
omega=i*omega
# Definition of weights and mean reversions in the approximation
h=np.linspace(0,N-1,N)
rpowerN=np.power(rN,h-N/2)
# weights
c=(rN**(1-alpha)-1)*(rpowerN**(1-alpha))/(gamma(alpha)*gamma(2-alpha))
# mean reversions
gammas=((1-alpha)/(2-alpha))*((rN**(2-alpha)-1)/(rN**(1-alpha)-1))*rpowerN
# Definition of the initial curve
g = lambda t: V0+lamb*theta*np.dot(c/gammas,1-np.exp(-t*gammas))
# Time steps for the approximation of psi
delta = T/M;
t=np.linspace(0,M,M+1)
t = t * delta
# Function F
F = lambda u,v : 0.5*(u**2-u)+(rho*nu*u-lamb)*v+.5*nu**2*v**2
# Iteration for approximation of psi - see Slide 87
psi=np.zeros((M+1,N),dtype=complex)
for k in range (1,M+1):
psi[k,:] = (np.ones(N)/(1+delta*gammas))*(psi[k-1,:]+delta*F(omega,np.dot(c,psi[k-1,:]))*np.ones(N))
# Invert g_0 to calculate phi - see Slide 87
g_0=np.zeros((1,M+1))
for k in range(1,M+2):
g_0[0,k-1]=g(T-t[k-1])
Y=np.zeros((1,M+1),dtype=complex)
phi=0
Y=F(omega,np.dot(c,psi.transpose()))*g_0
# Trapezoid rule to calculate phi
weights=np.ones(M+1)*delta
weights[0]=delta/2
weights[M]=delta/2
phi=np.dot(weights,Y.transpose())
phi=np.exp(omega*np.log(S0)+phi)
return phi
def psi_Lifted_Heston(K_,r_,omega,S0,T,rho,lamb,theta,nu,V0,N,rN,alpha,M):
k_ = np.log(K_)
phi = Ch_Lifted_Heston(omega,S0,T,rho,lamb,theta,nu,V0,N,rN,alpha,M)
F = phi*np.exp(-1j*omega.real*k_)
d = (1+1j*omega.real)*(2+1j*omega.real)
return np.exp(-r_*T-k_)/np.pi*(F/d).real
import scipy as scp
def C_Lifted_Heston(K_,r_,S0,T,rho,lamb,theta,nu,V0,N,rN,alpha,M,L_):
I = scp.integrate.quad(lambda x: psi_Lifted_Heston(K_,r_,x-2*1j,S0,T,rho,lamb,theta,nu,V0,N,rN,alpha,M) , 0, L_)
return I[0]
C_Lifted_Heston(90,0.03,100,0.5,-0.7,2,0.04,0.5,0.04,20,2.5,0.6,100,50)
```
|
github_jupyter
|
```
#Write a Python programming to create a pie chart of the popularity of programming Languages.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
plt.figure(figsize=(8,8))
languages=['Java', 'Python', 'PHP', 'JavaScript','c#','c++']
Popularity=[22.2, 17.6, 8.8, 8, 7.7, 6.7]
plt.pie(Popularity,labels=languages,startangle=60,explode=[0.1,0.09,0,0,0,0],autopct="%.f",shadow=True)
plt.show()
#Write a Python programming to create a pie chart with a title of the popularity of programming Languages.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
plt.figure(figsize=(8,8))
languages=['Java', 'Python', 'PHP', 'JavaScript','c#','c++']
Popularity=[22.2, 17.6, 8.8, 8, 7.7, 6.7]
plt.pie(Popularity,labels=languages,startangle=140,explode=[0.1,0,0,0,0,0],autopct="%1.1f%%",shadow=True)
plt.title("Pie chart example",bbox={'facecolor':'0.8', 'pad':5})
plt.show()
#Write a Python programming to create a pie chart with a title of the popularity of programming Languages.
#Make multiple wedges of the pie.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
plt.figure(figsize=(8,8))
languages=['Java', 'Python', 'PHP', 'JavaScript','c#','c++']
Popularity=[22.2, 17.6, 8.8, 8, 7.7, 6.7]
plt.pie(Popularity,labels=languages,startangle=140,explode=[0.1,0,0,0,0,0.1],autopct="%1.1f%%",shadow=True)
plt.title("Pie chart example",bbox={'facecolor':'0.8', 'pad':5})
plt.show()
#Write a Python programming to create a pie chart of gold medal achievements of five most successful
#countries in 2016 Summer Olympics. Read the data from a csv file.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
with open("medal.csv","r") as f:
x=f.read()
print(x)
#read method is not possible because of spaces.
plt.figure(figsize=(10,6))
df=pd.read_csv("medal.csv")
country_name=df['country']
gold_medals=df['gold_medal']
plt.pie(gold_medals,labels=country_name,autopct="%.f",explode=[0.1,0,0,0,0])
plt.title("Gold medal in olympic")
plt.show()
import matplotlib.pyplot as plt
with open("test.txt") as f:
data = f.read()
print(data)
data=data.split('\n')
print("----------")
print(data)
print("----------------")
# for i in zip(*data):
# print(i)
print(data[0])
x=[a.split(' ')[0] for a in x]
x
import matplotlib.pyplot as plt
import numpy
import pandas as pd
labels = 'Frogs', 'Hogs', 'Dogs'
sizes = numpy.array([5860, 677, 3200])
colors = ['yellowgreen', 'gold', 'lightskyblue']
p, tx, autotexts = plt.pie(sizes, labels=labels, colors=colors,
autopct="", shadow=True)
for i, a in enumerate(autotexts):
a.set_text("{}".format(sizes[i]))
plt.axis('equal')
plt.show()
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import stellargraph as sg
from stellargraph.mapper import PaddedGraphGenerator
from stellargraph.layer import DeepGraphCNN
from stellargraph import StellarGraph
from stellargraph import datasets
from sklearn import model_selection
from IPython.display import display, HTML
from tensorflow.keras import Model
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.layers import Dense, Conv1D, MaxPool1D, Dropout, Flatten
from tensorflow.keras.losses import binary_crossentropy
import tensorflow as tf
conspiracy_5G_path = '/Users/maria/Desktop/twitterAnalysis/FakeNews/dataset/graphs/5g_corona_conspiracy/'
conspiracy_other_path = '/Users/maria/Desktop/twitterAnalysis/FakeNews/dataset/graphs/non_conspiracy/'
non_conspiracy_path = '/Users/maria/Desktop/twitterAnalysis/FakeNews/dataset/graphs/other_conspiracy/'
test_graphs_path = '/Users/maria/Desktop/twitterAnalysis/FakeNews/dataset/graphs/test_graphs/'
conspiracy_5G_N = 270
conspiracy_other_N = 1660
non_conspiracy_N = 397
test_graphs_N = 1165
conspiracy_5G = list()
for i in range(conspiracy_5G_N):
g_id = i+1
nodes_path = conspiracy_5G_path + str(g_id) + '/nodes.csv'
edges_path = conspiracy_5G_path + str(g_id) + '/edges.txt'
g_nodes = pd.read_csv(nodes_path)
g_nodes = g_nodes.set_index('id')
g_edges = pd.read_csv(edges_path, header = None, sep=' ')
g_edges = g_edges.rename(columns={0: 'source', 1: 'target'})
g = StellarGraph(g_nodes, edges=g_edges)
conspiracy_5G.append(g)
conspiracy_other = list()
for i in range(conspiracy_other_N):
g_id = i+1
nodes_path = conspiracy_other_path + str(g_id) + '/nodes.csv'
edges_path = conspiracy_other_path + str(g_id) + '/edges.txt'
g_nodes = pd.read_csv(nodes_path)
g_nodes = g_nodes.set_index('id')
g_edges = pd.read_csv(edges_path, header = None, sep=' ')
g_edges = g_edges.rename(columns={0: 'source', 1: 'target'})
g = StellarGraph(g_nodes, edges=g_edges)
conspiracy_other.append(g)
non_conspiracy = list()
for i in range(non_conspiracy_N):
g_id = i+1
nodes_path = non_conspiracy_path + str(g_id) + '/nodes.csv'
edges_path = non_conspiracy_path + str(g_id) + '/edges.txt'
g_nodes = pd.read_csv(nodes_path)
g_nodes = g_nodes.set_index('id')
g_edges = pd.read_csv(edges_path, header = None, sep=' ')
g_edges = g_edges.rename(columns={0: 'source', 1: 'target'})
g = StellarGraph(g_nodes, edges=g_edges)
non_conspiracy.append(g)
test_graphs_off = list()
for i in range(test_graphs_N):
g_id = i+1
nodes_path = test_graphs_path + str(g_id) + '/nodes.csv'
edges_path = test_graphs_path + str(g_id) + '/edges.txt'
g_nodes = pd.read_csv(nodes_path)
g_nodes = g_nodes.set_index('id')
g_edges = pd.read_csv(edges_path, header = None, sep=' ')
g_edges = g_edges.rename(columns={0: 'source', 1: 'target'})
g = StellarGraph(g_nodes, edges=g_edges)
test_graphs_off.append(g)
graphs = conspiracy_5G + conspiracy_other + non_conspiracy
graph_labels = pd.Series(np.repeat([1, -1], [conspiracy_5G_N, conspiracy_other_N+non_conspiracy_N], axis=0))
graph_labels = pd.get_dummies(graph_labels, drop_first=True)
generator = PaddedGraphGenerator(graphs=graphs)
k = 35 # the number of rows for the output tensor
layer_sizes = [32, 32, 32, 1]
dgcnn_model = DeepGraphCNN(
layer_sizes=layer_sizes,
activations=["tanh", "tanh", "tanh", "tanh"],
k=k,
bias=False,
generator=generator,
)
x_inp, x_out = dgcnn_model.in_out_tensors()
x_out = Conv1D(filters=16, kernel_size=sum(layer_sizes), strides=sum(layer_sizes))(x_out)
x_out = MaxPool1D(pool_size=2)(x_out)
x_out = Conv1D(filters=32, kernel_size=5, strides=1)(x_out)
x_out = Flatten()(x_out)
x_out = Dense(units=128, activation="relu")(x_out)
x_out = Dropout(rate=0.5)(x_out)
predictions = Dense(units=1, activation="sigmoid")(x_out)
model = Model(inputs=x_inp, outputs=predictions)
model.compile(
optimizer=Adam(lr=0.0001), loss=binary_crossentropy, metrics=["acc"],
)
train_graphs, test_graphs = model_selection.train_test_split(
graph_labels, train_size=0.9, test_size=None, stratify=graph_labels,
)
gen = PaddedGraphGenerator(graphs=graphs)
train_gen = gen.flow(
list(train_graphs.index - 1),
targets=train_graphs.values,
batch_size=50,
symmetric_normalization=False,
)
test_gen = gen.flow(
list(test_graphs.index - 1),
targets=test_graphs.values,
batch_size=1,
symmetric_normalization=False,
)
epochs = 100
history = model.fit(
train_gen, epochs=epochs, verbose=1, validation_data=test_gen, shuffle=True,
)
sg.utils.plot_history(history)
test_gen_off = PaddedGraphGenerator(graphs=test_graphs_off)
test_gen_off_f = test_gen_off.flow(graphs=test_graphs_off)
preds = model.predict(test_gen_off_f)
import matplotlib.pyplot as plt
plt.hist(preds)
print(preds)
# Sources
# https://stellargraph.readthedocs.io/en/stable/demos/graph-classification/dgcnn-graph-classification.html
```
|
github_jupyter
|
```
import logging
import torch
import torch.optim as optim
import torch.nn as nn
import torch.nn.functional as F
import argparse
import os
import random
import numpy as np
from torch.autograd import Variable
from torch.utils.data import DataLoader
import utils
import itertools
from tqdm import tqdm_notebook
import models.dcgan_unet_64 as dcgan_unet_models
import models.dcgan_64 as dcgan_models
import models.classifiers as classifiers
import models.my_model as my_model
from data.moving_mnist import MovingMNIST
torch.cuda.set_device(0)
```
Constant definition
```
np.random.seed(1)
random.seed(1)
torch.manual_seed(1)
torch.cuda.manual_seed_all(1)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
lr = 2e-3
seq_len = 12
beta1 = 0.5
content_dim = 128
pose_dim = 10
channels = 3
normalize = False
sd_nf = 100
image_width = 64
batch_size = 100
log_dir = './logs/0522_my_model_CVAE_ourDisc_newPair/'
os.makedirs(os.path.join(log_dir, 'rec'), exist_ok=True)
os.makedirs(os.path.join(log_dir, 'analogy'), exist_ok=True)
logging.basicConfig(filename=os.path.join(log_dir, 'record.txt'), level=logging.DEBUG)
```
Data Loader
```
train_data = MovingMNIST(True, '../data_uni/', seq_len=seq_len)
test_data = MovingMNIST(False, '../data_uni/', seq_len=seq_len)
train_loader = DataLoader(
train_data,
batch_size=batch_size,
num_workers=16,
shuffle=True,
drop_last=True,
pin_memory=True
)
test_loader = DataLoader(
test_data,
batch_size=batch_size,
num_workers=0,
shuffle=True,
drop_last=True,
pin_memory=True
)
```
Model definition
```
# # netEC = dcgan_unet_models.content_encoder(content_dim, channels).to(device)
# netEC = dcgan_models.content_encoder(content_dim, channels).to(device)
# netEP = dcgan_models.pose_encoder(pose_dim, channels).to(device)
# # netD = dcgan_unet_models.decoder(content_dim, pose_dim, channels).to(device)
# netD = dcgan_models.decoder(content_dim, pose_dim, channels).to(device)
# netC = classifiers.scene_discriminator(pose_dim, sd_nf).to(device)
netEC = my_model.content_encoder(content_dim, channels).to(device)
netEP = my_model.pose_encoder(pose_dim, channels, conditional=True).to(device)
netD = my_model.decoder(content_dim, pose_dim, channels).to(device)
# netC = my_model.scene_discriminator(pose_dim, sd_nf).to(device)
netC = my_model.Discriminator(channels).to(device)
netEC.apply(utils.weights_init)
netEP.apply(utils.weights_init)
netD.apply(utils.weights_init)
netC.apply(utils.weights_init)
print(netEC)
print(netEP)
print(netD)
print(netC)
optimizerEC = optim.Adam(netEC.parameters(), lr=lr, betas=(beta1, 0.999))
optimizerEP = optim.Adam(netEP.parameters(), lr=lr, betas=(beta1, 0.999))
optimizerD = optim.Adam(netD.parameters(), lr=lr, betas=(beta1, 0.999))
optimizerC = optim.Adam(netC.parameters(), lr=lr, betas=(beta1, 0.999))
```
Plot function
```
# --------- plotting funtions ------------------------------------
def plot_rec(x, epoch, dtype):
x_c = x[0]
x_p = x[np.random.randint(1, len(x))]
h_c = netEC(x_c)
h_p = netEP(x_p, h_c)
rec = netD([h_c, h_p])
x_c, x_p, rec = x_c.data, x_p.data, rec.data
fname = '{}-{}.png'.format(dtype, epoch)
fname = os.path.join(log_dir, 'rec', fname)
to_plot = []
row_sz = 5
nplot = 20
for i in range(0, nplot-row_sz, row_sz):
row = [[xc, xp, xr] for xc, xp, xr in zip(x_c[i:i+row_sz], x_p[i:i+row_sz], rec[i:i+row_sz])]
to_plot.append(list(itertools.chain(*row)))
utils.save_tensors_image(fname, to_plot)
def plot_analogy(x, epoch, dtype):
x_c = x[0]
h_c = netEC(x_c)
nrow = 10
row_sz = len(x)
to_plot = []
row = [xi[0].data for xi in x]
zeros = torch.zeros(channels, image_width, image_width)
to_plot.append([zeros] + row)
for i in range(nrow):
to_plot.append([x[0][i].data])
for j in range(0, row_sz):
# for each time step
h_p = netEP(x[j], h_c).data
# first 10 pose vector, equal to first pose vector
for i in range(nrow):
h_p[i] = h_p[0]
rec = netD([h_c, h_p])
for i in range(nrow):
to_plot[i+1].append(rec[i].data.clone())
fname = '{}-{}.png'.format(dtype, epoch)
fname = os.path.join(log_dir, 'analogy', fname)
utils.save_tensors_image(fname, to_plot)
```
Training function
```
def train(x):
optimizerEC.zero_grad()
optimizerEP.zero_grad()
optimizerD.zero_grad()
# x_c1 = x[0]
# x_c2 = x[1]
# x_p1 = x[2]
# x_p2 = x[3]
x_c1 = x[np.random.randint(len(x))]
x_c2 = x[np.random.randint(len(x))]
x_p1 = x[np.random.randint(len(x))]
x_p2 = x[np.random.randint(len(x))]
h_c1 = netEC(x_c1)
# h_c2 = netEC(x_c2)[0].detach()
h_c2 = netEC(x_c2).detach()
h_p1 = netEP(x_p1, h_c1.detach()) # used for scene discriminator
h_p2 = netEP(x_p2, h_c1.detach())
# similarity loss: ||h_c1 - h_c2||
# sim_loss = F.mse_loss(h_c1[0], h_c2)
sim_loss = F.mse_loss(h_c1, h_c2)
# reconstruction loss: ||D(h_c1, h_p1), x_p1||
rec = netD([h_c1, h_p1])
rec_loss = F.mse_loss(rec, x_p1)
# scene discriminator loss: maximize entropy of output
# target = torch.FloatTensor(batch_size, 1).fill_(0.5).to(device)
# out = netC([h_p1, h_p2])
# sd_loss = F.binary_cross_entropy(out, target)
# Swap pose vector to train the discriminator
target = torch.FloatTensor(batch_size, 1).fill_(1).to(device)
idx = torch.randperm(batch_size)
h_p2 = h_p2[idx]
rec_swap = netD([h_c1, h_p2])
out = netC([x_c1.detach(), rec_swap]).view(-1, 1)
D_G_fake = out.mean().item()
adv_loss = F.binary_cross_entropy(out, target)
# full loss
loss = sim_loss + rec_loss + 0.1 * adv_loss
loss.backward()
optimizerEC.step()
optimizerEP.step()
optimizerD.step()
return sim_loss.item(), rec_loss.item(), adv_loss.item(), D_G_fake
def train_scene_discriminator(x):
optimizerC.zero_grad()
target = torch.FloatTensor(batch_size, 1).to(device)
# condition
h_c = netEC(x[np.random.randint(len(x))]).detach()
x1 = x[0]
x2 = x[1]
h_p1 = netEP(x1, h_c).detach()
h_p2 = netEP(x2, h_c).detach()
half = batch_size // 2
rp = torch.randperm(half).cuda()
h_p2[:half] = h_p2[rp]
target[:half] = 0
target[half:] = 1
out = netC([h_p1, h_p2])
bce = F.binary_cross_entropy(out, target)
bce.backward()
optimizerC.step()
acc =out[:half].le(0.5).sum() + out[half:].gt(0.5).sum()
return bce.data.cpu().numpy(), acc.data.cpu().numpy() / batch_size
def train_discriminator(x):
optimizerC.zero_grad()
real_lbl = torch.FloatTensor(batch_size, 1).fill_(1).to(device)
fake_lbl = torch.FloatTensor(batch_size, 1).fill_(0).to(device)
x1 = x[np.random.randint(len(x))]
x2 = x[np.random.randint(len(x))]
x3 = x[np.random.randint(len(x))]
# real pair
# 1. x1
# 2. reconstructed frames by pose(x2) and content(x1)
h_c = netEC(x1).detach()
h_p = netEP(x3, h_c)
x_rec = netD([h_c, h_p]).detach()
out_real = netC([x1, x_rec]).view(-1, 1)
loss_real = F.binary_cross_entropy(out_real, real_lbl)
D_real = loss_real.mean().item()
# fake pair
# 1. x1
# 2. swapped reconstructed frames
# by swapped pose(x3) and content(x1)
idx = torch.randperm(batch_size)
h_p = netEP(x3, h_c)
h_p = h_p[idx]
x_swap = netD([h_c, h_p]).detach()
out_fake = netC([x1, x_swap]).view(-1, 1)
loss_fake = F.binary_cross_entropy(out_fake, fake_lbl)
D_fake = loss_fake.mean().item()
bce = 0.5*loss_real + 0.5*loss_fake
bce.backward()
optimizerC.step()
return bce.item(), D_real, D_fake
epoch_size = len(train_loader)
test_x = next(iter(test_loader))
test_x = torch.transpose(test_x, 0, 1)
test_x = test_x.to(device)
for epoch in tqdm_notebook(range(200), desc='EPOCH'):
netEP.train()
netEC.train()
netD.train()
netC.train()
epoch_sim_loss, epoch_rec_loss, epoch_adv_loss, epoch_sd_loss = 0, 0, 0, 0
epoch_D_real, epoch_D_fake, epoch_D_G_fake = 0, 0, 0
for i, x in enumerate(tqdm_notebook(train_loader, desc='BATCH')):
# x to device
x = torch.transpose(x, 0, 1)
x = x.to(device)
# train scene discriminator
# sd_loss, sd_acc = train_scene_discriminator(x)
sd_loss, D_real, D_fake = train_discriminator(x)
epoch_sd_loss += sd_loss
epoch_D_real += D_real
epoch_D_fake += D_fake
# train main model
sim_loss, rec_loss, adv_loss, D_G_fake = train(x)
epoch_sim_loss += sim_loss
epoch_rec_loss += rec_loss
epoch_adv_loss += adv_loss
epoch_D_G_fake += D_G_fake
log_str='[%02d]rec loss: %.4f |sim loss: %.4f|adv loss: %.4f |sd loss: %.4f \
|D(real): %.2f |D(fake): %.2f |D(G(fake)): %.2f' %\
(epoch,
epoch_rec_loss/epoch_size,
epoch_sim_loss/epoch_size,
epoch_adv_loss/epoch_size,
epoch_sd_loss/epoch_size,
epoch_D_real/epoch_size,
epoch_D_fake/epoch_size,
epoch_D_G_fake/epoch_size)
print(log_str)
logging.info(log_str)
netEP.eval()
netEC.eval()
netD.eval()
with torch.no_grad():
plot_rec(test_x, epoch, 'test')
plot_analogy(test_x, epoch, 'test')
# save the model
torch.save({
'netD': netD,
'netEP': netEP,
'netEC': netEC},
'%s/model.pth' % log_dir)
len(train_loader)
for i, x in enumerate(train_loader):
if i == 0:
with torch.no_grad():
x = torch.transpose(x, 0, 1)
x = x.to(device)
plot_rec(x, 200)
plot_analogy(x, 200)
```
|
github_jupyter
|
# $H(curl, \Omega)$ Elliptic Problems
$\newcommand{\dd}{\,{\rm d}}$
$\newcommand{\uu}{\mathbf{u}}$
$\newcommand{\vv}{\mathbf{v}}$
$\newcommand{\nn}{\mathbf{n}}$
$\newcommand{\ff}{\mathbf{f}}$
$\newcommand{\Hcurlzero}{\mathbf{H}_0(\mbox{curl}, \Omega)}$
$\newcommand{\Curl}{\nabla \times}$
Let $\Omega \subset \mathbb{R}^d$ be an open Liptschitz bounded set, and we look for the solution of the following problem
\begin{align}
\left\{
\begin{array}{rl}
\Curl \Curl \uu + \mu \uu &= \ff, \quad \Omega
\\
\uu \times \nn &= 0, \quad \partial\Omega
\end{array} \right.
\label{eq:elliptic_hcurl}
\end{align}
where $\ff \in \mathbf{L}^2(\Omega)$, $\mu \in L^\infty(\Omega)$ and there exists $\mu_0 > 0$ such that $\mu \geq \mu_0$ almost everywhere.
We take the Hilbert space $V := \Hcurlzero$, in which case the variational formulation corresponding to \eqref{eq:elliptic_hcurl} writes
---
Find $\uu \in V$ such that
\begin{align}
a(\uu,\vv) = l(\vv) \quad \forall \vv \in V
\label{eq:abs_var_elliptic_hcurl}
\end{align}
where
\begin{align}
\left\{
\begin{array}{rll}
a(\uu, \vv) &:= \int_{\Omega} \Curl \uu \cdot \Curl \vv + \int_{\Omega} \mu \uu \cdot \vv, & \forall \uu, \vv \in V \\
l(\vv) &:= \int_{\Omega} \vv \cdot \ff, & \forall \vv \in V
\end{array} \right.
\label{tcb:elliptic_hcurl}
\end{align}
---
We recall that in $\Hcurlzero$, the bilinear form $a$ is equivalent to the inner product and is therefor continuous and coercive. Hence, our abstract theory applies and there exists a unique solution to the problem \eqref{eq:abs_var_elliptic_hcurl}.
```
import numpy as np
from sympy import pi, cos, sin, sqrt, Matrix, Tuple, lambdify
from scipy.sparse.linalg import spsolve
from scipy.sparse.linalg import gmres as sp_gmres
from scipy.sparse.linalg import minres as sp_minres
from scipy.sparse.linalg import cg as sp_cg
from scipy.sparse.linalg import bicg as sp_bicg
from scipy.sparse.linalg import bicgstab as sp_bicgstab
from sympde.calculus import grad, dot, inner, div, curl, cross
from sympde.topology import NormalVector
from sympde.topology import ScalarFunctionSpace, VectorFunctionSpace
from sympde.topology import ProductSpace
from sympde.topology import element_of, elements_of
from sympde.topology import Square
from sympde.expr import BilinearForm, LinearForm, integral
from sympde.expr import Norm
from sympde.expr import find, EssentialBC
from psydac.fem.basic import FemField
from psydac.fem.vector import ProductFemSpace
from psydac.api.discretization import discretize
from psydac.linalg.utilities import array_to_stencil
from psydac.linalg.iterative_solvers import pcg, bicg
# ... abstract model
domain = Square('A')
B_dirichlet_0 = domain.boundary
x, y = domain.coordinates
alpha = 1.
uex = Tuple(sin(pi*y), sin(pi*x)*cos(pi*y))
f = Tuple(alpha*sin(pi*y) - pi**2*sin(pi*y)*cos(pi*x) + pi**2*sin(pi*y),
alpha*sin(pi*x)*cos(pi*y) + pi**2*sin(pi*x)*cos(pi*y))
V = VectorFunctionSpace('V', domain, kind='hcurl')
u = element_of(V, name='u')
v = element_of(V, name='v')
F = element_of(V, name='F')
# Bilinear form a: V x V --> R
a = BilinearForm((u, v), integral(domain, curl(u)*curl(v) + alpha*dot(u,v)))
nn = NormalVector('nn')
a_bc = BilinearForm((u, v), integral(domain.boundary, 1e30 * cross(u, nn) * cross(v, nn)))
# Linear form l: V --> R
l = LinearForm(v, integral(domain, dot(f,v)))
# l2 error
error = Matrix([F[0]-uex[0],F[1]-uex[1]])
l2norm = Norm(error, domain, kind='l2')
ncells = [2**3, 2**3]
degree = [2, 2]
# Create computational domain from topological domain
domain_h = discretize(domain, ncells=ncells)
# Discrete spaces
Vh = discretize(V, domain_h, degree=degree)
# Discretize bi-linear and linear form
a_h = discretize(a, domain_h, [Vh, Vh])
a_bc_h = discretize(a_bc, domain_h, [Vh, Vh])
l_h = discretize(l, domain_h, Vh)
l2_norm_h = discretize(l2norm, domain_h, Vh)
M = a_h.assemble() + a_bc_h.assemble()
b = l_h.assemble()
# Solve linear system
sol, info = pcg(M ,b, pc='jacobi', tol=1e-8)
uh = FemField( Vh, sol )
l2_error = l2_norm_h.assemble(F=uh)
print(l2_error)
```
|
github_jupyter
|
# Emotion recognition using Emo-DB dataset and scikit-learn
### Database: Emo-DB database (free) 7 emotions
The data can be downloaded from http://emodb.bilderbar.info/index-1024.html
Code of emotions
W->Anger->Wut
L->Boredom->Langeweile
E->Disgust->Ekel
A->Anxiety/Fear->Angst
F->Happiness->Freude
T->Sadness->Trauer
N->Neutral

```
import requests
import zipfile
import os
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as st
import itertools
import sys
sys.path.append("../")
from plots_examples import plot_confusion_matrix, plot_ROC, plot_histogram
# disvoice imports
from phonation.phonation import Phonation
from articulation.articulation import Articulation
from prosody.prosody import Prosody
from phonological.phonological import Phonological
from replearning.replearning import RepLearning
# sklearn methods
from sklearn.model_selection import RandomizedSearchCV, train_test_split
from sklearn import preprocessing
from sklearn import metrics
from sklearn import svm
```
## Download and unzip data
```
def download_url(url, save_path, chunk_size=128):
r = requests.get(url, stream=True)
with open(save_path, 'wb') as fd:
for chunk in r.iter_content(chunk_size=chunk_size):
fd.write(chunk)
PATH_data="http://emodb.bilderbar.info/download/download.zip"
download_url(PATH_data, "./download.zip")
with zipfile.ZipFile("./download.zip", 'r') as zip_ref:
zip_ref.extractall("./emo-db/")
```
## prepare labels from the dataset
we will get labels for two classification problems:
1. high vs. low arousal emotions
2. positive vs. negative emotions
```
PATH_AUDIO=os.path.abspath("./emo-db/wav")+"/"
labelsd='WLEAFTN'
labelshl= [0, 1, 0, 0, 0, 1, 1] # 0 high arousal emotion, 1 low arousal emotions
labelspn= [0, 0, 0, 0, 1, 0, 1] # 0 negative valence emotion, 1 positive valence emotion
hf=os.listdir(PATH_AUDIO)
hf.sort()
yArousal=np.zeros(len(hf))
yValence=np.zeros(len(hf))
for j in range(len(hf)):
name_file=hf[j]
label=hf[j][5]
poslabel=labelsd.find(label)
yArousal[j]=labelshl[poslabel]
yValence[j]=labelspn[poslabel]
```
## compute features using disvoice: phonation, articulation, prosody, phonological
```
phonationf=Phonation()
articulationf=Articulation()
prosodyf=Prosody()
phonologicalf=Phonological()
replearningf=RepLearning('CAE')
```
### phonation features
```
Xphonation=phonationf.extract_features_path(PATH_AUDIO, static=True, plots=False, fmt="npy")
print(Xphonation.shape)
```
### articulation features
```
Xarticulation=articulationf.extract_features_path(PATH_AUDIO, static=True, plots=False, fmt="npy")
print(Xarticulation.shape)
```
### prosody features
```
Xprosody=prosodyf.extract_features_path(PATH_AUDIO, static=True, plots=False, fmt="npy")
print(Xprosody.shape)
```
### phonological features
```
Xphonological=phonologicalf.extract_features_path(PATH_AUDIO, static=True, plots=False, fmt="npy")
print(Xphonological.shape)
```
### representation learning features
```
Xrep=replearningf.extract_features_path(PATH_AUDIO, static=True, plots=False, fmt="npy")
print(Xrep.shape)
```
### Emotion classification using an SVM classifier
```
def classify(X, y):
# train test split
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, test_size=0.30, random_state=42)
# z-score standarization
scaler = preprocessing.StandardScaler().fit(Xtrain)
Xtrain=scaler.transform(Xtrain)
Xtest=scaler.transform(Xtest)
Results=[]
# randomized search cross-validation to optimize hyper-parameters of SVM
parameters = {'kernel':['rbf'], 'class_weight': ['balanced'],
'C':st.expon(scale=10),
'gamma':st.expon(scale=0.01)}
svc = svm.SVC()
clf=RandomizedSearchCV(svc, parameters, n_jobs=4, cv=10, verbose=1, n_iter=200, scoring='balanced_accuracy')
clf.fit(Xtrain, ytrain) # train the SVM
accDev= clf.best_score_ # validation accuracy
Copt=clf.best_params_.get('C') # best C
gammaopt=clf.best_params_.get('gamma') # best gamma
# train the SVM with the optimal hyper-parameters
cls=svm.SVC(kernel='rbf', C=Copt, gamma=gammaopt, class_weight='balanced')
cls.fit(Xtrain, ytrain)
ypred=cls.predict(Xtest) # test predictions
# check the results
acc=metrics.accuracy_score(ytest, ypred)
score_test=cls.decision_function(Xtest)
dfclass=metrics.classification_report(ytest, ypred,digits=4)
# display the results
plot_confusion_matrix(ytest, ypred, classes=["class 0", "class 1"], normalize=True)
plot_ROC(ytest, score_test)
plot_histogram(ytest, score_test, name_clases=["class 0", "class 1"])
print("Accuracy: ", acc)
print(dfclass)
```
## classify high vs. low arousal with the different feature sets
```
classify(Xphonation, yArousal)
classify(Xarticulation, yArousal)
classify(Xprosody, yArousal)
classify(Xphonological, yArousal)
classify(Xrep, yArousal)
```
## classify positive vs. negative valence with the different feature sets
```
classify(Xphonation, yValence)
classify(Xarticulation, yValence)
classify(Xprosody, yValence)
classify(Xphonological, yValence)
classify(Xrep, yValence)
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/Nikhitha-S-Pavan/Deep-learning-examples-using-keras/blob/main/Keras_mnist_digit_dataset.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
!pip install keras-tuner
import tensorflow as tf
from tensorflow import keras
import numpy as np
from matplotlib import pyplot
mnist=keras.datasets.mnist
(train_x, train_y), (test_x, test_y) = mnist.load_data()
for i in range(9):
# define subplot
pyplot.subplot(330 + 1 + i)
# plot raw pixel data
pyplot.imshow(train_x[i], cmap=pyplot.get_cmap('gray'))
# show the figure
pyplot.show()
train_images=train_x.reshape(len(train_x),28,28,1)
test_images=test_x.reshape(len(test_x),28,28,1)
train_x.shape
train_images=train_images/255
test_images = test_images/255
from kerastuner import RandomSearch
from kerastuner.engine.hyperparameters import HyperParameters
def build_model(hp):
model = keras.Sequential([
keras.layers.Conv2D(
filters=hp.Int('conv_1_filter', min_value=32, max_value=128, step=16),
kernel_size=hp.Choice('conv_1_kernel', values = [3,5]),
activation='relu',
input_shape=(28,28,1)
),
keras.layers.Conv2D(
filters=hp.Int('conv_2_filter', min_value=32, max_value=64, step=16),
kernel_size=hp.Choice('conv_2_kernel', values = [3,5]),
activation='relu'
),
keras.layers.Flatten(),
keras.layers.Dense(
units=hp.Int('dense_1_units', min_value=32, max_value=128, step=16),
activation='relu'
),
keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer=keras.optimizers.Adam(hp.Choice('learning_rate', values=[1e-2, 1e-3])),
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.summary()
return model
tuner_search=RandomSearch(build_model,
objective='val_accuracy',
max_trials=2,directory='output',project_name="Mnist")
tuner_search.search(train_images,train_y,epochs=3,validation_split=0.1)
model=tuner_search.get_best_models(num_models=1)[0]
model.fit(train_images, train_y, epochs=10, validation_split=0.1, initial_epoch=3)
"""
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
batch_size = 128
num_classes = 10
epochs = 12
# input image dimensions
img_rows, img_cols = 28, 28
# the data, split between train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# convert class vectors to binary class matrices
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3),
activation='relu',
input_shape=input_shape))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.Adadelta(),
metrics=['accuracy'])
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=5,
verbose=1,
validation_data=(x_test, y_test))
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
model.save_weights("model.h5")"""
model.summary()
```
|
github_jupyter
|
# 07 - Ensemble Methods
by [Alejandro Correa Bahnsen](http://www.albahnsen.com/) & [Iván Torroledo](http://www.ivantorroledo.com/)
version 1.3, June 2018
## Part of the class [Applied Deep Learning](https://github.com/albahnsen/AppliedDeepLearningClass)
This notebook is licensed under a [Creative Commons Attribution-ShareAlike 3.0 Unported License](http://creativecommons.org/licenses/by-sa/3.0/deed.en_US). Special thanks goes to [Kevin Markham](https://github.com/justmarkham)
Why are we learning about ensembling?
- Very popular method for improving the predictive performance of machine learning models
- Provides a foundation for understanding more sophisticated models
## Lesson objectives
Students will be able to:
- Define ensembling and its requirements
- Identify the two basic methods of ensembling
- Decide whether manual ensembling is a useful approach for a given problem
- Explain bagging and how it can be applied to decision trees
- Explain how out-of-bag error and feature importances are calculated from bagged trees
- Explain the difference between bagged trees and Random Forests
- Build and tune a Random Forest model in scikit-learn
- Decide whether a decision tree or a Random Forest is a better model for a given problem
# Part 1: Introduction
Ensemble learning is a widely studied topic in the machine learning community. The main idea behind
the ensemble methodology is to combine several individual base classifiers in order to have a
classifier that outperforms each of them.
Nowadays, ensemble methods are one
of the most popular and well studied machine learning techniques, and it can be
noted that since 2009 all the first-place and second-place winners of the KDD-Cup https://www.sigkdd.org/kddcup/ used ensemble methods. The core
principle in ensemble learning, is to induce random perturbations into the learning procedure in
order to produce several different base classifiers from a single training set, then combining the
base classifiers in order to make the final prediction. In order to induce the random permutations
and therefore create the different base classifiers, several methods have been proposed, in
particular:
* bagging
* pasting
* random forests
* random patches
Finally, after the base classifiers
are trained, they are typically combined using either:
* majority voting
* weighted voting
* stacking
There are three main reasons regarding why ensemble
methods perform better than single models: statistical, computational and representational . First, from a statistical point of view, when the learning set is too
small, an algorithm can find several good models within the search space, that arise to the same
performance on the training set $\mathcal{S}$. Nevertheless, without a validation set, there is
a risk of choosing the wrong model. The second reason is computational; in general, algorithms
rely on some local search optimization and may get stuck in a local optima. Then, an ensemble may
solve this by focusing different algorithms to different spaces across the training set. The last
reason is representational. In most cases, for a learning set of finite size, the true function
$f$ cannot be represented by any of the candidate models. By combining several models in an
ensemble, it may be possible to obtain a model with a larger coverage across the space of
representable functions.

## Example
Let's pretend that instead of building a single model to solve a binary classification problem, you created **five independent models**, and each model was correct about 70% of the time. If you combined these models into an "ensemble" and used their majority vote as a prediction, how often would the ensemble be correct?
```
import numpy as np
# set a seed for reproducibility
np.random.seed(1234)
# generate 1000 random numbers (between 0 and 1) for each model, representing 1000 observations
mod1 = np.random.rand(1000)
mod2 = np.random.rand(1000)
mod3 = np.random.rand(1000)
mod4 = np.random.rand(1000)
mod5 = np.random.rand(1000)
# each model independently predicts 1 (the "correct response") if random number was at least 0.3
preds1 = np.where(mod1 > 0.3, 1, 0)
preds2 = np.where(mod2 > 0.3, 1, 0)
preds3 = np.where(mod3 > 0.3, 1, 0)
preds4 = np.where(mod4 > 0.3, 1, 0)
preds5 = np.where(mod5 > 0.3, 1, 0)
# print the first 20 predictions from each model
print(preds1[:20])
print(preds2[:20])
print(preds3[:20])
print(preds4[:20])
print(preds5[:20])
# average the predictions and then round to 0 or 1
ensemble_preds = np.round((preds1 + preds2 + preds3 + preds4 + preds5)/5.0).astype(int)
# print the ensemble's first 20 predictions
print(ensemble_preds[:20])
# how accurate was each individual model?
print(preds1.mean())
print(preds2.mean())
print(preds3.mean())
print(preds4.mean())
print(preds5.mean())
# how accurate was the ensemble?
print(ensemble_preds.mean())
```
**Note:** As you add more models to the voting process, the probability of error decreases, which is known as [Condorcet's Jury Theorem](http://en.wikipedia.org/wiki/Condorcet%27s_jury_theorem).
## What is ensembling?
**Ensemble learning (or "ensembling")** is the process of combining several predictive models in order to produce a combined model that is more accurate than any individual model.
- **Regression:** take the average of the predictions
- **Classification:** take a vote and use the most common prediction, or take the average of the predicted probabilities
For ensembling to work well, the models must have the following characteristics:
- **Accurate:** they outperform the null model
- **Independent:** their predictions are generated using different processes
**The big idea:** If you have a collection of individually imperfect (and independent) models, the "one-off" mistakes made by each model are probably not going to be made by the rest of the models, and thus the mistakes will be discarded when averaging the models.
There are two basic **methods for ensembling:**
- Manually ensemble your individual models
- Use a model that ensembles for you
### Theoretical performance of an ensemble
If we assume that each one of the $T$ base classifiers has a probability $\rho$ of
being correct, the probability of an ensemble making the correct decision, assuming independence,
denoted by $P_c$, can be calculated using the binomial distribution
$$P_c = \sum_{j>T/2}^{T} {{T}\choose{j}} \rho^j(1-\rho)^{T-j}.$$
Furthermore, as shown, if $T\ge3$ then:
$$
\lim_{T \to \infty} P_c= \begin{cases}
1 &\mbox{if } \rho>0.5 \\
0 &\mbox{if } \rho<0.5 \\
0.5 &\mbox{if } \rho=0.5 ,
\end{cases}
$$
leading to the conclusion that
$$
\rho \ge 0.5 \quad \text{and} \quad T\ge3 \quad \Rightarrow \quad P_c\ge \rho.
$$
# Part 2: Manual ensembling
What makes a good manual ensemble?
- Different types of **models**
- Different combinations of **features**
- Different **tuning parameters**
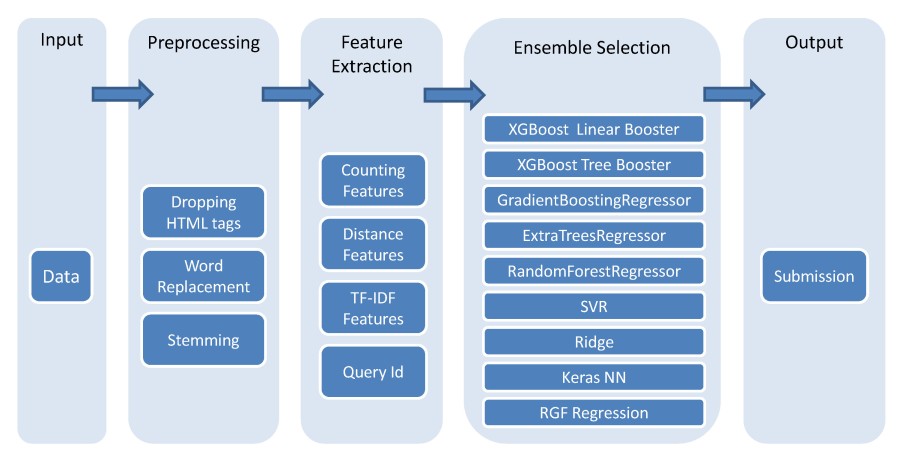
*Machine learning flowchart created by the [winner](https://github.com/ChenglongChen/Kaggle_CrowdFlower) of Kaggle's [CrowdFlower competition](https://www.kaggle.com/c/crowdflower-search-relevance)*
```
# read in and prepare the vehicle training data
import zipfile
import pandas as pd
with zipfile.ZipFile('../datasets/vehicles_train.csv.zip', 'r') as z:
f = z.open('vehicles_train.csv')
train = pd.io.parsers.read_table(f, index_col=False, sep=',')
with zipfile.ZipFile('../datasets/vehicles_test.csv.zip', 'r') as z:
f = z.open('vehicles_test.csv')
test = pd.io.parsers.read_table(f, index_col=False, sep=',')
train['vtype'] = train.vtype.map({'car':0, 'truck':1})
# read in and prepare the vehicle testing data
test['vtype'] = test.vtype.map({'car':0, 'truck':1})
train.head()
```
### Train different models
```
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
from sklearn.naive_bayes import GaussianNB
from sklearn.neighbors import KNeighborsRegressor
models = {'lr': LinearRegression(),
'dt': DecisionTreeRegressor(),
'nb': GaussianNB(),
'nn': KNeighborsRegressor()}
# Train all the models
X_train = train.iloc[:, 1:]
X_test = test.iloc[:, 1:]
y_train = train.price
y_test = test.price
for model in models.keys():
models[model].fit(X_train, y_train)
# predict test for each model
y_pred = pd.DataFrame(index=test.index, columns=models.keys())
for model in models.keys():
y_pred[model] = models[model].predict(X_test)
# Evaluate each model
from sklearn.metrics import mean_squared_error
for model in models.keys():
print(model,np.sqrt(mean_squared_error(y_pred[model], y_test)))
```
### Evaluate the error of the mean of the predictions
```
np.sqrt(mean_squared_error(y_pred.mean(axis=1), y_test))
```
## Comparing manual ensembling with a single model approach
**Advantages of manual ensembling:**
- Increases predictive accuracy
- Easy to get started
**Disadvantages of manual ensembling:**
- Decreases interpretability
- Takes longer to train
- Takes longer to predict
- More complex to automate and maintain
- Small gains in accuracy may not be worth the added complexity
# Part 3: Bagging
The primary weakness of **decision trees** is that they don't tend to have the best predictive accuracy. This is partially due to **high variance**, meaning that different splits in the training data can lead to very different trees.
**Bagging** is a general purpose procedure for reducing the variance of a machine learning method, but is particularly useful for decision trees. Bagging is short for **bootstrap aggregation**, meaning the aggregation of bootstrap samples.
What is a **bootstrap sample**? A random sample with replacement:
```
# set a seed for reproducibility
np.random.seed(1)
# create an array of 1 through 20
nums = np.arange(1, 21)
print(nums)
# sample that array 20 times with replacement
print(np.random.choice(a=nums, size=20, replace=True))
```
**How does bagging work (for decision trees)?**
1. Grow B trees using B bootstrap samples from the training data.
2. Train each tree on its bootstrap sample and make predictions.
3. Combine the predictions:
- Average the predictions for **regression trees**
- Take a vote for **classification trees**
Notes:
- **Each bootstrap sample** should be the same size as the original training set.
- **B** should be a large enough value that the error seems to have "stabilized".
- The trees are **grown deep** so that they have low bias/high variance.
Bagging increases predictive accuracy by **reducing the variance**, similar to how cross-validation reduces the variance associated with train/test split (for estimating out-of-sample error) by splitting many times an averaging the results.
```
# set a seed for reproducibility
np.random.seed(123)
n_samples = train.shape[0]
n_B = 10
# create ten bootstrap samples (will be used to select rows from the DataFrame)
samples = [np.random.choice(a=n_samples, size=n_samples, replace=True) for _ in range(1, n_B +1 )]
samples
# show the rows for the first decision tree
train.iloc[samples[0], :]
```
Build one tree for each sample
```
from sklearn.tree import DecisionTreeRegressor
# grow each tree deep
treereg = DecisionTreeRegressor(max_depth=None, random_state=123)
# DataFrame for storing predicted price from each tree
y_pred = pd.DataFrame(index=test.index, columns=[list(range(n_B))])
# grow one tree for each bootstrap sample and make predictions on testing data
for i, sample in enumerate(samples):
X_train = train.iloc[sample, 1:]
y_train = train.iloc[sample, 0]
treereg.fit(X_train, y_train)
y_pred[i] = treereg.predict(X_test)
y_pred
```
Results of each tree
```
for i in range(n_B):
print(i, np.sqrt(mean_squared_error(y_pred[i], y_test)))
```
Results of the ensemble
```
y_pred.mean(axis=1)
np.sqrt(mean_squared_error(y_test, y_pred.mean(axis=1)))
```
## Bagged decision trees in scikit-learn (with B=500)
```
# define the training and testing sets
X_train = train.iloc[:, 1:]
y_train = train.iloc[:, 0]
X_test = test.iloc[:, 1:]
y_test = test.iloc[:, 0]
# instruct BaggingRegressor to use DecisionTreeRegressor as the "base estimator"
from sklearn.ensemble import BaggingRegressor
bagreg = BaggingRegressor(DecisionTreeRegressor(), n_estimators=500,
bootstrap=True, oob_score=True, random_state=1)
# fit and predict
bagreg.fit(X_train, y_train)
y_pred = bagreg.predict(X_test)
y_pred
# calculate RMSE
np.sqrt(mean_squared_error(y_test, y_pred))
```
## Estimating out-of-sample error
For bagged models, out-of-sample error can be estimated without using **train/test split** or **cross-validation**!
On average, each bagged tree uses about **two-thirds** of the observations. For each tree, the **remaining observations** are called "out-of-bag" observations.
```
# show the first bootstrap sample
samples[0]
# show the "in-bag" observations for each sample
for sample in samples:
print(set(sample))
# show the "out-of-bag" observations for each sample
for sample in samples:
print(sorted(set(range(n_samples)) - set(sample)))
```
How to calculate **"out-of-bag error":**
1. For every observation in the training data, predict its response value using **only** the trees in which that observation was out-of-bag. Average those predictions (for regression) or take a vote (for classification).
2. Compare all predictions to the actual response values in order to compute the out-of-bag error.
When B is sufficiently large, the **out-of-bag error** is an accurate estimate of **out-of-sample error**.
```
# compute the out-of-bag R-squared score (not MSE, unfortunately!) for B=500
bagreg.oob_score_
```
## Estimating feature importance
Bagging increases **predictive accuracy**, but decreases **model interpretability** because it's no longer possible to visualize the tree to understand the importance of each feature.
However, we can still obtain an overall summary of **feature importance** from bagged models:
- **Bagged regression trees:** calculate the total amount that **MSE** is decreased due to splits over a given feature, averaged over all trees
- **Bagged classification trees:** calculate the total amount that **Gini index** is decreased due to splits over a given feature, averaged over all trees
# Part 4: Random Forests
Random Forests is a **slight variation of bagged trees** that has even better performance:
- Exactly like bagging, we create an ensemble of decision trees using bootstrapped samples of the training set.
- However, when building each tree, each time a split is considered, a **random sample of m features** is chosen as split candidates from the **full set of p features**. The split is only allowed to use **one of those m features**.
- A new random sample of features is chosen for **every single tree at every single split**.
- For **classification**, m is typically chosen to be the square root of p.
- For **regression**, m is typically chosen to be somewhere between p/3 and p.
What's the point?
- Suppose there is **one very strong feature** in the data set. When using bagged trees, most of the trees will use that feature as the top split, resulting in an ensemble of similar trees that are **highly correlated**.
- Averaging highly correlated quantities does not significantly reduce variance (which is the entire goal of bagging).
- By randomly leaving out candidate features from each split, **Random Forests "decorrelates" the trees**, such that the averaging process can reduce the variance of the resulting model.
# Part 5: Building and tuning decision trees and Random Forests
- Major League Baseball player data from 1986-87: [data](https://github.com/justmarkham/DAT8/blob/master/data/hitters.csv), [data dictionary](https://cran.r-project.org/web/packages/ISLR/ISLR.pdf) (page 7)
- Each observation represents a player
- **Goal:** Predict player salary
```
# read in the data
with zipfile.ZipFile('../datasets/hitters.csv.zip', 'r') as z:
f = z.open('hitters.csv')
hitters = pd.read_csv(f, sep=',', index_col=False)
# remove rows with missing values
hitters.dropna(inplace=True)
hitters.head()
# encode categorical variables as integers
hitters['League'] = pd.factorize(hitters.League)[0]
hitters['Division'] = pd.factorize(hitters.Division)[0]
hitters['NewLeague'] = pd.factorize(hitters.NewLeague)[0]
hitters.head()
# allow plots to appear in the notebook
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
# scatter plot of Years versus Hits colored by Salary
hitters.plot(kind='scatter', x='Years', y='Hits', c='Salary', colormap='jet', xlim=(0, 25), ylim=(0, 250))
# define features: exclude career statistics (which start with "C") and the response (Salary)
feature_cols = hitters.columns[hitters.columns.str.startswith('C') == False].drop('Salary')
feature_cols
# define X and y
X = hitters[feature_cols]
y = hitters.Salary
```
## Predicting salary with a decision tree
Find the best **max_depth** for a decision tree using cross-validation:
```
# list of values to try for max_depth
max_depth_range = range(1, 21)
# list to store the average RMSE for each value of max_depth
RMSE_scores = []
# use 10-fold cross-validation with each value of max_depth
from sklearn.model_selection import cross_val_score
for depth in max_depth_range:
treereg = DecisionTreeRegressor(max_depth=depth, random_state=1)
MSE_scores = cross_val_score(treereg, X, y, cv=10, scoring='neg_mean_squared_error')
RMSE_scores.append(np.mean(np.sqrt(-MSE_scores)))
# plot max_depth (x-axis) versus RMSE (y-axis)
plt.plot(max_depth_range, RMSE_scores)
plt.xlabel('max_depth')
plt.ylabel('RMSE (lower is better)')
# show the best RMSE and the corresponding max_depth
sorted(zip(RMSE_scores, max_depth_range))[0]
# max_depth=2 was best, so fit a tree using that parameter
treereg = DecisionTreeRegressor(max_depth=2, random_state=1)
treereg.fit(X, y)
# compute feature importances
pd.DataFrame({'feature':feature_cols, 'importance':treereg.feature_importances_}).sort_values('importance')
```
## Predicting salary with a Random Forest
```
from sklearn.ensemble import RandomForestRegressor
rfreg = RandomForestRegressor()
rfreg
```
### Tuning n_estimators
One important tuning parameter is **n_estimators**, which is the number of trees that should be grown. It should be a large enough value that the error seems to have "stabilized".
```
# list of values to try for n_estimators
estimator_range = range(10, 310, 10)
# list to store the average RMSE for each value of n_estimators
RMSE_scores = []
# use 5-fold cross-validation with each value of n_estimators (WARNING: SLOW!)
for estimator in estimator_range:
rfreg = RandomForestRegressor(n_estimators=estimator, random_state=1, n_jobs=-1)
MSE_scores = cross_val_score(rfreg, X, y, cv=5, scoring='neg_mean_squared_error')
RMSE_scores.append(np.mean(np.sqrt(-MSE_scores)))
# plot n_estimators (x-axis) versus RMSE (y-axis)
plt.plot(estimator_range, RMSE_scores)
plt.xlabel('n_estimators')
plt.ylabel('RMSE (lower is better)')
```
### Tuning max_features
The other important tuning parameter is **max_features**, which is the number of features that should be considered at each split.
```
# list of values to try for max_features
feature_range = range(1, len(feature_cols)+1)
# list to store the average RMSE for each value of max_features
RMSE_scores = []
# use 10-fold cross-validation with each value of max_features (WARNING: SLOW!)
for feature in feature_range:
rfreg = RandomForestRegressor(n_estimators=150, max_features=feature, random_state=1, n_jobs=-1)
MSE_scores = cross_val_score(rfreg, X, y, cv=10, scoring='neg_mean_squared_error')
RMSE_scores.append(np.mean(np.sqrt(-MSE_scores)))
# plot max_features (x-axis) versus RMSE (y-axis)
plt.plot(feature_range, RMSE_scores)
plt.xlabel('max_features')
plt.ylabel('RMSE (lower is better)')
# show the best RMSE and the corresponding max_features
sorted(zip(RMSE_scores, feature_range))[0]
```
### Fitting a Random Forest with the best parameters
```
# max_features=8 is best and n_estimators=150 is sufficiently large
rfreg = RandomForestRegressor(n_estimators=150, max_features=8, max_depth=3, oob_score=True, random_state=1)
rfreg.fit(X, y)
# compute feature importances
pd.DataFrame({'feature':feature_cols, 'importance':rfreg.feature_importances_}).sort_values('importance')
# compute the out-of-bag R-squared score
rfreg.oob_score_
```
### Reducing X to its most important features
```
# check the shape of X
X.shape
rfreg
# set a threshold for which features to include
from sklearn.feature_selection import SelectFromModel
print(SelectFromModel(rfreg, threshold=0.1, prefit=True).transform(X).shape)
print(SelectFromModel(rfreg, threshold='mean', prefit=True).transform(X).shape)
print(SelectFromModel(rfreg, threshold='median', prefit=True).transform(X).shape)
# create a new feature matrix that only includes important features
X_important = SelectFromModel(rfreg, threshold='mean', prefit=True).transform(X)
# check the RMSE for a Random Forest that only includes important features
rfreg = RandomForestRegressor(n_estimators=150, max_features=3, random_state=1)
scores = cross_val_score(rfreg, X_important, y, cv=10, scoring='neg_mean_squared_error')
np.mean(np.sqrt(-scores))
```
## Comparing Random Forests with decision trees
**Advantages of Random Forests:**
- Performance is competitive with the best supervised learning methods
- Provides a more reliable estimate of feature importance
- Allows you to estimate out-of-sample error without using train/test split or cross-validation
**Disadvantages of Random Forests:**
- Less interpretable
- Slower to train
- Slower to predict
|
github_jupyter
|
```
import os
for dirname, _, filenames in os.walk('../input/covid19-image-dataset'):
for filename in filenames:
print(os.path.join(dirname, filename))
import tensorflow as tf
import numpy as np
import os
from matplotlib import pyplot as plt
import cv2
from tensorflow import keras
from keras.models import Sequential
from keras.layers import Conv2D #images are two dimensional. Videos are three dimension.
from keras.layers import MaxPooling2D
from keras.layers import Flatten
from keras.layers import Dense
from keras.preprocessing import image
from tensorflow.keras.preprocessing.image import ImageDataGenerator
```
# Plotting Various Scan Reports
**Covid Patient**
```
plt.imshow(cv2.imread("../input/covid19-image-dataset/Covid19-dataset/train/Covid/022.jpeg"))
```
**Pneumomnia Patient**
```
plt.imshow(cv2.imread("../input/covid19-image-dataset/Covid19-dataset/train/Viral Pneumonia/020.jpeg"))
```
**Normal Patient**
```
plt.imshow(cv2.imread("../input/covid19-image-dataset/Covid19-dataset/train/Normal/018.jpeg"))
```
# Preprocessing the images
```
train_datagen=ImageDataGenerator(rescale=1/255,
shear_range=0.2,
zoom_range=2,
horizontal_flip=True)
training_set=train_datagen.flow_from_directory('../input/covid19-image-dataset/Covid19-dataset/train',
target_size=(224,224),
batch_size=32)
training_set.class_indices
test_datagen=ImageDataGenerator(rescale=1/255,
shear_range=0.2,
zoom_range=2,
horizontal_flip=True)
test_set=test_datagen.flow_from_directory('../input/covid19-image-dataset/Covid19-dataset/test',
target_size=(224,224),
batch_size=32)
test_set.class_indices
```
# Building VGG-16 architecture & Neural Network
```
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32,(3,3),strides=(1, 1),activation='relu',padding='same', input_shape=(224, 224, 3)),
tf.keras.layers.MaxPooling2D(pool_size=(2,2)),
tf.keras.layers.Conv2D(64,(3,3),strides=(1, 1) ,padding='same',activation='relu'),
tf.keras.layers.MaxPooling2D(pool_size=(2,2)),
tf.keras.layers.Conv2D(128,(3,3),strides=(1, 1),padding='same', activation='relu'),
tf.keras.layers.MaxPooling2D(pool_size=(2,2)),
tf.keras.layers.Conv2D(256,(3,3),strides=(1, 1),padding='same', activation='relu'),
tf.keras.layers.MaxPooling2D(pool_size=(2,2)),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(3, activation='softmax'),
])
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
model_fit = model.fit(training_set,
epochs = 71,
validation_data = test_set)
```
# Prediction
```
import numpy as np
from keras.preprocessing import image
test_image = image.load_img('../input/covid19-image-dataset/Covid19-dataset/test/Viral Pneumonia/0112.jpeg', target_size = (224, 224))
test_image = image.img_to_array(test_image)
test_image = np.expand_dims(test_image, axis = 0)
result = model.predict(test_image)
training_set.class_indices
print(result)
```
[0,0,1] which means Pneumonia. Hence our model is accurate
|
github_jupyter
|
# Collaborative filtering on Google Analytics data
This notebook demonstrates how to implement a WALS matrix refactorization approach to do collaborative filtering.
```
import os
PROJECT = "cloud-training-demos" # REPLACE WITH YOUR PROJECT ID
BUCKET = "cloud-training-demos-ml" # REPLACE WITH YOUR BUCKET NAME
REGION = "us-central1" # REPLACE WITH YOUR BUCKET REGION e.g. us-central1
# Do not change these
os.environ["PROJECT"] = PROJECT
os.environ["BUCKET"] = BUCKET
os.environ["REGION"] = REGION
os.environ["TFVERSION"] = "1.13"
%%bash
gcloud config set project $PROJECT
gcloud config set compute/region $REGION
import tensorflow as tf
print(tf.__version__)
```
## Create raw dataset
<p>
For collaborative filtering, we don't need to know anything about either the users or the content. Essentially, all we need to know is userId, itemId, and rating that the particular user gave the particular item.
<p>
In this case, we are working with newspaper articles. The company doesn't ask their users to rate the articles. However, we can use the time-spent on the page as a proxy for rating.
<p>
Normally, we would also add a time filter to this ("latest 7 days"), but our dataset is itself limited to a few days.
```
from google.cloud import bigquery
bq = bigquery.Client(project = PROJECT)
sql = """
WITH CTE_visitor_page_content AS (
SELECT
# Schema: https://support.google.com/analytics/answer/3437719?hl=en
# For a completely unique visit-session ID, we combine combination of fullVisitorId and visitNumber:
CONCAT(fullVisitorID,'-',CAST(visitNumber AS STRING)) AS visitorId,
(SELECT MAX(IF(index=10, value, NULL)) FROM UNNEST(hits.customDimensions)) AS latestContentId,
(LEAD(hits.time, 1) OVER (PARTITION BY fullVisitorId ORDER BY hits.time ASC) - hits.time) AS session_duration
FROM
`cloud-training-demos.GA360_test.ga_sessions_sample`,
UNNEST(hits) AS hits
WHERE
# only include hits on pages
hits.type = "PAGE"
GROUP BY
fullVisitorId,
visitNumber,
latestContentId,
hits.time )
-- Aggregate web stats
SELECT
visitorId,
latestContentId as contentId,
SUM(session_duration) AS session_duration
FROM
CTE_visitor_page_content
WHERE
latestContentId IS NOT NULL
GROUP BY
visitorId,
latestContentId
HAVING
session_duration > 0
"""
df = bq.query(sql).to_dataframe()
df.head()
stats = df.describe()
stats
df[["session_duration"]].plot(kind="hist", logy=True, bins=100, figsize=[8,5])
# The rating is the session_duration scaled to be in the range 0-1. This will help with training.
median = stats.loc["50%", "session_duration"]
df["rating"] = 0.3 * df["session_duration"] / median
df.loc[df["rating"] > 1, "rating"] = 1
df[["rating"]].plot(kind="hist", logy=True, bins=100, figsize=[8,5])
del df["session_duration"]
%%bash
rm -rf data
mkdir data
df.to_csv(path_or_buf = "data/collab_raw.csv", index = False, header = False)
!head data/collab_raw.csv
```
## Create dataset for WALS
<p>
The raw dataset (above) won't work for WALS:
<ol>
<li> The userId and itemId have to be 0,1,2 ... so we need to create a mapping from visitorId (in the raw data) to userId and contentId (in the raw data) to itemId.
<li> We will need to save the above mapping to a file because at prediction time, we'll need to know how to map the contentId in the table above to the itemId.
<li> We'll need two files: a "rows" dataset where all the items for a particular user are listed; and a "columns" dataset where all the users for a particular item are listed.
</ol>
<p>
### Mapping
```
import pandas as pd
import numpy as np
def create_mapping(values, filename):
with open(filename, 'w') as ofp:
value_to_id = {value:idx for idx, value in enumerate(values.unique())}
for value, idx in value_to_id.items():
ofp.write("{},{}\n".format(value, idx))
return value_to_id
df = pd.read_csv(filepath_or_buffer = "data/collab_raw.csv",
header = None,
names = ["visitorId", "contentId", "rating"],
dtype = {"visitorId": str, "contentId": str, "rating": np.float})
df.to_csv(path_or_buf = "data/collab_raw.csv", index = False, header = False)
user_mapping = create_mapping(df["visitorId"], "data/users.csv")
item_mapping = create_mapping(df["contentId"], "data/items.csv")
!head -3 data/*.csv
df["userId"] = df["visitorId"].map(user_mapping.get)
df["itemId"] = df["contentId"].map(item_mapping.get)
mapped_df = df[["userId", "itemId", "rating"]]
mapped_df.to_csv(path_or_buf = "data/collab_mapped.csv", index = False, header = False)
mapped_df.head()
```
### Creating rows and columns datasets
```
import pandas as pd
import numpy as np
mapped_df = pd.read_csv(filepath_or_buffer = "data/collab_mapped.csv", header = None, names = ["userId", "itemId", "rating"])
mapped_df.head()
NITEMS = np.max(mapped_df["itemId"]) + 1
NUSERS = np.max(mapped_df["userId"]) + 1
mapped_df["rating"] = np.round(mapped_df["rating"].values, 2)
print("{} items, {} users, {} interactions".format( NITEMS, NUSERS, len(mapped_df) ))
grouped_by_items = mapped_df.groupby("itemId")
iter = 0
for item, grouped in grouped_by_items:
print(item, grouped["userId"].values, grouped["rating"].values)
iter = iter + 1
if iter > 5:
break
import tensorflow as tf
grouped_by_items = mapped_df.groupby("itemId")
with tf.python_io.TFRecordWriter("data/users_for_item") as ofp:
for item, grouped in grouped_by_items:
example = tf.train.Example(features = tf.train.Features(feature = {
"key": tf.train.Feature(int64_list = tf.train.Int64List(value = [item])),
"indices": tf.train.Feature(int64_list = tf.train.Int64List(value = grouped["userId"].values)),
"values": tf.train.Feature(float_list = tf.train.FloatList(value = grouped["rating"].values))
}))
ofp.write(example.SerializeToString())
grouped_by_users = mapped_df.groupby("userId")
with tf.python_io.TFRecordWriter("data/items_for_user") as ofp:
for user, grouped in grouped_by_users:
example = tf.train.Example(features = tf.train.Features(feature = {
"key": tf.train.Feature(int64_list = tf.train.Int64List(value = [user])),
"indices": tf.train.Feature(int64_list = tf.train.Int64List(value = grouped["itemId"].values)),
"values": tf.train.Feature(float_list = tf.train.FloatList(value = grouped["rating"].values))
}))
ofp.write(example.SerializeToString())
!ls -lrt data
```
To summarize, we created the following data files from collab_raw.csv:
<ol>
<li> ```collab_mapped.csv``` is essentially the same data as in ```collab_raw.csv``` except that ```visitorId``` and ```contentId``` which are business-specific have been mapped to ```userId``` and ```itemId``` which are enumerated in 0,1,2,.... The mappings themselves are stored in ```items.csv``` and ```users.csv``` so that they can be used during inference.
<li> ```users_for_item``` contains all the users/ratings for each item in TFExample format
<li> ```items_for_user``` contains all the items/ratings for each user in TFExample format
</ol>
## Train with WALS
Once you have the dataset, do matrix factorization with WALS using the [WALSMatrixFactorization](https://www.tensorflow.org/versions/master/api_docs/python/tf/contrib/factorization/WALSMatrixFactorization) in the contrib directory.
This is an estimator model, so it should be relatively familiar.
<p>
As usual, we write an input_fn to provide the data to the model, and then create the Estimator to do train_and_evaluate.
Because it is in contrib and hasn't moved over to tf.estimator yet, we use tf.contrib.learn.Experiment to handle the training loop.<p>
Make sure to replace <strong># TODO</strong> in below code.
```
import os
import tensorflow as tf
from tensorflow.python.lib.io import file_io
from tensorflow.contrib.factorization import WALSMatrixFactorization
def read_dataset(mode, args):
def decode_example(protos, vocab_size):
# TODO
return
def remap_keys(sparse_tensor):
# Current indices of our SparseTensor that we need to fix
bad_indices = sparse_tensor.indices # shape = (current_batch_size * (number_of_items/users[i] + 1), 2)
# Current values of our SparseTensor that we need to fix
bad_values = sparse_tensor.values # shape = (current_batch_size * (number_of_items/users[i] + 1),)
# Since batch is ordered, the last value for a batch index is the user
# Find where the batch index chages to extract the user rows
# 1 where user, else 0
user_mask = tf.concat(values = [bad_indices[1:,0] - bad_indices[:-1,0], tf.constant(value = [1], dtype = tf.int64)], axis = 0) # shape = (current_batch_size * (number_of_items/users[i] + 1), 2)
# Mask out the user rows from the values
good_values = tf.boolean_mask(tensor = bad_values, mask = tf.equal(x = user_mask, y = 0)) # shape = (current_batch_size * number_of_items/users[i],)
item_indices = tf.boolean_mask(tensor = bad_indices, mask = tf.equal(x = user_mask, y = 0)) # shape = (current_batch_size * number_of_items/users[i],)
user_indices = tf.boolean_mask(tensor = bad_indices, mask = tf.equal(x = user_mask, y = 1))[:, 1] # shape = (current_batch_size,)
good_user_indices = tf.gather(params = user_indices, indices = item_indices[:,0]) # shape = (current_batch_size * number_of_items/users[i],)
# User and item indices are rank 1, need to make rank 1 to concat
good_user_indices_expanded = tf.expand_dims(input = good_user_indices, axis = -1) # shape = (current_batch_size * number_of_items/users[i], 1)
good_item_indices_expanded = tf.expand_dims(input = item_indices[:, 1], axis = -1) # shape = (current_batch_size * number_of_items/users[i], 1)
good_indices = tf.concat(values = [good_user_indices_expanded, good_item_indices_expanded], axis = 1) # shape = (current_batch_size * number_of_items/users[i], 2)
remapped_sparse_tensor = tf.SparseTensor(indices = good_indices, values = good_values, dense_shape = sparse_tensor.dense_shape)
return remapped_sparse_tensor
def parse_tfrecords(filename, vocab_size):
if mode == tf.estimator.ModeKeys.TRAIN:
num_epochs = None # indefinitely
else:
num_epochs = 1 # end-of-input after this
files = tf.gfile.Glob(filename = os.path.join(args["input_path"], filename))
# Create dataset from file list
dataset = tf.data.TFRecordDataset(files)
dataset = dataset.map(map_func = lambda x: decode_example(x, vocab_size))
dataset = dataset.repeat(count = num_epochs)
dataset = dataset.batch(batch_size = args["batch_size"])
dataset = dataset.map(map_func = lambda x: remap_keys(x))
return dataset.make_one_shot_iterator().get_next()
def _input_fn():
features = {
WALSMatrixFactorization.INPUT_ROWS: parse_tfrecords("items_for_user", args["nitems"]),
WALSMatrixFactorization.INPUT_COLS: parse_tfrecords("users_for_item", args["nusers"]),
WALSMatrixFactorization.PROJECT_ROW: tf.constant(True)
}
return features, None
return _input_fn
def input_cols():
return parse_tfrecords("users_for_item", args["nusers"])
return _input_fn#_subset
```
This code is helpful in developing the input function. You don't need it in production.
```
def try_out():
with tf.Session() as sess:
fn = read_dataset(
mode = tf.estimator.ModeKeys.EVAL,
args = {"input_path": "data", "batch_size": 4, "nitems": NITEMS, "nusers": NUSERS})
feats, _ = fn()
print(feats["input_rows"].eval())
print(feats["input_rows"].eval())
try_out()
def find_top_k(user, item_factors, k):
all_items = tf.matmul(a = tf.expand_dims(input = user, axis = 0), b = tf.transpose(a = item_factors))
topk = tf.nn.top_k(input = all_items, k = k)
return tf.cast(x = topk.indices, dtype = tf.int64)
def batch_predict(args):
import numpy as np
with tf.Session() as sess:
estimator = tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"])
# This is how you would get the row factors for out-of-vocab user data
# row_factors = list(estimator.get_projections(input_fn=read_dataset(tf.estimator.ModeKeys.EVAL, args)))
# user_factors = tf.convert_to_tensor(np.array(row_factors))
# But for in-vocab data, the row factors are already in the checkpoint
user_factors = tf.convert_to_tensor(value = estimator.get_row_factors()[0]) # (nusers, nembeds)
# In either case, we have to assume catalog doesn"t change, so col_factors are read in
item_factors = tf.convert_to_tensor(value = estimator.get_col_factors()[0])# (nitems, nembeds)
# For each user, find the top K items
topk = tf.squeeze(input = tf.map_fn(fn = lambda user: find_top_k(user, item_factors, args["topk"]), elems = user_factors, dtype = tf.int64))
with file_io.FileIO(os.path.join(args["output_dir"], "batch_pred.txt"), mode = 'w') as f:
for best_items_for_user in topk.eval():
f.write(",".join(str(x) for x in best_items_for_user) + '\n')
def train_and_evaluate(args):
train_steps = int(0.5 + (1.0 * args["num_epochs"] * args["nusers"]) / args["batch_size"])
steps_in_epoch = int(0.5 + args["nusers"] / args["batch_size"])
print("Will train for {} steps, evaluating once every {} steps".format(train_steps, steps_in_epoch))
def experiment_fn(output_dir):
return tf.contrib.learn.Experiment(
tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"]),
train_input_fn = read_dataset(tf.estimator.ModeKeys.TRAIN, args),
eval_input_fn = read_dataset(tf.estimator.ModeKeys.EVAL, args),
train_steps = train_steps,
eval_steps = 1,
min_eval_frequency = steps_in_epoch
)
from tensorflow.contrib.learn.python.learn import learn_runner
learn_runner.run(experiment_fn = experiment_fn, output_dir = args["output_dir"])
batch_predict(args)
import shutil
shutil.rmtree(path = "wals_trained", ignore_errors=True)
train_and_evaluate({
"output_dir": "wals_trained",
"input_path": "data/",
"num_epochs": 0.05,
"nitems": NITEMS,
"nusers": NUSERS,
"batch_size": 512,
"n_embeds": 10,
"topk": 3
})
!ls wals_trained
!head wals_trained/batch_pred.txt
```
## Run as a Python module
Let's run it as Python module for just a few steps.
```
os.environ["NITEMS"] = str(NITEMS)
os.environ["NUSERS"] = str(NUSERS)
%%bash
rm -rf wals.tar.gz wals_trained
gcloud ai-platform local train \
--module-name=walsmodel.task \
--package-path=${PWD}/walsmodel \
-- \
--output_dir=${PWD}/wals_trained \
--input_path=${PWD}/data \
--num_epochs=0.01 --nitems=${NITEMS} --nusers=${NUSERS} \
--job-dir=./tmp
```
## Run on Cloud
```
%%bash
gsutil -m cp data/* gs://${BUCKET}/wals/data
%%bash
OUTDIR=gs://${BUCKET}/wals/model_trained
JOBNAME=wals_$(date -u +%y%m%d_%H%M%S)
echo $OUTDIR $REGION $JOBNAME
gsutil -m rm -rf $OUTDIR
gcloud ai-platform jobs submit training $JOBNAME \
--region=$REGION \
--module-name=walsmodel.task \
--package-path=${PWD}/walsmodel \
--job-dir=$OUTDIR \
--staging-bucket=gs://$BUCKET \
--scale-tier=BASIC_GPU \
--runtime-version=$TFVERSION \
-- \
--output_dir=$OUTDIR \
--input_path=gs://${BUCKET}/wals/data \
--num_epochs=10 --nitems=${NITEMS} --nusers=${NUSERS}
```
This took <b>10 minutes</b> for me.
## Get row and column factors
Once you have a trained WALS model, you can get row and column factors (user and item embeddings) from the checkpoint file. We'll look at how to use these in the section on building a recommendation system using deep neural networks.
```
def get_factors(args):
with tf.Session() as sess:
estimator = tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"])
row_factors = estimator.get_row_factors()[0]
col_factors = estimator.get_col_factors()[0]
return row_factors, col_factors
args = {
"output_dir": "gs://{}/wals/model_trained".format(BUCKET),
"nitems": NITEMS,
"nusers": NUSERS,
"n_embeds": 10
}
user_embeddings, item_embeddings = get_factors(args)
print(user_embeddings[:3])
print(item_embeddings[:3])
```
You can visualize the embedding vectors using dimensional reduction techniques such as PCA.
```
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.decomposition import PCA
pca = PCA(n_components = 3)
pca.fit(user_embeddings)
user_embeddings_pca = pca.transform(user_embeddings)
fig = plt.figure(figsize = (8,8))
ax = fig.add_subplot(111, projection = "3d")
xs, ys, zs = user_embeddings_pca[::150].T
ax.scatter(xs, ys, zs)
```
<pre>
# Copyright 2018 Google Inc. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
</pre>
|
github_jupyter
|
<!--BOOK_INFORMATION-->
<img align="left" style="padding-right:10px;" src="figures/PDSH-cover-small.png">
*This notebook contains an excerpt from the [Python Data Science Handbook](http://shop.oreilly.com/product/0636920034919.do) by Jake VanderPlas; the content is available [on GitHub](https://github.com/jakevdp/PythonDataScienceHandbook).*
*The text is released under the [CC-BY-NC-ND license](https://creativecommons.org/licenses/by-nc-nd/3.0/us/legalcode), and code is released under the [MIT license](https://opensource.org/licenses/MIT). If you find this content useful, please consider supporting the work by [buying the book](http://shop.oreilly.com/product/0636920034919.do)!*
<!--NAVIGATION-->
< [Machine Learning](05.00-Machine-Learning.ipynb) | [Contents](Index.ipynb) | [Introducing Scikit-Learn](05.02-Introducing-Scikit-Learn.ipynb) >
<a href="https://colab.research.google.com/github/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/05.01-What-Is-Machine-Learning.ipynb"><img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open and Execute in Google Colaboratory"></a>
# What Is Machine Learning?
Before we take a look at the details of various machine learning methods, let's start by looking at what machine learning is, and what it isn't.
Machine learning is often categorized as a subfield of artificial intelligence, but I find that categorization can often be misleading at first brush.
The study of machine learning certainly arose from research in this context, but in the data science application of machine learning methods, it's more helpful to think of machine learning as a means of *building models of data*.
Fundamentally, machine learning involves building mathematical models to help understand data.
"Learning" enters the fray when we give these models *tunable parameters* that can be adapted to observed data; in this way the program can be considered to be "learning" from the data.
Once these models have been fit to previously seen data, they can be used to predict and understand aspects of newly observed data.
I'll leave to the reader the more philosophical digression regarding the extent to which this type of mathematical, model-based "learning" is similar to the "learning" exhibited by the human brain.
Understanding the problem setting in machine learning is essential to using these tools effectively, and so we will start with some broad categorizations of the types of approaches we'll discuss here.
## Categories of Machine Learning
At the most fundamental level, machine learning can be categorized into two main types: supervised learning and unsupervised learning.
*Supervised learning* involves somehow modeling the relationship between measured features of data and some label associated with the data; once this model is determined, it can be used to apply labels to new, unknown data.
This is further subdivided into *classification* tasks and *regression* tasks: in classification, the labels are discrete categories, while in regression, the labels are continuous quantities.
We will see examples of both types of supervised learning in the following section.
*Unsupervised learning* involves modeling the features of a dataset without reference to any label, and is often described as "letting the dataset speak for itself."
These models include tasks such as *clustering* and *dimensionality reduction.*
Clustering algorithms identify distinct groups of data, while dimensionality reduction algorithms search for more succinct representations of the data.
We will see examples of both types of unsupervised learning in the following section.
In addition, there are so-called *semi-supervised learning* methods, which falls somewhere between supervised learning and unsupervised learning.
Semi-supervised learning methods are often useful when only incomplete labels are available.
## Qualitative Examples of Machine Learning Applications
To make these ideas more concrete, let's take a look at a few very simple examples of a machine learning task.
These examples are meant to give an intuitive, non-quantitative overview of the types of machine learning tasks we will be looking at in this chapter.
In later sections, we will go into more depth regarding the particular models and how they are used.
For a preview of these more technical aspects, you can find the Python source that generates the following figures in the [Appendix: Figure Code](06.00-Figure-Code.ipynb).
### Classification: Predicting discrete labels
We will first take a look at a simple *classification* task, in which you are given a set of labeled points and want to use these to classify some unlabeled points.
Imagine that we have the data shown in this figure:

[figure source in Appendix](06.00-Figure-Code.ipynb#Classification-Example-Figure-1)
Here we have two-dimensional data: that is, we have two *features* for each point, represented by the *(x,y)* positions of the points on the plane.
In addition, we have one of two *class labels* for each point, here represented by the colors of the points.
From these features and labels, we would like to create a model that will let us decide whether a new point should be labeled "blue" or "red."
There are a number of possible models for such a classification task, but here we will use an extremely simple one. We will make the assumption that the two groups can be separated by drawing a straight line through the plane between them, such that points on each side of the line fall in the same group.
Here the *model* is a quantitative version of the statement "a straight line separates the classes", while the *model parameters* are the particular numbers describing the location and orientation of that line for our data.
The optimal values for these model parameters are learned from the data (this is the "learning" in machine learning), which is often called *training the model*.
The following figure shows a visual representation of what the trained model looks like for this data:

[figure source in Appendix](06.00-Figure-Code.ipynb#Classification-Example-Figure-2)
Now that this model has been trained, it can be generalized to new, unlabeled data.
In other words, we can take a new set of data, draw this model line through it, and assign labels to the new points based on this model.
This stage is usually called *prediction*. See the following figure:

[figure source in Appendix](06.00-Figure-Code.ipynb#Classification-Example-Figure-3)
This is the basic idea of a classification task in machine learning, where "classification" indicates that the data has discrete class labels.
At first glance this may look fairly trivial: it would be relatively easy to simply look at this data and draw such a discriminatory line to accomplish this classification.
A benefit of the machine learning approach, however, is that it can generalize to much larger datasets in many more dimensions.
For example, this is similar to the task of automated spam detection for email; in this case, we might use the following features and labels:
- *feature 1*, *feature 2*, etc. $\to$ normalized counts of important words or phrases ("Viagra", "Nigerian prince", etc.)
- *label* $\to$ "spam" or "not spam"
For the training set, these labels might be determined by individual inspection of a small representative sample of emails; for the remaining emails, the label would be determined using the model.
For a suitably trained classification algorithm with enough well-constructed features (typically thousands or millions of words or phrases), this type of approach can be very effective.
We will see an example of such text-based classification in [In Depth: Naive Bayes Classification](05.05-Naive-Bayes.ipynb).
Some important classification algorithms that we will discuss in more detail are Gaussian naive Bayes (see [In Depth: Naive Bayes Classification](05.05-Naive-Bayes.ipynb)), support vector machines (see [In-Depth: Support Vector Machines](05.07-Support-Vector-Machines.ipynb)), and random forest classification (see [In-Depth: Decision Trees and Random Forests](05.08-Random-Forests.ipynb)).
### Regression: Predicting continuous labels
In contrast with the discrete labels of a classification algorithm, we will next look at a simple *regression* task in which the labels are continuous quantities.
Consider the data shown in the following figure, which consists of a set of points each with a continuous label:

[figure source in Appendix](06.00-Figure-Code.ipynb#Regression-Example-Figure-1)
As with the classification example, we have two-dimensional data: that is, there are two features describing each data point.
The color of each point represents the continuous label for that point.
There are a number of possible regression models we might use for this type of data, but here we will use a simple linear regression to predict the points.
This simple linear regression model assumes that if we treat the label as a third spatial dimension, we can fit a plane to the data.
This is a higher-level generalization of the well-known problem of fitting a line to data with two coordinates.
We can visualize this setup as shown in the following figure:

[figure source in Appendix](06.00-Figure-Code.ipynb#Regression-Example-Figure-2)
Notice that the *feature 1-feature 2* plane here is the same as in the two-dimensional plot from before; in this case, however, we have represented the labels by both color and three-dimensional axis position.
From this view, it seems reasonable that fitting a plane through this three-dimensional data would allow us to predict the expected label for any set of input parameters.
Returning to the two-dimensional projection, when we fit such a plane we get the result shown in the following figure:

[figure source in Appendix](06.00-Figure-Code.ipynb#Regression-Example-Figure-3)
This plane of fit gives us what we need to predict labels for new points.
Visually, we find the results shown in the following figure:

[figure source in Appendix](06.00-Figure-Code.ipynb#Regression-Example-Figure-4)
As with the classification example, this may seem rather trivial in a low number of dimensions.
But the power of these methods is that they can be straightforwardly applied and evaluated in the case of data with many, many features.
For example, this is similar to the task of computing the distance to galaxies observed through a telescope—in this case, we might use the following features and labels:
- *feature 1*, *feature 2*, etc. $\to$ brightness of each galaxy at one of several wave lengths or colors
- *label* $\to$ distance or redshift of the galaxy
The distances for a small number of these galaxies might be determined through an independent set of (typically more expensive) observations.
Distances to remaining galaxies could then be estimated using a suitable regression model, without the need to employ the more expensive observation across the entire set.
In astronomy circles, this is known as the "photometric redshift" problem.
Some important regression algorithms that we will discuss are linear regression (see [In Depth: Linear Regression](05.06-Linear-Regression.ipynb)), support vector machines (see [In-Depth: Support Vector Machines](05.07-Support-Vector-Machines.ipynb)), and random forest regression (see [In-Depth: Decision Trees and Random Forests](05.08-Random-Forests.ipynb)).
### Clustering: Inferring labels on unlabeled data
The classification and regression illustrations we just looked at are examples of supervised learning algorithms, in which we are trying to build a model that will predict labels for new data.
Unsupervised learning involves models that describe data without reference to any known labels.
One common case of unsupervised learning is "clustering," in which data is automatically assigned to some number of discrete groups.
For example, we might have some two-dimensional data like that shown in the following figure:

[figure source in Appendix](06.00-Figure-Code.ipynb#Clustering-Example-Figure-2)
By eye, it is clear that each of these points is part of a distinct group.
Given this input, a clustering model will use the intrinsic structure of the data to determine which points are related.
Using the very fast and intuitive *k*-means algorithm (see [In Depth: K-Means Clustering](05.11-K-Means.ipynb)), we find the clusters shown in the following figure:

[figure source in Appendix](06.00-Figure-Code.ipynb#Clustering-Example-Figure-2)
*k*-means fits a model consisting of *k* cluster centers; the optimal centers are assumed to be those that minimize the distance of each point from its assigned center.
Again, this might seem like a trivial exercise in two dimensions, but as our data becomes larger and more complex, such clustering algorithms can be employed to extract useful information from the dataset.
We will discuss the *k*-means algorithm in more depth in [In Depth: K-Means Clustering](05.11-K-Means.ipynb).
Other important clustering algorithms include Gaussian mixture models (See [In Depth: Gaussian Mixture Models](05.12-Gaussian-Mixtures.ipynb)) and spectral clustering (See [Scikit-Learn's clustering documentation](http://scikit-learn.org/stable/modules/clustering.html)).
### Dimensionality reduction: Inferring structure of unlabeled data
Dimensionality reduction is another example of an unsupervised algorithm, in which labels or other information are inferred from the structure of the dataset itself.
Dimensionality reduction is a bit more abstract than the examples we looked at before, but generally it seeks to pull out some low-dimensional representation of data that in some way preserves relevant qualities of the full dataset.
Different dimensionality reduction routines measure these relevant qualities in different ways, as we will see in [In-Depth: Manifold Learning](05.10-Manifold-Learning.ipynb).
As an example of this, consider the data shown in the following figure:

[figure source in Appendix](06.00-Figure-Code.ipynb#Dimensionality-Reduction-Example-Figure-1)
Visually, it is clear that there is some structure in this data: it is drawn from a one-dimensional line that is arranged in a spiral within this two-dimensional space.
In a sense, you could say that this data is "intrinsically" only one dimensional, though this one-dimensional data is embedded in higher-dimensional space.
A suitable dimensionality reduction model in this case would be sensitive to this nonlinear embedded structure, and be able to pull out this lower-dimensionality representation.
The following figure shows a visualization of the results of the Isomap algorithm, a manifold learning algorithm that does exactly this:

[figure source in Appendix](06.00-Figure-Code.ipynb#Dimensionality-Reduction-Example-Figure-2)
Notice that the colors (which represent the extracted one-dimensional latent variable) change uniformly along the spiral, which indicates that the algorithm did in fact detect the structure we saw by eye.
As with the previous examples, the power of dimensionality reduction algorithms becomes clearer in higher-dimensional cases.
For example, we might wish to visualize important relationships within a dataset that has 100 or 1,000 features.
Visualizing 1,000-dimensional data is a challenge, and one way we can make this more manageable is to use a dimensionality reduction technique to reduce the data to two or three dimensions.
Some important dimensionality reduction algorithms that we will discuss are principal component analysis (see [In Depth: Principal Component Analysis](05.09-Principal-Component-Analysis.ipynb)) and various manifold learning algorithms, including Isomap and locally linear embedding (See [In-Depth: Manifold Learning](05.10-Manifold-Learning.ipynb)).
## Summary
Here we have seen a few simple examples of some of the basic types of machine learning approaches.
Needless to say, there are a number of important practical details that we have glossed over, but I hope this section was enough to give you a basic idea of what types of problems machine learning approaches can solve.
In short, we saw the following:
- *Supervised learning*: Models that can predict labels based on labeled training data
- *Classification*: Models that predict labels as two or more discrete categories
- *Regression*: Models that predict continuous labels
- *Unsupervised learning*: Models that identify structure in unlabeled data
- *Clustering*: Models that detect and identify distinct groups in the data
- *Dimensionality reduction*: Models that detect and identify lower-dimensional structure in higher-dimensional data
In the following sections we will go into much greater depth within these categories, and see some more interesting examples of where these concepts can be useful.
All of the figures in the preceding discussion are generated based on actual machine learning computations; the code behind them can be found in [Appendix: Figure Code](06.00-Figure-Code.ipynb).
<!--NAVIGATION-->
< [Machine Learning](05.00-Machine-Learning.ipynb) | [Contents](Index.ipynb) | [Introducing Scikit-Learn](05.02-Introducing-Scikit-Learn.ipynb) >
<a href="https://colab.research.google.com/github/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/05.01-What-Is-Machine-Learning.ipynb"><img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open and Execute in Google Colaboratory"></a>
|
github_jupyter
|
## Building a Stack in Python
Before we start let us reiterate they key components of a stack. A stack is a data structure that consists of two main operations: push and pop. A push is when you add an element to the **top of the stack** and a pop is when you remove an element from **the top of the stack**. Python 3.x conviently allows us to demonstate this functionality with a list. When you have a list such as [2,4,5,6] you can decide which end of the list is the bottom and the top of the stack respectivley. Once you decide that, you can use the append, pop or insert function to simulate a stack. We will choose the first element to be the bottom of our stack and therefore be using the append and pop functions to simulate it. Give it a try by implementing the function below!
#### Try Building a Stack
```
class Stack:
def __init__(self):
# TODO: Initialize the Stack
def size(self):
# TODO: Check the size of the Stack
def push(self, item):
# TODO: Push item onto Stack
def pop(self):
# TODO: Pop item off of the Stack
```
#### Test the Stack
```
MyStack = Stack()
MyStack.push("Web Page 1")
MyStack.push("Web Page 2")
MyStack.push("Web Page 3")
print (MyStack.items)
MyStack.pop()
MyStack.pop()
print ("Pass" if (MyStack.items[0] == 'Web Page 1') else "Fail")
MyStack.pop()
print ("Pass" if (MyStack.pop() == None) else "Fail")
```
<span class="graffiti-highlight graffiti-id_3l78doc-id_l2kcjcz"><i></i><button>Hide Solution</button></span>
```
# Solution
class Stack:
def __init__(self):
self.items = []
def size(self):
return len(self.items)
def push(self, item):
self.items.append(item)
def pop(self):
if self.size()==0:
return None
else:
return self.items.pop()
MyStack = Stack()
MyStack.push("Web Page 1")
MyStack.push("Web Page 2")
MyStack.push("Web Page 3")
print (MyStack.items)
MyStack.pop()
MyStack.pop()
print ("Pass" if (MyStack.items[0] == 'Web Page 1') else "Fail")
MyStack.pop()
print ("Pass" if (MyStack.pop() == None) else "Fail")# Solution
class Stack:
def __init__(self):
self.items = []
def size(self):
return len(self.items)
def push(self, item):
self.items.append(item)
def pop(self):
if self.size()==0:
return None
else:
return self.items.pop()
MyStack = Stack()
MyStack.push("Web Page 1")
MyStack.push("Web Page 2")
MyStack.push("Web Page 3")
print (MyStack.items)
MyStack.pop()
MyStack.pop()
print ("Pass" if (MyStack.items[0] == 'Web Page 1') else "Fail")
MyStack.pop()
print ("Pass" if (MyStack.pop() == None) else "Fail")# Solution
class Stack:
def __init__(self):
self.items = []
def size(self):
return len(self.items)
def push(self, item):
self.items.append(item)
def pop(self):
if self.size()==0:
return None
else:
return self.items.pop()
MyStack = Stack()
MyStack.push("Web Page 1")
MyStack.push("Web Page 2")
MyStack.push("Web Page 3")
print (MyStack.items)
MyStack.pop()
MyStack.pop()
print ("Pass" if (MyStack.items[0] == 'Web Page 1') else "Fail")
MyStack.pop()
print ("Pass" if (MyStack.pop() == None) else "Fail")
```
|
github_jupyter
|
```
# hide
%load_ext nb_black
# nb_black if using jupyter
```
# Helsinki Machine Learning Project Template
Template for open source ML and predictive analytics projects.

[](https://github.com/psf/black)
[](https://badge.fury.io/gh/City-of-Helsinki%2Fml_project_template)





NOTE: Once you begin your work, rewrite this notebook (index.ipynb) so that it describes your project, and regenerate README by calling `nbdev_build_docs`
## About
This is a git repository template for Python-based open source ML and analytics projects.
The template assumes the concept of Notebook Development.
This means, that you do all the data science work inside notebooks.
There is no copy-pasting! We use the [nbdev](https://nbdev.fast.ai/) tool to build python modules and doc pages from the notebooks, automatically.
This way you always have your code, results and documentation as one.
Notebooks can be executed with the [papermill](https://papermill.readthedocs.io/) tool for an automatic,
well documented model update workflow. Handy, isn't it?
The template assumes that you divide your machine learning project into 5 parts:
0. Data - loading & preprocessing
1. Model - Python class code & algorithm development
2. Loss - model training & evaluation
3. Workflow - automatic model update (reproduce steps 0.-2.)
4. API - an interface to interact with a trained model
Each part has their own notebook template, that you can follow to plan and do your development.
In addition, the template comes with a working Dockerfile and .devcontainer for doing your development easily with any device.
You can extend these for your needs and for building a runtime container for your machine learning app.
The template is completely open source and environment agnostic.
Follow the installation instructions to create a new,
independent repository with clean commit history,
but with a copy of all the files and folders presented.
The authors of this template will not be contributors to your project,
although we are more hear what you have achieved with it!
Also, if you don't like something or know an improvement, your contribution is very welcome!
Note, that updates to the template can not be automatically pulled to child projects.
The template is developed and maintained by the data and analytics team of the city of Helsinki.
The template is published under the Apache-2.0 licence and open source utilization is encouraged!
## Contents
The core structure of the repository is the following:
## EDITABLE:
data/ # Folder for storing data files. Ignored by git by default.
|- raw_data/ # To store raw data files
|- preprocessed_data/ # To store cleaned data
results/ # Save results here. Ignored by git by default.
|- notebooks/ # Save automatically executed notebooks here
00_data.ipynb # Extract, transfer, load data here & define related functions.
01_model.ipynb # Create and code test your ML model
02_loss.ipynb # Train and evaluate ML model, deploy or save for later use
03_workflow.ipynb # Define ML workflow and parameterization
04_api.ipynb # Define runtime API for using trained ML model
project-requirements.in # Add here the Python packages you want to install
update_install_dev_reqs.sh # run this script to install new python packages
settings.ini # Project specific settings. Build instructions for lib and docs.
Dockerfile # Define docker image build instructions
.devcontainer # Codespaces / VSC dev environment instructions
## AUTOMATICALLY GENERATED: (Do not edit unless otherwise specified!)
docs/ # Project documentation (html)
[your_module]/ # Python module built from the notebooks (follow the installation instructions).
README.md # The frontpage of your project, generated from index.ipynb
requirements.txt # dev / default requirements. automatically generated by pip-tools
min-requirements.txt # lighter requirements without dev tools. automatically generated by pip-tools
## STATIC NON-EDITABLE: (Edit only if you know what you're doing!)
base-requirements.in # core tools that every project built based on the template always requires
requirements.in # development tools + project spesific requirements
LISENCE # lisence information
MANIFEST.in # metadata for building python distributable
setup.py # settings for the python module of your project
CODE_OF_CONDUCT.md # code of conduct. Please review before contributing.
## How to install
> Note: if you are doing a project on personal data for the City of Helsinki, contact the data and analytics team of the city before proceeding any further!
### 1. On your GitHub homepage
0. (Create [GitHub account](https://github.com/) if you do not have one already.
1. Sign into your GitHub homepage
2. Go to [github.com/City-of-Helsinki/ml_project_template](https://github.com/City-of-Helsinki/ml_project_template) and click the green button that says 'Use this template'.
3. Give your project a name. Do not use the dash symbol '-', but rather the underscore '_', because the name of the repo will become the name of your Python module.
4. If you are creating a project for your organization, change the owner of the repo. From the drop down bar, select your organization GitHub account (e.g. City-of-Helsinki). You need to be included as a team member to the GitHub of the organization.
5. Define your project publicity (you can change this later, but most likely you want to begin with a private repo).
6. Click 'Create repository from template'
This will create a new repository for you copying everything from this template, but with clean commit history.
### 2. Setting up your development environment
#### a) Recommended: Codespaces
If your organization has [Codespaces](https://github.com/features/codespaces) enabled (requires GitHub Enterprise & Azure subscription), you are now ready to begin development. Just launch the repository in a codespace, and a dev container is automatically set up!
#### b) Can't use Codespaces: Local installation with Docker
You can build a development environment locally with docker.
The recommended way is to use VSC in container development mode ([link to instructions](https://code.visualstudio.com/docs/remote/containers)).
#### c) Can't use Docker: Local manual installation
You can also do your development 'the good old way':
0. Create an SSH key and add it to your github profile ([instructions](https://docs.github.com/en/authentication/connecting-to-github-with-ssh))
1. Configure your git user name and email adress if you haven't done it already: `git config --global user.name "Firstname Lastname" && git config --global user.email "your@email.com"`
2. Clone your new repository: `git clone git@github.com:[repository_owner]/[your_repository]`
3. Go inside the repository folder: `cd [your_repository]`
4. Create and activate virtual environment of your choice. Remember to define the Python version to 3.8! (Instructions: [conda](https://docs.conda.io/projects/conda/en/latest/user-guide/tasks/manage-environments.html), [venv](https://packaging.python.org/en/latest/guides/installing-using-pip-and-virtual-environments/))
5. Install pip-tools: `python -m pip install pip-tools`
6. Install requirements: `pip-sync requirements.txt`
7. Create an ipython kernel for running the notebooks: `python -m ipykernel install --user --name python38myenv`
8. The default development enviroment contains basic Jupyter, and many IDEs have built-in support notebooks. If you wish, you can install JupyterLab by uncommenting it in `requirements.in` and re-running pip-sync. To launch JupyterLab, run `jupyter-lab --allow-root --config .devcontainer/jupyter-server-config.py`
#### d) Can't connect to internet: Offline install with Docker
Sometimes you have to work in an environment that can not be connected to the internet, for example for privacy or cybersecurity reasons. In this case, first install the template and all packages that you assume you will require to an environment with internet, and build the docker image as in 2c). Then, save the docker image and transfer it to your offline environment following [these instructions](https://stackoverflow.com/questions/48125169/how-run-docker-images-without-connect-to-internet/48125632#48125632).
### 3. Initializing your project
Few last tweaks before you are good to go:
1. Edit `LICENCE`, `Makefile`, `settings.ini`, `docs/_config.yml` and `docs/_data/topnav.yml` according to your project details. Don't worry - you can continue editing them in the future.
2. Remove the folder `ml_project_template` with the command `git rm -r ml_project_template`. A new folder with the name of your repository will be created automatically when calling `nbdev_build_lib`.
3. Recreate the python module: `nbdev_build_lib`. In the future, repeat this step every time you move between notebooks to ensure your python modules are up to date.
4. Recreate the html doc pages & README: `nbdev_build_docs`. In the future, repeat this step every time you push code to ensure your documentation is up to date.
5. Make initial commit: `git add . && git commit -m "initialized repository from City-of-Helsinki/ml_project_template"`
6. Push changes `git push -u origin master`
You are now ready to begin your ML project development. Remember to track your changes with git!
## How to use
1. Install this template as basis of your new project (see above).
2. If you are not working inside a container, remember to activate your virtual environment every time you begin work: `conda activate [environment name]` with anaconda or `source [environment name]/bin/activate` with virtualenv.
3. Develop your ML solution! (Follow the notebooks!)
4. Save your notebooks and call `nbdev_build_lib` to build python modules of your notebooks - needed if you want to share code between notebooks or create a modules.
This will export all notebook cells with `# export` tag to corresponding .py files under the module (the folder inside your repository named after your repository).
Do this every time you make changes to any exportable parts of the code.
5. Save your notebooks and call `nbdev_build_docs` to create doc pages based on your notebooks (see below).
This will convert the notebooks into HTML files under `docs/` and update README based on the `index.ipynb`.
If you want to host your project pages on GitHub (like [the doc pages of this template](https://city-of-helsinki.github.io/ml_project_template/)), you will have to make your project public and enable github pages in repo > Settings > Pages : set Source to `docs/`.
Alternatively you can build the pages locally with jekyll.
## Installing & updating project libraries
Python has a rich and wide ecosystem of libraries to help with machine learning tasks among other things.
Pandas, Matplotlib, Scipy, PyTorch to name a few.
If base libraries in this template aren't sufficient you can add more with `pip install library`.
However, `pip` command installs libraries into your local Python environment.
To achieve consistent reproducibility we need to gather information about requirements into project repository.
New libraries are added to **`project-requirements.in`** file. When you change this file remember to run:
```bash
pip-compile --generate-hashes --allow-unsafe -o requirements.txt base-requirements.in requirements.in project-requirements.in
pip-compile --generate-hashes --allow-unsafe -o min-requirements.txt base-requirements.in project-requirements.in
```
These update full requirements for development environments and lighter, more focused requirements for server usage.
After requirements are updated you should run:
```bash
pip-sync requirements.txt
```
This way libraries you and other users will have the same Python environment.
NOTE: run `./update_install_dev_reqs.sh` for short - it contains the three above pip commands for updating and installing the requirements!
WARNING: if you don't update package names and versions next time you or anybody else tries to use this project in another environment its code might not work. Worse, it might *seem to* work, but does so incorrectly.
## Ethical aspects
Please involve ethical consideration in the documentation ML application.
For example:
* Can you recognize ethical issues with your ML project?
* Is there a risk for bias, discrimination, violation of privacy or conflict with the local or global laws?
* Could your results or algorithms be misused for malicious acts?
* Can data or model updates include bias in your model?
* How have you tackled these issues in your implementation?
* You most certainly make ethical choises in your code. Do you document & highlight them?
* If you build an actual application, how can contribute if they notice an unresolved ethical issue?
## How to cite (optional)
If you are doing a research project, you can add bibtex and other citation templates here.
You can also get a doi for your code by adding it to a code archive,
so your code can be cited directly! Most archives also provide repository badges.
To cite this work, use:
@misc{sten2022helsinki,
title = {Helsinki Machine Learning Project Template},
author = {Nuutti A Sten and Jussi Arpalahti},
year = {2022},
howpublished = {City of Helsinki. Available at: \url{https://github.com/City-of-Helsinki/ml_project_template}}
}
## Contributing
See [CONTRIBUTING.md](https://github.com/City-of-Helsinki/ml_project_template/blob/master/CONTRIBUTING.md) on how to contribute to the development of this template.
## Copyright
Copyright 2022 City-of-Helsinki. Licensed under the Apache License, Version 2.0 (the "License");
you may not use this project's files except in compliance with the License.
A copy of the License is provided in the LICENSE file in this repository.
The Helsinki logo is a registered trademark, and may only be used by the city of Helsinki.
NOTE: If you are using this template for other than city of Helsinki projects, remove the files `favicon.ico` and `company_logo.png` from `docs/assets/images/`.
# to remove remove helsinki logo and favicon, run:
git rm docs/assets/images/favicon.ico docs/assets/images/company_logo.png
git commit -m "removed Helsinki logo and favicon"
This template was built using [nbdev](https://nbdev.fast.ai/) on top of the fast.ai [nbdev_template](https://github.com/fastai/nbdev_template).
|
github_jupyter
|
## Install the packages
```
!pip install -Uqq datasets pythainlp==2.2.4 transformers==4.4.0 tensorflow==2.4.0 tensorflow_text emoji seqeval sentencepiece fuzzywuzzy
!npx degit --force https://github.com/vistec-AI/thai2transformers#dev
%load_ext autoreload
%autoreload 2
import pythainlp, transformers
pythainlp.__version__, transformers.__version__ #fix pythainlp to stabilize word tokenization for metrics
import collections
import logging
import pprint
import re
from tqdm.auto import tqdm
import numpy as np
import torch
#datasets
from datasets import (
load_dataset,
load_metric,
concatenate_datasets,
load_from_disk,
)
#transformers
from transformers import (
AutoConfig,
AutoTokenizer,
AutoModelForQuestionAnswering,
TrainingArguments,
Trainer,
default_data_collator,
)
#thai2transformers
import thai2transformers
from thai2transformers.metrics import (
squad_newmm_metric,
question_answering_metrics,
)
from thai2transformers.preprocess import (
prepare_qa_train_features
)
from thai2transformers.tokenizers import (
ThaiRobertaTokenizer,
ThaiWordsNewmmTokenizer,
ThaiWordsSyllableTokenizer,
FakeSefrCutTokenizer,
SEFR_SPLIT_TOKEN
)
from tqdm import tqdm
model_names = [
'wangchanberta-base-att-spm-uncased',
'xlm-roberta-base',
'bert-base-multilingual-cased',
'wangchanberta-base-wiki-newmm',
'wangchanberta-base-wiki-ssg',
'wangchanberta-base-wiki-sefr',
'wangchanberta-base-wiki-spm',
]
tokenizers = {
'wangchanberta-base-att-spm-uncased': AutoTokenizer,
'xlm-roberta-base': AutoTokenizer,
'bert-base-multilingual-cased': AutoTokenizer,
'wangchanberta-base-wiki-newmm': ThaiWordsNewmmTokenizer,
'wangchanberta-base-wiki-ssg': ThaiWordsSyllableTokenizer,
'wangchanberta-base-wiki-sefr': FakeSefrCutTokenizer,
'wangchanberta-base-wiki-spm': ThaiRobertaTokenizer,
}
public_models = ['xlm-roberta-base', 'bert-base-multilingual-cased']
#@title Choose Pretrained Model
model_name = "wangchanberta-base-att-spm-uncased" #@param ["wangchanberta-base-att-spm-uncased", "xlm-roberta-base", "bert-base-multilingual-cased", "wangchanberta-base-wiki-newmm", "wangchanberta-base-wiki-syllable", "wangchanberta-base-wiki-sefr", "wangchanberta-base-wiki-spm"]
#create tokenizer
tokenizer = tokenizers[model_name].from_pretrained(
f'airesearch/{model_name}' if model_name not in public_models else f'{model_name}',
revision='main',
model_max_length=416,)
```
## Prepare function for calculate metrics
```
!pip install rouge
from rouge import Rouge
rouge = Rouge()
def cal_rouge_score(hyps, refs, get_average_f1=True):
'''
argument: cands, refs [list of string], get_average_f1=True
return dict of r1, r2, rl score
if get_average_f1 == True return mean of rouge-1, rouge-2, rouge-L
'''
r1 = dict(); r1['precision'] = []; r1['recall'] = []; r1['f1'] = []
r2 = dict(); r2['precision'] = []; r2['recall'] = []; r2['f1'] = []
rl = dict(); rl['precision'] = []; rl['recall'] = []; rl['f1'] = []
for hyp, ref in zip(hyps, refs):
score = {}
if(len(hyp)==0 or len(ref)==0):
score = {
'rouge-1': {
'p': 0,
'r': 0,
'f': 0
},
'rouge-2': {
'p': 0,
'r': 0,
'f': 0
},
'rouge-l': {
'p': 0,
'r': 0,
'f': 0
}
}
else: score = rouge.get_scores(hyp, ref)[0]
r1['precision'].append(score['rouge-1']['p'])
r1['recall'].append(score['rouge-1']['r'])
r1['f1'].append(score['rouge-1']['f'])
r2['precision'].append(score['rouge-2']['f'])
r2['recall'].append(score['rouge-2']['f'])
r2['f1'].append(score['rouge-2']['f'])
rl['precision'].append(score['rouge-l']['f'])
rl['recall'].append(score['rouge-l']['f'])
rl['f1'].append(score['rouge-l']['f'])
if(get_average_f1==True): return sum(r1['f1'])/len(r1['f1']), sum(r2['f1'])/len(r2['f1']), sum(rl['f1'])/len(rl['f1'])
else: return r1, r2, rl
cands = ['test test test test test test bad']
refs = ['test test']
r1, r2, rl = cal_rouge_score(cands, refs)
print(r1)
print(r2)
print(rl)
```
## Utility functions for calculate label in our use.
```
def tokenize_with_space(texts, tokenizer):
output = []
encoded_texts = tokenizer(texts, max_length=416, truncation=True)
for text in encoded_texts['input_ids']:
tokenized_text = " ".join(tokenizer.convert_ids_to_tokens(text, skip_special_tokens=True))
if(len(tokenized_text)==0):
output.append("")
continue
if(tokenized_text[0]=="▁"):
tokenized_text = tokenized_text[1:]
output.append(tokenized_text.strip())
return output
def selection_start_end(paragraphs_raw, summaries_raw, tokenizer, length_sum_max = 10, metric='rouge-l'):
"""
Select the start position and end postion for each paragraph to make a summary and maximize the Rouge-L score
Args:
paragraphs [#number of paragraph, #number of word, #number of character] (must be tokenized with space and space change to '_')
summaries [#number of summary, #number of word, #number of character] (must be tokenized with space and space change to '_')
"""
paragraphs = tokenize_with_space(paragraphs_raw, tokenizer)
summaries = tokenize_with_space(summaries_raw, tokenizer)
start_position = []
end_position = []
texts_all = []
for paragraph_raw, summary in zip(paragraphs, summaries):
paragraph = paragraph_raw.split(" ")
len_paragraph = len(paragraph)
max_score = 0
s = 0
e = len_paragraph
text = ""
for length in range(1, length_sum_max):
for start_pos in range(len_paragraph-length+1):
t_summary = " ".join(paragraph[start_pos:start_pos+length])
try:
r1, r2, score = cal_rouge_score([summary], [t_summary])
if(max_score < score):
max_score = score
s = start_pos
e = start_pos + length
text = "".join(paragraph[s:e])
except:
pass
start_position.append(s)
end_position.append(e)
texts_all.append(text)
return start_position, end_position, texts_all
import collections as coll
# stopwords = pkgutil.get_data(__package__, 'smart_common_words.txt')
# stopwords = stopwords.decode('ascii').split('\n')
# stopwords = {key.strip(): 1 for key in stopwords}
def _get_ngrams_count(n, text):
"""Calcualtes n-grams.
Args:
n: which n-grams to calculate
text: An array of tokens
Returns:
A set of n-grams
"""
ngram_dic = coll.defaultdict(int)
text_length = len(text)
max_index_ngram_start = text_length - n
for i in range(max_index_ngram_start + 1):
ngram_dic[tuple(text[i:i + n])] += 1
return ngram_dic
def _get_ngrams(n, text):
"""Calcualtes n-grams.
Args:
n: which n-grams to calculate
text: An array of tokens
Returns:
A set of n-grams
"""
ngram_set = set()
text_length = len(text)
max_index_ngram_start = text_length - n
for i in range(max_index_ngram_start + 1):
ngram_set.add(tuple(text[i:i + n]))
return ngram_set
def _get_word_ngrams_list(n, text):
"""Calcualtes n-grams.
Args:
n: which n-grams to calculate
text: An array of tokens
Returns:
A set of n-grams
"""
text = sum(text, [])
ngram_set = []
text_length = len(text)
max_index_ngram_start = text_length - n
for i in range(max_index_ngram_start + 1):
ngram_set.append(tuple(text[i:i + n]))
return ngram_set
def _get_word_ngrams(n, sentences, do_count=False):
"""Calculates word n-grams for multiple sentences.
"""
assert len(sentences) > 0
assert n > 0
# words = _split_into_words(sentences)
words = sum(sentences, [])
# words = [w for w in words if w not in stopwords]
if do_count:
return _get_ngrams_count(n, words)
return _get_ngrams(n, words)
def cal_rouge(evaluated_ngrams, reference_ngrams):
reference_count = len(reference_ngrams)
evaluated_count = len(evaluated_ngrams)
overlapping_ngrams = evaluated_ngrams.intersection(reference_ngrams)
overlapping_count = len(overlapping_ngrams)
if evaluated_count == 0:
precision = 0.0
else:
precision = overlapping_count / evaluated_count
if reference_count == 0:
recall = 0.0
else:
recall = overlapping_count / reference_count
f1_score = 2.0 * ((precision * recall) / (precision + recall + 1e-8))
return {"f": f1_score, "p": precision, "r": recall}
def selection_start_end_r1_r2(doc, abstract, tokenizer, summary_size = 50):
"""
Select the start position and end postion for each paragraph to make a summary and maximize the Rouge-L score
Args:
paragraphs [#number of paragraph, #number of word, #number of character] (must be tokenized with space and space change to '_')
summaries [#number of summary, #number of word, #number of character] (must be tokenized with space and space change to '_')
"""
max_rouge = 0.0
tokenized_doc = tokenize_with_space([doc], tokenizer)[0].split(" ")
tokenized_abstract = tokenize_with_space([abstract], tokenizer)[0].split(" ")
# abstract = sum(abstract_sent_list, [])
# abstract = ' '.join(abstract).split()
# sents = [' '.join(s).split() for s in doc_sent_list]
evaluated_1grams = _get_word_ngrams_list(1, [tokenized_doc])
reference_1grams = _get_word_ngrams(1, [tokenized_abstract])
evaluated_2grams = _get_word_ngrams_list(2, [tokenized_doc])
reference_2grams = _get_word_ngrams(2, [tokenized_abstract])
start = 0
end = 0
text = ""
max_rouge = 0
for s in range(1,summary_size):
for i in range(len(tokenized_doc)-s+1):
# if (i in selected):
# continue
c = range(i,i+s)
candidates_1 = set(evaluated_1grams[i:i+s])
# candidates_1 = set.union(*map(set, candidates_1))
rouge = cal_rouge(candidates_1, reference_1grams)['f']
if(s > 1):
candidates_2 = set(evaluated_1grams[i:i+s-1])
rouge += cal_rouge(candidates_2, reference_2grams)['f']
if rouge > max_rouge:
max_rouge = rouge
start = i
end = i+s
text = "".join(tokenized_doc[i:i+s])
return start, end, text
```
## Preprocess data
```
!gdown --id 1-8IU8qyry-yPXwQ7AXz0GHIgn19QKGZP
!gdown --id 1-J0eqf4ig7cP8bMPRgSFUejshnBFTZoq
!gdown --id 1-IIJFl4AGNr7rRax4YSQTTm7j12YJ0ya
import pandas as pd
df = pd.read_csv('thaisum.csv')
val_df = pd.read_csv('validation_set.csv')
test_df = pd.read_csv('test_set.csv')
df = pd.concat([df, val_df, test_df], axis=0)
df = df.reset_index(drop=True)
df['body'][358868+11000]
def gold_summary(df, num_train, num_val, num_test):
return df.iloc[num_train+num_val:num_train+num_val+num_test,:]['summary'].tolist()
def get_tokenized_df(df):
df = df.reset_index(drop=True)
res = pd.DataFrame(columns=['attention_mask', 'input_ids', 'start_positions', 'end_positions'])
for i in tqdm(range(len(df))):
sent1 = df['body'][i].lower()
sent2 = df['summary'][i].lower()
start, end, _ = selection_start_end_r1_r2(sent1, sent2, tokenizer)
inp_ids = tokenizer(df['body'][i], max_length=416, truncation=True, padding='max_length')['input_ids']
att_mask = tokenizer(df['body'][i], max_length=416, truncation=True, padding='max_length')['attention_mask']
res = res.append({'attention_mask': att_mask,
'input_ids': inp_ids,
'start_positions': start,
'end_positions': end}, ignore_index=True)
return res
'''
return {'input_ids': res['input_ids'].tolist(),
'attention_mask': res['attention_mask'].tolist(),
'start_positions': res['start_positions'].tolist(),
'end_positions': res['end_positions'].tolist()}
'''
def get_tokenized_dict(df, num_train, num_val, num_test):
train_df = df.iloc[:num_train, :]
val_df = df.iloc[num_train:num_train+num_val, :]
test_df = df.iloc[num_train+num_val:num_train+num_val+num_test, :]
return {'train': get_tokenized_df(train_df),
'validation': get_tokenized_df(val_df),
'test': get_tokenized_df(test_df)}
def get_tokenized_dict_test_val(df, num_train, num_val, num_test):
val_df = df.iloc[num_train:num_train+num_val, :]
test_df = df.iloc[num_train+num_val:num_train+num_val+num_test, :]
return {'validation': get_tokenized_df(val_df),
'test': get_tokenized_df(test_df)}
def get_tokenized_dict_test(df, num_train, num_val, num_test):
test_df = df.iloc[num_train+num_val:num_train+num_val+num_test, :]
return {'test': get_tokenized_df(test_df)}
tokenize_with_space([df['body'][369868]], tokenizer)
```
Usually tokenizing takes a lot of time, you can choose to tokenize only some part of data by uncommenting.
```
# %%time
tokenized_datasets = get_tokenized_dict(df, 358868, 11000, 11000)
# tokenized_datasets = get_tokenized_dict_test_val(df, 358868, 11000, 11000)
# tokenized_datasets = get_tokenized_dict_test(df, 358868, 11000, 11000)
gold_summaries = gold_summary(df, 358868, 11000, 11000)
```
You can choose to save the data after preprocessing and load it.
```
# tokenized_datasets['train'].to_json('train.json', orient='records', lines=True)
# tokenized_datasets['validation'].to_json('/content/drive/MyDrive/validation_true_set.json', orient='records', lines=True)
# tokenized_datasets['test'].to_json('/content/drive/MyDrive/test_true_lower.json', orient='records', lines=True)
tokenized_datasets = load_dataset('json', data_files={'train': '/content/drive/MyDrive/train.json', 'validation': '/content/drive/MyDrive/validation_true.json', 'test': '/content/drive/MyDrive/test_true.json'})
tokenized_datasets
#8 in datasets['validation'] points to both 8 and 9 in tokenized_datasets['validation'] due to overflowing tokens
i = 8
example = tokenized_datasets['validation'][i]
combined_text = tokenizer.decode(example['input_ids'])
answer_with_token_idx = tokenizer.decode(example['input_ids'][example['start_positions']:example['end_positions']])
#there are quite a few more
len(tokenized_datasets['validation']), answer_with_token_idx, combined_text
```
## Fine-tuning model
```
model = AutoModelForQuestionAnswering.from_pretrained(
f'airesearch/{model_name}' if model_name not in public_models else f'{model_name}',
revision='main',)
batch_size = 16
learning_rate = 4e-5
args = TrainingArguments(
f"finetune_thaiSum",
evaluation_strategy = "epoch",
learning_rate=learning_rate,
per_device_train_batch_size=batch_size,
per_device_eval_batch_size=batch_size*2,
num_train_epochs=6,
warmup_ratio=0.15,
weight_decay=0.01,
fp16=True,
save_total_limit=3,
load_best_model_at_end=True,
)
data_collator = default_data_collator
trainer = Trainer(
model=model,
args=args,
train_dataset=tokenized_datasets["train"],
eval_dataset=tokenized_datasets["validation"],
data_collator=data_collator,
tokenizer=tokenizer,
)
trainer.train()
trainer.save_model("/content/drive/MyDrive/finetune_thaiSum4")
```
## Postprocess and metrics(BERTscore since rouge we already import at the beginning)
```
def post_process_index(data, raw_predictions, tokenizer, n_best_size = 20, max_answer_length=50):
all_start_logits, all_end_logits = raw_predictions
predictions = []
for start_logits, end_logits, example in zip(all_start_logits, all_end_logits, data):
start_indexes = np.argsort(start_logits)[-1 : -n_best_size - 1 : -1].tolist()
end_indexes = np.argsort(end_logits)[-1 : -n_best_size - 1 : -1].tolist()
valid_answers = []
for start_index in start_indexes:
for end_index in end_indexes:
# Don't consider answers with a length that is either < 0 or > max_answer_length.
if end_index < start_index or end_index - start_index + 1 > max_answer_length:
continue
valid_answers.append(
{
"score": start_logits[start_index] + end_logits[end_index],
"text": tokenizer.decode(example['input_ids'][start_index+1:end_index+1], skip_special_tokens=True)
}
)
if len(valid_answers) > 0:
best_answer = sorted(valid_answers, key=lambda x: x["score"], reverse=True)[0]
else:
# In the very rare edge case we have not a single non-null prediction, we create a fake prediction to avoid failure.
best_answer = {"text": "", "score": 0.0}
predictions.append(best_answer["text"])
return predictions
```
### BERTScore
```
!pip install bert_score==0.3.7
from bert_score import score
import numpy as np
import gc
def cal_bert_score(cands, refs, get_average_f1=True):
'''
arguments: cands, refs
return array of presicion, recall, f1, presicion_average, recall_average, f1_average
if get_average == True return mean of BERTScore
'''
p, r, f1 = score(cands, refs, lang="others", verbose=False)
p = p.numpy()
r = r.numpy()
f1 = f1.numpy()
if(get_average_f1==True): return f1.mean()
else: return p, r, f1
def cal_batch_bert_score(cands, refs, get_average_f1=True, batch_size=8):
f1_average = []
for i in tqdm(range(0,len(cands),batch_size)):
cand_batch = cands[i:i+batch_size]
ref_batch = refs[i:i+batch_size]
res = cal_bert_score(cand_batch, ref_batch)
f1_average.append(res)
gc.collect()
print(f1_average)
return sum(f1_average)/len(f1_average)
%%time
refs = ['เมื่อวันที่ 6 ม.ค.60 ที่ทำเนียบรัฐบาล นายวิษณุ เครืองาม รองนายกรัฐมนตรี กล่าวถึงกรณี ที่ นายสุรชัย เลี้ยงบุญเลิศชัย รองประธานสภานิติบัญญัติแห่งชาติ (สนช.) ออกมาระบุว่า การเลือกตั้งจะถูกเลื่อนออกไปถึงปี 2561 ว่า ขอให้ไปสอบถามกับ สนช. แต่เชื่อว่าคงไม่กล้าพูดอีก เพราะทำให้คนเข้าใจผิด ซึ่งที่ สนช.พูดเนื่องจากผูกกับกฎหมายของกรรมการร่างรัฐธรรมนูญ(กรธ.) ตนจึงไม่ขอวิพากษ์วิจารณ์ แต่รัฐบาลยืนยันว่ายังเดินตามโรดแม็ป ซึ่งโรดแม็ปมองได้สองแบบ คือ มีลำดับขั้นตอนและการกำหนดช่วงเวลา โดยเริ่มต้นจากการประกาศใช้รัฐธรรมนูญ แต่ขณะนี้รัฐธรรมนูญยังไม่ประกาศใช้ จึงยังเริ่มนับหนึ่งไม่ถูก จากนั้นเข้าสู่ขั้นตอนการร่างกฎหมายประกอบร่างรัฐธรรมนูญหรือกฎหมายลูก ภายใน 240 วัน ก่อนจะส่งกลับให้ สนช.พิจารณา ภายใน 2 เดือน\xa0,นายวิษณุ กล่าวต่อว่า หากมีการแก้ไขก็จะมีการพิจารณาร่วมกับ กรธ.อีก 1 เดือน ก่อนนำขึ้นทูลเกล้าฯ ทรงลงพระปรมาภิไธย ภายใน 90 วัน และจะเข้าสู่การเลือกตั้งภายในระยะเวลา 5 เดือน ซึ่งทั้งหมดนี้คือโรดแม็ปที่ยังเป็นแบบเดิมอยู่ ส่วนเดิมที่กำหนดวันเลือกตั้งไว้ภายในปี 60 นั้น เพราะมาจากสมมติฐานของขั้นตอนเดิมทั้งหมด แต่เมื่อมีเหตุสวรรคตทุกอย่างจึงต้องเลื่อนออกไป ส่วนการพิจารณากฎหมายลูกทั้งหมด 4 ฉบับ ขณะนี้กรธ.พิจารณาแล้วเสร็จ 2 ฉบับ คือ พ.ร.ป.พรรคการเมือง และพ.ร.ป. คณะกรรมการการเลือกตั้ง แต่ พ.ร.ป.การเลือกตั้งควรจะพิจารณาได้เร็วกลับล่าช้า ดังนั้น กรธ.จะต้องออกชี้แจงถึงเหตุผลว่าทำไมพิจารณากฎหมายดังกล่าวล่าช้ากว่ากำหนด ส่งผลให้เกิดข้อสงสัยจนถึงทุกวันนี้ ส่วนกรณีที่ สนช. ระบุว่า มีกฎหมายเข้าสู่การพิจารณาของ สนช.เป็นจำนวนมาก ทำให้ส่งผลกระทบต่อโรดแม็ปนั้น รัฐบาลเคยบอกไว้แล้วว่าในช่วงนี้ของโรดแม็ปกฎหมายจะเยอะกว่าที่ผ่านมา ดังนั้น สนช.จะต้องบริหารจัดการกันเอง เพราะได้มีการเพิ่มสมาชิก สนช.ให้แล้ว.']
cands = ['เมื่อวันที่ 6 ม.ค.60 ที่ทำเนียบรัฐบาล นายวิษณุ เครืองาม รองนายกรัฐมนตรี กล่าวถึงกรณี ที่ นายสุรชัย เลี้ยงบุญเลิศชัย รองประธานสภานิติบัญญัติแห่งชาติ (สนช.)']
f1_average = cal_bert_score(cands, refs)
print(f1_average)
```
### Evaluate
```
def evaluate_rouge(cands, refs, tokenizer):
cands_tokenized = tokenize_with_space(cands, tokenizer)
refs_tokenized = tokenize_with_space(refs, tokenizer)
r1, r2, rl = cal_rouge_score(refs_tokenized, cands_tokenized)
return r1, r2, rl
raw_predictions = trainer.predict(tokenized_datasets['test'])
predictions = post_process_index(tokenized_datasets['test'], raw_predictions[0], tokenizer)
predictions[:3]
display(predictions[:3], gold_summaries[:3])
r1, r2, rl = evaluate_rouge(predictions, gold_summaries, tokenizer)
print(r1, r2, rl)
%%time
BERTScore = cal_batch_bert_score(predictions, gold_summaries, tokenizer, batch_size=128)
print(BERTScore)
```
|
github_jupyter
|
##### Copyright 2018 The TensorFlow Authors.
Licensed under the Apache License, Version 2.0 (the "License");
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Get Started with Eager Execution
<table align="left"><td>
<a target="_blank" href="https://colab.sandbox.google.com/github/tensorflow/models/blob/master/samples/core/get_started/eager.ipynb">
<img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td><td>
<a target="_blank" href="https://github.com/tensorflow/models/blob/master/samples/core/get_started/eager.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on Github</a></td></table>
This guide uses machine learning to *categorize* Iris flowers by species. It uses [TensorFlow](https://www.tensorflow.org)'s eager execution to:
1. Build a model,
2. Train this model on example data, and
3. Use the model to make predictions about unknown data.
Machine learning experience isn't required, but you'll need to read some Python code.
## TensorFlow programming
There are many [TensorFlow APIs](https://www.tensorflow.org/api_docs/python/) available, but start with these high-level TensorFlow concepts:
* Enable an [eager execution](https://www.tensorflow.org/programmers_guide/eager) development environment,
* Import data with the [Datasets API](https://www.tensorflow.org/programmers_guide/datasets),
* Build models and layers with TensorFlow's [Keras API](https://keras.io/getting-started/sequential-model-guide/).
This tutorial is structured like many TensorFlow programs:
1. Import and parse the data sets.
2. Select the type of model.
3. Train the model.
4. Evaluate the model's effectiveness.
5. Use the trained model to make predictions.
For more TensorFlow examples, see the [Get Started](https://www.tensorflow.org/get_started/) and [Tutorials](https://www.tensorflow.org/tutorials/) sections. To learn machine learning basics, consider taking the [Machine Learning Crash Course](https://developers.google.com/machine-learning/crash-course/).
## Run the notebook
This tutorial is available as an interactive [Colab notebook](https://colab.research.google.com) that can execute and modify Python code directly in the browser. The notebook handles setup and dependencies while you "play" cells to run the code blocks. This is a fun way to explore the program and test ideas.
If you are unfamiliar with Python notebook environments, there are a couple of things to keep in mind:
1. Executing code requires connecting to a runtime environment. In the Colab notebook menu, select *Runtime > Connect to runtime...*
2. Notebook cells are arranged sequentially to gradually build the program. Typically, later code cells depend on prior code cells, though you can always rerun a code block. To execute the entire notebook in order, select *Runtime > Run all*. To rerun a code cell, select the cell and click the *play icon* on the left.
## Setup program
### Install the latest version of TensorFlow
This tutorial uses eager execution, which is available in [TensorFlow 1.8](https://www.tensorflow.org/install/). (You may need to restart the runtime after upgrading.)
```
!pip install --upgrade tensorflow
```
### Configure imports and eager execution
Import the required Python modules—including TensorFlow—and enable eager execution for this program. Eager execution makes TensorFlow evaluate operations immediately, returning concrete values instead of creating a [computational graph](https://www.tensorflow.org/programmers_guide/graphs) that is executed later. If you are used to a REPL or the `python` interactive console, this feels familiar.
Once eager execution is enabled, it *cannot* be disabled within the same program. See the [eager execution guide](https://www.tensorflow.org/programmers_guide/eager) for more details.
```
from __future__ import absolute_import, division, print_function
import os
import matplotlib.pyplot as plt
import tensorflow as tf
import tensorflow.contrib.eager as tfe
tf.enable_eager_execution()
print("TensorFlow version: {}".format(tf.VERSION))
print("Eager execution: {}".format(tf.executing_eagerly()))
```
## The Iris classification problem
Imagine you are a botanist seeking an automated way to categorize each Iris flower you find. Machine learning provides many algorithms to statistically classify flowers. For instance, a sophisticated machine learning program could classify flowers based on photographs. Our ambitions are more modest—we're going to classify Iris flowers based on the length and width measurements of their [sepals](https://en.wikipedia.org/wiki/Sepal) and [petals](https://en.wikipedia.org/wiki/Petal).
The Iris genus entails about 300 species, but our program will only classify the following three:
* Iris setosa
* Iris virginica
* Iris versicolor
<table>
<tr><td>
<img src="https://www.tensorflow.org/images/iris_three_species.jpg"
alt="Petal geometry compared for three iris species: Iris setosa, Iris virginica, and Iris versicolor">
</td></tr>
<tr><td align="center">
<b>Figure 1.</b> <a href="https://commons.wikimedia.org/w/index.php?curid=170298">Iris setosa</a> (by <a href="https://commons.wikimedia.org/wiki/User:Radomil">Radomil</a>, CC BY-SA 3.0), <a href="https://commons.wikimedia.org/w/index.php?curid=248095">Iris versicolor</a>, (by <a href="https://commons.wikimedia.org/wiki/User:Dlanglois">Dlanglois</a>, CC BY-SA 3.0), and <a href="https://www.flickr.com/photos/33397993@N05/3352169862">Iris virginica</a> (by <a href="https://www.flickr.com/photos/33397993@N05">Frank Mayfield</a>, CC BY-SA 2.0).<br/>
</td></tr>
</table>
Fortunately, someone has already created a [data set of 120 Iris flowers](https://en.wikipedia.org/wiki/Iris_flower_data_set) with the sepal and petal measurements. This is a classic dataset that is popular for beginner machine learning classification problems.
## Import and parse the training dataset
Download the dataset file and convert it to a structure that can be used by this Python program.
### Download the dataset
Download the training dataset file using the [tf.keras.utils.get_file](https://www.tensorflow.org/api_docs/python/tf/keras/utils/get_file) function. This returns the file path of the downloaded file.
```
train_dataset_url = "http://download.tensorflow.org/data/iris_training.csv"
train_dataset_fp = tf.keras.utils.get_file(fname=os.path.basename(train_dataset_url),
origin=train_dataset_url)
print("Local copy of the dataset file: {}".format(train_dataset_fp))
```
### Inspect the data
This dataset, `iris_training.csv`, is a plain text file that stores tabular data formatted as comma-separated values (CSV). Use the `head -n5` command to take a peak at the first five entries:
```
!head -n5 {train_dataset_fp}
```
From this view of the dataset, notice the following:
1. The first line is a header containing information about the dataset:
* There are 120 total examples. Each example has four features and one of three possible label names.
2. Subsequent rows are data records, one *[example](https://developers.google.com/machine-learning/glossary/#example)* per line, where:
* The first four fields are *[features](https://developers.google.com/machine-learning/glossary/#feature)*: these are characteristics of an example. Here, the fields hold float numbers representing flower measurements.
* The last column is the *[label](https://developers.google.com/machine-learning/glossary/#label)*: this is the value we want to predict. For this dataset, it's an integer value of 0, 1, or 2 that corresponds to a flower name.
Let's write that out in code:
```
# column order in CSV file
column_names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'species']
feature_names = column_names[:-1]
label_name = column_names[-1]
print("Features: {}".format(feature_names))
print("Label: {}".format(label_name))
```
Each label is associated with string name (for example, "setosa"), but machine learning typically relies on numeric values. The label numbers are mapped to a named representation, such as:
* `0`: Iris setosa
* `1`: Iris versicolor
* `2`: Iris virginica
For more information about features and labels, see the [ML Terminology section of the Machine Learning Crash Course](https://developers.google.com/machine-learning/crash-course/framing/ml-terminology).
```
class_names = ['Iris setosa', 'Iris versicolor', 'Iris virginica']
```
### Create a `tf.data.Dataset`
TensorFlow's [Dataset API](https://www.tensorflow.org/programmers_guide/datasets) handles many common cases for loading data into a model. This is a high-level API for reading data and transforming it into a form used for training. See the [Datasets Quick Start guide](https://www.tensorflow.org/get_started/datasets_quickstart) for more information.
Since the dataset is a CSV-formatted text file, use the the [make_csv_dataset](https://www.tensorflow.org/api_docs/python/tf/contrib/data/make_csv_dataset) function to parse the data into a suitable format. Since this function generates data for training models, the default behavior is to shuffle the data (`shuffle=True, shuffle_buffer_size=10000`), and repeat the dataset forever (`num_epochs=None`). We also set the [batch_size](https://developers.google.com/machine-learning/glossary/#batch_size) parameter.
```
batch_size = 32
train_dataset = tf.contrib.data.make_csv_dataset(
train_dataset_fp,
batch_size,
column_names=column_names,
label_name=label_name,
num_epochs=1)
```
The `make_csv_dataset` function returns a `tf.data.Dataset` of `(features, label)` pairs, where `features` is a dictionary: `{'feature_name': value}`
With eager execution enabled, these `Dataset` objects are iterable. Let's look at a batch of features:
```
features, labels = next(iter(train_dataset))
features
```
Notice that like-features are grouped together, or *batched*. Each example row's fields are appended to the corresponding feature array. Change the `batch_size` to set the number of examples stored in these feature arrays.
You can start to see some clusters by plotting a few features from the batch:
```
plt.scatter(features['petal_length'],
features['sepal_length'],
c=labels,
cmap='viridis')
plt.xlabel("Petal length")
plt.ylabel("Sepal length");
```
To simplify the model building step, create a function to repackage the features dictionary into a single array with shape: `(batch_size, num_features)`.
This function uses the [tf.stack](https://www.tensorflow.org/api_docs/python/tf/stack) method which takes values from a list of tensors and creates a combined tensor at the specified dimension.
```
def pack_features_vector(features, labels):
"""Pack the features into a single array."""
features = tf.stack(list(features.values()), axis=1)
return features, labels
```
Then use the [tf.data.Dataset.map](https://www.tensorflow.org/api_docs/python/tf/data/dataset/map) method to pack the `features` of each `(features,label)` pair into the training dataset:
```
train_dataset = train_dataset.map(pack_features_vector)
```
The features element of the `Dataset` are now arrays with shape `(batch_size, num_features)`. Let's look at the first few examples:
```
features, labels = next(iter(train_dataset))
print(features[:5])
```
## Select the type of model
### Why model?
A *[model](https://developers.google.com/machine-learning/crash-course/glossary#model)* is the relationship between features and the label. For the Iris classification problem, the model defines the relationship between the sepal and petal measurements and the predicted Iris species. Some simple models can be described with a few lines of algebra, but complex machine learning models have a large number of parameters that are difficult to summarize.
Could you determine the relationship between the four features and the Iris species *without* using machine learning? That is, could you use traditional programming techniques (for example, a lot of conditional statements) to create a model? Perhaps—if you analyzed the dataset long enough to determine the relationships between petal and sepal measurements to a particular species. And this becomes difficult—maybe impossible—on more complicated datasets. A good machine learning approach *determines the model for you*. If you feed enough representative examples into the right machine learning model type, the program will figure out the relationships for you.
### Select the model
We need to select the kind of model to train. There are many types of models and picking a good one takes experience. This tutorial uses a neural network to solve the Iris classification problem. *[Neural networks](https://developers.google.com/machine-learning/glossary/#neural_network)* can find complex relationships between features and the label. It is a highly-structured graph, organized into one or more *[hidden layers](https://developers.google.com/machine-learning/glossary/#hidden_layer)*. Each hidden layer consists of one or more *[neurons](https://developers.google.com/machine-learning/glossary/#neuron)*. There are several categories of neural networks and this program uses a dense, or *[fully-connected neural network](https://developers.google.com/machine-learning/glossary/#fully_connected_layer)*: the neurons in one layer receive input connections from *every* neuron in the previous layer. For example, Figure 2 illustrates a dense neural network consisting of an input layer, two hidden layers, and an output layer:
<table>
<tr><td>
<img src="https://www.tensorflow.org/images/custom_estimators/full_network.png"
alt="A diagram of the network architecture: Inputs, 2 hidden layers, and outputs">
</td></tr>
<tr><td align="center">
<b>Figure 2.</b> A neural network with features, hidden layers, and predictions.<br/>
</td></tr>
</table>
When the model from Figure 2 is trained and fed an unlabeled example, it yields three predictions: the likelihood that this flower is the given Iris species. This prediction is called *[inference](https://developers.google.com/machine-learning/crash-course/glossary#inference)*. For this example, the sum of the output predictions is 1.0. In Figure 2, this prediction breaks down as: `0.03` for *Iris setosa*, `0.95` for *Iris versicolor*, and `0.02` for *Iris virginica*. This means that the model predicts—with 95% probability—that an unlabeled example flower is an *Iris versicolor*.
### Create a model using Keras
The TensorFlow [tf.keras](https://www.tensorflow.org/api_docs/python/tf/keras) API is the preferred way to create models and layers. This makes it easy to build models and experiment while Keras handles the complexity of connecting everything together.
The [tf.keras.Sequential](https://www.tensorflow.org/api_docs/python/tf/keras/Sequential) model is a linear stack of layers. Its constructor takes a list of layer instances, in this case, two [Dense](https://www.tensorflow.org/api_docs/python/tf/keras/layers/Dense) layers with 10 nodes each, and an output layer with 3 nodes representing our label predictions. The first layer's `input_shape` parameter corresponds to the number of features from the dataset, and is required.
```
model = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation="relu", input_shape=(4,)), # input shape required
tf.keras.layers.Dense(10, activation="relu"),
tf.keras.layers.Dense(3)
])
```
The *[activation function](https://developers.google.com/machine-learning/crash-course/glossary#activation_function)* determines the output shape of each node in the layer. These non-linearities are important—without them the model would be equivalent to a single layer. There are many [available activations](https://www.tensorflow.org/api_docs/python/tf/keras/activations), but [ReLU](https://developers.google.com/machine-learning/crash-course/glossary#ReLU) is common for hidden layers.
The ideal number of hidden layers and neurons depends on the problem and the dataset. Like many aspects of machine learning, picking the best shape of the neural network requires a mixture of knowledge and experimentation. As a rule of thumb, increasing the number of hidden layers and neurons typically creates a more powerful model, which requires more data to train effectively.
### Using the model
Let's have a quick look at what this model does to a batch of features:
```
predictions = model(features)
predictions[:5]
```
Here, each example returns a [logit](https://developers.google.com/machine-learning/crash-course/glossary#logit) for each class.
To convert these logits to a probability for each class, use the [softmax](https://developers.google.com/machine-learning/crash-course/glossary#softmax) function:
```
tf.nn.softmax(predictions[:5])
```
Taking the `tf.argmax` across classes gives us the predicted class index. But, the model hasn't been trained yet, so these aren't good predictions.
```
print("Prediction: {}".format(tf.argmax(predictions, axis=1)))
print(" Labels: {}".format(labels))
```
## Train the model
*[Training](https://developers.google.com/machine-learning/crash-course/glossary#training)* is the stage of machine learning when the model is gradually optimized, or the model *learns* the dataset. The goal is to learn enough about the structure of the training dataset to make predictions about unseen data. If you learn *too much* about the training dataset, then the predictions only work for the data it has seen and will not be generalizable. This problem is called *[overfitting](https://developers.google.com/machine-learning/crash-course/glossary#overfitting)*—it's like memorizing the answers instead of understanding how to solve a problem.
The Iris classification problem is an example of *[supervised machine learning](https://developers.google.com/machine-learning/glossary/#supervised_machine_learning)*: the model is trained from examples that contain labels. In *[unsupervised machine learning](https://developers.google.com/machine-learning/glossary/#unsupervised_machine_learning)*, the examples don't contain labels. Instead, the model typically finds patterns among the features.
### Define the loss and gradient function
Both training and evaluation stages need to calculate the model's *[loss](https://developers.google.com/machine-learning/crash-course/glossary#loss)*. This measures how off a model's predictions are from the desired label, in other words, how bad the model is performing. We want to minimize, or optimize, this value.
Our model will calculate its loss using the [tf.keras.losses.categorical_crossentropy](https://www.tensorflow.org/api_docs/python/tf/losses/sparse_softmax_cross_entropy) function which takes the model's class probability predictions and the desired label, and returns the average loss across the examples.
```
def loss(model, x, y):
y_ = model(x)
return tf.losses.sparse_softmax_cross_entropy(labels=y, logits=y_)
l = loss(model, features, labels)
print("Loss test: {}".format(l))
```
Use the [tf.GradientTape](https://www.tensorflow.org/api_docs/python/tf/GradientTape) context to calculate the *[gradients](https://developers.google.com/machine-learning/crash-course/glossary#gradient)* used to optimize our model. For more examples of this, see the [eager execution guide](https://www.tensorflow.org/programmers_guide/eager).
```
def grad(model, inputs, targets):
with tf.GradientTape() as tape:
loss_value = loss(model, inputs, targets)
return loss_value, tape.gradient(loss_value, model.trainable_variables)
```
### Create an optimizer
An *[optimizer](https://developers.google.com/machine-learning/crash-course/glossary#optimizer)* applies the computed gradients to the model's variables to minimize the `loss` function. You can think of the loss function as a curved surface (see Figure 3) and we want to find its lowest point by walking around. The gradients point in the direction of steepest ascent—so we'll travel the opposite way and move down the hill. By iteratively calculating the loss and gradient for each batch, we'll adjust the model during training. Gradually, the model will find the best combination of weights and bias to minimize loss. And the lower the loss, the better the model's predictions.
<table>
<tr><td>
<img src="https://cs231n.github.io/assets/nn3/opt1.gif" width="70%"
alt="Optimization algorthims visualized over time in 3D space.">
</td></tr>
<tr><td align="center">
<b>Figure 3.</b> Optimization algorithms visualized over time in 3D space. (Source: <a href="http://cs231n.github.io/neural-networks-3/">Stanford class CS231n</a>, MIT License)<br/>
</td></tr>
</table>
TensorFlow has many [optimization algorithms](https://www.tensorflow.org/api_guides/python/train) available for training. This model uses the [tf.train.GradientDescentOptimizer](https://www.tensorflow.org/api_docs/python/tf/train/GradientDescentOptimizer) that implements the *[stochastic gradient descent](https://developers.google.com/machine-learning/crash-course/glossary#gradient_descent)* (SGD) algorithm. The `learning_rate` sets the step size to take for each iteration down the hill. This is a *hyperparameter* that you'll commonly adjust to achieve better results.
Let's setup the optimizer and the `global_step` counter:
```
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01)
global_step = tf.train.get_or_create_global_step()
```
We'll use this to calculate a single optimization step:
```
loss_value, grads = grad(model, features, labels)
print("Step: {}, Initial Loss: {}".format(global_step.numpy(),
loss_value.numpy()))
optimizer.apply_gradients(zip(grads, model.variables), global_step)
print("Step: {}, Loss: {}".format(global_step.numpy(),
loss(model, features, labels).numpy()))
```
### Training loop
With all the pieces in place, the model is ready for training! A training loop feeds the dataset examples into the model to help it make better predictions. The following code block sets up these training steps:
1. Iterate each *epoch*. An epoch is one pass through the dataset.
2. Within an epoch, iterate over each example in the training `Dataset` grabbing its *features* (`x`) and *label* (`y`).
3. Using the example's features, make a prediction and compare it with the label. Measure the inaccuracy of the prediction and use that to calculate the model's loss and gradients.
4. Use an `optimizer` to update the model's variables.
5. Keep track of some stats for visualization.
6. Repeat for each epoch.
The `num_epochs` variable is the amount of times to loop over the dataset collection. Counter-intuitively, training a model longer does not guarantee a better model. `num_epochs` is a *[hyperparameter](https://developers.google.com/machine-learning/glossary/#hyperparameter)* that you can tune. Choosing the right number usually requires both experience and experimentation.
```
## Note: Rerunning this cell uses the same model variables
# keep results for plotting
train_loss_results = []
train_accuracy_results = []
num_epochs = 201
for epoch in range(num_epochs):
epoch_loss_avg = tfe.metrics.Mean()
epoch_accuracy = tfe.metrics.Accuracy()
# Training loop - using batches of 32
for x, y in train_dataset:
# Optimize the model
loss_value, grads = grad(model, x, y)
optimizer.apply_gradients(zip(grads, model.variables),
global_step)
# Track progress
epoch_loss_avg(loss_value) # add current batch loss
# compare predicted label to actual label
epoch_accuracy(tf.argmax(model(x), axis=1, output_type=tf.int32), y)
# end epoch
train_loss_results.append(epoch_loss_avg.result())
train_accuracy_results.append(epoch_accuracy.result())
if epoch % 50 == 0:
print("Epoch {:03d}: Loss: {:.3f}, Accuracy: {:.3%}".format(epoch,
epoch_loss_avg.result(),
epoch_accuracy.result()))
```
### Visualize the loss function over time
While it's helpful to print out the model's training progress, it's often *more* helpful to see this progress. [TensorBoard](https://www.tensorflow.org/programmers_guide/summaries_and_tensorboard) is a nice visualization tool that is packaged with TensorFlow, but we can create basic charts using the `matplotlib` module.
Interpreting these charts takes some experience, but you really want to see the *loss* go down and the *accuracy* go up.
```
fig, axes = plt.subplots(2, sharex=True, figsize=(12, 8))
fig.suptitle('Training Metrics')
axes[0].set_ylabel("Loss", fontsize=14)
axes[0].plot(train_loss_results)
axes[1].set_ylabel("Accuracy", fontsize=14)
axes[1].set_xlabel("Epoch", fontsize=14)
axes[1].plot(train_accuracy_results);
```
## Evaluate the model's effectiveness
Now that the model is trained, we can get some statistics on its performance.
*Evaluating* means determining how effectively the model makes predictions. To determine the model's effectiveness at Iris classification, pass some sepal and petal measurements to the model and ask the model to predict what Iris species they represent. Then compare the model's prediction against the actual label. For example, a model that picked the correct species on half the input examples has an *[accuracy](https://developers.google.com/machine-learning/glossary/#accuracy)* of `0.5`. Figure 4 shows a slightly more effective model, getting 4 out of 5 predictions correct at 80% accuracy:
<table cellpadding="8" border="0">
<colgroup>
<col span="4" >
<col span="1" bgcolor="lightblue">
<col span="1" bgcolor="lightgreen">
</colgroup>
<tr bgcolor="lightgray">
<th colspan="4">Example features</th>
<th colspan="1">Label</th>
<th colspan="1" >Model prediction</th>
</tr>
<tr>
<td>5.9</td><td>3.0</td><td>4.3</td><td>1.5</td><td align="center">1</td><td align="center">1</td>
</tr>
<tr>
<td>6.9</td><td>3.1</td><td>5.4</td><td>2.1</td><td align="center">2</td><td align="center">2</td>
</tr>
<tr>
<td>5.1</td><td>3.3</td><td>1.7</td><td>0.5</td><td align="center">0</td><td align="center">0</td>
</tr>
<tr>
<td>6.0</td> <td>3.4</td> <td>4.5</td> <td>1.6</td> <td align="center">1</td><td align="center" bgcolor="red">2</td>
</tr>
<tr>
<td>5.5</td><td>2.5</td><td>4.0</td><td>1.3</td><td align="center">1</td><td align="center">1</td>
</tr>
<tr><td align="center" colspan="6">
<b>Figure 4.</b> An Iris classifier that is 80% accurate.<br/>
</td></tr>
</table>
### Setup the test dataset
Evaluating the model is similar to training the model. The biggest difference is the examples come from a separate *[test set](https://developers.google.com/machine-learning/crash-course/glossary#test_set)* rather than the training set. To fairly assess a model's effectiveness, the examples used to evaluate a model must be different from the examples used to train the model.
The setup for the test `Dataset` is similar to the setup for training `Dataset`. Download the CSV text file and parse that values, then give it a little shuffle:
```
test_url = "http://download.tensorflow.org/data/iris_test.csv"
test_fp = tf.keras.utils.get_file(fname=os.path.basename(test_url),
origin=test_url)
test_dataset = tf.contrib.data.make_csv_dataset(
train_dataset_fp,
batch_size,
column_names=column_names,
label_name='species',
num_epochs=1,
shuffle=False)
test_dataset = test_dataset.map(pack_features_vector)
```
### Evaluate the model on the test dataset
Unlike the training stage, the model only evaluates a single [epoch](https://developers.google.com/machine-learning/glossary/#epoch) of the test data. In the following code cell, we iterate over each example in the test set and compare the model's prediction against the actual label. This is used to measure the model's accuracy across the entire test set.
```
test_accuracy = tfe.metrics.Accuracy()
for (x, y) in test_dataset:
logits = model(x)
prediction = tf.argmax(logits, axis=1, output_type=tf.int32)
test_accuracy(prediction, y)
print("Test set accuracy: {:.3%}".format(test_accuracy.result()))
```
We can see on the last batch, for example, the model is usually correct:
```
tf.stack([y,prediction],axis=1)
```
## Use the trained model to make predictions
We've trained a model and "proven" that it's good—but not perfect—at classifying Iris species. Now let's use the trained model to make some predictions on [unlabeled examples](https://developers.google.com/machine-learning/glossary/#unlabeled_example); that is, on examples that contain features but not a label.
In real-life, the unlabeled examples could come from lots of different sources including apps, CSV files, and data feeds. For now, we're going to manually provide three unlabeled examples to predict their labels. Recall, the label numbers are mapped to a named representation as:
* `0`: Iris setosa
* `1`: Iris versicolor
* `2`: Iris virginica
```
predict_dataset = tf.convert_to_tensor([
[5.1, 3.3, 1.7, 0.5,],
[5.9, 3.0, 4.2, 1.5,],
[6.9, 3.1, 5.4, 2.1]
])
predictions = model(predict_dataset)
for i, logits in enumerate(predictions):
class_idx = tf.argmax(logits).numpy()
p = tf.nn.softmax(logits)[class_idx]
name = class_names[class_idx]
print("Example {} prediction: {} ({:4.1f}%)".format(i, name, 100*p))
```
These predictions look good!
To dig deeper into machine learning models, take a look at the TensorFlow [Programmer's Guide](https://www.tensorflow.org/programmers_guide/) and check out the [community](https://www.tensorflow.org/community/).
|
github_jupyter
|
# How to make the perfect time-lapse of the Earth
This tutorial shows a detail coverage of making time-lapse animations from satellite imagery like a pro.
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#0.-Prerequisites" data-toc-modified-id="0.-Prerequisites-1">0. Prerequisites</a></span></li><li><span><a href="#1.-Removing-clouds" data-toc-modified-id="1.-Removing-clouds-2">1. Removing clouds</a></span></li><li><span><a href="#2.-Applying-co-registration" data-toc-modified-id="2.-Applying-co-registration-3">2. Applying co-registration</a></span></li><li><span><a href="#3.-Large-Area-Example" data-toc-modified-id="3.-Large-Area-Example-4">3. Large Area Example</a></span></li><li><span><a href="#4.-Split-Image" data-toc-modified-id="4.-Split-Image-5">4. Split Image</a></span></li></ul></div>
Note: This notebook requires an installation of additional packages `ffmpeg-python` and `ipyleaflet`.
```
%load_ext autoreload
%autoreload 2
import datetime as dt
import json
import os
import subprocess
from concurrent.futures import ProcessPoolExecutor
from datetime import date, datetime, time, timedelta
from functools import partial
from glob import glob
import ffmpeg
import geopandas as gpd
import imageio
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import shapely
from ipyleaflet import GeoJSON, Map, basemaps
from shapely.geometry import Polygon
from tqdm.auto import tqdm
from eolearn.core import (EOExecutor, EOPatch, EOTask, FeatureType,
LinearWorkflow, LoadTask, OverwritePermission,
SaveTask, ZipFeatureTask)
from eolearn.coregistration import ECCRegistration
from eolearn.features import LinearInterpolation, SimpleFilterTask
from eolearn.io import ExportToTiff, ImportFromTiff, SentinelHubInputTask
from eolearn.mask import CloudMaskTask
from sentinelhub import (CRS, BatchSplitter, BBox, BBoxSplitter,
DataCollection, Geometry, MimeType, SentinelHubBatch,
SentinelHubRequest, SHConfig, bbox_to_dimensions)
```
## 0. Prerequisites
In order to set everything up and make the credentials work, please check [this notebook](https://github.com/sentinel-hub/eo-learn/blob/master/examples/io/SentinelHubIO.ipynb).
```
class AnimateTask(EOTask):
def __init__(self, image_dir, out_dir, out_name, feature=(FeatureType.DATA, 'RGB'), scale_factor=2.5, duration=3, dpi=150, pad_inches=None, shape=None):
self.image_dir = image_dir
self.out_name = out_name
self.out_dir = out_dir
self.feature = feature
self.scale_factor = scale_factor
self.duration = duration
self.dpi = dpi
self.pad_inches = pad_inches
self.shape = shape
def execute(self, eopatch):
images = np.clip(eopatch[self.feature]*self.scale_factor, 0, 1)
fps = len(images)/self.duration
subprocess.run(f'rm -rf {self.image_dir} && mkdir {self.image_dir}', shell=True)
for idx, image in enumerate(images):
if self.shape:
fig = plt.figure(figsize=(self.shape[0], self.shape[1]))
plt.imshow(image)
plt.axis(False)
plt.savefig(f'{self.image_dir}/image_{idx:03d}.png', bbox_inches='tight', dpi=self.dpi, pad_inches = self.pad_inches)
plt.close()
# video related
stream = ffmpeg.input(f'{self.image_dir}/image_*.png', pattern_type='glob', framerate=fps)
stream = stream.filter('pad', w='ceil(iw/2)*2', h='ceil(ih/2)*2', color='white')
split = stream.split()
video = split[0]
# gif related
palette = split[1].filter('palettegen', reserve_transparent=True, stats_mode='diff')
gif = ffmpeg.filter([split[2], palette], 'paletteuse', dither='bayer', bayer_scale=5, diff_mode='rectangle')
# save output
os.makedirs(self.out_dir, exist_ok=True)
video.output(f'{self.out_dir}/{self.out_name}.mp4', crf=15, pix_fmt='yuv420p', vcodec='libx264', an=None).run(overwrite_output=True)
gif.output(f'{self.out_dir}/{self.out_name}.gif').run(overwrite_output=True)
return eopatch
```
## 1. Removing clouds
```
# https://twitter.com/Valtzen/status/1270269337061019648
bbox = BBox(bbox=[-73.558102,45.447728,-73.488750,45.491908], crs=CRS.WGS84)
resolution = 10
time_interval = ('2018-01-01', '2020-01-01')
print(f'Image size: {bbox_to_dimensions(bbox, resolution)}')
geom, crs = bbox.geometry, bbox.crs
wgs84_geometry = Geometry(geom, crs).transform(CRS.WGS84)
geometry_center = wgs84_geometry.geometry.centroid
map1 = Map(
basemap=basemaps.Esri.WorldImagery,
center=(geometry_center.y, geometry_center.x),
zoom=13
)
area_geojson = GeoJSON(data=wgs84_geometry.geojson)
map1.add_layer(area_geojson)
map1
download_task = SentinelHubInputTask(
bands = ['B04', 'B03', 'B02'],
bands_feature = (FeatureType.DATA, 'RGB'),
resolution=resolution,
maxcc=0.9,
time_difference=timedelta(minutes=120),
data_collection=DataCollection.SENTINEL2_L2A,
max_threads=10,
mosaicking_order='leastCC',
additional_data=[
(FeatureType.MASK, 'CLM'),
(FeatureType.MASK, 'dataMask')
]
)
def valid_coverage_thresholder_f(valid_mask, more_than=0.95):
coverage = np.count_nonzero(valid_mask)/np.prod(valid_mask.shape)
return coverage > more_than
valid_mask_task = ZipFeatureTask({FeatureType.MASK: ['CLM', 'dataMask']}, (FeatureType.MASK, 'VALID_DATA'),
lambda clm, dm: np.all([clm == 0, dm], axis=0))
filter_task = SimpleFilterTask((FeatureType.MASK, 'VALID_DATA'), valid_coverage_thresholder_f)
name = 'clm_service'
anim_task = AnimateTask(image_dir = './images', out_dir = './animations', out_name=name, duration=5, dpi=200)
params = {'MaxIters': 500}
coreg_task = ECCRegistration((FeatureType.DATA, 'RGB'), channel=2, params=params)
name = 'clm_service_coreg'
anim_task_after = AnimateTask(image_dir='./images', out_dir='./animations', out_name=name, duration=5, dpi=200)
workflow = LinearWorkflow(
download_task,
valid_mask_task,
filter_task,
anim_task,
coreg_task,
anim_task_after
)
result = workflow.execute({
download_task: {'bbox': bbox, 'time_interval': time_interval}
})
```
## 2. Applying co-registration
```
bbox = BBox(bbox=[34.716, 30.950, 34.743, 30.975], crs=CRS.WGS84)
resolution = 10
time_interval = ('2020-01-01', '2021-01-01')
print(f'BBox size: {bbox_to_dimensions(bbox, resolution)}')
geom, crs = bbox.geometry, bbox.crs
wgs84_geometry = Geometry(geom, crs).transform(CRS.WGS84)
geometry_center = wgs84_geometry.geometry.centroid
map1 = Map(
basemap=basemaps.Esri.WorldImagery,
center=(geometry_center.y, geometry_center.x),
zoom=14
)
area_geojson = GeoJSON(data=wgs84_geometry.geojson)
map1.add_layer(area_geojson)
map1
download_task_l2a = SentinelHubInputTask(
bands = ['B04', 'B03', 'B02'],
bands_feature = (FeatureType.DATA, 'RGB'),
resolution=resolution,
maxcc=0.9,
time_difference=timedelta(minutes=120),
data_collection=DataCollection.SENTINEL2_L2A,
max_threads=10,
additional_data=[
(FeatureType.MASK, 'dataMask', 'dataMask_l2a')
]
)
download_task_l1c = SentinelHubInputTask(
bands_feature = (FeatureType.DATA, 'BANDS'),
resolution=resolution,
maxcc=0.9,
time_difference=timedelta(minutes=120),
data_collection=DataCollection.SENTINEL2_L1C,
max_threads=10,
additional_data=[
(FeatureType.MASK, 'dataMask', 'dataMask_l1c')
]
)
data_mask_merge = ZipFeatureTask({FeatureType.MASK: ['dataMask_l1c', 'dataMask_l2a']}, (FeatureType.MASK, 'dataMask'),
lambda dm1, dm2: np.all([dm1, dm2], axis=0))
cloud_masking_task = CloudMaskTask(
data_feature=(FeatureType.DATA, 'BANDS'),
is_data_feature='dataMask',
all_bands=True,
processing_resolution=120,
mono_features=None,
mask_feature='CLM',
average_over=16,
dilation_size=12,
mono_threshold=0.2
)
valid_mask_task = ZipFeatureTask({FeatureType.MASK: ['CLM', 'dataMask']}, (FeatureType.MASK, 'VALID_DATA'),
lambda clm, dm: np.all([clm == 0, dm], axis=0))
filter_task = SimpleFilterTask((FeatureType.MASK, 'VALID_DATA'), valid_coverage_thresholder_f)
name = 'wo_coreg_anim'
anim_task_before = AnimateTask(image_dir='./images', out_dir='./animations', out_name=name, duration=5, dpi=200)
params = {'MaxIters': 500}
coreg_task = ECCRegistration((FeatureType.DATA, 'RGB'), channel=2, params=params)
name = 'coreg_anim'
anim_task_after = AnimateTask(image_dir='./images', out_dir='./animations', out_name=name, duration=5, dpi=200)
workflow = LinearWorkflow(
download_task_l2a,
download_task_l1c,
data_mask_merge,
cloud_masking_task,
valid_mask_task,
filter_task,
anim_task_before,
coreg_task,
anim_task_after
)
result = workflow.execute({
download_task_l2a: {'bbox': bbox, 'time_interval': time_interval}
})
```
## 3. Large Area Example
```
bbox = BBox(bbox=[21.4,-20.0,23.9,-18.0], crs=CRS.WGS84)
time_interval = ('2017-09-01', '2019-04-01')
# time_interval = ('2017-09-01', '2017-10-01')
resolution = 640
print(f'BBox size: {bbox_to_dimensions(bbox, resolution)}')
geom, crs = bbox.geometry, bbox.crs
wgs84_geometry = Geometry(geom, crs).transform(CRS.WGS84)
geometry_center = wgs84_geometry.geometry.centroid
map1 = Map(
basemap=basemaps.Esri.WorldImagery,
center=(geometry_center.y, geometry_center.x),
zoom=8
)
area_geojson = GeoJSON(data=wgs84_geometry.geojson)
map1.add_layer(area_geojson)
map1
download_task_l2a = SentinelHubInputTask(
bands = ['B04', 'B03', 'B02'],
bands_feature = (FeatureType.DATA, 'RGB'),
resolution=resolution,
maxcc=0.9,
time_difference=timedelta(minutes=120),
data_collection=DataCollection.SENTINEL2_L2A,
max_threads=10,
additional_data=[
(FeatureType.MASK, 'dataMask', 'dataMask_l2a')
],
aux_request_args={'dataFilter': {'previewMode': 'PREVIEW'}}
)
download_task_l1c = SentinelHubInputTask(
bands_feature = (FeatureType.DATA, 'BANDS'),
resolution=resolution,
maxcc=0.9,
time_difference=timedelta(minutes=120),
data_collection=DataCollection.SENTINEL2_L1C,
max_threads=10,
additional_data=[
(FeatureType.MASK, 'dataMask', 'dataMask_l1c')
],
aux_request_args={'dataFilter': {'previewMode': 'PREVIEW'}}
)
data_mask_merge = ZipFeatureTask({FeatureType.MASK: ['dataMask_l1c', 'dataMask_l2a']}, (FeatureType.MASK, 'dataMask'),
lambda dm1, dm2: np.all([dm1, dm2], axis=0))
cloud_masking_task = CloudMaskTask(
data_feature='BANDS',
is_data_feature='dataMask',
all_bands=True,
processing_resolution=resolution,
mono_features=('CLP', 'CLM'),
mask_feature=None,
mono_threshold=0.3,
average_over=1,
dilation_size=4
)
valid_mask_task = ZipFeatureTask({FeatureType.MASK: ['CLM', 'dataMask']}, (FeatureType.MASK, 'VALID_DATA'),
lambda clm, dm: np.all([clm == 0, dm], axis=0))
resampled_range = ('2018-01-01', '2019-01-01', 10)
interp_task = LinearInterpolation(
feature=(FeatureType.DATA, 'RGB'),
mask_feature=(FeatureType.MASK, 'VALID_DATA'),
resample_range=resampled_range,
bounds_error=False
)
name = 'botswana_single_raw'
anim_task_raw = AnimateTask(image_dir='./images', out_dir='./animations', out_name=name, duration=5, dpi=200)
name = 'botswana_single'
anim_task = AnimateTask(image_dir='./images', out_dir='./animations', out_name=name, duration=3, dpi=200)
workflow = LinearWorkflow(
download_task_l2a,
# anim_task_raw
download_task_l1c,
data_mask_merge,
cloud_masking_task,
valid_mask_task,
interp_task,
anim_task
)
result = workflow.execute({
download_task_l2a:{'bbox': bbox, 'time_interval': time_interval},
})
```
## 4. Split Image
```
bbox = BBox(bbox=[21.3,-20.0,24.0,-18.0], crs=CRS.WGS84)
time_interval = ('2018-09-01', '2020-04-01')
resolution = 120
bbox_splitter = BBoxSplitter([bbox.geometry], bbox.crs, (6,5))
bbox_list = np.array(bbox_splitter.get_bbox_list())
info_list = np.array(bbox_splitter.get_info_list())
print(f'{len(bbox_list)} patches of size: {bbox_to_dimensions(bbox_list[0], resolution)}')
gdf = gpd.GeoDataFrame(None, crs=int(bbox.crs.epsg), geometry=[bbox.geometry for bbox in bbox_list])
geom, crs = gdf.unary_union, CRS.WGS84
wgs84_geometry = Geometry(geom, crs).transform(CRS.WGS84)
geometry_center = wgs84_geometry.geometry.centroid
map1 = Map(
basemap=basemaps.Esri.WorldImagery,
center=(geometry_center.y, geometry_center.x),
zoom=8
)
for geo in gdf.geometry:
area_geojson = GeoJSON(data=Geometry(geo, crs).geojson)
map1.add_layer(area_geojson)
map1
download_task = SentinelHubInputTask(
bands = ['B04', 'B03', 'B02'],
bands_feature = (FeatureType.DATA, 'RGB'),
resolution=resolution,
maxcc=0.9,
time_difference=timedelta(minutes=120),
data_collection=DataCollection.SENTINEL2_L2A,
max_threads=10,
additional_data=[
(FeatureType.MASK, 'CLM'),
(FeatureType.DATA, 'CLP'),
(FeatureType.MASK, 'dataMask')
]
)
valid_mask_task = ZipFeatureTask([(FeatureType.MASK, 'dataMask'), (FeatureType.MASK, 'CLM'), (FeatureType.DATA, 'CLP')], (FeatureType.MASK, 'VALID_DATA'),
lambda dm, clm, clp: np.all([dm, clm == 0, clp/255 < 0.3], axis=0))
resampled_range = ('2019-01-01', '2020-01-01', 10)
interp_task = LinearInterpolation(
feature=(FeatureType.DATA, 'RGB'),
mask_feature=(FeatureType.MASK, 'VALID_DATA'),
resample_range=resampled_range,
bounds_error=False
)
export_r = ExportToTiff(feature=(FeatureType.DATA, 'RGB'), folder='./tiffs/', band_indices=[0])
export_g = ExportToTiff(feature=(FeatureType.DATA, 'RGB'), folder='./tiffs/', band_indices=[1])
export_b = ExportToTiff(feature=(FeatureType.DATA, 'RGB'), folder='./tiffs/', band_indices=[2])
convert_to_uint16 = ZipFeatureTask([(FeatureType.DATA, 'RGB')], (FeatureType.DATA, 'RGB'),
lambda x: (x*1e4).astype(np.uint16))
os.system('rm -rf ./tiffs && mkdir ./tiffs')
workflow = LinearWorkflow(
download_task,
valid_mask_task,
interp_task,
convert_to_uint16,
export_r,
export_g,
export_b
)
# Execute the workflow
execution_args = []
for idx, bbox in enumerate(bbox_list):
execution_args.append({
download_task: {'bbox': bbox, 'time_interval': time_interval},
export_r: {'filename': f'r_patch_{idx}.tiff'},
export_g: {'filename': f'g_patch_{idx}.tiff'},
export_b: {'filename': f'b_patch_{idx}.tiff'}
})
executor = EOExecutor(workflow, execution_args, save_logs=True)
executor.run(workers=10, multiprocess=False)
executor.make_report()
# spatial merge
subprocess.run(f'gdal_merge.py -n 0 -a_nodata 0 -o tiffs/r.tiff -co compress=LZW tiffs/r_patch_*.tiff && rm -rf tiffs/r_patch_*.tiff', shell=True);
subprocess.run(f'gdal_merge.py -n 0 -a_nodata 0 -o tiffs/g.tiff -co compress=LZW tiffs/g_patch_*.tiff && rm -rf tiffs/g_patch_*.tiff', shell=True);
subprocess.run(f'gdal_merge.py -n 0 -a_nodata 0 -o tiffs/b.tiff -co compress=LZW tiffs/b_patch_*.tiff && rm -rf tiffs/b_patch_*.tiff', shell=True);
dates = pd.date_range('2019-01-01', '2020-01-01', freq='10D').to_pydatetime()
import_r = ImportFromTiff((FeatureType.DATA, 'R'), f'tiffs/r.tiff', timestamp_size=len(dates))
import_g = ImportFromTiff((FeatureType.DATA, 'G'), f'tiffs/g.tiff', timestamp_size=len(dates))
import_b = ImportFromTiff((FeatureType.DATA, 'B'), f'tiffs/b.tiff', timestamp_size=len(dates))
merge_bands_task = ZipFeatureTask({FeatureType.DATA: ['R', 'G', 'B']}, (FeatureType.DATA, 'RGB'),
lambda r, g, b: np.moveaxis(np.array([r[...,0], g[...,0], b[...,0]]), 0, -1))
def temporal_ma_f(f):
k = np.array([0.05, 0.6, 1, 0.6, 0.05])
k = k/np.sum(k)
w = len(k)//2
return np.array([np.sum([f[(i-w+j)%len(f)]*k[j] for j in range(len(k))], axis=0) for i in range(len(f))])
temporal_smoothing = ZipFeatureTask([(FeatureType.DATA, 'RGB')], (FeatureType.DATA, 'RGB'), temporal_ma_f)
name = 'botswana_multi_ma'
anim_task = AnimateTask(image_dir='./images', out_dir='./animations', out_name=name, duration=3,
dpi=400, scale_factor=3.0/1e4)
workflow = LinearWorkflow(
import_r,
import_g,
import_b,
merge_bands_task,
temporal_smoothing,
anim_task
)
result = workflow.execute()
```
## 5. Batch request
Use the evalscript from the [custom scripts repository](https://github.com/sentinel-hub/custom-scripts/tree/master/sentinel-2/interpolated_time_series) and see how to use it in the batch example in our [sentinelhub-py](https://github.com/sentinel-hub/sentinelhub-py/blob/master/examples/batch_processing.ipynb) library.
|
github_jupyter
|
```
%load_ext autoreload
%autoreload 2|
import os
import pickle
from utils.config import *
event = 'thread'
file = os.path.join(SANDY_ATTR_PATH, f'corpus.{event}.pkl')
corpus = pickle.load(open(file, "rb" ))
attr = pickle.load(open(os.path.join(SANDY_ATTR_PATH, f'attr.{event}.pkl'), "rb" ))
targets = attr['target_arr']
print(len(corpus))
# 8 Malware executions
summ = 0
for exe in attr['target_arr']:
summ += len(exe)
#attr['target_arr']
import pandas as pd
import numpy as np
df = pd.DataFrame(corpus, columns=['APIs'])
df['target'] = np.concatenate(attr['target_arr'])
df
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(df['APIs']).toarray()
df2 = pd.DataFrame(X)
df2[df2.any(axis=1)]
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer
from sklearn.decomposition import PCA, SparsePCA, TruncatedSVD
ngram = (1, 4)
min_df = 2
n = 2
def generate_ngrams(corpus, ngram=None, min_df=2, n=2):
if isinstance(ngram, tuple):
start, finish = 1, 1
else:
start, finish = 4, 4
for i in range(start):
for j in range(i, finish):
ngram = (i + 1, j + 1)# if ngram is None else ngram
print(ngram)
# idf vectorizer
vectorizer = TfidfVectorizer(ngram_range=ngram, min_df=min_df)
# ngram vectorizer
#vectorizer = CountVectorizer(ngram_range=ngram, min_df=2)
vec = vectorizer.fit_transform(corpus)
print(f"vec shape: {vec.shape}")
svd = TruncatedSVD(n_components=n, n_iter=5).fit(vec)
var = svd.explained_variance_ratio_
print(f"NGRAM {i+1}:{j+1} VARIANCE SUM | {svd.explained_variance_ratio_.sum():.3f}")
x_transformed = svd.transform(vec)
return x_transformed, var
vec, var = generate_ngrams(corpus, ngram=None, min_df=min_df, n=n)
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
target_flat = [item for sublist in targets for item in sublist]
for i in range(len(vec)):
ax.scatter(vec[i, 0], vec[i, 1], color='red' if target_flat[i] == 1 else 'green', alpha=0.5)
ax.set_xlabel(f'PC1 ({var[0]*100:.1f}%)', fontsize=15)
ax.set_ylabel(f'PC2 ({var[1]*100:.1f}%)', fontsize=15)
#ax.set_title(f'ngram={str(ngram)} | n_components={str(n)}', fontsize=15)
ax.grid(True)
fig.tight_layout()
plt.savefig("thread-14-2.png", bbox_inches='tight', dpi=150)
plt.show()
import matplotlib.pyplot as plt
#for graph in master_g[1]:
graph = master_g[4]
node_color = ['red' if g[1].get('target', 0) == 1 else 'green' for g in graph.nodes(data=True)]
node_name = {g[0] : g[1].get('name', 0) for g in graph.nodes(data=True)}
nx.draw(graph, pos=nx.spring_layout(graph, k=0.4), with_labels=True, node_color=node_color, labels=node_name, font_weight='bold', node_size=30, font_size=8)
```
|
github_jupyter
|
##### 训练PNet
```
#导入公共文件
import os
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torchvision
import torchvision.transforms as transforms
from torch.autograd import Variable
import sys
sys.path.append('../')
# add other package
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
from tool.plotcm import plot_confusion_matrix
import pdb
from collections import OrderedDict
from collections import namedtuple
from itertools import product
#torch.set_printoptions(linewidth=120)
from mtcnn.PNet import PNet
from mtcnn.mtcnn import RunBuilder
from mtcnn.LossFn import LossFn
from tool.imagedb import ImageDB
from tool.imagedb import TrainImageReader
from tool import image_tools
import datetime
torch.set_grad_enabled(True)
def compute_accuracy(prob_cls, gt_cls):
prob_cls = torch.squeeze(prob_cls)
gt_cls = torch.squeeze(gt_cls)
#we only need the detection which >= 0
mask = torch.ge(gt_cls,0)
#get valid element
valid_gt_cls = torch.masked_select(gt_cls,mask)
valid_prob_cls = torch.masked_select(prob_cls,mask)
size = min(valid_gt_cls.size()[0], valid_prob_cls.size()[0])
prob_ones = torch.ge(valid_prob_cls,0.6).float()
right_ones = torch.eq(prob_ones,valid_gt_cls).float()
#cms = confusion_matrix(prob_ones,right_ones,[0,1])
#print(cms)
#names = ('0','1')
#plot_confusion_matrix(cms, names)
#print(prob_cls.shape,gt_cls.shape,valid_prob_cls.shape,right_ones.shape)
## if size == 0 meaning that your gt_labels are all negative, landmark or part
return torch.div(torch.mul(torch.sum(right_ones),float(1.0)),float(size))
## divided by zero meaning that your gt_labels are all negative, landmark or part
#annotation_file = './image/imglist_anno_12.txt'
annotation_file = '../image/12/imglist_anno_12.txt' #'./image/wider_face/wider_face_train_bbx_gt.txt' #'./image/anno_train.txt'
model_store_path = '../model/Pnet'
params = OrderedDict(
lr = [.01]
,batch_size = [2000]
#,device = ["cuda", "cpu"]
,shuffle = [True]
)
end_epoch = 10
frequent = 10
#runs = RunBuilder.get_runs(params)
def train_net(imdb=None):
if imdb == None:
imagedb = ImageDB(annotation_file)
imdb = imagedb.load_imdb()
#print(imdb.num_images)
imdb = imagedb.append_flipped_images(imdb)
for run in RunBuilder.get_runs(params):
#create model path
if not os.path.exists(model_store_path):
os.makedirs(model_store_path)
#create data_loader
train_data=TrainImageReader(imdb,12,batch_size=run.batch_size,shuffle=run.shuffle)
#print(train_data.data[0].shape,len(train_data.data))
#Sprint(train_data.label[0][0])
acc=0.0
comment = f'-{run}'
lossfn = LossFn()
network = PNet()
optimizer = torch.optim.Adam(network.parameters(), lr=run.lr)
for epoch in range(end_epoch):
train_data.reset() # shuffle
epoch_acc = 0.0
#for batch_idx,(image,(gt_label,gt_bbox,gt_landmark))in enumerate(train_dat)
for batch_idx,(image,(gt_label,gt_bbox,gt_landmark))in enumerate(train_data):
im_tensor = [ image_tools.convert_image_to_tensor(image[i,:,:,:]) for i in range(image.shape[0]) ]
im_tensor = torch.stack(im_tensor)
im_tensor = Variable(im_tensor)
gt_label = Variable(torch.from_numpy(gt_label).float())
gt_bbox = Variable(torch.from_numpy(gt_bbox).float())
#gt_landmark = Variable(torch.from_numpy(gt_landmark).float())
cls_pred, box_offset_pred = network(im_tensor)
cls_loss = lossfn.cls_loss(gt_label,cls_pred)
box_offset_loss = lossfn.box_loss(gt_label,gt_bbox,box_offset_pred)
all_loss = cls_loss*1.0+box_offset_loss*0.5
if batch_idx%frequent==0:
accuracy=compute_accuracy(cls_pred,gt_label)
accuracy=compute_accuracy(cls_pred,gt_label)
show1 = accuracy.data.cpu().numpy()
show2 = cls_loss.data.cpu().numpy()
show3 = box_offset_loss.data.cpu().numpy()
# show4 = landmark_loss.data.cpu().numpy()
show5 = all_loss.data.cpu().numpy()
print("%s : Epoch: %d, Step: %d, accuracy: %s, det loss: %s, bbox loss: %s, all_loss: %s, lr:%s "%
(datetime.datetime.now(),epoch,batch_idx, show1,show2,show3,show5,run.lr))
epoch_acc = show1
#计算偏差矩阵
optimizer.zero_grad()
all_loss.backward()
optimizer.step()
pass
pass
print('save modle acc:', epoch_acc)
torch.save(network.state_dict(), os.path.join(model_store_path,"pnet_epoch_%d.pt" % epoch))
torch.save(network, os.path.join(model_store_path,"pnet_epoch_model_%d.pkl" % epoch))
pass
pass
pass
if __name__ == '__main__':
print('train Pnet Process:...')
#加载图片文件
#imagedb = ImageDB(annotation_file,'./image/train')
#gt_imdb = imagedb.load_imdb()
#gt_imdb = imagedb.append_flipped_images(gt_imdb)
train_net()
print('finish....')
#print(gt_imdb[2])
```
|
github_jupyter
|
## Segmenting and Clustering Neighborhoods in Toronto
In this project we explore, segment, and cluster the neighborhoods in the city of Toronto. Since the data is not available in the Internet on a simple presentation, we have to scrape a Wikipedia page wrangle the data, clean it, and then read it into a structured format.
```
import numpy as np # library to handle data in a vectorized manner
import pandas as pd # library for data analsysis
pd.set_option('display.max_columns', None)
pd.set_option('display.max_rows', None)
import json # library to handle JSON files
#!conda install -c conda-forge geopy --yes # uncomment this line if you haven't completed the Foursquare API lab
from geopy.geocoders import Nominatim # convert an address into latitude and longitude values
import requests # library to handle requests
from pandas.io.json import json_normalize # tranform JSON file into a pandas dataframe
# Matplotlib and associated plotting modules
import matplotlib.cm as cm
import matplotlib.colors as colors
# import k-means from clustering stage
from sklearn.cluster import KMeans
import folium # map rendering library
```
### Scraping the Data
Use the Notebook to build the code to scrape the following Wikipedia page, https://en.wikipedia.org/wiki/List_of_postal_codes_of_Canada:_M, in order to obtain the data that is in the table of postal codes and to transform the data into a pandas dataframe like the one shown below:
```
toronto='https://en.wikipedia.org/wiki/List_of_postal_codes_of_Canada:_M'
df = pd.read_html(toronto, header=0)[0]
df.head()
```
### Eliminating cells with a borough that is Not assigned
Only process the cells that have an assigned borough. Ignore cells with a borough that is Not assigned.
```
df.drop(df[df['Borough']=="Not assigned"].index,axis=0, inplace=True)
```
### Grouping by Postal Code
More than one neighborhood can exist in one postal code area. For example, in the table on the Wikipedia page, you will notice that M5A is listed twice and has two neighborhoods: Harbourfront and Regent Park. These two rows will be combined into one row with the neighborhoods separated with a comma as shown in row 11 in the above table.
```
df1=df.groupby('Postcode')['Neighbourhood'].agg(lambda x: ','.join(x))
df3=pd.DataFrame(df1)
df3.reset_index().head()
df2=df.groupby('Postcode')['Borough'].unique()
df4=pd.DataFrame(df2)
df4.reset_index().head()
df4['Borough']=[df4['Borough'][i][0] for i in range(df4.shape[0])]
df4.reset_index().head()
df4['Neighbourhood']=df3['Neighbourhood']
df4.reset_index().head()
df4.loc[df4['Neighbourhood']=="Not assigned",'Neighbourhood']=df4.loc[df4['Neighbourhood']=="Not assigned",'Borough']
df4.reset_index().head()
df4.shape
```
### Including the Latitude and Longitude to the Dataframe
Now in order to utilize the Foursquare location data, we need to get the latitude and the longitude coordinates of each neighborhood.
```
coords=r'http://cocl.us/Geospatial_data'
coord_df=pd.read_csv(coords)
df4['Latitude']=coord_df['Latitude'].values
df4['Longitude']=coord_df['Longitude'].values
df4.reset_index().head()
```
### Explore and cluster the neighborhoods in Toronto.
```
import folium
CLIENT_ID = 'IVUX2ATVRIVIAT3MYAOI3BNB0N5X2BCPEGK3W0FCX5RNN1HN' # my Foursquare ID
CLIENT_SECRET = '1UKWCBE54WZK50IHDYJXAK3GJCXPGQELW5QE30LXCGRA4MG2' # my Foursquare Secret
VERSION = '20180605' # Foursquare API version
print('Your credentails:')
print('CLIENT_ID: ' + CLIENT_ID)
print('CLIENT_SECRET:' + CLIENT_SECRET)
def getNearbyVenues(names, latitudes, longitudes, radius=500):
venues_list=[]
for name, lat, lng in zip(names, latitudes, longitudes):
print(name)
# create the API request URL
url = 'https://api.foursquare.com/v2/venues/explore?&client_id={}&client_secret={}&v={}&ll={},{}&radius={}&limit={}'.format(
CLIENT_ID,
CLIENT_SECRET,
VERSION,
lat,
lng,
radius,
LIMIT)
# make the GET request
results = requests.get(url).json()["response"]['groups'][0]['items']
# return only relevant information for each nearby venue
venues_list.append([(
name,
lat,
lng,
v['venue']['name'],
v['venue']['location']['lat'],
v['venue']['location']['lng'],
v['venue']['categories'][0]['name']) for v in results])
nearby_venues = pd.DataFrame([item for venue_list in venues_list for item in venue_list])
nearby_venues.columns = ['Neighbourhood',
'Neighbourhood Latitude',
'Neighbourhood Longitude',
'Venue',
'Venue Latitude',
'Venue Longitude',
'Venue Category']
return(nearby_venues)
LIMIT=100
toronto_venues = getNearbyVenues(names=df4['Neighbourhood'],
latitudes=df4['Latitude'],
longitudes=df4['Longitude']
)
toronto_venues.groupby('Neighbourhood').count().head()
print('There are {} uniques categories.'.format(len(toronto_venues['Venue Category'].unique())))
```
#### Encoding the variables
```
# one hot encoding
toronto_onehot = pd.get_dummies(toronto_venues[['Venue Category']], prefix="", prefix_sep="")
# add neighborhood column back to dataframe
toronto_onehot['Neighbourhood'] = toronto_venues['Neighbourhood']
# move neighborhood column to the first column
fixed_columns = [toronto_onehot.columns[-1]] + list(toronto_onehot.columns[:-1])
toronto_onehot = toronto_onehot[fixed_columns]
toronto_grouped = toronto_onehot.groupby('Neighbourhood').mean().reset_index()
num_top_venues = 5
for hood in toronto_grouped['Neighbourhood']:
#print("----"+hood+"----")
temp = toronto_grouped[toronto_grouped['Neighbourhood'] == hood].T.reset_index()
temp.columns = ['venue','freq']
temp = temp.iloc[1:]
temp['freq'] = temp['freq'].astype(float)
temp = temp.round({'freq': 2})
#print(
temp.sort_values('freq', ascending=False).reset_index(drop=True).head(num_top_venues)
# print('\n')
def return_most_common_venues(row, num_top_venues):
row_categories = row.iloc[1:]
row_categories_sorted = row_categories.sort_values(ascending=False)
return row_categories_sorted.index.values[0:num_top_venues]
num_top_venues = 10
indicators = ['st', 'nd', 'rd']
# create columns according to number of top venues
columns = ['Neighbourhood']
for ind in np.arange(num_top_venues):
try:
columns.append('{}{} Most Common Venue'.format(ind+1, indicators[ind]))
except:
columns.append('{}th Most Common Venue'.format(ind+1))
# create a new dataframe
neighborhoods_venues_sorted = pd.DataFrame(columns=columns)
neighborhoods_venues_sorted['Neighbourhood'] = toronto_grouped['Neighbourhood']
for ind in np.arange(toronto_grouped.shape[0]):
neighborhoods_venues_sorted.iloc[ind, 1:] = return_most_common_venues(toronto_grouped.iloc[ind, :], num_top_venues)
neighborhoods_venues_sorted.head()
```
### K Clusters
```
# set number of clusters
kclusters = 7
toronto_grouped_clustering = toronto_grouped.drop('Neighbourhood', 1)
# run k-means clustering
kmeans = KMeans(n_clusters=kclusters, random_state=0).fit(toronto_grouped_clustering)
# check cluster labels generated for each row in the dataframe
kmeans.labels_[0:10]
# add clustering labels
neighborhoods_venues_sorted.insert(0, 'Cluster Labels', kmeans.labels_)
toronto_merged = df4
# merge toronto_grouped with toronto_data to add latitude/longitude for each neighborhood
toronto_merged = toronto_merged.join(neighborhoods_venues_sorted.set_index('Neighbourhood'), on='Neighbourhood')
toronto_merged.reset_index()
toronto_merged.dropna(inplace=True)
# create map
address='Toronto'
geolocator = Nominatim(user_agent="toronto_explorer")
location = geolocator.geocode(address)
latitude = location.latitude
longitude = location.longitude
map_clusters = folium.Map(location=[latitude, longitude], zoom_start=11)
# set color scheme for the clusters
x = np.arange(kclusters)
ys = [i + x + (i*x)**2 for i in range(kclusters)]
colors_array = cm.rainbow(np.linspace(0, 1, len(ys)))
rainbow = [colors.rgb2hex(i) for i in colors_array]
# add markers to the map
markers_colors = []
for lat, lon, poi, cluster in zip(toronto_merged['Latitude'], toronto_merged['Longitude'], toronto_merged['Neighbourhood'], toronto_merged['Cluster Labels']):
label = folium.Popup(str(poi) + ' Cluster ' + str(cluster), parse_html=True)
folium.CircleMarker(
[lat, lon],
radius=5,
popup=label,
color=rainbow[int(cluster)-1],
fill=True,
fill_color=rainbow[int(cluster)-1],
fill_opacity=0.7).add_to(map_clusters)
map_clusters
```
|
github_jupyter
|
```
import numpy as np
import pandas as pd
import os
import gc
import seaborn as sns # for plotting graphs
import matplotlib.pyplot as plt # for plotting graphs aswell
import glob
from datetime import datetime
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn import preprocessing
from sklearn.metrics import log_loss,roc_auc_score
from sklearn.preprocessing import OneHotEncoder
from scipy.sparse import coo_matrix, hstack
import lightgbm
from lightgbm import LGBMClassifier
from sklearn.model_selection import KFold
%matplotlib inline
# to display maximum rows and columns
pd.set_option('display.max_rows', None)
pd.set_option('display.max_columns', None)
# function to set all numerical data to int16 or float16, to save on memory use
def dtype_conver(Dataframe):
for col in Dataframe:
if Dataframe[col].dtype in ['float32','float64']:
Dataframe[col] = Dataframe[col].astype(np.float16)
if Dataframe[col].dtype in ['int32','float64']:
Dataframe[col] = Dataframe[col].astype(np.int16)
#Parameters for lightGBM classification
model_lgb = LGBMClassifier(
n_jobs=4,
n_estimators=100000,
boost_from_average='false',
learning_rate=0.02,
num_leaves=64,
num_threads=4,
max_depth=7,
tree_learner = "serial",
feature_fraction = 0.7,
bagging_freq = 5,
bagging_fraction = 0.5,
# min_data_in_leaf = 75,
# min_sum_hessian_in_leaf = 50.0,
silent=-1,
verbose=-1,
device='cpu',
)
#Parameters for RFC classification
clf = RandomForestClassifier(n_estimators=1000, max_depth=7,random_state=0,max_leaf_nodes=64,verbose=1,n_jobs=-1)
# import OneHotEncoder & define it
from sklearn.preprocessing import OneHotEncoder
ohe = OneHotEncoder(categories = 'auto',sparse=True)
kf = KFold(n_splits=5, random_state=10, shuffle=True)
def master_pipe(X_ohe,y):
# place holder for k-fold scores
scores = []
# to differentiate files names produced by plt.savefig
n = 1
# model pipeline calculates model score and saves feature importance graph as .png file
for i,(tr_idx, val_idx) in enumerate(kf.split(X_ohe,y)):
print('Fold :{}'.format(i))
tr_X = X_ohe[tr_idx] # training for this loop
tr_y = y[tr_idx] #
val_X = X_ohe[val_idx]# validation data for this loop
val_y = y[val_idx]
# here build your models
model = model_lgb
model.fit(tr_X, tr_y, eval_set=[(tr_X, tr_y), (val_X, val_y)], eval_metric = 'auc', verbose=100,
early_stopping_rounds= 50)
#picking best model?
pred_val_y = model.predict_proba(val_X,num_iteration=model.best_iteration_)[:,1]
#measuring model vs validation
score = roc_auc_score(val_y,pred_val_y)
scores.append(score)
print('current performance by auc:{}'.format(score))
lightgbm.plot_importance(model, ax=None, height=0.2, xlim=None, ylim=None, title='Feature importance',
xlabel='Feature importance', ylabel='Features', importance_type='split',
max_num_features=20, ignore_zero=True, figsize=None, grid=True, precision=3)
# in python plots dir will be auto-created
#plt.show()
plt.savefig('..(in jupyter, point destination here and remove plots dir ->)plots/feature_importance{}.png'.format(n))
plt.close()
n=n+1
def master_pipe_RFC(X_ohe,y):
# place holder for k-fold scores
scores_rfc = []
# model pipeline calculates model score and saves feature importance graph as .png file
for i,(tr_idx, val_idx) in enumerate(kf.split(X_ohe,y)):
print('Fold :{}'.format(i))
tr_X = X_ohe[tr_idx] # training for this loop
tr_y = y[tr_idx] #
val_X = X_ohe[val_idx]# validation data for this loop
val_y = y[val_idx]
# here build your models
model = clf
model.fit(tr_X, tr_y)
#picking best model?
pred_val_y = model.predict(val_X)
#measuring model vs validation
score_rfc = roc_auc_score(val_y,pred_val_y)
scores_rfc.append(score_rfc)
print('current performance by auc:{}'.format(score_rfc))
# Read in filepath
DATA_PATH = r'C:/Users/t891199/Desktop/Big_Data_Diploma/CEBD_1260_Machine_learning/Data Files/Class_3/'
file_name = os.path.join(DATA_PATH,'train.csv')
# pandas reads in csv file using filepath
old_train_df = pd.read_csv(file_name)
print(old_train_df.shape)
#original_quote_date is time-series
#Feature Engineering
old_train_df['Original_Quote_Date'] = pd.to_datetime(old_train_df['Original_Quote_Date'])
old_train_df['year'] = old_train_df['Original_Quote_Date'].dt.year
old_train_df['month'] = old_train_df['Original_Quote_Date'].dt.month
old_train_df['day'] = old_train_df['Original_Quote_Date'].dt.day
train_df = old_train_df.drop(["Original_Quote_Date"], axis = 1)
# lets see how many NaN or Null values are in each column
nan_info = pd.DataFrame(train_df.isnull().sum()).reset_index()
nan_info.columns = ['col','nan_cnt']
#sort them in descending order and print 1st 10
nan_info.sort_values(by = 'nan_cnt',ascending=False,inplace=True)
nan_info.head(10)
# extract column names with NaNs and Nulls
# in numerical cols
num_cols_with_missing = ['PersonalField84','PropertyField29']
# extract column names with NaNs and Nulls
# in boolean type cols
bool_cols_with_missing = ['PropertyField3','PropertyField4','PersonalField7','PropertyField32',
'PropertyField34','PropertyField36','PropertyField38']
# fill in null and NaN values with 'U' in boolean type cols ( 'Y','N')
for cols in bool_cols_with_missing:
train_df[cols].fillna('U',inplace=True)
# fill in null and NaN values with -1 in numerical missing values
for cols in num_cols_with_missing:
train_df[cols].fillna(-1, inplace=True)
# define target
y = old_train_df["QuoteConversion_Flag"].values
# drop target column from data
# and static columns GeographicField10A & PropertyField6
X = train_df.drop(["QuoteConversion_Flag","GeographicField10A","PropertyField6"], axis = 1)
#QuoteNumber setting as index
X = X.set_index("QuoteNumber")
dtype_conver(X)
# select all columns that are categorical i.e with unique categories less than 40 in our case
X_for_ohe = [cols for cols in X.columns if X[cols].nunique() < 40 or X[cols].dtype in['object']]
X_not_ohe = [cols for cols in X.columns if X[cols].nunique() > 40 and X[cols].dtype not in['object']]
#numerical column that we will not encode
X[X_not_ohe].head()
#to keep track of our columns, how many are remaining after we removed 4 so far?
len(X_for_ohe)
X['SalesField8'].head()
nan_info = pd.DataFrame(X[X_for_ohe].isnull().sum()).reset_index()
nan_info.columns = ['col','nan_cnt']
#sort them in descending order and print 1st 10
nan_info.sort_values(by = 'nan_cnt',ascending=False,inplace=True)
nan_info.head(10)
# apply OneHotEncoder on categorical feature columns
X_ohe = ohe.fit_transform(X[X_for_ohe])
# we are pretty much done for now here, apparently we can set 'sparse = True' in OneHotEncoder and we get a
#csr_matrix. I left it as false so that you can see the sparse matrix
X_ohe
# SalesField8 was kept out of sparse matrix, now we need to bring it back
# scaledown SalesField8 for easy handling using log(), then convert to float16
SF8 = np.log(X['SalesField8']).astype(np.float16)
hstack((X_ohe,np.array(SF8)[:,None]))
# lets get the model k-fold scores for RFC
master_pipe_RFC(X_ohe,y)
# lets get the model k-fold scores and print feature importance graphs
master_pipe(X_ohe,y)
```
|
github_jupyter
|
```
import sys
import os
project_root = os.path.abspath("../..")
# project_root = os.path.abspath(os.path.join(script_path, "../.."))
if project_root not in sys.path:
sys.path.append(project_root)
print(f"Project_root: {project_root}")
import pandas as pd
from analysis.utils.constants import stats_2021_path, projected_2022_path
projected_stats = pd.read_csv(projected_2022_path).dropna()
last_year_stats = pd.read_csv(stats_2021_path).dropna()
data_set = {"last_year": last_year_stats, "projected": projected_stats}
from analysis.player_rating import (
get_players_pool,
get_player_ratings,
combine_player_data,
get_expected_salary,
)
n_teams = 13
players_pool = get_players_pool(n_teams=n_teams, n_players=17, over_write=1100)
rating_projected = get_player_ratings(projected_stats, players_pool=players_pool)
rating_last_year = get_player_ratings(last_year_stats, players_pool=players_pool)
player_ratings = combine_player_data(
data_last_year=rating_last_year, data_projected=rating_projected
)
player_stats = combine_player_data(
data_last_year=last_year_stats.set_index("name"),
data_projected=projected_stats.set_index("name"),
)
for n_expensive in range(5, 14, 2):
player_ratings[f"salary_{n_expensive}"] = get_expected_salary(
player_ratings,
players_per_team=13,
n_teams=n_teams,
one_dollar_rank=13 * n_expensive,
).round(2)
```
## Stats Scarcity Plot
```
import holoviews as hv
import hvplot.pandas
from analysis.utils.constants import stats_counts
rating_cols = ["overall"]
summary_data = (
pd.concat([player_stats[stats_counts], player_ratings[rating_cols]], axis=1)
.sort_values(by="overall", ascending=False)
.round(2)
.reset_index()
)
summary_data["rank"] = summary_data.index + 1
def get_reverse_cumsum_fraction(col_data):
this_total = col_data.sum()
this_resverse_cumsum = this_total - col_data.cumsum()
return this_resverse_cumsum / this_total
decay_lines = {}
for col in ["PTS", "AST", "REB", "3PTM", "BLK", "STL"]:
summary_data[f"cf_{col}"] = get_reverse_cumsum_fraction(summary_data[col])
this_line = summary_data.hvplot.line(x="rank", y=f"cf_{col}", label=col)
decay_lines[col] = this_line
import holoviews as hv
hv.Overlay(list(decay_lines.values())).opts(
xlabel="Rank",
ylabel="Fraction",
title="Stats Scarcity",
width=800,
height=500,
xlim=(0, 13 * 13),
ylim=(0.4, 1),
legend_position="bottom_left",
)
```
## Component Scatter
```
x_cols = ["AST", "FTR"]
y_cols = ["BLK", "FGR"]
salary_threshold = 35
plot_data = player_ratings.copy().reset_index()
plot_data["x_data"] = plot_data[x_cols].sum(axis=1)
plot_data["y_data"] = plot_data[y_cols].sum(axis=1)
plot_data["strategy_focus"] = plot_data[x_cols + y_cols].sum(axis=1)
from analysis.visualization import plot_player_ratings_scatter
strategy_scatter = plot_player_ratings_scatter(
player_ratings=plot_data,
x_col="x_data",
y_col="y_data",
color_col="strategy_focus",
width=600,
height=400,
xlabel=" + ".join(x_cols),
ylabel=" + ".join(y_cols),
)
positive_x = plot_data["x_data"] > 0
positive_y = plot_data["y_data"] > 0
plot_data["wasted_value"] = plot_data["overall"] - plot_data["strategy_focus"]
target_scatter = plot_player_ratings_scatter(
player_ratings=plot_data,
x_col="overall",
y_col="wasted_value",
width=600,
height=400,
)
wasted_value = plot_data["wasted_value"] > 0
not_too_expensive = plot_data["salary_13"] < salary_threshold
sorted_target = plot_data[wasted_value & not_too_expensive].sort_values(
by="overall", ascending=False
)
(strategy_scatter + target_scatter).cols(1)
sleeper_list = [
"Cade Cunningham",
"Jalen Suggs",
"Evan Mobley",
"Killian Hayes",
"Scottie Barnes",
"Jordan Poole",
]
injured_list = [
"Kawhi Leonard",
"Jonanthan Issac",
"Klay Thompson",
]
guard_list = [
"Trae Young",
"De'Aaron Fox",
"Jrue Holiday",
"Zach LaVine",
"Shai Gilgeous-Alexander",
"DeMar DeRozan",
"Lonzo Ball",
"Marcus Smart",
"Tyrese Haliburton",
"T.J. McConnell",
]
forward_list = [
"Domantas Sabonis",
"Brandon Ingram",
"Tobias Harris",
"Joe Harris",
"Duncan Robinson",
]
center_list = [
"Rudy Gobert",
"Deandre Ayton",
"Draymond Green",
"Bam Adebayo",
"Isaiah Stewart",
"Jonas Valanciunas",
"Jakob Poeltl",
"Jarrett Allen",
"Robert Williams III",
"Nerlens Noel",
"Mo Bamba",
]
target_list = guard_list + center_list + forward_list + sleeper_list
draft_targets = plot_data[plot_data["name"].isin(target_list)]
assert (set(target_list) - set(draft_targets["name"])) == set()
print(draft_targets.shape[0])
# plot_data.sort_values(by="AST", ascending=False).head(10)
# plot_data[plot_data.name.str.contains("Smart")]
draft_targets[["name", "overall", "strategy_focus", "salary_5", "salary_13"]]
```
## Target Players
## Salary Projection Plot
```
player_ratings.stats_type.value_counts()
plot_data = player_ratings.reset_index().copy()
plot_data["rank"] = plot_data.index + 1
overall_scatter = plot_data.hvplot.scatter(
x="rank", y="overall", c="overall", s=50, hover_cols=["name", "overall"],
)
overall_line = plot_data.hvplot.line(
x="rank", y="overall", hover_cols=["name", "overall"]
)
overall_plot = overall_line * overall_scatter
salary_lines = {}
for n_expensive in range(5, 14, 2):
this_scatter = plot_data.hvplot.scatter(
x="rank", y=f"salary_{n_expensive}", hover_cols=["name", "overall"]
)
this_line = plot_data.hvplot.line(
x="rank", y=f"salary_{n_expensive}", hover_cols=["name", "overall"]
)
salary_lines[n_expensive] = this_scatter * this_line
overall_plot.opts(height=600) + hv.Overlay(list(salary_lines.values())).opts(height=600)
```
|
github_jupyter
|
```
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python Docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the read-only "../input/" directory
# For example, running this (by clicking run or pressing Shift+Enter) will list all files under the input directory
import os
for dirname, _, filenames in os.walk('/kaggle/input'):
for filename in filenames:
print(os.path.join(dirname, filename))
# You can write up to 20GB to the current directory (/kaggle/working/) that gets preserved as output when you create a version using "Save & Run All"
# You can also write temporary files to /kaggle/temp/, but they won't be saved outside of the current session
```
# Installing important modules for proper functioning. #
```
!pip install tld
```
# Importing all required modules #
```
import re
import seaborn as sns
import matplotlib.pyplot as plt
from colorama import Fore
from urllib.parse import urlparse
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, classification_report, accuracy_score
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier, ExtraTreesClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import SGDClassifier
from sklearn.naive_bayes import GaussianNB
from tld import get_tld, is_tld
from sklearn.metrics import plot_confusion_matrix
from sklearn.metrics import plot_roc_curve
```
# Reading the contents from the imported (csv) file provided by the Kaggle #
```
data = pd.read_csv('/kaggle/input/malicious-urls-dataset/malicious_phish.csv')
data.head()
data.isnull().sum()
count = data.type.value_counts()
count
```
# Checking data types #
## Counting the numbers of phising, malware, etc types of links from the given csv files ##
```
sns.barplot(x=count.index, y=count)
plt.xlabel('Types of links')
plt.ylabel('Counts');
```
# Representing the types of links based on their categories and types #
## removing 'www" from the given dataset ##
```
data['url'] = data['url'].replace('www.', '', regex=True)
data
```
### Removing (WWW) from the given list and allowing only http:// ###
```
rem = {"Category": {"benign": 0, "defacement": 1, "phishing":2, "malware":3}}
data['Category'] = data['type']
data = data.replace(rem)
data['url_len'] = data['url'].apply(lambda x: len(str(x)))
def process_tld(url):
try:
res = get_tld(url, as_object = True, fail_silently=False,fix_protocol=True)
pri_domain= res.parsed_url.netloc
except :
pri_domain= None
return pri_domain
data['domain'] = data['url'].apply(lambda i: process_tld(i))
data.head()
```
# 👇 extracting number of feature = ['@','?','-','=','.','#','%','+','$','!','*',',','//'] from given data set. #
```
feature = ['@','?','-','=','.','#','%','+','$','!','*',',','//']
for a in feature:
data[a] = data['url'].apply(lambda i: i.count(a))
def abnormal_url(url):
hostname = urlparse(url).hostname
hostname = str(hostname)
match = re.search(hostname, url)
if match:
return 1
else:
return 0
data['abnormal_url'] = data['url'].apply(lambda i: abnormal_url(i))
sns.countplot(x='abnormal_url', data=data);
def httpSecure(url):
htp = urlparse(url).scheme
match = str(htp)
if match=='https':
return 1
else:
return 0
data['https'] = data['url'].apply(lambda i: httpSecure(i))
sns.countplot(x='https', data=data);
```
# Training the model for realtime use #
```
def digit_count(url):
digits = 0
for i in url:
if i.isnumeric():
digits = digits + 1
return digits
data['digits']= data['url'].apply(lambda i: digit_count(i))
def letter_count(url):
letters = 0
for i in url:
if i.isalpha():
letters = letters + 1
return letters
data['letters']= data['url'].apply(lambda i: letter_count(i))
data.head()
def Shortining_Service(url):
match = re.search('bit\.ly|goo\.gl|shorte\.st|go2l\.ink|x\.co|ow\.ly|t\.co|tinyurl|tr\.im|is\.gd|cli\.gs|'
'yfrog\.com|migre\.me|ff\.im|tiny\.cc|url4\.eu|twit\.ac|su\.pr|twurl\.nl|snipurl\.com|'
'short\.to|BudURL\.com|ping\.fm|post\.ly|Just\.as|bkite\.com|snipr\.com|fic\.kr|loopt\.us|'
'doiop\.com|short\.ie|kl\.am|wp\.me|rubyurl\.com|om\.ly|to\.ly|bit\.do|t\.co|lnkd\.in|'
'db\.tt|qr\.ae|adf\.ly|goo\.gl|bitly\.com|cur\.lv|tinyurl\.com|ow\.ly|bit\.ly|ity\.im|'
'q\.gs|is\.gd|po\.st|bc\.vc|twitthis\.com|u\.to|j\.mp|buzurl\.com|cutt\.us|u\.bb|yourls\.org|'
'x\.co|prettylinkpro\.com|scrnch\.me|filoops\.info|vzturl\.com|qr\.net|1url\.com|tweez\.me|v\.gd|'
'tr\.im|link\.zip\.net',
url)
if match:
return 1
else:
return 0
data['Shortining_Service'] = data['url'].apply(lambda x: Shortining_Service(x))
sns.countplot(x='Shortining_Service', data=data);
def having_ip_address(url):
match = re.search(
'(([01]?\\d\\d?|2[0-4]\\d|25[0-5])\\.([01]?\\d\\d?|2[0-4]\\d|25[0-5])\\.([01]?\\d\\d?|2[0-4]\\d|25[0-5])\\.'
'([01]?\\d\\d?|2[0-4]\\d|25[0-5])\\/)|' # IPv4
'(([01]?\\d\\d?|2[0-4]\\d|25[0-5])\\.([01]?\\d\\d?|2[0-4]\\d|25[0-5])\\.([01]?\\d\\d?|2[0-4]\\d|25[0-5])\\.'
'([01]?\\d\\d?|2[0-4]\\d|25[0-5])\\/)|' # IPv4 with port
'((0x[0-9a-fA-F]{1,2})\\.(0x[0-9a-fA-F]{1,2})\\.(0x[0-9a-fA-F]{1,2})\\.(0x[0-9a-fA-F]{1,2})\\/)' # IPv4 in hexadecimal
'(?:[a-fA-F0-9]{1,4}:){7}[a-fA-F0-9]{1,4}|'
'([0-9]+(?:\.[0-9]+){3}:[0-9]+)|'
'((?:(?:\d|[01]?\d\d|2[0-4]\d|25[0-5])\.){3}(?:25[0-5]|2[0-4]\d|[01]?\d\d|\d)(?:\/\d{1,2})?)', url) # Ipv6
if match:
return 1
else:
return 0
data['having_ip_address'] = data['url'].apply(lambda i: having_ip_address(i))
data["having_ip_address"].value_counts()
plt.figure(figsize=(15, 15))
sns.heatmap(data.corr(), linewidths=.5)
X = data.drop(['url','type','Category','domain'],axis=1)
y = data['Category']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=2)
models = [DecisionTreeClassifier,RandomForestClassifier,AdaBoostClassifier,KNeighborsClassifier,SGDClassifier,
ExtraTreesClassifier,GaussianNB]
accuracy_test=[]
for m in models:
print('Model =>\033[07m {} \033[0m'.format(m))
model_ = m()
model_.fit(X_train, y_train)
pred = model_.predict(X_test)
acc = accuracy_score(pred, y_test)
accuracy_test.append(acc)
print('Test Accuracy :\033[32m \033[01m {:.2f}% \033[30m \033[0m'.format(acc*100))
print('\033[01m Classification_report \033[0m')
print(classification_report(y_test, pred))
print('\033[01m Confusion_matrix \033[0m')
cf_matrix = confusion_matrix(y_test, pred)
plot_ = sns.heatmap(cf_matrix/np.sum(cf_matrix), annot=True,fmt= '0.2%')
plt.show()
print('\033[31m End \033[0m')
output = pd.DataFrame({"Model":['Decision Tree Classifier','Random Forest Classifier',
'AdaBoost Classifier','KNeighbors Classifier','SGD Classifier',
'Extra Trees Classifier','Gaussian NB'],
"Accuracy":accuracy_test})
plt.figure(figsize=(10, 5))
plots = sns.barplot(x='Model', y='Accuracy', data=output)
for bar in plots.patches:
plots.annotate(format(bar.get_height(), '.2f'),
(bar.get_x() + bar.get_width() / 2,
bar.get_height()), ha='center', va='center',
size=15, xytext=(0, 8),
textcoords='offset points')
plt.xlabel("Models", size=14)
plt.xticks(rotation=20);
plt.ylabel("Accuracy", size=14)
plt.show()
```
|
github_jupyter
|
```
from splinter import Browser
from bs4 import BeautifulSoup as bs
import pymongo
import time
import pandas as pd
conn = 'mongodb://localhost:27017'
client = pymongo.MongoClient(conn)
db = client.mars_db
collection = db.titles
executable_path = {"executable_path":"C:/Users/cgrinstead12/Desktop/Mission to Mars/chromedriver.exe"}
browser = Browser("chrome", **executable_path, headless = False)
url = "https://mars.nasa.gov/news/"
browser.visit(url)
html = browser.html
soup = bs(html,"html.parser")
news_title = soup.find('div', class_='content_title').text
news_para = soup.find('div', class_='article_teaser_body').text
print(news_title)
print(news_para)
image_url = "https://www.jpl.nasa.gov/spaceimages/?search=&category=Mars"
browser.visit(image_url)
browser.click_link_by_partial_text('FULL IMAGE')
time.sleep(1)
browser.click_link_by_partial_text('more info')
image_html = browser.html
soup = bs(image_html, "html.parser")
image_url = soup.find('img', class_="main_image")['src']
print(image_url)
main_url = 'https://www.jpl.nasa.gov/'
image_url_combined = main_url + image_url
print(image_url_combined)
browser.visit(image_url_combined)
```
Step 3 - Twitter Data https://twitter.com/marswxreport?lang=en - Visit the Mars Weather twitter account here and scrape the latest Mars weather tweet from the page. Save the tweet text for the weather report as a variable called mars_weather.
```
url = 'https://twitter.com/marswxreport?lang=en'
browser.visit(url)
twitter_html = browser.html
soup = bs(twitter_html, "html.parser")
mars_weather = soup.find('p', class_="TweetTextSize TweetTextSize--normal js-tweet-text tweet-text").text
print(mars_weather)
```
Mars Facts
Visit the Mars Facts webpage here and use Pandas to scrape the table containing facts about the planet including Diameter, Mass, etc.
Use Pandas to convert the data to a HTML table string.
```
url = "https://space-facts.com/mars/"
browser.visit(url)
facts_html = browser.html
soup = bs(facts_html, "html.parser")
mars_dict = {}
results = soup.find('tbody').find_all('tr')
for result in results:
column_description = result.find('td', class_="column-1").text
column_fact = result.find('td', class_="column-2").text
mars_dict[column_description] = column_fact
df = pd.DataFrame(list(mars_dict.items()), columns=['Facts', 'Data'])
df
```
Mars Hemispheres Visit the USGS Astrogeology site here to obtain high resolution images for each of Mar's hemispheres.
```
executable_path = {"executable_path":"C:/Users/cgrinstead12/Desktop/Mission to Mars/chromedriver.exe"}
browser = Browser("chrome", **executable_path, headless = False)
url = 'https://astrogeology.usgs.gov/search/results?q=hemisphere+enhanced&k1=target&v1=Mars'
hemispheres = ['Cerberus Hemisphere Enhanced',
'Schiaparelli Hemisphere Enhanced',
'Syrtis Major Hemisphere Enhanced',
'Valles Marineris Hemisphere Enhanced']
links = []
for hemisphere in hemispheres:
browser.visit(url)
browser.click_link_by_partial_text(hemisphere)
highresMars_html = browser.html
soup = bs(highresMars_html, "html.parser")
image_url_hemisphere = soup.find('div', class_='downloads').a['href']
links.append(image_url_hemisphere)
hemisphere_links = dict(zip(hemispheres, links))
print(hemisphere_links)
```
STEP 2 Use MongoDB with Flask templating to create a new HTML page that displays all of the information that was scraped from the URLs above.
|
github_jupyter
|
```
# Initialize Otter
import otter
grader = otter.Notebook("lab04.ipynb")
```
# Lab 4: Functions and Visualizations
Welcome to Lab 4! This week, we'll learn about functions, table methods such as `apply`, and how to generate visualizations!
Recommended Reading:
* [Applying a Function to a Column](https://www.inferentialthinking.com/chapters/08/1/applying-a-function-to-a-column.html)
* [Visualizations](https://www.inferentialthinking.com/chapters/07/visualization.html)
First, set up the notebook by running the cell below.
```
import numpy as np
from datascience import *
# These lines set up graphing capabilities.
import matplotlib
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
import warnings
warnings.simplefilter('ignore', FutureWarning)
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
```
**Deadline**: If you are not attending lab physically, you have to complete this lab and submit by Wednesday, February 12th before 8:59 A.M. in order to receive lab credit. Otherwise, please attend the lab you are enrolled in, get checked off with your (u)GSI or learning assistant **AND** submit this assignment by the end of the lab section (with whatever progress you've made) to receive lab credit.
**Submission**: Once you're finished, select "Save and Checkpoint" in the File menu and then execute the submit cell at the end. The result will contain a link that you can use to check that your assignment has been submitted successfully.
## 1. Defining functions
Let's write a very simple function that converts a proportion to a percentage by multiplying it by 100. For example, the value of `to_percentage(.5)` should be the number 50 (no percent sign).
A function definition has a few parts.
##### `def`
It always starts with `def` (short for **def**ine):
def
##### Name
Next comes the name of the function. Like other names we've defined, it can't start with a number or contain spaces. Let's call our function `to_percentage`:
def to_percentage
##### Signature
Next comes something called the *signature* of the function. This tells Python how many arguments your function should have, and what names you'll use to refer to those arguments in the function's code. A function can have any number of arguments (including 0!).
`to_percentage` should take one argument, and we'll call that argument `proportion` since it should be a proportion.
def to_percentage(proportion)
If we want our function to take more than one argument, we add a comma between each argument name. Note that if we had zero arguments, we'd still place the parentheses () after than name.
We put a colon after the signature to tell Python it's over. If you're getting a syntax error after defining a function, check to make sure you remembered the colon!
def to_percentage(proportion):
##### Documentation
Functions can do complicated things, so you should write an explanation of what your function does. For small functions, this is less important, but it's a good habit to learn from the start. Conventionally, Python functions are documented by writing an **indented** triple-quoted string:
def to_percentage(proportion):
"""Converts a proportion to a percentage."""
##### Body
Now we start writing code that runs when the function is called. This is called the *body* of the function and every line **must be indented with a tab**. Any lines that are *not* indented and left-aligned with the def statement is considered outside the function.
Some notes about the body of the function:
- We can write code that we would write anywhere else.
- We use the arguments defined in the function signature. We can do this because we assume that when we call the function, values are already assigned to those arguments.
- We generally avoid referencing variables defined *outside* the function. If you would like to reference variables outside of the function, pass them through as arguments!
Now, let's give a name to the number we multiply a proportion by to get a percentage:
def to_percentage(proportion):
"""Converts a proportion to a percentage."""
factor = 100
##### `return`
The special instruction `return` is part of the function's body and tells Python to make the value of the function call equal to whatever comes right after `return`. We want the value of `to_percentage(.5)` to be the proportion .5 times the factor 100, so we write:
def to_percentage(proportion):
"""Converts a proportion to a percentage."""
factor = 100
return proportion * factor
`return` only makes sense in the context of a function, and **can never be used outside of a function**. `return` is always the last line of the function because Python stops executing the body of a function once it hits a `return` statement.
*Note:* `return` inside a function tells Python what value the function evaluates to. However, there are other functions, like `print`, that have no `return` value. For example, `print` simply prints a certain value out to the console.
`return` and `print` are **very** different.
**Question 1.1.** Define `to_percentage` in the cell below. Call your function to convert the proportion .2 to a percentage. Name that percentage `twenty_percent`.
<!--
BEGIN QUESTION
name: q11
-->
```
...
"""" Converts a proportion to a percentage"""
factor = ...
...
twenty_percent = ...
twenty_percent
grader.check("q11")
```
Like you’ve done with built-in functions in previous labs (max, abs, etc.), you can pass in named values as arguments to your function.
**Question 1.2.** Use `to_percentage` again to convert the proportion named `a_proportion` (defined below) to a percentage called `a_percentage`.
*Note:* You don't need to define `to_percentage` again! Like other named values, functions stick around after you define them.
<!--
BEGIN QUESTION
name: q12
-->
```
a_proportion = 2**(.5) / 2
a_percentage = ...
a_percentage
grader.check("q12")
```
Here's something important about functions: the names assigned *within* a function body are only accessible within the function body. Once the function has returned, those names are gone. So even if you created a variable called `factor` and defined `factor = 100` inside of the body of the `to_percentage` function and then called `to_percentage`, `factor` would not have a value assigned to it outside of the body of `to_percentage`:
```
# You should see an error when you run this. (If you don't, you might
# have defined factor somewhere above.)
factor
```
As we've seen with built-in functions, functions can also take strings (or arrays, or tables) as arguments, and they can return those things, too.
**Question 1.3.** Define a function called `disemvowel`. It should take a single string as its argument. (You can call that argument whatever you want.) It should return a copy of that string, but with all the characters that are vowels removed. (In English, the vowels are the characters "a", "e", "i", "o", and "u".) You can use as many lines inside of the function to do this as you’d like.
*Hint:* To remove all the "a"s from a string, you can use `that_string.replace("a", "")`. The `.replace` method for strings returns a new string, so you can call `replace` multiple times, one after the other.
<!--
BEGIN QUESTION
name: q13
-->
```
def disemvowel(a_string):
"""Removes all vowels from a string."""
...
# An example call to your function. (It's often helpful to run
# an example call from time to time while you're writing a function,
# to see how it currently works.)
disemvowel("Can you read this without vowels?")
grader.check("q13")
```
##### Calls on calls on calls
Just as you write a series of lines to build up a complex computation, it's useful to define a series of small functions that build on each other. Since you can write any code inside a function's body, you can call other functions you've written.
If a function is a like a recipe, defining a function in terms of other functions is like having a recipe for cake telling you to follow another recipe to make the frosting, and another to make the jam filling. This makes the cake recipe shorter and clearer, and it avoids having a bunch of duplicated frosting recipes. It's a foundation of productive programming.
For example, suppose you want to count the number of characters *that aren't vowels* in a piece of text. One way to do that is this to remove all the vowels and count the size of the remaining string.
**Question 1.4.** Write a function called `num_non_vowels`. It should take a string as its argument and return a number. That number should be the number of characters in the argument string that aren't vowels. You should use the `disemvowel` function you wrote above inside of the `num_non_vowels` function.
*Hint:* The function `len` takes a string as its argument and returns the number of characters in it.
<!--
BEGIN QUESTION
name: q14
-->
```
def num_non_vowels(a_string):
"""The number of characters in a string, minus the vowels."""
...
# Try calling your function yourself to make sure the output is what
# you expect. You can also use the interact function in the next cell if you'd like.
grader.check("q14")
```
Functions can also encapsulate code that *displays output* instead of computing a value. For example, if you call `print` inside a function, and then call that function, something will get printed.
The `movies_by_year` dataset in the textbook has information about movie sales in recent years. Suppose you'd like to display the year with the 5th-highest total gross movie sales, printed in a human-readable way. You might do this:
```
movies_by_year = Table.read_table("movies_by_year.csv")
rank = 5
fifth_from_top_movie_year = movies_by_year.sort("Total Gross", descending=True).column("Year").item(rank-1)
print("Year number", rank, "for total gross movie sales was:", fifth_from_top_movie_year)
```
After writing this, you realize you also wanted to print out the 2nd and 3rd-highest years. Instead of copying your code, you decide to put it in a function. Since the rank varies, you make that an argument to your function.
**Question 1.5.** Write a function called `print_kth_top_movie_year`. It should take a single argument, the rank of the year (like 2, 3, or 5 in the above examples). It should print out a message like the one above.
*Note:* Your function shouldn't have a `return` statement.
<!--
BEGIN QUESTION
name: q15
-->
```
...
print(...)
...
# Example calls to your function:
print_kth_top_movie_year(2)
print_kth_top_movie_year(3)
grader.check("q15")
# interact also allows you to pass in an array for a function argument. It will
# then present a dropdown menu of options.
_ = interact(print_kth_top_movie_year, k=np.arange(1, 10))
```
### `print` is not the same as `return`
The `print_kth_top_movie_year(k)` function prints the total gross movie sales for the year that was provided! However, since we did not return any value in this function, we can not use it after we call it. Let's look at an example of another function that prints a value but does not return it.
```
def print_number_five():
print(5)
print_number_five()
```
However, if we try to use the output of `print_number_five()`, we see that the value `5` is printed but we get a TypeError when we try to add the number 2 to it!
```
print_number_five_output = print_number_five()
print_number_five_output + 2
```
It may seem that `print_number_five()` is returning a value, 5. In reality, it just displays the number 5 to you without giving you the actual value! If your function prints out a value without returning it and you try to use that value, you will run into errors, so be careful!
Explain to your neighbor how you might add a line of code to the `print_number_five` function (after `print(5)`) so that the code `print_number_five_output + 5` would result in the value `10`, rather than an error.
## 2. Functions and CEO Incomes
In this question, we'll look at the 2015 compensation of CEOs at the 100 largest companies in California. The data was compiled from a [Los Angeles Times analysis](http://spreadsheets.latimes.com/california-ceo-compensation/), and ultimately came from [filings](https://www.sec.gov/answers/proxyhtf.htm) mandated by the SEC from all publicly-traded companies. Two companies have two CEOs, so there are 102 CEOs in the dataset.
We've copied the raw data from the LA Times page into a file called `raw_compensation.csv`. (The page notes that all dollar amounts are in **millions of dollars**.)
```
raw_compensation = Table.read_table('raw_compensation.csv')
raw_compensation
```
We want to compute the average of the CEOs' pay. Try running the cell below.
```
np.average(raw_compensation.column("Total Pay"))
```
You should see a TypeError. Let's examine why this error occurred by looking at the values in the `Total Pay` column.
**Question 2.1.** Use the `type` function and set `total_pay_type` to the type of the first value in the "Total Pay" column.
<!--
BEGIN QUESTION
name: q21
-->
```
total_pay_type = ...
total_pay_type
grader.check("q21")
```
**Question 2.2.** You should have found that the values in the `Total Pay` column are strings. It doesn't make sense to take the average of string values, so we need to convert them to numbers if we want to do this. Extract the first value in `Total Pay`. It's Mark Hurd's pay in 2015, in *millions* of dollars. Call it `mark_hurd_pay_string`.
<!--
BEGIN QUESTION
name: q22
-->
```
mark_hurd_pay_string = ...
mark_hurd_pay_string
grader.check("q22")
```
**Question 2.3.** Convert `mark_hurd_pay_string` to a number of *dollars*.
Some hints, as this question requires multiple steps:
- The string method `strip` will be useful for removing the dollar sign; it removes a specified character from the start or end of a string. For example, the value of `"100%".strip("%")` is the string `"100"`.
- You'll also need the function `float`, which converts a string that looks like a number to an actual number.
- Finally, remember that the answer should be in dollars, not millions of dollars.
<!--
BEGIN QUESTION
name: q23
-->
```
mark_hurd_pay = ...
mark_hurd_pay
grader.check("q23")
```
To compute the average pay, we need to do this for every CEO. But that looks like it would involve copying this code 102 times.
This is where functions come in. First, we'll define a new function, giving a name to the expression that converts "total pay" strings to numeric values. Later in this lab, we'll see the payoff: we can call that function on every pay string in the dataset at once.
The next section of this lab explains how to define a function For now, just fill in the ellipses in the cell below.
**Question 2.4.** Copy the expression you used to compute `mark_hurd_pay`, and use it as the return expression of the function below. But make sure you replace the specific `mark_hurd_pay_string` with the generic `pay_string` name specified in the first line in the `def` statement.
*Hint*: When dealing with functions, you should generally not be referencing any variable outside of the function. Usually, you want to be working with the arguments that are passed into it, such as `pay_string` for this function. If you're using `mark_hurd_pay_string` within your function, you're referencing an outside variable!
<!--
BEGIN QUESTION
name: q24
-->
```
def convert_pay_string_to_number(pay_string):
"""Converts a pay string like '$100' (in millions) to a number of
dollars."""
...
grader.check("q24")
```
Running that cell doesn't convert any particular pay string. Instead, it creates a function called `convert_pay_string_to_number` that can convert *any* string with the right format to a number representing millions of dollars.
We can call our function just like we call the built-in functions we've seen. It takes one argument -- a string -- and it returns a float.
```
convert_pay_string_to_number('$42')
convert_pay_string_to_number(mark_hurd_pay_string)
# We can also compute Safra Catz's pay in the same way:
convert_pay_string_to_number(raw_compensation.where("Name", are.containing("Safra")).column("Total Pay").item(0))
```
So, what have we gained by defining the `convert_pay_string_to_number` function?
Well, without it, we'd have to copy the code `10**6 * float(some_pay_string.strip("$"))` each time we wanted to convert a pay string. Now we just call a function whose name says exactly what it's doing.
## 3. `apply`ing functions
Defining a function is a lot like giving a name to a value with `=`. In fact, a function is a value just like the number 1 or the text "data"!
For example, we can make a new name for the built-in function `max` if we want:
```
our_name_for_max = max
our_name_for_max(2, 6)
```
The old name for `max` is still around:
```
max(2, 6)
```
Try just writing `max` or `our_name_for_max` (or the name of any other function) in a cell, and run that cell. Python will print out a (very brief) description of the function.
```
max
```
Now try writing `?max` or `?our_name_for_max` (or the name of any other function) in a cell, and run that cell. A information box should show up at the bottom of your screen a longer description of the function
*Note: You can also press Shift+Tab after clicking on a name to see similar information!*
```
?our_name_for_max
```
Let's look at what happens when we set `max`to a non-function value. You'll notice that a TypeError will occur when you try calling `max`. Things like integers and strings are not callable. Look out for any functions that might have been renamed when you encounter this type of error
```
max = 6
max(2, 6)
# This cell resets max to the built-in function. Just run this cell, don't change its contents
import builtins
max = builtins.max
```
Why is this useful? Since functions are just values, it's possible to pass them as arguments to other functions. Here's a simple but not-so-practical example: we can make an array of functions.
```
make_array(max, np.average, are.equal_to)
```
**Question 3.1.** Make an array containing any 3 other functions you've seen. Call it `some_functions`.
<!--
BEGIN QUESTION
name: q31
-->
```
some_functions = ...
some_functions
grader.check("q31")
```
Working with functions as values can lead to some funny-looking code. For example, see if you can figure out why the following code works. Check your explanation with a neighbor or a staff member.
```
make_array(max, np.average, are.equal_to).item(0)(4, -2, 7)
```
A more useful example of passing functions to other functions as arguments is the table method `apply`.
`apply` calls a function many times, once on *each* element in a column of a table. It produces an *array* of the results. Here we use `apply` to convert every CEO's pay to a number, using the function you defined:
```
raw_compensation.apply(convert_pay_string_to_number, "Total Pay")
```
Here's an illustration of what that did:
<img src="apply.png"/>
Note that we didn’t write `raw_compensation.apply(convert_pay_string_to_number(), “Total Pay”)` or `raw_compensation.apply(convert_pay_string_to_number(“Total Pay”))`. We just passed the name of the function, with no parentheses, to `apply`, because all we want to do is let `apply` know the name of the function we’d like to use and the name of the column we’d like to use it on. `apply` will then call the function `convert_pay_string_to_number` on each value in the column for us!
**Question 3.2.** Using `apply`, make a table that's a copy of `raw_compensation` with one additional column called `Total Pay ($)`. That column should contain the result of applying `convert_pay_string_to_number` to the `Total Pay` column (as we did above). Call the new table `compensation`.
<!--
BEGIN QUESTION
name: q32
-->
```
compensation = raw_compensation.with_column(
"Total Pay ($)",
...
)
compensation
grader.check("q32")
```
Now that we have all the pays as numbers, we can learn more about them through computation.
**Question 3.3.** Compute the average total pay of the CEOs in the dataset.
<!--
BEGIN QUESTION
name: q33
-->
```
average_total_pay = ...
average_total_pay
grader.check("q33")
```
**Question 3.4.** Companies pay executives in a variety of ways: in cash, by granting stock or other equity in the company, or with ancillary benefits (like private jets). Compute the proportion of each CEO's pay that was cash. (Your answer should be an array of numbers, one for each CEO in the dataset.)
*Note:* When you answer this question, you'll encounter a red box appearing below your code cell that says something like `RuntimeWarning: invalid value encountered in true_divide`. Don't worry too much about the message. Warnings are raised by Python when it encounters an unusual condition in your code, but the condition is not severe enough to warrant throwing an error.
The warning below is Python's cryptic way of telling you that you're dividing a number by zero. If you extract the values in `Total Pay ($)` as an array, you'll see that the last element is 0.
<!--
BEGIN QUESTION
name: q34
-->
```
cash_proportion = ...
cash_proportion
grader.check("q34")
```
Check out the `% Change` column in `compensation`. It shows the percentage increase in the CEO's pay from the previous year. For CEOs with no previous year on record, it instead says "(No previous year)". The values in this column are *strings*, not numbers, so like the `Total Pay` column, it's not usable without a bit of extra work.
Given your current pay and the percentage increase from the previous year, you can compute your previous year's pay. For example, if your pay is $\$120$ this year, and that's an increase of 50% from the previous year, then your previous year's pay was $\frac{\$120}{1 + \frac{50}{100}}$, or \$80.
**Question 3.5.** Create a new table called `with_previous_compensation`. It should be a copy of `compensation`, but with the "(No previous year)" CEOs filtered out, and with an extra column called `2014 Total Pay ($)`. That column should have each CEO's pay in 2014.
*Hint 1:* You can print out your results after each step to make sure you're on the right track.
*Hint 2:* We've provided a structure that you can use to get to the answer. However, if it's confusing, feel free to delete the current structure and approach the problem your own way!
<!--
BEGIN QUESTION
name: q35
-->
```
# Definition to turn percent to number
def percent_string_to_num(percent_string):
"""Converts a percentage string to a number."""
return ...
# Compensation table where there is a previous year
having_previous_year = ...
# Get the percent changes as numbers instead of strings
# We're still working off the table having_previous_year
percent_changes = ...
# Calculate the previous year's pay
# We're still working off the table having_previous_year
previous_pay = ...
# Put the previous pay column into the having_previous_year table
with_previous_compensation = ...
with_previous_compensation
grader.check("q35")
```
**Question 3.6.** What was the average pay of these CEOs in 2014?
<!--
BEGIN QUESTION
name: q36
-->
```
average_pay_2014 = np.average(with_previous_compensation.column("2014 Total Pay ($)"))
average_pay_2014
grader.check("q36")
```
**Why is `apply` useful?**
For operations like arithmetic, or the functions in the NumPy library, you don't need to use `apply`, because they automatically work on each element of an array. But there are many things that don't. The string manipulation we did in today's lab is one example. Since you can write any code you want in a function, `apply` gives you total control over how you operate on data.
## 4. Histograms
Earlier, we computed the average pay among the CEOs in our 102-CEO dataset. The average doesn't tell us everything about the amounts CEOs are paid, though. Maybe just a few CEOs make the bulk of the money, even among these 102.
We can use a *histogram* method to display the *distribution* of a set of numbers. The table method `hist` takes a single argument, the name of a column of numbers. It produces a histogram of the numbers in that column.
**Question 4.1.** Make a histogram of the total pay of the CEOs in `compensation`. Check with your neighbor or a staff member to make sure you have the right plot.
<!--
BEGIN QUESTION
name: q41
-->
```
...
```
**Question 4.2.** How many CEOs made more than $30 million in total pay? Find the value using code, then check that the value you found is consistent with what you see in the histogram.
*Hint:* Use the table method `where` and the property `num_rows`.
<!--
BEGIN QUESTION
name: q42
-->
```
num_ceos_more_than_30_million_2 = compensation.where("Total Pay ($)", are.above(30000000)).num_rows
num_ceos_more_than_30_million_2
grader.check("q42")
```
## 5. Project 1 Partner Form
Project 1 will be released this Friday! You have the option of working with a partner that is enrolled in your lab. Your GSI will be sending out a form to match you up with a partner for this project. You may also indicate if you're working alone or have already found a partner and do not need to be paired up. This form is **mandatory** - please fill it out before submitting your lab. Set `submitted` to `True` once you've submitted the form.
Note: If you are completing this lab before the early submission deadline, the form may not have been sent out yet. Set `submitted` to `True` for now, and keep an eye out for an email from your GSI later this week.
<!--
BEGIN QUESTION
name: q5
-->
```
submitted = ...
grader.check("q5")
```
Great job! You're finished with lab 4! Be sure to...
* **run all the tests** (the next cell has a shortcut for that),
* **Save and Checkpoint** from the File menu,
* **run the last cell to submit your work**,
* and **ask one of the staff members to check you off**.
---
To double-check your work, the cell below will rerun all of the autograder tests.
```
grader.check_all()
```
## Submission
Make sure you have run all cells in your notebook in order before running the cell below, so that all images/graphs appear in the output. The cell below will generate a zip file for you to submit. **Please save before exporting!**
```
# Save your notebook first, then run this cell to export your submission.
grader.export()
```
|
github_jupyter
|
```
import sys
from PyQt5 import QtCore, QtWidgets, QtWebEngineWidgets
from lxml import html as htmlRenderer
import requests
import json
from datetime import date, datetime, timedelta
def render(source_url):
"""Fully render HTML, JavaScript and all."""
import sys
from PyQt5.QtWidgets import QApplication
from PyQt5.QtCore import QUrl
from PyQt5.QtWebEngineWidgets import QWebEngineView
class Render(QWebEngineView):
def __init__(self, url):
self.html = None
self.app = QApplication(sys.argv)
QWebEngineView.__init__(self)
self.loadFinished.connect(self._loadFinished)
#self.setHtml(html)
self.load(QUrl(url))
self.app.exec_()
def _loadFinished(self, result):
# This is an async call, you need to wait for this
# to be called before closing the app
self.page().toHtml(self._callable)
def _callable(self, data):
self.html = data
# Data has been stored, it's safe to quit the app
self.app.quit()
return Render(source_url).html
```
# Aux Functions
```
def generateDates(start=date(2019, 1, 1), end=date(2019, 8, 31), delta=timedelta(days=1), strFormat=""):
curr = start
dates = []
while curr < end:
if strFormat == "":
dates.append(str(curr))
else:
dates.append(curr.strftime(strFormat))
curr += delta
return dates
len(generateDates(date(2019, 1, 1), date(2019, 8, 31)))
a = generateDates(date(2019, 1, 1), date(2019, 8, 31))
date_1 =a[0]
date_1.strftime("%Y/%m/%d")
date_1.day.to_bytes()
date_1.day
str(date_1).replace('-', '/')
dateFormat = "%Y/%m/%d"
datesBase = generateDates(date(2019, 1, 1), date(2019, 8, 31), strFormat=dateFormat)
extraDateInfo = ["m", "t", "n"]
urlTemplate = "https://elpais.com/hemeroteca/elpais/{date}/{partOfDay}/portada.html"
def generateHemerotecaUrls(urlBase, dates, extraInfo):
urlsPerDay = []
print(" \t Url-Base: {}".format(urlBase))
for d in dates:
partOfDayUrls = [ urlBase.format(date=d, partOfDay=p) for p in extraInfo ]
urlsPerDay = urlsPerDay + partOfDayUrls
print(" \t -> urlsPerDay length: {}".format(len(urlsPerDay)))
return urlsPerDay
urlTemplate
generateHemerotecaUrls(urlTemplate, datesBase, extraDateInfo)
```
# Getting urls
```
url="https://www.elpais.com/"
renderUrl = render(url)
renderedPage = htmlRenderer.fromstring(renderUrl)
auxLinks = renderedPage.xpath("//a/@href")
# obtener links, cuidado que alguno ya empieza por http...
auxFinalLinks = list(dict.fromkeys([link for link in auxLinks
if not link.endswith("/")
and not "#comentarios" in link
and not link.endswith("=home")]))
auxFinalLinks
len(auxFinalLinks)
finalLinks = []
for l in auxFinalLinks:
if l.startswith("http"):
finalLinks.append(l)
elif l.startswith("//"):
finalLinks.append("https:{}".format(l))
else:
finalLinks.append("https://www.elpais.com{}".format(l))
print(" -> TOtal of url retrieved to extract comments: {}".format(len(finalLinks)))
finalLinks
# Url get info = https://elpais.com/ThreadeskupSimple?action=info&th=1564664936-bca025601586bc5a00ef0c26fdd878f6&rnd=1232123123
# # Url get comments =
# https://elpais.com/OuteskupSimple?s=&rnd=0.7131093272405999&th=2&msg=1564664936-bca025601586bc5a00ef0c26fdd878f6&p=1&nummsg=40&tt=1
# https://elpais.com/OuteskupSimple?s=&rnd=0.4308991070814918&th=2&msg=1564664936-bca025601586bc5a00ef0c26fdd878f6&p=2&nummsg=40&tt=1
# https://elpais.com/OuteskupSimple?s=&rnd=0.17594169864899367&th=2&msg=1564664936-bca025601586bc5a00ef0c26fdd878f6&p=3&nummsg=40&tt=1
```
|
github_jupyter
|
```
import math
import json
import pandas as pd
import numpy as np
from Bio import SeqIO
from Bio.Seq import Seq
from Bio.SeqRecord import SeqRecord
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
#make test data set to sanity check
outgroup_test = ['ATGGAGATT']
test_seqs = ['ATGGAGATT', 'ATGGAGAAT', 'ATGGAGATT',
'ATGGAGAAT', 'ATGGAGATC', 'ATCGAGATT',
'ATGGAGACT', 'ATGGAGATT', 'ATGGAGATT',
'ATGGGGATT', 'ATGCAGATT', 'ATGCAGATT', 'ATGGAGATT']
test_dates = [2010, 2010, 2011,
2012, 2012,
2013, 2013, 2013,
2014, 2014, 2014, 2014]
#given a polymorphism frequency, return bin
def frequency_binning(x):
#nan frequencies are when there is no sequence coverage at the given position
if math.isnan(x):
f_bin = float('nan')
else:
if x == 1.0:
f_bin = 'f'
elif x>=0.75:
f_bin = 'h'
elif x<0.75 and x>=0.15:
f_bin = 'm'
elif x<0.15:
f_bin='l'
return f_bin
def walk_through_sites(outgroup_seq, outgroup_aa_seq, input_file_alignment, viruses):
#at each site, count number of viruses with polymorphism
count_polymorphic = np.zeros(len(outgroup_seq))
#at each site, count totaly number of viruses
count_total_unambiguous = np.zeros(len(outgroup_seq))
count_replacement_mutations = np.zeros(len(outgroup_seq))
count_silent_mutations = np.zeros(len(outgroup_seq))
#at each site, list of nucleotide from each virus
ingroup_bases = [[] for x in range(len(outgroup_seq))]
with open(input_file_alignment, "r") as aligned_handle:
for virus in SeqIO.parse(aligned_handle, "fasta"):
#Only viruses in time window
if virus.id in viruses:
#check
if len(virus.seq) != len(outgroup_seq):
print(virus)
elif len(virus.seq) == len(outgroup_seq):
for pos in range(len(outgroup_seq)):
outgroup_nt = str(outgroup_seq[pos])
virus_nt = str(virus.seq[pos])
#skip ambiguous sites
if virus_nt != 'N':
ingroup_bases[pos].append(virus_nt)
count_total_unambiguous[pos]+=1
if virus_nt != outgroup_nt:
count_polymorphic[pos]+=1
#determine silent or replacement
codon = math.floor(pos/3)
codon_pos = pos-(codon*3)
if codon_pos == 0:
codon_nt = virus.seq[pos:(pos+3)]
elif codon_pos == 1:
codon_nt = virus.seq[(pos-1):(pos+2)]
elif codon_pos == 2:
codon_nt = virus.seq[(pos-2):(pos+1)]
codon_aa = codon_nt.translate()
outgroup_aa = outgroup_aa_seq[codon]
if codon_aa != outgroup_aa:
count_replacement_mutations[pos]+=1
elif codon_aa == outgroup_aa:
count_silent_mutations[pos]+=1
polymorphic_frequencies = count_polymorphic/count_total_unambiguous
replacement_score = count_replacement_mutations/count_total_unambiguous
freq_bins = [frequency_binning(x) for x in polymorphic_frequencies]
return freq_bins, replacement_score, ingroup_bases
def determine_site_type(outgroup, ingroup):
ingroup_bases_nan = set(ingroup)
#remove 'nan's
ingroup_bases = {x for x in ingroup_bases_nan if pd.notna(x)}
if len(ingroup_bases) == 0:
site_type = None
elif len(ingroup_bases) != 0:
#all ingroup bases are identical
if len(ingroup_bases) == 1:
if outgroup in ingroup_bases:
site_type = 1
elif outgroup not in ingroup_bases:
site_type = 2
#2 different bases in ingroup
elif len(ingroup_bases) == 2:
if outgroup in ingroup_bases:
site_type = 3
elif outgroup not in ingroup_bases:
site_type = 4
#3 different bases in ingroup
elif len(ingroup_bases) == 3:
if outgroup in ingroup_bases:
site_type = 5
elif outgroup not in ingroup_bases:
site_type = 6
#4 different bases in ingroup
elif len(ingroup_bases) == 4:
site_type = 7
return site_type
def fixation_polymorphism_score(outgroup, ingroup):
site_type = determine_site_type(outgroup, ingroup)
if site_type == None:
Fi = float('nan')
Pi = float('nan')
if site_type == 1:
Fi = 0
Pi = 0
elif site_type == 2:
Fi = 1
Pi = 0
elif site_type in [3,5,7]:
Fi = 0
Pi = 1
elif site_type == 4:
Fi = 0.5
Pi = 0.5
elif site_type == 6:
Fi = (1/3)
Pi = (2/3)
return Fi, Pi
def assign_fi_pi(outgroup_seq, ingroup_bases):
#at each site, record Fi
Fi_all = np.zeros(len(outgroup_seq))
#at each site, record Pi
Pi_all = np.zeros(len(outgroup_seq))
for pos in range(len(outgroup_seq)):
outgroup_nt = outgroup_seq[pos]
ingroup_nts = ingroup_bases[pos]
Fi, Pi = fixation_polymorphism_score(outgroup_nt, ingroup_nts)
Fi_all[pos] = Fi
Pi_all[pos] = Pi
return Fi_all, Pi_all
def calc_site_stats(cov, gene, window):
#Find percent polymorphism at each site
#Also determine whether polymorphism is silent or replacement
input_file_outgroup = '../'+str(cov)+'/auspice/seasonal_corona_'+str(cov)+'_'+str(gene)+'_root-sequence.json'
input_file_alignment = '../'+str(cov)+'/results/aligned_'+str(cov)+'_'+str(gene)+'.fasta'
metafile = '../'+str(cov)+'/results/metadata_'+str(cov)+'_'+str(gene)+'.tsv'
#Subset data based on time windows
meta = pd.read_csv(metafile, sep = '\t')
meta.drop(meta[meta['date']=='?'].index, inplace=True)
meta.dropna(subset=['date'], inplace=True)
meta['year'] = meta['date'].str[:4].astype('int')
date_range = meta['year'].max() - meta['year'].min()
#Group viruses by time windows
virus_time_subset = {}
if window == 'all':
years = str(meta['year'].min()) + '-' + str(meta['year'].max())
virus_time_subset[years] = meta['strain'].tolist()
else:
date_window_start = meta['year'].min()
date_window_end = meta['year'].min() + window
while date_window_end <= meta['year'].max():
years = str(date_window_start) + '-' + str(date_window_end)
strains = meta[(meta['year']>=date_window_start) & (meta['year']<date_window_end)]['strain'].tolist()
virus_time_subset[years] = strains
#sliding window
date_window_end += 1
date_window_start += 1
#Find outgroup sequence
outgroup_seq = ''
outgroup_aa_seq = ''
with open(input_file_outgroup, "r") as outgroup_handle:
outgroup = json.load(outgroup_handle)
outgroup_seq = SeqRecord(Seq(outgroup['nuc']))
outgroup_aa_seq = outgroup_seq.translate()
#initiate lists to record all time windows
year_windows = []
seqs_in_window = []
frequency_bins = []
fixation_scores = []
polymorphism_scores = []
replacement_scores = []
silent_scores = []
#each time window separately
for years, subset_viruses in virus_time_subset.items():
if len(subset_viruses) != 0:
year_windows.append(years)
seqs_in_window.append(len(subset_viruses))
freq_bins, replacement_score, ingroup_bases = walk_through_sites(outgroup_seq, outgroup_aa_seq,
input_file_alignment, subset_viruses)
Fi_all, Pi_all = assign_fi_pi(outgroup_seq, ingroup_bases)
silent_score = 1-replacement_score
frequency_bins.append(freq_bins)
fixation_scores.append(Fi_all)
polymorphism_scores.append(Pi_all)
replacement_scores.append(replacement_score)
silent_scores.append(silent_score)
return year_windows, seqs_in_window, frequency_bins, fixation_scores, polymorphism_scores, replacement_scores, silent_scores
#M=rm/sm
#not expected to vary through time provided that long-term effective population sizes remain sufficiently large
#For each gene, calculate M by combining site count among time points
def calc_m_ratio(cov, gene):
if gene=='spike' or gene=='s1':
(year_windows, seqs_in_window, frequency_bins,
fixation_scores, polymorphism_scores, replacement_scores, silent_scores) = calc_site_stats(cov, 's2', 'all')
else:
(year_windows, seqs_in_window, frequency_bins,
fixation_scores, polymorphism_scores, replacement_scores, silent_scores) = calc_site_stats(cov, gene, 'all')
sm = 0
rm = 0
for site in range(len(frequency_bins[0])):
freq_bin = frequency_bins[0][site]
if freq_bin == 'm':
sm+= (polymorphism_scores[0][site]*silent_scores[0][site])
rm+= (polymorphism_scores[0][site]*replacement_scores[0][site])
m_ratio = rm/sm
return m_ratio
def bhatt_estimators(cov, gene, window):
(year_windows, seqs_in_window, frequency_bins,
fixation_scores, polymorphism_scores,
replacement_scores, silent_scores) = calc_site_stats(cov, gene, window)
m_ratio = calc_m_ratio(cov, gene)
#Initiate lists to store a values
window_midpoint = []
adaptive_substitutions = []
#for each window, calculate bhatt estimators
for years_window in range(len(frequency_bins)):
#don't use windows with fewer than 5 sequences
if seqs_in_window[years_window] >= 5:
window_start = int(year_windows[years_window][0:4])
window_end = int(year_windows[years_window][-4:])
window_midpoint.append((window_start + window_end)/2)
sf = 0
rf = 0
sh = 0
rh = 0
sm = 0
rm = 0
sl = 0
rl = 0
#calculate number of sites in different catagories (defined by polymorphic freq at that site)
window_freq_bins = frequency_bins[years_window]
for site in range(len(window_freq_bins)):
freq_bin = window_freq_bins[site]
#ignore sites with no polymorphisms?
if freq_bin!='nan':
if freq_bin == 'f':
sf+= (fixation_scores[years_window][site]*silent_scores[years_window][site])
rf+= (fixation_scores[years_window][site]*replacement_scores[years_window][site])
elif freq_bin == 'h':
sh+= (polymorphism_scores[years_window][site]*silent_scores[years_window][site])
rh+= (polymorphism_scores[years_window][site]*replacement_scores[years_window][site])
elif freq_bin == 'm':
sm+= (polymorphism_scores[years_window][site]*silent_scores[years_window][site])
rm+= (polymorphism_scores[years_window][site]*replacement_scores[years_window][site])
elif freq_bin == 'l':
sl+= (polymorphism_scores[years_window][site]*silent_scores[years_window][site])
rl+= (polymorphism_scores[years_window][site]*replacement_scores[years_window][site])
# print(year_windows[years_window])
# print(sf, rf, sh, rh, sm, rm, sl, rl)
#Calculate equation 1: number of nonneutral sites
al = rl - sl*m_ratio
ah = rh - sh*m_ratio
af = rf - sf*m_ratio
#set negative a values to zero
if al < 0:
al = 0
if ah < 0:
ah = 0
if af < 0:
af = 0
# print(al, ah, af)
#Calculate the number and proportion of all fixed or high-freq sites that have undergone adaptive change
number_adaptive_substitutions = af + ah
adaptive_substitutions.append(number_adaptive_substitutions)
proportion_adaptive_sites = (af + ah)/(rf +rh)
# get coeffs of linear fit
slope, intercept, r_value, p_value, std_err = stats.linregress(window_midpoint, adaptive_substitutions)
ax = sns.regplot(x= window_midpoint, y=adaptive_substitutions,
line_kws={'label':"y={0:.1f}x+{1:.1f}".format(slope,intercept)})
plt.ylabel('number of adaptive substitutions')
plt.xlabel('year')
ax.legend()
plt.show()
```
|
github_jupyter
|
```
%matplotlib inline
```
# Wasserstein 1D with PyTorch
In this small example, we consider the following minization problem:
\begin{align}\mu^* = \min_\mu W(\mu,\nu)\end{align}
where $\nu$ is a reference 1D measure. The problem is handled
by a projected gradient descent method, where the gradient is computed
by pyTorch automatic differentiation. The projection on the simplex
ensures that the iterate will remain on the probability simplex.
This example illustrates both `wasserstein_1d` function and backend use within
the POT framework.
```
# Author: Nicolas Courty <ncourty@irisa.fr>
# Rémi Flamary <remi.flamary@polytechnique.edu>
#
# License: MIT License
import numpy as np
import matplotlib.pylab as pl
import matplotlib as mpl
import torch
from ot.lp import wasserstein_1d
from ot.datasets import make_1D_gauss as gauss
from ot.utils import proj_simplex
red = np.array(mpl.colors.to_rgb('red'))
blue = np.array(mpl.colors.to_rgb('blue'))
n = 100 # nb bins
# bin positions
x = np.arange(n, dtype=np.float64)
# Gaussian distributions
a = gauss(n, m=20, s=5) # m= mean, s= std
b = gauss(n, m=60, s=10)
# enforce sum to one on the support
a = a / a.sum()
b = b / b.sum()
device = "cuda" if torch.cuda.is_available() else "cpu"
# use pyTorch for our data
x_torch = torch.tensor(x).to(device=device)
a_torch = torch.tensor(a).to(device=device).requires_grad_(True)
b_torch = torch.tensor(b).to(device=device)
lr = 1e-6
nb_iter_max = 800
loss_iter = []
pl.figure(1, figsize=(8, 4))
pl.plot(x, a, 'b', label='Source distribution')
pl.plot(x, b, 'r', label='Target distribution')
for i in range(nb_iter_max):
# Compute the Wasserstein 1D with torch backend
loss = wasserstein_1d(x_torch, x_torch, a_torch, b_torch, p=2)
# record the corresponding loss value
loss_iter.append(loss.clone().detach().cpu().numpy())
loss.backward()
# performs a step of projected gradient descent
with torch.no_grad():
grad = a_torch.grad
a_torch -= a_torch.grad * lr # step
a_torch.grad.zero_()
a_torch.data = proj_simplex(a_torch) # projection onto the simplex
# plot one curve every 10 iterations
if i % 10 == 0:
mix = float(i) / nb_iter_max
pl.plot(x, a_torch.clone().detach().cpu().numpy(), c=(1 - mix) * blue + mix * red)
pl.legend()
pl.title('Distribution along the iterations of the projected gradient descent')
pl.show()
pl.figure(2)
pl.plot(range(nb_iter_max), loss_iter, lw=3)
pl.title('Evolution of the loss along iterations', fontsize=16)
pl.show()
```
## Wasserstein barycenter
In this example, we consider the following Wasserstein barycenter problem
$$ \\eta^* = \\min_\\eta\;\;\; (1-t)W(\\mu,\\eta) + tW(\\eta,\\nu)$$
where $\\mu$ and $\\nu$ are reference 1D measures, and $t$
is a parameter $\in [0,1]$. The problem is handled by a project gradient
descent method, where the gradient is computed by pyTorch automatic differentiation.
The projection on the simplex ensures that the iterate will remain on the
probability simplex.
This example illustrates both `wasserstein_1d` function and backend use within the
POT framework.
```
device = "cuda" if torch.cuda.is_available() else "cpu"
# use pyTorch for our data
x_torch = torch.tensor(x).to(device=device)
a_torch = torch.tensor(a).to(device=device)
b_torch = torch.tensor(b).to(device=device)
bary_torch = torch.tensor((a + b).copy() / 2).to(device=device).requires_grad_(True)
lr = 1e-6
nb_iter_max = 2000
loss_iter = []
# instant of the interpolation
t = 0.5
for i in range(nb_iter_max):
# Compute the Wasserstein 1D with torch backend
loss = (1 - t) * wasserstein_1d(x_torch, x_torch, a_torch.detach(), bary_torch, p=2) + t * wasserstein_1d(x_torch, x_torch, b_torch, bary_torch, p=2)
# record the corresponding loss value
loss_iter.append(loss.clone().detach().cpu().numpy())
loss.backward()
# performs a step of projected gradient descent
with torch.no_grad():
grad = bary_torch.grad
bary_torch -= bary_torch.grad * lr # step
bary_torch.grad.zero_()
bary_torch.data = proj_simplex(bary_torch) # projection onto the simplex
pl.figure(3, figsize=(8, 4))
pl.plot(x, a, 'b', label='Source distribution')
pl.plot(x, b, 'r', label='Target distribution')
pl.plot(x, bary_torch.clone().detach().cpu().numpy(), c='green', label='W barycenter')
pl.legend()
pl.title('Wasserstein barycenter computed by gradient descent')
pl.show()
pl.figure(4)
pl.plot(range(nb_iter_max), loss_iter, lw=3)
pl.title('Evolution of the loss along iterations', fontsize=16)
pl.show()
```
|
github_jupyter
|
```
from github import Github
import tqdm
# First create a Github instance:
g = Github("5c103d46120d27b0fac5d9d1b9df0b91c77c5d42")
org = g.get_organization("applied-ml-spring-18")
repos = org.get_repos()
repos_list = list(repos)
hw4 = [repo for repo in repos_list if "homework-4" in repo.full_name]
import os
os.chdir("/home/andy/Dropbox/columbia_safe/applied_machine_learning_spring_2018/submissions/")
import shutil
from os import listdir
for repo in tqdm.tqdm(hw4):
#print(repo.ssh_url)
if not os.path.exists(repo.name):
os.system("git clone {}".format(repo.ssh_url))
```
## Remove empty folders
```
import shutil
from os import listdir
for repo in hw4:
try:
l = listdir(repo.name)
except FileNotFoundError:
pass
if len(l) < 2:
# has .git folder
shutil.rmtree(repo.name)
```
### Convert notebooks to python files
```
from glob import glob
notebooks = glob("*/*.ipynb")
import nbconvert
import shlex
for notebook in tqdm.tqdm(notebooks):
#print(notebook)
# fixme: whitespace in names?
if not os.path.exists(notebook.replace("ipynb", "py")):
os.system("jupyter-nbconvert {} --to script".format(shlex.quote(notebook)))
import mosspy
userid = 321
m = mosspy.Moss(userid, "python")
m.setDirectoryMode(1)
# Submission Files
m.addFilesByWildcard("*/*.py")
url = m.send() # Submission Report URL
print ("Report Url: " + url)
```
http://moss.stanford.edu/results/374137986
```
# Save report file
m.saveWebPage(url, "report2.html")
# Download whole report locally including code diff links
mosspy.download_report(url, "submission2/", connections=8, log_level=20)
import logging
logging.DEBUG
logging.WARNING
# TODO: use absolute paths everywhere...
def clone_repos(pattern="homework-1", store_at="/tmp/homework"):
if not os.path.exists(store_at):
os.mkdir(store_at)
os.chdir(store_at)
g = Github("5c103d46120d27b0fac5d9d1b9df0b91c77c5d42")
org = g.get_organization("applied-ml-spring-18")
repos = org.get_repos()
these = [repo for repo in repos_list if pattern in repo.full_name]
for repo in tqdm.tqdm(these):
#print(repo.ssh_url)
if not os.path.exists(repo.name):
os.system("git clone {}".format(repo.ssh_url))
for repo in hw4:
try:
l = listdir(repo.name)
except FileNotFoundError:
#print(repo.name)
continue
if len(l) < 2:
# has .git folder
shutil.rmtree(repo.name)
return repos
def convert_notebooks():
notebooks = glob("*/*.ipynb")
for notebook in tqdm.tqdm(notebooks):
#print(notebook)
if not os.path.exists(notebook.replace("ipynb", "py")):
os.system("jupyter-nbconvert {} --to script".format(shlex.quote(notebook)))
def submit_moss():
import mosspy
userid = 321
m = mosspy.Moss(userid, "python")
m.setDirectoryMode(1)
m.addFilesByWildcard("*/*.py")
m.addFilesByWildcard("*/*/*.py")
url = m.send() # Submission Report URL
print ("Report Url: " + url)
return m, url
clone_repos(pattern="homework-3", store_at="/home/andy/Dropbox/columbia_safe/applied_machine_learning_spring_2018/submissions_hw3/")
convert_notebooks()
m = submit_moss()
mosspy.download_report(url, "hw3_report/", connections=8, log_level=20)
clone_repos(pattern="homework-2", store_at="/home/andy/Dropbox/columbia_safe/applied_machine_learning_spring_2018/submissions_hw2/")
convert_notebooks()
m, url = submit_moss()
#mosspy.download_report(url, "hw2_report/", connections=8, log_level=20)
#mosspy.download_report("http://moss.stanford.edu/results/136599236", "hw2_report/", connections=8, log_level=20)
clone_repos(pattern="homework-1", store_at="/home/andy/Dropbox/columbia_safe/applied_machine_learning_spring_2018/submissions_hw1/")
convert_notebooks()
m, url = submit_moss()
mosspy.download_report(url, "hw1_report/", connections=8, log_level=20)
```
|
github_jupyter
|
```
%run ../common-imports.ipynb
```
# Tidy Data with Pandas
```
# Reading the csv files into a pandas data frame
temperature = pd.read_csv("../../datasets/temperature.csv")
humidity = pd.read_csv("../../datasets/humidity.csv")
wind_speed = pd.read_csv("../../datasets/wind_speed.csv")
temperature.head()
# Importing the libraries
import pandas as pd
import numpy as np# Displaying the first 5 rows of the data frame
temperature.describe(include='all').transpose()
```
# Data Manipulation
Let us unpivot, or melt: convert from wide format to long format, as tidy-data thinking recommends.
Tidy data essentially says:
- Each row should be an observation
- Each column should be a variable. Roughly, each column that is not an identifier or dimension should be a measure.
- A dataframe should represent a logical unit of observables
```
tidy_temperature = pd.melt(temperature,
id_vars="datetime",
var_name="city", value_name="temperature")
tidy_temperature.describe(include='all')
tidy_temperature.head()
tidy_temperature.sample(20)
tidy_humidity = pd.melt(humidity,
id_vars="datetime",
var_name="city", value_name="humidity")
tidy_windspeed = pd.melt(wind_speed,
id_vars="datetime",
var_name="city", value_name="wind_speed")
raw_weather = tidy_temperature\
.join(tidy_humidity.set_index(['datetime', 'city']), on=['datetime', 'city'])\
.join(tidy_windspeed.set_index(['datetime', 'city']), on=['datetime', 'city'])
raw_weather.sample(20)
```
# Let's cleanup the data
There are many strategies to deal with NaN data. Here, since it is weather, perhaps a reasonable way would be interpolating the temperature, humidity and wind_speed. In other words, the tempeture today is reasonable between that of yesterday and tomorrow, as a good approximation.
```
raw_weather.describe()
# The amount of missing values
raw_weather.isna().sum()
weather = raw_weather.interpolate()
weather.isna().sum()
```
This is because we could not interpolate into the first row! Therefore, let us omit it.
```
weather = weather.dropna()
weather.isna().sum()
# Filter down to only San Francisco weather
sf_weather = weather[weather['city'] == 'San Francisco']
sf_weather.sample(10)
# Project down to only temperature and humidity
data = weather[['datetime', 'city','temperature', 'humidity']]
data.sample(10)
# The average weather for each city
means = weather.groupby('city')['temperature', 'humidity', 'wind_speed'].mean()
means.columns = ['mean_temperature', 'mean_humidity', 'mean_speed']
means.sample(10)
```
Note the two-levels of the columns above. Let us now flatten the data:
```
means = means.reset_index()
means.head()
```
Now, let's join it back with the original data
```
means.sample(10)
df = means.set_index('city')
```
Therefore, now we can remove the unnecessary column city.
```
means_data = means.drop(['city'], axis=1)
means_data.sample(10)
cor = means_data.corr()
cor
data = weather.merge(means, left_on='city', right_on='city')
data.sample(10)
```
|
github_jupyter
|
```
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
import numpy as np; np.random.seed(0)
import seaborn as sns
data = pd.read_csv("avocado.csv")
pd.set_option('display.max_rows', 100)
print(data)
data.head()
data.tail()
#BoxPlot_Avocado
columna_1 = data["Small Bags"]
columna_2 = data["Large Bags"]
columna_3 = data["XLarge Bags"]
columna_4 = data["Total Bags"]
myData = [columna_1,columna_2,columna_3,columna_4]
fig = plt.figure(figsize =(10, 7))
ax = fig.add_axes([0, 0, 1, 1])
bp = ax.boxplot(myData)
plt.title("Bags Boxplot")
ax.set_xticklabels(['Small Bags', 'Large Bags',
'XLarge Bags','Total Bags'])
plt.show()
#Histograma Precios Promedio
np.random.seed(10**7)
mu = 121
sigma = 21
x = mu + sigma * np.random.randn(1000)
num_bins = 100
n, bins, patches = plt.hist(data["AveragePrice"], num_bins,
density = 1,
color ='purple',
alpha = 0.7)
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
plt.plot(bins, y, '--', color ='black')
plt.xlabel('X-Axis')
plt.ylabel('Y-Axis')
plt.title('Precio Promedio',
fontweight ="bold")
plt.show()
#Histograma de Volumen total
np.random.seed(10**7)
mu = 121
sigma = 21
x = mu + sigma * np.random.randn(1000)
num_bins = 100
n, bins, patches = plt.hist(data["Total Volume"], num_bins,
density = 1,
color ='red',
alpha = 0.7)
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
plt.plot(bins, y, '--', color ='orange')
plt.xlabel('X-Axis')
plt.ylabel('Y-Axis')
plt.title('Volumen Total',
fontweight ="bold")
#Histograma de Large Bags
np.random.seed(10**7)
mu = 121
sigma = 21
x = mu + sigma * np.random.randn(1000)
num_bins = 100
n, bins, patches = plt.hist(data["Large Bags"], num_bins,
density = 3,
color ='red',
alpha = 0.7)
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
plt.plot(bins, y, '--', color ='red')
plt.xlabel('X-Axis')
plt.ylabel('Y-Axis')
plt.title('Bolsas Grandes',
fontweight ="bold")
#Histograma de Small Bags
np.random.seed(10**7)
mu = 121
sigma = 21
x = mu + sigma * np.random.randn(1000)
num_bins = 100
n, bins, patches = plt.hist(data["Small Bags"], num_bins,
density = 3,
color ='blue',
alpha = 0.7)
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
plt.plot(bins, y, '--', color ='orange')
plt.xlabel('X-Axis')
plt.ylabel('Y-Axis')
plt.title('Bolsas Pequeñas',
fontweight ="bold")
#Histograma Bolsas Extra Grandes
np.random.seed(10**7)
mu = 121
sigma = 21
x = mu + sigma * np.random.randn(1000)
num_bins = 100
n, bins, patches = plt.hist(data["XLarge Bags"], num_bins,
density = 3,
color ='brown',
alpha = 0.7)
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
plt.plot(bins, y, '--', color ='brown')
plt.xlabel('X-Axis')
plt.ylabel('Y-Axis')
plt.title('Bolsas Extra Grandes',
fontweight ="bold")
np.random.seed(10**7)
mu = 121
sigma = 21
x = mu + sigma * np.random.randn(1000)
num_bins = 100
n, bins, patches = plt.hist(data["Total Bags"], num_bins,
density = 3,
color ='yellow',
alpha = 0.7)
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
plt.plot(bins, y, '--', color ='red')
plt.xlabel('X-Axis')
plt.ylabel('Y-Axis')
plt.title('Bolsas Grandes',
fontweight ="bold")
newdf = data.copy()
newdf = newdf.drop(['Date','type','year','region', 'XLarge Bags'], axis=1)
print(data.head())
data.describe(include=np.object).transpose()
ax = sns.heatmap(data)
```
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.