code
stringlengths 2.5k
150k
| kind
stringclasses 1
value |
|---|---|
<!--NOTEBOOK_HEADER-->
*This notebook contains material from [Controlling Natural Watersheds](https://jckantor.github.io/Controlling-Natural-Watersheds);
content is available [on Github](https://github.com/jckantor/Controlling-Natural-Watersheds.git).*
<!--NAVIGATION-->
< [Control](http://nbviewer.jupyter.org/github/jckantor/Controlling-Natural-Watersheds/blob/master/notebooks/05.00-Control.ipynb) | [Contents](toc.ipynb) | [Implementation of Rainy Lake Rule Curves with Feedback Control](http://nbviewer.jupyter.org/github/jckantor/Controlling-Natural-Watersheds/blob/master/notebooks/05.02-Implementation_of_Rainy_Lake_Rule_Curves_with_Feedback_Control.ipynb) ><p><a href="https://colab.research.google.com/github/jckantor/Controlling-Natural-Watersheds/blob/master/notebooks/05.01-Lumped_Parameter_Model_for_Lake_Dynamics.ipynb"><img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open in Google Colaboratory"></a><p><a href="https://raw.githubusercontent.com/jckantor/Controlling-Natural-Watersheds/master/notebooks/05.01-Lumped_Parameter_Model_for_Lake_Dynamics.ipynb"><img align="left" src="https://img.shields.io/badge/Github-Download-blue.svg" alt="Download" title="Download Notebook"></a>
# Lumped Parameter Model for Lake Dynamics
```
# Display graphics inline with the notebook
%matplotlib inline
# Standard Python modules
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import pandas as pd
import os
import datetime
# Module to enhance matplotlib plotting
import seaborn
seaborn.set()
# Modules to display images and data tables
from IPython.display import Image
from IPython.core.display import display
# Data Directory
dir = './data/'
# Styles
from IPython.core.display import HTML
HTML(open("styles/custom.css", "r").read())
```
## Stage-Volume Relationships
$$ V(h) = a_0 + a_1 h + a_2 h^2 $$
$$\begin{align*}
A(h) & = \frac{d V}{d h} \\
& = a_1 + 2 a_2 h \\
& = \underbrace{\left(a_1 + 2 a_2 h_0\right)}_{b_0} \; + \; \underbrace{2 a_2}_{b_1} \left(h-h_0\right)\end{align*}$$
### Rainy Lake
```
h = np.array([335.0, 336.0, 336.5, 337.0, 337.5, 338.0, 339.0, 340.0])
v = np.array([112.67, 798.00, 1176.42, 1577.25, 2002.06, 2450.57, 3416.85, 4458.97])
plt.subplot(2,1,1)
plt.scatter(h,v)
plt.xlim(h.min(),h.max())
plt.ylim(0,plt.ylim()[1])
plt.title('Rainy Lake Stage-Volume Relationship')
plt.xlabel('Water Elevation (m)')
plt.ylabel('Volume (million cu. m)')
pf = sp.polyfit(h,v,2)
VRL= sp.poly1d(pf)
plt.hold(True)
plt.plot(h,VRL(h))
plt.hold(False)
ARL = sp.poly1d(np.array([2.0*pf[0],pf[1]]))
plt.subplot(2,1,2)
plt.plot(h,ARL(h))
plt.title('Rainy Lake Stage-Surface Area Relationship')
plt.xlabel('Elevation (m)')
plt.ylabel('Area (sq. km.)')
plt.tight_layout()
df = pd.DataFrame(zip(h,v,VRL(h),ARL(h)),columns=['h','V','Vhat','Ahat'])
print df.to_string(formatters={'V':' {:.0f}'.format,
'Vhat':' {:.0f}'.format,
'Ahat':' {:.0f}'.format})
h = np.array([337.0, 338.0, 338.5, 339.0, 339.5, 340.0,
340.5, 341.0, 341.5, 342.0, 343.0])
v = np.array([65.33, 259.95, 364.20, 475.58, 592.46, 712.28,
836.56, 966.17, 1099.79, 1239.68, 1540.75])
plt.subplot(2,1,1)
plt.scatter(h,v)
plt.xlim(h.min(),h.max())
plt.ylim(0,plt.ylim()[1])
plt.title('Namakan Lake Stage-Volume Relationship')
plt.xlabel('Water Elevation (m)')
plt.ylabel('Volume (million cu. m)')
pf = sp.polyfit(h,v,2)
VNL= sp.poly1d(pf)
plt.hold(True)
plt.plot(h,VNL(h))
plt.hold(False)
ANL = sp.poly1d(np.array([2.0*pf[0],pf[1]]))
plt.subplot(2,1,2)
plt.plot(h,ANL(h))
plt.title('Namakan Lake Stage-Surface Area Relationship')
plt.xlabel('Elevation (m)')
plt.ylabel('Area (sq. km.)')
plt.tight_layout()
df = pd.DataFrame(zip(h,v,VNL(h),ANL(h)),columns=['h','V','Vhat','Ahat'])
print df.to_string(formatters={'V':' {:.0f}'.format,
'Vhat':' {:.0f}'.format,
'Ahat':' {:.0f}'.format})
```
## Stage-Discharge Relationships
### Rainy Lake
```
h = np.array([335.4, 336.0, 336.5, 336.75, 337.0, 337.25, 337.5,
337.75, 338.0, 338.5, 339, 339.5, 340.0])
d = np.array([0.0, 399., 425., 443., 589., 704., 792., 909.,
1014., 1156., 1324., 1550., 1778.])
#plt.subplot(2,1,1)
plt.hold(True)
plt.scatter(d,h)
plt.plot(d,h)
plt.ylim(h.min(),h.max())
plt.xlim(0,plt.xlim()[1])
plt.title('Rainy Lake Stage-Discharge Relationship')
plt.ylabel('Water Elevation (m)')
plt.xlabel('Discharge (cu. per sec.)')
# Get historical flowrates and levels on RR and RL
RR = pd.read_pickle(dir+'RR.pkl')['1970':]
RL = pd.read_pickle(dir+'RL.pkl')['1970':]
Q = pd.concat([RR,RL],axis=1)
Q.columns = ['RR','RL']
A = Q['1970':'2000']
plt.scatter(A['RR'],A['RL'],marker='+',color='b')
B = Q['2000':]
plt.scatter(B['RR'],B['RL'],marker='+',color='r')
ax = plt.axis()
plt.plot([ax[0],ax[1]],[336.70,336.70],'y--')
plt.plot([ax[0],ax[1]],[337.20,337.20],'y--')
plt.plot([ax[0],ax[1]],[337.75,337.75],'m--')
plt.plot([ax[0],ax[1]],[337.90,337.90],'c--')
plt.xlabel('Upper Rainy River Flow [cubic meters/sec]')
plt.ylabel('Rainy Lake Level [meters]')
ax = plt.axis()
plt.axis([0,ax[1],ax[2],ax[3]])
plt.legend(['Winter Drought Line','Summer Drought Line','URC_max','All Gates Open','1970-2000','2000-2010'],loc="upper left")
plt.hold(False)
#plt.savefig('./images/RainyRiverDischarge.png')
Q = lambda x: np.interp(x,h,d)
x = np.linspace(336.,339.)
plt.plot(x,Q(x))
```
<!--NAVIGATION-->
< [Control](http://nbviewer.jupyter.org/github/jckantor/Controlling-Natural-Watersheds/blob/master/notebooks/05.00-Control.ipynb) | [Contents](toc.ipynb) | [Implementation of Rainy Lake Rule Curves with Feedback Control](http://nbviewer.jupyter.org/github/jckantor/Controlling-Natural-Watersheds/blob/master/notebooks/05.02-Implementation_of_Rainy_Lake_Rule_Curves_with_Feedback_Control.ipynb) ><p><a href="https://colab.research.google.com/github/jckantor/Controlling-Natural-Watersheds/blob/master/notebooks/05.01-Lumped_Parameter_Model_for_Lake_Dynamics.ipynb"><img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open in Google Colaboratory"></a><p><a href="https://raw.githubusercontent.com/jckantor/Controlling-Natural-Watersheds/master/notebooks/05.01-Lumped_Parameter_Model_for_Lake_Dynamics.ipynb"><img align="left" src="https://img.shields.io/badge/Github-Download-blue.svg" alt="Download" title="Download Notebook"></a>
|
github_jupyter
|
# "Proof" of noise ceiling by simulation
```
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from sklearn.preprocessing import StandardScaler, OneHotEncoder
from sklearn.model_selection import StratifiedKFold, cross_val_predict, GroupKFold
from sklearn.pipeline import make_pipeline
from sklearn.svm import SVC
from sklearn.metrics import roc_auc_score
from tqdm import tqdm_notebook
```
Define functions.
```
class Dataset:
def __init__(self, P, N_per_class, K, R, verbose=False):
self.P = P
self.N_per_class = N_per_class
self.N = N_per_class * K
self.K = K
self.R = R
self.verbose = verbose
self.rep_idx = np.repeat(np.arange(self.N), R)
self.y = None
self.X = None
self.ohe = None # added later
def generate(self, signal=0.1, inconsistency=5):
""" Generates pseudo-random data (X, y).
Parameters
----------
signal : float
"Amount" of signal added to X to induce corr(X, y)
"""
X_unrep = np.random.normal(0, 1, (self.N, self.P))
self.X = np.concatenate([X_unrep for _ in range(self.R)]) # repeat R times!
# Generate "unrepeated" labels
y_unrep = np.repeat(np.arange(self.K), self.N_per_class)
# Generate random labels, repeated R times, simulating
# inconsistency in subject ratings (sometimes anger, sometimes happiness, etc.)
shifts = np.random.normal(0, inconsistency, R).astype(int)
self.y = np.concatenate([np.roll(y_unrep, shifts[ii]) for ii in range(R)])
# Add signal
for k in range(self.K):
self.X[self.y == k, k] += signal
self.ohe = OneHotEncoder(sparse=False, categories='auto')
self.ohe.fit(y_unrep[:, np.newaxis])
def compute_noise_ceiling(self, use_prob=True):
""" Estimates the best prediction and score (noise ceiling) given the
inconsistency in the labels.
Parameters
----------
use_prob : bool
Whether to evaluate probabilistic performance or binarized
"""
# Get 2d version of y, shape (N / reps, reps)
y2d = np.c_[[self.y[self.N*i:self.N*(i+1)] for i in range(self.R)]].T
# Magic below! Count the number of classes across repetitions of the same sample ...
counts = np.apply_along_axis(np.bincount, 1, y2d, minlength=self.K)
# Pre-allocate best prediction array
best_pred = np.zeros_like(counts, dtype=float)
for ii in range(counts.shape[0]):
# Determine most frequent label across reps
opt_class = np.where(counts[ii, :] == counts[ii, :].max())[0]
if use_prob:
# Set prediction of the "optimal class" to 1 / num_opt_classes (ties)
best_pred[ii, opt_class] = 1 / len(opt_class)
else:
rnd_class = np.random.choice(opt_class, size=1)
best_pred[ii, rnd_class] = 1
# Repeat best possible prediction R times
best_pred = np.tile(best_pred.T, R).T
# Convert y to one-hot-encoded array
y_ohe = self.ohe.transform(self.y[:, np.newaxis])
# Compute best possible score ("ceiling")
self.ceiling = roc_auc_score(
y_ohe,
best_pred,
average=None if use_prob else 'micro'
)
if self.verbose:
print(f"Ceiling: {np.round(self.ceiling, 2)}")
def compute_model_performance(self, estimator, use_prob=True, cv=None, stratify_reps=False):
# Fit actual model
if cv is None:
estimator.fit(self.X, self.y)
preds = estimator.predict(self.X)
else:
preds = cross_val_predict(
estimator, self.X, self.y, cv=cv,
groups=self.rep_idx if stratify_reps else None
)
# Compute actual score (should be > ceiling)
y_ohe = self.ohe.transform(self.y[:, np.newaxis])
self.score = roc_auc_score(
self.ohe.transform(self.y[:, np.newaxis]),
self.ohe.transform(preds[:, np.newaxis]),
average=None if use_prob else 'micro'
)
if self.verbose:
print(f"Score: {np.round(self.score, 2)}")
self.diff = self.ceiling - self.score
```
## 1. Within-subject, no CV
First, let's check it out for within-subject ratings. We'll define some simulation parameters.
```
P = 1000 # number of features
N_per_class = 10 # number of samples per class
K = 3 # number of classes [0 - K]
R = 4 # how many repetitions of each sample
estimator = make_pipeline(StandardScaler(), SVC(kernel='linear'))
iters = 100
ds = Dataset(P=P, N_per_class=N_per_class, K=K, R=R, verbose=False)
scores = np.zeros((iters, K))
ceilings = np.zeros((iters, K))
diffs = np.zeros((iters, K))
for i in tqdm_notebook(range(iters)):
ds.generate(signal=0, inconsistency=5)
ds.compute_noise_ceiling()
ds.compute_model_performance(estimator)
scores[i, :] = ds.score
ceilings[i, :] = ds.ceiling
diffs[i, :] = ds.diff
fig, axes = plt.subplots(ncols=2, figsize=(15, 5), gridspec_kw={'width_ratios': [1, 3]})
for i in range(K):
sns.distplot(diffs[:, i], kde=False, ax=axes[0])
axes[0].set_xlabel('Score - ceiling')
axes[0].set_ylabel('Freq')
axes[0].legend([f'class {i+1}' for i in range(ds.K)], frameon=False)
axes[1].plot(ceilings.mean(axis=1), ls='--')
axes[1].plot(scores.mean(axis=1))
axes[1].set_xlabel('Iteration')
axes[1].set_ylabel('Model performance')
axes[1].legend(['ceiling', 'score'], frameon=False)
sns.despine()
```
## 2. With CV
```
ds = Dataset(P=P, N_per_class=N_per_class, K=K, R=R, verbose=False)
scores = np.zeros((iters, K))
ceilings = np.zeros((iters, K))
diffs = np.zeros((iters, K))
for i in tqdm_notebook(range(iters)):
ds.generate(signal=0, inconsistency=5)
ds.compute_noise_ceiling()
ds.compute_model_performance(estimator, cv=GroupKFold(n_splits=10), stratify_reps=True)
scores[i, :] = ds.score
ceilings[i, :] = ds.ceiling
diffs[i, :] = ds.diff
fig, axes = plt.subplots(ncols=2, figsize=(15, 5), gridspec_kw={'width_ratios': [1, 3]})
for i in range(K):
sns.distplot(diffs[:, i], kde=False, ax=axes[0])
axes[0].set_xlabel('Score - ceiling')
axes[0].set_ylabel('Freq')
axes[0].legend([f'class {i+1}' for i in range(ds.K)], frameon=False)
axes[1].plot(ceilings.mean(axis=1), ls='--')
axes[1].plot(scores.mean(axis=1))
axes[1].set_xlabel('Iteration')
axes[1].set_ylabel('Model performance')
axes[1].legend(['ceiling', 'score'], frameon=False)
sns.despine()
```
|
github_jupyter
|
```
import numpy as np
from keras.preprocessing.image import img_to_array
from keras.preprocessing.image import load_img
import matplotlib.pyplot as plt
from pathlib import Path
from functools import partial
from PIL import Image
img = load_img('../data/91-image/t2.bmp')
x = img_to_array(img)
plt.imshow(x/255.)
plt.show()
print(x.shape)
def load_image_pair(path, scale=3):
image = load_img(path)
image = image.convert('YCbCr')
hr_image = modcrop(image, scale)
lr_image = bicubic_rescale(hr_image, 1 / scale)
return lr_image, hr_image
def generate_sub_images(image, size, stride):
for i in range(0, image.size[0] - size + 1, stride):
for j in range(0, image.size[1] - size + 1, stride):
yield image.crop([i, j, i + size, j + size])
def array_to_img(x, mode='YCbCr'):
return Image.fromarray(x.astype('uint8'), mode=mode)
def bicubic_rescale(image, scale):
if isinstance(scale, (float, int)):
size = (np.array(image.size) * scale).astype(int)
return image.resize(size, resample=Image.BICUBIC)
def modcrop(image, scale):
size = np.array(image.size)
size -= size % scale
return image.crop([0, 0, *size])
repo_dir = Path('..')
data_dir = repo_dir / 'data'
i=0
dataset_name = '91-image'
for path in (data_dir / dataset_name).glob('*'):
i+=1
print(path)
if i%4==0:
break
lr_sub_size=11
lr_sub_stride=5
scale=3
dataset_name = '91-image'
hr_sub_size = lr_sub_size * scale # 33
hr_sub_stride = lr_sub_stride * scale # 15
lr_gen_sub = partial(generate_sub_images, size=lr_sub_size,
stride=lr_sub_stride)
hr_gen_sub = partial(generate_sub_images, size=hr_sub_size,
stride=hr_sub_stride)
lr_sub_arrays = []
hr_sub_arrays = []
for path in (data_dir / dataset_name).glob('*'):
image = load_img(path)
image = image.convert('YCbCr')
hr_image = modcrop(image, scale)
lr_image = bicubic_rescale(hr_image, 1 / scale)
lr_sub_arrays += [img_to_array(img) for img in lr_gen_sub(lr_image)]
hr_sub_arrays += [img_to_array(img) for img in hr_gen_sub(hr_image)]
x = np.stack(lr_sub_arrays)
y = np.stack(hr_sub_arrays)
# len(y)
len(x)
lr_image, hr_image = load_image_pair(str(path), scale=scale)
hr_imagecov = hr_image.convert('RGB')
lr_imagecov = lr_image.convert('RGB')
plt.subplot(2,2,1)
plt.imshow(np.asarray(hr_image))
plt.subplot(2,2,2)
plt.imshow(np.asarray(hr_imagecov))
print(type(hr_imagecov))
print(lr_image.size)
print(hr_image.size)
plt.imshow(img_to_array(hr_imagecov)/255.0)
plt.show()
plt.imshow(lr_sub_arrays[0]/255.0)
lr_sub_arrays[0].shape
len(lr_sub_arrays)
lr_sub_arrays[0].shape
len(hr_sub_arrays)
lr_sub_arrays=[]
hr_sub_arrays=[]
for path in (data_dir / dataset_name).glob('*'):
image = load_img(path)
# image = image.convert('YCbCr')
hr_image = modcrop(image, scale)
lr_image = bicubic_rescale(hr_image, 1 / scale)
lr_sub_arrays += [img for img in lr_gen_sub(lr_image)]
hr_sub_arrays += [img for img in hr_gen_sub(hr_image)]
len([img for img in lr_gen_sub(lr_image)])
x.shape[1:]
```
|
github_jupyter
|
```
import gym
#import moviepy.editor as mpy
import os
from pyvirtualdisplay import Display
# Filter tensorflow version warnings
import os
# https://stackoverflow.com/questions/40426502/is-there-a-way-to-suppress-the-messages-tensorflow-prints/40426709
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3' # or any {'0', '1', '2'}
import warnings
# https://stackoverflow.com/questions/15777951/how-to-suppress-pandas-future-warning
warnings.simplefilter(action='ignore', category=FutureWarning)
warnings.simplefilter(action='ignore', category=Warning)
import tensorflow as tf
tf.get_logger().setLevel('INFO')
tf.autograph.set_verbosity(0)
import logging
tf.get_logger().setLevel(logging.ERROR)
from matplotlib import pyplot as plt
from IPython.display import clear_output
import numpy as np
from stable_baselines import PPO2
#cargo el env original de OpenAI
env = gym.make('CarRacing-v0')
env.action_space
env.action_space.high, env.action_space.low
env.observation_space
```
```
#modelos propios multi-frame, segun el env_v1 de Mike que lo permite
#param comunes de imagenes usados en train
G=1 #rgb o grayscale o green
discre=True
intro=45
acc_prev=0
#model = PPO2.load('gym-master/ppo2_v1_mike_cnn_gray.pkl') #cuidado 2 frames
C=2
model = PPO2.load('gym-master/ppo2_v1_mike_cnn_4f_green_bs1600.pkl')
C=4
G=2
```
```
#mike's training discretization
act=[]
act.append([0, 0, 0])
act.append([-1,0, 0])
act.append([1, 0, 0])
act.append([0,1,0])
act.append([0, 0,0.8])
#setup
plot=False #si plot no render grande
if plot:
display = Display(visible=0, size=(1024, 768))
display.start()
os.environ["DISPLAY"] = ":" + str(display.display) + "." + str(display.screen)
rgb=env.reset()
#salteo la intro si uso 45 frames, lo pongo a acelerar segun env entretanto
for i in range(intro):
rgb, reward, done, info = env.step([0, acc_prev, 0])
#armo array de obser inicial
#--> hay sendos wrapper para esto, pero no puedo agregarle a TU entorno la
# opcion de quedarme solo con el canal green de rgb (G=2)
obser=np.zeros((96,96,C))
for i in range(C):
if G==1:
obs=np.average(rgb, weights=[0.299, 0.587, 0.114], axis=2)
elif G==2:
obs=rgb[:,:,1]
else:
obs=rgb[:,:,i]
obser[:,:,i]=obs
# rgb, reward, done, info = env.step([0, acc_prev, 0]) #acelero segun env estos C frames...
env.render()
obser.shape
#play
episode = intro
total_reward = 0
rewards = []
total_rewards = []
done = False
np.set_printoptions(precision=4)
#si plot no render grande
while not done and episode<1003: #a los mil corta el env() automaticamente
mod_act, _states = model.predict(obser, deterministic=True)
action=act[mod_act] if discre else mod_act
rgb, reward, done, info = env.step(action)
#obs=np.average(rgb, weights=[0.299, 0.587, 0.114], axis=2) if G else rgb
if G==1:
obs=np.average(rgb, weights=[0.299, 0.587, 0.114], axis=2)
elif G==2:
obs=rgb[:,:,1]
else:
obs=rgb
if C>1:
obser=np.roll(obser,1,2)
obser[:,:,0]=obs
else:
obser=obs
total_reward += reward
rewards.append(reward)
total_rewards.append(total_reward)
if plot:
clear_output(wait=True)
plt.subplots(1,2,figsize=(15,10))
plt.subplot(1,2, 1)
plt.imshow(obs,cmap='gray') #imagen mas nueva que ve la red para decidir, guarda C anteriores
plt.subplot(1,2,2)
plt.imshow(rgb) #el juego en estado natural
plt.show()
#print(f'\r{model.action_probability(obser):.4f}')
print(model.action_probability(obser))
else:
env.render()
episode+=1
#print(mod_act, act[mod_act])
print(f'\r{reward:.2f}, {action}, {total_reward:.2f}, {episode}', end=' ')
print('')
print('')
print('env() lo dio por finalizado: ', done)
print(f'\r{info}, {total_reward:.2f}, {episode}')
env.close()
plt.plot(rewards[:episode-1])
plt.plot(total_rewards[:episode])
plt.plot(rewards, marker='.')
env.close()
```
|
github_jupyter
|
## CS536: Perceptrons
#### Done by - Vedant Choudhary, vc389
In the usual way, we need data that we can fit and analyze using perceptrons. Consider generating data points (X, Y) in the following way:
- For $i = 1,....,k-1$, let $X_i ~ N(0, 1)$ (i.e. each $X_i$ is an i.i.d. standard normal)
- For $i = k$, generate $X_k$ in the following way: let $D ~ Exp(1)$, and for a parameter $\epsilon > 0$ take
$X_k = (\epsilon + D)$ with probability 1/2
$X_k = -(\epsilon + D)$ with probability 1/2
The effect of this is that while $X_1,...X_{k-1}$ are i.i.d. standard normals, $X_k$ is distributed randomly with some gap (of size $2\epsilon$ around $X_k = 0$. We can then classify each point according to the following:
$Y = 1$ if $X_k$ > 0
$Y = -1$ if $X_k$ < 0
We see that the class of each data point is determined entirely by the value of the $X_k$ feature
#### 1. Show that there is a perceptron that correctly classifies this data. Is this perceptron unique? What is the ‘best’ perceptron for this data set, theoretically?
**Solution:** The perceptron generated when the data is linearly separable is unique. Best perceptron for a data would be the perceptron that relies heaviliy on the last feature of the dataset, as target value is governed by that.
```
# Importing required libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import pprint
from tqdm import tqdm
%matplotlib inline
# Creating X (feature) vectors for the data
def create_data(k, m, D, epsilon):
X_k_minus_1 = np.random.normal(0, 1, (m,k-1))
X_k = []
for i in range(m):
temp = np.random.choice(2, 1, p=[0.5,0.5])
# print(temp)
if temp == 1:
X_k.append(epsilon + D)
else:
X_k.append(-(epsilon + D))
X_k = np.asarray(X_k).reshape((1,m))
# print(X_k_minus_1)
# print(X_k)
return np.concatenate((X_k_minus_1, X_k.T), axis=1)
# Creating target column for the data
def create_y(X, m):
y = []
for i in range(m):
if X[i][-1] > 0:
y.append(1)
else:
y.append(-1)
return y
# Combining all the sub data points into a dataframe
def create_dataset(k, m, epsilon, D):
X = np.asarray(create_data(k, m, epsilon, D))
y = np.asarray(create_y(X, m)).reshape((m,1))
# print(X.shape,y.shape)
# Training data is an appended version of X and y arrays
data = pd.DataFrame(np.append(X, y, axis=1), columns=["X" + str(i) for i in range(1,k+1)]+['Y'])
return data
# Global Variables - k = 20, m = 100, epsilon = 1
k, m, epsilon = 20, 100, 1
D = float(np.random.exponential(1, 1))
train_data = create_dataset(k, m, epsilon, D)
train_data.head()
```
#### 2. We want to consider the problem of learning perceptrons from data sets. Generate a set of data of size m = 100 with k = 20, $\epsilon$ = 1
##### - Implement the perceptron learning algorithm. This data is separable, so the algorithm will terminate. How does the output perceptron compare to your theoretical answer in the previous problem?
```
# Class for Perceptron
class Perceptron():
def __init__(self):
pass
'''
Calculates the sign of the predicted value
Input: dot product (X.w + b)
Return: Predicted sign of f_x
'''
def sign_function(self, data_vec):
return np.array([1 if val >= 1 else -1 for val in data_vec])[:, np.newaxis]
'''
Perceptron learning algorithm according to the notes posted
Input: dataset
Return: final weights and biases, along with number of steps for convergence
and upper bound of theoretical convergence
'''
def pla(self, data):
X = np.asarray(data.iloc[:,:-1])
y = np.asarray(data.iloc[:,-1:])
num_samples, num_features = X.shape
# Initialize weight and bias parameters
self.w = np.zeros(shape=(num_features, 1))
self.bias = 0
count_till_solution = 0
f_x = [0]*num_samples
i = 0
theoretical_termination = []
while True:
mismatch = 0
for i in range(num_samples):
# Calculate the mapping function f(x)
f_x[i] = float(self.sign_function(np.dot(X[i].reshape((num_features, 1)).T, self.w) + self.bias))
# Compute weights if f_x != y
if float(f_x[i]) != float(y[i]):
mismatch += 1
self.w += np.dot(X[i].reshape((num_features, 1)), y[i].reshape((1,1)))
self.bias += y[i]
count_till_solution += 1
min_margin = 99999
for i in range(num_samples):
margin = abs(np.dot(self.w.T, X[i].reshape(-1,1))/(np.linalg.norm(self.w)))
if margin < min_margin:
min_margin = margin
theoretical_termination.append(int(1/(min_margin**2)))
f_x = np.asarray(f_x).reshape((num_samples, 1))
i += 1
if (np.array_equal(y, f_x)) or (mismatch >= 0.3*num_samples and count_till_solution >= 5000):
break
return self.w, self.bias, count_till_solution, max(theoretical_termination)
'''
Predicts the target value based on a data vector
Input - a single row of dataset or a single X vector
Return - predicted value
'''
def predict(self, instance_data):
instance_data = np.asarray(instance_data)
prediction = self.sign_function(np.dot(self.w.T, instance_data.reshape((len(instance_data),1))) + self.bias)
return prediction
'''
Predicts the target value and then calculates error based on the predictions
Input - dataset, decision tree built
Return - error
'''
def fit(self, data):
error = 0
for i in range(len(data)):
prediction = self.predict(data.iloc[i][:-1])
if prediction != data.iloc[i][-1]:
print("Not equal")
error += 1
return error/len(data)
perceptron = Perceptron()
final_w, final_b, num_steps, theoretical_steps = perceptron.pla(train_data)
print("Final weights:\n",final_w)
print("Final bias:\n", final_b)
print("Number of steps till convergence: \n", num_steps)
print("Theoretical number of steps till convergence can be found for linear separation: ", theoretical_steps)
error = perceptron.fit(train_data)
error
plt.plot(np.linspace(0, 20, 20), list(final_w))
plt.title("Weight vector by feature")
plt.xlabel("Feature number")
plt.ylabel("Weights")
plt.show()
```
**Solution:** On implementing the perceptron learning algorithm on the dataset provided, we see that it is similar to our theoretical answer. The last feature has highest weight associated to it (as can be seen from the graph generated above). This is so because the data is created such that the target value depends solely on the last feature value.
#### 3. For any given data set, there may be multiple separators with multiple margins - but for our data set, we can effectively control the size of the margin with the parameter $\epsilon$ - the bigger this value, the bigger the margin of our separator.
#### – For m = 100, k = 20, generate a data set for a given value of $\epsilon$ and run the learning algorithm to completion. Plot, as a function of $\epsilon$ ∈ [0, 1], the average or typical number of steps the algorithm needs to terminate. Characterize the dependence.
```
def varied_margin():
k, m = 20, 100
epsilon = list(np.arange(0, 1.05, 0.02))
avg_steps = []
for i in tqdm(range(len(epsilon))):
steps = []
for j in range(100):
train_data = create_dataset(k, m, epsilon[i], D)
perceptron = Perceptron()
final_w, final_b, num_steps, theoretical_steps = perceptron.pla(train_data)
steps.append(num_steps)
avg_steps.append(sum(steps)/len(steps))
plt.plot(epsilon, avg_steps)
plt.title("Number of steps w.r.t. margin")
plt.xlabel("Margin value")
plt.ylabel("#Steps")
plt.show()
varied_margin()
```
**Solution:** On plotting average number of steps needed for termination of a linearly separable data w.r.t. $\epsilon$, we observe that bigger the margin, lesser the number of steps are needed for the perceptron to terminate. This dependence can be proved by the Perceptron Convergence Theorem - If data is linearly separable, perceptron algorithm will find a linear classifier that classifies all data correctly, whose convergence is inversely proportional to the square of margin.
This means as the margin increases, the convergence steps decrease.
#### 4. One of the nice properties of the perceptron learning algorithm (and perceptrons generally) is that learning the weight vector w and bias value b is typically independent of the ambient dimension. To see this, consider the following experiment:
#### – Fixing m = 100, $\epsilon$ = 1, consider generating a data set on k features and running the learning algorithm on it. Plot, as a function k (for k = 2, . . . , 40), the typical number of steps to learn a perceptron on a data set of this size. How does the number of steps vary with k? Repeat for m = 1000.
```
def varied_features(m):
epsilon = 1
D = float(np.random.exponential(1, 1))
k = list(np.arange(2, 40, 1))
steps = []
for i in range(len(k)):
train_data = create_dataset(k[i], m, epsilon, D)
perceptron = Perceptron()
final_w, final_b, num_steps, theoretical_steps = perceptron.pla(train_data)
steps.append(num_steps)
plt.plot(k, steps)
plt.title("Number of steps w.r.t. features")
plt.xlabel("#Features")
plt.ylabel("#Steps")
plt.show()
varied_features(100)
varied_features(1000)
```
**Solution:** The number of steps needed for convergence of a linearly separable data through perceptrons is usually independent of number of features the data has. This is shown through the above experiment too. For this case, I see no change in number of steps, but some different runs have shown very random change in number of steps, that also by just 1 step more or less. We cannot establish a trend of convergence w.r.t. the number of features.
#### 5. As shown in class, the perceptron learning algorithm always terminates in finite time - if there is a separator. Consider generating non-separable data in the following way: generate each $X_1, . . . , X_k$ as i.i.d. standard normals N(0, 1). Define Y by
$$Y = 1 if \sum_{i=1}^k{X_i^2} \ge k $$
$$Y = -1 else$$
```
def create_non_separable_data(k, m):
X = np.random.normal(0, 1, (m,k))
y = []
for i in range(m):
total = 0
for j in range(k):
total += X[i][j]**2
if total >= k:
y.append(1)
else:
y.append(-1)
return X, y
def create_non_separable_dataset(k, m):
X, y = create_non_separable_data(k, m)
X = np.asarray(X)
y = np.asarray(y).reshape((m,1))
# Training data is an appended version of X and y arrays
data = pd.DataFrame(np.append(X, y, axis=1), columns=["X" + str(i) for i in range(1,k+1)]+['Y'])
return data
k, m = 2, 100
train_ns_data = create_non_separable_dataset(k, m)
train_ns_data.head()
perceptron2 = Perceptron()
final_w2, final_b2, num_steps2, theoretical_steps = perceptron2.pla(train_ns_data)
plt.scatter(X1, X2, c=y2)
plt.title("Dataset")
plt.xlabel("First feature")
plt.ylabel("Second feature")
plt.show()
```
The data represented above is the data generated from the new rules of creating a non separable data. As can be seen, this data cannot be linearly separated through Perceptrons. A kernel method has to be applied to this data to find a separable hyper-plane.
```
def plot_hyperplane(x1, x2, y, w, b):
slope = -w[0]/w[1]
intercept = -b/w[1]
x_hyperplane = np.linspace(-3,3,20)
y_hyperplane = slope*x_hyperplane + intercept
plt.scatter(x1, x2, c=y)
plt.plot(x_hyperplane, y_hyperplane, 'b-')
plt.title("Dataset with fitted hyperplane")
plt.xlabel("First feature")
plt.ylabel("Second feature")
plt.show()
X2_1 = train_ns_data.iloc[:,:-2]
X2_2 = train_ns_data.iloc[:,1:-1]
y2 = train_ns_data.iloc[:,-1:]
plot_hyperplane(X2_1, X2_2, y2, final_w2, final_b2)
```
**Solution:** For a linearly non-separable data, perceptron is not a good algorithm to use, because it will never converge. Theoretically, it is possible to find an upper bound on number of steps required to converge (if the data is linearly separable). But, it cannot be put into practice easily, as to compute that, we first need to find the weight vector.
Another thing to note is that, even if there is a convergence, the number of steps needed might be too large, which might bring the problem of computation power.
For this assignment, I have established a heurisitc that if the mismatch % is approximately 30% of the total number of samples and the iterations have been more than 10000, then that means that possibly the data is not separable linearly. My reasoning for this is very straight forward, if 30% of data is still mismatched, it is likely that the mismatch will continue to happen for long, which is not computationally feasible.
|
github_jupyter
|
```
# installs
# imports
import scipy.io
import cv2
from google.colab.patches import cv2_imshow
from skimage import io
import numpy as np
import pandas as pd
from PIL import Image
import matplotlib.pylab as plt
import pickle
from skimage import transform
from sklearn.model_selection import train_test_split
import tensorflow as tf
from nltk.tokenize import word_tokenize
from nltk.stem import WordNetLemmatizer, LancasterStemmer
import spacy
import nltk
import keras.backend as K
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
nltk.download('punkt') #tokenizer
nltk.download('wordnet') #lemmatization
lemmatizer = WordNetLemmatizer() #lemmatizer
sp = spacy.load('en_core_web_sm') #lexical importance find
ls = LancasterStemmer()
# data loading
!gdown --id 1mrjvJq6XNM8QAgajSgrVGpsj8Vrm3BEm #PASCAL50S
mat = scipy.io.loadmat('/content/pascal50S.mat')
print(type(mat))
classes = ['person',
'bird',
'cat',
'cow',
'dog',
'horse',
'sheep',
'aeroplane',
'bicycle',
'boat',
'bus',
'car',
'motorbike',
'train',
'bottle',
'chair',
'dining table',
'potted plant',
'sofa',
'tv/monitor']
dict_classes = {'person':0, 'man':0, 'human':0, 'people':0, 'men': 0, 'girl':0, 'boy':0,
'serviceman':0, 'homo':0, 'valet':0, 'child':0, 'family':0, 'group':0,
'woman':0, 'women':0, 'couple':0, 'her':0, 'his':0, 'rider':0, 'him':0,
'he':0, 'she':0, 'child':0, 'children':0, 'baby':0, 'guy':0, 'gentleman':0,
'lady':0, 'grandma':0, 'friend':0, 'mother':0, 'father':0, 'teen':0, 'kid':0,
'teenager':0, 'cowboy':0, 'daughter':0, 'dad':0, 'son':0,
'bird':1, 'penguin':1, 'parrot':1, 'sparrow':1, 'dame':1, 'boo':1, 'eagle':1,
'cockatoo':1, 'hummingbird':1, 'duck':1, 'goose':1, 'songbird':1, 'dove':1,
'chicken':1, 'rooster':1, 'chick':1, 'crow':1, 'hawk':1, 'canary':1, 'peacock':1,
'magpie':1, 'swan':1, 'kingfisher':1, 'kookaburra':1, 'owl':1, 'woodpecker':1,
'crane':1,
'cat':2, 'pussy':2, 'kitty':2, 'wildcat':2, 'kitten':2,
'cow':3, 'calf':3, 'bullock':3, 'bull':3, 'ox':3,
'dog':4, 'greyhound':4, 'pug':4, 'puppy':4, 'schnauzer':4, 'pooch':4, 'tyke':4,
'labrador':4, 'bulldog':4, 'chihuahua':4, 'pomeranian':4, 'bernard':4, 'bitch':4,
'horse':5, 'stallion':5, 'pony':5, 'mare':5,
'sheep':6, 'goat':6, 'ram':6, 'ewe':6, 'lamb':6,
'aeroplane':7, 'airplane':7, 'flight':7, 'plane':7, 'jet':7, 'aircraft':7, 'biplane':7,
'bicycle':8, 'cycle':8, 'bike':8,
'boat':9, 'ship':9, 'cruise':9, 'canoe':9, 'kayak':9, 'barge':9,
'bus':10, 'van': 10,
'car':11, 'corvette':11, 'truck':11, 'supercar':11, 'coupe':11, 'sedan':11, 'roadster':11,
'hatchback':11, 'minivan':11,
'motorbike':12, 'motorcycle':12,
'train':13, 'locomotive':13, 'freight':13,
'bottle':14, 'flask':14,
'chair':15, 'armchair':15, 'rocker':15, 'recliner':15,
'dining':16, 'table':16,
'plant':17, 'sapling':17, 'flowerpot':17, 'potted':17,
'sofa':18, 'couch':18, 'lounge':18,
'tv':19, 'monitor':19, 'television':19, 'desktop':19, 'computer':19}
rever_dict_classes = {
0: 'person',
1: 'bird',
2: 'cat',
3: 'cow',
4: 'dog',
5: 'horse',
6: 'sheep',
7: 'aeroplane',
8: 'bicycle',
9: 'boat',
10: 'bus',
11: 'car',
12: 'motorbike',
13: 'train',
14: 'bottle',
15: 'chair',
16: 'dining table',
17: 'potted plant',
18: 'sofa',
19: 'tv/monitor'}
count = {'0':0, #person
'1':0, #bird
'2':0, #cat
'3':0, #cow
'4':0, #dog
'5':0, #horse
'6':0, #sheep
'7':0, #aeroplane
'8':0, #bicycle
'9':0, #boat
'10':0, #bus
'11':0, #car
'12':0, #motorbike
'13':0, #train
'14':0, #bottle
'15':0, #chair
'16':0, #dining
'17':0, #potted plant
'18':0, #sofa
'19':0} #tv/monitor
# observing data
data = []
idx=0
for sample in mat["train_sent_final"][0]:
# image = io.imread(i[0][0])
# cv2_imshow(image)
link = [sample[0][0]] #image link
cls = set()
for k in sample[1]:
for sent in k:
# if idx==10:
# break
# idx+=1
for word in sent[0].split():
pre_word = lemmatizer.lemmatize(ls.stem(word.lower()))
if(pre_word in dict_classes.keys()):
cls.add(dict_classes[pre_word])
for cl in cls:
count[str(cl)]+=1
data.append([link, list(cls)])
file = open("data.pkl", "wb")
pickle.dump(data, file)
file.close()
# preprocessing the dataset
'''
data -> url -> image -> array -> resized array
TrainX = array of images resized to (224x224x3)
TrainY = array of labels with size (20x1) in ones-zeros vector like [1, 1, 0, ....]
'''
# TrainX
new_shape = (224, 224, 3)
TrainX1 = []
for point in data:
photo = io.imread(point[0][0])
photo = transform.resize(image=photo, output_shape=new_shape)
TrainX1.append(photo)
TrainX1 = np.array(TrainX1)
file = open("TrainX1.pkl", "wb")
pickle.dump(TrainX1, file)
file.close()
```
**Loading the TrainX1 Pickle file**
```
pickle_in = open("TrainX1.pkl","rb")
TrainX1 = pickle.load(pickle_in)
# TrainY
TrainY = []
for points in data:
full_label = np.zeros(shape=(20, ))
for label in points[1]:
full_label[label] = 1
TrainY.append(full_label)
TrainY = np.array(TrainY)
```
**Models**
```
# model making(Image to Vector)
# input layer
input1 = tf.keras.Input(shape=(224, 224, 3), name='input1')
# Transfer Learning with VGG16 model with weights as imagenet
vgg16 = tf.keras.applications.VGG16(include_top=False, weights="imagenet", classes=20)
vgg16.trainable = False
x = vgg16(input1)
# Dense Layers
x = tf.keras.layers.Flatten(name='flatten')(x)
x = tf.keras.layers.BatchNormalization(name='norm1')(x)
x = tf.keras.layers.Dense(192, activation='relu', name='dense1')(x)
x = tf.keras.layers.BatchNormalization(name='norm2')(x)
x = tf.keras.layers.Dense(84, activation='relu', name='dense2')(x)
x = tf.keras.layers.BatchNormalization(name='norm3')(x)
x = tf.keras.layers.Dense(64, activation='relu', name='dense3')(x)
x = tf.keras.layers.BatchNormalization(name='norm4')(x)
#Output layer
output = tf.keras.layers.Dense(500, activation="linear", name='output')(x)
model1 = tf.keras.models.Model(inputs=input1, outputs=output, name='model1')
model1.summary()
```
**Text Model(Model2)**
#**Data Preprocessing**
```
# observing data for text Model
data2 = []
stringX2 = []
idx=0
for sample in mat["train_sent_final"][0]:
# image = io.imread(i[0][0])
# cv2_imshow(image)
link = [sample[0][0]] #image link
cls = set()
for k in sample[1]:
for sent in k:
# if idx==10:
# break
# idx+=1
for word in sent[0].split():
pre_word = lemmatizer.lemmatize(ls.stem(word.lower()))
if(pre_word in dict_classes.keys()):
cls.add(dict_classes[pre_word])
for cl in cls:
count[str(cl)]+=1
for k in sample[1]:
for sent in k:
stringX2.append(sent[0])
temp = np.zeros(shape=20)
for ele in list(cls):
temp[ele] = 1
data2.append([sent, temp])
#Preparation of TrainX2 and Trainy2 for Text Model(Model2)
tk = Tokenizer(filters='!"#$%&()*+,-./:;<=>?@[\]^`{|}~\t\n')
tk.fit_on_texts(stringX2)
X_seq = tk.texts_to_sequences(stringX2)
X_pad = pad_sequences(X_seq, maxlen=100, padding='post')
X_pad.shape
TrainX2 = X_pad
Trainy2 = np.zeros(shape=(len(data2), 20))
i = 0
for d in data2:
Trainy2[i] = np.array(d[1])
i = i + 1
INP_LEN1 = 100 #(Text to Vector)
input2 = tf.keras.Input(shape=(INP_LEN1,), name='input')
embed = tf.keras.layers.Embedding((len(tk.word_counts)+1),INP_LEN1)(input2)
rnn1 = tf.keras.layers.GRU(192, return_sequences=True, dropout=0.3)(embed)
pool = tf.keras.layers.MaxPool1D()(rnn1)
rnn2 = tf.keras.layers.GRU(128, dropout=0.2)(pool)
dense1 = tf.keras.layers.Dense(84, activation='relu')(rnn2)
drop1 = tf.keras.layers.Dropout(0.2)(dense1)
norm1 = tf.keras.layers.BatchNormalization()(drop1)
output = tf.keras.layers.Dense(500, activation='linear')(norm1)
model2 = tf.keras.models.Model(inputs=input2, outputs=output, name='model2')
model2.summary()
```
**Concatenating the Image Model(Model1) and Text Model(Model2)**
```
concate = tf.keras.layers.Concatenate(axis=-1)([model1.output, model2.output])
final_dense = tf.keras.layers.Dense(256, activation='relu')(concate)
Output = tf.keras.layers.Dense(20, activation='sigmoid')(final_dense)
finalModel = tf.keras.models.Model(inputs=[input1,input2],outputs=Output)
finalModel.summary()
tf.keras.utils.plot_model(finalModel,to_file="finalModel.png")
```
**Train the MultiModal**
```
finalModel.compile(optimizer=tf.keras.optimizers.Adam(lr = 0.0001), loss='binary_crossentropy',metrics=[tf.keras.metrics.BinaryAccuracy()])
finalModel.fit([TrainX1, TrainX2], TrainY, validation_split=0.2, epochs=100)
```
**Predictions**
```
rnd = np.random.randint(0, len(TrainX1))
sampleX1 = np.expand_dims(TrainX1[rnd], axis=0)
sampleX2 = np.expand_dims(TrainX2[rnd], axis=0)
label = TrainY[rnd]
pred = finalModel.predict([sampleX1, sampleX2])[0]
pred = (pred > 0.5)
pred = pred.astype(int)
plt.imshow(TrainX1[rnd])
true = []
approx = []
for i in range(20):
if label[i] == 1:
true.append(rever_dict_classes[i])
if pred[i] == 1:
approx.append(rever_dict_classes[i])
print("True Classes in the image: ", true)
print("Predicted Classes in the image: ", approx)
```
**Save the Model**
```
tf.keras.utils.plot_model(finalModel, to_file="finalModel.png")
```
|
github_jupyter
|
Fashion-MNIST is a dataset of Zalando's article images—consisting of a training set of 60,000 examples and a test set of 10,000 examples. Each example is a 28x28 grayscale image, associated with a label from 10 classes. It shares the same image size and structure of training and testing splits.
- ## Try to build a classifier for the Fashion-MNIST dataset that achieves over 85% accuracy on the test set.
- ## Use only classifiers that are used in the Chapter 3 of the textbook.
- ## Do the error analysis following the textbook.
```
# Check GPU
import tensorflow as tf
tf.test.gpu_device_name()
# !mkdir -p my_drive
# !google-drive-ocamlfuse my_drive
# #!mkdir -p my_drive/Fashion
# !python3 /content/my_drive/Fashion/mnist_reader.py
import sys
sys.path.append('/content/my_drive/Fashion')
```
----------Everything above this is for Google Coloab----------
```
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
import mnist_reader
X_train, y_train = mnist_reader.load_mnist('/content/my_drive/Fashion', kind='train')
X_test, y_test = mnist_reader.load_mnist('/content/my_drive/Fashion', kind='t10k')
X_train.shape
y_train.shape
```
### Labels
Each training and test example is assigned to one of the following labels:
Label Description
- 0 T-shirt/top
- 1 Trouser
- 2 Pullover
- 3 Dress
- 4 Coat
- 5 Sandal
- 6 Shirt
- 7 Sneaker
- 8 Bag
- 9 Ankle boot
```
def plot_digit(data):
image = data.reshape(28, 28)
plt.imshow(image, cmap = matplotlib.cm.binary, interpolation="nearest")
plt.axis("off")
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
some_digit = X_train[36001]
some_digit_image = some_digit.reshape(28, 28)
plt.imshow(some_digit_image, cmap = matplotlib.cm.binary, interpolation="nearest")
plt.axis("off");
y_train[36001]
plot_digit(X_train[40000])
y_train[40000]
def plot_digits(instances, images_per_row=10, **options):
size = 28
images_per_row = min(len(instances), images_per_row)
images = [instance.reshape(size,size) for instance in instances]
n_rows = (len(instances) - 1) // images_per_row + 1
row_images = []
n_empty = n_rows * images_per_row - len(instances)
images.append(np.zeros((size, size * n_empty)))
for row in range(n_rows):
rimages = images[row * images_per_row : (row + 1) * images_per_row]
row_images.append(np.concatenate(rimages, axis=1))
image = np.concatenate(row_images, axis=0)
plt.imshow(image, cmap = matplotlib.cm.binary, **options)
plt.axis("off")
plt.figure(figsize=(9,9))
X_0 = X_train[(y_train == 0)]
example_images = X_0[:100]
plot_digits(example_images, images_per_row=10)
plt.figure(figsize=(9,9))
X_6 = X_train[(y_train == 6)]
example_images = X_6[:100]
plot_digits(example_images, images_per_row=10)
plt.figure(figsize=(9,9))
X_1 = X_train[(y_train == 1)]
example_images = X_1[:100]
plot_digits(example_images, images_per_row=10)
plt.figure(figsize=(9,9))
X_2 = X_train[(y_train == 2)]
example_images = X_2[:100]
plot_digits(example_images, images_per_row=10)
plt.figure(figsize=(9,9))
X_3 = X_train[(y_train == 3)]
example_images = X_3[:100]
plot_digits(example_images, images_per_row=10)
some_article = X_train[1014]
plot_digit(some_article)
y_train[1014]
```
# Training a Binary classifier to identify the shirt
```
y_train_shirt = (y_train == 6)
y_test_shirt = (y_train == 6)
from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(max_iter=1000, tol=1e-3, random_state=42)
sgd_clf.fit(X_train, y_train_shirt)
```
# Performance measures
```
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_shirt, cv=3, scoring="accuracy")
# from sklearn.model_selection import StratifiedKFold
# from sklearn.base import clone
# skfolds = StratifiedKFold(n_splits=3, random_state=42)
# for train_index, test_index in skfolds.split(X_train, y_train_sneaker):
# clone_clf = clone(sgd_clf)
# X_train_folds = X_train[train_index]
# y_train_folds = y_train_sneaker[train_index]
# X_test_fold = X_train[test_index]
# y_test_fold = y_train_sneaker[test_index]
# clone_clf.fit(X_train_folds, y_train_folds)
# y_pred = clone_clf.predict(X_test_fold)
# n_correct = sum(y_pred == y_test_fold)
# print(n_correct / len(y_pred))
from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_shirt, cv=3)
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_shirt, y_train_pred)
y_train_perfect_predictions = y_train_shirt # pretend we reached perfection
confusion_matrix(y_train_shirt, y_train_perfect_predictions)
from sklearn.metrics import precision_score, recall_score
precision_score(y_train_shirt, y_train_pred)
recall_score(y_train_shirt, y_train_pred)
from sklearn.metrics import f1_score
f1_score(y_train_shirt, y_train_pred)
y_scores = cross_val_predict(sgd_clf, X_train, y_train_shirt, cv=3, method="decision_function")
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_shirt, y_scores)
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)
plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)
plt.legend(loc="center right", fontsize=16) # Not shown in the book
plt.xlabel("Threshold", fontsize=16) # Not shown
plt.grid(True) # Not shown
plt.axis([-50000, 50000, 0, 1]) # Not shown
plt.figure(figsize=(8, 4)) # Not shown
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
#save_fig("precision_recall_vs_threshold_plot") # Not shown
plt.show()
def plot_precision_vs_recall(precisions, recalls):
plt.plot(recalls, precisions, "b-", linewidth=2)
plt.xlabel("Recall", fontsize=16)
plt.ylabel("Precision", fontsize=16)
plt.axis([0, 1, 0, 1])
plt.grid(True)
plt.figure(figsize=(8, 6))
plot_precision_vs_recall(precisions, recalls)
#save_fig("precision_vs_recall_plot")
plt.show()
```
Sneaker Binary Classifier for comparison
```
y_train_sneaker = (y_train == 7)
y_scores_sneaker = cross_val_predict(sgd_clf, X_train, y_train_sneaker, cv=3, method="decision_function")
precisions, recalls, thresholds = precision_recall_curve(y_train_sneaker, y_scores_sneaker)
plt.figure(figsize=(8, 4)) # Not shown
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
#save_fig("precision_recall_vs_threshold_plot") # Not shown
plt.show()
plt.figure(figsize=(8, 6))
plot_precision_vs_recall(precisions, recalls)
plt.show()
```
# ROC Curves
```
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_shirt, y_scores)
def plot_roc_curve(fpr, tpr, label=None):
plt.plot(fpr, tpr, linewidth=2, label=label)
plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal
plt.axis([0, 1, 0, 1]) # Not shown in the book
plt.xlabel('False Positive Rate (Fall-Out)', fontsize=16) # Not shown
plt.ylabel('True Positive Rate (Recall)', fontsize=16) # Not shown
plt.grid(True) # Not shown
plt.figure(figsize=(8, 6)) # Not shown
plot_roc_curve(fpr, tpr)
#save_fig("roc_curve_plot") # Not shown
plt.show()
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_shirt, y_scores)
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(n_estimators=100, random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_shirt, cv=3, method="predict_proba")
y_scores_forest = y_probas_forest[:, 1] # score = proba of positive class
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_shirt,y_scores_forest)
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, "b:", linewidth=2, label="SGD")
plot_roc_curve(fpr_forest, tpr_forest, "Random Forest")
plt.grid(True)
plt.legend(loc="lower right", fontsize=16)
#save_fig("roc_curve_comparison_plot")
plt.show()
roc_auc_score(y_train_shirt, y_scores_forest)
y_train_pred_forest = cross_val_predict(forest_clf, X_train, y_train_shirt, cv=3)
precision_score(y_train_shirt, y_train_pred_forest)
recall_score(y_train_shirt, y_train_pred_forest)
```
# Multiclass classification
```
#from sklearn.svm import SVC
#from sklearn.multiclass import OneVsRestClassifier
#ovr_clf = OneVsRestClassifier(SVC(gamma="auto", random_state=42))
#ovr_clf.fit(X_train, y_train)
forest_clf = RandomForestClassifier(n_estimators=100, random_state=42)
forest_clf.fit(X_train, y_train)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train.astype(np.float64))
y_train_pred_forest = cross_val_predict(forest_clf, X_train_scaled, y_train, cv=3)
from sklearn.metrics import accuracy_score
accuracy_score(y_train, y_train_pred_forest)
```
88% Accuracy
```
#cross_val_score(forest_clf, X_train_scaled, y_train, cv=3, scoring="accuracy")
```
# Error Analysis
```
conf_mx = confusion_matrix(y_train, y_train_pred_forest)
conf_mx
plt.matshow(conf_mx, cmap=plt.cm.gray)
plt.show()
row_sums = conf_mx.sum(axis=1, keepdims=True)
norm_conf_mx = conf_mx / row_sums
np.fill_diagonal(norm_conf_mx, 0)
plt.matshow(norm_conf_mx, cmap=plt.cm.gray)
plt.show()
```
6(shirt) is confused with 0(T-shirt/top) the most
```
cl_a, cl_b = 6, 0
X_aa = X_train[(y_train == cl_a) & (y_train_pred_forest == cl_a)]
X_ab = X_train[(y_train == cl_a) & (y_train_pred_forest == cl_b)]
X_ba = X_train[(y_train == cl_b) & (y_train_pred_forest == cl_a)]
X_bb = X_train[(y_train == cl_b) & (y_train_pred_forest == cl_b)]
plt.figure(figsize=(8,8))
plt.subplot(221); plot_digits(X_aa[:25], images_per_row=5)
plt.subplot(222); plot_digits(X_ab[:25], images_per_row=5)
plt.subplot(223); plot_digits(X_ba[:25], images_per_row=5)
plt.subplot(224); plot_digits(X_bb[:25], images_per_row=5)
plt.show()
```
The error / loss in accuraccy is mostly coming from the shirt being confused for a T-shirt or top. This confusion is from the length of the sleeves and is not easy to tell.
# Testing test sample
```
y_test_pred = forest_clf.predict(X_test)
accuracy_score(y_test, y_test_pred)
```
87% Accuracy
|
github_jupyter
|
##### Copyright 2018 Google LLC.
Licensed under the Apache License, Version 2.0 (the "License");
```
#@title Default title text
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Simple, Distributed, and Accelerated Probabilistic Programming
This notebook is a companion webpage for the NIPS 2018 paper, ["Simple, Distributed, and Accelerated Probabilistic Programming"](https://arxiv.org/abs/1811.02091) (Tran et al., 2018). See the [README.md](https://github.com/google/edward2) for details on how to interact with data, models, probabilistic inference, and more. It assumes the following dependencies:
```
!pip install scipy==1.0.0
!pip install tensor2tensor==1.9.0
!pip install tensorflow==1.12.0rc2 # alternatively, tensorflow-gpu==1.12.0rc2
import numpy as np
import tensorflow as tf
from contextlib import contextmanager
from scipy import stats
from tensor2tensor.layers import common_attention
from tensor2tensor.layers import common_image_attention as cia
from tensor2tensor.models import image_transformer as imgtransformer
from tensor2tensor.models import transformer
tfb = tf.contrib.distributions.bijectors
tfe = tf.contrib.eager
```
This notebook also requires importing files in this Github repository:
```
import edward2 as ed
import no_u_turn_sampler # local file import
```
Certain snippets require eager execution. This is run with the command below.
```
tf.enable_eager_execution()
```
## Section 2. Random Variables Are All You Need
__Figure 1__. Beta-Bernoulli program. In eager mode, `model()` generates a binary vector of $50$ elements. In graph mode, `model()` returns an op to be evaluated in a TensorFlow session.
```
def model():
p = ed.Beta(1., 1., name="p")
x = ed.Bernoulli(probs=p,
sample_shape=50,
name="x")
return x
x = model()
print(x)
```
__Figure 2__. Variational program (Ranganath et al., 2016), available in eager mode. Python control flow is applicable to generative processes: given a coin flip, the program generates from one of two neural nets. Their outputs can have differing shape (and structure).
```
def neural_net_negative(noise, inputs):
net = noise + inputs
net = tf.layers.dense(net, 512, activation=tf.nn.relu)
net = tf.layers.dense(net, 64, activation=None)
return net
def neural_net_positive(noise, inputs):
del noise, inputs # unused
return "Hello. I'm a different output type."
def variational(x):
eps = ed.Normal(0., 1., sample_shape=2)
if eps[0] > 0:
return neural_net_positive(eps[1], x)
else:
return neural_net_negative(eps[1], x)
if not tf.executing_eagerly():
raise ValueError("This code snippet requires eager execution.")
x = tf.random_normal([4, 64, 64, 3]) # batch of, e.g., 64x64x3 images
z = variational(x)
if isinstance(z, tf.Tensor):
print(type(z), z.shape) # to avoid printing a huge Tensor
else:
print(z)
```
__Figure 3.__ Distributed autoregressive flows. The default length is 8, each with 4 independent flows (Papamakarios et al., 2017). Each flow transforms inputs via layers respecting autoregressive ordering. Flows are partitioned across a virtual topology of 4x4 cores (rectangles); each core computes 2 flows and is locally connected; a final core aggregates. The virtual topology aligns with the physical TPU topology: for 4x4 TPUs, it is exact; for 16x16 TPUs, it is duplicated for data parallelism.
```
class SplitAutoregressiveFlow(tfb.Bijector):
def __init__(flow_size=[4]*8):
self.flows = []
for num_splits in flow_size:
flow = SplitAutoregressiveFlow(masked_network, num_splits)
self.flows.append(flow)
self.flows.append(SplitAutoregressiveFlow(masked_network, 1))
super(SplitAutoregressiveFlow, self).__init__()
def _forward(self, x):
for l, flow in enumerate(self.flows):
with tf.device(tf.contrib.tpu.core(l%4)):
x = flow.forward(x)
return x
def _inverse_and_log_det_jacobian(self, y):
ldj = 0.
for l, flow in enumerate(self.flows[::-1]):
with tf.device(tf.contrib.tpu.core(l%4)):
y, new_ldj = flow.inverse_and_log_det_jacobian(y)
ldj += new_ldj
return y, ldj
class DistributedAutoregressiveFlow(tfb.Bijector):
def __init__(flow_size=[4]*8):
self.flows = []
for num_splits in flow_size:
flow = SplitAutoregressiveFlow(masked_network, num_splits)
self.flows.append(flow)
self.flows.append(SplitAutoregressiveFlow(masked_network, 1))
super(DistributedAutoregressiveFlow, self).__init__()
def _forward(self, x):
for l, flow in enumerate(self.flows):
with tf.device(tf.contrib.tpu.core(l%4)):
x = flow.forward(x)
return x
def _inverse_and_log_det_jacobian(self, y):
ldj = 0.
for l, flow in enumerate(self.flows[::-1]):
with tf.device(tf.contrib.tpu.core(l%4)):
y, new_ldj = flow.inverse_and_log_det_jacobian(y)
ldj += new_ldj
return y, ldj
```
__Figure 4.__
Model-parallel VAE with TPUs, generating 16-bit audio from 8-bit latents. The prior and decoder split computation according to distributed autoregressive flows. The encoder may split computation according to `compressor`; we omit it for space.
```
def prior():
"""Uniform noise to 8-bit latent, [u1,...,u(T/2)] -> [z1,...,z(T/2)]"""
dist = ed.Independent(ed.Uniform(low=tf.zeros([batch_size, T/2])))
return ed.TransformedDistribution(dist, DistributedAutoregressiveFlow(flow_size))
def decoder(z):
"""Uniform noise + latent to 16-bit audio, [u1,...,uT], [z1,...,z(T/2)] -> [x1,...,xT]"""
dist = ed.Independent(ed.Uniform(low=tf.zeros([batch_size, T])))
dist = ed.TransformedDistribution(dist, tfb.Affine(shift=decompressor(z)))
return ed.TransformedDistribution(dist, DistributedAutoregressiveFlow(flow_size))
def encoder(x):
"""16-bit audio to 8-bit latent, [x1,...,xT] -> [z1,...,z(T/2)]"""
loc, log_scale = tf.split(compressor(x), 2, axis=-1)
return ed.MultivariateNormalDiag(loc=loc, scale=tf.exp(log_scale))
```
__Figure 5__. Edward2's core.
`trace` defines a context; any traceable ops executed during it are replaced by calls to `tracer`. `traceable` registers these ops; we register Edward random variables.
```
STACK = [lambda f, *a, **k: f(*a, **k)]
@contextmanager
def trace(tracer):
STACK.append(tracer)
yield
STACK.pop()
def traceable(f):
def f_wrapped(*a, **k):
STACK[-1](f, *a, **k)
return f_wrapped
```
__Figure 7__. A higher-order function which takes a `model` program as input and returns its log-joint density function.
```
def make_log_joint_fn(model):
def log_joint_fn(**model_kwargs):
def tracer(rv_call, *args, **kwargs):
name = kwargs.get("name")
kwargs["value"] = model_kwargs.get(name)
rv = rv_call(*args, **kwargs)
log_probs.append(tf.reduce_sum(rv.distribution.log_prob(rv)))
return rv
log_probs = []
with ed.trace(tracer):
model()
return sum(log_probs)
return log_joint_fn
try:
model
except NameError:
raise NameError("This code snippet requires `model` from above.")
log_joint = make_log_joint_fn(model)
p = np.random.uniform()
x = np.round(np.random.normal(size=[50])).astype(np.int32)
out = log_joint(p=p, x=x)
print(out)
```
__Figure 8__. A higher-order function which takes a `model` program as input and returns its causally intervened program. Intervention differs from conditioning: it does not change the sampled value but the distribution.
```
def mutilate(model, **do_kwargs):
def mutilated_model(*args, **kwargs):
def tracer(rv_call, *args, **kwargs):
name = kwargs.get("name")
if name in do_kwargs:
return do_kwargs[name]
return rv_call(*args, **kwargs)
with ed.trace(tracer):
return model(*args, **kwargs)
return mutilated_model
try:
model
except NameError:
raise NameError("This code snippet requires `model` from above.")
mutilated_model = mutilate(model, p=0.999)
x = mutilated_model()
print(x)
```
## Section 3. Learning with Low-Level Functions
__FIgure 9__. Data-parallel Image Transformer with TPUs (Parmar et al., 2018). It is a neural autoregressive model which computes the log-probability of a batch of images with self-attention. Edward2 enables representing and training the model as a log-probability function; this is more efficient than the typical representation of programs as a generative process.
```
get_channel_embeddings = cia.get_channel_embeddings
add_positional_embedding = common_attention.add_positional_embedding
local_attention_1d = cia.local_attention_1d
def image_transformer(inputs, hparams):
x = get_channel_embeddings(3, inputs, hparams.hidden_size)
x = tf.reshape(x, [-1, 32*32*3, hparams.hidden_size])
x = tf.pad(x, [[0, 0], [1, 0], [0, 0]])[:, :-1, :] # shift pixels right
x = add_positional_embedding(x, max_length=32*32*3+3, name="pos_embed")
x = tf.nn.dropout(x, keep_prob=0.7)
for _ in range(hparams.num_decoder_layers):
with tf.variable_scope(None, default_name="decoder_layer"):
y = local_attention_1d(x, hparams, attention_type="local_mask_right",
q_padding="LEFT", kv_padding="LEFT")
x = tf.contrib.layers.layer_norm(tf.nn.dropout(y, keep_prob=0.7) + x, begin_norm_axis=-1)
y = tf.layers.dense(x, hparams.filter_size, activation=tf.nn.relu)
y = tf.layers.dense(y, hparams.hidden_size, activation=None)
x = tf.contrib.layers.layer_norm(tf.nn.dropout(y, keep_prob=0.7) + x, begin_norm_axis=-1)
x = tf.reshape(x, [-1, 32, 32, 3, hparams.hidden_size])
logits = tf.layers.dense(x, 256, activation=None)
return ed.Categorical(logits=logits).distribution.log_prob(inputs)
if tf.executing_eagerly():
raise ValueError("This code snippet does not support eager execution.")
batch_size = 4
inputs = tf.random_uniform([batch_size, 32, 32, 3], minval=0, maxval=256, dtype=tf.int32)
hparams = imgtransformer.imagetransformer_cifar10_base()
loss = -tf.reduce_sum(image_transformer(inputs, hparams))
train_op = tf.contrib.tpu.CrossShardOptimizer(tf.train.AdamOptimizer()).minimize(loss)
print(loss)
```
__Figure 10__. Core logic in No-U-Turn Sampler (Hoffman and Gelman, 2014). This algorithm has data-dependent non-tail recursion.
See [`no_u_turn_sampler/`](https://github.com/google/edward2/tree/master/examples/no_u_turn_sampler/) in the Github repository for its full implementation.
__Figure 11__. Variational inference with preconditioned gradient descent. Edward2 offers writing the probabilistic program and performing arbitrary TensorFlow computation for learning.
```
try:
model
make_log_joint_fn
except NameError:
raise NameError("This code snippet requires `model`, `make_log_joint_fn` "
" from above.")
class Variational(object):
def __init__(self):
self.parameters = tf.random_normal([2])
def __call__(self, x):
del x # unused; it is a non-amortized approximation
return ed.Deterministic(loc=tf.sigmoid(self.parameters[0]), name="qp")
variational = Variational()
x = tf.random_uniform([50], minval=0, maxval=2, dtype=tf.int32)
alignment = {"qp": "p"}
def loss(x):
qz = variational(x)
log_joint_fn = make_log_joint_fn(model)
kwargs = {alignment[rv.distribution.name]: rv.value
for rv in [qz]}
energy = log_joint_fn(x=x, **kwargs)
entropy = sum([rv.distribution.entropy() for rv in [qz]])
return -energy - entropy
def grad():
with tf.GradientTape() as tape:
tape.watch(variational.parameters)
loss_value = loss(x)
return tape.gradient(loss_value, variational.parameters)
def train(precond):
for _ in range(5):
grads = tf.tensordot(precond, grad(), [[1], [0]])
variational.parameters -= 0.1 * grads
return loss(x)
if not tf.executing_eagerly():
raise ValueError("This code snippet requires eager execution.")
precond = tf.eye(2)
loss_value = train(precond)
print(loss_value)
```
__Figure 12__. Learning-to-learn. It finds the optimal preconditioner for `train` (__Figure 11__) by differentiating the entire learning algorithm with respect to the preconditioner.
```
if not tf.executing_eagerly():
raise ValueError("This code snippet requires eager execution.")
precond = tfe.Variable(tf.random_normal([2, 2]))
optimizer = tf.train.AdamOptimizer(1.)
for _ in range(10):
with tf.GradientTape() as tape:
loss_value = train(precond)
grads = tape.gradient(loss_value, [precond])
optimizer.apply_gradients(zip(grads, [precond]))
print(loss_value.numpy(), precond.numpy())
```
## Appendix A. Edward2 on SciPy
We illustrate the broad applicability of Edward2’s tracing by implementing Edward2 on top of SciPy.
For this notebook, we mimick a namespace using a struct so that one can play with the traceable scipy stats here.
```
class FakeEdward2ScipyNamespace(object):
pass
for _name in sorted(dir(stats)):
_candidate = getattr(stats, _name)
if isinstance(_candidate, (stats._multivariate.multi_rv_generic,
stats.rv_continuous,
stats.rv_discrete,
stats.rv_histogram)):
_candidate.rvs = ed.traceable(_candidate.rvs)
setattr(FakeEdward2ScipyNamespace, _name, _candidate)
del _candidate
scipy_stats = FakeEdward2ScipyNamespace()
print([name for name in dir(scipy_stats) if not name.startswith("__")])
```
Below is an Edward2 linear regression program on SciPy.
```
def make_log_joint_fn(model):
def log_joint_fn(*model_args, **model_kwargs):
def tracer(rv_call, *args, **kwargs):
name = kwargs.pop("name", None)
kwargs.pop("size", None)
kwargs.pop("random_state", None)
value = model_kwargs.get(name)
log_prob_fn = getattr(scipy_stats, rv_call.im_class.__name__[:-4]).logpdf
log_prob = np.sum(log_prob_fn(value, *args, **kwargs))
log_probs.append(log_prob)
return value
log_probs = []
with ed.trace(tracer):
model(*model_args)
return sum(log_probs)
return log_joint_fn
def linear_regression(X):
beta = scipy_stats.norm.rvs(loc=0.0, scale=0.1, size=X.shape[1], name="beta")
loc = np.einsum('ij,j->i', X, beta)
y = scipy_stats.norm.rvs(loc=loc, scale=1., size=1, name="y")
return y
log_joint = make_log_joint_fn(linear_regression)
X = np.random.normal(size=[3, 2])
beta = np.random.normal(size=[2])
y = np.random.normal(size=[3])
out = log_joint(X, beta=beta, y=y)
print(out)
```
## Appendix B. Grammar Variational Auto-Encoder
The grammar variational auto-encoder (VAE) (Kusner et al., 2017) posits a generative model over
productions from a context-free grammar, and it posits an amortized variational
approximation for efficient posterior inference. We train the grammar VAE
on synthetic data using the grammar from Kusner et al. (2017; Figure 1).
This example showcases eager execution in order to train the model where data
points have a variable number of time steps. However, note that this requires a
batch size of 1. In this example, we assume data points arrive in a stream, one
at a time. Such a setting requires handling a variable number of time steps
as the maximum length is unbounded.
```
class SmilesGrammar(object):
"""Context-free grammar for SMILES strings."""
nonterminal_symbols = {"smiles", "chain", "branched atom", "atom", "ringbond",
"aromatic organic", "aliphatic organic", "digit"}
alphabet = {"c", "C", "N", "1", "2"}
production_rules = [
("smiles", ["chain"]),
("chain", ["chain", "branched atom"]),
("chain", ["branched atom"]),
("branched atom", ["atom", "ringbond"]),
("branched atom", ["atom"]),
("atom", ["aromatic organic"]),
("atom", ["aliphatic organic"]),
("ringbond", ["digit"]),
("aromatic organic", ["c"]),
("aliphatic organic", ["C"]),
("aliphatic organic", ["N"]),
("digit", ["1"]),
("digit", ["2"]),
]
start_symbol = "smiles"
def mask(self, symbol, on_value=0., off_value=-1e9):
"""Produces a masking tensor for (in)valid production rules."""
mask_values = []
for lhs, _ in self.production_rules:
if symbol in lhs:
mask_value = on_value
else:
mask_value = off_value
mask_values.append(mask_value)
mask_values = tf.reshape(mask_values, [1, len(self.production_rules)])
return mask_values
class ProbabilisticGrammar(tf.python.keras.Model):
"""Deep generative model over productions which follow a grammar."""
def __init__(self, grammar, latent_size, num_units):
"""Constructs a probabilistic grammar."""
super(ProbabilisticGrammar, self).__init__()
self.grammar = grammar
self.latent_size = latent_size
self.lstm = tf.nn.rnn_cell.LSTMCell(num_units)
self.output_layer = tf.python.keras.layers.Dense(len(grammar.production_rules))
def call(self, inputs):
"""Runs the model forward to generate a sequence of productions."""
del inputs # unused
latent_code = ed.MultivariateNormalDiag(loc=tf.zeros(self.latent_size),
sample_shape=1,
name="latent_code")
state = self.lstm.zero_state(1, dtype=tf.float32)
t = 0
productions = []
stack = [self.grammar.start_symbol]
while stack:
symbol = stack.pop()
net, state = self.lstm(latent_code, state)
logits = self.output_layer(net) + self.grammar.mask(symbol)
production = ed.OneHotCategorical(logits=logits,
name="production_" + str(t))
_, rhs = self.grammar.production_rules[tf.argmax(production, axis=1)]
for symbol in rhs:
if symbol in self.grammar.nonterminal_symbols:
stack.append(symbol)
productions.append(production)
t += 1
return tf.stack(productions, axis=1)
class ProbabilisticGrammarVariational(tf.python.keras.Model):
"""Amortized variational posterior for a probabilistic grammar."""
def __init__(self, latent_size):
"""Constructs a variational posterior for a probabilistic grammar."""
super(ProbabilisticGrammarVariational, self).__init__()
self.latent_size = latent_size
self.encoder_net = tf.python.keras.Sequential([
tf.python.keras.layers.Conv1D(64, 3, padding="SAME"),
tf.python.keras.layers.BatchNormalization(),
tf.python.keras.layers.Activation(tf.nn.elu),
tf.python.keras.layers.Conv1D(128, 3, padding="SAME"),
tf.python.keras.layers.BatchNormalization(),
tf.python.keras.layers.Activation(tf.nn.elu),
tf.python.keras.layers.Dropout(0.1),
tf.python.keras.layers.GlobalAveragePooling1D(),
tf.python.keras.layers.Dense(latent_size * 2, activation=None),
])
def call(self, inputs):
"""Runs the model forward to return a stochastic encoding."""
net = self.encoder_net(tf.cast(inputs, tf.float32))
return ed.MultivariateNormalDiag(
loc=net[..., :self.latent_size],
scale_diag=tf.nn.softplus(net[..., self.latent_size:]),
name="latent_code_posterior")
if not tf.executing_eagerly():
raise ValueError("This code snippet requires eager execution.")
grammar = SmilesGrammar()
probabilistic_grammar = ProbabilisticGrammar(
grammar=grammar, latent_size=8, num_units=128)
probabilistic_grammar_variational = ProbabilisticGrammarVariational(
latent_size=8)
for _ in range(5):
productions = probabilistic_grammar(_)
print("Production Shape: {}".format(productions.shape))
string = grammar.convert_to_string(productions)
print("String: {}".format(string))
encoded_production = probabilistic_grammar_variational(productions)
print("Encoded Productions: {}".format(encoded_production.numpy()))
```
See [`tensorflow_probability/examples/grammar_vae.py`](https://github.com/tensorflow/probability/blob/master/tensorflow_probability/examples/grammar_vae.py) for the full example.
## Appendix C. Markov chain Monte Carlo within Variational Inference
We demonstrate another level of composability: inference within a probabilistic program. Namely, we apply MCMC to construct a flexible family of distributions for variational inference
(Salimans et al., 2015; Hoffman, 2017). We apply a chain of transition kernels specified by NUTS (`nuts`) in Section 3.3 and the variational inference algorithm specified by `train` in __Figure 12__.
```
class DeepLatentGaussianModel(tf.python.keras.Model):
"""Deep generative model."""
def __init__(self, latent_size, data_shape, batch_size):
super(DeepLatentGaussianModel, self).__init__()
self.latent_size = latent_size
self.data_shape = data_shape
self.batch_size = batch_size
self.decoder_net = tf.python.keras.Sequential([
tf.python.keras.layers.Dense(512, activation=tf.nn.relu),
tf.python.keras.layers.Dense(np.prod(data_shape), activation=None),
tf.python.keras.layers.Reshape(data_shape),
])
def call(self, inputs):
del inputs # unused
latent_code = ed.MultivariateNormalDiag(
loc=tf.zeros([self.batch_size, self.latent_size]),
scale_diag=tf.ones([self.batch_size, self.latent_size]),
name="latent_code")
data = ed.Categorical(logits=self.decoder_net(latent_code), name="data")
return data
class DeepLatentGaussianModelVariational(tf.python.keras.Model):
"""Amortized variational posterior."""
def __init__(self,
latent_size,
data_shape,
num_transitions,
target_log_prob_fn,
step_size):
super(DeepLatentGaussianModelVariational, self).__init__()
self.latent_size = latent_size
self.data_shape = data_shape
self.num_transitions = num_transitions
self.target_log_prob_fn = target_log_prob_fn
self.step_size = step_size
self.encoder_net = tf.python.keras.Sequential([
tf.python.keras.layers.Reshape(np.prod(data_shape)),
tf.python.keras.layers.Dense(512, activation=tf.nn.relu),
tf.python.keras.layers.Dense(latent_size * 2, activation=None),
])
def call(self, inputs):
net = encoder_net(inputs)
qz = ed.MultivariateNormalDiag(
loc=net[..., :self.latent_size],
scale_diag=tf.nn.softplus(net[..., self.latent_size:]),
name="latent_code_posterior")
current_target_log_prob = None
current_grads_target_log_prob = None
for _ in range(self.num_transitions):
[
[qz],
current_target_log_prob,
current_grads_target_log_prob,
] = self._kernel(
current_state=[qz],
current_target_log_prob=current_target_log_prob,
current_grads_target_log_prob=current_grads_target_log_prob)
return qz
def _kernel(self, current_state, current_target_log_prob,
current_grads_target_log_prob):
return no_u_turn_sampler.kernel(
current_state=current_state,
target_log_prob_fn=self.target_log_prob_fn,
step_size=self.step_size,
current_target_log_prob=current_target_log_prob,
current_grads_target_log_prob=current_grads_target_log_prob)
latent_size = 50
data_shape = [32, 32, 3, 256]
batch_size = 4
features = tf.random_normal([batch_size] + data_shape)
model = DeepLatentGaussianModel(
latent_size=latent_size,
data_shape=data_shape,
batch_size=batch_size)
variational = DeepLatentGaussianModelVariational(
latent_size=latent_size,
data_shape=data_shape,
step_size=[0.1],
target_log_prob_fn=lambda z: ed.make_log_joint(model)(x=x, z=z),
num_transitions=10)
alignment = {"latent_code_posterior": "latent_code"}
optimizer = tf.train.AdamOptimizer(1e-2)
for _ in range(10):
with tf.GradientTape() as tape:
with ed.trace() as variational_tape:
_ = variational(features)
log_joint_fn = make_log_joint_fn(model)
kwargs = {alignment[rv.distribution.name]: rv.value
for rv in variational_tape.values()}
energy = log_joint_fn(data=features, **kwargs)
entropy = sum([rv.distribution.entropy()
for rv in variational_tape.values()])
loss_value = -energy - entropy
grads = tape.gradient(loss_value, variational.variables)
optimizer.apply_gradients(zip(grads, variational.variables))
print("Step: {:>3d} Loss: {:.3f}".format(step, loss_value))
```
## Appendix D. No-U-Turn Sampler
We implement an Edward program for Bayesian logistic regression with NUTS (Hoffman and Gelman, 2014).
```
def logistic_regression(features):
"""Bayesian logistic regression, which returns labels given features."""
coeffs = ed.MultivariateNormalDiag(
loc=tf.zeros(features.shape[1]), name="coeffs")
labels = ed.Bernoulli(
logits=tf.tensordot(features, coeffs, [[1], [0]]), name="labels")
return labels
features = tf.random_uniform([500, 55])
true_coeffs = 5. * tf.random_normal([55])
labels = tf.cast(tf.tensordot(features, true_coeffs, [[1], [0]]) > 0,
dtype=tf.int32)
log_joint = ed.make_log_joint_fn(logistic_regression)
def target_log_prob_fn(coeffs):
return log_joint(features=features, coeffs=coeffs, labels=labels)
if not tf.executing_eagerly():
raise ValueError("This code snippet requires eager execution.")
coeffs_samples = []
target_log_prob = None
grads_target_log_prob = None
for step in range(500):
[
[coeffs],
target_log_prob,
grads_target_log_prob,
] = kernel(target_log_prob_fn=target_log_prob_fn,
current_state=[coeffs],
step_size=[0.1],
current_target_log_prob=target_log_prob,
current_grads_target_log_prob=grads_target_log_prob)
coeffs_samples.append(coeffs)
for coeffs_sample in coeffs_samples:
plt.plot(coeffs_sample.numpy())
plt.show()
```
See [`no_u_turn_sampler/logistic_regression.py`](https://github.com/google/edward2/tree/master/examples/no_u_turn_sampler/logistic_regression.py) for the full example.
## References
1. Hoffman, M. D. (2017). Learning deep latent Gaussian models with Markov chain Monte Carlo. In _International Conference on Machine Learning_.
2. Hoffman, M. D. and Gelman, A. (2014). The No-U-turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. _Journal of Machine Learning Research_, 15(1):1593–1623.
3. Kusner, M. J., Paige, B., and Hernández-Lobato, J. M. (2017). Grammar variational auto-encoder. In _International Conference on Machine Learning_.
4. Papamakarios, G., Murray, I., and Pavlakou, T. (2017). Masked autoregressive flow for density estimation. In _Neural Information Processing Systems_.
5. Parmar, N., Vaswani, A., Uszkoreit, J., Kaiser, Ł., Shazeer, N., Ku, A., and Tran, D. (2018). Image transformer. In _International Conference on Machine Learning_.
6. Ranganath, R., Altosaar, J., Tran, D., and Blei, D. M. (2016). Operator variational inference. In _Neural Information Processing Systems_.
7. Salimans, T., Kingma, D., and Welling, M. (2015). Markov chain Monte Carlo and variational inference: Bridging the gap. In _International Conference on Machine Learning_.
8. Tran, D., Hoffman, M. D., Moore, D., Suter, C., Vasudevan S., Radul A., Johnson M., and Saurous R. A. (2018). Simple, Distributed, and Accelerated Probabilistic Programming. In _Neural Information Processing Systems_.
|
github_jupyter
|
# 5章 線形回帰
```
# 必要ライブラリの導入
!pip install japanize_matplotlib | tail -n 1
!pip install torchviz | tail -n 1
!pip install torchinfo | tail -n 1
# 必要ライブラリのインポート
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from IPython.display import display
import torch
import torch.nn as nn
import torch.optim as optim
from torchviz import make_dot
# デフォルトフォントサイズ変更
plt.rcParams['font.size'] = 14
# デフォルトグラフサイズ変更
plt.rcParams['figure.figsize'] = (6,6)
# デフォルトで方眼表示ON
plt.rcParams['axes.grid'] = True
# numpyの浮動小数点の表示精度
np.set_printoptions(suppress=True, precision=4)
```
## 5.3 線形関数(nn.Linear)
### 入力:1 出力:1 の線形関数
```
# 乱数の種固定
torch.manual_seed(123)
# 入力:1 出力:1 の線形関数の定義
l1 = nn.Linear(1, 1)
# 線形関数の表示
print(l1)
# パラメータ名、パラメータ値、shapeの表示
for param in l1.named_parameters():
print('name: ', param[0])
print('tensor: ', param[1])
print('shape: ', param[1].shape)
# 初期値設定
nn.init.constant_(l1.weight, 2.0)
nn.init.constant_(l1.bias, 1.0)
# 結果確認
print(l1.weight)
print(l1.bias)
# テスト用データ生成
# x_npをnumpy配列で定義
x_np = np.arange(-2, 2.1, 1)
# Tensor化
x = torch.tensor(x_np).float()
# サイズを(N,1)に変更
x = x.view(-1,1)
# 結果確認
print(x.shape)
print(x)
# 1次関数のテスト
y = l1(x)
print(y.shape)
print(y.data)
```
### 入力:2 出力:1 の線形関数
```
# 入力:2 出力:1 の線形関数の定義
l2 = nn.Linear(2, 1)
# 初期値設定
nn.init.constant_(l2.weight, 1.0)
nn.init.constant_(l2.bias, 2.0)
# 結果確認
print(l2.weight)
print(l2.bias)
# 2次元numpy配列
x2_np = np.array([[0, 0], [0, 1], [1, 0], [1,1]])
# Tensor化
x2 = torch.tensor(x2_np).float()
# 結果確認
print(x2.shape)
print(x2)
# 関数値計算
y2 = l2(x2)
# shape確認
print(y2.shape)
# 値確認
print(y2.data)
```
### 入力:2 出力:3 の線形関数
```
# 入力:2 出力:3 の線形関数の定義
l3 = nn.Linear(2, 3)
# 初期値設定
nn.init.constant_(l3.weight[0,:], 1.0)
nn.init.constant_(l3.weight[1,:], 2.0)
nn.init.constant_(l3.weight[2,:], 3.0)
nn.init.constant_(l3.bias, 2.0)
# 結果確認
print(l3.weight)
print(l3.bias)
# 関数値計算
y3 = l3(x2)
# shape確認
print(y3.shape)
# 値確認
print(y3.data)
```
## 5.4 カスタムクラスを利用したモデル定義
```
# モデルのクラス定義
class Net(nn.Module):
def __init__(self, n_input, n_output):
# 親クラスnn.Modulesの初期化呼び出し
super().__init__()
# 出力層の定義
self.l1 = nn.Linear(n_input, n_output)
# 予測関数の定義
def forward(self, x):
x1 = self.l1(x) # 線形回帰
return x1
# ダミー入力
inputs = torch.ones(100,1)
# インスタンスの生成 (1入力1出力の線形モデル)
n_input = 1
n_output = 1
net = Net(n_input, n_output)
# 予測
outputs = net(inputs)
```
## 5.6 データ準備
UCI公開データセットのうち、回帰でよく使われる「ボストン・データセット」を用いる。
https://www.cs.toronto.edu/~delve/data/boston/bostonDetail.html
オリジナルのデーセットは、17項目の入力値から、不動産価格を予測する目的のものだが、
一番単純な「単回帰モデル」(1入力)のモデルを作るため、このうち``RM``の1項目だけを抽出する。
```
# 学習用データ準備
# ライブラリのインポート
from sklearn.datasets import load_boston
# データ読み込み
boston = load_boston()
# 入力データと正解データ取得
x_org, yt = boston.data, boston.target
# 項目名リスト取得
feature_names = boston.feature_names
# 結果確認
print('元データ', x_org.shape, yt.shape)
print('項目名: ', feature_names)
# データ絞り込み (項目 RMのみ)
x = x_org[:,feature_names == 'RM']
print('絞り込み後', x.shape)
print(x[:5,:])
# 正解データ yの表示
print('正解データ')
print(yt[:5])
# 散布図の表示
plt.scatter(x, yt, s=10, c='b')
plt.xlabel('部屋数')
plt.ylabel('価格')
plt.title('部屋数と価格の散布図')
plt.show()
```
## 5.7 モデル定義
```
# 変数定義
# 入力次元数
n_input= x.shape[1]
# 出力次元数
n_output = 1
print(f'入力次元数: {n_input} 出力次元数: {n_output}')
# 機械学習モデル(予測モデル)クラス定義
class Net(nn.Module):
def __init__(self, n_input, n_output):
# 親クラスnn.Modulesの初期化呼び出し
super().__init__()
# 出力層の定義
self.l1 = nn.Linear(n_input, n_output)
# 初期値を全部1にする
# 「ディープラーニングの数学」と条件を合わせる目的
nn.init.constant_(self.l1.weight, 1.0)
nn.init.constant_(self.l1.bias, 1.0)
# 予測関数の定義
def forward(self, x):
x1 = self.l1(x) # 線形回帰
return x1
# インスタンスの生成
# 1入力1出力の線形モデル
net = Net(n_input, n_output)
# モデル内のパラメータの確認
# モデル内の変数取得にはnamed_parameters関数を利用する
# 結果の第1要素が名前、第2要素が値
#
# predict.weightとpredict.biasがあることがわかる
# 初期値はどちらも1.0になっている
for parameter in net.named_parameters():
print(f'変数名: {parameter[0]}')
print(f'変数値: {parameter[1].data}')
# パラメータのリスト取得にはparameters関数を利用する
for parameter in net.parameters():
print(parameter)
```
### モデル確認
```
# モデルの概要表示
print(net)
# モデルのサマリー表示
from torchinfo import summary
summary(net, (1,))
```
### 損失関数と最適化関数
```
# 損失関数: 平均2乗誤差
criterion = nn.MSELoss()
# 学習率
lr = 0.01
# 最適化関数: 勾配降下法
optimizer = optim.SGD(net.parameters(), lr=lr)
```
## 5.8 勾配降下法
```
# 入力変数x と正解値 ytのテンソル変数化
inputs = torch.tensor(x).float()
labels = torch.tensor(yt).float()
# 次元数確認
print(inputs.shape)
print(labels.shape)
# 損失値計算用にlabels変数を(N,1)次元の行列に変換する
labels1 = labels.view((-1, 1))
# 次元数確認
print(labels1.shape)
# 予測計算
outputs = net(inputs)
# 損失計算
loss = criterion(outputs, labels1)
# 損失値の取得
print(f'{loss.item():.5f}')
# 損失の計算グラフ可視化
g = make_dot(loss, params=dict(net.named_parameters()))
display(g)
# 予測計算
outputs = net(inputs)
# 損失計算
loss = criterion(outputs, labels1)
# 勾配計算
loss.backward()
# 勾配の結果が取得可能に
print(net.l1.weight.grad)
print(net.l1.bias.grad)
# パラメータ修正
optimizer.step()
# パラメータ値が変わる
print(net.l1.weight)
print(net.l1.bias)
# 勾配値の初期化
optimizer.zero_grad()
# 勾配値がすべてゼロになっている
print(net.l1.weight.grad)
print(net.l1.bias.grad)
```
### 繰り返し計算
```
# 学習率
lr = 0.01
# インスタンス生成 (パラメータ値初期化)
net = Net(n_input, n_output)
# 損失関数: 平均2乗誤差
criterion = nn.MSELoss()
# 最適化関数: 勾配降下法
optimizer = optim.SGD(net.parameters(), lr=lr)
# 繰り返し回数
num_epochs = 50000
# 評価結果記録用 (損失関数値のみ記録)
history = np.zeros((0,2))
# 繰り返し計算メインループ
for epoch in range(num_epochs):
# 勾配値初期化
optimizer.zero_grad()
# 予測計算
outputs = net(inputs)
# 損失計算
# 「ディープラーニングの数学」に合わせて2で割った値を損失とした
loss = criterion(outputs, labels1) / 2.0
# 勾配計算
loss.backward()
# パラメータ修正
optimizer.step()
# 100回ごとに途中経過を記録する
if ( epoch % 100 == 0):
history = np.vstack((history, np.array([epoch, loss.item()])))
print(f'Epoch {epoch} loss: {loss.item():.5f}')
```
## 5.9 結果確認
```
# 損失初期値と最終値
print(f'損失初期値: {history[0,1]:.5f}')
print(f'損失最終値: {history[-1,1]:.5f}')
# 学習曲線の表示 (損失)
# 最初の1つを除く
plt.plot(history[1:,0], history[1:,1], 'b')
plt.xlabel('繰り返し回数')
plt.ylabel('損失')
plt.title('学習曲線(損失)')
plt.show()
# 回帰直線の算出
# xの最小値、最大値
xse = np.array((x.min(), x.max())).reshape(-1,1)
Xse = torch.tensor(xse).float()
with torch.no_grad():
Yse = net(Xse)
print(Yse.numpy())
# 散布図と回帰直線の描画
plt.scatter(x, yt, s=10, c='b')
plt.xlabel('部屋数')
plt.ylabel('価格')
plt.plot(Xse.data, Yse.data, c='k')
plt.title('散布図と回帰直線')
plt.show()
```
## 5.10 重回帰モデルへの拡張
```
# 列(LSTAT: 低所得者率)の追加
x_add = x_org[:,feature_names == 'LSTAT']
x2 = np.hstack((x, x_add))
# shapeの表示
print(x2.shape)
# 入力データxの表示
print(x2[:5,:])
# 今度は入力次元数=2
n_input = x2.shape[1]
print(n_input)
# モデルインスタンスの生成
net = Net(n_input, n_output)
# モデル内のパラメータの確認
# predict.weight が2次元に変わった
for parameter in net.named_parameters():
print(f'変数名: {parameter[0]}')
print(f'変数値: {parameter[1].data}')
# モデルの概要表示
print(net)
# モデルのサマリー表示
from torchinfo import summary
summary(net, (2,))
# 入力変数x2 のテンソル変数化
# labels, labels1は前のものをそのまま利用
inputs = torch.tensor(x2).float()
```
### くり返し計算
```
# 初期化処理
# 学習率
lr = 0.01
# インスタンス生成 (パラメータ値初期化)
net = Net(n_input, n_output)
# 損失関数: 平均2乗誤差
criterion = nn.MSELoss()
# 最適化関数: 勾配降下法
optimizer = optim.SGD(net.parameters(), lr=lr)
# 繰り返し回数
num_epochs = 50000
# 評価結果記録用 (損失関数値のみ記録)
history = np.zeros((0,2))
# 繰り返し計算メインループ
for epoch in range(num_epochs):
# 勾配値初期化
optimizer.zero_grad()
# 予測計算
outputs = net(inputs)
# 誤差計算
# 「ディープラーニングの数学」に合わせて2で割った値を損失とした
loss = criterion(outputs, labels1) / 2.0
# 勾配計算
loss.backward()
# パラメータ修正
optimizer.step()
# 100回ごとに途中経過を記録する
if ( epoch % 100 == 0):
history = np.vstack((history, np.array([epoch, loss.item()])))
print(f'Epoch {epoch} loss: {loss.item():.5f}')
```
## 5.11 学習率の変更
```
# 繰り返し回数
#num_epochs = 50000
num_epochs = 2000
# 学習率
#l r = 0.01
lr = 0.001
# モデルインスタンスの生成
net = Net(n_input, n_output)
# 損失関数: 平均2乗誤差
criterion = nn.MSELoss()
# 最適化関数: 勾配降下法
optimizer = optim.SGD(net.parameters(), lr=lr)
# 繰り返し計算メインループ
# 評価結果記録用 (損失関数値のみ記録)
history = np.zeros((0,2))
for epoch in range(num_epochs):
# 勾配値初期化
optimizer.zero_grad()
# 予測計算
outputs = net(inputs)
# 誤差計算
loss = criterion(outputs, labels1) / 2.0
#勾配計算
loss.backward()
# パラメータ修正
optimizer.step()
# 100回ごとに途中経過を記録する
if ( epoch % 100 == 0):
history = np.vstack((history, np.array([epoch, loss.item()])))
print(f'Epoch {epoch} loss: {loss.item():.5f}')
# 損失初期値、最終値
print(f'損失初期値: {history[0,1]:.5f}')
print(f'損失最終値: {history[-1,1]:.5f}')
# 学習曲線の表示 (損失)
plt.plot(history[:,0], history[:,1], 'b')
plt.xlabel('繰り返し回数')
plt.ylabel('損失')
plt.title('学習曲線(損失)')
plt.show()
```
|
github_jupyter
|
```
import os
import numpy as np
np.set_printoptions(suppress=True)
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from matplotlib.ticker import LinearLocator
from matplotlib import gridspec
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()
%matplotlib inline
print("Package is ready.")
plt.rcParams['figure.figsize'] = ((8/2.54), (6/2.54))
plt.rcParams["font.family"] = "Arial"
plt.rcParams["mathtext.default"] = "rm"
plt.rcParams.update({'font.size': 11})
MARKER_SIZE = 15
cmap_m = ["#f4a6ad", "#f6957e", "#fccfa2", "#8de7be", "#86d6f2", "#24a9e4", "#b586e0", "#d7f293"]
cmap = ["#e94d5b", "#ef4d28", "#f9a54f", "#25b575", "#1bb1e7", "#1477a2", "#a662e5", "#c2f442"]
plt.rcParams['axes.spines.top'] = False
# plt.rcParams['axes.edgecolor'] =
plt.rcParams['axes.linewidth'] = 1
plt.rcParams['lines.linewidth'] = 1.5
plt.rcParams['xtick.major.width'] = 1
plt.rcParams['xtick.minor.width'] = 1
plt.rcParams['ytick.major.width'] = 1
plt.rcParams['ytick.minor.width'] = 1
```
# 2020 Summer
## Control weight
```
SW2_df = pd.read_csv('./results/2020_S/SW2_greenhouse.csv', index_col='Unnamed: 0')
SW2_df.index = pd.DatetimeIndex(SW2_df.index)
```
### Cultivation period
```
SW2_df = SW2_df.loc['2020-03-05 00:00:00': '2020-07-03 23:59:00']
SW2_df = SW2_df.interpolate()
```
### Rockwool weight
```
rockwool_mean = 656.50/1000
```
### water weight
```
substrate_volume = (120*12*7.5 + 10*10*6.5*4)/1000
water_w_df = substrate_volume*SW2_df['subs_VWC']/100
SW2_df['water'] = water_w_df
```
### Calculating aerial weight
```
SW2_df.loc[:, 'loadcell_1'] = SW2_df.loc[:, 'loadcell_1'] - rockwool_mean
SW2_df.loc[:, 'loadcell_2'] = SW2_df.loc[:, 'loadcell_2'] - rockwool_mean
SW2_df.loc[:, 'loadcell_3'] = SW2_df.loc[:, 'loadcell_3'] - rockwool_mean
```
### Destructive crop weight
```
weight_df = pd.read_csv('./results/2020_S/weight_ct.csv', index_col='Unnamed: 0')
weight_df.index = pd.DatetimeIndex(weight_df.index)
weight_df.index = np.append(weight_df.index[:-20], pd.DatetimeIndex(['2020-07-03']*20))
wweight_df = weight_df[['Stem FW', 'Leaf FW', 'petiole FW', 'Idv fruit FW']].sum(axis=1)
```
### Root DW to FW
```
roots_DW_mean = 297.27
DW_sum_df = weight_df.loc[:, [_ for _ in weight_df.columns if _.endswith('DW')]].sum(axis=1)
rs_ratio_df = (roots_DW_mean/(DW_sum_df.loc['2020-07-03']*4)).mean()
roots_df = pd.DataFrame(DW_sum_df * rs_ratio_df)
roots_df.columns = ['root DW']
roots_df['root FW'] = roots_df['root DW']/0.1325
roots_df.index = pd.DatetimeIndex(roots_df.index)
wweight_wr_df = wweight_df.add(roots_df['root FW'])
```
### Excepting irrigation disturbance
```
night_df = SW2_df.loc[SW2_df['rad'] <= 0.2, 'loadcell_1':'loadcell_3']
fig = plt.figure(figsize=((8/2.54*2.5), (6/2.54*1.2)))
ax0 = plt.subplot()
ax0.spines['right'].set_visible(False)
ax0.spines['left'].set_position(('outward', 5))
ax0.spines['bottom'].set_position(('outward', 5))
ax0.plot(SW2_df.index, SW2_df['loadcell_1']/4, c=cmap[3], alpha=0.5)
ax0.plot(SW2_df.index, SW2_df['loadcell_2']/4, c=cmap[0], alpha=0.5)
ax0.plot(SW2_df.index, SW2_df['loadcell_3']/4, c=cmap[4], alpha=0.5)
ax0.plot(night_df.resample('1d').mean().index, ((night_df.resample('1d').mean()['loadcell_1'] - SW2_df['water'].resample('1d').mean())/4), '-o', ms=5, mec='k', mew=0.5, c=cmap[3])
ax0.plot(night_df.resample('1d').mean().index, ((night_df.resample('1d').mean()['loadcell_2'] - SW2_df['water'].resample('1d').mean())/4), '-o', ms=5, mec='k', mew=0.5, c=cmap[0])
ax0.plot(night_df.resample('1d').mean().index, ((night_df.resample('1d').mean()['loadcell_3'] - SW2_df['water'].resample('1d').mean())/4), '-o', ms=5, mec='k', mew=0.5, c=cmap[4])
ax0.plot(wweight_df.index, wweight_wr_df/1000, 'o', ms=5, c='k')
ax0.set_xbound(SW2_df.index.min(), SW2_df.index.max())
ax0.xaxis.set_major_locator(LinearLocator(10))
ax0.xaxis.set_major_formatter(mdates.DateFormatter('%m-%d'))
ax0.yaxis.set_major_locator(LinearLocator(6))
ax0.set_ybound(0, 5)
ax0.set_xlabel('Date')
ax0.set_ylabel('Weight (kg)')
fig.tight_layout()
plt.show()
fw_labels = pd.concat([(night_df.resample('1d').mean()['loadcell_1'] - SW2_df['water'].resample('1d').mean())/4,
(night_df.resample('1d').mean()['loadcell_2'] - SW2_df['water'].resample('1d').mean())/4,
(night_df.resample('1d').mean()['loadcell_3'] - SW2_df['water'].resample('1d').mean())/4], axis=1)
fw_labels.columns = ['CT_1', 'CT_2', 'CT_3']
fw_labels.to_csv('./results/2020_S/ct_fw_labels.csv')
```
# 2020 Winter
## Control weight
```
SW2_df = pd.read_csv('./results/2020_W/SW_CT_greenhouse.csv', index_col='Unnamed: 0')
SW2_df.index = pd.DatetimeIndex(SW2_df.index)
```
### Cultivation period
```
SW2_df = SW2_df.loc['2020-08-26 00:00:00': '2021-01-25 23:59:00']
SW2_df = SW2_df.interpolate()
```
### Rockwool weight
```
rockwool_mean = 887.20/1000
```
### water weight
```
substrate_volume = (120*12*7.5 + 10*10*6.5*3)/1000
water_w_df = substrate_volume*SW2_df['subs_VWC']/100
SW2_df['water'] = water_w_df
```
### Calculating aerial weight
```
SW2_df.loc[:, 'loadcell_1'] = SW2_df.loc[:, 'loadcell_1'] - rockwool_mean
SW2_df.loc[:, 'loadcell_2'] = SW2_df.loc[:, 'loadcell_2'] - rockwool_mean
SW2_df.loc[:, 'loadcell_3'] = SW2_df.loc[:, 'loadcell_3'] - rockwool_mean
```
### Destructive crop weight
```
weight_df = pd.read_csv('./results/2020_W/weight_ct.csv', index_col='Unnamed: 0')
weight_df.index = pd.DatetimeIndex(weight_df.index)
wweight_df = weight_df[['Stem FW', 'Leaf FW', 'petiole FW', 'Idv fruit FW']].sum(axis=1)
```
### Root DW to FW
```
roots_DW_mean = 355.37
DW_sum_df = weight_df.loc[:, [_ for _ in weight_df.columns if _.endswith('DW')]].sum(axis=1)
rs_ratio_df = (roots_DW_mean/(DW_sum_df.loc['2021-01-25']*3)).mean()
roots_df = pd.DataFrame(DW_sum_df * rs_ratio_df)
roots_df.columns = ['root DW']
roots_df['root FW'] = roots_df['root DW']/0.1325
roots_df.index = pd.DatetimeIndex(roots_df.index)
wweight_wr_df = wweight_df.add(roots_df['root FW'])
```
### Excepting irrigation disturbance
```
night_df = SW2_df.loc[SW2_df['rad'] <= 0.2, 'loadcell_1':'loadcell_3']
fig = plt.figure(figsize=((8/2.54*2.5), (6/2.54*1.2)))
ax0 = plt.subplot()
ax0.spines['right'].set_visible(False)
ax0.spines['left'].set_position(('outward', 5))
ax0.spines['bottom'].set_position(('outward', 5))
ax0.plot(SW2_df.index, SW2_df['loadcell_1']/3, c=cmap[3], alpha=0.5)
ax0.plot(SW2_df.index, SW2_df['loadcell_2']/3, c=cmap[0], alpha=0.5)
ax0.plot(SW2_df.index, SW2_df['loadcell_3']/3, c=cmap[4], alpha=0.5)
ax0.plot(night_df.resample('1d').mean().index, ((night_df.resample('1d').mean()['loadcell_1'] - SW2_df['water'].resample('1d').mean())/3), '-o', ms=5, mec='k', mew=0.5, c=cmap[3])
ax0.plot(night_df.resample('1d').mean().index, ((night_df.resample('1d').mean()['loadcell_2'] - SW2_df['water'].resample('1d').mean())/3), '-o', ms=5, mec='k', mew=0.5, c=cmap[0])
ax0.plot(night_df.resample('1d').mean().index, ((night_df.resample('1d').mean()['loadcell_3'] - SW2_df['water'].resample('1d').mean())/3), '-o', ms=5, mec='k', mew=0.5, c=cmap[4])
ax0.plot(wweight_df.index, wweight_wr_df/1000, 'o', ms=5, c='k')
ax0.set_xbound(SW2_df.index.min(), SW2_df.index.max())
ax0.xaxis.set_major_locator(LinearLocator(10))
ax0.xaxis.set_major_formatter(mdates.DateFormatter('%m-%d'))
ax0.yaxis.set_major_locator(LinearLocator(6))
ax0.set_ybound(0, 6)
ax0.set_xlabel('Date')
ax0.set_ylabel('Weight (kg)')
fig.tight_layout()
plt.show()
fw_labels = pd.concat([(night_df.resample('1d').mean()['loadcell_1'] - SW2_df['water'].resample('1d').mean())/3,
(night_df.resample('1d').mean()['loadcell_2'] - SW2_df['water'].resample('1d').mean())/3,
(night_df.resample('1d').mean()['loadcell_3'] - SW2_df['water'].resample('1d').mean())/3], axis=1)
fw_labels.columns = ['CT_1', 'CT_2', 'CT_3']
fw_labels.to_csv('./results/2020_W/ct_fw_labels.csv')
```
|
github_jupyter
|
# XGBoost vs LightGBM
In this notebook we collect the results from all the experiments and reports the comparative difference between XGBoost and LightGBM
```
import matplotlib.pyplot as plt
import nbformat
import json
from toolz import pipe, juxt
import pandas as pd
import seaborn
from toolz import curry
from bokeh.io import show, output_notebook
from bokeh.charts import Bar
from bokeh.models.renderers import GlyphRenderer
from bokeh.models.glyphs import Rect
from bokeh.models import Range1d
from toolz import curry
from bokeh.io import export_svgs
from IPython.display import SVG, display
import warnings
warnings.filterwarnings("ignore")
%matplotlib inline
output_notebook()
```
We are going to read the results from the following notebooks
```
notebooks = {
'Airline':'01_airline.ipynb',
'Airline_GPU': '01_airline_GPU.ipynb',
'BCI': '02_BCI.ipynb',
'BCI_GPU': '02_BCI_GPU.ipynb',
'Football': '03_football.ipynb',
'Football_GPU': '03_football_GPU.ipynb',
'Planet': '04_PlanetKaggle.ipynb',
'Plannet_GPU': '04_PlanetKaggle_GPU.ipynb',
'Fraud': '05_FraudDetection.ipynb',
'Fraud_GPU': '05_FraudDetection_GPU.ipynb',
'HIGGS': '06_HIGGS.ipynb',
'HIGGS_GPU': '06_HIGGS_GPU.ipynb'
}
def read_notebook(notebook_name):
with open(notebook_name) as f:
return nbformat.read(f, as_version=4)
def results_cell_from(nb):
for cell in nb.cells:
if cell['cell_type']=='code' and cell['source'].startswith('# Results'):
return cell
def extract_text(cell):
return cell['outputs'][0]['text']
@curry
def remove_line_with(match_str, json_string):
return '\n'.join(filter(lambda x: match_str not in x, json_string.split('\n')))
def process_nb(notebook_name):
return pipe(notebook_name,
read_notebook,
results_cell_from,
extract_text,
remove_line_with('total RAM usage'),
json.loads)
```
Here we collect the results from all the exeperiment notebooks. The method simply searches the notebooks for a cell that starts with # Results. It then reads that cells output in as JSON.
```
results = {nb_key:process_nb(nb_name) for nb_key, nb_name in notebooks.items()}
results
datasets = [k for k in results.keys()]
print(datasets)
algos = [a for a in results[datasets[0]].keys()]
print(algos)
```
We wish to compare LightGBM and XGBoost both in terms of performance as well as how long they took to train.
```
def average_performance_diff(dataset):
lgbm_series = pd.Series(dataset['lgbm']['performance'])
try:
perf = 100*((lgbm_series-pd.Series(dataset['xgb']['performance']))/lgbm_series).mean()
except KeyError:
perf = None
return perf
def train_time_ratio(dataset):
try:
val = dataset['xgb']['train_time']/dataset['lgbm']['train_time']
except KeyError:
val = None
return val
def train_time_ratio_hist(dataset):
try:
val = dataset['xgb_hist']['train_time']/dataset['lgbm']['train_time']
except KeyError:
val = None
return val
def test_time_ratio(dataset):
try:
val = dataset['xgb']['test_time']/dataset['lgbm']['test_time']
except KeyError:
val = None
return val
metrics = juxt(average_performance_diff, train_time_ratio, train_time_ratio_hist, test_time_ratio)
res_per_dataset = {dataset_key:metrics(dataset) for dataset_key, dataset in results.items()}
results_df = pd.DataFrame(res_per_dataset, index=['Perf. Difference(%)',
'Train Time Ratio',
'Train Time Ratio Hist',
'Test Time Ratio']).T
results_df
results_gpu = results_df.ix[[idx for idx in results_df.index if idx.endswith('GPU')]]
results_cpu = results_df.ix[~results_df.index.isin(results_gpu.index)]
```
Plot of train time ratio for CPU experiments.
```
data = {
'Ratio': results_cpu['Train Time Ratio'].values.tolist() + results_cpu['Train Time Ratio Hist'].values.tolist(),
'label': results_cpu.index.values.tolist()*2,
'group': ['xgb/lgb']*len(results_cpu.index.values) + ['xgb_hist/lgb']*len(results_cpu.index.values)
}
bar = Bar(data, values='Ratio', agg='mean', label='label', group='group',
plot_width=600, plot_height=400, bar_width=0.7, color=['#5975a4','#99ccff'], legend='top_right')
bar.axis[0].axis_label=''
bar.axis[1].axis_label='Train Time Ratio (XGBoost/LightGBM)'
bar.axis[1].axis_label_text_font_size='12pt'
bar.y_range = Range1d(0, 30)
bar.toolbar_location='above'
bar.legend[0].visible=True
show(bar)
bar.output_backend = "svg"
export_svgs(bar, filename="xgb_vs_lgbm_train_time.svg")
display(SVG('xgb_vs_lgbm_train_time.svg'))
```
Plot of train time ratio for GPU experiments.
```
data = {
'Ratio': results_gpu['Train Time Ratio'].values.tolist() + results_gpu['Train Time Ratio Hist'].values.tolist(),
'label': results_gpu.index.values.tolist()*2,
'group': ['xgb/lgb']*len(results_gpu.index.values) + ['xgb_hist/lgb']*len(results_gpu.index.values)
}
bar = Bar(data, values='Ratio', agg='mean', label='label', group='group',
plot_width=600, plot_height=400, bar_width=0.5, color=['#ff8533','#ffd1b3'], legend='top_right')
bar.axis[0].axis_label=''
bar.y_range = Range1d(0, 30)
bar.axis[1].axis_label='Train Time Ratio (XGBoost/LightGBM)'
bar.axis[1].axis_label_text_font_size='12pt'
bar.toolbar_location='above'
bar.legend[0].visible=True
show(bar)
bar.output_backend = "svg"
export_svgs(bar, filename="xgb_vs_lgbm_train_time_gpu.svg")
display(SVG('xgb_vs_lgbm_train_time_gpu.svg'))
data = {
'Perf. Difference(%)': results_df['Perf. Difference(%)'].values,
'label': results_df.index.values
}
bar = Bar(data, values='Perf. Difference(%)', agg='mean', label=['label'],
plot_width=600, plot_height=400, bar_width=0.7, color='#5975a4')
bar.axis[0].axis_label=''
bar.axis[1].axis_label='Perf. Difference(%)'
bar.toolbar_location='above'
bar.legend[0].visible=False
show(bar)
bar.output_backend = "svg"
export_svgs(bar, filename="xgb_vs_lgbm_performance.svg")
display(SVG('xgb_vs_lgbm_performance.svg'))
```
For the speed results we can see that LightGBM is on average 5 times faster than the CPU and GPU versions of XGBoost and XGBoost histogram. In regards to the performance, we can see that LightGBM is sometimes better and sometimes worse.
Analyzing the results of XGBoost in CPU we can see that XGBoost histogram is faster than XGBoost in the Airline, Fraud and HIGGS datasets, but much slower in Planet and BCI dataset. In these two cases there is a memory overhead due to the high number of features. In the case of football dataset, the histogram implementation is slightly slower, we believe that there could be a slight principle of memory overhead.
Finally, if we look at the results of XGBoost in GPU we see that there are several values missing. This is due to an out of memory of the standard version. In our experiments we observed that XGBoost's memory consumption is around 10 times higher than LightGBM and 5 times higher than XGBoost histogram. We see that the histogram version is faster except in the BCI dataset, where there could be a memory overhead like in the CPU version.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/NeuromatchAcademy/course-content/blob/master/tutorials/W3D3_NetworkCausality/W3D3_Tutorial3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Neuromatch Academy 2020 -- Week 3 Day 3 Tutorial 3
# Causality Day - Simultaneous fitting/regression
**Content creators**: Ari Benjamin, Tony Liu, Konrad Kording
**Content reviewers**: Mike X Cohen, Madineh Sarvestani, Ella Batty, Michael Waskom
---
# Tutorial objectives
This is tutorial 3 on our day of examining causality. Below is the high level outline of what we'll cover today, with the sections we will focus on in this notebook in bold:
1. Master definitions of causality
2. Understand that estimating causality is possible
3. Learn 4 different methods and understand when they fail
1. perturbations
2. correlations
3. **simultaneous fitting/regression**
4. instrumental variables
### Notebook 3 objectives
In tutorial 2 we explored correlation as an approximation for causation and learned that correlation $\neq$ causation for larger networks. However, computing correlations is a rather simple approach, and you may be wondering: will more sophisticated techniques allow us to better estimate causality? Can't we control for things?
Here we'll use some common advanced (but controversial) methods that estimate causality from observational data. These methods rely on fitting a function to our data directly, instead of trying to use perturbations or correlations. Since we have the full closed-form equation of our system, we can try these methods and see how well they work in estimating causal connectivity when there are no perturbations. Specifically, we will:
- Learn about more advanced (but also controversial) techniques for estimating causality
- conditional probabilities (**regression**)
- Explore limitations and failure modes
- understand the problem of **omitted variable bias**
---
# Setup
```
import numpy as np
import matplotlib.pyplot as plt
from sklearn.multioutput import MultiOutputRegressor
from sklearn.linear_model import Lasso
#@title Figure settings
import ipywidgets as widgets # interactive display
%config InlineBackend.figure_format = 'retina'
plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/nma.mplstyle")
# @title Helper functions
def sigmoid(x):
"""
Compute sigmoid nonlinearity element-wise on x.
Args:
x (np.ndarray): the numpy data array we want to transform
Returns
(np.ndarray): x with sigmoid nonlinearity applied
"""
return 1 / (1 + np.exp(-x))
def logit(x):
"""
Applies the logit (inverse sigmoid) transformation
Args:
x (np.ndarray): the numpy data array we want to transform
Returns
(np.ndarray): x with logit nonlinearity applied
"""
return np.log(x/(1-x))
def create_connectivity(n_neurons, random_state=42, p=0.9):
"""
Generate our nxn causal connectivity matrix.
Args:
n_neurons (int): the number of neurons in our system.
random_state (int): random seed for reproducibility
Returns:
A (np.ndarray): our 0.1 sparse connectivity matrix
"""
np.random.seed(random_state)
A_0 = np.random.choice([0, 1], size=(n_neurons, n_neurons), p=[p, 1 - p])
# set the timescale of the dynamical system to about 100 steps
_, s_vals, _ = np.linalg.svd(A_0)
A = A_0 / (1.01 * s_vals[0])
# _, s_val_test, _ = np.linalg.svd(A)
# assert s_val_test[0] < 1, "largest singular value >= 1"
return A
def get_regression_estimate_full_connectivity(X):
"""
Estimates the connectivity matrix using lasso regression.
Args:
X (np.ndarray): our simulated system of shape (n_neurons, timesteps)
neuron_idx (int): optionally provide a neuron idx to compute connectivity for
Returns:
V (np.ndarray): estimated connectivity matrix of shape (n_neurons, n_neurons).
if neuron_idx is specified, V is of shape (n_neurons,).
"""
n_neurons = X.shape[0]
# Extract Y and W as defined above
W = X[:, :-1].transpose()
Y = X[:, 1:].transpose()
# apply inverse sigmoid transformation
Y = logit(Y)
# fit multioutput regression
reg = MultiOutputRegressor(Lasso(fit_intercept=False,
alpha=0.01, max_iter=250 ), n_jobs=-1)
reg.fit(W, Y)
V = np.zeros((n_neurons, n_neurons))
for i, estimator in enumerate(reg.estimators_):
V[i, :] = estimator.coef_
return V
def get_regression_corr_full_connectivity(n_neurons, A, X, observed_ratio, regression_args):
"""
A wrapper function for our correlation calculations between A and the V estimated
from regression.
Args:
n_neurons (int): number of neurons
A (np.ndarray): connectivity matrix
X (np.ndarray): dynamical system
observed_ratio (float): the proportion of n_neurons observed, must be betweem 0 and 1.
regression_args (dict): dictionary of lasso regression arguments and hyperparameters
Returns:
A single float correlation value representing the similarity between A and R
"""
assert (observed_ratio > 0) and (observed_ratio <= 1)
sel_idx = np.clip(int(n_neurons*observed_ratio), 1, n_neurons)
sel_X = X[:sel_idx, :]
sel_A = A[:sel_idx, :sel_idx]
sel_V = get_regression_estimate_full_connectivity(sel_X)
return np.corrcoef(sel_A.flatten(), sel_V.flatten())[1,0], sel_V
def see_neurons(A, ax, ratio_observed=1, arrows=True):
"""
Visualizes the connectivity matrix.
Args:
A (np.ndarray): the connectivity matrix of shape (n_neurons, n_neurons)
ax (plt.axis): the matplotlib axis to display on
Returns:
Nothing, but visualizes A.
"""
n = len(A)
ax.set_aspect('equal')
thetas = np.linspace(0, np.pi * 2, n, endpoint=False)
x, y = np.cos(thetas), np.sin(thetas),
if arrows:
for i in range(n):
for j in range(n):
if A[i, j] > 0:
ax.arrow(x[i], y[i], x[j] - x[i], y[j] - y[i], color='k', head_width=.05,
width = A[i, j] / 25,shape='right', length_includes_head=True,
alpha = .2)
if ratio_observed < 1:
nn = int(n * ratio_observed)
ax.scatter(x[:nn], y[:nn], c='r', s=150, label='Observed')
ax.scatter(x[nn:], y[nn:], c='b', s=150, label='Unobserved')
ax.legend(fontsize=15)
else:
ax.scatter(x, y, c='k', s=150)
ax.axis('off')
def simulate_neurons(A, timesteps, random_state=42):
"""
Simulates a dynamical system for the specified number of neurons and timesteps.
Args:
A (np.array): the connectivity matrix
timesteps (int): the number of timesteps to simulate our system.
random_state (int): random seed for reproducibility
Returns:
- X has shape (n_neurons, timeteps).
"""
np.random.seed(random_state)
n_neurons = len(A)
X = np.zeros((n_neurons, timesteps))
for t in range(timesteps - 1):
# solution
epsilon = np.random.multivariate_normal(np.zeros(n_neurons), np.eye(n_neurons))
X[:, t + 1] = sigmoid(A.dot(X[:, t]) + epsilon)
assert epsilon.shape == (n_neurons,)
return X
def correlation_for_all_neurons(X):
"""Computes the connectivity matrix for the all neurons using correlations
Args:
X: the matrix of activities
Returns:
estimated_connectivity (np.ndarray): estimated connectivity for the selected neuron, of shape (n_neurons,)
"""
n_neurons = len(X)
S = np.concatenate([X[:, 1:], X[:, :-1]], axis=0)
R = np.corrcoef(S)[:n_neurons, n_neurons:]
return R
def get_sys_corr(n_neurons, timesteps, random_state=42, neuron_idx=None):
"""
A wrapper function for our correlation calculations between A and R.
Args:
n_neurons (int): the number of neurons in our system.
timesteps (int): the number of timesteps to simulate our system.
random_state (int): seed for reproducibility
neuron_idx (int): optionally provide a neuron idx to slice out
Returns:
A single float correlation value representing the similarity between A and R
"""
A = create_connectivity(n_neurons, random_state)
X = simulate_neurons(A, timesteps)
R = correlation_for_all_neurons(X)
return np.corrcoef(A.flatten(), R.flatten())[0, 1]
def get_regression_corr(n_neurons, A, X, observed_ratio, regression_args, neuron_idx=None):
"""
A wrapper function for our correlation calculations between A and the V estimated
from regression.
Args:
n_neurons (int): the number of neurons in our system.
A (np.array): the true connectivity
X (np.array): the simulated system
observed_ratio (float): the proportion of n_neurons observed, must be between 0 and 1.
regression_args (dict): dictionary of lasso regression arguments and hyperparameters
neuron_idx (int): optionally provide a neuron idx to compute connectivity for
Returns:
A single float correlation value representing the similarity between A and R
"""
assert (observed_ratio > 0) and (observed_ratio <= 1)
sel_idx = np.clip(int(n_neurons * observed_ratio), 1, n_neurons)
selected_X = X[:sel_idx, :]
selected_connectivity = A[:sel_idx, :sel_idx]
estimated_selected_connectivity = get_regression_estimate(selected_X, neuron_idx=neuron_idx)
if neuron_idx is None:
return np.corrcoef(selected_connectivity.flatten(),
estimated_selected_connectivity.flatten())[1, 0], estimated_selected_connectivity
else:
return np.corrcoef(selected_connectivity[neuron_idx, :],
estimated_selected_connectivity)[1, 0], estimated_selected_connectivity
def plot_connectivity_matrix(A, ax=None):
"""Plot the (weighted) connectivity matrix A as a heatmap
Args:
A (ndarray): connectivity matrix (n_neurons by n_neurons)
ax: axis on which to display connectivity matrix
"""
if ax is None:
ax = plt.gca()
lim = np.abs(A).max()
ax.imshow(A, vmin=-lim, vmax=lim, cmap="coolwarm")
```
---
# Section 1: Regression
```
#@title Video 1: Regression approach
# Insert the ID of the corresponding youtube video
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="Av4LaXZdgDo", width=854, height=480, fs=1)
print("Video available at https://youtu.be/" + video.id)
video
```
You may be familiar with the idea that correlation only implies causation when there no hidden *confounders*. This aligns with our intuition that correlation only implies causality when no alternative variables could explain away a correlation.
**A confounding example**:
Suppose you observe that people who sleep more do better in school. It's a nice correlation. But what else could explain it? Maybe people who sleep more are richer, don't work a second job, and have time to actually do homework. If you want to ask if sleep *causes* better grades, and want to answer that with correlations, you have to control for all possible confounds.
A confound is any variable that affects both the outcome and your original covariate. In our example, confounds are things that affect both sleep and grades.
**Controlling for a confound**:
Confonds can be controlled for by adding them as covariates in a regression. But for your coefficients to be causal effects, you need three things:
1. **All** confounds are included as covariates
2. Your regression assumes the same mathematical form of how covariates relate to outcomes (linear, GLM, etc.)
3. No covariates are caused *by* both the treatment (original variable) and the outcome. These are [colliders](https://en.wikipedia.org/wiki/Collider_(statistics)); we won't introduce it today (but Google it on your own time! Colliders are very counterintuitive.)
In the real world it is very hard to guarantee these conditions are met. In the brain it's even harder (as we can't measure all neurons). Luckily today we simulated the system ourselves.
```
#@title Video 2: Fitting a GLM
# Insert the ID of the corresponding youtube video
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="GvMj9hRv5Ak", width=854, height=480, fs=1)
print("Video available at https://youtu.be/" + video.id)
video
```
## Section 1.1: Recovering connectivity by model fitting
Recall that in our system each neuron effects every other via:
$$
\vec{x}_{t+1} = \sigma(A\vec{x}_t + \epsilon_t),
$$
where $\sigma$ is our sigmoid nonlinearity from before: $\sigma(x) = \frac{1}{1 + e^{-x}}$
Our system is a closed system, too, so there are no omitted variables. The regression coefficients should be the causal effect. Are they?
We will use a regression approach to estimate the causal influence of all neurons to neuron #1. Specifically, we will use linear regression to determine the $A$ in:
$$
\sigma^{-1}(\vec{x}_{t+1}) = A\vec{x}_t + \epsilon_t ,
$$
where $\sigma^{-1}$ is the inverse sigmoid transformation, also sometimes referred to as the **logit** transformation: $\sigma^{-1}(x) = \log(\frac{x}{1-x})$.
Let $W$ be the $\vec{x}_t$ values, up to the second-to-last timestep $T-1$:
$$
W =
\begin{bmatrix}
\mid & \mid & ... & \mid \\
\vec{x}_0 & \vec{x}_1 & ... & \vec{x}_{T-1} \\
\mid & \mid & ... & \mid
\end{bmatrix}_{n \times (T-1)}
$$
Let $Y$ be the $\vec{x}_{t+1}$ values for a selected neuron, indexed by $i$, starting from the second timestep up to the last timestep $T$:
$$
Y =
\begin{bmatrix}
x_{i,1} & x_{i,2} & ... & x_{i, T} \\
\end{bmatrix}_{1 \times (T-1)}
$$
You will then fit the following model:
$$
\sigma^{-1}(Y^T) = W^TV
$$
where $V$ is the $n \times 1$ coefficient matrix of this regression, which will be the estimated connectivity matrix between the selected neuron and the rest of the neurons.
**Review**: As you learned Friday of Week 1, *lasso* a.k.a. **$L_1$ regularization** causes the coefficients to be sparse, containing mostly zeros. Think about why we want this here.
## Exercise 1: Use linear regression plus lasso to estimate causal connectivities
You will now create a function to fit the above regression model and V. We will then call this function to examine how close the regression vs the correlation is to true causality.
**Code**:
You'll notice that we've transposed both $Y$ and $W$ here and in the code we've already provided below. Why is that?
This is because the machine learning models provided in scikit-learn expect the *rows* of the input data to be the observations, while the *columns* are the variables. We have that inverted in our definitions of $Y$ and $W$, with the timesteps of our system (the observations) as the columns. So we transpose both matrices to make the matrix orientation correct for scikit-learn.
- Because of the abstraction provided by scikit-learn, fitting this regression will just be a call to initialize the `Lasso()` estimator and a call to the `fit()` function
- Use the following hyperparameters for the `Lasso` estimator:
- `alpha = 0.01`
- `fit_intercept = False`
- How do we obtain $V$ from the fitted model?
```
def get_regression_estimate(X, neuron_idx):
"""
Estimates the connectivity matrix using lasso regression.
Args:
X (np.ndarray): our simulated system of shape (n_neurons, timesteps)
neuron_idx (int): a neuron index to compute connectivity for
Returns:
V (np.ndarray): estimated connectivity matrix of shape (n_neurons, n_neurons).
if neuron_idx is specified, V is of shape (n_neurons,).
"""
# Extract Y and W as defined above
W = X[:, :-1].transpose()
Y = X[[neuron_idx], 1:].transpose()
# Apply inverse sigmoid transformation
Y = logit(Y)
############################################################################
## TODO: Insert your code here to fit a regressor with Lasso. Lasso captures
## our assumption that most connections are precisely 0.
## Fill in function and remove
raise NotImplementedError("Please complete the regression exercise")
############################################################################
# Initialize regression model with no intercept and alpha=0.01
regression = ...
# Fit regression to the data
regression.fit(...)
V = regression.coef_
return V
# Parameters
n_neurons = 50 # the size of our system
timesteps = 10000 # the number of timesteps to take
random_state = 42
neuron_idx = 1
A = create_connectivity(n_neurons, random_state)
X = simulate_neurons(A, timesteps)
# Uncomment below to test your function
# V = get_regression_estimate(X, neuron_idx)
#print("Regression: correlation of estimated connectivity with true connectivity: {:.3f}".format(np.corrcoef(A[neuron_idx, :], V)[1, 0]))
#print("Lagged correlation of estimated connectivity with true connectivity: {:.3f}".format(get_sys_corr(n_neurons, timesteps, random_state, neuron_idx=neuron_idx)))
# to_remove solution
def get_regression_estimate(X, neuron_idx):
"""
Estimates the connectivity matrix using lasso regression.
Args:
X (np.ndarray): our simulated system of shape (n_neurons, timesteps)
neuron_idx (int): a neuron index to compute connectivity for
Returns:
V (np.ndarray): estimated connectivity matrix of shape (n_neurons, n_neurons).
if neuron_idx is specified, V is of shape (n_neurons,).
"""
# Extract Y and W as defined above
W = X[:, :-1].transpose()
Y = X[[neuron_idx], 1:].transpose()
# Apply inverse sigmoid transformation
Y = logit(Y)
# Initialize regression model with no intercept and alpha=0.01
regression = Lasso(fit_intercept=False, alpha=0.01)
# Fit regression to the data
regression.fit(W, Y)
V = regression.coef_
return V
# Parameters
n_neurons = 50 # the size of our system
timesteps = 10000 # the number of timesteps to take
random_state = 42
neuron_idx = 1
A = create_connectivity(n_neurons, random_state)
X = simulate_neurons(A, timesteps)
# Uncomment below to test your function
V = get_regression_estimate(X, neuron_idx)
print("Regression: correlation of estimated connectivity with true connectivity: {:.3f}".format(np.corrcoef(A[neuron_idx, :], V)[1, 0]))
print("Lagged correlation of estimated connectivity with true connectivity: {:.3f}".format(get_sys_corr(n_neurons, timesteps, random_state, neuron_idx=neuron_idx)))
```
You should find that using regression, our estimated connectivity matrix has a correlation of 0.865 with the true connectivity matrix. With correlation, our estimated connectivity matrix has a correlation of 0.703 with the true connectivity matrix.
We can see from these numbers that multiple regression is better than simple correlation for estimating connectivity.
---
# Section 2: Omitted Variable Bias
If we are unable to observe the entire system, **omitted variable bias** becomes a problem. If we don't have access to all the neurons, and so therefore can't control for them, can we still estimate the causal effect accurately?
## Section 2.1: Visualizing subsets of the connectivity matrix
We first visualize different subsets of the connectivity matrix when we observe 75% of the neurons vs 25%.
Recall the meaning of entries in our connectivity matrix: $A[i,j] = 1$ means a connectivity **from** neuron $i$ **to** neuron $j$ with strength $1$.
```
#@markdown Execute this cell to visualize subsets of connectivity matrix
# Run this cell to visualize the subsets of variables we observe
n_neurons = 25
A = create_connectivity(n_neurons)
fig, axs = plt.subplots(2, 2, figsize=(10, 10))
ratio_observed = [0.75, 0.25] # the proportion of neurons observed in our system
for i, ratio in enumerate(ratio_observed):
sel_idx = int(n_neurons * ratio)
offset = np.zeros((n_neurons, n_neurons))
axs[i,1].title.set_text("{}% neurons observed".format(int(ratio * 100)))
offset[:sel_idx, :sel_idx] = 1 + A[:sel_idx, :sel_idx]
im = axs[i, 1].imshow(offset, cmap="coolwarm", vmin=0, vmax=A.max() + 1)
axs[i, 1].set_xlabel("Connectivity from")
axs[i, 1].set_ylabel("Connectivity to")
plt.colorbar(im, ax=axs[i, 1], fraction=0.046, pad=0.04)
see_neurons(A,axs[i, 0],ratio)
plt.suptitle("Visualizing subsets of the connectivity matrix", y = 1.05)
plt.show()
```
## Section 2.2: Effects of partial observability
```
#@title Video 3: Omitted variable bias
# Insert the ID of the corresponding youtube video
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="5CCib6CTMac", width=854, height=480, fs=1)
print("Video available at https://youtu.be/" + video.id)
video
```
**Video correction**: the labels "connectivity from"/"connectivity to" are swapped in the video but fixed in the figures/demos below
### Interactive Demo: Regression performance as a function of the number of observed neurons
We will first change the number of observed neurons in the network and inspect the resulting estimates of connectivity in this interactive demo. How does the estimated connectivity differ?
**Note:** the plots will take a moment or so to update after moving the slider.
```
#@markdown Execute this cell to enable demo
n_neurons = 50
A = create_connectivity(n_neurons, random_state=42)
X = simulate_neurons(A, 4000, random_state=42)
reg_args = {
"fit_intercept": False,
"alpha": 0.001
}
@widgets.interact
def plot_observed(n_observed=(5, 45, 5)):
to_neuron = 0
fig, axs = plt.subplots(1, 3, figsize=(15, 5))
sel_idx = n_observed
ratio = (n_observed) / n_neurons
offset = np.zeros((n_neurons, n_neurons))
axs[0].title.set_text("{}% neurons observed".format(int(ratio * 100)))
offset[:sel_idx, :sel_idx] = 1 + A[:sel_idx, :sel_idx]
im = axs[1].imshow(offset, cmap="coolwarm", vmin=0, vmax=A.max() + 1)
plt.colorbar(im, ax=axs[1], fraction=0.046, pad=0.04)
see_neurons(A,axs[0], ratio, False)
corr, R = get_regression_corr_full_connectivity(n_neurons,
A,
X,
ratio,
reg_args)
#rect = patches.Rectangle((-.5,to_neuron-.5),n_observed,1,linewidth=2,edgecolor='k',facecolor='none')
#axs[1].add_patch(rect)
big_R = np.zeros(A.shape)
big_R[:sel_idx, :sel_idx] = 1 + R
#big_R[to_neuron, :sel_idx] = 1 + R
im = axs[2].imshow(big_R, cmap="coolwarm", vmin=0, vmax=A.max() + 1)
plt.colorbar(im, ax=axs[2],fraction=0.046, pad=0.04)
c = 'w' if n_observed<(n_neurons-3) else 'k'
axs[2].text(0,n_observed+3,"Correlation : {:.2f}".format(corr), color=c, size=15)
#axs[2].axis("off")
axs[1].title.set_text("True connectivity")
axs[1].set_xlabel("Connectivity from")
axs[1].set_ylabel("Connectivity to")
axs[2].title.set_text("Estimated connectivity")
axs[2].set_xlabel("Connectivity from")
#axs[2].set_ylabel("Connectivity to")
```
Next, we will inspect a plot of the correlation between true and estimated connectivity matrices vs the percent of neurons observed over multiple trials.
What is the relationship that you see between performance and the number of neurons observed?
**Note:** the cell below will take about 25-30 seconds to run.
```
#@title
#@markdown Plot correlation vs. subsampling
import warnings
warnings.filterwarnings('ignore')
# we'll simulate many systems for various ratios of observed neurons
n_neurons = 50
timesteps = 5000
ratio_observed = [1, 0.75, 0.5, .25, .12] # the proportion of neurons observed in our system
n_trials = 3 # run it this many times to get variability in our results
reg_args = {
"fit_intercept": False,
"alpha": 0.001
}
corr_data = np.zeros((n_trials, len(ratio_observed)))
for trial in range(n_trials):
A = create_connectivity(n_neurons, random_state=trial)
X = simulate_neurons(A, timesteps)
print("simulating trial {} of {}".format(trial + 1, n_trials))
for j, ratio in enumerate(ratio_observed):
result,_ = get_regression_corr_full_connectivity(n_neurons,
A,
X,
ratio,
reg_args)
corr_data[trial, j] = result
corr_mean = np.nanmean(corr_data, axis=0)
corr_std = np.nanstd(corr_data, axis=0)
plt.plot(np.asarray(ratio_observed) * 100, corr_mean)
plt.fill_between(np.asarray(ratio_observed) * 100,
corr_mean - corr_std,
corr_mean + corr_std,
alpha=.2)
plt.xlim([100, 10])
plt.xlabel("Percent of neurons observed")
plt.ylabel("connectivity matrices correlation")
plt.title("Performance of regression as a function of the number of neurons observed");
```
---
# Summary
```
#@title Video 4: Summary
# Insert the ID of the corresponding youtube video
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="T1uGf1H31wE", width=854, height=480, fs=1)
print("Video available at https://youtu.be/" + video.id)
video
```
In this tutorial, we explored:
1) Using regression for estimating causality
2) The problem of ommitted variable bias, and how it arises in practice
|
github_jupyter
|
```
# Setup Sets
cities = ["C1", "C2", "C3", "C4", "C5", "C6", "C7", "C8", "C9"]
power_plants = ["P1", "P2", "P3", "P4", "P5", "P6"]
connections = [("C1", "P1"), ("C1", "P3"), ("C1","P5"), \
("C2", "P1"), ("C2", "P2"), ("C2","P4"), \
("C3", "P2"), ("C3", "P3"), ("C3","P4"), \
("C4", "P2"), ("C4", "P4"), ("C4","P6"), \
("C5", "P2"), ("C5", "P5"), ("C5","P6"), \
("C6", "P3"), ("C6", "P4"), ("C6","P6"), \
("C7", "P1"), ("C7", "P3"), ("C7","P6"), \
("C8", "P2"), ("C8", "P3"), ("C8","P4"), \
("C9", "P3"), ("C9", "P5"), ("C9","P6")]
# Setup Parameters
max_power_generation = {"P1":100, "P2":150, "P3":250, "P4":125, "P5": 175, "P6":165}
startup_cost = {"P1":50, "P2":80, "P3":90, "P4":60, "P5": 60, "P6":70}
power_cost = {"P1":2, "P2":1.5, "P3":1.2, "P4":1.8, "P5": 0.8, "P6":1.1}
power_required = {"C1":25, "C2":35, "C3":30, "C4":29, "C5":40, "C6":35, "C7":50, "C8":45, "C9":38}
# Import PuLP Library
from pulp import *
# Create Decision Variables
run_power_plant = LpVariable.dicts("StartPlant", power_plants, 0, 1, LpInteger)
power_generation = LpVariable.dicts("PowerGeneration", power_plants, 0, None, LpContinuous)
power_sent = LpVariable.dicts("PowerSent", connections, 0, None, LpContinuous)
# Create Problem object
problem = LpProblem("PowerPlanning", LpMinimize)
# Add the Objective Function
problem += lpSum([run_power_plant[p] * startup_cost[p] + power_generation[p] * power_cost[p] for p in power_plants])
# Add Power Capacity Constraints
for p in power_plants:
problem += power_generation[p] <= max_power_generation[p] * run_power_plant[p], f"PowerCapacity_{p}"
# Add Power Balance Constraints
for p in power_plants:
problem += power_generation[p] == lpSum([power_sent[(c,p)] for c in cities if (c, p) in connections]), f"PowerSent_{p}"
# Add Cities Powered Constraints
for c in cities:
problem += power_required[c] == lpSum([power_sent[(c,p)] for p in power_plants if (c, p) in connections]), f"PowerRequired_{c}"
# Solve the problem
problem.solve()
# Check the status of the solution
status = LpStatus[problem.status]
print(status)
# Print the results
for v in problem.variables():
if v.varValue != 0:
print(v.name, "=", v.varValue)
# Let's look at the Plant Utilization
for p in power_plants:
if power_generation[p].varValue > 0:
utilization = (power_generation[p].varValue / max_power_generation[p]) * 100
print(f"Plant: {p} Generation: {power_generation[p].varValue} Utilization: {utilization:.2f}%")
```
|
github_jupyter
|
# In-Class Coding Lab: Iterations
The goals of this lab are to help you to understand:
- How loops work.
- The difference between definite and indefinite loops, and when to use each.
- How to build an indefinite loop with complex exit conditions.
- How to create a program from a complex idea.
# Understanding Iterations
Iterations permit us to repeat code until a Boolean expression is `False`. Iterations or **loops** allow us to write succint, compact code. Here's an example, which counts to 3 before [Blitzing the Quarterback in backyard American Football](https://www.quora.com/What-is-the-significance-of-counting-one-Mississippi-two-Mississippi-and-so-on):
```
i = 1
while i <= 3:
print(i,"Mississippi...")
i=i+1
print("Blitz!")
```
## Breaking it down...
The `while` statement on line 2 starts the loop. The code indented beneath it (lines 3-4) will repeat, in a linear fashion until the Boolean expression on line 2 `i <= 3` is `False`, at which time the program continues with line 5.
### Some Terminology
We call `i <=3` the loop's **exit condition**. The variable `i` inside the exit condition is the only thing that we can change to make the exit condition `False`, therefore it is the **loop control variable**. On line 4 we change the loop control variable by adding one to it, this is called an **increment**.
Furthermore, we know how many times this loop will execute before it actually runs: 3. Even if we allowed the user to enter a number, and looped that many times, we would still know. We call this a **definite loop**. Whenever we iterate over a fixed number of values, regardless of whether those values are determined at run-time or not, we're using a definite loop.
If the loop control variable never forces the exit condition to be `False`, we have an **infinite loop**. As the name implies, an Infinite loop never ends and typically causes our computer to crash or lock up.
```
## WARNING!!! INFINITE LOOP AHEAD
## IF YOU RUN THIS CODE YOU WILL NEED TO KILL YOUR BROWSER AND SHUT DOWN JUPYTER NOTEBOOK
i = 1
while i <= 3:
print(i,"Mississippi...")
# i=i+1
print("Blitz!")
```
### For loops
To prevent an infinite loop when the loop is definite, we use the `for` statement. Here's the same program using `for`:
```
for i in range(1,4):
print(i,"Mississippi...")
print("Blitz!")
```
One confusing aspect of this loop is `range(1,4)` why does this loop from 1 to 3? Why not 1 to 4? Well it has to do with the fact that computers start counting at zero. The easier way to understand it is if you subtract the two numbers you get the number of times it will loop. So for example, 4-1 == 3.
### Now Try It
In the space below, Re-Write the above program to count from 10 to 15. Note: How many times will that loop?
```
# TODO Write code here
for i in range(10,16):
print(i,"Mississippi...")
print("Blitz!")
```
## Indefinite loops
With **indefinite loops** we do not know how many times the program will execute. This is typically based on user action, and therefore our loop is subject to the whims of whoever interacts with it. Most applications like spreadsheets, photo editors, and games use indefinite loops. They'll run on your computer, seemingly forever, until you choose to quit the application.
The classic indefinite loop pattern involves getting input from the user inside the loop. We then inspect the input and based on that input we might exit the loop. Here's an example:
```
name = ""
while name != 'mike':
name = input("Say my name! : ")
print("Nope, my name is not %s! " %(name))
```
The classic problem with indefinite loops is that its really difficult to get the application's logic to line up with the exit condition. For example we need to set `name = ""` in line 1 so that line 2 start out as `True`. Also we have this wonky logic where when we say `'mike'` it still prints `Nope, my name is not mike!` before exiting.
### Break statement
The solution to this problem is to use the break statement. **break** tells Python to exit the loop immediately. We then re-structure all of our indefinite loops to look like this:
```
while True:
if exit-condition:
break
```
Here's our program we-written with the break statement. This is the recommended way to write indefinite loops in this course.
```
while True:
name = input("Say my name!: ")
if name == 'mike':
break
print("Nope, my name is not %s!" %(name))
```
### Multiple exit conditions
This indefinite loop pattern makes it easy to add additional exit conditions. For example, here's the program again, but it now stops when you say my name or type in 3 wrong names. Make sure to run this program a couple of times. First enter mike to exit the program, next enter the wrong name 3 times.
```
times = 0
while True:
name = input("Say my name!: ")
times = times + 1
if name == 'mike':
print("You got it!")
break
if times == 3:
print("Game over. Too many tries!")
break
print("Nope, my name is not %s!" %(name))
```
# Number sums
Let's conclude the lab with you writing your own program which
uses an indefinite loop. We'll provide the to-do list, you write the code. This program should ask for floating point numbers as input and stops looping when **the total of the numbers entered is over 100**, or **more than 5 numbers have been entered**. Those are your two exit conditions. After the loop stops print out the total of the numbers entered and the count of numbers entered.
```
## TO-DO List
#1 count = 0
#2 total = 0
#3 loop Indefinitely
#4. input a number
#5 increment count
#6 add number to total
#7 if count equals 5 stop looping
#8 if total greater than 100 stop looping
#9 print total and count
# Write Code here:
count = 0
total = 0
while True:
total = float(input("Enter floating point numbers: "))
count = count + 1
total = total + total
if count == 5:
print("More than 5 numbers have been entered")
break
if total >= 100:
print("Your total is greater than 100.")
break
print("The total is", total, "and the count is", count)
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
import seaborn as sns
from Bio import SeqIO
import datasets
data_path = '../../data/PI_DataSet.tsv'
dataset_root = '../../datasets/'
results_root = '../../results/'
shuffle_stream = np.random.RandomState(seed = 1234)
df = pd.read_csv(data_path, sep = '\t')
df['id'] = df['SeqID'].map(str)
df.head()
```
## Cleaning
First, we need to convert the "difference from reference" format back into a normal sequence.
Using the Uniprot reference we can add back in the missing information.
```
pr_seq = 'PQITLWQRPLVTIKIGGQLKEALLDTGADDTVLEEMNLPGRWKPKMIGGIGGFIKVRQYDQILIEICGHKAIGTVLVGPTPVNIIGRNLLTQIGCTLNF'
# REF: https://hivdb.stanford.edu/pages/documentPage/consensus_amino_acid_sequences.html
seq_cols = [f'P{i}' for i in range(1,100)]
rep_dict = {}
for col, pr in zip(seq_cols, pr_seq):
rep_dict[col] = {'-': pr, '*': ''}
make_seq = lambda row: ''.join(row.reindex(seq_cols).fillna(''))
seq_ser = df[seq_cols].replace(rep_dict).apply(make_seq, axis=1)
df['sequence'] = seq_ser
df.head()
```
We also need to account for the data sparseness.
The subset of drugs: FPV, IDV, NFV, and SQV have the highest mutual coverage.
We'll use only those for downstream predictions.
```
wanted = ['FPV', 'IDV', 'NFV', 'SQV']
df.dropna(subset = wanted, inplace = True)
cutoff = 4 # fold increase over WT
resist = df[wanted]>4
resist['MULTI'] = resist.sum(axis=1)>0
resist.sum()
```
## Dataset Creation
```
# TODO: Add BibTeX citation
# Find for instance the citation on arxiv or on the dataset repo/website
_CITATION = """\
@InProceedings{huggingface:dataset,
title = {HIV Protease Drug Resistance Prediction Dataset},
author={Will Dampier
},
year={2021}
}
"""
# TODO: Add a link to an official homepage for the dataset here
_HOMEPAGE = ""
# TODO: Add the licence for the dataset here if you can find it
_LICENSE = ""
# TODO: Add description of the dataset here
# You can copy an official description
_DESCRIPTION = """\
This dataset was constructed the Stanford HIV Drug Resistance Database.
https://hivdb.stanford.edu/pages/genopheno.dataset.html
The sequences were interpolated from the protease high-quality dataset.
Sequences with >4-fold increased resistance relative to wild-type was labeled as True.
"""
features = datasets.Features({
'sequence': datasets.Value('string'),
'id': datasets.Value('string'),
'FPV': datasets.Value('bool'),
'IDV': datasets.Value('bool'),
'NFV': datasets.Value('bool'),
'SQV': datasets.Value('bool'),
'fold': datasets.Value('int32')
})
training_folds = shuffle_stream.randint(0,5, size = df['sequence'].values.shape)
df['fold'] = training_folds
info = datasets.DatasetInfo(description = _DESCRIPTION,
features = features,
homepage=_HOMEPAGE, license = _LICENSE, citation=_CITATION)
processed_df = df[wanted] > cutoff
processed_df['id'] = df['id']
processed_df['fold'] = df['fold']
processed_df['sequence'] = df['sequence']
dset = datasets.Dataset.from_pandas(processed_df,
info = info,
features = features)
#corecpt_dset
dset.save_to_disk(dataset_root + 'PR_resist')
```
|
github_jupyter
|
```
import pandas as pd
disp_url = 'https://raw.githubusercontent.com/PacktWorkshops/The-Data-Science-Workshop/master/Chapter12/Dataset/disp.csv'
trans_url = 'https://raw.githubusercontent.com/PacktWorkshops/The-Data-Science-Workshop/master/Chapter12/Dataset/trans.csv'
account_url = 'https://raw.githubusercontent.com/PacktWorkshops/The-Data-Science-Workshop/master/Chapter12/Dataset/account.csv'
client_url = 'https://raw.githubusercontent.com/PacktWorkshops/The-Data-Science-Workshop/master/Chapter12/Dataset/client.csv'
df_disp = pd.read_csv(disp_url, sep=';')
df_trans = pd.read_csv(trans_url, sep=';')
df_account = pd.read_csv(account_url, sep=';')
df_client = pd.read_csv(client_url, sep=';')
df_trans.head()
df_trans.shape
df_account.head()
df_trans_acc = pd.merge(df_trans, df_account, how='left', on='account_id')
df_trans_acc.shape
df_disp.head()
df_disp_owner = df_disp[df_disp['type'] == 'OWNER']
df_disp_owner.duplicated(subset='account_id').sum()
df_trans_acc_disp = pd.merge(df_trans_acc, df_disp_owner, how='left', on='account_id')
df_trans_acc_disp.shape
df_client.head()
df_merged = pd.merge(df_trans_acc_disp, df_client, how='left', on=['client_id', 'district_id'])
df_merged.shape
df_merged.columns
df_merged.rename(columns={'date_x': 'trans_date', 'type_x': 'trans_type', 'date_y':'account_creation', 'type_y':'client_type'}, inplace=True)
df_merged.head()
df_merged.dtypes
df_merged['trans_date'] = pd.to_datetime(df_merged['trans_date'], format="%y%m%d")
df_merged['account_creation'] = pd.to_datetime(df_merged['account_creation'], format="%y%m%d")
df_merged.dtypes
df_merged['is_female'] = (df_merged['birth_number'] % 10000) / 5000 > 1
df_merged['birth_number'].head()
df_merged.loc[df_merged['is_female'] == True, 'birth_number'] -= 5000
df_merged['birth_number'].head()
pd.to_datetime(df_merged['birth_number'], format="%y%m%d", errors='coerce')
df_merged['birth_number'] = df_merged['birth_number'].astype(str)
df_merged['birth_number'].head()
import numpy as np
df_merged.loc[df_merged['birth_number'] == 'nan', 'birth_number'] = np.nan
df_merged['birth_number'].head()
df_merged.loc[~df_merged['birth_number'].isna(), 'birth_number'] = '19' + df_merged.loc[~df_merged['birth_number'].isna(), 'birth_number']
df_merged['birth_number'].head()
df_merged['birth_number'] = pd.to_datetime(df_merged['birth_number'], format="%Y%m%d", errors='coerce')
df_merged['birth_number'].head(20)
df_merged['age_at_creation'] = df_merged['account_creation'] - df_merged['birth_number']
df_merged['age_at_creation'] = df_merged['age_at_creation'] / np.timedelta64(1,'Y')
df_merged['age_at_creation'] = df_merged['age_at_creation'].round()
df_merged.head()
```
|
github_jupyter
|
# Self-Driving Car Engineer Nanodegree
## Project: **Finding Lane Lines on the Road**
***
In this project, you will use the tools you learned about in the lesson to identify lane lines on the road. You can develop your pipeline on a series of individual images, and later apply the result to a video stream (really just a series of images). Check out the video clip "raw-lines-example.mp4" (also contained in this repository) to see what the output should look like after using the helper functions below.
Once you have a result that looks roughly like "raw-lines-example.mp4", you'll need to get creative and try to average and/or extrapolate the line segments you've detected to map out the full extent of the lane lines. You can see an example of the result you're going for in the video "P1_example.mp4". Ultimately, you would like to draw just one line for the left side of the lane, and one for the right.
In addition to implementing code, there is a brief writeup to complete. The writeup should be completed in a separate file, which can be either a markdown file or a pdf document. There is a [write up template](https://github.com/udacity/CarND-LaneLines-P1/blob/master/writeup_template.md) that can be used to guide the writing process. Completing both the code in the Ipython notebook and the writeup template will cover all of the [rubric points](https://review.udacity.com/#!/rubrics/322/view) for this project.
---
Let's have a look at our first image called 'test_images/solidWhiteRight.jpg'. Run the 2 cells below (hit Shift-Enter or the "play" button above) to display the image.
**Note: If, at any point, you encounter frozen display windows or other confounding issues, you can always start again with a clean slate by going to the "Kernel" menu above and selecting "Restart & Clear Output".**
---
**The tools you have are color selection, region of interest selection, grayscaling, Gaussian smoothing, Canny Edge Detection and Hough Tranform line detection. You are also free to explore and try other techniques that were not presented in the lesson. Your goal is piece together a pipeline to detect the line segments in the image, then average/extrapolate them and draw them onto the image for display (as below). Once you have a working pipeline, try it out on the video stream below.**
---
<figure>
<img src="examples/line-segments-example.jpg" width="380" alt="Combined Image" />
<figcaption>
<p></p>
<p style="text-align: center;"> Your output should look something like this (above) after detecting line segments using the helper functions below </p>
</figcaption>
</figure>
<p></p>
<figure>
<img src="examples/laneLines_thirdPass.jpg" width="380" alt="Combined Image" />
<figcaption>
<p></p>
<p style="text-align: center;"> Your goal is to connect/average/extrapolate line segments to get output like this</p>
</figcaption>
</figure>
**Run the cell below to import some packages. If you get an `import error` for a package you've already installed, try changing your kernel (select the Kernel menu above --> Change Kernel). Still have problems? Try relaunching Jupyter Notebook from the terminal prompt. Also, consult the forums for more troubleshooting tips.**
## Import Packages
```
#importing some useful packages
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import numpy as np
import cv2
import os
%matplotlib inline
```
## Read in an Image
```
#reading in an image
image = mpimg.imread('test_images/solidWhiteRight.jpg')
#printing out some stats and plotting
print('This image is:', type(image), 'with dimensions:', image.shape)
plt.imshow(image) # if you wanted to show a single color channel image called 'gray', for example, call as plt.imshow(gray, cmap='gray')
```
## Ideas for Lane Detection Pipeline
**Some OpenCV functions (beyond those introduced in the lesson) that might be useful for this project are:**
`cv2.inRange()` for color selection
`cv2.fillPoly()` for regions selection
`cv2.line()` to draw lines on an image given endpoints
`cv2.addWeighted()` to coadd / overlay two images
`cv2.cvtColor()` to grayscale or change color
`cv2.imwrite()` to output images to file
`cv2.bitwise_and()` to apply a mask to an image
**Check out the OpenCV documentation to learn about these and discover even more awesome functionality!**
## Helper Functions
Below are some helper functions to help get you started. They should look familiar from the lesson!
```
import math
def grayscale(img):
"""Applies Grayscale transform"""
return cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
def canny(img, low_threshold, high_threshold):
"""Applies the Canny transform"""
return cv2.Canny(img, low_threshold, high_threshold)
def gaussian_blur(img, kernel_size):
"""Applies a Gaussian Noise kernel"""
return cv2.GaussianBlur(img, (kernel_size, kernel_size), 0)
def region_of_interest(img, vertices):
"""
Applies an image mask, only keep the region of the image defined by the polygon
"""
#defining a blank mask to start with
mask = np.zeros_like(img)
#defining a 3 channel or 1 channel color to fill the mask with depending on the input image
if len(img.shape) > 2:
channel_count = img.shape[2] # i.e. 3 or 4 depending on your image
ignore_mask_color = (255,) * channel_count
else:
ignore_mask_color = 255
#filling pixels inside the polygon defined by "vertices" with the fill color
cv2.fillPoly(mask, vertices, ignore_mask_color)
#returning the image only where mask pixels are nonzero
masked_image = cv2.bitwise_and(img, mask)
return masked_image
def line_fit(img, x, y, color=[255, 0, 0], thickness=20):
fit = np.polyfit(x,y,1)
m, b = fit
#Define y Values
y_1 = img.shape[0]
y_2 = int(y_1 / 2) + 50
# Define x Values
# y = mx + b ----> x = (y - b) / m
x_1 = int((y_1 - b) / m)
x_2 = int((y_2 - b) / m)
cv2.line(img, (x_1, y_1), (x_2, y_2), color, thickness)
def draw_lines(img, lines):
"""
Draw the lines with the line fit
"""
left_x = []
left_y = []
right_x = []
right_y = []
for line in lines:
for x1,y1,x2,y2 in line:
m = (y2 - y1) / (x2 - x1)
if m < 0:
left_x.append(x1)
left_x.append(x2)
left_y.append(y1)
left_y.append(y2)
else:
right_x.append(x1)
right_x.append(x2)
right_y.append(y1)
right_y.append(y2)
line_fit(img, left_x, left_y)
line_fit(img, right_x, right_y)
def hough_lines(img, rho, theta, threshold, min_line_len, max_line_gap):
"""
`img` should be the output of a Canny transform. Returns an image with hough lines drawn.
"""
lines = cv2.HoughLinesP(img, rho, theta, threshold, np.array([]), minLineLength=min_line_len, maxLineGap=max_line_gap)
line_img = np.zeros((img.shape[0], img.shape[1], 3), dtype=np.uint8)
draw_lines(line_img, lines)
return line_img
# Python 3 has support for cool math symbols.
def weighted_img(img, initial_img, α=0.8, β=1., γ=0.):
"""
`img` is the output of the hough_lines(), An image with lines drawn on it.
"""
return cv2.addWeighted(initial_img, α, img, β, γ)
```
## Test Images
Build your pipeline to work on the images in the directory "test_images"
**You should make sure your pipeline works well on these images before you try the videos.**
```
# Use a single Image to test the Pipeline
image = mpimg.imread('test_images/' + 'solidWhiteCurve.jpg')
#Start with Grayscale
ip_gray = grayscale(image)
plt.imshow(ip_gray)
# Apply Gaussian Blur
ip_gaussian = gaussian_blur(ip_gray, 3)
plt.imshow(ip_gaussian)
# Experiment with Canny Edge Parameters
ip_canny1 = canny(ip_gaussian, 10, 30)
ip_canny2 = canny(ip_gaussian, 30, 90)
ip_canny3 = canny(ip_gaussian, 50, 150)
ip_canny4 = canny(ip_gaussian, 60, 120)
plt.subplot(221)
plt.imshow(ip_canny1)
plt.subplot(222)
plt.imshow(ip_canny2)
plt.subplot(223)
plt.imshow(ip_canny3)
plt.subplot(224)
plt.imshow(ip_canny4)
ip_canny = canny(ip_gaussian, 60, 120)
#Set mask verticies to limit range of interest within image
vertices = np.array([[(90,image.shape[0]),(450, 330), (510, 330), (image.shape[1],image.shape[0])]], dtype=np.int32)
ip_mask = region_of_interest(ip_canny, vertices)
plt.imshow(ip_mask)
# Set Hough Threshold Parameters
rho = 2
theta = np.pi/180
threshold = 10
min_line_len = 20
max_line_gap = 10
ip_hough = hough_lines(ip_mask, rho, theta, threshold, min_line_len, max_line_gap)
plt.imshow(ip_hough)
# Overlay the Hough Lines with the Original Image
ip_weighted = weighted_img(ip_hough, image)
plt.imshow(ip_weighted)
```
## Build a Lane Finding Pipeline
Build the pipeline and run your solution on all test_images. Make copies into the `test_images_output` directory, and you can use the images in your writeup report.
Try tuning the various parameters, especially the low and high Canny thresholds as well as the Hough lines parameters.
```
def image_processing(image):
# Set Hough Parameters
rho = 2
theta = np.pi/180
threshold = 20 #Originally 10
min_line_len = 40 #Originally 20
max_line_gap = 10
#Set Canny Parameters
low_threshold = 60
high_threshold = 120
#Set Mask Vertices
vertices = np.array([[(90,image.shape[0]),(450, 320), (510, 320), (image.shape[1],image.shape[0])]], dtype=np.int32)
# Build Pipeline: Grayscale -> Gaussian -> Canny -> Mask -> Hough -> Weighted
ip_gray = grayscale(image)
ip_gaussian = gaussian_blur(ip_gray, 3)
ip_canny = canny(ip_gaussian, low_threshold, high_threshold)
ip_mask = region_of_interest(ip_canny, vertices)
ip_hough = hough_lines(ip_mask, rho, theta, threshold, min_line_len, max_line_gap)
ip_weighted = weighted_img(ip_hough, image)
return ip_weighted
#Run through the pipeline with all images in directory
output_list = []
for img in os.listdir("test_images/"):
image = mpimg.imread('test_images/' + img)
output = image_processing(image)
output_list.append(output)
mpimg.imsave('test_images_output/' + img, output)
# Plot All Output Images
plt.figure(figsize=(12,8))
plt.subplot(231)
plt.imshow(output_list[0])
plt.subplot(232)
plt.imshow(output_list[1])
plt.subplot(233)
plt.imshow(output_list[2])
plt.subplot(234)
plt.imshow(output_list[3])
plt.subplot(235)
plt.imshow(output_list[4])
plt.subplot(236)
plt.imshow(output_list[5])
plt.subplots_adjust(top=0.95, bottom=0.42, left=0.10, right=0.95, hspace=0.35,
wspace=0.15)
```
## Test on Videos
You know what's cooler than drawing lanes over images? Drawing lanes over video!
We can test our solution on two provided videos:
`solidWhiteRight.mp4`
`solidYellowLeft.mp4`
**Note: if you get an import error when you run the next cell, try changing your kernel (select the Kernel menu above --> Change Kernel). Still have problems? Try relaunching Jupyter Notebook from the terminal prompt. Also, consult the forums for more troubleshooting tips.**
**If you get an error that looks like this:**
```
NeedDownloadError: Need ffmpeg exe.
You can download it by calling:
imageio.plugins.ffmpeg.download()
```
**Follow the instructions in the error message and check out [this forum post](https://discussions.udacity.com/t/project-error-of-test-on-videos/274082) for more troubleshooting tips across operating systems.**
```
# Import everything needed to edit/save/watch video clips
from moviepy.editor import VideoFileClip
from IPython.display import HTML
```
Let's try the one with the solid white lane on the right first ...
```
white_output = 'test_videos_output/solidWhiteRight.mp4'
clip1 = VideoFileClip("test_videos/solidWhiteRight.mp4")
white_clip = clip1.fl_image(image_processing) #NOTE: this function expects color images!!
%time white_clip.write_videofile(white_output, audio=False)
```
Play the video inline, or if you prefer find the video in your filesystem (should be in the same directory) and play it in your video player of choice.
```
HTML("""
<video width="960" height="540" controls>
<source src="{0}">
</video>
""".format(white_output))
```
## Improve the draw_lines() function
**At this point, if you were successful with making the pipeline and tuning parameters, you probably have the Hough line segments drawn onto the road, but what about identifying the full extent of the lane and marking it clearly as in the example video (P1_example.mp4)? Think about defining a line to run the full length of the visible lane based on the line segments you identified with the Hough Transform. As mentioned previously, try to average and/or extrapolate the line segments you've detected to map out the full extent of the lane lines. You can see an example of the result you're going for in the video "P1_example.mp4".**
**Go back and modify your draw_lines function accordingly and try re-running your pipeline. The new output should draw a single, solid line over the left lane line and a single, solid line over the right lane line. The lines should start from the bottom of the image and extend out to the top of the region of interest.**
Now for the one with the solid yellow lane on the left. This one's more tricky!
```
yellow_output = 'test_videos_output/solidYellowLeft_houghTest.mp4'
clip2 = VideoFileClip('test_videos/solidYellowLeft.mp4')
yellow_clip = clip2.fl_image(image_processing)
%time yellow_clip.write_videofile(yellow_output, audio=False)
HTML("""
<video width="960" height="540" controls>
<source src="{0}">
</video>
""".format(yellow_output))
# This video showed that the weighted lines jumped. Let's jump through each step to determine the culprit
# Copy from image_processing function for reference:
def image_test(image):
rho = 2
theta = np.pi/180
threshold = 20
min_line_len = 40
max_line_gap = 10
#Set Canny Parameters
low_threshold = 60
high_threshold = 120
#Set Mask Vertices
vertices = np.array([[(90,image.shape[0]),(450, 320), (510, 320), (image.shape[1],image.shape[0])]], dtype=np.int32)
# Build Pipeline: Grayscale -> Gaussian -> Canny -> Mask -> Hough -> Weighted
ip_gray = grayscale(image)
ip_gaussian = gaussian_blur(ip_gray, 3)
ip_canny = canny(ip_gaussian, low_threshold, high_threshold)
ip_mask = region_of_interest(ip_canny, vertices)
ip_hough = hough_lines(ip_mask, rho, theta, threshold, min_line_len, max_line_gap)
ip_weighted = weighted_img(ip_hough, image)
return ip_weighted
yellow_output = 'test_videos_output/solidYellowLeft_houghTest.mp4'
clip2 = VideoFileClip('test_videos/solidYellowLeft.mp4')
yellow_clip = clip2.fl_image(image_test)
%time yellow_clip.write_videofile(yellow_output, audio=False)
HTML("""
<video width="960" height="540" controls>
<source src="{0}">
</video>
""".format(yellow_output))
```
## Writeup and Submission
If you're satisfied with your video outputs, it's time to make the report writeup in a pdf or markdown file. Once you have this Ipython notebook ready along with the writeup, it's time to submit for review! Here is a [link](https://github.com/udacity/CarND-LaneLines-P1/blob/master/writeup_template.md) to the writeup template file.
## Optional Challenge
Try your lane finding pipeline on the video below. Does it still work? Can you figure out a way to make it more robust? If you're up for the challenge, modify your pipeline so it works with this video and submit it along with the rest of your project!
```
challenge_output = 'test_videos_output/challenge.mp4'
## To speed up the testing process you may want to try your pipeline on a shorter subclip of the video
## To do so add .subclip(start_second,end_second) to the end of the line below
## Where start_second and end_second are integer values representing the start and end of the subclip
## You may also uncomment the following line for a subclip of the first 5 seconds
##clip3 = VideoFileClip('test_videos/challenge.mp4').subclip(0,5)
clip3 = VideoFileClip('test_videos/challenge.mp4')
challenge_clip = clip3.fl_image(process_image)
%time challenge_clip.write_videofile(challenge_output, audio=False)
HTML("""
<video width="960" height="540" controls>
<source src="{0}">
</video>
""".format(challenge_output))
```
|
github_jupyter
|
# TensorFlow Transfer Learning
This notebook shows how to use pre-trained models from [TensorFlowHub](https://www.tensorflow.org/hub). Sometimes, there is not enough data, computational resources, or time to train a model from scratch to solve a particular problem. We'll use a pre-trained model to classify flowers with better accuracy than a new model for use in a mobile application.
## Learning Objectives
1. Know how to apply image augmentation
2. Know how to download and use a TensorFlow Hub module as a layer in Keras.
```
import os
import pathlib
import IPython.display as display
import matplotlib.pylab as plt
import numpy as np
import tensorflow as tf
import tensorflow_hub as hub
from PIL import Image
from tensorflow.keras import Sequential
from tensorflow.keras.layers import (
Conv2D,
Dense,
Dropout,
Flatten,
MaxPooling2D,
Softmax,
)
```
## Exploring the data
As usual, let's take a look at the data before we start building our model. We'll be using a creative-commons licensed flower photo dataset of 3670 images falling into 5 categories: 'daisy', 'roses', 'dandelion', 'sunflowers', and 'tulips'.
The below [tf.keras.utils.get_file](https://www.tensorflow.org/api_docs/python/tf/keras/utils/get_file) command downloads a dataset to the local Keras cache. To see the files through a terminal, copy the output of the cell below.
```
data_dir = tf.keras.utils.get_file(
"flower_photos",
"https://storage.googleapis.com/download.tensorflow.org/example_images/flower_photos.tgz",
untar=True,
)
# Print data path
print("cd", data_dir)
```
We can use python's built in [pathlib](https://docs.python.org/3/library/pathlib.html) tool to get a sense of this unstructured data.
```
data_dir = pathlib.Path(data_dir)
image_count = len(list(data_dir.glob("*/*.jpg")))
print("There are", image_count, "images.")
CLASS_NAMES = np.array(
[item.name for item in data_dir.glob("*") if item.name != "LICENSE.txt"]
)
print("These are the available classes:", CLASS_NAMES)
```
Let's display the images so we can see what our model will be trying to learn.
```
roses = list(data_dir.glob("roses/*"))
for image_path in roses[:3]:
display.display(Image.open(str(image_path)))
```
## Building the dataset
Keras has some convenient methods to read in image data. For instance [tf.keras.preprocessing.image.ImageDataGenerator](https://www.tensorflow.org/api_docs/python/tf/keras/preprocessing/image/ImageDataGenerator) is great for small local datasets. A tutorial on how to use it can be found [here](https://www.tensorflow.org/tutorials/load_data/images), but what if we have so many images, it doesn't fit on a local machine? We can use [tf.data.datasets](https://www.tensorflow.org/api_docs/python/tf/data/Dataset) to build a generator based on files in a Google Cloud Storage Bucket.
We have already prepared these images to be stored on the cloud in `gs://cloud-ml-data/img/flower_photos/`. The images are randomly split into a training set with 90% data and an iterable with 10% data listed in CSV files:
Training set: [train_set.csv](https://storage.cloud.google.com/cloud-ml-data/img/flower_photos/train_set.csv)
Evaluation set: [eval_set.csv](https://storage.cloud.google.com/cloud-ml-data/img/flower_photos/eval_set.csv)
Explore the format and contents of the train.csv by running:
```
!gsutil cat gs://cloud-ml-data/img/flower_photos/train_set.csv \
| head -5 > /tmp/input.csv
!cat /tmp/input.csv
!gsutil cat gs://cloud-ml-data/img/flower_photos/train_set.csv | \
sed 's/,/ /g' | awk '{print $2}' | sort | uniq > /tmp/labels.txt
!cat /tmp/labels.txt
```
Let's figure out how to read one of these images from the cloud. TensorFlow's [tf.io.read_file](https://www.tensorflow.org/api_docs/python/tf/io/read_file) can help us read the file contents, but the result will be a [Base64 image string](https://en.wikipedia.org/wiki/Base64). Hmm... not very readable for humans or Tensorflow.
Thankfully, TensorFlow's [tf.image.decode_jpeg](https://www.tensorflow.org/api_docs/python/tf/io/decode_jpeg) function can decode this string into an integer array, and [tf.image.convert_image_dtype](https://www.tensorflow.org/api_docs/python/tf/image/convert_image_dtype) can cast it into a 0 - 1 range float. Finally, we'll use [tf.image.resize](https://www.tensorflow.org/api_docs/python/tf/image/resize) to force image dimensions to be consistent for our neural network.
We'll wrap these into a function as we'll be calling these repeatedly. While we're at it, let's also define our constants for our neural network.
```
IMG_HEIGHT = 224
IMG_WIDTH = 224
IMG_CHANNELS = 3
BATCH_SIZE = 32
# 10 is a magic number tuned for local training of this dataset.
SHUFFLE_BUFFER = 10 * BATCH_SIZE
AUTOTUNE = tf.data.experimental.AUTOTUNE
VALIDATION_IMAGES = 370
VALIDATION_STEPS = VALIDATION_IMAGES // BATCH_SIZE
def decode_img(img, reshape_dims):
# Convert the compressed string to a 3D uint8 tensor.
img = tf.image.decode_jpeg(img, channels=IMG_CHANNELS)
# Use `convert_image_dtype` to convert to floats in the [0,1] range.
img = tf.image.convert_image_dtype(img, tf.float32)
# Resize the image to the desired size.
return tf.image.resize(img, reshape_dims)
```
Is it working? Let's see!
**TODO 1.a:** Run the `decode_img` function and plot it to see a happy looking daisy.
```
img = tf.io.read_file(
"gs://cloud-ml-data/img/flower_photos/daisy/754296579_30a9ae018c_n.jpg"
)
# Uncomment to see the image string.
# print(img)
img = decode_img(img, [IMG_WIDTH, IMG_HEIGHT])
plt.imshow(img.numpy());
```
One flower down, 3669 more of them to go. Rather than load all the photos in directly, we'll use the file paths given to us in the csv and load the images when we batch. [tf.io.decode_csv](https://www.tensorflow.org/api_docs/python/tf/io/decode_csv) reads in csv rows (or each line in a csv file), while [tf.math.equal](https://www.tensorflow.org/api_docs/python/tf/math/equal) will help us format our label such that it's a boolean array with a truth value corresponding to the class in `CLASS_NAMES`, much like the labels for the MNIST Lab.
```
def decode_csv(csv_row):
record_defaults = ["path", "flower"]
filename, label_string = tf.io.decode_csv(csv_row, record_defaults)
image_bytes = tf.io.read_file(filename=filename)
label = tf.math.equal(CLASS_NAMES, label_string)
return image_bytes, label
```
Next, we'll transform the images to give our network more variety to train on. There are a number of [image manipulation functions](https://www.tensorflow.org/api_docs/python/tf/image). We'll cover just a few:
* [tf.image.random_crop](https://www.tensorflow.org/api_docs/python/tf/image/random_crop) - Randomly deletes the top/bottom rows and left/right columns down to the dimensions specified.
* [tf.image.random_flip_left_right](https://www.tensorflow.org/api_docs/python/tf/image/random_flip_left_right) - Randomly flips the image horizontally
* [tf.image.random_brightness](https://www.tensorflow.org/api_docs/python/tf/image/random_brightness) - Randomly adjusts how dark or light the image is.
* [tf.image.random_contrast](https://www.tensorflow.org/api_docs/python/tf/image/random_contrast) - Randomly adjusts image contrast.
**TODO 1.b:** Add the missing parameters from the random augment functions.
```
MAX_DELTA = 63.0 / 255.0 # Change brightness by at most 17.7%
CONTRAST_LOWER = 0.2
CONTRAST_UPPER = 1.8
def read_and_preprocess(image_bytes, label, random_augment=False):
if random_augment:
img = decode_img(image_bytes, [IMG_HEIGHT + 10, IMG_WIDTH + 10])
img = tf.image.random_crop(img, [IMG_HEIGHT, IMG_WIDTH, IMG_CHANNELS])
img = tf.image.random_flip_left_right(img)
img = tf.image.random_brightness(img, MAX_DELTA)
img = tf.image.random_contrast(img, CONTRAST_LOWER, CONTRAST_UPPER)
else:
img = decode_img(image_bytes, [IMG_WIDTH, IMG_HEIGHT])
return img, label
def read_and_preprocess_with_augment(image_bytes, label):
return read_and_preprocess(image_bytes, label, random_augment=True)
```
Finally, we'll make a function to craft our full dataset using [tf.data.dataset](https://www.tensorflow.org/api_docs/python/tf/data/Dataset). The [tf.data.TextLineDataset](https://www.tensorflow.org/api_docs/python/tf/data/TextLineDataset) will read in each line in our train/eval csv files to our `decode_csv` function.
[.cache](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#cache) is key here. It will store the dataset in memory
```
def load_dataset(csv_of_filenames, batch_size, training=True):
dataset = (
tf.data.TextLineDataset(filenames=csv_of_filenames)
.map(decode_csv)
.cache()
)
if training:
dataset = (
dataset.map(read_and_preprocess_with_augment)
.shuffle(SHUFFLE_BUFFER)
.repeat(count=None)
) # Indefinately.
else:
dataset = dataset.map(read_and_preprocess).repeat(
count=1
) # Each photo used once.
# Prefetch prepares the next set of batches while current batch is in use.
return dataset.batch(batch_size=batch_size).prefetch(buffer_size=AUTOTUNE)
```
We'll test it out with our training set. A batch size of one will allow us to easily look at each augmented image.
```
train_path = "gs://cloud-ml-data/img/flower_photos/train_set.csv"
train_data = load_dataset(train_path, 1)
itr = iter(train_data)
```
**TODO 1.c:** Run the below cell repeatedly to see the results of different batches. The images have been un-normalized for human eyes. Can you tell what type of flowers they are? Is it fair for the AI to learn on?
```
image_batch, label_batch = next(itr)
img = image_batch[0]
plt.imshow(img)
print(label_batch[0])
```
**Note:** It may take a 4-5 minutes to see result of different batches.
## MobileNetV2
These flower photos are much larger than handwritting recognition images in MNIST. They are about 10 times as many pixels per axis **and** there are three color channels, making the information here over 200 times larger!
How do our current techniques stand up? Copy your best model architecture over from the <a href="2_mnist_models.ipynb">MNIST models lab</a> and see how well it does after training for 5 epochs of 50 steps.
**TODO 2.a** Copy over the most accurate model from 2_mnist_models.ipynb or build a new CNN Keras model.
```
eval_path = "gs://cloud-ml-data/img/flower_photos/eval_set.csv"
nclasses = len(CLASS_NAMES)
hidden_layer_1_neurons = 400
hidden_layer_2_neurons = 100
dropout_rate = 0.25
num_filters_1 = 64
kernel_size_1 = 3
pooling_size_1 = 2
num_filters_2 = 32
kernel_size_2 = 3
pooling_size_2 = 2
layers = [
Conv2D(
num_filters_1,
kernel_size=kernel_size_1,
activation="relu",
input_shape=(IMG_WIDTH, IMG_HEIGHT, IMG_CHANNELS),
),
MaxPooling2D(pooling_size_1),
Conv2D(num_filters_2, kernel_size=kernel_size_2, activation="relu"),
MaxPooling2D(pooling_size_2),
Flatten(),
Dense(hidden_layer_1_neurons, activation="relu"),
Dense(hidden_layer_2_neurons, activation="relu"),
Dropout(dropout_rate),
Dense(nclasses),
Softmax(),
]
old_model = Sequential(layers)
old_model.compile(
optimizer="adam", loss="categorical_crossentropy", metrics=["accuracy"]
)
train_ds = load_dataset(train_path, BATCH_SIZE)
eval_ds = load_dataset(eval_path, BATCH_SIZE, training=False)
old_model.fit(
train_ds,
epochs=5,
steps_per_epoch=5,
validation_data=eval_ds,
validation_steps=VALIDATION_STEPS,
)
```
If your model is like mine, it learns a little bit, slightly better then random, but *ugh*, it's too slow! With a batch size of 32, 5 epochs of 5 steps is only getting through about a quarter of our images. Not to mention, this is a much larger problem then MNIST, so wouldn't we need a larger model? But how big do we need to make it?
Enter Transfer Learning. Why not take advantage of someone else's hard work? We can take the layers of a model that's been trained on a similar problem to ours and splice it into our own model.
[Tensorflow Hub](https://tfhub.dev/s?module-type=image-augmentation,image-classification,image-others,image-style-transfer,image-rnn-agent) is a database of models, many of which can be used for Transfer Learning. We'll use a model called [MobileNet](https://tfhub.dev/google/imagenet/mobilenet_v2_035_224/feature_vector/4) which is an architecture optimized for image classification on mobile devices, which can be done with [TensorFlow Lite](https://github.com/tensorflow/hub/blob/master/examples/colab/tf2_image_retraining.ipynb). Let's compare how a model trained on [ImageNet](http://www.image-net.org/) data compares to one built from scratch.
The `tensorflow_hub` python package has a function to include a Hub model as a [layer in Keras](https://www.tensorflow.org/hub/api_docs/python/hub/KerasLayer). We'll set the weights of this model as un-trainable. Even though this is a compressed version of full scale image classification models, it still has over four hundred thousand paramaters! Training all these would not only add to our computation, but it is also prone to over-fitting. We'll add some L2 regularization and Dropout to prevent that from happening to our trainable weights.
**TODO 2.b**: Add a Hub Keras Layer at the top of the model using the handle provided.
```
module_selection = "mobilenet_v2_100_224"
module_handle = "https://tfhub.dev/google/imagenet/{}/feature_vector/4".format(
module_selection
)
transfer_model = tf.keras.Sequential(
[
hub.KerasLayer(module_handle, trainable=False),
tf.keras.layers.Dropout(rate=0.2),
tf.keras.layers.Dense(
nclasses,
activation="softmax",
kernel_regularizer=tf.keras.regularizers.l2(0.0001),
),
]
)
transfer_model.build((None,) + (IMG_HEIGHT, IMG_WIDTH, IMG_CHANNELS))
transfer_model.summary()
```
Even though we're only adding one more `Dense` layer in order to get the probabilities for each of the 5 flower types, we end up with over six thousand parameters to train ourselves. Wow!
Moment of truth. Let's compile this new model and see how it compares to our MNIST architecture.
```
transfer_model.compile(
optimizer="adam", loss="categorical_crossentropy", metrics=["accuracy"]
)
train_ds = load_dataset(train_path, BATCH_SIZE)
eval_ds = load_dataset(eval_path, BATCH_SIZE, training=False)
transfer_model.fit(
train_ds,
epochs=5,
steps_per_epoch=5,
validation_data=eval_ds,
validation_steps=VALIDATION_STEPS,
)
```
Alright, looking better!
Still, there's clear room to improve. Data bottlenecks are especially prevalent with image data due to the size of the image files. There's much to consider such as the computation of augmenting images and the bandwidth to transfer images between machines.
Think life is too short, and there has to be a better way? In the next lab, we'll blast away these problems by developing a cloud strategy to train with TPUs!
## Bonus Exercise
Keras has a [local way](https://keras.io/models/sequential/) to do distributed training, but we'll be using a different technique in the next lab. Want to give the local way a try? Check out this excellent [blog post](https://stanford.edu/~shervine/blog/keras-how-to-generate-data-on-the-fly) to get started. Or want to go full-blown Keras? It also has a number of [pre-trained models](https://keras.io/applications/) ready to use.
Copyright 2019 Google Inc.
Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
|
github_jupyter
|
```
import os
import sys
import time
import matplotlib.pyplot as plt
import numpy as np
import GCode
import GRBL
# Flip a 2D array. Effectively reversing the path.
flip2 = np.array([
[0, 1],
[1, 0],
])
flip2
# Flip a 2x3 array. Effectively reversing the path.
flip3 = np.array([
[0, 0, 1],
[0, 1, 0],
[1, 0, 0],
])
flip3
A = np.array([
[1, 2],
[3, 4],
])
A
np.matmul(flip2, A)
B = np.array([
[1, 2],
[3, 4],
[5, 6],
])
B
np.matmul(flip3, B)
B.shape[0]
np.eye(B.shape[0])
flip_n_reverseit = np.eye(B.shape[0])[:, ::-1]
flip_n_reverseit
def reverse(self, points):
flip_n_reverseit = np.eye(points.shape[0])[:, ::-1]
return np.matmul(flip_n_reverseit, points)
reverse(None, B)
```
# Code:
Draw a 10 mm line from (0, 0) to (10, 0).
```
line_len = 10
line_n_points = 2
p = np.linspace(0, line_len, line_n_points, endpoint=True)
p
line_n_points = 3
p = np.linspace(0, line_len, line_n_points, endpoint=True)
p
line_n_points = 4
p = np.linspace(0, line_len, line_n_points, endpoint=True)
p
p
Y=0
for X in np.linspace(0, line_len, line_n_points, endpoint=True):
def HorzLine(X0=0, Xf=10, Y=0, n_points=2):
p = np.linspace(X0, Xf, n_points, endpoint=True)
line_points = np.array([
p,
Y*np.ones(p.shape),
])
return line_points.transpose()
HorzLine()
def VertLine(X=0, Y0=0, Yf=10, n_points=2):
p = np.linspace(Y0, Yf, n_points, endpoint=True)
line_points = np.array([
X*np.ones(p.shape),
p,
])
return line_points.transpose()
VertLine()
points = HorzLine(X0=0, Xf=10, Y=0, n_points=2)
points
line = GCode.Line(points=points)
line
line.__repr__()
prog_cfg={
"points": points
}
prog_cfg
line_cfg = {
"X0": 0,
"Xf": 10,
"Y": 0,
"n_points": 2
}
line_cfg
help(GCode.Line)
help(GCode.Program)
progs = list()
for n_points in range(2, 10):
line_cfg = {
"X0": 0,
"Xf": 10,
"Y": 0,
"n_points": n_points
}
points = HorzLine(**line_cfg)
line_cfg = {
"points": points,
"feed":120,
"power":128,
"dynamic_power": True,
}
line = GCode.Line(points=points)
prog_cfg={
"lines": [line, line],
"feed": 120
}
prog = GCode.Program(**prog_cfg)
progs.append(prog)
progs
for prog in progs:
print(len(prog.buffer))
for prog in progs:
prog.generate_gcode()
print(len(prog.buffer))
list(map(lambda prog: prog.generate_gcode(), progs))
list(map(lambda prog: len(prog.buffer), progs))
import threading
def concurrent_map(func, data):
"""
Similar to the bultin function map(). But spawn a thread for each argument
and apply `func` concurrently.
Note: unlike map(), we cannot take an iterable argument. `data` should be an
indexable sequence.
"""
N = len(data)
result = [None] * N
# wrapper to dispose the result in the right slot
def task_wrapper(i):
result[i] = func(data[i])
threads = [threading.Thread(target=task_wrapper, args=(i,)) for i in range(N)]
for t in threads:
t.start()
for t in threads:
t.join()
return result
concurrent_map(lambda prog: prog.generate_gcode(), progs)
concurrent_map(lambda prog: len(prog.buffer), progs)
concurrent_map(lambda prog: prog.__repr__(), progs)
concurrent_map(lambda prog: prog.dist, progs)
concurrent_map(lambda prog: prog.jog_dist, progs)
concurrent_map(lambda prog: prog.laserin_dist, progs)
m=concurrent_map(lambda prog: prog.laserin_dist, progs)
np.diff(m)
np.diff(m)==0
np.all(np.diff(m)==0)
assert(np.all(np.diff(m)==0))
flip2
reverse(None, progs[1].lines[0].points)
progs
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
raw_data = pd.read_excel("hydrogen_test_classification.xlsx")
raw_data.head()
# 分开特征值和标签值
X = raw_data.drop("TRUE VALUE", axis=1).copy()
y = raw_data["TRUE VALUE"]
y.unique()
from sklearn.model_selection import train_test_split
# 分训练集、验证集和测试集
X_train_full, X_test, y_train_full, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
X_train, Y_valid, X_label, Y_label = train_test_split(X_train_full, y_train_full, test_size=0.2, random_state=42)
print(X_train.shape)
print(Y_valid.shape)
print(X_label.shape)
print(Y_label.shape)
#将数据进行转化成四个通道,方便使用卷积神经网络进行分类
def transform(X):
X=X.values
X=X.reshape(X.shape[0:1][0],5,5)
X=np.expand_dims(X,-1)
print("转化后的维度大小为:")
print(X.shape)
return X
#首先对X—train进行维度转换
X_train=transform(X_train)
X_train.shape
Y_valid=transform(Y_valid)
Y_valid.shape
Y_valid.shape
#将label的标签值,转化为1和0
def only_one_and_zero(y):
y=y.values#将pandas当中的dateframe对象转化为numpy-ndarray对象
length=y.shape[0:1][0]
i=0
while i<length:
if(y[i]==-1):
y[i]=0
i+=1
print("当前的y为",y)
print(type(y))
return y
X_label=only_one_and_zero(X_label)
Y_label=only_one_and_zero(Y_label)
X_train
Y_label
X_train.shape
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Flatten, Dense
#初步想法,将5*5的数据进行卷积操作,然后使用卷积神经网络进行图像识别
# input_shape 填特征的维度,将特征变为一维特征的形式
model = Sequential()
# model.add(Flatten(input_shape=[25]))、
model.add(tf.keras.layers.Conv2D(50,(2,2),input_shape=X_train.shape[1:],activation="relu"))
model.add(tf.keras.layers.BatchNormalization())
model.add(tf.keras.layers.Conv2D(100,(2,2),activation="relu"))
model.add(tf.keras.layers.MaxPool2D())
model.add(tf.keras.layers.Flatten())
#model.add(Dense(1024, activation="relu", input_shape=X_train.shape[1:]))
model.add(Dense(500, activation="relu"))
model.add(Dense(250, activation="relu"))
model.add(Dense(125, activation="relu"))
model.add(Dense(50, activation="relu"))
model.add(Dense(1, activation="sigmoid"))
model.summary()
#from tensorflow.keras.utils import plot_model
#plot_model(model, to_file='model.png',show_shapes=True)
#如果在本机安装pydot和pyfotprint这两个库的情况下,可以直接将神经网络进行可视化
model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.0001),
loss='binary_crossentropy',
metrics=['acc']
)
#创建checkpoint,在模型训练是进行回调,这样可以让训练完之后的模型得以保存
import os
checkpoint_path = "training_1/cnn.ckpt"
checkpoint_dir = os.path.dirname(checkpoint_path)
# 创建一个保存模型权重的回调
cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_path,
save_weights_only=True,
verbose=1)
#verbose=1,表示在模型训练的时候返回some imformation
history = model.fit(X_train,X_label, epochs=200,
validation_data=(Y_valid, Y_label),
callbacks=[cp_callback])
# 在一张图上画出loss和accuracy的
pd.DataFrame(history.history).plot(figsize=(8, 5))
plt.xlabel("epoch")
plt.grid(True)
# plt.gca().set_ylim(0, 1)
#save_fig("keras_learning_curves_plot")
plt.show()
plt.plot(history.epoch,history.history.get('loss'),label="loss")
plt.plot(history.epoch,history.history.get('val_loss'),label="val_loss")
plt.legend()
#络的重要信息
history.params
history.history.keys()
a = ["acc", "val_acc"]
plt.figure(figsize=(8, 5))
for i in a:
plt.plot(history.history[i], label=i)
plt.legend()
plt.grid(True)
model.evaluate(Y_valid, Y_label)
```
|
github_jupyter
|
```
import os, csv
from pprint import pprint
from pathlib import Path
import pandas as pd
from pandas.errors import ParserError
pd.set_option('display.max_columns', 999)
from icecream import ic
from tqdm.notebook import tqdm#, tqdm_notebook
temp_csvs = Path('/media/share/store_240a/data_downloads/noaa_daily_avg_temps')
len(os.listdir(temp_csvs))
#print(os.listdir(temp_csvs))
first_file = temp_csvs / os.listdir(temp_csvs)[0]
first_file = str(first_file)
first_file
df1 = pd.read_csv(first_file)
len(df1)
df1
df1['TEMP'].mean()
def unique_values_only_one(column: str):
value_l = column.unique()
if len(value_l) > 1:
return 'X'
return value_l[0]
def year_complete(year):
with open('complete.csv', 'a+', newline='') as f:
f.write(f'{year}')
f.write('\n')
def get_complete():
with open('complete.csv', 'r') as f:
year_l = [x[0] for x in csv.reader(f)]
return year_l
file_folders = os.listdir(temp_csvs)
for year in file_folders:
print(year)
file_folders_full = os.listdir(temp_csvs)
file_folders_full.sort()
print('All years:')
print(file_folders_full)
file_folders, done = [], []
complete_years = get_complete()
for year in file_folders_full:
if year not in complete_years:
file_folders.append(year)
else:
done.append(year)
print("Years completed already:")
print(done)
for year in tqdm(file_folders, desc='Overall Progress', position=0):
try:
years_complete = get_complete()
if year not in years_complete:
sites_in_folder = os.listdir(temp_csvs / year)
columns = ['SITE_NUMBER','LATITUDE','LONGITUDE','ELEVATION','AVERAGE_TEMP']
rows_l = []
for site in tqdm(sites_in_folder, desc=f'{year} Progress', position=1):
try:
df1 = pd.read_csv(temp_csvs / year / site)
average_temp = df1['TEMP'].mean()
site_number = unique_values_only_one(df1['STATION'])
latitude = unique_values_only_one(df1['LATITUDE'])
longitude = unique_values_only_one(df1['LONGITUDE'])
elevation = unique_values_only_one(df1['ELEVATION'])
if site_number == 'X' \
or latitude == 'X' \
or longitude == 'X' \
or elevation == 'X':
with open('non_unique', 'w', newline='') as f2:
f2.write(f'Non-unique column: {temp_csvs}, {year}, {site}')
rows_l.append([site_number,latitude,longitude,elevation,average_temp])
except ParserError as e:
print(e)
print(year, site)
with open(f'explor_year_temps_files/results_{year}.csv', 'w', newline='') as f:
write = csv.writer(f)
write.writerow(columns)
write.writerows(rows_l)
year_complete(year)
else:
print(f'{year} marked as complete already.')
except FileNotFoundError as e:
if not str(e).startswith("[Errno 2] No such file or directory: 'complete.csv'"):
raise FileNotFoundError(e)
year_complete('0000')
_2012 = temp_csvs / '2012' / '44275099999.csv'
with open(_2012, 'r') as f:
csv.reader(f)
year_l = [x[0] for x in csv.reader(f)]
year_l
_2012 = temp_csvs / '2012' / '30635099999.csv'
with open(_2012, 'r') as f:
csv.reader(f)
year_l = [x[0] for x in csv.reader(f)]
year_l
```
|
github_jupyter
|
# Supervised Learning
Supervised learning consists in learning the link between two datasets: the observed data X and an external variable y that we are trying to predict, usually called “target” or “labels”. Most often, y is a 1D array of length n_samples.
If the prediction task is to classify the observations in a set of finite labels, in other words to “name” the objects observed, the task is said to be a **classification** task. On the other hand, if the goal is to predict a continuous target variable, it is said to be a **regression** task.
Clustering, which we've just done with K means, is a type of *unsupervised* learning similar to classification. Here, the difference is that we'll be using the labels in our data in our algorithm.
## Classification
"The problem of identifying to which of a set of categories (sub-populations) a new observation belongs, on the basis of a training set of data containing observations (or instances) whose category membership is known." (Wikipedia)
We've seen one classification example already, the iris dataset. In this dataset, iris flowers are classified based on their petal and sepal geometries.
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA
def pca_plot(data):
pca = PCA(n_components=2)
pca.fit(data.data)
data_pca = pca.transform(data.data)
for label in range(len(data.target_names)):
plt.scatter(data_pca[data.target==label, 0],
data_pca[data.target==label, 1],
label=data.target_names[label])
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
from sklearn.datasets import load_iris
iris = load_iris()
pca_plot(iris)
```
Another dataset with more features is the wine classification dataset, which tries to determine the original cultivar, or plant family, of three different Italian wines. A chemical analysis determined the following samples:
1. Alcohol
2. Malic acid
3. Ash
4. Alcalinity of ash
5. Magnesium
6. Total phenols
7. Flavanoids
8. Nonflavanoid phenols
9. Proanthocyanins
10. Color intensity
11. Hue
12. OD280/OD315 of diluted wines
13. Proline
```
from sklearn.datasets import load_wine
wine = load_wine()
pca_plot(wine)
```
A final and more difficult dataset is a sample from the National Institute of Standards and Technology (NIST) dataset on handwritten numbers. A modified and larger version of this, Modified NIST or MNIST, is a current standard benchmark for state of the art machine learning algorithms. In this problem, each datapoint is an 8x8 pixel image (64 features) and the classification task is to label each image as the correct number.
```
from sklearn.datasets import load_digits
digits = load_digits()
images_and_labels = list(zip(digits.images, digits.target))
for index, (image, label) in enumerate(images_and_labels[:8]):
plt.subplot(2, 4, index + 1)
plt.axis('off')
plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
plt.title('Label: %i' % label)
plt.show()
pca_plot(digits)
```
## Regression
"In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships among variables. It includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables (or 'predictors'). More specifically, regression analysis helps one understand how the typical value of the dependent variable (or 'criterion variable') changes when any one of the independent variables is varied, while the other independent variables are held fixed." (Wikipedia)
In regression, each set of features doesn't correspond to a label but rather to a value. The task of the regression algorithm is to correctly predict this value based on the feature data. One way to think about regression and classification is that regression is continuous while classification is discrete.
Scikit learn also comes with a number of sample regression datasets.
In our example regression dataset, health metrics of diabetes patients were measured and then the progress of their diabetes was quantitatively measured after 1 year. The features are:
1. age
2. sex
3. body mass index
4. average blood pressure
+ 5-10 six blood serum measurements
```
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
y = diabetes.target
features = ["AGE", "SEX", "BMI", "BP", "BL1", "BL2", "BL3", "BL4", "BL5", "BL6"]
plt.figure(figsize=(20,20))
for i in range(10):
plt.subplot(4, 4, i + 1)
plt.scatter(diabetes.data[:, i], y, edgecolors=(0, 0, 0));
plt.title('Feature: %s' % features[i])
```
<div class="alert alert-success">
<b>EXERCISE: UCI datasets</b>
<ul>
<li>
Many of these datasets originally come from the UCI Machine Learning Repository. Visit https://archive.ics.uci.edu/ml/index.php and select a dataset. What is the dataset describing? What are the features? Is it classification or regression? How many data samples are there?
</li>
</ul>
</div>
|
github_jupyter
|
# Your first neural network
In this project, you'll build your first neural network and use it to predict daily bike rental ridership. We've provided some of the code, but left the implementation of the neural network up to you (for the most part). After you've submitted this project, feel free to explore the data and the model more.
```
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
```
## Load and prepare the data
A critical step in working with neural networks is preparing the data correctly. Variables on different scales make it difficult for the network to efficiently learn the correct weights. Below, we've written the code to load and prepare the data. You'll learn more about this soon!
```
data_path = 'Bike-Sharing-Dataset/hour.csv'
rides = pd.read_csv(data_path)
rides.head()
```
## Checking out the data
This dataset has the number of riders for each hour of each day from January 1 2011 to December 31 2012. The number of riders is split between casual and registered, summed up in the `cnt` column. You can see the first few rows of the data above.
Below is a plot showing the number of bike riders over the first 10 days in the data set. You can see the hourly rentals here. This data is pretty complicated! The weekends have lower over all ridership and there are spikes when people are biking to and from work during the week. Looking at the data above, we also have information about temperature, humidity, and windspeed, all of these likely affecting the number of riders. You'll be trying to capture all this with your model.
```
rides[:24*10].plot(x='dteday', y='cnt')
```
### Dummy variables
Here we have some categorical variables like season, weather, month. To include these in our model, we'll need to make binary dummy variables. This is simple to do with Pandas thanks to `get_dummies()`.
```
dummy_fields = ['season', 'weathersit', 'mnth', 'hr', 'weekday']
for each in dummy_fields:
dummies = pd.get_dummies(rides[each], prefix=each, drop_first=False)
rides = pd.concat([rides, dummies], axis=1)
fields_to_drop = ['instant', 'dteday', 'season', 'weathersit',
'weekday', 'atemp', 'mnth', 'workingday', 'hr']
data = rides.drop(fields_to_drop, axis=1)
data.head()
```
### Scaling target variables
To make training the network easier, we'll standardize each of the continuous variables. That is, we'll shift and scale the variables such that they have zero mean and a standard deviation of 1.
The scaling factors are saved so we can go backwards when we use the network for predictions.
```
quant_features = ['casual', 'registered', 'cnt', 'temp', 'hum', 'windspeed']
# Store scalings in a dictionary so we can convert back later
scaled_features = {}
for each in quant_features:
mean, std = data[each].mean(), data[each].std()
scaled_features[each] = [mean, std]
data.loc[:, each] = (data[each] - mean)/std
```
### Splitting the data into training, testing, and validation sets
We'll save the last 21 days of the data to use as a test set after we've trained the network. We'll use this set to make predictions and compare them with the actual number of riders.
```
# Save the last 21 days
test_data = data[-21*24:]
data = data[:-21*24]
# Separate the data into features and targets
target_fields = ['cnt', 'casual', 'registered']
features, targets = data.drop(target_fields, axis=1), data[target_fields]
test_features, test_targets = test_data.drop(target_fields, axis=1), test_data[target_fields]
```
We'll split the data into two sets, one for training and one for validating as the network is being trained. Since this is time series data, we'll train on historical data, then try to predict on future data (the validation set).
```
# Hold out the last 60 days of the remaining data as a validation set
train_features, train_targets = features[:-60*24], targets[:-60*24]
val_features, val_targets = features[-60*24:], targets[-60*24:]
```
## Time to build the network
Below you'll build your network. We've built out the structure and the backwards pass. You'll implement the forward pass through the network. You'll also set the hyperparameters: the learning rate, the number of hidden units, and the number of training passes.
The network has two layers, a hidden layer and an output layer. The hidden layer will use the sigmoid function for activations. The output layer has only one node and is used for the regression, the output of the node is the same as the input of the node. That is, the activation function is $f(x)=x$. A function that takes the input signal and generates an output signal, but takes into account the threshold, is called an activation function. We work through each layer of our network calculating the outputs for each neuron. All of the outputs from one layer become inputs to the neurons on the next layer. This process is called *forward propagation*.
We use the weights to propagate signals forward from the input to the output layers in a neural network. We use the weights to also propagate error backwards from the output back into the network to update our weights. This is called *backpropagation*.
> **Hint:** You'll need the derivative of the output activation function ($f(x) = x$) for the backpropagation implementation. If you aren't familiar with calculus, this function is equivalent to the equation $y = x$. What is the slope of that equation? That is the derivative of $f(x)$.
Below, you have these tasks:
1. Implement the sigmoid function to use as the activation function. Set `self.activation_function` in `__init__` to your sigmoid function.
2. Implement the forward pass in the `train` method.
3. Implement the backpropagation algorithm in the `train` method, including calculating the output error.
4. Implement the forward pass in the `run` method.
```
class NeuralNetwork(object):
def __init__(self, input_nodes, hidden_nodes, output_nodes, learning_rate):
# Set number of nodes in input, hidden and output layers.
self.input_nodes = input_nodes
self.hidden_nodes = hidden_nodes
self.output_nodes = output_nodes
# Initialize weights
self.weights_input_to_hidden = np.random.normal(0.0, self.hidden_nodes**-0.5,
(self.hidden_nodes, self.input_nodes))
self.weights_hidden_to_output = np.random.normal(0.0, self.output_nodes**-0.5,
(self.output_nodes, self.hidden_nodes))
self.lr = learning_rate
#### Set this to your implemented sigmoid function ####
# Activation function is the sigmoid function
self.activation_function = lambda x: 1. / (1. + np.exp(-x))
def train(self, inputs_list, targets_list):
# Convert inputs list to 2d array
inputs = np.array(inputs_list, ndmin=2).T
targets = np.array(targets_list, ndmin=2).T
#### Implement the forward pass here ####
### Forward pass ###
# TODO: Hidden layer
hidden_inputs = np.dot(self.weights_input_to_hidden, inputs)
hidden_outputs = self.activation_function(hidden_inputs)
# TODO: Output layer
final_inputs = np.dot(self.weights_hidden_to_output, hidden_outputs)
final_outputs = final_inputs
#### Implement the backward pass here ####
### Backward pass ###
# TODO: Output error
output_errors = targets - final_outputs
# TODO: Backpropagated error
hidden_errors = np.dot(self.weights_hidden_to_output.T, output_errors)
hidden_grad = hidden_outputs * (1 - hidden_outputs)
# TODO: Update the weights
self.weights_hidden_to_output += self.lr * np.dot(output_errors, hidden_outputs.T)
self.weights_input_to_hidden += self.lr * np.dot(hidden_errors * hidden_grad, inputs.T)
def run(self, inputs_list):
# Run a forward pass through the network
inputs = np.array(inputs_list, ndmin=2).T
#### Implement the forward pass here ####
# TODO: Hidden layer
hidden_inputs = np.dot(self.weights_input_to_hidden, inputs)
hidden_outputs = self.activation_function(hidden_inputs)
# TODO: Output layer
final_inputs = np.dot(self.weights_hidden_to_output, hidden_outputs)
final_outputs = final_inputs
return final_outputs
def MSE(y, Y):
return np.mean((y-Y)**2)
```
## Training the network
Here you'll set the hyperparameters for the network. The strategy here is to find hyperparameters such that the error on the training set is low, but you're not overfitting to the data. If you train the network too long or have too many hidden nodes, it can become overly specific to the training set and will fail to generalize to the validation set. That is, the loss on the validation set will start increasing as the training set loss drops.
You'll also be using a method know as Stochastic Gradient Descent (SGD) to train the network. The idea is that for each training pass, you grab a random sample of the data instead of using the whole data set. You use many more training passes than with normal gradient descent, but each pass is much faster. This ends up training the network more efficiently. You'll learn more about SGD later.
### Choose the number of epochs
This is the number of times the dataset will pass through the network, each time updating the weights. As the number of epochs increases, the network becomes better and better at predicting the targets in the training set. You'll need to choose enough epochs to train the network well but not too many or you'll be overfitting.
### Choose the learning rate
This scales the size of weight updates. If this is too big, the weights tend to explode and the network fails to fit the data. A good choice to start at is 0.1. If the network has problems fitting the data, try reducing the learning rate. Note that the lower the learning rate, the smaller the steps are in the weight updates and the longer it takes for the neural network to converge.
### Choose the number of hidden nodes
The more hidden nodes you have, the more accurate predictions the model will make. Try a few different numbers and see how it affects the performance. You can look at the losses dictionary for a metric of the network performance. If the number of hidden units is too low, then the model won't have enough space to learn and if it is too high there are too many options for the direction that the learning can take. The trick here is to find the right balance in number of hidden units you choose.
```
import sys
### Set the hyperparameters here ###
epochs = 1000
learning_rate = 0.1
hidden_nodes = 10
output_nodes = 1
N_i = train_features.shape[1]
network = NeuralNetwork(N_i, hidden_nodes, output_nodes, learning_rate)
losses = {'train':[], 'validation':[]}
for e in range(epochs):
# Go through a random batch of 128 records from the training data set
batch = np.random.choice(train_features.index, size=128)
for record, target in zip(train_features.ix[batch].values,
train_targets.ix[batch]['cnt']):
network.train(record, target)
# Printing out the training progress
train_loss = MSE(network.run(train_features), train_targets['cnt'].values)
val_loss = MSE(network.run(val_features), val_targets['cnt'].values)
sys.stdout.write("\rProgress: " + str(100 * e/float(epochs))[:4] \
+ "% ... Training loss: " + str(train_loss)[:5] \
+ " ... Validation loss: " + str(val_loss)[:5])
losses['train'].append(train_loss)
losses['validation'].append(val_loss)
plt.plot(losses['train'], label='Training loss')
plt.plot(losses['validation'], label='Validation loss')
plt.legend()
plt.ylim(ymax=0.5)
```
## Check out your predictions
Here, use the test data to view how well your network is modeling the data. If something is completely wrong here, make sure each step in your network is implemented correctly.
```
fig, ax = plt.subplots(figsize=(8,4))
mean, std = scaled_features['cnt']
predictions = network.run(test_features)*std + mean
ax.plot(predictions[0], label='Prediction')
ax.plot((test_targets['cnt']*std + mean).values, label='Data')
ax.set_xlim(right=len(predictions))
ax.legend()
dates = pd.to_datetime(rides.ix[test_data.index]['dteday'])
dates = dates.apply(lambda d: d.strftime('%b %d'))
ax.set_xticks(np.arange(len(dates))[12::24])
_ = ax.set_xticklabels(dates[12::24], rotation=45)
```
## Thinking about your results
Answer these questions about your results. How well does the model predict the data? Where does it fail? Why does it fail where it does?
> **Note:** You can edit the text in this cell by double clicking on it. When you want to render the text, press control + enter
#### Your answer below
Before Dec 21 model fits well. From Dec 22 model fits bad, because the amount of data decrease.
## Unit tests
Run these unit tests to check the correctness of your network implementation. These tests must all be successful to pass the project.
```
import unittest
inputs = [0.5, -0.2, 0.1]
targets = [0.4]
test_w_i_h = np.array([[0.1, 0.4, -0.3],
[-0.2, 0.5, 0.2]])
test_w_h_o = np.array([[0.3, -0.1]])
class TestMethods(unittest.TestCase):
##########
# Unit tests for data loading
##########
def test_data_path(self):
# Test that file path to dataset has been unaltered
self.assertTrue(data_path.lower() == 'bike-sharing-dataset/hour.csv')
def test_data_loaded(self):
# Test that data frame loaded
self.assertTrue(isinstance(rides, pd.DataFrame))
##########
# Unit tests for network functionality
##########
def test_activation(self):
network = NeuralNetwork(3, 2, 1, 0.5)
# Test that the activation function is a sigmoid
self.assertTrue(np.all(network.activation_function(0.5) == 1/(1+np.exp(-0.5))))
def test_train(self):
# Test that weights are updated correctly on training
network = NeuralNetwork(3, 2, 1, 0.5)
network.weights_input_to_hidden = test_w_i_h.copy()
network.weights_hidden_to_output = test_w_h_o.copy()
network.train(inputs, targets)
self.assertTrue(np.allclose(network.weights_hidden_to_output,
np.array([[ 0.37275328, -0.03172939]])))
self.assertTrue(np.allclose(network.weights_input_to_hidden,
np.array([[ 0.10562014, 0.39775194, -0.29887597],
[-0.20185996, 0.50074398, 0.19962801]])))
def test_run(self):
# Test correctness of run method
network = NeuralNetwork(3, 2, 1, 0.5)
network.weights_input_to_hidden = test_w_i_h.copy()
network.weights_hidden_to_output = test_w_h_o.copy()
self.assertTrue(np.allclose(network.run(inputs), 0.09998924))
suite = unittest.TestLoader().loadTestsFromModule(TestMethods())
unittest.TextTestRunner().run(suite)
```
|
github_jupyter
|
```
# Author: Robert Guthrie
from copy import copy
import torch
import torch.autograd as autograd
import torch.nn as nn
import torch.optim as optim
torch.manual_seed(1)
def argmax(vec):
# return the argmax as a python int
_, idx = torch.max(vec, 1)
return idx.item()
def prepare_sequence(seq, to_ix):
idxs = [to_ix[w] for w in seq]
return torch.tensor(idxs, dtype=torch.long)
# Compute log sum exp in a numerically stable way for the forward algorithm
def log_sum_exp(vec):
max_score = vec[0, argmax(vec)]
max_score_broadcast = max_score.view(1, -1).expand(1, vec.size()[1])
return max_score + \
torch.log(torch.sum(torch.exp(vec - max_score_broadcast)))
class BiLSTM_CRF(nn.Module):
def __init__(self, vocab_size, tag_to_ix, embedding_dim, hidden_dim):
super(BiLSTM_CRF, self).__init__()
self.embedding_dim = embedding_dim
self.hidden_dim = hidden_dim
self.vocab_size = vocab_size
self.tag_to_ix = tag_to_ix
self.tagset_size = len(tag_to_ix)
self.word_embeds = nn.Embedding(vocab_size, embedding_dim)
self.lstm = nn.LSTM(embedding_dim, hidden_dim // 2,
num_layers=1, bidirectional=True)
# Maps the output of the LSTM into tag space.
self.hidden2tag = nn.Linear(hidden_dim, self.tagset_size)
# Matrix of transition parameters. Entry i,j is the score of
# transitioning *to* i *from* j.
self.transitions = nn.Parameter(
torch.randn(self.tagset_size, self.tagset_size))
# These two statements enforce the constraint that we never transfer
# to the start tag and we never transfer from the stop tag
self.transitions.data[tag_to_ix[START_TAG], :] = -10000
self.transitions.data[:, tag_to_ix[STOP_TAG]] = -10000
self.hidden = self.init_hidden()
def init_hidden(self):
return (torch.randn(2, 1, self.hidden_dim // 2),
torch.randn(2, 1, self.hidden_dim // 2))
def _forward_alg(self, feats):
# Do the forward algorithm to compute the partition function
init_alphas = torch.full((1, self.tagset_size), -10000.)
# START_TAG has all of the score.
init_alphas[0][self.tag_to_ix[START_TAG]] = 0.
# Wrap in a variable so that we will get automatic backprop
forward_var = init_alphas
# Iterate through the sentence
for feat in feats:
alphas_t = [] # The forward tensors at this timestep
for next_tag in range(self.tagset_size):
# broadcast the emission score: it is the same regardless of
# the previous tag
emit_score = feat[next_tag].view(
1, -1).expand(1, self.tagset_size)
# the ith entry of trans_score is the score of transitioning to
# next_tag from i
trans_score = self.transitions[next_tag].view(1, -1)
# The ith entry of next_tag_var is the value for the
# edge (i -> next_tag) before we do log-sum-exp
next_tag_var = forward_var + trans_score + emit_score
# The forward variable for this tag is log-sum-exp of all the
# scores.
alphas_t.append(log_sum_exp(next_tag_var).view(1))
forward_var = torch.cat(alphas_t).view(1, -1)
terminal_var = forward_var + self.transitions[self.tag_to_ix[STOP_TAG]]
alpha = log_sum_exp(terminal_var)
return alpha
def _get_lstm_features(self, sentence):
self.hidden = self.init_hidden()
embeds = self.word_embeds(sentence).view(len(sentence), 1, -1)
lstm_out, self.hidden = self.lstm(embeds, self.hidden)
lstm_out = lstm_out.view(len(sentence), self.hidden_dim)
lstm_feats = self.hidden2tag(lstm_out)
return lstm_feats
def _score_sentence(self, feats, tags):
# Gives the score of a provided tag sequence
score = torch.zeros(1)
tags = torch.cat([torch.tensor([self.tag_to_ix[START_TAG]], dtype=torch.long), tags])
for i, feat in enumerate(feats):
score = score + \
self.transitions[tags[i + 1], tags[i]] + feat[tags[i + 1]]
score = score + self.transitions[self.tag_to_ix[STOP_TAG], tags[-1]]
return score
def _viterbi_decode(self, feats):
backpointers = []
# Initialize the viterbi variables in log space
init_vvars = torch.full((1, self.tagset_size), -10000.)
init_vvars[0][self.tag_to_ix[START_TAG]] = 0
# forward_var at step i holds the viterbi variables for step i-1
forward_var = init_vvars
for feat in feats:
bptrs_t = [] # holds the backpointers for this step
viterbivars_t = [] # holds the viterbi variables for this step
for next_tag in range(self.tagset_size):
# next_tag_var[i] holds the viterbi variable for tag i at the
# previous step, plus the score of transitioning
# from tag i to next_tag.
# We don't include the emission scores here because the max
# does not depend on them (we add them in below)
next_tag_var = forward_var + self.transitions[next_tag]
best_tag_id = argmax(next_tag_var)
bptrs_t.append(best_tag_id)
viterbivars_t.append(next_tag_var[0][best_tag_id].view(1))
# Now add in the emission scores, and assign forward_var to the set
# of viterbi variables we just computed
forward_var = (torch.cat(viterbivars_t) + feat).view(1, -1)
backpointers.append(bptrs_t)
# Transition to STOP_TAG
terminal_var = forward_var + self.transitions[self.tag_to_ix[STOP_TAG]]
best_tag_id = argmax(terminal_var)
path_score = terminal_var[0][best_tag_id]
# Follow the back pointers to decode the best path.
best_path = [best_tag_id]
for bptrs_t in reversed(backpointers):
best_tag_id = bptrs_t[best_tag_id]
best_path.append(best_tag_id)
# Pop off the start tag (we dont want to return that to the caller)
start = best_path.pop()
assert start == self.tag_to_ix[START_TAG] # Sanity check
best_path.reverse()
return path_score, best_path
def neg_log_likelihood(self, sentence, tags):
feats = self._get_lstm_features(sentence)
forward_score = self._forward_alg(feats)
gold_score = self._score_sentence(feats, tags)
return forward_score - gold_score
def forward(self, sentence): # dont confuse this with _forward_alg above.
# Get the emission scores from the BiLSTM
lstm_feats = self._get_lstm_features(sentence)
# Find the best path, given the features.
score, tag_seq = self._viterbi_decode(lstm_feats)
return score, tag_seq
START_TAG = "<START>"
STOP_TAG = "<STOP>"
EMBEDDING_DIM = 5
HIDDEN_DIM = 4
# Make up some training data
training_data = [(
"the wall street journal reported today that apple corporation made money".split(),
"B I I I O O O B I O O".split()
), (
"georgia tech is a university in georgia".split(),
"B I O O O O B".split()
)]
word_to_ix = {}
for sentence, tags in training_data:
for word in sentence:
if word not in word_to_ix:
word_to_ix[word] = len(word_to_ix)
tag_to_ix = {"B": 0, "I": 1, "O": 2, START_TAG: 3, STOP_TAG: 4}
model = BiLSTM_CRF(len(word_to_ix), tag_to_ix, EMBEDDING_DIM, HIDDEN_DIM)
optimizer = optim.SGD(model.parameters(), lr=0.01, weight_decay=1e-4)
# Check predictions before training
with torch.no_grad():
precheck_sent = prepare_sequence(training_data[0][0], word_to_ix)
precheck_tags = torch.tensor([tag_to_ix[t] for t in training_data[0][1]], dtype=torch.long)
print(model(precheck_sent))
# Make sure prepare_sequence from earlier in the LSTM section is loaded
for epoch in range(
300): # again, normally you would NOT do 300 epochs, it is toy data
for sentence, tags in training_data:
# Step 1. Remember that Pytorch accumulates gradients.
# We need to clear them out before each instance
model.zero_grad()
# Step 2. Get our inputs ready for the network, that is,
# turn them into Tensors of word indices.
sentence_in = prepare_sequence(sentence, word_to_ix)
targets = torch.tensor([tag_to_ix[t] for t in tags], dtype=torch.long)
# Step 3. Run our forward pass.
loss = model.neg_log_likelihood(sentence_in, targets)
# Step 4. Compute the loss, gradients, and update the parameters by
# calling optimizer.step()
loss.backward()
optimizer.step()
# Check predictions after training
with torch.no_grad():
precheck_sent = prepare_sequence(training_data[0][0], word_to_ix)
print(model(precheck_sent))
# We got it!
```
# model
```
import sys
sys.path.append('..')
from utils.dataset.ec import ECDataset
from utils.dataloader.ec import ECDataLoader
from models.han.word_model import WordAttention
from models.han.sentence_model import SentenceWithPosition
device = torch.device('cuda: 0')
batch_size = 16
vocab_size = 23071
num_classes = 2
sequence_length = 41
embedding_dim = 300
dropout = 0.5
word_rnn_size = 300
word_rnn_layer = 2
sentence_rnn_size = 300
sentence_rnn_layer = 2
pos_size = 103
pos_embedding_dim = 300
pos_embedding_file= '/data/wujipeng/ec/data/embedding/pos_embedding.pkl'
train_dataset = ECDataset(data_root='/data/wujipeng/ec/data/test/', vocab_root='/data/wujipeng/ec/data/raw_data/', train=True)
test_dataset = ECDataset(data_root='/data/wujipeng/ec/data/test/', vocab_root='/data/wujipeng/ec/data/raw_data/', train=False)
train_loader = ECDataLoader(dataset=train_dataset, clause_length=sequence_length, batch_size=16, shuffle=True, sort=True, collate_fn=train_dataset.collate_fn)
for batch in train_loader:
clauses, keywords, poses = ECDataset.batch2input(batch)
labels = ECDataset.batch2target(batch)
clauses = torch.from_numpy(clauses).to(device)
keywords = torch.from_numpy(keywords).to(device)
poses = torch.from_numpy(poses).to(device)
labels = torch.from_numpy(labels).to(device)
targets = labels
break
class HierachicalAttentionModelCRF:
def __init__(self,
vocab_size,
num_classes,
embedding_dim,
hidden_size,
word_model,
sentence_model,
dropout=0.5,
fix_embed=True,
name='HAN'):
super(HierachicalAttentionModelCRF, self).__init__()
self.num_classes = num_classes
self.fix_embed = fix_embed
self.name = name
self.Embedding = nn.Embedding(vocab_size, embedding_dim, padding_idx=0)
self.word_rnn = WordAttention(
vocab_size=vocab_size,
embedding_dim=embedding_dim,
batch_size=batch_size,
sequence_length=sequence_length,
rnn_size=word_rnn_size,
rnn_layers=word_rnn_layer,
dropout=dropout)
self.sentence_rnn = SentenceAttention(
batch_size=batch_size,
word_rnn_size = word_rnn_size,
rnn_size = sentence_rnn_size,
rnn_layers=sentence_rnn_layer,
pos_size=pos_size,
pos_embedding_dim=pos_embedding_dim,
pos_embedding_file=pos_embedding_file
)
self.fc = nn.Linear(
2 * self.word_rnn_size + 2 * self.sentence_rnn_size, num_classes)
self.dropout = nn.Dropout(dropout)
# self.fc = nn.Sequential(
# nn.Linear(2 * self.sentence_rnn_size, linear_hidden_dim),
# nn.ReLU(inplace=True),
# nn.Dropout(dropout),
# nn.Linear(linear_hidden_dim, num_classes)
# )
def init_weights(self, embeddings):
if embeddings is not None:
self.Embedding = self.Embedding.from_pretrained(embeddings)
def forward(self, clauses, keywords, poses):
inputs = self.linear(self.Embedding(clauses))
queries = self.linear(self.Embedding(keywords))
documents, word_attn = self.word_rnn(inputs, queries)
outputs, sentence_attn = self.sentence_rnn(documents, poses)
# outputs = self.fc(outputs)
s_c = torch.cat((documents, outputs), dim=-1)
outputs = self.fc(self.dropout(s_c))
return outputs, word_attn, sentence_attn
```
## init
```
def argmax(vec):
# return the argmax as a python int
_, idx = torch.max(vec, 1)
return idx.item()
def prepare_sequence(seq, to_ix):
idxs = [to_ix[w] for w in seq]
return torch.tensor(idxs, dtype=torch.long)
# Compute log sum exp in a numerically stable way for the forward algorithm
def log_sum_exp(vec):
max_score = vec[0, argmax(vec)]
max_score_broadcast = max_score.view(1, -1).expand(1, vec.size()[1])
return max_score + \
torch.log(torch.sum(torch.exp(vec - max_score_broadcast)))
START_TAG = "<START>"
STOP_TAG = "<STOP>"
tag_to_ix = {0: 0, 1: 1, START_TAG: 2, STOP_TAG: 3}
tagsize = len(tag_to_ix)
Embedding = nn.Embedding(vocab_size, embedding_dim, padding_idx=0).to(device)
word_rnn = WordAttention(
vocab_size=vocab_size,
embedding_dim=embedding_dim,
batch_size=batch_size,
sequence_length=sequence_length,
rnn_size=word_rnn_size,
rnn_layers=word_rnn_layer,
dropout=dropout).to(device)
sentence_rnn = SentenceWithPosition(
batch_size=batch_size,
word_rnn_size = word_rnn_size,
rnn_size = sentence_rnn_size,
rnn_layers=sentence_rnn_layer,
pos_size=pos_size,
pos_embedding_dim=pos_embedding_dim,
pos_embedding_file=pos_embedding_file
).to(device)
fc = nn.Linear(2 * word_rnn_size + 2 * sentence_rnn_size, num_classes+2).to(device)
drop = nn.Dropout(dropout).to(device)
transitions = nn.Parameter(torch.randn(tagset_size, tagset_size)).to(device)
transitions.data[tag_to_ix[START_TAG], :] = -10000
transitions.data[:, tag_to_ix[STOP_TAG]] = -10000
```
## forward
```
inputs = Embedding(clauses)
queries = Embedding(keywords)
documents, word_attn = word_rnn(inputs, queries)
outputs, sentence_attn = sentence_rnn(documents, poses)
s_c = torch.cat((documents, outputs), dim=-1)
outputs = fc(drop(s_c))
outputs.size()
lstm_feats = copy(outputs)
lstm_feats.size()
```
### _forward_alg
```
init_alphas = torch.full((1, tagset_size), -10000.).to(device)
# START_TAG has all of the score.
init_alphas[0][tag_to_ix[START_TAG]] = 0.
# Wrap in a variable so that we will get automatic backprop
forward_var = init_alphas
# Iterate through the sentence
for feat in lstm_feats:
alphas_t = [] # The forward tensors at this timestep
for next_tag in range(tagset_size):
# broadcast the emission score: it is the same regardless of
# the previous tag
emit_score = feat[next_tag].view(1, -1).expand(1, tagset_size)
# the ith entry of trans_score is the score of transitioning to
# next_tag from i
trans_score = transitions[next_tag].view(1, -1)
# The ith entry of next_tag_var is the value for the
# edge (i -> next_tag) before we do log-sum-exp
next_tag_var = forward_var + trans_score + emit_score
# The forward variable for this tag is log-sum-exp of all the
# scores.
alphas_t.append(log_sum_exp(next_tag_var).view(1))
forward_var = torch.cat(alphas_t).view(1, -1)
terminal_var = forward_var + transitions[tag_to_ix[STOP_TAG]]
alpha = log_sum_exp(terminal_var)
forward_score = alpha
init_alphas
```
### _score_sentence
```
lstm_feats.size()
tags = copy(targets)
score = torch.zeros(1).to(device)
tags = torch.cat((torch.full((tags.size(0), 1), tag_to_ix[START_TAG], dtype=torch.long).to(device), tags), dim=-1)
for feats, tag in zip(lstm_feats, tags):
score = torch.zeros(1).to(device)
tag = torch.cat([torch.LongTensor([tag_to_ix[START_TAG]]).to(device), tag])
for i, feat in enumerate(feats):
score = score + transitions[tags[i + 1], tags[i]] + feat[tags[i + 1]]
score = score + transitions[tag_to_ix[STOP_TAG], tags[-1]]
tag
score = forward_score - gold_score
forward_score, gold_score, score
```
### _viterbi_decode
```
backpointers = []
# Initialize the viterbi variables in log space
init_vvars = torch.full((1, tagset_size), -10000.).to(device)
init_vvars[0][tag_to_ix[START_TAG]] = 0
# forward_var at step i holds the viterbi variables for step i-1
forward_var = init_vvars
for feat in lstm_feats:
bptrs_t = [] # holds the backpointers for this step
viterbivars_t = [] # holds the viterbi variables for this step
for next_tag in range(tagset_size):
# next_tag_var[i] holds the viterbi variable for tag i at the
# previous step, plus the score of transitioning
# from tag i to next_tag.
# We don't include the emission scores here because the max
# does not depend on them (we add them in below)
next_tag_var = forward_var + transitions[next_tag]
best_tag_id = argmax(next_tag_var)
bptrs_t.append(best_tag_id)
viterbivars_t.append(next_tag_var[0][best_tag_id].view(1))
# Now add in the emission scores, and assign forward_var to the set
# of viterbi variables we just computed
forward_var = (torch.cat(viterbivars_t) + feat).view(1, -1)
backpointers.append(bptrs_t)
# Transition to STOP_TAG
terminal_var = forward_var + transitions[tag_to_ix[STOP_TAG]]
best_tag_id = argmax(terminal_var)
path_score = terminal_var[0][best_tag_id]
# Follow the back pointers to decode the best path.
best_path = [best_tag_id]
for bptrs_t in reversed(backpointers):
best_tag_id = bptrs_t[best_tag_id]
best_path.append(best_tag_id)
# Pop off the start tag (we dont want to return that to the caller)
start = best_path.pop()
assert start == tag_to_ix[START_TAG] # Sanity check
best_path.reverse()
path_score.data, len(best_path)
best_path
```
|
github_jupyter
|
Lambda School Data Science
*Unit 2, Sprint 1, Module 3*
---
```
%%capture
import sys
# If you're on Colab:
if 'google.colab' in sys.modules:
DATA_PATH = 'https://raw.githubusercontent.com/LambdaSchool/DS-Unit-2-Applied-Modeling/master/data/'
!pip install category_encoders==2.*
# If you're working locally:
else:
DATA_PATH = '../data/'
```
# Module Project: Ridge Regression
For this project, you'll return to the Tribecca Condo dataset. But this time, you'll look at the _entire_ dataset and try to predict property sale prices.
The [NYC Department of Finance](https://www1.nyc.gov/site/finance/taxes/property-rolling-sales-data.page) has a glossary of property sales terms and NYC Building Class Code Descriptions. The data comes from the [NYC OpenData](https://data.cityofnewyork.us/browse?q=NYC%20calendar%20sales) portal.
## Directions
The tasks for this project are the following:
- **Task 1:** Import `csv` file using `wrangle` function.
- **Task 2:** Conduct exploratory data analysis (EDA), and modify `wrangle` function to engineer two subset your dataset to one-family dwellings whose price is between \\$100,000 and \\$2,000,000.
- **Task 3:** Split data into feature matrix `X` and target vector `y`.
- **Task 4:** Split feature matrix `X` and target vector `y` into training and test sets.
- **Task 5:** Establish the baseline mean absolute error for your dataset.
- **Task 6:** Build and train a `OneHotEncoder`, and transform `X_train` and `X_test`.
- **Task 7:** Build and train a `LinearRegression` model.
- **Task 8:** Build and train a `Ridge` model.
- **Task 9:** Calculate the training and test mean absolute error for your `LinearRegression` model.
- **Task 10:** Calculate the training and test mean absolute error for your `Ridge` model.
- **Task 11:** Create a horizontal bar chart showing the 10 most influencial features for your `Ridge` model.
**Note**
You should limit yourself to the following libraries for this project:
- `category_encoders`
- `matplotlib`
- `pandas`
- `sklearn`
# I. Wrangle Data
```
def wrangle(filepath):
# Import csv file
cols = ['BOROUGH', 'NEIGHBORHOOD',
'BUILDING CLASS CATEGORY', 'GROSS SQUARE FEET',
'YEAR BUILT', 'SALE PRICE', 'SALE DATE']
df = pd.read_csv(filepath, usecols=cols)
return df
filepath = DATA_PATH+'condos/NYC_Citywide_Rolling_Calendar_Sales.csv'
```
**Task 1:** Use the above `wrangle` function to import the `NYC_Citywide_Rolling_Calendar_Sales.csv` file into a DataFrame named `df`.
```
df = ...
```
**Task 2:** Modify the above `wrangle` function so that:
- The column `'SALE DATE'` becomes the `DatetimeIndex`.
- The dtype for the `'BOROUGH'` column is `object`, not `int`.
- The dtype for the `'SALE PRICE'` column is `int`, not `object`.
- The dataset includes only one-family dwellings (`BUILDING CLASS CATEGORY == '01 ONE FAMILY DWELLINGS'`).
- The dataset includes only properties whose sale price is between \\$100,000 and \\$2,000,000.
```
# Perform your exploratory data analysis here and
# modify the wrangle function above
```
# II. Split Data
**Task 3:** Split your dataset into the feature matrix `X` and the target vector `y`. You want to predict `'SALE_PRICE'`.
```
X = ...
y = ...
```
**Task 4:** Split `X` and `y` into a training set (`X_train`, `y_train`) and a test set (`X_test`, `y_test`).
- Your training set should include data from January to March 2019.
- Your test set should include data from April 2019.
```
X_train, y_train = ..., ...
X_test, y_test = ..., ...
```
# III. Establish Baseline
**Task 5:** Since this is a **regression** problem, you need to calculate the baseline mean absolute error for your model.
```
baseline_mae = ...
print('Baseline MAE:', baseline_mae)
```
# IV. Build Model
**Task 6:** Build and train a `OneHotEncoder` and then use it to transform `X_train` and `X_test`.
```
ohe = ...
XT_train = ...
XT_test = ...
```
**Task 7:** Build and train a `LinearRegression` model named `model_lr`. Remember to train your model using your _transformed_ feature matrix.
```
model_lr = ...
```
**Task 8:** Build and train a `Ridge` model named `model_r`. Remember to train your model using your _transformed_ feature matrix.
```
model_r = ...
```
# V. Check Metrics
**Task 9:** Check the training and test metrics for `model_lr`.
```
training_mae_lr = ...
test_mae_lr = ...
print('Linear Training MAE:', training_mae_lr)
print('Linear Test MAE:', test_mae_lr)
```
**Task 10:** Check the training and test metrics for `model_r`.
```
training_mae_r = ...
test_mae_r = ...
print('Ridge Training MAE:', training_mae_r)
print('Ridge Test MAE:', test_mae_r)
```
**Stretch Goal:** Calculate the training and test $R^2$ scores `model_r`.
```
# Caculate R^2 score
```
# IV. Communicate Results
**Task 11:** Create a horizontal barchart that plots the 10 most important coefficients for `model_r`, sorted by absolute value. Your figure should look like our example from class:

**Note:** Your figure shouldn't be identical to the one above. Your model will have different coefficients since it's been trained on different data. Only the formatting should be the same.
|
github_jupyter
|
# Simple ARIMAX
This code template is for Time Series Analysis and Forecasting to make scientific predictions based on historical time stamped data with the help of ARIMAX algorithm
### Required Packages
```
import warnings
import numpy as np
import pandas as pd
import seaborn as se
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.statespace.sarimax import SARIMAX
from sklearn.metrics import mean_absolute_error, mean_squared_error
warnings.filterwarnings("ignore")
```
### Initialization
Filepath of CSV file
```
file_path = ""
```
Variable containing the date time column name of the Time Series data
```
date = ""
```
Target feature for prediction.
```
target = ""
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df = pd.read_csv(file_path)
df.head()
```
### Data Preprocessing
Since the majority of the machine learning models for Time Series Forecasting doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippets have functions, which removes the rows containing null value if any exists. And convert the string classes date column in the datasets to proper Date-time classes.
After the proper date conversions are done and null values are dropped, we set the Date column as the index value.
```
def data_preprocess(df, target, date):
df = df.dropna(axis=0, how = 'any')
df[date] = pd.to_datetime(df[date])
df = df.set_index(date)
return df
df = data_preprocess(df,target,date)
df.head()
df.plot(figsize = (15,8))
plt.show()
```
### Seasonality decomposition
Since Simple ARIMAX for non-seasonal data, we need to check for any seasonality in our time series and decompose it.
We use the Dickey Fuller Test for testing the seasonality and if the ADF Statistic value is positive, it means that the data has seasonality.
#### Dickey Fuller Test
The Dickey Fuller test is a common statistical test used to test whether a given Time series is stationary or not. The Augmented Dickey Fuller (ADF) test expands the Dickey-Fuller test equation to include high order regressive process in the model. We can implement the ADF test via the **adfuller()** function. It returns the following outputs:
1. adf : float
> The test statistic.
2. pvalue : float
> MacKinnon's approximate p-value based on MacKinnon(1994, 2010). It is used alongwith the test statistic to reject or accept the null hypothesis.
3. usedlag : int
> Number of lags considered for the test
4. critical values : dict
> Critical values for the test statistic at the 1 %, 5 %, and 10 % levels. Based on MacKinnon (2010).
For more information on the adfuller() function [click here](https://www.statsmodels.org/stable/generated/statsmodels.tsa.stattools.adfuller.html)
```
def dickeyFuller(df,target):
# Applying Dickey Fuller Test
X = df.values
result = adfuller(X)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Number of lags used: %d' % result[2])
print('Critical Values:')
for key, value in result[4].items():
print('\t%s: %.3f' % (key, value))
# Decomposing Seasonality if it exists
if result[0]>0:
df[target] = df[target].rolling(12).mean()
return df
```
To remove the seasonality we use the rolling mean technique for smoothing our data and decomposing any seasonality.
This method provides rolling windows over the data. On the resulting windows, we can perform calculations using a statistical function (in this case the mean) in order to decompose the seasonality.
For more information about rolling function [click here](https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.rolling.html)
```
df = dickeyFuller(df,target)
```
### Autocorrelation Plot
We can calculate the correlation for time series observations with observations with previous time steps, called lags. Because the correlation of the time series observations is calculated with values of the same series at previous times, this is called a serial correlation, or an autocorrelation.
A plot of the autocorrelation of a time series by lag is called the AutoCorrelation Function, or the acronym ACF.
An autocorrelation plot shows whether the elements of a time series are positively correlated, negatively correlated, or independent of each other.
The plot shows the value of the autocorrelation function (acf) on the vertical axis ranging from –1 to 1.
There are vertical lines (a “spike”) corresponding to each lag and the height of each spike shows the value of the autocorrelation function for the lag.
[API](https://www.statsmodels.org/stable/generated/statsmodels.graphics.tsaplots.plot_acf.html)
```
x = plot_acf(df, lags=40)
x.set_size_inches(15, 10, forward=True)
plt.show()
```
### Partial Autocorrelation Plot
A partial autocorrelation is a summary of the relationship between an observation in a time series with observations at prior time steps with the relationships of intervening observations removed.
The partial autocorrelation at lag k is the correlation that results after removing the effect of any correlations due to the terms at shorter lags. By examining the spikes at each lag we can determine whether they are significant or not. A significant spike will extend beyond the significant limits, which indicates that the correlation for that lag doesn't equal zero.
[API](https://www.statsmodels.org/stable/generated/statsmodels.graphics.tsaplots.plot_pacf.html)
```
y = plot_pacf(df, lags=40)
y.set_size_inches(15, 10, forward=True)
plt.show()
```
### Data Splitting
Since we are using a univariate dataset, we can directly split our data into training and testing subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
size = int(len(df)*0.9)
df_train, df_test = df.iloc[:size], df.iloc[size:]
```
### Model
The ARIMAX model is an extended version of the ARIMA model. It includes also other independent (predictor) variables. The model is also referred to as the vector ARIMA or the dynamic regression model.
The ARIMAX model is similar to a multivariate regression model, but allows to take advantage of autocorrelation that may be present in residuals of the regression to improve the accuracy of a forecast.
The API used here is from the statsmodels library. Statsmodels does not have a dedicated API for ARIMAX but the model can be created via <Code>SARIMAX</Code> API by setting the parameter <Code>seasonal_order</Code> = (0,0,0,0) i.e., no seasonality
#### Model Tuning Parameters
1. endog: array_like
>The observed time-series process
2. exog: array_like, optional
>Array of exogenous regressors, shaped nobs x k.
3. order: iterable or iterable of iterables, optional
>The (p,d,q) order of the model for the number of AR parameters, differences, and MA parameters. d must be an integer indicating the integration order of the process, while p and q may either be an integers indicating the AR and MA orders (so that all lags up to those orders are included) or else iterables giving specific AR and / or MA lags to include. Default is an AR(1) model: (1,0,0).
4. seasonal_order: iterable, optional
>The (P,D,Q,s) order of the seasonal component of the model for the AR parameters, differences, MA parameters, and periodicity. D must be an integer indicating the integration order of the process, while P and Q may either be an integers indicating the AR and MA orders (so that all lags up to those orders are included) or else iterables giving specific AR and / or MA lags to include. s is an integer giving the periodicity (number of periods in season), often it is 4 for quarterly data or 12 for monthly data. Default is no seasonal effect.
5. trend: str{‘n’,’c’,’t’,’ct’} or iterable, optional
>Parameter controlling the deterministic trend polynomial . Can be specified as a string where ‘c’ indicates a constant (i.e. a degree zero component of the trend polynomial), ‘t’ indicates a linear trend with time, and ‘ct’ is both. Can also be specified as an iterable defining the non-zero polynomial exponents to include, in increasing order. For example, [1,1,0,1] denotes
. Default is to not include a trend component.
6. measurement_error: bool, optional
>Whether or not to assume the endogenous observations endog were measured with error. Default is False.
7. time_varying_regression: bool, optional
>Used when an explanatory variables, exog, are provided provided to select whether or not coefficients on the exogenous regressors are allowed to vary over time. Default is False.
8. mle_regression: bool, optional
>Whether or not to use estimate the regression coefficients for the exogenous variables as part of maximum likelihood estimation or through the Kalman filter (i.e. recursive least squares). If time_varying_regression is True, this must be set to False. Default is True.
Refer to the official documentation at [statsmodels](https://www.statsmodels.org/dev/generated/statsmodels.tsa.statespace.sarimax.SARIMAX.html) for more parameters and information
```
model=SARIMAX(df[target],order=(1, 0, 0),seasonal_order=(0,0,0,0))
result=model.fit()
```
### Model Summary
After fitting the training data into our ARIMAX and training it, we can take a look at a brief summary of our model by using the **summary()** function. The followings aspects are included in our model summary:
1. Basic Model Details: The first column of our summary table contains the basic details regarding our model such as:
a. Name of dependent variable
b. Model used along with parameters
c. Date and time of model deployment
d. Time Series sample used to train the model
2. Probablistic Statistical Measures: The second column gives the values of the probablistic measures obtained by our model:
a. Number of observations
b. Log-likelihood, which comes from Maximum Likelihood Estimation, a technique for finding or optimizing the
parameters of a model in response to a training dataset.
c. Standard Deviation of the innovations
d. Akaike Information Criterion (AIC), which is derived from frequentist probability.
e. Bayesian Information Criterion (BIC), which is derived from Bayesian probability.
f. Hannan-Quinn Information Criterion (HQIC), which is an alternative to AIC and is derived using the log-likelihood and
the number of observartions.
3. Statistical Measures and Roots: The summary table also consists of certain other statistical measures such as z-value, standard error as well as the information on the characteristic roots of the model.
```
result.summary()
```
#### Simple Forecasting
```
df_train.tail()
```
### Predictions
By specifying the start and end time for our predictions, we can easily predict the future points in our time series with the help of our model.
```
d = df.drop([target], axis = 1)
start_date = d.iloc[size].name
end_date = d.iloc[len(df)-1].name
df_pred = result.predict(start = start_date, end = end_date)
df_pred.head()
```
## Model Accuracy
We will use the three most popular metrics for model evaluation: Mean absolute error (MAE), Mean squared error (MSE), or Root mean squared error (RMSE).
```
test = df_test[target]
print("Mean Absolute Error {:.2f}".format(mean_absolute_error(test,df_pred)))
print("Mean Squared Error {:.2f}".format(mean_squared_error(test,df_pred)))
print("Root Mean Squared Error {:.2f}".format(np.sqrt(mean_squared_error(test,df_pred))))
```
## Predictions Plot
First we make use of plot to plot the predicted values returned by our model based on the test data.
After that we plot the actual test data to compare our predictions.
```
plt.figure(figsize=(18,5))
plt.plot(df_pred[start_date:end_date], color = "red")
plt.plot(df_test, color = "blue")
plt.title("Predictions vs Actual", size = 24)
plt.plot(fontsize="x-large")
plt.show()
```
#### Creator: Viraj Jayant, Github: [Profile](https://github.com/Viraj-Jayant)
|
github_jupyter
|
```
%matplotlib inline
```
# STARmap processing example
This notebook demonstrates the processing of STARmap data using starfish. The
data we present here is a subset of the data used in this
[publication](https://doi.org/10.1126/science.aat5691) and was generously provided to us by the authors.
```
from pprint import pprint
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import starfish
import starfish.data
from starfish.types import Axes
from starfish.util.plot import (
diagnose_registration, imshow_plane, intensity_histogram
)
matplotlib.rcParams["figure.dpi"] = 150
```
## Visualize raw data
In this starmap experiment, starfish exposes a test dataset containing a
single field of view. This dataset contains 672 images spanning 6 rounds
`(r)`, 4 channels `(ch)`, and 28 z-planes `(z)`. Each image
is `1024x1024 (y, x)`
To examine this data, the vignette displays the max projection of channels and
rounds. Ideally, these should form fairly coherent spots, indicating that the
data are well registered. By contrast, if there are patterns whereby pairs of
spots are consistently present at small shifts, that can indicate systematic
registration offsets which should be corrected prior to analysis.
```
experiment = starfish.data.STARmap(use_test_data=True)
stack = experiment['fov_000'].get_image('primary')
ch_r_projection = stack.max_proj(Axes.CH, Axes.ROUND)
f = plt.figure(dpi=150)
imshow_plane(ch_r_projection, sel={Axes.ZPLANE: 15})
```
Visualize the codebook
----------------------
The STARmap codebook maps pixel intensities across the rounds and channels to
the corresponding barcodes and genes that those pixels code for. For this
dataset, the codebook specifies 160 gene targets.
```
print(experiment.codebook)
```
## Registration
Starfish exposes some simple tooling to identify registration shifts.
`starfish.util.plot.diagnose_registration` takes an ImageStack and a
set of selectors, each of which maps `Axes` objects
to indices that specify a particular 2d image.
Below the vignette projects the channels and z-planes and examines the
registration of those max projections across channels 0 and 1. To make the
difference more obvious, we zoom in by selecting a subset of the image, and
display the data before and after registration.
It looks like there is a small shift approximately the size of a spot
in the `x = -y` direction for at least the plotted rounds
The starfish package can attempt a translation registration to fix this
registration error.
```
projection = stack.max_proj(Axes.CH, Axes.ZPLANE)
reference_image = projection.sel({Axes.ROUND: 1})
ltt = starfish.image.LearnTransform.Translation(
reference_stack=reference_image,
axes=Axes.ROUND,
upsampling=1000,
)
transforms = ltt.run(projection)
```
How big are the identified translations?
```
pprint([t[2].translation for t in transforms.transforms])
```
Apply the translations
```
warp = starfish.image.ApplyTransform.Warp()
stack = warp.run(
stack=stack,
transforms_list=transforms,
)
```
Show the effect of registration.
```
post_projection = stack.max_proj(Axes.CH, Axes.ZPLANE)
f, (ax1, ax2) = plt.subplots(ncols=2)
sel_0 = {Axes.ROUND: 0, Axes.X: (500, 600), Axes.Y: (500, 600)}
sel_1 = {Axes.ROUND: 1, Axes.X: (500, 600), Axes.Y: (500, 600)}
diagnose_registration(
projection, sel_0, sel_1, ax=ax1, title='pre-registered'
)
diagnose_registration(
post_projection, sel_0, sel_1, ax=ax2, title='registered'
)
f.tight_layout()
```
The plot shows that the slight offset has been corrected.
Equalize channel intensities
----------------------------
The second stage of the STARmap pipeline is to align the intensity
distributions across channels and rounds. Here we calculate a reference
distribution by sorting each image's intensities in increasing order and
averaging the ordered intensities across rounds and channels. All `(z, y, x)`
volumes from each round and channel are quantile normalized against this
reference.
Note that this type of histogram matching has an implied assumption that each
channel has relatively similar numbers of spots. In the case of this data
this assumption is reasonably accurate, but for other datasets it can be
problematic to apply filters that match this stringently.
```
mh = starfish.image.Filter.MatchHistograms({Axes.CH, Axes.ROUND})
scaled = mh.run(stack, in_place=False, verbose=True, n_processes=8)
def plot_scaling_result(
template: starfish.ImageStack, scaled: starfish.ImageStack
):
f, (before, after) = plt.subplots(ncols=4, nrows=2)
for channel, ax in enumerate(before):
title = f'Before scaling\nChannel {channel}'
intensity_histogram(
template, sel={Axes.CH: channel, Axes.ROUND: 0}, ax=ax, title=title,
log=True, bins=50,
)
ax.set_xlim((0, 1))
for channel, ax in enumerate(after):
title = f'After scaling\nChannel {channel}'
intensity_histogram(
scaled, sel={Axes.CH: channel, Axes.ROUND: 0}, ax=ax, title=title,
log=True, bins=50,
)
ax.set_xlim((0, 1))
f.tight_layout()
return f
f = plot_scaling_result(stack, scaled)
```
Find spots
----------
Finally, a local blob detector that finds spots in each (z, y, x) volume
separately is applied. The user selects an "anchor round" and spots found in
all channels of that round are used to seed a local search across other rounds
and channels. The closest spot is selected, and any spots outside the search
radius (here 10 pixels) is discarded.
The Spot finder returns an IntensityTable containing all spots from round
zero. Note that many of the spots do _not_ identify spots in other rounds and
channels and will therefore fail decoding. Because of the stringency built
into the STARmap codebook, it is OK to be relatively permissive with the spot
finding parameters for this assay.
```
lsbd = starfish.spots.DetectSpots.LocalSearchBlobDetector(
min_sigma=1,
max_sigma=8,
num_sigma=10,
threshold=np.percentile(np.ravel(stack.xarray.values), 95),
exclude_border=2,
anchor_round=0,
search_radius=10,
)
intensities = lsbd.run(scaled, n_processes=8)
```
Decode spots
------------
Next, spots are decoded. There is really no good way to display 3-d spot
detection in 2-d planes, so we encourage you to grab this notebook and
uncomment the below lines.
```
decoded = experiment.codebook.decode_per_round_max(intensities.fillna(0))
decode_mask = decoded['target'] != 'nan'
# %gui qt
# viewer = starfish.display(
# stack, decoded[decode_mask], radius_multiplier=2, mask_intensities=0.1
# )
```
|
github_jupyter
|
# Plotting with matplotlib
### Setup
```
%matplotlib inline
import numpy as np
import pandas as pd
pd.set_option('display.max_columns', 10)
pd.set_option('display.max_rows', 10)
```
### Getting the pop2019 DataFrame
```
csv ='../csvs/nc-est2019-agesex-res.csv'
pops = pd.read_csv(csv, usecols=['SEX', 'AGE', 'POPESTIMATE2019'])
def fix_sex(sex):
if sex == 0:
return 'T'
elif sex == 1:
return 'M'
else: # 2
return 'F'
pops.SEX = pops.SEX.apply(fix_sex)
pops = pops.pivot(index='AGE', columns='SEX', values='POPESTIMATE2019')
pops
pops.plot();
```
### Create a Line Plot
```
# Create the plot.
plt_pop = pops.plot(
title = "Population by Age: 2019",
style=['b--', 'm^', 'k-'],
figsize=(12, 6),
lw=2
)
# Include gridlines.
plt_pop.grid(True)
# Set the x and y labels.
plt_pop.set_xlabel('Age')
plt_pop.set_ylabel('Population')
# Create the legend.
plt_pop.legend(['M', 'F', 'A'], loc="lower left")
# Set x and y ticks.
plt_pop.set_xticks(np.arange(0, 101, 10))
yticks = np.arange(500000, 5000001, 500000)
ytick_labels = pd.Series(yticks).apply(lambda y: "{:,}".format(y))
plt_pop.set_yticks(yticks)
plt_pop.set_yticklabels(ytick_labels);
```
### Create a Bar Plot
```
csv ='../csvs/mantle.csv'
mantle = pd.read_csv(csv, index_col='Year',
usecols=['Year', '2B', '3B', 'HR'])
mantle
# Create the plot.
plt_mantle = mantle.plot(
kind='bar',
title = 'Mickey Mantle: Doubles, Triples, and Home Runs',
figsize=(12, 6),
width=.8,
fontsize=16
)
# Include gridlines.
plt_mantle.grid(True)
# Set the x and y labels.
plt_mantle.set_ylabel('Number', fontsize=20)
plt_mantle.set_xlabel('Year', fontsize=20)
# Hatch the bars.
bars = plt_mantle.patches
for i in np.arange(0, 18):
bars[i].set_hatch('+')
for i in np.arange(18, 36):
bars[i].set_hatch('o')
for i in np.arange(36, 54):
bars[i].set_hatch('/')
# Create the legend.
plt_mantle.legend(['Doubles', 'Triples', 'Home Runs'],
loc="upper right", fontsize='xx-large');
plt_mantle = mantle.plot(kind='bar',
title = 'Mickey Mantle: Doubles, Triples, and Home Runs',
figsize=(12, 6),
width=.8,
fontsize=16,
stacked=True)
plt_mantle.set_ylabel('Number', fontsize=20)
plt_mantle.set_xlabel('Year', fontsize=20)
plt_mantle.grid(True)
bars = plt_mantle.patches
for i in np.arange(0, 18):
bars[i].set_hatch('-')
for i in np.arange(18, 36):
bars[i].set_hatch('o')
for i in np.arange(36, 54):
bars[i].set_hatch('/')
plt_mantle.legend(['Doubles','Triples','Home Runs'],
loc="upper right", fontsize='xx-large');
```
|
github_jupyter
|
```
a =[]
import torch
from torch import nn
a = torch.rand(4,10,20)
b = torch.rand(4,10,20)
loss = nn.MSELoss()
[loss(x,y).item() for x,y in zip(a,b)]
import numpy as np
np.mean(list(range(10)))
np.std(list(range(10)))
np.quantile(list(range(10)),0.5)
import sys,os
sys.path.append(os.path.abspath('../'))
from models import get_model
model,config = get_model('ae0')
import argparse
exam_code = '''
e.g)
python evaluate.py -p ./ae/models/ae0_80.pt
'''
parser = argparse.ArgumentParser("Evaluate AE models",epilog=exam_code)
parser.add_argument('-d' ,'--directory' ,default='models' ,metavar='{...}' ,help='directory path containing the models')
parser.add_argument('-p' ,'--path' ,default=None , help='Specify the model path')
parser.add_argument('-th',default=None,help='Value of threshold to classify')
parser.add_argument('--dataset_path' ,default='./data/split/test.csv' , help='test dataset path')
parser.add_argument('-s','--save' ,default=True, type=bool , help='whether to save')
args = parser.parse_args()
import torch
from dataset import ProteinDataset
from sklearn.metrics import accuracy_score
from sklearn.metrics import recall_score
from sklearn.metrics import precision_score
from sklearn.metrics import f1_score
# from sklearn.metrics import make_scorer
# from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
def evaluate(dl,model,lossf,epoch=None):
model.eval()
size, _ , losses = len(dl.dataset) ,0,0
pre_l,gt_l = [],[]
with torch.no_grad():
for x,y in dl:
x,y = x.to(device),y.to(device)
pre = model(x)
loss = lossf(pre,y)
losses += loss.item()
pre_l.extend(pre.argmax(1).cpu().numpy().tolist())
gt_l .extend(y.cpu().numpy().tolist())
loss = losses/size
acc = accuracy_score(gt_l,pre_l)
recall = recall_score(gt_l,pre_l)
precision= precision_score(gt_l,pre_l)
f1 = f1_score(gt_l,pre_l)
confusion= confusion_matrix(gt_l,pre_l)
metrics = {'acc':acc,'recall':recall,'precision':precision,'f1':f1,'confusion':confusion,'loss':loss}
return metrics
device = 'cuda' if torch.cuda.is_available() else 'cpu'
from models import *
import os
results = {}
model_paths = []
if args.path is not None:
m_path = args.path
model_paths.append(m_path)
model_name = os.path.basename(m_path).split('_')[0].lower()
print(model_name)
# model = 'lstm0'
model,transform = get_model(model_name)
model = model.to(device)
# config
transform = config['transform']
batch_size = config['batch_size']
tedt = ProteinDataset(args.dataset_path,transform=transform)
tedl = torch.utils.data.DataLoader(tedt, batch_size=batch_size, num_workers=4)
loss = nn.CrossEntropyLoss()
params = [p for p in model.parameters() if p.requires_grad]
opt = torch.optim.Adam(params)
model.load_state_dict(torch.load(m_path))
result = evaluate(tedl,model,loss)
print(f'{model_name}: {result}')
results[model_name] = result
else:
files = os.listdir(args.directory)
model_paths = [os.path.join('./models',file) for file in files if file.endswith('.pt')]
for m_path in model_paths:
model_name = os.path.basename(m_path).split('_')[0].lower()
print(model_name)
model,config = get_model(model_name)
model = model.to(device)
# config
transform = config['transform']
batch_size = config['batch_size']
tedt = ProteinDataset(args.dataset_path,transform=transform)
tedl = torch.utils.data.DataLoader(tedt, batch_size=batch_size, num_workers=4)
loss = nn.CrossEntropyLoss()
params = [p for p in model.parameters() if p.requires_grad]
opt = torch.optim.Adam(params)
model.load_state_dict(torch.load(m_path))
result = evaluate(tedl,model,loss)
print(f'{model_name}: {result}')
results[model_name] = result
# save the results
print(type(args.save ))
if args.save:
import pandas as pd
df = pd.DataFrame(results).T
models = [os.path.splitext( os.path.basename(path) )[0] for path in model_paths]
df.to_csv(f"assets/{'&'.join(models)}.csv")
print(f"result was saved in assets/{'&'.join(models)}.csv")
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/RihaChri/ImageClassificationBreastCancer/blob/main/CNNBreatCancer.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import os
import glob
import cv2
import numpy as np
from sklearn.model_selection import train_test_split
from re import search
from tensorflow import keras
#-----------------------load images---------------------------------------------
#imageDir=os.path.abspath('/content/drive/MyDrive/Colab Notebooks/ImageClassificationBreastCancerCNN/images')
imageDir=os.path.abspath('/content/drive/MyDrive/Colab Notebooks/ImageClassificationBreastCancerCNN/images/validation')
subDirList=[x[0] for x in os.walk(imageDir)]
fileList=[]
for folder in subDirList:
for file in glob.glob(folder+'/*.png'):
fileList.append(file)
images=[]
y=np.zeros(len(fileList))
for i in range(len(fileList)):
image = cv2.imread(fileList[i])
image = cv2.resize(image, (700, 460), cv2.INTER_LINEAR)
images.append(image)
if search('SOB_M', fileList[i]): y[i]=1
elif search('SOB_B', fileList[i]): y[i]=0
else: raise Exception('the file ',fileList[i],'is not a valid file')
if i%1000==0: print(i,' images out of', len(fileList), ' are loaded')
assert len(images)==y.size
X=np.asarray(images)
print('Loading images succesful')
print('Data shape: ',X.shape)
print('Labels shape: ',y.shape)
#------------------------split data---------------------------------------------
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=1)
X_train, X_val, y_train, y_val = train_test_split(
X_train, y_train, test_size=0.25, random_state=1)
print('X_train: ',X_train.shape)
print('y_train: ',y_train.shape)
print('X_test: ',X_test.shape)
print('y_test: ',y_test.shape)
print('X_val: ',X_val.shape)
print('y_val: ',y_val.shape)
#-------------------Define Model------------------------------------------------
model = keras.Sequential()
# Convolutional layer and maxpool layer 1
model.add(keras.layers.Conv2D(32,(3,3),activation='relu',input_shape=(460,700,3)))
model.add(keras.layers.MaxPool2D(2,2))
# Convolutional layer and maxpool layer 2
model.add(keras.layers.Conv2D(64,(3,3),activation='relu'))
model.add(keras.layers.MaxPool2D(2,2))
# Convolutional layer and maxpool layer 3
model.add(keras.layers.Conv2D(128,(3,3),activation='relu'))
model.add(keras.layers.MaxPool2D(2,2))
# Convolutional layer and maxpool layer 4
model.add(keras.layers.Conv2D(128,(3,3),activation='relu'))
model.add(keras.layers.MaxPool2D(2,2))
# This layer flattens the resulting image array to 1D array
model.add(keras.layers.Flatten())
# Hidden layer with 512 neurons and Rectified Linear Unit activation function
model.add(keras.layers.Dense(512,activation='relu'))
# Output layer with single neuron which gives 0 for benign or 1 for malign
#Here we use sigmoid activation function which makes our model output to lie between 0 and 1
model.add(keras.layers.Dense(1,activation='sigmoid'))
model.compile(loss='binary_crossentropy',
optimizer='rmsprop',
metrics=['accuracy'])
batch_size = 32
model.summary()
#-----------------Define callback-----------------------------------------------
checkpoint_path = "/content/drive/MyDrive/Colab Notebooks/ImageClassificationBreastCancerCNN/checkpoints/cp.ckpt"
checkpoint_dir = os.path.dirname(checkpoint_path)
# Create a callback that saves the model's weights
cp_callback = keras.callbacks.ModelCheckpoint(filepath=checkpoint_path,
save_weights_only=True,
verbose=1)
#model.load_weights(checkpoint_path)
#----------------Train the model------------------------------------------------
model.fit(X_train,
y_train,
epochs=10,
validation_data=(X_val, y_val),
callbacks=[cp_callback]) # Pass callback to training
#evaluate model
loss, acc = model.evaluate(X_test, y_test, verbose=2)
print("Restored model, accuracy: {:5.2f}%".format(100 * acc))
```
|
github_jupyter
|
```
# Import all libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")
data = pd.read_csv('bank-marketing.csv')
data_copy = data.copy()
data.head()
Itemlist = []
for col in data.columns:
Itemlist.append([col, data[col].dtype, data[col].isnull().sum(),
round(data[col].isnull().sum()/len(data[col])*100,2),
data[col].nunique(),
list(data[col].sample(5).drop_duplicates().values)])
dfDesc = pd.DataFrame(columns=['dataFeatures', 'dataType', 'null', 'nullPct', 'unique', 'uniqueSample'], data=Itemlist)
dfDesc
data.describe()
```
#### We notice that pdays is having [25, 50, 75] percentiles as -1 which indicates that missing values are denoted by -1.
```
data[data.duplicated()]
```
### Which age was targeted most and which one of them responded positively?
```
plt.figure(figsize=(13,5))
plt.subplot(1, 2, 1)
sns.distplot(data['age']).set_title('Age distribution')
plt.subplot(1, 2, 2)
sns.violinplot(x = 'response', y = 'age', data=data).set_title('Relationship between age and response')
```
* We see from the above graph that most people targeted in the campaign lie in the age group of 25 to 50.
* It is clear that people lying in the age group of 25 to 40 respond positively than any other age group.
### Does job description affect the chances of success?
```
grouped_job = pd.DataFrame(data.groupby(['job'])['response'].value_counts(normalize=True))
grouped_job.rename(columns={"response" : "pct"}, inplace=True)
grouped_job.reset_index(inplace=True)
plt.figure(figsize=(15,5))
sns.barplot(x='job', y='pct', hue='response', data=grouped_job).set_title('Response by job description')
```
* From the above plot it can be said that customers responding positively to the camapign are very less.
* Customer with job role as management seems to interested more than any other job role.
### Does people with high profile job and high salary have greater chances of positive response?
```
job_salary = pd.DataFrame(data.groupby('job')['salary'].unique().apply(lambda x : x[0])).reset_index()
job_response = pd.crosstab(data['job'], data['response']).reset_index()
data1 = pd.merge(job_salary, job_response)
data1.sort_values('yes', ascending=False)
plt.figure(figsize=(15,5))
plt.subplot(1, 2, 1)
g = sns.barplot(x='job', y='salary', data=data)
g.set_title('Salary by job description')
g.set_xticklabels(g.get_xticklabels(), rotation=45)
plt.subplot(1, 2, 2)
g1 = sns.barplot(x='job', y='yes', data=data1)
g1.set_title('Positive response based on job description')
g1.set_xticklabels(g1.get_xticklabels(), rotation=45)
plt.show()
```
Yes, it is clearly visible that people with high job profile and salary tend to be more interested.
### Does marital status decide the response type?
```
np.log(pd.crosstab(data['marital'], data['response'])).plot.bar(title = 'Response based on marital status')
```
Positive response is almost neutral in case of marital status.
### Does married people of younger age responds positively to the campaign?
```
data2 = data[(data['marital']=='married') & (data['age']<25)]
sns.barplot(x='response', y='age', data=data2)
```
Ratio of yes/no among married young customer seems to be equal.
### Age distribution based on marital status
```
m = sns.FacetGrid(data, col='marital', height = 4)
m.map(plt.hist, 'age')
```
* From the 1st plot it can be seen that mostly married people lie around 25 to 56.
* Single people lie in the age group of 25 to 37.
* Most probably divorced people lie in the age group of 30 to 60.
### What is the relationship between education level and salary?
```
sns.boxplot(x='education', y='salary', data=data).set_title('Boxplot distribution of salary based on education level')
plt.show()
```
It is clear from the above graph that people with high level of education tend to have high salary.
### Are customer of low job profile and married are most responsive one?
```
grouped_job_married = pd.DataFrame(data[data['marital']=='married'].groupby(['job'])['response'].value_counts(normalize=True))
grouped_job_married.rename(columns={"response" : "pct"}, inplace=True)
grouped_job_married.reset_index(inplace=True)
plt.figure(figsize=(15,5))
sns.barplot(x='job', y='pct', hue='response', data=grouped_job_married).set_title('Response of married and low job profile customers')
```
Yes, people who are married and have low job profile tend to response more positvely than any other job profile.
### Are the targeted customers interested in such campaigns?
```
data.head()
```
In order to answer this questions checking of previous campaign records would be appropriate.
```
grouped_poutcome = pd.DataFrame(data['poutcome'].value_counts(normalize=True))
grouped_poutcome = grouped_poutcome.reset_index().rename(columns={"index" : "poutcome", "poutcome" : "pct"})
sns.barplot(x='poutcome', y='pct', data=grouped_poutcome).set_title('Results of previous campaign')
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
sns.distplot(data['pdays'], bins=10).set_title('Days passed after last contact')
plt.subplot(1, 2, 2)
sns.boxplot(y=data['pdays']).set_title('Boxplot of Days passed after last contact')
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
sns.distplot(data['previous'], bins=10).set_title('Contacts performed before this campaign')
plt.subplot(1, 2, 2)
sns.boxplot(y=data['previous']).set_title('Boxplot of Contacts performed before this campaign')
```
It seems that mostly people were contacted within few days still people dosen't seems to be interested in such campaigns.
### Does targeted customer with high job profile and high salary interested in such campaigns anymore?
```
data.groupby('job')['salary'].unique().apply(lambda x : x[0]).sort_values(ascending=False)
data3 = data[(data['salary']>50000) & (data['targeted']=='yes')]['response'].value_counts(normalize=True)
data3 = pd.DataFrame(data3)
data3 = data3.reset_index().rename(columns={'index' : 'response', 'response' : 'pct'})
grouped_high_job = pd.DataFrame(data[data['salary']>50000]['response'].value_counts(normalize=True)).reset_index().rename(columns={'index' : 'response', 'response' : 'pct'})
sns.barplot(x='response', y = 'pct', data=grouped_high_job).set_title('Response of high job profile customer on previous campaigns')
sns.barplot(x='response', y = 'pct', data=data3).set_title('Response of targeted customer with high job profile')
(data[data['salary']>50000]['response'].value_counts(normalize=True) - data3['response'].value_counts(normalize=True)).plot.bar(title='Diff in response of previous v current campaign')
```
There is not much significant difference in the response of high job profile customers from previous to current campaign.
### Distribution of diff in salary and balance.
```
data['expenditure'] = data['salary'] - data['balance']
plt.figure(figsize=(15,5))
sns.distplot(data['expenditure'], bins=10).set_title('Distribution of expenditure')
```
It seems there are people with varying limit in terms of expenditure.
### What is the response of customer with high expenditure?
```
data['expenditure'].plot.box()
threshold = data['expenditure'].quantile(0.90)
less_exp = pd.DataFrame(data[data['expenditure']<threshold]['response'].value_counts(normalize=True))
less_exp = less_exp.reset_index().rename(columns={'index' : 'response', 'response' : 'pct'})
high_exp = pd.DataFrame(data[data['expenditure']>=threshold]['response'].value_counts(normalize=True))
high_exp = high_exp.reset_index().rename(columns={'index' : 'response', 'response' : 'pct'})
plt.figure(figsize=(14,5))
plt.subplot(1, 2, 1)
sns.barplot(x='response', y='pct', data = less_exp).set_title('Response by expenditure less than cutoff')
plt.subplot(1, 2, 2)
sns.barplot(x='response', y='pct', data = high_exp).set_title('Response by expenditure with greater or equal to cutoff')
```
Although, the response from customers are very few. But, those who spend less have greater chances of postive response as compared to those who spend more.
### Is there any relationship between education level and bank balance?
```
sns.boxplot(x='education', y='balance', data=data).set_title('Boxplot distribution of balance by education level')
```
There is not much difference in the statistical measure of balance by education. Rather, it depends on person-to-person.
### What are the chances of customer responding positively who already have home and personal loan?
```
data[(data['housing']=='yes') & (data['loan']=='yes')]['response'].value_counts(normalize=True).plot.bar(title='Customer response having home and personal loan')
```
Not much people are interested in such campaigns who already have loans.
### What are the ways of contacting a customer. And which contact types are most effective?
```
grouped_contact = pd.DataFrame(data['contact'].value_counts(normalize=True)).reset_index().rename(columns={'index' : 'contact_type', 'contact' : 'pct'})
sns.barplot(x='contact_type', y ='pct', data=grouped_contact).set_title('Different contact types for contacting customers')
grouped_contact_response = pd.DataFrame(data.groupby(['contact'])['response'].value_counts(normalize=True)).rename(columns={"response" : "pct"}).reset_index()
sns.barplot(x='contact', y='pct' , data=grouped_contact_response, hue='response').set_title('Response by contact type')
```
Most of the people use cell phones as a communication device and it would be better if we target customer who use cell phones.
### In which month and day most customer were addressed?
```
grouped_month = pd.DataFrame(data['month'].value_counts(normalize=True)).reset_index().rename(columns={"index" : "month", "month" : "pct"})
grouped_day = pd.DataFrame(data['day'].value_counts(normalize=True)).reset_index().rename(columns={"index" : "day", "day" : "pct"})
plt.figure(figsize=(15, 5))
plt.subplot(1, 2, 1)
sns.barplot(x='month', y='pct', data=grouped_month).set_title('Customer addressed by month')
plt.subplot(1, 2, 2)
sns.barplot(x='day', y='pct', data=grouped_day).set_title('Customer addressed by day')
```
It seems in the month of may most customers are handled and this may be due to the fact that vacations are going on at that point of time.
### What is the effect of regular campaigning to a customer?
```
grouped_camp = pd.DataFrame(data['campaign'].value_counts(normalize=True)).reset_index().rename(columns={"index" : "campaign_freq", "campaign" : "pct"})
plt.figure(figsize=(15,5))
plt.subplot(1, 2, 1)
sns.barplot(x='campaign_freq', y='pct', data=grouped_camp).set_title('No of times a customer was contacted during a campaign')
plt.subplot(1, 2, 2)
sns.boxplot(y = data['campaign'])
data['campaign'].describe()
bins = [0, 10, 25, 40, 55, 70]
labels = ['0-10', '10-25', '25-40', '40-55', '55-70']
data['campaign_size'] = pd.cut(data['campaign'], bins =bins, labels = labels)
plt.figure(figsize=(15,5))
sns.countplot(data['campaign_size'], hue=data['response']).set_title('Response based on the campaign size')
plt.yscale('log')
```
* It is clear from above graph that as people are being contacted more and more for a particular contact they seems to lose interest.
* The campaign team also needs to keep track of these records as it will save their time and focus on things which will add value to them.
### Modelling
```
def get_dummies(x,df):
temp = pd.get_dummies(df[x], prefix = x, prefix_sep = '_', drop_first = True)
df = pd.concat([df, temp], axis = 1)
df.drop([x], axis = 1, inplace = True)
return df
X = data.drop(['response', 'campaign_size'], axis=1)
y = data.response
X.loc[X['pdays']==-1, 'pdays'] = 10000
# Create a new column: recent_pdays
X['recent_pdays'] = np.where(X['pdays'], 1/X.pdays, 1/X.pdays)
# Drop 'pdays'
X.drop('pdays', axis=1, inplace = True)
cols = X.select_dtypes('object').columns.tolist()
cols = cols + X.select_dtypes('number').columns.tolist()
X[cols].shape
categoric_cols = X.select_dtypes('object').columns
numeric_cols = data.select_dtypes('number').columns.tolist()
numeric_cols.remove('pdays')
numeric_cols.append('recent_pdays')
for col in categoric_cols:
X = get_dummies(col, X)
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
X[numeric_cols] = scaler.fit_transform(X[numeric_cols])
y.replace({'yes' : 1, 'no' : 0}, inplace=True)
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.feature_selection import RFE
from statsmodels.stats.outliers_influence import variance_inflation_factor
from sklearn.metrics import classification_report, f1_score
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import RandomizedSearchCV
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state = 121)
rf = RandomForestClassifier()
rf.fit(X_train, y_train)
rfe = RFE(rf, 15)
rfe = rfe.fit(X_train, y_train)
list(zip(X_train.columns,rfe.support_,rfe.ranking_))
X_train.columns[rfe.support_]
X_train_rfe = X_train[X_train.columns[rfe.support_]]
params_grid = {'n_estimators' : [10,20,35,50],
'criterion' : ['gini', 'entropy'],
'max_depth' : [10,20,30,50]
}
```
### Random Forest Classifier
```
rfc = RandomForestClassifier()
random_search = RandomizedSearchCV(rfc, param_distributions=params_grid, n_iter=10, cv=10)
random_search.fit(X_train, y_train)
random_search.best_estimator_.n_estimators
random_search.best_estimator_.criterion
random_search.best_estimator_.max_depth
rfc2 = RandomForestClassifier(n_estimators=50, criterion='entropy', max_depth=20)
rfc2.fit(X_train_rfe, y_train)
X_test_rfe = X_test[X_test.columns[rfe.support_]]
y_pred = rfc2.predict(X_test_rfe)
print(classification_report(y_test, y_pred))
```
|
github_jupyter
|
```
import string
import random
from deap import base, creator, tools
## Create a Finess base class which is to be minimized
# weights is a tuple -sign tells to minimize, +1 to maximize
creator.create("FitnessMax", base.Fitness, weights=(1.0,))
```
This will define a class ```FitnessMax``` which inherits the Fitness class of deep.base module. The attribute weight which is a tuple is used to specify whether fitness function is to be maximized (weights=1.0) or minimized weights=-1.0. The DEAP library allows multi-objective Fitness function.
### Individual
Next we create a ```Individual``` class, which inherits the class ```list``` and has the ```FitnessMax``` class in its Fitness attribute.
```
# Now we create a individual class
creator.create("Individual", list, fitness=creator.FitnessMax)
```
# Population
Once the individuals are created we need to create population and define gene pool, to do this we use DEAP toolbox. All the objects that we will need now onwards- an individual, the population, the functions, the operators and the arguments are stored in the container called ```Toolbox```
We can add or remove content in the container ```Toolbox``` using ```register()``` and ```unregister()``` methods
```
toolbox = base.Toolbox()
# Gene Pool
toolbox.register("attr_string", random.choice, string.ascii_letters + string.digits )
#Number of characters in word
word = list('hello')
N = len(word)
# Initialize population
toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attr_string, N )
toolbox.register("population",tools.initRepeat, list, toolbox.individual)
def evalWord(individual, word):
#word = list('hello')
return sum(individual[i] == word[i] for i in range(len(individual))),
toolbox.register("evaluate", evalWord, word)
toolbox.register("mate", tools.cxTwoPoint)
toolbox.register("mutate", tools.mutShuffleIndexes, indpb=0.05)
toolbox.register("select", tools.selTournament, tournsize=3)
```
We define the other operators/functions we will need by registering them in the toolbox. This allows us to easily switch between the operators if desired.
## Evolving the Population
Once the representation and the genetic operators are chosen, we will define an algorithm combining all the individual parts and performing the evolution of our population until the One Max problem is solved. It is good style in programming to do so within a function, generally named main().
Creating the Population
First of all, we need to actually instantiate our population. But this step is effortlessly done using the population() method we registered in our toolbox earlier on.
```
def main():
random.seed(64)
# create an initial population of 300 individuals (where
# each individual is a list of integers)
pop = toolbox.population(n=300)
# CXPB is the probability with which two individuals
# are crossed
#
# MUTPB is the probability for mutating an individual
CXPB, MUTPB = 0.5, 0.2
print("Start of evolution")
# Evaluate the entire population
fitnesses = list(map(toolbox.evaluate, pop))
for ind, fit in zip(pop, fitnesses):
#print(ind, fit)
ind.fitness.values = fit
print(" Evaluated %i individuals" % len(pop))
# Extracting all the fitnesses of
fits = [ind.fitness.values[0] for ind in pop]
# Variable keeping track of the number of generations
g = 0
# Begin the evolution
while max(fits) < 5 and g < 1000:
# A new generation
g = g + 1
print("-- Generation %i --" % g)
# Select the next generation individuals
offspring = toolbox.select(pop, len(pop))
# Clone the selected individuals
offspring = list(map(toolbox.clone, offspring))
# Apply crossover and mutation on the offspring
for child1, child2 in zip(offspring[::2], offspring[1::2]):
# cross two individuals with probability CXPB
if random.random() < CXPB:
toolbox.mate(child1, child2)
# fitness values of the children
# must be recalculated later
del child1.fitness.values
del child2.fitness.values
for mutant in offspring:
# mutate an individual with probability MUTPB
if random.random() < MUTPB:
toolbox.mutate(mutant)
del mutant.fitness.values
# Evaluate the individuals with an invalid fitness
invalid_ind = [ind for ind in offspring if not ind.fitness.valid]
fitnesses = map(toolbox.evaluate, invalid_ind)
for ind, fit in zip(invalid_ind, fitnesses):
ind.fitness.values = fit
print(" Evaluated %i individuals" % len(invalid_ind))
# The population is entirely replaced by the offspring
pop[:] = offspring
# Gather all the fitnesses in one list and print the stats
fits = [ind.fitness.values[0] for ind in pop]
length = len(pop)
mean = sum(fits) / length
sum2 = sum(x*x for x in fits)
std = abs(sum2 / length - mean**2)**0.5
print(" Min %s" % min(fits))
print(" Max %s" % max(fits))
print(" Avg %s" % mean)
print(" Std %s" % std)
print("-- End of (successful) evolution --")
best_ind = tools.selBest(pop, 1)[0]
print("Best individual is %s, %s" % (''.join(best_ind), best_ind.fitness.values))
main()
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/kumarikumari/Keras-Deep-Learning-Cookbook/blob/master/Sentiment_Analysis_Series_part_2(4000samplesonsent140).ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
from google.colab import drive
drive.mount('/content/drive')
!nvidia-smi
!pip install transformers
!pip install -q -U watermark
%reload_ext watermark
%watermark -v -p numpy,pandas,torch,transformers
!pip install sklearn
import sklearn
```
### Making the necessary imports
```
import transformers
from transformers import XLNetTokenizer, XLNetModel, AdamW, get_linear_schedule_with_warmup
import torch
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib import rc
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score
from collections import defaultdict
from textwrap import wrap
from pylab import rcParams
from torch import nn, optim
from keras.preprocessing.sequence import pad_sequences
from torch.utils.data import TensorDataset,RandomSampler,SequentialSampler
from torch.utils.data import Dataset, DataLoader
import torch.nn.functional as F
%matplotlib inline
%config InlineBackend.figure_format='retina'
sns.set(style='whitegrid', palette='muted', font_scale=1.2)
HAPPY_COLORS_PALETTE = ["#01BEFE", "#FFDD00", "#FF7D00", "#FF006D", "#ADFF02", "#8F00FF"]
sns.set_palette(sns.color_palette(HAPPY_COLORS_PALETTE))
rcParams['figure.figsize'] = 12, 8
RANDOM_SEED = 42
np.random.seed(RANDOM_SEED)
torch.manual_seed(RANDOM_SEED)
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
device
```
### Data Preprocessing
```
from google.colab import files
files.upload()
df = pd.read_csv('sent140_preprocessed.csv')
df.head()
from sklearn.utils import shuffle
df = shuffle(df)
df.head(20)
df = df[:4000]
len(df)
import re
def clean_text(text1):
text = re.sub(r"@[A-Za-z0-9]+", ' ', text)
text = re.sub(r"https?://[A-Za-z0-9./]+", ' ', text)
text = re.sub(r"[^a-zA-z.!?'0-9]", ' ', text)
text = re.sub('\t', ' ', text)
text = re.sub(r" +", ' ', text)
return text1
#df_new = df.rename(columns={'text': 'review'})
#df_new
#data = df_new[['review', 'polarity']]
#data.polarity.replace(4, 1, inplace=True)
#data
#df['text'] = df_new['text'].apply(clean_text)
rcParams['figure.figsize'] = 10, 8
sns.countplot(data.polarity)
plt.xlabel('review score');
def sentiment2label(polarity):
if polarity == "positive":
return 1
else :
return 0
df['polarity'] = df['polarity'].apply(sentiment2label)
df['polarity'].value_counts()
#class_names = ['negative', 'positive']
```
### Playing with XLNetTokenizer
```
from transformers import XLNetTokenizer, XLNetModel
PRE_TRAINED_MODEL_NAME = 'xlnet-base-cased'
tokenizer = XLNetTokenizer.from_pretrained(PRE_TRAINED_MODEL_NAME)
input_txt = "India is my country. All Indians are my brothers and sisters"
encodings = tokenizer.encode_plus(input_txt, add_special_tokens=True, max_length=16, return_tensors='pt', return_token_type_ids=False, return_attention_mask=True, pad_to_max_length=False)
print('input_ids : ',encodings['input_ids'])
tokenizer.convert_ids_to_tokens(encodings['input_ids'][0])
type(encodings['attention_mask'])
attention_mask = pad_sequences(encodings['attention_mask'], maxlen=512, dtype=torch.Tensor ,truncating="post",padding="post")
attention_mask = attention_mask.astype(dtype = 'int64')
attention_mask = torch.tensor(attention_mask)
attention_mask.flatten()
encodings['input_ids']
```
### Checking the distribution of token lengths
```
token_lens = []
for txt in df['text']:
tokens = tokenizer.encode(txt, max_length=512)
token_lens.append(len(tokens))
sns.distplot(token_lens)
plt.xlim([0, 1024]);
plt.xlabel('Token count');
MAX_LEN = 512
```
### Custom Dataset class
```
class sent140(Dataset):
def __init__(self, reviews, targets, tokenizer, max_len):
self.reviews = reviews
self.targets = targets
self.tokenizer = tokenizer
self.max_len = max_len
def __len__(self):
return len(self.reviews)
def __getitem__(self, item):
review = str(self.reviews[item])
target = self.targets[item]
encoding = self.tokenizer.encode_plus(
review,
add_special_tokens=True,
max_length=self.max_len,
return_token_type_ids=False,
pad_to_max_length=False,
return_attention_mask=True,
return_tensors='pt',
)
input_ids = pad_sequences(encoding['input_ids'], maxlen=MAX_LEN, dtype=torch.Tensor ,truncating="post",padding="post")
input_ids = input_ids.astype(dtype = 'int64')
input_ids = torch.tensor(input_ids)
attention_mask = pad_sequences(encoding['attention_mask'], maxlen=MAX_LEN, dtype=torch.Tensor ,truncating="post",padding="post")
attention_mask = attention_mask.astype(dtype = 'int64')
attention_mask = torch.tensor(attention_mask)
return {
'review_text': review,
'input_ids': input_ids,
'attention_mask': attention_mask.flatten(),
'targets': torch.tensor(target, dtype=torch.long)
}
df_train, df_test = train_test_split(df, test_size=0.5, random_state=101)
df_val, df_test = train_test_split(df_test, test_size=0.5, random_state=101)
df_train.shape, df_val.shape, df_test.shape
```
### Custom Dataloader
```
def create_data_loader(df, tokenizer, max_len, batch_size):
ds = sent140(
reviews=df.text.to_numpy(),
targets=df.polarity.to_numpy(),
tokenizer=tokenizer,
max_len=max_len
)
return DataLoader(
ds,
batch_size=batch_size,
num_workers=4
)
BATCH_SIZE = 4
train_data_loader = create_data_loader(df_train, tokenizer, MAX_LEN, BATCH_SIZE)
val_data_loader = create_data_loader(df_val, tokenizer, MAX_LEN, BATCH_SIZE)
test_data_loader = create_data_loader(df_test, tokenizer, MAX_LEN, BATCH_SIZE)
```
### Loading the Pre-trained XLNet model for sequence classification from huggingface transformers
```
from transformers import XLNetForSequenceClassification
model = XLNetForSequenceClassification.from_pretrained('xlnet-base-cased', num_labels = 2)
model = model.to(device)
model
```
### Setting Hyperparameters
```
EPOCHS = 3
param_optimizer = list(model.named_parameters())
no_decay = ['bias', 'LayerNorm.bias', 'LayerNorm.weight']
optimizer_grouped_parameters = [
{'params': [p for n, p in param_optimizer if not any(nd in n for nd in no_decay)], 'weight_decay': 0.01},
{'params': [p for n, p in param_optimizer if any(nd in n for nd in no_decay)], 'weight_decay':0.0}
]
optimizer = AdamW(optimizer_grouped_parameters, lr=3e-5)
total_steps = len(train_data_loader) * EPOCHS
scheduler = get_linear_schedule_with_warmup(
optimizer,
num_warmup_steps=0,
num_training_steps=total_steps
)
```
### Sanity check with one batch
```
data = next(iter(val_data_loader))
data.keys()
input_ids = data['input_ids'].to(device)
attention_mask = data['attention_mask'].to(device)
targets = data['targets'].to(device)
print(input_ids.reshape(4,512).shape) # batch size x seq length
print(attention_mask.shape) # batch size x seq length
input_ids[0]
outputs = model(input_ids.reshape(4,512), token_type_ids=None, attention_mask=attention_mask, labels=targets)
outputs
type(outputs[0])
```
### Defining the training step function
```
from sklearn import metrics
def train_epoch(model, data_loader, optimizer, device, scheduler, n_examples):
model = model.train()
losses = []
acc = 0
counter = 0
for d in data_loader:
input_ids = d["input_ids"].reshape(4,512).to(device)
attention_mask = d["attention_mask"].to(device)
targets = d["targets"].to(device)
outputs = model(input_ids=input_ids, token_type_ids=None, attention_mask=attention_mask, labels = targets)
loss = outputs[0]
logits = outputs[1]
# preds = preds.cpu().detach().numpy()
_, prediction = torch.max(outputs[1], dim=1)
targets = targets.cpu().detach().numpy()
prediction = prediction.cpu().detach().numpy()
accuracy = metrics.accuracy_score(targets, prediction)
acc += accuracy
losses.append(loss.item())
loss.backward()
nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)
optimizer.step()
scheduler.step()
optimizer.zero_grad()
counter = counter + 1
return acc / counter, np.mean(losses)
```
### Defining the evaluation function
```
def eval_model(model, data_loader, device, n_examples):
model = model.eval()
losses = []
acc = 0
counter = 0
with torch.no_grad():
for d in data_loader:
input_ids = d["input_ids"].reshape(4,512).to(device)
attention_mask = d["attention_mask"].to(device)
targets = d["targets"].to(device)
outputs = model(input_ids=input_ids, token_type_ids=None, attention_mask=attention_mask, labels = targets)
loss = outputs[0]
logits = outputs[1]
_, prediction = torch.max(outputs[1], dim=1)
targets = targets.cpu().detach().numpy()
prediction = prediction.cpu().detach().numpy()
accuracy = metrics.accuracy_score(targets, prediction)
acc += accuracy
losses.append(loss.item())
counter += 1
return acc / counter, np.mean(losses)
```
### Fine-tuning the pre-trained model
```
%%time
history = defaultdict(list)
best_accuracy = 0
for epoch in range(EPOCHS):
print(f'Epoch {epoch + 1}/{EPOCHS}')
print('-' * 10)
train_acc, train_loss = train_epoch(
model,
train_data_loader,
optimizer,
device,
scheduler,
len(df_train)
)
print(f'Train loss {train_loss} Train accuracy {train_acc}')
val_acc, val_loss = eval_model(
model,
val_data_loader,
device,
len(df_val)
)
print(f'Val loss {val_loss} Val accuracy {val_acc}')
print()
history['train_acc'].append(train_acc)
history['train_loss'].append(train_loss)
history['val_acc'].append(val_acc)
history['val_loss'].append(val_loss)
if val_acc > best_accuracy:
torch.save(model.state_dict(), 'C:\\Users\\BUJJI\\Desktop\\NLP\\models\\xlnet_model1.bin')
best_accuracy = val_acc
```
### Evaluation of the fine-tuned model
```
model.load_state_dict(torch.load('C:\\Users\\BUJJI\\Desktop\\NLP\\models\\xlnet_model1.bin'))
model = model.to(device)
test_acc, test_loss = eval_model(
model,
test_data_loader,
device,
len(df_test)
)
print('Test Accuracy :', test_acc)
print('Test Loss :', test_loss)
def get_predictions(model, data_loader):
model = model.eval()
review_texts = []
predictions = []
prediction_probs = []
real_values = []
with torch.no_grad():
for d in data_loader:
texts = d["review_text"]
input_ids = d["input_ids"].reshape(4,512).to(device)
attention_mask = d["attention_mask"].to(device)
targets = d["targets"].to(device)
outputs = model(input_ids=input_ids, token_type_ids=None, attention_mask=attention_mask, labels = targets)
loss = outputs[0]
logits = outputs[1]
_, preds = torch.max(outputs[1], dim=1)
probs = F.softmax(outputs[1], dim=1)
review_texts.extend(texts)
predictions.extend(preds)
prediction_probs.extend(probs)
real_values.extend(targets)
predictions = torch.stack(predictions).cpu()
prediction_probs = torch.stack(prediction_probs).cpu()
real_values = torch.stack(real_values).cpu()
return review_texts, predictions, prediction_probs, real_values
y_review_texts, y_pred, y_pred_probs, y_test = get_predictions(
model,
test_data_loader
)
print(classification_report(y_test, y_pred, target_names=class_names))
```
### Custom prediction function on raw text
```
def predict_sentiment(text):
review_text = text
encoded_review = tokenizer.encode_plus(
review_text,
max_length=MAX_LEN,
add_special_tokens=True,
return_token_type_ids=False,
pad_to_max_length=False,
return_attention_mask=True,
return_tensors='pt',
)
input_ids = pad_sequences(encoded_review['input_ids'], maxlen=MAX_LEN, dtype=torch.Tensor ,truncating="post",padding="post")
input_ids = input_ids.astype(dtype = 'int64')
input_ids = torch.tensor(input_ids)
attention_mask = pad_sequences(encoded_review['attention_mask'], maxlen=MAX_LEN, dtype=torch.Tensor ,truncating="post",padding="post")
attention_mask = attention_mask.astype(dtype = 'int64')
attention_mask = torch.tensor(attention_mask)
input_ids = input_ids.reshape(1,512).to(device)
attention_mask = attention_mask.to(device)
outputs = model(input_ids=input_ids, attention_mask=attention_mask)
outputs = outputs[0][0].cpu().detach()
probs = F.softmax(outputs, dim=-1).cpu().detach().numpy().tolist()
_, prediction = torch.max(outputs, dim =-1)
print("Positive score:", probs[1])
print("Negative score:", probs[0])
print(f'Review text: {review_text}')
print(f'Sentiment : {class_names[prediction]}')
text = "Movie is the worst one I have ever seen!! The story has no meaning at all"
predict_sentiment(text)
text = "This is the best movie I have ever seen!! The story is such a motivation"
predict_sentiment(text)
```
|
github_jupyter
|
# 06_Business_Insights
In this section, we will expend upon the features used by the model and attempt to explain its significance as well as contributions to the pricing model.
Accordingly, in Section Four, we identified the following key features that that are strong predictors of housing price based upon a combination of feature engineering coupled with recursive feature elimination.
$$
\hat{y} = \beta_0 + \begin{align} \beta_1\textit{(age_since_built)} + \beta_2\textit{(Gr_Liv_Area)} + \beta_3\textit{(Total_Bsmt_SF)} + \beta_4\textit{(house_exter_score)} + \beta_j\textit{(Land_Contour)}_j
\end{align}$$
Where:
$\textit{house_exter_score}$ = ['Overall Qual'] + ['Overall Cond'] +['Exter Qual'] + ['Exter Cond']
| Score |
| --- |
|age_since_built |
|Total Bsmt SF |
|Land Contour_Lvl |
|house_exter_score |
|Gr Liv Area |
|Land Contour_Low |
|Land Contour_HLS |
```
# model coefficients
prod_model_rfe
```
## Import Libraries
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import matplotlib.ticker as ticker
%matplotlib inline
rfe_columns = ['Total Bsmt SF', 'Gr Liv Area', 'age_since_built', 'house_exter_score',
'Land Contour_HLS', 'Land Contour_Low', 'Land Contour_Lvl']
```
## Load in Training Set for Exploration
```
train = pd.read_csv('./datasets/imputed_train.csv')
new_train = train[(train['Total Bsmt SF']<4000) & (train['Total Bsmt SF']>0)]
plt.figure(figsize=(15,10))
ax = sns.scatterplot(x='Total Bsmt SF',y='SalePrice',data=new_train,hue='Total Bsmt SF')
ax.set_title("Total Basement Area against Sale Prices", fontname='Helvetica', fontsize=18,loc='left')
ax.set_xlabel('Total Basement Area / SqFt',fontname='Helvetica',fontsize=12)
ax.set_ylabel('Sale Price / $',fontname='Helvetica',fontsize=12)
plt.savefig("./img/bsmt_area.png",dpi=300)
plt.figure(figsize=(15,10))
ax = sns.scatterplot(x='age_since_built',y='SalePrice',data=new_train,hue='age_since_built')
ax.set_title("Building Age against Sale Prices", fontname='Helvetica', fontsize=18,loc='left')
ax.set_xlabel('Building Age / yr',fontname='Helvetica',fontsize=12)
ax.set_ylabel('Sale Price / $',fontname='Helvetica',fontsize=12)
plt.savefig("./img/building_age.png",dpi=300)
train.columns
plt.figure(figsize=(15,10))
ax = sns.pointplot(x='house_exter_score',y='SalePrice',data=new_train)
ax.set_title("Housing Scores against Sale Prices", fontname='Helvetica', fontsize=18,loc='left')
ax.set_xlabel('Score',fontname='Helvetica',fontsize=12)
ax.set_ylabel('Sale Price / $',fontname='Helvetica',fontsize=12)
for ind, label in enumerate(ax.get_xticklabels()):
if ind % 5 == 0: # every 10th label is kept
label.set_visible(True)
else:
label.set_visible(False)
plt.savefig("./img/housing_score.png",dpi=300)
plt.figure(figsize=(15,10))
ax = sns.scatterplot(x='Gr Liv Area',y='SalePrice',data=new_train,hue='Gr Liv Area')
ax.set_title("Living Area against Sale Prices", fontname='Helvetica', fontsize=18,loc='left')
ax.set_xlabel('Living Area / Sqft',fontname='Helvetica',fontsize=12)
ax.set_ylabel('Sale Price / $',fontname='Helvetica',fontsize=12)
plt.savefig("./img/living_area.png",dpi=300)
new_train_melt = new_train[['Land Contour_Low', 'Land Contour_HLS','Land Contour_Lvl','SalePrice']].melt(id_vars='SalePrice' ,value_vars=['Land Contour_Low', 'Land Contour_HLS','Land Contour_Lvl'])
plt.figure(figsize=(15,10))
ax = sns.boxplot(x='variable',y='SalePrice',order=['Land Contour_Lvl','Land Contour_Low','Land Contour_HLS'],data=new_train_melt[new_train_melt['value']!=0])
ax.set_title("Land Contours and relationship to Sale Prices", fontname='Helvetica', fontsize=18,loc='left')
ax.set_xlabel('Score',fontname='Helvetica',fontsize=12)
ax.set_ylabel('Sale Price / $',fontname='Helvetica',fontsize=12)
plt.savefig("./img/contour_plot.png",dpi=300)
```
## Key Takeaways
## Conclusion And Recommendations
House age, Land Contours, Housing Scores as well as Gross floor areas are strong predictors of housing prices. Using these few variables, a prospective home seller can look into improving areas such as home quality, condition as well as look at expanding gross floor areas via careful remodelling of their homes.
To make this model location agnostic, we may impute features such as accessibility to the city (via distances) and crime rates which can affect buyer's judgement.
|
github_jupyter
|
# Bulk RNA-seq eQTL analysis
This notebook provide a command generator on the XQTL workflow so it can automate the work for data preprocessing and association testing on multiple data collection as proposed.
```
%preview ../images/eqtl_command.png
```
This master control notebook is mainly to serve the 8 tissues snuc_bulk_expression analysis, but should be functional on all analysis where expression data are are a tsv table in a bed.gz like format.
Input:
A recipe file,each row is a data collection and with the following column:
Theme
name of dataset, must be different, each uni_study analysis will be performed in a folder named after each, meta analysis will be performed in a folder named as {study1}_{study2}
The column name must contain the # and be the first column
genotype_file
{Path to a whole genome genotype file}
molecular_pheno
{Path to file}
covariate_file
{Path to file}
### note: Only data collection from the same Populations and conditions will me merged to perform Fix effect meta analysis
A genotype list, with two column, `#chr` and `path`
This can be generated by the genotype session of this command generator.
Output:
1 set of association_scan result for each tissue (each row in the recipe)
```
pd.DataFrame({"Theme":"MWE","molecular_pheno":"MWE.log2cpm.tsv","genotype_file":"MWE.bed","covariate_file":"MWE.covariate.cov.gz"}).to_csv("/mnt/vast/hpc/csg/snuc_pseudo_bulk/eight_tissue_analysis/MWE/command_generator",sep = "\t",index = 0)
```
| Theme | molecular_pheno | genotype_file |covariate_file|
| ----------- | ----------- |-----------||
| MWE | MWE.log2cpm.tsv | /data/genotype_data/GRCh38_liftedover_sorted_all.add_chr.leftnorm.filtered.bed |MWE.covariate.cov.gz|
## Minimal Working Example
### Genotype
The MWE for the genotype session can be ran with the following commands, please be noted that a [seperated MWE genoFile]( https://drive.google.com/file/d/1zaacRlZ63Nf_oEUv2nIiqekpQmt2EDch/view?usp=sharing) was needed.
```
sos run pipeline/eQTL_analysis_commands.ipynb plink_per_chrom \
--ref_fasta reference_data/GRCh38_full_analysis_set_plus_decoy_hla.noALT_noHLA_noDecoy_ERCC.fasta \
--genoFile mwe_genotype.vcf.gz \
--dbSNP_vcf reference_data/00-All.vcf.gz \
--sample_participant_lookup reference_data/sampleSheetAfterQC.txt -n
```
### Per tissue analysis
A MWE for the core per tissue analysis can be ran with the following commands, a complete collection of input file as well as intermediate output of the analysis can be found at [here](https://drive.google.com/drive/folders/16ZUsciZHqCeeEWwZQR46Hvh5OtS8lFtA?usp=sharing).
```
sos run pipeline/eQTL_analysis_commands.ipynb sumstat_merge \
--recipe MWE.recipe \
--genotype_list plink_files_list.txt \
--annotation_gtf reference_data/genes.reformatted.gene.gtf \
--sample_participant_lookup reference_data/sampleSheetAfterQC.txt \
--Association_option "TensorQTL" -n
sos run pipeline/eQTL_analysis_commands.ipynb sumstat_merge \
--recipe MWE.recipe \
--genotype_list plink_files_list.txt \
--annotation_gtf /mnt/vast/hpc/csg/snuc_pseudo_bulk/data/reference_data/genes.reformatted.gene.gtf \
--sample_participant_lookup /mnt/vast/hpc/csg/snuc_pseudo_bulk/data/reference_data/sampleSheetAfterQC.txt \
--Association_option "APEX" -n
```
## Example for running the workflow
This will run the workflow from via several submission
```
sos run ~/GIT/xqtl-pipeline/pipeline/eQTL_analysis_commands.ipynb sumstat_merge \
--recipe /mnt/vast/hpc/csg/snuc_pseudo_bulk//data/recipe_8tissue_new \
--genotype_list /mnt/vast/hpc/csg/snuc_pseudo_bulk/data/genotype_qced/plink_files_list.txt \
--annotation_gtf /mnt/vast/hpc/csg/snuc_pseudo_bulk/data/reference_data/genes.reformatted.gene.gtf \
--sample_participant_lookup /mnt/vast/hpc/csg/snuc_pseudo_bulk/data/reference_data/sampleSheetAfterQC.txt \
--Association_option "TensorQTL" --run &
sos run ~/GIT/xqtl-pipeline/pipeline/eQTL_analysis_commands.ipynb sumstat_merge \
--recipe <(cat /mnt/vast/hpc/csg/snuc_pseudo_bulk//data/recipe_8tissue_new | head -2) \
--genotype_list /mnt/vast/hpc/csg/snuc_pseudo_bulk/data/genotype_qced/plink_files_list.txt \
--annotation_gtf /mnt/vast/hpc/csg/snuc_pseudo_bulk/data/reference_data/genes.reformatted.gene.gtf \
--sample_participant_lookup /mnt/vast/hpc/csg/snuc_pseudo_bulk/data/reference_data/sampleSheetAfterQC.txt \
--factor_option "PEER" --Association_option "TensorQTL" -n
[global]
## The aforementioned input recipe
parameter: recipe = path(".") # Added option to run genotype part without the recipe input, which was not used.
## Overall wd, the file structure of analysis is wd/[steps]/[sub_dir for each steps]
parameter: cwd = path("output")
## Diretory to the excutable
parameter: exe_dir = path("~/GIT/xqtl-pipeline/")
parameter: container_base_bioinfo = 'containers/bioinfo.sif'
parameter: container_apex = 'containers/apex.sif'
parameter: container_PEER = 'containers/PEER.sif'
parameter: container_TensorQTL = 'containers//TensorQTL.sif'
parameter: container_rnaquant = 'containers/rna_quantification.sif'
parameter: container_flashpca = 'containers/flashpcaR.sif'
parameter: container_susie = 'containers/stephenslab.sif'
parameter: sample_participant_lookup = path
parameter: phenotype_id_type = "gene_name"
parameter: yml = path("csg.yml")
parameter: run = False
interpreter = 'cat' if not run else 'bash'
import pandas as pd
if recipe.is_file():
input_inv = pd.read_csv(recipe, sep = "\t").to_dict("records")
import os
parameter: jobs = 50 # Number of jobs that are submitted to the cluster
parameter: queue = "csg" # The queue that jobs are submitted to
submission = f'-J {jobs} -c {yml} -q {queue}'
## Control of the workflow
### Factor option (PEER vs BiCV)
parameter: factor_option = "PEER"
### Association scan option (APEX vs TensorQTL)
parameter: Association_option = "TensorQTL"
```
## Data Preprocessing
### Genotype Preprocessing (Once for all tissues)
```
[dbSNP]
parameter: dbSNP_vcf = path
input: dbSNP_vcf
parameter: add_chr = True
output: f'{cwd}/reference_data/{_input:bnn}.add_chr.variants.gz'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output}.stderr', stdout = f'{_output}.stdout'
sos run $[exe_dir]/pipeline//VCF_QC.ipynb dbsnp_annotate \
--genoFile $[_input] \
--cwd $[_output:d] \
--container $[container_base_bioinfo] \
$[submission if yml.is_file() else "" ] $["--add_chr" if add_chr else "--no-add_chr" ]
[VCF_QC]
parameter: genoFile = path
parameter: ref_fasta = path
parameter: add_chr = True
input: genoFile, output_from("dbSNP")
output: f'{cwd}/data_preprocessing/{_input[0]:bnn}.{"add_chr." if add_chr else False}leftnorm.filtered.bed'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output}.stderr', stdout = f'{_output}.stdout'
sos run $[exe_dir]//pipeline/VCF_QC.ipynb qc \
--genoFile $[_input[0]] \
--dbsnp-variants $[_input[1]] \
--reference-genome $[ref_fasta] \
--cwd $[_output:d] \
--container $[container_base_bioinfo] \
--walltime "24h" \
$[submission if yml.is_file() else "" ] $["--add_chr" if add_chr else "--no-add_chr" ]
[plink_QC]
# minimum MAF filter to use. 0 means do not apply this filter.
parameter: maf_filter = 0.05
# maximum MAF filter to use. 0 means do not apply this filter.
parameter: maf_max_filter = 0.0
# Maximum missingess per-variant
parameter: geno_filter = 0.1
# Maximum missingness per-sample
parameter: mind_filter = 0.1
# HWE filter
parameter: hwe_filter = 1e-06
input: output_from("VCF_QC")
output: f'{_input:n}.filtered.bed'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output}.stderr', stdout = f'{_output}.stdout'
sos run $[exe_dir]//pipeline/GWAS_QC.ipynb qc_no_prune \
--cwd $[_output:d] \
--genoFile $[_input] \
--maf-filter $[maf_filter] \
--geno-filter $[geno_filter] \
--mind-filter $[mind_filter] \
--hwe-filter $[hwe_filter] \
--mem 40G \
--container $[container_base_bioinfo] $[submission if yml.is_file() else "" ]
[plink_per_chrom]
input: output_from("plink_QC")
output: f'{cwd:a}/data_preprocessing/{_input:bn}.plink_files_list.txt'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output}.stderr', stdout = f'{_output}.stdout'
sos run $[exe_dir]//pipeline/genotype_formatting.ipynb plink_by_chrom \
--genoFile $[_input] \
--cwd $[_output:d] \
--chrom `cut -f 1 $[_input:n].bim | uniq | sed "s/chr//g"` \
--container $[container_base_bioinfo] $[submission if yml.is_file() else "" ]
[plink_to_vcf]
parameter: genotype_list = path
input: genotype_list
import pandas as pd
parameter: genotype_file_name = pd.read_csv(_input,"\t",nrows = 1).values.tolist()[0][1]
output: f'{cwd:a}/data_preprocessing/{path(genotype_file_name):bnn}.vcf_files_list.txt'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output}.stderr', stdout = f'{_output}.stdout'
sos run $[exe_dir]//pipeline/genotype_formatting.ipynb plink_to_vcf \
--genoFile $[_input] \
--cwd $[_output:d] \
--container $[container_base_bioinfo] $[submission if yml.is_file() else "" ]
[plink_per_gene]
# The plink genotype file
parameter: genoFile = path
input: output_from("region_list_concat"),genoFile
output: f'{cwd:a}/{_input[1]:bn}.plink_files_list.txt'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output}.stderr', stdout = f'{_output}.stdout'
sos run $[exe_dir]/pipeline//genotype_formatting.ipynb plink_by_gene \
--genoFile $[_input[1]] \
--cwd $[_output:d] \
--region_list $[_input[0]] \
--container $[container_base_bioinfo] $[submission if yml.is_file() else "" ]
```
### Molecular Phenotype Processing
```
[annotation]
stop_if(not recipe.is_file(), msg = "Please specify a valid recipe as input")
import os
parameter: annotation_gtf = path
input: for_each = "input_inv"
output: f'{cwd:a}/data_preprocessing/{_input_inv["Theme"]}/phenotype_data/{path(_input_inv["molecular_pheno"]):bn}.bed.gz'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output}.stderr', stdout = f'{_output}.stdout'
sos run $[exe_dir]/pipeline/gene_annotation.ipynb annotate_coord \
--cwd $[_output:d] \
--phenoFile $[_input_inv["molecular_pheno"]] \
--annotation-gtf $[annotation_gtf] \
--sample-participant-lookup $[sample_participant_lookup] \
--container $[container_rnaquant] \
--phenotype-id-type $[phenotype_id_type] $[submission if yml.is_file() else "" ]
[region_list_generation]
parameter: annotation_gtf = path
input: output_from("annotation"), group_with = "input_inv"
output: pheno_mod = f'{cwd:a}/data_preprocessing/{_input_inv["Theme"]}/phenotype_data/{_input:bnn}.region_list'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output[0]}.stderr', stdout = f'{_output[0]}.stdout'
sos run $[exe_dir]/pipeline/gene_annotation.ipynb region_list_generation \
--cwd $[_output:d] \
--phenoFile $[_input]\
--annotation-gtf $[annotation_gtf] \
--sample-participant-lookup $[sample_participant_lookup] \
--container $[container_rnaquant] \
--phenotype-id-type $[phenotype_id_type] $[submission if yml.is_file() else "" ]
[region_list_concat]
input: output_from("region_list_generation"), group_by = "all"
output: f'{cwd:a}/data_preprocessing/phenotype_data/concat.region_list'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output[0]}.stderr', stdout = f'{_output[0]}.stdout'
cat $[_input:a] | sort | uniq > $[_output:a]
[phenotype_partition_by_chrom]
input: output_from("annotation"),output_from("region_list_generation"), group_with = "input_inv"
output: per_chrom_pheno_list = f'{cwd:a}/data_preprocessing/{_input_inv["Theme"]}/phenotype_data/{_input[0]:bn}.processed_phenotype.per_chrom.recipe'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output[0]}.stderr', stdout = f'{_output[0]}.stdout'
sos run $[exe_dir]/pipeline/phenotype_formatting.ipynb partition_by_chrom \
--cwd $[_output:d] \
--phenoFile $[_input[0]:a] \
--region-list $[_input[1]:a] \
--container $[container_rnaquant] \
--mem 4G $[submission if yml.is_file() else "" ]
```
### Genotype Processing
Since genotype is shared among the eight tissue, the QC of whole genome file is not needed. Only pca needed to be run again.
```
[sample_match]
input: for_each = "input_inv"
output: f'{cwd:a}/data_preprocessing/{_input_inv["Theme"]}/{sample_participant_lookup:bn}.filtered.txt',
geno = f'{cwd:a}/data_preprocessing/{_input_inv["Theme"]}/{sample_participant_lookup:bn}.filtered_geno.txt'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output[0]}.stderr', stdout = f'{_output[0]}.stdout'
sos run $[exe_dir]/pipeline/sample_matcher.ipynb filtered_sample_list \
--cwd $[_output[0]:d] \
--phenoFile $[_input_inv["molecular_pheno"]] \
--genoFile $[path(_input_inv["genotype_file"]):n].fam \
--sample-participant-lookup $[sample_participant_lookup] \
--container $[container_rnaquant] \
--translated_phenoFile $[submission if yml.is_file() else "" ]
[king]
parameter: maximize_unrelated = False
input:output_from("sample_match")["geno"], group_with = "input_inv"
output: related = f'{cwd:a}/data_preprocessing/{_input_inv["Theme"]}/genotype_data/{path(_input_inv["genotype_file"]):bn}.{_input_inv["Theme"]}.related.bed',
unrelated = f'{cwd:a}/data_preprocessing/{_input_inv["Theme"]}/genotype_data/{path(_input_inv["genotype_file"]):bn}.{_input_inv["Theme"]}.unrelated.bed'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output[0]}.stderr', stdout = f'{_output[0]}.stdout'
sos run $[exe_dir]/pipeline/GWAS_QC.ipynb king \
--cwd $[_output[0]:d] \
--genoFile $[_input_inv["genotype_file"]] \
--name $[_input_inv["Theme"]] \
--keep-samples $[_input] \
--container $[container_base_bioinfo] \
--walltime 48h $[submission if yml.is_file() else "" ] $["--maximize_unrelated" if maximize_unrelated else "--no-maximize_unrelated"]
[unrelated_QC]
input: output_from("king")["unrelated"]
output: unrelated_bed = f'{_input:n}.filtered.prune.bed',
prune = f'{_input:n}.filtered.prune.in'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output[0]}.stderr', stdout = f'{_output[0]}.stdout'
sos run $[exe_dir]/pipeline/GWAS_QC.ipynb qc \
--cwd $[_output[0]:d] \
--genoFile $[_input] \
--exclude-variants /mnt/vast/hpc/csg/snuc_pseudo_bulk/Ast/genotype/dupe_snp_to_exclude \
--maf-filter 0.05 \
--container $[container_base_bioinfo] \
--mem 40G $[submission if yml.is_file() else "" ]
[related_QC]
input: output_from("king")["related"],output_from("unrelated_QC")["prune"]
output: f'{_input[0]:n}.filtered.extracted.bed'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output[0]}.stderr', stdout = f'{_output[0]}.stdout'
sos run $[exe_dir]/pipeline/GWAS_QC.ipynb qc_no_prune \
--cwd $[_output[0]:d] \
--genoFile $[_input[0]] \
--maf-filter 0 \
--geno-filter 0 \
--mind-filter 0.1 \
--hwe-filter 0 \
--keep-variants $[_input[1]] \
--container $[container_base_bioinfo] \
--mem 40G $[submission if yml.is_file() else "" ]
```
## Factor Analysis
```
[pca]
input: output_from("unrelated_QC")["unrelated_bed"],group_with = "input_inv"
output: f'{cwd}/data_preprocessing/{_input_inv["Theme"]}/pca/{_input:bn}.pca.rds',
f'{cwd}/data_preprocessing/{_input_inv["Theme"]}/pca/{_input:bn}.pca.scree.txt'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output[0]}.stderr', stdout = f'{_output[0]}.stdout'
sos run $[exe_dir]/pipeline/PCA.ipynb flashpca \
--cwd $[_output:d] \
--genoFile $[_input] \
--container $[container_flashpca] $[submission if yml.is_file() else "" ]
[projected_sample]
# The percentage of PVE explained
parameter: PVE_treshold = 0.7
input: output_from("related_QC"),output_from("pca"), group_with = "input_inv"
output: f'{cwd}/data_preprocessing/{_input_inv["Theme"]}/pca/{_input[0]:bn}.pca.projected.rds',
f'{cwd}/data_preprocessing/{_input_inv["Theme"]}/pca/{_input[0]:bn}.pca.projected.scree.txt'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output[0]}.stderr', stdout = f'{_output[0]}.stdout'
sos run $[exe_dir]/pipeline/PCA.ipynb project_samples \
--cwd $[_output:d] \
--genoFile $[_input[0]] \
--pca-model $[_input[1]] \
--maha-k `awk '$3 < $[PVE_treshold]' $[_input[2]] | tail -1 | cut -f 1 ` \
--container $[container_flashpca] $[submission if yml.is_file() else "" ]
[merge_pca_covariate]
# The percentage of PVE explained
parameter: PVE_treshold = 0.7
input: output_from("projected_sample"),group_with = "input_inv"
output: f'{cwd}/data_preprocessing/{_input_inv["Theme"]}/covariates/{path(_input_inv["covariate_file"]):bn}.pca.gz'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output[0]}.stderr', stdout = f'{_output[0]}.stdout'
sos run $[exe_dir]/pipeline/covariate_formatting.ipynb merge_pca_covariate \
--cwd $[_output:d] \
--pcaFile $[_input[0]:a] \
--covFile $[path(_input_inv["covariate_file"])] \
--tol_cov 0.3 \
--k `awk '$3 < $[PVE_treshold]' $[_input[1]] | tail -1 | cut -f 1 ` \
--container $[container_base_bioinfo] $[submission if yml.is_file() else "" ] --name $[_output:bn] --outliersFile $[_input[0]:an].outliers
[resid_exp]
input: output_from("merge_pca_covariate"),output_from("annotation"),group_with = "input_inv"
output: f'{cwd}/data_preprocessing/{_input_inv["Theme"]}/resid_phenotype/{_input[1]:bnn}.{_input[0]:bn}.resid.bed.gz'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output[0]}.stderr', stdout = f'{_output[0]}.stdout'
sos run $[exe_dir]/pipeline/covariate_formatting.ipynb compute_residual \
--cwd $[_output:d] \
--phenoFile $[_input[1]:a] \
--covFile $[_input[0]:a] \
--container $[container_base_bioinfo] $[submission if yml.is_file() else "" ]
[factor]
parameter: N = 0
input: output_from("resid_exp"),group_with = "input_inv"
output: f'{cwd}/data_preprocessing/{_input_inv["Theme"]}/covariates/{_input[0]:bnn}.{factor_option}.gz'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output}.stderr', stdout = f'{_output}.stdout'
sos run $[exe_dir]/pipeline/$[factor_option]_factor.ipynb $[factor_option] \
--cwd $[_output:d] \
--phenoFile $[_input[0]:a] \
--container $[container_apex if factor_option == "BiCV" else container_PEER] \
--walltime 24h \
--numThreads 8 \
--iteration 1000 \
--N $[N] $[submission if yml.is_file() else "" ]
[merge_factor_covariate]
# The percentage of PVE explained
parameter: PVE_treshold = 0.7
input: output_from("factor"),output_from("merge_pca_covariate"),group_with = "input_inv"
output: f'{cwd}/data_preprocessing/{_input_inv["Theme"]}/covariates/{_input[0]:bn}.cov.gz'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output}.stderr', stdout = f'{_output}.stdout'
sos run $[exe_dir]/pipeline/covariate_formatting.ipynb merge_factor_covariate \
--cwd $[_output:d] \
--factorFile $[_input[0]:a] \
--covFile $[_input[1]:a] \
--container $[container_base_bioinfo] $[submission if yml.is_file() else "" ] --name $[_output:bn]
```
## Association Scan
```
[TensorQTL]
# The number of minor allele count as treshold for the analysis
parameter: MAC = 0
# The minor allele frequency as treshold for the analysis, overwrite MAC
parameter: maf_threshold = 0
parameter: genotype_list = path
input: genotype_list, output_from("phenotype_partition_by_chrom"),output_from("merge_factor_covariate"),group_with = "input_inv"
output: f'{cwd:a}/association_scan/{_input_inv["Theme"]}/TensorQTL/TensorQTL.cis._recipe.tsv'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output[0]}.stderr', stdout = f'{_output[0]}.stdout'
sos run $[exe_dir]/pipeline/TensorQTL.ipynb cis \
--genotype-list $[_input[0]] \
--phenotype-list $[_input[1]] \
--covariate-file $[_input[2]] \
--cwd $[_output:d] \
--container $[container_TensorQTL] $[submission if yml.is_file() else "" ] $[f'--MAC {MAC}' if MAC else ""] $[f'--maf_threshold {maf_threshold}' if maf_threshold else ""]
[APEX]
parameter: genotype_list = path
input: output_from("plink_to_vcf"), output_from("phenotype_partition_by_chrom"),output_from("merge_factor_covariate"),group_with = "input_inv"
output: f'{cwd:a}/association_scan/{_input_inv["Theme"]}/APEX/APEX_QTL_recipe.tsv'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output[0]}.stderr', stdout = f'{_output[0]}.stdout'
sos run $[exe_dir]/pipeline/APEX.ipynb cis \
--genotype-list $[_input[0]] \
--phenotype-list $[_input[1]] \
--covariate-file $[_input[2]] \
--cwd $[_output:d] \
--container $[container_apex] $[submission if yml.is_file() else "" ] --name $[_input[1]:bnn]
```
## Trans Association Scan
```
[TensorQTL_Trans]
parameter: MAC = 0
# The minor allele frequency as treshold for the analysis, overwrite MAC
parameter: maf_threshold = 0
parameter: genotype_list = path
parameter: region_list = path
input: genotype_list, output_from("phenotype_partition_by_chrom"),output_from("merge_factor_covariate"),group_with = "input_inv"
output: f'{cwd:a}/association_scan/{_input_inv["Theme"]}/Trans/TensorQTL.trans._recipe.tsv'
script: interpreter = interpreter, expand = "$[ ]", stderr = f'{_output[0]}.stderr', stdout = f'{_output[0]}.stdout'
sos run $[exe_dir]/pipeline/TensorQTL.ipynb trans \
--genotype-list $[_input[0]] \
--phenotype-list $[_input[1]] \
--covariate-file $[_input[2]] \
--cwd $[_output:d] \
--region_list $[region_list] \
--container $[container_TensorQTL] $[submission if yml.is_file() else "" ] $[f'--MAC {MAC}' if MAC else ""] $[f'--maf_threshold {maf_threshold}' if maf_threshold else ""]
```
## SuSiE
```
[UniSuSiE]
input: output_from("plink_per_gene"), output_from("annotation"),output_from("factor"), output_from("region_list_concat"), group_by = "all"
output: f'{cwd:a}/Fine_mapping/UniSuSiE/UniSuSiE_recipe.tsv'
script: interpreter = interpreter, expand = "$[ ]"
sos run $[exe_dir]/pipeline/SuSiE.ipynb uni_susie \
--genoFile $[_input[0]] \
--phenoFile $[" ".join([str(x) for x in _input[1:len(input_inv)+1]])] \
--covFile $[" ".join([str(x) for x in _input[len(input_inv)+1:len(input_inv)*2+1]])] \
--cwd $[_output:d] \
--tissues $[" ".join([x["Theme"] for x in input_inv])] \
--region-list $[_input[3]] \
--container $[container_susie] $[submission if yml.is_file() else "" ]
```
## Sumstat Merger
```
[yml_generation]
parameter: TARGET_list = path("./")
input: output_from(Association_option), group_by = "all"
output: f'{cwd:a}/data_intergration/{Association_option}/qced_sumstat_list.txt',f'{cwd:a}/data_intergration/{Association_option}/yml_list.txt'
script: interpreter = interpreter, expand = "$[ ]"
sos run $[exe_dir]/pipeline/yml_generator.ipynb yml_list \
--sumstat-list $[_input] \
--cwd $[_output[1]:d] --name $[" ".join([str(x).split("/")[-3] for x in _input])] --TARGET_list $[TARGET_list]
[sumstat_merge]
input: output_from("yml_generation")
script: interpreter = interpreter, expand = "$[ ]"
sos run $[exe_dir]/pipeline/summary_stats_merger.ipynb \
--sumstat-list $[_input[0]] \
--yml-list $[_input[1]] \
--cwd $[_input[0]:d] $[submission if yml.is_file() else "" ] --mem 50G --walltime 48h
```
|
github_jupyter
|
```
import os
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import plotly.plotly as py
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
import plotly.graph_objs as go
init_notebook_mode(connected=True)
%matplotlib inline
data_folder = r'C:\Users\ocni\PycharmProjects\delphin_6_automation\data_process\simtime_prediction\data'
excel_file = os.path.join(data_folder, 'sim_time.xlsx')
data = pd.read_excel(excel_file)
data.shape
plt.figure(figsize=(16, 8), dpi= 80, facecolor='w', edgecolor='k')
(data['time'][data['time'] < 1500 * 60] / 60).plot('hist', bins=50, color='#003399')
plt.xlabel('Simulation Time in minutes')
#plt.savefig('simulation_time_histogram.pdf')
(data['time'][data['time'] < 1500 * 60] / 60).describe()
hist, edges = np.histogram((data['time'][data['time'] < 1500 * 60] / 60), density=True, bins=50)
dx = edges[1] - edges[0]
cdf = np.cumsum(hist) * dx
plt.figure(figsize=(16, 8), dpi= 80, facecolor='w', edgecolor='k')
plt.plot(edges[:-1], cdf)
from sklearn.model_selection import train_test_split
from sklearn import linear_model
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import PolynomialFeatures
from sklearn.neighbors import KNeighborsRegressor
y_data = data['time']
x_data = data.loc[:, data.columns != 'time']
x_data.loc[:, 'exterior_climate'] = np.ones(len(x_data['exterior_climate']))
x_data = x_data.fillna(0.0)
x_data.loc[x_data.loc[:, 'interior_climate'] == 'a', 'interior_climate'] = 0.0
x_data.loc[x_data.loc[:, 'interior_climate'] == 'b', 'interior_climate'] = 1.0
x_data.loc[x_data.loc[:, 'system_name'] == 'ClimateBoard', 'system_name'] = 1.0
x_data.head()
x_data.columns
processed_data = x_data.assign(time=y_data/60)
plt_data = [
go.Parcoords(
line = dict(color = processed_data['time'],
colorscale = 'Jet',
showscale = True,
cmin = 0,
cmax = 1500),
dimensions = list([
dict(range = [0,1440],
label = 'Time', values = processed_data['time'],
tickformat='r'),
dict(range = [0, 5],
label = 'Ext. Heat\nTransfer Coef. Slope',
values = processed_data['exterior_heat_transfer_coefficient_slope']),
dict(range = [4 * 10 ** -9, 10 ** -8],
label = 'Ext. Moisture Transfer Coef.',
values = processed_data['exterior_moisture_transfer_coefficient'],
tickformat='e'),
dict(range = [0.4, 0.8],
label = 'Solar Absorption', values = processed_data['solar_absorption'],
tickformat='.1f'),
dict(range = [0.0, 2.0],
label = 'Rain Scale Factor', values = processed_data['rain_scale_factor']),
dict(range = [0.0, 1.0],
label = 'Int. Climate', values = processed_data['interior_climate']),
dict(range = [4.0, 11.0],
label = 'Int. Heat Transfer Coef.',
values = processed_data['interior_heat_transfer_coefficient']),
dict(range = [4 * 10 ** -9, 10 ** -8],
label = 'Int. Moisture Transfer Coef.',
values = processed_data['interior_moisture_transfer_coefficient'],
tickformat='e'),
dict(range = [0.0, 0.6],
label = 'Int. Sd Value', values = processed_data['interior_sd_value'],
tickformat='.1f'),
dict(range = [0.0, 360.0],
label = 'Wall Orientation', values = processed_data['wall_orientation']),
dict(range = [0.0, 1.0],
label = 'Wall Core Width', values = processed_data['wall_core_width']),
dict(range = [0.0, 1000],
label = 'Wall Core Material', values = processed_data['wall_core_material'],
tickformat='r'),
dict(range = [0.01, 0.02],
label = 'Plaster Width', values = processed_data['plaster_width'],
tickformat='.2f'),
dict(range = [0.0, 1000],
label = 'Plaster Material', values = processed_data['plaster_material'],
tickformat='r'),
dict(range = [0.0, 1.0],
label = 'Ext. Plaster', values = processed_data['exterior_plaster']),
dict(range = [0.0, 1.0],
label = 'System', values = processed_data['system_name']),
dict(range = [0.0, 1000],
label = 'Insulation Material', values = processed_data['insulation_material'],
tickformat='r'),
dict(range = [0.0, 1000],
label = 'Finish Material', values = processed_data['finish_material'],
tickformat='r'),
dict(range = [0.0, 1000],
label = 'Detail Material', values = processed_data['detail_material'],
tickformat='r'),
dict(range = [0.0, 200],
label = 'Insulation Thickness', values = processed_data['insulation_thickness']),
])
)
]
layout = go.Layout(
plot_bgcolor = '#E5E5E5',
paper_bgcolor = '#E5E5E5'
)
fig = go.Figure(data = plt_data, layout = layout)
plot(fig, filename = 'sim_time.html')
X_train, X_test, y_train, y_test = train_test_split(x_data, y_data, random_state=0)
# Linear Model
linreg = linear_model.LinearRegression(normalize=True)
linreg.fit(X_train, y_train)
print('linear model intercept: {}'.format(linreg.intercept_))
print('linear model coeff:\n{}'.format(linreg.coef_))
print('R-squared score (training): {:.3f}'.format(linreg.score(X_train, y_train)))
print('R-squared score (test): {:.3f}'.format(linreg.score(X_test, y_test)))
print('Number of non-zero features: {}'.format(np.sum(linreg.coef_ != 0)))
# Ridge Model
linridge = linear_model.Ridge(alpha=20.0).fit(X_train, y_train)
print('ridge regression linear model intercept: {}'.format(linridge.intercept_))
print('ridge regression linear model coeff:\n{}'.format(linridge.coef_))
print('R-squared score (training): {:.3f}'.format(linridge.score(X_train, y_train)))
print('R-squared score (test): {:.3f}'.format(linridge.score(X_test, y_test)))
print('Number of non-zero features: {}'.format(np.sum(linridge.coef_ != 0)))
# Ridge Model Normalized
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
linridge_normal = linear_model.Ridge(alpha=20.0).fit(X_train_scaled, y_train)
print('ridge regression linear model intercept: {}'.format(linridge_normal.intercept_))
print('ridge regression linear model coeff:\n{}'.format(linridge_normal.coef_))
print('R-squared score (training): {:.3f}'.format(linridge_normal.score(X_train_scaled, y_train)))
print('R-squared score (test): {:.3f}'.format(linridge_normal.score(X_test_scaled, y_test)))
print('Number of non-zero features: {}'.format(np.sum(linridge_normal.coef_ != 0)))
# K-nearest regression - 5 neighbors
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
knn_reg5_uni = KNeighborsRegressor(n_neighbors=5).fit(X_train_scaled, y_train)
#print(knn_reg5_uni.predict(X_test_scaled))
print('R-squared train score: {:.5f}'.format(knn_reg5_uni.score(X_train_scaled, y_train)))
print('R-squared test score: {:.5f}'.format(knn_reg5_uni.score(X_test_scaled, y_test)))
# K-nearest regression - 3 neighbors
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
knn_reg5_uni = KNeighborsRegressor(n_neighbors=3).fit(X_train_scaled, y_train)
#print(knn_reg5_uni.predict(X_test_scaled))
print('R-squared train score: {:.5f}'.format(knn_reg5_uni.score(X_train_scaled, y_train)))
print('R-squared test score: {:.5f}'.format(knn_reg5_uni.score(X_test_scaled, y_test)))
# K-nearest regression - 5 neighbors, weights = distance
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
knn_reg5 = KNeighborsRegressor(n_neighbors=3, weights='distance').fit(X_train_scaled, y_train)
#print(knn_reg5.predict(X_test_scaled))
print('R-squared train score: {:.5f}'.format(knn_reg5.score(X_train_scaled, y_train)))
print('R-squared test score: {:.5f}'.format(knn_reg5.score(X_test_scaled, y_test)))
from sklearn.model_selection import ShuffleSplit
ss = ShuffleSplit(n_splits=5, test_size=0.25, random_state=47)
scaler = MinMaxScaler()
test_scores = []
for train_index, test_index in ss.split(x_data):
x_train = scaler.fit_transform(x_data.iloc[train_index, :])
x_test = scaler.transform(x_data.iloc[test_index, :])
y_train = y_data.iloc[train_index]
y_test = y_data.iloc[test_index]
knn_reg = KNeighborsRegressor(n_neighbors=5, weights='distance').fit(x_train, y_train)
#knn_reg = KNeighborsRegressor(n_neighbors=5).fit(x_train, y_train)
test_scores.append(knn_reg.score(x_test, y_test))
mean_score = np.mean(test_scores)
print(f'Average R-squared test score: {mean_score:.5f}')
# Cross Validation Score
from sklearn.model_selection import ShuffleSplit
from sklearn.model_selection import cross_val_score
ss = ShuffleSplit(n_splits=5, test_size=0.25, random_state=47)
scaler = MinMaxScaler()
knn_reg = KNeighborsRegressor(n_neighbors=5, weights='distance')
#knn_reg = KNeighborsRegressor(n_neighbors=5)
validated_test_scores = cross_val_score(knn_reg, scaler.fit_transform(x_data), y_data, cv=ss)
print(f'Accuracy: {validated_test_scores.mean():.5f} (+/- {validated_test_scores.std()*2:.5f})')
# Feature Importance
features = x_data.columns
col_del = []
feature_scores = []
for feat in features:
feature_less_data = x_data.loc[:, x_data.columns != feat]
test_scores = cross_val_score(knn_reg, scaler.fit_transform(feature_less_data), y_data, cv=ss, scoring='r2')
feature_scores.append((feat, test_scores.mean()))
if test_scores.mean() >= validated_test_scores.mean():
col_del.append(feat)
feature_scores = sorted(feature_scores, key=lambda x: x[1])
width = len('exterior heat transfer coefficient slope')
print('Feature'.ljust(width, ' ') + ' Accuracy')
for i in feature_scores:
print(f'{i[0].ljust(width, " ")} - {i[1]:.5f}')
print('Columns to delete:\n')
for col in col_del:
print(f'\t{col}')
clean_col = x_data.columns[[c not in col_del for c in x_data.columns.tolist()]]
cleaned_data = x_data.loc[:, clean_col]
clean_scores = cross_val_score(knn_reg, scaler.fit_transform(cleaned_data), y_data, cv=ss, scoring='r2')
print(f'Accuracy: {clean_scores.mean():.5f} (+/- {clean_scores.std()*2:.5f})')
```
|
github_jupyter
|
# Artificial Intelligence Nanodegree
## Convolutional Neural Networks
---
In this notebook, we visualize four activation maps in a CNN layer.
### 1. Import the Image
```
import cv2
import scipy.misc
import matplotlib.pyplot as plt
%matplotlib inline
# TODO: Feel free to try out your own images here by changing img_path
# to a file path to another image on your computer!
img_path = 'part12/udacity_sdc.png'
# load color image
bgr_img = cv2.imread(img_path)
# convert to grayscale
gray_img = cv2.cvtColor(bgr_img, cv2.COLOR_BGR2GRAY)
# resize to smaller
small_img = scipy.misc.imresize(gray_img, 0.3)
# rescale entries to lie in [0,1]
small_img = small_img.astype("float32")/255
# plot image
plt.imshow(small_img, cmap='gray')
plt.show()
```
### 2. Specify the Filters
```
import numpy as np
# TODO: Feel free to modify the numbers here, to try out another filter!
# Please don't change the size of the array ~ :D
filter_vals = np.array([[-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1]])
### do not modify the code below this line ###
# define four filters
filter_1 = filter_vals
filter_2 = -filter_1
filter_3 = filter_1.T
filter_4 = -filter_3
filters = [filter_1, filter_2, filter_3, filter_4]
# visualize all filters
fig = plt.figure(figsize=(10, 5))
for i in range(4):
ax = fig.add_subplot(1, 4, i+1, xticks=[], yticks=[])
ax.imshow(filters[i], cmap='gray')
ax.set_title('Filter %s' % str(i+1))
width, height = filters[i].shape
for x in range(width):
for y in range(height):
ax.annotate(str(filters[i][x][y]), xy=(y,x),
horizontalalignment='center',
verticalalignment='center',
color='white' if filters[i][x][y]<0 else 'black')
```
### 3. Visualize the Activation Maps for Each Filter
```
from keras.models import Sequential
from keras.layers.convolutional import Convolution2D
import matplotlib.cm as cm
# plot image
plt.imshow(small_img, cmap='gray')
# define a neural network with a single convolutional layer with one filter
model = Sequential()
model.add(Convolution2D(1, (4, 4), activation='relu', input_shape=(small_img.shape[0], small_img.shape[1], 1)))
# apply convolutional filter and return output
def apply_filter(img, index, filter_list, ax):
# set the weights of the filter in the convolutional layer to filter_list[i]
model.layers[0].set_weights([np.reshape(filter_list[i], (4,4,1,1)), np.array([0])])
# plot the corresponding activation map
ax.imshow(np.squeeze(model.predict(np.reshape(img, (1, img.shape[0], img.shape[1], 1)))), cmap='gray')
# visualize all filters
fig = plt.figure(figsize=(12, 6))
fig.subplots_adjust(left=0, right=1.5, bottom=0.8, top=1, hspace=0.05, wspace=0.05)
for i in range(4):
ax = fig.add_subplot(1, 4, i+1, xticks=[], yticks=[])
ax.imshow(filters[i], cmap='gray')
ax.set_title('Filter %s' % str(i+1))
# visualize all activation maps
fig = plt.figure(figsize=(20, 20))
for i in range(4):
ax = fig.add_subplot(1, 4, i+1, xticks=[], yticks=[])
apply_filter(small_img, i, filters, ax)
ax.set_title('Activation Map for Filter %s' % str(i+1))
```
|
github_jupyter
|
```
# Import All Libraries
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt
import nltk
import re
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
from sklearn.model_selection import train_test_split
from nltk.corpus import stopwords
# Import Data
data = pd.read_csv("./Corona_NLP.csv", encoding='ISO-8859-1')
data.head()
# Check Data Type
data.info(memory_usage=False)
# Check Data Null
print("Data Empty:", data.isnull().sum().sum())
# Drop Data Null
data.dropna(inplace=True)
print("Data Empty:", data.isnull().sum().sum())
# Drop column
data.drop(columns=['UserName', 'ScreenName',
'Location', 'TweetAt'], inplace=True)
# Simplify Data
data['Sentiment'] = data['Sentiment'].map({
"Neutral": "Neutral",
"Positive": "Positive",
"Negative": "Negative",
"Extremely Positive": "Positive",
"Extremely Negative": "Negative"
})
sentiment = pd.get_dummies(data['Sentiment'])
df = pd.concat([data, sentiment], axis=1)
df.drop(columns='Sentiment', inplace=True)
# Data Cleaning with regex
def data_cleaner(tweet):
# hapus link
tweet = re.sub(r'http\S+', ' ', tweet)
# hapus html tags
tweet = re.sub(r'<.*?>',' ', tweet)
# hapus angka
tweet = re.sub(r'\d+',' ', tweet)
# hapus hashtags
tweet = re.sub(r'#\w+',' ', tweet)
# hapus tag
tweet = re.sub(r'@\w+',' ', tweet)
# hapus kata tambahan
tweet = tweet.split()
tweet = " ".join([word for word in tweet if not word in stop_words])
return tweet
nltk.download('stopwords')
stop_words = stopwords.words('english')
df['OriginalTweet'] = df['OriginalTweet'].apply(lambda x: x.lower()).apply(data_cleaner)
df.head()
# Split Data
tweet = df['OriginalTweet'].values
sentiment = df[['Negative', 'Neutral', 'Positive']].values
tweet_train, tweet_test, sentiment_train, sentiment_test = train_test_split(
tweet, sentiment, test_size=0.2, random_state=69
)
# Tokenizer Data
tokenizer = Tokenizer(num_words=36000, oov_token='-')
tokenizer.fit_on_texts(tweet_train)
tokenizer.fit_on_texts(tweet_test)
sequens_train = tokenizer.texts_to_sequences(tweet_train)
sequens_test = tokenizer.texts_to_sequences(tweet_test)
padded_train = pad_sequences(sequens_train, padding='post')
padded_test = pad_sequences(sequens_test, padding='post')
# Create Model NN
model = tf.keras.models.Sequential([
tf.keras.layers.Embedding(input_dim=36000, output_dim=16),
tf.keras.layers.LSTM(128),
tf.keras.layers.Dense(32, activation='relu'),
tf.keras.layers.Dense(3, activation='softmax')
])
model.compile(
optimizer='adam',
loss='categorical_crossentropy',
metrics='accuracy'
)
# Create Callback
class Callback(tf.keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs={}):
if logs.get('val_accuracy') > 0.9:
print("\nValidasi Akurasi telah mencapai > 90%!")
self.model.stop_training = True
callback0 = Callback()
callback1 = tf.keras.callbacks.EarlyStopping(
min_delta=0.001,
patience=20,
restore_best_weights=True
)
# Train Model
history = model.fit(
padded_train,
sentiment_train,
validation_data=(padded_test, sentiment_test),
epochs=5,
callbacks=[callback0, callback1],
)
# Plot Accuracy Model
plt.figure(figsize=(20, 10))
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('Akurasi Model', fontsize=20)
plt.xlabel('Epoch', fontsize=20)
plt.ylabel('Accuracy', fontsize=20)
plt.legend(['train', 'test'], loc='upper left')
plt.show()
# Plot Loss Model
plt.figure(figsize=(20, 10))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('Loss Model', fontsize=20)
plt.ylabel('loss', fontsize=20)
plt.xlabel('epoch', fontsize=20)
plt.legend(['train', 'test'], loc='upper left')
plt.show()
```
|
github_jupyter
|
# Part - 2: COVID-19 Time Series Analysis and Prediction using ML.Net framework
## COVID-19
- As per [Wiki](https://en.wikipedia.org/wiki/Coronavirus_disease_2019) **Coronavirus disease 2019** (**COVID-19**) is an infectious disease caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). The disease was first identified in 2019 in Wuhan, the capital of China's Hubei province, and has since spread globally, resulting in the ongoing 2019–20 coronavirus pandemic.
- The virus had caused a pandemic across the globe and spreading/affecting most of the nations.
- The purpose of notebook is to visualize the trends of virus spread in various countries and explore features present in ML.Net such as DataFrame.
### Acknowledgement
- [Johns Hopkins CSSE](https://github.com/CSSEGISandData/COVID-19/raw/master/csse_covid_19_data) for dataset
- [COVID-19 data visualization](https://www.kaggle.com/akshaysb/covid-19-data-visualization) by Akshay Sb
### Dataset
- [2019 Novel Coronavirus COVID-19 (2019-nCoV) Data Repository by Johns Hopkins CSSE - Time Series](https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data/csse_covid_19_time_series).
### Introduction
This is **Part-2** of our analysis on the COVID-19 dataset provided by Johns Hopkins CSSE. In [**Part-1**](https://github.com/praveenraghuvanshi1512/TechnicalSessions/tree/31052020-virtualmlnet/31052020-virtualmlnet/src/part-1), I did data analysis on the dataset and created some tables and plots for getting insights from it. In Part-2, I'll focus on applying machine learning for making a prediction using time-series API's provided by ML.Net framework. I'll be building a model from scratch on the number of confirmed cases and predicting for the next 7 days. Later on, I'll plot these numbers for better visualization.
[**ML.Net**](https://dotnet.microsoft.com/apps/machinelearning-ai/ml-dotnet) is a cross-platform framework from Microsoft for developing Machine learning models in the .Net ecosystem. It allows .Net developers to solve business problems using machine learning algorithms leveraging their preferred language such as C#/F#. It's highly scalable and used within Microsoft in many of its products such as Bing, Powerpoint, etc.
**Disclaimer**: This is an exercise to explore different features present in ML.Net. The actual and predicted numbers might vary due to several factors such as size and features in a dataset.
### Summary
Below is the summary of steps we'll be performing
1. Define application level items
- Nuget packages
- Namespaces
- Constants
2. Utility Functions
- Formatters
3. Dataset and Transformations
- Actual from [Johns Hopkins CSSE](https://github.com/CSSEGISandData/COVID-19/blob/master/csse_covid_19_data/csse_covid_19_time_series)
- Transformed [time_series_covid19_confirmed_global_transposed.csv](time_series_covid19_confirmed_global_transposed.csv)
4. Data Classes
- ConfirmedData : Provides a map between columns in a dataset
- ConfirmedForecast : Holds predicted values
5. Data Analysis
- Visualize Data using DataFrame API
- Display Top 10 Rows - dataframe.Head(10)
- Display Last 10 Rows - dataframe.Tail(10)
- Display Dataset Statistics - dataframe.Description()
- Plot of TotalConfimed cases vs Date
6. Load Data - MLContext
7. ML Pipeline
8. Train Model
9. Prediction/Forecasting
10. Prediction Visualization
11. Prediction Analysis
12. Conclusion
**Note** : Graphs/Plots may not render in GitHub due to secutiry reasons, however if you run this notebook locally/binder they will render.
```
#!about
```
### 1. Define Application wide Items
#### Nuget Packages
```
// ML.NET Nuget packages installation
#r "nuget:Microsoft.ML"
#r "nuget:Microsoft.ML.TimeSeries"
#r "nuget:Microsoft.Data.Analysis"
// Install XPlot package
#r "nuget:XPlot.Plotly"
```
#### Namespaces
```
using System;
using System.Collections.Generic;
using System.Linq;
using Microsoft.ML;
using Microsoft.ML.Data;
using Microsoft.Data.Analysis;
using Microsoft.ML.Transforms.TimeSeries;
using Microsoft.AspNetCore.Html;
using XPlot.Plotly;
```
#### Constants
```
const string CONFIRMED_DATASET_FILE = "time_series_covid19_confirmed_global_transposed.csv";
// Forecast API
const int WINDOW_SIZE = 5;
const int SERIES_LENGTH = 10;
const int TRAIN_SIZE = 100;
const int HORIZON = 7;
// Dataset
const int DEFAULT_ROW_COUNT = 10;
const string TOTAL_CONFIRMED_COLUMN = "TotalConfirmed";
const string DATE_COLUMN = "Date";
```
### 2. Utility Functions - TBR
#### Formatters
By default the output of DataFrame is not proper and in order to display it as a table, we need to have a custom formatter implemented as shown in next cell.
```
Formatter<DataFrame>.Register((df, writer) =>
{
var headers = new List<IHtmlContent>();
headers.Add(th(i("index")));
headers.AddRange(df.Columns.Select(c => (IHtmlContent) th(c.Name)));
var rows = new List<List<IHtmlContent>>();
var take = DEFAULT_ROW_COUNT;
for (var i = 0; i < Math.Min(take, df.Rows.Count); i++)
{
var cells = new List<IHtmlContent>();
cells.Add(td(i));
foreach (var obj in df.Rows[i])
{
cells.Add(td(obj));
}
rows.Add(cells);
}
var t = table(
thead(
headers),
tbody(
rows.Select(
r => tr(r))));
writer.Write(t);
}, "text/html");
```
### 3. Dataset and Transformations
#### Download Dataset
- Actual Dataset: [Johns Hopkins CSSE](https://github.com/CSSEGISandData/COVID-19/blob/master/csse_covid_19_data/csse_covid_19_time_series)
- Transformed Dataset: [time_series_covid19_confirmed_global_transposed.csv](time_series_covid19_confirmed_global_transposed.csv)
I'll be using COVID-19 time series dataset from [Johns Hopkins CSSE](https://github.com/CSSEGISandData/COVID-19/blob/master/csse_covid_19_data/csse_covid_19_time_series) and will be performing predictions using **time_series_covid19_confirmed_global.csv** file.
The data present in these files have name of the countries as Rows and dates as columns which makes it difficult to map to our classes while loading data from csv. Also, it contains data per country wise. In order to keep things simple I'll work with global count of COVID-19 cases and not specific country.
I have done few transformations to the dataset as below and created transformed csv's
- Sum cases from all the countries for a specific date
- Just have two rows with Date and Total
- Applied transformation to the csv for converting Rows into Columns and vice-versa. [Refer](https://support.office.com/en-us/article/transpose-rotate-data-from-rows-to-columns-or-vice-versa-3419f2e3-beab-4318-aae5-d0f862209744) for transformation.
- Below transposed files have been saved in the current github directory. There is no change in dataset. The files have data till 05-27-2020
- [time_series_covid19_confirmed_global_transposed.csv](time_series_covid19_confirmed_global_transposed.csv) : Columns - **Date, TotalConfirmed**
##### Before transformation
<img src=".\assets\time-series-before-transformation.png" alt="Time Series data before transofmation" style="zoom: 80%;" />
#### After transformation
<img src=".\assets\time-series-after-transformation.png" alt="Time Series data after transofmation" style="zoom: 80%;" />
### 4. Data Classes
Now, we need to create few data structures to map to columns within our dataset.
#### Confirmed cases
```
/// <summary>
/// Represent data for confirmed cases with a mapping to columns in a dataset
/// </summary>
public class ConfirmedData
{
/// <summary>
/// Date of confirmed case
/// </summary>
[LoadColumn(0)]
public DateTime Date;
/// <summary>
/// Total no of confirmed cases on a particular date
/// </summary>
[LoadColumn(1)]
public float TotalConfirmed;
}
/// <summary>
/// Prediction/Forecast for Confirmed cases
/// </summary>
internal class ConfirmedForecast
{
/// <summary>
/// No of predicted confirmed cases for multiple days
/// </summary>
public float[] Forecast { get; set; }
}
```
### 5. Data Analysis
For loading data from csv, first we need to create MLContext that acts as a starting point for creating a machine learning model in ML.Net. Few things to note
- Set hasHeader as true as our dataset has header
- Add separatorChar to ',' as its a csv
#### Visualize Data - DataFrame
```
var predictedDf = DataFrame.LoadCsv(CONFIRMED_DATASET_FILE);
predictedDf.Head(DEFAULT_ROW_COUNT)
predictedDf.Tail(DEFAULT_ROW_COUNT)
predictedDf.Description()
```
##### Number of Confirmed cases over Time
```
// Number of confirmed cases over time
var totalConfirmedDateColumn = predictedDf.Columns[DATE_COLUMN];
var totalConfirmedColumn = predictedDf.Columns[TOTAL_CONFIRMED_COLUMN];
var dates = new List<string>();
var totalConfirmedCases = new List<string>();
for (int index = 0; index < totalConfirmedDateColumn.Length; index++)
{
dates.Add(totalConfirmedDateColumn[index].ToString());
totalConfirmedCases.Add(totalConfirmedColumn[index].ToString());
}
var title = "Number of Confirmed Cases over Time";
var confirmedTimeGraph = new Graph.Scattergl()
{
x = dates.ToArray(),
y = totalConfirmedCases.ToArray(),
mode = "lines+markers"
};
var chart = Chart.Plot(confirmedTimeGraph);
chart.WithTitle(title);
display(chart);
```
**Analysis**
- Duration: 1/22/2020 through 5/27/2020
- Total records: 127
- Case on first day: 555
- Case on last day: 5691790
- No of confirmed cases was low in the beginning, there was first jump around 2/12/2020 and an exponential jump around 3/22/2020.
- Cases have been increasing at an alarming rate in the past two months.
### 6. Load Data - MLContext
```
var context = new MLContext();
var data = context.Data.LoadFromTextFile<ConfirmedData>(CONFIRMED_DATASET_FILE, hasHeader: true, separatorChar: ',');
```
### 7. ML Pipeline
For creating ML Pipeline for a time-series analysis, we'll use [Single Spectrum Analysis](https://en.wikipedia.org/wiki/Singular_spectrum_analysis). ML.Net provides built in API for same, more details could be found at [TimeSeriesCatalog.ForecastBySsa](https://docs.microsoft.com/en-us/dotnet/api/microsoft.ml.timeseriescatalog.forecastbyssa?view=ml-dotnet)
```
var pipeline = context.Forecasting.ForecastBySsa(
nameof(ConfirmedForecast.Forecast),
nameof(ConfirmedData.TotalConfirmed),
WINDOW_SIZE,
SERIES_LENGTH,
TRAIN_SIZE,
HORIZON);
```
### 8. Train Model
We are ready with our pipeline and ready to train the model
```
var model = pipeline.Fit(data);
```
### 9. Prediction/Forecasting - 7 days
Our model is trained and we need to do prediction for next 7(Horizon) days.
Time-series provides its own engine for making prediction which is similar to PredictionEngine present in ML.Net. Predicted values show an increasing trend which is in alignment with recent past values.
```
var forecastingEngine = model.CreateTimeSeriesEngine<ConfirmedData, ConfirmedForecast>(context);
var forecasts = forecastingEngine.Predict();
display(forecasts.Forecast.Select(x => (int) x))
```
### 10. Prediction Visualization
```
var lastDate = DateTime.Parse(dates.LastOrDefault());
var predictionStartDate = lastDate.AddDays(1);
for (int index = 0; index < HORIZON; index++)
{
dates.Add(lastDate.AddDays(index + 1).ToShortDateString());
totalConfirmedCases.Add(forecasts.Forecast[index].ToString());
}
var title = "Number of Confirmed Cases over Time";
var layout = new Layout.Layout();
layout.shapes = new List<Graph.Shape>
{
new Graph.Shape
{
x0 = predictionStartDate.ToShortDateString(),
x1 = predictionStartDate.ToShortDateString(),
y0 = "0",
y1 = "1",
xref = 'x',
yref = "paper",
line = new Graph.Line() {color = "red", width = 2}
}
};
var chart1 = Chart.Plot(
new []
{
new Graph.Scattergl()
{
x = dates.ToArray(),
y = totalConfirmedCases.ToArray(),
mode = "lines+markers"
}
},
layout
);
chart1.WithTitle(title);
display(chart1);
```
### 11. Analysis
Comparing the plots before and after prediction, it seems our ML model has performed reasonably well. The red line represents the data on future date(5/8/2020). Beyond this, we predicted for 7 days. Looking at the plot, there is a sudden drop on 5/8/2020 which could be accounted due to insufficient data as we have only 127 records. However we see an increasing trend for next 7 days in alignment with previous confirmed cases. We can extend this model for predicting confirmed cases for any number of days by changing HORIZON constant value. This plot is helpful in analysing the increased number of cases and allow authorities to take precautionary measures to keep the numbers low.
## Conclusion
I hope you have enjoyed reading the notebook, and might have got some idea on the powerful framework ML.Net. ML.Net is a very fast emerging framework for .Net developers which abstracts lot of complexity present in the field of Data science and Machine Learning. The focus of Part-2 notebook is leverage ML.Net for making predictions using time-series API. The model generated can be saved as a zip file and used in different applications.
Feedback/Suggestion are welcome. Please reach out to me through below channels
**Contact**
**Email :** praveenraghuvanshi@gmail.com
**LinkedIn :** https://in.linkedin.com/in/praveenraghuvanshi
**Github :** https://github.com/praveenraghuvanshi1512
**Twitter :** @praveenraghuvan
## References
- [Tutorial: Forecast bike rental service demand with time series analysis and ML.NET](https://docs.microsoft.com/en-us/dotnet/machine-learning/tutorials/time-series-demand-forecasting#evaluate-the-model)
- [Time Series Forecasting in ML.NET and Azure ML notebooks](https://github.com/gvashishtha/time-series-mlnet/blob/master/time-series-forecast.ipynb) by Gopal Vashishtha
# ******************** Be Safe **********************
|
github_jupyter
|
[](https://colab.research.google.com/github/JohnSnowLabs/spark-nlp-workshop/blob/master/jupyter/transformers/HuggingFace%20in%20Spark%20NLP%20-%20RoBertaForTokenClassification.ipynb)
## Import RoBertaForTokenClassification models from HuggingFace 🤗 into Spark NLP 🚀
Let's keep in mind a few things before we start 😊
- This feature is only in `Spark NLP 3.3.x` and after. So please make sure you have upgraded to the latest Spark NLP release
- You can import RoBERTa models trained/fine-tuned for token classification via `RobertaForTokenClassification` or `TFRobertaForTokenClassification`. These models are usually under `Token Classification` category and have `roberta` in their labels
- Reference: [TFRobertaForTokenClassification](https://huggingface.co/transformers/model_doc/roberta.html#tfrobertafortokenclassification)
- Some [example models](https://huggingface.co/models?filter=roberta&pipeline_tag=token-classification)
## Export and Save HuggingFace model
- Let's install `HuggingFace` and `TensorFlow`. You don't need `TensorFlow` to be installed for Spark NLP, however, we need it to load and save models from HuggingFace.
- We lock TensorFlow on `2.4.1` version and Transformers on `4.10.0`. This doesn't mean it won't work with the future releases, but we wanted you to know which versions have been tested successfully.
```
!pip install -q transformers==4.10.0 tensorflow==2.4.1
```
- HuggingFace comes with a native `saved_model` feature inside `save_pretrained` function for TensorFlow based models. We will use that to save it as TF `SavedModel`.
- We'll use [philschmid/distilroberta-base-ner-wikiann-conll2003-3-class](https://huggingface.co/philschmid/distilroberta-base-ner-wikiann-conll2003-3-class) model from HuggingFace as an example
- In addition to `TFRobertaForTokenClassification` we also need to save the `RobertaTokenizer`. This is the same for every model, these are assets needed for tokenization inside Spark NLP.
```
from transformers import TFRobertaForTokenClassification, RobertaTokenizer
MODEL_NAME = 'philschmid/distilroberta-base-ner-wikiann-conll2003-3-class'
tokenizer = RobertaTokenizer.from_pretrained(MODEL_NAME)
tokenizer.save_pretrained('./{}_tokenizer/'.format(MODEL_NAME))
# just in case if there is no TF/Keras file provided in the model
# we can just use `from_pt` and convert PyTorch to TensorFlow
try:
print('try downloading TF weights')
model = TFRobertaForTokenClassification.from_pretrained(MODEL_NAME)
except:
print('try downloading PyTorch weights')
model = TFRobertaForTokenClassification.from_pretrained(MODEL_NAME, from_pt=True)
model.save_pretrained("./{}".format(MODEL_NAME), saved_model=True)
```
Let's have a look inside these two directories and see what we are dealing with:
```
!ls -l {MODEL_NAME}
!ls -l {MODEL_NAME}/saved_model/1
!ls -l {MODEL_NAME}_tokenizer
```
- as you can see, we need the SavedModel from `saved_model/1/` path
- we also be needing `vocab.json` and `merges.txt` files from the tokenizer
- all we need is to first convert `vocab.json` to `vocab.txt` and copy both `vocab.txt` and `merges.txt` into `saved_model/1/assets` which Spark NLP will look for
- in addition to vocabs, we also need `labels` and their `ids` which is saved inside the model's config. We will save this inside `labels.txt`
```
asset_path = '{}/saved_model/1/assets'.format(MODEL_NAME)
# let's save the vocab as txt file
with open('{}_tokenizer/vocab.txt'.format(MODEL_NAME), 'w') as f:
for item in tokenizer.get_vocab().keys():
f.write("%s\n" % item)
# let's copy both vocab.txt and merges.txt files to saved_model/1/assets
!cp {MODEL_NAME}_tokenizer/vocab.txt {asset_path}
!cp {MODEL_NAME}_tokenizer/merges.txt {asset_path}
# get label2id dictionary
labels = model.config.label2id
# sort the dictionary based on the id
labels = sorted(labels, key=labels.get)
with open(asset_path+'/labels.txt', 'w') as f:
f.write('\n'.join(labels))
```
Voila! We have our `vocab.txt` and `labels.txt` inside assets directory
```
!ls -l {MODEL_NAME}/saved_model/1/assets
```
## Import and Save RobertaForTokenClassification in Spark NLP
- Let's install and setup Spark NLP in Google Colab
- This part is pretty easy via our simple script
```
! wget http://setup.johnsnowlabs.com/colab.sh -O - | bash
```
Let's start Spark with Spark NLP included via our simple `start()` function
```
import sparknlp
# let's start Spark with Spark NLP
spark = sparknlp.start()
```
- Let's use `loadSavedModel` functon in `RoBertaForTokenClassification` which allows us to load TensorFlow model in SavedModel format
- Most params can be set later when you are loading this model in `RoBertaForTokenClassification` in runtime like `setMaxSentenceLength`, so don't worry what you are setting them now
- `loadSavedModel` accepts two params, first is the path to the TF SavedModel. The second is the SparkSession that is `spark` variable we previously started via `sparknlp.start()`
- NOTE: `loadSavedModel` only accepts local paths and not distributed file systems such as `HDFS`, `S3`, `DBFS`, etc. That is why we use `write.save` so we can use `.load()` from any file systems
```
from sparknlp.annotator import *
tokenClassifier = RoBertaForTokenClassification\
.loadSavedModel('{}/saved_model/1'.format(MODEL_NAME), spark)\
.setInputCols(["sentence",'token'])\
.setOutputCol("ner")\
.setCaseSensitive(True)\
.setMaxSentenceLength(128)
```
- Let's save it on disk so it is easier to be moved around and also be used later via `.load` function
```
tokenClassifier.write().overwrite().save("./{}_spark_nlp".format(MODEL_NAME))
```
Let's clean up stuff we don't need anymore
```
!rm -rf {MODEL_NAME}_tokenizer {MODEL_NAME}
```
Awesome 😎 !
This is your RoBertaForTokenClassification model from HuggingFace 🤗 loaded and saved by Spark NLP 🚀
```
! ls -l {MODEL_NAME}_spark_nlp
```
Now let's see how we can use it on other machines, clusters, or any place you wish to use your new and shiny RoBertaForTokenClassification model 😊
```
tokenClassifier_loaded = RoBertaForTokenClassification.load("./{}_spark_nlp".format(MODEL_NAME))\
.setInputCols(["sentence",'token'])\
.setOutputCol("ner")
tokenClassifier_loaded.getCaseSensitive()
```
That's it! You can now go wild and use hundreds of `RoBertaForTokenClassification` models from HuggingFace 🤗 in Spark NLP 🚀
|
github_jupyter
|
# Section 2.1 `xarray`, `az.InferenceData`, and NetCDF for Markov Chain Monte Carlo
_How do we generate, store, and save Markov chain Monte Carlo results_
```
import numpy as np
import pandas as pd
import scipy.stats as stats
import matplotlib.pyplot as plt
import arviz as az
import pystan
import xarray as xr
from IPython.display import Video
np.random.seed(0)
plt.style.use('arviz-white')
```
## Learning Objectives
* Understand Markov chain Monte Carlo fundamentals
* Recognize the meaning of sample, draws, and chains in MCMC context
* Understand relationship between Xarray, az.InferenceData, and NetCDF
* Gain profiency with Xarray, NetCDF, and az.InferenceData objects
## Markov Chain Monte Carlo
**Pop quiz**: Why do we use Markov chain Monte Carlo in Bayesian inference?
**Highlight for answer:** C<span style="color:white">alculating the posterior distribution is hard</span>!
**Example:** If a flight has cancellation rate $r$, alternate tickets cost you $c$, and these distributions are modelled by $p(r, c)$, then expected cost of insuring a flight is
$$
\text{risk} = \int_{r=0}^{1}\int_{c=0}^{\infty} r\cdot c~dp(r, c)
$$
This can be hard to calculate for any number of reasons! If, instead, we have samples
$$
\{r_j, c_j\}_{j=1}^N \sim p(r, c)
$$
then
$$
\text{risk} \approx \frac{1}{N}\sum_{j=1}^N r_j \cdot c_j
$$
In python code, this would just be
```
risk = np.dot(r, c) / N
```
## Markov Chain Monte Carlo algorithm (greatly simplified)
Step 1: Start at a random spot
Step 2: Propose a new spot, possibly based on the previous spot
Step 3: Accept or reject this proposal based on some mathematical book keeping
Step 4: If accepted, move to proposed spot, if rejected, stay where you are
Step 5: Write down where you're standing
Step 6: Go back to step 2
The accepted proposals are called draws (or samples).
When animated this algorithm looks like this:
```
Video("../../img/medium_steps.mp4")
```
In MCMC Step 2 and Step 4 is where most MCMC variants differentiate themselves. Algorithms like Hamiltonian Monte Carlo and Sequential Monte Carlo are better at picking that next step for certain tasks. Richard McElreath has a great visual explainer [on his blog]([http://elevanth.org/blog/2017/11/28/build-a-better-markov-chain/)
Chain: A Markov chain
Sample/Draw: A single element of that chain
Regardless of algorithm in MCMC we end up with the same thing, a chain of accepted proposals with a fixed size. There is a rich literature to show that these algorithms produce samples that are eventually distributed according to the distribution we care about.
## Markov chain Monte Carlo with Metropolis-Hastings
Below is a working Metropolis-Hastings sampler, taken from [Thomas Wiecki's blog](https://twiecki.io/blog/2015/11/10/mcmc-sampling/). For the purposes of this tutorial focus more on the return value than the algorithm details.
It is important to note that this for simplicity's sake we have also hard coded the likelihood and prior in the sampler below. In mathematical notation our model looks like this. We are adding 20 to the estimation of mu to make it easier to recognize the distribution of **parameters** from the distribution of **observed data**
$$
\mu \sim \mathcal{N}(0, 1) \\
y \sim \mathcal{N}(\mu+20, 1)
$$
```
def mh_sampler(data, samples=4, mu_init=.5):
mu_current = mu_init
posterior = []
prior_logpdf = stats.norm(0, 1).logpdf
for i in range(samples):
# suggest new position
mu_proposal = stats.norm(mu_current, 0.5).rvs()
# Compute likelihood by multiplying probabilities of each data point
likelihood_current = stats.norm(mu_current + 20, 1).logpdf(data).sum()
likelihood_proposal = stats.norm(mu_proposal + 20, 1).logpdf(data).sum()
# Compute prior probability of current and proposed mu
prior_current = prior_logpdf(mu_current)
prior_proposal = prior_logpdf(mu_proposal)
# log(p(x|θ) p(θ)) = log(p(x|θ)) + log(p(θ))
p_current = likelihood_current + prior_current
p_proposal = likelihood_proposal + prior_proposal
# Accept proposal?
p_accept = np.exp(p_proposal - p_current)
accept = np.random.rand() < p_accept
if accept:
# Update position
mu_current = mu_proposal
else:
# don't move
pass
posterior.append(mu_current)
return np.array(posterior)
```
## Setup
Before using the sampler let's generate some data to test our Metropolis Hasting Implementation. In the code block below we are generating a bimodal distribution for the sampler.
```
data = stats.norm.rvs(loc=30, scale=1, size=1000).flatten()
```
We'll also plot our samples to get a sense of what the distribution of data looks like. Note how the histogram centers around 30. This should intuitively make sense as we're specified a mean of 30 when generating random values.
```
fig, ax = plt.subplots()
ax.hist(data)
fig.suptitle("Histogram of observed data");
```
As humans we can intuit *data mean* of **30** + an offset of **20** will lead to a parameter mean for *mu* of **10**. We want to see if our inference algorithm can recover our parameters.
## Single Variable Single Chain Inference Run
The simplest MCMC run we can perform is with a single variable and a single chain. We'll do so by putting our sampler function and data to use.
```
samples = 200
chain = mh_sampler(data=data, samples=samples)
chain[:100]
```
And just like that we've performed an inference run! We can generate a traceplot
```
fig, ax = plt.subplots(figsize=(10, 7))
x = np.arange(samples)
ax.plot(x, chain);
```
In terms of data structures, for a **single** variable **single** chain inference run, an array suffices for storing samples.
## Single Variable Multiple Chain Inference Run
As Bayesian modelers, life would be relatively easy if a single chain worked well every time, but unfortunately this is not the case. To understand why look at the above inference run. While the sampler started at *mu=8*, it took a 50 or so steps before the sampler honed in on the "correct" value of 10.
MCMC algorithms are sensitive to their starting points and in finite runs it's **not** guaranteed that the Markov Chain will approach the true underlying distribution. A common method to get around this is to sample from many chains in parallel and see if we get to the same place. We will discuss this further when we get to single model diagnostics.
```
chain_0 = mh_sampler(data=data, samples=samples)
chain_1 = mh_sampler(data=data, samples=samples, mu_init=13)
data_df = pd.DataFrame({"x_0":chain_0, "x_1":chain_1})
fig, ax = plt.subplots()
x = np.arange(samples)
ax.plot(x, data_df["x_0"], c="g")
ax.plot(x, data_df["x_1"])
```
With two chains converging to approximately a single value we can be more confident that the sampler reached the true underlying parameter. We can also store the results in a 2D data structures, such as Pandas Dataframes in python memory, and csvs or sql tables for persistent on disk storage.
## Multiple Variable Multiple Chain Inference Runs
A Bayesian modelers, life would be relatively easy if all models only had one variable (univariate models in math speak). Unfortunately many types of models require 2 or more variables. For example in a linear regression we are interested in estimating both <b>m</b> and <b>b</b>:
$$ y \sim mx+b$$
With at least 3 things to track (chains, samples, and variables) a 2d data structures become limiting. This problem exists in many domains and is the focus of the *xarray* project.
A motivating example comes from climate sciences. In this image from the xarray documentation the researcher might want to measure the temperature and humidity, across a 2D region at a point in time. Or they may want to plot the temperature over a time interval. xarray simplifies the data handling in cases like these.

### Xarray
In ArviZ an xarray DataSet object would look like the one below, where the variables are the Inference run variables, and the coordinates are at a minimum chains, draws.
```
posterior = xr.Dataset(
{"mu": (["chain", "draw"], [[11,12,13],[22,23,24]]), "sd": (["chain", "draw"], [[33,34,35],[44,45,46]])},
coords={"draw": [1,2,3], "chain": [0,1]},
)
posterior
```
## Multiple Variable Multiple Chain Inference runs and associated datasets
As a Bayesian modelers, life would be relatively easy if we were only concerned about posterior distributions. Looking back at the full end to end workflow, recall that there are other datasets, such as prior predictive samples, posterior predictive samples, among others. To aid the ArviZ user we present `az.InferenceData`.
### az.InferenceData
az.InferenceData serves as a data container for the various xarray datasets that are generated from an end-to-end Bayesian workflow. Consider our earlier simple model, and this time let's use `stan` to run a full analysis with multiple chains, multiple runs, and generate all sorts of datasets common in Bayesian analysis.
### Calculating prior
```
stan_code_prior = """
data {
int<lower=1> N;
}
parameters {
real mu; // Estimated parameter
}
model {
mu ~ normal(0, 1);
}
generated quantities {
real y_hat[N]; // prior prediction
for (n in 1:N) {
y_hat[n] = normal_rng(mu+20, 1);
}
}
"""
stan_prior = pystan.StanModel(model_code=stan_code_prior)
stan_data_prior = {"N" : len(data)}
stan_fit_prior = stan_prior.sampling(data=stan_data_prior)
stan_code_posterior = """
data {
int N;
real y[N]; // Observed data
}
parameters {
real mu; // Estimated parameter
}
model {
mu ~ normal(0, 1);
y ~ normal(mu+20, 1);
}
generated quantities {
real y_hat[N]; // posterior prediction
real log_lik[N]; // log_likelihood
for (n in 1:N) {
// Stan normal functions https://mc-stan.org/docs/2_19/functions-reference/normal-distribution.html
y_hat[n] = normal_rng(mu, 1);
log_lik[n] = normal_lpdf(y[n] | mu, 1);
}
}
"""
stan_model_posterior = pystan.StanModel(model_code=stan_code_posterior)
stan_data_posterior = dict(
y=data,
N=len(data)
)
stan_fit_posterior = stan_model_posterior.sampling(data=stan_data_posterior)
stan_inference_data = az.from_pystan(posterior=stan_fit_posterior,
observed_data="y",
# Other Bayesian Datasets that we have not discussed yet!
posterior_predictive="y_hat",
prior=stan_fit_prior,
prior_predictive="y_hat",
log_likelihood="log_lik",
)
```
### NetCDF
Calculating the various datasets is usually not trivial. Network Common Data Form (NetCDF) is an open standard for storing multidimensional datasets, and `xarray` is a library for doing high performance analysis on those datasets. NetCDF even comes with "group" support, making it easy to serialize az.InferenceData straight to disk. ArviZ uses NetCDF to save the results to disk, allowing reproducible analyses, multiple experiments, and sharing with others.
ArviZ even ships with sample datasets, serialized in NetCDF
https://github.com/arviz-devs/arviz/tree/master/arviz/data/_datasets
In short: like SQL is to Pandas DataFrame, NetCDF is to az.InferenceData.
```
data = az.load_arviz_data("centered_eight")
data
```
## The benefits of az.InferenceData
One of the goals for the ArviZ developers is to ensure that Bayesian practioners can share and reproduce analyses regardless of PPl, regardless of language and az.InferenceData was the implementation of this idea.
In summary az.InferenceData
* provides a consistent format for Bayesian datasets.
* makes it easy to save results
* makes use of ArviZ plotting and statistics functions simpler
* stores metadata for ease of reproducibility
## InferenceData in practice
In practice it's rare to ever generate a xarray manually for use in ArviZ. Instead ArviZ provides methods for instantiating InferenceData from plain Python objects, mappings to various PPLs, as well as methods to save and load NetCDF files.
For further references consider the ArviZ cookbook, and data structure tutorial.
https://arviz-devs.github.io/arviz/notebooks/InferenceDataCookbook.html
https://arviz-devs.github.io/arviz/notebooks/XarrayforArviZ.html
## Examples
See below for some useful methods of interacting with az.InferenceData, Xarray, and NetCDF
For Xarray methods we only demo a subset of the available API. For a much more comprehensive explanation view the indexing and selection page from the xarray docs
http://xarray.pydata.org/en/stable/indexing.html
### Creating InferenceData objects
We can create an InferenceData objects from our "home built" chain, not just from the output of supported PPLs
```
data_dict = {"mu": [chain_0, chain_1]}
home_built_data = az.from_dict(data_dict)
home_built_data
# Load NetCDF from disk into memory
## Replace with NetCDF that's "visible"
data = az.load_arviz_data("centered_eight")
# Reference posterior directly
posterior = data.posterior
posterior
# Select specific variables
posterior[["mu", "tau"]]
# Select specific chains and draws
posterior.sel(chain=[0,2], draw=slice(0,5))
# Get first 10 samples of mu from chain 0
posterior["mu"].sel(chain=0, draw=slice(0,10)).values
```
## Extra Credit
* xarray supports numpy "ufuncs" (https://docs.scipy.org/doc/numpy/reference/ufuncs.html). ArviZ uses these under the hood for efficient calculations.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/NeuromatchAcademy/course-content/blob/master/tutorials/W1D1_ModelTypes/student/W1D1_Tutorial1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Tutorial 1: "What" models
**Week 1, Day 1: Model Types**
**By Neuromatch Academy**
__Content creators:__ Matt Laporte, Byron Galbraith, Konrad Kording
__Content reviewers:__ Dalin Guo, Aishwarya Balwani, Madineh Sarvestani, Maryam Vaziri-Pashkam, Michael Waskom
We would like to acknowledge [Steinmetz _et al._ (2019)](https://www.nature.com/articles/s41586-019-1787-x) for sharing their data, a subset of which is used here.
**Our 2021 Sponsors, including Presenting Sponsor Facebook Reality Labs**
<p align='center'><img src='https://github.com/NeuromatchAcademy/widgets/blob/master/sponsors.png?raw=True'/></p>
___
# Tutorial Objectives
This is tutorial 1 of a 3-part series on different flavors of models used to understand neural data. In this tutorial we will explore 'What' models, used to describe the data. To understand what our data looks like, we will visualize it in different ways. Then we will compare it to simple mathematical models. Specifically, we will:
- Load a dataset with spiking activity from hundreds of neurons and understand how it is organized
- Make plots to visualize characteristics of the spiking activity across the population
- Compute the distribution of "inter-spike intervals" (ISIs) for a single neuron
- Consider several formal models of this distribution's shape and fit them to the data "by hand"
```
# @title Video 1: "What" Models
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = 'https://player.bilibili.com/player.html?bvid={0}&page={1}'.format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id="", width=854, height=480, fs=1)
print('Video available at https://www.bilibili.com/video/{0}'.format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="KgqR_jbjMQg", width=854, height=480, fs=1, rel=0)
print('Video available at https://youtube.com/watch?v=' + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
display(out)
```
# Setup
Python requires you to explictly "import" libraries before their functions are available to use. We will always specify our imports at the beginning of each notebook or script.
```
import numpy as np
import matplotlib.pyplot as plt
```
Tutorial notebooks typically begin with several set-up steps that are hidden from view by default.
**Important:** Even though the code is hidden, you still need to run it so that the rest of the notebook can work properly. Step through each cell, either by pressing the play button in the upper-left-hand corner or with a keyboard shortcut (`Cmd-Return` on a Mac, `Ctrl-Enter` otherwise). A number will appear inside the brackets (e.g. `[3]`) to tell you that the cell was executed and what order that happened in.
If you are curious to see what is going on inside each cell, you can double click to expand. Once expanded, double-click the white space to the right of the editor to collapse again.
```
#@title Figure Settings
import ipywidgets as widgets #interactive display
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/nma.mplstyle")
#@title Helper functions
#@markdown Most of the tutorials make use of helper functions
#@markdown to simplify the code that you need to write. They are defined here.
# Please don't edit these, or worry about understanding them now!
def restrict_spike_times(spike_times, interval):
"""Given a spike_time dataset, restrict to spikes within given interval.
Args:
spike_times (sequence of np.ndarray): List or array of arrays,
each inner array has spike times for a single neuron.
interval (tuple): Min, max time values; keep min <= t < max.
Returns:
np.ndarray: like `spike_times`, but only within `interval`
"""
interval_spike_times = []
for spikes in spike_times:
interval_mask = (spikes >= interval[0]) & (spikes < interval[1])
interval_spike_times.append(spikes[interval_mask])
return np.array(interval_spike_times, object)
#@title Data retrieval
#@markdown This cell downloads the example dataset that we will use in this tutorial.
import io
import requests
r = requests.get('https://osf.io/sy5xt/download')
if r.status_code != 200:
print('Failed to download data')
else:
spike_times = np.load(io.BytesIO(r.content), allow_pickle=True)['spike_times']
```
---
# Section 1: Exploring the Steinmetz dataset
In this tutorial we will explore the structure of a neuroscience dataset.
We consider a subset of data from a study of [Steinmetz _et al._ (2019)](https://www.nature.com/articles/s41586-019-1787-x). In this study, Neuropixels probes were implanted in the brains of mice. Electrical potentials were measured by hundreds of electrodes along the length of each probe. Each electrode's measurements captured local variations in the electric field due to nearby spiking neurons. A spike sorting algorithm was used to infer spike times and cluster spikes according to common origin: a single cluster of sorted spikes is causally attributed to a single neuron.
In particular, a single recording session of spike times and neuron assignments was loaded and assigned to `spike_times` in the preceding setup.
Typically a dataset comes with some information about its structure. However, this information may be incomplete. You might also apply some transformations or "pre-processing" to create a working representation of the data of interest, which might go partly undocumented depending on the circumstances. In any case it is important to be able to use the available tools to investigate unfamiliar aspects of a data structure.
Let's see what our data looks like...
## Section 1.1: Warming up with `spike_times`
What is the Python type of our variable?
```
type(spike_times)
```
You should see `numpy.ndarray`, which means that it's a normal NumPy array.
If you see an error message, it probably means that you did not execute the set-up cells at the top of the notebook. So go ahead and make sure to do that.
Once everything is running properly, we can ask the next question about the dataset: what's its shape?
```
spike_times.shape
```
There are 734 entries in one dimension, and no other dimensions. What is the Python type of the first entry, and what is *its* shape?
```
idx = 0
print(
type(spike_times[idx]),
spike_times[idx].shape,
sep="\n",
)
```
It's also a NumPy array with a 1D shape! Why didn't this show up as a second dimension in the shape of `spike_times`? That is, why not `spike_times.shape == (734, 826)`?
To investigate, let's check another entry.
```
idx = 321
print(
type(spike_times[idx]),
spike_times[idx].shape,
sep="\n",
)
```
It's also a 1D NumPy array, but it has a different shape. Checking the NumPy types of the values in these arrays, and their first few elements, we see they are composed of floating point numbers (not another level of `np.ndarray`):
```
i_neurons = [0, 321]
i_print = slice(0, 5)
for i in i_neurons:
print(
"Neuron {}:".format(i),
spike_times[i].dtype,
spike_times[i][i_print],
"\n",
sep="\n"
)
```
Note that this time we've checked the NumPy `dtype` rather than the Python variable type. These two arrays contain floating point numbers ("floats") with 32 bits of precision.
The basic picture is coming together:
- `spike_times` is 1D, its entries are NumPy arrays, and its length is the number of neurons (734): by indexing it, we select a subset of neurons.
- An array in `spike_times` is also 1D and corresponds to a single neuron; its entries are floating point numbers, and its length is the number of spikes attributed to that neuron. By indexing it, we select a subset of spike times for that neuron.
Visually, you can think of the data structure as looking something like this:
```
| . . . . . |
| . . . . . . . . |
| . . . |
| . . . . . . . |
```
Before moving on, we'll calculate and store the number of neurons in the dataset and the number of spikes per neuron:
```
n_neurons = len(spike_times)
total_spikes_per_neuron = [len(spike_times_i) for spike_times_i in spike_times]
print(f"Number of neurons: {n_neurons}")
print(f"Number of spikes for first five neurons: {total_spikes_per_neuron[:5]}")
# @title Video 2: Exploring the dataset
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = 'https://player.bilibili.com/player.html?bvid={0}&page={1}'.format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id="", width=854, height=480, fs=1)
print('Video available at https://www.bilibili.com/video/{0}'.format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="oHwYWUI_o1U", width=854, height=480, fs=1, rel=0)
print('Video available at https://youtube.com/watch?v=' + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
display(out)
```
## Section 1.2: Getting warmer: counting and plotting total spike counts
As we've seen, the number of spikes over the entire recording is variable between neurons. More generally, some neurons tend to spike more than others in a given period. Lets explore what the distribution of spiking looks like across all the neurons in the dataset.
Are most neurons "loud" or "quiet", compared to the average? To see, we'll define bins of constant width in terms of total spikes and count the neurons that fall in each bin. This is known as a "histogram".
You can plot a histogram with the matplotlib function `plt.hist`. If you just need to compute it, you can use the numpy function `np.histogram` instead.
```
plt.hist(total_spikes_per_neuron, bins=50, histtype="stepfilled")
plt.xlabel("Total spikes per neuron")
plt.ylabel("Number of neurons");
```
Let's see what percentage of neurons have a below-average spike count:
```
mean_spike_count = np.mean(total_spikes_per_neuron)
frac_below_mean = (total_spikes_per_neuron < mean_spike_count).mean()
print(f"{frac_below_mean:2.1%} of neurons are below the mean")
```
We can also see this by adding the average spike count to the histogram plot:
```
plt.hist(total_spikes_per_neuron, bins=50, histtype="stepfilled")
plt.xlabel("Total spikes per neuron")
plt.ylabel("Number of neurons")
plt.axvline(mean_spike_count, color="orange", label="Mean neuron")
plt.legend();
```
This shows that the majority of neurons are relatively "quiet" compared to the mean, while a small number of neurons are exceptionally "loud": they must have spiked more often to reach a large count.
### Exercise 1: Comparing mean and median neurons
If the mean neuron is more active than 68% of the population, what does that imply about the relationship between the mean neuron and the median neuron?
*Exercise objective:* Reproduce the plot above, but add the median neuron.
```
# To complete the exercise, fill in the missing parts (...) and uncomment the code
median_spike_count = ... # Hint: Try the function np.median
# plt.hist(..., bins=50, histtype="stepfilled")
# plt.axvline(..., color="limegreen", label="Median neuron")
# plt.axvline(mean_spike_count, color="orange", label="Mean neuron")
# plt.xlabel("Total spikes per neuron")
# plt.ylabel("Number of neurons")
# plt.legend()
```
[*Click for solution*](https://github.com/NeuromatchAcademy/course-content/tree/master//tutorials/W1D1_ModelTypes/solutions/W1D1_Tutorial1_Solution_b3411d5d.py)
*Example output:*
<img alt='Solution hint' align='left' width=558 height=414 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W1D1_ModelTypes/static/W1D1_Tutorial1_Solution_b3411d5d_0.png>
*Bonus:* The median is the 50th percentile. What about other percentiles? Can you show the interquartile range on the histogram?
---
# Section 2: Visualizing neuronal spiking activity
## Section 2.1: Getting a subset of the data
Now we'll visualize trains of spikes. Because the recordings are long, we will first define a short time interval and restrict the visualization to only the spikes in this interval. We defined a utility function, `restrict_spike_times`, to do this for you. If you call `help()` on the function, it will tell you a little bit about itself:
```
help(restrict_spike_times)
t_interval = (5, 15) # units are seconds after start of recording
interval_spike_times = restrict_spike_times(spike_times, t_interval)
```
Is this a representative interval? What fraction of the total spikes fall in this interval?
```
original_counts = sum([len(spikes) for spikes in spike_times])
interval_counts = sum([len(spikes) for spikes in interval_spike_times])
frac_interval_spikes = interval_counts / original_counts
print(f"{frac_interval_spikes:.2%} of the total spikes are in the interval")
```
How does this compare to the ratio between the interval duration and the experiment duration? (What fraction of the total time is in this interval?)
We can approximate the experiment duration by taking the minimum and maximum spike time in the whole dataset. To do that, we "concatenate" all of the neurons into one array and then use `np.ptp` ("peak-to-peak") to get the difference between the maximum and minimum value:
```
spike_times_flat = np.concatenate(spike_times)
experiment_duration = np.ptp(spike_times_flat)
interval_duration = t_interval[1] - t_interval[0]
frac_interval_time = interval_duration / experiment_duration
print(f"{frac_interval_time:.2%} of the total time is in the interval")
```
These two values—the fraction of total spikes and the fraction of total time—are similar. This suggests the average spike rate of the neuronal population is not very different in this interval compared to the entire recording.
## Section 2.2: Plotting spike trains and rasters
Now that we have a representative subset, we're ready to plot the spikes, using the matplotlib `plt.eventplot` function. Let's look at a single neuron first:
```
neuron_idx = 1
plt.eventplot(interval_spike_times[neuron_idx], color=".2")
plt.xlabel("Time (s)")
plt.yticks([]);
```
We can also plot multiple neurons. Here are three:
```
neuron_idx = [1, 11, 51]
plt.eventplot(interval_spike_times[neuron_idx], color=".2")
plt.xlabel("Time (s)")
plt.yticks([]);
```
This makes a "raster" plot, where the spikes from each neuron appear in a different row.
Plotting a large number of neurons can give you a sense for the characteristics in the population. Let's show every 5th neuron that was recorded:
```
neuron_idx = np.arange(0, len(spike_times), 5)
plt.eventplot(interval_spike_times[neuron_idx], color=".2")
plt.xlabel("Time (s)")
plt.yticks([]);
```
*Question*: How does the information in this plot relate to the histogram of total spike counts that you saw above?
```
# @title Video 3: Visualizing activity
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = 'https://player.bilibili.com/player.html?bvid={0}&page={1}'.format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id="", width=854, height=480, fs=1)
print('Video available at https://www.bilibili.com/video/{0}'.format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="QGA5FCW7kkA", width=854, height=480, fs=1, rel=0)
print('Video available at https://youtube.com/watch?v=' + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
display(out)
```
---
# Section 3: Inter-spike intervals and their distributions
Given the ordered arrays of spike times for each neuron in `spike_times`, which we've just visualized, what can we ask next?
Scientific questions are informed by existing models. So, what knowledge do we already have that can inform questions about this data?
We know that there are physical constraints on neuron spiking. Spiking costs energy, which the neuron's cellular machinery can only obtain at a finite rate. Therefore neurons should have a refractory period: they can only fire as quickly as their metabolic processes can support, and there is a minimum delay between consecutive spikes of the same neuron.
More generally, we can ask "how long does a neuron wait to spike again?" or "what is the longest a neuron will wait?" Can we transform spike times into something else, to address questions like these more directly?
We can consider the inter-spike times (or interspike intervals: ISIs). These are simply the time differences between consecutive spikes of the same neuron.
### Exercise 2: Plot the distribution of ISIs for a single neuron
*Exercise objective:* make a histogram, like we did for spike counts, to show the distribution of ISIs for one of the neurons in the dataset.
Do this in three steps:
1. Extract the spike times for one of the neurons
2. Compute the ISIs (the amount of time between spikes, or equivalently, the difference between adjacent spike times)
3. Plot a histogram with the array of individual ISIs
```
def compute_single_neuron_isis(spike_times, neuron_idx):
"""Compute a vector of ISIs for a single neuron given spike times.
Args:
spike_times (list of 1D arrays): Spike time dataset, with the first
dimension corresponding to different neurons.
neuron_idx (int): Index of the unit to compute ISIs for.
Returns:
isis (1D array): Duration of time between each spike from one neuron.
"""
#############################################################################
# Students: Fill in missing code (...) and comment or remove the next line
raise NotImplementedError("Exercise: compute single neuron ISIs")
#############################################################################
# Extract the spike times for the specified neuron
single_neuron_spikes = ...
# Compute the ISIs for this set of spikes
# Hint: the function np.diff computes discrete differences along an array
isis = ...
return isis
# Uncomment the following lines when you are ready to test your function
# single_neuron_isis = compute_single_neuron_isis(spike_times, neuron_idx=283)
# plt.hist(single_neuron_isis, bins=50, histtype="stepfilled")
# plt.axvline(single_neuron_isis.mean(), color="orange", label="Mean ISI")
# plt.xlabel("ISI duration (s)")
# plt.ylabel("Number of spikes")
# plt.legend()
```
[*Click for solution*](https://github.com/NeuromatchAcademy/course-content/tree/master//tutorials/W1D1_ModelTypes/solutions/W1D1_Tutorial1_Solution_4792dbfa.py)
*Example output:*
<img alt='Solution hint' align='left' width=558 height=414 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W1D1_ModelTypes/static/W1D1_Tutorial1_Solution_4792dbfa_0.png>
---
In general, the shorter ISIs are predominant, with counts decreasing rapidly (and smoothly, more or less) with increasing ISI. However, counts also rapidly decrease to zero with _decreasing_ ISI, below the maximum of the distribution (8-11 ms). The absence of these very low ISIs agrees with the refractory period hypothesis: the neuron cannot fire quickly enough to populate this region of the ISI distribution.
Check the distributions of some other neurons. To resolve various features of the distributions, you might need to play with the value of `n_bins`. Using too few bins might smooth over interesting details, but if you use too many bins, the random variability will start to dominate.
You might also want to restrict the range to see the shape of the distribution when focusing on relatively short or long ISIs. *Hint:* `plt.hist` takes a `range` argument
---
# Section 4: What is the functional form of an ISI distribution?
```
# @title Video 4: ISI distribution
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = 'https://player.bilibili.com/player.html?bvid={0}&page={1}'.format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id="", width=854, height=480, fs=1)
print('Video available at https://www.bilibili.com/video/{0}'.format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="DHhM80MOTe8", width=854, height=480, fs=1, rel=0)
print('Video available at https://youtube.com/watch?v=' + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
display(out)
```
The ISI histograms seem to follow continuous, monotonically decreasing functions above their maxima. The function is clearly non-linear. Could it belong to a single family of functions?
To motivate the idea of using a mathematical function to explain physiological phenomena, let's define a few different function forms that we might expect the relationship to follow: exponential, inverse, and linear.
```
def exponential(xs, scale, rate, x0):
"""A simple parametrized exponential function, applied element-wise.
Args:
xs (np.ndarray or float): Input(s) to the function.
scale (float): Linear scaling factor.
rate (float): Exponential growth (positive) or decay (negative) rate.
x0 (float): Horizontal offset.
"""
ys = scale * np.exp(rate * (xs - x0))
return ys
def inverse(xs, scale, x0):
"""A simple parametrized inverse function (`1/x`), applied element-wise.
Args:
xs (np.ndarray or float): Input(s) to the function.
scale (float): Linear scaling factor.
x0 (float): Horizontal offset.
"""
ys = scale / (xs - x0)
return ys
def linear(xs, slope, y0):
"""A simple linear function, applied element-wise.
Args:
xs (np.ndarray or float): Input(s) to the function.
slope (float): Slope of the line.
y0 (float): y-intercept of the line.
"""
ys = slope * xs + y0
return ys
```
### Interactive Demo: ISI functions explorer
Here is an interactive demo where you can vary the parameters of these functions and see how well the resulting outputs correspond to the data. Adjust the parameters by moving the sliders and see how close you can get the lines to follow the falling curve of the histogram. This will give you a taste of what you're trying to do when you *fit a model* to data.
"Interactive demo" cells have hidden code that defines an interface where you can play with the parameters of some function using sliders. You don't need to worry about how the code works – but you do need to **run the cell** to enable the sliders.
```
#@title
#@markdown Be sure to run this cell to enable the demo
# Don't worry about understanding this code! It's to setup an interactive plot.
single_neuron_idx = 283
single_neuron_spikes = spike_times[single_neuron_idx]
single_neuron_isis = np.diff(single_neuron_spikes)
counts, edges = np.histogram(
single_neuron_isis,
bins=50,
range=(0, single_neuron_isis.max())
)
functions = dict(
exponential=exponential,
inverse=inverse,
linear=linear,
)
colors = dict(
exponential="C1",
inverse="C2",
linear="C4",
)
@widgets.interact(
exp_scale=widgets.FloatSlider(1000, min=0, max=20000, step=250),
exp_rate=widgets.FloatSlider(-10, min=-200, max=50, step=1),
exp_x0=widgets.FloatSlider(0.1, min=-0.5, max=0.5, step=0.005),
inv_scale=widgets.FloatSlider(1000, min=0, max=3e2, step=10),
inv_x0=widgets.FloatSlider(0, min=-0.2, max=0.2, step=0.01),
lin_slope=widgets.FloatSlider(-1e5, min=-6e5, max=1e5, step=10000),
lin_y0=widgets.FloatSlider(10000, min=0, max=4e4, step=1000),
)
def fit_plot(
exp_scale=1000, exp_rate=-10, exp_x0=0.1,
inv_scale=1000, inv_x0=0,
lin_slope=-1e5, lin_y0=2000,
):
"""Helper function for plotting function fits with interactive sliders."""
func_params = dict(
exponential=(exp_scale, exp_rate, exp_x0),
inverse=(inv_scale, inv_x0),
linear=(lin_slope, lin_y0),
)
f, ax = plt.subplots()
ax.fill_between(edges[:-1], counts, step="post", alpha=.5)
xs = np.linspace(1e-10, edges.max())
for name, function in functions.items():
ys = function(xs, *func_params[name])
ax.plot(xs, ys, lw=3, color=colors[name], label=name);
ax.set(
xlim=(edges.min(), edges.max()),
ylim=(0, counts.max() * 1.1),
xlabel="ISI (s)",
ylabel="Number of spikes",
)
ax.legend()
# @title Video 5: Fitting models by hand
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = 'https://player.bilibili.com/player.html?bvid={0}&page={1}'.format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id="", width=854, height=480, fs=1)
print('Video available at https://www.bilibili.com/video/{0}'.format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="uW2HDk_4-wk", width=854, height=480, fs=1, rel=0)
print('Video available at https://youtube.com/watch?v=' + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
display(out)
```
# Summary
In this tutorial, we loaded some neural data and poked at it to understand how the dataset is organized. Then we made some basic plots to visualize (1) the average level of activity across the population and (2) the distribution of ISIs for an individual neuron. In the very last bit, we started to think about using mathematical formalisms to understand or explain some physiological phenomenon. All of this only allowed us to understand "What" the data looks like.
This is the first step towards developing models that can tell us something about the brain. That's what we'll focus on in the next two tutorials.
|
github_jupyter
|
# Introduction
Try writing some **SELECT** statements of your own to explore a large dataset of air pollution measurements.
Run the cell below to set up the feedback system.
```
# Set up feedback system
from learntools.core import binder
binder.bind(globals())
from learntools.sql.ex2 import *
print("Setup Complete")
```
The code cell below fetches the `global_air_quality` table from the `openaq` dataset. We also preview the first five rows of the table.
```
from google.cloud import bigquery
# Create a "Client" object
client = bigquery.Client()
# Construct a reference to the "openaq" dataset
dataset_ref = client.dataset("openaq", project="bigquery-public-data")
# API request - fetch the dataset
dataset = client.get_dataset(dataset_ref)
# Construct a reference to the "global_air_quality" table
table_ref = dataset_ref.table("global_air_quality")
# API request - fetch the table
table = client.get_table(table_ref)
# Preview the first five lines of the "global_air_quality" table
client.list_rows(table, max_results=5).to_dataframe()
```
# Exercises
### 1) Units of measurement
Which countries have reported pollution levels in units of "ppm"? In the code cell below, set `first_query` to an SQL query that pulls the appropriate entries from the `country` column.
In case it's useful to see an example query, here's some code from the tutorial:
```
query = """
SELECT city
FROM `bigquery-public-data.openaq.global_air_quality`
WHERE country = 'US'
"""
```
```
# Query to select countries with units of "ppm"
first_query = ____ # Your code goes here
# Set up the query (cancel the query if it would use too much of
# your quota, with the limit set to 1 GB)
safe_config = bigquery.QueryJobConfig(maximum_bytes_billed=1e9)
first_query_job = client.query(first_query, job_config=safe_config)
# API request - run the query, and return a pandas DataFrame
first_results = first_query_job.to_dataframe()
# View top few rows of results
print(first_results.head())
# Check your answer
q_1.check()
```
For the solution, uncomment the line below.
```
#q_1.solution()
```
### 2) High air quality
Which pollution levels were reported to be exactly 0?
- Set `zero_pollution_query` to select **all columns** of the rows where the `value` column is 0.
- Set `zero_pollution_results` to a pandas DataFrame containing the query results.
```
# Query to select all columns where pollution levels are exactly 0
zero_pollution_query = ____ # Your code goes here
# Set up the query
query_job = client.query(zero_pollution_query, job_config=safe_config)
# API request - run the query and return a pandas DataFrame
zero_pollution_results = ____ # Your code goes here
print(zero_pollution_results.head())
# Check your answer
q_2.check()
```
For the solution, uncomment the line below.
```
#q_2.solution()
```
That query wasn't too complicated, and it got the data you want. But these **SELECT** queries don't organizing data in a way that answers the most interesting questions. For that, we'll need the **GROUP BY** command.
If you know how to use [`groupby()`](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.groupby.html) in pandas, this is similar. But BigQuery works quickly with far larger datasets.
Fortunately, that's next.
# Keep going
**[GROUP BY](#$NEXT_NOTEBOOK_URL$)** clauses and their extensions give you the power to pull interesting statistics out of data, rather than receiving it in just its raw format.
|
github_jupyter
|
# ETL Pipeline Preparation
Follow the instructions below to help you create your ETL pipeline.
### 1. Import libraries and load datasets.
- Import Python libraries
- Load `messages.csv` into a dataframe and inspect the first few lines.
- Load `categories.csv` into a dataframe and inspect the first few lines.
```
# import libraries
import pandas as pd
import numpy as np
# load messages dataset
messages = pd.read_csv("../data/disaster_messages.csv")
messages.head()
# load categories dataset
categories = pd.read_csv("../data/disaster_categories.csv")
categories.head()
```
### 2. Merge datasets.
- Merge the messages and categories datasets using the common id
- Assign this combined dataset to `df`, which will be cleaned in the following steps
```
# merge datasets
df = pd.merge(messages, categories, on="id")
df.head()
df['categories'].unique()
```
### 3. Split `categories` into separate category columns.
- Split the values in the `categories` column on the `;` character so that each value becomes a separate column. You'll find [this method](https://pandas.pydata.org/pandas-docs/version/0.23/generated/pandas.Series.str.split.html) very helpful! Make sure to set `expand=True`.
- Use the first row of categories dataframe to create column names for the categories data.
- Rename columns of `categories` with new column names.
- Update the total value of the items to be 0 or 1
```
# create a dataframe of the 36 individual category columns
df_tmp = df['categories'].str.split(";", expand=True)
cols = [w.split("-")[0] for w in df_tmp.iloc[0, :].tolist()]
df_tmp.columns = cols
df_tmp = df_tmp.apply(lambda x: x.str.replace(".*?-([0-9]+)", r"\g<1>").astype(int)).clip(0, 1)
df = pd.concat([df.iloc[:, :-1], df_tmp], axis=1)
```
### 4. Remove duplicates.
- Check how many duplicates are in this dataset.
- Drop the duplicates.
- Confirm duplicates were removed.
```
# check number of duplicates
df_dub = df[df.duplicated(subset=None)]
print("Duplicates: {}".format(df_dub.shape[0]))
df_dub.head()
# drop duplicates
df = df.drop_duplicates()
# check number of duplicates
df[df.duplicated(subset=None)]
```
Check for items with a very low mean
```
desc = df.describe()
desc[desc.columns[desc.loc['std', :] < 0.01]]
# since child_alone holds no relevant information, remove:
df = df.drop('child_alone', axis=1)
```
### 5. Save the clean dataset into an sqlite database.
You can do this with pandas [`to_sql` method](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.to_sql.html) combined with the SQLAlchemy library. Remember to import SQLAlchemy's `create_engine` in the first cell of this notebook to use it below.
```
from sqlalchemy import create_engine
engine = create_engine('sqlite:///../data/disaster_data.db')
df.to_sql('texts', engine, index=False)
```
### 6. Use this notebook to complete `etl_pipeline.py`
Use the template file attached in the Resources folder to write a script that runs the steps above to create a database based on new datasets specified by the user. Alternatively, you can complete `etl_pipeline.py` in the classroom on the `Project Workspace IDE` coming later.
|
github_jupyter
|
# 选择
## 布尔类型、数值和表达式

- 注意:比较运算符的相等是两个等到,一个等到代表赋值
- 在Python中可以用整型0来代表False,其他数字来代表True
- 后面还会讲到 is 在判断语句中的用发
```
b=100
aa = eval(input('请输入密码: '))
bb = 123456
if aa == bb:
a = eval(input('请输入取多少钱: '))
if a <= b:
c = b-a
print('取钱成功')
b=c
print('余额',c)
# send_message()
else:
print('失败')
else:
print('密码错误')
```
## 字符串的比较使用ASCII值
## Markdown
- https://github.com/younghz/Markdown
## EP:
- <img src="../Photo/34.png"></img>
- 输入一个数字,判断其实奇数还是偶数
## 产生随机数字
- 函数random.randint(a,b) 可以用来产生一个a和b之间且包括a和b的随机整数
## 其他random方法
- random.random 返回0.0到1.0之间前闭后开区间的随机浮点
- random.randrange(a,b) 前闭后开
## EP:
- 产生两个随机整数number1和number2,然后显示给用户,使用户输入数字的和,并判定其是否正确
- 进阶:写一个随机序号点名程序
```
import random
a = random.randint(1,10)
b = random.randint(1,6)
if b < 5:
print('请第',a,'行','第',b,'个同学回答问题')
else:
print('请第 9 行','第',b,'个同学回答问题')
```
## if语句
- 如果条件正确就执行一个单向if语句,亦即当条件为真的时候才执行if内部的语句
- Python有很多选择语句:
> - 单向if
- 双向if-else
- 嵌套if
- 多向if-elif-else
- 注意:当语句含有子语句的时候,那么一定至少要有一个缩进,也就是说如果有儿子存在,那么一定要缩进
- 切记不可tab键和space混用,单用tab 或者 space
- 当你输出的结果是无论if是否为真时都需要显示时,语句应该与if对齐
## EP:
- 用户输入一个数字,判断其实奇数还是偶数
- 进阶:可以查看下4.5实例研究猜生日
## 双向if-else 语句
- 如果条件为真,那么走if内部语句,否则走else内部语句
## EP:
- 产生两个随机整数number1和number2,然后显示给用户,使用户输入数字,并判定其是否正确,如果正确打印“you‘re correct”,否则打印正确错误
## 嵌套if 和多向if-elif-else

## EP:
- 提示用户输入一个年份,然后显示表示这一年的动物

- 计算身体质量指数的程序
- BMI = 以千克为单位的体重除以以米为单位的身高

```
tz = eval(input('请输入体重(KG): '))
sg = eval(input('身高(m): '))
aa = tz / sg
if aa<18.5:
print('超轻')
if 18.5<=aa<25.0:
print('标准')
if 25.0<=aa<30.0:
print('超重')
if 30.0<=aa:
print('吃肥')
year = eval(input('请输入年份: '))
b = year % 12
if b == 0:
print('猴')
elif b== 1:
print('鸡')
elif b== 2:
print('狗')
elif b== 3:
print('猪')
elif b== 4:
print('鼠')
elif b== 5:
print('牛')
elif b== 6:
print('虎')
elif b== 7:
print('兔')
elif b== 8:
print('龙')
elif b== 9:
print('蛇')
elif b== 10:
print('马')
elif b== 11:
print('羊')
```
## 逻辑运算符



## EP:
- 判定闰年:一个年份如果能被4整除但不能被100整除,或者能被400整除,那么这个年份就是闰年
- 提示用户输入一个年份,并返回是否是闰年
- 提示用户输入一个数字,判断其是否为水仙花数
```
for i in range(100,1000):
a = i % 10
b = i // 100
c = (i // 10) % 10
e = a ** 3 + b ** 3 + c ** 3
if e == i:
print(e)
stri = 'asdsad'
stri[1]
year = eval(input('nianfen: '))
if (year % 4 ==0 and year % 100 != 0) or year % 400 ==0:
print('闰年')
else:
print('非')
```
## 实例研究:彩票

```
import random
a = input('请输入一个两位数: ')
b = str(random.randint(10,99))
print('随机生成: ',b)
if a == (b[0]+b[1]):
print('恭喜获得10000$')
elif a == (b[1]+b[0]):
print('恭喜获得3000$')
elif a[0] == b[0] or a[0] == b[1] or a[1] == b[0] or a[1] == b[1]:
print('恭喜获得1000$')
else:
print('抱歉什么也没有!')
```
# Homework
- 1

```
import math
a,b,c = eval(input('Enter a,b,c'))
e = b**2 -4*a*c
if e > 0:
r1=(-b+math.sqrt(e))/2*a
r2=(-b-math.sqrt(e))/2*a
print('r1=',round(r1,6),'\nr2',round(r2,6))
elif e == 0:
r =-b / 2*a
print('r=',int(r))
else:
print('没有实根!')
```
- 2

```
import random
a = random.randint(0,100)
b = random.randint(0,100)
print('生成2个数为: ',a,' ',b)
c = eval(input('请输入整和: '))
if b + a == c:
print('真')
else:
print('假')
```
- 3

```
a = eval(input('今天星期几: '))
b = eval(input('未来几天后: '))
c = (a+b)%7
if c==0:
print('今天是星期日',b,'天后星期日')
else:
print('今天是星期',a,b,'天后星期',c)
```
- 4

```
a,b,c = eval(input('请输入3个数: '))
d=max(a,b,c)
e=min(a,b,c)
f=a+b+c-d-e
print(e,f,d)
```
- 5

```
a,b = eval(input('请输入1号重量和价钱: '))
c,d = eval(input('请输入2号重量和价钱: '))
e=a/b
f=c/d
if e>f:
print('1号食品性价比更好!')
else:
print('2号食品性价比更好!')
```
- 6

```
yue = eval(input('月份: '))
year = eval(input('年份: '))
if yue == 2:
if ((year % 4 ==0 and year % 100 != 0) or year % 400 ==0):
print(year,'年的2月有29天!')
else:
print(year,'年的2月有28天!')
elif yue == 1 or yue ==3 or yue ==5 or yue ==7 or yue ==8 or yue ==10 or yue ==12:
print(year,'年的',yue,'月有31天!')
elif yue == 4 or yue ==6 or yue ==9 or yue ==11:
print(year,'年的',yue,'月有30天!')
```
- 7

```
import random
a = random.randint(2,3)
print('(测试程序是否正确2为正,3为反)',a)
#2为正面,3为反面
b = input('请猜测硬币正反面: ')
if b == '正面' and a == 2:
print('猜对了!')
elif b == '反面' and a==3:
print('猜对了!')
else:
print('猜错了!')
```
- 8

```
import random
a = eval(input('请输入你要出什么(0=剪刀,1=石头,2=布): '))
b = random.randint(0,2)
print(b)
if a == 0 and b == 2:
print('玩家获胜!')
elif a == 1 and b == 0:
print('玩家获胜!')
elif a == 2 and b == 1:
print('玩家获胜!')
elif a == b:
print('平局!')
else:
print('电脑获胜!')
h =(q+(26*(m+1))/10+k+k/4+j/4+5*j)%7
```
- 9

```
year = eval(input('输入年份:'))
months = eval(input('输入月份:'))
days = eval(input('输入当前月份的某天:'))
hdayDict = {0:'星期六',1:'星期日', 2: '星期一', 3: '星期二', 4: '星期三', 5: '星期四', 6: '星期五'}
monDict = {1: '13', 2: '14', 3: '3', 4: '4', 5: '5', 6: '6', 7: '7', 8: '8', 9: '9', 10: '10', \
11: '11', 12: '12'}
if months == 1 or months == 2:
year = year - 1
shijishu = year // 100
shijiyear = year % 100
h = (days + (26 * (eval(monDict[months]) + 1)) // 10 + shijiyear + shijiyear // 4 + shijishu // 4 + 5 * shijishu) % 7
print('Day of the week is ' + hdayDict[h])
```
- 10

```
import random
a = random.randint(1,13)
huase ={1:'梅花',2:'红桃',3:'方块',4:'黑桃'}
c = random.randint(1,4)
d = huase[c]+str(a)
print(d)
```
- 11

```
a = input('请输入一个3位数: ')
b = a[2]+a[1]+a[0]
if a == b:
print('是回文数')
else:
print('不是回文数')
```
- 12

```
a,b,c =eval(input('输入三边:'))
if a+b>c and a-b<c:
d=a+b+c
print(d)
else:
print('输入非法')
```
|
github_jupyter
|
# LOGISTIC REGRESSION WITH MNIST
```
import numpy as np
# import tensorflow as tf
import tensorflow.compat.v1 as tf
import matplotlib.pyplot as plt
# tf.disable_eager_execution()
# tf.enable_eager_execution()
print ("PACKAGES LOADED")
```
# DOWNLOAD AND EXTRACT MNIST DATASET
```
def OnehotEncoding(target):
from sklearn.preprocessing import OneHotEncoder
target_re = target.reshape(-1,1)
enc = OneHotEncoder()
enc.fit(target_re)
return enc.transform(target_re).toarray()
def SuffleWithNumpy(data_x, data_y):
idx = np.random.permutation(len(data_x))
x,y = data_x[idx], data_y[idx]
return x,y
```
## download with keras dataset
```
print ("Download and Extract MNIST dataset")
# mnist = input_data.read_data_sets('data/', one_hot=True)
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
print
print (" tpye of 'mnist' is %s" % (type(mnist)))
print (" number of train data is %d" % (len(x_train)))
print (" number of test data is %d" % (len(x_test)))
num_train_data = len(x_train)
trainimg = x_train
trainimg = trainimg.reshape(len(trainimg),784)
trainlabel = OnehotEncoding(y_train)
testimg = x_test
testimg = testimg.reshape(len(testimg),784)
testlabel = OnehotEncoding(y_test)
print ("MNIST loaded")
tf.disable_eager_execution()
```
## Download with tfds
```
import tensorflow_datasets as tfds
print ("Batch Learning? ")
tf.enable_eager_execution()
dataset, metadata = tfds.load('mnist', as_supervised=True, with_info=True)
train_dataset, test_dataset = dataset['train'], dataset['test']
num_train_examples = metadata.splits['train'].num_examples
num_test_examples = metadata.splits['test'].num_examples
print("Number of training examples: {}".format(num_train_examples))
print("Number of test examples: {}".format(num_test_examples))
def normalize(images, labels):
images = tf.cast(images, tf.float32)
images /= 255
return images, labels
# The map function applies the normalize function to each element in the train
# and test datasets
train_dataset = train_dataset.map(normalize)
test_dataset = test_dataset.map(normalize)
# The first time you use the dataset, the images will be loaded from disk
# Caching will keep them in memory, making training faster
train_dataset = train_dataset.cache()
test_dataset = test_dataset.cache()
train_dataset=train_dataset.shuffle(num_train_examples,reshuffle_each_iteration=True)
train_to_np=tf.compat.v1.data.make_one_shot_iterator(train_dataset.batch(num_train_examples)).get_next()
x_train=train_to_np[0].numpy()
y_train=train_to_np[1].numpy()
test_to_np=tf.compat.v1.data.make_one_shot_iterator(test_dataset.batch(num_test_examples)).get_next()
x_test = test_to_np[0].numpy()
y_test = test_to_np[1].numpy()
num_train_data = len(x_train)
trainimg = x_train
trainlabel = OnehotEncoding(y_train)
trainimg = trainimg.reshape(len(trainimg),784)
testimg = x_test
testimg = testimg.reshape(len(testimg),784)
testlabel = OnehotEncoding(y_test)
tf.disable_eager_execution()
trainimg.shape, trainlabel.shape
```
## CREATE TENSOR GRAPH FOR LOGISTIC REGRESSION
```
x = tf.placeholder(tf.float32, shape = (None, 784))
y = tf.placeholder(tf.float32, shape = (None, 10)) # None is for infinite
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
# LOGISTIC REGRESSION MODEL
actv = tf.nn.softmax(tf.matmul(x, W) + b)
# COST FUNCTION
cost = tf.reduce_mean(-tf.reduce_sum(y*tf.math.log(actv), axis=1))
# OPTIMIZER
learning_rate = 0.01
optm = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)
```
## PREDICTION AND ACCURACY
```
# PREDICTION
pred = tf.equal(tf.argmax(actv, 1), tf.argmax(y, 1))
# ACCURACY
accr = tf.reduce_mean(tf.cast(pred, "float"))
# INITIALIZER
initializer = tf.global_variables_initializer()
```
# TRAIN MODEL
```
training_epochs = 50
batch_size = 100
display_step = 5
# SESSION
sess = tf.Session()
sess.run(initializer)
# MINI-BATCH LEARNING
for epoch in range(training_epochs):
avg_cost = 0.
num_batch = int(num_train_data/batch_size)
for i in range(num_batch):
batch_xs=trainimg[i*batch_size:(i+1)*batch_size]
batch_ys=trainlabel[i*batch_size:(i+1)*batch_size]
sess.run(optm, feed_dict={x: batch_xs, y: batch_ys})
feeds = {x: batch_xs, y: batch_ys}
avg_cost += sess.run(cost, feed_dict=feeds)/num_batch
# DISPLAY
if epoch % display_step == 0:
feeds_train = {x: batch_xs, y: batch_ys}
feeds_test = {x: testimg, y: testlabel}
train_acc = sess.run(accr, feed_dict=feeds_train)
test_acc = sess.run(accr, feed_dict=feeds_test)
print ("Epoch: %03d/%03d cost: %.9f train_acc: %.3f test_acc: %.3f"
% (epoch, training_epochs, avg_cost, train_acc, test_acc))
#shuffle in each epoch
trainimg,trainlabel = SuffleWithNumpy(trainimg,trainlabel)
print ("DONE")
```
|
github_jupyter
|
[View in Colaboratory](https://colab.research.google.com/github/anaurora/WineClassification/blob/master/WineClassification.ipynb)
#Wine Type Prediction (Multi-class Classification)
This data set is taken from the UCI repository (link [here](https://archive.ics.uci.edu/ml/datasets/wine)). I have done some basic pre-processing of the data in Excel, like adding headers based on the dataset description and converting the dataset to the CSV format. As usual, I've ingested this data from my personal Drive, and this project's GitHub repository has the pre-processed dataset (in CSV format).
###Dataset Information:
**Winelab.csv**: To quote the UCI dataset description:
> *These data are the results of a chemical analysis of
wines grown in the same region in Italy but derived from three
different cultivars.
The analysis determined the quantities of 13 constituents
found in each of the three types of wines. *
Basically, there are 3 different types of wines and their attributes are their chemical compositions (Alcohol, Malic Acid, Ash etc.). Fortunately, this is a dataset with continuous quantitative features only. This makes our life a lot easier!
## Install and import necessary libraries
```
!pip3 install -U -q PyDrive #Only if you are loading your data from Google Drive
from pydrive.auth import GoogleAuth
from pydrive.drive import GoogleDrive
from google.colab import auth
from oauth2client.client import GoogleCredentials
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split,GridSearchCV,KFold,cross_val_score
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import f1_score, accuracy_score, classification_report
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
from sklearn.calibration import CalibratedClassifierCV
```
## Authorize Google Drive (if your data is stored in Drive)
```
%%capture
auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)
```
## Data Ingestion
I have saved the file in my personal drive storage and read it from there into a pandas data frame. Please modify the following cells to read the CSV files into a Pandas dataframe as per your storage location.
```
%%capture
downloaded = drive.CreateFile({'id':'1Tghlhn7nTZv_WOV7typp9fFZil4TjZ_9'}) # replace the id with id of file you want to access
downloaded.GetContentFile('Winelab.csv')
winedata = pd.read_csv('Winelab.csv')
```
Let's take a sneak peek at the data
```
winedata.head()
winedata.info()
```
As we can see, we have 13 attributes for each wine with one class label (*Wine_Class*).
##Data Preparation
To prepare the data for analysis, we need to convert our Wine Class feature to a categorical one and scale the features, to prepare for dimensionality reduction using Principal Component Analysis (PCA).
```
winedata['Wine_Class']=winedata['Wine_Class'].astype('category')
```
In the previous section, we noticed that all 13 attributes of each wine are measured on completely different scales. To run PCA, and most machine learning algorithms, we need to focus on keeping the data around the same scale, so that no one feature can overpower the others with pure magnitude.
```
scaler = StandardScaler()
winedatapc=winedata.copy()
scaler.fit(winedatapc.iloc[:,1:])
winedatapc.iloc[:,1:]=scaler.transform(winedatapc.iloc[:,1:])
```
Now, one can see that all data has been scaled i.e. each feature (except the class label, of course) has been centered and scaled to unit variance (Z scores).
```
winedatapc.head()
```
##Dimension Reduction (using PCA)
We are going to generate all possible Principal Components for our dataset (13), plot them to see how well segregated the classes are, and decide on the number of components we are going to use for our prediction algorithm.
The following lines of code generate the Principal Component scores of all the observations, for all 13 principal components (PC0 through PC12).
```
pca = PCA(n_components=13,random_state=0)
PCAscores=pd.DataFrame(pca.fit_transform(winedatapc.iloc[:,1:]))
PCAscores=PCAscores.rename('PC{}'.format, axis='columns')
PCAscores['Wine_Class']=winedatapc.Wine_Class
PCAscores.head()
```
To see what these Principal Components mean, we create a loadings dataframe for each attribute of the dataframe (columns), for each Principal Component (index)
```
load=pd.DataFrame(pca.components_,columns=winedatapc.iloc[:,1:].columns)
load=load.rename('PC{}'.format, axis='index')
load
```
To interpret the above table, we take an example of the first row (PC0 i.e. the first Principal Component). The highest dependence of this PC is on *Flavanoids* and the dependence is positive. This implies that the higher the amount of Flavanoids in this wine, the higher the score of the first principal component. The highest negative dependence is on *Nonflavanoid_phenols*, which implies the higher the *Nonflavanoid_phenols* attribute for a wine, the lower the PC score will be. This can be extended to all other PCs.
We now visualize all the wines (observations) using the first 2 Principal Components to see if the class distributions are well separated.
```
PC=sns.pairplot(x_vars=['PC0'], y_vars=['PC1'], data=PCAscores, hue="Wine_Class", size=8)
plt.xlabel('Principal Component 0')
plt.ylabel('Principal Component 1')
plt.title('Visual Representation of all observations')
plt.show()
```
We can see that the 3 categories of wine, are pretty well segregated. This is good, as we have distinct features for each type of wine. This will improve the accuracy of our prediction algorithm.
The next task is to use these Principal Components to reduce the dimension of the problem. To see how many Principal Components we need, we are going to try 2 approaches:
1) Scree Plot
2) Percentage of Variance Explained
```
scree=plt.plot(pca.explained_variance_,'o-')
plt.title('Scree Plot')
plt.ylabel('Eigen Values')
plt.xlabel('Component/Dimension')
plt.xticks(range(0,13))
plt.show()
var1=np.cumsum(np.round(pca.explained_variance_ratio_, decimals=4)*100)
cumsum=plt.plot(var1,'o-')
plt.xlabel('Component/Dimension')
plt.ylabel('Percentage of Explained Variance')
plt.title('Cumulative Percentage of Variance Explained')
plt.xticks(range(0,13))
plt.show()
```
According to Kaiser's Rule, we should select the number of components that have eigen values greater than 1, and according to the variance rule, we should select the number of components that explain 95% of the variance in the data.
From Kaiser's Rule, we should select approximately 3 components (scree plot), and from the Variance Rule, we should select approximately 8 components. For this case, I'm going to be leaning towards the Variance Rule, but not exactly. I'm going to select the number of components that explain approximately 80% of the variation of the data.
**This implies that I'm going to choose 5 components.**
The code below selects only the first 5 principal component scores.
```
X=PCAscores.iloc[:,:5].copy()
X=X.values
y=PCAscores.Wine_Class.astype(np.int64).values
```
##Prediction
###Split Data: Training and Testing
**We split the data to use 70% of it for training our machine learning models, and the remaining 30% for testing.**
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
```
###Class distribution
**A large part of how we decide which Machine Learning model to choose will depend on the class distribution. **
```
unique, counts = np.unique(y, return_counts=True)
print(np.asarray((unique, counts)).T)
```
**So we have a noticeably uneven class distribution. This skew can introduce a bias in our model, and hence we need to be careful with our scoring method.**
**We chose the F1 micro score as a measure of model performance as we have an uneven class distribution (we have more ones than zeros in our class labels). For a more detailed explanation (and formulae), please see [this link.](https://blogs.msdn.microsoft.com/andreasderuiter/2015/02/09/performance-measures-in-azure-ml-accuracy-precision-recall-and-f1-score/)**
###Method 1: K-Nearest Neighbours (KNN)
####Hyperparameter Tuning
**In the case of KNN, we tune the type of distance metric used and the number of nearest neigbours considered in classification.**
```
def knn_param_selection(X, y, nfolds):
n_neighborss = [3,4,5,6,7,8,9,10,11,12,13,14,15]
metrics=['minkowski','euclidean','manhattan']
param_grid = {'n_neighbors': n_neighborss,'metric':metrics}
grid_search = GridSearchCV(KNeighborsClassifier(), param_grid, cv=nfolds,scoring='f1_micro')
grid_search.fit(X, y)
grid_search.best_params_
return grid_search.best_params_
knn_param_selection(X_train, y_train, 10)
```
**The grid search reveals that we should use the *minkowski* distance metric and the *5 nearest neighbours* to maximize the F1 (micro) score. Since we have a class imbalance, we have used the F1 Micro score.**
####Model Fitting and Analysis
```
knnclass = KNeighborsClassifier(n_neighbors=5,metric='minkowski')
knnclass.fit(X_train, y_train)
y_pred = knnclass.predict(X_test)
print('K-Nearest Neighbors predicts the correct class label with a',str(round(accuracy_score(y_test, y_pred)*100,2)),'% accuracy.')
kfold=KFold(n_splits=10, random_state=0)
modelCV = KNeighborsClassifier(n_neighbors=5,metric='minkowski')
scoring = 'f1_micro'
results = cross_val_score(modelCV, X, y, cv=kfold,scoring=scoring)
print("10-fold average cross validation average F1 micro score: %.3f" % (results.mean()))
```
###Method 2: Logistic Regression
####Hyperparameter Tuning
**We tune the regularization parameter (*C*) for logistic regression using a 10 fold cross validated Grid Search, using our training set. Notice, that we have set the grid search to maximize the F1 micro score for our model. **
```
def lgr_param_selection(X, y, nfolds):
Cs = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1,1.5,2,2.5,3]
param_grid = {'C': Cs}
grid_search = GridSearchCV(LogisticRegression(max_iter=1000,solver='sag',penalty='l2',random_state=0), param_grid, cv=nfolds,scoring='f1_micro')
grid_search.fit(X, y)
grid_search.best_params_
return grid_search.best_params_
lgr_param_selection(X_train, y_train, 10)
```
**The Grid Search has yielded a regularization parameter (C) of 0.5. Note that we have used the L2 norm penalty, as L1/Elastic Net would perform automatic feature selection for us, which we have already done in the previous section.**
**We now apply this parameter to create a logistic regression model for analysis, and then run a 10 fold cross validation to check if we have a good model that is not overfitted.**
####Model Fitting and Analysis
```
logreg = LogisticRegression(max_iter=1000,solver='sag',penalty='l2',C=0.5,random_state=0)
logreg.fit(X_train, y_train)
y_pred = logreg.predict(X_test)
print('Logistic Regression predicts the correct class label with a',str(round(accuracy_score(y_test, y_pred)*100,2)),'% accuracy.')
kfold=KFold(n_splits=10, random_state=0)
modelCV = LogisticRegression(max_iter=1000,solver='sag',penalty='l2',C=0.5,random_state=0)
scoring = 'f1_micro'
results = cross_val_score(modelCV, X, y, cv=kfold,scoring=scoring)
print("10-fold average cross validation average F1 micro score: %.3f" % (results.mean()))
```
###Method 3: Support Vector Classifier with Linear Kernel
####Hyperparameter Tuning
```
def linsvc_param_selection(X, y, nfolds):
Cs = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1,1.5,2,2.5,3]
param_grid = {'C': Cs}
grid_search = GridSearchCV(LinearSVC(random_state=0), param_grid, cv=nfolds,scoring='f1_micro')
grid_search.fit(X, y)
grid_search.best_params_
return grid_search.best_params_
linsvc_param_selection(X_train, y_train, 10)
```
####Model Fitting and Analysis
```
clf = LinearSVC(C=0.1,random_state=0)
linsvc = CalibratedClassifierCV(clf)
linsvc.fit(X_train, y_train)
y_pred=linsvc.predict(X_test)
print('Linear SVC predicts the correct class label with a',str(round(accuracy_score(y_test, y_pred)*100,2)),'% accuracy.')
kfold=KFold(n_splits=10, random_state=0)
modelCV = CalibratedClassifierCV(LinearSVC(C=0.1,random_state=0))
scoring = 'f1_micro'
results = cross_val_score(modelCV, X, y, cv=kfold,scoring=scoring)
print("10-fold average cross validation average F1 micro score: %.3f" % (results.mean()))
```
###Summary
We have seen a multi-class dataset, and have more than halved the number of features using Principal Component Analysis. As we can see, PCA is an extremely powerful tool for feature selection (or feature engineering, in a way!), and one major advantage it has is that it produces orthogonal, independent components. We used the Principal Components in 3 machine learning algorithms, to predict our class labels. Since we had a class imbalance, we used the F1 Micro score as our primary measure of effectiveness. The average scores of a 10 fold cross validation set (on the whole dataset) for each algorithm are tabulated below:
| Classifier | F1 Micro (10 fold CV) |
| --- | --- |
| K-Nearest Neighbours | 0.950
| Logistic Regression | 0.933
| Linear SVC | 0.944
It can be seen that the highest score is when we used the K-Nearest Neighbours algorithm, while the worst (not bad by any measure) was Logistic Regression. The power of simplicity really shines in this dataset. KNN is one of the simplest classifiers and yet was able to outperform far more complex classifiers. This can be attributed to the fact that our classes are very well segregated (see wine class scatter plot), and while the other two algorithms were able to predict the classes with 100% accuracy, they generalize worse, over the whole dataset. This is why KNN comes out on top. Simple, elegant and fast!
|
github_jupyter
|
```
import numpy as np
import pandas as pd
import json
import shap
import matplotlib.pyplot as plt
from matplotlib import rc
from colour import Color
from matplotlib.colors import ListedColormap, LinearSegmentedColormap
import collections
import pickle
colors = ['#3f7f93','#da3b46','#F6AE2D', '#98b83b', '#825FC3']
cmp_5 = LinearSegmentedColormap.from_list('my_list', [Color(c1).rgb for c1 in colors], N=len(colors))
seed = 42
def abs_shap(df_shap, df, shap_plot, names, class_names, cmp):
''' A function to plot the bar plot for the mean abs SHAP values
arguments:
df_shap: the dataframe of the SHAP values
df: the dataframe for the feature values for which the SHAP values have been determined
shap_plot: The name of the output file for the plot
names: The names of the variables
class_names: names of the classes
cmp: the colour map
'''
rc('text', usetex=True)
plt.rcParams['text.latex.preamble'] = r"\usepackage{amsmath}"
plt.figure(figsize=(5,5))
shap.summary_plot(df_shap, df, color=cmp, class_names=class_names, class_inds='original', plot_size=(5,5), show=False)#, feature_names=names)
ax = plt.gca()
handles, labels = ax.get_legend_handles_labels()
ax.legend(reversed(handles), reversed(labels), loc='lower right', fontsize=15)
plt.xlabel(r'$\overline{|S_v|}$', fontsize=15)
ax = plt.gca()
ax.spines["top"].set_visible(True)
ax.spines["right"].set_visible(True)
ax.spines["left"].set_visible(True)
vals = ax.get_xticks()
ax.tick_params(axis='both', which='major', labelsize=15)
for tick in vals:
ax.axvline(x=tick, linestyle='dashed', alpha=0.7, color='#808080', zorder=0, linewidth=0.5)
plt.tight_layout()
plt.savefig(shap_plot, dpi=300)
rc('text', usetex=False)
def get_mclass(i, df_array, weight_array, ps_exp_class, seed=seed):
""" This function is used to create the confusion matrix
arguments:
i: integer corresponding to the class number
df_array: the array of the dataframes of the different classes
weight_array: the array of the weights for the different classes
ps_exp_class: the collection of the pseudo experiment events
seed: the seed for the random number generator
returns:
nevents: the number of events
sif: the significance
"""
mclass = []
nchannels = len(df_array)
for j in range(nchannels):
mclass.append(collections.Counter(classifier.predict(df_array[j].iloc[:,:-2].values))[i]/len(df_array[j])*weight_array[j]/weight_array[i])
sig = np.sqrt(ps_exp_class[i])*mclass[i]/np.sum(mclass)
nevents = np.round(ps_exp_class[i]/np.sum(mclass)*np.array(mclass)).astype(int)
if nchannels == 5: print('sig: {:2.2f}, klam events: {}, hhsm events: {}, tth events: {}, bbh events: {}, bbxaa events: {}'.format(sig, nevents[4], nevents[3], nevents[2], nevents[1], nevents[0]))
if nchannels == 4: print('sig: {:2.2f}, hhsm events: {}, tth events: {}, bbh events: {}, bbxaa events: {}'.format(sig, nevents[3], nevents[2], nevents[1], nevents[0]))
if nchannels == 2: print('sig: {:2.2f}, ku events: {}, hhsm events: {}'.format(sig, nevents[1], nevents[0]))
return nevents, sig
prefix = '../WORK/klm1/'
df_sig_test = pd.read_json(prefix+'test_files/sig_test.json')
df_bkg_test = pd.read_json(prefix+'test_files/bkg_test.json')
df_bbh_test = pd.read_json(prefix+'test_files/bbh_test.json')
df_tth_test = pd.read_json(prefix+'test_files/tth_test.json')
df_bbxaa_test = pd.read_json(prefix+'test_files/bbxaa_test.json')
X_shap = pd.read_json(prefix+'shapley_files/shapley_X.json')
with open(prefix+'shapley_files/shapley_values.json', 'r') as f:
shapley_values = json.load(f)['shap_values']
shapley_values = [np.array(elem) for elem in shapley_values]
weight_sig = df_sig_test['weight'].sum()
weight_bkg = df_bkg_test['weight'].mean()
weight_bbh = df_bbh_test['weight'].mean()
weight_tth = df_tth_test['weight'].mean()
weight_bbxaa = df_bbxaa_test['weight'].mean()
classifier = pickle.load(open(prefix+'hbb-BDT-5class-hhsm-klm1.csv.pickle.dat', 'rb'))
with open(prefix+'test_files/weights.json', 'r') as f:
weights = json.load(f)
class_names = [r'$bb\gamma\gamma$', r'$b\bar{b}h$', r'$t\bar{t}h$', r'$hh^{SM}$', r'$hh^{\kappa_u}$']
names = list(df_bbxaa_test.columns)[:-2]
shap_plot = '../plots/shap-klm1.pdf'
abs_shap(shapley_values, X_shap, shap_plot, names, class_names, cmp=cmp_5)
df_array = [df_bbxaa_test, df_bbh_test, df_tth_test, df_bkg_test, df_sig_test]
weight_array = [weights['weight_bbxaa']*1.5, weights['weight_bbh'],
weights['weight_tth']*1.2, weights['weight_bkg']*1.72, weights['weight_sig']*1.28]
ps_exp_class = collections.Counter(classifier.predict(pd.concat([df_array[4].iloc[:,:-2].sample(n=round(weight_array[4]), random_state=seed, replace=True),
df_array[3].iloc[:,:-2].sample(n=round(weight_array[3]), random_state=seed, replace=True),
df_array[2].iloc[:,:-2].sample(n=round(weight_array[2]), random_state=seed, replace=True),
df_array[1].iloc[:,:-2].sample(n=round(weight_array[1]), random_state=seed, replace=True),
df_array[0].iloc[:,:-2].sample(n=round(weight_array[0]), random_state=seed, replace=True)]).values))
nevents_ku, sig_ku = get_mclass(4, df_array, weight_array, ps_exp_class)
nevents_hhsm, sig_hhsm = get_mclass(3, df_array, weight_array, ps_exp_class)
nevents_tth, sig_tth = get_mclass(2, df_array, weight_array, ps_exp_class)
nevents_bbh, sig_bbh = get_mclass(1, df_array, weight_array, ps_exp_class)
nevents_bbxaa, sig_bbxaa = get_mclass(0, df_array, weight_array, ps_exp_class)
confusion = np.column_stack((nevents_ku, nevents_hhsm, nevents_tth, nevents_bbh, nevents_bbxaa))
```
|
github_jupyter
|
```
%load_ext autoreload
%autoreload 2
import pandas as pd
import time
from pandarallel import pandarallel
import math
import numpy as np
```
# Initialize pandarallel
```
pandarallel.initialize()
```
# DataFrame.apply
```
df_size = int(5e6)
df = pd.DataFrame(dict(a=np.random.randint(1, 8, df_size),
b=np.random.rand(df_size)))
def func(x):
return math.sin(x.a**2) + math.sin(x.b**2)
%%time
res = df.apply(func, axis=1)
%%time
res_parallel = df.parallel_apply(func, axis=1)
res.equals(res_parallel)
```
# DataFrame.applymap
```
df_size = int(1e7)
df = pd.DataFrame(dict(a=np.random.randint(1, 8, df_size),
b=np.random.rand(df_size)))
def func(x):
return math.sin(x**2) - math.cos(x**2)
%%time
res = df.applymap(func)
%%time
res_parallel = df.parallel_applymap(func)
res.equals(res_parallel)
```
# DataFrame.groupby.apply
```
df_size = int(3e7)
df = pd.DataFrame(dict(a=np.random.randint(1, 1000, df_size),
b=np.random.rand(df_size)))
def func(df):
dum = 0
for item in df.b:
dum += math.log10(math.sqrt(math.exp(item**2)))
return dum / len(df.b)
%%time
res = df.groupby("a").apply(func)
%%time
res_parallel = df.groupby("a").parallel_apply(func)
res.equals(res_parallel)
```
# DataFrame.groupby.rolling.apply
```
df_size = int(1e6)
df = pd.DataFrame(dict(a=np.random.randint(1, 300, df_size),
b=np.random.rand(df_size)))
def func(x):
return x.iloc[0] + x.iloc[1] ** 2 + x.iloc[2] ** 3 + x.iloc[3] ** 4
%%time
res = df.groupby('a').b.rolling(4).apply(func, raw=False)
%%time
res_parallel = df.groupby('a').b.rolling(4).parallel_apply(func, raw=False)
res.equals(res_parallel)
```
# DataFrame.groupby.expanding.apply
```
df_size = int(1e6)
df = pd.DataFrame(dict(a=np.random.randint(1, 300, df_size),
b=np.random.rand(df_size)))
def func(x):
return x.iloc[0] + x.iloc[1] ** 2 + x.iloc[2] ** 3 + x.iloc[3] ** 4
%%time
res = df.groupby('a').b.expanding(4).apply(func, raw=False)
%%time
res_parallel = df.groupby('a').b.expanding(4).parallel_apply(func, raw=False)
```
# Series.map
```
df_size = int(5e7)
df = pd.DataFrame(dict(a=np.random.rand(df_size) + 1))
def func(x):
return math.log10(math.sqrt(math.exp(x**2)))
%%time
res = df.a.map(func)
%%time
res_parallel = df.a.parallel_map(func)
res.equals(res_parallel)
```
# Series.apply
```
df_size = int(3.5e7)
df = pd.DataFrame(dict(a=np.random.rand(df_size) + 1))
def func(x, power, bias=0):
return math.log10(math.sqrt(math.exp(x**power))) + bias
%%time
res = df.a.apply(func, args=(2,), bias=3)
%%time
res_parallel = df.a.parallel_apply(func, args=(2,), bias=3)
res.equals(res_parallel)
```
# Series.rolling.apply
```
df_size = int(1e6)
df = pd.DataFrame(dict(a=np.random.randint(1, 8, df_size),
b=list(range(df_size))))
def func(x):
return x.iloc[0] + x.iloc[1] ** 2 + x.iloc[2] ** 3 + x.iloc[3] ** 4
%%time
res = df.b.rolling(4).apply(func, raw=False)
%%time
res_parallel = df.b.rolling(4).parallel_apply(func, raw=False)
res.equals(res_parallel)
```
|
github_jupyter
|
# What is the most popular start station and most popular end station?
```
#one
import csv
from pprint import pprint
"""This takes the file and returns dict of values. """
with open('chicago.csv', newline='') as csv_file:
reader = [{key: value for key, value in row.items()} #list comprehimsion or one liners {} its s dictionary
for row in csv.DictReader(csv_file, skipinitialspace=True)]
"""creates a mini chicogo file called testing"""
testing=(reader[0:15])
pprint(testing[0:1])
from collections import Counter
"""start/end station popular"""
station_start = []
station_end = []
for x in testing:
station_start.append(x['Start Station'])
station_end.append(x['End Station'])
y=Counter(station_start)
d= max(y,key=y.get)
z=Counter(station_end)
e= max(z,key=z.get)
print('popular start station is {} and popular end station is {}'.format(d,e) )
#one
import csv
from pprint import pprint
from collections import Counter
"""This takes the file and returns dict of values. """
with open('chicago.csv', newline='') as csv_file:
reader = [{key: value for key, value in row.items()} #list comprehimsion or one liners {} its s dictionary
for row in csv.DictReader(csv_file, skipinitialspace=True)]
"""start/end station popular"""
station_start = []
station_end = []
for x in reader:
station_start.append(x['Start Station'])
station_end.append(x['End Station'])
y=Counter(station_start)
d= max(y,key=y.get)
z=Counter(station_end)
e= max(z,key=z.get)
print('popular start station is {} and popular end station is {}'.format(d,e) )
station_start = []
station_end = []
pop_start = []
pop_end = []
elif time_period == 'month' :
"""filter month wise"""
for x in city_file:
a=(calendar.month_name[int(x['Start Time'][5:7])]) #month name
b=x['Start Station']
c=x['End Station']
popular_start += [(a,b)]
popular_end += [(a,b)]
x= Counter (pop_start)
y= max(x, key=x.get)
xx= Counter (pop_end)
yy= max(xx, key=x.get)
return (y,yy)
else:
"""filter by day"""
for x in city_file:
a=parser.parse(x['Start Time']).strftime("%a") # day name
b=x['Start Station']
c=x['End Station']
popular_start += [(a,b)]
popular_end += [(a,b)]
x= Counter (pop_start)
y= max(x, key=x.get)
xx= Counter (pop_end)
yy= max(xx, key=x.get)
return (y,yy)
popular_hour_day = []
for x in file_st:
a=parser.parse(x['Start Time']).strftime("%a") # day name
b=hour(x)
popular_day += [(a,b)]
xx= Counter(popular_hour)
yy= max(xx, key=xx.get) #retund the filtered month and popular day example june:friday
return (yy)
elif time_period == 'month' :
"""filter month wise"""
for x in file_st:
a=(calendar.month_name[int(x['Start Time'][5:7])]) #month name
b=hour(x)
popular_day += [(a,b)]
x= Counter (popular_hour)
y= max(x, key=x.get) #retund the filtered month and popular day example june:friday
return (y)
else:
"""filter by day"""
popular_hour_day = []
for x in file_st:
a=parser.parse(x['Start Time']).strftime("%a") # day name
b=hour(x)
popular_day += [(a,b)]
xx= Counter(popular_hour)
yy= max(xx, key=xx.get) #retund the filtered month and popular day example june:friday
return (yy)
```
|
github_jupyter
|
<a href="https://www.bigdatauniversity.com"><img src="https://ibm.box.com/shared/static/cw2c7r3o20w9zn8gkecaeyjhgw3xdgbj.png" width="400" align="center"></a>
<h1 align=center><font size="5"> SVM (Support Vector Machines)</font></h1>
In this notebook, you will use SVM (Support Vector Machines) to build and train a model using human cell records, and classify cells to whether the samples are benign or malignant.
SVM works by mapping data to a high-dimensional feature space so that data points can be categorized, even when the data are not otherwise linearly separable. A separator between the categories is found, then the data is transformed in such a way that the separator could be drawn as a hyperplane. Following this, characteristics of new data can be used to predict the group to which a new record should belong.
<h1>Table of contents</h1>
<div class="alert alert-block alert-info" style="margin-top: 20px">
<ol>
<li><a href="#load_dataset">Load the Cancer data</a></li>
<li><a href="#modeling">Modeling</a></li>
<li><a href="#evaluation">Evaluation</a></li>
<li><a href="#practice">Practice</a></li>
</ol>
</div>
<br>
<hr>
```
import pandas as pd
import pylab as pl
import numpy as np
import scipy.optimize as opt
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
%matplotlib inline
import matplotlib.pyplot as plt
```
<h2 id="load_dataset">Load the Cancer data</h2>
The example is based on a dataset that is publicly available from the UCI Machine Learning Repository (Asuncion and Newman, 2007)[http://mlearn.ics.uci.edu/MLRepository.html]. The dataset consists of several hundred human cell sample records, each of which contains the values of a set of cell characteristics. The fields in each record are:
|Field name|Description|
|--- |--- |
|ID|Clump thickness|
|Clump|Clump thickness|
|UnifSize|Uniformity of cell size|
|UnifShape|Uniformity of cell shape|
|MargAdh|Marginal adhesion|
|SingEpiSize|Single epithelial cell size|
|BareNuc|Bare nuclei|
|BlandChrom|Bland chromatin|
|NormNucl|Normal nucleoli|
|Mit|Mitoses|
|Class|Benign or malignant|
<br>
<br>
For the purposes of this example, we're using a dataset that has a relatively small number of predictors in each record. To download the data, we will use `!wget` to download it from IBM Object Storage.
__Did you know?__ When it comes to Machine Learning, you will likely be working with large datasets. As a business, where can you host your data? IBM is offering a unique opportunity for businesses, with 10 Tb of IBM Cloud Object Storage: [Sign up now for free](http://cocl.us/ML0101EN-IBM-Offer-CC)
```
#Click here and press Shift+Enter
!wget -O cell_samples.csv https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/ML0101ENv3/labs/cell_samples.csv
```
### Load Data From CSV File
```
cell_df = pd.read_csv("cell_samples.csv")
cell_df.head()
cell_df.describe
```
The ID field contains the patient identifiers. The characteristics of the cell samples from each patient are contained in fields Clump to Mit. The values are graded from 1 to 10, with 1 being the closest to benign.
The Class field contains the diagnosis, as confirmed by separate medical procedures, as to whether the samples are benign (value = 2) or malignant (value = 4).
Lets look at the distribution of the classes based on Clump thickness and Uniformity of cell size:
```
ax = cell_df[cell_df['Class'] == 4][0:50].plot(kind='scatter', x='Clump', y='UnifSize', color='DarkBlue', label='malignant');
cell_df[cell_df['Class'] == 2][0:50].plot(kind='scatter', x='Clump', y='UnifSize', color='Yellow', label='benign', ax=ax);
plt.show()
```
## Data pre-processing and selection
Lets first look at columns data types:
```
cell_df.dtypes
```
It looks like the __BareNuc__ column includes some values that are not numerical. We can drop those rows:
```
cell_df = cell_df[pd.to_numeric(cell_df['BareNuc'], errors='coerce').notnull()]
cell_df['BareNuc'] = cell_df['BareNuc'].astype('int')
cell_df.dtypes
feature_df = cell_df[['Clump', 'UnifSize', 'UnifShape', 'MargAdh', 'SingEpiSize', 'BareNuc', 'BlandChrom', 'NormNucl', 'Mit']]
X = np.asarray(feature_df)
X[0:5]
```
We want the model to predict the value of Class (that is, benign (=2) or malignant (=4)). As this field can have one of only two possible values, we need to change its measurement level to reflect this.
```
cell_df['Class'] = cell_df['Class'].astype('int')
y = np.asarray(cell_df['Class'])
y [0:5]
```
## Train/Test dataset
Okay, we split our dataset into train and test set:
```
X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.2, random_state=4)
print ('Train set:', X_train.shape, y_train.shape)
print ('Test set:', X_test.shape, y_test.shape)
```
<h2 id="modeling">Modeling (SVM with Scikit-learn)</h2>
The SVM algorithm offers a choice of kernel functions for performing its processing. Basically, mapping data into a higher dimensional space is called kernelling. The mathematical function used for the transformation is known as the kernel function, and can be of different types, such as:
1.Linear
2.Polynomial
3.Radial basis function (RBF)
4.Sigmoid
Each of these functions has its characteristics, its pros and cons, and its equation, but as there's no easy way of knowing which function performs best with any given dataset, we usually choose different functions in turn and compare the results. Let's just use the default, RBF (Radial Basis Function) for this lab.
```
from sklearn import svm
clf = svm.SVC(kernel='rbf')
clf.fit(X_train, y_train)
```
After being fitted, the model can then be used to predict new values:
```
yhat = clf.predict(X_test)
yhat [0:5]
```
<h2 id="evaluation">Evaluation</h2>
```
from sklearn.metrics import classification_report, confusion_matrix
import itertools
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test, yhat, labels=[2,4])
np.set_printoptions(precision=2)
print (classification_report(y_test, yhat))
# Plot non-normalized confusion matrix
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=['Benign(2)','Malignant(4)'],normalize= False, title='Confusion matrix')
```
You can also easily use the __f1_score__ from sklearn library:
```
from sklearn.metrics import f1_score
f1_score(y_test, yhat, average='weighted')
```
Lets try jaccard index for accuracy:
```
from sklearn.metrics import jaccard_similarity_score
jaccard_similarity_score(y_test, yhat)
```
<h2 id="practice">Practice</h2>
Can you rebuild the model, but this time with a __linear__ kernel? You can use __kernel='linear'__ option, when you define the svm. How the accuracy changes with the new kernel function?
```
# write your code here
```
Double-click __here__ for the solution.
<!-- Your answer is below:
clf2 = svm.SVC(kernel='linear')
clf2.fit(X_train, y_train)
yhat2 = clf2.predict(X_test)
print("Avg F1-score: %.4f" % f1_score(y_test, yhat2, average='weighted'))
print("Jaccard score: %.4f" % jaccard_similarity_score(y_test, yhat2))
-->
<h2>Want to learn more?</h2>
IBM SPSS Modeler is a comprehensive analytics platform that has many machine learning algorithms. It has been designed to bring predictive intelligence to decisions made by individuals, by groups, by systems – by your enterprise as a whole. A free trial is available through this course, available here: <a href="http://cocl.us/ML0101EN-SPSSModeler">SPSS Modeler</a>
Also, you can use Watson Studio to run these notebooks faster with bigger datasets. Watson Studio is IBM's leading cloud solution for data scientists, built by data scientists. With Jupyter notebooks, RStudio, Apache Spark and popular libraries pre-packaged in the cloud, Watson Studio enables data scientists to collaborate on their projects without having to install anything. Join the fast-growing community of Watson Studio users today with a free account at <a href="https://cocl.us/ML0101EN_DSX">Watson Studio</a>
<h3>Thanks for completing this lesson!</h3>
<h4>Author: <a href="https://ca.linkedin.com/in/saeedaghabozorgi">Saeed Aghabozorgi</a></h4>
<p><a href="https://ca.linkedin.com/in/saeedaghabozorgi">Saeed Aghabozorgi</a>, PhD is a Data Scientist in IBM with a track record of developing enterprise level applications that substantially increases clients’ ability to turn data into actionable knowledge. He is a researcher in data mining field and expert in developing advanced analytic methods like machine learning and statistical modelling on large datasets.</p>
<hr>
<p>Copyright © 2018 <a href="https://cocl.us/DX0108EN_CC">Cognitive Class</a>. This notebook and its source code are released under the terms of the <a href="https://bigdatauniversity.com/mit-license/">MIT License</a>.</p>
|
github_jupyter
|
# Iteration
**CS1302 Introduction to Computer Programming**
___
```
%reload_ext mytutor
from ipywidgets import interact
```
## Motivation
Many tasks are repetitive:
- To print from 1 up to a user-specified number *arbitrarily large*.
- To compute the maximum of a sequence of numbers *arbitrarily long*.
- To get user input *repeatedly until* it is within a certain range.
**How to write code to perform repetitive tasks?**
E.g., can you complete the following code to print from 1 up to a user-specified number?
```
%%mytutor -h 400
num = int(input(">"))
if 1 <= num:
print(1)
if 2 <= num:
print(2)
if 3 <= num:
print(3)
# YOUR CODE HERE
```
*Code duplication* is not good because:
- Duplicate code is hard to read/write/maintain.
(Imagine what you need to do to change some code.)
- The number of repetitions may not be known before runtime.
Instead, programmers write a *loop* which specifies a piece of code to be executed iteratively.
## For Loop
### Iterate over a sequence
**How to print from 1 up to 4?**
We can use a [`for` statement](https://docs.python.org/3.3/tutorial/controlflow.html#for-statements) as follows:
```
%%mytutor -h 300
for i in 1, 2, 3, 4:
print(i)
```
- `i` is automatically assigned to each element in the sequence `1, 2, 3, 4` one-by-one from left to right.
- After each assignment, the body `print(i)` is executed.
N.b., if `i` is defined before the for loop, its value will be overwritten.
The assignment is not restricted to integers and can also be a tuple assignment. The expression list can also be an [iterable object](https://docs.python.org/3.3/glossary.html#term-iterable) instead.
```
tuples = (0, "l"), (1, "o"), (2, "o"), (3, "p")
for i, c in tuples:
print(i, c)
```
An even shorter code...
```
for i, c in enumerate("loop"):
print(i, c)
```
### Iterate over a range
**How to print up to a user-specified number?**
We can use [`range`](https://docs.python.org/3/library/stdtypes.html#range):
```
%%mytutor -h 300
stop = int(input(">")) + 1
for i in range(stop):
print(i)
```
**Why add 1 to the user input number?**
`range(stop)` generates a sequence of integers from `0` up to *but excluding* `stop`.
**How to start from a number different from `0`?**
```
for i in range(1, 5):
print(i)
```
**What about a step size different from `1`?**
```
for i in range(0, 5, 2): print(i) # starting number must also be specified. Why?
```
**Exercise** How to count down from 4 to 0? Try doing it without addition or subtraction.
```
# YOUR CODE HERE
raise NotImplementedError()
```
**Exercise** Print from `0` to a user-specified number but in steps of `0.5`.
E.g., if the user inputs `2`, the program should print:
```
0.0
0.5
1.0
1.5
2.0
```
*Note:* `range` only accepts integer arguments.
```
%%mytutor -h 300
num = int(input(">"))
# YOUR CODE HERE
raise NotImplementedError()
```
**Exercise** How to print the character `'*'` repeatedly for `m` rows and `n` columns?
Try using a *nested for loop*: Write a for loop (*inner loop*) inside the body of another for loop (*outer loop*).
```
@interact(m=(0, 10), n=(0, 10))
def draw_rectangle(m=5, n=5):
# YOUR CODE HERE
raise NotImplementedError()
```
### Iterate over a string
**What does the following do?**
```
%%mytutor -h 300
for character in "loop":
print(character)
```
`str` is a [sequence type](https://docs.python.org/3/library/stdtypes.html#textseq) because a string is regarded as a sequence of characters.
- The function [`len`](https://docs.python.org/3/library/functions.html#len) can return the length of a string.
- The indexing operator `[]` can return the character of a string at a specified location.
```
message = "loop"
print("length:", len(message))
print("characters:", message[0], message[1], message[2], message[3])
```
We can also iterate over a string as follows although it is less elegant:
```
for i in range(len("loop")):
print("loop"[i])
```
**Exercise** Print a string assigned to `message` in reverse.
E.g., `'loop'` should be printed as `'pool'`. Try using the for loop and indexing operator.
```
@interact(message="loop")
def reverse_print(message):
# YOUR CODE HERE
raise NotImplementedError()
```
## While Loop
**How to ensure user input is non-empty?**
Python provides the [`while` statement](https://docs.python.org/3/reference/compound_stmts.html#while) to loop until a specified condition is false.
```
%%mytutor -h 300
while not input("Input something please:"):
pass
```
As long as the condition after `while` is true, the body gets executed repeatedly. In the above example,
- if user inputs nothing,
- `input` returns an empty string `''`, which is [regarded as `False`](https://docs.python.org/3/reference/expressions.html#booleans), and so
- the looping condition `not input('...')` is `True`.
**Is it possible to use a for loop instead of a while loop?**
- Not without hacks because the for loop is a *definite loop* which has a definite number of iterations before the execution of the loop.
- `while` statement is useful for an *indefinite loop* where the number of iterations is unknown before the execution of the loop.
It is possible, however, to replace a for loop by a while loop.
E.g., the following code prints from `0` to `4` using a while loop instead of a for loop.
```
i = 0
while i <= 4:
print(i)
i += 1
```
- A while loop may not be as elegant, c.f.,
```Python
for i in range(5): print(i)
```
- but it can be as efficient.
**Should we just use while loop?**
Consider using the following while loop to print from `0` to a user-specified value.
```
%%mytutor -h 310
num = int(input(">"))
i = 0
while i != num + 1:
print(i)
i += 1
```
**Exercise** Is the above while loop doing the same thing as the for loop below?
```
%%mytutor -h 300
for i in range(int(input(">")) + 1):
print(i)
```
YOUR ANSWER HERE
We have to be careful not to create unintended *infinite loops*.
The computer can't always detect whether there is an infinite loop. ([Why not?](https://en.wikipedia.org/wiki/Halting_problem))
## Break/Continue/Else Constructs of a Loop
### Breaking out of a loop
**Is the following an infinite loop?**
```
%%mytutor -h 310
while True:
message = input("Input something please:")
if message:
break
print("You entered:", message)
```
The loop is terminated by the [`break` statement](https://docs.python.org/3/tutorial/controlflow.html#break-and-continue-statements-and-else-clauses-on-loops) when user input is non-empty.
**Why is the `break` statement useful?**
Recall the earlier `while` loop:
```
%%mytutor -h 300
while not input("Input something please:"):
pass
```
This while loop is not useful because it does not store the user input.
**Is the `break` statement strictly necessary?**
- We can use the assignment expression but it is not supported by Python version <3.8.
- We can avoid `break` statement by using *flags*, which are boolean variables for flow control:
```
%%mytutor -h 350
has_no_input = True
while has_no_input:
message = input("Input something please:")
if message:
has_no_input = False
print("You entered:", message)
```
Using flags makes the program more readable, and we can use multiple flags for more complicated behavior.
The variable names for flags are often `is_...`, `has_...`, etc.
### Continue to Next Iteration
**What does the following program do?
Is it an infinite loop?**
```
%%mytutor -h 310
while True:
message = input("Input something please:")
if not message:
continue
print("You entered:", message)
```
- The program repeatedly asks the user for input.
- If the input is empty, the `continue` statement will skip to the next iteration.
- The loop can only be terminated by interrupting the kernel.
- Such an infinite loop can be useful. E.g., your computer clock continuously updates the current time.
**Exercise** Is the `continue` statement strictly necessary? Can you rewrite the above program without the `continue` statement?
```
%%mytutor -h 350
while True:
message = input("Input something please:")
# YOUR CODE HERE
raise NotImplementedError()
```
### Else construct for a loop
The following program checks whether a number is composite, namely,
- a positive integer that is
- a product of two strictly smaller positive integers.
```
@interact(num="1")
def check_composite(num):
if num.isdigit():
num = int(num)
for divisor in range(2, num): # why starts from 2 instead of 1
if num % divisor:
continue # where will this go?
else:
print("It is composite.")
break # where will this go?
else:
print("It is not composite.") # how to get here?
else:
print("Not a positive integer.") # how to get here?
```
**Exercise** There are three else claues in the earlier code. Which one is for the loop?
- The second else clause that `print('It is not composite.')`.
- The clause is called when there is no divisor found in the range from `2` to `num`.
If program flow is confusing, try stepping through executation:
```
%%mytutor -h 520
def check_composite(num):
if num.isdigit():
num = int(num)
for divisor in range(2, num):
if num % divisor:
continue
else:
print("It is composite.")
break
else:
print("It is not composite.")
else:
print("Not a positive integer.")
check_composite("1")
check_composite("2")
check_composite("3")
check_composite("4")
```
- In addition to using `continue` and `break` in an elegant way,
- the code also uses an else clause that is executed only when the loop terminates *normally* not by `break`.
**Exercise** Convert the for loop to a while loop. Try to make the code as efficient as possible with less computation and storage.
```
@interact(num="1")
def check_composite(num):
if num.isdigit():
num = int(num)
# YOUR CODE HERE
raise NotImplementedError()
else:
print("Not a positive integer.")
```
|
github_jupyter
|
# Use Spark to predict credit risk with `ibm-watson-machine-learning`
This notebook introduces commands for model persistance to Watson Machine Learning repository, model deployment, and scoring.
Some familiarity with Python is helpful. This notebook uses Python 3.6 and Apache® Spark 2.4.
You will use **German Credit Risk** dataset.
## Learning goals
The learning goals of this notebook are:
- Load a CSV file into an Apache® Spark DataFrame.
- Explore data.
- Prepare data for training and evaluation.
- Persist a pipeline and model in Watson Machine Learning repository from tar.gz files.
- Deploy a model for online scoring using Wastson Machine Learning API.
- Score sample scoring data using the Watson Machine Learning API.
- Explore and visualize prediction result using the plotly package.
## Contents
This notebook contains the following parts:
1. [Set up](#setup)
2. [Load and explore data](#load)
3. [Persist model](#persistence)
4. [Predict locally](#visualization)
5. [Deploy and score](#scoring)
6. [Clean up](#cleanup)
7. [Summary and next steps](#summary)
<a id="setup"></a>
## 1. Set up the environment
Before you use the sample code in this notebook, you must perform the following setup tasks:
- Contact with your Cloud Pack for Data administrator and ask him for your account credentials
### Connection to WML
Authenticate the Watson Machine Learning service on IBM Cloud Pack for Data. You need to provide platform `url`, your `username` and `password`.
```
username = 'PASTE YOUR USERNAME HERE'
password = 'PASTE YOUR PASSWORD HERE'
url = 'PASTE THE PLATFORM URL HERE'
wml_credentials = {
"username": username,
"password": password,
"url": url,
"instance_id": 'openshift',
"version": '3.5'
}
```
### Install and import the `ibm-watson-machine-learning` package
**Note:** `ibm-watson-machine-learning` documentation can be found <a href="http://ibm-wml-api-pyclient.mybluemix.net/" target="_blank" rel="noopener no referrer">here</a>.
```
!pip install -U ibm-watson-machine-learning
from ibm_watson_machine_learning import APIClient
client = APIClient(wml_credentials)
```
### Working with spaces
First of all, you need to create a space that will be used for your work. If you do not have space already created, you can use `{PLATFORM_URL}/ml-runtime/spaces?context=icp4data` to create one.
- Click New Deployment Space
- Create an empty space
- Go to space `Settings` tab
- Copy `space_id` and paste it below
**Tip**: You can also use SDK to prepare the space for your work. More information can be found [here](https://github.com/IBM/watson-machine-learning-samples/blob/master/cpd3.5/notebooks/python_sdk/instance-management/Space%20management.ipynb).
**Action**: Assign space ID below
```
space_id = 'PASTE YOUR SPACE ID HERE'
```
You can use `list` method to print all existing spaces.
```
client.spaces.list(limit=10)
```
To be able to interact with all resources available in Watson Machine Learning, you need to set **space** which you will be using.
```
client.set.default_space(space_id)
```
### Test Spark
```
try:
from pyspark.sql import SparkSession
except:
print('Error: Spark runtime is missing. If you are using Watson Studio change the notebook runtime to Spark.')
raise
```
<a id="load"></a>
## 2. Load and explore data
In this section you will load the data as an Apache® Spark DataFrame and perform a basic exploration.
The csv file for German Credit Risk is available on the same repository as this notebook. Load the file to Apache® Spark DataFrame using code below.
```
import os
from wget import download
sample_dir = 'spark_sample_model'
if not os.path.isdir(sample_dir):
os.mkdir(sample_dir)
filename = os.path.join(sample_dir, 'credit_risk_training.csv')
if not os.path.isfile(filename):
filename = download('https://github.com/IBM/watson-machine-learning-samples/raw/master/cpd3.5/data/credit_risk/credit_risk_training.csv', out=sample_dir)
spark = SparkSession.builder.getOrCreate()
df_data = spark.read\
.format('org.apache.spark.sql.execution.datasources.csv.CSVFileFormat')\
.option('header', 'true')\
.option('inferSchema', 'true')\
.load(filename)
```
Explore the loaded data by using the following Apache® Spark DataFrame methods:
- print schema
- print top ten records
- count all records
```
df_data.printSchema()
```
As you can see, the data contains 21 fields. Risk field is the one we would like to predict (label).
```
df_data.show(n=5, truncate=False, vertical=True)
print("Number of records: " + str(df_data.count()))
```
As you can see, the data set contains 5000 records.
### 2.1 Prepare data
In this subsection you will split your data into: train, test and predict datasets.
```
splitted_data = df_data.randomSplit([0.8, 0.18, 0.02], 24)
train_data = splitted_data[0]
test_data = splitted_data[1]
predict_data = splitted_data[2]
print("Number of training records: " + str(train_data.count()))
print("Number of testing records : " + str(test_data.count()))
print("Number of prediction records : " + str(predict_data.count()))
```
As you can see our data has been successfully split into three datasets:
- The train data set, which is the largest group, is used for training.
- The test data set will be used for model evaluation and is used to test the assumptions of the model.
- The predict data set will be used for prediction.
<a id="persistence"></a>
## 3. Persist model
In this section you will learn how to store your pipeline and model in Watson Machine Learning repository by using python client libraries.
**Note**: Apache® Spark 2.4 is required.
### 3.1: Save pipeline and model
In this subsection you will learn how to save pipeline and model artifacts to your Watson Machine Learning instance.
**Download pipeline and model archives**
```
import os
from wget import download
sample_dir = 'spark_sample_model'
if not os.path.isdir(sample_dir):
os.mkdir(sample_dir)
pipeline_filename = os.path.join(sample_dir, 'credit_risk_spark_pipeline.tar.gz')
if not os.path.isfile(pipeline_filename):
pipeline_filename = download('https://github.com/IBM/watson-machine-learning-samples/raw/master/cpd3.5/models/spark/credit-risk/model/credit_risk_spark_pipeline.tar.gz', out=sample_dir)
model_filename = os.path.join(sample_dir, 'credit_risk_spark_model.gz')
if not os.path.isfile(model_filename):
model_filename = download('https://github.com/IBM/watson-machine-learning-samples/raw/master/cpd3.5/models/spark/credit-risk/model/credit_risk_spark_model.gz', out=sample_dir)
```
**Store piepline and model**
To be able to store your Spark model, you need to provide a training data reference, this will allow to read the model schema automatically.
```
training_data_references = [
{
"type": "fs",
"connection": {},
"location": {},
"schema": {
"id": "training_schema",
"fields": [
{
"metadata": {},
"name": "CheckingStatus",
"nullable": True,
"type": "string"
},
{
"metadata": {},
"name": "LoanDuration",
"nullable": True,
"type": "integer"
},
{
"metadata": {},
"name": "CreditHistory",
"nullable": True,
"type": "string"
},
{
"metadata": {},
"name": "LoanPurpose",
"nullable": True,
"type": "string"
},
{
"metadata": {},
"name": "LoanAmount",
"nullable": True,
"type": "integer"
},
{
"metadata": {},
"name": "ExistingSavings",
"nullable": True,
"type": "string"
},
{
"metadata": {},
"name": "EmploymentDuration",
"nullable": True,
"type": "string"
},
{
"metadata": {},
"name": "InstallmentPercent",
"nullable": True,
"type": "integer"
},
{
"metadata": {},
"name": "Sex",
"nullable": True,
"type": "string"
},
{
"metadata": {},
"name": "OthersOnLoan",
"nullable": True,
"type": "string"
},
{
"metadata": {},
"name": "CurrentResidenceDuration",
"nullable": True,
"type": "integer"
},
{
"metadata": {},
"name": "OwnsProperty",
"nullable": True,
"type": "string"
},
{
"metadata": {},
"name": "Age",
"nullable": True,
"type": "integer"
},
{
"metadata": {},
"name": "InstallmentPlans",
"nullable": True,
"type": "string"
},
{
"metadata": {},
"name": "Housing",
"nullable": True,
"type": "string"
},
{
"metadata": {},
"name": "ExistingCreditsCount",
"nullable": True,
"type": "integer"
},
{
"metadata": {},
"name": "Job",
"nullable": True,
"type": "string"
},
{
"metadata": {},
"name": "Dependents",
"nullable": True,
"type": "integer"
},
{
"metadata": {},
"name": "Telephone",
"nullable": True,
"type": "string"
},
{
"metadata": {},
"name": "ForeignWorker",
"nullable": True,
"type": "string"
},
{
"metadata": {
"modeling_role": "target"
},
"name": "Risk",
"nullable": True,
"type": "string"
}
]
}
}
]
published_model_details = client.repository.store_model(
model=model_filename,
meta_props={
client.repository.ModelMetaNames.NAME:'Credit Risk model',
client.repository.ModelMetaNames.TYPE: "mllib_2.4",
client.repository.ModelMetaNames.SOFTWARE_SPEC_UID: client.software_specifications.get_id_by_name('spark-mllib_2.4'),
client.repository.ModelMetaNames.TRAINING_DATA_REFERENCES: training_data_references,
client.repository.ModelMetaNames.LABEL_FIELD: "Risk",
},
training_data=train_data,
pipeline=pipeline_filename)
model_uid = client.repository.get_model_uid(published_model_details)
print(model_uid)
client.repository.get_model_details(model_uid)
```
Get saved model metadata from Watson Machine Learning.
**Tip**: Use `client.repository.ModelMetaNames.show()` to get the list of available props.
```
client.repository.ModelMetaNames.show()
```
### 3.2: Load model
In this subsection you will learn how to load back saved model from specified instance of Watson Machine Learning.
```
loaded_model = client.repository.load(model_uid)
```
You can print for example model name to make sure that model has been loaded correctly.
```
print(type(loaded_model))
```
<a id="visualization"></a>
## 4. Predict locally
In this section you will learn how to score test data using loaded model.
### 4.1: Make local prediction using previously loaded model and test data
In this subsection you will score *predict_data* data set.
```
predictions = loaded_model.transform(predict_data)
```
Preview the results by calling the *show()* method on the predictions DataFrame.
```
predictions.show(5)
```
By tabulating a count, you can see which product line is the most popular.
```
predictions.select("predictedLabel").groupBy("predictedLabel").count().show(truncate=False)
```
<a id="scoring"></a>
## 5. Deploy and score
In this section you will learn how to create online scoring and to score a new data record using `ibm-watson-machine-learning`.
**Note:** You can also use REST API to deploy and score.
For more information about REST APIs, see the [Swagger Documentation](https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Deployments/deployments_create).
### 5.1: Create online scoring endpoint
Now you can create an online scoring endpoint.
#### Create online deployment for published model
```
deployment_details = client.deployments.create(
model_uid,
meta_props={
client.deployments.ConfigurationMetaNames.NAME: "Credit Risk model deployment",
client.deployments.ConfigurationMetaNames.ONLINE: {}
}
)
deployment_details
```
Now, you can send new scoring records (new data) for which you would like to get predictions. To do that, execute the following sample code:
```
fields = ["CheckingStatus", "LoanDuration", "CreditHistory", "LoanPurpose", "LoanAmount", "ExistingSavings",
"EmploymentDuration", "InstallmentPercent", "Sex", "OthersOnLoan", "CurrentResidenceDuration",
"OwnsProperty", "Age", "InstallmentPlans", "Housing", "ExistingCreditsCount", "Job", "Dependents",
"Telephone", "ForeignWorker"]
values = [
["no_checking", 13, "credits_paid_to_date", "car_new", 1343, "100_to_500", "1_to_4", 2, "female", "none", 3,
"savings_insurance", 46, "none", "own", 2, "skilled", 1, "none", "yes"],
["no_checking", 24, "prior_payments_delayed", "furniture", 4567, "500_to_1000", "1_to_4", 4, "male", "none",
4, "savings_insurance", 36, "none", "free", 2, "management_self-employed", 1, "none", "yes"],
["0_to_200", 26, "all_credits_paid_back", "car_new", 863, "less_100", "less_1", 2, "female", "co-applicant",
2, "real_estate", 38, "none", "own", 1, "skilled", 1, "none", "yes"],
["0_to_200", 14, "no_credits", "car_new", 2368, "less_100", "1_to_4", 3, "female", "none", 3, "real_estate",
29, "none", "own", 1, "skilled", 1, "none", "yes"],
["0_to_200", 4, "no_credits", "car_new", 250, "less_100", "unemployed", 2, "female", "none", 3,
"real_estate", 23, "none", "rent", 1, "management_self-employed", 1, "none", "yes"],
["no_checking", 17, "credits_paid_to_date", "car_new", 832, "100_to_500", "1_to_4", 2, "male", "none", 2,
"real_estate", 42, "none", "own", 1, "skilled", 1, "none", "yes"],
["no_checking", 33, "outstanding_credit", "appliances", 5696, "unknown", "greater_7", 4, "male",
"co-applicant", 4, "unknown", 54, "none", "free", 2, "skilled", 1, "yes", "yes"],
["0_to_200", 13, "prior_payments_delayed", "retraining", 1375, "100_to_500", "4_to_7", 3, "male", "none", 3,
"real_estate", 37, "none", "own", 2, "management_self-employed", 1, "none", "yes"]
]
payload_scoring = {"input_data": [{"fields": fields, "values": values}]}
deployment_id = client.deployments.get_id(deployment_details)
client.deployments.score(deployment_id, payload_scoring)
```
<a id="cleanup"></a>
## 6. Clean up
If you want to clean up all created assets:
- experiments
- trainings
- pipelines
- model definitions
- models
- functions
- deployments
please follow up this sample [notebook](https://github.com/IBM/watson-machine-learning-samples/blob/master/cpd3.5/notebooks/python_sdk/instance-management/Machine%20Learning%20artifacts%20management.ipynb).
<a id="summary"></a>
## 7. Summary and next steps
You successfully completed this notebook! You learned how to use Apache Spark machine learning as well as Watson Machine Learning for model creation and deployment.
Check out our [Online Documentation](https://dataplatform.cloud.ibm.com/docs/content/analyze-data/wml-setup.html) for more samples, tutorials, documentation, how-tos, and blog posts.
### Authors
**Amadeusz Masny**, Python Software Developer in Watson Machine Learning at IBM
Copyright © 2020, 2021 IBM. This notebook and its source code are released under the terms of the MIT License.
|
github_jupyter
|
```
import numpy as np
import pandas as pd
import os
import joblib
import sklearn
import matplotlib
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
#Regressions:
from sklearn.multioutput import MultiOutputRegressor
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.linear_model import ElasticNet
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import RidgeCV
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import AdaBoostRegressor
from sklearn.tree import DecisionTreeRegressor
#Metric
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import r2_score
from pandas import DataFrame
# Show progress bar
from tqdm import tqdm
df = pd.read_csv('dataset_CdSe_augmented_adjusted.csv')
df
input_col = ['Growth Temp (Celsius)', 'Metal_mmol (mmol)', 'Chalcogen_mmol (mmol)',
'Amines_mmol (mmol)', 'CA_mmol (mmol)', 'Phosphines_mmol (mmol)',
'S_I_amount (g)', 'S_II_amount (g)', 'Time_min (min)',
'x0_cadmium acetate', 'x0_cadmium acetate dihydrate',
'x0_cadmium oxide', 'x0_cadmium stearate', 'x0_dimethylcadmium',
'x1_None', 'x1_benzoic acid', 'x1_dodecylphosphonic acid',
'x1_ethylphosphonic acid', 'x1_lauric acid',
'x1_myrstic acid', 'x1_oleic acid', 'x1_stearic acid',
'x2_2-6-dimethylpyridine', 'x2_None', 'x2_aniline',
'x2_benzylamine', 'x2_dioctylamine/hexadecylamine',
'x2_dodecylamine', 'x2_heptylamine', 'x2_hexadecylamine',
'x2_octadecylamine', 'x2_octylamine', 'x2_oleylamine',
'x2_pyridine', 'x2_trioctylamine', 'x3_None', 'x3_diphenylphosphine',
'x3_tributylphosphine', 'x3_trioctylphosphine',
'x3_triphenylphosphine', 'x4_None', 'x4_liquid parafin',
'x4_octadecene', 'x4_phenyl ether', 'x4_trioctylphosphine oxide',
'x5_None', 'x5_phosphinic acid', 'x5_trioctylphosphine oxide'
]
#Three individual outputs:
diameter = ['diameter_nm']
emission = ['emission_nm']
absorbance = ['abs_nm']
#Splitting dataset
X = df[input_col]
Y_d = df[diameter]
Y_e = df[emission]
Y_a = df[absorbance]
X_train_d, X_test_d, Y_train_d, Y_test_d = train_test_split(X, Y_d, test_size=0.15, random_state=45, shuffle=True)
X_train_e, X_test_e, Y_train_e, Y_test_e = train_test_split(X, Y_e, test_size=0.15, random_state=45, shuffle=True)
X_train_a, X_test_a, Y_train_a, Y_test_a = train_test_split(X, Y_a, test_size=0.15, random_state=45, shuffle=True)
```
## D - Optimizing diameter model
### 1D. Extra Trees
```
# This is a grid search for three parameters in the Extra Trees algorithm.
# Parameters are: random_state, n_estimators, max_features.
# This gives the best combination of the three parameters for the smallest mean squared error.
min_mae = 99999
min_i, min_j, min_k = 0, 0, 0
for i in tqdm(range(1, 25)):
for j in range(1, 25):
for k in range(2, 50, 1):
ET_regr = ExtraTreesRegressor(n_estimators=i,
max_features=j,
random_state=k)
ET_regr.fit(X_train_d, np.ravel(Y_train_d))
ET_Y_pred_d = pd.DataFrame(ET_regr.predict(X_test_d))
mae = mean_absolute_error(Y_test_d, ET_Y_pred_d)
if (min_mae > mae):
min_mae = mae
min_i = i
min_j = j
min_k = k
print(min_mae, min_i, min_j, min_k)
ET_regr_d = ExtraTreesRegressor(n_estimators=2,
max_features=23,
random_state=20)
ET_regr_d.fit(X_train_d, np.ravel(Y_train_d))
ET_Y_pred_d = pd.DataFrame(ET_regr_d.predict(X_test_d))
D_mae = mean_absolute_error(Y_test_d, ET_Y_pred_d)
D_r_2 = r2_score(Y_test_d, ET_Y_pred_d)
D_mse = mean_squared_error(Y_test_d, ET_Y_pred_d)
D_rmse = mean_squared_error(Y_test_d, ET_Y_pred_d, squared=False)
from tabulate import tabulate
d = ["Diameter", D_r_2, D_mae, D_mse, D_rmse],
print(tabulate(d, headers=["Outputs", "R2", "Mean absolute error", "Mean squared error", "Root mean squared error"]))
```
### 2D. Decision Tree
```
# This is a grid search for three parameters in the Decision Trees algorithm.
# Parameters are: max_depth, max_features, random_state.
# This gives the best combination of the three parameters for the smallest mean squared error.
min_mae = 99999
min_i, min_j, min_k = 0, 0, 0
for i in tqdm(range(1, 30)):
for j in range(1, 30):
for k in range(4, 80, 2):
DT_regr = DecisionTreeRegressor(max_depth=i,
max_features=j,
random_state=k)
DT_regr.fit(X_train_d, np.ravel(Y_train_d))
DT_Y_pred_d = pd.DataFrame(DT_regr.predict(X_test_d))
mae = mean_absolute_error(Y_test_d, DT_Y_pred_d)
if (min_mae > mae):
min_mae = mae
min_i = i
min_j = j
min_k = k
print(min_mae, min_i, min_j, min_k)
DT_regr_d = DecisionTreeRegressor(max_depth=12,
max_features=25,
random_state=62)
DT_regr_d.fit(X_train_d, np.ravel(Y_train_d))
DT_Y_pred_d = pd.DataFrame(DT_regr_d.predict(X_test_d))
DT_regr_d.fit(X_train_d, np.ravel(Y_train_d))
DT_Y_pred_d = pd.DataFrame(DT_regr_d.predict(X_test_d))
D_mae = mean_absolute_error(Y_test_d, DT_Y_pred_d)
D_r_2 = r2_score(Y_test_d, DT_Y_pred_d)
D_mse = mean_squared_error(Y_test_d, DT_Y_pred_d)
D_rmse = mean_squared_error(Y_test_d, DT_Y_pred_d, squared=False)
from tabulate import tabulate
d = ["Diameter", D_r_2, D_mae, D_mse, D_rmse],
print(tabulate(d, headers=["Outputs", "R2", "Mean absolute error", "Mean squared error", "Root mean squared error"]))
```
### 3D. Random Forest
```
# This is a grid search for three parameters in the Random Forest algorithm.
# Parameters are: max_depth, n_estimators, max_features.
# Random_state is set to 45.
# This gives the best combination of the three parameters for the smallest mean squared error.
min_mae = 99999
min_i, min_j, min_k = 0, 0, 0
for i in tqdm(range(1, 21)):
for j in range(1, 21):
for k in range(2, 40, 1):
RF_regr = RandomForestRegressor(max_depth=i,
n_estimators=j,
max_features=k,
random_state=45)
RF_regr.fit(X_train_d, np.ravel(Y_train_d))
RF_Y_pred_d = pd.DataFrame(RF_regr.predict(X_test_d))
mae = mean_absolute_error(Y_test_d, RF_Y_pred_d)
if (min_mae > mae):
min_mae = mae
min_i = i
min_j = j
min_k = k
print(min_mae, min_i, min_j, min_k)
```
### 4D. K Neighbors
```
min_mae = 99999
min_i, min_j = 0, 0
for i in tqdm(range(1, 40)):
for j in range(1, 40):
KNN_reg_d = KNeighborsRegressor(n_neighbors=i,
p=j).fit(X_train_d, np.ravel(Y_train_d))
KNN_Y_pred_d = KNN_reg_d.predict(X_test_d)
mae = mean_absolute_error(Y_test_d, KNN_Y_pred_d)
if (min_mae > mae):
min_mae = mae
min_i = i
min_j = j
print(min_mae, min_i, min_j)
```
### Saving Decision Tree model
```
ET_regr_d = ExtraTreesRegressor(n_estimators=2,
max_features=23,
random_state=20)
ET_regr_d.fit(X_train_d, np.ravel(Y_train_d))
ET_Y_pred_d = pd.DataFrame(ET_regr.predict(X_test_d))
joblib.dump(ET_regr_d, "./model_CdSe_SO_diameter_ExtraTrees.joblib")
```
## E - Optimizing emission model
### 1E. Extra Trees
```
# This is a grid search for three parameters in the Extra Trees algorithm.
# Parameters are: random_state, n_estimators, max_features.
# This gives the best combination of the three parameters for the smallest mean squared error.
min_mae = 99999
min_i, min_j, min_k = 0, 0, 0
for i in tqdm(range(1, 25)):
for j in range(1, 25):
for k in range(2, 50, 1):
ET_regr_e = ExtraTreesRegressor(n_estimators=i,
max_features=j,
random_state=k)
ET_regr_e.fit(X_train_e, np.ravel(Y_train_e))
ET_Y_pred_e = pd.DataFrame(ET_regr_e.predict(X_test_e))
mae = mean_absolute_error(Y_test_e, ET_Y_pred_e)
if (min_mae > mae):
min_mae = mae
min_i = i
min_j = j
min_k = k
print(min_mae, min_i, min_j, min_k)
ET_regr_e = ExtraTreesRegressor(n_estimators=8,
max_features=2,
random_state=13)
ET_regr_e.fit(X_train_e, np.ravel(Y_train_e))
ET_Y_pred_e = pd.DataFrame(ET_regr_e.predict(X_test_e))
D_mae = mean_absolute_error(Y_test_e, ET_Y_pred_e)
D_r_2 = r2_score(Y_test_e, ET_Y_pred_e)
D_mse = mean_squared_error(Y_test_e, ET_Y_pred_e)
D_rmse = mean_squared_error(Y_test_e, ET_Y_pred_e, squared=False)
from tabulate import tabulate
d = ["Diameter", D_r_2, D_mae, D_mse, D_rmse],
print(tabulate(d, headers=["Outputs", "R2", "Mean absolute error", "Mean squared error", "Root mean squared error"]))
```
### 2E. Decision Trees
```
# This is a grid search for three parameters in the Decision Trees algorithm.
# This gives the best combination of the three parameters for the smallest mean squared error.
min_mae = 99999
min_i, min_j, min_k = 0, 0, 0
for i in tqdm(range(1, 30)):
for j in range(1, 30):
for k in range(4, 70, 2):
DT_regr_e = DecisionTreeRegressor(max_depth=i,
max_features=j,
random_state=k)
DT_regr_e.fit(X_train_e, np.ravel(Y_train_e))
DT_Y_pred_e = pd.DataFrame(DT_regr_e.predict(X_test_e))
mae = mean_absolute_error(Y_test_e, DT_Y_pred_e)
if (min_mae > mae):
min_mae = mae
min_i = i
min_j = j
min_k = k
print(min_mae, min_i, min_j, min_k)
DT_regr_e = DecisionTreeRegressor(max_depth=13,
max_features=5,
random_state=32)
DT_regr_e.fit(X_train_e, np.ravel(Y_train_e))
DT_Y_pred_e = pd.DataFrame(DT_regr_e.predict(X_test_e))
DT_regr_e.fit(X_train_e, np.ravel(Y_train_e))
DT_Y_pred_e = pd.DataFrame(DT_regr_e.predict(X_test_e))
D_mae = mean_absolute_error(Y_test_e, DT_Y_pred_e)
D_r_2 = r2_score(Y_test_e, DT_Y_pred_e)
D_mse = mean_squared_error(Y_test_e, DT_Y_pred_e)
D_rmse = mean_squared_error(Y_test_e, DT_Y_pred_e, squared=False)
from tabulate import tabulate
d = ["Diameter", D_r_2, D_mae, D_mse, D_rmse],
print(tabulate(d, headers=["Outputs", "R2", "Mean absolute error", "Mean squared error", "Root mean squared error"]))
```
### 3E. Random Forest
```
min_mae = 99999
min_i, min_j, min_k = 0, 0, 0
for i in tqdm(range(1, 21)):
for j in range(1, 21):
for k in range(2, 30, 1):
RF_regr_e = RandomForestRegressor(max_depth=i,
n_estimators=j,
max_features=k,
random_state=45)
RF_regr_e.fit(X_train_e, np.ravel(Y_train_e))
RF_Y_pred_e = pd.DataFrame(RF_regr_e.predict(X_test_e))
mae = mean_absolute_error(Y_test_e, RF_Y_pred_e)
if (min_mae > mae):
min_mae = mae
min_i = i
min_j = j
min_k = k
print(min_mae, min_i, min_j, min_k)
```
### 4E. K Neighbors
```
min_mae = 99999
min_i, min_j = 0, 0
for i in tqdm(range(1, 40)):
for j in range(1, 40):
KNN_reg_e = KNeighborsRegressor(n_neighbors=i,
p=j).fit(X_train_e, np.ravel(Y_train_e))
KNN_Y_pred_e = KNN_reg_e.predict(X_test_e)
mae = mean_absolute_error(Y_test_e, KNN_Y_pred_e)
if (min_mae > mae):
min_mae = mae
min_i = i
min_j = j
print(min_mae, min_i, min_j)
```
### Saving Extra Trees model
```
DT_regr_e = DecisionTreeRegressor(max_depth=13,
max_features=5,
random_state=32)
DT_regr_e.fit(X_train_e, np.ravel(Y_train_e))
DT_Y_pred_e = pd.DataFrame(DT_regr_e.predict(X_test_e))
joblib.dump(ET_regr_e, "./model_CdSe_SO_emission_DecisionTree.joblib")
```
## A - Optimizing absorption model
### 1A: Extra Trees
```
# This is a grid search for three parameters in the Extra Trees algorithm.
# Parameters are: random_state, n_estimators, max_features.
# This gives the best combination of the three parameters for the smallest mean squared error.
min_mae = 99999
min_i, min_j, min_k = 0, 0, 0
for i in tqdm(range(1, 30)):
for j in range(1, 30):
for k in range(2, 50, 1):
ET_regr_a = ExtraTreesRegressor(n_estimators=i,
max_features=j,
random_state=k)
ET_regr_a.fit(X_train_a, np.ravel(Y_train_a))
ET_Y_pred_a = pd.DataFrame(ET_regr_a.predict(X_test_a))
mae = mean_absolute_error(Y_test_a, ET_Y_pred_a)
if (min_mae > mae):
min_mae = mae
min_i = i
min_j = j
min_k = k
print(min_mae, min_i, min_j, min_k)
ET_regr_a = ExtraTreesRegressor(n_estimators=3,
max_features=28,
random_state=12)
ET_regr_a.fit(X_train_a, np.ravel(Y_train_a))
ET_Y_pred_a = pd.DataFrame(ET_regr_a.predict(X_test_a))
D_mae = mean_absolute_error(Y_test_a, ET_Y_pred_a)
D_r_2 = r2_score(Y_test_a, ET_Y_pred_a)
D_mse = mean_squared_error(Y_test_a, ET_Y_pred_a)
D_rmse = mean_squared_error(Y_test_a, ET_Y_pred_a, squared=False)
from tabulate import tabulate
d = ["Diameter", D_r_2, D_mae, D_mse, D_rmse],
print(tabulate(d, headers=["Outputs", "R2", "Mean absolute error", "Mean squared error", "Root mean squared error"]))
```
### 2A. Decision Trees
```
# This is a grid search for three parameters in the Decision Trees algorithm.
# This gives the best combination of the three parameters for the smallest mean squared error.
min_mae = 99999
min_i, min_j, min_k = 0, 0, 0
for i in tqdm(range(1, 30)):
for j in range(1, 30):
for k in range(4, 60, 2):
DT_regr_a = DecisionTreeRegressor(max_depth=i,
max_features=j,
random_state=k)
DT_regr_a.fit(X_train_a, np.ravel(Y_train_a))
DT_Y_pred_a = pd.DataFrame(DT_regr_a.predict(X_test_a))
mae = mean_absolute_error(Y_test_a, DT_Y_pred_a)
if (min_mae > mae):
min_mae = mae
min_i = i
min_j = j
min_k = k
print(min_mae, min_i, min_j, min_k)
DT_regr_a = DecisionTreeRegressor(max_depth=11,
max_features=11,
random_state=38)
DT_regr_a.fit(X_train_a, np.ravel(Y_train_a))
DT_Y_pred_a = pd.DataFrame(DT_regr_a.predict(X_test_a))
DT_regr_a.fit(X_train_a, np.ravel(Y_train_a))
DT_Y_pred_a = pd.DataFrame(DT_regr_a.predict(X_test_a))
D_mae = mean_absolute_error(Y_test_a, DT_Y_pred_a)
D_r_2 = r2_score(Y_test_a, DT_Y_pred_a)
D_mse = mean_squared_error(Y_test_a, DT_Y_pred_a)
D_rmse = mean_squared_error(Y_test_a, DT_Y_pred_a, squared=False)
from tabulate import tabulate
d = ["Diameter", D_r_2, D_mae, D_mse, D_rmse],
print(tabulate(d, headers=["Outputs", "R2", "Mean absolute error", "Mean squared error", "Root mean squared error"]))
```
### 3A. Random Forest
```
min_mae = 99999
min_i, min_j, min_k = 0, 0, 0
for i in tqdm(range(1, 21)):
for j in range(1, 21):
for k in range(2, 31, 1):
RF_regr_a = RandomForestRegressor(max_depth=i,
n_estimators=j,
max_features=k,
random_state=45)
RF_regr_a.fit(X_train_a, np.ravel(Y_train_a))
RF_Y_pred_a = pd.DataFrame(RF_regr_a.predict(X_test_a))
mae = mean_absolute_error(Y_test_a, RF_Y_pred_a)
if (min_mae > mae):
min_mae = mae
min_i = i
min_j = j
min_k = k
print(min_mae, min_i, min_j, min_k)
```
### 4A. K Neighbors
```
min_mae = 99999
min_i, min_j = 0, 0
for i in tqdm(range(1, 40)):
for j in range(1, 40):
KNN_reg_a = KNeighborsRegressor(n_neighbors=i,
p=j).fit(X_train_a, np.ravel(Y_train_a))
KNN_Y_pred_a = KNN_reg_a.predict(X_test_a)
mae = mean_absolute_error(Y_test_a, KNN_Y_pred_a)
if (min_mae > mae):
min_mae = mae
min_i = i
min_j = j
print(min_mae, min_i, min_j)
```
### Saving model
```
DT_regr_a = DecisionTreeRegressor(max_depth=11,
max_features=11,
random_state=38)
DT_regr_a.fit(X_train_a, np.ravel(Y_train_a))
DT_Y_pred_a = pd.DataFrame(DT_regr_a.predict(X_test_a))
joblib.dump(DT_regr_a, "./model_CdSe_SO_abs_DecisionTree.joblib")
```
## Analyzing
```
## Diameter
ET_regr_d = ExtraTreesRegressor(n_estimators=2,
max_features=23,
random_state=20)
ET_regr_d.fit(X_train_d, np.ravel(Y_train_d))
ET_Y_pred_d = pd.DataFrame(ET_regr_d.predict(X_test_d))
D_mae = mean_absolute_error(Y_test_d, ET_Y_pred_d)
D_r_2 = r2_score(Y_test_d, ET_Y_pred_d)
D_mse = mean_squared_error(Y_test_d, ET_Y_pred_d)
D_rmse = mean_squared_error(Y_test_d, ET_Y_pred_d, squared=False)
## Emission
DT_regr_e = DecisionTreeRegressor(max_depth=13,
max_features=5,
random_state=32)
DT_regr_e.fit(X_train_e, np.ravel(Y_train_e))
DT_Y_pred_e = pd.DataFrame(DT_regr_e.predict(X_test_e))
E_mae = mean_absolute_error(Y_test_e, DT_Y_pred_e)
E_r_2 = r2_score(Y_test_e, DT_Y_pred_e)
E_mse = mean_squared_error(Y_test_e, DT_Y_pred_e)
E_rmse = mean_squared_error(Y_test_e, DT_Y_pred_e, squared=False)
### Absorption
DT_regr_a = DecisionTreeRegressor(max_depth=11,
max_features=11,
random_state=38).fit(X_train_a, np.ravel(Y_train_a))
DT_Y_pred_a = DT_regr_a.predict(X_test_a)
A_mae = mean_absolute_error(Y_test_a, DT_Y_pred_a)
A_r_2 = r2_score(Y_test_a, DT_Y_pred_a)
A_mse = mean_squared_error(Y_test_a, DT_Y_pred_a)
A_rmse = mean_squared_error(Y_test_a, DT_Y_pred_a, squared=False)
from tabulate import tabulate
d = [ ["Diameter", D_r_2, D_mae, D_mse, D_rmse],
["Absorption", A_r_2, A_mae, A_mse, A_rmse],
["Emission", E_r_2, E_mae, E_mse, E_rmse]]
print(tabulate(d, headers=["Outputs", "R2", "Mean absolute error", "Mean squared error", "Root mean squared error"]))
## Diameter
ET_regr_d = ExtraTreesRegressor(n_estimators=2,
max_features=23,
random_state=20)
ET_regr_d.fit(X_train_d, np.ravel(Y_train_d))
ET_Y_pred_d = ET_regr_d.predict(X_test_d)
D_mae = mean_absolute_error(Y_test_d, ET_Y_pred_d)
D_r_2 = r2_score(Y_test_d, ET_Y_pred_d)
D_mse = mean_squared_error(Y_test_d, ET_Y_pred_d)
D_rmse = mean_squared_error(Y_test_d, ET_Y_pred_d, squared=False)
## Emission
DT_regr_e = DecisionTreeRegressor(max_depth=13,
max_features=5,
random_state=32)
DT_regr_e.fit(X_train_e, np.ravel(Y_train_e))
DT_Y_pred_e =DT_regr_e.predict(X_test_e)
E_mae = mean_absolute_error(Y_test_e, DT_Y_pred_e)
E_r_2 = r2_score(Y_test_e, DT_Y_pred_e)
E_mse = mean_squared_error(Y_test_e, DT_Y_pred_e)
E_rmse = mean_squared_error(Y_test_e, DT_Y_pred_e, squared=False)
### Absorption
DT_regr_a = DecisionTreeRegressor(max_depth=11,
max_features=11,
random_state=38).fit(X_train_a, np.ravel(Y_train_a))
DT_Y_pred_a = DT_regr_a.predict(X_test_a)
A_mae = mean_absolute_error(Y_test_a, DT_Y_pred_a)
A_r_2 = r2_score(Y_test_a, DT_Y_pred_a)
A_mse = mean_squared_error(Y_test_a, DT_Y_pred_a)
A_rmse = mean_squared_error(Y_test_a, DT_Y_pred_a, squared=False)
from tabulate import tabulate
d = [ ["Diameter", D_r_2, D_mae, D_mse, D_rmse],
["Absorption", A_r_2, A_mae, A_mse, A_rmse],
["Emission", E_r_2, E_mae, E_mse, E_rmse]]
print(tabulate(d, headers=["Outputs", "R2", "Mean absolute error", "Mean squared error", "Root mean squared error"]))
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(20,5))
fig.suptitle('Single Outputs', fontsize=25)
ax1.plot(Y_test_d, ET_Y_pred_d,'o')
ax1.plot([1,6],[1,6], color = 'r')
ax1.set_title('Diameter')
ax1.set(xlabel='Observed Values (nm)', ylabel='Predicted Values (nm)')
ax2.plot(Y_test_a, DT_Y_pred_a,'o')
ax2.plot([350,650],[350,650], color = 'r')
ax2.set_title('Absorption')
ax2.set(xlabel='Observed Values (nm)', ylabel='Predicted Values (nm)')
ax3.plot(Y_test_e, DT_Y_pred_e,'o')
ax3.plot([450,650],[450,650], color = 'r')
ax3.set_title('Emission')
ax3.set(xlabel='Observed Values (nm)', ylabel='Predicted Values (nm)')
fig.tight_layout()
```
## Feature importance
### For diameter prediction
```
importance_dict_d = dict()
for i in range(0,48):
importance_dict_d[input_col[i]] = ET_regr_d.feature_importances_[i]
sorted_importance_d = sorted(importance_dict_d.items(), key=lambda x: x[1], reverse=True)
sorted_importance_d
top7_d = DataFrame(sorted_importance_d[0:7], columns=['features', 'importance score'])
others_d = DataFrame(sorted_importance_d[7:], columns=['features', 'importance score'])
import seaborn as sns
a4_dims = (20.7, 8.27)
fig, ax = plt.subplots(figsize=a4_dims)
sns.set_theme(style="whitegrid")
ax = sns.barplot(x="features", y="importance score", data=top7_d)
```
### Emission prediction
```
importance_dict_e = dict()
for i in range(0,48):
importance_dict_e[input_col[i]] = DT_regr_e.feature_importances_[i]
sorted_importance_e = sorted(importance_dict_e.items(), key=lambda x: x[1], reverse=True)
sorted_importance_e
top7_e = DataFrame(sorted_importance_e[0:7], columns=['features', 'importance score'])
others_e = DataFrame(sorted_importance_e[7:], columns=['features', 'importance score'])
# combined_others2 = pd.DataFrame(data = {
# 'features' : ['others'],
# 'importance score' : [others2['importance score'].sum()]
# })
# #combining top 10 with others
# imp_score2 = pd.concat([top7, combined_others2])
import seaborn as sns
a4_dims = (20.7, 8.27)
fig, ax = plt.subplots(figsize=a4_dims)
sns.set_theme(style="whitegrid")
ax = sns.barplot(x="features", y="importance score", data=top7_e)
```
### Absorption prediction
```
importance_dict_a = dict()
for i in range(0,48):
importance_dict_a[input_col[i]] = DT_regr_a.feature_importances_[i]
sorted_importance_a = sorted(importance_dict_a.items(), key=lambda x: x[1], reverse=True)
sorted_importance_a
top7_a = DataFrame(sorted_importance_a[0:7], columns=['features', 'importance score'])
others_a = DataFrame(sorted_importance_a[7:], columns=['features', 'importance score'])
import seaborn as sns
a4_dims = (20.7, 8.27)
fig, ax = plt.subplots(figsize=a4_dims)
sns.set_theme(style="whitegrid")
ax = sns.barplot(x="features", y="importance score", data=top7_a)
importance_dict_a
```
### Combine
```
sorted_a = sorted(importance_dict_a.items(), key=lambda x: x[0], reverse=False)
sorted_d = sorted(importance_dict_d.items(), key=lambda x: x[0], reverse=False)
sorted_e = sorted(importance_dict_e.items(), key=lambda x: x[0], reverse=False)
sorted_d
combined_importance = dict()
for i in range(0,48):
combined_importance[sorted_e[i][0]] = sorted_e[i][1] + sorted_a[i][1] + sorted_d[i][1]
combined_importance
sorted_combined_importance = sorted(combined_importance.items(), key=lambda x: x[1], reverse=True)
sorted_combined_importance
top7_combined = DataFrame(sorted_combined_importance[0:7], columns=['features', 'importance score'])
others_combined = DataFrame(sorted_combined_importance [7:], columns=['features', 'importance score'])
import seaborn as sns
a4_dims = (20.7, 8.27)
fig, ax = plt.subplots(figsize=a4_dims)
sns.set_theme(style="whitegrid")
ax = sns.barplot(x="features", y="importance score", data=top7_combined)
```
|
github_jupyter
|
```
# import esm
import torch
from argparse import Namespace
from esm.constants import proteinseq_toks
import math
import torch.nn as nn
import torch.nn.functional as F
from esm.modules import TransformerLayer, PositionalEmbedding # noqa
from esm.model import ProteinBertModel
# model, alphabet = torch.hub.load("facebookresearch/esm", "esm1_t34_670M_UR50S")
import esm
from ych_util import prepare_mlm_mask
import pandas as pd
import time
pfamA_balanced = pd.read_csv("../../data/esm/pfamA_motors_balanced.csv")
pfamA_balanced = pfamA_balanced.sample(frac = 1)
pfamA_balanced.head()
alphabet = esm.Alphabet.from_dict(proteinseq_toks)
# model_name = "esm1_t34_670M_UR50S"
model_name = "esm1_t12_85M_UR50S"
url = f"https://dl.fbaipublicfiles.com/fair-esm/models/{model_name}.pt"
if torch.cuda.is_available():
print("cuda")
model_data = torch.hub.load_state_dict_from_url(url, progress=False)
else:
model_data = torch.hub.load_state_dict_from_url(url, progress=False, map_location=torch.device('cpu'))
pra = lambda s: ''.join(s.split('decoder_')[1:] if 'decoder' in s else s)
prs = lambda s: ''.join(s.split('decoder.')[1:] if 'decoder' in s else s)
model_args = {pra(arg[0]): arg[1] for arg in vars(model_data["args"]).items()}
model_state = {prs(arg[0]): arg[1] for arg in model_data["model"].items()}
model = esm.ProteinBertModel(
Namespace(**model_args), len(alphabet), padding_idx=alphabet.padding_idx
)
model.load_state_dict(model_state)
# model.load_state_dict(torch.load("../../data/esm1_t12_85M_UR50S_balanced_201102.pt"))
model.cuda()
model.train()
batch_converter = alphabet.get_batch_converter()
criterion = nn.CrossEntropyLoss()
lr = 0.0001 # learning rate
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer)
start_time = time.time()
print_every = 10000
for j in range(10):
for i in range(pfamA_balanced.shape[0]):
if len(pfamA_balanced.iloc[i,3])>1024:
continue
data = [(pfamA_balanced.iloc[i,1], pfamA_balanced.iloc[i,3])]
batch_labels, batch_strs, batch_tokens = batch_converter(data)
true_aa,target_ind,masked_batch_tokens = prepare_mlm_mask(alphabet,batch_tokens)
optimizer.zero_grad()
results = model(masked_batch_tokens.to('cuda'), repr_layers=[34])
pred = results["logits"].squeeze(0)[target_ind,:]
target = true_aa.squeeze(0)
loss = criterion(pred.cpu(),target)
loss.backward()
optimizer.step()
if i % print_every == 0:
print(batch_labels)
print(batch_strs)
print(batch_tokens.size())
print(masked_batch_tokens.size())
print(results["logits"].size())
print(pred.size())
print(target.size())
print(f"At Epoch: %.1f"% i)
print(f"Loss %.4f"% loss)
elapsed = time.time() - start_time
print(f"time elapsed %.4f"% elapsed)
torch.save(model.state_dict(), "../../data/esm1_t12_85M_UR50S_balanced_201102.pt")
# loss_vector.append(loss)
# break
torch.save(model.state_dict(), "../../data/esm1_t12_85M_UR50S_balanced_201102.pt")
print("done")
```
|
github_jupyter
|
```
%pylab inline
import pandas as pd
import numpy as np
import pickle,itertools,sys,pdb
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import graphviz
from ultron.factor.genetic.accumulators import mutated_pool, cross_pool
from ultron.sentry.Analysis.SecurityValueHolders import SecurityValueHolder
from ultron.sentry.Analysis.SecurityValueHolders import SecurityCombinedValueHolder
from ultron.sentry.Analysis.SecurityValueHolders import SecurityLatestValueHolder
from ultron.sentry.Analysis.SecurityValueHolders import SecurityCurrentValueHolder
from ultron.sentry.Analysis.TechnicalAnalysis.StatelessTechnicalAnalysers import SecurityDiffValueHolder
from ultron.sentry.Analysis.TechnicalAnalysis.StatelessTechnicalAnalysers import SecuritySignValueHolder
from ultron.sentry.Analysis.TechnicalAnalysis.StatelessTechnicalAnalysers import SecurityExpValueHolder
from ultron.sentry.Analysis.TechnicalAnalysis.StatelessTechnicalAnalysers import SecurityLogValueHolder
from ultron.sentry.Analysis.TechnicalAnalysis.StatelessTechnicalAnalysers import SecuritySqrtValueHolder
from ultron.sentry.Analysis.TechnicalAnalysis.StatelessTechnicalAnalysers import SecurityAbsValueHolder
from ultron.sentry.Analysis.TechnicalAnalysis.StatelessTechnicalAnalysers import SecurityNormInvValueHolder
from ultron.sentry.Analysis.TechnicalAnalysis.StatelessTechnicalAnalysers import SecurityCeilValueHolder
from ultron.sentry.Analysis.TechnicalAnalysis.StatelessTechnicalAnalysers import SecurityFloorValueHolder
from ultron.sentry.Analysis.TechnicalAnalysis.StatelessTechnicalAnalysers import SecurityRoundValueHolder
from ultron.sentry.Analysis.TechnicalAnalysis.StatelessTechnicalAnalysers import SecuritySigmoidValueHolder
from ultron.sentry.Analysis.TechnicalAnalysis.StatelessTechnicalAnalysers import SecurityTanhValueHolder
from ultron.sentry.Analysis.CrossSectionValueHolders import CSRankedSecurityValueHolder
from ultron.sentry.Analysis.CrossSectionValueHolders import CSZScoreSecurityValueHolder
from ultron.sentry.Analysis.CrossSectionValueHolders import CSPercentileSecurityValueHolder
from ultron.sentry.Analysis.CrossSectionValueHolders import CSResidueSecurityValueHolder
from ultron.sentry.Analysis.SecurityValueHolders import SecurityAddedValueHolder
from ultron.sentry.Analysis.SecurityValueHolders import SecuritySubbedValueHolder
from ultron.sentry.Analysis.SecurityValueHolders import SecurityMultipliedValueHolder
from ultron.sentry.Analysis.SecurityValueHolders import SecurityDividedValueHolder
from ultron.sentry.Analysis.SecurityValueHolders import SecurityLtOperatorValueHolder
from ultron.sentry.Analysis.SecurityValueHolders import SecurityLeOperatorValueHolder
from ultron.sentry.Analysis.SecurityValueHolders import SecurityGtOperatorValueHolder
from ultron.sentry.Analysis.SecurityValueHolders import SecurityGeOperatorValueHolder
from ultron.sentry.Analysis.SecurityValueHolders import SecurityEqOperatorValueHolder
from ultron.sentry.Analysis.SecurityValueHolders import SecurityNeOperatorValueHolder
from ultron.sentry.Analysis.SecurityValueHolders import SecurityAndOperatorValueHolder
from ultron.sentry.Analysis.SecurityValueHolders import SecurityOrOperatorValueHolder
# 读取算子
mutated_list = list(mutated_pool.values())
cross_list = list(cross_pool.values())
with open('factor_data.pkl','rb') as file2:
total_data = pickle.load(file2)
facotr_sets = [i for i in list(set(total_data.columns)) if i not in ['trade_date','code','ret']]
#合并函数
mutated_sets = [{'activy':1,'function': f} for f in mutated_list]
cross_sets = [{'activy':2,'function': f} for f in cross_list]
function_sets = mutated_sets + cross_sets
def calcu_program(max_depth=4):
n_features = 2
function_obj = function_sets[np.random.randint(0,len(function_sets)-1)] # 随机选择函数
program = [function_obj]
terminal_stack = [function_obj['activy']]
while terminal_stack:
depth = len(terminal_stack)
choice = n_features + len(function_sets)
choice = np.random.randint(0,choice)
if depth < max_depth and choice <= len(function_sets):
function_obj = function_sets[np.random.randint(0,len(function_sets)-1)]
program.append(function_obj)
terminal_stack.append(function_obj['activy'])
else:
factor = facotr_sets[np.random.randint(0,len(facotr_sets)-1)]
program.append(factor)
terminal_stack[-1] -= 1
while terminal_stack[-1] == 0:
terminal_stack.pop()
if not terminal_stack:
return program
terminal_stack[-1] -= 1
def draw_program(program):
fade_nodes = None
terminals = []
if fade_nodes is None:
fade_nodes = []
output = 'digraph program {\nnode [style=filled]\n'
for i, node in enumerate(program):
fill = '#cecece'
if node in function_sets:
if i not in fade_nodes:
fill = '#2a5caa'
terminals.append([node['activy'], i])
output += ('%d [label="%s", fillcolor="%s"] ;\n'
% (i, node['function'].__name__, fill))
else:
if i not in fade_nodes:
fill = '#60a6f6'
if node in facotr_sets:
feature_name = node
else:
feature_name = 'X%s' % node
output += ('%d [label="%s", fillcolor="%s"] ;\n'
% (i, feature_name, fill))
if i == 0 :
output += '}'
return output
terminals[-1][0] -= 1
terminals[-1].append(i)
while terminals[-1][0] == 0:
output += '%d -> %d ;\n' % (terminals[-1][1],
terminals[-1][-1])
terminals[-1].pop()
if len(terminals[-1]) == 2:
parent = terminals[-1][-1]
terminals.pop()
if not terminals:
output += '}'
return output
terminals[-1].append(parent)
terminals[-1][0] -= 1
graph = graphviz.Source(draw_program(calcu_program()))
graph
graph.render('test-table3.gv', view=True)
```
# 繁衍计算
```
program = calcu_program()
graphviz.Source(draw_program(program))
def get_subtree(program):
probs = np.array([0.9 if node in function_sets else 0.1 for node in program])
probs = np.cumsum(probs / probs.sum())
start = np.searchsorted(probs, np.random.uniform(0, 1))
stack = 1
end = start
while stack > end - start:
node = program[end]
if node in function_sets:
stack += node['activy']
end += 1
return start, end
```
## 交叉计算
```
copy_program = program
donor_program = calcu_program()
start, end = get_subtree(copy_program)
removed = range(start, end)
donor_start, donor_end = get_subtree(donor_program)
donor_removed = list(set(range(len(donor_program))) -
set(range(donor_start, donor_end)))
crossover_program = copy_program[:start] + donor_program[donor_start:donor_end] + copy_program[end:]
graphviz.Source(draw_program(crossover_program))
```
## 变异计算
#### 树突变 - 等同于交叉计算
```
copy_program = program
chicken_program = calcu_program()
start, end = get_subtree(copy_program)
removed = range(start, end)
chicken_start, chicken_end = get_subtree(chicken_program)
chicken_removed = list(set(range(len(chicken_program))) -
set(range(chicken_start, chicken_end)))
crossover_program = copy_program[:start] + chicken_program[chicken_start:chicken_end] + copy_program[end:]
graphviz.Source(draw_program(crossover_program))
```
#### 提升突变
```
copy_program = program
start, end = get_subtree(copy_program)
subtree = program[start:end]
sub_start, sub_end = get_subtree(subtree)
hoist = subtree[sub_start:sub_end]
hosit_program = copy_program[:start] + hoist + copy_program[end:]
graphviz.Source(draw_program(hosit_program))
```
#### 节点突变
```
copy_program = copy(program)
mutate = np.where(np.random.uniform(size=len(copy_program)) < 0.5)[0]
for node in mutate:
if copy_program[node] in function_sets:
activy = copy_program[node]['activy']
#找到参数个数替换
if activy == 1:
replace_node = mutated_sets[np.random.randint(0,len(mutated_sets)-1)]
else:
replace_node = cross_sets[np.random.randint(0,len(cross_sets)-1)]
copy_program[node] = replace_node
else:
factor = facotr_sets[np.random.randint(0,len(facotr_sets)-1)]
copy_program[node] = factor
graphviz.Source(draw_program(copy_program))
```
## 计算因子值
```
def create_formual(apply_formual):
function = apply_formual[0]
formula = function['function'].__name__
formula +='('
for i in range(0,function['activy']):
if i != 0:
formula += ','
if apply_formual[i+1] in facotr_sets:
formula += '\'' + apply_formual[i+1] + '\''
else:
formula += apply_formual[i+1]
formula += ')'
return formula
apply_stack = []
for node in program:
if node in function_sets:
apply_stack.append([node])
else:
apply_stack[-1].append(node)
while len(apply_stack[-1]) == apply_stack[-1][0]['activy'] + 1:
result = create_formual(apply_stack[-1])
if len(apply_stack) != 1:
apply_stack.pop()
apply_stack[-1].append(result)
else:
print(result)
break
%%time
rt = eval(result).transform(total_data.set_index(['trade_date']), category_field='code', dropna=False)
rt
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/madhavjk/DataScience-ML_and_DL/blob/main/SESSION_20_(Decision_trees_and_Random_Forests).ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import numpy as np
import matplotlib.pyplot as plt
import h5py
from PIL import Image
from scipy import ndimage
with h5py.File('train_signs.h5', 'r') as hdf:
ls = list(hdf.keys())
print(ls)
train_set_x = np.array(hdf.get('train_set_x'))
train_set_y = np.array(hdf.get('train_set_y'))
print(train_set_x.shape)
print(train_set_y.shape)
with h5py.File('test_signs.h5', 'r') as hdf:
ls = list(hdf.keys())
print(ls)
test_set_x = np.array(hdf.get('test_set_x'))
test_set_y = np.array(hdf.get('test_set_y'))
print(test_set_x.shape)
print(test_set_y.shape)
plt.figure()
plt.imshow(train_set_x[0])
plt.figure()
plt.imshow(train_set_x[5])
plt.figure()
plt.imshow(train_set_x[14])
plt.figure()
plt.imshow(train_set_x[2])
plt.figure()
plt.imshow(train_set_x[9])
print(train_set_y[0])
print(train_set_y[5])
print(train_set_y[14])
print(train_set_y[2])
print(train_set_y[9])
m_train = train_set_x.shape[0]
m_test = test_set_x.shape[0]
num_px = train_set_x.shape[1]
train_set_y.shape = (1,m_train)
test_set_y.shape = (1,m_test)
print ("Number of training examples: m_train = " + str(m_train))
print ("Number of testing examples: m_test = " + str(m_test))
print ("Height/Width of each image: num_px = " + str(num_px))
print ("Each image is of size: (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("train_set_x shape: " + str(train_set_x.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x shape: " + str(test_set_x.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
# Reshape the training and test examples
# Each column represents a flattened image
# There are total m columns for m images
train_set_x_flatten = train_set_x.reshape(num_px*num_px*3, m_train)
test_set_x_flatten = test_set_x.reshape(num_px*num_px*3, m_test)
print ("train_set_x_flatten shape: " + str(train_set_x_flatten.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x_flatten shape: " + str(test_set_x_flatten.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
x_train = train_set_x_flatten/255.
x_test = test_set_x_flatten/255.
from sklearn.tree import DecisionTreeClassifier
classifier1 = DecisionTreeClassifier(criterion = 'gini', random_state = 0,max_depth = 300,min_samples_split = 10,min_samples_leaf = 5)
classifier1.fit(x_train.T,train_set_y.T)
y_pred1 = classifier1.predict(x_train.T)
y_pred2 = classifier1.predict(x_test.T)
from sklearn.metrics import accuracy_score
accuracy_score(train_set_y.T, y_pred1)
accuracy_score(test_set_y.T, y_pred2)
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/Shahid1993/colab-notebooks/blob/master/word_completion_prediction.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# [Making a Predictive Keyboard using Recurrent Neural Networks](https://medium.com/@curiousily/making-a-predictive-keyboard-using-recurrent-neural-networks-tensorflow-for-hackers-part-v-3f238d824218)
# Recurrent Neural Networks
In short, `RNN` models provide a way to not only examine the current input but the one that was provided one step back, as well. If we turn that around, we can say that the decision reached at time step t-1 directly affects the future at step t.
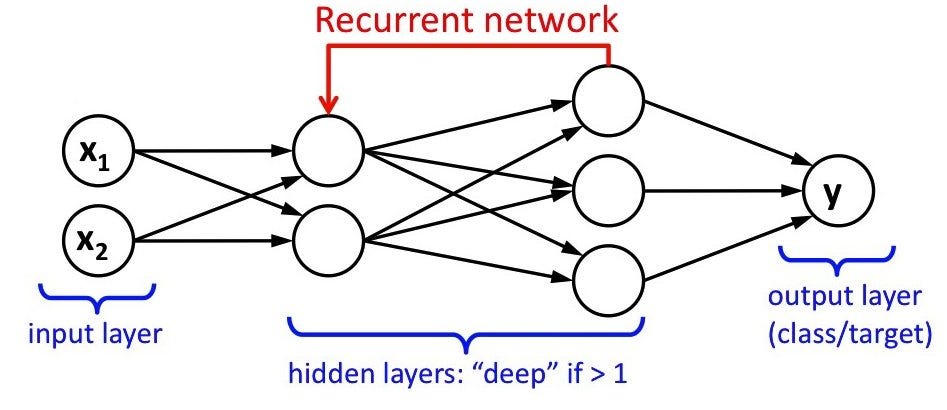
## Definition
RNNs define a recurrence relation over time steps which is given by:
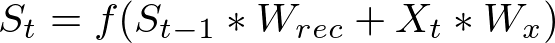
Where St is the state at time step t, Xt an exogenous input at time t, Wrec and Wx are weights parameters. The feedback loops gives memory to the model because it can remember information between time steps.
`RNNs` can compute the current state St from the current input Xt and previous state St−1 or predict the next state from St+1 from the current St and current input Xt. Concretely, we will pass a sequence of 40 characters and ask the model to predict the next one. We will append the new character and drop the first one and predict again. This will continue until we complete a whole word.
# LSTMs
Two major problems torment the `RNNs` — **vanishing** and **exploding gradients**. In traditional `RNNs` the gradient signal can be multiplied a large number of times by the weight matrix. Thus, the magnitude of the weights of the transition matrix can play an important role.
If the weights in the matrix are small, the gradient signal becomes smaller at every training step, thus making learning very slow or completely stops it. This is called vanishing gradient. Let’s have a look at applying the sigmoid function multiple times, thus simulating the effect of vanishing gradient:
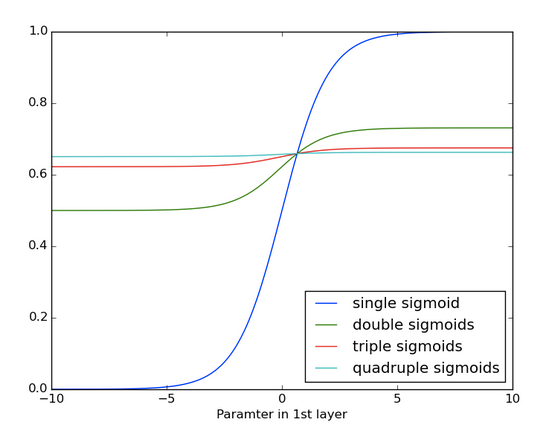
Conversely, the exploding gradient refers to the weights in this matrix being so large that it can cause learning to diverge.
`LSTM` model is a special kind of `RNN` that learns long-term dependencies. It introduces new structure — the memory cell that is composed of four elements: input, forget and output gates and a neuron that connects to itself:
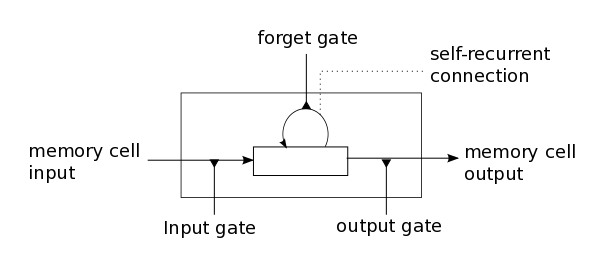
`LSTMs` *fight the gradient vanishing problem by preserving the error that can be backpropagated through time and layers*. By maintaining a more constant error, they allow for learning long-term dependencies. On another hand, *exploding is controlled with **gradient clipping***, that is the gradient is not allowed to go above some predefined value.
# Setup
Let’s properly seed our random number generator and import all required modules:
```
# Mounting Google Drive to Load Data
from google.colab import drive
drive.mount('/content/drive')
import numpy as np
np.random.seed(42)
import tensorflow as tf
tf.set_random_seed(42)
from keras.models import Sequential, load_model
from keras.layers import Dense, Activation
from keras.layers import LSTM, Dropout, CuDNNLSTM
from keras.layers import TimeDistributed
from keras.layers.core import Dense, Activation, Dropout, RepeatVector
from keras.optimizers import RMSprop
import matplotlib.pyplot as plt
import pickle
import sys
import heapq
import seaborn as sns
from pylab import rcParams
%matplotlib inline
sns.set(style='whitegrid', palette='muted', font_scale=1.5)
rcParams['figure.figsize'] = 12, 5
```
# Loading the data
```
#path = 'nietzsche.txt'
path = "./drive/My Drive/ML/data/nietzsche.txt"
#path = "./drive/My Drive/ML/data/1-billion-word-language-modeling-benchmark-r13output/training-monolingual.tokenized.shuffled/news.en-00001-of-00100"
text = open(path).read().lower()
print('corpus length:', len(text))
```
# Preprocessing
Let’s find all unique chars in the corpus and create char to index and index to char maps:
```
chars = sorted(list(set(text)))
char_indices = dict((c, i) for i, c in enumerate(chars))
indices_char = dict((i, c) for i, c in enumerate(chars))
print(f'unique chars: {len(chars)}')
print(chars)
print(''.join(map(str, chars)))
# def clean_special_chars(text, punct):
# for p in punct:
# text = text.replace(p, '')
# return text
# def preprocess(data):
# output = []
# punct = '\n#$<=>[\\]@^{|}~¡¢£¤¥©«¬®°²´µ¶·º»¼½¾¿×àáâãäåæçèéêëíîïñóôõöøùúüþąćĕěœšŵžʼ˚а‐‑‚‟†•′₤€∆④●♥fi()£�'
# for line in data:
# pline= clean_special_chars(line.lower(), punct)
# output.append(pline)
# return output
# text = preprocess(text)
def preprocess(data):
punct = '\n#$<=>[\\]@^{|}~¡¢£¤¥©«¬®°²´µ¶·º»¼½¾¿×àáâãäåæçèéêëíîïñóôõöøùúüþąćĕěœšŵžʼ˚а‐‑‚‟†•′₤€∆④●♥fi()£�'
for p in punct:
data = data.replace(p, '')
return data
text = preprocess(text)
chars = sorted(list(set(text)))
char_indices = dict((c, i) for i, c in enumerate(chars))
indices_char = dict((i, c) for i, c in enumerate(chars))
print(f'unique chars: {len(chars)}')
print(chars)
print(''.join(map(str, chars)))
print('corpus length:', len(text))
```
Next, let’s cut the corpus into chunks of `40` characters, spacing the sequences by `3` characters. Additionally, we will store the next character (the one we need to predict) for every sequence:
```
SEQUENCE_LENGTH = 40
step = 3
sentences = []
next_chars = []
for i in range(0, len(text) - SEQUENCE_LENGTH, step):
sentences.append(text[i: i + SEQUENCE_LENGTH])
next_chars.append(text[i + SEQUENCE_LENGTH])
print(f'num training examples: {len(sentences)}')
```
It is time for generating our features and labels. We will use the previously generated sequences and characters that need to be predicted to create one-hot encoded vectors using the `char_indices` map:
```
X = np.zeros((len(sentences), SEQUENCE_LENGTH, len(chars)), dtype=np.bool)
y = np.zeros((len(sentences), len(chars)), dtype=np.bool)
for i, sentence in enumerate(sentences):
for t, char in enumerate(sentence):
X[i, t, char_indices[char]] = 1
y[i, char_indices[next_chars[i]]] = 1
```
Let’s have a look at a single training sequence:
```
sentences[1091]
```
The character that needs to be predicted for it is:
```
next_chars[1091]
```
The encoded (one-hot) data looks like this:
```
X[0]
y[0]
```
And for the dimensions:
```
X.shape
y.shape
```
We have `200285` training examples, each sequence has length of `40` with `57` unique chars.
# Building the model
The model we’re going to train is pretty straight forward. Single `LSTM` layer with `128` neurons which accepts input of shape (`40` — the length of a sequence, `57` — the number of unique characters in our dataset). A fully connected layer (for our output) is added after that. It has `57` neurons and softmax for activation function:
```
model = Sequential()
#model.add(LSTM(128, input_shape=(SEQUENCE_LENGTH, len(chars))))
#model.add(CuDNNLSTM(128, input_shape=(None, len(chars))))
model.add(CuDNNLSTM(128, input_shape=(None, len(chars)), return_sequences=True))
model.add(CuDNNLSTM(128, return_sequences=True))
model.add(CuDNNLSTM(128))
#Dropout added to avoid overfitting
model.add(Dropout(rate = 0.2))
# build model using keras documentation recommended optimizer initialization
optimizer = RMSprop(lr=0.001, rho=0.9, epsilon=1e-08, decay=0.0)
model.add(Dense(len(chars)))
model.add(Activation('softmax'))
model.summary()
```
# Training
Our model is trained for `20` epochs using `RMSProp` optimizer and uses `5%` of the data for validation:
```
#optimizer = RMSprop(lr=0.01)
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
history = model.fit(X, y, validation_split=0.05, batch_size=128, epochs=15, shuffle=True).history
```
# Saving
```
model.save('predictive_keyboard_keras_model.h5')
pickle.dump(history, open("predictive_keyboard_history.p", "wb"))
```
And load it back, just to make sure it works:
```
model = load_model('predictive_keyboard_keras_model.h5')
history = pickle.load(open("predictive_keyboard_history.p", "rb"))
```
# Evaluation
Let’s have a look at how our accuracy and loss change over training epochs:
```
plt.plot(history['acc'])
plt.plot(history['val_acc'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left');
plt.plot(history['loss'])
plt.plot(history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left');
```
# Let’s put our model to the test
```
# def prepare_input(text):
# x = np.zeros((1, SEQUENCE_LENGTH, len(chars)))
# for t, char in enumerate(text):
# x[0, t, char_indices[char]] = 1.
# return x
def prepare_input(text):
x = np.zeros((1, len(text), len(chars)))
for t, char in enumerate(text):
x[0, t, char_indices[char]] = 1.
return x
```
Remember that our sequences must be `40` characters long. So we make a tensor with shape `(1, 40, 59)`, initialized with zeros. Then, a value of 1 is placed for each character in the passed text. We must not forget to use the lowercase version of the text:
```
prepare_input("This is an example of input for our LSTM".lower())
#prepare_input("Tests".lower())
```
#### Next up, the sample function:
This function allows us to ask our model what are the next `n` most probable characters.
```
def sample(preds, top_n=3):
preds = np.asarray(preds).astype('float64')
preds = np.log(preds)
exp_preds = np.exp(preds)
preds = exp_preds / np.sum(exp_preds)
return heapq.nlargest(top_n, range(len(preds)), preds.take)
```
Now for the **prediction functions** themselves:
This function predicts next character until space is predicted (you can extend that to punctuation symbols, right?). It does so by repeatedly preparing input, asking our model for predictions and sampling from them.
```
def predict_completion(text):
original_text = text
generated = text
completion = ''
while True:
x = prepare_input(text)
preds = model.predict(x, verbose=0)[0]
next_index = sample(preds, top_n=1)[0]
next_char = indices_char[next_index]
text = text[1:] + next_char
completion += next_char
if len(original_text + completion) + 2 > len(original_text) and next_char == ' ':
return completion
```
The final piece of the puzzle — `predict_completions` wraps everything and allow us to predict multiple completions:
```
def predict_completions(text, n=3):
x = prepare_input(text)
preds = model.predict(x, verbose=0)[0]
next_indices = sample(preds, n)
return [indices_char[idx] + predict_completion(text[1:] + indices_char[idx]) for idx in next_indices]
```
Let’s use sequences of 40 characters that we will use as seed for our completions. All of these are quotes from Friedrich Nietzsche himself:
```
# actual_text = [
# "It is not a lack of love, but a lack of friendship that makes unhappy marriages.",
# "That which does not kill us makes us stronger.",
# "I'm not upset that you lied to me, I'm upset that from now on I can't believe you.",
# "And those who were seen dancing were thought to be insane by those who could not hear the music.",
# "It is hard enough to remember my opinions, without also remembering my reasons for them!",
# "A man lying on a comfortable sofa is listening to his wi",
# "Assuming the predictions are probabilistic, novel sequences can be generated from a trai",
# "The networks performance is competitive with state-of-the-art language models, and it works almost",
# "This document is the initial part of a study to predict next words from a text dataset"
# ]
input = [
"It is not a lack of lov",
"That which does not kill us makes us stro",
"I'm not upset that you lied to me, I'm upset that from now on I can't bel",
"And those who were seen dan",
"It is hard enough to remember my opini",
"A man lying on a comfortable ch",
"Assuming the pre",
"The networks performance is competi",
"The networks performance is competitive with state-of-the-art lan",
"This document is the initial part of a study to pre",
"This document is the initial part of a study to pred",
"Assuming the prediction",
"Assuming the predictions are probabilistic, novel sequences can be gene",
"Assuming the predictions are probabilistic, novel sequences can be generat"
]
for i in input:
seq = i.lower()
print(seq)
print(predict_completions(seq, 5))
print()
```
Apart from the fact that the completions look like proper words (remember, we are training our model on characters, not words), they look pretty reasonable as well! Perhaps better model and/or more training will provide even better results?
# Conclusion
We’ve built a model using just a few lines of code in `Keras` that performs reasonably well after just 20 training epochs. Can you try it with your own text? Why not predict whole sentences? Will it work that well in other languages?
# Testing Already Created Models
### Load Model from Google Drive
```
# Mounting Google Drive to Load Data
from google.colab import drive
drive.mount('/content/drive')
model = load_model('./drive/My Drive/ML/Models/word_completion_prediction/word_completion_prediction_keras_model.h5')
history = pickle.load(open("./drive/My Drive/ML/Models/word_completion_prediction/word_completion_prediction_history.p", "rb"))
def prepare_input(text):
x = np.zeros((1, len(text), len(chars)))
for t, char in enumerate(text):
x[0, t, char_indices[char]] = 1.
return x
def sample(preds, top_n=3):
preds = np.asarray(preds).astype('float64')
preds = np.log(preds)
exp_preds = np.exp(preds)
preds = exp_preds / np.sum(exp_preds)
return heapq.nlargest(top_n, range(len(preds)), preds.take)
def predict_completion(text):
original_text = text
generated = text
completion = ''
while True:
x = prepare_input(text)
preds = model.predict(x, verbose=0)[0]
next_index = sample(preds, top_n=1)[0]
next_char = indices_char[next_index]
text = text[1:] + next_char
completion += next_char
if len(original_text + completion) + 2 > len(original_text) and next_char == ' ':
return completion
def predict_completions(text, n=3):
x = prepare_input(text)
preds = model.predict(x, verbose=0)[0]
next_indices = sample(preds, n)
return [indices_char[idx] + predict_completion(text[1:] + indices_char[idx]) for idx in next_indices]
# actual_text = [
# "It is not a lack of love, but a lack of friendship that makes unhappy marriages.",
# "That which does not kill us makes us stronger.",
# "I'm not upset that you lied to me, I'm upset that from now on I can't believe you.",
# "And those who were seen dancing were thought to be insane by those who could not hear the music.",
# "It is hard enough to remember my opinions, without also remembering my reasons for them!",
# "A man lying on a comfortable sofa is listening to his wi",
# "Assuming the predictions are probabilistic, novel sequences can be generated from a trai",
# "The networks performance is competitive with state-of-the-art language models, and it works almost",
# "This document is the initial part of a study to predict next words from a text dataset"
# ]
input = [
"It is not a lack of lov",
"That which does not kill us makes us stro",
"I'm not upset that you lied to me, I'm upset that from now on I can't bel",
"And those who were seen dan",
"It is hard enough to remember my opini",
"A man lying on a comfortable ch",
"The networks perf",
"The networks performance is competi",
"The networks performance is competitive with state-of-the-art lan",
"This document is the initial part of a study to pre",
"This document is the initial part of a study to pred",
"Assuming the prediction",
"Assuming the predictions are probabilistic, novel sequences can be gene",
"Assuming the predictions are probabilistic, novel sequences can be generat"
]
for i in input:
seq = i.lower()
print(seq)
print(predict_completions(seq, 5))
print()
```
|
github_jupyter
|
# Extract barrier island metrics along transects
Author: Emily Sturdivant, esturdivant@usgs.gov
***
Extract barrier island metrics along transects for Barrier Island Geomorphology Bayesian Network. See the project [README](https://github.com/esturdivant-usgs/BI-geomorph-extraction/blob/master/README.md) and the Methods Report (Zeigler et al., in review).
## Pre-requisites:
- All the input layers (transects, shoreline, etc.) must be ready. This is performed with the notebook file prepper.ipynb.
- The files servars.py and configmap.py may need to be updated for the current dataset.
## Notes:
- This notebook includes interactive quality checking, which requires the user's attention. For thorough QC'ing, we recommend displaying the layers in ArcGIS, especially to confirm the integrity of values for variables such as distance to inlet (__Dist2Inlet__) and widths of the landmass (__WidthPart__, etc.).
***
## Import modules
```
import os
import sys
import pandas as pd
import numpy as np
import io
import arcpy
import pyproj
import datetime
import matplotlib.pyplot as plt
import matplotlib
matplotlib.style.use('ggplot')
import core.functions_warcpy as fwa
import core.functions as fun
print("Date: {}".format(datetime.date.today()))
# print(os.__version__)
# print(sys.__version__)
print('pandas version: {}'.format(pd.__version__))
print('numpy version: {}'.format(np.__version__))
print('matplotlib version: {}'.format(matplotlib.__version__))
# print(io.__version__)
# print(arcpy.__version__)
print('pyproj version: {}'.format(pyproj.__version__))
# print(fwa.__version__)
```
### Initialize variables
This cell prompts you for the site, year, and project directory path. `setvars.py` retrieves the pre-determined values for that site in that year from `configmap.py`. The project directory will be used to set up your workspace. It's hidden for security – sorry! I recommend that you type the path somewhere and paste it in.
```
from core.setvars import *
```
Change the filename variables to match your local files. They should be in an Esri file geodatabase named site+year.gdb in your project directory, which you input above and is the value of the variable `home`.
```
# Extended transects: NASC transects extended and sorted, ready to be the base geometry for processing
extendedTrans = os.path.join(home, 'Monomoy2014_extTrans_null')
# Tidied transects: Extended transects without overlapping transects
extTrans_tidy = os.path.join(home, 'Monomoy_tidyTrans')
# Geomorphology points: positions of indicated geomorphic features
ShorelinePts = os.path.join(home, 'Monomoy2014_SLpts') # shoreline
dlPts = os.path.join(home, 'Monomoy2014_DLpts') # dune toe
dhPts = os.path.join(home, 'Monomoy2014_DHpts') # dune crest
# Inlet lines: polyline feature classes delimiting inlet position. Must intersect the full island shoreline
inletLines = os.path.join(home, 'Monomoy2014_inletLines')
# Full island shoreline: polygon that outlines the island shoreline, MHW on oceanside and MTL on bayside
barrierBoundary = os.path.join(home, 'Monomoy2014_bndpoly_2sl')
# Elevation grid: DEM of island elevation at either 5 m or 1 m resolution
elevGrid = os.path.join(home, 'Monomoy2014_DEM_5m')
# ---
# OPTIONAL - comment out each one that is not available
# ---
#
# morphdata_prefix = '14CNT01'
# Study area boundary; manually digitize if the barrier island study area does not end at an inlet.
# SA_bounds = os.path.join(home, 'SA_bounds')
# Armoring lines: digitize lines of shorefront armoring to be used if dune toe points are not available.
# armorLines = os.path.join(home, 'armorLines')
# Extended transects with Construction, Development, and Nourishment coding
# tr_w_anthro = os.path.join(home, 'extTrans_wAnthro')
# Piping Plover Habitat BN raster layers
SubType = os.path.join(home, 'SubType') # substrate type
VegType = os.path.join(home, 'VegType') # vegetation type
VegDens = os.path.join(home, 'VegDens') # vegetation density
GeoSet = os.path.join(home, 'GeoSet') # geomorphic setting
# Derivatives of inputs: They will be generated during process if they are not found.
shoreline = os.path.join(home, 'ShoreBetweenInlets') # oceanside shoreline between inlets; generated from shoreline polygon, inlet lines, and SA bounds
slopeGrid = os.path.join(home, 'slope_5m') # Slope at 5 m resolution; generated from DEM
```
## Transect-averaged values
We work with the shapefile/feature class as a pandas DataFrame as much as possible to speed processing and minimize reliance on the ArcGIS GUI display.
1. Add the bearing of each transect line to the attribute table from the LINE_BEARING geometry attribute.
1. Create a pandas dataframe from the transects feature class. In the process, remove some of the unnecessary fields. The resulting dataframe is indexed by __sort_ID__ with columns corresponding to the attribute fields in the transects feature class.
2. Add __DD_ID__.
3. Join the values from the transect file that includes the three anthropologic development fields, __Construction__, __Development__, and __Nourishment__.
```
# Add BEARING field to extendedTrans feature class
arcpy.AddGeometryAttributes_management (extendedTrans, 'LINE_BEARING')
print("Adding line bearing field to transects.")
# Copy feature class to dataframe.
trans_df = fwa.FCtoDF(extendedTrans, id_fld=tID_fld, extra_fields=extra_fields)
trans_df['DD_ID'] = trans_df[tID_fld] + sitevals['id_init_val']
trans_df.drop('Azimuth', axis=1, inplace=True)
trans_df.rename_axis({"BEARING": "Azimuth"}, axis=1, inplace=True)
# Get anthro fields and join to DF
if 'tr_w_anthro' in locals():
trdf_anthro = fwa.FCtoDF(tr_w_anthro, id_fld=tID_fld, dffields=['Development', 'Nourishment','Construction'])
trans_df = fun.join_columns(trans_df, trdf_anthro)
# Save
trans_df.to_pickle(os.path.join(scratch_dir, 'trans_df.pkl'))
# Display
print("\nHeader of transects dataframe (rows 1-5 out of {}): ".format(len(trans_df)))
trans_df.head()
print(extra_fields)
```
### Get XY and Z/slope from SL, DH, DL points within 25 m of transects
Add to each transect row the positions of the nearest pre-created beach geomorphic features (shoreline, dune toe, and dune crest).
#### If needed, convert morphology points stored locally to feature classes for use.
After which, view the new feature classes in a GIS. Isolate the points to the region of interest. Quality check them. Then copy them for use with this code, which will require setting the filenames to match those included here or changing the values included here to match the final filenames.
```
if "morphdata_prefix" in locals():
csvpath = os.path.join(proj_dir, 'Input_Data', '{}_morphology'.format(morphdata_prefix),
'{}_morphology.csv'.format(morphdata_prefix))
dt_fc, dc_fc, sl_fc = fwa.MorphologyCSV_to_FCsByFeature(csvpath, state, proj_code,
csv_fill = 999, fc_fill = -99999, csv_epsg=4326)
print("OUTPUT: morphology point feature classes in the scratch gdb. We recommend QC before proceeding.")
```
#### Shoreline
The MHW shoreline easting and northing (__SL_x__, __SL_y__) are the coordinates of the intersection of the oceanside shoreline with the transect. Each transect is assigned the foreshore slope (__Bslope__) from the nearest shoreline point within 25 m. These values are populated for each transect as follows:
1. get __SL_x__ and __SL_y__ at the point where the transect crosses the oceanside shoreline;
2. find the closest shoreline point to the intersection point (must be within 25 m) and copy the slope value from the point to the transect in the field __Bslope__.
```
if not arcpy.Exists(inletLines):
# manually create lines that correspond to end of land and cross the MHW line (refer to shoreline polygon)
arcpy.CreateFeatureclass_management(home, os.path.basename(inletLines), 'POLYLINE', spatial_reference=utmSR)
print("OUTPUT: {}. Interrupt execution to manually create lines at each inlet.".format(inletLines))
if not arcpy.Exists(shoreline):
if not 'SA_bounds' in locals():
SA_bounds = ''
shoreline = fwa.CreateShoreBetweenInlets(barrierBoundary, inletLines, shoreline, ShorelinePts, proj_code, SA_bounds)
# Get the XY position where transect crosses the oceanside shoreline
sl2trans_df, ShorelinePts = fwa.add_shorelinePts2Trans(extendedTrans, ShorelinePts, shoreline,
tID_fld, proximity=pt2trans_disttolerance)
# Save and print sample
sl2trans_df.to_pickle(os.path.join(scratch_dir, 'sl2trans.pkl'))
sl2trans_df.sample(5)
# Export the inlet delineation and shoreline polygons to the scratch directory ultimately for publication
arcpy.FeatureClassToFeatureClass_conversion(inletLines, scratch_dir, pts_name.split('_')[0] + '_inletLines.shp')
arcpy.FeatureClassToFeatureClass_conversion(barrierBoundary, scratch_dir, pts_name.split('_')[0] + '_shoreline.shp')
print('OUTPUT: Saved inletLines and shoreline shapefiles in the scratch directory.')
# fun.AddGeographicCoordinates(ShorelinePts)
# Convert to pandas DF
slpts_df = fwa.FCtoDF(ShorelinePts)
slpts_df.head()
# Report values
xmlfile = os.path.join(scratch_dir, pts_name.split('_')[0] + '_SLpts_eainfo.xml')
sl_extra_flds = fun.report_fc_values(slpts_df, field_defs, xmlfile)
# Delete extra fields from points feature class and dataframe (which will become CSV)
if len(sl_extra_flds) > 0:
for fld in sl_extra_flds:
try:
arcpy.DeleteField_management(ShorelinePts, fld)
print('Deleted field "{}"'.format(fld))
except:
print('WARNING: Failed to delete field "{}"'.format(fld))
pass
arcpy.Delete_management(pts_name.split('_')[0] + '_SLpts.shp')
arcpy.FeatureClassToFeatureClass_conversion(ShorelinePts, scratch_dir, pts_name.split('_')[0] + '_SLpts.shp')
print("\nOUTPUT: {} in specified scratch_dir.".format(os.path.basename(pts_name.split('_')[0] + '_SLpts.shp')))
# Save CSV in scratch_dir
slpts_df.drop(sl_extra_flds, axis=1, inplace=True)
csv_fname = os.path.join(scratch_dir, pts_name.split('_')[0] + '_SLpts.csv')
slpts_df.to_csv(csv_fname, na_rep=fill, index=False)
print("\nOUTPUT: {} in specified scratch_dir.".format(os.path.basename(csv_fname)))
```
#### Dune positions along transects
__DL_x__, __DL_y__, and __DL_z__ are the easting, northing, and elevation, respectively, of the nearest dune toe point within 25 meters of the transect. __DH_x__, __DH_y__, and __DH_z__ are the easting, northing, and elevation, respectively, of the nearest dune crest point within 25 meters.
__DL_snapX__, __DL_snapY__, __DH_snapX__, and __DH_snapY__ are the eastings and northings of the points "snapped" to the transect. "Snapping" finds the position along the transect nearest to the point, i.e. orthogonal to the transect. These values are used to find the beach width. The elevation values are not snapped; we use the elevation values straight from the original points.
These values are populated as follows:
1. Find the nearest dune crest/toe point to the transect and proceed if the distance is less than 25 m. If there are no points within 25 m of the transect, populate the row with Null values.
2. Get the X, Y, and Z values of the point.
3. Find the position along the transect of an orthogonal line drawn to the dune point (__DL_snapX__, __DL_snapY__, __DH_snapX__, and __DH_snapY__). This is considered the 'snapped' XY position and is calculated using the arcpy geometry method.
```
# Create dataframe for both dune crest and dune toe positions
dune2trans_df, dhPts, dlPts = fwa.find_ClosestPt2Trans_snap(extendedTrans, dhPts, dlPts, trans_df,
tID_fld, proximity=pt2trans_disttolerance)
# Save and print sample
dune2trans_df.to_pickle(os.path.join(scratch_dir, 'dune2trans.pkl'))
dune2trans_df.sample(5)
# Convert to pandas DF
dlpts_df = fwa.FCtoDF(dlPts)
# Report values
xmlfile = os.path.join(scratch_dir, pts_name.split('_')[0] + '_DTpts_eainfo.xml')
dl_extra_flds = fun.report_fc_values(dlpts_df, field_defs, xmlfile)
# Delete extra fields from points feature class and dataframe (which will become CSV)
for fld in dl_extra_flds:
try:
arcpy.DeleteField_management(dlPts, fld)
print('Deleted field "{}"'.format(fld))
except:
print('WARNING: Failed to delete field "{}"'.format(fld))
pass
arcpy.FeatureClassToFeatureClass_conversion(dlPts, scratch_dir, pts_name.split('_')[0] + '_DTpts.shp')
# Save CSV in scratch_dir
dlpts_df.drop(dl_extra_flds, axis=1, inplace=True)
csv_fname = os.path.join(scratch_dir, pts_name.split('_')[0] + '_DTpts.csv')
dlpts_df.to_csv(csv_fname, na_rep=fill, index=False)
print("\nOUTPUT: {} in specified scratch_dir.\n".format(os.path.basename(csv_fname)))
# Convert to pandas DF
dhpts_df = fwa.FCtoDF(dhPts)
# Report values
xmlfile = os.path.join(scratch_dir, pts_name.split('_')[0] + '_DCpts_eainfo.xml')
dh_extra_flds = fun.report_fc_values(dhpts_df, field_defs, xmlfile)
# Delete extra fields from points feature class and dataframe (which will become CSV)
for fld in dh_extra_flds:
try:
arcpy.DeleteField_management(dhPts, fld)
print('Deleted field "{}"'.format(fld))
except:
print('WARNING: Failed to delete field "{}"'.format(fld))
pass
arcpy.FeatureClassToFeatureClass_conversion(dhPts, scratch_dir, pts_name.split('_')[0] + '_DCpts.shp')
# Save CSV in scratch_dir
dhpts_df.drop(dh_extra_flds, axis=1, inplace=True)
csv_fname = os.path.join(scratch_dir, pts_name.split('_')[0] + '_DCpts.csv')
dhpts_df.to_csv(csv_fname, na_rep=fill, index=False)
print("\nOUTPUT: {} in specified scratch_dir.".format(os.path.basename(csv_fname)))
```
#### Armoring
__Arm_x__, __Arm_y__, and __Arm_z__ are the easting, northing, and elevation, respectively, where an artificial structure crosses the transect in the vicinity of the beach. These features are meant to supplement the dune toe data set by providing an upper limit to the beach in areas where dune toe extraction was confounded by the presence of an artificial structure. Values are populated for each transect as follows:
1. Get the positions of intersection between the digitized armoring lines and the transects (Intersect tool from the Overlay toolset);
2. Extract the elevation value at each intersection point from the DEM (Extract Multi Values to Points tool from Spatial Analyst);
```
# Create elevation raster at 5-m resolution if not already
elevGrid = fwa.ProcessDEM_2(elevGrid, utmSR)
# Armoring line
if not arcpy.Exists(armorLines):
arcpy.CreateFeatureclass_management(home, os.path.basename(armorLines), 'POLYLINE', spatial_reference=utmSR)
print("{} created. If shorefront armoring exists, interrupt execution to manually digitize.".format(armorLines))
arm2trans_df = fwa.ArmorLineToTrans_PD(extendedTrans, armorLines, sl2trans_df, tID_fld, proj_code, elevGrid)
# Save and print sample
arm2trans_df.to_pickle(os.path.join(scratch_dir, 'arm2trans.pkl'))
try:
arm2trans_df.sample(5)
except:
pass
```
### Add all the positions to the trans_df
Join the new dataframes to the transect dataframe. Before it performs the join, `join_columns_id_check()` checks the index and the ID field for potential errors such as whether they are the equal and whether there are duplicated IDs or null values in either.
```
# Load saved dataframes
trans_df = pd.read_pickle(os.path.join(scratch_dir, 'trans_df.pkl'))
sl2trans_df = pd.read_pickle(os.path.join(scratch_dir, 'sl2trans.pkl'))
dune2trans_df = pd.read_pickle(os.path.join(scratch_dir, 'dune2trans.pkl'))
arm2trans_df = pd.read_pickle(os.path.join(scratch_dir, 'arm2trans.pkl'))
# Join positions of shoreline, dune crest, dune toe, armoring
trans_df = fun.join_columns_id_check(trans_df, sl2trans_df, tID_fld)
trans_df = fun.join_columns_id_check(trans_df, dune2trans_df, tID_fld)
trans_df = fun.join_columns_id_check(trans_df, arm2trans_df, tID_fld)
# Save and print sample
trans_df.to_pickle(os.path.join(scratch_dir, 'trans_df_beachmetrics.pkl'))
trans_df.sample(5)
```
### Check for errors
*Optional*
Display summary stats / histograms and create feature classes. The feature classes display the locations that will be used to calculate beach width. Review the output feature classes in a GIS to validate.
```
plots = trans_df.hist(['DH_z', 'DL_z', 'Arm_z'])
# Subplot Labels
plots[0][0].set_xlabel("Elevation (m in NAVD88)")
plots[0][0].set_ylabel("Frequency")
plots[0][1].set_xlabel("Elevation (m in NAVD88)")
plots[0][1].set_ylabel("Frequency")
try:
plots[0][2].set_xlabel("Elevation (m in NAVD88)")
plots[0][2].set_ylabel("Frequency")
except:
pass
plt.show()
plt.close()
# Convert dataframe to feature class - shoreline points with slope
fwa.DFtoFC(sl2trans_df, os.path.join(arcpy.env.workspace, 'pts2trans_SL'),
spatial_ref=utmSR, id_fld=tID_fld, xy=["SL_x", "SL_y"], keep_fields=['Bslope'])
print('OUTPUT: pts2trans_SL in designated scratch geodatabase.')
# Dune crests
try:
fwa.DFtoFC(dune2trans_df, os.path.join(arcpy.env.workspace, 'ptSnap2trans_DH'),
spatial_ref=utmSR, id_fld=tID_fld, xy=["DH_snapX", "DH_snapY"], keep_fields=['DH_z'])
print('OUTPUT: ptSnap2trans_DH in designated scratch geodatabase.')
except Exception as err:
print(err)
pass
# Dune toes
try:
fwa.DFtoFC(dune2trans_df, os.path.join(arcpy.env.workspace, 'ptSnap2trans_DL'),
spatial_ref=utmSR, id_fld=tID_fld, xy=["DL_snapX", "DL_snapY"], keep_fields=['DL_z'])
print('OUTPUT: ptSnap2trans_DL in designated scratch geodatabase.')
except Exception as err:
print(err)
pass
```
### Calculate upper beach width and height
Upper beach width (__uBW__) and upper beach height (__uBH__) are calculated based on the difference in position between two points: the position of MHW along the transect (__SL_x__, __SL_y__) and the dune toe position or equivalent (usually __DL_snapX__, __DL_snapY__). In some cases, the dune toe is not appropriate to designate the "top of beach" so beach width and height are calculated from either the position of the dune toe, the dune crest, or the base of an armoring structure. The dune crest was only considered a possibility if the dune crest elevation (__DH_zMHW__) was less than or equal to `maxDH`.
They are calculated as follows:
2. Calculate distances from MHW to the position along the transect of the dune toe (__DistDL__), dune crest (__DistDH__), and armoring (__DistArm__).
2. Adjust the elevations to MHW, populating fields __DH_zmhw__, __DL_zmhw__, and __Arm_zmhw__.
3. Conditionally select the appropriate feature to represent "top of beach." Dune toe is prioritized. If it is not available and __DH_zmhw__ is less than or equal to maxDH, use dune crest. If neither of the dune positions satisfy the conditions and an armoring feature intersects with the transect, use the armoring position. If none of the three are possible, __uBW__ and __uBH__ will be null.
4. Copy the distance to shoreline and height above MHW (__Dist--__, __---zmhw__) to __uBW__ and __uBH__, respectively.
Notes:
- In some morphology datasets, missing elevation values at a point indicate that the point should not be used to measure beach width. In those cases, use the `skip_missing_z` argument to select whether or not to skip these points.
```
# Load saved dataframe
trans_df = pd.read_pickle(os.path.join(scratch_dir, 'trans_df_beachmetrics.pkl'))
# Calculate distances from shore to dunes, etc.
trans_df = fwa.calc_BeachWidth_fill(extendedTrans, trans_df, maxDH, tID_fld,
sitevals['MHW'], fill, skip_missing_z=True)
```
### Dist2Inlet
Distance to nearest tidal inlet (__Dist2Inlet__) is computed as alongshore distance of each sampling transect from the nearest tidal inlet. This distance includes changes in the path of the shoreline instead of simply a Euclidean distance and reflects sediment transport pathways. It is measured using the oceanside shoreline between inlets (ShoreBetweenInlets).
Note that the ShoreBetweenInlets feature class must be both 'dissolved' and 'singlepart' so that each feature represents one-and-only-one shoreline that runs the entire distance between two inlets or equivalent. If the shoreline is bounded on both sides by an inlet, measure the distance to both and assign the minimum distance of the two. If the shoreline meets only one inlet (meaning the study area ends before the island ends), use the distance to the only inlet.
The process uses the cut, disjoint, and length geometry methods and properties in ArcPy data access module. The function measure_Dist2Inlet() prints a warning when the difference in Dist2Inlet between two consecutive transects is greater than 300.
```
# Calc Dist2Inlet in new dataframe
dist_df = fwa.measure_Dist2Inlet(shoreline, extendedTrans, inletLines, tID_fld)
# Join to transects
trans_df = fun.join_columns_id_check(trans_df, pd.DataFrame(dist_df.Dist2Inlet), tID_fld, fill=fill)
# Save and view last 10 rows
dist_df.to_pickle(os.path.join(scratch_dir, 'dist2inlet_df.pkl'))
dist_df.tail(10)
```
### Clip transects, get barrier widths
Calculates __WidthLand__, __WidthFull__, and __WidthPart__, which measure different flavors of the cross-shore width of the barrier island. __WidthLand__ is the above-water distance between the back-barrier and seaward MHW shorelines. __WidthLand__ only includes regions of the barrier within the shoreline polygon (bndpoly_2sl) and does not extend into any of the sinuous or intervening back-barrier waterways and islands. __WidthFull__ is the total distance between the back-barrier and seaward MHW shorelines (including space occupied by waterways). __WidthPart__ is the width of only the most seaward portion of land within the shoreline.
These are calculated as follows:
1. Clip the transect to the full island shoreline (Clip in the Analysis toolbox);
2. For __WidthLand__, get the length of the multipart line segment from "SHAPE@LENGTH" feature class attribute. When the feature is multipart, this will include only the remaining portions of the transect;
3. For __WidthPart__, convert the clipped transect from multipart to singlepart and get the length of the first line segment, which should be the most seaward;
4. For __WidthFull__, calculate the distance between the first vertex and the last vertex of the clipped transect (Feature Class to NumPy Array with explode to points, pandas groupby, numpy hypot).
```
# Clip transects, get barrier widths
widths_df = fwa.calc_IslandWidths(extendedTrans, barrierBoundary, tID_fld=tID_fld)
# # Save
widths_df.to_pickle(os.path.join(scratch_dir, 'widths_df.pkl'))
# Join
trans_df = fun.join_columns_id_check(trans_df, widths_df, tID_fld, fill=fill)
# Save
trans_df.to_pickle(os.path.join(scratch_dir, trans_name+'_null_prePts.pkl'))
trans_df.sample(5)
```
## 5-m Points
The point dataset samples the land every 5 m along each shore-normal transect.
### Split transects into points at 5-m intervals.
The point dataset is created from the tidied transects (tidyTrans, created during pre-processing) as follows:
1. Clip the tidied transects (tidyTrans) to the shoreline polygon (bndpoly_2sl) , retaining only those portions of the transects that represent land.
2. Produce a dataframe of point positions along each transect every 5 m starting from the ocean-side shoreline. This uses the positionAlongLine geometry method accessed with a Search Cursor and saves the outputs in a new dataframe.
3. Create a point feature class from the dataframe.
Note: Sometimes the system doesn't seem to register the new feature class (transPts_unsorted) for a while. I'm not sure how to work around that, other than just to wait.
```
pts_df, pts_presort = fwa.TransectsToPointsDF(extTrans_tidy, barrierBoundary, fc_out=pts_presort)
print("OUTPUT: '{}' in scratch geodatabase.".format(os.path.basename(pts_presort)))
# Save
pts_df.to_pickle(os.path.join(scratch_dir, 'pts_presort.pkl'))
```
### Add Elevation and Slope to points
__ptZ__ (later __ptZmhw__) and __ptSlp__ are the elevation and slope at the 5-m cell corresponding to the point.
1. Create the slope and DEM rasters if they don't already exist. We use the 5-m DEM to generate a slope surface (Slope tool in 3D Analyst).
2. Use Extract Multi Values to Points tool in Spatial Analyst.
3. Convert the feature class back to a dataframe.
```
# Create slope raster from DEM
if not arcpy.Exists(slopeGrid):
arcpy.Slope_3d(elevGrid, slopeGrid, 'PERCENT_RISE')
print("OUTPUT: slope file in designated home geodatabase.")
# Add elevation and slope values at points.
arcpy.sa.ExtractMultiValuesToPoints(pts_presort, [[elevGrid, 'ptZ'], [slopeGrid, 'ptSlp']])
print("OUTPUT: added slope and elevation to '{}' in designated scratch geodatabase.".format(os.path.basename(pts_presort)))
if 'SubType' in locals():
# Add substrate type, geomorphic setting, veg type, veg density values at points.
arcpy.sa.ExtractMultiValuesToPoints(pts_presort, [[SubType, 'SubType'], [VegType, 'VegType'],
[VegDens, 'VegDens'], [GeoSet, 'GeoSet']])
# Convert to dataframe
pts_df = fwa.FCtoDF(pts_presort, xy=True, dffields=[tID_fld,'ptZ', 'ptSlp', 'SubType',
'VegType', 'VegDens', 'GeoSet'])
# Recode fill values
pts_df.replace({'GeoSet': {9999:np.nan}, 'SubType': {9999:np.nan}, 'VegType': {9999:np.nan},
'VegDens': {9999:np.nan}}, inplace=True)
else:
print("Plover BN layers not specified (we only check for SubType), so we'll proceed without them. ")
# Convert to dataframe
pts_df = fwa.FCtoDF(pts_presort, xy=True, dffields=[tID_fld,'ptZ', 'ptSlp'])
# Save and view sample
pts_df.to_pickle(os.path.join(scratch_dir, 'pts_extractedvalues_presort.pkl'))
pts_df.sample(5)
# Print histogram of elevation extracted to points
plots = pts_df.hist('ptZ')
# Subplot Labels
plots[0][0].set_xlabel("Elevation (m in NAVD88)")
plots[0][0].set_ylabel("Frequency")
# Display
plt.show()
plt.close()
```
### Calculate distances and sort points
__SplitSort__ is a unique numeric identifier of the 5-m points at the study site, sorted by order along shoreline and by distance from oceanside. __SplitSort__ values are populated by sorting the points by __sort_ID__ and __Dist_Seg__ (see below).
__Dist_Seg__ is the Euclidean distance between the point and the seaward shoreline (__SL_x__, __SL_y__). __Dist_MHWbay__ is the distance between the point and the bayside shoreline and is calculated by subtracting the __Dist_Seg__ value from the __WidthPart__ value of the transect.
__DistSegDH__, __DistSegDL__, and __DistSegArm__ measure the distance of each 5-m point from the dune crest and dune toe position along a particular transect. They are calculated as the Euclidean distance between the 5-m point and the given feature.
```
# Load saved dataframes
pts_df = pd.read_pickle(os.path.join(scratch_dir, 'pts_extractedvalues_presort.pkl'))
trans_df = pd.read_pickle(os.path.join(scratch_dir, trans_name+'_null_prePts.pkl'))
print(sorted_pt_flds)
# Calculate DistSeg, Dist_MHWbay, DistSegDH, DistSegDL, DistSegArm, and sort points (SplitSort)
pts_df = fun.join_columns(pts_df, trans_df, tID_fld)
pts_df = fun.prep_points(pts_df, tID_fld, pID_fld, sitevals['MHW'], fill)
# Aggregate ptZmhw to max and mean and join to transects
pts_df, zmhw = fun.aggregate_z(pts_df, sitevals['MHW'], tID_fld, 'ptZ', fill)
trans_df = fun.join_columns(trans_df, zmhw)
# Join transect values to pts
pts_df = fun.join_columns(pts_df, trans_df, tID_fld)
# pID_fld needs to be among the columns
if not pID_fld in pts_df.columns:
pts_df.reset_index(drop=False, inplace=True)
# Match field names to those in sorted_pt_flds list
for fld in pts_df.columns:
if fld not in sorted_pt_flds:
for i, fldi in enumerate(sorted_pt_flds):
if fldi.lower() == fld.lower():
sorted_pt_flds[i] = fld
print(fld)
# Drop extra fields and sort columns
trans_df.drop(extra_fields, axis=1, inplace=True, errors='ignore')
for i, f in enumerate(sorted_pt_flds):
for c in pts_df.columns:
if f.lower() == c.lower():
sorted_pt_flds[i] = c
pts_df = pts_df.reindex_axis(sorted_pt_flds, axis=1)
# Save dataframes
trans_df.to_pickle(os.path.join(scratch_dir, trans_name+'_null.pkl'))
pts_df.to_pickle(os.path.join(scratch_dir, pts_name+'_null.pkl'))
# View random rows from the points DF
pts_df.sample(5)
# Use pyproj to convert projected coordinates to geographic coordinates (lat, lon in NAD83)
utm = pyproj.Proj(init='epsg:{}'.format(proj_code))
nad = pyproj.Proj(init='epsg:4269') # NAD83
in_y = pts_df['seg_y'].tolist()
in_x = pts_df['seg_x'].tolist()
lon, lat = pyproj.transform(utm, nad, in_x,in_y)
lon_col = 'seg_lon'
lat_col = 'seg_lat'
pts_df[lon_col] = lon
pts_df[lat_col] = lat
```
### Recode the values for CSV output and model running
```
# Recode
pts_df4csv = pts_df.replace({'SubType': {7777:'{1111, 2222}', 1000:'{1111, 3333}'},
'VegType': {77:'{11, 22}', 88:'{22, 33}', 99:'{33, 44}'},
'VegDens': {666: '{111, 222}', 777: '{222, 333}',
888: '{333, 444}', 999: '{222, 333, 444}'}})
# Fill NAs
pts_df4csv.fillna(fill, inplace=True)
# Save and view sample
pts_df4csv.to_pickle(os.path.join(scratch_dir, pts_name+'_csv.pkl'))
pts_df4csv.sample(5)
```
## Quality checking
Look at extracted profiles from around the island. Enter the transect ID within the available range when prompted. Evaluate the plots for consistency among variables. Repeat various times until you can be satisfied that the variables are consistent with each other and appear to represent reality. View areas with inconsistencies in a GIS.
```
desccols = ['DL_zmhw', 'DH_zmhw', 'Arm_zmhw', 'uBW', 'uBH', 'Dist2Inlet',
'WidthPart', 'WidthLand', 'WidthFull', 'mean_Zmhw', 'max_Zmhw']
# Histograms
trans_df.hist(desccols, sharey=True, figsize=[15, 10], bins=20)
plt.show()
plt.close('all')
flds_dist = ['SplitSort', 'Dist_Seg', 'Dist_MHWbay', 'DistSegDH', 'DistSegDL', 'DistSegArm']
flds_z = ['ptZmhw', 'ptZ', 'ptSlp']
pts_df.loc[:,flds_dist+flds_z].describe()
pts_df.hist(flds_dist, sharey=True, figsize=[15, 8], layout=(2,3))
pts_df.hist(flds_z, sharey=True, figsize=[15, 4], layout=(1,3))
plt.show()
plt.close('all')
# Prompt for transect identifier (sort_ID) and get all points from that transect.
trans_in = int(input('Transect ID ("sort_ID" {:d}-{:d}): '.format(int(pts_df[tID_fld].head(1)), int(pts_df[tID_fld].tail(1)))))
pts_set = pts_df[pts_df[tID_fld] == trans_in]
# Plot
fig = plt.figure(figsize=(13,10))
# Plot the width of the island.
ax1 = fig.add_subplot(211)
try:
fun.plot_island_profile(ax1, pts_set, sitevals['MHW'], sitevals['MTL'])
except TypeError as err:
print('TypeError: {}'.format(err))
pass
# Zoom in on the upper beach.
ax2 = fig.add_subplot(212)
try:
fun.plot_beach_profile(ax2, pts_set, sitevals['MHW'], sitevals['MTL'], maxDH)
except TypeError as err:
print('TypeError: {}'.format(err))
pass
# Display
plt.show()
plt.close('all')
```
### Report field values
```
# Load dataframe
pts_df4csv = pd.read_pickle(os.path.join(scratch_dir, pts_name+'_csv.pkl'))
xmlfile = os.path.join(scratch_dir, pts_name+'_eainfo.xml')
fun.report_fc_values(pts_df4csv, field_defs, xmlfile)
```
## Outputs
### Transect-averaged
Output the transect-averaged metrics in the following formats:
- transects, unpopulated except for ID values, as gdb feature class
- transects, unpopulated except for ID values, as shapefile
- populated transects with fill values as gdb feature class
- populated transects with null values as gdb feature class
- populated transects with fill values as shapefile
- raster of beach width (__uBW__) by transect
```
# Load the dataframe
trans_df = pd.read_pickle(os.path.join(scratch_dir, trans_name+'_null.pkl'))
trans_df['Construction'] = 111
trans_df['Nourishment'] = 111
trans_df['Development'] = 111
```
#### Vector format
```
# Create transect file with only ID values and geometry to publish.
trans_flds = ['TRANSECTID', 'TRANSORDER', 'DD_ID']
for i, f in enumerate(trans_flds):
for c in trans_df.columns:
if f.lower() == c.lower():
trans_flds[i] = c
trans_4pub = fwa.JoinDFtoFC(trans_df.loc[:,trans_flds], extendedTrans, tID_fld, out_fc=sitevals['code']+'_trans')
out_shp = arcpy.FeatureClassToFeatureClass_conversion(trans_4pub, scratch_dir, sitevals['code']+'_trans.shp')
print("OUTPUT: {} in specified scratch_dir.".format(os.path.basename(str(out_shp))))
trans_4pub
trans_4pubdf = fwa.FCtoDF(trans_4pub)
xmlfile = os.path.join(scratch_dir, trans_4pub + '_eainfo.xml')
trans_df_extra_flds = fun.report_fc_values(trans_4pubdf, field_defs, xmlfile)
# Create transect FC with fill values - Join values from trans_df to the transect FC as a new file.
trans_fc = fwa.JoinDFtoFC(trans_df, extendedTrans, tID_fld, out_fc=trans_name+'_fill')
# Create transect FC with null values
fwa.CopyFCandReplaceValues(trans_fc, fill, None, out_fc=trans_name+'_null', out_dir=home)
# Save final transect SHP with fill values
out_shp = arcpy.FeatureClassToFeatureClass_conversion(trans_fc, scratch_dir, trans_name+'_shp.shp')
print("OUTPUT: {} in specified scratch_dir.".format(os.path.basename(str(out_shp))))
```
#### Raster - beach width
It may be necessary to close any Arc sessions you have open.
```
# Create a template raster corresponding to the transects.
if not arcpy.Exists(rst_transID):
print("{} was not found so we will create the base raster.".format(os.path.basename(rst_transID)))
outEucAll = arcpy.sa.EucAllocation(extTrans_tidy, maximum_distance=50, cell_size=cell_size, source_field=tID_fld)
outEucAll.save(os.path.basename(rst_transID))
# Create raster of uBW values by joining trans_df to the template raster.
out_rst = fwa.JoinDFtoRaster(trans_df, os.path.basename(rst_transID), bw_rst, fill, tID_fld, 'uBW')
```
### 5-m points
Output the point metrics in the following formats:
- tabular, in CSV
- populated points with fill values as gdb feature class
- populated points with null values as gdb feature class
- populated points with fill values as shapefile
```
# Load the saved dataframes
pts_df4csv = pd.read_pickle(os.path.join(scratch_dir, pts_name+'_csv.pkl'))
pts_df = pd.read_pickle(os.path.join(scratch_dir, pts_name+'_null.pkl'))
pts_df4csv['Construction'] = 111
pts_df4csv['Nourishment'] = 111
pts_df4csv['Development'] = 111
pts_df['Construction'] = 111
pts_df['Nourishment'] = 111
pts_df['Development'] = 111
```
#### Tabular format
```
# Save CSV in scratch_dir
csv_fname = os.path.join(scratch_dir, pts_name +'.csv')
pts_df4csv.to_csv(csv_fname, na_rep=fill, index=False)
sz_mb = os.stat(csv_fname).st_size/(1024.0 * 1024.0)
print("OUTPUT: {} [{} MB] in specified scratch_dir. ".format(os.path.basename(csv_fname), sz_mb))
```
#### Vector format
```
# Convert pts_df to FC - automatically converts NaNs to fills (default fill is -99999)
pts_fc = fwa.DFtoFC_large(pts_df, out_fc=os.path.join(arcpy.env.workspace, pts_name+'_fill'),
spatial_ref=utmSR, df_id=pID_fld, xy=["seg_x", "seg_y"])
# Save final FCs with null values
fwa.CopyFCandReplaceValues(pts_fc, fill, None, out_fc=pts_name+'_null', out_dir=home)
# Save final points as SHP with fill values
out_pts_shp = arcpy.FeatureClassToFeatureClass_conversion(pts_fc, scratch_dir, pts_name+'_shp.shp')
print("OUTPUT: {} in specified scratch_dir.".format(os.path.basename(str(out_pts_shp))))
```
## Rerun create transects with values
|
github_jupyter
|
# MOwNiT – arytmetyka komputerowa

```
import numpy as np
import matplotlib.pyplot as plt
x1 = 4
n = 30
def visualize(points):
plt.figure(figsize=(12,6))
plt.axhline(y=3.14159, color='r', linestyle='--')
plt.xlabel("Xi")
plt.ylabel("points")
plt.plot(points, marker="o", markersize=10)
plt.show()
```
## Informacje o używanych typach danych:
```
print(np.finfo(np.float32))
print(np.finfo(np.double))
print(np.finfo(np.longdouble))
```
## Rozwiązanie dla liczb typu float:
```
def float_32_sequence_default():
res = [np.float32(0) for _ in range(n)]
res[0] = np.float32(x1)
for k in range(n-1):
calc_sqrt = np.sqrt(1 + (res[k]**2 / 2**(2*(k+2))))
new_xk = 2**(2*(k+2)+1) * ((calc_sqrt - 1)/res[k])
res[k+1] = np.float32(new_xk)
return res
def float_32_sequence_reshaped():
res = [np.float32(0) for _ in range(n)]
res[0] = np.float32(x1)
for k in range(n-1):
calc_sqrt = np.sqrt(1 + (res[k]**2 / 2**(2*(k+2))))
new_xk = 2*res[k]/(calc_sqrt+1)
res[k+1] = np.float32(new_xk)
return res
```
### Porównanie wyników oraz ich wizualizacja:
**Dla nieprzekształconego wzoru:**
```
f32_def_res = float_32_sequence_default()
f32_def_res
f32_def_res[-1]
visualize(f32_def_res)
```
**Dla przekształconego wzoru:**
```
f32_resh_res = float_32_sequence_reshaped()
f32_resh_res
f32_resh_res[-1]
visualize(f32_resh_res)
```
## Rozwiązanie dla liczb typu double:
```
def double_sequence_default():
res = [np.double(0) for _ in range(n)]
res[0] = np.double(x1)
for k in range(n-1):
calc_sqrt = np.sqrt(1 + (res[k]**2 / 2**(2*(k+2))))
new_xk = 2**(2*(k+2)+1) * ((calc_sqrt - 1)/res[k])
res[k+1] = np.double(new_xk)
return res
def double_sequence_reshaped():
res = [np.double(0) for _ in range(n)]
res[0] = np.double(x1)
for k in range(n-1):
calc_sqrt = np.sqrt(1 + (res[k]**2 / 2**(2*(k+2))))
new_xk = 2*res[k]/(calc_sqrt+1)
res[k+1] = np.double(new_xk)
return res
```
### Porównanie wyników:
**Dla nieprzekształconego wzoru:**
```
doub_def_res = double_sequence_default()
doub_def_res
doub_def_res[-1]
visualize(doub_def_res)
```
**Dla przekształconego wzoru:**
```
doub_resh_res = double_sequence_reshaped()
doub_resh_res
doub_resh_res[-1]
visualize(doub_resh_res)
```
## Rozwiązanie dla liczb typu long double:
```
def longdouble_sequence_default():
res = [np.longdouble(0) for _ in range(n)]
res[0] = np.longdouble(x1)
for k in range(n-1):
calc_sqrt = np.sqrt(1 + (res[k]**2 / 2**(2*(k+2))))
new_xk = 2**(2*(k+2)+1) * ((calc_sqrt - 1)/res[k])
res[k+1] = np.longdouble(new_xk)
return res
def longdouble_sequence_reshaped():
res = [np.longdouble(0) for _ in range(n)]
res[0] = np.longdouble(x1)
for k in range(n-1):
calc_sqrt = np.sqrt(1 + (res[k]**2 / 2**(2*(k+2))))
new_xk = 2*res[k]/(calc_sqrt+1)
res[k+1] = np.longdouble(new_xk)
return res
```
### Porównanie wyników:
**Dla nieprzekształconego wzoru:**
```
l_doub_def_res = longdouble_sequence_default()
l_doub_def_res
l_doub_def_res[-1]
visualize(l_doub_def_res)
```
**Dla przekształconego wzoru:**
```
l_doub_resh_res = longdouble_sequence_reshaped()
l_doub_resh_res
l_doub_resh_res[-1]
visualize(l_doub_resh_res)
```
|
github_jupyter
|
```
import sys
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from astropy import constants as const
# remove this line if you installed platypos with pip
sys.path.append('/work2/lketzer/work/gitlab/platypos_group/platypos/')
import platypos
from platypos import Planet_LoFo14
from platypos import Planet_Ot20
# import the classes with fixed step size for completeness
from platypos.planet_LoFo14_PAPER import Planet_LoFo14_PAPER
from platypos.planet_Ot20_PAPER import Planet_Ot20_PAPER
import platypos.planet_models_LoFo14 as plmoLoFo14
```
# Create Planet object and stellar evolutionary track
## Example planet 1.1 - V1298Tau c with 5 Eearth mass core and measured radius (var. step)
```
# (David et al. 2019, Chandra observation)
L_bol, mass_star, radius_star = 0.934, 1.101, 1.345 # solar units
age_star = 23. # Myr
Lx_age = Lx_chandra = 1.3e30 # erg/s in energy band: (0.1-2.4 keV)
Lx_age_error = 1.4e29
# use dictionary to store star-parameters
star_V1298Tau = {'star_id': 'V1298Tau', 'mass': mass_star, 'radius': radius_star, 'age': age_star, 'L_bol': L_bol, 'Lx_age': Lx_age}
Lx_1Gyr, Lx_5Gyr = 2.10*10**28, 1.65*10**27
track_low = {"t_start": star_V1298Tau["age"], "t_sat": star_V1298Tau["age"], "t_curr": 1000., "t_5Gyr": 5000., "Lx_max": Lx_age,
"Lx_curr": Lx_1Gyr, "Lx_5Gyr": Lx_5Gyr, "dt_drop": 20., "Lx_drop_factor": 16.}
track_med = {"t_start": star_V1298Tau["age"], "t_sat": star_V1298Tau["age"], "t_curr": 1000., "t_5Gyr": 5000., "Lx_max": Lx_age,
"Lx_curr": Lx_1Gyr, "Lx_5Gyr": Lx_5Gyr, "dt_drop": 0., "Lx_drop_factor": 0.}
track_high = {"t_start": star_V1298Tau["age"], "t_sat": 240., "t_curr": 1000., "t_5Gyr": 5000., "Lx_max": Lx_age,
"Lx_curr": Lx_1Gyr, "Lx_5Gyr": Lx_5Gyr, "dt_drop": 0., "Lx_drop_factor": 0.}
# planet c
planet = {"core_mass": 5.0, "radius": 5.59, "distance": 0.0825, "metallicity": "solarZ"}
pl = Planet_LoFo14(star_V1298Tau, planet)
pl.__dict__
```
### Example planet 1.1.1 - V1298Tau c with 5 Eearth mass core and measured radius (fixed step)
```
pl = Planet_LoFo14_PAPER(star_V1298Tau, planet)
```
## Example planet 1.2 - V1298Tau c with mass estimate from Otegi et al. (2020) and measured radius (var step)
```
pl = Planet_Ot20(star_V1298Tau, planet)
pl.__dict__
```
### Example planet 1.2.1 - V1298Tau c with mass estimate from Otegi et al. (2020) and measured radius (fixed step)
```
pl = Planet_Ot20_PAPER(star_V1298Tau, planet)
pl.__dict__
```
## Example planet 2 - artificial planet with specified core mass and envelope mass fraction
```
Lx_1Gyr, Lx_5Gyr = 2.10*10**28, 1.65*10**27
dict_star = {'star_id': 'star_age1.0_mass0.89',
'mass': 0.8879632311581124,
'radius': None,
'age': 1.0,
'L_bol': 1.9992811847525246e+33/const.L_sun.cgs.value,
'Lx_age': 1.298868513129789e+30}
dict_pl = {'distance': 0.12248611607793611,
'metallicity': 'solarZ',
'fenv': 3.7544067802231664,
'core_mass': 4.490153906104026}
track = {"t_start": dict_star["age"], "t_sat": 100., "t_curr": 1000., "t_5Gyr": 5000., "Lx_max": Lx_age,
"Lx_curr": Lx_1Gyr, "Lx_5Gyr": Lx_5Gyr, "dt_drop": 0., "Lx_drop_factor": 0.}
pl = Planet_LoFo14(dict_star, dict_pl)
#pl.__dict__
```
# Evolve & create outputs
```
%%time
folder_id = "dummy"
path_save = os.getcwd() + "/" + folder_id +"/"
if not os.path.exists(path_save):
os.makedirs(path_save)
else:
os.system("rm -r " + path_save[:-1])
os.makedirs(path_save)
t_final = 5007.
pl.evolve_forward_and_create_full_output(t_final, 0.1, 0.1, "yes", "yes", track_high, path_save, folder_id)
```
# Read in results and plot
```
df_pl = pl.read_results(path_save)
df_pl.head()
df_pl.tail()
# fig, ax = plt.subplots(figsize=(10,5))
# ax.plot(df_pl["Time"], df_pl["Lx"])
# ax.loglog()
# plt.show()
fig, ax = plt.subplots(figsize=(10,5))
age_arr = np.logspace(np.log10(pl.age), np.log10(t_final), 100)
if (type(pl) == platypos.planet_LoFo14.Planet_LoFo14
or type(pl) == platypos.planet_LoFo14_PAPER.Planet_LoFo14_PAPER):
ax.plot(age_arr, plmoLoFo14.calculate_planet_radius(pl.core_mass, pl.fenv, age_arr, pl.flux, pl.metallicity), \
lw=2.5, label='thermal contraction only', color="blue")
ax.plot(df_pl["Time"], df_pl["Radius"],
marker="None", ls="--", label='with photoevaporation', color="red")
else:
ax.plot(df_pl["Time"], df_pl["Radius"], marker="None", ls="--", label='with photoevaporation', color="red")
ax.legend(fontsize=10)
ax.set_xlabel("Time [Myr]", fontsize=16)
ax.set_ylabel("Radius [R$_\oplus$]", fontsize=16)
ax.set_xscale('log')
#ax.set_ylim(5.15, 5.62)
plt.show()
```
|
github_jupyter
|
### Prepare the Dataset for Building a Predictive Model
As a first step we will build a graph convolution model predict ERK2 activity. We will train the model to distinguish a set of ERK2 active compounds from a set of decoy compounds. The active and decoy compounds are derived from the DUD-E database. In order to generate the best model, we would like to decoys with property distributions similar to those of our active compounds. Let's say this was not the case and the inactive compounds had lower molecular weight than the active compounds. In this case our classifer may be trained to simply separate low molecular compounds from
high molecular weight compounds. This classifer will have very limited utility in preactice.
As a first step, we will examine a few calculated properties of our active and decoy molecules. In order to build a reliable model, we need to ensure that the properties of the active molecules are similar to those of the decoy molecules.
First lets import the libraries we will need.
```
from rdkit import Chem
from rdkit.Chem import Draw
from rdkit.Chem.Draw import IPythonConsole
import pandas as pd
from rdkit.Chem import PandasTools
from rdkit.Chem import Descriptors
from rdkit.Chem import rdmolops
import seaborn as sns
```
Now we can read a SMILES file into a Pandas dataframe and add an RDKit molecule to the dataframe.
```
active_df = pd.read_csv("mk01/actives_final.ism",header=None,sep=" ")
active_rows,active_cols = active_df.shape
active_df.columns = ["SMILES","ID","ChEMBL_ID"]
active_df["label"] = ["Active"]*active_rows
PandasTools.AddMoleculeColumnToFrame(active_df,"SMILES","Mol")
```
Let's define a function to add caculated properties to a dataframe
```
def add_property_columns_to_df(df_in):
df_in["mw"] = [Descriptors.MolWt(mol) for mol in df_in.Mol]
df_in["logP"] = [Descriptors.MolLogP(mol) for mol in df_in.Mol]
df_in["charge"] = [rdmolops.GetFormalCharge(mol) for mol in df_in.Mol]
```
With this function in hand, we can calculate the molecular weight, LogP and formal charge of the molecules. Once we have these properties we can compare the distributions for the active and decoy sets.
```
add_property_columns_to_df(active_df)
```
Let's look at the frist few rows of our dataframe to ensure that it makes sense.
```
active_df.head()
```
Now let's do the same thing with the decoy molecules
```
decoy_df = pd.read_csv("mk01/decoys_final.ism",header=None,sep=" ")
decoy_df.columns = ["SMILES","ID"]
decoy_rows, decoy_cols = decoy_df.shape
decoy_df["label"] = ["Decoy"]*decoy_rows
PandasTools.AddMoleculeColumnToFrame(decoy_df,"SMILES","Mol")
add_property_columns_to_df(decoy_df)
tmp_df = active_df.append(decoy_df)
```
With properties calculated for both the active and the decoy sets, we can compare the properties of the two compound sets. To do the comparison, we will use violin plots. A violin plot can be thought of as analogous to a boxplot. The violin plot provides a mirrored, horizontal view of a frequency distribution. Ideally, we would
like to see similar distributions for the active and decoy sets.
```
sns.violinplot(tmp_df["label"],tmp_df["mw"])
```
An examination of the distributions in the figures above show that the molecular weight distributions for the two sets
are roughly equivalent. The decoy set has more low molecular weight molecules, but the center of the distribution, show as a box in the middle of each violin plot is in a similar location in both plots.
We can use violin plots to perform a similar comparison of the LogP distributions. Again, we can see that the
distributions are similar with a few more decoys at the lower end of the distribution.
```
sns.violinplot(tmp_df["label"],tmp_df["logP"])
```
Finally, we will do the same comparison with the formal charges of the molecules.
```
sns.violinplot(tmp_df["label"],tmp_df["charge"])
```
In this case, we see a signficant difference. All of the active molecules are neutral, while some of the decoys
are charged. Let see what fraction of the decoy molecules are charged. We can do this by creating a new dataframe
with just the charged molecules.
```
charged = decoy_df[decoy_df["charge"] != 0]
```
A pandas dataframe has a property, shape, that returns the number of rows and columns in the dataframe. As such,
element[0] in the shape property will be the number of rows. Let's divide the number of rows in our dataframe of
charged molecules by the total number of rows in the decoy dataframe.
```
charged.shape[0]/decoy_df.shape[0]
```
The fact that 16% of the decoy compounds are charged, while none of the active compounds are is a concern. An examination of both sets indicate that charge states were assigned to the decoys, but not to the active molecules. In order to be consistent, we will use some code from the RDKit Cookbook to neutralize the molecules. First, we will import an RDKit function to neutralize charges.
```
from neutralize import NeutraliseCharges
```
Now we will create a new dataframe with the SMILES, ID, and label for the decoys.
```
revised_decoy_df = decoy_df[["SMILES","ID","label"]].copy()
```
With this new dataframe in hand, we can replace the SMILES with the SMILES for the neutral form of the molecule. The
NeutraliseCharges function returns two values. The first is the SMILES for the neutral form of the molecule and the second is a boolean variable indicating whether the molecule was changed. In the code below, we only need the SMILES, so we will use the first element of the tuple returned by NeutraliseCharges.
```
revised_decoy_df["SMILES"] = [NeutraliseCharges(x)[0] for x in revised_decoy_df["SMILES"]]
```
Once we've replaced the SMILES, we can add a molecule column to our new dataframe and calculated properties again.
```
PandasTools.AddMoleculeColumnToFrame(revised_decoy_df,"SMILES","Mol")
add_property_columns_to_df(revised_decoy_df)
```
We can now append the dataframe with the active molecules to the one with the revised, neutral decoys and calculate
another box plot.
```
new_tmp_df = active_df.append(revised_decoy_df)
sns.violinplot(new_tmp_df["label"],new_tmp_df["charge"])
```
An examination of the plot about show that there are very few charged molecules in the decoy set. We can use the same
technique we used above to create a dataframe with only the charged molecules. We can then use this dataframe to determine the number of charged molecules remaining in the set.
```
charged = revised_decoy_df[revised_decoy_df["charge"] != 0]
charged.shape[0]/revised_decoy_df.shape[0]
```
We have now reduced the fraction of charged compounds from 16% to 0.3%. We can now be confident that our active and decoy sets are reasonbly well balanced.
In order to use these datasets with DeepChem we need to write the molecules out as a csv file consisting of SMILES, Name, and an integer value indicating whether the compounds are active (labeled as 1) or inactive (labeled as 0).
```
active_df["is_active"] = [1] * active_df.shape[0]
revised_decoy_df["is_active"] = [0] * revised_decoy_df.shape[0]
combined_df = active_df.append(revised_decoy_df)[["SMILES","ID","is_active"]]
combined_df.head()
```
Our final step in this section is to save our new combined_df as a csv file. The index=False option causes Pandas to not include the row number in the first column.
```
combined_df.to_csv("dude_erk1_mk01.csv")
```
|
github_jupyter
|
```
import cv2
import numpy as np
from matplotlib import pyplot as plt
import os
import xlsxwriter
import pandas as pd # Excel
import struct # Binary writing
import scipy.io as sio # Read .mat files
import h5py
import time
from grading__old import *
from ipywidgets import FloatProgress
from IPython.display import display
import scipy.signal
import scipy.ndimage
import sklearn.metrics as skmet
import sklearn.decomposition as skdec
import sklearn.linear_model as sklin
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.model_selection import LeaveOneOut
from sklearn.model_selection import KFold
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import RandomForestRegressor
from sklearn.preprocessing import normalize
from sklearn import svm
from sklearn import neighbors
def pipeline_lbp(impath, savepath, save, dtype='dat'):
#Start time
start_time = time.time()
# Calculate MRELBP from dataset
# Parameters
dict = {'N':8, 'R':9,'r':3,'wc':5,'wr':(5,5)}
mapping = getmapping(dict['N']) # mapping
files = os.listdir(impath)
files.sort()
#print(files[32 * 2])
#files.pop(32 * 2)
#files.pop(32 * 2)
#print(files)
features = None # Reset feature array
p = FloatProgress(min=0, max=len(files), description='Features:')
display(p)
for k in range(len(files)):
#Load file
if dtype == 'dat':
p.value += 2
if k > len(files) / 2 - 1:
break
file = os.path.join(impath,files[2 * k])
try:
Mz = loadbinary(file, np.float64)
except:
continue
file = os.path.join(impath,files[2 * k + 1])
try:
sz = loadbinary(file, np.float64)
except:
continue
else:
file = os.path.join(impath,files[k])
p.value += 1
try:
file = sio.loadmat(file)
Mz = file['Mz']
sz = file['sz']
except NotImplementedError:
file = h5py.File(file)
Mz = file['Mz'][()]
sz = file['sz'][()]
#Combine mean and sd images
image = Mz+sz
#Grayscale normalization
image = localstandard(image,23,5,5,1)
# LBP
Chist,Lhist,Shist,Rhist, lbpIL, lbpIS, lbpIR = MRELBP(image,dict['N'],dict['R'],dict['r'],dict['wc'],dict['wr'])
f1 = Chist
f2 = maplbp(Lhist,mapping)
f3 = maplbp(Shist,mapping)
f4 = maplbp(Rhist,mapping)
#Concatenate features
f = np.concatenate((f1.T,f2.T,f3.T,f4.T),axis=0)
try:
features = np.concatenate((features,f),axis=1)
except ValueError:
features = f
# Save images
if dtype == 'dat':
cv2.imwrite(savepath + '\\' + files[2 * k][:-9] + '.png', lbpIS)
else:
cv2.imwrite(savepath + '\\' + files[k][:-9] + '.png', lbpIS)
# Plot LBP images
#plt.imshow(lbpIS); plt.show()
#plt.imshow(lbpIL); plt.show()
#plt.imshow(lbpIR); plt.show()
# Save features
writer = pd.ExcelWriter(save + r'\LBP_features_python.xlsx')
df1 = pd.DataFrame(features)
df1.to_excel(writer, sheet_name='LBP_features')
writer.save()
t = time.time()-start_time
print('Elapsed time: {0}s'.format(t))
def pipeline_load(featurepath, gpath, save, choice):
#Start time
start_time = time.time()
# Load grades to array
grades = pd.read_excel(gpath, 'Sheet1')
grades = pd.DataFrame(grades).values
fnames = grades[:,0].astype('str')
g = list(grades[:,choice].astype('int'))
#g.pop(32)
g = np.array(g)
print('Max grade: {0}, min grade: {1}'.format(max(g), min(g)))
# Load features
features = pd.read_excel(featurepath, 'LBP_features')
features = pd.DataFrame(features).values.astype('int')
print(features.shape)
#PCA
# PCA parameters: whitening, svd solver (auto/full)
pca, score = ScikitPCA(features.T, 10, True, 'auto')
#pca, score = PCA(features,10)
print(score[0,:])
print(score.shape)
# Regression
if min(g) > 0:
g = g - min(g)
pred1 = regress(score, g)
pred2 = logreg(score, g>min(g))
for p in range(len(pred1)):
if pred1[p]<0:
pred1[p] = 0
if pred1[p] > max(g):
pred1[p]=max(g)
#Plotting PCA
a = g
b = np.round(pred1).astype('int')
# ROC curve
C1 = skmet.confusion_matrix(a,b)
MSE1 = skmet.mean_squared_error(a,pred1)
fpr, tpr, thresholds = skmet.roc_curve(a>0, np.round(pred1)>0, pos_label=1)
AUC1 = skmet.auc(fpr,tpr)
AUC2 = skmet.roc_auc_score(a>0,pred2)
m, b = np.polyfit(a, pred1.flatten(), 1)
R2 = skmet.r2_score(a,pred1.flatten())
fig0 = plt.figure(figsize=(6,6))
ax0 = fig0.add_subplot(111)
ax0.plot(fpr,tpr)
# Save prediction
stats = np.zeros(len(g))
stats[0] = MSE1
stats[1] = AUC1
stats[2] = AUC2
tuples = list(zip(fnames, g, pred1[:,0], abs(g - pred1[:,0]), pred2, stats))
writer = pd.ExcelWriter(save + r'\prediction_python.xlsx')
df1 = pd.DataFrame(tuples, columns=['Sample', 'Actual grade', 'Prediction', 'Difference', 'Logistic prediction', 'MSE, AUC1, AUC2'])
df1.to_excel(writer, sheet_name='Prediction')
writer.save()
print('Confusion matrix')
print(C1)
print('Mean squared error, Area under curve 1 and 2')
print(MSE1, AUC1, AUC2)#,MSE2,MSE3,MSE4)
print('R2 score')
print(R2)
#print('Sample, grade, prediction')
#for k in range(len(fnames)):
# print(fnames[k],a[k],pred1[k])#,pred3[k])
x = score[:,0]
y = score[:,1]
fig = plt.figure(figsize=(6,6))
ax1 = fig.add_subplot(111)
ax1.scatter(score[g<2,0],score[g<2,1],marker='o',color='b',label='Normal')
ax1.scatter(score[g>1,0],score[g>1,1],marker='s',color='r',label='OA')
for k in range(len(g)):
txt = fnames[k][0:-4]+str(g[k])
if g[k] >= 2:
ax1.scatter(x[k],y[k],marker='s',color='r')
else:
ax1.scatter(x[k],y[k],marker='o',color='b')
# Scatter plot actual vs prediction
fig = plt.figure(figsize=(6,6))
ax2 = fig.add_subplot(111)
ax2.scatter(a,pred1.flatten())
ax2.plot(a,m*a,'-',color='r')
ax2.set_xlabel('Actual grade')
ax2.set_ylabel('Predicted')
for k in range(len(g)):
txt = fnames[k]
txt = txt+str(g[k])
ax2.annotate(txt,xy=(a[k],pred1[k]),color='r')
plt.show()
```
### Load features
```
featurepath = r'Z:\3DHistoData\Grading\LBP_features_surface.xlsx'
gpath = r'Z:\3DHistoData\Grading\PTAgreiditjanaytteet.xls'
save = r'Z:\3DHistoData\Grading'
total = 1
surf = 2
deep = 5
cc = 6
deepcell = 7
deepECM = 8
ccECM = 9
ccVasc = 10
choice = surf
pipeline_load(featurepath, gpath, save, choice)
```
### Calculate LBP features from .dat mean and std images
```
impath = r'Z:\3DHistoData\SurfaceImages\Deep'
impath = r'V:\Tuomas\PTASurfaceImages'
dtype = 'dat'
dtype = 'mat'
savepath = r'Z:\3DHistoData\Grading\LBP'
save = r'Z:\3DHistoData\Grading'
pipeline_lbp(impath, savepath, save, dtype)
```
|
github_jupyter
|
# Desafio 5
Neste desafio, vamos praticar sobre redução de dimensionalidade com PCA e seleção de variáveis com RFE. Utilizaremos o _data set_ [Fifa 2019](https://www.kaggle.com/karangadiya/fifa19), contendo originalmente 89 variáveis de mais de 18 mil jogadores do _game_ FIFA 2019.
> Obs.: Por favor, não modifique o nome das funções de resposta.
## _Setup_ geral
```
from math import sqrt
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as sct
import seaborn as sns
import statsmodels.api as sm
import statsmodels.stats as st
from sklearn.decomposition import PCA
from loguru import logger
from sklearn.linear_model import LinearRegression
from sklearn.feature_selection import RFE
# Algumas configurações para o matplotlib.
"""
%matplotlib inline
from IPython.core.pylabtools import figsize
figsize(12, 8)
sns.set()
"""
fifa = pd.read_csv("fifa.csv")
columns_to_drop = ["Unnamed: 0", "ID", "Name", "Photo", "Nationality", "Flag",
"Club", "Club Logo", "Value", "Wage", "Special", "Preferred Foot",
"International Reputation", "Weak Foot", "Skill Moves", "Work Rate",
"Body Type", "Real Face", "Position", "Jersey Number", "Joined",
"Loaned From", "Contract Valid Until", "Height", "Weight", "LS",
"ST", "RS", "LW", "LF", "CF", "RF", "RW", "LAM", "CAM", "RAM", "LM",
"LCM", "CM", "RCM", "RM", "LWB", "LDM", "CDM", "RDM", "RWB", "LB", "LCB",
"CB", "RCB", "RB", "Release Clause"
]
try:
fifa.drop(columns_to_drop, axis=1, inplace=True)
except KeyError:
logger.warning(f"Columns already dropped")
```
## Inicia sua análise a partir daqui
```
# Sua análise começa aqui.
fifa.dropna(inplace= True)
```
## Questão 1
Qual fração da variância consegue ser explicada pelo primeiro componente principal de `fifa`? Responda como um único float (entre 0 e 1) arredondado para três casas decimais.
```
def q1():
# Retorne aqui o resultado da questão 1.
pca = PCA(n_components = 1)
project = pca.fit(fifa)
varianciaExplicada = project.explained_variance_ratio_[0]
return varianciaExplicada.round(3)
pass
```
## Questão 2
Quantos componentes principais precisamos para explicar 95% da variância total? Responda como un único escalar inteiro.
```
def q2():
# Retorne aqui o resultado da questão 2.
pca095 = PCA(n_components= 0.95)
project = pca095.fit_transform(fifa)
numeroComponentesPrincipais = project.shape[1]
return numeroComponentesPrincipais
pass
```
## Questão 3
Qual são as coordenadas (primeiro e segundo componentes principais) do ponto `x` abaixo? O vetor abaixo já está centralizado. Cuidado para __não__ centralizar o vetor novamente (por exemplo, invocando `PCA.transform()` nele). Responda como uma tupla de float arredondados para três casas decimais.
```
x = [0.87747123, -1.24990363, -1.3191255, -36.7341814,
-35.55091139, -37.29814417, -28.68671182, -30.90902583,
-42.37100061, -32.17082438, -28.86315326, -22.71193348,
-38.36945867, -20.61407566, -22.72696734, -25.50360703,
2.16339005, -27.96657305, -33.46004736, -5.08943224,
-30.21994603, 3.68803348, -36.10997302, -30.86899058,
-22.69827634, -37.95847789, -22.40090313, -30.54859849,
-26.64827358, -19.28162344, -34.69783578, -34.6614351,
48.38377664, 47.60840355, 45.76793876, 44.61110193,
49.28911284
]
def q3():
# Retorne aqui o resultado da questão 3.
pca = PCA().fit(fifa)
c1,c2 = pca.components_.dot(x)[0:2].round(3)
return c1,c2
pass
```
## Questão 4
Realiza RFE com estimador de regressão linear para selecionar cinco variáveis, eliminando uma a uma. Quais são as variáveis selecionadas? Responda como uma lista de nomes de variáveis.
```
def q4():
# Retorne aqui o resultado da questão 4.
x = fifa.drop(columns="Overall")
y = fifa["Overall"]
rfe = RFE(estimator= LinearRegression(), n_features_to_select= 5)
rfe.fit(x,y)
indexFeatureSelect = rfe.get_support(indices=True)
featureSelect = list(x.columns[indexFeatureSelect])
return featureSelect
pass
```
|
github_jupyter
|
# Exercises
## Simple array manipulation
Investigate the behavior of the statements below by looking
at the values of the arrays a and b after assignments:
```
a = np.arange(5)
b = a
b[2] = -1
b = a[:]
b[1] = -1
b = a.copy()
b[0] = -1
```
Generate a 1D NumPy array containing numbers from -2 to 2
in increments of 0.2. Use optional start and step arguments
of **np.arange()** function.
Generate another 1D NumPy array containing 11 equally
spaced values between 0.5 and 1.5. Extract every second
element of the array
Create a 4x4 array with arbitrary values.
Extract every element from the second row
Extract every element from the third column
Assign a value of 0.21 to upper left 2x2 subarray.
## Simple plotting
Plot to the same graph **sin** and **cos** functions in the interval $[-\pi/2, \pi/2]$. Use $\theta$ as x-label and insert also legends.
## Pie chart
The file "../data/csc_usage.txt" contains the usage of CSC servers by different disciplines. Plot a pie chart about the resource usage.
## Bonus exercises
### Numerical derivative with finite differences
Derivatives can be calculated numerically with the finite-difference method
as:
$$ f'(x_i) = \frac{f(x_i + \Delta x)- f(x_i - \Delta x)}{2 \Delta x} $$
Construct 1D Numpy array containing the values of xi in the interval $[0, \pi/2]$ with spacing
$\Delta x = 0.1$. Evaluate numerically the derivative of **sin** in this
interval (excluding the end points) using the above formula. Try to avoid
`for` loops. Compare the result to function **cos** in the same interval.
### Game of Life
Game of life is a cellular automaton devised by John Conway
in 70's: http://en.wikipedia.org/wiki/Conway's_Game_of_Life
The game consists of two dimensional orthogonal grid of
cells. Cells are in two possible states, alive or dead. Each cell
interacts with its eight neighbours, and at each time step the
following transitions occur:
* Any live cell with fewer than two live neighbours dies, as if
caused by underpopulation
* Any live cell with more than three live neighbours dies, as if
by overcrowding
* Any live cell with two or three live neighbours lives on to
the next generation
* Any dead cell with exactly three live neighbours becomes a
live cell
The initial pattern constitutes the seed of the system, and
the system is left to evolve according to rules. Deads and
births happen simultaneously.
Implement the Game of Life using Numpy, and visualize the
evolution with Matplotlib's **imshow**. Try first 32x32
square grid and cross-shaped initial pattern:

Try also other grids and initial patterns (e.g. random
pattern). Try to avoid **for** loops.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/everestso/Fall21Spring22/blob/main/c164s22ch3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Tile Sliding Domain
```
import random
import heapq
random.seed(13)
StateDimension=3
# StateDimension=4
#InitialState = [1,2,3,4,5,6,0,7,8]
InitialState = "123456078"
#GoalState=[1,2,3,4,5,6,7,8,0]
GoalState = "123456780"
# GoalState = "123456789ABCDEF0"
Actions = lambda s: ['u', 'd', 'l', 'r']
Opposite=dict([('u','d'),('d','u'),('l','r'),('r','l'), (None, None)])
def Result(state, action):
i = state.index('0')
newState = list(state)
row,col=i//StateDimension, i % StateDimension
if ( (action=='u' and row==0) or
(action=='d' and row==StateDimension-1) or
(action=='l' and col==0) or
(action=='r' and col==StateDimension-1)):
return newState
if action=='u':
l,r = row*StateDimension+col, (row-1)*StateDimension+col
elif action=='d':
l,r = row*StateDimension+col, (row+1)*StateDimension+col
elif action=='l':
l,r = row*StateDimension+col, row*StateDimension+col-1
elif action=='r' :
l,r = row*StateDimension+col, row*StateDimension+col+1
newState[l], newState[r] = newState[r], newState[l]
return ''.join(newState)
def PrintState(s):
for i in range(0,len(s),StateDimension):
print(s[i:i+StateDimension])
def LegalMove(state, action):
i = state.index('0')
row,col=i//StateDimension, i % StateDimension
if ( (action=='u' and row==0) or
(action=='d' and row==StateDimension-1) or
(action=='l' and col==0) or
(action=='r' and col==StateDimension-1)):
return False
return True
def SingleTileManhattanDistance(tile, left, right):
leftIndex = left.index(tile)
rightIndex = right.index(tile)
return (abs(leftIndex//StateDimension-rightIndex//StateDimension) +
abs(leftIndex%StateDimension-rightIndex%StateDimension))
def ManhattanDistance(left, right):
distances = [SingleTileManhattanDistance(tile, left, right)
for tile in [str(c) for c in range(1, StateDimension**2)]]
### print ("Distances= ", distances)
return sum(distances)
def OutOfPlace(left, right):
distances = [left[i]!=right[i] and right[i] != '0'
for i in range(StateDimension**2)]
return sum(distances)
PrintState(InitialState)
PrintState(GoalState)
print("ManhattanDistance= ", ManhattanDistance(InitialState, GoalState))
print("OutOfPlace= ", OutOfPlace(InitialState, GoalState))
PrintState(InitialState)
print()
state1 = Result(InitialState, 'u')
PrintState(state1)
print()
state1 = Result(state1, 'r')
PrintState(state1)
```
# Random Walk
```
def RandomWalk(state, steps):
actionSequence = []
actionLast = None
for i in range(steps):
action = None
while action==None:
action = random.choice(Actions(state))
action = action if (LegalMove(state, action)
and action!= Opposite[actionLast]) else None
actionLast = action
state = Result(state, action)
actionSequence.append(action)
return state, actionSequence
state1, sol = RandomWalk(InitialState, 50)
PrintState(state1)
print (ManhattanDistance(state1, GoalState), sol)
state1, sol = RandomWalk(InitialState, 5)
PrintState(InitialState)
print (sol)
PrintState(state1)
def ApplyMoves(actions, state):
for action in actions:
state = Result(state, action)
return state
PrintState(InitialState)
print(['r','r'])
PrintState(ApplyMoves(['r','r'],InitialState))
def ReverseMoves(actions):
ret = [Opposite[a] for a in actions]
ret.reverse()
return ret
state1, sol = RandomWalk(GoalState, 5)
PrintState(state1)
print (sol)
print(ReverseMoves(sol))
PrintState (ApplyMoves(ReverseMoves(sol), state1))
```
# Example 1
```
Problems = [RandomWalk(GoalState, 5) for _ in range(10)]
for i, s in Problems:
print ('"', i, '" , "', ''.join(map(str, ReverseMoves(s))), '",',
ManhattanDistance(i, GoalState), sep='')
NewState = ApplyMoves("dldrr", "103526478")
print (NewState)
PrintState("123456780")
print()
PrintState("103526478")
print(OutOfPlace("103526478", "123456780"))
MD=[(1,0), (2, 1), (3, 0), (4, 1), (5, 1), (6, 0), (7, 1), (8, 1)]
print(ManhattanDistance("103526478", "123456780"))
InitialState = "412053786"
GoalState = "123456780"
print ("ManhattanDistance=", ManhattanDistance(InitialState, GoalState))
print ("Out of Place= ", OutOfPlace(InitialState, GoalState))
```
# Example 2
```
Problems = [RandomWalk(GoalState, 100) for _ in range(20)]
for i, s in Problems:
print ('"', i, '", ', ''.join(map(str, ReverseMoves(s))), '",',
OutOfPlace(i, GoalState), " ", ManhattanDistance(i, GoalState), sep='')
InitialState = "281607543"
GoalState = "123456780"
print ("ManhattanDistance=", ManhattanDistance(InitialState, GoalState))
print ("Out of Place= ", OutOfPlace(InitialState, GoalState))
InitialState = "076581324"
GoalState = "123456780"
print ("ManhattanDistance=", ManhattanDistance(InitialState, GoalState))
print ("Out of Place= ", OutOfPlace(InitialState, GoalState))
PrintState(InitialState)
sol = "drdlurrullddruruldlurrddlluurrddluldrruulddruullddrruullddrurdlulurrddluurdlulddrulurdldrurdluuldrdr"
print (len(sol))
print(ApplyMoves(sol, InitialState))
```
# Simple 15 Puzzle Test
```
GoalState = "123456789ABCDEF0"
s15a = Result(GoalState, "l")
s15b = Result(GoalState, "u")
PrintState(GoalState)
print()
PrintState(s15a)
print('')
PrintState(s15b)
```
# Discussion
```
StateDimension=3
s1 = "821357064"
sol1="ruurdllurrdlurddllurrdllurrd"
r = ApplyMoves(sol1, s1)
PrintState(r)
StateDimension=4
s1 = "13275AE069C4DF8B"
sol1="dluullddrrruuldrddlurdlluulurrrddd"
r = ApplyMoves(sol1, s1)
PrintState(r)
StateDimension=4
s="FAC42B061D89E537"
sol1="LLURDLDRDRURDLUULDDRUUULLDRDDRUULURDRDDLLLURURRDLDR".lower()
sol2="ddluuuldddrruluuldddruulddruulddruurruldlurrdlddluldrruuurdlddruuuldddruldlurrdllluruurdddllurrdlurdluldrruulurdldruuldddrruldlurrdlluurddlurulddrulurddr"
print(len(sol1))
print(len(sol2))
r = ApplyMoves(sol1, s)
print("------Solution 1-------")
PrintState(r)
r = ApplyMoves(sol2, s)
print("------Solution 2-------")
PrintState(r)
```
## Assignment Challenge Problems
```
StateDimension=4
s="71A92CE03DB4658F "
sol1="LLLDDRURURDLDRULLULURRRDDLUULDDRUULDLDDRURULLDRRRD".lower()
print(len(sol1))
r = ApplyMoves(sol1, s)
PrintState(r)
StateDimension=4
s="02348697DF5A1EBC"
sol1="RDDRDLULDRUURDLULDDRRURULLULDDRRRULDRD".lower()
print(len(sol1))
r = ApplyMoves(sol1, s)
PrintState(r)
StateDimension=4
s="39A1D0EC7BF86452"
sol1="DLUURRRDDLLDRRULULDDRUULURDLLURDDDLUURDDRUURULLDDRRULDDR".lower()
print(len(sol1))
r = ApplyMoves(sol1, s)
PrintState(r)
StateDimension=4
s="EAB480FC19D56237"
sol1="LDRRUULLDDRDRURULLDRULDDLUURURDDLDRRUULDLUURDDDLUURDRD".lower()
print(len(sol1))
r = ApplyMoves(sol1, s)
PrintState(r)
StateDimension=4
s="7DB13C52F46E80A9"
sol1="RULLDRRRULLUULDRRURDDLLLURDDRRULULULDRURRDLLLURRDLDDLURDRR".lower()
print(len(sol1))
r = ApplyMoves(sol1, s)
PrintState(r)
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/Tessellate-Imaging/monk_v1/blob/master/study_roadmaps/2_transfer_learning_roadmap/3_effect_of_number_of_classes_in_dataset/3)%20Understand%20transfer%20learning%20and%20the%20role%20of%20number%20of%20dataset%20classes%20in%20it%20-%20Keras.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Goals
### 1. Visualize deep learning network
### 2. Understand how the final layer would change when number of classes in dataset changes
# What do you do with a deep learning model in transfer learning
- These are the steps already done by contributors in pytorch, keras and mxnet
- You take a deep learning architecture, such as resnet, densenet, or even custom network
- Train the architecture on large datasets such as imagenet, coco, etc
- The trained wieghts become your starting point for transfer learning
- The final layer of this pretrained model has number of neurons = number of classes in the large dataset
- In transfer learning
- You take the network and load the pretrained weights on the network
- Then remove the final layer that has the extra(or less) number of neurons
- You add a new layer with number of neurons = number of classes in your custom dataset
- Optionally you can add more layers in between this newly added final layer and the old network
- Now you have two parts in your network
- One that already existed, the pretrained one, the base network
- The new sub-network or a single layer you added
- The hyper-parameter we can see here: Freeze base network
- Freezing base network makes the base network untrainable
- The base network now acts as a feature extractor and only the next half is trained
- If you do not freeze the base network the entire network is trained
(You will take this part in next sessions)
# Table of Contents
## [Install](#0)
## [Setup Default Params with Cats-Dogs dataset](#1)
## [Visualize network](#2)
## [Reset Default Params with new dataset - Logo classification](#3)
## [Visualize the new network](#4)
<a id='0'></a>
# Install Monk
## Using pip (Recommended)
- colab (gpu)
- All bakcends: `pip install -U monk-colab`
- kaggle (gpu)
- All backends: `pip install -U monk-kaggle`
- cuda 10.2
- All backends: `pip install -U monk-cuda102`
- Gluon bakcned: `pip install -U monk-gluon-cuda102`
- Pytorch backend: `pip install -U monk-pytorch-cuda102`
- Keras backend: `pip install -U monk-keras-cuda102`
- cuda 10.1
- All backend: `pip install -U monk-cuda101`
- Gluon bakcned: `pip install -U monk-gluon-cuda101`
- Pytorch backend: `pip install -U monk-pytorch-cuda101`
- Keras backend: `pip install -U monk-keras-cuda101`
- cuda 10.0
- All backend: `pip install -U monk-cuda100`
- Gluon bakcned: `pip install -U monk-gluon-cuda100`
- Pytorch backend: `pip install -U monk-pytorch-cuda100`
- Keras backend: `pip install -U monk-keras-cuda100`
- cuda 9.2
- All backend: `pip install -U monk-cuda92`
- Gluon bakcned: `pip install -U monk-gluon-cuda92`
- Pytorch backend: `pip install -U monk-pytorch-cuda92`
- Keras backend: `pip install -U monk-keras-cuda92`
- cuda 9.0
- All backend: `pip install -U monk-cuda90`
- Gluon bakcned: `pip install -U monk-gluon-cuda90`
- Pytorch backend: `pip install -U monk-pytorch-cuda90`
- Keras backend: `pip install -U monk-keras-cuda90`
- cpu
- All backend: `pip install -U monk-cpu`
- Gluon bakcned: `pip install -U monk-gluon-cpu`
- Pytorch backend: `pip install -U monk-pytorch-cpu`
- Keras backend: `pip install -U monk-keras-cpu`
## Install Monk Manually (Not recommended)
### Step 1: Clone the library
- git clone https://github.com/Tessellate-Imaging/monk_v1.git
### Step 2: Install requirements
- Linux
- Cuda 9.0
- `cd monk_v1/installation/Linux && pip install -r requirements_cu90.txt`
- Cuda 9.2
- `cd monk_v1/installation/Linux && pip install -r requirements_cu92.txt`
- Cuda 10.0
- `cd monk_v1/installation/Linux && pip install -r requirements_cu100.txt`
- Cuda 10.1
- `cd monk_v1/installation/Linux && pip install -r requirements_cu101.txt`
- Cuda 10.2
- `cd monk_v1/installation/Linux && pip install -r requirements_cu102.txt`
- CPU (Non gpu system)
- `cd monk_v1/installation/Linux && pip install -r requirements_cpu.txt`
- Windows
- Cuda 9.0 (Experimental support)
- `cd monk_v1/installation/Windows && pip install -r requirements_cu90.txt`
- Cuda 9.2 (Experimental support)
- `cd monk_v1/installation/Windows && pip install -r requirements_cu92.txt`
- Cuda 10.0 (Experimental support)
- `cd monk_v1/installation/Windows && pip install -r requirements_cu100.txt`
- Cuda 10.1 (Experimental support)
- `cd monk_v1/installation/Windows && pip install -r requirements_cu101.txt`
- Cuda 10.2 (Experimental support)
- `cd monk_v1/installation/Windows && pip install -r requirements_cu102.txt`
- CPU (Non gpu system)
- `cd monk_v1/installation/Windows && pip install -r requirements_cpu.txt`
- Mac
- CPU (Non gpu system)
- `cd monk_v1/installation/Mac && pip install -r requirements_cpu.txt`
- Misc
- Colab (GPU)
- `cd monk_v1/installation/Misc && pip install -r requirements_colab.txt`
- Kaggle (GPU)
- `cd monk_v1/installation/Misc && pip install -r requirements_kaggle.txt`
### Step 3: Add to system path (Required for every terminal or kernel run)
- `import sys`
- `sys.path.append("monk_v1/");`
## Dataset - Sample
- one having 2 classes
- other having 16 classes
```
! wget --load-cookies /tmp/cookies.txt "https://docs.google.com/uc?export=download&confirm=$(wget --save-cookies /tmp/cookies.txt --keep-session-cookies --no-check-certificate 'https://docs.google.com/uc?export=download&id=1jE-ckk0JbrdbJvIBaKMJWkTfbRDR2MaF' -O- | sed -rn 's/.*confirm=([0-9A-Za-z_]+).*/\1\n/p')&id=1jE-ckk0JbrdbJvIBaKMJWkTfbRDR2MaF" -O study_classes.zip && rm -rf /tmp/cookies.txt
! unzip -qq study_classes.zip
```
# Imports
```
#Using keras backend
# When installed using pip
from monk.keras_prototype import prototype
# When installed manually (Uncomment the following)
#import os
#import sys
#sys.path.append("monk_v1/");
#sys.path.append("monk_v1/monk/");
#from monk.keras_prototype import prototype
```
### Creating and managing experiments
- Provide project name
- Provide experiment name
```
gtf = prototype(verbose=1);
gtf.Prototype("Project", "study-num-classes");
```
### This creates files and directories as per the following structure
workspace
|
|--------Project
|
|-----study-num-classes
|
|-----experiment-state.json
|
|-----output
|
|------logs (All training logs and graphs saved here)
|
|------models (all trained models saved here)
<a id='1'></a>
# Setup Default Params with Cats-Dogs dataset
```
gtf.Default(dataset_path="study_classes/dogs_vs_cats",
model_name="resnet50",
num_epochs=5);
```
### From Data summary - Num classes: 2
<a id='2'></a>
# Visualize network
```
gtf.Visualize_With_Netron(data_shape=(3, 224, 224), port=8081);
```
## The final layer
```
from IPython.display import Image
Image(filename='imgs/2_classes_base_keras.png')
```
<a id='3'></a>
# Reset Default Params with new dataset - Logo classification
```
gtf = prototype(verbose=1);
gtf.Prototype("Project", "study-num-classes");
gtf.Default(dataset_path="study_classes/logos",
model_name="resnet50",
num_epochs=5);
```
### From Data summary - Num classes: 16
<a id='4'></a>
# Visualize network
```
gtf.Visualize_With_Netron(data_shape=(3, 224, 224), port=8082);
```
## The final layer
```
from IPython.display import Image
Image(filename='imgs/16_classes_base_keras.png')
```
# Goals Completed
### 1. Visualize deep learning network
### 2. Understand how the final layer would change when number of classes in dataset changes
|
github_jupyter
|
```
# Automatically reload custom code modules when there are changes:
%load_ext autoreload
%autoreload 2
# Adjust relative path so that the notebook can find the code modules:
import sys
sys.path.append('../code/')
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib notebook
# Import code modules:
from structures import RingRoad
from animations import Animation
# Hide warnings about safe distance violation (still in development):
import warnings
warnings.filterwarnings("ignore", category=UserWarning)
```
# Baseline:
```
# Define simulation:
env = RingRoad(
num_vehicles = 22, # The vechicles at index 0 is an A.V.
ring_length = 230.0, # The road is a cicle.
starting_noise = 4.0, # Uniformly add noise to starting positions.
temporal_res = 0.3, # Set the size of simulation steps (seconds).
av_activate = 30, # Set when the PID controller is activated.
seed = 286, # Set a random seed.
)
# Run the simulation for set number of time steps:
total_time = 90 # In seconds.
total_steps = int(np.ceil(total_time/env.dt))
env.run(steps=total_steps)
# Build animation:
anim = Animation(env, speedup=5.0, interval=5, mode='notebook')
anim.animate_dashboard(draw_cars_to_scale=True, draw_safety_buffer=False, show_sigma=True)
# # Show animation:
# anim.show()
# # Save animation as GIF:
# anim.save_gif(filepath="../outputs/baseline.gif", overwrite=True)
# # Stop animation:
# anim.stop()
```
<a href='https://github.com/chickert/autonomous_vehicles/blob/main/outputs/baseline.gif'><img src='https://github.com/chickert/autonomous_vehicles/raw/main/outputs/baseline.gif' /></a>
# Extension 1
```
# Define simulation:
num_vehicles = 22
num_avs = 11
env = RingRoad(
num_vehicles=num_vehicles, # The vechicles at index 0 is an A.V.
ring_length=230.0, # The road is a cicle.
starting_noise=4.0, # Uniformly add noise to starting positions.
temporal_res=0.3, # Set the size of simulation steps (seconds).
av_activate=30, # Set when the PID controller is activated.
seed=286, # Set a random seed.
num_avs=num_avs
)
# Run the simulation for set number of time steps:
total_time = 90 # In seconds.
total_steps = int(np.ceil(total_time/env.dt))
env.run(steps=total_steps)
# Build animation:
anim = Animation(env, speedup=5.0, interval=5, mode='notebook')
anim.animate_dashboard(draw_cars_to_scale=True, draw_safety_buffer=False, show_sigma=True)
# # Show animation:
# anim.show()
# # Save animation as GIF:
# anim.save_gif(filepath="../outputs/extension1.gif", overwrite=True)
# # Stop animation:
# anim.stop()
```
<a href='https://github.com/chickert/autonomous_vehicles/blob/main/outputs/extension1.gif'><img src='https://github.com/chickert/autonomous_vehicles/raw/main/outputs/extension1.gif' /></a>
# Extension 2
```
# Define simulation:
a_sigma = 0.04
b_sigma = 0.5
env = RingRoad(
num_vehicles=22, # The vechicles at index 0 is an A.V.
ring_length=230.0, # The road is a cicle.
starting_noise=0., # Uniformly add noise to starting positions.
temporal_res=0.3, # Set the size of simulation steps (seconds).
av_activate=30, # Set when the PID controller is activated.
seed=286, # Set a random seed.
a_sigma=a_sigma,
b_sigma=b_sigma,
hv_heterogeneity=True,
)
# Run the simulation for set number of time steps:
total_time = 90 # In seconds.
total_steps = int(np.ceil(total_time/env.dt))
env.run(steps=total_steps)
# Build animation:
anim = Animation(env, speedup=5.0, interval=5, mode='notebook')
anim.animate_dashboard(draw_cars_to_scale=True, draw_safety_buffer=False, show_sigma=True)
# # Show animation:
# anim.show()
# # Save animation as GIF:
# anim.save_gif(filepath="../outputs/extension2.gif", overwrite=True)
# # Stop animation:
# anim.stop()
```
<a href='https://github.com/chickert/autonomous_vehicles/blob/main/outputs/extension2.gif'><img src='https://github.com/chickert/autonomous_vehicles/raw/main/outputs/extension2.gif' /></a>
# Extension 3
```
# Define simulation:
sigma_pct = 40
env = RingRoad(
num_vehicles=22, # The vechicles at index 0 is an A.V.
ring_length=230.0, # The road is a cicle.
starting_noise=4.0, # Uniformly add noise to starting positions.
temporal_res=0.3, # Set the size of simulation steps (seconds).
av_activate=30, # Set when the PID controller is activated.
seed=286, # Set a random seed.
uncertain_avs=True,
sigma_pct=sigma_pct
)
# Run the simulation for set number of time steps:
total_time = 50 # In seconds.
total_steps = int(np.ceil(total_time/env.dt))
env.run(steps=total_steps)
# Build animation:
anim = Animation(env, speedup=5.0, interval=5, mode='notebook')
anim.animate_dashboard(draw_cars_to_scale=True, draw_safety_buffer=False, show_sigma=True)
# # Show animation:
# anim.show()
# # Save animation as GIF:
# anim.save_gif(filepath="../outputs/extension3.gif", overwrite=True)
# # Stop animation:
# anim.stop()
```
<a href='https://github.com/chickert/autonomous_vehicles/blob/main/outputs/extension3.gif'><img src='https://github.com/chickert/autonomous_vehicles/raw/main/outputs/extension3.gif' /></a>
|
github_jupyter
|
# **Neural Networks Summary**
```
from keras.models import Sequential
from keras.layers import Dense, Dropout, Conv2D, MaxPool2D, Flatten
from keras.utils import to_categorical
```
## Regression
```
model = Sequential()
n_cols = data.shape[1]
model.add(Dense(5, activation='relu', input_shape=(n_cols, ))) # input shape has to be the same as number of columns
model.add(Dense(5, activation='relu'))
model.add(Dense(1)) # output layer
model.compile(optimizer='adam', loss='mean_square_error')
# adam is more effcicient than gradient descent.
# it adapts the learning rate automatically
model.fit(predictors, target)
predictions = model.predict(test_data)
```
## Classification
```
model = Sequential()
n_cols = data.shape[1]
target = to_categorical(target)
model.add(Dense(5, activation='relu', input_shape=(n_cols, )))
model.add(Dropout(0.2)) # dropout is a regularization technique to prevent overfitting. Normally ~0.2-0.4
model.add(Dense(5, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(num_classes, activation='softmax'))
# for classification the last layer has an activation function which ussually is softmax
# in addition, the output dimension has to be the same as the calsses in the target
model.compile(optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy']) # to measure accuracy in classification
model.fit(predictors, target,
epochs=20, # number of iterations
batch_size=50, # size of the splitted bachs (this only works with SGD?)
validation_split=0.2, )
predictions = model.predict(test_data)
```
## Convolutional Neural Networks (CNN) - supervised
This are mainly use for images as they reduce dimensionality. Check this [link](https://courses.edx.org/courses/course-v1:IBM+DL0101EN+3T2019/courseware/89227024130b43f684d95376901b65c8/052a444d45914712a597f0c58cbc4391/?child=first)
```
model = Sequential()
input_shape = (N, N, 3) # 3 for RGB images and 1 for gray scale images
model.add(Conv2D(16, kernel_size=(2, 2), # size of the filter to use
strides=(1, 1), # steps the filter is moved
activation='relu',
input_shape=input_shape))
model.add(MaxPool2D(pool_size(2, 2), strides=(1, 1))
model.add(Conv2D(16, kernel_size=(2, 2), strides=(1, 1), activation='relu')
model.add(MaxPool2D(pool_size(2, 2))
model.add(Flatten()) # so the data can proceed to the fully-connected layer
model.add(Dense(100, activation='relu'))
model.add(Dense(num_classes, activation='sotmax'))
model.compile(optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy']) # to measure accuracy in classification
model.fit(predictors, target)
predictions = model.predict(test_data)
```
## Recurrent Neural Networks (RNN) - supervised
This are networks with loops that take into account dependency of data like images in a movie.
## Autoencoders - unsupervised
These commpress and decompress functions learned from data. For this reason they are data-specific.
These are used in data de-noising and dimensionality reduction for data visualisation.
|
github_jupyter
|
```
import swat
import pandas as pd
import os
from sys import platform
import riskpy
from os.path import join as path
if "CASHOST" in os.environ:
# Create a session to the CASHOST and CASPORT variables set in your environment
conn = riskpy.SessionContext(session=swat.CAS(),
caslib="CASUSER")
else:
# Otherwise set this to your host and port:
host = "riskpy.rqs-cloud.sashq-d.openstack.sas.com"
port = 5570
conn = riskpy.SessionContext(session=swat.CAS(host, port), caslib="CASUSER")
base_dir = '.'
# Set output location
if platform == "win32":
# Windows...
output_dir = 'u:\\temp'
else:
# platform == "linux" or platform == "linux2" or platform == "darwin":
output_dir = '/tmp'
mkt_data = riskpy.MarketData(
current = pd.DataFrame(data={'uerate': 6.0}, index=[0]),
risk_factors = ['uerate'])
my_scens = riskpy.Scenarios(
name = "my_scens",
market_data = mkt_data,
data = path("datasources","CreditRisk",'uerate_scenario.xlsx'))
my_scens
cpty_df = pd.read_excel(path("datasources","CreditRisk",'uerate_cpty.xlsx'))
loan_groups = riskpy.Counterparties(data=pd.read_excel(
path("datasources","CreditRisk",'uerate_cpty.xlsx')))
loan_groups.mapping = {"cpty1": "score_uerate"}
loan_groups
score_code_file=(path("methods","CreditRisk",'score_uerate.sas'))
scoring_methods = riskpy.MethodLib(
method_code=path("methods","CreditRisk",'score_uerate.sas'))
scoring_methods
my_scores = riskpy.Scores(counterparties=loan_groups,
scenarios=my_scens,
method_lib=scoring_methods)
my_scores.generate(session_context=conn, write_allscore=True)
print(my_scores.allscore.head())
allscore_file = path(output_dir, 'simple_allscores.xlsx')
my_scores.allscore.to_excel(allscore_file)
my_scores
portfolio = riskpy.Portfolio(
data=path("datasources","CreditRisk",'retail_portfolio.xlsx'),
class_variables = ["region", "cptyid"])
eval_methods = riskpy.MethodLib(
method_code=path("methods","CreditRisk",'credit_method2.sas'))
my_values = riskpy.Values(
session_context=conn,
portfolio=portfolio,
output_variables=["Expected_Credit_Loss"],
scenarios=my_scens,
scores=my_scores,
method_lib=eval_methods,
mapping = {"Retail": "ecl_method"})
my_values
my_values.evaluate(write_prices=True)
allprice_df = my_values.fetch_prices(max_rows=100000)
print(my_values.allprice.head())
allprice_file = path(output_dir, 'creditrisk_allprice.xlsx')
allprice_df.to_excel(allprice_file)
results = riskpy.Results(
session_context=conn,
values=my_values,
requests=["_TOP_", ["region"]],
out_type="values"
)
results_df = results.query().to_frame()
print(results_df.head())
rollup_file = path(output_dir, 'creditrisk_rollup_by_region.xlsx')
results_df.to_excel(rollup_file)
results
```
|
github_jupyter
|
```
import pandas as pd
from openpyxl import Workbook
from openpyxl.styles import Border, Side, Font, Alignment
from openpyxl.utils.dataframe import dataframe_to_rows
```
# 測試資料
```
# 表格資料title
data = [
{"route_id": "0001", "route_desc": "路線1", "num_of_people": 100,
"origin_amt": 1000, "act_amt": 600, "subsidy_amt": 400, "avg_subsidy_amt_by_people": 4},
{"route_id": "0002", "route_desc": "路線2", "num_of_people": 100,
"origin_amt": 1000, "act_amt": 600, "subsidy_amt": 400, "avg_subsidy_amt_by_people": 4},
{"route_id": "0003", "route_desc": "路線3", "num_of_people": 100,
"origin_amt": 1000, "act_amt": 600, "subsidy_amt": 400, "avg_subsidy_amt_by_people": 4},
]
df = pd.DataFrame(data, columns=["route_id", "route_desc", "num_of_people", "origin_amt",
"act_amt", "subsidy_amt", "avg_subsidy_amt_by_people"])
df
df.columns=["路線\n編號", "路線\n名稱", "使用轉乘優惠\n人數", "原始票收金額", "實際交易金額",
"優惠補貼金額", "平均每人\n優惠金額"]
```
# EXCEL輸出格式產生
```
wb = Workbook()
ws = wb.active
# 設定print area
# https://openpyxl.readthedocs.io/en/stable/print_settings.html
ws.print_options.horizontalCentered = True
# ws.print_options.verticalCentered = True
ws.print_area = 'A1:G10'
# 設定輸出表格字體參數
table_title_ft = Font(name='標楷體', color='000000', size=14, bold=True)
table_ft = Font(name='標楷體', color='000000', size=14)
# 表格格線設定
table_border = Border(left=Side(border_style='thin', color='000000'),
right=Side(border_style='thin', color='000000'),
top=Side(border_style='thin', color='000000'),
bottom=Side(border_style='thin', color='000000'))
ws.insert_rows(1) # 在第一行插入一行
ws.merge_cells('A1:G1') # 欄位
ws["A1"] = '表1 ○年○月○○客運公司○○○公車轉乘第一段票免費補貼金額申請表'
ws["A1"].font = table_title_ft
ws["A1"].alignment = Alignment(horizontal='center')
# DataFrame資料填入sheet row
for row in dataframe_to_rows(df, index=False, header=True):
ws.append(row)
# Table加入格線
rows = ws["A3:G6"]
for row in rows:
for cell in row:
cell.border = table_border
cell.font = table_ft
# 自動指定欄位寬度
# https://stackoverflow.com/questions/13197574/openpyxl-adjust-column-width-size
# from openpyxl.utils import get_column_letter
# column_widths = []
# for row in data:
# for i, cell in enumerate(row):
# if len(column_widths) > i:
# if len(cell) > column_widths[i]:
# column_widths[i] = len(cell)
# else:
# column_widths += [len(cell)]
# for i, column_width in enumerate(column_widths):
# ws.column_dimensions[get_column_letter(i+1)].width = column_width
# 直接指定欄位寬度
# https://stackoverflow.com/questions/53906532/is-it-possible-to-change-the-column-width-using-openpyxl/53906585
ws.column_dimensions['A'].width = 10
ws.column_dimensions['B'].width = 10
ws.column_dimensions['C'].width = 23
ws.column_dimensions['D'].width = 23
ws.column_dimensions['E'].width = 23
ws.column_dimensions['F'].width = 23
ws.column_dimensions['G'].width = 23
# Table欄位title style設定
table_align_style = Alignment(wrapText=True, horizontal='center', vertical='center')
for rows in ws['A3':'G3']:
for cell in rows:
cell.alignment = table_align_style
# ws["A":"G"].alignment = Alignment(wrapText=True, horizontal='center')
# ws['A1'].alignment = Alignment(wrapText=True)
# rows = sheet["A1:C3"]
# for row in rows:
# for cell in row:
# cell.border = border
wb.save("report_01_output.xlsx")
```
|
github_jupyter
|
# Semantic Function Species (part 2)
```
from scripts.imports import *
out = Exporter(
paths['outdir'],
'semantics'
)
from IPython.display import HTML, display
df.columns
```
# Miscellaneous Functions
```
df[df.funct_type == 'secondary'].function.value_counts()
funct2names = {
'purposive_ext':['purpext', 'Purposive Extent'],
'dist_posterior': ['distpost', 'Distance Posterior'],
'anterior_limitive': ['antlimit', 'Anterior Limitive'],
'dist_prospective': ['distprosp', 'Distance Prospective'],
'purposive': ['purp', 'Purposive'],
'anterior_dur_except': ['antdurex', 'Anterior Durative with "Except"'],
'posterior_dur_future': ['postdurfut', 'Posterior Durative Future'],
}
# automatically show examples
for funct in funct2names:
exdf = df[df.function == funct].sort_values(by='notes').head(10)
print(funct)
display(
ts.show(exdf, extra=['notes'], spread=-1)
)
print('-'*50)
```
# Pull Out Examples
## Purposive Extent
```
purpext_df = df[df.function == 'purposive_ext']
out.number(
purpext_df.shape[0],
'purpext_N'
)
antlim_df = df[df.function == 'anterior_limitive']
out.number(
antlim_df.shape[0],
'antlim_N'
)
```
# Difficult Cases
# Compound Time Adverbials
```
compound_ct = df[df.funct_type == 'compound'].function.value_counts()
out.table(
compound_ct,
'compound_funct_ct',
caption='Sampled Compound Time Adverbial Frequencies',
)
comp_clusters = {
'begin-to-end': [
'begin_to_end',
'habitual + begin_to_end',
'begin_to_end_habitual',
'simultaneous + begin_to_end',
'simultaneous + multi_begin_to_end',
'posterior_dur + begin_to_end + atelic_ext',
'begin_to_end + multi_antdur',
],
'coordinated location': [
'simultaneous_calendar',
'multi_simuls',
'simultaneous + anterior',
'simul_to_end',
'simultaneous + anterior_limitive?',
'simultaneous + anterior_dist',
'simultaneous + posterior',
'simultaneous + posteriors',
'simultaneous + dist_posterior',
'posterior + simultaneous',
'multi_antdur',
'anterior_dur + anterior',
'anterior + posterior',
'multi_posterior_dur',
'simultaneous + purposive_ext',
],
'coordinated extent': [
'multi_atelic_ext',
],
'location + extent': [
'simultaneous + atelic_ext',
'atelic_ext + simultaneous',
'anterior + atelic_ext',
'anterior + distance',
'atelic_ext + anterior + atelic_ext',
'anterior_dur + duration',
'dur_to_end',
'posterior + atelic_ext',
'dist_fut + atelic_ext',
'reg_recurr + atelic_ext',
'atelic_ext + habitual',
],
'distance sequential': [
'posterior + distance',
],
}
attested = set(cl for name, functs in comp_clusters.items() for cl in functs)
set(compound_ct.index) - attested
```
## Auto Export Examples for Compounds
```
for cluster, labels in comp_clusters.items():
display(HTML(f'<h2>{cluster.title()}</h2>'))
for label in labels:
print(label)
ex_df = df[df.function == label]
display(
ts.show(
ex_df
)
)
display(HTML('<hr>'))
```
# Manually Extract Specific Cases
## Begin-to-end
```
b2edf = df[df.function.isin(comp_clusters['begin-to-end'])]
out.number(
b2edf.shape[0],
'begintoend_N'
)
```
## Calendricals
```
caldf = df[df.function == 'simultaneous_calendar']
out.number(
caldf.shape[0],
'N_simul_calendar'
)
caldf.times_utf8.value_counts()
```
|
github_jupyter
|
# COMP4096 Business Intelligence Group Project
## COVID-19 Data Analysis and Prediction
#### This part is written by Wong Tin Yau David (18207871).
##### Datasets below are downloaded from https://raw.githubusercontent.com/owid/covid-19-data/master/public/data/owid-covid-data.csv, which is provided by https://ourworldindata.org/. (An Open Source Project). With Filtering (only select data after 2021 because vaccines releases in this year and we would like to see the effectiveness)
### 1. Import Data 'owid-covid-data_2021.csv'
```
import pandas as pd
import numpy as np
pd.options.mode.chained_assignment = None # default='warn'
df = pd.read_csv('owid-covid-data_2021.csv')
df.head()
df.shape
```
### 2. Select the data only from G20 Countries only
```
g20df = df[(df["location"]=='Australia')|(df["location"]=='Canada')|(df["location"]=='Saudi Arabia')|(df["location"]=='United States')|(df["location"]=='India')|(df["location"]=='Russia')|(df["location"]=='South Africa')|(df["location"]=='Turkey')|(df["location"]=='Argentina')|(df["location"]=='Brazil')|(df["location"]=='Mexico')|(df["location"]=='France')|(df["location"]=='Italy')|(df["location"]=='Germany')|(df["location"]=='United Kingdom')|(df["location"]=='China')|(df["location"]=='Indonesia')|(df["location"]=='Japan')|(df["location"]=='South Korea')]
g20df.shape
droppable_features = []
```
### 3. Seach columns with mostly-missing values and drop columns with over 99% values
```
(g20df.isnull().sum()/g20df.shape[0]).sort_values(ascending=False)
droppable_features.append('weekly_icu_admissions_per_million')
droppable_features.append('weekly_icu_admissions')
droppable_features.append('weekly_hosp_admissions')
droppable_features.append('weekly_hosp_admissions_per_million')
```
### 4. Find Too Skewed Columns and Remove
```
pd.options.display.float_format = '{:,.4f}'.format
sk_df = pd.DataFrame([{'column': c, 'uniq': g20df[c].nunique(), 'skewness': g20df[c].value_counts(normalize=True).values[0] * 100} for c in g20df.columns])
sk_df = sk_df.sort_values('skewness', ascending=False)
sk_df
```
### 5. Find columns that have more than 10% of missing values and filled with means
```
null_counts = g20df.isnull().sum()
null_counts = null_counts / g20df.shape[0]
null_counts[null_counts > 0.1]
g20df.drop(droppable_features, axis=1, inplace=True)
g20df.shape
g20df['icu_patients'].fillna((g20df['icu_patients'].mean()), inplace=True)
g20df['icu_patients_per_million'].fillna((g20df['icu_patients_per_million'].mean()), inplace=True)
g20df['hosp_patients'].fillna((g20df['hosp_patients'].mean()), inplace=True)
g20df['hosp_patients_per_million'].fillna((g20df['hosp_patients_per_million'].mean()), inplace=True)
g20df['new_tests'].fillna((g20df['new_tests'].mean()), inplace=True)
g20df['total_tests'].fillna((g20df['total_tests'].mean()), inplace=True)
g20df['total_tests_per_thousand'].fillna((g20df['total_tests_per_thousand'].mean()), inplace=True)
g20df['new_tests_per_thousand'].fillna((g20df['new_tests_per_thousand'].mean()), inplace=True)
g20df['new_tests_smoothed'].fillna((g20df['new_tests_smoothed'].mean()), inplace=True)
g20df['new_tests_smoothed_per_thousand'].fillna((g20df['new_tests_smoothed_per_thousand'].mean()), inplace=True)
g20df['total_vaccinations'].fillna((g20df['total_vaccinations'].mean()), inplace=True)
```
### 6. Find correlations between each attributes
```
cols = g20df.columns.tolist()
import seaborn as sns
import matplotlib.pyplot as plt
plt.figure(figsize=(10,10))
co_cols = cols[:10]
co_cols.append('new_vaccinations')
sns.heatmap(g20df[co_cols].corr(), cmap='RdBu_r', annot=True, center=0.0)
plt.title('Correlation between 1 ~ 10th columns')
plt.show()
corr_remove = []
co_cols = cols[10:20]
co_cols.append('new_vaccinations')
plt.figure(figsize=(10,10))
sns.heatmap(g20df[co_cols].corr(), cmap='RdBu_r', annot=True, center=0.0)
plt.title('Correlation between 11 ~ 20th columns')
plt.show()
corr_remove = []
co_cols = cols[20:30]
co_cols.append('new_vaccinations')
plt.figure(figsize=(10,10))
sns.heatmap(g20df[co_cols].corr(), cmap='RdBu_r', annot=True, center=0.0)
plt.title('Correlation between 21 ~ 30th columns')
plt.show()
corr_remove = []
co_cols = cols[30:40]
co_cols.append('new_vaccinations')
plt.figure(figsize=(10,10))
sns.heatmap(g20df[co_cols].corr(), cmap='RdBu_r', annot=True, center=0.0)
plt.title('Correlation between 31 ~ 40th columns')
plt.show()
corr_remove = []
co_cols = cols[40:50]
co_cols.append('new_vaccinations')
plt.figure(figsize=(10,10))
sns.heatmap(g20df[co_cols].corr(), cmap='RdBu_r', annot=True, center=0.0)
plt.title('Correlation between 41 ~ 50th columns')
plt.show()
corr_remove = []
co_cols = cols[50:]
co_cols.append('new_vaccinations')
plt.figure(figsize=(10,10))
sns.heatmap(g20df[co_cols].corr(), cmap='RdBu_r', annot=True, center=0)
plt.title('Correlation between from 51th to the last columns')
plt.show()
corr = g20df.corr()
high_corr = (corr >= 0.99).astype('uint8')
plt.figure(figsize=(15,15))
sns.heatmap(high_corr, cmap='RdBu_r', annot=True, center=0.0)
plt.show()
fig, ax = plt.subplots()
ax.plot(organizedg20df['bymonth'],organizedg20df['total_new_cases_from_2021Jan'],color='green', linestyle=':', label='line 1')
ax.plot(organizedg20df['bymonth'],organizedg20df['total_vaccinations'], linestyle='--', label = 'line 2')
ax.legend(loc=1) #
ax.set_title('COVID-19 Cases versus Vaccinations', fontweight='bold',fontsize=18)
ax.set_xlabel('x label') # add xlabel
ax.set_ylabel('y label'); # add ylabel
```
|
github_jupyter
|
TSG108 - View the controller upgrade config map
===============================================
Description
-----------
When running a Big Data Cluster upgrade using `azdata bdc upgrade`:
`azdata bdc upgrade --name <namespace> --tag <tag>`
It may fail with:
> Upgrading cluster to version 15.0.4003.10029\_2
>
> NOTE: Cluster upgrade can take a significant amount of time depending
> on configuration, network speed, and the number of nodes in the
> cluster.
>
> Upgrading Control Plane. Control plane upgrade failed. Failed to
> upgrade controller.
Steps
-----
Use these steps to troubelshoot the problem.
### Common functions
Define helper functions used in this notebook.
```
# Define `run` function for transient fault handling, suggestions on error, and scrolling updates on Windows
import sys
import os
import re
import platform
import shlex
import shutil
import datetime
from subprocess import Popen, PIPE
from IPython.display import Markdown
retry_hints = {} # Output in stderr known to be transient, therefore automatically retry
error_hints = {} # Output in stderr where a known SOP/TSG exists which will be HINTed for further help
install_hint = {} # The SOP to help install the executable if it cannot be found
def run(cmd, return_output=False, no_output=False, retry_count=0, base64_decode=False, return_as_json=False, regex_mask=None):
"""Run shell command, stream stdout, print stderr and optionally return output
NOTES:
1. Commands that need this kind of ' quoting on Windows e.g.:
kubectl get nodes -o jsonpath={.items[?(@.metadata.annotations.pv-candidate=='data-pool')].metadata.name}
Need to actually pass in as '"':
kubectl get nodes -o jsonpath={.items[?(@.metadata.annotations.pv-candidate=='"'data-pool'"')].metadata.name}
The ' quote approach, although correct when pasting into Windows cmd, will hang at the line:
`iter(p.stdout.readline, b'')`
The shlex.split call does the right thing for each platform, just use the '"' pattern for a '
"""
MAX_RETRIES = 5
output = ""
retry = False
# When running `azdata sql query` on Windows, replace any \n in """ strings, with " ", otherwise we see:
#
# ('HY090', '[HY090] [Microsoft][ODBC Driver Manager] Invalid string or buffer length (0) (SQLExecDirectW)')
#
if platform.system() == "Windows" and cmd.startswith("azdata sql query"):
cmd = cmd.replace("\n", " ")
# shlex.split is required on bash and for Windows paths with spaces
#
cmd_actual = shlex.split(cmd)
# Store this (i.e. kubectl, python etc.) to support binary context aware error_hints and retries
#
user_provided_exe_name = cmd_actual[0].lower()
# When running python, use the python in the ADS sandbox ({sys.executable})
#
if cmd.startswith("python "):
cmd_actual[0] = cmd_actual[0].replace("python", sys.executable)
# On Mac, when ADS is not launched from terminal, LC_ALL may not be set, which causes pip installs to fail
# with:
#
# UnicodeDecodeError: 'ascii' codec can't decode byte 0xc5 in position 4969: ordinal not in range(128)
#
# Setting it to a default value of "en_US.UTF-8" enables pip install to complete
#
if platform.system() == "Darwin" and "LC_ALL" not in os.environ:
os.environ["LC_ALL"] = "en_US.UTF-8"
# When running `kubectl`, if AZDATA_OPENSHIFT is set, use `oc`
#
if cmd.startswith("kubectl ") and "AZDATA_OPENSHIFT" in os.environ:
cmd_actual[0] = cmd_actual[0].replace("kubectl", "oc")
# To aid supportability, determine which binary file will actually be executed on the machine
#
which_binary = None
# Special case for CURL on Windows. The version of CURL in Windows System32 does not work to
# get JWT tokens, it returns "(56) Failure when receiving data from the peer". If another instance
# of CURL exists on the machine use that one. (Unfortunately the curl.exe in System32 is almost
# always the first curl.exe in the path, and it can't be uninstalled from System32, so here we
# look for the 2nd installation of CURL in the path)
if platform.system() == "Windows" and cmd.startswith("curl "):
path = os.getenv('PATH')
for p in path.split(os.path.pathsep):
p = os.path.join(p, "curl.exe")
if os.path.exists(p) and os.access(p, os.X_OK):
if p.lower().find("system32") == -1:
cmd_actual[0] = p
which_binary = p
break
# Find the path based location (shutil.which) of the executable that will be run (and display it to aid supportability), this
# seems to be required for .msi installs of azdata.cmd/az.cmd. (otherwise Popen returns FileNotFound)
#
# NOTE: Bash needs cmd to be the list of the space separated values hence shlex.split.
#
if which_binary == None:
which_binary = shutil.which(cmd_actual[0])
# Display an install HINT, so the user can click on a SOP to install the missing binary
#
if which_binary == None:
print(f"The path used to search for '{cmd_actual[0]}' was:")
print(sys.path)
if user_provided_exe_name in install_hint and install_hint[user_provided_exe_name] is not None:
display(Markdown(f'HINT: Use [{install_hint[user_provided_exe_name][0]}]({install_hint[user_provided_exe_name][1]}) to resolve this issue.'))
raise FileNotFoundError(f"Executable '{cmd_actual[0]}' not found in path (where/which)")
else:
cmd_actual[0] = which_binary
start_time = datetime.datetime.now().replace(microsecond=0)
cmd_display = cmd
if regex_mask is not None:
regex = re.compile(regex_mask)
cmd_display = re.sub(regex, '******', cmd)
print(f"START: {cmd_display} @ {start_time} ({datetime.datetime.utcnow().replace(microsecond=0)} UTC)")
print(f" using: {which_binary} ({platform.system()} {platform.release()} on {platform.machine()})")
print(f" cwd: {os.getcwd()}")
# Command-line tools such as CURL and AZDATA HDFS commands output
# scrolling progress bars, which causes Jupyter to hang forever, to
# workaround this, use no_output=True
#
# Work around a infinite hang when a notebook generates a non-zero return code, break out, and do not wait
#
wait = True
try:
if no_output:
p = Popen(cmd_actual)
else:
p = Popen(cmd_actual, stdout=PIPE, stderr=PIPE, bufsize=1)
with p.stdout:
for line in iter(p.stdout.readline, b''):
line = line.decode()
if return_output:
output = output + line
else:
if cmd.startswith("azdata notebook run"): # Hyperlink the .ipynb file
regex = re.compile(' "(.*)"\: "(.*)"')
match = regex.match(line)
if match:
if match.group(1).find("HTML") != -1:
display(Markdown(f' - "{match.group(1)}": "{match.group(2)}"'))
else:
display(Markdown(f' - "{match.group(1)}": "[{match.group(2)}]({match.group(2)})"'))
wait = False
break # otherwise infinite hang, have not worked out why yet.
else:
print(line, end='')
if wait:
p.wait()
except FileNotFoundError as e:
if install_hint is not None:
display(Markdown(f'HINT: Use {install_hint} to resolve this issue.'))
raise FileNotFoundError(f"Executable '{cmd_actual[0]}' not found in path (where/which)") from e
exit_code_workaround = 0 # WORKAROUND: azdata hangs on exception from notebook on p.wait()
if not no_output:
for line in iter(p.stderr.readline, b''):
try:
line_decoded = line.decode()
except UnicodeDecodeError:
# NOTE: Sometimes we get characters back that cannot be decoded(), e.g.
#
# \xa0
#
# For example see this in the response from `az group create`:
#
# ERROR: Get Token request returned http error: 400 and server
# response: {"error":"invalid_grant",# "error_description":"AADSTS700082:
# The refresh token has expired due to inactivity.\xa0The token was
# issued on 2018-10-25T23:35:11.9832872Z
#
# which generates the exception:
#
# UnicodeDecodeError: 'utf-8' codec can't decode byte 0xa0 in position 179: invalid start byte
#
print("WARNING: Unable to decode stderr line, printing raw bytes:")
print(line)
line_decoded = ""
pass
else:
# azdata emits a single empty line to stderr when doing an hdfs cp, don't
# print this empty "ERR:" as it confuses.
#
if line_decoded == "":
continue
print(f"STDERR: {line_decoded}", end='')
if line_decoded.startswith("An exception has occurred") or line_decoded.startswith("ERROR: An error occurred while executing the following cell"):
exit_code_workaround = 1
# inject HINTs to next TSG/SOP based on output in stderr
#
if user_provided_exe_name in error_hints:
for error_hint in error_hints[user_provided_exe_name]:
if line_decoded.find(error_hint[0]) != -1:
display(Markdown(f'HINT: Use [{error_hint[1]}]({error_hint[2]}) to resolve this issue.'))
# Verify if a transient error, if so automatically retry (recursive)
#
if user_provided_exe_name in retry_hints:
for retry_hint in retry_hints[user_provided_exe_name]:
if line_decoded.find(retry_hint) != -1:
if retry_count < MAX_RETRIES:
print(f"RETRY: {retry_count} (due to: {retry_hint})")
retry_count = retry_count + 1
output = run(cmd, return_output=return_output, retry_count=retry_count)
if return_output:
if base64_decode:
import base64
return base64.b64decode(output).decode('utf-8')
else:
return output
elapsed = datetime.datetime.now().replace(microsecond=0) - start_time
# WORKAROUND: We avoid infinite hang above in the `azdata notebook run` failure case, by inferring success (from stdout output), so
# don't wait here, if success known above
#
if wait:
if p.returncode != 0:
raise SystemExit(f'Shell command:\n\n\t{cmd_display} ({elapsed}s elapsed)\n\nreturned non-zero exit code: {str(p.returncode)}.\n')
else:
if exit_code_workaround !=0 :
raise SystemExit(f'Shell command:\n\n\t{cmd_display} ({elapsed}s elapsed)\n\nreturned non-zero exit code: {str(exit_code_workaround)}.\n')
print(f'\nSUCCESS: {elapsed}s elapsed.\n')
if return_output:
if base64_decode:
import base64
return base64.b64decode(output).decode('utf-8')
else:
return output
# Hints for tool retry (on transient fault), known errors and install guide
#
retry_hints = {'azdata': ['Endpoint sql-server-master does not exist', 'Endpoint livy does not exist', 'Failed to get state for cluster', 'Endpoint webhdfs does not exist', 'Adaptive Server is unavailable or does not exist', 'Error: Address already in use', 'Login timeout expired (0) (SQLDriverConnect)', 'SSPI Provider: No Kerberos credentials available', ], 'kubectl': ['A connection attempt failed because the connected party did not properly respond after a period of time, or established connection failed because connected host has failed to respond', ], 'python': [ ], }
error_hints = {'azdata': [['Please run \'azdata login\' to first authenticate', 'SOP028 - azdata login', '../common/sop028-azdata-login.ipynb'], ['The token is expired', 'SOP028 - azdata login', '../common/sop028-azdata-login.ipynb'], ['Reason: Unauthorized', 'SOP028 - azdata login', '../common/sop028-azdata-login.ipynb'], ['Max retries exceeded with url: /api/v1/bdc/endpoints', 'SOP028 - azdata login', '../common/sop028-azdata-login.ipynb'], ['Look at the controller logs for more details', 'TSG027 - Observe cluster deployment', '../diagnose/tsg027-observe-bdc-create.ipynb'], ['provided port is already allocated', 'TSG062 - Get tail of all previous container logs for pods in BDC namespace', '../log-files/tsg062-tail-bdc-previous-container-logs.ipynb'], ['Create cluster failed since the existing namespace', 'SOP061 - Delete a big data cluster', '../install/sop061-delete-bdc.ipynb'], ['Failed to complete kube config setup', 'TSG067 - Failed to complete kube config setup', '../repair/tsg067-failed-to-complete-kube-config-setup.ipynb'], ['Data source name not found and no default driver specified', 'SOP069 - Install ODBC for SQL Server', '../install/sop069-install-odbc-driver-for-sql-server.ipynb'], ['Can\'t open lib \'ODBC Driver 17 for SQL Server', 'SOP069 - Install ODBC for SQL Server', '../install/sop069-install-odbc-driver-for-sql-server.ipynb'], ['Control plane upgrade failed. Failed to upgrade controller.', 'TSG108 - View the controller upgrade config map', '../diagnose/tsg108-controller-failed-to-upgrade.ipynb'], ['NameError: name \'azdata_login_secret_name\' is not defined', 'SOP013 - Create secret for azdata login (inside cluster)', '../common/sop013-create-secret-for-azdata-login.ipynb'], ['ERROR: No credentials were supplied, or the credentials were unavailable or inaccessible.', 'TSG124 - \'No credentials were supplied\' error from azdata login', '../repair/tsg124-no-credentials-were-supplied.ipynb'], ['Please accept the license terms to use this product through', 'TSG126 - azdata fails with \'accept the license terms to use this product\'', '../repair/tsg126-accept-license-terms.ipynb'], ], 'kubectl': [['no such host', 'TSG010 - Get configuration contexts', '../monitor-k8s/tsg010-get-kubernetes-contexts.ipynb'], ['No connection could be made because the target machine actively refused it', 'TSG056 - Kubectl fails with No connection could be made because the target machine actively refused it', '../repair/tsg056-kubectl-no-connection-could-be-made.ipynb'], ], 'python': [['Library not loaded: /usr/local/opt/unixodbc', 'SOP012 - Install unixodbc for Mac', '../install/sop012-brew-install-odbc-for-sql-server.ipynb'], ['WARNING: You are using pip version', 'SOP040 - Upgrade pip in ADS Python sandbox', '../install/sop040-upgrade-pip.ipynb'], ], }
install_hint = {'azdata': [ 'SOP063 - Install azdata CLI (using package manager)', '../install/sop063-packman-install-azdata.ipynb' ], 'kubectl': [ 'SOP036 - Install kubectl command line interface', '../install/sop036-install-kubectl.ipynb' ], }
print('Common functions defined successfully.')
```
### Get the Kubernetes namespace for the big data cluster
Get the namespace of the Big Data Cluster use the kubectl command line
interface .
**NOTE:**
If there is more than one Big Data Cluster in the target Kubernetes
cluster, then either:
- set \[0\] to the correct value for the big data cluster.
- set the environment variable AZDATA\_NAMESPACE, before starting
Azure Data Studio.
```
# Place Kubernetes namespace name for BDC into 'namespace' variable
if "AZDATA_NAMESPACE" in os.environ:
namespace = os.environ["AZDATA_NAMESPACE"]
else:
try:
namespace = run(f'kubectl get namespace --selector=MSSQL_CLUSTER -o jsonpath={{.items[0].metadata.name}}', return_output=True)
except:
from IPython.display import Markdown
print(f"ERROR: Unable to find a Kubernetes namespace with label 'MSSQL_CLUSTER'. SQL Server Big Data Cluster Kubernetes namespaces contain the label 'MSSQL_CLUSTER'.")
display(Markdown(f'HINT: Use [TSG081 - Get namespaces (Kubernetes)](../monitor-k8s/tsg081-get-kubernetes-namespaces.ipynb) to resolve this issue.'))
display(Markdown(f'HINT: Use [TSG010 - Get configuration contexts](../monitor-k8s/tsg010-get-kubernetes-contexts.ipynb) to resolve this issue.'))
display(Markdown(f'HINT: Use [SOP011 - Set kubernetes configuration context](../common/sop011-set-kubernetes-context.ipynb) to resolve this issue.'))
raise
print(f'The SQL Server Big Data Cluster Kubernetes namespace is: {namespace}')
```
### View the upgrade configmap
```
run(f'kubectl get configmap -n {namespace} controller-upgrade-configmap -o yaml')
print("Notebook execution is complete.")
```
Related
-------
- [TSG109 - Set upgrade timeouts](../repair/tsg109-upgrade-stalled.ipynb)
|
github_jupyter
|
```
import re
import numpy as np
import os
os.sys.path.append('../1/')
from z2 import loader
from math import log
import sys
import heapq
import collections
import operator
vowels = list('aeioóuyąę') + list('aeioóuyąę'.upper())
compacted_vovels = ['i' + x for x in vowels if x != 'i']
word2tag = dict()
tag2word = dict()
dataPath = 'data/'
def stringNorm(sent, num=False):
regex = re.compile(f'[,\.!?:;\'{"0-9" if not num else ""}\*\-“…\(\)„”—»«–––=\[\]’]')
return regex.sub('',sent.lower())
def bigrams2unigrams(bigrams):
return {w1: sum([float(bigrams[w1][w2]) for w2 in bigrams[w1]])/2 for w1 in bigrams}
def count_syllable(phrase, verose=False):
res = 0
for i, letter in enumerate(phrase):
if letter in vowels:
res += 1
if verose:
print(letter)
if phrase[i:i+2] in compacted_vovels:
res -= 1
if verose:
print(phrase[i:i+2])
return res
with open(dataPath + "supertags.txt") as tags:
for line in tags:
word, tag = stringNorm(line, num=True).split()
word2tag[word] = tag
if tag in tag2word:
tag2word[tag].append(word)
else:
tag2word[tag] = [word]
base = {}
with open(dataPath + "superbazy.txt") as file:
for line in file:
word, base_word = line.split()
base[word] = base_word
vectors = {}
with open(dataPath + "poleval_base_vectors.txt") as file:
for line in file:
vec = line.split()
if 150< len(vec) < 250:
x = np.array([float(x) for x in vec[1:]])
vectors[vec[0]] = x / np.sqrt(x.T @ x)
with open(dataPath + 'rytmiczne_zdania_z_korpusu.txt') as f:
sentences = [
tuple(
[
[
x for x in y.split()
]
for y in line.split('RYM:')[1].rstrip(' .\n').split('[*]')
]
)
for line in f
]
PMI = lambda w1, w2: log(
float(bigrams[w1][w2] if w1 in bigrams and w2 in bigrams[w1] else 1) * uniSum / (unigrams[w1] * unigrams[w2])
+ sys.float_info.min)
for i, x in enumerate(vectors):
if i < 10:
print(vectors[x].T@vectors[x].T)
else:
break
def get_rym(w):
best = None
for i in range(len(w)):
if count_syllable(w[i:]) == 2:
best = w[i:]
return best
def sample_verset():
index = np.random.choice(np.arange(len(sentences)))
return sentences[index]
def get_accents(phrase):
return [count_syllable(x) for x in phrase]
def sameTags(w):
if w in word2tag:
return tag2word[word2tag[w]]
elif ('^' + w)[-3:] in word2tag:
return tag2word[word2tag[('^' + w)[-3:]]]
else:
return []
def createAltWords(accent, verse, rime=None):
return [list(
set(
filter(
lambda x: count_syllable(x) == accent[i] ,
sameTags(w)
)
).intersection(
{y for y in safeGrams}
))
for i, w in enumerate(verse)
]
def createAltWords(accent, w, rime=None):
return list(
filter(
lambda x: count_syllable(x) == accent and x != w and(rime is None or get_rym(x) == rime),
sameTags(w)
)
)
def get_rime_set(alts):
return {get_rym(x) for x in alts}
def change_word(accent, word, rime=None):
alts = createAltWords(accent, word, rime=rime)
vec = vectors[base[word]]
values = list(
map(
lambda x: vectors[base[x]].T @ vec if x in base and base[x] in vectors else 0,
alts
))
if len(alts) > 0:
x = np.argmax(np.array(values))
choosen = alts[x]
return choosen, values[x]
return None, 0
def find_common_rime(a1,w1,a2,w2):
alts1 = createAltWords(a1, w1, rime=None)
alts2 = createAltWords(a2, w2, rime=None)
common_rimes = get_rime_set(alts1).intersection(get_rime_set(alts2) )
if len(common_rimes) == 0:
return None
vec1 = vectors[base[w1]]
values1 = list(
map(
lambda x: vectors[base[x]].T @ vec1 if x in base and base[x] in vectors and get_rym(x) in common_rimes else 0,
alts1
))
x = np.argmax(np.array(values1))
choosen1 = alts1[x]
choosen2 = change_word(a2, w2, rime=get_rym(choosen1))[0]
return choosen1, choosen2
def change_last(a1,w1,a2,w2):
alt1 = change_word(a1, v1[-1], get_rym(v2[-1]))
alt2 = change_word(a2, v2[-1], get_rym(v1[-1]))
# print(alt1, alt2)
if alt1[1] <= alt2[1] and alt2[1] > 0:
return w1, alt2[0]
elif alt2[1] < alt1[1] and alt1[1] > 0:
return alt1[0], w2
else:
return find_common_rime(a1, v1[-1], a2, v2[-1])
def pretty_print(v1,v2):
print(' '.join(v1)+'\n'+' '.join(v2)+'\n')
for _ in range(20):
v1,v2 = sample_verset()
a1 = [count_syllable(i) for i in v1]
a2 = [count_syllable(i) for i in v2]
pretty_print(v1,v2)
for i, w1 in enumerate(v1):
if np.random.rand(1) > 0.8:
try:
if i < len(v1) - 1:
v1[i] = change_word(a1[i], w1)[0]
else:
v1[-1], v2[-1] = change_last(a1[i],w1,a2[-1],v2[-1])
pretty_print(v1,v2)
except:
print('.')
print('<->')
for i, w2 in enumerate(v2):
if np.random.rand(1) > 0.8:
try:
if i < len(v2) - 1:
v2[i] = change_word(a2[i], w2)[0]
else:
v1[-1], v2[-1] = change_last(a1[-1],v1[-1],a2[i],w2)
pretty_print(v1,v2)
except:
print('.')
print('************')
```
|
github_jupyter
|
# 15天入门Python3
CopyRight by 黑板客
转载请联系heibanke_at_aliyun.com
**上节作业**
八皇后
```
%load day08/eight_queen.py
a = gen_n_queen(5)
printsolution(next(a))
```
## day09:谈对象—高富帅和白富美
1. <a href="#1">面向对象编程</a>
2. <a href="#2">**封装**, 属性和方法</a>
3. <a href="#3">**继承**</a>
4. <a href="#4">**多态** 与 重载</a>
5. <a href="#5">作业</a>
## <a name="1">面向对象编程</a>
面向对象和面向过程的区别:
1. 面向过程编程 (OPP) 定义各种数据,定义各种函数,然后操作数据和函数输出结果,解决一类问题。面向过程适合解决特定的简单问题。
2. 面向对象编程 (OOP) 最重要的是把用到的数据和方法抽象成为类。使用不同的类进行建模。达到代码模块化。适合解决多变,复杂,不断更新的问题。
三大特性:封装,继承,多态。
```
class A(object):
nums_A = 0
def __init__(self, data):
# 初始化
self.data = data
A.nums_A += 1
def methods(self):
self.data -= 1
a = A(3)
print(a.data, A.nums_A)
b = A(5)
print(b.data, A.nums_A)
a.methods()
c = A(6)
print(a.data, A.nums_A)
%%html
<style>
.rendered_html td, .rendered_html th {text-align: left;}
</style>
```
| A |
| :- |
|- data|
|+ methods()|
举个王者荣耀简化版的例子说明一下:
你要开发一个游戏,游戏中每个玩家都是一个英雄。英雄有两种,比如亚瑟是近战英雄,后羿是远程英雄。
每种英雄都有不同的属性。
1. name
2. defence
3. attack
4. life
请模拟游戏里两个英雄互相PK的过程。看谁先game over。
<img src="day09/yase_vs_houyi_small.png" width=600></img>
```
# %load day09/pk_opp_01.py
# 面向过程
def cal_damage(A, B):
"""
计算A对B造成的伤害
"""
return A['attack'] * (1-B['defence']/(B['defence']+400))
tank = {'name':'亚瑟1', 'defence':200, 'attack':80, 'life':600}
archer = {'name':'后羿1', 'defence':100, 'attack':200, 'life':300}
def game_test(A, B):
while A['life']>0 and B['life']>0:
damage1 = cal_damage(A, B) #A对B造成伤害
damage2 = cal_damage(B, A) #B对A造成伤害
A['life'] -= damage2
print('%s 对 %s 造成 %.2f 伤害,%s 还剩 %.2f 生命。'%(B['name'], A['name'], damage2, A['name'], A['life']))
B['life'] -= damage1
print('%s 对 %s 造成 %.2f 伤害,%s 还剩 %.2f 生命。'%(A['name'], B['name'], damage1, B['name'], B['life']))
if A['life']<0:
print('%s 被打败了'%(A['name']))
if B['life']<0:
print('%s 被打败了'%(B['name']))
game_test(tank, archer)
```
## <a name="2">封装,属性和方法</a>
|Hero|
| :- |
|- name <br> - defence <br> - attack <br> - life|
|+ \__init\__ (name, defence, attack, life) <br> + damage (enemy) <br> + alive ()|
|Game|
| :- |
|- A <br> - B|
|+ \__init\__ (A, B) <br> + start () <br> + end ()|
```
# %load day09/pk_oop_01.py
class Hero(object):
def __init__(self, name, defence, attack, life):
self.name = name
self.defence = defence
self.attack = attack
self.life = life
def damage(self, enemy):
d = self.attack * (1-enemy.defence/(enemy.defence+400))
enemy.life -= d
print('%s 对 %s 造成 %.2f 伤害,%s 还剩 %.2f 生命。'%(self.name, enemy.name, d, enemy.name, enemy.life))
def alive(self):
return self.life > 0
class Game(object):
def __init__(self, A, B):
self.A = A
self.B = B
def start(self):
while self.A.alive() and self.B.alive():
self.A.damage(self.B)
self.B.damage(self.A)
self.end()
def end(self):
if not self.B.alive():
print('%s 被打败了'%(self.B.name))
if not self.A.alive():
print('%s 被打败了'%(self.A.name))
def game_test():
A = Hero('亚瑟1', 200, 80, 600)
B = Hero('后羿1', 100, 200, 300)
game = Game(A, B)
game.start()
game_test()
```
封装:对象的属性建议只能通过调用对象的方法来修改。只对对象的方法可见。
问题:当玩家很多时,生成亚瑟和后羿的属性只需要改变name,而其他属性是统一的。怎么更简化?
## <a name="3">继承</a>
子类继承父类的属性和方法。
```
# %load day09/pk_oop_02.py
from day09.pk_oop_01 import Game
class Hero(object):
nums = 0
def __init__(self, name, defence, attack, life):
self.name = name
self.defence = defence
self.attack = attack
self.life = life
Hero.nums += 1
def damage(self, enemy):
d = self.attack * (1-enemy.defence/(enemy.defence+400))
enemy.life -= d
print('%s 对 %s 造成 %.2f 伤害,%s 还剩 %.2f 生命。'%(self.name, enemy.name, d, enemy.name, enemy.life))
def alive(self):
return self.life > 0
class YaSe(Hero):
nums = 0
def __init__(self, name):
Hero.__init__(self, name, 200, 80, 600)
YaSe.nums += 1
class HouYi(Hero):
nums = 0
def __init__(self, name):
Hero.__init__(self, name, 100, 200, 300)
HouYi.nums += 1
def game_test():
A = YaSe('亚瑟1')
B = HouYi('后羿1')
game = Game(A, B)
game.start()
game_test()
class YaSe(Hero):
nums = 0
def __init__(self, name):
Hero.__init__(self, name, 200, 80, 600)
YaSe.nums += 1
game_test()
print(Hero.nums, YaSe.nums, HouYi.nums)
```
## <a name="4">多态和重载
多态,方法和子类动态绑定
重载,多个同名的方法,参数不同。
让亚瑟的攻击带有吸血功能,每次将伤害的10%转化成自己的生命,看能否打败后羿。
```
class YaSe(Hero):
def __init__(self, name):
Hero.__init__(self, name, 200, 80, 2000)
def damage(self, enemy, xixie = 0.1):
d = self.attack * (1-enemy.defence/(enemy.defence+400))
enemy.life -= d
self.life += d * xixie
print('%s 对 %s 造成 %.2f 伤害,%s 还剩 %.2f 生命。'%(self.name, enemy.name, d, enemy.name, enemy.life))
game_test()
```
<a name="5">作业:(面向对象角度实现选做)</a>
1. 如何让英雄可以使用道具,比如铠甲能够增加defence,增加生命。弓箭可以增加attack。
2. 如果考虑装备有其他更多的作用,比如弓箭可以减少对方的一部分defence,铠甲受到伤害可以反弹一部分给对方,如何设计?
3. 如果道具能让英雄有吸血功能,而且很多种英雄都有吸血功能,如何设计代码?
4. 从面向过程和面向对象两个角度考虑实现上面的功能,对比不同。
欢迎大家把做好的作业分享到讨论区。
|
github_jupyter
|
Starting with Chollet's advice -- program simple programs that can solve the first 10 tasks
```
import numpy as np
import json
from PIL import Image, ImageDraw
from IPython.display import Image as Im
import matplotlib.pyplot as plt
import collections
colorMap = {0:"black",1:"blue",2:"red", 3:"green",4:"yellow",5:"grey",6:"magenta",7:"orange",8:"cyan",9:"brown"}
# accuracy of predicted output to actual output (simply the sum of the differences)
def accuracy(inputGrid,outputGrid):
inputGrid, outputGrid = returnArrays(inputGrid,outputGrid)
acc = 0
if inputGrid.shape != outputGrid.shape:
return np.inf
for i in range(inputGrid.shape[0]):
for j in range(inputGrid.shape[1]):
acc += np.abs(inputGrid[i][j]-outputGrid[i][j])
return acc
```
### Functions for displaying grids
```
# displaying a single grid
def DisplayGrid(grid):
grid = np.asarray(grid)
nrows = len(grid[:,0])
ncols = len(grid[0,:])
height, width = nrows*50, ncols*50
image = Image.new(size=(width,height),mode='RGB',color=(255,255,255))
draw = ImageDraw.Draw(image)
r = 0
for row in grid:
c = 0
for col in row:
draw.rectangle(xy=[c*50,r*50,(c+1)*50,(r+1)*50], fill=colorMap[np.abs(grid[r][c])])
c += 1
r += 1
for i in range(ncols):
draw.line([(i+1)*50,0,(i+1)*50,height],fill="grey")
for i in range(nrows):
draw.line([0,(i+1)*50,width,(i+1)*50],fill="grey")
display(image)
# displaying two grids side by side
def DisplayGrids(grid1,grid2):
# Grid 1
grid1 = np.asarray(grid1)
nrows = len(grid1[:,0])
ncols = len(grid1[0,:])
height, width = nrows*50, ncols*50
image1 = Image.new(size=(width,height),mode='RGB',color=(255,255,255))
draw = ImageDraw.Draw(image1)
r = 0
for row in grid1:
c = 0
for col in row:
draw.rectangle(xy=[c*50,r*50,(c+1)*50,(r+1)*50], fill=colorMap[np.abs(grid1[r][c])])
c += 1
r += 1
for i in range(ncols):
draw.line([(i+1)*50,0,(i+1)*50,height],fill="grey")
for i in range(nrows):
draw.line([0,(i+1)*50,width,(i+1)*50],fill="grey")
# Grid 2
grid2 = np.asarray(grid2)
nrows = len(grid2[:,0])
ncols = len(grid2[0,:])
height, width = nrows*50, ncols*50
image2 = Image.new(size=(width,height),mode='RGB',color=(255,255,255))
draw = ImageDraw.Draw(image2)
r = 0
for row in grid2:
c = 0
for col in row:
draw.rectangle(xy=[c*50,r*50,(c+1)*50,(r+1)*50], fill=colorMap[np.abs(grid2[r][c])])
c += 1
r += 1
for i in range(ncols):
draw.line([(i+1)*50,0,(i+1)*50,height],fill="grey")
for i in range(nrows):
draw.line([0,(i+1)*50,width,(i+1)*50],fill="grey")
# Displaying
fig, ax = plt.subplots(1,2,figsize=(50,50))
ax[0].imshow(image1)
ax[0].axis("off")
ax[1].imshow(image2)
ax[1].axis("off")
```
## Solving grid 1
```
filename = "/Users/aysjajohnson/Desktop/ARC-master/data/training/007bbfb7.json"
with open(filename, 'r') as f:
grid = json.load(f)
inGrid = grid["train"][0]["input"]
outGrid = grid["train"][0]["output"]
def returnArrays(inputGrid, outputGrid):
return(np.asarray(inputGrid),np.asarray(outputGrid))
def inDim2outDim(inputGrid,outputGrid):
inputGrid, outputGrid = returnArrays(inputGrid,outputGrid)
if inputGrid.shape != outputGrid.shape:
return(np.zeros((outputGrid.shape[0],outputGrid.shape[1])))
else:
return(inputGrid)
# the thing that actually solves this is mapping each square to a 3x3 area on the output and whenever there's a color,
# copy and paste the input... so... very complicated. I'm just going to write a function that solves this and then
# simplify
# need to get these not to rely on outputGrid... you need to save that info somewhere though. For now I'm just going
# to focus on ones where the size is the same
def copyPaste(inputGrid, outputGrid):
inputGrid, outputGrid = returnArrays(inputGrid,outputGrid)
inputHeight = inputGrid.shape[0]
inputWidth = inputGrid.shape[1]
outputHeight = outputGrid.shape[0]
outputWidth = outputGrid.shape[1]
outputBigger = (inputHeight*inputWidth)<(outputHeight*outputWidth)
if outputBigger and (outputHeight%inputHeight == 0 or outputWidth%inputWidth == 0):
output = np.zeros((outputHeight,outputWidth))
for i in range(outputHeight)[::inputHeight]:
for j in range(outputWidth)[::inputWidth]:
output[i:i+inputHeight,j:j+inputWidth] = inputGrid
return(output)
else:
return(inputGrid)
DisplayGrid(copyPaste(inGrid,outGrid))
def mask(inputGrid,outputGrid):
inputGrid, outputGrid = returnArrays(inputGrid,outputGrid)
inputHeight = inputGrid.shape[0]
inputWidth = inputGrid.shape[1]
outputHeight = outputGrid.shape[0]
outputWidth = outputGrid.shape[1]
outputBigger = (inputHeight*inputWidth)<(outputHeight*outputWidth)
if outputBigger and outputHeight%inputHeight == 0 and outputWidth%inputWidth == 0:
output = np.ones((outputHeight,outputWidth))
mask = np.zeros((inputHeight,inputWidth))
for i in range(outputHeight)[::3]:
for j in range(outputWidth)[::3]:
if inputGrid[int(i/inputHeight),int(j/inputWidth)] == 0:
output[i:i+inputHeight,j:j+inputWidth] = mask
return(output)
else:
return(inputGrid)
DisplayGrid(np.multiply(copyPaste(inGrid,outGrid),mask(inGrid,outGrid)))
for i in range(len(grid["train"])):
inGrid = grid["train"][i]["input"]
outGrid = grid["train"][i]["output"]
DisplayGrids(inGrid, np.multiply(copyPaste(inGrid,outGrid),mask(inGrid,outGrid)))
accuracy(grid["test"][0]["output"],np.multiply(copyPaste(grid["test"][0]["input"],grid["train"][0]["output"]),mask(grid["test"][0]["input"],grid["train"][0]["output"])))
DisplayGrid(np.multiply(copyPaste(grid["test"][0]["input"],grid["train"][0]["output"]),mask(grid["test"][0]["input"],grid["train"][0]["output"])))
```
## Solving Grid 2
```
filename = "/Users/aysjajohnson/Desktop/ARC-master/data/training/00d62c1b.json"
with open(filename, 'r') as f:
grid = json.load(f)
inGrid = grid["train"][3]["input"]
outGrid = grid["train"][0]["output"]
DisplayGrids(inGrid,outGrid)
def bfs(grid, start, width, height, wall=3):
goal = 10
queue = collections.deque([[start]])
seen = set([start])
if grid[start[0],start[1]] == wall:
return False
while queue:
path = queue.popleft()
# print("current path", path)
x, y = path[-1]
if grid[x][y] == goal:
return False
for x2, y2 in ((x+1,y), (x-1,y), (x,y+1), (x,y-1)):
# print("considering", (x2,y2))
if 0 <= x2 < height and 0 <= y2 < width and grid[x2][y2] != wall and (x2, y2) not in seen:
queue.append(path + [(x2, y2)])
seen.add((x2, y2))
# print("expanding queue", queue)
# print("no path", path)
return True
def fillBorders(grid, color=1):
grid = np.asarray(grid)
height = grid.shape[0]
width = grid.shape[1]
grid[:,0] = np.where(grid[:,0]==0,10,grid[:,0])
grid[:,-1] = np.where(grid[:,-1]==0,10,grid[:,-1])
grid[0,:] = np.where(grid[0,:]==0,10,grid[0,:])
grid[-1,:] = np.where(grid[-1,:]==0,10,grid[-1,:])
# bfs(grid,(2,3),width,height)
for i in range(1,height-1):
for j in range(1,width-1):
# print(i,j)
if bfs(grid,(i,j),width,height):
grid[i][j] = color
grid = np.where(grid==10,0,grid)
return(grid)
DisplayGrids(inGrid,fillBorders(inGrid,4))
accuracy(grid["test"][0]["output"],fillBorders(grid["test"][0]["input"],4))
DisplayGrids(grid["test"][0]["output"],fillBorders(grid["test"][0]["input"],4))
```
## Solving Grid 3
```
filename = "/Users/aysjajohnson/Desktop/ARC-master/data/training/017c7c7b.json"
with open(filename, 'r') as f:
grid = json.load(f)
inGrid = grid["train"][0]["input"]
outGrid = grid["train"][0]["output"]
DisplayGrids(inGrid,outGrid)
# making copy and paste more general
def patternCompletion(inputGrid, outputGrid, color=1, pattern_length = 2):
inputGrid, outputGrid = returnArrays(inputGrid,outputGrid)
inputHeight = inputGrid.shape[0]
inputWidth = inputGrid.shape[1]
outputHeight = outputGrid.shape[0]
outputWidth = outputGrid.shape[1]
output = np.zeros((outputHeight,outputWidth))
if inputHeight == outputHeight:
ouputPattern = np.zeros((outputHeight-inputHeight,inputWidth))
elif inputWidth == outputWidth:
pattern = inputGrid[-pattern_length:,:]
for i in range(inputHeight-pattern_length):
if np.all(inputGrid[i:i+pattern_length,:] == np.asarray(pattern)):
output[inputHeight:,:] = inputGrid[i+pattern_length:i+pattern_length + outputHeight-inputHeight,:]
output[:inputHeight,:] = inputGrid
return output
else:
return(inputGrid)
def changeColor(grid,color=1):
grid = np.asarray(grid)
return np.where(grid!=0, color,0)
DisplayGrid(changeColor(patternCompletion(inGrid,outGrid),2))
accuracy(grid["test"][0]["output"],changeColor(patternCompletion(grid["test"][0]["input"],grid["train"][0]["output"]),2))
DisplayGrids(grid["test"][0]["output"],changeColor(patternCompletion(grid["test"][0]["input"],grid["train"][0]["output"]),2))
```
## Solving Grid 4
```
filename = "/Users/aysjajohnson/Desktop/ARC-master/data/training/025d127b.json"
with open(filename, 'r') as f:
grid = json.load(f)
inGrid = grid["train"][0]["input"]
outGrid = grid["train"][0]["output"]
DisplayGrids(inGrid,outGrid)
def moveRight(grid):
grid = np.asarray(grid)
height = grid.shape[0]
width = grid.shape[1]
for i in range(height-1):
for j in range(width-1):
if grid[i][j]
```
|
github_jupyter
|
# Introdução ao Pandas - Viagens do Governo | Tratamento de dados
*Esse notebook usa o arquivo sobre [viagens de funcionários do governo](http://www.portaltransparencia.gov.br/viagens) disponibilizado no portal da transparência.*
```
import pandas as pd
df_viagem = pd.read_csv('viagens_2019.csv', encoding='latin-1', sep=';')
```
**Saber informações sobre uma coluna específica**
```
df_viagem['Valor passagens']
```
**Mudar as virgulas dos valores por pontos**
```
# o str é pra sinalizar que a troca do replace é uma string
df_viagem['Valor passagens'] = df_viagem['Valor passagens'].str.replace(',','.')
```
**Mudar o tipo de dado da coluna**
```
df_viagem['Valor passagens'] = df_viagem['Valor passagens'].astype(float)
```
**Contar quantas vezes aparece uma determinada coisa**
```
df_viagem['Destinos'].value_counts()
```
**Separar as cidades dos Estados ou Países**<br><br>
O `split()` guarda o resultado em uma **lista**
```
# O parametro 'expand = True' indica que os elementos devem ser separados em diferentes colunas
col = df_viagem['Destinos'].str.split('/',1,expand = True)
```
**Incluir a coluna nova no dataframe**
```
df_viagem['cidade_destino'] = col[0]
```
**Separar conteudos diferentes que estão na mesma coluna**
A coluna do dataframe possui valores nulos, estados e países misturados. Para resolver isso é preciso identificar **padrões**. No caso desse dataframe, o padrão é: <br>
- **Estados** tem só **2 caracteres**
- **Paises** estão escritos com nome completo, ou seja tem mais caracteres
- Valores **nulos** estão escritos **None**
Antes de tudo, vou armazenar o conteudo bagunçado em uma coluna que chamarei de 'Provisoria'
```
df_viagem['Provisoria'] = col[1]
```
**Criando um dataframe para cada conteudo separado**<br><br>
Todos os dataframes vão ter uma coluna chamda 'Provisoria' com o conteudo separado por conteudo que foi filtrado a partir do dataframe original 'df_viagem'. Para isso filtrarei usando a função `len()`. Essa função apresenta a quantidade de conteúdo que for passado por parametro.
Criando um dataframe com o conteudo de estados
```
#Estou colocando na coluna estado o conteudo da coluna provisória que tenha apenas dois caracteres
estado = df_viagem[df_viagem['Provisoria'].str.len()==2]
```
Agora vou criar um dataframe com o conteudo de paises, incluindo nele todo conteudo que tenha informações maior que dois caracteres
```
pais = df_viagem[df_viagem['Provisoria'].str.len() > 2]
```
E por fim vou criar um dataframe com o conteudo None. A função `isnull()` identifica os valores nulos no dataframe. No caso do exemplo está identificando na coluna 'Provisoria'
```
nulo = df_viagem[df_viagem['Provisoria'].isnull()]
```
**Renomeado as colunas dos dataframes**
Se na coluna 'Provisoria' do dataframe 'estado' só tem o conteudo relacionado aos estados, basta renomear a coluna 'Provisoria' para 'estado'.
```
#No dicionario é passado na chave o nome da coluna antiga e no valor o nome que quer renomear
#O inplace serve para tornar a mudança definitiva
estado.rename(columns = {'Provisoria' : 'estado'}, inplace = True)
```
Todas os estados são relacionados ao Brasil. Então vou criar dentro do dataframe 'estado' a coluna 'pais' e incluir o conteudo 'Brasil'
```
estado['país'] = 'Brasil'
```
No dataframe 'pais' vou renomear a coluna 'Provisoria' para 'país'
```
pais.rename(columns = {'Provisoria' : 'país'}, inplace = True)
```
Como os outros paises não tem a informação do estado (no caso desse dataframe), vou criar uma coluna 'estado' e incluir o conteudo 'Sem informação'
```
pais['estado'] = 'Sem informação'
```
No dataframe nulo, vou renomear a coluna 'Provisoria' para 'estado'
```
nulo.rename(columns = {'Provisoria' : 'estado'}, inplace = True)
```
E inserir uma coluna 'país' com o conteudo 'Sem informação'
```
nulo['país'] = 'Sem informação'
```
Vou mudar o conteudo 'None' da coluna 'Estado' para 'Sem informação'
```
nulo['estado'] = 'Sem informação'
```
**Ordenando Colunas** <br><br>
A ordem das colunas novas nos novos dataframes deveria ser 'cidade_destino', 'estado' e 'pais', mas essa ordem está diferente no dataframe 'pais'. Vou reordenar para todos ficarem iguais.
1. Pegarei o nome de todas as colunas
```
pais.columns
```
2. Agora copio todas as colunas dentro dos colchetes duplos na ordem que eu considerar certa
```
pais = pais[['Identificador do processo de viagem', 'Situação',
'Código do órgão superior', 'Nome do órgão superior',
'Código órgão solicitante', 'Nome órgão solicitante', 'CPF viajante',
'Nome', 'Cargo', 'Período - Data de início', 'Período - Data de fim',
'Destinos', 'Motivo', 'Valor diárias', 'Valor passagens',
'Valor outros gastos', 'cidade_destino', 'estado', 'país']]
```
**Juntar os 3 dataframes em 1**
```
#ignore_true serve pra ignorar o indice de cada dataframe, se não vai ser impossivel junta-los
df_final = pd.concat([estado, pais, nulo], ignore_index = True)
```
**Removendo uma coluna**<br>
Agora não faz mais sentido ter a coluna 'Destinos' afinal ela já foi tratada. Usarei o método `drop()` para fazer isso.
```
#O axis indica se eu quero fazer minha alteração em uma linha ou em uma coluna. 1 é coluna, 0 é linha.
df_final.drop('Destinos', inplace = True, axis = 1)
```
**Salvando um arquivo em csv**<br>
É importante depois de tratado gerar um arquivo novo para não precisar rodar tudo e novo.
```
df_final.to_csv('viagens_tratado_2019.csv', encoding = 'latin-1', sep = ';')
```
|
github_jupyter
|
```
import torch
import matplotlib.pyplot as plt
import tqdm
import utils
import dataloaders
import numpy as np
import torchvision
import os
from trainer import Trainer
torch.random.manual_seed(0)
np.random.seed(0)
torch.backends.cudnn.benchmark = False
torch.backends.cuda.deterministic = True
```
### Model Definition
```
class LeNet(torch.nn.Module):
def __init__(self):
super().__init__()
### START YOUR CODE HERE ### (You can change anything inside this block)
num_input_nodes = 32*32
num_hidden_nodes = 64
num_classes = 10
self.classifier = torch.nn.Sequential(
torch.nn.Linear(num_input_nodes, num_hidden_nodes),
torch.nn.ReLU(),
torch.nn.Linear(num_hidden_nodes, num_classes)
)
### END YOUR CODE HERE ###
def forward(self, x):
### START YOUR CODE HERE ### (You can change anything inside this block)
x = x.view(-1, 32*32)
x = self.classifier(x)
return x
### END YOUR CODE HERE ###
```
### Hyperparameters & Loss function
```
# Hyperparameters
batch_size = 64
learning_rate = 0.0192
num_epochs = 4
# Use CrossEntropyLoss for multi-class classification
loss_function = torch.nn.CrossEntropyLoss()
```
### Train model
```
image_transform = torchvision.transforms.Compose([
torchvision.transforms.Resize((32, 32)),
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize([0.5], [0.25])
])
dataloader_train, dataloader_val = dataloaders.load_dataset(batch_size, image_transform)
# Model definition
model = LeNet()
# Transfer model to GPU memory (if possible)
model = utils.to_cuda(model)
# Define optimizer (Stochastic Gradient Descent)
optimizer = torch.optim.SGD(model.parameters(),
lr=learning_rate)
trainer = Trainer(
model=model,
dataloader_train=dataloader_train,
dataloader_val=dataloader_val,
batch_size=batch_size,
loss_function=loss_function,
optimizer=optimizer
)
train_loss_dict, val_loss_dict = trainer.train(num_epochs)
```
### Train Model
```
utils.plot_loss(train_loss_dict, label="Train Loss")
utils.plot_loss(val_loss_dict, label="Test Loss")
# Limit the y-axis of the plot (The range should not be increased!)
plt.ylim([0, .4])
plt.legend()
plt.xlabel("Global Training Step")
plt.ylabel("Cross Entropy Loss")
os.makedirs("image_processed", exist_ok=True)
plt.savefig(os.path.join("image_processed", "task2.png"))
plt.show()
torch.save(model.state_dict(), "saved_model.torch")
# %%
final_loss, final_acc = utils.compute_loss_and_accuracy(
dataloader_val, model, loss_function)
print(f"Final Validation loss: {final_loss}. Final Validation accuracy: {final_acc}")
# %%
```
|
github_jupyter
|
# HW7
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
%matplotlib inline
```
In order to ensure your plots are inline, make sure to run the matplotlib magic command.
# Q1
You are provided with a csv file (shoes.csv) on canvas that contains 2 columns.
The first column is the height of the individuals being surveyed and the second column is their shoe size. We do not know anything else about the individuals.
Using the information in that file do the following:
1. Create a scatter plot displaying shoe size on the y-axis and height on the x-axis.
2. Compute the correlation between shoe size and height.
3. Fit a linear regression line through this data.
4. Use the linear regression line to predict what your shoe size would be. For this question just write down what your height is (in inches), then write down the predicted shoe size (based on the linear regression ). Finally write your own actual shoe size. How far off is the model’s prediction?
```
shoes = pd.read_csv('shoes.csv')
plt.scatter(shoes['HEIGHT (IN)'], shoes['SHOE SIZE (FT)'])
plt.xlabel('Height (in inches)')
plt.ylabel('Shoe Size (in feet)')
plt.title('Shoe Size by Height')
#computing the correlation coefficient using the long method:
def standardize(anylist):
'''convert any array of numbers to std units '''
return (anylist - np.mean(anylist)) / np.std(anylist)
standardize_x = standardize(shoes['HEIGHT (IN)'])
standardize_y = standardize(shoes['SHOE SIZE (FT)'])
#correlation coefficient r
r = np.mean(standardize_x * standardize_y)
r
#computing the correlation coefficient using np.corrcoef()
np.corrcoef(shoes['HEIGHT (IN)'], shoes['SHOE SIZE (FT)'])
#fitting a linear regression line
plt.scatter(standardize_x, standardize_y) #graphs the scatter plot of data
xvals = np.arange(-4, 3, 0.3) #setting the range of x values for regression line
yvals = r * xvals #the regression y values (correlation coefficient * x values)
plt.plot(xvals, yvals, color = 'g') #graphing the linear regression
plt.title('Distribution of Shoe Sizes by Height')
plt.xlabel('Height (in inches)')
plt.ylabel('Shoe Size (in feet)')
#predicting shoe size
m, b = np.polyfit(shoes['HEIGHT (IN)'], shoes['SHOE SIZE (FT)'], 1)
m, b
# predicting using the linear regression: y = mx + b
# My height: 63 inches
my_height = 63
my_shoe_size = (m * my_height) + b
my_shoe_size
```
- My actual shoe size is an 8. The model is off by about a size.
# Q2
The department of transportation releases flight delay information annually.
We will use a small sample of this data to check if Chebychev's inequality holds.
Use the airline_data.csv file. Plot the distribution of arrival delays.
Compute the mean and standard deviation of the arrival delays. As per Chebychev's inequality, as least 88.88% of the data should be within 3 standard deviations of the mean. Is that true for this dataset? (support your answer with actual code)
Based on this sample (and this sample alone), which airline would you avoid? Why?
```
delays = pd.read_excel('flightdelays.xlsx')
delays.shape
#cleaning data
delays = delays.dropna(subset=['ARRIVAL_DELAY'])
delays.shape
plt.style.use('fivethirtyeight')
plt.hist(delays['ARRIVAL_DELAY'], normed = True, bins = 15, ec = 'k')
plt.title('distribution of arrival delays', size = 'medium')
plt.xlabel('Delay Amount')
plt.ylabel('Frequency')
```
- As per Chebychev's inequality, as least 88.88% of the data should be within 3 standard deviations of the mean...
```
standardized_delays = (delays['ARRIVAL_DELAY'] - np.mean(delays['ARRIVAL_DELAY'])) / np.std(delays['ARRIVAL_DELAY'])
upper_bound = np.mean(delays['ARRIVAL_DELAY']) + 3 * np.std(delays['ARRIVAL_DELAY'])
lower_bound = np.mean(delays['ARRIVAL_DELAY']) - 3 * np.std(delays['ARRIVAL_DELAY'])
within_3_SDs = np.sum(np.logical_and(delays['ARRIVAL_DELAY'] < upper_bound, delays['ARRIVAL_DELAY'] > lower_bound))
print(within_3_SDs / len(delays) * 100)
```
- Yes, Chebychev's inequality is true for this dataset.
```
# Determining which airline to avoid...
grouped_delays = delays.groupby(['AIRLINE'], as_index=False)
grouped_delays.agg({'ARRIVAL_DELAY' : 'mean'}).sort_values('ARRIVAL_DELAY', ascending = False)
```
- Based on this data alone, it would be a good idea to avoid Hawaii Airlines (HA) because it has the highest average of delay time.
# Q3
The NFL players data has the heights and weights of some players in the NFL. It also tells you what position they play in.
1. Plot a histogram of the heights. Does this seem normally distributed? What is the mean? What is the median? Are there any significant outliers?
2. Plot a histogram of the weights. Does this seem normally distributed? What is the mean? What is the median? Are there any significant outliers?
3. Does the distribution of weights depend on the position? If so, please convey that is a visual form.
#### 1: Heights
```
nfl = pd.read_csv('nfl_players.csv', encoding='latin-1')
nfl.head()
#Plot a histogram of the heights.
plt.hist(nfl['Height'], bins = np.arange(60, 85), ec = 'blue', color = 'lightskyblue')
plt.title('distribution of heights', size = 'medium')
plt.xlabel('Player Height')
plt.ylabel('Frequency')
```
- The distribution looks vaguely but not quite normal.
```
# Mean?
np.mean(nfl['Height'])
```
- The mean height of NFL players is 74.013
```
# Median?
np.median(nfl['Height'])
```
- The median height of NFL players is 74
```
# Outliers?
np.max(nfl['Height']), np.min(nfl['Height'])
```
- The minimum and maximum values are not significant enough to be outliers.
#### 2: Weights
```
#Plot a histogram of the weights.
plt.hist(nfl['Weight'], bins = np.arange(150, 370, 10), ec = 'blue', color = 'lightskyblue')
plt.title('distribution of weights', size = 'medium')
plt.xlabel('player weight')
plt.ylabel('frequency')
```
- The distribution of weights is not normal.
```
# Mean?
np.mean(nfl['Weight'])
# Median?
np.median(nfl['Weight'])
# Outliers?
np.max(nfl['Weight']), np.min(nfl['Weight'])
nfl[['Weight']].sort_values('Weight', ascending=True)[:5]
nfl[['Weight']].sort_values('Weight', ascending=False)[:5]
```
- There seem to be no significantly large outliers because the data for both ends of the weight spectrum seem to be gradually increasing/decreasing.
#### 3. Does the distribution of weights depend on the position?
```
nfl.columns
weight_position = nfl[['Position', 'Weight']]
weight_position.head()
# Histogramming the Distributions of Weights per Position
mpl.style.use('seaborn')
nfl.hist(column = ['Weight'], by= ['Position'], figsize = (15, 40),
layout = (12, 2), sharey = False, sharex = False,
bins = np.arange(150, 364, 5))
```
- As we can see in the histograms above, the distribution of weights among players of different positions changes. Therefore, yes, the distribution of weights depends on the position.
# Q4
According to a fun statistics blog
"The consumption of ice cream (pints per person) and the number of murders in New York are positively correlated. That is, as the amount of ice cream sold per person increases, the number of murders increases."
Does this mean that ice cream causes murder? Why or why not? What could explain this positive association?
- No. Correlation does not imply cause; just because a mutual relationship can be observed between two variablies doesn't mean that one causes the other. One possible explanation for this positive association may be may be that there is some unknown variable that seperately influences ice cream sales and murders. In this case, it could be high temperatures; more ice cream sales as the temperature increases, and more murders on hotter days when the windows are left open.
# Q5
Use the music dataset to explore what goes into the making of a popular song.
Use the following stepwise approach to build a model that helps predict the popularity of a song.
1. Understand the data. The data was taken from https://think.cs.vt.edu/corgis/csv/music/music.html. Take a look at the description of the data. If you do not understand what a particular column means, either remove it from the data or do some research to figure it out.
2. Who are the top 10 artists in terms of artist hotness (basically recent popularity)? Which are the top 10 songs in terms of hotness?
3. Create 5 different scatter plots with song hotness as the dependent variable and your choice of 5 columns as the independent variables. For each choice of independent variable, provide a one line explanation of why you think that column could influence song hotness.
4. Create a linear regression model that helps predict song hotness. You can choose any or all of the 5 columns you picked to be part of the model.
#### a) Understanding the data, cleaning...
```
music = pd.read_csv('music.csv')
music.shape, music.columns
music = music.rename(columns = {'terms' : 'genre'})
print(music.shape)
music.head(5)
#removing songs where song.hottnesss is 0 (outliers)
music = music[music['song.hotttnesss'] != 0]
```
#### b. Who are the top 10 artists in terms of artist hotness?
```
sorted_hot_artists = music.sort_values(['artist.hotttnesss'], ascending=False)
top10 = sorted_hot_artists['artist.name'].unique()[:10]
print('These are the top 10 artists by hotness:')
for x in top10:
print(x)
```
#### Which are the top 10 songs in terms of hotness?
```
song_hotness = music[['song.hotttnesss', 'artist.name', 'title']]
top_10_songs = song_hotness.sort_values('song.hotttnesss', ascending = False)[:10]
top_10_songs[['title', 'song.hotttnesss', 'artist.name']]
```
- These are the top 10 songs in terms of hotness.
### c. Create 5 different scatter plots
#### 1) Tempo's Effect on Song Hotness.
```
music = music.dropna(subset = ['familiarity', 'song.hotttnesss'])
r = np.corrcoef(music['familiarity'], music['song.hotttnesss'])
r
```
- the correlation coefficient r, 0.5439, tells us that there is a significant relationship between familiarity and song hotness.
```
m, b = np.polyfit(music['familiarity'], music['song.hotttnesss'], 1)
plt.figure(figsize=(10,5))
plt.scatter(music['familiarity'], music['song.hotttnesss'], color = 'dodgerblue')
#regression line
xvals = np.arange(0, 1.1, 0.1)
yvals = m * xvals + b
plt.plot(xvals, yvals, color = 'navy')
plt.title('Song Hotness by Familiarity', size = 'medium')
plt.xlabel('familiarity')
plt.ylabel('hotness')
```
- The scatterplot shows that higher familiarity is significantly correlated with more popular songs; in general, the higher the familiarity, the hotter the song should be. This may be because people like to listen to songs over and over, familiar songs are catchy and easy to sing along to.
#### 2) Duration's Effect on Song Hotness.
```
music = music.dropna(subset = ['duration', 'song.hotttnesss'])
#removing that one nasty outlier song that lasted over 2,050
cleaned_music = music[music['duration'] < np.max(music['duration'])]
r = np.corrcoef(cleaned_music['duration'], cleaned_music['song.hotttnesss'])
r
plt.figure(figsize=(10,5))
m, b = np.polyfit(cleaned_music['duration'], cleaned_music['song.hotttnesss'], 1)
plt.scatter(cleaned_music['duration'], cleaned_music['song.hotttnesss'], color = 'royalblue')
#regression line
xvals = np.arange(0, 1760, 5)
yvals = m * xvals + b
plt.plot(xvals, yvals, color = 'k')
plt.title('Song Hotness by Duration', size = 'medium')
plt.xlabel('duration')
plt.ylabel('hotness')
```
- The scatter plot shows that as song duration increases past 750, there are fewer songs with high hotness. This is probably because people have short attention spans and like music in the 3 - 4 minute range; 30 minute songs are too long to hit the popular charts.
#### 3) Key's Effect on Song Hotness.
```
music = music.dropna(subset = ['key', 'song.hotttnesss'])
r = np.corrcoef(music['key'], music['song.hotttnesss'])
r
#removing that one nasty outlier key:
cleaned_music = music[music['key'] < np.max(music['key'])]
r = np.corrcoef(cleaned_music['key'], cleaned_music['song.hotttnesss'])
r
```
- The correlation coefficient 0.001238 tells us that there is basically no linear relationship between key and song hottness.
```
plt.figure(figsize=(10,5))
m, b = np.polyfit(cleaned_music['key'], cleaned_music['song.hotttnesss'], 1)
plt.scatter(cleaned_music['key'], cleaned_music['song.hotttnesss'], color = 'blue')
#regression line
xvals = np.arange(0, 10, 5)
yvals = m * xvals + b
plt.title('Song Hotness by Key', size = 'medium')
plt.xlabel('key')
plt.ylabel('hotness')
```
- The scatter plot shows that there is generally an even distribution of hot songs by key. Therefore key has very little to no influence on the song's hotness.
#### 4) Loudness' Effect on Song Hotness.
```
music = music.dropna(subset = ['loudness', 'song.hotttnesss'])
r = np.corrcoef(music['loudness'], music['song.hotttnesss'])
r
```
- the correlation coefficient r, 0.22587, tells us that there is a very slight linear relationship between song loudness and song hotness.
```
plt.figure(figsize=(10,5))
m, b = np.polyfit(music['loudness'], music['song.hotttnesss'], 1)
plt.scatter(music['loudness'], music['song.hotttnesss'], color = 'dodgerblue')
#regression line
xvals = np.arange(-45, 0, 1)
yvals = m * xvals + b
plt.plot(xvals, yvals, color = 'navy')
plt.title('Song Hotness by Loudness', size = 'medium')
plt.xlabel('loudness')
plt.ylabel('hotness')
```
- The scatter plot shows that the number of hot songs is concentrated around louder songs; loudness has somewhat of an influence on the song's hotness. This might be because loud songs are popular among young adults for dancing.
```
music.columns
```
#### 5) Artist's hotness on song's hotness
```
music = music.dropna(subset = ['artist.hotttnesss', 'song.hotttnesss'])
r = np.corrcoef(music['artist.hotttnesss'], music['song.hotttnesss'])
r
```
- The correlation coefficient r = 0.5223 shows that there is a relatively strong linear relationship between an artist's hotness and the song's hotness.
```
plt.figure(figsize=(10,5))
m, b = np.polyfit(music['artist.hotttnesss'], music['song.hotttnesss'], 1)
plt.scatter(music['artist.hotttnesss'], music['song.hotttnesss'], color = 'royalblue')
#regression line
xvals = np.arange(0, 1.2, .1)
yvals = m * xvals + b
plt.plot(xvals, yvals, color = 'navy')
plt.title('Song Hotness by Artist Hotness', size = 'medium')
plt.xlabel('artist hotness')
plt.ylabel('song hotness')
```
- The scatterplot shows that there is a considerable relationship between an artist's hotness and their song's hotness. An explanation: the hotter an artist is, the larger their fanbase is. The larger the fanbase, the larger potential receptive audience for the song which means higher hotness.
#### d) Create a linear regression model that helps predict song hotness. You can choose any or all of the 5 columns you picked to be part of the model.
```
import statsmodels.api as sm
# create a df of the independent variables
X = music[['artist.hotttnesss', 'familiarity', 'loudness']]
# dependent variable. what are we predicting?
y = music['song.hotttnesss']
#we are fitting y = ax_1 + bx_2+ c and not just ax_1 + bx_2
X = sm.add_constant(X)
# OLS - ordinary least squares.
# best possible hyperplane through the data
# best = minimize sum of square distances
est = sm.OLS(y, X).fit()
est.summary()
```
#### - The model is:
##### predicted song hotness = 0.1273 + 0.3121x + 0.3652y + 0.0032z
.... where x is the song artist's hotness, y is the song's familiarity, and z is the song's loudness.
# Q6
Use the automobilie dataset
Plot the distribution of the car mileage. Does this look like a normal distribution?
Plot 3 different distributions based on the origin of the car. Which of the 3 is most normally distributed?
Use the dataset to create a linear regression model that predicts the mileage of a car.
There are 3 values of the origin column - 1 means USA, 2 means Germany, and 3 means Japan.
After you have made your linear regression model, use it to predict the mpg of the following cars. Which one of these 3 cars does your model do best on?
https://www.caranddriver.com/chevrolet/camaro/specs
https://www.caranddriver.com/smart/fortwo/specs
https://www.caranddriver.com/toyota/86/specs
```
automobiles = pd.read_csv('auto-mpg.csv')
automobiles = automobiles.dropna(subset= ['mpg', 'origin', 'weight', 'horsepower',
'model year', 'displacement', 'acceleration'])
```
#### Plot the distribution of the car mileage. Does this look like a normal distribution?
```
plt.hist(automobiles['mpg'], normed = True, bins = np.arange(5, 50), ec = 'k')
plt.xlabel('Mileage', size = 'medium')
plt.ylabel('Frequency', size = 'medium')
plt.title('Mileage Distribution for All Cars')
```
- no, the distribution does not completely look like a normal distribution but it looks vaguely like one.
#### Plot 3 different distributions based on the origin of the car. Which of the 3 is most normally distributed?
```
np.unique(automobiles['origin'])
origin_1 = automobiles[automobiles['origin'] == 1]
origin_2 = automobiles[automobiles['origin'] == 2]
origin_3 = automobiles[automobiles['origin'] == 3]
```
#### mileage distribution for origin 1, USA
```
# mileage distribution for origin 1, USA
plt.hist(standardize(origin_1['mpg']), normed = True, bins = 20, ec = 'k')
plt.xlabel('Mileage for Origin 1 (USA)', size = 'medium')
plt.ylabel('Frequency', size = 'medium')
plt.title('Mileage Distribution for Origin 1 (USA) Cars')
```
- If you squint, this looks vaguely normally distributed.
```
# looking at the percent of data that lies between k standard deviations.
k = 1
upper_bound = np.mean(origin_1['mpg']) + k * np.std(origin_1['mpg'])
lower_bound = np.mean(origin_1['mpg']) - k * np.std(origin_1['mpg'])
within_3_SDs = np.sum(np.logical_and(origin_1['mpg'] < upper_bound, origin_1['mpg'] > lower_bound))
print(within_3_SDs / len(origin_1) * 100)
```
- We see that about 69% of the data lies between 1 standard dev. from the mean for origin 1 mileage.
#### mileage distribution for origin 2, Germany
```
# mileage distribution for origin 2, Germany
plt.hist(standardize(origin_2['mpg']), normed = True, bins = 20, ec = 'k')
plt.xlabel('Mileage for Origin 2 (GER) Cars', size = 'medium')
plt.ylabel('Frequency', size = 'medium')
plt.title('Mileage Distribution for Origin 2 (German) Cars')
# looking at the percent of data that lies between k standard deviations.
k = 1
upper_bound = np.mean(origin_2['mpg']) + k * np.std(origin_2['mpg'])
lower_bound = np.mean(origin_2['mpg']) - k * np.std(origin_2['mpg'])
within_3_SDs = np.sum(np.logical_and(origin_2['mpg'] < upper_bound, origin_2['mpg'] > lower_bound))
print(within_3_SDs / len(origin_2) * 100)
```
- We see that about 70% of the data lies between 1 standard dev. from the mean for origin 2 mileage.
```
# mileage distribution for origin 3, Japan
plt.hist(standardize(origin_3['mpg']), normed = True, bins = 20, ec = 'k')
plt.xlabel('Mileage for Origin 3 (JPN) Cars', size = 'medium')
plt.ylabel('Frequency', size = 'medium')
plt.title('Mileage Distribution for Origin 3 (Japanese) Cars')
# looking at the percent of data that lies between k standard deviations.
k = 1
upper_bound = np.mean(origin_3['mpg']) + k * np.std(origin_3['mpg'])
lower_bound = np.mean(origin_3['mpg']) - k * np.std(origin_3['mpg'])
within_3_SDs = np.sum(np.logical_and(origin_3['mpg'] < upper_bound, origin_3['mpg'] > lower_bound))
print(within_3_SDs / len(origin_3) * 100)
```
- We see that about 61% of the data lies between 1 standard dev. from the mean for origin 2 mileage.
- Of the 3 origins, the mileage distribution for origin 1 (USA) visually looks the most normally distributed but origin 2 (Germany) actually has more data (70%) for grouped within 1 SD of the mean than origin 1 (68%)
#### Use the dataset to create a linear regression model that predicts the mileage of a car.
```
# cleaning dataframe, removing rows with '?'
vect_float = np.vectorize(float)
automobiles = automobiles[automobiles['horsepower'] != '?']
automobiles['horsepower'] = automobiles['horsepower'].apply(vect_float)
# create a df of the independent variables
X = automobiles[['weight', 'displacement', 'horsepower']]
# dependent variable. what are we predicting?
y = automobiles['mpg']
#we are fitting y = ax_1 + bx_2+ c and not just ax_1 + bx_2
X = sm.add_constant(X)
# OLS - ordinary least squares.
# best possible hyperplane through the data
# best = minimize sum of square distances
est = sm.OLS(y, X).fit()
est.summary()
```
#### - The model is:
##### predicted mpg = 44.8559 - 0.0054x -0.0058y -0.0417z
.... where x is the weight, y is the displacement, and z is the horsepower.
### Testing the model for the 3 different cars' mileages.
- we will compare the predicted mileages to the Fuel Economy Est-Combined MPG from the website.
```
#Car 1: 2018 Chevrolet Camaro
actual_mileage = 25
x = 3339 #weight
y = 122 #displacement
z = 275 #horsepower
predicted_mpg = 44.8559 - 0.0054*x - 0.0058*y - 0.0417*z
print('The predicted mpg for the 2018 Chevrolet Camaro is: ' + str(predicted_mpg))
print('The difference between the predicted and actual milelage:')
print(str(actual_mileage - predicted_mpg))
#Car 2: 2017 Smart Fortwo
actual_mileage = 34
x = 2050 #weight
y = 55 #displacement
z = 89 #horsepower
predicted_mpg = 44.8559 - 0.0054*x - 0.0058*y - 0.0417*z
print('The predicted mpg for the 2017 Smart Fortwo is: ' + str(predicted_mpg))
print('The difference between the predicted and actual milelage:')
print(str(actual_mileage - predicted_mpg))
#Car 3: 2018 Toyota 86
actual_mileage = 24
x = 2774 #weight
y = 122 #displacement
z = 205 #horsepower
predicted_mpg = 44.8559 - 0.0054*x - 0.0058*y - 0.0417*z
print('The predicted mpg for the 2018 Toyota 86 is: ' + str(predicted_mpg))
print('The difference between the predicted and actual milelage:')
print(str(actual_mileage - predicted_mpg))
```
- The model is most accurate for the 2018 Toyota 86 because the difference between the actual and predicted mileages is the smallest.
# Q7
Using the bodyfat.csv file, create a regression model that predicts the bodyfat based on other factors in the dataset.
Remember that you have to first identify correlations before you decide to put a variable into your regression model.
```
bodyfat = pd.read_excel('BodyFat.xls')
bodyfat.head()
def correlation(df, x, y):
# r = avg(standardize(x) * standardize(y))
x_std = standardize(df[x])
y_std = standardize(df[y])
return np.mean(x_std * y_std)
# The variables below have significant correlations with bodyfat
print(correlation(bodyfat, 'BODYFAT', 'WEIGHT'))
print(correlation(bodyfat, 'BODYFAT', 'DENSITY'))
print(correlation(bodyfat, 'BODYFAT', 'ADIPOSITY'))
print(correlation(bodyfat, 'BODYFAT', 'CHEST'))
print(correlation(bodyfat, 'BODYFAT', 'ABDOMEN'))
print(correlation(bodyfat, 'BODYFAT', 'HIP'))
print(correlation(bodyfat, 'BODYFAT', 'THIGH'))
```
#### Making the linear regression model for bodyfat
```
# create a df of the independent variables
X = bodyfat[['WEIGHT', 'DENSITY', 'ADIPOSITY', 'CHEST', 'ABDOMEN', 'HIP', 'THIGH']]
# dependent variable. what are we predicting?
y = bodyfat['BODYFAT']
X = sm.add_constant(X)
# OLS - ordinary least squares.
# best possible hyperplane through the data
# best = minimize sum of square distances
est = sm.OLS(y, X).fit()
est.summary()
```
#### - The model is:
##### predicted bodyfat = 415.1138 - 0.0033x - 381.1288y - 0.0422z + 0.0338a + 0.0428b + 0.0214c - 0.0285d
.... where x is the weight, y is the density, and z is the adiposity, a is the chest size, b is the abdomen size, c is the hip size, and d is the thigh size.
|
github_jupyter
|
```
# These are all the modules we'll be using later. Make sure you can import them
# before proceeding further.
from __future__ import print_function
import os
import numpy as np
import random
import math
import string
import tensorflow as tf
import zipfile
from six.moves import range
from six.moves.urllib.request import urlretrieve
url = 'http://mattmahoney.net/dc/'
def maybe_download(filename, expected_bytes):
"""Download a file if not present, and make sure it's the right size."""
if not os.path.exists(filename):
filename, _ = urlretrieve(url + filename, filename)
statinfo = os.stat(filename)
if statinfo.st_size == expected_bytes:
print('Found and verified %s' % filename)
else:
print(statinfo.st_size)
raise Exception(
'Failed to verify ' + filename + '. Can you get to it with a browser?')
return filename
filename = maybe_download('text8.zip', 31344016)
def read_data(filename):
with zipfile.ZipFile(filename) as f:
name = f.namelist()[0]
data = tf.compat.as_str(f.read(name))
return data
text = read_data(filename)
print('Data size %d' % len(text))
valid_size = 1000
valid_text = text[:valid_size]
train_text = text[valid_size:]
train_size = len(train_text)
print(train_size, train_text[:64])
print(valid_size, valid_text[:64])
vocabulary_size = len(string.ascii_lowercase) + 1 # [a-z] + ' '
first_letter = ord(string.ascii_lowercase[0])
def char2id(char):
if char in string.ascii_lowercase:
return ord(char) - first_letter + 1
elif char == ' ':
return 0
else:
print('Unexpected character: %s' % char)
return 0
def id2char(dictid):
if dictid > 0:
return chr(dictid + first_letter - 1)
else:
return ' '
print(char2id('a'), char2id('z'), char2id(' '), char2id('ï'))
print(id2char(1), id2char(26), id2char(0))
batch_size=64
num_unrollings=10
embedding_size=27
class BatchGenerator(object):
def __init__(self, text, batch_size, num_unrollings):
self._text = text
self._text_size = len(text)
self._batch_size = batch_size
self._num_unrollings = num_unrollings
segment = self._text_size // batch_size
self._cursor = [ offset * segment for offset in range(batch_size)]
self._last_batch = self._next_batch()
def _next_batch(self):
"""Generate a single batch from the current cursor position in the data."""
batch = np.zeros(shape=(self._batch_size,2), dtype=np.int32)
for b in range(self._batch_size):
batch[b,0] = char2id(self._text[self._cursor[b]])
batch[b,1] = char2id(self._text[self._cursor[b]+1])
self._cursor[b] = (self._cursor[b] +1) % self._text_size
return batch
def next(self):
"""Generate the next array of batches from the data. The array consists of
the last batch of the previous array, followed by num_unrollings new ones.
"""
batches = [self._last_batch]
for step in range(self._num_unrollings):
batches.append(self._next_batch())
self._last_batch = batches[-1]
return batches
def characters(batches):
"""Turn a 1-hot encoding or a probability distribution over the possible
characters back into its (most likely) character representation."""
batches=list(map(list, zip(*batches)))
s=list("")
for b in batches:
ss=""
for c in b:
ss+=id2char(int(c[0]))
#ss+=id2char(int(c[1]))
s.append(ss)
return s
def characters2(probabilities):
"""Turn a 1-hot encoding or a probability distribution over the possible
characters back into its (most likely) character representation."""
s=[id2char(np.floor_divide(c,27)) for c in np.argmax(probabilities, 1)]
s+=[id2char(c-27*np.floor_divide(c,27)) for c in np.argmax(probabilities, 1)]
return s
def batches2string(batches):
"""Convert a sequence of batches back into their (most likely) string
representation."""
s = [''] * batches[0].shape[0]
for b in batches:
s = [''.join(x) for x in zip(s, characters(b))]
return s
train_batches = BatchGenerator(train_text, batch_size, num_unrollings)
valid_batches = BatchGenerator(valid_text, 1, 1)
print((np.array(train_batches.next())).shape)
print(characters(train_batches.next()))
print(characters(train_batches.next()))
print(characters(valid_batches.next()))
print(characters(valid_batches.next()))
# ==========================
# OTHER EVALUATION FUNCTIONS
# ==========================
def logprob(predictions, labels):
"""Log-probability of the true labels in a predicted batch."""
predictions[predictions < 1e-10] = 1e-10
return np.sum(np.multiply(labels, -np.log(predictions))) / labels.shape[0]
def sample_distribution(distribution):
"""Sample one element from a distribution assumed to be an array of normalized
probabilities.
"""
r = random.uniform(0, 1)
s = 0
for i in range(len(distribution)):
s += distribution[i]
if s >= r:
return i
return len(distribution) - 1
def sample(prediction):
"""Turn a (column) prediction into 1-hot encoded samples."""
p = np.zeros(shape=[1, vocabulary_size], dtype=np.float)
p[0, sample_distribution(prediction[0])] = 1.0
return p
def random_distribution():
"""Generate a random column of probabilities."""
b = np.random.uniform(0.0, 26.0, size=[1, 1])
return b[:,None]
num_nodes = 64
vocabulary_size=27*27
graph = tf.Graph()
with graph.as_default():
# Parameters:
# first parameter of each gate in 1 matrix:
i_all = tf.Variable(tf.truncated_normal([embedding_size, 4*num_nodes], -0.1, 0.1))
# second parameter of each gate in 1 matrix
o_all = tf.Variable(tf.truncated_normal([num_nodes, 4*num_nodes], -0.1, 0.1))
# Input gate: input, previous output, and bias.
ib = tf.Variable(tf.zeros([1, num_nodes]))
# Forget gate: input, previous output, and bias.
fb = tf.Variable(tf.zeros([1, num_nodes]))
# Memory cell: input, state and bias.
cb = tf.Variable(tf.zeros([1, num_nodes]))
# Output gate: input, previous output, and bias.
ob = tf.Variable(tf.zeros([1, num_nodes]))
# Variables saving state across unrollings.
saved_output = tf.Variable(tf.zeros([batch_size, num_nodes]), trainable=False)
saved_state = tf.Variable(tf.zeros([batch_size, num_nodes]), trainable=False)
# Classifier weights and biases.
#embeddings
embeddings = tf.Variable(tf.random_uniform([vocabulary_size, embedding_size], -1.0, 1.0))
w = tf.Variable(tf.truncated_normal([num_nodes, vocabulary_size],-0.1,0.1))
b = tf.Variable(tf.zeros([vocabulary_size]))
# Definition of the cell computation.
def lstm_cell(i, o, state):
"""Create a LSTM cell. See e.g.: http://arxiv.org/pdf/1402.1128v1.pdf
Note that in this formulation, we omit the various connections between the
previous state and the gates."""
input_mat=tf.matmul(i,i_all)
output_mat=tf.matmul(o,o_all)
input_gate = tf.sigmoid(input_mat[:,0:num_nodes] + output_mat[:,0:num_nodes] + ib)
forget_gate = tf.sigmoid(input_mat[:,num_nodes:2*num_nodes] + output_mat[:,num_nodes:2*num_nodes] + fb)
update = input_mat[:,2*num_nodes:3*num_nodes] + output_mat[:,2*num_nodes:3*num_nodes] + cb
state = forget_gate * state + input_gate * tf.tanh(update)
output_gate = tf.sigmoid(input_mat[:,3*num_nodes:] + output_mat[:,3*num_nodes:] + ob)
return output_gate * tf.tanh(state), state
# Input data.
train_data = list()
for _ in range(num_unrollings+1):
train_data.append(tf.placeholder(tf.int32, shape=[batch_size,2]))
train_inputs = train_data[:num_unrollings]
train_labels = train_data[1:] # labels are inputs shifted by one time step.
# Unrolled LSTM loop.
outputs = list()
output = saved_output
state = saved_state
for i in train_inputs:
i_concat=27*i[:,0]+i[:,1]
embedded_i=tf.nn.embedding_lookup(embeddings,i_concat)
output, state = lstm_cell(embedded_i, output, state)
outputs.append(output)
# State saving across unrollings.
with tf.control_dependencies([saved_output.assign(output),
saved_state.assign(state)]):
# Classifier.
outputs_concat=tf.concat(outputs,0)
#try to compute similarity here as well
logits=tf.nn.xw_plus_b(outputs_concat,w,b)
print((logits).shape)
#Compute one hot encodings
label_batch=tf.concat(train_labels,0)
label_batch=27*label_batch[:,0]+label_batch[:,1]
print(label_batch.shape)
sparse_labels = tf.reshape(label_batch, [-1, 1])
derived_size = tf.shape(label_batch)[0]
indices = tf.reshape(tf.range(0, derived_size, 1), [-1, 1])
print(indices.shape,'indices.shape')
concated = tf.concat([indices, sparse_labels],1)
outshape = tf.stack([derived_size, vocabulary_size])
labels = tf.sparse_to_dense(concated, outshape, 1.0, 0.0)
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=logits))
# Optimizer.
global_step = tf.Variable(0)
learning_rate = tf.train.exponential_decay(
10.0, global_step, 5000, 0.1, staircase=True)
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
gradients, v = zip(*optimizer.compute_gradients(loss))
gradients, _ = tf.clip_by_global_norm(gradients, 1.25)
optimizer = optimizer.apply_gradients(
zip(gradients, v), global_step=global_step)
# Predictions.
train_prediction = tf.nn.softmax(logits)
print(train_prediction.shape)
# Sampling and validation eval: batch 1, no unrolling.
norm = tf.sqrt(tf.reduce_sum(tf.square(embeddings), 1, keep_dims=True))
normalized_embeddings = embeddings / norm
#valid_dataset=np.array([i for i in range(27)])
#valid_embeddings = tf.nn.embedding_lookup(normalized_embeddings, valid_dataset)
sample_input = tf.placeholder(tf.int32, shape=[1])
saved_sample_output = tf.Variable(tf.zeros([1, num_nodes]))
saved_sample_state = tf.Variable(tf.zeros([1, num_nodes]))
reset_sample_state = tf.group(
saved_sample_output.assign(tf.zeros([1, num_nodes])),
saved_sample_state.assign(tf.zeros([1, num_nodes])))
embedded_sample=tf.nn.embedding_lookup(embeddings,sample_input)
sample_output, sample_state = lstm_cell(embedded_sample, saved_sample_output, saved_sample_state)
with tf.control_dependencies([saved_sample_output.assign(sample_output),
saved_sample_state.assign(sample_state)]):
sample_prediction = tf.nn.softmax(tf.nn.xw_plus_b(sample_output, w, b))
#similarity = tf.matmul(sample_prediction, tf.transpose(normalized_embeddings))
print(sample_prediction.shape)
num_steps = 50001
summary_frequency = 500
with tf.Session(graph=graph) as session:
tf.global_variables_initializer().run()
print('Initialized')
mean_loss = 0
for step in range(num_steps):
batches = train_batches.next()
feed_dict = dict()
for i in range(num_unrollings + 1):
feed_dict[train_data[i]] = batches[i]
#print((feed_dict[train_data[i]]).shape)
_, l, predictions, lr,train_lab = session.run([optimizer, loss, train_prediction, learning_rate,train_labels], feed_dict=feed_dict)
mean_loss += l
if step % summary_frequency == 0:
if step > 0:
mean_loss = mean_loss / summary_frequency
# The mean loss is an estimate of the loss over the last few batches.
print('Average loss at step %d: %f learning rate: %f' % (step, mean_loss, lr))
mean_loss = 0
#print(train_lab)
#print(labels.shape[0])
#print('Minibatch perplexity: ',np.exp(logprob(predictions, labels)))
if step % (summary_frequency * 2) == 0:
# Generate some samples.
print('=' * 80)
for _ in range(5):
feed = np.zeros(shape=(1,), dtype=np.int32)
feed[0,] =np.random.randint(0,729)
sentence=id2char(np.floor_divide(feed[0],27))
sentence+=id2char(feed[0]-27*np.floor_divide(feed[0],27))
reset_sample_state.run()
for _ in range(50):
prediction=sample_prediction.eval({sample_input:feed})
k = sample(prediction)
k=characters2(k)
#print(k)
feed = np.zeros(shape=(1,), dtype=np.int32)
feed[0,] = 27*char2id(k[0])+char2id(k[1])
sentence += k[0]
#sentence+=k[1]
#feed = np.zeros(shape=(1,), dtype=np.int32)
#feed[0,] = np.argmax(prediction)
#print(feed.shape)
#sentence += id2char(feed[0,])
print(sentence)
print('=' * 80)
# Measure validation set perplexity.
reset_sample_state.run()
valid_logprob = 0
#for _ in range(valid_size):
# b = valid_batches.next()
#predictions = sample_prediction.eval({sample_input: b[0]})
#valid_logprob = valid_logprob + logprob(predictions, b[1])
#print('Validation set perplexity: %.2f' % float(np.exp(valid_logprob / valid_size)))
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/b15145456/1st-ML-Marathon/blob/main/Day_010_HW.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# 作業 : (Kaggle)房價預測
# [作業目標]
- 試著模仿範例寫法, 在房價預測中, 觀察去除離群值的影響
# [作業重點]
- 觀察將極端值以上下限值取代, 對於分布與迴歸分數的影響 (In[5], Out[5])
- 觀察將極端值資料直接刪除, 對於分布與迴歸分數的影響 (In[6], Out[6])
```
# 做完特徵工程前的所有準備 (與前範例相同)
import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
# data_path = 'data/'
df_train = pd.read_csv('house_train.csv.gz')
train_Y = np.log1p(df_train['SalePrice'])
df = df_train.drop(['Id', 'SalePrice'] , axis=1)
df.head()
#只取 int64, float64 兩種數值型欄位, 存於 num_features 中
num_features = []
for dtype, feature in zip(df.dtypes, df.columns):
if dtype == 'float64' or dtype == 'int64':
num_features.append(feature)
print(f'{len(num_features)} Numeric Features : {num_features}\n')
# 削減文字型欄位, 只剩數值型欄位
df = df[num_features]
df = df.fillna(-1)
MMEncoder = MinMaxScaler()
train_num = train_Y.shape[0]
df.head()
```
# 作業1
* 試著限制 '1樓地板面積(平方英尺)' (1stFlrSF) 欄位的上下限, 看看能否再進一步提高分數?
```
# 顯示 1stFlrSF 與目標值的散佈圖
import seaborn as sns
import matplotlib.pyplot as plt
sns.regplot(x = df['1stFlrSF'][:train_num], y=train_Y)
plt.show()
# 做線性迴歸, 觀察分數
train_X = MMEncoder.fit_transform(df)
estimator = LinearRegression()
cross_val_score(estimator, train_X, train_Y, cv=5).mean()
# 將 1stFlrSF 限制在你覺得適合的範圍內, 調整離群值
"""
Your Code Here
"""
# df1 = df
# df1.loc[df1['1stFlrSF'] > 2000,'1stFlrSF'] = 2000
# df1.loc[df1['1stFlrSF'] <500,'1stFlrSF'] = 500
df['1stFlrSF'] = df['1stFlrSF'].clip(500, 2250)
sns.regplot(x = df['1stFlrSF'], y=train_Y)
plt.show()
# 做線性迴歸, 觀察分數
train_X = MMEncoder.fit_transform(df1)
estimator = LinearRegression()
cross_val_score(estimator, train_X, train_Y, cv=5).mean()
```
# 作業2
* 續前題, 去除離群值有兩類方式 : 捨棄離群值(刪除離群的資料) 以及調整離群值,
請試著用同樣的上下限, 改為 '捨棄離群值' 的方法, 看看結果會變好還是變差? 並試著解釋原因。
```
# 將 1stFlrSF 限制在你覺得適合的範圍內, 捨棄離群值
"""
Your Code Here
"""
keep_indexs = (df['1stFlrSF']> 500) & (df['1stFlrSF']< 2250)
df = df[keep_indexs]
train_Y = train_Y[keep_indexs]
sns.regplot(x = df['1stFlrSF'], y=train_Y)
plt.show()
# df2 = df
# del_id = df2.loc[df2['1stFlrSF']>2000].index
# del_id.append(df2.loc[df2['1stFlrSF']<500].index)
# df2.drop(del_id, inplace=True)
# train_Y.drop(del_id, inplace=True)
# 做線性迴歸, 觀察分數
train_X = MMEncoder.fit_transform(df)
estimator = LinearRegression()
cross_val_score(estimator, train_X, train_Y, cv=5).mean()
```
```
del_id
```
|
github_jupyter
|
## February and April 2020 precipitation anomalies
In this notebook, we will analyze precipitation anomalies of February and April 2020, which seemed to be very contrasting in weather. We use the EOBS dataset.
### Import packages
```
##This is so variables get printed within jupyter
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
##import packages
import os
import xarray as xr
import numpy as np
import matplotlib.pyplot as plt
import cartopy
import cartopy.crs as ccrs
import matplotlib.ticker as mticker
os.chdir(os.path.abspath('../../')) # Change the working directory to UNSEEN-open
os.getcwd() #print the working directory
### Set plot font size
plt.rcParams['font.size'] = 10 ## change font size
```
### Load EOBS
I downloaded EOBS (from 1950 - 2019) and the most recent EOBS data (2020) [here](https://surfobs.climate.copernicus.eu/dataaccess/access_eobs.php). Note, you have to register as E-OBS user.
The data has a daily timestep. I resample the data into monthly average mm/day. I chose not to use the total monthly precipitation because of leap days.
```
EOBS = xr.open_dataset('../UK_example/EOBS/rr_ens_mean_0.25deg_reg_v20.0e.nc') ## open the data
EOBS = EOBS.resample(time='1m').mean() ## Monthly averages
# EOBS = EOBS.sel(time=EOBS['time.month'] == 2) ## Select only February
EOBS
```
Here I define the attributes, that xarray uses when plotting
```
EOBS['rr'].attrs = {'long_name': 'rainfall', ##Define the name
'units': 'mm/day', ## unit
'standard_name': 'thickness_of_rainfall_amount'} ## original name, not used
EOBS['rr'].mean('time').plot() ## and show the 1950-2019 average February precipitation
```
The 2020 data file is separate and needs the same preprocessing:
```
EOBS2020 = xr.open_dataset('../UK_example/EOBS/rr_0.25deg_day_2020_grid_ensmean.nc.1') #open
EOBS2020 = EOBS2020.resample(time='1m').mean() #Monthly mean
EOBS2020['rr'].sel(time='2020-04').plot() #show map
EOBS2020 ## display dataset
```
### Plot the 2020 event
I calculate the anomaly (deviation from the mean in mm/d) and divide this by the standard deviation to obtain the standardized anomalies.
```
EOBS2020_anomaly = EOBS2020['rr'].groupby('time.month') - EOBS['rr'].groupby('time.month').mean('time')
EOBS2020_anomaly
EOBS2020_sd_anomaly = EOBS2020_anomaly.groupby('time.month') / EOBS['rr'].groupby('time.month').std('time')
EOBS2020_sd_anomaly.attrs = {
'long_name': 'Monthly precipitation standardized anomaly',
'units': '-'
}
EOBS2020_sd_anomaly
```
I select February and April (tips on how to select this are appreciated)
```
EOBS2020_sd_anomaly
# EOBS2020_sd_anomaly.sel(time = ['2020-02','2020-04']) ## Dont know how to select this by label?
EOBS2020_sd_anomaly[[1,3],:,:] ## Dont know how to select this by label?
```
And plot using cartopy!
```
EOBS_plots = EOBS2020_sd_anomaly[[1, 3], :, :].plot(
transform=ccrs.PlateCarree(),
robust=True,
extend = 'both',
col='time',
cmap=plt.cm.twilight_shifted_r,
subplot_kws={'projection': ccrs.EuroPP()})
for ax in EOBS_plots.axes.flat:
ax.add_feature(cartopy.feature.BORDERS, linestyle=':')
ax.coastlines(resolution='50m')
gl = ax.gridlines(crs=ccrs.PlateCarree(),
draw_labels=False,
linewidth=1,
color='gray',
alpha=0.5,
linestyle='--')
# plt.savefig('graphs/February_April_2020_precipAnomaly.png', dpi=300)
```
|
github_jupyter
|
# Collaboration Patterns By Year (International, Domestic, Internal)
Using the count capability of the API, Dimensions allows you to quickly identify international, domestic, and inernal Collaboration
This notebook shows how to quickly identify international, domestic, and internal collaboration using the [Organizations data source](https://docs.dimensions.ai/dsl/datasource-organizations.html) and the [Publications data source](https://docs.dimensions.ai/dsl/datasource-publications.html) available via the [Dimensions Analytics API](https://docs.dimensions.ai/dsl/).
## Prerequisites
Please install the latest versions of these libraries to run this notebook.
```
!pip install dimcli plotly -U --quiet
#
# load libraries
import dimcli
from dimcli.utils import *
import json, sys, time
import pandas as pd
import plotly.express as px # plotly>=4.8.1
if not 'google.colab' in sys.modules:
# make js dependecies local / needed by html exports
from plotly.offline import init_notebook_mode
init_notebook_mode(connected=True)
print("==\nLogging in..")
# https://digital-science.github.io/dimcli/getting-started.html#authentication
ENDPOINT = "https://app.dimensions.ai"
if 'google.colab' in sys.modules:
import getpass
KEY = getpass.getpass(prompt='API Key: ')
dimcli.login(key=KEY, endpoint=ENDPOINT)
else:
KEY = ""
dimcli.login(key=KEY, endpoint=ENDPOINT)
dsl = dimcli.Dsl()
```
## 1. Lookup the University that you are interested in
```
dsl.query("""
search organizations for "melbourne" return organizations
""").as_dataframe()
institution = "grid.1008.9"
```
## 2. Publications output by year
```
allpubs = dsl.query(f"""
search publications
where research_orgs.id = "{institution}"
and type="article"
and year > 2010
return year
""").as_dataframe()
allpubs.columns = ['year', 'pubs']
px.bar(allpubs, x="year", y="pubs")
```
## 3. International publications
```
international = dsl.query(f"""
search publications
where research_orgs.id = "{institution}"
and type="article"
and count(research_org_countries) > 1
and year > 2010
return year
""").as_dataframe()
international.columns = ['year', 'international_count']
px.bar(international, x="year", y="international_count")
```
## 4. Domestic
```
domestic = dsl.query(f"""
search publications
where research_orgs.id = "{institution}"
and type="article"
and count(research_org_countries) = 1
and year > 2010
return year
""").as_dataframe()
domestic.columns = ['year', 'domestic_count']
px.bar(domestic, x="year", y="domestic_count")
```
## 5. Internal
```
internal = dsl.query(f"""
search publications
where research_orgs.id = "{institution}"
and type="article"
and count(research_orgs) = 1
and year > 2010
return year
""").as_dataframe()
internal.columns = ['year', 'internal_count']
px.bar(internal, x="year", y="internal_count")
```
## 6. Joining up All metrics together
```
jdf = allpubs.set_index('year'). \
join(international.set_index('year')). \
join(domestic.set_index('year')). \
join(internal.set_index('year'))
jdf
px.bar(jdf, title="University of Melbourne: publications collaboration")
```
## 7. How does this compare to Australia?
```
auallpubs = dsl.query("""
search publications
where research_org_countries.name= "Australia"
and type="article"
and year > 2010
return year
""").as_dataframe()
auallpubs.columns = ['year', 'all_count']
auintpubs = dsl.query("""
search publications
where research_org_countries.name= "Australia"
and type="article"
and year > 2010
and count(research_org_countries) > 1
return year
""").as_dataframe()
auintpubs.columns = ['year', 'all_int_count']
audompubs = dsl.query("""
search publications
where research_org_countries.name= "Australia"
and type="article"
and year > 2010
and count(research_org_countries) = 1
return year
""").as_dataframe()
audompubs.columns = ['year', 'all_dom_count']
auinternalpubs = dsl.query("""
search publications
where
research_org_countries.name= "Australia"
and count(research_orgs) = 1
and type="article"
and year > 2010
return year
""").as_dataframe()
auinternalpubs.columns = ['year', 'all_internal_count']
audf = auallpubs.set_index('year'). \
join(auintpubs.set_index('year')). \
join(audompubs.set_index('year')). \
join(auinternalpubs.set_index('year')). \
sort_values(by=['year'])
px.bar(audf, title="Australia: publications collaboration")
```
## 8. How does this compare to a different Institution (University of Toronto)?
```
institution = "grid.17063.33"
allpubs = dsl.query(f"""
search publications
where research_orgs.id = "{institution}"
and type="article"
and year > 2010
return year
""").as_dataframe()
allpubs.columns = ['year', 'pubs']
international = dsl.query(f"""
search publications
where research_orgs.id = "{institution}"
and type="article"
and count(research_org_countries) > 1
and year > 2010
return year
""").as_dataframe()
international.columns = ['year', 'international_count']
domestic = dsl.query(f"""
search publications
where research_orgs.id = "{institution}"
and type="article"
and count(research_org_countries) = 1
and year > 2010
return year
""").as_dataframe()
domestic.columns = ['year', 'domestic_count']
internal = dsl.query(f"""
search publications
where research_orgs.id = "{institution}"
and type="article"
and count(research_orgs) = 1
and year > 2010
return year
""").as_dataframe()
internal.columns = ['year', 'internal_count']
jdf = allpubs.set_index('year'). \
join(international.set_index('year')). \
join(domestic.set_index('year')). \
join(internal.set_index('year'))
px.bar(jdf, title="Univ. of Toronto: publications collaboration")
```
---
## Want to learn more?
Check out the [Dimensions API Lab](https://api-lab.dimensions.ai/) website, which contains many tutorials and reusable Jupyter notebooks for scholarly data analytics.
|
github_jupyter
|
# LANL Earthquake Prediction
<a href="https://www.kaggle.com/c/LANL-Earthquake-Prediction/overview">Link to competition on Kaggle</a>
This notebook is a reimplementation of <a href="https://www.kaggle.com/tunguz/andrews-features-only">Andrews Feature Only</a>, with some modifications.
## Feature Engineering
The large training dataset needs to be prepared to closely match the test data, which comprise independent series of 150,000 acoustic measurements. Thus, the training data shall be sliced into separate series of 150,000 measurements, and then summary features will be computed across the training and test series to serve as inputs for modelling.
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from tqdm import tqdm_notebook
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import MinMaxScaler
from scipy.signal import hilbert
from scipy.signal import hann
from scipy.signal import convolve
from scipy import stats
import warnings
warnings.filterwarnings("ignore")
```
### Load Data
```
%%time
train = pd.read_csv('data/raw/train.csv', dtype={'acoustic_data': np.int16, 'time_to_failure': np.float32})
print(train.shape)
train.head()
train.info()
```
The dataset is large, occupying 3.5 GB of memory and comprising over 600 million rows. The data can be visualised by sampling a small portion of it.
```
train_acoustic_data_small = train['acoustic_data'].values[::50]
train_time_to_failure_small = train['time_to_failure'].values[::50]
fig, ax1 = plt.subplots(figsize=(16, 8))
plt.title("acoustic_data vs time_to_failure (2% of data sampled)")
plt.plot(train_acoustic_data_small, color='b')
ax1.set_ylabel('acoustic_data', color='b')
plt.legend(['acoustic_data'])
ax2 = ax1.twinx()
plt.plot(train_time_to_failure_small, color='r')
ax2.set_ylabel('time_to_failure', color='r')
plt.legend(['time_to_failure'], loc=(0.875, 0.9))
plt.grid(False)
plt.savefig('reports/figures/acoustic_data_vs_time_to_failure.png')
del train_acoustic_data_small
del train_time_to_failure_small
```
### Create Segments
Slice the training data into series of 150,000 measurements.
```
rows = 150000
segments = int(np.floor(train.shape[0] / rows))
X_tr = pd.DataFrame(index=range(segments), dtype=np.float64)
y_tr = pd.DataFrame(index=range(segments), dtype=np.float64, columns=['time_to_failure'])
```
### Generate Features
Compute features for the training and test segments.
```
def add_trend_feature(arr, abs_values=False):
idx = np.array(range(len(arr)))
if abs_values:
arr = np.abs(arr)
lr = LinearRegression()
lr.fit(idx.reshape(-1, 1), arr)
return lr.coef_[0]
def classic_sta_lta(x, length_sta, length_lta):
# Short Term Average and Long Term Average
sta = np.cumsum(x ** 2)
# Convert to float
sta = np.require(sta, dtype=np.float)
# Copy for LTA
lta = sta.copy()
# Compute the STA and the LTA
sta[length_sta:] = sta[length_sta:] - sta[:-length_sta]
sta /= length_sta
lta[length_lta:] = lta[length_lta:] - lta[:-length_lta]
lta /= length_lta
# Pad zeros
sta[:length_lta - 1] = 0
# Avoid division by zero by setting zero values to tiny float
dtiny = np.finfo(0.0).tiny
idx = lta < dtiny
lta[idx] = dtiny
return sta / lta
for segment in tqdm_notebook(range(segments)):
seg = train.iloc[segment*rows:segment*rows+rows]
x = pd.Series(seg['acoustic_data'].values)
y = seg['time_to_failure'].values[-1]
y_tr.loc[segment, 'time_to_failure'] = y
X_tr.loc[segment, 'mean'] = x.mean()
X_tr.loc[segment, 'std'] = x.std()
X_tr.loc[segment, 'max'] = x.max()
X_tr.loc[segment, 'min'] = x.min()
X_tr.loc[segment, 'mean_change_abs'] = np.mean(np.diff(x))
X_tr.loc[segment, 'mean_change_rate'] = np.mean(np.nonzero((np.diff(x) / x[:-1]))[0])
X_tr.loc[segment, 'abs_max'] = np.abs(x).max()
X_tr.loc[segment, 'abs_min'] = np.abs(x).min()
X_tr.loc[segment, 'std_first_50000'] = x[:50000].std()
X_tr.loc[segment, 'std_last_50000'] = x[-50000:].std()
X_tr.loc[segment, 'std_first_10000'] = x[:10000].std()
X_tr.loc[segment, 'std_last_10000'] = x[-10000:].std()
X_tr.loc[segment, 'avg_first_50000'] = x[:50000].mean()
X_tr.loc[segment, 'avg_last_50000'] = x[-50000:].mean()
X_tr.loc[segment, 'avg_first_10000'] = x[:10000].mean()
X_tr.loc[segment, 'avg_last_10000'] = x[-10000:].mean()
X_tr.loc[segment, 'min_first_50000'] = x[:50000].min()
X_tr.loc[segment, 'min_last_50000'] = x[-50000:].min()
X_tr.loc[segment, 'min_first_10000'] = x[:10000].min()
X_tr.loc[segment, 'min_last_10000'] = x[-10000:].min()
X_tr.loc[segment, 'max_first_50000'] = x[:50000].max()
X_tr.loc[segment, 'max_last_50000'] = x[-50000:].max()
X_tr.loc[segment, 'max_first_10000'] = x[:10000].max()
X_tr.loc[segment, 'max_last_10000'] = x[-10000:].max()
X_tr.loc[segment, 'max_to_min'] = x.max() / np.abs(x.min())
X_tr.loc[segment, 'max_to_min_diff'] = x.max() - np.abs(x.min())
X_tr.loc[segment, 'count_big'] = len(x[np.abs(x) > 500])
X_tr.loc[segment, 'sum'] = x.sum()
X_tr.loc[segment, 'mean_change_rate_first_50000'] = np.mean(np.nonzero((np.diff(x[:50000]) / x[:50000][:-1]))[0])
X_tr.loc[segment, 'mean_change_rate_last_50000'] = np.mean(np.nonzero((np.diff(x[-50000:]) / x[-50000:][:-1]))[0])
X_tr.loc[segment, 'mean_change_rate_first_10000'] = np.mean(np.nonzero((np.diff(x[:10000]) / x[:10000][:-1]))[0])
X_tr.loc[segment, 'mean_change_rate_last_10000'] = np.mean(np.nonzero((np.diff(x[-10000:]) / x[-10000:][:-1]))[0])
X_tr.loc[segment, 'q95'] = np.quantile(x, 0.95)
X_tr.loc[segment, 'q99'] = np.quantile(x, 0.99)
X_tr.loc[segment, 'q05'] = np.quantile(x, 0.05)
X_tr.loc[segment, 'q01'] = np.quantile(x, 0.01)
X_tr.loc[segment, 'abs_q95'] = np.quantile(np.abs(x), 0.95)
X_tr.loc[segment, 'abs_q99'] = np.quantile(np.abs(x), 0.99)
X_tr.loc[segment, 'abs_q05'] = np.quantile(np.abs(x), 0.05)
X_tr.loc[segment, 'abs_q01'] = np.quantile(np.abs(x), 0.01)
X_tr.loc[segment, 'trend'] = add_trend_feature(x)
X_tr.loc[segment, 'abs_trend'] = add_trend_feature(x, abs_values=True)
X_tr.loc[segment, 'abs_mean'] = np.abs(x).mean()
X_tr.loc[segment, 'abs_std'] = np.abs(x).std()
X_tr.loc[segment, 'mad'] = x.mad()
X_tr.loc[segment, 'kurt'] = x.kurtosis()
X_tr.loc[segment, 'skew'] = x.skew()
X_tr.loc[segment, 'med'] = x.median()
X_tr.loc[segment, 'Hilbert_mean'] = np.abs(hilbert(x)).mean()
X_tr.loc[segment, 'Hann_window_mean'] = (convolve(x, hann(150), mode='same') / sum(hann(150))).mean()
X_tr.loc[segment, 'classic_sta_lta1_mean'] = classic_sta_lta(x, 500, 10000).mean()
X_tr.loc[segment, 'classic_sta_lta2_mean'] = classic_sta_lta(x, 5000, 100000).mean()
X_tr.loc[segment, 'classic_sta_lta3_mean'] = classic_sta_lta(x, 3333, 6666).mean()
X_tr.loc[segment, 'classic_sta_lta4_mean'] = classic_sta_lta(x, 10000, 25000).mean()
X_tr.loc[segment, 'Moving_average_700_mean'] = x.rolling(window=700).mean().mean(skipna=True)
X_tr.loc[segment, 'Moving_average_1500_mean'] = x.rolling(window=1500).mean().mean(skipna=True)
X_tr.loc[segment, 'Moving_average_3000_mean'] = x.rolling(window=3000).mean().mean(skipna=True)
X_tr.loc[segment, 'Moving_average_6000_mean'] = x.rolling(window=6000).mean().mean(skipna=True)
ewma = pd.Series.ewm
X_tr.loc[segment, 'exp_Moving_average_300_mean'] = (ewma(x, span=300).mean()).mean(skipna=True)
X_tr.loc[segment, 'exp_Moving_average_3000_mean'] = ewma(x, span=3000).mean().mean(skipna=True)
X_tr.loc[segment, 'exp_Moving_average_30000_mean'] = ewma(x, span=6000).mean().mean(skipna=True)
no_of_std = 2
X_tr.loc[segment, 'MA_700MA_std_mean'] = x.rolling(window=700).std().mean()
X_tr.loc[segment,'MA_700MA_BB_high_mean'] = (X_tr.loc[segment, 'Moving_average_700_mean'] + no_of_std * X_tr.loc[segment, 'MA_700MA_std_mean']).mean()
X_tr.loc[segment,'MA_700MA_BB_low_mean'] = (X_tr.loc[segment, 'Moving_average_700_mean'] - no_of_std * X_tr.loc[segment, 'MA_700MA_std_mean']).mean()
X_tr.loc[segment, 'MA_400MA_std_mean'] = x.rolling(window=400).std().mean()
X_tr.loc[segment,'MA_400MA_BB_high_mean'] = (X_tr.loc[segment, 'Moving_average_700_mean'] + no_of_std * X_tr.loc[segment, 'MA_400MA_std_mean']).mean()
X_tr.loc[segment,'MA_400MA_BB_low_mean'] = (X_tr.loc[segment, 'Moving_average_700_mean'] - no_of_std * X_tr.loc[segment, 'MA_400MA_std_mean']).mean()
X_tr.loc[segment, 'MA_1000MA_std_mean'] = x.rolling(window=1000).std().mean()
X_tr.loc[segment, 'iqr'] = np.subtract(*np.percentile(x, [75, 25]))
X_tr.loc[segment, 'q999'] = np.quantile(x,0.999)
X_tr.loc[segment, 'q001'] = np.quantile(x,0.001)
X_tr.loc[segment, 'ave10'] = stats.trim_mean(x, 0.1)
for windows in [10, 100, 1000]:
x_roll_std = x.rolling(windows).std().dropna().values
x_roll_mean = x.rolling(windows).mean().dropna().values
X_tr.loc[segment, 'ave_roll_std_' + str(windows)] = x_roll_std.mean()
X_tr.loc[segment, 'std_roll_std_' + str(windows)] = x_roll_std.std()
X_tr.loc[segment, 'max_roll_std_' + str(windows)] = x_roll_std.max()
X_tr.loc[segment, 'min_roll_std_' + str(windows)] = x_roll_std.min()
X_tr.loc[segment, 'q01_roll_std_' + str(windows)] = np.quantile(x_roll_std, 0.01)
X_tr.loc[segment, 'q05_roll_std_' + str(windows)] = np.quantile(x_roll_std, 0.05)
X_tr.loc[segment, 'q95_roll_std_' + str(windows)] = np.quantile(x_roll_std, 0.95)
X_tr.loc[segment, 'q99_roll_std_' + str(windows)] = np.quantile(x_roll_std, 0.99)
X_tr.loc[segment, 'av_change_abs_roll_std_' + str(windows)] = np.mean(np.diff(x_roll_std))
X_tr.loc[segment, 'av_change_rate_roll_std_' + str(windows)] = np.mean(np.nonzero((np.diff(x_roll_std) / x_roll_std[:-1]))[0])
X_tr.loc[segment, 'abs_max_roll_std_' + str(windows)] = np.abs(x_roll_std).max()
X_tr.loc[segment, 'ave_roll_mean_' + str(windows)] = x_roll_mean.mean()
X_tr.loc[segment, 'std_roll_mean_' + str(windows)] = x_roll_mean.std()
X_tr.loc[segment, 'max_roll_mean_' + str(windows)] = x_roll_mean.max()
X_tr.loc[segment, 'min_roll_mean_' + str(windows)] = x_roll_mean.min()
X_tr.loc[segment, 'q01_roll_mean_' + str(windows)] = np.quantile(x_roll_mean, 0.01)
X_tr.loc[segment, 'q05_roll_mean_' + str(windows)] = np.quantile(x_roll_mean, 0.05)
X_tr.loc[segment, 'q95_roll_mean_' + str(windows)] = np.quantile(x_roll_mean, 0.95)
X_tr.loc[segment, 'q99_roll_mean_' + str(windows)] = np.quantile(x_roll_mean, 0.99)
X_tr.loc[segment, 'av_change_abs_roll_mean_' + str(windows)] = np.mean(np.diff(x_roll_mean))
X_tr.loc[segment, 'av_change_rate_roll_mean_' + str(windows)] = np.mean(np.nonzero((np.diff(x_roll_mean) / x_roll_mean[:-1]))[0])
X_tr.loc[segment, 'abs_max_roll_mean_' + str(windows)] = np.abs(x_roll_mean).max()
print("Number of training segments: {}".format(X_tr.shape[0]))
print("Number of features: {}".format(X_tr.shape[1]))
X_tr.head()
plt.figure(figsize=(44, 24))
cols = list(np.abs(X_tr.corrwith(y_tr['time_to_failure'])).sort_values(ascending=False).head(24).index)
mms = MinMaxScaler()
X_tr_scaled = pd.DataFrame(columns=cols, data=mms.fit_transform(X_tr[cols]))
y_tr_scaled = mms.fit_transform(y_tr)
for i, col in enumerate(cols):
plt.subplot(6, 4, i + 1)
plt.plot(X_tr_scaled[col], color='b')
plt.title(col)
ax1.set_ylabel(col, color='b')
ax2 = ax1.twinx()
plt.plot(y_tr_scaled, color='r')
ax2.set_ylabel('time_to_failure', color='r')
plt.legend([col, 'time_to_failure'], loc=(0.875, 0.9))
plt.grid(False)
plt.savefig('reports/figures/feature_correlations.png')
submission = pd.read_csv('data/sample_submission.csv', index_col='seg_id')
X_test = pd.DataFrame(columns=X_tr.columns, dtype=np.float64, index=submission.index)
for i, seg_id in enumerate(tqdm_notebook(X_test.index)):
seg = pd.read_csv('data/test/' + seg_id + '.csv')
x = pd.Series(seg['acoustic_data'].values)
X_test.loc[seg_id, 'mean'] = x.mean()
X_test.loc[seg_id, 'std'] = x.std()
X_test.loc[seg_id, 'max'] = x.max()
X_test.loc[seg_id, 'min'] = x.min()
X_test.loc[seg_id, 'mean_change_abs'] = np.mean(np.diff(x))
X_test.loc[seg_id, 'mean_change_rate'] = np.mean(np.nonzero((np.diff(x) / x[:-1]))[0])
X_test.loc[seg_id, 'abs_max'] = np.abs(x).max()
X_test.loc[seg_id, 'abs_min'] = np.abs(x).min()
X_test.loc[seg_id, 'std_first_50000'] = x[:50000].std()
X_test.loc[seg_id, 'std_last_50000'] = x[-50000:].std()
X_test.loc[seg_id, 'std_first_10000'] = x[:10000].std()
X_test.loc[seg_id, 'std_last_10000'] = x[-10000:].std()
X_test.loc[seg_id, 'avg_first_50000'] = x[:50000].mean()
X_test.loc[seg_id, 'avg_last_50000'] = x[-50000:].mean()
X_test.loc[seg_id, 'avg_first_10000'] = x[:10000].mean()
X_test.loc[seg_id, 'avg_last_10000'] = x[-10000:].mean()
X_test.loc[seg_id, 'min_first_50000'] = x[:50000].min()
X_test.loc[seg_id, 'min_last_50000'] = x[-50000:].min()
X_test.loc[seg_id, 'min_first_10000'] = x[:10000].min()
X_test.loc[seg_id, 'min_last_10000'] = x[-10000:].min()
X_test.loc[seg_id, 'max_first_50000'] = x[:50000].max()
X_test.loc[seg_id, 'max_last_50000'] = x[-50000:].max()
X_test.loc[seg_id, 'max_first_10000'] = x[:10000].max()
X_test.loc[seg_id, 'max_last_10000'] = x[-10000:].max()
X_test.loc[seg_id, 'max_to_min'] = x.max() / np.abs(x.min())
X_test.loc[seg_id, 'max_to_min_diff'] = x.max() - np.abs(x.min())
X_test.loc[seg_id, 'count_big'] = len(x[np.abs(x) > 500])
X_test.loc[seg_id, 'sum'] = x.sum()
X_test.loc[seg_id, 'mean_change_rate_first_50000'] = np.mean(np.nonzero((np.diff(x[:50000]) / x[:50000][:-1]))[0])
X_test.loc[seg_id, 'mean_change_rate_last_50000'] = np.mean(np.nonzero((np.diff(x[-50000:]) / x[-50000:][:-1]))[0])
X_test.loc[seg_id, 'mean_change_rate_first_10000'] = np.mean(np.nonzero((np.diff(x[:10000]) / x[:10000][:-1]))[0])
X_test.loc[seg_id, 'mean_change_rate_last_10000'] = np.mean(np.nonzero((np.diff(x[-10000:]) / x[-10000:][:-1]))[0])
X_test.loc[seg_id, 'q95'] = np.quantile(x,0.95)
X_test.loc[seg_id, 'q99'] = np.quantile(x,0.99)
X_test.loc[seg_id, 'q05'] = np.quantile(x,0.05)
X_test.loc[seg_id, 'q01'] = np.quantile(x,0.01)
X_test.loc[seg_id, 'abs_q95'] = np.quantile(np.abs(x), 0.95)
X_test.loc[seg_id, 'abs_q99'] = np.quantile(np.abs(x), 0.99)
X_test.loc[seg_id, 'abs_q05'] = np.quantile(np.abs(x), 0.05)
X_test.loc[seg_id, 'abs_q01'] = np.quantile(np.abs(x), 0.01)
X_test.loc[seg_id, 'trend'] = add_trend_feature(x)
X_test.loc[seg_id, 'abs_trend'] = add_trend_feature(x, abs_values=True)
X_test.loc[seg_id, 'abs_mean'] = np.abs(x).mean()
X_test.loc[seg_id, 'abs_std'] = np.abs(x).std()
X_test.loc[seg_id, 'mad'] = x.mad()
X_test.loc[seg_id, 'kurt'] = x.kurtosis()
X_test.loc[seg_id, 'skew'] = x.skew()
X_test.loc[seg_id, 'med'] = x.median()
X_test.loc[seg_id, 'Hilbert_mean'] = np.abs(hilbert(x)).mean()
X_test.loc[seg_id, 'Hann_window_mean'] = (convolve(x, hann(150), mode='same') / sum(hann(150))).mean()
X_test.loc[seg_id, 'classic_sta_lta1_mean'] = classic_sta_lta(x, 500, 10000).mean()
X_test.loc[seg_id, 'classic_sta_lta2_mean'] = classic_sta_lta(x, 5000, 100000).mean()
X_test.loc[seg_id, 'classic_sta_lta3_mean'] = classic_sta_lta(x, 3333, 6666).mean()
X_test.loc[seg_id, 'classic_sta_lta4_mean'] = classic_sta_lta(x, 10000, 25000).mean()
X_test.loc[seg_id, 'Moving_average_700_mean'] = x.rolling(window=700).mean().mean(skipna=True)
X_test.loc[seg_id, 'Moving_average_1500_mean'] = x.rolling(window=1500).mean().mean(skipna=True)
X_test.loc[seg_id, 'Moving_average_3000_mean'] = x.rolling(window=3000).mean().mean(skipna=True)
X_test.loc[seg_id, 'Moving_average_6000_mean'] = x.rolling(window=6000).mean().mean(skipna=True)
ewma = pd.Series.ewm
X_test.loc[seg_id, 'exp_Moving_average_300_mean'] = (ewma(x, span=300).mean()).mean(skipna=True)
X_test.loc[seg_id, 'exp_Moving_average_3000_mean'] = ewma(x, span=3000).mean().mean(skipna=True)
X_test.loc[seg_id, 'exp_Moving_average_30000_mean'] = ewma(x, span=6000).mean().mean(skipna=True)
no_of_std = 2
X_test.loc[seg_id, 'MA_700MA_std_mean'] = x.rolling(window=700).std().mean()
X_test.loc[seg_id,'MA_700MA_BB_high_mean'] = (X_test.loc[seg_id, 'Moving_average_700_mean'] + no_of_std * X_test.loc[seg_id, 'MA_700MA_std_mean']).mean()
X_test.loc[seg_id,'MA_700MA_BB_low_mean'] = (X_test.loc[seg_id, 'Moving_average_700_mean'] - no_of_std * X_test.loc[seg_id, 'MA_700MA_std_mean']).mean()
X_test.loc[seg_id, 'MA_400MA_std_mean'] = x.rolling(window=400).std().mean()
X_test.loc[seg_id,'MA_400MA_BB_high_mean'] = (X_test.loc[seg_id, 'Moving_average_700_mean'] + no_of_std * X_test.loc[seg_id, 'MA_400MA_std_mean']).mean()
X_test.loc[seg_id,'MA_400MA_BB_low_mean'] = (X_test.loc[seg_id, 'Moving_average_700_mean'] - no_of_std * X_test.loc[seg_id, 'MA_400MA_std_mean']).mean()
X_test.loc[seg_id, 'MA_1000MA_std_mean'] = x.rolling(window=1000).std().mean()
X_test.loc[seg_id, 'iqr'] = np.subtract(*np.percentile(x, [75, 25]))
X_test.loc[seg_id, 'q999'] = np.quantile(x,0.999)
X_test.loc[seg_id, 'q001'] = np.quantile(x,0.001)
X_test.loc[seg_id, 'ave10'] = stats.trim_mean(x, 0.1)
for windows in [10, 100, 1000]:
x_roll_std = x.rolling(windows).std().dropna().values
x_roll_mean = x.rolling(windows).mean().dropna().values
X_test.loc[seg_id, 'ave_roll_std_' + str(windows)] = x_roll_std.mean()
X_test.loc[seg_id, 'std_roll_std_' + str(windows)] = x_roll_std.std()
X_test.loc[seg_id, 'max_roll_std_' + str(windows)] = x_roll_std.max()
X_test.loc[seg_id, 'min_roll_std_' + str(windows)] = x_roll_std.min()
X_test.loc[seg_id, 'q01_roll_std_' + str(windows)] = np.quantile(x_roll_std, 0.01)
X_test.loc[seg_id, 'q05_roll_std_' + str(windows)] = np.quantile(x_roll_std, 0.05)
X_test.loc[seg_id, 'q95_roll_std_' + str(windows)] = np.quantile(x_roll_std, 0.95)
X_test.loc[seg_id, 'q99_roll_std_' + str(windows)] = np.quantile(x_roll_std, 0.99)
X_test.loc[seg_id, 'av_change_abs_roll_std_' + str(windows)] = np.mean(np.diff(x_roll_std))
X_test.loc[seg_id, 'av_change_rate_roll_std_' + str(windows)] = np.mean(np.nonzero((np.diff(x_roll_std) / x_roll_std[:-1]))[0])
X_test.loc[seg_id, 'abs_max_roll_std_' + str(windows)] = np.abs(x_roll_std).max()
X_test.loc[seg_id, 'ave_roll_mean_' + str(windows)] = x_roll_mean.mean()
X_test.loc[seg_id, 'std_roll_mean_' + str(windows)] = x_roll_mean.std()
X_test.loc[seg_id, 'max_roll_mean_' + str(windows)] = x_roll_mean.max()
X_test.loc[seg_id, 'min_roll_mean_' + str(windows)] = x_roll_mean.min()
X_test.loc[seg_id, 'q01_roll_mean_' + str(windows)] = np.quantile(x_roll_mean, 0.01)
X_test.loc[seg_id, 'q05_roll_mean_' + str(windows)] = np.quantile(x_roll_mean, 0.05)
X_test.loc[seg_id, 'q95_roll_mean_' + str(windows)] = np.quantile(x_roll_mean, 0.95)
X_test.loc[seg_id, 'q99_roll_mean_' + str(windows)] = np.quantile(x_roll_mean, 0.99)
X_test.loc[seg_id, 'av_change_abs_roll_mean_' + str(windows)] = np.mean(np.diff(x_roll_mean))
X_test.loc[seg_id, 'av_change_rate_roll_mean_' + str(windows)] = np.mean(np.nonzero((np.diff(x_roll_mean) / x_roll_mean[:-1]))[0])
X_test.loc[seg_id, 'abs_max_roll_mean_' + str(windows)] = np.abs(x_roll_mean).max()
X_test.head()
```
## Save Prepared Datasets
```
X_tr.to_csv('data/processed/010_train_features.csv', index=False)
y_tr.to_csv('data/processed/010_train_target.csv', index=False)
X_test.to_csv('data/processed/010_test_features.csv', index=True)
```
|
github_jupyter
|
```
import warnings
warnings.filterwarnings("ignore")
import sys
import itertools
from keras.layers import Input, Dense, Reshape, Flatten
from keras import layers, initializers
from keras.models import Model, load_model
import keras.backend as K
import numpy as np
from seqtools import SequenceTools as ST
from gfp_gp import SequenceGP
from util import AA, AA_IDX
from util import build_vae
from sklearn.model_selection import train_test_split, ShuffleSplit
from keras.callbacks import EarlyStopping
import matplotlib.pyplot as plt
import pandas as pd
from gan import WGAN
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, ConstantKernel as C
import scipy.stats
from scipy.stats import norm
from scipy.optimize import minimize
from keras.utils.generic_utils import get_custom_objects
from util import one_hot_encode_aa, partition_data, get_balaji_predictions, get_samples
from util import convert_idx_array_to_aas, build_pred_vae_model, get_experimental_X_y
from util import get_gfp_X_y_aa
from losses import neg_log_likelihood
import json
plt.rcParams['figure.dpi'] = 300
class color:
PURPLE = '\033[95m'
CYAN = '\033[96m'
DARKCYAN = '\033[36m'
BLUE = '\033[94m'
GREEN = '\033[92m'
YELLOW = '\033[93m'
RED = '\033[91m'
BOLD = '\033[1m'
UNDERLINE = '\033[4m'
END = '\033[0m'
import tensorflow as tf
from keras.backend.tensorflow_backend import set_session
def contain_tf_gpu_mem_usage() :
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
sess = tf.Session(config=config)
set_session(sess)
contain_tf_gpu_mem_usage()
#Load GFP training dataset
it = 0
TRAIN_SIZE = 5000
train_size_str = "%ik" % (TRAIN_SIZE/1000)
num_models = [1, 5, 20][it]
RANDOM_STATE = it + 1
X_train, y_train, gt_train = get_experimental_X_y(random_state=RANDOM_STATE, train_size=TRAIN_SIZE)
#Print the 50th, 80th, 95th and 100th percentile of oracle scores
print(np.percentile(y_train, 50))
print(np.percentile(y_train, 80))
print(np.percentile(y_train, 95))
print(np.percentile(y_train, 100))
def build_model(M):
x = Input(shape=(M, 20,))
y = Flatten()(x)
y = Dense(50, activation='elu')(y)
y = Dense(2)(y)
model = Model(inputs=x, outputs=y)
return model
def evaluate_ground_truth(X_aa, ground_truth, save_file=None):
y_gt = ground_truth.predict(X_aa, print_every=100000)[:, 0]
if save_file is not None:
np.save(save_file, y_gt)
def train_and_save_oracles(X_train, y_train, n=10, suffix='', batch_size=100):
for i in range(n):
model = build_model(X_train.shape[1])
model.compile(optimizer='adam',
loss=neg_log_likelihood,
)
early_stop = EarlyStopping(monitor='val_loss',
min_delta=0,
patience=5,
verbose=1)
model.fit(X_train, y_train,
epochs=100,
batch_size=batch_size,
validation_split=0.1,
callbacks=[early_stop],
verbose=2)
model.save("models/oracle_%i%s.h5" % (i, suffix))
import editdistance
def compute_edit_distance(seqs, opt_len=None) :
shuffle_index = np.arange(len(seqs))
shuffle_index = shuffle_index[::-1]
seqs_shuffled = [seqs[shuffle_index[i]] for i in range(len(seqs))]
edit_distances = np.ravel([float(editdistance.eval(seq_1, seq_2)) for seq_1, seq_2 in zip(seqs, seqs_shuffled)])
if opt_len is not None :
edit_distances /= opt_len
return edit_distances
def weighted_ml_opt(X_train, oracles, ground_truth, vae_0, weights_type='dbas',
LD=20, iters=20, samples=500, homoscedastic=False, homo_y_var=0.1,
quantile=0.95, verbose=False, alpha=1, train_gt_evals=None,
cutoff=1e-6, it_epochs=10, enc1_units=50):
assert weights_type in ['cbas', 'dbas','rwr', 'cem-pi', 'fbvae']
L = X_train.shape[1]
vae = build_vae(latent_dim=LD,
n_tokens=20, seq_length=L,
enc1_units=enc1_units)
traj = np.zeros((iters, 7))
oracle_samples = np.zeros((iters, samples))
gt_samples = np.zeros((iters, samples))
edit_distance_samples = np.zeros((iters, samples))
oracle_max_seq = None
oracle_max = -np.inf
gt_of_oracle_max = -np.inf
y_star = -np.inf
# FOR REVIEW:
all_seqs = pd.DataFrame(0, index=range(int((iters-1)*samples)), columns=['seq', 'val'])
l_ = 0
for t in range(iters):
### Take Samples ###
zt = np.random.randn(samples, LD)
if t > 0:
Xt_p = vae.decoder_.predict(zt)
Xt = get_samples(Xt_p)
else:
Xt = X_train
### Evaluate ground truth and oracle ###
yt, yt_var = get_balaji_predictions(oracles, Xt)
if homoscedastic:
yt_var = np.ones_like(yt) * homo_y_var
Xt_aa = np.argmax(Xt, axis=-1)
if t == 0 and train_gt_evals is not None:
yt_gt = train_gt_evals
else:
yt_gt = ground_truth.predict(Xt_aa, print_every=1000000)[:, 0]
### Calculate weights for different schemes ###
if t > 0:
if weights_type == 'cbas':
log_pxt = np.sum(np.log(Xt_p) * Xt, axis=(1, 2))
X0_p = vae_0.decoder_.predict(zt)
log_px0 = np.sum(np.log(X0_p) * Xt, axis=(1, 2))
w1 = np.exp(log_px0-log_pxt)
y_star_1 = np.percentile(yt, quantile*100)
if y_star_1 > y_star:
y_star = y_star_1
w2= scipy.stats.norm.sf(y_star, loc=yt, scale=np.sqrt(yt_var))
weights = w1*w2
elif weights_type == 'cem-pi':
pi = scipy.stats.norm.sf(max_train_gt, loc=yt, scale=np.sqrt(yt_var))
pi_thresh = np.percentile(pi, quantile*100)
weights = (pi > pi_thresh).astype(int)
elif weights_type == 'dbas':
y_star_1 = np.percentile(yt, quantile*100)
if y_star_1 > y_star:
y_star = y_star_1
weights = scipy.stats.norm.sf(y_star, loc=yt, scale=np.sqrt(yt_var))
elif weights_type == 'rwr':
weights = np.exp(alpha*yt)
weights /= np.sum(weights)
else:
weights = np.ones(yt.shape[0])
max_train_gt = np.max(yt_gt)
yt_max_idx = np.argmax(yt)
yt_max = yt[yt_max_idx]
if yt_max > oracle_max:
oracle_max = yt_max
try:
oracle_max_seq = convert_idx_array_to_aas(Xt_aa[yt_max_idx-1:yt_max_idx])[0]
except IndexError:
print(Xt_aa[yt_max_idx-1:yt_max_idx])
gt_of_oracle_max = yt_gt[yt_max_idx]
### Record and print results ##
if t == 0:
rand_idx = np.random.randint(0, len(yt), samples)
oracle_samples[t, :] = yt[rand_idx]
gt_samples[t, :] = yt_gt[rand_idx]
edit_distance_samples[t, :] = compute_edit_distance(convert_idx_array_to_aas(Xt_aa[rand_idx, ...]))
if t > 0:
oracle_samples[t, :] = yt
gt_samples[t, :] = yt_gt
edit_distance_samples[t, :] = compute_edit_distance(convert_idx_array_to_aas(Xt_aa))
traj[t, 0] = np.max(yt_gt)
traj[t, 1] = np.mean(yt_gt)
traj[t, 2] = np.std(yt_gt)
traj[t, 3] = np.max(yt)
traj[t, 4] = np.mean(yt)
traj[t, 5] = np.std(yt)
traj[t, 6] = np.mean(yt_var)
if verbose:
print(weights_type.upper(), t, traj[t, 0], color.BOLD + str(traj[t, 1]) + color.END,
traj[t, 2], traj[t, 3], color.BOLD + str(traj[t, 4]) + color.END, traj[t, 5], traj[t, 6], np.median(edit_distance_samples[t, :]))
### Train model ###
if t == 0:
vae.encoder_.set_weights(vae_0.encoder_.get_weights())
vae.decoder_.set_weights(vae_0.decoder_.get_weights())
vae.vae_.set_weights(vae_0.vae_.get_weights())
else:
cutoff_idx = np.where(weights < cutoff)
Xt = np.delete(Xt, cutoff_idx, axis=0)
yt = np.delete(yt, cutoff_idx, axis=0)
weights = np.delete(weights, cutoff_idx, axis=0)
vae.fit([Xt], [Xt, np.zeros(Xt.shape[0])],
epochs=it_epochs,
batch_size=10,
shuffle=False,
sample_weight=[weights, weights],
verbose=0)
max_dict = {'oracle_max' : oracle_max,
'oracle_max_seq': oracle_max_seq,
'gt_of_oracle_max': gt_of_oracle_max}
return traj, oracle_samples, gt_samples, edit_distance_samples, max_dict
def fb_opt(X_train, oracles, ground_truth, vae_0, weights_type='fbvae',
LD=20, iters=20, samples=500,
quantile=0.8, verbose=False, train_gt_evals=None,
it_epochs=10, enc1_units=50):
assert weights_type in ['fbvae']
L = X_train.shape[1]
vae = build_vae(latent_dim=LD,
n_tokens=20, seq_length=L,
enc1_units=enc1_units)
traj = np.zeros((iters, 7))
oracle_samples = np.zeros((iters, samples))
gt_samples = np.zeros((iters, samples))
edit_distance_samples = np.zeros((iters, samples))
oracle_max_seq = None
oracle_max = -np.inf
gt_of_oracle_max = -np.inf
y_star = - np.inf
for t in range(iters):
### Take Samples and evaluate ground truth and oracle ##
zt = np.random.randn(samples, LD)
if t > 0:
Xt_sample_p = vae.decoder_.predict(zt)
Xt_sample = get_samples(Xt_sample_p)
yt_sample, _ = get_balaji_predictions(oracles, Xt_sample)
Xt_aa_sample = np.argmax(Xt_sample, axis=-1)
yt_gt_sample = ground_truth.predict(Xt_aa_sample, print_every=1000000)[:, 0]
else:
Xt = X_train
yt, _ = get_balaji_predictions(oracles, Xt)
Xt_aa = np.argmax(Xt, axis=-1)
fb_thresh = np.percentile(yt, quantile*100)
if train_gt_evals is not None:
yt_gt = train_gt_evals
else:
yt_gt = ground_truth.predict(Xt_aa, print_every=1000000)[:, 0]
### Calculate threshold ###
if t > 0:
threshold_idx = np.where(yt_sample >= fb_thresh)[0]
n_top = len(threshold_idx)
sample_arrs = [Xt_sample, yt_sample, yt_gt_sample, Xt_aa_sample]
full_arrs = [Xt, yt, yt_gt, Xt_aa]
for l in range(len(full_arrs)):
sample_arr = sample_arrs[l]
full_arr = full_arrs[l]
sample_top = sample_arr[threshold_idx]
full_arr = np.concatenate([sample_top, full_arr])
full_arr = np.delete(full_arr, range(full_arr.shape[0]-n_top, full_arr.shape[0]), axis=0)
full_arrs[l] = full_arr
Xt, yt, yt_gt, Xt_aa = full_arrs
yt_max_idx = np.argmax(yt)
yt_max = yt[yt_max_idx]
if yt_max > oracle_max:
oracle_max = yt_max
try:
oracle_max_seq = convert_idx_array_to_aas(Xt_aa[yt_max_idx-1:yt_max_idx])[0]
except IndexError:
print(Xt_aa[yt_max_idx-1:yt_max_idx])
gt_of_oracle_max = yt_gt[yt_max_idx]
### Record and print results ##
rand_idx = np.random.randint(0, len(yt), samples)
oracle_samples[t, :] = yt[rand_idx]
gt_samples[t, :] = yt_gt[rand_idx]
edit_distance_samples[t, :] = compute_edit_distance(convert_idx_array_to_aas(Xt_aa[rand_idx, ...]))
traj[t, 0] = np.max(yt_gt)
traj[t, 1] = np.mean(yt_gt)
traj[t, 2] = np.std(yt_gt)
traj[t, 3] = np.max(yt)
traj[t, 4] = np.mean(yt)
traj[t, 5] = np.std(yt)
if t > 0:
traj[t, 6] = n_top
else:
traj[t, 6] = 0
if verbose:
print(weights_type.upper(), t, traj[t, 0], color.BOLD + str(traj[t, 1]) + color.END,
traj[t, 2], traj[t, 3], color.BOLD + str(traj[t, 4]) + color.END, traj[t, 5], traj[t, 6], np.median(edit_distance_samples[t, :]))
### Train model ###
if t == 0:
vae.encoder_.set_weights(vae_0.encoder_.get_weights())
vae.decoder_.set_weights(vae_0.decoder_.get_weights())
vae.vae_.set_weights(vae_0.vae_.get_weights())
else:
vae.fit([Xt], [Xt, np.zeros(Xt.shape[0])],
epochs=1,
batch_size=10,
shuffle=False,
verbose=0)
max_dict = {'oracle_max' : oracle_max,
'oracle_max_seq': oracle_max_seq,
'gt_of_oracle_max': gt_of_oracle_max}
return traj, oracle_samples, gt_samples, edit_distance_samples, max_dict
def train_experimental_oracles():
TRAIN_SIZE = 5000
train_size_str = "%ik" % (TRAIN_SIZE/1000)
i = 1
num_models = [1, 5, 20]
for i in range(len(num_models)):
RANDOM_STATE = i+1
nm = num_models[i]
X_train, y_train, _ = get_experimental_X_y(random_state=RANDOM_STATE, train_size=TRAIN_SIZE)
suffix = '_%s_%i_%i' % (train_size_str, nm, RANDOM_STATE)
train_and_save_oracles(X_train, y_train, batch_size=10, n=nm, suffix=suffix)
def train_experimental_vaes(i_list=[0, 2]):
TRAIN_SIZE = 5000
train_size_str = "%ik" % (TRAIN_SIZE/1000)
suffix = '_%s' % train_size_str
for i in i_list:
RANDOM_STATE = i + 1
X_train, _, _ = get_experimental_X_y(random_state=RANDOM_STATE, train_size=TRAIN_SIZE)
vae_0 = build_vae(latent_dim=20,
n_tokens=20,
seq_length=X_train.shape[1],
enc1_units=50)
vae_0.fit([X_train], [X_train, np.zeros(X_train.shape[0])],
epochs=100,
batch_size=10,
verbose=2)
vae_0.encoder_.save_weights("models/vae_0_encoder_weights%s_%i.h5"% (suffix, RANDOM_STATE))
vae_0.decoder_.save_weights("models/vae_0_decoder_weights%s_%i.h5"% (suffix, RANDOM_STATE))
vae_0.vae_.save_weights("models/vae_0_vae_weights%s_%i.h5"% (suffix, RANDOM_STATE))
def run_experimental_weighted_ml(it, repeat_start=0, repeats=3):
assert it in [0, 1, 2]
TRAIN_SIZE = 5000
train_size_str = "%ik" % (TRAIN_SIZE/1000)
num_models = [1, 5, 20][it]
RANDOM_STATE = it + 1
X_train, y_train, gt_train = get_experimental_X_y(random_state=RANDOM_STATE, train_size=TRAIN_SIZE)
vae_suffix = '_%s_%i' % (train_size_str, RANDOM_STATE)
oracle_suffix = '_%s_%i_%i' % (train_size_str, num_models, RANDOM_STATE)
vae_0 = build_vae(latent_dim=20,
n_tokens=20,
seq_length=X_train.shape[1],
enc1_units=50)
vae_0.encoder_.load_weights("models/vae_0_encoder_weights%s.h5" % vae_suffix)
vae_0.decoder_.load_weights("models/vae_0_decoder_weights%s.h5"% vae_suffix)
vae_0.vae_.load_weights("models/vae_0_vae_weights%s.h5"% vae_suffix)
ground_truth = SequenceGP(load=True, load_prefix="data/gfp_gp")
loss = neg_log_likelihood
get_custom_objects().update({"neg_log_likelihood": loss})
oracles = [build_model(X_train.shape[1]) for i in range(num_models)]
for i in range(num_models) :
oracles[i].load_weights("models/oracle_%i%s.h5" % (i, oracle_suffix))
test_kwargs = [
{'weights_type':'cbas', 'quantile': 1},
{'weights_type':'rwr', 'alpha': 20},
{'weights_type':'dbas', 'quantile': 0.95},
{'weights_type':'cem-pi', 'quantile': 0.8},
{'weights_type': 'fbvae', 'quantile': 0.8}
]
base_kwargs = {
'homoscedastic': False,
'homo_y_var': 0.01,
'train_gt_evals':gt_train,
'samples':100,
'cutoff':1e-6,
'it_epochs':10,
'verbose':True,
'LD': 20,
'enc1_units':50,
'iters': 50
}
if num_models==1:
base_kwargs['homoscedastic'] = True
base_kwargs['homo_y_var'] = np.mean((get_balaji_predictions(oracles, X_train)[0] - y_train)**2)
for k in range(repeat_start, repeats):
for j in range(len(test_kwargs)):
test_name = test_kwargs[j]['weights_type']
suffix = "_%s_%i_%i_w_edit_distances" % (train_size_str, RANDOM_STATE, k)
if test_name == 'fbvae':
if base_kwargs['iters'] > 100:
suffix += '_long'
print(suffix)
kwargs = {}
kwargs.update(test_kwargs[j])
kwargs.update(base_kwargs)
[kwargs.pop(k) for k in ['homoscedastic', 'homo_y_var', 'cutoff', 'it_epochs']]
test_traj, test_oracle_samples, test_gt_samples, test_edit_distance_samples, test_max = fb_opt(np.copy(X_train), oracles, ground_truth, vae_0, **kwargs)
else:
if base_kwargs['iters'] > 100:
suffix += '_long'
kwargs = {}
kwargs.update(test_kwargs[j])
kwargs.update(base_kwargs)
test_traj, test_oracle_samples, test_gt_samples, test_edit_distance_samples, test_max = weighted_ml_opt(np.copy(X_train), oracles, ground_truth, vae_0, **kwargs)
np.save('results/%s_traj%s.npy' %(test_name, suffix), test_traj)
np.save('results/%s_oracle_samples%s.npy' % (test_name, suffix), test_oracle_samples)
np.save('results/%s_gt_samples%s.npy'%(test_name, suffix), test_gt_samples )
np.save('results/%s_edit_distance_samples%s.npy'%(test_name, suffix), test_edit_distance_samples )
with open('results/%s_max%s.json'% (test_name, suffix), 'w') as outfile:
json.dump(test_max, outfile)
train_experimental_oracles()
train_experimental_vaes()
run_experimental_weighted_ml(0, repeat_start=0, repeats=1)
run_experimental_weighted_ml(1, repeat_start=0, repeats=1)
run_experimental_weighted_ml(2, repeat_start=0, repeats=1)
run_experimental_weighted_ml(0, repeat_start=1, repeats=3)
run_experimental_weighted_ml(1, repeat_start=1, repeats=3)
run_experimental_weighted_ml(2, repeat_start=1, repeats=3)
```
|
github_jupyter
|
```
import numpy as np
class NelderMeadSimplexOptimizer:
reflection_coeff = 1.0
expansion_coeff = 2.0
contraction_coeff = 0.5
shrinking_coeff = 0.5
# <objective_function>: objective function, should match the specified dimension
# <dimension>: dimension of parameter vector (integer)
# <initial values>: list of <dimension+1> np.arrays of length <dimension> each
# <stop_thresh>: float value stopping criterion, absolute of objective function value of best vs. worst vertex
# <max_iter>: stopping criterion, maximum number of iterations
def __init__(self, objective_function, dimension, initial_values, stop_thresh=1e-4, max_iter=500):
self.obj_func = objective_function
self.dimension = dimension
self.vertices_and_values = []
self.stop_thresh = stop_thresh
self.max_iter = max_iter
for vertex_iterator in initial_values:
# create list of tuples (objective function value, vertex)
self.vertices_and_values.append( (self.obj_func(vertex_iterator), vertex_iterator) )
@staticmethod
def create_random_vertices(dimension, center, scale):
vertex_list = []
rng = np.random.default_rng()
for i in range(dimension+1):
vertex_list.append( center + float(scale) * rng.random((dimension,)) )
return vertex_list
def calculate_centroid(self):
# calculate center of all vertices except the worst
self.centroid = np.zeros(self.dimension)
for i in range(len(self.vertices_and_values)-1):
self.centroid += self.vertices_and_values[i][1]
self.centroid /= float( len(self.vertices_and_values) - 1 )
def sort_vertices(self):
# sort obj. func. values and their vertices by the obj. func. value
self.vertices_and_values = sorted(self.vertices_and_values, key=lambda tup: tup[0])
# store 2 best and 2 worst values and vertices separately
self.best = self.vertices_and_values[0]
self.second_best = self.vertices_and_values[1]
self.second_worst = self.vertices_and_values[-2]
self.worst = self.vertices_and_values[-1]
def reflect(self):
new_vertex = self.centroid * ( 1.0 + self.reflection_coeff ) - self.reflection_coeff * self.worst[1]
new_obj_func_value = self.obj_func(new_vertex)
return (new_obj_func_value, new_vertex)
def expand(self):
new_vertex = self.centroid * ( 1.0 + self.expansion_coeff ) - self.expansion_coeff * self.worst[1]
new_obj_func_value = self.obj_func(new_vertex)
return (new_obj_func_value, new_vertex)
def contract(self, _vertex):
new_vertex = self.centroid * ( 1.0 - self.contraction_coeff ) + self.contraction_coeff * _vertex
new_obj_func_value = self.obj_func(new_vertex)
return (new_obj_func_value, new_vertex)
def shrink(self):
# iterate over all vertices except the best (first) one
for i in range(1, len(self.vertices_and_values)):
# shrink
new_vertex = self.best[1] * (1.0 - self.shrinking_coeff) + self.shrinking_coeff * self.vertices_and_values[i][1]
new_obj_func_value = self.obj_func(new_vertex)
# replace vertices and new objective function values
self.vertices_and_values[i] = (new_obj_func_value, new_vertex)
def find_minimum(self, verbose=False):
num_iterations = 0
while(True):
num_iterations += 1
self.sort_vertices()
self.calculate_centroid()
# do reflection
(reflection_value, reflection_vertex) = self.reflect()
if( (reflection_value < self.second_worst[0]) and (reflection_value <= self.best[0]) ):
# accept reflection, replace worst vertex by reflection
self.vertices_and_values[-1] = (reflection_value, reflection_vertex)
if(verbose):
print("reflection")
elif( reflection_value < self.best[0] ):
# do expansion
(expansion_value, expansion_vertex) = self.expand()
if( expansion_value <= reflection_value):
# accept expansion, replace worst vertex by expansion
self.vertices_and_values[-1] = (expansion_value, expansion_vertex)
if(verbose):
print("expansion")
else:
# accept reflection, replace worst vertex by reflection
self.vertices_and_values[-1] = (reflection_value, reflection_vertex)
elif( (reflection_value < self.worst[0]) and (reflection_value >= self.second_worst[0]) ):
# do outside contraction towards reflection
(outside_contraction_value, outside_contraction_vertex) = self.contract(reflection_vertex)
if( outside_contraction_value <= reflection_value ):
# accept outside contraction, replace worst vertex by outside contraction
self.vertices_and_values[-1] = (outside_contraction_value, outside_contraction_vertex)
if(verbose):
print("outside contraction")
else:
# shrink
self.shrink()
if(verbose):
print("shrink")
else: # reflection_value >= self.worst[0]
# do inside contraction towards worst
(inside_contraction_value, inside_contraction_vertex) = self.contract(self.worst[1])
if( inside_contraction_value <= self.worst[0]):
# accept inside contraction, replace worst vertex by inside contraction
self.vertices_and_values[-1] = (inside_contraction_value, inside_contraction_vertex)
if(verbose):
print("inside contraction")
else:
# shrink
self.shrink()
if(verbose):
print("shrink")
if(verbose):
print("minimum:", self.best[0], "vertex:", self.best[1])
distance = abs(self.worst[0] - self.best[0])
if(verbose):
print("dist:", distance)
if( distance < self.stop_thresh ):
break
self.sort_vertices()
return (self.best)
# use Rosenbrock a.k.a. Banana-function as our test objective function
def banana(x):
return pow(1-x[0], 2) + 100.0 * pow( x[1] - pow(x[0], 2), 2)
# create random initial vertices centered around (1, 1) with a maximum deviation of 2
# i.e. the initial points will lie somewhere inside (-1..3, -1..3)
init_vertices = NelderMeadSimplexOptimizer.create_random_vertices(2, np.array([1,1]), 2.0)
print("initial simplex:")
for vertex in init_vertices:
print(vertex)
# create a NMS-optimizer instance with our objective function, initial vertices and a dimension of 2
optimizer = NelderMeadSimplexOptimizer(banana, 2, init_vertices)
# run optimizer
(min_value, min_vertex) = optimizer.find_minimum()
print("\nfound minimum", min_value, "at", min_vertex)
```
|
github_jupyter
|
```
from google.colab import drive
drive.mount('/content/gdrive')
import tarfile
tfile = tarfile.open("/content/gdrive/My Drive/Deep Learning Groupwork/Project/Data.tar")
tfile.extractall()
training_dir = '/content/Data/Train'
val_dir = '/content/Data/Validation'
finetunedir = '/content/Data/FineTune'
testdir = '/content/Data/Test'
import os
from os import listdir
from os.path import isfile, join
mypath = '/content/Data/Test/Fake'
print(mypath)
for f in listdir(mypath):
#print(f[0])
if f[0] == '.':
try:
os.remove(join(mypath, f))
except:
print("file not deleted")
mypath = '/content/Data/Test/Real'
print(mypath)
for f in listdir(mypath):
#print(f[0])
if f[0] == '.':
try:
os.remove(join(mypath, f))
except:
print("file not deleted")
mypath = '/content/Data/Train/Fake'
print(mypath)
for f in listdir(mypath):
#print(f[0])
if f[0] == '.':
try:
os.remove(join(mypath, f))
except:
print("file not deleted")
mypath = '/content/Data/Train/Real'
print(mypath)
for f in listdir(mypath):
#print(f[0])
if f[0] == '.':
try:
os.remove(join(mypath, f))
except:
print("file not deleted")
mypath = '/content/Data/Validation/Real'
print(mypath)
for f in listdir(mypath):
#print(f[0])
if f[0] == '.':
try:
os.remove(join(mypath, f))
except:
print("file not deleted")
mypath = '/content/Data/Validation/Fake'
print(mypath)
for f in listdir(mypath):
#print(f[0])
if f[0] == '.':
try:
os.remove(join(mypath, f))
except:
print("file not deleted")
mypath = '/content/Data/FineTune/Real'
print(mypath)
for f in listdir(mypath):
#print(f[0])
if f[0] == '.':
try:
os.remove(join(mypath, f))
except:
print("file not deleted")
mypath = '/content/Data/FineTune/Fake'
print(mypath)
for f in listdir(mypath):
#print(f[0])
if f[0] == '.':
try:
os.remove(join(mypath, f))
except:
print("file not deleted")
import os
os.chdir('/content/gdrive/My Drive/Deep Learning Groupwork/Project/Code - Kabir/Code/FDFtNet')
print(os.getcwd())
!python3 pretrain.py -network='denseNet' -train_dir='/content/Data/Train' -val_dir='/content/Data/Validation' -batch_size=128 -reduce_patience=100 -step=200 -epochs=100
!python3 '/content/gdrive/My Drive/Deep Learning Groupwork/Project/Code - Kabir/Code/FDFtNet/network/DenseNet.py'
!python3 test.py -test_dir='/content/Data/Test' -model='/content/gdrive/My Drive/Deep Learning Groupwork/Project/Code - Kabir/Code/FDFtNet/models/weights-densenet-million'
!python3 fdft.py -model='/content/gdrive/My Drive/Deep Learning Groupwork/Project/Code - Kabir/Code/FDFtNet/models/weights-densenet-million' -ft_dir='/content/Data/FineTune' -val_dir='/content/Data/Validation' -network='denseNet' -test_dir='/content/Data/Test'
```
|
github_jupyter
|
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Datasets/Terrain/srtm_landforms.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Datasets/Terrain/srtm_landforms.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=Datasets/Terrain/srtm_landforms.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Datasets/Terrain/srtm_landforms.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geehydro](https://github.com/giswqs/geehydro). The **geehydro** Python package builds on the [folium](https://github.com/python-visualization/folium) package and implements several methods for displaying Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, `Map.centerObject()`, and `Map.setOptions()`.
The magic command `%%capture` can be used to hide output from a specific cell. Uncomment these lines if you are running this notebook for the first time.
```
# %%capture
# !pip install earthengine-api
# !pip install geehydro
```
Import libraries
```
import ee
import folium
import geehydro
```
Authenticate and initialize Earth Engine API. You only need to authenticate the Earth Engine API once. Uncomment the line `ee.Authenticate()`
if you are running this notebook for the first time or if you are getting an authentication error.
```
# ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
This step creates an interactive map using [folium](https://github.com/python-visualization/folium). The default basemap is the OpenStreetMap. Additional basemaps can be added using the `Map.setOptions()` function.
The optional basemaps can be `ROADMAP`, `SATELLITE`, `HYBRID`, `TERRAIN`, or `ESRI`.
```
Map = folium.Map(location=[40, -100], zoom_start=4)
Map.setOptions('HYBRID')
```
## Add Earth Engine Python script
```
dataset = ee.Image('CSP/ERGo/1_0/Global/SRTM_landforms')
landforms = dataset.select('constant')
landformsVis = {
'min': 11.0,
'max': 42.0,
'palette': [
'141414', '383838', '808080', 'EBEB8F', 'F7D311', 'AA0000', 'D89382',
'DDC9C9', 'DCCDCE', '1C6330', '68AA63', 'B5C98E', 'E1F0E5', 'a975ba',
'6f198c'
],
}
Map.setCenter(-105.58, 40.5498, 11)
Map.addLayer(landforms, landformsVis, 'Landforms')
```
## Display Earth Engine data layers
```
Map.setControlVisibility(layerControl=True, fullscreenControl=True, latLngPopup=True)
Map
```
|
github_jupyter
|
```
from bokeh.io import output_notebook, show, reset_output
import numpy as np
output_notebook()
from IPython.display import IFrame
IFrame('https://demo.bokehplots.com/apps/sliders', width=900, height=500)
```
### Basic scatterplot
```
from bokeh.io import output_notebook, show
from bokeh.plotting import figure
# create a new plot with default tools, using figure
p = figure(plot_width=400, plot_height=400)
# add a circle renderer with a size, color, and alpha
p.circle([1, 2, 3, 4, 5], [6, 7, 2, 4, 5], size=15, line_color="navy", fill_color="orange", fill_alpha=0.5)
show(p) # show the results
```
### Interactive visualization using sliders
```
from bokeh.layouts import row, column
from bokeh.models import CustomJS, ColumnDataSource, Slider
import matplotlib.pyplot as plt
x = [x*0.005 for x in range(0, 201)]
output_notebook()
source = ColumnDataSource(data=dict(x=x, y=x))
plot = figure(plot_width=400, plot_height=400)
plot.scatter('x', 'y', source=source, line_width=3, line_alpha=0.6)
slider = Slider(start=0.1, end=6, value=1, step=.1, title="power")
update_curve = CustomJS(args=dict(source=source, slider=slider), code="""
var data = source.get('data');
var f = slider.value;
x = data['x']
y = data['y']
for (i = 0; i < x.length; i++) {
y[i] = Math.pow(x[i], f)
}
source.change.emit();
""")
slider.js_on_change('value', update_curve)
show(row(slider, plot))
#scatterplot using sliders
x = [x*0.005 for x in range(0, 21)]
output_notebook()
source = ColumnDataSource(data=dict(x=x, y=x))
plot = figure(plot_width=400, plot_height=400)
plot.scatter('x', 'y', source=source, line_width=3, line_alpha=0.6)
slider = Slider(start=0.1, end=6, value=1, step=.1, title="power")
update_curve = CustomJS(args=dict(source=source, slider=slider), code="""
var data = source.get('data');
var f = slider.value;
x = data['x']
y = data['y']
for (i = 0; i < x.length; i++) {
y[i] = Math.pow(x[i], f)
}
source.change.emit();
""")
slider.js_on_change('value', update_curve)
print source.data['y']
show(row(slider, plot))
#Making equivalent of diffusion
Arr = np.random.rand(2,100)
source = ColumnDataSource(data=dict(x=Arr[0,], y=Arr[1,]))
plot = figure(plot_width=400, plot_height=400)
plot.scatter('x', 'y', source=source, line_width=3, line_alpha=0.6)
slider = Slider(start=1, end=8, value=1, step=1, title="Diffusion_steps")
slider2 = Slider(start=1, end=8, value=1, step=1, title="Anti_Diffusion_steps")
update_curve = CustomJS(args=dict(source=source, slider=slider), code="""
var data = source.get('data');
var f = slider.value;
x = data['x']
y = data['y']
for (i = 0; i < x.length; i++) {
x[i] = Math.pow(x[i], f)
y[i] = Math.pow(y[i], f)
}
source.change.emit();
""")
update_curve2 = CustomJS(args=dict(source=source, slider=slider2), code="""
var data = source.get('data');
var f = slider.value;
x = data['x']
y = data['y']
for (i = 0; i < x.length; i++) {
x[i] = Math.pow(x[i], 1/f)
y[i] = Math.pow(y[i], 1/f)
}
source.change.emit();
""")
slider.js_on_change('value', update_curve)
slider2.js_on_change('value', update_curve2)
show(row(column(slider,slider2), plot))
from bokeh.models import TapTool, CustomJS, ColumnDataSource
callback = CustomJS(code="alert('hello world')")
tap = TapTool(callback=callback)
p = figure(plot_width=600, plot_height=300, tools=[tap])
p.circle(x=[1, 2, 3, 4, 5], y=[2, 5, 8, 2, 7], size=20)
show(p)
from bokeh.models import ColumnDataSource, OpenURL, TapTool
from bokeh.plotting import figure, output_file, show
output_file("openurl.html")
p = figure(plot_width=400, plot_height=400,
tools="tap", title="Click the Dots")
source = ColumnDataSource(data=dict(
x=[1, 2, 3, 4, 5],
y=[2, 5, 8, 2, 7],
color=["navy", "orange", "olive", "firebrick", "gold"]
))
p.circle('x', 'y', color='color', size=20, source=source)
url = "http://www.colors.commutercreative.com/@color/"
taptool = p.select(type=TapTool)
taptool.callback = OpenURL(url=url)
show(p)
from bokeh.models import ColumnDataSource, TapTool, DataRange1d, Plot, LinearAxis, Grid, HoverTool
from bokeh.plotting import figure, output_file, show
from bokeh.models.glyphs import HBar
p = figure(plot_width=400, plot_height=400,
tools="tap", title="Click the Dots")
source = ColumnDataSource(data=dict(
x=[1, 2, 3, 4, 5],
y=[2, 5, 8, 2, 7],
color=["navy", "orange", "olive", "firebrick", "gold"]
))
p.circle('x', 'y', color='color', size=20, source=source)
source2 = ColumnDataSource(data=dict(
x=[1,2],
y=[1,2]))
callback = CustomJS(args=dict(source2=source2), code="""
var data = source2.get('data');
var geom = cb_data['geometries'];
data['x'] = [geom[0].x+1,geom[0].x-1]
data['y'] = [geom[0].y+1,geom[0].y-1]
source2.trigger('change');
""")
def callback2(source2 = source2):
data = source2.get('data')
geom = cb_obj.get('geometries')
data['x'] = [geom['x']+1,geom['x']-1]
data['y'] = [geom['y']+1,geom['y']-1]
source2.trigger('change')
taptool = p.select(type=TapTool)
taptool.callback = CustomJS.from_py_func(callback2);
xdr = DataRange1d()
ydr = DataRange1d()
p2 = figure(plot_width=400, plot_height=400)
p2.vbar(x=source2.data['x'], width=0.5, bottom=0,
top=source2.data['y'], color="firebrick")
#glyph = HBar(source2.data['x'], source2.data['y'], left=0, height=0.5, fill_color="#b3de69")
#p2.add_glyph(source2, glyph)
#p2.add_glyph(source, glyph)
show(row(p,p2))
update()
source = ColumnDataSource(data=dict(
x=[1, 2, 3, 4, 5],
y=[2, 5, 8, 2, 7],
color=["navy", "orange", "olive", "firebrick", "gold"]
))
source2.data['x']
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/jimfhahn/Machine-Learning-Tutorials/blob/master/C3_W3_Lab_1_Distributed_Training.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Ungraded lab: Distributed Strategies with TF and Keras
------------------------
Welcome, during this ungraded lab you are going to perform a distributed training strategy using TensorFlow and Keras, specifically the [`tf.distribute.MultiWorkerMirroredStrategy`](https://www.tensorflow.org/api_docs/python/tf/distribute/MultiWorkerMirroredStrategy).
With the help of this strategy, a Keras model that was designed to run on single-worker can seamlessly work on multiple workers with minimal code change. In particular you will:
1. Perform training with a single worker.
2. Understand the requirements for a multi-worker setup (`tf_config` variable) and using context managers for implementing distributed strategies.
3. Use magic commands to simulate different machines.
4. Perform a multi-worker training strategy.
This notebook is based on the official [Multi-worker training with Keras](https://www.tensorflow.org/tutorials/distribute/multi_worker_with_keras) notebook, which covers some additional topics in case you want a deeper dive into this topic.
[Distributed Training with TensorFlow](https://www.tensorflow.org/guide/distributed_training) guide is also available for an overview of the distribution strategies TensorFlow supports for those interested in a deeper understanding of `tf.distribute.Strategy` APIs.
Let's get started!
## Setup
First, some necessary imports.
```
import os
import sys
import json
import time
```
Before importing TensorFlow, make a few changes to the environment.
- Disable all GPUs. This prevents errors caused by the workers all trying to use the same GPU. **For a real application each worker would be on a different machine.**
- Add the current directory to python's path so modules in this directory can be imported.
```
# Disable GPUs
os.environ["CUDA_VISIBLE_DEVICES"] = "-1"
# Add current directory to path
if '.' not in sys.path:
sys.path.insert(0, '.')
```
The previous step is important since this notebook relies on writting files using the magic command `%%writefile` and then importing them as modules.
Now that the environment configuration is ready, import TensorFlow.
```
import tensorflow as tf
# Ignore warnings
tf.get_logger().setLevel('ERROR')
```
### Dataset and model definition
Next create an `mnist.py` file with a simple model and dataset setup. This python file will be used by the worker-processes in this tutorial.
The name of this file derives from the dataset you will be using which is called [mnist](https://keras.io/api/datasets/mnist/) and consists of 60,000 28x28 grayscale images of the first 10 digits.
```
%%writefile mnist.py
# import os
import tensorflow as tf
import numpy as np
def mnist_dataset(batch_size):
# Load the data
(x_train, y_train), _ = tf.keras.datasets.mnist.load_data()
# Normalize pixel values for x_train and cast to float32
x_train = x_train / np.float32(255)
# Cast y_train to int64
y_train = y_train.astype(np.int64)
# Define repeated and shuffled dataset
train_dataset = tf.data.Dataset.from_tensor_slices((x_train, y_train)).shuffle(60000).repeat().batch(batch_size)
return train_dataset
def build_and_compile_cnn_model():
# Define simple CNN model using Keras Sequential
model = tf.keras.Sequential([
tf.keras.layers.InputLayer(input_shape=(28, 28)),
tf.keras.layers.Reshape(target_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(32, 3, activation='relu'),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10)
])
# Compile model
model.compile(
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.SGD(learning_rate=0.001),
metrics=['accuracy'])
return model
```
Check that the file was succesfully created:
```
!ls *.py
```
Import the mnist module you just created and try training the model for a small number of epochs to observe the results of a single worker to make sure everything works correctly.
```
# Import your mnist model
import mnist
# Set batch size
batch_size = 64
# Load the dataset
single_worker_dataset = mnist.mnist_dataset(batch_size)
# Load compiled CNN model
single_worker_model = mnist.build_and_compile_cnn_model()
# As training progresses, the loss should drop and the accuracy should increase.
single_worker_model.fit(single_worker_dataset, epochs=3, steps_per_epoch=70)
```
Everything is working as expected!
Now you will see how multiple workers can be used as a distributed strategy.
## Multi-worker Configuration
Now let's enter the world of multi-worker training. In TensorFlow, the `TF_CONFIG` environment variable is required for training on multiple machines, each of which possibly has a different role. `TF_CONFIG` is a JSON string used to specify the cluster configuration on each worker that is part of the cluster.
There are two components of `TF_CONFIG`: `cluster` and `task`.
Let's dive into how they are used:
`cluster`:
- **It is the same for all workers** and provides information about the training cluster, which is a dict consisting of different types of jobs such as `worker`.
- In multi-worker training with `MultiWorkerMirroredStrategy`, there is usually one `worker` that takes on a little more responsibility like saving checkpoint and writing summary file for TensorBoard in addition to what a regular `worker` does.
-Such a worker is referred to as the `chief` worker, and it is customary that the `worker` with `index` 0 is appointed as the chief `worker` (in fact this is how `tf.distribute.Strategy` is implemented).
`task`:
- Provides information of the current task and is different on each worker. It specifies the `type` and `index` of that worker.
Here is an example configuration:
```
tf_config = {
'cluster': {
'worker': ['localhost:12345', 'localhost:23456']
},
'task': {'type': 'worker', 'index': 0}
}
```
Here is the same `TF_CONFIG` serialized as a JSON string:
```
json.dumps(tf_config)
```
### Explaining the TF_CONFIG example
In this example you set a `TF_CONFIG` with 2 workers on `localhost`. In practice, users would create multiple workers on external IP addresses/ports, and set `TF_CONFIG` on each worker appropriately.
Since you set the task `type` to `"worker"` and the task `index` to `0`, **this machine is the first worker and will be appointed as the chief worker**.
Note that other machines will need to have the `TF_CONFIG` environment variable set as well, and it should have the same `cluster` dict, but different task `type` or task `index` depending on what the roles of those machines are. For instance, for the second worker you would set `tf_config['task']['index']=1`.
### Quick Note on Environment variables and subprocesses in notebooks
Above, `tf_config` is just a local variable in python. To actually use it to configure training, this dictionary needs to be serialized as JSON, and placed in the `TF_CONFIG` environment variable.
In the next section, you'll spawn new subprocesses for each worker using the `%%bash` magic command. Subprocesses inherit environment variables from their parent, so they can access `TF_CONFIG`.
You would never really launch your jobs this way (as subprocesses of an interactive Python runtime), but it's how you will do it for the purposes of this tutorial.
## Choose the right strategy
In TensorFlow there are two main forms of distributed training:
* Synchronous training, where the steps of training are synced across the workers and replicas, and
* Asynchronous training, where the training steps are not strictly synced.
`MultiWorkerMirroredStrategy`, which is the recommended strategy for synchronous multi-worker training is the one you will be using.
To train the model, use an instance of `tf.distribute.MultiWorkerMirroredStrategy`.
```
strategy = tf.distribute.MultiWorkerMirroredStrategy()
```
`MultiWorkerMirroredStrategy` creates copies of all variables in the model's layers on each device across all workers. It uses `CollectiveOps`, a TensorFlow op for collective communication, to aggregate gradients and keep the variables in sync. The [official TF distributed training guide](https://www.tensorflow.org/guide/distributed_training) has more details about this.
### Implement Distributed Training via Context Managers
To distribute the training to multiple-workers all you need to do is to enclose the model building and `model.compile()` call inside `strategy.scope()`.
The distribution strategy's scope dictates how and where the variables are created, and in the case of `MultiWorkerMirroredStrategy`, the variables created are `MirroredVariable`s, and they are replicated on each of the workers.
```
# Implementing distributed strategy via a context manager
with strategy.scope():
multi_worker_model = mnist.build_and_compile_cnn_model()
```
Note: `TF_CONFIG` is parsed and TensorFlow's GRPC servers are started at the time `MultiWorkerMirroredStrategy()` is called, so the `TF_CONFIG` environment variable must be set before a `tf.distribute.Strategy` instance is created.
**Since `TF_CONFIG` is not set yet the above strategy is effectively single-worker training**.
## Train the model
### Create training script
To actually run with `MultiWorkerMirroredStrategy` you'll need to run worker processes and pass a `TF_CONFIG` to them.
Like the `mnist.py` file written earlier, here is the `main.py` that each of the workers will run:
```
%%writefile main.py
import os
import json
import tensorflow as tf
import mnist # Your module
# Define batch size
per_worker_batch_size = 64
# Get TF_CONFIG from the env variables and save it as JSON
tf_config = json.loads(os.environ['TF_CONFIG'])
# Infer number of workers from tf_config
num_workers = len(tf_config['cluster']['worker'])
# Define strategy
strategy = tf.distribute.MultiWorkerMirroredStrategy()
# Define global batch size
global_batch_size = per_worker_batch_size * num_workers
# Load dataset
multi_worker_dataset = mnist.mnist_dataset(global_batch_size)
# Create and compile model following the distributed strategy
with strategy.scope():
multi_worker_model = mnist.build_and_compile_cnn_model()
# Train the model
multi_worker_model.fit(multi_worker_dataset, epochs=3, steps_per_epoch=70)
```
In the code snippet above note that the `global_batch_size`, which gets passed to `Dataset.batch`, is set to `per_worker_batch_size * num_workers`. This ensures that each worker processes batches of `per_worker_batch_size` examples regardless of the number of workers.
The current directory should now contain both Python files:
```
!ls *.py
```
### Set TF_CONFIG environment variable
Now json-serialize the `TF_CONFIG` and add it to the environment variables:
```
# Set TF_CONFIG env variable
os.environ['TF_CONFIG'] = json.dumps(tf_config)
```
And terminate all background processes:
```
# first kill any previous runs
%killbgscripts
```
### Launch the first worker
Now, you can launch a worker process that will run the `main.py` and use the `TF_CONFIG`:
```
%%bash --bg
python main.py &> job_0.log
```
There are a few things to note about the above command:
1. It uses the `%%bash` which is a [notebook "magic"](https://ipython.readthedocs.io/en/stable/interactive/magics.html) to run some bash commands.
2. It uses the `--bg` flag to run the `bash` process in the background, because this worker will not terminate. It waits for all the workers before it starts.
The backgrounded worker process won't print output to this notebook, so the `&>` redirects its output to a file, so you can see what happened.
So, wait a few seconds for the process to start up:
```
# Wait for logs to be written to the file
time.sleep(10)
```
Now look what's been output to the worker's logfile so far using the `cat` command:
```
%%bash
cat job_0.log
```
The last line of the log file should say: `Started server with target: grpc://localhost:12345`. The first worker is now ready, and is waiting for all the other worker(s) to be ready to proceed.
### Launch the second worker
Now update the `tf_config` for the second worker's process to pick up:
```
tf_config['task']['index'] = 1
os.environ['TF_CONFIG'] = json.dumps(tf_config)
```
Now launch the second worker. This will start the training since all the workers are active (so there's no need to background this process):
```
%%bash
python main.py
```
Now if you recheck the logs written by the first worker you'll see that it participated in training that model:
```
%%bash
cat job_0.log
```
Unsurprisingly this ran _slower_ than the the test run at the beginning of this tutorial. **Running multiple workers on a single machine only adds overhead**. The goal here was not to improve the training time, but only to give an example of multi-worker training.
-----------------------------
**Congratulations on finishing this ungraded lab!** Now you should have a clearer understanding of how to implement distributed strategies with Tensorflow and Keras.
Although this tutorial didn't show the true power of a distributed strategy since this will require multiple machines operating under the same network, you now know how this process looks like at a high level.
In practice and especially with very big models, distributed strategies are commonly used as they provide a way of better managing resources to perform time-consuming tasks, such as training in a fraction of the time that it will take without the strategy.
**Keep it up!**
|
github_jupyter
|
```
%matplotlib notebook
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from astropy.time import Time
def convert_to_ap_Time(df, key):
print(key)
df[key] = pd.to_datetime(df[key])
df[key] = Time([t1.astype(str) for t1 in df[key].values], format="isot")
return df
def convert_times_to_datetime(df):
columns = ["Gun Time", "Chip Time", "TOD", "Beat the Bridge", "Beat the Bridge.1"]
for key in columns:
df = convert_to_ap_Time(df, key)
df = convert_Time_to_seconds(df, key)
return df
def convert_Time_to_seconds(df, key):
t0 = Time("2017-05-04T00:00:00.000", format="isot")
df["sub" + key] = df[key] - t0
df["sub" + key] = [t.sec for t in df["sub" + key].values]
return df
def find_astronomers(df):
astronomers = ("Robert FIRTH", "Stephen BROWETT", "Mathew SMITH", "Sadie JONES")
astro_df = df[df["Name"].isin((astronomers))]
return astro_df
def plot_hist_with_astronomers(df, astro_df, key):
rob_time = astro_df[key][158]/60.
mat_time = astro_df[key][737]/60.
steve_time = astro_df[key][1302]/60.
sadie_time = astro_df[key][576]/60.
mean_time = df[key].mean()/60
median_time = df[key].median()/60
plt.hist(df[key]/60., bins = 100)
plt.plot([rob_time, rob_time], [0, 70], lw = 2, label = "Rob")
plt.plot([mat_time, mat_time], [0, 70], lw = 2, label = "Mat")
plt.plot([steve_time, steve_time], [0, 70], lw = 2, label = "Steve")
plt.plot([sadie_time, sadie_time], [0, 70], lw = 2, label = "Sadie")
plt.plot([mean_time, mean_time], [0, 70], lw = 2, color = "Black", ls = ":", label = "Mean")
plt.plot([median_time, median_time], [0, 70], lw = 2, color = "Black", ls = "--", label = "Median")
plt.xlabel(key.replace("sub", "") + " Minutes")
plt.legend()
results_path = "/Users/berto/Code/zoidberg/ABPSoton10k/data/Results10k.csv"
df = pd.read_csv(results_path)
# df = df.drop(df.index[len(df)-10:])
df = df.drop(df.loc[df["Gun Time"] == "DNF"].index)
df = df.drop(df.loc[df["Gun Time"] == "QRY"].index)
df = df.drop(df.loc[df["Beat the Bridge"] == "99:99:99"].index)
df.columns
df = convert_times_to_datetime(df)
astro_df = find_astronomers(df)
astro_df
# key = "subGun Time"
key = "subChip Time"
rob_time = astro_df[key][158]/60.
mat_time = astro_df[key][737]/60.
steve_time = astro_df[key][1302]/60.
sadie_time = astro_df[key][576]/60.
mean_time = df[key].mean()/60
median_time = df[key].median()/60
plt.hist(df[key]/60., bins = 100)
plt.plot([rob_time, rob_time], [0, 70], lw = 2, label = "Rob")
plt.plot([mat_time, mat_time], [0, 70], lw = 2, label = "Mat")
plt.plot([steve_time, steve_time], [0, 70], lw = 2, label = "Steve")
plt.plot([sadie_time, sadie_time], [0, 70], lw = 2, label = "Sadie")
plt.plot([mean_time, mean_time], [0, 70], lw = 2, color = "Black", ls = ":", label = "Mean")
plt.plot([median_time, median_time], [0, 70], lw = 2, color = "Black", ls = "--", label = "Median")
plt.xlabel(key.replace("sub", "") + " Minutes")
plt.legend()
plot_hist_with_astronomers(df=df, astro_df=astro_df, key="subBeat the Bridge")
```
## Chip Time vs Bridge Time
```
keyx = "subChip Time"
keyy = "subBeat the Bridge"
corr_co = np.corrcoef(df[keyx]/60., df[keyy]/60.)
plt.scatter(df[keyx]/60., df[keyy]/60.)
plt.xlabel(keyx.replace("sub", "") + " Minutes")
plt.ylabel(keyy.replace("sub", "") + " Minutes")
print(corr_co[1,0])
```
## Time vs Bib Number
```
keyx = "subChip Time"
keyy = "Bib No"
corr_co = np.corrcoef(df[keyx]/60., df[keyy])
plt.scatter(df[keyx]/60., df[keyy])
plt.xlabel(keyx.replace("sub", "") + " Minutes")
plt.ylabel(keyy.replace("sub", ""))
print(corr_co[1,0])
# plt.scatter(df["Pos"], df["subChip Time"])
# plt.scatter(df["subChip Time"], df["subBeat the Bridge"])
plt.scatter(df["Pos"], df["G/Pos"])
# print(df.groupby("Gender"))
plt.scatter((df["subGun Time"] - df["subChip Time"])/60., df["subGun Time"]/60.)
# plt.scatter(df["subChip Time"]/60., df["Bib No"])
# df.
# df.columns
# fig = plt.figure(figsize=[8, 4])
# fig.subplots_adjust(left = 0.09, bottom = 0.13, top = 0.99,
# right = 0.99, hspace=0, wspace = 0)
# ax1 = fig.add_subplot(111)
# ax1.scatter(df[df["Club"] == "NaN"]["subChip Time"]/60., df[df["Club"] == "NaN"]["subBeat the Bridge"]/60., color = "Orange")
# ax1.scatter(df[df["Club"] != "NaN"]["subChip Time"]/60., df[df["Club"] != "NaN"]["subBeat the Bridge"]/60., color = "Blue")
clubs = df["Club"].unique()
clubs = [clubs[i] for i in np.arange(len(clubs)) if i != 1]
keyx = "subChip Time"
keyy = "subBeat the Bridge"
corr_co = np.corrcoef(df[keyx][df["Club"].isin(clubs)]/60., df[keyy][df["Club"].isin(clubs)]/60.)
plt.scatter(df[keyx][df["Club"].isin(clubs)]/60., df[keyy][df["Club"].isin(clubs)]/60., label = "clubbed")
# plt.scatter(df[keyx][df["Club"].isin(np.invert(clubs))]/60., df[keyy][df["Club"].isin(np.invert(clubs))]/60.)
keyx = "subChip Time"
keyy = "subBeat the Bridge"
corr_co = np.corrcoef(df[keyx]/60., df[keyy]/60.)
plt.scatter(df[keyx]/60., df[keyy]/60., label = "unclubbed", zorder = -9)
plt.xlabel(keyx.replace("sub", "") + " Minutes")
plt.ylabel(keyy.replace("sub", "") + " Minutes")
plt.legend()
plt.hist(df[keyx][df["Club"].isin(clubs)]/60,label = "clubbed", normed = True, alpha = 0.7)
plt.hist(df[keyx]/60,label = "unclubbed", zorder = -99, normed= True, alpha = 0.7)
plt.scatter((df["subGun Time"][df["Club"].isin(clubs)] - df["subChip Time"][df["Club"].isin(clubs)])/60., df["subGun Time"][df["Club"].isin(clubs)]/60.)
plt.scatter((df["subGun Time"] - df["subChip Time"])/60., df["subGun Time"]/60., zorder = -99)
print(df[keyx].mean()/60.)
print(df[keyx][df["Club"].isin(clubs)].mean()/60.)
df[["Club", "Name", "subChip Time"]][df["Club"].isin(clubs)]
# convert_to_ap_Time(df)
t0 = Time("2017-04-26T00:00:00.000", format="isot")
t1 = df["Gun Time"].values[0]
t1
t1 - t0
col = df["Gun Time"] - t0
x = col[0]
x.
col.sec
```
|
github_jupyter
|
```
#default_exp neighbors
#hide
from nbdev.showdoc import *
#hide
%load_ext autoreload
%autoreload 2
import sys
sys.path.append('..')
```
- weighted NN based on (possibly batch) grad descent of feature weights
- find optimizer engine
- find fast KNN for query time
- Define metric specific sampling function (based on distance)) (possibly optimize func hyperparams during training, like $\alpha$ for $P_{sample} = Dist^{-\alpha}$ and others)
- Define cost function (possibly a product of entropy/variance divided by the KL div from percentiles dist and flat dirichlet (hypercube))
- Study cvxpy
- study metric learn
```
import os
from functools import partial
import numpy as np
from scipy import sparse
from scipy.optimize import minimize
from skdensity.utils import cos_sim_query, sample_from_dist_array, sparse_mul_row, make_bimodal_regression,make_distplot
from skdensity.metrics import kde_entropy, quantile, bimodal_variance, marginal_variance
```
## Training data
```
X_train, y_train, X_test, y_test = make_bimodal_regression(10000, random_state = 42, bimodal_inbalance = 5)
```
# Weighted KNN density estimator cvxpy
```
from time import time
def train_func(x):
# draw batch from x
#X_train, y_train,
n_samples = 40
batch_size = X_train.shape[0]//5
tic = time()
n_neighbors = max(2, int(x[-1]))
weights = x[:-1]
idx = np.random.choice([*range(X_train.shape[0])], size = batch_size, replace = False)
X_batch,y_batch = X_train[idx], y_train[idx]
# transform search space and query vector through weights
X_batch = sparse_mul_row(X_batch, weights)
X_ = sparse_mul_row(X_train, weights)
# make query of idx and wieghts
idx, sim = cos_sim_query(X_batch, X_, n_neighbors = n_neighbors)
# draw samples from y
sampled_idxs = sample_from_dist_array(arr = idx, size = n_samples, weights = sim)[:,:,-1]
samples = np.take(y_train, indices = sampled_idxs, axis = 0)
# calculate variance
loss = bimodal_var(samples).mean()
#loss = -kde_entropy(quantile(y_batch,samples))[0]
toc = time()
print(f'iteration took {round(toc-tic,2)}s | loss: {loss}')
return loss
x0 = np.concatenate([np.ones(X_train.shape[1]), 8*np.ones(1)])
f = train_func
params = minimize(fun = f, x0 = x0,method = 'CG',options = {'maxiter':1000},)
params
```
# Weighted KNN DensityEstimator PyTorch
```
import pytorch_lightning as pl
from torch.utils.data import TensorDataset, DataLoader
import torch
from torch import nn
from torch.autograd import Variable as V
def update_tensor(tensor, new_values):
try:
tensor = tensor.data.fill_(1)*torch.Tensor(new_values)
except: print(tensor.shape, new_values.shape); raise
return tensor
class WeightedKNNTorch(pl.LightningModule):
@property
def weighted_query_space(self,):
return sparse_mul_row(self.raw_query_space,self.weights.clone().detach().numpy()).astype('double')
def __init__(self, X, y, n_neighbors, n_samples, layers = [], batch_size = 256):
super().__init__()
self.weights = torch.ones(X.shape[1], requires_grad = True)
self.weights = nn.Parameter(self.weights, requires_grad=True)
self.raw_query_space = sparse.csr_matrix(X)#X should be a sparse matrix
self.y_ = y
self.n_neighbors = n_neighbors
self.n_samples = n_samples
self.samples_tensor = torch.zeros(batch_size, n_samples, y.shape[-1], requires_grad = True)
def _cos_sim_query(self,query_vector,query_space, n_neighbors):
idx,sim = cos_sim_query(query_vector,query_space,n_neighbors)
#drops the closest match which is the similarity of the row with itself
#maybe n_neighbors > 1 deals with it
#idx, sim = idx[:,1:], sim[:,1:]
return idx,sim
def _sample_values(self, idx, sim, n_samples):
sampled_idxs = sample_from_dist_array(arr = idx, size = n_samples, weights = sim)[:,:,-1]
samples = np.take(self.y_, indices = sampled_idxs, axis = 0)
return update_tensor(self.samples_tensor, samples)
def forward(self, x):
# in lightning, forward defines the prediction/inference actions
x = sparse_mul_row(
x.numpy(),
self.weights.clone().detach().numpy()
).astype('double')
idx, sim = self._cos_sim_query(x,self.weighted_query_space, self.n_neighbors)
samples = self._sample_values(idx,sim,self.n_samples)
update_tensor(self.samples_tensor, samples)
return self.samples_tensor
def training_step(self, batch, batch_idx):
if batch_idx == 0:
self.loss_tensor = torch.ones(1).data.fill_(1000)
self.loss_tensor.requires_grad = True
# training_step defined the train loop. It is independent of forward
X, y = batch
samples = self.forward(X)
loss_tensor = self.loss_tensor
#minimize uncertainty
if batch_idx%2 == 0:
loss = np.array([bimodal_variance(samples.clone().detach()).mean()])
update_tensor(loss_tensor,loss)
#loss = -kde_entropy(quantile(y.numpy(),samples))
else:
#maximize entropy
loss = np.array([bimodal_variance(samples.clone().detach()).mean()])
update_tensor(loss_tensor,loss)
#loss = -kde_entropy(quantile(y.numpy(),samples))
self.log('train_loss', loss_tensor)
return loss_tensor
def configure_optimizers(self):
optimizer = torch.optim.Adam(self.parameters(), lr=1e-3)
return optimizer
model = WeightedKNNTorch(X_train,y_train,50,200)
tensor_x = torch.Tensor(X_train) # transform to torch tensor
tensor_y = torch.Tensor(y_train)
my_dataset = TensorDataset(tensor_x,tensor_y) # create your datset
my_dataloader = DataLoader(my_dataset, batch_size = 256) # create your dataloader
trainer = pl.Trainer(max_epochs=10)
trainer.fit(model, my_dataloader)
i += 45
sample = model.forward(torch.Tensor(X_test[i]))
true_value = y_test[i]
import seaborn as sns
import matplotlib.pyplot as plt
make_distplot(sample,true_value ,y_test)
class LitAutoEncoder(pl.LightningModule):
def training_step(self, batch, batch_idx, optimizer_idx):
# access your optimizers with use_pl_optimizer=False. Default is True
(opt_a, opt_b) = self.optimizers(use_pl_optimizer=True)
loss_a = ...
self.manual_backward(loss_a, opt_a)
opt_a.step()
opt_a.zero_grad()
loss_b = ...
self.manual_backward(loss_b, opt_b, retain_graph=True)
self.manual_backward(loss_b, opt_b)
opt_b.step()
opt_b.zero_grad()
```
|
github_jupyter
|
```
%reload_ext autoreload
%autoreload 2
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_digits, load_iris
from sklearn.model_selection import train_test_split
from pca import pca as MyPCA
```
# Load Digit Dataset
```
digits = load_digits()
def draw_digits(X, y):
fig = plt.figure(1, figsize=(8, 8))
plt.scatter(X[:, 0], X[:, 1],
c=y, edgecolor='none', alpha=0.5,
cmap=plt.cm.get_cmap('Spectral', 10))
plt.xlabel('component 1')
plt.ylabel('component 2')
plt.colorbar()
plt.show();
```
# sklearn PCA
```
pca = PCA(n_components=2, random_state=17).fit(digits.data)
data_pca = pca.transform(digits.data)
pca.explained_variance_ratio_, pca.explained_variance_, pca.singular_values_, pca.components_
data_pca
draw_digits(data_pca, digits.target)
```
# Our Implementation
```
pca1 = MyPCA(n_components=2, solver='svd')
pca1.fit(digits.data)
data_pca1 = pca1.transform(digits.data)
pca1.explained_variance_ratio_, pca1.explained_variance_, pca1.singular_values_, pca1.components_
data_pca1
draw_digits(data_pca1, digits.target)
```
### eig solver
```
pca_eig = MyPCA(n_components=2, solver='eig')
pca_eig.fit(digits.data)
data_eig = pca_eig.transform(digits.data)
pca_eig.explained_variance_ratio_, pca_eig.explained_variance_, pca_eig.singular_values_, pca_eig.components_
data_eig
draw_digits(data_eig, digits.target)
```
# Iris Dataset
Let's try to plot 3 components after PCA.<br>
https://scikit-learn.org/stable/auto_examples/decomposition/plot_pca_iris.html#sphx-glr-auto-examples-decomposition-plot-pca-iris-py
```
from mpl_toolkits.mplot3d import Axes3D
def plot_components(X, y):
fig = plt.figure(1, figsize=(12, 8))
plt.clf()
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
for name, label in [('Setosa', 0), ('Versicolour', 1), ('Virginica', 2)]:
ax.text3D(X[y == label, 0].mean(),
X[y == label, 1].mean() + 1.5,
X[y == label, 2].mean(), name,
horizontalalignment='center',
bbox=dict(alpha=.5, edgecolor='w', facecolor='w'))
# Reorder the labels to have colors matching the cluster results
y = np.choose(y, [1, 2, 0]).astype(np.float)
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y, cmap=plt.cm.nipy_spectral,
edgecolor='k')
ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
plt.show()
iris = load_iris()
X, y = iris.data, iris.target
```
# sklearn
```
pca_3d = PCA(n_components=3, random_state=17).fit(X)
X_3d = pca_3d.transform(X)
plot_components(X_3d, y)
```
# Our's: Solver:svd
```
pca_3d_svd = MyPCA(n_components=3)
pca_3d_svd.fit(X)
X_3d_svd = pca_3d_svd.transform(X)
plot_components(X_3d_svd, y)
```
# Our's: Solver:eig fit_transform
```
pca_3d_eig = MyPCA(n_components=3, solver='eig')
X_3d_eig = pca_3d_eig.fit_transform(X)
plot_components(X_3d_eig, y)
```
|
github_jupyter
|
```
import cv2
import numpy as np
img = cv2.imread("hough.jpg", 0)
print(type(img))
img = np.asarray(img)
#Fetching the rows and columns
rows = len(img)
cols = len(img[0])
```
# Sobel Operator
```
#initializing Sobel Operator
gx_sobel = [[-1,-2,-1],
[0,0,0],
[1,2,1]]
gy_sobel = [[-1,0,1],
[-2,0,2],
[-1,0,1]]
x_sobel = list(map(list,zip(*gx_sobel)))
y_sobel = list(map(list,zip(*gy_sobel)))
```
# Applying Gradient
```
#Used to pad the image
img_x = [[0]*902 for i in range(602)]
img_y= [[0]*902 for i in range(602)]
#Finding the Gradient to distinguish the images clearly. Especially the edges of the images
#Along X Axis
for i in range(1,img.shape[0]-1):
for j in range(1,img.shape[1]-1):
img_x[i][j] = img[i+1][j] - img[i-1][j] #Subtract the neighbouring pixels on the x-axis
#Along Y Axis
for i in range(1,img.shape[0]-1):
for j in range(1,img.shape[1]-1):
img_y[i][j] = img[i][j+1] - img[i][j-1] #Subtract the neighbouring pixels on the y-axis
img_x = np.asarray(img_x)
img_y = np.asarray(img_y)
cv2.imwrite('T3_Images/Gradient_X.png',(img_x))
cv2.imwrite('T3_Images/Gradient_Y.png',(img_y))
```
# Convolution
```
#Convolution
import math
sobelgx = [[0]*img.shape[1] for i in range(img.shape[0])] #Creating empty 2D Lists
sobelgy = [[0]*img.shape[1] for i in range(img.shape[0])]
sobel = [[0]*img.shape[1] for i in range(img.shape[0])]
sobel_add = [[0]*img.shape[1] for i in range(img.shape[0])]
#Multiplying the sobel operator with the corresponding image pixel for that patch of the image to find the covoluted pixel value for (x,y)
for x in range(1, rows-1):
for y in range (1, cols-1):
gx = x_sobel[0][0] * img[x-1][y-1] + x_sobel[0][1] * img[x][y-1] + x_sobel[0][2] * img[x+1][y-1] + (x_sobel[1][0] * img[x-1][y]) + (x_sobel[1][1] * img[x][y]) + (x_sobel[1][2] * img[x+1][y]) + (x_sobel[2][0] * img[x-1][y+1]) + (x_sobel[2][1] * img[x][y+1]) + (x_sobel[2][2] * img[x+1][y+1])
sobelgy[x-1][y-1] = gx
gy = (y_sobel[0][0] * img[x-1][y-1]) + (y_sobel[0][1] * img[x][y-1]) + (y_sobel[0][2] * img[x+1][y-1]) + (y_sobel[1][0] * img[x-1][y]) + (y_sobel[1][1] * img[x][y]) + (y_sobel[1][2] * img[x+1][y]) + (y_sobel[2][0] * img[x-1][y+1]) + (y_sobel[2][1] * img[x][y+1]) + (y_sobel[2][2] * img[x+1][y+1])
sobelgx[x-1][y-1] = gy
sobel[x-1][y-1] = math.sqrt((gx*gx + gy*gy)) #Combining the outputs of the Sobel-X and Sobel-Y by Root of Squared Sum.
sobel_add[x-1][y-1] = (gx + gy)/2 #Combining the outputs of the Sobel-x and Sobel-Y by adding the values
cv2.imwrite('T3_Images/Sobel_X.png',np.asarray(sobelgx))
cv2.imwrite('T3_Images/Sobel_Y.png',np.asarray(sobelgy))
cv2.imwrite('T3_Images/Sobel.png',np.asarray(sobel))
cv2.imwrite('T3_Images/Sobel_add.png',np.asarray(sobel_add))
```
# Normalization
```
theta = []
for i in range(0,360):
theta.append(i)
theta = np.asarray(theta)
img = cv2.imread("T3_Images/Sobel_Y.png", 0)
print (img)
R = 22
thres_img = np.zeros((img.shape[0], img.shape[1]))
for i in range(img.shape[0]):
for j in range(img.shape[1]):
if img[i][j] > 100:
thres_img[i][j] = 255
thres_img = np.asarray(thres_img)
cv2.imwrite("T3_Images/T_sobel.jpg", thres_img)
thres_img.shape, img.shape
def circumference_point(x,y, theta, R):
points = []
for t in theta:
a = int((y - R*np.cos(math.radians(t))))
b = int((x - R*np.sin(math.radians(t))))
points.append([a,b])
return points
def accumulator_matrix(thres_img,theta, R):
acc = np.zeros((2*thres_img.shape[0], 2*thres_img.shape[1]))
for x in range(thres_img.shape[0]):
for y in range(thres_img.shape[1]):
if thres_img[x][y] == 255:
circum_points = circumference_point(x,y,theta,R)
#print (circum_points)
for point in circum_points:
acc[point[0]][point[1]] += 1
cv2.imwrite("Bonus_accumulator.jpg",acc)
return acc
import math
acc = accumulator_matrix(thres_img, theta, R)
cv2.imwrite("T3_Images/Bonus_acc.jpg",acc)
# sobelgx = cv2.imread("red_img.jpg", 0)
# cv2.imwrite("gray_red_img.jpg",sobelgx)
def max_indices(arr, k):
'''
Returns the indices of the k first largest elements of arr
(in descending order in values)
'''
assert k <= arr.size, 'k should be smaller or equal to the array size'
arr_ = arr.astype(float) # make a copy of arr
max_idxs = []
for _ in range(k):
max_element = np.max(arr_)
if np.isinf(max_element):
break
else:
idx = np.where(arr_ == max_element)
max_idxs.append(idx)
arr_[idx] = -np.inf
return convert(np.asarray(max_idxs))
def convert(k):
edge_points = []
for i in range(k.shape[0]):
n = k[i][0].shape[0]
if n>1:
for j in range(n):
edge_points.append([k[i][0][j], k[i][1][j]])
else:
edge_points.append([k[i][0][0], k[i][1][0]])
return edge_points
e = []
edge_points = max_indices(acc, 60)
#edge_points
for i in range(len(edge_points)):
if (i in range(50,56)):
print (i)
else:
print (i)
e.append(edge_points[i])
print (len(e), len(edge_points))
edge_points = e
len(edge_points)
e
o_img = cv2.imread("hough.jpg")
print (edge_points[0][0], edge_points[0][1])
for i in range(len(edge_points)):
cv2.circle(o_img, (edge_points[i][0],edge_points[i][1]), R, (0,255,0))
cv2.imwrite("T3_Images/circle.jpg",o_img)
```
|
github_jupyter
|
**Important**: This notebook is different from the other as it directly calls **ImageJ Kappa plugin** using the [`scyjava` ImageJ brige](https://github.com/scijava/scyjava).
Since Kappa uses ImageJ1 features, you might not be able to run this notebook on an headless machine (need to be tested).
```
from pathlib import Path
import pandas as pd
import numpy as np
from tqdm.auto import tqdm
import sys; sys.path.append("../../")
import pykappa
# Init ImageJ with Fiji plugins
# It can take a while if Java artifacts are not yet cached.
import imagej
java_deps = []
java_deps.append('org.scijava:Kappa:1.7.1')
ij = imagej.init("+".join(java_deps), headless=False)
import jnius
# Load Java classes
KappaFrame = jnius.autoclass('sc.fiji.kappa.gui.KappaFrame')
CurvesExporter = jnius.autoclass('sc.fiji.kappa.gui.CurvesExporter')
# Load ImageJ services
dsio = ij.context.getService(jnius.autoclass('io.scif.services.DatasetIOService'))
dsio = jnius.cast('io.scif.services.DatasetIOService', dsio)
# Set data path
data_dir = Path("/home/hadim/.data/Postdoc/Kappa/spiral_curve_SDM/")
# Pixel size used when fixed
fixed_pixel_size = 0.16
# Used to select pixels around the initialization curves
base_radius_um = 1.6
enable_control_points_adjustment = True
# "Point Distance Minimization" or "Squared Distance Minimization"
if '_SDM' in data_dir.name:
fitting_algorithm = "Squared Distance Minimization"
else:
fitting_algorithm = "Point Distance Minimization"
fitting_algorithm
experiment_names = ['variable_snr', 'variable_initial_position', 'variable_pixel_size', 'variable_psf_size']
experiment_names = ['variable_psf_size']
for experiment_name in tqdm(experiment_names, total=len(experiment_names)):
experiment_path = data_dir / experiment_name
fnames = sorted(list(experiment_path.glob("*.tif")))
n = len(fnames)
for fname in tqdm(fnames, total=n, leave=False):
tqdm.write(str(fname))
kappa_path = fname.with_suffix(".kapp")
assert kappa_path.exists(), f'{kappa_path} does not exist.'
curvatures_path = fname.with_suffix(".csv")
if not curvatures_path.is_file():
frame = KappaFrame(ij.context)
frame.getKappaMenubar().openImageFile(str(fname))
frame.resetCurves()
frame.getKappaMenubar().loadCurveFile(str(kappa_path))
frame.getCurves().setAllSelected()
# Compute threshold according to the image
dataset = dsio.open(str(fname))
mean = ij.op().stats().mean(dataset).getRealDouble()
std = ij.op().stats().stdDev(dataset).getRealDouble()
threshold = int(mean + std * 2)
# Used fixed pixel size or the one in the filename
if fname.stem.startswith('pixel_size'):
pixel_size = float(fname.stem.split("_")[-2])
if experiment_name == 'variable_psf_size':
pixel_size = 0.01
else:
pixel_size = fixed_pixel_size
base_radius = int(np.round(base_radius_um / pixel_size))
# Set curve fitting parameters
frame.setEnableCtrlPtAdjustment(enable_control_points_adjustment)
frame.setFittingAlgorithm(fitting_algorithm)
frame.getInfoPanel().thresholdRadiusSpinner.setValue(ij.py.to_java(base_radius))
frame.getInfoPanel().thresholdSlider.setValue(threshold)
frame.getInfoPanel().updateConversionField(str(pixel_size))
# Fit the curves
frame.fitCurves()
# Save fitted curves
frame.getKappaMenubar().saveCurveFile(str(fname.with_suffix(".FITTED.kapp")))
# Export results
exporter = CurvesExporter(frame)
exporter.exportToFile(str(curvatures_path), False)
# Remove duplicate rows during CSV export.
df = pd.read_csv(curvatures_path)
df = df.drop_duplicates()
df.to_csv(curvatures_path)
0.13**2
```
|
github_jupyter
|
# Classification 2
## Exercise 1: Exploratory Data Analysis
### Overview
The objective of this course is to build models to predict customer churn for a fictitious telco company. Before we start creating models, let's begin by having a closer look at our data and doing some basic data wrangling.
Go through this notebook and modify the code accordingly (i.e. #TASK) based on the text and/or the comments.
### Data
Download data from here:
https://public.dhe.ibm.com/software/data/sw-library/cognos/mobile/C11/data/Telco_customer_churn.xlsx
Description of data (for a newer version)
https://community.ibm.com/community/user/businessanalytics/blogs/steven-macko/2019/07/11/telco-customer-churn-1113
### Importing Libraries
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# TASK: Import visualization libraries, matplotlib and seaborn using standard aliases plt and sns respectively
import warnings
# silence all warnings
warnings.filterwarnings("ignore")
# plotting settings
plt.style.use(['seaborn-paper'])
plt.rcParams['font.family'] = 'helvetica'
```
### Reading in the Data
```
# TASK: Read in the Excel file. Use the parameter na_values=" " to convert any empty cells to a NA value.
# You may also need to use parameter engine='openpyxl') in newer versions of pandas if you encounter an XLRD error.
data = pd.read_excel('../../data/raw/Telco_customer_churn.xlsx', na_values='NA',engine='openpyxl') # TASK: Use pandas to read in an Excel file.
data.head()
data.info()
# Define columns to keep and filter the original dataset
cols_to_keep = ['CustomerID', 'Gender', 'Senior Citizen', 'Partner', 'Dependents', 'Tenure Months', 'Phone Service', 'Multiple Lines', 'Internet Service', 'Online Security', 'Online Backup', 'Device Protection', 'Tech Support', 'Streaming TV', 'Streaming Movies', 'Contract', 'Paperless Billing', 'Payment Method', 'Monthly Charges', 'Total Charges', 'Churn Label']
data = data[cols_to_keep]
# TASK: Rename the multi-worded columns to remove the space
# HINT: You can either manually remove the spaces in the column name list or use a loop to remove the space
data.columns = [('').join(col.split(' ')) for col in data.columns]
data.columns
```
### Basic Information
```
# TASK: Display the number of rows and columns for the dataset
print("Rows & Columns: {}".format(data.shape))
data.info()
# TASK: Display the datatypes for the columns in the dataframe i.e. use the dtypes variable
# How many columns are numerical and how many are non-numerical
obj_cols = data.select_dtypes(include="object").columns
print("Number of non-numerical columns: {}".format(len(obj_cols)))
num_cols = data.select_dtypes(exclude="object").columns
print("Number of numerical columns: {}".format(len(num_cols)))
# check that cat + num = total
assert(len(obj_cols) + len(num_cols) == len(data.columns))
data.dtypes
# TASK: use count() on the dataframe to count the number of entries for each of the column. Are there any columns with missing values?
print(data.count())
# to check for missing %
print("\n")
print(data.isnull().mean()) # TotalCharges has null values, but relatively small 0.001562
# ChurnReason has ~73% mising values
# TASK: Use nunique() on the dataframe to count the number of unique values for each of the columns
print(data.nunique())
data.iloc[20,2:]
data.head(10)
```
TASK: Display first few values of the dataframe
Based on this and the previous display, how would you describe the columns with a small number (less than 10) of unique values?
Based from above, we can say that all the customers are in the same country and state. Most of the columns are categorical like <code>Gender</code> with *Male* or *Female* values, <code>SeniorCitizen</code> with *Yes* or *No* values, <code>ChurnLabel</code> with Yes or No with equivalent <code>ChrunValue</code> of 1 or 0 respectively, etc. It can be observed that there are columns with many different unique values such as the <code>CustomerID</code> which makes sense as each customer should have its own unique id. <code>ZipCode</code>, <code>Latitude</code> and <code>Longitude</code> which have the same number of possible values make sense as the state has the limited number of zip codes.
We have also observed that there are continuous values in the columns: <code>TotalCharges</code> and <code>MothlyCharges</code> and discrete values in the column <code>TenureMonths</code> which indicates the number of months that the customer use the Telco service.
```
# TASK: Let's analyze the values for the categorical features (columns with less than 10 unique values)
for id, row in data.nunique().iteritems(): # this counts the number of unique values for each feature and returns the result as a dictionary
if(row < 10):
# TASK: Print out the unique values for the feature
print("{}\t{}".format(id, row))
# For columns with 3 or 4 unique values, display them to see if they make sense
for col in ['MultipleLines', 'InternetService', 'OnlineSecurity', 'OnlineBackup', 'DeviceProtection', 'TechSupport', 'StreamingTV', 'StreamingMovies', 'Contract', "PaymentMethod"]:
print("{} : {}".format(col, np.unique(data[col].values)))
```
**Observations**
- The value 'No phone service' found in MultipleLines is already captured by the PhoneService feature ('No' value)
- The value 'No internet service' found in the several features is already captured by InternetService feature ('No' value)
- Values that are longer or more complex may need to be simplified.
Conclusion: These values can be considered duplicated information as they are found in the PhoneService and InternetService features. There are several options to consider here:
- Retain all features and values as is
- Convert the 'No Internet Service'/'No phone service' to 'No' in the features as PhoneService and InternetService features has already captured this information
- Remove the PhoneService feature as MultipleLines feature has this information. To remove the InternetService feature, we would have to 'fold in' the values in the other features e.g. the values for OnlineSecurity could be changed to ['DSL_No','DSL_Yes','FiberOptic_No','FiberOptic_Yes','No internet service']
For this course, we will be using the second option (without justification). You are encouraged to test the others options during modelling to see if there are any impact.
### Data Wrangling
Based on the discoveries made above, we will be modifying our data before continuing the exploration.
```
# Replace 'No phone service'
data['MultipleLines'] = data['MultipleLines'].replace({'No phone service':'No'})
# TASK: Replace 'No internet service'
for col in ['OnlineSecurity', 'OnlineBackup', 'DeviceProtection', 'TechSupport', 'StreamingTV', 'StreamingMovies']:
# similar to the operation for 'No phone service' above
data[col] = data[col].replace({'No internet service':'No'})
# Simplify the values made up of phrases
data['PaymentMethod'] = data['PaymentMethod'].replace({
'Bank transfer (automatic)':'transfer',
'Credit card (automatic)':'creditcard',
'Electronic check':'echeck',
'Mailed check':'mcheck'
})
data['InternetService'] = data['InternetService'].replace({
'Fiber optic':'FiberOptic'
})
data['Contract'] = data['Contract'].replace({
'Month-to-month':'M2M',
'One year':'OneYear',
'Two year':'TwoYear'
})
# Remove the rows with empty TotalCharges value
data = data[data["TotalCharges"].notnull()]
data.shape
data.info()
# we can see that the TotalCharges column is of object data type, we must change it into float
# After data wrangling, repeat prints
print("Rows & Columns: {}".format(data.shape))
print("################################################")
# Number of unique values for each of the columns
print(data.nunique())
print("################################################")
# Check the data types
print(data.dtypes)
print("################################################")
# Display first few values
print(data.head())
# Randomly display 1 row from the dataframe
print(data.sample(n=1).iloc[0])
# TASK: Save the data as a CSV fiile
data.to_csv("../../data/interim/0telco_churn.csv", index=False)
```
### Additional Exploration
**TASK:** This is the open-ended section of the exercise. Use any exploration techniques that you know to further explore and understand your data. We expect a number of visualizations that can show the relationships between features as well as between features and the outcome variable 'ChurnLabel'. Some of the questions in the quiz may require you to perform additional analyses.
From the initial exploration above, the following questions have been answered:
* What is the shape of your data? Number of rows and columns.
* How many of the columns are numerical and how many are categorical?
* What is the name of the column to be predicted?
* For the numerical columns, how many missing values are there for each column?
* For the categorical columns, how many missing values are there for each column?
However, we will still need to do further exploration using visualizations to better understand the data using the following questions as the goal:
* For the numerical columns, what does the distributions look like?
* How are the various attributes correlated to the outcome variable?
* What visualizations can you use to highlight outliers in the data?
**Recapping on the columns**
Before we begin to decide on the type of visualisations to use to aim our understanding, let's recap on the columns we have and the data type of it.
```
print("Categorical columns: {}\n".format(obj_cols))
print("Numerical columns: {}\n".format(num_cols))
print("Total columns: {} categorical, {} numerical.".format(len(obj_cols), len(num_cols)))
```
**Utilities Functions**
Let's define some helper functions that will help us iterate through all the columns with same datatype.
```
# Example: Look at Churn vs MonthCharges
plt.clf()
for label in ['Yes','No']:
subset = data[data.ChurnLabel==label]
# Draw the density plot
sns.distplot(subset['MonthlyCharges'], hist = False, kde = True,
kde_kws = {'linewidth': 3, 'shade':True},
label = label)
# Plot formatting
plt.legend(prop={'size': 16}, title = 'ChurnLabel')
plt.title('Density Plot with ChurnLabel')
plt.xlabel('') # Monthly Charges
plt.ylabel('Density')
plt.show()
# Additional Exploration
```
|
github_jupyter
|
```
import util
import jax
import jax.numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import numpy as base_np
from epiweeks import Week, Year
start = '2020-03-15'
forecast_start = '2020-04-19'
num_weeks = 8
data = util.load_state_data()
places = sorted(list(data.keys()))
#places = ['AK', 'AL']
allQuantiles = [0.01,0.025]+list(np.arange(0.05,0.95+0.05,0.05)) + [0.975,0.99]
forecast_date = pd.to_datetime('2020-04-19')
currentEpiWeek = Week.fromdate(forecast_date) - 1
forecast = {'quantile':[], 'value':[], 'type':[], 'location':[], 'target':[]}
print (currentEpiWeek)
for place in places:
prior_samples, mcmc_samples, post_pred_samples = util.load_samples(place, path='out')
forecast_samples = post_pred_samples['z_future']
t = pd.date_range(start=forecast_start, periods=forecast_samples.shape[1], freq='D')
weekly_df = pd.DataFrame(index=t, data=np.transpose(forecast_samples)).resample("1w",label='right').last()
weekly_df[weekly_df<0.] = 0.
for time, samples in weekly_df.iterrows():
for q in allQuantiles:
deathPrediction = base_np.percentile(samples,q*100)
forecast["quantile"].append("{:.3f}".format(q))
forecast["value"].append(deathPrediction)
forecast["type"].append("quantile")
forecast["location"].append(place)
horizon_date = Week.fromdate(time)
week_ahead = horizon_date.week - currentEpiWeek.week
forecast["target"].append("{:d} wk ahead cum death".format(week_ahead))
currentEpiWeek_datetime = currentEpiWeek.startdate()
forecast["forecast_date"] = "{:4d}-{:02d}-{:02d}".format(currentEpiWeek_datetime.year,currentEpiWeek_datetime.month,currentEpiWeek_datetime.day)
if q==0.50:
forecast["quantile"].append("NA")
forecast["value"].append(deathPrediction)
forecast["type"].append("point")
forecast["location"].append(place)
forecast["target"].append("{:d} wk ahead cum death".format(week_ahead))
forecast["forecast_date"] = "{:4d}-{:02d}-{:02d}".format(currentEpiWeek_datetime.year,currentEpiWeek_datetime.month,currentEpiWeek_datetime.day)
#base_np.quantile(hosp,axis=1,q=allQuantiles)
forecast = pd.DataFrame(forecast)
forecast.loc[forecast.type=="point"]
fips_codes = pd.read_csv('/Users/gcgibson/covid19-forecast-hub/template/state_fips_codes.csv')
df_truth = forecast.merge(fips_codes, left_on='location', right_on='state', how='left')
df_truth["state_code"] = df_truth["state_code"].astype(int)
df_truth = df_truth[["quantile", "value", "type", "state_code","target","forecast_date"]]
df_truth = df_truth.rename(columns={"state_code": "location"})
import datetime
df_truth['location'] = df_truth['location'].apply(lambda x: '{0:0>2}'.format(x))
#df_truth['forecast_date'] = datetime.datetime(2020, 4, 19)
df_truth.to_csv(f'out/sub.csv', float_format="%.0f")
df_truth
```
|
github_jupyter
|
# Estimating the biomass of terrestrial arthropods
To estimate the biomass of terrestrial arthropods, we rely on two parallel methods - a method based on average biomass densities of arthropods extrapolated to the global ice-free land surface, and a method based on estimates of the average carbon content of a characteristic arthropod and the total number of terrestrial arthropods.
## Average biomass densities method
We collected values from the literature on the biomass densities of arthropods per unit area. We assume, based on [Stork et al.](http://dx.doi.org/10.1007/978-94-009-1685-2_1), most of the biomass is located in the soil, litter or in the canopy of trees. We thus estimate a mean biomass density of arhtropods in soil, litter and in canopies, sum those biomass densities and apply them across the entire ice-free land surface.
### Litter arthropod biomass
We complied a list of values from several different habitats. Most of the measurements are from forests and savannas. For some of the older studies, we did not have access to the original data, but to a summary of the data made by two main studies: [Gist & Crossley](http://dx.doi.org/10.2307/2424109) and [Brockie & Moeed](http://dx.doi.org/10.1007/BF00377108). Here is a sample of the data from Gist & Grossley:
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gmean
import sys
sys.path.insert(0, '../../statistics_helper/')
from CI_helper import *
pd.options.display.float_format = '{:,.1f}'.format
# Load global stocks data
gc_data = pd.read_excel('terrestrial_arthropods_data.xlsx','Gist & Crossley',skiprows=1)
gc_data.head()
```
Here is a sample from Brockie & Moeed:
```
bm_data = pd.read_excel('terrestrial_arthropods_data.xlsx','Brockie & Moeed',skiprows=1)
bm_data.head()
```
We calculate the sum of biomass of all the groups of arthropods in each study to provide an estimate for the total biomass density of arthropods in litter:
```
gc_study = gc_data.groupby('Study').sum()
bm_study = bm_data.groupby('Study').sum()
print('The estimate from Brockie & Moeed:')
bm_study
print('The estimate from Gist & Crossley:')
gc_study
```
In cases where data is coflicting between the two studies, we calculate the mean. We merge the data from the papers to generate a list of estimates on the total biomass density of arhtropods
```
# Concat the data from the two studies
conc = pd.concat([gc_study,bm_study])
conc_mean = conc.groupby(conc.index).mean()
conc_mean
```
We calculate from the dry weight and wet weight estimates the biomass density in g C $m^{-2}$ by assuming 70% water content and 50% carbon in dry mass:
```
# Fill places with no dry weight estimate with 30% of the wet weight estimate
conc_mean['Dry weight [g m^-2]'].fillna(conc_mean['Wet weight [g m^-2]']*0.3,inplace=True)
# Calculate carbon biomass as 50% of dry weight
conc_mean['Biomass density [g C m^-2]'] = conc_mean['Dry weight [g m^-2]']/2
conc_mean['Biomass density [g C m^-2]']
```
We calculate the geometric mean of the estimates from the different studies as our best estimate of the biomass density of litter arthropods.
```
litter_biomass_density = gmean(conc_mean.iloc[0:5,3])
print('Our best estimate for the biomass density of arthropods in litter is ≈%.0f g C m^-2' %litter_biomass_density)
```
### Soil arthropod biomass
As our source for estimating the biomass of soil arthropods, we use these data collected from the literature, which are detailed below:
```
# Load additional data
soil_data = pd.read_excel('terrestrial_arthropods_data.xlsx','Soil',index_col='Reference')
soil_data
```
We calculate the geometric mean of the estimate for the biomass density of arthropods in soils:
```
# Calculate the geometric mean of the estimates of the biomass density of soil arthropods
soil_biomass_density = gmean(soil_data['Biomass density [g C m^-2]'])
print('Our best estimate for the biomass density of arthropods in soils is ≈%.0f g C m^-2' %soil_biomass_density)
```
If we sum the biomass density of soil and litter arthropods, we arrive at an estimate of ≈2 g C m^-2, which is inline with the data from Kitazawa et al. of 1-2 g C m^-2.
### Canopy arthropod biomass
Data on the biomass density of canopy arthropods is much less abundant. We extracted from the literature the following values:
```
# Load the data on the biomass density of canopy arthropods
canopy_data = pd.read_excel('terrestrial_arthropods_data.xlsx', 'Canopy',index_col='Reference')
canopy_data
```
We calculate the geometric mean of the estimates for the biomass density of arthropods in canopies:
```
# Calculate the geometric mean of the estimates of biomass densitiy of canopy arthropods
canopy_biomass_density = gmean(canopy_data['Biomass density [g C m^-2]'])
print('Our best estimate for the biomass density of arthropods in canopies is ≈%.1f g C m^-2' %canopy_biomass_density)
```
To generate our best estimate for the biomass of arthropods using estimates of biomass densities, we sum the estimates for the biomass density of arthropods in soils and in canopies, and apply this density over the entire ice-free land surface of $1.3×10^{14} \: m^2$:
```
# Sum the biomass densities of arthropods in soils and in canopies
total_denisty = litter_biomass_density+soil_biomass_density+canopy_biomass_density
# Apply the average biomass density across the entire ice-free land surface
method1_estimate = total_denisty*1.3e14
print('Our best estimate for the biomass of terrestrial arthropods using average biomass densities is ≈%.1f Gt C' %(method1_estimate/1e15))
```
## Average carbon content method
In this method, in order to estimate the total biomass of arthropods, we calculate the carbon content of a characteristic arthropod, and multiply this carbon content by an estimate for the total number of arthropods.
We rely both on data from Gist & Crossley which detail the total number of arthropods per unit area as well as the total biomass of arthropods per unit area for serveal studies. Form this data we can calculate the characteristic carbon content of a single arthropod assuming 50% carbon in dry mass:
```
pd.options.display.float_format = '{:,.1e}'.format
# Calculate the carbon content of a single arthropod by dividing the dry weight by 2 (assuming 50% carbon in
# dry weight) and dividing the result by the total number of individuals
gc_study['Carbon content [g C per individual]'] = gc_study['Dry weight [g m^-2]']/2/gc_study['Density of individuals [N m^-2]']
gc_study
```
We combine the data from these studies with data from additional sources detailed below:
```
# Load additional data sources
other_carbon_content_data = pd.read_excel('terrestrial_arthropods_data.xlsx', 'Carbon content',index_col='Reference')
other_carbon_content_data
```
We calculate the geometric mean of the estimates from the difference studies and use it as our best estimate for the carbon content of a characteristic arthropod:
```
# Calculate the geometric mean of the estimates from the different studies on the average carbon content of a single arthropod.
average_carbon_content = gmean(pd.concat([other_carbon_content_data,gc_study])['Carbon content [g C per individual]'])
print('Our best estimate for the carbon content of a characteristic arthropod is %.1e g C' % average_carbon_content)
```
To estimate the total biomass of arthropods using the characteristic carbon content method, we multiply our best estiamte of the carbon content of a single arthropod by an estimate of the total number of arthropods made by [Williams](http://dx.doi.org/10.1086/282115). Williams estiamted a total of $~10^{18}$ individual insects in soils. We assume this estimate of the total number of insects is close to the total number of arthropods (noting that in this estimate Williams also included collembola which back in 1960 were considered insects, and are usually very numerous because of their small size). To estimate the total biomass of arthropods, we multiply the carbon content of a single arthropod by the the estimate for the total number of arthropods:
```
# Total number of insects estimated by Williams
tot_num_arthropods = 1e18
# Calculate the total biomass of arthropods
method2_estimate = average_carbon_content*tot_num_arthropods
print('Our best estimate for the biomass of terrestrial arthropods using average biomass densities is ≈%.1f Gt C' %(method2_estimate/1e15))
```
Our best estimate for the biomass of arthropods is the geometric mean of the estimates from the two methods:
```
# Calculate the geometric mean of the estimates using the two methods
best_estimate = gmean([method1_estimate,method2_estimate])
print('Our best estimate for the biomass of terrestrial arthropods is ≈%.1f Gt C' %(best_estimate/1e15))
```
# Uncertainty analysis
To assess the uncertainty associated with the estimate of the biomass of terrestrial arthropods, we compile a collection of the different sources of uncertainty, and combine them to project the total uncertainty. We survey the interstudy uncertainty for estimates within each method, the total uncertainty of each method and the uncertainty of the geometric mean of the values from the two methods.
## Average biomass densities method
We calculate the 95% confidence interval for the geometric mean of the biomass densities reported for soil and canopy arthropods:
```
litter_CI = geo_CI_calc(conc_mean['Biomass density [g C m^-2]'])
soil_CI = geo_CI_calc(soil_data['Biomass density [g C m^-2]'])
canopy_CI = geo_CI_calc(canopy_data['Biomass density [g C m^-2]'])
print('The 95 percent confidence interval for the average biomass density of soil arthropods is ≈%.1f-fold' %litter_CI)
print('The 95 percent confidence interval for the average biomass density of soil arthropods is ≈%.1f-fold' %soil_CI)
print('The 95 percent confidence interval for the average biomass density of canopy arthropods is ≈%.1f-fold' %canopy_CI)
```
To estimate the uncertainty of the global biomass estimate using the average biomass density method, we propagate the uncertainties of the soil and canopy biomass density:
```
method1_CI = CI_sum_prop(estimates=np.array([litter_biomass_density,soil_biomass_density,canopy_biomass_density]),mul_CIs=np.array([litter_CI,soil_CI,canopy_CI]))
print('The 95 percent confidence interval biomass of arthropods using the biomass densities method is ≈%.1f-fold' %method1_CI)
```
## Average carbon content method
As a measure of the uncertainty of the estimate of the total biomass of arthropods using the average carbon content method, we calculate the 95% confidence interval of the geometric mean of the estimates from different studies of the carbon content of a single arthropod:
```
carbon_content_CI = geo_CI_calc(pd.concat([other_carbon_content_data,gc_study])['Carbon content [g C per individual]'])
print('The 95 percent confidence interval of the carbon content of a single arthropod is ≈%.1f-fold' %carbon_content_CI)
```
We combine this uncertainty of the average carbon content of a single arthropod with the uncertainty reported in Williams on the total number of insects of about one order of magnitude. This provides us with a measure of the uncertainty of the estimate of the biomass of arthropods using the average carbon content method.
```
# The uncertainty of the total number of insects from Williams
tot_num_arthropods_CI = 10
# Combine the uncertainties of the average carbon content of a single arthropod and the uncertainty of
# the total number of arthropods
method2_CI = CI_prod_prop(np.array([carbon_content_CI,tot_num_arthropods_CI]))
print('The 95 percent confidence interval biomass of arthropods using the average carbon content method is ≈%.1f-fold' %method2_CI)
```
## Inter-method uncertainty
We calculate the 95% conficence interval of the geometric mean of the estimates of the biomass of arthropods using the average biomass density or the average carbon content:
```
inter_CI = geo_CI_calc(np.array([method1_estimate,method2_estimate]))
print('The inter-method uncertainty of the geometric mean of the estimates of the biomass of arthropods is ≈%.1f' % inter_CI)
```
As our best projection for the uncertainty associated with the estimate of the biomass of terrestrial arthropods, we take the highest uncertainty among the collection of uncertainties we generate, which is the ≈15-fold uncertainty of the average carbon content method.
```
mul_CI = np.max([inter_CI,method1_CI,method2_CI])
print('Our best projection for the uncertainty associated with the estimate of the biomass of terrestrial arthropods is ≈%.1f-fold' %mul_CI)
```
## The biomass of termites
As we state in the Supplementary Information, there are some groups of terrestrial arthropods for which better estimates are available. An example is the biomass of termites. We use the data in [Sanderson](http://dx.doi.org/10.1029/96GB01893) to estimate the global biomass of termites:
```
# Load termite data
termite_data = pd.read_excel('terrestrial_arthropods_data.xlsx', 'Sanderson', skiprows=1, index_col=0)
# Multiply biomass density by biome area and sum over biomes
termite_biomass = (termite_data['Area [m^2]']* termite_data['Biomass density [g wet weight m^-2]']).sum()
# Calculate carbon mass assuming carbon is 15% of wet weight
termite_biomass *= 0.15
print('The estimate of the total biomass of termites based on Sanderson is ≈%.2f Gt C' %(termite_biomass/1e15))
```
|
github_jupyter
|
# Pandas Exercise
```
import matplotlib.pyplot as plt
import numpy as np
np.random.seed(0)
import pandas as pd
def df_info(df: pd.DataFrame) -> None:
return df.head(n=20).style
```
## Cars Auction Dataset
| Feature | Type | Description |
|--------------|---------|-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| Price | Integer | The sale price of the vehicle in the ad |
| Years | Integer | The vehicle registration year |
| Brand | String | The brand of car |
| Model | String | model of the vehicle |
| Color | String | Color of the vehicle |
| State/City | String | The location in which the car is being available for purchase |
| Mileage | Float | miles traveled by vehicle |
| Title Status | String | This feature included binary classification, which are clean title vehicles and salvage insurance |
| Condition | String | Time |
```
df = pd.read_csv("../data/USA_cars_datasets.csv")
print(df.columns)
df.head()
```
## Exercise 1
- Get the counts for the us states
## Exercise 2
- Get all cars from the state of new mexico
## Exercise 3
- Compute the mean mileage of all cars from new york
## Exercise 4
- Remove all entries where the year is below 2019
## Exercise 5
- Replace all color values by the first character of the color name
E.g.: 'blue' => 'b'
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.