code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
import pandas as pd
import numpy as np
# +
base = pd.read_csv('base_info.csv')
container = pd.read_csv('container_info.csv')
base.loc[:,'bid'] = base['id']
del base['id']
container = container.dropna()
container = container[container['service_name'] != 'NONE_NONE.0']
del container['id']
# -
print base.columns
base.info()
# +
base.loc[:,'sec'] = np.array((base['bid'] - 253) / 3, dtype=np.int32) * 10
base.loc[base.node_ip=='172.16.1.90','node_id'] = '0'
base.loc[base.node_ip=='172.16.1.91','node_id'] = '1'
base.loc[base.node_ip=='172.16.1.101','node_id'] = '2'
base.loc[:,'hour'] = np.array(base['sec'] / 3600, dtype=np.int32)
base.loc[:,'min'] = np.array(base['sec'] / 60, dtype=np.int32)
base.loc[:,'mem_rate'] = base['mem_use'] / base['mem_total']
base.loc[:,'disk_rate'] = base['disk_use'] / base['disk_total']
base
# -
# +
container.loc[:, "cpu"] = container['cpu'].replace(r"\%", '', regex = True).astype(np.float32)
container.loc[:, "mem"] = container['mem'].replace(r"\%", '', regex = True).astype(np.float32)
# 切割特征
container.loc[:, "mem_use"] = container['mem_limit'].replace(r"B\/\d*\.?[0-9]*(Gi|G|M|k)?B", 'B', regex = True)
container.loc[:, "mem_total"] = container['mem_limit'].replace(r".*B\/", '', regex = True)
# netio中包含科学计数法得数值:1.4MB/1e+03kB
container.loc[:, "net_in"] = container['netio'].replace(r"B\/.*(Gi|G|M|k)?B", 'B', regex = True)
container.loc[:, "net_out"] = container['netio'].replace(r".*B\/", '', regex = True)
container.loc[:, "disk_in"] = container['io'].replace(r"B\/\d*\.?[0-9]*(Gi|G|M|k)?B", 'B', regex = True)
container.loc[:, "disk_out"] = container['io'].replace(r".*B\/", '', regex = True)
# 统一特征单位
# 此时container的数据类型大多为object,需要转换为float32
cols = ['mem_use','mem_total','net_in','net_out','disk_in','disk_out']
for col in cols:
# 注意科学计数表示,提取单位
temp_unit = container[col].replace(r'.*[0-9]+','',regex=True)
# 默认特征项单位为k
temp_unit[temp_unit=='B'] = 0.001
temp_unit[temp_unit=='MiB'] = 1024
temp_unit[temp_unit=='GiB'] = 1024*1024
temp_unit[temp_unit=='kB'] = 1
temp_unit[temp_unit=='MB'] = 1000
temp_unit[temp_unit=='GB'] = 1000*1000
# 提取数值
temp_num = container[col].replace(r'(Gi|G|Mi|M|k)?B','',regex=True).astype(np.float32)
# 数值乘以转化后的单位得到真实的数值大小
container.loc[:,col] = temp_num * temp_unit.astype(np.float32)
index = container.groupby('service_name').size().index
print index
for i in range(len(index)):
container["service_name"].replace(index[i], i, inplace=True)
#del container['netio'],container['mem_limit'],container['io']
container
# -
container.columns
# +
# 合并两个表
new_df = pd.merge(container, base, on=['bid'], how='left')
# 由于没有container_id,缺乏对sample的唯一标识,合并相同<service, sec>的样例
#avg_cols = ['cpu','mem','mem_use','mem_total','net_in','net_out','disk_in','disk_out']
id_cols = ['sec','service_name']
# 一个时间点只存在一个相同service_name 记录,对多个记录取平均值
new_df = new_df.groupby(id_cols).mean().reset_index()
#new_df.groupby(['sec','service_name']).size()
new_df
# -
new_df.columns
# 查看各属性得分布情况,没变化得属性不进行特征提取
for col in new_df.columns:
print new_df[new_df.service_name==0][col].describe()
print '*'*10
# +
import time
def feat_last_time(df_data, col, time_col, interval):
# 上一个时间点的特征值
# e.g. last_10_sec_net_in_x
new_col = 'last_'+str(interval)+'_'+time_col+'_'+col
print 'Parsing %s ...'%new_col
df_data.loc[:, new_col] = 0.0
for service in set(df_data.service_name):
cond = (df_data.service_name==service)
t1 = [] # 存储过去秒数
t2 = [] # 存储当前秒数
bi = df_data[cond].index[0]
for i in df_data[cond].index[1:]:
if df_data.loc[bi,'sec'] + interval == df_data.loc[i,'sec']:
# 检测相同服务且相隔10秒的数据行
t1.append(df_data.loc[bi,'sec'])
t2.append(df_data.loc[i,'sec'])
bi = i
cond1 = cond&(df_data.sec.isin(t1))
cond2 = cond&(df_data.sec.isin(t2))
df_data.loc[cond2, new_col] = list(df_data[cond1][col])
def feat_past_time(df_data, col, time_col, interval):
# **必须先提取last特征**
# 过去一段时间内的特征值: avg, max, min
# e.g. past_10_sec_net_in_x_avg
col = '_' + time_col + '_' + col
new_col = 'past_' + str(interval) + col
print 'Parsing %s ...'%new_col
cols = ['last_10'+col]
for t in range(20, interval+1, 10):
cols.append('last_'+str(t)+col)
df_data.loc[:,new_col+'_sum'] = list(df_data[cols].sum(axis=1))
df_data.loc[:,new_col+'_avg'] = list(df_data[cols].mean(axis=1))
df_data.loc[:,new_col+'_min'] = list(df_data[cols].min(axis=1))
df_data.loc[:,new_col+'_max'] = list(df_data[cols].max(axis=1))
start = time.time()
# 特征工程
# last_10_sec_net_in_x 表示10秒前的net_in值
for interval in range(10, 61, 10):
# 提取半分钟前每隔10s的特征值
feat_last_time(new_df, 'cpu', 'sec', interval)
feat_last_time(new_df, 'mem', 'sec', interval)
feat_last_time(new_df, 'mem_use_x', 'sec', interval)
feat_last_time(new_df, 'mem_use_y', 'sec', interval)
feat_last_time(new_df, 'net_in_x', 'sec', interval)
feat_last_time(new_df, 'net_in_y', 'sec', interval)
feat_last_time(new_df, 'net_out_x', 'sec', interval)
feat_last_time(new_df, 'net_out_y', 'sec', interval)
feat_last_time(new_df, 'disk_in', 'sec', interval)
feat_last_time(new_df, 'disk_out', 'sec', interval)
feat_last_time(new_df, 'bi', 'sec', interval)
feat_last_time(new_df, 'bo', 'sec', interval)
feat_last_time(new_df, 'cpu_userate', 'sec', interval)
feat_last_time(new_df, 'container_num', 'sec', interval)
feat_last_time(new_df, 'image_num', 'sec', interval)
feat_last_time(new_df, 'disk_use', 'sec', interval)
feat_last_time(new_df, 'min', 'sec', interval)
feat_last_time(new_df, 'mem_rate', 'sec', interval)
feat_last_time(new_df, 'disk_rate', 'sec', interval)
for interval in range(20, 61, 10):
# 提取半分钟前每隔10s的特征值
feat_past_time(new_df, 'cpu', 'sec', interval)
feat_past_time(new_df, 'mem', 'sec', interval)
feat_past_time(new_df, 'mem_use_x', 'sec', interval)
feat_past_time(new_df, 'mem_use_y', 'sec', interval)
feat_past_time(new_df, 'net_in_x', 'sec', interval)
feat_past_time(new_df, 'net_in_y', 'sec', interval)
feat_past_time(new_df, 'net_out_x', 'sec', interval)
feat_past_time(new_df, 'net_out_y', 'sec', interval)
feat_past_time(new_df, 'disk_in', 'sec', interval)
feat_past_time(new_df, 'disk_out', 'sec', interval)
feat_past_time(new_df, 'bi', 'sec', interval)
feat_past_time(new_df, 'bo', 'sec', interval)
feat_past_time(new_df, 'cpu_userate', 'sec', interval)
feat_past_time(new_df, 'container_num', 'sec', interval)
feat_past_time(new_df, 'image_num', 'sec', interval)
feat_past_time(new_df, 'disk_use', 'sec', interval)
feat_past_time(new_df, 'min', 'sec', interval)
feat_past_time(new_df, 'mem_rate', 'sec', interval)
feat_past_time(new_df, 'disk_rate', 'sec', interval)
print 'Feature Engineering cost: %.6fs'%(time.time() - start)
# -
import xgboost as xgb
from sklearn.model_selection import train_test_split
# 划分数据集:假设所有提取得过去数据为X,预测得y值为 mem_use_x
'''
for col_y in ['mem_use_x','cpu']:
col_X = []
for col in new_df.columns:
if col.find('past') >= 0 or col.find('last') >= 0:
# 只使用特征工程得到得过去特征
col_X.append(col)
X_train, X_test, y_train, y_test = train_test_split(new_df[col_X], new_df[col_y],
test_size=0.3, random_state=42)
print np.shape(X_train), np.shape(y_train)
reg = xgb.XGBRegressor( max_depth=6,
learning_rate=0.025,
n_estimators=80,
silent=True,
objective='reg:linear',
booster='gbtree',
n_jobs=6,
min_child_weight=3,
max_delta_step=0,
subsample=1,
colsample_bytree=1,
colsample_bylevel=1,
reg_alpha=0,
reg_lambda=1,
scale_pos_weight=1,
base_score=0.5,
random_state=0,
seed=10)
reg.fit(X_train, y_train, eval_set=[(X_test, y_test)], eval_metric='rmse') # 使用均方误差rmse作为评价指标
print '测试数据预测结果(前5):'
print reg.predict(X_test)[:5]
print '测试数据真实结果(前5):'
print y_test[:5]'''
print
col_y = 'cpu'
col_X = []
for col in new_df.columns:
if col.find('past') >= 0 or col.find('last') >= 0:
# 只使用特征工程得到得过去特征
col_X.append(col)
temp_df = new_df[(new_df[col_y]<20)&(new_df[col_y]>0.2)]
X_train, X_test, y_train, y_test = train_test_split(temp_df[col_X], temp_df[col_y],
test_size=0.1, random_state=42)
new_df[(new_df[col_y]<1)][col_y].describe()
# +
print np.shape(X_train), np.shape(y_train)
reg = xgb.XGBRegressor( max_depth=5,
learning_rate=0.05,
n_estimators=200,
silent=True,
objective='reg:linear',
booster='gbtree',
n_jobs=6,
min_child_weight=3,
max_delta_step=0,
subsample=1,
colsample_bytree=1,
colsample_bylevel=1,
reg_alpha=0,
reg_lambda=1,
scale_pos_weight=1.5,
base_score=0.5,
random_state=0,
seed=10)
reg.fit(X_train, y_train, eval_set=[(X_train, y_train),(X_test, y_test)], eval_metric='rmse') # 使用均方误差rmse作为评价指标
print '测试数据预测结果(前5):'
print reg.predict(X_test)[5:10]
print '测试数据真实结果(前5):'
print y_test[5:10]
# -
import matplotlib.pyplot as plt
converge_df = pd.read_csv('cpu_curve.csv', names=['index', 'rmse_train','rmse_val'], sep='\t')
converge_df.loc[:,'rmse_train'] = converge_df.rmse_train.replace(r'.*:','',regex=True).astype(np.float32)
converge_df.loc[:,'rmse_val'] = converge_df.rmse_val.replace(r'.*:','',regex=True).astype(np.float32)
del converge_df['index']
converge_df
plt.plot(range(len(converge_df)), converge_df.rmse_train, 'b-')
plt.plot(range(len(converge_df)), converge_df.rmse_val, 'g-')
plt.title('RMSE Convergence Curve of CPU Rate Prediction')
plt.grid(True)
plt.legend(('Train Set Error','Valid Set Error'), loc=1, framealpha=1)
plt.xlabel('iter (step)')
plt.ylabel('RMSE (%)')
plt.xticks(range(0,151,15))
plt.xlim(0,150)
#plt.show()
plt.savefig('cpu_rmse_curve.jpg', dpi=150, bbox_inches='tight')
plt.close()
reg.predict(X_test)
from sklearn.metrics import mean_squared_error
min_ = 100
min_seed = 1
for seed in range(574,575,1):
np.random.seed(seed)
rand = np.random.randint(0,len(y_test)-1,200)
pred_y = reg.predict(X_test)
pred_y = [pred_y[i] for i in rand]
y_test_ = [list(y_test)[i] for i in rand]
plt.plot(range(len(y_test_)), y_test_, 'b.')
plt.plot(range(len(pred_y)), pred_y, 'r.')
plt.title('Predict and Ground-True Memory Usage Distribution')
plt.grid(True)
plt.legend(('Ground True','Prediction'), loc=1, framealpha=1)
plt.xlabel('sample')
plt.ylabel('memory use (kiB)')
#plt.yticks(range(0,21,2))
#plt.xlim(0,201)
#plt.ylim(-1,1100000)
#plt.show()
plt.savefig('mem_usage.jpg', dpi=150, bbox_inches='tight')
plt.close()
s = mean_squared_error(y_test_,pred_y)
if s < min_:
min_ = s
min_seed = seed
print (min_, min_seed)
print min_seed
# +
# SVR
from sklearn.svm import SVR
from sklearn.metrics import mean_squared_error
clf = SVR(C=1.0, epsilon=0.2, max_iter=500)
clf.fit(X_train, y_train)
pred_y_train = clf.predict(X_train)
pred_y_test = clf.predict(X_test)
print 'SVR训练误差:%.6f'%np.sqrt(mean_squared_error(y_train, pred_y_train))
print 'SVR测试误差:%.6f'%np.sqrt(mean_squared_error(y_test, pred_y_test))
# -
from sklearn.ensemble import GradientBoostingRegressor
clf = GradientBoostingRegressor(n_estimators=200, learning_rate=0.05,max_depth=5, random_state=0, loss='ls', max_features=200)
clf.fit(X_train, y_train)
pred_y_train = clf.predict(X_train)
pred_y_test = clf.predict(X_test)
print 'GBRT训练误差:%.6f'%np.sqrt(mean_squared_error(y_train, pred_y_train))
print 'GBRT测试误差:%.6f'%np.sqrt(mean_squared_error(y_test, pred_y_test))
from sklearn.ensemble import RandomForestRegressor
clf = RandomForestRegressor(n_estimators=200,n_jobs=6,max_depth=6)
clf.fit(X_train, y_train)
pred_y_train = clf.predict(X_train)
pred_y_test = clf.predict(X_test)
print 'RF训练误差:%.6f'%np.sqrt(mean_squared_error(y_train, pred_y_train))
print 'RF测试误差:%.6f'%np.sqrt(mean_squared_error(y_test, pred_y_test))
|
LoadPrediction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 成都市教育局教育服务专题下的学前教育、义务教育、高中教育的内容全部拉下来.
# http://edu.chengdu.gov.cn/cdedu/c131243/jyxw.shtml
# http://edu.chengdu.gov.cn/cdedu/c131244/jyxw.shtml
# http://edu.chengdu.gov.cn/cdedu/c131245/jyxw.shtml
# http://edu.chengdu.gov.cn/cdedu/c131244/jyxw.shtml
#
# http://edu.chengdu.gov.cn/cdedu/c131244/2020-07/16/content_41a17a8926e3494f9983ceea33b9569c.shtml
#
# http://edu.chengdu.gov.cn/cdedu/c131244/2020-07/16/content_540d8dc2c16949bf9d3d22b5b55779aa.shtml
#
# +
# encoding = 'utf-8'
import requests
import pandas as pd
import numpy as np
from bs4 import BeautifulSoup
# 定义函数,抓取目标网页的目录urls
def get_page_links(url):
headers = {'user-agent':'Mozilla/5.0 (Macintosh; Intel Mac OS X 10_15_7) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/86.0.4240.75 Safari/537.36'}
req = requests.get(url,headers = headers)
req.encoding = 'utf-8'
req = req.text
soup = BeautifulSoup(req, 'html.parser')
# print(soup)
#确定抓取链接的区域,并找到所有的'a'标签
all_a = soup.find('td', class_ = 'listitems').find_all('a')
print(all_a)
out_urls = []
for a in all_a:
link = a['href']
# title = a.get_text(strip = True)
if link[:4] != 'http':
link = 'http://edu.sh.gov.cn' + link # 相对路径转成完整网址
out_urls.append(link)
# print(out_urls)
return out_urls
url = 'http://edu.chengdu.gov.cn/cdedu/c131244/jyxw.shtml'
links = get_page_links(url)
print(links)
# +
# encoding = 'utf-8'
import requests
import pandas as pd
import numpy as np
from bs4 import BeautifulSoup
url = 'http://edu.chengdu.gov.cn/cdedu/c131244/jyxw.shtml'
headers = {'user-agent':'Mozilla/5.0 (Macintosh; Intel Mac OS X 10_15_7) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/86.0.4240.75 Safari/537.36'}
req = requests.get(url,headers = headers)
req.encoding = 'utf-8'
req = req.text
soup = BeautifulSoup(req, 'html.parser')
# print(soup)
#确定抓取链接的区域,并找到所有的'a'标签
all_a = soup.find('td', class_ = 'list')
print(all_a)
# out_urls = []
# for a in all_a:
# link = a['href']
# # title = a.get_text(strip = True)
# if link[:4] != 'http':
# link = 'http://edu.sh.gov.cn' + link # 相对路径转成完整网址
# out_urls.append(link)
# # print(out_urls)
|
Untitled3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import math
import pandas as pd
import json
import numpy as np
import matplotlib.pyplot as plt
# +
# Reach per year
reach15 = pd.read_json('reach_2015.json', orient='values')
reach16 = pd.read_json('reach_2016.json', orient='values')
reach17 = pd.read_json('reach_2017.json', orient='values')
reach18 = pd.read_json('reach_2018.json', orient='values')
xindex = list(range(max(len(reach15), len(reach16), len(reach17), len(reach18))))[:140000]
plt.figure(figsize=(8,6), dpi=90)
plt.rcParams.update({'font.size': 14})
plt.xlabel('Number of Packages (Ranked by Reach)')
plt.ylabel('Package Reach')
plt.plot(xindex, reach15[:140000], label="2015")
plt.plot(xindex, reach16[:140000], label="2016")
plt.plot(xindex, reach17[:140000], label="2017")
plt.plot(xindex, reach18[:140000], label="2018")
plt.gca().set_yscale("log")
plt.gca().set_yticklabels(['{:.0f}'.format(x) for x in plt.gca().get_yticks()])
plt.legend(loc='best', frameon=False)
plt.savefig("reachYearEvolution.png")
# -
|
jupyterlab/graphs/ReachEvolution.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/mittshah2/Pneumonia-Detection/blob/master/pneumonia.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="9HQhsA2cjcXy" colab_type="code" colab={}
# !unzip /content/drive/'My Drive'/pneumonia/train_images.zip -d /content/drive/'My Drive'/pneumonia
# + id="8Oh90ziqkzkc" colab_type="code" outputId="70d1db97-d5ec-4f06-d96a-086f0c59a44c" colab={"base_uri": "https://localhost:8080/", "height": 131}
# !pip install pydicom
# + id="an-bpYHBjcaH" colab_type="code" colab={}
import shutil
import pydicom as dicom
from skimage.transform import resize
from tqdm import tqdm
import os
import matplotlib.pyplot as plt
for i in tqdm(os.listdir('/content/drive/My Drive/pneumonia/train_images')):
if i.endswith('dcm'):
img=dicom.read_file(os.path.join('/content/drive/My Drive/pneumonia/train_images',i)).pixel_array
plt.imsave('/content/drive/My Drive/pneumonia/train_images/'+i[:-4]+'.jpg',img,cmap='gray')
shutil.move(os.path.join('/content/drive/My Drive/pneumonia/train_images',i),os.path.join('/content/drive/My Drive/pneumonia/dicom_files',i))
# + id="UVltNdmo0Tv_" colab_type="code" outputId="2ce6d4f2-7cde-4658-b176-b2513d7d0584" colab={"base_uri": "https://localhost:8080/", "height": 111}
# clone darknet repo
# !git clone https://github.com/AlexeyAB/darknet
# + id="lvkOisvu0ULI" colab_type="code" outputId="dc8de335-fcd7-45ca-a279-306800594aa6" colab={"base_uri": "https://localhost:8080/", "height": 36}
# change makefile to have GPU and OPENCV enabled
# %cd darknet
# !sed -i 's/OPENCV=0/OPENCV=1/' Makefile
# !sed -i 's/GPU=0/GPU=1/' Makefile
# !sed -i 's/CUDNN=0/CUDNN=1/' Makefile
# + id="yfULdSJW0URr" colab_type="code" colab={}
# make darknet (build)
# !make
# + id="wrXmdZA30Uap" colab_type="code" colab={}
# get yolov3 pretrained coco dataset weights
# !wget https://pjreddie.com/media/files/yolov3.weights
# + id="Tr6tk5c40e8M" colab_type="code" colab={}
# define helper functions
def imShow(path):
import cv2
import matplotlib.pyplot as plt
# %matplotlib inline
image = cv2.imread(path)
height, width = image.shape[:2]
resized_image = cv2.resize(image,(3*width, 3*height), interpolation = cv2.INTER_CUBIC)
fig = plt.gcf()
fig.set_size_inches(18, 10)
plt.axis("off")
plt.imshow(cv2.cvtColor(resized_image, cv2.COLOR_BGR2RGB))
plt.show()
# use this to upload files
def upload():
from google.colab import files
uploaded = files.upload()
for name, data in uploaded.items():
with open(name, 'wb') as f:
f.write(data)
print ('saved file', name)
# use this to download a file
def download(path):
from google.colab import files
files.download(path)
# + id="3g0EiVIrjciR" colab_type="code" colab={}
# !cp cfg/yolov3.cfg /content/drive/'My Drive'/pneumonia/yolov3_custom.cfg
# + id="Ms0xarDBaIrq" colab_type="code" colab={}
assert False
# + [markdown] id="lTyPLqSDaMmz" colab_type="text"
# change the config file
# + id="SWiFqRA5jcmI" colab_type="code" colab={}
# !cp /content/drive/'My Drive'/pneumonia/yolov3_custom.cfg ./cfg
# + id="AAuYsbqOw1Vw" colab_type="code" colab={}
# !cp /content/drive/'My Drive'/pneumonia/obj.names ./data
# !cp /content/drive/'My Drive'/pneumonia/obj.data ./data
# + id="xtL3P0i0w1Yl" colab_type="code" colab={}
# !python /content/drive/'My Drive'/pneumonia/generate_train.py
# + id="kt8dzWqow1bU" colab_type="code" outputId="dfd85428-73d6-4b81-b786-f0213c0c6bb7" colab={"base_uri": "https://localhost:8080/", "height": 241}
# !wget http://pjreddie.com/media/files/darknet53.conv.74
# + id="wodsul2H8Icd" colab_type="code" colab={}
# !cp /content/drive/'My Drive'/pneumonia/train.txt ./data
# + id="i8zj9G8L2oLb" colab_type="code" colab={}
# !ln -s /content/drive/My\ Drive /drive
# + id="BCAGPjCTw1dl" colab_type="code" colab={}
# !./darknet detector train data/obj.data cfg/yolov3_custom.cfg /content/drive/'My Drive'/pneumonia/backup/yolov3_custom_last.weights -dont_show
# + [markdown] id="A8KK8FptHLJD" colab_type="text"
# **Predictions**
# + id="CyB_sTqjAU9_" colab_type="code" outputId="d8133cad-5e98-45be-f7dd-19dcbf2ca039" colab={"base_uri": "https://localhost:8080/", "height": 54}
# %cd cfg
# !sed -i 's/batch=64/batch=1/' yolov3_custom.cfg
# !sed -i 's/subdivisions=16/subdivisions=1/' yolov3_custom.cfg
# %cd ..
# + id="gRg5GIjTApQ2" colab_type="code" outputId="89b5b109-3615-4566-8e15-5eca02a37174" colab={"base_uri": "https://localhost:8080/", "height": 575}
imShow('chart.png')
# + id="xq1QZJ0kA0HS" colab_type="code" colab={}
# !./darknet detector test data/obj.data cfg/yolov3_custom.cfg /content/drive/'My Drive'/pneumonia/backup/yolov3_custom_last.weights /content/drive/'My Drive'/pneumonia/train_images/01cd2ba5-2baf-44b2-bf15-ee57e1ea4599.jpg -thresh 0.3
# + id="JguN_yd7IZwY" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 575} outputId="2d57e305-4c82-422e-ce32-3354c67a48d5"
imShow('predictions.jpg')
# + [markdown] id="fUEA4aJJEhh_" colab_type="text"
# **Real Bounding boxes**
# + id="eWZO4L_PDTHc" colab_type="code" outputId="5fda888e-444c-4270-9d69-4b07d9e4741a" colab={"base_uri": "https://localhost:8080/", "height": 877}
import pandas as pd
import os
import matplotlib.pyplot as plt
import cv2
plt.figure(figsize=(20,15))
df=pd.read_csv('/content/drive/My Drive/pneumonia/csv.csv')
name='01cd2ba5-2baf-44b2-bf15-ee57e1ea4599'
s = df[df['patientId'] == name]
path=os.path.join('/content/drive/My Drive/pneumonia/train_images',name+'.jpg')
img=plt.imread(path)
for _,row in s.iterrows():
x=int(row['x'])
y=int(row['y'])
w=int(row['width'])
h=int(row['height'])
cv2.rectangle(img,(x,y),(x+w,y+h),(255,0,0),3)
plt.imshow(img,cmap='gray')
|
pneumonia_yolo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Gaia Data Workshop - Heidelberg, November 21-24, 2016
# ## The Gaia Service at AIP
# <NAME> // <EMAIL>
# ## Hands-on Tutorial
#
# This notebook will cover the access of the AIP's Gaia service through the UWS (Universal Worker Service) interface. More information about the UWS standard can be found <a href="http://www.ivoa.net/documents/UWS/">here</a>. Another two very useful sources (in pdf format) on the topic are available from <a href="http://www.g-vo.org/tutorials/uwsintro.pdf">here</a> and <a href="http://wiki.ivoa.net/internal/IVOA/InterOpMay2016-GWS/uws-client.pdf">here</a>.
#
# In this tutorial we will be using the <a href='https://github.com/aipescience/uws-client'>`uws-client`</a> for python.
# ### Basics
# First, let us import the packages we will need in this tutorial:
# +
import time
from subprocess import Popen, PIPE
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import matplotlib
matplotlib.rcParams.update(matplotlib.rcParamsDefault)
import uws.UWS.client as client
# %matplotlib inline
# #%config InlineBackend.figure_format = 'retina'
# -
# The connection to the database is established very easly through the `Client` object. We need to supply it with the url and the user credentials (same as the ones used in the web interface):
# +
# Option 1
#username = ''
#password = ''
# Option 2
#p = Popen(['pass', '<PASSWORD>'],
# stdout=PIPE, stderr=PIPE)
#stdout = p.communicate()
#username, password = stdout[0].split(b'\n')[:-1]
# Option 3
import json
with open('gaia.aip.de.json') as data_file:
username, password = json.load(data_file).values()
url = 'https://gaia.aip.de/uws/query'
cli = client.Client(url, username, password)
# -
# To list all `PENDING` or `COMPLETED` jobs we can use the `get_job_list()` function (it might take a second or two):
filters = {'phases': ['PENDING', 'COMPLETED']}
job_list = cli.get_job_list(filters)
for ref in job_list.job_reference:
print ref.ownerId, ref.creationTime, ref.phase[0]
# Similar job list can also be shown for other `phases` such as `ABORTED`, `QUEUED` and so on. We can also list the jobs based on their creation time (`after` keyword) or print out the last few jobs using the `last` keyword.
filters = {'last': 2}
job_list = cli.get_job_list(filters)
for ref in job_list.job_reference:
print ref
# ### Controlling jobs
# Adding a new job to the stack is done with the `new_job()` function. It requires a query and a queue to be passed to it. We wrap both into a dictionary called `parameters`:
parameters = {'query': 'SELECT ra, `dec` FROM GDR1.tgas_source LIMIT 10',
'queue': 'long'}
job = cli.new_job(parameters)
print job.phase
# We can now run it with `run_job()` function. To check the phase of the job we use the `get_job()` to query its state for up to the specified amount of seconds and see if the phase has changed from `QUEUED`.
run = cli.run_job(job.job_id)
job = cli.get_job(run.job_id, wait='10', phase='QUEUED')
print job.phase[0]
# If it is still `EXECUTING` we can re-check the phase with
print job.phase[0]
# If we look at the job list in the web interface we will see the submitted job in the list on the left.
# Now we need to fetch the results that the query has generated. We can download the data returned by the query in a few different formats. We will be using the `csv` format as it is easly parsed by the `pandas` package that we will use to read the data into the notebook:
if job.phase[0] == 'COMPLETED':
fileurl = str(job.results[0].reference)
cli.connection.download_file(fileurl, username, password,
file_name='res.csv')
data = pd.read_csv('res.csv')
data
# Finally, we can delete the job from the stack so it does not hog our limited user space. We do that using the `delete_job()` function:
deleted = cli.delete_job(job.job_id)
print deleted
# The operation of submitting a query, downloading a file, converting it to a `pandas` frame, and deleteing a job will be something will re-use again so let us wrap this procedure into a couple of functions:
# +
def submit_query(client, query, queue):
parameters = {'query': query, 'queue': queue}
job = client.new_job(parameters)
time.sleep(1)
run = client.run_job(job.job_id)
return run
def get_data(client, run, username, password, wait='30',
filename='res.csv'):
time.sleep(1)
job = client.get_job(run.job_id, wait=wait, phase='QUEUED')
if job.phase[0] == 'COMPLETED':
fileurl = str(job.results[0].reference)
client.connection.download_file(fileurl, username, password,
file_name=filename)
data = pd.read_csv(filename)
success = client.delete_job(job.job_id)
print 'Job is %s' % (job.phase[0])
return data
else:
print 'Job is %s' % (job.phase[0])
# -
# ### Example queries
# ##### 1. Magnitude histogram
# Executing a query and fetching the results can now be done in a couple of lines. A histogram of G magnitudes of TGAS stars can be produced with the following query:
query = '''
SELECT FLOOR(phot_g_mean_mag * 10) / 10.0 AS gmag,
COUNT(FLOOR(phot_g_mean_mag)) AS count
FROM GDR1.tgas_source
GROUP BY FLOOR(phot_g_mean_mag * 10)
'''
run = submit_query(cli, query, queue='long')
data = get_data(cli, run, username, password)
# We can print it out to see we really got what we expected.
data
# And plot it:
ax = plt.subplot(111)
ax.step(data['gmag'], data['count'])
ax.set_yscale('log')
ax.set_xlabel('gmag')
ax.set_ylabel('count')
ax.set_xlim(3.2, 18)
ax.set_ylim(1.1, 2e5);
# ##### 2. RAVE-TGAS color-magnitude diagram using APASS photometry
# Here is a slightly more elaborate example combining the positions of TGAS stars with the cross-matched magnitude values of the APASS catalog and atmospheric parameters from RAVE DR5 (<a href="https://arxiv.org/abs/1609.03210">Kunder et al.</a>). It joins the two tables that are linked by the `source_id` columns.
query = '''
SELECT tgas.parallax AS par,
rave.Bmag_APASSDR9 AS bmag, rave.Vmag_APASSDR9 AS vmag,
rave.logg_K AS logg, rave.Met_K AS met
FROM GDR1.tgas_source AS tgas, RAVE.RAVE_DR5 AS rave
WHERE rave.Bmag_APASSDR9 > 0 AND rave.Vmag_APASSDR9 > 0
AND tgas.parallax > 0
AND tgas.parallax_error < 0.25
AND tgas.source_id = rave.source_id
'''
run = submit_query(cli, query, queue='long')
data = get_data(cli, run, username, password)
Mv = data['vmag'] + 5.0 * np.log10(data['par']) - 10.0
bmv = data['bmag'] - data['vmag']
# +
fig = plt.figure(figsize=(10, 6))
for i, c in enumerate([('logg', 0, 5.0), ('met', -1.0, 0.2)]):
ax = plt.subplot(1, 2, i + 1)
sc = ax.scatter(bmv, Mv, c=data[c[0]], s=1.5, alpha=0.3, lw=0, vmin=c[1], vmax=c[2])
ax.axis((-0.1, 1.8, 9, -3))
ax.set_xlabel('B-V')
ax.set_ylabel('M_V')
cbar = plt.colorbar(sc)
cbar.set_label(c[0])
cbar.set_alpha(1.0)
cbar.draw_all()
# -
# ##### 3. Radial velocities from RAVE
query = '''
SELECT tgas.l AS l, tgas.b AS b, tgas.parallax AS par,
rave.HRV AS rv, rave.logg_K AS logg
FROM GDR1.tgas_source AS tgas, RAVE.RAVE_DR5 AS rave
WHERE rave.ALGO_CONV = 0 AND rave.logg_K > 0
AND tgas.source_id = rave.source_id
LIMIT 50000
'''
run = submit_query(cli, query, queue='long')
data = get_data(cli, run, username, password)
# +
def pscatter(ax, x, y, c='k', size=5, alpha=1.0):
x = np.remainder(x + 360.0, 360.0)
x[x > 180.0] -= 360.0
sc = ax.scatter(np.radians(-x), np.radians(y), c=c, s=size,
lw=0, alpha=alpha)
return sc
fig = plt.figure(figsize=(9, 4))
ax = plt.subplot(111, projection='aitoff')
rv = np.clip(data['rv'], -50, 50)
sc = pscatter(ax, data['l'], data['b'], c=rv, size=2, alpha=1)
cbar = plt.colorbar(sc)
cbar.set_label('HRV [km/s]')
ax.set_xticklabels([])
plt.grid()
# -
# For added fanciness, we can plot the distribution in 3D using the TGAS parallax as a distance estimator (where we just naively assume the distance is the inverse of the parallax). In this example we start a simple HTTP server to host the 3D viewer. Afterwards, the server has to be stopped using the `kill()` command.
color = plt.cm.RdBu((rv + 50.0) / 100.0)
data['rc'] = color[:, 0]
data['gc'] = color[:, 1]
data['bc'] = color[:, 2]
data.to_csv('threedviewer/res.csv')
# +
# Galaxy image credit: <NAME> (SSC), JPL-Caltech, NASA
import subprocess
from IPython.core.display import display, HTML
server = subprocess.Popen(['python', '-m', 'SimpleHTTPServer', '8891'])
url_viewer = 'http://localhost:8891/threedviewer'
display(HTML('<iframe src="http://localhost:8891/threedviewer"' +\
'width=768 height=512 frameborder=0></iframe>'))
plt.figure(figsize=(9, 0.5))
ax = plt.axes([0.0, 0.0, 0.3, 1.0]); ax.axis('off');
ax = plt.axes([0.7, 0.7, 0.3, 0.3]); ax.axis('off');
ax = plt.axes([0.3, 0.7, 0.4, 0.3])
cmap = plt.cm.RdBu
norm = matplotlib.colors.Normalize(vmin=-50, vmax=50)
cb = matplotlib.colorbar.ColorbarBase(ax, cmap=cmap, norm=norm, orientation='horizontal')
ax.set_xlabel('HRV [km/s]');
# -
server.kill()
# ##### 4. HEALPix density plots (using `healpy`)
# To replicate the TGAS star density diagrams from <a href="https://arxiv.org/abs/1609.04303"> Lindegren et al.</a>, we use the following query. Gaia catalog `source_id` also encodes HEALPix values in nested ordering up to the resolution index of 12. To get HEALPix values at lower resolutions we need to divide the `source_id` column with an appropriate factor. Similar query can be performed on the whole Gaia catalog, however, it typically takes a few minutes to run.
query = '''
SELECT hpix, COUNT(hpix) AS number
FROM
(
SELECT FLOOR(source_id / (POW(2, 35) * POW(4, 12 - 6))) AS hpix
FROM GDR1.tgas_source
) AS hq
GROUP BY hpix
'''
run = submit_query(cli, query, queue='long')
data = get_data(cli, run, username, password)
# +
import healpy as hp
density = np.ones(12 * (2 ** 6) ** 2) * np.inf
density[data['hpix'].values] = data['number']
density /= 0.8393 # area in deg^2 of one HEALPix with NSIDE=64
cmap = plt.cm.magma
vmin = 1
vmax = 220
hp.mollview(density, nest=True, title='Source density [deg^2]', cmap=cmap,
coord='C', norm='log', min=vmin, max=vmax, cbar=False)
hp.graticule(verbose=False)
hp.mollview(density, nest=True, title='', cmap=cmap,
coord='CG', norm='log', min=vmin, max=vmax, cbar=False)
hp.graticule(verbose=False)
fig = plt.gcf()
ax = plt.gca()
image = ax.get_images()[0]
cbar = fig.colorbar(image, ax=ax, orientation='horizontal',
fraction=0.04, pad=-0.05)
cbar.set_ticks([1, 2, 5, 10, 20, 50, 100, 220])
# -
|
AIP-gdw.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/szymbor2/ATMS-597-Project-4-Group-C/blob/master/project4_0327_SS.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="yO3amLYIvTjR" colab_type="text"
# ## Imports
# + [markdown] id="eNOPQKvWvV8-" colab_type="text"
# <b>Import Libraries</b>
# + id="55pWVpDPHiUl" colab_type="code" colab={}
import tarfile
import pandas as pd
import os
# + id="Klp25IS9HgpD" colab_type="code" colab={}
# Import Libraries for section "Linear regression model"
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from math import sqrt
# + id="aHABP3T2tqeI" colab_type="code" outputId="1c24509f-3aff-4e49-fef4-6b823da6ca40" colab={"base_uri": "https://localhost:8080/", "height": 34}
from google.colab import drive
drive.mount('/content/drive')
# + [markdown] id="hIpjQNvXvc6J" colab_type="text"
# <b>Set Your Directory</b>
# + id="W_UolI2kvJ9Y" colab_type="code" colab={}
YOUR_DIRECTORY = '/content/drive/My Drive/Colab Notebooks/ATMS597/project4/' #Sarah
# YOUR_DIRECTORY = '/content/drive/My Drive/Colab Notebooks/ATMS 597/P04/' #Cathy
# YOUR_DIRECTORY = '/content/drive/My Drive/ATMS597 Weather Climate Data Analysis/Module 4/Project 4/' #Chu-Chun
# + [markdown] id="qJTBAVi9veNy" colab_type="text"
# ### <b>Import</b> GFS data - Daily
# + id="cxJsR6LYvuI1" colab_type="code" outputId="b106fbc7-fbf6-4de9-c0c2-c9a72c220960" colab={"base_uri": "https://localhost:8080/", "height": 589}
daily = tarfile.open(name = YOUR_DIRECTORY + 'daily.tar.gz') # Set the archive for opening
# Aggregate to PD DataFrame
cur_file = daily.next() # Initiate while loop using the first file in the tar archive
daily_gfs = pd.DataFrame(columns=['TMAX', 'TMIN', 'WMAX', 'RTOT'])
i = 0
while cur_file != None:
i += 1
if i % 350 == 0:
print(float(i/3500))
working_file = YOUR_DIRECTORY + cur_file.name
daily.extract(cur_file, path=YOUR_DIRECTORY) # Extract TarInfo Object
convert_to_df = pd.read_csv(working_file, index_col=0, parse_dates=True,
infer_datetime_format=True) # Convert cur_file
# (TarInfo Object) to string, then to PD; convert
# index col to DateTime
daily_gfs = daily_gfs.append(convert_to_df) # Append PD to DF
os.remove(working_file) # Remove file extracted in directory
cur_file = daily.next() # Go to next file in archive
daily.close() # Close .tar
daily_gfs
# + id="_ktAkzfMXFaT" colab_type="code" outputId="a9b446b5-08ab-49d2-e40c-5216bc262c53" colab={"base_uri": "https://localhost:8080/", "height": 357}
# Find missing dates
missing_daily_gfs = pd.date_range(start = '2010-01-01 12:00:00', end = '2020-01-31 12:00:00', freq='D').difference(daily_gfs.index)
missing_daily_gfs
# + [markdown] id="u_LLYDftICqX" colab_type="text"
# ### <b>Import</b> GFS data - Profiles
# + id="0_YlLGtdnKqQ" colab_type="code" outputId="5a01443b-59a3-430b-90a7-2a2f7861daab" colab={"base_uri": "https://localhost:8080/", "height": 929}
# Profile gfs data
prof = tarfile.open(name = YOUR_DIRECTORY + 'prof.tar.gz') # Set the archive for opening
# Aggregate to PD DataFrame
cur_file = prof.next() # Initiate while loop using the first file in the tar archive
prof_gfs = pd.DataFrame(columns=['DWPC','HGHT','PRES','TMPC','UWND','VWND'])
i = 0
while cur_file != None:
i += 1
if i % 350 == 0:
print(float(i/3500))
working_file = YOUR_DIRECTORY + cur_file.name
prof.extract(cur_file, path=YOUR_DIRECTORY) # Extract TarInfo Object
convert_to_df = pd.read_csv(working_file, index_col=0, parse_dates=True,
infer_datetime_format=True) # Convert cur_file
# (TarInfo Object) to string, then to PD; convert
# index col to DateTime
prof_gfs = prof_gfs.append(convert_to_df) # Append PD to DF
os.remove(working_file) # Remove file extracted in directory
cur_file = prof.next() # Go to next file in archive
prof.close() # Close .tar
prof_gfs
# + id="p14tBcz5pTsg" colab_type="code" outputId="e9974ac3-1335-4269-ddb1-b68a9231e8d7" colab={"base_uri": "https://localhost:8080/", "height": 221}
# Find missing times
missing_prof_gfs = pd.date_range(start = '2010-01-02 06:00:00', end = '2020-02-02 06:00:00', freq='6H').difference(prof_gfs.index)
missing_prof_gfs
# the result shows that len(missing_prof_gfs) < 4*len(missing_daily_gfs)...not sure how to go from here.
# + [markdown] id="gXgKT9jZIIc-" colab_type="text"
# ### <b>Import</b> GFS data - Surface
# + id="3uO0BDALtuyx" colab_type="code" outputId="29d3f6d8-92f2-4b74-9ba4-cad1be355021" colab={"base_uri": "https://localhost:8080/", "height": 589}
# Surface gfs data
sfc = tarfile.open(name = YOUR_DIRECTORY + 'sfc.tar.gz') # Set the archive for opening
# Aggregate to PD DataFrame
cur_file = sfc.next() # Initiate while loop using the first file in the tar archive
sfc_gfs = pd.DataFrame()
i = 0
while cur_file != None:
i += 1
if i % 350 == 0:
print(float(i/3500))
working_file = YOUR_DIRECTORY + cur_file.name
sfc.extract(cur_file, path=YOUR_DIRECTORY) # Extract TarInfo Object
convert_to_df = pd.read_csv(working_file, index_col=0).T # Convert cur_file
# (TarInfo Object) to string, then to PD. Note that
# the sfc files are transposed, i.e. they have
# variables as rows and timestamps as columns, hence .T
sfc_gfs = sfc_gfs.append(convert_to_df) # Append PD to DF
os.remove(working_file) # Remove file extracted in directory
cur_file = sfc.next() # Go to next file in archive
sfc.close() # Close .tar
sfc_gfs
# + id="cjkukFWC20TT" colab_type="code" outputId="2e7441d7-3d5a-4bff-a33f-7516136fb2da" colab={"base_uri": "https://localhost:8080/", "height": 221}
# Find missing times
missing_sfc_gfs = pd.date_range(start = '2010-01-02 06:00:00', end = '2020-02-02 06:00:00', freq='3H').difference(sfc_gfs.index)
missing_sfc_gfs
# the result shows that len(missing_sfc_gfs) < (24/3)*len(missing_daily_gfs)...not sure how to go from here.
# + [markdown] id="PIDh60eWBYHX" colab_type="text"
# ### <b>Import</b> obs daily data
# + id="iewpNIUB_Ume" colab_type="code" outputId="103127a7-be85-4038-82f1-0284171a0c66" colab={"base_uri": "https://localhost:8080/", "height": 450}
daily_obs = pd.read_csv(YOUR_DIRECTORY + 'KCMI_daily.csv', header=4, usecols=[0,1,2,3,4], index_col='Date')[:-7] # ignore the last 7 lines
daily_obs
# + id="X-YwzXGL--AJ" colab_type="code" outputId="5fd43f4a-4b24-4ce1-99b3-120af36193d7" colab={"base_uri": "https://localhost:8080/", "height": 34}
# Check for missing dates - there's none
missing_dates_obs = pd.date_range(start = '2010-01-01', end = '2019-12-31', freq='D').difference(daily_obs.index)
missing_dates_obs
# + [markdown] id="GQo90ECpc3FO" colab_type="text"
# ### <b>Import</b> obs hourly data
# + id="6OSS7dSxZvj0" colab_type="code" outputId="26e0595a-f6b1-403e-a634-044eea893a39" colab={"base_uri": "https://localhost:8080/", "height": 450}
hourly_obs = pd.read_csv(YOUR_DIRECTORY + 'KCMI_hourly.csv', #header=1, usecols=[0,1,2,3,4], comment='#',
index_col=0, parse_dates=True, infer_datetime_format=True)
hourly_obs
# + [markdown] id="1RWsthDEkkdp" colab_type="text"
# ### <b>Resample</b> hourly precip data into daily freq and add to daily_obs
# + id="RYm_g2ppeZ2X" colab_type="code" outputId="778769f9-5e3d-4ff5-a84f-698998e6b51c" colab={"base_uri": "https://localhost:8080/", "height": 238}
hourly_obs[hourly_obs['pr1h'] < 0] = 0 # Counts trace precip (-0.1) as 0
hourly_obs_res = hourly_obs.resample('24H',base=6).sum()
precip_daily = hourly_obs_res['pr1h']['2010-01-01 06:00:00':'2019-12-31 06:00:00'].resample('D').sum()
precip_daily
# + id="PgPfXfXefrih" colab_type="code" outputId="96133f63-8de2-40f1-c18b-c784b1862790" colab={"base_uri": "https://localhost:8080/", "height": 450}
daily_obs['Total Precip from Hourly (in)'] = precip_daily
daily_obs
# + [markdown] id="AZP8Xi3QJjU3" colab_type="text"
# ## TMAX
# + [markdown] id="nQCfMMOPGVRb" colab_type="text"
# ### Plot the TMAX from GFS and observation
# + id="dR5NU9FyC0W7" colab_type="code" outputId="b6375a27-34b1-405a-91a2-4b31f366ce7b" colab={"base_uri": "https://localhost:8080/", "height": 0}
GFS_TMAX = daily_gfs['TMAX']['2010-01-01 12:00:00':'2018-12-30 12:00:00'] # select 2010-01-01 to 2018-12-30
GFS_TMAX.index = GFS_TMAX.index.strftime('%Y-%m-%d') # to be consistent with observation index
print(GFS_TMAX)
GFS_TMAX.plot()
# + id="J9vUzEnRCUyI" colab_type="code" outputId="69ccb7d2-128f-4403-c43e-f97328e70797" colab={"base_uri": "https://localhost:8080/", "height": 0}
# Select 2010-01-02 to 2018-12-31 (one day after GFS model) and Mask Missing Data
mask_missing = daily_obs['Max Hourly Temp (F)'] == 'M'
OBS_TMAX = daily_obs['Max Hourly Temp (F)'].mask(mask_missing).dropna().astype(float)['2010-01-02':'2018-12-31']
print(OBS_TMAX)
OBS_TMAX.plot()
# + [markdown] id="y-lRkDv0ySpb" colab_type="text"
# ### Delete missing days for GFS daily, GFS sfc, and Obs
# + [markdown] id="oK_V4gK_GewP" colab_type="text"
# <b>Find the overlap dates between GFS daily and observation (one day after GFS model)</b> and delete the missing dates.
# + id="UHJEzf3FsqZX" colab_type="code" colab={}
GFS_TMAX_plus1day = pd.to_datetime(GFS_TMAX.index) + pd.Timedelta('1 day') # OBS dates are one day after GFS timestamps
mismatch_dates = GFS_TMAX_plus1day.difference(pd.to_datetime(OBS_TMAX.index)) # OBS doesn't have these dates
OBS_TMAX_dates = GFS_TMAX_plus1day.drop(mismatch_dates) # dates derived from available GFS dates and OBS dates
GFS_TMAX_dates = OBS_TMAX_dates - pd.Timedelta('1 day')
# + [markdown] id="XVr8I6M6KoNz" colab_type="text"
# <b>Update the dates in both GFS and obs TMAX</b>
# + id="dDg3EyTkuLLx" colab_type="code" outputId="86f28d98-4ba3-4d5f-d66d-39eb31bec67f" colab={"base_uri": "https://localhost:8080/", "height": 0}
GFS_TMAX[GFS_TMAX_dates.strftime('%Y-%m-%d')]
OBS_TMAX[OBS_TMAX_dates.strftime('%Y-%m-%d')]
# + [markdown] id="jKpsB-E-QuNy" colab_type="text"
# <b>Find the max temperature from sfc GFS dataset between 06Z to 06Z</b>
# + id="AWm_XxTooqEG" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 0} outputId="503701a5-e562-4af3-cd19-dd8c60b82a4f"
sfc_gfs.index = pd.to_datetime(sfc_gfs.index, format='%Y-%m-%d %H:%M:%S')
GFS_sfc_TMPC_daily_max = sfc_gfs['TMPC'].astype(float).resample('24H',base=6).max()['2010-01-02 06:00:00':'2018-12-31 06:00:00'].resample('D').mean()
GFS_sfc_TMPC_daily_max
# + [markdown] id="2GpNVQLLnYN2" colab_type="text"
# <b> Drop the dates that don't exist </b>
# + id="7jekUYI616gN" colab_type="code" outputId="cbfeb59b-411f-408e-fa98-97a2a04580a0" colab={"base_uri": "https://localhost:8080/", "height": 0}
mismatch_dates = pd.to_datetime(GFS_sfc_TMPC_daily_max.index).difference(pd.to_datetime(OBS_TMAX_dates)) # OBS_TMAX_dates doesn't have these dates
GFS_sfc_TMPC_max = GFS_sfc_TMPC_daily_max.drop(mismatch_dates)
GFS_sfc_TMPC_max
# + [markdown] id="QSz0Z9ACP27Z" colab_type="text"
# ## TMIN
# + [markdown] id="UbAkTQ0AP6_a" colab_type="text"
# ### Plot the TMIN from GFS and observation
# + id="3fZNXLN5P6ZE" colab_type="code" outputId="405bc2f5-5e35-497c-c3b4-3f2c98eca7cf" colab={"base_uri": "https://localhost:8080/", "height": 0}
GFS_TMIN = daily_gfs['TMIN']['2010-01-01 12:00:00':'2018-12-30 12:00:00'] # select 2010-01-01 to 2018-12-30
GFS_TMIN.index = GFS_TMIN.index.strftime('%Y-%m-%d') # to be consistent with observation index
print(GFS_TMIN)
GFS_TMIN.plot()
# + id="JA9eySHTQE48" colab_type="code" outputId="e2f0afa2-2611-4ccd-c6d9-4a7449d27c8b" colab={"base_uri": "https://localhost:8080/", "height": 0}
# Select 2010-01-02 to 2018-12-31 (one day after GFS model) and Mask Missing Data
mask_missing = daily_obs['Min Hourly Temp (F)'] == 'M'
OBS_TMIN = daily_obs['Min Hourly Temp (F)'].mask(mask_missing).dropna().astype(float)['2010-01-02':'2018-12-31']
print(OBS_TMIN)
OBS_TMIN.plot()
# + [markdown] id="kgovcdNfyeXi" colab_type="text"
# ### Delete missing days for GFS daily, GFS sfc, and Obs
# + [markdown] id="jKinAB19QUpG" colab_type="text"
# <b>Find the overlap dates between GFS daily and observation (one day after GFS model)</b> and delete the missing dates.
# + id="Bug9ZyGNQUSF" colab_type="code" colab={}
GFS_TMIN_plus1day = pd.to_datetime(GFS_TMIN.index) + pd.Timedelta('1 day') # OBS dates are one day after GFS timestamps
mismatch_dates = GFS_TMIN_plus1day.difference(pd.to_datetime(OBS_TMIN.index)) # OBS doesn't have these dates
OBS_TMIN_dates = GFS_TMIN_plus1day.drop(mismatch_dates) # dates derived from available GFS dates and OBS dates
GFS_TMIN_dates = OBS_TMIN_dates - pd.Timedelta('1 day')
# + [markdown] id="A1y6VR-hQjEJ" colab_type="text"
# <b>Update the dates in both GFS and obs TMAX</b>
# + id="4e1IrwUyQjxa" colab_type="code" outputId="529ea792-b908-4120-c16d-474a67358d02" colab={"base_uri": "https://localhost:8080/", "height": 0}
GFS_TMIN[GFS_TMIN_dates.strftime('%Y-%m-%d')]
OBS_TMIN[OBS_TMIN_dates.strftime('%Y-%m-%d')]
# + [markdown] id="3Bw9MoCgtD3t" colab_type="text"
# <b>Find the min temperature from sfc GFS dataset between 06Z to 06Z</b>
# + id="nbg8N1JDtD_U" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 0} outputId="f69db1d8-fcbf-4e43-bf1b-7720899806d6"
sfc_gfs.index = pd.to_datetime(sfc_gfs.index, format='%Y-%m-%d %H:%M:%S')
GFS_sfc_TMPC_daily_min = sfc_gfs['TMPC'].astype(float).resample('24H',base=6).min()['2010-01-02 06:00:00':'2018-12-31 06:00:00'].resample('D').mean()
GFS_sfc_TMPC_daily_min
# + [markdown] id="bxZC95VHtEIA" colab_type="text"
# <b> Drop the dates that don't exist </b>
# + id="c7lGWJz1tEP5" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 0} outputId="2df1365d-4afb-4d02-cfe1-53357a729010"
mismatch_dates = pd.to_datetime(GFS_sfc_TMPC_daily_min.index).difference(pd.to_datetime(OBS_TMIN_dates)) # OBS_TMAX_dates doesn't have these dates
GFS_sfc_TMPC_min = GFS_sfc_TMPC_daily_min.drop(mismatch_dates)
GFS_sfc_TMPC_min
# + [markdown] id="FlgEjyE73OUq" colab_type="text"
# ## Max Wind
# + [markdown] id="mBIUETZJ3VZn" colab_type="text"
# ### Plot the WMAX from GFS and observation
# + id="nfOUKfnl3Zoq" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 0} outputId="3f7cf44b-c106-4e2b-bd9d-86b3f8721f6c"
GFS_WMAX = daily_gfs['WMAX']['2010-01-01 12:00:00':'2018-12-30 12:00:00'] # select 2010-01-01 to 2018-12-30
GFS_WMAX.index = GFS_WMAX.index.strftime('%Y-%m-%d') # to be consistent with observation index
print(GFS_WMAX)
GFS_WMAX.plot()
# + id="caLYoNlw3uta" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 0} outputId="60b660e4-0e6e-4bc7-a61b-76701a743539"
# Select 2010-01-02 to 2018-12-31 (one day after GFS model) and Mask Missing Data
mask_missing = daily_obs['Max Wind Speed (mph)'] == 'M'
OBS_WMAX = daily_obs['Max Wind Speed (mph)'].mask(mask_missing).dropna().astype(float)['2010-01-02':'2018-12-31']
print(OBS_WMAX)
OBS_WMAX.plot()
# + [markdown] id="2I8e1EiK3-P8" colab_type="text"
# ### Delete missing days for GFS daily, GFS sfc, and Obs
# + [markdown] id="8NtASHwc4ACE" colab_type="text"
# <b>Find the overlap dates between GFS daily and observation (one day after GFS model)</b> and delete the missing dates.
# + id="AP4I4gpJ3_bq" colab_type="code" colab={}
GFS_WMAX_plus1day = pd.to_datetime(GFS_WMAX.index) + pd.Timedelta('1 day') # OBS dates are one day after GFS timestamps
mismatch_dates = GFS_WMAX_plus1day.difference(pd.to_datetime(OBS_WMAX.index)) # OBS doesn't have these dates
OBS_WMAX_dates = GFS_WMAX_plus1day.drop(mismatch_dates) # dates derived from available GFS dates and OBS dates
GFS_WMAX_dates = OBS_WMAX_dates - pd.Timedelta('1 day')
# + [markdown] id="NwPdWEDD4A1M" colab_type="text"
# <b>Update the dates in both GFS and obs TMAX</b>
# + id="WifNhLei4BCT" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 0} outputId="cee5aa7f-4491-4af0-ddf3-64ffc7ac3bbc"
GFS_WMAX[GFS_WMAX_dates.strftime('%Y-%m-%d')]
OBS_WMAX[OBS_WMAX_dates.strftime('%Y-%m-%d')]
# + [markdown] id="QkWw0pHM4BMP" colab_type="text"
# <b>Find the max wind from sfc GFS dataset between 06Z to 06Z</b>
# + id="GNMvYNwr4BZt" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 0} outputId="ff8b900e-cd48-4cd6-91a4-282d7f956042"
sfc_gfs.index = pd.to_datetime(sfc_gfs.index, format='%Y-%m-%d %H:%M:%S')
GFS_sfc_WMAX_daily = sfc_gfs['WSPD'].astype(float).resample('24H',base=6).max()['2010-01-02 06:00:00':'2018-12-31 06:00:00'].resample('D').mean()
GFS_sfc_WMAX_daily
# + [markdown] id="F_cdd_w85erH" colab_type="text"
# <b> Drop the dates that don't exist </b>
# + id="989qFhz25ext" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 0} outputId="b077f300-90aa-4faa-aa6b-97812109d192"
mismatch_dates = pd.to_datetime(GFS_sfc_WMAX_daily.index).difference(pd.to_datetime(OBS_WMAX_dates)) # OBS_TMAX_dates doesn't have these dates
GFS_sfc_WMAX = GFS_sfc_WMAX_daily.drop(mismatch_dates)
GFS_sfc_WMAX
# + [markdown] id="L0LPqM2h3QtB" colab_type="text"
# ## Precipitation
# + [markdown] id="DQhGl-8e9Hwp" colab_type="text"
# ### Plot the WMAX from GFS and observation
# + id="RYeav9Qw9QgE" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 486} outputId="f8e6260f-96ed-42ce-cb71-05009d421def"
daily_gfs[daily_gfs['RTOT'] < 0] = 0 # Takes care of trace precip
GFS_PRCP = daily_gfs['RTOT']['2010-01-01 12:00:00':'2018-12-30 12:00:00'] # select 2010-01-01 to 2018-12-30
GFS_PRCP.index = GFS_PRCP.index.strftime('%Y-%m-%d') # to be consistent with observation index
print(GFS_PRCP)
GFS_PRCP.plot()
# + id="lw-AC0PTCADC" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 571} outputId="cbc6bcb2-3c4e-4c8e-ce12-1bb7a4b6c229"
# Select 2010-01-02 to 2018-12-31 (one day after GFS model) and Mask Missing Data
mask_missing = daily_obs['Total Precip from Hourly (in)'] == 'M'
OBS_PRCP = daily_obs['Total Precip from Hourly (in)'].mask(mask_missing).dropna().astype(float)['2010-01-02':'2018-12-31']
print(OBS_PRCP)
OBS_PRCP.plot()
# + [markdown] id="st4YB7i89Kxw" colab_type="text"
# ### Delete missing days for GFS daily, GFS sfc, and Obs
# + [markdown] id="fJMPqfWJ9RAw" colab_type="text"
# <b>Find the overlap dates between GFS daily and observation (one day after GFS model)</b> and delete the missing dates.
# + id="wmRJtGTp9RHW" colab_type="code" colab={}
GFS_PRCP_plus1day = pd.to_datetime(GFS_PRCP.index) + pd.Timedelta('1 day') # OBS dates are one day after GFS timestamps
mismatch_dates = GFS_PRCP_plus1day.difference(pd.to_datetime(OBS_PRCP.index)) # OBS doesn't have these dates
OBS_PRCP_dates = GFS_PRCP_plus1day.drop(mismatch_dates) # dates derived from available GFS dates and OBS dates
GFS_PRCP_dates = OBS_PRCP_dates - pd.Timedelta('1 day')
# + [markdown] id="uW4jL-IH9RPE" colab_type="text"
# <b>Update the dates in both GFS and obs TMAX</b>
# + id="l83p2zMU9RWU" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 221} outputId="89fa4267-8408-4840-d5ab-0f4568f3e4bb"
GFS_PRCP[GFS_PRCP_dates.strftime('%Y-%m-%d')]
OBS_PRCP[OBS_PRCP_dates.strftime('%Y-%m-%d')]
# + [markdown] id="pEG96La69ReS" colab_type="text"
# <b>Find the total precip from sfc GFS dataset between 06Z to 06Z</b>
# + id="Z-nvIu709RlH" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 221} outputId="edb255f8-5c72-42f3-85e8-720a02c56d8e"
sfc_gfs.index = pd.to_datetime(sfc_gfs.index, format='%Y-%m-%d %H:%M:%S')
sfc_gfs[sfc_gfs['PRCP'] < 0] = 0 # Takes care of trace precip
GFS_sfc_PRCP_daily = sfc_gfs['PRCP'].astype(float).resample('24H',base=6).sum()['2010-01-02 06:00:00':'2018-12-31 06:00:00'].resample('D').mean()
GFS_sfc_PRCP_daily
# + [markdown] id="r3QzUVt0Cgg4" colab_type="text"
# <b> Drop the dates that don't exist </b>
# + id="AVFIaTyoCgos" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 221} outputId="db1d09e8-362e-4d4c-d111-3aede9b2b4a0"
mismatch_dates = pd.to_datetime(GFS_sfc_PRCP_daily.index).difference(pd.to_datetime(OBS_PRCP_dates)) # OBS_TMAX_dates doesn't have these dates
GFS_sfc_PRCP = GFS_sfc_PRCP_daily.drop(mismatch_dates)
GFS_sfc_PRCP
# + [markdown] id="NzuvQ41RAeEg" colab_type="text"
# # Linear regression model
#
# + [markdown] id="XehD6volQ53U" colab_type="text"
# ## TMAX
# + id="iYHN-qlL_4xu" colab_type="code" outputId="936093fd-568d-4079-fbd7-f8bd6d32a96d" colab={"base_uri": "https://localhost:8080/", "height": 0}
X = np.column_stack((GFS_TMAX[GFS_TMAX_dates.strftime('%Y-%m-%d')].values, GFS_sfc_TMPC_max.values)) # GFS model daily and sfc max TMPC
y = (OBS_TMAX[OBS_TMAX_dates.strftime('%Y-%m-%d')].values-32)*5/9 # Observation, converted from F to C
model = LinearRegression(fit_intercept=False)
model.fit(X, y)
y_predict = model.predict(X) # linear regression model prediction
print("Model slope: ", model.coef_)
print("Model intercept:", model.intercept_)
# y_predict = X[:, 0] * model.coef_[0] + X[:, 1] * model.coef_[1] + model.intercept_ # another form to write the equation
plt.figure(figsize=(20, 8.5))
# plt.plot(OBS_TMAX_dates, X, alpha=0.5)
plt.plot(OBS_TMAX_dates, y, alpha=0.5, label='Observation')
plt.plot(OBS_TMAX_dates, y_predict, alpha=0.5, label='Prediction')
plt.legend()
plt.show()
rms = sqrt(mean_squared_error(y, y_predict))
print('RMS: ', rms)
# + [markdown] id="fB-Q74GkQ7M2" colab_type="text"
# ## TMIN
# + id="1aoSDf0hMBRP" colab_type="code" outputId="12dd5ed4-f501-482e-f18a-b362ce7590aa" colab={"base_uri": "https://localhost:8080/", "height": 0}
X = np.column_stack((GFS_TMIN[GFS_TMIN_dates.strftime('%Y-%m-%d')].values, GFS_sfc_TMPC_min.values)) # GFS model daily and sfc min TMPC
y = (OBS_TMIN[OBS_TMIN_dates.strftime('%Y-%m-%d')].values-32)*5/9 # Observation, converted from F to C
model = LinearRegression(fit_intercept=False)
model.fit(X, y)
y_predict = model.predict(X) # linear regression model prediction
print("Model slope: ", model.coef_)
print("Model intercept:", model.intercept_)
# y_predict = X[:, 0] * model.coef_[0] + X[:, 1] * model.coef_[1] + model.intercept_ # another form to write the equation
plt.figure(figsize=(20, 8.5))
# plt.plot(OBS_TMIN_dates, X, alpha=0.5)
plt.plot(OBS_TMIN_dates, y, alpha=0.5, label='Observation')
plt.plot(OBS_TMIN_dates, y_predict, alpha=0.5, label='Prediction')
plt.legend()
plt.show()
rms = sqrt(mean_squared_error(y, y_predict))
print('RMS: ', rms)
# + [markdown] id="fH8JUYUDyoxU" colab_type="text"
# ## Max Wind
# + id="MRgc5o-FRRWf" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 0} outputId="43d1ad90-67f1-4078-a540-1c4fc3040eb9"
X = np.column_stack((GFS_WMAX[GFS_WMAX_dates.strftime('%Y-%m-%d')].values, GFS_sfc_WMAX.values)) # GFS model daily and sfc WMAX
y = (OBS_WMAX[OBS_WMAX_dates.strftime('%Y-%m-%d')].values)*0.44704 # Observation, converted from mph to m/s
model = LinearRegression(fit_intercept=False)
model.fit(X, y)
y_predict = model.predict(X) # linear regression model prediction
print("Model slope: ", model.coef_)
print("Model intercept:", model.intercept_)
# y_predict = X[:, 0] * model.coef_[0] + X[:, 1] * model.coef_[1] + model.intercept_ # another form to write the equation
plt.figure(figsize=(20, 8.5))
# plt.plot(OBS_WMAX_dates, X, alpha=0.5)
plt.plot(OBS_WMAX_dates, y, alpha=0.5, label='Observation')
plt.plot(OBS_WMAX_dates, y_predict, alpha=0.5, label='Prediction')
plt.legend()
plt.show()
rms = sqrt(mean_squared_error(y, y_predict))
print('RMS: ', rms)
# + [markdown] id="zprl2YRzyryx" colab_type="text"
# ## Precipitation
# + id="bgmln_4Oys48" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 547} outputId="13fac761-5e80-40f3-e56d-da38100c8a60"
X = np.column_stack((GFS_PRCP[GFS_PRCP_dates.strftime('%Y-%m-%d')].values, GFS_sfc_PRCP.values)) # GFS model daily and sfc total PRCP
y = (OBS_PRCP[OBS_PRCP_dates.strftime('%Y-%m-%d')].values)*0.039370 # Observation, converted from mm to inches
model = LinearRegression(fit_intercept=False)
model.fit(X, y)
y_predict = model.predict(X) # linear regression model prediction
print("Model slope: ", model.coef_)
print("Model intercept:", model.intercept_)
# y_predict = X[:, 0] * model.coef_[0] + X[:, 1] * model.coef_[1] + model.intercept_ # another form to write the equation
plt.figure(figsize=(20, 8.5))
# plt.plot(OBS_PRCP_dates, X, alpha=0.5)
plt.plot(OBS_PRCP_dates, y, alpha=0.5, label='Observation')
plt.plot(OBS_PRCP_dates, y_predict, alpha=0.5, label='Prediction')
plt.legend()
plt.show()
rms = sqrt(mean_squared_error(y, y_predict))
print('RMS: ', rms)
|
Developing_ipynb/project4_0327_SS.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/RodriCalle/ComplejidadAlgoritmica/blob/main/14_Prim.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="NFIMRIvf8o9J"
import graphviz as gv
import numpy as np
import pandas as pd
import heapq as hq
import math
def readAdjl(fn, haslabels=False, weighted=False, sep="|"):
with open(fn) as f:
labels = None
if haslabels:
labels = f.readline().strip().split()
L = []
for line in f:
if weighted:
L.append([tuple(map(int, p.split(sep))) for p in line.strip().split()])
# line => "1|3 2|5 4|4" ==> [(1, 3), (2, 5), (4, 4)]
else:
L.append(list(map(int, line.strip().split()))) # "1 3 5" => [1, 3, 5]
# L.append([int(x) for x in line.strip().split()])
return L, labels
def adjlShow(L, labels=None, directed=False, weighted=False, path=[],
layout="sfdp"):
g = gv.Digraph("G") if directed else gv.Graph("G")
g.graph_attr["layout"] = layout
g.edge_attr["color"] = "gray"
g.node_attr["color"] = "orangered"
g.node_attr["width"] = "0.1"
g.node_attr["height"] = "0.1"
g.node_attr["fontsize"] = "8"
g.node_attr["fontcolor"] = "mediumslateblue"
g.node_attr["fontname"] = "monospace"
g.edge_attr["fontsize"] = "8"
g.edge_attr["fontname"] = "monospace"
n = len(L)
for u in range(n):
g.node(str(u), labels[u] if labels else str(u))
added = set()
for v, u in enumerate(path):
if u != None:
if weighted:
for vi, w in G[u]:
if vi == v:
break
g.edge(str(u), str(v), str(w), dir="forward", penwidth="2", color="orange")
else:
g.edge(str(u), str(v), dir="forward", penwidth="2", color="orange")
added.add(f"{u},{v}")
added.add(f"{v},{u}")
if weighted:
for u in range(n):
for v, w in L[u]:
if not directed and not f"{u},{v}" in added:
added.add(f"{u},{v}")
added.add(f"{v},{u}")
g.edge(str(u), str(v), str(w))
elif directed:
g.edge(str(u), str(v), str(w))
else:
for u in range(n):
for v in L[u]:
if not directed and not f"{u},{v}" in added:
added.add(f"{u},{v}")
added.add(f"{v},{u}")
g.edge(str(u), str(v))
elif directed:
g.edge(str(u), str(v))
return g
# + id="tg9_K_--1FUP"
import math
def prim(G):
n = len(G)
visited = [False]*n
path = [None]*n
cost = [math.inf]*n
q = [(0, 0)]
while q:
_, u = hq.heappop(q)
if not visited[u]:
visited[u] = True
for v, w in G[u]:
if not visited[v] and w < cost[v]:
cost[v] = w
path[v] = u
hq.heappush(q, (w, v))
return path, cost
# + colab={"base_uri": "https://localhost:8080/"} id="ybD83SIfAxAe" outputId="8d4367ee-c754-4c9b-ef69-0a2f9a0f636b"
# %%file 1.in
2|3 3|8 4|9
2|1 3|7 5|7
0|3 1|1 4|8 6|7
0|8 1|7 5|2
0|9 2|8 7|6
1|7 3|2 6|2 7|9
2|7 5|2 7|1
4|6 5|9 6|1
# + colab={"base_uri": "https://localhost:8080/", "height": 349} id="rj0TzOABA0VS" outputId="3a17d135-b9e8-4df5-c84c-9c6a6b705ad0"
G, _ = readAdjl("1.in", weighted=True)
adjlShow(G, weighted=True)
# + colab={"base_uri": "https://localhost:8080/", "height": 382} id="aelolawZA-xh" outputId="6d9d911c-9041-40ba-8ea1-c08269cd3961"
path, cost = prim(G)
print(path)
print(cost)
adjlShow(G, weighted=True, path=path)
|
14_Prim.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Convert FIRE data
#
# This script will convert the FIRE .hdf5 files into a .json data files that can be read into Firefly.
#
# FIREreader is the class that will allow you to read in files within a directory, create the dictionary, and write out the json files
#
# +
# %load_ext autoreload
# %autoreload 2
from FIREreader import FIREreader
import numpy as np
# -
# ### Set the defaults and create the .json files
# +
reader = FIREreader()
reader.directory = "/Users/ageller/Visualizations/Firefly"
reader.snapnum = 440
reader.names = {'PartType0':'Gas',
'PartType1':'HRDM',
'PartType2':'LRDM',
'PartType4':'Stars' }
#define the defaults; this must be run first if you want to change the defaults below
reader.defineDefaults()
decimate = 100.
for i,p in enumerate(reader.returnParts):
reader.decimate[p] = decimate
#make the file
reader.run()
# -
|
data/convertFIREdata_simple.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Now we will continue on the [Conversation AI](https://conversationai.github.io/) dataset seen in [week 4 homework and lab](https://github.com/MIDS-scaling-up/v2/tree/master/week04).
# We shall use a version of pytorch BERT for classifying comments found at [https://github.com/huggingface/pytorch-pretrained-BERT](https://github.com/huggingface/pytorch-pretrained-BERT).
#
# The original implementation of BERT is optimised for TPU. Google released some amazing performance improvements on TPU over GPU, for example, see [here](https://medium.com/@ranko.mosic/googles-bert-nlp-5b2bb1236d78) - *BERT relies on massive compute for pre-training ( 4 days on 4 to 16 Cloud TPUs; pre-training on 8 GPUs would take 40–70 days).*. In response, Nvidia released [apex](https://devblogs.nvidia.com/apex-pytorch-easy-mixed-precision-training/), which gave mixed precision training. Weights are stored in float32 format, but calculations, like forward and backward propagation happen in float16 - this allows these calculations to be made with a [4X speed up](https://github.com/huggingface/pytorch-pretrained-BERT/issues/149).
#
# We shall apply BERT to the problem for classifiying toxicity, using apex from Nvidia. We shall compare the impact of hardware by running the model on a V100 and P100 and comparing the speed and accuracy in both cases.
#
# This script relies heavily on an existing [Kaggle kernel](https://www.kaggle.com/yuval6967/toxic-bert-plain-vanila) from [yuval r](https://www.kaggle.com/yuval6967).
#
# *Disclaimer: the dataset used contains text that may be considered profane, vulgar, or offensive.*
import sys, os
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import torch.utils.data
import torch.nn.functional as F
from sklearn.metrics import roc_auc_score
# %load_ext autoreload
# %autoreload 2
# %matplotlib inline
from tqdm import tqdm, tqdm_notebook
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
import warnings
warnings.filterwarnings(action='once')
import pickle
from apex import amp
import shutil
# Let's activate CUDA for GPU based operations
device=torch.device('cuda')
# Change the PATH variable to whereever your `week06/hw` directory is located.
# **For the final run we would like you to have a train_size of at least 1 Million rows, and a valid size of at least 500K rows. When you first run the script, feel free to work with a reduced train and valid size for speed.**
# +
# In bert we need all inputs to have the same length, we will use the first 220 characters.
MAX_SEQUENCE_LENGTH = 220
SEED = 1234
# We shall run a single epoch (ie. one pass over the data)
EPOCHS = 1
PATH = '/root/v2/week06/hw' # /root/v2/week06/hw"
DATA_DIR = os.path.join(PATH, "data")
WORK_DIR = os.path.join(PATH, "workingdir")
# Validation and training sizes are here.
train_size= 1000000 # 1000000
valid_size= 500000 # 500000
# -
# This should be the files you downloaded earlier when you ran `download.sh`
os.listdir(DATA_DIR)
# We shall install pytorch BERT implementation.
# If you would like to experiment with or view any code (purely optional, and not graded :) ), you can copy the files from the repo https://github.com/huggingface/pytorch-pretrained-BERT
# %%capture
from pytorch_pretrained_bert import convert_tf_checkpoint_to_pytorch
from pytorch_pretrained_bert import BertTokenizer, BertForSequenceClassification,BertAdam
from pytorch_pretrained_bert.modeling import BertModel
from pytorch_pretrained_bert import BertConfig
# We shall now load the model. When you run this, comment out the `capture` command to understand the archecture.
# +
# #%%capture
# Translate model from tensorflow to pytorch
BERT_MODEL_PATH = os.path.join(DATA_DIR, 'uncased_L-12_H-768_A-12')
convert_tf_checkpoint_to_pytorch.convert_tf_checkpoint_to_pytorch(
os.path.join(BERT_MODEL_PATH, 'bert_model.ckpt'),
os.path.join(BERT_MODEL_PATH, 'bert_config.json'),
os.path.join(WORK_DIR, 'pytorch_model.bin'))
shutil.copyfile(os.path.join(BERT_MODEL_PATH, 'bert_config.json'), \
os.path.join(WORK_DIR, 'bert_config.json'))
# This is the Bert configuration file
bert_config = BertConfig(os.path.join(WORK_DIR, 'bert_config.json'))
# -
# Bert needs a special formatting of sentences, so we have a sentence start and end token, as well as separators.
# Thanks to this [script](https://www.kaggle.com/httpwwwfszyc/bert-in-keras-taming) for a fast convertor of the sentences.
def convert_lines(example, max_seq_length,tokenizer):
max_seq_length -=2
all_tokens = []
longer = 0
for text in tqdm_notebook(example):
tokens_a = tokenizer.tokenize(text)
if len(tokens_a)>max_seq_length:
tokens_a = tokens_a[:max_seq_length]
longer += 1
one_token = tokenizer.convert_tokens_to_ids(["[CLS]"]+tokens_a+["[SEP]"])+[0] * (max_seq_length - len(tokens_a))
all_tokens.append(one_token)
print(longer)
return np.array(all_tokens)
# Now we load the BERT tokenizer and convert the sentences.
# +
# %%time
tokenizer = BertTokenizer.from_pretrained(BERT_MODEL_PATH, cache_dir=None,do_lower_case=True)
train_all = pd.read_csv(os.path.join(DATA_DIR, "train.csv")).sample(train_size+valid_size,random_state=SEED)
print('loaded %d records' % len(train_all))
# Make sure all comment_text values are strings
train_all['comment_text'] = train_all['comment_text'].astype(str)
sequences = convert_lines(train_all["comment_text"].fillna("DUMMY_VALUE"),MAX_SEQUENCE_LENGTH,tokenizer)
train_all=train_all.fillna(0)
# -
# Let us look at how the tokenising works in BERT, see below how it recongizes misspellings - words the model never saw.
train_all.head(10)
train_all[["comment_text", 'target']].head()
# Lets tokenize some text (I intentionally mispelled some words to check berts subword information handling)
text = 'Hi, I am learning new things in w251 about deep learning the cloud and teh edge.'
tokens = tokenizer.tokenize(text)
' '.join(tokens)
# Added start and end token and convert to ids. This is how it is fed into BERT.
tokens = ["[CLS]"] + tokens + ["[SEP]"]
input_ids = tokenizer.convert_tokens_to_ids(tokens)
' '.join(map(str, input_ids))
# When BERT converts this sentence to a torch tensor below is shape of the stored tensors.
# We have 12 input tensors, while the sentence tokens has length 23; where are can you see the 23 tokens in the tensors ?... **Feel free to post in slack or discuss in class**
# +
# put input on gpu and make prediction
bert = BertModel.from_pretrained(WORK_DIR).cuda()
bert_output = bert(torch.tensor([input_ids]).cuda())
print('Sentence tokens {}'.format(tokens))
print('Number of tokens {}'.format(len(tokens)))
print('Tensor shapes : {}'.format([b.cpu().detach().numpy().shape for b in bert_output[0]]))
print('Number of torch tensors : {}'.format(len(bert_output[0])))
# -
# As it is a binary problem, we change our target to [0,1], instead of float.
# We also split the dataset into a training and validation set,
train_all['target']=(train_all['target']>=0.5).astype(float)
# Training data - sentences
X = sequences[:train_size]
# Target - the toxicity.
y = train_all[['target']].values[:train_size]
X_val = sequences[train_size:]
y_val = train_all[['target']].values[train_size:]
train_all[['id',"comment_text",'target']].head(10)
test_df=train_all.tail(valid_size).copy()
train_df=train_all.head(train_size)
# **From here on in we would like you to run BERT.**
# **Please do rely on the script available - [Kaggle kernel](https://www.kaggle.com/yuval6967/toxic-bert-plain-vanila) from [yuval r](https://www.kaggle.com/yuval6967) - for at least the first few steps up to training and prediction.**
#
# **1)**
# **Load the training set to a training dataset. For this you need to load the X sequences and y objects to torch tensors**
# **You can use `torch.utils.data.TensorDataset` to input these into a train_dataset.**
# Training data creations
train_dataset = torch.utils.data.TensorDataset(torch.tensor(X,dtype=torch.long), torch.tensor(y,dtype=torch.float))
# **2)**
# **Set your learning rate and batch size; and optionally random seeds if you want reproducable results**
# **Load your pretrained BERT using `BertForSequenceClassification`**
# **Initialise the gradients and place the model on cuda, set up your optimiser and decay parameters**
# **Initialise the model with `apex` (we imprted this as `amp`) for mixed precision training**
# +
# %%time
output_model_file = "bert_pytorch.bin"
lr=2e-5
batch_size = 32
accumulation_steps=2
np.random.seed(SEED)
torch.manual_seed(SEED)
torch.cuda.manual_seed(SEED)
torch.backends.cudnn.deterministic = True
model = BertForSequenceClassification.from_pretrained(WORK_DIR,cache_dir=None,num_labels=1) #len(y_columns)
model.zero_grad()
model = model.to(device)
param_optimizer = list(model.named_parameters())
no_decay = ['bias', 'LayerNorm.bias', 'LayerNorm.weight']
optimizer_grouped_parameters = [
{'params': [p for n, p in param_optimizer if not any(nd in n for nd in no_decay)], 'weight_decay': 0.01},
{'params': [p for n, p in param_optimizer if any(nd in n for nd in no_decay)], 'weight_decay': 0.0}
]
train = train_dataset
num_train_optimization_steps = int(EPOCHS*len(train)/batch_size/accumulation_steps)
optimizer = BertAdam(optimizer_grouped_parameters,
lr=lr,
warmup=0.05,
t_total=num_train_optimization_steps)
model, optimizer = amp.initialize(model, optimizer, opt_level="O1",verbosity=0)
# -
# **3)**
# **Start training your model by iterating through batches in a single epoch of the data**
# +
# %%time
model=model.train()
tq = tqdm_notebook(range(EPOCHS))
for epoch in tq:
train_loader = torch.utils.data.DataLoader(train, batch_size=batch_size, shuffle=True)
avg_loss = 0.
avg_accuracy = 0.
lossf=None
tk0 = tqdm_notebook(enumerate(train_loader),total=len(train_loader),leave=False)
optimizer.zero_grad() # Bug fix - thanks to @chinhuic
for i,(x_batch, y_batch) in tk0:
# optimizer.zero_grad()
y_pred = model(x_batch.to(device), attention_mask=(x_batch>0).to(device), labels=None)
loss = F.binary_cross_entropy_with_logits(y_pred,y_batch.to(device))
with amp.scale_loss(loss, optimizer) as scaled_loss:
scaled_loss.backward()
if (i+1) % accumulation_steps == 0: # Wait for several backward steps
optimizer.step() # Now we can do an optimizer step
optimizer.zero_grad()
if lossf:
lossf = 0.98*lossf+0.02*loss.item()
else:
lossf = loss.item()
tk0.set_postfix(loss = lossf)
avg_loss += loss.item() / len(train_loader)
avg_accuracy += torch.mean(((torch.sigmoid(y_pred[:,0])>0.5) == (y_batch[:,0]>0.5).to(device)).to(torch.float) ).item()/len(train_loader)
tq.set_postfix(avg_loss=avg_loss,avg_accuracy=avg_accuracy)
# -
# **4)**
# **Store your trained model to disk, you will need it if you choose section 8C.**
torch.save(model.state_dict(), output_model_file)
# **5)**
# **Now make a prediction for your validation set.**
# +
# Run validation
# The following 2 lines are not needed but show how to download the model for prediction
model = BertForSequenceClassification(bert_config,num_labels=1) #len(y_columns)
model.load_state_dict(torch.load(output_model_file ))
model.to(device)
for param in model.parameters():
param.requires_grad=False
model.eval()
valid_preds = np.zeros((len(X_val)))
valid = torch.utils.data.TensorDataset(torch.tensor(X_val,dtype=torch.long))
valid_loader = torch.utils.data.DataLoader(valid, batch_size=32, shuffle=False)
tk0 = tqdm_notebook(valid_loader)
for i,(x_batch,) in enumerate(tk0):
pred = model(x_batch.to(device), attention_mask=(x_batch>0).to(device), labels=None)
valid_preds[i*32:(i+1)*32]=pred[:,0].detach().cpu().squeeze().numpy()
test_pred = torch.sigmoid(torch.tensor(valid_preds)).numpy().ravel()
# -
# **6)**
# **In the yuval's kernel he get a metric based on the metric for the jigsaw competition - it is quite complicated. Instead, we would like you to measure the `AUC`, similar to how you did in homework 04. You can compare the results to HW04**
# *A tip, if your score is lower than homework 04 something is wrong....*
from sklearn.metrics import roc_auc_score
print('AUC score : {:.5f}'.format(roc_auc_score(y_val, valid_preds)))
#rue_labels = test_df['target']
#predicted_labels = torch.sigmoid(torch.tensor(valid_preds)).numpy()
#print(true_labels)
#print(predicted_labels)
#print('AUC score : {:.5f}'.format(roc_auc_score(true_labels, predicted_labels)))
# **7)**
# **Can you show/print the validation sentences predicted with the highest and lowest toxicity ?**
MODEL_NAME = 'model1'
test_df[MODEL_NAME]=torch.sigmoid(torch.tensor(valid_preds)).numpy()
test_df['comment_text'].loc[test_df['model1'].idxmax()]
test_df['comment_text'].loc[test_df['model1'].idxmin()]
# **8)**
# **Pick only one of the below items and complete it. The last two will take a good amount of time (and partial success on them is fine), so proceed with caution on your choice of items :)**
#
#
# **A. Can you train on two epochs ?**
#
# **B. Can you change the learning rate and improve validation score ?**
#
# **C. Make a prediction on the test data set with your downloaded model and submit to Kaggle to see where you score on public LB - check out [Abhishek's](https://www.kaggle.com/abhishek) script - https://www.kaggle.com/abhishek/pytorch-bert-inference**
#
# **D. Get BERT running on the tx2 for a sample of the data.**
#
# **E. Finally, and very challenging -- the `BertAdam` optimiser proved to be suboptimal for this task. There is a better optimiser for this dataset in this script [here](https://www.kaggle.com/cristinasierra/pretext-lstm-tuning-v3). Check out the `custom_loss` function. Can you implement it ? It means getting under the hood of the `BertForSequenceClassification` at the source repo and implementing a modified version locally . `https://github.com/huggingface/pytorch-pretrained-BERT/blob/master/pytorch_pretrained_bert/modeling.py`**
|
hw6/BERT_classifying_toxicity_p100.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Mean Normalization
#
# In machine learning we use large amounts of data to train our models. Some machine learning algorithms may require that the data is *normalized* in order to work correctly. The idea of normalization, also known as *feature scaling*, is to ensure that all the data is on a similar scale, *i.e.* that all the data takes on a similar range of values. For example, we might have a dataset that has values between 0 and 5,000. By normalizing the data we can make the range of values be between 0 and 1.
#
# In this lab, you will be performing a different kind of feature scaling known as *mean normalization*. Mean normalization will scale the data, but instead of making the values be between 0 and 1, it will distribute the values evenly in some small interval around zero. For example, if we have a dataset that has values between 0 and 5,000, after mean normalization the range of values will be distributed in some small range around 0, for example between -3 to 3. Because the range of values are distributed evenly around zero, this guarantees that the average (mean) of all elements will be zero. Therefore, when you perform *mean normalization* your data will not only be scaled but it will also have an average of zero.
#
# # To Do:
#
# You will start by importing NumPy and creating a rank 2 ndarray of random integers between 0 and 5,000 (inclusive) with 1000 rows and 20 columns. This array will simulate a dataset with a wide range of values. Fill in the code below
# +
# import NumPy into Python
import numpy as np
# Create a 1000 x 20 ndarray with random integers in the half-open interval [0, 5001).
X = np.random.randint(0, 5000, (1000, 20))
# print the shape of X
print(X.shape)
# -
# Now that you created the array we will mean normalize it. We will perform mean normalization using the following equation:
#
# $\mbox{Norm_Col}_i = \frac{\mbox{Col}_i - \mu_i}{\sigma_i}$
#
# where $\mbox{Col}_i$ is the $i$th column of $X$, $\mu_i$ is average of the values in the $i$th column of $X$, and $\sigma_i$ is the standard deviation of the values in the $i$th column of $X$. In other words, mean normalization is performed by subtracting from each column of $X$ the average of its values, and then by dividing by the standard deviation of its values. In the space below, you will first calculate the average and standard deviation of each column of $X$.
# +
# Average of the values in each column of X
ave_cols = X.mean(axis=0)
# Standard Deviation of the values in each column of X
std_cols = X.std(axis=0)
# -
# If you have done the above calculations correctly, then `ave_cols` and `std_cols`, should both be vectors with shape `(20,)` since $X$ has 20 columns. You can verify this by filling the code below:
# +
# Print the shape of ave_cols
print(ave_cols.shape)
# Print the shape of std_cols
print(std_cols.shape)
# -
# You can now take advantage of Broadcasting to calculate the mean normalized version of $X$ in just one line of code using the equation above. Fill in the code below
# Mean normalize X
X_norm = (X - ave_cols)/std_cols
# If you have performed the mean normalization correctly, then the average of all the elements in $X_{\tiny{\mbox{norm}}}$ should be close to zero, and they should be evenly distributed in some small interval around zero. You can verify this by filing the code below:
# +
# Print the average of all the values of X_norm
print(X_norm.mean())
# Print the average of the minimum value in each column of X_norm
print(X_norm.min(axis=0).mean())
# Print the average of the maximum value in each column of X_norm
print(X_norm.max(axis=0).mean())
# -
# You should note that since $X$ was created using random integers, the above values will vary.
#
# # Data Separation
#
# After the data has been mean normalized, it is customary in machine learning to split our dataset into three sets:
#
# 1. A Training Set
# 2. A Cross Validation Set
# 3. A Test Set
#
# The dataset is usually divided such that the Training Set contains 60% of the data, the Cross Validation Set contains 20% of the data, and the Test Set contains 20% of the data.
#
# In this part of the lab you will separate `X_norm` into a Training Set, Cross Validation Set, and a Test Set. Each data set will contain rows of `X_norm` chosen at random, making sure that we don't pick the same row twice. This will guarantee that all the rows of `X_norm` are chosen and randomly distributed among the three new sets.
#
# You will start by creating a rank 1 ndarray that contains a random permutation of the row indices of `X_norm`. You can do this by using the `np.random.permutation()` function. The `np.random.permutation(N)` function creates a random permutation of integers from 0 to `N - 1`. Let's see an example:
# We create a random permutation of integers 0 to 4
np.random.permutation(5)
# # To Do
#
# In the space below create a rank 1 ndarray that contains a random permutation of the row indices of `X_norm`. You can do this in one line of code by extracting the number of rows of `X_norm` using the `shape` attribute and then passing it to the `np.random.permutation()` function. Remember the `shape` attribute returns a tuple with two numbers in the form `(rows,columns)`.
# Create a rank 1 ndarray that contains a random permutation of the row indices of `X_norm`
row_indices = np.random.permutation(X_norm.shape[0])
# Now you can create the three datasets using the `row_indices` ndarray to select the rows that will go into each dataset. Rememeber that the Training Set contains 60% of the data, the Cross Validation Set contains 20% of the data, and the Test Set contains 20% of the data. Each set requires just one line of code to create. Fill in the code below
# +
# Make any necessary calculations.
# You can save your calculations into variables to use later.
training_set = row_indices[:int(len(row_indices)*0.6)]
cross_val_set = row_indices[int(len(row_indices)*0.6):int(len(row_indices)*0.8)]
test_set = row_indices[int(len(row_indices)*0.8):]
# Create a Training Set
X_train = X_norm[training_set]
# Create a Cross Validation Set
X_crossVal = X_norm[cross_val_set]
# Create a Test Set
X_test = X_norm[test_set]
# -
# If you performed the above calculations correctly, then `X_train` should have 600 rows and 20 columns, `X_crossVal` should have 200 rows and 20 columns, and `X_test` should have 200 rows and 20 columns. You can verify this by filling the code below:
# +
# Print the shape of X_train
print(X_train.shape)
# Print the shape of X_crossVal
print(X_crossVal.shape)
# Print the shape of X_test
print(X_test.shape)
# -
|
NumPy Mini-Project/Mean Normalization and Data Separation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.6 64-bit (''venv'': venv)'
# name: python_defaultSpec_1599460568056
# ---
# +
import math
import arviz as az
import matplotlib.pyplot as plt
import pandas as pd
from causalgraphicalmodels import CausalGraphicalModel
from IPython.display import Image, set_matplotlib_formats
from matplotlib.patches import Ellipse, transforms
import jax.numpy as jnp
from jax import ops, random, vmap
from jax.scipy.special import expit
import numpy as onp
import numpyro as numpyro
import numpyro.distributions as dist
from numpyro.diagnostics import effective_sample_size, print_summary
from numpyro.infer import MCMC, NUTS, Predictive
az.style.use("arviz-darkgrid")
numpyro.set_host_device_count(4)
# -
# Replicate sim
#
# +
def make_df(rho=-0.7):
a = 3.5 # average morning wait time
b = -1 # average difference afternoon wait time
sigma_a = 1 # std dev in intercepts
sigma_b = 0.5 # std dev in slopes
# rho = -0.7 # correlation between intercepts and slopes
Mu = jnp.array([a, b])
cov_ab = sigma_a * sigma_b * rho
Sigma = jnp.array([[sigma_a ** 2, cov_ab], [cov_ab, sigma_b ** 2]])
jnp.array([1, 2, 3, 4]).reshape(2, 2).T
sigmas = jnp.array([sigma_a, sigma_b]) # standard deviations
Rho = jnp.array([[1, rho], [rho, 1]]) # correlation matrix
# now matrix multiply to get covariance matrix
Sigma = jnp.diag(sigmas) @ Rho @ jnp.diag(sigmas)
N_cafes = 20
seed = random.PRNGKey(5) # used to replicate example
vary_effects = dist.MultivariateNormal(Mu, Sigma).sample(seed, (N_cafes,))
a_cafe = vary_effects[:, 0]
b_cafe = vary_effects[:, 1]
#---
seed = random.PRNGKey(22)
N_visits = 10
afternoon = jnp.tile(jnp.arange(2), N_visits * N_cafes // 2)
cafe_id = jnp.repeat(jnp.arange(N_cafes), N_visits)
mu = a_cafe[cafe_id] + b_cafe[cafe_id] * afternoon
sigma = 0.5 # std dev within cafes
wait = dist.Normal(mu, sigma).sample(seed)
return pd.DataFrame(dict(cafe=cafe_id, afternoon=afternoon, wait=wait))
d_rho0 = make_df(0)
d = make_df()
# +
def model(cafe, afternoon, wait):
a = numpyro.sample("a", dist.Normal(5, 2))
b = numpyro.sample("b", dist.Normal(-1, 0.5))
sigma_cafe = numpyro.sample("sigma_cafe", dist.Exponential(1).expand([2]))
sigma = numpyro.sample("sigma", dist.Exponential(1))
Rho = numpyro.sample("Rho", dist.LKJ(2, 2))
cov = numpyro.deterministic("cov", jnp.outer(sigma_cafe, sigma_cafe) * Rho)
a_cafe_b_cafe = numpyro.sample(
"a_cafe_b_cafe", dist.MultivariateNormal(jnp.stack([a, b]), cov).expand([20])
)
a_cafe, b_cafe = a_cafe_b_cafe[:, 0], a_cafe_b_cafe[:, 1]
mu = a_cafe[cafe] + b_cafe[cafe] * afternoon
numpyro.sample("wait", dist.Normal(mu, sigma), obs=wait)
m14_1 = MCMC(NUTS(model), 500, 500, num_chains=4)
m14_1.run(random.PRNGKey(0), d_rho0.cafe.values, d_rho0.afternoon.values, d_rho0.wait.values)
# -
post = m14_1.get_samples()
az.plot_kde(post["Rho"][:, 0, 1], bw=2)
plt.show()
# ---
m14_2a = MCMC(NUTS(model), 500, 500, num_chains=4)
m14_2a.run(random.PRNGKey(0), d.cafe.values, d.afternoon.values, d.wait.values)
# + tags=[]
def model(cafe, afternoon, wait):
n_cafes = len(set(cafe))
a = numpyro.sample("a", dist.Normal(0, 10))
b = numpyro.sample("b", dist.Normal(0, 10))
sigma_a = numpyro.sample("sigma_a", dist.HalfCauchy(2))
sigma_b = numpyro.sample("sigma_b", dist.HalfCauchy(2))
a_cafe = numpyro.sample("a_cafe", dist.Normal(a, sigma_a), sample_shape=(n_cafes,))
b_cafe = numpyro.sample("b_cafe", dist.Normal(b, sigma_b), sample_shape=(n_cafes,))
mu = a_cafe[cafe] + b_cafe[cafe] * afternoon
sigma = numpyro.sample("sigma", dist.HalfCauchy(2))
numpyro.sample("wait", dist.Normal(mu, sigma), obs=wait)
m14_2b = MCMC(NUTS(model), 500, 500, num_chains=4)
m14_2b.run(random.PRNGKey(1), d.cafe.values, d.afternoon.values, d.wait.values)
# -
az.compare(
{
"m14_2a": az.from_numpyro(m14_2a),
"m14_2b": az.from_numpyro(m14_2b),
},
ic="waic",
scale="deviance",
)
# + tags=[]
post_2a = m14_2a.get_samples()
post_2b = m14_2b.get_samples()
print(post_2a["a_cafe_b_cafe"].shape)
print(post_2b["a_cafe"].shape)
a_cafe_2a = jnp.mean(post_2a['a_cafe_b_cafe'], 0)[:,0]
b_cafe_2a = jnp.mean(post_2a['a_cafe_b_cafe'], 0)[:,1]
a_cafe_2b = jnp.mean(post_2b['a_cafe'], 0)
b_cafe_2b = jnp.mean(post_2b['b_cafe'], 0)
# + tags=[]
rho_2a = post_2a["Rho"]
sigma_cafe_2a = post_2a["sigma_cafe"]
cov_2a = sigma_cafe_2a[:,:,None] * sigma_cafe_2a[:,None,:] * rho_2a
print(rho_2a[:2])
print(sigma_cafe_2a.shape)
print(post_2a["cov"].shape)
print(cov_2a.shape)
assert jnp.array_equal(post_2a["cov"], cov_2a)
# + tags=[]
a_mean_2a = jnp.mean(post_2a['a'], 0)
b_mean_2a = jnp.mean(post_2a['b'], 0)
print(a_mean_2a, b_mean_2a)
rho_est = jnp.mean(post_2a['Rho'][:,0,1], 0)
sa_est = jnp.mean(post_2a["sigma_cafe"][:,0], 0)
sb_est = jnp.mean(post_2a["sigma_cafe"][:,1], 0)
cov_ab = sa_est * sb_est * rho_est
rho_est, sa_est, sb_est, cov_ab
Sigma_est = jnp.array([[sa_est**2, cov_ab], [cov_ab, sb_est**2]])
Sigma_est
# + tags=[]
plt.plot(a_cafe_2a, b_cafe_2a, "o", color='k', alpha=0.7)
plt.plot(a_cafe_2b, b_cafe_2b, "o", color='b', alpha=0.7)
for i in range(len(a_cafe_2a)):
plt.plot([a_cafe_2a, a_cafe_2b], [b_cafe_2a, b_cafe_2b], "k", lw=0.5)
# overlay population distribution
# Ref: https://matplotlib.org/gallery/statistics/confidence_ellipse.html
for l in [0.1, 0.3, 0.5, 0.8, 0.99]:
pearson = Sigma_est[0, 1] / jnp.sqrt(Sigma_est[0, 0] * Sigma_est[1, 1])
ellipse = Ellipse(
(0, 0),
jnp.sqrt(1 + pearson),
jnp.sqrt(1 - pearson),
edgecolor="k",
alpha=0.2,
facecolor="none",
)
std_dev = dist.Normal().icdf((1 + jnp.sqrt(l)) / 2)
scale_x = 2 * std_dev * jnp.sqrt(Sigma_est[0, 0])
scale_y = 2 * std_dev * jnp.sqrt(Sigma_est[1, 1])
scale = transforms.Affine2D().rotate_deg(45).scale(scale_x, scale_y)
ellipse.set_transform(scale.translate(a_mean_2a, b_mean_2a) + plt.gca().transData)
plt.gca().add_patch(ellipse)
# -
# ---
ucbadmit = pd.read_csv('../data/UCBadmit.csv', sep=';')
d = ucbadmit
d.columns = [c.replace('.', '_') for c in d.columns]
d["male"] = d.applicant_gender.map({"male": 1, "female": 0})
d["dept_id"] = pd.factorize(d.dept)[0]
d["acc_rate"] = d.admit / d.applications
d.head()
# + tags=[]
def model(admit, applications, dept_id, male):
n_depts = len(set(dept_id))
a = numpyro.sample("a", dist.Normal(0, 10))
bm = numpyro.sample("bm", dist.Normal(0, 10))
sigma_dept = numpyro.sample("sigma_dept", dist.HalfCauchy(2).expand([2]))
Rho = numpyro.sample("Rho", dist.LKJ(2, 2))
cov = jnp.outer(sigma_dept, sigma_dept) * Rho
a_dept_bm_dept = numpyro.sample(
"a_dept_bm_dept", dist.MultivariateNormal(
jnp.stack([a, bm]), cov
).expand([n_depts])
)
a_dept = numpyro.deterministic("a_dept", a_dept_bm_dept[:, 0])
bm_dept = numpyro.deterministic("bm_dept", a_dept_bm_dept[:, 1])
logit_p = a_dept[dept_id] + bm_dept[dept_id] * male
numpyro.sample("admit", dist.Binomial(applications, logits=logit_p), obs=admit)
m14_3a = MCMC(NUTS(model), 500, 500, num_chains=4)
m14_3a.run(random.PRNGKey(3),
d.admit.values, d.applications.values, d.dept_id.values, d.male.values
)
m14_3a.print_summary()
# + tags=[]
def model(admit, applications, dept_id, male):
n_depts = len(set(dept_id))
sigma_dept = numpyro.sample("sigma_dept", dist.HalfCauchy(2).expand([2]))
L_Rho_dept = numpyro.sample("L_Rho_dept", dist.LKJCholesky(2, 2))
z_dept = numpyro.sample("z_dept", dist.Normal(0, 1).expand([2, n_depts]))
a_dept_bm_dept = ((sigma_dept[..., None] * L_Rho_dept) @ z_dept).T
a_dept = numpyro.deterministic("a_dept", a_dept_bm_dept[:, 0])
bm_dept = numpyro.deterministic("bm_dept", a_dept_bm_dept[:, 1])
logit_p = a_dept[dept_id] + bm_dept[dept_id] * male
numpyro.sample("admit", dist.Binomial(applications, logits=logit_p), obs=admit)
m14_3b = MCMC(NUTS(model), 500, 500, num_chains=4)
m14_3b.run(random.PRNGKey(234),
d.admit.values, d.applications.values, d.dept_id.values, d.male.values
)
m14_3b.print_summary()
# -
az.compare(
{
"m14_3a": az.from_numpyro(m14_3a),
"m14_3b": az.from_numpyro(m14_3b),
},
ic="waic",
scale="deviance",
)
az.plot_forest(
m14_3a, var_names=["a_dept", "bm_dept"], combined=True, hdi_prob=0.95
)
az.plot_forest(
m14_3b, var_names=["a_dept", "bm_dept"], combined=True, hdi_prob=0.95
)
# +
post_c = m14_3a.get_samples(group_by_chain=True)
neff_c = jnp.concatenate(
[effective_sample_size(post_c[k].copy()).reshape(-1)
for k in ["a_dept", "bm_dept"]]
)
post_nc = m14_3b.get_samples(group_by_chain=True)
neff_nc = jnp.concatenate(
[effective_sample_size(post_nc[k].copy()).reshape(-1)
for k in ["a_dept", "bm_dept"]]
)
# -
plt.plot(neff_c, neff_nc, 'o')
x = jnp.linspace(0, 2000, 100)
plt.gca().set(xlabel="centered", ylabel="non-centered")
plt.plot(x, x, "--")
# ---
|
practice/14.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # PC lab 10: Artificial Neural Networks
# ---
# <img src="img/neural_nets_art.jpg">
# ## Introduction
# Although artificial neural networks enjoy a lot of progress today, they were first described by [<NAME> and <NAME>](https://link.springer.com/article/10.1007%2FBF02478259) in 1943. Early progress in training competitive neural networks was stalled by a multitude of reasons, such as the limited computer resources, sub-optimal network architectures and the use of smaller datasets. In this PC-lab we will implement a custom neural network on a step-by-step basis, allowing an in-depth comprehension of the essential elements of deep learning
#
# ### Artificial Neuron
# The core unit of every (artificial) neural network is considered the neuron. The neuron can be observed as a switch. It receives **one or more inputs** $\mathbf{x}$, processes a **weighted sum** $z$ (adding **bias** $b$) that is sent through the **sigmoid activation function $\sigma()$**, outputing a **single response** $a$:
#
# $$
# z = \sum\limits_{i=1}^{n}(w_ix_i) + b = \sum\limits_{i=0}^{n}(w_ix_i)$$ with $$ x_0 = 1 \tag{1}\\
# $$
#
# $$ a = \sigma(z) $$
# <img src="img/neuron_bishop.jpg" style="width:40%">
# The default recommended activation function is the **Rectified Linear Unit**, or **ReLU**.
#
# $$ ReLU(z) = max\{0,z\} $$
#
# <img src="img/relu.png" style="width:30%">
#
# The ReLU function has many properties that make optimization easy using gradient-based methods. It can be seen as a switch giving no response for $z < 0$ and giving a response $z$ for $z > 0$.
#
#
# ### Artificial Neural Networks
# The most basic artificial neural network is the **feedforward neural network**. There are no feedback connections such as can be found in **recurrent neural networks**. A feedforward neural network is called a network as it is composed out of many inheriting functions making up the model, e.g. $f(\textbf{x})= f^{(3)}(f^{(2)}(f^{(1)}(\textbf{x})))$. Neural networks typically are constructed in different layers of neurons in which every neuron is connected with all the neurons of the previous layer, eventually resulting in a set of **output neurons** $\mathbf{\hat{\textbf{y}}}$.
# <img src="img/nn_bishop_adapted.png" style="width:70%">
#
# To train the network, samples are processed in batches. This allows for faster training and improved convergence of the loss during gradient descent. Advantages of stochastic gradient descent or other optimization algorithms for loss calculation are not discussed in this PC-lab, but have been [extensively discussed](https://ruder.io/optimizing-gradient-descent/) before.
# Practically, the first fully-connected layer of the network using batch size $B$ is computed by matrix combination of the input $X \in \mathbb{R}^{B, D}$ with a set of weights $W^{(12)} \in \mathbb{R}^{D, M}$.
#
# \begin{equation}
# XW^{(12)} =
# \begin{bmatrix}
# 1 & x_{0,1} & ... & x_{0,D-1} & x_{0,D} \\
# 1 & x_{1,1} & ... & x_{1,D-1} & x_{1,D} \\
# ... & ... & ... & ... & ...\\
# 1 & x_{B-1,1} & ... & x_{B-1,D-1} & x_{B-1,D} \\
# 1 & x_{B,1} & ... & x_{B,D-1} & x_{B,D} \\
# \end{bmatrix}
# \begin{bmatrix}
# W_{0,0} & W_{0,1} & ... & W_{0,M-1} & W_{0,M} \\
# W_{1,0} & W_{1,1} & ... & W_{1,M-1} & W_{1,M} \\
# ... & ... & ... & ... & ...\\
# W_{D-1,0} & W_{D-1,1} & ... & W_{D-1,M-1} & W_{D-1,M} \\
# W_{D,0} & W_{D,1} & ... & W_{D,M-1} & W_{D,M} \\
# \end{bmatrix}
# \end{equation}
# <div class="alert alert-warning">
# <h2>Structure of the exercise</h2>
# <p>The idea of this PC-Lab will be to construct our very own neural network from scratch. Every exercize will introduce a new feature necessary to train a working model.</p>
# <p>We define the class <code>Neural_Network</code> for which the structural architecture is given at initialization. Let's start by creating a neural network with one hidden layer. To include the bias term, we add a scalar to the weights vector for every layer.</p>
#
# <code>
# class Neural_Network(object):
# def __init__(self, input_nodes, output_nodes, hlayer_nodes):
# self.input_nodes = input_nodes
# self.output_nodes = output_nodes
# self.hlayer_nodes = hlayer_nodes
# # initialize weights + bias in the first layer
# self.W_12 = np.random.randn(self.input_nodes+1, self.hlayer_nodes))
# # initialize weights + bias in the second layer
# self.W_23 = append(np.random.randn(self.hlayer_nodes+1, self.output_nodes))
# </code>
#
#
#
# </div>
# <div class="alert alert-success">
#
# <h3>EXERCISE</h3> <p><b>Complete</b> the attribute function <code>Neural_Net.forward()</code> and <code>Neural_Net.relu()</code></p>
# </div>
# |Code Symbol | Math Symbol | Definition | Dimensions
# | :-: | :-: | :-: | :-: |
# |X|$$X$$|Input Data| (batch_size, input_nodes) |
# |y|$$y$$|label| (batch_size, output_nodes) |
# |y_hat| $$\hat{y}$$| Output Data | (batch_size, output_nodes) |
# |W_12 | $$W^{(12)}$$ | Layer 1 weights | (input_nodes + 1, hlayer_nodes) |
# |W_23 | $$W^{(23)}$$ | Layer 2 weights | (hlayer_nodes + 1, output_nodes) |
# |a_1 | $$a^{(1)}$$ | Layer 1 activity (inputs) | (batch_size, input_nodes + 1) |
# |z_2 | $$z^{(2)}$$ | Layer 2 linear combination | (batch_size, hlayer_nodes) |
# |a_2 | $$a^{(2)}$$ | Layer 2 activity | (batch_size, hlayer_nodes + 1) |
# | y_hat | $\hat{y}$ | Layer 3 linear combination | (batch_size, output_nodes) |
# $$
# \textbf{z}^{(2)} = \textbf{a}^{(1)}\textbf{W}^{(12)} \tag{2}\\
# $$
# $$
# \textbf{a}^{(2)} = ReLU(\textbf{z}^{(2)}) \tag{3}\\
# $$
# $$
# \hat{\textbf{y}} = \textbf{a}^{(2)}\textbf{W}^{(23)} \tag{4}\\
# $$
#
import numpy as np
class Neural_Network(object):
def __init__(self, input_nodes, output_nodes, hlayer_nodes):
self.input_nodes = input_nodes
self.output_nodes = output_nodes
self.hlayer_nodes = hlayer_nodes
# initialize weights + bias in the first layer
self.W_12 = np.random.randn(self.input_nodes+1, self.hlayer_nodes)
# initialize weights + bias in the second layer
self.W_23 = np.random.randn(self.hlayer_nodes+1, self.output_nodes)
def forward(self, X):
# add bias to input samples
self.a_1 = np.hstack((np.ones((len(X),1)), X)) # add one acting as a bias to all samples
#//solution
self.z_2 = np.matmul(self.a_1, self.W_12)
self.a_2 = np.hstack((np.ones((len(X),1)), self.relu(self.z_2)))
self.y_hat = np.matmul(self.a_2, self.W_23)
#//solution
return np.clip(self.y_hat, -10e6, 10e6)
def relu(self, z):
#//solution
return np.maximum(0., z)
#//solution
def relu_prime(self, z):
return (z>0)*1
np.random.seed(1)
# Initialize neural network with 1 input, 1 output and 2 nodes in hidden layer
NN = Neural_Network(1,1,3)
# Input two samples, each with one input
NN.forward([[2],[3]])
# ## Backpropagation
# Let's construct a dataset that follows the function $\mathbf{y = sin(x)}$. To train the neural network we have to evaluate how the prediction $\hat{y}$ compares to the true label $y$. This is done through the loss function $L$. The formula used for L is dependent upon the problem we are trying to solve. In line with previous methods fitting a **regression** problem, we consider the **MSE** :
#
# $$
# L = \frac{1}{n}\sum_{i=1}^{n}{(y_i-\hat{y_i})^2}\tag{6}
# $$
# +
import matplotlib.pyplot as plt
# %matplotlib inline
def squared_error(y, y_hat):
return (y-y_hat)**2
X = np.random.uniform(-3, 3, size=(1000,1)) # sample random points for x=[0, pi]
y = -26*X + 145*X**2 + 28*X**3 - 26*X**4 - 2*X**5 + X**6 - 80
#y = np.sum(np.sin(X),axis=1).reshape(-1,1) # sinus transform
NN = Neural_Network(1,1,40)
y_hat = NN.forward(X) # predict values
loss = squared_error(y, y_hat)
fig, (ax_1, ax_2, ax_3) = plt.subplots(1,3, figsize=(15,4))
ax_1.set_title("sample data")
ax_1.scatter(X, y)
ax_2.set_title("predictions on sample data")
ax_2.scatter(X, y_hat)
ax_3.set_title("loss function at each sample")
ax_3.scatter(X, loss)
# -
# To train our model, we must find a set of weights that minimizes the overall loss function. An exhaustive method would be to try all possible combinations of weights, a solution that blows up with increasing dimensionality. In order to reduce processing times to obtain the optimal set of weights, we evaluate the influence of each weight on the loss function. If we consider the different equations to obtain our loss:
# $$
# \textbf{z}^{(2)} = \textbf{a}^{(1)}\textbf{W}^{(12)} \tag{2}\\
# $$
# $$
# \textbf{a}^{(2)} = ReLU(\textbf{z}^{(2)}) \tag{3}\\
# $$
# $$
# \hat{\textbf{y}} = \textbf{a}^{(2)}\textbf{W}^{(23)} \tag{4}\\
# $$
# $$
# L = \frac{1}{n} \sum_{i=0}^{n}{(y_{i}-\hat{y_{i}})^2} \tag{6}\\
# $$
# To evaluate the influence of $W^{(23)}$ on the loss $L$, we can find the **partial derivative** of the loss in function of $W^{(23)}$. Using the **chain rule**, this can be calculated using a step-by-step approach.
# $$ \frac{\delta L}{\delta W^{(23)}} = \frac{\delta \textbf{L}}{\delta \hat{\textbf{y}}} \cdot \frac{\delta \hat{\textbf{y}}}{\delta \textbf{W}^{(23)}} = \delta_{1} \cdot \frac{\delta \hat{\textbf{y}}}{\delta \textbf{W}^{(23)}} \tag{7}$$
#
#
#
# Backpropagation is the step-by-step evaluation of the partial derivatives of the loss in function of the network weights, performed by backward iteration over the different transformations performed by the network. The values obtained when iterating down from the loss function are recyclable when calculating the derivative of weights further down in the chain rule, making **a substantial difference** in the amount of processing power needed to obtain all derivatives. The use of backpropagation is a major element in making training of deep neural networks possible. For example, to obtain the derivatives of the weights in the first layer ($\textbf{W}^{(12)}$) we apply:
#
# $$ \frac{\delta L}{\delta W^{(12)}} = \delta_{1} \cdot \frac{\delta \hat{\textbf{y}}}{\delta \textbf{a}^{(2)}} \cdot \frac{\delta \textbf{a}^{(2)}}{\delta \textbf{z}^{(2)}} \cdot \frac{\delta \textbf{z}^{(2)}}{\delta \textbf{W}^{(12)}} = \delta_{2} \cdot \frac{\delta \textbf{z}^{(2)}}{\delta \textbf{W}^{(12)}} \tag{8} $$
#
#
# $\delta_{1}$ and $\delta_{2}$ are solely introduced as variables to which the intermediate values can be assigned. Using these variables when implementing backpropagation into the neural network will make things easier.
#
# <div class="alert alert-success">
#
# <b>EXERCISE:</b>
# <p><b>Write out</b> the following partial derivatives as found in the chain rule.</p>
#
# $$\frac{\delta L}{\delta \hat{y}}$$
# <hr>
# $$\frac{\delta \hat{y}}{\delta a^{(2)}}$$
# <hr>
# $$\frac{\delta a^{(2)}}{\delta z^{(2)}}$$
# <hr>
# $$\frac{\delta z^{(2)}}{\delta W^{(12)}}$$
#
# </div>
# <div class="alert alert-success">
#
# <b>EXERCISE:</b>
# <p><b>Write out</b> the following partial derivatives as found in the chain rule.</p>
#
# $$\frac{\delta L}{\delta \hat{y}} = \frac{1}{n}\sum_{i=0}^{n}{2*(\hat{y_{i}} - y_{i})}$$
# <hr>
# $$\frac{\delta \hat{y}}{\delta a^{(2)}} = W^{(23)}$$
# <hr>
# $$\frac{\delta a^{(2)}}{\delta z^{(2)}} =
# \begin{cases}
# 0 & \text{if } (z^{(2)}) < 0 \\
# 1 & \text{if } (z^{(2)}) > 0 \\
# \end{cases}$$
# <hr>
# $$\frac{\delta z^{(2)}}{\delta W^{(12)}} = a^{(1)}$$
#
# </div>
# <hr>
# <div class="alert alert-success">
#
# <h3>EXERCISE</h3>
# <p><b>Complete</b> the attribute functions <code>NN.backpropagate()</code> and <code>NN.relu_prime()</code>, and the function <code>loss_prime</code>. Use the partial derivatives of the previous exercise to get an overview of the sequential steps executed in backpropagation.</p>
# </div>
# </div>
class Neural_Network(object):
def __init__(self, input_nodes, output_nodes, hlayer_nodes):
self.input_nodes = input_nodes
self.output_nodes = output_nodes
self.hlayer_nodes = hlayer_nodes
# initialize weights + bias in the first layer
self.W_12 = np.random.randn(self.input_nodes+1, self.hlayer_nodes)
# initialize weights + bias in the second layer
self.W_23 = np.random.randn(self.hlayer_nodes+1, self.output_nodes)
def forward(self, X):
# add bias to input samples
self.a_1 = np.hstack((np.ones((len(X),1)), X)) # add one acting as a bias to all samples
#//solution
self.z_2 = np.matmul(self.a_1, self.W_12)
self.a_2 = np.hstack((np.ones((len(X),1)), self.relu(self.z_2)))
self.y_hat = np.matmul(self.a_2, self.W_23)
#//solution
return np.clip(self.y_hat, -10e6, 10e6) # stability
def relu(self, z):
#//solution
return np.maximum(0., z)
#//solution
def relu_prime(self, z):
return (z>0)*1
def backpropagate(self, X, y, get_loss_prime):
self.y_hat = self.forward(X)
self.delta_1 = get_loss_prime(self.y_hat,y) # derivative of cost function
self.dLdW_23 = np.matmul(self.delta_1.T, self.a_2)
self.dLda_2 = np.matmul(self.delta_1, self.W_23[1:].T)
self.delta_2 = self.dLda_2*self.relu_prime(self.z_2)
self.dLdW_12 = np.matmul(self.a_1.T, self.delta_2)
# join two flattened arrays in one vector
return np.concatenate((self.dLdW_12.ravel(), self.dLdW_23.ravel()))
NN.a_2.shape
from pdb import set_trace
NN.delta_1
NN.a_2
# +
def get_loss_prime(y_hat, y):
return 2*(y_hat-y) # Cost function over all batches, divided by # batches
np.random.seed(1)
NN = Neural_Network(1,1,3)
NN.backpropagate(X[:2], y[:2], get_loss_prime)
# -
# <div class="alert alert-success">
#
# <b>EXERCISE:</b>
# <p><b>Evaluate</b> the values and shapes of <i>dLdW_12</i> and <i>dLdW_23</i> separately, and compare the size of vectors. Can you differentiate the updates for weights from the updates for the biases? Can you predict the shapes of these values after changing the amount of nodes of the different layers within the neural network? Don't forget to run <code>NN.backpropagation()</code> with updated arguments when changing the hyperparameters of the network!</p>
# </div>
#
NN = Neural_Network(1,1,2)
NN.backpropagate([[1],[2]], [[np.sin(1)],[np.sin(2)]], get_loss_prime)
print("dLdW_12:\n {}".format(NN.dLdW_12))
print("dLdW_23:\n {}".format(NN.dLdW_23))
# ## Gradient Descent
# Our simple neural network is close to completion now. One more important element is the ability to train this network. To adjust the weights based on the partial derivatives we need to apply the obtained gradient to perform an update to the actual weights. As we are dealing with a **non-convex** and **non-linear optimization problem**, updates are performed using the well-known **gradient descent** algorithm. Small variations on the gradient descent method have shown to drastically increase the speed at which deep neural networks can be trained (i.e. [momentum, adam, ...](http://ruder.io/optimizing-gradient-descent/index.html)).
# ### A brief recap: Gradient Descent
#
#
#
# $$W_{t+1} = W_{t} - \eta \nabla L(\theta)$$
#
#
# where
#
# $\eta$: learning rate (default: 1e-4)
#
#
# >**input** starting point $\textbf{x}\in$ **dom** $f$.
# >
# >**repeat**
# >
# >> 1. $\Delta \textbf{x} := -\nabla f(\textbf{x})$.
# >> 3. *Update*. $\textbf{x}:=\textbf{x}+\eta\Delta \textbf{x}$.
# >
# >**until** stopping criterion is satisfied.
#
# >**output** $x$
#
# The stopping criterion is usually expressed as the amount of times the dataset is iterated. An **epoch** is one iteration over the whole dataset.
from sklearn.utils import shuffle
class Neural_Network(object):
def __init__(self, input_nodes, output_nodes, hlayer_nodes):
self.input_nodes = input_nodes
self.output_nodes = output_nodes
self.hlayer_nodes = hlayer_nodes
# initialize weights + bias in the first layer
self.W_12 = np.random.randn(self.input_nodes+1, self.hlayer_nodes)
# initialize weights + bias in the second layer
self.W_23 = np.random.randn(self.hlayer_nodes+1, self.output_nodes)
def forward(self, X):
# add bias to input samples
self.a_1 = np.hstack((np.ones((len(X),1)), X)) # add one acting as a bias to all samples
#//solution
self.z_2 = np.matmul(self.a_1, self.W_12)
self.a_2 = np.hstack((np.ones((len(X),1)), self.relu(self.z_2)))
self.y_hat = np.matmul(self.a_2, self.W_23)
#//solution
return np.clip(self.y_hat, -10e6, 10e6)
def relu(self, z):
#//solution
return np.maximum(0., z)
#//solution
def relu_prime(self, z):
return (z>0)*1
def backpropagate(self, X, y, get_loss_prime):
self.y_hat = self.forward(X)
self.delta_1 = get_loss_prime(self.y_hat,y) # derivative of cost function
self.dLdW_23 = np.matmul(self.delta_1.T, self.a_2)
self.dLda_2 = np.matmul(self.delta_1, self.W_23[1:].T)
self.delta_2 = self.dLda_2*self.relu_prime(self.z_2)
self.dLdW_12 = np.matmul(self.a_1.T, self.delta_2)
# join two flattened arrays in one vector
return np.concatenate((self.dLdW_12.ravel(), self.dLdW_23.ravel()))
def set_weights(self, weights):
self.W_12 = weights[:len(self.W_12.ravel())].reshape(self.W_12.shape)
self.W_23 = weights[len(self.W_12.ravel()):].reshape(self.W_23.shape)
def get_weights(self):
return np.concatenate((self.W_12.ravel(), self.W_23.ravel()))
def compile(self, optimizer_f, loss_f, loss_prime_f):
self.optimizer = optimizer_f
self.get_loss = loss_f
self.get_loss_prime = loss_prime_f
def fit(self, X, y, batch_size=8, epochs=50, eta=1e-5):
epoch = 0 # set starting epoch
pool = np.arange(len(X)//batch_size) # setup batch pool
avg_loss_all = [] # initialize loss vector
while epoch<epochs:
print("\repoch: {}".format(epoch), end="")
epoch +=1
# shuffle X, y
X_scrambled, y_scrambled = shuffle(X,y)
avg_loss = 0
for i in shuffle(pool): # select random batch
# select batch data
X_batch = X_scrambled[i*batch_size:(i+1)*batch_size]
y_batch = y_scrambled[i*batch_size:(i+1)*batch_size]
# get prediction
y_hat = self.forward(X_batch)
# get loss on prediction
avg_loss += self.get_loss(y_hat, y_batch)
# get gradients on weights
dLdW = self.backpropagate(X_batch, y_batch, self.get_loss_prime)
# get update values with weight gradients
dLdW_update = self.optimizer(dLdW, eta)
self.set_weights(self.get_weights()+dLdW_update) # set new weights with update values
avg_loss_all.append(avg_loss)
return avg_loss_all
# <div class="alert alert-success">
#
# <h3>EXERCISE</h3>
# <p><b>Complete</b> the function <code>gradient_descent()</code>. The different steps as explained above have already been partially implemented in the <code>Neural_Network.fit()</code> function, make sure to analyze it before completing the code for the <code>gradient_descent</code> function. <code>gradient_descent</code> is one way to optimize your weights given a loss, and is stored in <code>Neural_Network.optimizer</code> when running <code>Neural_Network.compile()</code></p>
# </div>
# +
def MSE_loss(y_hat, y):
return np.mean((y-y_hat)**2)/(len(y))
def MSE_loss_prime(y_hat, y):
return np.minimum(2*(y_hat-y), 10e6)
def gradient_descent(dLdW, eta):
return dLdW*-eta
# -
# <div class="alert alert-success">
#
# <h3>EXERCISE</h3>
# <p><b>Run</b> the code below and <b>evaluate</b> how the network trains when tweaking with specific functions such as the amount of hidden nodes, epochs and step size of the gradient update.</p>
# </div>
# +
np.random.seed(1)
NN = Neural_Network(1,1,160)
NN.compile(gradient_descent, MSE_loss, MSE_loss_prime)
fig, ax = plt.subplots(2,2, figsize=(10,10))
ax_1, ax_2, ax_3, ax_4 = ax.ravel()
ax_1.scatter(X , NN.forward(X))
ax_1.set_title("Predicted y values BEFORE GD")
loss = NN.fit(X, y, epochs=200, batch_size=5, eta=1e-5)
ax_2.scatter(X, NN.forward(X))
ax_2.set_title("Predicted y values AFTER GD")
ax_3.scatter(X,y)
ax_3.set_title("True y values")
ax_4.set_title("Loss function throughout training")
ax_4.plot(range(len(loss)),loss, 'r')
# +
np.random.seed(1)
NN = Neural_Network(1,1,320)
NN.compile(gradient_descent, MSE_loss, MSE_loss_prime)
fig, ax = plt.subplots(2,2, figsize=(10,10))
ax_1, ax_2, ax_3, ax_4 = ax.ravel()
ax_1.scatter(X , NN.forward(X))
ax_1.set_title("Predicted y values BEFORE GD")
loss = NN.fit(X, y, epochs=200, batch_size=5, eta=1e-5)
ax_2.scatter(X, NN.forward(X))
ax_2.set_title("Predicted y values AFTER GD")
ax_3.scatter(X,y)
ax_3.set_title("True y values")
ax_4.set_title("Loss function throughout training")
ax_4.plot(range(len(loss)),loss, 'r')
# -
# <div class="alert alert-success">
#
# <h3>Optional EXERCISE</h3>
# <p>Tweak the network to allow for classification purposes. For this, a sigmoid layer has to be added as the final step in
# <code>NN.forward()</code>. Make sure to adjust the backpropagate step and the loss function accordingly.</p>
# </div>
|
predmod/lab4/PClab012_ANN_solved.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:cta] *
# language: python
# name: conda-env-cta-py
# ---
# # Timing for a Toymodel Cherenkov Shower
#
# Currently the ImageModel classes in ctapipe only provide methods for obtaining charge. In order for us to create realistic toymodel waveforms, we also need to generate "time images", indicating the pulse time in each pixel.
# +
from ctapipe.image.toymodel import Gaussian
from ctapipe.instrument import CameraGeometry
from ctapipe.visualization import CameraDisplay
from ctapipe.image.hillas import camera_to_shower_coordinates
from astropy import units as u
from astropy.coordinates import Angle
import numpy as np
from matplotlib import pyplot as plt
camera = CameraGeometry.from_name("CHEC")
# -
# ## Obtain Image
# +
centroid_x = u.Quantity(0.05, u.m)
centroid_y = u.Quantity(0.05, u.m)
length = u.Quantity(0.03, u.m)
width = u.Quantity(0.008, u.m)
psi = Angle(u.Quantity(70, u.deg))
model = Gaussian(centroid_x, centroid_y, length, width, psi)
_, charge, _ = model.generate_image(camera, 10000)
# -
display = CameraDisplay(camera)
display.image = charge
display.add_colorbar()
# ## Obtain longitudinal coordinates
#
# Based on this image, we wish to obtain the coordinates along the major axis.
#
# The `camera_to_shower_coordinates` method in ctapipe already contains the required transformations, and takes in the same parameters we used to define the image.
longitudinal, transverse = camera_to_shower_coordinates(
camera.pix_x,
camera.pix_y,
centroid_x,
centroid_y,
psi
)
display = CameraDisplay(camera, title="longitudinal")
display.image = longitudinal.value
display.add_colorbar()
# ## Obtain Time Image
#
# As a Cherenkov shower's most significant time development is along its major axis, we will solely consider a time development along the longitudinal axis for this toy model. We will also assume a linear development of time along this axis.
#
# The only things remaining to define are therefore the `time_gradient` and the `time_intercept`
def obtain_time_image(longitudinal, time_gradient, time_intercept):
return longitudinal * time_gradient + time_intercept
time_gradient = u.Quantity(3, u.s/u.m)
time_intercept = u.Quantity(40, u.s)
time = obtain_time_image(longitudinal, time_gradient, time_intercept)
display = CameraDisplay(camera)
display.image = time
display.add_colorbar()
|
d200326_ctapipe_charge_sampling_rate/image_timing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="9mEq66v4PziL"
import matplotlib.pyplot as plt
import numpy as np
import numpy.random as rnd
# + id="xuQDD_oiQDC0"
#2-D Rosenbrock function
def Rosenbrock(x1, x2):
return ((1-x1)**2 + 100*(x2 -x1**2)**2)
# + colab={"base_uri": "https://localhost:8080/"} id="bS6qfA6jQLQL" outputId="260819a9-a582-415d-db23-339d977fa701"
N = 100000 ## no of random points
D = 2 ##Dimension
lb = -4 ## lower bound
ub = 4 ## upper bound
X1=[]
X2=[]
Y=[]
#randomly generate N points
X1 = np.random.uniform(lb, ub, N)
X2 = np.random.uniform(lb, ub, N)
#Evaluate the function
for i in range(N):
Y.append(Rosenbrock(X1[i], X2[i]))
#display Results
print('\n Monte Carlo Simulation Optimisation\n')
print( 'Best decision variable : ', X1[np.argmin(Y)], X2[np.argmin(Y)])
print('Best objective : ', min(Y))
X_optimum = [1,1] #Known from theory
print("Known Optimal decision variables:",X_optimum)
print("Known Optimal objective =",Rosenbrock(X_optimum[0], X_optimum[1]))
# + [markdown] id="cnTVEuMvRZEf"
# 'Optimise' above model for different values of N. Observe how just randomly searching the soultion space yields pretty good results!
# + [markdown] id="42bS-uuXQiTP"
# ##To Do
#
# You can find some single objective unconstrained test functions at [Wiki page](https://en.wikipedia.org/wiki/Test_functions_for_optimization)
#
# 1. Through simulation, find the optimum solution of any one of the function: Beale or Goldstein-Price or Booth
#
# 2. 'Optimise' either Himmelblau's function OR Cross-in-Tray function. These functions have 4 alternate solutions. Do 20 sets of 'simulation-optimisation' runs, with N ~= 200000. Compute the number of times we are close to a particular known solution.
# + [markdown] id="-szzuQWl8doy"
# #Q-1
# + colab={"base_uri": "https://localhost:8080/"} id="D7OqW1u8KQsR" outputId="0c5bd59e-dcc2-47f1-b87d-227939cbaa7e"
# Goldstein function:
def Goldstein(x1, x2):
z= (1 + (19 - 14*x1 + 3*x1**2 - 14*x2 + 6*x1*x2 + 3*x2**2)*((x1+x2+1)**2))*(30 + (18 - 32*x1 + 12*x1**2 + 48*x2 - 36*x1*x2 + 27*x2**2)*((2*x1 - 3*x2)**2))
return z
N = 200000 ## no of random points
D = 2 ## dimension
lb = -2 ## lower bound
ub = 2 ## upper bound
X1=[rnd.uniform(lb,ub) for i in range(N)]
X2=[rnd.uniform(lb,ub) for i in range(N)]
Y=[Goldstein(X1[i],X2[i]) for i in range(N)]
#display results
print('Monte Carlo Simulation Optimization: ')
print('Best Decision Variables: ', X1[np.argmin(Y)],X2[np.argmin(Y)])
print('The best objective: ', min(Y))
X_optimum = [0,-1] #known from theory
print('Optimal decision variables:', X_optimum)
print('Optimal objective value: ', Goldstein(X_optimum[0],X_optimum[1]))
# + [markdown] id="jNE0Bvd88i4d"
# #Q-2
# + colab={"base_uri": "https://localhost:8080/"} id="EI1aGKjORT5f" outputId="39eb31a5-4bd4-4ab0-d37c-f62b8a6247c9"
# Himmelblau's function
def Himmelblau(x1, x2):
return (x1**2 + x2 - 11)**2 + (x1 + x2**2 - 7)**2
R = 20 #replication number
N = 200000 ## no of random points
D = 2 ##dimension
lb = -5 ## lower bound+
ub = 5 ## upper bound
Dec_Var = []
obj = []
for k in range(R):
X1 = [rnd.uniform(lb,ub) for i in range(N)]
X2 = [rnd.uniform(lb,ub) for i in range(N)]
Y = [Himmelblau(X1[i],X2[i]) for i in range(N)]
#display the results:
Dec_Var.append([round(X1[np.argmin(Y)],3),round(X2[np.argmin(Y)],3)])
obj.append(min(Y))
for k in range(R):
print(k+1,': Decision Variable: ',Dec_Var[k],'|| Objective Value: ',round(obj[k],4),)
print()
#known solutions are:
soln = [[3.0,2.0],[-2.805118,3.131312],[-3.77931,-3.28318],[3.584428,-1.848126]]
eps = 0.05
count = [0 for i in range(4)]
# counting the number of solutions close to each of the known solutions
for k in range(R):
for i in range(4):
if Dec_Var[k][0] >= soln[i][0] - eps and Dec_Var[k][0] <= soln[i][0] + eps and Dec_Var[k][1] >= soln[i][1] - eps and Dec_Var[k][1] <= soln[i][1] + eps :
count[i] = count[i] + 1
for i in range(4):
print('Number of Solutions close to ',soln[i],' is: ', count[i])
print('\nOut of',R,' solutions found, ', sum(count), 'were found close to the particular known solutions')
|
Python Simulation/SimOptClass.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Jupyter Setup
#
# Hello! You've successfully opened this Jupyter Notebook in Google Colab. Congrats!
#
# Throughout the club, we will use pink & green sticky notes to keep tabs on how everyone is doing. If at any time you want help from a facilitator, put your **pink** sticky note on your laptop like this:
#
# <img src="https://raw.githubusercontent.com/GWC-DCMB/curriculum-notebooks/master/Figures/pink_sticky.jpg" style="width: 300px;"/>
#
# Don't hesitate to ask for help if you get stuck, have a question, or something just doesn't make sense. We're here to help you!
#
# When you reach the end of this practice notebook, put up your **green** sticky note so the facilitators know you've finished. A green sticky means "Everything is working great!"
# ## Writing code
#
# A Jupyter Notebook is a file that lets us run code and see the output right below it. Every chunk of code is called a cell. You can run a code cell by pressing the play button next to it. Hover your mouse over the brackets in cell below (or click on the cell) and press the play button to the left to see what happens!
2 + 3
# Isn't that cool? Python did the math for us and showed us the answer. Like many programming languages, you can use Python just like a calculator.
#
# You can create new code cells by pressing the button `+ Code` in the upper left corner of the toolbar. (Hint: first select the cell you want the new one to appear beneath.)
#
# Try it here! Create a new code cell and add two numbers together.
# any two numbers with an addition sign between them
5 + 4
# ## Writing comments
#
# Sometimes we want to write a comment inside a code cell as a note to our future selves or other coders, but we don't want Python to interpret the comment as code. Code is meant to be read by computers _and_ humans, while comments are meant to be read by humans only.
# You can begin a line with the hash symbol (`#`) so Python will know it's a comment, like this:
# this line is a comment. it doesn't get run as code
11 + 23 # the first part of this line is code, but everything after # is a comment
# Throughout the Lessons and Practices you will see code cells that begin with a comment that instructs you to do something, and a blank line below it where you should write code -- like this:
# add together the number of letters in your first & last name
# Besides addition with the plus symbol (`+`), Python can do lots of other operations including subtraction (`-`), multiplication (`*`), and division (`/`).
#
# Practice using them below!
# subtract the year you were born from the current year
# multiply the number of days in a week with the number of weeks in a year
# divide the number of facilitators in the room by the total number of people
# Next week, we'll continue to practice using Python as a calculator and learn how to reuse the results.
# ## Writing Text
#
# We can use text cells (this is one!) to write descriptions of what our code does, why we wrote it, and ideas for future work. We can use underscores (`_`) to make text _italicized_ and double asterisks (`**`) to make text **bold**. We can also make a bulleted list using dashes `-` with on item on each line:
# - item 1
# - item 2
# - item 3
#
# Press the button `+ Text` in the toolbar to create a new text cell below this one. Then, write a list of 3 things you're looking forward to about this club. Make the one you're most excited about **bold**. Share your answer with your neighbor!
# _Here, students should have written what they're looking forward to in the GWC club._
# ## Moving cells
#
# You can move cells around to change the order in the notebook by pressing the arrow buttons in the upper right corner of the cell. Try moving the cells below so that they're in ascending order.
# **This is cell 1** _(it should be first)_
# **This is cell 2** _(it should be second)_
# **This is cell 3** _(it should be third)_
# # Saving notebooks
#
# Throughout the club, be sure to save your notebooks so you can access your work later! To save a notebook, press `Copy to Drive` in the upper left corner. Once you've copied a notebook to Google Drive, you can use the keyboard shortcut `Ctrl` + `S` to save it again as you make changes and write new code.
#
# Save this notebook if you haven't already!
# Now let's make sure you have access to your Jupyter notebooks. Go to your [Google Drive](https://drive.google.com) and open the folder `Colab Notebooks`. There should be a copy of this notebook -- double-click it and select `Open with Google Colaboratory`. You should see all of your work in it.
#
# If you've gotten to this point and everything worked, put up your **green** sticky note.
# If you run into any problems, put up your **pink** sticky note and a facilitator will come help.
|
Practices/_Keys/KEY_Practice01_Jupyter-Setup.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Vornoi Tesellation
#
# The Voronoi diagram, or tessellation of point clouds, is a method used to partition the input space of molecular localizations into regions according to the Euclidean distance between he seed points. The resultant polygonal regions re called Voronoi cells, where each cell is centered around one seed. The Voronoi edges are equidistant from the two nearest molecules. Specifically, the projected perpendicular line from every seed to any one of its Voronoi cell edges is the shortest distance between every neighboring pair of seeds. Hence, there is no intersection between any Voronoi cells.
#
# The Voronoi geometric characteristics for every seed might be different based on the density and data organization and therefore could be used to describe the the neighborhood of the seeds. For instance, the Voronoi cell area is inversely proportional to the density of the seeds.
#
# Here we aim to see the if voronoi cell poperties could be used to describe the crowding in tissue images with labelled nuclei.
#import libraries
# %load_ext autoreload
import sys
sys.path.append("..")
from tifffile import imread
from skimage import measure
import pandas as pd
import numpy as np
import src.spatial_features.Voronoi_tessellation as VT
# So we read in a image after nuclear segmentation. We use the centroids of the nuclei as inputs for the voronoi diagram. Below is the results for a given input image. The colors indicates unique nuclear labels and the white dots represents the nuclear centroids.
# +
# Read in the image
img= imread('/home/pathy_s/Documents/TMA/Stardist_seg_results/Instance_segmentation/BR2082B_H15.tif')
img=img[4000:6000,5000:7000]
image_width=img.shape[1]
image_height=img.shape[0]
#measure nuclear positions
features=measure.regionprops_table(img,properties=('label','centroid'))
#get voronoi map
vor_image=VT.get_voronoi_map(centroids=np.stack((features['centroid-0'],features['centroid-1']),axis=1),
labels=features['label'],img_height=image_height,img_width=image_height)
VT.plot_voronoi_map(img,vor_image)
# -
# As we can see, most of the nuclei sit with the voronoi edges, but however there are some that overlap. This is because we just use nuclear centroids for computations and ignore the size of the nuclei.
#
# Now that we have a labelled voronoi cell image can also extract its geometric features. As noted above te size of a nucleus's voronoi cell is indicative of its local density; tighly packed nuclei with many neighbours will have smaller cells with more uniform shapes. An elongated cell is indicative of a cells with asymmetrically distribution of neighbours, like around the edges of clusters.
#extract geometric features
VT.extract_voronoi_cell_features(vor_image)
# For a quick extraction of features given a segmented image use the following code:
# +
from src.utlis.Run_voronoi_features import extract_voronoi_features
Voronoi_features=extract_voronoi_features('/home/pathy_s/Documents/TMA/Stardist_seg_results/Instance_segmentation/BR2082B_H15.tif',
False)
Voronoi_features
# -
# #### Tissue level summary:
#
# In order to characterise the nuclear density/crowding in a given tissue, we compute the distribution characteristics of each of the above features.
#
# The measures available are: Median, Min, Max, Standard Deviation (SD) Coefficient of Variation (CV) and Coefficient of Dispersion (CD), Inter_Quartile_Range(IQR) and Quartile Coeeffient of Dispersrion (QCD).
from src.utlis.summarising_features import summarise_feature_table
summarise_feature_table(Voronoi_features.drop(['centroid-0','centroid-1','orientation'], axis=1))
# ### Reference
#
# 1. <NAME>. "Spatial tessellations." International Encyclopedia of Geography: People, the Earth, Environment and Technology: People, the Earth, Environment and Technology (2016): 1-11.
|
notes_on_feature_extraction/voronoi_tesselation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # Lecture 18
# ## Wednesday, November 8th, 2017
# ## Databases with `SQlite`
# -
# # `SQLite` Exercises
# Today you will work with the candidates and contributors datasets to create a database in `Python` using `SQLite`.
#
# The exercises will consist of a sequence of steps to help illustrate basic commands.
# + [markdown] slideshow={"slide_type": "subslide"}
# <a id='deliverables'></a>
# # Exercise Deliverables
# 1. Create a `Jupyter` notebook called `Exercises-Final.ipynb` inside the `L18` directory. This is the one we will grade.
# 2. For each step in this lecture, there were instructions labeled "Do the following:". Put all the code from those instructions in a single `Jupyter` notebook cell. It should look like a `Python` script. You *must* comment where appropriate to demonstrate that you understand what you are doing.
# 3. Save and close your database. Be sure to upload your database with the lecture exercises. You must name your database **`L18DB.sqlite`**.
# -
# ## Table of Contents
# [Setting the Stage](#setting_the_stage)
#
# [Step 1](#step_1)
#
# [Interlude](#interlude): Not required but highly recommended.
#
# [Step 2](#step_2)
#
# [Step 3](#step_3)
#
# [Step 4](#step_4)
#
# [Step 5](#step_5)
#
# [Step 6](#step_6)
#
# [Step 7](#step_7)
#
# [Step 8](#step_8)
# ---
# <a id='setting_the_stage'></a>
# # Setting the Stage
# You should import `sqlite3` again like last time.
import sqlite3
# We will also use a basic a `pandas` feature to display tables in the database. Although this lecture isn't on `pandas`, I will still have you use it a little bit.
import pandas as pd
pd.set_option('display.width', 500)
pd.set_option('display.max_columns', 100)
pd.set_option('display.notebook_repr_html', True)
# Now we create the tables in the database (just like last time).
# +
db = sqlite3.connect('L18DB_demo.sqlite')
cursor = db.cursor()
cursor.execute("DROP TABLE IF EXISTS candidates")
cursor.execute("DROP TABLE IF EXISTS contributors")
cursor.execute("PRAGMA foreign_keys=1")
cursor.execute('''CREATE TABLE candidates (
id INTEGER PRIMARY KEY NOT NULL,
first_name TEXT,
last_name TEXT,
middle_init TEXT,
party TEXT NOT NULL)''')
db.commit() # Commit changes to the database
cursor.execute('''CREATE TABLE contributors (
id INTEGER PRIMARY KEY AUTOINCREMENT NOT NULL,
last_name TEXT,
first_name TEXT,
middle_name TEXT,
street_1 TEXT,
street_2 TEXT,
city TEXT,
state TEXT,
zip TEXT,
amount REAL,
date DATETIME,
candidate_id INTEGER NOT NULL,
FOREIGN KEY(candidate_id) REFERENCES candidates(id))''')
db.commit()
# -
# <a id='step_1'></a>
# # Step 1
# Read `candidates.txt` and `contributors.txt` and insert their values into the respective tables.
with open ("candidates.txt") as candidates:
next(candidates) # jump over the header
for line in candidates.readlines():
cid, first_name, last_name, middle_name, party = line.strip().split('|')
vals_to_insert = (int(cid), first_name, last_name, middle_name, party)
cursor.execute('''INSERT INTO candidates
(id, first_name, last_name, middle_init, party)
VALUES (?, ?, ?, ?, ?)''', vals_to_insert)
with open ("contributors.txt") as contributors:
next(contributors)
for line in contributors.readlines():
cid, last_name, first_name, middle_name, street_1, street_2, \
city, state, zip_code, amount, date, candidate_id = line.strip().split('|')
vals_to_insert = (last_name, first_name, middle_name, street_1, street_2,
city, state, int(zip_code), amount, date, candidate_id)
cursor.execute('''INSERT INTO contributors (last_name, first_name, middle_name,
street_1, street_2, city, state, zip, amount, date, candidate_id)
VALUES (?, ?, ?, ?, ?, ?, ?, ?, ?, ?, ?)''', vals_to_insert)
# ---
# <a id='interlude'></a>
# ## Interlude
# Now that you have values in the tables of the database, it would be convenient to be able to visualize those tables in some way. We'll write a little helper function to accomplish this.
def viz_tables(cols, query):
q = cursor.execute(query).fetchall()
framelist = []
for i, col_name in enumerate(cols):
framelist.append((col_name, [col[i] for col in q]))
return pd.DataFrame.from_items(framelist)
# Here's how we can use our helper function. It gives a pretty nice visualization of our table. You should do the same thing with the `contributors` table.
candidate_cols = [col[1] for col in cursor.execute("PRAGMA table_info(candidates)")]
query = '''SELECT * FROM candidates'''
viz_tables(candidate_cols, query)
# <a id='step_2'></a>
# # Step 2: Various Queries
# We can query our database for entries with certain characteristics. For example, we can query the `candidates` table for entries who's middle name fields are not empty.
query = '''SELECT * FROM candidates WHERE middle_init <> ""'''
viz_tables(candidate_cols, query)
# We can also see how many entries satisfy the query:
print("{} candidates have a middle initial.".format(viz_tables(candidate_cols, query).shape[0]))
# ### Do the following queries:
# * Display the contributors where the state is "PA"
# * Display the contributors where the amount contributed is greater than $\$1000.00$.
# * Display the contributors from "UT" where the amount contributed is greater than $\$1000.00$.
# * Display the contributors who didn't list their state
# - **Hint**: Match `state` to the empty string
# * Display the contributors from "WA" and "PA"
# - **Hint**: You will need to use `IN ("WA", "PA")` in your `SELECT` statement.
# * Display the contributors who contributed between $\$100.00$ and $\$200.00$.
# - **Hint**: You can use the `BETWEEN 100.00 and 200.00` clause.
# <a id='step_3'></a>
# # Step 3: Sorting
# It could be beneficial to sort by one of the attributes in the database. The following cell contains a basic sorting demo.
query = '''SELECT * FROM candidates ORDER BY id DESC'''
viz_tables(candidate_cols, query)
# ### Do the following sorts on the `contributors` table:
# * Sort the `contributors` table by `last_name`.
# * Sort by the `amount` in decending order where `amount` is restricted to be between $\$1000.00$ and $\$5000.00$.
# * Sort the contributors who donted between $\$1000.00$ and $\$5000.00$ by `candidate_id` and then by `amount` in descending order.
# - **Hint**: Multiple orderings can be accomplished by separating requests after `ORDER BY` with commas.
# - e.g. `ORDER BY amount ASC, last_name DESC`
# <a id='step_4'></a>
# # Step 4: Selecting Columns
# So far, we've been selecting all columns from a table (i.e. `SELECT * FROM`). Often, we just want to select specific columns (e.g. `SELECT amount FROM`).
query = '''SELECT last_name, party FROM candidates'''
viz_tables(['last_name', 'party'], query)
# Using the `DISTINCT` clause, you remove duplicate rows.
query = '''SELECT DISTINCT party FROM candidates'''
viz_tables(['party'], query)
# ### Do the following:
# * Get the first and last name of contributors. Make sure each row has distinct values.
# <a id='step_5'></a>
# # Step 5: Altering Tables
# The `ALTER` clause allows us to modify tables in our database. Here, we had a new column to our candidates table called `nick_name`.
cursor.execute('''ALTER TABLE candidates ADD COLUMN full_name TEXT''')
candidate_cols = [col[1] for col in cursor.execute("PRAGMA table_info(candidates)")]
viz_tables(candidate_cols, '''SELECT * FROM candidates''')
# What if we want to rename or delete a columm? It can't be done with `SQLite` with a single command. We need to follow some roundabout steps (see [`SQLite` ALTER TABLE](http://www.sqlitetutorial.net/sqlite-alter-table/)). We won't consider this case at the moment.
# For now, let's put a few commands together to populate the `full_name` column.
# +
candidate_cols = [col[1] for col in cursor.execute("PRAGMA table_info(candidates)")] # regenerate columns with full_name
query = '''SELECT id, last_name, first_name FROM candidates''' # Select a few columns
full_name_and_id = [(attr[1] + ", " + attr[2], attr[0]) for attr in cursor.execute(query).fetchall()] # List of tuples: (full_name, id)
update = '''UPDATE candidates SET full_name = ? WHERE id = ?''' # Update the table
for rows in full_name_and_id:
cursor.execute(update, rows)
query = '''SELECT * FROM candidates'''
viz_tables(candidate_cols, query)
# -
# Here's another update, this time on an existing column.
update = '''UPDATE candidates SET full_name = "<NAME>" WHERE last_name = "Obama"'''
cursor.execute(update)
update = '''UPDATE candidates SET full_name = "<NAME>" WHERE last_name = "McCain"'''
cursor.execute(update)
viz_tables(candidate_cols, query)
# ### Do the following:
# * Add a new column to the contributors table called `full_name`. The value in that column should be in the form `last_name, first_name`.
# * Change the value in the `full_name` column to the string `"Too Much"` if someone donated more than $\$1000.00$.
# <a id='step_6'></a>
# # Step 6: Aggregation
# You can perform some nice operations on the values in the database. For example, you can compute the maximum, minimum, and sum of a set. You can also count the number of items in a given set. Here's a little example. You can do the rest.
contributor_cols = [col[1] for col in cursor.execute("PRAGMA table_info(contributors)")] # You've already done this part. I just need to do it here b/c I haven't yet.
function = '''SELECT *, MAX(amount) AS max_amount FROM contributors'''
viz_tables(contributor_cols, function)
# ### Do the following:
#
# * Count how many donations there were above $\$1000.00$.
# * Calculate the average donation.
# * Calculate the average contribution from each state and display in a table.
# - **Hint**: Use code that looks like:
#
# ```python
# "SELECT state,SUM(amount) FROM contributors GROUP BY state"
# ```
# <a id='step_7'></a>
# # Step 7: DELETE
# We have already noted that `SQLite` can't drop columns in a straightfoward manner. However, it can delete rows quite simply. Here's the syntax:
# ```python
# deletion = '''DELETE FROM table_name WHERE condition'''
# ```
#
# ### Do the following:
# * Delete rows in the `contributors` table with last name "Ahrens".
# <a id='step_8'></a>
# # Step 8: LIMIT
# The `LIMIT` clause offers convenient functionality. It allows you to constrain the number of rows returned by your query. It shows up in many guises.
query = '''SELECT * FROM candidates LIMIT 3'''
viz_tables(candidate_cols, query)
query = '''SELECT * FROM candidates LIMIT 4 OFFSET 5'''
viz_tables(candidate_cols, query)
query = '''SELECT * FROM candidates ORDER BY last_name LIMIT 4 OFFSET 5'''
viz_tables(candidate_cols, query)
# ### Do the following:
# * Query and display the ten most generous donors.
# * Query and display the ten least generous donors who donated a positive amount of money (since the data we have has some negative numbers in it...).
# # Save
# Don't forget to save all of these changes to your database using `db.commit()`. Before closing shop, be sure to close the database connection with `db.close()`.
|
lectures/L18/L18.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
ratings = pd.read_csv("data/ratings.csv", sep = ',')
movies = pd.read_csv("data/movies.csv", sep = ',')
tags = pd.read_csv("data/tags.csv", sep = ',')
# +
import numpy as np
import math
# build a TF dataframe
tf = tags.groupby(['movieId','tag'], as_index=False, sort=False)\
.count()\
.rename(columns = {'userId':'tag_count_tf'})[['movieId','tag','tag_count_tf']]
tag_distinct = tags[['tag','movieId']].drop_duplicates()
# build a DF dataframe
df = tag_distinct.groupby(['tag'], as_index=False, sort=False)\
.count()\
.rename(columns = {'movieId':'tag_count_df'})[['tag','tag_count_df']]
# compute TF-IDF values
idf = math.log10(len(np.unique(tags['movieId'])))
df['idf'] = idf-np.log10(df['tag_count_df'])
tf = pd.merge(tf, df, on='tag', how='left', sort=False)
tf['tf-idf'] = tf['tag_count_tf']*tf['idf']
# show TF-IDF values for each movie
#tf[['movieId','tag','tf-idf']].head()
# +
# get the vector length with rows of movieId and columns of TF-IDF
vect_length = tf.loc[:,('movieId','tf-idf')]
# normalize the vector by unit length
vect_length['tf-idf-sq'] = vect_length['tf-idf']**2
vect_length = vect_length.groupby(['movieId'], as_index=False, sort=False)\
.sum()\
.rename(columns = {'tf-idf-sq':'tf-idf-sq-total'})[['movieId','tf-idf-sq-total']]
vect_length['vect_length'] = np.sqrt(vect_length[['tf-idf-sq-total']].sum(axis=1))
tf = pd.merge(tf, vect_length, on='movieId', how='left', sort=False)
tf['tag_vec'] = tf['tf-idf']/tf['vect_length']
# display the feature unit length vector of each movie: 'tag_vec'
#tf[tf['movieId'] == 60756][['movieId','tag','tf-idf','vect_length','tag_vec']].head()
# -
# Compute user profile vector
# ---------------------------------
#
# # Step 3-1. Calculate user profile: sum of the item-tag vectors of all items with positive ratings (>=3)
# +
import pandas as pd
ratings_filter = ratings[ratings['rating']>=3]
user_distinct = np.unique(ratings['userId'])
user_tag_pref = pd.DataFrame()
i = 1
# enter userId for analysis
userId = 65
# compute the profile vector for the selected user
user_index = user_distinct.tolist().index(userId)
for user in user_distinct[user_index:user_index+1]:
user_data= ratings_filter[ratings_filter['userId']==user]
user_data = pd.merge(tf,user_data, on = 'movieId', how = 'inner', sort = False)
user_data_itr = user_data.groupby(['tag'], as_index = False, sort = False)\
.sum()\
.rename(columns = {'tag_vec': 'tag_pref'})[['tag','tag_pref']]
user_tag_pref = user_tag_pref.append(user_data_itr, ignore_index=True)
# display the user profile vector: 'tag_pref'
user_tag_pref['userId'] = userId
# +
user_tag_pref_all = user_tag_pref
movie_distinct = np.unique(tf['movieId'])
tag_merge_all = pd.DataFrame()
movie = 123
tf_movie = tf[tf['movieId']==movie]
tag_merge = pd.merge(tf_movie, user_tag_pref_all, on = 'tag', how = 'left', sort = False)
tag_merge['tag_pref'] = tag_merge['tag_pref'].fillna(0)
tag_merge['tag_value'] = tag_merge['tag_vec']*tag_merge['tag_pref']
tag_vec_val = np.sqrt(np.sum(np.square(tag_merge['tag_vec']), axis=0))
tag_pref_val = np.sqrt(np.sum(np.square(user_tag_pref_all['tag_pref']), axis=0))
tag_merge_final = tag_merge.groupby(['userId','movieId'])[['tag_value']]\
.sum()\
.rename(columns = {'tag_value': 'rating'})\
.reset_index()
tag_merge_final['rating']=tag_merge_final['rating']/(tag_vec_val*tag_pref_val)
tag_merge_final.head()
# for movie in movie_distinct:
# tf_movie = tf[tf['movieId']==movie]
# tag_merge = pd.merge(tf_movie, user_tag_pref_all, on = 'tag', how = 'left', sort = False)
# tag_merge['tag_pref'] = tag_merge['tag_pref'].fillna(0)
# tag_merge['tag_value'] = tag_merge['tag_vec']*tag_merge['tag_pref']
# tag_vec_val = np.sqrt(np.sum(np.square(tag_merge['tag_vec']), axis=0))
# tag_pref_val = np.sqrt(np.sum(np.square(user_tag_pref_all['tag_pref']), axis=0))
# tag_merge_final = tag_merge.groupby(['userId','movieId'])[['tag_value']]\
# .sum()\
# .rename(columns = {'tag_value': 'rating'})\
# .reset_index()
# tag_merge_final['rating']=tag_merge_final['rating']/(tag_vec_val*tag_pref_val)
# tag_merge_all = tag_merge_all.append(tag_merge_final, ignore_index=True)
# # remove movies already rated by user
# movies_rated = ratings[ratings['userId'] == userId]['movieId']
# tag_merge_all = tag_merge_all[~tag_merge_all['movieId'].isin(movies_rated)]
# tag_merge_all['userId'] = tag_merge_all['userId'].apply(np.int64)
# print(tag_merge_all.shape)
# # display the top 10 movies by rating
# tag_merge_all = tag_merge_all.head(15)
# tag_merge_all = pd.merge(tag_merge_all, movies, on = 'movieId', how = 'left')
# tag_merge_all.head(20)
# -
|
recommender/rest-api/Content Based SKLearn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Advertisement CTR (Click-Through Rate) Prediction
# By <NAME>
#
# In this logistic regression based project I will try to predict whether or not a particular internet user clicked on an Advertisement on a company website using NumPy, Pandas, Matplotlib, Seaborn, and SciKitLearn.
#
# I will work on a fake advertising dataset which contains the following features:
# * 'Daily Time Spent on Site': consumer time on site in minutes
# * 'Age': cutomer age in years
# * 'Area Income': Avg. Income of geographical area of consumer
# * 'Daily Internet Usage': Avg. minutes a day consumer is on the internet
# * 'Ad Topic Line': Headline of the advertisement
# * 'City': City of consumer
# * 'Male': Whether or not consumer was male
# * 'Country': Country of consumer
# * 'Timestamp': Time at which consumer clicked on Ad or closed window
# * 'Clicked on Ad': 0 or 1 indicated clicking on Ad
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
import seaborn as sns
sns.set_style('whitegrid')
# **Getting the Data**
# +
# Extracting the data from csv file
adv_data = pd.read_csv('advertising.csv')
adv_data.head()
# +
# Info of the data
adv_data.info()
# +
# Statistical description of the data
adv_data.describe()
# -
# **Exploratory Data Analysis**
# +
# Histogram of the 'Age' column
adv_data['Age'].hist(bins=30)
plt.xlabel('Age')
# +
# Jointplot showing Area Income vs Age
sns.jointplot(data=adv_data, x='Age', y='Area Income')
# +
# Jointplot showing the kde distributions of Daily Time spent on site vs Age
sns.jointplot(data=adv_data, x='Age', y='Daily Time Spent on Site', color='green', kind='kde', fill=True);
# +
# Jointplot of Daily Time Spent on Site vs Daily Internet Usage
sns.jointplot(data=adv_data, x='Daily Time Spent on Site', y='Daily Internet Usage', color='red')
# +
# Pairplot of adv_data with hue by 'Clicked on Ad' column
sns.pairplot(adv_data, hue='Clicked on Ad', diag_kind='hist', height=2, palette='bwr')
# -
# **Logistic Regression Model**
# +
# Splitting the data in training and testing data
X = adv_data[['Daily Time Spent on Site', 'Age', 'Area Income','Daily Internet Usage', 'Male']]
y = adv_data['Clicked on Ad']
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=101)
# +
# Training the model on training data
from sklearn.linear_model import LogisticRegression
logReg = LogisticRegression()
logReg.fit(X_train, y_train)
# +
# Predicting from the model
predictions = logReg.predict(X_test)
# +
# Evaluation the model
from sklearn import metrics
print(metrics.confusion_matrix(y_test, predictions)) # Confusion Matrix
# -
# Classification report
print(metrics.classification_report(y_test, predictions))
|
Advertisement-CTR-Prediction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="UEBilEjLj5wY"
# STAT 453: Deep Learning (Spring 2020)
# Instructor: <NAME> (<EMAIL>)
# - Course website: http://pages.stat.wisc.edu/~sraschka/teaching/stat453-ss2020/
# - GitHub repository: https://github.com/rasbt/stat453-deep-learning-ss20
# + [markdown] colab_type="text" id="MEu9MiOxj5wk"
# - Runs on CPU (not recommended here) or GPU (if available)
# + [markdown] colab_type="text" id="rH4XmErYj5wm"
# # ResNet-34 Convolutional Neural Network
# + [markdown] colab_type="text" id="MkoGLH_Tj5wn"
# ## Imports
# + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="ORj09gnrj5wp"
import time
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision import datasets
from torchvision import transforms
from torch.utils.data import DataLoader
if torch.cuda.is_available():
torch.backends.cudnn.deterministic = True
# -
import matplotlib.pyplot as plt
# %matplotlib inline
# + [markdown] colab_type="text" id="PvgJ_0i7j5wt"
# ## Settings and Dataset
# + colab={"autoexec": {"startup": false, "wait_interval": 0}, "base_uri": "https://localhost:8080/", "height": 85} colab_type="code" executionInfo={"elapsed": 23936, "status": "ok", "timestamp": 1524974497505, "user": {"displayName": "<NAME>", "photoUrl": "//lh6.googleusercontent.com/-cxK6yOSQ6uE/AAAAAAAAAAI/AAAAAAAAIfw/P9ar_CHsKOQ/s50-c-k-no/photo.jpg", "userId": "118404394130788869227"}, "user_tz": 240} id="NnT0sZIwj5wu" outputId="55aed925-d17e-4c6a-8c71-0d9b3bde5637"
##########################
### SETTINGS
##########################
# Hyperparameters
RANDOM_SEED = 1
LEARNING_RATE = 0.001
NUM_EPOCHS = 50
# Architecture
NUM_FEATURES = 128*128
NUM_CLASSES = 10
BATCH_SIZE = 256
DEVICE = 'cuda:0' # default GPU device
GRAYSCALE = False
##########################
### MNIST DATASET
##########################
# Note transforms.ToTensor() scales input images
# to 0-1 range
train_dataset = datasets.CIFAR10(root='data',
train=True,
transform=transforms.ToTensor(),
download=True)
test_dataset = datasets.CIFAR10(root='data',
train=False,
transform=transforms.ToTensor())
train_loader = DataLoader(dataset=train_dataset,
batch_size=BATCH_SIZE,
shuffle=True)
test_loader = DataLoader(dataset=test_dataset,
batch_size=BATCH_SIZE,
shuffle=False)
# Checking the dataset
for images, labels in train_loader:
print('Image batch dimensions:', images.shape)
print('Image label dimensions:', labels.shape)
break
# + [markdown] colab_type="text" id="I<KEY>"
# ## Model
# + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="_lza9t_uj5w1"
##########################
### MODEL
##########################
def conv3x3(in_planes, out_planes, stride=1):
"""3x3 convolution with padding"""
return nn.Conv2d(in_planes, out_planes, kernel_size=3, stride=stride,
padding=1, bias=False)
class BasicBlock(nn.Module):
expansion = 1
def __init__(self, inplanes, planes, stride=1, downsample=None):
super(BasicBlock, self).__init__()
self.conv1 = conv3x3(inplanes, planes, stride)
self.bn1 = nn.BatchNorm2d(planes)
self.relu = nn.ReLU(inplace=True)
self.conv2 = conv3x3(planes, planes)
self.bn2 = nn.BatchNorm2d(planes)
self.downsample = downsample
self.stride = stride
def forward(self, x):
residual = x
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
if self.downsample is not None:
residual = self.downsample(x)
out += residual
out = self.relu(out)
return out
class ResNet(nn.Module):
def __init__(self, block, layers, num_classes, grayscale):
self.inplanes = 64
if grayscale:
in_dim = 1
else:
in_dim = 3
super(ResNet, self).__init__()
self.conv1 = nn.Conv2d(in_dim, 64, kernel_size=7, stride=2, padding=3,
bias=False)
self.bn1 = nn.BatchNorm2d(64)
self.relu = nn.ReLU(inplace=True)
self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
self.layer1 = self._make_layer(block, 64, layers[0])
self.layer2 = self._make_layer(block, 128, layers[1], stride=2)
self.layer3 = self._make_layer(block, 256, layers[2], stride=2)
self.layer4 = self._make_layer(block, 512, layers[3], stride=2)
self.avgpool = nn.AvgPool2d(7, stride=1)
self.fc = nn.Linear(512 * block.expansion, num_classes)
for m in self.modules():
if isinstance(m, nn.Conv2d):
n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
m.weight.data.normal_(0, (2. / n)**.5)
elif isinstance(m, nn.BatchNorm2d):
m.weight.data.fill_(1)
m.bias.data.zero_()
def _make_layer(self, block, planes, blocks, stride=1):
downsample = None
if stride != 1 or self.inplanes != planes * block.expansion:
downsample = nn.Sequential(
nn.Conv2d(self.inplanes, planes * block.expansion,
kernel_size=1, stride=stride, bias=False),
nn.BatchNorm2d(planes * block.expansion),
)
layers = []
layers.append(block(self.inplanes, planes, stride, downsample))
self.inplanes = planes * block.expansion
for i in range(1, blocks):
layers.append(block(self.inplanes, planes))
return nn.Sequential(*layers)
def forward(self, x):
x = self.conv1(x)
x = self.bn1(x)
x = self.relu(x)
x = self.maxpool(x)
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
x = self.layer4(x)
# because MNIST is already 1x1 here:
# disable avg pooling
#x = self.avgpool(x)
x = x.view(x.size(0), -1)
logits = self.fc(x)
probas = F.softmax(logits, dim=1)
return logits, probas
def resnet34(num_classes):
"""Constructs a ResNet-34 model."""
model = ResNet(block=BasicBlock,
layers=[3, 4, 6, 3],
num_classes=NUM_CLASSES,
grayscale=GRAYSCALE)
return model
# +
torch.manual_seed(RANDOM_SEED)
##########################
### COST AND OPTIMIZER
##########################
model = resnet34(NUM_CLASSES)
model.to(DEVICE)
optimizer = torch.optim.Adam(model.parameters(), lr=LEARNING_RATE)
# + [markdown] colab_type="text" id="RAodboScj5w6"
# ## Training
# + colab={"autoexec": {"startup": false, "wait_interval": 0}, "base_uri": "https://localhost:8080/", "height": 1547} colab_type="code" executionInfo={"elapsed": 2384585, "status": "ok", "timestamp": 1524976888520, "user": {"displayName": "<NAME>", "photoUrl": "//lh6.googleusercontent.com/-cxK6yOSQ6uE/AAAAAAAAAAI/AAAAAAAAIfw/P9ar_CHsKOQ/s50-c-k-no/photo.jpg", "userId": "118404394130788869227"}, "user_tz": 240} id="Dzh3ROmRj5w7" outputId="5f8fd8c9-b076-403a-b0b7-fd2d498b48d7"
def compute_accuracy(model, data_loader):
model.eval()
correct_pred, num_examples = 0, 0
for i, (features, targets) in enumerate(data_loader):
features = features.to(DEVICE)
targets = targets.to(DEVICE)
logits, probas = model(features)
_, predicted_labels = torch.max(probas, 1)
num_examples += targets.size(0)
correct_pred += (predicted_labels == targets).sum()
return correct_pred.float()/num_examples * 100
def compute_epoch_loss(model, data_loader):
model.eval()
curr_loss, num_examples = 0., 0
with torch.no_grad():
for features, targets in data_loader:
features = features.to(DEVICE)
targets = targets.to(DEVICE)
logits, probas = model(features)
loss = F.cross_entropy(logits, targets, reduction='sum')
num_examples += targets.size(0)
curr_loss += loss
curr_loss = curr_loss / num_examples
return curr_loss
minibatch_cost, epoch_cost = [], []
all_train_acc, all_test_acc = [], []
start_time = time.time()
for epoch in range(NUM_EPOCHS):
model.train()
for batch_idx, (features, targets) in enumerate(train_loader):
features = features.to(DEVICE)
targets = targets.to(DEVICE)
### FORWARD AND BACK PROP
logits, probas = model(features)
cost = F.cross_entropy(logits, targets)
optimizer.zero_grad()
cost.backward()
minibatch_cost.append(cost)
### UPDATE MODEL PARAMETERS
optimizer.step()
### LOGGING
if not batch_idx % 50:
print ('Epoch: %03d/%03d | Batch %04d/%04d | Cost: %.4f'
%(epoch+1, NUM_EPOCHS, batch_idx,
len(train_loader), cost))
model.eval()
with torch.set_grad_enabled(False): # save memory during inference
train_acc = compute_accuracy(model, train_loader)
test_acc = compute_accuracy(model, test_loader)
print('Epoch: %03d/%03d | Train: %.3f%% | Test: %.3f%%' % (
epoch+1, NUM_EPOCHS, train_acc, test_acc))
all_train_acc.append(train_acc)
all_test_acc.append(test_acc)
cost = compute_epoch_loss(model, train_loader)
epoch_cost.append(cost)
print('Time elapsed: %.2f min' % ((time.time() - start_time)/60))
print('Total Training Time: %.2f min' % ((time.time() - start_time)/60))
# + [markdown] colab_type="text" id="paaeEQHQj5xC"
# ## Evaluation
# + colab={"autoexec": {"startup": false, "wait_interval": 0}, "base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 6514, "status": "ok", "timestamp": 1524976895054, "user": {"displayName": "<NAME>", "photoUrl": "//lh6.googleusercontent.com/-cxK6yOSQ6uE/AAAAAAAAAAI/AAAAAAAAIfw/P9ar_CHsKOQ/s50-c-k-no/photo.jpg", "userId": "118404394130788869227"}, "user_tz": 240} id="gzQMWKq5j5xE" outputId="de7dc005-5eeb-4177-9f9f-d9b5d1358db9"
with torch.set_grad_enabled(False): # save memory during inference
print('Test accuracy: %.2f%%' % (compute_accuracy(model, test_loader)))
# +
plt.plot(range(len(minibatch_cost)), minibatch_cost)
plt.ylabel('Cross Entropy')
plt.xlabel('Minibatch')
plt.ylim([0, 2])
plt.show()
plt.plot(range(len(epoch_cost)), epoch_cost)
plt.ylabel('Cross Entropy')
plt.xlabel('Epoch')
plt.ylim([0, 2])
plt.show()
plt.plot(range(len(all_test_acc)), all_test_acc, label='Test (in practice, use validation set)')
plt.plot(range(len(all_train_acc)), all_train_acc, linestyle='--', label='train')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.ylim([0, 100])
plt.legend()
plt.show()
|
L13-cnns-part2/code/resnet-34.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from sagas.ofbiz.entities import OfEntity as e, oc, finder
hub=oc.component('entity_event_hub')
forms=oc.component('form_mgr')
# form_loc="component://content/widget/forum/BlogForms.xml;EditBlog;en_US"
# form_loc='component://party/widget/partymgr/LookupForms.xml;LookupPartyName;en_US'
form_loc='component://party/widget/partymgr/LookupForms.xml;LookupPartyName;zh'
form=forms.getMetaForm(form_loc)
print(form)
# +
from forms_pb2 import MetaForm, MetaMappingPackage, MetaFieldMapping, MetaFieldMappings, SUBMIT, RESET
def extract_key(original):
return original.replace('${uiLabelMap.', '').replace('}', '').strip()
py_form=MetaForm()
form_data=form.toByteString().toByteArray()
py_form.ParseFromString(form_data)
package={}
for fld in py_form.fields:
if fld.titleOriginal is not None and len(fld.titleOriginal)>0 and fld.fieldType not in (SUBMIT, RESET):
key=extract_key(fld.titleOriginal)
print(fld.name, '♯', fld.title, fld.titleOriginal, '♯', key)
mapping=MetaFieldMapping(key=key, fieldName=fld.name,
fieldTitle=fld.title,
fieldTitleOriginal=fld.titleOriginal,
formUri=form_loc
)
if key in package:
package[key].fields.append(mapping)
# print('+', package[key])
else:
# print('add', key)
package[key]=MetaFieldMappings(fields=[mapping])
meta_package=MetaMappingPackage(mappings=package)
print(meta_package)
# +
def component_loc(loc):
prefix="component://"
pkg_prefixes = ['ofbiz-framework/applications',
'ofbiz-framework/framework',
'ofbiz-framework/plugins']
for pkg_prefix in pkg_prefixes:
idx = loc.find(pkg_prefix)
if idx != -1:
return prefix+loc[idx + len(pkg_prefix) + 1:]
raise ValueError('Cannot normalize the location ' + loc)
component_loc('/Users/xiaofeiwu/jcloud/vagrant/fedora/fedora-28/ofbiz/ofbiz-framework/applications/workeffort/widget/TimesheetForms.xml')
# -
from sagas.ofbiz.util import norm_loc
norm_loc('/Users/xiaofeiwu/jcloud/vagrant/fedora/fedora-28/ofbiz/ofbiz-framework/applications/workeffort/widget/TimesheetForms.xml')
from sagas.ofbiz.entity_prefabs import all_components
all_components()
# +
class FormResource(object):
def __init__(self, comp, name, location):
self.comp=comp
self.name=name
self.location=location
self.forms=[]
class FormDescriptor(object):
def __init__(self, tag, name, type, target, extends):
self.tag=tag
self.name=name
self.type=type
self.target=target
self.extends=extends
# + code_folding=[]
from sagas.ofbiz.entities import OfEntity as e, oc, finder
import os
import io_utils
oc.import_package('org.apache.ofbiz.base.component.ComponentConfig')
allComponents = oc.j.ComponentConfig.getAllComponents()
form_list=[]
for c in allComponents:
# print(c.getRootLocation())
widget_dir=c.getRootLocation()+"widget"
if os.path.isdir(widget_dir):
files=io_utils.list_files(widget_dir)
print(c.getGlobalName(), len(files))
counts={'forms':0, 'screens':0, 'menus':0, 'trees':0, 'others':0}
for f in files:
base=os.path.basename(f)
name=os.path.splitext(base)[0]
if 'Form' in name:
counts['forms']=counts['forms']+1
form_list.append(FormResource(c.getGlobalName(), name, f))
elif 'Screen' in name:
counts['screens']=counts['screens']+1
elif 'Menu' in name:
counts['menus']=counts['menus']+1
elif 'Tree' in name:
counts['trees']=counts['trees']+1
elif name=='Theme':
pass
else:
counts['others']=counts['others']+1
print('** get unexpected file type', name)
print('\t', counts)
print(len(form_list))
# +
import xml.etree.ElementTree as ET
total=0
form_index={}
for form_res in form_list:
tree = ET.parse(form_res.location)
root = tree.getroot()
for child in root:
# tag, name, type, target
fd=FormDescriptor(child.tag, child.get('name'),
child.get('type'),
child.get('target'),
child.get('extends')
)
form_res.forms.append(fd)
if fd.name not in form_index:
form_index[fd.name]=[form_res]
else:
form_index[fd.name].append(form_res)
print('duplicate form name %s, extends -> %s'%(fd.name, fd.extends))
total=total+1
print(total)
# -
import json
form=form_list[0]
print(form.name, form.location)
# print(form.forms)
printstr=json.dumps(form, default=lambda o: o.__dict__,
sort_keys=True, indent=4)
print(printstr)
locs=form_index['ListTaskInfo']
for loc in locs:
print(loc.name, loc.location)
# AddTimesheetEntry
locs=form_index['AddTimesheetEntry']
for loc in locs:
print(loc.name, loc.location)
|
notebook/procs-ofbiz-form.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: dlnd
# language: python
# name: dlnd
# ---
# https://keras.io/preprocessing/image/
# # TensorFlow 2.0
# +
import tensorflow as tf
from tensorflow.keras import layers
from tensorflow.keras import datasets
from tensorflow.keras.preprocessing.image import ImageDataGenerator
# -
import os
from glob import glob
os.listdir('../../dataset/mnist_png/mnist_png/training')
# +
train_dir = '../../dataset/mnist_png/mnist_png/training'
test_dir = '../../dataset/mnist_png/mnist_png/testing'
# -
# ## Hyperparameter Tunning
# +
num_epochs = 10
batch_size = 32
learning_rate = 0.001
dropout_rate = 0.5
input_shape = (28, 28, 1)
num_classes = 10
# -
# ## Preprocess
# +
train_datagen = ImageDataGenerator(
rescale=1./255,
width_shift_range=0.3,
zoom_range=0.2,
horizontal_flip=True)
test_datagen = ImageDataGenerator(rescale=1./255)
# +
train_generator = train_datagen.flow_from_directory(
train_dir,
target_size=input_shape[:2],
batch_size=batch_size,
color_mode='grayscale'
)
validation_generator = test_datagen.flow_from_directory(
test_dir,
target_size=input_shape[:2],
batch_size=batch_size,
color_mode='grayscale'
)
# -
# ## Build Model
# +
inputs = layers.Input(input_shape)
net = layers.Conv2D(32, (3, 3), padding='SAME')(inputs)
net = layers.Activation('relu')(net)
net = layers.Conv2D(32, (3, 3), padding='SAME')(net)
net = layers.Activation('relu')(net)
net = layers.MaxPooling2D(pool_size=(2, 2))(net)
net = layers.Dropout(dropout_rate)(net)
net = layers.Conv2D(64, (3, 3), padding='SAME')(net)
net = layers.Activation('relu')(net)
net = layers.Conv2D(64, (3, 3), padding='SAME')(net)
net = layers.Activation('relu')(net)
net = layers.MaxPooling2D(pool_size=(2, 2))(net)
net = layers.Dropout(dropout_rate)(net)
net = layers.Flatten()(net)
net = layers.Dense(512)(net)
net = layers.Activation('relu')(net)
net = layers.Dropout(dropout_rate)(net)
net = layers.Dense(num_classes)(net)
net = layers.Activation('softmax')(net)
model = tf.keras.Model(inputs=inputs, outputs=net, name='Basic_CNN')
# -
# Model is the full model w/o custom layers
model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate), # Optimization
loss='categorical_crossentropy', # Loss Function
metrics=['accuracy']) # Metrics / Accuracy
# ## Training
model.fit_generator(
train_generator,
steps_per_epoch=len(train_generator),
epochs=num_epochs,
validation_data=validation_generator,
validation_steps=len(validation_generator))
|
DL_TF20/Part 11 - fit_generator - flow from directory-Antonio.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.3 64-bit (''base'': conda)'
# language: python
# name: python373jvsc74a57bd0210f9608a45c0278a93c9e0b10db32a427986ab48cfc0d20c139811eb78c4bbc
# ---
test_index = 0
# #### testing
from load_data import *
# +
# load_data()
# -
# ## Loading the data
from load_data import *
X_train,X_test,y_train,y_test = load_data()
len(X_train),len(y_train)
len(X_test),len(y_test)
# ## Test Modelling
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
class Test_Model(nn.Module):
def __init__(self) -> None:
super().__init__()
self.c1 = nn.Conv2d(1,64,5)
self.c2 = nn.Conv2d(64,128,5)
self.c3 = nn.Conv2d(128,256,5)
self.fc4 = nn.Linear(256*10*10,256)
self.fc6 = nn.Linear(256,128)
self.fc5 = nn.Linear(128,4)
def forward(self,X):
preds = F.max_pool2d(F.relu(self.c1(X)),(2,2))
preds = F.max_pool2d(F.relu(self.c2(preds)),(2,2))
preds = F.max_pool2d(F.relu(self.c3(preds)),(2,2))
# print(preds.shape)
preds = preds.view(-1,256*10*10)
preds = F.relu(self.fc4(preds))
preds = F.relu(self.fc6(preds))
preds = self.fc5(preds)
return preds
device = torch.device('cuda')
BATCH_SIZE = 32
IMG_SIZE = 112
model = Test_Model().to(device)
optimizer = optim.SGD(model.parameters(),lr=0.1)
criterion = nn.CrossEntropyLoss()
EPOCHS = 125
from tqdm import tqdm
PROJECT_NAME = 'Weather-Clf'
import wandb
test_index += 1
wandb.init(project=PROJECT_NAME,name=f'test-{test_index}')
for _ in tqdm(range(EPOCHS)):
for i in range(0,len(X_train),BATCH_SIZE):
X_batch = X_train[i:i+BATCH_SIZE].view(-1,1,112,112).to(device)
y_batch = y_train[i:i+BATCH_SIZE].to(device)
model.to(device)
preds = model(X_batch.float())
preds.to(device)
loss = criterion(preds,torch.tensor(y_batch,dtype=torch.long))
optimizer.zero_grad()
loss.backward()
optimizer.step()
wandb.log({'loss':loss.item()})
wandb.finish()
for index in range(10):
print(torch.argmax(preds[index]))
print(y_batch[index])
print('\n')
class Test_Model(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1,16,5)
self.conv2 = nn.Conv2d(16,32,5)
self.conv3 = nn.Conv2d(32,64,5)
self.fc1 = nn.Linear(64*10*10,16)
self.fc2 = nn.Linear(16,32)
self.fc3 = nn.Linear(32,64)
self.fc4 = nn.Linear(64,32)
self.fc5 = nn.Linear(32,6)
def forward(self,X):
preds = F.max_pool2d(F.relu(self.conv1(X)),(2,2))
preds = F.max_pool2d(F.relu(self.conv2(preds)),(2,2))
preds = F.max_pool2d(F.relu(self.conv3(preds)),(2,2))
# print(preds.shape)
preds = preds.view(-1,64*10*10)
preds = F.relu(self.fc1(preds))
preds = F.relu(self.fc2(preds))
preds = F.relu(self.fc3(preds))
preds = F.relu(self.fc4(preds))
preds = F.relu(self.fc5(preds))
return preds
model = Test_Model().to(device)
optimizer = optim.SGD(model.parameters(),lr=0.1)
criterion = nn.CrossEntropyLoss()
test_index += 1
wandb.init(project=PROJECT_NAME,name=f'test-{test_index}')
for _ in tqdm(range(EPOCHS)):
for i in range(0,len(X_train),BATCH_SIZE):
X_batch = X_train[i:i+BATCH_SIZE].view(-1,1,112,112).to(device)
y_batch = y_train[i:i+BATCH_SIZE].to(device)
model.to(device)
preds = model(X_batch.float())
preds.to(device)
loss = criterion(preds,torch.tensor(y_batch,dtype=torch.long))
optimizer.zero_grad()
loss.backward()
optimizer.step()
wandb.log({'loss':loss.item()})
wandb.finish()
for index in range(10):
print(torch.argmax(preds[index]))
print(y_batch[index])
print('\n')
|
wandb/run-20210518_221159-1q566nef/tmp/code/00-main.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import arff
import numpy as np
import json
from sklearn.model_selection import train_test_split, KFold
dataset = arff.loadarff(open('dataset.arff', 'r'))
data = np.array(dataset[0])
print('The dataset has {0} datapoints with {1} features'.format(data.shape[0], data.shape[1]-1))
print('Features: {0}'.format([feature[0] for feature in dataset['attributes']]))
data = data[:, [0, 1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 16, 22, 30]]
X, y = data[:, :-1], data[:, -1]
y.reshape(y.shape[0])
print('Before spliting')
print('X:{0}, y:{1}'.format(X.shape, y.shape))
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
print('After spliting')
print('X_train:{0}, y_train:{1}, X_test:{2}, y_test:{3}'.format(X_train.shape, y_train.shape, X_test.shape, y_test.shape))
np.save('X_train.npy', X_train)
np.save('X_test.npy', X_test)
np.save('y_train.npy', y_train)
np.save('y_test.npy', y_test)
print('Saved!')
test_data = dict()
test_data['X_test'] = X_test.tolist()
test_data['y_test'] = y_test.tolist()
with open('../../static/testdata.json', 'w') as tdfile:
json.dump(test_data, tdfile)
print('Test Data written to testdata.json')
|
backend/dataset/preprocess.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R
# language: ''
# name: ir
# ---
# ## Winpython with R : comparing DPLYR and Pandas
#
#
# It is based on the Thomas Augspurger comparison [Notebook](
# http://nbviewer.ipython.org/urls/gist.githubusercontent.com/TomAugspurger/6e052140eaa5fdb6e8c0/raw/674f99243eec162e17499eb0e2e0ee881e17b960/dplyr_pandas.ipynb)
#
# This is the [introductory dplyr vignette](http://cran.r-project.org/web/packages/dplyr/vignettes/introduction.html) to analyze some flight data, played via an Ipython/Jupyter notebook.
#
# We just play the "R" code part, this time
#
# Nota: <NAME> would recommand you to add more package to the list: caret, reader, shiny
#
# https://gist.github.com/hadley/820f09ded347c62c2864
# ##### Transform this Markdown cell to a Code cell, if ever you need to re-feed a basic R environnement
#
# # %R install.packages("tidyr")
#
# # %R install.packages("dplyr")
#
# # %R install.packages("ggplot2")
#
# # %R install.packages("rvest")
#
# # %R install.packages('RSQLite')
#
# # %R install.packages("zoo")
#
# # %R install.packages("forecast")
#
# # %R install.packages('R.utils')
#
# # %R install.packages("nycflights13")
#
# # %R install.packages('hflights')
#
# # %R update.packages()
library("dplyr") # for functions
library("nycflights13")
write.csv(flights, "flights.csv")
# # Data: nycflights13
dim(flights)
head(flights)
# # Single table verbs
# ``dplyr`` has a small set of nicely defined verbs. I've listed their closest pandas verbs.
#
#
# <table>
# <tr>
# <td><b>dplyr</b></td>
# <td><b>pandas</b></td>
# </tr>
# <tr>
# <td>filter() (and slice())</td>
# <td>query() (and loc[], iloc[])</td>
# </tr>
# <tr>
# <td>arrange()</td>
# <td>sort()</td>
# </tr>
# <tr>
# <td>select() (and rename())</td>
# <td>\_\_getitem\_\_ (and rename())</td>
# </tr>
# <tr>
# <td>distinct()</td>
# <td>drop_duplicates()</td>
# </tr>
# <tr>
# <td>mutate() (and transmute())</td>
# <td>None</td>
# </tr>
# <tr>
# <td>summarise()</td>
# <td>None</td>
# </tr>
# <tr>
# <td>sample_n() and sample_frac()</td>
# <td>None</td>
# </tr>
# </table>
#
#
# Some of the "missing" verbs in pandas are because there are other, different ways of achieving the same goal. For example `summarise` is spread across `mean`, `std`, etc. Others, like `sample_n`, just haven't been implemented yet.
# # Filter rows with filter(), query()
#
# filter() allows you to select a subset of the rows of a data frame. The first argument is the name of the data frame, and the second and subsequent are filtering expressions evaluated in the context of that data frame:
#
# For example, we can select all flights on January 1st with:
filter(flights, month == 1, day == 1)
# The more verbose version:
flights[flights$month == 1 & flights$day == 1, ]
# filter() works similarly to subset() except that you can give it any number of filtering conditions which are joined together with & (not && which is easy to do accidentally!). You can use other boolean operators explicitly:
filter(flights, month == 1 | month == 2)
# ####To select rows by position, use slice():
slice(flights, 1:10)
# # Arrange rows with arrange(), sort()
#
# arrange() works similarly to filter() except that instead of filtering or selecting rows, it reorders them. It takes a data frame, and a set of column names (or more complicated expressions) to order by. If you provide more than one column name, each additional column will be used to break ties in the values of preceding columns:
arrange(flights, year, month, day)
# Use desc() to order a column in descending order:
arrange(flights, desc(arr_delay))
# # Select columns with select()
#
# Often you work with large datasets with many columns where only a few are actually of interest to you. select() allows you to rapidly zoom in on a useful subset using operations that usually only work on numeric variable positions:
select(flights, year, month, day)
select(flights, year:day)
select(flights, -(year:day))
select(flights, tail_num = tailnum)
# But like Hadley mentions, not that useful since it only returns the one column. ``dplyr`` and ``pandas`` compare well here.
rename(flights, tail_num = tailnum)
# # Extract distinct (unique) rows
distinct(select(flights, tailnum))
# FYI this returns a numpy array instead of a Series.
distinct(select(flights, origin, dest))
# # Add new columns with mutate()
mutate(flights, gain = arr_delay - dep_delay, speed = distance / air_time * 60)
mutate(flights, gain = arr_delay - dep_delay, gain_per_hour = gain / (air_time / 60) )
# +
# mutate(flights,
# gain = arr_delay - dep_delay,
# gain_per_hour = gain / (air_time / 60)
# )
flights['gain'] = flights.arr_delay - flights.dep_delay
flights['gain_per_hour'] = flights.gain / (flights.air_time / 60)
flights
# -
# ``dplyr's`` approach may be nicer here since you get to refer to the variables in subsequent statements within the ``mutate()``. To achieve this with pandas, you have to add the `gain` variable as another column in ``flights``. If I don't want it around I would have to explicitly drop it.
transmute(flights, gain = arr_delay - dep_delay, gain_per_hour = gain / (air_time / 60) )
# # Summarise values with summarise()
summarise(flights,
delay = mean(dep_delay, na.rm = TRUE))
# # Randomly sample rows with sample_n() and sample_frac()
sample_n(flights, 10)
sample_frac(flights, 0.01)
# # Grouped operations
# +
library("ggplot2")
by_tailnum <- group_by(flights, tailnum)
delay <- summarise(by_tailnum,
count = n(),
dist = mean(distance, na.rm = TRUE),
delay = mean(arr_delay, na.rm = TRUE))
delay <- filter(delay, count > 20, dist < 2000)
# Interestingly, the average delay is only slightly related to the
# average distance flown by a plane.
ggplot(delay, aes(dist, delay)) +
geom_point(aes(size = count), alpha = 1/2) +
geom_smooth() +
scale_size_area()
# -
destinations <- group_by(flights, dest)
summarise(destinations,
planes = n_distinct(tailnum),
flights = n()
)
filter(
summarise(
select(
group_by(flights, year, month, day),
arr_delay, dep_delay
),
arr = mean(arr_delay, na.rm = TRUE),
dep = mean(dep_delay, na.rm = TRUE)
),
arr > 30 | dep > 30
)
# Similar to how ``dplyr`` provides optimized C++ versions of most of the `summarise` functions, pandas uses [cython](http://cython.org) optimized versions for most of the `agg` methods.
daily <- group_by(flights, year, month, day)
(per_day <- summarise(daily, flights = n()))
(per_month <- summarise(per_day, flights = sum(flights)))
(per_year <- summarise(per_month, flights = sum(flights)))
# I'm not sure how ``dplyr`` is handling the other columns, like `year`, in the last example. With pandas, it's clear that we're grouping by them since they're included in the groupby. For the last example, we didn't group by anything, so they aren't included in the result.
# # Chaining
# Any follower of Hadley's [twitter account](https://twitter.com/hadleywickham/) will know how much R users *love* the ``%>%`` (pipe) operator. And for good reason!
flights %>%
group_by(year, month, day) %>%
select(arr_delay, dep_delay) %>%
summarise(
arr = mean(arr_delay, na.rm = TRUE),
dep = mean(dep_delay, na.rm = TRUE)
) %>%
filter(arr > 30 | dep > 30)
# # Other Data Sources
# Pandas has tons [IO tools](http://pandas.pydata.org/pandas-docs/version/0.15.0/io.html) to help you get data in and out, including SQL databases via [SQLAlchemy](http://www.sqlalchemy.org).
# # Summary
# I think pandas held up pretty well, considering this was a vignette written for dplyr. I found the degree of similarity more interesting than the differences. The most difficult task was renaming of columns within an operation; they had to be followed up with a call to ``rename`` *after* the operation, which isn't that burdensome honestly.
#
# More and more it looks like we're moving towards future where being a language or package partisan just doesn't make sense. Not when you can load up a [Jupyter](http://jupyter.org) (formerly IPython) notebook to call up a library written in R, and hand those results off to python or Julia or whatever for followup, before going back to R to make a cool [shiny](http://shiny.rstudio.com) web app.
#
# There will always be a place for your "utility belt" package like dplyr or pandas, but it wouldn't hurt to be familiar with both.
#
# If you want to contribute to pandas, we're always looking for help at https://github.com/pydata/pandas/.
# You can get ahold of me directly on [twitter](https://twitter.com/tomaugspurger).
|
docs/FlavorR/dplyr_vignette_in_R_kernel.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from pyrep import PyRep
from pyrep.objects.shape import Shape
from pyrep.const import PrimitiveShape
from pyrep.errors import ConfigurationPathError
import time
import numpy as np
import math
import matplotlib.pyplot as plt
from scipy.interpolate import UnivariateSpline
import os
os.environ["CUDA_DEVICE_ORDER"] = "PCI_BUS_ID"
os.environ["CUDA_VISIBLE_DEVICES"] = ""
import tensorflow as tf
import keras
from keras.layers import Softmax,Input,TimeDistributed,Dense,Average,GlobalAveragePooling1D
from keras.layers import Concatenate,Lambda,RepeatVector,Conv2D,ConvLSTM2D,MaxPooling2D,BatchNormalization,Flatten,Reshape,UpSampling2D
from keras.models import Model, load_model
from keras.optimizers import Adam
from keras.utils import plot_model
import numpy as np
import matplotlib.pyplot as plt
import math
import time
import random
import pylab as pl
from IPython import display
from IPython.core.display import HTML
from IPython.core.display import display as html_width
import tensorflow_probability as tfp
from tensorflow.keras.utils import Sequence
import matplotlib.image as mpimg
from keras.models import load_model
html_width(HTML("<style>.container { width:90% !important; }</style>"))
# -
# #### The LfD part of the code is taken from https://github.com/rssCNMP/CNMP
# ## Initializing scene
# +
from pyrep.robots.arms.arm import Arm
class Trobot(Arm):
def __init__(self, count: int = 0):
super().__init__(count, 'Trobot', num_joints=3)
# +
pr = PyRep()
# Launch the application with a scene file in headless mode
pr.launch('table.ttt', headless=False)
pr.start() # Start the simulation
# Do some stuff
# -
pr.start()
# +
#pr.shutdown() # to shut down the scene
# -
pr.stop() # to initialize the scene
cnmp_traj=np.load('CNMP_pushing_solution.npy')
print(np.shape(cnmp_traj))
Threedof_starting_position = [-0.50009131, 2.42891255, -0.91733952]
# ## Playing initial LfD solution
agent_model = pr.import_model('Trobot3Dof.ttm')
agent=Trobot()
agent.set_joint_target_positions(Threedof_starting_position)
for i in range(50):
pr.step()
cylinder_object_position = [0.281, -0.0613, 0.125]
end_goal_position = [-0.257, 0.238, 0.125]
# +
target_object = Shape.create(type=PrimitiveShape.CYLINDER,
color=[0,0,0], size=[0.05, 0.05, 0.05],
position=cylinder_object_position)
print(agent.get_joint_positions())
goal_pos = Shape.create(type=PrimitiveShape.CYLINDER,
color=[1,0,0], size=[0.06, 0.06, 0.005],
position=end_goal_position,
static=True, respondable=False)
pr.step()
# -
pr.step()
for i in range(300):
agent.set_joint_target_positions(cnmp_traj[i])
pr.step()
pr.step()
pr.step()
pr.step()
pr.step()
pr.step()
target_object.remove()
goal_pos.remove()
agent_model.remove()
pr.step()
# ## Loading data for ACNMP
#
# * <b>parameters</b>: Task_parameters corresponding to goal positions.
# * <b>reward_true</b>: Recorded object trajectories during demonstrations
#
# * <b>y</b>: Joint trajectories for 10 skill
#
# * The last skill will be predicted in the code, for interpolation, places of skills should be swapped by uncommenting.
#
# +
time_N = 300
times = np.linspace(0.,1.,time_N)
len_files=10
class Demonstration:
def __init__(self):
self.target_position= []
self.object_position= []
self.obj_trajectory = []
self.joint_trajectory = []
A=Demonstration()
A.joint_trajectory=np.load('Threedofpushing_joint_trajectories.npy')
A.obj_trajectory = np.load('Threedofpushing_obj_trajectories.npy')
A.object_position = np.load ('Threedofpushing_object_position.npy')
A.target_position = np.load('Threedofpushing_target_position.npy')
print(np.shape(A.joint_trajectory))
print(np.shape(A.obj_trajectory))
print(np.shape(A.object_position))
print(np.shape(A.target_position))
parameters=np.zeros((10,2))
parameters[:,0] = A.target_position[:,0]
parameters[:,1] = A.target_position[:,1]
reward_true = np.zeros((10,300,2))
reward_true[:,:,0] = A.obj_trajectory[:,:,0]
reward_true[:,:,1] = A.obj_trajectory[:,:,1]
max_par=parameters.max()
min_par=parameters.min()
parameters=(parameters-min_par)/(max_par-min_par)+0.01
y = np.zeros((len_files,time_N,3))
y = A.joint_trajectory
# Uncomment the following for interpolation example
#ch_num = 7
#y[[ch_num,9]] = y[[9,ch_num]]
#parameters[[ch_num,9]] = parameters[[9,ch_num]]
#reward_true[[ch_num,9]] = reward_true[[9,ch_num]]
for xyz in range(3):
for i in range(len_files):
plt.plot(times,y[i,:,xyz])
plt.scatter(times[0],y[9,0,xyz])
plt.scatter(times[time_N-1],y[9,time_N-1,xyz])
plt.show()
# -
# ## Loading model inputs
#
# * <b>n_max</b>: Hyperparameter that decides to the maximum number of observations CNMP uses. In this experiment, it is set to 5.
# * <b>n</b>: Number of observations taken for one time step.
#
# * <b>p</b>: Number that specifies the taken expert demonstration.
#
# * <b>observation</b>: The input vector for CNMP network, which consists of n observations.
#
# * <b>target</b>: A random time point concatenated with task parameters used for the training
#
# * <b>Y</b>: The matrix that contains expert demonstrations.
#
n_max = 5
def get_train_sample():
observation = np.zeros((1,n_max,6))
observation_flag = np.zeros((1,1,n_max))
target = np.zeros((1,1,3))
p = random.randint(0, 8)
n = random.randint(1,n_max)
perm = np.random.permutation(time_N)
for i in range(n):
observation[0,i] = [times[perm[i]],parameters[p,0],parameters[p,1],y[p,perm[i],0],y[p,perm[i],1],y[p,perm[i],2]]
observation_flag[0,0,i] = 1./n
target[0,0,0] = times[perm[n]]
target[0,0,1] = parameters[p,0]
target[0,0,2] = parameters[p,1]
return [observation,observation_flag,target], [[[y[p,perm[n],0],y[p,perm[n],1],y[p,perm[n],2],0.,0.,0.]]],p
# ### custom_loss2():
# * The policy gradient loss where a Gaussian distribution is used for action values .
import keras.backend as K
def custom_loss2(taken, predicted):
predicted_action_mean, predicted_action_sigma = tf.split(predicted, 2, axis=-1)
taken_action, q_value =tf.split(taken,2,axis=-1)
square_loss=tf.math.square(taken_action-predicted_action_mean)
loss=(1./4.)*tf.math.multiply(square_loss,q_value)
return K.mean(loss)
# ## The reinforcement learning model:
#
# * Same as LfD network
#
# +
observation_layer = Input(shape=(n_max,6))
observation_flag_layer=Input(shape=(1,n_max))
observation_encoded = TimeDistributed(Dense(128, activation='relu'))(observation_layer)
observation_encoded = TimeDistributed(Dense(128, activation='relu'))(observation_encoded)
observation_encoded = TimeDistributed(Dense(64, activation='relu'))(observation_encoded)
observation_encoded = TimeDistributed(Dense(32))(observation_encoded)
matmul_layer=Lambda(lambda x:(tf.matmul(x[0],x[1])), output_shape =(1,32))
representation=matmul_layer([observation_flag_layer,observation_encoded])
target_layer = Input(shape=(1,3))
decoder_input = Concatenate(axis=-1)([representation, target_layer])
decoder = Dense(128, activation='relu')(decoder_input)
decoder = Dense(128, activation='relu')(decoder)
decoder = Dense(128, activation='relu')(decoder)
output_layer = Dense(6)(decoder)
#next_model_input=Concatenate(axis=2)([decoder_input, output_layer])
rl_input=decoder_input
model2 = Model(inputs=[observation_layer,observation_flag_layer,target_layer],outputs=output_layer)
model2.compile(optimizer = Adam(lr = 5e-5),loss=custom_loss2)
model2.summary()
representation_model2 = Model(inputs=[observation_layer,observation_flag_layer,target_layer],outputs=rl_input)
# -
# #### The weights of LfD network are copied to bootstrap reinforcement learning agent
# +
model2.load_weights('naive_cnmp_3dof_pushing.h5')
#Uncomment this for interpolation case
#model2.load_weights('naive_cnmp_3dof_pushing_7.h5')
# -
# ### Mismatch function to measure the differences of old and new policy
def mismatch_func(actions1,actions2):
error=0
for i in range(time_N):
error2=np.square(actions1[i]-actions2[i])
error=max(error,error2)
return error
# #### Gaussian Pdf
def normpdf(x, mean, sd):
denom = sd*(2*math.pi)**0.5
num= math.exp(-0.5*((x-mean)/float(sd))**2)
return num/denom
# ### The states are recorded by only using the start point and task parameters as observation.
# +
pred_y = np.zeros(time_N)
pred_std = np.zeros(time_N)
states1=[]
states2=[]
states3=[]
observation = np.zeros((1,n_max,6))
observation_flag = np.zeros((1,1,n_max))
target = np.zeros((1,1,3))
observation[0,0] = [times[0],parameters[9,0], parameters[9,1], -0.51061333, 2.42277872, -0.914231]
observation_flag[0,0,0] = 1.
for i in range(time_N):
target[0,0,0] = times[i]
target[0,0,1] = parameters[9,0]
target[0,0,2] = parameters[9,1]
if(i==0):
states1=observation
states2=observation_flag
states3=target
else:
states1=np.concatenate((states1,observation),axis=0)
states2=np.concatenate((states2,observation_flag),axis=0)
states3=np.concatenate((states3,target),axis=0)
states=[states1,states2,states3]
# -
def square_error(arr1,arr2):
errsum=0
for j in range(2):
errsum+=np.square(arr1[j]-arr2[j])
return errsum
max_reward = 5
var = 0.05
reward_array = []
saved_trajectory = np.zeros((300,3))
def rl_agent(c_t,c):
global max_reward
global var
global saved_trajectory
for i in range(100): #supervised_learning
inp,out,sample = get_train_sample()
out[0][0][3]=1
out[0][0][4]=1
out[0][0][5]=1
data = model2.fit(inp,out,batch_size=1,verbose=0)
actions, rewards, rewards2 = [], [], [] #arrays to record
action_prob=[]
actions_mean=[]
agent_model = pr.import_model('Trobot.ttm') #for each step robot and objects are recreated.
agent=Trobot()
pr.step()
agent.set_joint_target_positions(Threedof_starting_position)
for i in range(50):
pr.step()
cylinder_object_position = A.object_position[9]
end_goal_position = A.target_position[9]
#cylinder_object_position = A.object_position[7] #uncomment for interpolation
#end_goal_position = A.target_position[7]
target_object = Shape.create(type=PrimitiveShape.CYLINDER,
color=[0,0,0], size=[0.05, 0.05, 0.05],
position=cylinder_object_position)
goal_pos = Shape.create(type=PrimitiveShape.CYLINDER,
color=[1,0,0], size=[0.06, 0.06, 0.005],
position=end_goal_position,
static=True, respondable=False)
pr.step()
#Rewards for mean of the policy ditribution are observed
traj_list = []
for i in range(time_N):
pred= model2.predict([[states1[i]],[states2[i]],[states3[i]]])[0][0]
reward2= 0
agent.set_joint_positions(pred[:3])
traj_list.append(pred[:3])
obj=target_object.get_position()
reward2=-square_error(reward_true[9,i] ,obj)
reward2=reward2/1.
rewards2.append(reward2)
observed_reward=np.absolute(np.sum(rewards2))
reward_array.append(observed_reward)
var = min(observed_reward/10,0.05)
if observed_reward<max_reward:
max_reward = observed_reward
saved_trajectory = np.asarray(traj_list)
print("new_best")
target_object.remove()
agent_model.remove()
goal_pos.remove()
pr.step()
agent_model = pr.import_model('Trobot.ttm') # robot and objects are recreated.
agent=Trobot()
pr.step()
agent.set_joint_target_positions(Threedof_starting_position)
for i in range(50):
pr.step()
starting_joints=agent.get_joint_positions()
cylinder_object_position = A.object_position[9]
end_goal_position = A.target_position[9]
#cylinder_object_position = A.object_position[7] #uncomment for interpolation
#end_goal_position = A.target_position[7]
target_object = Shape.create(type=PrimitiveShape.CYLINDER,
color=[0,0,0], size=[0.05, 0.05, 0.05],
position=cylinder_object_position)
goal_pos = Shape.create(type=PrimitiveShape.CYLINDER,
color=[1,0,0], size=[0.06, 0.06, 0.005],
position=end_goal_position,
static=True, respondable=False)
pr.step()
samples2=[]
#smoothed gaussian noise is added on top of policy mean.
for i in range (3):
mean = 0
std = var
num_samples = 20
samples = np.random.normal(mean, std, size=num_samples)
old_indices = np.arange(0,len(samples))
new_length = 300
new_indices = np.linspace(0,len(samples)-1,new_length)
spl = UnivariateSpline(old_indices,samples,k=3,s=0.1)
samples2.append(spl(new_indices))
# rewards for sampled policy are obtained
for i in range(time_N):
pred= model2.predict([[states1[i]],[states2[i]],[states3[i]]])[0][0]
selected_action=[pred[0]+samples2[0][i],pred[1]+samples2[1][i],pred[2]+samples2[2][i]]
#selected_action = [np.random.normal(pred[0], 0.1, 1)[0], np.random.normal(pred[1], 0.1, 1)[0], np.random.normal(pred[2], 0.1, 1)[0]]
action_prob.append([normpdf(selected_action[0], pred[0], var),normpdf(selected_action[1], pred[1], var),normpdf(selected_action[2], pred[2], var)])
actions.append(selected_action)
actions_mean.append(pred[:3])
object_trajectory = []
for i in range(time_N):
reward = 0
agent.set_joint_positions(actions[i])
obj=target_object.get_position()
object_trajectory.append(obj)
reward=-square_error(reward_true[9,i] ,obj)
reward=reward*1.0
rewards.append(reward)
object_trajectory = np.asarray(object_trajectory)
target_object.remove()
agent_model.remove()
goal_pos.remove()
pr.step()
gradient_rewards = np.zeros((time_N))
for i in range(time_N):
gradient_rewards[i]=rewards[i]-rewards2[i]
gradient_rewards /= np.std(gradient_rewards)
advantages=np.zeros((time_N,1,6))
for i in range(time_N):
for j in range(3):
advantages[i][0][j]=actions[i][j]
advantages[i][0][j+3]=gradient_rewards[i]
data = model2.fit(states,advantages,verbose=0)
counter=0
while(var>0.1): # off-policy learning
counter=counter+1
actions2=[]
action_prob2=[]
for i in range(50): #supervised learning
inp,out,sample = get_train_sample()
out[0][0][3]=1
out[0][0][4]=1
out[0][0][5]=1
data = model2.fit(inp,out,batch_size=1,verbose=0)
for i in range(time_N): #reinforcement learning
pred= model2.predict([[states1[i]],[states2[i]],[states3[i]]])[0][0]
selected_action = actions[i]
selected_action2 = [np.random.normal(pred[0], var, 1)[0], np.random.normal(pred[1], var, 1)[0], np.random.normal(pred[2], var, 1)[0]]
action_prob2.append([normpdf(selected_action[0], pred[0], var),normpdf(selected_action[1], pred[1], var),normpdf(selected_action[2], pred[2], var)])
actions2.append(pred[:3])
advantages2=np.zeros((time_N,1,6))
for i in range(time_N):
for j in range(3):
advantages2[i][0][j]=actions[i][j]
advantages2[i][0][3+j]=gradient_rewards[i]*min(1,(action_prob2[i][j]/action_prob[i][j]))
#data = model2.fit(states,advantages2,verbose=0)
act1=np.transpose(actions_mean)
act2=np.transpose(actions2)
plcy_diff1=mismatch_func(act1[0],act2[0])
plcy_diff2=mismatch_func(act1[1],act2[1])
plcy_diff3=mismatch_func(act1[2],act2[2])
plcy_diff=max(plcy_diff1,plcy_diff2,plcy_diff3)
if plcy_diff>0.001:
break
elif counter>50: #check for infinite loop
break
else:
print("offpolicy")
data = model2.fit(states,advantages2,verbose=0)
#print(KL_diff)
return observed_reward
pr.start()
#target_object.remove()
#agent_model.remove()
#goal_pos.remove()
pr.step()
training_loss = np.zeros(2000)
reward_array_list = []
reward_array_list.append(reward_array)
for kk in range(10):
model2.load_weights('naive_cnmp_3dof_pushing.h5')
#Uncomment this for interpolation case
#model2.load_weights('naive_cnmp_3dof_pushing_7.h5')
reward_array = []
for step in range(100):
rrr=rl_agent([times[0],times[299]],[y[9,0],y[9,299]])
print(step)
reward_array_list.append(reward_array)
saved_trajectory
pr.stop() # Stop the simulation
pr.start()
# +
extra_reward = np.load('extrapolation_reward2.npy')
#extra_reward = reward_array_list #uncomment to use training result
for i in range(10):
for j in range(100):
extra_reward[i,j]=extra_reward[i,j]*(-1)
mean_extrapolation = np.mean(extra_reward,axis=0)
std_extrapolation = np.std(extra_reward,axis=0)
# -
inter_reward = np.load('intrapolation_reward2.npy')
mean_interpolation = np.mean(inter_reward,axis=0)
std_interpolation = np.std(inter_reward,axis=0)
# +
plt.errorbar(range(100), mean_interpolation, yerr=std_interpolation, color = 'b' , label = 'interpolation')
plt.errorbar(range(100), mean_extrapolation, yerr=std_extrapolation, color = 'r' , label = 'extrapolation')
plt.legend()
plt.xlabel('Iteration', fontsize=12)
plt.ylabel('Reward (in m)', fontsize=12)
# -
pr.shutdown() # Close the application
|
Experiment2/ACNMP-SecondExperiment-Cylinder_pushing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
# this is to test the Bergen County mismatch from the email
import pandas as pd
import os
data_path='/Users/anastasiaclark/irs_nyc_migration/data'
county_pep=pd.read_csv(os.path.join(data_path, 'census_pop_est','co-est2016-alldata.csv'), converters={'STATE':str,'COUNTY':str},encoding='LATIN-1')
# -
county_pep['fips']=county_pep.STATE+county_pep.COUNTY
county_pep.set_index('fips',inplace=True)
pop_cng_cols=[c for c in county_pep.columns if 'NPOPCHG' in c]
pop_cng_cols
county_pep[pop_cng_cols].loc['34003'].sum()
county_pep['POPESTIMATE2016'].loc['34003']-county_pep['POPESTIMATE2010'].loc['34003']
|
scripts/.ipynb_checkpoints/test-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Effect of including average bonus + save + card points
from airsenal.framework.utils import *
from airsenal.framework.prediction_utils import *
# +
df_bonus = fit_bonus_points()[0]
df_cards = fit_card_points()
df_saves = fit_save_points()
df = pd.DataFrame({"bonus": df_bonus, "cards": df_cards, "saves": df_saves})
df.fillna(0, inplace=True)
df["TOTAL"] = df.sum(axis=1)
players = pd.read_sql(session.query(Player).statement, engine)
df = pd.merge(df, players, how="left", left_on="player_id", right_on="player_id")
current_players = list_players()
current_ids = [p.player_id for p in current_players]
current_positions = pd.Series({p.player_id: p.position(CURRENT_SEASON) for p in current_players}, name="position")
df = df[df.player_id.isin(current_ids)]
df = pd.merge(df, current_positions, how="left", left_on="player_id", right_index=True)
df.set_index(["player_id", "name"], inplace=True)
# -
# ## Gain most overall
df.sort_values(by="TOTAL", ascending=False).head(20)
# ## Lose most overall
df.sort_values(by="TOTAL", ascending=True).head(20)
# ## Top GK
df[df.position == "GK"].sort_values(by="TOTAL", ascending=False).head(20)
# ## Top DEF
df[df.position == "DEF"].sort_values(by="TOTAL", ascending=False).head(20)
# ## Top MID
df[df.position == "MID"].sort_values(by="TOTAL", ascending=False).head(20)
# ## Top FWD
df[df.position == "FWD"].sort_values(by="TOTAL", ascending=False).head(20)
# ## Specific player
p = get_player("Fabinho").player_id
df[df.index.get_level_values(0) == p]
|
notebooks/total_saves_bonus_cards.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + deletable=true editable=true
n = int(input('请输入一个整数,以回车结束'))
i = 1
total = 1
while i < n:
i = i + 1
total = total * i
print(total)
# + deletable=true editable=true
name = input('请输入你的名字,以回车结束')
print('你好!', name)
total = 0
m = int(input('请输入你要输入的整数个数,以回车结束'))
i = 0
while m > i:
i += 1
n = int(input('请输入一个整数,以回车结束'))
total += n
print('你输入的所有整数和为', total)
print('再见!', name)
# + deletable=true editable=true
name = input('请输入你的名字,以回车结束')
print('你好!', name)
start = int(input('如果你想输入数字,请输入1,否则请输入2。'))
m = 2
while m > start:
n = int(input('请输入你想输入的数字,以回车结束'))
start = int(input('如果你想输入数字,请输入1,否则请输入2。'))
print('再见!', name)
# +
name = input('请输入你的名字,以回车结束')
print('你好!', name)
total = 0
m = 1
start = int(input('如果你想输入数字,请输入1,否则请输入2,以回车结束'))
m = 2
while m > start:
n = int(input('请输入你想输入的数字,以回车结束'))
total += n
m *= n
while total < n and m < n**2:
print('end')
print('再见', name)
|
chapter1/homework/localization/3-15/201611680132.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Neural Network
#
# In this jupyter notebook we will focus on $\textit{Neural Netowrks}$ (also called MultiLayer Perceptrons), which is computing system, that is based on biological neural networks that constitute animal brains.
#
# <img src="Neural_net/neural_net.jpg" height="40%" width="40%">
# # Problem
# For a given set $D = \{(x_n, y_n)\}_{n=1}^N$ classify $\textit{y}$ for the new $\textbf{x}$. To do it we will have to teach our neural network how to predict the class basing on input data.
#
# <h3>Example</h3>
# Given a dataset from MNIST (set of handwritten digits) we have to predict proper digit according to the input image:
# <img src="Neural_net/example.jpg" height="70%" width="70%">
import numpy as np
import matplotlib.pyplot as plt
import utils
from tqdm import tqdm_notebook
from matplotlib.gridspec import GridSpec
# # Simple example
# We want our model to learn if the output is ture of false, according to input data that will represent the xor logical gate, with A and B as inputs and O as output. The xor is a logical gate that gives a true output, when number of true inputs is odd.
# <img src="Neural_net/xor.jpg" height="70%" width="70%">
#
#
# Neural network have to learn itself what weights it has set to the inputs, so it can easliy decide if the output is true or not. For example it can develop weights to detect features like this:
#
# <img src="Neural_net/neural_net_xor.jpeg" height="70%" width="70%">
# # Input data
# We have to prepare some input data, for example four pairs A, B like in table above, but we will store it in just single variable x, and the output O in variable y.
def prepare_data():
X = np.array([[0, 0], [1, 0], [0, 1], [1, 1]])
Y = np.array([[0],[1],[1],[0]])
return X, Y
X, Y = prepare_data()
print('Input shape: {}'.format(X.shape))
print('Output shape: {}'.format(Y.shape))
# # Neural Network Model
# Our model is a simple neural network with one hidden layer. That consists of input layer, where the "x" is given, hidden layer, and output layer, where we predict 'y'. In each layer there is addidtional node, which is not connected with the previous layer called bias. This neuron allows us to provide some independency between inputs.
#
# <img src="Neural_net/neural_net_bias.jpg" height="40%" width="40%">
# # Sigmoid
# We are going to use sigmoid non-linear function, that is defined:
#
# $\sigma(x) = \frac{1}{1+e^{-x}}$
#
# And looks like this below:
# <img src="Neural_net/sigmoid.jpg" height="40%" width="40%">
#
# We also need to know sigmoid derivative which is equal to:
# $\frac{\delta \sigma}{\delta x} = \sigma(x) \cdot (1 - \sigma(x)) $
def sigmoid(x):
'''
param x: input matrix of size NxM
'''
return 1/(1+np.exp(-x))
print('Sigmoid for small value f.e. -100 equals: {:.3f}'.format(sigmoid(-100)))
print('Sigmoid of big values f.e. 100 equals: {:.3f}'.format(sigmoid(100)))
# # Forward pass
# Now we are going to implement steps:
# 1. We are multiplying inputs by weights and adding bias to get $z_1$ values at the hidden layer.
# 3. On the $z_1$ we are applaying non-linear function to 'activate' the layer.
# 4. We are multiplying values from the hidden layer by next weights and adding another bias to get $z_2$ value on output layer
# 6. At the end we need to apply another non-linear function on output layer.
#
# $z_1 = (a_0 \times w_1) + b_1 $
#
# $a_1 = \sigma(z_1) $
#
# $z_2 = (a_1 \times w_2 ) + b_2 $
#
# $a_2 = \sigma(z_2) $
def forward_pass(x, w, b):
'''
param x: vector of input training values NxM, where N is the number of examples & M number of features
param w: tuple of two matrixes, which describes weights between layers
param b: tuple of two vectors, which describes biases for layers
returns: function returns cache, which is tuple, that includes values of activated layers.
'''
w1, w2 = w # unpacking tuple to single matrixes
b1, b2 = b # unpacking tuple to single vectors
a0 = x
z1 = (a0 @ w1) + b1
a1 = sigmoid(z1)
z2 = (a1 @ w2) + b2
a2 = sigmoid(z2)
cache = (a1, a2)
return cache
# # Cost Function
# At start weights are random numbers, so we need to find parameters that will predict output with the smallest error. we are going to search for them using gradient descent, which is a method that allows to reach local minimum by substracting derivatives values from weights.
#
# Before computing the gradient we need to define cost function, which in our case will be mean squared error:
# $J = \frac{1}{2N}\lVert{\textbf{y}} - \overline{\textbf{y}}\rVert_2^2$
#
# The cost function will let us measure how bad our model works.
#
#
# $\lVert \textbf{y} - \overline{\textbf{y}}\rVert_2$ is called Norm 2 <br>
# In linear algebra, functional analysis, and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to each vector in a vector space
# <br>
#
# $\lVert\textbf{x}\rVert_2 = \sqrt[2]{\sum_{n=1}^{N} x_n^2}$
def initialize_random_weights(inputs_amount, hidden_nodes_amount, outputs_amount):
'''
param inputs_amount: number of cells in input layer
param output_amount: number of cells in output layer
return: pair of tuples of weights and biases for proper layers
'''
np.random.seed(100)
w1 = np.random.normal(0, 1 / np.sqrt(hidden_nodes_amount), (inputs_amount, hidden_nodes_amount))
b1 = np.random.normal(0, 1, hidden_nodes_amount)
w2 = np.random.normal(0, 1 / np.sqrt(outputs_amount), (hidden_nodes_amount, outputs_amount))
b2 = np.random.normal(0, 1, outputs_amount)
return (w1, w2), (b1, b2)
# +
#example usage
w, b = initialize_random_weights(inputs_amount = 2, hidden_nodes_amount = 3, outputs_amount=1)
w1, w2 = w
b1, b2 = b
print("W1 (from input layer to hidden layer) shape: {}".format(w1.shape))
print("b1 (bias added to hidden layer) shape: {}".format(b1.shape))
print("W2 (from hidden layer to outputs layer) shape: {}".format(w2.shape))
print("b2 (bias added to outplut layer) shape: {}".format(b2.shape))
# -
# # Backpropagation
# To make some improvements to our weights we need to compute the error, and then following the chain rule change the parameters as follows:
# <h3>Steps of gradeint descent</h3>
# 1. Compute the cost (the error on our last layer)
# 2. Compute the error on not activated values $z_2$
# 3. Compute the gradient on weights $w_2$ and bias $b_2$
# 4. Compute the error on layer $a_1$
# 5. Compute the error on not activated values $z_1$
# 6. compute the gradient on weights $w_1$ and bias $b_1$
#
# <h3> How are we going to compute those errors</h3>
# We need to compute derivative of our cost function with coressponding to our weights and biases, so after substracting computed values from weights and biases we become closer to minimum of cost function.
# <p><i>When the cost function grows the derivative is positive, so substracting it will make a 'step back' in direction of minimum.
#
# When the function decreases the derivative is negative, so substracting it will make a 'step forward' in direction of minimum.
#
# If this is hard to imagine - draw yourself a $x^2$ function and place yourself on the left and right of the minimum, compute derivative and substract it from x.
# </i></p>
#
# <h4>Detailed steps of gradient descent using chain rule (for people familiar with calculus) </h4>
# 1. Compute the cost: $ J = \frac{1}{2N}\lVert{\textbf{y} - \textbf{a}_2}\rVert_2^2$
#
# 2. Compute the derivative of cost with respect to $ a_2 = \space \frac{\delta J}{\delta a_2} = -2 \cdot(y - a_2) $
#
# 3. Compute the derivative of cost with respect to $ z_2 = \space \frac{\delta J}{\delta z_2} = \frac{\delta J}{\delta a_2} \cdot \frac{\delta a_2}{\delta z_2} = \frac{\delta J}{\delta a_2} \cdot (a_2 \cdot (1 -a_2)) \space,$because $ \frac{\delta a_2}{\delta z_2} = a_2 \cdot (1-a_2) \space $ as $a_2$ is the $\sigma(z_2)$
#
# 4. 1. Compute the derivative of cost with respect to $ w_2 = \space \frac{\delta J}{\delta w_2} = \frac{\delta J}{\delta a_2} \cdot \frac{\delta a_2}{\delta z_2} \cdot \frac{\delta z_2}{\delta w_2} =\frac{\delta J}{\delta z_2} \cdot \frac{\delta z_2}{\delta w_2} = \frac{\delta J}{\delta z_2} \cdot a_1 \space$, beacuse $\frac{\delta z_2}{\delta w_2} = a_1 \space$ as $z_2 = a_1 \cdot w_2 + b_2 $
#
# 2. Compute the derivative of cost with respect to $ b_2 = \space \frac{\delta J}{\delta b_2} = \frac{\delta J}{\delta a_2} \cdot \frac{\delta a_2}{\delta z_2} \cdot \frac{\delta z_2}{\delta b_2} =\frac{\delta J}{\delta z_2} \cdot \frac{\delta z_2}{\delta b_2} = \frac{\delta J}{\delta z_2} \cdot 1 \space$, beacuse $\frac{\delta z_2}{\delta b_2} = 1 \space$ as $z_2 = a_1 \cdot w_2 + b_2 $
# 3. Compute the derivative of cost with respect to $ a_1 = \space \frac{\delta J}{\delta a_1} = \frac{\delta J}{\delta a_2} \cdot \frac{\delta a_2}{\delta z_2} \cdot \frac{\delta z_2}{\delta a_1} =\frac{\delta J}{\delta z_2} \cdot \frac{\delta z_2}{\delta a_1} = \frac{\delta J}{\delta z_2} \cdot w_2 \space$, beacuse $\frac{\delta z_2}{\delta b_2} = w_2 \space$ as $z_2 = a_1 \cdot w_2 + b_2 $
# 5. Compute the derivative of cost with respect to $z_1 =\space \frac{\delta J}{\delta z_1} =\frac{\delta J}{\delta a_2} \cdot \frac{\delta a_2}{\delta z_2} \cdot \frac{\delta z_2}{\delta a_1} \cdot \frac{\delta a_1}{\delta z_1} = \frac{\delta J}{\delta a_1} \cdot \frac{\delta a_1}{\delta z_1} = \frac{\delta J}{\delta a_1} \cdot (a_1 \cdot ( 1 - a_1 )), \space $because $\frac{\delta a_1}{\delta z_1} = a_1 \cdot ( 1 - a_1 )$ as $a_1 = \sigma(z_1)$
# 6. 1. Compute the derivative of cost with respect to $w_1 =\space \frac{\delta J}{\delta w_1} = \frac{\delta J}{\delta a_2} \cdot \frac{\delta a_2}{\delta z_2} \cdot \frac{\delta z_2}{\delta a_1} \cdot \frac{\delta a_1}{\delta z_1} \cdot \frac{\delta z_1}{\delta w_1} = \frac{\delta J}{\delta z_1} \cdot \frac{\delta z_1}{\delta w_1} = \frac{\delta J}{\delta z_1} \cdot a_0, \space $ beacuse $\frac{\delta z_1}{\delta w_1} = a_0, \space$ as $z_1 = a_0 \cdot w_1 + b_1$
# 2. Compute the derivative of cost with respect to $b_1 =\space \frac{\delta J}{\delta b_1} = \frac{\delta J}{\delta a_2} \cdot \frac{\delta a_2}{\delta z_2} \cdot \frac{\delta z_2}{\delta a_1} \cdot \frac{\delta a_1}{\delta z_1} \cdot \frac{\delta z_1}{\delta b_1} = \frac{\delta J}{\delta z_1} \cdot \frac{\delta z_1}{\delta b_1} = \frac{\delta J}{\delta z_1} \cdot 1, \space $ because $\frac{\delta z_1}{\delta b_1} = 1, \space$ as $z_1 = a_0 \cdot w_1 + b_1$
#
# We don't need to calculate our derivative with respect to a_0, as this is our input, which we are not going to change.
# Now, when we have our derivatives computed, or rather <b>gradients</b>, as this are operations on matrices.
# In code those operations may bit a lit differ, as we are operating on matrices and sometimes you need to transpose them or compute it in proper order, to make it right. (In matrices $A \times B \neq B \times A$) And we are going to compute the mean gradient over all training examples.
def backward_pass(x, w, b, y, cache):
'''
param x: input matrix of size NxM
param w: tuple of weights
param b: tuple of biases
param y: matrix of size NxO
param cache: tuple of values in layers a1,a2 from forward propagation
'''
w1, w2 = w # unpacking tuple to single matrixes
b1, b2 = b # unpacking tuple to single vectors
a1, a2 = cache
N = y.shape[0]
a0 = x
dJ_da2 = -2 *(y - a2)
dJ_dz2 = dJ_da2 * a2*(1-a2)
dJ_dw2 = 1/N * a1.T @ dJ_dz2
dJ_db2 = np.mean(dJ_dz2 * 1, axis=0)
dJ_da1 = dJ_dz2 @ w2.T
dJ_dz1 = dJ_da1 * a1 * (1-a1)
dJ_dw1 = 1/N * a0.T @ dJ_dz1
dJ_db1 = np.mean(dJ_dz1 * 1, axis=0)
cache = (dJ_dw1, dJ_dw2), (dJ_db1, dJ_db2)
return cache
# # Training
#
# <h3>Steps for training</h3>
# After backpropagation we can update weights and biases by substracting from them those gradients multiplied by hyperparamter called learning rate, which defines how fast our model is learning itself.
#
# $w_2 := w_2 - learning\_rate \cdot \frac{\delta J}{\delta w_2}$
#
# $b_2 := b_2 - learning\_rate \cdot \frac{\delta J}{\delta b_2}$
#
# $w_1 := w_1 - learning\_rate \cdot \frac{\delta J}{\delta w_1}$
#
# $b_1 := b_1 - learning\_rate \cdot \frac{\delta J}{\delta b_1}$
#
# 0 - Initialize weights and biases with random values
#
# For k times (where k is number of epochs)
#
# 1. Process forward pass to get values at layers
# 2. Process backward pass to get error at weighst and biases
# 3. Update weights and biases to be closer to Cost function minimum
#
def train(x, y, hidden_nodes_amount = 2, epochs = 10000, learning_rate = 1e-3):
'''
param x: input data of shape NxM
param y: output data of shape NxO
param hidden_nodes_amount: number of nodes in hidden layer
param epochs: nubmer of epochs
param learning_rate: rate of learning speed
return: funcion return weights, biases, costs
'''
inputs_amount = x.shape[1]
outputs_amount = y.shape[1]
N = x.shape[0]
costs=[]
w, b = initialize_random_weights(inputs_amount, hidden_nodes_amount, outputs_amount)
for epoch in tqdm_notebook(range(epochs)):
#cache is (a1,a2), values in layers
cache = forward_pass(x, w, b)
_, a2 = cache
(dw1, dw2), (db1, db2) = backward_pass(x, w, b, y, cache)
cost = np.mean((y-a2)**2/2)
costs.append(cost)
w1, w2 = w
b1, b2 = b
w1 -= dw1
w2 -= dw2
b1 -= db1
b2 -= db2
w = (w1, w2)
b = (b1, b2)
return w,b,costs
# # Prediction
# Prediction is a single feed forward part for each input, to generate classified output.
def predict(x, w, b):
'''
param x: input matrix NxM
param w: tuple of weights
param b: tuple of biases
param threshold_value: decision border
'''
w1, w2 = w
b1, b2 = b
_, result = forward_pass(x, w, b)
return result
w, b, _ = train(x=X, y=Y)
prediction = predict(X, w, b)
for i in range(prediction.shape[0]):
print('Input: {}, Real output: {}, Prediction: {}'.format(X[i], Y[i], prediction[i]))
# # More complicated classification task - MNIST Dataset
# Mnist is a popular database of handwritten images created for people who are new to machine learning. There are many courses on the internet that include classification problem using MNIST dataset.
#
# This dataset contains 55000 images and labels. Each image is 28x28 pixels large, but for the purpose of the classification task they are flattened to 784x1 arrays $(28 \cdot 28 = 784)$. Summing up our training set is a matrix of size $[55000, 784]$ = [amount of images, size of image]. Each label is size of $[10, 1]$, beacuse it is in 'one-hot' format. In this format we are using only 'zeros' and single 'one' to represent a number. For instance:
#
# $3_{10} = \begin{bmatrix}0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix}_{one\_hot}$
#
# $7_{10} = \begin{bmatrix}0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \end{bmatrix}_{one\_hot}$
#
# It is done to ease neural network learning.
#
# It also contains 5000 test images and labels, which are used for testing purpose. We are going to test results on diffrent set than training to avoid overfitting and get "true" accuracy on new inputs.
#
#
#
#
# <h3>Mnist Data Example</h3>
# <img src="Neural_net/mnist_example.jpg" height="70%" width="70%">
#
# Now we are going to download this dataset and split it into test and train sets.
#
#
# +
train_data, test = utils.get_mnist_dataset()
train_images, train_labels = train_data
test_images, test_labels = test
print("Training images matrix size: {}".format(train_images.shape))
print("Training labels matrix size: {}".format(train_labels.shape))
print("Testing images matrix size: {}".format(test_images.shape))
print("Testing labels matrix size: {}".format(test_labels.shape))
# -
# # Visualisation
# Visualisation isn't necessery to the problem, but it helps to understand what are we doing.
def show_few(images):
'''
param images: vecotr of images of size 28x28 to plot
'''
ax =[]
fig = plt.figure(figsize=(10, 10))
gs = GridSpec(2, 4, wspace=0.0, hspace=-0.5)
for i in range(2):
for j in range(4):
ax.append(fig.add_subplot(gs[i,j]))
for i, axis in enumerate(ax):
axis.imshow(images[i])
plt.show()
first_8_images = train_images[:8]
resized = np.reshape(first_8_images, (-1,28,28))
print('First 8 images of train data:')
show_few(resized)
# # Some intuition
#
# Without neural network you have to perform following steps:
# 1. Extract features from image
# 2. Choose and inplement the model
# 3. Choose and implement learning algorithm
# 4. (Learn model if necessary) and predict class for the new image with this model
#
# In neural network you can skip some of those, as network learns how to extract features by itslef in hidden layers. You need only to specify its size and hyperparameters (learning rate, regularization, etc.)
# <img src="Neural_net/neural_intuition.jpg" height="50%" width="50%">
#
# To provide some more intuition about how is neural network perforing binary classification and extracting features there is another example below:
# <img src="Neural_net/neural_intuition2.jpg" height="50%" width="50%">
#
#
#
#
# # Mutliclass classification
# In the previous problem we had only 2 classes - True or False in the last node. It was an example of binary classification. In MNIST task we have 10 classes, so in the ouptput layer we need 10 neurons.
# <img src="Neural_net/neural_one_hot.jpg" height="75%" width="75%">
#
# # Accuracy counting
# As our model is never returning 1 or 0, due to activation function sigmoid on output layer, we have to find maximum argument, to detect class predicted by network.
#
# <h3>Example</h3>
# $[0.2 ;\space 0.123; \space 0.5] \stackrel{arg\_max}{\implies} [0;\space 0;\space 1]$
#
def count_accuracy(prediction, y):
'''
param prediction: the output of neural network
param y: the true output values
'''
hits = np.argmax(prediction, axis=1) == np.argmax(y, axis = 1)
accuracy = np.mean(hits, axis = 0)
return accuracy
# +
w, b, costs = train(x=train_images, y=train_labels, hidden_nodes_amount = 100, epochs=600, learning_rate=5e-3)
prediction = predict(test_images, w, b)
accuracy = count_accuracy(prediction, test_labels)
print("Accuracy {:.3f} %".format(accuracy * 100))
plt.plot(costs)
plt.xlabel('Epoch number')
plt.ylabel('Cost value')
plt.title('Cost')
plt.grid()
plt.show()
# -
# # Conclusion
#
# Accuracy on mnist dataset should be about 90% which is quite poor. To get better results you are supposed to add another hidden layers, or even better - use diffrent types of neural networks like Convolutional Neural Networks.
#
# If you are intrested in machine learning topic we recommend:
#
# https://www.coursera.org/learn/machine-learning - great introduction to machine learning by Prof. <NAME>, unfortunately the course is written in matlab, but provides necessary software. If you don't want to work in matlab, you can still get theoretical background.
#
# https://www.coursera.org/specializations/deep-learning - a next step into deep learning with more details, prepared as well by Prof. Andrew Ng, written in python.
#
# https://www.youtube.com/channel/UCYO_jab_esuFRV4b17AJtAw - a great youtube channel where you can gain essential knowledge of math - linear algebra, calculus and other stuff - especially neural networks.
# # Sources:
# Following sources were used to create this notebook:
#
# http://mlg.ii.pwr.edu.pl/sz/#/courses - Wrocław University of Science and Technology, <NAME> Ph.D. - neural network intuintion first image
#
# https://think-data.github.io/machine%20learning/python/2016/12/03/simple-neural-network-using-tensorflow.html - mnist network visualisation with one-hot output layer
#
# https://www.youtube.com/watch?v=BR9h47Jtqyw - neural net intuintion second image (feature extraction)
#
# https://becominghuman.ai/neural-network-xor-application-and-fundamentals-6b1d539941ed - the XOR neural network image
#
# http://www.vlsiinterviewquestions.org/2012/04/17/xor-gate-using-21-mux/ - xor logical gate with table image
#
# https://db-blog.web.cern.ch/ - first example image
#
# http://web.stanford.edu/class/cs20si/syllabus.html - Stanford computer science course with presentation about deep learning
#
# https://www.coursera.org/learn/nlp-sequence-models/notebook/acNYU/emojify - one_hot function from utils
#
# https://www.kaggle.com/pablotab/mnistpklgz - mnist dataset
|
Neural_net.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # library
# +
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import keras
# keras: for data processing
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
from sklearn.model_selection import train_test_split
from keras.utils.np_utils import to_categorical
# keras: for Deep-learing
from keras.layers import *
from keras.models import *
from keras.activations import *
from keras.callbacks import EarlyStopping
# -
# # data processing
# data load
data = pd.read_csv('./data/uci_news_aggregator.csv', delimiter = ',', skiprows = 1,
names = ['ID', 'TITLE', 'URL', 'PUBLISHER', 'CATEGORY', 'STORY',
'HOSTNAME', 'TIMESTAMP'], usecols=['TITLE', 'CATEGORY'])
data.head(5)
np.array(data).shape
# +
# # remove punctuation and lowercase
# def normalize_text(s):
# s = s.lower()
# # remove punctuation that is not word-internal (e.g., hyphens, apostrophes)
# s = re.sub('\s\W',' ',s)
# s = re.sub('\W\s',' ',s)
# # make sure we didn't introduce any double spaces
# s = re.sub('\s+',' ',s)
# return s
# +
# news['TEXT'] = [normalize_text(s) for s in news['TITLE']]
# -
# # construct label
# +
# [1. 0. 0. 0.] e
# [0. 1. 0. 0.] b
# [0. 0. 1. 0.] t
# [0. 0. 0. 1.] m
# -
data.CATEGORY.value_counts()
# +
# data slicing
num_of_categories = 45000
shuffled = data.reindex(np.random.permutation(data.index))
e = shuffled[shuffled['CATEGORY'] == 'e'][:num_of_categories]
b = shuffled[shuffled['CATEGORY'] == 'b'][:num_of_categories]
t = shuffled[shuffled['CATEGORY'] == 't'][:num_of_categories]
m = shuffled[shuffled['CATEGORY'] == 'm'][:num_of_categories]
concated = pd.concat([e,b,t,m], ignore_index=True)
# -
np.array(concated).shape
# label col
concated['LABEL'] = 0
concated.head(5)
np.array(concated).shape
# +
concated = concated.reindex(np.random.permutation(concated.index))
concated.loc[concated['CATEGORY'] == 'e', 'LABEL'] = 0
concated.loc[concated['CATEGORY'] == 'b', 'LABEL'] = 1
concated.loc[concated['CATEGORY'] == 't', 'LABEL'] = 2
concated.loc[concated['CATEGORY'] == 'm', 'LABEL'] = 3
# -
concated['LABEL'][:10]
# one-hot encoding
labels = to_categorical(concated['LABEL'], num_classes=4)
labels[:10]
# # construct train & test dataset
n_most_common_words = 8000
max_len = 130
tokenizer = Tokenizer(num_words=n_most_common_words, filters='!"#$%&()*+,-./:;<=>?@[\]^_`{|}~', lower=True)
concated['TITLE'].values
tokenizer.fit_on_texts(concated['TITLE'].values)
sequences = tokenizer.texts_to_sequences(concated['TITLE'].values)
sequences[:10]
word_index = tokenizer.word_index
word_index
X = pad_sequences(sequences, maxlen=max_len)
print(X.shape)
print(labels.shape)
X_train, X_test, y_train, y_test = train_test_split(X , labels, test_size=0.2, random_state=42)
# +
# X_train = np.expand_dims(X_train, -1)
# X_test = np.expand_dims(X_test, -1)
# y_train = np.expand_dims(X_train, -1)
# y_test = np.expand_dims(X_test, -1)
# -
print((X_train.shape, y_train.shape, X_test.shape, y_test.shape))
# # model
# model param
emb_dim = 128
def get_model():
inp = Input(shape=(max_len,))
emb = Embedding(n_most_common_words, emb_dim, input_length=max_len)(inp)
_ = SpatialDropout1D(0.7)(emb)
# _ = LSTM(64, dropout=0.7, recurrent_dropout=0.7)(_)
_ = Bidirectional(LSTM(64, dropout=0.6, recurrent_dropout=0.6))(_)
_ = Dense(64, activation="relu")(_)
_ = Dropout(0.25)(_)
out = Dense(4, activation='softmax')(_)
return Model(inputs=inp, outputs=out)
model = get_model()
model.summary()
# # train
# train param
epochs = 15
batch_size = 512
learning_rate = 0.001
decay = 1e-06
model.compile(optimizer = optimizers.adam(lr = learning_rate, decay = decay), loss='categorical_crossentropy', metrics=['acc'])
history = model.fit(X_train, y_train, epochs=epochs, batch_size=batch_size,validation_split=0.2,callbacks=[EarlyStopping(monitor='val_loss',patience=7, min_delta=0.0001)])
model.save('model.h5')
# # test
# +
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(acc) + 1)
# +
# visualization
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
# +
# test
labels = ['entertainment', 'bussiness', 'science/tech', 'health']
txt_list = [["Regular fast food eating linked to fertility issues in women"], ["Chinese ethnic group biggest earners in the UK"],
["Dozens of arrests in Copenhagen for drunk scooter driving"]]
for txt in txt_list:
print(txt)
sequence = tokenizer.texts_to_sequences(txt)
padded = pad_sequences(sequence, maxlen=max_len)
pred = model.predict(padded)
print(pred, labels[np.argmax(pred)])
# -
|
News_classifier_bidirectional_LSTM.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Test Case 5 Calculating interaction of randomly generated sphecial gaussian charge distribution with varying r_ext in 3D space
import numpy as np
from fast_multipole_method import operation as op
from scipy.special import erf
from scipy.special import erfc
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# %matplotlib inline
plt.style.use('ggplot')
def plot_3d(x):
"""plot particles in 3 dimentional"""
y = np.transpose(x)
fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(y[0], y[1], y[2])
ax = ax.view_init(30)
plt.show()
return
#case 4.1 construction: random sphecial distributions, similar extend to make WS<=2
num_distribution = 100
x_i = np.ndarray(shape=(3, num_distribution))
x_i[0] = 20 * np.random.rand(num_distribution) - 10
x_i[1] = 20 * np.random.rand(num_distribution) - 10
x_i[2] = 20 * np.random.rand(num_distribution) - 10
x_i = np.transpose(x_i)
K_i = np.ones(num_distribution)
a_i = 10 * np.random.rand(num_distribution)
# +
#case 4.2 constuction: uniform distributed sphecial distributions, same WS index
num_distribution_in_a_box = 1
num_distribution_1D = 3
num_distribution = num_distribution_in_a_box * num_distribution_1D **3
x_i = np.zeros(shape=(num_distribution,3))
for i in range(0,num_distribution_1D):
for j in range(0,num_distribution_1D):
for k in range(0,num_distribution_1D):
x_i[i*num_distribution_1D*num_distribution_1D+j*num_distribution_1D+k] = [i,j,k]
K_i = np.ones(num_distribution)
a_i = 10 * np.random.rand(num_distribution)
# -
[x0_i, scale_factor] = op.cartesian_scaling_to_unit_range(x_i)
plot_3d(x0_i)
a_i
WS_max = 2 * (erfc(1-1e-16) * 8) * np.sqrt(2/min(a_i))
WS_max
# +
# analytical answer
pair_potential = np.zeros(shape=(num_distribution,num_distribution))
pre_factor = np.power(np.pi, 3)
for i in range(0, num_distribution):
for j in range(i+1, num_distribution):
pre_factor2 = K_i[i] * K_i[j] / ( np.power(a_i[i]*a_i[j], 1.5) * op.distance_cal(x0_i[i], x0_i[j]))
t_sqrt = np.sqrt(a_i[i]*a_i[j]/(a_i[i]+a_i[j])) * op.distance_cal(x0_i[i], x0_i[j]) * scale_factor[1]
pair_potential[i][j] = pre_factor * pre_factor2 * erf(t_sqrt)
pair_potential /= scale_factor[1]
pair_potential
# +
J_analytic = np.zeros(num_distribution)
for i in range(0, num_distribution):
for j in range(0, num_distribution):
if j<i:
J_analytic[i] += pair_potential[j][i]
if j>i:
J_analytic[i] += pair_potential[i][j]
J_analytic
# -
total_energy = 0.5 * sum(J_analytic)
total_energy
from continuous_fast_multipole_method import cfmm
from fast_multipole_method import fmm
from fast_multipole_method import fmm_q_gaussain_distribution as fq
# build list of q_source
q_source = np.ndarray(shape=(len(x0_i)), dtype=fq)
for i in range(0, len(x0_i)):
q_source[i] = fq(x0_i[i], a_i[i], K_i[i])
btm_level = 3
p = 10
ws_ref = 3
[J_far_field, J_near_field] = cfmm(q_source, btm_level, p, scale_factor[1], ws_ref)
J_far_field
a_i
J_near_field
J_total = J_far_field + J_near_field
J_total
total_energy = 0.5 * sum(J_total)
total_energy
J_error = np.abs(J_total-J_analytic) / J_analytic
J_error
a_i[6]
btm_level = 3
p = 20
ws_ref = 3
[J_far_field, J_near_field] = fmm(q_source, btm_level, p, scale_factor[1], ws_ref)
J_total = J_far_field + J_near_field
J_error = np.abs(J_total-J_analytic) / J_analytic
J_error
J_far_field
J_near_field
|
.ipynb_checkpoints/test _case_5-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="7QUQgep6nsyW"
#
# Problem Statement and Objective: A hospital readmission is when a patient who is discharged from the hospital, gets re-admitted again within a certain period of time. Hospital readmission rates for certain conditions are now considered an indicator of hospital quality, and also affect the cost of care adversely. For this reason, Centers for Medicare & Medicaid Services established the Hospital Readmissions Reduction Program which aims to improve quality of care for patients and reduce health care spending by applying payment penalties to hospitals that have more than expected readmission rates for certain conditions. Although diabetes is not yet included in the penalty measures, the program is regularly adding new disease conditions to the list, now totaling 6 for FY2018. In 2011, American hospitals spent over $41 billion on diabetic patients who got readmitted within 30 days of discharge. Being able to determine factors that lead to higher readmission in such patients, and correspondingly being able to predict which patients will get readmitted can help hospitals save millions of dollars while improving quality of care. So, with that background in mind, we used a medical claims dataset (description below), to answer these questions:
#
# What factors are the strongest predictors of hospital readmission in diabetic patients?
# How well can we predict hospital readmission in this dataset with limited features?
#
# + [markdown] id="Fb7xXOvLtzAS"
# **Data Set Description**
#
# VARIABLE NAMES: DESCRIPTION
#
# **Encounter ID**: Unique identifier of an encounter
#
# **Patient number**: Unique identifier of a patient
#
# **Race Values**: Caucasian, Asian, African American, Hispanic, and other
#
# **Gender Values**: male, female, and unknown/invalid
#
# **Age**: Grouped in 10-year intervals: 0, 10), 10, 20), …, 90, 100)
#
# **Weight**: Weight in pounds
#
# **Admission type**: Integer identifier corresponding to 9 distinct values, for example, emergency, urgent, elective, newborn, and not available
#
# **Discharge disposition**: Integer identifier corresponding to 29 distinct values, for example, discharged to home, expired, and not available
#
# **Admission source**: Integer identifier corresponding to 21 distinct values, for example, physician referral, emergency room, and transfer from a hospital
#
# **Time in hospital**: Integer number of days between admission and discharge
#
# **Payer code**: Integer identifier corresponding to 23 distinct values, for example, Blue Cross/Blue Shield, Medicare, and self-pay Medical
#
# **Medical specialty**: Integer identifier of a specialty of the admitting physician, corresponding to 84 distinct values, for example, cardiology, internal medicine, family/general practice, and surgeon
#
# **Number of lab procedures**: Number of lab tests performed during the encounter
#
# **Number of procedures**: Numeric Number of procedures (other than lab tests) performed during the encounter
#
# **Number of medications**: Number of distinct generic names administered during the encounter
#
# **Number of outpatient visits**: Number of outpatient visits of the patient in the year preceding the encounter
#
#
# **Number of emergency**: visits Number of emergency visits of the patient in the year preceding the encounter
#
#
# **Number of inpatient visits**: Number of inpatient visits of the patient in the year preceding the encounter
#
#
# **Diagnosis 1**: The primary diagnosis (coded as first three digits of ICD9); 848 distinct values
#
#
# **Diagnosis 2**: Secondary diagnosis (coded as first three digits of ICD9); 923 distinct values
#
#
# **Diagnosis 3**: Additional secondary diagnosis (coded as first three digits of ICD9); 954 distinct values
#
#
# **Number of diagnoses**: entered to the system 0%
#
#
# **Glucose serum test result**: Indicates the range of the result or if the test was not taken. Values: “>200,” “>300,” “normal,” and “none” if not measured
#
#
# **A1c test result**: Indicates the range of the result or if the test was not taken. Values: “>8” if the result was greater than 8%, “>7” if the result was greater than 7% but less than 8%, “normal” if the result was less than 7%, and “none” if not measured.
#
#
# **Change of medications**: Indicates if there was a change in diabetic medications (either dosage or generic name). Values: “change” and “no change”
#
#
# **Diabetes medications**: Indicates if there was any diabetic medication prescribed. Values: “yes” and “no”
#
#
# 24 features for medications For the generic names: **metformin, repaglinide, nateglinide, chlorpropamide, glimepiride, acetohexamide, glipizide, glyburide, tolbutamide, pioglitazone, rosiglitazone, acarbose, miglitol, troglitazone, tolazamide, examide, sitagliptin, insulin, glyburide-metformin, glipizide-metformin, glimepiride- pioglitazone, metformin-rosiglitazone, and metformin- pioglitazone**, the feature indicates whether the drug was prescribed or there was a change in the dosage. Values: “up” if the dosage was increased during the encounter, “down” if the dosage was decreased, “steady” if the dosage did not change, and “no” if the drug was not prescribed
#
#
# **Readmitted**: Days to inpatient readmission. Values: “<30” if the patient was readmitted in less than 30 days, “>30” if the patient was readmitted in more than 30 days, and “No” for no record of readmission
# + [markdown] id="4D7ySLZOykJJ"
# ### Data preparation and Exploration
# + id="cRFK3rk4GmSo"
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import re
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler,LabelEncoder, OrdinalEncoder
from sklearn.model_selection import train_test_split, GridSearchCV, cross_val_score
from sklearn.metrics import (confusion_matrix, accuracy_score,f1_score,recall_score,mean_squared_error, r2_score,
roc_auc_score, roc_curve, classification_report,precision_recall_fscore_support)
from sklearn.metrics import roc_auc_score, accuracy_score, precision_score, recall_score,f1_score
from sklearn.metrics import confusion_matrix as cm
from sklearn.linear_model import LogisticRegression
from sklearn.linear_model import SGDClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.neural_network import MLPClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import GradientBoostingClassifier
from xgboost import XGBClassifier
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
# + colab={"base_uri": "https://localhost:8080/"} id="sO05tsdSHdGp" outputId="a8a8e4d5-c2d4-44f6-f7b9-3c0ab64e54a8"
from google.colab import drive
drive.mount('/content/drive')
# + id="rKVGvXemI64T"
data = pd.read_csv('/content/drive/My Drive/diabetic_data.csv')
# + id="rDkhnAxEWfuW" colab={"base_uri": "https://localhost:8080/", "height": 308} outputId="14bc3aec-b8d2-4ed4-e792-6e6f178f5c71"
data.head()
# + colab={"base_uri": "https://localhost:8080/"} id="jjV1s5WLUgpk" outputId="de8ba572-3b56-45fb-a46c-bf8995535649"
data.shape
# + id="uBDlCN7xXqNU"
data.readmitted = [1 if each=='<30' else 0 for each in data.readmitted]
# + id="EUWj6EwAXyeI"
def cat(data, column, labels=[]):
fig, ax=plt.subplots(nrows=1,ncols=2, figsize=(12,5))
sns.countplot(x=data[column], data=data, ax=ax[0])
data[column].value_counts().plot.pie(labels=labels,autopct="%1.2f%%",explode = (0, 0.05))
plt.show()
# + id="9_YoS3YYX-Ak" colab={"base_uri": "https://localhost:8080/", "height": 333} outputId="45f65f42-895d-4a5a-cd14-1f2e01d37f4e"
cat(data,'readmitted',labels=['0','1'])
# + id="-EHj6GEjX6ku"
data.replace('?', np.nan , inplace=True)
# + id="sqIhinKA85Qu"
data.replace('Unknown/Ivalid', np.nan, inplace=True)
# + [markdown] id="ynUNzlCB1dmd"
# ### Dealing with Missing Values
# + [markdown] id="k_5uxCbI-ujM"
# Weight” is missing in over 98% records. “Payer code” and “Medical specialty” also have 40-50% missing values. The best thing is to drop them because the poor interpretability and little predictive generalizability to ptients. Two medications named “Citoglipton” and “Examide” were deleted because all records have the same value.
# + id="7lf_4kQg9zla"
drop_l = ['examide' , 'citoglipton', 'weight','encounter_id','patient_nbr','payer_code','medical_specialty']
data.drop(drop_l,axis=1, inplace=True)
# + colab={"base_uri": "https://localhost:8080/"} id="2s_vcuIK_iBU" outputId="b0932563-c3b4-4f02-b284-2d7499a84f3e"
data.shape
# + id="6qmQ4bVk_18t"
data.dropna(subset=['gender'], how='all', inplace = True)
# + id="kSCdkAkT1yR5"
data["race"].fillna(data["race"].mode()[0], inplace = True)
# + colab={"base_uri": "https://localhost:8080/", "height": 297} id="weMuq1V9ApDq" outputId="f2673333-ff14-4140-877a-6481cbcb93de"
data.describe()
# + [markdown] id="Q4mUrkim14cM"
# ## Feature Engineering
#
# + [markdown] id="AvbDUdZp4wh-"
# Based on some common sense: Since the objective is to predict readmissions, those patients who died during this hospital admission were excluded. Encounters with “Discharge disposition” values of 11, 13, 14, 19, 20, or 21 are related to death or hospice which mean these patients cannot be readmitted.
#
# + colab={"base_uri": "https://localhost:8080/"} id="w37W7fnZCDhV" outputId="79dbf716-5328-455e-bfc6-07b3c93da155"
data['discharge_disposition_id'].nunique()
# + colab={"base_uri": "https://localhost:8080/"} id="XaVLRcZtEXGO" outputId="881642ff-fb92-4d0a-9d81-8074b892cd50"
data.discharge_disposition_id.unique()
# + id="t3wtTOPVEtHT"
data = data.loc[~data.discharge_disposition_id.isin([11,13,14,19,20,21])]
# + colab={"base_uri": "https://localhost:8080/"} id="jxAiqLd8HeUP" outputId="f265380b-4ff3-4f90-9795-9b7b2df8c280"
~data.discharge_disposition_id.isin([11,13,14,19,20,21])
# + id="XTozeldmIJtP"
data=data.loc[~data.discharge_disposition_id.isin([11,13,14,19,20,21])]
# + colab={"base_uri": "https://localhost:8080/"} id="OsTTSffzI0N9" outputId="5a50b2ab-4b98-454a-de6c-aee3ad8b91af"
data.shape
# + [markdown] id="NaFlIIfj47Xm"
# Admission type has 9 values, including emergency, urgent, elective, newborn, and not available..
# + id="ZtZDaBZHJKBx"
data.admission_type_id.replace([2,7,6,8],[1,1,5,5], inplace=True)
# + id="z11yObs5K-6a"
data.admission_type_id.replace([1,5,3,4],["Emergency","Other","Elective","Newborn"], inplace=True)
# + [markdown] id="eyql3nOE4_nZ"
# Admission source has 21 values, including physician referral, emergency room, and transfer from a hospital.....
# + id="IPRd2m4DNjb3"
data.admission_source_id.replace([1,2,3], 'Physician Referral', inplace=True)
# + id="KyVercpsPgms"
data.admission_source_id.replace([4,5,6,8,9,10,11,12,13,14,15,17,18,19,20,21,22,23,24,25,26],
'Other', inplace=True)
# + colab={"base_uri": "https://localhost:8080/"} id="h_si020eROhs" outputId="95c482b9-ed82-4bdc-bbf0-25aed457cdc8"
data.admission_source_id.unique()
# + id="3Sz7u2BbP98g"
data.admission_source_id.replace(7, 'Emergency Room', inplace=True)
# + [markdown] id="fPUClqza5fzA"
# Discharge disposition has 29 values, for example, discharged to home, expired, and not available......
# + colab={"base_uri": "https://localhost:8080/"} id="OBTYS5nVQ0fT" outputId="cfe6105f-92f2-48c2-8184-cbe0aaff3d78"
data.discharge_disposition_id.unique()
# + id="wHsTVLwESx1S"
data.discharge_disposition_id.replace([25, 3, 6, 2, 5, 7, 10, 4, 18, 8, 12, 16, 17, 22, 23, 9,
15, 24, 28, 27],'other', inplace=True)
# + id="9GVfU8okTG2f"
data.discharge_disposition_id.replace(1,'Home', inplace=True)
# + [markdown] id="l5272tsI5qw4"
# The 'diag_1',diag_2,diag_3 contained three diagnoses for a given patient (primary, secondary and additional). However, each of these had 700-900 unique ICD codes and it is extremely difficult to include them in the model and interpret them meaningfully. Therefore, these diagnosis codes were collapsed into 9 disease categories, which include Circulatory, Respiratory, Digestive, Diabetes, Injury, Musculoskeletal, Genitourinary, Neoplasms, and Others
# + id="dpzw0r-fTqHK"
import re
import numpy as np
def transformFunc(value):
value = re.sub("V[0-9]*", "0", value) # V
value = re.sub("E[0-9]*", "0", value) # E
value = re.sub('NaN', "-1", value) # Nan
return value
# + id="4F1OoFaFHqLg"
diag_list = ['diag_1','diag_2','diag_3']
# + id="Nv71uWsiVacF"
for col in diag_list:
data[col] = data[col].astype(str)
data[col] = data[col].apply(transformFunc)
data[col] = data[col].astype(float)
# + id="7AB9M1AFXXGB"
def transformCategory(value):
if value>=390 and value<=459 or value==785:
category = 'Circulatory'
elif value>=460 and value<=519 or value==786:
category = 'Respiratory'
elif value>=520 and value<=579 or value==787:
category = 'Digestive'
elif value==250:
category = 'Diabetes'
elif value>=800 and value<=999:
category = 'Injury'
elif value>=710 and value<=739:
category = 'Musculoskeletal'
elif value>=580 and value<=629 or value==788:
category = 'Genitourinary'
elif value>=140 and value<=239 :
category = 'Neoplasms'
elif value==-1:
category = 'NAN'
else :
category = 'Other'
return category
for col in diag_list:
data[col] = data[col].apply(transformCategory)
# + id="xz82_Pi0XaB8"
keys = ['metformin', 'repaglinide', 'nateglinide', 'chlorpropamide', 'glimepiride', 'glipizide', 'glyburide', 'pioglitazone',
'rosiglitazone', 'acarbose', 'miglitol', 'insulin', 'glyburide-metformin', 'tolazamide', 'metformin-pioglitazone',
'metformin-rosiglitazone', 'glimepiride-pioglitazone', 'glipizide-metformin', 'troglitazone', 'tolbutamide', 'acetohexamide']
for col in keys:
data[col] = data[col].replace(['No','Steady','Up','Down'],[0,1,1,1])
data[col] = data[col].astype(int)
# + id="3_wTpRnYaDz4"
# A1Cresult and max_glu_serum
data['A1Cresult'] = data['A1Cresult'].replace(['>7','>8','Norm','None'],[1,1,0,-99])
data['max_glu_serum'] = data['max_glu_serum'].replace(['>200','>300','Norm','None'],[1,1,0,-99])
# + colab={"base_uri": "https://localhost:8080/"} id="-RZBLZlhaIW-" outputId="5a478f87-6735-4a78-c303-a5789876c209"
data.isnull().sum()
# + [markdown] id="ElNFnRVf7ihN"
# ##Encoding of data
# + id="rA6_vU6TIdaG"
data = pd.get_dummies(data, columns=['race'], prefix=["enc"])
# + id="uQYX4YCqJIQu"
ordinal_enc = OrdinalEncoder()
data.age = ordinal_enc.fit_transform(data.age.values.reshape(-1, 1))
# + id="BIBDXnBSKAnu"
for col in diag_list:
label_enc = LabelEncoder()
data[col] = label_enc.fit_transform(data[col])
# + colab={"base_uri": "https://localhost:8080/"} id="MB6yMH78Kkt1" outputId="eecc5fca-89e9-4d4c-b4f1-ea9241035719"
# !pip install Category_encoders
# + colab={"base_uri": "https://localhost:8080/"} id="_KQ9qDL6KX9H" outputId="43c50b82-1e9c-4cd0-ef3e-eca6d4b68ba8"
binary = ['change', 'diabetesMed', 'gender']
from category_encoders import BinaryEncoder
binary_enc = BinaryEncoder(cols=binary)
data = binary_enc.fit_transform(data)
# + id="srBpZdaCK4pA"
data = pd.get_dummies(data, columns=['admission_type_id', 'discharge_disposition_id', 'admission_source_id'])
# + [markdown] id="rwBtWRHy7ufW"
# ## Train-test splitting
# + id="2kARqEpXLM6B"
df = data.copy()
X = df.drop(columns="readmitted", axis=1)
Y = df.readmitted
# + id="Z-S64HemLaiG"
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.20, random_state = 42)
# + [markdown] id="cY1MHoMs70_5"
# ## resampling
# the data is not balanced
# + colab={"base_uri": "https://localhost:8080/"} id="tdJp8m9Talf9" outputId="61a60fb3-7f8c-49d4-f767-b12ff47c3b28"
from sklearn.utils import resample
X = pd.concat([X_train, y_train], axis=1)
not_readmitted = X[X.readmitted==0]
readmitted = X[X.readmitted==1]
not_readmitted_sampled = resample(not_readmitted,
replace = False,
n_samples = len(readmitted),
random_state = 42)
downsampled = pd.concat([not_readmitted_sampled, readmitted])
downsampled.readmitted.value_counts()
# + id="ywJlwtpAa7eh"
y_train = downsampled.readmitted
X_train = downsampled.drop('readmitted', axis=1)
# + [markdown] id="iVYFeQ218DX8"
# ##train val splitting
# + id="OQUBcyljLplA"
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train, test_size = 0.30, random_state = 42)
# + [markdown] id="nVB6ODCg8hA5"
# ## Base model
# + [markdown] id="5TKh_un69sMD"
# ### Logistic regression
# + id="4-bnEM8pLv4W"
log_model = LogisticRegression(solver = "liblinear",class_weight="balanced",random_state = 42).fit(X_train, y_train)
# + colab={"base_uri": "https://localhost:8080/"} id="CP9A8Dg7QL3x" outputId="30d9ad28-9c2a-452e-9561-18a62aa9590b"
y_train_preds = log_model.predict_proba(X_train)[:,1]
y_val_preds = log_model.predict_proba(X_val)[:,1]
print("Logistic Regression")
print('Training:')
lr_train_auc = roc_auc_score(y_train, y_train_preds)
lr_train_accuracy = accuracy_score(y_train, (y_train_preds>0.5))
lr_train_recall = recall_score(y_train, (y_train_preds>0.5))
lr_train_precision = precision_score(y_train, (y_train_preds>0.5))
lr_train_fscore = f1_score(y_train, (y_train_preds>0.5))
print('AUC: ', lr_train_auc)
print('accuracy: ', lr_train_accuracy)
print('recall: ',lr_train_recall)
print('precision: ',lr_train_precision)
print('fscore: ',lr_train_fscore)
print('Validation:')
lr_val_auc = roc_auc_score(y_val, y_val_preds)
lr_val_accuracy = accuracy_score(y_val, (y_val_preds>0.5))
lr_val_recall = recall_score(y_val, (y_val_preds>0.5))
lr_val_precision = precision_score(y_val, (y_val_preds>0.5))
lr_val_fscore = f1_score(y_val, (y_val_preds>0.5))
print('AUC: ', lr_val_auc)
print('accuracy: ', lr_val_accuracy)
print('recall: ', lr_val_precision)
print('fscore: ', lr_val_fscore)
# + colab={"base_uri": "https://localhost:8080/", "height": 352} id="Sq2mNOcmUUE-" outputId="ecef66de-4fb7-4ce7-d0d5-d265b4b4eaee"
# Confusion Matrix
predictions = log_model.predict(X_train)
train_score = round(accuracy_score(y_train, predictions), 3)
cm_train = cm(y_train, predictions)
predictions = log_model.predict(X_val)
val_score = round(accuracy_score(y_val, predictions), 3)
cm_val = cm(y_val, predictions)
fig, (ax1,ax2) = plt.subplots(nrows=1,ncols=2,figsize=(15,5))
sns.heatmap(cm_train, annot=True, fmt=".0f",ax=ax1)
ax1.set_xlabel('Predicted Values')
ax1.set_ylabel('Actual Values')
ax1.set_title('Train Accuracy Score: {0}'.format(train_score), size = 15)
sns.heatmap(cm_val, annot=True, fmt=".0f",ax=ax2)
ax2.set_xlabel('Predicted Values')
ax2.set_ylabel('Actual Values')
ax2.set_title('Validation Accuracy Score: {0}'.format(val_score), size = 15)
plt.show()
# + [markdown] id="bNmgSVel-UNr"
# ### Random Forest
# + colab={"base_uri": "https://localhost:8080/"} id="RdQ7ZDZ0Uxbb" outputId="935b1191-1925-41b6-b270-36478a4b84db"
random_forest_model = RandomForestClassifier(random_state=42, n_jobs=-1, n_estimators=100, max_depth=3)
random_forest_model.fit(X_train, y_train)
# + colab={"base_uri": "https://localhost:8080/"} id="HVK7ZFnmUxhf" outputId="0f800992-7e32-4fe5-e7bc-65706b48adf3"
y_train_preds = random_forest_model.predict_proba(X_train)[:,1]
y_val_preds = random_forest_model.predict_proba(X_val)[:,1]
print("Random Forest")
print('Training:')
rf_train_auc = roc_auc_score(y_train, y_train_preds)
rf_train_accuracy = accuracy_score(y_train, (y_train_preds>0.5))
rf_train_recall = recall_score(y_train, (y_train_preds>0.5))
rf_train_precision = precision_score(y_train, (y_train_preds>0.5))
rf_train_fscore = f1_score(y_train, (y_train_preds>0.5))
print('AUC: ', rf_train_auc)
print('accuracy: ', rf_train_accuracy)
print('recall: ',rf_train_recall)
print('precision: ',rf_train_precision)
print('fscore: ',rf_train_fscore)
print('Validation:')
rf_val_auc = roc_auc_score(y_val, y_val_preds)
rf_val_accuracy = accuracy_score(y_val, (y_val_preds>0.5))
rf_val_recall = recall_score(y_val, (y_val_preds>0.5))
rf_val_precision = precision_score(y_val, (y_val_preds>0.5))
rf_val_fscore = f1_score(y_val, (y_val_preds>0.5))
print('AUC: ', rf_val_auc)
print('accuracy: ', rf_val_accuracy)
print('recall: ', rf_val_precision)
print('fscore: ', rf_val_fscore)
# + colab={"base_uri": "https://localhost:8080/", "height": 352} id="S6r5z7IbUxnu" outputId="200e5a32-3a06-4d57-d180-45b9592992f0"
predictions = random_forest_model.predict(X_train)
train_score = round(accuracy_score(y_train, predictions), 3)
cm_train = cm(y_train, predictions)
predictions = random_forest_model.predict(X_val)
val_score = round(accuracy_score(y_val, predictions), 3)
cm_val = cm(y_val, predictions)
fig, (ax1,ax2) = plt.subplots(nrows=1,ncols=2,figsize=(15,5))
sns.heatmap(cm_train, annot=True, fmt=".0f",ax=ax1)
ax1.set_xlabel('Predicted Values')
ax1.set_ylabel('Actual Values')
ax1.set_title('Train Accuracy Score: {0}'.format(train_score), size = 15)
sns.heatmap(cm_val, annot=True, fmt=".0f",ax=ax2)
ax2.set_xlabel('Predicted Values')
ax2.set_ylabel('Actual Values')
ax2.set_title('Validation Accuracy Score: {0}'.format(val_score), size = 15)
plt.show()
# + [markdown] id="j1VT0JPe-epD"
# ### xgb
# + colab={"base_uri": "https://localhost:8080/"} id="LF-Vpf_LUxrx" outputId="5880ced9-16dd-4d41-a389-499ee69368bb"
xgb_model = XGBClassifier(random_state=42, n_jobs=-1,max_depth=3)
xgb_model.fit(X_train, y_train)
# + colab={"base_uri": "https://localhost:8080/"} id="F7m0YhksUxxX" outputId="d6053bec-e6df-48c6-eb2f-f1534767b2e4"
print("XGBOOST")
y_train_preds = xgb_model.predict_proba(X_train)[:,1]
y_val_preds = xgb_model.predict_proba(X_val)[:,1]
print('Training:')
xgb_train_auc = roc_auc_score(y_train, y_train_preds)
xgb_train_accuracy = accuracy_score(y_train, (y_train_preds>0.5))
xgb_train_recall = recall_score(y_train, (y_train_preds>0.5))
xgb_train_precision = precision_score(y_train, (y_train_preds>0.5))
xgb_train_fscore = f1_score(y_train, (y_train_preds>0.5))
print('AUC: ', xgb_train_auc)
print('accuracy: ', xgb_train_accuracy)
print('recall: ',xgb_train_recall)
print('precision: ',xgb_train_precision)
print('fscore: ',xgb_train_fscore)
print('Validation:')
xgb_val_auc = roc_auc_score(y_val, y_val_preds)
xgb_val_accuracy = accuracy_score(y_val, (y_val_preds>0.5))
xgb_val_recall = recall_score(y_val, (y_val_preds>0.5))
xgb_val_precision = precision_score(y_val, (y_val_preds>0.5))
xgb_val_fscore = f1_score(y_val, (y_val_preds>0.5))
print('AUC: ', xgb_val_auc)
print('accuracy: ', xgb_val_accuracy)
print('recall: ', xgb_val_precision)
print('fscore: ', xgb_val_fscore)
# + colab={"base_uri": "https://localhost:8080/", "height": 352} id="ND2nFTFfUx02" outputId="fa7b00af-680e-41cb-e2b1-84fcc3dae38f"
# Confusion Matrix
predictions = xgb_model.predict(X_train)
train_score = round(accuracy_score(y_train, predictions), 3)
cm_train = cm(y_train, predictions)
predictions = xgb_model.predict(X_val)
val_score = round(accuracy_score(y_val, predictions), 3)
cm_val = cm(y_val, predictions)
fig, (ax1,ax2) = plt.subplots(nrows=1,ncols=2,figsize=(15,5))
sns.heatmap(cm_train, annot=True, fmt=".0f",ax=ax1)
ax1.set_xlabel('Predicted Values')
ax1.set_ylabel('Actual Values')
ax1.set_title('Train Accuracy Score: {0}'.format(train_score), size = 15)
sns.heatmap(cm_val, annot=True, fmt=".0f",ax=ax2)
ax2.set_xlabel('Predicted Values')
ax2.set_ylabel('Actual Values')
ax2.set_title('Validation Accuracy Score: {0}'.format(val_score), size = 15)
plt.show()
# + [markdown] id="QanZIpd--454"
# ### lightgbm
# + colab={"base_uri": "https://localhost:8080/"} id="0OEtBk-AUx3Z" outputId="cfa05b15-e6ce-43e1-d7e8-3af23fa0cfa3"
from lightgbm import LGBMClassifier
lgbm_model = LGBMClassifier(random_state = 42,max_depth=3)
lgbm_model.fit(X_train, y_train)
# + colab={"base_uri": "https://localhost:8080/"} id="SyemeEj5Ux55" outputId="134be672-c688-4dc3-8183-88a49d36f961"
y_train_preds = lgbm_model.predict_proba(X_train)[:,1]
y_val_preds = lgbm_model.predict_proba(X_val)[:,1]
print("LGBM")
print('Training:')
lgbm_train_auc = roc_auc_score(y_train, y_train_preds)
lgbm_train_accuracy = accuracy_score(y_train, (y_train_preds>0.5))
lgbm_train_recall = recall_score(y_train, (y_train_preds>0.5))
lgbm_train_precision = precision_score(y_train, (y_train_preds>0.5))
lgbm_train_fscore = f1_score(y_train, (y_train_preds>0.5))
print('AUC: ', lgbm_train_auc)
print('accuracy: ', lgbm_train_accuracy)
print('recall: ',lgbm_train_recall)
print('precision: ',lgbm_train_precision)
print('fscore: ',lgbm_train_fscore)
print('Validation:')
lgbm_val_auc = roc_auc_score(y_val, y_val_preds)
lgbm_val_accuracy = accuracy_score(y_val, (y_val_preds>0.5))
lgbm_val_recall = recall_score(y_val, (y_val_preds>0.5))
lgbm_val_precision = precision_score(y_val, (y_val_preds>0.5))
lgbm_val_fscore = f1_score(y_val, (y_val_preds>0.5))
print('AUC: ', lgbm_val_auc)
print('accuracy: ', lgbm_val_accuracy)
print('recall: ', lgbm_val_precision)
print('fscore: ', lgbm_val_fscore)
# + colab={"base_uri": "https://localhost:8080/", "height": 369} id="NZ4YAP90Ux9B" outputId="fe57b7e5-19f1-4ff9-a9c1-4f149f49ccd3"
# Confusion Matrix
predictions = lgbm_model.predict(X_train)
train_score = round(accuracy_score(y_train, predictions), 3)
cm_train = cm(y_train, predictions)
predictions = lgbm_model.predict(X_val)
val_score = round(accuracy_score(y_val, predictions), 3)
cm_val = cm(y_val, predictions)
fig, (ax1,ax2) = plt.subplots(nrows=1,ncols=2,figsize=(15,5))
sns.heatmap(cm_train, annot=True, fmt=".0f",ax=ax1)
ax1.set_xlabel('Predicted Values')
ax1.set_ylabel('Actual Values')
ax1.set_title('Train Accuracy Score: {0}'.format(train_score), size = 15)
sns.heatmap(cm_val, annot=True, fmt=".0f",ax=ax2)
ax2.set_xlabel('Predicted Values')
ax2.set_ylabel('Actual Values')
ax2.set_title('Validation Accuracy Score: {0}'.format(val_score), size = 15)
# + [markdown] id="WFnCNYHmY9RY"
# ## Feature Importance
#
# + colab={"base_uri": "https://localhost:8080/", "height": 621} id="OWOT8lEJUyEJ" outputId="0ec9b315-034c-4e49-93a5-f2486e65e5a3"
import lightgbm as lgb
plt.rcParams["figure.figsize"] = (18, 10)
lgb.plot_importance(lgbm_model)
feature_imp = pd.Series(lgbm_model.feature_importances_, index = X_train.columns)
best_features = feature_imp.nlargest(25)
# + id="Rh7om0ZJUyHk"
X_train_importance = X_train[best_features.index]
X_val_importance = X_val[best_features.index]
X_test_importance = X_test[best_features.index]
# + [markdown] id="DRq-ihT7_p1g"
# ### Training after feature importance
# + id="qIhe0WxkUyKf"
lgbm=LGBMClassifier()
# + id="6HroffRtUyOS"
lgbm_params = {"learning_rate":[0.01,0.1,0.05],
"n_estimators": [100,200,500],
"subsample":[0.1,0.2],
"max_depth":[2,3,5,8]}
# + colab={"base_uri": "https://localhost:8080/"} id="xJK6IxIVUyR_" outputId="88dc26ab-7e2f-4fe1-b025-c6d4c295524c"
lgbm_cv_model=GridSearchCV(lgbm,lgbm_params,cv=3,n_jobs=-1,verbose=2).fit(X_train_importance,y_train)
# + colab={"base_uri": "https://localhost:8080/"} id="hTXXBBm3UyVz" outputId="e98ea6e3-e778-4950-bf46-9d9db6928c06"
lgbm_cv_model.best_params_
# + id="IFOl0l-VZrX1"
lgbm_tuned=LGBMClassifier(learning_rate=0.1,max_depth=2,n_estimators=200,subsample= 0.1).fit(X_train_importance, y_train)
# + colab={"base_uri": "https://localhost:8080/"} id="k5YpKx7LZrgP" outputId="9fd8cbba-79f2-4ae8-f24c-1f7befc4d634"
y_train_preds = lgbm_model.predict_proba(X_train)[:,1]
y_val_preds = lgbm_model.predict_proba(X_val)[:,1]
print('Baseline LGBM')
lgbm_train_auc_base = roc_auc_score(y_train, y_train_preds)
lgbm_val_auc_base = roc_auc_score(y_val, y_val_preds)
print('Training AUC:%.3f'%(lgbm_train_auc_base))
print('Validation AUC:%.3f'%(lgbm_val_auc_base))
print('Optimized LGBM')
y_train_preds_lgbm = lgbm_tuned.predict_proba(X_train_importance)[:,1]
y_val_preds_lgbm = lgbm_tuned.predict_proba(X_val_importance)[:,1]
lgbm_train_auc = roc_auc_score(y_train, y_train_preds_lgbm)
lgbm_val_auc = roc_auc_score(y_val, y_val_preds_lgbm)
print('Training AUC:%.3f'%(lgbm_train_auc))
print('Validation AUC:%.3f'%(lgbm_val_auc))
# + colab={"base_uri": "https://localhost:8080/"} id="KLSkoySFOxyy" outputId="9c6e1634-e3f6-4343-f52c-2c1c6ba63372"
# !pip install catboost
# + id="dDJNnpwbZrnv"
from catboost import CatBoostClassifier
catb=CatBoostClassifier()
# + id="VQ88eKNRZrqR"
catb_params={"iterations":[200,500,1000],
"learning_rate":[0.05,0.1],
"depth":[4,5,8],
}
# + colab={"base_uri": "https://localhost:8080/"} id="7--uvFmUZrtx" outputId="c8e97758-5a3b-4086-f0bb-bfdd540991a1"
catb_cv_model=GridSearchCV(catb,catb_params, cv=3, n_jobs=-1, verbose=2).fit(X_train_importance,y_train)
# + colab={"base_uri": "https://localhost:8080/"} id="wqk_deHZZrxO" outputId="4cab78a7-5ad0-4763-e3d0-140256944ef8"
catb_cv_model.best_params_
# + colab={"base_uri": "https://localhost:8080/"} id="3a4VJ-m3Zr2G" outputId="d2138135-44c6-4038-e9ae-1cac8f54cc06"
catb_tuned =CatBoostClassifier(depth=5,iterations=200,learning_rate=0.05).fit(X_train_importance, y_train)
# + colab={"base_uri": "https://localhost:8080/"} id="w4surzz-Zr71" outputId="c97d65eb-232e-46f6-c3aa-2d8fa65eb107"
print('Optimized CATBOOST')
y_train_preds_catb = catb_tuned.predict_proba(X_train_importance)[:,1]
y_val_preds_catb = catb_tuned.predict_proba(X_val_importance)[:,1]
catb_train_auc = roc_auc_score(y_train, y_train_preds_catb)
catb_val_auc = roc_auc_score(y_val, y_val_preds_catb)
print('Training AUC:%.3f'%(catb_train_auc))
print('Validation AUC:%.3f'%(catb_val_auc))
# + [markdown] id="LexiF8TTA-vT"
# ## choosing best model
# + id="V_KHc_W4Zr_n"
classifiers = [
lgbm_tuned,
catb_tuned]
# Define a result table as a DataFrame
result_table = pd.DataFrame(columns=['classifiers', 'fpr','tpr','auc'])
# Train the models and record the results
for cls in classifiers:
yproba = cls.predict_proba(X_test_importance)[::,1]
fpr, tpr, _ = roc_curve(y_test, yproba)
auc = roc_auc_score(y_test, yproba)
result_table = result_table.append({'classifiers':cls.__class__.__name__,
'fpr':fpr,
'tpr':tpr,
'auc':auc}, ignore_index=True)
# Set name of the classifiers as index labels
result_table.set_index('classifiers', inplace=True)
result_table.sort_values('auc',ascending=False,inplace=True)
# + colab={"base_uri": "https://localhost:8080/", "height": 410} id="kE_0wRkPZsH2" outputId="a059b6c0-9593-409d-b8bd-b7878dfe13eb"
fig = plt.figure(figsize=(10,6))
for i in result_table.index:
plt.plot(result_table.loc[i]['fpr'],
result_table.loc[i]['tpr'],
label="{}, AUC={:.3f}".format(i, result_table.loc[i]['auc']))
plt.plot([0,1], [0,1], color='black', linestyle='--')
plt.xticks(np.arange(0.0, 1.1, step=0.1))
plt.xlabel("False Positive Rate", fontsize=14)
plt.yticks(np.arange(0.0, 1.1, step=0.1))
plt.ylabel("True Positive Rate", fontsize=14)
plt.title('ROC Curve Analysis', fontweight='bold', fontsize=15)
plt.legend(prop={'size':10}, loc='lower right')
plt.show()
# + id="puOyvvJzO02_"
def test_scores(y_actual, y_pred, thresh):
auc = roc_auc_score(y_actual, y_pred)
accuracy = accuracy_score(y_actual, (y_pred > thresh))
recall = recall_score(y_actual, (y_pred > thresh))
return auc, accuracy, recall
classifiers = [
lgbm_tuned,
catb_tuned]
# Define a result table as a DataFrame
test_result = pd.DataFrame(columns=['classifiers', 'accuracy','recall','auc'])
# Train the models and record the results
for cls in classifiers:
y_test_preds = cls.predict_proba(X_test_importance)[:,1]
test_auc, test_accuracy, test_recall = test_scores(y_test,y_test_preds, 0.5) # thresh = 0.5
test_result = test_result.append({'classifiers':cls.__class__.__name__,
'accuracy':test_accuracy,
'recall':test_recall,
'auc':test_auc}, ignore_index=True)
# Set name of the classifiers as index labels
test_result.set_index('classifiers', inplace=True)
test_result.sort_values('auc',ascending=False,inplace=True)
# + colab={"base_uri": "https://localhost:8080/", "height": 133} id="oYNwLRa2jX7l" outputId="5c772239-43c8-4fb5-9aa2-4ea80a4bc261"
test_result
# + [markdown] id="Ts7L9l-3BQ2M"
# Conclusion: Going by this,i would use catboost_classifier
# + id="Wp8efGkijYMO"
# + id="o_ioCPiVjYR2"
# + id="-hWCTq1ojYWL"
# + id="XyvwgjnujYbX"
# + id="1xez7T6OjYfQ"
# + id="zZBg3sJqjYiv"
# + id="1NW6NM4MPY96"
|
sca_project (3).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python2
# ---
# # Intro. to Snorkel: Extracting Spouse Relations from the News
# ## Part III: Creating or Loading Evaluation Labels
# +
# %load_ext autoreload
# %autoreload 2
import os
# TO USE A DATABASE OTHER THAN SQLITE, USE THIS LINE
# Note that this is necessary for parallel execution amongst other things...
# os.environ['SNORKELDB'] = 'postgres:///snorkel-intro'
from snorkel import SnorkelSession
session = SnorkelSession()
# -
# ## Part III(a): Creating Evaluation Labels in the `Viewer`
# We repeat our definition of the `Spouse` `Candidate` subclass from Part II.
from snorkel.models import candidate_subclass
Spouse = candidate_subclass('Spouse', ['person1', 'person2'])
dev_cands = session.query(Spouse).filter(Spouse.split == 1).all()
len(dev_cands)
test_cands = session.query(Spouse).filter(Spouse.split == 2).all()
len(test_cands)
# ## Labeling by hand in the `Viewer`
# +
from snorkel.viewer import SentenceNgramViewer
# NOTE: This if-then statement is only to avoid opening the viewer during automated testing of this notebook
# You should ignore this!
import os
if 'CI' not in os.environ:
sv = SentenceNgramViewer(dev_cands, session)
else:
sv = None
# -
# We now open the Viewer. You can mark each `Candidate` as true or false. Try it! These labels are automatically saved in the database backend, and can be accessed using the annotator's name as the AnnotationKey.
sv
# ## Part III(b): Loading External Evaluation Labels
#
# We have already annotated the dev and test set for this tutorial, and now use it as an excuse to go through a basic procedure of loading in _externally annotated_ labels.
#
# Snorkel stores all labels that are manually annotated in a **stable** format (called `StableLabels`), which is somewhat independent from the rest of Snorkel's data model, does not get deleted when you delete the candidates, corpus, or any other objects, and can be recovered even if the rest of the data changes or is deleted.
#
# If we have external labels from another source, we can also load them in via the `stable_label` table:
# +
import pandas as pd
from snorkel.models import StableLabel
gold_labels = pd.read_csv('data/gold_labels.tsv', sep="\t")
name = 'gold'
for index, row in gold_labels.iterrows():
# We check if the label already exists, in case this cell was already executed
context_stable_ids = "~~".join([row['person1'], row['person2']])
query = session.query(StableLabel).filter(StableLabel.context_stable_ids == context_stable_ids)
query = query.filter(StableLabel.annotator_name == name)
if query.count() == 0:
session.add(StableLabel(context_stable_ids=context_stable_ids, annotator_name=name, value=row['label']))
# Because it's a symmetric relation, load both directions...
context_stable_ids = "~~".join([row['person2'], row['person1']])
query = session.query(StableLabel).filter(StableLabel.context_stable_ids == context_stable_ids)
query = query.filter(StableLabel.annotator_name == name)
if query.count() == 0:
session.add(StableLabel(context_stable_ids=context_stable_ids, annotator_name=name, value=row['label']))
session.commit()
# -
# Then, we use a helper function to restore `Labels` from the `StableLabels` we just loaded
#
# _Note that we "miss" a few due to parsing discrepancies with original candidates labeled; specifically, you should be able to reload 220/223 on the dev set and 273/279 on the test set._
from snorkel.db_helpers import reload_annotator_labels
reload_annotator_labels(session, Spouse, 'gold', split=1, filter_label_split=False)
reload_annotator_labels(session, Spouse, 'gold', split=2, filter_label_split=False)
# If you want to confirm that these labels are loaded, you can reload the `SentenceNgramViewer` with `annotator_name=gold` to see them! Next, in Part IV, we will build a model to predict these labels using data programming.
|
tutorials/intro/Intro_Tutorial_3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + [markdown] tags=[] id="44e9b83a-a610-44f0-838e-cd2c072c4519"
# # MScFE 640 - Portfolio Theory and Asset Pricing
# # Group Assignment - Group 3 - Submission 2
# + id="77IcsxVlrP3J"
# %%capture
# !pip install yfinance
import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt
import warnings
import pandas as pd
warnings.filterwarnings('ignore')
# + colab={"base_uri": "https://localhost:8080/"} id="cl8sPXDYrQLB" outputId="56faeb59-fec8-42f6-f052-54e526c9cd68"
etfs_lst = ['IYR', 'IYZ', 'XLB', 'XLE', 'XLF', 'XLI', 'XLK', 'XLP', 'XLU', 'XLV', 'XLY']
etfsPrices = yf.download(etfs_lst)['Adj Close']
# + colab={"base_uri": "https://localhost:8080/", "height": 455} id="-jstbTagrQQv" outputId="b03dcc72-c9bd-4ad3-b018-6eb7920bee79"
#returns of all etfs
returns=etfsPrices.pct_change()
returns
# + id="68rYxAuvsDNK"
# 2.1 Select 2 of the Select SPDR ETFs. Form an equally weighted portfolio of these 2 securities.
# + colab={"base_uri": "https://localhost:8080/", "height": 290} id="Me8AZD7CsDR-" outputId="18bd61de-4644-4658-d9f8-82e4ac41a75c"
etfs =['XLK','XLI']
# giving equal weights
Weights=np.array([0.5,0.5])
combine_returns = returns[etfs]
combine_returns['EWP'] = combine_returns[etfs].dot(Weights)
#plot performance of individual and combined
combine_plot = ( 1+ combine_returns).cumprod()
combine_plot.plot()
# + id="aIMhRRQOsDWE"
# 2.2 Compute the standard deviation of each of the securities
# + colab={"base_uri": "https://localhost:8080/"} id="QWo3pMoisDcN" outputId="ad98ba3a-5015-4ea1-8cda-ea60da620acd"
combine_returns.std()
# + id="c9-uwB3esDiK"
#2.3 Compute the correlation between the securities
# + colab={"base_uri": "https://localhost:8080/", "height": 144} id="-sdXD7rJsDk7" outputId="b02e6d05-e228-4777-8405-2a0f81ff2041"
combine_returns.corr()
# + id="AvCe0QS7sDpw"
#2.4 Write a function that computes the weighted return of a portfolio.
# + id="oxNIBKfIrQVw"
def weighted_returns(item_returns, weights):
return item_returns.dot(weights).mean()
# + id="eu6Bv-h1sWlq"
#2.5 Write a function that computes the portfolio standard deviation.
# + id="FngQuAbssWrL"
def standard_deviation(item_returns, weights, correlation='actual'):
covariance_matrix = item_returns.cov()
if correlation != 'actual':
# calculated covariance from correlation
ex_covar = correlation * item_returns.std().prod()
covariance_matrix.iloc[1,0] = covariance_matrix.iloc[0,1] = ex_covar
return np.sqrt(weights.dot(covariance_matrix).dot(weights))
# + id="4e-DDY2PsWw7"
# 3.1 Write a function showing the efficient frontier (EF) of your portfolio. Be sure to vary the weights of the security from (0, 100%), (1%, 99%), … (100%,0%).
# + colab={"base_uri": "https://localhost:8080/"} id="bsicgvhIsW2H" outputId="5a3fbc3d-f607-4e9e-f503-4d3e9ad30e37"
weighted_returns(combine_returns[etfs],Weights), standard_deviation(combine_returns[etfs],Weights)
# + id="0R82LE4fsW7W"
import matplotlib.pyplot as plt
def EF(returns, corr='actual'):
efs_data=pd.DataFrame()
for ranges in np.arange(0,1.01,0.02):
weighted=np.array([ranges,1-ranges])
efs_data.loc[ranges,'Return']= weighted_returns(returns,weighted)*252
efs_data.loc[ranges,'StDev'] = standard_deviation(returns,weighted, corr)*np.sqrt(252)
plt.plot(efs_data.StDev,efs_data.Return, label = 'correlation =' + (str(np.round(returns.corr().iloc[0,1],3))) + "(Actual)" if corr == 'actual' else str(corr))
plt.title('EF')
plt.xlabel('STD')
plt.ylabel('Returns')
plt.legend()
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="kDGQ7VhxsgWz" outputId="4e52bd51-383b-46d7-fc85-87aa577cf1d3"
# returns of 2 ETFs
both=combine_returns[etfs]
EF(both)
# + id="BxEwcWHvsgd3"
#3.2 What is the leftmost point of the EF called?
# + [markdown] id="95mlFJSXsgkq"
# Answer: Minimum Variance Portfolio
# + id="AeK3JHrFsgqK"
# 3.3 Rerun your function, but pretend the correlation between the securities is -1. Graph the EF. Comment on the shape
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="oa8Th2nosgv9" outputId="453c0b6a-4669-48c6-8d1e-b5803c12a669"
EF(both)
EF(both, corr= -1)
# + [markdown] id="bAXNeQgfsg1I"
# The slight Straight line show the EF with the perfect correlation
# + id="4Ygna5xxsg5-"
# 3.4 Return your function, but pretend the correlation between the securities is 0. Graph the EF. Comment on the shape.
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="ifGoTSTcswfJ" outputId="36fbe5c9-6b22-4a8d-fa27-5d00a91371d0"
EF(both)
EF(both, corr= -1)
EF(both, corr= 0)
# + [markdown] id="xQpKWdzkswkQ"
# The zero-correlation EF is located between the actual-correlation 0.728 EF and the perfectly negative correlation EF.
# + id="CsjLMsP1swpD"
# 3.5 Return your function, but pretend the correlation between the securities is 1. Graph the EF. Comment on the shape.
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="pUKbK_Tgswt-" outputId="7b15eb6a-2c76-41b5-a842-84f5d577f663"
EF(both)
EF(both, corr= -1)
EF(both, corr= 0)
EF(both, corr= 1)
# + [markdown] id="qTgefP53swyM"
# The negative correlation EF is connected by a perfect correlation of EF.
#
# + id="TqAX0N7Is8hh"
# 3.6 Apply 5% trim to the data. Recompute the correlation. Return the EF.
# + colab={"base_uri": "https://localhost:8080/", "height": 314} id="q3WrXDeRs8lP" outputId="442eedd5-0f99-402e-c3e2-012c866b4efa"
#%5 and 95% - triming
quartile_5, quartile_95 = np.quantile(combine_returns.EWP.dropna(),[0.05,0.95], axis=0)
trimmed_returns = combine_returns[((combine_returns.EWP>quartile_5) & (combine_returns.EWP<quartile_95))]
trimmed_returns = trimmed_returns[etfs]
correlation_trimmed = trimmed_returns.corr().iloc[0,1]# trimmed correlation
print('trimmed correlation:',correlation_trimmed)
EF(trimmed_returns,correlation_trimmed)
EF(both)
# + id="MTXnyDwms8pP"
# 3.7 How does the EF from the actual data compare to the EF from the trimmed data?
# + [markdown] id="5spNyY7ks8tC"
# Answer: The correlation of the actual is much better than the correlation of the trimmed.
# + id="j53-EJnKs8yX"
#3.8 Use a robust method of portfolio (see FRAPO R Library or pyportfolioopt Python module, for example).
#3.10 How does this EF compare with the other 2
# + id="3ejXvDMss82J"
# %%capture
# !pip install PyPortfolioOpt
from pypfopt.expected_returns import mean_historical_return
from pypfopt.risk_models import sample_cov, CovarianceShrinkage
from pypfopt.efficient_frontier import EfficientFrontier
import pypfopt as pf
from pypfopt import plotting
# + colab={"base_uri": "https://localhost:8080/", "height": 313} id="lth7n2J5s867" outputId="6fb29ae8-397f-492c-e15a-1db6b0049d22"
#mean returns (annual)
etf_prices=etfsPrices[etfs] # taking same common etfs used before
mean_value = mean_historical_return(etf_prices,compounding=False)
# covar matrix (shrink)
Shrink = CovarianceShrinkage(etf_prices).ledoit_wolf()
EF_shrink = EfficientFrontier(mean_value,Shrink)
# covariance shrinkage EF
plotting.plot_efficient_frontier(EF_shrink)
EF(both)
EF(both, corr= -1)
EF(both, corr= 0)
EF(both, corr= 1)
# + [markdown] id="jzypdFars88-"
# The addition of robust estimation of covariance matrix hasn't resulted in a significant change in the output.
# + id="ho7haHnYs8_s"
# 4.1 Add 1 ETF to your portfolio. Calculate the correlation matrix for 3 ETFs chosen.
# + colab={"base_uri": "https://localhost:8080/", "height": 144} id="NhkoeVm6tTux" outputId="85cd9775-19ef-4e02-eecc-882d7ced0e0a"
three_etfs =['XLK','XLI','XLY']
W3=np.array([1/3]*3) #equal weights
rets3 = returns[three_etfs].copy()
rets3.corr()
# + id="ArZVMNk8tTzL"
triple=rets3[three_etfs]
# + id="8ptmmeN4tT3j"
# 4.2 Graph the efficeint frontier of this 3-security portfolio.
# + colab={"base_uri": "https://localhost:8080/", "height": 315} id="XHCmEnictT80" outputId="422e6b4e-d4f5-42cf-f049-0d8b18f535fe"
etf_prices=etfsPrices[three_etfs] # taking same common etfs used before
mean_value = mean_historical_return(etf_prices,compounding=False)
# covar matrix (shrink)
Shrink = CovarianceShrinkage(etf_prices).ledoit_wolf()
EF_shrink = EfficientFrontier(mean_value,Shrink)
# covariance shrinkage EF
plotting.plot_efficient_frontier(EF_shrink)
# + id="6-VQz0YLtUAH"
# 4.3 Is there a diversification benefits to adding Security?
# + [markdown] id="CUKPWSLftUEE"
# Yes, there is a diversification benefits.
#
# + tags=[] id="7ace0ea9-b868-4eb5-b116-56addeb3749e"
from itertools import combinations
from scipy.optimize import curve_fit
from scipy.optimize import differential_evolution
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from pypfopt.expected_returns import mean_historical_return
from pypfopt import efficient_frontier
from pypfopt.risk_models import sample_cov, CovarianceShrinkage
#from pypfopt import hierarchical_portfolio
from pypfopt import cla
# + [markdown] tags=[] id="9dddb8e9-5eda-4876-a05d-809e9562fe01"
# ## Part 5: Category 3 Portfolios: All Combinations
# + [markdown] id="efa927a0-5155-4e44-84c4-8e7e6960746b"
# ### 5.1 Use 2019 daily return data. Apply a robust method of calculating the efficient frontier for all 165 (11 choose 3) combinations of 3 Select SPDR portfolios. DO NOT GRAPH THESE! You are allowed to be short securities. Call these the trained portfolios.
#
# ### 5.2 Assume a fixed amount of risk. Use each portfolio's EF to determine the weights of each of the 3 securities.
# + [markdown] id="07134f50-1a23-4dc3-8024-50518865f734"
# #### Critical Line Algorithm (Robust Approach) to Derive Efficient Frontier and Determine Weights for the Trained Portfolios
# + [markdown] id="55124e18-02e4-4317-8e4f-28c8e8eafe2f"
# Daily adjusted closing price data for 2019 is imported for the following ETFs covering 11 US sectors, based on which dialy log returns are calculated.
# - IYR: iShares U.S. Real Estate ETF
# - IYZ: iShares U.S. Telecommunications ETF
# - XLB: Materials Select Sector SPDR Fund
# - XLE: Energy Select Sector SPDR Fund
# - XLF: Financial Select Sector SPDR Fund
# - XLI: Industrial Select Sector SPDR Fund
# - XLK: Technology Select Sector SPDR Fund
# - XLP: Consumer Staples Select Sector SPDR Fund
# - XLU: Utilities Select Sector SPDR Fund
# - XLV: Health Care Select Sector SPDR Fund
# - XLY: Consumer Discretionary Select Sector SPDR Fund
#
# The above ETFs were also used in Submission 1, for categorisation into the LEI, CEI and LAG buckets.
# + id="e537b9fa-f8b6-4576-8fe9-a53fec7f15ad" outputId="b7924285-e047-4799-b026-8457f83a2ead"
# Using same list but taking data only of 2019
# etfs_lst = ['IYR', 'IYZ', 'XLB', 'XLE', 'XLF', 'XLI', 'XLK', 'XLP', 'XLU', 'XLV', 'XLY']
etfsPrices = yf.download(etfs_lst, '2019-01-01', '2019-12-31')['Adj Close']
etfsPrices
# + tags=[] id="d510e295-6081-4a2a-a524-4af1bc8a9257" outputId="a51c4fc1-a408-451f-f768-e05052dce66c"
etfsDailyLogRet = np.log(etfsPrices/etfsPrices.shift(1))[1:]
etfsDailyLogRet
# + [markdown] id="1a346828-11e1-4040-ace7-e86f7c629986"
# The annualised mean historical returns calculated below from the above daily log returns over 2019 are used as estimates of expected returns for the 11 ETFs.
# + id="5ad622af-ed3a-4fc1-b442-e6471610c56b" outputId="dfeb51ce-9b00-4ee7-e57f-5d5e84ca5d4c"
etfsExpLogRet = mean_historical_return(etfsPrices, returns_data=False, compounding=True, frequency=251, log_returns=True)
etfsExpLogRet
# + [markdown] id="f17365a0-ae9f-4809-93af-cf669cdd5322"
# We now use these expected returns and the covariance matrix to trace out the efficient frontiers for all possible 3-ETF portfolios which can be constructed from our 11 ETFs. There are 165 such portfolios (11C3) and, therefore, 165 efficient frontiers.
#
# The Critical Line Algorithm (CLA) has been used to estimate these frontiers. CLA was developed by <NAME> to optimise general quadratic functions subject to linear inequality constraints. CLA solves any portfolio optimisation problem that can be represented in such terms, like the standard Efficient Frontier problem. The posterior mean and posterior covariance derived by Black-Litterman also lead to a quadratic programming problem, thus CLA is also a useful tool in that Bayesian framework. However, portfolio optimisation problems which cannot be represented in a quadratic form cannot be solved by CLA.
#
# As required in the assignment, we assume volatility to be 0.08% and find the expected return and ETF weights for the portfolio lying on each of the 165 efficient frontiers. Since the efficient frontier is given as a set of discrete points instead of an equation, we use the expected return and weights available for the volatility level nearest to our assumed volatility level.
#
# The expected returns and weights thus obtained are stored in a dataframe.
# + id="fd8c9631-c644-4020-8127-ad7fa3ef8b8e"
# Function to find the value in an array which is nearest to a pre-specified value
def find_nearest(array, value):
array = np.asarray(array)
idx = (np.abs(array - value)).argmin()
return (idx, array[idx])
# + id="60b64cd4-22e9-4a9d-bed2-af6256d85fe3"
lst3etfComb = list(combinations(etfsPrices.columns,3))
constVol = 0.008
matrix3etf_constVol = np.zeros((165, 4))
for i in lst3etfComb:
ret3etf = [etfsExpLogRet[i[0]], etfsExpLogRet[i[1]], etfsExpLogRet[i[2]]]
cov3etfRobust = CovarianceShrinkage(pd.DataFrame([etfsPrices[i[0]], etfsPrices[i[1]], etfsPrices[i[2]]]).transpose()).ledoit_wolf()
claClass = cla.CLA(ret3etf, cov3etfRobust, weight_bounds = (-1,1))
efRet, efStdev, efWeights = claClass.efficient_frontier(points = 100)
idx, val = find_nearest(efStdev, constVol)
efWeights_constVol = efWeights[idx]
efRet_constVol = efRet[idx]
# print(efRet_constVol1, np.around(efWeights_constVol1, 2))
matrix3etf_constVol[lst3etfComb.index(i), 0] = efRet_constVol
matrix3etf_constVol[lst3etfComb.index(i), 1] = efWeights_constVol[0]
matrix3etf_constVol[lst3etfComb.index(i), 2] = efWeights_constVol[1]
matrix3etf_constVol[lst3etfComb.index(i), 3] = efWeights_constVol[2]
# print(np.around(np.mean(np.array(efStdev)), 3))
# plt.plot(efStdev, efRet)
# + id="1d09d0db-2221-4efe-9022-3842841784dc"
df3etf_constVol = pd.DataFrame(matrix3etf_constVol, columns = ['ExpRet2019', 'OptWt_ETF1', 'OptWt_ETF2', 'OptWt_ETF3'])
df3etf_constVol.insert(0, 'Portfolio' , lst3etfComb)
#with pd.option_context("display.max_rows", 2000, "display.max_columns", 100):
# display(df3etf_constVol)
#np.std(df3etf_constVol['OptWt_ETF3'])
# + [markdown] id="49b8a4b6-8fd0-47f1-9b95-446cd188c5ae"
# ### 5.3 Rank the 2019 portfolio returns.
# + id="65edc83b-551d-4621-b32c-a287772e8f23" outputId="24a4673b-1ba2-4a04-afd8-d228ada8e7a8"
rank = df3etf_constVol['ExpRet2019'].rank(ascending = False)
df3etf_constVol.insert(1, 'Rank2019' , rank)
df3etf_constVol.sort_values(by = 'ExpRet2019', ascending = False)
# + [markdown] id="a34efffb-7f3d-438b-be84-f5e0ef77d0c4"
# ### 5.4 Test each of the 165 portfolios using 2020 daily return data.
# + [markdown] id="6e8da1df-07cf-4070-8864-6f790f03a095"
# After importing the 2020 Adjusted Close prices for the ETFs and calculating daily log returns based on these, we apply the weights calculated above to estimate the 2020 expected return for all 165 3-ETF portfolio combinations as a weighted average of the individual ETFs' 2020 expected returns.
# + id="74cae740-b729-49ba-8724-0e9034495660" outputId="0c6bb5c7-de28-44a7-dd43-10bfdab2a61c"
etfsPrices2020 = yf.download(etfs_lst, '2020-01-01', '2020-12-31')['Adj Close']
#etfsPrices2020
# + id="d4754ea6-0701-4565-9add-3c3752877a8b"
etfsExpLogRet2020 = mean_historical_return(etfsPrices2020, returns_data=False, compounding=True, frequency=252, log_returns=True)
#etfsExpLogRet2020
# + id="2222f8c9-4a6e-4c15-be61-a81ddbaa08ae"
expRet2020 = np.zeros((165, 3))
for (i, j) in zip(df3etf_constVol['Portfolio'], df3etf_constVol.index):
expRet2020[j, 0] = etfsExpLogRet2020[i[0]]
expRet2020[j, 1] = etfsExpLogRet2020[i[1]]
expRet2020[j, 2] = etfsExpLogRet2020[i[2]]
optWtMatrix = np.array([df3etf_constVol['OptWt_ETF1'], df3etf_constVol['OptWt_ETF2'], df3etf_constVol['OptWt_ETF3']]).transpose()
df3etf_constVol.insert(3, 'ExpRet2020' , np.sum(expRet2020 * optWtMatrix, axis = 1))
# + [markdown] id="c2e08285-1941-431a-a3f5-b51e736f5d98"
# ### 5.5 Rank the 2020 portfolio returns.
# + id="2aa1fdbf-22fa-477d-a804-3b0375231eb4" outputId="41d777cb-6459-4588-cce4-f3ec4ed35d9e"
rank2020 = df3etf_constVol['ExpRet2020'].rank(ascending = False)
df3etf_constVol.insert(2, 'Rank2020', rank2020)
df3etf_constVol.sort_values(by = 'ExpRet2020', ascending = False)
# + id="61ad1919-aed5-4e7a-973d-09d17e12db4c" outputId="8f459e64-2863-4502-8f58-c270b0883a92"
plt.plot(df3etf_constVol['Rank2019'], df3etf_constVol['Rank2020'], '.')
plt.title('3-ETF Portfolio Return 2019 Rank vs. 2020 Rank')
plt.xlabel('Rank based on 2019 Expected Return')
plt.ylabel('Rank based on 2020 Expected Return')
# + id="620b68f4-39ea-4022-bc14-2158e122b02f" outputId="99892997-f11c-453e-d24b-cb098f1411c9"
plt.plot(df3etf_constVol['ExpRet2019'], df3etf_constVol['ExpRet2020'], '.')
plt.title('3-ETF Portfolio 2019 Return vs. 2020 Return')
plt.xlabel('2019 Expected Return')
plt.ylabel('2020 Expected Return')
# + [markdown] id="61ad1c3e-04d0-4d10-a7b5-06c587cbeb81"
# The above two plots show that the expected return/ rank for 2019 is not a good predictor of the expected return/ rank for 2020 respectively.
# + [markdown] tags=[] id="bc5112f2-f9b4-4e1a-bba9-e08064f8d474"
# ## Part 6: Analysing 3-Security Portfolio
# + [markdown] id="91276cd7-516e-42fc-833d-f40ad76fe62f"
# ### 6.1 Relabel the ETF with a + sign if the weight >0, or a - sign if the weight <0. Then add the assigned Economic Indicator.
# + [markdown] id="13e38667-c0a0-4fcb-a1be-ef04891c655c"
# The below dataframe summarises how 3 supervised learning models used in submission 1 place each of the 11 ETFs into the 3 economic indicator buckets (LEI, CEI, LAG). The final category used for each ETF is LEI unless at least one of the models places it into a bucket other than LEI, in which case the other bucket is taken to be the final category.
# + id="0690a08a-5824-4abe-9268-8ce20a37350c" outputId="f671bf1c-8531-4d10-a7fc-f2e2845666be"
etfsCategories = pd.read_excel('ETF Categories_GWP 1.xlsx')
etfsCategories
# + id="e9af2fce-d001-40ad-836c-5b52cdfae5e9" outputId="a7229ed9-ef51-473b-9e2d-15ed8231761e"
etfsCategories['FinalCat'] = ['LEI', 'CEI', 'LEI', 'LEI', 'LEI', 'CEI', 'LEI', 'LEI', 'LAG', 'LEI', 'LAG']
etfsCategories.set_index('ETF', drop = True, inplace = True)
etfsCategories
# + id="6725b177-ffec-4d8c-b819-3f49124ce86d" outputId="eb781728-bd27-4303-f26c-6420548d78ec"
indicCat = list()
for (i, j) in zip(df3etf_constVol['Portfolio'], df3etf_constVol.index):
catEtf1 = etfsCategories['FinalCat'].loc[i[0]]
catEtf2 = etfsCategories['FinalCat'].loc[i[1]]
catEtf3 = etfsCategories['FinalCat'].loc[i[2]]
if (df3etf_constVol['OptWt_ETF1'][j] >= 0): wtSignEtf1 = '+'
else: wtSignEtf1 = '-'
if (df3etf_constVol['OptWt_ETF2'][j] >= 0): wtSignEtf2 = '+'
else: wtSignEtf2 = '-'
if (df3etf_constVol['OptWt_ETF3'][j] >= 0): wtSignEtf3 = '+'
else: wtSignEtf3 = '-'
indicCat.append((wtSignEtf1 + catEtf1, wtSignEtf2 + catEtf2, wtSignEtf3 + catEtf3))
df3etf_constVol['IndicCat'] = indicCat
df3etf_constVol
# + [markdown] id="5513b213-38d8-449d-9644-c9e600a248ea"
# ### 6.2 Using the ranks from 5.5, determine which combinations tend to be the best performing. Interpret the results.
# + id="dfd353ba-4a2e-4293-802d-0fb048555b56"
indicComb = df3etf_constVol[['IndicCat', 'ExpRet2019', 'ExpRet2020']].groupby('IndicCat').mean()
indicRank2019 = indicComb['ExpRet2019'].rank(ascending = False)
indicRank2020 = indicComb['ExpRet2020'].rank(ascending = False)
indicComb.insert(2, 'Rank2019', indicRank2019)
indicComb.insert(3, 'Rank2020', indicRank2020)
# + id="dc93e523-0929-4e9d-bb1a-b3f618f8b9db" outputId="b86d69bc-9c7e-424e-a11c-cdf70773720d"
indicComb.sort_values(by = 'ExpRet2019', ascending = False)
# + id="51e944c7-5b3d-4c86-b78f-9dc843c746e6" outputId="7ff0f737-f2af-466e-8014-d503618dc967"
indicComb.sort_values(by = 'ExpRet2020', ascending = False)
# + [markdown] id="f8409df7-1f03-453d-81c3-28a4d9a4d99f"
# After specifying the indicator (LEI, CEI, LAG) and positional (long + / short -) categories for each ETF in each portfolio, the above two dataframes identify the unique indicator combinations resulting from these portfolios and rank the 2019 and 2020 returns for these combinations. However, this does not reveal much about which indicators tend to perform better.
#
# So, we calculate the weights which each portfolio attributes to LEI, CEI and LAG. This is done by looking at the indicator bucket for each asset in the portfolio, and assigning the weight for that asset to its indicator bucket.
#
# If more than one asset in the portfolio are assigned to the same indicator bucket, the weights for those two assets are summed and the result is assigned to the indicator bucket. If no asset is assigned to an indicator bucket, the weight of that bucket in the portfolio is taken to be 0.
# + id="6ba1b351-0ec5-4689-9572-288966bd5ee3" outputId="3a504826-74b0-46e9-c970-63118284b540"
indicComb2 = pd.DataFrame(index = df3etf_constVol.index, columns = ['OptWt_LEI', 'OptWt_CEI', 'OptWt_LAG'])
for (i, j) in zip(df3etf_constVol['IndicCat'], df3etf_constVol['IndicCat'].index):
indicComb2['OptWt_LEI'].loc[j] = ((df3etf_constVol['OptWt_ETF1'].loc[j] * (i[0][-3:] == 'LEI')) +
(df3etf_constVol['OptWt_ETF2'].loc[j] * (i[1][-3:] == 'LEI')) +
(df3etf_constVol['OptWt_ETF3'].loc[j] * (i[2][-3:] == 'LEI')))
indicComb2['OptWt_CEI'].loc[j] = ((df3etf_constVol['OptWt_ETF1'].loc[j] * (i[0][-3:] == 'CEI')) +
(df3etf_constVol['OptWt_ETF2'].loc[j] * (i[1][-3:] == 'CEI')) +
(df3etf_constVol['OptWt_ETF3'].loc[j] * (i[2][-3:] == 'CEI')))
indicComb2['OptWt_LAG'].loc[j] = ((df3etf_constVol['OptWt_ETF1'].loc[j] * (i[0][-3:] == 'LAG')) +
(df3etf_constVol['OptWt_ETF2'].loc[j] * (i[1][-3:] == 'LAG')) +
(df3etf_constVol['OptWt_ETF3'].loc[j] * (i[2][-3:] == 'LAG')))
indicComb2.insert(0, 'Portfolio', df3etf_constVol['Portfolio'])
indicComb2.insert(1, 'IndicCat', df3etf_constVol['IndicCat'])
indicComb2.insert(5, 'ExpRet2019', df3etf_constVol['ExpRet2019'])
indicComb2.insert(6, 'ExpRet2020', df3etf_constVol['ExpRet2020'])
indicComb2
# + [markdown] id="400b37b3-fc47-42e6-8568-efb3bde2bb8d"
# We now visualise how the 2019 and 2020 expected returns evolve as the weight allocated to a certain indicator bucket increases.
# + id="d4b07f2d-97f0-4d09-92b5-41b87132e42b" outputId="82aa0cc0-c71b-4341-a413-c57a6063691a"
dataPlotLeiRet19 = indicComb2[['OptWt_LEI', 'ExpRet2019']].sort_values(by = 'OptWt_LEI', ascending = True)
plt.plot(dataPlotLeiRet19['OptWt_LEI'], dataPlotLeiRet19['ExpRet2019'], '.')
plt.title('Impact of Exposure to LEI on Portfolio Return in 2019')
plt.xlabel('Weight Allocated to LEI')
plt.ylabel('Portfolio Expected Return')
# + id="16794b9a-87d9-4874-a78d-1d20fc1b90a6" outputId="61a5b143-8613-4cc1-e9a8-f394224cdd76"
dataPlotLeiRet20 = indicComb2[['OptWt_LEI', 'ExpRet2020']].sort_values(by = 'OptWt_LEI', ascending = True)
plt.plot(dataPlotLeiRet20['OptWt_LEI'], dataPlotLeiRet20['ExpRet2020'], '.')
plt.title('Impact of Exposure to LEI on Portfolio Return in 2020')
plt.xlabel('Weight Allocated to LEI')
plt.ylabel('Portfolio Expected Return')
# + [markdown] id="c472a5dd-91b9-41a9-a82d-7f9907f4d1e6"
# Increasing a portfolio's exposure to LEI tended to increase returns over 2019 and decrease returns over 2020.
# + id="5c6b7563-63c6-4c1c-b24a-ed5727f65b1c" outputId="b5b0c24e-612d-47e5-c1b0-cae240cac8fe"
dataPlotCeiRet19 = indicComb2[['OptWt_CEI', 'ExpRet2019']].sort_values(by = 'OptWt_CEI', ascending = True)
plt.plot(dataPlotCeiRet19['OptWt_CEI'], dataPlotCeiRet19['ExpRet2019'], '.')
plt.title('Impact of Exposure to CEI on Portfolio Return in 2019')
plt.xlabel('Weight Allocated to CEI')
plt.ylabel('Portfolio Expected Return')
# + id="9d4055ab-2156-420a-b63d-42afefb7b6f8" outputId="57686870-dd92-4cab-8650-0cf725ef75d1"
dataPlotCeiRet20 = indicComb2[['OptWt_CEI', 'ExpRet2020']].sort_values(by = 'OptWt_CEI', ascending = True)
plt.plot(dataPlotCeiRet20['OptWt_CEI'], dataPlotCeiRet20['ExpRet2020'], '.')
plt.title('Impact of Exposure to CEI on Portfolio Return in 2020')
plt.xlabel('Weight Allocated to CEI')
plt.ylabel('Portfolio Expected Return')
# + [markdown] id="4937dd2f-c29d-4185-ada0-b2419b6d76fc"
# Increasing a portfolio's exposure to CEI tended to decrease returns over 2019. However, the effect of CEI on 2020 returns appears to be ambiguous upon visual inspection.
# + id="422937d4-fdb0-401d-8929-f9f8e8713d15" outputId="269dd356-c0e5-4c12-a4e4-e5633c42d5d4"
dataPlotLagRet19 = indicComb2[['OptWt_LAG', 'ExpRet2019']].sort_values(by = 'OptWt_LAG', ascending = True)
plt.plot(dataPlotLagRet19['OptWt_LAG'], dataPlotLagRet19['ExpRet2019'], '.')
plt.title('Impact of Exposure to LAG on Portfolio Return in 2019')
plt.xlabel('Weight Allocated to LAG')
plt.ylabel('Portfolio Expected Return')
# + id="ec45e96a-cc2d-4874-aba4-d7f1edf90b76" outputId="bcbc82e5-0110-4d4c-800e-c31d6857489e"
dataPlotLagRet20 = indicComb2[['OptWt_LAG', 'ExpRet2020']].sort_values(by = 'OptWt_LAG', ascending = True)
plt.plot(dataPlotLagRet20['OptWt_LAG'], dataPlotLagRet20['ExpRet2020'], '.')
plt.title('Impact of Exposure to LAG on Portfolio Return in 2020')
plt.xlabel('Weight Allocated to LAG')
plt.ylabel('Portfolio Expected Return')
# + [markdown] id="4d6bfb20-eaf9-4909-afa0-826b91a98cb3"
# Increasing a portfolio's exposure to LAG appears to have a marginal negative impact on 2019 returns and a relatively stronger positive impact on 2020 returns.
# + [markdown] tags=[] id="20308934-695d-469f-b8c3-0920b2e354c9"
# ## Part 7: Category 4 Portfolios: Using Principal Components
# + [markdown] tags=[] id="dd5b9292-c27b-477f-bd63-1fec4fbd1712"
# ### 7.1 Compute the PCA from the correlation matrix of the 11 ETFs.
# + [markdown] id="3752e20e-2041-4f7f-9838-e666cb51231d"
# We use daily returns instead of log returns for this analysis since the mean_historical_return function does not take log returns as an input.
# + id="c3f79e8b-4faa-4932-a8c1-27879542a767" outputId="976b4ca0-c70f-4ae4-957f-0ba00f45ae69"
etfsDailyRet2019 = (etfsPrices/etfsPrices.shift(1)-1)[1:]
etfsDailyRet2019
# + [markdown] id="db397f8d-db44-419d-a693-559fc0509ee6"
# The above 11-dimensional dataset is reduced to a 3-dimensional dataset using Principal Component Analysis. Since the implementation of the PCA algorithm in sci-kit learn automatically computes the covariance matrix, we do not compute it explicitly here.
# + id="74b06e22-0449-45ce-acfc-d20b3eb84b36" outputId="be301d17-e6fe-4f10-9323-0fa7eb5c4178"
pc2019 = PCA(n_components = 3).fit_transform(etfsDailyRet2019)
pc2019
# + [markdown] tags=[] id="eb59655e-aa7e-42ea-b60b-8b7ec945f1e3"
# ### 7.2 Using 2019 data, compute the EF for the first 3 principal components portfolio.
# + [markdown] id="9f143af3-55cc-405c-b8e4-77ab1c9ee349"
# The above 3 PCs are used to estimate 2019 expected return and covariances, which are then fed into the Critical Line Algorithm to obtain the efficient frontier resulting from a portfolio of the 3 PCs.
# + id="7b99065d-dde0-41a4-b265-cfdfaa7f2f60" outputId="ea912974-6c7d-4e69-f43a-81eebc6da4f8"
pcExpRet2019 = mean_historical_return(pd.DataFrame(pc2019, columns = ['PC1', 'PC2','PC3']), returns_data = True, compounding = True, frequency = 251, log_returns = False)
pcCovMat2019 = np.cov(pc2019.transpose())
pcClaClass = cla.CLA(pcExpRet2019, pcCovMat2019, weight_bounds = (-1,1))
pcEfRet, pcEfStdev, pcEfWeights = pcClaClass.efficient_frontier(points = 100)
plt.plot(pcEfStdev, pcEfRet)
plt.title('Efficient Frontier of the 3-Principal Components Portfolio')
plt.xlabel('Portfolio Standard Deviation')
plt.ylabel('Portfolio Expected Return')
# + [markdown] tags=[] id="23bd3feb-0cea-4f0c-8b67-d0b5918c030d"
# ### 7.3 How does the PCA portfolio return compare to the 2019 3-security portfolio returns?
# + [markdown] id="ea99c482-76e7-4a28-93df-03a95c0419df"
# We now use the 0.8% volatility and the approach laid out in 5.2 to get the expected return and weights for the 3-PC portfolio lying on the efficient frontier for the assumed volatility level.
# + id="b079667b-eeb0-435e-92a2-32c0065ab645" outputId="ace60e46-22b1-47c0-ce76-2eee4970cf5b"
idx, val = find_nearest(pcEfStdev, constVol)
pcEfWeights_constVol = np.around(pcEfWeights[idx], 2)
pcEfRet_constVol = pcEfRet[idx]
print('PCA Portfolio Weights:',pcEfWeights_constVol)
print('2019 PCA Portfolio Return:', pcEfRet_constVol)
print('Average 2019 3-security Portfolio Return across all 165 Combinations:', df3etf_constVol['ExpRet2019'].mean())
# + [markdown] id="61f8e317-5954-43c9-8c8b-d3b1063f191c"
# The PCA portfolio return of 0.176% is much lower than the average of the 2019 returns across 165 portfolios, which stands at 23.566%.
# + [markdown] tags=[] id="1d34c534-a8ac-4daf-93f2-3eed0ae20c53"
# ### 7.4 Assuming a fixed amount of risk, and 2020 data, use the PC weights to compute the 3-PC portfolio returns.
# + id="3caf7b1b-ad73-4b12-966d-1d172331683a" outputId="e0d02040-9280-417b-e236-f65775218461"
etfsDailyRet2020 = (etfsPrices2020/etfsPrices2020.shift(1)-1)[1:]
etfsDailyRet2020
# + [markdown] id="3b5b423b-7ab2-4500-b132-c3dd60a45e9b"
# Using sci-kit learn's PCA implementation to get the 3 PCs from 2020 daily return data.
# + id="04744054-55fc-4381-9e33-b0ecad7f6223" outputId="f036fadc-3342-4622-92b7-f5e484f73b5b"
pc2020 = PCA(n_components = 3).fit_transform(etfsDailyRet2020)
pcExpRet2020 = mean_historical_return(pd.DataFrame(pc2020, columns = ['PC1', 'PC2','PC3']), returns_data = True, compounding = True, frequency = 252, log_returns = False)
pcExpRet2020
# + [markdown] id="4b38914a-9a44-4220-9774-01b1d8d0bbc1"
# The historical estimates of expected returns given above are used with the 2019 weights calculated in 7.3 to get the expected return for the 2020 3-PC portfolio. This stands at 3.89%, higher than the expected return for the 2019 3-PC portfolio.
# + id="7bb77856-120d-4c8a-a5a4-f9be7e7b9d00" outputId="824baa52-d72b-4499-89d9-dd2fd7edc41e"
pcPortExpRet2020 = np.sum(pcEfWeights_constVol * np.array(pcExpRet2020).reshape(3,1))
pcPortExpRet2020
|
WQU MScFE 640 - Portfolio Theory and Asset Pricing (C21-S1)/Group Work/Final Submissions/Submission 2/Final Submission/MScFE_640_PTAP_Group_Submission_2_Group_3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [Root]
# language: python
# name: Python [Root]
# ---
# +
# This is an initial device test run to see if the user feels all the nodes or if they need adjustmet
import serial
import csv
import time
import struct
testmatrix = []
num = 0
# with open('C:/Users/santiago.arconada/Downloads/sensogram.txt') as csvfile:
with open('sensogram.txt') as csvfile:
inputfile = csv.reader(csvfile)
for row in inputfile:
testmatrix.append(row)
for i in range(len(row)):
testmatrix[num][i] = int(row[i])
num = num+1
# At this point we get all values in packets of data being integer, good job, had to loop through each array
# as it comes in to convert it from a string to an integer.
# Might have to change the tty.usbserial to Mac specific address
ser = serial.Serial('/dev/cu.usbmodem1411',9600)
# ser = serial.Serial('/dev/cu.usbmodem53',9600)
node_matrix = []
# This section is for parsing the data inside the testmatrix
activ_array_new = []
# Counter = [13,50,5,50,7,50,8,50,9,50,13,50,10,50,11,50,6,50,13,50]
# Test run for all the nodes in a sequence
strength = 100
Counter = [13,200,3,strength,13,200,4,strength,13,200,5,strength,13,200,6,strength,13,200,7,strength,13,200,8,strength,13,200,9,strength,13,200,10,strength,13,200,11,strength,13,200,12,strength,13,200,13,strength]
b = 0
while b<1:
line = ser.readline()
print(line)
if (ser.readline() == b'ready\r\n'):
ser.write(b'1') # Need to include the b so that data can be sent
# this is python 3 syntax
# ser.write(b'1') # This will be the initiate Serial listening command
ser.write(struct.pack('>B', len(Counter))) # Something is working here, but I am not sure what it is haha
print(struct.pack('>B', len(Counter)))
c = 0
# for y in range(len(Counter)//2):
for y in range(21):
ser.write(struct.pack('>B', Counter[c]))
ser.write(struct.pack('>B', Counter[c+1]))
print('Im sending %d %d' % (Counter[c], Counter[c+1]))
c = c+2
# ser.write(b Counter '\r') # This defines how many to wait for
time.sleep(0.2)
else:
time.sleep(0.2)
# So this part of the code is what defines the reading speed of the 'control board'
# Each 100ms it checks the serial to see if there are any responses from the "display board"
# # This way I can send values only when the Arduino is ready.
# ser.close()
b = b+1
# -
Counter = [9,40,1,20,5,60]
print(Counter[0])
print(struct.pack('>B', 12))
for i in range(3):
print(i)
activ_array_new = []
for i in range(1):
activ_array = []
for q in range(7):
if (testmatrix[i][testmatrix[i][q+6]] == 1):
activ_array.append(testmatrix[i][q+6])
activ_array.append(testmatrix[i][q+13])
activ_array_new.append(activ_array) # We could send this as a packet of data to the Arduino (node,delay)
print(activ_array)
print(len(activ_array))
Counter = len(activ_array) # How many values am I sending
print('Counter is', Counter)
# ser.write(Counter)
n = 0
for j in range(Counter//2):
print('Node %d and delay %d', activ_array_new[i][n], activ_array_new[i][n+1]) # Substitute this by sending value on Serial
#ser.write(activ_array_new[i][j] 0D 0A)
n = n+2
# +
# print(testmatrix)
# +
# Code for the Arduino
void setup() {
pinMode(3,OUTPUT);
# And all others
Serial.begin(9600);
}
void loop() {
if (Serial.available()) {
while (# Command to start communication isn't there yet) {
# Just wait
}
values = #read incoming data with count of how many im doing
for (i=0; i<values,i++) {
node_array[i] = #serialdata;
delay_array[i] = #serialdata;
}
# Maybe I could combine these two for loops together
# for loop reading x values of the serial
for (i=0; i<values,i++) {
digitalWrite(node_array[i],HIGH);
# Maybe put a print to test out if it works
delay(delay_array[i]);
digitalWrite(node_array[i],LOW);
}
Serial.write('done'); # To tell python that we are done with the sequence
}
}
# +
# This code is to be run as the final version, but I don't want to modify the code that works already above
# so I will use this as my testing platform
import serial
import csv
import time
import struct
from PIL import Image
import random
# %run _Functions.ipynb
testmatrix = LoadSensogram()
picmatrix = LoadImages('Picorder.txt')
# Connect to Arduino
ser = serial.Serial('/dev/cu.usbmodem1421',9600)
sampledown = 0
sampleup = 6
# # Define order array, need to change this up for the second round, i.e range(10,20)
order = list(range(sampledown,sampleup))
# Randomize the order
random.shuffle(order)
# This establishes serial communication and data sending
for i in order: # Loop through 20 images for the experiment
TestPattern(ser,testmatrix,i)
img = Image.open(','.join(picmatrix[i]))
img.show()
time.sleep(2)
# +
# This is the testing code, used to run through the patterns but not displaying the associated
# image, that the user will select among 5 presented.
import serial
import random
# %run _Functions.ipynb
testmatrix = LoadSensogram()
picmatrix = LoadImages('Picorder.txt')
# Connect to Arduino
ser = serial.Serial('/dev/cu.usbmodem1421',9600)
# ser = 'hi'
# Define the results matrix
results = []
# Re-randomize for testing round, need to change this up for the second round, i.e range(10,20)
order = list(range(sampledown,sampleup))
# Randomize the order
random.shuffle(order)
# This establishes serial communication and data sending
for i in order:
TestPattern(ser,testmatrix,i)
# MIGHT HAVE TO REDUCE THE DELAY TIME, IT IS TOO MUCH, OR MAYBE MOVE THE TEST FUNCTION UP
time.sleep(1.5)
#After the data has been sent to the sensogram display the pictures and test the subject
TestFunction(i,picmatrix,order)
time.sleep(0.5)
# -
PrintScore(results)
DetailedInfo(results,order,1)
|
Test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# +
import param
import parambokeh
from bokeh.io import output_notebook
import numpy as np
import pandas as pd
output_notebook()
# -
# The paramBokeh library provides an easy way to manipulate parameters on ``Parameterized`` using the widgets on bokeh server and within the notebook. In addition to controlling input parameters a common usecase for using widgets in the notebook is to dynamically control some visual display output. In addition to all the standard parameters supplied by the ``param`` library, ``paramBokeh`` also supplies so called ``View`` parameters, which render bokeh plot output in a widget area. The output parameters may be updated simply by setting the parameter on the class.
#
# In the first simple example we will declare a Parameterized class with a ``Number`` parameter called magnitude and an ``HTML`` parameter which will let us display some arbitrary HTML. In this case we will simply generate a pandas dataframe with random data within the update method and use the ``to_html`` method to convert it to an HTML table. If we define the ``update`` method as the callback of the widgets the table will now update whenever the slider is dragged. To ensure that the output is drawn on initialization we set ``on_init=True``.
# +
class HTMLExample(param.Parameterized):
magnitude = param.Number(1, bounds=(0, 10))
output = parambokeh.view.HTML()
def update(self, **kwargs):
self.output = pd.DataFrame(np.random.rand(10,2)*self.magnitude).to_html()
example = HTMLExample(name='HTMLExample')
layout = parambokeh.Widgets(example, on_init=True, callback=example.update)
# -
# The ``HTML`` parameter accepts any arbitrary HTML string but for convenience paramBokeh also allows rendering bokeh and HoloViews plots using the ``Plot`` parameter. Note however that we can only replace a plot when deploying on bokeh server, within the notebook we may only update a plot:
#
# Additionally we can declare the ``view_position``, which specifies where the viewing widget will be placed in relation to the input widgets:
# +
import holoviews as hv
class CurveExample(hv.streams.Stream):
color = param.Color(default='#000000', precedence=0)
element = param.ObjectSelector(default=hv.Curve,
objects=[hv.Curve, hv.Scatter, hv.Area],
precedence=0)
amplitude = param.Number(default=2, bounds=(2, 5))
frequency = param.Number(default=2, bounds=(1, 10))
output = parambokeh.view.Plot()
def view(self, *args, **kwargs):
return self.element(self.amplitude*np.sin(np.linspace(0, np.pi*self.frequency)),
vdims=[hv.Dimension('y', range=(-5, 5))]).opts(style=dict(color=self.color))
def event(self, **kwargs):
if not self.output or any(k in kwargs for k in ['color', 'element']):
self.output = hv.DynamicMap(self.view, streams=[self], cache_size=0)
else:
super(CurveExample, self).event(**kwargs)
example = CurveExample(name='HoloViews Example')
parambokeh.Widgets(example, callback=example.event, on_init=True, view_position='right')
|
examples/user_guide/View_Parameters.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
# ## Anonymize Enbridge data
enbridge = pd.read_csv("./enbridge_data.csv")
enbridge.columns
del enbridge["Account ID"]
del enbridge[" Name"]
del enbridge[" Invoice Number"]
enbridge.to_csv("./enbridge_data.csv", index=False)
|
anonymize_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %load_ext autoreload
# %autoreload 2
# %matplotlib inline
# -
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import matplotlib.pyplot as plt
import seaborn as sns
from pathlib import Path
import os
from collections import Counter
import datetime
path=Path('/opt/data/john_hopkins/COVID-19/csse_covid_19_data')
assert path.exists()
# !ls -la {path}
# !git -C {path} remote -v
# !git -C {path} pull
# +
# # !ls -la {path/'csse_covid_19_daily_reports'}
# -
last_day = pd.read_csv(path/'csse_covid_19_daily_reports/05-17-2020.csv')
last_day
last_day['Country_Region'].unique()
len(last_day['Country_Region'].unique())
# !ls {path}
# Extract meaningful columns and concatenate all csv files
# +
full_data_set = None
col_counter = Counter()
for i, p in enumerate(Path(path/'csse_covid_19_daily_reports').rglob('*.csv')):
df = pd.read_csv(p)
df.rename(columns={'Country/Region': 'Country_Region', 'Last Update': 'Last_Update'}, inplace=True)
col_counter.update(df.columns)
cleansed_df = df[['Country_Region', 'Last_Update', 'Confirmed', 'Deaths', 'Recovered']]
if full_data_set is None:
full_data_set = cleansed_df
else:
full_data_set = pd.concat([full_data_set, cleansed_df], axis=0, sort=False)
print(f'There are {i + 1} items', len(full_data_set))
# -
col_counter
len(full_data_set.Country_Region.unique()), len(full_data_set.Last_Update.unique())
# Date conversion
full_data_set["Last_Update"] = pd.to_datetime(full_data_set["Last_Update"])
full_data_set["Date"] = full_data_set["Last_Update"].dt.date
full_data_set[(full_data_set['Country_Region'] == 'US') & (full_data_set['Date'] == datetime.date(2020, 4, 22))]['Confirmed'].sum()
full_data_set[full_data_set['Country_Region'].str.contains("Congo")]
# There are problems with synonyms in the datasets. Like e.g. 'Mainland China', 'China', 'Congo (Brazzaville)', 'Congo (Kinshasa)'
full_data_set[full_data_set['Country_Region'].str.contains("China")].sort_values(['Date'])
full_data_set['Country_Region'] = full_data_set['Country_Region'].str.replace('Mainland China', 'China')
# full_data_set['Country_Region'] = full_data_set['Country_Region'].str.replace('Congo (Brazzaville)', 'Congo')
# full_data_set['Country_Region'] = full_data_set['Country_Region'].str.replace('Congo (Kinshasa)', 'Congo')
# We are intterested in daily results and some countries are providing results multiple times a day.
full_data_set_grouped = full_data_set.groupby(['Country_Region', 'Date']).agg({
'Confirmed': 'sum', 'Deaths': 'sum', 'Recovered': 'sum', 'Last_Update': 'last'})
full_data_set_grouped.reset_index(inplace=True)
full_data_set_grouped
# Change the type of the numeric fields
for c in ['Confirmed', 'Deaths', 'Recovered']:
full_data_set_grouped[c] = full_data_set_grouped[c].astype('uint32')
# Add the active cases columns
full_data_set_grouped.fillna(0, inplace=True)
full_data_set_grouped['Active'] = full_data_set_grouped['Confirmed'] - full_data_set_grouped['Deaths'] - full_data_set_grouped['Recovered']
# Create percent changes on confirmed
full_data_set_grouped.sort_values(['Country_Region', 'Date'], inplace=True)
full_data_set_grouped['Confirmed_Pct'] = full_data_set_grouped.groupby(['Country_Region'])['Confirmed'].pct_change(7)
full_data_set_grouped[full_data_set_grouped['Country_Region'] == 'US']
full_data_set_grouped.info()
# +
import matplotlib.style as style
style.use('fivethirtyeight')
def plot_country(countries, fields=['Confirmed'], save_fig=False, target_folder='export/images'):
fig_size = plt.rcParams["figure.figsize"]
fig_size[0] = 9
fig_size[1] = 6
fig, ax = plt.subplots(dpi=80)
for country in countries:
for field in fields:
full_data_set_grouped_country = full_data_set_grouped[full_data_set_grouped['Country_Region'] == country]
plt.plot(full_data_set_grouped_country['Date'], full_data_set_grouped_country[field], label=field)
ax.legend();
ax.set_title(','.join(countries))
plt.xticks(rotation=45)
if save_fig == True:
plt.gcf().subplots_adjust(bottom=0.18)
plt.gcf().subplots_adjust(left=0.12)
plt.savefig(f'{target_folder}/{countries[0]}.jpg')
return full_data_set_grouped_country
full_data_set_grouped_country = plot_country(['US'], ['Confirmed', 'Deaths', 'Recovered', 'Active'])
# -
full_data_set_grouped_country = plot_country(['Germany'], ['Confirmed', 'Deaths', 'Recovered', 'Active'])
full_data_set_grouped_country = plot_country(['China'], ['Confirmed_Pct'])
full_data_set_grouped_country = plot_country(['China'], ['Confirmed', 'Deaths', 'Recovered', 'Active'])
full_data_set_grouped_country = plot_country(['United Kingdom'], ['Confirmed', 'Deaths', 'Active'])
full_data_set_grouped_country.sort_values(['Date']).tail(40)
full_data_set_grouped_country = plot_country(['Portugal'], ['Confirmed', 'Deaths', 'Recovered', 'Active'])
full_data_set_grouped_country = plot_country(['Austria'], ['Confirmed', 'Deaths', 'Recovered', 'Active'])
full_data_set_grouped_country = plot_country(['South Korea'], ['Confirmed', 'Deaths', 'Recovered', 'Active'])
full_data_set_grouped_country = plot_country(['France'], ['Confirmed', 'Deaths', 'Recovered', 'Active'])
full_data_set_grouped_country = plot_country(['Italy'], ['Confirmed', 'Deaths', 'Recovered', 'Active'])
# ### Create a graph for each country
# !mkdir export
# !rm -rf export/images
# !mkdir export/images
plt.rcParams.update({'figure.max_open_warning': 0})
all_countries = full_data_set_grouped['Country_Region'].unique()
# %%capture
for country in all_countries:
plot_country([country], ['Confirmed', 'Deaths', 'Recovered', 'Active'], save_fig=True);
# ### Generate HTML
def escape_country_name(c):
return c.strip()
def generate_country_list():
country_list = ''
for c in all_countries:
c_strip = escape_country_name(c)
country_list += f"<li class='list-group-item'><a href='#{c_strip}'>{c_strip}</a></li>"
return country_list
def generate_country_plots():
country_plots = ''
for i, c in enumerate(all_countries):
if i % 2 == 0:
country_plots += '<div class="row">'
c_strip = escape_country_name(c)
country_plots += f'''
<div class="col-md-5">
<a id="{c_strip}">
<img class="img-fluid" src="../images/{c_strip}.jpg?token=<PASSWORD>" />
</a>
</div>
'''
if i % 2 == 1:
country_plots += '</div>'
return country_plots
now = datetime.datetime.now()
template = (f'''
<!DOCTYPE html>
<html>
<head>
<style>
#topButton {{
display: none; /* Hidden by default */
position: fixed; /* Fixed/sticky position */
bottom: 20px; /* Place the button at the bottom of the page */
right: 30px; /* Place the button 30px from the right */
z-index: 99; /* Make sure it does not overlap */
border: none; /* Remove borders */
outline: none; /* Remove outline */
background-color: red; /* Set a background color */
color: white; /* Text color */
cursor: pointer; /* Add a mouse pointer on hover */
padding: 15px; /* Some padding */
border-radius: 10px; /* Rounded corners */
font-size: 18px; /* Increase font size */
}}
</style>
<link rel="stylesheet" href="https://maxcdn.bootstrapcdn.com/bootstrap/4.0.0/css/bootstrap.min.css" integrity="<KEY>" crossorigin="anonymous">
</head>
<body>
<div class="container-fluid">
<h2>Covid-19 cases around the world</h2>
<p>Data sourced from John Hopkins Github repository at <a href='https://github.com/CSSEGISandData/COVID-19'>https://github.com/CSSEGISandData/COVID-19</a></p>
<p><small>Last updated: {now.strftime("%d-%b-%Y (%H:%M:%S)")}</small></p>
<div class="row">
<div class="col-md-2">
<ul class="list-group">
{generate_country_list()}
</ul>
</div>
<div class="col-md-10">
{generate_country_plots()}
</div>
</div>
</div>
<button class="btn btn-primary" id="topButton" onclick="javascript: topFunction()">Go to top</button>
<script>
//Get the button:
mybutton = document.getElementById("topButton");
// When the user scrolls down 20px from the top of the document, show the button
window.onscroll = function() {{scrollFunction()}};
function scrollFunction() {{
if (document.body.scrollTop > 20 || document.documentElement.scrollTop > 20) {{
mybutton.style.display = "block";
}} else {{
mybutton.style.display = "none";
}}
}}
// When the user clicks on the button, scroll to the top of the document
function topFunction() {{
document.body.scrollTop = 0; // For Safari
document.documentElement.scrollTop = 0; // For Chrome, Firefox, IE and Opera
}}
</script>
</body>
</html>
''')
# !rm -rf export/html
# !mkdir export/html
with(open('export/html/index.html', 'w')) as f:
f.write(template)
# !tar -czvf export.tgz export
|
nbs_gil/covid19/john_hopkins_dataset_creation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Step 0.0. Install LightAutoML
# Uncomment if doesn't clone repository by git. (ex.: colab, kaggle version)
# +
# #! pip install -U lightautoml
# -
# # Step 0.1. Import necessary libraries
# +
# Standard python libraries
import logging
import os
import time
import requests
logging.basicConfig(format='[%(asctime)s] (%(levelname)s): %(message)s', level=logging.INFO)
# Installed libraries
import numpy as np
import pandas as pd
from sklearn.metrics import roc_auc_score, log_loss
from sklearn.model_selection import train_test_split
import torch
# Imports from our package
from lightautoml.automl.base import AutoML
from lightautoml.automl.blend import WeightedBlender
from lightautoml.ml_algo.boost_lgbm import BoostLGBM
from lightautoml.ml_algo.linear_sklearn import LinearLBFGS
from lightautoml.ml_algo.tuning.optuna import OptunaTuner
from lightautoml.pipelines.features.lgb_pipeline import LGBSimpleFeatures, LGBAdvancedPipeline
from lightautoml.pipelines.features.linear_pipeline import LinearFeatures
from lightautoml.pipelines.ml.base import MLPipeline
from lightautoml.pipelines.selection.importance_based import ModelBasedImportanceEstimator, ImportanceCutoffSelector
from lightautoml.reader.base import PandasToPandasReader
from lightautoml.tasks import Task
from lightautoml.utils.profiler import Profiler
from lightautoml.utils.timer import PipelineTimer
# -
# # Step 0.2. Parameters
N_THREADS = 8 # threads cnt for lgbm and linear models
N_FOLDS = 5 # folds cnt for AutoML
RANDOM_STATE = 42 # fixed random state for various reasons
TEST_SIZE = 0.2 # Test size for metric check
TIMEOUT = 600 # Time in seconds for automl run
TARGET_NAME = 'TARGET' # Target column name
# # Step 0.3. Fix torch number of threads and numpy seed
np.random.seed(RANDOM_STATE)
torch.set_num_threads(N_THREADS)
# # Step 0.4. Change profiling decorators settings
# By default, profiling decorators are turned off for speed and memory reduction. If you want to see profiling report after using LAMA, you need to turn on the decorators using command below:
p = Profiler()
p.change_deco_settings({'enabled': True})
# # Step 0.5. Example data load
# Load a dataset from the repository if doesn't clone repository by git.
DATASET_DIR = './example_data/test_data_files'
DATASET_NAME = 'sampled_app_train.csv'
DATASET_FULLNAME = os.path.join(DATASET_DIR, DATASET_NAME)
DATASET_URL = 'https://raw.githubusercontent.com/sberbank-ai-lab/LightAutoML/master/example_data/test_data_files/sampled_app_train.csv'
# +
# %%time
if not os.path.exists(DATASET_FULLNAME):
os.makedirs(DATASET_DIR, exist_ok=True)
dataset = requests.get(DATASET_URL).text
with open(DATASET_FULLNAME, 'w') as output:
output.write(dataset)
# +
# %%time
data = pd.read_csv(DATASET_FULLNAME)
data.head()
# -
# # Step 0.6. (Optional) Some user feature preparation
# Cell below shows some user feature preparations to create task more difficult (this block can be omitted if you don't want to change the initial data):
# +
# %%time
data['BIRTH_DATE'] = (np.datetime64('2018-01-01') + data['DAYS_BIRTH'].astype(np.dtype('timedelta64[D]'))).astype(str)
data['EMP_DATE'] = (np.datetime64('2018-01-01') + np.clip(data['DAYS_EMPLOYED'], None, 0).astype(np.dtype('timedelta64[D]'))
).astype(str)
data['constant'] = 1
data['allnan'] = np.nan
data['report_dt'] = np.datetime64('2018-01-01')
data.drop(['DAYS_BIRTH', 'DAYS_EMPLOYED'], axis=1, inplace=True)
# -
# # Step 0.7. Create fake multiclass target
data[TARGET_NAME] = np.where(np.random.rand(data.shape[0]) > .5, 2, data[TARGET_NAME].values)
data[TARGET_NAME].value_counts()
# # Step 0.8. (Optional) Data splitting for train-test
# Block below can be omitted if you are going to train model only or you have specific train and test files:
# +
# %%time
train_data, test_data = train_test_split(data,
test_size=TEST_SIZE,
stratify=data[TARGET_NAME],
random_state=RANDOM_STATE)
logging.info('Data splitted. Parts sizes: train_data = {}, test_data = {}'
.format(train_data.shape, test_data.shape))
# -
train_data.head()
# # ========= AutoML creation =========
#
# 
#
#
# ## Step 1. Create Timer for pipeline
#
# Here we are going to use strict timer for AutoML pipeline, which helps not to go outside the limit:
# +
# %%time
timer = PipelineTimer(600, mode=2)
# -
# ## Step 2. Create feature selector
# +
# %%time
timer_gbm = timer.get_task_timer('gbm') # Get task timer from pipeline timer
feat_sel_0 = LGBSimpleFeatures()
mod_sel_0 = BoostLGBM(timer=timer_gbm)
imp_sel_0 = ModelBasedImportanceEstimator()
selector_0 = ImportanceCutoffSelector(feat_sel_0, mod_sel_0, imp_sel_0, cutoff=0, )
# -
# ## Step 3.1. Create GBMs pipeline for AutoML
# Our GBMs ML pipeline:
# - Advanced features for gradient boosting built on selected features (using step 2)
# - 2 different models:
# * LightGBM with params tuning (using OptunaTuner)
# * LightGBM with heuristic params
#
# +
# %%time
feats_gbm_0 = LGBAdvancedPipeline(top_intersections=4,
output_categories=True,
feats_imp=imp_sel_0)
timer_gbm_0 = timer.get_task_timer('gbm')
timer_gbm_1 = timer.get_task_timer('gbm')
gbm_0 = BoostLGBM(timer=timer_gbm_0)
gbm_1 = BoostLGBM(timer=timer_gbm_1)
tuner_0 = OptunaTuner(n_trials=20, timeout=30, fit_on_holdout=True)
gbm_lvl0 = MLPipeline([
(gbm_0, tuner_0),
gbm_1
],
pre_selection=selector_0,
features_pipeline=feats_gbm_0,
post_selection=None
)
# -
# ## Step 3.2. Create linear pipeline for AutoML
# Our linear pipeline:
# - Using features, special for linear models
# - LinearLBFGS as a model
# - Without feature selection here
# +
# %%time
feats_reg_0 = LinearFeatures(output_categories=True,
sparse_ohe='auto')
timer_reg = timer.get_task_timer('reg')
reg_0 = LinearLBFGS(timer=timer_reg)
reg_lvl0 = MLPipeline([
reg_0
],
pre_selection=None,
features_pipeline=feats_reg_0,
post_selection=None
)
# -
# ## Step 4. Create multiclass task and reader
# +
# %%time
task = Task('multiclass', metric = 'crossentropy', )
reader = PandasToPandasReader(task = task, samples = None, max_nan_rate = 1, max_constant_rate = 1,
advanced_roles = True, drop_score_co = -1, n_jobs = 4)
# -
# ## Step 5. Create blender for 2nd level
# To combine predictions from different models into one vector we use WeightedBlender:
# +
# %%time
blender = WeightedBlender()
# -
# ## Step 6. Create AutoML pipeline
# +
# %%time
automl = AutoML(reader=reader, levels=[
[gbm_lvl0, reg_lvl0]
], timer=timer, blender=blender, skip_conn=False)
# -
# ## Step 7. Train AutoML on loaded data
# In cell below we train AutoML with target column `TARGET` to receive fitted model and OOF predictions:
# +
# %%time
oof_pred = automl.fit_predict(train_data, roles={'target': TARGET_NAME})
logging.info('oof_pred:\n{}\nShape = {}'.format(oof_pred, oof_pred.shape))
# -
# ## Step 8. Predict to test data and check scores
# +
# %%time
test_pred = automl.predict(test_data)
logging.debug('Prediction for test data:\n{}\nShape = {}'
.format(test_pred, test_pred.shape))
logging.info('Check scores...')
logging.info('OOF score: {}'.format(log_loss(train_data[TARGET_NAME].values, oof_pred.data)))
logging.info('TEST score: {}'.format(log_loss(test_data[TARGET_NAME].values, test_pred.data)))
# -
# ## Step 9. Check AUCs for each class in train and test data
for dat, df, name in zip([oof_pred, test_pred], [train_data, test_data], ['train', 'test']):
logging.debug('Check aucs {0}...'.format(name))
for cl in range(3):
sc = roc_auc_score((df[TARGET_NAME].values == cl).astype(np.float32), dat.data[:, cl])
logging.info('Class {0} {1} auc score: {2}'.format(cl, name, sc))
# ## Step 10. Profiling AutoML
# To build report here, we must turn on decorators on step 0.4. Report is interactive and you can go as deep into functions call stack as you want:
# %%time
p.profile('my_report_profile.html')
assert os.path.exists('my_report_profile.html'), 'Profile report failed to build'
# # Appendix. Profiling report screenshots
# After loading HTML with profiling report, you can see fully folded report (please wait for green LOAD OK text for full load finish). If you click on triangle on the left, it unfolds and look like this:
#
# <img src="imgs/tutorial_3_initial_report.png" alt="Initial profiling report" style="width: 500px;"/>
#
# If we go even deeper we will receive situation like this:
#
# <img src="imgs/tutorial_3_unfolded_report.png" alt="Profiling report after several unfoldings on different levels" style="width: 500px;"/>
#
|
Tutorial_3. Multiclass task.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Perform MC simulation on the NPT ensemble using HOOMD-Blue and user defined potential (hard sphere double ramp Jagla model)
# ### Import necessary libraries and initialise hoomd on CPU.
import hoomd
import hoomd.hpmc
import hoomd.jit
import hoomd.hpmc.field
import numpy as np
import ase
import ase.io
from matplotlib import pyplot
hoomd.context.initialize('--mode=cpu');
# ### Input parameters: temperature, pressure and initial xyz configuration ###
# Note that the temperature is set by scaling the Jagla parameters appropriately - this is down when initialising the potential.
# Give the pressure value as in Jagla parameters - it is converted to hoomd units later.
at=ase.io.read("Jagla_hoomd_LDliq_N585.extxyz")
Temp=0.375 # temperature
Press=0.1 # pressure
# create HOOMD system
cell = at.get_cell()
pos = at.get_positions()
nd = 1 # if reading in a smaller cell, it can be multiplied to create a larger simulation box.
uc = hoomd.lattice.unitcell(N=len(at),
a1=cell[0],
a2=cell[1],
a3=cell[2],
dimensions=3,
position=pos,
type_name=['A']*len(at));
system = hoomd.init.create_lattice(unitcell=uc, n=[nd, nd, nd]);
# set HOOMD MC integrator
# initial stepsize = d
mc = hoomd.hpmc.integrate.sphere(seed=96241, d=0.1)
# hard sphere diameter = diameter
mc.shape_param.set('A', diameter=1.0)
mc.set_params(nselect=1)
# ### Jagla potential - set parameters
#
# ``patch.alpha_iso[0]`` = depth of potential well and ``patch.alpha_iso[1]`` = height of the repulsive ramp. In order to control the temperature of the simulation the calculation corresponds to, both of these parameters are divided by ``Temp``.
#
# ``r_cut`` = cutoff distance the potential is truncated
# +
# T* = kT/E
Jagla = """float rsq = dot(r_ij, r_ij);
if (sqrt(rsq) >= 1.72f)
return -alpha_iso[0] + alpha_iso[0]*((sqrt(rsq)-1.72f)/(3.0f-1.72f));
else
return alpha_iso[1] - ( alpha_iso[1] + alpha_iso[0]) * (sqrt(rsq) - 1.0f)/(1.72f-1.0f);
"""
patch = hoomd.jit.patch.user(mc=mc, r_cut=3.0, array_size=2, code=Jagla)
patch.alpha_iso[0]=1.0/Temp
patch.alpha_iso[1]=3.5/Temp
print(patch.alpha_iso)
# +
## Alternative potential model: Stepwise version of the Jagla model used e.g. in
## Luo et al. JOURNAL OF CHEMICAL PHYSICS 142, 224501 (2015)
#
## T* = kT/E
#Jagla_step = """float rsq = dot(r_ij, r_ij);
# if (sqrt(rsq) >= 1.8f)
# return -alpha_iso[0] + ((ceil((100.0*sqrt(rsq)-180.0)/16)))*0.125;
# else if (sqrt(rsq) > 1.72f && sqrt(rsq) < 1.80f)
# return -alpha_iso[0];
# else
# return alpha_iso[1]-((ceil((100.0*sqrt(rsq)-100.0)/2))-1)*0.125;
# """
#
#patch = hoomd.jit.patch.user(mc=mc, r_cut=3.0, array_size=2, code=Jagla_step)
#patch.alpha_iso[0]=1.0/Temp
#patch.alpha_iso[1]=3.5/Temp
#print(patch.alpha_iso)
# -
# quantities to be logged during MC run
quantities=["hpmc_patch_energy","volume","hpmc_overlap_count","pressure",'lx','ly','lz']
logfilename="LDliq_N585.out"
log = hoomd.analyze.log(filename=logfilename,quantities=quantities,period=100)
# set constant pressure and allow change of the simulation box
betap = Press/Temp # see HOOMD manual: betap=p/(k_t*T)
boxmc = hoomd.hpmc.update.boxmc(mc, betaP=betap, seed=74)
# set the stepsize for atom moves
mc.set_params(d=0.13)
# volume moves, stepsize controlled by delta, weight is the frequency of this type of box change
boxmc.volume(delta=10.0,weight=1.0)
# box length moves, stepsize controlled by a delta in each dimension,
# weight is the frequency of this type of box change. If zero, the shape of the box is kept constant.
boxmc.length(delta=(0.0,0.0,0.0), weight=0.0)
# ### Run simulation ###
hoomd.run(500)
# current state of the simulation
U = log.query(quantity="hpmc_patch_energy") # potential energy (this is scaled by Temp!)
OC = log.query(quantity="hpmc_overlap_count") # overlap count of hard spheres (should be zero)
V = log.query(quantity="volume") # volume of simulation box
print(U, OC, V)
data = np.genfromtxt(fname=logfilename, skip_header=True)
pyplot.figure(figsize=(8,4), dpi=100)
pyplot.plot(data[:,2]/len(at))
pyplot.grid(color='k', linestyle='-', linewidth=0.1)
pyplot.xlabel('MC step/100')
pyplot.ylabel('Volume/atom')
def save_config(hoomd_system,atom_types=["H"]):
lattice=np.array([hoomd_system.box.get_lattice_vector(i=i) for i in range(3)])
x2 = int(lattice[[0],[0]]) / 2
y2 = int(lattice[[1],[1]]) / 2
z2 = int(lattice[[2],[2]]) / 2
ase_atoms=ase.Atoms(pbc=[(True,True,True)],cell=lattice)
for i in range(system.particles.types.pdata.getN()):
i_type = hoomd_system.particles.types.pdata.getType(i)
i_pos = hoomd_system.particles.pdata.getPosition(i)
i_pos.x = i_pos.x + x2 ; i_pos.y = i_pos.y + y2 ; i_pos.z = i_pos.z + z2
ase_atoms.append(ase.Atom(atom_types[i_type],position=[i_pos.x,i_pos.y,i_pos.z]))
return ase_atoms
current_config = save_config(system)
ase.io.write("Jagla_LDliq_N585.final.extxyz", current_config)
|
HOOMD_simulation_scripts/hoomd_Jagla_NPT.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.8 64-bit (''base'': conda)'
# name: python3
# ---
# # Python Basics
# ## What is Python?
#
# Python is an interpreted high-level programming language that converts human-friendly commands into computer instructions. This means that it takes human-readable code as input and then interprets the code into machine language. In a sense, other computer languages involve a similar process; however languages like C/C++ or Fortran are much more efficient at it. But, those languages are categorized as compiled languages because they are converted to machine code once the compilation process is complete. Python programs are analyzed by the interpreter "on the fly", which causes Python to run much slower. Luckily, hardware and software (OS) improvements have been so dramatic over the past 30+ years that the hit to performance is not as noticeable. The advantage to coding in an interpreted language is that it is easier to tweak and debug because the variables are stored in local memory and there is no need to re-compile with every change.
#
# Additionally, Python can be easily run from the command-line, which allows users to experiment with Python commands without having to create a fully fledged program. For this course, we will make use of Juptyer notebooks, which are similar to notebooks in Mathematica. In the previous chapter, we experimented with storing variables and creating a numpy array. Python can be used for arthimetic tasks as well. Try this:
x = 4
y = 16
x*y
x**y
y/x
# In the first line, the notebood stores the integer (*int*) 4 into memory and gives it a label 'x', where in the second line a similar action is performed where the label is 'y'. Under most conditions, Python will assume the number is an 64-bit integer when there is not a decimal point. The product of two integers is also an integer and hence, the operation x*y returns 64 as an integer.
#
# An integer raised to an integer power (Note: Python uses \*\* for exponents instead of ^) is simply the repeated product of integers. Therefore x\*\*y is equivalent to $4^{16}$ and Python returns a large integer. The division of two numbers can sometimes be confusing for the interpreter and depend on the version of Python. In the past, the division of two integers would return an integer (e.g., 4/2 = 2), but **what would happen for 2/4**?
#
# A good practice is to use the decimal point during multiplaction or division. This removes the ambiguity for the interpreter and forces it to return a floating point number (*float*). For example:
int(2/4)
2./4.
# You may be asking where this might be important. Python includes a function for square root (e.g., $\sqrt{x}$ = sqrt(X)), but not for higher roots. Some Python (and C) programs will change 1/3 from a cube root into 0 and return 1.
# ## Comments
#
# Every programming language allows for the programmer to leave notes (or comments) within the code. Adding comments to your code is very important because
#
# - You and *future you* need to communicate; It is not uncommon to write some code and comeback to it more than 6 months later. After which, some unkind words maybe directed at *past you* from yourself for not leaving comments.
# - The *future person* to read the code may not be *future you* and they will not konw what you were thinking.
#
# Comments can be designated with the \# (hashtag) symbol, where the text that follows it is ignored by the interpreter until the next line. However this can be impractical if you are providing a description of a function that takes many lines. In this case, three \' (apostrophe) symbols are used to begin a *block comment*, where another three \' symbols are needed to end the block comment. Otherwise, the interpeter will either return an error or not do anything at all.
# ## Simple Input \& Output
#
# In the previous chapter, we read from a file using the *genfromtxt* function from Numpy, but you may want to take in some user input "on the fly". This can be accomplished using the *input* function, where you will need to designate a variable to store the user input. For example:
name = input("What is your name?")
print(name)
quest = input("What is your quest?")
print(quest)
airspeed = input("What is the airspeed of a laden swallow?")
print(airspeed, type(airspeed))
# Notice in the above examples that *input* stored the user input as a string of characters (*string* or *str*).
#
# Output can be directed to a file or the command prompt. For the command prompt, you can print stored variables using the *print* function. To determine the data type of a stored variable, use the *type* function. *Note: that type can return datatypes like ndarray for numpy array as well as string, int, or float.*
#
# Printing variables isn't limited to strings, but can be useful for probing numerical variatbles when debugging your code. For example, you might think your code is doing one thing, when in fact it is doing something else entirely. Python borrows a print syntax that is simlar to the one used in C/C++ programs. Let's look at the value of $\pi$.
import numpy as np
pi = np.pi
print(pi)
# In the above code, we imported the `numpy` module and gave it a label *np* for easier referencing. Then, the value of $\pi$ from numpy was stored as a float in the variable `pi`. Finally, $\pi$ was printed in machine (or double) precision (15 decimal places). *Note that some versions of Python default to single precision (8 decimal places).*
#
# Maybe we want to know $\pi$ to a four decimal places, as an integer, or in scientific notation. Then we can use the following:
"Pi to 4 decimal places is: %1.4f" % pi
"Pi as an integer is: %d" % pi
"10*Pi to 8 decimal places, but in Scientific Notation is: %1.8e" % (10*pi)
# Some of the common string formatting indicators are:
#
# | Format | Description |
# |--------|-------------|
# |%xd | Integer value with the total width *x*|
# |%x.yf | Floating point value with a pre-allocated width *x* and *y* decimal places. Note the total width will be expanded so that it includes the decimal places and the decimal point can count towards the total width.|
# |%x.ye | Scientific (exponential) notation with the total width *x* and *y* decimal places.|
# |%xs | String of characters with total width *x*|
#
# Python 3 introduced a new way to format strings using the *format* function. Let's use the example that `6 bananas cost \$1.74`
print('{0} {1} cost ${2}'.format(6,'bananas',1.74))
# 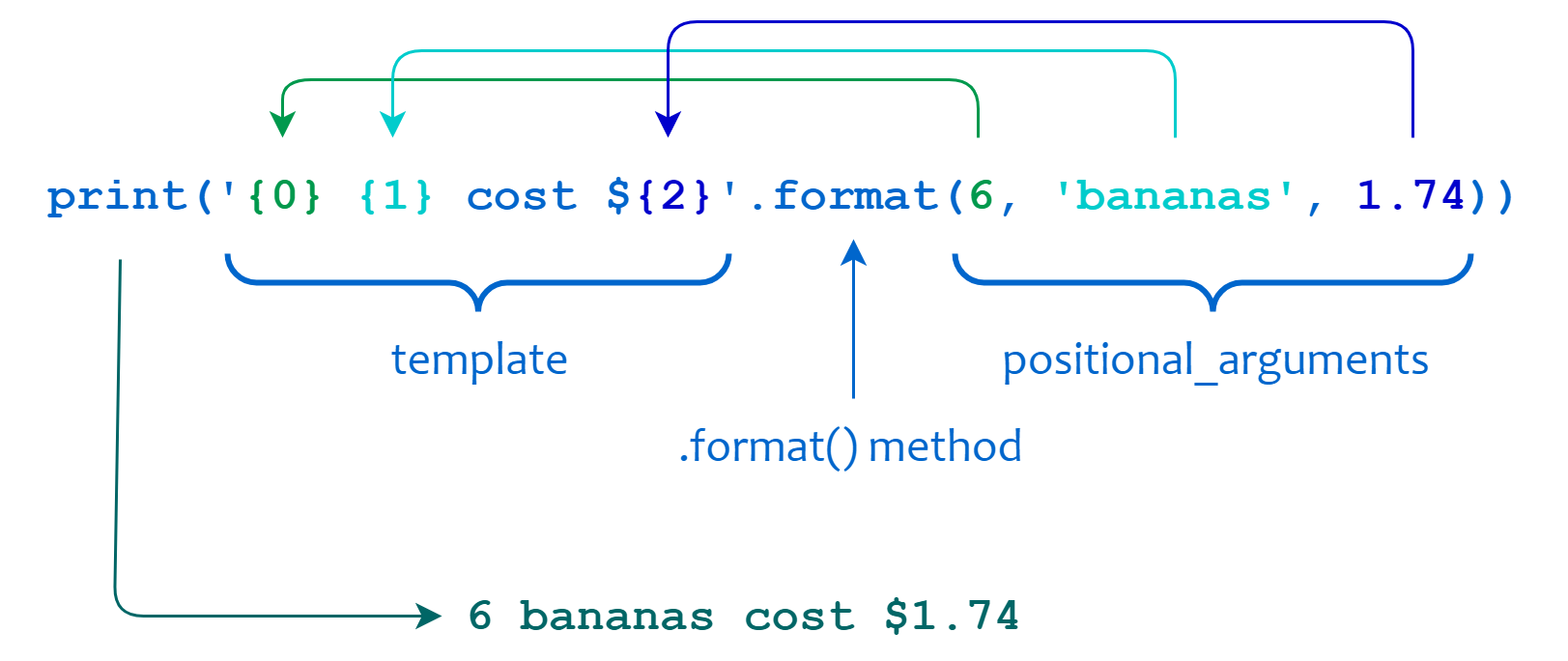|
# |:--:|
# |Example taken from [realpython.com](https://realpython.com/python-formatted-output/)|
#
# We can obtain the same functionality in defining the number formatting using `:x.yf` after the position in the {} of the format template.
print('{0:1d} {1} cost ${2:1.2f}'.format(6,'bananas',1.74))
# ## Variable Types
#
# Thus far, I hinted at the different types of variables in Python. Those are the typical variables that exist in all programming languates. However, there are two broad divisions in variable types in Python: a) *numeric* and *sequence* types. Numeric types hold a single number, such as an integer, floating point number, or a complex number (e.g., 2-3*i*). Sequence types hold multiple objects (imagine a filled grocery bag), which could be single numbers, characters, or even collections of different things.
#
# - Numeric Types
# - **Integer**: The integer is the simplest numeric type in Python. They are useful for counting items or tracking indices in an array. The maximum 32 bit integer is $2^{31}$ - 1 = 2,147,483,647
# - **Long Integer**: Integers larger than $2^{31}$ - 1 are stored automatically as long integers. When you use the *type* function on them, there is a trailing "L" to indicate it is a long integer.
# - **Float**: The *floating point* type is a number containing a decimal point. Floats require more memory to store and are slower in calculations. Python upconverts variable types (recall the 1/2 = 0 vs 1./2 = 0.5 distinction).
# - **Complex**: Complex numbers are naturally included in Python, but uses $j\equiv\sqrt{-1}$. For example, $x=0.5+1.2j$ is a valid complex number.
# - Sequence Types
# - **Tuple**: Tuples are indicated by parentheses (). Items in tuples can be any other data type, including other tuples. Tuples are *immutable*, meaning that once defined their contents cannot change.
# - **List**: Lists are indicated by square brackets [] and are almost the same as tuples. However, lists are *mutable*: individual items in a list can be changed.
# - **String**: A string is a sequence of characters. Strings are surrounded by either double \" or single \' quotes. Strings are *immutable* (like tuples), but can only include characters.
# - *Reserved characters*: Some characters are reserved (like \# for comments), but can be used with an escape \\.
# - *Tab and Newline*: To indicate a <tab> character, use an escape \\ + t ("\t"). A similar approach is used for a newline ("\n").
# - **Dictionary**: Dictionaries are indicated by curly brackets {}. The are different because they use "keys" (which are string labels) instead of numeric indices. Dictionaries are useful when managing data, where you want to assign the column header of a table as the key instead of referencing the column index.
#
# Here are some examples of sequence types
# +
Pythons = ("Cleese", "Palin", "Idle", "Chapman", "Jones", "Gilliam")
#Note that the index counting begins from zero and counting can be startied \
# from the end of the type using negative numbers (starting from 1)
print(Pythons[0],Pythons[2],Pythons[-1])
#One can also specify a slice of a sequence, where slices start on the first\
# index : terminate when reaching the second index (but do not include it)
print(Pythons[1:3])
#Let's see what happens if we try to replace an element of a tuple
Pythons[1] = "Atkinson"
# -
print("Pythons is a tuple and immutable; Let's change it to a list with []")
Pythons = ["Cleese", "Palin", "Idle", "Chapman", "Jones", "Gilliam"]
#Let's see what happens if we try to replace an element of a list
Pythons[1] = "Atkinson"
print(Pythons)
# Another example is creating a 2-dimensional array or matrix
matrix = [[1,2,3],[4,5,6],[7,8,9]]
#matrix is list of lists, where each row is its own list (columns)
print(matrix)
# Think about how to reference values constructed as a list of lists like `matrix`. **How can we reference `5`?** (Remember that indices start from zero!)
matrix[1]
print(matrix[1][1])
matrix[1][1] = 0
print(matrix[1][1])
# This type of list construction requires the [i][j] method of indexing and it applies to tuples of tuples as well. This is a little clumsy, where we it would be clearer to have [i,j] indexing, where i=>row and j=>column. This can be accomplished by converting `matrix` from a list into a Numpy matrix. (Recall that the numpy module was loaded earlier when converting strings.)
matrix = np.matrix(matrix)
print(matrix)
#Notice that the commas have been removed and the matrix starts \
# looking like a more traditional matrix
print("The element in the 0th row and 2nd column is: ",matrix[0,2])
# ### Sequence Tricks
#
# If you are needing to store of *N* numbers, but don't know the values beforehand. Here are two ways:
#
# 1. Create an empty list with the needed length
# 2. Create an empty array filled with ones/zeros
# +
N = 5
LongList = [None]*N
LongList[3] = np.pi
print(len(LongList),LongList)
LongList = np.zeros(N) #Note that this overwrites the previous variable
LongList[2] = np.pi/2
print(len(LongList),LongList)
# -
# where it depends on what you want to store. Approach #1 would be more useful if you were storing strings or different data types. Sometimes you may not know exactly how many list elements you need until after the fact. Elements can be added to the end of a list using the **[list].append()** function. Here's an example:
Values = []
print(Values)
#Some calculation is done and you need to store NewValue into the Values list for later
NewValue = 4
#The append function acts on the list object *Values* and takes the NewValue as input
Values.append(NewValue)
print(Values)
# Notice that we started with an *empty* list. In this case appending to it just adds one element. **Go back and fill Values with a few numbers. Then re-run the cell.** Now you can see the NewValue is indeed added to the end of the list.
# Another handy trick is sorting. There are two types of sorting: in-place (sort) or return (sorted). In some cases you may want to sort a list but also want to preserve the original list; this is where the second option becomse useful. Luckily, these two options are implemented differently to help distinguish between them. The **sort** function acts on a list object, where the **sorted** function takes the list as an argument (input) to return.
# +
ValueData = [5,3,7,6,2,7,2,9,4,0]
StringData =["Tommy","Dick","Harry","Sally","Mary","Nina"]
New_ValueData = sorted(ValueData) #returning the sorted list into a new variable
print("The original list: ",ValueData)
print("The sorted list: ", New_ValueData)
ValueData.sort()
print("Sorting in-place using sort: ",ValueData)
StringData.sort()
print("Sorting strings in-place: ", StringData)
ValueData[4] = StringData[3]
print("Replacing an element of ValueData with a string: ",ValueData)
# -
# The last two lines mixed the data types so that a string is now in the list of values. **Do you think a sort will work?**
# ### Iterables
#
# Python allows for special functions called *iterables* that can contain the instructions to generate a list without allocating the memory. A common iterable is the **range** function, which generates a list of *integers* given three parameters: starting value, stopping value, and increment (must be an integer). This is especially useful if you need to quickly generate a range of indices for a process or array.
#Create a list of 100 numbers for a graph axis
axis = list(range(0,100))
print(axis)
#Create a list of even numbers from 6 up to 17.
Evens = list(range(6,17,2))
print(Evens)
# We often need a more flexible means of generating a list of values. *Suppose that we want to generate a list of floating point numbers.* The previous trick can be modified.
# +
axis = [0.02 * i for i in range(0,100)]
#Only printing the first 10 values for this example
print(axis[:10])
#Another way is to use the **arange** function from Numpy, \
# where the difference is whether you need a list or array returned
np_axis = np.arange(0,100,0.02)
print(np_axis[:10])
# -
# List can become iterables themselves too.
# +
new_axis = [a*10 for a in axis]
print(new_axis[:10])
#Notice that some values are not exact.
#Axis was stored in memory as floating point numbers with \
# limited precision
#Iterating over floats like this can generate some \
# unexpected results due to the limitation of numerical precision
# -
# ## Mathematical Operators
#
# Thus far, you have seen typical arithmetic operators +-*/ on numerical values. However, these operators don't work the same way with lists. The + operator for two lists does not add them together, rather it **concatenates** them (i.e., joins the lists). A simliar process occurs with strings because they are lists of characters. The * operator makes copies of lists instead of multiplying the elements.
#
# Division (/) has a few quirks, where it works fine for floats. But it does *third-grade* math for integers (i.e., the result is the integer portion of the actual answer). There are instances when you might want the *third-grade* math behavior for floats, in which case you can use the floor division (//) operator. At the beginning of this chapter, you saw that ** is responsible for exponentiation. The modulo operator (%) returns the remainder, although it was also used for string conversions.
# +
#Examples of Operators
String_a = "<NAME>"
String_b = " went up the hill"
print(String_a + String_b) #Concatenation of strigs using +
List_a = ["Jack","and","Jill"]
List_b = ["went","up","the","hill"]
print(List_a+List_b) #Concatenation of lists using +
print(10//4)
print(2**4)
remainder = 10 % 3
print("Remainder of 10 % 3 is: ",remainder)
# -
# There are also some shortcut operators, that help reduce the amount of code. *Suppose you want to increment a counter*. The += operator is a shortcut for when you want to perfom an addition and immediately replace the value stored in the variable. Similar operators exist for other arithmetic operators as *=, /=, or -=. These operators are best for people to generate code more quickly, but do not affect the speed of the code. Sometimes they make the code harder to read by others, so use them cautiously.
#Create a counter and increment it
counter = 0
print("The initial value is ", counter)
counter = counter + 1 #this is the long way
print("The next value is ", counter)
counter += 1 #this is the short way
print("The next value is ", counter)
# ## Lines in Python
#
# Python uses spaces and indentation as part of the syntax. This is in contrast to C/C++, Fortran, or JAVA that use (), {}, or ; to separate out bits of code. The Python interpreter actually cares about blank spaces before commands on a line. As a result, there are two types of lines: **physical** or **logical** lines.
# +
#Show the differences between a physical line and a logical line
x = "This line is a physical line and a logical line"
print(x)
x = x.split() #The split function helps split a string into a list
print(x)
#Note that the \ at the end of a line creates a soft line \
# break (i.e., breaks the physical line, but not the logical one);
x = "this line is multiple \
physical lines but is \
just one logical line"
print(x)
x = x.split()
print(x) #Notice that split removes the extra spaces
# -
# ## Control Structures
#
# Control statements direct or modify the flow of logic within a program thereby allowing the program to be flexible depending on what happens. For example, "If you are hungry, then eat lunch" is a control statement. Control statements require a conditional (boolean) to evaluate before taking an action. Most control statments have a clear end point, where **While** does not (be careful with while loops).
#
# Conditionals
# A conditional is anything that can be evaluated as either **True** or **False**. In Python, the following things are always False:
# - The word **False** (note the captialization)
# - 0, 0L, or 0.0
# - "" or '' (an empty string)
# - (), [], or {} (an empty sequence)
#
# Almost everything else is True:
# - 1, 3.14, 42 (True because they aren't zero)
# - The word **True** (note the captialization)
# - "False", "0", or [0,False,(),""] (Why are these true?)
#
# Conditionals have operators to evaluate the relationship between objects, which may be true or false.
# - \< Less than
# - \> Greater than
# - \<= Less than including equal to
# - \>= Greater than including equal to
# - == Equal to
# - != **Not** equal to
#
# Note that = is an assignment (i.e., store something to a variable), where == is a conditional (i.e., are two obects congruent). *This is one of the most common bugs in Python programs, where an = is missed.* There are also the boolean operators **and**, **or**, **in** and **not**.
Name = input("What is your name?")
Cast = Pythons
if Name in Cast:
print("Yes, ",Name," is a member of Monty Python")
else:
print("No, you're an impostor!")
# In the above example, there are two print statements. Depending on the user input stored in *Name*, a different print statement is evaluated. This demonstrates the most basic control statement **If...Else**. More generally this can become:
# ```
# if (Check if these are the droids you're looking for): #The colon (:) signifies the end of a conditional
# Grab them
# elif (These might be them): #Check another condition, maybe there are many
# Ask your superiors
# else: #Finally after checking everything else
# Fall for the Jedi mind trick
#
# Go about your business, move along
# ```
# Python uses the indentation to determine where the conditional ends, so the non-indented lines are executed after the conditional statements are checked. In other computer languages, indentation is used to make the code easier to read; but the is a defining trait in Python. **The indentation is not optional**.
#
# The **while** statement is used to repeat a block of commands until a condition is met. The most common example is the instructions given on shampoo.
#
# ```
# while (in the shower):
# extract shampoo from bottle into hand
# apply to hair
# lather
# rinse
# ```
#
# In this statment that instructions are give while the condition (in the shower) is True and repeated until that condition is False. Notice that there is not a conditional to indicate *when to stop*. This is a common bug for new programmers, which results in an **infinite loop** and is most profitable for the shampoo manufacturers. A proper while loop has the following structure:
# ```
# while (in the shower):
# extract shampoo from bottle into hand
# apply to hair
# lather
# rinse
# if (hair is clean):
# get out of the shower!
# ```
# There are a few keywords that can be used in conjuction with a **while** loop.
# - **pass**: The pass keyword does nothing. Its purpose is to take up a line if there is a structural need for one. Sometimes you have a conditional for do something or nothing.
# - **continue**: The continue keyword moves the program execution back to the while (i.e., excludes the lines that come after and increments the loop)
# - **break**: The break keyword moves the program execution to outside the while ("breaks out").
# - **else**: The else command delineate a block of code that is executed only after the while block executes normally (no breaks)
# +
#Create a Python program to determine whether a number is prime. \
# DISCLAIMER: This is not the most efficient way
Number = int(input("What integer do you want to check?")) #need to make sure input is an integer
divisor = 2 #Use this to set floor on numbers to check
#Main loop to test each number
while divisor < Number:
if Number % divisor == 0: #if remainder is zero then Number is divisible by the number in divisor
print(Number," is divisible by ",divisor, " and thus, not prime")
break #since the number is not prime, we can stop (break out)
else:
#The remainder is not zero, we need to check another divisor
divisor += 1
else:
#all the possible divisors were checked and failed
#must be prime
print(Number," is a prime number")
# -
# Sometimes iterating over a sequence is very straight-forward. In that case, the **for** loop is the way to go. The most basic syntax is:
#
# ```
# #Item is a value within the Sequence (number, string, row of a matrix, etc.)
# for Item in Sequence:
# Do something with Item
# ```
# After executing the lines within the for loop, the next Item will be the next value in the Sequence. The most common for is `for i in range(start,stop)`, where the range function generates the sequence and *i* is simply the index within the range. **Make sure that the Sequence is not being changed within the for loop**.
# ## Functions
# ### Defining a function
# A **function** is a bit of code that you want to use more than once. It can be a calculation, such as find the distance between two points, or it could be an action like draw a graph or save some data to a file. Functions are defined using **def** and the function name must start with a letter, while the rest of the name can be composed of numbers, letters or underscore. After the function name, there is a set of () that contains a list of input variables that are passed to the function. The def command should end with a colon (:). The lines following the def command are an indented block and non-indented lines (relative to the def command) are outside the function.
#
# Generally, the first line of a function is a comment block that describes the use of the function, including any assumptions for the input variables (e.g., type, format). A function can return a value, but this is not required and depends on the inheritance of variables. The return value can be numerical or a boolean (True or False).
# +
#Write a function that calculates the factorial of a positive integer
def factorial(n):
"""
This function calculates n! by the simplest method imaginable
n: input integer
f: return value
"""
f = 1 #the smallest factorial is 1
for i in range(2,n+1): #starting from 2 and stopping at n
f *= i
return f
#Now that the function is created, you can call on it anytime you need to know the factorial of a number
print("%2s %7s" % ('n','n!'))
for j in range(0,10):
print("%2d %7d" % (j,factorial(j)))
# -
# Functions are often used to reduce the code needed to illustrate the big picture and make it more understandable. You are the boss and you delegate tasks to the functions because the boss can't do everything. Your morning might look like this:
# ```
# if (Time>=Morning):
# GetUp()
# GetDressed()
# EatBreakfast(Spam,eggs,Spam,Spam,Spam,Spam,bacon,baked_beans,Spam)
# else:
# ContinueSleeping()
# ```
# The functions *GetDressed()* and *EatBreakfast()* typically entail many actions (i.e., quite a bit of code); but writing them as separate functions allows one to bury the details. Writing the program as a set of functions gives you a modular flexibility (i.e., easy switching for the order of functions). The variables that are passed into the function only exist while the funciton is active (i.e., *local* variables).
#Here's the function definition
def sq(x):
#returns the square of a number x
x *= x #this step is to show that x is replaced locally
return x
#Here's the main program
x = 3 #first definition of x
print("x^2 = ", sq(x)) #the return squared value is printed
print("x = ",x) #the value of x is printed
# Note that the value of *x* is changed within the function, but the value of *x* is **not** changed in the main program. The reason is that the function stores the value of *x* as a separate copy in memory but uses the same label for the copy.
#
# Functions can have default values built-in, which is handy when on specific parameter doesn't change too much. This is done by puttin gthe value directly into the definition line, like this:
def answer2everything(A=42):
return A
#main program
print(answer2everything())
print(answer2everything("How many roads must a man walk down?"))
# At this point, it should be clear that *local* variables are in use locally. If a Python function can't find the value of some variable, it looks outside the function. This is handy: you can define some constants at the beginning of the program and call upon them whenever they are needed. This is in contrast to older versions of Fortran that required you to carry the variables around and pass to each function. Values used throughout the program are called **global** variables.
#
# *What happens in the function, stays in the function*. At least most of the time. There are occasions where you might want to change a value globally, in which case refer to that variable in the function as a **global**.
# +
a, b, c = 4, 5, 6
def fn(a):
d = a #local copy of the value a that is passed in
a = b #the global value b replaces a
global c #this defines c as a global variable
c = 9 #this changes the value of c everywhere
print("initial values ",a,b,c)
fn(b) #passing in the value of b into the fn (d=a=b=5 inside fn)
print("values after function call ",a,b,c) #What will these values be?
#Can we print d here?
print(d)
# -
# ### Passing functions
# Python treats functions just like any other variable. This means that you can store function in other variables or sequences. Even passing functions into other functions is allowed.
# +
"""
pass_trig.py
Demonstrates Python's ability to store functions as variables and pass those functions to other functions
--Assumes that 'import numpy as np' has been called
"""
import matplotlib.pyplot as plt
def plot_trig(f):
#plots the function f over the range(-pi,pi)
xstep = np.pi/20.
xvals = np.arange(-np.pi,np.pi+xstep,xstep)
ax.plot(xvals,f(xvals),'-',lw=2)
trig_func = (np.sin,np.cos,np.tan) #a tuple holding some trig functions
fig = plt.figure()
ax = fig.add_subplot(111)
for func in trig_func:
#for each trig function test a value and plot a graph
print("function value at pi/6 is: ",func(np.pi/6))
plot_trig(func)
ax.set_xlim(-np.pi,np.pi)
ax.set_ylim(-2,2)
fig.savefig("Trig_pass.png",bbox_inches='tight',dpi=300)
# -
# The functions in this example are stored in a list, referred to as elements in lists, and passed to other functions.
# ## Program Structure
#
# Python programs allow for a lot of flexibility, which is one of its strengths. However, this much freedom can also be a source of confusion. When we develop a program, we must employ some convention to make it easier for others to read and/or use. This is similar to how we choose to write from left to right or drive on the *right* side of the road (those silly Brits). As a result a common program structure is as follows:
#
# ```
# #Program title
# #short description
#
# Import block #all import statements (numpy,scipy,matplotlib,etc.)
#
# Define constants #defining physical constants like G, k, c, etc.
#
# Function block # define each function (preferably in alpha order)
#
# Main program #this is where the magic happens
#
# Program end #sometimes you need to close the opened objects (files, figures, processing pool, etc.)
# ```
#
# ## Problems
# - Complete the following problems in a Jupyter notebook, where you will save your results as an external file (*.png).
# - Create a LaTex document with:
# - an abstract summary
# - sections for each problem that state the problem, summarize what you did, and display the results
# - include a reference for each solution (this can be textbooks)
#
# 1. Create a list holding the squares of the numbers between 10 and 20, including the endpoints.
#
# 2. Write a Python program to print out the first *N* number of the Fibonacci sequence, where *N* is provided by the user and is greater than 2.
#
# 3. Write a Python program that creates two lists (time and height) for a projectile thrown *vertically* at some initial velocity $v_i$. The program should ask the user for the initial height $y_i$ and velocity $v_i$, and produce a table containing 50 data points over 5 seconds.
#
# 4. The energy levels for a quantum particle in a 3D rectangular box of dimensions {$L_1$, $L_2$, and $L_3$} are given by:
# $E = \frac{\hbar^2\pi^2}{2m} \sum_{i=1}^{3} \left(\frac{n_i}{L_i} \right)^2$, where the $n_i\geq 1$ and an integer. Write a program that will calculate, and list in order of increasing energy, the *n*'s for the 10 lowest *different* energy levels, where $L_2 = 2L_1$ and $L_3 = 4L_1$.
#
# 5. Write a function that calculates the value of the *n*th triangular number. Triangular numbers are formed by adding a series of integers {1,n} (see [triangular numbers](https://en.wikipedia.org/wiki/Triangular_number)).
#
# 6. Write a Python program to make an $N \times N$ multiplication table and write this table to a file. Each row in the table should be a single line and tab-delimited. The program size of the table and the filename should be supplied by the user.
|
_build/jupyter_execute/courseware/Chapter_2/Python_Basics.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 基本程序设计
# - 一切代码输入,请使用英文输入法
print ('hello word')
# ## 编写一个简单的程序
# - 圆公式面积: area = radius \* radius \* 3.1415
radius =float ( input ('please input radius'))
#type (radius)
print (radius * radius * 3.1415)
# ### 在Python里面不需要定义数据的类型
# ## 控制台的读取与输入
# - input 输入进去的是字符串
# - eval
age =eval (input ('age'))
print (age)
# - 在jupyter用shift + tab 键可以跳出解释文档
# ## 变量命名的规范
# - 由字母、数字、下划线构成
# - 不能以数字开头 \*
# - 标识符不能是关键词(实际上是可以强制改变的,但是对于代码规范而言是极其不适合)
# - 可以是任意长度
# - 驼峰式命名
# ## 变量、赋值语句和赋值表达式
# - 变量: 通俗理解为可以变化的量
# - x = 2 \* x + 1 在数学中是一个方程,而在语言中它是一个表达式
# - test = test + 1 \* 变量在赋值之前必须有值
# ## 同时赋值
# var1, var2,var3... = exp1,exp2,exp3...
# ## 定义常量
# - 常量:表示一种定值标识符,适合于多次使用的场景。比如PI
# - 注意:在其他低级语言中如果定义了常量,那么,该常量是不可以被改变的,但是在Python中一切皆对象,常量也是可以被改变的
# ## 数值数据类型和运算符
# - 在Python中有两种数值类型(int 和 float)适用于加减乘除、模、幂次
# <img src = "../Photo/01.jpg"></img>
# ## 运算符 /、//、**
# ## 运算符 %
# ## EP:
# - 25/4 多少,如果要将其转变为整数该怎么改写
# - 输入一个数字判断是奇数还是偶数
# - 进阶: 输入一个秒数,写一个程序将其转换成分和秒:例如500秒等于8分20秒
# - 进阶: 如果今天是星期六,那么10天以后是星期几? 提示:每个星期的第0天是星期天
16% 7
'A'*'10'
x=eval(input('x'))
a=(10+x)%7
print('星期',a)
s=eval(input('s'))
a=s//60
b=s%60
print(a,'分',b,'秒')
int (25/4)
25//4
a=eval(input (' a'))
if a%2==0:
print ('偶数')
else :
print ('奇数')
import random
random.randint(1000,10000)
import random
res=random.randint(1000,10000)
print(res)
res1=input('输入验证码:')
if res == int (res1):
print ('ok')
else :
print ('not ok')
# ## 科学计数法
# - 1.234e+2
# - 1.234e-2
# ## 计算表达式和运算优先级
# <img src = "../Photo/02.png"></img>
# <img src = "../Photo/03.png"></img>
# ## 增强型赋值运算
# <img src = "../Photo/04.png"></img>
# ## 类型转换
# - float -> int
# - 四舍五入 round
round(100.0195,2)
# ## EP:
# - 如果一个年营业税为0.06%,那么对于197.55e+2的年收入,需要交税为多少?(结果保留2为小数)
# - 必须使用科学计数法
# # Project
# - 用Python写一个贷款计算器程序:输入的是月供(monthlyPayment) 输出的是总还款数(totalpayment)
# 
# # Homework
# - 1
# <img src="../Photo/06.png"></img>
celsius=eval(input ('celsius'))
fahrenheit = (9 / 5) * celsius + 32
print(fahrenheit)
# - 2
# <img src="../Photo/07.png"></img>
import math
radius,length=eval(input ('radius and length : '))
area=radius*radius*math.pi
volume=area*length
print('The area is ' , str(area)[:7])
print('The volume is' , round(volume,1))
# - 3
# <img src="../Photo/08.png"></img>
a=eval(input('a'))
m=a*0.305
print (a ,'feet is',m,'meters')
# - 4
# <img src="../Photo/10.png"></img>
M,initialTemperature,finalTemperature=eval(input('kilograms')),eval(input('initial temperature')),eval(input('final temperature'))
Q = M * (finalTemperature - initialTemperature) * 4184
print (Q)
# - 5
# <img src="../Photo/11.png"></img>
cae,lilv=eval(input('cae and lilv :'))
lixi = cae * (lilv/1200)
print ('The interest is',round(lixi,5))
# - 6
# <img src="../Photo/12.png"></img>
# +
v0,v1,t=eval(input('v0 and v1 and t : '))
a=(v1-v0)/t
print (round(a,4))
# -
# - 7 进阶
# <img src="../Photo/13.png"></img>
a=eval(input('cunru'))
sum = 0
for i in range(0,6):
sum = (sum+100)* (1+0.00417)
print (str(sum)[:6])
# - 8 进阶
# <img src="../Photo/14.png"></img>
a=eval(input('a'))
b=a%10
c=(a//10)%10
d=a//100
if 0<a<1000:
print (b+c+d)
1.0001*1.0001
|
7.16.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Proximas tareas :
#
# - Crear version secuencial de multiplicacion de matrices.
# - Crear Version Threading de multiplicacion de matrices
# * Usar representación de numpy.
# * Correr Numpy
|
Class/Untitled.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="view-in-github"
# <a href="https://colab.research.google.com/github/Team-16-B/VintageColorizer/blob/master/ImageColorizerColab.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# -
# ### **<font color='blue'> Artistic Colorizer </font>**
# + [markdown] colab_type="text" id="663IVxfrpIAb"
# #◢ Vintage Colorizer - Colorize your own photos!
#
#
# + [markdown] colab_type="text" id="ZjPqTBNoohK9"
#
#
# ---
#
#
# #◢ Verify Correct Runtime Settings
#
# **<font color='#FF000'> IMPORTANT </font>**
#
# In the "Runtime" menu for the notebook window, select "Change runtime type." Ensure that the following are selected:
# * Runtime Type = Python 3
# * Hardware Accelerator = GPU
#
# + [markdown] colab_type="text" id="gaEJBGDlptEo"
# #◢ Git clone and install Vintage Colorizer
# + colab={} colab_type="code" id="-T-svuHytJ-8"
# !git clone https://github.com/Team-16-B/VintageColorizer Vintage_Colorizer
# -
# cd Vintage_Colorizer
# + [markdown] colab_type="text" id="BDFjbNxaadNK"
# #◢ Setup
# + colab={} colab_type="code" id="00_GcC_trpdE"
#NOTE: This must be the first call in order to work properly!
from vintageColorizer import device
from vintageColorizer.device_id import DeviceId
#choices: CPU, GPU0...GPU7
device.set(device=DeviceId.GPU0)
import torch
if not torch.cuda.is_available():
print('GPU not available.')
# + colab={} colab_type="code" id="Lsx7xCXNSVt6"
# !pip install -r colab_requirements.txt
# + colab={} colab_type="code" id="MsJa69CMwj3l"
import fastai
from vintageColorizer.visualize import *
import warnings
warnings.filterwarnings("ignore", category=UserWarning, message=".*?Your .*? set is empty.*?")
# -
# !mkdir 'models'
# !wget https://data.deepai.org/deoldify/ColorizeArtistic_gen.pth -O ./models/ColorizeArtistic_gen.pth
# !wget https://raw.githubusercontent.com/Team-16-B/VintageColorizer/main/resource_images/watermark.png -O ./resource_images/watermark.png
# + colab={} colab_type="code" id="tzHVnegp21hC"
colorizer = get_image_colorizer(artistic=True)
# + [markdown] colab_type="text" id="BDFjbNxaadNJ"
# #◢ Instructions
# -
# ### source_url
# Type in a url to a direct link of an image. Usually that means they'll end in .png, .jpg, etc. NOTE: If you want to use your own image, upload it first to a site like Imgur.
#
# ### render_factor
# The default value of 35 has been carefully chosen and should work -ok- for most scenarios (but probably won't be the -best-). This determines resolution at which the color portion of the image is rendered. Lower resolution will render faster, and colors also tend to look more vibrant. Older and lower quality images in particular will generally benefit by lowering the render factor. Higher render factors are often better for higher quality images, but the colors may get slightly washed out.
#
# ### watermarked
# Selected by default, this places a watermark icon of a palette at the bottom left corner of the image. This is intended to be a standard way to convey to others viewing the image that it is colorized by AI. We want to help promote this as a standard, especially as the technology continues to improve and the distinction between real and fake becomes harder to discern.
#
# #### How to Download a Copy
# Simply right click on the displayed image and click "Save image as..."!
#
# ## Pro Tips
#
# You can evaluate how well the image is rendered at each render_factor by using the code at the bottom (that cell under "See how well render_factor values perform on a frame here").
# + [markdown] colab_type="text" id="sUQrbSYipiJn"
# #◢ Colorize!!
# +
source_url = '' #@param {type:"string"}
render_factor = 35 #@param {type: "slider", min: 7, max: 40}
watermarked = True #@param {type:"boolean"}
if source_url is not None and source_url !='':
image_path = colorizer.plot_transformed_image_from_url(url=source_url, render_factor=render_factor, compare=True, watermarked=watermarked)
show_image_in_notebook(image_path)
else:
print('Provide an image url and try again.')
# -
# ## See how well render_factor values perform on the image here
for i in range(10,40,2):
colorizer.plot_transformed_image('test_images/image.png', render_factor=i, display_render_factor=True, figsize=(8,8))
|
ImageColorizerColab.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Linear Regression
# __~ <NAME>__
# $ x_1 x_2 x_3 .. x_m $ --> $y_1 y_2 y_3 ... y_m$
#
#
# x --> y
#
#
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
X=pd.read_csv("Linear_X_Train.csv").values
Y=pd.read_csv("Linear_Y_Train.csv").values
plt.figure(figsize=(10, 7))
plt.scatter(X,Y)
plt.show()
# ## Cost Function
# __m__ = No. of points
#
# $$
# f(x_i) = \theta_0 + \theta_1 \cdot x
# $$
#
# $$
# J_{\theta}(x) = \frac{1}{m} \Sigma (f(x_i) - y_i) ^2
# $$
#
# $$
# $$
# # Normalise Data
#
# $$
# \mu = \bar{X} \\
# \sigma = std(X)
# $$
mu = X.mean()
sigma = X.std()
X = (X - mu) / sigma
X
# # Linear Regression
def hypothesis(theta, x):
return theta[0] + theta[1] * x
hypothesis([0, 2], np.array([1, 2, 3]))
# The cost function is defined as
# $$
# J_{\theta}(x) = \frac{1}{m} \Sigma (h_{\theta}(x_i) - y_i) ^2
# $$
#
# $$
# J_{\theta}(x) = \frac{1}{m} \Sigma |h_{\theta}(x_i) - y_i|
# $$
X
X.shape
Y
Y.shape
def error(theta, X, Y):
err = 0
m, _ = X.shape # number of entries
for i in range(m):
err += (hypothesis(theta, X[i]) - Y[i]) ** 2
return err / m
((hypothesis([0, 200/3], X) - Y) ** 2).sum() / X.shape[0]
X.shape[0]
# vectorized
def error_advanced(theta, X, Y):
return ((hypothesis(theta, X) - Y) ** 2).mean()
error([1, 2], X, Y)
error_advanced([1, 2], X, Y)
# The Gradient of the hypothesis is defined as
# $$
# \frac{\delta J_{\theta}(x)}{\delta \theta_{0}} = \frac{1}{m} \Sigma (f_{\theta}(x_i) - y_i)
# $$
#
# $$
# \frac{\delta J_{\theta}(x)}{\delta \theta_{1}} = \frac{1}{m} \Sigma (f_{\theta}(x_i) - y_i) \cdot x_i
# $$
def gradient(theta, X, Y):
m, _ = X.shape
grad = np.zeros((2,))
for i in range(m):
hx = hypothesis(theta, X[i])
grad[0] += hx -Y[i]
grad[1] += (hx - Y[i]) * X[i]
# return [dJ/dtheta_0 dJ/ d theta_1]
return grad / m
gradient([0, 0], X, Y)
((hypothesis([1, 2], X) - Y) * X).sum() / 3750
def gradient_vectorized(theta, X, Y):
f = hypothesis(theta, X)
m = X.shape[0]
grad = np.zeros(2,)
grad[0] = (f - Y).sum()
grad[1] = ((f - Y) * X).sum()
return grad / m
gradient([1, 2], X, Y)
gradient_vectorized([1, 2], X, Y)
def gradient_descent(X, Y, lr=0.1, max_itr=100):
m, _ = X.shape
theta = np.zeros((2,))
error_list = []
theta_list = []
for i in range(max_itr):
err = error(theta, X, Y) # cost
error_list.append(err)
theta_list.append((theta[0], theta[1]))
# learn
theta += -lr * gradient(theta, X, Y)
if i % 10 == 0:
print(f'Iteration no {i}, cost of the parameters are {err}')
return theta, theta_list, error_list
# training our parameters on our data
theta, theta_list, error_list = gradient_descent(X, Y, max_itr=200, lr=1)
theta
plt.plot(error_list)
Y_pred = hypothesis(theta, X)
Y_pred
plt.scatter(X, Y)
plt.plot(X, Y_pred, color='red')
plt.show()
hypothesis(theta, 100)
# # Predict for New Datafor X_test
X_test = pd.read_csv("Linear_X_test.csv").values
# normalizing the data
X_test = (X_test - mu) / sigma
X_test
Y_pred = hypothesis(theta, X_test)
Y_pred
df = pd.DataFrame(data=Y_pred, columns=['y'])
df.to_csv("ans.csv", index=False)
# # Evaluation
def evaluate(Y_actual, Y_pred):
num = ((Y_actual - Y_pred) ** 2).sum()
denom = ((Y_actual - Y_actual.mean()) ** 2).sum()
return (1 - (num / denom)) * 100
evaluate(hypothesis(theta, X), Y)
# ## Scikit -Learn Linear Regression
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X, Y)
Y_pred = model.predict(X)
Y_pred
model.score(X, Y)
|
notebooks/linear-regression/linear-regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import time
import math
import numpy as np
import pandas as pd
from pandas import DataFrame
from pandas import concat
from matplotlib import pyplot
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_recall_curve
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.ensemble import AdaBoostClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.model_selection import GridSearchCV
import pickle
# -
extra_data=pd.read_csv('new_corrected_data-v1-7-24-2019.csv')# loading extra genereated data genereated by LSTM #prediction_of_1_0007.csv
original_data=pd.read_csv('train_Data.csv')#original data
extra_data.head()#displaying LSTM generated data
extra=np.array(extra_data)# getting the original shape
print(extra.shape)
extra[0] # showing first row vector
# Setting predictions of all generated data to 1 because their outputs are mostly 0.98, 0.99 etc.
for i in range(0,len(extra),1):
extra[i][9]=int(1)
extra #showing LSTM generated extra data ready for training
original_data.head() #showing original data
#loading data values from original dataset(Pima)
val=original_data.values
X=val[:,:9].astype(float)# getting the feature values
Y=val[:,9].astype(int)# getting prediction
# +
#extra_X denotes the extra training data generated by LSTM
extra_X=extra[:,:9].astype(float)
#extra_Y denotes extra training prediction data for training the algorithm
extra_Y=extra[:,9].astype(int)
# +
# extrain=original training data + LSTM generated training data
# eytrain=original training prediction + LSTM generated
extrain=np.concatenate((X,extra_X),axis=0)
eytrain=np.concatenate((Y,extra_Y),axis=0)
# -
print(extrain.shape)
print(eytrain.shape)
test_Data=pd.read_csv('test_Data.csv')
test_Data=np.array(test_Data)
test_Data.shape
X_test=test_Data[:,:9].astype(float)
Y_test=test_Data[:,9].astype(int)
def svc_param_selection(X, y, nfolds):
Cs = [0.0001,0.001, 0.01, 0.1, 1, 10,100,1000]
gammas = [0.0001,0.001, 0.01, 0.1, 1,10]
param_grid = {'C': Cs, 'gamma' : gammas}
grid_search = GridSearchCV(SVC(kernel='rbf',probability=True),param_grid, cv=nfolds)
grid_search.fit(X, y)
grid_search.best_params_
return grid_search.best_estimator_
# setting seed =7 to produce same results over and over again, it was maintained during different experiments
seed=11
# +
# first rbf_svc for training on just the original training data
#rbf_svc = SVC(kernel='rbf', gamma=0.00001, C=1000,probability=True).fit(X_train,Y_train)
rbf_svc=svc_param_selection(X,Y,5)
# secondly rbf_svc_extra for training on original+LSTM
rbf_svc_extra = svc_param_selection(extrain,eytrain,5)
# +
# fitting the data
rbf_svc.fit(X,Y)
rbf_svc_extra.fit(extrain,eytrain)
# +
# loading the validation dataset previously set up by validation split(this data was not included in any training procedure)
Prediction_data=X_test
#producing the shape
Prediction_data.shape
# +
# making predictions on validation dataset using svc trained only on original training data
prediction_on_real_dataset=rbf_svc.predict_proba(Prediction_data)
#saving probabilities
predictions=rbf_svc.predict(Prediction_data)
# making predictions on validation dataset using svc trained on original training data + LSTM generated data
prediction_on_real_dataset_adding_extra=rbf_svc_extra.predict_proba(Prediction_data)
#saving probabilities
predictions_extra=rbf_svc_extra.predict(Prediction_data)
# +
print(len(prediction_on_real_dataset))
print(len(prediction_on_real_dataset_adding_extra))
# +
from sklearn.metrics import f1_score
from sklearn.metrics import auc
from sklearn.metrics import average_precision_score
from sklearn.metrics import roc_curve, roc_auc_score
# -
f1_score(Y_test,predictions)#without_extra
f1_score(Y_test,predictions_extra)#with_extra
prediction_on_real_dataset[0]# probabilities of 2 class
# +
# getting AUC score for classifier trained on only original data
fpr, tpr, thres=roc_curve(Y_test,prediction_on_real_dataset[:,1],pos_label=1)
#getting AUC score for classifier trained on original + LSTM generated data
efpr, etpr, ethres=roc_curve(Y_test,prediction_on_real_dataset_adding_extra[:,1],pos_label=1)
with_=auc(fpr,tpr)
without_=auc(efpr,etpr)
print('Without extra: ',auc(fpr,tpr))
print('With extra: ',auc(efpr,etpr))
# +
# plotting data ( for minority predictions , here minority class = 1)
Y_probs=prediction_on_real_dataset[:,1]
fpr,tpr,_=roc_curve(Y_test,Y_probs)
Y_probs_extra=prediction_on_real_dataset_adding_extra[:,1]
efpr,etpr,_=roc_curve(Y_test,Y_probs_extra)
original=auc(fpr,tpr)
lstm_with_extra=auc(efpr,etpr)
original=original.astype(float)
lstm_with_extra=lstm_with_extra.astype(float)
pyplot.clf()
pyplot.plot(fpr, tpr,label='original (AUC : %5.4f)'%(with_),linewidth='1.2')
pyplot.plot(efpr,etpr,label='LSTM generated+original(AUC : %5.4f)'%(without_),linewidth='1.2')
pyplot.xlabel('FPR')
pyplot.ylabel('TPR')
pyplot.title('ROC curve ')
pyplot.legend(loc=4)
pyplot.savefig('ROC curve .png',dpi=500)
pyplot.show()
# +
Y_probs=prediction_on_real_dataset[:,0]
fpr,tpr,_=roc_curve(Y_test,Y_probs)
Y_probs_extra=prediction_on_real_dataset_adding_extra[:,0]
efpr,etpr,_=roc_curve(Y_test,Y_probs_extra)
pyplot.clf()
pyplot.plot(fpr, tpr,label='original')
pyplot.plot(efpr,etpr,label='LSTM generated')
pyplot.xlabel('FPR')
pyplot.ylabel('TPR(recall)')
pyplot.title('ROC curve ')
pyplot.legend(loc=2)
pyplot.show()
# -
prediction_on_real_dataset
prediction_on_real_dataset_adding_extra
|
glass1-seed -11/Training SVM Getting AUC glass1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 4.2.2 Dependence on the Node Degree
# %load_ext autoreload
# %autoreload 2
# %matplotlib notebook
from sensible_raw.loaders import loader
from world_viewer.cns_world import CNSWorld
from world_viewer.glasses import Glasses
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import networkx as nx
from matplotlib.colors import LogNorm
from sklearn.utils import shuffle
# +
#load data
cns = CNSWorld()
cns.load_world(opinions = ['fitness'], read_cached = False, stop=False, write_pickle = False, continous_op=False)
cns_glasses = Glasses(cns)
# load exposure
exposure = pd.read_pickle("tmp/fitness_exposure_tx7.pkl")#.set_index(['node_id','time'])
# alternative: recalculate exposure value
# exposure = cns_glasses.calc_exposure("expo_frac", "op_fitness", exposure_time = 7)
# -
# set analysis params
analysis = 'expo_frac'
opinion_type = "op_fitness"
binning = True
n_bins = 10
save_plots = True
show_plot = True
# +
# filter by degre
degree = exposure.groupby("node_id").n_nbs.mean().to_frame("avg").reset_index()
exposure = exposure.loc[degree.loc[degree.avg >= 4,"node_id"]]
exposure = exposure[exposure.n_nbs_mean > 1/7]
# column "exposure" equals relative exposure
# column "n_influencer_summed" equals absolute exposure
# use absolute exposure for further calculations
exposure.rename(columns={"exposure":"exposure_old", "n_influencer_summed":"exposure"},inplace=True)
# select time period: spring
start = "2014-02-01"
end = "2014-04-30"
exposure.reset_index(inplace=True)
exposure = exposure.loc[(exposure.time >= pd.to_datetime(start)) & (exposure.time <= pd.to_datetime(end))]
exposure.set_index(['node_id','time'],inplace=True)
# +
# plot fig. 6.2
plt.subplots()
exposure.n_nbs_mean.hist( cumulative=True,bins=100, density=True)
plt.xlabel(r"$\bar n$")
plt.ylabel("cummulative distribution function")
plt.savefig("tmp/final/n_bar_cdf.pdf")
# -
# calculate if nodes changed trait after experiencing a certain exposure
# save value as column "op_change" (bool)
data, expo_agg = cns_glasses.opinion_change_per_exposure(exposure, opinion_type, opinion_change_time = 1)
# +
# plot drf for different t_x (fig 4.12)
cns_glasses.output_folder = "final/"
suffix = "min_degree"
x_max = 330
fig,ax = plt.subplots(2,3,subplot_kw = {"adjustable":'box', "aspect":x_max/0.2})
index = 0
lables = [r"(a) $\bar n > 1/7$", r"(b) $\bar n > 1$", r"(c) $\bar n > 10$"]
q_binning = False
for min_degree in [1/7, 1, 10]:
expo_tmp = exposure[exposure.n_nbs_mean > min_degree]
data, expo_agg = cns_glasses.opinion_change_per_exposure(expo_tmp, opinion_type, opinion_change_time = 1)
data = data[data.exposure < x_max]
_,_,l1 = cns_glasses.plot_opinion_change_per_exposure_number(data[data.op_fitness == True], "expo_nmb", binning, n_bins=15, bin_width=15, \
save_plots=False, show_plot=show_plot, y_lower_lim=-0.01, y_upper_lim = 0.2, fig=fig, ax=ax[1][index], \
label="become active", q_binning = q_binning, loglog=False, step_plot=True, color="forestgreen", \
suffix=suffix,legend_loc="upper left", legend=False, min_bin_size = 30, x_lim=x_max, xlabel=r"abs. exposure $K$")
_,_,l2 = cns_glasses.plot_opinion_change_per_exposure_number(data[data.op_fitness == False], "expo_nmb", binning, n_bins=15, bin_width=15, \
save_plots=False, show_plot=show_plot, y_lower_lim=-0.01, y_upper_lim = 0.2, fig=fig, ax=ax[0][index], \
label="become passive", loglog=False, q_binning=q_binning, step_plot=True, color="darkorange", \
suffix=suffix,legend_loc="upper left", legend=False, min_bin_size = 30, x_lim=x_max)
index += 1
for i in range(2):
for j in range(3):
ax[i][j].set_xticks((0,100,200, 300))
ax[1][0].set_title(lables[0], y=-0.5)
ax[1][1].set_title(lables[1], y=-0.5)
ax[1][2].set_title(lables[2], y=-0.5)
fig.legend((l2,l1), ("become passive","become active"),"upper left")
fig.subplots_adjust(hspace=0)
#fig.tight_layout()
fig.savefig("tmp/final/degree_comparison_absolute_qbin.pdf" , bbox_inches='tight')
|
CNS_Sensitivity_k_tilde_min.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <h1>INTERPOLATIONS</h1>
# <b>Group 8</b> <br>
# <NAME> (2301902296)
# <h2>When do we need interpolation?</h2>
# Interpolation is drawing conclusions from within a set of known information. For example, if we know that 0 is the lowest number and 10 being the maximum, we can determine that the number 5 must lie in between. Interpolation has many real-life applications, such as: <br>
# <ul>
# <li>When you have the cost of catering for 25 and 100 people, but you need an estimate for the cost of catering for 50 people.</li>
# <li>When deciding what laptop to buy and you know the price tag and capabilities of laptops at both the lower and higher ends, interpolation can be used to get the most optimal price and specs out of your budget.</li>
# <li>Finding the amount of employees needed to complete a task with the most optimal cost.</li>
# <li>And more...</li>
# </ul>
# There are a number of ways or methods to do interpolation. Two of them, for example, is Lagrange's method and Newton's Divided Difference method. In this notebook, we will be learning about these two and how we can implement them using Python. Strap youselves in, because at the end of every section there will be a playground area for you to explore and mess around! Let's go!
# <h2>Lagrange Interpolation</h2>
# <h3>The Theory</h3>
# Lagrange's method is one of the ways for data interpolation from a set of known data points. With this method, we can interpolate the value of f(x) from any value of x from within the data set. Here is the formula:
# 
# Where: <br>
# <b>n</b> = the degree of polynomial (for linear n = 1, quadratic n = 2, and so on) <br>
# <b>Li(x)</b> = the weighting function
# To get the weighting function, the formula is:
# 
# For some people this formula might seem quite daunting or scary even. However, this formula is just the equivalent of
# 
# <h3>Doing it in Python</h3>
# First let's make a list of the data points we know.
# +
xy_values = []
#Initialize x and y values (make sure the X values are in order)
xy_values.append([0, 0])
xy_values.append([10, 227.04])
xy_values.append([15, 362.78])
xy_values.append([20, 517.35])
xy_values.append([22.5, 602.97])
xy_values.append([30, 901.67])
xy_values
# -
# Next let's decide on the order of polynomial to interpolate our data with. We will store it in a variable called <i>n</i>. For reference, to do a linear interpolation, we put our <i>n</i> value as 1. For quadratic <i>n</i> = 2, cubic <i>n</i> = 3, and so on.
n = 1
# Now let's choose a value of <i>x</i> to interpolate. Obviously, the value of <i>x</i> needs to be within our known data points, otherwise we won't be able to interpolate (that would be extrapolation).
xVal = 16
# Next we need to pick <b>two</b> points from our known data points that sandwhiches our <i>xVal</i>. We will be keeping track on the indexes. So if our <i>xVal</i> is <b>16</b>, we will be picking the x values <b>15</b> and <b>20</b> because 16 lies between them. As we see in our <i>xy_values</i> list, 15 and 20 are positioned in the indexes <b>2</b> and <b>3</b> respectively. Hence, we take a note of that in a new list.
# +
def get_first2_indexes(xy_values, xVal):
indexes = []
for i in range(len(xy_values)-1):
if xy_values[i][0] < xVal and xy_values[i+1][0] > xVal:
indexes.append(i)
indexes.append(i+1)
return indexes
indexes = get_first2_indexes(xy_values, xVal)
indexes
# -
# If <i>n</i> = 1 (linear), we can go directly to finding the weighting function. However, when <i>n</i> > 1, we have to also select adjacent x values from our two chosen data points. Take note to always pick the data point closest to <i>xVal</i>.
#
# For example when <b><i>n</i> = 3</b>:
# 1. Compare <b>10</b> and <b>22.5</b>
# 2. <b>10</b> is closer to <b>16</b> than 22.5. So we choose that.
# 3. <b><i>indexes</i></b> will now house [1, 2, 3]. Take note to keep track the indexes in ascending order.
#
# For example when <b><i>n</i> = 4</b>:
# 1. We add one more data point from when <i>n</i> = 3.
# 2. Compare <b>0</b> and <b>22.5</b>
# 2. <b>22.5</b> is closer to <b>16</b> than 0. So we choose that.
# 3. <b><i>indexes</i></b> will now house [1, 2, 3, 4].
# +
def get_remaining_indexes(xy_values, indexes, xVal, n):
for _ in range(n-1):
#find the value nearest to xVal
leftIndex = indexes[0]-1
rightIndex = indexes[len(indexes)-1] + 1
#Check if the adjacent index exists in the given xy_values data
if (leftIndex > -1):
if (rightIndex < len(xy_values)):
#Check which one is closer to xVal
if (abs(xy_values[leftIndex][0] - xVal) < abs(xy_values[rightIndex][0] - xVal)):
indexes.insert(0, leftIndex)
else:
indexes.append(rightIndex)
else:
indexes.insert(0, leftIndex)
elif (rightIndex < len(xy_values)):
indexes.append(rightIndex)
get_remaining_indexes(xy_values, indexes, xVal, n)
indexes
# -
# Now we can go ahead and try to find the weighting functions. We will be using <b>Sympy</b> to help us keep track of variables and automatically calculate the final result. Let's start by importing Sympy library.
# +
import sympy as sp
x = sp.Symbol('x');
# -
# We will now proceed in determining the weighting function. Recall that the formula is
# 
# +
def gather_weighting_functions(polynomial):
wFunc = [] #Collection of Ln(x)
for i in range(polynomial+1):
subFunc = [] #Collection of individual (x - xj)/(xi-xj)
for j in range(polynomial+1):
#j != i
if i != j:
#(t - xj)/(xi-xj)
#sub = [i, j]
#sub[0] = xi
#sub[1] = xj
sub = []
sub.append(i)
sub.append(j)
subFunc.append(sub)
wFunc.append(subFunc)
return wFunc
wFunc = gather_weighting_functions(n)
wFunc
# -
# The code above simply stores the values i and j in each of their respective iterations.
# Recall the formula for lagrange's interpolation to be
# 
# We will now put <b>fn(x)</b> together with the code below (Sympy has the benefit of automatically simplifying our otherwise very long equation):
# +
def get_equation(xy_values, wFunc, indexes, x_symbol):
total = 0
for i in range(len(wFunc)):
weight_function_prod = 1
for a in range(len(wFunc[i])):
iIndex = wFunc[i][a][0]
index = indexes[iIndex]
xi = xy_values[index][0]
jIndex = wFunc[i][a][1]
index = indexes[jIndex]
xj = xy_values[index][0]
sub = (x_symbol - xj)/ (xi - xj)
weight_function_prod *= sub
#Multiply by f(i)
total += weight_function_prod * xy_values[indexes[i]][1]
return sp.simplify(total)
equation = get_equation(xy_values, wFunc, indexes, x)
equation
# -
# We are not done however, because we are interested in the value of <b>y</b> when x is our <b><i>xVal</i></b>, which is <b>16</b>. To solve this, we can call Sympy's <b>evalf()</b> function on our <i>equation</i> variable.
# +
#Solve for xVal
result = equation.evalf(subs={x : xVal})
result
# -
# If we graph our findings it will look like this
# +
def graph_lagrange(xy_values, equation, xVal, result, x_symbol):
#Graphing
# %matplotlib inline
import matplotlib.pyplot as plt
#split x and y
x_values = []
y_values = []
for i in range(len(xy_values)):
x_values.append(xy_values[i][0])
y_values.append(xy_values[i][1])
#Generate x and y
new_x_values = []
new_y_values = []
for i in range(int(min(x_values) * 100), int(max(x_values) * 100), 1):
new_x_values.append(i/100)
new_y_values.append(equation.evalf(subs={x_symbol:i/100}))
plt.plot(x_values, y_values, 'o', label='data')
plt.plot(new_x_values, new_y_values, '-', label='equation')
plt.plot([xVal], [result], '+', label="interpolated data")
plt.legend()
plt.xlabel("X")
plt.ylabel("Y")
print("y =", equation)
plt.show()
graph_lagrange(xy_values, equation, xVal, result, x)
# -
# Notice how our interpolated <i>xVal</i> lies within our predicted equation, but not all of our known data points. There are some that are relatively quite far away from the equation line. In order to reduce this, we need to use a <b>higher</b> level polynomial (a higher value for <b>n</b>). Do take note that the highest level of polynomial you can do is equal to the number of data points you have minus 1. This is because you do not have enough data points to use a higher degree polynomial.
# <h3>Try it Yourself!</h3>
# Try experimenting with Lagrange's Interpolation yourself with your own data inputs. <br>
# Let's start with the data points that you know:
# +
xy_values = []
#Initialize x and y values (make sure the X values are in order)
xy_values.append([0, 0])
xy_values.append([10, 227.04])
xy_values.append([15, 362.78])
xy_values.append([20, 517.35])
xy_values.append([22.5, 602.97])
xy_values.append([30, 901.67])
xy_values
# -
# Now for what value of x do you want to find?
xVal = 16
xVal
# And what order of polynomial would you like to use? <br>
# Note: Be sure to set your value of <b>n</b> to be the amount of data points -1. If you have 6 data points, your max value for <b>n</b> is 5.
n = 3 #Order/degree of polynomial
#n = len(xy_values) - 1 #Use this to use the highest possible degree of polynomial
n
# Your inputs are now in! (Don't change anything in the code below)
# +
import sympy as sp
x = sp.Symbol('x');
indexes = get_first2_indexes(xy_values, xVal)
get_remaining_indexes(xy_values, indexes, xVal, n)
wFunc = gather_weighting_functions(n)
equation = get_equation(xy_values, wFunc, indexes, x)
result = equation.evalf(subs={x : xVal})
equation
# -
# The code has been baked and here is the result!
result
# Now let's see how that looks like in a graph.
graph_lagrange(xy_values, equation, xVal, result, x)
# How did your graph turn out? Were you able to line up your known data points with your equation line? Maybe try with a higher value of n, or try with an entire different data set. Play around!
# <h2>Newton Interpolation</h2>
# <h3>The Theory</h3>
# To do interpolation with Newton's method, we use Newton's Divided Difference Polynomial (NDDP) method. With this method, we wil be able to interpolate the equation of the line using the known data points. Here is the formula:
# 
# Where: <br>
# <b>n</b> = the degree of polynomial <br>
# <b>a<i>n</i></b> = is the divided difference
# Solving for <b>a<i>n</i></b> is quite tricky, and so that part will be discussed as we learn to solve NDDP using Python.
# <h3>Solving it with Python</h3>
# Similar to what we did in Lagrange's, we first make a list of the data points we know.
# +
xy_values = []
#Initialize x and y values (make sure the X values are in order)
xy_values.append([0, 0])
xy_values.append([10, 227.04])
xy_values.append([15, 362.78])
xy_values.append([20, 517.35])
xy_values.append([22.5, 602.97])
xy_values.append([30, 901.67])
# -
# The beauty with Newton's method is that we do not need to specify what order of polynomial we want to use. That is determined by the amount of data points we have -1. So if we have 6 data points, we will be using a 5 degree polynomial. Our next step is to create the divided difference table, so let's do that.
# +
#Initialize divided difference table
def init_table():
table = []
for _ in range(len(xy_values)):
temp = []
for _ in range(len(xy_values) + 1):
temp.append(-1)
table.append(temp)
#Insert x and y values to table
for i in range(len(xy_values)):
table[i][0] = xy_values[i][0]
table[i][1] = xy_values[i][1]
return table
table = init_table()
table
# -
# We first initialize an empty table by flagging all values with -1. Then we insert our known x and y values there. Our table will look something like this.
# 
# Next we need to populate the table and fill in the remaining empty cells. Here is the way to fill in the table in general:
# 
# Try taking a look at it carefully. You will see a particular pattern. Let's go ahead and fill the values in.
#Do the divided difference table
def compute_table(table):
y_bound = 1
for col in range(2, len(table[0])):
for row in range(y_bound, len(table)):
try:
delta = (table[row][col-1] - table[y_bound-1][col-1]) / (table[row][0] - table[y_bound-1][0])
except:
delta = 0
#print(table[row][col-1], '-', table[y_bound-1][col-1], "divide", table[row][0], '-', table[y_bound-1][0], '=', delta)
table[row][col] = delta
y_bound += 1
compute_table(table)
table
# Next we need to get the values for our <b>a0, a1, a2,...., an</b>. Since we already did the divided difference table, we can just "steal" the values from it. This is how you can get the values from the table:
# 
# +
#Get an values
def get_an_values(table):
an = []
col = 1
for row in range(0, len(table)):
an.append(table[row][col])
col += 1
return an
an = get_an_values(table)
an
# -
# We now have all the pieces to put our NDDP puzzle together. Let's recall the formula again.
# 
# Alright let's do it in Python now.
# +
import sympy as sp
x = sp.Symbol('x')
def get_equation_newton(an, x_symb):
func = 0
for a in range(len(an)):
product = an[a]
for i in range(a):
product *= (x_symb - xy_values[i][0])
func += product
func = sp.simplify(func)
return func
func = get_equation_newton(an, x)
func
# -
# Great! We now have our equation line. Let's plot it and see how it looks.
# +
# %matplotlib inline
import matplotlib.pyplot as plt
def graph_newton(xy_values, func, x_symb):
#split n and y
x_values = []
y_values = []
for i in range(len(xy_values)):
x_values.append(xy_values[i][0])
y_values.append(xy_values[i][1])
#Generate x and y
new_x_values = []
new_y_values = []
for i in range(int(min(x_values) * 100), int(max(x_values) * 100), 1):
new_x_values.append(i/100)
new_y_values.append(func.evalf(subs={x_symb:i/100}))
plt.plot(x_values, y_values, 'o', label='data')
plt.plot(new_x_values, new_y_values, '-', label='equation')
plt.legend()
plt.xlabel("X")
plt.ylabel("Y")
plt.show()
def graph_newton_with_interpolation(xy_values, func, x_symb, xVal, yVal):
#split n and y
x_values = []
y_values = []
for i in range(len(xy_values)):
x_values.append(xy_values[i][0])
y_values.append(xy_values[i][1])
#Generate x and y
new_x_values = []
new_y_values = []
for i in range(int(min(x_values) * 100), int(max(x_values) * 100), 1):
new_x_values.append(i/100)
new_y_values.append(func.evalf(subs={x_symb:i/100}))
plt.plot(x_values, y_values, 'o', label='data')
plt.plot(new_x_values, new_y_values, '-', label='equation')
plt.plot([xVal], [yVal], '+', label="interpolated data")
plt.legend()
plt.xlabel("X")
plt.ylabel("Y")
plt.show()
print("y =", func)
graph_newton(xy_values, func, x)
# -
# Well would you look at that. The graph looks quite nicely; all the data points are inside the graph line. Much better than lagrange's method using a polynomial degree of 1. And we didn't even specify the order of polynomial with Newton's.
# <h3>Try it Yourself!</h3>
# Try experimenting with Newton's Divided Difference method yourself with your own datasets. <br>
# Let's start with the data points that you know:
# +
xy_values = []
#Initialize x and y values (make sure the X values are in order)
xy_values.append([0, 0])
xy_values.append([10, 227.04])
xy_values.append([15, 362.78])
xy_values.append([20, 517.35])
xy_values.append([22.5, 602.97])
xy_values.append([30, 901.67])
xy_values
# -
# Your inputs are now in! Let's process it.
# +
x = sp.Symbol('x')
table = init_table()
compute_table(table)
an = get_an_values(table)
func = get_equation_newton(an, x)
# -
# The code has been baked and here is the line equation you get:
func
# Let's see how it looks in a graph
print("y =", func)
graph_newton(xy_values, func, x)
# How does your graph look? Are all the data points lined up nicely? Maybe try with a higher value of <i>n</i>, or try with an entirely different data set. Play around!
# Perhaps you would like to interpolate a value of y? What value for x would you like to try?
xVal = 16
xVal
# +
yVal = func.evalf(subs={x: xVal})
yVal
# -
# Let's see where does that lie in the graph
graph_newton_with_interpolation(xy_values, func, x, xVal, yVal)
# Does your interpolated data lie somewhere in the graph? Mess around with more interpolation and enjoy your graph :)
# <h3>Conclusion</h3>
# Alright, now that we've explored both Langrange's and Newton's method to do interpolations, let's do a recap!
# Interpolation is all about making an educated guess from within a set of known data. Two methods we can use to do interpolation is Lagrange's and Newton's Divided Difference method. With Lagrange's we can control the degree of polynomial we want to use to produce different accuracies and therefore control the speed at which our program is going to run. Newton's method, on the other hand, would use the highest possible degree of polynomial to produce the most accurate and precise interpolation, but that means it will also use the max amount of time to compute. So which one to use? It all depends on you. Use the method that suits you best.
|
Interpolation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
###HEADERS
#get_ipython().magic(u'pylab inline')
import pandas as pd
from scipy import stats
import numpy as np
import scipy as sp
from IPython.display import Image, HTML
import time
#Importing Biopython to use KEGG API
import Bio
Bio.__version__
from Bio import SeqIO
from Bio.KEGG.REST import *
from Bio.KEGG.KGML import KGML_parser
from Bio.KEGG import REST
import random
##read in data as a dataframe
import csv
#read in file and checks to make sure file exist
while True:
try:
#input file
df = raw_input("Enter File location and name ex.(/Users/nne1s/Documents/Nneka.csv): \n")
f = open(df)
break
#if error will run exception and ask user again
except IOError as e:
print "Oops! That was not a valid file location name. Try again..."
continue
outfile = raw_input("Enter Output File name ex. (C:/Users/nne1s/Documents/Ede-DATA.csv): \n")
correlation_file = raw_input("Enter file location and name for Correlation Map ex. ('C:/Users/nne1s/Documents/Ede-CorrelationMap.csv'): \n")
df = pd.read_csv(df)
# +
df = pd.read_table("DATAFILE.txt", sep= '\t', header=0)
v1 = pd.read_table("V1.txt", sep ='\t', header=0)
v2 = pd.read_table("V2.txt", sep ='\t', header=0)
v3 = pd.read_table("V3.txt", sep ='\t', header=0)
v4 = pd.read_table("V4.txt", sep ='\t', header=0)
# combine all dataframes
df = pd.concat([df["GENE_SYMBOL"],v1["VALUE"], v2["VALUE"], v3["VALUE"], v4["VALUE"]], axis=1) #combine all data to a dataframe
df = df.dropna(axis = 0, how = 'any') #will delete zeros
df.columns = ['GENE_SYMBOL', 'VALUE1',"VALUE2", "VALUE3", "VALUE4"] #change header names for each row in the DF
#data = df.loc[:,"VALUE1":"VALUE4"] #will access data without gene names
#print data
df = pd.read_table("ASTRO W_O OLI NEU all replicas NORM MED-NO RED.csv", sep= '\t', header=0)
df = pd.read_csv("ASTRO W_O OLI NEU all replicas NORM MED-NO RED.csv", header=0)
print df
print df["GeneName"]
data = pd.concat([df["C1"],df["C2"], df["C3"], df["C4"]], axis=1) #combine all data to a dataframe
data2 = pd.concat([df["I1"],df["I2"], df["I3"], df["I4"]], axis=1)
print data
print data2
# +
###FIND MEAN, STD, COV, MEDIAN OF COV, EXPRESSION CONTROL, LOG BASE VALUES
mean = np.mean(data, axis = 1) #mean
#mean = pd.DataFrame(mean)
std = np.std(data, axis = 1) #standard deviation
#cov1 = stats.variation(data, axis = 1) #coeffient of variation
cov1 = std/mean
cov = pd.Series(cov1)
median = np.median(cov1) #median of cov
expcon = median / cov #expression control
logvalues = np.log2(data)
mean2 = np.mean(data2, axis = 1)
std2 = np.std(data2, axis = 1)
cov2 = std2/mean2
cov2 = pd.Series(cov2)
print mean2
print data2
print cov2
##Table of all calculations
#al = pd.concat([df["GENE_SYMBOL"],mean, std, cov, expcon, logvalues], axis = 1, ignore_index=True)
#al.columns = ["GENE_SYMBOL", "Mean", "Standard Deviation", "Coefficient of Variation",
# "Expression Control", "Log of Value1", "Log of Value2", "Log Value3", "Log Value4"]
#print "\n\n HERE \n", al
#print al
#al = al.set_index(df['GENE_SYMBOL'].values)
filename = outfile
#al.to_csv(filename, sep=',')
# +
##FIND CORRELATION COEFFICIENT
results = (logvalues.T).corr(method='pearson') #transpose and find correlation
print "\n \n correlation map \n", results
pearsons_df = pd.DataFrame(results.values, columns = df['GeneName'], index = df['GeneName'].values) ## change to dataframe
print "\n \n here \n", pearsons_df
#export to csv
#filename = correlation_file
#pearsons_df.to_csv(filename, sep=',')
# -
#calculate the sum across the dataframe 'results'
thesum = results.sum(axis = 0)
print thesum
# +
#gene commanding height
gch = expcon * np.exp((4*thesum-1)/len(pearsons_df.index)-1)
print gch
#place all info in dataframe
al = pd.concat([df["GeneName"],mean, std, cov, expcon, logvalues, gch], axis = 1, ignore_index=True)
al.columns = ["GeneName", "Mean", "Standard Deviation", "Coefficient of Variation - 1",
"Expression Control", "Log of Value1", "Log of Value2", "Log Value3", "Log Value4", "GCH"]
#order by gene commanding height
print al
al = al.sort_values(by='GCH', ascending=False)
print al
#print "\n\n HERE \n", al
# -
#fold change
foldchange = []
if cov2 > cov:
fold = cov2 - cov
foldchange = np.append(foldchange,fold)
al.to_csv(filename, sep=',')
# +
### THIS FUNCTION WILL OUTPUT THE KEGG DATABASE AND THE PATHWAYS
import csv
def letsrun (genes):
f = open('PATHWAY.csv', 'w')
with f:
writer = csv.writer(f,delimiter = ',', dialect = 'excel')
##Read in gene and species
xx = []
for gene in genes:
species = 'mmu' # will look at genes for mouse
try:
x = kegg_get(species+':' + gene).read() # will try to find genes
#if error (gene NOT FOUND) will run exception skip word
except Exception:
print gene + " -- was skipped"
continue
print gene
pp = []
pp = np.append(pp, [gene])
#xx = []
#xx = np.append(xx,[gene])
#PRINT OUTPUT OF THE KEGG DATABASE
#print'\n\n Species: '+species+ ' Gene:' +gene+'\n'+ (kegg_get(species+':' + gene).read())
gene = REST.kegg_get(species+':'+gene).read()
#WILL PARSE DATA TO ONLY PRINT PATHWAY DATA
print "Pathways Found:"
for line in gene.rstrip().split("\n"): #splits each line
section = line[:12].strip() # section names are within 12 columns in KEGG so split 12 ways
if not section == "":
current_section = section
#Find the section named pathway and print all pathways
if current_section == "PATHWAY":
gene_identifiers= line[12:].split("; ") #Splits each line based on ';'
print gene_identifiers
pp = np.append([pp], [gene_identifiers])
#xx.append[gene_identifiers]
#xx = np.append(xx, gene_identifiers)
##with open(csvfile, "w") as output:
print "HERE >>>>>", list(pp)
writer.writerows([list(pp)])
#xx = np.append([xx], [pp], axis = 0)
#print "HERE>>>>", xx
#print "\n"
return xx
# -
#will use run the function "letsrun"
# will access the KEGG database using KEGG API
#and find all pathways for each gene
ans = letsrun(al['GeneName'])
ans
print "done"
# +
#sorting algorithm
#sorts all genes based on which pathways they are in
#save data to a dictionary where the keys are the pathways
#and values are an ARRAY(LIST) OF GENES
from collections import defaultdict
d = defaultdict(list)
#read in from
with open('PATHWAY.csv', 'rb') as csvfile:
readcsv = csv.reader(csvfile, delimiter=',')
for c, row in enumerate(readcsv): # will iterate through each row in csv
length = len(row)
intial = 1
genename = row[0]
while intial < length: # will get all pathway names
d[row[intial]].append(genename)
#print genename
#print row[intial]
intial += 1
print d
# print(row)
# +
###weighted pathway regulation
al2 = al.set_index(al["GeneName"])# made genes the index values for .at function
df2 = df.set_index(df["GeneName"])#made gene names the index values for input file
# REMEBER TO GO BACK AN MANUAL DO FC!!!!
#calc WPR for each pathway
for i in d: # i is name of pathway
print i
length = len(d[i])
avg_gch = 0 #intialized value to find avg
fc = [] #foldchange of all genes in a certain pathway
p_val=[] #p value of all genes in a certain values
for j in d[i]: #j is the name of gene
#avg gch
print j
avg_gch = avg_gch + al2.at[j, "GCH"] #[0] # calc sum of all GCH in each pathway
#fold change
fc = np.append(fc, df2.loc[j, 'X'])
#p value
p_val = np.append(p_val, df2.loc[j,'P'])
avg_gch = avg_gch / length #avg of GCH of the genes in a certain pathway
print 'AVG GCH: ', avg_gch
print "FC: ", fc
print "P value: ", p_val
wpr = np.median(avg_gch * (abs(fc)-1) * (1-p_val))
print "WPR: ", wpr, "\n"
# -
#CUT
#for i in df["GeneName"]:
CUT = 1 + np.sqrt( 2 * ( np.square(df["CV-C"]) + np.square(df["CV-I"]) ) )
print CUT
al2 = al.set_index(al["GENE_SYMBOL"])
print al2.at["Shh", "GCH"][0]
print al2
from __future__ import print_function
import sys
for i in xrange(0,10): sys.stdout.write('.')
|
Master regulators.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.9 64-bit (''venv'': venv)'
# name: python389jvsc74a57bd00f83d342e98484a010df626dda691e8b4833dc694f818ed4313faeed5486bc82
# ---
# # Лабораторная работы №3 "Сезонные модели"
# ## Импортирование библиотек
# +
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.pyplot import figure
from matplotlib.gridspec import GridSpec
from sklearn import metrics
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
import statsmodels
from statsmodels.graphics.tsaplots import plot_pacf,plot_acf
from statsmodels.graphics.api import qqplot
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.tsa.statespace.sarimax import SARIMAX
from statsmodels.tsa.stattools import adfuller
from scipy import stats
from tabulate import tabulate
from itertools import product
import warnings
warnings.filterwarnings("ignore")
# -
# ## Загрузка входных данных
dist = pd.read_csv('data/season.csv')
season = dist["liquor"].dropna()
season
# ## График процесса, его АКФ и ЧАКФ
# +
lagCount = 30
fig = plt.figure(figsize=(12, 8))
gs = GridSpec(2, 2, wspace=0.2, hspace=0.2)
ax1 = fig.add_subplot(gs[0, :])
ax1.set_title('Season model')
ax1.plot(season)
ax2 = fig.add_subplot(gs[1, :-1])
_ = plot_acf(season, ax = ax2, lags = lagCount)
ax3 = fig.add_subplot(gs[1:, -1])
_ = plot_pacf(season, ax = ax3, lags = lagCount)
plt.show()
# -
# ## Удаление тренда
diff = list()
for i in range(1, len(season)):
value = season[i] - season[i - 1]
diff.append(value)
plt.plot(season, label='season')
plt.plot(diff, label='not trend')
plt.show()
# ## График процесса, его АКФ и ЧАКФ без тренда
# +
lagCount = 30
fig = plt.figure(figsize=(12, 8))
gs = GridSpec(2, 2, wspace=0.2, hspace=0.2)
ax1 = fig.add_subplot(gs[0, :])
ax1.set_title('Diff model')
ax1.plot(diff)
ax2 = fig.add_subplot(gs[1, :-1])
_ = plot_acf(diff, ax = ax2, lags = lagCount)
ax3 = fig.add_subplot(gs[1:, -1])
_ = plot_pacf(diff, ax = ax3, lags = lagCount)
plt.show()
# -
# ### Проанализируем графики АКФ и ЧАКФ, для определения максимальных порядков модели
#
# ### Проведём обучение для всех моделей, порядок которых ниже максимального порядка модели.
# +
pSeason = [0, 1, 2]
qSeason = [0, 1, 2]
pOrder = [0, 1, 2]
qOrder = [0, 1, 2]
models = {}
for i in pOrder:
for j in qOrder:
for k in pSeason:
for l in qSeason:
if ((i, j ,k, l) == (0, 0, 0, 0)):
continue
arimax = SARIMAX(np.array(diff), order=(i, 0, j), seasonal_order=(k, 0, l, 12), initialization='approximate_diffuse').fit()
pVal = arimax.pvalues
if all(i <= 0.05 for i in pVal):
models[i, j, k, l] = arimax
# -
# ### Количество моделей, имеющих значимые коэффициенты, то есть pVal < 0.05
print(f'Количество моделей: {len(models.keys())}')
# ### Разделение данных на обучающую и тестовую выборки
split_diff = int(len(diff) * 0.7)
diff_train, diff_test = diff[:split_diff], diff[split_diff:]
diff_train = np.array(diff_train)
diff_test = np.array(diff_test)
# ## Вычисление стандартной ошибки для моделей
def standard_error(y, y_1, order):
return np.sqrt(np.sum(np.square((y_1 - y))) / (len(y) - order))
def standard_error_model(train, test, model):
k = max(model.model_orders['ar'], model.model_orders['ma'])
standard_error_train = standard_error(train, model.predict(0, len(train) - 1), k)
standard_error_test = standard_error(test, model.forecast(len(test)), k)
return standard_error_train, standard_error_test
# +
m = {}
dict_se_train = {}
dict_se_test = {}
dict_aic = {}
dict_bic = {}
for name, model in models.items():
tmp_dict = {}
se_train, se_test = standard_error_model(diff_train, diff_test, model)
dict_se_train[name] = se_train
dict_se_test[name] = se_test
dict_aic[name] = model.aic
dict_bic[name] = model.bic
tmp_dict['SE Train'] = se_train
tmp_dict['SE Test'] = se_test
tmp_dict['AIC'] = model.aic
tmp_dict['BIC'] = model.bic
m[name] = tmp_dict
data = {
'Model': list(m.keys()),
'SE Train': list(dict_se_train.values()),
'SE Test': list(dict_se_test.values()),
'AIC': list(dict_aic.values()),
'BIC': list(dict_bic.values())
}
df = pd.DataFrame.from_dict(data)
# df.set_index('Model')
dfAIC = df.sort_values("AIC")
# -
# ## Таблица результатов моделей, отсортированных по критерию Акаике
dfAIC.head(10)
# ## Анализ остатков моделей
# ### Отсортировав все модели по критерию акаике, выберем первые 5
#
# ### Построим их АКФ и ЧАКФ
# +
lagCount = 30
top_model = 5
width = 2
height = 4
fig = plt.figure( figsize=( width * len(dfAIC.head(top_model)['Model']), height * len(dfAIC.head(top_model)['Model'] ) ) )
for idx, elem in enumerate(dfAIC.head(top_model)['Model']):
gs = GridSpec(len(dfAIC.head(top_model)['Model']), 2, wspace = 0.2, hspace = 0.3)
m = models[elem]
ax1 = fig.add_subplot(gs[idx, 0])
ax2 = fig.add_subplot(gs[idx, 1])
_ = plot_acf(m.resid, ax = ax1, lags = lagCount, title=f'АКФ {elem}')
_ = plot_pacf(m.resid, ax = ax2, lags = lagCount, title=f'ЧАКФ {elem}')
plt.show()
|
lab3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import time
import random
import numpy as np
from tqdm import tqdm
from bs4 import BeautifulSoup
import click
from whyclick.chrome import open_chrome, remove_popups
from whyclick import whyq
import torch
from collections import Counter
# +
query = {'username': "*****", 'password': "*****"}
driver = whyq.login(query['username'], query['password'], headless=False)
# -
order_json = whyq.download_previous_orders(driver)
ordered_items = [o['Item Name'] for o in order_json]
ordered_items[-10:]
from transformers import DistilBertTokenizer, DistilBertModel, DistilBertForSequenceClassification
tokenizer = DistilBertTokenizer.from_pretrained('distilbert-base-uncased')
model = DistilBertModel.from_pretrained('distilbert-base-uncased')
def vectorize(text):
input_ids = torch.tensor(tokenizer.encode(text)).unsqueeze(0)
ff = model(input_ids)
output = ff[0].squeeze().squeeze()[0]
return output.detach().numpy()
# Converts sentences to arrays of floats.
vectorized_sents = [vectorize(s) for s in tqdm(ordered_items)]
vectorized_sents = torch.tensor(np.array(vectorized_sents))
driver.get('http://whyq.sg')
def smartly_order_one_day(driver, element_day, simple_max=False, halal=False, healthy=False, vegetarian=False):
time.sleep(1)
loop_count = 0 # Sanity break.
global tempered_vectorized_sents
while True:
try:
# Apply dietary filter
whyq.apply_dietary_filters(driver, halal, healthy, vegetarian)
# Find meals.
meals = [b for b in element_day.find_elements_by_xpath('//button')
if b and b.text == "ADD"]
meals_str = [h6.text for h6 in element_day.find_elements_by_xpath('//h6')][:len(meals)]
meals_vec = torch.tensor(np.array([vectorize(m) for m in meals_str]))
# For every meal choice, I find what's most similar, by scores with temperature.
sim_scores = torch.tensor(np.dot(meals_vec, tempered_vectorized_sents.T))
if simple_max:
""" Old neural top-1 choice.
top_m, top_m_score = -1, -1
for i, m in enumerate(meals_vec):
for s in vectorized_sents:
if np.dot(m, s.T) > top_m_score:
top_m = i
"""
top_m = int(torch.max(torch.max(sim_scores, dim=1).values, dim=0).indices)
else:
# For every meal choice, pick from a multinomial distribution.
top_m = int(torch.multinomial(torch.max(sim_scores, dim=1).values, 1).view(-1))
meals[top_m].click()
# Randomly choose one.
##random.choice(meals).click()
# Check if you've ordered already.
time.sleep(0.3)
msg = element_day.find_element_by_xpath('//div[@id="notify_msg"]')
break
except IndexError: # No meals from dietary restriction.
# Repeat the loop so that the filters are undone.
pass
if loop_count > 3: # Sanity break.
break # If everything fails, go to next day.
loop_count += 1
return driver, element_day, msg.text
# +
temperature = 0.7
tempered_vectorized_sents = vectorized_sents.div(temperature).exp().cpu()
#tempered_vectorized_sents = vectorized_sents
days = driver.find_elements_by_xpath("//div[@class='owl-item active']")
for element_day in days:
element_day.click()
driver, element_day, msg = smartly_order_one_day(
driver, element_day, #simple_max=True
)
time.sleep(3)
# -
driver.find_element_by_link_text("PLACE ORDER").click()
|
Neural Clicks.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="Y8V2E13xR5nX"
# # How to train StarCraft II Bots
#
# In this notebook, we will get started with StarCraft II Machine Learning on Google Colab
# + [markdown] colab_type="text" id="AwYYNIbITWgr"
# # Prerequisite steps
# + colab={} colab_type="code" id="LLOlLbH2R7Aa"
# Uncomment the line below to use dev branch of pysc2
# #!pip install git+https://github.com/deepmind/pysc2.git@dev
# Note: Colab does not have an X Server, installing a virtual one
# !pip install -q pysc2 pyvirtualdisplay
# !apt-get install -y xvfb python-opengl mesa-utils libosmesa6-dev xorg x11-xserver-utils
# + [markdown] colab_type="text" id="J5NEmiwgSLR5"
# ## Download StarCraft II
# + [markdown] colab_type="text" id="ZX0JoA3dZB2h"
# Note: By typing in the password ‘<PASSWORD>’ you agree to be bound by the terms of Blizzard's [AI and Machine Learning License](http://blzdistsc2-a.akamaihd.net/AI_AND_MACHINE_LEARNING_LICENSE.html)
#
# Blizzard's CDNs are not very fast, so if you have space free in your Google Drive, I highly recommend uploading StarCraft II onto Google Drive and download from there.
# + colab={} colab_type="code" id="9viW3ESbSNhy"
# !wget http://blzdistsc2-a.akamaihd.net/Linux/SC2.4.10.zip
# !unzip -P iagreetotheeula -oq SC2.4.10.zip -d ~
# + [markdown] colab_type="text" id="WvMu0KmvSF8j"
# ## Getting the maps
#
# Like StarCraft II itself, I recommend downloading all the maps and uploading it to Google Drive for it to download faster
# + colab={} colab_type="code" id="nRk95lbLSFL9"
# !wget https://github.com/deepmind/pysc2/releases/download/v1.0/mini_games.zip
# !unzip -P iagreetotheeula -oq mini_games.zip -d ~/StarCraftII/Maps/
map_packs = ["Ladder2017Season1.zip", "Ladder2017Season2.zip", "Ladder2017Season3_Updated.zip", "Ladder2017Season4.zip", "Ladder2018Season1.zip", "Melee.zip"]
for file in map_packs:
# !wget https://blzdistsc2-a.akamaihd.net/MapPacks/{file}
# !unzip -P iagreetotheeula -oq {file} -d ~/StarCraftII/Maps/
# + [markdown] colab_type="text" id="ckLzQaqYrHO8"
# ## Remove TCMalloc
#
# This is the main roadblock stopping us originally from using Google's free GPUS
#
# Note that you will get a lot of errors looking like this
#
#
# ```
# ERROR: ld.so: object '/usr/lib/x86_64-linux-gnu/libtcmalloc.so.4' from LD_PRELOAD cannot be preloaded (cannot open shared object file): ignored.
# ```
# This is normal, since we had to get rid of TCMalloc to run StarCraft
# + colab={} colab_type="code" id="Ucy1pZnzjYg7"
# Important - remove libtcmalloc
# !apt-get remove libtcmalloc*
# + [markdown] colab_type="text" id="I0YGj3m3W3qQ"
# # Mount your google drive to save your model's learned parameters
# + colab={} colab_type="code" id="hMsCgMFOZJJ9"
from google.colab import drive
drive.mount('/content/drive')
# + [markdown] colab_type="text" id="XkwqHBCTW6TA"
# # Load Tensorboard for monitoring
# + colab={} colab_type="code" id="wyYldjbLXXSl"
# %load_ext tensorboard
# %tensorboard --logdir=/content/ --port=6006
# + [markdown] colab_type="text" id="jR_BrGryTM5q"
# # Now we can start Machine Learning
#
# This is an example applying NaiveDQN to a PySC2 Agent.
#
# + [markdown] colab_type="text" id="Zthxww_IBxjZ"
#
# + colab={} colab_type="code" id="YQ_qv6HUBz1o"
import random
import time
import math
import os.path
import numpy as np
import pandas as pd
from collections import deque
import pickle
from pysc2.agents import base_agent
from pysc2.env import sc2_env
from pysc2.lib import actions, features, units
from absl import app
import torch
from torch.utils.tensorboard import SummaryWriter
#from skdrl.pytorch.model.mlp import NaiveMultiLayerPerceptron
#from skdrl.common.memory.memory import ExperienceReplayMemory
# + colab={} colab_type="code" id="d2QrwG8jpDTW"
DATA_FILE_QNET = '/content/drive/My Drive/rlagent_with_vanilla_dqn_qnet'
DATA_FILE_QNET_TARGET = '/content/drive/My Drive/rlagent_with_vanilla_dqn_qnet_target'
SCORE_FILE = '/content/drive/My Drive/rlagent_with_vanilla_dqn_score'
scores = [] # list containing scores from each episode
scores_window = deque(maxlen=100) # last 100 scores
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
writer = SummaryWriter()
# + colab={} colab_type="code" id="EverEUVZHX7d"
import torch
import torch.nn as nn
class NaiveMultiLayerPerceptron(nn.Module):
def __init__(self,
input_dim: int,
output_dim: int,
num_neurons: list = [64, 32],
hidden_act_func: str = 'ReLU',
out_act_func: str = 'Identity'):
super(NaiveMultiLayerPerceptron, self).__init__()
self.input_dim = input_dim
self.output_dim = output_dim
self.num_neurons = num_neurons
self.hidden_act_func = getattr(nn, hidden_act_func)()
self.out_act_func = getattr(nn, out_act_func)()
input_dims = [input_dim] + num_neurons
output_dims = num_neurons + [output_dim]
self.layers = nn.ModuleList()
for i, (in_dim, out_dim) in enumerate(zip(input_dims, output_dims)):
is_last = True if i == len(input_dims) - 1 else False
self.layers.append(nn.Linear(in_dim, out_dim))
if is_last:
self.layers.append(self.out_act_func)
else:
self.layers.append(self.hidden_act_func)
def forward(self, xs):
for layer in self.layers:
xs = layer(xs)
return xs
if __name__ == '__main__':
net = NaiveMultiLayerPerceptron(10, 1, [20, 12], 'ReLU', 'Identity')
print(net)
xs = torch.randn(size=(12, 10))
ys = net(xs)
print(ys)
# + colab={} colab_type="code" id="C6JDCzjTHXQc"
from random import sample
class ExperienceReplayMemory:
def __init__(self, max_size):
# deque object that we've used for 'episodic_memory' is not suitable for random sampling
# here, we instead use a fix-size array to implement 'buffer'
self.buffer = [None] * max_size
self.max_size = max_size
self.index = 0
self.size = 0
def push(self, obj):
self.buffer[self.index] = obj
self.size = min(self.size + 1, self.max_size)
self.index = (self.index + 1) % self.max_size
def sample(self, batch_size):
indices = sample(range(self.size), batch_size)
return [self.buffer[index] for index in indices]
def __len__(self):
return self.size
# + colab={} colab_type="code" id="ehj0EAv7CD-B"
import torch
import torch.nn as nn
import numpy as np
import random
class DQN(nn.Module):
def __init__(self,
state_dim: int,
action_dim: int,
qnet: nn.Module,
qnet_target: nn.Module,
lr: float,
gamma: float,
epsilon: float):
"""
:param state_dim: input state dimension
:param action_dim: action dimension
:param qnet: main q network
:param qnet_target: target q network
:param lr: learning rate
:param gamma: discount factor of MDP
:param epsilon: E-greedy factor
"""
super(DQN, self).__init__()
self.state_dim = state_dim
self.action_dim = action_dim
self.qnet = qnet
self.lr = lr
self.gamma = gamma
self.opt = torch.optim.Adam(params=self.qnet.parameters(), lr=lr)
self.register_buffer('epsilon', torch.ones(1) * epsilon)
# target network related
qnet_target.load_state_dict(qnet.state_dict())
self.qnet_target = qnet_target
self.criteria = nn.SmoothL1Loss()
def choose_action(self, state):
qs = self.qnet(state)
#prob = np.random.uniform(0.0, 1.0, 1)
#if torch.from_numpy(prob).float() <= self.epsilon: # random
if random.random() <= self.epsilon: # random
action = np.random.choice(range(self.action_dim))
else: # greedy
action = qs.argmax(dim=-1)
return int(action)
def learn(self, state, action, reward, next_state, done):
s, a, r, ns = state, action, reward, next_state
# compute Q-Learning target with 'target network'
with torch.no_grad():
q_max, _ = self.qnet_target(ns).max(dim=-1, keepdims=True)
q_target = r + self.gamma * q_max * (1 - done)
q_val = self.qnet(s).gather(1, a)
loss = self.criteria(q_val, q_target)
self.opt.zero_grad()
loss.backward()
self.opt.step()
def prepare_training_inputs(sampled_exps, device='cpu'):
states = []
actions = []
rewards = []
next_states = []
dones = []
for sampled_exp in sampled_exps:
states.append(sampled_exp[0])
actions.append(sampled_exp[1])
rewards.append(sampled_exp[2])
next_states.append(sampled_exp[3])
dones.append(sampled_exp[4])
states = torch.cat(states, dim=0).float().to(device)
actions = torch.cat(actions, dim=0).to(device)
rewards = torch.cat(rewards, dim=0).float().to(device)
next_states = torch.cat(next_states, dim=0).float().to(device)
dones = torch.cat(dones, dim=0).float().to(device)
return states, actions, rewards, next_states, dones
# + colab={} colab_type="code" id="nlcHcXAoCUNq"
class TerranAgentWithRawActsAndRawObs(base_agent.BaseAgent):
actions = ("do_nothing",
"harvest_minerals",
"build_supply_depot",
"build_barracks",
"train_marine",
"attack")
def get_my_units_by_type(self, obs, unit_type):
return [unit for unit in obs.observation.raw_units
if unit.unit_type == unit_type
and unit.alliance == features.PlayerRelative.SELF]
def get_enemy_units_by_type(self, obs, unit_type):
return [unit for unit in obs.observation.raw_units
if unit.unit_type == unit_type
and unit.alliance == features.PlayerRelative.ENEMY]
def get_my_completed_units_by_type(self, obs, unit_type):
return [unit for unit in obs.observation.raw_units
if unit.unit_type == unit_type
and unit.build_progress == 100
and unit.alliance == features.PlayerRelative.SELF]
def get_enemy_completed_units_by_type(self, obs, unit_type):
return [unit for unit in obs.observation.raw_units
if unit.unit_type == unit_type
and unit.build_progress == 100
and unit.alliance == features.PlayerRelative.ENEMY]
def get_distances(self, obs, units, xy):
units_xy = [(unit.x, unit.y) for unit in units]
return np.linalg.norm(np.array(units_xy) - np.array(xy), axis=1)
def step(self, obs):
super(TerranAgentWithRawActsAndRawObs, self).step(obs)
if obs.first():
command_center = self.get_my_units_by_type(
obs, units.Terran.CommandCenter)[0]
self.base_top_left = (command_center.x < 32)
def do_nothing(self, obs):
return actions.RAW_FUNCTIONS.no_op()
def harvest_minerals(self, obs):
scvs = self.get_my_units_by_type(obs, units.Terran.SCV)
idle_scvs = [scv for scv in scvs if scv.order_length == 0]
if len(idle_scvs) > 0:
mineral_patches = [unit for unit in obs.observation.raw_units
if unit.unit_type in [
units.Neutral.BattleStationMineralField,
units.Neutral.BattleStationMineralField750,
units.Neutral.LabMineralField,
units.Neutral.LabMineralField750,
units.Neutral.MineralField,
units.Neutral.MineralField750,
units.Neutral.PurifierMineralField,
units.Neutral.PurifierMineralField750,
units.Neutral.PurifierRichMineralField,
units.Neutral.PurifierRichMineralField750,
units.Neutral.RichMineralField,
units.Neutral.RichMineralField750
]]
scv = random.choice(idle_scvs)
distances = self.get_distances(obs, mineral_patches, (scv.x, scv.y))
mineral_patch = mineral_patches[np.argmin(distances)]
return actions.RAW_FUNCTIONS.Harvest_Gather_unit(
"now", scv.tag, mineral_patch.tag)
return actions.RAW_FUNCTIONS.no_op()
def build_supply_depot(self, obs):
supply_depots = self.get_my_units_by_type(obs, units.Terran.SupplyDepot)
scvs = self.get_my_units_by_type(obs, units.Terran.SCV)
if (len(supply_depots) == 0 and obs.observation.player.minerals >= 100 and
len(scvs) > 0):
supply_depot_xy = (22, 26) if self.base_top_left else (35, 42)
distances = self.get_distances(obs, scvs, supply_depot_xy)
scv = scvs[np.argmin(distances)]
return actions.RAW_FUNCTIONS.Build_SupplyDepot_pt(
"now", scv.tag, supply_depot_xy)
return actions.RAW_FUNCTIONS.no_op()
def build_barracks(self, obs):
completed_supply_depots = self.get_my_completed_units_by_type(
obs, units.Terran.SupplyDepot)
barrackses = self.get_my_units_by_type(obs, units.Terran.Barracks)
scvs = self.get_my_units_by_type(obs, units.Terran.SCV)
if (len(completed_supply_depots) > 0 and len(barrackses) == 0 and
obs.observation.player.minerals >= 150 and len(scvs) > 0):
barracks_xy = (22, 21) if self.base_top_left else (35, 45)
distances = self.get_distances(obs, scvs, barracks_xy)
scv = scvs[np.argmin(distances)]
return actions.RAW_FUNCTIONS.Build_Barracks_pt(
"now", scv.tag, barracks_xy)
return actions.RAW_FUNCTIONS.no_op()
def train_marine(self, obs):
completed_barrackses = self.get_my_completed_units_by_type(
obs, units.Terran.Barracks)
free_supply = (obs.observation.player.food_cap -
obs.observation.player.food_used)
if (len(completed_barrackses) > 0 and obs.observation.player.minerals >= 100
and free_supply > 0):
barracks = self.get_my_units_by_type(obs, units.Terran.Barracks)[0]
if barracks.order_length < 5:
return actions.RAW_FUNCTIONS.Train_Marine_quick("now", barracks.tag)
return actions.RAW_FUNCTIONS.no_op()
def attack(self, obs):
marines = self.get_my_units_by_type(obs, units.Terran.Marine)
if len(marines) > 0:
attack_xy = (38, 44) if self.base_top_left else (19, 23)
distances = self.get_distances(obs, marines, attack_xy)
marine = marines[np.argmax(distances)]
x_offset = random.randint(-4, 4)
y_offset = random.randint(-4, 4)
return actions.RAW_FUNCTIONS.Attack_pt(
"now", marine.tag, (attack_xy[0] + x_offset, attack_xy[1] + y_offset))
return actions.RAW_FUNCTIONS.no_op()
# + colab={} colab_type="code" id="6t35XWVbCc8h"
class TerranRandomAgent(TerranAgentWithRawActsAndRawObs):
def step(self, obs):
super(TerranRandomAgent, self).step(obs)
action = random.choice(self.actions)
return getattr(self, action)(obs)
# + colab={} colab_type="code" id="O0ZqigqbCuk2"
class TerranRLAgentWithRawActsAndRawObs(TerranAgentWithRawActsAndRawObs):
def __init__(self):
super(TerranRLAgentWithRawActsAndRawObs, self).__init__()
self.s_dim = 21
self.a_dim = 6
self.lr = 1e-4 * 1
self.batch_size = 32
self.gamma = 0.99
self.memory_size = 200000
self.eps_max = 1.0
self.eps_min = 0.01
self.epsilon = 1.0
self.init_sampling = 4000
self.target_update_interval = 10
self.data_file_qnet = DATA_FILE_QNET
self.data_file_qnet_target = DATA_FILE_QNET_TARGET
self.score_file = SCORE_FILE
self.qnetwork = NaiveMultiLayerPerceptron(input_dim=self.s_dim,
output_dim=self.a_dim,
num_neurons=[128],
hidden_act_func='ReLU',
out_act_func='Identity').to(device)
self.qnetwork_target = NaiveMultiLayerPerceptron(input_dim=self.s_dim,
output_dim=self.a_dim,
num_neurons=[128],
hidden_act_func='ReLU',
out_act_func='Identity').to(device)
if os.path.isfile(self.data_file_qnet + '.pt'):
self.qnetwork.load_state_dict(torch.load(self.data_file_qnet + '.pt', map_location=device))
if os.path.isfile(self.data_file_qnet_target + '.pt'):
self.qnetwork_target.load_state_dict(torch.load(self.data_file_qnet_target + '.pt', map_location=device))
# initialize target network same as the main network.
self.qnetwork_target.load_state_dict(self.qnetwork.state_dict())
self.dqn = DQN(state_dim=self.s_dim,
action_dim=self.a_dim,
qnet=self.qnetwork,
qnet_target=self.qnetwork_target,
lr=self.lr,
gamma=self.gamma,
epsilon=self.epsilon).to(device)
self.memory = ExperienceReplayMemory(self.memory_size)
self.print_every = 1
self.cum_reward = 0
self.cum_loss = 0
self.episode_count = 0
self.new_game()
def reset(self):
super(TerranRLAgentWithRawActsAndRawObs, self).reset()
self.new_game()
def new_game(self):
self.base_top_left = None
self.previous_state = None
self.previous_action = None
self.cum_reward = 0
self.cum_loss = 0
# epsilon scheduling
# slowly decaying_epsilon
self.epsilon = max(self.eps_min, self.eps_max - self.eps_min * (self.episode_count / 50))
self.dqn.epsilon = torch.tensor(self.epsilon).to(device)
def get_state(self, obs):
scvs = self.get_my_units_by_type(obs, units.Terran.SCV)
idle_scvs = [scv for scv in scvs if scv.order_length == 0]
command_centers = self.get_my_units_by_type(obs, units.Terran.CommandCenter)
supply_depots = self.get_my_units_by_type(obs, units.Terran.SupplyDepot)
completed_supply_depots = self.get_my_completed_units_by_type(
obs, units.Terran.SupplyDepot)
barrackses = self.get_my_units_by_type(obs, units.Terran.Barracks)
completed_barrackses = self.get_my_completed_units_by_type(
obs, units.Terran.Barracks)
marines = self.get_my_units_by_type(obs, units.Terran.Marine)
queued_marines = (completed_barrackses[0].order_length
if len(completed_barrackses) > 0 else 0)
free_supply = (obs.observation.player.food_cap -
obs.observation.player.food_used)
can_afford_supply_depot = obs.observation.player.minerals >= 100
can_afford_barracks = obs.observation.player.minerals >= 150
can_afford_marine = obs.observation.player.minerals >= 100
enemy_scvs = self.get_enemy_units_by_type(obs, units.Terran.SCV)
enemy_idle_scvs = [scv for scv in enemy_scvs if scv.order_length == 0]
enemy_command_centers = self.get_enemy_units_by_type(
obs, units.Terran.CommandCenter)
enemy_supply_depots = self.get_enemy_units_by_type(
obs, units.Terran.SupplyDepot)
enemy_completed_supply_depots = self.get_enemy_completed_units_by_type(
obs, units.Terran.SupplyDepot)
enemy_barrackses = self.get_enemy_units_by_type(obs, units.Terran.Barracks)
enemy_completed_barrackses = self.get_enemy_completed_units_by_type(
obs, units.Terran.Barracks)
enemy_marines = self.get_enemy_units_by_type(obs, units.Terran.Marine)
return (len(command_centers),
len(scvs),
len(idle_scvs),
len(supply_depots),
len(completed_supply_depots),
len(barrackses),
len(completed_barrackses),
len(marines),
queued_marines,
free_supply,
can_afford_supply_depot,
can_afford_barracks,
can_afford_marine,
len(enemy_command_centers),
len(enemy_scvs),
len(enemy_idle_scvs),
len(enemy_supply_depots),
len(enemy_completed_supply_depots),
len(enemy_barrackses),
len(enemy_completed_barrackses),
len(enemy_marines))
def step(self, obs):
super(TerranRLAgentWithRawActsAndRawObs, self).step(obs)
#time.sleep(0.5)
state = self.get_state(obs)
state = torch.tensor(state).float().view(1, self.s_dim).to(device)
action_idx = self.dqn.choose_action(state)
action = self.actions[action_idx]
done = True if obs.last() else False
if self.previous_action is not None:
experience = (self.previous_state.to(device),
torch.tensor(self.previous_action).view(1, 1).to(device),
torch.tensor(obs.reward).view(1, 1).to(device),
state.to(device),
torch.tensor(done).view(1, 1).to(device))
self.memory.push(experience)
self.cum_reward += obs.reward
self.previous_state = state
self.previous_action = action_idx
if obs.last():
self.episode_count = self.episode_count + 1
if len(self.memory) >= self.init_sampling:
# training dqn
sampled_exps = self.memory.sample(self.batch_size)
sampled_exps = prepare_training_inputs(sampled_exps, device)
self.dqn.learn(*sampled_exps)
if self.episode_count % self.target_update_interval == 0:
self.dqn.qnet_target.load_state_dict(self.dqn.qnet.state_dict())
if self.episode_count % self.print_every == 0:
msg = (self.episode_count, self.cum_reward, self.epsilon)
print("Episode : {:4.0f} | Cumulative Reward : {:4.0f} | Epsilon : {:.3f}".format(*msg))
torch.save(self.dqn.qnet.state_dict(), self.data_file_qnet + '.pt')
torch.save(self.dqn.qnet_target.state_dict(), self.data_file_qnet_target + '.pt')
scores_window.append(obs.reward) # save most recent reward
win_rate = scores_window.count(1)/len(scores_window)*100
tie_rate = scores_window.count(0)/len(scores_window)*100
lost_rate = scores_window.count(-1)/len(scores_window)*100
scores.append([win_rate, tie_rate, lost_rate]) # save most recent score(win_rate, tie_rate, lost_rate)
with open(self.score_file + '.txt', "wb") as fp:
pickle.dump(scores, fp)
#writer.add_scalar("Loss/train", self.cum_loss/obs.observation.game_loop, self.episode_count)
writer.add_scalar("Score", self.cum_reward, self.episode_count)
return getattr(self, action)(obs)
# + colab={} colab_type="code" id="v0FxrDQgTMW1"
### unfortunately, PySC2 uses Abseil, which treats python code as if its run like an app
# This does not play well with jupyter notebook
# So we will need to monkeypatch sys.argv
import sys
#sys.argv = ["python", "--map", "AbyssalReef"]
sys.argv = ["python", "--map", "Simple64"]
# Copyright 2017 Google Inc. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS-IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
"""Run an agent."""
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import importlib
import threading
from absl import app
from absl import flags
from future.builtins import range # pylint: disable=redefined-builtin
from pysc2 import maps
from pysc2.env import available_actions_printer
from pysc2.env import run_loop
from pysc2.env import sc2_env
from pysc2.lib import point_flag
from pysc2.lib import stopwatch
from pysc2.lib import actions
FLAGS = flags.FLAGS
# because of Abseil's horrible design for running code underneath Colabs
# We have to pull out this ugly hack from the hat
if "flags_defined" not in globals():
flags.DEFINE_bool("render", False, "Whether to render with pygame.")
point_flag.DEFINE_point("feature_screen_size", "84",
"Resolution for screen feature layers.")
point_flag.DEFINE_point("feature_minimap_size", "64",
"Resolution for minimap feature layers.")
point_flag.DEFINE_point("rgb_screen_size", None,
"Resolution for rendered screen.")
point_flag.DEFINE_point("rgb_minimap_size", None,
"Resolution for rendered minimap.")
flags.DEFINE_enum("action_space", "RAW", sc2_env.ActionSpace._member_names_, # pylint: disable=protected-access
"Which action space to use. Needed if you take both feature "
"and rgb observations.")
flags.DEFINE_bool("use_feature_units", False,
"Whether to include feature units.")
flags.DEFINE_bool("use_raw_units", True,
"Whether to include raw units.")
flags.DEFINE_integer("raw_resolution", 64, "Raw Resolution.")
flags.DEFINE_bool("disable_fog", True, "Whether to disable Fog of War.")
flags.DEFINE_integer("max_agent_steps", 0, "Total agent steps.")
flags.DEFINE_integer("game_steps_per_episode", None, "Game steps per episode.")
flags.DEFINE_integer("max_episodes", 0, "Total episodes.")
flags.DEFINE_integer("step_mul", 8, "Game steps per agent step.")
flags.DEFINE_float("fps", 22.4, "Frames per second to run the game.")
#flags.DEFINE_string("agent", "sc2.agent.BasicAgent.ZergBasicAgent",
# "Which agent to run, as a python path to an Agent class.")
#flags.DEFINE_enum("agent_race", "zerg", sc2_env.Race._member_names_, # pylint: disable=protected-access
# "Agent 1's race.")
flags.DEFINE_string("agent", "TerranRLAgentWithRawActsAndRawObs",
"Which agent to run, as a python path to an Agent class.")
flags.DEFINE_enum("agent_race", "terran", sc2_env.Race._member_names_, # pylint: disable=protected-access
"Agent 1's race.")
flags.DEFINE_string("agent2", "Bot", "Second agent, either Bot or agent class.")
flags.DEFINE_enum("agent2_race", "terran", sc2_env.Race._member_names_, # pylint: disable=protected-access
"Agent 2's race.")
flags.DEFINE_enum("difficulty", "very_easy", sc2_env.Difficulty._member_names_, # pylint: disable=protected-access
"If agent2 is a built-in Bot, it's strength.")
flags.DEFINE_bool("profile", False, "Whether to turn on code profiling.")
flags.DEFINE_bool("trace", False, "Whether to trace the code execution.")
flags.DEFINE_integer("parallel", 1, "How many instances to run in parallel.")
flags.DEFINE_bool("save_replay", True, "Whether to save a replay at the end.")
flags.DEFINE_string("map", None, "Name of a map to use.")
flags.mark_flag_as_required("map")
flags_defined = True
def run_thread(agent_classes, players, map_name, visualize):
"""Run one thread worth of the environment with agents."""
with sc2_env.SC2Env(
map_name=map_name,
players=players,
agent_interface_format=sc2_env.parse_agent_interface_format(
feature_screen=FLAGS.feature_screen_size,
feature_minimap=FLAGS.feature_minimap_size,
rgb_screen=FLAGS.rgb_screen_size,
rgb_minimap=FLAGS.rgb_minimap_size,
action_space=FLAGS.action_space,
use_raw_units=FLAGS.use_raw_units,
raw_resolution=FLAGS.raw_resolution),
step_mul=FLAGS.step_mul,
game_steps_per_episode=FLAGS.game_steps_per_episode,
disable_fog=FLAGS.disable_fog,
visualize=visualize) as env:
#env = available_actions_printer.AvailableActionsPrinter(env)
agents = [agent_cls() for agent_cls in agent_classes]
run_loop.run_loop(agents, env, FLAGS.max_agent_steps, FLAGS.max_episodes)
if FLAGS.save_replay:
env.save_replay(agent_classes[0].__name__)
def main(unused_argv):
"""Run an agent."""
#stopwatch.sw.enabled = FLAGS.profile or FLAGS.trace
#stopwatch.sw.trace = FLAGS.trace
map_inst = maps.get(FLAGS.map)
agent_classes = []
players = []
#agent_module, agent_name = FLAGS.agent.rsplit(".", 1)
#agent_cls = getattr(importlib.import_module(agent_module), agent_name)
#agent_classes.append(agent_cls)
agent_classes.append(TerranRLAgentWithRawActsAndRawObs)
players.append(sc2_env.Agent(sc2_env.Race[FLAGS.agent_race]))
if map_inst.players >= 2:
if FLAGS.agent2 == "Bot":
players.append(sc2_env.Bot(sc2_env.Race[FLAGS.agent2_race],
sc2_env.Difficulty[FLAGS.difficulty]))
else:
#agent_module, agent_name = FLAGS.agent2.rsplit(".", 1)
#agent_cls = getattr(importlib.import_module(agent_module), agent_name)
agent_classes.append(TerranRandomAgent)
players.append(sc2_env.Agent(sc2_env.Race[FLAGS.agent2_race]))
threads = []
for _ in range(FLAGS.parallel - 1):
t = threading.Thread(target=run_thread,
args=(agent_classes, players, FLAGS.map, False))
threads.append(t)
t.start()
run_thread(agent_classes, players, FLAGS.map, FLAGS.render)
for t in threads:
t.join()
if FLAGS.profile:
pass
#print(stopwatch.sw)
# + colab={} colab_type="code" id="wwFx7U8CGC3Z"
if __name__ == "__main__":
app.run(main)
# + colab={} colab_type="code" id="36uEfbuUGGwS"
|
Training_StarCraft_2_Agent_under_Colab.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Exercise: CBS Innovation
import requests
from bs4 import BeautifulSoup
import time
www = 'https://www.cbs.nl'
r = requests.get(f'{www}/en-gb/our-services/innovation')
print(r.status_code)
soup = BeautifulSoup(r.text,'lxml')
# - Retrieve a list of titles of all innovation articles on this page using a CSS selector and print them
# Solution using a CSS selector:
for h3 in soup.select('section div div h3'):
print(h3.text)
# An alternative solution using find_all:
for i in soup.find_all('div', class_='caption'):
print(i.h3.text)
# - For each innovation article page retrieve the first 500 characters of the text and print it
# First try your code for one article
r = requests.get('https://www.cbs.nl/en-gb/our-services/innovation/project/innovation-in-small-businesses')
s = BeautifulSoup(r.text, 'lxml')
sel = s.select('section')
print(sel)
print(sel[0].text[:500].strip())
# Then loop through all articles
for a in soup.select('section div div a'):
art = a['href']
r = requests.get(f'{www}{art}')
s = BeautifulSoup(r.text, 'lxml')
sel = s.select('section')
print(sel[0].text[:500].strip())
print('********************')
time.sleep(1) # in robots.txt CBS advises a delay of 1 second
# - Option: retrieve all urls to images in all innovation articles and show them
|
20191008/Exercises/CBS_Innovation.ipynb
|
# ---
# jupyter:
# jupytext:
# formats: ipynb,md
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Modulo
#
# Given 10 non-negative integers, if we divide each by 42,
# how many different remainders do we get?
from test import test
# ## Official solution
#
# As we compute the remainder for each input number,
# we keep track of which values have already been obtained,
# so that we don't double-count them.
# This can be achieved with one Boolean for each possible remainder (0 to 41)
# and counting only those set to true.
# +
# %%writefile modulo.py
obtained = [False] * 42
for line in range(10):
modulo = int(input()) % 42
obtained[modulo] = True
counter = 0
for modulo in range(42):
if obtained[modulo]:
counter = counter + 1
print(counter)
# -
test('modulo')
# ### Variations
# I tend to use the 'anonymous name' `_` when a variable is not referred to.
# The second part of the algorithm can be shortened with the `count` method:
# it computes how often a given value occurs in a list.
# +
# %%writefile modulo.py
obtained = [False] * 42
for _ in range(10):
modulo = int(input()) % 42
obtained[modulo] = True
print(obtained.count(True))
# -
test('modulo')
# A slightly more efficient version doesn't iterate over all 42 Booleans to count those true.
# As each remainder is computed, we increment the counter if it wasn't computed before.
# +
# %%writefile modulo.py
obtained = [False] * 42
counter = 0
for _ in range(10):
modulo = int(input()) % 42
if not obtained[modulo]:
counter = counter + 1
obtained[modulo] = True
print(counter)
# -
test('modulo')
# ## Sets
#
# The distinct remainder values form a set, a collection of items without duplicates.
# Python has a built-in data type for sets.
# We simply add each computed remainder to the initially empty set;
# adding a duplicate is automatically ignored.
# Finally, we compute the size of the set with the `len` function.
# +
# %%writefile modulo.py
obtained = set()
for _ in range(10):
obtained.add(int(input()) % 42)
print(len(obtained))
# -
test('modulo')
# With set comprehensions, the above code can be written in a single line.
# +
# %%writefile modulo.py
print(len({int(input()) % 42 for _ in range(10)}))
# -
test('modulo')
# ## Concluding remarks
#
# Due to the small input size, just 10 integers,
# neither solution is substantially faster than the others.
# When a set can only contain a very small number of integers,
# in this case at most 10 of the 42 different remainders,
# a Boolean list is usually faster and uses less memory than the set type.
|
coci/2006-1/modulo.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.0.1
# language: julia
# name: julia-1.0
# ---
# >This is another post in the ongoing series in which I try to learn 2D vector graphics using Julia. It doesn't contain any revelations or new material, and you should visit the following sites if you're looking for a good introduction to the subject of noise in graphics:
# - [red blob games](https://www.redblobgames.com/articles/noise/introduction.html)
# - [adrianbiagioli](http://flafla2.github.io/2014/08/09/perlinnoise.html)
# - [khan academy](https://www.khanacademy.org/partner-content/pixar/pattern/perlin-noise/v/patterns-9)
# I'm using Julia version 1.0 if you want to play along; you can find the source files and notebooks on the github. If you do, you'll need the packages [Luxor](https://github.com/JuliaGraphics/Luxor.jl), [Colors](https://github.com/JuliaGraphics/Colors.jl), and [ColorSchemes](https://github.com/JuliaGraphics/ColorSchemes.jl). I used [Literate.jl](https://github.com/fredrikekre/Literate.jl) to produce the Markdown and Jupyter notebook versions.
# ### Random versus Noise
# Luxor provides a function called `noise()`. This can accept a single floating-point number as input, and it returns a value between 0.0 and 1.0.
# +
using Luxor
noise(0.0)
# -
noise(1.0)
noise(2.0)
# It will be easier to draw some graphs. Here's a quick throwaway function to draw a simple graph.
# +
function graph(a, width = 800;
startnumber = 0,
endnumber = 1,
style = :line,
margin = 30)
setline(1)
bars(a, labels =false,
xwidth = (width - 2margin)/length(a),
yheight =40,
barfunction = (bottom::Point, top::Point, value;
extremes=extrema(a), barnumber=0, bartotal=0) ->
begin
if style == :line
line(bottom, top, :stroke)
else
circle(top, 1, :fill)
end
end)
sethue("black")
label(string(startnumber), :S,
Point(0, 0), offset=10)
label(string(endnumber), :S,
Point(width - 2margin, 0), offset=10)
end
function drawgraph(startvalue, endvalue, filename)
Drawing(800, 150, filename)
background("white")
origin()
# move to top left corner
margin=30
translate(BoundingBox()[1] + (margin, boxheight(BoundingBox()/2)))
sethue("black")
graph(noise.(range(startvalue, endvalue, length=200)),
startnumber=startvalue,
endnumber=endvalue)
finish(); preview()
end
# -
# To test this out, graph 200 random integers:
Drawing(800, 150, "images/noise/graph-random.png")
background("white")
origin() ## move to top left corner
margin=30
translate(BoundingBox()[1] + (margin, boxheight(BoundingBox()/2)))
sethue("black")
graph(rand(200))
finish(); preview()
# 
# To start with, let's graph the output of the `noise()` function for the first 200 integers:
drawgraph(0, 200, "images/noise/graph-0-200.png")
# 
# It looks very random. But let's look at 200 values between 0 and 10:
drawgraph(0, 10, "images/noise/graph-0-10.png")
# 
# There's some randomness, but it's smoother, and looks more natural.
# Zoom and enhance, between 0 and 5:
drawgraph(0, 5, "images/noise/graph-5.png")
# 
# You can see that the left half of the 0 to 10 graph has been stretched.
# Between 0 and 1:
drawgraph(0, 1, "images/noise/graph-0-1.png")
# 
# One more for luck:
drawgraph(0, 0.5, "images/noise/graph-0-05.png")
# 
# The more often you sample the noise space (ie the shorter the gaps between the set of values passed to `noise()`, the closer together the output values will be.
# So the `noise()` function provides gently changing undulations rather than the unpredictable jumps of randomness. Here's a slowly changing color pattern in the LCHab color space, using a set of noisy values to choose the hue. We'll change the length of each line as well just for fun:
using Colors
@svg begin ## switch to SVG for better graphic quality
rate = .009
setline(2)
for x in -250:2:250
yn = noise(x * rate)
hue = rescale(yn, 0, 1, 0, 359)
sethue(LCHab(50, 100, hue))
ht = rescale(yn, 0, 1, 10, 100)
line(Point(x, -ht/2), Point(x, ht/2), :stroke)
end
end 600 200 "images/noise/colorbars.svg"
# 
# You can use noisy values to specify other changing parameters. For example, let's place some pebbles at random, and control their size using a noisy distribution, to give the illusion of a naturally changing distribution.
# +
function drawpebble(pt, radius)
sethue("grey60")
@layer begin
transform([rand(0.5:0.1:1) 0 0 rand(0.5:0.1:1) 0 0])
circle(pt, radius, :fill)
for i in 1:-0.02:0.2
sethue(rescale(i, 1, 0, 0.5 + rand(0:0.1:0.3), 1.0),
rescale(i, 1, 0.1, 0.4 + rand(0:0.1:0.5), 1.0),
rescale(i, 1, 0.3, 0.5, 1.0))
setopacity(1 - i)
circle(pt + (-2i, -2i), i * radius, :fill)
end
end
end
@png begin
# switch to PNG, SVG can't handle this
background("palegoldenrod")
pebblesize = 12
for i in 1:6000
pt = Point(rand(-400:400), rand(-200:200))
n = noise(pt.x * 0.002)
drawpebble(pt, pebblesize * n)
end
end 800 400 "images/noise/pebbles.png"
# -
# 
# ### Detail and persistence
# The `noise()` function has two optional keyword arguments that let you tweak the knobs of the noise generator.
# The first is `detail`, an integer. Increasing it from the default value of 1 upwards will add finer detail to the basic noise. The second is `persistence`, a floating-point value between 0 and 1 (or more).
# 'detail` is graphed here with values from 1 to 12. As the level increases, you can see that the same overall noise contours are gradually modulated with finer variations.
function detailgraph()
@svg begin
margin=30
translate(BoundingBox()[1] + (margin, 0))
setline(.5)
sethue("black")
stopat = 2
r = range(0, length=400, stop=stopat)
for detail in 1:2:12
translate(0, 100)
sethue("red")
graph(noise.(r), style=:circle, endnumber=stopat)
sethue("black")
text("detail = $detail, persistence = 0.9", Point(200, 15))
graph(noise.(r, detail=detail, persistence=0.9), endnumber=stopat)
end
end 800 650 "images/noise/detail-graph.svg"
end
detailgraph()
# {: .center-image}
# You can see the original noisy curve (in red) behind each more detailed graph. The noise generator is doubling the frequency but halving the amplitude every time you go one level higher. Noise, like music, can have octaves of higher frequencies mixed with lower fundamental frequency. The `detail` keyword is adding one or more octaves of noise.
# The `persistence` argument defaults to zero. The value controls the amplitude of each successive octave of noise, with higher values of persistence producing higher levels of finer detail, as the values persist for longer.
# +
function persistencegraph()
@svg begin
setline(.5)
sethue("black")
margin=30
translate(BoundingBox()[1] + (margin, 0))
stopat = 10
r = range(0, length=400, stop=stopat)
for p in 0:0.25:2
translate(0, 70)
sethue("red")
graph(noise.(r, detail=4, persistence=0),
endnumber=stopat, style=:circle)
sethue("black")
text("detail = 4, persistence = $p", Point(200, 15))
graph(noise.(r, detail=4, persistence=p),
endnumber=stopat)
end
end 800 675 "images/noise/persistence-graph.svg"
end
persistencegraph()
# -
# 
# Here, the detail is kept at 4, and the persistence varies from 0 upwards. As the persistence increases, the effects accumulate, until the original curve is barely visible.
# There are many uses for noisy input, such as generating varying shapes that don't have that undesirable 'too random' quality.
# +
using ColorSchemes
function treerings()
@svg begin
nrate = 0.01
npoints= 500
nrings = 400
rad = 20
setline(0.5)
for ring in nrings:-5:1
pts = Point[]
for i in 1:npoints
push!(pts, polar(rad + (ring * noise(i * nrate)),
rescale(i, 1, npoints, 0, 2pi)))
end
sethue(get(ColorSchemes.sienna, noise(ring * 5nrate)))
poly(pts, :fill, close=false)
sethue("black")
poly(pts, :stroke, close=false)
end
end 800 800 "images/noise/treerings.svg"
end
treerings()
# -
# {: .center-image}
# Here's a more questionable idea, using noise to control the setting of a line of text.
# +
function drawtextline(t, point, fsize; rate=0.1)
for (n, c) in enumerate(split(t, ""))
f = fsize * noise(n * rate, persistence=0, detail=4)
fontsize(f)
te = textextents(c)
text(c, point)
point = Point(point.x + te[5] * 0.98, 0) ## tightness is tight
move(point)
end
end
@png begin
fontface("Bodoni")
drawtextline("variablefontsizetextsettingiscool,orisit?",
O - (380, 0), 50, rate=.11)
end 800 120 "images/noise/text-setting.png"
# -
# 
# I then used the `readpng()` and `placeimage()` functions to add a background image (the original Tenniel illustration), with the following result:
# {: .center-image}
# ### Why noise?
# The first use of computer graphics in movies is generally considered to be Tron (1981).
# Tron lies at the very beginning of the history of CGI in the movies, and the technology available to the artists, mathematicians, and programmers making Tron was amazingly underpowered compared with the computing power that we have today on our wrists, let alone on our phones.
# <NAME> was a mathematician and programmer who worked on Tron, and (I think after the film was released) he realised that there was room for using mathematical techniques for realistic-looking surfaces and textures, such as terrain.
# 
# Ken's noise, or Perlin Noise as it became known, was quickly adodpted as the best way to generate naturalistic surfaces.
# I think the reason why natural scenes appear to us as variable but not completely random is due to the (possibly hidden) larger scale processes that make smaller and more visible details clump together, and appear to work together and change gradually. For example, clouds, mountains, and pebble beaches have large scale structure controlled by unseen forces like heat, pressure, and gravity. We mostly see the objects that are subject to these forces, rather than the forces themselves.
# ### Moving into 2D
# So far the noise we've been producing has been one-dimensional, although we've been using 2D graphics to draw it.
# The `noise()` function can accept two floating-point numbers as input. These effectively define a rectangular grid of varying noise values: the x and y inputs produce a third value which requires representation.
# A simple way of doing this is to draw a table and vary the color of each square, giving a type of heat map.
# +
using ColorSchemes
@svg begin
nrows = 40
ncols = 40
cellwidth = 15
cellheight = 15
table = Table(nrows, ncols, cellwidth, cellheight)
rate = 0.1
fontsize(5)
for row in 1:nrows
for col in 1:ncols
zvalue = noise(row * rate, col * rate)
sethue(get(ColorSchemes.temperaturemap, zvalue))
box(table[row, col], table.colwidths[1], table.rowheights[1], :fill)
sethue("black")
text(string(round(zvalue, digits=1)), table[row, col], halign=:center, valign=:middle)
end
end
end 800 700 "images/noise/table.svg"
# -
# 
# Alternatively, we can create a 3D surface and use the noise values for the height at each point. Normally this would require a visit to Julia's colorful and generally awesome Swedish-nightclub-themed Package manager, Pkg:
# 
# to download some of the cool plotting packages available, not least Simon Danisch's impressive [Makie.jl](https://github.com/JuliaPlots/Makie.jl).
# But, just to be contrary, I decided to whip up a simple isometric projection:
# +
function project(x, y, z;
scalingfactor = 3, heightmultiplier = -1)
# negative because y is positive downwards!
u = (x - y)/sqrt(2)
v = (x + 2(heightmultiplier * z) + y)/sqrt(6)
return Point(scalingfactor * u, scalingfactor * v)
end
project(t; kwargs...) = project(t[1], t[2], t[3]; kwargs...)
function generatenoisearray(sx=100, sy=100;
rate=0.5,
detail=1,
persistence=0)
a = Array{Float64}(undef, sx, sy)
for x in 1:sx
for y in 1:sy
a[x, y] = noise(x * rate, y * rate,
detail=detail, persistence=persistence)
end
end
return a
end
function isograph(a)
@svg begin
background("grey30")
translate(0, -300)
setline(0.5)
sx, sy = size(a)
scalingfactor = 5
heightmultiplier = -6
for x in 1:sx-1
newpath()
move(project(x, sy, -10,
scalingfactor = scalingfactor,
heightmultiplier = heightmultiplier))
for y in sy-1:-1:1
toppolygon = project.([
(x, y, a[x, y]),
(x + 1, y, a[x + 1, y]),
(x + 1, y + 1, a[x + 1, y + 1]),
(x, y + 1, a[x, y + 1])],
scalingfactor = scalingfactor,
heightmultiplier = heightmultiplier)
centroid = polycentroid(toppolygon)
line(centroid)
end
line(project(x, 1, -10,
scalingfactor = scalingfactor,
heightmultiplier = heightmultiplier))
sethue("grey20")
fillpreserve()
sethue("grey85")
strokepath()
end
end 800 700 "images/noise/isograph.svg"
end
isograph(generatenoisearray(80, 80, rate=0.08))
# -
# 
# (This image reminds me of the famous Joy Division LP cover and T-shirt image, which features plots of the first ever pulsar discovered by <NAME> and <NAME> in 1967. This then became the basis of many entertaining blog posts, such as [this one](https://adamcap.com/2011/05/19/history-of-joy-division-unknown-pleasures-album-art/){:target="_blank"}.)
# 
# A more conventional surface rendering is also possible:
# +
function isograph(a)
@png begin
background("grey20")
translate(0, -200)
setline(0.5)
sx, sy = size(a)
for x in 1:sx-1
for y in sy-1:-1:1
toppolygon = project.([
(x, y, a[x, y]),
(x + 1, y, a[x + 1, y]),
(x + 1, y + 1, a[x + 1, y + 1]),
(x, y + 1, a[x, y + 1])],
heightmultiplier=-10,
scalingfactor=5)
sethue("black")
poly(toppolygon, close=true, :stroke)
sethue(get(ColorSchemes.inferno, a[x, y]))
poly(toppolygon, close=true, :fill)
end
end
end 800 500 "images/noise/isosurface-2.png"
end
isograph(generatenoisearray(100, 100, rate=0.08))
# -
# 
# ### What, more dimensions?
# So far we've been generating 2D noise. The `noise()` function can also accept three floating-point numbers as input. This produces noise values in 3D space, where each 3D point can have a noise value between 0 and 1. Rendering these point clouds is definitely a job for something other than a simple 2D graphics system. But, while we're here, let's have a go:
# +
function buildarray(a::AbstractArray; rate=20)
sx, sy, sz = size(a)
for x in 1:sx
for y in 1:sy
for z in 1:sz
a[x, y, z] = noise(x * rate, y * rate, z * rate)
end
end
end
return a
end
function iso3d(a)
background("grey20")
sethue("gray80")
setline(0.15)
rule.([Point(0, y) for y in -400:10:400])
sx, sy, sz = size(a)
for x in 1:sx
for y in 1:sy
for z in 1:sz
noisevalue = a[x, y, z]
sethue(get(ColorSchemes.plasma, noisevalue))
pt = project(x, y, z, scalingfactor=8)
setopacity(noisevalue)
circle(pt, rescale(noisevalue, 0, 1, 0.05, 6), :fill)
end
end
end
end
const A = Array{Float64, 3}(undef, 50, 50, 50)
@png begin
iso3d(buildarray(A, rate=0.05))
end 800 800 "images/noise/isosolid.png"
# -
# 
# The noise values nearer 1 look like hot plasma, whereas values nearer 0 are almost translucent. It suggests what you might expect to see from a real volume visualization tool.
# ## Journey to Algorithmia
# The final images in this post combine 2D noise and 1D noise; 2D noise for the sky, and 1D noise to create the contours.
# There's a `seednoise()` function. This takes an array of 512 integers between 1 and 12, and is broadly the equivalent of the `Random.seed!()` function in Julia. This is useful when you want the noise to vary from image to image.
# +
function layer(leftminheight, rightminheight, noiserate;
detail=1, persistence=0)
c1, c2, c3, c4 = box(BoundingBox(), vertices=true)
ip1 = between(c4, c1, leftminheight)
ip2 = between(c3, c2, rightminheight)
topedge = Point[]
seednoise(rand(1:12, 512))
for x in ip1.x:2:ip2.x
ypos = between(ip1, ip2, rescale(x, ip1.x, ip2.x, 0, 1)).y
ypos *= noise(x/noiserate,
detail=detail, persistence=persistence)
push!(topedge, Point(x, ypos))
end
p = [c4, topedge..., c3]
poly(p, :fill, close=true)
end
function clouds()
tiles = Tiler(boxwidth(BoundingBox()),
boxheight(BoundingBox()),
800, 800, margin=0)
@layer begin
transform([3 0 0 1 0 0])
setopacity(0.3)
noiserate = 0.01
for (pos, n) in tiles
nv = noise(pos.x * noiserate,
pos.y * noiserate,
detail=4, persistence=.4)
setgray(nv)
box(pos, tiles.tilewidth, tiles.tileheight, :fill)
end
end
end
function colorblend(fromcolor, tocolor, n=0.5)
f = clamp(n, 0, 1)
nc1 = convert(RGBA, fromcolor)
nc2 = convert(RGBA, tocolor)
from📕, from📗, from📘, from💡 =
convert.(Float64, (nc1.r, nc1.g, nc1.b, nc1.alpha))
to📕, to📗, to📘, to💡 =
convert.(Float64, (nc2.r, nc2.g, nc2.b, nc1.alpha))
new📕 = (f * (to📕 - from📕)) + from📕
new📗 = (f * (to📗 - from📗)) + from📗
new📘 = (f * (to📘 - from📘)) + from📘
new💡 = (f * (to💡 - from💡)) + from💡
return RGBA(new📕, new📗, new📘, new💡)
end
function landscape(scheme, filename)
Drawing(800, 300, "$(filename).png")
origin()
# sky is gradient mesh
bb = BoundingBox()
mesh1 = mesh(box(bb, vertices=true), [
get(scheme, rand()),
get(scheme, rand()),
get(scheme, rand()),
get(scheme, rand())
])
setmesh(mesh1)
box(bb, :fill)
# clouds are 2D noise
clouds()
# the sun is a disk placed at random
@layer begin
setopacity(0.25)
sethue(get(scheme, .95))
sunposition = boxtop(bb) +
(rand(-boxwidth(bb)/3:boxwidth(bb)/3), boxheight(bb)/10)
circle(sunposition, boxdiagonal(bb)/30, :fill)
end
setopacity(0.8)
# how many layers
len = 6
noiselevels = range(1000, length=len, stop=200)
detaillevels = 1:len
persistencelevels = range(0.5, length=len, stop=0.85 )
for (n, i) in enumerate(range(1, length=len, stop=0))
# avoid extremes of range
sethue(colorblend(get(scheme, .05), get(scheme, .95), i))
layer(i - rand()/2, i - rand()/2,
noiselevels[n], detail=detaillevels[n],
persistence=persistencelevels[n])
end
finish()
preview()
end
landscape(ColorSchemes.leonardo, "images/noise/landscape-leonardo")
# -
# 
landscape(ColorSchemes.starrynight, "images/noise/landscapes-starrynight")
# 
# I generated a few hundred of these (there are over 300 colorschemes that can be selected at random) and, scrolling through them quickly, I found that sometimes the results were good, sometimes they weren't. Randomness—and noise—can be hard to predict.
# [2018-10-16]
# 
# *This notebook was generated using [Literate.jl](https://github.com/fredrikekre/Literate.jl).*
|
src/notebooks/noise.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # [LEGALST-190] Lab 4/12: Morality and Sentiment Analysis
# This lab will cover morality and sentiment analysis using the *Moral Foundations Theory* with dictionary-based analysis, connecting to topic modeling and classifications ideas from previous labs.
#
# ### Table of Contents
# [The Data](#section data)<br>
# [Goal and Question](#section goal)<br>
# 1 - [Text Pre-processing](#section 1)<br>
# 2 - [Polarity](#section 2)<br>
# 3 - [Moral Foundations Theory](#section 3)<br>
# 4 - [Non-negative matrix factorization](#section 4)<br>
#
# **Dependencies:**
# +
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
import json
from sklearn.decomposition import NMF, LatentDirichletAllocation
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer
import nltk
from nltk.stem.snowball import SnowballStemmer
import seaborn as sns
# !pip install textblob
from textblob import TextBlob
# -
# ----
# ## The Data<a id='section data'></a>
#
# For this lab, we'll use the Old Bailey dataset, something you all should be familiar with now. The size of the dataset is also rather large so we will compare two year-long periods, one from before 1827 and one after. Read the question to better understand why we look at 1827.
# ## Goal and Question<a id='section goal'></a>
#
# The goal of today's lab is to explore sentiment analysis with three different approaches – [polarity scoring](#section 2), [topic-specific dictionary methods](#section 3), and [topic modeling](#section 4).
#
# We'll look at sentiment in the context of the following question:
#
# **Did the way judges, prosecutors, and witnesses talk about moral culpability change after the Bloody Code was mostly repealed in 1827 (at the leading edge of a wave of legal reform in England)?**
#
# *Note: this is a question that could encompass an entire research project. Today's lab uses a very small subset of data due to datahub memory limitations, and skips over many of the steps needed for truly robust conclusions. *
#
# Something to think about: What are some things you would need to consider before answering this question?
#
# ----
# ## Section 1: Text Pre-processing<a id='section 1'></a>
#
# ### Before we start
# This dataset we are about to look at is incredibly large, so to avoid crashing our datahub kernel, we only consider two years: 1822 and 1832. These two years were chosen as periods that were equally far from 1827 (when the Bloody Code was mostly repealed), while not being so far from each other that we'd expect to see major language usage change due only to time.
#
# ----
#
# ### Getting started
#
# Let's get working with the data.
# contains Old Bailey trial data from 1822 and 1832
old_bailey = pd.read_csv('data/obc_1822_1832.csv', index_col='trial_id')
# select only the columns we need for this lab
old_bailey = old_bailey.loc[:, ['year', 'transcript']]
old_bailey.head()
# Awesome! We now have data we can work with. Before we start anything, we must clean the text!
#
# Just to review, we want to process our text by:<br>
# 1) Lowercasing the words<br>
# 2) Cleaning up punctuation<br>
# 3) Splitting into individual words<br>
# 4) Stemming the word tokens<br>
#
# For the sake of time (and to get to the good stuff), we've provided the pre-processing code below. This a big data set, so the code will take up to a minute to run.
# +
# pre-process the data
lower_cased = old_bailey['transcript'].str.lower()
punct_re = r'[^\w\s]'
lower_no_punc = lower_cased.str.replace(punct_re, ' ')
tokens = lower_no_punc.str.split()
old_bailey['tokens'] = tokens
stemmer = SnowballStemmer('english')
stem_lists = []
for token_list in old_bailey['tokens']:
stem_lists.append([stemmer.stem(wd) for wd in token_list])
old_bailey['stemmed_tokens'] = stem_lists
old_bailey.head()
# -
# ----
#
# ## Section 2: Polarity <a id='section 2'></a>
#
# One way to measure the tone of a text is to look at the text **polarity**: a measure of how positive or negative it is perceived to be. For example, a sentence like "I love Berkeley!" would be considered positive, while a sentence like "Stanford is terrible!" would be negative. And, because polarity is represented as a scale, some words have stronger positive or negative sentiment than others- "I like data science" is positive, but not as positive as "I love data science."
#
# We will use the [TextBlob](https://textblob.readthedocs.io/en/dev/quickstart.html#sentiment-analysis) tools to analyze the sentiment of Old Bailey. TextBlob provides access to many common text-processing operations, and includes a lexicon and rule-based sentiment analysis tool.
#
# A TextBlob is created around string of text:
# creates a sentiment analyzer
blob = TextBlob("This is a super exciting, totally awesome test sentence.")
blob
# We can access the sentiment by using `.sentiment`.
blob.sentiment
# `sentiment` returns two values: the **polarity** and the **subjectivity**. The polarity ranges between -1 and 1 where -1 is a very negative text and 1 is a very positive text. Subjectivity ranges between 0 and 1 where 0 is a very objective text and 1 is a very subjective text (i.e. one that can be interpreted many different ways). You can get the polarity by using `.polarity`.
blob.sentiment.polarity
# Polarity is calculated fairly simply: TextBlob accesses a dictionary of words that have been assigned polarity and subjectivity scores, looks up each word in the given text, and averages over the sentence. It also employs a few rules, such as changing the polarity of a word that comes after a negation.
# +
happy = TextBlob('Happy')
print(happy.sentiment.polarity)
negation = TextBlob('Not')
print(negation.sentiment.polarity)
negated_happy = TextBlob('Not happy')
print(negated_happy.sentiment.polarity)
# -
# **QUESTION:** Try calculating the polarity scores of a few of your own sentences in the cell below.
# test the polarity scoring for different sentences
my_blob = ...
...
# Next, we want to get the average polarity for each transcript.
#
# **EXERCISE:** define a function that will take in a string of text and return the polarity of that text.
def get_polarity(text):
"""Return the polarity of TEXT"""
...
return ...
# SOLUTION
def get_polarity(text):
"""Return the polarity of TEXT"""
blob = TextBlob(text)
return blob.sentiment.polarity
# **EXERCISE**: Using `.apply` and your `get_polarity` function, get the polarity of every transcript in the Old Bailey data.
polarities = ...
# SOLUTION
polarities = old_bailey['transcript'].apply(get_polarity)
# add the polarities as a column
old_bailey['polarity'] = polarities
old_bailey.head()
# **QUESTION:**
# - What was the most negative transcript/transcripts?
# - What was the most positive transcript/transcripts?
#
# find the transcript with the highest polarity
most_pos = ...
most_pos
# +
# SOLUTION
# find the transcript with the highest polarity
most_pos = old_bailey[old_bailey.polarity == old_bailey.polarity.max()]
print(most_pos.transcript)
# -
# find the transcript with the lowest polarity
most_neg = ...
most_neg
# +
# SOLUTION
# find the transcript with the lowest polarity
most_neg = old_bailey[old_bailey.polarity == old_bailey.polarity.min()]
print(most_neg.transcript)
# -
# **EXERCISE:** Let's take a look at violin plots of these two datasets to better compare how the average compound polarity is distributed for each of the two years, before and after 1827.
#
# To show both years at once, it's easiest to use the Seaborn (abbreviated as `sns`) visualization library function. `y` is set to the name of the variable (a string) whose distributions we want to see. `x` is set to the name of the variable (also a string)that we want to compare distributions for . `data` is set to the dataframe (not a string) with all the values.
# +
# uncomment the next line and fill in the code to create the violin plots
#sns.violinplot(x=..., y=..., data=...)
# -
#SOLUTION
sns.violinplot(x="year", y="polarity", data=old_bailey);
# **QUESTION:** What does this plot show us?
#
# What are some advantages to using polarity as a way to measure moral tone? What are some issues with this approach? Consider also how these answers might change for a different data set.
# *Write your answer here.*
# **SOLUTION**
# The plot shows that the violin plots are about the same shape and have about the same median around 0.
#
# Polarity is a nice metric because it's easy to calculate and interpret. It might run into issues because it will ignore words that aren't in its dictionary; this is especially an issue for this data, which has text from almost 200 years ago and may contain a significant number of more archaic words.
# ----
# ## Section 3: Moral Foundations Theory<a id='section 3'></a>
#
# Another approach is to create specialized dictionaries containing specific words of interest to try to analyze sentiment from a particular angle (i.e. use a **dictionary method**). One set of researchers did just that from the perspective of [Moral Foundations Theory](http://moralfoundations.org/). We will now use it to see if we can understand more about the moral tone of Old Bailey transcripts than by using general polarity. You should be doing something like this for your homework. We will be using a provided moral foundations dictionary.
with open('data/haidt_dict.json') as json_data:
mft_dict = json.load(json_data)
# Moral Foundations Theory posits that there are five (with an occasional sixth) innane, universal psychological foundations of morality, and that those foundations shape human cultures and institutions (including legal). The keys of the dictionary correspond to the five foundations.
#look at the keys of the dictionary provided
keys = mft_dict.keys()
list(keys)
# And the values of the dictionary are lists of words associated with each foundation.
mft_dict[list(keys)[0]] #one example of the values provided for the first key
# ### Calculating Percentages
#
# In this approach, we'll use the frequency of Moral Foundations-related words as a measure of how the transcripts talk about morality and see if there's a difference between pre- and post-1827 trends.
#
# As a first step, we need to know the total number of words in each transcript.
#
# **EXERCISE:** Add a column to `old_bailey` with the number of words corresponding to each transcript.
# create a new column called 'total_words'
old_bailey['total_words'] = ...
old_bailey.head()
# SOLUTION
old_bailey['total_words'] = old_bailey['tokens'].apply(len)
old_bailey.head()
# Next, we need to calculate the number of matches to entries in our dictionary for each foundation for each speech.
#
# Run the next cell to add six new columns to `old_bailey`, one per foundation, that show the number of word matches. This cell will also likely take some time to run (no more than a minute). Note that by now, you have the skills to write all the code in the next cell- we're just giving it to you because it's long, fiddly, and writing nested for-loops is not the focus of this lab. Make sure you know what it does before you move on, though.
# +
# Will take a bit of time to run due to the large size.
# do the following code for each foundation
for foundation in mft_dict.keys():
# create a new, empty column
num_match_words = np.zeros(len(old_bailey))
stems = mft_dict[foundation]
# do the following code for each foundation word
for stem in stems:
# find related word matches
wd_count = np.array([sum([wd == stem for wd in transcript])for transcript in old_bailey['stemmed_tokens']])
# add the number of matches to the total
num_match_words += wd_count
# create a new column for each foundation with the number of related words per transcript
old_bailey[foundation] = num_match_words
old_bailey.head()
# -
# **EXERCISE:** The columns for each foundation currently contain the number of words related to that foundation for each of the trials. Calculate the *percentage* of foundation words per trial by dividing the number of matched words by the number of total words and multiplying by 100.
# +
# do this for each foundation column
for foundation in mft_dict.keys():
old_bailey[foundation] = old_bailey[foundation] # fill in your code to transform the values here
old_bailey.head()
# +
#SOLUTION
for foundation in mft_dict.keys():
old_bailey[foundation] = (old_bailey[foundation] / old_bailey['total_words']) * 100
old_bailey.head()
# -
# Let's compare the average percentage of foundation words per transcript for the two dates, 1822, and 1832.
#
# **EXERCISE**: Create a dataframe that only has columns for the five foundations plus the year. Then, use the pandas dataframe function `groupby` to group rows by the year, and call the `mean` function on the `groupby` output to get the averages for each foundation.
# +
# the names of the columns we want to keep
mft_columns = ['authority/subversion', 'care/harm', 'fairness/cheating', 'loyalty/betrayal',
'sanctity/degradation', 'year']
# create a data frame with only the above columns included
mft_df = ...
# groups the rows of mft_df by year, then take the mean
foundation_avgs = ...
foundation_avgs
# +
# SOLUTION
# the names of the columns we want to keep
mft_columns = ['authority/subversion', 'care/harm', 'fairness/cheating', 'loyalty/betrayal',
'sanctity/degradation', 'year']
# create a data frame with only the above columns included
mft_df = old_bailey.loc[:, mft_columns]
# groups the rows by year, then take the mean
foundation_avgs = mft_df.groupby('year').mean()
foundation_avgs
# -
# Next, create a bar graph. The simplest way is to call `.plot.barh()` on your dataframe of the averages.
#
# Also try calling `.transpose()` on your averages dataframe, then making a bar graph of that. The transpose function flips the rows and columns and can make it easier to compare the percentages.
# create a bar graph
...
# SOLUTION
# create a bar graph
foundation_avgs.transpose().plot.barh()
# **QUESTION:** What do you see from the bar graphs you created?
#
# Why would this be a good approach to answering the question of how talk about morality changed between these two periods? What are some limitations of this approach (Hint: look at the values on the graphs you calculated, and remember: these are *percentages*, not proportions)?
# *Write your answer here.*
# *Potential answer: The proportion of care/harm words is greater before the repeal, and the proportion of authority/subversion words is greater after the repeal. Rarity of words means results may not be significant. And, since this dictionary was not designed specifically for this data set, it also may be missing relevant words.*
# ----
# ## Section 4: Non-negative matrix factorization<a id='section 4'></a>
#
# In this section, you can get an idea of sentiment using topic modeling algorithms, something you touched on in the 4/10 lab earlier this week, to help look for patterns.
#
# On Tuesday, you explored Latent Dirichlet Allocation (LDA) in gensim to look for topics in a corpus. Non-negative matrix factorization (NMF), not included in gensim, is another such way to look for topics in unstructured text data. The two methods differ in what kinds of math they use 'under the hood': LDA relies on probabilistic graphical modeling, while NMF uses linear algebra.
#
# We want to generate the topics found for 1822 and 1832 trials, look for topics related to tone or morality, and see if there's a difference between the two.
#
# Run the cell below to make two lists: one list of the trial transcripts for each year.
# +
# trial transcripts for 1822
transcripts_1822 = old_bailey[old_bailey['year'] == 1822]['transcript']
# trial transcripts for 1832
transcripts_1832 = old_bailey[old_bailey['year'] == 1832]['transcript']
# -
# We'll start by looking at 1822. The following cell creates the tfidf vectorizer, fits the text data, and assigns the list of feature name (i.e. the words in the document) to `tfidf_feature_names_1822`.
#
# Check out the [documentation for TfidfVectorizer](http://scikit-learn.org/stable/modules/generated/sklearn.feature_extraction.text.TfidfVectorizer.html) if you need a refresher on what it does.
# create the vectorizer
tfidf_vectorizer_1822 = TfidfVectorizer(max_df=0.95, min_df=2, max_features=1000, stop_words='english')
# fit the data
tfidf_1822 = tfidf_vectorizer_1822.fit_transform(transcripts_1822)
# get the feature names
tfidf_feature_names_1822 = tfidf_vectorizer_1822.get_feature_names()
# **EXERCISE:** Create the TfidfVectorizer, fit_transform the data, and get the feature names for 1832.
# create the vectorizer
tfidf_vectorizer_1832 = ...
# fit the data
tfidf_1832 = ...
# get the feature names
tfidf_feature_names_1832 = ...
# SOLUTION
tfidf_vectorizer_1832 = TfidfVectorizer(max_df=0.95, min_df=2, max_features=1000, stop_words='english')
tfidf_1832 = tfidf_vectorizer_1832.fit_transform(transcripts_1832)
tfidf_feature_names_1832 = tfidf_vectorizer_1832.get_feature_names()
# As mentioned previously the algorithms are not able to automatically determine the number of topics and this value must be set when running the algorithm. Initialising NMF with ‘nndsvd’ rather than random initialisation improves the time it takes for NMF to converge.`random_state` gives the seed for the random number generator to use: this lets us reproduce our results in the future.
#
num_topics = 20
# Run NMF for 1822
nmf_1822 = NMF(n_components=num_topics, random_state=1, init='nndsvd').fit(tfidf_1822)
# **EXERCISE:** Run NMF using `num_topics` for the number of components on the data from 1832.
# Run NMF for 1832
nmf_1832 = ...
# SOLUTION
nmf_1832 = NMF(n_components=num_topics, random_state=1, init='nndsvd').fit(tfidf_1832)
# We've provided you the function to display the topics shown by the NMF.
# +
def display_topics(model, feature_names, num_top_words):
"""Displays NUM_TOP_WORDS topics for MODEL """
for topic_idx, topic in enumerate(model.components_):
print("Topic %d:" % (topic_idx))
print(" ".join([feature_names[i]
for i in topic.argsort()[:-num_top_words - 1:-1]]))
# the number of words to display per topic
num_top_words = 10
# display the topics for 1822
display_topics(nmf_1822, tfidf_feature_names_1822, num_top_words)
# -
# display the topics for 1832
display_topics(nmf_1832, tfidf_feature_names_1832, num_top_words)
# As in LDA, it often takes some hyperparameter tuning before you get a coherent set of topics. Go back and tune the parameters for tfidf and NMF to see if you can get topics that show something about the moral sentiment of the transcripts. `num_topics` usually makes the most dramatic difference.
#
# Once you've compared several sets of topics, answer the next question:
# **QUESTION:** What did the best set of topics you found tell you about the tone of the documents for the two periods? Why might this approach be a good way to study sentiment? What are some issues with this approach?
# *Write your answer here.*
# *Potential answer: NMF can be good for uncovering patterns in unstructured data without imposing structure like in dictionary methods. But, unstructured data means you might have to dig a lot to find relevant topics.*
# ----
# Fantastic! Now you know how to approach sentiment analysis several ways using general sentiment analysis with `VADER`, Moral Foundations Theory, and Non-negative matrix factorization.
#
# Ultimately, there were limitations to all of these methods. In your homework, you'll explore how to generate your own dictionary to try to overcome some of these limitations.
#
# ----
# ## Bibliography
#
#
# - Moral Foundations Theory background and dictionary: *<NAME> and <NAME> http://moralfoundations.org/*
# - Moral Foundations analysis code adapted from *https://github.com/ds-modules/XRHETOR-R1A/blob/master/02-Moral-Foundations-Analysis/02-Moral-Foundations-Analysis.ipynb*
# - NMF code and explanation adapted from *Aneesha Bakharia. 'Topic Modeling With Scikit-Learn.' https://medium.com/mlreview/topic-modeling-with-scikit-learn-e80d33668730*
#
# ----
# Notebook developed by: <NAME>, <NAME>
#
# Data Science Modules: http://data.berkeley.edu/education/modules
|
labs/24_Sentiment Morality/.ipynb_checkpoints/4-12_Morality_Sentiment_Analysis_SOLUTIONS-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# default_exp core.spells
# -
# # Spells
#
# > Describe spells within sequences
# ## Overview
#
# Spells are exclusively recurrent n-grams (the same element repeated a number of times), and are a useful prerequisite for a number of distance measures and other descriptive statistics. The `pysan.core.spells` module contains methods for understanding the prevalence and extremes of spells in sequences, plus some basic visualisation functionality.
# ## Methods
#export
def get_spells(sequence):
"Returns a list of tuples where each tuple holds the element and the length of the spell (also known as run or episode) for each spell in the sequence."
# get each spell and its length
spells = [(k, sum(1 for x in v)) for k,v in itertools.groupby(sequence)]
# this is functionally equivalent to the following;
# spells = [(k, len(list(v))) for k,v in itertools.groupby(sequence)]
return spells
#export
def get_longest_spell(sequence):
"Returns a dict containing the element, count, and starting position of the longest spell in the sequence. The keys of this dict are 'element, 'count', and 'start'."
spells = get_spells(sequence)
longest_spell = max(count for element, count in spells)
for i, (element, count) in enumerate(spells):
if count == longest_spell:
# sum the counts of all previous spells to get its starting position
position_in_sequence = sum(count for _,count in spells[:i])
return {'element':element, 'count':count,'start':position_in_sequence}
#export
def get_spell_durations(sequence):
"Computes the durations of each spell in the sequence, returning a list."
spells = get_spells(sequence)
durations = [spell[1] for spell in spells]
return durations
# # Plotting
# todo: add plot_spell_durations
|
15_core_spells.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.5.3
# language: julia
# name: julia-1.5
# ---
# - By [lazarusA](https://lazarusa.github.io/Webpage/index.html)
# +
using CairoMakie, Random
include("makieTheme1.jl") # don't forget to include the theme.
Random.seed!(123)
fig = Figure(resolution = (500, 400), font =:serif)
ax = Axis(fig, aspect = 1,xlabel = "x", ylabel = "y", xgridvisible = false, ygridvisible = false)
hmap = heatmap!(rand(10,20), colormap = :thermal)
cbar = Colorbar(fig, hmap, label = "value", labelpadding = -5, flipaxisposition= false,
ticklabelpad = 30)
fig[1, 1] = cbar
fig[1, 2] = ax
#save("/results/FigHeatCbarLeft.svg", scene, pt_per_unit = 0.7);
save("./results/FigHeatCbarLeft.png", fig, px_per_unit = 2)
fig
|
FigHeatCbarLeft.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Simple linear regression
#
# 선형모형은 입력 특성에 대한 선형 함수를 만들어 예측을 수행한다.
# 선형회귀에서는 최소제곱법을 사용하여 회귀계수를 계산한다.
#
# **최소제곱법 : 예측값과 훈련세트의 target Y 사이의 평균제곱오차를 최소화하는 회귀계수를 찾는 방법이다.**
# ## Import the relevant libraries
# +
# For these lessons we will need NumPy, pandas, matplotlib
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# and of course the actual regression (machine learning) module
from sklearn.linear_model import LinearRegression
# -
# ## Load the data
# We start by loading the data
data = pd.read_csv('../../data/1.01. Simple linear regression.csv')
# Let's explore the top 5 rows of the df
data.head()
plt.plot(data['SAT'], data['GPA'], 'o')
plt.xlabel('SAT', fontsize = 20)
plt.ylabel('GPA', fontsize = 20)
# ## Create the regression
# ### Declare the dependent and independent variables
# +
# There is a single independent variable: 'SAT'
x = data['SAT']
# and a single depended variable: 'GPA'
y = data['GPA']
# -
# Often it is useful to check the shapes of the features
x.shape
y.shape
# +
# scikit learn 에서 데이터를 입력으로 사용하기 위해서는 2D 배열을 사용해야 한다.
x_matrix = x.values.reshape(-1,1)
# Check the shape just in case
x_matrix.shape
# -
# ### Regression 모형을 생성하자.
# 참고 문서: https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html
# We start by creating a linear regression object
reg = LinearRegression()
# 최소제곱법을 사용하여 회귀 직선식을 생성한다.
# 첫번째 인수는 독립변수를 두번째 인수는 종속변수
reg.fit(x_matrix,y)
# ### R-squared
# 모형의 설명력은 R 결정계수로 확인한다.
# 1에 가까울수록 설명력이 좋은 모형이다.
# To get the R-squared in sklearn we must call the appropriate method
reg.score(x_matrix,y)
# ### Coefficients
#
# 회귀계수 값을 확인한다.
#
# **회귀계수의 해석**
# 회귀계수는 x의 값이 1단위 변경할때 y값이 변하는 정도를 말한다.
# 예를 들어 이 예제에서 회귀계수가 0.00167769라는 것은 SAT가 1 증가하면 GPA는 0.00167769변경된다는 뜻이다.
# Getting the coefficients of the regression
# Note that the output is an array, as we usually expect several coefficients
reg.coef_
# ### Intercept
# Getting the intercept of the regression
# Note that the result is a float as we usually expect a single value
reg.intercept_
# ### Making predictions
#
# 새로운 값으로 예측을 해보자.
# There is a dedicated method should we want to predict values
# Note that the result is an array, as we can predict more than one value at a time
reg.predict([[1740]])
# To be in line with our knowledge so far, we can create a pandas data frame with several different values of SAT
new_data = pd.DataFrame(data=[1740,1760],columns=['SAT'])
new_data
# We can predict the whole data frame in bulk
# Note that the result is an array, this time with 2 elements
reg.predict(new_data)
# Finally, we can directly store the predictions in a new series of the same dataframe
new_data['Predicted_GPA'] = reg.predict(new_data)
new_data
# ### 회귀식을 산점도에 그래프로 표현해 보자.
# +
# There are different ways to plot the data - here's the matplotlib code
plt.scatter(x,y)
# Parametrized version of the regression line
yhat = reg.coef_*x_matrix + reg.intercept_
# Plotting the regression line
fig = plt.plot(x, yhat, lw=4, c='orange', label ='regression line')
# Labelling our axes
plt.xlabel('SAT', fontsize = 20)
plt.ylabel('GPA', fontsize = 20)
plt.show()
# -
|
02ML/02Supervised/01Regression/01SimpleRegression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# +
from PIL import Image
import pytesseract
# Install software to complete ocr recognition
# https://www.simplifiedpython.net/how-to-extract-text-from-image-in-python/
# https://digi.bib.uni-mannheim.de/tesseract/tesseract-ocr-w64-setup-v4.1.0-bibtag19.exe
# -
# picture path
# %cd ..
# %cd pics
# +
# Include tesseract executable in your path
pytesseract.pytesseract.tesseract_cmd = r"C:\Program Files\Tesseract-OCR\tesseract.exe"
# Create an image object of PIL library
image = Image.open('Capture.jpg')
# pass image into pytesseract module
# pytesseract is trained in many languages
image_to_text = pytesseract.image_to_string(image, lang='eng')
# -
# Print the text
print(image_to_text)
|
notebooks/ocrTest.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
"""
Basic imgae load, plot, resize, etc..
<NAME> (<EMAIL>)
"""
# Import packs
import numpy as np
import os
from imageio import imread
import matplotlib.pyplot as plt
import skimage.io
import skimage.transform
from skimage.transform import resize
# import tensorflow as tf
# %matplotlib inline
print ("Packs loaded")
# +
# Print Current Folder
cwd = os.getcwd()
print ("Current folder is %s" % (cwd) )
# Useful function
def print_typeshape(img):
print("Type is %s" % (type(img)))
print("Shape is %s" % (img.shape,))
# -
# # Load & plot
# Load
cat = imread(cwd + "/images/cat.jpg")
print_typeshape(cat)
# Plot
plt.figure(0)
plt.imshow(cat)
plt.title("Original Image with imread")
plt.draw()
# Load
cat2 = imread(cwd + "/images/cat.jpg").astype(np.float)
print_typeshape(cat2)
# Plot
plt.figure(0)
plt.imshow(cat2)
plt.title("Original Image with imread.astype(np.float)")
plt.draw()
# Load
cat3 = imread(cwd + "/images/cat.jpg").astype(np.float)
print_typeshape(cat3)
# Plot
plt.figure(0)
plt.imshow(cat3/255.)
plt.title("Original Image with imread.astype(np.float)/255.")
plt.draw()
# # Resize
# Resize
catsmall = resize(cat, [100, 100, 3])
print_typeshape(catsmall)
# Plot
plt.figure(1)
plt.imshow(catsmall)
plt.title("Resized Image")
plt.draw()
# # Grayscale
# +
# Grayscale
def rgb2gray(rgb):
if len(rgb.shape) is 3:
return np.dot(rgb[...,:3], [0.299, 0.587, 0.114])
else:
print ("Current Image if GRAY!")
return rgb
catsmallgray = rgb2gray(catsmall)
print ("size of catsmallgray is %s" % (catsmallgray.shape,))
print ("type of catsmallgray is", type(catsmallgray))
plt.figure(2)
plt.imshow(catsmallgray, cmap=plt.get_cmap("gray"))
plt.title("[imshow] Gray Image")
plt.colorbar()
plt.draw()
# -
# # Reshape
# +
# Convert to Vector
#한줄로 펴라
catrowvec = np.reshape(catsmallgray, (1, -1));
print ("size of catrowvec is %s" % (catrowvec.shape,))
print ("type of catrowvec is", type(catrowvec))
# Convert to Matrix
catmatrix = np.reshape(catrowvec, (100, 100));
print ("size of catmatrix is %s" % (catmatrix.shape,))
print ("type of catmatrix is", type(catmatrix))
# -
# # Load from folder
# +
# Load from Folder
cwd = os.getcwd()
path = cwd + "/images/cats"
valid_exts = [".jpg",".gif",".png",".tga", ".jpeg"]
# print ("Images in %s are: \n %s" % (path, os.listdir(path)))
print ("%d files in %s" % (len(os.listdir(path)), path))
# Append Images and their Names to Lists
imgs = []
names = []
for f in os.listdir(path):
# For all files
ext = os.path.splitext(f)[1]
# Check types
if ext.lower() not in valid_exts:
continue
fullpath = os.path.join(path,f)
imgs.append(imread(fullpath))
names.append(os.path.splitext(f)[0]+os.path.splitext(f)[1])
print ("%d images loaded" % (len(imgs)))
# -
# Check
nimgs = len(imgs)
randidx = np.sort(np.random.randint(nimgs, size=3))
print ("Type of 'imgs': ", type(imgs))
print ("Length of 'imgs': ", len(imgs))
for curr_img, curr_name, i \
in zip([imgs[j] for j in randidx]
, [names[j] for j in randidx]
, range(len(randidx))):
print ("[%d] Type of 'curr_img': %s" % (i, type(curr_img)))
print (" Name is: %s" % (curr_name))
print (" Size of 'curr_img': %s" % (curr_img.shape,))
# Plot Images in 'imgs' list
nimgs = len(imgs)
randidx = np.sort(np.random.randint(nimgs, size=3))
for curr_img, curr_name, i \
in zip([imgs[j] for j in randidx]
, [names[j] for j in randidx], range(len(randidx))):
plt.figure(i)
plt.imshow(curr_img)
plt.title("["+ curr_name +", " + str(i) + "] ")
plt.draw()
print "That was all!"
|
notebooks/basic_imgprocess.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# +
import torch
import torch.nn.functional as F
import torchsde
import math
import matplotlib.pyplot as plt
import numpy as np
from tqdm.notebook import tqdm
from torch import _vmap_internals
# -
# cd ..
from cfollmer.objectives import log_g, relative_entropy_control_cost, stl_relative_entropy_control_cost
from cfollmer.sampler_utils import FollmerSDE, SimpleForwardNet
from cfollmer.trainers import basic_batched_trainer
# # The Model
#
# \begin{align}
# \theta &\sim \mathcal{N}(\theta | 0, \sigma_w^2 \mathbb{I}) \\
# y_i | x_i, \theta &\sim \mathrm{Bernouli}\left[\mathrm{sigmoid}\left(\theta^\top x_i + \theta_0\right)\right]
# \end{align}
#
# We want samples from $p(\theta | \{(y_i, x_i)\})$. Note $f(x; \theta)$ is a neural net with params $\theta$
# ## Loading the iris dataset
# +
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
device = "cuda" if torch.cuda.is_available() else "cpu"
iris = load_iris()
X = iris['data']
y = iris['target']
# Binary classification
X = X[~(y==2)][:,[0,1]]
y = y[~(y==2)]
# dummy dims
X = np.concatenate((torch.ones(X.shape[0],1), torch.tensor(X) ), axis=1)
names = iris['target_names']
feature_names = iris['feature_names']
# Scale data to have mean 0 and variance 1
# which is importance for convergence of the neural network
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# Split the data set into training and testing
X_train, X_test, y_train, y_test = train_test_split(
X_scaled, y, test_size=0.2, random_state=2)
X_train, X_test, y_train, y_test = \
torch.tensor(X_train, dtype=torch.float32, device=device), \
torch.tensor(X_test, dtype=torch.float32, device=device), \
torch.tensor(y_train, dtype=torch.float32, device=device), \
torch.tensor(y_test, dtype=torch.float32, device=device)
# -
fig, ax1 = plt.subplots(1, 1, figsize=(16, 6))
for target, target_name in enumerate(names[0:2]):
X_plot = X[y == target]
ax1.plot(X_plot[:, 1], X_plot[:, 2],
linestyle='none',
marker='o',
label=target_name)
ax1.set_xlabel(feature_names[0])
ax1.set_ylabel(feature_names[1])
ax1.axis('equal')
ax1.legend();
# $$\DeclareMathOperator*{\argmin}{arg\,min}$$
# $$\def\E{{\mathbb{E}}}$$
# $$\def\rvu{{\mathbf{u}}}$$
# $$\def\rvTheta{{\bm{\Theta}}}$$
# $$\def\gU{{\mathcal{U}}}$$
# $$\def\mX{{\mathbf{X}}}$$
# ## Controlled Schrodinger Follmer Sampler
#
# The objevtive we are trying to implement is:
#
# \begin{align}
# \mathbf{u}_t^{*}= \argmin_{\rvu_t \in \mathcal{U}}\mathbb{E}\left[\frac{1}{2\gamma}\int_0^1||\rvu(t, \Theta_t)||^2 dt - \ln\left(\frac{ p(\mX | \Theta_1)p(\Theta_1)}{\mathcal{N}(\Theta_1|\mathbf{0}, \gamma \mathbb{I} )}\right)\right] \
# \end{align}
#
# Where:
# \begin{align}
# d\Theta_t = \rvu(t, \Theta_t)dt + \sqrt{\gamma} dB_t
# \end{align}
#
# To do so we use the EM discretisation.
# +
def gaussian_prior(Θ, σ_w=1.0):
"""
Logistic regresion bayesian prior
"""
return -0.5 * (Θ**2).sum(axis=1) / σ_w
def log_likelihood(Θ, X, y):
"""
Slow implementation of logistic log likleihood
as a function of the parameters
"""
logits = X.mm(Θ.T)
vector_loss = - (torch.einsum("a,ab->b", y, torch.nn.functional.logsigmoid(logits)) +
torch.einsum("a,ab->b", (1-y), torch.log(1-torch.sigmoid(logits)))
)
return vector_loss
def log_likelihood_vmap(Θ, X, y):
"""
Hoping this implementation is less buggy / faster
still feels a bit slow.
"""
logits = X.mm(Θ.T)
pos_weights = torch.ones(logits.shape[0], device=device)
loss = torch.nn.BCEWithLogitsLoss(pos_weight=pos_weights, reduction="sum")
# TODO: Double check this is right, changed to a minus sign here
loss_ = lambda x: -1.0 * loss(x, y)
batched_loss = torch._vmap_internals.vmap(loss_)
return batched_loss(logits.T)
# +
γ = 1.0
Δt=0.05
dim=3
sde, losses = basic_batched_trainer(
γ, Δt, gaussian_prior, log_likelihood_vmap, dim, X_train, y_train,
method="euler", stl=True, adjoint=False, optimizer=None,
num_steps=400, batch_size_data=X_train.shape[0], batch_size_Θ=20,
batchnorm=False, device=device#, drift = None, lr=0.001
)
# -
losses
plt.plot(losses[:])
t_size = int(math.ceil(1.0/Δt))
ts = torch.linspace(0, 1, t_size).to(device)
Θ_0 = torch.zeros((50, dim)).to(device)
torchsde.sdeint(sde, Θ_0, ts, method="euler", dt=Δt).shape
X_train.shape
# +
t_size = int(math.ceil(1.0/Δt))
ts = torch.linspace(0, 1, t_size).to(device)
no_posterior_samples = 100
Θ_0 = torch.zeros((no_posterior_samples, 3)).to(device)
Θ_1 = torchsde.sdeint(sde, Θ_0, ts, dt=Δt)[-1,...]
# +
fig, (ax1,ax2,ax3) = plt.subplots(1,3)
ax1.hist(Θ_1[:,0].cpu().detach().numpy())
ax2.hist(Θ_1[:,1].cpu().detach().numpy())
ax3.hist(Θ_1[:,2].cpu().detach().numpy())
# -
pred = torch.sigmoid(X_train.mm(Θ_1.T)).mean(axis=1)
((pred > 0.5).float() == y_train).float().mean()
pred_test = torch.sigmoid(X_test.float().mm(Θ_1.T)).mean(axis=1)
((pred_test > 0.5).float() == y_test).float().mean()
Θ_1.mean(axis=0)
y_test, (pred_test < 0.5).long()
# +
plt.clf()
scaler = StandardScaler()
X_scaled2 = scaler.fit_transform(X)
plt.plot(X_scaled2[y==1, 1], X_scaled2[y==1, 2], 'bx')
plt.plot(X_scaled2[y==0, 1], X_scaled2[y==0, 2], 'ro')
plt.legend(('y=1', 'y=0'))
# # Overlay contour plot of approximate predictive distribution:
x_grid = np.arange(-4, 4, 0.005)
X1, X2 = np.meshgrid(x_grid, x_grid)
NG = X1.size
X_test_2 = np.hstack((np.ones((NG,1)), X1.reshape(NG,1), X2.reshape(NG,1)))
X_test_2.shape
X_test_2_tt = torch.tensor(X_test_2).to(device).float()
p_test = torch.sigmoid(X_test_2_tt.cpu().mm(Θ_1.cpu().T)).mean(axis=1).detach().cpu().numpy()
# kappa = 1.0 / np.sqrt(1 + (np.pi/8)*np.sum(np.dot(X_test,V)*X_test, 1))
# p_test = 1.0 / (1+np.exp(-np.dot(X_test,mm)*kappa))
P = np.reshape(p_test, X1.shape)
CS = plt.contour(X1, X2, P, [0.1,0.25,0.5,0.75,0.9])
plt.clabel(CS)
plt.xlabel('x_1')
plt.ylabel('x_2')
plt.title('Contours of p(y=1|x,D)')
plt.show()
# -
# ## MAP Baseline
#
# We run the point estimate approximation (Maximum a posteriori) to double check what the learned weights look like. We get the exact same training accuracy as with the controlled model and similarly large weights for the non bias weights.
X.shape
# +
Θ_map = torch.zeros((1, dim), requires_grad=True, device=device)
optimizer_map = torch.optim.Adam([Θ_map], lr=0.05)
# optimizer = torch.optim.LBFGS(gpr.parameters(), lr=0.01)
losses_map = []
num_steps = 1000
for i in tqdm(range(num_steps)):
optimizer_map.zero_grad()
if isinstance(optimizer_map, torch.optim.LBFGS):
def closure_map():
loss_map = log_likelihood_vmap()
optimizer_map.zero_grad()
loss_map.backward()
return loss
optimizer_map.step(closure_map)
losses_map.append(closure_map().item())
else:
loss_map = -(log_likelihood_vmap(Θ_map, X_train, y_train) + gaussian_prior(Θ_map))
optimizer_map.zero_grad()
loss_map.backward()
print(loss_map.item())
optimizer_map.step()
losses_map.append(loss_map.item())
Θ_map
pred_map = torch.sigmoid(X_train.mm(Θ_map.T)).mean(axis=1)
((pred_map < 0.5).float() == y_train).float().mean(), Θ_map
# -
# ## Pyro Bayesian Logistic Regeression
#
# As a baseline we run pyro with SVI on this same example atm we get very different results which is a bit worrying.
#
# #### EDIT:
#
# I think results are actually in agreement what was happening is the priors in the pyro code where much more confident thus the smaller weights. I just tried changing the prior of this pyro model and the posterior is not changing much, this is a bit fishy maybe worth investigating.
#
# I think it might just be the case that this model is not very good.
# +
import numpy as np
import scipy.special as ssp
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.distributions.constraints as constraints
from torch.utils.data import DataLoader
from torch.utils.data.sampler import SubsetRandomSampler
import pyro
import pyro.distributions as dist
from pyro.infer import SVI, Trace_ELBO
from pyro.optim import Adam, SGD
pyro.enable_validation(True)
torch.set_default_dtype(torch.double) # this was necessary on the CPU
# +
# these were adapted from the Pyro VAE tutorial
def train(svi, train_loader, n_train):
# initialize loss accumulator
epoch_loss = 0.
# do a training epoch over each mini-batch x returned
# by the data loader
for _, xs in enumerate(train_loader):
# do ELBO gradient and accumulate loss
epoch_loss += svi.step(*xs)
# return epoch loss
total_epoch_loss_train = epoch_loss / n_train
return total_epoch_loss_train
def evaluate(svi, test_loader, n_test):
# initialize loss accumulator
test_loss = 0.
# compute the loss over the entire test set
for _, xs in enumerate(test_loader):
# compute ELBO estimate and accumulate loss
test_loss += svi.evaluate_loss(*xs)
total_epoch_loss_test = test_loss / n_test
return total_epoch_loss_test
def plot_llk(train_elbo, test_elbo, test_int):
plt.figure(figsize=(8, 6))
x = np.arange(len(train_elbo))
plt.plot(x, train_elbo, marker='o', label='Train ELBO')
plt.plot(x[::test_int], test_elbo, marker='o', label='Test ELBO')
plt.xlabel('Training Epoch')
plt.legend()
plt.show()
# -
class LogRegressionModel(nn.Module):
def __init__(self, p):
super(LogRegressionModel, self).__init__()
self.p = p
# hyperparameters for normal priors
self.alpha_h_loc = torch.zeros(1, p)
self.alpha_h_scale = 0.0001 * torch.ones(1, p)
self.beta_h_loc = torch.zeros(1)
self.beta_h_scale = 0.0001 * torch.ones(1)
# initial values of variational parameters
self.alpha_0 = np.zeros((1, p))
self.alpha_0_scale = np.ones((1, p))
self.beta_0 = np.zeros((1,))
self.beta_0_scale = np.ones((1,))
def model(self, x, y):
# sample from prior
a = pyro.sample(
"weight", dist.Normal(self.alpha_h_loc, self.alpha_h_scale, validate_args=True).independent(1)
).float()
b = pyro.sample(
"bias", dist.Normal(self.beta_h_loc, self.beta_h_scale, validate_args=True).independent(1)
).float()
with pyro.iarange("data", x.size(0)):
# import pdb; pdb.set_trace()
model_logits = (torch.matmul(x, a.permute(1, 0)) + b).squeeze()
pyro.sample(
"obs",
dist.Bernoulli(logits=model_logits, validate_args=True),
obs=y.squeeze()
)
def guide(self, x, y):
# register variational parameters with pyro
alpha_loc = pyro.param("alpha_loc", torch.tensor(self.alpha_0))
alpha_scale = pyro.param("alpha_scale", torch.tensor(self.alpha_0_scale),
constraint=constraints.positive)
beta_loc = pyro.param("beta_loc", torch.tensor(self.beta_0))
beta_scale = pyro.param("beta_scale", torch.tensor(self.beta_0_scale),
constraint=constraints.positive)
pyro.sample(
"weight", dist.Normal(alpha_loc, alpha_scale, validate_args=True).independent(1)
)
pyro.sample(
"bias", dist.Normal(beta_loc, beta_scale, validate_args=True).independent(1)
)
def guide_(self, x, y, N=100):
# register variational parameters with pyro
alpha_loc = pyro.param("alpha_loc", torch.tensor(self.alpha_0))
alpha_scale = pyro.param("alpha_scale", torch.tensor(self.alpha_0_scale),
constraint=constraints.positive)
beta_loc = pyro.param("beta_loc", torch.tensor(self.beta_0))
beta_scale = pyro.param("beta_scale", torch.tensor(self.beta_0_scale),
constraint=constraints.positive)
w = []
b = []
for _ in range(N):
w.append(torch.tensor(pyro.sample(
"weight", dist.Normal(alpha_loc, alpha_scale, validate_args=True).independent(1)
)))
b.append(torch.tensor(pyro.sample(
"bias", dist.Normal(beta_loc, beta_scale, validate_args=True).independent(1)
)))
# import pdb;pdb.set_trace()
return torch.vstack(w), torch.vstack(b)
# +
pyro.clear_param_store()
optim = Adam({'lr': 0.01})
num_epochs = 1000
batch_size = 50
N = X.shape[0]
p = 2
n_train = X_train.shape[0]
example_indices = np.random.permutation(N)
n_test = N - n_train
test_iter = 50
# +
lr_model = LogRegressionModel(p=p)
svi = SVI(
lr_model.model, lr_model.guide, optim,
loss=Trace_ELBO()
)
lr_dataset = torch.utils.data.TensorDataset(torch.tensor(X[:,1:]).float(), torch.tensor(y.reshape(-1,1)).float())
data_loader_train = DataLoader(
dataset=lr_dataset, batch_size=batch_size, pin_memory=False,
sampler=SubsetRandomSampler(example_indices[:n_train]),
)
data_loader_test = DataLoader(
dataset=lr_dataset, batch_size=batch_size, pin_memory=False,
sampler=SubsetRandomSampler(example_indices[n_train:]),
)
train_elbo = []
test_elbo = []
for epoch in range(num_epochs):
total_epoch_loss_train = train(svi, data_loader_train, n_train)
train_elbo.append(-total_epoch_loss_train)
if epoch % test_iter == 0:
print("[epoch %03d] average training loss: %.4f" % (epoch, total_epoch_loss_train))
# report test diagnostics
total_epoch_loss_test = evaluate(svi, data_loader_test, n_test)
test_elbo.append(-total_epoch_loss_test)
# -
plot_llk(train_elbo, test_elbo, test_iter)
W, b = lr_model.guide_(X_train.float(), y_train.float())
# +
fig, (ax1,ax2,ax3) = plt.subplots(1,3)
# ax1.hist(Θ_1[:,0].detach().numpy())
# ax2.hist(Θ_1[:,1].detach().numpy())
# ax3.hist(Θ_1[:,2].detach().numpy())
ax1.hist(b.detach().numpy(), color="red")
ax2.hist(W[:,0].detach().numpy(), color="red")
ax3.hist(W[:,1].detach().numpy(), color="red")
# -
b.mean(), W.mean(axis=0)
|
notebooks/outdated_notebooks/LogisticRegressionExample.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <h1>Data Cleaning in Python</h1>
# <h2>Errors with Dirty data</h2>
# <p>
# <ul>
# <li>Formatting and encoding errors (e.g. extra whitespace, misspellings)</li>
# <li>Incorrect data type (e.g. numerical or string entries)</li>
# <li>Nonsensical data entries(e.g. age is less than 0)</li>
# <li>Duplicate entries (duplicate rows or columns)</li>
# <li>Missing data (e.g. NaN)</li>
# <li>Saturated data (e.g. value beyond a measurement limit)</li>
# <li>Systematic and individual errors (error affects many entries or only one)</li>
# <li>Confidential information (e.g. personally identifying or private information)</li>
# </ul>
# <p>
# <h1>In this tutorial, we will discuss how to clear some of the errors that occur in the dataset, we import.</h1>
import pandas as pd
import numpy as np
# <h2>Loading and Reading of .csv file</h2>
# <p><ul>
# <li>Encoding error</li>
# <li>Inconsistent rows</li>
# </ul>
# </p>
df=pd.read_csv('food_coded.csv')
# <p>The above error is due to wrong `encoding` of the data.<br>
# Encoding is the process of converting the data or a given sequence of characters, symbols, alphabets etc., into a specified format, for the secured transmission of data.</p>
# +
#To know the encoding of the data
import chardet
import pandas as pd
with open(r'food_coded.csv', 'rb') as f:
result = chardet.detect(f.read()) # or readline if the file is large
print(result)
df=pd.read_csv(r'food_coded.csv',encoding=result['encoding'])
# -
df
df.head() #For the first five rows of the data
df.tail() #For the last 5 rows of the data
# <h2>Inconsistent column names</h2>
# <p><ul>
# <li>Convert case</li>
# <li>Convert names if necessary</li>
# </ul>
# </p>
df.columns
df.columns.str.upper()
df.columns=df.columns.str.upper()
df.columns
#Renaming of column names
df.rename(columns={'COMFORT_FOOD':'JUNK' , 'COMFORT_FOOD_REASONS':'JUNK_REASONS'})
# <h2>Missing data</h2>
# <p><ul>
# <li><b>Add a default value or mean to fill the missing values.</b></li></p>
df.isnull() #'True' represent presence of NAN(not a number)
df.isnull().sum() #Total number of missing values in every column
df.isnull().sum().sum() #Total number of missing values in the entire dataset
df_with_zeros=df.fillna(0) #See the nan in 'CALORIES_DAY' column(first row) has been replaced by a default value which, in our case is 0.
df_with_zeros
#If we want to replace 'nan' with the mean in every column
df[df.columns].mean() #If want to do this in a particuar column, say 'Calories_Day', just write:df['CALORIES_DAY'].mean()
df_with_mean=df.fillna(df[df.columns].mean()) #df.fillna(df['CALORIES_DAY'].mean())
df_with_mean
# <p><ul>
# <li><b>Dropping the rows having 'nan' values</b></li>
# </ul>
# </p>
df_drop1=df.dropna(how='any') # drop rows having atleast one 'nan' values
df_drop=df_drop1
df_drop1
#See what's written in 73rd row of 'GPA' column(XD), its hilarious!
#I had to change it.The dataset had this previously, I didn't wrote that(XD)
df_drop['GPA'][73]='3.79'
df_drop
#See the difference after dropping the rows with any nan values
print(df.shape)
print(df_drop.shape)
df_drop_all_with_nan=df.dropna(how='all') # drop rows having all values as 'nan'
df_drop_all_with_nan
#You will see there is no row with all values as 'nan'
print(df.shape)
print(df_drop_all_with_nan.shape)
# <p><ul>
# <li><b>Dropping the rows having 'nan' values with a threshold</b></li>
# </ul>
# </p>
#Thresh is the number of non-values that should be in a row to not to drop it.
df_with_condition=df.dropna(thresh=3)
df_with_condition
df_with_no_duplicates=df.drop_duplicates(keep='first')
print(df.shape)
print(df_with_no_duplicates.shape)
# <h2>Some more functions to play with</h2>
df.GPA.describe()
df_drop.to_csv('cleanfile_droppednan.csv' , encoding='UTF-16')
df[df['GPA'] > 3.5]
#Since datatype of contents in GPA is 'str', we need to convert them to 'float' to make the above code work
df=pd.read_csv('cleanfile_droppednan.csv' , dtype={'GPA':float} , encoding='UTF-16')
df[df['GPA'] > 3.5]
# <h2>Try by yourself</h2>
# <p> <ul>
# <li>Select a column: df[‘calories_day’]</li>
# <li>Select the first 10 rows of a column: df[‘calories_day’][:10]</li>
# <li>Select multiple columns: df[[‘Gender’,’coffee’]]</li>
# </p>
# <h2>Have a good day and make this world a better place to live!!</h2>
|
dataPreprocessing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda root]
# language: python
# name: conda-root-py
# ---
# # Kaggle-kilpailu: Gene Expression Prediction
# ### <NAME>, [pekkoo](https://www.kaggle.com/pekkoo) @ Kaggle
# https://inclass.kaggle.com/c/gene-expression-prediction
#
# ## Taustaa
# Kilpailu järjestettiin osana TTY:n SGN-41007 Pattern Recognition and Machine Learning -kurssia ja se oli avoinna myös kurssin ulkopuolelle. Tavoitteena oli ennustaa geeniekspressiotaso histonimuokkaussignaalien pohjalta. Geeniekspressiotasoja oli kaksi, korkea ja matala, joten kyseessä oli binäärinen luokitteluongelma. Kilpailun arviointikriteerinä toimi Area Under Curve (AUC), joten ennusteiden tuli olla korkean geeniekspressiotason todennäköisyyksiä.
#
# Ryhmäämme "Group 40" kuuluivat lisäkseni Inkariina Simola ja <NAME>. Päädyimme sijalle **4/125**. Jaoimme työt ryhmän kesken suurin piirtein siten, että Inkariina teki data-analyysia ja visualisointia etsien uusia featureita, Bahareh kokeili muutamia scikit-learniin implementoituja algoritmeja ja minä keskityin tunkkaamaan XGBoostia, neuroverkkoja sekä näistä ja muutamasta muusta mallista koostuvaa lopullista ensembleä.
#
# Tässä raportissa esittelen vaihe vaiheelta siistityn koodini, mikä tuottaa neljännelle sijalle asettuvan ratkaisun ongelmaan. Suuri osa eksperimentoinnista on poistettu, jottei raportti olisi loputtoman pitkä. Myös koodisolujen tulosteet on poistettu, sillä kilpailun tuiskeessa soluja ajettiin epämääräisessä järjestyksessä, jolloin tulosteet olivat lopulta keskenään ristiriidassa. Raportti etenee luontevasti datan esikäsittelystä ja featureiden luomisesta kohti lopullisen ensemblen syntymistä. Lopuksi pohditaan mitä kilpailusta opittiin ja mitä olisi kenties voinut tehdä paremmin.
# ## Koodi
#
# Aluksi ladataan tarvittavat kirjastot ja tehdään muutamia asetuksia, jotka varmistavat tulosten toistettavuuden tai säätävät tulostuksia.
# +
import os
import numpy as np
import pandas as pd
from bayes_opt import BayesianOptimization
import xgboost as xgb
# Scikit-learn
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score, StratifiedKFold
from sklearn.metrics import roc_auc_score
from sklearn.neighbors import KNeighborsClassifier
# Keras
from keras.models import Sequential
from keras.layers import Convolution1D, MaxPooling1D, Flatten, Dense, Dropout, BatchNormalization, LSTM
from keras.layers.advanced_activations import PReLU
from keras.callbacks import ModelCheckpoint
# Asetukset
pd.options.display.max_columns = 999
np.random.seed(123)
random_state = 2017
cv = StratifiedKFold(n_splits=5, shuffle=True, random_state=random_state)
# -
# Määritetään funktiot datan lataamiseen, skaalaamiseen sekä neuroverkkojen rakentamiseen.
#
# Funktio **load_data** tarjottiin professori Heikki Huttusen puolesta kilpailun foorumilla ja sitä on muokattu vain tekemällä datan uudelleenmuotoilu valinnaiseksi. Muokkaus johtuu siitä, että ratkaisussamme dataa tarvitaan kahdessa eri muodossa riippuen siitä syötetäänkö sitä neuroverkoille vai ei.
#
# Neuroverkkojen arkkitehtuuri ja hyperparametrit etsittiin manuaalisesti kokeilemalla ja hieman [DeepChrome-arkkitehtuurista](https://arxiv.org/abs/1607.02078) inspiroituen. Kokeilua hankaloitti huomattavasti se, että neuroverkkoja pyöritettiin läppärillä ilman kunnollista näytönohjainta. Tämä oli melko hidasta ja uskoisin, että kunnollisella laskentateholla oltaisiin päädytty ainakin hieman erilaiseen lopputulokseen.
#
# Funktio **rnn_model** rakentaa CNN+RNN-yhdistelmän, mikä saattaa näin jälkikäteen mietittynä olla tarpeettoman monimutkaista, sillä se toimii suunnilleen yhtä hyvin kuin pelkkä CNN-malli. Toisaalta se sisältää huomattavasti vähemmän parametreja kuin pelkkä CNN, mikä on suotavaa etenkin tässä tilanteessa, kun koulutusdataa ei ole kovin paljoa (15 485 observaatiota).
# +
def load_data(ravel=True):
print("Loading data...")
x_train = np.loadtxt("x_train.csv", delimiter = ",", skiprows = 1)
x_test = np.loadtxt("x_test.csv", delimiter = ",", skiprows = 1)
y_train = np.loadtxt("y_train.csv", delimiter = ",", skiprows = 1)
print("All files loaded. Preprocessing...")
# remove the first column(Id)
x_train = x_train[:,1:]
x_test = x_test[:,1:]
y_train = y_train[:,1:]
# Every 100 rows correspond to one gene.
# Extract all 100-row-blocks into a list using np.split.
num_genes_train = x_train.shape[0] / 100
num_genes_test = x_test.shape[0] / 100
print("Train / test data has %d / %d genes." % \
(num_genes_train, num_genes_test))
x_train = np.split(x_train, num_genes_train)
x_test = np.split(x_test, num_genes_test)
if ravel:
# Reshape by raveling each 100x5 array into a 500-length vector
x_train = [g.ravel() for g in x_train]
x_test = [g.ravel() for g in x_test]
# convert data from list to array
x_train = np.array(x_train)
y_train = np.array(y_train)
x_test = np.array(x_test)
y_train = np.ravel(y_train)
# Now x_train should be 15485 x 500 and x_test 3871 x 500.
# y_train is 15485-long vector.
print("x_train shape is %s" % str(x_train.shape))
print("y_train shape is %s" % str(y_train.shape))
print("x_test shape is %s" % str(x_test.shape))
print('Data preprocessing done...')
return(x_train, y_train, x_test)
def minmax_scale(array, minimum=0, maximum=1):
array_std = (array - array.min(axis=0)) / (array.max(axis=0) - array.min(axis=0))
return array_std * (maximum - minimum) + minimum
def cnn_model():
model = Sequential()
model.add(Convolution1D(nb_filter=50, filter_length=10, border_mode='same',
input_shape=(100, 5)))
model.add(PReLU())
model.add(MaxPooling1D(5, border_mode='same'))
model.add(Dropout(.3))
model.add(BatchNormalization())
model.add(Flatten())
model.add(Dense(100))
model.add(PReLU())
model.add(Dropout(.3))
model.add(BatchNormalization())
model.add(Dense(100))
model.add(PReLU())
model.add(Dropout(.3))
model.add(BatchNormalization())
model.add(Dense(1, activation = 'sigmoid'))
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
return model
def rnn_model():
model = Sequential()
model.add(Convolution1D(nb_filter=50, filter_length=10, border_mode='same',
input_shape=(100, 5)))
model.add(PReLU())
model.add(MaxPooling1D(5, border_mode='same'))
model.add(Dropout(.4))
model.add(BatchNormalization())
model.add(LSTM(100))
model.add(Dropout(.4))
model.add(BatchNormalization())
model.add(Dense(125))
model.add(PReLU())
model.add(Dropout(.2))
model.add(BatchNormalization())
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
return model
# -
# ### Datan esikäsittely
# Ladataan data 15485 x 500 -muodossa ja muutetaan dataframeiksi featureiden käsittelyn ja lisäämisen helpottamiseksi *pandas*-kirjaston avulla.
x_train, y_train, x_test = load_data()
x_train_df = pd.DataFrame(x_train)
x_test_df = pd.DataFrame(x_test)
# Ladataan data erikseen neuroverkoille soveltuvassa muodossa. Tällä kertaa muoto pysyy alkuperäisenä eikä tarvetta ole käsitellä featureita tai muuntaa dataa matriiseista dataframeiksi, sillä neuroverkkomme löytävät sopivat featuret itse. Neuroverkkojen oppimisen jouhevoittamiseksi data skaalataan välille 0 - 1.
x_train_100_5, y_train, x_test_100_5 = load_data(ravel=False)
x_train_100_5 = minmax_scale(x_train_100_5)
x_test_100_5 = minmax_scale(x_test_100_5)
# Luodaan funktio, mikä laskee statistiikkoja eri "markereille". Markerit esiintyvät dataframen kolumneissa viiden välein. Paljon muitakin statistiikkoja kokeiltiin (esim. mediaani, varianssi, minimi/maksimi ja summat), mutta nämä kolme muodostivat cross-validation-proseduurin perusteella parhaan joukon.
def get_stats(row, index=0, stat='mean'):
if stat == 'mean':
return row[index:500:5].mean()
elif stat == 'perc0': # Nollien prosentuaalinen osuus markerille
return np.mean(row[index:500:5] == 0)
elif stat == 'std':
return np.std(row[index:500:5])
else:
raise ValueError(stat + ' currently not supported.')
# Hyödyntäen funktiota yllä, luodaan kolumnit jokaiselle markerille jokaisesta statistiikasta sekä koulutus- että testausdataframeille.
# +
markers = ['H3K4me3', 'H3K4me1', 'H3K36me3', 'H3K9me3', 'H3K27me3']
dataframes = [x_train_df, x_test_df]
stats = ['mean', 'perc0', 'std']
for df in dataframes:
for stat in stats:
for i, j in enumerate(markers):
df[j + '_' + stat] = df.apply(get_stats, args=(i, stat), axis=1)
# -
# ### Ennustavien mallien rakentaminen
# Luodaan DMatrix XGBoostia varten.
xg_train = xgb.DMatrix(x_train_df, label=y_train)
# Etsitään optimaalisia hyperparametreja XGBoostille Bayesilaisen optimoinnin avulla. Koodi on napattu käytännössä suoraan BayesianOptimization-kirjaston [Github-esimerkistä](https://github.com/fmfn/BayesianOptimization/blob/master/examples/xgboost_example.py).
# +
def xgb_evaluate(min_child_weight,
colsample_bytree,
max_depth,
subsample,
gamma,
alpha):
params['min_child_weight'] = int(min_child_weight)
params['colsample_bytree'] = max(min(colsample_bytree, 1), 0)
params['max_depth'] = int(max_depth)
params['subsample'] = max(min(subsample, 1), 0)
params['gamma'] = max(gamma, 0)
params['alpha'] = max(alpha, 0)
cv_result = xgb.cv(params, xg_train, num_boost_round=num_rounds,
nfold=5, seed=random_state, stratified=True,
metrics='auc', callbacks=[xgb.callback.early_stop(100)])
return cv_result['test-auc-mean'].values[-1]
num_rounds = 3000
num_iter = 120
init_points = 5
params = {
'objective': 'binary:logistic',
'eta': .01,
'silent': 1,
'verbose_eval': True,
'seed': random_state
}
xgbBO = BayesianOptimization(xgb_evaluate, {'min_child_weight': (1, 20),
'colsample_bytree': (.1, 1),
'max_depth': (1, 40),
'subsample': (.6, 1),
'gamma': (0, 8),
'alpha': (0, 8),
})
xgbBO.maximize(init_points=init_points, n_iter=num_iter)
# -
# Alla parhaat löydetyt hyperparametrit. Puista tuli huomattavan syviä.
bayes_params3 = {
'objective': 'binary:logistic',
'eta': .01,
'alpha': 0.9939,
'colsample_bytree': .1066,
'gamma': 1.8422,
'max_depth': 39,
'min_child_weight': 7,
'subsample': .8101,
'seed': random_state,
'silent': 1
}
# Rullataan XGBoostin oma cross-validation-proseduuri löydetyillä parametreilla, jolloin saadaan optimaalinen puiden lukumäärä.
xgb_cv = xgb.cv(bayes_params_3, xg_train, num_boost_round=10000, early_stopping_rounds=200, nfold=5,
stratified=True, verbose_eval=True, metrics='auc', seed=random_state)
# Luodaan meta-versio koulutus- ja testausdataframeista ensemblen rakentamista varten. Lisätään näihin tyhjät kolumnit kaikille käytettäville malleille. Ensemble rakennetaan [Kagglen blogissa julkaistun ohjeen](http://blog.kaggle.com/2016/12/27/a-kagglers-guide-to-model-stacking-in-practice/) mukaisesti. Lopulliset käytettävät mallit valikoitiin rakentamalla erilaisia ensemblejä ja cross-validoimalla.
# +
x_train_df_meta = x_train_df.copy()
x_train_df_meta['XGB'] = np.nan
x_train_df_meta['CNN'] = np.nan
x_train_df_meta['RNN'] = np.nan
x_train_df_meta['LR'] = np.nan
x_train_df_meta['ET'] = np.nan
x_train_df_meta['RF'] = np.nan
x_test_df_meta = x_test_df.copy()
x_test_df_meta['XGB'] = np.nan
x_test_df_meta['CNN'] = np.nan
x_test_df_meta['RNN'] = np.nan
x_test_df_meta['LR'] = np.nan
x_test_df_meta['ET'] = np.nan
x_test_df_meta['RF'] = np.nan
# -
# Tehdään lista ensemblessä käytettävistä scikit-learn-algoritmeista ja niille annettavista nimistä. Jokaisen mallin hyperparametrit valittiin yksittäin cross-validoiden koulutusdatalla.
# +
clfs = [LogisticRegression(C=.01, penalty='l1'),
ExtraTreesClassifier(n_estimators=800, n_jobs=2),
RandomForestClassifier(n_estimators=800, n_jobs=2, criterion='entropy')]
clf_names = ['LR', 'ET', 'RF']
# -
# Sitten rakennetaan itse ensemble. Koulutusdata jaetaan viiteen osaan ja jokaisella kierroksella koulutetaan mallit neljällä osalla sekä ennustetaan korkean geeniekspressiotason todennäköisyydet viidennelle. Näitä ennustuksia tallennetaan jokaisella kierroksella koulutusdatan meta-version tietyille riveille, josta niitä myöhemmin käytetään koulutusdatana seuraavan tason mallissa.
#
# Optimaalinen epochien määrä neuroverkoille tuntui vaihtelevan merkittävästi, joten mallit päädyttiin tallentamaan jokaiselta epochilta ja testaamaan niitä kaikkia kunkin kierroksen validointidatalla. Parhaat pisteet saava malli valittiin ja muut poistettiin. Tämä saattoi tarpeettomasti lisätä monimutkaisuutta, enkä ole varma oliko se nerokasta vai typerää.
#
# Ensemblen rakentaminen kesti läppärilläni noin 14 tuntia.
# +
num_fold = 0
n_epochs = 25
CNN_test_preds = []
RNN_test_preds = []
neural_nets = ['CNN', 'RNN']
for train_index, test_index in cv.split(x_train_df, y_train):
# Valitaan data sekä neuroverkoille että muille käytettäville malleille
X_cvtrain = x_train_df.iloc[train_index]
X_cvtest = x_train_df.iloc[test_index]
X_cvtrain_100_5 = x_train_100_5[train_index]
X_cvtest_100_5 = x_train_100_5[test_index]
y_cvtrain = y_train[train_index]
y_cvtest = y_train[test_index]
num_fold += 1
# Valmiiksi oltiin luotu viisi kansiota hakemistoon, yksi kutakin kierrosta varten
os.chdir('/Users/peks/Documents/Studies/ML/Competition/Keras_models/Fold' + str(num_fold))
# Koulutetaan molemmat neuroverkot loopissa, CNN ja CNN+RNN
for net in neural_nets:
if net == 'CNN':
model = cnn_model()
else:
model = rnn_model()
# Tallennetaan malli jokaiselta epochilta hakemistoon
callbacks = [
ModelCheckpoint(filepath='weights.-{epoch:02d}-{val_acc:.4f}.hdf5', monitor='val_acc')
]
# Sovitetaan malli
model.fit(X_cvtrain_100_5, y_cvtrain, validation_data=[X_cvtest_100_5, y_cvtest],
nb_epoch=n_epochs, callbacks=callbacks, batch_size=16)
# Haetaan jokaisen epochin mallien nimet
fold_model_names = os.listdir()[1:]
epoch_aucs = np.array([])
# Testataan jokaisen epochin mallia validointidatalla ja lisätään AUC-pisteytys listaan
for epoch_model in fold_model_names:
model.load_weights(epoch_model)
epoch_auc = roc_auc_score(y_cvtest, model.predict(X_cvtest_100_5).ravel())
epoch_aucs = np.append(epoch_aucs, epoch_auc)
# Valitaan malleista parhaiten validointidatalla toimiva ja ladataan sen painotukset
model.load_weights(fold_model_names[epoch_aucs.argmax()])
# Poistetaan tallennetut epoch-mallit
for file in fold_model_names:
os.remove(file)
# Ennustetaan sekä validointidatalla koulutus-metaa varten että
# testidatalla testi-metaa varten
nn_fold_pred = model.predict(X_cvtest_100_5).ravel()
x_train_df_meta.loc[test_index, net] = nn_fold_pred
nn_test_pred = model.predict(x_test_100_5).ravel()
# Listään testidatan ennusteet oikeaan listaan
if net == 'CNN':
CNN_test_preds.append(nn_test_pred)
else:
RNN_test_preds.append(nn_test_pred)
# Tulostetaan kierroksen tulokset validointidatalla neuroverkoille
print('Fold', num_fold, net, 'CV AUC:', roc_auc_score(y_cvtest, nn_fold_pred))
# Rullataan scikit-learn mallit läpi ja ennustetaan jokaisella
for i, clf in enumerate(clfs):
clf.fit(X_cvtrain, y_cvtrain)
clf_pred = clf.predict_proba(X_cvtest)[:, 1]
x_train_df_meta.loc[test_index, clf_names[i]] = clf_pred
print('Fold', num_fold, clf_names[i], 'CV AUC:', roc_auc_score(y_cvtest, clf_pred))
# Koulutetaan XGBoost-malli aiemmin löydetyillä parametreilla
xg_cvtrain = xgb.DMatrix(X_cvtrain, label=y_cvtrain)
xg_cvtest = xgb.DMatrix(X_cvtest)
xgb_model = xgb.train(bayes_params3, xg_cvtrain, num_boost_round=1184)
xgb_cvpred = xgb_model.predict(xg_cvtest)
x_train_df_meta.loc[test_index, 'XGB'] = xgb_cvpred
print('Fold', num_fold, 'XGB CV AUC:', roc_auc_score(y_cvtest, xgb_cvpred))
print('Fold', num_fold, 'completed.')
print(50 * '-')
print('Train meta filled. Thank you.')
os.chdir('/Users/peks/Documents/Studies/ML/Competition/')
# -
# Tallennetaan tämänhetkinen koulutus-meta-dataframe CSV-tiedostoon varmuuden vuoksi.
x_train_df_meta.to_csv('train_meta.csv', index=False)
# Tarkistetaan CV-pisteet sovittamalla logistinen regressio meta-ennusteiden päälle.
# +
LR = LogisticRegression()
used_cols = ['XGB', 'CNN', 'RNN', 'LR', 'ET', 'RF']
cross_val_score(LR, x_train_df_meta[used_cols], y_train, scoring='roc_auc', cv=cv).mean()
# -
# Tutkitaan josko parantamisen varaa löytyisi lisäämällä alkuperäisiä marker-statistiikkoihin liittyviä featureita. Pyörittelemällä tätä hetken aikaa eri kombinaatioilla saatiin CV-pisteitä nostettua hieman.
# +
stat_cols = x_train_df_meta.columns[500:-7].values
used_cols = ['XGB', 'CNN', 'RNN', 'LR', 'ET','H3K27me3_std',
'H3K27me3_mean', 'H3K4me1_perc0', 'H3K9me3_std']
print('Baseline:', cross_val_score(LR, x_train_df_meta[used_cols],
y_train, scoring='roc_auc', cv=cv).mean())
# Printataan uudet CV-pisteet featureita yksi kerrallaan lisäillen
for i in range(len(stat_cols)):
print(stat_cols[i], cross_val_score(LR, x_train_df_meta[used_cols + [stat_cols[i]]],
y_train, scoring='roc_auc', cv=cv).mean())
# -
# Aivan kilpailun viime hetkillä päätin testata vielä XGBoost-mallien rakentamista eri seedeillä ja näistä keskiarvon ottamista. Tämä paransi tulostamme vielä yllättävän paljon. Jos tämän olisi tajunnut tehdä aikaisemmin, olisin nostanut loopattavien seedien lukumäärää vielä hieman. Nyt tuli kiire niin piti rajoittaa.
# +
xgbs = []
xg_train = xgb.DMatrix(x_train_df, label=y_train)
xg_test = xgb.DMatrix(x_test_df)
for i in range(1, 8):
complete_xgb_model = xgb.train(bayes_params3, xg_train, num_boost_round=int(1184/.8))
xgb_pred = complete_xgb_model.predict(xg_test)
xgbs.append(xgb_pred)
x_test_df_meta['XGB'] = np.mean(xgbs, axis=0)
# -
# Tehdään lopulliset yksittäisennusteet muilla scikit-learn-malleilla testidatalle.
# +
final_clfs = [LogisticRegression(C=.01, penalty='l1'),
ExtraTreesClassifier(n_estimators=800, n_jobs=2)]
final_clf_names = ['LR', 'ET']
x_test_df_meta.drop('RF', axis=1, inplace=True) # Random forest huomattiin haitalliseksi ensemblessä
x_test_df_meta['CNN'] = np.mean(CNN_test_preds, axis=0)
x_test_df_meta['RNN'] = np.mean(RNN_test_preds, axis=0)
for i, clf in enumerate(final_clfs):
clf.fit(x_train_df, y_train)
x_test_df_meta[final_clf_names[i]] = clf.predict_proba(x_test_df)[:, 1]
# -
# Viimeisen tason mallina meta-featureiden päällä käytetään jälleen XGBoostia, jolle etsitään taas optimaalisia hyperparametreja Bayesilaisella optimoinnilla.
xg_train_meta = xgb.DMatrix(x_train_df_meta[used_cols], label=y_train)
xg_test_meta = xgb.DMatrix(x_test_df_meta[used_cols])
# +
def xgb_evaluate(min_child_weight,
colsample_bytree,
max_depth,
subsample,
gamma,
alpha):
params['min_child_weight'] = int(min_child_weight)
params['colsample_bytree'] = max(min(colsample_bytree, 1), 0)
params['max_depth'] = int(max_depth)
params['subsample'] = max(min(subsample, 1), 0)
params['gamma'] = max(gamma, 0)
params['alpha'] = max(alpha, 0)
cv_result = xgb.cv(params, xg_train_meta, num_boost_round=num_rounds,
nfold=5, seed=random_state, stratified=True,
metrics='auc', callbacks=[xgb.callback.early_stop(100)])
return cv_result['test-auc-mean'].values[-1]
num_rounds = 3000
num_iter = 120
init_points = 5
params = {
'objective': 'binary:logistic',
'eta': .01,
'silent': 1,
'verbose_eval': True,
'seed': random_state
}
xgbBO = BayesianOptimization(xgb_evaluate, {'min_child_weight': (1, 20),
'colsample_bytree': (.1, 1),
'max_depth': (1, 40),
'subsample': (.6, 1),
'gamma': (0, 8),
'alpha': (0, 8),
})
xgbBO.maximize(init_points=init_points, n_iter=num_iter)
# -
bayes_params_final = {
'objective': 'binary:logistic',
'eta': .01,
'alpha': .0748,
'colsample_bytree': .8819,
'gamma': .8596,
'max_depth': 1,
'min_child_weight': 2,
'subsample': .6542,
'seed': random_state,
'silent': 1
}
# Hyvät parametrit on löydetty, joten on aika tehdä lopulliset ennusteet.
final_xgb_ = xgb.train(bayes_params_final, xg_train_meta, num_boost_round=int(912/.8))
xgb_pred = final_xgb_model.predict(xg_test_meta)
# Luodaan data frame geenitunnisteista ja lopullisista ennusteista. Tallennetaan tämä CSV-tiedostona ja lähetetään kilpailuun. Lopullinen AUC-pisteytys on 0.92787 Kagglen yksityisellä pistetaululla.
pred_df = pd.DataFrame({'GeneId': np.arange(1, x_test.shape[0] + 1),
'Prediction': xgb_pred})
pred_df.to_csv('submission.csv', index=False)
# ## Mietteitä
#
# Opin kilpailussa todella paljon ja osallistuminen oli lystiä. Ensimmäistä kertaa rakensin kunnon ensemblen, käytin Bayesilaista optimointia hyperparametrien löytämiseksi sekä käytin neuroverkkoja Kaggle-kilpailussa. Nähdäkseni parantamisen varaa jäi etenkin neuroverkkojen hyödyntämisen suhteen, sillä esimerkiksi [Kagglen foorumiketjussa](https://inclass.kaggle.com/c/gene-expression-prediction/forums/t/29637/congratulations-to-the-winners) toiseksi tulleet kertoivat käyttäneensä pelkästään CNN:ää, ottaen mediaanin 10-osaisen cross-validation-proseduurin ennusteista testidatalle. Neuroverkkojen tutkimista rajoitti kuitenkin pelkkä läppärin käyttö. Kaksi erilaista neuroverkkomallia tuli silti rakennettua, mikä oli luultavasti hieman ylitseampuvaa, vaikka se ensembleä tässä vähän kohensikin.
#
# Parempien neuroverkkoarkkitehtuurien lisäksi olen lähes varma, että 10-osainen cross-validation olisi nostanut pisteitämme nykyisilläkin malleilla. Erityisesti se olisi uskoakseni hyödyttänyt juurikin neuroverkkoja, jotka olisivat nauttineet kasvaneesta koulutusdatan määrästä, ja joiden ennusteet testidatalla luotiin nimenomaan cross-validation-proseduurin aikana. Laskentatehon puutteen vuoksi käytin vain viittä osaa ristiinvalidoidessa. Myös XGBoostin seedejä olisi voinut rullata enemmän läpi, jos olisi sen aikasemmin tajunnut tehdä.
#
# Neljänteen sijaan voi kuitenkin olla sangen tyytyväinen. Ero kolmanneksi ja toiseksi sijoittuneisiin joukkueisiin jäi pieneksi. Kilpailun voittaja sen sijaan paini täysin omassa sarjassaan. Ero muihin oli niinkin suuri, että haistelisimme voittajan löytäneen internetistä [oikeat vastaukset testidatalle](http://egg2.wustl.edu/roadmap/data/byDataType/rna/expression/).
|
Kaggle_gene_expression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # ***Introduction to Radar Using Python and MATLAB***
# ## <NAME> - Copyright (C) 2019 Artech House
# <br/>
#
# # Rounded Nose Cone Radar Cross Section
# ***
# Referring to Section 7.4.1.6, for cones with rounded nose tips, as shown in Figure 7.12, the physical optics approximation with axial incidence is given by (Equation 7.55)
#
# $$
# \sigma = \pi b^2\Bigg[ 1 - \frac{\sin\big(2kb(1-\sin\alpha)\big)}{kb\cos^2\alpha} + \frac{1 + \cos^4\alpha}{4(kb)^2\cos^4\alpha} - \frac{\cos\big(2kb(1-\sin\alpha)\big)}{2(kb^2)\cos^2\alpha} \Bigg] \hspace{0.5in} \text{(m}^2\text{)},
# $$
#
#
# where $b$ is the radius of the rounded nose tip. For incident angles other than axial, but less than the cone angle ($\theta_i \le \alpha$), (Equation 7.56)
#
# $$
# \sigma = \pi b^2 \frac{1 + \theta_i^2}{4(kb)^2} \Big[A_1 + A_2 \cos\big(2k\cos\theta_i (1 - \sin\alpha)\big) + A_3\sin\big(2k\cos\theta_i(1-\sin\alpha)\big)\Big]\hspace{0.25in} \text{(m}^2\text{)},
# $$
#
# where
#
# \begin{align}
# A_1 = \; &2 + 2\alpha^2 - 2\theta_i^2 + \alpha^4 - \alpha^2\theta_i^2 + 0.5\theta_i^4 + 2\alpha^4\theta_i^2 + 4(kb)^2 - 2(kb)^2\theta_i^2 \nonumber \\[5pt]
# &- 8(kb)^3\theta_i^2 + (kb)^2\theta_i^4 + 6(kb)^2\alpha^2\theta_i^2 + 8(kb)^3\theta_i^4 + 13(kb)^4\theta_i^4, \\ \nonumber \\
# A_2 = &-2 -2\alpha^2 + 2\theta_i^2 + \alpha^2\theta_i^2 - 0.5\theta_i^4 - 6(kb)^2\theta_i^2 + 8(kb)^4\theta_i^3 + 3(kb)^2\theta_i^4, \\ \nonumber \\
# A_3 = &-4\big(1 + \alpha^2 - 0.5\theta_i^2 + 3(kb\theta_i)^2\big)\big(kb - kb\theta_i^2 - (kb\theta_i)^2\big) - 4(kb\theta_i)^3.\nonumber
# \end{align}
# ***
# Begin by getting the library path
import lib_path
# Set the operating frequency (Hz), the cone half angle (radians), and the nose radius (m)
# +
from numpy import radians
frequency = 1e9
cone_half_angle = radians(20.0)
nose_radius = 1.4
# -
# Set the incident angles using the `linspace` routine from `scipy`
# +
from numpy import linspace
incident_angle = linspace(0, cone_half_angle, 1801)
# -
# Calculate the radar cross section (m^2) for the rounded nose cone
# +
from Libs.rcs.rounded_nose_cone import radar_cross_section
from numpy import array
rcs = array([radar_cross_section(frequency, cone_half_angle, nose_radius, ia) for ia in incident_angle])
# -
# Display the radar cross section (m^2) for the rounded nose cone using the routines from `matplotlib`
# +
from matplotlib import pyplot as plt
from numpy import log10, degrees
# Set the figure size
plt.rcParams["figure.figsize"] = (15, 10)
# Display the results
plt.plot(degrees(incident_angle), 10.0 * log10(abs(rcs)), '')
# Set the plot title and labels
plt.title('RCS vs Incident Angle', size=14)
plt.ylabel('RCS (dBsm)', size=12)
plt.xlabel('Incident Angle (deg)', size=12)
# Set the tick label size
plt.tick_params(labelsize=12)
# Turn on the grid
plt.grid(linestyle=':', linewidth=0.5)
# -
|
jupyter/Chapter07/rounded_nose_cone.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Built on
# !date
# ## Status
#
# [](https://github.com/cranmer/stats-ds-book/actions?query=workflow%3A%22Deploy+Jupyter+Book%22+branch%3Amaster)
#
|
book/built-on.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # Introduction to Strings
#
# Algorithms PERG – Mar. 5<sup>th</sup>, 2020
#
# by <NAME>
# + [markdown] slideshow={"slide_type": "slide"}
# ## What is a string?
# + [markdown] slideshow={"slide_type": "fragment"}
# - **Goal:**
# Represent text in a computer
#
# - **Problem:**
# Computers only understand numbers
#
# - **Solution:**
# Store letters as numbers!
# + [markdown] slideshow={"slide_type": "slide"}
# ## String = Sequence of numbers
# + slideshow={"slide_type": "fragment"}
list(b"Hello World!")
# + [markdown] slideshow={"slide_type": "fragment"}
# Any structure as long as it's ordered:
# array, linked list, tree…
# + [markdown] slideshow={"slide_type": "slide"}
# ## How do strings work?
#
# Matching letters to numbers = **Encoding**
# + [markdown] slideshow={"slide_type": "fragment"}
# Binary text encoding is _much_ older than computers:
# * Baudot code: 1874
# * Colossus computer: 1944
# + [markdown] slideshow={"slide_type": "slide"}
# ## The ASCII Encoding
#
# - 7-bit code (128 characters)
# - Published in 1963
# - Designed for Teletype / Teleprinters
# - Base of practically all other encodings created since
# + [markdown] slideshow={"slide_type": "subslide"}
# ## The ASCII Encoding
# + slideshow={"slide_type": "skip"}
import numpy as np
import pandas as pd
ascii_chars = [
"␀␁␂␃␄␅␆␇␈␉␊␋␌␍␎␏",
"␐␑␒␓␔␕␖␗␘␙␚␛␜␝␞␟",
" !\"#$%&'()*+,-./",
"0123456789:;<=>?",
"@ABCDEFGHIJKLMNO",
"PQRSTUVWXZY[\\]^_",
"`abcdefghijklmno",
"pqrstuvwxyz{|}~␡",
]
ascii_col = [f"_{n:x}" for n in range(16)]
ascii_row = [f"{n:x}_" for n in range(8)]
np_ascii = np.array([list(line) for line in ascii_chars])
ascii_table = pd.DataFrame(np_ascii, columns=ascii_col, index=ascii_row)
# + slideshow={"slide_type": "-"}
ascii_table
# + [markdown] slideshow={"slide_type": "slide"}
# ## What about other languages?
#
# "Extended ASCII" codes use the 8<sup>th</sup> bit for 128 extra characters.
# + [markdown] slideshow={"slide_type": "fragment"}
# - ISO-8859
# - KOI8
# - Windows-1252
# - Mac OS Roman
# - …
# + [markdown] slideshow={"slide_type": "slide"}
# ## Unicode
#
# Having all these encodings is inconvenient, because Internet.
# + [markdown] slideshow={"slide_type": "fragment"}
# **Unicode** = international standard for encoding text.
# Currently includes 137,994 characters!
# + [markdown] slideshow={"slide_type": "subslide"}
# ## UTF-8
#
# UTF-8 is the most popular way to encode Unicode.
# + [markdown] slideshow={"slide_type": "fragment"}
# - Superset of ASCII
# - Uses between 1 and 4 bytes per character
# - Never produces null bytes except for `U+0`
# + [markdown] slideshow={"slide_type": "subslide"}
# ## ⚠ Unicode ≠ UTF-8 ⚠
#
# - **Unicode:**
# Assigns _code points_ to characters
# - **UTF-8:**
# Converts code points into _bytes_
#
# Alternatives to UTF-8 exist, e.g. UTF-16.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Demonstration
# + slideshow={"slide_type": "-"}
s = "Pandora \U0001F44D\U0001F3FF"
s
# + slideshow={"slide_type": "fragment"}
s.encode('utf-8')
# + slideshow={"slide_type": "fragment"}
s.encode('utf-8').decode('cp1252', 'replace')
# + [markdown] slideshow={"slide_type": "slide"}
# ## Implementations
# + [markdown] slideshow={"slide_type": "fragment"}
# - **Python 3:** Sequence of Unicode code points
# - **Java / JavaScript:** Sequence of UTF-16 codes
# - **Go / Rust:** Sequence of bytes, UTF-8 encoded
# - **C:** ¯\\_(ツ)_/¯
# + [markdown] slideshow={"slide_type": "slide"}
# # Thank You!
|
intro_to_strings/intro_to_strings-PERG_2020-03-05.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:larval_gonad]
# language: python
# name: conda-env-larval_gonad-py
# ---
# # Create all possible tSNE
# This is a quick and dirty script to create all possible tSNEs.
# +
# # %load ../start.py
# Imports
import os
import sys
from pathlib import Path
from tempfile import TemporaryDirectory
import string
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
# Project level imports
sys.path.insert(0, '../../lib')
from larval_gonad.notebook import Nb
from larval_gonad.plotting import TSNEPlot
# Setup notebook
nbconfig = Nb.setup_notebook()
# Turn on cache
from joblib import Memory
memory = Memory(cachedir=nbconfig.cache, verbose=0)
# +
REF = os.environ['REFERENCES_DIR']
OUTPUT = '../../output/testes_scRNAseq_pilot'
Path(OUTPUT).mkdir(exist_ok=True)
FIGS = '../../output/figures/testis_tsne'
Path(FIGS).mkdir(exist_ok=True)
# Import gene annotations
fbgn2symbol = pd.read_csv(str(Path(REF, 'dmel/r6-16/fb_annotation/dmel_r6-16.fb_annotation')), sep='\t',
usecols=['gene_symbol', 'primary_FBgn'], index_col='primary_FBgn').to_dict()['gene_symbol']
symbol2fbgn = pd.read_csv(str(Path(REF, 'dmel/r6-16/fb_annotation/dmel_r6-16.fb_annotation')), sep='\t',
usecols=['gene_symbol', 'primary_FBgn'], index_col='gene_symbol').to_dict()['primary_FBgn']
# -
tsne = pd.read_csv(Path(OUTPUT, 'tsne.tsv'), sep='\t')
norm = pd.read_csv(Path(OUTPUT, 'normalized_read_counts.tsv'), sep='\t')
data = tsne.join(norm.T)
# +
def sanitize_fname(fname):
valid_chars = "-_.%s%s" % (string.ascii_letters, string.digits)
return ''.join([x for x in fname if x in valid_chars])
def plot_gene(data, fbgn, symbol, **kwargs):
symbol = sanitize_fname(symbol)
fname = str(Path(FIGS, f'{fbgn}_{symbol}.png'))
if Path(fname).exists():
return
df = data[['tSNE_1', 'tSNE_2', fbgn]]
with plt.style.context(['paper-wide', 'default']):
fig, (ax1, ax2) = plt.subplots(1, 2, gridspec_kw={'width_ratios': [1.3, 1]})
TSNEPlot('tSNE_2', 'tSNE_1', data=df, hue=fbgn, s=10,
ax=ax1, title='Normalized Expression\n(Continuous)', **kwargs)
TSNEPlot('tSNE_2', 'tSNE_1', data=df, hue=df[fbgn] > 0,
cmap={
'0': 'w',
'1': 'k',
}, s=10, ax=ax2, alpha=.6, edgecolor='k', title='Normalized Expression\n(Binary)', **kwargs)
fig.suptitle(f'{symbol} ({fbgn})');
plt.tight_layout(rect=[0, 0, .9, .9])
plt.savefig(fname)
plt.close()
# +
colors = sns.color_palette('Reds')
color2 = sns.color_palette('Greys')
colors[0] = color2[0]
for fbgn in data.columns[2:]:
symbol = fbgn2symbol[fbgn]
plot_gene(data, fbgn, symbol, palette=colors)
# -
|
notebook/2017-12-08_iter_code.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
# %matplotlib inline
from zipline.data.data_portal import DataPortal
from zipline.data import bundles
from zipline.utils.calendars import get_calendar
bundle_data = bundles.load("quandl")
print(type(bundle_data))
end_date = pd.Timestamp("2014-01-01", tz="utc")
bundle_data.equity_daily_bar_reader.first_trading_day
data_por = DataPortal(
asset_finder=bundle_data.asset_finder,
trading_calendar=get_calendar("NYSE"),
first_trading_day=bundle_data.equity_daily_bar_reader.first_trading_day,
equity_daily_reader=bundle_data.equity_daily_bar_reader
)
TSLA = data_por.asset_finder.lookup_symbol(
"TSLA",
as_of_date=None
)
df = data_por.get_history_window(
assets=[TSLA],
end_dt=end_date,
bar_count=31 * 12,
frequency='1d',
data_frequency='daily',
field="open"
)
df.head()
df.describe()
df.index = pd.DatetimeIndex(df.index)
list(df.columns)[0]
df['open'] = df[list(df.columns)[0]]
df.head()
df = df.drop(columns=[list(df.columns)[0]])
df.head()
df['close'] = data_por.get_history_window(
assets=[TSLA],
end_dt=end_date,
bar_count=31 * 12,
frequency='1d',
data_frequency='daily',
field="close"
)
df['low'] = data_por.get_history_window(
assets=[TSLA],
end_dt=end_date,
bar_count=31 * 12,
frequency='1d',
data_frequency='daily',
field="low"
)
df['high'] = data_por.get_history_window(
assets=[TSLA],
end_dt=end_date,
bar_count=31 * 12,
frequency='1d',
data_frequency='daily',
field="high"
)
df.head()
df.tail()
# +
from zipline.data.data_portal import OHLCV_FIELDS
print(OHLCV_FIELDS)
# +
from matplotlib.dates import MonthLocator, date2num, DateFormatter
fig, ax = plt.subplots()
fig.subplots_adjust(bottom=0.3)
fig.set_figwidth(16)
fig.set_figheight(8)
ax.plot(df.index, df.open)
ax.plot(df.index, df.close)
lctr = MonthLocator() # every month
frmt = DateFormatter('%b') # %b gives us Jan, Feb...
ax.xaxis.set_major_locator(lctr)
ax.xaxis.set_major_formatter(frmt)
ax.legend()
plt.xticks(rotation=70)
plt.tight_layout()
plt.show();
# -
# #### Link <a href="https://www.forbes.com/sites/jimgorzelany/2013/10/02/tesla-model-s-catches-fire-stock-price-drops/#27f44d49781a"> Read More </a>
# +
from mpl_finance import candlestick2_ohlc
fig, ax = plt.subplots()
fig.subplots_adjust(bottom=0.3)
fig.set_figwidth(16)
fig.set_figheight(8)
lctr = MonthLocator() # every month
frmt = DateFormatter('%b') # %b gives us Jan, Feb...
ax.xaxis.set_major_locator(lctr)
ax.xaxis.set_major_formatter(frmt)
candlestick2_ohlc(ax,
opens=df.open,
closes=df.close,
highs=df.high,
lows=df.low,
width=0.8,
colorup='r',
colordown='k')
plt.xticks(rotation=70)
plt.tight_layout()
plt.show()
# -
|
section 0001/SEC001 VID004 Fetching and understanding the Dataset.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Introduction
#
# This is an open-source implementation of the paper **Hiding Images in Plain Sight: Deep Steganography, by <NAME> (Google), at NIPS 2017**. The paper is available [here](https://papers.nips.cc/paper/6802-hiding-images-in-plain-sight-deep-steganography).
#
# This code was initially produced with the goal of reproducing to a reasonable degree the results achieved and described in the paper, for the **[Global NIPS Paper Implementation Challenge](https://nurture.ai/nips-challenge/)**.
#
# **Abstract**: Steganography is the practice of concealing a secret message within another, ordinary, message. Commonly, steganography is used to unobtrusively hide a small message within the noisy regions of a larger image. In this study, we attempt to place a full size color image within another image of the same size. Deep neural networks are simultaneously trained to create the hiding and revealing processes and are designed to specifically work as a pair. The system is trained on images drawn randomly from the ImageNet database, and works well on natural images from a wide variety of sources. Beyond demonstrating the successful application of deep learning to hiding images, we carefully examine how the result is achieved and explore extensions. Unlike many popular steganographic methods that encode the secret message within the least significant bits of the carrier image, our approach compresses and distributes the secret image's representation across all of the available bits.
# +
### Imports接口 ###
from keras.callbacks import ModelCheckpoint, LearningRateScheduler, TensorBoard
from keras.engine.topology import Container
from keras.layers import *
from keras.models import Model
from keras.preprocessing import image
import keras.backend as K
import matplotlib.pyplot as plt
import numpy as np
import os
import random
import scipy.misc
from tqdm import *
import sys
from PIL import Image
sys.modules['Image'] = Image
# %matplotlib inline
# -
# ## Config
# +
### 常量定义(目录) ###
DATA_DIR = "./data"
TRAIN_DIR = os.path.join(DATA_DIR, "train")
TEST_DIR = os.path.join(DATA_DIR, "test")
IMG_SHAPE = (64, 64)
# -
# ## Dataset creation
# The Dataset we used is Tiny ImageNet Visual Recognition Challenge. It can be downloaded [here](https://tiny-imagenet.herokuapp.com/).
#
# Our training set is made of a random subset of images from all 200 classes.
def load_dataset_small(num_images_per_class_train=10, num_images_test=500):
"""从ImageNet数据集获得测试数据
num_images_per_class_train: 要加载到培训数据集中的每个类的图像数。
num_images_test:要加载到训练数据集中的图像总数。
"""
X_train = []
X_test = []
# 创建训练集
for c in os.listdir(TRAIN_DIR):
c_dir = os.path.join(TRAIN_DIR, c, 'images')
c_imgs = os.listdir(c_dir)
random.shuffle(c_imgs)
for img_name_i in c_imgs[0:num_images_per_class_train]:
img_i = image.load_img(os.path.join(c_dir, img_name_i))
x = image.img_to_array(img_i)
X_train.append(x)
random.shuffle(X_train)
# 创建测试集
test_dir = os.path.join(TEST_DIR, 'images')
test_imgs = os.listdir(test_dir)
random.shuffle(test_imgs)
for img_name_i in test_imgs[0:num_images_test]:
img_i = image.load_img(os.path.join(test_dir, img_name_i))
x = image.img_to_array(img_i)
X_test.append(x)
# 将训练和测试的数据以numpy数组的格式返回
return np.array(X_train), np.array(X_test)
# +
# 加载数据
X_train_orig, X_test_orig = load_dataset_small()
# 图像矢量规范化
X_train = X_train_orig/255.
X_test = X_test_orig/255.
# 打印统计信息
print ("Number of training examples = " + str(X_train.shape[0]))
print ("Number of test examples = " + str(X_train.shape[0]))
print ("X_train shape: " + str(X_train.shape)) # Should be (train_size, 64, 64, 3).
# +
# 把训练集分为两部分
# 前半部分用于秘密图像的训练,后半部分用于容器图像的训练
# S: 秘密图像
input_S = X_train[0:X_train.shape[0] // 2]
# C: 容器图像
input_C = X_train[X_train.shape[0] // 2:]
# -
# 显示训练数据集中的示例图像
fig=plt.figure(figsize=(8, 8))
columns = 4
rows = 5
for i in range(1, columns*rows +1):
# 从训练数据集中随机抽样
img_idx = np.random.choice(X_train.shape[0])
fig.add_subplot(rows, columns, i)
plt.imshow(X_train[img_idx])
plt.show()
# ## Model
#
# The model is composed of three parts: The **Preparation Network**, **Hiding Network** (Encoder) and the **Reveal Network**. Its goal is to be able to encode information about the secret image S into the cover image C, generating C' that closely resembles C, while still being able to decode information from C' to generate the decoded secret image S', which should resemble S as closely as possible.
#
# The Preparation Network has the responsibility of preparing data from the secret image to be concatenated with the cover image and fed to the Hiding Network. The Hiding Network than transforms that input into the encoded cover image C'. Finally, the Reveal Network decodes the secret image S' from C'. For stability, we add noise before the Reveal Network, as suggested by the paper. Although the author of the paper didn't originally specify the architecture of the three networks, we discovered aggregated layers showed good results. For both the Hiding and Reveal networks, we use 5 layers of 65 filters (50 3x3 filters, 10 4x4 filters and 5 5x5 filters). For the preparation network, we use only 2 layers with the same structure.
#
# Note that the loss function for the Reveal Network is different from the loss function for the Preparation and Hiding Networks. In order to correctly implement the updates for the weights in the networks, we create stacked Keras models, one for the Preparation and Hiding Network (which share the same loss function) and one for the Reveal Network. To make sure weights are updated only once, we freeze the weights on the layers of the Reveal Network before adding it to the full model.
#
# 
# +
# 用于衡量秘密图像和容器图像损失的变量
beta = 1.0
# 显示网络的反馈
def rev_loss(s_true, s_pred):
# Loss for reveal network is: beta * |S-S'|
return beta * K.sum(K.square(s_true - s_pred))
#整个模型的反馈,用于准备网络和隐藏网络
def full_loss(y_true, y_pred):
# 整个模型的反馈公式为: |C-C'| + beta * |S-S'|
s_true, c_true = y_true[...,0:3], y_true[...,3:6]
s_pred, c_pred = y_pred[...,0:3], y_pred[...,3:6]
s_loss = rev_loss(s_true, s_pred)
c_loss = K.sum(K.square(c_true - c_pred))
return s_loss + c_loss
#encoder编码器由准备网络和隐藏网络构成
# Returns the encoder as a Keras model, composed by Preparation and Hiding Networks.
def make_encoder(input_size):
input_S = Input(shape=(input_size))
input_C= Input(shape=(input_size))
# 准备网络2层
x3 = Conv2D(50, (3, 3), strides = (1, 1), padding='same', activation='relu', name='conv_prep0_3x3')(input_S)
x4 = Conv2D(10, (4, 4), strides = (1, 1), padding='same', activation='relu', name='conv_prep0_4x4')(input_S)
x5 = Conv2D(5, (5, 5), strides = (1, 1), padding='same', activation='relu', name='conv_prep0_5x5')(input_S)
x = concatenate([x3, x4, x5])
x3 = Conv2D(50, (3, 3), strides = (1, 1), padding='same', activation='relu', name='conv_prep1_3x3')(x)
x4 = Conv2D(10, (4, 4), strides = (1, 1), padding='same', activation='relu', name='conv_prep1_4x4')(x)
x5 = Conv2D(5, (5, 5), strides = (1, 1), padding='same', activation='relu', name='conv_prep1_5x5')(x)
x = concatenate([x3, x4, x5])
x = concatenate([input_C, x])
# 隐藏网络5层
x3 = Conv2D(50, (3, 3), strides = (1, 1), padding='same', activation='relu', name='conv_hid0_3x3')(x)
x4 = Conv2D(10, (4, 4), strides = (1, 1), padding='same', activation='relu', name='conv_hid0_4x4')(x)
x5 = Conv2D(5, (5, 5), strides = (1, 1), padding='same', activation='relu', name='conv_hid0_5x5')(x)
x = concatenate([x3, x4, x5])
x3 = Conv2D(50, (3, 3), strides = (1, 1), padding='same', activation='relu', name='conv_hid1_3x3')(x)
x4 = Conv2D(10, (4, 4), strides = (1, 1), padding='same', activation='relu', name='conv_hid1_4x4')(x)
x5 = Conv2D(5, (5, 5), strides = (1, 1), padding='same', activation='relu', name='conv_hid1_5x5')(x)
x = concatenate([x3, x4, x5])
x3 = Conv2D(50, (3, 3), strides = (1, 1), padding='same', activation='relu', name='conv_hid2_3x3')(x)
x4 = Conv2D(10, (4, 4), strides = (1, 1), padding='same', activation='relu', name='conv_hid2_4x4')(x)
x5 = Conv2D(5, (5, 5), strides = (1, 1), padding='same', activation='relu', name='conv_hid2_5x5')(x)
x = concatenate([x3, x4, x5])
x3 = Conv2D(50, (3, 3), strides = (1, 1), padding='same', activation='relu', name='conv_hid3_3x3')(x)
x4 = Conv2D(10, (4, 4), strides = (1, 1), padding='same', activation='relu', name='conv_hid3_4x4')(x)
x5 = Conv2D(5, (5, 5), strides = (1, 1), padding='same', activation='relu', name='conv_hid3_5x5')(x)
x = concatenate([x3, x4, x5])
x3 = Conv2D(50, (3, 3), strides = (1, 1), padding='same', activation='relu', name='conv_hid4_3x3')(x)
x4 = Conv2D(10, (4, 4), strides = (1, 1), padding='same', activation='relu', name='conv_hid4_4x4')(x)
x5 = Conv2D(5, (5, 5), strides = (1, 1), padding='same', activation='relu', name='conv_hid5_5x5')(x)
x = concatenate([x3, x4, x5])
output_Cprime = Conv2D(3, (3, 3), strides = (1, 1), padding='same', activation='relu', name='output_C')(x)
return Model(inputs=[input_S, input_C],
outputs=output_Cprime,
name = 'Encoder')
#decoder解码器由显示网络构成
# Returns the decoder as a Keras model, composed by the Reveal Network
def make_decoder(input_size, fixed=False):
# 显示网络
reveal_input = Input(shape=(input_size))
#加上高斯噪声,标准偏差为0.01。
# Adding Gaussian noise with 0.01 standard deviation.
input_with_noise = GaussianNoise(0.01, name='output_C_noise')(reveal_input)
x3 = Conv2D(50, (3, 3), strides = (1, 1), padding='same', activation='relu', name='conv_rev0_3x3')(input_with_noise)
x4 = Conv2D(10, (4, 4), strides = (1, 1), padding='same', activation='relu', name='conv_rev0_4x4')(input_with_noise)
x5 = Conv2D(5, (5, 5), strides = (1, 1), padding='same', activation='relu', name='conv_rev0_5x5')(input_with_noise)
x = concatenate([x3, x4, x5])
x3 = Conv2D(50, (3, 3), strides = (1, 1), padding='same', activation='relu', name='conv_rev1_3x3')(x)
x4 = Conv2D(10, (4, 4), strides = (1, 1), padding='same', activation='relu', name='conv_rev1_4x4')(x)
x5 = Conv2D(5, (5, 5), strides = (1, 1), padding='same', activation='relu', name='conv_rev1_5x5')(x)
x = concatenate([x3, x4, x5])
x3 = Conv2D(50, (3, 3), strides = (1, 1), padding='same', activation='relu', name='conv_rev2_3x3')(x)
x4 = Conv2D(10, (4, 4), strides = (1, 1), padding='same', activation='relu', name='conv_rev2_4x4')(x)
x5 = Conv2D(5, (5, 5), strides = (1, 1), padding='same', activation='relu', name='conv_rev2_5x5')(x)
x = concatenate([x3, x4, x5])
x3 = Conv2D(50, (3, 3), strides = (1, 1), padding='same', activation='relu', name='conv_rev3_3x3')(x)
x4 = Conv2D(10, (4, 4), strides = (1, 1), padding='same', activation='relu', name='conv_rev3_4x4')(x)
x5 = Conv2D(5, (5, 5), strides = (1, 1), padding='same', activation='relu', name='conv_rev3_5x5')(x)
x = concatenate([x3, x4, x5])
x3 = Conv2D(50, (3, 3), strides = (1, 1), padding='same', activation='relu', name='conv_rev4_3x3')(x)
x4 = Conv2D(10, (4, 4), strides = (1, 1), padding='same', activation='relu', name='conv_rev4_4x4')(x)
x5 = Conv2D(5, (5, 5), strides = (1, 1), padding='same', activation='relu', name='conv_rev5_5x5')(x)
x = concatenate([x3, x4, x5])
output_Sprime = Conv2D(3, (3, 3), strides = (1, 1), padding='same', activation='relu', name='output_S')(x)
if not fixed:
return Model(inputs=reveal_input,
outputs=output_Sprime,
name = 'Decoder')
else:
return Container(inputs=reveal_input,
outputs=output_Sprime,
name = 'DecoderFixed')
# 整个模型的构建
def make_model(input_size):
input_S = Input(shape=(input_size))
input_C= Input(shape=(input_size))
encoder = make_encoder(input_size)
decoder = make_decoder(input_size)
decoder.compile(optimizer='adam', loss=rev_loss)
decoder.trainable = False
output_Cprime = encoder([input_S, input_C])
output_Sprime = decoder(output_Cprime)
autoencoder = Model(inputs=[input_S, input_C],
outputs=concatenate([output_Sprime, output_Cprime]))
autoencoder.compile(optimizer='adam', loss=full_loss)
return encoder, decoder, autoencoder
# -
encoder_model, reveal_model, autoencoder_model = make_model(input_S.shape[1:])
# ## Training
#
# Although the author of the paper didn't explicitly described the learning rate schedule or the optimizer properties, we used our own schedule with ADAM optimizer. We train for 1000 epochs with a batch size of 32.
def lr_schedule(epoch_idx):
if epoch_idx < 200:
return 0.001
elif epoch_idx < 400:
return 0.0003
elif epoch_idx < 600:
return 0.0001
else:
return 0.00003
#绘制
# Plot loss through epochs
plt.plot(loss_history)
plt.title('Model loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.show()
# +
NB_EPOCHS = 1000
BATCH_SIZE = 32
m = input_S.shape[0]
loss_history = []
for epoch in range(NB_EPOCHS):
np.random.shuffle(input_S)
np.random.shuffle(input_C)
t = tqdm(range(0, input_S.shape[0], BATCH_SIZE),mininterval=0)
ae_loss = []
rev_loss = []
for idx in t:
batch_S = input_S[idx:min(idx + BATCH_SIZE, m)]
batch_C = input_C[idx:min(idx + BATCH_SIZE, m)]
C_prime = encoder_model.predict([batch_S, batch_C])
ae_loss.append(autoencoder_model.train_on_batch(x=[batch_S, batch_C],
y=np.concatenate((batch_S, batch_C),axis=3)))
rev_loss.append(reveal_model.train_on_batch(x=C_prime,
y=batch_S))
#更新学习率
# Update learning rate
K.set_value(autoencoder_model.optimizer.lr, lr_schedule(epoch))
K.set_value(reveal_model.optimizer.lr, lr_schedule(epoch))
t.set_description('Epoch {} | Batch: {:3} of {}. Loss AE {:10.2f} | Loss Rev {:10.2f}'.format(epoch + 1, idx, m, np.mean(ae_loss), np.mean(rev_loss)))
loss_history.append(np.mean(ae_loss))
# -
# 保存模型
autoencoder_model.save_weights('models/model.hdf5')
# 加载模型
autoencoder_model.load_weights('models/weights_final.hdf5')
# ## Results
# +
#返回解码的预测值
# Retrieve decoded predictions.
decoded = autoencoder_model.predict([input_S, input_C])
decoded_S, decoded_C = decoded[...,0:3], decoded[...,3:6]
#得到输出和预测值之间的绝对差
# Get absolute difference between the outputs and the expected values.
diff_S, diff_C = np.abs(decoded_S - input_S), np.abs(decoded_C - input_C)
# +
def pixel_errors(input_S, input_C, decoded_S, decoded_C):
"""Calculates mean of Sum of Squared Errors per pixel for cover and secret images. """
see_Spixel = np.sqrt(np.mean(np.square(255*(input_S - decoded_S))))
see_Cpixel = np.sqrt(np.mean(np.square(255*(input_C - decoded_C))))
return see_Spixel, see_Cpixel
def pixel_histogram(diff_S, diff_C):
"""Calculates histograms of errors for cover and secret image. """
diff_Sflat = diff_S.flatten()
diff_Cflat = diff_C.flatten()
fig = plt.figure(figsize=(15, 5))
a=fig.add_subplot(1,2,1)
imgplot = plt.hist(255* diff_Cflat, 100, density=1, alpha=0.75, facecolor='red')
a.set_title('Distribution of error in the Cover image.')
plt.axis([0, 250, 0, 0.2])
a=fig.add_subplot(1,2,2)
imgplot = plt.hist(255* diff_Sflat, 100, density=1, alpha=0.75, facecolor='red')
a.set_title('Distribution of errors in the Secret image.')
plt.axis([0, 250, 0, 0.2])
plt.show()
# +
#打印像素平均错误
# Print pixel-wise average errors in a 256 scale.
S_error, C_error = pixel_errors(input_S, input_C, decoded_S, decoded_C)
print ("S error per pixel [0, 255]:", S_error)
print ("C error per pixel [0, 255]:", C_error)
# -
#绘制秘密图像和容器图像中错误的分布。
# Plot distribution of errors in cover and secret images.
pixel_histogram(diff_S, diff_C)
# +
#结果显示
# Configs for results display
#显示灰度图像
# Show images in gray scale
SHOW_GRAY = False
#显示预测和输出的差别
# Show difference bettwen predictions and ground truth.
SHOW_DIFF = True
#差分增强幅度
# Diff enhance magnitude
ENHANCE = 1
#要显示的秘密图像和容器图像的数目
# Number of secret and cover pairs to show.
n = 6
def rgb2gray(rgb):
return np.dot(rgb[...,:3], [0.299, 0.587, 0.114])
def show_image(img, n_rows, n_col, idx, gray=False, first_row=False, title=None):
ax = plt.subplot(n_rows, n_col, idx)
if gray:
plt.imshow(rgb2gray(img), cmap = plt.get_cmap('gray'))
else:
plt.imshow(img)
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
if first_row:
plt.title(title)
plt.figure(figsize=(14, 15))
rand_indx = [random.randint(0, 10) for x in range(n)]
#随机显示0到n之间的图像
# for i, idx in enumerate(range(0, n)):
for i, idx in enumerate(rand_indx):
n_col = 6 if SHOW_DIFF else 4
show_image(input_C[idx], n, n_col, i * n_col + 1, gray=SHOW_GRAY, first_row=i==0, title='Cover')
show_image(input_S[idx], n, n_col, i * n_col + 2, gray=SHOW_GRAY, first_row=i==0, title='Secret')
show_image(decoded_C[idx], n, n_col, i * n_col + 3, gray=SHOW_GRAY, first_row=i==0, title='Encoded Cover')
show_image(decoded_S[idx], n, n_col, i * n_col + 4, gray=SHOW_GRAY, first_row=i==0, title='Decoded Secret')
if SHOW_DIFF:
show_image(np.multiply(diff_C[idx], ENHANCE), n, n_col, i * n_col + 5, gray=SHOW_GRAY, first_row=i==0, title='Diff Cover')
show_image(np.multiply(diff_S[idx], ENHANCE), n, n_col, i * n_col + 6, gray=SHOW_GRAY, first_row=i==0, title='Diff Secret')
plt.show()
# -
|
deep_steg.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# ## <NAME> convective aggregation classification
#
# Uses VISST data to derive convective aggregation index
# Load required libraries
from netCDF4 import Dataset
import numpy as np
from mpl_toolkits.basemap import Basemap
import matplotlib.pyplot as plt
import datetime
from matplotlib import dates
import math
import glob
import os
from skimage import measure
# %matplotlib inline
from scipy import interpolate, ndimage
from copy import deepcopy
import cartopy.crs as ccrs
from cartopy.mpl.ticker import LongitudeFormatter, LatitudeFormatter
# Input time for algorithm to run on
# +
# Input the range of dates and time wanted for the collection of images
year = 2006
start_day = 1
start_month = 1
start_hour = 1
start_minute = 0
start_second = 0
end_month = 3
end_day = 1
end_hour = 1
end_minute = 10
end_second = 00
start_time = datetime.datetime(year,
start_month,
start_day,
start_hour,
start_minute,
start_second)
end_time = datetime.datetime(year,
end_month,
end_day,
end_hour,
end_minute,
end_second)
deltatime = end_time - start_time
if(deltatime.seconds > 0 or deltatime.minute > 0):
no_days = deltatime.days + 1
else:
no_days = deltatime.days
days = np.arange(0, no_days, 1)
print('We are about to load grid files for ' + str(no_days) + ' days')
data_path = '/home/rjackson/data/visst/'
# Find the list of files for each day
cur_time = start_time
file_list = []
time_list = []
for i in days:
year_str = "%04d" % cur_time.year
day_str = "%02d" % cur_time.day
month_str = "%02d" % cur_time.month
print('Looking for files with format ' +
data_path +
'twpvisstpx04*' +
year_str +
month_str +
day_str +
'*.cdf')
data_list = glob.glob(data_path +
'twpvisstpx04*' +
year_str +
month_str +
day_str +
'*.cdf')
if(data_list):
file_list.append(data_list[0])
time_list.append(cur_time)
cur_time = cur_time + datetime.timedelta(days=1)
# +
# Convert degrees minutes seconds to decimal
def dms_to_decimal(deg, minutes, seconds):
return deg+minutes/60+seconds/3600
# Convert seconds to midnight to a string format
def seconds_to_midnight_to_string(time_secs_after_midnight):
hours = math.floor(time_secs_after_midnight/3600)
minutes = math.floor((time_secs_after_midnight - hours*3600)/60)
temp = datetime.time(int(hours), int(minutes), )
return temp.strftime('%H%M%S')
def seconds_to_midnight_to_hm(time_secs_after_midnight):
hours = math.floor(time_secs_after_midnight/3600)
minutes = math.floor((time_secs_after_midnight - hours*3600)/60)
return hours, minutes
# -
# Load image data. Mask out all regions with Tb > 240 K to only include convective regions as defined by Tobin et al. (2012)
# +
i = 2
cdf_data = Dataset(file_list[i], mode='r')
# Load lat, lon, and time parameters - try statement for 24-hourly data, except for daily data
Latitude = cdf_data.variables['latitude']
Longitude = cdf_data.variables['longitude']
Time = cdf_data.variables['image_times']
NumPixels = cdf_data.variables['image_numpix']
# Load brightness temperature
IRBrightness = cdf_data.variables['temperature_ir']
frame = 20
j = frame
convective_regions = IRBrightness[:] < 240
Darwin_Lat = dms_to_decimal(-12, 25, 28.56)
Darwin_Lon = dms_to_decimal(130, 53, 29.75)
cpol_latitude = -12.249166
cpol_longitude = 131.04445
# Get Lat and Lon for specific frame
Lat = Latitude[(int(j)*int(NumPixels[j])):(int(j+1)*int(NumPixels[j])-1)]
Lon = Longitude[(int(j)*int(NumPixels[j])):(int(j+1)*int(NumPixels[j])-1)]
print(Lon)
# Set up projection
plt.clf()
m = Basemap(width=500000, height=500000,
resolution='l', projection='stere',
lat_0=cpol_latitude,
lon_0=cpol_longitude)
xi, yi = m(Lon, Lat)
darwin_x, darwin_y = m(cpol_latitude, cpol_longitude)
# Regrid data to 2D
x,y = np.meshgrid(np.arange(min(xi),max(xi),5000),np.arange(min(yi),max(yi),5000))
index = j
data = IRBrightness[(int(j)*int(NumPixels[j])):(int(j+1)*int(NumPixels[j])-1)]
data_gridded = interpolate.griddata((xi,yi), data, (x,y))
lat_gridded = interpolate.griddata((xi,yi), Lat, (x,y))
lon_gridded = interpolate.griddata((xi,yi), Lon, (x,y))
lat_bounds = np.logical_or(lat_gridded > cpol_latitude+1.5,
lat_gridded < cpol_latitude-1.5)
lon_bounds = np.logical_or(lon_gridded < cpol_longitude-1.5,
lon_gridded > cpol_longitude+1.5)
masked_region = np.logical_or(lat_bounds, lon_bounds)
masked_region = np.logical_or(masked_region, data_gridded > 240)
data_masked = np.ma.array(data_gridded)
data_masked = np.ma.masked_where(masked_region, data_gridded)
# Plot the masked data
colors = m.pcolormesh(x,y,data_masked, cmap='gray_r', vmin=190, vmax=270)
plt.text(darwin_x,
darwin_y,
'Darwin',
fontweight='bold',
color='white')
plt.plot(darwin_x*0.98, darwin_y*1.01, 'w.')
m.drawparallels(np.arange(-80., 81., 10.),
labels=[1, 0, 0, 0],
fontsize=10)
m.drawmeridians(np.arange(-180., 181., 10.),
labels=[0, 0, 0, 1],
fontsize=10)
m.drawcoastlines()
m.drawcountries()
m.colorbar()
year_str = "%04d" % year
day_str = "%02d" % time_list[i].month
month_str = "%02d" % time_list[i].day
plt.title('IR Brightness Temperature '
+ str(year)
+ '-'
+ str(day_str)
+ '-'
+ str(month_str)
+ ' '
+ seconds_to_midnight_to_string(Time[index]))
if not os.path.exists('./output_plots'):
os.makedirs('./output_plots')
print('Domain:' + str(np.min(Lon)) + ' '
+ str(np.max(Lon)) +
str(np.min(Lat))
+ ' '
+ str(np.max(Lat)))
blobs = ~data_masked.mask
blobs_labels = measure.label(blobs, background=0)
print(blobs_labels.shape)
array = ndimage.measurements.center_of_mass(blobs, blobs_labels, [1,2,3,4,5,6,7])
m.scatter(array[0], array[1])
# -
# ## Find all of the blobs in the image. Number of blobs = number of clusters
# +
def scale_bar(ax, length, location=(0.5, 0.05), linewidth=3):
"""
ax is the axes to draw the scalebar on.
location is center of the scalebar in axis coordinates ie. 0.5 is the middle of the plot
length is the length of the scalebar in km.
linewidth is the thickness of the scalebar.
"""
#Projection in metres, need to change this to suit your own figure
utm = ccrs.UTM(53)
#Get the extent of the plotted area in coordinates in metres
x0, x1, y0, y1 = ax.get_extent(utm)
#Turn the specified scalebar location into coordinates in metres
sbcx, sbcy = x0 + (x1 - x0) * location[0], y0 + (y1 - y0) * location[1]
#Generate the x coordinate for the ends of the scalebar
bar_xs = [sbcx - length * 500, sbcx + length * 500]
#Plot the scalebar
ax.plot(bar_xs, [sbcy, sbcy], transform=utm, color='k', linewidth=linewidth)
#Plot the scalebar label
ax.text(sbcx, sbcy, str(length) + ' km', transform=utm,
horizontalalignment='center', verticalalignment='bottom')
# Make image to where 1 = convective, 0 = not convective
blobs = deepcopy(data_masked)
blobs[~blobs.mask] = 1
blobs[blobs.mask] = 0
blobs.mask = False
# Get locations of blobs
blobs_labels, num_blobs = ndimage.measurements.label(blobs)
locs = ndimage.measurements.center_of_mass(blobs, blobs_labels, range(2, num_blobs))
List = [(elem2, elem1) for elem1, elem2 in locs]
lat_points = []
lon_points = []
for element in List:
lat_points.append(lat_gridded[element[1], element[0]])
lon_points.append(lon_gridded[element[1], element[0]])
# Label 0 = masked data, 1 = background, clusters start at label 2
print('N = ' + str(num_blobs-2))
print('Locations: ')
print(List)
# Plot the blobs
figure = plt.figure(figsize=(13,6))
plt.rcParams.update({'font.size': 12})
ax = plt.axes(projection=ccrs.PlateCarree())
ax.coastlines(resolution='10m')
print(lat_gridded.shape)
handle = plt.contourf(lon_gridded, lat_gridded,
data_masked, cmap=plt.get_cmap('gray'))
ax.set_xticks([129, 130, 131, 132, 133], crs=ccrs.PlateCarree())
ax.set_yticks([-14, -13.5, -13, -12.5, -12,
-11.5, -11,-10.5,], crs=ccrs.PlateCarree())
lon_formatter = LongitudeFormatter(zero_direction_label=True)
lat_formatter = LatitudeFormatter()
ax.xaxis.set_major_formatter(lon_formatter)
ax.yaxis.set_major_formatter(lat_formatter)
plt.scatter(lon_points, lat_points, color='b')
plt.title('IR Brightness Temperature '
+ str(year)
+ '-'
+ str(day_str)
+ '-'
+ str(month_str)
+ ' '
+ seconds_to_midnight_to_string(Time[index]))
plt.text(cpol_longitude, cpol_latitude,
'CPOL', fontweight='bold', fontsize=15)
cbar = plt.colorbar(handle)
cbar.set_label('Brightness temperature [k]')
print(ax.get_extent())
scale_bar(ax, 100, location=(0.1, 0.9),)
plt.clim([190, 240])
plt.xlim((129, 133))
plt.ylim((-14, -10.5))
# -
# ## Calculate SCAI N/Nmax * D/L
#
# N = number of clusters
# Nmax = theoretical maximum number of clusters
# D = product of distances between cells
# L = characteristic length of domain (about 350 km here)
#
# Tobin et al. (2012) show that N is sufficient to categorize degree of aggregation,
# SCAI depends on domain size and on resolution, N does not.
# +
L = 350.0
a = 5.0
Nmax = pow((L/a),2)
print('Expected pairs: ' + str((num_blobs-2)*(num_blobs-3)/2))
distances = []
for point1 in List:
for point2 in List:
if(point1 != point2):
d = math.sqrt(pow(point1[0]-point2[0],2) + pow(point1[1]-point2[1],2))
distances.append(d)
n = (num_blobs-2)*(num_blobs-3)/2
d1 = 1/float(n)*np.sum(distances*5)
print(Nmax)
scai = ((num_blobs-2))/Nmax*d1/(L)*1000
plt.figure
plt.hist(distances)
plt.xlabel('Distances between cells')
plt.ylabel('Count')
plt.title('SCAI for scene:' + str(scai))
# -
# ## Make NetCDF for time period
N = []
years = []
days = []
months = []
hours = []
minutes = []
d1 = []
year = 2006
j = 0
k = 0
for satellite_file in file_list:
cdf_data = Dataset(satellite_file, mode='r')
# Load lat, lon, and time parameters
Latitude = cdf_data.variables['latitude']
Longitude = cdf_data.variables['longitude']
Time = cdf_data.variables['image_times']
NumPixels = cdf_data.variables['image_numpix']
for i in range(0, len(NumPixels)):
# Load brightness temperature
IRBrightness = cdf_data.variables['temperature_ir']
# Get Lat and Lon for specific frame
Lat = Latitude[(int(i)*int(NumPixels[i])):(int(i+1)*int(NumPixels[i])-1)]
Lon = Longitude[(int(i)*int(NumPixels[i])):(int(i+1)*int(NumPixels[i])-1)]
plt.clf()
m = Basemap(width=500000, height=500000,
resolution='l', projection='stere',
lat_0=cpol_latitude,
lon_0=cpol_longitude)
xi, yi = m(Lon, Lat)
darwin_x, darwin_y = m(cpol_latitude, cpol_longitude)
# Regrid data to 2D
x,y = np.meshgrid(np.arange(min(xi),max(xi),5000),
np.arange(min(yi),max(yi),5000))
index = j
data = IRBrightness[(int(i)*int(NumPixels[i])):(int(i+1)*int(NumPixels[i])-1)]
data_gridded = interpolate.griddata((xi,yi), data, (x,y))
lat_gridded = interpolate.griddata((xi,yi), Lat, (x,y))
lon_gridded = interpolate.griddata((xi,yi), Lon, (x,y))
lat_bounds = np.logical_or(lat_gridded > cpol_latitude+1.5,
lat_gridded < cpol_latitude-1.5)
lon_bounds = np.logical_or(lon_gridded < cpol_longitude-1.5,
lon_gridded > cpol_longitude+1.5)
masked_region = np.logical_or(lat_bounds, lon_bounds)
masked_region = np.logical_or(masked_region, data_gridded > 240)
data_masked = np.ma.array(data_gridded)
data_masked = np.ma.masked_where(masked_region, data_gridded)
# Make image to where 1 = convective, 0 = not convective
blobs = deepcopy(data_masked)
blobs[~blobs.mask] = 1
blobs[blobs.mask] = 0
blobs.mask = False
blobs_labels, num_blobs = ndimage.measurements.label(blobs)
locs = ndimage.measurements.center_of_mass(blobs,
blobs_labels,
range(2, num_blobs))
# Label 0 = masked data, 1 = background, clusters start at label 2
List = [(elem2, elem1) for elem1, elem2 in locs]
N.append(num_blobs-2)
distances = []
for point1 in List:
for point2 in List:
if(point1 != point2):
d = math.sqrt(pow(point1[0]-point2[0],2) + pow(point1[1]-point2[1],2))
distances.append(d)
n = (num_blobs-2)*(num_blobs-3)/2
if(n > 0):
d1.append(1/float(n)*np.sum(distances))
else:
d1.append(float('nan'))
years.append(year)
days.append(time_list[k].day)
months.append(time_list[k].month)
h, m = seconds_to_midnight_to_hm(Time[i])
hours.append(h)
minutes.append(m)
j = j + 1
if(j % 100 == 0):
print(j)
k = k + 1
# +
# Make netCDF file
out_netcdf = Dataset('num_clusters.cdf', mode='w')
out_netcdf.createDimension('time', len(N))
print(len(N))
groups_file = out_netcdf.createVariable('N', 'i4', ('time',))
groups_file.long_name = 'Number of convective clusters'
groups_file.units = '#'
groups_file[:] = N
d1_file = out_netcdf.createVariable('d1', 'f4', ('time',))
d1_file.long_name = 'Distance between clusters'
d1_file.units = '#'
d1_file[:] = d1
years_file = out_netcdf.createVariable('year', int, ('time',))
years_file.long_name = 'Year'
years_file.units = 'YYYY'
years_file[:] = year
month_file = out_netcdf.createVariable('month', int, ('time',))
month_file.long_name = 'Month'
month_file.units = 'MM'
month_file[:] = months
day_file = out_netcdf.createVariable('day', int, ('time',))
day_file.long_name = 'Day'
day_file.units = 'DD'
day_file[:] = days
hour_file = out_netcdf.createVariable('hour', int, ('time',))
hour_file.long_name = 'Hour'
hour_file.units = 'HH'
hour_file[:] = hours
minute_file = out_netcdf.createVariable('minute', int, ('time',))
minute_file.long_name = 'Hour'
minute_file.units = 'MM'
minute_file[:] = minutes
out_netcdf.close()
# -
# ## Plot aggregation index as a function of time
# +
CY_cdf = Dataset('/home/rjackson/data/num_clusters.cdf', mode='r')
classification = CY_cdf.variables['d1'][:]
year = CY_cdf.variables['year'][:]
month = CY_cdf.variables['month'][:]
day = CY_cdf.variables['day'][:]
hour = CY_cdf.variables['hour'][:]
minute = CY_cdf.variables['minute'][:]
print(hour[0:50])
date_array = []
for i in range(0,len(year)):
dat = datetime.datetime(year=int(year[i]),
month=int(month[i]),
day=int(day[i]),
hour=int(hour[i]),
minute=int(minute[i]),)
date_array.append(dat)
CY_cdf.close()
plt.figure(figsize=(20,5))
plt.plot_date(dates.date2num(date_array[250:-400]), classification[250:-400])
# -
|
notebooks/Tobin aggregation index.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 0.5.0-rc4
# language: julia
# name: julia-0.5
# ---
addprocs(3)
nprocs()
@everywhere include("../src/UNSflow.jl")
#@everywhere include("../src/UNSflow.jl")
#@everywhere using UNSflow
@everywhere include("../src/UNSflow.jl")
# # Recreate Antonio 3D results using a strip theory approach and LDVM
using UNSflow
# +
c = 0.2
u = 10
f = 0.8889
k = 2*pi*f*c/(2*u)
c = 1
u = 1
w = 2*k
b = 6
T = (2*pi/w)
ncyc = 4
t_tot = ncyc*T
# -
#The bending mode which we wish to simulate
data = readdlm("../test/anto_mode1.dat");
plot(data[:,3],data[:,4])
# ### Let's place strips at -3, -2, -1 and 0. Set up 2D problems at these positions.
#
#
# +
#Strip at y = -3
nsteps = 50
h_amp = 0.45/c #input is nondimensional
alpha_amp = 5*pi/180 #Root incidence
dtstar = 0.015*0.2*2/(k*h_amp)
dt = dtstar*c/u
nsteps =round(Int,t_tot/dt)+1
alphadef = ConstDef(alpha_amp)
hdef = CosDef(0., h_amp, w, 0.)
udef = ConstDef(u)
full_kinem = KinemDef(alphadef, hdef, udef)
pvt = 0.0 #Doesnt matter, no pitch
lespcrit = [21;] #high value to turn off LEV shedding
surf = TwoDSurf(c, u, "FlatPlate", pvt, 70, 35, "Prescribed", full_kinem, lespcrit)
curfield = TwoDFlowField()
del = DelVortDef(1, 500, 10)
# -
nsteps
mat, surf, curfield = ldvm(surf, curfield, nsteps, dtstar)
range = round(Int,(ncyc-1)*nsteps/ncyc)+1:nsteps
tbyT = (mat[range,1]-mat[range[1]])/T
plot(tbyT,mat[range,5])
# +
##Store these values so we can get back to it later
mat1, surf1, curfield1 = mat, surf, curfield
# +
# Second strip
#Strip at y = -2
h_amp = (0.1638 + 0.1407)/(2*c) #m #Roughly calculated from file
alpha_amp = 5*pi/180 # built incidence
dtstar = 0.015*0.2*4/(k*h_amp)
dt = dtstar*c/u
nsteps =round(Int,t_tot/dt)+1
alphadef = ConstDef(alpha_amp)
hdef = CosDef(0., h_amp, w, 0.)
udef = ConstDef(u)
full_kinem = KinemDef(alphadef, hdef, udef)
pvt = 0.0 #Doesnt matter, no pitch
lespcrit = [21;] #high value to turn off LEV shedding
surf = TwoDSurf(c, u, "FlatPlate", pvt, 70, 35, "Prescribed", full_kinem, lespcrit)
curfield = TwoDFlowField()
del = DelVortDef(1, 500, 10)
# -
mat, surf, curfield = ldvm(surf, curfield, nsteps, dtstar)
range = round(Int,(ncyc-1)*nsteps/ncyc)+1:nsteps
tbyT = (mat[range,1]-mat[range[1]])/T
plot(tbyT,mat[range,6])
# +
##Store these values so we can get back to it later
mat2, surf2, curfield2 = mat, surf, curfield
# +
# Third strip
#Strip at y = -1
h_amp = (-0.0912 - 0.1107)/(2*c) #m #Roughly calculated from file
alpha_amp = 5*pi/180 #Since we are using the airfoil file, no need to consider built incidence?
dtstar = 0.015*0.2*2/(k*abs(h_amp))
dt = dtstar*c/u
nsteps =round(Int,t_tot/dt)+1
alphadef = ConstDef(alpha_amp)
hdef = CosDef(0., h_amp, w, 0.)
udef = ConstDef(u)
full_kinem = KinemDef(alphadef, hdef, udef)
pvt = 0.0 #Doesnt matter, no pitch
lespcrit = [21;] #high value to turn off LEV shedding
surf = TwoDSurf(c, u, "FlatPlate", pvt, 70, 35, "Prescribed", full_kinem, lespcrit)
curfield = TwoDFlowField()
del = DelVortDef(1, 500, 10)
# -
mat, surf, curfield = ldvm(surf, curfield, nsteps, dtstar)
range = round(Int,(ncyc-1)*nsteps/ncyc)+1:nsteps
tbyT = (mat[range,1]-mat[range[1]])/T
plot(tbyT,mat[range,6])
# +
##Store these values so we can get back to it later
mat3, surf3, curfield3 = mat, surf, curfield
# +
# Second strip
#Strip at y = 0
h_amp = -0.2040/c #m #Roughly calculated from file
alpha_amp = 5*pi/180 #Since we are using the airfoil file, no need to consider built incidence?
dtstar = 0.015*0.2*2/(k*abs(h_amp))
dt = dtstar*c/u
nsteps =round(Int,t_tot/dt)+1
alphadef = ConstDef(alpha_amp)
hdef = CosDef(0., h_amp, w, 0.)
udef = ConstDef(u)
full_kinem = KinemDef(alphadef, hdef, udef)
pvt = 0.0 #Doesnt matter, no pitch
lespcrit = [21;] #high value to turn off LEV shedding
surf = TwoDSurf(c, u, "FlatPlate", pvt, 70, 35, "Prescribed", full_kinem, lespcrit)
curfield = TwoDFlowField()
del = DelVortDef(1, 500, 10)
# -
mat, surf, curfield = ldvm(surf, curfield, nsteps, dtstar)
range = round(Int,(ncyc-1)*nsteps/ncyc)+1:nsteps
tbyT = (mat[range,1]-mat[range[1]])/T
plot(tbyT,mat[range,6])
# +
##Store these values so we can get back to it later
mat4, surf4, curfield4 = mat, surf, curfield
# -
# ## Let's try and gather the results
# +
#Using nondimensional quantities here
time = [0:0.001:t_tot;]
cl1_spl = Spline1D(mat1[:,1],mat1[:,6])
cl2_spl = Spline1D(mat2[:,1],mat2[:,6])
cl3_spl = Spline1D(mat3[:,1],mat3[:,6])
cl4_spl = Spline1D(mat4[:,1],mat4[:,6])
cm1_spl = Spline1D(mat1[:,1],mat1[:,8])
cm2_spl = Spline1D(mat2[:,1],mat2[:,8])
cm3_spl = Spline1D(mat3[:,1],mat3[:,8])
cm4_spl = Spline1D(mat4[:,1],mat4[:,8])
cd1_spl = Spline1D(mat1[:,1],mat1[:,7])
cd2_spl = Spline1D(mat2[:,1],mat2[:,7])
cd3_spl = Spline1D(mat3[:,1],mat3[:,7])
cd4_spl = Spline1D(mat4[:,1],mat4[:,7])
cl1 = evaluate(cl1_spl,time)
cl2 = evaluate(cl2_spl,time)
cl3 = evaluate(cl3_spl,time)
cl4 = evaluate(cl4_spl,time)
cm1 = evaluate(cm1_spl,time)
cm2 = evaluate(cm2_spl,time)
cm3 = evaluate(cm3_spl,time)
cm4 = evaluate(cm4_spl,time)
cd1 = evaluate(cd1_spl,time)
cd2 = evaluate(cd2_spl,time)
cd3 = evaluate(cd3_spl,time)
cd4 = evaluate(cd4_spl,time)
range = round(Int,(ncyc-1)*length(time)/ncyc)+1:length(time)
tbyT = (time[range]-time[range[1]])/(T)
# +
#Now consider that there are 6 strips
# at strip 1 and 6 , cl = 0.5*(cl1+cl2)
dy = 1
cl_tot = (cl1 + cl2 + cl2 + cl3 + cl3 + cl4)*dy*c/b
#plot(tbyT,cl1[range])
#plot(tbyT,cl2[range])
#plot(tbyT,cl3[range])
#plot(tbyT,cl4[range])
#plot(tbyT,cl_tot[range])
#cm_tot = (cm1 + cm2 + cm2 + cm3 + cm3 + cm4)*dy*c/b
#plot(tbyT,cm_tot[range])
cd_tot = (cd1 + cd2 + cd2 + cd3 + cd3 + cd4)*dy*c/b
plot(tbyT,cd_tot[range])
# +
### Visualise the 3D problem
fig = figure()
ax = gca(projection="3d")
plot3D(map(q->q.x, surf1.bv),map(q->q.z,surf1.bv),-3,"y",color = "black",linewidth=2.0)
plot3D(map(q->q.x, surf2.bv),map(q->q.z,surf2.bv),-2,"y",color = "black",linewidth=2.0)
plot3D(map(q->q.x, surf3.bv),map(q->q.z,surf3.bv),-1,"y",color = "black",linewidth=2.0)
plot3D(map(q->q.x, surf4.bv),map(q->q.z,surf4.bv),0, "y",color = "black",linewidth=2.0)
plot3D(map(q->q.x, surf1.bv),map(q->q.z,surf1.bv),3, "y",color = "black",linewidth=2.0)
plot3D(map(q->q.x, surf2.bv),map(q->q.z,surf2.bv),2, "y",color = "black",linewidth=2.0)
plot3D(map(q->q.x, surf3.bv),map(q->q.z,surf3.bv),1, "y",color = "black",linewidth=2.0)
scatter3D(map(q->q.x, curfield1.tev),map(q->q.z,curfield1.tev),-3,"z",s=20,c=map(q->q.s,curfield1.tev),cmap=ColorMap("jet"),edgecolors="none")
scatter3D(map(q->q.x, curfield2.tev),map(q->q.z,curfield2.tev),-2,"z",s=20,c=map(q->q.s,curfield2.tev),cmap=ColorMap("jet"),edgecolors="none")
scatter3D(map(q->q.x, curfield3.tev),map(q->q.z,curfield3.tev),-1,"z",s=20,c=map(q->q.s,curfield3.tev),cmap=ColorMap("jet"),edgecolors="none")
scatter3D(map(q->q.x, curfield4.tev),map(q->q.z,curfield4.tev),0,"z",s=20,c=map(q->q.s,curfield4.tev),cmap=ColorMap("jet"),edgecolors="none")
scatter3D(map(q->q.x, curfield1.tev),map(q->q.z,curfield1.tev),3,"z",s=20,c=map(q->q.s,curfield1.tev),cmap=ColorMap("jet"),edgecolors="none")
scatter3D(map(q->q.x, curfield2.tev),map(q->q.z,curfield2.tev),2,"z",s=20,c=map(q->q.s,curfield2.tev),cmap=ColorMap("jet"),edgecolors="none")
scatter3D(map(q->q.x, curfield3.tev),map(q->q.z,curfield3.tev),1,"z",s=20,c=map(q->q.s,curfield3.tev),cmap=ColorMap("jet"),edgecolors="none")
#axis("equal")
#ax[:view_init](20, 120)
# -
#
# # Now we atttempt the same problem with a basic LLT correction - circulation goes to zero at the wingtips
#
# +
#Construct dimensionless quantities from given values
c_d = 0.2
b_d = 6
AR = b_d/c_d
u_d = 10
f_d = 0.8889
k = 2*pi*f_d*c_d/(2*u_d)
#_dAll values below are nondimensional
c = 1
u = 1
w = 2*k
T = (2*pi/w)
ncyc = 8
t_tot = ncyc*T
modedata = readdlm("../test/anto_mode1.dat");
mode_spl = Spline1D(modedata[:,3],modedata[:,4])
n_span = 12
n_bterm = 40
psi = zeros(n_span)
dpsi = pi/n_span
for i = 1:n_span
psi[i] = (real(i)-0.5)*dpsi
end
scale = 0.02
#Run LDVM at all these locations:
alpha_amp = 5*pi/180
h_amp = zeros(n_span)
for i = 1:n_span
y_d = -b_d*cos(psi[i])/2.
h_amp[i] = evaluate(mode_spl,y_d)*scale/c_d
end
dtstar = min(0.015*8,0.015*0.2*4/(k*maximum(h_amp)))
nsteps =round(Int,t_tot/dtstar)+1
alphadef = ConstDef(alpha_amp)
udef = ConstDef(u)
pvt = 0.0 #Doesnt matter, no pitch
lespcrit = [21;] #high value to turn off LEV shedding
# -
nsteps = 200
# +
#Time parallel and serial runs
#Parallel
W_mat = SharedArray{Float64,2}[]
W_surf = TwoDSurf[]
W_curfield = TwoDFlowField[]
@time for i = 1:Int(n_span/2) #Since problem is symmetric
hdef = CosDef(0., h_amp[i], w, 0.)
full_kinem = KinemDef(alphadef, hdef, udef)
surf = TwoDSurf("FlatPlate", pvt, full_kinem, lespcrit)
curfield = TwoDFlowField()
del = DelVortDef(1, 500, 10)
mt, st, ct = fetch(@spawn ldvm(surf, curfield, nsteps, dtstar))
push!(W_mat, mt)
push!(W_surf, st)
push!(W_curfield, ct)
end
# -
@time for i = 1:Int(n_span/2) #Since problem is symmetric
hdef = CosDef(0., h_amp[i], w, 0.)
full_kinem = KinemDef(alphadef, hdef, udef)
surf = TwoDSurf("FlatPlate", pvt, full_kinem, lespcrit)
curfield = TwoDFlowField()
del = DelVortDef(1, 500, 10)
mt, st, ct = ldvm(surf, curfield, nsteps, dtstar)
push!(W_mat, mt)
push!(W_surf, st)
push!(W_curfield, ct)
end
#Mirror image for the rest of the span
for i = Int(n_span/2)+1:n_span
mt = W_mat[n_span - i + 1]
st = W_surf[n_span - i + 1]
ct = W_curfield[n_span - i + 1]
push!(W_mat, mt)
push!(W_surf, st)
push!(W_curfield, ct)
end
# +
lhs = zeros(n_span,n_bterm)
rhs = zeros(n_span)
b_coeff = zeros(nsteps,n_bterm)
sp_gam = zeros(nsteps,n_span)
dt = W_mat[1][2,1] - W_mat[1][1,1]
cnc_f = zeros(nsteps)
cnnc_f = zeros(nsteps)
# +
bdot = zeros(nsteps,n_bterm)
for i = 1:nsteps
for j = 1:n_span
for n = 1:n_bterm
lhs[j,n] = sin(n*psi[j])*(sin(psi[j]) + (n*pi/(2*AR)))
end
rhs[j] = pi*sin(psi[j])*W_mat[j][i,9]/(2*AR)
end
b_coeff[i,:] = \(lhs, rhs)
if i >= 2
bdot[i,:] = (b_coeff[i,:] - b_coeff[i-1,:])/dt
end
end
# +
a03d = zeros(nsteps,n_span)
cd_ind = zeros(nsteps)
a0dot3d = zeros(nsteps,n_span)
gam_other = zeros(nsteps,n_span)
for i = 1:nsteps
for j = 1:n_span
sp_gam[i,j] = 0
for n = 1:n_bterm
sp_gam[i,j] = sp_gam[i,j] + 2*b_d*u*b_coeff[i,n]*sin(n*psi[j])
end
end
end
for i = 1:nsteps
cd_ind[i] = 0
for n = 1:n_bterm
cd_ind[i] = cd_ind[i] + real(n)*b_coeff[i,n]^2
end
cd_ind[i] = cd_ind[i]*pi*AR
for j = 1:n_span
a03d[i,j] = 0
for n = 1:n_bterm
a03d[i,j] = a03d[i,j] - real(n)*b_coeff[i,n]*sin(n*psi[j])/sin(psi[j])
a0dot3d[i,j] = a0dot3d[i,j] - real(n)*bdot[i,n]*sin(n*psi[j])/sin(psi[j])
end
gam_other[i,j] = u*c_d*pi*(W_mat[j][i,9] + a03d[i,j])
end
end
# -
plot(sp_gam[10,1:n_span])
plot(gam_other[10,:])
plot(a03d[10,:])
plot(a0dot3d[10,:])
W_alpha = zeros(nsteps,n_span)
W_h = zeros(nsteps,n_span)
W_hdot = zeros(nsteps,n_span)
W_u = zeros(nsteps,n_span)
W_u[:,:] = 1
W_alpha[:,:] = 5*pi/180
for i = 1:nsteps
for j = 1:n_span
hdef = CosDef(0., h_amp[j], w, 0.)
tt = W_mat[1][i,1]
W_h[i,j] = hdef(tt)*c
W_hdot[i,j] = ForwardDiff.derivative(hdef,tt)*u
end
end
# +
W_cn = zeros(nsteps)
W_cs = zeros(nsteps)
W_cl = zeros(nsteps)
W_cd = zeros(nsteps)
W_cdi = zeros(nsteps)
cn3d = zeros(nsteps, n_span)
cs3d = zeros(nsteps, n_span)
cl3d = zeros(nsteps, n_span)
cd3d = zeros(nsteps, n_span)
for i = 1:nsteps
W_cn[i] = 0
W_cs[i] = 0
for j = 1:n_span
cn3d[i,j] = W_mat[j][i,10] + (2*pi/u)*(W_u[i,j]*cos(W_alpha[i,j]) + W_hdot[i,j]*sin(W_alpha[i,j]))*a03d[1,j] + (2*pi*c/u)*(3*a0dot3d[i,j]/4)
cs3d[i,j] = W_mat[j][i,11] + 2*pi*a03d[i,j]^2
cl3d[i,j] = cn3d[i,j]*cos(W_alpha[i,j]) + cs3d[i,j]*sin(W_alpha[i,j])
cd3d[i,j] = cn3d[i,j]*sin(W_alpha[i,j]) - cs3d[i,j]*cos(W_alpha[i,j])
W_cn[i] = W_cn[i] + cn3d[i,j]*sin(psi[j])*dpsi/2
W_cs[i] = W_cs[i] + cs3d[i,j]*sin(psi[j])*dpsi/2
W_cl[i] = W_cl[i] + cl3d[i,j]*sin(psi[j])*dpsi/2
W_cd[i] = W_cd[i] + cd3d[i,j]*sin(psi[j])*dpsi/2
end
end
#cn_w =
#sum_bcoeff = 0
# for n = 1:n_bterm
# if rem(n,2) != 0
# sum_bcoeff = sum_bcoeff + b_coeff[n]
# end
# end
# cnc_f[i] = -2*pi*(u[i]*cos(alpha[i])/surf.uref + hdot[i]*sin(alpha[i])/surf.uref)*(sum_bcoeff)
# sum_bdot = 0
# for n = 1:n_bterm
# if rem(n,2) != 0
# sum_bdot = sum_bdot + bdot[n]
# end
# end
# cnnc_f[i] = -(2*pi*surf.c/(surf.uref))*(3*sum_bdot/4)
# end
# +
dlt = readcsv("../test/anto_cl.csv")
plot(dlt[:,1]/T,dlt[:,2])
t_th = W_mat[1][:,1]*c_d/u_d
range = round(Int,(ncyc-1)*nsteps/ncyc)+1:nsteps
tbyT = (t_th-t_th[1])/T
plot(tbyT,W_cl[range])
# -
plot(W_mat[1][:,1]*c_d/u_d,W_cl)
PyPlot.axis([0,4,0.0,0.7])
plot(W_mat[1][:,1]*c_d/u_d,cd_ind/6)
#PyPlot.axis([0,120,0,1])
W_mat[1]
W_mat[2]
|
Notebooks/.ipynb_checkpoints/Flexible_firstBending-Parallel-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: PyCharm (F-MT126-1)
# language: python
# name: pycharm-47e98d46
# ---
# ## Imports
import os
from IPython.display import Image
import pandas as pd
pd.set_option("display.max_rows", None)
pd.set_option("display.width", 180)
# ## Paths
data_dir = 'C:\\Users\\obarn\\Projects\\F-MT126-1\\vilio\\data'
feature_dir = os.path.join(data_dir, 'features')
anno_dir = os.path.join(feature_dir, 'annotations')
gt_dir = os.path.join(anno_dir, 'gt')
img_dir = os.path.join(feature_dir, 'img')
# ## Display
img_id = '78251'
img = Image(filename=os.path.join(img_dir, f'{img_id}.png'))
train = pd.read_json(os.path.join(anno_dir, "dev_all.entity.jsonl"), lines=True, orient="records")
print(train[train.id == int(img_id)].partition_description.values)
print(train[train.id == int(img_id)].label.values)
display(img)
|
notebooks/entity.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# name: python2
# ---
# + [markdown] id="MV-CWK2kI-iH" colab_type="text"
# ## TFMA Notebook example
#
# This notebook describes how to export your model for TFMA and demonstrates the analysis tooling it offers.
#
# ## Setup
#
# Import necessary packages.
# + id="xFbGgkXAJCJ7" colab_type="code" colab={}
import apache_beam as beam
import os
import preprocess
import shutil
import tensorflow as tf
import tensorflow_data_validation as tfdv
import tensorflow_model_analysis as tfma
from google.protobuf import text_format
from tensorflow.python.lib.io import file_io
from tensorflow_transform.beam.tft_beam_io import transform_fn_io
from tensorflow_transform.coders import example_proto_coder
from tensorflow_transform.saved import saved_transform_io
from tensorflow_transform.tf_metadata import dataset_schema
from tensorflow_transform.tf_metadata import schema_utils
from trainer import task
from trainer import taxi
# + [markdown] id="zpCt_emiJDeb" colab_type="text"
# Helper functions and some constants for running the notebook locally.
# + id="1Axm8YxCJF7K" colab_type="code" colab={}
BASE_DIR = os.getcwd()
DATA_DIR = os.path.join(BASE_DIR, 'data')
OUTPUT_DIR = os.path.join(BASE_DIR, 'chicago_taxi_output')
# Base dir containing train and eval data
TRAIN_DATA_DIR = os.path.join(DATA_DIR, 'train')
EVAL_DATA_DIR = os.path.join(DATA_DIR, 'eval')
# Base dir where TFT writes training data
TFT_TRAIN_OUTPUT_BASE_DIR = os.path.join(OUTPUT_DIR, 'tft_train')
TFT_TRAIN_FILE_PREFIX = 'train_transformed'
# Base dir where TFT writes eval data
TFT_EVAL_OUTPUT_BASE_DIR = os.path.join(OUTPUT_DIR, 'tft_eval')
TFT_EVAL_FILE_PREFIX = 'eval_transformed'
TF_OUTPUT_BASE_DIR = os.path.join(OUTPUT_DIR, 'tf')
# Base dir where TFMA writes eval data
TFMA_OUTPUT_BASE_DIR = os.path.join(OUTPUT_DIR, 'tfma')
SERVING_MODEL_DIR = 'serving_model_dir'
EVAL_MODEL_DIR = 'eval_model_dir'
def get_tft_train_output_dir(run_id):
return _get_output_dir(TFT_TRAIN_OUTPUT_BASE_DIR, run_id)
def get_tft_eval_output_dir(run_id):
return _get_output_dir(TFT_EVAL_OUTPUT_BASE_DIR, run_id)
def get_tf_output_dir(run_id):
return _get_output_dir(TF_OUTPUT_BASE_DIR, run_id)
def get_tfma_output_dir(run_id):
return _get_output_dir(TFMA_OUTPUT_BASE_DIR, run_id)
def _get_output_dir(base_dir, run_id):
return os.path.join(base_dir, 'run_' + str(run_id))
def get_schema_file():
return os.path.join(OUTPUT_DIR, 'schema.pbtxt')
# + [markdown] id="YDaWlFehJH7r" colab_type="text"
# Clean up output directories.
# + id="E7zx4bAOJKZN" colab_type="code" colab={}
shutil.rmtree(TFT_TRAIN_OUTPUT_BASE_DIR, ignore_errors=True)
shutil.rmtree(TFT_EVAL_OUTPUT_BASE_DIR, ignore_errors=True)
shutil.rmtree(TF_OUTPUT_BASE_DIR, ignore_errors=True)
shutil.rmtree(get_schema_file(), ignore_errors=True)
# + [markdown] id="ZXK_1T-JJL9s" colab_type="text"
# ## Compute and visualize descriptive data statistics
# + id="hXYNl387JOfp" colab_type="code" colab={}
# Compute stats over training data.
train_stats = tfdv.generate_statistics_from_csv(data_location=os.path.join(TRAIN_DATA_DIR, 'data.csv'))
# + id="baGGqXSaJQeT" colab_type="code" colab={}
# Visualize training data stats.
tfdv.visualize_statistics(train_stats)
# + [markdown] id="AsOJi9U3JR35" colab_type="text"
# ## Infer a schema
# + id="JSUFwSKoJTtT" colab_type="code" colab={}
# Infer a schema from the training data stats.
schema = tfdv.infer_schema(statistics=train_stats, infer_feature_shape=False)
tfdv.display_schema(schema=schema)
# + [markdown] id="kzLwrYqEJWcD" colab_type="text"
# ## Check evaluation data for errors
# + id="NVA5Bor4JaxL" colab_type="code" colab={}
# Compute stats over eval data.
eval_stats = tfdv.generate_statistics_from_csv(data_location=os.path.join(EVAL_DATA_DIR, 'data.csv'))
# + id="NvxUKVMJJcSk" colab_type="code" colab={}
# Compare stats of eval data with training data.
tfdv.visualize_statistics(lhs_statistics=eval_stats, rhs_statistics=train_stats,
lhs_name='EVAL_DATASET', rhs_name='TRAIN_DATASET')
# + id="5QqFQ29tJhEi" colab_type="code" colab={}
# Check eval data for errors by validating the eval data stats using the previously inferred schema.
anomalies = tfdv.validate_statistics(statistics=eval_stats, schema=schema)
tfdv.display_anomalies(anomalies)
# + id="MZ_xsJgUJiGL" colab_type="code" colab={}
# Update the schema based on the observed anomalies.
# Relax the minimum fraction of values that must come from the domain for feature company.
company = tfdv.get_feature(schema, 'company')
company.distribution_constraints.min_domain_mass = 0.9
# Add new value to the domain of feature payment_type.
payment_type_domain = tfdv.get_domain(schema, 'payment_type')
payment_type_domain.value.append('Prcard')
# Validate eval stats after updating the schema
updated_anomalies = tfdv.validate_statistics(eval_stats, schema)
tfdv.display_anomalies(updated_anomalies)
# + [markdown] id="gR81RJidJlJT" colab_type="text"
# ## Freeze the schema
#
# Now that the schema has been reviewed and curated, we will store it in a file to reflect its "frozen" state.
# + id="MBC7_QnbJmar" colab_type="code" colab={}
file_io.recursive_create_dir(OUTPUT_DIR)
file_io.write_string_to_file(get_schema_file(), text_format.MessageToString(schema))
# + [markdown] id="q1aDkWP3Jn9a" colab_type="text"
# ## Preprocess Inputs
#
# transform_data is defined in preprocess.py and uses the tensorflow_transform library to perform preprocessing. The same code is used for both local preprocessing in this notebook and preprocessing in the Cloud (via Dataflow).
# + id="7i00wLcIJqEb" colab_type="code" colab={}
# Transform eval data
preprocess.transform_data(input_handle=os.path.join(EVAL_DATA_DIR, 'data.csv'),
outfile_prefix=TFT_EVAL_FILE_PREFIX,
working_dir=get_tft_eval_output_dir(0),
schema_file=get_schema_file(),
pipeline_args=['--runner=DirectRunner'])
print('Done')
# + id="8Onber05Jr46" colab_type="code" colab={}
# Transform training data
preprocess.transform_data(input_handle=os.path.join(TRAIN_DATA_DIR, 'data.csv'),
outfile_prefix=TFT_TRAIN_FILE_PREFIX,
working_dir=get_tft_train_output_dir(0),
schema_file=get_schema_file(),
pipeline_args=['--runner=DirectRunner'])
print('Done')
# + [markdown] id="0LUjgM3AJtwj" colab_type="text"
# ## Compute statistics over transformed data
# + id="Kzks-t0sJxOL" colab_type="code" colab={}
# Compute stats over transformed training data.
TRANSFORMED_TRAIN_DATA = os.path.join(get_tft_train_output_dir(0), TFT_TRAIN_FILE_PREFIX + "*")
transformed_train_stats = tfdv.generate_statistics_from_tfrecord(data_location=TRANSFORMED_TRAIN_DATA)
# + id="w83Kd3fXJyga" colab_type="code" colab={}
# Visualize transformed training data stats and compare to raw training data.
# Use 'Feature search' to focus on a feature and see statistics pre- and post-transformation.
tfdv.visualize_statistics(transformed_train_stats, train_stats, lhs_name='TRANSFORMED', rhs_name='RAW')
# + [markdown] id="j-SN2NaKJ1Wq" colab_type="text"
# ## Prepare the Model
#
# To use TFMA, export the model into an **EvalSavedModel** by calling ``tfma.export.export_eval_savedmodel``.
#
# ``tfma.export.export_eval_savedmodel`` is analogous to ``estimator.export_savedmodel`` but exports the evaluation graph as opposed to the training or inference graph. Notice that one of the inputs is ``eval_input_receiver_fn`` which is analogous to ``serving_input_receiver_fn`` for ``estimator.export_savedmodel``. For more details, refer to the documentation for TFMA on Github.
#
# Contruct the **EvalSavedModel** after training is completed.
# + id="a35ueyufJ2bj" colab_type="code" colab={}
def run_experiment(hparams):
"""Run the training and evaluate using the high level API"""
# Train and evaluate the model as usual.
estimator = task.train_and_maybe_evaluate(hparams)
# Export TFMA's sepcial EvalSavedModel
eval_model_dir = os.path.join(hparams.output_dir, EVAL_MODEL_DIR)
receiver_fn = lambda: eval_input_receiver_fn(hparams.tf_transform_dir)
tfma.export.export_eval_savedmodel(
estimator=estimator,
export_dir_base=eval_model_dir,
eval_input_receiver_fn=receiver_fn)
def eval_input_receiver_fn(working_dir):
# Extract feature spec from the schema.
raw_feature_spec = schema_utils.schema_as_feature_spec(schema).feature_spec
serialized_tf_example = tf.placeholder(
dtype=tf.string, shape=[None], name='input_example_tensor')
# First we deserialize our examples using the raw schema.
features = tf.parse_example(serialized_tf_example, raw_feature_spec)
# Now that we have our raw examples, we must process them through tft
_, transformed_features = (
saved_transform_io.partially_apply_saved_transform(
os.path.join(working_dir, transform_fn_io.TRANSFORM_FN_DIR),
features))
# The key MUST be 'examples'.
receiver_tensors = {'examples': serialized_tf_example}
# NOTE: Model is driven by transformed features (since training works on the
# materialized output of TFT, but slicing will happen on raw features.
features.update(transformed_features)
return tfma.export.EvalInputReceiver(
features=features,
receiver_tensors=receiver_tensors,
labels=transformed_features[taxi.transformed_name(taxi.LABEL_KEY)])
print('Done')
# + [markdown] id="wZV47rcxJ6aC" colab_type="text"
# ## Train and export the model for TFMA
# + id="wXlW87u8J8vb" colab_type="code" colab={}
def run_local_experiment(tft_run_id, tf_run_id, num_layers, first_layer_size, scale_factor):
"""Helper method to train and export the model for TFMA
The caller specifies the input and output directory by providing run ids. The optional parameters
allows the user to change the modelfor time series view.
Args:
tft_run_id: The run id for the preprocessing. Identifies the folder containing training data.
tf_run_id: The run for this training run. Identify where the exported model will be written to.
num_layers: The number of layers used by the hiden layer.
first_layer_size: The size of the first hidden layer.
scale_factor: The scale factor between each layer in in hidden layers.
"""
hparams = tf.contrib.training.HParams(
# Inputs: are tf-transformed materialized features
train_files=os.path.join(get_tft_train_output_dir(tft_run_id), TFT_TRAIN_FILE_PREFIX + '-00000-of-*'),
eval_files=os.path.join(get_tft_eval_output_dir(tft_run_id), TFT_EVAL_FILE_PREFIX + '-00000-of-*'),
schema_file=get_schema_file(),
# Output: dir for trained model
job_dir=get_tf_output_dir(tf_run_id),
tf_transform_dir=get_tft_train_output_dir(tft_run_id),
# Output: dir for both the serving model and eval_model which will go into tfma
# evaluation
output_dir=get_tf_output_dir(tf_run_id),
train_steps=10000,
eval_steps=5000,
num_layers=num_layers,
first_layer_size=first_layer_size,
scale_factor=scale_factor,
num_epochs=None,
train_batch_size=40,
eval_batch_size=40)
run_experiment(hparams)
print('Done')
# + id="LVqhulOSKAly" colab_type="code" colab={}
run_local_experiment(tft_run_id=0,
tf_run_id=0,
num_layers=4,
first_layer_size=100,
scale_factor=0.7)
print('Done')
# + [markdown] id="8Y6sRSPZKCjs" colab_type="text"
# ## Run TFMA to compute metrics
# For local analysis, TFMA offers a helper method ``tfma.run_model_analysis``
# + id="ZB7n3o1YKErx" colab_type="code" colab={}
help(tfma.run_model_analysis)
# + [markdown] id="uOKlvwTLKH8T" colab_type="text"
# #### You can also write your own custom pipeline if you want to perform extra transformations on the data before evaluation.
# + id="ZKCj7orAKKpq" colab_type="code" colab={}
def run_tfma(slice_spec, tf_run_id, tfma_run_id, input_csv, schema_file, add_metrics_callbacks=None):
"""A simple wrapper function that runs tfma locally.
A function that does extra transformations on the data and then run model analysis.
Args:
slice_spec: The slicing spec for how to slice the data.
tf_run_id: An id to contruct the model directories with.
tfma_run_id: An id to construct output directories with.
input_csv: The evaluation data in csv format.
schema_file: The file holding a text-serialized schema for the input data.
add_metrics_callback: Optional list of callbacks for computing extra metrics.
Returns:
An EvalResult that can be used with TFMA visualization functions.
"""
eval_model_base_dir = os.path.join(get_tf_output_dir(tf_run_id), EVAL_MODEL_DIR)
eval_model_dir = os.path.join(eval_model_base_dir, next(os.walk(eval_model_base_dir))[1][0])
eval_shared_model = tfma.default_eval_shared_model(
eval_saved_model_path=eval_model_dir,
add_metrics_callbacks=add_metrics_callbacks)
schema = taxi.read_schema(schema_file)
print(eval_model_dir)
display_only_data_location = input_csv
with beam.Pipeline() as pipeline:
csv_coder = taxi.make_csv_coder(schema)
raw_data = (
pipeline
| 'ReadFromText' >> beam.io.ReadFromText(
input_csv,
coder=beam.coders.BytesCoder(),
skip_header_lines=True)
| 'ParseCSV' >> beam.Map(csv_coder.decode))
# Examples must be in clean tf-example format.
coder = taxi.make_proto_coder(schema)
raw_data = (
raw_data
| 'ToSerializedTFExample' >> beam.Map(coder.encode))
_ = (raw_data
| 'ExtractEvaluateAndWriteResults' >>
tfma.ExtractEvaluateAndWriteResults(
eval_shared_model=eval_shared_model,
slice_spec=slice_spec,
output_path=get_tfma_output_dir(tfma_run_id),
display_only_data_location=input_csv))
return tfma.load_eval_result(output_path=get_tfma_output_dir(tfma_run_id))
print('Done')
# + [markdown] id="DC70sAOfKMo7" colab_type="text"
# #### You can also compute metrics on slices of your data in TFMA. Slices can be specified using ``tfma.slicer.SingleSliceSpec``.
#
# Below are examples of how slices can be specified.
# + id="n2JA6QRGKPCr" colab_type="code" colab={}
# An empty slice spec means the overall slice, that is, the whole dataset.
OVERALL_SLICE_SPEC = tfma.slicer.SingleSliceSpec()
# Data can be sliced along a feature column
# In this case, data is sliced along feature column trip_start_hour.
FEATURE_COLUMN_SLICE_SPEC = tfma.slicer.SingleSliceSpec(columns=['trip_start_hour'])
# Data can be sliced by crossing feature columns
# In this case, slices are computed for trip_start_day x trip_start_month.
FEATURE_COLUMN_CROSS_SPEC = tfma.slicer.SingleSliceSpec(columns=['trip_start_day', 'trip_start_month'])
# Metrics can be computed for a particular feature value.
# In this case, metrics is computed for all data where trip_start_hour is 12.
FEATURE_VALUE_SPEC = tfma.slicer.SingleSliceSpec(features=[('trip_start_hour', 12)])
# It is also possible to mix column cross and feature value cross.
# In this case, data where trip_start_hour is 12 will be sliced by trip_start_day.
COLUMN_CROSS_VALUE_SPEC = tfma.slicer.SingleSliceSpec(columns=['trip_start_day'], features=[('trip_start_hour', 12)])
ALL_SPECS = [
OVERALL_SLICE_SPEC,
FEATURE_COLUMN_SLICE_SPEC,
FEATURE_COLUMN_CROSS_SPEC,
FEATURE_VALUE_SPEC,
COLUMN_CROSS_VALUE_SPEC
]
# + [markdown] id="As53x7HhKRVn" colab_type="text"
# #### Let's run TFMA!
# + id="9ffmUVhlKUBz" colab_type="code" colab={}
tf.logging.set_verbosity(tf.logging.INFO)
tfma_result_1 = run_tfma(input_csv=os.path.join(EVAL_DATA_DIR, 'data.csv'),
tf_run_id=0,
tfma_run_id=1,
slice_spec=ALL_SPECS,
schema_file=get_schema_file())
print('Done')
# + [markdown] id="XdNnyYg0KVwi" colab_type="text"
# ## Visualization: Slicing Metrics
#
# To see the slices, either use the name of the column (by setting slicing_column) or provide a tfma.slicer.SingleSliceSpec (by setting slicing_spec). If neither is provided, the overall will be displayed.
#
# The default visualization is **slice overview** when the number of slices is small. It shows the value of a metric for each slice sorted by the another metric. It is also possible to set a threshold to filter out slices with smaller weights.
#
# This view also supports **metrics histogram** as an alternative visualization. It is also the defautl view when the number of slices is large. The results will be divided into buckets and the number of slices / total weights / both can be visualized. Slices with small weights can be fitlered out by setting the threshold. Further filtering can be applied by dragging the grey band. To reset the range, double click the band. Filtering can be used to remove outliers in the visualization and the metrics table below.
# + id="VtptlAgnKXt6" colab_type="code" colab={}
# Show data sliced along feature column trip_start_hour.
tfma.view.render_slicing_metrics(
tfma_result_1, slicing_column='trip_start_hour')
# + id="J2CGlSfHKZ71" colab_type="code" colab={}
# Show metrics sliced by COLUMN_CROSS_VALUE_SPEC above.
tfma.view.render_slicing_metrics(tfma_result_1, slicing_spec=COLUMN_CROSS_VALUE_SPEC)
# + id="6lkVP_RQKbgz" colab_type="code" colab={}
# Show overall metrics.
tfma.view.render_slicing_metrics(tfma_result_1)
# + [markdown] id="585hmemUKc6L" colab_type="text"
# ## Visualization: Plots
#
# TFMA offers a number of built-in plots. To see them, add them to ``add_metrics_callbacks``
# + id="rSUDOrnYKemd" colab_type="code" colab={}
tf.logging.set_verbosity(tf.logging.INFO)
tfma_vis = run_tfma(input_csv=os.path.join(EVAL_DATA_DIR, 'data.csv'),
tf_run_id=0,
tfma_run_id='vis',
slice_spec=ALL_SPECS,
schema_file=get_schema_file(),
add_metrics_callbacks=[
# calibration_plot_and_prediction_histogram computes calibration plot and prediction
# distribution at different thresholds.
tfma.post_export_metrics.calibration_plot_and_prediction_histogram(),
# auc_plots enables precision-recall curve and ROC visualization at different thresholds.
tfma.post_export_metrics.auc_plots()
])
print('Done')
# + [markdown] id="XCpJn307KhHZ" colab_type="text"
# Plots must be visualized for an individual slice. To specify a slice, use ``tfma.slicer.SingleSliceSpec``.
#
# In the example below, we are using ``tfma.slicer.SingleSliceSpec(features=[('trip_start_hour', 1)])`` to specify the slice where trip_start_hour is 1.
#
# Plots are interactive:
# - Drag to pan
# - Scroll to zoom
# - Right click to reset the view
#
# Simply hover over the desired data point to see more details.
# + id="8ajak6hvKjvz" colab_type="code" colab={}
tfma.view.render_plot(tfma_vis, tfma.slicer.SingleSliceSpec(features=[('trip_start_hour', 1)]))
# + [markdown] id="JEQxCwlmKlMS" colab_type="text"
# #### Custom metrics
#
# In addition to plots, it is also possible to compute additional metrics not present at export time or custom metrics metrics using ``add_metrics_callbacks``.
#
# All metrics in ``tf.metrics`` are supported in the callback and can be used to compose other metrics:
# https://www.tensorflow.org/api_docs/python/tf/metrics
#
# In the cells below, false negative rate is computed as an example.
# + id="G6YlvQLrKmvz" colab_type="code" colab={}
# Defines a callback that adds FNR to the result.
def add_fnr_for_threshold(threshold):
def _add_fnr_callback(features_dict, predictions_dict, labels_dict):
metric_ops = {}
prediction_tensor = tf.cast(
predictions_dict.get(tf.contrib.learn.PredictionKey.LOGISTIC), tf.float64)
fn_value_op, fn_update_op = tf.metrics.false_negatives_at_thresholds(tf.squeeze(labels_dict),
tf.squeeze(prediction_tensor),
[threshold])
tp_value_op, tp_update_op = tf.metrics.true_positives_at_thresholds(tf.squeeze(labels_dict),
tf.squeeze(prediction_tensor),
[threshold])
fnr = fn_value_op[0] / (fn_value_op[0] + tp_value_op[0])
metric_ops['FNR@' + str(threshold)] = (fnr, tf.group(fn_update_op, tp_update_op))
return metric_ops
return _add_fnr_callback
# + id="9pWXzEMvKpm6" colab_type="code" colab={}
tf.logging.set_verbosity(tf.logging.INFO)
tfma_fnr = run_tfma(input_csv=os.path.join(EVAL_DATA_DIR, 'data.csv'),
tf_run_id=0,
tfma_run_id='fnr',
slice_spec=ALL_SPECS,
schema_file=get_schema_file(),
add_metrics_callbacks=[
# Simply add the call here.
add_fnr_for_threshold(0.75)
])
tfma.view.render_slicing_metrics(tfma_fnr, slicing_spec=FEATURE_COLUMN_SLICE_SPEC)
# + [markdown] id="brWQBOnuKrJq" colab_type="text"
# ## Visualization: Time Series
#
# It is important to track how your model is doing over time. TFMA offers two modes to show your model performs over time.
#
# **Multiple model analysis** shows how model perfoms from one version to another. This is useful early on to see how the addition of new features, change in modeling technique, etc, affects the performance. TFMA offers a convenient method.
# + id="EnsBKnmrKtdJ" colab_type="code" colab={}
help(tfma.multiple_model_analysis)
# + [markdown] id="JtHDM1sPKvBx" colab_type="text"
# **Multiple data analysis** shows how a model perfoms under different evaluation data set. This is useful to ensure that model performance does not degrade over time. TFMA offer a conveneient method.
# + id="kG7Ff-2YKwsK" colab_type="code" colab={}
help(tfma.multiple_data_analysis)
# + [markdown] id="OsfW6L2QKyGq" colab_type="text"
# It is also possible to compose a time series manually.
# + id="cxzmxsJyKzxC" colab_type="code" colab={}
# Create different models.
# Run some experiments with different hidden layer configurations.
run_local_experiment(tft_run_id=0,
tf_run_id=1,
num_layers=3,
first_layer_size=200,
scale_factor=0.7)
run_local_experiment(tft_run_id=0,
tf_run_id=2,
num_layers=4,
first_layer_size=240,
scale_factor=0.5)
print('Done')
# + id="SLBflNxyK14D" colab_type="code" colab={}
tfma_result_2 = run_tfma(input_csv=os.path.join(EVAL_DATA_DIR, 'data.csv'),
tf_run_id=1,
tfma_run_id=2,
slice_spec=ALL_SPECS,
schema_file=get_schema_file())
tfma_result_3 = run_tfma(input_csv=os.path.join(EVAL_DATA_DIR, 'data.csv'),
tf_run_id=2,
tfma_run_id=3,
slice_spec=ALL_SPECS,
schema_file=get_schema_file())
print('Done')
# + [markdown] id="N5ZVlsu3K3s6" colab_type="text"
# Like plots, time series view must visualized for a slice too.
#
# In the example below, we are showing the overall slice.
#
# Select a metric to see its time series graph. Hover over each data point to get more details.
# + id="d52jgg8WK51T" colab_type="code" colab={}
eval_results = tfma.make_eval_results([tfma_result_1, tfma_result_2, tfma_result_3],
tfma.constants.MODEL_CENTRIC_MODE)
tfma.view.render_time_series(eval_results, OVERALL_SLICE_SPEC)
# + [markdown] id="T9o8bZWRK8Fi" colab_type="text"
# Serialized results can also be used to construct a time series. Thus, there is no need to re-run TFMA for models already evaluated for a long running pipeline.
# + id="zYyVJEWWK90c" colab_type="code" colab={}
# Visualize the results in a Time Series. In this case, we are showing the slice specified.
eval_results_from_disk = tfma.load_eval_results([get_tfma_output_dir(1),
get_tfma_output_dir(2),
get_tfma_output_dir(3)],
tfma.constants.MODEL_CENTRIC_MODE)
tfma.view.render_time_series(eval_results_from_disk, FEATURE_VALUE_SPEC)
|
examples/chicago_taxi/chicago_taxi_tfma_local_playground.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:anaconda3]
# language: python
# name: conda-env-anaconda3-py
# ---
# # 文法特征
#
# 第 6 章中我们通过检测文本的特征建立分类器,那些特征可能非常简单,如提取一个单词的最后一个字母等。本章中,我们将探讨特征在建立基于规则的文法中的作用。与第 6 章中自动提取的特征不同,这里我们手动声明词和短语的特征:
kim = {'CAT': 'NP', 'ORTH': 'Kim', 'REF': 'k'}
chase = {'CAT': 'V', 'ORTH': 'chased', 'REL': 'chase'}
# 字典对象 kim 和 chase 存储了两组特征值,CAT 代表文法类别,ORTH 代表单词的拼写,还有一些其它面向语义的特征:kim 的 REF 意在给出 kim 的指示物,chase 的 REL 则给出 chase 表示的关系。这样的特征和特征值对被称为**特征结构**。
#
# 特征结构包含了各种有关文法实体的信息,我们可以进一步增加属性。例如:对于 chase, 主语扮演施事(agent)角色,而宾语扮演受事(patient)角色。我们添加这些信息:
chase['AGT'] = 'sbj'
chase['PAT'] = 'obj'
# 现在我们来处理句子 Kim chased Lee,我们要“绑定”动词的施事角色给主语,受事角色给宾语,可以通过链接 NP 的 REF 特征来达到这一目的(这里假设了动词左侧和右侧的 NP 分别是主语和宾语):
# +
sent = 'Kim chased Lee'
tokens = sent.split()
lee = {'CAT': 'NP', 'ORTH': 'Lee', 'REF': 'l'}
def lex2fs(word):
for fs in [kim, lee, chase]:
if fs['ORTH'] == word:
return fs
subj, verb, obj = lex2fs(tokens[0]), lex2fs(tokens[1]), lex2fs(tokens[2])
verb['AGT'] = subj['REF']
verb['PAT'] = obj['REF']
for k in ['ORTH', 'REL', 'AGT', 'PAT']:
print('%-5s => %s' % (k, verb[k]))
# -
# 同样的方法可以适用不同的动词,例如 surprise,不同之处在于这种情况下,主语将扮演来源(source,SRC)角色,宾语将扮演体验者(experiencer,EXP)角色:
surprise = {'CAT': 'V', 'ORTH': 'surprised', 'REL': 'surprise',
'SRC': 'sbj', 'EXP': 'obj'}
# 特征结构是非常强大的,接下来我们将分析如何将上下文无关文法扩展到合适的特征结构。
# ## 句法协议
#
# 在英语中,名词通常被标记为单数或附属,例如 this dog 和 these dogs 是符合语法的,而 these dog 和 this dogs 则不是,也就是说名词短语中使用的指示词和名词搭配是由限制的。动词的现在时态也有类似的变化,例如 the dog runs 和 the dogs run。这种同时的变化被称为**协议(agreement)**,下表展示了英语中规则动词的协议规范:
#
# | | 单数 | 复数 |
# |----------|----------------|----------|
# | 第一人称 | I run | we run |
# | 第二人称 | you run | you run |
# | 第三人称 | he/she/it runs | they run |
#
# 让我们看看当我们在一个上下文无关文法中编码这些协议约束会发生什么。我们从一个简单的 CFG 开始:
#
# S -> NP VP
# NP -> Det N
# VP -> V
#
# Det -> 'this'
# N -> 'dog'
# V -> 'runs'
#
# 该文法可以产生句子 this dog runs,然而我们真正想要做的是也能产生 these dogs run,同时阻止不必要的序列如 this dogs run 和 these dog runs:
#
# S -> NP_SG VP_SG
# S -> NP_PL VP_PL
# NP_SG -> Det_SG N_SG
# NP_PL -> Det_PL N_PL
# VP_SG -> V_SG
# VP_PL -> V_PL
#
# Det_SG -> 'this'
# Det_PL -> 'these'
# N_SG -> 'dog'
# N_PL -> 'dogs'
# V_SG -> 'runs'
# V_PL -> 'run'
#
# 在扩展 S 的地方,我们现在有两个产生式,一个覆盖单数主语 NP 和 VP,另一个覆盖复数主语 NP 和 VP,原始文法的所有产生式都有两个与之对应。在小规模文法中这不是什么问题,但是在更大的涵盖了一定量英语成分的文法中,产生式的数量会成爆炸式地增长。
# ## 使用属性和约束
#
# 非正式的语言类别都具有属性,例如:名词具有复数的属性,我们可以用如下符号来表示,它的意思是类别 N 有一个**(文法)特征**叫做 NUM(数字 number 的简写),此特征的值是 pl(复数 plural 的简写):
#
# N[NUM=pl]
#
# 我们可以添加类似的注解给其他类别:
#
# Det[NUM=sg] -> 'this'
# Det[NUM=pl] -> 'these'
#
# N[NUM=sg] -> 'dog'
# N[NUM=pl] -> 'dogs'
# V[NUM=sg] -> 'runs'
# V[NUM=pl] -> 'run'
#
# 当我们在产生式中允许使用特征值变量时,事情变得有趣了起来:
#
# S -> NP[NUM=?n] VP[NUM=?n]
# NP[NUM=?n] -> Det[NUM=?n] N[NUM=?n]
# VP[NUM=?n] -> V[NUM=?n]
#
# 这里我们使用 ?n 来作为 NUM 值得变量,它可以在给定的产生式中被实例化为 sg 或 pl。值得注意的是,在一个产生式中所有的 ?n 需要取同样的值,也就是在 S -> NP VP 中,不管 NP 为特征 NUM 取什么值,VP 必须取同样的值。
#
# 我们用树的形式来思考这些特征限制是如何工作的。首先词汇产生式承认下面深度为 1 的树:
#
# 
#
# 接下来通过 NP -> Det N 来产生深度为 2 的树,可以看出后两种情况是不允许的,用顶端节点值为 FAIL 来表示,这是由于它们字数的根节点 NUM 值不同。
#
# 
#
# 再结合扩展 S 的产生式,可以得到 these dogs run 的解析树:
#
# 
#
# 在上面的例子中限定词 Det 有 this 和 these 两种形式,然而英语中的其他限定词对与它们结合的名词数量并不挑剔:
#
# Det[NUM=sg] -> 'the' | 'some' | 'any'
# Det[NUM=pl] -> 'the' | 'some' | 'any'
#
# 一个更优雅的写法是保留 NUM 的值为未指定,让它匹配与它结合的任何名词的数量:
#
# Det[NUM=?n] -> 'the' | 'some' | 'any'
#
# 事实上我们可以更简单些,在这样的产生式中不给 NUM 任何指定:
#
# Det -> 'the' | 'some' | 'any'
#
# 下面是一个较为完整的基于特征的文法的例子:
# +
import nltk
nltk.data.show_cfg('grammars/book_grammars/feat0.fcfg')
# -
# 文法开头的 % start S 告诉分析器以 S 作为文法的开始符号,同时一个句法类别可以有多个特征,如 IV[TENSE=pres, NUM=pl],可以添加任意数量的特征。
#
# 我们可以使用 [nltk.load_parse](http://www.nltk.org/_modules/nltk/parse/util.html#load_parser) 函数来加载基于特征的文法:
tokens = 'Kim likes children'.split()
cp = nltk.load_parser('grammars/book_grammars/feat0.fcfg', trace=2)
for tree in cp.parse(tokens):
print(tree)
# ## 术语
#
# 前面我们看到了像 sg 和 pl 这样的特征值,这些简单的值通常被称为**原子**,也就是说它们不能被分解成更小的部分。原子值得一种特殊情况时**布尔值**,也就是说值仅仅指定一个属性是真还是假。例如:我们用布尔特征 AUX 区分**助动词**,如 can、may、will 和 do,就可以写成 AUX=+ 或 AUX=-,有一个广泛采用的缩写约定为 +AUX 和 -AUX。
#
# V[TENSE=pres, +AUX] -> 'can'
# V[TENSE=pres, +AUX] -> 'may'
# V[TENSE=pres, -AUX] -> 'walks'
# V[TENSE=pres, -AUX] -> 'likes'
#
# 除了原子值特征以外,特征可能本省就是特征结构的值。例如:我们可以将协议特征组合在一起(如:人称、数量和性别)作为一个类别的不同部分,表示为 AGR,这种情况下,AGR 就是一个**复杂值**,在格式上称为**属性值矩阵**(attribute value matrix,AVM)。
#
# [POS = N ]
# [ ]
# [AGR = [PER = 3 ]]
# [ [NUM = pl ]]
# [ [GND = fem ]]
#
# 当我们有可能使用像 AGR 这样的特征时,我们可以重构前面的文法,使协议特征捆绑在一起:
#
# S -> NP[AGR=?n] VP[AGR=?n]
# NP[AGR=?n] -> PropN[AGR=?n]
# VP[TENSE=?t, AGR=?n] -> Cop[TENSE=?t, AGR=?n] Adj
#
# Cop[TENSE=pres, AGR=[NUM=sg, PER=3]] -> 'is'
# PropN[AGR=[NUM=sg, PER=3]] -> 'Kim'
# Adj -> 'happy'
|
9.1-grammatical-features.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/brilianputraa/dyncontrol/blob/master/ODE/ODE_Supplementary_v1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="i3sUibvBvC_g" colab_type="code" colab={}
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] id="WwxGQpY7VJr-" colab_type="text"
# # ODE Supplementary v1
#
#
# This notebook will provide the intuition about the use of Ordinary Differential Equation (ODE) on the Control Systems Field. Also gives refreshment about Numerical ODE topics which widely employed on Dynamical Systems and Control.
#
#
# <a href="https://github.com/brilianputraa/dyncontrol/blob/master/ODE" source="blank" ><img src="https://i.ibb.co/6NxqGSF/pinpng-com-github-logo-png-small.png"></a>
#
# + [markdown] id="ea6hKFl2MiF-" colab_type="text"
# ### Simple Cruise Control Systems
# Suppose we have very simple and straightforward first order linear system such as cruise control systems
#
#
#
#
#
# 
#
#
#
# Source : [Control Tutorials for MATLAB and Simulink, Michigan University](http://ctms.engin.umich.edu/CTMS/index.php?example=CruiseControl§ion=SystemModeling)
#
#
# With the systems equations denoted below,
# \begin{align}
# m\dot{v}+bv= u
# \end{align}
# Since the aim of our system is to control the velocity so the output is (but in this occasion we don't control the systems, conversely we only simulate the dynamics)
#
# \begin{align} y = v \end{align}
#
# Where v is the vehicle velocity in (m/s), u is the control input force (N), m is the vehicle mass (kg), and b is the damping coefficient (Ns/m)
#
# Then, we can derive the state space equation for the system as
#
# \begin{align} x = v \end{align}
#
# \begin{align} \dot{v} = \dot{x} \end{align}
#
# \begin{align} \dot{x} = -\frac{b}{m}x\, + \frac{1}{m} u \end{align}
#
# \begin{align} y = x \end{align}
#
# So we get the state space matrix (in this case scalar because our system just first order system),
#
# $ A = -\frac{b}{m}$
#
# $ B = \frac{1}{m}$
#
# $ C = 1 $
#
# Assuming that our system have parameter below,
#
# $m = 1500\, \text{kg}$
#
# $b = 70\, \text{Ns/m}$
# + [markdown] id="SmKZ5jcuwLFr" colab_type="text"
# #### Cook Up the System State Space
# + id="HpvAPszgiDjq" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 181} outputId="a66d8d9b-4b04-4bf4-f262-b06e3a3eada6"
import numpy as np
from numpy.linalg import inv, eig
import scipy
import matplotlib.pyplot as plt
# Plugging the parameter into the state space matrix, be obtained
# Params
m = 1500
b = 70
# State Space Matrix
A = -np.array([[np.divide(b,m)]])
B = np.divide(1,m)
C = 1
# Check the stability
print(eig(np.dot(A, np.eye(A.shape[0])))),
print('The System is stable because the eigenvalue is real negative')
print()
print("The State Space Matrix"),
print(f"A : {A}")
print()
print(f"B : {B}")
print()
print(f"C : {C}")
# Okay in this case not matrix but it's scalar, but I often call it state space matrix
# + [markdown] id="BN7qS2fGQ5v0" colab_type="text"
# ### The Numerical Integration
# There are several ways to do a numerical integration for knowing the trajectory of our dynamical system, from the simplest one into the complex but wholly more accurate compared to the simple method.
#
# The list of numerical integration methods:
#
#
# 1. Forward Euler
# 2. Backward Euler
# 3. Runge Kutta 3rd Order (ODE23)
# 4. Runge Kutta 4th Order (ODE45)
# 5. Etcetera.
#
# There are comparison according to the accuracy of the integrator which state that ODE45 has best accuracy among the others, the error comparison can be seen below
#
# <img src="https://beltoforion.de/en/runge-kutta_vs_euler//images/analytic_accuracy_vs_stepsize.svg" height = "400" width = "400" align="center" />
#
# Source : [A Comparison of Numeric Integration Schemes, Beltoforion.de](https://beltoforion.de/article.php?a=runge-kutta_vs_euler&p=calculation_samples)
#
# So because of that factor ODE45 is vastly used on the numerical integration scheme of dynamical systems, though it only had order of 4th it is very well tuned algorithm.
# + [markdown] id="eAW1kZKwMcTL" colab_type="text"
# #### 1. Forward Euler Method
# \begin{align} X_{k+1} = X_k + X'_k * \Delta_t \end{align}
#
# Also we can write that equation as,
#
# \begin{align} X_{k+1}=[I + \Delta_tA]X_k \end{align}
# + id="Zg1fqv4geeRj" colab_type="code" colab={}
def forward_euler(init_pos, steps, A, B, u):
nextstate = np.dot(np.eye(init_pos.shape[0]) + np.multiply(A + np.multiply(B, u), steps), init_pos)
return nextstate
# + [markdown] id="o3urRZXFX7qF" colab_type="text"
# #### 2. Backward Euler Method
# \begin{align} X_{k+1} = X_k + X'_{k+1}*\Delta_t \end{align}
#
# Also we can write that equation as,
#
# \begin{align} X_{k+1} = [I-\Delta_tA]^{-1} X_k \end{align}
# + id="TJ_7YCNre4_K" colab_type="code" colab={}
def backward_euler(init_pos, steps, A, B, u):
nextstate = np.dot(inv(np.eye(init_pos.shape[0]) - np.multiply(A + np.multiply(B,u), steps)), init_pos)
return nextstate
# + [markdown] id="M23nGB-AcxWE" colab_type="text"
# #### 3. Runge Kutta 3rd Order (ODE23)
# \begin{align} X_{k+1} = X_k + \frac{\Delta_t}{6}[f_1+4f_2+f_3] \end{align}
#
# Where,
#
# \begin{align} f_1 = f(k, X_k) \end{align}
#
# \begin{align} f_2 = f(k + \frac{\Delta_t}{2}, X_k + \frac{\Delta_t}{2}f_1) \end{align}
#
# \begin{align} f_3 = f(k+ \Delta_t, X_k+2f_1 -f_2) \end{align}
#
# Caveat:
# Function f is your system function
#
# + id="ptXXsSXoBq_N" colab_type="code" colab={}
def sode23(time, steps, init_pos):
k = time
f1 = fun(k, init_pos)
f2 = fun(np.add(k, np.divide(steps, 2)), np.add(init_pos, np.multiply(np.divide(steps, 2), f1)))
f3 = fun(np.add(k, steps), np.add(init_pos, -f2, 2*f1))
nextstate = np.add(init_pos, np.multiply(steps/6, f1 + 4*f2 + f3))
return nextstate
# + [markdown] id="b7gquO-4BrNG" colab_type="text"
# #### 4. Runge Kutta 4th Order (ODE45)
# \begin{align} X_{k+1} = X_k + \frac{\Delta_t}{6}[f_1+2f_2+2f_3+f_4] \end{align}
#
# Where,
#
# \begin{align} f_1 = f(k, X_k) \end{align}
#
# \begin{align} f_2 = f(k + \frac{\Delta_t}{2}, X_k + \frac{\Delta_t}{2}f_1) \end{align}
#
# \begin{align} f_3 = f(k + \frac{\Delta_t}{2}, X_k + \frac{\Delta_t}{2}f_2) \end{align}
#
# \begin{align} f_4 = f(k+ \Delta_t,X_k + \Delta_tf_3) \end{align}
# + id="Mqho3Vu9BrdO" colab_type="code" colab={}
def sode45(time, steps, init_pos):
k = time
f1 = fun(k, init_pos)
f2 = fun(np.add(k, np.divide(steps, 2)), np.add(init_pos, np.multiply(np.divide(steps, 2), f1)))
f3 = fun(np.add(k, np.divide(steps, 2)), np.add(init_pos, np.multiply(np.divide(steps, 2), f2)))
f4 = fun(np.add(k, steps), np.add(init_pos, f3 * steps))
nextstate = np.add(init_pos, np.multiply(steps/6, f1 + 2*f2 + 2*f3 + f4))
return nextstate
# + [markdown] id="16OBNn36Brtb" colab_type="text"
# ### Let's Do The Simulation
# + id="yPtSI8BSsP8H" colab_type="code" colab={}
## System function
def fun(time, pos):
time = int(time)
dx = np.dot(A, pos) + np.dot(B, u[time])
return dx
# + id="RbfoDiaTBt-G" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 279} outputId="54e21aa5-60a7-4f97-ea4b-8c3c7ed82d1c"
init_state = 10
steps = 0.01 # Try to explore the algorithm by changing the step time
T = 100 # Maximum simulation time
totalsteps = int(T / steps)
d = 1
w = 2* np.pi
t = np.linspace(0, T, totalsteps) # Simulation time
u = np.heaviside(t, 1) # Step input
x = np.array([[init_state]])
xb = x
xf = x
xkd = x
xkf = x
## Forward Euler
for k in range(0, t.shape[0]-1):
xf = np.concatenate((xf, forward_euler(xf[k,:].T, steps, A, B, u[k]).T.reshape(x.shape)), axis = 0)
## Backward Euler
for k in range(0, t.shape[0]-1):
xb = np.concatenate((xb, backward_euler(xb[k,:].T, steps, A, B, u[k]).T.reshape(x.shape)), axis = 0)
## ODE23
for k in range(0, t.shape[0]-1):
xkd = np.concatenate((xkd, sode23(k, steps, xkd[k,:].T).T.reshape(x.shape)), axis = 0)
## ODE45
for k in range(0, t.shape[0]-1):
xkf = np.concatenate((xkf, sode45(k, steps, xkf[k,:].T).T.reshape(x.shape)), axis = 0)
xf = np.dot(xf, np.array(C).T)
xb = np.dot(xb, np.array(C).T)
xkd = np.dot(xkd, np.array(C).T)
xkf = np.dot(xkf, np.array(C).T)
plt.plot(t,xf, label = 'Forward Euler')
plt.plot(t,xb, label = 'Backward Euler')
plt.plot(t,xkd, label = 'ODE23')
plt.plot(t,xkf, label = 'ODE45')
plt.xlabel('Time (s)')
plt.ylabel('Velocity')
plt.legend(loc = 0)
plt.show()
# + [markdown] id="hO6uC-d0kam4" colab_type="text"
# It's looks like the system were converge to zero and that's great
#
#
|
ODE/ODE_Supplementary_v1.ipynb
|
# <!-- dom:TITLE: Many-body Hamiltonians, basic linear algebra and Second Quantization -->
# # Many-body Hamiltonians, basic linear algebra and Second Quantization
# <!-- dom:AUTHOR: [<NAME>](http://mhjgit.github.io/info/doc/web/), National Superconducting Cyclotron Laboratory and Department of Physics and Astronomy, Michigan State University, East Lansing, MI 48824, USA & Department of Physics, University of Oslo, Oslo, Norway -->
# <!-- Author: -->
# **[<NAME>](http://mhjgit.github.io/info/doc/web/), National Superconducting Cyclotron Laboratory and Department of Physics and Astronomy, Michigan State University, East Lansing, MI 48824, USA & Department of Physics, University of Oslo, Oslo, Norway**
#
# Date: **Jul 10, 2018**
#
# ## Definitions and notations
#
# Before we proceed we need some definitions.
# We will assume that the interacting part of the Hamiltonian
# can be approximated by a two-body interaction.
# This means that our Hamiltonian is written as the sum of some onebody part and a twobody part
# <!-- Equation labels as ordinary links -->
# <div id="Hnuclei"></div>
#
# $$
# \begin{equation}
# \hat{H} = \hat{H}_0 + \hat{H}_I
# = \sum_{i=1}^A \hat{h}_0(x_i) + \sum_{i < j}^A \hat{v}(r_{ij}),
# \label{Hnuclei} \tag{1}
# \end{equation}
# $$
# with
# <!-- Equation labels as ordinary links -->
# <div id="hinuclei"></div>
#
# $$
# \begin{equation}
# H_0=\sum_{i=1}^A \hat{h}_0(x_i).
# \label{hinuclei} \tag{2}
# \end{equation}
# $$
# The onebody part $u_{\mathrm{ext}}(x_i)$ is normally approximated by a harmonic oscillator potential or the Coulomb interaction an electron feels from the nucleus. However, other potentials are fully possible, such as
# one derived from the self-consistent solution of the Hartree-Fock equations to be discussed here.
#
#
#
# Our Hamiltonian is invariant under the permutation (interchange) of two particles.
# Since we deal with fermions however, the total wave function is antisymmetric.
# Let $\hat{P}$ be an operator which interchanges two particles.
# Due to the symmetries we have ascribed to our Hamiltonian, this operator commutes with the total Hamiltonian,
# $$
# [\hat{H},\hat{P}] = 0,
# $$
# meaning that $\Psi_{\lambda}(x_1, x_2, \dots , x_A)$ is an eigenfunction of
# $\hat{P}$ as well, that is
# $$
# \hat{P}_{ij}\Psi_{\lambda}(x_1, x_2, \dots,x_i,\dots,x_j,\dots,x_A)=
# \beta\Psi_{\lambda}(x_1, x_2, \dots,x_i,\dots,x_j,\dots,x_A),
# $$
# where $\beta$ is the eigenvalue of $\hat{P}$. We have introduced the suffix $ij$ in order to indicate that we permute particles $i$ and $j$.
# The Pauli principle tells us that the total wave function for a system of fermions
# has to be antisymmetric, resulting in the eigenvalue $\beta = -1$.
#
#
#
# In our case we assume that we can approximate the exact eigenfunction with a Slater determinant
# <!-- Equation labels as ordinary links -->
# <div id="eq:HartreeFockDet"></div>
#
# $$
# \begin{equation}
# \Phi(x_1, x_2,\dots ,x_A,\alpha,\beta,\dots, \sigma)=\frac{1}{\sqrt{A!}}
# \left| \begin{array}{ccccc} \psi_{\alpha}(x_1)& \psi_{\alpha}(x_2)& \dots & \dots & \psi_{\alpha}(x_A)\\
# \psi_{\beta}(x_1)&\psi_{\beta}(x_2)& \dots & \dots & \psi_{\beta}(x_A)\\
# \dots & \dots & \dots & \dots & \dots \\
# \dots & \dots & \dots & \dots & \dots \\
# \psi_{\sigma}(x_1)&\psi_{\sigma}(x_2)& \dots & \dots & \psi_{\sigma}(x_A)\end{array} \right|, \label{eq:HartreeFockDet} \tag{3}
# \end{equation}
# $$
# where $x_i$ stand for the coordinates and spin values of a particle $i$ and $\alpha,\beta,\dots, \gamma$
# are quantum numbers needed to describe remaining quantum numbers.
#
#
# ### Brief reminder on some linear algebra properties
#
# Before we proceed with a more compact representation of a Slater determinant, we would like to repeat some linear algebra properties which will be useful for our derivations of the energy as function of a Slater determinant, Hartree-Fock theory and later the nuclear shell model.
#
# The inverse of a matrix is defined by
# $$
# \mathbf{A}^{-1} \cdot \mathbf{A} = I
# $$
# A unitary matrix $\mathbf{A}$ is one whose inverse is its adjoint
# $$
# \mathbf{A}^{-1}=\mathbf{A}^{\dagger}
# $$
# A real unitary matrix is called orthogonal and its inverse is equal to its transpose.
# A hermitian matrix is its own self-adjoint, that is
# $$
# \mathbf{A}=\mathbf{A}^{\dagger}.
# $$
# <table border="1">
# <thead>
# <tr><th align="center"> Relations </th> <th align="center"> Name </th> <th align="center"> matrix elements </th> </tr>
# </thead>
# <tbody>
# <tr><td align="center"> $A = A^{T}$ </td> <td align="center"> symmetric </td> <td align="center"> $a_{ij} = a_{ji}$ </td> </tr>
# <tr><td align="center"> $A = \left (A^{T} \right )^{-1}$ </td> <td align="center"> real orthogonal </td> <td align="center"> $\sum_k a_{ik} a_{jk} = \sum_k a_{ki} a_{kj} = \delta_{ij}$ </td> </tr>
# <tr><td align="center"> $A = A^{ * }$ </td> <td align="center"> real matrix </td> <td align="center"> $a_{ij} = a_{ij}^{ * }$ </td> </tr>
# <tr><td align="center"> $A = A^{\dagger}$ </td> <td align="center"> hermitian </td> <td align="center"> $a_{ij} = a_{ji}^{ * }$ </td> </tr>
# <tr><td align="center"> $A = \left (A^{\dagger} \right )^{-1}$ </td> <td align="center"> unitary </td> <td align="center"> $\sum_k a_{ik} a_{jk}^{ * } = \sum_k a_{ki}^{ * } a_{kj} = \delta_{ij}$ </td> </tr>
# </tbody>
# </table>
#
#
#
#
# Since we will deal with Fermions (identical and indistinguishable particles) we will
# form an ansatz for a given state in terms of so-called Slater determinants determined
# by a chosen basis of single-particle functions.
#
# For a given $n\times n$ matrix $\mathbf{A}$ we can write its determinant
# $$
# det(\mathbf{A})=|\mathbf{A}|=
# \left| \begin{array}{ccccc} a_{11}& a_{12}& \dots & \dots & a_{1n}\\
# a_{21}&a_{22}& \dots & \dots & a_{2n}\\
# \dots & \dots & \dots & \dots & \dots \\
# \dots & \dots & \dots & \dots & \dots \\
# a_{n1}& a_{n2}& \dots & \dots & a_{nn}\end{array} \right|,
# $$
# in a more compact form as
# $$
# |\mathbf{A}|= \sum_{i=1}^{n!}(-1)^{p_i}\hat{P}_i a_{11}a_{22}\dots a_{nn},
# $$
# where $\hat{P}_i$ is a permutation operator which permutes the column indices $1,2,3,\dots,n$
# and the sum runs over all $n!$ permutations. The quantity $p_i$ represents the number of transpositions of column indices that are needed in order to bring a given permutation back to its initial ordering, in our case given by $a_{11}a_{22}\dots a_{nn}$ here.
#
#
#
#
# A simple $2\times 2$ determinant illustrates this. We have
# $$
# det(\mathbf{A})=
# \left| \begin{array}{cc} a_{11}& a_{12}\\
# a_{21}&a_{22}\end{array} \right|= (-1)^0a_{11}a_{22}+(-1)^1a_{12}a_{21},
# $$
# where in the last term we have interchanged the column indices $1$ and $2$. The natural ordering we have chosen is $a_{11}a_{22}$.
#
#
# ### Back to the derivation of the energy
#
# The single-particle function $\psi_{\alpha}(x_i)$ are eigenfunctions of the onebody
# Hamiltonian $h_i$, that is
# $$
# \hat{h}_0(x_i)=\hat{t}(x_i) + \hat{u}_{\mathrm{ext}}(x_i),
# $$
# with eigenvalues
# $$
# \hat{h}_0(x_i) \psi_{\alpha}(x_i)=\left(\hat{t}(x_i) + \hat{u}_{\mathrm{ext}}(x_i)\right)\psi_{\alpha}(x_i)=\varepsilon_{\alpha}\psi_{\alpha}(x_i).
# $$
# The energies $\varepsilon_{\alpha}$ are the so-called non-interacting single-particle energies, or unperturbed energies.
# The total energy is in this case the sum over all single-particle energies, if no two-body or more complicated
# many-body interactions are present.
#
#
#
# Let us denote the ground state energy by $E_0$. According to the
# variational principle we have
# $$
# E_0 \le E[\Phi] = \int \Phi^*\hat{H}\Phi d\mathbf{\tau}
# $$
# where $\Phi$ is a trial function which we assume to be normalized
# $$
# \int \Phi^*\Phi d\mathbf{\tau} = 1,
# $$
# where we have used the shorthand $d\mathbf{\tau}=dx_1dr_2\dots dr_A$.
#
#
#
#
# In the Hartree-Fock method the trial function is the Slater
# determinant of Eq. ([eq:HartreeFockDet](#eq:HartreeFockDet)) which can be rewritten as
# $$
# \Phi(x_1,x_2,\dots,x_A,\alpha,\beta,\dots,\nu) = \frac{1}{\sqrt{A!}}\sum_{P} (-)^P\hat{P}\psi_{\alpha}(x_1)
# \psi_{\beta}(x_2)\dots\psi_{\nu}(x_A)=\sqrt{A!}\hat{A}\Phi_H,
# $$
# where we have introduced the antisymmetrization operator $\hat{A}$ defined by the
# summation over all possible permutations of two particles.
#
#
#
# It is defined as
# <!-- Equation labels as ordinary links -->
# <div id="antiSymmetryOperator"></div>
#
# $$
# \begin{equation}
# \hat{A} = \frac{1}{A!}\sum_{p} (-)^p\hat{P},
# \label{antiSymmetryOperator} \tag{4}
# \end{equation}
# $$
# with $p$ standing for the number of permutations. We have introduced for later use the so-called
# Hartree-function, defined by the simple product of all possible single-particle functions
# $$
# \Phi_H(x_1,x_2,\dots,x_A,\alpha,\beta,\dots,\nu) =
# \psi_{\alpha}(x_1)
# \psi_{\beta}(x_2)\dots\psi_{\nu}(x_A).
# $$
# Both $\hat{H}_0$ and $\hat{H}_I$ are invariant under all possible permutations of any two particles
# and hence commute with $\hat{A}$
# <!-- Equation labels as ordinary links -->
# <div id="commutionAntiSym"></div>
#
# $$
# \begin{equation}
# [H_0,\hat{A}] = [H_I,\hat{A}] = 0. \label{commutionAntiSym} \tag{5}
# \end{equation}
# $$
# Furthermore, $\hat{A}$ satisfies
# <!-- Equation labels as ordinary links -->
# <div id="AntiSymSquared"></div>
#
# $$
# \begin{equation}
# \hat{A}^2 = \hat{A}, \label{AntiSymSquared} \tag{6}
# \end{equation}
# $$
# since every permutation of the Slater
# determinant reproduces it.
#
#
#
# The expectation value of $\hat{H}_0$
# $$
# \int \Phi^*\hat{H}_0\Phi d\mathbf{\tau}
# = A! \int \Phi_H^*\hat{A}\hat{H}_0\hat{A}\Phi_H d\mathbf{\tau}
# $$
# is readily reduced to
# $$
# \int \Phi^*\hat{H}_0\Phi d\mathbf{\tau}
# = A! \int \Phi_H^*\hat{H}_0\hat{A}\Phi_H d\mathbf{\tau},
# $$
# where we have used Eqs. ([commutionAntiSym](#commutionAntiSym)) and
# ([AntiSymSquared](#AntiSymSquared)). The next step is to replace the antisymmetrization
# operator by its definition and to
# replace $\hat{H}_0$ with the sum of one-body operators
# $$
# \int \Phi^*\hat{H}_0\Phi d\mathbf{\tau}
# = \sum_{i=1}^A \sum_{p} (-)^p\int
# \Phi_H^*\hat{h}_0\hat{P}\Phi_H d\mathbf{\tau}.
# $$
# The integral vanishes if two or more particles are permuted in only one
# of the Hartree-functions $\Phi_H$ because the individual single-particle wave functions are
# orthogonal. We obtain then
# $$
# \int \Phi^*\hat{H}_0\Phi d\mathbf{\tau}= \sum_{i=1}^A \int \Phi_H^*\hat{h}_0\Phi_H d\mathbf{\tau}.
# $$
# Orthogonality of the single-particle functions allows us to further simplify the integral, and we
# arrive at the following expression for the expectation values of the
# sum of one-body Hamiltonians
# <!-- Equation labels as ordinary links -->
# <div id="H1Expectation"></div>
#
# $$
# \begin{equation}
# \int \Phi^*\hat{H}_0\Phi d\mathbf{\tau}
# = \sum_{\mu=1}^A \int \psi_{\mu}^*(x)\hat{h}_0\psi_{\mu}(x)dx
# d\mathbf{r}.
# \label{H1Expectation} \tag{7}
# \end{equation}
# $$
# We introduce the following shorthand for the above integral
# $$
# \langle \mu | \hat{h}_0 | \mu \rangle = \int \psi_{\mu}^*(x)\hat{h}_0\psi_{\mu}(x)dx,
# $$
# and rewrite Eq. ([H1Expectation](#H1Expectation)) as
# <!-- Equation labels as ordinary links -->
# <div id="H1Expectation1"></div>
#
# $$
# \begin{equation}
# \int \Phi^*\hat{H}_0\Phi d\tau
# = \sum_{\mu=1}^A \langle \mu | \hat{h}_0 | \mu \rangle.
# \label{H1Expectation1} \tag{8}
# \end{equation}
# $$
# The expectation value of the two-body part of the Hamiltonian is obtained in a
# similar manner. We have
# $$
# \int \Phi^*\hat{H}_I\Phi d\mathbf{\tau}
# = A! \int \Phi_H^*\hat{A}\hat{H}_I\hat{A}\Phi_H d\mathbf{\tau},
# $$
# which reduces to
# $$
# \int \Phi^*\hat{H}_I\Phi d\mathbf{\tau}
# = \sum_{i\le j=1}^A \sum_{p} (-)^p\int
# \Phi_H^*\hat{v}(r_{ij})\hat{P}\Phi_H d\mathbf{\tau},
# $$
# by following the same arguments as for the one-body
# Hamiltonian.
#
#
#
# Because of the dependence on the inter-particle distance $r_{ij}$, permutations of
# any two particles no longer vanish, and we get
# $$
# \int \Phi^*\hat{H}_I\Phi d\mathbf{\tau}
# = \sum_{i < j=1}^A \int
# \Phi_H^*\hat{v}(r_{ij})(1-P_{ij})\Phi_H d\mathbf{\tau}.
# $$
# where $P_{ij}$ is the permutation operator that interchanges
# particle $i$ and particle $j$. Again we use the assumption that the single-particle wave functions
# are orthogonal.
#
#
#
#
#
# We obtain
# <!-- Equation labels as ordinary links -->
# <div id="_auto1"></div>
#
# $$
# \begin{equation}
# \int \Phi^*\hat{H}_I\Phi d\mathbf{\tau}
# = \frac{1}{2}\sum_{\mu=1}^A\sum_{\nu=1}^A
# \left[ \int \psi_{\mu}^*(x_i)\psi_{\nu}^*(x_j)\hat{v}(r_{ij})\psi_{\mu}(x_i)\psi_{\nu}(x_j)
# dx_idx_j \right.
# \label{_auto1} \tag{9}
# \end{equation}
# $$
# <!-- Equation labels as ordinary links -->
# <div id="H2Expectation"></div>
#
# $$
# \begin{equation}
# \left.
# - \int \psi_{\mu}^*(x_i)\psi_{\nu}^*(x_j)
# \hat{v}(r_{ij})\psi_{\nu}(x_i)\psi_{\mu}(x_j)
# dx_idx_j
# \right]. \label{H2Expectation} \tag{10}
# \end{equation}
# $$
# The first term is the so-called direct term. It is frequently also called the Hartree term,
# while the second is due to the Pauli principle and is called
# the exchange term or just the Fock term.
# The factor $1/2$ is introduced because we now run over
# all pairs twice.
#
#
#
#
# The last equation allows us to introduce some further definitions.
# The single-particle wave functions $\psi_{\mu}(x)$, defined by the quantum numbers $\mu$ and $x$
# are defined as the overlap
# $$
# \psi_{\alpha}(x) = \langle x | \alpha \rangle .
# $$
# We introduce the following shorthands for the above two integrals
# $$
# \langle \mu\nu|\hat{v}|\mu\nu\rangle = \int \psi_{\mu}^*(x_i)\psi_{\nu}^*(x_j)\hat{v}(r_{ij})\psi_{\mu}(x_i)\psi_{\nu}(x_j)
# dx_idx_j,
# $$
# and
# $$
# \langle \mu\nu|\hat{v}|\nu\mu\rangle = \int \psi_{\mu}^*(x_i)\psi_{\nu}^*(x_j)
# \hat{v}(r_{ij})\psi_{\nu}(x_i)\psi_{\mu}(x_j)
# dx_idx_j.
# $$
# ## Preparing for later studies: varying the coefficients of a wave function expansion and orthogonal transformations
#
# It is common to expand the single-particle functions in a known basis and vary the coefficients,
# that is, the new single-particle wave function is written as a linear expansion
# in terms of a fixed chosen orthogonal basis (for example the well-known harmonic oscillator functions or the hydrogen-like functions etc).
# We define our new single-particle basis (this is a normal approach for Hartree-Fock theory) by performing a unitary transformation
# on our previous basis (labelled with greek indices) as
# <!-- Equation labels as ordinary links -->
# <div id="eq:newbasis"></div>
#
# $$
# \begin{equation}
# \psi_p^{new} = \sum_{\lambda} C_{p\lambda}\phi_{\lambda}. \label{eq:newbasis} \tag{11}
# \end{equation}
# $$
# In this case we vary the coefficients $C_{p\lambda}$. If the basis has infinitely many solutions, we need
# to truncate the above sum. We assume that the basis $\phi_{\lambda}$ is orthogonal.
#
#
#
#
# It is normal to choose a single-particle basis defined as the eigenfunctions
# of parts of the full Hamiltonian. The typical situation consists of the solutions of the one-body part of the Hamiltonian, that is we have
# $$
# \hat{h}_0\phi_{\lambda}=\epsilon_{\lambda}\phi_{\lambda}.
# $$
# The single-particle wave functions $\phi_{\lambda}(\mathbf{r})$, defined by the quantum numbers $\lambda$ and $\mathbf{r}$
# are defined as the overlap
# $$
# \phi_{\lambda}(\mathbf{r}) = \langle \mathbf{r} | \lambda \rangle .
# $$
# In deriving the Hartree-Fock equations, we will expand the single-particle functions in a known basis and vary the coefficients,
# that is, the new single-particle wave function is written as a linear expansion
# in terms of a fixed chosen orthogonal basis (for example the well-known harmonic oscillator functions or the hydrogen-like functions etc).
#
# We stated that a unitary transformation keeps the orthogonality. To see this consider first a basis of vectors $\mathbf{v}_i$,
# $$
# \mathbf{v}_i = \begin{bmatrix} v_{i1} \\ \dots \\ \dots \\v_{in} \end{bmatrix}
# $$
# We assume that the basis is orthogonal, that is
# $$
# \mathbf{v}_j^T\mathbf{v}_i = \delta_{ij}.
# $$
# An orthogonal or unitary transformation
# $$
# \mathbf{w}_i=\mathbf{U}\mathbf{v}_i,
# $$
# preserves the dot product and orthogonality since
# $$
# \mathbf{w}_j^T\mathbf{w}_i=(\mathbf{U}\mathbf{v}_j)^T\mathbf{U}\mathbf{v}_i=\mathbf{v}_j^T\mathbf{U}^T\mathbf{U}\mathbf{v}_i= \mathbf{v}_j^T\mathbf{v}_i = \delta_{ij}.
# $$
# This means that if the coefficients $C_{p\lambda}$ belong to a unitary or orthogonal trasformation (using the Dirac bra-ket notation)
# $$
# \vert p\rangle = \sum_{\lambda} C_{p\lambda}\vert\lambda\rangle,
# $$
# orthogonality is preserved, that is $\langle \alpha \vert \beta\rangle = \delta_{\alpha\beta}$
# and $\langle p \vert q\rangle = \delta_{pq}$.
#
# This propertry is extremely useful when we build up a basis of many-body Stater determinant based states.
#
# **Note also that although a basis $\vert \alpha\rangle$ contains an infinity of states, for practical calculations we have always to make some truncations.**
#
#
#
#
#
# Before we develop for example the Hartree-Fock equations, there is another very useful property of determinants that we will use both in connection with Hartree-Fock calculations and later shell-model calculations.
#
# Consider the following determinant
# $$
# \left| \begin{array}{cc} \alpha_1b_{11}+\alpha_2sb_{12}& a_{12}\\
# \alpha_1b_{21}+\alpha_2b_{22}&a_{22}\end{array} \right|=\alpha_1\left|\begin{array}{cc} b_{11}& a_{12}\\
# b_{21}&a_{22}\end{array} \right|+\alpha_2\left| \begin{array}{cc} b_{12}& a_{12}\\b_{22}&a_{22}\end{array} \right|
# $$
# We can generalize this to an $n\times n$ matrix and have
# $$
# \left| \begin{array}{cccccc} a_{11}& a_{12} & \dots & \sum_{k=1}^n c_k b_{1k} &\dots & a_{1n}\\
# a_{21}& a_{22} & \dots & \sum_{k=1}^n c_k b_{2k} &\dots & a_{2n}\\
# \dots & \dots & \dots & \dots & \dots & \dots \\
# \dots & \dots & \dots & \dots & \dots & \dots \\
# a_{n1}& a_{n2} & \dots & \sum_{k=1}^n c_k b_{nk} &\dots & a_{nn}\end{array} \right|=
# \sum_{k=1}^n c_k\left| \begin{array}{cccccc} a_{11}& a_{12} & \dots & b_{1k} &\dots & a_{1n}\\
# a_{21}& a_{22} & \dots & b_{2k} &\dots & a_{2n}\\
# \dots & \dots & \dots & \dots & \dots & \dots\\
# \dots & \dots & \dots & \dots & \dots & \dots\\
# a_{n1}& a_{n2} & \dots & b_{nk} &\dots & a_{nn}\end{array} \right| .
# $$
# This is a property we will use in our Hartree-Fock discussions.
#
#
#
#
# We can generalize the previous results, now
# with all elements $a_{ij}$ being given as functions of
# linear combinations of various coefficients $c$ and elements $b_{ij}$,
# $$
# \left| \begin{array}{cccccc} \sum_{k=1}^n b_{1k}c_{k1}& \sum_{k=1}^n b_{1k}c_{k2} & \dots & \sum_{k=1}^n b_{1k}c_{kj} &\dots & \sum_{k=1}^n b_{1k}c_{kn}\\
# \sum_{k=1}^n b_{2k}c_{k1}& \sum_{k=1}^n b_{2k}c_{k2} & \dots & \sum_{k=1}^n b_{2k}c_{kj} &\dots & \sum_{k=1}^n b_{2k}c_{kn}\\
# \dots & \dots & \dots & \dots & \dots & \dots \\
# \dots & \dots & \dots & \dots & \dots &\dots \\
# \sum_{k=1}^n b_{nk}c_{k1}& \sum_{k=1}^n b_{nk}c_{k2} & \dots & \sum_{k=1}^n b_{nk}c_{kj} &\dots & \sum_{k=1}^n b_{nk}c_{kn}\end{array} \right|=det(\mathbf{C})det(\mathbf{B}),
# $$
# where $det(\mathbf{C})$ and $det(\mathbf{B})$ are the determinants of $n\times n$ matrices
# with elements $c_{ij}$ and $b_{ij}$ respectively.
# This is a property we will use in our Hartree-Fock discussions. Convince yourself about the correctness of the above expression by setting $n=2$.
#
#
#
#
#
#
# With our definition of the new basis in terms of an orthogonal basis we have
# $$
# \psi_p(x) = \sum_{\lambda} C_{p\lambda}\phi_{\lambda}(x).
# $$
# If the coefficients $C_{p\lambda}$ belong to an orthogonal or unitary matrix, the new basis
# is also orthogonal.
# Our Slater determinant in the new basis $\psi_p(x)$ is written as
# $$
# \frac{1}{\sqrt{A!}}
# \left| \begin{array}{ccccc} \psi_{p}(x_1)& \psi_{p}(x_2)& \dots & \dots & \psi_{p}(x_A)\\
# \psi_{q}(x_1)&\psi_{q}(x_2)& \dots & \dots & \psi_{q}(x_A)\\
# \dots & \dots & \dots & \dots & \dots \\
# \dots & \dots & \dots & \dots & \dots \\
# \psi_{t}(x_1)&\psi_{t}(x_2)& \dots & \dots & \psi_{t}(x_A)\end{array} \right|=\frac{1}{\sqrt{A!}}
# \left| \begin{array}{ccccc} \sum_{\lambda} C_{p\lambda}\phi_{\lambda}(x_1)& \sum_{\lambda} C_{p\lambda}\phi_{\lambda}(x_2)& \dots & \dots & \sum_{\lambda} C_{p\lambda}\phi_{\lambda}(x_A)\\
# \sum_{\lambda} C_{q\lambda}\phi_{\lambda}(x_1)&\sum_{\lambda} C_{q\lambda}\phi_{\lambda}(x_2)& \dots & \dots & \sum_{\lambda} C_{q\lambda}\phi_{\lambda}(x_A)\\
# \dots & \dots & \dots & \dots & \dots \\
# \dots & \dots & \dots & \dots & \dots \\
# \sum_{\lambda} C_{t\lambda}\phi_{\lambda}(x_1)&\sum_{\lambda} C_{t\lambda}\phi_{\lambda}(x_2)& \dots & \dots & \sum_{\lambda} C_{t\lambda}\phi_{\lambda}(x_A)\end{array} \right|,
# $$
# which is nothing but $det(\mathbf{C})det(\Phi)$, with $det(\Phi)$ being the determinant given by the basis functions $\phi_{\lambda}(x)$.
#
#
#
# In our discussions hereafter we will use our definitions of single-particle states above and below the Fermi ($F$) level given by the labels
# $ijkl\dots \le F$ for so-called single-hole states and $abcd\dots > F$ for so-called particle states.
# For general single-particle states we employ the labels $pqrs\dots$.
#
#
#
#
# The energy functional is
# $$
# E[\Phi]
# = \sum_{\mu=1}^A \langle \mu | h | \mu \rangle +
# \frac{1}{2}\sum_{{\mu}=1}^A\sum_{{\nu}=1}^A \langle \mu\nu|\hat{v}|\mu\nu\rangle_{AS},
# $$
# we found the expression for the energy functional in terms of the basis function $\phi_{\lambda}(\mathbf{r})$. We then varied the above energy functional with respect to the basis functions $|\mu \rangle$.
# Now we are interested in defining a new basis defined in terms of
# a chosen basis as defined in Eq. ([eq:newbasis](#eq:newbasis)). We can then rewrite the energy functional as
# <!-- Equation labels as ordinary links -->
# <div id="FunctionalEPhi2"></div>
#
# $$
# \begin{equation}
# E[\Phi^{New}]
# = \sum_{i=1}^A \langle i | h | i \rangle +
# \frac{1}{2}\sum_{ij=1}^A\langle ij|\hat{v}|ij\rangle_{AS}, \label{FunctionalEPhi2} \tag{12}
# \end{equation}
# $$
# where $\Phi^{New}$ is the new Slater determinant defined by the new basis of Eq. ([eq:newbasis](#eq:newbasis)).
#
#
#
#
#
# Using Eq. ([eq:newbasis](#eq:newbasis)) we can rewrite Eq. ([FunctionalEPhi2](#FunctionalEPhi2)) as
# <!-- Equation labels as ordinary links -->
# <div id="FunctionalEPhi3"></div>
#
# $$
# \begin{equation}
# E[\Psi]
# = \sum_{i=1}^A \sum_{\alpha\beta} C^*_{i\alpha}C_{i\beta}\langle \alpha | h | \beta \rangle +
# \frac{1}{2}\sum_{ij=1}^A\sum_{{\alpha\beta\gamma\delta}} C^*_{i\alpha}C^*_{j\beta}C_{i\gamma}C_{j\delta}\langle \alpha\beta|\hat{v}|\gamma\delta\rangle_{AS}. \label{FunctionalEPhi3} \tag{13}
# \end{equation}
# $$
# # Definitions and Second quantization
#
# We introduce the time-independent operators
# $a_\alpha^{\dagger}$ and $a_\alpha$ which create and annihilate, respectively, a particle
# in the single-particle state
# $\varphi_\alpha$.
# We define the fermion creation operator
# $a_\alpha^{\dagger}$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-1a"></div>
#
# $$
# \begin{equation}
# a_\alpha^{\dagger}|0\rangle \equiv |\alpha\rangle \label{eq:2-1a} \tag{14},
# \end{equation}
# $$
# and
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-1b"></div>
#
# $$
# \begin{equation}
# a_\alpha^{\dagger}|\alpha_1\dots \alpha_n\rangle_{\mathrm{AS}} \equiv |\alpha\alpha_1\dots \alpha_n\rangle_{\mathrm{AS}} \label{eq:2-1b} \tag{15}
# \end{equation}
# $$
# In Eq. ([eq:2-1a](#eq:2-1a))
# the operator $a_\alpha^{\dagger}$ acts on the vacuum state
# $|0\rangle$, which does not contain any particles. Alternatively, we could define a closed-shell nucleus or atom as our new vacuum, but then
# we need to introduce the particle-hole formalism, see the discussion to come.
#
# In Eq. ([eq:2-1b](#eq:2-1b)) $a_\alpha^{\dagger}$ acts on an antisymmetric $n$-particle state and
# creates an antisymmetric $(n+1)$-particle state, where the one-body state
# $\varphi_\alpha$ is occupied, under the condition that
# $\alpha \ne \alpha_1, \alpha_2, \dots, \alpha_n$.
# It follows that we can express an antisymmetric state as the product of the creation
# operators acting on the vacuum state.
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-2"></div>
#
# $$
# \begin{equation}
# |\alpha_1\dots \alpha_n\rangle_{\mathrm{AS}} = a_{\alpha_1}^{\dagger} a_{\alpha_2}^{\dagger} \dots a_{\alpha_n}^{\dagger} |0\rangle \label{eq:2-2} \tag{16}
# \end{equation}
# $$
# It is easy to derive the commutation and anticommutation rules for the fermionic creation operators
# $a_\alpha^{\dagger}$. Using the antisymmetry of the states
# ([eq:2-2](#eq:2-2))
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-3a"></div>
#
# $$
# \begin{equation}
# |\alpha_1\dots \alpha_i\dots \alpha_k\dots \alpha_n\rangle_{\mathrm{AS}} =
# - |\alpha_1\dots \alpha_k\dots \alpha_i\dots \alpha_n\rangle_{\mathrm{AS}} \label{eq:2-3a} \tag{17}
# \end{equation}
# $$
# we obtain
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-3b"></div>
#
# $$
# \begin{equation}
# a_{\alpha_i}^{\dagger} a_{\alpha_k}^{\dagger} = - a_{\alpha_k}^{\dagger} a_{\alpha_i}^{\dagger} \label{eq:2-3b} \tag{18}
# \end{equation}
# $$
# Using the Pauli principle
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-4a"></div>
#
# $$
# \begin{equation}
# |\alpha_1\dots \alpha_i\dots \alpha_i\dots \alpha_n\rangle_{\mathrm{AS}} = 0 \label{eq:2-4a} \tag{19}
# \end{equation}
# $$
# it follows that
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-4b"></div>
#
# $$
# \begin{equation}
# a_{\alpha_i}^{\dagger} a_{\alpha_i}^{\dagger} = 0. \label{eq:2-4b} \tag{20}
# \end{equation}
# $$
# If we combine Eqs. ([eq:2-3b](#eq:2-3b)) and ([eq:2-4b](#eq:2-4b)), we obtain the well-known anti-commutation rule
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-5"></div>
#
# $$
# \begin{equation}
# a_{\alpha}^{\dagger} a_{\beta}^{\dagger} + a_{\beta}^{\dagger} a_{\alpha}^{\dagger} \equiv
# \{a_{\alpha}^{\dagger},a_{\beta}^{\dagger}\} = 0 \label{eq:2-5} \tag{21}
# \end{equation}
# $$
# The hermitian conjugate of $a_\alpha^{\dagger}$ is
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-6"></div>
#
# $$
# \begin{equation}
# a_{\alpha} = ( a_{\alpha}^{\dagger} )^{\dagger} \label{eq:2-6} \tag{22}
# \end{equation}
# $$
# If we take the hermitian conjugate of Eq. ([eq:2-5](#eq:2-5)), we arrive at
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-7"></div>
#
# $$
# \begin{equation}
# \{a_{\alpha},a_{\beta}\} = 0 \label{eq:2-7} \tag{23}
# \end{equation}
# $$
# What is the physical interpretation of the operator $a_\alpha$ and what is the effect of
# $a_\alpha$ on a given state $|\alpha_1\alpha_2\dots\alpha_n\rangle_{\mathrm{AS}}$?
# Consider the following matrix element
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-8"></div>
#
# $$
# \begin{equation}
# \langle\alpha_1\alpha_2 \dots \alpha_n|a_\alpha|\alpha_1'\alpha_2' \dots \alpha_m'\rangle \label{eq:2-8} \tag{24}
# \end{equation}
# $$
# where both sides are antisymmetric. We distinguish between two cases. The first (1) is when
# $\alpha \in \{\alpha_i\}$. Using the Pauli principle of Eq. ([eq:2-4a](#eq:2-4a)) it follows
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-9a"></div>
#
# $$
# \begin{equation}
# \langle\alpha_1\alpha_2 \dots \alpha_n|a_\alpha = 0 \label{eq:2-9a} \tag{25}
# \end{equation}
# $$
# The second (2) case is when $\alpha \notin \{\alpha_i\}$. It follows that an hermitian conjugation
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-9b"></div>
#
# $$
# \begin{equation}
# \langle \alpha_1\alpha_2 \dots \alpha_n|a_\alpha = \langle\alpha\alpha_1\alpha_2 \dots \alpha_n| \label{eq:2-9b} \tag{26}
# \end{equation}
# $$
# Eq. ([eq:2-9b](#eq:2-9b)) holds for case (1) since the lefthand side is zero due to the Pauli principle. We write
# Eq. ([eq:2-8](#eq:2-8)) as
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-10"></div>
#
# $$
# \begin{equation}
# \langle\alpha_1\alpha_2 \dots \alpha_n|a_\alpha|\alpha_1'\alpha_2' \dots \alpha_m'\rangle =
# \langle \alpha_1\alpha_2 \dots \alpha_n|\alpha\alpha_1'\alpha_2' \dots \alpha_m'\rangle \label{eq:2-10} \tag{27}
# \end{equation}
# $$
# Here we must have $m = n+1$ if Eq. ([eq:2-10](#eq:2-10)) has to be trivially different from zero.
#
#
#
# For the last case, the minus and plus signs apply when the sequence
# $\alpha ,\alpha_1, \alpha_2, \dots, \alpha_n$ and
# $\alpha_1', \alpha_2', \dots, \alpha_{n+1}'$ are related to each other via even and odd permutations.
# If we assume that $\alpha \notin \{\alpha_i\}$ we obtain
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-12"></div>
#
# $$
# \begin{equation}
# \langle\alpha_1\alpha_2 \dots \alpha_n|a_\alpha|\alpha_1'\alpha_2' \dots \alpha_{n+1}'\rangle = 0 \label{eq:2-12} \tag{28}
# \end{equation}
# $$
# when $\alpha \in \{\alpha_i'\}$. If $\alpha \notin \{\alpha_i'\}$, we obtain
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-13a"></div>
#
# $$
# \begin{equation}
# a_\alpha\underbrace{|\alpha_1'\alpha_2' \dots \alpha_{n+1}'}\rangle_{\neq \alpha} = 0 \label{eq:2-13a} \tag{29}
# \end{equation}
# $$
# and in particular
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-13b"></div>
#
# $$
# \begin{equation}
# a_\alpha |0\rangle = 0 \label{eq:2-13b} \tag{30}
# \end{equation}
# $$
# If $\{\alpha\alpha_i\} = \{\alpha_i'\}$, performing the right permutations, the sequence
# $\alpha ,\alpha_1, \alpha_2, \dots, \alpha_n$ is identical with the sequence
# $\alpha_1', \alpha_2', \dots, \alpha_{n+1}'$. This results in
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-14"></div>
#
# $$
# \begin{equation}
# \langle\alpha_1\alpha_2 \dots \alpha_n|a_\alpha|\alpha\alpha_1\alpha_2 \dots \alpha_{n}\rangle = 1 \label{eq:2-14} \tag{31}
# \end{equation}
# $$
# and thus
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-15"></div>
#
# $$
# \begin{equation}
# a_\alpha |\alpha\alpha_1\alpha_2 \dots \alpha_{n}\rangle = |\alpha_1\alpha_2 \dots \alpha_{n}\rangle \label{eq:2-15} \tag{32}
# \end{equation}
# $$
# The action of the operator
# $a_\alpha$ from the left on a state vector is to to remove one particle in the state
# $\alpha$.
# If the state vector does not contain the single-particle state $\alpha$, the outcome of the operation is zero.
# The operator $a_\alpha$ is normally called for a destruction or annihilation operator.
#
# The next step is to establish the commutator algebra of $a_\alpha^{\dagger}$ and
# $a_\beta$.
#
#
#
# The action of the anti-commutator
# $\{a_\alpha^{\dagger}$,$a_\alpha\}$ on a given $n$-particle state is
# $$
# a_\alpha^{\dagger} a_\alpha \underbrace{|\alpha_1\alpha_2 \dots \alpha_{n}\rangle}_{\neq \alpha} = 0 \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-16a"></div>
#
# $$
# \begin{equation}
# a_\alpha a_\alpha^{\dagger} \underbrace{|\alpha_1\alpha_2 \dots \alpha_{n}\rangle}_{\neq \alpha} =
# a_\alpha \underbrace{|\alpha \alpha_1\alpha_2 \dots \alpha_{n}\rangle}_{\neq \alpha} =
# \underbrace{|\alpha_1\alpha_2 \dots \alpha_{n}\rangle}_{\neq \alpha} \label{eq:2-16a} \tag{33}
# \end{equation}
# $$
# if the single-particle state $\alpha$ is not contained in the state.
#
#
#
#
# If it is present
# we arrive at
# $$
# a_\alpha^{\dagger} a_\alpha |\alpha_1\alpha_2 \dots \alpha_{k}\alpha \alpha_{k+1} \dots \alpha_{n-1}\rangle =
# a_\alpha^{\dagger} a_\alpha (-1)^k |\alpha \alpha_1\alpha_2 \dots \alpha_{n-1}\rangle \nonumber
# $$
# $$
# = (-1)^k |\alpha \alpha_1\alpha_2 \dots \alpha_{n-1}\rangle =
# |\alpha_1\alpha_2 \dots \alpha_{k}\alpha \alpha_{k+1} \dots \alpha_{n-1}\rangle \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-16b"></div>
#
# $$
# \begin{equation}
# a_\alpha a_\alpha^{\dagger}|\alpha_1\alpha_2 \dots \alpha_{k}\alpha \alpha_{k+1} \dots \alpha_{n-1}\rangle = 0 \label{eq:2-16b} \tag{34}
# \end{equation}
# $$
# From Eqs. ([eq:2-16a](#eq:2-16a)) and ([eq:2-16b](#eq:2-16b)) we arrive at
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-17"></div>
#
# $$
# \begin{equation}
# \{a_\alpha^{\dagger} , a_\alpha \} = a_\alpha^{\dagger} a_\alpha + a_\alpha a_\alpha^{\dagger} = 1 \label{eq:2-17} \tag{35}
# \end{equation}
# $$
# The action of $\left\{a_\alpha^{\dagger}, a_\beta\right\}$, with
# $\alpha \ne \beta$ on a given state yields three possibilities.
# The first case is a state vector which contains both $\alpha$ and $\beta$, then either
# $\alpha$ or $\beta$ and finally none of them.
#
#
#
# The first case results in
# $$
# a_\alpha^{\dagger} a_\beta |\alpha\beta\alpha_1\alpha_2 \dots \alpha_{n-2}\rangle = 0 \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-18a"></div>
#
# $$
# \begin{equation}
# a_\beta a_\alpha^{\dagger} |\alpha\beta\alpha_1\alpha_2 \dots \alpha_{n-2}\rangle = 0 \label{eq:2-18a} \tag{36}
# \end{equation}
# $$
# while the second case gives
# $$
# a_\alpha^{\dagger} a_\beta |\beta \underbrace{\alpha_1\alpha_2 \dots \alpha_{n-1}}_{\neq \alpha}\rangle =
# |\alpha \underbrace{\alpha_1\alpha_2 \dots \alpha_{n-1}}_{\neq \alpha}\rangle \nonumber
# $$
# $$
# a_\beta a_\alpha^{\dagger} |\beta \underbrace{\alpha_1\alpha_2 \dots \alpha_{n-1}}_{\neq \alpha}\rangle =
# a_\beta |\alpha\beta\underbrace{\beta \alpha_1\alpha_2 \dots \alpha_{n-1}}_{\neq \alpha}\rangle \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-18b"></div>
#
# $$
# \begin{equation}
# = - |\alpha\underbrace{\alpha_1\alpha_2 \dots \alpha_{n-1}}_{\neq \alpha}\rangle \label{eq:2-18b} \tag{37}
# \end{equation}
# $$
# Finally if the state vector does not contain $\alpha$ and $\beta$
# $$
# a_\alpha^{\dagger} a_\beta |\underbrace{\alpha_1\alpha_2 \dots \alpha_{n}}_{\neq \alpha,\beta}\rangle = 0 \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-18c"></div>
#
# $$
# \begin{equation}
# a_\beta a_\alpha^{\dagger} |\underbrace{\alpha_1\alpha_2 \dots \alpha_{n}}_{\neq \alpha,\beta}\rangle =
# a_\beta |\alpha \underbrace{\alpha_1\alpha_2 \dots \alpha_{n}}_{\neq \alpha,\beta}\rangle = 0 \label{eq:2-18c} \tag{38}
# \end{equation}
# $$
# For all three cases we have
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-19"></div>
#
# $$
# \begin{equation}
# \{a_\alpha^{\dagger},a_\beta \} = a_\alpha^{\dagger} a_\beta + a_\beta a_\alpha^{\dagger} = 0, \quad \alpha \neq \beta \label{eq:2-19} \tag{39}
# \end{equation}
# $$
# We can summarize our findings in Eqs. ([eq:2-17](#eq:2-17)) and ([eq:2-19](#eq:2-19)) as
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-20"></div>
#
# $$
# \begin{equation}
# \{a_\alpha^{\dagger},a_\beta \} = \delta_{\alpha\beta} \label{eq:2-20} \tag{40}
# \end{equation}
# $$
# with $\delta_{\alpha\beta}$ is the Kroenecker $\delta$-symbol.
#
# The properties of the creation and annihilation operators can be summarized as (for fermions)
# $$
# a_\alpha^{\dagger}|0\rangle \equiv |\alpha\rangle,
# $$
# and
# $$
# a_\alpha^{\dagger}|\alpha_1\dots \alpha_n\rangle_{\mathrm{AS}} \equiv |\alpha\alpha_1\dots \alpha_n\rangle_{\mathrm{AS}}.
# $$
# from which follows
# $$
# |\alpha_1\dots \alpha_n\rangle_{\mathrm{AS}} = a_{\alpha_1}^{\dagger} a_{\alpha_2}^{\dagger} \dots a_{\alpha_n}^{\dagger} |0\rangle.
# $$
# The hermitian conjugate has the folowing properties
# $$
# a_{\alpha} = ( a_{\alpha}^{\dagger} )^{\dagger}.
# $$
# Finally we found
# $$
# a_\alpha\underbrace{|\alpha_1'\alpha_2' \dots \alpha_{n+1}'}\rangle_{\neq \alpha} = 0, \quad
# \textrm{in particular } a_\alpha |0\rangle = 0,
# $$
# and
# $$
# a_\alpha |\alpha\alpha_1\alpha_2 \dots \alpha_{n}\rangle = |\alpha_1\alpha_2 \dots \alpha_{n}\rangle,
# $$
# and the corresponding commutator algebra
# $$
# \{a_{\alpha}^{\dagger},a_{\beta}^{\dagger}\} = \{a_{\alpha},a_{\beta}\} = 0 \hspace{0.5cm}
# \{a_\alpha^{\dagger},a_\beta \} = \delta_{\alpha\beta}.
# $$
# # One-body operators in second quantization
#
# A very useful operator is the so-called number-operator. Most physics cases we will
# study in this text conserve the total number of particles. The number operator is therefore
# a useful quantity which allows us to test that our many-body formalism conserves the number of particles.
# In for example $(d,p)$ or $(p,d)$ reactions it is important to be able to describe quantum mechanical states
# where particles get added or removed.
# A creation operator $a_\alpha^{\dagger}$ adds one particle to the single-particle state
# $\alpha$ of a give many-body state vector, while an annihilation operator $a_\alpha$
# removes a particle from a single-particle
# state $\alpha$.
#
#
#
#
#
# Let us consider an operator proportional with $a_\alpha^{\dagger} a_\beta$ and
# $\alpha=\beta$. It acts on an $n$-particle state
# resulting in
# <!-- Equation labels as ordinary links -->
# <div id="_auto2"></div>
#
# $$
# \begin{equation}
# a_\alpha^{\dagger} a_\alpha |\alpha_1\alpha_2 \dots \alpha_{n}\rangle =
# \begin{cases}
# 0 &\alpha \notin \{\alpha_i\} \\
# \\
# |\alpha_1\alpha_2 \dots \alpha_{n}\rangle & \alpha \in \{\alpha_i\}
# \end{cases}
# \label{_auto2} \tag{41}
# \end{equation}
# $$
# Summing over all possible one-particle states we arrive at
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-21"></div>
#
# $$
# \begin{equation}
# \left( \sum_\alpha a_\alpha^{\dagger} a_\alpha \right) |\alpha_1\alpha_2 \dots \alpha_{n}\rangle =
# n |\alpha_1\alpha_2 \dots \alpha_{n}\rangle \label{eq:2-21} \tag{42}
# \end{equation}
# $$
# The operator
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-22"></div>
#
# $$
# \begin{equation}
# \hat{N} = \sum_\alpha a_\alpha^{\dagger} a_\alpha \label{eq:2-22} \tag{43}
# \end{equation}
# $$
# is called the number operator since it counts the number of particles in a give state vector when it acts
# on the different single-particle states. It acts on one single-particle state at the time and falls
# therefore under category one-body operators.
# Next we look at another important one-body operator, namely $\hat{H}_0$ and study its operator form in the
# occupation number representation.
#
#
#
#
# We want to obtain an expression for a one-body operator which conserves the number of particles.
# Here we study the one-body operator for the kinetic energy plus an eventual external one-body potential.
# The action of this operator on a particular $n$-body state with its pertinent expectation value has already
# been studied in coordinate space.
# In coordinate space the operator reads
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-23"></div>
#
# $$
# \begin{equation}
# \hat{H}_0 = \sum_i \hat{h}_0(x_i) \label{eq:2-23} \tag{44}
# \end{equation}
# $$
# and the anti-symmetric $n$-particle Slater determinant is defined as
# $$
# \Phi(x_1, x_2,\dots ,x_n,\alpha_1,\alpha_2,\dots, \alpha_n)= \frac{1}{\sqrt{n!}} \sum_p (-1)^p\hat{P}\psi_{\alpha_1}(x_1)\psi_{\alpha_2}(x_2) \dots \psi_{\alpha_n}(x_n).
# $$
# Defining
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-25"></div>
#
# $$
# \begin{equation}
# \hat{h}_0(x_i) \psi_{\alpha_i}(x_i) = \sum_{\alpha_k'} \psi_{\alpha_k'}(x_i) \langle\alpha_k'|\hat{h}_0|\alpha_k\rangle \label{eq:2-25} \tag{45}
# \end{equation}
# $$
# we can easily evaluate the action of $\hat{H}_0$ on each product of one-particle functions in Slater determinant.
# From Eq. ([eq:2-25](#eq:2-25)) we obtain the following result without permuting any particle pair
# $$
# \left( \sum_i \hat{h}_0(x_i) \right) \psi_{\alpha_1}(x_1)\psi_{\alpha_2}(x_2) \dots \psi_{\alpha_n}(x_n) \nonumber
# $$
# $$
# =\sum_{\alpha_1'} \langle \alpha_1'|\hat{h}_0|\alpha_1\rangle
# \psi_{\alpha_1'}(x_1)\psi_{\alpha_2}(x_2) \dots \psi_{\alpha_n}(x_n) \nonumber
# $$
# $$
# +\sum_{\alpha_2'} \langle \alpha_2'|\hat{h}_0|\alpha_2\rangle
# \psi_{\alpha_1}(x_1)\psi_{\alpha_2'}(x_2) \dots \psi_{\alpha_n}(x_n) \nonumber
# $$
# $$
# + \dots \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-26"></div>
#
# $$
# \begin{equation}
# +\sum_{\alpha_n'} \langle \alpha_n'|\hat{h}_0|\alpha_n\rangle
# \psi_{\alpha_1}(x_1)\psi_{\alpha_2}(x_2) \dots \psi_{\alpha_n'}(x_n) \label{eq:2-26} \tag{46}
# \end{equation}
# $$
# If we interchange particles $1$ and $2$ we obtain
# $$
# \left( \sum_i \hat{h}_0(x_i) \right) \psi_{\alpha_1}(x_2)\psi_{\alpha_1}(x_2) \dots \psi_{\alpha_n}(x_n) \nonumber
# $$
# $$
# =\sum_{\alpha_2'} \langle \alpha_2'|\hat{h}_0|\alpha_2\rangle
# \psi_{\alpha_1}(x_2)\psi_{\alpha_2'}(x_1) \dots \psi_{\alpha_n}(x_n) \nonumber
# $$
# $$
# +\sum_{\alpha_1'} \langle \alpha_1'|\hat{h}_0|\alpha_1\rangle
# \psi_{\alpha_1'}(x_2)\psi_{\alpha_2}(x_1) \dots \psi_{\alpha_n}(x_n) \nonumber
# $$
# $$
# + \dots \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-27"></div>
#
# $$
# \begin{equation}
# +\sum_{\alpha_n'} \langle \alpha_n'|\hat{h}_0|\alpha_n\rangle
# \psi_{\alpha_1}(x_2)\psi_{\alpha_1}(x_2) \dots \psi_{\alpha_n'}(x_n) \label{eq:2-27} \tag{47}
# \end{equation}
# $$
# We can continue by computing all possible permutations.
# We rewrite also our Slater determinant in its second quantized form and skip the dependence on the quantum numbers $x_i.$
# Summing up all contributions and taking care of all phases
# $(-1)^p$ we arrive at
# $$
# \hat{H}_0|\alpha_1,\alpha_2,\dots, \alpha_n\rangle = \sum_{\alpha_1'}\langle \alpha_1'|\hat{h}_0|\alpha_1\rangle
# |\alpha_1'\alpha_2 \dots \alpha_{n}\rangle \nonumber
# $$
# $$
# + \sum_{\alpha_2'} \langle \alpha_2'|\hat{h}_0|\alpha_2\rangle
# |\alpha_1\alpha_2' \dots \alpha_{n}\rangle \nonumber
# $$
# $$
# + \dots \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-28"></div>
#
# $$
# \begin{equation}
# + \sum_{\alpha_n'} \langle \alpha_n'|\hat{h}_0|\alpha_n\rangle
# |\alpha_1\alpha_2 \dots \alpha_{n}'\rangle \label{eq:2-28} \tag{48}
# \end{equation}
# $$
# In Eq. ([eq:2-28](#eq:2-28))
# we have expressed the action of the one-body operator
# of Eq. ([eq:2-23](#eq:2-23)) on the $n$-body state in its second quantized form.
# This equation can be further manipulated if we use the properties of the creation and annihilation operator
# on each primed quantum number, that is
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-29"></div>
#
# $$
# \begin{equation}
# |\alpha_1\alpha_2 \dots \alpha_k' \dots \alpha_{n}\rangle =
# a_{\alpha_k'}^{\dagger} a_{\alpha_k} |\alpha_1\alpha_2 \dots \alpha_k \dots \alpha_{n}\rangle \label{eq:2-29} \tag{49}
# \end{equation}
# $$
# Inserting this in the right-hand side of Eq. ([eq:2-28](#eq:2-28)) results in
# $$
# \hat{H}_0|\alpha_1\alpha_2 \dots \alpha_{n}\rangle = \sum_{\alpha_1'}\langle \alpha_1'|\hat{h}_0|\alpha_1\rangle
# a_{\alpha_1'}^{\dagger} a_{\alpha_1} |\alpha_1\alpha_2 \dots \alpha_{n}\rangle \nonumber
# $$
# $$
# + \sum_{\alpha_2'} \langle \alpha_2'|\hat{h}_0|\alpha_2\rangle
# a_{\alpha_2'}^{\dagger} a_{\alpha_2} |\alpha_1\alpha_2 \dots \alpha_{n}\rangle \nonumber
# $$
# $$
# + \dots \nonumber
# $$
# $$
# + \sum_{\alpha_n'} \langle \alpha_n'|\hat{h}_0|\alpha_n\rangle
# a_{\alpha_n'}^{\dagger} a_{\alpha_n} |\alpha_1\alpha_2 \dots \alpha_{n}\rangle \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-30a"></div>
#
# $$
# \begin{equation}
# = \sum_{\alpha, \beta} \langle \alpha|\hat{h}_0|\beta\rangle a_\alpha^{\dagger} a_\beta
# |\alpha_1\alpha_2 \dots \alpha_{n}\rangle \label{eq:2-30a} \tag{50}
# \end{equation}
# $$
# In the number occupation representation or second quantization we get the following expression for a one-body
# operator which conserves the number of particles
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-30b"></div>
#
# $$
# \begin{equation}
# \hat{H}_0 = \sum_{\alpha\beta} \langle \alpha|\hat{h}_0|\beta\rangle a_\alpha^{\dagger} a_\beta \label{eq:2-30b} \tag{51}
# \end{equation}
# $$
# Obviously, $\hat{H}_0$ can be replaced by any other one-body operator which preserved the number
# of particles. The stucture of the operator is therefore not limited to say the kinetic or single-particle energy only.
#
# The opearator $\hat{H}_0$ takes a particle from the single-particle state $\beta$ to the single-particle state $\alpha$
# with a probability for the transition given by the expectation value $\langle \alpha|\hat{h}_0|\beta\rangle$.
#
#
#
#
#
# It is instructive to verify Eq. ([eq:2-30b](#eq:2-30b)) by computing the expectation value of $\hat{H}_0$
# between two single-particle states
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-30c"></div>
#
# $$
# \begin{equation}
# \langle \alpha_1|\hat{h}_0|\alpha_2\rangle = \sum_{\alpha\beta} \langle \alpha|\hat{h}_0|\beta\rangle
# \langle 0|a_{\alpha_1}a_\alpha^{\dagger} a_\beta a_{\alpha_2}^{\dagger}|0\rangle \label{eq:2-30c} \tag{52}
# \end{equation}
# $$
# Using the commutation relations for the creation and annihilation operators we have
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-30d"></div>
#
# $$
# \begin{equation}
# a_{\alpha_1}a_\alpha^{\dagger} a_\beta a_{\alpha_2}^{\dagger} = (\delta_{\alpha \alpha_1} - a_\alpha^{\dagger} a_{\alpha_1} )(\delta_{\beta \alpha_2} - a_{\alpha_2}^{\dagger} a_{\beta} ), \label{eq:2-30d} \tag{53}
# \end{equation}
# $$
# which results in
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-30e"></div>
#
# $$
# \begin{equation}
# \langle 0|a_{\alpha_1}a_\alpha^{\dagger} a_\beta a_{\alpha_2}^{\dagger}|0\rangle = \delta_{\alpha \alpha_1} \delta_{\beta \alpha_2} \label{eq:2-30e} \tag{54}
# \end{equation}
# $$
# and
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-30f"></div>
#
# $$
# \begin{equation}
# \langle \alpha_1|\hat{h}_0|\alpha_2\rangle = \sum_{\alpha\beta} \langle \alpha|\hat{h}_0|\beta\rangle\delta_{\alpha \alpha_1} \delta_{\beta \alpha_2} = \langle \alpha_1|\hat{h}_0|\alpha_2\rangle \label{eq:2-30f} \tag{55}
# \end{equation}
# $$
# # Two-body operators in second quantization
#
# Let us now derive the expression for our two-body interaction part, which also conserves the number of particles.
# We can proceed in exactly the same way as for the one-body operator. In the coordinate representation our
# two-body interaction part takes the following expression
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-31"></div>
#
# $$
# \begin{equation}
# \hat{H}_I = \sum_{i < j} V(x_i,x_j) \label{eq:2-31} \tag{56}
# \end{equation}
# $$
# where the summation runs over distinct pairs. The term $V$ can be an interaction model for the nucleon-nucleon interaction
# or the interaction between two electrons. It can also include additional two-body interaction terms.
#
# The action of this operator on a product of
# two single-particle functions is defined as
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-32"></div>
#
# $$
# \begin{equation}
# V(x_i,x_j) \psi_{\alpha_k}(x_i) \psi_{\alpha_l}(x_j) = \sum_{\alpha_k'\alpha_l'}
# \psi_{\alpha_k}'(x_i)\psi_{\alpha_l}'(x_j)
# \langle \alpha_k'\alpha_l'|\hat{v}|\alpha_k\alpha_l\rangle \label{eq:2-32} \tag{57}
# \end{equation}
# $$
# We can now let $\hat{H}_I$ act on all terms in the linear combination for $|\alpha_1\alpha_2\dots\alpha_n\rangle$. Without any permutations we have
# $$
# \left( \sum_{i < j} V(x_i,x_j) \right) \psi_{\alpha_1}(x_1)\psi_{\alpha_2}(x_2)\dots \psi_{\alpha_n}(x_n) \nonumber
# $$
# $$
# = \sum_{\alpha_1'\alpha_2'} \langle \alpha_1'\alpha_2'|\hat{v}|\alpha_1\alpha_2\rangle
# \psi_{\alpha_1}'(x_1)\psi_{\alpha_2}'(x_2)\dots \psi_{\alpha_n}(x_n) \nonumber
# $$
# $$
# + \dots \nonumber
# $$
# $$
# + \sum_{\alpha_1'\alpha_n'} \langle \alpha_1'\alpha_n'|\hat{v}|\alpha_1\alpha_n\rangle
# \psi_{\alpha_1}'(x_1)\psi_{\alpha_2}(x_2)\dots \psi_{\alpha_n}'(x_n) \nonumber
# $$
# $$
# + \dots \nonumber
# $$
# $$
# + \sum_{\alpha_2'\alpha_n'} \langle \alpha_2'\alpha_n'|\hat{v}|\alpha_2\alpha_n\rangle
# \psi_{\alpha_1}(x_1)\psi_{\alpha_2}'(x_2)\dots \psi_{\alpha_n}'(x_n) \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-33"></div>
#
# $$
# \begin{equation}
# + \dots \label{eq:2-33} \tag{58}
# \end{equation}
# $$
# where on the rhs we have a term for each distinct pairs.
#
#
#
#
# For the other terms on the rhs we obtain similar expressions and summing over all terms we obtain
# $$
# H_I |\alpha_1\alpha_2\dots\alpha_n\rangle = \sum_{\alpha_1', \alpha_2'} \langle \alpha_1'\alpha_2'|\hat{v}|\alpha_1\alpha_2\rangle
# |\alpha_1'\alpha_2'\dots\alpha_n\rangle \nonumber
# $$
# $$
# + \dots \nonumber
# $$
# $$
# + \sum_{\alpha_1', \alpha_n'} \langle \alpha_1'\alpha_n'|\hat{v}|\alpha_1\alpha_n\rangle
# |\alpha_1'\alpha_2\dots\alpha_n'\rangle \nonumber
# $$
# $$
# + \dots \nonumber
# $$
# $$
# + \sum_{\alpha_2', \alpha_n'} \langle \alpha_2'\alpha_n'|\hat{v}|\alpha_2\alpha_n\rangle
# |\alpha_1\alpha_2'\dots\alpha_n'\rangle \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-34"></div>
#
# $$
# \begin{equation}
# + \dots \label{eq:2-34} \tag{59}
# \end{equation}
# $$
# We introduce second quantization via the relation
# $$
# a_{\alpha_k'}^{\dagger} a_{\alpha_l'}^{\dagger} a_{\alpha_l} a_{\alpha_k}
# |\alpha_1\alpha_2\dots\alpha_k\dots\alpha_l\dots\alpha_n\rangle \nonumber
# $$
# $$
# = (-1)^{k-1} (-1)^{l-2} a_{\alpha_k'}^{\dagger} a_{\alpha_l'}^{\dagger} a_{\alpha_l} a_{\alpha_k}
# |\alpha_k\alpha_l \underbrace{\alpha_1\alpha_2\dots\alpha_n}_{\neq \alpha_k,\alpha_l}\rangle \nonumber
# $$
# $$
# = (-1)^{k-1} (-1)^{l-2}
# |\alpha_k'\alpha_l' \underbrace{\alpha_1\alpha_2\dots\alpha_n}_{\neq \alpha_k',\alpha_l'}\rangle \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-35"></div>
#
# $$
# \begin{equation}
# = |\alpha_1\alpha_2\dots\alpha_k'\dots\alpha_l'\dots\alpha_n\rangle \label{eq:2-35} \tag{60}
# \end{equation}
# $$
# Inserting this in ([eq:2-34](#eq:2-34)) gives
# $$
# H_I |\alpha_1\alpha_2\dots\alpha_n\rangle
# = \sum_{\alpha_1', \alpha_2'} \langle \alpha_1'\alpha_2'|\hat{v}|\alpha_1\alpha_2\rangle
# a_{\alpha_1'}^{\dagger} a_{\alpha_2'}^{\dagger} a_{\alpha_2} a_{\alpha_1}
# |\alpha_1\alpha_2\dots\alpha_n\rangle \nonumber
# $$
# $$
# + \dots \nonumber
# $$
# $$
# = \sum_{\alpha_1', \alpha_n'} \langle \alpha_1'\alpha_n'|\hat{v}|\alpha_1\alpha_n\rangle
# a_{\alpha_1'}^{\dagger} a_{\alpha_n'}^{\dagger} a_{\alpha_n} a_{\alpha_1}
# |\alpha_1\alpha_2\dots\alpha_n\rangle \nonumber
# $$
# $$
# + \dots \nonumber
# $$
# $$
# = \sum_{\alpha_2', \alpha_n'} \langle \alpha_2'\alpha_n'|\hat{v}|\alpha_2\alpha_n\rangle
# a_{\alpha_2'}^{\dagger} a_{\alpha_n'}^{\dagger} a_{\alpha_n} a_{\alpha_2}
# |\alpha_1\alpha_2\dots\alpha_n\rangle \nonumber
# $$
# $$
# + \dots \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-36"></div>
#
# $$
# \begin{equation}
# = \sum_{\alpha, \beta, \gamma, \delta} ' \langle \alpha\beta|\hat{v}|\gamma\delta\rangle
# a^{\dagger}_\alpha a^{\dagger}_\beta a_\delta a_\gamma
# |\alpha_1\alpha_2\dots\alpha_n\rangle \label{eq:2-36} \tag{61}
# \end{equation}
# $$
# Here we let $\sum'$ indicate that the sums running over $\alpha$ and $\beta$ run over all
# single-particle states, while the summations $\gamma$ and $\delta$
# run over all pairs of single-particle states. We wish to remove this restriction and since
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-37"></div>
#
# $$
# \begin{equation}
# \langle \alpha\beta|\hat{v}|\gamma\delta\rangle = \langle \beta\alpha|\hat{v}|\delta\gamma\rangle \label{eq:2-37} \tag{62}
# \end{equation}
# $$
# we get
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-38a"></div>
#
# $$
# \begin{equation}
# \sum_{\alpha\beta} \langle \alpha\beta|\hat{v}|\gamma\delta\rangle a^{\dagger}_\alpha a^{\dagger}_\beta a_\delta a_\gamma =
# \sum_{\alpha\beta} \langle \beta\alpha|\hat{v}|\delta\gamma\rangle
# a^{\dagger}_\alpha a^{\dagger}_\beta a_\delta a_\gamma \label{eq:2-38a} \tag{63}
# \end{equation}
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-38b"></div>
#
# $$
# \begin{equation}
# = \sum_{\alpha\beta}\langle \beta\alpha|\hat{v}|\delta\gamma\rangle
# a^{\dagger}_\beta a^{\dagger}_\alpha a_\gamma a_\delta \label{eq:2-38b} \tag{64}
# \end{equation}
# $$
# where we have used the anti-commutation rules.
#
#
#
#
# Changing the summation indices
# $\alpha$ and $\beta$ in ([eq:2-38b](#eq:2-38b)) we obtain
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-38c"></div>
#
# $$
# \begin{equation}
# \sum_{\alpha\beta} \langle \alpha\beta|\hat{v}|\gamma\delta\rangle a^{\dagger}_\alpha a^{\dagger}_\beta a_\delta a_\gamma =
# \sum_{\alpha\beta} \langle \alpha\beta|\hat{v}|\delta\gamma\rangle
# a^{\dagger}_\alpha a^{\dagger}_\beta a_\gamma a_\delta \label{eq:2-38c} \tag{65}
# \end{equation}
# $$
# From this it follows that the restriction on the summation over $\gamma$ and $\delta$ can be removed if we multiply with a factor $\frac{1}{2}$, resulting in
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-39"></div>
#
# $$
# \begin{equation}
# \hat{H}_I = \frac{1}{2} \sum_{\alpha\beta\gamma\delta} \langle \alpha\beta|\hat{v}|\gamma\delta\rangle
# a^{\dagger}_\alpha a^{\dagger}_\beta a_\delta a_\gamma \label{eq:2-39} \tag{66}
# \end{equation}
# $$
# where we sum freely over all single-particle states $\alpha$,
# $\beta$, $\gamma$ og $\delta$.
#
#
#
#
#
#
# With this expression we can now verify that the second quantization form of $\hat{H}_I$ in Eq. ([eq:2-39](#eq:2-39))
# results in the same matrix between two anti-symmetrized two-particle states as its corresponding coordinate
# space representation. We have
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-40"></div>
#
# $$
# \begin{equation}
# \langle \alpha_1 \alpha_2|\hat{H}_I|\beta_1 \beta_2\rangle =
# \frac{1}{2} \sum_{\alpha\beta\gamma\delta}
# \langle \alpha\beta|\hat{v}|\gamma\delta\rangle \langle 0|a_{\alpha_2} a_{\alpha_1}
# a^{\dagger}_\alpha a^{\dagger}_\beta a_\delta a_\gamma
# a_{\beta_1}^{\dagger} a_{\beta_2}^{\dagger}|0\rangle. \label{eq:2-40} \tag{67}
# \end{equation}
# $$
# Using the commutation relations we get
# $$
# a_{\alpha_2} a_{\alpha_1}a^{\dagger}_\alpha a^{\dagger}_\beta
# a_\delta a_\gamma a_{\beta_1}^{\dagger} a_{\beta_2}^{\dagger} \nonumber
# $$
# $$
# = a_{\alpha_2} a_{\alpha_1}a^{\dagger}_\alpha a^{\dagger}_\beta
# ( a_\delta \delta_{\gamma \beta_1} a_{\beta_2}^{\dagger} -
# a_\delta a_{\beta_1}^{\dagger} a_\gamma a_{\beta_2}^{\dagger} ) \nonumber
# $$
# $$
# = a_{\alpha_2} a_{\alpha_1}a^{\dagger}_\alpha a^{\dagger}_\beta
# (\delta_{\gamma \beta_1} \delta_{\delta \beta_2} - \delta_{\gamma \beta_1} a_{\beta_2}^{\dagger} a_\delta -
# a_\delta a_{\beta_1}^{\dagger}\delta_{\gamma \beta_2} +
# a_\delta a_{\beta_1}^{\dagger} a_{\beta_2}^{\dagger} a_\gamma ) \nonumber
# $$
# $$
# = a_{\alpha_2} a_{\alpha_1}a^{\dagger}_\alpha a^{\dagger}_\beta
# (\delta_{\gamma \beta_1} \delta_{\delta \beta_2} - \delta_{\gamma \beta_1} a_{\beta_2}^{\dagger} a_\delta \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-41"></div>
#
# $$
# \begin{equation}
# \qquad - \delta_{\delta \beta_1} \delta_{\gamma \beta_2} + \delta_{\gamma \beta_2} a_{\beta_1}^{\dagger} a_\delta
# + a_\delta a_{\beta_1}^{\dagger} a_{\beta_2}^{\dagger} a_\gamma ) \label{eq:2-41} \tag{68}
# \end{equation}
# $$
# The vacuum expectation value of this product of operators becomes
# $$
# \langle 0|a_{\alpha_2} a_{\alpha_1} a^{\dagger}_\alpha a^{\dagger}_\beta a_\delta a_\gamma
# a_{\beta_1}^{\dagger} a_{\beta_2}^{\dagger}|0\rangle \nonumber
# $$
# $$
# = (\delta_{\gamma \beta_1} \delta_{\delta \beta_2} -
# \delta_{\delta \beta_1} \delta_{\gamma \beta_2} )
# \langle 0|a_{\alpha_2} a_{\alpha_1}a^{\dagger}_\alpha a^{\dagger}_\beta|0\rangle \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-42b"></div>
#
# $$
# \begin{equation}
# = (\delta_{\gamma \beta_1} \delta_{\delta \beta_2} -\delta_{\delta \beta_1} \delta_{\gamma \beta_2} )
# (\delta_{\alpha \alpha_1} \delta_{\beta \alpha_2} -\delta_{\beta \alpha_1} \delta_{\alpha \alpha_2} ) \label{eq:2-42b} \tag{69}
# \end{equation}
# $$
# Insertion of
# Eq. ([eq:2-42b](#eq:2-42b)) in Eq. ([eq:2-40](#eq:2-40)) results in
# $$
# \langle \alpha_1\alpha_2|\hat{H}_I|\beta_1\beta_2\rangle = \frac{1}{2} \big[
# \langle \alpha_1\alpha_2|\hat{v}|\beta_1\beta_2\rangle- \langle \alpha_1\alpha_2|\hat{v}|\beta_2\beta_1\rangle \nonumber
# $$
# $$
# - \langle \alpha_2\alpha_1|\hat{v}|\beta_1\beta_2\rangle + \langle \alpha_2\alpha_1|\hat{v}|\beta_2\beta_1\rangle \big] \nonumber
# $$
# $$
# = \langle \alpha_1\alpha_2|\hat{v}|\beta_1\beta_2\rangle - \langle \alpha_1\alpha_2|\hat{v}|\beta_2\beta_1\rangle \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-43b"></div>
#
# $$
# \begin{equation}
# = \langle \alpha_1\alpha_2|\hat{v}|\beta_1\beta_2\rangle_{\mathrm{AS}}. \label{eq:2-43b} \tag{70}
# \end{equation}
# $$
# The two-body operator can also be expressed in terms of the anti-symmetrized matrix elements we discussed previously as
# $$
# \hat{H}_I = \frac{1}{2} \sum_{\alpha\beta\gamma\delta} \langle \alpha \beta|\hat{v}|\gamma \delta\rangle
# a_\alpha^{\dagger} a_\beta^{\dagger} a_\delta a_\gamma \nonumber
# $$
# $$
# = \frac{1}{4} \sum_{\alpha\beta\gamma\delta} \left[ \langle \alpha \beta|\hat{v}|\gamma \delta\rangle -
# \langle \alpha \beta|\hat{v}|\delta\gamma \rangle \right]
# a_\alpha^{\dagger} a_\beta^{\dagger} a_\delta a_\gamma \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-45"></div>
#
# $$
# \begin{equation}
# = \frac{1}{4} \sum_{\alpha\beta\gamma\delta} \langle \alpha \beta|\hat{v}|\gamma \delta\rangle_{\mathrm{AS}}
# a_\alpha^{\dagger} a_\beta^{\dagger} a_\delta a_\gamma \label{eq:2-45} \tag{71}
# \end{equation}
# $$
# The factors in front of the operator, either $\frac{1}{4}$ or
# $\frac{1}{2}$ tells whether we use antisymmetrized matrix elements or not.
#
# We can now express the Hamiltonian operator for a many-fermion system in the occupation basis representation
# as
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-46b"></div>
#
# $$
# \begin{equation}
# H = \sum_{\alpha, \beta} \langle \alpha|\hat{t}+\hat{u}_{\mathrm{ext}}|\beta\rangle a_\alpha^{\dagger} a_\beta + \frac{1}{4} \sum_{\alpha\beta\gamma\delta}
# \langle \alpha \beta|\hat{v}|\gamma \delta\rangle a_\alpha^{\dagger} a_\beta^{\dagger} a_\delta a_\gamma. \label{eq:2-46b} \tag{72}
# \end{equation}
# $$
# This is the form we will use in the rest of these lectures, assuming that we work with anti-symmetrized two-body matrix elements.
#
#
#
#
#
# # Particle-hole formalism
#
# Second quantization is a useful and elegant formalism for constructing many-body states and
# quantum mechanical operators. One can express and translate many physical processes
# into simple pictures such as Feynman diagrams. Expecation values of many-body states are also easily calculated.
# However, although the equations are seemingly easy to set up, from a practical point of view, that is
# the solution of Schroedinger's equation, there is no particular gain.
# The many-body equation is equally hard to solve, irrespective of representation.
# The cliche that
# there is no free lunch brings us down to earth again.
# Note however that a transformation to a particular
# basis, for cases where the interaction obeys specific symmetries, can ease the solution of Schroedinger's equation.
#
# But there is at least one important case where second quantization comes to our rescue.
# It is namely easy to introduce another reference state than the pure vacuum $|0\rangle $, where all single-particle states are active.
# With many particles present it is often useful to introduce another reference state than the vacuum state$|0\rangle $. We will label this state $|c\rangle$ ($c$ for core) and as we will see it can reduce
# considerably the complexity and thereby the dimensionality of the many-body problem. It allows us to sum up to infinite order specific many-body correlations. The particle-hole representation is one of these handy representations.
#
#
#
#
#
# In the original particle representation these states are products of the creation operators $a_{\alpha_i}^\dagger$ acting on the true vacuum $|0\rangle $.
# Following Eq. ([eq:2-2](#eq:2-2)) we have
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-47a"></div>
#
# $$
# \begin{equation}
# |\alpha_1\alpha_2\dots\alpha_{n-1}\alpha_n\rangle = a_{\alpha_1}^\dagger a_{\alpha_2}^\dagger \dots
# a_{\alpha_{n-1}}^\dagger a_{\alpha_n}^\dagger |0\rangle \label{eq:2-47a} \tag{73}
# \end{equation}
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-47b"></div>
#
# $$
# \begin{equation}
# |\alpha_1\alpha_2\dots\alpha_{n-1}\alpha_n\alpha_{n+1}\rangle =
# a_{\alpha_1}^\dagger a_{\alpha_2}^\dagger \dots a_{\alpha_{n-1}}^\dagger a_{\alpha_n}^\dagger
# a_{\alpha_{n+1}}^\dagger |0\rangle \label{eq:2-47b} \tag{74}
# \end{equation}
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-47c"></div>
#
# $$
# \begin{equation}
# |\alpha_1\alpha_2\dots\alpha_{n-1}\rangle = a_{\alpha_1}^\dagger a_{\alpha_2}^\dagger \dots
# a_{\alpha_{n-1}}^\dagger |0\rangle \label{eq:2-47c} \tag{75}
# \end{equation}
# $$
# If we use Eq. ([eq:2-47a](#eq:2-47a)) as our new reference state, we can simplify considerably the representation of
# this state
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-48a"></div>
#
# $$
# \begin{equation}
# |c\rangle \equiv |\alpha_1\alpha_2\dots\alpha_{n-1}\alpha_n\rangle =
# a_{\alpha_1}^\dagger a_{\alpha_2}^\dagger \dots a_{\alpha_{n-1}}^\dagger a_{\alpha_n}^\dagger |0\rangle \label{eq:2-48a} \tag{76}
# \end{equation}
# $$
# The new reference states for the $n+1$ and $n-1$ states can then be written as
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-48b"></div>
#
# $$
# \begin{equation}
# |\alpha_1\alpha_2\dots\alpha_{n-1}\alpha_n\alpha_{n+1}\rangle = (-1)^n a_{\alpha_{n+1}}^\dagger |c\rangle
# \equiv (-1)^n |\alpha_{n+1}\rangle_c \label{eq:2-48b} \tag{77}
# \end{equation}
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-48c"></div>
#
# $$
# \begin{equation}
# |\alpha_1\alpha_2\dots\alpha_{n-1}\rangle = (-1)^{n-1} a_{\alpha_n} |c\rangle
# \equiv (-1)^{n-1} |\alpha_{n-1}\rangle_c \label{eq:2-48c} \tag{78}
# \end{equation}
# $$
# The first state has one additional particle with respect to the new vacuum state
# $|c\rangle $ and is normally referred to as a one-particle state or one particle added to the
# many-body reference state.
# The second state has one particle less than the reference vacuum state $|c\rangle $ and is referred to as
# a one-hole state.
# When dealing with a new reference state it is often convenient to introduce
# new creation and annihilation operators since we have
# from Eq. ([eq:2-48c](#eq:2-48c))
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-49"></div>
#
# $$
# \begin{equation}
# a_\alpha |c\rangle \neq 0 \label{eq:2-49} \tag{79}
# \end{equation}
# $$
# since $\alpha$ is contained in $|c\rangle $, while for the true vacuum we have
# $a_\alpha |0\rangle = 0$ for all $\alpha$.
#
# The new reference state leads to the definition of new creation and annihilation operators
# which satisfy the following relations
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-50a"></div>
#
# $$
# \begin{equation}
# b_\alpha |c\rangle = 0 \label{eq:2-50a} \tag{80}
# \end{equation}
# $$
# $$
# \{b_\alpha^\dagger , b_\beta^\dagger \} = \{b_\alpha , b_\beta \} = 0 \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-50c"></div>
#
# $$
# \begin{equation}
# \{b_\alpha^\dagger , b_\beta \} = \delta_{\alpha \beta} \label{eq:2-50c} \tag{81}
# \end{equation}
# $$
# We assume also that the new reference state is properly normalized
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-51"></div>
#
# $$
# \begin{equation}
# \langle c | c \rangle = 1 \label{eq:2-51} \tag{82}
# \end{equation}
# $$
# The physical interpretation of these new operators is that of so-called quasiparticle states.
# This means that a state defined by the addition of one extra particle to a reference state $|c\rangle $ may not necesseraly be interpreted as one particle coupled to a core.
# We define now new creation operators that act on a state $\alpha$ creating a new quasiparticle state
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-52"></div>
#
# $$
# \begin{equation}
# b_\alpha^\dagger|c\rangle = \Bigg\{ \begin{array}{ll}
# a_\alpha^\dagger |c\rangle = |\alpha\rangle, & \alpha > F \\
# \\
# a_\alpha |c\rangle = |\alpha^{-1}\rangle, & \alpha \leq F
# \end{array} \label{eq:2-52} \tag{83}
# \end{equation}
# $$
# where $F$ is the Fermi level representing the last occupied single-particle orbit
# of the new reference state $|c\rangle $.
#
#
# The annihilation is the hermitian conjugate of the creation operator
# $$
# b_\alpha = (b_\alpha^\dagger)^\dagger,
# $$
# resulting in
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-54"></div>
#
# $$
# \begin{equation}
# b_\alpha^\dagger = \Bigg\{ \begin{array}{ll}
# a_\alpha^\dagger & \alpha > F \\
# \\
# a_\alpha & \alpha \leq F
# \end{array} \qquad
# b_\alpha = \Bigg\{ \begin{array}{ll}
# a_\alpha & \alpha > F \\
# \\
# a_\alpha^\dagger & \alpha \leq F
# \end{array} \label{eq:2-54} \tag{84}
# \end{equation}
# $$
# With the new creation and annihilation operator we can now construct
# many-body quasiparticle states, with one-particle-one-hole states, two-particle-two-hole
# states etc in the same fashion as we previously constructed many-particle states.
# We can write a general particle-hole state as
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-56"></div>
#
# $$
# \begin{equation}
# |\beta_1\beta_2\dots \beta_{n_p} \gamma_1^{-1} \gamma_2^{-1} \dots \gamma_{n_h}^{-1}\rangle \equiv
# \underbrace{b_{\beta_1}^\dagger b_{\beta_2}^\dagger \dots b_{\beta_{n_p}}^\dagger}_{>F}
# \underbrace{b_{\gamma_1}^\dagger b_{\gamma_2}^\dagger \dots b_{\gamma_{n_h}}^\dagger}_{\leq F} |c\rangle \label{eq:2-56} \tag{85}
# \end{equation}
# $$
# We can now rewrite our one-body and two-body operators in terms of the new creation and annihilation operators.
# The number operator becomes
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-57b"></div>
#
# $$
# \begin{equation}
# \hat{N} = \sum_\alpha a_\alpha^\dagger a_\alpha=
# \sum_{\alpha > F} b_\alpha^\dagger b_\alpha + n_c - \sum_{\alpha \leq F} b_\alpha^\dagger b_\alpha \label{eq:2-57b} \tag{86}
# \end{equation}
# $$
# where $n_c$ is the number of particle in the new vacuum state $|c\rangle $.
# The action of $\hat{N}$ on a many-body state results in
# <!-- Equation labels as ordinary links -->
# <div id="2-59"></div>
#
# $$
# \begin{equation}
# N |\beta_1\beta_2\dots \beta_{n_p} \gamma_1^{-1} \gamma_2^{-1} \dots \gamma_{n_h}^{-1}\rangle = (n_p + n_c - n_h) |\beta_1\beta_2\dots \beta_{n_p} \gamma_1^{-1} \gamma_2^{-1} \dots \gamma_{n_h}^{-1}\rangle \label{2-59} \tag{87}
# \end{equation}
# $$
# Here $n=n_p +n_c - n_h$ is the total number of particles in the quasi-particle state of
# Eq. ([eq:2-56](#eq:2-56)). Note that $\hat{N}$ counts the total number of particles present
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-60"></div>
#
# $$
# \begin{equation}
# N_{qp} = \sum_\alpha b_\alpha^\dagger b_\alpha, \label{eq:2-60} \tag{88}
# \end{equation}
# $$
# gives us the number of quasi-particles as can be seen by computing
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-61"></div>
#
# $$
# \begin{equation}
# N_{qp}= |\beta_1\beta_2\dots \beta_{n_p} \gamma_1^{-1} \gamma_2^{-1} \dots \gamma_{n_h}^{-1}\rangle
# = (n_p + n_h)|\beta_1\beta_2\dots \beta_{n_p} \gamma_1^{-1} \gamma_2^{-1} \dots \gamma_{n_h}^{-1}\rangle \label{eq:2-61} \tag{89}
# \end{equation}
# $$
# where $n_{qp} = n_p + n_h$ is the total number of quasi-particles.
#
#
#
#
# We express the one-body operator $\hat{H}_0$ in terms of the quasi-particle creation and annihilation operators, resulting in
# $$
# \hat{H}_0 = \sum_{\alpha\beta > F} \langle \alpha|\hat{h}_0|\beta\rangle b_\alpha^\dagger b_\beta +
# \sum_{\alpha > F, \beta \leq F } \left[\langle \alpha|\hat{h}_0|\beta\rangle b_\alpha^\dagger b_\beta^\dagger + \langle \beta|\hat{h}_0|\alpha\rangle b_\beta b_\alpha \right] \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-63b"></div>
#
# $$
# \begin{equation}
# + \sum_{\alpha \leq F} \langle \alpha|\hat{h}_0|\alpha\rangle - \sum_{\alpha\beta \leq F} \langle \beta|\hat{h}_0|\alpha\rangle b_\alpha^\dagger b_\beta \label{eq:2-63b} \tag{90}
# \end{equation}
# $$
# The first term gives contribution only for particle states, while the last one
# contributes only for holestates. The second term can create or destroy a set of
# quasi-particles and
# the third term is the contribution from the vacuum state $|c\rangle$.
#
#
#
#
#
# Before we continue with the expressions for the two-body operator, we introduce a nomenclature we will use for the rest of this
# text. It is inspired by the notation used in quantum chemistry.
# We reserve the labels $i,j,k,\dots$ for hole states and $a,b,c,\dots$ for states above $F$, viz. particle states.
# This means also that we will skip the constraint $\leq F$ or $> F$ in the summation symbols.
# Our operator $\hat{H}_0$ reads now
# $$
# \hat{H}_0 = \sum_{ab} \langle a|\hat{h}|b\rangle b_a^\dagger b_b +
# \sum_{ai} \left[
# \langle a|\hat{h}|i\rangle b_a^\dagger b_i^\dagger +
# \langle i|\hat{h}|a\rangle b_i b_a \right] \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-63c"></div>
#
# $$
# \begin{equation}
# + \sum_{i} \langle i|\hat{h}|i\rangle -
# \sum_{ij} \langle j|\hat{h}|i\rangle
# b_i^\dagger b_j \label{eq:2-63c} \tag{91}
# \end{equation}
# $$
# The two-particle operator in the particle-hole formalism is more complicated since we have
# to translate four indices $\alpha\beta\gamma\delta$ to the possible combinations of particle and hole
# states. When performing the commutator algebra we can regroup the operator in five different terms
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-65"></div>
#
# $$
# \begin{equation}
# \hat{H}_I = \hat{H}_I^{(a)} + \hat{H}_I^{(b)} + \hat{H}_I^{(c)} + \hat{H}_I^{(d)} + \hat{H}_I^{(e)} \label{eq:2-65} \tag{92}
# \end{equation}
# $$
# Using anti-symmetrized matrix elements,
# bthe term $\hat{H}_I^{(a)}$ is
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-66"></div>
#
# $$
# \begin{equation}
# \hat{H}_I^{(a)} = \frac{1}{4}
# \sum_{abcd} \langle ab|\hat{V}|cd\rangle
# b_a^\dagger b_b^\dagger b_d b_c \label{eq:2-66} \tag{93}
# \end{equation}
# $$
# The next term $\hat{H}_I^{(b)}$ reads
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-67b"></div>
#
# $$
# \begin{equation}
# \hat{H}_I^{(b)} = \frac{1}{4} \sum_{abci}\left(\langle ab|\hat{V}|ci\rangle b_a^\dagger b_b^\dagger b_i^\dagger b_c +\langle ai|\hat{V}|cb\rangle b_a^\dagger b_i b_b b_c\right) \label{eq:2-67b} \tag{94}
# \end{equation}
# $$
# This term conserves the number of quasiparticles but creates or removes a
# three-particle-one-hole state.
# For $\hat{H}_I^{(c)}$ we have
# $$
# \hat{H}_I^{(c)} = \frac{1}{4}
# \sum_{abij}\left(\langle ab|\hat{V}|ij\rangle b_a^\dagger b_b^\dagger b_j^\dagger b_i^\dagger +
# \langle ij|\hat{V}|ab\rangle b_a b_b b_j b_i \right)+ \nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-68c"></div>
#
# $$
# \begin{equation}
# \frac{1}{2}\sum_{abij}\langle ai|\hat{V}|bj\rangle b_a^\dagger b_j^\dagger b_b b_i +
# \frac{1}{2}\sum_{abi}\langle ai|\hat{V}|bi\rangle b_a^\dagger b_b. \label{eq:2-68c} \tag{95}
# \end{equation}
# $$
# The first line stands for the creation of a two-particle-two-hole state, while the second line represents
# the creation to two one-particle-one-hole pairs
# while the last term represents a contribution to the particle single-particle energy
# from the hole states, that is an interaction between the particle states and the hole states
# within the new vacuum state.
# The fourth term reads
# $$
# \hat{H}_I^{(d)} = \frac{1}{4}
# \sum_{aijk}\left(\langle ai|\hat{V}|jk\rangle b_a^\dagger b_k^\dagger b_j^\dagger b_i+
# \langle ji|\hat{V}|ak\rangle b_k^\dagger b_j b_i b_a\right)+\nonumber
# $$
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-69d"></div>
#
# $$
# \begin{equation}
# \frac{1}{4}\sum_{aij}\left(\langle ai|\hat{V}|ji\rangle b_a^\dagger b_j^\dagger+
# \langle ji|\hat{V}|ai\rangle - \langle ji|\hat{V}|ia\rangle b_j b_a \right). \label{eq:2-69d} \tag{96}
# \end{equation}
# $$
# The terms in the first line stand for the creation of a particle-hole state
# interacting with hole states, we will label this as a two-hole-one-particle contribution.
# The remaining terms are a particle-hole state interacting with the holes in the vacuum state.
# Finally we have
# <!-- Equation labels as ordinary links -->
# <div id="eq:2-70d"></div>
#
# $$
# \begin{equation}
# \hat{H}_I^{(e)} = \frac{1}{4}
# \sum_{ijkl}
# \langle kl|\hat{V}|ij\rangle b_i^\dagger b_j^\dagger b_l b_k+
# \frac{1}{2}\sum_{ijk}\langle ij|\hat{V}|kj\rangle b_k^\dagger b_i
# +\frac{1}{2}\sum_{ij}\langle ij|\hat{V}|ij\rangle \label{eq:2-70d} \tag{97}
# \end{equation}
# $$
# The first terms represents the
# interaction between two holes while the second stands for the interaction between a hole and the remaining holes in the vacuum state.
# It represents a contribution to single-hole energy to first order.
# The last term collects all contributions to the energy of the ground state of a closed-shell system arising
# from hole-hole correlations.
#
#
#
#
# # Summarizing and defining a normal-ordered Hamiltonian
# $$
# \Phi_{AS}(\alpha_1, \dots, \alpha_A; x_1, \dots x_A)=
# \frac{1}{\sqrt{A}} \sum_{\hat{P}} (-1)^P \hat{P} \prod_{i=1}^A \psi_{\alpha_i}(x_i),
# $$
# which is equivalent with $|\alpha_1 \dots \alpha_A\rangle= a_{\alpha_1}^{\dagger} \dots a_{\alpha_A}^{\dagger} |0\rangle$. We have also
# 2
# 0
# 3
#
# <
# <
# <
# !
# !
# M
# A
# T
# H
# _
# B
# L
# O
# C
# K
# $$
# \delta_{pq} = \left\{a_p, a_q^\dagger \right\},
# $$
# and
# 2
# 0
# 5
#
# <
# <
# <
# !
# !
# M
# A
# T
# H
# _
# B
# L
# O
# C
# K
# $$
# |\Phi_0\rangle = |\alpha_1 \dots \alpha_A\rangle, \quad \alpha_1, \dots, \alpha_A \leq \alpha_F
# $$
# 2
# 0
# 7
#
# <
# <
# <
# !
# !
# M
# A
# T
# H
# _
# B
# L
# O
# C
# K
# $$
# \left\{a_p, a_q^\dagger \right\} = \delta_{pq}, p, q > \alpha_F
# $$
# with $i,j,\ldots \leq \alpha_F, \quad a,b,\ldots > \alpha_F, \quad p,q, \ldots - \textrm{any}$
# $$
# a_i|\Phi_0\rangle = |\Phi_i\rangle, \hspace{0.5cm} a_a^\dagger|\Phi_0\rangle = |\Phi^a\rangle
# $$
# and
# $$
# a_i^\dagger|\Phi_0\rangle = 0 \hspace{0.5cm} a_a|\Phi_0\rangle = 0
# $$
# The one-body operator is defined as
# $$
# \hat{F} = \sum_{pq} \langle p|\hat{f}|q\rangle a_p^\dagger a_q
# $$
# while the two-body opreator is defined as
# $$
# \hat{V} = \frac{1}{4} \sum_{pqrs} \langle pq|\hat{v}|rs\rangle_{AS} a_p^\dagger a_q^\dagger a_s a_r
# $$
# where we have defined the antisymmetric matrix elements
# $$
# \langle pq|\hat{v}|rs\rangle_{AS} = \langle pq|\hat{v}|rs\rangle - \langle pq|\hat{v}|sr\rangle.
# $$
# We can also define a three-body operator
# $$
# \hat{V}_3 = \frac{1}{36} \sum_{pqrstu} \langle pqr|\hat{v}_3|stu\rangle_{AS}
# a_p^\dagger a_q^\dagger a_r^\dagger a_u a_t a_s
# $$
# with the antisymmetrized matrix element
# <!-- Equation labels as ordinary links -->
# <div id="_auto3"></div>
#
# $$
# \begin{equation}
# \langle pqr|\hat{v}_3|stu\rangle_{AS} = \langle pqr|\hat{v}_3|stu\rangle + \langle pqr|\hat{v}_3|tus\rangle + \langle pqr|\hat{v}_3|ust\rangle- \langle pqr|\hat{v}_3|sut\rangle - \langle pqr|\hat{v}_3|tsu\rangle - \langle pqr|\hat{v}_3|uts\rangle.
# \label{_auto3} \tag{98}
# \end{equation}
# $$
# # Hartree-Fock in second quantization and stability of HF solution
#
# We wish now to derive the Hartree-Fock equations using our second-quantized formalism and study the stability of the equations.
# Our ansatz for the ground state of the system is approximated as (this is our representation of a Slater determinant in second quantization)
# $$
# |\Phi_0\rangle = |c\rangle = a^{\dagger}_i a^{\dagger}_j \dots a^{\dagger}_l|0\rangle.
# $$
# We wish to determine $\hat{u}^{HF}$ so that
# $E_0^{HF}= \langle c|\hat{H}| c\rangle$ becomes a local minimum.
#
# In our analysis here we will need Thouless' theorem, which states that
# an arbitrary Slater determinant $|c'\rangle$ which is not orthogonal to a determinant
# $| c\rangle ={\displaystyle\prod_{i=1}^{n}}
# a_{\alpha_{i}}^{\dagger}|0\rangle$, can be written as
# $$
# |c'\rangle=exp\left\{\sum_{a>F}\sum_{i\le F}C_{ai}a_{a}^{\dagger}a_{i}\right\}| c\rangle
# $$
# Let us give a simple proof of Thouless' theorem. The theorem states that we can make a linear combination av particle-hole excitations with respect to a given reference state $\vert c\rangle$. With this linear combination, we can make a new Slater determinant $\vert c'\rangle $ which is not orthogonal to
# $\vert c\rangle$, that is
# $$
# \langle c|c'\rangle \ne 0.
# $$
# To show this we need some intermediate steps. The exponential product of two operators $\exp{\hat{A}}\times\exp{\hat{B}}$ is equal to $\exp{(\hat{A}+\hat{B})}$ only if the two operators commute, that is
# $$
# [\hat{A},\hat{B}] = 0.
# $$
# ## Thouless' theorem
#
#
# If the operators do not commute, we need to resort to the [Baker-Campbell-Hauersdorf](http://www.encyclopediaofmath.org/index.php/Campbell%E2%80%93Hausdorff_formula). This relation states that
# $$
# \exp{\hat{C}}=\exp{\hat{A}}\exp{\hat{B}},
# $$
# with
# $$
# \hat{C}=\hat{A}+\hat{B}+\frac{1}{2}[\hat{A},\hat{B}]+\frac{1}{12}[[\hat{A},\hat{B}],\hat{B}]-\frac{1}{12}[[\hat{A},\hat{B}],\hat{A}]+\dots
# $$
# From these relations, we note that
# in our expression for $|c'\rangle$ we have commutators of the type
# $$
# [a_{a}^{\dagger}a_{i},a_{b}^{\dagger}a_{j}],
# $$
# and it is easy to convince oneself that these commutators, or higher powers thereof, are all zero. This means that we can write out our new representation of a Slater determinant as
# $$
# |c'\rangle=exp\left\{\sum_{a>F}\sum_{i\le F}C_{ai}a_{a}^{\dagger}a_{i}\right\}| c\rangle=\prod_{i}\left\{1+\sum_{a>F}C_{ai}a_{a}^{\dagger}a_{i}+\left(\sum_{a>F}C_{ai}a_{a}^{\dagger}a_{i}\right)^2+\dots\right\}| c\rangle
# $$
# We note that
# $$
# \prod_{i}\sum_{a>F}C_{ai}a_{a}^{\dagger}a_{i}\sum_{b>F}C_{bi}a_{b}^{\dagger}a_{i}| c\rangle =0,
# $$
# and all higher-order powers of these combinations of creation and annihilation operators disappear
# due to the fact that $(a_i)^n| c\rangle =0$ when $n > 1$. This allows us to rewrite the expression for $|c'\rangle $ as
# $$
# |c'\rangle=\prod_{i}\left\{1+\sum_{a>F}C_{ai}a_{a}^{\dagger}a_{i}\right\}| c\rangle,
# $$
# which we can rewrite as
# $$
# |c'\rangle=\prod_{i}\left\{1+\sum_{a>F}C_{ai}a_{a}^{\dagger}a_{i}\right\}| a^{\dagger}_{i_1} a^{\dagger}_{i_2} \dots a^{\dagger}_{i_n}|0\rangle.
# $$
# The last equation can be written as
# <!-- Equation labels as ordinary links -->
# <div id="_auto4"></div>
#
# $$
# \begin{equation}
# |c'\rangle=\prod_{i}\left\{1+\sum_{a>F}C_{ai}a_{a}^{\dagger}a_{i}\right\}| a^{\dagger}_{i_1} a^{\dagger}_{i_2} \dots a^{\dagger}_{i_n}|0\rangle=\left(1+\sum_{a>F}C_{ai_1}a_{a}^{\dagger}a_{i_1}\right)a^{\dagger}_{i_1}
# \label{_auto4} \tag{99}
# \end{equation}
# $$
# <!-- Equation labels as ordinary links -->
# <div id="_auto5"></div>
#
# $$
# \begin{equation}
# \times\left(1+\sum_{a>F}C_{ai_2}a_{a}^{\dagger}a_{i_2}\right)a^{\dagger}_{i_2} \dots |0\rangle=\prod_{i}\left(a^{\dagger}_{i}+\sum_{a>F}C_{ai}a_{a}^{\dagger}\right)|0\rangle.
# \label{_auto5} \tag{100}
# \end{equation}
# $$
# ## New operators
#
#
# If we define a new creation operator
# <!-- Equation labels as ordinary links -->
# <div id="eq:newb"></div>
#
# $$
# \begin{equation}
# b^{\dagger}_{i}=a^{\dagger}_{i}+\sum_{a>F}C_{ai}a_{a}^{\dagger}, \label{eq:newb} \tag{101}
# \end{equation}
# $$
# we have
# $$
# |c'\rangle=\prod_{i}b^{\dagger}_{i}|0\rangle=\prod_{i}\left(a^{\dagger}_{i}+\sum_{a>F}C_{ai}a_{a}^{\dagger}\right)|0\rangle,
# $$
# meaning that the new representation of the Slater determinant in second quantization, $|c'\rangle$, looks like our previous ones. However, this representation is not general enough since we have a restriction on the sum over single-particle states in Eq. ([eq:newb](#eq:newb)). The single-particle states have all to be above the Fermi level.
# The question then is whether we can construct a general representation of a Slater determinant with a creation operator
# $$
# \tilde{b}^{\dagger}_{i}=\sum_{p}f_{ip}a_{p}^{\dagger},
# $$
# where $f_{ip}$ is a matrix element of a unitary matrix which transforms our creation and annihilation operators
# $a^{\dagger}$ and $a$ to $\tilde{b}^{\dagger}$ and $\tilde{b}$. These new operators define a new representation of a Slater determinant as
# $$
# |\tilde{c}\rangle=\prod_{i}\tilde{b}^{\dagger}_{i}|0\rangle.
# $$
# ## Showing that $|\tilde{c}\rangle= |c'\rangle$
#
#
#
# We need to show that $|\tilde{c}\rangle= |c'\rangle$. We need also to assume that the new state
# is not orthogonal to $|c\rangle$, that is $\langle c| \tilde{c}\rangle \ne 0$. From this it follows that
# $$
# \langle c| \tilde{c}\rangle=\langle 0| a_{i_n}\dots a_{i_1}\left(\sum_{p=i_1}^{i_n}f_{i_1p}a_{p}^{\dagger} \right)\left(\sum_{q=i_1}^{i_n}f_{i_2q}a_{q}^{\dagger} \right)\dots \left(\sum_{t=i_1}^{i_n}f_{i_nt}a_{t}^{\dagger} \right)|0\rangle,
# $$
# which is nothing but the determinant $det(f_{ip})$ which we can, using the intermediate normalization condition,
# normalize to one, that is
# $$
# det(f_{ip})=1,
# $$
# meaning that $f$ has an inverse defined as (since we are dealing with orthogonal, and in our case unitary as well, transformations)
# $$
# \sum_{k} f_{ik}f^{-1}_{kj} = \delta_{ij},
# $$
# and
# $$
# \sum_{j} f^{-1}_{ij}f_{jk} = \delta_{ik}.
# $$
# Using these relations we can then define the linear combination of creation (and annihilation as well)
# operators as
# $$
# \sum_{i}f^{-1}_{ki}\tilde{b}^{\dagger}_{i}=\sum_{i}f^{-1}_{ki}\sum_{p=i_1}^{\infty}f_{ip}a_{p}^{\dagger}=a_{k}^{\dagger}+\sum_{i}\sum_{p=i_{n+1}}^{\infty}f^{-1}_{ki}f_{ip}a_{p}^{\dagger}.
# $$
# Defining
# $$
# c_{kp}=\sum_{i \le F}f^{-1}_{ki}f_{ip},
# $$
# we can redefine
# $$
# a_{k}^{\dagger}+\sum_{i}\sum_{p=i_{n+1}}^{\infty}f^{-1}_{ki}f_{ip}a_{p}^{\dagger}=a_{k}^{\dagger}+\sum_{p=i_{n+1}}^{\infty}c_{kp}a_{p}^{\dagger}=b_k^{\dagger},
# $$
# our starting point. We have shown that our general representation of a Slater determinant
# $$
# |\tilde{c}\rangle=\prod_{i}\tilde{b}^{\dagger}_{i}|0\rangle=|c'\rangle=\prod_{i}b^{\dagger}_{i}|0\rangle,
# $$
# with
# $$
# b_k^{\dagger}=a_{k}^{\dagger}+\sum_{p=i_{n+1}}^{\infty}c_{kp}a_{p}^{\dagger}.
# $$
# This means that we can actually write an ansatz for the ground state of the system as a linear combination of
# terms which contain the ansatz itself $|c\rangle$ with an admixture from an infinity of one-particle-one-hole states. The latter has important consequences when we wish to interpret the Hartree-Fock equations and their stability. We can rewrite the new representation as
# $$
# |c'\rangle = |c\rangle+|\delta c\rangle,
# $$
# where $|\delta c\rangle$ can now be interpreted as a small variation. If we approximate this term with
# contributions from one-particle-one-hole (*1p-1h*) states only, we arrive at
# $$
# |c'\rangle = \left(1+\sum_{ai}\delta C_{ai}a_{a}^{\dagger}a_i\right)|c\rangle.
# $$
# In our derivation of the Hartree-Fock equations we have shown that
# $$
# \langle \delta c| \hat{H} | c\rangle =0,
# $$
# which means that we have to satisfy
# $$
# \langle c|\sum_{ai}\delta C_{ai}\left\{a_{a}^{\dagger}a_i\right\} \hat{H} | c\rangle =0.
# $$
# With this as a background, we are now ready to study the stability of the Hartree-Fock equations.
#
#
#
# ## Hartree-Fock in second quantization and stability of HF solution
#
# The variational condition for deriving the Hartree-Fock equations guarantees only that the expectation value $\langle c | \hat{H} | c \rangle$ has an extreme value, not necessarily a minimum. To figure out whether the extreme value we have found is a minimum, we can use second quantization to analyze our results and find a criterion
# for the above expectation value to a local minimum. We will use Thouless' theorem and show that
# $$
# \frac{\langle c' |\hat{H} | c'\rangle}{\langle c' |c'\rangle} \ge \langle c |\hat{H} | c\rangle= E_0,
# $$
# with
# $$
# {|c'\rangle} = {|c\rangle + |\delta c\rangle}.
# $$
# Using Thouless' theorem we can write out $|c'\rangle$ as
# <!-- Equation labels as ordinary links -->
# <div id="_auto6"></div>
#
# $$
# \begin{equation}
# {|c'\rangle}=\exp\left\{\sum_{a > F}\sum_{i \le F}\delta C_{ai}a_{a}^{\dagger}a_{i}\right\}| c\rangle
# \label{_auto6} \tag{102}
# \end{equation}
# $$
# <!-- Equation labels as ordinary links -->
# <div id="_auto7"></div>
#
# $$
# \begin{equation}
# =\left\{1+\sum_{a > F}\sum_{i \le F}\delta C_{ai}a_{a}^{\dagger}
# a_{i}+\frac{1}{2!}\sum_{ab > F}\sum_{ij \le F}\delta C_{ai}\delta C_{bj}a_{a}^{\dagger}a_{i}a_{b}^{\dagger}a_{j}+\dots\right\}
# \label{_auto7} \tag{103}
# \end{equation}
# $$
# where the amplitudes $\delta C$ are small.
#
#
# The norm of $|c'\rangle$ is given by (using the intermediate normalization condition $\langle c' |c\rangle=1$)
# $$
# \langle c' | c'\rangle = 1+\sum_{a>F}
# \sum_{i\le F}|\delta C_{ai}|^2+O(\delta C_{ai}^3).
# $$
# The expectation value for the energy is now given by (using the Hartree-Fock condition)
# 2
# 5
# 1
#
# <
# <
# <
# !
# !
# M
# A
# T
# H
# _
# B
# L
# O
# C
# K
# $$
# \frac{1}{2!}\sum_{ab>F}
# \sum_{ij\le F}\delta C_{ai}\delta C_{bj}\langle c |\hat{H}a_{a}^{\dagger}a_{i}a_{b}^{\dagger}a_{j}|c\rangle+\frac{1}{2!}\sum_{ab>F}
# \sum_{ij\le F}\delta C_{ai}^*\delta C_{bj}^*\langle c|a_{j}^{\dagger}a_{b}a_{i}^{\dagger}a_{a}\hat{H}|c\rangle
# +\dots
# $$
# We have already calculated the second term on the right-hand side of the previous equation
# <!-- Equation labels as ordinary links -->
# <div id="_auto8"></div>
#
# $$
# \begin{equation}
# \langle c | \left(\{a^\dagger_i a_a\} \hat{H} \{a^\dagger_b a_j\} \right) | c\rangle=\sum_{pq} \sum_{ijab}\delta C_{ai}^*\delta C_{bj} \langle p|\hat{h}_0 |q\rangle
# \langle c | \left(\{a^{\dagger}_i a_a\}\{a^{\dagger}_pa_q\}
# \{a^{\dagger}_b a_j\} \right)| c\rangle
# \label{_auto8} \tag{104}
# \end{equation}
# $$
# <!-- Equation labels as ordinary links -->
# <div id="_auto9"></div>
#
# $$
# \begin{equation}
# +\frac{1}{4} \sum_{pqrs} \sum_{ijab}\delta C_{ai}^*\delta C_{bj} \langle pq| \hat{v}|rs\rangle
# \langle c | \left(\{a^\dagger_i a_a\}\{a^{\dagger}_p a^{\dagger}_q a_s a_r\} \{a^{\dagger}_b a_j\} \right)| c\rangle ,
# \label{_auto9} \tag{105}
# \end{equation}
# $$
# resulting in
# $$
# E_0\sum_{ai}|\delta C_{ai}|^2+\sum_{ai}|\delta C_{ai}|^2(\varepsilon_a-\varepsilon_i)-\sum_{ijab} \langle aj|\hat{v}| bi\rangle \delta C_{ai}^*\delta C_{bj}.
# $$
# $$
# \frac{1}{2!}\langle c |\left(\{a^\dagger_j a_b\} \{a^\dagger_i a_a\} \hat{V}_N \right) | c\rangle =
# \frac{1}{2!}\langle c |\left( \hat{V}_N \{a^\dagger_a a_i\} \{a^\dagger_b a_j\} \right)^{\dagger} | c\rangle
# $$
# which is nothing but
# $$
# \frac{1}{2!}\langle c | \left( \hat{V}_N \{a^\dagger_a a_i\} \{a^\dagger_b a_j\} \right) | c\rangle^*
# =\frac{1}{2} \sum_{ijab} (\langle ij|\hat{v}|ab\rangle)^*\delta C_{ai}^*\delta C_{bj}^*
# $$
# or
# $$
# \frac{1}{2} \sum_{ijab} (\langle ab|\hat{v}|ij\rangle)\delta C_{ai}^*\delta C_{bj}^*
# $$
# where we have used the relation
# $$
# \langle a |\hat{A} | b\rangle = (\langle b |\hat{A}^{\dagger} | a\rangle)^*
# $$
# due to the hermiticity of $\hat{H}$ and $\hat{V}$.
#
#
# We define two matrix elements
# $$
# A_{ai,bj}=-\langle aj|\hat{v} bi\rangle
# $$
# and
# $$
# B_{ai,bj}=\langle ab|\hat{v}|ij\rangle
# $$
# both being anti-symmetrized.
#
#
#
# With these definitions we write out the energy as
# <!-- Equation labels as ordinary links -->
# <div id="_auto10"></div>
#
# $$
# \begin{equation}
# \langle c'|H|c'\rangle = \left(1+\sum_{ai}|\delta C_{ai}|^2\right)\langle c |H|c\rangle+\sum_{ai}|\delta C_{ai}|^2(\varepsilon_a^{HF}-\varepsilon_i^{HF})+\sum_{ijab}A_{ai,bj}\delta C_{ai}^*\delta C_{bj}+
# \label{_auto10} \tag{106}
# \end{equation}
# $$
# <!-- Equation labels as ordinary links -->
# <div id="_auto11"></div>
#
# $$
# \begin{equation}
# \frac{1}{2} \sum_{ijab} B_{ai,bj}^*\delta C_{ai}\delta C_{bj}+\frac{1}{2} \sum_{ijab} B_{ai,bj}\delta C_{ai}^*\delta C_{bj}^*
# +O(\delta C_{ai}^3),
# \label{_auto11} \tag{107}
# \end{equation}
# $$
# which can be rewritten as
# $$
# \langle c'|H|c'\rangle = \left(1+\sum_{ai}|\delta C_{ai}|^2\right)\langle c |H|c\rangle+\Delta E+O(\delta C_{ai}^3),
# $$
# and skipping higher-order terms we arrived
# $$
# \frac{\langle c' |\hat{H} | c'\rangle}{\langle c' |c'\rangle} =E_0+\frac{\Delta E}{\left(1+\sum_{ai}|\delta C_{ai}|^2\right)}.
# $$
# We have defined
# $$
# \Delta E = \frac{1}{2} \langle \chi | \hat{M}| \chi \rangle
# $$
# with the vectors
# $$
# \chi = \left[ \delta C\hspace{0.2cm} \delta C^*\right]^T
# $$
# and the matrix
# $$
# \hat{M}=\left(\begin{array}{cc} \Delta + A & B \\ B^* & \Delta + A^*\end{array}\right),
# $$
# with $\Delta_{ai,bj} = (\varepsilon_a-\varepsilon_i)\delta_{ab}\delta_{ij}$.
#
#
#
# The condition
# $$
# \Delta E = \frac{1}{2} \langle \chi | \hat{M}| \chi \rangle \ge 0
# $$
# for an arbitrary vector
# $$
# \chi = \left[ \delta C\hspace{0.2cm} \delta C^*\right]^T
# $$
# means that all eigenvalues of the matrix have to be larger than or equal zero.
# A necessary (but no sufficient) condition is that the matrix elements (for all $ai$ )
# $$
# (\varepsilon_a-\varepsilon_i)\delta_{ab}\delta_{ij}+A_{ai,bj} \ge 0.
# $$
# This equation can be used as a first test of the stability of the Hartree-Fock equation.
#
#
#
#
#
#
#
# # Operators in second quantization
#
# In the build-up of a shell-model or FCI code that is meant to tackle large dimensionalities
# is the action of the Hamiltonian $\hat{H}$ on a
# Slater determinant represented in second quantization as
# $$
# |\alpha_1\dots \alpha_n\rangle = a_{\alpha_1}^{\dagger} a_{\alpha_2}^{\dagger} \dots a_{\alpha_n}^{\dagger} |0\rangle.
# $$
# The time consuming part stems from the action of the Hamiltonian
# on the above determinant,
# $$
# \left(\sum_{\alpha\beta} \langle \alpha|t+u|\beta\rangle a_\alpha^{\dagger} a_\beta + \frac{1}{4} \sum_{\alpha\beta\gamma\delta}
# \langle \alpha \beta|\hat{v}|\gamma \delta\rangle a_\alpha^{\dagger} a_\beta^{\dagger} a_\delta a_\gamma\right)a_{\alpha_1}^{\dagger} a_{\alpha_2}^{\dagger} \dots a_{\alpha_n}^{\dagger} |0\rangle.
# $$
# A practically useful way to implement this action is to encode a Slater determinant as a bit pattern.
#
#
#
# Assume that we have at our disposal $n$ different single-particle orbits
# $\alpha_0,\alpha_2,\dots,\alpha_{n-1}$ and that we can distribute among these orbits $N\le n$ particles.
#
# A Slater determinant can then be coded as an integer of $n$ bits. As an example, if we have $n=16$ single-particle states
# $\alpha_0,\alpha_1,\dots,\alpha_{15}$ and $N=4$ fermions occupying the states $\alpha_3$, $\alpha_6$, $\alpha_{10}$ and $\alpha_{13}$
# we could write this Slater determinant as
# $$
# \Phi_{\Lambda} = a_{\alpha_3}^{\dagger} a_{\alpha_6}^{\dagger} a_{\alpha_{10}}^{\dagger} a_{\alpha_{13}}^{\dagger} |0\rangle.
# $$
# The unoccupied single-particle states have bit value $0$ while the occupied ones are represented by bit state $1$.
# In the binary notation we would write this 16 bits long integer as
# $$
# \begin{array}{cccccccccccccccc}
# {\alpha_0}&{\alpha_1}&{\alpha_2}&{\alpha_3}&{\alpha_4}&{\alpha_5}&{\alpha_6}&{\alpha_7} & {\alpha_8} &{\alpha_9} & {\alpha_{10}} &{\alpha_{11}} &{\alpha_{12}} &{\alpha_{13}} &{\alpha_{14}} & {\alpha_{15}} \\
# {0} & {0} &{0} &{1} &{0} &{0} &{1} &{0} &{0} &{0} &{1} &{0} &{0} &{1} &{0} & {0} \\
# \end{array}
# $$
# which translates into the decimal number
# $$
# 2^3+2^6+2^{10}+2^{13}=9288.
# $$
# We can thus encode a Slater determinant as a bit pattern.
#
#
#
# With $N$ particles that can be distributed over $n$ single-particle states, the total number of Slater determinats (and defining thereby the dimensionality of the system) is
# $$
# \mathrm{dim}(\mathcal{H}) = \left(\begin{array}{c} n \\N\end{array}\right).
# $$
# The total number of bit patterns is $2^n$.
#
#
# We assume again that we have at our disposal $n$ different single-particle orbits
# $\alpha_0,\alpha_2,\dots,\alpha_{n-1}$ and that we can distribute among these orbits $N\le n$ particles.
# The ordering among these states is important as it defines the order of the creation operators.
# We will write the determinant
# $$
# \Phi_{\Lambda} = a_{\alpha_3}^{\dagger} a_{\alpha_6}^{\dagger} a_{\alpha_{10}}^{\dagger} a_{\alpha_{13}}^{\dagger} |0\rangle,
# $$
# in a more compact way as
# $$
# \Phi_{3,6,10,13} = |0001001000100100\rangle.
# $$
# The action of a creation operator is thus
# $$
# a^{\dagger}_{\alpha_4}\Phi_{3,6,10,13} = a^{\dagger}_{\alpha_4}|0001001000100100\rangle=a^{\dagger}_{\alpha_4}a_{\alpha_3}^{\dagger} a_{\alpha_6}^{\dagger} a_{\alpha_{10}}^{\dagger} a_{\alpha_{13}}^{\dagger} |0\rangle,
# $$
# which becomes
# $$
# -a_{\alpha_3}^{\dagger} a^{\dagger}_{\alpha_4} a_{\alpha_6}^{\dagger} a_{\alpha_{10}}^{\dagger} a_{\alpha_{13}}^{\dagger} |0\rangle=-|0001101000100100\rangle.
# $$
# Similarly
# $$
# a^{\dagger}_{\alpha_6}\Phi_{3,6,10,13} = a^{\dagger}_{\alpha_6}|0001001000100100\rangle=a^{\dagger}_{\alpha_6}a_{\alpha_3}^{\dagger} a_{\alpha_6}^{\dagger} a_{\alpha_{10}}^{\dagger} a_{\alpha_{13}}^{\dagger} |0\rangle,
# $$
# which becomes
# $$
# -a^{\dagger}_{\alpha_4} (a_{\alpha_6}^{\dagger})^ 2 a_{\alpha_{10}}^{\dagger} a_{\alpha_{13}}^{\dagger} |0\rangle=0!
# $$
# This gives a simple recipe:
# * If one of the bits $b_j$ is $1$ and we act with a creation operator on this bit, we return a null vector
#
# * If $b_j=0$, we set it to $1$ and return a sign factor $(-1)^l$, where $l$ is the number of bits set before bit $j$.
#
# Consider the action of $a^{\dagger}_{\alpha_2}$ on various slater determinants:
# $$
# \begin{array}{ccc}
# a^{\dagger}_{\alpha_2}\Phi_{00111}& = a^{\dagger}_{\alpha_2}|00111\rangle&=0\times |00111\rangle\\
# a^{\dagger}_{\alpha_2}\Phi_{01011}& = a^{\dagger}_{\alpha_2}|01011\rangle&=(-1)\times |01111\rangle\\
# a^{\dagger}_{\alpha_2}\Phi_{01101}& = a^{\dagger}_{\alpha_2}|01101\rangle&=0\times |01101\rangle\\
# a^{\dagger}_{\alpha_2}\Phi_{01110}& = a^{\dagger}_{\alpha_2}|01110\rangle&=0\times |01110\rangle\\
# a^{\dagger}_{\alpha_2}\Phi_{10011}& = a^{\dagger}_{\alpha_2}|10011\rangle&=(-1)\times |10111\rangle\\
# a^{\dagger}_{\alpha_2}\Phi_{10101}& = a^{\dagger}_{\alpha_2}|10101\rangle&=0\times |10101\rangle\\
# a^{\dagger}_{\alpha_2}\Phi_{10110}& = a^{\dagger}_{\alpha_2}|10110\rangle&=0\times |10110\rangle\\
# a^{\dagger}_{\alpha_2}\Phi_{11001}& = a^{\dagger}_{\alpha_2}|11001\rangle&=(+1)\times |11101\rangle\\
# a^{\dagger}_{\alpha_2}\Phi_{11010}& = a^{\dagger}_{\alpha_2}|11010\rangle&=(+1)\times |11110\rangle\\
# \end{array}
# $$
# What is the simplest way to obtain the phase when we act with one annihilation(creation) operator
# on the given Slater determinant representation?
#
#
#
#
# We have an SD representation
# $$
# \Phi_{\Lambda} = a_{\alpha_0}^{\dagger} a_{\alpha_3}^{\dagger} a_{\alpha_6}^{\dagger} a_{\alpha_{10}}^{\dagger} a_{\alpha_{13}}^{\dagger} |0\rangle,
# $$
# in a more compact way as
# $$
# \Phi_{0,3,6,10,13} = |1001001000100100\rangle.
# $$
# The action of
# $$
# a^{\dagger}_{\alpha_4}a_{\alpha_0}\Phi_{0,3,6,10,13} = a^{\dagger}_{\alpha_4}|0001001000100100\rangle=a^{\dagger}_{\alpha_4}a_{\alpha_3}^{\dagger} a_{\alpha_6}^{\dagger} a_{\alpha_{10}}^{\dagger} a_{\alpha_{13}}^{\dagger} |0\rangle,
# $$
# which becomes
# $$
# -a_{\alpha_3}^{\dagger} a^{\dagger}_{\alpha_4} a_{\alpha_6}^{\dagger} a_{\alpha_{10}}^{\dagger} a_{\alpha_{13}}^{\dagger} |0\rangle=-|0001101000100100\rangle.
# $$
# The action
# $$
# a_{\alpha_0}\Phi_{0,3,6,10,13} = |0001001000100100\rangle,
# $$
# can be obtained by subtracting the logical sum (AND operation) of $\Phi_{0,3,6,10,13}$ and
# a word which represents only $\alpha_0$, that is
# $$
# |1000000000000000\rangle,
# $$
# from $\Phi_{0,3,6,10,13}= |1001001000100100\rangle$.
#
# This operation gives $|0001001000100100\rangle$.
#
# Similarly, we can form $a^{\dagger}_{\alpha_4}a_{\alpha_0}\Phi_{0,3,6,10,13}$, say, by adding
# $|0000100000000000\rangle$ to $a_{\alpha_0}\Phi_{0,3,6,10,13}$, first checking that their logical sum
# is zero in order to make sure that orbital $\alpha_4$ is not already occupied.
#
#
#
#
#
#
#
# It is trickier however to get the phase $(-1)^l$.
# One possibility is as follows
# * Let $S_1$ be a word that represents the $1-$bit to be removed and all others set to zero.
#
# In the previous example $S_1=|1000000000000000\rangle$
# * Define $S_2$ as the similar word that represents the bit to be added, that is in our case
#
# $S_2=|0000100000000000\rangle$.
# * Compute then $S=S_1-S_2$, which here becomes
# $$
# S=|0111000000000000\rangle
# $$
# * Perform then the logical AND operation of $S$ with the word containing
# $$
# \Phi_{0,3,6,10,13} = |1001001000100100\rangle,
# $$
# which results in $|0001000000000000\rangle$. Counting the number of $1-$bits gives the phase. Here you need however an algorithm for bitcounting. Several efficient ones available.
#
#
#
#
#
#
#
# <!-- --- begin exercise --- -->
#
# ## Exercise 1: Relation between basis functions
#
# This exercise serves to convince you about the relation between
# two different single-particle bases, where one could be our new Hartree-Fock basis and the other a harmonic oscillator basis.
#
# Consider a Slater determinant built up of single-particle orbitals $\psi_{\lambda}$,
# with $\lambda = 1,2,\dots,A$. The unitary transformation
# $$
# \psi_a = \sum_{\lambda} C_{a\lambda}\phi_{\lambda},
# $$
# brings us into the new basis.
# The new basis has quantum numbers $a=1,2,\dots,A$.
# Show that the new basis is orthonormal.
# Show that the new Slater determinant constructed from the new single-particle wave functions can be
# written as the determinant based on the previous basis and the determinant of the matrix $C$.
# Show that the old and the new Slater determinants are equal up to a complex constant with absolute value unity.
# (Hint, $C$ is a unitary matrix).
#
# Starting with the second quantization representation of the Slater determinant
# $$
# \Phi_{0}=\prod_{i=1}^{n}a_{\alpha_{i}}^{\dagger}|0\rangle,
# $$
# use Wick's theorem to compute the normalization integral
# $\langle\Phi_{0}|\Phi_{0}\rangle$.
#
# <!-- --- end exercise --- -->
#
#
#
#
# <!-- --- begin exercise --- -->
#
# ## Exercise 2: Matrix elements
#
# Calculate the matrix elements
# $$
# \langle \alpha_{1}\alpha_{2}|\hat{F}|\alpha_{1}\alpha_{2}\rangle
# $$
# and
# $$
# \langle \alpha_{1}\alpha_{2}|\hat{G}|\alpha_{1}\alpha_{2}\rangle
# $$
# with
# 2
# 9
# 7
#
# <
# <
# <
# !
# !
# M
# A
# T
# H
# _
# B
# L
# O
# C
# K
# 2
# 9
# 8
#
# <
# <
# <
# !
# !
# M
# A
# T
# H
# _
# B
# L
# O
# C
# K
# 2
# 9
# 9
#
# <
# <
# <
# !
# !
# M
# A
# T
# H
# _
# B
# L
# O
# C
# K
# $$
# \hat{G} = \frac{1}{2}\sum_{\alpha\beta\gamma\delta}
# \langle \alpha\beta |\hat{g}|\gamma\delta\rangle
# a_{\alpha}^{\dagger}a_{\beta}^{\dagger}a_{\delta}a_{\gamma} ,
# $$
# and
# $$
# \langle \alpha\beta |\hat{g}|\gamma\delta\rangle=
# \int\int \psi_{\alpha}^{*}(x_{1})\psi_{\beta}^{*}(x_{2})g(x_{1},
# x_{2})\psi_{\gamma}(x_{1})\psi_{\delta}(x_{2})dx_{1}dx_{2}
# $$
# Compare these results with those from exercise 3c).
#
# <!-- --- end exercise --- -->
#
#
#
#
# <!-- --- begin exercise --- -->
#
# ## Exercise 3: Normal-ordered one-body operator
#
# Show that the onebody part of the Hamiltonian
# $$
# \hat{H}_0 = \sum_{pq} \langle p|\hat{h}_0|q\rangle a^{\dagger}_p a_q,
# $$
# can be written, using standard annihilation and creation operators, in normal-ordered form as
# $$
# \hat{H}_0 = \sum_{pq} \langle p|\hat{h}_0|q\rangle \left\{a^\dagger_p a_q\right\} +
# \sum_i \langle i|\hat{h}_0|i\rangle.
# $$
# Explain the meaning of the various symbols. Which reference
# vacuum has been used?
#
# <!-- --- end exercise --- -->
#
#
#
#
# <!-- --- begin exercise --- -->
#
# ## Exercise 4: Normal-ordered two-body operator
#
# Show that the twobody part of the Hamiltonian
# $$
# \hat{H}_I = \frac{1}{4} \sum_{pqrs} \langle pq|\hat{v}|rs\rangle a^\dagger_p a^\dagger_q a_s a_r,
# $$
# can be written, using standard annihilation and creation operators, in normal-ordered form as
# $$
# \hat{H}_I =\frac{1}{4} \sum_{pqrs} \langle pq|\hat{v}|rs\rangle \left\{a^\dagger_p a^\dagger_q a_s a_r\right\}
# + \sum_{pqi} \langle pi|\hat{v}|qi\rangle \left\{a^\dagger_p a_q\right\}
# + \frac{1}{2} \sum_{ij}\langle ij|\hat{v}|ij\rangle.
# $$
# Explain again the meaning of the various symbols.
#
# This exercise is optional: Derive the normal-ordered form of the threebody part of the Hamiltonian.
# $$
# \hat{H}_3 = \frac{1}{36} \sum_{\substack{pqr \\ stu}}
# \langle pqr|\hat{v}_3|stu\rangle a^\dagger_p a^\dagger_q a^\dagger_r a_u a_t a_s,
# $$
# and specify the contributions to the twobody, onebody and the scalar part.
#
# <!-- --- end exercise --- -->
#
#
#
#
# <!-- --- begin exercise --- -->
#
# ## Exercise 5: Matrix elements using the Slater-Condon rule
#
# The aim of this exercise is to set up specific matrix elements that will turn useful when we start our discussions of the nuclear shell model. In particular you will notice, depending on the character of the operator, that many matrix elements will actually be zero.
#
# Consider three $N$-particle Slater determinants $|\Phi_0$, $|\Phi_i^a\rangle$ and $|\Phi_{ij}^{ab}\rangle$, where the notation means that
# Slater determinant $|\Phi_i^a\rangle$ differs from $|\Phi_0\rangle$ by one single-particle state, that is a single-particle
# state $\psi_i$ is replaced by a single-particle state $\psi_a$.
# It is often interpreted as a so-called one-particle-one-hole excitation.
# Similarly, the Slater determinant $|\Phi_{ij}^{ab}\rangle$
# differs by two single-particle states from $|\Phi_0\rangle$ and is normally thought of as a two-particle-two-hole excitation.
# We assume also that $|\Phi_0\rangle$ represents our new vacuum reference state
# and the labels $ijk\dots$ represent single-particle states below the Fermi level and $abc\dots$ represent states above the Fermi level, so-called particle states.
# We define thereafter a general onebody normal-ordered (with respect to the new vacuum state) operator
# as
# $$
# \hat{F}_N=\sum_{pq}\langle p |f |\beta\rangle \left\{a_{p}^{\dagger}a_{q}\right\} ,
# $$
# with
# $$
# \langle p |f| q\rangle=\int \psi_{p}^{*}(x)f(x)\psi_{q}(x)dx ,
# $$
# and a general normal-ordered two-body operator
# $$
# \hat{G}_N = \frac{1}{4}\sum_{pqrs}
# \langle pq |g| rs\rangle_{AS} \left\{a_{p}^{\dagger}a_{q}^{\dagger}a_{s}a_{r}\right\} ,
# $$
# with for example the direct matrix element given as
# $$
# \langle pq |g| rs\rangle=
# \int\int \psi_{p}^{*}(x_{1})\psi_{q}^{*}(x_{2})g(x_{1}, x_{2})\psi_{r}(x_{1})\psi_{s}(x_{2})dx_{1}dx_{2}
# $$
# with $g$ being invariant under the interchange of the coordinates of two particles.
# The single-particle states $\psi_i$ are not necessarily eigenstates of $\hat{f}$. The curly brackets mean that the operators are normal-ordered with respect to the new vacuum reference state.
#
# How would you write the above Slater determinants in a second quantization formalism, utilizing the fact that we have defined a new reference state?
#
# Use thereafter Wick's theorem to find the expectation values of
# $$
# \langle \Phi_0 \vert\hat{F}_N\vert\Phi_0\rangle,
# $$
# and
# $$
# \langle \Phi_0\hat{G}_N|\Phi_0\rangle.
# $$
# Find thereafter
# $$
# \langle \Phi_0 |\hat{F}_N|\Phi_i^a\rangle,
# $$
# and
# $$
# \langle \Phi_0|\hat{G}_N|\Phi_i^a\rangle,
# $$
# Finally, find
# $$
# \langle \Phi_0 |\hat{F}_N|\Phi_{ij}^{ab}\rangle,
# $$
# and
# $$
# \langle \Phi_0|\hat{G}_N|\Phi_{ij}^{ab}\rangle.
# $$
# What happens with the two-body operator if we have a transition probability of the type
# $$
# \langle \Phi_0|\hat{G}_N|\Phi_{ijk}^{abc}\rangle,
# $$
# where the Slater determinant to the right of the operator differs by more than two single-particle states?
#
# <!-- --- end exercise --- -->
#
#
#
#
# <!-- --- begin exercise --- -->
#
# ## Exercise 6: Program to set up Slater determinants
#
# Write a program which sets up all possible Slater determinants given $N=4$ eletrons which can occupy
# the atomic single-particle states defined by the $1s$, $2s2p$ and $3s3p3d$ shells. How many single-particle
# states $n$ are there in total? Include the spin degrees of freedom as well.
#
# <!-- --- end exercise --- -->
#
#
#
#
# <!-- --- begin exercise --- -->
#
# ## Exercise 7: Using sympy to compute matrix elements
#
# Compute the matrix element
# $$
# \langle\alpha_{1}\alpha_{2}\alpha_{3}|\hat{G}|\alpha_{1}'\alpha_{2}'\alpha_{3}'\rangle,
# $$
# using Wick's theorem and express the two-body operator
# $G$ in the occupation number (second quantization)
# representation.
#
# <!-- --- end exercise --- -->
#
#
#
#
# <!-- --- begin exercise --- -->
#
# ## Exercise 8: Using sympy to compute matrix elements
#
# The last exercise can be solved using the symbolic Python package called *SymPy*. SymPy is a Python
# package for general purpose symbolic algebra. There is a physics module with several interesting submodules.
# Among these, the submodule called *secondquant*, contains several functionalities that allow us to test
# our algebraic manipulations using Wick's theorem and operators for second quantization.
# +
from sympy import *
from sympy.physics.secondquant import *
i, j = symbols('i,j', below_fermi=True)
a, b = symbols('a,b', above_fermi=True)
p, q = symbols('p,q')
print simplify(wicks(Fd(i)*F(a)*Fd(p)*F(q)*Fd(b)*F(j), keep_only_fully_contracted=True))
# -
# The code defines single-particle states above and below the Fermi level, in addition to the genereal symbols
# $pq$ which can refer to any type of state below or above the Fermi level. Wick's theorem is implemented between
# the creation and annihilation operators *Fd* and *F*, respectively. Using the simplify option, one can lump together several Kronecker-$\delta$ functions.
#
# <!-- --- end exercise --- -->
#
#
#
#
# <!-- --- begin exercise --- -->
#
# ## Exercise 9: Using sympy to compute matrix elements
#
# We can expand the above Python code by defining one-body and two-body operators using the following SymPy code
# +
# This code sets up a two-body Hamiltonian for fermions
from sympy import symbols, latex, WildFunction, collect, Rational
from sympy.physics.secondquant import F, Fd, wicks, AntiSymmetricTensor, substitute_dummies, NO
# setup hamiltonian
p,q,r,s = symbols('p q r s',dummy=True)
f = AntiSymmetricTensor('f',(p,),(q,))
pr = NO((Fd(p)*F(q)))
v = AntiSymmetricTensor('v',(p,q),(r,s))
pqsr = NO(Fd(p)*Fd(q)*F(s)*F(r))
Hamiltonian=f*pr + Rational(1)/Rational(4)*v*pqsr
print "Hamiltonian defined as:", latex(Hamiltonian)
# -
# Here we have used the *AntiSymmetricTensor* functionality, together with normal-ordering defined by the *NO* function.
# Using the *latex* option, this program produces the following output
# $$
# f^{p}_{q} \left\{a^\dagger_{p} a_{q}\right\} - \frac{1}{4} v^{qp}_{sr} \left\{a^\dagger_{p} a^\dagger_{q} a_{r} a_{s}\right\}
# $$
# <!-- --- end exercise --- -->
#
#
#
#
# <!-- --- begin exercise --- -->
#
# ## Exercise 10: Using sympy to compute matrix elements
#
# We can now use this code to compute the matrix elements between two two-body Slater determinants using Wick's theorem.
# +
from sympy import symbols, latex, WildFunction, collect, Rational, simplify
from sympy.physics.secondquant import F, Fd, wicks, AntiSymmetricTensor, substitute_dummies, NO, evaluate_deltas
# setup hamiltonian
p,q,r,s = symbols('p q r s',dummy=True)
f = AntiSymmetricTensor('f',(p,),(q,))
pr = NO((Fd(p)*F(q)))
v = AntiSymmetricTensor('v',(p,q),(r,s))
pqsr = NO(Fd(p)*Fd(q)*F(s)*F(r))
Hamiltonian=f*pr + Rational(1)/Rational(4)*v*pqsr
c,d = symbols('c, d',above_fermi=True)
a,b = symbols('a, b',above_fermi=True)
expression = wicks(F(b)*F(a)*Hamiltonian*Fd(c)*Fd(d),keep_only_fully_contracted=True, simplify_kronecker_deltas=True)
expression = evaluate_deltas(expression)
expression = simplify(expression)
print "Hamiltonian defined as:", latex(expression)
# -
# The result is as expected,
# $$
# \delta_{a c} f^{b}_{d} - \delta_{a d} f^{b}_{c} - \delta_{b c} f^{a}_{d} + \delta_{b d} f^{a}_{c} + v^{ab}_{cd}.
# $$
# <!-- --- end exercise --- -->
#
#
#
#
# <!-- --- begin exercise --- -->
#
# ## Exercise 11: Using sympy to compute matrix elements
#
# We can continue along these lines and define a normal-ordered Hamiltonian with respect to a given reference state.
# In our first step we just define the Hamiltonian
from sympy import symbols, latex, WildFunction, collect, Rational, simplify
from sympy.physics.secondquant import F, Fd, wicks, AntiSymmetricTensor, substitute_dummies, NO, evaluate_deltas
# setup hamiltonian
p,q,r,s = symbols('p q r s',dummy=True)
f = AntiSymmetricTensor('f',(p,),(q,))
pr = Fd(p)*F(q)
v = AntiSymmetricTensor('v',(p,q),(r,s))
pqsr = Fd(p)*Fd(q)*F(s)*F(r)
#define the Hamiltonian
Hamiltonian = f*pr + Rational(1)/Rational(4)*v*pqsr
#define indices for states above and below the Fermi level
index_rule = {
'below': 'kl',
'above': 'cd',
'general': 'pqrs'
}
Hnormal = substitute_dummies(Hamiltonian,new_indices=True, pretty_indices=index_rule)
print "Hamiltonian defined as:", latex(Hnormal)
# which results in
# $$
# f^{q}_{p} a^\dagger_{q} a_{p} + \frac{1}{4} v^{sr}_{qp} a^\dagger_{s} a^\dagger_{r} a_{p} a_{q}
# $$
# <!-- --- end exercise --- -->
#
#
#
#
# <!-- --- begin exercise --- -->
#
# ## Exercise 12: Using sympy to compute matrix elements
#
# In our next step we define the reference energy $E_0$ and redefine the Hamiltonian by subtracting the reference energy and collecting the coefficients for all normal-ordered products (given by the *NO* function).
from sympy import symbols, latex, WildFunction, collect, Rational, simplify
from sympy.physics.secondquant import F, Fd, wicks, AntiSymmetricTensor, substitute_dummies, NO, evaluate_deltas
# setup hamiltonian
p,q,r,s = symbols('p q r s',dummy=True)
f = AntiSymmetricTensor('f',(p,),(q,))
pr = Fd(p)*F(q)
v = AntiSymmetricTensor('v',(p,q),(r,s))
pqsr = Fd(p)*Fd(q)*F(s)*F(r)
#define the Hamiltonian
Hamiltonian=f*pr + Rational(1)/Rational(4)*v*pqsr
#define indices for states above and below the Fermi level
index_rule = {
'below': 'kl',
'above': 'cd',
'general': 'pqrs'
}
Hnormal = substitute_dummies(Hamiltonian,new_indices=True, pretty_indices=index_rule)
E0 = wicks(Hnormal,keep_only_fully_contracted=True)
Hnormal = Hnormal-E0
w = WildFunction('w')
Hnormal = collect(Hnormal, NO(w))
Hnormal = evaluate_deltas(Hnormal)
print latex(Hnormal)
# which gives us
# $$
# - f^{i}_{i} + f^{q}_{p} a^\dagger_{q} a_{p} - \frac{1}{4} v^{ii}_{ii} - \frac{1}{4} v^{ii}_{ii} + \frac{1}{4} v^{sr}_{qp} a^\dagger_{r} a^\dagger_{s} a_{q} a_{p},
# $$
# again as expected, with the reference energy to be subtracted.
#
# <!-- --- end exercise --- -->
#
#
#
#
# <!-- --- begin exercise --- -->
#
# ## Exercise 13: Using sympy to compute matrix elements
#
# We can now go back to exercise 7 and define the Hamiltonian and the second-quantized representation of a three-body Slater determinant.
# +
from sympy import symbols, latex, WildFunction, collect, Rational, simplify
from sympy.physics.secondquant import F, Fd, wicks, AntiSymmetricTensor, substitute_dummies, NO, evaluate_deltas
# setup hamiltonian
p,q,r,s = symbols('p q r s',dummy=True)
v = AntiSymmetricTensor('v',(p,q),(r,s))
pqsr = NO(Fd(p)*Fd(q)*F(s)*F(r))
Hamiltonian=Rational(1)/Rational(4)*v*pqsr
a,b,c,d,e,f = symbols('a,b, c, d, e, f',above_fermi=True)
expression = wicks(F(c)*F(b)*F(a)*Hamiltonian*Fd(d)*Fd(e)*Fd(f),keep_only_fully_contracted=True, simplify_kronecker_deltas=True)
expression = evaluate_deltas(expression)
expression = simplify(expression)
print latex(expression)
# -
# resulting in nine terms (as expected),
# $$
# - \delta_{a d} v^{cb}_{ef} - \delta_{a e} v^{cb}_{fd} + \delta_{a f} v^{cb}_{ed} - \delta_{b d} v^{ac}_{ef} - \delta_{b e} v^{ac}_{fd} + \delta_{b f} v^{ac}_{ed} + \delta_{c d} v^{ab}_{ef} + \delta_{c e} v^{ab}_{fd} - \delta_{c f} v^{ab}_{ed}
# $$
# <!-- --- end exercise --- -->
#
#
#
#
# <!-- --- begin exercise --- -->
#
# ## Exercise 14: Diagrammatic representation of Hartree-Fock equations
#
# What is the diagrammatic representation of the HF equation?
# $$
# -\langle\alpha_{k}|u^{HF}|\alpha_{i}\rangle+\sum_{j=1}^{n}
# \left[\langle\alpha_{k}\alpha_{j}|\hat{v}|\alpha_{i}\alpha_{j}\rangle-
# \langle\alpha_{k}\alpha_{j}|v|\alpha_{j}\alpha_{i}\rangle\right]=0
# $$
# (Represent $(-u^{HF})$ by the symbol $---$X .)
#
# <!-- --- end exercise --- -->
#
#
#
#
# <!-- --- begin exercise --- -->
#
# ## Exercise 15: Derivation of Hartree-Fock equations
#
# Consider the ground state $|\Phi\rangle$
# of a bound many-particle system of fermions. Assume that we remove one particle
# from the single-particle state $\lambda$ and that our system ends in a new state
# $|\Phi_{n}\rangle$.
# Define the energy needed to remove this particle as
# $$
# E_{\lambda}=\sum_{n}\vert\langle\Phi_{n}|a_{\lambda}|\Phi\rangle\vert^{2}(E_{0}-E_{n}),
# $$
# where $E_{0}$ and $E_{n}$ are the ground state energies of the states
# $|\Phi\rangle$ and $|\Phi_{n}\rangle$, respectively.
# * Show that
# $$
# E_{\lambda}=\langle\Phi|a_{\lambda}^{\dagger}\left[
# a_{\lambda},H \right]|\Phi\rangle,
# $$
# where $H$ is the Hamiltonian of this system.
# * If we assume that $\Phi$ is the Hartree-Fock result, find the
#
# relation between $E_{\lambda}$ and the single-particle energy
# $\varepsilon_{\lambda}$
# for states $\lambda \leq F$ and $\lambda >F$, with
# $$
# \varepsilon_{\lambda}=\langle\lambda|\hat{t}+\hat{u}|\lambda\rangle,
# $$
# and
# $$
# \langle\lambda|\hat{u}|\lambda\rangle=\sum_{\beta \leq F}
# \langle\lambda\beta|\hat{v}|\lambda\beta\rangle.
# $$
# We have assumed an antisymmetrized matrix element here.
# Discuss the result.
#
# The Hamiltonian operator is defined as
# $$
# H=\sum_{\alpha\beta}\langle\alpha|\hat{t}|\beta\rangle a_{\alpha}^{\dagger}a_{\beta}+
# \frac{1}{2}\sum_{\alpha\beta\gamma\delta}\langle\alpha\beta|\hat{v}|\gamma\delta\rangle a_{\alpha}^{\dagger}a_{\beta}^{\dagger}a_{\delta}a_{\gamma}.
# $$
# <!-- --- end exercise --- -->
|
doc/pub/secondquant/ipynb/secondquant.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Tabular data preprocessing
# + hide_input=true
from fastai.gen_doc.nbdoc import *
from fastai.tabular import *
# -
# ## Overview
# This package contains the basic class to define a transformation for preprocessing dataframes of tabular data, as well as basic [`TabularTransform`](/tabular.transform.html#TabularTransform). Preprocessing includes things like
# - replacing non-numerical variables by categories, then their ids,
# - filling missing values,
# - normalizing continuous variables.
#
# In all those steps we have to be careful to use the correspondance we decide on our training set (which id we give to each category, what is the value we put for missing data, or how the mean/std we use to normalize) on our validation or test set. To deal with this, we use a speciall class called [`TabularTransform`](/tabular.transform.html#TabularTransform).
#
# The data used in this document page is a subset of the [adult dataset](https://archive.ics.uci.edu/ml/datasets/adult). It gives a certain amount of data on individuals to train a model to predict wether their salary is greater than \$50k or not.
path = untar_data(URLs.ADULT_SAMPLE)
df = pd.read_csv(path/'adult.csv')
train_df, valid_df = df.iloc[:800].copy(), df.iloc[800:1000].copy()
train_df.head()
# We see it contains numerical variables (like `age` or `education-num`) as well as categorical ones (like `workclass` or `relationship`). The original dataset is clean, but we removed a few values to give examples of dealing with missing variables.
cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race', 'sex', 'native-country']
cont_names = ['age', 'fnlwgt', 'education-num', 'capital-gain', 'capital-loss', 'hours-per-week']
# ## Transforms for tabular data
# + hide_input=true
show_doc(TabularProc)
# -
# Base class for creating transforms for dataframes with categorical variables `cat_names` and continuous variables `cont_names`. Note that any column not in one of those lists won't be touched.
# + hide_input=true
show_doc(TabularProc.__call__)
# + hide_input=true
show_doc(TabularProc.apply_train)
# + hide_input=true
show_doc(TabularProc.apply_test)
# + hide_input=true
jekyll_important("Those two functions must be implemented in a subclass. `apply_test` defaults to `apply_train`.")
# -
# The following [`TabularTransform`](/tabular.transform.html#TabularTransform) are implemented in the fastai library. Note that the replacement from categories to codes as well as the normalization of continuous variables are automatically done in a [`TabularDataset`](/tabular.data.html#TabularDataset).
# + hide_input=true
show_doc(Categorify)
# -
# Variables in `cont_names` aren't affected.
# + hide_input=true
show_doc(Categorify.apply_train)
# + hide_input=true
show_doc(Categorify.apply_test)
# -
tfm = Categorify(cat_names, cont_names)
tfm(train_df)
tfm(valid_df, test=True)
# Since we haven't changed the categories by their codes, nothing visible has changed in the dataframe yet, but we can check that the variables are now categorical and view their corresponding codes.
train_df['workclass'].cat.categories
# The test set will be given the same category codes as the training set.
valid_df['workclass'].cat.categories
# + hide_input=true
show_doc(FillMissing)
# -
# `cat_names` variables are left untouched (their missing value will be repalced by code 0 in the [`TabularDataset`](/tabular.data.html#TabularDataset)). [`fill_strategy`](#FillStrategy) is adopted to replace those nans and if `add_col` is True, whenever a column `c` has missing values, a column named `c_nan` is added and flags the line where the value was missing.
# + hide_input=true
show_doc(FillMissing.apply_train)
# + hide_input=true
show_doc(FillMissing.apply_test)
# -
# Fills the missing values in the `cont_names` columns with the ones picked during train.
train_df[cont_names].head()
tfm = FillMissing(cat_names, cont_names)
tfm(train_df)
tfm(valid_df, test=True)
train_df[cont_names].head()
# Values issing in the `education-num` column are replaced by 10, which is the median of the column in `train_df`. Categorical variables are not changed, since `nan` is simply used as another category.
valid_df[cont_names].head()
# + hide_input=true
show_doc(FillStrategy, alt_doc_string='Enum flag represents determines how `FillMissing` should handle missing/nan values', arg_comments={
'MEDIAN':'nans are replaced by the median value of the column',
'COMMON': 'nans are replaced by the most common value of the column',
'CONSTANT': 'nans are replaced by `fill_val`'
})
# + hide_input=true
show_doc(Normalize)
# + hide_input=true
show_doc(Normalize.apply_train)
# + hide_input=true
show_doc(Normalize.apply_test)
# -
# ## Treating date columns
# + hide_input=true
show_doc(add_datepart)
# -
# Will `drop` the column in `df` if the flag is `True`. The `time` flag decides if we go down to the time parts or stick to the date parts.
# ## Undocumented Methods - Methods moved below this line will intentionally be hidden
# ## New Methods - Please document or move to the undocumented section
# + hide_input=false
show_doc(add_datepart)
# -
#
|
docs_src/tabular.transform.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # QCoDeS Example with Tektronix Keithley 2450 Source Meter
#
# In this example we will setup a number of [four-wire measurements](https://en.wikipedia.org/wiki/Four-terminal_sensing) with the 2540 source meter. We attach a variable resistor to the front terminals and determine if we can measure the correct resistance.
import qcodes as qc
from qcodes.instrument_drivers.tektronix.Keithley_2450 import Keithley2450
from qcodes.dataset import initialise_database, Measurement, new_experiment
from qcodes.dataset.plotting import plot_dataset
from visa import VisaIOError
keithley = Keithley2450("keithley", "GPIB0::18::INSTR")
keithley.reset()
# ## Single point measurements
# Attach a variable resistor to the front and source a current
# +
keithley.terminals("front")
keithley.source.function("current")
keithley.source.current(1E-6) # Put 1uA through the resistor
current_setpoint = keithley.source.current()
voltage = keithley.sense.function("voltage")
with keithley.output_enabled.set_to(True):
voltage = keithley.sense.voltage()
print(f"Approx. resistance: ", voltage/current_setpoint)
# -
# We can also directly measure the resistance
# +
voltage = keithley.sense.function("resistance")
with keithley.output_enabled.set_to(True):
resistance = keithley.sense.resistance()
print(f"Measured resistance: ", resistance)
# -
# In 'current' mode, we cannot set/get a voltage and vice versa
try:
keithley.source.voltage()
except AttributeError as err:
function = keithley.source.function()
print(f"In the '{function}' source mode the source module does not have a 'voltage' attribute")
# This goes for both the source and sense subsystems
try:
keithley.sense.current()
except AttributeError as err:
function = keithley.sense.function()
print(f"In the '{function}' sense mode the sense module does not have a 'current' attribute")
# We also need to make sure the output is enabled for use the measure (or 'sense') a current or voltage
# ## Sweeping measurements
# The instrument has a build-in sweep system. For the first measurement, we drive a current through the resistor and measure the voltage accross it.
initialise_database()
experiment = new_experiment(name='Keithley_2450_example', sample_name="no sample")
# Sweep the current from 0 to 1uA in 10 steps and measure voltage
# +
keithley.sense.function("voltage")
keithley.sense.auto_range(True)
keithley.source.function("current")
keithley.source.auto_range(True)
keithley.source.limit(2)
keithley.source.sweep_setup(0, 1E-6, 10)
keithley.sense.four_wire_measurement(True)
# +
meas = Measurement(exp=experiment)
meas.register_parameter(keithley.sense.sweep)
with meas.run() as datasaver:
datasaver.add_result((keithley.source.sweep_axis, keithley.source.sweep_axis()),
(keithley.sense.sweep, keithley.sense.sweep()))
dataid = datasaver.run_id
plot_dataset(datasaver.dataset)
# -
# Sweep the voltage from 10mV in 10 steps and measure current
# +
keithley.sense.function("current")
keithley.sense.range(1E-5)
keithley.sense.four_wire_measurement(True)
keithley.source.function("voltage")
keithley.source.range(0.2)
keithley.source.sweep_setup(0, 0.01, 10)
# +
meas = Measurement(exp=experiment)
meas.register_parameter(keithley.sense.sweep)
with meas.run() as datasaver:
datasaver.add_result((keithley.source.sweep_axis, keithley.source.sweep_axis()),
(keithley.sense.sweep, keithley.sense.sweep()))
dataid = datasaver.run_id
plot_dataset(datasaver.dataset)
# -
# ## To perform measurements with user-defined reading buffer
keithley.reset()
# By default, when performing measurement, the value is stored in the default buffer "defbuffer1".
keithley.sense_function('current')
with keithley.output_enabled.set_to(True):
data_point01 = keithley.sense.current()
data_point02 = keithley.sense.current()
data_point03 = keithley.sense.current()
print(f"The current measurements are {data_point01}, {data_point02}, {data_point03} A.")
# We can use a user-defined reading buffer for measurement. The following example is to do a sweep measurement, and read extra data elements in addition to the measurement value with the new method "elements".
buffer_name = 'userbuff1'
buffer_size = 100
with keithley.buffer(buffer_name, buffer_size) as buff1:
buff1.elements(['time', 'date', 'measurement', 'source_value_formatted'])
keithley.source.sweep_setup(0, 1E-6, 10, buffer_name=buff1.buffer_name)
data = keithley.sense.sweep()
all_data = keithley.sense.sweep.get_selected()
# "data" includes the numerical value of the measurement:
data
# "all_data" includes extra information specified by the "elements()" method:
all_data
# By using "with ... as ...:" to perform the measurement, there user-defined buffer is automatically removed after the measurement. **This is the recommanded way to use the user-defined buffer.**
try:
buff1.size()
except VisaIOError as err:
print(err)
# And we can still access the data in the default buffer:
buffer_name = 'defbuffer1'
buffer = keithley.buffer(buffer_name)
print(f"There are {buffer.number_of_readings()} data points in '{buffer_name}'.")
# The last reading is:
buffer.get_last_reading()
# We can get all 3 previously measured data as following:
buffer.get_data(1,3)
# And the original infomration are still there:
buffer.elements(["time", "measurement_formatted"])
buffer.get_data(1, 3)
# This is all the available elements, if none is requested, "measurement" will be used:
buffer.available_elements
# If the user gives a incorrect element name, error message will show which ones are correct:
try:
buffer.elements(['dates'])
except ValueError as err:
print(err)
|
docs/examples/driver_examples/Qcodes example with keithley 2450.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### 1 Short Answer
# 1.False
# MV optimization considers the covariance matrix as a factor. Even if one asset has a high sharpe ratio, it may has a high correlation with other assets in the portfolio or with the market ratio. Based on the MF optimization, we don't include this kinf of asset in out portfolio.
#
#
# 2.True
# The logic is tha log returns are i.i.d., then the annualized average (log) return will converge to the population mean. Thus, if the population mean of equities is higher than other asset classes, the h-period return is almost certainly larger for equities as ℎ gets large.
# A long-term investor without special need for liquidity, they are willing to maximize the total h-period return even if the one-year returns are riskier.
#
# 3.With an intercept.
# Usually times, regression with or without an intercept won't make much difference. Depends on whether we want to focuse on the variation or the trend. If we want to best replicate the variation, maximize correlation, and ignore the in-sample mean---then we need to include an intercept. Also, the most important reason is that we don't trust the historical data since it's such a short period, so we need to include an intercept to prevent following the historical data.
# 4 HDG is effective at tracking HFRI in-samplea based on the case study we discussed. HDG is a modified version of the ML Factor Model, MLFM-ES.
#
# In case study, it showed that HDG tracks the standard ML Factor Model with a correlation of more than 90% from 2011-2013. And even out of the sample, it still has a high R square. HDG is valuable by delivering complicated or expensive beta to investors. Especially if delivered in a low-cost ETF.
# The out-of-sample replication performs very well with respect to the target. It has a very high correlation to the HFRI.
# 5. Alpha is the portion of mean return that is not explained by our regressor "x". A negative alpha means that the mean return of the un explained part of the portfolio has a negative return. A hedge fund claims to beat the market by having a very high alpha, it may still be negative because in that time period, other parts of the portfolio,for example, SPY had a outstanding performance than all others in the porfolio. Taking out the SPY, the alpha may be negative
# ### 2. Allocation
import pandas as pd
import numpy as np
import statsmodels.api as sm
from statsmodels.regression.rolling import RollingOLS
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")
# +
hf_data = pd.read_excel('/Users/beckygong/Desktop/2021 UChicago/2020 Autumn/367 Portfolio Theory and Risk Management I/proshares_analysis_data.xlsx', sheet_name = 'hedge_fund_series')
hf_data = hf_data.set_index('date')
factor_data = pd.read_excel('/Users/beckygong/Desktop/2021 UChicago/2020 Autumn/367 Portfolio Theory and Risk Management I/proshares_analysis_data.xlsx', sheet_name = 'merrill_factors')
factor_data = factor_data.set_index('date')
other_data = pd.read_excel('/Users/beckygong/Desktop/2021 UChicago/2020 Autumn/367 Portfolio Theory and Risk Management I/proshares_analysis_data.xlsx', sheet_name = 'other_data')
other_data = other_data.set_index('date')
other_data['USGG3M Index'] = factor_data['USGG3M Index']
# -
def summary_stats(df, annual_fac):
report = pd.DataFrame()
report['Mean'] = df.mean() * annual_fac
report['Vol'] = df.std() * np.sqrt(annual_fac)
report['Sharpe'] = report['Mean'] / report['Vol']
return round(report, 4)
#
# ### 2.1
# +
def compute_tangency(factor_data, diagonalize_Sigma=False):
"""Compute tangency portfolio given a set of excess returns.
Also, for convenience, this returns the associated vector of average
returns and the variance-covariance matrix.
Parameters
----------
diagonalize_Sigma: bool
When `True`, set the off diagonal elements of the variance-covariance
matrix to zero.
"""
Sigma = factor_data.cov()
#print(Sigma) = cov matrix
# N is the number of assets
N = Sigma.shape[0]
# print(N) = 11
Sigma_adj = Sigma.copy()
if diagonalize_Sigma:
Sigma_adj.loc[:,:] = np.diag(np.diag(Sigma_adj))
mu_tilde = factor_data.mean()
Sigma_inv = np.linalg.inv(Sigma_adj)
weights = Sigma_inv @ mu_tilde / (np.ones(N) @ Sigma_inv @ mu_tilde)
# For convenience, I'll wrap the solution back into a pandas.Series object.
omega_tangency = pd.Series(weights, index=mu_tilde.index)
return omega_tangency, mu_tilde, Sigma_adj
omega_tangency, mu_tilde, Sigma = compute_tangency(hf_data) ### 需要改
omega_tangency.to_frame('Tangency Weights')
# -
# ### 2.2
# +
def target_mv_portfolio(factor_data, target_return=0.02, diagonalize_Sigma=False):
"""Compute MV optimal portfolio, given target return and set of excess returns.
Parameters
----------
diagonalize_Sigma: bool
When `True`, set the off diagonal elements of the variance-covariance
matrix to zero.
"""
omega_tangency, mu_tilde, Sigma = compute_tangency(factor_data.loc[:'2018'], diagonalize_Sigma=diagonalize_Sigma)
Sigma_adj = Sigma.copy()
if diagonalize_Sigma:
Sigma_adj.loc[:,:] = np.diag(np.diag(Sigma_adj))
Sigma_inv = np.linalg.inv(Sigma_adj)
N = Sigma_adj.shape[0]
delta_tilde = ((np.ones(N) @ Sigma_inv @ mu_tilde)/(mu_tilde @ Sigma_inv @ mu_tilde)) * target_return
omega_star = delta_tilde * omega_tangency
return omega_star, mu_tilde, Sigma_adj
omega_star, mu_tilde, Sigma = target_mv_portfolio(hf_data) ### 需要改
omega_star_df = omega_star.to_frame('MV Portfolio Weights')
omega_star_df
# -
portfolio_stats(omega_star, mu_tilde, Sigma, 12)
# ### 2.3
# +
def portfolio_stats(omega, mu_tilde, Sigma, annualize_fac):
# Mean
mean = (mu_tilde @ omega) * annualize_fac
# Volatility
vol = np.sqrt(omega @ Sigma @ omega) * np.sqrt(annualize_fac)
# Sharpe ratio
sharpe_ratio = mean / vol
return round(pd.DataFrame(data = [mean, vol, sharpe_ratio],
index = ['Mean', 'Volatility', 'Sharpe'],
columns = ['Portfolio Stats']), 4)
portfolio_stats(omega_tangency, mu_tilde, Sigma, 12)
portfolio_stats(omega_star, mu_tilde, Sigma, 12)
# -
# ### 2.4
# +
def target_mv_portfolio(factor_data, target_return=0.02, diagonalize_Sigma=False):
"""Compute MV optimal portfolio, given target return and set of excess returns.
Parameters
----------
diagonalize_Sigma: bool
When `True`, set the off diagonal elements of the variance-covariance
matrix to zero.
"""
omega_tangency, mu_tilde, Sigma = compute_tangency(factor_data, diagonalize_Sigma=diagonalize_Sigma)
Sigma_adj = Sigma.copy()
if diagonalize_Sigma:
Sigma_adj.loc[:,:] = np.diag(np.diag(Sigma_adj))
Sigma_inv = np.linalg.inv(Sigma_adj)
N = Sigma_adj.shape[0]
delta_tilde = ((np.ones(N) @ Sigma_inv @ mu_tilde)/(mu_tilde @ Sigma_inv @ mu_tilde)) * target_return
omega_star = delta_tilde * omega_tangency
return omega_star, mu_tilde, Sigma_adj
omega_star, mu_tilde, Sigma = target_mv_portfolio(hf_data)
omega_star_df = omega_star.to_frame('MV Portfolio Weights')
omega_star_df
# -
# ### 2.5
# I think that the out-of-sample performance for 5 commodities would be better. Because commodities has lower volatility
# than risky assets, the historical data would have a better predictrion for commodities.
# ### 3.1
# +
filepath_data = '/Users/beckygong/Desktop/2021 UChicago/2020 Autumn/367 Portfolio Theory and Risk Management I/proshares_analysis_data.xlsx'
info = pd.read_excel(filepath_data,sheet_name='descriptions')
info.rename(columns={'Unnamed: 0':'Symbol'},inplace=True)
info.set_index('Symbol',inplace=True)
hf = pd.read_excel(filepath_data,sheet_name='hedge_fund_series')
hf.set_index('date',inplace=True)
ml = pd.read_excel(filepath_data,sheet_name='merrill_factors')
ml.set_index('date',inplace=True)
# -
info.loc[list(hf.columns) + list(ml.columns)]
y = factor_data['EEM US Equity']
X = factor_data['SPY US Equity']
static_model = sm.OLS(y,X).fit()
static_model.summary()
# This is, each dollar I invest on EEM, I invest 0.9241 in SPY
# ### 3.2
summary_stats(factor_data,12)
summary_stats(factor_data,12)
# ### 3.3
# The original mean for EEM is 0.043495. It is different because the
# weight of EEM changes, so it has a different mean return.
#
The mean for EEM is 0.043495. It is different because the weight of it has changes, so the mean return has changed.
# ### 3.4
def display_correlation(factor_data,list_maxmin=True):
corrmat = factor_data.corr()
#ignore self-correlation
corrmat[corrmat==1] = None
sns.heatmap(corrmat)
if list_maxmin:
corr_rank = corrmat.unstack().sort_values().dropna()
pair_max = corr_rank.index[-1]
pair_min = corr_rank.index[0]
print(f'MIN Correlation pair is {pair_min}')
print(f'MAX Correlation pair is {pair_max}')
display_correlation(factor_data)
# We can tell the SPY has a high correlation with IWM, when adding IWM as another regressor,
# the high correlation between the two regressors will highly impect the regression result.
# ### 4.1
# Since it's log return, then we can add the returns together to get the total return.
def summary_stats(df, annual_fac):
report = pd.DataFrame()
report['Mean'] = df.mean() * annual_fac
report['Vol'] = df.std() * np.sqrt(annual_fac)
report['Sharpe'] = report['Mean'] / report['Vol']
return round(report, 4)
summary_stats(factor_data, 122)
# ### 4.2
factor_data.head()
factor_data['tilde_r'] = factor_data['SPY US Equity'] - factor_data['USGG3M Index']
#part (a)
var_hist = factor_data['tilde_r'].shift(1).expanding(60).quantile(0.05).dropna()
plt.plot(var_hist)
plt.ylabel('VaR')
plt.title("Historical VaR")
freq = np.size(var_hist[factor_data.iloc[60:]['tilde_r']<var_hist])
print("Frequency of r_tilde < r_tilde_VaR: %d" %freq)
print("The percentage is", np.round(freq*100/np.size(var_hist.index),2))
|
solutions/mid1/submissions/gongjinruo_167940_6241789_Jinruo Gong 2021 Midterm (1).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:Anaconda3]
# language: python
# name: conda-env-Anaconda3-py
# ---
# ## Transfer MNIST-M domain adaptation to Fashion MIST Images
from __future__ import print_function, division
import scipy
import pandas as pd
import numpy as np
import os
#from keras.datasets import mnist
from keras.datasets import fashion_mnist
from keras_contrib.layers.normalization.instancenormalization import InstanceNormalization
from keras.layers import Input, Dense, Reshape, Flatten, Dropout, Concatenate
from keras.layers import BatchNormalization, Activation, ZeroPadding2D, Add
from keras.layers.advanced_activations import LeakyReLU
from keras.layers.convolutional import UpSampling2D, Conv2D
from keras.models import Sequential, Model
from keras.optimizers import Adam
from keras.utils import to_categorical
import datetime
import matplotlib.pyplot as plt
import sys
import scipy
from glob import glob
from keras.datasets import mnist
from skimage.transform import resize as imresize
import pickle
import os
import urllib
import gzip
class DataLoader():
"""Loads images from MNIST (domain A) and MNIST-M (domain B)"""
def __init__(self, img_res=(28, 28)):
self.img_res = img_res
self.mnistm_url = 'https://github.com/VanushVaswani/keras_mnistm/releases/download/1.0/keras_mnistm.pkl.gz'
self.setup_mnist(img_res)
self.setup_mnistm(img_res)
def normalize(self, images):
return images.astype(np.float32) / 127.5 - 1.
def setup_mnist(self, img_res):
print ("Setting up MNIST...")
if os.path.exists('datasets/mnist_x.npy'):
# Load the dataset
(mnist_X, mnist_y), (_, _) = fashion_mnist.load_data()
# Normalize and rescale images
mnist_X = self.normalize(mnist_X)
mnist_X = np.array([imresize(x, img_res) for x in mnist_X])
mnist_X = np.expand_dims(mnist_X, axis=-1)
mnist_X = np.repeat(mnist_X, 3, axis=-1)
self.mnist_X, self.mnist_y = mnist_X, mnist_y
# Save formatted images
np.save('datasets/mnist_x.npy', self.mnist_X)
np.save('datasets/mnist_y.npy', self.mnist_y)
else:
self.mnist_X = np.load('datasets/mnist_x.npy')
self.mnist_y = np.load('datasets/mnist_y.npy')
print ("+ Done.")
def setup_mnistm(self, img_res):
print ("Setting up MNIST-M...")
if not os.path.exists('datasets/mnistm_x.npy'):
# Download the MNIST-M pkl file
filepath = 'datasets/keras_mnistm.pkl.gz'
if not os.path.exists(filepath.replace('.gz', '')):
print('+ Downloading ' + self.mnistm_url)
data = urllib.request.urlopen(self.mnistm_url)
with open(filepath, 'wb') as f:
f.write(data.read())
with open(filepath.replace('.gz', ''), 'wb') as out_f, \
gzip.GzipFile(filepath) as zip_f:
out_f.write(zip_f.read())
os.unlink(filepath)
# load MNIST-M images from pkl file
with open('datasets/keras_mnistm.pkl', "rb") as f:
data = pickle.load(f, encoding='bytes')
# Normalize and rescale images
mnistm_X = np.array(data[b'train'])
mnistm_X = self.normalize(mnistm_X)
mnistm_X = np.array([imresize(x, img_res) for x in mnistm_X])
self.mnistm_X, self.mnistm_y = mnistm_X, self.mnist_y.copy()
# Save formatted images
np.save('datasets/mnistm_x.npy', self.mnistm_X)
np.save('datasets/mnistm_y.npy', self.mnistm_y)
else:
self.mnistm_X = np.load('datasets/mnistm_x.npy')
self.mnistm_y = np.load('datasets/mnistm_y.npy')
print ("+ Done.")
def load_data(self, domain, batch_size=1):
X = self.mnist_X if domain == 'A' else self.mnistm_X
y = self.mnist_y if domain == 'A' else self.mnistm_y
idx = np.random.choice(list(range(len(X))), size=batch_size)
return X[idx], y[idx]
class PixelDA():
def __init__(self):
# Input shape
self.img_rows = 28
self.img_cols = 28
self.channels = 3
self.img_shape = (self.img_rows, self.img_cols, self.channels)
self.num_classes = 10
# Configure MNIST and MNIST-M data loader
self.data_loader = DataLoader(img_res=(self.img_rows, self.img_cols))
# Loss weights
lambda_adv = 10
lambda_clf = 1
# Calculate output shape of D (PatchGAN)
#patch = int(self.img_rows / 2**4)
patch = 2
self.disc_patch = (patch, patch, 1)
# Number of residual blocks in the generator
self.residual_blocks = 6
optimizer = Adam(0.0002, 0.5)
# Number of filters in first layer of discriminator and classifier
self.df = 64
self.cf = 64
# Build and compile the discriminators
self.discriminator = self.build_discriminator()
self.discriminator.compile(loss='mse',
optimizer=optimizer,
metrics=['accuracy'])
# Build the generator
self.generator = self.build_generator()
# Build the task (classification) network
self.clf = self.build_classifier()
# Input images from both domains
img_A = Input(shape=self.img_shape)
img_B = Input(shape=self.img_shape)
# Translate images from domain A to domain B
fake_B = self.generator(img_A)
# Classify the translated image
class_pred = self.clf(fake_B)
# For the combined model we will only train the generator and classifier
self.discriminator.trainable = False
# Discriminator determines validity of translated images
valid = self.discriminator(fake_B)
self.combined = Model(img_A, [valid, class_pred])
self.combined.compile(loss=['mse', 'categorical_crossentropy'],
loss_weights=[lambda_adv, lambda_clf],
optimizer=optimizer,
metrics=['accuracy'])
def build_generator(self):
"""Resnet Generator"""
def residual_block(layer_input):
"""Residual block described in paper"""
d = Conv2D(64, kernel_size=3, strides=1, padding='same')(layer_input)
d = BatchNormalization(momentum=0.8)(d)
d = Activation('relu')(d)
d = Conv2D(64, kernel_size=3, strides=1, padding='same')(d)
d = BatchNormalization(momentum=0.8)(d)
d = Add()([d, layer_input])
return d
# Image input
img = Input(shape=self.img_shape)
l1 = Conv2D(64, kernel_size=3, padding='same', activation='relu')(img)
# Propogate signal through residual blocks
r = residual_block(l1)
for _ in range(self.residual_blocks - 1):
r = residual_block(r)
output_img = Conv2D(self.channels, kernel_size=3, padding='same', activation='tanh')(r)
return Model(img, output_img)
def build_discriminator(self):
def d_layer(layer_input, filters, f_size=4, normalization=True):
"""Discriminator layer"""
d = Conv2D(filters, kernel_size=f_size, strides=2, padding='same')(layer_input)
d = LeakyReLU(alpha=0.2)(d)
if normalization:
d = InstanceNormalization()(d)
return d
img = Input(shape=self.img_shape)
d1 = d_layer(img, self.df, normalization=False)
d2 = d_layer(d1, self.df*2)
d3 = d_layer(d2, self.df*4)
d4 = d_layer(d3, self.df*8)
validity = Conv2D(1, kernel_size=4, strides=1, padding='same')(d4)
return Model(img, validity)
def build_classifier(self):
def clf_layer(layer_input, filters, f_size=4, normalization=True):
"""Classifier layer"""
d = Conv2D(filters, kernel_size=f_size, strides=2, padding='same')(layer_input)
d = LeakyReLU(alpha=0.2)(d)
if normalization:
d = InstanceNormalization()(d)
return d
img = Input(shape=self.img_shape)
c1 = clf_layer(img, self.cf, normalization=False)
c2 = clf_layer(c1, self.cf*2)
c3 = clf_layer(c2, self.cf*4)
c4 = clf_layer(c3, self.cf*8)
c5 = clf_layer(c4, self.cf*8)
class_pred = Dense(self.num_classes, activation='softmax')(Flatten()(c5))
return Model(img, class_pred)
def train(self, epochs, batch_size=128, sample_interval=50):
half_batch = int(batch_size / 2)
# Classification accuracy on 100 last batches of domain B
test_accs = []
# Adversarial ground truths
valid = np.ones((batch_size, *self.disc_patch))
fake = np.zeros((batch_size, *self.disc_patch))
for epoch in range(epochs):
# ---------------------
# Train Discriminator
# ---------------------
imgs_A, labels_A = self.data_loader.load_data(domain="B", batch_size=batch_size)
imgs_B, labels_B = self.data_loader.load_data(domain="A", batch_size=batch_size)
# Translate images from domain A to domain B
fake_B = self.generator.predict(imgs_A)
# Train the discriminators (original images = real / translated = Fake)
d_loss_real = self.discriminator.train_on_batch(imgs_B, valid)
d_loss_fake = self.discriminator.train_on_batch(fake_B, fake)
d_loss = 0.5 * np.add(d_loss_real, d_loss_fake)
# --------------------------------
# Train Generator and Classifier
# --------------------------------
# One-hot encoding of labels
labels_A = to_categorical(labels_A, num_classes=self.num_classes)
# Train the generator and classifier
g_loss = self.combined.train_on_batch(imgs_A, [valid, labels_A])
#-----------------------
# Evaluation (domain B)
#-----------------------
pred_B = self.clf.predict(imgs_B)
test_acc = np.mean(np.argmax(pred_B, axis=1) == labels_B)
# Add accuracy to list of last 100 accuracy measurements
test_accs.append(test_acc)
if len(test_accs) > 100:
test_accs.pop(0)
# Plot the progress
# print ( "%d : [D - loss: %.5f, acc: %3d%%], [G - loss: %.5f], [clf - loss: %.5f, acc: %3d%%, test_acc: %3d%% (%3d%%)]" % \
# (epoch, d_loss[0], 100*float(d_loss[1]),
# g_loss[1], g_loss[2], 100*float(g_loss[-1]),
# 100*float(test_acc), 100*float(np.mean(test_accs))))
# If at save interval => save generated image samples
if epoch % sample_interval == 0:
self.sample_images(epoch)
print ( "%d : [D - loss: %.5f, acc: %3d%%], [G - loss: %.5f], [clf - loss: %.5f, acc: %3d%%, test_acc: %3d%% (%3d%%)]" % \
(epoch, d_loss[0], 100*float(d_loss[1]),
g_loss[1], g_loss[2], 100*float(g_loss[-1]),
100*float(test_acc), 100*float(np.mean(test_accs))))
def sample_images(self, epoch):
r, c = 2, 5
imgs_A, _ = self.data_loader.load_data(domain="A", batch_size=5)
# Translate images to the other domain
fake_B = self.generator.predict(imgs_A)
gen_imgs = np.concatenate([imgs_A, fake_B])
# Rescale images 0 - 1
gen_imgs = 0.5 * gen_imgs + 0.5
#titles = ['Original', 'Translated']
fig, axs = plt.subplots(r, c)
cnt = 0
for i in range(r):
for j in range(c):
axs[i,j].imshow(gen_imgs[cnt])
#axs[i, j].set_title(titles[i])
axs[i,j].axis('off')
cnt += 1
fig.savefig("images/%d.png" % (epoch))
plt.imread("images/%d.png" % (epoch))
plt.show()
plt.close()
gan = PixelDA()
gan.train(epochs=10000, batch_size=8, sample_interval=1000)
|
Transfer_MNIST_M_domain_adaptation_to_Fashion_MIST_Images_PixelDA.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Problem Sheet Tensorflow
# ## 1. Use Tensorflow to create model
# The following has been adapted from an example provided by [<NAME>](https://github.com/ianmcloughlin), included in the module resources: https://github.com/emerging-technologies/keras-iris/blob/master/iris_nn.py.
# ### Imports
import numpy as n
import keras as k
from sklearn.datasets import load_iris
from sklearn.preprocessing import OneHotEncoder
from sklearn.model_selection import train_test_split
# ### Data Preparation
# The data is loaded from **Scikit Learn**, using the sklearn.datasets module: http://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_iris.html.
# To subsquently process the data, I utilized the sklearn.preprocessing module: http://scikit-learn.org/stable/modules/preprocessing.html. I then implemented sklearn.preprocessing's OneHotEncoder feature to transform the possible species into corresponding matrices of binary integers, since machines cannot comprehend strings of categorical data as we would.
# +
# load data
data = load_iris()
# derive necessary data
x, y_ = data.data, data.target.reshape(-1,1)
enc = OneHotEncoder(sparse = False)
y = enc.fit_transform(y_)
# -
# ### Model Creation
# **Keras** is an API that allows for a high level implementation of a neural network: https://keras.io/. Keras can use **Tensorflow** as it's backend, and does so on default.
#
# Tensorflow allows for numerical computation using data flow graphs, which is what is utilized to build the following neural network: https://www.tensorflow.org/. The beginning of the graphs are constant nodes or tensors (the input layer) that are input into a hidden layer of nodes to perform comutations. The ouputs can be passed into another hidden layer of nodes, or left as the output layer.
# +
# create a model with a linear/sequential stack of layers.
model = k.models.Sequential()
# using the add() method, add input layer of 4 nodes, and a fully connected hidden layer of 16 nodes.
model.add(k.layers.Dense(16, input_shape=(4,)))
# then apply the sigmoid activation function to that layer.
model.add(k.layers.Activation("sigmoid"))
# add and fully connect another layer (the output layer) of three nodes.
model.add(k.layers.Dense(3))
# add the softmax function to the output layer as the activation function.
model.add(k.layers.Activation("softmax"))
# use the adam optimizer - algorithm used when datasets have a seemingly random pattern.
# https://keras.io/optimizers/
optimizer = k.optimizers.Adam(lr=0.001)
# configure the model for training.
# uses categorical cross entropy as the loss function because iris a catergorical based dataset.
model.compile(optimizer, loss="categorical_crossentropy", metrics=["accuracy"])
# -
# ## 2. Split the data into training and testing
# Why would we want to split the data into two seperate sets? If we input the whole datasets and then test it with the same data, the machines predictions will be unproven as it will already have been given the exact data and corresponding classification.
#
# Originally I had assumed the application of the Pareto principle would surfice - 80% would be split into the training sets and 20% for the test sets. Upon futher research, I noticed the most common answer was from 60% to 80%: https://www.researchgate.net/post/What_is_the_best_way_to_divide_a_dataset_into_training_and_test_sets , https://stackoverflow.com/questions/13610074/is-there-a-rule-of-thumb-for-how-to-divide-a-dataset-into-training-and-validatio , https://www.researchgate.net/post/Is_there_an_ideal_ratio_between_a_training_set_and_validation_set_Which_trade-off_would_you_suggest.
# However, where does this leave us in the terms of our small data set? Since the data set is small I decided to stay with the 80% to 20% ratio to ensure the set has been trained extensively enough.
#
# Similar to the data preperation above, I used Scikit Learn's functionality to restructure data for machine learning methods. I used the model_selection module to split the arrays of data into seperate arrays for training and testing: http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html
# the training arrays will be 80% of the original, while the test arrays will be 20%.
train_x, test_x, train_y, test_y = train_test_split(x, y, test_size=0.2)
# ## 3. Train the model
# train the model with relevant set.
# verbose set to 0 - no output while fitting model
# epochs - the iteration limit
model.fit(train_x, train_y, epochs=500, batch_size=25, verbose=0)
# ## 4. Test the model
# +
# evaluate the model using the test data set.
loss, accuracy = model.evaluate(test_x, test_y, verbose=0)
# print results.
print("\n\nLoss: %6.4f\tAccuracy: %6.4f" % (loss, accuracy))
|
solutions/solution.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] pycharm={"name": "#%% md\n"}
# ---
# sidebar_position: 1
# ---
# + [markdown] pycharm={"name": "#%% md\n"}
# # Combining signals
#
# In this tutorial, you'll learn how to combine signals and how to perform scalar operations.
#
# As a reminder, timeseries are often expressed as a [combination of 3 components](https://otexts.com/fpp2/components.html): trend, seasonality and noise.
# If the interaction is **additive** the formula is: **$y_t = S_t + T_t + N_t$**, with $S_t$ the seasonal component, $T_t$ the trend-cycle component and $N_t$ the Noise component, at period $t$.
# Alternatively, if the interaction is **multiplicative**, the relation is: **$y_t = S_t * T_t * N_t$**.
#
# The point is: **to combine signals, you add or multiply them**.
# It's easy in **mockseries**: just use the standard operators `+` and `*` !
# You can write complex signals mixing **additive** and **multiplicative** interactions, such as:
# $$
# y_t = noise * (flat\_trend + (seasonal\_1 * linear\_trend) + seasonal\_2)
# $$
#
# ## Simple examples
# Lets add a linear trend and a sinusoidal signal:
# + pycharm={"name": "#%%\n"}
# matplotlib config for whole tutorial
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (20,7)
from datetime import timedelta
from mockseries.trend import LinearTrend
from mockseries.seasonality import SinusoidalSeasonality
linear_trend = LinearTrend(coefficient=2, time_unit=timedelta(days=1))
seasonality = SinusoidalSeasonality(amplitude=2, period=timedelta(hours=12))
additive_timeseries = linear_trend + seasonality
# quick preview function !
additive_timeseries.preview_week()
# + [markdown] pycharm={"name": "#%% md\n"}
# Now if we multiply them:
# + pycharm={"name": "#%%\n"}
multiplicative_timeseries = linear_trend * seasonality
multiplicative_timeseries.preview_week()
# + [markdown] pycharm={"name": "#%% md\n"}
# ## Complex example
# Let's implement the example in the introduction:
# $y_t = noise * (flat\_trend + (seasonal\_1 * linear\_trend) + seasonal\_2)$.
#
# To give more context, it could represent something like the temperature on Earth:
# - the temperature has an average value ($flat\_trend$)
# - the temperature is rising $linear\_trend$
# - the yearly pattern $seasonal\_1$ is multiplicative with the trend: this means global warming results in bigger yearly patterns
# - the daily pattern is additive: it's not impacted by the trend.
# - a noise is multiplicative by all of the above: this means it tends to get bigger when temperatures are bigger
#
# *NB: This model is an un-documented simulation, it is not linked to any research and is obviously incorrect.*
# *NB: For the sake of simplicity, we'll use sinusoidal signals for seasonalities. Check out the next tutorial for more realistic patterns !*
# + pycharm={"name": "#%%\n"}
from mockseries.trend import FlatTrend
from mockseries.noise import GaussianNoise
noise = GaussianNoise(mean=1, std=0.05)
average = FlatTrend(12)
warming = LinearTrend(0.1, timedelta(days=365.25), flat_base=1)
yearly_seasonality = SinusoidalSeasonality(amplitude=15, period=timedelta(days=365.25))
daily_seasonality = SinusoidalSeasonality(amplitude=5, period=timedelta(days=1))
temperature = noise * ( average + (warming * yearly_seasonality) + daily_seasonality)
temperature.preview_year(num_years=4)
# + [markdown] pycharm={"name": "#%% md\n"}
# ## Scalars operations:
#
# **mockseries** also supports simple scalar operations:
# - negate a signal: `-my_signal`
# - add a constant to a signal: `3 + my_signal`
# - multiply a signal: `3 * my_signal`
# + pycharm={"name": "#%% \n"}
# negate a signal:
from datetime import datetime
from mockseries.utils.dates import datetime_range
from mockseries.utils.plot import plot_timeseries
one_week_index = datetime_range(
granularity=timedelta(hours=1),
start_time=datetime(2021, 8, 23),
end_time=datetime(2021, 8, 23) + timedelta(days=7),
)
trend = LinearTrend(coefficient=3, time_unit=timedelta(days=1))
negated_trend = -trend
plot_timeseries(
one_week_index,
[trend.generate(one_week_index), negated_trend.generate(one_week_index)]
)
# + pycharm={"name": "#%% \n"}
# add a constant to a signal
sinusoid = SinusoidalSeasonality(1, timedelta(days=1))
sinusoid_plus_three = 3 + sinusoid
plot_timeseries(
one_week_index,
[sinusoid.generate(one_week_index),sinusoid_plus_three.generate(one_week_index)]
)
# + pycharm={"name": "#%% \n"}
# multiply a signal
sinusoid = SinusoidalSeasonality(1, timedelta(days=1))
sinusoid_times_three = 3 * sinusoid
plot_timeseries(
one_week_index,
[sinusoid.generate(one_week_index),sinusoid_times_three.generate(one_week_index)]
)
# + [markdown] pycharm={"name": "#%% md\n"}
# You're now able to combine timeseries and use scalar broadcasting!
# You should be able to build all kinds of timeseries with this simple primitives.
#
# Go to the next page to learn how to create periodic signals based on `(time, value)` constraints. This is helpful when you simulate real life timeseries.
#
|
tutorials/interaction-scalar-operations.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] pycharm={"name": "#%% md\n"}
# # Metadata to standardize datasets in memory
# + pycharm={"name": "#%%\n", "is_executing": false}
datasets = {
'ushhs': 'breach_report.csv',
'iib': 'visualisation-data.csv' # Information is beautiful
}
# Standardize Column Names. Create a dictionary for each data set with original name and standardized column name
standardized_names = {
'iib': {
'Entity': 'entity',
'records lost': 'records',
'YEAR': 'year',
'SECTOR': 'sector',
'METHOD': 'method'
},
'ushhs': {
'Name of Covered Entity': 'entity',
'Individuals Affected': 'records',
'Breach Submission Date': 'year',
'Covered Entity Type': 'sector',
'Type of Breach': 'method'
}
}
# -
# # Load the datasets
# + pycharm={"is_executing": false}
import csv
import os
data = {}
#load data from CSV files
for key in datasets:
with (open(os.path.join('data', datasets[key]))) as csvfile:
reader = csv.DictReader(csvfile, escapechar='\\')
data[key] = [r for r in reader]
# + pycharm={"is_executing": false}
# standardize column names
std_cols = {}
for key in data:
std_names = standardized_names[key]
std_rows = []
raw_data = data[key]
for row in raw_data:
std_row = {}
for name in std_names:
std_row[std_names[name]] = row[name]
std_rows.append(std_row)
std_cols[key] = std_rows
print(std_rows[0])
# + pycharm={"name": "#%%\n", "is_executing": false}
# Standardize values
import locale
import datetime
locale.setlocale( locale.LC_ALL, 'en_US.UTF-8' )
def atoi(s):
if s is None or len(s) == 0:
return 0
else:
return locale.atoi(s)
def year_for_ushhs(date):
return datetime.datetime.strptime(date, '%m/%d/%Y').year
def year_for_iib(year):
return int(year)
std_funcs = {
'iib': {
'records': atoi,
'year': year_for_iib
},
'ushhs': {
'records': atoi,
'year': year_for_ushhs
}
}
std_data = []
for key in std_cols:
std_rows = []
for row in std_cols[key]:
std_row = {}
for col in row:
if col in std_funcs[key]:
std_row[col] = std_funcs[key][col](row[col])
else:
std_row[col] = row[col]
std_rows.append(std_row)
std_data.extend(std_rows)
# + pycharm={"name": "#%%\n", "is_executing": false}
# Aggregrate by method and create a pie chart
method_count = {}
row_count = {}
def standardize_method_name(method_name):
if method_name == "hacked":
return "Hacking/IT Incident"
return method_name
for row in std_data:
if len(row['method']) > 0:
method = standardize_method_name(row['method'])
if method in method_count:
method_count[method] += 1
row_count[method] += row['records']
else:
method_count[method] =1
row_count[method] = row['records']
print(method_count)
print(row_count)
# + pycharm={"name": "#%%\n", "is_executing": false}
import matplotlib.pyplot as plt
fig1, ax1 = plt.subplots()
ax1.pie([method_count[k] for k in sorted(method_count.keys())],
labels=sorted(method_count.keys()))
ax1.axis('equal')
plt.show()
# + pycharm={"name": "#%%\n", "is_executing": false}
import matplotlib.pyplot as plt
fig1, ax1 = plt.subplots()
ax1.pie([row_count[k] for k in sorted(method_count.keys())],
labels=sorted(method_count.keys()))
ax1.axis('equal')
plt.show()
|
data-breach-report.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.9.7 64-bit (''tectosaur2'': conda)'
# language: python
# name: python3
# ---
# The classical free term coefficient for a smooth surface is either 0.5 or -0.5, depending on whether we are evaluating from the interior or the exterior. But with a halfspace surface, the free term can end up being either 0 or 1. The integrations below demonstrate this fact.
# +
import numpy as np
import sympy as sp
from tectosaur2 import gauss_rule, refine_surfaces, integrate_term
from tectosaur2.laplace2d import double_layer
from tectosaur2.elastic2d import elastic_t
qx, qw = gauss_rule(12)
t = sp.var("t")
circle = refine_surfaces(
[(t, sp.cos(sp.pi * t), sp.sin(sp.pi * t))], (qx, qw), max_curvature=0.125
)
A = integrate_term(double_layer, circle.pts, circle)
print(A[:, 0, :, 0].sum(axis=1)[0])
A2 = integrate_term(double_layer, circle.pts, circle, limit_direction=-1)
print(A2[:, 0, :, 0].sum(axis=1)[0])
line = refine_surfaces(
[(t, 100 * t, 0.0 * t)],
(qx, qw),
control_points=np.array([[0, 0, 100, 1]]),
)
A3 = integrate_term(
double_layer, line.pts, line, singularities=np.array([[-100, 0], [100, 0]])
)
print(A3[:, 0, :, 0].sum(axis=1)[A3.shape[0] // 2])
A4 = integrate_term(
double_layer,
line.pts,
line,
limit_direction=-1,
singularities=np.array([[-100, 0], [100, 0]]),
)
print(A4[:, 0, :, 0].sum(axis=1)[A3.shape[0] // 2])
# +
qx, qw = gauss_rule(12)
t = sp.var("t")
circle = refine_surfaces(
[(t, sp.cos(sp.pi * t), sp.sin(sp.pi * t))], (qx, qw), max_curvature=0.125
)
A = integrate_term(elastic_t(0.25), circle.pts, circle)
print(A[:, :, :, :].sum(axis=2)[0])
A2 = integrate_term(elastic_t(0.25), circle.pts, circle, limit_direction=-1)
print(A2[:, :, :, :].sum(axis=2)[0])
line = refine_surfaces(
[(t, 100 * t, 0.0 * t)], (qx, qw), control_points=np.array([[0, 0, 100, 1]])
)
A3 = integrate_term(
elastic_t(0.25),
line.pts,
line,
singularities=np.array([[-100, 0], [100, 0]]),
)
print(A3[:, :, :, :].sum(axis=2)[A3.shape[0] // 2])
A4 = integrate_term(
elastic_t(0.25),
line.pts,
line,
singularities=np.array([[-100, 0], [100, 0]]),
limit_direction=-1,
)
print(A4[:, :, :, :].sum(axis=2)[A3.shape[0] // 2])
# -
|
experiments/free_terms.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python uois3d
# language: python
# name: uois3d
# ---
# # Unseen Object Instance Segmentation
# +
# %matplotlib inline
import os
os.environ['CUDA_VISIBLE_DEVICES'] = "0" # TODO: Change this if you have more than 1 GPU
import sys
import json
from time import time
import glob
import torch
import numpy as np
import matplotlib.pyplot as plt
import cv2
# My libraries. Ugly hack to import from sister directory
import src.data_augmentation as data_augmentation
import src.segmentation as segmentation
import src.evaluation as evaluation
import src.util.utilities as util_
import src.util.flowlib as flowlib
# -
# ## Depth Seeding Network Parameters
# +
dsn_config = {
# Sizes
'feature_dim' : 64, # 32 would be normal
# Mean Shift parameters (for 3D voting)
'max_GMS_iters' : 10,
'epsilon' : 0.05, # Connected Components parameter
'sigma' : 0.02, # Gaussian bandwidth parameter
'num_seeds' : 200, # Used for MeanShift, but not BlurringMeanShift
'subsample_factor' : 5,
# Misc
'min_pixels_thresh' : 500,
'tau' : 15.,
}
# -
# ## Region Refinement Network parameters
# +
rrn_config = {
# Sizes
'feature_dim' : 64, # 32 would be normal
'img_H' : 224,
'img_W' : 224,
# architecture parameters
'use_coordconv' : False,
}
# -
# # UOIS-Net-3D Parameters
# +
uois3d_config = {
# Padding for RGB Refinement Network
'padding_percentage' : 0.25,
# Open/Close Morphology for IMP (Initial Mask Processing) module
'use_open_close_morphology' : True,
'open_close_morphology_ksize' : 9,
# Largest Connected Component for IMP module
'use_largest_connected_component' : True,
}
# -
checkpoint_dir = '/home/chrisxie/projects/uois/checkpoints/' # TODO: change this to directory of downloaded models
dsn_filename = checkpoint_dir + 'DepthSeedingNetwork_3D_TOD_checkpoint.pth'
rrn_filename = checkpoint_dir + 'RRN_OID_checkpoint.pth'
uois3d_config['final_close_morphology'] = 'TableTop_v5' in rrn_filename
uois_net_3d = segmentation.UOISNet3D(uois3d_config,
dsn_filename,
dsn_config,
rrn_filename,
rrn_config
)
# ## Run on example OSD/OCID images
#
# We provide a few [OSD](https://www.acin.tuwien.ac.at/en/vision-for-robotics/software-tools/osd/) and [OCID](https://www.acin.tuwien.ac.at/en/vision-for-robotics/software-tools/object-clutter-indoor-dataset/) images and run the network on them. Evaluation metrics are shown for each of the images.
# +
example_images_dir = os.path.abspath('.') + '/example_images/'
OSD_image_files = sorted(glob.glob(example_images_dir + '/OSD_*.npy'))
OCID_image_files = sorted(glob.glob(example_images_dir + '/OCID_*.npy'))
N = len(OSD_image_files) + len(OCID_image_files)
rgb_imgs = np.zeros((N, 480, 640, 3), dtype=np.float32)
xyz_imgs = np.zeros((N, 480, 640, 3), dtype=np.float32)
label_imgs = np.zeros((N, 480, 640), dtype=np.uint8)
for i, img_file in enumerate(OSD_image_files + OCID_image_files):
d = np.load(img_file, allow_pickle=True, encoding='bytes').item()
# RGB
rgb_img = d['rgb']
rgb_imgs[i] = data_augmentation.standardize_image(rgb_img)
# XYZ
xyz_imgs[i] = d['xyz']
# Label
label_imgs[i] = d['label']
batch = {
'rgb' : data_augmentation.array_to_tensor(rgb_imgs),
'xyz' : data_augmentation.array_to_tensor(xyz_imgs),
}
# +
print("Number of images: {0}".format(N))
### Compute segmentation masks ###
st_time = time()
fg_masks, center_offsets, initial_masks, seg_masks = uois_net_3d.run_on_batch(batch)
total_time = time() - st_time
print('Total time taken for Segmentation: {0} seconds'.format(round(total_time, 3)))
print('FPS: {0}'.format(round(N / total_time,3)))
# Get results in numpy
seg_masks = seg_masks.cpu().numpy()
fg_masks = fg_masks.cpu().numpy()
center_offsets = center_offsets.cpu().numpy().transpose(0,2,3,1)
initial_masks = initial_masks.cpu().numpy()
# +
rgb_imgs = util_.torch_to_numpy(batch['rgb'].cpu(), is_standardized_image=True)
total_subplots = 6
fig_index = 1
for i in range(N):
num_objs = max(np.unique(seg_masks[i,...]).max(), np.unique(label_imgs[i,...]).max()) + 1
rgb = rgb_imgs[i].astype(np.uint8)
depth = xyz_imgs[i,...,2]
seg_mask_plot = util_.get_color_mask(seg_masks[i,...], nc=num_objs)
gt_masks = util_.get_color_mask(label_imgs[i,...], nc=num_objs)
images = [rgb, depth, seg_mask_plot, gt_masks]
titles = [f'Image {i+1}', 'Depth',
f"Refined Masks. #objects: {np.unique(seg_masks[i,...]).shape[0]-1}",
f"Ground Truth. #objects: {np.unique(label_imgs[i,...]).shape[0]-1}"
]
util_.subplotter(images, titles, fig_num=i+1)
# Run evaluation metric
eval_metrics = evaluation.multilabel_metrics(seg_masks[i,...], label_imgs[i])
print(f"Image {i+1} Metrics:")
print(eval_metrics)
# -
|
uois_3D_example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Copy/move files from CSV files
# This notebook allow to copy or move files based on two columns of a CSV file
# ### Load libraries
import os
import shutil
import pandas
# ### Settings
inputdir = 'PATH_TO_INPUT_FOLDER' # Image folder, including subfolders
filetypes = set(['.png', '.jpg', '.jpeg', '.bmp']) # Define filetypes to include
outputdir = 'PATH_TO_OUTPUT_FOLDER' # Output folder
move_files = False # Move files to destination, otherwise copy the files
csv_path = 'FULL_PATH_TO_CSV_FILE' # Path to the CSV file
csv_column1 = 'COL1' # First column of CSV containing filenames
csv_column2 = 'COL2' # Second column of CSV containing sort variable, e.g. 'Fracture'
csv_delimiter = ',' # CSV column delimiter
# ### Main code
# + tags=["outputPrepend"]
if not os.path.exists(inputdir) or inputdir == outputdir or not os.path.isfile(csv_path):
print('ERROR (Directory/file issues): Please check paths.')
exit()
# Fill dictionary from columns
df = pandas.read_csv(os.path.normpath(csv_path), dtype=str, sep=csv_delimiter,
usecols=[csv_column1, csv_column2]).dropna()
csv = df.set_index(csv_column1)[csv_column2].to_dict()
# Iterate over FILES in folder and subfolders
def main():
for paths, _, files in os.walk(os.path.normpath(inputdir), topdown=True):
for file in files:
if any(x in file.lower() for x in filetypes) == True:
filestem = os.path.basename(file).split('.')[0]
inputfile = os.path.join(paths, file)
if filestem in csv and csv[filestem]:
outputpath = os.path.normpath(os.path.join(outputdir, csv.get(filestem, '')))
outputfile = os.path.join(outputpath, file)
if os.path.isfile(outputfile) == True:
print('SKIPPED (File exists), '+inputfile)
continue
if not os.path.exists(outputpath): os.makedirs(outputpath)
if move_files == True: shutil.move(inputfile, outputfile)
else: shutil.copy2(inputfile, outputfile)
print('SUCCESS (File processed), ' + outputfile)
else:
print('SKIPPED (Value empty), '+ inputfile)
if __name__ == '__main__':
main()
|
copy_files_by_csv.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
# ### Use scikit-learn's built-in *make_classification* method to generate syntehtic classificiation data
from sklearn.datasets import make_classification
# #### I used two informative features (Temp, Humidity) and one redundant feature 'Crime'
X,y = make_classification(n_samples=35040,n_classes=2,n_features=3,n_informative=2,n_redundant=1,
weights=[0.999,0.001],class_sep=1.0)
df=pd.DataFrame(data=X,columns=['Temp','Humidity','Crime'])
df['y']=y
df['Temp']=df['Temp']-min(df['Temp'])
maxt=max(df['Temp'])
df['Temp']=90*df['Temp']/maxt
df['Humidity']=df['Humidity']-min(df['Humidity'])
maxh=max(df['Humidity'])
df['Humidity']=100*df['Humidity']/maxh
df['Crime']=df['Crime']-min(df['Crime'])
maxc=max(df['Crime'])
df['Crime']=10*df['Crime']/maxc
df.hist('Temp')
df.hist('Humidity')
df.hist('Crime')
# ### Take a sum on the Boolean array with df['y']==1 to count the number of positive examples
sum(df['y']==1)
# ** That means only 223 responses out of 35040 samples are positive **
df.head(10)
df.describe()
# ## Logistic Regression undersampling
from sklearn.model_selection import StratifiedKFold
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegressionCV
from sklearn.metrics import classification_report
# ### Under-sampling the negative class to limited number
df0=df[df['y']==0].sample(800)
df1=df[df['y']==1]
df_balanced = pd.concat([df0,df1],axis=0)
df_balanced.describe()
df_balanced.hist('y')
plt.title("Relative frequency of positive and negative classes\n in the balanced (under-sampled) dataset")
log_model_balanced = LogisticRegressionCV(cv=5,class_weight='balanced')
X_train, X_test, y_train, y_test = train_test_split(df_balanced.drop('y',axis=1),
df_balanced['y'], test_size=0.30)
from sklearn.preprocessing import MinMaxScaler
scaler=MinMaxScaler()
X_train = scaler.fit_transform(X_train)
log_model_balanced.fit(X_train,y_train)
print(classification_report(y_test,log_model_balanced.predict(X_test)))
# ### I did an experiment with how the degree of under-sampling affects _F1-score_, _precision_, and _recall_
from sklearn.metrics import f1_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
# +
n_neg = [i for i in range(200,4200,200)]
df1=df[df['y']==1]
F1_scores=[]
precision_scores=[]
recall_scores=[]
for num in n_neg:
# Create under-sampled data sets
df0=df[df['y']==0].sample(num)
df_balanced = pd.concat([df0,df1],axis=0)
# Create model with 'class_weight=balanced' and 5-fold cross-validation
log_models=LogisticRegressionCV(cv=5,class_weight='balanced')
# Create test/train splits
X_train, X_test, y_train, y_test = train_test_split(df_balanced.drop('y',axis=1),
df_balanced['y'], test_size=0.30)
# Min-max scale the training data
X_train = scaler.fit_transform(X_train)
# Fit the logistic regression model
log_models.fit(X_train,y_train)
# Calculate various scores
F1_scores.append(f1_score(y_test,log_models.predict(X_test)))
precision_scores.append(precision_score(y_test,log_models.predict(X_test)))
recall_scores.append(recall_score(y_test,log_models.predict(X_test)))
# -
plt.scatter(n_neg,F1_scores,color='green',edgecolor='black',alpha=0.6,s=100)
plt.title("F1-score as function of negative samples")
plt.grid(True)
plt.ylabel("F1-score")
plt.xlabel("Number of negative samples")
plt.scatter(n_neg,precision_scores,color='orange',edgecolor='black',alpha=0.6,s=100)
plt.title("Precision score as function of negative samples")
plt.grid(True)
plt.ylabel("Precision score")
plt.xlabel("Number of negative samples")
plt.scatter(n_neg,recall_scores,color='blue',edgecolor='black',alpha=0.6,s=100)
plt.title("Recall score as function of negative samples")
plt.grid(True)
plt.ylabel("Recall score")
plt.xlabel("Number of negative samples")
# ### So, precision goes down rapidly with more negative samples and so does F1-score. Recall is largely unaffected by mixing negative samples with the positive ones.
|
Classification/Logistic Regression Skewed.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %%time
import malaya
# ## List available deep learning NER models
malaya.entity.available_deep_model()
# ## Describe supported entities
malaya.describe_entities()
string = 'KUALA LUMPUR: Sempena sambutan Aidilfitri minggu depan, Perdana Menteri Tun Dr <NAME> dan <NAME> <NAME> menitipkan pesanan khas kepada orang ramai yang mahu pulang ke kampung halaman masing-masing. Dalam video pendek terbitan Jabatan Keselamatan Jalan Raya (JKJR) itu, Dr Mahathir menasihati mereka supaya berhenti berehat dan tidur sebentar sekiranya mengantuk ketika memandu.'
# ## Load CRF model
crf = malaya.entity.crf()
crf.predict(string)
crf.analyze(string)
# ## Load Case-Sensitive CRF model
crf = malaya.entity.crf(sensitive = True)
crf.predict(string)
# ## Print important features from CRF model
crf.print_features(10)
# ## Print important transitions from CRF Model
crf.print_transitions(10)
# ## Load deep learning models
for i in malaya.entity.available_deep_model():
print('Testing %s model'%(i))
model = malaya.entity.deep_model(i)
print(model.predict(string))
print()
# ## Load Case-Sensitive deep learning models
for i in malaya.entity.available_deep_model():
print('Testing %s model'%(i))
model = malaya.entity.deep_model(i, sensitive = True)
print(model.predict(string))
print()
bahdanau = malaya.entity.deep_model('bahdanau')
bahdanau.analyze(string)
# ## Print important features from deep learning model
bahdanau = malaya.entity.deep_model('bahdanau')
bahdanau.print_features(10)
# ## Print important transitions from deep learning model
bahdanau.print_transitions(10)
# ## Visualize output alignment from attention
#
# This visualization only can call from `bahdanau` or `luong` model.
d_object, predicted, state_fw, state_bw = bahdanau.get_alignment(string)
d_object.to_graphvis()
# ## Voting stack model
entity_network = malaya.entity.deep_model('entity-network')
bahdanau = malaya.entity.deep_model('bahdanau')
luong = malaya.entity.deep_model('luong')
malaya.stack.voting_stack([entity_network, bahdanau, luong], string)
entity_network = malaya.entity.deep_model('entity-network')
bahdanau = malaya.entity.deep_model('bahdanau')
luong = malaya.entity.deep_model('luong')
malaya.stack.voting_stack([entity_network, bahdanau, luong], 'Husein lapar nak makan rm10k punya ayam goreng')
|
example/entities/load-entities.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.9.5 64-bit
# language: python
# name: python3
# ---
# # Semana 13
#
# ## Módulo 4a: Ferramentas digitais e o ensino de história
#
# **Período**: 24/01/2022 a 28/01/2022
#
# **CH**: 2h
# ### Atividade Assíncrona 7 (AA)
#
# Tutorial 03: **Construindo apresentações interativas com Reveal.js**
#
# > EM BREVE O TUTORIAL ESTARÁ DISPONÍVEL AQUI
|
cclhm0069/_build/jupyter_execute/mod4a/sem13.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: python3
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Dependencies and Setup
import pandas as pd
# File to Load (Remember to Change These)
file_to_load = "Resources/purchase_data.csv"
# Read Purchasing File and store into Pandas data frame
purchase_data = pd.read_csv(file_to_load)
# -
purchase_data.head()
total_players = len(purchase_data['SN'].unique())
player_counts_df = pd.DataFrame({'Total Players': [total_players]})
player_counts_df
number_unique_items = len(purchase_data['Item ID'].unique())
number_of_purchases = len(purchase_data['Purchase ID'].unique())
average_price = purchase_data['Price'].mean()
total_revenue = purchase_data['Price'].sum()
average_price
# +
purchasing_analysis_df = pd.DataFrame({'Number of Unique Items': [number_unique_items],
'Average Price':[average_price],
'Number of Purchases':[number_of_purchases],
'Total Revenue':[total_revenue]})
purchasing_analysis_df['Average Price'] = purchasing_analysis_df['Average Price'].map("${:,.2f}".format)
purchasing_analysis_df['Total Revenue'] = purchasing_analysis_df['Total Revenue'].map("${:,.2f}".format)
purchasing_analysis_df
# -
player_demo_df = purchase_data[['SN','Gender','Age']].drop_duplicates()
gender_percentage = player_demo_df['Gender'].value_counts(normalize = True).mul(100).round(1).astype(str) + '%'
gender = player_demo_df['Gender'].value_counts()
gender_demo_df = pd.DataFrame({'Total Counts':gender,
'Percentage of Players':gender_percentage})
gender_demo_df
# +
groupby_gender_df = purchase_data[['Gender','SN','Price','Age']]
groupby_gender = groupby_gender_df.groupby(['Gender'])
Purchase_Counts = groupby_gender['SN'].count()
Average_Purchase_Price = groupby_gender['Price'].mean()
Total_Purchase_Value = Purchase_Counts*Average_Purchase_Price
Average_Total_Purchase_Per_Person = Total_Purchase_Value/gender_demo_df['Total Counts']
gender_purchasing_analysis_df = pd.DataFrame({'Purchase Count':Purchase_Counts,
'Average Purchase Price':Average_Purchase_Price,
'Total Purchase Value':Total_Purchase_Value,
'Average Total Purchase Per Person':Average_Total_Purchase_Per_Person})
# Changing the format of the displayed units
gender_purchasing_analysis_df['Average Purchase Price']= gender_purchasing_analysis_df['Average Purchase Price'].map("${:,.2f}".format)
gender_purchasing_analysis_df['Average Total Purchase Per Person'] = gender_purchasing_analysis_df['Average Total Purchase Per Person'].map("${:,.2f}".format)
gender_purchasing_analysis_df
# -
# Establish bins for ages
bins = [0, 9.9, 14.9, 19.9, 24.9, 29.9, 34.9, 39.9,100]
labels = ["<10", "10-14", "15-19", "20-24", "25-29", "30-34", "35-39", "40+"]
player_demo_df["Age Groups"] = pd.cut(player_demo_df["Age"], bins, labels=labels)
age_group_counts = player_demo_df['Age Groups'].value_counts()
age_group_counts_percentage = player_demo_df['Age Groups'].value_counts(normalize = True).mul(100).round(2).astype(str) + '%'
cleaned_age_demo_df = pd.DataFrame({'Total Count':age_group_counts,
'Percentage of Players':age_group_counts_percentage})
cleaned_age_demo_df.sort_index()
# +
bins = [0, 9.9, 14.9, 19.9, 24.9, 29.9, 34.9, 39.9,100]
labels = ["<10", "10-14", "15-19", "20-24", "25-29", "30-34", "35-39", "40+"]
purchase_data['Age Groups']= pd.cut(purchase_data["Age"], bins, labels=labels)
groupby_age = purchase_data.groupby(['Age Groups'])
total_purchase_value = purchase_data.groupby('Age Groups')["Price"].sum()
total_purchase_count = purchase_data.groupby('Age Groups')['SN'].count()
idewe = purchase_data.groupby('Age Groups')['SN'].unique()
avg_price = purchase_data.groupby('Age Groups')['Price'].mean().map("${:,.2f}".format)
avg_purchase_person = total_purchase_value/cleaned_age_demo_df['Total Count']
age_group_purchase_analysis_df = pd.DataFrame({'Purchase Count':total_purchase_count,
'Average Purchase Price':avg_price,
'Total Purchase Value':total_purchase_value,
'Average Total Purchase Per Person':avg_purchase_person})
age_group_purchase_analysis_df['Total Purchase Value']=age_group_purchase_analysis_df['Total Purchase Value'].map("${:,.2f}".format)
age_group_purchase_analysis_df['Average Total Purchase Per Person']=age_group_purchase_analysis_df['Average Total Purchase Per Person'].map("${:,.2f}".format)
age_group_purchase_analysis_df.sort_index()
# -
TS_purchase_value = purchase_data.groupby('SN')["Price"].sum()
TS_purchase_count = purchase_data.groupby('SN')['SN'].count()
TS_avg_price = purchase_data.groupby('SN')['Price'].mean().map("${:,.2f}".format)
top_spender_df =pd.DataFrame({'Purchase Count':TS_purchase_count,
'Average Purchase Price':TS_avg_price,
'Total Purchase Value':TS_purchase_value})
top_spender_df['Total Purchase Value']=top_spender_df['Total Purchase Value']
top_spender_df.sort_values('Total Purchase Value', ascending=False).head()
# +
popular_items_group = purchase_data.groupby(["Item ID", "Item Name"])
purchase_count = popular_items_group['Price'].count()
item_price = popular_items_group['Price'].mean()
purchase_value = popular_items_group["Price"].sum()
popular_item_df = pd.DataFrame({'Purchase Count':purchase_count,
'Item Price': item_price,
'Purchase Value':purchase_value})
popular_item_df['Item Price'] = popular_item_df['Item Price'].map("${:,.2f}".format)
popular_item_df['Purchase Value']= popular_item_df['Purchase Value'].map("${:,.2f}".format)
popular_item_df.sort_values('Purchase Count', ascending=False).head()
# -
# ## Most Popular Items
# * Retrieve the Item ID, Item Name, and Item Price columns
#
#
# * Group by Item ID and Item Name. Perform calculations to obtain purchase count, item price, and total purchase value
#
#
# * Create a summary data frame to hold the results
#
#
# * Sort the purchase count column in descending order
#
#
# * Optional: give the displayed data cleaner formatting
#
#
# * Display a preview of the summary data frame
#
#
# ## Most Profitable Items
# * Sort the above table by total purchase value in descending order
#
#
# * Optional: give the displayed data cleaner formatting
#
#
# * Display a preview of the data frame
#
#
|
HeroesOfPymoli/.ipynb_checkpoints/HeroesOfPymoli-Completed-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <img src="images/dask_horizontal.svg" align="right" width="30%">
# # Bag: Parallel Lists for semi-structured data
# Dask-bag excels in processing data that can be represented as a sequence of arbitrary inputs. We'll refer to this as "messy" data, because it can contain complex nested structures, missing fields, mixtures of data types, etc. The *functional* programming style fits very nicely with standard Python iteration, such as can be found in the `itertools` module.
#
# Messy data is often encountered at the beginning of data processing pipelines when large volumes of raw data are first consumed. The initial set of data might be JSON, CSV, XML, or any other format that does not enforce strict structure and datatypes.
# For this reason, the initial data massaging and processing is often done with Python `list`s, `dict`s, and `set`s.
#
# These core data structures are optimized for general-purpose storage and processing. Adding streaming computation with iterators/generator expressions or libraries like `itertools` or [`toolz`](https://toolz.readthedocs.io/en/latest/) let us process large volumes in a small space. If we combine this with parallel processing then we can churn through a fair amount of data.
#
# Dask.bag is a high level Dask collection to automate common workloads of this form. In a nutshell
#
# dask.bag = map, filter, toolz + parallel execution
#
# **Related Documentation**
#
# * [Bag Documenation](http://dask.pydata.org/en/latest/bag.html)
# * [Bag API](http://dask.pydata.org/en/latest/bag-api.html)
# ## Creation
# You can create a `Bag` from a Python sequence, from files, from data on S3, etc.
# We demonstrate using `.take()` to show elements of the data. (Doing `.take(1)` results in a tuple with one element)
#
# Note that the data are partitioned into blocks, and there are many items per block. In the first example, the two partitions contain five elements each, and in the following two, each file is partitioned into one or more bytes blocks.
# each element is an integer
import dask.bag as db
b = db.from_sequence([1, 2, 3, 4, 5, 6, 7, 8, 9, 10], npartitions=2)
b.take(3)
# each element is a text file, where each line is a JSON object
# note that the compression is handled automatically
import os
b = db.read_text(os.path.join('data', 'accounts.*.json.gz'))
b.take(1)
# Requires `s3fs` library
# each partition is a remote CSV text file
b = db.read_text('s3://dask-data/nyc-taxi/2015/yellow_tripdata_2015-01.csv',
storage_options={'anon': True})
b.take(1)
# ## Manipulation
# `Bag` objects hold the standard functional API found in projects like the Python standard library, `toolz`, or `pyspark`, including `map`, `filter`, `groupby`, etc..
#
# Operations on `Bag` objects create new bags. Call the `.compute()` method to trigger execution, as we saw for `Delayed` objects.
# +
def is_even(n):
return n % 2 == 0
b = db.from_sequence([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
c = b.filter(is_even).map(lambda x: x ** 2)
c
# -
# blocking form: wait for completion (which is very fast in this case)
c.compute()
# ### Example: Accounts JSON data
# We've created a fake dataset of gzipped JSON data in your data directory. This is like the example used in the `DataFrame` example we will see later, except that it has bundled up all of the entires for each individual `id` into a single record. This is similar to data that you might collect off of a document store database or a web API.
#
# Each line is a JSON encoded dictionary with the following keys
#
# * id: Unique identifier of the customer
# * name: Name of the customer
# * transactions: List of `transaction-id`, `amount` pairs, one for each transaction for the customer in that file
filename = os.path.join('data', 'accounts.*.json.gz')
lines = db.read_text(filename)
lines.take(3)
# Our data comes out of the file as lines of text. Notice that file decompression happened automatically. We can make this data look more reasonable by mapping the `json.loads` function onto our bag.
import json
js = lines.map(json.loads)
# take: inspect first few elements
js.take(3)
# ### Basic Queries
# Once we parse our JSON data into proper Python objects (`dict`s, `list`s, etc.) we can perform more interesting queries by creating small Python functions to run on our data.
# filter: keep only some elements of the sequence
js.filter(lambda record: record['name'] == 'Alice').take(5)
# +
def count_transactions(d):
return {'name': d['name'], 'count': len(d['transactions'])}
# map: apply a function to each element
(js.filter(lambda record: record['name'] == 'Alice')
.map(count_transactions)
.take(5))
# -
# pluck: select a field, as from a dictionary, element[field]
(js.filter(lambda record: record['name'] == 'Alice')
.map(count_transactions)
.pluck('count')
.take(5))
# Average number of transactions for all of the Alice entries
(js.filter(lambda record: record['name'] == 'Alice')
.map(count_transactions)
.pluck('count')
.mean()
.compute())
# ### Use `flatten` to de-nest
# In the example below we see the use of `.flatten()` to flatten results. We compute the average amount for all transactions for all Alices.
js.filter(lambda record: record['name'] == 'Alice').pluck('transactions').take(3)
(js.filter(lambda record: record['name'] == 'Alice')
.pluck('transactions')
.flatten()
.take(3))
(js.filter(lambda record: record['name'] == 'Alice')
.pluck('transactions')
.flatten()
.pluck('amount')
.take(3))
(js.filter(lambda record: record['name'] == 'Alice')
.pluck('transactions')
.flatten()
.pluck('amount')
.mean()
.compute())
# ### Groupby and Foldby
# Often we want to group data by some function or key. We can do this either with the `.groupby` method, which is straightforward but forces a full shuffle of the data (expensive) or with the harder-to-use but faster `.foldby` method, which does a streaming combined groupby and reduction.
#
# * `groupby`: Shuffles data so that all items with the same key are in the same key-value pair
# * `foldby`: Walks through the data accumulating a result per key
#
# *Note: the full groupby is particularly bad. In actual workloads you would do well to use `foldby` or switch to `DataFrame`s if possible.*
# ### `groupby`
# Groupby collects items in your collection so that all items with the same value under some function are collected together into a key-value pair.
b = db.from_sequence(['Alice', 'Bob', 'Charlie', 'Dan', 'Edith', 'Frank'])
b.groupby(len).compute() # names grouped by length
b = db.from_sequence(list(range(10)))
b.groupby(lambda x: x % 2).compute()
b.groupby(lambda x: x % 2).starmap(lambda k, v: (k, max(v))).compute()
# ### `foldby`
# Foldby can be quite odd at first. It is similar to the following functions from other libraries:
#
# * [`toolz.reduceby`](http://toolz.readthedocs.io/en/latest/streaming-analytics.html#streaming-split-apply-combine)
# * [`pyspark.RDD.combineByKey`](http://abshinn.github.io/python/apache-spark/2014/10/11/using-combinebykey-in-apache-spark/)
#
# When using `foldby` you provide
#
# 1. A key function on which to group elements
# 2. A binary operator such as you would pass to `reduce` that you use to perform reduction per each group
# 3. A combine binary operator that can combine the results of two `reduce` calls on different parts of your dataset.
#
# Your reduction must be associative. It will happen in parallel in each of the partitions of your dataset. Then all of these intermediate results will be combined by the `combine` binary operator.
is_even = lambda x: x % 2
b.foldby(is_even, binop=max, combine=max).compute()
# ### Example with account data
# We find the number of people with the same name.
# %%time
# Warning, this one takes a while...
result = js.groupby(lambda item: item['name']).starmap(lambda k, v: (k, len(v))).compute()
print(sorted(result))
# +
# %%time
# This one is comparatively fast and produces the same result.
from operator import add
def incr(tot, _):
return tot+1
result = js.foldby(key='name',
binop=incr,
initial=0,
combine=add,
combine_initial=0).compute()
print(sorted(result))
# -
# ### Exercise: compute total amount per name
# We want to groupby (or foldby) the `name` key, then add up the all of the amounts for each name.
#
# Steps
#
# 1. Create a small function that, given a dictionary like
#
# {'name': 'Alice', 'transactions': [{'amount': 1, 'id': 123}, {'amount': 2, 'id': 456}]}
#
# produces the sum of the amounts, e.g. `3`
#
# 2. Slightly change the binary operator of the `foldby` example above so that the binary operator doesn't count the number of entries, but instead accumulates the sum of the amounts.
# +
# Your code here...
# -
# ## DataFrames
# For the same reasons that Pandas is often faster than pure Python, `dask.dataframe` can be faster than `dask.bag`. We will work more with DataFrames later, but from for the bag point of view, they are frequently the end-point of the "messy" part of data ingestion—once the data can be made into a data-frame, then complex split-apply-combine logic will become much more straight-forward and efficient.
#
# You can transform a bag with a simple tuple or flat dictionary structure into a `dask.dataframe` with the `to_dataframe` method.
df1 = js.to_dataframe()
df1.head()
# This now looks like a well-defined DataFrame, and we can apply Pandas-like computations to it efficiently.
# Using a Dask DataFrame, how long does it take to do our prior computation of numbers of people with the same name? It turns out that `dask.dataframe.groupby()` beats `dask.bag.groupby()` more than an order of magnitude; but it still cannot match `dask.bag.foldby()` for this case.
# %time df1.groupby('name').id.count().compute().head()
# ### Denormalization
# This DataFrame format is less-than-optimal because the `transactions` column is filled with nested data so Pandas has to revert to `object` dtype, which is quite slow in Pandas. Ideally we want to transform to a dataframe only after we have flattened our data so that each record is a single `int`, `string`, `float`, etc..
# +
def denormalize(record):
# returns a list for every nested item, each transaction of each person
return [{'id': record['id'],
'name': record['name'],
'amount': transaction['amount'],
'transaction-id': transaction['transaction-id']}
for transaction in record['transactions']]
transactions = js.map(denormalize).flatten()
transactions.take(3)
# -
df = transactions.to_dataframe()
df.head()
# %%time
# number of transactions per name
# note that the time here includes the data load and ingestion
df.groupby('name')['transaction-id'].count().compute()
# ## Limitations
# Bags provide very general computation (any Python function.) This generality
# comes at cost. Bags have the following known limitations
#
# 1. Bag operations tend to be slower than array/dataframe computations in the
# same way that Python tends to be slower than NumPy/Pandas
# 2. ``Bag.groupby`` is slow. You should try to use ``Bag.foldby`` if possible.
# Using ``Bag.foldby`` requires more thought. Even better, consider creating
# a normalised dataframe.
|
02_bag.ipynb
|
#
# ## Figuring out Natural Language Processing
# As I have never worked on NLP before, the purpose of this notebook was to play arround with a dataset and try to figure out a bunch of stuff on the subject.
# Here we will be working on the IMDB dataset which provides 50k movies text reviews and their corresponding sentiment "Positive" or "Negative".
#
# Our job will be to find a way to learn some features that can predict the sentiment based on a textual review.
# ### Load the data
# We will be getting the data from my google drive. I have downloaded those data from Kaggle https://www.kaggle.com/lakshmi25npathi/imdb-dataset-of-50k-movie-reviews .
# +
import pandas as pd
import requests
from io import StringIO
orig_url='https://drive.google.com/file/d/1Tl9AMNkExM5mFw3xDuIeZ1RiDIEu4Oci/view?usp=sharing'
file_id = orig_url.split('/')[-2]
dwn_url='https://drive.google.com/uc?export=download&id=' + file_id
url = requests.get(dwn_url).text
csv_raw = StringIO(url)
df_dwnld = pd.read_csv(csv_raw)
df = df_dwnld.copy()
df.head()
# -
df.iloc[0,0]
# ## Cleaning
# Now that we have the data, and displayed some of those data, we know that there is cleaning to be made.
#
# For this analysis, I will assume that numbers are meaningless and that we need only words to predict the sentiment.
# Therefore, we will get rid of :
# * numbers,
# * html tags,
# * uppercases,
# * any special characters
# +
# Remove numbers
df['clean_review'] = df['review'].str.replace('\d+', '')
# Remove any <> and everything inside
df['clean_review'] = df['clean_review'].str.replace('<[^<]+?>', '')
# Remove anything that is not alphanumeric
df['clean_review'] = df['clean_review'].str.replace(r'[^A-Za-z0-9 ]+', '')
# Remove any uppercase character
df['clean_review'] = df['clean_review'].str.lower()
# Remove any one character words
df['clean_review'] = df['clean_review'].str.replace(r'\b\w\b', '')
# Remove multiple spaces
df['clean_review'] = df['clean_review'].str.replace(r'\s+', ' ')
# Strip data
df['clean_review'] = df['clean_review'].str.strip()
df['clean_review'][0]
# -
# ## What direction ?
# Now, we have a text that seems to be way more clean.
#
# Obviously, we will have to create some features out of all these words in order to extract the sentiment.
#
# What I mean by that is that we need to create a standardized framework in which any review could fit. The problem with those textual input is that they are of random sizes, and any model that we might create will need inputs of pre-defined sizes.
#
# What we will be using here is some kind of one-hot-encoding technic. The concept is simple, you take a categorical variable and transform it in vector space. ie:
#
# | category |
# |---|
# | A |
# | B |
# | C |
#
# | A | B | C |
# |---|---|---|
# | 1 | 0 | 0 |
# | 0 | 1 | 0 |
# | 0 | 0 | 1 |
#
# -----------
#
# Here, the columns will be some relevants words that we believe to have predictive power.
#
# In order to find them, let's play arround with the data.
# The columns 'words' will contains a list of all the words in the 'clean' column
df['words_'] = df.clean_review.str.split('\s+')
df.words_[0][:10]
# ## Feature engineering
# Now we will identify ALL the words that have been used and count how many time they have been used.
#
# It is important to split your data in training and testing set. Therefore we will do it right now by spliting the dataset in half and we will be doing ou analysis only on the first half.
# +
# Here we define the lenght of our training set. which will be half of the dataset.
total = x.shape[0]
n = total // 2
dict_count = {}
data = list(df.itertuples(index=False, name=None))
# We will loop only on the first n reviews
for d in data[:n]:
for w in d[3]:
if not w in dict_count:
dict_count[w] = 1
else:
dict_count[w] +=1
df_count = pd.DataFrame(dict_count, index=['Count']).T.sort_values('Count')
df_count.tail()
# -
# ## Stop words problem
# And here we are, the famous stop words problems.
# This was indeed pretty well expected, the words that are the most common will be completely useless in our case.
#
# A good practice is to get rid of them.
# The sklearn library has a english stop word frozen set, we will use it.
#
from sklearn.feature_extraction import stop_words
df_count = df_count.loc[~df_count.index.isin(stop_words.ENGLISH_STOP_WORDS)]
df_count.tail()
# #### Next step
# Now for each of these words, I will add a column to the DataFrame and I want to count how many time each of them appear in each review. This is where we use "some kind" of one-hot-encoding technics as we will not populate with 1 or 0 but with a number of occurence.
# +
top_words = df_count.tail(1500).index.tolist()
# Rename the columns as their name might appear in the list of words
df = df.rename({
"sentiment": '_predict',
"review": "_review"
}, axis=1)
for word in top_words:
df[word] = df.clean_review.str.count(word)
df.head()
# -
# ## Where are the interesting stuff ??
# Alright, now that we have counted everything, why don't we group our data by sentiment, positive or negative, and see if any words appears way more often in a group and not in the other
result = df[['_predict',*top_words]].groupby('_predict').mean().T
result['diff_'] = (result.negative / result.positive) -1
result.diff_.sort_values()
# ### That is interesting
# So here we are, words such as beautiful and wonderful are way more often used in a positive review than in a negative review. And words like worst, and awful are more often used in a negative review.
#
# Again, I believe those results are pretty obvious, that is just common sense. However it still took us less time than coming up with 1500 words by ourself.
#
# By looking at the data so far, I'm assuming that there should be some predictive power in our variable. Let's prepare our data and try to fit a simple model.
predict_df = df[['_predict', *top_words]]
x = predict_df.drop('_predict', axis=1)
y = predict_df['_predict']
y = y.replace({'positive':1,'negative':0})
# +
n_test = total - n
x_train = x.iloc[:n,:].values
y_train = y.iloc[:n].values
x_test = x.iloc[n:,:].values
y_test = y.iloc[n:].values
# -
# ## Standardize the data
# Some learning models require the data to be normalize in some way.
# Here we will just standardize them.
x_train_std = (x_train - x_train.mean(axis=0)) / x_train.std(axis=0)
x_test_std = (x_test - x_train.mean(axis=0)) / x_train.std(axis=0)
# # Learn
# It is time to create our model.
#
# This problem is a classification problem. Therefore we can choose among the following learning technics :
#
# * Linear Models
# * Logistic Regression
# * Support Vector Machines
# * Nonlinear models
# * K-nearest Neighbors (KNN)
# * Kernel Support Vector Machines (SVM)
# * Naïve Bayes
# * Decision Tree Classification
# * Random Forest Classification
#
# For this type of classification problem, I usually run a simple logistic regression as well as a Random forest classification.
# Now, we will just look into the logistic regression
#
# In order to evaluate the quality of our model we will be using the following metrics:
#
# * Accuracy: Correct Predictions / Total predictions
# * Precision: True Positive / (True Positive + False Positive)
# * Recall: True Positive / (True Positive + False Negative)
from sklearn.metrics import confusion_matrix,plot_confusion_matrix, accuracy_score, recall_score, precision_score
def scores(y, y_pred):
precision = precision_score(y, y_pred)
accuracy = accuracy_score(y, y_pred)
recall = recall_score(y, y_pred)
print('-----------------')
print('Precision')
print(precision)
print('-----------------')
print('Accuracy')
print(accuracy)
print('-----------------')
print('Recall')
print(recall)
cnf_mat = confusion_matrix(y,y_pred)
print('-----------------')
print('Confusion Matrix')
print(cnf_mat)
# ## Logistic Regression
#
# This regression is used when the variable to predict is categorical (1 or 0).
#
# For our convenience, we will be using the LogisticRegressionCV class from scikit-learn which is doing the Cross-validation for us.
# What it does is playing with a list of lambda values which defines the strenght of the penalty term and a list of l1_ratios which makes our penalty term closer to either L1 or L2 when using the elasticnet penalty term.
#
# As the default solver only supports the l2 penalty term, we will be fine with that and our CV will decide only which lambda fits better.
#
#
from sklearn.linear_model import LogisticRegressionCV
from sklearn.ensemble import RandomForestClassifier
clf = LogisticRegressionCV()
clf.fit(x_train_std, y_train)
y_pred = clf.predict(x_test_std)
scores(y_test, y_pred)
# The results are pretty good as we have not been doing any extensive feature engineering here.
# On the back of those results, we are now able to read some review that the model was not able to predict and try to identify a pattern that our model can't handle. This would help us improving our feature engineering process.
#
# However, for the purpose of this notebook, I will just stop here. Feel free to play with the data and find better alternatives.
output = df.clean_review.iloc[:n].to_frame()
output.loc[:,'prediction'] = (y_test - y_pred)
# Wrong prediction
output.query('prediction==1').iloc[0,0]
# Wrong prediction
output.query('prediction==-1').iloc[0,0]
# Good prediction
output.query('prediction==-1').iloc[0,0]
|
projects/discovering_nlp/script.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ---
#
# _You are currently looking at **version 1.5** of this notebook. To download notebooks and datafiles, as well as get help on Jupyter notebooks in the Coursera platform, visit the [Jupyter Notebook FAQ](https://www.coursera.org/learn/python-machine-learning/resources/bANLa) course resource._
#
# ---
# # Assignment 2
#
# In this assignment you'll explore the relationship between model complexity and generalization performance, by adjusting key parameters of various supervised learning models. Part 1 of this assignment will look at regression and Part 2 will look at classification.
#
# ## Part 1 - Regression
# First, run the following block to set up the variables needed for later sections.
# +
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
np.random.seed(0)
n = 15
x = np.linspace(0,10,n) + np.random.randn(n)/5
y = np.sin(x)+x/6 + np.random.randn(n)/10
X_train, X_test, y_train, y_test = train_test_split(x, y, random_state=0)
# You can use this function to help you visualize the dataset by
# plotting a scatterplot of the data points
# in the training and test sets.
def part1_scatter():
import matplotlib.pyplot as plt
# %matplotlib notebook
plt.figure()
plt.scatter(X_train, y_train, label='training data')
plt.scatter(X_test, y_test, label='test data')
plt.legend(loc=4);
# NOTE: Uncomment the function below to visualize the data, but be sure
# to **re-comment it before submitting this assignment to the autograder**.
part1_scatter()
# -
# ### Question 1
#
# Write a function that fits a polynomial LinearRegression model on the *training data* `X_train` for degrees 1, 3, 6, and 9. (Use PolynomialFeatures in sklearn.preprocessing to create the polynomial features and then fit a linear regression model) For each model, find 100 predicted values over the interval x = 0 to 10 (e.g. `np.linspace(0,10,100)`) and store this in a numpy array. The first row of this array should correspond to the output from the model trained on degree 1, the second row degree 3, the third row degree 6, and the fourth row degree 9.
#
# <img src="readonly/polynomialreg1.png" style="width: 1000px;"/>
#
# The figure above shows the fitted models plotted on top of the original data (using `plot_one()`).
#
# <br>
# *This function should return a numpy array with shape `(4, 100)`*
def answer_one():
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
np.random.seed(0)
n = 15
x = np.linspace(0,10,n) + np.random.randn(n)/5
y = np.sin(x)+x/6 + np.random.randn(n)/10
X_train, X_test, y_train, y_test = train_test_split(x, y, random_state=0)
# Reshaping for fit_transform
predicted = np.linspace(0,10,100).reshape(-1,1)
X_train = X_train.reshape(-1,1)
degrees = [1,3,6,9]
y_predicted = []
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
# Iterate over all degree levels
for i in degrees:
poly = PolynomialFeatures(degree=i)
xpoly_features = poly.fit_transform(X_train)
#anything done to the training set should be done to the test set
ypoly_features = poly.fit_transform(predicted)
poly_reg_model = LinearRegression()
poly_reg_model.fit(xpoly_features, y_train)
new_prediction = poly_reg_model.predict(ypoly_features)
#append to the y_predicted list
y_predicted.append(new_prediction)
#Converting list to array datatype
y_predicted = np.array(y_predicted)
return y_predicted
# +
# feel free to use the function plot_one() to replicate the figure
# from the prompt once you have completed question one
def plot_one(degree_predictions):
import matplotlib.pyplot as plt
# %matplotlib notebook
plt.figure(figsize=(10,5))
plt.plot(X_train, y_train, 'o', label='training data', markersize=10)
plt.plot(X_test, y_test, 'o', label='test data', markersize=10)
for i,degree in enumerate([1,3,6,9]):
plt.plot(np.linspace(0,10,100), degree_predictions[i], alpha=0.8, lw=2, label='degree={}'.format(degree))
plt.ylim(-1,2.5)
plt.legend(loc=4)
plot_one(answer_one())
# -
# ### Question 2
#
# Write a function that fits a polynomial LinearRegression model on the training data `X_train` for degrees 0 through 9. For each model compute the $R^2$ (coefficient of determination) regression score on the training data as well as the the test data, and return both of these arrays in a tuple.
#
# *This function should return one tuple of numpy arrays `(r2_train, r2_test)`. Both arrays should have shape `(10,)`*
def answer_two():
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
np.random.seed(0)
n = 15
x = np.linspace(0,10,n) + np.random.randn(n)/5
y = np.sin(x)+x/6 + np.random.randn(n)/10
X_train, X_test, y_train, y_test = train_test_split(x, y, random_state=0)
# Reshaping for fit_transform
X_train = X_train.reshape(-1,1)
X_test = X_test.reshape(-1,1)
degrees = [*range(10)]
r2_train, r2_test = [],[]
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics.regression import r2_score
# Iterate over all degree levels
for i in degrees:
poly = PolynomialFeatures(degree=i)
train_poly_features = poly.fit_transform(X_train)
test_poly_features = poly.fit_transform(X_test)
poly_reg_model = LinearRegression()
train = poly_reg_model.fit(train_poly_features, y_train)
train_score = train.score(train_poly_features, y_train)
r2_train.append(train_score)
test_score = train.score(test_poly_features, y_test)
r2_test.append(test_score)
#Converting list to array datatype
r2_train, r2_test = np.array(r2_train), np.array(r2_test)
return (r2_train, r2_test)
# ### Question 3
#
# Based on the $R^2$ scores from question 2 (degree levels 0 through 9), what degree level corresponds to a model that is underfitting? What degree level corresponds to a model that is overfitting? What choice of degree level would provide a model with good generalization performance on this dataset?
#
# Hint: Try plotting the $R^2$ scores from question 2 to visualize the relationship between degree level and $R^2$. Remember to comment out the import matplotlib line before submission.
#
# *This function should return one tuple with the degree values in this order: `(Underfitting, Overfitting, Good_Generalization)`. There might be multiple correct solutions, however, you only need to return one possible solution, for example, (1,2,3).*
def answer_three():
# Your code here
return # Return your answer
# ### Question 4
#
# Training models on high degree polynomial features can result in overly complex models that overfit, so we often use regularized versions of the model to constrain model complexity, as we saw with Ridge and Lasso linear regression.
#
# For this question, train two models: a non-regularized LinearRegression model (default parameters) and a regularized Lasso Regression model (with parameters `alpha=0.01`, `max_iter=10000`) both on polynomial features of degree 12. Return the $R^2$ score for both the LinearRegression and Lasso model's test sets.
#
# *This function should return one tuple `(LinearRegression_R2_test_score, Lasso_R2_test_score)`*
def answer_four():
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import Lasso, LinearRegression
from sklearn.metrics.regression import r2_score
# Your code here
return # Your answer here
# ## Part 2 - Classification
#
# Here's an application of machine learning that could save your life! For this section of the assignment we will be working with the [UCI Mushroom Data Set](http://archive.ics.uci.edu/ml/datasets/Mushroom?ref=datanews.io) stored in `readonly/mushrooms.csv`. The data will be used to train a model to predict whether or not a mushroom is poisonous. The following attributes are provided:
#
# *Attribute Information:*
#
# 1. cap-shape: bell=b, conical=c, convex=x, flat=f, knobbed=k, sunken=s
# 2. cap-surface: fibrous=f, grooves=g, scaly=y, smooth=s
# 3. cap-color: brown=n, buff=b, cinnamon=c, gray=g, green=r, pink=p, purple=u, red=e, white=w, yellow=y
# 4. bruises?: bruises=t, no=f
# 5. odor: almond=a, anise=l, creosote=c, fishy=y, foul=f, musty=m, none=n, pungent=p, spicy=s
# 6. gill-attachment: attached=a, descending=d, free=f, notched=n
# 7. gill-spacing: close=c, crowded=w, distant=d
# 8. gill-size: broad=b, narrow=n
# 9. gill-color: black=k, brown=n, buff=b, chocolate=h, gray=g, green=r, orange=o, pink=p, purple=u, red=e, white=w, yellow=y
# 10. stalk-shape: enlarging=e, tapering=t
# 11. stalk-root: bulbous=b, club=c, cup=u, equal=e, rhizomorphs=z, rooted=r, missing=?
# 12. stalk-surface-above-ring: fibrous=f, scaly=y, silky=k, smooth=s
# 13. stalk-surface-below-ring: fibrous=f, scaly=y, silky=k, smooth=s
# 14. stalk-color-above-ring: brown=n, buff=b, cinnamon=c, gray=g, orange=o, pink=p, red=e, white=w, yellow=y
# 15. stalk-color-below-ring: brown=n, buff=b, cinnamon=c, gray=g, orange=o, pink=p, red=e, white=w, yellow=y
# 16. veil-type: partial=p, universal=u
# 17. veil-color: brown=n, orange=o, white=w, yellow=y
# 18. ring-number: none=n, one=o, two=t
# 19. ring-type: cobwebby=c, evanescent=e, flaring=f, large=l, none=n, pendant=p, sheathing=s, zone=z
# 20. spore-print-color: black=k, brown=n, buff=b, chocolate=h, green=r, orange=o, purple=u, white=w, yellow=y
# 21. population: abundant=a, clustered=c, numerous=n, scattered=s, several=v, solitary=y
# 22. habitat: grasses=g, leaves=l, meadows=m, paths=p, urban=u, waste=w, woods=d
#
# <br>
#
# The data in the mushrooms dataset is currently encoded with strings. These values will need to be encoded to numeric to work with sklearn. We'll use pd.get_dummies to convert the categorical variables into indicator variables.
# +
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
mush_df = pd.read_csv('mushrooms.csv')
mush_df2 = pd.get_dummies(mush_df)
X_mush = mush_df2.iloc[:,2:]
y_mush = mush_df2.iloc[:,1]
# use the variables X_train2, y_train2 for Question 5
X_train2, X_test2, y_train2, y_test2 = train_test_split(X_mush, y_mush, random_state=0)
# For performance reasons in Questions 6 and 7, we will create a smaller version of the
# entire mushroom dataset for use in those questions. For simplicity we'll just re-use
# the 25% test split created above as the representative subset.
#
# Use the variables X_subset, y_subset for Questions 6 and 7.
X_subset = X_test2
y_subset = y_test2
# -
# ### Question 5
#
# Using `X_train2` and `y_train2` from the preceeding cell, train a DecisionTreeClassifier with default parameters and random_state=0. What are the 5 most important features found by the decision tree?
#
# As a reminder, the feature names are available in the `X_train2.columns` property, and the order of the features in `X_train2.columns` matches the order of the feature importance values in the classifier's `feature_importances_` property.
#
# *This function should return a list of length 5 containing the feature names in descending order of importance.*
#
# *Note: remember that you also need to set random_state in the DecisionTreeClassifier.*
def answer_five():
from sklearn.tree import DecisionTreeClassifier
# Your code here
return # Your answer here
# ### Question 6
#
# For this question, we're going to use the `validation_curve` function in `sklearn.model_selection` to determine training and test scores for a Support Vector Classifier (`SVC`) with varying parameter values. Recall that the validation_curve function, in addition to taking an initialized unfitted classifier object, takes a dataset as input and does its own internal train-test splits to compute results.
#
# **Because creating a validation curve requires fitting multiple models, for performance reasons this question will use just a subset of the original mushroom dataset: please use the variables X_subset and y_subset as input to the validation curve function (instead of X_mush and y_mush) to reduce computation time.**
#
# The initialized unfitted classifier object we'll be using is a Support Vector Classifier with radial basis kernel. So your first step is to create an `SVC` object with default parameters (i.e. `kernel='rbf', C=1`) and `random_state=0`. Recall that the kernel width of the RBF kernel is controlled using the `gamma` parameter.
#
# With this classifier, and the dataset in X_subset, y_subset, explore the effect of `gamma` on classifier accuracy by using the `validation_curve` function to find the training and test scores for 6 values of `gamma` from `0.0001` to `10` (i.e. `np.logspace(-4,1,6)`). Recall that you can specify what scoring metric you want validation_curve to use by setting the "scoring" parameter. In this case, we want to use "accuracy" as the scoring metric.
#
# For each level of `gamma`, `validation_curve` will fit 3 models on different subsets of the data, returning two 6x3 (6 levels of gamma x 3 fits per level) arrays of the scores for the training and test sets.
#
# Find the mean score across the three models for each level of `gamma` for both arrays, creating two arrays of length 6, and return a tuple with the two arrays.
#
# e.g.
#
# if one of your array of scores is
#
# array([[ 0.5, 0.4, 0.6],
# [ 0.7, 0.8, 0.7],
# [ 0.9, 0.8, 0.8],
# [ 0.8, 0.7, 0.8],
# [ 0.7, 0.6, 0.6],
# [ 0.4, 0.6, 0.5]])
#
# it should then become
#
# array([ 0.5, 0.73333333, 0.83333333, 0.76666667, 0.63333333, 0.5])
#
# *This function should return one tuple of numpy arrays `(training_scores, test_scores)` where each array in the tuple has shape `(6,)`.*
def answer_six():
from sklearn.svm import SVC
from sklearn.model_selection import validation_curve
# Your code here
return # Your answer here
# ### Question 7
#
# Based on the scores from question 6, what gamma value corresponds to a model that is underfitting (and has the worst test set accuracy)? What gamma value corresponds to a model that is overfitting (and has the worst test set accuracy)? What choice of gamma would be the best choice for a model with good generalization performance on this dataset (high accuracy on both training and test set)?
#
# Hint: Try plotting the scores from question 6 to visualize the relationship between gamma and accuracy. Remember to comment out the import matplotlib line before submission.
#
# *This function should return one tuple with the degree values in this order: `(Underfitting, Overfitting, Good_Generalization)` Please note there is only one correct solution.*
def answer_seven():
# Your code here
return # Return your answer
|
Assignments Submitted/Week 2/Assignment+2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Notebook Template
#
# This Notebook is stubbed out with some project paths, loading of enviroment variables, and common package imports to speed up the process of starting a new project.
#
# It is highly recommended you copy and rename this notebook following the naming convention outlined in the readme of naming notebooks with a double number such as `01-first-thing`, and `02-next-thing`. This way the order of notebooks is apparent, and each notebook does not need to be needlesssly long, complex, and difficult to follow.
# +
import importlib
import os
from pathlib import Path
import sys
from arcgis.features import GeoAccessor, GeoSeriesAccessor
from arcgis.gis import GIS
from dotenv import load_dotenv, find_dotenv
import pandas as pd
# import arcpy if available
if importlib.util.find_spec("arcpy") is not None:
import arcpy
# +
# paths to common data locations - NOTE: to convert any path to a raw string, simply use str(path_instance)
dir_prj = Path.cwd().parent
dir_data = dir_prj/'data'
dir_raw = dir_data/'raw'
dir_ext = dir_data/'external'
dir_int = dir_data/'interim'
dir_out = dir_data/'processed'
gdb_raw = dir_raw/'raw.gdb'
gdb_int = dir_int/'interim.gdb'
gdb_out = dir_out/'processed.gdb'
# import the project package from the project package path - only necessary if you are not using a unique environemnt for this project
sys.path.append(str(dir_prj/'src'))
import river_levels
# load the "autoreload" extension so that code can change, & always reload modules so that as you change code in src, it gets loaded
# %load_ext autoreload
# %autoreload 2
# load environment variables from .env
load_dotenv(find_dotenv())
# create a GIS object instance; if you did not enter any information here, it defaults to anonymous access to ArcGIS Online
gis = GIS(
url=os.getenv('ESRI_GIS_URL'),
username=os.getenv('ESRI_GIS_USERNAME'),
password=None if len(os.getenv('ESRI_GIS_PASSWORD')) is 0 else os.getenv('ESRI_GIS_PASSWORD')
)
gis
# -
# Licensing
#
# Copyright 2020 Esri
#
# Licensed under the Apache License, Version 2.0 (the "License"); You
# may not use this file except in compliance with the License. You may
# obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or
# implied. See the License for the specific language governing
# permissions and limitations under the License.
#
# A copy of the license is available in the repository's
# LICENSE file.
|
notebooks/notebook-template.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/futureCodersSE/python-fundamentals/blob/main/Operators1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="3O7iro_BV0mL"
# # Operators - arithmetic
#
# ---
# + [markdown] id="Nk7bg_hfLzu7"
# In Python, we can use the following arithmetic operators:
#
# 
#
#
#
#
#
#
#
#
#
#
# + [markdown] id="ohKiZuy-OnDN"
# ---
# ### Exercise 1 - multiplication of integers
# Write a function called **print_dog_human_age()** which will:
#
# * ask the user to input their dog's age and assign this to an integer variable called **dog_age**
# * calculate the dog’s age in human years by multiplying it by 7, assigning it to a new variable called **dog_human_age**
# * print the age in human years (`dog_human_age`)
#
# Test Input:
# 4
#
# Expected output:
# 28
#
# + id="kWpM2m4nO7Ir"
# + [markdown] id="fvxtRRcfOnGr"
# ---
# ### Exercise 2 - BIDMAS
# Write a function called **calculate_average()** which will:
#
# * ask the user for 3 seperate numbers, **num1**, **num2**, **num3**
# * calculate the **average** of the three numbers
# * print the `average`, rounded to 2 decimal places
#
# *Hint 1: to round a number, use round(), e.g. round(`average`) *
# *Hint 2: remember the BIDMAS order of operators and use brackets to change the order if necessary.*
#
# Test Input:
# 3
# 5
# 9
#
# Expected output:
# 5.67
# + id="jYtLq8olPRZM"
# + [markdown] id="r9w0fiW-PR2D"
# ---
# ### Exercise 3 - BIDMAS
#
# Write a function called **calculate_avg_height()** which will:
#
# * ask the user to input their **height**
# * convert `height` to **height_centimeters** (multiply by 100)
# * print `height_centimeters`
#
# *Remember, height in metres is usually a decimal, so data type matters*
#
# Test Input:
# 1.67
#
# Expected output:
# 167
#
# + id="2dMgvQlUPirV"
# + [markdown] id="QTprQ2zhPi9L"
# ---
# ### Exercise 4 - float and formatting printing
#
# At the time of writing, the exchange rate from Pounds (£) to Euros (€) is 1.16 (£1 = €1.16).
#
# Write a function called **convert_currency(**) which will:
#
# * ask a user to input an amount in **pounds**
# * calculate the equivalent number of **euros**
# * print `euros`, rounded to 2 decimal places
#
# Test Input:
# £60
#
# Expected output:
# €69.6
#
# *Remember, pounds is likely to be a decimal number and that the user should not enter the £ sign.*
# + id="DXqxS75kQWOm"
# + [markdown] id="Eur4tRWUQWYL"
# ---
# ### Exercise 5 - rounding
#
# Write a function called **calculate_stats()** which will:
#
# * assign the numbers 3.145, 5.6723 and 9.34 to the variables **num1**, **num2** and **num3** respectively
# * calculate the **total** of the three numbers, rounded to 2 decimal places
# * calculate the **average** of the numbers, rounded to 3 decimal places
# * print `total` and `average` in a message that labels them.
#
# Expected output:
#
# The total of the three numbers is 18.16
# The average of the three numbers is 6.053
#
# *Remember to calculate the average you divide the total by the quantity of numbers, e.g. total/3*
#
# + id="pD1lMOhuRZvd"
# + [markdown] id="jsV3uF5aRZ56"
# ---
# ### Exercise 6 - calculating volume
#
# Bill is moving house. He needs to know how much space his cardboard packing boxes have.
#
# Write a function called **calculate_volume()** which will:
#
# * assign the value 3.2, 5.6 and 7.8 to the variables **base**, **width** and **height** respectively
# * calculate the **box_volume** rounded to 1 decimal place
# * print the `box_volume`
#
# *Hint: volume = base x width x height*
#
# Expected output:
# 139.8
#
# + id="WVLFFYayRwcN"
# + [markdown] id="Apy8QqKIB3_c"
# ---
# ***Floor Division***
# *So far, we have been using standard arithmetic operators. If we would like to divide without remainders (eg. no decimals) we can use floor division using the // operator. This will always round down*.
#
# *For example*:
# *42/8 = 5.75*
# *BUT*
# 4*2//8 = 5*
# + [markdown] id="eGo_VENXRwo0"
# ---
# ### Exercise 7 - calculating with volumes
#
# Bill needs to work out how many boxes he will need.
#
# Building on what you did in the last exercise, write a function called **calculate_boxes(base, width, height)** which will:
#
# * calculate the volume of a box, using the **base**, **width** and **height** supplied in the brackets
# * ask Bill for the **total_volume** of his stuff
# * calculate the total **number_of_boxes** he will need, and print the `number_of_boxes`
#
# *Hint: the `total` will not be a decimal number - you should use floor division and add one to the answer (for the box that will have the leftovers).*
#
# Test Input:
# 1500
#
# Expected output:
# 11
#
# + id="0X6TKFubSIpT"
def calculate_boxes(base, width, height):
# add your code below here to calculate the boxVolume, ask for totalVolume and calculate number of boxes
calculate_boxes(3.2, 5.6, 7.8)
# + [markdown] id="paxj6AccSIwy"
# ---
# ### Exercise 8 - floor division
#
# Write a function called **calculate_parcel_weight()** which will:
#
# * ask the user to enter the weights, in kg, of four parcels (**weight1, weight2, weight3, weight4**)
# * calculate the total **parcel_weight** and display this in a whole number of kg, rounded up
# * print the `parcel_weight`
#
# *Hint: round() could either round up or down. Floor division could be a better option*
#
# Test Inputs:
# 1.23
# 2.84
# 1.675
# 3.03
#
# Expected output:
# 9kg
#
# + id="Lulkpg6rStwT"
# + [markdown] id="SduMAQwsXKiA"
# ---
# ### Exercise 9 - modulus
#
# Write a function called **get_pm_minutes()** which will:
#
# * ask the user to enter an afternoon **time** in 24 hour clock (e.g. 1350)
# * use floor division to get the **hour** (ie divide by 100)
# * use modulus to get the **minutes**
# * subtract 12 to get the 12 hour clock storing the result back in `hour`
# * print a message to say that It is `minutes` minutes past `hour` PM
#
# Test Input:
# 1350
#
# Expected output:
# It is 50 minutes past 1 PM
#
# *(Is it possible to use this code to get the right hour for a morning time? You will do this in the section that allows selection depending on value)*
#
#
# + id="dSxM7C1dXK9g"
# + [markdown] id="HUwYL72HSt5b"
# ---
# ### Exercise 10 - How many tins of beans?
#
# Write a function called **calculate_tins()** that will calculate how many tins of beans will fit in a cardboard box. Bean tins are *11cm tall* and *8cm* diameter. All tins will be standing up and can be stacked in layers.
#
# * use the **height**, **width** and **depth** of the box supplied in the function’s brackets.
# * calculate the **number_of_tins** that can fit in the box
# * print the `number_of_tins` that can fit
#
# *Hint: you will need to calculate the number of layers, and the number that will fit in each direction, the product (all of the numbers multiplied together) will tell you how many tins. All answers must be whole numbers*
#
#
# Expected output:
# 24 tins will fit in this box
#
# + id="HNTLnqrDVdAW"
def calculate_tins(height, width, depth):
# add your code below here
calculate_tins(24, 50, 18)
|
Operators1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # High-level CNTK Example
# + tags=["parameters"]
# Parameters
EPOCHS = 10
N_CLASSES=10
BATCHSIZE = 64
LR = 0.01
MOMENTUM = 0.9
GPU = True
LOGGER_URL='msdlvm.southcentralus.cloudapp.azure.com'
LOGGER_USRENAME='admin'
LOGGER_PASSWORD='password'
LOGGER_DB='gpudata'
LOGGER_SERIES='gpu'
# +
import numpy as np
import os
import sys
import cntk
from cntk.layers import Convolution2D, MaxPooling, Dense, Dropout
from os import path
from utils import cifar_for_library, yield_mb, create_logger, Timer
from gpumon.influxdb import log_context
from influxdb import InfluxDBClient
# -
client = InfluxDBClient(LOGGER_URL, 8086, LOGGER_USRENAME, LOGGER_PASSWORD, LOGGER_DB)
node_id = os.getenv('AZ_BATCH_NODE_ID', default='node')
task_id = os.getenv('AZ_BATCH_TASK_ID', default='cntk')
job_id = os.getenv('AZ_BATCH_JOB_ID', default='cntk')
logger = create_logger(client, node_id=node_id, task_id=task_id, job_id=job_id)
print("OS: ", sys.platform)
print("Python: ", sys.version)
print("Numpy: ", np.__version__)
print("CNTK: ", cntk.__version__)
data_path = path.join(os.getenv('AZ_BATCHAI_INPUT_DATASET'), 'cifar-10-batches-py')
def create_network():
# Weight initialiser from uniform distribution
# Activation (unless states) is None
with cntk.layers.default_options(init = cntk.glorot_uniform(), activation = cntk.relu):
x = Convolution2D(filter_shape=(3, 3), num_filters=50, pad=True)(features)
x = Convolution2D(filter_shape=(3, 3), num_filters=50, pad=True)(x)
x = MaxPooling((2, 2), strides=(2, 2), pad=False)(x)
x = Dropout(0.25)(x)
x = Convolution2D(filter_shape=(3, 3), num_filters=100, pad=True)(x)
x = Convolution2D(filter_shape=(3, 3), num_filters=100, pad=True)(x)
x = MaxPooling((2, 2), strides=(2, 2), pad=False)(x)
x = Dropout(0.25)(x)
x = Dense(512)(x)
x = Dropout(0.5)(x)
x = Dense(N_CLASSES, activation=None)(x)
return x
def init_model(m):
# Loss (dense labels); check if support for sparse labels
loss = cntk.cross_entropy_with_softmax(m, labels)
# Momentum SGD
# https://github.com/Microsoft/CNTK/blob/master/Manual/Manual_How_to_use_learners.ipynb
# unit_gain=False: momentum_direction = momentum*old_momentum_direction + gradient
# if unit_gain=True then ...(1-momentum)*gradient
learner = cntk.momentum_sgd(m.parameters,
lr=cntk.learning_rate_schedule(LR, cntk.UnitType.minibatch) ,
momentum=cntk.momentum_schedule(MOMENTUM),
unit_gain=False)
trainer = cntk.Trainer(m, (loss, cntk.classification_error(m, labels)), [learner])
return trainer
# %%time
# Data into format for library
x_train, x_test, y_train, y_test = cifar_for_library(data_path, channel_first=True, one_hot=True)
# CNTK format
y_train = y_train.astype(np.float32)
y_test = y_test.astype(np.float32)
print(x_train.shape, x_test.shape, y_train.shape, y_test.shape)
print(x_train.dtype, x_test.dtype, y_train.dtype, y_test.dtype)
# %%time
# Placeholders
features = cntk.input_variable((3, 32, 32), np.float32)
labels = cntk.input_variable(N_CLASSES, np.float32)
# Load symbol
sym = create_network()
# %%time
trainer = init_model(sym)
with Timer() as t:
with log_context(LOGGER_URL, LOGGER_USRENAME, LOGGER_PASSWORD, LOGGER_DB, LOGGER_SERIES,
node_id=node_id, task_id=task_id, job_id=job_id):
# Train model
for j in range(EPOCHS):
for data, label in yield_mb(x_train, y_train, BATCHSIZE, shuffle=True):
trainer.train_minibatch({features: data, labels: label})
# Log (this is just last batch in epoch, not average of batches)
eval_error = trainer.previous_minibatch_evaluation_average
print("Epoch %d | Accuracy: %.6f" % (j+1, (1-eval_error)))
print('Training took %.03f sec.' % t.interval)
logger('training duration', value=t.interval)
# %%time
# Predict and then score accuracy
# Apply softmax since that is only applied at training
# with cross-entropy loss
z = cntk.softmax(sym)
n_samples = (y_test.shape[0]//BATCHSIZE)*BATCHSIZE
y_guess = np.zeros(n_samples, dtype=np.int)
y_truth = np.argmax(y_test[:n_samples], axis=-1)
c = 0
for data, label in yield_mb(x_test, y_test, BATCHSIZE):
predicted_label_probs = z.eval({features : data})
y_guess[c*BATCHSIZE:(c+1)*BATCHSIZE] = np.argmax(predicted_label_probs, axis=-1)
c += 1
acc=sum(y_guess == y_truth)/len(y_guess)
print("Accuracy: ", acc)
logger('accuracy', value=acc)
|
{{cookiecutter.repo_name}}/exec_src/CNTK_CIFAR.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.0.1
# language: julia
# name: julia-1.0
# ---
# # Quantum Harmonic Osscilator
# ### <NAME>
# ### Prerequisites: Quantum Mechanics
# <b>Slinkies</b>. They started out as toys. I still have one to play with on my desk.
# <b>Rubber bands</b> What was once something useful, is now a wonderful projectile weapon.
# <b> Swings</b> I still love them, but people seem to not make them in adult sizes for some reason.
#
# A person's perception of these objects start to change as they enter their first physics class. Even in that beginning classical mechanics, the problems are filled with harmonic osscilators, like slinkies, rubber bands, or swings, which exert a force proportional to their displacement
# \begin{equation}
# F=-kx
# \end{equation}
# and therefore a quadratic potential
# \begin{equation}
# V(x)=\frac{1}{2} k x^2
# \end{equation}
#
# This is all extremely fun and useful in the classical regime, but we add Quantum Mechanics to the mix, and LOW AND BEHOLD! we have one of the few exactly solvable models in Quantum Mechanics. Moreso, this solution demonstrates some extremely important properties of quantum mechanical systems.
#
# ##### The Hamiltonian
# \begin{equation}
# {\cal H}= \frac{p^2}{2 m} + \frac{1}{2} m \omega ^2 x^2
# \end{equation}
#
# ##### The Solution
# \begin{equation}
# \Psi (x) = \frac{1}{\sqrt{2^n n!}} \left(\frac{m \omega}{\hbar \pi}\right)^{1/4} \mathrm{e}^{-m \omega x^2/2 \hbar} H_n \left( \sqrt{\frac{m \omega}{\hbar}} x \right)
# \end{equation}
# Today, I just intend to present the form of the solution, calculate this equation numerically, and visualize the results. If you wish to know how the equation is derived, you can find a standard quantum mechanics textbook, or stay tuned till I manage to write it up.
#
# ### Physicists' Hermite Polynomials
# Note: These are not the same as the "probabilists' Hermite Polynomial". The two functions differ by scaling factors.
#
# Physicists' Hermite polynomials are defined as eigenfunctions for the differential equation
# \begin{equation}
# u^{\prime \prime}-2xu^{\prime} = -2 \lambda u
# \end{equation}
#
# \begin{equation}
# H_n(x) = (-1)^n \mathrm{e}^{x^2} \frac{\mathrm{d}^n}{\mathrm{d}x^n}
# \left( e^{-x^2} \right)
# \end{equation}
#
# I leave it as an exercise to the reader (muahahahaha) to
# * demonstrate othogonality with respect to the measure $e^{-x^2}$, ie
# \begin{equation}
# \int_{-\infty}^{\infty} H_m(x) H_n(x) e^{-x^2} \mathrm{d}x = \sqrt{\pi} 2^n n! \delta_{mn}
# \end{equation}
# * demonstrate completeness. This means we can describe every function by a linear combination of Hermite polynomials, provided it is suitably well behaved.
#
#
# Though a formula exists or calculating a function at n directly, the most efficient method at low n for calculating polynomials relies on recurrence relationships. These recurrence relationships will also be quite handy if you ever need to show orthogonality, or expectation values.
# ##### Recurrence Relations
# \begin{equation}
# H_{n+1}(x) = 2xH_n(x) - H^{\prime}_n(x)
# \end{equation}
# \begin{equation}
# H^{\prime}_n(x) = 2n H_{n-1}(x)
# \end{equation}
# \begin{equation}
# H_{n+1}(x) = 2x H_n(x) - 2n H_{n-1}(x)
# \end{equation}
using Pkg
Pkg.add("Roots")
using Roots;
using Plots
gr()
# #### Programming Tip!
# Since Hermite polynomials are generated recursively, I wanted to generate and save all the functions up to a designated value at once. In order to do so, I created an array, whose values are anonymous functions.
function GenerateHermite(n)
Hermite=Function[]
push!(Hermite,x->1);
push!(Hermite,x->2*x);
for ni in 3:n
push!(Hermite,x->2*x.*Hermite[ni-1](x)-2*n.*Hermite[ni-2](x))
end
return Hermite
end
# So lets generate some Hermite polynomials and look at them.
# <b> Make sure you don't call a Hermite you haven't generated yet!
Hermite=GenerateHermite(5)
# #### Programming Tip!
# Since the Hermite polynomials, and the wavefunctions after them, are composed on anonymous functions, we need to use `map(f,x)` in order to map the function `f` onto the array `x`. Otherwise our polynomials only work on single values.
x=collect(-2:.01:2);
plot(ylims=(-50,50))
for j in 1:5
plot!(x,map(Hermite[j],x),label="H_$j (x)")
end
plot!()
# +
# Lets make our life easy and set all units to 1
m=1
ω=1
ħ=1
#Finally, we define Ψ
Ψ(n,x)=1/sqrt(factorial(n)*2^n)*(m*ω/(ħ*π))^(1/4)*exp(-m*ω*x^2/(2*ħ))*Hermite[n](sqrt(m*ω/ħ)*x)
# -
# ### Finding Zeros
# The eigenvalue maps to the number of zeros in the wavefunction. Below, I use Julia's roots package to indentify roots on the interval from -3 to 3.
zeds=Array{Array{Float64}}(undef,1)
zeds[1]=[] #ground state has no zeros
for j in 2:4
push!(zeds,fzeros(y->Ψ(j,y),-3,3))
end
zeds[3]
# +
# AHHHHH! So Much code!
# Don't worry; it's all just plotting
x=collect(-3:.01:3) #Set some good axes
plot(xlim=(-3,3),ylim=(-.5,4.5))
for j in 1:4 #how many do you want to view?
plot!(x,map.(y->Ψ(j,y),x).+j.-1,label="| $j >")
plot!(x,(j-1)*ones(length(x)),
color="black",label="")
scatter!(zeds[j],(j-1)*ones(length(zeds[j])),
label="")
end
plot!(x,.5*m*ω^2*x.^2,label="Potential")
scatter!([],[],label="Zeros")
plot!(xlabel="x",ylabel="Ψ+n",
title="Eigenstates of a Harmonic Osscilator")
# -
# ## Example Result
#
# 
#
# ## More to come
# This barely scratched the surface into the richness that can be seen in the quantum harmonic osscilator. Here, just we developed a way for calculating the functions, and visualized the results. Stay tuned to hear here about ground state energy, ladder operators, and atomic trapping.
|
Prerequisites/QHO.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:py38] *
# language: python
# name: conda-env-py38-py
# ---
# # Model/Reanalysis SST
# ## Data Sources and Description
#
# There are lots of sst products - either derived from sat data or gridded from insitu data or modelled or some combination.
#
# Best to focus on just a few: Sat product (OISST), Highres product (MUR) and non-US product (UKMet)
#
# Retrieve regional subsets of SST including any error and ice information (these should be in seperate datasets?).
#
# An ultimate dataset would have each drifter/ship/other point collocated with the one datapoint from the models)
#
# +
#avhrr only data from ncei - this is highres oi V2.1 data - 0.25deg resolution
erddap_path_avhrr_only="https://coastwatch.pfeg.noaa.gov/erddap/griddap/ncdcOisst2Agg"
erddap_path_hroisst="https://coastwatch.pfeg.noaa.gov/erddap/griddap/ncdcOisst21Agg" #newer v2.1
#avhrr+amsr data is available for 2002-2011 from ncei
erddap_path_avhrramsre="https://coastwatch.pfeg.noaa.gov/erddap/griddap/ncdcOisst2AmsrAgg" #version 2... not 2.1 if one exists
#gh1sst data - ROMS from JPL - .01deg
erddap_path_ghsst="https://coastwatch.pfeg.noaa.gov/erddap/griddap/jplG1SST" #project not encouraged via coastwatch - push for MUR
# JPL MUR - OI using wavelets... theres a .01deg and .25 (not on coastwatch erddap)
erddap_path_ghsst="https://coastwatch.pfeg.noaa.gov/erddap/griddap/jplMURSST41"
# https://podaac-tools.jpl.nasa.gov/drive/files/allData/ghrsst/data/GDS2/L4/GLOB/JPL/MUR25/v4.2
#blended product from Remote Sensing Systems http://www.remss.com/ - does not span entire time series
erddap_path_blended = "https://coastwatch.pfeg.noaa.gov/erddap/griddap/erdG1ssta1day"
#gh1sst data - UKMET 0.05deg resolution
erddap_UKMET= "https://coastwatch.pfeg.noaa.gov/erddap/griddap/jplUKMO_OSTIAv20"
# -
# ## General Modelset Details
#
# (PSL - https://psl.noaa.gov/data/gridded/tables/sst.html)
# (JPL - https://podaac.jpl.nasa.gov)
#
# NCEP OISSTV2 - 0.25deg resolution (0:360 degE)
# + lots of good details on this page (https://www.ncdc.noaa.gov/oisst/optimum-interpolation-sea-surface-temperature-oisst-v21 and https://www.ncei.noaa.gov/metadata/geoportal/rest/metadata/item/gov.noaa.ncdc:C01606/html)
# + (podaac doesn't have it?)
#
# JPL MUR - 0.01deg resolution https://podaac.jpl.nasa.gov/dataset/MUR-JPL-L4-GLOB-v4.1 (there is a 0.25deg version too... v4.2) : uses nighttime skin/subkin temps and "The ice concentration data are from the archives at the EUMETSAT Ocean and Sea Ice Satellite Application Facility (OSI SAF) High Latitude Processing Center and are also used for an improved SST parameterization for the high-latitudes."
#
# UKMET - (via jpl) - 0.05deg resolution (-180:180 degE)
#
# Canadian Model - 0.1 or 0.2deg resolution (not on coastwatch erddap) - https://podaac.jpl.nasa.gov/dataset/CMC0.1deg-CMC-L4-GLOB-v3.0?ids=Keywords:Processing%20Levels&values=Oceans:Ocean%20Temperature::4%20-%20Gridded%20Model%20Output)
#
# REMSS V5 SST (no in-situ data used)
# https://podaac.jpl.nasa.gov/dataset/MW_OI-REMSS-L4-GLOB-v5.0?ids=Keywords:Processing%20Levels&values=Oceans:Ocean%20Temperature::4%20-%20Gridded%20Model%20Output
#
# and a subskin AMSRE satellite retrieval dataset - https://podaac.jpl.nasa.gov/dataset/AMSR2-REMSS-L3U-v8a?ids=Keywords&values=Oceans:Ocean%20Temperature:Sea%20Surface%20Temperature
# or
# maybe use the AMSRE+AVHRR datasets?
# or
# a modis dataset? (https://coastwatch.pfeg.noaa.gov/erddap/griddap/erdMH1sstd1dayR20190SQ)
#
# ## SUBSET FOR 2010+ ONLY
#
# ***Dataset/Programming Note:***
#
# Xarray's `open_dataset` function lazyloads and allows exploration, `load_dataset` pulls it to memory and `da.sel().load()` will load a subset to memory. If the data has to be retrieved every datapoint, that will take forever. Local loading of data is more convenient by far.
#
# **ADVICE:**
# Either call via erddap a subset location over a year and process expected in-situ data (works well for argos_NRT datasets) _or_ download dataset locally to work from so there is no network call.
import xarray as xa
#four times a year breakdown - run on system with strong memory or network speed
xa_UKMET = xa.open_dataset(erddap_UKMET)
for i in range(2010,2011,1):
print(i)
xa_UKMET_subset = xa_UKMET.sel(time=slice(str(i)+'-01-01',str(i)+'-3-30'),
latitude=slice(57,90),longitude=slice(-180,-150)).load()
xa_UKMET_subset.to_netcdf('NBS_CK_UKMET_'+str(i)+'.0.nc')
xa_UKMET_subset = xa_UKMET.sel(time=slice(str(i)+'-04-01',str(i)+'-6-30'),
latitude=slice(57,90),longitude=slice(-180,-150)).load()
xa_UKMET_subset.to_netcdf('NBS_CK_UKMET_'+str(i)+'.1.nc')
xa_UKMET_subset = xa_UKMET.sel(time=slice(str(i)+'-07-01',str(i)+'-9-30'),
latitude=slice(57,90),longitude=slice(-180,-150)).load()
xa_UKMET_subset.to_netcdf('NBS_CK_UKMET_'+str(i)+'.2.nc')
xa_UKMET_subset = xa_UKMET.sel(time=slice(str(i)+'-10-01',str(i)+'-12-31'),
latitude=slice(57,90),longitude=slice(-180,-150)).load()
xa_UKMET_subset.to_netcdf('NBS_CK_UKMET_'+str(i)+'.3.nc')
xa_UKMET_subset
#open_dataset vs load_dataset
erddap_path_hroisst="http://coastwatch.pfeg.noaa.gov/erddap/griddap/ncdcOisst21Agg" #newer
xa_HROISST = xa.open_dataset(erddap_path_hroisst)
for i in range(2010,2021,1):
print(i)
xa_HROISST_subset = xa_HROISST.sel(time=slice(str(i)+'-01-01',str(i)+'-12-31'),
latitude=slice(55,90),longitude=slice(170,210)).load()
xa_HROISST_subset.to_netcdf('NBS_CK_HROISST_'+str(i)+'.nc')
xa_HROISST_subset
xa_ghsst = xa.open_dataset(erddap_path_ghsst)
xa_ghsst_subset= xa_ghsst['analysed_sst'].sel(time=slice('2010-2','2010-2'),latitude=slice(55,66),longitude=slice(-180,-150)).load()
xa_ghsst_subset.to_netcdf('NBS_CK_MUR_'+str(i)+'.1.nc')
#monthly breakdown
xa_ghsst = xa.open_dataset(erddap_path_ghsst)
for i in range(2010,2021,1):
print(i)
xa_ghsst_subset = xa_ghsst['analysed_sst'].sel(time=slice(str(i)+'-1'),
latitude=slice(57,90),longitude=slice(-180,-150)).load()
#xa_UKMET_subset.load()
xa_ghsst_subset.to_netcdf('NBS_CK_MUR_'+str(i)+'.1.nc')
xa_ghsst_subset
xa_ghsst = xa.open_dataset(erddap_path_ghsst)
xa_ghsst
xa_ghsst_subset = xa_ghsst['analysed_sst'].sel(time=slice(str(i)+'-06-01',str(i)+'-12-31'),
latitude=slice(57,90),longitude=slice(170,210))
|
2020/NBS_SST_Analysis/SST_ModelandReAnalysis.ipynb
|