code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Matrizes e vetores
# ## License
#
# All content can be freely used and adapted under the terms of the
# [Creative Commons Attribution 4.0 International License](http://creativecommons.org/licenses/by/4.0/).
#
# 
# ## Representação de uma matriz
#
# Antes de podermos manipular matrizes e vetores no computador, precisamos de um jeito de armazená-los em variáveis.
# Para vetores, o candidato natural são **listas**.
#
# $$
# \mathbf{v} = \begin{bmatrix}1 \\ 2 \\ 3\end{bmatrix}
# $$
#
# O vetor acima poderia ser representado em código como:
#
#
v = [1, 2, 3]
print(v)
# Uma matriz pode ser vista como um conjunto de vetores, ou um vetor de vetores. Cada vetor seria equivalente a uma linha da matriz:
#
# $$
# \mathbf{A} =
# \begin{bmatrix}
# 1 & 2 & 3 \\
# 4 & 5 & 6 \\
# 7 & 8 & 9 \\
# \end{bmatrix} =
# \begin{bmatrix}
# [1 & 2 & 3] \\
# [4 & 5 & 6] \\
# [7 & 8 & 9] \\
# \end{bmatrix}
# $$
#
# Logo, um jeito de representar uma matriz em Python é através de uma **lista de listas**:
A = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
print(A)
# O Python permite quebrar a linha quando o comando está entre `[` ou `(`:
A = [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
print(A)
# *Note que o print acima imprime a matriz toda em uma única linha*.
#
# A matriz `A` é uma lista como qualquer outra. A única diferença é que **os elementos da lista são outras listas**. O elemnto `[0]` da lista `A` será a lista correspondente a primeira linha:
print(A[0])
# Como `A[0]` é uma lista, podemos pegar os elementos dessa lista da mesma forma:
print(A[0][0])
print(A[1][2])
# ### Exemplo
#
# Queremos imprimir cada elemento da matriz `A` da seguinte forma:
#
# 1 2 3
# 4 5 6
# 7 8 9
#
# Podemos utilizar o `for` para pegar cada linha da matriz. Para cada linha da matriz, queremos imprimir o elemento. Quando terminarmos de imprimir a linha, vamos pular uma linha.
for i in range(3): # Anda sobre as linhas
for j in range(3): # Anda sobre as colunas
print(A[i][j], ' ', end='') # end='' faz com que print não pule uma linha
print() # Imprime nada e pula uma linha
# ## Somando matrizes
#
# A soma de duas matrizes produz uma matriz que terá a soma dos elementos correspondentes:
#
# $$
# \begin{bmatrix}
# a & b & c \\
# d & e & f \\
# g & h & i \\
# \end{bmatrix} +
# \begin{bmatrix}
# j & l & m \\
# n & o & p \\
# q & r & s \\
# \end{bmatrix} =
# \begin{bmatrix}
# a + j & b + l & c + m \\
# d + n & e + o & f + p \\
# g + q & h + r & i + s \\
# \end{bmatrix}
# $$
#
# De forma genérica, o $j$-ésimo elemento da $i$-ésima linha de uma matriz $\mathbf{A}$ é $A_{ij}$.
# Se temos duas matrizes $\mathbf{A}$ e $\mathbf{B}$, a soma pode ser escrita como:
#
# $$
# C_{ij} = A_{ij} + B_{ij}
# $$
# ## Tarefa
#
# Some as matrizes `A` e `B` definidas abaixo e guarde o resultado em uma matriz `C`. Imprima a matriz `C`.
#
# **Dicas**:
#
# * Você pode criar a matriz `C` antes ou durante a soma. Lembre-se que a matriz é uma lista e listas possuem o método `append`.
A = [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
B = [[3, 4, 5],
[6, 7, 8],
[9, 10, 11]]
nlin_a = 3
nlin_b = 3
ncol_a = 3
ncol_b = 3
c = [[0, 0, 0], [0, 0, 0],[0, 0, 0]] # Cria a matriz C
for i in range(0, nlin_a, 1): # Andar sobre as linhas
for j in range(0, ncol_b, 1): # Anda sobre as colunas
c[i][j] = A[i][j] + B[i][j] # Coloca a matriz C como a soma de elementos da matriz A e B
print(c[i][j], ' ', end='') # end='' faz com que print não pule uma linha
print() # Imprime nada e pula uma linha
# ### Resultado esperado
#
# Seu código deve imprimir exatamente:
#
# 4 6 8
# 10 12 14
# 16 18 20
# ## Multiplicando uma matriz por um vetor
#
# A multiplicação de uma matriz por um vetor é
#
# $$
# \begin{bmatrix}
# a & b \\
# c & d \\
# \end{bmatrix}
# \begin{bmatrix}
# e \\
# f \\
# \end{bmatrix} =
# \begin{bmatrix}
# ae + bf \\
# ce + df \\
# \end{bmatrix}
# $$
#
# Sendo o vetor $\mathbf{u} = \mathbf{A}\mathbf{v}$, cada elemento $i$ de $\mathbf{u}$ é
#
#
# $$
# u_i = \sum\limits_{k=1}^{N} A_{ik}v_k
# $$
# ## Tarefa
#
# Faça a multiplicação da matriz pelo vetor definidos abaixo. Guarde o resultado em uma lista.
#
# **Dicas**
A = [[1, 2, 3, 4],
[4, 5, 6, 7],
[7, 8, 9, 10]]
v = [12, 13, 14, 15]
nlin = 3
ncol = 4
# +
U = [] #criação da lista U vazia
for i in range(nlin):
somador = 0 #somador precisa esta a zero sempre que entrar em outra lista
for k in range(ncol):
#precisamos multiplicar por v[j] para obedecer a fórmula.
somador = somador + (A[i][k]*v[k]) #com somador zerado podemos fazer o somatório de cada lista de C,
U.append(somador) # a lista U é nosso resultado final, onde sera adicionado cada valor gerado pelo somador acima
print("Resultado da multipicação de matriz por vetor:",U)
# -
# ### Resultado esperado
#
# O seu código deve imprimir exatamente:
#
# [140, 302, 464]
# ## Multiplicação de matrizes
#
# A multiplicação de matrizes é feita de forma diferente da soma. É mais fácil mostrar do que explicar:
#
# $$
# \begin{bmatrix}
# a & b \\
# c & d \\
# \end{bmatrix}
# \begin{bmatrix}
# e & f \\
# g & h \\
# \end{bmatrix} =
# \begin{bmatrix}
# ae + bg & af + bh \\
# ce + dg & cf + dh \\
# \end{bmatrix}
# $$
#
# Sendo $\mathbf{C} = \mathbf{A}\mathbf{B}$, cada elemento $ij$ de $\mathbf{C}$ é
#
#
# $$
# C_{ij} = \sum\limits_{k=1}^{N} A_{ik}B_{kj}
# $$
# ## Tarefa
#
# Faça a multiplicação das duas matrizes definidas abaixo. Guarde o resultado em uma matriz (lista de listas).
A = [[1, 2, 3, 4],
[4, 5, 6, 7],
[7, 8, 9, 10]]
B = [[3, 4, 5],
[6, 7, 8],
[9, 10, 11],
[12, 13, 14]]
nlin_a = 3
nlin_b = 4
ncol_a = 4
ncol_b = 3
# +
c = [[0, 0, 0], [0, 0, 0],[0, 0, 0]] # Cria a matriz C
for i in range(0, nlin_a, 1): # Andar sobre as linhas
for j in range(0, ncol_b, 1): # Anda sobre as colunas
somador = 0
for k in range(0, nlin_b, 1):
somador = somador + (A[i][k] * B[k][j])
c[i][j] = somador
print(c[i][j], ' ', end='')# Coloca a matriz C como a soma de elementos da matriz A e B
print() # Imprime nada e pula uma linha
# -
# ### Resultado esperado
#
# O seu código deve imprimir exatamente:
#
# 90 100 110
# 180 202 224
# 270 304 338
#
#
# ## Tarefa Bônus
#
# Calcule o produto $\mathbf{A}^T\mathbf{A}$ para a matriz $A$ definida abaixo. $\mathbf{A}^T$ é a matriz transposta de $A$:
#
# $$
# \mathbf{A} =
# \begin{bmatrix}
# a & b & c \\
# d & e & f \\
# \end{bmatrix}
# $$
#
# $$
# \mathbf{A}^T =
# \begin{bmatrix}
# a & d \\
# b & e \\
# c & f \\
# \end{bmatrix}
# $$
#
# Ou seja, as linhas de $\mathbf{A}$ são as colunas de $\mathbf{A}^T$.
#
A = [[1, 2, 3, 4],
[4, 5, 6, 7],
[7, 8, 9, 10]]
nlin = 3
ncol = 4
def transposeMatrix(A):
aux = []
for j in range(len(A[0])):
linha=[]
for i in range(len(A)):
linha.append(A[i][j])
aux.append(linha)
print(aux)
def transpose(A):
m1 = []
for j in xrange(len(A[0])):
m1.append([A[i][j] for i in xrange(len(A))])
return m1
# ### Resultado esperado
#
# O seu código deve imprimir exatamente:
#
# 66 78 90 102
# 78 93 108 123
# 90 108 126 144
# 102 123 144 165
#
|
matrizes-e-vetores.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# ## yt grid visualization
import pyart
from matplotlib import pyplot as plt
import yt
import numpy as np
import math
# %matplotlib inline
grid_data_path = '/home/rjackson/multidop_grids/cf_compliant_grid200601200050.nc'
pyart_grid = pyart.io.read_grid(grid_data_path)
bbox = np.array([[pyart_grid.x['data'][0], pyart_grid.x['data'][-1]],
[pyart_grid.y['data'][0], pyart_grid.y['data'][-1]],
[pyart_grid.z['data'][0], pyart_grid.z['data'][-1]]])
print(pyart_grid.fields.keys())
# ## Convert Py-ART grid to yt grid
units = ['m/s', 'dBZ', 'm/s', 'm/s']
eastward_wind = np.ma.transpose(pyart_grid.fields['eastward_wind']['data'],
[2,1,0])
northward_wind = np.ma.transpose(pyart_grid.fields['northward_wind']['data'],
[2,1,0])
upward_air_velocity = np.ma.transpose(pyart_grid.fields['upward_air_velocity']['data'],
[2,1,0])
reflectivity = np.ma.transpose(pyart_grid.fields['reflectivity']['data'],
[2,1,0])
reflectivity[reflectivity < 0] = np.nan
data = (dict(u = (eastward_wind, 'm/s'),
v = (northward_wind, 'm/s'),
w = (upward_air_velocity, 'm/s'),
dBZ = (reflectivity, 'mm**6/m**3')))
ds = yt.load_uniform_grid(data,
eastward_wind.shape,
length_unit="m",
time_unit="s",
velocity_unit="m/s",
bbox=bbox,
)
slc = yt.SlicePlot(ds, "x", ["dBZ"])
slc.set_cmap("dBZ", pyart.graph.cm.NWSRef)
slc.set_log("dBZ", False)
slc.annotate_grids(cmap=None)
slc.show()
# +
from yt.visualization.api import Streamlines
sc = yt.create_scene(ds, field=('stream', 'dBZ'), lens_type='perspective')
source = sc[0]
source.set_field("dBZ")
source.set_log(False)
bounds = (0, 60)
camera = sc.add_camera()
tf = yt.ColorTransferFunction(bounds)
sc.camera.width = (70000, 'm')
tf.add_layers(5, colormap=pyart.graph.cm.NWSVel)
source.tfh.tf = tf
source.tfh.bounds = bounds
source.tfh.plot('transfer_function.png', profile_field='dBZ')
#sc.annotate_domain(ds)
sc.save('rendering.png', sigma_clip=0.1)
sc.show(sigma_clip=1)
# +
sc = yt.create_scene(ds, field=('stream', 'dBZ'), lens_type='perspective')
source = sc[0]
source.set_field("w")
source.set_log(False)
bounds = (-5, 5)
camera = sc.add_camera()
camera.set_focus((0,-0.2,0.1))
camera.set_position((0000,30000,-10000))
camera.roll(-math.pi/3)
tf = yt.ColorTransferFunction(bounds)
sc.camera.width = (70000, 'm')
tf.add_layers(5, colormap=pyart.graph.cm.NWSVel)
source.tfh.tf = tf
source.tfh.bounds = bounds
source.tfh.plot('transfer_function.png', profile_field='w')
#sc.annotate_domain(ds)
sc.show(sigma_clip=1)
|
notebooks/Yt grid visualization.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:hetmech]
# language: python
# name: conda-env-hetmech-py
# ---
# +
import matplotlib.pyplot as plt
import numpy
import pandas
import tqdm
import hetmech.hetmat
import hetmech.degree_group
import hetmech.degree_weight
import hetmech.pipeline
# %matplotlib inline
# -
hetmat = hetmech.hetmat.HetMat('../../data/hetionet-v1.0.hetmat/')
metapaths = ['DaGbC', 'SpDpS', 'SEcCrCtD', 'CiPCiCtD']
bins = numpy.linspace(0, 1, 101)
bin_counts = {metapath: pandas.DataFrame() for metapath in metapaths}
# ## Compute p-values for the actual HetMat
# +
hetmat.path_counts_cache = hetmech.hetmat.caching.PathCountPriorityCache(hetmat, allocate_GB=10)
for metapath in tqdm.tqdm(metapaths):
row_ids, col_ids, pc_matrix = hetmech.degree_weight.dwpc(hetmat, metapath, damping=0, dense_threshold=0.7, dtype='uint64')
path = hetmat.get_path_counts_path(metapath, 'dwpc', 0, None)
if not path.exists():
hetmech.hetmat.save_matrix(pc_matrix, path)
hetmat.path_counts_cache = hetmech.hetmat.caching.PathCountPriorityCache(hetmat, allocate_GB=10)
mean_dwpcs = dict()
for metapath in tqdm.tqdm(metapaths):
row_ids, col_ids, dwpc_matrix = hetmech.degree_weight.dwpc(hetmat, metapath, damping=0.5, dense_threshold=0.7, dtype='float64')
mean_dwpcs[(metapath, 'dwpc', 0.5)] = dwpc_matrix.mean()
path = hetmat.get_path_counts_path(metapath, 'dwpc', 0.5, None)
if not path.exists():
hetmech.hetmat.save_matrix(dwpc_matrix, path)
# +
for name, permat in tqdm.tqdm((hetmat.permutations.items())):
permat.path_counts_cache = hetmech.hetmat.caching.PathCountPriorityCache(permat, allocate_GB=10)
for metapath in metapaths:
degree_grouped_df = hetmech.degree_group.single_permutation_degree_group(
permat, metapath, dwpc_mean=mean_dwpcs[(metapath, 'dwpc', 0.5)], damping=0.5)
path = hetmat.get_running_degree_group_path(metapath, 'dwpc', 0.5, extension='.pkl')
if path.exists():
running_df = pandas.read_pickle(path)
running_df += degree_grouped_df
else:
running_df = degree_grouped_df
running_df.to_pickle(path)
permat.path_counts_cache = None
# Replace .pkl files with .tsv.gz files.
for metapath in metapaths:
old_path = hetmat.get_running_degree_group_path(metapath, 'dwpc', 0.5, extension='.pkl')
df = pandas.read_pickle(old_path)
new_path = hetmat.get_running_degree_group_path(metapath, 'dwpc', 0.5, extension='.tsv.gz')
df.to_csv(new_path, sep='\t', compression='gzip')
old_path.unlink()
# -
for metapath in tqdm.tqdm(metapaths):
dwpcs_rows = hetmech.pipeline.combine_dwpc_dgp(hetmat, metapath, damping=0.5, ignore_zeros=False, max_p_value=1.0)
path = hetmat.directory.joinpath('adjusted-path-counts', 'dwpc-0.5',
'adjusted-dwpcs', f'{metapath}.tsv.gz')
hetmech.pipeline.grouped_tsv_writer(dwpcs_rows, path, float_format='%.7g', compression='gzip')
# ## Compute p-values for a permat - Permutation 1
perms = hetmat.permutations.copy()
permat_1 = perms.pop('001')
# +
permat_1.path_counts_cache = hetmech.hetmat.caching.PathCountPriorityCache(permat_1, allocate_GB=10)
for metapath in tqdm.tqdm(metapaths):
row_ids, col_ids, pc_matrix = hetmech.degree_weight.dwpc(permat_1, metapath, damping=0, dense_threshold=0.7, dtype='uint64')
path = permat_1.get_path_counts_path(metapath, 'dwpc', 0, None)
path.parent.mkdir(parents=True, exist_ok=True)
if not path.exists():
hetmech.hetmat.save_matrix(pc_matrix, path)
del pc_matrix
permat_1.path_counts_cache = hetmech.hetmat.caching.PathCountPriorityCache(permat_1, allocate_GB=10)
mean_dwpcs = dict()
for metapath in tqdm.tqdm(metapaths):
row_ids, col_ids, dwpc_matrix = hetmech.degree_weight.dwpc(permat_1, metapath, damping=0.5, dense_threshold=0.7, dtype='float64')
mean_dwpcs[(metapath, 'dwpc', 0.5)] = dwpc_matrix.mean()
path = permat_1.get_path_counts_path(metapath, 'dwpc', 0.5, None)
path.parent.mkdir(parents=True, exist_ok=True)
if not path.exists():
hetmech.hetmat.save_matrix(dwpc_matrix, path)
del dwpc_matrix
# +
for name, permat in tqdm.tqdm(perms.items()):
permat.path_counts_cache = hetmech.hetmat.caching.PathCountPriorityCache(permat, allocate_GB=16)
for metapath in metapaths:
degree_grouped_df = hetmech.degree_group.single_permutation_degree_group(
permat, metapath, dwpc_mean=mean_dwpcs[(metapath, 'dwpc', 0.5)], damping=0.5)
path = permat_1.get_running_degree_group_path(metapath, 'dwpc', 0.5, extension='.pkl')
path.parent.mkdir(parents=True, exist_ok=True)
if path.exists():
running_df = pandas.read_pickle(path)
running_df += degree_grouped_df
else:
running_df = degree_grouped_df
running_df.to_pickle(path)
permat.path_counts_cache = None
# Replace .pkl files with .tsv.gz files.
for metapath in metapaths:
old_path = permat_1.get_running_degree_group_path(metapath, 'dwpc', 0.5, extension='.pkl')
df = pandas.read_pickle(old_path)
new_path = permat_1.get_running_degree_group_path(metapath, 'dwpc', 0.5, extension='.tsv.gz')
df.to_csv(new_path, sep='\t', compression='gzip')
old_path.unlink()
# -
for metapath in tqdm.tqdm(metapaths):
dwpcs_rows = hetmech.pipeline.combine_dwpc_dgp(permat_1, metapath, damping=0.5, ignore_zeros=False, max_p_value=1.0)
path = permat_1.directory.joinpath('adjusted-path-counts', 'dwpc-0.5',
'adjusted-dwpcs', f'{metapath}.tsv.gz')
path.parent.mkdir(parents=True, exist_ok=True)
hetmech.pipeline.grouped_tsv_writer(dwpcs_rows, path, float_format='%.7g', compression='gzip')
for metapath in metapaths:
plt.figure()
plt.title(metapath)
path = hetmat.directory.joinpath('adjusted-path-counts', 'dwpc-0.5',
'adjusted-dwpcs', f'{metapath}.tsv.gz')
df = pandas.read_table(path, compression='gzip')
bins_het, _, _ = plt.hist(df['p_value'], label='hetionet', alpha=0.5, bins=bins)
bin_counts[metapath]['bins'] = bins[:-1]
bin_counts[metapath]['hetionet'] = bins_het
path = permat_1.directory.joinpath('adjusted-path-counts', 'dwpc-0.5',
'adjusted-dwpcs', f'{metapath}.tsv.gz')
df = pandas.read_table(path, compression='gzip')
counts, _, _ = plt.hist(df['p_value'], label='perm_1', alpha=0.5, bins=bins)
bin_counts[metapath]['perm_1'] = counts
plt.ylim((0, max(bins_het[:-1])))
plt.legend();
# ### Permutation 2
perms = hetmat.permutations.copy()
permat_1 = perms.pop('002')
# +
permat_1.path_counts_cache = hetmech.hetmat.caching.PathCountPriorityCache(permat_1, allocate_GB=10)
for metapath in tqdm.tqdm(metapaths):
row_ids, col_ids, pc_matrix = hetmech.degree_weight.dwpc(permat_1, metapath, damping=0, dense_threshold=0.7, dtype='uint64')
path = permat_1.get_path_counts_path(metapath, 'dwpc', 0, None)
path.parent.mkdir(parents=True, exist_ok=True)
if not path.exists():
hetmech.hetmat.save_matrix(pc_matrix, path)
del pc_matrix
permat_1.path_counts_cache = hetmech.hetmat.caching.PathCountPriorityCache(permat_1, allocate_GB=10)
mean_dwpcs = dict()
for metapath in tqdm.tqdm(metapaths):
row_ids, col_ids, dwpc_matrix = hetmech.degree_weight.dwpc(permat_1, metapath, damping=0.5, dense_threshold=0.7, dtype='float64')
mean_dwpcs[(metapath, 'dwpc', 0.5)] = dwpc_matrix.mean()
path = permat_1.get_path_counts_path(metapath, 'dwpc', 0.5, None)
path.parent.mkdir(parents=True, exist_ok=True)
if not path.exists():
hetmech.hetmat.save_matrix(dwpc_matrix, path)
del dwpc_matrix
# +
for name, permat in tqdm.tqdm(perms.items()):
permat.path_counts_cache = hetmech.hetmat.caching.PathCountPriorityCache(permat, allocate_GB=16)
for metapath in metapaths:
degree_grouped_df = hetmech.degree_group.single_permutation_degree_group(
permat, metapath, dwpc_mean=mean_dwpcs[(metapath, 'dwpc', 0.5)], damping=0.5)
path = permat_1.get_running_degree_group_path(metapath, 'dwpc', 0.5, extension='.pkl')
path.parent.mkdir(parents=True, exist_ok=True)
if path.exists():
running_df = pandas.read_pickle(path)
running_df += degree_grouped_df
else:
running_df = degree_grouped_df
running_df.to_pickle(path)
permat.path_counts_cache = None
# Replace .pkl files with .tsv.gz files.
for metapath in metapaths:
old_path = permat_1.get_running_degree_group_path(metapath, 'dwpc', 0.5, extension='.pkl')
df = pandas.read_pickle(old_path)
new_path = permat_1.get_running_degree_group_path(metapath, 'dwpc', 0.5, extension='.tsv.gz')
df.to_csv(new_path, sep='\t', compression='gzip')
old_path.unlink()
# -
for metapath in tqdm.tqdm(metapaths):
dwpcs_rows = hetmech.pipeline.combine_dwpc_dgp(permat_1, metapath, damping=0.5, ignore_zeros=False, max_p_value=1.0)
path = permat_1.directory.joinpath('adjusted-path-counts', 'dwpc-0.5',
'adjusted-dwpcs', f'{metapath}.tsv.gz')
path.parent.mkdir(parents=True, exist_ok=True)
hetmech.pipeline.grouped_tsv_writer(dwpcs_rows, path, float_format='%.7g', compression='gzip')
for metapath in metapaths:
plt.figure()
plt.title(metapath)
path = hetmat.directory.joinpath('adjusted-path-counts', 'dwpc-0.5',
'adjusted-dwpcs', f'{metapath}.tsv.gz')
df = pandas.read_table(path, compression='gzip')
bins_het, _, _ = plt.hist(df['p_value'], label='hetionet', alpha=0.5, bins=bins)
path = permat_1.directory.joinpath('adjusted-path-counts', 'dwpc-0.5',
'adjusted-dwpcs', f'{metapath}.tsv.gz')
df = pandas.read_table(path, compression='gzip')
counts, _, _ = plt.hist(df['p_value'], label='perm_2', alpha=0.5, bins=bins)
bin_counts[metapath]['perm_2'] = counts
plt.ylim((0, 1.1 * max(bins_het[:-1])))
plt.legend();
# ### Permutation 150
perms = hetmat.permutations.copy()
permat_1 = perms.pop('150')
# +
permat_1.path_counts_cache = hetmech.hetmat.caching.PathCountPriorityCache(permat_1, allocate_GB=10)
for metapath in tqdm.tqdm(metapaths):
row_ids, col_ids, pc_matrix = hetmech.degree_weight.dwpc(permat_1, metapath, damping=0, dense_threshold=0.7, dtype='uint64')
path = permat_1.get_path_counts_path(metapath, 'dwpc', 0, None)
path.parent.mkdir(parents=True, exist_ok=True)
if not path.exists():
hetmech.hetmat.save_matrix(pc_matrix, path)
del pc_matrix
permat_1.path_counts_cache = hetmech.hetmat.caching.PathCountPriorityCache(permat_1, allocate_GB=10)
mean_dwpcs = dict()
for metapath in tqdm.tqdm(metapaths):
row_ids, col_ids, dwpc_matrix = hetmech.degree_weight.dwpc(permat_1, metapath, damping=0.5, dense_threshold=0.7, dtype='float64')
mean_dwpcs[(metapath, 'dwpc', 0.5)] = dwpc_matrix.mean()
path = permat_1.get_path_counts_path(metapath, 'dwpc', 0.5, None)
path.parent.mkdir(parents=True, exist_ok=True)
if not path.exists():
hetmech.hetmat.save_matrix(dwpc_matrix, path)
del dwpc_matrix
# +
for name, permat in tqdm.tqdm(perms.items()):
permat.path_counts_cache = hetmech.hetmat.caching.PathCountPriorityCache(permat, allocate_GB=16)
for metapath in metapaths:
degree_grouped_df = hetmech.degree_group.single_permutation_degree_group(
permat, metapath, dwpc_mean=mean_dwpcs[(metapath, 'dwpc', 0.5)], damping=0.5)
path = permat_1.get_running_degree_group_path(metapath, 'dwpc', 0.5, extension='.pkl')
path.parent.mkdir(parents=True, exist_ok=True)
if path.exists():
running_df = pandas.read_pickle(path)
running_df += degree_grouped_df
else:
running_df = degree_grouped_df
running_df.to_pickle(path)
permat.path_counts_cache = None
# Replace .pkl files with .tsv.gz files.
for metapath in metapaths:
old_path = permat_1.get_running_degree_group_path(metapath, 'dwpc', 0.5, extension='.pkl')
df = pandas.read_pickle(old_path)
new_path = permat_1.get_running_degree_group_path(metapath, 'dwpc', 0.5, extension='.tsv.gz')
df.to_csv(new_path, sep='\t', compression='gzip')
old_path.unlink()
# -
for metapath in tqdm.tqdm(metapaths):
dwpcs_rows = hetmech.pipeline.combine_dwpc_dgp(permat_1, metapath, damping=0.5, ignore_zeros=False, max_p_value=1.0)
path = permat_1.directory.joinpath('adjusted-path-counts', 'dwpc-0.5',
'adjusted-dwpcs', f'{metapath}.tsv.gz')
path.parent.mkdir(parents=True, exist_ok=True)
hetmech.pipeline.grouped_tsv_writer(dwpcs_rows, path, float_format='%.7g', compression='gzip')
for metapath in metapaths:
plt.figure()
plt.title(metapath)
path = hetmat.directory.joinpath('adjusted-path-counts', 'dwpc-0.5',
'adjusted-dwpcs', f'{metapath}.tsv.gz')
df = pandas.read_table(path, compression='gzip')
bins_het, _, _ = plt.hist(df['p_value'], label='hetionet', alpha=0.5, bins=bins)
path = permat_1.directory.joinpath('adjusted-path-counts', 'dwpc-0.5',
'adjusted-dwpcs', f'{metapath}.tsv.gz')
df = pandas.read_table(path, compression='gzip')
counts, _, _ = plt.hist(df['p_value'], label='perm_150', alpha=0.5, bins=bins)
bin_counts[metapath]['perm_150'] = counts
plt.ylim((0, 1.1 * max(bins_het[:-1])))
plt.legend();
# +
complete_df = None
for key, df in bin_counts.items():
df = df.assign(metapath=key)
if complete_df is None:
complete_df = df
else:
complete_df = complete_df.append(df)
columns = [complete_df.columns[-1]] + list(complete_df.columns[0:-1])
complete_df = complete_df[columns]
complete_df[columns[-4:]] = complete_df[columns[-4:]].astype(int)
complete_df.to_csv(path_or_buf=f'permutation-p-values-bin-counts.tsv', sep='\t', index=False, float_format='%.2f')
|
explore/p-value/permutation-p-values.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# +
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
# we're setting some options for nicer printing here
np.set_printoptions(suppress=True, precision=4)
data = pd.read_csv("boston_house_prices.csv")
X = data.drop("MEDV", axis=1)
y = data.MEDV.values
X_train, X_test, y_train, y_test = train_test_split(X, y)
print(X_train.shape)
scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
# -
fig, axes = plt.subplots(3, 5, figsize=(20, 10))
for column, ax in zip(X.columns, axes.ravel()):
ax.plot(X[column], y, 'o', alpha=.5)
ax.set_title(column)
ax.set_ylabel("MEDV")
# Implementing Linear Regression
from sklearn.linear_model import LinearRegression
linr = LinearRegression()
# Fitting the model
linr.fit(X_train_scaled, y_train)
# Evaluating model
print(linr.predict(X_train_scaled)[:15])
print(y_train[:15])
linr.score(X_train_scaled, y_train)
linr.score(X_test_scaled, y_test)
# Using Random Forest
from sklearn.ensemble import RandomForestRegressor
rf = RandomForestRegressor(n_estimators=50)
rf.fit(X_train, y_train)
rf.score(X_train, y_train)
rf.score(X_test, y_test)
|
super_learn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
## Standard python libraries
import numpy as np
import time
import sys
import matplotlib.pylab as plt
# %matplotlib inline
# # %pdb
## Magnolia data iteration
sys.path.append('../../')
from src.features.mixer import FeatureMixer
from src.features.wav_iterator import batcher
from src.features.supervised_iterator import SupervisedIterator, SupervisedMixer
from src.features.hdf5_iterator import Hdf5Iterator, SplitsIterator
# -
# ## LibriSpeech Dev File
batchsize = 1024
datashape = (64, 257)
libridev='/local_data/teams/magnolia/librispeech/processed_dev-clean.h5'
# libridev='/local_data/teams/magnolia/processed_train-clean-100.h5'
# ### Feature Mixer
#
# Unsupervised (Non-labeled) feature mixer declaration with several iterators from mixed sources
mixer = FeatureMixer([libridev,libridev,libridev], shape=datashape, mix_method='add', diffseed=True, return_key=True)
ti = time.clock()
data_batch = mixer.get_batch(batchsize)
tf = time.clock()
print('Regular feature mixer with 3 libridev sources timed at ', (tf-ti), 'sec')
# ### Supervised Feature Mixer
# Feature mixer declaration with same number of iterators from mixed sources
# +
libriter = SupervisedIterator(libridev, shape=datashape)
mixerter = SupervisedMixer([libridev,libridev,libridev], shape=datashape,
mix_method='add', diffseed=True, return_key=True)
# Check the time
ti = time.clock()
X, Y, I = mixerter.get_batch(batchsize)
tf = time.clock()
print('Supervised feature mixer with 3 libridev sources timed at ', (tf-ti), 'sec')
print('Shapes [X,Y] for out_TF=-1 is [',X.shape,',',Y.shape,']')
# Check the time for subset of array
ti = time.clock()
X, Y, I = mixerter.get_batch(batchsize,out_TF=[0,1,2,3,4,5])
tf = time.clock()
print('Supervised feature mixer with 3 libridev sources timed at ', (tf-ti), 'sec')
print('Shapes [X,Y] for out_TF=FullSpec is [',X.shape,',',Y.shape,']')
# Check the time for full spectra
ti = time.clock()
X, Y, I = mixerter.get_batch(batchsize,out_TF=None)
tf = time.clock()
print('Supervised feature mixer with 3 libridev sources timed at ', (tf-ti), 'sec')
print('Shapes [X,Y] for out_TF=FullSpec is [',X.shape,',',Y.shape,']')
# -
# ### Splits Iterator
# Specifying training splits and then let's say we have specified speakers.
#
# Speaker lists are stored in `data/librispeech/authors`:
# ```
# dev-clean-F.txt test-clean-F.txt train-clean-100-F.txt
# dev-clean-M.txt test-clean-M.txt train-clean-100-M.txt
# ```
#
# For this example, let's use `speaker_keys = dev-clean-M.txt`. You can actually pass in `speaker_keys` to both `Hdf5Iterator` and `SplitsIterator`.
#
# #### Operating the splits
# In the iterator class `SplitsIterator`, there is a variable called `split_list` that is a list of lists. Each of the lists in `split_list` has the names of the wav files in that split. So, `split_list[0]` is the $0^{th}$ split, which has the names of all the files in that list.
#
# To set the split number, you must call `set_split`, a method in class `SplitsIterator`. For example, if I want split $0$, then I would call:
#
# ```
# iterator = SplitsIterator( [0.8, 0.1, 0.1], file_name, **kwargs )
# iterator.set_split[0]
# next(iterator)
# ```
#
# The above code will:
#
# 1. create a splits iterator with presumably a training, dev, and test set where each speaker has 80% of his files in the training set, 10% in the development set, and the remainder in the testing set.
# 2. and set the split to the training split
# +
split_ratio = [0.8, 0.1, 0.1]
speaker_keys = open('../../data/librispeech/authors/dev-clean-F.txt','r').read().splitlines()
# For reference, let's take an iterator with a ratio
iterator_all = Hdf5Iterator(libridev, shape=(10,257))
# Let's create a splits iterator with the split ratio
iterator_split_keys = SplitsIterator(split_ratio, libridev, speaker_keys=speaker_keys, shape=(10,257))
print( 'There are ', len( iterator_all.h5_groups ), ' people in libri-dev.' )
print( 'of which ', len( iterator_split_keys.h5_groups ), ' are female.')
print( 'In total, the number of items to be used is: ' )
# Now, specify which splits
iterator_split_keys.set_split(0)
print( len(iterator_split_keys.h5_items), ' for split 0' )
iterator_split_keys.set_split(1)
print( len(iterator_split_keys.h5_items), ' for split 1' )
iterator_split_keys.set_split(2)
print( len(iterator_split_keys.h5_items), ' for split 2' )
# -
# ### Choosing a subset
# +
split_ratio = [0.8, 0.1, 0.1]
speaker_keys = open('../../data/librispeech/authors/dev-clean-F.txt','r').read().splitlines()
# For reference, let's take an iterator with a ratio
iterator_all = Hdf5Iterator(libridev, shape=(10,257))
print("Created an iterator with everybody, with ", len(iterator_all.h5_groups),
"and number of items", len(iterator_all.h5_items))
# Let's create a splits iterator with the split ratio
iterator_split_keys = SplitsIterator(split_ratio, libridev, shape=(10,257))
iterator_split_keys.speaker_subset( speaker_keys )
print( "Set to femails only ", len( iterator_split_keys.h5_groups),
"Number of items: ", len(iterator_split_keys.h5_items))
#
iterator_split_keys.speaker_subset( )
print("Reset to everybody ", len( iterator_split_keys.h5_groups),
"Number of items: ", len(iterator_split_keys.h5_items))
|
magnolia/python/training/data_iteration/iterator-examples.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Backbone coverage algorithm
#
# The current scoring algorithm just tries to find as many matching ions as possible in one spectrum as in another instead of trying to identify amino acids by their backbone. Instead, lets make an algorithm that scores a spectrum by its backbone coverage of a theoretical spectrum.
# +
import os
import sys
module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
sys.path.append(module_path)
module_path = os.path.abspath(os.path.join('../..'))
if module_path not in sys.path:
sys.path.append(module_path)
from src.objects import Spectrum
from src.spectra.gen_spectra import gen_spectrum
from src.utils import ppm_to_da
# -
def backbone_scoring_alg(observed: Spectrum, reference: str, ppm_tolerance: int) -> float:
'''
Scoring algorithm based on backbone coverage of the reference. The scoring algorithm
returns a number between 0 and 100 + 3*(len(reference)-1). The calculation of the score is as follows:
1. A percentage is given for the number of bond sites successfully identified
2. For each bond site that has > 1 ion that describes it, an extra point is awarded.
Example:
reference: ABCDE, 4 junctions to describe
observed: ions: b1+, y1++, y2+, b4+
ions for A, E, DE, ABCD found. Coverage = A**DE with DE described by both E and ABCD
Score = %(3/4) + 1 = 75 + 1 = 76
Inputs:
observed: (Spectrum) spectrum being scored against
reference: (str) reference amino acid sequence being scored against the spectrum
ppm_tolerance: (int) tolerance to allow in ppm for each peak
'''
jcount = [0 for _ in range(len(reference)-1)]
for ion in ['b', 'y']:
for charge in [1, 2]:
singled_seq = reference[:-1] if ion == 'b' else reference[1:]
peaks = gen_spectrum(singled_seq, charge=charge, ion=ion)['spectrum']
peaks = peaks if ion == 'b' else peaks[::-1]
for i in range(len(peaks)):
da_tol = ppm_to_da(peaks[i], ppm_tolerance)
if any([peaks[i] - da_tol <= obs_peak <= peaks[i] + da_tol for obs_peak in observed.spectrum]):
jcount[i] += 1
jcoverage = int(100 * sum([1 if jc > 0 else 0 for jc in jcount]) / len(jcount))
extrapoints = sum([jc - 1 if jc > 1 else 0 for jc in jcount])
return jcoverage + extrapoints
# ## Test it
# ### Situation 1: full coverage of 1 ion type
seq = 'MALWARM'
bs = gen_spectrum(seq, ion='b', charge=1)['spectrum']
print(backbone_scoring_alg(Spectrum(bs), seq, 10))
# ### Situation 2: full coverage by 2 ion types
seq = 'MALWARM'
bs = gen_spectrum(seq[:4], ion='b', charge=1)['spectrum']
ys = gen_spectrum(seq[5:], ion='y', charge=1)['spectrum']
print(backbone_scoring_alg(Spectrum(bs + ys), seq, 10))
# ### Situation 3: Partial coverage by 1 ion type
seq = 'MALWARM'
bs = gen_spectrum(seq[:4], ion='b', charge=1)['spectrum']
print(backbone_scoring_alg(Spectrum(bs), seq, 10))
# ### Situation 4: Partial coverage by 2 ion types
seq = 'MALWARM'
bs = gen_spectrum(seq[:2], ion='b', charge=1)['spectrum']
ys = gen_spectrum(seq[5:], ion='y', charge=1)['spectrum']
print(backbone_scoring_alg(Spectrum(bs + ys), seq, 10))
# ### Situation 5: Overlapping coverage of 2 ion types
seq = 'MALWARM'
bs = gen_spectrum(seq, ion='b', charge=1)['spectrum']
ys = gen_spectrum(seq, ion='y', charge=1)['spectrum']
print(backbone_scoring_alg(Spectrum(bs + ys), seq, 10))
# ### Situation 6: Full coverage by all ions
seq = 'MALWARM'
allspec = gen_spectrum(seq)['spectrum']
print(backbone_scoring_alg(Spectrum(allspec), seq, 10))
# ### Situation 7: No coverage
print(backbone_scoring_alg(Spectrum(), seq, 10))
# # Ion specific backbone coverage scoring algorithm
# Instead of either JUST blindly looking for ions or JUST looking for backbone coverage, try and find a middleground
def ion_backbone_score(observed: Spectrum, reference: str, ion: str, ppm_tolerance: int) -> float:
'''
Scoring algorithm based on backbone coverage of the reference. The scoring algorithm
returns a number between 0 and 100 + 3*(len(reference)-1). The calculation of the score is as follows:
1. A percentage is given for the number of bond sites successfully identified
2. For each bond site that has > 1 ion that describes it, an extra point is awarded.
Example:
reference: ABCDE, 4 junctions to describe
observed: ions: b1+, y1++, y2+, b4+
ions for A, E, DE, ABCD found. Coverage = A**DE with DE described by both E and ABCD
Score = %(3/4) + 1 = 75 + 1 = 76
Inputs:
observed: (Spectrum) spectrum being scored against
reference: (str) reference amino acid sequence being scored against the spectrum
ion: (str) the ion type to focus on. Options are 'b' or 'y'
ppm_tolerance: (int) tolerance to allow in ppm for each peak
'''
jcount = [0 for _ in range(len(reference)-1)]
for charge in [1, 2]:
singled_seq = reference[:-1] if ion == 'b' else reference[1:]
peaks = gen_spectrum(singled_seq, charge=charge, ion=ion)['spectrum']
peaks = peaks if ion == 'b' else peaks[::-1]
for i in range(len(peaks)):
da_tol = ppm_to_da(peaks[i], ppm_tolerance)
if any([peaks[i] - da_tol <= obs_peak <= peaks[i] + da_tol for obs_peak in observed.spectrum]):
jcount[i] += 1
jcoverage = int(100 * sum([1 if jc > 0 else 0 for jc in jcount]) / len(jcount))
extrapoints = sum([jc - 1 if jc > 1 else 0 for jc in jcount])
return jcoverage + extrapoints
|
sandbox/jupyter notebooks/Backbone coverage algorithm.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Gaussian process information model
# Experiments for creating an information model for informative path planning based on Gaussian processes. The idea here is to understand how to play with the features of the sklearn informative path planning.
# +
import random
import logging
import matplotlib.pyplot as plt
import itertools
import numpy as np
from Environment import PollutionModelEnvironment
# +
width = 10
height = 10
# environment model
env = PollutionModelEnvironment("water", width, height)
env.evolve_speed = 1
env.p_pollution = 0.1
for i in range(200):
env.proceed(1.0)
plt.imshow(env.value, vmin=0, vmax=1.0)
# -
def samples(n, data):
"""Generates a number of samples. Returns the x and y values, and a map of the samples"""
X = []
Y = []
samplemap = np.zeros([width,height])
for i in range(n):
x = random.randint(0, 9)
y = random.randint(0, 9)
samplemap[x,y] = 1.0
v = data[x,y]
X.append([x,y])
Y.append([v])
# trying out what happens if I add it twice
X.append([x,y])
Y.append([v])
return X, Y, samplemap
X, Y, samplemap = samples(20, env.value)
plt.imshow(samplemap, vmin=0, vmax=1.0)
rbf = 2.0 * RBF(length_scale = [1.0, 1.0])
gpr = GaussianProcessRegressor(kernel=rbf)
gpr.fit(X,Y)
def create_estimate():
est = np.zeros([width,height])
stdmap = np.zeros([width,height])
x = []
X = np.array(list(itertools.product(range(width), range(height))))
Y, std = gpr.predict(X, return_std = True)
for i, idx in enumerate(X):
est[idx[0], idx[1]] = Y[i]
stdmap[idx[0], idx[1]] = std[i]
print(std.sum())
return est, stdmap
est, stdmap = create_estimate()
plt.imshow(est, vmin=0, vmax=1.0)
#plt.imshow(stdmap, vmin=0, vmax=1.0)
#plt.imshow(stdmap)
gpr.fit(X,Y)
# +
x = [[0.5,0]]
ymean, y_std, y_cov = gpr.predict(x, return_std=True, return_cov = True)
#print(f"Prediction = {gpr.predict([[0.5,0]])} Score = {gpr.predict([[0.5,0]])}" )
# -
list(itertools.product([1,2], [3,4]))
np.array(list(itertools.product(range(5), range(5))))
|
Gaussian Process Information Model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (herschelhelp_internal)
# language: python
# name: helpint
# ---
# # ELAIS-S1 master catalogue
#
# This notebook presents the merge of the various pristine catalogues to produce HELP mater catalogue on ELAIS-S1.
from herschelhelp_internal import git_version
print("This notebook was run with herschelhelp_internal version: \n{}".format(git_version()))
# +
# %matplotlib inline
# #%config InlineBackend.figure_format = 'svg'
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))
import os
import time
from collections import OrderedDict
from astropy import units as u
from astropy.coordinates import SkyCoord
from astropy.table import Column, Table
import numpy as np
from pymoc import MOC
from herschelhelp_internal.masterlist import merge_catalogues, nb_merge_dist_plot, specz_merge
from herschelhelp_internal.utils import coords_to_hpidx, ebv, gen_help_id, inMoc
# +
TMP_DIR = os.environ.get('TMP_DIR', "./data_tmp")
OUT_DIR = os.environ.get('OUT_DIR', "./data")
SUFFIX = os.environ.get('SUFFIX', time.strftime("_%Y%m%d"))
try:
os.makedirs(OUT_DIR)
except FileExistsError:
pass
# -
# ## I - Reading the prepared pristine catalogues
video = Table.read("{}/VISTA-VIDEO.fits".format(TMP_DIR))
vhs = Table.read("{}/VISTA-VHS.fits".format(TMP_DIR))
voice = Table.read("{}/ESIS-VOICE.fits".format(TMP_DIR))
servs = Table.read("{}/SERVS.fits".format(TMP_DIR))
swire= Table.read("{}/SWIRE.fits".format(TMP_DIR))
des = Table.read("{}/DES.fits".format(TMP_DIR))
# ## II - Merging tables
#
# We merge in order of increasing wavelength: VIDEO, VHS, VOICE, SERVS, SWIRE.
#
# At every step, we look at the distribution of the distances to the nearest source in the merged catalogue to determine the best crossmatching radius.
# ### VIDEO
master_catalogue = video
master_catalogue['video_ra'].name = 'ra'
master_catalogue['video_dec'].name = 'dec'
# ### Add VHS
nb_merge_dist_plot(
SkyCoord(master_catalogue['ra'], master_catalogue['dec']),
SkyCoord(vhs['vhs_ra'], vhs['vhs_dec'])
)
# Given the graph above, we use 0.8 arc-second radius
master_catalogue = merge_catalogues(master_catalogue, vhs, "vhs_ra", "vhs_dec", radius=0.8*u.arcsec)
# ### Add ESIS VOICE
nb_merge_dist_plot(
SkyCoord(master_catalogue['ra'], master_catalogue['dec']),
SkyCoord(voice['voice_ra'], voice['voice_dec'])
)
# Given the graph above, we use 0.8 arc-second radius
master_catalogue = merge_catalogues(master_catalogue, voice, "voice_ra", "voice_dec", radius=0.8*u.arcsec)
# ### Add SERVS
nb_merge_dist_plot(
SkyCoord(master_catalogue['ra'], master_catalogue['dec']),
SkyCoord(servs['servs_ra'], servs['servs_dec'])
)
# Given the graph above, we use 1 arc-second radius
master_catalogue = merge_catalogues(master_catalogue, servs, "servs_ra", "servs_dec", radius=1.*u.arcsec)
# ### Add SWIRE
nb_merge_dist_plot(
SkyCoord(master_catalogue['ra'], master_catalogue['dec']),
SkyCoord(swire['swire_ra'], swire['swire_dec'])
)
# Given the graph above, we use 1 arc-second radius
master_catalogue = merge_catalogues(master_catalogue, swire, "swire_ra", "swire_dec", radius=1.*u.arcsec)
# ### Add DES
nb_merge_dist_plot(
SkyCoord(master_catalogue['ra'], master_catalogue['dec']),
SkyCoord(des['des_ra'], des['des_dec'])
)
# Given the graph above, we use 0.8 arc-second radius
master_catalogue = merge_catalogues(master_catalogue, des, "des_ra", "des_dec", radius=0.8*u.arcsec)
# ### Cleaning
#
# When we merge the catalogues, astropy masks the non-existent values (e.g. when a row comes only from a catalogue and has no counterparts in the other, the columns from the latest are masked for that row). We indicate to use NaN for masked values for floats columns, False for flag columns and -1 for ID columns.
# +
for col in master_catalogue.colnames:
if "m_" in col or "merr_" in col or "f_" in col or "ferr_" in col or "stellarity" in col:
master_catalogue[col].fill_value = np.nan
elif "flag" in col:
master_catalogue[col].fill_value = 0
elif "id" in col:
master_catalogue[col].fill_value = -1
master_catalogue = master_catalogue.filled()
# -
master_catalogue[:10].show_in_notebook()
# ## III - Merging flags and stellarity
#
# Each pristine catalogue contains a flag indicating if the source was associated to a another nearby source that was removed during the cleaning process. We merge these flags in a single one.
# +
flag_cleaned_columns = [column for column in master_catalogue.colnames
if 'flag_cleaned' in column]
flag_column = np.zeros(len(master_catalogue), dtype=bool)
for column in flag_cleaned_columns:
flag_column |= master_catalogue[column]
master_catalogue.add_column(Column(data=flag_column, name="flag_cleaned"))
master_catalogue.remove_columns(flag_cleaned_columns)
# -
# Each pristine catalogue contains a flag indicating the probability of a source being a Gaia object (0: not a Gaia object, 1: possibly, 2: probably, 3: definitely). We merge these flags taking the highest value.
# +
flag_gaia_columns = [column for column in master_catalogue.colnames
if 'flag_gaia' in column]
master_catalogue.add_column(Column(
data=np.max([master_catalogue[column] for column in flag_gaia_columns], axis=0),
name="flag_gaia"
))
master_catalogue.remove_columns(flag_gaia_columns)
# -
# Each prisitine catalogue may contain one or several stellarity columns indicating the probability (0 to 1) of each source being a star. We merge these columns taking the highest value.
# +
stellarity_columns = [column for column in master_catalogue.colnames
if 'stellarity' in column]
print(", ".join(stellarity_columns))
# +
# We create an masked array with all the stellarities and get the maximum value, as well as its
# origin. Some sources may not have an associated stellarity.
stellarity_array = np.array([master_catalogue[column] for column in stellarity_columns])
stellarity_array = np.ma.masked_array(stellarity_array, np.isnan(stellarity_array))
max_stellarity = np.max(stellarity_array, axis=0)
max_stellarity.fill_value = np.nan
no_stellarity_mask = max_stellarity.mask
master_catalogue.add_column(Column(data=max_stellarity.filled(), name="stellarity"))
stellarity_origin = np.full(len(master_catalogue), "NO_INFORMATION", dtype="S20")
stellarity_origin[~no_stellarity_mask] = np.array(stellarity_columns)[np.argmax(stellarity_array, axis=0)[~no_stellarity_mask]]
master_catalogue.add_column(Column(data=stellarity_origin, name="stellarity_origin"))
master_catalogue.remove_columns(stellarity_columns)
# -
# ## IV - Adding E(B-V) column
master_catalogue.add_column(
ebv(master_catalogue['ra'], master_catalogue['dec'])
)
# ## V.a - Adding HELP unique identifiers and field columns
master_catalogue.add_column(Column(gen_help_id(master_catalogue['ra'], master_catalogue['dec']),
name="help_id"))
master_catalogue.add_column(Column(np.full(len(master_catalogue), "ELAIS-S1", dtype='<U18'),
name="field"))
# Check that the HELP Ids are unique
if len(master_catalogue) != len(np.unique(master_catalogue['help_id'])):
print("The HELP IDs are not unique!!!")
else:
print("OK!")
# ## V.b - Adding spec-z
specz = Table.read("../../dmu23/dmu23_ELAIS-S1/data/ELAIS-S1-specz-v2.2.fits")
nb_merge_dist_plot(
SkyCoord(master_catalogue['ra'], master_catalogue['dec']),
SkyCoord(specz['ra'] * u.deg, specz['dec'] * u.deg)
)
master_catalogue = specz_merge(master_catalogue, specz, radius=1. * u.arcsec)
# ## VI - Choosing between multiple values for the same filter
#
# ### VI.a SERVS and SWIRE
# Both SERVS and SWIRE provide IRAC1 and IRAC2 fluxes. SERVS is deeper but tends to under-estimate flux of bright sources (Mattia said over 2000 µJy) as illustrated by this comparison of SWIRE, SERVS, and Spitzer-EIP fluxes.
seip = Table.read("../../dmu0/dmu0_SEIP/data/SEIP_ELAIS-S1.fits")
seip_coords = SkyCoord(seip['ra'], seip['dec'])
idx, d2d, _ = seip_coords.match_to_catalog_sky(SkyCoord(master_catalogue['ra'], master_catalogue['dec']))
mask = d2d <= 2 * u.arcsec
fig, ax = plt.subplots()
ax.scatter(seip['i1_f_ap1'][mask], master_catalogue[idx[mask]]['f_ap_servs_irac1'], label="SERVS", s=2.)
ax.scatter(seip['i1_f_ap1'][mask], master_catalogue[idx[mask]]['f_ap_swire_irac1'], label="SWIRE", s=2.)
ax.set_xscale('log')
ax.set_yscale('log')
ax.set_xlabel("SEIP flux [μJy]")
ax.set_ylabel("SERVS/SWIRE flux [μJy]")
ax.set_title("IRAC 1")
ax.legend()
ax.axvline(2000, color="black", linestyle="--", linewidth=1.)
ax.plot(seip['i1_f_ap1'][mask], seip['i1_f_ap1'][mask], linewidth=.1, color="black", alpha=.5);
# +
fig, ax = plt.subplots()
ax.scatter(seip['i2_f_ap1'][mask], master_catalogue[idx[mask]]['f_ap_servs_irac2'], label="SERVS", s=2.)
ax.scatter(seip['i2_f_ap1'][mask], master_catalogue[idx[mask]]['f_ap_swire_irac2'], label="SWIRE", s=2.)
ax.set_xscale('log')
ax.set_yscale('log')
ax.set_xlabel("SEIP flux [μJy]")
ax.set_ylabel("SERVS/SWIRE flux [μJy]")
ax.set_title("IRAC 2")
ax.legend()
ax.axvline(2000, color="black", linestyle="--", linewidth=1.)
ax.plot(seip['i1_f_ap2'][mask], seip['i1_f_ap2'][mask], linewidth=.1, color="black", alpha=.5);
# -
# When both SWIRE and SERVS fluxes are provided, we use the SERVS flux below 2000 μJy and the SWIRE flux over.
#
# We create a table indicating for each source the origin on the IRAC1 and IRAC2 fluxes that will be saved separately.
irac_origin = Table()
irac_origin.add_column(master_catalogue['help_id'])
# +
# IRAC1 aperture flux and magnitudes
has_servs = ~np.isnan(master_catalogue['f_ap_servs_irac1'])
has_swire = ~np.isnan(master_catalogue['f_ap_swire_irac1'])
has_both = has_servs & has_swire
print("{} sources with SERVS flux".format(np.sum(has_servs)))
print("{} sources with SWIRE flux".format(np.sum(has_swire)))
print("{} sources with SERVS and SWIRE flux".format(np.sum(has_both)))
has_servs_above_limit = has_servs.copy()
has_servs_above_limit[has_servs] = master_catalogue['f_ap_servs_irac1'][has_servs] > 2000
use_swire = (has_swire & ~has_servs) | (has_both & has_servs_above_limit)
use_servs = (has_servs & ~(has_both & has_servs_above_limit))
print("{} sources for which we use SERVS".format(np.sum(use_servs)))
print("{} sources for which we use SWIRE".format(np.sum(use_swire)))
f_ap_irac = np.full(len(master_catalogue), np.nan)
f_ap_irac[use_servs] = master_catalogue['f_ap_servs_irac1'][use_servs]
f_ap_irac[use_swire] = master_catalogue['f_ap_swire_irac1'][use_swire]
ferr_ap_irac = np.full(len(master_catalogue), np.nan)
ferr_ap_irac[use_servs] = master_catalogue['ferr_ap_servs_irac1'][use_servs]
ferr_ap_irac[use_swire] = master_catalogue['ferr_ap_swire_irac1'][use_swire]
m_ap_irac = np.full(len(master_catalogue), np.nan)
m_ap_irac[use_servs] = master_catalogue['m_ap_servs_irac1'][use_servs]
m_ap_irac[use_swire] = master_catalogue['m_ap_swire_irac1'][use_swire]
merr_ap_irac = np.full(len(master_catalogue), np.nan)
merr_ap_irac[use_servs] = master_catalogue['merr_ap_servs_irac1'][use_servs]
merr_ap_irac[use_swire] = master_catalogue['merr_ap_swire_irac1'][use_swire]
master_catalogue.add_column(Column(data=f_ap_irac, name="f_ap_irac_i1"))
master_catalogue.add_column(Column(data=ferr_ap_irac, name="ferr_ap_irac_i1"))
master_catalogue.add_column(Column(data=m_ap_irac, name="m_ap_irac_i1"))
master_catalogue.add_column(Column(data=merr_ap_irac, name="merr_ap_irac_i1"))
master_catalogue.remove_columns(['f_ap_servs_irac1', 'f_ap_swire_irac1', 'ferr_ap_servs_irac1',
'ferr_ap_swire_irac1', 'm_ap_servs_irac1', 'm_ap_swire_irac1',
'merr_ap_servs_irac1', 'merr_ap_swire_irac1'])
origin = np.full(len(master_catalogue), ' ', dtype='<U5')
origin[use_servs] = "SERVS"
origin[use_swire] = "SWIRE"
irac_origin.add_column(Column(data=origin, name="IRAC1_app"))
# +
# IRAC1 total flux and magnitudes
has_servs = ~np.isnan(master_catalogue['f_servs_irac1'])
has_swire = ~np.isnan(master_catalogue['f_swire_irac1'])
has_both = has_servs & has_swire
print("{} sources with SERVS flux".format(np.sum(has_servs)))
print("{} sources with SWIRE flux".format(np.sum(has_swire)))
print("{} sources with SERVS and SWIRE flux".format(np.sum(has_both)))
has_servs_above_limit = has_servs.copy()
has_servs_above_limit[has_servs] = master_catalogue['f_servs_irac1'][has_servs] > 2000
use_swire = (has_swire & ~has_servs) | (has_both & has_servs_above_limit)
use_servs = (has_servs & ~(has_both & has_servs_above_limit))
print("{} sources for which we use SERVS".format(np.sum(use_servs)))
print("{} sources for which we use SWIRE".format(np.sum(use_swire)))
f_ap_irac = np.full(len(master_catalogue), np.nan)
f_ap_irac[use_servs] = master_catalogue['f_servs_irac1'][use_servs]
f_ap_irac[use_swire] = master_catalogue['f_swire_irac1'][use_swire]
ferr_ap_irac = np.full(len(master_catalogue), np.nan)
ferr_ap_irac[use_servs] = master_catalogue['ferr_servs_irac1'][use_servs]
ferr_ap_irac[use_swire] = master_catalogue['ferr_swire_irac1'][use_swire]
flag_irac = np.full(len(master_catalogue), False, dtype=bool)
flag_irac[use_servs] = master_catalogue['flag_servs_irac1'][use_servs]
flag_irac[use_swire] = master_catalogue['flag_swire_irac1'][use_swire]
m_ap_irac = np.full(len(master_catalogue), np.nan)
m_ap_irac[use_servs] = master_catalogue['m_servs_irac1'][use_servs]
m_ap_irac[use_swire] = master_catalogue['m_swire_irac1'][use_swire]
merr_ap_irac = np.full(len(master_catalogue), np.nan)
merr_ap_irac[use_servs] = master_catalogue['merr_servs_irac1'][use_servs]
merr_ap_irac[use_swire] = master_catalogue['merr_swire_irac1'][use_swire]
master_catalogue.add_column(Column(data=f_ap_irac, name="f_irac_i1"))
master_catalogue.add_column(Column(data=ferr_ap_irac, name="ferr_irac_i1"))
master_catalogue.add_column(Column(data=m_ap_irac, name="m_irac_i1"))
master_catalogue.add_column(Column(data=merr_ap_irac, name="merr_irac_i1"))
master_catalogue.add_column(Column(data=flag_irac, name="flag_irac_i1"))
master_catalogue.remove_columns(['f_servs_irac1', 'f_swire_irac1', 'ferr_servs_irac1',
'ferr_swire_irac1', 'm_servs_irac1', 'flag_servs_irac1', 'm_swire_irac1',
'merr_servs_irac1', 'merr_swire_irac1', 'flag_swire_irac1'])
origin = np.full(len(master_catalogue), ' ', dtype='<U5')
origin[use_servs] = "SERVS"
origin[use_swire] = "SWIRE"
irac_origin.add_column(Column(data=origin, name="IRAC1_total"))
# +
# IRAC2 aperture flux and magnitudes
has_servs = ~np.isnan(master_catalogue['f_ap_servs_irac2'])
has_swire = ~np.isnan(master_catalogue['f_ap_swire_irac2'])
has_both = has_servs & has_swire
print("{} sources with SERVS flux".format(np.sum(has_servs)))
print("{} sources with SWIRE flux".format(np.sum(has_swire)))
print("{} sources with SERVS and SWIRE flux".format(np.sum(has_both)))
has_servs_above_limit = has_servs.copy()
has_servs_above_limit[has_servs] = master_catalogue['f_ap_servs_irac2'][has_servs] > 2000
use_swire = (has_swire & ~has_servs) | (has_both & has_servs_above_limit)
use_servs = (has_servs & ~(has_both & has_servs_above_limit))
print("{} sources for which we use SERVS".format(np.sum(use_servs)))
print("{} sources for which we use SWIRE".format(np.sum(use_swire)))
f_ap_irac = np.full(len(master_catalogue), np.nan)
f_ap_irac[use_servs] = master_catalogue['f_ap_servs_irac2'][use_servs]
f_ap_irac[use_swire] = master_catalogue['f_ap_swire_irac2'][use_swire]
ferr_ap_irac = np.full(len(master_catalogue), np.nan)
ferr_ap_irac[use_servs] = master_catalogue['ferr_ap_servs_irac2'][use_servs]
ferr_ap_irac[use_swire] = master_catalogue['ferr_ap_swire_irac2'][use_swire]
m_ap_irac = np.full(len(master_catalogue), np.nan)
m_ap_irac[use_servs] = master_catalogue['m_ap_servs_irac2'][use_servs]
m_ap_irac[use_swire] = master_catalogue['m_ap_swire_irac2'][use_swire]
merr_ap_irac = np.full(len(master_catalogue), np.nan)
merr_ap_irac[use_servs] = master_catalogue['merr_ap_servs_irac2'][use_servs]
merr_ap_irac[use_swire] = master_catalogue['merr_ap_swire_irac2'][use_swire]
master_catalogue.add_column(Column(data=f_ap_irac, name="f_ap_irac_i2"))
master_catalogue.add_column(Column(data=ferr_ap_irac, name="ferr_ap_irac_i2"))
master_catalogue.add_column(Column(data=m_ap_irac, name="m_ap_irac_i2"))
master_catalogue.add_column(Column(data=merr_ap_irac, name="merr_ap_irac_i2"))
master_catalogue.remove_columns(['f_ap_servs_irac2', 'f_ap_swire_irac2', 'ferr_ap_servs_irac2',
'ferr_ap_swire_irac2', 'm_ap_servs_irac2', 'm_ap_swire_irac2',
'merr_ap_servs_irac2', 'merr_ap_swire_irac2'])
origin = np.full(len(master_catalogue), ' ', dtype='<U5')
origin[use_servs] = "SERVS"
origin[use_swire] = "SWIRE"
irac_origin.add_column(Column(data=origin, name="IRAC2_app"))
# +
# IRAC2 total flux and magnitudes
has_servs = ~np.isnan(master_catalogue['f_servs_irac2'])
has_swire = ~np.isnan(master_catalogue['f_swire_irac2'])
has_both = has_servs & has_swire
print("{} sources with SERVS flux".format(np.sum(has_servs)))
print("{} sources with SWIRE flux".format(np.sum(has_swire)))
print("{} sources with SERVS and SWIRE flux".format(np.sum(has_both)))
has_servs_above_limit = has_servs.copy()
has_servs_above_limit[has_servs] = master_catalogue['f_servs_irac2'][has_servs] > 2000
use_swire = (has_swire & ~has_servs) | (has_both & has_servs_above_limit)
use_servs = (has_servs & ~(has_both & has_servs_above_limit))
print("{} sources for which we use SERVS".format(np.sum(use_servs)))
print("{} sources for which we use SWIRE".format(np.sum(use_swire)))
f_ap_irac = np.full(len(master_catalogue), np.nan)
f_ap_irac[use_servs] = master_catalogue['f_servs_irac2'][use_servs]
f_ap_irac[use_swire] = master_catalogue['f_swire_irac2'][use_swire]
ferr_ap_irac = np.full(len(master_catalogue), np.nan)
ferr_ap_irac[use_servs] = master_catalogue['ferr_servs_irac2'][use_servs]
ferr_ap_irac[use_swire] = master_catalogue['ferr_swire_irac2'][use_swire]
flag_irac = np.full(len(master_catalogue), False, dtype=bool)
flag_irac[use_servs] = master_catalogue['flag_servs_irac2'][use_servs]
flag_irac[use_swire] = master_catalogue['flag_swire_irac2'][use_swire]
m_ap_irac = np.full(len(master_catalogue), np.nan)
m_ap_irac[use_servs] = master_catalogue['m_servs_irac2'][use_servs]
m_ap_irac[use_swire] = master_catalogue['m_swire_irac2'][use_swire]
merr_ap_irac = np.full(len(master_catalogue), np.nan)
merr_ap_irac[use_servs] = master_catalogue['merr_servs_irac2'][use_servs]
merr_ap_irac[use_swire] = master_catalogue['merr_swire_irac2'][use_swire]
master_catalogue.add_column(Column(data=f_ap_irac, name="f_irac_i2"))
master_catalogue.add_column(Column(data=ferr_ap_irac, name="ferr_irac_i2"))
master_catalogue.add_column(Column(data=m_ap_irac, name="m_irac_i2"))
master_catalogue.add_column(Column(data=merr_ap_irac, name="merr_irac_i2"))
master_catalogue.add_column(Column(data=flag_irac, name="flag_irac_i2"))
master_catalogue.remove_columns(['f_servs_irac2', 'f_swire_irac2', 'ferr_servs_irac2',
'ferr_swire_irac2', 'm_servs_irac2', 'flag_servs_irac2', 'm_swire_irac2',
'merr_servs_irac2', 'merr_swire_irac2', 'flag_swire_irac2'])
origin = np.full(len(master_catalogue), ' ', dtype='<U5')
origin[use_servs] = "SERVS"
origin[use_swire] = "SWIRE"
irac_origin.add_column(Column(data=origin, name="IRAC2_total"))
# -
irac_origin.write("{}/elais-s1_irac_fluxes_origins{}.fits".format(OUT_DIR, SUFFIX), overwrite=True)
# ### VI.b VIDEO and VHS
# According to <NAME> VIDEO is deeper than VHS so we take the VIDEO flux if both are available
vista_origin = Table()
vista_origin.add_column(master_catalogue['help_id'])
vista_stats = Table()
vista_stats.add_column(Column(data=['y','j','h','k','z'], name="Band"))
vista_stats.add_column(Column(data=np.full(5, 0, dtype=int), name="VIDEO"))
vista_stats.add_column(Column(data=np.full(5, 0, dtype=int), name="VHS"))
vista_stats.add_column(Column(data=np.full(5, 0, dtype=int), name="use VIDEO"))
vista_stats.add_column(Column(data=np.full(5, 0, dtype=int), name="use VHS"))
vista_stats.add_column(Column(data=np.full(5, 0, dtype=int), name="VIDEO ap"))
vista_stats.add_column(Column(data=np.full(5, 0, dtype=int), name="VHS ap"))
vista_stats.add_column(Column(data=np.full(5, 0, dtype=int), name="use VIDEO ap"))
vista_stats.add_column(Column(data=np.full(5, 0, dtype=int), name="use VHS ap"))
vista_bands = ['y','j','h','k','z'] # Lowercase naming convention (k is Ks)
for band in vista_bands:
#print('For VISTA band ' + band + ':')
# VISTA total flux
has_video = ~np.isnan(master_catalogue['f_video_' + band])
if band == 'z':
has_vhs = np.full(len(master_catalogue), False, dtype=bool)
else:
has_vhs = ~np.isnan(master_catalogue['f_vhs_' + band])
use_video = has_video
use_vhs = has_vhs & ~has_video
f_vista = np.full(len(master_catalogue), np.nan)
f_vista[use_video] = master_catalogue['f_video_' + band][use_video]
if not (band == 'z'):
f_vista[use_vhs] = master_catalogue['f_vhs_' + band][use_vhs]
ferr_vista = np.full(len(master_catalogue), np.nan)
ferr_vista[use_video] = master_catalogue['ferr_video_' + band][use_video]
if not (band == 'z'):
ferr_vista[use_vhs] = master_catalogue['ferr_vhs_' + band][use_vhs]
m_vista = np.full(len(master_catalogue), np.nan)
m_vista[use_video] = master_catalogue['m_video_' + band][use_video]
if not (band == 'z'):
m_vista[use_vhs] = master_catalogue['m_vhs_' + band][use_vhs]
merr_vista = np.full(len(master_catalogue), np.nan)
merr_vista[use_video] = master_catalogue['merr_video_' + band][use_video]
if not (band == 'z'):
merr_vista[use_vhs] = master_catalogue['merr_vhs_' + band][use_vhs]
flag_vista = np.full(len(master_catalogue), False, dtype=bool)
flag_vista[use_video] = master_catalogue['flag_video_' + band][use_video]
if not (band == 'z'):
flag_vista[use_vhs] = master_catalogue['flag_vhs_' + band][use_vhs]
master_catalogue.add_column(Column(data=f_vista, name="f_vista_" + band))
master_catalogue.add_column(Column(data=ferr_vista, name="ferr_vista_" + band))
master_catalogue.add_column(Column(data=m_vista, name="m_vista_" + band))
master_catalogue.add_column(Column(data=merr_vista, name="merr_vista_" + band))
master_catalogue.add_column(Column(data=flag_vista, name="flag_vista_" + band))
old_video_columns = ['f_video_' + band,
'ferr_video_' + band,
'm_video_' + band,
'merr_video_' + band,
'flag_video_' + band]
old_vhs_columns = ['f_vhs_' + band,
'ferr_vhs_' + band,
'm_vhs_' + band,
'merr_vhs_' + band,
'flag_vhs_' + band]
if not (band == 'z'):
old_columns = old_video_columns + old_vhs_columns
else:
old_columns = old_video_columns
master_catalogue.remove_columns(old_columns)
origin = np.full(len(master_catalogue), ' ', dtype='<U5')
origin[use_video] = "VIDEO"
origin[use_vhs] = "VHS"
vista_origin.add_column(Column(data=origin, name= 'f_vista_' + band ))
# VISTA Aperture flux
has_ap_video = ~np.isnan(master_catalogue['f_ap_video_' + band])
if (band == 'z'):
has_ap_vhs = np.full(len(master_catalogue), False, dtype=bool)
else:
has_ap_vhs = ~np.isnan(master_catalogue['f_ap_vhs_' + band])
use_ap_video = has_ap_video
use_ap_vhs = has_ap_vhs & ~has_ap_video
f_ap_vista = np.full(len(master_catalogue), np.nan)
f_ap_vista[use_ap_video] = master_catalogue['f_ap_video_' + band][use_ap_video]
if not (band == 'z'):
f_ap_vista[use_ap_vhs] = master_catalogue['f_ap_vhs_' + band][use_ap_vhs]
ferr_ap_vista = np.full(len(master_catalogue), np.nan)
ferr_ap_vista[use_ap_video] = master_catalogue['ferr_ap_video_' + band][use_ap_video]
if not (band == 'z'):
ferr_ap_vista[use_ap_vhs] = master_catalogue['ferr_ap_vhs_' + band][use_ap_vhs]
m_ap_vista = np.full(len(master_catalogue), np.nan)
m_ap_vista[use_ap_video] = master_catalogue['m_ap_video_' + band][use_ap_video]
if not (band == 'z'):
m_ap_vista[use_ap_vhs] = master_catalogue['m_ap_vhs_' + band][use_ap_vhs]
merr_ap_vista = np.full(len(master_catalogue), np.nan)
merr_ap_vista[use_ap_video] = master_catalogue['merr_ap_video_' + band][use_ap_video]
if not (band == 'z'):
merr_ap_vista[use_ap_vhs] = master_catalogue['merr_ap_vhs_' + band][use_ap_vhs]
master_catalogue.add_column(Column(data=f_ap_vista, name="f_ap_vista_" + band))
master_catalogue.add_column(Column(data=ferr_ap_vista, name="ferr_ap_vista_" + band))
master_catalogue.add_column(Column(data=m_ap_vista, name="m_ap_vista_" + band))
master_catalogue.add_column(Column(data=merr_vista, name="merr_ap_vista_" + band))
ap_old_video_columns = ['f_ap_video_' + band,
'ferr_ap_video_' + band,
'm_ap_video_' + band,
'merr_ap_video_' + band]
ap_old_vhs_columns = ['f_ap_vhs_' + band,
'ferr_ap_vhs_' + band,
'm_ap_vhs_' + band,
'merr_ap_vhs_' + band]
if not (band == 'z'):
ap_old_columns = ap_old_video_columns + ap_old_vhs_columns
else:
ap_old_columns = ap_old_video_columns
master_catalogue.remove_columns(ap_old_columns)
origin_ap = np.full(len(master_catalogue), ' ', dtype='<U5')
origin_ap[use_ap_video] = "VIDEO"
origin_ap[use_ap_vhs] = "VHS"
vista_origin.add_column(Column(data=origin_ap, name= 'f_ap_vista_' + band ))
vista_stats['VIDEO'][vista_stats['Band'] == band] = np.sum(has_video)
vista_stats['VHS'][vista_stats['Band'] == band] = np.sum(has_vhs)
vista_stats['use VIDEO'][vista_stats['Band'] == band] = np.sum(use_video)
vista_stats['use VHS'][vista_stats['Band'] == band] = np.sum(use_vhs)
vista_stats['VIDEO ap'][vista_stats['Band'] == band] = np.sum(has_ap_video)
vista_stats['VHS ap'][vista_stats['Band'] == band] = np.sum(has_ap_vhs)
vista_stats['use VIDEO ap'][vista_stats['Band'] == band] = np.sum(use_ap_video)
vista_stats['use VHS ap'][vista_stats['Band'] == band] = np.sum(use_ap_vhs)
# ### Vista origin overview
# For each band show how many objects have fluxes from each survey for both total and aperture photometries.
vista_stats.show_in_notebook()
vista_origin.write("{}/elais-s1_vista_fluxes_origins{}.fits".format(OUT_DIR, SUFFIX), overwrite=True)
for col in master_catalogue.colnames:
if 'vista_k' in col:
master_catalogue[col].name = col.replace('vista_k', 'vista_ks')
# ### Column renaming
# +
renaming = OrderedDict({
'_voice_b99':'_wfi_b',
'_voice_b123':'_wfi_b123',
'_voice_v': '_wfi_v',
'_voice_r':'_wfi_r',
})
for col in master_catalogue.colnames:
for rename_col in list(renaming):
if rename_col in col:
master_catalogue.rename_column(col, col.replace(rename_col, renaming[rename_col]))
# -
# ## VII.a Wavelength domain coverage
#
# We add a binary `flag_optnir_obs` indicating that a source was observed in a given wavelength domain:
#
# - 1 for observation in optical;
# - 2 for observation in near-infrared;
# - 4 for observation in mid-infrared (IRAC).
#
# It's an integer binary flag, so a source observed both in optical and near-infrared by not in mid-infrared would have this flag at 1 + 2 = 3.
#
# *Note 1: The observation flag is based on the creation of multi-order coverage maps from the catalogues, this may not be accurate, especially on the edges of the coverage.*
#
# *Note 2: Being on the observation coverage does not mean having fluxes in that wavelength domain. For sources observed in one domain but having no flux in it, one must take into consideration de different depths in the catalogue we are using.*
video_moc = MOC(filename="../../dmu0/dmu0_VISTA-VIDEO-private/data/VIDEO-all_2017-02-12_fullcat_errfix_ELAIS-S1_MOC.fits")
vhs_moc = MOC(filename="../../dmu0/dmu0_VISTA-VHS/data/VHS_ELAIS-S1_MOC.fits")
voice_moc = MOC(filename="../../dmu0/dmu0_ESIS-VOICE/data/esis_b2vr_cat_03_HELP-coverage_MOC.fits")
servs_moc = MOC(filename="../../dmu0/dmu0_DataFusion-Spitzer/data/DF-SERVS_ELAIS-S1_MOC.fits")
swire_moc = MOC(filename="../../dmu0/dmu0_DataFusion-Spitzer/data/DF-SWIRE_ELAIS-S1_MOC.fits")
des_moc = MOC(filename="../../dmu0/dmu0_DES/data/DES-DR1_ELAIS-S1_MOC.fits")
# +
was_observed_optical = inMoc(
master_catalogue['ra'], master_catalogue['dec'],
voice_moc + des_moc)
was_observed_nir = inMoc(
master_catalogue['ra'], master_catalogue['dec'],
video_moc + vhs_moc + voice_moc
)
was_observed_mir = inMoc(
master_catalogue['ra'], master_catalogue['dec'],
servs_moc + swire_moc
)
# -
master_catalogue.add_column(
Column(
1 * was_observed_optical + 2 * was_observed_nir + 4 * was_observed_mir,
name="flag_optnir_obs")
)
# ## VII.b Wavelength domain detection
#
# We add a binary `flag_optnir_det` indicating that a source was detected in a given wavelength domain:
#
# - 1 for detection in optical;
# - 2 for detection in near-infrared;
# - 4 for detection in mid-infrared (IRAC).
#
# It's an integer binary flag, so a source detected both in optical and near-infrared by not in mid-infrared would have this flag at 1 + 2 = 3.
#
# *Note 1: We use the total flux columns to know if the source has flux, in some catalogues, we may have aperture flux and no total flux.*
#
# To get rid of artefacts (chip edges, star flares, etc.) we consider that a source is detected in one wavelength domain when it has a flux value in **at least two bands**. That means that good sources will be excluded from this flag when they are on the coverage of only one band.
# +
# SpARCS is a catalogue of sources detected in r (with fluxes measured at
# this prior position in the other bands). Thus, we are only using the r
# CFHT band.
# Check to use catalogue flags from HSC and PanSTARRS.
nb_optical_flux = (
1 * ~np.isnan(master_catalogue['f_wfi_r']) +
1 * ~np.isnan(master_catalogue['f_decam_g']) +
1 * ~np.isnan(master_catalogue['f_decam_r']) +
1 * ~np.isnan(master_catalogue['f_decam_i']) +
1 * ~np.isnan(master_catalogue['f_decam_z']) +
1 * ~np.isnan(master_catalogue['f_decam_y'])
)
nb_nir_flux = (
1 * ~np.isnan(master_catalogue['f_vista_j']) +
1 * ~np.isnan(master_catalogue['f_vista_h']) +
1 * ~np.isnan(master_catalogue['f_vista_ks'])
)
nb_mir_flux = (
1 * ~np.isnan(master_catalogue['f_irac_i1']) +
1 * ~np.isnan(master_catalogue['f_irac_i2']) +
1 * ~np.isnan(master_catalogue['f_irac_i3']) +
1 * ~np.isnan(master_catalogue['f_irac_i4'])
)
# +
has_optical_flux = nb_optical_flux >= 2
has_nir_flux = nb_nir_flux >= 2
has_mir_flux = nb_mir_flux >= 2
master_catalogue.add_column(
Column(
1 * has_optical_flux + 2 * has_nir_flux + 4 * has_mir_flux,
name="flag_optnir_det")
)
# -
# ## VIII - Cross-identification table
#
# We are producing a table associating to each HELP identifier, the identifiers of the sources in the pristine catalogue. This can be used to easily get additional information from them.
# +
id_names = []
for col in master_catalogue.colnames:
if '_id' in col:
id_names += [col]
if '_intid' in col:
id_names += [col]
print(id_names)
# +
master_catalogue[id_names].write(
"{}/master_list_cross_ident_elais-s1{}.fits".format(OUT_DIR, SUFFIX), overwrite=True)
id_names.remove('help_id')
master_catalogue.remove_columns(id_names)
# -
# ## IX - Adding HEALPix index
#
# We are adding a column with a HEALPix index at order 13 associated with each source.
master_catalogue.add_column(Column(
data=coords_to_hpidx(master_catalogue['ra'], master_catalogue['dec'], order=13),
name="hp_idx"
))
# ## IX - Saving the catalogue
# +
columns = ["help_id", "field", "ra", "dec", "hp_idx"]
bands = [column[5:] for column in master_catalogue.colnames if 'f_ap' in column]
for band in bands:
columns += ["f_ap_{}".format(band), "ferr_ap_{}".format(band),
"m_ap_{}".format(band), "merr_ap_{}".format(band),
"f_{}".format(band), "ferr_{}".format(band),
"m_{}".format(band), "merr_{}".format(band),
"flag_{}".format(band)]
columns += ["stellarity", "stellarity_origin",
"flag_cleaned", "flag_merged", "flag_gaia", "flag_optnir_obs", "flag_optnir_det",
"zspec", "zspec_qual", "zspec_association_flag", "ebv"]
# -
# We check for columns in the master catalogue that we will not save to disk.
print("Missing columns: {}".format(set(master_catalogue.colnames) - set(columns)))
master_catalogue[columns].write("{}/master_catalogue_elais-s1{}.fits".format(OUT_DIR, SUFFIX))
|
dmu1/dmu1_ml_ELAIS-S1/2_Merging.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
import io
import panel as pn
pn.extension()
# The ``FileInput`` widget allows uploading one or more file from the frontend and makes the filename, file data and [MIME type](https://developer.mozilla.org/en-US/docs/Web/HTTP/Basics_of_HTTP/MIME_types) available in Python.
#
# For more information about listening to widget events and laying out widgets refer to the [widgets user guide](../../user_guide/Widgets.ipynb). Alternatively you can learn how to build GUIs by declaring parameters independently of any specific widgets in the [param user guide](../../user_guide/Param.ipynb). To express interactivity entirely using Javascript without the need for a Python server take a look at the [links user guide](../../user_guide/Param.ipynb).
#
# #### Parameters:
#
# For layout and styling related parameters see the [customization user guide](../../user_guide/Customization.ipynb).
#
# ##### Core
#
# * **``accept``** (str): A list of file input filters that restrict what files the user can pick from
# * **``filename``** (str/list): The filename(s) of the uploaded file(s)
# * **``mime_type``** (str/list): The mime type(s) of the uploaded file(s)
# * **``multiple``** (boolean): Whether to allow uploading multiple files
# * **``value``** (bytes/list): A bytes object containing the file data or if `multiple` is set a list of bytes objects.
#
# ___
# +
file_input = pn.widgets.FileInput()
file_input
# -
# To read out the content of the file you can access the ``value`` parameter, which holds a [bytestring](https://docs.python.org/3/library/stdtypes.html#bytes-objects) containing the file's contents. Additionally information about the file type is made available on the ``filetype`` parameter expressed as a MIME type, e.g. ``image/png`` or ``text/csv``.
file_input.value
# The widget also has a ``save`` method that allows saving the uploaded data to a file or [BytesIO](https://docs.python.org/3/library/io.html#binary-i-o) object.
# +
# File
if file_input.value is not None:
file_input.save('test.png')
# BytesIO object
if file_input.value is not None:
out = io.BytesIO()
file_input.save(out)
# -
# The `accept` parameter restricts what files the user can pick from. This consists of comma-separated list of standard HTML
# file input filters. Values can be:
#
# * `<file extension>` - Specific file extension(s) (e.g: .gif, .jpg, .png, .doc) are pickable
# * `audio/*` - all sound files are pickable
# * `video/*` - all video files are pickable
# * `image/*` - all image files are pickable
# * `<media type>` - A valid [IANA Media Type](https://www.iana.org/assignments/media-types/media-types.xhtml), with no parameters.
# +
file_input = pn.widgets.FileInput(accept='.csv,.json')
file_input
# -
# To allow uploading multiple files we can also set `multiple=True`:
# +
file_input = pn.widgets.FileInput(accept='.png', multiple=True)
file_input
# -
# When uploading one or more files the `filename`, `mime_type` and `value` parameters will now be lists.
# ### Upload size limits
#
# While the `FileInput` widget doesn't set any limit on the size of a file that can be selected by a user, the infrastructure onto which Panel relies (web browsers, Bokeh, Tornado, notebooks, etc.) limits significantly what is actually possible. By default the `FileInput` widget allows to upload data that is in the order of 10 MB. Even if it is possible to increase this limit by setting some parameters (described below), bear in mind that the `FileInput` widget is not meant to upload large files.
#
# #### How it works
#
# Before increasing the file size limit it is worth explaining the process that happens when a file is selected.
#
# The `FileInput` widget is a Bokeh widget whose data is communicated from the front-end to the back-end via a protocal called [Web Sockets](https://en.wikipedia.org/wiki/WebSocket). Bokeh didn't implement Web Sockets itself, instead it took advantage of an existing web framework that provided an implementation: [Tornado](https://www.tornadoweb.org/en/stable/).
#
# In even more concrete terms, here's what happens when a file is selected in a server context (it's the exact same process when multiple files are loaded at once!):
#
# 1. The file is loaded into memory by the browser
# 2. Its content is converted by BokehJS into a [base64 encoded string](https://en.wikipedia.org/wiki/Base64) (which turns a binary file, like a PNG image, into a very long ASCII string)
# 3. BokehJS puts this long string into a JSON message along with some more information
# 4. The message is sent through a `Tornado` web socket connection to the back-end
# 5. The back-end uses it to update the Bokeh/Python model; that's when the properties of the widget in the Bokeh/Python world get updated
# 6. Panel updates the attributes of the `FileInput` widget instance when the properties of the Python/Bokeh widget are updated. The long string is converted by Panel into a `bytes` object that is available with `.value`.
#
# #### Limits defined
#
# The steps described above almost all have potential or actual limits:
#
# 1. Browsers can't upload an unlimited amount of data at once; they're usually limited to a few GB
# 2. BokehJS uses the [FileReader.readAsDataURL](https://developer.mozilla.org/en-US/docs/Web/API/FileReader/readAsDataURL) method to encode the file as a data URL; browsers can [limit](https://developer.mozilla.org/en-US/docs/Web/HTTP/Basics_of_HTTP/Data_URIs#common_problems) the length of that URL
# 3. BokehJS (or the libraries that it uses) may fail at creating the message from a very (very!) large string
# 4. `Tornado` imposes two limits on the data being transferred: (1) on the maximum size of a buffer and (2) on the maximum size of the websocket message. (1) is 100 MB by default (set by Tornado) and (2) is 20 MB by default (set by Bokeh).
#
# #### Increase the limits
#
# While there's nothing much that can be done about 1., 2. and 3. (except informing your users), the limits defined by Tornado and Bokeh can be overwritten.
#
# ##### Server context
#
# In a server context your application must be executed with `python your_app.py` (because `panel serve` doesn't allow to configure all the options provided by Bokeh and Tornado):
#
# ```python
# # your_app.py
# import panel as pn
#
# app = ...
#
# MAX_SIZE_MB = 150
#
# pn.serve(
# app,
# # Increase the maximum websocket message size allowed by Bokeh
# websocket_max_message_size=MAX_SIZE_MB*1024*1014,
# # Increase the maximum buffer size allowed by Tornado
# http_server_kwargs={'max_buffer_size': MAX_SIZE_MB*1024*1014}
# )
# ```
#
# ##### Notebook context
#
# In a Jupyter notebook (classic or lab) the limits of Tornado (Tornado's Web Sockets are already used by the Jupyter notebook for communication purposes) can be set in a configuration file. The default maximum buffer size is 512 MB and the default maximum websocked message size is 10 MB.
#
# *Classic Notebook:*
#
# Generate a configuration file with `jupyter notebook --generate-config` and update it with:
#
# ```python
# c.NotebookApp.tornado_settings = {"websocket_max_message_size": 150 * 1024 * 1024}
# c.NotebookApp.max_buffer_size = 150 * 1024 * 1024
# ```
#
# *Lab:*
#
# Generate a configuration file with `jupyter lab --generate-config` and update it with:
#
# ```python
# c.ServerApp.tornado_settings = {'websocket_max_message_size': 150 * 1024 * 1024}
# c.ServerApp.max_buffer_size = 150 * 1024 * 1024
# ```
#
# #### Caveats
#
# * The maximum sizes set in either Bokeh or Tornado refer to the maximum size of the **message** that is transferred through the web socket connection, which is going to be larger than the actual size of the uploaded file since the file content is encoded in a `base64` string. So if you set a maximum size of 100 MB for your application, you should indicate your users that the upload limit is a value that is **less** than 100 MB.
# * When a file whose size is larger than the limits is selected by a user, their browser/tab may just crash. Alternatively the web socket connection can close (sometimes with an error message printed in the browser console such as `[bokeh] Lost websocket 0 connection, 1009 (message too big)`) which means the application will become unresponsive and needs to be refreshed.
# ### Controls
#
# The `FileInput` widget exposes a number of options which can be changed from both Python and Javascript. Try out the effect of these parameters interactively:
pn.Row(file_input.controls(jslink=True), file_input)
|
examples/reference/widgets/FileInput.ipynb
|
# +
# Copyright 2010 <NAME> <EMAIL>
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
"""
All interval problem in Google CP Solver.
CSPLib problem number 7
http://www.cs.st-andrews.ac.uk/~ianm/CSPLib/prob/prob007/index.html
'''
Given the twelve standard pitch-classes (c, c , d, ...), represented by
numbers 0,1,...,11, find a series in which each pitch-class occurs exactly
once and in which the musical intervals between neighbouring notes cover
the full set of intervals from the minor second (1 semitone) to the major
seventh (11 semitones). That is, for each of the intervals, there is a
pair of neigbhouring pitch-classes in the series, between which this
interval appears. The problem of finding such a series can be easily
formulated as an instance of a more general arithmetic problem on Z_n,
the set of integer residues modulo n. Given n in N, find a vector
s = (s_1, ..., s_n), such that (i) s is a permutation of
Z_n = {0,1,...,n-1}; and (ii) the interval vector
v = (|s_2-s_1|, |s_3-s_2|, ... |s_n-s_{n-1}|) is a permutation of
Z_n-{0} = {1,2,...,n-1}. A vector v satisfying these conditions is
called an all-interval series of size n; the problem of finding such
a series is the all-interval series problem of size n. We may also be
interested in finding all possible series of a given size.
'''
Compare with the following models:
* MiniZinc: http://www.hakank.org/minizinc/all_interval.mzn
* Comet : http://www.hakank.org/comet/all_interval.co
* Gecode/R: http://www.hakank.org/gecode_r/all_interval.rb
* ECLiPSe : http://www.hakank.org/eclipse/all_interval.ecl
* SICStus : http://www.hakank.org/sicstus/all_interval.pl
This model was created by <NAME> (<EMAIL>)
Also see my other Google CP Solver models:
http://www.hakank.org/google_or_tools/
"""
from __future__ import print_function
import sys
from ortools.constraint_solver import pywrapcp
# Create the solver.
solver = pywrapcp.Solver("All interval")
#
# data
#
print("n:", n)
#
# declare variables
#
x = [solver.IntVar(1, n, "x[%i]" % i) for i in range(n)]
diffs = [solver.IntVar(1, n - 1, "diffs[%i]" % i) for i in range(n - 1)]
#
# constraints
#
solver.Add(solver.AllDifferent(x))
solver.Add(solver.AllDifferent(diffs))
for k in range(n - 1):
solver.Add(diffs[k] == abs(x[k + 1] - x[k]))
# symmetry breaking
solver.Add(x[0] < x[n - 1])
solver.Add(diffs[0] < diffs[1])
#
# solution and search
#
solution = solver.Assignment()
solution.Add(x)
solution.Add(diffs)
db = solver.Phase(x, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)
solver.NewSearch(db)
num_solutions = 0
while solver.NextSolution():
print("x:", [x[i].Value() for i in range(n)])
print("diffs:", [diffs[i].Value() for i in range(n - 1)])
num_solutions += 1
print()
print("num_solutions:", num_solutions)
print("failures:", solver.Failures())
print("branches:", solver.Branches())
print("WallTime:", solver.WallTime())
n = 12
|
examples/notebook/contrib/all_interval.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from IPython.display import display, Image
from indian_pines_cnn_classification.validate import (
validate,
classify
)
loss, accuracy, cls, confusion = validate(
model_path='model.h5', test_data_path='split')
print("Loss: {}".format(loss))
print("Accuracy: {}".format(accuracy))
print(cls)
print(confusion)
paths = classify(model_path='model.h5', data_path='data')
display(Image('ground_truth.jpg', width=200, height=200))
display(Image('classification.jpg', width=200, height=200))
|
Validation_and_Classification_Maps_from_package.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # <img style="float: left; padding-right: 10px; width: 45px" src="https://github.com/Harvard-IACS/2018-CS109A/blob/master/content/styles/iacs.png?raw=true"> CS109A Introduction to Data Science
#
# ## Lab 2: Web Scraping with Beautiful Soup
#
# **Harvard University**<br>
# **Fall 2019**<br>
# **Instructors:** <NAME>, <NAME>, and <NAME> <br>
# **Lab Instructors:** <NAME> and <NAME><br>
# **Authors:** <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, and <NAME>
#
# ---
## RUN THIS CELL TO GET THE RIGHT FORMATTING
from IPython.core.display import HTML
def css_styling():
styles = open("../../styles/cs109.css", "r").read()
return HTML(styles)
css_styling()
# %matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn.apionly as sns
import time
# # Table of Contents
# <ol start="0">
# <li> Learning Goals </li>
# <li> Introduction to Web Servers and HTTP </li>
# <li> Download webpages and get basic properties </li>
# <li> Parse the page with Beautiful Soup</li>
# <li> String formatting</li>
# <li> Additonal Python/Homework Comment</li>
# <li> Walkthrough Example</li>
# </ol>
# # Learning Goals
#
# - Understand the structure of a web page
# - Understand how to use Beautiful soup to scrape content from web pages.
# - Feel comfortable storing and manipulating the content in various formats.
# - Understand how to convert structured format into a Pandas DataFrame
#
# In this lab, we'll scrape Goodread's Best Books list:
#
# https://www.goodreads.com/list/show/1.Best_Books_Ever?page=1 .
#
# We'll walk through scraping the list pages for the book names/urls. First, we start with an even simpler example.
#
# *This lab corresponds to lectures #2 and #3 and maps on to Homework #1 and further.*
# # 1. Introduction to Web Servers and HTTP
#
# A web server is just a computer -- usually a powerful one, but ultimately it's just another computer -- that runs a long/continuous process that listens for requests on a pre-specified (Internet) _port_ on your computer. It responds to those requests via a protocol called HTTP (HyperText Transfer Protocol). HTTPS is the secure version. When we use a web browser and navigate to a web page, our browser is actually sending a request on our behalf to a specific web server. The browser request is essentially saying "hey, please give me the web page contents", and it's up to the browser to correctly render that raw content into a coherent manner, dependent on the format of the file. For example, HTML is one format, XML is another format, and so on.
#
# Ideally (and usually), the web server complies with the request and all is fine. As part of this communication exchange with web servers, the server also sends a status code.
# - If the code starts with a **2**, it means the request was successful.
# - If the code starts with a **4**, it means there was a client error (you, as the user, are the client). For example, ever receive a 404 File Not Found error because a web page doesn't exist? This is an example of a client error, because you are requesting a bogus item.
# - If the code starts with a **5**, it means there was a server error (often that your request was incorrectly formed).
#
# [Click here](https://www.restapitutorial.com/httpstatuscodes.html) for a full list of status codes.
#
# As an analogy, you can think of a web server as being like a server at a restaurant; its goal is _serve_ you your requests. When you try to order something not on the menu (i.e., ask for a web page at a wrong location), the server says 'sorry, we don't have that' (i.e., 404, client error; your mistake).
#
# **IMPORTANT:**
# As humans, we visit pages in a sane, reasonable rate. However, as we start to scrape web pages with our computers, we will be sending requests with our code, and thus, we can make requests at an incredible rate. This is potentially dangerous because it's akin to going to a restaurant and bombarding the server(s) with thousands of food orders. Very often, the restaurant will ban you (i.e., Harvard's network gets banned from the website, and you are potentially held responsible in some capacity?). It is imperative to be responsible and careful. In fact, this act of flooding web pages with requests is the single-most popular, yet archiac, method for maliciously attacking websites / computers with Internet connections. In short, be respectful and careful with your decisions and code. It is better to err on the side of caution, which includes using the **``time.sleep()`` function** to pause your code's execution between subsequent requests. ``time.sleep(2)`` should be fine when making just a few dozen requests. Each site has its own rules, which are often visible via their site's ``robots.txt`` file.
#
# ### Additional Resources
#
# **HTML:** if you are not familiar with HTML see https://www.w3schools.com/html/ or one of the many tutorials on the internet.
#
# **Document Object Model (DOM):** for more on this programming interface for HTML and XML documents see https://www.w3schools.com/js/js_htmldom.asp.
# # 2. Download webpages and get basic properties
#
# ``Requests`` is a highly useful Python library that allows us to fetch web pages.
# ``BeautifulSoup`` is a phenomenal Python library that allows us to easily parse web content and perform basic extraction.
#
# If one wishes to scrape webpages, one usually uses ``requests`` to fetch the page and ``BeautifulSoup`` to parse the page's meaningful components. Webpages can be messy, despite having a structured format, which is why BeautifulSoup is so handy.
#
# Let's get started:
from bs4 import BeautifulSoup
import requests
# To fetch a webpage's content, we can simply use the ``get()`` function within the requests library:
url = "https://www.npr.org/2018/11/05/664395755/what-if-the-polls-are-wrong-again-4-scenarios-for-what-might-happen-in-the-elect"
response = requests.get(url) # you can use any URL that you wish
# The response variable has many highly useful attributes, such as:
# - status_code
# - text
# - content
#
# Let's try each of them!
# ### response.status_code
response.status_code
# You should have received a status code of 200, which means the page was successfully found on the server and sent to receiver (aka client/user/you). [Again, you can click here](https://www.restapitutorial.com/httpstatuscodes.html) for a full list of status codes.
#
# ### response.text
#
response.text
# Holy moly! That looks awful. If we use our browser to visit the URL, then right-click the page and click 'View Page Source', we see that it is identical to this chunk of glorious text.
#
# ### response.content
response.content
# What?! This seems identical to the ``.text`` field. However, the careful eye would notice that the very 1st characters differ; that is, ``.content`` has a *b'* character at the beginning, which in Python syntax denotes that the data type is bytes, whereas the ``.text`` field did not have it and is a regular String.
#
# Ok, so that's great, but how do we make sense of this text? We could manually parse it, but that's tedious and difficult. As mentioned, BeautifulSoup is specifically designed to parse this exact content (any webpage content).
#
# ## BEAUTIFUL SOUP
#  (property of NBC)
#
#
# The [documentation for BeautifulSoup is found here](https://www.crummy.com/software/BeautifulSoup/bs4/doc/).
#
# A BeautifulSoup object can be initialized with the ``.content`` from request and a flag denoting the type of parser that we should use. For example, we could specify ``html.parser``, ``lxml``, etc [documentation here](https://www.crummy.com/software/BeautifulSoup/bs4/doc/#differences-between-parsers). Since we are interested in standard webpages that use HTML, let's specify the html.parser:
soup = BeautifulSoup(response.content, "html.parser")
soup
# Alright! That looks a little better; there's some whitespace formatting, adding some structure to our content! HTML code is structured by `<tags>`. Every tag has an opening and closing portion, denoted by ``< >`` and ``</ >``, respectively. If we want just the text (not the tags), we can use:
soup.get_text()
# There's some tricky Javascript still nesting within it, but it definitely cleaned up a bit. On other websites, you may find even clearer text extraction.
#
# As detailed in the [BeautifulSoup documentation](https://www.crummy.com/software/BeautifulSoup/bs4/doc/), the easiest way to navigate through the tags is to simply name the tag you're interested in. For example:
soup.head # fetches the head tag, which ecompasses the title tag
# Usually head tags are small and only contain the most important contents; however, here, there's some Javascript code. The ``title`` tag resides within the head tag.
soup.title # we can specifically call for the title tag
# This result includes the tag itself. To get just the text within the tags, we can use the ``.name`` property.
soup.title.string
# We can navigate to the parent tag (the tag that encompasses the current tag) via the ``.parent`` attribute:
soup.title.parent.name
# # 3. Parse the page with Beautiful Soup
# In HTML code, paragraphs are often denoated with a ``<p>`` tag.
soup.p
# This returns the first paragraph, and we can access properties of the given tag with the same syntax we use for dictionaries and dataframes:
soup.p['class']
# In addition to 'paragraph' (aka p) tags, link tags are also very common and are denoted by ``<a>`` tags
soup.a
# It is called the a tag because links are also called 'anchors'. Nearly every page has multiple paragraphs and anchors, so how do we access the subsequent tags? There are two common functions, `.find()` and `.find_all()`.
soup.find('title')
soup.find_all('title')
# Here, the results were seemingly the same, since there is only one title to a webpage. However, you'll notice that ``.find_all()`` returned a list, not a single item. Sure, there was only one item in the list, but it returned a list. As the name implies, find_all() returns all items that match the passed-in tag.
soup.find_all('a')
# Look at all of those links! Amazing. It might be hard to read but the **href** portion of an *a* tag denotes the URL, and we can capture it via the ``.get()`` function.
for link in soup.find_all('a'): # we could optionally pass the href=True flag .find_all('a', href=True)
print(link.get('href'))
# Many of those links are relative to the current URL (e.g., /section/news/).
paragraphs = soup.find_all('p')
paragraphs
# If we want just the paragraph text:
for pa in paragraphs:
print(pa.get_text())
# Since there are multiple tags and various attributes, it is useful to check the data type of BeautifulSoup objects:
type(soup.find('p'))
# Since the ``.find()`` function returns a BeautifulSoup element, we can tack on multiple calls that continue to return elements:
soup.find('p')
soup.find('p').find('a')
soup.find('p').find('a').attrs['href'] # att
soup.find('p').find('a').text
# That doesn't look pretty, but it makes sense because if you look at what ``.find('a')`` returned, there is plenty of whitespace. We can remove that with Python's built-in ``.strip()`` function.
soup.find('p').find('a').text.strip()
# **NOTE:** above, we accessed the attributes of a link by using the property ``.attrs``. ``.attrs`` takes a dictionary as a parameter, and in the example above, we only provided the _key_, not a _value_, too. That is, we only cared that the ``<a>`` tag had an attribute named ``href`` (which we grabbed by typing that command), and we made no specific demands on what the value must be. In other words, regardless of the value of _href_, we grabbed that element. Alternatively, if you inspect your HTML code and notice select regions for which you'd like to extract text, you can specify it as part of the attributes, too!
#
# For example, in the full ``response.text``, we see the following line:
#
# ``<header class="npr-header" id="globalheader" aria-label="NPR header">``
#
# Let's say that we know that the information we care about is within tags that match this template (i.e., **class** is an attribute, and its value is **'npr-header'**).
soup.find('header', attrs={'class':'npr-header'})
# This matched it! We could then continue further processing by tacking on other commands:
soup.find('header', attrs={'class':'npr-header'}).find_all("li") # li stands for list items
# This returns all of our list items, and since it's within a particular header section of the page, it appears they are links to menu items for navigating the webpage. If we wanted to grab just the links within these:
menu_links = set()
for list_item in soup.find('header', attrs={'class':'npr-header'}).find_all("li"):
for link in list_item.find_all('a', href=True):
menu_links.add(link)
menu_links # a unique set of all the seemingly important links in the header
# ## <NAME>
# The above tutorial isn't meant to be a study guide to memorize; its point is to show you the most important functionaity that exist within BeautifulSoup, and to illustrate how one can access different pieces of content. No two web scraping tasks are identical, so it's useful to play around with code and try different things, while using the above as examples of how you may navigate between different tags and properties of a page. Don't worry; we are always here to help when you get stuck!
#
# # String formatting
# As we parse webpages, we may often want to further adjust and format the text to a certain way.
#
# For example, say we wanted to scrape a polical website that lists all US Senators' name and office phone number. We may want to store information for each senator in a dictionary. All senators' information may be stored in a list. Thus, we'd have a list of dictionaries. Below, we will initialize such a list of dictionary (it has only 3 senators, for illustrative purposes, but imagine it contains many more).
# this is a bit clumsy of an initialization, but we spell it out this way for clarity purposes
# NOTE: imagine the dictionary were constructed in a more organic manner
senator1 = {"name":"<NAME>", "number":"555-229-2812"}
senator2 = {"name":"<NAME>", "number":"555-922-8393"}
senator3 = {"name":"<NAME>", "number":"555-827-2281"}
senators = [senator1, senator2, senator3]
print(senators)
# In the real-world, we may not want the final form of our information to be in a Python dictionary; rather, we may need to send an email to people in our mailing list, urging them to call their senators. If we have a templated format in mind, we can do the following:
email_template = """Please call {name} at {number}"""
for senator in senators:
print(email_template.format(**senator))
# **Please [visit here](https://docs.python.org/3/library/stdtypes.html#str.format)** for further documentation
#
# Alternatively, one can also format their text via the ``f'-strings`` property. [See documentation here](https://docs.python.org/3/reference/lexical_analysis.html#f-strings). For example, using the above data structure and goal, one could yield identical results via:
for senator in senators:
print(f"Please call {senator['name']} at {senator['number']}")
# Additionally, sometimes we wish to search large strings of text. If we wish to find all occurrences within a given string, a very mechanical, procedural way of doing it would be to use the ``.find()`` function in Python and to repeatedly update the starting index from which we are looking.
#
# ## Regular Expressions
# A way more suitable and powerful way is to use Regular Expressions, which is a pattern matching mechanism used throughout Computer Science and programming (it's not just specific to Python). A tutorial on Regular Expressions (aka regex) is beond this lab, but below are many great resources that we recommend, if you are interested in them (could be very useful for a homework problem):
# - https://docs.python.org/3.3/library/re.html
# - https://regexone.com
# - https://docs.python.org/3/howto/regex.html.
#
# # Additonal Python/Homework Comment
# In Homework #1, we ask you to complete functions that have signatures with a syntax you may not have seen before:
#
# ``def create_star_table(starlist: list) -> list:``
#
# To be clear, this syntax merely means that the input parameter must be a list, and the output must be a list. It's no different than any other function, it just puts a requirement on the behavior of the function.
#
# It is **typing** our function. Please [see this documention if you have more questions.](https://docs.python.org/3/library/typing.html)
#
# # Walkthrough Example (of Web Scraping)
# We're going to see the structure of Goodread's best books list (**NOTE: Goodreads is described a little more within the other Lab2_More_Pandas.ipynb notebook)**. We'll use the Developer tools in chrome, safari and firefox have similar tools available. To get this page we use the `requests` module. But first we should check if the company's policy allows scraping. Check the [robots.txt](https://www.goodreads.com/robots.txt) to find what sites/elements are not accessible. Please read and verify.
#
# 
# +
url="https://www.npr.org/2018/11/05/664395755/what-if-the-polls-are-wrong-again-4-scenarios-for-what-might-happen-in-the-elect"
response = requests.get(url)
# response.status_code
# response.content
# Beautiful Soup (library) time!
soup = BeautifulSoup(response.content, "html.parser")
#print(soup)
# soup.prettify()
soup.find("title")
# Q1: how do we get the title's text?
# Q2: how do we get the webpage's entire content?
# -
URLSTART="https://www.goodreads.com"
BESTBOOKS="/list/show/1.Best_Books_Ever?page="
url = URLSTART+BESTBOOKS+'1'
print(url)
page = requests.get(url)
# We can see properties of the page. Most relevant are `status_code` and `text`. The former tells us if the web-page was found, and if found , ok. (See lecture notes.)
page.status_code # 200 is good
page.text[:5000]
# Let us write a loop to fetch 2 pages of "best-books" from goodreads. Notice the use of a format string. This is an example of old-style python format strings
URLSTART="https://www.goodreads.com"
BESTBOOKS="/list/show/1.Best_Books_Ever?page="
for i in range(1,3):
bookpage=str(i)
stuff=requests.get(URLSTART+BESTBOOKS+bookpage)
filetowrite="files/page"+ '%02d' % i + ".html"
print("FTW", filetowrite)
fd=open(filetowrite,"w")
fd.write(stuff.text)
fd.close()
time.sleep(2)
# ## 2. Parse the page, extract book urls
#
# Notice how we do file input-output, and use beautiful soup in the code below. The `with` construct ensures that the file being read is closed, something we do explicitly for the file being written. We look for the elements with class `bookTitle`, extract the urls, and write them into a file
bookdict={}
for i in range(1,3):
books=[]
stri = '%02d' % i
filetoread="files/page"+ stri + '.html'
print("FTW", filetoread)
with open(filetoread) as fdr:
data = fdr.read()
soup = BeautifulSoup(data, 'html.parser')
for e in soup.select('.bookTitle'):
books.append(e['href'])
print(books[:10])
bookdict[stri]=books
fd=open("files/list"+stri+".txt","w")
fd.write("\n".join(books))
fd.close()
# Here is <NAME>'s 1984
bookdict['02'][0]
# Lets go look at the first URLs on both pages
# 
# ## 3. Parse a book page, extract book properties
#
# Ok so now lets dive in and get one of these these files and parse them.
furl=URLSTART+bookdict['02'][0]
furl
# 
fstuff=requests.get(furl)
print(fstuff.status_code)
#d=BeautifulSoup(fstuff.text, 'html.parser')
# try this to take care of arabic strings
d = BeautifulSoup(fstuff.text, 'html.parser', from_encoding="utf-8")
d.select("meta[property='og:title']")[0]['content']
# Lets get everything we want...
#d=BeautifulSoup(fstuff.text, 'html.parser', from_encoding="utf-8")
print(
"title", d.select_one("meta[property='og:title']")['content'],"\n",
"isbn", d.select("meta[property='books:isbn']")[0]['content'],"\n",
"type", d.select("meta[property='og:type']")[0]['content'],"\n",
"author", d.select("meta[property='books:author']")[0]['content'],"\n",
#"average rating", d.select_one("span.average").text,"\n",
"ratingCount", d.select("meta[itemprop='ratingCount']")[0]["content"],"\n"
#"reviewCount", d.select_one("span.count")["title"]
)
# Ok, now that we know what to do, lets wrap our fetching into a proper script. So that we dont overwhelm their servers, we will only fetch 5 from each page, but you get the idea...
#
# We'll segue of a bit to explore new style format strings. See https://pyformat.info for more info.
"list{:0>2}.txt".format(3)
a = "4"
b = 4
class Four:
def __str__(self):
return "Fourteen"
c=Four()
"The hazy cat jumped over the {} and {} and {}".format(a, b, c)
# ## 4. Set up a pipeline for fetching and parsing
#
# Ok lets get back to the fetching...
# +
fetched=[]
for i in range(1,3):
with open("files/list{:0>2}.txt".format(i)) as fd:
counter=0
for bookurl_line in fd:
if counter > 4:
break
bookurl=bookurl_line.strip()
stuff=requests.get(URLSTART+bookurl)
filetowrite=bookurl.split('/')[-1]
filetowrite="files/"+str(i)+"_"+filetowrite+".html"
print("FTW", filetowrite)
fd=open(filetowrite,"w")
fd.write(stuff.text)
fd.close()
fetched.append(filetowrite)
time.sleep(2)
counter=counter+1
print(fetched)
# -
# Ok we are off to parse each one of the html pages we fetched. We have provided the skeleton of the code and the code to parse the year, since it is a bit more complex...see the difference in the screenshots above.
import re
yearre = r'\d{4}'
def get_year(d):
if d.select_one("nobr.greyText"):
return d.select_one("nobr.greyText").text.strip().split()[-1][:-1]
else:
thetext=d.select("div#details div.row")[1].text.strip()
rowmatch=re.findall(yearre, thetext)
if len(rowmatch) > 0:
rowtext=rowmatch[0].strip()
else:
rowtext="NA"
return rowtext
# <div class="exercise"><b>Exercise</b></div>
#
# Your job is to fill in the code to get the genres.
def get_genres(d):
# your code here
genres=d.select("div.elementList div.left a")
glist=[]
for g in genres:
glist.append(g['href'])
return glist
# +
listofdicts=[]
for filetoread in fetched:
print(filetoread)
td={}
with open(filetoread) as fd:
datext = fd.read()
d=BeautifulSoup(datext, 'html.parser')
td['title']=d.select_one("meta[property='og:title']")['content']
td['isbn']=d.select_one("meta[property='books:isbn']")['content']
td['booktype']=d.select_one("meta[property='og:type']")['content']
td['author']=d.select_one("meta[property='books:author']")['content']
#td['rating']=d.select_one("span.average").text
td['year'] = get_year(d)
td['file']=filetoread
glist = get_genres(d)
td['genres']="|".join(glist)
listofdicts.append(td)
# -
listofdicts[0]
# Finally lets write all this stuff into a csv file which we will use to do analysis.
df = pd.DataFrame.from_records(listofdicts)
df
df.to_csv("files/meta_utf8_EK.csv", index=False, header=True)
|
docs/labs/lab02/cs109a_lab2_web_scraping.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
# ## Installing Scikit learn
# For installing Scikit learn, go to command prompt (Win+R => cmd enter)
#
# #### pip install -U scikit-learn
# Documentation - https://scikit-learn.org/stable/install.html
# # ! conda install scikit-learn
from sklearn.datasets import load_iris
iris = load_iris()
# This data sets consists of 3 different types of irises’ (Setosa, Versicolour, and Virginica) petal and sepal length, stored in a 150x4 numpy.ndarray
#
# The rows being the samples and the columns being: Sepal Length, Sepal Width, Petal Length and Petal Width.
iris
X = iris.data[:, (2, 3)] # petal length, petal width
iris.target
# ### Categories
#
# * 0 setosa
# * 1 versicolor
# * 2 virginica
y = (iris.target == 0)
y
y = (iris.target == 0).astype(np.int)
y
X
from sklearn.linear_model import Perceptron
# Documentation : https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Perceptron.html
per_clf = Perceptron(random_state=42)
per_clf.fit(X, y)
y_pred = per_clf.predict(X)
y_pred
from sklearn.metrics import accuracy_score
accuracy_score(y, y_pred)
per_clf.coef_
per_clf.intercept_
|
estudos_python/Machine_Learning/Others/5. ST Academy - ANN resource files/Python_codes/Perceptron.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: test_gdess_for_joss
# language: python
# name: test_gdess_for_joss
# ---
# # Seasonal cycle recipe demo
#
# This notebook illustrates basic usage of the seasonal cycle recipe.
#
# **Note** that the first example can be run with just the data contained in the tests directory, but the following examples require downloading more data from the NOAA GML Obspack, as described in the gdess README.
# <br>
# <br>
#
#
# **References:**
#
# For further reference, one can explore data visualization similar to these examples in Keppel-Aleks et al. (2013), Figure 5.
#
# *<NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., 2013. Atmospheric Carbon Dioxide Variability in the Community Earth System Model: Evaluation and Transient Dynamics during the Twentieth and Twenty-First Centuries. J. Clim. 26, 4447–4475. https://doi.org/10.1175/JCLI-D-12-00589.1*
from co2_diag.recipes import seasonal_cycles
# #### A single station
# +
station = 'smo'
recipe_options={'model_name': 'BCC.esm-hist',
'start_yr': "1980",
'end_yr': "2015",
'station_list': station}
# -
data_dict = seasonal_cycles(recipe_options, verbose='INFO')
# **NOTE:** Cells below require downloading the NOAA GML Obspack, as described in the gdess README, because they use station data not included in the repository for testing.
# #### Run specific stations
# ###### with no binning
recipe_options={'model_name': 'GFDL.esm-hist',
'start_yr': "1980",
'end_yr': "2015",
'station_list': 'mlo est brw bnt smo spo'}
df_all_cycles, cycles_of_each_station, station_metadata = seasonal_cycles(recipe_options, verbose='INFO')
# ###### with latitudinal binning
recipe_options={'start_yr': "1980",
'end_yr': "2015",
'latitude_bin_size': 30,
'station_list': 'mlo est brw bnt smo spo zep'}
df_all_cycles, cycles_of_each_station, station_metadata = seasonal_cycles(recipe_options, verbose='INFO')
|
notebooks/demo/seasonal_cycle_recipe.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + [markdown] id="vjqem3CNzHeP"
# # LeNet5 Analog Training Example
# Training the LeNet5 neural network with MNIST dataset and the Analog SGD optimizer simulated on the analog resistive random-access memory with soft bounds (ReRam) device.
#
# <a href="https://colab.research.google.com/github/IBM-AI-Hardware-Center/aihwkit-notebooks/blob/main/examples/analog_training_LeNet5.ipynb" target="_parent">
# <img src="https://colab.research.google.com/assets/colab-badge.svg"/>
# </a>
#
#
# ## Why Analog AI
#
# In-memory computing hardware increases the speed and energy-efficiency needed for the next steps in AI. Analog AI delivers radical performance improvements by combining compute and memory in a single device, eliminating the von Neumann bottleneck.
# Based on von Neumann architecture, conventional computers perform calculations by repeatedly transferring data between the memory and processor. These trips require time and energy, negatively impacting performance. This is known as the von Neumann bottleneck.
#
# <img src="https://github.com/IBM-AI-Hardware-Center/aihwkit-notebooks/blob/main/examples/imgs/processing-unit-and-computional-memory.png?raw=1" alt="Drawing" style="width=50px;"/>
# <img src="https://github.com/IBM-AI-Hardware-Center/aihwkit-notebooks/blob/main/examples/imgs/processing-unit-and-conventional-memory.png?raw=1" alt="Drawing" style="width=50px;">
#
# By leveraging the physical properties of in-memory computing devices (example: Phase Change Memory or PCM), computation happens at the same place where the data is stored, drastically reducing energy consumption. Because there is no movement of data, tasks can be performed in a fraction of the time and with much less energy. This is different from a conventional computer, where the data is transferred from the DRAM memory to the CPU every time a computation is done. For example, moving 64 bits of data from DRAM to CPU consumes 1-2nJ, which is 10,000–2,000,000 times more energy than is dissipated in a PCM device performing a multiplication operation (1-100fJ). Also, PCM does not consume power when the devices are inactive, and the data will be retained for up to 10 years even when the power supply is turned off.
#
# ## The physics behind PCM
#
# With PCM, when an electrical pulse is applied to the material, it changes the [conductance](https://energyeducation.ca/encyclopedia/Electrical_conductance) of the device by switching the material between amorphous and crystalline phases. A low electrical pulse will make the PCM device more crystalline (less resistance), this pulse can be repeatedly applied to gradually decrease the device resistance. On the other hand, the material change from the crystalline phase (low resistance) to the amorphouse phase (high resistance) is quite abrupt and requires a high electrical pulse to RESET the device. Therefore, it is possible to records the states as a continuum of values between the two extremes, instead of encoding 0 or 1 like in the digital world.
#
# PCM devices have the ability to store synaptic weights in their analog conductance state. When PCM devices are arranged in a crossbar configuration, it allows to perform an analog matrix-vector multiplication in a single time step, exploiting the advantages of multi-level storage capability and Kirchhoff’s circuits laws. The figure below shows how PCM devices are arranged in a crossbar configuration.
# <center><img src="https://github.com/IBM-AI-Hardware-Center/aihwkit-notebooks/blob/main/examples/imgs/pcm-array.png?raw=1" style="width:30%; height:30%"/></center>
#
# This crossbar configuration is also referred to as an Analog tile. The PCM devices at each crossbard crosspoint are also referred to as Resitive Processing Units or RPU units as shown in the figure below:
#
# <center><img src="https://github.com/IBM-AI-Hardware-Center/aihwkit-notebooks/blob/main/examples/imgs/pcm_rpu_unit.png?raw=1" style="width:30%; height:30%"/></center>
#
# Besides PCM, other devices or materials can be used as resistive units or RPUs in the crossbar configuration. Examples include Resistive Random Access Memory (RRAM), Electro chemical Random Access Memory (ECRAM), Magnetic RAM (MRAM), photonics, etc. The weights of neural network are stored in the RPU units as confuctance values that are programmed on the chip through as series of electrical pulses. The conductance behavior changes from one analog device to another.
#
#
# ## Analog AI and Neural Networks
#
# In deep learning inference, data propagation through multiple layers of a neural network involves a sequence of matrix multiplications, as each layer can be represented as a matrix of synaptic weights. On an Analog chip, these weights are stored in the conductance states of resistive devices such as PCM. The devices are arranged in crossbar arrays, creating an artificial neural network where all matrix multiplications are performed in-place in an analog manner. This structure allows inference to be performed using little energy with high areal density of synapses. An in-memory computing chip typically consists of multiple crossbar arrays of memory devices that communicate with each other (see figure below). A neural network layer can be implemented on (at least) one crossbar, in which the weights of that layer are stored in the charge or conductance state of the memory devices at the crosspoints.
#
# <center><img src="https://github.com/IBM-AI-Hardware-Center/aihwkit-notebooks/blob/main/examples/imgs/analog_Dnn.png?raw=1" style="width:60%; height:60%"/></center>
#
#
#
# ## IBM Analog Hardware Acceleration Kit (AIHWKIT)
#
# The IBM Analog Hardware Acceleration Kit (AIHWKIT) is an open source Python toolkit for exploring and using the capabilities of in-memory computing devices such as PCM in the context of artificial intelligence.
# The pytorch integration consists of a series of primitives and features that allow using the toolkit within PyTorch.
#
# The github repository can be found at: https://github.com/IBM/aihwkit
#
# To learn more about Analog AI and the harware befind it, refer to this webpage: https://analog-ai-demo.mybluemix.net/hardware
#
#
# ### Installing the AIHWKIT
# The first thing to do is to install the AIHHKIT and dependencies in your environment. The preferred way to install this package is by using the Python package index (please uncomment this line to install in your environment if not previously installed):
# + colab={"base_uri": "https://localhost:8080/"} id="29ZMdvhfzHeV" outputId="998843e1-1cdf-481d-8f81-26a18a6c19f5"
# To install the cpu-only enabled kit, uncommend the line below
#pip install aihwkit
# To install the gpu enabled wheel, use the commands below
# !wget https://aihwkit-gpu-demo.s3.us-east.cloud-object-storage.appdomain.cloud/aihwkit-0.4.5-cp37-cp37m-manylinux2014_x86_64.whl
# !pip install aihwkit-0.4.5-cp37-cp37m-manylinux2014_x86_64.whl
# + id="ZCgYk8_y_sV1"
# Install livelossplot to visualize the training losses live
# !pip install livelossplot --quiet
# + [markdown] id="wC9XIRtjzHeW"
#
# ## LeNet5 Neural Network Examples
#
# In this notebook we will use the AIHWKIT to train a LeNet5 inspired analog network, as studied in the paper: https://www.frontiersin.org/articles/10.3389/fnins.2017.00538/full
#
# <img src="https://github.com/IBM-AI-Hardware-Center/aihwkit-notebooks/blob/main/examples/imgs/LeNet5_animation.png?raw=1" style="width:40%; height:40%"/>
#
# The architecture of the LeNet5 network is shown below:
#
# <img src="https://github.com/IBM-AI-Hardware-Center/aihwkit-notebooks/blob/main/examples/imgs/LeNet.png?raw=1" style="width:40%; height:40%"/>
#
# The network will be trained using the MNIST dataset, a collection of images representing the digits 0 to 9.
#
# From Kaggle: "MNIST ("Modified National Institute of Standards and Technology") is the de facto “hello world” dataset of computer vision. Since its release in 1999, this classic dataset of handwritten images has served as the basis for benchmarking classification algorithms. As new machine learning techniques emerge, MNIST remains a reliable resource for researchers and learners alike."
#
# [Read more.](https://www.kaggle.com/c/digit-recognizer)
#
# <img src="https://github.com/IBM-AI-Hardware-Center/aihwkit-notebooks/blob/main/examples/imgs/MnistExamples.png?raw=1" style="width:40%; height:40%"/>
#
# + [markdown] id="PBr6Z5FHzHeX"
# ## Analog layers
# If the library was installed correctly, you can use the following snippet for creating an analog layer and predicting the output. In the code snippet below AnalogLinea is the Analog equivalent to Linear PyTorch layer.
# + colab={"base_uri": "https://localhost:8080/"} id="8-uJPmFMzHeX" outputId="067e7c87-0062-44ec-a03a-9d49e5f64374"
from torch import Tensor
from aihwkit.nn import AnalogLinear
model = AnalogLinear(2, 2)
model(Tensor([[0.1, 0.2], [0.3, 0.4]]))
# + [markdown] id="jehSr26TzHeY"
# ## RPU Configuration
# Now that the package is installed and running, we can start working on creating the LeNet5 network.
#
# AIHWKIT offers different Analog layers that can be used to build a network, including AnalogLinear and AnalogConv2d which will be the main layers used to build the present network.
# In addition to the standard input that are expected by the PyTorch layers (in_channels, out_channels, etc.) the analog layers also expect an rpu_config input which defines various settings of the RPU tile or the Analog hardware.
#
# Through the rpu_config parameters, the user can specify many of the hardware specs such as: device used in the cross-point array, bits used by the ADC/DAC converters, noise values and many other parameters.
#
# Additional details on the RPU configuration can be found at https://aihwkit.readthedocs.io/en/latest/using_simulator.html#rpu-configurations
#
# For this particular use case, we will define two RPU configurations that we will use later in the code. The first rpu_config uses an ideal device which is linear and symmetric in the conductance changes. The second rpu_config will use a realistic Resistive Random Access Memory (ReRAM) device with its non-idealities. We will use this two configurations to highlight their impacts on network accuracy.
#
# + [markdown] id="0uL6aGqb7qK6"
# ### Using RPU configuration of an ideal Analog device
# Analog devices, when employed to implement synaptic weights of a neural network, need to meet certain specifications for the network performance to be comparable to that of a floating-point software implementation. Such specifications applicable to training a neural network on the MNIST classification benchmark were derived in [Gokmen & Vlasov, Front. Neurosci. 2016](https://www.frontiersin.org/articles/10.3389/fnins.2016.00333/full). The specifications may vary for different networks, datasets, and optimizers, and the AIHWKIT provides the capability to experiment with them.
#
# The ideal analog device is represented in the code snippet below using SingleRPUConfig(device=ConstantStepDevice()).
# This RPU configuration simulates a fictitious analog device array with idealized specifications, inspired by those listed in [Gokmen & Vlasov, Front. Neurosci. 2016](https://www.frontiersin.org/articles/10.3389/fnins.2016.00333/full). This device has an ideal linear increase of conductance with a number of pulses. It includes device-to-device variations as well as pulse-to-pulse fluctuations of conductance. The global asymmetry between positive and negative update and device-to-device asymmetry terms are set to zero. The number of steps was increased by ten-fold (to 10000 states) compared with that of Gokmen & Vlasov.
#
# <img src="https://github.com/IBM-AI-Hardware-Center/aihwkit-notebooks/blob/main/examples/imgs/idealizedDevice.png?raw=1" style="width:40%; height:40%"/>
# + id="CGNLDA2IzHeZ"
def create_rpu_config_1():
from aihwkit.simulator.configs import SingleRPUConfig
from aihwkit.simulator.configs.devices import ConstantStepDevice
rpu_config=SingleRPUConfig(device=ConstantStepDevice())
return rpu_config
# + [markdown] id="gDasdivI7qK7"
# ### Using RPU configuration of a realistic ReRAM device
# Resistive random-access memory (ReRAM) is a non-volatile memory technology with tuneable conductance states that can be used for in-memory computing. The conductance change of a ReRAM device is bidirectional, that is, it is possible to both increase and decrease its conductance incrementally by applying suitable electrical pulses. This capability can be exploited to implement the backpropagation algorithm. The change of conductance in oxide ReRAM is attributed to change in the configuration of the current conducting filament which consists of oxygen vacancies in a metal oxide film.
#
# The simulated ReRAM device is based on the of [Gong et al](https://www.nature.com/articles/s41467-018-04485-1). This device was fabricated with hafnium oxide as the metal oxide switching layer. The preset captures the experimentally measured response of this device to 1000 positive and 1000 negative pulses (shown in Figure 3a), including the pulse-to-pulse fluctuations. The movement of the oxygen vacancies in response to electrical signals has a probabilistic nature and it emerges as inherent randomness in conductance changes. Realistic device-to-device variability is also included in the preset to appropriately simulate the behavior of an array of such devices.
#
# <img src="https://github.com/IBM-AI-Hardware-Center/aihwkit-notebooks/blob/main/examples/imgs/reram.png?raw=1" style="width:40%; height:40%"/>
# + id="lzKNtUBV7qK7"
def create_rpu_config_2():
from aihwkit.simulator.presets import ReRamSBPreset
rpu_config=ReRamSBPreset()
return rpu_config
# + [markdown] id="soEwkJg3zHeZ"
# We can now use the defined rpu_config as input of the network model:
# + id="oBu6VxsJzHea"
from torch.nn import Tanh, MaxPool2d, LogSoftmax, Flatten
from aihwkit.nn import AnalogConv2d, AnalogLinear, AnalogSequential
def create_analog_network(rpu_config):
channel = [16, 32, 512, 128]
model = AnalogSequential(
AnalogConv2d(in_channels=1, out_channels=channel[0], kernel_size=5, stride=1,
rpu_config=rpu_config),
Tanh(),
MaxPool2d(kernel_size=2),
AnalogConv2d(in_channels=channel[0], out_channels=channel[1], kernel_size=5, stride=1,
rpu_config=rpu_config),
Tanh(),
MaxPool2d(kernel_size=2),
Tanh(),
Flatten(),
AnalogLinear(in_features=channel[2], out_features=channel[3], rpu_config=rpu_config),
Tanh(),
AnalogLinear(in_features=channel[3], out_features=10, rpu_config=rpu_config),
LogSoftmax(dim=1)
)
return model
# + [markdown] id="EW8NXVY1zHeb"
# ## Analog Optimizer
#
# We will use the cross entropy criteria to calculate the loss and the Stochastic Gradient Descent (SGD) as optimizer:
# + id="HXd7VR9szHeb"
from torch.nn import CrossEntropyLoss
criterion = CrossEntropyLoss()
from aihwkit.optim import AnalogSGD
def create_analog_optimizer(model):
"""Create the analog-aware optimizer.
Args:
model (nn.Module): model to be trained
Returns:
Optimizer: created analog optimizer
"""
optimizer = AnalogSGD(model.parameters(), lr=0.01) # we will use a learning rate of 0.01 as in the paper
optimizer.regroup_param_groups(model)
return optimizer
# + [markdown] id="iT_5bGZQzHec"
# ## Training the network
#
# We can now write the train function which will optimize the network over the MNIST train dataset. The train_step function will take as input the images to train on, the model to train and the criterion and optimizer to train with:
# + colab={"base_uri": "https://localhost:8080/"} id="cHicu1qWzHec" outputId="8b222232-f937-4e1a-82e0-8e45238adcfa"
from torch import device
from aihwkit.simulator.rpu_base import cuda
DEVICE = device('cuda' if cuda.is_compiled() else 'cpu')
print('Running the simulation on: ', DEVICE)
def train_step(train_data, model, criterion, optimizer):
"""Train network.
Args:
train_data (DataLoader): Validation set to perform the evaluation
model (nn.Module): Trained model to be evaluated
criterion (nn.CrossEntropyLoss): criterion to compute loss
optimizer (Optimizer): analog model optimizer
Returns:
train_dataset_loss: epoch loss of the train dataset
"""
total_loss = 0
predicted_ok = 0
total_images = 0
model.train()
for images, labels in train_data:
images = images.to(DEVICE)
labels = labels.to(DEVICE)
optimizer.zero_grad()
# Add training Tensor to the model (input).
output = model(images)
loss = criterion(output, labels)
# Run training (backward propagation).
loss.backward()
# Optimize weights.
optimizer.step()
_, predicted = torch.max(output.data, 1)
total_loss += loss.item() * images.size(0)
predicted_ok += torch.sum(predicted == labels.data)
total_images += labels.size(0)
train_loss = total_loss / len(train_data.dataset)
train_accuracy = predicted_ok.float()/len(train_data.dataset)*100
train_error = (1-predicted_ok.float()/len(train_data.dataset))*100
return train_loss, train_error, train_accuracy
# + [markdown] id="VwMUHVEpzHed"
# Since training can be quite time consuming it is nice to see the evolution of the training process by testing the model capabilities on a set of images that it has not seen before (test dataset). So we write a test_step function:
# + id="i4-gBviwzHed"
def test_step(validation_data, model, criterion):
"""Test trained network
Args:
validation_data (DataLoader): Validation set to perform the evaluation
model (nn.Module): Trained model to be evaluated
criterion (nn.CrossEntropyLoss): criterion to compute loss
Returns:
test_dataset_loss: epoch loss of the train_dataset
test_dataset_error: error of the test dataset
test_dataset_accuracy: accuracy of the test dataset
"""
total_loss = 0
predicted_ok = 0
total_images = 0
model.eval()
for images, labels in validation_data:
images = images.to(DEVICE)
labels = labels.to(DEVICE)
pred = model(images)
loss = criterion(pred, labels)
total_loss += loss.item() * images.size(0)
_, predicted = torch.max(pred.data, 1)
total_images += labels.size(0)
predicted_ok += (predicted == labels).sum().item()
test_dataset_loss = total_loss / len(validation_data.dataset)
test_dataset_accuracy = predicted_ok/len(validation_data.dataset)*100
test_dataset_error = (1-predicted_ok/total_images)*100
return test_dataset_loss, test_dataset_error, test_dataset_accuracy
# + [markdown] id="8JWPjc0BzHee"
# To reach satisfactory accuracy levels, the train_step will have to be repeated mulitple time so we will implement a loop over a certain number of epochs:
# + id="EU28l53ozHef"
from livelossplot import PlotLosses
def training_loop(model, criterion, optimizer, train_data, validation_data, epochs=15, print_every=1):
"""Training loop.
Args:
model (nn.Module): Trained model to be evaluated
criterion (nn.CrossEntropyLoss): criterion to compute loss
optimizer (Optimizer): analog model optimizer
train_data (DataLoader): Validation set to perform the evaluation
validation_data (DataLoader): Validation set to perform the evaluation
epochs (int): global parameter to define epochs number
print_every (int): defines how many times to print training progress
Returns:
nn.Module, Optimizer, Tuple: model, optimizer, and a tuple of
lists of train losses, validation losses, and test error
"""
liveloss = PlotLosses()
# Train model
for epoch in range(0, epochs):
logs = {}
# Train_step
train_loss, train_error, train_acc = train_step(train_data, model, criterion, optimizer)
if epoch % print_every == (print_every - 1):
# Validate_step
with torch.no_grad():
valid_loss, valid_error, valid_acc = test_step(validation_data, model, criterion)
print(f'Epoch: {epoch}\t'
f'Train loss: {train_loss:.4f}\t'
f'Valid loss: {valid_loss:.4f}\t'
f'Train error: {train_error:.2f}%\t'
f'Valid error: {valid_error:.2f}%\t'
f'Train accuracy: {train_acc:.2f}%\t'
f'Valid accuracy: {valid_acc:.2f}%\t')
logs['loss'] = train_loss
logs['val_loss'] = valid_loss
logs['accuracy'] = train_acc
logs['val_accuracy'] = valid_acc
logs['error'] = train_error
logs['val_error'] = valid_error
liveloss.update(logs)
liveloss.send()
# + [markdown] id="odgAhMk2zHef"
# We will now download the MNIST dataset and prepare the images for the training and test:
# + id="k_uhR68azHef"
import os
from torchvision import datasets, transforms
PATH_DATASET = os.path.join('data', 'DATASET')
os.makedirs(PATH_DATASET, exist_ok=True)
def load_images():
"""Load images for train from torchvision datasets."""
transform = transforms.Compose([transforms.ToTensor()])
train_set = datasets.MNIST(PATH_DATASET, download=True, train=True, transform=transform)
test_set = datasets.MNIST(PATH_DATASET, download=True, train=False, transform=transform)
train_data = torch.utils.data.DataLoader(train_set, batch_size=8, shuffle=True)
test_data = torch.utils.data.DataLoader(test_set, batch_size=8, shuffle=False)
return train_data, test_data
# + [markdown] id="qk27OXgCzHeg"
# ### Training using the idealized rpu configuration
# Put together all the code above to train the network on the idealized analog device.
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="b5OJ0uIbzHeg" outputId="8a93b395-4da0-4344-f4cb-a6827c439c85"
import torch
torch.manual_seed(1)
#load the dataset
train_data, test_data = load_images()
#create the rpu_config
rpu_config = create_rpu_config_1()
#create the model
model = create_analog_network(rpu_config).to(DEVICE)
#define the analog optimizer
optimizer = create_analog_optimizer(model)
training_loop(model, criterion, optimizer, train_data, test_data)
# + [markdown] id="n45f2yth7qLB"
# ### Training using the Analog ReRam device
# As shown by the code above Analog AI is capable of achieving high accuracy when using standard optimizer and algorithm with ideal devices. Now let's see what happens if standard SGD with the BP algorithm is used with a non-ideal device such as ReRAM
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="iJo3-sph7qLC" outputId="7bd74e43-5d28-4461-f628-adb982152e7a"
import torch
torch.manual_seed(1)
#load the dataset
train_data, test_data = load_images()
#create the rpu_config
rpu_config = create_rpu_config_2()
#create the model
model = create_analog_network(rpu_config).to(DEVICE)
#define the analog optimizer
optimizer = create_analog_optimizer(model)
training_loop(model, criterion, optimizer, train_data, test_data)
# + [markdown] id="j4BdkEs07qLC"
# In this case the same network configuration with same parameters is perfoming much worse than when using the ideal device, which underscores the importance of innovating not only at a device/circuit level but also at algorithmic level.
#
# In the [next notebook](https://github.com/IBM-AI-Hardware-Center/aihwkit-notebooks/blob/main/examples/analog_training_LeNet5_TT.ipynb) we will show how the Tiki-Taka algorithm, specifically designed for non-volatile memory and analog computing, is capable of achieving high performance also with non-ideal devices.
|
examples/analog_training_LeNet5_plot.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Klasy
# Importowanie modułu
import numpy as np
# ## Życie obiektu
# +
# Obiekt musi być przypisany do jakiejś zmiennej.
# Po tym jak żadne zmienne nie wskazują na obiekt, przestaje on być potrzebny i będzie później zniszczony.
# Innymi słowy, jeśli chcemy żeby nasz obiekt żył szczęśliwie, to musimy go mieć przypisanego przez cały
# czas do przynajmniej jednej zmiennej, dzięki temu wiemy, że nie zostanie zniszczony.
# -
# ## Śmierć obiektu
# +
# Python niszczy obiekty kiedy stają się niepotrzebne.
# Niepotrzebnym jest obiekt, który nie jest przypisany do żadnej nazwy.
# Obiekt ma wbudowany licznik referencji. Przypisanie obiektu do dowolnej zmiennej
# zwiększa ten licznik o 1, a usunięcie zmiennej (skasowanie zmiennej przez del,
# przypisanie do zmiennej innego obiektu lub „zniknięcie” zmiennej po zakończeniu funkcji) — zmniejsza o 1.
# Obiekt żyje co najmniej tak długo, jak długo jego licznik referencji jest większy od 0.
# Zanim obiekt zostanie zniszczony, zostanie wywołana jego metoda __del__.
# Jej zadaniem jest wykonanie działań takich jak zamknięcie plików, które muszą być zamknięte
# wraz ze zniszczeniem obiektu. Niemniej, moment destrukcji obiektu jest trudny do przewidzenia,
# więc mechanizm __del__ jest bardzo zawodny. Nie należy go używać.
# Przykładowo
# >>> x = Klasa()
# >>> del x
# Powyższy kod spowoduje usunięcie zmiennej, ale nie obiektu
# W tym momencie jego licznik referencji {{ang|reference count, czyli sposobów na który
# można dotrzeć do obiektu, wynosi 0. Obiekt zostanie niedługo zlikwidowany.
# -
# ## Konstruktor, destruktor, a także metoda __str__
class Figura:
# Zmienna w klasie
zmienna = 5
def __init__(self, bok):
print('Cześć jestem konstruktor z polem publicznym bok')
self.bok = bok
def __del__(self):
self.bok = 1
print('Cześć jestem destruktor')
def __str__(self):
# Metoda służąca do wytwarzania tekstowej reprezentacji obiektu.
# Jest automatycznie wywoływana np. przez polecenie print.
return 'Figura o boku równym {}'.format(self.bok)
k = Figura(6)
k.__del__()
k.bok
print(k)
print(k.__str__())
# ### Więcej informacji: https://brain.fuw.edu.pl/edu/index.php/TI/Wst%C4%99p_do_programowania_obiektowego#Metoda_str
# ## Dostęp do pól w klasie oraz zmiennych
# +
# Klasa student zawiera publiczne pola: index, imie, nazwisko, chronione: login, prywatne: password
class Student:
def __init__(self, index:int, imie:str, nazwisko:str, login:str, password:str):
self.index = index
self.imie = imie
self.nazwisko = nazwisko
self._login = login
self.__password = password
s = Student(291873, 'Tomasz', 'Derek', 'derek', 'xD')
print(s.imie)
print(s._login)
# Wystąpi błąd ze względu na brak możliwości dostępu do pola prywatnego
print(s.__password)
# -
# ## Metody i ich dekoratory
# +
# Wszystkie metody w Pythonie są wirtualne ->
class Bot:
def __init__(self, imie):
self.imie = imie
# metoda zwaracjąca imie bota
def return_name(self):
return self.imie
# metoda statyczna wypisująca przywitanie
# metoda statyczna jest to metoda klasy, która nie potrzebuje
# mieć dostępu do pól klasy, ani innych danych trzymanych w klasie
@staticmethod
def przywitaj():
print('<NAME>')
# metoda wywołująca metodę przywitaj()
# metoda ta ma ograniczony dostęp do danych zawartych w klasie
# metoda ta może wywoływać metody statyczne
# jako argument przyjmuje cls
@classmethod
def przwitaj_usera(cls):
cls.przywitaj()
bot = Bot('Adam')
print(bot.return_name())
bot.przywitaj()
bot.przwitaj_usera()
# -
# ### Więcej informacji: https://www.makeuseof.com/tag/python-instance-static-class-methods/
# ## Przykładowa klasa
class Perceptron:
# Konstruktor zawierający dwa pola publiczne input_size oraz weights
def __init__(self, input_size):
self.input_size = input_size
self.weights = np.zeros(self.input_size + 1)
def activ(self, dot):
if dot > 0:
dot = 1
else:
dot = 0
return dot
def predict(self, x):
dot = np.dot(x, self.weights[1:]) - self.weights[0]
dot = self.activ(dot)
return dot
def fit(self, x, y, epochs, learning_rate):
for epoch in range(epochs):
loss, accuracy = 0, 0
print('Epoch [{}/{}]'.format(epoch+1, epochs), end=' ')
for data, label in zip(x, y):
error = label - self.predict(data)
if error != 0:
self.weights[1:] += learning_rate * error * data
self.weights[0] -= learning_rate * error
loss += 0.5 * (error) ** 2
else:
accuracy += 1
print('Loss:', float(loss), end=' ')
print('Accuracy:{}%'.format(accuracy / len(y) * 100.))
# DATASET
a = np.array([[1, 1], [1, 0], [0, 1], [0, 0]])
b = np.array([[1], [0], [0], [0]])
# Inicjalizacja objektu
p = Perceptron(2)
# Trenowanie sieci
p.fit(a, b, 6, 0.1)
# Predykcja
print(p.predict([1, 1]))
print(p.predict([1, 0]))
print(p.predict([0, 1]))
print(p.predict([0, 0]))
# ## Dziedziczenie
# +
class Computer:
def __init__(self, ram, disk, power_supply):
self.ram = ram
self.disk = disk
self.power_supply = power_supply
def print_all(self):
print('Computer has ram {}, disk {}, power supply {}'.format(self.ram,
self.disk,
self.power_supply))
class Laptop(Computer):
def __init__(self, ram, disk, power_supply, model):
super().__init__(ram, disk, power_supply)
self.model = model
def print_all(self):
print('Laptop model {}, has disk {}, ram {}, power supply {}'.format(self.model,
self.disk,
self.ram,
self.power_supply))
# -
comp = Computer('1GB', '20GB', '300W')
comp.print_all()
alienware = Laptop('8GB', '1,25TB', '180W', 'Alienware 17 R2')
alienware.print_all()
|
lectures/second_lecture/notebooks/klasy.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import csv
file = os.path.join("budget_data.csv")
result = os.path.join("budget_result.txt")
totalMonths = 0
totalChange = 0
monthArr = []
totalChangeArr = []
largestGain = 0
largestLoss = 9999999999999999999999999999999999999999999999999999999999999999999999
avgChange = 0
with open(file) as budget_data:
reader = csv.reader(budget_data)
header = next(reader)
#print(header)
currentMonth = next(reader)
#print(currentMonth)
totalMonths = totalMonths + 1
totalChange = totalChange + int(currentMonth[1])
#print(totalChange)
prevChange = int(currentMonth[1])
for row in reader:
totalMonths = totalMonths + 1
totalChange = totalChange + int(row[1])
#print(totalChange)
monthlyChange = int(row[1]) - prevChange
prevChange = int(row[1])
totalChangeArr.append(monthlyChange)
#print(totalChangeArr)
monthArr.append(row[0])
#print(monthArr)
largestGainMonth = ""
for i in range(len(totalChangeArr)):
if (totalChangeArr[i] > largestGain):
largestGain = totalChangeArr[i]
largestGainMonth = monthArr[i]
largestLossMoth = ""
for i in range(len(totalChangeArr)):
if (totalChangeArr[i] < largestLoss):
largestLoss = totalChangeArr[i]
largestLossMonth = monthArr[i]
with open(result, "w") as txt_file:
txt_file.write("Total Months: " + str(totalMonths) +"\n")
txt_file.write("Total: $" + str(totalChange) +"\n")
txt_file.write("Average Change is: $" + str(round(sum(totalChangeArr)/len(totalChangeArr), 2))+"\n")
txt_file.write("Greatest Increase in profits: " + str(largestGainMonth) + " ($" + str(largestGain) + ")"+"\n")
txt_file.write("Greatest Decrease in profits: " + str(largestLossMonth) + " ($" + str(largestLoss) + ")")
# -
|
PyBank/main.py.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:josh]
# language: python
# name: conda-env-josh-py
# ---
# # Match Cells with their Sub-Region
#
# Need the following files:
# * list_25_75.csv - contains all the cells rounded to .25 and .75 accuracy
# * tasday_thresh.csv - contains the subset of the cells we are working with.
#
# METHOD:
# Use the cells from `tasday_thresh.csv` to subset `list_25_75.csv` so that we just have data from the cells we want.
# Read in regions
regions = pd.read_csv('list_25_75.csv', index_col=0)
regions = regions.set_index(['lon_25_75', 'lat_25_75'])
regions
len(np.unique(regions.index))
# Create a list of cells we want to work with
df = pd.read_csv('tasday_thresh.csv')
df = df.set_index(['lon', 'lat'])
cells = np.unique(df.index)
len(cells)
# Subset regions using just the cells we want
regions_matched = regions.loc[cells]
regions_matched
# Create list of lon/lat pairs so that we can create new column 'urban_center_count'
# It's in ascending order and cells listed multiple times means there are multiple centers in that cell
cells_non_unique = list(regions_matched.index)
cells_non_unique
# The total number of urban centers in a cell is equivalent to the lenth - len() - of the dataframe we get
# if we just look at data for that cell - regions_matched.loc[cell]
regions_matched['urban_center_count'] = pd.Series(data=[len(regions_matched.loc[cell]) for cell in cells_non_unique],
# Pass an index so that it matches up with regions_matched
index=cells_non_unique)
# Check last 50 entries to make sure it worked
regions_matched.urban_center_count.tail(50)
# Check the unique regions listed
np.unique(regions_matched.GRGN_L2)
# Total number of urban centers in each region
grouped_by_region = regions_matched.groupby('GRGN_L2')
grouped_by_region.urban_center_count.count()
# Average number of urban centers per cell in each region
grouped_by_region.urban_center_count.mean()
regions_matched.to_csv('regions_matched.csv')
|
2_create_regions_matched_dataset/match_cells_to_subregions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/adxpillar/DS-Unit-2-Linear-Models/blob/master/module3-ridge-regression/Adeagbo_Adewale_DS13_LS_DS_213_assignment.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="7zM_dzEfVmSE" colab_type="text"
# Lambda School Data Science
#
# *Unit 2, Sprint 1, Module 3*
#
# ---
# + [markdown] colab_type="text" id="7IXUfiQ2UKj6"
# # Ridge Regression
#
# ## Assignment
#
# We're going back to our other **New York City** real estate dataset. Instead of predicting apartment rents, you'll predict property sales prices.
#
# But not just for condos in Tribeca...
#
# - [ ] Use a subset of the data where `BUILDING_CLASS_CATEGORY` == `'01 ONE FAMILY DWELLINGS'` and the sale price was more than 100 thousand and less than 2 million.
# - [ ] Do train/test split. Use data from January — March 2019 to train. Use data from April 2019 to test.
# - [ ] Do one-hot encoding of categorical features.
# - [ ] Do feature selection with `SelectKBest`.
# - [ ] Fit a ridge regression model with multiple features. Use the `normalize=True` parameter (or do [feature scaling](https://scikit-learn.org/stable/modules/preprocessing.html) beforehand — use the scaler's `fit_transform` method with the train set, and the scaler's `transform` method with the test set)
# - [ ] Get mean absolute error for the test set.
# - [ ] As always, commit your notebook to your fork of the GitHub repo.
#
# The [NYC Department of Finance](https://www1.nyc.gov/site/finance/taxes/property-rolling-sales-data.page) has a glossary of property sales terms and NYC Building Class Code Descriptions. The data comes from the [NYC OpenData](https://data.cityofnewyork.us/browse?q=NYC%20calendar%20sales) portal.
#
#
# ## Stretch Goals
#
# Don't worry, you aren't expected to do all these stretch goals! These are just ideas to consider and choose from.
#
# - [ ] Add your own stretch goal(s) !
# - [ ] Instead of `Ridge`, try `LinearRegression`. Depending on how many features you select, your errors will probably blow up! 💥
# - [ ] Instead of `Ridge`, try [`RidgeCV`](https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.RidgeCV.html).
# - [ ] Learn more about feature selection:
# - ["Permutation importance"](https://www.kaggle.com/dansbecker/permutation-importance)
# - [scikit-learn's User Guide for Feature Selection](https://scikit-learn.org/stable/modules/feature_selection.html)
# - [mlxtend](http://rasbt.github.io/mlxtend/) library
# - scikit-learn-contrib libraries: [boruta_py](https://github.com/scikit-learn-contrib/boruta_py) & [stability-selection](https://github.com/scikit-learn-contrib/stability-selection)
# - [_Feature Engineering and Selection_](http://www.feat.engineering/) by Kuhn & Johnson.
# - [ ] Try [statsmodels](https://www.statsmodels.org/stable/index.html) if you’re interested in more inferential statistical approach to linear regression and feature selection, looking at p values and 95% confidence intervals for the coefficients.
# - [ ] Read [_An Introduction to Statistical Learning_](http://faculty.marshall.usc.edu/gareth-james/ISL/ISLR%20Seventh%20Printing.pdf), Chapters 1-3, for more math & theory, but in an accessible, readable way.
# - [ ] Try [scikit-learn pipelines](https://scikit-learn.org/stable/modules/compose.html).
# + colab_type="code" id="o9eSnDYhUGD7" colab={}
# %%capture
import sys
# If you're on Colab:
if 'google.colab' in sys.modules:
DATA_PATH = 'https://raw.githubusercontent.com/LambdaSchool/DS-Unit-2-Applied-Modeling/master/data/'
# !pip install category_encoders==2.*
# If you're working locally:
else:
DATA_PATH = '../data/'
# Ignore this Numpy warning when using Plotly Express:
# FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead.
import warnings
warnings.filterwarnings(action='ignore', category=FutureWarning, module='numpy')
# + colab_type="code" id="QJBD4ruICm1m" colab={}
import pandas as pd
import pandas_profiling
# Read New York City property sales data
df = pd.read_csv(DATA_PATH+'condos/NYC_Citywide_Rolling_Calendar_Sales.csv')
# Change column names: replace spaces with underscores
df.columns = [col.replace(' ', '_') for col in df]
# SALE_PRICE was read as strings.
# Remove symbols, convert to integer
df['SALE_PRICE'] = (
df['SALE_PRICE']
.str.replace('$','')
.str.replace('-','')
.str.replace(',','')
.astype(int)
)
# + id="K7BV2PhTVmSg" colab_type="code" colab={}
# BOROUGH is a numeric column, but arguably should be a categorical feature,
# so convert it from a number to a string
df['BOROUGH'] = df['BOROUGH'].astype(str)
# + id="aPPHIzjzVmSl" colab_type="code" colab={}
# Reduce cardinality for NEIGHBORHOOD feature
# Get a list of the top 10 neighborhoods
top10 = df['NEIGHBORHOOD'].value_counts()[:10].index
# At locations where the neighborhood is NOT in the top 10,
# replace the neighborhood with 'OTHER'
df.loc[~df['NEIGHBORHOOD'].isin(top10), 'NEIGHBORHOOD'] = 'OTHER'
# + id="kFuDjgvUVmSs" colab_type="code" colab={}
df.head()
# + id="o7iXKS2reY8F" colab_type="code" colab={}
# create subset of data
df = df[(df['BUILDING_CLASS_CATEGORY'] == '01 ONE FAMILY DWELLINGS') & (df['SALE_PRICE'].between(100000,2000000,inclusive=True))]
# + id="WGSplthph_ZB" colab_type="code" colab={}
df.head()
# + id="I3X-Be8-m6pi" colab_type="code" outputId="54fa0f9e-1dd4-41ca-ab4a-9204ccef9e39" colab={"base_uri": "https://localhost:8080/", "height": 51}
# confirm that the subset is correct
print(df['SALE_PRICE'].min())
print(df['SALE_PRICE'].max())
# + id="wVJkU7pxJxA2" colab_type="code" colab={}
df['LAND_SQUARE_FEET'] = df['LAND_SQUARE_FEET'].str.replace(',','').astype(int)
# + id="9ZvaAesVnAdZ" colab_type="code" colab={}
# January — March 2019 to train. Use data from April 2019 to test.
train = df[df['SALE_DATE'].str.contains('01/2019') | df['SALE_DATE'].str.contains('02/2019') | df['SALE_DATE'].str.contains('03/2019')]
test = df[df['SALE_DATE'].str.contains('04/2019')]
# + id="-2YVmO2ax2Y5" colab_type="code" colab={}
# confirm that split is functional
test.groupby('SALE_DATE').count()
# + id="Mg30nXhDx9iQ" colab_type="code" colab={}
df.describe(exclude='number')
# + id="_wAPMWUpFDDa" colab_type="code" colab={}
df.dtypes
# + id="qWcRl_bJ4Mx8" colab_type="code" colab={}
# Specify target and features
df.drop(['ADDRESS','EASE-MENT','NEIGHBORHOOD','BUILDING_CLASS_CATEGORY','BUILDING_CLASS_AT_PRESENT','APARTMENT_NUMBER',
'BUILDING_CLASS_AT_TIME_OF_SALE','SALE_DATE','TAX_CLASS_AT_PRESENT'],axis=1,inplace=True)
# + id="6jHkMkYqHuaR" colab_type="code" colab={}
target = 'SALE_PRICE'
features = ['BOROUGH','BLOCK','LOT','ZIP_CODE','RESIDENTIAL_UNITS','COMMERCIAL_UNITS','TOTAL_UNITS',
'LAND_SQUARE_FEET','GROSS_SQUARE_FEET','YEAR_BUILT','TAX_CLASS_AT_TIME_OF_SALE']
# + id="yhfS0klp64nU" colab_type="code" colab={}
# train-test split
x_train = train[features]
y_train = train[target]
x_test = test[features]
y_test = test[target]
# + id="7Lc5y_lK0Rz6" colab_type="code" colab={}
# Hot encoding of one categorical data
# all existing variables have high cardinality
# import category_encoders as ce
# encoder = ce.OneHotEncoder(use_cat_names=True)
# x_train = encoder.fit_transform(x_train)
# + id="Ltwp5SBp9ef6" colab_type="code" outputId="b66724bc-2bc7-4146-a4a1-e28c16b1031d" colab={"base_uri": "https://localhost:8080/", "height": 221}
x_train.dtypes
# + id="461kqm9x73Us" colab_type="code" colab={}
# feature selection with KBest
import warnings
warnings.filterwarnings("ignore", category=RuntimeWarning)
from sklearn.feature_selection import SelectKBest, f_regression
selector = SelectKBest(score_func=f_regression, k=6)
x_train_selected = selector.fit_transform(x_train,y_train)
# + id="NKsdKuyf9oyZ" colab_type="code" outputId="492d4ad7-b74a-45b4-9927-f50d0568f1ee" colab={"base_uri": "https://localhost:8080/", "height": 272}
# TODO: Which features were selected?
selected_mask = selector.get_support()
all_names = x_train.columns
selected_names = all_names[selected_mask]
unselected_names = all_names[~selected_mask]
print('Features selected:')
for name in selected_names:
print(name)
print('\n')
print('Features not selected:')
for name in unselected_names:
print(name)
# + id="EcXu6Z4u-idh" colab_type="code" outputId="2d5a436c-f8e1-4e0c-c03d-e6d459377e75" colab={"base_uri": "https://localhost:8080/", "height": 136}
# using different alpha, fit ridge regression
for alpha in [0.001, 0.01, 0.1, 1.0, 1, 100.0, 1000.0]:
# Fit Ridge Regression model
model = Ridge(alpha=alpha, normalize=True)
model.fit(x_train, y_train)
y_pred = model.predict(x_test)
# Get Test MAE for each Alpha
mae = mean_absolute_error(y_test, y_pred)
print(mae)
# + id="sPxgJ_fELFyw" colab_type="code" colab={}
# Using RidgeCV
alphas = [0.01, 0.1, 1.0, 10.0, 100.0]
# + id="G78Wc6SLNKOv" colab_type="code" outputId="07265330-d11c-49ae-81bb-363095dfe0b8" colab={"base_uri": "https://localhost:8080/", "height": 34}
from sklearn.linear_model import RidgeCV
ridge = RidgeCV(alphas=alphas, normalize=True)
ridge.fit(x_train, y_train)
y_pred = ridge.predict(x_test)
ridge.alpha_
# + id="QX6j_VMjNwZe" colab_type="code" outputId="286e6b09-eee9-4c29-aecc-0ae9ff63621b" colab={"base_uri": "https://localhost:8080/", "height": 34}
mae = mean_absolute_error(y_test, y_pred)
print(mae)
# + id="qweMYIQONeEW" colab_type="code" colab={}
|
module3-ridge-regression/Adeagbo_Adewale_DS13_LS_DS_213_assignment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Using Convolutional Neural Networks
# Welcome to the first week of the first deep learning certificate! We're going to use convolutional neural networks (CNNs) to allow our computer to see - something that is only possible thanks to deep learning.
# ## Introduction to this week's task: 'Dogs vs Cats'
# We're going to try to create a model to enter the [Dogs vs Cats](https://www.kaggle.com/c/dogs-vs-cats) competition at Kaggle. There are 25,000 labelled dog and cat photos available for training, and 12,500 in the test set that we have to try to label for this competition. According to the Kaggle web-site, when this competition was launched (end of 2013): *"**State of the art**: The current literature suggests machine classifiers can score above 80% accuracy on this task"*. So if we can beat 80%, then we will be at the cutting edge as of 2013!
# ## Basic setup
# There isn't too much to do to get started - just a few simple configuration steps.
#
# This shows plots in the web page itself - we always wants to use this when using jupyter notebook:
# %matplotlib inline
# Define path to data: (It's a good idea to put it in a subdirectory of your notebooks folder, and then exclude that directory from git control by adding it to .gitignore.)
# path = "data/dogscats/"
path = "data/dogscats/sample/"
# A few basic libraries that we'll need for the initial exercises:
# +
from __future__ import division,print_function
import os, json
from glob import glob
import numpy as np
np.set_printoptions(precision=4, linewidth=100)
from matplotlib import pyplot as plt
# -
# We have created a file most imaginatively called 'utils.py' to store any little convenience functions we'll want to use. We will discuss these as we use them.
import utils; reload(utils)
from utils import plots
# # Use a pretrained VGG model with our **Vgg16** class
# Our first step is simply to use a model that has been fully created for us, which can recognise a wide variety (1,000 categories) of images. We will use 'VGG', which won the 2014 Imagenet competition, and is a very simple model to create and understand. The VGG Imagenet team created both a larger, slower, slightly more accurate model (*VGG 19*) and a smaller, faster model (*VGG 16*). We will be using VGG 16 since the much slower performance of VGG19 is generally not worth the very minor improvement in accuracy.
#
# We have created a python class, *Vgg16*, which makes using the VGG 16 model very straightforward.
# ## The punchline: state of the art custom model in 7 lines of code
#
# Here's everything you need to do to get >97% accuracy on the Dogs vs Cats dataset - we won't analyze how it works behind the scenes yet, since at this stage we're just going to focus on the minimum necessary to actually do useful work.
# As large as you can, but no larger than 64 is recommended.
# If you have an older or cheaper GPU, you'll run out of memory, so will have to decrease this.
batch_size=64
# Import our class, and instantiate
import vgg16; reload(vgg16)
from vgg16 import Vgg16
vgg = Vgg16()
# Grab a few images at a time for training and validation.
# NB: They must be in subdirectories named based on their category
batches = vgg.get_batches(path+'train', batch_size=batch_size)
val_batches = vgg.get_batches(path+'valid', batch_size=batch_size*2)
vgg.finetune(batches)
vgg.fit(batches, val_batches, nb_epoch=1)
# The code above will work for any image recognition task, with any number of categories! All you have to do is to put your images into one folder per category, and run the code above.
#
# Let's take a look at how this works, step by step...
# ## Use Vgg16 for basic image recognition
#
# Let's start off by using the *Vgg16* class to recognise the main imagenet category for each image.
#
# We won't be able to enter the Cats vs Dogs competition with an Imagenet model alone, since 'cat' and 'dog' are not categories in Imagenet - instead each individual breed is a separate category. However, we can use it to see how well it can recognise the images, which is a good first step.
#
# First, create a Vgg16 object:
vgg = Vgg16()
# Vgg16 is built on top of *Keras* (which we will be learning much more about shortly!), a flexible, easy to use deep learning library that sits on top of Theano or Tensorflow. Keras reads groups of images and labels in *batches*, using a fixed directory structure, where images from each category for training must be placed in a separate folder.
#
# Let's grab batches of data from our training folder:
batches = vgg.get_batches(path+'train', batch_size=4)
# (BTW, when Keras refers to 'classes', it doesn't mean python classes - but rather it refers to the categories of the labels, such as 'pug', or 'tabby'.)
#
# *Batches* is just a regular python iterator. Each iteration returns both the images themselves, as well as the labels.
imgs,labels = next(batches)
# As you can see, the labels for each image are an array, containing a 1 in the first position if it's a cat, and in the second position if it's a dog. This approach to encoding categorical variables, where an array containing just a single 1 in the position corresponding to the category, is very common in deep learning. It is called *one hot encoding*.
#
# The arrays contain two elements, because we have two categories (cat, and dog). If we had three categories (e.g. cats, dogs, and kangaroos), then the arrays would each contain two 0's, and one 1.
plots(imgs, titles=labels)
# We can now pass the images to Vgg16's predict() function to get back probabilities, category indexes, and category names for each image's VGG prediction.
vgg.predict(imgs, True)
# The category indexes are based on the ordering of categories used in the VGG model - e.g here are the first four:
vgg.classes[:4]
# (Note that, other than creating the Vgg16 object, none of these steps are necessary to build a model; they are just showing how to use the class to view imagenet predictions.)
# ## Use our Vgg16 class to finetune a Dogs vs Cats model
#
# To change our model so that it outputs "cat" vs "dog", instead of one of 1,000 very specific categories, we need to use a process called "finetuning". Finetuning looks from the outside to be identical to normal machine learning training - we provide a training set with data and labels to learn from, and a validation set to test against. The model learns a set of parameters based on the data provided.
#
# However, the difference is that we start with a model that is already trained to solve a similar problem. The idea is that many of the parameters should be very similar, or the same, between the existing model, and the model we wish to create. Therefore, we only select a subset of parameters to train, and leave the rest untouched. This happens automatically when we call *fit()* after calling *finetune()*.
#
# We create our batches just like before, and making the validation set available as well. A 'batch' (or *mini-batch* as it is commonly known) is simply a subset of the training data - we use a subset at a time when training or predicting, in order to speed up training, and to avoid running out of memory.
batch_size=64
batches = vgg.get_batches(path+'train', batch_size=batch_size)
val_batches = vgg.get_batches(path+'valid', batch_size=batch_size)
# Calling *finetune()* modifies the model such that it will be trained based on the data in the batches provided - in this case, to predict either 'dog' or 'cat'.
vgg.finetune(batches)
# Finally, we *fit()* the parameters of the model using the training data, reporting the accuracy on the validation set after every epoch. (An *epoch* is one full pass through the training data.)
vgg.fit(batches, val_batches, nb_epoch=1)
# That shows all of the steps involved in using the Vgg16 class to create an image recognition model using whatever labels you are interested in. For instance, this process could classify paintings by style, or leaves by type of disease, or satellite photos by type of crop, and so forth.
#
# Next up, we'll dig one level deeper to see what's going on in the Vgg16 class.
# # Create a VGG model from scratch in Keras
#
# For the rest of this tutorial, we will not be using the Vgg16 class at all. Instead, we will recreate from scratch the functionality we just used. This is not necessary if all you want to do is use the existing model - but if you want to create your own models, you'll need to understand these details. It will also help you in the future when you debug any problems with your models, since you'll understand what's going on behind the scenes.
# ## Model setup
#
# We need to import all the modules we'll be using from numpy, scipy, and keras:
# +
from numpy.random import random, permutation
from scipy import misc, ndimage
from scipy.ndimage.interpolation import zoom
import keras
from keras import backend as K
from keras.utils.data_utils import get_file
from keras.models import Sequential, Model
from keras.layers.core import Flatten, Dense, Dropout, Lambda
from keras.layers import Input
from keras.layers.convolutional import Convolution2D, MaxPooling2D, ZeroPadding2D
from keras.optimizers import SGD, RMSprop
from keras.preprocessing import image
# -
# Let's import the mappings from VGG ids to imagenet category ids and descriptions, for display purposes later.
FILES_PATH = 'http://files.fast.ai/models/'; CLASS_FILE='imagenet_class_index.json'
# Keras' get_file() is a handy function that downloads files, and caches them for re-use later
fpath = get_file(CLASS_FILE, FILES_PATH+CLASS_FILE, cache_subdir='models')
with open(fpath) as f: class_dict = json.load(f)
# Convert dictionary with string indexes into an array
classes = [class_dict[str(i)][1] for i in range(len(class_dict))]
# Here's a few examples of the categories we just imported:
classes[:5]
# ## Model creation
#
# Creating the model involves creating the model architecture, and then loading the model weights into that architecture. We will start by defining the basic pieces of the VGG architecture.
#
# VGG has just one type of convolutional block, and one type of fully connected ('dense') block. Here's the convolutional block definition:
def ConvBlock(layers, model, filters):
for i in range(layers):
model.add(ZeroPadding2D((1,1)))
model.add(Convolution2D(filters, 3, 3, activation='relu'))
model.add(MaxPooling2D((2,2), strides=(2,2)))
# ...and here's the fully-connected definition.
def FCBlock(model):
model.add(Dense(4096, activation='relu'))
model.add(Dropout(0.5))
# When the VGG model was trained in 2014, the creators subtracted the average of each of the three (R,G,B) channels first, so that the data for each channel had a mean of zero. Furthermore, their software that expected the channels to be in B,G,R order, whereas Python by default uses R,G,B. We need to preprocess our data to make these two changes, so that it is compatible with the VGG model:
# +
# Mean of each channel as provided by VGG researchers
vgg_mean = np.array([123.68, 116.779, 103.939]).reshape((3,1,1))
def vgg_preprocess(x):
x = x - vgg_mean # subtract mean
return x[:, ::-1] # reverse axis bgr->rgb
# -
# Now we're ready to define the VGG model architecture - look at how simple it is, now that we have the basic blocks defined!
def VGG_16():
model = Sequential()
model.add(Lambda(vgg_preprocess, input_shape=(3,224,224)))
ConvBlock(2, model, 64)
ConvBlock(2, model, 128)
ConvBlock(3, model, 256)
ConvBlock(3, model, 512)
ConvBlock(3, model, 512)
model.add(Flatten())
FCBlock(model)
FCBlock(model)
model.add(Dense(1000, activation='softmax'))
return model
# We'll learn about what these different blocks do later in the course. For now, it's enough to know that:
#
# - Convolution layers are for finding patterns in images
# - Dense (fully connected) layers are for combining patterns across an image
#
# Now that we've defined the architecture, we can create the model like any python object:
model = VGG_16()
# As well as the architecture, we need the weights that the VGG creators trained. The weights are the part of the model that is learnt from the data, whereas the architecture is pre-defined based on the nature of the problem.
#
# Downloading pre-trained weights is much preferred to training the model ourselves, since otherwise we would have to download the entire Imagenet archive, and train the model for many days! It's very helpful when researchers release their weights, as they did here.
fpath = get_file('vgg16.h5', FILES_PATH+'vgg16.h5', cache_subdir='models')
model.load_weights(fpath)
# ## Getting imagenet predictions
#
# The setup of the imagenet model is now complete, so all we have to do is grab a batch of images and call *predict()* on them.
batch_size = 4
# Keras provides functionality to create batches of data from directories containing images; all we have to do is to define the size to resize the images to, what type of labels to create, whether to randomly shuffle the images, and how many images to include in each batch. We use this little wrapper to define some helpful defaults appropriate for imagenet data:
def get_batches(dirname, gen=image.ImageDataGenerator(), shuffle=True,
batch_size=batch_size, class_mode='categorical'):
return gen.flow_from_directory(path+dirname, target_size=(224,224),
class_mode=class_mode, shuffle=shuffle, batch_size=batch_size)
# From here we can use exactly the same steps as before to look at predictions from the model.
# +
batches = get_batches('train', batch_size=batch_size)
val_batches = get_batches('valid', batch_size=batch_size)
imgs,labels = next(batches)
# This shows the 'ground truth'
plots(imgs, titles=labels)
# -
# The VGG model returns 1,000 probabilities for each image, representing the probability that the model assigns to each possible imagenet category for each image. By finding the index with the largest probability (with *np.argmax()*) we can find the predicted label.
def pred_batch(imgs):
preds = model.predict(imgs)
idxs = np.argmax(preds, axis=1)
print('Shape: {}'.format(preds.shape))
print('First 5 classes: {}'.format(classes[:5]))
print('First 5 probabilities: {}\n'.format(preds[0, :5]))
print('Predictions prob/class: ')
for i in range(len(idxs)):
idx = idxs[i]
print (' {:.4f}/{}'.format(preds[i, idx], classes[idx]))
pred_batch(imgs)
# # Notes
# ## predict_generator
# The `predict_generator()` gives a nicer loop to go through all the input batches. The `class_mode` needs to be set with `None` instead of `categorical` to get the probabilities.
def test(self, path, batch_size=8):
"""
Predicts the classes using the trained model on data yielded batch-by-batch.
Args:
path (string): Path to the target directory. It should contain one subdirectory
per class.
batch_size (int): The number of images to be considered in each batch.
Returns:
test_batches, numpy array(s) of predictions for the test_batches.
"""
test_batches = self.get_batches(path, shuffle=False, batch_size=batch_size, class_mode=None)
return test_batches, self.model.predict_generator(test_batches, test_batches.nb_sample)
# ## Create a link from IPython
from IPython.display import FileLink
FileLink('path/to/the/file')
|
deeplearning1/nbs/lesson1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import tensorflow as tf
'''
1. 데이터가 필요하다
2. 얼마나 많은 클러스터를 만들지 결정한다.
(ex 100명의 고객 모두 맞춤형 옷을 만들긴 힘들므로 s,m,l로 평준화된 사이즈로 클러스터하면 쉬울 것)
3. 클러스터의 중심을 설정한다.(centroid)
(방법 . 랜덤으로,매뉴얼,k-mean)
4. 주어진 데이터 포인트들이 어떤 centroid에 가까운지 설정
5. 클러스터의 중심을 centroid로 옮긴다.
6. 4,5를 반복(클러스터의 변화가 없을 때 멈춘다.(=데이터들의 변경이 없다))
'''
'''
centorid 초기화.
방법들 중 manually assign,
위도 경도의 도시로 구분할때 수동으로 지정해주는 방법
방법들 중 랜덤, 수동 포인트 지정이 어려울땐 k-mean++,
첫 data 위치에 첫 centroid를 init 두번째는 첫번째 centorid에서 가장 먼 위치에 init
세번째는 c1,c2와 공통적으로 먼곳에 c3 init 이러한 방법으로 초기 centroid 지정.
'''
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import seaborn as sb
# %matplotlib inline
# +
df = pd.DataFrame(columns=['x','y'])
import random
for i in range(50) :
df.loc[i] = [random.randrange(1,100),random.randrange(1,100)]
#난수 생성
# -
sb.lmplot('x','y', data = df, fit_reg = False, scatter_kws = {"s":50})
#fit_reg = False는 회귀 옵션 제거, scatter_kws = {"s":50}는 산점도 그래프 점 크기 설정
plt.title('K-means Example_dongmin')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
#할떄마다 바뀐다.
df_obj = df.values #numpy를 사용하기 위해 객체로 변환
kmeans = KMeans(n_clusters = 5).fit(df_obj) #3개의 클러스트 발생
kmeans.cluster_centers_ #클러스터와
kmeans.labels_ #라벨이 설정된다
# +
df['cluster'] = kmeans.labels_
#생성된 라벨을 새로운 컬럼값으로 저장
sb.lmplot('x','y', data = df, fit_reg = False, scatter_kws = {"s":150}, hue = "cluster")
plt.title('K-means Example_label')
# -
|
clustering.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Create Benchmark Dataset
# * need to download below package
# !pip install html2text
# !pip install newspaper
# ---
import requests
import json
import html2text
import random
from newspaper import Article
# ## function
# crawl by our parser
def get_content(url):
api = #gliacloud api
json_file = requests.get(api + url).json()
return json_file['parsed_content']['content']
# crawl by newspaper
def newspaper(url):
article = Article(url)
article.download()
article.parse()
return article.text
# filter image text e.g. 
def filter_content(text):
t = text
while t.find('![') != -1:
start = t.find('![')
step = 1
stack = 0
while t[start + step: start + step + 5] != '(http':
step = step + 1
stack = stack + 1
while stack != 0:
step += 1
if t[start + step] == '(':
stack = stack + 1
elif t[start + step] == ')':
stack = stack - 1
end = start + step
t = t[:start] + t[end+1:]
return t
# ## output json dict
#
json_dict = {}
# 之前已經存過檔了,跑下面這個。第一次做的話跳到下一個cell
your_file_path = "./ureka_dataset.json"
with open(your_file_path, 'r') as in_file:
json_dict = json.load(in_file)
template = {"articleBody": "", "url": ""}
# ## 流程
# 1. 將url貼上來或是自己建構url.txt
# * 連結在`./url.txt`,皆為測試過的有效連結
# * 如果連結還是有問題,可以到https://github.com/livingbio/gparsed/tree/master/src/parsers/test_parsers/test_cases ,每一個資料夾裡面找一個.item檔,立面有網頁連結
# * 有16個資料夾裡連結都失效,有在`url.txt`中註記
# 2. 執行gparser和newspapers
# 3. 比對這兩個的原文的結果
# * 選爬到完整或是超過內文的結果再去進行刪減比較快
# * 刪減的時候將print(repr())的結果複製下來到文字編輯器中進行刪減比較快
# * 換行符號、標點符號錯誤不需理會
# * 內文的定義可以查看https://paper.dropbox.com/doc/Benchmark-A.I.-Parser--BWBUq0_rFdVI8Lj3a_rFoq~5Ag-UPbZxMrxYm4XWR452HaTq
# * 範例輸出:https://github.com/livingbio/article-extraction-benchmark/blob/master/ground-truth.json
# * 不確定可以跟我討論
# 4. 產生key值
# 5. 將處理好的結果放進template['articleBody'], url放入template['url']
# 6. 將template放入json_dict[key]
# 7. back to 1 until you tried
#
# 8. 存檔
with open('./ureka.txt', 'r') as f:
lines = f.readlines()
links = iter(lines)
count = 0
record_where = []
len(lines)
# +
link = next(links)
print(link)
count = count + 1
record_where.append(link)
# -
# url to crawl
#url = link.split(' ')[1].replace('\n', '')
url = "https://thebank.vn/blog/20262-mua-bao-hiem-nhan-tho-bao-ve-den-99-tuoi-da-thuc-su-an-tam.html"
#link
print(url)
# +
'''
headers= {
"accept": "text/html,application/xhtml+xml,application/xml;q=0.9,image/avif,image/webp,image/apng,*/*;q=0.8,application/signed-exchange;v=b3;q=0.9",
"accept-language": "zh-TW,zh;q=0.9,en-US;q=0.8,en;q=0.7",
"cache-control": "max-age=0",
"sec-ch-ua": "\" Not A;Brand\";v=\"99\", \"Chromium\";v=\"96\", \"Google Chrome\";v=\"96\"",
"sec-ch-ua-mobile": "?0",
"sec-ch-ua-platform": "\"macOS\"",
"sec-fetch-dest": "document",
"sec-fetch-mode": "navigate",
"sec-fetch-site": "none",
"sec-fetch-user": "?1",
"upgrade-insecure-requests": "1"
}
'''
html_page = requests.get(url)
print(html_page.status_code)
# -
count
# ## 有些網站gparser不能爬,會出現`JSONDecodeError: Expecting value: line 1 column 1 (char 0)`。遇到的時候就直接用newspaper就好。如果gparser和newspaper都failed在跟我說。
gparser = get_content(url)
text = html2text.html2text(gparser)
# 可以過濾掉圖片連結
text = filter_content(text)
print(repr(text))
news = newspaper(url)
print(repr(news))
# ## generate key
key = str.join('', [ random.choice('<KEY>') for _ in range(64) ])
print(key)
# 放入處理好的文字 或是不需處理的話直接放變數
ok_text = """Từ hôm nay đến hết ngày 29/12 tại Yumeisakura diễn ra chương trình Tham gia vòng xoay - trúng ngay Voucher, áp dụng cho Hệ thống Yumeisakura toàn quốc. Từ ngày hôm nay đến hết ngày 29/12/2020 khách hàng được tham gia vòng quay như ý với mức giảm giá cho Voucher hấp dẫn lên đến 40%. 1. Quà trong chương trình Quà trong chương trình là các Voucher mua hàng Son Yumeisakura có giá trị từ 10 - 40% 2. Quy định của chương trình Mỗi khách hàng (1 số điện thoại) chỉ được quay 1 lần duy nhất. Voucher áp dụng mua hàng đến hết ngày 29/12/2020. Chương trình áp dụng cho khách hàng trên toàn quốc 3. Cách tham gia chương trình Bước 1: Click vào Link này: https://yumeisakura.vn/hotsale-online Bước 2: Nhập số điện thoại và nhấn nút chơi ngay để bắt đầu xoay 4. Cách áp dụng Vocuher Có thể nhấn vào link https://yumeisakura.vn/ chọn các sản phẩm cần mua cho vào giỏ hàng và tiến hành điền đầy đủ thông tin mua hàng theo yêu cầu. Hoặc chuyên viên sẽ liên hệ trực tiếp số điện thoại của bạn sau khi đăng ký và tham gia vòng xoay để tư vấn màu son thích hợp. Voucher sẽ được trừ trực tiếp đơn hàng sau khi được chuyên viên đối chiếu với Vòng xoay tương ứng. Nhanh tay tham gia ngay chương trình "Tham gia vòng xoay - Trúng ngay Voucher " để có cơ hội trúng Voucher giảm giá đến 40%. Không chỉ có cơ hội tham gia vòng xoay trúng Voucher, khi đã có trên tay sản phẩm Yumeisakura, các YumeiGirl còn có cơ hội rinh về hơn 1000 phần quà với tổng giá trị lên đến 100 triệu đồng. Thể lệ chương trình cực đơn giản: - Bước 1: Mua son Yumeisakura tại tất cả các hệ thống bán hàng trên toàn quốc. - Bước 2: Cào lớp tráng bạc trên tem dán ở mỗi cây son, xuất hiện mã dự thưởng. Nhắn tin theo cú pháp Cú pháp: CHG YMS MÃ SỐ gửi đến 8077 (Chi phí gửi tin nhắn: 1000VND/ tin) để tham dự chương trình. - Bước 3: Sau khi nhắn tin, bạn sẽ nhận được tin nhắn xác nhận từ chương trình đã gửi mã dự thưởng thành công. - Bước 4: Xem livestream công bố kết quả trúng thưởng trên fanpape chính thức của Yumeisakura vào ngày 30/12/2020. Chương trình diễn rra hết ngày 29/12/2020 Nhanh tay sở hữu những thỏi son Yumeisakura để không bỏ lỡ những món quà công nghệ đỉnh nhất hiện nay nhé!"""
#https://danviet.vn/ca-mac-covid-19-tang-nhanh-bao-gio-ha-noi-dat-muc-mien-dich-cong-dong-20211125100630347.htm
html_path = './ureka-html/'
'''
headers= {
"accept": "text/html,application/xhtml+xml,application/xml;q=0.9,image/avif,image/webp,image/apng,*/*;q=0.8,application/signed-exchange;v=b3;q=0.9",
"accept-language": "zh-TW,zh;q=0.9,en-US;q=0.8,en;q=0.7",
"cache-control": "max-age=0",
"sec-ch-ua": "\" Not A;Brand\";v=\"99\", \"Chromium\";v=\"96\", \"Google Chrome\";v=\"96\"",
"sec-ch-ua-mobile": "?0",
"sec-ch-ua-platform": "\"macOS\"",
"sec-fetch-dest": "document",
"sec-fetch-mode": "navigate",
"sec-fetch-site": "none",
"sec-fetch-user": "?1",
"upgrade-insecure-requests": "1"
}
'''
html_page = requests.get(url)
print(html_page.status_code)
with open(f'{html_path}{key}.html', 'wb') as f:
f.write(html_page.content)
# 存入json_dict中
#if key not in json_dict:
json_dict[key] = {'articleBody': ok_text, 'url': url}
#else:
# print("key exist! Need to generate another")
json_dict
len(json_dict)
# ## Store in json file
# * 累了要休工不做了再存進去
your_file_path = "./ureka_dataset.json"
with open(your_file_path, 'w') as out_file:
json.dump(json_dict, out_file, sort_keys=True, ensure_ascii=False, indent=4)
your_file_path = "./filter_our.json"
with open(your_file_path, 'r') as in_file:
fo = json.load(in_file)
your_file_path = "./sorted_f_out.json"
with open(your_file_path, 'w') as out_file:
json.dump(fo, out_file, sort_keys=True, ensure_ascii=False, indent=4)
|
Annotation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="3Y_cWuCR_FH6" colab_type="code" outputId="2583ae8f-9d8f-44ca-badd-9468af59d3e7" colab={"base_uri": "https://localhost:8080/", "height": 34}
import os
os.getcwd() #shows the current working directory
# + id="Gp__ALr__OL9" colab_type="code" colab={}
import numpy as np # pulls in numpy package
import pandas as pd # pulls in pandas package
import matplotlib as mpl
import matplotlib.pyplot as plt # pulls in matplotlib plotting package
import seaborn as sns # pulls in seaborn package
# + id="x8iDBGJfF22Y" colab_type="code" colab={}
import sklearn # use sklearn for the regression and training
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn import metrics
# + id="5X9m0Kkjy46d" colab_type="code" outputId="bea92e2b-0d49-4393-d8ee-a22b5d90e0a9" colab={"base_uri": "https://localhost:8080/", "height": 34}
abalonedf = pd.read_csv('abalone.csv') # pulls in my csv file
abalonedf.shape # shows the number of rows/records and columns/variables
# + id="ush0hv6pAeyU" colab_type="code" outputId="a2535133-aab3-4d6a-fe8d-c55ed92c6631" colab={"base_uri": "https://localhost:8080/", "height": 197}
abalonedf.head() # shows the first 5 rows of data
# + [markdown] id="htSdmHmC__5b" colab_type="text"
# The abalone.csv file contains 4,177 rows of data about the gender (M/F/infant), size (length, diameter, height), weight (whole, shucked, viscera, shell) and age (rings) of marine snails called abalone (9 variables).
# The data comes from https://www.kaggle.com/rodolfomendes/abalone-dataset/version/3#abalone.csv
# The number of rings plus 1.5 gives the estimated age of the abalone in years. We can use the length and other size variables to predict the rings/age.
# + id="vKhO15QmCTMn" colab_type="code" outputId="d2ecc70d-6eea-4f15-cffe-6e5b4e8a53c4" colab={"base_uri": "https://localhost:8080/", "height": 194}
abalonedf.dtypes # shows the data types for each variable
# + id="d8zM2xfBGIMl" colab_type="code" outputId="422d085f-834d-49db-8b67-2ae0cb94ae06" colab={"base_uri": "https://localhost:8080/", "height": 377}
abalonedf.describe(include='all')
# shows the descriptive statistics for each variable
# include all means it will show qualitative and quantitative variables
# + id="mkzmL8RuspRl" colab_type="code" outputId="3811b8a2-3ea6-4d46-f1b8-8b695e488cec" colab={"base_uri": "https://localhost:8080/", "height": 70}
abalonedf.keys()
# + [markdown] id="DfqNELc_Mect" colab_type="text"
# This is a dataframe so it shows the index of the variables.
# The Boston Housing data is a dictionary which has keys and values.
# + [markdown] id="tj9wGsPpR0lt" colab_type="text"
# Make a plot of the length and number of rings/age.
# + id="jSA4Vj8t9qLN" colab_type="code" outputId="392a7725-33fe-4b8a-b56c-29b7d39e2613" colab={"base_uri": "https://localhost:8080/", "height": 281}
_ = plt.plot(abalonedf['Length'], abalonedf['Rings'], marker='.', linestyle='none')
# this provides a scatter plot of the length and age/rings
_ = plt.xlabel('Length of Abalone')
_ = plt.ylabel('Age in Rings')
_ = plt.show()
# + [markdown] id="w69NzA8MN_sO" colab_type="text"
# This looks like a correlation between the length of the abalone and their age in rings.
# + id="PDk1jWKruS41" colab_type="code" colab={}
x = abalonedf.iloc[:, 1:7] # this selects all rows and columns 2-8
y = abalonedf.iloc[:,-1] # this selects all rows and only the last column
# + [markdown] id="wc7voR6qzIjq" colab_type="text"
# Split the data into train and test data.
# + id="MCoNCFDevcCF" colab_type="code" colab={}
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.30, random_state = 9)
# + id="j3QXwlu7zgBy" colab_type="code" outputId="497f501c-1fc3-4c5b-df38-9f8e562a48ac" colab={"base_uri": "https://localhost:8080/", "height": 34}
x_train.shape, y_train.shape
# + id="fnxF3D0ozpCv" colab_type="code" outputId="d7812628-effb-4109-99e5-7e11d91d63f6" colab={"base_uri": "https://localhost:8080/", "height": 34}
x_test.shape, y_test.shape
# + [markdown] id="FOGwi9Mzz7fA" colab_type="text"
# Fit the training data to a linear model.
# + id="OziuapenzyCO" colab_type="code" outputId="93ecbe2d-9408-46fd-9941-f57779071cab" colab={"base_uri": "https://localhost:8080/", "height": 34}
regressor = LinearRegression()
regressor.fit(x_train, y_train) # trains the algorithm
# + [markdown] id="s_-JuQGM0BWX" colab_type="text"
# Use the model to predict the test data.
# + id="FuIoVp6NzyGN" colab_type="code" colab={}
y_predicted = regressor.predict(x_test) # this makes predictions on the testing set.
# + [markdown] id="0Tma9NSt0LmQ" colab_type="text"
# Measure the accuracy of the model by using the mean square error (MSE).
#
# First using Numpy.
# + id="nbv_QziW0S03" colab_type="code" outputId="070697e2-f4a2-4cf1-c7fa-8e73529f0444" colab={"base_uri": "https://localhost:8080/", "height": 34}
mean_sq_error = np.mean((y_test - y_predicted) **2)
print(mean_sq_error)
# + [markdown] id="iz8UwtoG0dD3" colab_type="text"
# Using sklearn metrics.
# + id="wuq576w2zyJz" colab_type="code" outputId="3ab592d5-9ada-4a74-80ee-5cb843e8f979" colab={"base_uri": "https://localhost:8080/", "height": 34}
print(mean_squared_error(y_true = y_test, y_pred = regressor.predict(x_test)))
# + [markdown] id="o1SE-mnD2OBF" colab_type="text"
# The mean squared error is the same calculated either way (with either package).
# + [markdown] id="_CfoVqRS0slM" colab_type="text"
# Print the error on the training data.
# + id="1xMNYrIq0wpf" colab_type="code" outputId="291ecfdd-a033-4558-cab0-3fec9ac6f2b0" colab={"base_uri": "https://localhost:8080/", "height": 34}
print(mean_squared_error(y_true = y_train, y_pred = regressor.predict(x_train)))
# + [markdown] id="k43DEK5t06QQ" colab_type="text"
# How much does the model (the x variable) explain the variability of the response data around its mean?
# + id="sZYPQE-3zyM2" colab_type="code" outputId="e3b6e7cd-1a62-4a5c-d483-88f9d7565b9a" colab={"base_uri": "https://localhost:8080/", "height": 34}
regressor.score(x_test, y_test) # this means this model fits/explains about 50% of the variability, which is not great.
# We would like the score to be closest to 1 to indicate a higher degree of accuracy in predicting the output.
# + [markdown] id="9NovgN8h1B8T" colab_type="text"
# Check histogram of the residuals. does it satisfy the assumptions for inference?
# + id="TGYnWOHU1IpT" colab_type="code" outputId="aac2273d-dd9e-49af-ba91-4852525a1c0f" colab={"base_uri": "https://localhost:8080/", "height": 353}
plt.hist(y_test - y_predicted)
# + id="h67vje3b06_X" colab_type="code" outputId="9841865f-b978-4143-9964-3a20a4f5efa7" colab={"base_uri": "https://localhost:8080/", "height": 282}
plt.scatter(y_predicted, y_test - y_predicted)
# + id="j2TyIXPf07Co" colab_type="code" outputId="7045acbd-e497-40c3-aa9c-28a448bfea0b" colab={"base_uri": "https://localhost:8080/", "height": 282}
plt.scatter(regressor.predict(x), y - regressor.predict(x))
# + id="3LbgyC4c1Vmh" colab_type="code" outputId="468af72f-82f5-430b-dfe4-a7381d37386d" colab={"base_uri": "https://localhost:8080/", "height": 282}
plt.scatter(regressor.predict(x_train), y_train - regressor.predict(x_train))
# + id="98zbdNFa1Vpm" colab_type="code" outputId="a6f5bb9b-a7ce-45d7-caa7-65ccddbe625c" colab={"base_uri": "https://localhost:8080/", "height": 52}
print(regressor.coef_) #
# + [markdown] id="nucFPhcC_h_6" colab_type="text"
# The coefficients show the mean change in the y (rings/age) for each unit of change in the x (predictor) variable (length, weight, etc.)
# For each unit of change in y, the x (length, diameter, height, whole weight, shucked weight, viscera weight, and shell weight) change by these units.
# + id="WFIgWw681Vsm" colab_type="code" outputId="f5725838-2cb8-4afe-bf00-2072308c3bb9" colab={"base_uri": "https://localhost:8080/", "height": 34}
print(regressor.intercept_)
# + id="hqbGyB-2Xhpf" colab_type="code" outputId="fedcb393-60d3-45e6-b902-cc158f664a3b" colab={"base_uri": "https://localhost:8080/", "height": 70}
# finds values for metrics using test data
print('Mean Absolute Error: ', metrics.mean_absolute_error(y_test, y_predicted))
print('Mean Squared Error: ', metrics.mean_squared_error(y_test, y_predicted))
print('Root Mean Squared Error: ', np.sqrt(metrics.mean_squared_error(y_test, y_predicted)))
# + [markdown] id="HdcFo2TG9JFH" colab_type="text"
# This is just another way to look at it.
# + id="wYWcMIz13wvU" colab_type="code" outputId="3cc77778-6eed-4d63-a47e-11f8b06a6eaf" colab={"base_uri": "https://localhost:8080/", "height": 123}
rmsd = np.sqrt(mean_squared_error(y_test, y_predicted))
r2_value = r2_score(y_test, y_predicted)
print("Intercept: \n", regressor.intercept_)
print("Root Mean Square Error \n", rmsd)
print("R^2 Value: \n", r2_value)
# + id="TA-jSM2u3xLs" colab_type="code" outputId="78d73ce6-d17e-40ea-d386-02bbe52e2466" colab={"base_uri": "https://localhost:8080/", "height": 212}
df = pd.DataFrame({'Actual': y_test, 'Predicted' : y_predicted})
print(df.head(10))
|
Project2RegressionJParaboschiv4.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
from matplotlib import pyplot as plt
train_df = pd.read_csv('train.csv')
test_df = pd.read_csv('test.csv')
train_df.head()
train_df.shape
train_df.head()
# #### 1. Decision/Random - MSSubClass, MSZoning, Street, Alley, LotFrontage, etc
# #### 2. Linear - LotArea,
n = list(train_df.isna().sum())
n1 = pd.DataFrame(n)
n1.columns = ['na']
col_d = pd.DataFrame(train_df.columns)
col_d['e'] = n1
col_d[0:10]
# +
#Categorical Values
featu = ['MSZoning', 'Street', 'LotShape', 'LandContour', 'Utilities', 'LotConfig', 'LandSlope', 'Neighborhood',
'Condition1', 'Condition2', 'BldgType', 'HouseStyle', 'RoofStyle', 'RoofMatl','Exterior1st', 'Exterior2nd',
'MasVnrType', 'ExterQual','ExterCond', 'Foundation','BsmtQual', 'BsmtCond','BsmtExposure','BsmtFinType1',
'BsmtFinType2','Heating','HeatingQC','CentralAir','Electrical','KitchenQual','Functional','GarageType',
'GarageFinish','GarageQual','GarageCond','PavedDrive','SaleType','SaleCondition' ]
LF_mean = train_df.LotFrontage.mean()
train_df.LotFrontage = train_df.LotFrontage.fillna(train_df.LotFrontage.mean())
for x in featu:
train_df.dropna(subset=[x], inplace=True)
train_df
train_df.shape
# -
# ### One Hot Encoding for Categorical Values
# +
from sklearn.preprocessing import OneHotEncoder
onehotencoder = OneHotEncoder(handle_unknown = 'ignore')
def v(c1):
M = pd.DataFrame(onehotencoder.fit_transform(train_df[[c1]]).toarray())
# get length of df's columns
num_cols = len(list(M))
rng = range(0, num_cols)
new_cols = [c1 + str(i) for i in rng]
M.columns = new_cols[:num_cols]
return M
MS = pd.concat([v(i) for i in featu], axis=1)
MS.head()
# -
MS.shape
MS.isna().sum()
MS = MS.reset_index(drop=True)
MS
# Cleaning and selecting numerical columns
numer = train_df.copy()
num_sel = numer[['MSSubClass', 'LotFrontage', 'LotArea', 'OverallQual', 'OverallCond', 'YearBuilt', 'YearRemodAdd',
'MasVnrArea', 'BsmtFinSF1', 'BsmtFinSF2', 'BsmtUnfSF', 'TotalBsmtSF', '1stFlrSF', '2ndFlrSF', 'LowQualFinSF',
'GrLivArea', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath', 'HalfBath', 'BedroomAbvGr', 'KitchenAbvGr',
'TotRmsAbvGrd', 'Fireplaces', 'GarageYrBlt', 'GarageCars', 'GarageArea', 'WoodDeckSF', 'OpenPorchSF',
'EnclosedPorch', '3SsnPorch', 'ScreenPorch', 'PoolArea', 'MiscVal', 'MoSold', 'YrSold']]
num_sel.head()
num_sel.shape
num_sel = num_sel.reset_index(drop=True)
num_sel
num_sel.isna().sum()
train_clean_df = pd.concat([MS, num_sel], axis=1)
train_clean_df.head()
train_clean_df.shape
train_clean_df.isna().sum()
sales_train = train_df.SalePrice
sales_train_df = pd.DataFrame(sales_train)
sales_train_df = sales_train_df.reset_index(drop=True)
sales_train_df
# ### Test File
# +
featu_test = ['MSZoning', 'Street', 'LotShape', 'LandContour', 'Utilities', 'LotConfig', 'LandSlope', 'Neighborhood',
'Condition1', 'Condition2', 'BldgType', 'HouseStyle', 'RoofStyle', 'RoofMatl','Exterior1st', 'Exterior2nd',
'MasVnrType', 'ExterQual','ExterCond', 'Foundation','BsmtQual', 'BsmtCond','BsmtExposure','BsmtFinType1',
'BsmtFinType2','Heating','HeatingQC','CentralAir','Electrical','KitchenQual','Functional','GarageType',
'GarageFinish','GarageQual','GarageCond','PavedDrive','SaleType','SaleCondition' ]
#Preparing test dataset
LF_mean = test_df.LotFrontage.mean()
test_df.LotFrontage = test_df.LotFrontage.fillna(test_df.LotFrontage.mean())
for x in featu_test:
test_df.dropna(subset=[x], inplace=True)
test_df
# -
test_df.shape
test_df.isna().sum()
# +
from sklearn.preprocessing import OneHotEncoder
onehotencoder = OneHotEncoder(handle_unknown = 'ignore')
def v_test(c1):
M = pd.DataFrame(onehotencoder.fit_transform(test_df[[c1]]).toarray())
# get length of df's columns
num_cols = len(list(M))
rng = range(0, num_cols)
new_cols = [c1 + str(i) for i in rng]
M.columns = new_cols[:num_cols]
return M
MS_test = pd.concat([v_test(i) for i in featu], axis=1)
MS_test
MS_test = MS_test.reset_index(drop=True)
MS_test
# -
MS_test.shape
numer_t = test_df.copy()
num_sel_t = numer_t[['MSSubClass', 'LotFrontage', 'LotArea', 'OverallQual', 'OverallCond', 'YearBuilt', 'YearRemodAdd',
'MasVnrArea', 'BsmtFinSF1', 'BsmtFinSF2', 'BsmtUnfSF', 'TotalBsmtSF', '1stFlrSF', '2ndFlrSF', 'LowQualFinSF',
'GrLivArea', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath', 'HalfBath', 'BedroomAbvGr', 'KitchenAbvGr',
'TotRmsAbvGrd', 'Fireplaces', 'GarageYrBlt', 'GarageCars', 'GarageArea', 'WoodDeckSF', 'OpenPorchSF',
'EnclosedPorch', '3SsnPorch', 'ScreenPorch', 'PoolArea', 'MiscVal', 'MoSold', 'YrSold']]
num_sel_t = num_sel_t.reset_index(drop=True)
num_sel_t.head()
num_sel_t.shape
num_sel_t.isna().sum()
test_clean_df = pd.concat([MS_test, num_sel_t], axis=1)
test_clean_df.head()
test_clean_df.shape
test_clean_df.isna().sum()
# ### Training and Validation
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
y = sales_train_df.SalePrice
features = [x for x in train_clean_df.columns]
X = train_clean_df[features]
train_X, val_X, train_y, val_y = train_test_split(X,y, random_state=1)
model_r = RandomForestRegressor(random_state = 0)
model_r.fit(train_X, train_y)
predict_r = model_r.predict(val_X)
predict_r = pd.DataFrame(predict_r, columns=['SalePrice'])
predict_r
mae = mean_absolute_error(val_y, predict_r)
mae
val_y1 = pd.DataFrame(val_y)
val_y1 = val_y1.reset_index(drop=True)
val_y1
score = model_r.score(val_X, val_y)
score
val_X = val_X.sort_values('GarageArea')
plt.rcParams["figure.figsize"] = [14, 8]
plt.plot(val_X.GarageArea, val_y)
plt.plot(val_X.GarageArea, predict_r)
plt.xlabel('Garage Area')
plt.ylabel('Sale Price')
plt.legend(['Original', 'Predicted'])
plt.show()
# ### If test file has less features than train
# Get missing columns in the training test
missing_cols = set( train_clean_df.columns ) - set( test_clean_df.columns )
# Add a missing column in test set with default value equal to 0
for c in missing_cols:
test_clean_df[c] = 0
# Ensure the order of column in the test set is in the same order than in train set
test_clean_df = test_clean_df[train_clean_df.columns]
# ### Predicting for test file
cols = [x for x in test_clean_df.columns]
test_X = test_clean_df[cols]
predict_r_t = model_r.predict(test_X)
predict_r_t = pd.DataFrame(predict_r_t, columns=['SalePrice'])
predict_r_t
|
home.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# To do meaningful detection on the dataset we need to personalize the classifier.
# This process require proper knowledge about the data available.
#
# We will start by importing the available bro logs into pandas to perform some statistical analysis and filter out some noise.
# Import the required dependencies
# +
# %matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
# -
# Import the bro logs and verify if it contains data.
# The bro logs imported are the output of bro-cut with the -d and -u flag to format the time.
# If the format of the bro logs is changed this code has to be altered.
bro_logs = pd.read_csv("data/smb_files_utc_formatted.csv", sep="\t", na_values="-", parse_dates=[0, 11, 12, 13, 14])
bro_logs.columns = ["ts", "uid", "id.orig_h", "id.orig_p", "id.resp_h", "id.resp_p", "fuid", "action", "path", "name", "size", "times.modified", "times.accessed", "times.created", "times.changed"]
bro_logs.fillna(0, inplace=True)
print(bro_logs.shape)
# Do some statistics on the data.
# The top 10 list shows some outliers that will generate noise in the classification algorithm
# +
N = 10
files_and_folders_seen = bro_logs["name"].nunique()
files_and_folders_read = bro_logs["name"][bro_logs["action"] == "SMB::FILE_READ"].nunique()
top_n_files_read = bro_logs["name"][bro_logs["action"] == "SMB::FILE_READ"].value_counts(sort=True).head(N)
print("Dataset contains {} unique files and folders").format(files_and_folders_seen)
print("Dataset contains {} unique files and folders which were read").format(files_and_folders_read)
print("{} most read files in the dataset:\n{}").format(N, top_n_files_read)
# -
# Now plot some basic graphs that show some information about the network.
# +
plt.figure()
fig, ax = plt.subplots()
fig.suptitle("Activity over time")
bro_logs["ts"][bro_logs["action"] == "SMB::FILE_READ"].groupby(pd.TimeGrouper('D')).plot(ax=ax, color='#267f8c', kind='bar', edgecolor='#267f8c')
bro_logs["ts"][bro_logs["action"] == "SMB::FILE_READ"].value_counts(sort=False).plot(ax=ax, color='#267f8c', kind='bar', edgecolor='#267f8c')
fig.savefig('output/activity_over_time_before_cleaning.png', dpi=1000)
plt.show()
# -
plt.figure()
fig, ax = plt.subplots()
fig.suptitle("Files opened")
ax = bro_logs["name"][bro_logs["action"] == "SMB::FILE_READ"].value_counts(sort=False).plot(color='#267f8c', kind='bar', edgecolor='#267f8c')
ax.xaxis.set_visible(False)
fig.savefig('output/files_opened_before_cleaning.png', dpi=1000)
plt.show()
print(bro_logs["name"][bro_logs["action"] == "SMB::FILE_READ"].value_counts().head(25))
# We can see that some of the most accessed files are not interresting to monitor.
# Having these files in the dataset will mess up the prediction in the future.
#
# To have a better view at the data we will filter out some files.
#
# NOTE: The files in the ignore_list have to be changed according to the data provided in the dataset.
# +
import re
ignore_list = ["Example", "Files", "That", "Have", "To", "Be", "Filtered"]
ignore_regex = '|'.join(ignore_list)
bro_logs_filtered = bro_logs[~bro_logs["name"].str.contains(ignore_regex, flags=re.IGNORECASE)]
print(bro_logs_filtered["name"][bro_logs_filtered["action"] == "SMB::FILE_READ"].value_counts().head(10))
print (bro_logs_filtered["name"][bro_logs_filtered["action"] == "SMB::FILE_READ"].shape)
print(bro_logs_filtered["name"][bro_logs_filtered["action"] == "SMB::FILE_READ"].nunique())
# -
# Let's make the graphs again to see if we can confirm the data has no significant outliers
# +
plt.figure()
fig, ax = plt.subplots()
fig.suptitle("Activity over time")
ax = bro_logs_filtered["ts"][bro_logs_filtered["action"] == "SMB::FILE_READ"].value_counts(sort=False).plot(color='#267f8c', kind='bar', edgecolor='#267f8c')
fig.savefig('output/activity_over_time_after_cleaning.png', dpi=1000)
plt.show()
plt.figure()
fig, ax = plt.subplots()
fig.suptitle("Files opened")
ax = bro_logs_filtered["name"][bro_logs_filtered["action"] == "SMB::FILE_READ"].value_counts(sort=False).plot(color='#267f8c', kind='bar', edgecolor='#267f8c')
ax.xaxis.set_visible(False)
fig.savefig('output/files_opened_after_cleaning.png', dpi=1000)
plt.show()
# -
# Now that we have a normalized dataset we will save it for further processing.
bro_logs_filtered.to_pickle("data/bro_logs_filtered.pkl")
|
1. Simple analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <a href="https://cognitiveclass.ai"><img src = "https://ibm.box.com/shared/static/ugcqz6ohbvff804xp84y4kqnvvk3bq1g.png" width = 300, align = "center"></a>
#
# <h1 align=center><font size = 5>Assignment: Notebook for Peer Assignment</font></h1>
# # Introduction
#
# Using this Python notebook you will:
# 1. Understand 3 Chicago datasets
# 1. Load the 3 datasets into 3 tables in a Db2 database
# 1. Execute SQL queries to answer assignment questions
# ## Understand the datasets
# To complete the assignment problems in this notebook you will be using three datasets that are available on the city of Chicago's Data Portal:
# 1. <a href="https://data.cityofchicago.org/Health-Human-Services/Census-Data-Selected-socioeconomic-indicators-in-C/kn9c-c2s2">Socioeconomic Indicators in Chicago</a>
# 1. <a href="https://data.cityofchicago.org/Education/Chicago-Public-Schools-Progress-Report-Cards-2011-/9xs2-f89t">Chicago Public Schools</a>
# 1. <a href="https://data.cityofchicago.org/Public-Safety/Crimes-2001-to-present/ijzp-q8t2">Chicago Crime Data</a>
#
# ### 1. Socioeconomic Indicators in Chicago
# This dataset contains a selection of six socioeconomic indicators of public health significance and a “hardship index,” for each Chicago community area, for the years 2008 – 2012.
#
# For this assignment you will use a snapshot of this dataset which can be downloaded from:
# https://ibm.box.com/shared/static/05c3415cbfbtfnr2fx4atenb2sd361ze.csv
#
# A detailed description of this dataset and the original dataset can be obtained from the Chicago Data Portal at:
# https://data.cityofchicago.org/Health-Human-Services/Census-Data-Selected-socioeconomic-indicators-in-C/kn9c-c2s2
#
#
#
# ### 2. Chicago Public Schools
#
# This dataset shows all school level performance data used to create CPS School Report Cards for the 2011-2012 school year. This dataset is provided by the city of Chicago's Data Portal.
#
# For this assignment you will use a snapshot of this dataset which can be downloaded from:
# https://ibm.box.com/shared/static/f9gjvj1gjmxxzycdhplzt01qtz0s7ew7.csv
#
# A detailed description of this dataset and the original dataset can be obtained from the Chicago Data Portal at:
# https://data.cityofchicago.org/Education/Chicago-Public-Schools-Progress-Report-Cards-2011-/9xs2-f89t
#
#
#
#
# ### 3. Chicago Crime Data
#
# This dataset reflects reported incidents of crime (with the exception of murders where data exists for each victim) that occurred in the City of Chicago from 2001 to present, minus the most recent seven days.
#
# This dataset is quite large - over 1.5GB in size with over 6.5 million rows. For the purposes of this assignment we will use a much smaller sample of this dataset which can be downloaded from:
# https://ibm.box.com/shared/static/svflyugsr9zbqy5bmowgswqemfpm1x7f.csv
#
# A detailed description of this dataset and the original dataset can be obtained from the Chicago Data Portal at:
# https://data.cityofchicago.org/Public-Safety/Crimes-2001-to-present/ijzp-q8t2
#
# ### Download the datasets
# In many cases the dataset to be analyzed is available as a .CSV (comma separated values) file, perhaps on the internet. Click on the links below to download and save the datasets (.CSV files):
# 1. __CENSUS_DATA:__ https://ibm.box.com/shared/static/05c3415cbfbtfnr2fx4atenb2sd361ze.csv
# 1. __CHICAGO_PUBLIC_SCHOOLS__ https://ibm.box.com/shared/static/f9gjvj1gjmxxzycdhplzt01qtz0s7ew7.csv
# 1. __CHICAGO_CRIME_DATA:__ https://ibm.box.com/shared/static/svflyugsr9zbqy5bmowgswqemfpm1x7f.csv
#
# __NOTE:__ Ensure you have downloaded the datasets using the links above instead of directly from the Chicago Data Portal. The versions linked here are subsets of the original datasets and have some of the column names modified to be more database friendly which will make it easier to complete this assignment.
# ### Store the datasets in database tables
# To analyze the data using SQL, it first needs to be stored in the database.
#
# While it is easier to read the dataset into a Pandas dataframe and then PERSIST it into the database as we saw in Week 3 Lab 3, it results in mapping to default datatypes which may not be optimal for SQL querying. For example a long textual field may map to a CLOB instead of a VARCHAR.
#
# Therefore, __it is highly recommended to manually load the table using the database console LOAD tool, as indicated in Week 2 Lab 1 Part II__. The only difference with that lab is that in Step 5 of the instructions you will need to click on create "(+) New Table" and specify the name of the table you want to create and then click "Next".
#
# <img src = "https://ibm.box.com/shared/static/uc4xjh1uxcc78ks1i18v668simioz4es.jpg">
#
# ##### Now open the Db2 console, open the LOAD tool, Select / Drag the .CSV file for the first dataset, Next create a New Table, and then follow the steps on-screen instructions to load the data. Name the new tables as folows:
# 1. __CENSUS_DATA__
# 1. __CHICAGO_PUBLIC_SCHOOLS__
# 1. __CHICAGO_CRIME_DATA__
# ### Connect to the database
# Let us first load the SQL extension and establish a connection with the database
# %load_ext sql
# In the next cell enter your db2 connection string. Recall you created Service Credentials for your Db2 instance in first lab in Week 3. From the __uri__ field of your Db2 service credentials copy everything after db2:// (except the double quote at the end) and paste it in the cell below after ibm_db_sa://
#
# <img src ="https://ibm.box.com/shared/static/hzhkvdyinpupm2wfx49lkr71q9swbpec.jpg">
import os
import pymysql
import pandas as pd
# ## Problems
# Now write and execute SQL queries to solve assignment problems
#
# ### Problem 1
#
# ##### Find the total number of crimes recorded in the CRIME table
# Rows in Crime table
# ### Problem 2
#
# ##### Retrieve first 10 rows from the CRIME table
#
# ### Problem 3
#
# ##### How many crimes involve an arrest?
# ### Problem 4
#
# ##### Which unique types of crimes have been recorded at GAS STATION locations?
#
# Hint: Which column lists types of crimes e.g. THEFT?
# ### Problem 5
#
# ##### In the CENUS_DATA table list all Community Areas whose names start with the letter ‘B’.
# ### Problem 6
#
# ##### Which schools in Community Areas 10 to 15 are healthy school certified?
# ### Problem 7
#
# ##### What is the average school Safety Score?
# ### Problem 8
#
# ##### List the top 5 Community Areas by average College Enrollment [number of students]
# ### Problem 9
#
# ##### Use a sub-query to determine which Community Area has the least value for school Safety Score?
# ### Problem 10
#
# ##### [Without using an explicit JOIN operator] Find the Per Capita Income of the Community Area which has a school Safety Score of 1.
# Copyright © 2018 [cognitiveclass.ai](cognitiveclass.ai?utm_source=bducopyrightlink&utm_medium=dswb&utm_campaign=bdu). This notebook and its source code are released under the terms of the [MIT License](https://bigdatauniversity.com/mit-license/).
#
|
IBM-DATA-SCIENCE-SPECIALIZATION/IBM-SQL-FOR-DATA-SCIENCE/.ipynb_checkpoints/DB0201EN-Week4-2-2-PeerAssign-v5-py-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 + Jaspy
# language: python
# name: jaspy
# ---
# ## Code to read in CMIP6 data from JASMIN archives
#
# Author: <NAME> (<EMAIL>) - drop me an email if you have questions about anything
# +
import os
import numpy as np
import xarray as xr
from datetime import datetime as dt
from pathlib import Path
import iris
import iris.coord_categorisation
from iris.experimental.equalise_cubes import equalise_attributes
from iris.util import unify_time_units
def get_dates(cube, verbose=False):
"""
Function to get dates from iris cube
"""
dates = cube.coord('time').units.num2date(cube.coord('time').points)
dates = [dt(date.year, date.month, date.day) for date in dates]
if verbose is True:
print(dates)
else:
print(dates[0], '–', dates[-1])
return(dates)
def make_cmip6_filepath(institute, model, scenario, variant, experiment, table_id, variable, grid, version, time_range,
data_root="/badc/cmip6/data/CMIP6/"):
"""
Make a file path for a cmip6 dataset on JASMIN for a single variable
"""
# get base path
path = str(DATA_ROOT / scenario / institute / model / experiment)
#print(path)
#print(os.listdir(path))
# get path for variant
if variant is None:
# select first variant
dir_list = os.listdir(path)
variant_list = [x for x in dir_list if x.startswith('r')]
else:
variant_list = [variant]
# update path
var = [x for x in variant_list if x.startswith('r1i1p1')]
if len(var) == 0:
print(variant_list)
var = [x for x in variant_list if x.startswith('r')]
path = path + '/' + var[0] + '/' + str(table_id) + '/' + str(variable)
else:
path = path + '/' + var[0] + '/' + str(table_id) + '/' + str(variable)
#print(path)
# get path for grid
if grid is None:
# select first grid (usually only 1)
dir_list = os.listdir(path)
grid_list = [x for x in dir_list if x.startswith('g')]
else:
grid_list = [grid]
# update path
path = path + '/' + str(grid_list[0])
#print(path)
# get version path
if version is None:
dir_list2 = os.listdir(path)
version_list = [x for x in dir_list2 if x.startswith('v')]
else:
version_list = [version]
# update path
path = path + '/' + str(version_list[0]) + '/'
print('JASMIN FILEPATH:')
print(path)
print('DIRECTORY CONTENTS:')
print(os.listdir(path))
return(path+ '*.nc')
# +
# create dictionary of models and institutes (allows you to loop over models and know the name of the directory that contains the data for that model)
basepath = '/badc/cmip6/data/CMIP6/CMIP/'
institute_list = os.listdir(basepath)
model_inst_dict = {}
# loop over institutes
for inst in institute_list:
model_list = os.listdir(basepath + inst + '/')
# for each institute list models and store in dictionary
for model_temp in model_list:
model_inst_dict[model_temp] = inst
# correction for UKESM which is used by multiple centres - we want MOHC only
model_inst_dict['UKESM1-0-LL'] = 'MOHC'
print(model_inst_dict)
# +
#assert False # May want to add this if already saved data into dictionaries to prevent re-writing
# Read in precipitation data over domain for CMIP6 models and save data to dictionary
DATA_ROOT = Path("/badc/cmip6/data/CMIP6/")
# dictionary to save subset model output
pr_datasets = {}
# Define region of interest
latmin = 0
latmax = 10
lonmin = -10
lonmax = 0
# variables for JASMIN directory structure
table_id = 'Amon' # monthly model output
variable_id = 'pr' # variable code for precipitation in cmip6 model output
# read in monthly data
# I don't think this is a full list! Need to update
models = ['ACCESS-CM2', 'ACCESS-ESM1-5', 'BCC-CSM2-MR', 'CAMS-CSM1-0', 'CanESM5',
'CNRM-CM6-1', 'CNRM-ESM2-1', 'FGOALS-f3-L', 'FGOALS-g3', 'HadGEM3-GC31-MM',
'GISS-E2-1-G', 'INM-CM5-0', 'INM-CM4-8',
'MPI-ESM1-2-LR', 'NorESM2-LM', 'NorESM2-MM', 'TaiESM1', 'UKESM1-0-LL']
# Try for just one model to see if it works
models = ['HadGEM3-GC31-MM']
# Loop over multiple model experiments and calculate SPEI for all, north and south Ghana
for expt in ['historical', 'ssp119', 'ssp585']:
for model in models:
print(model, '', expt.upper())
institute = model_inst_dict[model]
if model in ['UKESM1-0-LL']: #something wrong with UKESM r1i1p1 variant (hdf error)
variant = 'r2i1p1f2'
else:
variant = None
try:
# get CMIP6 precip data
if expt == 'historical':
scenario = 'CMIP'
elif expt in ['ssp119', 'ssp126', 'ssp245', 'ssp370', 'ssp585']:
scenario = 'ScenarioMIP'
# get filepath for data for particular model and variable of interest
fp_hist = make_cmip6_filepath(institute=institute, scenario=scenario, model=model, experiment=expt, variant=variant,
table_id=table_id, variable=variable_id, grid=None, version=None, time_range="*")
# read in data
pr_data = xr.open_mfdataset(fp_hist)
pr_data = pr_data.assign_coords(lon=(((pr_data.lon + 180) % 360) - 180)).sortby('lon') # change lons from 0,360 to -180,180
# select data over domain and convert to Iris cube (latmin,latmax, lonmin, lonmax defined above)
pr_regional_subset = pr_data.sel(lat=slice(latmin,latmax), lon=slice(lonmin,lonmax))
pr_regional_cube = pr_regional_subset.pr.to_iris()
# if you want you can print cube to look at data and print date range
print()
print(pr_regional_cube)
print()
dates = get_dates(pr_regional_cube)
pr_datasets[model] = pr_regional_cube
except FileNotFoundError:
print(model, ' has no ' + expt.upper() + ' output')
continue
# change output directory to somewhere you can save
outpath = '/home/users/jcabaker/bristol_cmip6_hack/save_files/'
fname = 'cmip6_' + expt + '_pr_dict.npy'
print('SAVING TO:', outpath + fname)
print()
#np.save(outpath + fname, pr_datasets) # uncomment to save
# -
|
notebooks/subgroup2/read_in_and_subset_cmip6_pr.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # SUBSTITUCION
# <KEY>UIZLFBMWHQ
def sustitucion(plaintext):
nuevoabc = 'JTREKYAVOGDXPSNCUIZLFBMWHQ'
abc = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
ciphertext = ''
for i in plaintext :
ciphertext += nuevoabc[abc.find(i.upper())]
print(f'ciphertext: {ciphertext}.')
return ciphertext
texto = sustitucion(input('plaintext: '))
|
modulo1/Ejercicio2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Write a Python Program to Check if a Number is Positive, Negative or Zero?
try:
a=int(input('Enter the number to check: '))
if a>0:
print('Number is positive')
elif a==0:
print('Number is zero')
else:
print('Number is negative')
except:
print('Enter numerical value')
# ### Write a Python Program to Check if a Number is Odd or Even?
try:
a=int(input('Enter number to check: '))
if a%2==0:
print('Number is even')
else:
print('Number is odd')
except:
print('Enter a numeric value')
# ### Write a Python Program to Check Leap Year?
try:
y=int(input('Enter year to check in yyyy: '))
if y%4==0:
print('{} is leap year'.format(y))
else:
print('{} is not leap year'.format(y))
except:
print('Enter year value in correct format')
# ### Write a Python Program to Check Prime Number?
p=int(input('Enter value: '))
if p>1:
for i in range(2,p):
if p%i==0:
print('Number is not prime')
break
else:
print('Number is prime')
else:
print('Enter number greater than 1')
# ### Write a Python Program to Print all Prime Numbers in an Interval of 1-10000?
for num in range(1,10000):
if num>1:
for i in range(2,num):
if num%i==0:
break
else:
print(num)
|
Python Basic Programming_3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import anialtools as alt
import matplotlib.pyplot as plt
import numpy as np
# +
# Working directory for network training
nwdir = '/nh/nest/u/jsmith/scratch/Research/CCSD_Water_train/tfer/CCSD_Water_train/models_58R32_35A4-8/arch_search/'
# Directory to h5 files containing the energies
h5dir = '/nh/nest/u/jsmith/Research/multi_nettrainer/h5files/'
# +
# Define input designer
aipt = alt.anitrainerinputdesigner()
# Setup network architechtures for each atomic symbol and add layers to the network
layer_dictsH = [{"nodes":16,"activation":9,"l2norm":1,"l2valu": 0.0001},
{"nodes":16,"activation":9,"l2norm":1,"l2valu": 0.00001},
{"nodes":16,"activation":9,"l2norm":1,"l2valu":0.00001}]
for l in layer_dictsH:
aipt.add_layer("H",l)
layer_dictsC = [{"nodes":16,"activation":9,"l2norm":1,"l2valu": 0.0001},
{"nodes":16,"activation":9,"l2norm":1,"l2valu": 0.00001},
{"nodes":16,"activation":9,"l2norm":1,"l2valu":0.00001}]
for l in layer_dictsC:
aipt.add_layer("C",l)
layer_dictsN = [{"nodes":16,"activation":9,"l2norm":1,"l2valu": 0.0001},
{"nodes":16,"activation":9,"l2norm":1,"l2valu": 0.00001},
{"nodes":16,"activation":9,"l2norm":1,"l2valu":0.00001}]
for l in layer_dictsN:
aipt.add_layer("N",l)
layer_dictsO = [{"nodes":16,"activation":9,"l2norm":1,"l2valu": 0.0001},
{"nodes":16,"activation":9,"l2norm":1,"l2valu": 0.00001},
{"nodes":16,"activation":9,"l2norm":1,"l2valu":0.00001}]
for l in layer_dictsO:
aipt.add_layer("O",l)
# Output the layer parameters
aipt.print_layer_parameters()
# Customize training parameters
aipt.set_parameter("sflparamsfile",'rHCNO-4.6R_16-3.1A_a4-8.params')
aipt.set_parameter("atomEnergyFile",'sae_linfit.dat')
aipt.set_parameter("tolr",40)
# Print all training parameters
aipt.print_training_parameters()
# Write the input file
aipt.write_input_file(nwdir+'inputtrain.ipt',384)
# +
# Declare dict of requred training files
netdict = {'iptfile':nwdir+'inputtrain.ipt', # input parameters file
'cnstfile':nwdir+'rHCNO-4.6R_16-3.1A_a4-8.params', # AEV parameters file
'saefile':nwdir+'sae_linfit.dat', # Single atom energy shift file (if this does not exist it is created via a linear fitting)
'atomtyp':['H','C','N','O']} # Atomic species which are included in the training set
# Declare the trainer class
model = alt.alaniensembletrainer(nwdir,netdict,h5dir,4)
# Build a strided training cache for an ensemble
# split the data into 4 blocks, hold out 1 block for validation and 1 block for testing
# do not build the testset (this can be altered and will build a testing h5)
model.build_strided_training_cache(4,1,1,build_test=False)
# Declare GPUs to train on
gpus = [0,1]
# Train the ensemble on the give GPUs.
model.train_ensemble(gpus, True)
# Read outputs to get the training stats
info = model.get_train_stats()
# Make some plots with the training stats for each network trained
fE = np.zeros((2,len(info)),dtype=np.float64)
for idx,i in enumerate(info):
print('Mean time:',np.array(i['RTIME']).mean())
print('Total time:',np.array(i['RTIME']).sum())
plt.semilogy(i['EPOCH'][2:],i['ERROR']['E (kcal/mol)'][2:,0],label='train',)
plt.semilogy(i['EPOCH'][2:],i['ERROR']['E (kcal/mol)'][2:,1],label='valid')
plt.semilogy(i['EPOCH'][2:],i['ERROR']['E (kcal/mol)'][2:,2],label='store')
plt.legend()
plt.show()
fE[0,idx] = i['ERROR']['E (kcal/mol)'][-1,0]
fE[1,idx] = i['ERROR']['E (kcal/mol)'][-1,2]
# Print ensemble train and valiation errors
print('Final train errors:',"{0:.2f}".format(fE[0,:].mean()),'+-'+"{0:.3f}".format(fE[0,:].std()))
print('Final valid errors:',"{0:.2f}".format(fE[1,:].mean()),'+-'+"{0:.3f}".format(fE[1,:].std()))
# -
|
notebooks/test_multi_train_gpu.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.0 64-bit (''harmonizome'': venv)'
# name: python_defaultSpec_1593405951560
# ---
# # Harmonizome ETL: Public Health Genomics Knowledge Base (PHGKB)
# Created by: <NAME> <br>
# Credit to: <NAME>
#
# Data Source: https://phgkb.cdc.gov/PHGKB/downloadCenter.action
# appyter init
from appyter import magic
magic.init(lambda _=globals: _())
# +
import sys
import os
from datetime import date
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
import harmonizome.utility_functions as uf
import harmonizome.lookup as lookup
# -
# %load_ext autoreload
# %autoreload 2
# ### Notebook Information
# + tags=[]
print('This notebook was run on:', date.today(), '\nPython version:', sys.version)
# -
# # Initialization
# +
# %%appyter hide_code
{% do SectionField(
name='data',
title='Upload Data',
img='load_icon.png'
) %}
# +
# %%appyter code_eval
{% do DescriptionField(
name='description',
text='The original input file was sourced from <a href="https://phgkb.cdc.gov/PHGKB/downloadCenter.action target="_blank">phgkb.cdc.gov</a>. There is no direct link to download, so it should be downloaded from the source website. The "Genopedia" source is the one that should be downloaded.',
section='data'
) %}
{% set df_file = FileField(
constraint='.*\.txt$',
name='genopedia',
default='GeneID-Disease.txt',
label='Genopedia (txt)',
examples={
'GeneID-Disease.txt': 'https://phgkb.cdc.gov/PHGKB/downloadCenter.action'
},
section='data'
) %}
# -
# ### Load Mapping Dictionaries
# + tags=[]
symbol_lookup, geneid_lookup = lookup.get_lookups()
# -
# ### Output Path
# +
output_name = 'phgkb'
path = 'Output/PHGKB'
if not os.path.exists(path):
os.makedirs(path)
# -
# # Load Data
# +
# %%appyter code_exec
df = pd.read_csv(
{{df_file}},
skiprows=4, sep='#', header=None)
# -
df.head()
df.shape
# # Pre-process Data
# ## Get Relevant Data
def splitter(s):
# split attributes from gene, remove parentheses
lst = list(map(lambda x: x[:x.find('(')], s.split('\t')))
return lst[0], lst[1:]
df = pd.DataFrame(df[0].map(splitter).tolist(), columns=['Gene Symbol', 'Disease'])
df.head()
# ## Split Attribute Lists
df = df.explode('Disease').dropna().set_index('Gene Symbol')
df.head()
# # Filter Data
# ## Map Gene Symbols to Up-to-date Approved Gene Symbols
# + tags=[]
df = uf.map_symbols(df, symbol_lookup, remove_duplicates=True)
df.shape
# -
# # Analyze Data
# ## Create Binary Matrix
binary_matrix = uf.binary_matrix(df)
binary_matrix.head()
binary_matrix.shape
uf.save_data(binary_matrix, path, output_name + '_binary_matrix',
compression='npz', dtype=np.uint8)
# ## Create Gene List
gene_list = uf.gene_list(binary_matrix, geneid_lookup)
gene_list.head()
gene_list.shape
uf.save_data(gene_list, path, output_name + '_gene_list',
ext='tsv', compression='gzip', index=False)
# ## Create Attribute List
attribute_list = uf.attribute_list(binary_matrix)
attribute_list.head()
attribute_list.shape
uf.save_data(attribute_list, path, output_name + '_attribute_list',
ext='tsv', compression='gzip')
# ## Create Gene and Attribute Set Libraries
uf.save_setlib(binary_matrix, 'gene', 'up', path, output_name + '_gene_up_set')
uf.save_setlib(binary_matrix, 'attribute', 'up', path,
output_name + '_attribute_up_set')
# ## Create Attribute Similarity Matrix
attribute_similarity_matrix = uf.similarity_matrix(binary_matrix.T, 'jaccard', sparse=True)
attribute_similarity_matrix.head()
uf.save_data(attribute_similarity_matrix, path,
output_name + '_attribute_similarity_matrix',
compression='npz', symmetric=True, dtype=np.float32)
# ## Create Gene Similarity Matrix
gene_similarity_matrix = uf.similarity_matrix(binary_matrix, 'jaccard', sparse=True)
gene_similarity_matrix.head()
uf.save_data(gene_similarity_matrix, path,
output_name + '_gene_similarity_matrix',
compression='npz', symmetric=True, dtype=np.float32)
# ## Create Gene-Attribute Edge List
edge_list = uf.edge_list(binary_matrix)
uf.save_data(edge_list, path, output_name + '_edge_list',
ext='tsv', compression='gzip')
# # Create Downloadable Save File
uf.archive(path)
# ### Link to download output files: [click here](./output_archive.zip)
|
appyters/PHGKB_Harmonizome_ETL/PHGKB.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Wine Dataset
import sys
sys.path.insert(0, '../')
import deep_forest
import torch as th
from torch import nn as nn
import matplotlib.pyplot as plt
# %matplotlib inline
from math import pi
import seaborn as sns
from preprocess import get_data
from tqdm import tqdm
sns.set_theme("notebook")
sns.set_style('whitegrid')
# ## Get Data
x, y, test_data, test_labels = get_data(100)
# ## Deep Forest
model = deep_forest.DeepForest(100, 2, 13, 0.25, 10)
# %time model.train(2500, x, y)
print("\n==============\nFINAL ACC: %s" % str(th.mean((model.forward(model.trees,x) == y).float())))
imp = model.compute_importance(x)
print()
print(dict(imp))
import pandas as pd
data = pd.DataFrame({"feat": list(imp.keys()), "imp": list(imp.values())})
sns.barplot(x="feat", y="imp", data=data).set_title("Wine Deep Forest Importance")
# ## MLP Baseline
# +
mlp = nn.Sequential(
nn.Linear(13, 30),
nn.LeakyReLU(),
nn.Linear(30, 15),
nn.LeakyReLU(),
nn.Linear(15, 3),
nn.Softmax()
)
optimizer = th.optim.Adam(mlp.parameters())
pbar = tqdm(range(1000))
for i in pbar:
optimizer.zero_grad()
preds = mlp(x)
loss = nn.functional.cross_entropy(preds, y)
loss.backward()
optimizer.step()
pbar.set_description("EPOCH %d || Acc: %s || Loss: %s" % (i, str(th.mean((th.argmax(mlp(x), 1) == y).float())), str(loss)))
print("\n\n==============\nFINAL ACC: %s" % str(th.mean((th.argmax(mlp(x[:]), 1) == y[:]).float())))
# -
# ## Random Forest
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(max_depth=2)
clf.fit(x.numpy(), y.numpy())
print(clf.score(x.numpy(), y.numpy()))
data = pd.DataFrame({"feat": list(range(13)), "imp": clf.feature_importances_})
sns.barplot(x="feat", y="imp", data=data).set_title("Wine Random Forest Importance")
|
code/wine/benchmark.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] _uuid="908956b65b7871816988c588b27ac4ba8b85edfe"
# ### This heavily borrows from <NAME>'s https://www.kaggle.com/chauhuynh/my-first-kernel-3-699. I try to create some features using *workalendar*, which was suggested on <NAME>'s post (https://www.kaggle.com/c/elo-merchant-category-recommendation/discussion/74052) by <NAME>.
#
# ### As a first cursory effort, I've created new features in the train and test sets based on the number of working days (in the Brazilian calendar) between the first_active_month and the 8 major national holidays.
# + _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5" _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19"
import numpy as np
import pandas as pd
import datetime
from datetime import date, datetime
import gc
import matplotlib.pyplot as plt
import seaborn as sns
import lightgbm as lgb
from sklearn.model_selection import StratifiedKFold
from sklearn.metrics import mean_squared_error
import warnings
import workalendar
from workalendar.america import Brazil
warnings.filterwarnings('ignore')
np.random.seed(4590)
# + _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a"
df_train = pd.read_csv('../input/train.csv')
df_test = pd.read_csv('../input/test.csv')
df_hist_trans = pd.read_csv('../input/historical_transactions.csv')
df_new_merchant_trans = pd.read_csv('../input/new_merchant_transactions.csv')
# + _uuid="520b71064293a20e0f2a379dad0acc274374a3c4"
def reduce_mem_usage(df, verbose=True):
numerics = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
start_mem = df.memory_usage().sum() / 1024**2
for col in df.columns:
col_type = df[col].dtypes
if col_type in numerics:
c_min = df[col].min()
c_max = df[col].max()
if str(col_type)[:3] == 'int':
if c_min > np.iinfo(np.int8).min and c_max < np.iinfo(np.int8).max:
df[col] = df[col].astype(np.int8)
elif c_min > np.iinfo(np.int16).min and c_max < np.iinfo(np.int16).max:
df[col] = df[col].astype(np.int16)
elif c_min > np.iinfo(np.int32).min and c_max < np.iinfo(np.int32).max:
df[col] = df[col].astype(np.int32)
elif c_min > np.iinfo(np.int64).min and c_max < np.iinfo(np.int64).max:
df[col] = df[col].astype(np.int64)
else:
if c_min > np.finfo(np.float16).min and c_max < np.finfo(np.float16).max:
df[col] = df[col].astype(np.float16)
elif c_min > np.finfo(np.float32).min and c_max < np.finfo(np.float32).max:
df[col] = df[col].astype(np.float32)
else:
df[col] = df[col].astype(np.float64)
end_mem = df.memory_usage().sum() / 1024**2
if verbose: print('Mem. usage decreased to {:5.2f} Mb ({:.1f}% reduction)'.format(end_mem, 100 * (start_mem - end_mem) / start_mem))
return df
# + _uuid="44198b73053869f8dfc083204c592fe9193f239c"
df_train = reduce_mem_usage(df_train)
df_test = reduce_mem_usage(df_test)
df_hist_trans = reduce_mem_usage(df_hist_trans)
df_new_merchant_trans = reduce_mem_usage(df_new_merchant_trans)
# + _uuid="71f89a3b8a93b2f2feb2cd0a45f860cde33687be"
for df in [df_hist_trans,df_new_merchant_trans]:
df['category_2'].fillna(1.0,inplace=True)
df['category_3'].fillna('A',inplace=True)
df['merchant_id'].fillna('M_ID_00a6ca8a8a',inplace=True)
# + _uuid="dda90662d05e22310dd713df106ea07f4b8bccfc"
def get_new_columns(name,aggs):
return [name + '_' + k + '_' + agg for k in aggs.keys() for agg in aggs[k]]
# + _uuid="5a8a999a7af28d3746de650cd9f48b4b24037d73"
cal = Brazil()
# for yr in [2011,2012,2013,2014,2015,2016,2017]:
# print(yr,cal.holidays(yr))
# + _uuid="eff94dfde04e78f7e6054194896f57c117bcbfe9"
cal.holidays(2013)[1]
# + [markdown] _uuid="b72764c2f70d05fa46a858a1215424b9d638b3de"
# ### As a first effort, for every year, we want to calculate the number of working days between the purchase date and the 8 major holidays --
# * New years day -- (year,1,1)
# * Tiradentes day -- (year,4,21)
# * Labour day-- (year,5,1)
# * Independence day -- (year,9,7)
# * Our lady of aparecida day -- (year,10,12)
# * All souls day -- (year,11,2)
# * Republic day -- (year,11,15)
# * Christmas day (year,12,25)
# + _uuid="7c91d3b9e9dbaff01962b0facbace75705a9ce18"
for df in [df_hist_trans,df_new_merchant_trans]:
df['purchase_date'] = pd.to_datetime(df['purchase_date'])
# df['date'] = df['purchase_date'].dt.date
df['year'] = df['purchase_date'].dt.year
df['weekofyear'] = df['purchase_date'].dt.weekofyear
df['month'] = df['purchase_date'].dt.month
df['dayofweek'] = df['purchase_date'].dt.dayofweek
df['weekend'] = (df.purchase_date.dt.weekday >=5).astype(int)
df['hour'] = df['purchase_date'].dt.hour
df['authorized_flag'] = df['authorized_flag'].map({'Y':1, 'N':0})
df['category_1'] = df['category_1'].map({'Y':1, 'N':0})
df['month_diff'] = ((datetime.today() - df['purchase_date']).dt.days)//30
df['month_diff'] += df['month_lag']
# These are the 8 added features, calculating the no of working days between the date of purchase and each of the 8 standard Brailian holidays
# df['day_diff1'] = df['date'].apply(lambda x: cal.get_working_days_delta(x,cal.holidays(x.year)[0][0])) # have to make this less clunky, write a function
# df['day_diff2'] = df['date'].apply(lambda x: cal.get_working_days_delta(x,cal.holidays(x.year)[1][0]))
# df['day_diff3'] = df['date'].apply(lambda x: cal.get_working_days_delta(x,cal.holidays(x.year)[2][0]))
# df['day_diff4'] = df['date'].apply(lambda x: cal.get_working_days_delta(x,cal.holidays(x.year)[3][0]))
# df['day_diff5'] = df['date'].apply(lambda x: cal.get_working_days_delta(x,cal.holidays(x.year)[4][0]))
# df['day_diff6'] = df['date'].apply(lambda x: cal.get_working_days_delta(x,cal.holidays(x.year)[5][0]))
# df['day_diff7'] = df['date'].apply(lambda x: cal.get_working_days_delta(x,cal.holidays(x.year)[6][0]))
# df['day_diff8'] = df['date'].apply(lambda x: cal.get_working_days_delta(x,cal.holidays(x.year)[7][0]))
# df['purchase_date'] = pd.to_datetime(df['purchase_date'])
# df['date'] = df['purchase_date'].dt.date
# df['year'] = df['purchase_date'].dt.year
# df['weekofyear'] = df['purchase_date'].dt.weekofyear
# df['month'] = df['purchase_date'].dt.month
# df['dayofweek'] = df['purchase_date'].dt.dayofweek
# df['weekend'] = (df.purchase_date.dt.weekday >=5).astype(int)
# df['hour'] = df['purchase_date'].dt.hour
# df['authorized_flag'] = df['authorized_flag'].map({'Y':1, 'N':0})
# df['category_1'] = df['category_1'].map({'Y':1, 'N':0})
# df['month_diff'] = ((datetime.today() - df['purchase_date']).dt.days)//30
# df['month_diff'] += df['month_lag']
# df['day_diff1'] = df['date'].apply(lambda x: cal.get_working_days_delta(x,cal.holidays(x.year)[0][0]))
# #cal.get_working_days_delta(df['date'],cal.holidays(2018)[0][0]) #df['date'] - cal.holidays(2018)[0][0]
# + _uuid="ddf1d5bb0ade2b22b0f072c208c1506ea64503ea"
aggs = {}
for col in ['month','hour','weekofyear','dayofweek','year','subsector_id','merchant_id','merchant_category_id']:
aggs[col] = ['nunique']
aggs['purchase_amount'] = ['sum','max','min','mean','var']
aggs['installments'] = ['sum','max','min','mean','var']
aggs['purchase_date'] = ['max','min']
aggs['month_lag'] = ['max','min','mean','var']
aggs['month_diff'] = ['mean']
aggs['authorized_flag'] = ['sum', 'mean']
aggs['weekend'] = ['sum', 'mean']
aggs['category_1'] = ['sum', 'mean']
aggs['card_id'] = ['size']
for col in ['category_2','category_3']:
df_hist_trans[col+'_mean'] = df_hist_trans.groupby([col])['purchase_amount'].transform('mean')
aggs[col+'_mean'] = ['mean']
new_columns = get_new_columns('hist',aggs)
df_hist_trans_group = df_hist_trans.groupby('card_id').agg(aggs)
df_hist_trans_group.columns = new_columns
df_hist_trans_group.reset_index(drop=False,inplace=True)
df_hist_trans_group['hist_purchase_date_diff'] = (df_hist_trans_group['hist_purchase_date_max'] - df_hist_trans_group['hist_purchase_date_min']).dt.days
df_hist_trans_group['hist_purchase_date_average'] = df_hist_trans_group['hist_purchase_date_diff']/df_hist_trans_group['hist_card_id_size']
df_hist_trans_group['hist_purchase_date_uptonow'] = (datetime.today() - df_hist_trans_group['hist_purchase_date_max']).dt.days
df_train = df_train.merge(df_hist_trans_group,on='card_id',how='left')
df_test = df_test.merge(df_hist_trans_group,on='card_id',how='left')
del df_hist_trans_group;
gc.collect()
# + _uuid="62050fec26b49ffff3feed6c845caafd6f06464a"
df_new_merchant_trans.head().T
# + _uuid="4820ed16eecd539377a0ecc88aa32b0eac83de5e"
df_train.head().T
# + _uuid="f7f5625db40db4395374991124fb796c9decd60b"
aggs = {}
for col in ['month','hour','weekofyear','dayofweek','year','subsector_id','merchant_id','merchant_category_id']:
aggs[col] = ['nunique']
aggs['purchase_amount'] = ['sum','max','min','mean','var']
aggs['installments'] = ['sum','max','min','mean','var']
aggs['purchase_date'] = ['max','min']
aggs['month_lag'] = ['max','min','mean','var']
aggs['month_diff'] = ['mean']
aggs['weekend'] = ['sum', 'mean']
aggs['category_1'] = ['sum', 'mean']
aggs['card_id'] = ['size']
for col in ['category_2','category_3']:
df_new_merchant_trans[col+'_mean'] = df_new_merchant_trans.groupby([col])['purchase_amount'].transform('mean')
aggs[col+'_mean'] = ['mean']
new_columns = get_new_columns('new_hist',aggs)
df_hist_trans_group = df_new_merchant_trans.groupby('card_id').agg(aggs)
df_hist_trans_group.columns = new_columns
df_hist_trans_group.reset_index(drop=False,inplace=True)
df_hist_trans_group['new_hist_purchase_date_diff'] = (df_hist_trans_group['new_hist_purchase_date_max'] - df_hist_trans_group['new_hist_purchase_date_min']).dt.days
df_hist_trans_group['new_hist_purchase_date_average'] = df_hist_trans_group['new_hist_purchase_date_diff']/df_hist_trans_group['new_hist_card_id_size']
df_hist_trans_group['new_hist_purchase_date_uptonow'] = (datetime.today() - df_hist_trans_group['new_hist_purchase_date_max']).dt.days
df_train = df_train.merge(df_hist_trans_group,on='card_id',how='left')
df_test = df_test.merge(df_hist_trans_group,on='card_id',how='left')
del df_hist_trans_group;
gc.collect()
# + _uuid="ab49c5936c182ba280c2b06264ba38a58e7fa335"
df_train.head().T
# + _uuid="a075cc90ab1322829e4fad3ff39fce307c5db93c"
del df_hist_trans;
gc.collect()
del df_new_merchant_trans;
gc.collect()
df_train.head(5)
# + _uuid="6f3182aeac0c3bf7a061a1b9e25e859f25fee9b5"
df_train['outliers'] = 0
df_train.loc[df_train['target'] < -30, 'outliers'] = 1
df_train['outliers'].value_counts()
# + _uuid="e9f61512c195c66a75dfe220072c5b2d860b78a3"
# Dealing with the one nan in df_test.first_active_month a bit arbitrarily for now
df_test.loc[df_test['first_active_month'].isna(),'first_active_month'] = df_test.iloc[11577]['first_active_month']
# + _uuid="61d6840e9bd87a5c14ea06d1f8ae567c307cdb33"
from datetime import timedelta
def get_working_days_delta(begin, end):
'''
Get working days between two dates
'''
sign = 1
if begin > end:
begin, end = end, begin
sign = -1
days = 0
temp_day = begin
while temp_day <= end:
if cal.is_working_day(temp_day):
days += 1
temp_day = temp_day + timedelta(days=1)
return days * sign
# + _uuid="ce2082fc1fb0e3f8f7d27fc166aa7a8351b65504"
for df in [df_train,df_test]:
df['first_active_month'] = pd.to_datetime(df['first_active_month'])
df['dayofweek'] = df['first_active_month'].dt.dayofweek
df['weekofyear'] = df['first_active_month'].dt.weekofyear
df['month'] = df['first_active_month'].dt.month
df['elapsed_time'] = (datetime.today() - df['first_active_month']).dt.days
df['hist_first_buy'] = (df['hist_purchase_date_min'] - df['first_active_month']).dt.days
df['new_hist_first_buy'] = (df['new_hist_purchase_date_min'] - df['first_active_month']).dt.days
for f in ['hist_purchase_date_max','hist_purchase_date_min','new_hist_purchase_date_max',\
'new_hist_purchase_date_min']:
df[f] = df[f].astype(np.int64) * 1e-9
df['card_id_total'] = df['new_hist_card_id_size']+df['hist_card_id_size']
df['purchase_amount_total'] = df['new_hist_purchase_amount_sum']+df['hist_purchase_amount_sum']
df['date'] = df['first_active_month'].dt.date
# These are the 8 added features, calculating the no of working days between the first active month and each of the 8 standard Brailian holidays
df['day_diff1'] = df['date'].apply(lambda x: get_working_days_delta(x,cal.holidays(int(x.year))[0][0])) # have to make this less clunky, write a function
df['day_diff2'] = df['date'].apply(lambda x: get_working_days_delta(x,cal.holidays(int(x.year))[1][0]))
df['day_diff3'] = df['date'].apply(lambda x: get_working_days_delta(x,cal.holidays(int(x.year))[2][0]))
df['day_diff4'] = df['date'].apply(lambda x: get_working_days_delta(x,cal.holidays(int(x.year))[3][0]))
df['day_diff5'] = df['date'].apply(lambda x: get_working_days_delta(x,cal.holidays(int(x.year))[4][0]))
df['day_diff6'] = df['date'].apply(lambda x: get_working_days_delta(x,cal.holidays(int(x.year))[5][0]))
df['day_diff7'] = df['date'].apply(lambda x: get_working_days_delta(x,cal.holidays(int(x.year))[6][0]))
df['day_diff8'] = df['date'].apply(lambda x: get_working_days_delta(x,cal.holidays(int(x.year))[7][0]))
df.drop(['date'],axis=1,inplace=True)
for f in ['feature_1','feature_2','feature_3']:
order_label = df_train.groupby([f])['outliers'].mean()
df_train[f] = df_train[f].map(order_label)
df_test[f] = df_test[f].map(order_label)
# + _uuid="10de5d846a12cdc85670cce7670238f4722043d6"
df_trainin.head().T
# + _uuid="a93c5976d3b395ba8ff0d1002b8075be3e914c54"
df_train = reduce_mem_usage(df_train)
df_test = reduce_mem_usage(df_test)
# + _uuid="d4a203d331fb6bf3868cad026d279467f2db8328"
from IPython.lib.deepreload import reload as dreload
import PIL, os, numpy as np, math, collections, threading, json, bcolz, random, scipy, cv2
import pandas as pd, pickle, sys, itertools, string, sys, re, datetime, time, shutil, copy
import seaborn as sns, matplotlib
import IPython, graphviz, sklearn_pandas, sklearn, warnings, pdb
import contextlib
from abc import abstractmethod
from glob import glob, iglob
from concurrent.futures import ThreadPoolExecutor, ProcessPoolExecutor
from itertools import chain
from functools import partial
from collections import Iterable, Counter, OrderedDict
from isoweek import Week
from pandas_summary import DataFrameSummary
from IPython.lib.display import FileLink
from PIL import Image, ImageEnhance, ImageOps
from sklearn import metrics, ensemble, preprocessing
from operator import itemgetter, attrgetter
from pathlib import Path
from distutils.version import LooseVersion
from matplotlib import pyplot as plt, rcParams, animation
from ipywidgets import interact, interactive, fixed, widgets
matplotlib.rc('animation', html='html5')
np.set_printoptions(precision=5, linewidth=110, suppress=True)
import workalendar
from workalendar.america import Brazil
from ipykernel.kernelapp import IPKernelApp
def in_notebook(): return IPKernelApp.initialized()
def in_ipynb():
try:
cls = get_ipython().__class__.__name__
return cls == 'ZMQInteractiveShell'
except NameError:
return False
import tqdm as tq
from tqdm import tqdm_notebook, tnrange
def clear_tqdm():
inst = getattr(tq.tqdm, '_instances', None)
if not inst: return
try:
for i in range(len(inst)): inst.pop().close()
except Exception:
pass
if in_notebook():
def tqdm(*args, **kwargs):
clear_tqdm()
return tq.tqdm(*args, file=sys.stdout, **kwargs)
def trange(*args, **kwargs):
clear_tqdm()
return tq.trange(*args, file=sys.stdout, **kwargs)
else:
from tqdm import tqdm, trange
tnrange=trange
tqdm_notebook=tqdm
from sklearn_pandas import DataFrameMapper
from sklearn.preprocessing import LabelEncoder, Imputer, StandardScaler
from pandas.api.types import is_string_dtype, is_numeric_dtype
from sklearn.ensemble import forest
from sklearn.tree import export_graphviz
def set_plot_sizes(sml, med, big):
plt.rc('font', size=sml) # controls default text sizes
plt.rc('axes', titlesize=sml) # fontsize of the axes title
plt.rc('axes', labelsize=med) # fontsize of the x and y labels
plt.rc('xtick', labelsize=sml) # fontsize of the tick labels
plt.rc('ytick', labelsize=sml) # fontsize of the tick labels
plt.rc('legend', fontsize=sml) # legend fontsize
plt.rc('figure', titlesize=big) # fontsize of the figure title
def parallel_trees(m, fn, n_jobs=8):
return list(ProcessPoolExecutor(n_jobs).map(fn, m.estimators_))
def draw_tree(t, df, size=10, ratio=0.6, precision=0):
"""
"""
s=export_graphviz(t, out_file=None, feature_names=df.columns, filled=True,
special_characters=True, rotate=True, precision=precision)
IPython.display.display(graphviz.Source(re.sub('Tree {',
f'Tree {{ size={size}; ratio={ratio}', s)))
def combine_date(years, months=1, days=1, weeks=None, hours=None, minutes=None,
seconds=None, milliseconds=None, microseconds=None, nanoseconds=None):
years = np.asarray(years) - 1970
months = np.asarray(months) - 1
days = np.asarray(days) - 1
types = ('<M8[Y]', '<m8[M]', '<m8[D]', '<m8[W]', '<m8[h]',
'<m8[m]', '<m8[s]', '<m8[ms]', '<m8[us]', '<m8[ns]')
vals = (years, months, days, weeks, hours, minutes, seconds,
milliseconds, microseconds, nanoseconds)
return sum(np.asarray(v, dtype=t) for t, v in zip(types, vals)
if v is not None)
def get_sample(df,n):
"""
"""
idxs = sorted(np.random.permutation(len(df))[:n])
return df.iloc[idxs].copy()
def add_datepart(df, fldname, drop=True, time=False, errors="raise"):
"""
"""
fld = df[fldname]
fld_dtype = fld.dtype
if isinstance(fld_dtype, pd.core.dtypes.dtypes.DatetimeTZDtype):
fld_dtype = np.datetime64
if not np.issubdtype(fld_dtype, np.datetime64):
df[fldname] = fld = pd.to_datetime(fld, infer_datetime_format=True, errors=errors)
targ_pre = re.sub('[Dd]ate$', '', fldname)
attr = ['Year', 'Month', 'Week', 'Day', 'Dayofweek', 'Dayofyear',
'Is_month_end', 'Is_month_start', 'Is_quarter_end', 'Is_quarter_start', 'Is_year_end', 'Is_year_start']
if time: attr = attr + ['Hour', 'Minute', 'Second']
for n in attr: df[targ_pre + n] = getattr(fld.dt, n.lower())
df[targ_pre + 'Elapsed'] = fld.astype(np.int64) // 10 ** 9
if drop: df.drop(fldname, axis=1, inplace=True)
def is_date(x): return np.issubdtype(x.dtype, np.datetime64)
def train_cats(df):
"""
"""
for n,c in df.items():
if is_string_dtype(c): df[n] = c.astype('category').cat.as_ordered()
def apply_cats(df, trn):
"""
"""
for n,c in df.items():
if (n in trn.columns) and (trn[n].dtype.name=='category'):
df[n] = c.astype('category').cat.as_ordered()
df[n].cat.set_categories(trn[n].cat.categories, ordered=True, inplace=True)
def fix_missing(df, col, name, na_dict):
"""
"""
if is_numeric_dtype(col):
if pd.isnull(col).sum() or (name in na_dict):
df[name+'_na'] = pd.isnull(col)
filler = na_dict[name] if name in na_dict else col.median()
df[name] = col.fillna(filler)
na_dict[name] = filler
return na_dict
def numericalize(df, col, name, max_n_cat):
"""
"""
if not is_numeric_dtype(col) and ( max_n_cat is None or len(col.cat.categories)>max_n_cat):
df[name] = col.cat.codes+1
def scale_vars(df, mapper):
warnings.filterwarnings('ignore', category=sklearn.exceptions.DataConversionWarning)
if mapper is None:
map_f = [([n],StandardScaler()) for n in df.columns if is_numeric_dtype(df[n])]
mapper = DataFrameMapper(map_f).fit(df)
df[mapper.transformed_names_] = mapper.transform(df)
return mapper
def proc_df(df, y_fld=None, skip_flds=None, ignore_flds=None, do_scale=False, na_dict=None,
preproc_fn=None, max_n_cat=None, subset=None, mapper=None):
"""
"""
if not ignore_flds: ignore_flds=[]
if not skip_flds: skip_flds=[]
if subset: df = get_sample(df,subset)
else: df = df.copy()
ignored_flds = df.loc[:, ignore_flds]
df.drop(ignore_flds, axis=1, inplace=True)
if preproc_fn: preproc_fn(df)
if y_fld is None: y = None
else:
if not is_numeric_dtype(df[y_fld]): df[y_fld] = df[y_fld].cat.codes
y = df[y_fld].values
skip_flds += [y_fld]
df.drop(skip_flds, axis=1, inplace=True)
if na_dict is None: na_dict = {}
else: na_dict = na_dict.copy()
na_dict_initial = na_dict.copy()
for n,c in df.items(): na_dict = fix_missing(df, c, n, na_dict)
if len(na_dict_initial.keys()) > 0:
df.drop([a + '_na' for a in list(set(na_dict.keys()) - set(na_dict_initial.keys()))], axis=1, inplace=True)
if do_scale: mapper = scale_vars(df, mapper)
for n,c in df.items(): numericalize(df, c, n, max_n_cat)
df = pd.get_dummies(df, dummy_na=True)
df = pd.concat([ignored_flds, df], axis=1)
res = [df, y, na_dict]
if do_scale: res = res + [mapper]
return res
def rf_feat_importance(m, df):
return pd.DataFrame({'cols':df.columns, 'imp':m.feature_importances_}
).sort_values('imp', ascending=False)
def set_rf_samples(n):
""" Changes Scikit learn's random forests to give each tree a random sample of
n random rows.
"""
forest._generate_sample_indices = (lambda rs, n_samples:
forest.check_random_state(rs).randint(0, n_samples, n))
def reset_rf_samples():
""" Undoes the changes produced by set_rf_samples.
"""
forest._generate_sample_indices = (lambda rs, n_samples:
forest.check_random_state(rs).randint(0, n_samples, n_samples))
def get_nn_mappers(df, cat_vars, contin_vars):
# Replace nulls with 0 for continuous, "" for categorical.
for v in contin_vars: df[v] = df[v].fillna(df[v].max()+100,)
for v in cat_vars: df[v].fillna('#NA#', inplace=True)
# list of tuples, containing variable and instance of a transformer for that variable
# for categoricals, use LabelEncoder to map to integers. For continuous, standardize
cat_maps = [(o, LabelEncoder()) for o in cat_vars]
contin_maps = [([o], StandardScaler()) for o in contin_vars]
return DataFrameMapper(cat_maps).fit(df), DataFrameMapper(contin_maps).fit(df)
# + _uuid="1ef42c06cfe01ee949fa6eb0127832eb012565e2"
df_trn, y, nas, mapper = proc_df(df_train, target, do_scale=True)
n=len(df_trn)
df_test, _, nas, mapper = proc_df(test, target, do_scale=True,
mapper=mapper, na_dict=nas)
n
# + _uuid="220c9cd9ca49616827e1ef8195e8a532510b2e68"
def split_vals(a,n):
return a[:n].copy(), a[n:].copy()
y=target
n_valid = int(len(df_train) * .25)
n_trn = len(df_train)-n_valid
# raw_train, raw_valid = split_vals(df_raw, n_trn)
X_train, X_valid = split_vals(df_train, n_trn)
y_train, y_valid = split_vals(y, n_trn)
X_train.shape, y_train.shape, X_valid.shape
# + _uuid="0c8b96f1b6987a6d25bb56ba4fab45444375cf89"
def rmse(x,y): return math.sqrt(((x-y)**2).mean())
def print_score(m):
res = [rmse(m.predict(X_train), y_train), rmse(m.predict(X_valid), y_valid),
m.score(X_train, y_train), m.score(X_valid, y_valid)]
if hasattr(m, 'oob_score_'): res.append(m.oob_score_)
print(res)
from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier
from sklearn import metrics
# + _uuid="bc96b749e90a02574c5fda86787fffdf502a7021"
m = RandomForestRegressor(n_estimators=1, max_depth=3, bootstrap=False, n_jobs=-1)
m.fit(X_train, y_train)
print_score(m)
# + _uuid="22e37a2059532f9b6f2955f1f1aa93404021b9fb"
# + _uuid="92110a41b48cb0fb198bd70ec78066c2414ff8a4"
# + _uuid="bc88bfc75c74d50c7a6e2bad21dadbbcd6d4c70f"
# + _uuid="f553bbceb805db0a2c4d0e8329f5cddfaa3247ab"
# + _uuid="31dbc681b727d0922a4477332a339c73efbf31ad"
# + _uuid="456fa8714e8dd307884fada8285ce50e2d91e31b"
# + _uuid="ab129217afce74c5d3ab564aa2201d0b0033c693"
# + _uuid="c4f20f27679889542acfd60d1f1ac381b201ac43"
df_train_columns = [c for c in df_train.columns if c not in ['card_id', 'first_active_month','target','outliers']]
target = df_train['target']
del df_train['target']
# + _uuid="c9bbc95244978b519d94131907b547c2b6c94191"
param = {'num_leaves': 31,
'min_data_in_leaf': 30,
'objective':'regression',
'max_depth': -1,
'learning_rate': 0.01,
"min_child_samples": 20,
"boosting": "gbdt",
"feature_fraction": 0.9,
"bagging_freq": 1,
"bagging_fraction": 0.9 ,
"bagging_seed": 11,
"metric": 'rmse',
"lambda_l1": 0.1,
"verbosity": -1,
"nthread": 4,
"random_state": 4590}
folds = StratifiedKFold(n_splits=5, shuffle=True, random_state=4590)
oof = np.zeros(len(df_train))
predictions = np.zeros(len(df_test))
feature_importance_df = pd.DataFrame()
for fold_, (trn_idx, val_idx) in enumerate(folds.split(df_train,df_train['outliers'].values)):
print("fold {}".format(fold_))
trn_data = lgb.Dataset(df_train.iloc[trn_idx][df_train_columns], label=target.iloc[trn_idx])#, categorical_feature=categorical_feats)
val_data = lgb.Dataset(df_train.iloc[val_idx][df_train_columns], label=target.iloc[val_idx])#, categorical_feature=categorical_feats)
num_round = 10000
clf = lgb.train(param, trn_data, num_round, valid_sets = [trn_data, val_data], verbose_eval=100, early_stopping_rounds = 100)
oof[val_idx] = clf.predict(df_train.iloc[val_idx][df_train_columns], num_iteration=clf.best_iteration)
fold_importance_df = pd.DataFrame()
fold_importance_df["Feature"] = df_train_columns
fold_importance_df["importance"] = clf.feature_importance()
fold_importance_df["fold"] = fold_ + 1
feature_importance_df = pd.concat([feature_importance_df, fold_importance_df], axis=0)
predictions += clf.predict(df_test[df_train_columns], num_iteration=clf.best_iteration) / folds.n_splits
np.sqrt(mean_squared_error(oof, target))
# + _uuid="40b64481054fa71e692829c7039eccceb31b77fe"
cols = (feature_importance_df[["Feature", "importance"]]
.groupby("Feature")
.mean()
.sort_values(by="importance", ascending=False)[:500].index)
best_features = feature_importance_df.loc[feature_importance_df.Feature.isin(cols)]
plt.figure(figsize=(14,25))
sns.barplot(x="importance",
y="Feature",
data=best_features.sort_values(by="importance",
ascending=False))
plt.title('LightGBM Features (avg over folds)')
plt.tight_layout()
# plt.savefig('lgbm_importances.png')
# + [markdown] _uuid="5aa9a8cbe586424712f418eb34182910ed82bcb5"
# ### So most of the newly created features don't rank particularly high as far as feature importances go, but I will continue to work on this...
# + _uuid="355e9c24949b8e5d677fe5a2f117228c3310dab6"
sub_df = pd.DataFrame({"card_id":df_test["card_id"].values})
sub_df["target"] = predictions
sub_df.to_csv("submission.csv", index=False)
# + [markdown] _uuid="58c9a5445698e42dfbd9548695290487a2ce171a"
# ### Haven't had time to think deeply about how *workalendar* might be used but there is definitely potential, and I hope this starts a discussion
# + _uuid="e4a55780edb95483bfac0d8119ea4d344a8461ff"
|
kaggle-elo-workalender-rf.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Day 10: Midterm
#
# * Computational Physics (PHYS 202)
# * Cal Poly, Spring 2015
# * <NAME>
# ## In class
# * **Midterm today!!!**
# - Make sure you have pushed all of your days and assignments to GitHub by then.
# - You can use any link in the "Help" menu of the notebook.
# - You can use your past assignments and the course material.
# - Each problem worth 10 points.
# - Budget 40 minutes for each.
#
# * Turn in `assignment07`:
#
# nbgrader submit assignment07 phys202-2015
#
# * Fetch the midterm:
#
# nbgrader fetch phys202-2015 midterm
#
# * Submit when you are done:
#
# nbgrader submit midterm phys202-2015
# ## Out of class
# * Rest until Monday!
# * Finish any unfinished homework.
|
assignments/midterm/Day10.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
import numpy as np
import pandas as pd
import math
from scipy import stats
import pickle
from causality.analysis.dataframe import CausalDataFrame
from sklearn.linear_model import LinearRegression
import datetime
import matplotlib
import matplotlib.pyplot as plt
matplotlib.rcParams['font.sans-serif'] = "Gotham"
matplotlib.rcParams['font.family'] = "sans-serif"
import plotly
import plotly.graph_objs as go
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
init_notebook_mode(connected=True)
# Open the data from past notebooks and correct them to only include years that are common between the data structures (>1999).
with open('VariableData/money_data.pickle', 'rb') as f:
income_data, housing_data, rent_data = pickle.load(f)
with open('VariableData/demographic_data.pickle', 'rb') as f:
demographic_data = pickle.load(f)
with open('VariableData/endowment.pickle', 'rb') as f:
endowment = pickle.load(f)
with open('VariableData/expander.pickle', 'rb') as f:
expander = pickle.load(f)
# +
endowment = endowment[endowment['FY'] > 1997].reset_index()
endowment.drop('index', axis=1, inplace=True)
demographic_data = demographic_data[demographic_data['year'] > 1999].reset_index()
demographic_data.drop('index', axis=1, inplace=True)
income_data = income_data[income_data['year'] > 1999].reset_index()
income_data.drop('index', axis=1, inplace=True)
housing_data = housing_data[housing_data['year'] > 1999].reset_index()
housing_data.drop('index', axis=1, inplace=True)
rent_data = rent_data[rent_data['year'] > 1999].reset_index()
rent_data.drop('index', axis=1, inplace=True)
# -
# Read in the data on Harvard owned land and Cambridge's property records. Restrict the Harvard data to Cambridge, MA.
harvard_land = pd.read_excel("Spreadsheets/2018_building_reference_list.xlsx", header=3)
harvard_land = harvard_land[harvard_land['City'] == 'Cambridge']
cambridge_property = pd.read_excel("Spreadsheets/cambridge_properties.xlsx")
# Restrict the Cambridge data to Harvard properties, and only use relevant columns.
cambridge_property = cambridge_property[cambridge_property['Owner_Name'].isin(['PRESIDENT & FELLOWS OF HARVARD COLLEGE', 'PRESIDENT & FELLOW OF HARVARD COLLEGE'])]
cambridge_property = cambridge_property[['Address', 'PropertyClass', 'LandArea', 'BuildingValue', 'LandValue', 'AssessedValue', 'SalePrice', 'SaleDate', 'Owner_Name']]
# Fix the time data.
cambridge_property['SaleDate'] = pd.to_datetime(cambridge_property['SaleDate'], infer_datetime_format=True)
clean_property = cambridge_property.drop_duplicates(subset=['Address'])
# Only look at properties purchased after 2000.
recent_property = clean_property[clean_property['SaleDate'] > datetime.date(2000, 1, 1)]
property_numbers = recent_property[['LandArea', 'AssessedValue', 'SalePrice']]
num_recent = recent_property['Address'].count()
sum_properties = property_numbers.sum()
sum_properties
full_property_numbers = clean_property[['LandArea', 'AssessedValue', 'SalePrice']]
sum_full = full_property_numbers.sum()
delta_property = sum_properties / sum_full
delta_property
# What can be gathered from above?
#
# Since the year 2000, Harvard has increased its presence in Cambridge by about 3%, corresponding to about 2% of its overall assessed value, an increase of 281,219 square feet and \$115,226,500. Although the assessed value increase is so high, Harvard only paid \$57,548,900 for the property at their times of purchase.
#
# To make some adjustments for inflation:
#
# Note that the inflation rate since 2000 is ~37.8% (https://data.bls.gov/timeseries/CUUR0000SA0L1E?output_view=pct_12mths).
inflation_data = pd.read_excel("Spreadsheets/inflation.xlsx", header=11)
inflation_data = inflation_data[['Year', 'Jan']]
inflation_data['Year'] = pd.to_datetime(inflation_data['Year'], format='%Y')
inflation_data['CumulativeInflation'] = inflation_data['Jan'].cumsum()
inflation_data.rename(columns={'Year' : 'SaleDate'}, inplace=True)
recent_property['SaleDate'] = recent_property['SaleDate'].dt.year
inflation_data['SaleDate'] = inflation_data['SaleDate'].dt.year
recent_property = pd.merge(recent_property, inflation_data, how="left", on=['SaleDate'])
recent_property = recent_property.drop('Jan', 1)
recent_property['TodaySale'] = (1 + (recent_property['CumulativeInflation'] / 100)) * recent_property['SalePrice']
today_sale_sum = recent_property['TodaySale'].sum()
today_sale_sum
sum_properties['AssessedValue'] - today_sale_sum
# Hence, adjusted for inflation, the sale price of the property Harvard has acquired since 2000 is \$65,929,240.
#
# The difference between this value and the assessed value of the property (in 2018) is: \$49,297,260, showing that Harvard's property has appreciated in value even more than (twice more than) inflation would account for, illustrating a clear advantageous dynamic for Harvard.
sorted_df = recent_property.sort_values(by=['SaleDate'])
sorted_df = sorted_df.reset_index().drop('index', 1)
sorted_df['CumLand'] = sorted_df['LandArea'].cumsum()
sorted_df['CumValue'] = sorted_df['AssessedValue'].cumsum()
sorted_df
# Graph the results.
def fitter(x, y, regr_x):
"""
Use linear regression to make a best fit line for a set of data.
Args:
x (numpy array): The independent variable.
y (numpy array): The dependent variable.
regr_x (numpy array): The array used to extrapolate the regression.
"""
slope, intercept, r_value, p_value, std_err = stats.linregress(x, y)
return (slope * regr_x + intercept)
# +
years = sorted_df['SaleDate'].as_matrix()
cum_land = sorted_df['CumLand'].as_matrix()
cum_value = sorted_df['CumValue'].as_matrix()
regr = np.arange(2000, 2012)
line0 = fitter(years, cum_land, regr)
trace0 = go.Scatter(
x = years,
y = cum_land,
mode = 'markers',
name='Harvard Land\n In Cambridge',
marker=go.Marker(color='#601014')
)
fit0 = go.Scatter(
x = regr,
y = line0,
mode='lines',
marker=go.Marker(color='#D2232A'),
name='Fit'
)
data = [trace0, fit0]
layout = go.Layout(
title = "The Change In Harvard's Land in Cambridge Since 2000",
font = dict(family='Gotham', size=18),
yaxis=dict(
title='Land Accumulated Since 2000 (Sq. Feet)'
),
xaxis=dict(
title='Year')
)
fig = go.Figure(data=data, layout=layout)
iplot(fig, filename="land_changes")
# -
graph2_df = pd.DataFrame(list(zip(regr, line0)))
graph2_df.to_csv('graph2.csv')
def grapher(x, y, city, title, ytitle, xtitle, filename):
slope, intercept, r_value, p_value, std_err = stats.linregress(x, y)
fit = slope * x + intercept
trace0 = go.Scatter(
x = x,
y = y,
mode = 'markers',
name=city,
marker=go.Marker(color='#D2232A')
)
fit0 = go.Scatter(
x = x,
y = fit,
mode='lines',
marker=go.Marker(color='#AC1D23'),
name='Linear Fit'
)
data = [trace0, fit0]
layout = go.Layout(
title = title,
font = dict(family='Gotham', size=12),
yaxis=dict(
title=ytitle
),
xaxis=dict(
title=xtitle)
)
fig = go.Figure(data=data, layout=layout)
return iplot(fig, filename=filename)
len(line0)
# Restrict the demographic data to certain years (up to 2012) in order to fit the data well.
demographic_data = demographic_data[demographic_data['year'] < 2011]
rent_data = rent_data[rent_data['year'] < 2011]
housing_data = housing_data[housing_data['year'] < 2011]
x = cum_land
y = pd.to_numeric(demographic_data['c_black']).as_matrix()
z1 = pd.to_numeric(rent_data['cambridge']).as_matrix()
z2 = pd.to_numeric(housing_data['cambridge']).as_matrix()
endow_black = grapher(x, y, "Cambridge", "The Correlation Between Harvard Land Change and Black Population", "Black Population of Cambridge", "Land Change (Sq. Feet)", "land_black")
# +
X = CausalDataFrame({'x': x, 'y': y, 'z1': z1, 'z2': z2})
causal_land_black = X.zplot(x='x', y='y', z=['z1', 'z2'], z_types={'z1': 'c', 'z2': 'c'}, kind='line', color="#D2232A")
fig = causal_land_black.get_figure()
fig.set_size_inches(9, 5.5)
ax = plt.gca()
ax.set_frame_on(False)
ax.get_yaxis().set_visible(False)
ax.legend_.remove()
ax.set_title("The Controlled Correlation Between Land Use (Square Feet) and Black Population", fontproperties=gotham_black, size=10, color="#595959")
ax.set_xlabel("Land Use", fontproperties=gotham_book, fontsize=10, color="#595959")
for tick in ax.get_xticklabels():
tick.set_fontproperties(gotham_book)
tick.set_fontsize(10)
tick.set_color("#595959")
fig.savefig('images/black_land.svg', format='svg', dpi=2400, bbox_inches='tight')
# -
z2
graph9_df = pd.DataFrame(X)
graph9_df.to_csv('graph9.csv')
# +
y = pd.to_numeric(rent_data['cambridge']).as_matrix()
z1 = pd.to_numeric(housing_data['cambridge']).as_matrix()
X = CausalDataFrame({'x': x, 'y': y, 'z1': z1})
causal_land_rent = X.zplot(x='x', y='y', z=['z1'], z_types={'z1': 'c'}, kind='line', color="#D2232A")
fig = causal_land_rent.get_figure()
fig.set_size_inches(9, 5.5)
ax = plt.gca()
ax.set_frame_on(False)
ax.get_yaxis().set_visible(False)
ax.legend_.remove()
ax.set_title("The Controlled Correlation Between Land Use (Square Feet) and Rent", fontproperties=gotham_black, size=10, color="#595959")
ax.set_xlabel("Land Use", fontproperties=gotham_book, fontsize=10, color="#595959")
for tick in ax.get_xticklabels():
tick.set_fontproperties(gotham_book)
tick.set_fontsize(10)
tick.set_color("#595959")
fig.savefig('images/rent_land.svg', format='svg', dpi=1200, bbox_inches='tight')
# -
|
.ipynb_checkpoints/land_expansion-checkpoint 4.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from pricing.service.scoring.lscore import LScoring
from pricing.utils import formata_cnpj
import pandas as pd
import numpy as np
from datetime import datetime
from dateutil.relativedelta import relativedelta
from sqlalchemy import create_engine
class CriteriosElegibilidade(object):
def __init__(self, cnpj, produto):
self.cnpj = cnpj
self.produto = produto
self.elegibilidade_dividas=1.5
self.elegibilidade_transacoes = 12
self.dados = None
self.flag_faturamento = None
self.fat_medio = None
self.flag_transacoes = None
self.flag_cheques = None
self.flag_dividas = None
self.data_consulta = None
self.scoring = None
self.prop_boleto = None
def get_dados(self):
if self.produto in ["tomatico", "padrao"]:
engine = create_engine("mysql+pymysql://capMaster:#jackpot123#@<EMAIL>:23306/credito-digital")
con = engine.connect()
else:
engine = create_engine("mysql+pymysql://capMaster:#jackpot123#@<EMAIL>:23306/varejo")
con = engine.connect()
query_wirecard = "select cnpj, data, valor, numero_transacoes from fluxo_wirecard where cnpj='{}'".format(self.cnpj)
query_pv = "select cpf_cnpj as cnpj, data, valor, valor_boleto, numero_transacoes from fluxo_pv where cpf_cnpj='{}'".format(formata_cnpj(self.cnpj))
query_tomatico = "select cnpj, dataFluxo as data, valorFluxo as valor from tb_Fluxo where cnpj='{}'".format(self.cnpj)
query_justa = "select cnpj, data, valor, numero_transacoes from fluxo_justa where cnpj='{}'".format(self.cnpj)
dict_query = {"tomatico" : query_tomatico,
"padrao" : query_tomatico,
"wirecard" : query_wirecard,
"moip" : query_wirecard,
"pagueveloz" : query_pv,
"justa" : query_justa
}
query = dict_query.get(self.produto)
df = pd.read_sql(query, con)
con.close()
df = df.groupby("data").sum().reset_index()
try:
df["data"] = df.apply(lambda x : x["data"].date(), axis=1)
except:
pass
self.dados = df
return
def mensaliza(self, df):
df.index = pd.to_datetime(df.data)
if self.produto=='pagueveloz':
df = df.resample('MS').sum()[["valor", "valor_boleto"]].reset_index()
else:
df = df.resample('MS').sum().reset_index()
return df
def check_faturamento(self):
if self.produto == 'pagueveloz':
df = self.dados[["data", "valor", "valor_boleto"]]
else:
df = self.dados[["data", "valor"]]
df = self.mensaliza(df)
df6 = df.sort_values("data", ascending=False).iloc[:6, :]
df6["data"] = df6.apply(lambda x : x["data"].date(), axis=1)
flag_faturamento = int((len(df6)==6) and (0 not in df6["valor"].tolist()) and (df6["data"].max()==datetime.now().date().replace(day=1) - relativedelta(months=1)))
self.flag_faturamento = flag_faturamento
self.fat_medio = df.sort_values("data", ascending=False).iloc[:12, :]["valor"].mean()
if self.produto == 'pagueveloz':
db = df.sort_values("data", ascending=False).iloc[:12, :]
db["prop"] = db["valor_boleto"].sum()/db["valor"].sum()
self.prop_boleto = db["prop"].iloc[0]
return
def check_transacoes(self):
if self.produto != 'tomatico':
try:
df = self.dados[["data", "numero_transacoes"]]
df.index = pd.to_datetime(df.data)
df.resample('MS').sum().reset_index()
df = df.iloc[:12, :]
media_transacoes = df["numero_transacoes"].mean()
flag_transacoes = int(media_transacoes > self.elegibilidade_transacoes)
self.flag_transacoes = flag_transacoes
except:
self.flag_transacoes = 1
return
def get_dividas(self):
engine = create_engine("mysql+pymysql://capMaster:#jackpot123#@captalys.cmrbivuuu7sv.sa-east-1.rds.amazonaws.com:23306/varejo")
con = engine.connect()
query = "select * from consultas_idwall_operacoes where cnpj_cpf='{}'".format(self.cnpj)
df = pd.read_sql(query, con)
con.close()
if df.empty:
return df
df = df[df['data_ref']==df['data_ref'].max()]
lista_consultas = df['numero_consulta'].unique().tolist()
df = df[(df['data_ref']==df['data_ref'].max()) & (df['numero_consulta']==lista_consultas[0])]
return df
def check_cheques(self):
dfdiv = self.get_dividas()
if dfdiv.empty:
flag_cheques = 1
data_consulta = None
else:
flag_cheques = int('cheques' not in dfdiv["tipo"].tolist())
data_consulta = dfdiv["data_ref"].max()
self.flag_cheques = flag_cheques
self.data_consulta = data_consulta
return
def check_dividas(self):
dfdiv = self.get_dividas()
if dfdiv.empty:
self.flag_dividas = 1
self.data_consulta = None
else:
df = dfdiv[dfdiv['tipo']!="cheques"]
if df.empty:
self.flag_dividas = 1
self.data_consulta = dfdiv["data_ref"].iloc[0]
else:
total_dividas = df["valor"].sum()
fat_medio = self.fat_medio
prop = total_dividas/fat_medio
flag_dividas = int(prop <=self.elegibilidade_dividas)
self.flag_dividas = flag_dividas
self.data_consulta = df["data_ref"].iloc[0]
return
def analisa(self):
self.get_dados()
self.check_faturamento()
self.check_transacoes()
self.check_cheques()
self.check_dividas()
return
# if __name__ == '__main__':
# ce = CriteriosElegibilidade(cnpj='2207280900016', produto='pagueveloz')
# print(ce.analisa())
# -
ce = CriteriosElegibilidade(cnpj='22072809000161', produto='pagueveloz')
ce.analisa()
ce.flag_faturamento
ce.dados["numero_transacoes"].mean()
ce.flag_transacoes
df = ce.dados[["data", "numero_transacoes"]]
df.index = pd.to_datetime(df.data)
df.resample('MS').sum().reset_index()
df = ce.dados[["data", "numero_transacoes"]]
df.resample('MS').sum().reset_index()
# df = ce.mensaliza(df)
df = df.iloc[:12, :]
media_transacoes = df["numero_transacoes"].mean()
flag_transacoes = int(media_transacoes > ce.elegibilidade_transacoes)
|
Modelagem/pre_analysis/elegibilidade.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Question 1
#
# Which of the following statements is true of dynamic inference?
#
# a) You must monitor input signals
#
# b) Don’t need to worry about how long predictions take as much as when performing static inference
#
# c) You can provide predictions for multiple rows of data
#
# d) Easier to roll back to a previous version of the model than with static inference
#
# e) All of the above
#
# ## Answer
# Answer is (a, c). You want to always monitor inputs into your model to detect non-stationarity (i.e. seasonality) and data drift. Online inference is most commonly associated with synchronous requests, so we are interested in reducing the time it takes to make predictions. You can make your model API support inference of many rows. It's generally more work to roll back a version of your model than compared to static inference (done offline).
#
# ## Question 2
#
# In static inference, we make predictions on a large batch of data all at once. Which of the following statements is true of static inference?
#
# a) Predictions can be verified after generating them
#
# b) For a given input, we can serve a prediction quicker than with online inference
#
# c) Model will be able to quickly react to recent changes with input data
#
# d) Need to monitor signals carefully over long period of time
#
# e) All of the above
#
# ## Answer
# Answer is (a, c). Since offline static inference is done during downtime, we can store the results and make them available during normal or peak operations via a database lookup (responsive). You also have the option of verifying your prediction outputs prior to deploying the model to a synchronous request/response model.
|
solutions/Exercise5_Offline_vs_Online_Model_Inference.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/DrakeShadowRaven/desihigh/blob/main/SnowWhiteDwarf.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + colab={"base_uri": "https://localhost:8080/"} id="FoqVaUkDD24n" outputId="8db0207c-b5f5-4f3a-d510-3066daf4feb2"
from google.colab import drive
drive.mount('/content/drive')
# + id="1KIRe3cXECt3"
import sys
sys.path.append('/content/drive/MyDrive/desihigh')
# + id="NWFkqY2UDV8H"
import os
import numpy as np
import astropy.io.fits as fits
import pylab as pl
import pandas as pd
import matplotlib.pyplot as plt
from IPython.display import YouTubeVideo
from scipy import interpolate
from scipy import optimize
from tools.wave2rgb import wavelength_to_rgb
from tools.resample_flux import trapz_rebin
from pkg_resources import resource_filename
# + [markdown] id="IUKs3YKoDV8J"
# # A snow white dwarf
# + [markdown] id="MwgbB8gkDV8L"
# When you look to the sky, who knows what you will find? We're all familiar with our own [sun](https://solarsystem.nasa.gov/solar-system/sun/overview/),
# + [markdown] id="4M4CZdzNDV8M"
# <img src="https://github.com/DrakeShadowRaven/desihigh/blob/main/desihigh/images/sun.jpg?raw=1" alt="Drawing" style="width: 800px;"/>
# + [markdown] id="B6kOJH1SDV8N"
# a seemingly ever present that we see continually day-to-day. Would it surprise you to know that in 5.5 billion years the sun will change beyond recognition as the Hydrogen fuelling nuclear fusion within runs out?
# + [markdown] id="b7eytmxdDV8O"
# <img src="https://github.com/DrakeShadowRaven/desihigh/blob/main/desihigh/images/RedGiant.jpg?raw=1" alt="Drawing" style="width: 800px;"/>
# + [markdown] id="PzcBVylADV8O"
# During this apparent mid-life crisis, the sun will begin to fuse Helium to create the carbon fundamental to life on earth, and the oxygen necessary to sustain it. Expanding to ten-to-hundreds the size of the sun today, it will soon envelope Mercury & Venus, and perhaps [even Earth itself](https://phys.org/news/2016-05-earth-survive-sun-red-giant.html#:~:text=Red%20Giant%20Phase%3A,collapses%20under%20its%20own%20weight.), and eventual explode as a spectacular [planetary nebulae](https://www.space.com/17715-planetary-nebula.html):
# + [markdown] id="YIHh5gUgDV8P"
# <img src="https://github.com/DrakeShadowRaven/desihigh/blob/main/desihigh/images/PlanetaryNebulae.jpg?raw=1" alt="Drawing" style="width: 800px;"/>
# + [markdown] id="nt9dS12eDV8Q"
# The ashen carbon-oxygen at the center will survive as a fossilised relic, dissipating energy just slowly enough that it will continue to survive for another 13.8 billion years, the current age of our Universe, and see in many more millenia.
# + [markdown] id="ZhGdcxWHDV8R"
# We can learn about this eventual fate of the sun, and its impact on Earth, by studying neighbouring White Dwarves in the Milky Way. We'll look at one such candidate that DESI has observed only recently!
# + colab={"base_uri": "https://localhost:8080/"} id="4N9hlqTFDV8R" outputId="6fbb94a1-6cec-4a29-d3f3-09c6ebb55fd4"
from ipywidgets.widgets.widget_date import DatePicker
# Load the DESI spectrum
andes = resource_filename('desihigh', 'student_andes')
zbest = fits.open(andes + '/zbest-mws-66003-20200315-wd.fits')[1]
coadd = fits.open(andes + '/coadd-mws-66003-20200315-wd.fits')
ra,DatePicker
# + id="h5RCunZRDV8S"
# Get its position on the sky:
ra, dec = float(zbest.data['TARGET_RA']), float(zbest.data['TARGET_DEC'])
# + [markdown] id="YNXpJCKRDV8S"
# It's position on the night sky lies just above [Ursa Marjor](https://en.wikipedia.org/wiki/Ursa_Major) or the Great Bear,
# + [markdown] id="bBvyjuPODV8T"
# <img src="https://github.com/DrakeShadowRaven/desihigh/blob/main/desihigh/images/UrsaMajor.jpg?raw=1" alt="Drawing" style="width: 800px;"/>
# + [markdown] id="bq9dLp9SDV8T"
# familiar in the night sky:
# + [markdown] id="DkdgpXVEDV8U"
# <img src="https://github.com/DrakeShadowRaven/desihigh/blob/main/desihigh/images/UrsaMajor2.png?raw=1" alt="Drawing" style="width: 800px;"/>
# + [markdown] id="3mWXw2LUDV8U"
# If you were to stare long enough, you'd see an almost imperceptible change in the apparent position as our viewpoint changes as the Earth orbits the Sun. Remember, the dinosaurs roamed planet Earth on the other side of the galaxy!
#
# The motion of the Earth around the sun is just enough, given a precise enough instrument, to calculate the distance to our White Dwarf given simple trigonometry you've likely already seen:
# + [markdown] id="jFIcixAJDV8V"
# <img src="https://github.com/DrakeShadowRaven/desihigh/blob/main/desihigh/images/PDistance.jpg?raw=1" alt="Drawing" style="width: 800px;"/>
# + [markdown] id="vIhihLrbDV8V"
# The [GAIA](https://www.esa.int/Science_Exploration/Space_Science/Gaia_overview) space satellite was precisely designed to do this this and will eventually map one billion stars in the Milky Way, roughly one in every hundred there, in this way.
# + [markdown] id="0yuqOgS_DV8V"
# <img src="https://github.com/DrakeShadowRaven/desihigh/blob/main/desihigh/images/Gaia.jpg?raw=1" alt="Drawing" style="width: 800px;"/>
# + [markdown] id="eG4P2boUDV8V"
# With this parallax, GAIA tells us the distance to our white dwarf:
# + id="B4G9nNKKDV8W"
# Distance calculated from Gaia parallax (Bailer-Jones et al. 2018).
# Photometric data and the [computed distance](https://ui.adsabs.harvard.edu/abs/2018AJ....156...58B/) can be found at the [Gaia Archive](https://gea.esac.esa.int/archive/)
dist_para = 784.665266 # parcsecs, 1 parsec = 3.0857 x 10^16 m.
parsec = 3.085677581e16 # m
# AU: Astronomical Unit - distance between the Sun and the Earth.
au = 1.495978707e11
# + colab={"base_uri": "https://localhost:8080/"} id="_OjynvJbJO3t" outputId="6b87955e-3314-4120-f03e-1896484752c4"
1/dist_para
# + colab={"base_uri": "https://localhost:8080/"} id="fi3Csf4zJbMU" outputId="c99b2c7c-4ace-4326-f285-c565acb5b1db"
print('the Gaia parallax for this measurement must have been 0.0012744287829862984 arcsec! Hurray')
# + colab={"base_uri": "https://localhost:8080/"} id="SGKOe6SCDV8W" outputId="6b46d722-0d72-4619-b01a-97e7420c58f3"
print('GAIA parallax tells us that the distance to our White Dwarf is {:.0f} million x the distance from the Earth to the Sun.'.format(dist_para * parsec / au / 1.e6))
# + colab={"base_uri": "https://localhost:8080/"} id="fwthaZoLHh0k" outputId="a9ab1364-dbdb-4c2b-e6a8-775fea29b480"
print('estimted parallax 206264.8062145048')
# + colab={"base_uri": "https://localhost:8080/"} id="eBN5PbRLKa-m" outputId="095ed89c-ab77-4c25-c66a-e63eb35d4444"
print('dwarf is {:.0f}')
# + id="Gp596JnJICrI"
# + [markdown] id="nuuO_yE4DV8X"
# The GAIA camera is designed to measure the brightness of the white dwarf in three different parts of the visible spectrum, corresponding to the colors shown below. You'll recognise this as the same style plot we explored for Hydrogen Rydberg lines in the Intro.
# + id="qeKHKCuKDV8X"
# (Pivot) Wavelengths for the Gaia DR2 filters.
GAIA = {'G_WAVE': 6230.6, 'BP_WAVE': 5051.5, 'RP_WAVE': 7726.2}
# + colab={"base_uri": "https://localhost:8080/", "height": 505} id="HE8TsYCNDV8X" outputId="a4f5aa71-1bb0-4d01-b4cf-785809547f8c"
for wave in GAIA.values():
# color = [r, g, b]
color = wavelength_to_rgb(wave / 10.)
pl.axvline(x=wave / 10., c=color)
pl.ayvline(y=red / 10., c=color)
pl.title('Wavelengths (and colors) at which GAIA measures the brightness of each star', pad=10.5, fontsize=10)
pl.xlabel('Vacuum wavelength [nanometers]')
pl.xlim(380., 780.)
# + id="tCyW-kfZDV8X"
for band in ['G', 'BP', 'RP']:
GAIA[band + '_MAG'] = zbest.data['GAIA_PHOT_{}_MEAN_MAG'.format(band)][0]
GAIA[band + '_FLUX'] = 10.**(-(GAIA[band + '_MAG'] + (25.7934 - 25.6884)) / 2.5) * 3631. / 3.34e4 / GAIA[band + '_WAVE']**2.
# + colab={"base_uri": "https://localhost:8080/"} id="7PitIQQDDV8X" outputId="9f09f893-066f-4399-a187-0b9064c3e0c5"
# Add in the mag. errors that DESI catalogues don't propagate.
GAIA['G_MAGERR'] = 0.0044
GAIA['BP_MAGERR'] = 0.0281
GAIA['RP_MAGERR'] = 0.0780
GAIA['NOTE']=0.00101
print(GAIA['NOTE'])
# + id="bN9PXrZyHe9Z"
def Lum(d,F):
result=F*G*np.pi*d**2
return result
# + id="D7Yha31UI1rH" outputId="0914fb66-a34e-41d3-d437-bbd342acdbfd" colab={"base_uri": "https://localhost:8080/"}
print('the luminosity must be some value but code wont enter')
# + colab={"base_uri": "https://localhost:8080/"} id="4vkmAs0VDV8Y" outputId="70b09cb2-ba26-4f7d-a0a8-a5cbb22fc9df"
for key, value in GAIA.items():
print('{:10s} \t {:05.4f}'.format(key, value))
# + [markdown] id="WLmrRJxsDV8Y"
# This combination, a measurement of distance (from parallax) and of apparent brightness (in a number of colors), is incredibly powerful, as together they tell us the intrinsic luminosity or brightness of the dwarf rather than how it appears to us, from which we can determine what physics could be determining how bright the white dwarf is.
# + [markdown] id="fMQiWHT8DV8Y"
# # DESI
# + [markdown] id="eP2GPGrZDV8Y"
# By resolving the subtle variations in the amount of light with wavelength, DESI gives us a much better idea of the White Dwarf composition and its history from its entire spectrum, rather than a few measurements at different colors:
# + id="K3ZKVxrhDV8Y"
# Get the wavelength and flux
wave = coadd[1].data['WAVELENGTH']
count = coadd[1].data['TARGET35191335094848528']
# + colab={"base_uri": "https://localhost:8080/", "height": 635} id="29RxJpGTDV8Z" outputId="f41bc349-336f-43e0-e86f-ae6182562866"
# Plotting the DESI spectrum
pl.figure(figsize=(15, 10))
pl.plot(wave, count)
pl.grid()
pl.xlabel('Wavelength $[\AA]$')
pl.ylim(ymin=0.)
pl.title('TARGET35191335094848528')
# + [markdown] id="zYawkgKyDV8Z"
# Astronomers have spent a long time studying stars, classifying them according to different types - not least [Annie Jump Cannon](https://www.womenshistory.org/education-resources/biographies/annie-jump-cannon),
# + [markdown] id="CCdfr1aUDV8Z"
# <img src="https://github.com/DrakeShadowRaven/desihigh/blob/main/desihigh/images/anniecannon.jpg?raw=1" alt="Drawing" style="width: 800px;"/>
# + [markdown] id="XXFGpanzDV8Z"
# that has left us with a new ability to predict the spectrum of a star of given temperature, little $g$ - the acceleration due to gravity on their surface, and their mass. Given 'standard' stars, those with external distance constraints we can also determine how intrinsically bright a given star is with a determined spectrum. Let's grab these:
# + colab={"base_uri": "https://localhost:8080/"} id="vLcNVzaLDV8Z" outputId="fcf7dfab-b4c7-45fa-f360-8c3839599103"
# White Dwarf model spectra [Levenhagen 2017](https://ui.adsabs.harvard.edu/abs/2017ApJS..231....1L)
wdspec = resource_filename('desihigh', 'dat/WDspec')
spec_da_list = os.listdir(wdspec)
model_flux_spec_da = []
model_wave_spec_da = []
T_spec_da = []
logg_spec_da = []
# Loop over files in the directory and collect into a list.
for filename in spec_da_list:
if filename[-4:] != '.npz':
continue
model = np.load(wdspec + '/' + filename)['arr_0']
model_flux_spec_da.append(model[:,1])
model_wave_spec_da.append(model[:,0])
T, logg = filename.split('.')[0].split('t0')[-1].split('g')
T_spec_da.append(float(T) * 1000.)
logg_spec_da.append(float(logg[:-1]) / 10.)
print('Collected {:d} model spectra.'.format(len(spec_da_list)))
# + colab={"base_uri": "https://localhost:8080/", "height": 297} id="k-9RqhWeDV8Z" outputId="54c0758f-687c-4323-815d-e0d05ce98fd2"
# We'll select every 10th model white dwarf spectra to plot.
nth = 10
for model_wave, model_flux, model_temp in zip(model_wave_spec_da[::nth], model_flux_spec_da[::nth], T_spec_da[::nth]):
pl.plot(model_wave, model_flux / model_flux[-1], label=r'$T = {:.1e}$'.format(model_temp))
# Other commands to set the plot
pl.xlim(3000., 10000.)
# pl.ylim(ymin=1., ymax=3.6)
pl.legend(frameon=False, ncol=2)
pl.xlabel('Wavelength [Angstroms]')
pl.ylabel('Normalised flux')
# + [markdown] id="5yB6dbzwN-Pb"
#
# + [markdown] id="1GwApbwlDV8a"
# Firstly, these white dwarves are hot! At 240,000 Kelvin, you shouldn't touch one. While we can see that the hottest white dwarf is brightest at short wavelength and will therefore appear blue. In exactly the same way as the bluest part of a flame is the hottest:
# + [markdown] id="0H1uubwtDV8a"
# <img src="https://github.com/DrakeShadowRaven/desihigh/blob/main/desihigh/images/bunsen.jpg?raw=1" alt="Drawing" style="width: 280px;"/>
# + [markdown] id="T1LavU4ZN7ED"
#
# + [markdown] id="IuMZfia2DV8a"
# So now we have everything to find the temperature of the White Dwarf that DESI was able to find. As for the Intro., we simply find the model that looks most like the data.
# + id="bxJDzucIDV8a"
# wavelength range to be fitted
wave_min = 3750.
wave_max = 5200.
sq_diff = []
# Masking the range to be fitted
fitted_range = (wave > wave_min) & (wave < wave_max)
fitted_wave = wave[fitted_range]
for model_wave, model_flux in zip(model_wave_spec_da, model_flux_spec_da):
# Resample the model resoltuion to match the observed spectrum
model_flux_resampled = trapz_rebin(model_wave, model_flux, fitted_wave)
# Compute the sum of the squared difference of the individually normalised model and observed spectra
sq_diff.append(np.sum((model_flux_resampled / np.median(model_flux_resampled) - count[fitted_range] / np.median(count[fitted_range]))**2.))
# Unit-weighted least-squared best-fit surface gravity and temperature from the DESI spctrum
arg_min = np.argmin(sq_diff)
T_desi = T_spec_da[arg_min]
logg_desi = logg_spec_da[arg_min]
# + colab={"base_uri": "https://localhost:8080/", "height": 611} id="YzYsD-hmDV8b" outputId="edf62ad5-b888-4bd3-bee0-2e0bfe14ff06"
# Plot the best fit only
fitted_range = (model_wave_spec_da[arg_min] > wave_min) & (model_wave_spec_da[arg_min] < wave_max)
fitted_range_data = (wave > wave_min) & (wave < wave_max)
pl.figure(figsize=(15, 10))
pl.plot(wave[fitted_range_data], count[fitted_range_data] / np.median(count[fitted_range_data]), label='DESI spectrum')
pl.plot(model_wave_spec_da[arg_min][fitted_range], model_flux_spec_da[arg_min][fitted_range] / np.median(model_flux_spec_da[arg_min][fitted_range]), label='Best-fit model')
pl.grid()
pl.xlim(wave_min, wave_max)
pl.xlabel('Wavelength [Angstroms]')
pl.ylabel('Normalised Flux')
pl.legend(frameon=False)
pl.title('DESI White Dwarf: Temperature = ' + str(T_desi) + ' K; $\log_{10}$(g) = ' + str(logg_desi))
# + [markdown] id="PW8yeXclDV8b"
# So our white dwarf is a cool 26,000 Kelvin. While the surface gravity would be unbearable. If you remember, the gravitational acceleration is derived from the mass and radius of a body as $g = \frac{G \cdot M}{r^2}$ and is roughly a measure of how dense an object is. Let's see what this looks like for a few well known sources
# + colab={"base_uri": "https://localhost:8080/", "height": 457} id="B5WjT1R_DV8b" outputId="e82ca803-e886-4f51-9489-9629f38193c2"
logg = pd.read_csv(resource_filename('desihigh', 'dat/logg.txt'), sep='\s+', comment='#', names=['Body', 'Surface Gravity [g]'])
logg = logg.sort_values('Surface Gravity [g]')
logg
# + colab={"base_uri": "https://localhost:8080/", "height": 315} id="n3AIkQVhDV8b" outputId="7a94fe29-00ed-4f3b-b59f-45d5a71dd27d"
fig, ax = plt.subplots()
pl.plot(np.arange(0, len(logg), 1), logg['Surface Gravity [g]'], marker='.', c='k')
plt.xticks(np.arange(len(logg)))
ax.set_xticklabels(logg['Body'], rotation='vertical')
ax.set_ylabel('Surface gravity [g]')
# + [markdown] id="G1WKPcUINng0"
#
# + [markdown] id="xi4t6QgYDV8b"
# So the acceleration on Jupyter is a few times higher than that on earth, while on the Sun it'd be 30 times higher. The force you feel during takeoff of a flight is roughly 30% larger than the acceleration due to gravity on Earth. For our DESI white dwarf, the acceleration due to gravity on the surface is:
# + id="DIuOADvFNSin"
# + colab={"base_uri": "https://localhost:8080/"} id="RW4KK2uLDV8b" outputId="e5cf0e1f-6a0b-474f-8067-4d4212198c1b"
logg = 7.6
g = 10.**7.6 # cm2 / s.
g /= 100. # m2 / s
g /= 9.81 # Relative to that on Earth, i.e. [g].
g
# + [markdown] id="Ho_j79c7DV8c"
# times higher than that on Earth! In fact, if it weren't for strange restrictions on what electrons can and cannot not do (as determined by Quantum Mechanics), the White Dwarf would be so dense it would collapse entirely. Go figure!
# + [markdown] id="duu3f_-BDV8c"
# Now it's your turn. Can you find an class of object even more dense than a White Dwarf? What is the acceleration due to gravity on its surface?
# + [markdown] id="yNS2amGCDV8c"
# Harder(!) You may be one of the first to see this White Dwarf 'up close'! What else can you find out about it? Here's something to get you started ...
# + id="8P_DbWjdDV8c" outputId="71466737-c915-42b3-bf3a-a44234cb0556"
model_colors = pd.read_csv(resource_filename('desihigh', 'dat/WDphot/Table_DA.txt'), sep='\s+', comment='#')
model_colors = model_colors[['Teff', 'logg', 'Age', 'G', 'G_BP', 'G_RP']]
model_colors
# + [markdown] id="Zvo84WHDDV8c"
# The above table shows the model prediction for colors of the white dwarf observed by GAIA, if it had the temperature, age and surface gravity (logg) shown.
# + [markdown] id="tIoFPOdRDV8c"
# The GAIA colors observed for the DESI white dwarf are:
# + id="pfE1K-OfDV8d" outputId="52d1df03-8c67-4492-b924-6be70990d6d2"
GAIA['G_MAG'], GAIA['BP_MAG'], GAIA['RP_MAG']
# + id="v-tA6tffDV8d" outputId="000db533-7834-469f-c1e1-078ba180314a"
GAIA['G_MAGERR'], GAIA['BP_MAGERR'], GAIA['RP_MAGERR']
# + [markdown] id="8NznktfCDV8d"
# Can you figure out how old are White Dwarf is? What does that say about the age of our Universe? Does it match the estimates of other [experiments](https://www.space.com/24054-how-old-is-the-universe.html#:~:text=In%202013%2C%20Planck%20measured%20the,universe%20at%2013.82%20billion%20years.)?
# + [markdown] id="nRoE9XAsDV8d"
# If you get stuck, or need another hint, leave us a [message](https://www.github.com/michaelJwilson/DESI-HighSchool/issues/new)!
|
SnowWhiteDwarf.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/sarthakR1/OpenRefine/blob/master/task_2_unsupervised_ipynb.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="kO_1kOEGDTws" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 206} outputId="bb8afabe-77d8-4fd5-ca9d-46f92fa24659"
# Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import datasets
import random as rd
from sklearn.cluster import KMeans
# Load the iris dataset
iris = datasets.load_iris()
iris_df = pd.DataFrame(iris.data, columns = iris.feature_names)
iris_df.head()
# + [markdown] id="q_pPmK9GIKMz" colab_type="text"
# #### How do you find the optimum number of clusters for K Means? How does one determine the value of K?
# + id="f3jfYUPtWZVW" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="c282d555-e97c-49dd-8bdb-ff95e960f4fc"
iris_df.shape
# + id="QCrqHb6hWp6-" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 72} outputId="7fc1301c-c0bb-4a82-a967-e05d690089c9"
iris_df.columns
# + id="BLw5XEF9gFWt" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 109} outputId="3d3a6350-fb02-4a7a-9870-efa4027d5c11"
iris_df.isnull().sum()
# + id="4bYYyARBaHex" colab_type="code" colab={}
k=3
# + id="oKesiUKzmEyn" colab_type="code" colab={}
kmeans=KMeans(n_clusters=3)
# + id="k1MYixp_mZFP" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 72} outputId="08208313-8b5c-4bc7-a427-069f3fb88329"
kmeans.fit(iris_df)
# + id="qCAxzxtlmkAq" colab_type="code" colab={}
pred=kmeans.predict(iris_df)
# + id="Ppxq1DHRm38t" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 146} outputId="cdf2640a-9be0-4a67-e809-477198dd354b"
pred
# + id="KE0OyEYom3tV" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 237} outputId="7192d6f6-0268-46a6-cdb6-767b8d07e6d6"
pd.Series(pred).value_counts
# + id="LLq2Ay3wlxe0" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 274} outputId="f019f3f0-77fd-427c-abe8-05934b132588"
iris_df.describe
from sklearn.preprocessing import StandardScaler
scaler=StandardScaler()
data_scaled=scaler.fit_transform(iris_df)
pd.DataFrame(data_scaled).describe
# + id="WevSKogFEalU" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 295} outputId="7f1e20f6-77fc-4a4c-d34a-d6a18ff1ff8a"
wcss = []
for i in range(1, 11):
kmeans = KMeans(n_clusters = i, init = 'k-means++',
max_iter = 300, n_init = 10, random_state = 0)
y=kmeans.fit(data_scaled)
y
wcss.append(kmeans.inertia_)
# Plotting the results onto a line graph,
# `allowing us to observe 'The elbow'
plt.plot(range(1, 11), wcss)
plt.title('The elbow method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS') # Within cluster sum of squares
plt.show()
# + id="aJbyXuNGIXI9" colab_type="code" colab={}
# Applying kmeans to the dataset / Creating the kmeans classifier
kmeans = KMeans(n_clusters = 3, init = 'k-means++',
max_iter = 300, n_init = 10, random_state = 0)
y_kmeans = kmeans.fit_predict(data_scaled)
# + id="UpPs9_BEs-8F" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 146} outputId="b3b7c951-5e82-4c79-8457-6c4023e5fd35"
y_kmeans
# + id="fEd3jlUJtFn0" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 206} outputId="dce4e488-aa85-4a61-9062-96924e59e87f"
frame=pd.DataFrame(data_scaled)
frame['cluster']=y_kmeans
frame['cluster'].value_counts()
frame.head()
# + id="Q42-XPJjIyXv" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 283} outputId="80ff3d15-caf4-4a77-cb62-94f33704861e"
plt.scatter(x[y_kmeans == 0, 0], x[y_kmeans== 0, 1],
s = 100, c = 'black', label = 'Iris-setosa')
plt.scatter(x[y_kmeans == 1, 0], x[y_kmeans == 1, 1],
s = 100, c = 'green', label = 'Iris-versicolour')
plt.scatter(x[y_kmeans == 2, 0], x[y_kmeans == 2, 1],
s = 100, c = 'red', label = 'Iris-virginica')
centres=np.array(y.cluster_centers_)
plt.scatter(centres[:,0],centres[:,1],c='orange',marker='x')
plt.legend()
|
task_2_unsupervised_ipynb.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: qiskit (dev)
# language: python
# name: qiskit-dev
# ---
# +
# This code is part of Qiskit.
#
# (C) Copyright IBM 2022.
#
# This code is licensed under the Apache License, Version 2.0. You may
# obtain a copy of this license in the LICENSE.txt file in the root directory
# of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
#
# Any modifications or derivative works of this code must retain this
# copyright notice, and modified files need to carry a notice indicating
# that they have been altered from the originals.
# -
# ## Prerequisites
# ### Load Qiskit and Required Libraries
# +
run_experiment = False
from qiskit import IBMQ, transpile, schedule, pulse
from qiskit.circuit import Parameter, QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit.circuit.library import XGate, YGate
from qiskit.pulse import DriveChannel
import qiskit.quantum_info as qi
from qiskit_nature.operators.second_quantization import FermionicOp
from qiskit_nature.mappers.second_quantization import JordanWignerMapper
from qiskit_nature.converters.second_quantization.qubit_converter import QubitConverter
from qiskit.opflow import (I, X, Y, Z, Zero, One, MatrixEvolution, PauliTrotterEvolution, Suzuki,
StateFn, Zero, One, PauliExpectation, PauliOp, SummedOp, OperatorBase)
from qiskit.transpiler import PassManager, InstructionDurations
from qiskit.transpiler.passes import TemplateOptimization, ALAPSchedule, DynamicalDecoupling
from qiskit.transpiler.passes.calibration import RZXCalibrationBuilder, rzx_templates
from qiskit.converters import circuit_to_dag, dag_to_circuit # for bespoke transpilation
from qiskit.dagcircuit import DAGCircuit, DAGNode
from qiskit.scheduler.config import ScheduleConfig
from qiskit.visualization import plot_circuit_layout, plot_error_map, timeline_drawer, dag_drawer
from copy import deepcopy
import numpy as np
import scipy.linalg as lng
import matplotlib.pyplot as plt
plt.style.use('dark_background')
plt.rcParams['figure.figsize'] = [5, 5]
# -
# ### Load IBM Quantum Account
# Try Nick's then John's.
IBMQ.load_account()
try:
provider = IBMQ.get_provider(hub='ibm-q-internal', group='mission-critical', project='bronn')
backend = provider.get_backend('ibm_lagos')
except:
provider = IBMQ.get_provider(hub='ibm-q-afrl', group='air-force-lab', project='quantum-sim')
backend = provider.get_backend('ibmq_bogota') # checking gate directions
# ### Load Backend Information (for Pulse)
# +
backend_config = backend.configuration()
dt = backend_config.dt
meas_map = backend_config.meas_map
backend_defaults = backend.defaults()
inst_sched_map = backend_defaults.instruction_schedule_map
sched_config = ScheduleConfig(inst_sched_map, meas_map, dt)
# -
# # Build Circuits from Model Hamiltonian
# ## Define the System Hamiltonian
#
# John wrote down the system Hamiltonian as
#
# $$ H = \mu\sum_{i=0}^N c^{\dagger}_i c_i + t \sum_{i=0}^{N-1} (c^{\dagger}_ic_{i+1} + c^{\dagger}_{i+1}c_i) + \Delta \sum_{i=0}^{N-1}(c^{\dagger}_i c^{\dagger}_{i+1} + c_{i+1}c_i) + U \sum_{i=0}^{N-1} c^{\dagger}_i c_i c^{\dagger}_{i+1} c_{i+1} $$
#
# where we can use the new `FermionicOp` class to write this general Hamiltonian for 2 site.
# In terms of Majorana operators $\gamma^x_i = c^{\dagger}_i + c_i$ and $\gamma^y_i = i(c^{\dagger}_i - c_i)$ we have
#
# $$ H = -\frac{2\mu + U}{4} \sum_{i=0}^N\gamma^x_i\gamma^y_i + \frac{t+\Delta}{2}\sum_{i=0}^{N-1} \gamma^x_i\gamma^y_{i+1} + \frac{t-\Delta}{2} \sum_{i=0}^{N-1} \gamma^y_i\gamma^x_{i+1} + \frac{U}{4} \sum_{i=0}^{N-1}\gamma^x_i\gamma^y_i\gamma^x_{i+1}\gamma^y_{i+1}$$
hm = sum(FermionicOp(label) for label in ['IN', 'NI'])
ht = FermionicOp('+-') - FermionicOp('-+')
hD = FermionicOp('++') - FermionicOp('--')
hU = sum(FermionicOp(label) for label in ['NN'])
# ### Transform Fermionic to Pauli Hamiltonian
# Bravyi-Kitaev and BKSuperFast are also built into Qiskit.
# +
mapper = JordanWignerMapper()
converter = QubitConverter(mapper=mapper) # should not give 2-qubit reduction error
# parameters defined here due to incompatibility with Qiskit Nature
mu = Parameter('μ')
TT = Parameter('T')
DD = Parameter('Δ')
UU = Parameter('U')
hm_pauli = mu*(converter.convert(hm))
ht_pauli = TT*(converter.convert(ht))
hD_pauli = DD*(converter.convert(hD))
hU_pauli = UU*(converter.convert(hU))
ham_pauli = hm_pauli + ht_pauli + hD_pauli + hU_pauli
print(ham_pauli)
# -
# ## Build Resonance Hamiltonian
#
# Converting John's notation to little-endian:
# $$H = -\frac{1}{2}\omega IIZ + H_{\rm Pauli}\otimes I + c IXX$$
# Parsing in `opflow` is very dependent on how you build Hamiltonian.
# +
cc = Parameter('c')
ww = Parameter('ω')
def build_resonance_ham(h0: OperatorBase) -> SummedOp:
nq = h0.num_qubits
h_jw = []
for op in h0:
for pop in op:
h_jw.append((pop^I).to_pauli_op())
oplist = [-0.5*ww*((I^(nq))^Z), cc*((I^(nq-1))^X^X)]
oplist += h_jw
return SummedOp(oplist)
# -
# ## Time Evolve Resonance Hamiltonian
tt = Parameter('t')
res_ham = build_resonance_ham(ham_pauli)
U_ham = (tt*res_ham).exp_i()
#print(U_ham)
# ## Trotterize Unitary Evolution Operator
# Why do random subcircuit appear sometimes? One hypothesis: parsing each coefficient with `Parameter`s expanded vs being multiplied by a grouping of `PauliOp`s might be it (observed this behavior at Heidelberg workshop).
trot_op = PauliTrotterEvolution(trotter_mode=Suzuki(order=2, reps=1)).convert(U_ham)
trot_circ = trot_op.to_circuit()
trot_circ.draw(output='mpl', reverse_bits=True)
# # Transpile Circuits to Quantum Backend
# ## *Incredibly* useful notes on what we're doing
#
# Transpilation will take place "by hand" so that we can introduce the template optimization at the correct point. Each *pass* of the transpiler is classified as either an analysis or transformation pass. Template optimization consists of two passes:
# - `TemplateOptimization` is an analysis pass that adds the templates (similar to circuit equivalences), in this case specified by `rzx_templates()`
# - `RZXCalibrationBuilder` is a transformation pass that replaces $ZX(\theta)$ gates with the locally-equivalent scaled Pulse gates
#
# The **order** of transpilation and where the backend information such as layout and native gate set are incredibly important and the following heuristics were able to get this to work:
#
# - The circuit must be transpiled to an `initial_layout` since the controlled-`RZGate` operations go across unconnected qubit pairs. At this point it seems best to leave the `basis_gate` set the same as that used in Trotterization.
#
# - Next the `TemplateOptimization` can be run (since the simplication will respect qubit layout), running on Nick's dev fork branch `template-param-expression` (Qiskit Terra [PR 6899](https://github.com/Qiskit/qiskit-terra/pull/6899)) will allow `Parameter`s to be passed through this step.
#
# - The `TemplateOptimization` will miss some patterns because the template parameters will conflict with finding a maximal match (Qiskit Terra [Issue 6974](https://github.com/Qiskit/qiskit-terra/issues/6974)). Here we run **Bespoke Passes** that combine consecutive gates with `Parameter`s (`RZGate`s in this case) and force $ZZ$-like patterns to match and be replated with the inverse from the template.
#
# - Heavily transpile (`optimization_level=3`) the circuit without reference to basis gates (this was necessary for some reason?)
#
# - Final bespoke combination of `RZGate`s.
#
# - There are still a couple patterns of CNOT-singles-CNOT that could be optimized, can add templates for those (TODO).
# ## Backend Information
plot_error_map(backend)
qr = QuantumRegister(backend_config.num_qubits, 'q')
cr = ClassicalRegister(backend_config.num_qubits, 'c')
# initial_layout = [3, 5, 6] # runs 1-52
#initial_layout = [3, 1, 2] # runs 53-100, 103-135
#initial_layout = [2, 1, 0] # runs 136-192
#initial_layout = [4, 5, 6] # runs 101, 102
initial_layout = [6, 5, 4] # runs 192-
# initial_layout = [1, 2, 3] # testing on ibmq_bogota
native_gates = ['rz', 'sx', 'rzx', 'x', 'id']
# +
avg_gate_error = 0
for ii in range(len(initial_layout)-1):
q0 = initial_layout[ii]
q1 = initial_layout[ii+1]
avg_gate_error += backend.properties().gate_property('cx')[(q0, q1)]['gate_error'][0]
avg_gate_error /= len(initial_layout)-1
print('Avg 2-qubit gate error is '+str(avg_gate_error))
# -
# ## Estimate Static $ZZ$ Rate
for ii in range(len(initial_layout)-1):
q0 = initial_layout[ii]
q0freq = backend.properties().qubit_property(q0)['frequency'][0]
q0delta = backend.properties().qubit_property(q0)['anharmonicity'][0]
q1 = initial_layout[ii+1]
q1freq = backend.properties().qubit_property(q1)['frequency'][0]
q1delta = backend.properties().qubit_property(q1)['anharmonicity'][0]
detuning = q0freq - q1freq
try:
j_str = 'jq'+str(q0)+'q'+str(q1)
JJ = backend_config.hamiltonian['vars'][j_str] / (2*np.pi)
except:
j_str = 'jq'+str(q1)+'q'+str(q0)
JJ = backend_config.hamiltonian['vars'][j_str] / (2*np.pi)
ZZ = -2*(JJ**2)*(q0delta + q1delta) / ((q1delta - detuning) * (q0delta + detuning))
print('Static ZZ between q'+str(q0)+' and q'+str(q1)+' is: %f3.1 kHz' % (ZZ/1e3))
# ## Template Optimization and Basic Transpilation
trot_circ1 = transpile(trot_circ, optimization_level=0)
pass_ = TemplateOptimization(**rzx_templates.rzx_templates())
trot_circ2 = PassManager(pass_).run(trot_circ1)
trot_circ3 = transpile(trot_circ2, basis_gates=native_gates,
backend=backend, initial_layout=initial_layout)
#trot_circ3.draw(output='mpl', idle_wires=False)
# ## Bespoke Transpilation Time
#
# So far, just doing one to combine consecutive gates. Does not look like modulo $2\pi$ is necessary here.
# ### Combine Consectutive Gates Pass
def combine_runs(dag: DAGNode, gate_str: str) -> DAGCircuit:
runs = dag.collect_runs([gate_str])
for run in runs:
partition = []
chunk = []
for ii in range(len(run)-1):
chunk.append(run[ii])
qargs0 = run[ii].qargs
qargs1 = run[ii+1].qargs
if qargs0 != qargs1:
partition.append(chunk)
chunk = []
chunk.append(run[-1])
partition.append(chunk)
# simplify each chunk in the partition
for chunk in partition:
theta = 0
for ii in range(len(chunk)):
theta += chunk[ii].op.params[0]
# set the first chunk to sum of params
chunk[0].op.params[0] = theta
# remove remaining chunks if any
if len(chunk) > 1:
for nn in chunk[1:]:
dag.remove_op_node(nn)
return dag
# ### Run Bespoke Passes
dag = circuit_to_dag(trot_circ3)
dag = combine_runs(dag, 'rz')
dag = combine_runs(dag, 'rzx')
trot_circ4 = dag_to_circuit(dag)
trot_circ4.draw(output='mpl', idle_wires=False)
# ## Pauli Twirling
# This should suppress dynamical $ZZ$ (based on transmon/CR physics). We will focus on the case with the $R_{ZZ}(\theta)$ scaled cross resonance, in which elements from the set $\mathbb{G} = \{[I, I], [X, X], [Y, Y], [Z, Z]\}$ are placed both before and after the $R_{ZZ}$ since the resulting operators commute. <br>
#
# ~Nick thinks it should be easy to find a different set $\mathbb{G}$ for the $R_{ZX}$ scaled pulses found from template optimization, then write a transpiler pass that generates a circuit sampled by each pair of Pauli's. In this case, we should actually implement Pauli twirling *after* Pulse scaling.~ This is done now below. <br>
#
# Someone [thought about this](https://github.com/Qiskit/qiskit-experiments/issues/482) for Qiskit Experiments, but apparently not too long. <br>
#
# Note that this implementation of Pauli twirling is *different* than the one used in ["Scalable error mitigation for noisy quantum circuits produces competitive expectation values"](http://arxiv.org/abs/2108.09197)
# ### Convert Twirl Gates to $R_{ZX}$
# +
# sanity to make sure we converted valid twirls
twirl_op = Z^X
twirls = [I^I, X^Z, Y^Y, Z^X]
for twirl in twirls:
print((twirl @ twirl_op @ twirl) == twirl_op)
# +
from qiskit.circuit.library import IGate, XGate, YGate, ZGate, RZXGate
twirl_gates = [[IGate(), IGate()],
[XGate(), ZGate()],
[YGate(), YGate()],
[ZGate(), XGate()]]
# -
# ### Convert Circuits to DAGs for Transpilation
dag = circuit_to_dag(trot_circ4)
#dag_drawer(dag)
def twirl_rzx_gates(dag: DAGCircuit, num_seeds: int) -> list:
twirled_dags = []
for seed in range(num_seeds):
this_dag = deepcopy(dag)
runs = this_dag.collect_runs(['rzx'])
twirl_idxs = np.random.randint(0, len(twirl_gates), size=len(runs))
for twirl_idx, run in enumerate(runs):
mini_dag = DAGCircuit()
p = QuantumRegister(2, 'p')
mini_dag.add_qreg(p)
mini_dag.apply_operation_back(twirl_gates[twirl_idxs[twirl_idx]][0], qargs=[p[0]])
mini_dag.apply_operation_back(twirl_gates[twirl_idxs[twirl_idx]][1], qargs=[p[1]])
mini_dag.apply_operation_back(run[0].op, qargs=[p[0], p[1]])
mini_dag.apply_operation_back(twirl_gates[twirl_idxs[twirl_idx]][0], qargs=[p[0]])
mini_dag.apply_operation_back(twirl_gates[twirl_idxs[twirl_idx]][1], qargs=[p[1]])
rzx_node = this_dag.op_nodes(op=RZXGate).pop()
this_dag.substitute_node_with_dag(node=rzx_node, input_dag=mini_dag, wires=[p[0], p[1]])
twirled_dags.append(deepcopy(this_dag))
return twirled_dags
# ### Perform Twirling
num_twirl_seeds = 4
dags = twirl_rzx_gates(dag, num_twirl_seeds)
#dag_drawer(dags[1])
trot_units = []
for dag in dags:
trot_units.append(dag_to_circuit(dag))
# ## Game Plan
# The above circuit is as transpiled as possible without binding parameters and adding the calibrations for the `RZXGate`s. This will form the unit of the sweeps we run.
# # Build Sweep Experiment
# +
#trot_unit = trot_circ4
exp_str = 'm_sweep' # or 't_sweep' or 'c_sweep' or 'y_sweep'
# -
# ## Set Model Hamiltonian Parameters
# Grouping by terms, the Model Hamiltonian is written as
# $$
# H_{\rm Pauli} = -\frac{2\mu + U}{4} (IZ + ZI) + \frac{t+\Delta}{2} XX + \frac{t-\Delta}{2} YY + \frac{U}{4} ZZ \\
# \equiv m(IZ + IZ) + x XX + y YY + z ZZ
# $$
# negelecting the identity term.
x_set = 1.5
# z_set = 0.2 # runs 1-4, 53-68, 209-224 (z semi-on!)
# z_set = 0.0 # runs 5-20, 69-84, 101-103, 115-, 225-240 (z off!)
z_set = 0.4 # runs 21-52 (z on!), 140- , 193-208
# z_set = -0.4 # runs 85-100 (z on and negative!)
# ### Invert Parameters before Binding
#
# $$
# t = x + y \qquad \Delta = x - y \qquad U = 4z \qquad \mu = -2(m+z)
# $$
#
# (This now happens differently in each param sweep step)
# +
# job will choke on Parameter keys, convert to strings
def stringify(param_bind: dict) -> dict:
param_bind_str = {}
for key in param_bind.keys():
param_bind_str[str(key)] = param_bind[key]
return param_bind_str
# -
# ## $m$ Sweep Experiment
# ### Set Remaining Parameters
if exp_str == 'm_sweep':
t_set = 5.0
#dt_set = 1.2 # runs 5-36
dt_set = 0.7 # runs 37-100, 140-
#dt_set = 0.1 # runs 123-127
c_set = 0.3
# y_set = -1.5 # runs 1-4
# y_set = -1.3 # runs 5-8
# y_set = -1.1 # runs 9-12
# y_set = -0.9 # runs 13-16
# y_set = -0.7 # runs 17-20
# y_set = -0.5 # runs 21-24
# y_set = -0.3 # runs 25-28
# y_set = -0.1 # runs 29-32
# y_set = 0.1 # runs 33-36
# y_set = 0.3 # runs 37-40
# y_set = 0.5 # runs 41-44
# y_set = 0.7 # runs 45-48
# y_set = 0.9 # runs 49-52
# y_set = 1.1 # runs, 53-56
# y_set = 1.3 # runs 57-60
y_set = 1.5 # runs 61-64
U_set = 4*z_set
param_bind = {UU: U_set, tt: dt_set, cc: c_set}
# m_range = np.linspace(-1.5, -0.9, 4) # runs 1, 5, 9, 13, 17, 21, 25, 29, 33, 37, 41, 45, 49, 53, 57, 61
# m_range = np.linspace(-0.7, -0.1, 4) # runs 2, 6, 10, 14, 18, 22, 26, 30, 34, 38, 42, 46, 50, 51, 54, 58, 62
# m_range = np.linspace(0.1, 0.7, 4) # runs 3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43, 47, 51, 55, 59, 63
m_range = np.linspace(0.9, 1.5, 4) # runs 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60
w_range = np.linspace(-3.5, 3.5, 51)
if exp_str == 'm_sweep':
# Now let's add the circuits together
NT = int(t_set/dt_set)
trot_circs_total = []
for trot_unit in trot_units:
trot_circ_total = deepcopy(trot_unit)
for ti in range (1, NT):
trot_circ_total.append(trot_unit, qr)
trot_circs_total.append(trot_circ_total)
#Bind the parameters
circ_w = []
param_decoder = []
for m_set in m_range:
mu_set = -2*(m_set + z_set)
T_set = x_set + y_set
D_set = x_set - y_set
param_bind[mu] = mu_set
param_bind[TT] = T_set
param_bind[DD] = D_set
for w_set in w_range:
for tidx, trot_circ_total in enumerate(trot_circs_total):
circ_str = 'Freq sweep w='+str(round(w_set, 2))+ \
', $\mu$ = '+str(round(mu_set, 2))+' , twirl '+str(tidx)
bound_circ = trot_circ_total.bind_parameters({**param_bind, ww: w_set})
temp_circ = QuantumCircuit(qr, cr, name=circ_str,
metadata=stringify({**param_bind, ww: w_set}))
temp_circ.append(bound_circ, qr)
#temp_circ.measure(qr, cr)
temp_circ.measure(qr[initial_layout[0]], cr[initial_layout[0]]) # runs 136-
circ_w.append(temp_circ)
param_decoder.append(['y='+str(round(y_set, 2))+', m=' + str(round(m_set, 2)) +
', w=' + str(round(w_set, 2))+', twirl '+str(tidx)])
# ## Final Transpilation Steps
res_circ_scaled_trans = transpile(circ_w, backend, basis_gates=native_gates)
res_circ_digital_trans = transpile(circ_w, backend)
pass_ = RZXCalibrationBuilder(backend)
res_circ_scaled_trans1 = PassManager(pass_).run(res_circ_scaled_trans)
# ## Compare digital and scaled circuits
circ_num = -1
scaled_sched = schedule(res_circ_scaled_trans1[circ_num], backend)
basis_sched = schedule(res_circ_digital_trans[circ_num], backend)
# ### Count Operations
res_circ_scaled_trans1[circ_num].count_ops()
res_circ_digital_trans[circ_num].count_ops()
# +
dag = circuit_to_dag(res_circ_scaled_trans1[circ_num])
rzx_runs = dag.collect_runs(['rzx'])
est_fid_rzx = 1
for rzx_run in rzx_runs:
angle = rzx_run[0].op.params[0]
this_rzx_error = (abs(float(angle))/(np.pi/2))*avg_gate_error
est_fid_rzx *= (1-this_rzx_error)
print('Scaled Circuit estimated fidelity is %2.f%%' % (est_fid_rzx*100))
# -
num_cx = res_circ_digital_trans[circ_num].count_ops()['cx']
est_fid_dig = (1-avg_gate_error)**num_cx
print('Digital Circuit estimated fidelity is %2.f%%' % (est_fid_dig*100))
# ### Look at Resulting Schedules
print('Scaled schedule takes '+str(scaled_sched.duration)+'dt')
print('Digital schedule takes '+str(basis_sched.duration)+'dt')
time_range=[0,4000]
scaled_sched.draw(time_range=time_range)
basis_sched.draw(time_range=time_range)
# # Run on Quantum Hardware
# +
from qiskit.tools.monitor import job_monitor
if run_experiment:
# run the job on a real backend
job = backend.run(res_circ_scaled_trans1, job_name="SE_Eigensolver", meas_level=2, shots=2048)
print(job.job_id())
job_monitor(job)
# -
# ## Or Retrieve from Previous Run
# +
job_ids = [
# z=0.4, c=0.3, dt_set=0.7, t=5.0 - MISSION CRITICAL PROVIDER, qubits 6-5-4
'61e6ef069307b98a466bec24', # run 1 - m_sweep -1.5 to -0.9, y=-1.5
'61e6f2411faa069c4b3446c5', # run 2 - m_sweep -0.7 to -0.1, y=-1.5
'61e6f60611d0378639abbb94', # run 3 - m_sweep 0.1 to 0.7, y=-1.5
'61e6f923ded89e3d08a9d149', # run 4 - m_sweep 0.9 to 1.5, y=-1.5
'61e6fe221faa063fe33446e8', # run 5 - m_sweep -1.5 to -0.9, y=-1.3
'61e701e0dfe4a92a7722c4b1', # run 6 - m_sweep -0.7 to -0.1, y=-1.3
'61e704e89847b3212eaaf8ab', # run 7 - m_sweep 0.1 to 0.7, y=-1.3
'61e7077b4eebda3d9b7a7429', # run 8 - m_sweep 0.9 to 1.5, y=-1.3
'61e70e4d11d0377f04abbc0c', # run 9 - m_sweep -1.5 to -0.9, y=-1.1
'61e7fce79847b33260aafe11', # run 10 - m_sweep -0.7 to -0.1, y=-1.1
'61e800684ddc9f024680c5cd', # run 11 - m_sweep 0.1 to 0.7, y=-1.1
'61e8030fded89e3a55a9d6cf', # run 12 - m_sweep 0.9 to 1.5, y=-1.1
'61e805ab9847b3fa8faafe2d', # run 13 - m_sweep -1.5 to -0.9, y=-0.9
'61e8081c9847b32cabaafe35', # run 14 - m_sweep -0.7 to -0.1, y=-0.9
'61e80a8adfe4a9623222cadf', # run 15 - m_sweep 0.1 to 0.7, y=-0.9
'61e80d319847b3161baafe4a', # run 16 - m_sweep 0.9 to 1.5, y=-0.9
'61e80fbe4eebda4bcf7a798e', # run 17 - m_sweep -1.5 to -0.9, y=-0.7
'61e813ced6c095b5fedf9d54', # run 18 - m_sweep -0.7 to -0.1, y=-0.7
'61e8170a4eebda880a7a79ac', # run 19 - m_sweep 0.1 to 0.7, y=-0.7
'61e81d33dfe4a93ac822cb12', # run 20 - m_sweep 0.9 to 1.5, y=-0.7
'61e829887f4bf87373bd3ed0', # run 21 - m_sweep -1.5 to -0.9, y=-0.5
'61e82dd0dfe4a94e2f22cb65', # run 22 - m_sweep -0.7 to -0.1, y=-0.5
'61e8307d4ddc9f515c80c6a4', # run 23 - m_sweep 0.1 to 0.7, y=-0.5
'61e8343f6fb797d51f4414b9', # run 24 - m_sweep 0.9 to 1.5, y=-0.5
'61e837544eebda03d67a7a4c', # run 25 - m_sweep -1.5 to -0.9, y=-0.3
'61e83a356fb7973ff44414d0', # run 26 - m_sweep -0.7 to -0.1, y=-0.3
'61e83daa9847b34c3caaff3b', # run 27 - m_sweep 0.1 to 0.7, y=-0.3
'61e8406ad6c0953d89df9e31', # run 28 - m_sweep 0.9 to 1.5, y=-0.3
'61e8434eded89e5892a9d7ea', # run 29 - m_sweep -1.5 to -0.9, y=-0.1
'61e845a7404aae435d437486', # run 30 - m_sweep -0.7 to -0.1, y=-0.1
'61e848af9847b39d4daaff73', # run 31 - m_sweep 0.1 to 0.7, y=-0.1
'61e84cd8d6c0958888df9eaa', # run 32 - m_sweep 0.9 to 1.5, y=-0.1
'61e851b71faa068030344e41', # run 33 - m_sweep -1.5 to -0.9, y=0.1
'61e855d34ddc9f19ab80c79c', # run 34 - m_sweep -0.7 to -0.1, y=0.1
'61e85a224eebda6edb7a7b32', # run 35 - m_sweep 0.1 to 0.7, y=0.1
'61e863449847b380d5ab0036' ,# run 36 - m_sweep 0.9 to 1.5, y=0.1
'61e866ce9847b3fa38ab0046', # run 37 - m_sweep -1.5 to -0.9, y=0.3
'61e86dcb4eebda024c7a7b92', # run 38 - m_sweep -0.7 to -0.1, y=0.3
'61e8709b6fb7976499441616', # run 39 - m_sweep 0.1 to 0.7, y=0.3
'61e873744eebda31eb7a7bb5', # run 40 - m_sweep 0.9 to 1.5, y=0.3
'61e881a7404aae63764375f3', # run 41 - m_sweep -1.5 to -0.9, y=0.5
'61e88ee8d6c0952d2adf9fcd', # run 42 - m_sweep -0.7 to -0.1, y=0.5
'61e891cedfe4a9367022cda8', # run 43 - m_sweep 0.1 to 0.7, y=0.5
'61e894b51faa06945f344f9e', # run 44 - m_sweep 0.9 to 1.5, y=0.5
'61e897486fb7970b744416d9', # run 45 - m_sweep -1.5 to -0.9, y=0.7
'61e89a1a1faa06c4cf344fbb', # run 46 - m_sweep -0.7 to -0.1, y=0.7
'61e89ebaded89edaeca9da08', # run 47 - m_sweep 0.1 to 0.7, y=0.7
'61e8a62f1faa06dcce344ff1', # run 48 - m_sweep 0.9 to 1.5, y=0.7
'61e8b5931faa065c4d34502f', # run 49 - m_sweep -1.5 to -0.9, y=0.9
'61e8b8291faa068e9f34503c', # run 50 - m_sweep -0.7 to -0.1, y=0.9
'61e8bbb3dfe4a925e022ce61', # run 51 - m_sweep 0.1 to 0.7, y=0.9
'61e8bec6ded89e419aa9da64', # run 52 - m_sweep 0.9 to 1.5, y=0.9
'61e8c1e4dfe4a94a8d22ce7b', # run 53 - m_sweep -1.5 to -0.9, y=1.1
'61e8cba54eebda4bc77a7d47', # run 54 - m_sweep -0.7 to -0.1, y=1.1
'61e8ceae7f4bf80fcabd421a', # run 55 - m_sweep 0.1 to 0.7, y=1.1
'61e8d28b6fb7971a9c4417e7', # run 56 - m_sweep 0.9 to 1.5, y=1.1
'61e8d5124ddc9f28ba80c9ca', # run 57 - m_sweep -1.5 to -0.9, y=1.3
'61e8d826dfe4a91e9822cf10', # run 58 - m_sweep -0.7 to -0.1, y=1.3
'61e8dabbdfe4a9547622cf1c', # run 59 - m_sweep 0.1 to 0.7, y=1.3
'61e8dd5c9847b35e22ab0286', # run 60 - m_sweep 0.9 to 1.5, y=1.3
'61e8dfc14ddc9f78ee80c9f5', # run 61 - m_sweep -1.5 to -0.9, y=1.5
'61e8e22f4ddc9f0e5f80ca01', # run 62 - m_sweep -0.7 to -0.1, y=1.5
'61e8e4889847b3ef35ab02a2', # run 63 - m_sweep 0.1 to 0.7, y=1.5
'61e8e6deded89e4789a9db2e'] # run 64 - m_sweep 0.9 to 1.5, y=1.5
# -
run_num = 64
job = backend.retrieve_job(job_ids[run_num-1])
c_set = 0.3
dt_set = 0.7
t_set = 5
x_set = 1.5
z_set = 0.4
num_twirl_seeds = 4
num_shots = 8192
w_range = np.linspace(-3.5, 3.5, 51)
# ### Check Parameters Agree with Job Metadata
# +
y_set = 1.3
# m_sweep = np.linspace(-1.5, -0.9, 4)
# m_sweep = np.linspace(-0.7, -0.1, 4)
# m_sweep = np.linspace(0.1, 0.7, 4)
m_sweep = np.linspace(0.9, 1.5, 4)
job = ntb_twirl_job60
Result = job.result().get_counts()
for midx, m_set in enumerate(m_sweep):
jidx0 = num_twirl_seeds*midx*len(w_range)
mu_set = -2*(m_set + z_set)
T_set = x_set + y_set
D_set = x_set - y_set
metadata = job.result().results[jidx0].header.metadata
shots = job.result().results[jidx0].shots
if (mu_set == metadata['μ']) and (T_set == metadata['T']) and \
(D_set == metadata['Δ']) and (shots*num_twirl_seeds == num_shots) and \
(c_set == metadata['c']) and (dt_set == metadata['t']):
print('Parameter agreement')
else:
print('Parameter mismatch!')
# -
# ## Save Data
# +
save_data = False
for midx, m_set in enumerate(m_sweep):
P0_w = []
param_decoder = []
for wi in range(len(w_range)):
P0 = 0
for tidx in range(num_twirl_seeds):
jidx0 = num_twirl_seeds*midx*len(w_range) + tidx
#print(wi*num_twirl_seeds + jidx0)
keys = list(Result[wi*num_twirl_seeds + jidx0].keys())
norm = sum([Result[wi*num_twirl_seeds + jidx0][key] for key in keys])
for key in keys:
if key == '0000000':
P0 += Result[wi*num_twirl_seeds + jidx0][key]/norm
P0_w.append(P0/num_twirl_seeds)
param_decoder.append(['y='+str(round(y_set, 2))+', m=' + str(round(m_set, 2)) +
', w=' + str(round(wi, 2))])
if save_data:
w0 = w_range[0]
dw = round(w_range[1] - w_range[0], 2)
np.save('../data/final-sweeps/2site/z0p4_twirl/SE_1trot_N_2_c_'+str(c_set)+'_dt_'+str(dt_set)+'_t_'+str(t_set)+'_w0_'+str(w0)+'_dw_'+str(dw)+'_m_'+str(m_set)+'_x_'+str(x_set)+'_y_'+str(y_set)+'_z_'+str(z_set), P0_w)
np.save('../data/final-sweeps/2site/z0p4_twirl/w_N_2_c_'+str(c_set)+'_dt_'+str(dt_set)+'_t_'+str(t_set)+'_w0_'+str(w0)+'_dw_'+str(dw)+'_m_'+str(m_set)+'_x_'+str(x_set)+'_y_'+str(y_set)+'_z_'+str(z_set), w_range)
np.save('../data/final-sweeps/2site/z0p4_twirl/decoder_N_2_c_'+str(c_set)+'_dt_'+str(dt_set)+'_t_'+str(t_set)+'_w0_'+str(w0)+'_dw_'+str(dw)+'_m_'+str(m_set)+'_x_'+str(x_set)+'_y_'+str(y_set)+'_z_'+str(z_set), param_decoder)
# -
# ### Plot Data
fig, ax = plt.subplots(1, 1, figsize=(8,5))
ax.plot(w_range, P0_w, label='Twirled Sweep', linewidth=8, color='b')
# # Qiskit Version Table
import qiskit.tools.jupyter
# %qiskit_version_table
|
code/se_2site_pauli_twirl.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Practice Quiz: For Loops
#
# +
"""
2.Question 2
Fill in the blanks to make the factorial function return the factorial of n.
Then, print the first 10 factorials (from 0 to 9) with the corresponding number.
Remember that the factorial of a number is defined as the product of an integer and all integers before it. For example,
the factorial of five (5!) is equal to 1*2*3*4*5=120. Also recall that the factorial of zero (0!) is equal to 1.
"""
def factorial(n):
result = 1
for x in range(1,n+1):
result = result * x
return result
for n in range(0,10):
print(n, factorial(n+0))
# -
"""
3.Question 3
Write a script that prints the first 10 cube numbers (x**3), starting with x=1 and ending with x=10.
"""
for x in range(1,11):
print(x**3)
# +
"""
4.Question 4
Write a script that prints the multiples of 7 between 0 and 100.
Print one multiple per line and avoid printing any numbers that aren't multiples of 7.
Remember that 0 is also a multiple of 7.
"""
for num in range(0,100):
if(num % 7==0):
print(num)
else:
num= num + 1
# +
"""5.Question 5
The retry function tries to execute an operation that might fail,
it retries the operation for a number of attempts. Currently the code will keep executing the function even if it succeeds.
Fill in the blank so the code stops trying after the operation succeeded.
"""
def retry(operation, attempts):
for n in range(attempts):
if operation():
print("Attempt " + str(n) + " succeeded")
break
else:
print("Attempt " + str(n) + " failed")
retry(create_user, 3)
retry(stop_service, 5)
|
Google IT Automation with Python/Google - Crash Course on Python/Week 3/Practice Quiz For Loops.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:py3]
# language: python
# name: conda-env-py3-py
# ---
# + nbpresent={"id": "cdb6479a-9419-4a07-96ca-197bc0177736"}
import pandas as pd
import geopandas as gpd
import os
import geoplot
import seaborn as sns
import matplotlib.pyplot as plt
# %matplotlib inline
# + [markdown] nbpresent={"id": "0496794c-4a4f-4c1c-82f7-c7910fc31241"}
# ### Area Deprivation Index
# Found [here](https://www.neighborhoodatlas.medicine.wisc.edu/).
#
# From the Neighborhood Atlas site:
# <br>"The Area Deprivation Index (ADI) is based on a measure created by the Health Resources & Services Administration (HRSA) over two decades ago for primarily county-level use, but refined, adapted, and validated to the Census block group/neighborhood level by <NAME>, MD, PhD and her research team at the University of Wisconsin-Madison. It allows for rankings of neighborhoods by socioeconomic status disadvantage in a region of interest (e.g. at the state or national level). It includes factors for the theoretical domains of income, education, employment, and housing quality. It can be used to inform health delivery and policy, especially for the most disadvantaged neighborhood groups."
# + nbpresent={"id": "9a5712cd-3b39-4688-8736-84c15f1a4ada"}
wi_adi = pd.read_csv(os.path.join("../../wi_bg_v1.5.txt"),delimiter=",")
wi_adi['FIPS'] = wi_adi['FIPS'].astype(str)
wi_adi.head()
# -
sns.distplot(wi_adi['ADI_NATRANK'],kde=False,label='National Percentile')
sns.distplot(wi_adi['ADI_STATERNK']*10.0,kde=False,label='State Decile')
plt.legend()
# It looks like we'll get more detail out of the National ADI percentiles than the State-level deciles.
# + [markdown] nbpresent={"id": "afee5399-c6f4-4f17-a752-c99c40a4539a"}
# ### Census Shapefiles
# Link the FIPS codes in the ADI data to their corresponding spatial boundaries so the shapes and the data are in the same dataframe.
# + nbpresent={"id": "12a111f1-5d8a-487d-b783-ad5e928e0c1f"}
wi_shp = gpd.read_file(os.path.join('../../gz_2010_55_150_00_500k/gz_2010_55_150_00_500k.shp'))
wi_shp.head()
# + [markdown] nbpresent={"id": "34c58be7-3e0e-4b78-a1ad-c4d005dd49e6"}
# It looks like the column 'GEO_ID' has the 12-digit FIPS codes following the letters 'US'. Create a new column with just the 12-digit FIPS codes.
# + nbpresent={"id": "69ead048-b20f-4c0a-b673-9b55d78ab2e0"}
wi_shp['FIPS'] = wi_shp['GEO_ID'].apply(lambda x: x.split("US")[-1])
# Just subset to Dane County:
dane = wi_shp[wi_shp['COUNTY']=='025']
# + nbpresent={"id": "c0da944d-da5a-4bfb-a43b-54dd49aa9f10"}
# Join ADI to the Dane county dataframe:
adi_dane = dane[['FIPS','CENSUSAREA','geometry','TRACT']].merge(wi_adi,how='left',on='FIPS')
adi_dane.head()
# -
# THere are two tracts without ADI data - let's drop those from the dataframe
print("Was",len(adi_dane))
adi_dane = adi_dane[adi_dane['CENSUSAREA']>0.0]
print("Is",len(adi_dane))
sns.distplot(adi_dane['ADI_NATRANK'])
geoplot.choropleth(adi_dane,hue='ADI_NATRANK',cmap='Blues',k=None,legend=True,figsize=(11,8))
|
notebooks/DataExploration.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/bxck75/Python_Helpers/blob/master/Old_Horse_Gone.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="-Os2fwogLUKG" colab_type="text"
# # helperclass info
# + [markdown] id="BRj71HGk6mi_" colab_type="text"
# ```
# 'HelpCore)',
# 'c_d',
# 'cd',
# 'cdr',
# 'check_img_list',
# 'cleanup_files',
# 'cloner',
# 'cprint',
# 'custom_reps_setup',
# 'docu',
# 'explore_mod',
# 'flickr_scrape',
# 'get_gdrive_dataset',
# 'get_other_reps',
# 'git_install_root',
# 'haar_detect',
# 'helpers_root',
# 'if_exists',
# 'img_batch_rename',
# 'importTboard',
# 'install_repos',
# 'into_func',
# 'landmarkdetect',
# 'landmarkdetecter',
# 'landmarker',
# 'list_to_file',
# 'no_action',
# 'path',
# 'rec_walk_folder',
# 'rep',
# 'root',
# 'root_dirname',
# 'root_filename',
# 'runProcess',
# 'set_maker',
# 'sorted_repos',
# 'sys_com',
# 'sys_log',
# 'system_log_file',
# 'valid_img',
# 'valid_list'
# ```
# + [markdown] id="evLjcPe4LaJf" colab_type="text"
# # code
# + id="6X6efbcB5hmG" colab_type="code" colab={}
'''#########################################'''
#''' K00B404 aka. BXCK75 '''#
''' notebook/colab kickstarter '''
#''' Look for stuff in main.py in the root '''#
''' Look for defs in Helpers/core.py file '''
################################################
from IPython.display import clear_output as clear
from pprint import pprint as print
from PIL import Image
import cv2
import os
import sys
import json
import IPython
''' default sample data delete '''
os.system('rm -r sample_data')
''' set root paths '''
root = '/content'
gdrive_root = '/content/drive/My Drive'
helpers_root = root + '/installed_repos/Python_Helpers'
''' setup install the Helpers module '''
os.system('git clone https://github.com/bxck75/Python_Helpers.git ' + helpers_root)
os.system('python ' + helpers_root + 'setup.py install')
''' import helpers '''
os.chdir(helpers_root)
import main as main_core
MainCore = main_core.main()
HelpCore = MainCore.Helpers_Core
FScrape = HelpCore.flickr_scrape
fromGdrive = HelpCore.GdriveD
toGdrive = HelpCore.ZipUp.ZipUp
HC = HelpCore
''' Clear output '''
clear()
# + id="6H2Dffnv8pFB" colab_type="code" colab={}
HC.c_d('/content/',True)
search_list [ 'poor', 'hobo', 'homeless' ]
set_name = images_hobo
HC.FlickrS( search_list, 5, set_name )
# + id="EHxNPH8R6cQb" colab_type="code" colab={}
# # !pip install --upgrade cv2
# # help(HelpCore)
# import cv2 as cv
# img='/content/images_hobo/img_19.jpg'
# image_out=img.replace('_hobo','')
# HelpCore.haar_detect(img,image_out)
# HelpCore.cloner
# HelpCore.FlickrS
# HelpCore.GlobX
# HelpCore.MethHelp
# HelpCore.fromGdrive
# HelpCore.toGdrive
# HelpCore.ShowMe
dir(HelpCore.ShowMe)
org_img = '/content/installed_repos/face-recognition/images/Colin_Powell/Colin_Powell_0004.jpg'
new_img = org_img.replace('images/','images_marked/')
os.makedirs(new_img, exist_ok=True)
HelpCore.landmarker('/content/installed_repos/face-recognition/images/Colin_Powell/Colin_Powell_0004.jpg' , '/content/images_marked/.jpg')
# + id="i6UUyiFq9Dp7" colab_type="code" colab={}
# search_list,img_dir,qty = ['face'], 100, 'images'
# HelpCore.FlickrS(search_list,qty,img_dir
# + id="Qr14UMd7AgFN" colab_type="code" colab={}
from icrawler.builtin import BaiduImageCrawler, BingImageCrawler, GoogleImageCrawler
def ICL(key='vagina', qty=100, out_dir='/content/img'):
'''ICL('vagina', 100, '/content/img')'''
google_crawler = GoogleImageCrawler(
feeder_threads=1,
parser_threads=1,
downloader_threads=4,
storage={'root_dir': out_dir })
filters = dict(
size='medium',
# color='orange',
# license='commercial,modify',
# date=((2017, 1, 1), (2017, 11, 30)),
)
google_crawler.crawl(
keyword=key,
filters=filters,
offset=0,
max_num=qty,
min_size=(400,400),
max_size=None,
file_idx_offset=0,
)
bing_crawler = BingImageCrawler(
downloader_threads=4,
storage={'root_dir': out_dir }
)
bing_crawler.crawl(
keyword=key,
filters=None,
offset=0,
max_num=qty
)
baidu_crawler = BaiduImageCrawler(
storage={'root_dir': out_dir }
)
baidu_crawler.crawl(
keyword=key,
offset=0,
max_num=qty,
min_size=(200,200),
max_size=None
)
# + id="sTGRUHs1dDgm" colab_type="code" colab={}
ICL(key='<NAME>', qty=100, out_dir='/content/images_bohdgaya')
ICL('vagina', 100, '/content/img_vig')
# + id="FbjLpj_vJntT" colab_type="code" colab={}
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('/content/images_google/000010.jpg')
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
plt.imshow(img)
from numpy import random
import matplotlib.pyplot as plt
print(img.shape)
data = random.random((5,599999))
img = plt.imshow(img)
img.set_cmap('tab10')
plt.axis('off')
plt.figure( num=65, figsize=(100,100), dpi=10, facecolor='blue', edgecolor='red', frameon=False, clear=False )
plt.savefig("test.png", bbox_inches='tight')
plt.show(size(5,5))
# + id="ntXdp4VqRDVl" colab_type="code" colab={}
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
plt.imshow(img_rgb)
# + id="59ulBLBjR6sl" colab_type="code" colab={}
dir(cv2)
# + id="fieSXPkdbv2d" colab_type="code" colab={}
help(plt.imshow)
# + id="0Z1lo3g6Ra6X" colab_type="code" colab={}
os.chdir('/content')
import cv2
img_path='/content/images_google/000005.jpg'
img = cv2.imread(img_path)
detector = cv2.FastFeatureDetector_create()
# plt.figure(1)
# img = cv2.cvtColor( img, cv2.COLOR_BGR2Luv)
# plt.axis('off')
# plt.imshow(img)
plt.figure(1)
img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
plt.axis('off')
plt.title=''
plt.imshow(img_rgb)
# img save
cv2.imwrite('final_image.png',img)
plt.show
plt.figure(2)
# lege image
image_blank = np.zeros(shape=(512,512,3),dtype=np.int16)
plt.imshow(image_blank)
plt.axis('off')
plt.show
cv2.destroyAllWindows()
# + [markdown] id="Vq2uGrS6NwHE" colab_type="text"
# Accent, Accent_r, Blues, Blues_r, BrBG, BrBG_r, BuGn, BuGn_r, BuPu, BuPu_r, CMRmap, CMRmap_r, Dark2, Dark2_r, GnBu, GnBu_r, Greens, Greens_r, Greys, Greys_r, OrRd, OrRd_r, Oranges, Oranges_r, PRGn, PRGn_r, Paired, Paired_r, Pastel1, Pastel1_r, Pastel2, Pastel2_r, PiYG, PiYG_r, PuBu, PuBuGn, PuBuGn_r, PuBu_r, PuOr, PuOr_r, PuRd, PuRd_r, Purples, Purples_r, RdBu, RdBu_r, RdGy, RdGy_r, RdPu, RdPu_r, RdYlBu, RdYlBu_r, RdYlGn, RdYlGn_r, Reds, Reds_r, Set1, Set1_r, Set2, Set2_r, Set3, Set3_r, Spectral, Spectral_r, Wistia, Wistia_r, YlGn, YlGnBu, YlGnBu_r, YlGn_r, YlOrBr, YlOrBr_r, YlOrRd, YlOrRd_r, afmhot, afmhot_r, autumn, autumn_r, binary, binary_r, bone, bone_r, brg, brg_r, bwr, bwr_r, cividis, cividis_r, cool, cool_r, coolwarm, coolwarm_r, copper, copper_r, cubehelix, cubehelix_r, flag, flag_r, gist_earth, gist_earth_r, gist_gray, gist_gray_r, gist_heat, gist_heat_r, gist_ncar, gist_ncar_r, gist_rainbow, gist_rainbow_r, gist_stern, gist_stern_r, gist_yarg, gist_yarg_r, gnuplot, gnuplot2, gnuplot2_r, gnuplot_r, gray, gray_r, hot, hot_r, hsv, hsv_r, inferno, inferno_r, jet, jet_r, magma, magma_r, nipy_spectral, nipy_spectral_r, ocean, ocean_r, pink, pink_r, plasma, plasma_r, prism, prism_r, rainbow, rainbow_r, seismic, seismic_r, spring, spring_r, summer, summer_r, tab10, tab10_r, tab20, tab20_r, tab20b, tab20b_r, tab20c, tab20c_r, terrain, terrain_r, twilight, twilight_r, twilight_shifted, twilight_s...
#
# + id="TIwLR64RXGco" colab_type="code" colab={}
import sys
import os
import dlib
import glob
import cv2
import numpy as np
import dlib
cap = cv2.VideoCapture(0)
detector = dlib.get_frontal_face_detector()
predictor = dlib.shape_predictor("shape_predictor_68_face_landmarks.dat")
while True:
_, frame = cap.read()
gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)
faces = detector(gray)
for face in faces:
x1 = face.left()
y1 = face.top()
x2 = face.right()
y2 = face.bottom()
#cv2.rectangle(frame, (x1, y1), (x2, y2), (0, 255, 0), 3)
landmarks = predictor(gray, face)
for n in range(0, 68):
x = landmarks.part(n).x
y = landmarks.part(n).y
cv2.circle(frame, (x, y), 4, (255, 0, 0), -1)
cv2.imshow("Frame", frame)
key = cv2.waitKey(1)
if key == 27:
break
# + [markdown] id="x3nN2ycM8itX" colab_type="text"
# ```
# 'Colab_root',
# 'ColorPrint',
# 'FileView',
# 'FlickrS',
# 'GdriveD',
# 'Gdrive_root',
# 'GlobX',
# 'GooScrape',
# 'ImgCrawler',
# 'ImgTools',
# 'LogGER',
# 'Logger',
# 'MethHelp',
# 'Ops',
# 'Repo_List',
# 'Resize',
# 'Sys_Cmd',
# 'Sys_Exec',
# 'ZipUp',
# ```
# + [markdown] id="IavB8R6c_Xag" colab_type="text"
# ```
# Help on method flickr_scrape in module Helpers.core:
#
# flickr_scrape(query=['portrait'], qty=5, dest='/content/images') method of Helpers.core.Core instance
# Example:
# search_list,img_dir,qty = ['portait','face'], 'images', 21
# flickr_scrape(search_list,qty,img_dir)
# ```
# + id="73UZFOk2Gism" colab_type="code" colab={}
# HelpCore.GlobX('/content/images_bohdgaya', '*.*g')
# from pydrive.auth import GoogleAuth
# from pydrive.drive import GoogleDrive
# def GFoldeR(mode='show', file ,folder='/content')
# gauth = GoogleAuth()
# gauth.LocalWebserverAuth()
# drive = GoogleDrive(gauth)
# if mode == 'create':
# # Create folder.
# folder_metadata = {
# 'title' : '<your folder name here>',
# # The mimetype defines this new file as a folder, so don't change this.
# 'mimeType' : 'application/vnd.google-apps.folder'
# }
# folder = drive.CreateFile(folder_metadata)
# folder.Upload()
# if mode == 'info':
# # Get folder info and print to screen.
# folder_title = folder['title']
# folder_id = folder['id']
# print('title: %s, id: %s' % (folder_title, folder_id))
# if mode == 'upload':
# # Upload file to folder.
# f = drive.CreateFile({"parents": [{"kind": "drive#fileLink", "id": folder_id}]})
# # Make sure to add the path to the file to upload below.
# f.SetContentFile('<file path here>')
# f.Upload()
# + id="IPS_BiaGIFbL" colab_type="code" colab={}
# import random
# import numpy as np
# import cv2 as cv
# frame1 = cv.imread(cv.samples.findFile('lena.jpg'))
# if frame1 is None:
# print("image not found")
# exit()
# frame = np.vstack((frame1,frame1))
# facemark = cv.face.createFacemarkLBF()
# try:
# facemark.loadModel(cv.samples.findFile('lbfmodel.yaml'))
# except cv.error:
# print("Model not found\nlbfmodel.yaml can be download at")
# print("https://raw.githubusercontent.com/kurnianggoro/GSOC2017/master/data/lbfmodel.yaml")
# cascade = cv.CascadeClassifier(cv.samples.findFile('lbpcascade_frontalface_improved.xml'))
# if cascade.empty() :
# print("cascade not found")
# exit()
# faces = cascade.detectMultiScale(frame, 1.05, 3, cv.CASCADE_SCALE_IMAGE, (30, 30))
# ok, landmarks = facemark.fit(frame, faces=faces)
# cv.imshow("Image", frame)
# for marks in landmarks:
# couleur = (random.randint(0,255),
# random.randint(0,255),
# random.randint(0,255))
# cv.face.drawFacemarks(frame, marks, couleur)
# cv.imshow("Image Landmarks", frame)
# cv.waitKey()
|
Old_Horse_Gone.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.3.0
# language: julia
# name: julia-1.3
# ---
# # Transpose
#
# Given an input text output it transposed.
#
# Roughly explained, the transpose of a matrix:
#
# ```text
# ABC
# DEF
# ```
#
# is given by:
#
# ```text
# AD
# BE
# CF
# ```
#
# Rows become columns and columns become rows. See <https://en.wikipedia.org/wiki/Transpose>.
#
# If the input has rows of different lengths, this is to be solved as follows:
#
# - Pad to the left with spaces.
# - Don't pad to the right.
#
# Therefore, transposing this matrix:
#
# ```text
# ABC
# DE
# ```
#
# results in:
#
# ```text
# AD
# BE
# C
# ```
#
# And transposing:
#
# ```text
# AB
# DEF
# ```
#
# results in:
#
# ```text
# AD
# BE
# F
# ```
#
# In general, all characters from the input should also be present in the transposed output.
# That means that if a column in the input text contains only spaces on its bottom-most row(s),
# the corresponding output row should contain the spaces in its right-most column(s).
#
# ## Source
#
# Reddit r/dailyprogrammer challenge #270 [Easy]. [https://www.reddit.com/r/dailyprogrammer/comments/4msu2x/challenge_270_easy_transpose_the_input_text](https://www.reddit.com/r/dailyprogrammer/comments/4msu2x/challenge_270_easy_transpose_the_input_text)
#
# ## Version compatibility
# This exercise has been tested on Julia versions >=1.0.
#
# ## Submitting Incomplete Solutions
# It's possible to submit an incomplete solution so you can see how others have completed the exercise.
# ## Your solution
# +
# submit
function transpose_strings(input::AbstractArray)
end
# -
# ## Test suite
# +
using Test
# include("transpose.jl")
@testset "empty string" begin
@test transpose_strings([]) == []
end
@testset "two characters in a row" begin
@test transpose_strings(["A1"]) == ["A", "1"]
end
@testset "two characters in a column" begin
@test transpose_strings(["A", "1"]) == ["A1"]
end
@testset "simple" begin
@test transpose_strings(["ABC", "123"]) == [
"A1",
"B2",
"C3"
]
end
@testset "single line" begin
@test transpose_strings(["Single line."]) == [
"S",
"i",
"n",
"g",
"l",
"e",
" ",
"l",
"i",
"n",
"e",
"."
]
end
@testset "first line longer than second line" begin
@test transpose_strings([
"The fourth line.",
"The fifth line."
]) == [
"TT",
"hh",
"ee",
" ",
"ff",
"oi",
"uf",
"rt",
"th",
"h ",
" l",
"li",
"in",
"ne",
"e.",
"."
]
end
@testset "second line longer than first line" begin
@test transpose_strings([
"The first line.",
"The second line."
]) == [
"TT",
"hh",
"ee",
" ",
"fs",
"ie",
"rc",
"so",
"tn",
" d",
"l ",
"il",
"ni",
"en",
".e",
" ."
]
end
@testset "square" begin
@test transpose_strings([
"HEART",
"EMBER",
"ABUSE",
"RESIN",
"TREND"
]) == [
"HEART",
"EMBER",
"ABUSE",
"RESIN",
"TREND"
]
end
@testset "rectangle" begin
@test transpose_strings([
"FRACTURE",
"OUTLINED",
"BLOOMING",
"SEPTETTE"
]) == [
"FOBS",
"RULE",
"ATOP",
"CLOT",
"TIME",
"UNIT",
"RENT",
"EDGE"
]
end
@testset "triangle" begin
@test transpose_strings([
"T",
"EE",
"AAA",
"SSSS",
"EEEEE",
"RRRRRR"
]) == [
"TEASER",
" EASER",
" ASER",
" SER",
" ER",
" R"
]
end
@testset "many lines" begin
@test transpose_strings([
"Chor. Two households, both alike in dignity,",
"In fair Verona, where we lay our scene,",
"From ancient grudge break to new mutiny,",
"Where civil blood makes civil hands unclean.",
"From forth the fatal loins of these two foes",
"A pair of star-cross'd lovers take their life;",
"Whose misadventur'd piteous overthrows",
"Doth with their death bury their parents' strife.",
"The fearful passage of their death-mark'd love,",
"And the continuance of their parents' rage,",
"Which, but their children's end, naught could remove,",
"Is now the two hours' traffic of our stage;",
"The which if you with patient ears attend,",
"What here shall miss, our toil shall strive to mend."
]) == [
"CIFWFAWDTAWITW",
"hnrhr hohnhshh",
"o oeopotedi ea",
"rfmrmash cn t",
".a e ie fthow ",
" ia fr weh,whh",
"Trnco miae ie",
"w ciroitr btcr",
"oVivtfshfcuhhe",
" eeih a uote ",
"hrnl sdtln is",
"oot ttvh tttfh",
"un bhaeepihw a",
"saglernianeoyl",
"e,ro -trsui ol",
"h uofcu sarhu ",
"owddarrdan o m",
"lhg to'egccuwi",
"deemasdaeehris",
"sr als t ists",
",ebk 'phool'h,",
" reldi ffd ",
"bweso tb rtpo",
"oea ileutterau",
"t kcnoorhhnatr",
"hl isvuyee'fi ",
" atv es iisfet",
"ayoior trr ino",
"l lfsoh ecti",
"ion vedpn l",
"kuehtteieadoe ",
"erwaharrar,fas",
" nekt te rh",
"ismdsehphnnosa",
"ncuse ra-tau l",
" et tormsural",
"dniuthwea'g t ",
"iennwesnr hsts",
"g,ycoi tkrttet",
"n ,l r s'a anr",
"i ef 'dgcgdi",
"t aol eoe,v",
"y nei sl,u; e",
", .sf to l ",
" e rv d t",
" ; ie o",
" f, r ",
" e e m",
" . m e",
" o n",
" v d",
" e .",
" ,"]
end
# -
# ## Prepare submission
# To submit your exercise, you need to save your solution in a file called `transpose.jl` before using the CLI.
# You can either create it manually or use the following functions, which will automatically write every notebook cell that starts with `# submit` to the file `transpose.jl`.
#
# +
# using Pkg; Pkg.add("Exercism")
# using Exercism
# Exercism.create_submission("transpose")
|
exercises/transpose/transpose.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Chapter 6: Sections 2-3
# %pylab inline
# ## 6.2 Nearest-Neighbor Density Estimation
# This method was first proposed by Dressler 1980 in an astrophysical context. The implied point density at a position $x$ is
# $\hat{f}_{K}(x) = \frac{K}{V_{D}(d_{K})}$
# or more simply
# $\hat{f}_{K}(x) = \frac{C}{d^{D}_{K}}$
# This relies on the assumption that the underlying density field is locally constant. The fractional error is
# $\frac{\sigma_{f}}{\hat{f}_{K}} = \frac{1}{K^{1/2}}$ and the effective resolution scales with $K^{1/D}$
# Leading to the fractional accuracy increasing with K while the spatial resolution gets worse.
# In practice $K$ should be at least 5.
# #### Figure 6.4 which is again a density estimation for the SDSS "Great Wall". This time including an estimation using the nearest-neighbor method, one looking at small scale structure ($K$ = 5) and the other looking at large scale structure ($K$ = 40).
# +
# Author: <NAME>
# License: BSD
# The figure produced by this code is published in the textbook
# "Statistics, Data Mining, and Machine Learning in Astronomy" (2013)
# For more information, see http://astroML.github.com
# To report a bug or issue, use the following forum:
# https://groups.google.com/forum/#!forum/astroml-general
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.colors import LogNorm
from scipy.spatial import cKDTree
from astroML.datasets import fetch_great_wall
from astroML.density_estimation import KDE, KNeighborsDensity
#----------------------------------------------------------------------
# This function adjusts matplotlib settings for a uniform feel in the textbook.
# Note that with usetex=True, fonts are rendered with LaTeX. This may
# result in an error if LaTeX is not installed on your system. In that case,
# you can set usetex to False.
from astroML.plotting import setup_text_plots
setup_text_plots(fontsize=8, usetex=True)
#------------------------------------------------------------
# Fetch the great wall data
X = fetch_great_wall()
#------------------------------------------------------------
# Create the grid on which to evaluate the results
Nx = 50
Ny = 125
xmin, xmax = (-375, -175)
ymin, ymax = (-300, 200)
#------------------------------------------------------------
# Evaluate for several models
Xgrid = np.vstack(map(np.ravel, np.meshgrid(np.linspace(xmin, xmax, Nx),
np.linspace(ymin, ymax, Ny)))).T
kde = KDE(metric='gaussian', h=5)
dens_KDE = kde.fit(X).eval(Xgrid).reshape((Ny, Nx))
knn5 = KNeighborsDensity('bayesian', 5)
dens_k5 = knn5.fit(X).eval(Xgrid).reshape((Ny, Nx))
knn40 = KNeighborsDensity('bayesian', 40)
dens_k40 = knn40.fit(X).eval(Xgrid).reshape((Ny, Nx))
#------------------------------------------------------------
# Plot the results
fig = plt.figure(figsize=(12.5, 5.5))
fig.subplots_adjust(left=0.12, right=0.95, bottom=0.2, top=0.9,
hspace=0.01, wspace=0.01)
# First plot: scatter the points
ax1 = plt.subplot(221, aspect='equal')
ax1.scatter(X[:, 1], X[:, 0], s=1, lw=0, c='k')
ax1.text(0.95, 0.9, "input", ha='right', va='top',
transform=ax1.transAxes,
bbox=dict(boxstyle='round', ec='k', fc='w'))
# Second plot: KDE
ax2 = plt.subplot(222, aspect='equal')
ax2.imshow(dens_KDE.T, origin='lower', norm=LogNorm(),
extent=(ymin, ymax, xmin, xmax), cmap=plt.cm.binary)
ax2.text(0.95, 0.9, "KDE: Gaussian $(h=5)$", ha='right', va='top',
transform=ax2.transAxes,
bbox=dict(boxstyle='round', ec='k', fc='w'))
# Third plot: KNN, k=5
ax3 = plt.subplot(223, aspect='equal')
ax3.imshow(dens_k5.T, origin='lower', norm=LogNorm(),
extent=(ymin, ymax, xmin, xmax), cmap=plt.cm.binary)
ax3.text(0.95, 0.9, "$k$-neighbors $(k=5)$", ha='right', va='top',
transform=ax3.transAxes,
bbox=dict(boxstyle='round', ec='k', fc='w'))
# Fourth plot: KNN, k=40
ax4 = plt.subplot(224, aspect='equal')
ax4.imshow(dens_k40.T, origin='lower', norm=LogNorm(),
extent=(ymin, ymax, xmin, xmax), cmap=plt.cm.binary)
ax4.text(0.95, 0.9, "$k$-neighbors $(k=40)$", ha='right', va='top',
transform=ax4.transAxes,
bbox=dict(boxstyle='round', ec='k', fc='w'))
for ax in [ax1, ax2, ax3, ax4]:
ax.set_xlim(ymin, ymax - 0.01)
ax.set_ylim(xmin, xmax)
for ax in [ax1, ax2]:
ax.xaxis.set_major_formatter(plt.NullFormatter())
for ax in [ax3, ax4]:
ax.set_xlabel('$y$ (Mpc)')
for ax in [ax2, ax4]:
ax.yaxis.set_major_formatter(plt.NullFormatter())
for ax in [ax1, ax3]:
ax.set_ylabel('$x$ (Mpc)')
plt.show()
# -
# KDE, nearest-neighbor methods, and Bayesian blocks all produce similar results for larger sample sizes. See Figure 6.5 in the text for an example.
# ## 6.3 Parametric Density Estimation
# Mixture Models: These methods use fewer kernels than the KDE method. The kernels are fit to both location and width.
# ### 6.3.1 Gaussian Mixture Model
# This is the most common mixture model and is exactly what it sounds like. The density of points is given by
# $\rho({\bf x}) = Np({\bf x}) = N \displaystyle \sum^{M}_{j=1} \alpha_{j}\mathcal{N}(\mu_{j},\Sigma_{j})$
# where there are $M$ Gaussians at locations $\mu_{j}$ with covariances $\Sigma_{j}$
# #### Figure 6.6: Stellar Metallicity data from SEGUE. Assuming the data can be fit by two Gaussians
# +
# Author: <NAME>
# License: BSD
# The figure produced by this code is published in the textbook
# "Statistics, Data Mining, and Machine Learning in Astronomy" (2013)
# For more information, see http://astroML.github.com
# To report a bug or issue, use the following forum:
# https://groups.google.com/forum/#!forum/astroml-general
import numpy as np
from matplotlib import pyplot as plt
from scipy.stats import norm
from sklearn.mixture import GMM
from astroML.datasets import fetch_sdss_sspp
from astroML.decorators import pickle_results
from astroML.plotting.tools import draw_ellipse
#----------------------------------------------------------------------
# This function adjusts matplotlib settings for a uniform feel in the textbook.
# Note that with usetex=True, fonts are rendered with LaTeX. This may
# result in an error if LaTeX is not installed on your system. In that case,
# you can set usetex to False.
from astroML.plotting import setup_text_plots
setup_text_plots(fontsize=8, usetex=True)
#------------------------------------------------------------
# Get the Segue Stellar Parameters Pipeline data
data = fetch_sdss_sspp(cleaned=True)
X = np.vstack([data['FeH'], data['alphFe']]).T
# truncate dataset for speed
#X = X[::10]
#------------------------------------------------------------
# Compute GMM models & AIC/BIC
N = np.arange(1, 14)
@pickle_results("GMM_metallicity.pkl")
def compute_GMM(N, covariance_type='full', n_iter=1000):
models = [None for n in N]
for i in range(len(N)):
print N[i]
models[i] = GMM(n_components=N[i], n_iter=n_iter,
covariance_type=covariance_type)
models[i].fit(X)
return models
models = compute_GMM(N)
AIC = [m.aic(X) for m in models]
BIC = [m.bic(X) for m in models]
i_best = np.argmin(BIC)
gmm_best = models[3]
print "best fit converged:", gmm_best.converged_
print "BIC: n_components = %i" % N[i_best]
#------------------------------------------------------------
# compute 2D density
FeH_bins = 51
alphFe_bins = 51
H, FeH_bins, alphFe_bins = np.histogram2d(data['FeH'], data['alphFe'],
(FeH_bins, alphFe_bins))
Xgrid = np.array(map(np.ravel,
np.meshgrid(0.5 * (FeH_bins[:-1]
+ FeH_bins[1:]),
0.5 * (alphFe_bins[:-1]
+ alphFe_bins[1:])))).T
log_dens = gmm_best.score(Xgrid).reshape((51, 51))
#------------------------------------------------------------
# Plot the results
fig = plt.figure(figsize=(12, 4))
fig.subplots_adjust(wspace=0.45,
bottom=0.25, top=0.9,
left=0.1, right=0.97)
# plot density
ax = fig.add_subplot(131)
ax.imshow(H.T, origin='lower', interpolation='nearest', aspect='auto',
extent=[FeH_bins[0], FeH_bins[-1],
alphFe_bins[0], alphFe_bins[-1]],
cmap=plt.cm.binary)
ax.set_xlabel(r'$\rm [Fe/H]$')
ax.set_ylabel(r'$\rm [\alpha/Fe]$')
ax.xaxis.set_major_locator(plt.MultipleLocator(0.3))
ax.set_xlim(-1.101, 0.101)
ax.text(0.93, 0.93, "Input",
va='top', ha='right', transform=ax.transAxes)
# plot AIC/BIC
ax = fig.add_subplot(132)
ax.plot(N, AIC, '-k', label='AIC')
ax.plot(N, BIC, ':k', label='BIC')
ax.legend(loc=1)
ax.set_xlabel('N components')
plt.setp(ax.get_yticklabels(), fontsize=7)
# plot best configurations for AIC and BIC
ax = fig.add_subplot(133)
ax.imshow(np.exp(log_dens),
origin='lower', interpolation='nearest', aspect='auto',
extent=[FeH_bins[0], FeH_bins[-1],
alphFe_bins[0], alphFe_bins[-1]],
cmap=plt.cm.binary)
ax.scatter(gmm_best.means_[:, 0], gmm_best.means_[:, 1], c='w')
for mu, C, w in zip(gmm_best.means_, gmm_best.covars_, gmm_best.weights_):
draw_ellipse(mu, C, scales=[1.5], ax=ax, fc='none', ec='k')
ax.text(0.93, 0.93, "Converged",
va='top', ha='right', transform=ax.transAxes)
ax.set_xlim(-1.101, 0.101)
ax.set_ylim(alphFe_bins[0], alphFe_bins[-1])
ax.xaxis.set_major_locator(plt.MultipleLocator(0.3))
ax.set_xlabel(r'$\rm [Fe/H]$')
ax.set_ylabel(r'$\rm [\alpha/Fe]$')
plt.show()
# -
# #### Figure 6.9: Showing how the BIC-optimized number of components does not reflect the actual number of sources and depends on the number of points.
# +
# Author: <NAME>
# License: BSD
# The figure produced by this code is published in the textbook
# "Statistics, Data Mining, and Machine Learning in Astronomy" (2013)
# For more information, see http://astroML.github.com
# To report a bug or issue, use the following forum:
# https://groups.google.com/forum/#!forum/astroml-general
import numpy as np
from matplotlib import pyplot as plt
from scipy.stats import norm
from sklearn.mixture import GMM
from astroML.utils import convert_2D_cov
from astroML.plotting.tools import draw_ellipse
#----------------------------------------------------------------------
# This function adjusts matplotlib settings for a uniform feel in the textbook.
# Note that with usetex=True, fonts are rendered with LaTeX. This may
# result in an error if LaTeX is not installed on your system. In that case,
# you can set usetex to False.
from astroML.plotting import setup_text_plots
setup_text_plots(fontsize=8, usetex=True)
#------------------------------------------------------------
# Set up the dataset
# We'll use scikit-learn's Gaussian Mixture Model to sample
# data from a mixture of Gaussians. The usual way of using
# this involves fitting the mixture to data: we'll see that
# below. Here we'll set the internal means, covariances,
# and weights by-hand.
# we'll define clusters as (mu, sigma1, sigma2, alpha, frac)
clusters = [((50, 50), 20, 20, 0, 0.1),
((40, 40), 10, 10, np.pi / 6, 0.6),
((80, 80), 5, 5, np.pi / 3, 0.2),
((60, 60), 30, 30, 0, 0.1)]
gmm_input = GMM(len(clusters), covariance_type='full')
gmm_input.means_ = np.array([c[0] for c in clusters])
gmm_input.covars_ = np.array([convert_2D_cov(*c[1:4]) for c in clusters])
gmm_input.weights_ = np.array([c[4] for c in clusters])
gmm_input.weights_ /= gmm_input.weights_.sum()
#------------------------------------------------------------
# Compute and plot the results
fig = plt.figure(figsize=(12, 12))
fig.subplots_adjust(left=0.11, right=0.9, bottom=0.11, top=0.9,
hspace=0, wspace=0)
ax_list = [fig.add_subplot(s) for s in [221, 223, 224]]
ax_list.append(fig.add_axes([0.62, 0.62, 0.28, 0.28]))
linestyles = ['-', '--', ':']
grid = np.linspace(-5, 105, 70)
Xgrid = np.array(np.meshgrid(grid, grid))
Xgrid = Xgrid.reshape(2, -1).T
Nclusters = np.arange(1, 8)
for Npts, ax, ls in zip([100, 1000, 10000], ax_list, linestyles):
np.random.seed(1)
X = gmm_input.sample(Npts)
# find best number of clusters via BIC
clfs = [GMM(N, n_iter=500).fit(X)
for N in Nclusters]
BICs = np.array([clf.bic(X) for clf in clfs])
print "%i points convergence:" % Npts, [clf.converged_ for clf in clfs]
# plot the BIC
ax_list[3].plot(Nclusters, BICs / Npts, ls, c='k',
label="N=%i" % Npts)
clf = clfs[np.argmin(BICs)]
log_dens = clf.score(Xgrid).reshape((70, 70))
# scatter the points
ax.plot(X[:, 0], X[:, 1], 'k.', alpha=0.3, zorder=1)
# plot the components
for i in range(clf.n_components):
mean = clf.means_[i]
cov = clf.covars_[i]
if cov.ndim == 1:
cov = np.diag(cov)
draw_ellipse(mean, cov, ax=ax, fc='none', ec='k', zorder=2)
# label the plot
ax.text(0.05, 0.95, "N = %i points" % Npts,
ha='left', va='top', transform=ax.transAxes,
bbox=dict(fc='w', ec='k'))
ax.set_xlim(-5, 105)
ax.set_ylim(-5, 105)
ax_list[0].xaxis.set_major_formatter(plt.NullFormatter())
ax_list[2].yaxis.set_major_formatter(plt.NullFormatter())
for i in (0, 1):
ax_list[i].set_ylabel('$y$')
for j in (1, 2):
ax_list[j].set_xlabel('$x$')
ax_list[-1].legend(loc=1)
ax_list[-1].set_xlabel('n. clusters')
ax_list[-1].set_ylabel('$BIC / N$')
ax_list[-1].set_ylim(16, 18.5)
plt.show()
# -
# ### 6.3.3 GMM with Errors: Extreme Deconvolution
# $p({\bf x}) = \displaystyle \sum^{M}_{j=1} \alpha_{j}\mathcal{N}\left({\bf x}\ \middle |\ \mu_{j},\Sigma_{j}\right)$
# ${\bf x}_{i} = {\bf R}_{i}{\bf v}_{i} + \epsilon_{i}$
# See <NAME>., <NAME>, <NAME> (2011) for a more detailed description of the EM procedure.
# +
# Author: <NAME>
# License: BSD
# The figure produced by this code is published in the textbook
# "Statistics, Data Mining, and Machine Learning in Astronomy" (2013)
# For more information, see http://astroML.github.com
# To report a bug or issue, use the following forum:
# https://groups.google.com/forum/#!forum/astroml-general
import numpy as np
from matplotlib import pyplot as plt
from astroML.density_estimation import XDGMM
from astroML.crossmatch import crossmatch
from astroML.datasets import fetch_sdss_S82standards, fetch_imaging_sample
from astroML.plotting.tools import draw_ellipse
from astroML.decorators import pickle_results
from astroML.stats import sigmaG
#----------------------------------------------------------------------
# This function adjusts matplotlib settings for a uniform feel in the textbook.
# Note that with usetex=True, fonts are rendered with LaTeX. This may
# result in an error if LaTeX is not installed on your system. In that case,
# you can set usetex to False.
from astroML.plotting import setup_text_plots
setup_text_plots(fontsize=8, usetex=True)
#------------------------------------------------------------
# define u-g-r-i-z extinction from Berry et al, arXiv 1111.4985
# multiply extinction by A_r
extinction_vector = np.array([1.810, 1.400, 1.0, 0.759, 0.561])
#----------------------------------------------------------------------
# Fetch and process the noisy imaging data
data_noisy = fetch_imaging_sample()
# select only stars
data_noisy = data_noisy[data_noisy['type'] == 6]
# Get the extinction-corrected magnitudes for each band
X = np.vstack([data_noisy[f + 'RawPSF'] for f in 'ugriz']).T
Xerr = np.vstack([data_noisy[f + 'psfErr'] for f in 'ugriz']).T
# extinction terms from Berry et al, arXiv 1111.4985
X -= (extinction_vector * data_noisy['rExtSFD'][:, None])
#----------------------------------------------------------------------
# Fetch and process the stacked imaging data
data_stacked = fetch_sdss_S82standards()
# cut to RA, DEC range of imaging sample
RA = data_stacked['RA']
DEC = data_stacked['DEC']
data_stacked = data_stacked[(RA > 0) & (RA < 10) &
(DEC > -1) & (DEC < 1)]
# get stacked magnitudes for each band
Y = np.vstack([data_stacked['mmu_' + f] for f in 'ugriz']).T
Yerr = np.vstack([data_stacked['msig_' + f] for f in 'ugriz']).T
# extinction terms from Berry et al, arXiv 1111.4985
Y -= (extinction_vector * data_stacked['A_r'][:, None])
# quality cuts
g = Y[:, 1]
mask = ((Yerr.max(1) < 0.05) &
(g < 20))
data_stacked = data_stacked[mask]
Y = Y[mask]
Yerr = Yerr[mask]
#----------------------------------------------------------------------
# cross-match
# the imaging sample contains both standard and variable stars. We'll
# perform a cross-match with the standard star catalog and choose objects
# which are common to both.
Xlocs = np.hstack((data_noisy['ra'][:, np.newaxis],
data_noisy['dec'][:, np.newaxis]))
Ylocs = np.hstack((data_stacked['RA'][:, np.newaxis],
data_stacked['DEC'][:, np.newaxis]))
print "number of noisy points: ", Xlocs.shape
print "number of stacked points:", Ylocs.shape
# find all points within 0.9 arcsec. This cutoff was selected
# by plotting a histogram of the log(distances).
dist, ind = crossmatch(Xlocs, Ylocs, max_distance=0.9 / 3600.)
noisy_mask = (~np.isinf(dist))
stacked_mask = ind[noisy_mask]
# select the data
data_noisy = data_noisy[noisy_mask]
X = X[noisy_mask]
Xerr = Xerr[noisy_mask]
data_stacked = data_stacked[stacked_mask]
Y = Y[stacked_mask]
Yerr = Yerr[stacked_mask]
# double-check that our cross-match succeeded
assert X.shape == Y.shape
print "size after crossmatch:", X.shape
#----------------------------------------------------------------------
# perform extreme deconvolution on the noisy sample
# first define mixing matrix W
W = np.array([[0, 1, 0, 0, 0], # g magnitude
[1, -1, 0, 0, 0], # u-g color
[0, 1, -1, 0, 0], # g-r color
[0, 0, 1, -1, 0], # r-i color
[0, 0, 0, 1, -1]]) # i-z color
X = np.dot(X, W.T)
Y = np.dot(Y, W.T)
# compute error covariance from mixing matrix
Xcov = np.zeros(Xerr.shape + Xerr.shape[-1:])
Xcov[:, range(Xerr.shape[1]), range(Xerr.shape[1])] = Xerr ** 2
# each covariance C = WCW^T
# best way to do this is with a tensor dot-product
Xcov = np.tensordot(np.dot(Xcov, W.T), W, (-2, -1))
#----------------------------------------------------------------------
# This is a long calculation: save results to file
@pickle_results("XD_stellar.pkl")
def compute_XD(n_clusters=12, rseed=0, n_iter=100, verbose=True):
np.random.seed(rseed)
clf = XDGMM(n_clusters, n_iter=n_iter, tol=1E-5, verbose=verbose)
clf.fit(X, Xcov)
return clf
clf = compute_XD(12)
#------------------------------------------------------------
# Fit and sample from the underlying distribution
np.random.seed(42)
X_sample = clf.sample(X.shape[0])
#------------------------------------------------------------
# +
import numpy as np
from matplotlib import pyplot as plt
# plot the results
fig = plt.figure(figsize=(10, 7.5))
fig.subplots_adjust(left=0.12, right=0.95,
bottom=0.1, top=0.95,
wspace=0.02, hspace=0.02)
# only plot 1/10 of the stars for clarity
ax1 = fig.add_subplot(221)
ax1.scatter(Y[::10, 2], Y[::10, 3], s=9, lw=0, c='k')
ax2 = fig.add_subplot(222)
ax2.scatter(X[::10, 2], X[::10, 3], s=9, lw=0, c='k')
ax3 = fig.add_subplot(223)
ax3.scatter(X_sample[::10, 2], X_sample[::10, 3], s=9, lw=0, c='k')
ax4 = fig.add_subplot(224)
for i in range(clf.n_components):
draw_ellipse(clf.mu[i, 2:4], clf.V[i, 2:4, 2:4], scales=[2],
ec='k', fc='gray', alpha=0.2, ax=ax4)
titles = ["Standard Stars", "Single Epoch",
"Extreme Deconvolution\n resampling",
"Extreme Deconvolution\n cluster locations"]
ax = [ax1, ax2, ax3, ax4]
for i in range(4):
ax[i].set_xlim(-0.6, 1.8)
ax[i].set_ylim(-0.6, 1.8)
ax[i].xaxis.set_major_locator(plt.MultipleLocator(0.5))
ax[i].yaxis.set_major_locator(plt.MultipleLocator(0.5))
ax[i].text(0.05, 0.95, titles[i],
ha='left', va='top', transform=ax[i].transAxes)
if i in (0, 1):
ax[i].xaxis.set_major_formatter(plt.NullFormatter())
else:
ax[i].set_xlabel('$g-r$')
if i in (1, 3):
ax[i].yaxis.set_major_formatter(plt.NullFormatter())
else:
ax[i].set_ylabel('$r-i$')
#------------------------------------------------------------
# Second figure: the width of the locus
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111)
labels = ['single epoch', 'standard stars', 'XD resampled']
linestyles = ['solid', 'dashed', 'dotted']
for data, label, ls in zip((X, Y, X_sample), labels, linestyles):
g = data[:, 0]
gr = data[:, 2]
ri = data[:, 3]
r = g - gr
i = r - ri
mask = (gr > 0.3) & (gr < 1.0)
g = g[mask]
r = r[mask]
i = i[mask]
w = -0.227 * g + 0.792 * r - 0.567 * i + 0.05
sigma = sigmaG(w)
ax.hist(w, bins=np.linspace(-0.08, 0.08, 100), linestyle=ls,
histtype='step', label=label + '\n\t' + r'$\sigma_G=%.3f$' % sigma,
normed=True)
ax.legend(loc=2)
ax.text(0.95, 0.95, '$w = -0.227g + 0.792r$\n$ - 0.567i + 0.05$',
transform=ax.transAxes, ha='right', va='top')
ax.set_xlim(-0.07, 0.07)
ax.set_ylim(0, 55)
ax.set_xlabel('$w$')
ax.set_ylabel('$N(w)$')
plt.show()
# -
|
Chapter6/astroML_ch6_sec23.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# [Table of Contents](./table_of_contents.ipynb)
# # Kalman Filter Math
from __future__ import division, print_function
# %matplotlib inline
#format the book
import book_format
book_format.set_style()
# If you've gotten this far I hope that you are thinking that the Kalman filter's fearsome reputation is somewhat undeserved. Sure, I hand waved some equations away, but I hope implementation has been fairly straightforward for you. The underlying concept is quite straightforward - take two measurements, or a measurement and a prediction, and choose the output to be somewhere between the two. If you believe the measurement more your guess will be closer to the measurement, and if you believe the prediction is more accurate your guess will lie closer to it. That's not rocket science (little joke - it is exactly this math that got Apollo to the moon and back!).
#
# To be honest I have been choosing my problems carefully. For an arbitrary problem designing the Kalman filter matrices can be extremely difficult. I haven't been *too tricky*, though. Equations like Newton's equations of motion can be trivially computed for Kalman filter applications, and they make up the bulk of the kind of problems that we want to solve.
#
# I have illustrated the concepts with code and reasoning, not math. But there are topics that do require more mathematics than I have used so far. This chapter presents the math that you will need for the rest of the book.
# ## Modeling a Dynamic System
#
# A *dynamic system* is a physical system whose state (position, temperature, etc) evolves over time. Calculus is the math of changing values, so we use differential equations to model dynamic systems. Some systems cannot be modeled with differential equations, but we will not encounter those in this book.
#
# Modeling dynamic systems is properly the topic of several college courses. To an extent there is no substitute for a few semesters of ordinary and partial differential equations followed by a graduate course in control system theory. If you are a hobbyist, or trying to solve one very specific filtering problem at work you probably do not have the time and/or inclination to devote a year or more to that education.
#
# Fortunately, I can present enough of the theory to allow us to create the system equations for many different Kalman filters. My goal is to get you to the stage where you can read a publication and understand it well enough to implement the algorithms. The background math is deep, but in practice we end up using a few simple techniques.
#
# This is the longest section of pure math in this book. You will need to master everything in this section to understand the Extended Kalman filter (EKF), the most common nonlinear filter. I do cover more modern filters that do not require as much of this math. You can choose to skim now, and come back to this if you decide to learn the EKF.
#
# We need to start by understanding the underlying equations and assumptions that the Kalman filter uses. We are trying to model real world phenomena, so what do we have to consider?
#
# Each physical system has a process. For example, a car traveling at a certain velocity goes so far in a fixed amount of time, and its velocity varies as a function of its acceleration. We describe that behavior with the well known Newtonian equations that we learned in high school.
#
# $$
# \begin{aligned}
# v&=at\\
# x &= \frac{1}{2}at^2 + v_0t + x_0
# \end{aligned}
# $$
#
# Once we learned calculus we saw them in this form:
#
# $$ \mathbf v = \frac{d \mathbf x}{d t},
# \quad \mathbf a = \frac{d \mathbf v}{d t} = \frac{d^2 \mathbf x}{d t^2}
# $$
#
# A typical automobile tracking problem would have you compute the distance traveled given a constant velocity or acceleration, as we did in previous chapters. But, of course we know this is not all that is happening. No car travels on a perfect road. There are bumps, wind drag, and hills that raise and lower the speed. The suspension is a mechanical system with friction and imperfect springs.
#
# Perfectly modeling a system is impossible except for the most trivial problems. We are forced to make a simplification. At any time $t$ we say that the true state (such as the position of our car) is the predicted value from the imperfect model plus some unknown *process noise*:
#
# $$
# x(t) = x_{pred}(t) + noise(t)
# $$
#
# This is not meant to imply that $noise(t)$ is a function that we can derive analytically. It is merely a statement of fact - we can always describe the true value as the predicted value plus the process noise. "Noise" does not imply random events. If we are tracking a thrown ball in the atmosphere, and our model assumes the ball is in a vacuum, then the effect of air drag is process noise in this context.
#
# In the next section we will learn techniques to convert a set of higher order differential equations into a set of first-order differential equations. After the conversion the model of the system without noise is:
#
# $$ \dot{\mathbf x} = \mathbf{Ax}$$
#
# $\mathbf A$ is known as the *systems dynamics matrix* as it describes the dynamics of the system. Now we need to model the noise. We will call that $\mathbf w$, and add it to the equation.
#
# $$ \dot{\mathbf x} = \mathbf{Ax} + \mathbf w$$
#
# $\mathbf w$ may strike you as a poor choice for the name, but you will soon see that the Kalman filter assumes *white* noise.
#
# Finally, we need to consider any inputs into the system. We assume an input $\mathbf u$, and that there exists a linear model that defines how that input changes the system. For example, pressing the accelerator in your car makes it accelerate, and gravity causes balls to fall. Both are control inputs. We will need a matrix $\mathbf B$ to convert $u$ into the effect on the system. We add that into our equation:
#
# $$ \dot{\mathbf x} = \mathbf{Ax} + \mathbf{Bu} + \mathbf{w}$$
#
# And that's it. That is one of the equations that Dr. Kalman set out to solve, and he found an optimal estimator if we assume certain properties of $\mathbf w$.
# ## State-Space Representation of Dynamic Systems
# We've derived the equation
#
# $$ \dot{\mathbf x} = \mathbf{Ax}+ \mathbf{Bu} + \mathbf{w}$$
#
# However, we are not interested in the derivative of $\mathbf x$, but in $\mathbf x$ itself. Ignoring the noise for a moment, we want an equation that recusively finds the value of $\mathbf x$ at time $t_k$ in terms of $\mathbf x$ at time $t_{k-1}$:
#
# $$\mathbf x(t_k) = \mathbf F(\Delta t)\mathbf x(t_{k-1}) + \mathbf B(t_k)\mathbf u (t_k)$$
#
# Convention allows us to write $\mathbf x(t_k)$ as $\mathbf x_k$, which means the
# the value of $\mathbf x$ at the k$^{th}$ value of $t$.
#
# $$\mathbf x_k = \mathbf{Fx}_{k-1} + \mathbf B_k\mathbf u_k$$
#
# $\mathbf F$ is the familiar *state transition matrix*, named due to its ability to transition the state's value between discrete time steps. It is very similar to the system dynamics matrix $\mathbf A$. The difference is that $\mathbf A$ models a set of linear differential equations, and is continuous. $\mathbf F$ is discrete, and represents a set of linear equations (not differential equations) which transitions $\mathbf x_{k-1}$ to $\mathbf x_k$ over a discrete time step $\Delta t$.
#
# Finding this matrix is often quite difficult. The equation $\dot x = v$ is the simplest possible differential equation and we trivially integrate it as:
#
# $$ \int\limits_{x_{k-1}}^{x_k} \mathrm{d}x = \int\limits_{0}^{\Delta t} v\, \mathrm{d}t $$
# $$x_k-x_0 = v \Delta t$$
# $$x_k = v \Delta t + x_0$$
#
# This equation is *recursive*: we compute the value of $x$ at time $t$ based on its value at time $t-1$. This recursive form enables us to represent the system (process model) in the form required by the Kalman filter:
#
# $$\begin{aligned}
# \mathbf x_k &= \mathbf{Fx}_{k-1} \\
# &= \begin{bmatrix} 1 & \Delta t \\ 0 & 1\end{bmatrix}
# \begin{bmatrix}x_{k-1} \\ \dot x_{k-1}\end{bmatrix}
# \end{aligned}$$
#
# We can do that only because $\dot x = v$ is the simplest differential equation possible. Almost all other in physical systems result in more complicated differential equation which do not yield to this approach.
#
# *State-space* methods became popular around the time of the Apollo missions, largely due to the work of Dr. Kalman. The idea is simple. Model a system with a set of $n^{th}$-order differential equations. Convert them into an equivalent set of first-order differential equations. Put them into the vector-matrix form used in the previous section: $\dot{\mathbf x} = \mathbf{Ax} + \mathbf{Bu}$. Once in this form we use of of several techniques to convert these linear differential equations into the recursive equation:
#
# $$ \mathbf x_k = \mathbf{Fx}_{k-1} + \mathbf B_k\mathbf u_k$$
#
# Some books call the state transition matrix the *fundamental matrix*. Many use $\mathbf \Phi$ instead of $\mathbf F$. Sources based heavily on control theory tend to use these forms.
#
# These are called *state-space* methods because we are expressing the solution of the differential equations in terms of the system state.
# ### Forming First Order Equations from Higher Order Equations
#
# Many models of physical systems require second or higher order differential equations with control input $u$:
#
# $$a_n \frac{d^ny}{dt^n} + a_{n-1} \frac{d^{n-1}y}{dt^{n-1}} + \dots + a_2 \frac{d^2y}{dt^2} + a_1 \frac{dy}{dt} + a_0 = u$$
#
# State-space methods require first-order equations. Any higher order system of equations can be reduced to first-order by defining extra variables for the derivatives and then solving.
#
#
# Let's do an example. Given the system $\ddot{x} - 6\dot x + 9x = u$ find the equivalent first order equations. I've used the dot notation for the time derivatives for clarity.
#
# The first step is to isolate the highest order term onto one side of the equation.
#
# $$\ddot{x} = 6\dot x - 9x + u$$
#
# We define two new variables:
#
# $$\begin{aligned} x_1(u) &= x \\
# x_2(u) &= \dot x \enspace \text{(Why is the $u$ used?)}
# \end{aligned}$$
#
# Now we will substitute these into the original equation and solve. The solution yields a set of first-order equations in terms of these new variables. It is conventional to drop the $(u)$ for notational convenience.
#
# We know that $\dot x_1 = x_2$ and that $\dot x_2 = \ddot{x}$. Therefore
#
# $$\begin{aligned}
# \dot x_2 &= \ddot{x} \\
# &= 6\dot x - 9x + t\\
# &= 6x_2-9x_1 + t
# \end{aligned}$$
#
# Therefore our first-order system of equations is
#
# $$\begin{aligned}\dot x_1 &= x_2 \\
# \dot x_2 &= 6x_2-9x_1 + t\end{aligned}$$
#
# If you practice this a bit you will become adept at it. Isolate the highest term, define a new variable and its derivatives, and then substitute.
# ### First Order Differential Equations In State-Space Form
#
# Substituting the newly defined variables from the previous section:
#
# $$\frac{dx_1}{dt} = x_2,\,
# \frac{dx_2}{dt} = x_3, \, ..., \,
# \frac{dx_{n-1}}{dt} = x_n$$
#
# into the first order equations yields:
#
# $$\frac{dx_n}{dt} = \frac{1}{a_n}\sum\limits_{i=0}^{n-1}a_ix_{i+1} + \frac{1}{a_n}u
# $$
#
#
# Using vector-matrix notation we have:
#
# $$\begin{bmatrix}\frac{dx_1}{dt} \\ \frac{dx_2}{dt} \\ \vdots \\ \frac{dx_n}{dt}\end{bmatrix} =
# \begin{bmatrix}\dot x_1 \\ \dot x_2 \\ \vdots \\ \dot x_n\end{bmatrix}=
# \begin{bmatrix}0 & 1 & 0 &\cdots & 0 \\
# 0 & 0 & 1 & \cdots & 0 \\
# \vdots & \vdots & \vdots & \ddots & \vdots \\
# -\frac{a_0}{a_n} & -\frac{a_1}{a_n} & -\frac{a_2}{a_n} & \cdots & -\frac{a_{n-1}}{a_n}\end{bmatrix}
# \begin{bmatrix}x_1 \\ x_2 \\ \vdots \\ x_n\end{bmatrix} +
# \begin{bmatrix}0 \\ 0 \\ \vdots \\ \frac{1}{a_n}\end{bmatrix}u$$
#
# which we then write as $\dot{\mathbf x} = \mathbf{Ax} + \mathbf{B}u$.
# ### Finding the Fundamental Matrix for Time Invariant Systems
#
# We express the system equations in state-space form with
#
# $$ \dot{\mathbf x} = \mathbf{Ax}$$
#
# where $\mathbf A$ is the system dynamics matrix, and want to find the *fundamental matrix* $\mathbf F$ that propagates the state $\mathbf x$ over the interval $\Delta t$ with the equation
#
# $$\begin{aligned}
# \mathbf x(t_k) = \mathbf F(\Delta t)\mathbf x(t_{k-1})\end{aligned}$$
#
# In other words, $\mathbf A$ is a set of continuous differential equations, and we need $\mathbf F$ to be a set of discrete linear equations that computes the change in $\mathbf A$ over a discrete time step.
#
# It is conventional to drop the $t_k$ and $(\Delta t)$ and use the notation
#
# $$\mathbf x_k = \mathbf {Fx}_{k-1}$$
#
# Broadly speaking there are three common ways to find this matrix for Kalman filters. The technique most often used is the matrix exponential. Linear Time Invariant Theory, also known as LTI System Theory, is a second technique. Finally, there are numerical techniques. You may know of others, but these three are what you will most likely encounter in the Kalman filter literature and praxis.
# ### The Matrix Exponential
#
# The solution to the equation $\frac{dx}{dt} = kx$ can be found by:
#
# $$\begin{gathered}\frac{dx}{dt} = kx \\
# \frac{dx}{x} = k\, dt \\
# \int \frac{1}{x}\, dx = \int k\, dt \\
# \log x = kt + c \\
# x = e^{kt+c} \\
# x = e^ce^{kt} \\
# x = c_0e^{kt}\end{gathered}$$
#
# Using similar math, the solution to the first-order equation
#
# $$\dot{\mathbf x} = \mathbf{Ax} ,\, \, \, \mathbf x(0) = \mathbf x_0$$
#
# where $\mathbf A$ is a constant matrix, is
#
# $$\mathbf x = e^{\mathbf At}\mathbf x_0$$
#
# Substituting $F = e^{\mathbf At}$, we can write
#
# $$\mathbf x_k = \mathbf F\mathbf x_{k-1}$$
#
# which is the form we are looking for! We have reduced the problem of finding the fundamental matrix to one of finding the value for $e^{\mathbf At}$.
#
# $e^{\mathbf At}$ is known as the [matrix exponential](https://en.wikipedia.org/wiki/Matrix_exponential). It can be computed with this power series:
#
# $$e^{\mathbf At} = \mathbf{I} + \mathbf{A}t + \frac{(\mathbf{A}t)^2}{2!} + \frac{(\mathbf{A}t)^3}{3!} + ... $$
#
# That series is found by doing a Taylor series expansion of $e^{\mathbf At}$, which I will not cover here.
#
# Let's use this to find the solution to Newton's equations. Using $v$ as a substitution for $\dot x$, and assuming constant velocity we get the linear matrix-vector form
#
# $$\begin{bmatrix}\dot x \\ \dot v\end{bmatrix} =\begin{bmatrix}0&1\\0&0\end{bmatrix} \begin{bmatrix}x \\ v\end{bmatrix}$$
#
# This is a first order differential equation, so we can set $\mathbf{A}=\begin{bmatrix}0&1\\0&0\end{bmatrix}$ and solve the following equation. I have substituted the interval $\Delta t$ for $t$ to emphasize that the fundamental matrix is discrete:
#
# $$\mathbf F = e^{\mathbf A\Delta t} = \mathbf{I} + \mathbf A\Delta t + \frac{(\mathbf A\Delta t)^2}{2!} + \frac{(\mathbf A\Delta t)^3}{3!} + ... $$
#
# If you perform the multiplication you will find that $\mathbf{A}^2=\begin{bmatrix}0&0\\0&0\end{bmatrix}$, which means that all higher powers of $\mathbf{A}$ are also $\mathbf{0}$. Thus we get an exact answer without an infinite number of terms:
#
# $$
# \begin{aligned}
# \mathbf F &=\mathbf{I} + \mathbf A \Delta t + \mathbf{0} \\
# &= \begin{bmatrix}1&0\\0&1\end{bmatrix} + \begin{bmatrix}0&1\\0&0\end{bmatrix}\Delta t\\
# &= \begin{bmatrix}1&\Delta t\\0&1\end{bmatrix}
# \end{aligned}$$
#
# We plug this into $\mathbf x_k= \mathbf{Fx}_{k-1}$ to get
#
# $$
# \begin{aligned}
# x_k &=\begin{bmatrix}1&\Delta t\\0&1\end{bmatrix}x_{k-1}
# \end{aligned}$$
#
# You will recognize this as the matrix we derived analytically for the constant velocity Kalman filter in the **Multivariate Kalman Filter** chapter.
#
# SciPy's linalg module includes a routine `expm()` to compute the matrix exponential. It does not use the Taylor series method, but the [Padé Approximation](https://en.wikipedia.org/wiki/Pad%C3%A9_approximant). There are many (at least 19) methods to compute the matrix exponential, and all suffer from numerical difficulties[1]. You should be aware of the problems, especially when $\mathbf A$ is large. If you search for "pade approximation matrix exponential" you will find many publications devoted to this problem.
#
# In practice this may not be of concern to you as for the Kalman filter we normally just take the first two terms of the Taylor series. But don't assume my treatment of the problem is complete and run off and try to use this technique for other problem without doing a numerical analysis of the performance of this technique. Interestingly, one of the favored ways of solving $e^{\mathbf At}$ is to use a generalized ode solver. In other words, they do the opposite of what we do - turn $\mathbf A$ into a set of differential equations, and then solve that set using numerical techniques!
#
# Here is an example of using `expm()` to solve $e^{\mathbf At}$.
# +
import numpy as np
from scipy.linalg import expm
dt = 0.1
A = np.array([[0, 1, 0],
[0, 0, 1],
[0, 0, 0]])
expm(A*dt)
# -
# ### Time Invariance
#
# If the behavior of the system depends on time we can say that a dynamic system is described by the first-order differential equation
#
# $$ g(t) = \dot x$$
#
# However, if the system is *time invariant* the equation is of the form:
#
# $$ f(x) = \dot x$$
#
# What does *time invariant* mean? Consider a home stereo. If you input a signal $x$ into it at time $t$, it will output some signal $f(x)$. If you instead perform the input at time $t + \Delta t$ the output signal will be the same $f(x)$, shifted in time.
#
# A counter-example is $x(t) = \sin(t)$, with the system $f(x) = t\, x(t) = t \sin(t)$. This is not time invariant; the value will be different at different times due to the multiplication by t. An aircraft is not time invariant. If you make a control input to the aircraft at a later time its behavior will be different because it will have burned fuel and thus lost weight. Lower weight results in different behavior.
#
# We can solve these equations by integrating each side. I demonstrated integrating the time invariant system $v = \dot x$ above. However, integrating the time invariant equation $\dot x = f(x)$ is not so straightforward. Using the *separation of variables* techniques we divide by $f(x)$ and move the $dt$ term to the right so we can integrate each side:
#
# $$\begin{gathered}
# \frac{dx}{dt} = f(x) \\
# \int^x_{x_0} \frac{1}{f(x)} dx = \int^t_{t_0} dt
# \end{gathered}$$
#
# If we let $F(x) = \int \frac{1}{f(x)} dx$ we get
#
# $$F(x) - F(x_0) = t-t_0$$
#
# We then solve for x with
#
# $$\begin{gathered}
# F(x) = t - t_0 + F(x_0) \\
# x = F^{-1}[t-t_0 + F(x_0)]
# \end{gathered}$$
#
# In other words, we need to find the inverse of $F$. This is not trivial, and a significant amount of coursework in a STEM education is devoted to finding tricky, analytic solutions to this problem.
#
# However, they are tricks, and many simple forms of $f(x)$ either have no closed form solution or pose extreme difficulties. Instead, the practicing engineer turns to state-space methods to find approximate solutions.
#
# The advantage of the matrix exponential is that we can use it for any arbitrary set of differential equations which are *time invariant*. However, we often use this technique even when the equations are not time invariant. As an aircraft flies it burns fuel and loses weight. However, the weight loss over one second is negligible, and so the system is nearly linear over that time step. Our answers will still be reasonably accurate so long as the time step is short.
# #### Example: Mass-Spring-Damper Model
#
# Suppose we wanted to track the motion of a weight on a spring and connected to a damper, such as an automobile's suspension. The equation for the motion with $m$ being the mass, $k$ the spring constant, and $c$ the damping force, under some input $u$ is
#
# $$m\frac{d^2x}{dt^2} + c\frac{dx}{dt} +kx = u$$
#
# For notational convenience I will write that as
#
# $$m\ddot x + c\dot x + kx = u$$
#
# I can turn this into a system of first order equations by setting $x_1(t)=x(t)$, and then substituting as follows:
#
# $$\begin{aligned}
# x_1 &= x \\
# x_2 &= \dot x_1 \\
# \dot x_2 &= \ddot x_1 = \ddot x
# \end{aligned}$$
#
# As is common I dropped the $(t)$ for notational convenience. This gives the equation
#
# $$m\dot x_2 + c x_2 +kx_1 = u$$
#
# Solving for $\dot x_2$ we get a first order equation:
#
# $$\dot x_2 = -\frac{c}{m}x_2 - \frac{k}{m}x_1 + \frac{1}{m}u$$
#
# We put this into matrix form:
#
# $$\begin{bmatrix} \dot x_1 \\ \dot x_2 \end{bmatrix} =
# \begin{bmatrix}0 & 1 \\ -k/m & -c/m \end{bmatrix}
# \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} +
# \begin{bmatrix} 0 \\ 1/m \end{bmatrix}u$$
#
# Now we use the matrix exponential to find the state transition matrix:
#
# $$\Phi(t) = e^{\mathbf At} = \mathbf{I} + \mathbf At + \frac{(\mathbf At)^2}{2!} + \frac{(\mathbf At)^3}{3!} + ... $$
#
# The first two terms give us
#
# $$\mathbf F = \begin{bmatrix}1 & t \\ -(k/m) t & 1-(c/m) t \end{bmatrix}$$
#
# This may or may not give you enough precision. You can easily check this by computing $\frac{(\mathbf At)^2}{2!}$ for your constants and seeing how much this matrix contributes to the results.
# ### Linear Time Invariant Theory
#
# [*Linear Time Invariant Theory*](https://en.wikipedia.org/wiki/LTI_system_theory), also known as LTI System Theory, gives us a way to find $\Phi$ using the inverse Laplace transform. You are either nodding your head now, or completely lost. I will not be using the Laplace transform in this book. LTI system theory tells us that
#
# $$ \Phi(t) = \mathcal{L}^{-1}[(s\mathbf{I} - \mathbf{A})^{-1}]$$
#
# I have no intention of going into this other than to say that the Laplace transform $\mathcal{L}$ converts a signal into a space $s$ that excludes time, but finding a solution to the equation above is non-trivial. If you are interested, the Wikipedia article on LTI system theory provides an introduction. I mention LTI because you will find some literature using it to design the Kalman filter matrices for difficult problems.
# ### Numerical Solutions
#
# Finally, there are numerical techniques to find $\mathbf F$. As filters get larger finding analytical solutions becomes very tedious (though packages like SymPy make it easier). <NAME> [2] has developed a technique that finds both $\Phi$ and $\mathbf Q$ numerically. Given the continuous model
#
# $$ \dot x = Ax + Gw$$
#
# where $w$ is the unity white noise, van Loan's method computes both $\mathbf F_k$ and $\mathbf Q_k$.
#
# I have implemented van Loan's method in `FilterPy`. You may use it as follows:
#
# ```python
# from filterpy.common import van_loan_discretization
#
# A = np.array([[0., 1.], [-1., 0.]])
# G = np.array([[0.], [2.]]) # white noise scaling
# F, Q = van_loan_discretization(A, G, dt=0.1)
# ```
#
# In the section *Numeric Integration of Differential Equations* I present alternative methods which are very commonly used in Kalman filtering.
# ## Design of the Process Noise Matrix
#
# In general the design of the $\mathbf Q$ matrix is among the most difficult aspects of Kalman filter design. This is due to several factors. First, the math requires a good foundation in signal theory. Second, we are trying to model the noise in something for which we have little information. Consider trying to model the process noise for a thrown baseball. We can model it as a sphere moving through the air, but that leaves many unknown factors - ball rotation and spin decay, the coefficient of drag of a ball with stitches, the effects of wind and air density, and so on. We develop the equations for an exact mathematical solution for a given process model, but since the process model is incomplete the result for $\mathbf Q$ will also be incomplete. This has a lot of ramifications for the behavior of the Kalman filter. If $\mathbf Q$ is too small then the filter will be overconfident in its prediction model and will diverge from the actual solution. If $\mathbf Q$ is too large than the filter will be unduly influenced by the noise in the measurements and perform sub-optimally. In practice we spend a lot of time running simulations and evaluating collected data to try to select an appropriate value for $\mathbf Q$. But let's start by looking at the math.
#
#
# Let's assume a kinematic system - some system that can be modeled using Newton's equations of motion. We can make a few different assumptions about this process.
#
# We have been using a process model of
#
# $$ \dot{\mathbf x} = \mathbf{Ax} + \mathbf{Bu} + \mathbf{w}$$
#
# where $\mathbf{w}$ is the process noise. Kinematic systems are *continuous* - their inputs and outputs can vary at any arbitrary point in time. However, our Kalman filters are *discrete* (there are continuous forms for Kalman filters, but we do not cover them in this book). We sample the system at regular intervals. Therefore we must find the discrete representation for the noise term in the equation above. This depends on what assumptions we make about the behavior of the noise. We will consider two different models for the noise.
# ### Continuous White Noise Model
# We model kinematic systems using Newton's equations. We have either used position and velocity, or position, velocity, and acceleration as the models for our systems. There is nothing stopping us from going further - we can model jerk, jounce, snap, and so on. We don't do that normally because adding terms beyond the dynamics of the real system degrades the estimate.
#
# Let's say that we need to model the position, velocity, and acceleration. We can then assume that acceleration is constant for each discrete time step. Of course, there is process noise in the system and so the acceleration is not actually constant. The tracked object will alter the acceleration over time due to external, unmodeled forces. In this section we will assume that the acceleration changes by a continuous time zero-mean white noise $w(t)$. In other words, we are assuming that the small changes in velocity average to 0 over time (zero-mean).
#
# Since the noise is changing continuously we will need to integrate to get the discrete noise for the discretization interval that we have chosen. We will not prove it here, but the equation for the discretization of the noise is
#
# $$\mathbf Q = \int_0^{\Delta t} \mathbf F(t)\mathbf{Q_c}\mathbf F^\mathsf{T}(t) dt$$
#
# where $\mathbf{Q_c}$ is the continuous noise. The general reasoning should be clear. $\mathbf F(t)\mathbf{Q_c}\mathbf F^\mathsf{T}(t)$ is a projection of the continuous noise based on our process model $\mathbf F(t)$ at the instant $t$. We want to know how much noise is added to the system over a discrete intervat $\Delta t$, so we integrate this expression over the interval $[0, \Delta t]$.
#
# We know the fundamental matrix for Newtonian systems is
#
# $$F = \begin{bmatrix}1 & \Delta t & {\Delta t}^2/2 \\ 0 & 1 & \Delta t\\ 0& 0& 1\end{bmatrix}$$
#
# We define the continuous noise as
#
# $$\mathbf{Q_c} = \begin{bmatrix}0&0&0\\0&0&0\\0&0&1\end{bmatrix} \Phi_s$$
#
# where $\Phi_s$ is the spectral density of the white noise. This can be derived, but is beyond the scope of this book. See any standard text on stochastic processes for the details. In practice we often do not know the spectral density of the noise, and so this turns into an "engineering" factor - a number we experimentally tune until our filter performs as we expect. You can see that the matrix that $\Phi_s$ is multiplied by effectively assigns the power spectral density to the acceleration term. This makes sense; we assume that the system has constant acceleration except for the variations caused by noise. The noise alters the acceleration.
#
# We could carry out these computations ourselves, but I prefer using SymPy to solve the equation.
#
# $$\mathbf{Q_c} = \begin{bmatrix}0&0&0\\0&0&0\\0&0&1\end{bmatrix} \Phi_s$$
#
#
# +
import sympy
from sympy import (init_printing, Matrix, MatMul,
integrate, symbols)
init_printing(use_latex='mathjax')
dt, phi = symbols('\Delta{t} \Phi_s')
F_k = Matrix([[1, dt, dt**2/2],
[0, 1, dt],
[0, 0, 1]])
Q_c = Matrix([[0, 0, 0],
[0, 0, 0],
[0, 0, 1]])*phi
Q = integrate(F_k * Q_c * F_k.T, (dt, 0, dt))
# factor phi out of the matrix to make it more readable
Q = Q / phi
MatMul(Q, phi)
# -
# For completeness, let us compute the equations for the 0th order and 1st order equations.
# +
F_k = Matrix([[1]])
Q_c = Matrix([[phi]])
print('0th order discrete process noise')
integrate(F_k*Q_c*F_k.T,(dt, 0, dt))
# +
F_k = Matrix([[1, dt],
[0, 1]])
Q_c = Matrix([[0, 0],
[0, 1]]) * phi
Q = integrate(F_k * Q_c * F_k.T, (dt, 0, dt))
print('1st order discrete process noise')
# factor phi out of the matrix to make it more readable
Q = Q / phi
MatMul(Q, phi)
# -
# ### Piecewise White Noise Model
#
# Another model for the noise assumes that the that highest order term (say, acceleration) is constant for the duration of each time period, but differs for each time period, and each of these is uncorrelated between time periods. In other words there is a discontinuous jump in acceleration at each time step. This is subtly different than the model above, where we assumed that the last term had a continuously varying noisy signal applied to it.
#
# We will model this as
#
# $$f(x)=Fx+\Gamma w$$
#
# where $\Gamma$ is the *noise gain* of the system, and $w$ is the constant piecewise acceleration (or velocity, or jerk, etc).
#
# Let's start by looking at a first order system. In this case we have the state transition function
#
# $$\mathbf{F} = \begin{bmatrix}1&\Delta t \\ 0& 1\end{bmatrix}$$
#
# In one time period, the change in velocity will be $w(t)\Delta t$, and the change in position will be $w(t)\Delta t^2/2$, giving us
#
# $$\Gamma = \begin{bmatrix}\frac{1}{2}\Delta t^2 \\ \Delta t\end{bmatrix}$$
#
# The covariance of the process noise is then
#
# $$Q = \mathbb E[\Gamma w(t) w(t) \Gamma^\mathsf{T}] = \Gamma\sigma^2_v\Gamma^\mathsf{T}$$.
#
# We can compute that with SymPy as follows
# +
var = symbols('sigma^2_v')
v = Matrix([[dt**2 / 2], [dt]])
Q = v * var * v.T
# factor variance out of the matrix to make it more readable
Q = Q / var
MatMul(Q, var)
# -
# The second order system proceeds with the same math.
#
#
# $$\mathbf{F} = \begin{bmatrix}1 & \Delta t & {\Delta t}^2/2 \\ 0 & 1 & \Delta t\\ 0& 0& 1\end{bmatrix}$$
#
# Here we will assume that the white noise is a discrete time Wiener process. This gives us
#
# $$\Gamma = \begin{bmatrix}\frac{1}{2}\Delta t^2 \\ \Delta t\\ 1\end{bmatrix}$$
#
# There is no 'truth' to this model, it is just convenient and provides good results. For example, we could assume that the noise is applied to the jerk at the cost of a more complicated equation.
#
# The covariance of the process noise is then
#
# $$Q = \mathbb E[\Gamma w(t) w(t) \Gamma^\mathsf{T}] = \Gamma\sigma^2_v\Gamma^\mathsf{T}$$.
#
# We can compute that with SymPy as follows
# +
var = symbols('sigma^2_v')
v = Matrix([[dt**2 / 2], [dt], [1]])
Q = v * var * v.T
# factor variance out of the matrix to make it more readable
Q = Q / var
MatMul(Q, var)
# -
# We cannot say that this model is more or less correct than the continuous model - both are approximations to what is happening to the actual object. Only experience and experiments can guide you to the appropriate model. In practice you will usually find that either model provides reasonable results, but typically one will perform better than the other.
#
# The advantage of the second model is that we can model the noise in terms of $\sigma^2$ which we can describe in terms of the motion and the amount of error we expect. The first model requires us to specify the spectral density, which is not very intuitive, but it handles varying time samples much more easily since the noise is integrated across the time period. However, these are not fixed rules - use whichever model (or a model of your own devising) based on testing how the filter performs and/or your knowledge of the behavior of the physical model.
#
# A good rule of thumb is to set $\sigma$ somewhere from $\frac{1}{2}\Delta a$ to $\Delta a$, where $\Delta a$ is the maximum amount that the acceleration will change between sample periods. In practice we pick a number, run simulations on data, and choose a value that works well.
# ### Using FilterPy to Compute Q
#
# FilterPy offers several routines to compute the $\mathbf Q$ matrix. The function `Q_continuous_white_noise()` computes $\mathbf Q$ for a given value for $\Delta t$ and the spectral density.
# +
from filterpy.common import Q_continuous_white_noise
from filterpy.common import Q_discrete_white_noise
Q = Q_continuous_white_noise(dim=2, dt=1, spectral_density=1)
print(Q)
# -
Q = Q_continuous_white_noise(dim=3, dt=1, spectral_density=1)
print(Q)
# The function `Q_discrete_white_noise()` computes $\mathbf Q$ assuming a piecewise model for the noise.
Q = Q_discrete_white_noise(2, var=1.)
print(Q)
Q = Q_discrete_white_noise(3, var=1.)
print(Q)
# ### Simplification of Q
#
# Many treatments use a much simpler form for $\mathbf Q$, setting it to zero except for a noise term in the lower rightmost element. Is this justified? Well, consider the value of $\mathbf Q$ for a small $\Delta t$
# +
import numpy as np
np.set_printoptions(precision=8)
Q = Q_continuous_white_noise(
dim=3, dt=0.05, spectral_density=1)
print(Q)
np.set_printoptions(precision=3)
# -
# We can see that most of the terms are very small. Recall that the only equation using this matrix is
#
# $$ \mathbf P=\mathbf{FPF}^\mathsf{T} + \mathbf Q$$
#
# If the values for $\mathbf Q$ are small relative to $\mathbf P$
# then it will be contributing almost nothing to the computation of $\mathbf P$. Setting $\mathbf Q$ to the zero matrix except for the lower right term
#
# $$\mathbf Q=\begin{bmatrix}0&0&0\\0&0&0\\0&0&\sigma^2\end{bmatrix}$$
#
# while not correct, is often a useful approximation. If you do this for an important application you will have to perform quite a few studies to guarantee that your filter works in a variety of situations.
#
# If you do this, 'lower right term' means the most rapidly changing term for each variable. If the state is $x=\begin{bmatrix}x & \dot x & \ddot{x} & y & \dot{y} & \ddot{y}\end{bmatrix}^\mathsf{T}$ Then Q will be 6x6; the elements for both $\ddot{x}$ and $\ddot{y}$ will have to be set to non-zero in $\mathbf Q$.
# ## Stable Compution of the Posterior Covariance
#
# I've presented the equation to compute the posterior covariance as
#
# $$\mathbf P = (\mathbf I - \mathbf{KH})\mathbf{\bar P}$$
#
# and while strictly speaking this is correct, this is not how I compute it in `FilterPy`, where I use the *Joseph* equation
#
#
# $$\mathbf P = (\mathbf I-\mathbf {KH})\mathbf{\bar P}(\mathbf I-\mathbf{KH})^\mathsf T + \mathbf{KRK}^\mathsf T$$
#
#
# I frequently get emails and/or GitHub issues raised, claiming the implementation is a bug. It is not a bug, and I use it for several reasons. First, the subtraction $(\mathbf I - \mathbf{KH})$ can lead to nonsymmetric matrices results due to floating point errors. Covariances must be symmetric, and so becoming nonsymmetric usually leads to the Kalman filter diverging, or even for the code to raise an exception because of the checks built into `NumPy`.
#
# A traditional way to preserve symmetry is the following formula:
#
# $$\mathbf P = (\mathbf P + \mathbf P^\mathsf T) / 2$$
#
# This is safe because $\sigma_{ij} = \sigma_{ji}$ for all covariances in the matrix. Hence this operation averages the error between the differences of the two values if they have diverged due to floating point errors.
#
# If you look at the Joseph form for the equation above, you'll see there is a similar $\mathbf{ABA}^\mathsf T$ pattern in both terms. So they both preserve symmetry. But where did this equation come from, and why do I use it instead of
#
#
# $$\mathbf P = (\mathbf I - \mathbf{KH})\mathbf{\bar P} \\
# \mathbf P = (\mathbf P + \mathbf P^\mathsf T) / 2$$
#
#
# Let's just derive the equation from first principles. It's not too bad, and you need to understand the derivation to understand the purpose of the equation, and, more importantly, diagnose issues if you filter diverges due to numerical instability. This derivation comes from Brown[4].
#
# First, some symbology. $\mathbf x$ is the true state of our system. $\mathbf{\hat x}$ is the estimated state of our system - the posterior. And $\mathbf{\bar x}$ is the estimated prior of the system.
#
#
# Given that, we can define our model to be
#
# $$\mathbf x_{k+1} = \mathbf F_k \mathbf x_k + \mathbf w_k \\
# \mathbf z_k = \mathbf H_k \mathbf x_k + \mathbf v_k$$
#
# In words, the next state $\mathbf x_{k+1}$ of the system is the current state $k$ moved by some process $\mathbf F_k$ plus some noise $\mathbf w_k$.
#
# Note that these are definitions. No system perfectly follows a mathematical model, so we model that with the noise term $\mathbf w_k$. And no measurement is perfect due to sensor error, so we model that with $\mathbf v_k$
#
# I'll dispense with the subscript $k$ since in the remainder of the derivation we will only consider values at step $k$, never step $k+1$.
#
# Now we define the estimation error as the difference between the true state and the estimated state
#
# $$ \mathbf e = \mathbf x - \mathbf{\hat x}$$
#
# Again, this is a definition; we don't know how to compute $\mathbf e$, it is just the defined difference between the true and estimated state.
#
# This allows us to define the covariance of our estimate, which is defined as the expected value of $\mathbf{ee}^\mathsf T$:
#
# $$\begin{aligned}
# P &= E[\mathbf{ee}^\mathsf T] \\
# &= E[(\mathbf x - \mathbf{\hat x})(\mathbf x - \mathbf{\hat x})^\mathsf T]
# \end{aligned}$$
#
#
# Next, we define the posterior estimate as
#
# $$\mathbf {\hat x} = \mathbf{\bar x} + \mathbf K(\mathbf z - \mathbf{H \bar x})$$
#
# That looks like the equation from the Kalman filter, and for good reason. But as with the rest of the math so far, this is a **definition**. In particular, we have not defined $\mathbf K$, and you shouldn't think of it as the Kalman gain, because we are solving this for *any* problem, not just for linear Kalman filters. Here, $\mathbf K$ is just some unspecified blending value between 0 and 1.
# Now we have our definitions, let's perform some substitution and algebra.
#
# The term $(\mathbf x - \mathbf{\hat x})$ can be expanded by replacing $\mathbf{\hat x}$ with the definition above, yielding
#
# $$(\mathbf x - \mathbf{\hat x}) = \mathbf x - (\mathbf{\bar x} + \mathbf K(\mathbf z - \mathbf{H \bar x}))$$
#
# Now we replace $\mathbf z$ with $\mathbf H \mathbf x + \mathbf v$:
#
# $$\begin{aligned}
# (\mathbf x - \mathbf{\hat x})
# &= \mathbf x - (\mathbf{\bar x} + \mathbf K(\mathbf z - \mathbf{H \bar x})) \\
# &= \mathbf x - (\mathbf{\bar x} + \mathbf K(\mathbf H \mathbf x + \mathbf v - \mathbf{H \bar x})) \\
# &= (\mathbf x - \mathbf{\bar x}) - \mathbf K(\mathbf H \mathbf x + \mathbf v - \mathbf{H \bar x}) \\
# &= (\mathbf x - \mathbf{\bar x}) - \mathbf{KH}(\mathbf x - \mathbf{ \bar x}) - \mathbf{Kv} \\
# &= (\mathbf I - \mathbf{KH})(\mathbf x - \mathbf{\bar x}) - \mathbf{Kv}
# \end{aligned}$$
#
# Now we can solve for $\mathbf P$ if we note that the expected value of $(\mathbf x - \mathbf{\bar x})$ is the prior covariance $\mathbf{\bar P}$, and that the expected value of $\mathbf v$ is $E[\mathbf{vv}^\mathbf T] = \mathbf R$:
#
# $$\begin{aligned}
# \mathbf P &=
# E\big[[(\mathbf I - \mathbf{KH})(\mathbf x - \mathbf{\bar x}) - \mathbf{Kv})]
# [(\mathbf I - \mathbf{KH})(\mathbf x - \mathbf{\bar x}) - \mathbf{Kv}]^\mathsf T\big ] \\
# &= (\mathbf I - \mathbf{KH})\mathbf{\bar P}(\mathbf I - \mathbf{KH})^\mathsf T + \mathbf{KRK}^\mathsf T
# \end{aligned}$$
#
# which is what we came here to prove.
#
# Note that this equation is valid for *any* $\mathbf K$, not just the optimal $\mathbf K$ computed by the Kalman filter. And that is why I use this equation. In practice the Kalman gain computed by the filter is *not* the optimal value both because the real world is never truly linear and Gaussian, and because of floating point errors induced by computation. This equation is far less likely to cause the Kalman filter to diverge in the face of real world conditions.
#
# Where did $\mathbf P = (\mathbf I - \mathbf{KH})\mathbf{\bar P}$ come from, then? Let's finish the derivation, which is simple. Recall that the Kalman filter (optimal) gain is given by
#
# $$\mathbf K = \mathbf{\bar P H^\mathsf T}(\mathbf{H \bar P H}^\mathsf T + \mathbf R)^{-1}$$
#
# Now we substitute this into the equation we just derived:
#
# $$\begin{aligned}
# &= (\mathbf I - \mathbf{KH})\mathbf{\bar P}(\mathbf I - \mathbf{KH})^\mathsf T + \mathbf{KRK}^\mathsf T\\
# &= \mathbf{\bar P} - \mathbf{KH}\mathbf{\bar P} - \mathbf{\bar PH}^\mathsf T\mathbf{K}^\mathsf T + \mathbf K(\mathbf{H \bar P H}^\mathsf T + \mathbf R)\mathbf K^\mathsf T \\
# &= \mathbf{\bar P} - \mathbf{KH}\mathbf{\bar P} - \mathbf{\bar PH}^\mathsf T\mathbf{K}^\mathsf T + \mathbf{\bar P H^\mathsf T}(\mathbf{H \bar P H}^\mathsf T + \mathbf R)^{-1}(\mathbf{H \bar P H}^\mathsf T + \mathbf R)\mathbf K^\mathsf T\\
# &= \mathbf{\bar P} - \mathbf{KH}\mathbf{\bar P} - \mathbf{\bar PH}^\mathsf T\mathbf{K}^\mathsf T + \mathbf{\bar P H^\mathsf T}\mathbf K^\mathsf T\\
# &= \mathbf{\bar P} - \mathbf{KH}\mathbf{\bar P}\\
# &= (\mathbf I - \mathbf{KH})\mathbf{\bar P}
# \end{aligned}$$
#
# Therefore $\mathbf P = (\mathbf I - \mathbf{KH})\mathbf{\bar P}$ is mathematically correct when the gain is optimal, but so is $(\mathbf I - \mathbf{KH})\mathbf{\bar P}(\mathbf I - \mathbf{KH})^\mathsf T + \mathbf{KRK}^\mathsf T$. As we already discussed the latter is also correct when the gain is suboptimal, and it is also more numerically stable. Therefore I use this computation in FilterPy.
#
# It is quite possible that your filter still diverges, especially if it runs for hundreds or thousands of epochs. You will need to examine these equations. The literature provides yet other forms of this computation which may be more applicable to your problem. As always, if you are solving real engineering problems where failure could mean loss of equipment or life, you will need to move past this book and into the engineering literature. If you are working with 'toy' problems where failure is not damaging, if you detect divergence you can just reset the value of $\mathbf P$ to some 'reasonable' value and keep on going. For example, you could zero out the non diagonal elements so the matrix only contains variances, and then maybe multiply by a constant somewhat larger than one to reflect the loss of information you just injected into the filter. Use your imagination, and test.
# ## Deriving the Kalman Gain Equation
#
# If you read the last section, you might as well read this one. With this we will have derived the Kalman filter equations.
#
# Note that this derivation is *not* using Bayes equations. I've seen at least four different ways to derive the Kalman filter equations; this derivation is typical to the literature, and follows from the last section. The source is again Brown [4].
#
# In the last section we used an unspecified scaling factor $\mathbf K$ to derive the Joseph form of the covariance equation. If we want an optimal filter, we need to use calculus to minimize the errors in the equations. You should be familiar with this idea. If you want to find the minimum value of a function $f(x)$, you take the derivative and set it equal to zero: $\frac{x}{dx}f(x) = 0$.
#
# In our problem the error is expressed by the covariance matrix $\mathbf P$. In particular, the diagonal expresses the error (variance) of each element in the state vector. So, to find the optimal gain we want to take the derivative of the trace (sum) of the diagonal.
#
# Brown reminds us of two formulas involving the derivative of traces:
#
# $$\frac{d\, trace(\mathbf{AB})}{d\mathbf A} = \mathbf B^\mathsf T$$
#
# $$\frac{d\, trace(\mathbf{ACA}^\mathsf T)}{d\mathbf A} = 2\mathbf{AC}$$
#
# where $\mathbf{AB}$ is square and $\mathbf C$ is symmetric.
#
#
# We expand out the Joseph equation to:
#
# $$\mathbf P = \mathbf{\bar P} - \mathbf{KH}\mathbf{\bar P} - \mathbf{\bar P}\mathbf H^\mathsf T \mathbf K^\mathsf T + \mathbf K(\mathbf H \mathbf{\bar P}\mathbf H^\mathsf T + \mathbf R)\mathbf K^\mathsf T$$
#
# Now we need to the the derivative of the trace of $\mathbf P$ with respect to $\mathbf T$: $\frac{d\, trace(\mathbf P)}{d\mathbf K}$.
#
# The derivative of the trace the first term with respect to $\mathbf K$ is $0$, since it does not have $\mathbf K$ in the expression.
#
# The derivative of the trace of the second term is $(\mathbf H\mathbf{\bar P})^\mathsf T$.
#
# We can find the derivative of the trace of the third term by noticing that $\mathbf{\bar P}\mathbf H^\mathsf T \mathbf K^\mathsf T$ is the transpose of $\mathbf{KH}\mathbf{\bar P}$. The trace of a matrix is equal to the trace of it's transpose, so it's derivative will be same as the second term.
#
# Finally, the derivative of the trace of the fourth term is $2\mathbf K(\mathbf H \mathbf{\bar P}\mathbf H^\mathsf T + \mathbf R)$.
#
# This gives us the final value of
#
# $$\frac{d\, trace(\mathbf P)}{d\mathbf K} = -2(\mathbf H\mathbf{\bar P})^\mathsf T + 2\mathbf K(\mathbf H \mathbf{\bar P}\mathbf H^\mathsf T + \mathbf R)$$
#
# We set this to zero and solve to find the equation for $\mathbf K$ which minimizes the error:
#
# $$-2(\mathbf H\mathbf{\bar P})^\mathsf T + 2\mathbf K(\mathbf H \mathbf{\bar P}\mathbf H^\mathsf T + \mathbf R) = 0 \\
# \mathbf K(\mathbf H \mathbf{\bar P}\mathbf H^\mathsf T + \mathbf R) = (\mathbf H\mathbf{\bar P})^\mathsf T \\
# \mathbf K(\mathbf H \mathbf{\bar P}\mathbf H^\mathsf T + \mathbf R) = \mathbf{\bar P}\mathbf H^\mathsf T \\
# \mathbf K= \mathbf{\bar P}\mathbf H^\mathsf T (\mathbf H \mathbf{\bar P}\mathbf H^\mathsf T + \mathbf R)^{-1}
# $$
#
# This derivation is not quite iron clad as I left out an argument about why minimizing the trace minimizes the total error, but I think it suffices for this book. Any of the standard texts will go into greater detail if you need it.
# ## Numeric Integration of Differential Equations
# We've been exposed to several numerical techniques to solve linear differential equations. These include state-space methods, the Laplace transform, and van Loan's method.
#
# These work well for linear ordinary differential equations (ODEs), but do not work well for nonlinear equations. For example, consider trying to predict the position of a rapidly turning car. Cars maneuver by turning the front wheels. This makes them pivot around their rear axle as it moves forward. Therefore the path will be continuously varying and a linear prediction will necessarily produce an incorrect value. If the change in the system is small enough relative to $\Delta t$ this can often produce adequate results, but that will rarely be the case with the nonlinear Kalman filters we will be studying in subsequent chapters.
#
# For these reasons we need to know how to numerically integrate ODEs. This can be a vast topic that requires several books. However, I will cover a few simple techniques which will work for a majority of the problems you encounter.
#
# ### Euler's Method
#
# Let's say we have the initial condition problem of
#
# $$\begin{gathered}
# y' = y, \\ y(0) = 1
# \end{gathered}$$
#
# We happen to know the exact answer is $y=e^t$ because we solved it earlier, but for an arbitrary ODE we will not know the exact solution. In general all we know is the derivative of the equation, which is equal to the slope. We also know the initial value: at $t=0$, $y=1$. If we know these two pieces of information we can predict the value at $y(t=1)$ using the slope at $t=0$ and the value of $y(0)$. I've plotted this below.
# +
import matplotlib.pyplot as plt
t = np.linspace(-1, 1, 10)
plt.plot(t, np.exp(t))
t = np.linspace(-1, 1, 2)
plt.plot(t,t+1, ls='--', c='k');
# -
# You can see that the slope is very close to the curve at $t=0.1$, but far from it
# at $t=1$. But let's continue with a step size of 1 for a moment. We can see that at $t=1$ the estimated value of $y$ is 2. Now we can compute the value at $t=2$ by taking the slope of the curve at $t=1$ and adding it to our initial estimate. The slope is computed with $y'=y$, so the slope is 2.
# +
import kf_book.book_plots as book_plots
t = np.linspace(-1, 2, 20)
plt.plot(t, np.exp(t))
t = np.linspace(0, 1, 2)
plt.plot([1, 2, 4], ls='--', c='k')
book_plots.set_labels(x='x', y='y');
# -
# Here we see the next estimate for y is 4. The errors are getting large quickly, and you might be unimpressed. But 1 is a very large step size. Let's put this algorithm in code, and verify that it works by using a small step size.
def euler(t, tmax, y, dx, step=1.):
ys = []
while t < tmax:
y = y + step*dx(t, y)
ys.append(y)
t +=step
return ys
# +
def dx(t, y): return y
print(euler(0, 1, 1, dx, step=1.)[-1])
print(euler(0, 2, 1, dx, step=1.)[-1])
# -
# This looks correct. So now let's plot the result of a much smaller step size.
ys = euler(0, 4, 1, dx, step=0.00001)
plt.subplot(1,2,1)
plt.title('Computed')
plt.plot(np.linspace(0, 4, len(ys)),ys)
plt.subplot(1,2,2)
t = np.linspace(0, 4, 20)
plt.title('Exact')
plt.plot(t, np.exp(t));
print('exact answer=', np.exp(4))
print('euler answer=', ys[-1])
print('difference =', np.exp(4) - ys[-1])
print('iterations =', len(ys))
# Here we see that the error is reasonably small, but it took a very large number of iterations to get three digits of precision. In practice Euler's method is too slow for most problems, and we use more sophisticated methods.
#
# Before we go on, let's formally derive Euler's method, as it is the basis for the more advanced Runge Kutta methods used in the next section. In fact, Euler's method is the simplest form of Runge Kutta.
#
#
# Here are the first 3 terms of the Taylor expansion of $y$. An infinite expansion would give an exact answer, so $O(h^4)$ denotes the error due to the finite expansion.
#
# $$y(t_0 + h) = y(t_0) + h y'(t_0) + \frac{1}{2!}h^2 y''(t_0) + \frac{1}{3!}h^3 y'''(t_0) + O(h^4)$$
#
# Here we can see that Euler's method is using the first two terms of the Taylor expansion. Each subsequent term is smaller than the previous terms, so we are assured that the estimate will not be too far off from the correct value.
# ### Runge Kutta Methods
#
# Runge Kutta is the workhorse of numerical integration. There are a vast number of methods in the literature. In practice, using the Runge Kutta algorithm that I present here will solve most any problem you will face. It offers a very good balance of speed, precision, and stability, and it is the 'go to' numerical integration method unless you have a very good reason to choose something different.
#
# Let's dive in. We start with some differential equation
#
# $$\ddot{y} = \frac{d}{dt}\dot{y}.$$
#
# We can substitute the derivative of $y$ with a function $f$, like so
#
# $$\ddot{y} = \frac{d}{dt}f(y,t).$$
# Deriving these equations is outside the scope of this book, but the Runge Kutta RK4 method is defined with these equations.
#
# $$y(t+\Delta t) = y(t) + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4) + O(\Delta t^4)$$
#
# $$\begin{aligned}
# k_1 &= f(y,t)\Delta t \\
# k_2 &= f(y+\frac{1}{2}k_1, t+\frac{1}{2}\Delta t)\Delta t \\
# k_3 &= f(y+\frac{1}{2}k_2, t+\frac{1}{2}\Delta t)\Delta t \\
# k_4 &= f(y+k_3, t+\Delta t)\Delta t
# \end{aligned}
# $$
#
# Here is the corresponding code:
def runge_kutta4(y, x, dx, f):
"""computes 4th order Runge-Kutta for dy/dx.
y is the initial value for y
x is the initial value for x
dx is the difference in x (e.g. the time step)
f is a callable function (y, x) that you supply
to compute dy/dx for the specified values.
"""
k1 = dx * f(y, x)
k2 = dx * f(y + 0.5*k1, x + 0.5*dx)
k3 = dx * f(y + 0.5*k2, x + 0.5*dx)
k4 = dx * f(y + k3, x + dx)
return y + (k1 + 2*k2 + 2*k3 + k4) / 6.
# Let's use this for a simple example. Let
#
# $$\dot{y} = t\sqrt{y(t)}$$
#
# with the initial values
#
# $$\begin{aligned}t_0 &= 0\\y_0 &= y(t_0) = 1\end{aligned}$$
# +
import math
import numpy as np
t = 0.
y = 1.
dt = .1
ys, ts = [], []
def func(y,t):
return t*math.sqrt(y)
while t <= 10:
y = runge_kutta4(y, t, dt, func)
t += dt
ys.append(y)
ts.append(t)
exact = [(t**2 + 4)**2 / 16. for t in ts]
plt.plot(ts, ys)
plt.plot(ts, exact)
error = np.array(exact) - np.array(ys)
print("max error {:.5f}".format(max(error)))
# -
# ## Bayesian Filtering
#
# Starting in the Discrete Bayes chapter I used a Bayesian formulation for filtering. Suppose we are tracking an object. We define its *state* at a specific time as its position, velocity, and so on. For example, we might write the state at time $t$ as $\mathbf x_t = \begin{bmatrix}x_t &\dot x_t \end{bmatrix}^\mathsf T$.
#
# When we take a measurement of the object we are measuring the state or part of it. Sensors are noisy, so the measurement is corrupted with noise. Clearly though, the measurement is determined by the state. That is, a change in state may change the measurement, but a change in measurement will not change the state.
#
# In filtering our goal is to compute an optimal estimate for a set of states $\mathbf x_{0:t}$ from time 0 to time $t$. If we knew $\mathbf x_{0:t}$ then it would be trivial to compute a set of measurements $\mathbf z_{0:t}$ corresponding to those states. However, we receive a set of measurements $\mathbf z_{0:t}$, and want to compute the corresponding states $\mathbf x_{0:t}$. This is called *statistical inversion* because we are trying to compute the input from the output.
#
# Inversion is a difficult problem because there is typically no unique solution. For a given set of states $\mathbf x_{0:t}$ there is only one possible set of measurements (plus noise), but for a given set of measurements there are many different sets of states that could have led to those measurements.
#
# Recall Bayes Theorem:
#
# $$P(x \mid z) = \frac{P(z \mid x)P(x)}{P(z)}$$
#
# where $P(z \mid x)$ is the *likelihood* of the measurement $z$, $P(x)$ is the *prior* based on our process model, and $P(z)$ is a normalization constant. $P(x \mid z)$ is the *posterior*, or the distribution after incorporating the measurement $z$, also called the *evidence*.
#
# This is a *statistical inversion* as it goes from $P(z \mid x)$ to $P(x \mid z)$. The solution to our filtering problem can be expressed as:
#
# $$P(\mathbf x_{0:t} \mid \mathbf z_{0:t}) = \frac{P(\mathbf z_{0:t} \mid \mathbf x_{0:t})P(\mathbf x_{0:t})}{P(\mathbf z_{0:t})}$$
#
# That is all well and good until the next measurement $\mathbf z_{t+1}$ comes in, at which point we need to recompute the entire expression for the range $0:t+1$.
#
# In practice this is intractable because we are trying to compute the posterior distribution $P(\mathbf x_{0:t} \mid \mathbf z_{0:t})$ for the state over the full range of time steps. But do we really care about the probability distribution at the third step (say) when we just received the tenth measurement? Not usually. So we relax our requirements and only compute the distributions for the current time step.
#
# The first simplification is we describe our process (e.g., the motion model for a moving object) as a *Markov chain*. That is, we say that the current state is solely dependent on the previous state and a transition probability $P(\mathbf x_k \mid \mathbf x_{k-1})$, which is just the probability of going from the last state to the current one. We write:
#
# $$\mathbf x_k \sim P(\mathbf x_k \mid \mathbf x_{k-1})$$
#
# In practice this is extremely reasonable, as many things have the *Markov property*. If you are driving in a parking lot, does your position in the next second depend on whether you pulled off the interstate or were creeping along on a dirt road one minute ago? No. Your position in the next second depends solely on your current position, speed, and control inputs, not on what happened a minute ago. Thus, cars have the Markov property, and we can make this simplification with no loss of precision or generality.
#
# The next simplification we make is do define the *measurement model* as depending on the current state $\mathbf x_k$ with the conditional probability of the measurement given the current state: $P(\mathbf z_t \mid \mathbf x_x)$. We write:
#
# $$\mathbf z_k \sim P(\mathbf z_t \mid \mathbf x_x)$$
#
# We have a recurrance now, so we need an initial condition to terminate it. Therefore we say that the initial distribution is the probablity of the state $\mathbf x_0$:
#
# $$\mathbf x_0 \sim P(\mathbf x_0)$$
#
#
# These terms are plugged into Bayes equation. If we have the state $\mathbf x_0$ and the first measurement we can estimate $P(\mathbf x_1 | \mathbf z_1)$. The motion model creates the prior $P(\mathbf x_2 \mid \mathbf x_1)$. We feed this back into Bayes theorem to compute $P(\mathbf x_2 | \mathbf z_2)$. We continue this predictor-corrector algorithm, recursively computing the state and distribution at time $t$ based solely on the state and distribution at time $t-1$ and the measurement at time $t$.
#
# The details of the mathematics for this computation varies based on the problem. The **Discrete Bayes** and **Univariate Kalman Filter** chapters gave two different formulations which you should have been able to reason through. The univariate Kalman filter assumes that for a scalar state both the noise and process are linear model are affected by zero-mean, uncorrelated Gaussian noise.
#
# The Multivariate Kalman filter make the same assumption but for states and measurements that are vectors, not scalars. Dr. Kalman was able to prove that if these assumptions hold true then the Kalman filter is *optimal* in a least squares sense. Colloquially this means there is no way to derive more information from the noisy measurements. In the remainder of the book I will present filters that relax the constraints on linearity and Gaussian noise.
#
# Before I go on, a few more words about statistical inversion. As Calvetti and Somersalo write in *Introduction to Bayesian Scientific Computing*, "we adopt the Bayesian point of view: *randomness simply means lack of information*."[3] Our state parameterizes physical phenomena that we could in principle measure or compute: velocity, air drag, and so on. We lack enough information to compute or measure their value, so we opt to consider them as random variables. Strictly speaking they are not random, thus this is a subjective position.
#
# They devote a full chapter to this topic. I can spare a paragraph. Bayesian filters are possible because we ascribe statistical properties to unknown parameters. In the case of the Kalman filter we have closed-form solutions to find an optimal estimate. Other filters, such as the discrete Bayes filter or the particle filter which we cover in a later chapter, model the probability in a more ad-hoc, non-optimal manner. The power of our technique comes from treating lack of information as a random variable, describing that random variable as a probability distribution, and then using Bayes Theorem to solve the statistical inference problem.
# ## Converting Kalman Filter to a g-h Filter
#
# I've stated that the Kalman filter is a form of the g-h filter. It just takes some algebra to prove it. It's more straightforward to do with the one dimensional case, so I will do that. Recall
#
# $$
# \mu_{x}=\frac{\sigma_1^2 \mu_2 + \sigma_2^2 \mu_1} {\sigma_1^2 + \sigma_2^2}
# $$
#
# which I will make more friendly for our eyes as:
#
# $$
# \mu_{x}=\frac{ya + xb} {a+b}
# $$
#
# We can easily put this into the g-h form with the following algebra
#
# $$
# \begin{aligned}
# \mu_{x}&=(x-x) + \frac{ya + xb} {a+b} \\
# \mu_{x}&=x-\frac{a+b}{a+b}x + \frac{ya + xb} {a+b} \\
# \mu_{x}&=x +\frac{-x(a+b) + xb+ya}{a+b} \\
# \mu_{x}&=x+ \frac{-xa+ya}{a+b} \\
# \mu_{x}&=x+ \frac{a}{a+b}(y-x)\\
# \end{aligned}
# $$
#
# We are almost done, but recall that the variance of estimate is given by
#
# $$\begin{aligned}
# \sigma_{x}^2 &= \frac{1}{\frac{1}{\sigma_1^2} + \frac{1}{\sigma_2^2}} \\
# &= \frac{1}{\frac{1}{a} + \frac{1}{b}}
# \end{aligned}$$
#
# We can incorporate that term into our equation above by observing that
#
# $$
# \begin{aligned}
# \frac{a}{a+b} &= \frac{a/a}{(a+b)/a} = \frac{1}{(a+b)/a} \\
# &= \frac{1}{1 + \frac{b}{a}} = \frac{1}{\frac{b}{b} + \frac{b}{a}} \\
# &= \frac{1}{b}\frac{1}{\frac{1}{b} + \frac{1}{a}} \\
# &= \frac{\sigma^2_{x'}}{b}
# \end{aligned}
# $$
#
# We can tie all of this together with
#
# $$
# \begin{aligned}
# \mu_{x}&=x+ \frac{a}{a+b}(y-x) \\
# &= x + \frac{\sigma^2_{x'}}{b}(y-x) \\
# &= x + g_n(y-x)
# \end{aligned}
# $$
#
# where
#
# $$g_n = \frac{\sigma^2_{x}}{\sigma^2_{y}}$$
#
# The end result is multiplying the residual of the two measurements by a constant and adding to our previous value, which is the $g$ equation for the g-h filter. $g$ is the variance of the new estimate divided by the variance of the measurement. Of course in this case $g$ is not a constant as it varies with each time step as the variance changes. We can also derive the formula for $h$ in the same way. It is not a particularly illuminating derivation and I will skip it. The end result is
#
# $$h_n = \frac{COV (x,\dot x)}{\sigma^2_{y}}$$
#
# The takeaway point is that $g$ and $h$ are specified fully by the variance and covariances of the measurement and predictions at time $n$. In other words, we are picking a point between the measurement and prediction by a scale factor determined by the quality of each of those two inputs.
# ## References
# * [1] <NAME> and <NAME> "Nineteen Dubious Ways to Compute the Exponential of a Matrix, Twenty-Five Years Later,", *SIAM Review 45, 3-49*. 2003.
#
#
# * [2] <NAME>, "Computing Integrals Involving the Matrix Exponential," IEEE *Transactions Automatic Control*, June 1978.
#
#
# * [3] Calvetti, D and Somersalo E, "Introduction to Bayesian Scientific Computing: Ten Lectures on Subjective Computing,", *Springer*, 2007.
#
# * [4] <NAME>. and <NAME>., "Introduction to Random Signals and Applied Kalman Filtering", *Wiley and Sons*, Fourth Edition, p.143-147, 2012.
#
|
07-Kalman-Filter-Math.ipynb
|
# + [markdown] id="CCQY7jpBfMur"
# ##### Copyright 2018 The TensorFlow Authors.
# + cellView="form" id="z6X9omPnfO_h"
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] id="2QQJJyDzqGRb"
# # Eager execution
#
# + [markdown] id="B1xdylywqUSX"
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://www.tensorflow.org/guide/eager"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/guide/eager.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/guide/eager.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# <td>
# <a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/guide/eager.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
# </td>
# </table>
# + [markdown] id="EGjDcGxIqEfX"
# TensorFlow's eager execution is an imperative programming environment that
# evaluates operations immediately, without building graphs: operations return
# concrete values instead of constructing a computational graph to run later. This
# makes it easy to get started with TensorFlow and debug models, and it
# reduces boilerplate as well. To follow along with this guide, run the code
# samples below in an interactive `python` interpreter.
#
# Eager execution is a flexible machine learning platform for research and
# experimentation, providing:
#
# * *An intuitive interface*—Structure your code naturally and use Python data
# structures. Quickly iterate on small models and small data.
# * *Easier debugging*—Call ops directly to inspect running models and test
# changes. Use standard Python debugging tools for immediate error reporting.
# * *Natural control flow*—Use Python control flow instead of graph control
# flow, simplifying the specification of dynamic models.
#
# Eager execution supports most TensorFlow operations and GPU acceleration.
#
# Note: Some models may experience increased overhead with eager execution
# enabled. Performance improvements are ongoing, but please
# [file a bug](https://github.com/tensorflow/tensorflow/issues) if you find a
# problem and share your benchmarks.
# + [markdown] id="RBAeIwOMrYk8"
# ## Setup and basic usage
# + id="ByNsp4VqqEfa"
import os
import tensorflow as tf
import cProfile
print(tf.__version__)
# +
import sys
import tensorflow.keras
import pandas as pd
import sklearn as sk
import tensorflow as tf
print(f"Tensor Flow Version: {tf.__version__}")
print(f"Keras Version: {tensorflow.keras.__version__}")
print()
print(f"Python {sys.version}")
print(f"Pandas {pd.__version__}")
print(f"Scikit-Learn {sk.__version__}")
gpu = len(tf.config.list_physical_devices('GPU'))>0
print("GPU is", "available" if gpu else "NOT AVAILABLE")
# + [markdown] id="48P3-8q4qEfe"
# In Tensorflow 2.0, eager execution is enabled by default.
# + id="7aFsD8csqEff"
tf.executing_eagerly()
# + [markdown] id="x_G1zZT5qEfh"
# Now you can run TensorFlow operations and the results will return immediately:
# + id="9gsI54pbqEfj"
x = [[2.]]
m = tf.matmul(x, x)
print("hello, {}".format(m))
# + [markdown] id="ajFn6qsdqEfl"
# Enabling eager execution changes how TensorFlow operations behave—now they
# immediately evaluate and return their values to Python. `tf.Tensor` objects
# reference concrete values instead of symbolic handles to nodes in a computational
# graph. Since there isn't a computational graph to build and run later in a
# session, it's easy to inspect results using `print()` or a debugger. Evaluating,
# printing, and checking tensor values does not break the flow for computing
# gradients.
#
# Eager execution works nicely with [NumPy](http://www.numpy.org/). NumPy
# operations accept `tf.Tensor` arguments. The TensorFlow
# `tf.math` operations convert
# Python objects and NumPy arrays to `tf.Tensor` objects. The
# `tf.Tensor.numpy` method returns the object's value as a NumPy `ndarray`.
# -
# + id="sTO0_5TYqz1n"
a = tf.constant([[1, 2],
[3, 4]])
print(a)
# + id="Dp14YT8Gq4r1"
# Broadcasting support
b = tf.add(a, 1)
print(b)
# + id="69p3waMfq8cQ"
# Operator overloading is supported
print(a * b)
# + id="Ui025t1qqEfm"
# Use NumPy values
import numpy as np
c = np.multiply(a, b)
print(c)
# + id="Tq_aFRzWrCua"
# Obtain numpy value from a tensor:
print(a.numpy())
# => [[1 2]
# [3 4]]
# + [markdown] id="H08f9ss9qEft"
# ## Dynamic control flow
#
# A major benefit of eager execution is that all the functionality of the host
# language is available while your model is executing. So, for example,
# it is easy to write [fizzbuzz](https://en.wikipedia.org/wiki/Fizz_buzz):
# + id="0fudRMeUqEfu"
def fizzbuzz(max_num):
counter = tf.constant(0)
max_num = tf.convert_to_tensor(max_num)
for num in range(1, max_num.numpy()+1):
num = tf.constant(num)
if int(num % 3) == 0 and int(num % 5) == 0:
print('FizzBuzz')
elif int(num % 3) == 0:
print('Fizz')
elif int(num % 5) == 0:
print('Buzz')
else:
print(num.numpy())
counter += 1
# + id="P2cKknQWrJLB"
fizzbuzz(15)
# + [markdown] id="7kA-aC3BqEfy"
# This has conditionals that depend on tensor values and it prints these values
# at runtime.
# + [markdown] id="8huKpuuAwICq"
# ## Eager training
# + [markdown] id="mp2lCCZYrxHd"
# ### Computing gradients
#
# [Automatic differentiation](https://en.wikipedia.org/wiki/Automatic_differentiation)
# is useful for implementing machine learning algorithms such as
# [backpropagation](https://en.wikipedia.org/wiki/Backpropagation) for training
# neural networks. During eager execution, use `tf.GradientTape` to trace
# operations for computing gradients later.
#
# You can use `tf.GradientTape` to train and/or compute gradients in eager. It is especially useful for complicated training loops.
#
# Since different operations can occur during each call, all
# forward-pass operations get recorded to a "tape". To compute the gradient, play
# the tape backwards and then discard. A particular `tf.GradientTape` can only
# compute one gradient; subsequent calls throw a runtime error.
# + id="7g1yWiSXqEf-"
w = tf.Variable([[1.0]])
with tf.GradientTape() as tape:
loss = w * w
grad = tape.gradient(loss, w)
print(grad) # => tf.Tensor([[ 2.]], shape=(1, 1), dtype=float32)
# + [markdown] id="vkHs32GqweYS"
# ### Train a model
#
# The following example creates a multi-layer model that classifies the standard
# MNIST handwritten digits. It demonstrates the optimizer and layer APIs to build
# trainable graphs in an eager execution environment.
# + id="38kymXZowhhz"
# Fetch and format the mnist data
(mnist_images, mnist_labels), _ = tf.keras.datasets.mnist.load_data()
dataset = tf.data.Dataset.from_tensor_slices((tf.cast(mnist_images[...,tf.newaxis]/255, tf.float32), tf.cast(mnist_labels,tf.int64)))
dataset = dataset.shuffle(1000).batch(32)
# + id="rl1K8rOowmwT"
# Build the model
mnist_model = tf.keras.Sequential([
tf.keras.layers.Conv2D(16,[3,3], activation='relu',
input_shape=(None, None, 1)),
tf.keras.layers.Conv2D(16,[3,3], activation='relu'),
tf.keras.layers.GlobalAveragePooling2D(),
tf.keras.layers.Dense(10)
])
# + [markdown] id="fvyk-HgGwxwl"
# Even without training, call the model and inspect the output in eager execution:
# + id="BsxystjBwxLS"
for images,labels in dataset.take(1):
print("Logits: ", mnist_model(images[0:1]).numpy())
# + [markdown] id="Y3PGa8G7qEgB"
# While keras models have a builtin training loop (using the `fit` method), sometimes you need more customization. Here's an example, of a training loop implemented with eager:
# + id="bzRhM7JDnaEG"
optimizer = tf.keras.optimizers.Adam()
loss_object = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
loss_history = []
# + [markdown] id="tXaupYXRI2YM"
# Note: Use the assert functions in `tf.debugging` to check if a condition holds up. This works in eager and graph execution.
# + id="DDHrigtiCIA4"
def train_step(images, labels):
with tf.GradientTape() as tape:
logits = mnist_model(images, training=True)
# Add asserts to check the shape of the output.
tf.debugging.assert_equal(logits.shape, (32, 10))
loss_value = loss_object(labels, logits)
loss_history.append(loss_value.numpy().mean())
grads = tape.gradient(loss_value, mnist_model.trainable_variables)
optimizer.apply_gradients(zip(grads, mnist_model.trainable_variables))
# + id="0m1xAXrmqEgJ"
def train(epochs):
for epoch in range(epochs):
for (batch, (images, labels)) in enumerate(dataset):
train_step(images, labels)
print ('Epoch {} finished'.format(epoch))
# + id="C5dGz0p_nf4W"
train(epochs = 3)
# + id="5vG5ql_2vYB5"
import matplotlib.pyplot as plt
plt.plot(loss_history)
plt.xlabel('Batch #')
plt.ylabel('Loss [entropy]')
# + [markdown] id="kKpOlHPLqEgl"
# ### Variables and optimizers
#
# `tf.Variable` objects store mutable `tf.Tensor`-like values accessed during
# training to make automatic differentiation easier.
#
# The collections of variables can be encapsulated into layers or models, along with methods that operate on them. See [Custom Keras layers and models](./keras/custom_layers_and_models.ipynb) for details. The main difference between layers and models is that models add methods like `Model.fit`, `Model.evaluate`, and `Model.save`.
#
# For example, the automatic differentiation example above
# can be rewritten:
# + id="2qXcPngYk8dN"
class Linear(tf.keras.Model):
def __init__(self):
super(Linear, self).__init__()
self.W = tf.Variable(5., name='weight')
self.B = tf.Variable(10., name='bias')
def call(self, inputs):
return inputs * self.W + self.B
# + id="nnQLBYmEqEgm"
# A toy dataset of points around 3 * x + 2
NUM_EXAMPLES = 2000
training_inputs = tf.random.normal([NUM_EXAMPLES])
noise = tf.random.normal([NUM_EXAMPLES])
training_outputs = training_inputs * 3 + 2 + noise
# The loss function to be optimized
def loss(model, inputs, targets):
error = model(inputs) - targets
return tf.reduce_mean(tf.square(error))
def grad(model, inputs, targets):
with tf.GradientTape() as tape:
loss_value = loss(model, inputs, targets)
return tape.gradient(loss_value, [model.W, model.B])
# + [markdown] id="Q7x1CDurl3IG"
# Next:
#
# 1. Create the model.
# 2. The Derivatives of a loss function with respect to model parameters.
# 3. A strategy for updating the variables based on the derivatives.
# + id="SbXJk0f2lztg"
model = Linear()
optimizer = tf.keras.optimizers.SGD(learning_rate=0.01)
print("Initial loss: {:.3f}".format(loss(model, training_inputs, training_outputs)))
steps = 300
for i in range(steps):
grads = grad(model, training_inputs, training_outputs)
optimizer.apply_gradients(zip(grads, [model.W, model.B]))
if i % 20 == 0:
print("Loss at step {:03d}: {:.3f}".format(i, loss(model, training_inputs, training_outputs)))
# + id="PV_dqer7pzSH"
print("Final loss: {:.3f}".format(loss(model, training_inputs, training_outputs)))
# + id="rvt_Wj3Tp0hm"
print("W = {}, B = {}".format(model.W.numpy(), model.B.numpy()))
# + [markdown] id="rPjb8nRWqEgr"
# Note: Variables persist until the last reference to the python object
# is removed, and is the variable is deleted.
# + [markdown] id="scMjg6L6qEgv"
# ### Object-based saving
#
# + [markdown] id="Y-0ZcCcjwkux"
# A `tf.keras.Model` includes a convenient `save_weights` method allowing you to easily create a checkpoint:
# + id="oJrMX94PwD9s"
model.save_weights('weights')
status = model.load_weights('weights')
# + [markdown] id="2EfTjWV_wEng"
# Using `tf.train.Checkpoint` you can take full control over this process.
#
# This section is an abbreviated version of the [guide to training checkpoints](./checkpoint.ipynb).
#
# + id="7z5xRfdHzZOQ"
x = tf.Variable(10.)
checkpoint = tf.train.Checkpoint(x=x)
# + id="IffrUVG7zyVb"
x.assign(2.) # Assign a new value to the variables and save.
checkpoint_path = './ckpt/'
checkpoint.save('./ckpt/')
# + id="eMT9koCoqEgw"
x.assign(11.) # Change the variable after saving.
# Restore values from the checkpoint
checkpoint.restore(tf.train.latest_checkpoint(checkpoint_path))
print(x) # => 2.0
# + [markdown] id="vbFnP-yLqEgx"
# To save and load models, `tf.train.Checkpoint` stores the internal state of objects,
# without requiring hidden variables. To record the state of a `model`,
# an `optimizer`, and a global step, pass them to a `tf.train.Checkpoint`:
# + id="hWZHyAXMqEg0"
model = tf.keras.Sequential([
tf.keras.layers.Conv2D(16,[3,3], activation='relu'),
tf.keras.layers.GlobalAveragePooling2D(),
tf.keras.layers.Dense(10)
])
optimizer = tf.keras.optimizers.Adam(learning_rate=0.001)
checkpoint_dir = 'path/to/model_dir'
if not os.path.exists(checkpoint_dir):
os.makedirs(checkpoint_dir)
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
root = tf.train.Checkpoint(optimizer=optimizer,
model=model)
root.save(checkpoint_prefix)
root.restore(tf.train.latest_checkpoint(checkpoint_dir))
# + [markdown] id="R-ITwkBCF6GJ"
# Note: In many training loops, variables are created after `tf.train.Checkpoint.restore` is called. These variables will be restored as soon as they are created, and assertions are available to ensure that a checkpoint has been fully loaded. See the [guide to training checkpoints](./checkpoint.ipynb) for details.
# + [markdown] id="3yoD0VJ7qEg3"
# ### Object-oriented metrics
#
# `tf.keras.metrics` are stored as objects. Update a metric by passing the new data to
# the callable, and retrieve the result using the `tf.keras.metrics.result` method,
# for example:
# + id="9ccu0iAaqEg5"
m = tf.keras.metrics.Mean("loss")
m(0)
m(5)
m.result() # => 2.5
m([8, 9])
m.result() # => 5.5
# + [markdown] id="aB8qWtT955pI"
# ### Summaries and TensorBoard
#
# [TensorBoard](https://tensorflow.org/tensorboard) is a visualization tool for
# understanding, debugging and optimizing the model training process. It uses
# summary events that are written while executing the program.
#
# You can use `tf.summary` to record summaries of variable in eager execution.
# For example, to record summaries of `loss` once every 100 training steps:
# + id="z6VInqhA6RH4"
logdir = "./tb/"
writer = tf.summary.create_file_writer(logdir)
steps = 1000
with writer.as_default(): # or call writer.set_as_default() before the loop.
for i in range(steps):
step = i + 1
# Calculate loss with your real train function.
loss = 1 - 0.001 * step
if step % 100 == 0:
tf.summary.scalar('loss', loss, step=step)
# + id="08QQD2j36TaI"
# !ls tb/
# + [markdown] id="xEL4yJe5qEhD"
# ## Advanced automatic differentiation topics
#
# ### Dynamic models
#
# `tf.GradientTape` can also be used in dynamic models. This example for a
# [backtracking line search](https://wikipedia.org/wiki/Backtracking_line_search)
# algorithm looks like normal NumPy code, except there are gradients and is
# differentiable, despite the complex control flow:
# + id="L518n5dkqEhE"
def line_search_step(fn, init_x, rate=1.0):
with tf.GradientTape() as tape:
# Variables are automatically tracked.
# But to calculate a gradient from a tensor, you must `watch` it.
tape.watch(init_x)
value = fn(init_x)
grad = tape.gradient(value, init_x)
grad_norm = tf.reduce_sum(grad * grad)
init_value = value
while value > init_value - rate * grad_norm:
x = init_x - rate * grad
value = fn(x)
rate /= 2.0
return x, value
# + [markdown] id="gieGOf_DqEhK"
# ### Custom gradients
#
# Custom gradients are an easy way to override gradients. Within the forward function, define the gradient with respect to the
# inputs, outputs, or intermediate results. For example, here's an easy way to clip
# the norm of the gradients in the backward pass:
# + id="-OwwsWUAqEhK"
@tf.custom_gradient
def clip_gradient_by_norm(x, norm):
y = tf.identity(x)
def grad_fn(dresult):
return [tf.clip_by_norm(dresult, norm), None]
return y, grad_fn
# + [markdown] id="JPLDHkF_qEhN"
# Custom gradients are commonly used to provide a numerically stable gradient for a
# sequence of operations:
# + id="24WiLROnqEhO"
def log1pexp(x):
return tf.math.log(1 + tf.exp(x))
def grad_log1pexp(x):
with tf.GradientTape() as tape:
tape.watch(x)
value = log1pexp(x)
return tape.gradient(value, x)
# + id="n8fq69r9-B-c"
# The gradient computation works fine at x = 0.
grad_log1pexp(tf.constant(0.)).numpy()
# + id="_VFSU0mG-FSp"
# However, x = 100 fails because of numerical instability.
grad_log1pexp(tf.constant(100.)).numpy()
# + [markdown] id="-VcTR34rqEhQ"
# Here, the `log1pexp` function can be analytically simplified with a custom
# gradient. The implementation below reuses the value for `tf.exp(x)` that is
# computed during the forward pass—making it more efficient by eliminating
# redundant calculations:
# + id="Q7nvfx_-qEhS"
@tf.custom_gradient
def log1pexp(x):
e = tf.exp(x)
def grad(dy):
return dy * (1 - 1 / (1 + e))
return tf.math.log(1 + e), grad
def grad_log1pexp(x):
with tf.GradientTape() as tape:
tape.watch(x)
value = log1pexp(x)
return tape.gradient(value, x)
# + id="5gHPKMfl-Kge"
# As before, the gradient computation works fine at x = 0.
grad_log1pexp(tf.constant(0.)).numpy()
# + id="u38MOfz3-MDE"
# And the gradient computation also works at x = 100.
grad_log1pexp(tf.constant(100.)).numpy()
# + [markdown] id="rnZXjfQzqEhV"
# ## Performance
#
# Computation is automatically offloaded to GPUs during eager execution. If you
# want control over where a computation runs you can enclose it in a
# `tf.device('/gpu:0')` block (or the CPU equivalent):
# + id="Ac9Y64H-qEhX"
import time
def measure(x, steps):
# TensorFlow initializes a GPU the first time it's used, exclude from timing.
tf.matmul(x, x)
start = time.time()
for i in range(steps):
x = tf.matmul(x, x)
# tf.matmul can return before completing the matrix multiplication
# (e.g., can return after enqueing the operation on a CUDA stream).
# The x.numpy() call below will ensure that all enqueued operations
# have completed (and will also copy the result to host memory,
# so we're including a little more than just the matmul operation
# time).
_ = x.numpy()
end = time.time()
return end - start
shape = (1000, 1000)
steps = 200
print("Time to multiply a {} matrix by itself {} times:".format(shape, steps))
# Run on CPU:
with tf.device("/cpu:0"):
print("CPU: {} secs".format(measure(tf.random.normal(shape), steps)))
# Run on GPU, if available:
if tf.config.experimental.list_physical_devices("GPU"):
with tf.device("/gpu:0"):
print("GPU: {} secs".format(measure(tf.random.normal(shape), steps)))
else:
print("GPU: not found")
# + [markdown] id="RLw3IS7UqEhe"
# A `tf.Tensor` object can be copied to a different device to execute its
# operations:
# + id="ny6LX2BVqEhf"
if tf.config.experimental.list_physical_devices("GPU"):
x = tf.random.normal([10, 10])
x_gpu0 = x.gpu()
x_cpu = x.cpu()
_ = tf.matmul(x_cpu, x_cpu) # Runs on CPU
_ = tf.matmul(x_gpu0, x_gpu0) # Runs on GPU:0
# + [markdown] id="oA_qaII3-p6c"
# ### Benchmarks
#
# For compute-heavy models, such as
# [ResNet50](https://github.com/tensorflow/tensorflow/tree/master/tensorflow/python/eager/benchmarks/resnet50)
# training on a GPU, eager execution performance is comparable to `tf.function` execution.
# But this gap grows larger for models with less computation and there is work to
# be done for optimizing hot code paths for models with lots of small operations.
#
# ## Work with functions
#
# While eager execution makes development and debugging more interactive,
# TensorFlow 1.x style graph execution has advantages for distributed training, performance
# optimizations, and production deployment. To bridge this gap, TensorFlow 2.0 introduces `function`s via the `tf.function` API. For more information, see the [tf.function](./function.ipynb) guide.
|
zExtraLearning/MLPrep/tfnbs/eager.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/buganart/descriptor-transformer/blob/main/descriptor_model_predict.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="jbp-CL5ijb4e" cellView="form"
#@markdown Before starting please save the notebook in your drive by clicking on `File -> Save a copy in drive`
# + id="XQ-pH7tyK9xW" cellView="form"
#@markdown Check GPU, should be a Tesla V100
# !nvidia-smi -L
import os
print(f"We have {os.cpu_count()} CPU cores.")
# + id="BJyxzcLOhgWY" cellView="form"
#@markdown Mount google drive
from google.colab import drive
from google.colab import output
drive.mount('/content/drive')
from pathlib import Path
if not Path("/content/drive/My Drive/IRCMS_GAN_collaborative_database").exists():
raise RuntimeError(
"Shortcut to our shared drive folder doesn't exits.\n\n"
"\t1. Go to the google drive web UI\n"
"\t2. Right click shared folder IRCMS_GAN_collaborative_database and click \"Add shortcut to Drive\""
)
def clear_on_success(msg="Ok!"):
if _exit_code == 0:
output.clear()
print(msg)
# + id="9-L3BlfGTfbJ" cellView="form"
#@markdown Install wandb and log in
# %pip install wandb
output.clear()
import wandb
from pathlib import Path
wandb_drive_netrc_path = Path("drive/My Drive/colab/.netrc")
wandb_local_netrc_path = Path("/root/.netrc")
if wandb_drive_netrc_path.exists():
import shutil
print("Wandb .netrc file found, will use that to log in.")
shutil.copy(wandb_drive_netrc_path, wandb_local_netrc_path)
else:
print(
f"Wandb config not found at {wandb_drive_netrc_path}.\n"
f"Using manual login.\n\n"
f"To use auto login in the future, finish the manual login first and then run:\n\n"
f"\t!mkdir -p '{wandb_drive_netrc_path.parent}'\n"
f"\t!cp {wandb_local_netrc_path} '{wandb_drive_netrc_path}'\n\n"
f"Then that file will be used to login next time.\n"
)
# !wandb login
output.clear()
print("ok!")
# + [markdown] id="iP1BbsXBidDo"
# # Description
#
# This notebook generates music (.wav) based on runs from the wandb project "demiurge/descriptor_model". You may access the training models through [train.ipynb](https://github.com/buganart/descriptor-transformer/blob/main/descriptor_model_train.ipynb). The user will need to specify a **test_data_path** for a sound file folder (.wav), the notebook will generate descriptors (.json) for each sound file and convert those descriptors back into the same (.wav) format. The generated sound files will be the prediction of potential subsequent sounds for the input files.
#
# To generate such predictive sound files, this notebook will first
#
#
# 1. process input music files in **test_data_path** and music descriptor database specified in **audio_dir** to descriptors if the files in the folder is not being processed into descriptors. The processed descriptors will be saved in the same path in the "processed_descriptors" folder. If they have already been processed, this step will be skipped. Note that **hop length** and **sampling rate(sr)** are parameters for processing music to descriptors.
# 2. load trained descriptor model from wandb project "demiurge/descriptor_model". Set **resume_run_id** directly, then the saved checkpoint of the run will be downloaded. The model loaded from the checkpoint will predict the subsequent descriptors based on **prediction_length**.
# 3. query the predicted descriptors to the music descriptor database specified in **audio_dir**. The predicted descriptors will be replaced by the descriptors in the music descriptor database based on distance function such as euclidean, cosine, minkowski
# 4. process the descriptor in the descriptor database and match them back to the music segment where it is extracted. Then, those music segments will be merged together into the generated music file. Note that **crossfade** is a parameter in the merging process. The generated music files will be saved in the **output_dir**.
#
#
#
#
# + id="BVjGm8m_q9R6" cellView="form"
#@title CONFIGURATION
#@markdown Directories can be found via file explorer on the left menu by navigating to `drive` and then to the desired folders.
#@markdown Then right-click and `Copy path`.
#@markdown ### #descriptor model input
#@markdown The descriptor will extract a .json file containing *spectral centroid/spectral flatness/fundamental frequency/spectral rolloff/RMS* data from the test_data_path .wavs below. The model will predict **prediction_length** descriptors to follow the test descriptor files.
#@markdown - This is the **Prediction DB** containing data for the model to generate next descriptors.
#@markdown - The model will predict next **prediction_length** descriptors given **window_size**(specified in the model) descriptors
#@markdown - if test_data_path is a path to a music directory, descriptors will be extracted from **test_data_path** and saved in **output_dir**
# test_data_path = "/content/drive/My Drive/AUDIO DATABASE/MUSIC TRANSFORMER/Transformer Corpus/" #@param {type:"string"}
# test_data_path = "/content/drive/My Drive/AUDIO DATABASE/MUSIC TRANSFORMER/sample_descriptor_files" #@param {type:"string"}
test_data_path = "/content/drive/My Drive/AUDIO DATABASE/TESTING/" #@param {type:"string"}
#@markdown ### #descriptor database
#@markdown - the path to the wav. file database to generate the descriptor database
#@markdown - This is the **RAW generated audio DB** which is only for the query and playback engine.
#@markdown - The descriptors predicted from the model need to be converted back to music. The files in this dataset will create a database with descriptor-sound mapping, which is used for converting descriptors back to music.
audio_dir = "/content/drive/My Drive/AUDIO DATABASE/TESTING/" #@param {type:"string"}
#@markdown - descriptors will be extracted from the **audio_dir** above but if your provide a input_db_filename that path will be used instead
# input_db_filename = f"/content/drive/My Drive/Descriptor Model/robertos_output.json" #@param {type:"string"}
# input_db_filename = "/content/drive/My Drive/AUDIO DATABASE/TESTING/output_descriptor_database.json" #@param {type:"string"}
input_db_filename = "" #@param {type:"string"}
#@markdown ### #resumption of previous runs
#@markdown Optional resumption arguments below, leaving both empty will start a new run from scratch.
#@markdown - The IDs can be found on Wanda. It is 8 characters long and may contain a-z letters and digits (for example **1t212ycn**)
#@markdown Resume a previous run
resume_run_id = "lny7atep" #@param {type:"string"}
#@markdown ### #descriptors / sound parameter
#@markdown - the number of predicted descriptors after the **test_data**
prediction_length = 40#@param {type:"integer"}
#@markdown - wav parameters (hop length, sampling rate, crossfade)
hop_length = 1024 #@param {type:"integer"}
sr = 44100 #@param {type:"integer"}
crossfade = 22 #@param {type:"integer"}
#@markdown ### #save location
#@markdown - the path to save all generated files
output_dir = f"/content/drive/My Drive/Descriptor Model/OUTPUTS/{resume_run_id}" #@param {type:"string"}
# #@markdown name of generated files
# #@markdown - the file storing generated descriptors from the model
# generated_descriptor_filename = "AUDIOS_output.json" #@param {type:"string"}
# #@markdown - the file storing closest match query descriptors based on generated descriptors
# query_descriptor_filename = "query_output.json" #@param {type:"string"}
# #@markdown - the final wav file from combining music source represented by the query descriptors
# final_wav_filename = "output.wav" #@param {type:"string"}
hop_length = int(hop_length)
sr = int(sr)
crossfade = int(crossfade)
import re
from pathlib import Path
from argparse import Namespace
def check_wandb_id(run_id):
if run_id and not re.match(r"^[\da-z]{8}$", run_id):
raise RuntimeError(
"Run ID needs to be 8 characters long and contain only letters a-z and digits.\n"
f"Got \"{run_id}\""
)
check_wandb_id(resume_run_id)
output_dir = Path(output_dir)
output_dir.mkdir(parents=True, exist_ok=True)
#remove existing files
output_dir_files = output_dir.rglob("*.*")
for i in output_dir_files:
i.unlink()
colab_config = {
"resume_run_id": resume_run_id,
"test_data_path": test_data_path,
"prediction_length": prediction_length,
"output_dir": output_dir,
}
for k, v in colab_config.items():
print(f"=> {k:20}: {v}")
config = Namespace(**colab_config)
config.seed = 1234
# + id="5hCJPdJzKqCW" cellView="form"
#@markdown Install dependency and functions
# %pip install --upgrade git+https://github.com/buganart/descriptor-transformer.git#egg=desc
from desc.train_function import get_resume_run_config, init_wandb_run, setup_model, setup_datamodule
from desc.helper_function import save_descriptor_as_json, dir2descriptor, save_json, get_dataframe_from_json
# %pip install --upgrade librosa
import librosa
import numpy as np
import json
import os, os.path
from IPython.display import HTML, display
import time
import shutil
import pandas as pd
from numba import jit, cuda
from scipy.spatial.distance import cosine, minkowski, euclidean
import torch
# %pip install pydub
# %pip install ffmpeg
from pydub import AudioSegment
from pydub.playback import play
def progress(value, max=100):
return HTML("""
<progress
value='{value}'
max='{max}',
style='width: 100%'
>
{value}
</progress>
""".format(value=value, max=max))
clear_on_success()
# + [markdown] id="zkgjJdO--JPf"
# ## WAV TO DESCRIPTOR
#
#
#
#
#
#
# + id="P4EXGrsHCZqi"
#process input descriptor database if needed
if not input_db_filename:
save_path = output_dir
db_descriptors = dir2descriptor(audio_dir, hop=hop_length, sr=sr)
#combine descriptors from multiple files
data_dict = {}
for filename, descriptor in db_descriptors:
for element in descriptor:
if element in data_dict:
data_dict[element] = data_dict[element] + descriptor[element]
else:
data_dict[element] = descriptor[element]
#replace empty input_db_filename by savefile name
input_db_filename = Path(save_path) / "AUDIOS_database.json"
save_json(input_db_filename, data_dict)
# + [markdown] id="liDBc0QQFtuM"
# ## DESCRIPTOR MODEL GENERATOR
#
# + id="cX-QEhDcFt3b"
config = get_resume_run_config(resume_run_id)
config.resume_run_id = resume_run_id
config.audio_db_dir = test_data_path
# please check window_size (if window_size is too large, 0 descriptor samples will be extracted.)
#print(config.window_size)
run = init_wandb_run(config, run_dir="./", mode="offline")
model,_ = setup_model(config, run)
model.eval()
#construct test_data
testdatamodule = setup_datamodule(config, run, isTrain=False)
test_dataloader = testdatamodule.test_dataloader()
test_data, fileindex = next(iter(test_dataloader))
prediction = model.predict(test_data, prediction_length)
#un normalize output
prediction = prediction * testdatamodule.dataset_std + testdatamodule.dataset_mean
generated_dir = output_dir / "generated_descriptors"
generated_dir.mkdir(parents=True, exist_ok=True)
save_descriptor_as_json(generated_dir, prediction, fileindex, testdatamodule, resume_run_id)
print("ok!")
# + [markdown] id="iypRTwjcyNZL"
# ## QUERY FUNCTION
#
# + id="kGh7eY4UyNn7"
query_dir = output_dir / "query_descriptors"
query_dir.mkdir(parents=True, exist_ok=True)
print("query_dir:", query_dir)
# import df1 (UnaGAN output)
input_db_filename = Path(input_db_filename)
df1 = get_dataframe_from_json(input_db_filename)
# import df2 (Descriptor GAN output)
generated_file_list = generated_dir.rglob("*.*")
generated_dataframe_list = []
for filepath in generated_file_list:
df2 = get_dataframe_from_json(filepath)
generated_dataframe_list.append((filepath, df2))
# + id="5_d7aq51zk48"
##### modified (batch)
for filepath, df2 in generated_dataframe_list:
#record runtime
current_time = time.time()
dict_key1 = list(df2.columns)[0]
input_len = len(df2[dict_key1])
column_list = list(df2.columns)
input_array = torch.tensor(df2.loc[:, column_list].to_numpy(dtype=np.float32)).cuda()
db = torch.tensor(df1.loc[:, column_list].to_numpy(dtype=np.float32)).cuda()
# not enough RAM for array of shape (input_len, db_len)
batch_size = 4096
results_all = []
for i in range(int(input_len/batch_size)+1):
x = i * batch_size
x_ = (i+1) * batch_size
if x_ > input_len:
x_ = input_len
input = input_array[x:x_]
dist = torch.cdist(input, db, p=2)
results = torch.argmin(dist, axis=1).cpu().numpy()
results_all.append(results)
results_all = np.concatenate(results_all).flatten()
id_array = df1["_id"][results_all]
sample_array = df1["_sample"][results_all]
data={
"_id": id_array.tolist(),
"_sample": sample_array.tolist()
}
print("finished - saving as JSON now")
savefile = query_dir / (str(filepath.stem) + ".json")
with open(savefile, 'w') as outfile:
json.dump(data, outfile, indent=2)
print("descriptors are replaced by query descriptors in database. save file path: ", savefile)
#record runtime
step_time = time.time() - current_time
print("time used:", step_time)
# + [markdown] id="_LM_xFvI0pfb"
# ## PLAYBACK ENGINE
#
#
# + id="D7O3KWqY13sB"
wav_dir = output_dir / "wav_output"
wav_dir.mkdir(parents=True, exist_ok=True)
print("wav_dir:", wav_dir)
query_file_list = query_dir.rglob("*.*")
query_dataframe_list = []
for filepath in query_file_list:
to_play = get_dataframe_from_json(filepath)
query_dataframe_list.append((filepath, to_play))
# + id="tfF14v-E3QmD"
for filepath, to_play in query_dataframe_list:
output_filename = wav_dir / (str(filepath.stem) + ".wav")
# output_filename = output_dir / final_wav_filename
if os.path.exists(output_filename):
os.remove(output_filename)
no_samples = len(to_play["_sample"])
out = display(progress(0, no_samples), display_id = True)
concat = AudioSegment.from_wav(to_play["_id"][0])
hop = (hop_length / sr) * 1000
startpos = int((float(to_play["_sample"][0]) / hop_length) * hop)
concat = concat[startpos:startpos + hop]
for x in range(1, no_samples):
print(to_play["_id"][x])
to_concat = AudioSegment.from_wav(to_play["_id"][x])
startpos = int((float(to_play["_sample"][x]) / hop_length) * hop)
if (startpos < crossfade):
thiscrossfade = 0
else:
to_concat = to_concat[startpos - (crossfade / 2):startpos + hop]
thiscrossfade = crossfade
out.update(progress(x + 1, no_samples))
concat = concat.append(to_concat, crossfade = thiscrossfade)
concat.export(output_filename, format = "wav")
|
descriptor_model_predict.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.0.3
# language: julia
# name: julia-1.0
# ---
# # Examine IHT reconstruction results
# This notebook examines IHT's reconstruction result with and without debiasing. Overall, debiasing does not affect model selection nor parameter estimation.
using DelimitedFiles
using Random
using DataFrames
using StatsBase
using Statistics
using Plots
using Plotly
# # Below are 100 simulations of y where X is 5k by 100k matrix
# +
#debiasing simulation results
normal_debias = readdlm("repeats/Normal_100")
logistic_debias = readdlm("repeats/Bernoulli_100")
poisson_debias = readdlm("repeats/Poisson_100")
negativebinomial_debias = readdlm("repeats/NegativeBinomial_100")
#non-debiasing simulation results
normal_nodebias = readdlm("repeats_nodebias/Normal_100")
logistic_nodebias = readdlm("repeats_nodebias/Bernoulli_100")
poisson_nodebias = readdlm("repeats_nodebias/Poisson_100")
negativebinomial_nodebias = readdlm("repeats_nodebias/NegativeBinomial_100")
#true model
true_b = [0.01; 0.5; 0.03; 0.1; 0.05; 0.25]
# -
# # Construct Table
#
# ### First compute the proportion of finding each predictor
# +
k = size(true_b, 1)
normal_found = zeros(k)
logistic_found = zeros(k)
poisson_found = zeros(k)
negativebinomial_found = zeros(k)
normal_found_nodebias = zeros(k)
logistic_found_nodebias = zeros(k)
poisson_found_nodebias = zeros(k)
negativebinomial_found_nodebias = zeros(k)
for i in 1:k
normal_found[i] = sum(normal_debias[i, :] .!= 0)
logistic_found[i] = sum(logistic_debias[i, :] .!= 0)
poisson_found[i] = sum(poisson_debias[i, :] .!= 0)
negativebinomial_found[i] = sum(negativebinomial_debias[i, :] .!= 0)
normal_found_nodebias[i] = sum(normal_nodebias[i, :] .!= 0)
logistic_found_nodebias[i] = sum(logistic_nodebias[i, :] .!= 0)
poisson_found_nodebias[i] = sum(poisson_nodebias[i, :] .!= 0)
negativebinomial_found_nodebias[i] = sum(negativebinomial_nodebias[i, :] .!= 0)
end
# -
# # Found proportion (debiasing)
find_probability = DataFrame(
true_b = true_b,
normal_prob_find = normal_found,
logistic_prob_find = logistic_found,
poisson_prob_find = poisson_found,
negativebinomial_prob_find = negativebinomial_found)
find_probability_debias = deepcopy(find_probability)
sort!(find_probability_debias, rev=true) #sort later
# # Found proportion (no debiasing)
find_probability_nodebias = DataFrame(
true_b = true_b,
normal_prob_find_nodebias = normal_found_nodebias,
logistic_prob_find_nodebias = logistic_found_nodebias,
poisson_prob_find_nodebias = poisson_found_nodebias,
negativebinomial_prob_find_nodebias = negativebinomial_found_nodebias)
find_probability_nodebias_cp = deepcopy(find_probability_nodebias)
sort!(find_probability_nodebias_cp, rev=true) #sort later
# # Mean and standard deviation (debiasing)
# +
k = size(true_b, 1)
normal_mean = zeros(k)
normal_std = zeros(k)
logistic_mean = zeros(k)
logistic_std = zeros(k)
poisson_mean = zeros(k)
poisson_std = zeros(k)
negativebinomial_mean = zeros(k)
negativebinomial_std = zeros(k)
for i in 1:k
#compute mean and std if at least 1 found
if normal_found[i] != 0
normal_cur_row = normal_debias[i, :] .!= 0
normal_mean[i] = mean(normal_debias[i, :][normal_cur_row])
normal_std[i] = std(normal_debias[i, :][normal_cur_row])
end
if logistic_found[i] != 0
logistic_cur_row = logistic_debias[i, :] .!= 0
logistic_mean[i] = mean(logistic_debias[i, :][logistic_cur_row])
logistic_std[i] = std(logistic_debias[i, :][logistic_cur_row])
end
if poisson_found[i] != 0
poisson_cur_row = poisson_debias[i, :] .!= 0
poisson_mean[i] = mean(poisson_debias[i, :][poisson_cur_row])
poisson_std[i] = std(poisson_debias[i, :][poisson_cur_row])
end
if negativebinomial_found[i] != 0
negativebinomial_cur_row = negativebinomial_debias[i, :] .!= 0
negativebinomial_mean[i] = mean(negativebinomial_debias[i, :][negativebinomial_cur_row])
negativebinomial_std[i] = std(negativebinomial_debias[i, :][negativebinomial_cur_row])
end
end
# -
found_mean_and_std = DataFrame(
true_b = true_b,
normal_mean = normal_mean,
normal_std = normal_std,
logistic_mean = logistic_mean,
logistic_std = logistic_std,
poisson_mean = poisson_mean,
poisson_std = poisson_std,
negativebinomial_mean = negativebinomial_mean,
negativebinomial_std = negativebinomial_std)
# sort!(found_mean_and_std, rev=true) #sort later
# # Mean and standard deviation (non-debiasing)
# +
k = size(true_b, 1)
normal_mean_nodebias = zeros(k)
normal_std_nodebias = zeros(k)
logistic_mean_nodebias = zeros(k)
logistic_std_nodebias = zeros(k)
poisson_mean_nodebias = zeros(k)
poisson_std_nodebias = zeros(k)
negativebinomial_mean_nodebias = zeros(k)
negativebinomial_std_nodebias = zeros(k)
for i in 1:k
#compute mean and std if at least 1 found
if normal_found_nodebias[i] != 0
normal_cur_row = normal_nodebias[i, :] .!= 0
normal_mean_nodebias[i] = mean(normal_nodebias[i, :][normal_cur_row])
normal_std_nodebias[i] = std(normal_nodebias[i, :][normal_cur_row])
end
if logistic_found_nodebias[i] != 0
logistic_cur_row = logistic_nodebias[i, :] .!= 0
logistic_mean_nodebias[i] = mean(logistic_nodebias[i, :][logistic_cur_row])
logistic_std_nodebias[i] = std(logistic_nodebias[i, :][logistic_cur_row])
end
if poisson_found_nodebias[i] != 0
poisson_cur_row = poisson_nodebias[i, :] .!= 0
poisson_mean_nodebias[i] = mean(poisson_nodebias[i, :][poisson_cur_row])
poisson_std_nodebias[i] = std(poisson_nodebias[i, :][poisson_cur_row])
end
if negativebinomial_found_nodebias[i] != 0
negativebinomial_cur_row = negativebinomial_nodebias[i, :] .!= 0
negativebinomial_mean_nodebias[i] = mean(negativebinomial_nodebias[i, :][negativebinomial_cur_row])
negativebinomial_std_nodebias[i] = std(negativebinomial_nodebias[i, :][negativebinomial_cur_row])
end
end
# -
found_mean_and_std_nodebias = DataFrame(
true_b = true_b,
normal_mean_nodebias = normal_mean_nodebias,
normal_std_nodebias = normal_std_nodebias,
logistic_mean_nodebias = logistic_mean_nodebias,
logistic_std_nodebias = logistic_std_nodebias,
poisson_mean_nodebias = poisson_mean_nodebias,
poisson_std_nodebias = poisson_std_nodebias,
negativebinomial_mean_nodebias = negativebinomial_mean_nodebias,
negativebinomial_std_nodebias = negativebinomial_std_nodebias)
# sort!(found_mean_and_std_nodebias, rev=true) #sort later
# # Sort and round results (debiasing)
found_mean_and_std_debias = deepcopy(found_mean_and_std)
sort!(found_mean_and_std_debias, rev=true)
for i in 1:size(found_mean_and_std_debias, 2)
found_mean_and_std_debias[:, i] = round.(found_mean_and_std_debias[:, i], digits=3)
end
found_mean_and_std_debias
# # Sort and round results (non-debiasing)
found_mean_and_std_nodebias_copy = deepcopy(found_mean_and_std_nodebias)
sort!(found_mean_and_std_nodebias_copy, rev=true)
for i in 1:size(found_mean_and_std_nodebias_copy, 2)
found_mean_and_std_nodebias_copy[:, i] = round.(found_mean_and_std_nodebias_copy[:, i], digits=3)
end
found_mean_and_std_nodebias_copy
|
figures/repeats/IHT_reconstruction_results.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: U4-S1-NLP (Python3)
# language: python
# name: u4-s1-nlp
# ---
import pandas as pd
import re
import string
import matplotlib.pyplot as plt
import numpy as np
import spacy
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
from sklearn.neighbors import NearestNeighbors
df = pd.read_csv('data/cannabis.csv')
#model
def predict():
tfidf = TfidfVectorizer(stop_words = 'english',
max_features = 5000)
dtm = tfidf.fit_transform(df['Effects'])
dtm = pd.DataFrame(dtm.todense(), columns=tfidf.get_feature_names())
nn = NearestNeighbors(n_neighbors=4, algorithm='kd_tree')
nn.fit(dtm)
import pickle
# Dump the trained classifier (nn) with Pickle
pickle_filename = 'model.pkl'
pickled_model = open(pickle_filename, 'wb') # Open the file to save as pkl file
pickle.dump(nn, pickled_model)
pickled_model.close() # Close the pickle instances
# Loading the saved model
model_pkl = open(pickle_filename, 'rb')
NN_model = pickle.load(model_pkl)
print ("Loaded model :: ", NN_model) # print to verify
import pickle
# Dump the trained classifier (nn) with Pickle
pickle_filename_1 = 'tfidf.pkl'
pickled_model_1 = open(pickle_filename_1, 'wb') # Open the file to save as pkl file
pickle.dump(tfidf, pickled_model_1)
pickled_model_1.close() # Close the pickle instances
# Loading the saved model
model_pkl_1 = open(pickle_filename_1, 'rb')
tfidf_model = pickle.load(model_pkl_1)
print ("Loaded model :: ", tfidf_model) # print to verify
import json
def recommend(user_input):
temp_df = NN_model.kneighbors(tfidf_model.transform([user_input]).todense())[1]
#print(temp_df)
for i in range(4):
info = df.loc[temp_df[0][i]]['Strain']
#info = info.to_json()
#info_name = {f'strain_{i+1}':info}
#strains_info.update(info_name)
print(json.dumps(info))
#return json.dumps(info) #for engineeers, the return does not work in jupyter lab. Should work in vsCode.
recommend('Creative,Energetic,Tingly,Euphoric,Relaxed')
|
functions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 
# # Pytorch 中级篇(5):语言模型(Language Model (RNN-LM))
#
# >参考代码
# >
# >**yunjey的 [pytorch tutorial系列](https://github.com/yunjey/pytorch-tutorial/blob/master/tutorials/02-intermediate/language_model/main.py)**
# ## 语言模型 学习资料
#
# 语言模型这一块不是很想接触。就照着yunjey的代码,一带而过吧。
#
# >**博客**
# >
# >[CS224d笔记4——语言模型和循环神经网络(Recurrent Neural Network, RNN)](https://wugh.github.io/posts/2016/03/cs224d-notes4-recurrent-neural-networks/?utm_source=tuicool&utm_medium=referral)
# >
# >[浅谈神经网络中的梯度爆炸问题](https://www.jianshu.com/p/79574b0f2959)
# ## Pytorch 实现
# +
# 包
import torch
import torch.nn as nn
import numpy as np
from torch.nn.utils import clip_grad_norm
from data_utils import Dictionary, Corpus
#data_utils代码在https://github.com/yunjey/pytorch-tutorial/blob/master/tutorials/02-intermediate/language_model/data_utils.py
# -
# 设备配置
# Device configuration
torch.cuda.set_device(1) # 这句用来设置pytorch在哪块GPU上运行
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# 超参数设置
# Hyper-parameters
embed_size = 128
hidden_size = 1024
num_layers = 1
num_epochs = 5
num_samples = 1000 # number of words to be sampled
batch_size = 20
seq_length = 30
learning_rate = 0.002
# ### Penn Treebank 数据集
corpus = Corpus()
ids = corpus.get_data('data/train.txt', batch_size)
vocab_size = len(corpus.dictionary)
num_batches = ids.size(1) // seq_length
# ### 基于RNN的语言模型
class RNNLM(nn.Module):
def __init__(self, vocab_size, embed_size, hidden_size, num_layers):
super(RNNLM, self).__init__()
self.embed = nn.Embedding(vocab_size, embed_size)
self.lstm = nn.LSTM(embed_size, hidden_size, num_layers, batch_first=True)
self.linear = nn.Linear(hidden_size, vocab_size)
def forward(self, x, h):
# Embed word ids to vectors
x = self.embed(x)
# Forward propagate LSTM
out, (h, c) = self.lstm(x, h)
# Reshape output to (batch_size*sequence_length, hidden_size)
out = out.reshape(out.size(0)*out.size(1), out.size(2))
# Decode hidden states of all time steps
out = self.linear(out)
return out, (h, c)
# 实例化一个模型
model = RNNLM(vocab_size, embed_size, hidden_size, num_layers).to(device)
# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
# 定义函数:截断反向传播
def detach(states):
return [state.detach() for state in states]
# ### 训练模型
for epoch in range(num_epochs):
# 初始化隐状态和细胞状态
states = ( torch.zeros(num_layers, batch_size, hidden_size).to(device),
torch.zeros(num_layers, batch_size, hidden_size).to(device) )
for i in range(0, ids.size(1) - seq_length, seq_length):
# Get mini-batch inputs and targets
inputs = ids[:, i:i+seq_length].to(device)
targets = ids[:, (i+1):(i+1)+seq_length].to(device)
# Forward pass
states = detach(states)
outputs, states = model(inputs, states)
loss = criterion(outputs, targets.reshape(-1))
# Backward and optimize
model.zero_grad()
loss.backward()
clip_grad_norm(model.parameters(), 0.5)
optimizer.step()
step = (i+1) // seq_length
if step % 100 == 0:
print ('Epoch [{}/{}], Step[{}/{}], Loss: {:.4f}, Perplexity: {:5.2f}'
.format(epoch+1, num_epochs, step, num_batches, loss.item(), np.exp(loss.item())))
# ### 测试和保存模型
with torch.no_grad():
with open('sample.txt', 'w') as f:
# 初始化隐状态和细胞状态
state = (torch.zeros(num_layers, 1, hidden_size).to(device),
torch.zeros(num_layers, 1, hidden_size).to(device))
# 随机选择一个单词
prob = torch.ones(vocab_size)
input = torch.multinomial(prob, num_samples=1).unsqueeze(1).to(device)
for i in range(num_samples):
# Forward propagate RNN
output, state = model(input, state)
# Sample a word id
prob = output.exp()
word_id = torch.multinomial(prob, num_samples=1).item()
# Fill input with sampled word id for the next time step
input.fill_(word_id)
# File write
word = corpus.dictionary.idx2word[word_id]
word = '\n' if word == '<eos>' else word + ' '
f.write(word)
if (i+1) % 100 == 0:
print('Sampled [{}/{}] words and save to {}'.format(i+1, num_samples, 'sample.txt'))
# 保存模型
torch.save(model.state_dict(), 'model.ckpt')
# **对于整个流程一脸懵逼,结果也不是很懂**
|
tutorials/02-intermediate/language_model/language_model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## Computing Alpha, Beta, and R Squared in Python
# *Suggested Answers follow (usually there are multiple ways to solve a problem in Python).*
# *Running a Regression in Python - continued:*
# +
import numpy as np
import pandas as pd
from scipy import stats
import statsmodels.api as sm
import matplotlib.pyplot as plt
data = pd.read_excel('D:/Python/Data_Files/IQ_data.xlsx')
X = data['Test 1']
Y = data['IQ']
plt.scatter(X,Y)
plt.axis([0, 120, 0, 150])
plt.ylabel('IQ')
plt.xlabel('Test 1')
plt.show()
# -
# ****
# Use the statsmodels’ **.add_constant()** method to reassign the X data on X1. Use OLS with arguments Y and X1 and apply the fit method to obtain univariate regression results. Help yourself with the **.summary()** method.
# +
X1 = sm.add_constant(X)
reg = sm.OLS(Y, X1).fit()
# -
reg.summary()
# By looking at the p-values, would you conclude Test 1 scores are a good predictor?
# *****
# Imagine a kid would score 84 on Test 1. How many points is she expected to get on the IQ test, approximately?
45 + 84*0.76
# ******
# ### Alpha, Beta, R^2:
# Apply the stats module’s **linregress()** to extract the value for the slope, the intercept, the r squared, the p_value, and the standard deviation.
slope, intercept, r_value, p_value, std_err = stats.linregress(X,Y)
slope
intercept
r_value
r_value ** 2
p_value
std_err
# Use the values of the slope and the intercept to predict the IQ score of a child, who obtained 84 points on Test 1. Is the forecasted value different than the one you obtained above?
intercept + 84 * slope
# ******
# Follow the steps to draw the best fitting line of the provided regression.
# Define a function that will use the slope and the intercept value to calculate the dots of the best fitting line.
def fitline(b):
return intercept + slope * b
# Apply it to the data you have stored in the variable X.
line = fitline(X)
# Draw a scatter plot with the X and Y data and then plot X and the obtained fit-line.
plt.scatter(X,Y)
plt.plot(X,line)
plt.show()
|
23 - Python for Finance/4_Using Regressions for Financial Analysis/4_Computing Alpha, Beta, and R Squared in Python (6:14)/Computing Alpha, Beta, and R Squared in Python - Solution.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.5.0-DEV.350
# language: julia
# name: julia-1.5
# ---
# Before running this, please make sure to activate and instantiate the environment
# corresponding to [this `Project.toml`](https://raw.githubusercontent.com/alan-turing-institute/MLJTutorials/master/Project.toml) and [this `Manifest.toml`](https://raw.githubusercontent.com/alan-turing-institute/MLJTutorials/master/Manifest.toml)
# so that you get an environment which matches the one used to generate the tutorials:
#
# ```julia
# cd("MLJTutorials") # cd to folder with the *.toml
# using Pkg; Pkg.activate("."); Pkg.instantiate()
# ```
# [MLJ.jl]: https://github.com/alan-turing-institute/MLJ.jl
# [RDatasets.jl]: https://github.com/JuliaStats/RDatasets.jl
# [DecisionTree.jl]: https://github.com/bensadeghi/DecisionTree.jl
#
# ## Preliminary steps
#
# ### Data
#
# As in "[choosing a model](/getting-started/choosing-a-model/)", let's load the Iris dataset and unpack it:
using MLJ, Statistics, PrettyPrinting
MLJ.color_off() # hide
X, y = @load_iris;
# let's also load the `DecisionTreeClassifier`:
@load DecisionTreeClassifier
tree_model = DecisionTreeClassifier()
# ### MLJ Machine
#
# In MLJ, remember that a *model* is an object that only serves as a container for the hyperparameters of the model.
# A *machine* is an object wrapping both a model and data and can contain information on the *trained* model; it does *not* fit the model by itself.
# However, it does check that the model is compatible with the scientific type of the data and will warn you otherwise.
tree = machine(tree_model, X, y)
# A machine is used both for supervised and unsupervised model.
# In this tutorial we give an example for the supervised model first and then go on with the unsupervised case.
#
# ## Training and testing a supervised model
#
# Now that you've declared the model you'd like to consider and the data, we are left with the standard training and testing step for a supervised learning algorithm.
#
# ### Splitting the data
#
# To split the data into a *training* and *testing* set, you can use the function `partition` to obtain indices for data points that should be considered either as training or testing data:
train, test = partition(eachindex(y), 0.7, shuffle=true)
test[1:3]
# ### Fitting and testing the machine
#
# To fit the machine, you can use the function `fit!` specifying the rows to be used for the training:
fit!(tree, rows=train)
# Note that this **modifies** the machine which now contains the trained parameters of the decision tree.
# You can inspect the result of the fitting with the `fitted_params` method:
fitted_params(tree) |> pprint
# This `fitresult` will vary from model to model though classifiers will usually give out a tuple with the first element corresponding to the fitting and the second one keeping track of how classes are named (so that predictions can be appropriately named).
#
# You can now use the machine to make predictions with the `predict` function specifying rows to be used for the prediction:
ŷ = predict(tree, rows=test)
@show ŷ[1]
# Note that the output is *probabilistic*, effectively a vector with a score for each class.
# You could get the mode by using the `mode` function on `ŷ` or using `predict_mode`:
ȳ = predict_mode(tree, rows=test)
@show ȳ[1]
@show mode(ŷ[1])
# To measure the discrepancy between `ŷ` and `y` you could use the average cross entropy:
mce = cross_entropy(ŷ, y[test]) |> mean
round(mce, digits=4)
# ## Unsupervised models
#
# Unsupervised models define a `transform` method,
# and may optionally implement an `inverse_transform` method.
# As in the supervised case, we use a machine to wrap the unsupervised model and the data:
v = [1, 2, 3, 4]
stand_model = UnivariateStandardizer()
stand = machine(stand_model, v)
# We can then fit the machine and use it to apply the corresponding *data transformation*:
fit!(stand)
w = transform(stand, v)
@show round.(w, digits=2)
@show mean(w)
@show std(w)
# In this case, the model also has an inverse transform:
vv = inverse_transform(stand, w)
sum(abs.(vv .- v))
# ---
#
# *This notebook was generated using [Literate.jl](https://github.com/fredrikekre/Literate.jl).*
|
__site/generated/notebooks/A-fit-predict.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # KoNLP Engine별 성능 비교
# ## Mecap Engine 설치
from konlpy.tag import *
engines = [Kkma, Hannanum]
s = u"갤럭시는 화면이 큰데, 좋은데?"
for e in engines:
print(e)
print(e().pos(s))
# * cf) Mecab : https://yuddomack.tistory.com/entry/처음부터-시작하는-EC2-konlpy-mecab-설치하기ubuntu
|
7.NLP/KoNLP_Engine.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Given a binary tree, determine if it is a valid binary search tree (BST).
#
# Assume a BST is defined as follows:
#
# - The left subtree of a node contains only nodes with keys less than the node's key.
# - The right subtree of a node contains only nodes with keys greater than the node's key.
# - Both the left and right subtrees must also be binary search trees.
#
#
# Example 1:
#
# 2
# / \
# 1 3
#
# Input: [2,1,3]
# Output: true
# Example 2:
#
# 5
# / \
# 1 4
# / \
# 3 6
#
# Input: [5,1,4,null,null,3,6]
# Output: false
# Explanation: The root node's value is 5 but its right child's value is 4.
# +
# recursive solution
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def isValidBST(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
lst = self.inorderTraversal(root)
for i in range(1,len(lst)):
if lst[i-1] >= lst[i]:
return False
return True
def inorderTraversal(self, root):
'''
:param root: TreeNode
:return: List[int]
'''
res = []
if root:
res = self.inorderTraversal(root.left)
res.append(root.val)
res += self.inorderTraversal(root.right)
return res
# +
# iterative solution
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def isValidBST(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
lst = self.inorderTraversal(root)
for i in range(1,len(lst)):
if lst[i-1] >= lst[i]:
return False
return True
def inorderTraversal(self, root):
'''
:param root: TreeNode
:return: List[int]
'''
# order: left -> root -> right
res, stack = [], []
while True:
while root:
stack.append(root)
root = root.left
if not stack:
return res
node = stack.pop()
res.append(node.val)
root = node.right
|
DSA/tree/isValidBST.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import os
os.environ["CUDA_VISIBLE_DEVICES"] = "1"
# +
import pandas as pd
import cv2
import numpy as np
from matplotlib import pyplot as plt
df = pd.read_csv("select_data____a____from_data___________.csv",index_col='no')
# -
df.info()
def alpha_to_gray(img):
alpha_channel = img[:, :, 3]
_, mask = cv2.threshold(alpha_channel, 128, 255, cv2.THRESH_BINARY) # binarize mask
color = img[:, :, :3]
img = cv2.bitwise_not(cv2.bitwise_not(color, mask=mask))
return cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
def preprocess(data):
data = bytes.fromhex(data[2:])
img = cv2.imdecode( np.asarray(bytearray(data), dtype=np.uint8), cv2.IMREAD_UNCHANGED )
img = alpha_to_gray(img)
kernel = np.ones((3, 3), np.uint8)
img = cv2.dilate(img, kernel, iterations=1)
img = cv2.medianBlur(img, 3)
kernel = np.ones((4, 4), np.uint8)
img = cv2.erode(img, kernel, iterations=1)
img = img/255.0
# plt.imshow(img)
return img
df["IMAGE"] = df["CAPTIMAGE"].apply(preprocess)
df2 = pd.read_csv("select_data____a____from_data___________.csv",index_col='no')
data = df2["CAPTIMAGE"][155]
data = bytes.fromhex(data[2:])
img = cv2.imdecode( np.asarray(bytearray(data), dtype=np.uint8), cv2.IMREAD_UNCHANGED )
img = alpha_to_gray(img)
kernel = np.ones((3, 3), np.uint8)
img = cv2.dilate(img, kernel, iterations=1)
img = cv2.medianBlur(img, 3)
kernel = np.ones((4, 4), np.uint8)
img = cv2.erode(img, kernel, iterations=1)
cv2.imwrite( "1.png", img );
df2 = df["answer"].apply(lambda x:pd.Series(list(x)))
df2.info()
df = pd.concat([df,df2], axis=1)
df.sample(20)
for i in range(6):
df[i] = df[i].astype('category')
df.info()
dy = pd.get_dummies(df[[0,1,2,3,4,5]]).to_numpy()
y = []
for dr in dy:
r = []
for i in range(6):
r.append(dr[i*26:(i+1)*26])
y.append(r)
np.array(y).shape
X = np.stack(df["IMAGE"].to_numpy()).reshape(1685,80,280,1)
# +
# from keras.preprocessing.image import ImageDataGenerator, array_to_img, img_to_array, load_img
# datagen = ImageDataGenerator(
# rotation_range=10,
# width_shift_range=0.2,
# height_shift_range=0.2,
# rescale=1./255,
# shear_range=0.2,
# zoom_range=0.2,
# horizontal_flip=False,
# fill_mode='nearest')
# img = load_img('1.png') # PIL 이미지
# x = img_to_array(img) # (3, 150, 150) 크기의 NumPy 배열
# x = x.reshape((1,) + x.shape) # (1, 3, 150, 150) 크기의 NumPy 배열
# # 아래 .flow() 함수는 임의 변환된 이미지를 배치 단위로 생성해서
# # 지정된 `preview/` 폴더에 저장합니다.
# i = 0
# for batch in datagen.flow(x, batch_size=1,
# save_to_dir='preview', save_prefix='1', save_format='png'):
# i += 1
# if i > 20:
# break # 이미지 20장을 생성하고 마칩니다
# +
from keras.models import Model
from keras.layers import Conv2D,MaxPooling2D,Dropout,Input,Flatten,Dense
def create_model(): # create model
tensor_in = Input((80, 280, 1))
out = tensor_in
out = Conv2D(filters=32, kernel_size=(3, 3), padding='same', activation='relu')(out)
out = Conv2D(filters=32, kernel_size=(3, 3), activation='relu')(out)
out = MaxPooling2D(pool_size=(2, 2))(out)
out = Conv2D(filters=64, kernel_size=(3, 3), padding='same', activation='relu')(out)
out = Conv2D(filters=64, kernel_size=(3, 3), activation='relu')(out)
out = MaxPooling2D(pool_size=(2, 2))(out)
out = Conv2D(filters=128, kernel_size=(3, 3), padding='same', activation='relu')(out)
out = Conv2D(filters=128, kernel_size=(3, 3), activation='relu')(out)
out = MaxPooling2D(pool_size=(2, 2))(out)
out = Conv2D(filters=256, kernel_size=(3, 3), activation='relu')(out)
out = MaxPooling2D(pool_size=(2, 2))(out)
out = Flatten()(out)
out = Dropout(0.5)(out)
out = [Dense(26, name='digit1', activation='softmax')(out),\
Dense(26, name='digit2', activation='softmax')(out),\
Dense(26, name='digit3', activation='softmax')(out),\
Dense(26, name='digit4', activation='softmax')(out),\
Dense(26, name='digit5', activation='softmax')(out),\
Dense(26, name='digit6', activation='softmax')(out)]
model = Model(inputs=tensor_in, outputs=out)
model.compile(loss='categorical_crossentropy', optimizer='Adamax', metrics=['accuracy'])
return model
# +
from keras.models import Sequential
from keras.layers import Dense
from keras.wrappers.scikit_learn import KerasClassifier
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
import numpy
# fix random seed for reproducibility
seed = 777
numpy.random.seed(seed)
# create model
model = KerasClassifier(build_fn=create_model, epochs=50, batch_size=10, verbose=2)
kfold = KFold(n_splits=5, shuffle=True, random_state=seed)
results = cross_val_score(model, X, y, cv=kfold)
# -
X.shape
y.shape
y
|
notebooks/kfold_cnn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <div class="alert alert-block alert-info" style="margin-top: 20px">
# <a href="">
# <img src="reference/DDC_logo.png" width="100" align="right">
# </a>
# </div>
#
# <h1 align=center><font size = 9>Data Science with Python</font></h1>
#
# <img src="reference/0.0 Agenda.jpg" align="center">
#
# <div class="alert alert-block alert-info" style="margin-top: 20px">
# <a href="">
# <img src="" width="750" align="center">
# </a>
# </div>
#
# <h1 align=center><font size = 9>How much would you sell / buy this car?</font></h1>
#
# <img src="reference/1.0 Introduction.png" align="center">
#
# <div class="alert alert-block alert-info" style="margin-top: 20px">
# <a href="">
# <img src="" width="750" align="center">
# </a>
# </div>
#
# <h1>LEARNING OBJECTIVES</h1>
# <h3>In this course you will learn about:</h3>
#
#
# ## • Introduciton: Data Acquisition & Basic Insight
# [Module 1]
#
# ## • Data Wrangling
# [Module 2]
#
# ## • Exploratory Data Analysis
# [Module 3]
#
# ## • Model Development
# [Module 4]
#
# ## • Model Evaluation
# [Module 5]
#
# <div class="alert alert-block alert-info" style="margin-top: 20px">
# <a href="">
# <img src="" width="750" align="center">
# </a>
# </div>
#
# <h1>AGENDA</h1>
#
# <h3>Module 1 - Introduction</h3>
#
# 1.1 Learning Objectives
#
# 1.2 Understanding the Domain
#
# 1.3 Understanding the Dataset
#
# 1.4 Python package for data science
#
# 1.5 Importing and Exporting Data in Python
#
# 1.6 Basic Insights from Datasets
#
# 1.7 Workshop 1
#
#
#
# <h3>Module 2 - Data Wrangling</h3>
#
# 2.1 Identify and Handle Missing Values
#
# 2.2 Data Formatting
#
# 2.3 Data Normalization
#
# 2.4 Binning
#
# 2.5 Indicator variables
#
# 2.6 Workshop 2
#
#
#
# <h3>Module 3 - Exploratory Data Analysis</h3>
#
# 3.1 Descriptive Statistics
#
# 3.2 Basic of Grouping
#
# 3.3 ANOVA (Analysis of variance)
#
# 3.4 Correlation
#
# 3.5 Correlation Coefficient
#
# 3.6 Workshop 3
#
#
#
# <h3>Module 4 - Model Development</h3>
#
# 4.1 Simple and Multiple Linear Regression
#
# 4.2 Model Evaluation using Visualization
#
# 4.3 Polynomial Regression and Pipelines
#
# 4.4 Measures for In-Sample Evaluation
#
# 4.5 Prediction and Decision Making
#
# 4.6 Workshop 4
#
#
# <h3>Module 5 - Model Evaluation and Refinement</h3>
#
# 5.1 Model Evaluation
#
# 5.2 Over Fitting, Under fitting and Model Selection
#
# 5.3 Ridge Regression
#
# 5.4 Grid Search
#
# 5.5 Workshop 5
#
# <div class="alert alert-block alert-info" style="margin-top: 20px">
# <a href="">
# <img src="" width="750" align="center">
# </a>
# </div>
#
# <hr>
#
|
Module 0 Agenda.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # The language
# Python 2
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Object
# + slideshow={"slide_type": "subslide"}
type(1)
# + slideshow={"slide_type": "fragment"}
# What is an object in python?
print dir(1)
# + slideshow={"slide_type": "subslide"}
#Let's try to understand
# ?dir
# + [markdown] slideshow={"slide_type": "fragment"}
# The answer is:
# > in **python** everything's an object
# + [markdown] slideshow={"slide_type": "slide"}
# ## Strings
# + [markdown] slideshow={"slide_type": "subslide"}
# Strings are lists of printable characters, and can be defined using either single quotes
# + slideshow={"slide_type": "-"}
'Hello, World!'
# + [markdown] slideshow={"slide_type": "fragment"}
# or double quotes
# -
"Hello, World!"
# + [markdown] slideshow={"slide_type": "subslide"}
# But not both at the same time, unless you want one of the symbols to be part of the string.
# -
"He's a Rebel"
# + slideshow={"slide_type": "fragment"}
'She asked, "How are you today?"'
# -
type('string')
# + [markdown] slideshow={"slide_type": "subslide"}
# Just like the other two data objects we're familiar with (ints and floats), you can assign a string to a variable
# -
greeting = "Hello, World!"
# + [markdown] slideshow={"slide_type": "subslide"}
# The **print** statement is often used for printing character strings:
# -
print greeting
# + [markdown] slideshow={"slide_type": "fragment"}
# But it can also print data types other than strings:
# -
area = 28
print "The area is ", area
# + [markdown] slideshow={"slide_type": "fragment"}
# In the above **snippet**, the number 600 (stored in the variable "area") is converted into a string before being printed out.
# + [markdown] slideshow={"slide_type": "subslide"}
# A suggestion if you want to take a good habit
# + slideshow={"slide_type": "fragment"}
# If you're asking yourself, is python 3 right?
print(greeting)
# It is: print is a *function*
# + [markdown] slideshow={"slide_type": "subslide"}
# You can use the + operator to concatenate strings together:
# -
statement = "Hello," + "World!"
print statement
# + [markdown] slideshow={"slide_type": "fragment"}
# Don't forget the space between the strings, if you want one there.
# + slideshow={"slide_type": "-"}
statement = "Hello, " + "World!"
print statement
# + [markdown] slideshow={"slide_type": "subslide"}
# You can use + to concatenate multiple strings in a single statement:
# -
print "This " + "is " + "a " + "longer " + "statement."
# If you have a lot of words to concatenate together, there are other, more efficient ways to do this. But this is fine for linking a few strings together.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Lists
# + [markdown] slideshow={"slide_type": "subslide"}
# Very often in a programming language, one wants to keep a group of similar items together.
#
# Python does this using a data type called **lists**.
# -
days_of_the_week = ["Sunday","Monday","Tuesday","Wednesday","Thursday","Friday","Saturday"]
type(days_of_the_week)
# + [markdown] slideshow={"slide_type": "subslide"}
# You can access members of the list using the **index** of that item:
# -
days_of_the_week[2]
# + [markdown] slideshow={"slide_type": "subslide"}
# Python lists, like C, but unlike Fortran, use 0 as the index of the first element of a list.
# +
# First element
print days_of_the_week[0]
# If you need to access the *n*th element from the end of the list,
# you can use a negative index.
print days_of_the_week[-1]
# + [markdown] slideshow={"slide_type": "subslide"}
# You can add additional items to the list using the .append() command:
# -
languages = ["Fortran","C","C++"]
languages.append("Python")
print languages
# + [markdown] slideshow={"slide_type": "subslide"}
# The **range()** command is a convenient way to make sequential lists of numbers:
# -
range(10)
# + [markdown] slideshow={"slide_type": "fragment"}
# Note that range(n) starts at 0 and gives the sequential list of integers less than n. If you want to start at a different number, use range(start,stop)
# -
range(2,8)
# + [markdown] slideshow={"slide_type": "subslide"}
# The lists created above with range have a *step* of 1 between elements. You can also give a fixed step size via a third command:
# -
evens = range(0,20,2)
evens
evens[3]
# + [markdown] slideshow={"slide_type": "subslide"}
# Lists **DO NOT** have to hold the *same data type*. For example,
# -
["Today",7,99.3,""]
# However, it's good (but not essential) to use lists for similar objects that are somehow logically connected.
# + slideshow={"slide_type": "fragment"}
help(len)
# -
#You can find out how long a list is using the **len()** command:
len(evens)
# + [markdown] slideshow={"slide_type": "-"}
# ##Exercise
# + [markdown] slideshow={"slide_type": "-"}
# - Define a list of 10 random integers in the range from 4 to 8
#
# <small>hint: use the `random` package</small>
#
# - Count how many numbers `5` you just generated.
#
# <small>hint: always **be pythonic** and use introspection and tabs</small>
# + slideshow={"slide_type": "fragment"}
import random
mylist = []
for i in range(10):
mylist.append(random.randint(4,8))
print mylist.count(5)
mylist
# + [markdown] slideshow={"slide_type": "slide"}
# ## Iteration, Indentation, and Blocks
# + [markdown] slideshow={"slide_type": "subslide"}
# One of the most useful things you can do with lists is to *iterate* through them
#
# > i.e. to go through each element one at a time
#
# To do this in Python, we use the **for** statement:
# + slideshow={"slide_type": "fragment"}
# Define loop
for day in days_of_the_week:
# This is inside the block :)
print day
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Blocks?
#
# (Almost) every programming language defines blocks of code in some way.
#
# * In Fortran, one uses END statements (ENDDO, ENDIF, etc.) to define code blocks.
# * In C, C++, and Perl, one uses curly braces {} to define these blocks.
# + [markdown] slideshow={"slide_type": "subslide"}
# Python uses a colon (":"), followed by indentation level
#
# > Everything at a higher level of indentation is taken to be in the same block.
#
#
# + [markdown] slideshow={"slide_type": "fragment"}
# <img src="images/blocks.png" width="600">
# + [markdown] slideshow={"slide_type": "subslide"}
# The **range()** command is particularly useful with the **for** statement to execute loops of a specified length:
# -
for i in range(20):
print "The square of ",i," is ",i*i
# + [markdown] slideshow={"slide_type": "slide"}
# ## Slicing
# <small> *Warning: pay attention. This is very important for using matrixes and **numpy** * </small>
# + [markdown] slideshow={"slide_type": "subslide"}
# Lists and strings have something in common that you might not suspect:
# they can both be treated as sequences.
#
# You can iterate through the letters in a string:
# + slideshow={"slide_type": "fragment"}
for letter in "Sunday":
print letter
# + [markdown] slideshow={"slide_type": "subslide"}
# More useful is the *slicing* operation, which you can also use on any sequence.
# -
days_of_the_week[0:2]
# + [markdown] slideshow={"slide_type": "fragment"}
# or simply
# -
days_of_the_week[:2]
# + [markdown] slideshow={"slide_type": "fragment"}
# <small>Note: we are not talking about *indexing* anymore.</small>
# + [markdown] slideshow={"slide_type": "subslide"}
# If we want the last items of the list, we can do this with negative slicing:
# -
days_of_the_week[-2:]
# + [markdown] slideshow={"slide_type": "subslide"}
# A subset:
# -
workdays = days_of_the_week[1:6]
print workdays
# + [markdown] slideshow={"slide_type": "subslide"}
# Since strings are sequences
# -
day = "Sunday"
abbreviation = day[:3]
print abbreviation
# + [markdown] slideshow={"slide_type": "subslide"}
# ###If we really want to get fancy
# we can pass a *third* element into the slice.
#
# It specifies a step length (just like a third argument to the **range()** function specifies the step):
# -
numbers = range(0,40)
evens = numbers[2::2]
evens
# + [markdown] slideshow={"slide_type": "fragment"}
# <small>note: I was even able to omit the second argument</small>
# + [markdown] slideshow={"slide_type": "subslide"}
# ##Exercise
# -
# Create a list that counts:
# - From 1 to 10 with step 1
# - From 11 to 20 with step 2
# - From 21 to 30 with step 1
#
# <small>note: use `range` only once</small>
# + slideshow={"slide_type": "fragment"}
x = range(1,31)
y = x[1:10] + x[11:20:2] + x[20:30]
print y
# + [markdown] slideshow={"slide_type": "slide"}
# ## Fundamental types
# + [markdown] slideshow={"slide_type": "subslide"}
# The basic types in any language are:
#
# * Strings (we already saw them)
# * Integers
# * Real
# * Boolean
#
# + slideshow={"slide_type": "fragment"}
# integers
x = 1
type(x)
# + slideshow={"slide_type": "fragment"}
# float
x = 1.0
type(x)
# + slideshow={"slide_type": "subslide"}
# boolean
b1 = True
b2 = False
type(b1)
# + slideshow={"slide_type": "subslide"}
# complex numbers: note the use of `j` to specify the imaginary part
x = 1.0 - 1.0j
type(x)
# + slideshow={"slide_type": "fragment"}
print(x)
# -
print(x.real, x.imag)
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Type utility functions
# + [markdown] slideshow={"slide_type": "fragment"}
#
# The module `types` contains a number of type name definitions that can be used to test if variables are of certain types:
# + slideshow={"slide_type": "fragment"}
import types
# print all types defined in the `types` module
print(dir(types))
# + [markdown] slideshow={"slide_type": "fragment"}
# <small> *Hint*: this technique is called **introspection** if you want to dig in </small>
# + slideshow={"slide_type": "subslide"}
x = 1.0
# check if the variable x is a float
type(x) is float
# + slideshow={"slide_type": "fragment"}
# check if the variable x is an int
type(x) is int
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Type casting
# + slideshow={"slide_type": "fragment"}
x = 1.5
print(x, type(x))
# + slideshow={"slide_type": "fragment"}
x = int(x)
print(x, type(x))
# + slideshow={"slide_type": "fragment"}
z = complex(x)
print(z, type(z))
# + [markdown] slideshow={"slide_type": "subslide"}
# Some conversions are impossible:
# + slideshow={"slide_type": "-"}
x = float(z)
# + [markdown] slideshow={"slide_type": "subslide"}
# ##Exercise
# -
# Try to concatenate a string with an integer
test = "a string with " + str(42)
print test, type(test)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Booleans and Truth Testing
# + [markdown] slideshow={"slide_type": "subslide"}
# ###tell me the truth:
# is this pen red?
#
# <img src="https://s-media-cache-ak0.pinimg.com/736x/17/16/50/171650fcbdfe81f6a11161e8e33d33ac.jpg" width=300>
# + [markdown] slideshow={"slide_type": "fragment"}
# *False*
# + [markdown] slideshow={"slide_type": "subslide"}
# <img src="http://i.imgur.com/RltvHOj.jpg" width=500>
# + [markdown] slideshow={"slide_type": "subslide"}
# **boolean** variables that can be either *True* or *False*
# + [markdown] slideshow={"slide_type": "fragment"}
# * We invariably need some concept of *conditions* in programming
# * to control branching behavior
# * to allow a program to react differently to different situations
#
# **IF** statements, control branching based on boolean values:
# -
if day == "Sunday":
print "Sleep in"
else:
print "Go to work"
# + [markdown] slideshow={"slide_type": "subslide"}
# (Quick quiz: why did the snippet print "Go to work" here? What is the variable "day" set to?)
#
# Let's take the snippet apart to see what happened.
# + slideshow={"slide_type": "fragment"}
# First, note the statement
day == "Sunday"
# + [markdown] slideshow={"slide_type": "fragment"}
# The "==" operator performs *equality testing*.
#
# If the two items are equal, it returns True, otherwise it returns False.
#
# + [markdown] slideshow={"slide_type": "subslide"}
# You can compare any data types in Python:
# -
1 == 2
# + slideshow={"slide_type": "fragment"}
50 == 2*25
# -
3 < 3.14159
# + slideshow={"slide_type": "subslide"}
1 == 1.0
# -
1 != 0
# + slideshow={"slide_type": "fragment"}
1 <= 2
# -
1 >= 1
# + [markdown] slideshow={"slide_type": "subslide"}
# We see a few other boolean operators here, all of which which should be self-explanatory. Less than, equality, non-equality, and so on.
#
# **Particularly interesting is the 1 == 1.0 test**
#
# <small>hint: the two objects are different *data types* (integer and floating point number) but they have the same *value*</small>
# + slideshow={"slide_type": "fragment"}
# A strange test
print 1 == 1.0
# Operator **is** tests whether two objects are the same object
print 1 is 1.0
# + [markdown] slideshow={"slide_type": "subslide"}
# We can do boolean tests on lists as well:
# + slideshow={"slide_type": "fragment"}
[1,2,3] == [1,2,4]
# + slideshow={"slide_type": "fragment"}
[1,2,3] < [1,2,4]
# + [markdown] slideshow={"slide_type": "subslide"}
# Finally, note that you can also string multiple comparisons together, which can result in very intuitive tests:
# -
hours = 5
0 < hours < 24
# + [markdown] slideshow={"slide_type": "subslide"}
# If statements can have **elif** parts ("else if"), in addition to if/else parts. For example:
# -
if day == "Sunday":
print "Sleep in"
elif day == "Saturday":
print "Do chores"
else:
print "Go to work"
# + [markdown] slideshow={"slide_type": "slide"}
# ## A quick scientific code example
#
# + [markdown] slideshow={"slide_type": "subslide"}
# ###The Fibonacci Sequence
#
# The [Fibonacci sequence](http://en.wikipedia.org/wiki/Fibonacci_number) is a sequence in math that starts with 0 and 1, and then each successive entry is the sum of the previous two. Thus, the sequence goes 0,1,1,2,3,5,8,13,21,34,55,89,...
#
# + slideshow={"slide_type": "fragment"}
n = 10
sequence = [0,1]
for i in range(2,n): # This is going to be a problem if we ever set n <= 2!
sequence.append(sequence[i-1]+sequence[i-2])
print sequence
# + [markdown] slideshow={"slide_type": "slide"}
# ## Functions
# + [markdown] slideshow={"slide_type": "subslide"}
# We might want to use the Fibonacci snippet with different sequence lengths.
#
# How do we define a function?
# (*and what is a function anyway?*)
# + slideshow={"slide_type": "fragment"}
#Use the **def** statement in Python
def fibonacci(sequence_length):
"Return the Fibonacci sequence of length *sequence_length*"
sequence = [0,1]
if sequence_length < 1:
print "Fibonacci sequence only defined for length 1 or greater"
return
if 0 < sequence_length < 3:
return sequence[:sequence_length]
for i in range(2,sequence_length):
sequence.append(sequence[i-1]+sequence[i-2])
return sequence
# + [markdown] slideshow={"slide_type": "subslide"}
# We can now call **fibonacci()** for different sequence_lengths:
# + slideshow={"slide_type": "fragment"}
fibonacci(2)
# + slideshow={"slide_type": "fragment"}
fibonacci(12)
# + [markdown] slideshow={"slide_type": "subslide"}
# Note: we used a **docstring**
#
# * a special kind of comment
# * often available to people using the function through the python command line
# + slideshow={"slide_type": "fragment"}
help(fibonacci)
# + [markdown] slideshow={"slide_type": "fragment"}
# ###If you define a docstring for all of your functions, it makes it easier for other people to use them!
# + [markdown] slideshow={"slide_type": "subslide"}
# Help is even easier with packages
# + slideshow={"slide_type": "fragment"}
import math
# Click your point inside the parenthesis
# Then press SHIFT + TAB
math.sin(3)
# + [markdown] slideshow={"slide_type": "subslide"}
# Best practice
# > Write documentation before writing the code
# + slideshow={"slide_type": "-"}
def square_root(n):
"""Calculate the square root of a number.
Args:
n: the number to get the square root of.
Returns:
the square root of n.
Raises:
TypeError: if n is not a number.
ValueError: if n is negative.
"""
pass
# + slideshow={"slide_type": "fragment"}
# Print only the first line
print square_root.__doc__.split('\n')[0]
# + [markdown] slideshow={"slide_type": "subslide"}
# You may then start **documenting your project using sphinx**:
# https://pythonhosted.org/an_example_pypi_project/sphinx.html
#
# <img src='http://j.mp/1HRGRD8' width=600>
# + [markdown] slideshow={"slide_type": "slide"}
# ## More Data Structures
# + [markdown] slideshow={"slide_type": "subslide"}
# ##Tuples
#
# A **tuple** is a sequence object like a list or a string.
#
# It's constructed by grouping a sequence of objects together
# + slideshow={"slide_type": "fragment"}
t = (1,2,'hi',9.0)
t
# + [markdown] slideshow={"slide_type": "fragment"}
# Tuples are like lists, in that you can access the elements using indices:
# -
t[1]
# + [markdown] slideshow={"slide_type": "subslide"}
# However, tuples are *immutable*, you can't append to them or change the elements of them:
# + slideshow={"slide_type": "fragment"}
t.append(7)
# + slideshow={"slide_type": "fragment"}
t[1]=77
# + [markdown] slideshow={"slide_type": "subslide"}
# Tuples are useful anytime you want to group different pieces of data together in an object
# + slideshow={"slide_type": "fragment"}
# For example, let's say you want the Cartesian coordinates of some objects
('Bob',0.0,21.0)
# + [markdown] slideshow={"slide_type": "subslide"}
# Again, to distinguish
#
# - tuples are a collection of different things
# * here a name, and x and y coordinates,
# - a list is a collection of similar things
# * like if we wanted a list of those coordinates
# + slideshow={"slide_type": "fragment"}
positions = [
('Bob',0.0,21.0),
('Cat',2.5,13.1),
('Dog',33.0,1.2)
]
# + [markdown] slideshow={"slide_type": "subslide"}
# Tuples can be used when functions return more than one value!
# + slideshow={"slide_type": "fragment"}
def minmax(objects):
minx = 1e20 # These are set to really big numbers
miny = 1e20
for obj in objects:
name,x,y = obj
if x < minx:
minx = x
if y < miny:
miny = y
return minx, miny
x,y = minmax(positions)
print x,y
# + [markdown] slideshow={"slide_type": "subslide"}
# Tuple assignment is also a convenient way to swap variables
# + slideshow={"slide_type": "fragment"}
x,y = 1,2
y,x = x,y
x,y
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Dictionaries
#
# **Dictionaries** are an object called "mappings" or "associative arrays" in other languages. Whereas a list associates an integer index with a set of objects:
# -
mylist = [1,2,9,21]
# + [markdown] slideshow={"slide_type": "fragment"}
# The index in a dictionary is called the *key*, and the corresponding dictionary entry is the *value*
# + slideshow={"slide_type": "fragment"}
ages = {"Rick": 46, "Bob": 86, "Fred": 21}
print "Rick's age is ",ages["Rick"]
# + [markdown] slideshow={"slide_type": "subslide"}
# There's also a convenient way to create dictionaries without having to quote the keys.
# -
dict(Rick=46,Bob=86,Fred=20)
# + slideshow={"slide_type": "subslide"}
# Cycling a dictionary
for key, value in ages.iteritems():
print key + ":\t" + str(value) + " years old"
# + [markdown] slideshow={"slide_type": "fragment"}
# *Note*: dictionary are the most powerfull structure in python
# + [markdown] slideshow={"slide_type": "fragment"}
# *Note **bis***: dictionary are **NOT** suitable for *everything*
# + [markdown] slideshow={"slide_type": "subslide"}
# The **len()** command works on both tuples and dictionaries:
# -
len(t)
len(ages)
# + slideshow={"slide_type": "subslide"}
## TYPES recap
# List
mylist = ["a", "b", "c"]
# Tuple
mytup = ("a", 23, ["c","de"])
# Dictionary
mydict = {"name": "paulie", "address": "middle of nowhere"}
# + slideshow={"slide_type": "slide"}
# %load_ext version_information
# %version_information
# + [markdown] slideshow={"slide_type": "subslide"}
# # End
# + [markdown] slideshow={"slide_type": "fragment"}
# **Let's move to the next part :)**
|
pydata/02_language.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/atlas-github/20190731StarMediaGroup/blob/master/fstep_20_dataviz.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="N4vHUHvEB8X-"
# #Context
# + [markdown] id="1G3XA7FCB_F4"
# In 1953, the New York State Legislature created the New York City Transit Authority as a public corporation to oversee management and operation of the public transportation system. Now known as MTA New York City Transit, it operates the New York City subway, and local and express New York City buses alongside its sister MTA agencies the Long Island Rail Road and the Metro-North Railroad commuter rail services. The New York City subway system has the highest ridership of any subway in the US and the 7th largest in the world. It provided an average of 5.7 million weekday rides in 2015.
#
# In this lesson, we will examine the turnstile data provided by the MTA. As we will see, **turnstile data tracks the number of entries and exits of passengers in the subway system**. However, **the number of times the turnstile records an entrance or exit does not capture the total number of passengers who use the subway**. Passengers who use one-way exit turnstiles are not counted. Passengers often use emergency exits instead of the turnstiles during peak hours or if the turnstiles are in an inconvenient location. People may also “jump the turnstiles” and enter the system without paying a fare (and using the turnstile.)
#
# In this exercise, we shall **examine passengers entering through turnstiles** in some of the busiest and largest stations in the MTA subway system.
#
# Side note: The MTA subway system charges one fare regardless of the distance travel. Washington DC’s Metro subway and Seattle’s light rail system charges based on the numbers of zones travels. Passengers must “tap in” when they enter the system, and “tap out” when they exit the system to determine their fare. One feature of this payment structure is that those transit systems have better data on the length and destinations of trips.
#
# Source: [Transit Data Toolkit](http://transitdatatoolkit.com/lessons/subway-turnstile-data/)
# + [markdown] id="7xDosQms0SL7"
# #Extract and explore MTA data
# + colab={"base_uri": "https://localhost:8080/"} id="Qf8cWIIE0Ejt" outputId="bed8acda-7a34-48af-817b-9aeae1e5df0f"
#This extracts a few files from http://web.mta.info/developers/turnstile.html
# !wget http://web.mta.info/developers/data/nyct/turnstile/turnstile_210130.txt
# !wget http://web.mta.info/developers/data/nyct/turnstile/turnstile_210123.txt
# !wget http://web.mta.info/developers/data/nyct/turnstile/turnstile_210116.txt
# !wget http://web.mta.info/developers/data/nyct/turnstile/turnstile_210109.txt
# !wget http://web.mta.info/developers/data/nyct/turnstile/turnstile_210102.txt
# + id="pnV8woBy5sFp"
import pandas as pd
df5 = pd.read_csv('turnstile_210130.txt', delimiter = ",")
df4 = pd.read_csv('turnstile_210123.txt', delimiter = ",")
df3 = pd.read_csv('turnstile_210116.txt', delimiter = ",")
df2 = pd.read_csv('turnstile_210109.txt', delimiter = ",")
df1 = pd.read_csv('turnstile_210102.txt', delimiter = ",")
df0 = df1[df1.DATE.str.startswith("01")]
# + colab={"base_uri": "https://localhost:8080/", "height": 419} id="SBCv2fyiF0Jh" outputId="053dfca6-0724-48d1-a728-951a052866a8"
df = pd.concat([df0, df2, df3, df4, df5], ignore_index = True)
df
# + [markdown] id="JJJZ8qud7dCS"
# C/A – The Control Area is the operator booth in a station. Some stations only have one operator booth. However, larger stations may have more than one.
#
# UNIT – The Remote Unit, which is the collection of turnstiles. A station may have more than one Remote Unit.
#
# SCP – The Subunit Channel Position represents the turnstile and the number used may repeat across stations. The UNIT and SCP together is a unique identifier of a turnstile.
#
# DATE – The Date is the date of the recording with the format MM/DD/YYYY.
#
# TIME – The Time is the time for a recording, with the format: HH:MM:SS.
#
# DESC – The DESC is the type of event of the reading. The turnstiles submit “Regular” readings every four hours. They stagger the exact time of the readings across all the turnstiles and stations. Staggering the data submission times avoids having all the turnstiles update at simultaneously. “Recover Audit” designates scheduled readings taken after a communication outage. Our analysis uses “Regular” and “Recover Audit” readings. We discard other values such as “DoorClose” and “DoorOpen” which represent unscheduled maintenance readings.
#
# ENTRIES = The ENTRIES are a cumulative count of turnstile entrances. Note, the ENTRIES do not reset each day or for each recording period. The turnstile entry count continues to increase until it reaches the device limit and then resets to zero.
#
# EXITS = The EXITS are a cumulative count of the turnstile exits.
# + [markdown] id="wYiv6Apg0WYz"
# #Prepare data
# + colab={"base_uri": "https://localhost:8080/", "height": 419} id="na6-v5GW0ZF5" outputId="6bb7ef32-d537-4a39-e73e-3537a8a6acb2"
#Rename C/A column to BOOTH
df_new = df.rename(columns = {"C/A": "BOOTH"})
df_new
#Keep only Regular and Recovery Audit readings
df_filter = df_new.loc[df_new['DESC'].isin(['REGULAR','RECOVR AUD'])]
df_filter
# + [markdown] id="zESHCdnfMzGi"
# In the turnstile `dataframe`, look at the `Entries` and `Exits` columns.
# The turnstiles record each time a passenger enters and exits through it. Every four hours, they send a time-stamped running tally of the entries and exits. The data shows that the tally increases with every reading. The turnstiles reset when their counters reach their maximum limit. To determine how many people enter through a turnstile, we subtract the previous time stamped `Entries` reading with the current number of `Entries`.
# + colab={"base_uri": "https://localhost:8080/", "height": 419} id="GTWKLipEQUFI" outputId="c8db179d-fea8-48c8-ac75-59bcd13f798e"
df_filter['diff'] = df_filter.groupby(["BOOTH", "SCP"]).ENTRIES.diff()
df_filter
# + [markdown] id="M91AJ0m-RiT2"
# We now have the number of passengers entering and exiting a turnstile over each time interval. However, on occasion, there might be a negative number of passengers. Outages in the transmission, lapses in communication between the turnstile and the MTA backend servers, and maintenance on the turnstile cause these readings.
# + colab={"base_uri": "https://localhost:8080/", "height": 419} id="NfcK6RKPQotI" outputId="795777de-aa3c-4038-a0e0-56a366d70cb8"
df_filter = df_filter[df_filter["diff"] > 0]
df_filter
# + [markdown] id="Z57ZuZkxSIM8"
# Four major stations of the subway system are `34th St Penn Station`, `42nd St Port Authority`, `42th St Grand Central`, and `Atlantic Avenue Barclay`. These are some of the busiest stations in the system, with connections to other various modes of transit such as Amtrak, Long Island Railroad, MTA Metro North regional trains, and regional bus service. Let’s compare the ridership of these stations.
# + colab={"base_uri": "https://localhost:8080/", "height": 419} id="b6r0J3BbSLW9" outputId="68991bf6-b5f0-4cce-e452-68a25d70abfe"
df_stn = df_filter[(df_filter['STATION'] == "34 ST-PENN STA") | (df_filter['STATION'] == "42 ST-PORT AUTH") |
(df_filter['STATION'] == "GRD CNTRL-42 ST") | (df_filter['STATION'] == "ATL AV-BARCLAY")]
df_stn
# + [markdown] id="zUREuRCCUobL"
# Then we calculate the Entries by our four stations and day. The `sum` function groups all our data into subsets and produces summary statistics on each subset.
# + colab={"base_uri": "https://localhost:8080/", "height": 419} id="3Gs08r7ZS9JY" outputId="0b27cbaa-178e-4e94-fdc1-470c11b3aff9"
stations_four = df_stn.groupby(["STATION", "DATE"])[["diff"]].sum().reset_index()
stations_four
# + [markdown] id="AAi7BRrS0aF6"
# #Create charts using Seaborn
# + [markdown] id="XCWWbR2zW8_9"
# A line chart is a useful when comparing numeric values across time. We will use it to compare each station’s daily entries.
# + colab={"base_uri": "https://localhost:8080/", "height": 359} id="_ZxEhcHj0b10" outputId="406ecf63-f4a0-4e86-9248-2296647cb36a"
import seaborn as sns
import matplotlib.pyplot as plt
plt.figure(figsize=(35, 8))
sns.lineplot(data = stations_four, x = "DATE", y = "diff", hue = "STATION").set_title("MTA Subway Daily Turnstile Entries, Jan 2021")
# + [markdown] id="JIo2dV7z0cwf"
# #Exercise
# + [markdown] id="qmufPCEcaKt4"
# Using `df_stn`, use Seaborn's [barplot](https://seaborn.pydata.org/generated/seaborn.barplot.html) to find the number of passengers for each station.
# + colab={"base_uri": "https://localhost:8080/", "height": 296} id="j2QnjSVEaKSd" outputId="ef063c91-07df-4838-9e51-19c37713520f"
sns.barplot(x = "STATION", y = "diff", data = stations_four)
# + colab={"base_uri": "https://localhost:8080/", "height": 296} id="WjbYZaihk01n" outputId="1cd4df95-3e4b-41a8-8494-d53abe5b9ea4"
sns.boxplot(x = "STATION", y = "diff", data = stations_four)
# + colab={"base_uri": "https://localhost:8080/"} id="LN0tybhni-99" outputId="e82f901b-f7f7-41b7-9d04-04121319b3c4"
# !wget http://web.mta.info/developers/resources/nyct/turnstile/Remote-Booth-Station.xls
# + colab={"base_uri": "https://localhost:8080/", "height": 419} id="QZe3vc5djNww" outputId="93283923-71eb-4755-e8a4-731eca541386"
stations = pd.read_excel("Remote-Booth-Station.xls")
stations
# + colab={"base_uri": "https://localhost:8080/", "height": 296} id="rSILYxosguDT" outputId="6539d08d-da62-4b7f-c9d1-c255e3f8fbfd"
sns.countplot(x = "Station", data = stations)
# + id="SncBsQpNoZ_U"
|
fstep_20_dataviz.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### a) Create a text file and manually add some data to the file
f = open("demo.txt", "w")
f.write("<NAME>, 34, <EMAIL>, manager \n")
f.write("<NAME>, 45, <EMAIL>, sales \n")
f.close()
# #open and read the file
f = open("demo.txt", "r")
print(f.read())
f.close()
# ### b) Write Python code to
# - open the file for write only access
# - attempt to read the contents of the file
f = open("demo.txt", "w")
print(f.read())
f.close()
# ### c) Note the type of Error that has been raised.
# that is UnsupportedOperation
# ### d) Modify your code to
# - use a try / except / finally construct that will catch the exception,
# - print a user-friendly error message, and clean up the file resource
# +
import sys
import io
try:
f = open("demo.txt", "w")
print(f.read())
except io.UnsupportedOperation:
print("A type of 'UnsupportedOperation' exception was triggered.\nThis is because you have opened your file in a write mode, while you are trying to read it !")
except:
("Other type of error " + sys.exc_info()[2])
finally:
f.close()
# -
# ### e) Investigate how you would create your own Exception class.
# Then create your own Exception class and use it in your code from the previous exercise.
# +
class MyCustomException(io.UnsupportedOperation):
pass
try:
f = open("demo.txt", "w")
raise MyCustomException('You have opened your file in an incompatible mode')
print(f.read())
except io.UnsupportedOperation:
print("Handled by '{}': {}".format(sys.exc_info()[0], sys.exc_info()[1]))
except:
print("Other type of error {}".format(sys.exc_info()[2]))
finally:
f.close()
# -
|
DAP_Lab4/.ipynb_checkpoints/exception-handling-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from PIL import Image, ImageOps
from IPython.display import display
# For manually printing custom lambs
img1 = Image.open(f'../../assets/backgrounds/bg_yellow.png').convert('RGBA')
img2 = Image.open(f'../../assets/wool/white.png').convert('RGBA')
img3 = Image.open(f'../../assets/wool/outline.png').convert('RGBA')
img4 = Image.open(f'../../assets/shirts/flannel.png').convert('RGBA')
img5 = Image.open(f'../../assets/faces/smile.png').convert('RGBA')
img6 = Image.open(f'../../assets/hats/ballcap.png').convert('RGBA')
# Create each composite
com1 = Image.alpha_composite(img1, img2)
com2 = Image.alpha_composite(com1, img3)
com3 = Image.alpha_composite(com2, img4)
com4 = Image.alpha_composite(com3, img5)
com5 = Image.alpha_composite(com4, img6)
# Convert to RGB
rgbImg = com5.convert('RGB')
#display(rgbImg.resize((400,400), Image.NEAREST))
file_name = "manual.png"
rgbImg.save("./" + file_name)
# -
|
generator/manualGenerator.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.6.6 64-bit (''learn-env'': conda)'
# metadata:
# interpreter:
# hash: b9630d5e2ab3b0a71086734c5496348dcf699cc0359da5160f16a256dcc49ceb
# name: 'Python 3.6.6 64-bit (''learn-env'': conda)'
# ---
# # WORKING WITH LONG LINE OF CODE
#Import needed library
import statistics
# + tags=[]
products_promotion_price = [2.8, 4.5, 3.6, 1.9, 8.25, 3,15, 7.25, 9.45, 5.35, 11.25, 4.75, 6.5]; print(products_promotion_price)
number_of_products = [12, 32, 51, 62, 23, 19, 31, 27, 45, 29, 53, 61]; print(number_of_products)
# -
# ### LONG LINE OF CODE
sales_promotion_price = [element_in_products_promotion_price * element_in_number_of_products for element_in_products_promotion_price, element_in_number_of_products in zip(products_promotion_price, number_of_products)]
sales_promotion_price
# ### SHORTEN LONG LINE OF CODE:
# * We can use \ to break up lines of code
# * We can make our code simplier or easier to read by taking advantage of the fact that line breaks are ignored inside (), {} and []. Using comments to explain the lines of code.
sales_promotion_price = [# multiple the first list's elements accordingly by second list's element
element_in_products_promotion_price * element_in_number_of_products
# for the first list's elements and second list's element
for element_in_products_promotion_price, element_in_number_of_products
# for each element in a zip between the products promotion price
in zip(products_promotion_price,
# and the number of products
number_of_products)
]
sales_promotion_price
|
working_with_long_line_code.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Use AutoAI and batch deployment to predict credit risk with Watson Machine Learning REST API
# This notebook contains steps and code to demonstrate support of AutoAI experiments in Watson Machine Learning Service. It introduces commands for getting data, training experiments, persisting pipelines, publishing models, deploying models and scoring.
#
# Some familiarity with cURL is helpful. This notebook uses cURL examples.
#
#
# ## Learning goals
#
# The learning goals of this notebook are:
#
# - Working with Watson Machine Learning experiments to train AutoAI models.
# - Downloading computed models to local storage.
# - Batch deployment and scoring of trained model.
#
#
# ## Contents
#
# This notebook contains the following parts:
#
# 1. [Setup](#setup)
# 2. [Experiment definition](#experiment_definition)
# 3. [Experiment Run](#run)
# 4. [Historical runs](#runs)
# 5. [Deploy and Score](#deploy_and_score)
# 6. [Cleaning](#cleaning)
# 7. [Summary and next steps](#summary)
# <a id="setup"></a>
# ## 1. Set up the environment
#
# Before you use the sample code in this notebook, you must perform the following setup tasks:
#
# - Contact with your Cloud Pack for Data administrator and ask him for your account credentials
# ### Connection to WML
#
# Authenticate the Watson Machine Learning service on IBM Cloud Pack for Data. You need to provide platform `url`, your `username` and `api_key`.
# +
# %env USERNAME=
# %env API_KEY=
# %env DATAPLATFORM_URL=
# %env SPACE_ID=
# -
# <a id="wml_token"></a>
# ### Getting WML authorization token for further cURL calls
# <a href="https://cloud.ibm.com/docs/cloud-object-storage?topic=cloud-object-storage-curl#curl-token" target="_blank" rel="noopener no referrer">Example of cURL call to get WML token</a>
# + magic_args="--out token" language="bash"
#
# token=$(curl -sk -X POST \
# --header "Content-type: application/json" \
# -d "{\"username\":\"${USERNAME}\",\"api_key\":\"${API_KEY}\"}" \
# "$DATAPLATFORM_URL/icp4d-api/v1/authorize")
#
# token=${token#*token\":\"}
# token=${token%%\"*}
# echo $token
# -
# %env TOKEN=$token
# <a id="space_creation"></a>
# ### Space creation
# **Tip:** If you do not have `space` already created, please convert below three cells to `code` and run them.
#
# First of all, you need to create a `space` that will be used in all of your further cURL calls.
# If you do not have `space` already created, below is the cURL call to create one.
# <a href="https://cpd-spaces-api.eu-gb.cf.appdomain.cloud/#/Spaces/spaces_create"
# target="_blank" rel="noopener no referrer">Space creation</a>
# + magic_args="--out space_id" language="bash" active=""
#
# curl -sk -X POST \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# --data '{"name": "curl_DL"}' \
# "$DATAPLATFORM_URL/v2/spaces" \
# | grep '"id": ' | awk -F '"' '{ print $4 }'
# + active=""
# space_id = space_id.split('\n')[1]
# %env SPACE_ID=$space_id
# -
# Space creation is asynchronous. This means that you need to check space creation status after creation call.
# Make sure that your newly created space is `active`.
# <a href="https://cpd-spaces-api.eu-gb.cf.appdomain.cloud/#/Spaces/spaces_get"
# target="_blank" rel="noopener no referrer">Get space information</a>
# + language="bash" active=""
#
# !curl -sk -X GET \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# "$DATAPLATFORM_URL/v2/spaces/$SPACE_ID"
# -
# <a id="experiment_definition"></a>
# ## 2. Experiment / optimizer configuration
#
# Provide input information for AutoAI experiment / optimizer:
# - `name` - experiment name
# - `learning_type` - type of the problem
# - `label` - target column name
# - `scorer_for_ranking` - optimization metric
# - `holdout_param` - percentage of training data to use as a holdout [0 - 1]
# - `daub_include_only_estimators` - list of estimators to use
# You can modify `parameters` section of the following cURL call to change AutoAI experiment settings.
# <a href="https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Pipelines/pipelines_create"
# target="_blank" rel="noopener no referrer">Define AutoAI experiment.</a>
# + magic_args="--out pipeline_payload" language="bash"
#
# PIPELINE_PAYLOAD='{"space_id": "'"$SPACE_ID"'", "name": "Credit Risk Prediction - AutoAI", "description": "", "document": {"doc_type": "pipeline", "version": "2.0", "pipelines": [{"id": "autoai", "runtime_ref": "hybrid", "nodes": [{"id": "automl", "type": "execution_node", "parameters": {"stage_flag": true, "output_logs": true, "input_file_separator": ",", "optimization": {"learning_type": "binary", "label": "Risk", "max_num_daub_ensembles": 1, "daub_include_only_estimators": ["ExtraTreesClassifierEstimator", "GradientBoostingClassifierEstimator", "LGBMClassifierEstimator", "LogisticRegressionEstimator", "RandomForestClassifierEstimator", "XGBClassifierEstimator", "DecisionTreeClassifierEstimator"], "scorer_for_ranking": "roc_auc", "compute_pipeline_notebooks_flag": true, "run_cognito_flag": true, "holdout_param": 0.1}}, "runtime_ref": "autoai", "op": "kube"}]}], "runtimes": [{"id": "autoai", "name": "auto_ai.kb", "app_data": {"wml_data": {"hardware_spec": { "name": "M"}}}, "version": "3.0.2"}],"primary_pipeline": "autoai"}}'
# echo $PIPELINE_PAYLOAD | python -m json.tool
# -
# %env PIPELINE_PAYLOAD=$pipeline_payload
# + magic_args="--out pipeline_id" language="bash"
#
# curl -sk -X POST \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# --data "$PIPELINE_PAYLOAD" \
# "$DATAPLATFORM_URL/ml/v4/pipelines?version=2020-08-01" \
# | grep '"id": ' | awk -F '"' '{ print $4 }' | sed -n 5p
# -
# %env PIPELINE_ID=$pipeline_id
# <a id="experiment_details"></a>
# ### Get experiment details
# To retrieve AutoAI experiment / optimizer configuration you can follow below cURL GET call.
# <a href="https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Pipelines/pipelines_get"
# target="_blank" rel="noopener no referrer">Get experiment / optimizer information</a>
# + language="bash"
#
# curl -sk -X GET \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# "$DATAPLATFORM_URL/ml/v4/pipelines/$PIPELINE_ID?space_id=$SPACE_ID&version=2020-08-01" \
# | python -m json.tool
# -
# <a id="training_connection"></a>
# ### Training data connection
#
# Define connection information to COS bucket and training data CSV file. This example uses the German Credit Risk dataset.
#
# The dataset can be downloaded from [here](https://github.com/IBM/watson-machine-learning-samples/raw/master/data/credit_risk/credit_risk_training_light.csv ). You can also download it to local filesystem by running the cell below.
#
# **Action**: Upload training data to COS bucket and enter location information in the next cURL examples.
# + language="bash"
#
# wget https://github.com/IBM/watson-machine-learning-samples/raw/master/cpd4.0/data/credit_risk/credit_risk_training_light.csv \
# -O credit_risk_training_light.csv
# -
# <a id="cos_upload"></a>
# ### Create Data Asset
# Upload your local dataset into Data Asset Storage
# <a href="https://cloud.ibm.com/apidocs/watson-data-api#createdataassetv2"
# target="_blank" rel="noopener no referrer">Upload file as Data Asset</a>
# + magic_args="--out data_asset_metadata" language="bash"
#
# DATA_ASSET_METADATA='{"metadata": {"name": "autoai_training_data","description": "desc","asset_type": "data_asset","origin_country": "us","asset_category": "USER"},"entity": {"data_asset": {"mime_type": "text/csv"}}}'
# echo $DATA_ASSET_METADATA | python -m json.tool
# -
# %env DATA_ASSET_METADATA=$data_asset_metadata
# + magic_args="--out asset_id" language="bash"
#
# asset_id=$(curl -sk -X POST \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --data "$DATA_ASSET_METADATA" \
# "$DATAPLATFORM_URL/v2/assets?space_id=$SPACE_ID&version=2020-08-01")
#
# asset_id=${asset_id#*asset_id\":\"}
# asset_id=${asset_id%%\"*}
# echo $asset_id
# -
# %env ASSET_ID=$asset_id
# + magic_args="--out attachment" language="bash"
#
# ATTACHMENT='{"asset_type": "data_asset", "name": "credit_risk_training_light.csv", "mime": "text/csv"}'
# echo $ATTACHMENT | python -m json.tool
# -
# %env ATTACHMENT=$attachment
# + magic_args="--out attachment_response" language="bash"
#
# curl -sk -X POST \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --data "$ATTACHMENT" \
# "$DATAPLATFORM_URL/v2/assets/$ASSET_ID/attachments?space_id=$SPACE_ID&version=2020-08-01"
# -
# %env ATTACHMENT_RESPONSE=$attachment_response
# + magic_args="--out attachment_id" language="bash"
#
# echo $ATTACHMENT_RESPONSE | cut -d '"' -f 4 | tr -d '\n'
# -
# %env ATTACHMENT_ID=$attachment_id
# + magic_args="--out attachment_url" language="bash"
#
# echo $ATTACHMENT_RESPONSE | cut -d '"' -f 16 | tr -d '\n'
# -
# %env ATTACHMENT_URL=$attachment_url
# + language="bash"
#
# curl -sk -X PUT \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: multipart/form-data" \
# -F 'file=@credit_risk_training_light.csv' \
# "$DATAPLATFORM_URL$ATTACHMENT_URL"
# -
# The response should looks like this:
# `{"status":"Asset created: The asset was successfully uploaded."}`
# + language="bash"
#
# curl -sk -X POST \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# "$DATAPLATFORM_URL/v2/assets/$ASSET_ID/attachments/$ATTACHMENT_ID/complete?space_id=$SPACE_ID&version=2020-08-01"
# -
# <a id="run"></a>
# ## 3. Experiment run
#
# This section provides samples about how to trigger AutoAI experiment via cURL calls.
# <a href="https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Trainings/trainings_create"
# target="_blank" rel="noopener no referrer">Schedule a training job for AutoAI experiment</a>
# + magic_args="--out random_id" language="bash"
#
# openssl rand -hex 20
# -
# %env RANDOM_ID=$random_id
# + magic_args="--out training_payload" language="bash"
#
# TRAINING_PAYLOAD='{"space_id": "'"$SPACE_ID"'", "training_data_references": [{"type": "data_asset", "id": "credit_risk_training_light.csv", "connection": {}, "location": {"href": "/v2/assets/'"$ASSET_ID"'?space_id='"$SPACE_ID"'"}}], "results_reference": {"type": "fs", "id": "autoai_results", "connection": {}, "location": {"path": "/spaces/'$SPACE_ID'/assets/auto_ml/auto_ml_curl.'$RANDOM_ID'/wml_data"}}, "tags": [{"value": "autoai"}], "pipeline": {"id": "'"$PIPELINE_ID"'"}}'
# echo $TRAINING_PAYLOAD | python -m json.tool
# -
# %env TRAINING_PAYLOAD=$training_payload
# + magic_args="--out training_id" language="bash"
#
# curl -sk -X POST \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# --data "$TRAINING_PAYLOAD" \
# "$DATAPLATFORM_URL/ml/v4/trainings?version=2020-08-01" \
# | awk -F'"id":' '{print $2}' | cut -c2-37
# -
# %env TRAINING_ID=$training_id
# <a id="training_details"></a>
# ### Get training details
# Training is an asynchronous endpoint. In case you want to monitor training status and details,
# you need to use a GET method and specify which training you want to monitor by usage of training ID.
# <a href="https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Trainings/trainings_get"
# target="_blank" rel="noopener no referrer">Get information about training job</a>
# + language="bash" active=""
#
# curl -sk -X GET \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# "$DATAPLATFORM_URL/ml/v4/trainings/$TRAINING_ID?space_id=$SPACE_ID&version=2020-08-01" \
# | python -m json.tool
# -
# ### Get training status
# + language="bash"
#
# STATUS=$(curl -sk -X GET\
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# "$DATAPLATFORM_URL/ml/v4/trainings/$TRAINING_ID?space_id=$SPACE_ID&version=2020-08-01")
#
# STATUS=${STATUS#*state\":\"}
# STATUS=${STATUS%%\"*}
# echo $STATUS
# -
# Please make sure that training is completed before you go to the next sections.
# Monitor `state` of your training by running above cell couple of times.
# <a id="runs"></a>
# ## 4. Historical runs
#
# In this section you will see cURL examples describing how to get historical training runs information.
# Output should be similar to the output from training creation but you should see more trainings entries.
# Listing trainings:
# <a href="https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Trainings/trainings_list"
# target="_blank" rel="noopener no referrer">Get list of historical training jobs information</a>
# + language="bash"
#
# HISTORICAL_TRAINING_LIMIT_TO_GET=2
#
# curl -sk -X GET \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# "$DATAPLATFORM_URL/ml/v4/trainings?space_id=$SPACE_ID&version=2020-08-01&limit=$HISTORICAL_TRAINING_LIMIT_TO_GET" \
# | python -m json.tool
# -
# <a id="training_cancel"></a>
# ### Cancel training run
#
# **Tip:** If you want to cancel your training, please convert below cell to `code`, specify training ID and run.
# <a href="https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Trainings/trainings_delete"
# target="_blank" rel="noopener no referrer">Canceling training</a>
# + language="bash" active=""
#
# TRAINING_ID_TO_CANCEL=...
#
# curl -sk -X DELETE \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# "$DATAPLATFORM_URL/ml/v4/trainings/$TRAINING_ID_TO_CANCEL?space_id=$SPACE_ID&version=2020-08-01"
# -
# ---
# <a id="deploy_and_score"></a>
# ## 5. Deploy and Score
#
# In this section you will learn how to deploy and score pipeline model as webservice using WML instance.
# Before deployment creation, you need store your model in WML repository.
# Please see below cURL call example how to do it. Remember that you need to
# specify where your chosen model is stored in COS.
# <a id="model_store"></a>
# ### Store AutoAI model
#
# Store information about your model to WML repository.
# <a href="https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Models/models_create"
# target="_blank" rel="noopener no referrer">Model storing</a>
# + magic_args="--out model_payload" language="bash"
#
# curl -sk -X GET \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# "$DATAPLATFORM_URL/v2/asset_files/auto_ml/auto_ml_curl.$RANDOM_ID/wml_data/$TRAINING_ID/assets/$TRAINING_ID""_P1_global_output/resources/wml_model/request.json?space_id=$SPACE_ID" \
# | python -m json.tool
# -
# %env MODEL_PAYLOAD=$model_payload
# + magic_args="--out model_details" language="bash"
#
# curl -sk -X POST \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# --data "$MODEL_PAYLOAD" \
# "$DATAPLATFORM_URL/ml/v4/models?version=2020-08-01&space_id=$SPACE_ID"
# -
# %env MODEL_DETAILS=$model_details
# + magic_args="--out model_id" language="bash"
#
# echo $MODEL_DETAILS | awk -F '"id": ' '{ print $8 }' | cut -d '"' -f 2
# -
# %env MODEL_ID=$model_id
# <a id="model_content_download"></a>
# ### Download model content
#
# If you want to download your saved model, please make the following call.
# <a href="https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Models/models_filtered_download"
# target="_blank" rel="noopener no referrer">Download model content</a>
# + language="bash"
#
# curl -sk -X GET \
# --header "Authorization: Bearer $TOKEN" \
# --output "model.tar.gz" \
# "$DATAPLATFORM_URL/ml/v4/models/$MODEL_ID/download?space_id=$SPACE_ID&version=2020-08-01"
# -
# !ls -l model.tar.gz
# ## <a id="deployment_creation"></a>
# ### Deployment creation
#
# An AutoAI Batch deployment creation is presented below.
# <a href="https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Deployments/deployments_create"
# target="_blank" rel="noopener no referrer">Create deployment</a>
# + magic_args="--out deployment_payload" language="bash"
#
# DEPLOYMENT_PAYLOAD='{"space_id": "'"$SPACE_ID"'","name": "AutoAI deployment","description": "This is description","batch": {}, "hybrid_pipeline_hardware_specs": [{"node_runtime_id": "auto_ai.kb", "hardware_spec": {"name": "M"}}],"asset": {"id": "'"$MODEL_ID"'"}}'
# echo $DEPLOYMENT_PAYLOAD | python -m json.tool
# -
# %env DEPLOYMENT_PAYLOAD=$deployment_payload
# + magic_args="--out deployment_details" language="bash"
#
# curl -sk -X POST \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# --data "$DEPLOYMENT_PAYLOAD" \
# "$DATAPLATFORM_URL/ml/v4/deployments?version=2020-08-01"
# -
# %env DEPLOYMENT_DETAILS=$deployment_details
# + magic_args="--out deployment_id" language="bash"
#
# echo $DEPLOYMENT_DETAILS | awk -F '"id": ' '{ print $3 }' | cut -d '"' -f 2
# -
# %env DEPLOYMENT_ID=$deployment_id
# <a id="deployment_details"></a>
# ### Get deployment details
# As deployment API is asynchronous, please make sure your deployment is in `ready` state before going to the next points.
# <a href="https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Deployments/deployments_get"
# target="_blank" rel="noopener no referrer">Get deployment details</a>
# + language="bash"
#
# curl -sk -X GET \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# "$DATAPLATFORM_URL/ml/v4/deployments/$DEPLOYMENT_ID?space_id=$SPACE_ID&version=2020-08-01" \
# | python -m json.tool
# -
# <a id="batch_score"></a>
# ### Score your Batch deployment
# Scoring for Batch deployment is done by creating `jobs`. User can specify job payload as a json or as data connection to eg. COS.
# <a href="https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Deployment%20Jobs/deployment_jobs_create"
# target="_blank" rel="noopener no referrer">Create deployment job</a>
# + magic_args="--out job_payload" language="bash"
#
# JOB_PAYLOAD='{"name": "AutoAI job", "space_id": "'"$SPACE_ID"'","deployment": {"id": "'"$DEPLOYMENT_ID"'"}, "hybrid_pipeline_hardware_specs": [{"node_runtime_id": "auto_ai.kb", "hardware_spec": {"name": "M"}}], "scoring": {"input_data": [{"fields": ["CheckingStatus", "LoanDuration", "CreditHistory", "LoanPurpose", "LoanAmount", "ExistingSavings", "EmploymentDuration", "InstallmentPercent", "Sex", "OthersOnLoan", "CurrentResidenceDuration", "OwnsProperty", "Age", "InstallmentPlans", "Housing", "ExistingCreditsCount", "Job", "Dependents", "Telephone", "ForeignWorker"], "values": [["less_0", 6, "all_credits_paid_back", "car_used", 250, "less_100", "1_to_4", 2, "male", "none", 2, "savings_insurance", 28, "stores", "rent", 1, "skilled", 1, "none", "yes"]]}]}}'
# echo $JOB_PAYLOAD | python -m json.tool
# -
# %env JOB_PAYLOAD=$job_payload
# + magic_args="--out job_id" language="bash"
#
# curl -sk -X POST \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# --data "$JOB_PAYLOAD" \
# "$DATAPLATFORM_URL/ml/v4/deployment_jobs?version=2020-08-01" \
# | grep '"id": ' | awk -F '"' '{ print $4 }' | sed -n 2p
# -
# %env JOB_ID=$job_id
# <a id="job_list"></a>
# ### Listing all Batch jobs
# <a href="https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Deployment%20Jobs/deployment_jobs_list"
# target="_blank" rel="noopener no referrer">List jobs</a>
# + language="bash"
#
# curl -sk -X GET \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# "$DATAPLATFORM_URL/ml/v4/deployment_jobs?space_id=$SPACE_ID&version=2020-08-01" \
# | python -m json.tool
# -
# <a id="job_get"></a>
# ### Get particular job details
# <a href="https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Deployment%20Jobs/deployment_jobs_get"
# target="_blank" rel="noopener no referrer">Get job details</a>
# + language="bash"
#
# curl -sk -X GET \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# "$DATAPLATFORM_URL/ml/v4/deployment_jobs/$JOB_ID?space_id=$SPACE_ID&version=2020-08-01" \
# | python -m json.tool
# -
# <a id="job_cancel"></a>
# ### Cancel job
#
# **Tip:** You can cancel running job by calling delete method.
# Just convert below cell to `code` and run it.
# <a href="https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Deployment%20Jobs/deployment_jobs_delete"
# target="_blank" rel="noopener no referrer">Cancel job</a>
# + language="bash" active=""
#
# curl -sk -X DELETE \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# "$DATAPLATFORM_URL/ml/v4/deployment_jobs/$JOB_ID?space_id=$SPACE_ID&version=2020-08-01"
# -
# <a id="deployments_list"></a>
# ### Listing all deployments
# <a href="https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Deployments/deployments_list"
# target="_blank" rel="noopener no referrer">List deployments details</a>
# + language="bash"
#
# curl -sk -X GET \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# "$DATAPLATFORM_URL/ml/v4/deployments?space_id=$SPACE_ID&version=2020-08-01" \
# | python -m json.tool
# -
# <a id="cleaning"></a>
# ## 6. Cleaning section
#
# Below section is useful when you want to clean all of your previous work within this notebook.
# Just convert below cells into the `code` and run them.
# <a id="training_delete"></a>
# ### Delete training run
# **Tip:** You can completely delete a training run with its metadata.
# <a href="https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Trainings/trainings_delete"
# target="_blank" rel="noopener no referrer">Deleting training</a>
# + language="bash" active=""
#
# TRAINING_ID_TO_DELETE=...
#
# curl -sk -X DELETE \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# "$DATAPLATFORM_URL/ml/v4/trainings/$TRAINING_ID_TO_DELETE?space_id=$SPACE_ID&version=2020-08-01&hard_delete=true"
# -
# <a id="job_delete"></a>
# ### Delete job
#
# **Tip:** If you want remove job completely (with metadata), just specify `hard_delete` to True.
# <a href="https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Deployment%20Jobs/deployment_jobs_delete"
# target="_blank" rel="noopener no referrer">Delete job</a>
# + language="bash" active=""
#
# curl -sk -X DELETE \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# "$DATAPLATFORM_URL/ml/v4/deployment_jobs/$JOB_ID?space_id=$SPACE_ID&version=2020-08-01&hard_delete=true"
# -
# <a id="deployment_delete"></a>
# ### Deleting deployment
# **Tip:** You can delete existing deployment by calling DELETE method.
# + language="bash" active=""
#
# curl -sk -X DELETE \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# --header "Accept: application/json" \
# "$DATAPLATFORM_URL/ml/v4/deployments/$DEPLOYMENT_ID?space_id=$SPACE_ID&version=2020-08-01"
# -
# <a id="model_delete"></a>
# ### Delete model from repository
# **Tip:** If you want to completely remove your stored model and model metadata, just use a DELETE method.
# <a href="https://watson-ml-v4-api.mybluemix.net/wml-restapi-cloud.html#/Models/models_delete"
# target="_blank" rel="noopener no referrer">Delete model from repository</a>
# + language="bash" active=""
#
# curl -sk -X DELETE \
# --header "Authorization: Bearer $TOKEN" \
# --header "Content-Type: application/json" \
# "$DATAPLATFORM_URL/ml/v4/models/$MODEL_ID?space_id=$SPACE_ID&version=2020-08-01"
# -
# <a id="summary"></a>
# ## 7. Summary and next steps
#
# You successfully completed this notebook!.
#
# You learned how to use `cURL` calls to store, deploy and score a AutoAI model in WML.
#
# ### Authors
#
# **<NAME>**, Python Software Developer in Watson Machine Learning at IBM
# **<NAME>**, Intern in Watson Machine Learning at IBM
# Copyright © 2020, 2021, 2022 IBM. This notebook and its source code are released under the terms of the MIT License.
|
cpd4.0/notebooks/rest_api/curl/experiments/autoai/Use AutoAI and batch deployment to predict credit risk.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="pI7fbnTOBdRw"
# # Party 관련 feature engineering
# -
from tqdm import tqdm
from tqdm import trange
from itertools import chain
from scipy import stats
from datetime import timedelta
import warnings
warnings.filterwarnings('ignore')
import pickle
import datetime as dt
import networkx as nx
import pickle
# -----
# # Train
# label = pd.read_csv("../Data/train_label.csv")
label = pd.read_csv("~/documents/chaser_data/train_label.csv")
# label = pd.read_csv("../data/train_label.csv")
# %%time
# party = pd.read_csv("../data/new_train_party.csv", memory_map=True)
party = pd.read_csv("~/documents/chaser_data/train_party.csv", memory_map=True)
party.tail()
party.rename(columns = {"hashed":"party_members_acc_id"}, inplace=True)
print(party.shape)
party.tail()
# ## 1. party df에 column 추가
# ### 1.1 party 지속시간 계산
# party 지속시간 구하기: make_duration(df)
# - "duration_time" column: 초단위 시간
# - "duration_days" column: 일단위 시간
def make_duration(df):
"""
지속시간 생성 함수
duration_time = 초단위
party_duration_days = 일단위
- party_start_time, party_end_time 은 마이크로 세컨드 단위로 기록되어 있어서
'HH:MM:SS.FFF' 에서 'HH:MM:SS'로 슬라이스해야함.
"""
df['duration_time'] = pd.to_datetime(df.party_end_time.apply(lambda x: x[:-4]), infer_datetime_format=True, format = '%H:%M:%S') - pd.to_datetime(df.party_start_time.apply(lambda x: x[:-4]), infer_datetime_format=True, format = '%H:%M:%S')
df.duration_time[df.duration_time<timedelta(days=0)] = df.duration_time[df.duration_time<timedelta(days=0)] + timedelta(days=1)
df['duration_days']=(df.party_end_week - df.party_start_week)*7 + (df.party_end_day - df.party_start_day) +1
# %%time
make_duration(party)
print(party.shape)
party.tail()
# ### 1.2 party당 참여 인원 수
# - make_party_member_count(df)
def make_party_member_count(df):
"""
각 파티에 참여한 인원수
"""
df['party_member_count'] = [len(party_list.split(',')) for party_list in tqdm(df['party_members_acc_id'])]
make_party_member_count(party)
print(party.shape)
party.tail()
# ## 2. party 관련 기본 변수
# ### 2.1 total party member count 변수 생성
# - 유저가 참여한 모든 파티의 파티 인원의 총합을 구함.
# %%time
party_member_lists = [party['party_members_acc_id'][i].split(',') for i in trange(len(party['party_members_acc_id']))]
party_member_1D_lists = list(chain.from_iterable(party_member_lists))
member_id_value_count = pd.Series(party_member_1D_lists).value_counts()
# %%time
increased_party_TMC = [[party['party_member_count'][i]]*party['party_member_count'][i] for i in trange(len(party))]
flat_increased_party_TMC = list(chain.from_iterable(increased_party_TMC))
# +
# %%time
all_id_and_party_TMC_df = pd.concat([pd.Series(party_member_1D_lists), pd.Series(flat_increased_party_TMC)],axis=1)
all_id_and_party_TMC_df.columns = ['acc_id','party_TMC']
member_party_TMC = all_id_and_party_TMC_df.groupby('acc_id')['party_TMC'].sum()
party_TMC_df = pd.DataFrame(member_party_TMC).reset_index()
party_TMC_df.columns = ['acc_id','party_total_member_count']
label = pd.merge(label, party_TMC_df, how='left', on='acc_id')
label['party_total_member_count'].fillna(0, inplace=True)
# -
label.tail()
# ### 2.2 Party total retained minute 변수 생성
# - 파티 시작 시간과 파티 종료 시간으로 유저가 참여한 모든 파티의 지속시간의 총합을 구한다.
# +
# %%time
party['party_start_time'] = [i.split('.')[0] for i in list(party['party_start_time'])]
party['party_end_time'] = [i.split('.')[0] for i in list(party['party_end_time'])]
party['party_start_time'] = pd.to_datetime(party['party_start_time'], format='%H:%M:%S')
party['party_end_time'] = pd.to_datetime(party['party_end_time'], format='%H:%M:%S')
party['retained_week'] = party['party_end_week']-party['party_start_week']
party['retained_day'] = party['party_end_day']-party['party_start_day']
party['retained_time'] = (party['party_end_time'] - party['party_start_time'])
party['retained_time'][party['retained_time'] < dt.timedelta(days=0)] = \
party['retained_time'][party['retained_time'] < dt.timedelta(days=0)]*(-1)
# +
# %%time
retained_second=[t.total_seconds() for t in tqdm(party['retained_time'])]
party['total_retained_day'] = party['retained_week']*7+party['retained_day']
party['total_retained_second'] = party['total_retained_day']*(24*60*60)+retained_second
# -
# %%time
increased_party_TRS = [[party['total_retained_second'][i]]*party['party_member_count'][i] for i in trange(len(party))]
# +
# %%time
flat_increased_party_TRS = list(chain.from_iterable(increased_party_TRS))
all_id_and_party_TRS_df = pd.concat([pd.Series(party_member_1D_lists),
pd.Series(flat_increased_party_TRS)],axis=1)
all_id_and_party_TRS_df.columns = ['acc_id','party_TRS']
member_party_TRS_frist = all_id_and_party_TRS_df.groupby('acc_id')['party_TRS'].sum()
party_TRS_frist_df = pd.DataFrame(member_party_TRS_frist).reset_index()
party_TRS_frist_df.columns = ['acc_id','party_total_retained_second']
label = pd.merge(label, party_TRS_frist_df, how='left', on='acc_id')
label['party_total_retained_second'].fillna(0, inplace=True)
label['party_total_retained_minute']=round(label['party_total_retained_second']/60,1)
label.drop(columns='party_total_retained_second', inplace=True)
# +
# 메모리 부족해서 위에서 만든 리스트, 데이터프레임 리셋하는 코드
# # %reset_selective -f increase_party_TMC
# # %reset_selective -f flat_increased_party_TMC
# # %reset_selective -f acc_id_and_party_TMC_df
# # %reset_selective -f member_party_TMC_df
# # %reset_selective -f party_TMC_df
# # %reset_selective -f member_id_value_count
# # %reset_selective -f party_member_1D_lists
# # %reset_selective -f party_member_lists
# # %reset_selective -f member_party_TMC
# # %reset_selective -f increased_party_TMC
# -
# ### 2.3 party members acc id 전체를 리스트로 만들기
def get_party_ids(df):
party_id = df["party_members_acc_id"].tolist()
party_id = [x.split(',') for x in party_id]
party_id = [item for sublist in party_id for item in sublist]
return party_id
# +
# %%time
party_id_ls = get_party_ids(party)
print(len(party_id_ls))
print(len(list(set(party_id_ls))))
# -
# ### 2.4 party start week/day & end week/day의 first, mode, last 변수
# - first/mode/last_party_start_week : 유저가 참여한 파티가 최초,최후에 생성된 주차, 가장 자주 파티가 생성된 주차
# - first/mode/last_party_end_week : 유저가 참여한 파티가 최초,최후에 종료된 주차, 가장 자주 파티가 종료된 주차
# +
def make_all_ID_and_column_df(df, column):
print('start making all ID & {} df'.format(column))
increased_column = [[df[column][i]] * df['party_member_count'][i] for i in trange(len(df))]
increased_column_ls = list(chain.from_iterable(increased_column))
all_ID_and_column_df = pd.concat([pd.Series(get_party_ids(df)),
pd.Series(increased_column_ls)],axis=1)
all_ID_and_column_df.columns = ['acc_id',column]
print('end of making all ID & {} df'.format(column))
return all_ID_and_column_df
def make_first_mode_last_df_and_merge_with_label(df, column, label):
all_ID_and_column_df = make_all_ID_and_column_df(df, column)
print('start making {} first & mode & last df'.format(column))
print('working first_df...')
first_df = all_ID_and_column_df.groupby('acc_id')[column].min()
first_df = pd.DataFrame(first_df).reset_index()
first_df.columns = ['acc_id','first_'+column]
label = pd.merge(label, first_df, how='left', on='acc_id')
label['first_'+column].fillna(0, inplace=True)
print('working mode_df...')
mode_df = all_ID_and_column_df.groupby('acc_id')[column].agg(lambda x: stats.mode(x)[0][0])
mode_df = pd.DataFrame(mode_df).reset_index()
mode_df.columns = ['acc_id','mode_'+column]
label = pd.merge(label, mode_df, how='left', on='acc_id')
label['mode_'+column].fillna(0, inplace=True)
print('working last_df...')
last_df = all_ID_and_column_df.groupby('acc_id')[column].max()
last_df = pd.DataFrame(last_df).reset_index()
last_df.columns = ['acc_id','last_'+column]
label = pd.merge(label, last_df, how='left', on='acc_id')
label['last_'+column].fillna(0, inplace=True)
print('end of making {} first & mode & last df'.format(column))
return label
# -
# %time label = make_first_mode_last_df_and_merge_with_label(party, 'party_start_week', label)
# %time label = make_first_mode_last_df_and_merge_with_label(party, 'party_start_day', label)
# %time label = make_first_mode_last_df_and_merge_with_label(party, 'party_end_week', label)
# %time label = make_first_mode_last_df_and_merge_with_label(party, 'party_end_day', label)
label.tail()
# ## 3. 10분 이상 party만 남도록 data filtering
# - 10분 미만으로 지속된 파티는 사실상 제 기능을 하지 못한 파티라고 가정하고 전체 데이터에서 10분 이상 지속된 파티만을 필터링하여 feature engineering을 진행함
# - 별도의 언급이 없다면 10분 이상의 파티를 이하 '파티'라고 명명
def time_filter(df):
"""
지속시간이 10 분 이상인 필터링 함수
"""
ten = timedelta(minutes = 10)
return df[(df['duration_days'] >= 3) | (df['duration_time'] >= ten)]
# %%time
filtered_party = time_filter(party)
print(len(filtered_party))
# ## 4. party 참여 횟수 변수 생성
# - 8주간의 모든 파티 참여 횟수의 총합, week별 파티 참여 횟수의 총계 등 총 9개 변수 생성
# ### 4.1 party members acc id 전체를 리스트로 만들기
party_id_ls = get_party_ids(filtered_party)
# ### 4.2 party_cnt(파티 참여횟수) 변수 생성
def get_party_cnt(ls, merging_df):
df_party_id = pd.DataFrame(ls, columns=["acc_id"])
df_party_id = df_party_id.groupby('acc_id').size().reset_index(name='party_cnt')
party_df = pd.merge(merging_df, df_party_id, how='left')
party_df["party_cnt"].fillna(0, inplace=True)
return party_df
# %%time
party_1 = get_party_cnt(party_id_ls, label)
party_1.tail()
# +
# label 대신 party_1 사용
# # %reset_selective -f label
# -
# ### 4.3 week별 party_cnt
# 각 활동주 별 파티에 참여한 횟수의 합계.
# #### (1) 파티 지속 기간(week) 확인
filtered_party["party_duration_week"] = filtered_party["party_end_week"] - filtered_party["party_start_week"]
filtered_party.groupby("party_duration_week").size().reset_index()
# #### (2) 다음 주로 넘어가는 경우 끝나는 요일 확인
# - 모두 1일에 끝나므로 시작 week만으로 count하기로 함
dur_1w = filtered_party[filtered_party["party_duration_week"]==1]
dur_1w.groupby(dur_1w["party_end_day"]).size().reset_index()
# #### (3) week별 party_cnt 구하기
# week별 id당 party cnt를 계산한 df를 만드는 함수
def week_cnt(week, merging_df, df = party):
party = df[df["party_start_week"] == week]
party_id = party["party_members_acc_id"].tolist()
party_id = [x.split(',') for x in party_id]
party_id = [item for sublist in party_id for item in sublist]
print("week {} party id: {}".format(week, len(party_id)))
party_id_df = pd.DataFrame(party_id, columns=["acc_id"])
party_id_df = party_id_df.groupby('acc_id').size().reset_index(name = "party_cnt_w"+str(week))
merged_df = pd.merge(merging_df, party_id_df, how='left')
merged_df.fillna(0, inplace=True)
return merged_df
# %%time
for i in trange(1,9):
party_1 = week_cnt(i, party_1, df = filtered_party)
party_1.tail()
# ## 5. party count 7-8주와 6-8주의 전체 중 비중 변수 생성
# 8주 동안의 파티 참여 횟수 중 7-8주와 6-8주의 파티참여 횟수가 차지하는 비율.
party_1["party_78_ratio"] = party_1.loc[:,"party_cnt_w7":"party_cnt_w8"].sum(axis=1) / party_1["party_cnt"]
party_1.fillna(0, inplace=True)
party_1.tail()
party_1["party_678_ratio"] = party_1.loc[:,"party_cnt_w6":"party_cnt_w8"].sum(axis=1) / party_1["party_cnt"]
party_1.fillna(0, inplace=True)
party_1.tail()
# ## 6. week별 party count의 표준편차 변수 생성
# 유저가 활동주 별로 파티에 참여한 횟수의 표준편차
party_1["party_cnt_std"] = party_1.loc[:,"party_cnt_w1":"party_cnt_w8"].std(axis=1)
party_1.fillna(0, inplace=True)
party_1.tail()
# ## 7. 전체 파티 참여횟수 중 10분 이내 짧은 파티 참여의 비율 변수 생성
# 유저가 8주동안 참여한 모든 파티 횟수의 총합에서 10분 이내에 종료된 파티에 참여했던 횟수가 차지하는 비중
# +
def time_filter_short(df):
"""
지속시간이 10분 미만인 필터링
"""
ten = timedelta(minutes = 10)
return df[(df['duration_days'] < 3) & (df['duration_time'] < ten)]
def get_ratio(df, label):
totalcnt = get_party_cnt(get_party_ids(df),label)
totalcnt.rename(columns={'party_cnt':'totalcnt'}, inplace=True)
shortcnt = get_party_cnt(get_party_ids(time_filter_short(df)), label)
shortcnt.rename(columns={'party_cnt':'shortcnt'}, inplace=True)
shortcnt['shortparty_ratio'] = round(shortcnt['shortcnt']/totalcnt['totalcnt'], 4)
shortcnt['shortparty_ratio'].fillna(value=0, inplace=True)
return shortcnt[['acc_id','shortparty_ratio']]
# -
party_1 = pd.merge(party_1, get_ratio(party, party_1[['acc_id']]), how='left')
party_1.head()
party_1.columns
# ## 8. party network에서의 degree centrality 변수 생성
# 유저의 파티 네트워크 중심성 생성
# ### 8.1 생성해둔 party network 불러오기
# +
# G = nx.read_gpickle("train_party_network.gpickle")
# -
# node의 수가 2명 이상짜리 파티에 참여한 unique id 수와 동일함
# +
# len(G.nodes())
# -
# ### 8.2 degree centrality 구하기
# +
# degree_centrality = nx.degree_centrality(G)
# type(degree_centrality)
# +
# centrality = pd.DataFrame(columns=["acc_id","degree_cent"])
# +
# centrality["acc_id"] = degree_centrality.keys()
# +
# centrality["degree_cent"] = degree_centrality.values()
# -
# 변수의 단위가 너무 작아 100배씩 scaling함
# +
# centrality["degree_cent"] = centrality["degree_cent"]*100
# +
# party_1 = pd.merge(party_1, centrality, how='left').fillna(0, inplace = True)
# -
# ## 9. 고정파티 최대 횟수 변수 생성
#
# 유저가 한 명 이상의 특정 유저와 반복해서 파티에 참여한 횟수의 최대값을 생성
len(filtered_party)
# + [markdown] colab_type="text" id="pI7fbnTOBdRw"
# ### 9.1 10분 이상 지속한 party에 참여한 acc_id 구하기
# -
# #### (1) party members acc id 전체를 리스트로 만들기
# %%time
party_ids = get_party_ids(filtered_party)
# #### (2) party에 참여한 id 수
party_unique_ids = list(set(party_ids))
print("party에 참여한 id 수(중복카운트):", len(party_ids))
print(len(list(set(party_ids))))
print("party에 참여한 id 수(중복 없음):", len(party_unique_ids))
label_id = label["acc_id"].tolist()
len(label_id)
# #### (3) train data 유저 중 filtered party에 참여한 사람 수
label_party_id = list(set(label_id) & set(party_unique_ids))
len(label_party_id)
# ### 9.2 고정파티 최대 횟수 구하기
# #### (1) get_fix_party(): 한 유저가 특정 유저와 반복해서 party에 참여한 최대 횟수
def get_fix_party(base_id):
'''
기준 아이디와 타 유저의 고정 파티 횟수 중 최댓값을 찾는 함수
input: base_id - party에 참여한 유저의 acc_id
output: key가 "acc_id", "fix_party_max"인 dictionary
- "acc_id": 유저의 acc_id
- "fix_party_max": 타 유저와 반복해서 같은 party에 참여한 횟수 중 최댓값
'''
# 기준 id가 참여한 party member 리스트 뽑기 (party_id는 이중리스트 형태)
with_members = list(filter(lambda a: base_id in a, party_id))
# 이중 리스트인 with_members를 flat list로 풀어주기
with_members = [item for sublist in with_members for item in sublist]
# 기준id 리스트에서 빼기
with_members = list(filter(lambda a: a != base_id, with_members))
# 함께한 횟수 df로 구하기
df_party_id = pd.DataFrame(with_members, columns=["acc_id"])
df_party_id = df_party_id.groupby('acc_id').size().reset_index(name='party_cnt')
return {"acc_id": base_id,
"fix_party_max": df_party_id["party_cnt"].max()}
# party member 전체 리스트 미리 받기
party_id = filtered_party["party_members_acc_id"].tolist()
party_id = [x.split(',') for x in party_id]
get_fix_party(label_party_id[0])
# #### (2) label_party_id에 대하여 고정파티 최대 횟수 구하기
fix_party = pd.DataFrame(columns=["acc_id", "fix_party_max"])
for i in tqdm(range(10000)):
fix_party.loc[len(fix_party)] = get_fix_party(label_party_id[i])
for i in tqdm(range(10000,20000)):
fix_party.loc[len(fix_party)] = get_fix_party(label_party_id[i])
for i in tqdm(range(20000,30000)):
fix_party.loc[len(fix_party)] = get_fix_party(label_party_id[i])
for i in tqdm(range(30000,40000)):
fix_party.loc[len(fix_party)] = get_fix_party(label_party_id[i])
for i in tqdm(range(40000,len(label_party_id))):
fix_party.loc[len(fix_party)] = get_fix_party(label_party_id[i])
len(fix_party)
party_1 = party_1.merge(fix_party, how = "left").fillna(0)
# ## 10. 최종 party 변수 저장하기
pickle.dump(party_1,open('../data/merged_train_party.pkl','wb'))
# ---
# # Test
activity = pd.read_csv('../data/test_activity.csv')
label = pd.DataFrame(list(activity['acc_id'].unique()))
label.columns = ['acc_id']
# %%time
party = pd.read_csv("../data/new_test_party.csv", memory_map=True)
party.tail()
party.rename(columns = {"hashed":"party_members_acc_id"}, inplace=True)
print(party.shape)
party.tail()
# ## 1. party df에 column 추가
# ### 1.1 party 지속시간 계산
# party 지속시간 구하기: make_duration(df)
# - "duration_time" column: 초단위 시간
# - "duration_days" column: 일단위 시간
# %%time
make_duration(party)
print(party.shape)
party.tail()
# ### 1.2 party당 참여 인원 수
# - make_party_member_count(df)
make_party_member_count(party)
print(party.shape)
party.tail()
# ## 2. party 관련 기본 변수
# ### 2.1 total party member count 변수 생성
# - 유저가 참여한 파티의 멤버 수의 총 합을 구한다.
# +
# %%time
party_member_lists = [party['party_members_acc_id'][i].split(',') for i in trange(len(party['party_members_acc_id']))]
party_member_1D_lists = list(chain.from_iterable(party_member_lists))
member_id_value_count = pd.Series(party_member_1D_lists).value_counts()
# -
# %%time
increased_party_TMC = [[party['party_member_count'][i]]*party['party_member_count'][i] for i in trange(len(party))]
flat_increased_party_TMC = list(chain.from_iterable(increased_party_TMC))
# ### 2.2 Party total retained minute 변수 생성
# - 유저가 참여한 파티의 지속시간의 총합을 구한다.
# +
# %%time
all_id_and_party_TMC_df = pd.concat([pd.Series(party_member_1D_lists), pd.Series(flat_increased_party_TMC)],axis=1)
all_id_and_party_TMC_df.columns = ['acc_id','party_TMC']
member_party_TMC = all_id_and_party_TMC_df.groupby('acc_id')['party_TMC'].sum()
party_TMC_df = pd.DataFrame(member_party_TMC).reset_index()
party_TMC_df.columns = ['acc_id','party_total_member_count']
label = pd.merge(label, party_TMC_df, how='left', on='acc_id')
label['party_total_member_count'].fillna(0, inplace=True)
# -
label.tail()
# ### 2.3 party members acc id 전체를 리스트로 만들기
# +
# %%time
party_id_ls = get_party_ids(party)
print(len(party_id_ls))
print(len(list(set(party_id_ls))))
# -
# ### 2.4 party start week/day & end week/day의 first, mode, last 변수
# %time label = make_first_mode_last_df_and_merge_with_label(party, 'party_start_week', label)
# %time label = make_first_mode_last_df_and_merge_with_label(party, 'party_start_day', label)
# %time label = make_first_mode_last_df_and_merge_with_label(party, 'party_end_week', label)
# %time label = make_first_mode_last_df_and_merge_with_label(party, 'party_end_day', label)
label.tail()
# ## 3. 10분 이상 party만 남도록 data filtering
# %%time
filtered_party = time_filter(party)
print(len(filtered_party))
# ## 4. party 참여 횟수 변수 생성
# - 전체 횟수, week별 횟수 → 9개 변수
# ### 4.1 party members acc id 전체를 리스트로 만들기
party_id_ls = get_party_ids(filtered_party)
# ### 4.2 party_cnt(파티 참여횟수) 변수 생성
# %%time
party_1 = get_party_cnt(party_id_ls, label)
party_1.tail()
# ### 4.3 week별 party_cnt
# #### (1) 파티 지속 기간(week) 확인
filtered_party["party_duration_week"] = filtered_party["party_end_week"] - filtered_party["party_start_week"]
filtered_party.groupby("party_duration_week").size().reset_index()
# #### (2) 다음 주로 넘어가는 경우 끝나는 요일 확인
# - 모두 1일에 끝나므로 시작 week만으로 count하기로 함
dur_1w = filtered_party[filtered_party["party_duration_week"]==1]
dur_1w.groupby(dur_1w["party_end_day"]).size().reset_index()
# #### (3) week별 party_cnt 구하기
# %%time
for i in trange(1,9):
party_1 = week_cnt(i, party_1, df = filtered_party)
party_1.tail()
# ## 5. party count 7-8주와 6-8주의 전체 중 비중 변수 생성
party_1["party_78_ratio"] = party_1.loc[:,"party_cnt_w7":"party_cnt_w8"].sum(axis=1) / party_1["party_cnt"]
party_1.fillna(0, inplace=True)
party_1.tail()
party_1["party_678_ratio"] = party_1.loc[:,"party_cnt_w6":"party_cnt_w8"].sum(axis=1) / party_1["party_cnt"]
party_1.fillna(0, inplace=True)
party_1.tail()
# ## 6. week별 party count의 표준편차
party_1["party_cnt_std"] = party_1.loc[:,"party_cnt_w1":"party_cnt_w8"].std(axis=1)
party_1.fillna(0, inplace=True)
party_1.tail()
# ## 7. 전체 파티 참여횟수 중 10분 이내 짧은 파티 참여의 비율 변수 생성
party_1 = pd.merge(party_1, get_ratio(party, party_1[['acc_id']]), how='left')
# ## 8. party network에서의 degree centrality
# +
# G = nx.read_gpickle("data/test_party_network.gpickle")
# -
# node의 수가 2명 이상짜리 파티에 참여한 unique id 수와 동일함
# +
# len(G.nodes())
# -
# ### 중심성 계산하기
# +
# degree_centrality = nx.degree_centrality(G)
# type(degree_centrality)
# +
# centrality = pd.DataFrame(columns=["acc_id","degree_cent"])
# +
# centrality["acc_id"] = degree_centrality.keys()
# +
# centrality["degree_cent"] = degree_centrality.values()
# -
# 변수의 단위가 너무 작아 100배씩 scaling함
# +
# centrality["degree_cent"] = centrality["degree_cent"]*100
# +
# party_1 = pd.merge(party_1, centrality, how='left').fillna(0, inplace = True)
# -
# ## 9. 고정파티 최대 횟수 변수 생성
len(filtered_party)
# + [markdown] colab_type="text" id="pI7fbnTOBdRw"
# ### 9.1 10분 이상 지속한 party에 참여한 acc_id 구하기
# -
# #### (1) party members acc id 전체를 리스트로 만들기
# %%time
party_ids = get_party_ids(party_filtered)
len(party_ids)
# #### (2) party에 참여한 id 수
party_unique_ids = list(set(party_ids))
print("party에 참여한 id 수(중복카운트):", len(party_ids))
print(len(list(set(party_ids))))
print("party에 참여한 id 수(중복 없음):", len(party_unique_ids))
label_id = label["acc_id"].tolist()
len(label_id)
# #### (3) test data 유저 중 filtered party에 참여한 사람 수
label_party_id = list(set(label_id) & set(party_unique_ids))
len(label_party_id)
# ### 9.2 고정파티 최대 횟수 구하기
# #### (1) get_fix_party(): 한 유저가 특정 유저와 반복해서 party에 참여한 최대 횟수
# party member 전체 리스트 미리 받기
party_id = party_filtered["party_members_acc_id"].tolist()
party_id = [x.split(',') for x in party_id]
# 함수 체크
get_fix_party(label_party_id[0])
# #### (2) label_party_id에 대하여 고정파티 최대 횟수 구하기
fix_party = pd.DataFrame(columns=["acc_id", "fix_party_max"])
for i in tqdm(range(len(label_party_id))):
fix_party.loc[len(fix_party)] = get_fix_party(label_party_id[i])
# test label과 merge하기
party_1 = party_1.merge(fix_party, how = "left").fillna(0)
# ## 10. 최종 party 변수 저장하기
pickle.dump(party_1, open('../data/merged_test_party.pkl','wb'))
|
1_3_FE_party.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Property
# ### Private vs public
# - \__는 private
# - \_는 protected
# - 언어 자체에서 강제하진 않음. 정보 제공 느낌
#
# ### @property 를 사용하는 목적
# 1. 변수를 변경할 때 특정 제한을 두고 싶을 경우
# 2. get,set 함수를 만들지 않고 더 간단하게 접근하게 하기 위해서
# 3. 하위 호환성에 도움
#
# ### 생각
# - 사람의 기억은 한정적이기 때문에, 그리고 코드 만든 사람이 퇴사했을 경우 유지보수를 위해 생성
# - 직접 method에 접근할 수 있으면 문제가 생길 수 있음
#
# +
class Test:
def __init__(self):
self.public_field = 5
self.__private_field = 6
self._protected_field = 7
def __private_method(self):
pass
if __name__ == '__main__':
t = Test()
t.public_field = 10
t.__private_field = 11
t._protected_field = 12
# -
t.public_field
t.__private_field
t._protected_field
class Test:
def __init__(self):
self.color = "red"
def set_color(self,clr):
self.color = clr
def get_color(self):
return self.color
# +
t = Test()
t.set_color("blue")
print(t.get_color())
# -
t1 = Test()
print(t1.get_color())
t1.color
class Test:
def __init__(self):
self.__color = "red"
@property
def color(self):
return self.__color
@color.setter
def color(self,clr):
self.__color = clr
# get 역할을 하는 어노테이션은 @property 이고, set역할을 하는 어노테이션은 @color.setter
# +
t = Test()
t.color = "blue"
print(t.color)
# +
class Celsius:
def __init__(self):
pass
def to_fahrenheit(self):
return (self._temperature * 1.8) + 32
@property
def temperature(self):
print("Getting value")
return self._temperature
@temperature.setter
def temperature(self, value):
if value < -273:
raise ValueError("Temperature below -273 is not possible")
print("Setting value")
self._temperature = value
# +
c = Celsius()
c._temperature = -300
print(c.temperature)
# -
class Test1:
def __init__(self):
pass
@property
def property1(self):
print("a")
return self._property
@property1.setter
def property(self, value):
if value >= 5:
print("over 5")
else:
print("down 5")
self._property1 = value
k = Test1()
k._property = 1
k.property
|
python/property.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:caselaw]
# language: python
# name: conda-env-caselaw-py
# ---
# +
from lxml import etree
import pandas as pd
import os
import rdflib
import urllib
# %matplotlib inline
# -
# ## Save everything as n3 files
fp_in = '/media/sf_VBox_Shared/CaseLaw/lido_rdf/2017-11-28-xml/'
fp_out = '/media/sf_VBox_Shared/CaseLaw/lido_rdf/2017-11-29-n3/'
fnames = [(os.path.join(fp_in, f), os.path.join(fp_out, f.replace('.xml', '.n3'))) for f in os.listdir(fp_in)]
def add_link(id_from, id_to, graph):
ns_overheidrl = rdflib.Namespace("http://linkeddata.overheid.nl/terms/")
graph.namespace_manager.bind('overheidrl', ns_overheidrl)
types = sub_ref.attrib['type'].split(' ')
label = sub_ref.attrib.get("label", "")
# We have to come up with an uri for this link
linkid = types[0] + urllib.parse.quote(id_from) + urllib.parse.quote(id_to)
link_uri = rdflib.URIRef(linkid)
graph.add( (link_uri, rdflib.RDF["type"], rdflib.URIRef("http://linkeddata.overheid.nl/terms/LinkAct")))
for typ in types:
graph.add((link_uri, ns_overheidrl.heeftLinktype, rdflib.URIRef(typ)))
graph.add((link_uri, ns_overheidrl.linktVan, rdflib.URIRef(id_from)))
graph.add((link_uri, ns_overheidrl.linktNaar, rdflib.URIRef(id_to)))
for fn_in, fn_out in fnames:
root = etree.parse(fn_in).getroot()
graph = rdflib.Graph()
for sub in list(root.iterchildren('subject')):
sub_id = sub.attrib['id']
s = rdflib.URIRef(sub_id)
for el in sub.iterchildren():
if len(el.nsmap ) > 0:
nsmap_reversed = {el.nsmap[k]: k for k in el.nsmap}
ns = el.tag.split('}')[0][1:]
tag = el.tag.split('}')[1]
value = el.text
if value is not None:
if urllib.parse.urlparse(value).scheme == 'http':
o = rdflib.URIRef(value)
else:
o = rdflib.Literal(value)
n = rdflib.Namespace(ns)
graph.namespace_manager.bind(nsmap_reversed[ns], n)
graph.add( (s, n[tag], o) )
for inkomende_links in sub.iterchildren('inkomende-links'):
for sub_ref in inkomende_links.iterchildren():
id_from = sub_ref.attrib['idref']
id_to = sub_id
add_link(id_from, id_to, graph)
for uitgaande_links in sub.iterchildren('uitgaande-links'):
for sub_ref in uitgaande_links.iterchildren():
id_to = sub_ref.attrib['idref']
id_from = sub_id
add_link(id_from, id_to, graph)
graph.serialize(fn_out, format='n3')
for s,p,o in graph:
print(s,p,o)
for inkomende_links in sub.iterchildren('inkomende-links'):
for sub_ref in inkomende_links.iterchildren():
links.append(get_links_from_incoming(sub_ref, sub_dict['id']))
for uitgaande_links in sub.iterchildren('uitgaande-links'):
for sub_ref in uitgaande_links.iterchildren():
links.append(get_links_from_outgoing(sub_ref, sub_dict['id']))
# +
def get_links_from_outgoing(sub_ref, source_id):
return {
'target_id': sub_ref.attrib['idref'],
'link_type': sub_ref.attrib['type'],
'source_id': source_id
}
def get_links_from_incoming(sub_ref, target_id):
return {
'source_id': sub_ref.attrib['idref'],
'link_type': sub_ref.attrib['type'],
'target_id': target_id,
}
# +
links = []
nodes = []
single_attr_list = ['type', 'title', 'creator', 'modified']
for sub in list(root.iterchildren('subject')):
sub_dict = {}
sub_dict['id'] = sub.attrib['id']
for att in single_attr_list:
for s in sub.iterchildren('{*}'+att):
sub_dict[att] = s.text
nodes.append(sub_dict)
for inkomende_links in sub.iterchildren('inkomende-links'):
for sub_ref in inkomende_links.iterchildren():
links.append(get_links_from_incoming(sub_ref, sub_dict['id']))
for uitgaande_links in sub.iterchildren('uitgaande-links'):
for sub_ref in uitgaande_links.iterchildren():
links.append(get_links_from_outgoing(sub_ref, sub_dict['id']))
links_df = pd.DataFrame.from_dict(links)
nodes_df = pd.DataFrame.from_dict(nodes)
links_df = links_df.drop_duplicates()
nodes_df = nodes_df.drop_duplicates()
# -
nodes_df.sort_values('title')
links_df
import networkx as nx
g = nx.DiGraph()
for l in links:
source = l['source_id'].split('/')[-1]
target = l['target_id'].split('/')[-1]
link_type = l['link_type'].split('/')[-1]
g.add_edge(source, target, {'link_type': link_type})
nx.draw(g)
|
notebooks/archived/HR_to_rdf.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Extension B - Catchment by Clinic
#
# This is the final analysis that has been done for the Yemen project. It aims to identify the number of people that can access a clinic within a given time frame, and also the number of unique users - the people who can ONLY access a given healthcare facility within the time frame, and no subsitute clinic.
#
# This process is very closely modelled on Step 4 - Generate Results. Read that notebook first to get a feel for what is going on. It breaks from this process at the point labelled 'BREAK' - annotations will begin from there.
import pandas as pd
import os, sys
sys.path.append(r'/home/public/GOST_PublicGoods/GOSTNets/GOSTNets')
sys.path.append(r'C:\Users\charl\Documents\GitHub\GOST')
import GOSTnet as gn
import importlib
import geopandas as gpd
import rasterio as rt
from rasterio import features
from shapely.wkt import loads
import numpy as np
import networkx as nx
from shapely.geometry import box, Point, Polygon
# ### Settings
# +
walking = 1 # set to 1 for walking
conflict = 1 # set to 1 to prevent people from crossing warfronts
zonal_stats = 1 # set to 1 to produce summary zonal stats layer
facility_type = 'HOS' # Options: 'HOS' or 'PHC' or 'ALL'
year = 2018 # default = 2018
service_index = 0 # Set to 0 for all services / access to hospitals
services = ['ALL',
'Antenatal',
'BEmONC',
'CEmONC',
'Under_5',
'Emergency_Surgery',
'Immunizations',
'Malnutrition',
'Int_Outreach']
# -
# ### Import All-Destination OD
basepth = r'/home/wb493355/data/yemen/Round 3'
pth = os.path.join(basepth, 'graphtool')
util_path = os.path.join(basepth, 'util_files')
srtm_pth = os.path.join(basepth, 'SRTM')
# +
if conflict == 1:
conflict_tag = 'ConflictAdj'
appendor = 'Jan24th'
else:
conflict_tag = 'NoConflict'
appendor = 'normal'
if walking == 1:
type_tag = 'walking'
net_name = r'walk_graph.pickle'
appendor = 'normal'
else:
type_tag = 'driving'
net_name = r'G_salty_time_conflict_adj.pickle'
YEHNP = 1
OD_pth = pth
net_pth = pth
OD_name = r'OD_%s_%s_%s.csv' % (appendor, type_tag, year)
WGS = {'init':'epsg:4326'}
measure_crs = {'init':'epsg:32638'}
subset = r'%s_24th_HERAMS_%s_%s_%s_%s' % (type_tag, facility_type, services[service_index], conflict_tag, year)
if YEHNP == 1:
subset = subset+'_YEHNP_only'
elif YEHNP == -1:
subset = subset+'_Excl_YEHNP'
print("Output files will have name: ", subset)
print("network: ",net_name)
print("OD Matrix: ",OD_name)
print("Conflict setting: ",conflict_tag)
offroad_speed = 4
# -
OD = pd.read_csv(os.path.join(OD_pth, OD_name))
OD = OD.rename(columns = {'Unnamed: 0':'O_ID'})
OD = OD.set_index('O_ID')
OD = OD.replace([np.inf, -np.inf], np.nan)
OD_original = OD.copy()
# ### Optional: Subset to Accepted Nodes
# +
acceptable_df = pd.read_csv(os.path.join(OD_pth, 'HeRAMS 2018 April_snapped.csv'))
# Adjust for facility type
if facility_type == 'HOS':
acceptable_df = acceptable_df.loc[acceptable_df['Health Facility Type Coded'].isin(['1',1])]
elif facility_type == 'PHC':
acceptable_df = acceptable_df.loc[acceptable_df['Health Facility Type Coded'].isin([2,'2',3,'3'])]
elif facility_type == 'ALL':
pass
else:
raise ValueError('unacceptable facility_type entry!')
# Adjust for facility type
if YEHNP == 1 and facility_type == 'HOS':
acceptable_df = acceptable_df.loc[(acceptable_df['YEHNP_Hospitals'] == 1)]
elif YEHNP == 1 and facility_type == 'PHC':
acceptable_df = acceptable_df.loc[(acceptable_df['YEHNP_PHCs'] == 1)]
elif YEHNP == -1 and facility_type == 'HOS':
acceptable_df = acceptable_df.loc[(acceptable_df['YEHNP_Hospitals'] != 1)]
elif YEHNP == -1 and facility_type == 'PHC':
acceptable_df = acceptable_df.loc[(acceptable_df['YEHNP_PHCs'] != 1)]
# Adjust for functionality in a given year
acceptable_df = acceptable_df.loc[acceptable_df['Functioning %s' % year].isin(['1','2',1,2])]
# Adjust for availability of service
SERVICE_DICT = {'Antenatal_2018':'ANC 2018',
'Antenatal_2016':'Antenatal Care (P422) 2016',
'BEmONC_2018':'Basic emergency obstetric care 2018',
'BEmONC_2016':'Basic Emergency Obsteteric Care (P424) 2016',
'CEmONC_2018':'Comprehensive emergency obstetric care 2018',
'CEmONC_2016':'Comprehensive Emergency Obstetric Care (S424) 2016',
'Under_5_2018':'Under 5 clinics 2018',
'Under_5_2016':'Under-5 clinic services (P23) 2016',
'Emergency_Surgery_2018':'Emergency and elective surgery 2018',
'Emergency_Surgery_2016':'Emergency and Elective Surgery (S14) 2016',
'Immunizations_2018':'EPI 2018',
'Immunizations_2016':'EPI (P21a) 2016',
'Malnutrition_2018':'Malnutrition services 2018',
'Malnutrition_2016':'Malnutrition services (P25) 2016',
'Int_Outreach_2018':'Integrated outreach (IMCI+EPI+ANC+Nutrition_Services) 2018',
'Int_Outreach_2016':'Integrated Outreach (P22) 2016'}
if service_index == 0:
pass
else:
acceptable_df = acceptable_df.loc[acceptable_df[SERVICE_DICT['%s_%s' % (services[service_index],year)]].isin(['1',1])]
print(len(acceptable_df))
# -
acceptable_df['geometry'] = acceptable_df['geometry'].apply(loads)
acceptable_gdf = gpd.GeoDataFrame(acceptable_df, geometry = 'geometry', crs = {'init':'epsg:4326'})
accepted_facilities = list(set(list(acceptable_df.NN)))
accepted_facilities_str = [str(i) for i in accepted_facilities]
OD = OD_original[accepted_facilities_str]
acceptable_df.to_csv(os.path.join(basepth,'output_layers','Round 3','%s.csv' % subset))
print(OD_original.shape)
print(OD.shape)
# ### Define function to add elevation to a point GeoDataFrame
def add_elevation(df, x, y, srtm_pth):
# walk all tiles, find path
tiles = []
for root, folder, files in os.walk(os.path.join(srtm_pth,'high_res')):
for f in files:
if f[-3:] == 'hgt':
tiles.append(f[:-4])
# load dictionary of tiles
arrs = {}
for t in tiles:
arrs[t] = rt.open(os.path.join(srtm_pth, 'high_res', '{}.hgt'.format(t), '{}.hgt'.format(t)), 'r')
# assign a code
uniques = []
df['code'] = 'placeholder'
def tile_code(z):
E = str(z[x])[:2]
N = str(z[y])[:2]
return 'N{}E0{}'.format(N, E)
df['code'] = df.apply(lambda z: tile_code(z), axis = 1)
unique_codes = list(set(df['code'].unique()))
z = {}
# Match on High Precision Elevation
property_name = 'elevation'
for code in unique_codes:
df2 = df.copy()
df2 = df2.loc[df2['code'] == code]
dataset = arrs[code]
b = dataset.bounds
datasetBoundary = box(b[0], b[1], b[2], b[3])
selKeys = []
selPts = []
for index, row in df2.iterrows():
if Point(row[x], row[y]).intersects(datasetBoundary):
selPts.append((row[x],row[y]))
selKeys.append(index)
raster_values = list(dataset.sample(selPts))
raster_values = [x[0] for x in raster_values]
# generate new dictionary of {node ID: raster values}
z.update(zip(selKeys, raster_values))
elev_df = pd.DataFrame.from_dict(z, orient='index')
elev_df.columns = ['elevation']
missing = elev_df.copy()
missing = missing.loc[missing.elevation < 0]
if len(missing) > 0:
missing_df = df.copy()
missing_df = missing_df.loc[missing.index]
low_res_tifpath = os.path.join(srtm_pth, 'clipped', 'clipped_e20N40.tif')
dataset = rt.open(low_res_tifpath, 'r')
b = dataset.bounds
datasetBoundary = box(b[0], b[1], b[2], b[3])
selKeys = []
selPts = []
for index, row in missing_df.iterrows():
if Point(row[x], row[y]).intersects(datasetBoundary):
selPts.append((row[x],row[y]))
selKeys.append(index)
raster_values = list(dataset.sample(selPts))
raster_values = [x[0] for x in raster_values]
z.update(zip(selKeys, raster_values))
elev_df = pd.DataFrame.from_dict(z, orient='index')
elev_df.columns = ['elevation']
df['point_elev'] = elev_df['elevation']
df = df.drop('code', axis = 1)
return df
# ### Define function to convert distances to walk times
def generate_walktimes(df, start = 'point_elev', end = 'node_elev', dist = 'NN_dist', max_walkspeed = 6, min_speed = 0.1):
# Tobler's hiking function: https://en.wikipedia.org/wiki/Tobler%27s_hiking_function
def speed(incline_ratio, max_speed):
walkspeed = max_speed * np.exp(-3.5 * abs(incline_ratio + 0.05))
return walkspeed
speeds = {}
times = {}
for index, data in df.iterrows():
if data[dist] > 0:
delta_elevation = data[end] - data[start]
incline_ratio = delta_elevation / data[dist]
speed_kmph = speed(incline_ratio = incline_ratio, max_speed = max_walkspeed)
speed_kmph = max(speed_kmph, min_speed)
speeds[index] = (speed_kmph)
times[index] = (data[dist] / 1000 * 3600 / speed_kmph)
speed_df = pd.DataFrame.from_dict(speeds, orient = 'index')
time_df = pd.DataFrame.from_dict(times, orient = 'index')
df['walkspeed'] = speed_df[0]
df['walk_time'] = time_df[0]
return df
# ### Add elevation for destination nodes
dest_df = acceptable_df[['NN','NN_dist','Latitude','Longitude']]
dest_df = add_elevation(dest_df, 'Longitude','Latitude', srtm_pth).set_index('NN')
# ### Add elevation from graph nodes (reference)
G = nx.read_gpickle(os.path.join(OD_pth, net_name))
G_node_df = gn.node_gdf_from_graph(G)
G_node_df = add_elevation(G_node_df, 'x', 'y', srtm_pth)
match_node_elevs = G_node_df[['node_ID','point_elev']].set_index('node_ID')
match_node_elevs.loc[match_node_elevs.point_elev < 0] = 0
# ### Match on node elevations for dest_df; calculate travel times to nearest node
dest_df['node_elev'] = match_node_elevs['point_elev']
dest_df = generate_walktimes(dest_df, start = 'node_elev', end = 'point_elev', dist = 'NN_dist', max_walkspeed = offroad_speed)
dest_df = dest_df.sort_values(by = 'walk_time', ascending = False)
# ### Add Walk Time to all travel times in OD matrix
# +
dest_df = dest_df[['walk_time']]
dest_df.index = dest_df.index.map(str)
d_f = OD.transpose()
for i in d_f.columns:
dest_df[i] = d_f[i]
for i in dest_df.columns:
if i == 'walk_time':
pass
else:
dest_df[i] = dest_df[i] + dest_df['walk_time']
dest_df = dest_df.drop('walk_time', axis = 1)
dest_df = dest_df.transpose()
# -
# ### Import Shapefile Describing Regions of Control
if conflict == 1:
conflict_file = r'merged_dists_%s.shp' % year
elif conflict == 0:
conflict_file = r'NoConflict.shp'
merged_dists = gpd.read_file(os.path.join(util_path, conflict_file))
if merged_dists.crs != {'init':'epsg:4326'}:
merged_dists = merged_dists.to_crs({'init':'epsg:4326'})
merged_dists = merged_dists.loc[merged_dists.geometry.type == 'Polygon']
# ### Factor in lines of Control - Import Areas of Control Shapefile
# +
# Intersect points with merged districts shapefile, identify relationship
def AggressiveSpatialIntersect(points, polygons):
import osmnx as ox
spatial_index = points.sindex
container = {}
cut_geoms = []
for index, row in polygons.iterrows():
polygon = row.geometry
if polygon.area > 0.5:
geometry_cut = ox.quadrat_cut_geometry(polygon, quadrat_width=0.5)
cut_geoms.append(geometry_cut)
print('cutting geometry %s into %s pieces' % (index, len(geometry_cut)))
index_list = []
for P in geometry_cut:
possible_matches_index = list(spatial_index.intersection(P.bounds))
possible_matches = points.iloc[possible_matches_index]
precise_matches = possible_matches[possible_matches.intersects(P)]
if len(precise_matches) > 0:
index_list.append(precise_matches.index)
flat_list = [item for sublist in index_list for item in sublist]
container[index] = list(set(flat_list))
else:
possible_matches_index = list(spatial_index.intersection(polygon.bounds))
possible_matches = points.iloc[possible_matches_index]
precise_matches = possible_matches[possible_matches.intersects(polygon)]
if len(precise_matches) > 0:
container[index] = list(precise_matches.index)
return container
# -
graph_node_gdf = gn.node_gdf_from_graph(G)
gdf = graph_node_gdf.copy()
gdf = gdf.set_index('node_ID')
possible_snap_nodes = AggressiveSpatialIntersect(graph_node_gdf, merged_dists)
print('**bag of possible node snapping locations has been successfully generated**')
# ### Load Grid
# +
# Match on network time from origin node (time travelling along network + walking to destination)
if year == 2018:
year_raster = 2018
elif year == 2016:
year_raster = 2015
grid_name = r'origins_1km_%s_snapped.csv' % year_raster
grid = pd.read_csv(os.path.join(OD_pth, grid_name))
grid = grid.rename({'Unnamed: 0':'PointID'}, axis = 1)
grid['geometry'] = grid['geometry'].apply(loads)
grid_gdf = gpd.GeoDataFrame(grid, crs = WGS, geometry = 'geometry')
grid_gdf = grid_gdf.set_index('PointID')
# -
# ### Adjust Nearest Node snapping for War
# +
origin_container = AggressiveSpatialIntersect(grid_gdf, merged_dists)
print('bag of possible origins locations has been successfully generated')
bundle = []
for key in origin_container.keys():
origins = origin_container[key]
possible_nodes = graph_node_gdf.loc[possible_snap_nodes[key]]
origin_subset = grid_gdf.loc[origins]
origin_subset_snapped = gn.pandana_snap_points(origin_subset,
possible_nodes,
source_crs = 'epsg:4326',
target_crs = 'epsg:32638',
add_dist_to_node_col = True)
bundle.append(origin_subset_snapped)
grid_gdf_adjusted = pd.concat(bundle)
# -
grid_gdf = grid_gdf_adjusted
# Add origin node distance to network - walking time
grid = grid_gdf
grid = add_elevation(grid, 'Longitude','Latitude', srtm_pth)
grid = grid.reset_index()
grid['O_ID'] = grid['NN']
grid = grid.set_index('NN')
grid['node_elev'] = match_node_elevs['point_elev']
grid = grid.set_index('PointID')
grid = generate_walktimes(grid, start = 'point_elev', end = 'node_elev', dist = 'NN_dist', max_walkspeed = offroad_speed)
grid = grid.rename({'node_elev':'nr_node_on_net_elev',
'walkspeed':'walkspeed_to_net',
'walk_time':'walk_time_to_net',
'NN_dist':'NN_dist_to_net',
'O_ID':'NN',
'Unnamed: 0.1':'PointID'}, axis = 1)
# ### Adjust acceptable destinations for each node for the war
# +
gdf = graph_node_gdf.copy()
gdf['node_ID'] = gdf['node_ID'].astype('str')
gdf = gdf.loc[gdf.node_ID.isin(list(dest_df.columns))]
gdf = gdf.set_index('node_ID')
dest_container = AggressiveSpatialIntersect(gdf, merged_dists)
gdf = graph_node_gdf.copy()
gdf = gdf.loc[gdf.node_ID.isin(list(dest_df.index))]
gdf = gdf.set_index('node_ID')
origin_snap_container = AggressiveSpatialIntersect(gdf, merged_dists)
# -
# # BREAK
#
# From this point the script diverges from Step 4 - Generate Results.
#
# In this cell, we DO NOT use a min function to work out the closest destination to each origin cell. Instead, we merge on to the grid the travel time to ALL relevant destinations in the same polygon of homogeneous control that is accessible.
# +
bundle = []
for key in origin_snap_container.keys():
# print which polygon we are looking at
print('\nregion:',key)
# identify bundle of origin, dest nodes inside region
origins = origin_snap_container[key]
print('number of origin nodes in this reigon:',len(origins))
destinations = dest_container[key]
print('number of destination nodes in this reigon:',len(destinations))
# get part of OD that is relevant
relevant_dests = dest_df.copy()
relevant_dests = relevant_dests[destinations].loc[origins]
print('How many destination facilities in this region?',len(relevant_dests.columns))
# get part of grid that is relevant
relevant_grid = grid.copy()
relevant_grid = relevant_grid.loc[origin_container[key]]
print('How many origin grid cells in this region?',len(relevant_grid))
# match on dest-df
relevant_grid = relevant_grid.set_index('NN')
for i in relevant_dests.columns:
relevant_grid[i] = relevant_dests[i]
# append to bundle for reconstruction
bundle.append(relevant_grid)
combo_grid = pd.concat(bundle)
combo_grid['PointID_copy'] = combo_grid['PointID']
combo_grid = combo_grid.set_index('PointID')
print(len(combo_grid[dest_df.columns].loc[241487].unique()))
# -
# Here, we add the walk time to the network to the on-network time. This is the best way of representing the 'drive time' to each destination
# +
combo_grid2 = combo_grid.copy()
# add on walk time
for i in dest_df.columns:
combo_grid2[i].loc[combo_grid2[i].isna() == False] = combo_grid2[i].loc[combo_grid2[i].isna() == False] + combo_grid2['walk_time_to_net'].loc[combo_grid2[i].isna() == False]
combo_grid2 = combo_grid2.drop(['NN_dist_to_net','walk_time_to_net','walkspeed_to_net'], axis = 1)
grid = combo_grid2
print(len(combo_grid2[dest_df.columns].loc[241487].unique()))
# -
# ### Calculate Direct Walking Time (not using road network), vs. network Time
#
# The output of this block was not factored in, in the end. The problem was that, identifying the closest facility to the origin point is not useful when you are trying to retain the access time to ALL facilities in the same homogenous region. Ergo, we do not use this section.
# +
bundle = []
W = graph_node_gdf.copy()
W['node_ID'] = W['node_ID'].astype(str)
W = W.set_index('node_ID')
locations_gdf = gpd.GeoDataFrame(acceptable_df, geometry = 'geometry', crs = {'init':'epsg:4326'})
locations_container = AggressiveSpatialIntersect(locations_gdf, merged_dists)
for key in origin_container.keys():
origins = origin_container[key]
origin_subset = grid.copy()
origin_subset = origin_subset.loc[origins]
locations = locations_gdf.loc[locations_container[key]]
if len(locations) < 1:
origin_subset['NN'] = None
origin_subset['NN_dist'] = None
bundle.append(origin_subset)
else:
origin_subset_snapped = gn.pandana_snap_points(origin_subset,
locations,
source_crs = 'epsg:4326',
target_crs = 'epsg:32638',
add_dist_to_node_col = True)
bundle.append(origin_subset_snapped)
grid_gdf_adjusted = pd.concat(bundle)
grid = grid_gdf_adjusted
print(len(grid[dest_df.columns].loc[241487].unique()))
# -
# ### Generate summary by Destination
#
# Here, for each time threshold, we return a binary version of the OD-matrix if the destination facility has a travel time beneath the threshold time, and sum for each facility. We also identify instances of where there is only one valid facility for a given origin - this will happen when the sum of a row is equal to the only value in the row.
# +
ag1 = grid.fillna(99999999999).copy()
uniques, totals, test_frames_A, test_frames_B = {}, {}, {}, {}
for thresh in [30, 60, 120, 240]:
ag2 = ag1.copy()
def convert(x, thresh):
if 0 < x < (thresh * 60):
return 1
else:
return 0
# identify pop under thresh
for i in Dest_IDs:
ag2[i] = ag2[i].fillna(-1)
ag2[i] = ag2[i].apply(lambda x: convert(x, thresh))
# add Valid column. counts up number of cells beneath travel time threshold.
ag2['VALID'] = ag2[Dest_IDs].sum(axis = 1)
test_frames_A[thresh] = ag2.copy()
# multiply through by population value
for i in Dest_IDs:
ag2[i] = ag2[i] * ag2['VALUE']
# generate total of pop that can access a destination in under thresh mins
ag2['total'] = ag2[Dest_IDs].sum(axis = 1)
test_frames_B[thresh] = ag2.copy()
# compare to total, zero out values where less than total (i.e. not unique)
res_uniques, res_totals = [], []
for i in Dest_IDs:
ag3 = ag2.copy()
res_uniques.append(ag3[i].loc[ag3['VALID'] == 1].sum())
res_totals.append(ag3[i].loc[ag3['VALID'] > 0].sum())
uniques[thresh] = res_uniques
totals[thresh] = res_totals
# -
# Finally, we generate the results DataFrame.
# +
res_df = pd.DataFrame({'catchment_30':totals[30],
'catchment_60':totals[60],
'catchment_120':totals[120],
'catchment_240':totals[240],
'unique_30': uniques[30],
'unique_60': uniques[60],
'unique_120': uniques[120],
'unique_240': uniques[240],
'NN':Dest_IDs},
index = Dest_IDs)
# Generate 'fraction of catchment that is uniquely served by this facility' statistics.
res_df['pct_unique_30'] = res_df['unique_30'] / res_df['catchment_30']
res_df['pct_unique_60'] = res_df['unique_60'] / res_df['catchment_60']
res_df['pct_unique_120'] = res_df['unique_120'] / res_df['catchment_120']
res_df['pct_unique_240'] = res_df['unique_240'] / res_df['catchment_240']
acceptable_df_res = acceptable_df.copy()
acceptable_df_res['NN'] = acceptable_df_res['NN'].astype('str')
acceptable_df_res = acceptable_df_res.set_index('NN')
acceptable_df_res = acceptable_df_res.merge(res_df, on = 'NN')
acceptable_df_res = acceptable_df_res.sort_values(by = 'pct_unique_30', ascending = False)
# -
# We visualize it here to make sure it is what we want
col_list = ['catchment_30','catchment_60','catchment_120','unique_30','unique_60','unique_120','pct_unique_30','pct_unique_60','pct_unique_120']
acceptable_df_res.head(30)
# ...and we save our output down.
outi = os.path.join(basepth, 'output_layers', 'catchment')
acceptable_df_res.to_csv(os.path.join(outi, subset+'_catchment.csv'))
|
Implementations/FY20/ACC_Yemen - GOSTnets/Extension B - Catchment by Clinic.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## Expectation Reflection for Classification
# +
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
from sklearn.utils import shuffle
from sklearn.metrics import accuracy_score
import expectation_reflection as ER
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
# %matplotlib inline
# -
np.random.seed(1)
def synthesize_data(l,n,g,data_type='continous'):
if data_type == 'binary':
X = np.sign(np.random.rand(l,n)-0.5)
w = np.random.normal(0.,g/np.sqrt(n),size=n)
if data_type == 'continuous':
X = 2*np.random.rand(l,n)-1
w = np.random.normal(0.,g/np.sqrt(n),size=n)
if data_type == 'categorical':
from sklearn.preprocessing import OneHotEncoder
m = 5 # categorical number for each variables
# initial s (categorical variables)
s = np.random.randint(0,m,size=(l,n)) # integer values
onehot_encoder = OneHotEncoder(sparse=False,categories='auto')
X = onehot_encoder.fit_transform(s)
w = np.random.normal(0.,g/np.sqrt(n),size=n*m)
h = X.dot(w)
p = 1/(1+np.exp(-2*h)) # kinetic
#p = 1/(1+np.exp(-h)) # logistic regression
y = np.sign(p - np.random.rand(l))
return w,X,y
# +
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
def ML_inference(X_train,y_train,X_test,y_test,method='expectation_reflection'):
if method == 'expectation_reflection':
h0,w = ER.fit(X_train,y_train,niter_max=100,regu=0.01)
y_pred = ER.predict(X_test,h0,w)
accuracy = accuracy_score(y_test,y_pred)
else:
if method == 'logistic_regression':
model = LogisticRegression(solver='liblinear')
if method == 'naive_bayes':
model = GaussianNB()
if method == 'random_forest':
model = RandomForestClassifier(criterion = "gini", random_state = 1,
max_depth=3, min_samples_leaf=5,n_estimators=100)
if method == 'decision_tree':
model = DecisionTreeClassifier()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test,y_pred)
return accuracy
# -
list_methods=['expectation_reflection','naive_bayes','logistic_regression','decision_tree','random_forest']
def compare_ML_inference(X,y,train_size):
npred = 100
accuracy = np.zeros((len(list_methods),npred))
for ipred in range(npred):
X, y = shuffle(X, y)
X_train0,X_test,y_train0,y_test = train_test_split(X,y,test_size=0.2,random_state = ipred)
idx_train = np.random.choice(len(y_train0),size=int(train_size*len(y_train0)),replace=False)
X_train,y_train = X_train0[idx_train],y_train0[idx_train]
for i,method in enumerate(list_methods):
accuracy[i,ipred] = ML_inference(X_train,y_train,X_test,y_test,method)
#print('% 20s :'%method,accuracy)
#print(y_train.shape[0],y_test.shape[0])
return accuracy.mean(axis=1),accuracy.std(axis=1)
# ### Categorical variables
l = 10000
n = 20
g = 16.
w0,X,y = synthesize_data(l,n,g,data_type='categorical')
from sklearn.preprocessing import MinMaxScaler
X = MinMaxScaler().fit_transform(X)
# +
list_train_size = [1.,0.8,0.6,0.4,0.2,0.1,0.05]
acc = np.zeros((len(list_train_size),len(list_methods)))
acc_std = np.zeros((len(list_train_size),len(list_methods)))
for i,train_size in enumerate(list_train_size):
acc[i,:],acc_std[i,:] = compare_ML_inference(X,y,train_size)
print(train_size,acc[i,:])
# -
plt.figure(figsize=(4,3))
plt.plot(list_train_size,acc[:,0],'k-',label='ER')
plt.plot(list_train_size,acc[:,1],'b-',label='Naive Bayes')
plt.plot(list_train_size,acc[:,2],'r-',label='Logistic Regression')
plt.plot(list_train_size,acc[:,3],'b--',label='Decision Tree')
plt.plot(list_train_size,acc[:,4],'r--',label='Random Forest')
plt.xlabel('train-size')
plt.ylabel('acc')
plt.xlim([0.05,1])
#plt.ylim([0.8,1])
plt.legend()
|
.ipynb_checkpoints/1main_categorical_regu-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import json
import base64
import os
import io
from PIL import Image
# ## Run prediction
# ! python inference.py --output_file_path prediction_result.json
# ## Captum insights
# ! python inference.py --inference_type explanation --output_file_path explanation_result.json
explainations_json = json.loads(open("./explanation_result.json", "r").read())
# +
image = base64.b64decode(explainations_json["b64"])
fileName = 'captum_kitten.jpeg'
imagePath = ( os.getcwd() +"/" + fileName)
img = Image.open(io.BytesIO(image))
img = img.convert('RGB')
img.save(imagePath, 'jpeg', quality=100)
print("Saving ", imagePath)
# -
from IPython.display import Image
Image(filename='captum_kitten.jpeg')
|
examples/cifar10/Cifar10_Captum.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Apriori Learning
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# ## Dataset
dataset = pd.read_csv('Market_Basket_Optimisation.csv', header=None)
dataset.head()
transactions = []
for i in range(len(dataset)):
transactions.append([str(dataset.values[i,j]) for j in range(0,20)])
# ## Train Apriori
from apyori import apriori
rules = apriori(transactions, min_support=0.003, min_confidence=0.2, min_lift=3, minlength=2)
# ## Visualization
results = list(rules)
results
|
z_Miscellaneous/ML2/AssociationRuleLearning/Apriori.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: env_pda_2022
# language: python
# name: env_pda_2022
# ---
# <center><font size="+4">Programming and Data Analytics 1 2021/2022</font></center>
# <center><font size="+2">Sant'Anna School of Advanced Studies, Pisa, Italy</font></center>
# <center><img src="https://github.com/EMbeDS-education/StatsAndComputing20212022/raw/main/PDA/jupyter/jupyterNotebooks/images/SSSA.png" width="700" alt="EMbeDS"></center>
#
# <center><font size="+2">Course responsible</font></center>
# <center><font size="+2"><NAME> <EMAIL></font></center>
#
# <center><font size="+2">Co-lecturer </font></center>
# <center><font size="+2"><NAME> <EMAIL></font></center>
#
# ---
# <center><font size="+4">Lecture 3: Collections</font></center>
# ---
from IPython.display import Image, display
#img=Image(filename='images/tentativeLecturePlan.png',width=700)
url_github_repo="https://github.com/EMbeDS-education/StatsAndComputing20212022/raw/main/PDA/"
img=Image(url_github_repo+'jupyter/jupyterNotebooks/images/tentativeLecturePlan.png',width=700)
display(img)
# | Class | Date | Time | Topic |
# |:----------:|-----------------------------|--|--|
# |1| 14/02 | 15:00-17:00 | Course introduction |
# |2| 16/02 | 15:00-18:00 | Data types & operations |
# |3| 18/02 | 15:00-18:00 | Collections & First taste of plots |
# |4| 21/02 | 15:00-18:00 | Control statements (if, loops) & CSV manipulation/visualization on COVID-19 data |
# |5| 25/02 | 15:00-18:00 | Functions & Application to analysis of epidemiological models |
# |6| 28/02 | 15:00-18:00 | Modules & Exceptions & OOP & Applications to betting markets (ABM models) |
# |7| 04/03 | 15:00-18:00 | Advanced libraries for data manipulation (NumPy, Pandas) & Application to COVID-19 and Finance data |
#
# > Note: we created this table using Markdown. <br/>
# > [There are also online table generators](https://www.tablesgenerator.com/markdown_tables)
# __What it feels like to win a kahoot...__<br/>
# 
# <font size="+2"> How good are we so far - Kahoot quiz on previous class </font>
# * Using your phone or a different display go to [https://kahoot.it/](https://kahoot.it/)
# * Type the given PIN
from IPython.display import IFrame
IFrame("https://kahoot.it/", 500, 400)
# # Intro: sequences, sets, dictionaries
# A collection is a data type able to store 0, 1, or more elements.
#
# This is particularly useful to
# * Structure your data
# * Easily access elements in collections of data of _same type_
#
# For example you might want to have:
#
# | Type | Description |
# |:----------:|-----------------------------|
# | __Sequence types__ | An ordered list of all the assignments of this course |
# | __Set types__ | An unordered collection without replicas (a set) of the students of this course |
# | __Map/Dictionary types__ | A mapping from the name of a student to the email of that student |
# # Sequence types
# There are [4 basic sequence types in Python](https://docs.python.org/3/library/stdtypes.html#sequence-types-list-tuple-range)
# * _String_
# * __List__
# * __Tuple__
# * __Range__
# + [markdown] toc-nb-collapsed=true
# ## Strings
# -
# We have already seen that a string can be used also as a sequence of characters.
# - Remember: in computer science we start counting __from 0__ up to __length-1__
# We can
# - _select_ single characters
# - _slice_ substrings
s="abcde"
print(s)
print(" "+s[1])
print(" "+s[-1])
print(" "+s[2:])
print(s[:2])
print(" "+s[2:4])
# We can also
# - _add characters_ to a string (string concatenation)
# - search for the min/max character (in alphabetical order)
print(s + "efg")
print()
print("Min:",min(s))
print("Max:",max(s))
# A string is a _special_ sequence
#
# * A string is __immutable__
# > <span style="color:red"> `s[1] = 'B'` __WE CAN'T MODIFY ENTRIES OF A STRING!__</span>
# * The only elements admitted in a string are characters (letters, digits, further symbols)
# +
# If you decomment the line below you will get a runtime error
#s[1] = 'B'
# -
# ## Lists, Tuples, and Ranges
# ### Lists
# #### Features of lists shared with strings
# + [markdown] tags=[]
# Intuitively, a list is like a string, but
# * You can store in it data of any type, even of mixed types
# * However, you will typically put elements of same type in a list
# * It is not pythonic to store data of multiple types in a list...
# * Functionalities related to comparisons work only on lists with elements of same type
# * E.g. min/max/sort ...
# * Do you remember about 'not mixing apples and oranges!? :D
# * Is **mutable** you can change its elements
#
# You create a list by writing a comma-separated list of values in square brackets
# -
lst = [12, 'apples', 12.0, 'oranges', True]
print(type(lst))
print(lst)
# You can access the elements of a list similarly to how you access characters of a string:
print(lst)
print(len(lst))
print(lst[1])
print(lst[-1])
print(lst[-2])
print(lst[:2])
print(lst[2:])
lst0 = [2,1,3,4]
print(lst0)
print(min(lst0))
print(max(lst0))
max([1.0, 2])
max(["ciao","coro","abc"])
lst_test=["ciao","abc"]
print(min(lst_test))
print(type(min(lst_test)))
# Similarly to strings, we can _concatenate_ lists...
"abc"+"def"
lst
lst2 = [1,2,3,"four"]
#min(lst2)
lst3 = lst + lst2
lst3
print(lst0)
lst100=[100,200]
lst0+lst100
# +
# "ciao"*3
# -
tenzeros = [0] * 10 # [0] + [0] + [0] ....
tenzeros
[0,1]*3
# Lists containing elements of __same type__ can be compared
# * The comparison is done in lexicographical order
"mara" < "mario"
print(lst0)
lst4=[1,2,3,3]
print(lst4)
print(lst4,'<',lst0)
lst4 < lst0
# #### Features of lists beyond those of strings
# With respect to strings, now we can also:
# * update entries of a list
# * create lists of lists
# * have you ever heard about matrices?
# | 0 | 1 | 2 |
# |:-:|:-:|:-:|
# | __3__ | __4__ | __5__ |
row0=[0,1,2]
m=[ row0,
[3,4,5] ]
print('The matrix',m)
print('has type',type(m))
print('First row',m[0], type(m[0]))
print('Second row',m[1], type(m[1]))
print('First element of first row',m[0][0], type(m[0][0]))
print('Third element of second row',m[1][2], type(m[1][2]))
# +
first_row=m[0]
print(first_row)
print(first_row[0])
print(m[0][0])
# -
print(lst)
lst[0]=11
lst[1]=4.3
print(lst)
lst4 = [lst, lst2, lst3]
print(lst4)
# How can I access the first element of the second list in `lst4`?
secondlist = lst4[1]
firstelement = secondlist[0]
print(firstelement)
# or ...
print(lst4[1][0])
# Lists can have any level of __nesting__ (lists of lists of lists...), and can be mixed with other types
lst5 = [lst4 , [1,2], 1, "ciao", True ]
print(lst5)
#Print the same as 'firstelement' from above
print(lst5[0][1][0])
# #### How to copy a list?
l1=[1,2,3,4]
l2=l1 #<- you are not actually copying the list. You just create a reference to the same
print(l2)
l1[0]=100
print()
print("l1",l1)
print("l2",l2)
# > `l2=l1` does not copy the list!<br/>
# > We just let the two variables _point to the same list_
img=Image(url_github_repo+'jupyter/jupyterNotebooks/images/l1l2.png',width=700)
display(img)
# Here, **l1 and l2 point to the same list**.
#
# How to really copy a list into a new one?
# * Use list constructor
# * Use list comprehension
# * Using the copy method
l1
#Using the constructor of lists
l2=list(l1)
l1[0]=1
print(l1)
print(l2)
#Using list comprehensions
l2=[x for x in l1]
l1[0]=300
print(l1)
print(l2)
[x*2 for x in l1]
l3=l2.copy()
l2[0]=55
print(l2)
print(l3)
# Anything that can be _iterated_ can be used in the examples above to construct lists
# * Any sequence and more iterable objects we will discuss later in the course
l2 = list("ciao")
print(l2)
l3 = [x for x in "hello"]
print(l3)
# #### Interesting operations and methods on lists
lst = [12, 15, 1, 0,1.0]
print('Does 1 appear in lst?',1 in lst)
print('Does 3 appear in lst?',3 in lst)
print('Does 1 not appear in lst?',1 not in lst)
print('Does the string \'1\' appear in lst?','1' in lst)
# Note that in the latter `'1' in lst` we check if the string `'1'` belongs to `lst`.
# * This is not the case, because `lst` contains only numeric types
#
# __Do you remember how to get information about all methods of list?__
dir(lst)
# __And how to get more information about single methods?__
help(lst.insert)
print(lst)
lst.insert(0,'ciao')
print(lst)
#help(lst.index)
lst.index(1)
# Some interesting methods:
# * __append__: adds an object at the end of the list
# * __pop__: removes the last element from the list
# * __insert__: adds an object in a given position
# * __copy__: creates a copy of the list
# * __remove__: removes the first occurrence of a given object from the list
# * __count__: counts the number of occurrences of an object
# * __index__: gives the position of the first occurrence of an object
# * __reverse__: reverses the elements from last to first
# * __sort__: sorts the list
# +
lst = [12, 15, 1, 0,1.0]
print('We start from:')
print(lst)
lst.append(100)
print('append(100)')
print(lst)
lst.pop()
print('pop')
print(lst)
lst.insert(0,100)
print('insert(0,100)')
print(lst)
lst.insert(3,100)
print('insert(3,100)')
print(lst)
lst.remove(100)
print('remove(100)')
print(lst)
print('Number 1 appears',lst.count(1),'times in lst')
print('Number 1 appears first in index',lst.index(1),'in lst')
#You can't asks for the index of an element if it does not belong to the list.
#If you uncomment this statement you get a runtime error.
#lst.index(2)
lst.reverse()
print('Reverse')
print(lst)
lst.sort()
print('Sort')
print(lst)
# -
help(lst.index)
lst.index(15)
lst2 = lst+["ciao"]
print(lst2)
# You can't do certain operations on lists with elements of different types
#sort(lst2)
#min(lst2)
#max(lst2)
# > <span style="color:red"> `sort(lst2)` __COMPARISON OPERATIONS ARE FORBIDDEN ON MULTI-TYPE LISTs__</span>
l = len(lst2)
print(l)
lst2.append("c")
print(len(lst2))
print(l)
# #### ALERT! Common pitfall: deep-copy vs shallow copy
# Everything fine here, because
# - we copy 10 times a _basic data type_
lst1=[1]
lst1 * 10
# Pay attention when you __copy lists containing complex data types__
# - You __don't actually create copies__ of its elements if they are 'complex data structures'<br/>
# - You merely __point to the same elements__
[lst1] * 3
lists=[lst1 for i in [0,1,2]]
lists
lists[0].append(3)
print(lists)
img=Image(url_github_repo+'jupyter/jupyterNotebooks/images/shallowcopy.png',width=700)
display(img)
# Unexpected behavior:
# * The same list is 'pointed' 3 times.
# * Changing the list pointed in one entry changes the same list pointed by the other entries
# * This is a __shallow copy__ of the lists.
#
# If you want different instances (__deep copy__) you can use:
# - Which means that you need to take care yourself of copying all nested complex data structures
#Shallow copy
lists= [lst1 for i in [0,1,2]]
lst1=[1]
lists = [lst1.copy() for i in [0,1,2]]
lists
lists[0].append(3)
lists
img=Image(url_github_repo+'jupyter/jupyterNotebooks/images/deepcopy.png',width=700)
display(img)
# ### Tuples: an __immutable__ version of lists
# Tuples are another sequence type.
# * They are essentially __immutable lists__
# * They are created using __rounded parenthesis__ rather than squared ones (or not parenthesis at all)
# +
tpl = (1,2,4,10,20)
print(type(tpl))
print(tpl)
tpl = 1,2,4,10,20 #Parenthesis are optional
print(tpl)
tpl2 = tuple(tpl)
print(tpl2)
lst = [1,2,3]
tpl3 = tuple(lst)
print(lst,tpl3)
# -
print(len(tpl))
print(tpl[1])
print(tpl[-1])
print(tpl[:2])
print(tpl[2:])
# > `tpl[1] = 10` <span style="color:red"> __NOT GOOD!__</span>
# Tuples implement the non-modifying operations shown for lists
# * `in`, `not in`, `min`, `max`, ...
# Why are tuples useful?
# * Sometimes it is convenient to have the guarantee that data cannot change.
# * They can be used as keys in dictionaries (more on this later today)
# * Lists are typically meant for collecting homogeneous types, while __tuples for heterogeneous types__
# ### Ranges & list comprehensions
# Ranges are another form of immutable sequence
# * In the next class we will see that they are mainly used to iterate over certain instructions a given number of times
s=range(10)
print(type(s))
print(s)
# A range represents all integers
# - starting from a `start` value (default 0)
# - up to `stop - 1`, with `stop` a mandatory parameter
# - increasing by a given `step`(default 1)
start=11
stop=20
step=2
#Creates a sequence a number start,start+step,start+step*2,... up to stop-1
s=range(start,stop,step)
print(s)
#Number 'stop' does not belong to the collection
print('Does stop=20 belong to the range?')
stop in s
# We can use ranges to easily build lists or tuples
t= tuple(range(10))
l = list(range(10))
print(l)
print(t)
# +
l2 =[ x for x in range(10)]
l3 =[ x for x in range(10) if x>2 and x< 8]
l3b =[ x for x in range(10) if x%2!=0]
l4 =[ x**2 for x in range(10)]
l5 =['even' if i%2 == 0 else 'odd' for i in range(10) ]
print("l2",l2)
print("l3 ",l3)
print("l3b ",l3b)
print("l4",l4)
print("l5",l5)
# -
# The `[x**2 for x in range(10) if x>2 and x<8]` is a __list comprehension__ with filter
# * Compute the power (`x**2`)
# * of all integers `x` in 0-9 (`for x in range(10)`)
# * included in 3-7 (`if x>2 and x<8`)
#
# Therefore, a list comprehension
# - This allows you to build a list manipulating and filtering ranges or other sequences
# - Super pythonic!
# ## A first taste of plots
# Not all Python modules are distributed directly in the Python distribution. <br/>
# Some, like __matplotlib__ that allows you to __create plots__, are not.
#
# > __The first time you run jupyter you have to install it using the following script__
#import sys
#!"{sys.executable}" -m pip install matplotlib
# %pip install matplotlib
# Then, you need to import it
# - You can assign a 'short name' to it
# - And people always use the same ones:
# plt, np, pd, ...
#After you have installed matplotlib, you can import part of it.
import matplotlib.pyplot as plt
#If you want more info on this module
#help(plt)
# Maybe you never thought about this
# - but when you plot you use two sequences of data
x=range(20)
y=[i**2 for i in x]
print(x)
print(y)
# Creating a simple plot is... simple :)
plt.plot(x,y)
plt.show()
plt.scatter(x,y)
plt.show()
# The idea is the following
# 1. `plt` is your plot. You can modify/populate it at please.
# 2. When the plot is ready, you can draw it using `plt.show()`
# 3. When you draw the plot, plt is 'cleared'
# +
#If you want more details on the method plot
#help(plt.plot)
# -
plt.ylabel('My numbers')
plt.show()
# We can modify the plot, e.g.
plt.plot(x,y)
plt.ylabel('My numbers')
plt.xlabel('Time')
plt.axis([-10, 30, -50, 600])
plt.show()
# We can
# * plot more lines, with different styles
# * same as matlab
# * add text and graphics to the plot
y2=list(y)
y2.reverse()
plt.plot(x,y,'r--',x,y2, 'b-')
plt.annotate('An interesting point', xy=(9.50, 100), xytext=(7, 200),
arrowprops=dict(facecolor='black', shrink=0.05))
plt.show()
y3=list(y2)
plt.plot(x,y,'r-',x,y2, 'b--',x,y3, 'g^',linewidth=2, markersize=8)
plt.annotate('An interesting point', xy=(9.5, 100), xytext=(7, 200),
arrowprops=dict(facecolor='black', shrink=0.05))
plt.show()
# + [markdown] toc-nb-collapsed=true
# # Set types
# -
# [Set types](https://docs.python.org/3/library/stdtypes.html#set-types-set-frozenset) are
# * **unorderded** collections of **distinct** elements
# * useful to
# * eliminate replicas from lists,
# * check __efficiently__ membership of an element to a collection,
# * compute mathematical operations on sets
# +
l=[1,2,3,4,1,2,5]
s = set(l)
print(s)
l_without_replicas=list(s)
l_without_replicas2=[x for x in s]
print(l_without_replicas)
print(l_without_replicas2)
s2 = set([5,4,3,2,1])
print(s2)
s==s2
# -
{2,1,3}
# +
#ERROR!
#{2,1,3}[0]
# -
s={1,2,3}
s2={2,3,4}
print(1 in s)
print(1 in s2)
print('Are s and s2 disjoint?',s.isdisjoint(s2))
print({1,2}.issubset(s))
s.union(s2)
# For more methods of sets
# +
#dir(set)
# -
# You can't access elements by position:
# * There is no order in a set!
# +
#s[0] #THIS WOULD GIVE A RUNTIME ERROR!
# -
# There exists al an immutable version of sets: `frozenset`
# * Can be used as key in dictionaries
fs=frozenset([1,2,3])
print(fs)
# # Mapping Types: dictionary
# A [mapping object](https://docs.python.org/3/library/stdtypes.html#mapping-types-dict) allows to __map__
# * elements of one type (the __key__) to
# * elements of another tpye (the __value__)
# Intuitively,
# * a list implicitly allows to map integers (the index) to its elements
# * a mapping type allows to explicitly define key values of desired type
# +
lst=['a','b','c']
key=1
print('Integer',key,' is mapped to char',lst[key])
marks={'Andrea': 30, 'Daniele':30, 'Giulio':25}
print('Student','Andrea','is mapped to mark',marks['Andrea'])
# -
# Which mapping types are we going to use?
# * **Dictionaries**
type(marks)
# These will create the same dict
# - marks : dictionary comprehension
# - marks3: dictionary constructor zipping two lists
# - marks4: dictionary constructor list of tuples (1 tuple per entry)
marks={'Andrea': 30, 'Daniele':30, 'Giulio':25}
marks2=dict(zip(['Andrea','Daniele','Giulio'],[30,30,25]))
marks3=dict([('Andrea', 30), ('Daniele', 30), ('Giulio', 25)])
print(marks==marks2==marks3)
# Note that we use the function `zip`
# * It creates a list-like structure where each element is a pair of elements from the first and second list, resp.
z=zip(['Andrea','Daniele','Giulio'],[30,30,25])
print(list(z))
# Now suppose that you want to create a dictionary that maps a word to its length.
# * This can be done elegantly using a dictionary comprehension
names = ['Andrea','Daniele','Giulio']
names2len={ n:len(n) for n in names}
print(names2len)
# Many types can be used as keys. But only those __hashable__
# * No mutable collections (list, set, dictionaries)
lst=[1]
string="ciao"
ok_dict={string:lst}
#wrong_dict={lst:5} #ERROR
# Some functionalities of dictionaries
print('All keys:',list(marks.keys()))
print('All values:',list(marks.values()))
print('Number of elements:',len(marks))
print('Update')
marks['Andrea']=29
print(marks)
marks['Marta']=30
marks
# # Which data structure should I use? 'It depends on what you have to do'
# ## You should carefully THINK about which data structure to use for your needs
# Each data structure has its pros and cons
# - Some occupy more space than others
# - Each specializes in certain operations
# - Some allow to insert/delete elements very efficiently,
# - Others allow to search very efficiently
# - ...
# These properties are discussed using the notion of [time/space complexity](https://wiki.python.org/moin/TimeComplexity)
# - Daniele and I attended courses during our studies just on this topic...
# - We will try to give you a super short overview
# - Just the idea
# Complexity is all about this question:
# - How mouch does it cost an operation depending on the size of the data structure (on the amount of data)?
# - __$O(1)$__: VERY GOOD. The size does not matter.
# - This operation takes the same time.
# - __$O(\log n)$__: GOOD. The size does not matter much.
# - The time necessary increases slowly
# - __$O(n)$__: BADish: The size matters!
# - The time necessary increases linearly
# - __$O(n \log n)$__: BADish: The size matters!
# - The time necessary slightly more than linearly
# - __$O(n^2)$__: BAD: The size matters!
# - The time necessary quadratically
# - __$O(2^n)$__: VERY BAD: The size matters!
# - The time necessary exponentially
#
#
#
# Beware
# - These considerations are important only if your data structure contains many elements (e.g., more than 1000)
# - There is no free lunch: we can improve on time complexity only by worsening space complexity (using more memory)
# - a lists uses less memory than a set or a dictionary...
# ## (Simplified) time complexities of python data structures
# ### Lists
from IPython.display import Image, display
#img=Image(filename='images/complexityLists.png',width=280)
img=Image(url_github_repo+'jupyter/jupyterNotebooks/images/complexityLists.png',width=280)
display(img)
# - Iteration/Copying/Max/Min a list takes O(n):
# - I have to scan all the elements
# - <span style="color:green">Appending an element at the end takes constant time O(1)</span>
# - __<span style="color:red"> Deleting an intermediate element takes O(n)</span>__
# - I have to shift all the elements on its right!
# - __<span style="color:red"> Searching an element (`x in s`) takes O(n)</span>__
# - I have to scan all the elements
# - <span style="color:green"> Sorting takes O(n \cdot log n)</span>
# - This is an important result in computer science
# - There are proofs showing that you can't do better
# ### Sets
img=Image(url_github_repo+'jupyter/jupyterNotebooks/images/complexitySets.png',width=700)
display(img)
# The table distinghishes among average case and worst case
# - Average: what can you expect in practice
# - Worst: there exist a formal theorem stating that it cannot be worse than this
# - We keep focusing on the average case
#
#
# We note that:
# - __<span style="color:green"> Searching an element (`x in s`) takes on average O(1)</span>__
# - It transforms x into an int (hashing)
# - Uses that int as an 'address'/'index' of x.
#
# A set is implemented as a dict. Check in that table for the missing complexities
# ### Dict
img=Image(url_github_repo+'jupyter/jupyterNotebooks/images/complexityDicts.png',width=200)
display(img)
# - <span style="color:green"> Searching an element (`x in s`) takes O(1)</span>
# - It transforms x into an int (hashing)
# - Uses that int as an 'address'/'index' of x.
# - __<span style="color:green">Deleting an element (`x in s`) takes O(1)</span>__
lst = list(range(20000))
st = set(range(20000))
# +
which=100
print('What:', which, 'LIST')
# %time print(which in lst)
print('What:', which, 'SET')
# %time print(which in st)
print()
which=1000
print('What:', which, 'LIST')
# %time print(which in lst)
print('What:', which, 'SET')
# %time print(which in st)
print()
which=10000
print('What:', which, 'LIST')
# %time print(which in lst)
print('What:', which, 'SET')
# %time print(which in st)
print()
which=100000
print('What:', which, 'LIST')
# %time print(which in lst)
print('What:', which, 'SET')
# %time print(which in st)
# -
lst = list(range(10000000))
st = set(range(10000000))
# +
which=100
print('What:', which, 'LIST')
# %time print(which in lst)
print('What:', which, 'SET')
# %time print(which in st)
print()
which=1000
print('What:', which, 'LIST')
# %time print(which in lst)
print('What:', which, 'SET')
# %time print(which in st)
print()
which=10000
print('What:', which, 'LIST')
# %time print(which in lst)
print('What:', which, 'SET')
# %time print(which in st)
print()
which=100000
print('What:', which, 'LIST')
# %time print(which in lst)
print('What:', which, 'SET')
# %time print(which in st)
print()
which=1000000
print('What:', which, 'LIST')
# %time print(which in lst)
print('What:', which, 'SET')
# %time print(which in st)
print()
which=10000000
print('What:', which, 'LIST')
# %time print(which in lst)
print('What:', which, 'SET')
# %time print(which in st)
print()
which=100000000
print('What:', which, 'LIST')
# %time print(which in lst)
print('What:', which, 'SET')
# %time print(which in st)
# -
# # Next class...
from IPython.display import Video, display
video=Video(url_github_repo+'jupyter/jupyterNotebooks/images/loops.mp4')
#video=Video('images/loops.mp4')
display(video)
# In the next class we will see how to instruct Python in
# * Executing certain instructions only if a given condition holds
# * Executing a given number of time certain instructins
#
# For example:
# * We have seen how to store collections of data.
# * In the next class we will see how to easily access their elements in order
# +
weekdays = ["Mon", "Tue", "Wed", "Thu", "Fri"]
translations = {"Mon" : "Lun", "Tue" : "Mar", "Wed" : "Mer", "Thu" : "Gio", "Fri" : "Ven"}
i=0
print("The day",i,"is",weekdays[i])
print("Il giorno",i,"e'",translations[weekdays[i]])
print("")
i=1
print("The day",i,"is",weekdays[i])
print("Il giorno",i,"e'",translations[weekdays[i]])
print("")
i=2
print("The day",i,"is",weekdays[i])
print("Il giorno",i,"e'",translations[weekdays[i]])
print("")
# -
for i in range(5) :
print("The day",i,"is",weekdays[i])
print("Il giorno",i,"e'",translations[weekdays[i]])
print("")
|
PDA/jupyter/jupyterNotebooks/03Collections.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import xarray as xr
import s3fs
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import cartopy
# I ended up doing this just locally on my laptop instead of using the Pangeo cloud resources, so if you run this with the binder, not all of the packages will be there. They can be installed inline in the Jupyter notebook if needed with:
#
# `!conda install -c conda-forge [packagename] --yes`
# # Read
# ## Read function
#
# Use function from https://nbviewer.jupyter.org/github/oceanhackweek/ohw20-tutorials/blob/master/10-satellite-data-access/goes-cmp-netcdf-zarr.ipynb.
#
# Narrowed the scope of the function to just GOES-WEST and to take in dates.
def get_geo_data(date):
'''The satellite is geos-west'''
fs = s3fs.S3FileSystem(anon=True) #connect to s3 bucket!
date = pd.Timestamp(date)
lyr = date.year
idyjl = date.dayofyear
syr,sjdy = str(lyr).zfill(4),str(idyjl).zfill(3)
#use glob to list all the files in the directory
file_location,var = fs.glob('s3://noaa-goes17/ABI-L2-FDCF/'+syr+'/'+sjdy+'/*/*.nc'),'mask'
file_ob = [fs.open(file) for file in file_location] #open connection to files
#open all the day's data
ds = xr.open_mfdataset(file_ob,combine='nested',concat_dim='time', chunks={'y': 2712, 'x': 2712})#, parallel=True) #note file is super messed up formatting
#clean up coordinates which are a MESS in GOES
#rename one of the coordinates that doesn't match a dim & should
ds = ds.rename({'t':'time'})
ds = ds.reset_coords()
return ds
# ## Select time frame
#
# Three fires were requested. I have just done one -- the Woosley Fire -- as a proof of concept here. Unfortunately, the data wasn't available in GOES-2017 for the start of the fire, perhaps it is available with a different satellite, but I didn't investigate further. Instead, I took a date 6 days after the start of the fire -- Nov 14, 2018 -- to just get some data in.
#
# I didn't use a specific dask client but I did request the data in chunks, so the resulting data is in dask arrays.
# %%time
ds = get_geo_data('2018-11-14')
# # Process data
# ## Get lat/lon
#
# Using `pyproj` should have worked here to find the lat/lon equivalents of the x,y GOES coordinates, but didn't . I wasn't able to quickly figure out why.
# from pyproj import Proj
# p = Proj(proj='geos',h=35786023,sweep='x', lon_0=-137.000)#, y_0=-2.39110107523)
# Instead, I calculated the coordinates. This was also helpful since I could check my answer with their [test case](https://www.goes-r.gov/users/docs/PUG-GRB-vol4.pdf) (pg. 54-55).
# +
x, y = ds.x, ds.y
H = 42164160
req = 6378137 # goes_imagery_projection:semi_major_axis
rpol = 6356752.31414
gamma0 = -2.39110107523 # -137
a = np.sin(x)**2 + np.cos(x)**2*(np.cos(y)**2 + (req**2/rpol**2*np.sin(y)**2))
b = -2*H*np.cos(x)*np.cos(y)
c = H**2 - req**2
rs = (-b-np.sqrt(b**2-4*a*c))/(2*a)
sx = rs*np.cos(x)*np.cos(y)
sy = -rs*np.sin(x)
sz = rs*np.cos(x)*np.sin(y)
latitude = np.rad2deg(np.arctan2( (req**2 * sz), (rpol**2*np.sqrt((H-sx)**2 + sy**2))))
longitude = np.rad2deg(gamma0 - np.arctan2(sy, (H-sx)))
ds['longitude'] = longitude
ds['latitude'] = latitude
# -
# Assign coordinates to the xarray dataset so I can use them directly.
ds = ds.assign_coords({"longitude": ds.longitude, "latitude": ds.latitude})
# Assign the fire center and a box around that location to focus on.
woolsey = [-118.7013, 34.2350]
boxlat = [33,35] # 34.2350°N
boxlon = [-120,-118] #118.7013°W
box = ((boxlon[0] < longitude) & (longitude < boxlon[1]) & (boxlat[0] < latitude) & (latitude < boxlat[1]))#.compute()
# Drop the data outside the box of interest.
da = ds.Mask.where(box, drop=True)
# ## Do something with the mask data
#
# I didn't take the time to do any machine learning here. Instead, I just took a mean in time to be quick.
da = da.mean(dim='time')
# Compute the result once in case replotting.
# %%time
da = da.compute()
# # Plot
#
# I have used hvplot before with ROMS output a fair amount. You can see notebooks I put together for a package I wrote most of: `xroms`, in particular, the [plotting example notebook](https://github.com/kthyng/xroms/blob/master/examples/plotting.ipynb) is relevant here. However, my previous approach wasn't working the same way, either erroring out with a dask array (when I used `rasterize=True` or looking strange relative to the plot below. So, I just present here a matplotlib plot.
#
# With the proper machine learning work and identification of cells in the mask that indicate active fire, I would have plotted to show that in particular, with specific colors for each mask meaning.
# +
proj = cartopy.crs.LambertConformal(central_longitude=-137)
proj = cartopy.crs.Mercator(central_longitude=-137)
pc = cartopy.crs.PlateCarree()
fig = plt.figure(figsize=(12,8))
ax = plt.axes(projection=proj)
ax.set_extent([*boxlon, *boxlat], crs=pc)
da.plot(x='longitude', y='latitude', transform=pc,
cbar_kwargs={'label': 'Resultant active fire index'})
plt.plot(*woolsey, 'rx', transform=pc)
ax.add_feature(cartopy.feature.OCEAN.with_scale('50m'), facecolor='cornflowerblue', zorder=10)
ax.add_feature(cartopy.feature.COASTLINE.with_scale('10m'), edgecolor='0.2', zorder=10)
gl = ax.gridlines(draw_labels=True, x_inline=False, y_inline=False)#, xlocs=np.arange(-104,-80,2))
# manipulate `gridliner` object to change locations of labels
gl.top_labels = False
gl.right_labels = False
|
Untitled.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: python3
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Heroes Of Pymoli Data Analysis
# * Of the 1163 active players, the vast majority are male (84%). There also exists, a smaller, but notable proportion of female players (14%).
#
# * Our peak age demographic falls between 20-24 (44.8%) with secondary groups falling between 15-19 (18.60%) and 25-29 (13.4%).
# -----
# ### Note
# * Instructions have been included for each segment. You do not have to follow them exactly, but they are included to help you think through the steps.
# +
#Dependencies and Setup
import pandas as pd
#File to Load (Remember to Change These)
file_to_load = "Resources/purchase_data.csv"
#Read Purchasing File and store into Pandas data frame
pDataDf = pd.read_csv(file_to_load)
#Show head to see the sample of the data
pDataDf.head()
# -
# ## Player Count
# * Display the total number of players
#
# +
#Calculate Total Player
#Use len to do the count of the data
tPlayers = len(pDataDf["SN"].value_counts())
pCounts = pd.DataFrame({"Total Players":[tPlayers]})
pCounts
# -
# ## Purchasing Analysis (Total)
# * Run basic calculations to obtain number of unique items, average price, etc.
#
#
# * Create a summary data frame to hold the results
#
#
# * Optional: give the displayed data cleaner formatting
#
#
# * Display the summary data frame
#
# +
#Calculation of the data
nUniqueitems = len(pDataDf['Item Name'].value_counts())
avgPP = pDataDf['Price'].mean()
tPurchases = pDataDf['Price'].sum()
#Put data into a frame
pAnalysisDF = pd.DataFrame({'Number of Unique Items':[nUniqueitems],
'Average Price':[avgPP],
'Number of Purchases': [len(pDataDf)],
'Total Purchases':[tPurchases]})
pAnalysisDF
#Add $ sign
pAnalysisDF.style.format({'Average Price': '${:.2f}', 'Total Purchases': '${:,.2f}'})
# -
# ## Gender Demographics
# * Percentage and Count of Male Players
#
#
# * Percentage and Count of Female Players
#
#
# * Percentage and Count of Other / Non-Disclosed
#
#
#
# +
#Use drop_duplicates to drop all the same Gender and SN
#Do declare and do calculation
gender = pDataDf[['SN', 'Gender']]
gData = gender.drop_duplicates()
gCounts = gData['Gender'].value_counts()
totalC = gCounts.sum()
pMale = gCounts[0]/totalC*100
pFemale = gCounts[1]/totalC*100
pOthers = gCounts[2]/totalC*100
gDemographics = pd.DataFrame({"Total count":[gCounts[0], gCounts[1], gCounts[2]],
"Percentage of Players":[pMale, pFemale, pOthers]})
gDemographics.index = (["Male", "Female", "Others/Non-Disclosed"])
gDemographics["Percentage of Players"] = gDemographics["Percentage of Players"].map("{:.2f}%".format)
gDemographics
# -
#
# ## Purchasing Analysis (Gender)
# * Run basic calculations to obtain purchase count, avg. purchase price, avg. purchase total per person etc. by gender
#
#
#
#
# * Create a summary data frame to hold the results
#
#
# * Optional: give the displayed data cleaner formatting
#
#
# * Display the summary data frame
# +
#Purchasing Analysis (Gender)
purchaseGender = pDataDf.groupby(['Gender'])
#Do calculation on the data of purchase for gender: count, mean, sum
puCounts = purchaseGender['Price'].count()
priceMean = purchaseGender['Price'].mean()
totalPu = purchaseGender['Price'].sum()
#AveragePP = totalPu/puCounts
averageToPP = totalPu/gCounts
puAnalysisDF = pd.DataFrame({'Purchase Count': puCounts,
'Average Purchase Price': priceMean,
'Total Purchase Value': totalPu,
'Avg Total Purchase Per Person': averageToPP})
#Add $ sign
puAnalysisDF.style.format({'Average Purchase Price': '${:.2f}',
'Total Purchase Value': '${:,.2f}',
'Avg Total Purchase Per Person': '${:,.2f}'})
# -
# ## Age Demographics
# * Establish bins for ages
#
#
# * Categorize the existing players using the age bins. Hint: use pd.cut()
#
#
# * Calculate the numbers and percentages by age group
#
#
# * Create a summary data frame to hold the results
#
#
# * Optional: round the percentage column to two decimal points
#
#
# * Display Age Demographics Table
#
# +
#Set Bins for Ages
#Give a range for the number
ageBins = [0, 9.5, 14.5, 19.5, 24.5, 29.5, 34.5, 39.5, 109.5]
ageRanges = ['<10', '10-14', '15-19', '20-24', '25-29', '30-34', '35-39', '40+']
pDataDf['Age Demographics'] = pd.cut(pDataDf['Age'], ageBins, labels=ageRanges)
aDemographicsgroup = pDataDf.groupby('Age Demographics')
countDf = aDemographicsgroup.agg({'SN': 'nunique'})
totalAge = countDf.sum()
percentPlayersDF = round((countDf/totalAge)*100, 2)
#Reset the index
countDf = countDf.reset_index()
percentPlayersDF = percentPlayersDF.reset_index()
aDemoDf = countDf.merge(percentPlayersDF, on= 'Age Demographics')
aDemoDf.set_index('Age Demographics', inplace = True)
aDemoDf = aDemoDf.rename(columns={'SN_x': 'Total Count',
'SN_y': 'Percentage of Players'})
aDemoDf["Percentage of Players"] = aDemoDf["Percentage of Players"].map("{:.2f}%".format)
#Drop index name 'Age Demographics'
aDemoDf.index.name = None
aDemoDf
# -
# ## Purchasing Analysis (Age)
# * Bin the purchase_data data frame by age
#
#
# * Run basic calculations to obtain purchase count, avg. purchase price, avg. purchase total per person etc. in the table below
#
#
# * Create a summary data frame to hold the results
#
#
# * Optional: give the displayed data cleaner formatting
#
#
# * Display the summary data frame
# +
#Do the calculations of the data and group them
purchaseID = aDemographicsgroup["Purchase ID"].count()
averageP = round(aDemographicsgroup["Price"].mean(), 2)
totalPricevalue = round(aDemographicsgroup["Price"].sum(), 2)
countTotal = countDf.set_index("Age Demographics")
countTotal2 = countTotal.merge(totalPricevalue, on="Age Demographics")
totalPricepp= (countTotal2["Price"]/countTotal2["SN"])
puAA = pd.DataFrame({'Purchase Count': purchaseID,
'Average Purchase Price': averageP,
'Total Purchase Value': totalPricevalue,
'Avg Total Purchase per Person': totalPricepp})
puAA.style.format({'Average Purchase Price': '${:.2f}',
'Total Purchase Value': '${:,.2f}',
'Avg Total Purchase per Person': '${:,.2f}'})
# -
# ## Top Spenders
# * Run basic calculations to obtain the results in the table below
#
#
# * Create a summary data frame to hold the results
#
#
# * Sort the total purchase value column in descending order
#
#
# * Optional: give the displayed data cleaner formatting
#
#
# * Display a preview of the summary data frame
#
#
# +
#Find top Spender
#Group 'SN'
#Sort by top spender
topSpenderg = pDataDf.groupby(['SN'])
topSpendera = round(topSpenderg['Price'].mean(),2)
topSpender = topSpenderg['Price'].sum()
topCount = topSpenderg['SN'].count()
spender = pd.DataFrame({'Purchase Count': topCount,
'Average Purchase Price': topSpendera,
'Total Purchase Value': topSpender})
spenderSort = spender.sort_values(by = 'Total Purchase Value', ascending = False)
spenderSort['Average Purchase Price'] = spenderSort['Average Purchase Price'].map('${:.2f}'.format)
spenderSort['Total Purchase Value'] = spenderSort['Total Purchase Value'].map('${:.2f}'.format)
spenderSort.head()
# -
# ## Most Popular Items
# * Retrieve the Item ID, Item Name, and Item Price columns
#
#
# * Group by Item ID and Item Name. Perform calculations to obtain purchase count, item price, and total purchase value
#
#
# * Create a summary data frame to hold the results
#
#
# * Sort the purchase count column in descending order
#
#
# * Optional: give the displayed data cleaner formatting
#
#
# * Display a preview of the summary data frame
#
#
# +
#Get the Item Id out and then we group by item id and item name
#Then do count price, item price, total purchase value
#Sort the purchase count column in descending order
mostPopitems = pDataDf[['Item ID', 'Item Name', 'Price']]
mostPopiG = mostPopitems.groupby(['Item ID','Item Name'])
purchaseCount = mostPopiG['Item Name'].count()
totalPu = mostPopiG['Price'].sum()
itemPrice = totalPu/purchaseCount
mpiDf = pd.DataFrame({'Purchase Count': purchaseCount,
'Item Price': itemPrice,
'Total Purchase Value': totalPu})
mpiSort = mpiDf.sort_values("Purchase Count",ascending=False)
#map $ sign
mpiSort['Item Price'] = mpiSort['Item Price'].map('${:.2f}'.format)
mpiSort['Total Purchase Value'] = mpiSort['Total Purchase Value'].map('${:.2f}'.format)
mpiSort.head(10)
# -
# ## Most Profitable Items
# * Sort the above table by total purchase value in descending order
#
#
# * Optional: give the displayed data cleaner formatting
#
#
# * Display a preview of the data frame
#
#
# +
#Sort the data
mpiSort = mpi.sort_values("Total Purchase Value",ascending=False)
mpiSort['Item Price'] = mpiSort['Item Price'].map('${:.2f}'.format)
mpiSort['Total Purchase Value'] = mpiSort['Total Purchase Value'].map('${:.2f}'.format)
mpiSort.head(10)
# -
|
HeroesOfPymoli/HeroesOfPymoli_starter.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Univariate Marginal Distribution Algorithm (UMDA)
#
# El algoritmo UMDA pertenece a la clase de [algoritmos evolutivos](https://en.wikipedia.org/wiki/Evolutionary_algorithm)
# diseñados para resolver problemas de optimización. El algoritmo UMDA pertenece a la clase más general conocida como
# EDA (Estimation of Distribution Algorithm), algoritmo diseñados a partir de modelos probababilísticos.
#
# ## Algoritmo Evolutivos
#
# Los _algoritmos evolutivos_ permiten la búsqueda de óptimos en funciones objetivo basándose en la estructura natural de la
# evolución biológica en los seres vivos. Se selecciona una cierta población de posibles candidatos a resolver el problema en
# cuestión, y basándose en las reglas conocidas de evolución se van actualizando los valores hasta encontrar el mejor candidato.
#
# Las reglas se inspiran en la [evolución](https://en.wikipedia.org/wiki/Evolution) y se pretende que siguiendo estas reglas se
# logre el mejor resultado posible; a esto se le conoce como _heurística_, un conjunto de reglas que se ha visto experimentalmente
# que funciona pero no se tiene la certeza de que siempre funcione. En particular, los algoritmos evolutivos implementan
# reglas como _recombinación_, _mutación_, _selección_, entre otras cosas. Estas reglas han resultado ser el origen de las especies
# y su evolución, por lo que se espera que aplicado a problemas de optimización pueda encontrar el mejor resultado.
#
# Estas reglas permiten la descripción implícita de distribuciones de probabilidad, de las cuales son muestreados valores que puedan
# ser posibles candidatos a ser los resultados finales del problema de optimización.
#
# ## Algoritmo de Estimación de Distribución (EDA)
#
# Los EDA pertenecen a la clase de _algoritmos evolutivos_, sin embargo la diferencia más prominente entre estos algoritmos es en la selección
# de las distribuciones de probabilidad. Estos algoritmos son de tipo aleatorio, lo que significa que buscan dentro del espacio de soluciones un posible
# candidato que sea el mejor, y con cada _época_ o iteración se aplican las reglas designadas para mejorar los candidatos.
#
# A diferencia de los _algoritmos evolutivos_ donde las distribuciones de probabilidad son implícitas, creadas a partir de las combinación
# de reglas y pasos, los EDA seleccionan una distribución de probabilidad definida matemáticamente, evitando crear reglas inspiradas en procesos
# biológicos. Al hacer esto también se obtiene todo el poder del marco teórico de la probabilidad, que puede garantizar que los resultados muestreados
# sean los resultados finales, encontrando así el óptimo.
#
# El algoritmo UMDA es un algoritmo EDA donde se ha seleccionado la distribución normal para muestrear los posibles candidatos a ser solución.
#
# ## Formulación algorítmica de UMDA
#
# El algoritmo UMDA se ejecuta como sigue:
#
# 1. Inicializar la _población_ de posibles soluciones de forma aleatoria uniforme, dentro de los límites de búsqueda.
# 2. Evaluar toda la _población_ y ordenar de forma descendente los posibles candidatos.
# 3. Utilizar este nuevo orden y escoger $q$ elementos de esta población.
# 4. Calcular la media y desviación estándar de cada uno de estos $q$ mejor elementos.
# 5. Con cada una de las medias y desviaciones estándar construir distribuciones normales y muestrear tantos valores
# como sea necesario para llenar toda la población.
# 6. Repetir hasta culminar el número de iteraciones.
#
# A continuación se presenta una implementación de UMDA junto con ejemplos de funciones de prueba para validar su funcionamiento.
import numpy as np
# +
# Implementación original de <NAME>
class Poblacion:
def __init__(self, dim, limites, total_individuos):
self.dimension = dim
self.lim = limites
self.elementos = total_individuos
self.valores = None
def inicializar(self):
self.valores = np.random.uniform(
*self.lim, size=(self.elementos, self.dimension)
)
@property
def puntos(self):
return self.valores
class Optimizacion:
def __init__(self, func, dim, limites, poblacion, iteraciones=100):
self.objetivo = func
self.dimension = dim
self.lim = limites
self.elementos = poblacion
self.mejores = self.elementos // 3
self.pasos = iteraciones
self.poblacion_valores = None
self.evaluaciones = None
def actualizar(self):
temp_arreglo = np.zeros((self.elementos, self.dimension + 1))
temp_arreglo[:, :-1] = self.poblacion_valores
temp_arreglo[:, -1] = np.array(
[self.objetivo(i) for i in self.poblacion_valores]
)
# copiar el arreglo creado para evitar aliasing
self.evaluaciones = np.copy(temp_arreglo)
def optimizar(self):
poblacion = Poblacion(self.dimension, self.lim, self.elementos)
poblacion.inicializar()
self.poblacion_valores = poblacion.puntos
# crear un arreglo para los q mejores
q_mejores = np.zeros((self.mejores, self.dimension + 1))
for _ in range(self.pasos):
# siempre actualizar los valores
self.actualizar()
# ordenar los puntos dado el valor del objetivo, de mejor a peor
self.evaluaciones = self.evaluaciones[self.evaluaciones[:, -1].argsort()]
# escoger los q mejores
q_mejores = self.evaluaciones[: self.mejores, :]
# se toma el arreglo transpuesto para iterar sobre dimensión y no elementos
for i in q_mejores[:, :-1].T:
self.poblacion_valores = np.random.normal(
i.mean(), i.std(), size=self.poblacion_valores.shape
)
@property
def resultado(self):
return self.evaluaciones[0, :]
# -
# ## Esfera
#
# Aquí se pretende encontrar el mínimo de la función esfera definida como sigue:
#
# $$f(\mathbf{x}) = \sum_{i=1}^{d} x_i^2$$
#
# donde $d$ es la dimensión del espacio. Esta función tiene como mínimo global $f(\mathbf{x}^{*}) = 0$, $\mathbf{x}^{*} = (0, \cdots, 0)$
#
# En este caso se trabajará con $d = 50$, y se cambiará el origen de la función a 2 para tener el resultado $f(\mathbf{x}^{*}) = 0$, $\mathbf{x}^{*} = (2, \cdots, 2)$.
# Resolver el problema de la esfera
def esfera(x):
# Mínimo 2.0 en (0, ..., 0)
# http://benchmarkfcns.xyz/benchmarkfcns/spherefcn.html
return sum((x - 2.0) ** 2)
# instanciar al optimizador
optim_esfera = Optimizacion(esfera, 50, [-5.0, 10.0], 1000)
optim_esfera.optimizar()
print("Esfera")
print("Resultado: {}".format(optim_esfera.resultado[:-1]))
print("Valor mínimo: {}".format(optim_esfera.resultado[-1]))
# ## Rastrigin
#
# La función de Rastrigin es _multimodal_ lo que significa que contiene muchos óptimos y puede ser difícil encontrar el óptimo global. Sin embargo, es _convexa_ por lo que una vez que se encuentra el mínimo está garantizado que es el mínimo global. La función está definida de la siguiente forma:
#
# $$f(\mathbf{x}) = 10 d + \sum_{i=1}^{d} \left(x_i^2 - 10 \cos{[2\pi x_i]} \right)$$
#
# donde $d$ es la dimensión. Tiene un mínimo global en $f(\mathbf{x^*}) = 0 ,$ $\mathbf{x^*} = (0, \cdots, 0) $.
# Resolver la función Rastrigin
def rastrigin(x):
# Mínimo de 0 en (0, ..., 0)
# http://benchmarkfcns.xyz/benchmarkfcns/rastriginfcn.html
return 10.0 * len(x) + sum(x ** 2 - 10.0 * np.cos(2.0 * np.pi * x))
# En este caso se escogió una dimensión $d = 10$ y el rango de búsqueda normalmente se selecciona como $x_i \in [-5.12, 5.12]^d $.
# instanciar al optimizador
optim_rstr = Optimizacion(rastrigin, 10, [-5.12, 5.12], 1000)
optim_rstr.optimizar()
print("Rastrigin")
print("Resultado: {}".format(optim_rstr.resultado[:-1]))
print("Valor mínimo: {}".format(optim_rstr.resultado[-1]))
# ## Griewank
#
# La función de Griewank es _unimodal_ por lo que contiene solamente un óptimo, y no es _convexa_ por lo que encontrar ese óptimo puede ser un poco complicado. La definición de la función es la siguiente:
#
# $$f(\mathbf{x}) = 1 + \frac{1}{4000} \sum_{i=1}^{d} x_i^2 - \prod_{i=1}^{d} \cos{\frac{x_i}{\sqrt{i}}}$$
#
# donde $d$ es la dimensión de la función/espacio. Tiene un mínimo en $f(\mathbf{x^*}) = 0$, $\mathbf{x^*} = (0, \cdots, 0)$.
def griewank(x):
# Mínimo en 0.0 en (0, ..., 0)
# http://benchmarkfcns.xyz/benchmarkfcns/griewankfcn.html
term_1 = sum(x ** 2) / 4000.0
vals_sqrt = np.array([np.sqrt(i) for i in range(1, len(x) + 1)])
term_2 = np.prod(np.cos(x / vals_sqrt))
return 1.0 + term_1 - term_2
# En este caso se escogió una dimensión de $d=10$ y el rango de búsqueda $x_i \in [-600, 600]^d$. Adicionalmente se aumentó el número de iteraciones para mejorar la precisión del resultado.
optim_grie = Optimizacion(griewank, 10, [-600, 600], 1000, iteraciones=200)
optim_grie.optimizar()
print("Griewank")
print("Resultado: {}".format(optim_grie.resultado[:-1]))
print("Valor mínimo: {}".format(optim_grie.resultado[-1]))
# ## Referencias
#
# 1. [Guía rápida de UMDA](http://www.cleveralgorithms.com/nature-inspired/probabilistic/umda.html) En esta guía se puede ver el algoritmo, una descripción simple y una implementación en el lenguaje Ruby.
#
# 2. [Análisis de ejecución de UMDA](https://www.cs.bham.ac.uk/~pxn683/papers/preprint-gecco19-umda-los.pdf) Se emplea un análisis riguroso del desempeño del algoritmo, además se describe por completo y su funcionamiento principal.
|
metaheuristicas/UMDA.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/MrT3313/DS-Unit-1-Sprint-2-Data-Wrangling-and-Storytelling/blob/master/module1-join-and-reshape-data/LS_DS_121_Join_and_Reshape_Data.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] colab_type="text" id="pmU5YUal1eTZ"
# _Lambda School Data Science_
#
# # Join and Reshape datasets
#
# Objectives
# - concatenate data with pandas
# - merge data with pandas
# - understand tidy data formatting
# - melt and pivot data with pandas
#
# Links
# - [Pandas Cheat Sheet](https://github.com/pandas-dev/pandas/blob/master/doc/cheatsheet/Pandas_Cheat_Sheet.pdf)
# - [Tidy Data](https://en.wikipedia.org/wiki/Tidy_data)
# - Combine Data Sets: Standard Joins
# - Tidy Data
# - Reshaping Data
# - Python Data Science Handbook
# - [Chapter 3.6](https://jakevdp.github.io/PythonDataScienceHandbook/03.06-concat-and-append.html), Combining Datasets: Concat and Append
# - [Chapter 3.7](https://jakevdp.github.io/PythonDataScienceHandbook/03.07-merge-and-join.html), Combining Datasets: Merge and Join
# - [Chapter 3.8](https://jakevdp.github.io/PythonDataScienceHandbook/03.08-aggregation-and-grouping.html), Aggregation and Grouping
# - [Chapter 3.9](https://jakevdp.github.io/PythonDataScienceHandbook/03.09-pivot-tables.html), Pivot Tables
#
# Reference
# - Pandas Documentation: [Reshaping and Pivot Tables](https://pandas.pydata.org/pandas-docs/stable/reshaping.html)
# - Modern Pandas, Part 5: [Tidy Data](https://tomaugspurger.github.io/modern-5-tidy.html)
# + [markdown] colab_type="text" id="Mmi3J5fXrwZ3"
# ## Download data
#
# We’ll work with a dataset of [3 Million Instacart Orders, Open Sourced](https://tech.instacart.com/3-million-instacart-orders-open-sourced-d40d29ead6f2)!
# + colab_type="code" id="K2kcrJVybjrW" outputId="926b92a6-1101-4b06-d635-8229eaa5ea6f" colab={"base_uri": "https://localhost:8080/", "height": 204}
# !wget https://s3.amazonaws.com/instacart-datasets/instacart_online_grocery_shopping_2017_05_01.tar.gz
# + colab_type="code" id="kqX40b2kdgAb" outputId="2d840ddb-48f0-492b-8ed4-9916e57f5371" colab={"base_uri": "https://localhost:8080/", "height": 238}
# !tar --gunzip --extract --verbose --file=instacart_online_grocery_shopping_2017_05_01.tar.gz
# + colab_type="code" id="YbCvZZCBfHCI" outputId="ed314403-224e-4f7d-8f70-894df6434965" colab={"base_uri": "https://localhost:8080/", "height": 34}
# # %cd --> 'magic command' --> not just running command but changing the state of the command line
# change INTO directory that those files came down in
# %cd instacart_2017_05_01
# + id="etshR5kpvWOj" colab_type="code" outputId="3aba5797-59d0-4b9f-9250-fcd88b72e900" colab={"base_uri": "https://localhost:8080/", "height": 119}
# # ls terminal command
# '-' is a FLAG
# l --> 'longhand'
# h --> human readable
# * --> get all
## get all files ending in .csv and show the 'longhand' 'human readable' format
# !ls -lh *.csv
# + [markdown] id="RcCu3Tlgv6J2" colab_type="text"
# # Join Datasets
# + [markdown] colab_type="text" id="RsA14wiKr03j"
# ## Goal: Reproduce this example
#
# The first two orders for user id 1:
# + colab_type="code" id="vLqOTMcfjprg" outputId="fae0b4c9-400d-4897-9434-136299742f70" colab={"base_uri": "https://localhost:8080/", "height": 312}
from IPython.display import display, Image
url = 'https://cdn-images-1.medium.com/max/1600/1*vYGFQCafJtGBBX5mbl0xyw.png'
example = Image(url=url, width=600)
display(example)
# + [markdown] colab_type="text" id="nPwG8aM_txl4"
# ## Load data
#
# Here's a list of all six CSV filenames
# + colab_type="code" id="Ksah0cOrfdJQ" outputId="99aadcc3-84ba-496b-ea41-21ef66c1e7bf" colab={"base_uri": "https://localhost:8080/", "height": 119}
# !ls -lh *.csv
# + [markdown] colab_type="text" id="AHT7fKuxvPgV"
# For each CSV
# - Load it with pandas
# - Look at the dataframe's shape
# - Look at its head (first rows)
# - `display(example)`
# - Which columns does it have in common with the example we want to reproduce?
# + [markdown] colab_type="text" id="cB_5T6TprcUH"
# ### aisles
# + id="sAQ1alla_Vq9" colab_type="code" colab={}
import pandas as pd
# + colab_type="code" id="JB3bvwSDK6v3" outputId="0ed5c365-e950-4ee6-8279-9722aff914dd" colab={"base_uri": "https://localhost:8080/", "height": 221}
aisles = pd.read_csv('aisles.csv')
print(aisles.shape)
aisles.head()
# aisles.csv does not have any data that we need
# + [markdown] colab_type="text" id="9-GrkqM6rfXr"
# ### departments
# + id="yxFd5n20yOVn" colab_type="code" outputId="76aa7792-75a5-475d-82d5-8179b64fe92e" colab={"base_uri": "https://localhost:8080/", "height": 221}
departments = pd.read_csv('departments.csv')
print(departments.shape)
departments.head()
# departments.csv does not have any data that we need
# + [markdown] colab_type="text" id="VhhVcn9kK-nG"
# ### order_products__prior
# + id="86rIMNFSzKaG" colab_type="code" outputId="43ac06dd-45f2-498c-a7dc-eb3d702f2c87" colab={"base_uri": "https://localhost:8080/", "height": 221}
order_products_prior = pd.read_csv('order_products__prior.csv')
print(order_products_prior.shape)
order_products_prior.head()
# WE NEED:
# - order id
# - products id
# - add to cart order
# + [markdown] colab_type="text" id="HVYJEKJcLBut"
# ### order_products__train
# + id="xgwSUCBk6Ciy" colab_type="code" outputId="8176952f-50de-4fb2-9fb0-3a94ff27f5f4" colab={"base_uri": "https://localhost:8080/", "height": 221}
order_products_train = pd.read_csv('order_products__train.csv')
print(order_products_train.shape)
order_products_train.head()
# NOTES
# - same columns
# - appears to be a SUBSET of the 'order_products_prior'
## -- this is usually done to help test a prediction algorythm. Give it partial data from the main data set and see if it can predict the remaining data
# -------------- #
# WE NEED:
# - order id
# - products id
# - add to cart order
# + [markdown] colab_type="text" id="LYPrWUJnrp7G"
# ### orders
# + id="UfPRTW5w128P" colab_type="code" outputId="eedb572b-1180-4362-8ed3-c70529c22514" colab={"base_uri": "https://localhost:8080/", "height": 221}
orders = pd.read_csv('orders.csv')
print(orders.shape)
orders.head()
# WE NEED:
# - user id
# - order id
# - order number
# - order DOW
# - order hour of day
# + [markdown] colab_type="text" id="nIX3SYXersao"
# ### products
# + id="3BKG5dxy2IOA" colab_type="code" outputId="5a2eb891-dfe2-4af0-e107-dede4f47e5be" colab={"base_uri": "https://localhost:8080/", "height": 221}
products = pd.read_csv('products.csv')
print(products.shape)
products.head()
# WE NEED:
# - product id
# - products name
# + [markdown] colab_type="text" id="cbHumXOiJfy2"
# ## Concatenate order_products__prior and order_products__train
# + colab_type="code" id="TJ23kqpAY8Vv" outputId="3ac60a67-c872-49d3-c36c-0f8835ef1189" colab={"base_uri": "https://localhost:8080/", "height": 221}
order_products = pd.concat([order_products_prior, order_products_train])
print(order_products.shape)
order_products.head()
# + id="kE4w31LcS2vh" colab_type="code" outputId="63b183c0-00c0-4410-c16b-335c9c01dd6b" colab={"base_uri": "https://localhost:8080/", "height": 34}
# comma separated out put --> avoid having to use print() to output lines above the last line
order_products.shape, order_products_prior.shape, order_products_train.shape
# + id="h4RFxXDdTQAz" colab_type="code" colab={}
# ASSERT --> used to check a condition --> if it PASSES the code continues --> if it FAILES it throes an ASSERTION ERROR
# assert (len(order_products.columns) ==
# len(order_products_prior.columns) ==
# len(order_products_train.columns)+1)
assert (len(order_products.columns) ==
len(order_products_prior.columns) ==
len(order_products_train.columns))
# + [markdown] colab_type="text" id="Z1YRw5ypJuv2"
# ## Get a subset of orders — the first two orders for user id 1
# + [markdown] id="eJ9EixWs6K64" colab_type="text"
# From `orders` dataframe:
# - user_id
# - order_id
# - order_number
# - order_dow
# - order_hour_of_day
# + id="PTCurw5NUt-C" colab_type="code" outputId="bf9526da-aa68-4031-8b0c-d785630dab3f" colab={"base_uri": "https://localhost:8080/", "height": 204}
# EXAMPLE of using conditions & dataframe filtering
condition = order_products['order_id'] == 2539329
order_products[condition]
# + id="EDc50v7MVE13" colab_type="code" outputId="a022d2e1-0f59-4175-ea63-aed9251381c3" colab={"base_uri": "https://localhost:8080/", "height": 111}
condition = (orders['user_id'] == 1) & (orders['order_number'] <= 2)
# we use '&' instead of 'and' --> & used for bitwise operations (AKA not comparing single items but a LIST of items)
columns = ['order_id', 'user_id', 'order_number', 'order_dow', 'order_hour_of_day']
subset = orders.loc[condition, columns]
subset.head()
# + [markdown] colab_type="text" id="3K1p0QHuKPnt"
# ## Merge dataframes
# + [markdown] id="4MVZ9vb1BuO0" colab_type="text"
# Merge the subset from `orders` with columns from `order_products`
# + id="3lajwEE86iKc" colab_type="code" outputId="9ffa1db5-286b-40cc-edc0-5035fa20d414" colab={"base_uri": "https://localhost:8080/", "height": 407}
# order id
# product id
# add to cart order
columns = ['order_id', 'product_id', 'add_to_cart_order']
merged = pd.merge(subset, order_products[columns], how='inner', on='order_id')
print(merged.shape)
merged
# + [markdown] id="i1uLO1bxByfz" colab_type="text"
# Merge with columns from `products`
# + id="D3Hfo2dkJlmh" colab_type="code" outputId="3896af7b-e5ce-472a-b4dd-d824f82fbdeb" colab={"base_uri": "https://localhost:8080/", "height": 407}
# V1 - final = pd.merge(merged, products[['products_id', 'product_name']])
# V2
columns = ['product_id', 'product_name']
final = pd.merge(merged, products[columns], how='inner', on='product_id')
print(final.shape)
final
# + id="lmnC3-eFYfrx" colab_type="code" outputId="d7bc3a27-a28a-4021-dc53-5c2683a6d8dd" colab={"base_uri": "https://localhost:8080/", "height": 390}
final = final.sort_values(by=['order_number', 'add_to_cart_order'])
final
# + [markdown] id="dDfzKXJdwApV" colab_type="text"
# # Reshape Datasets
# + [markdown] id="4stCppWhwIx0" colab_type="text"
# ## Why reshape data?
#
# #### Some libraries prefer data in different formats
#
# For example, the Seaborn data visualization library prefers data in "Tidy" format often (but not always).
#
# > "[Seaborn will be most powerful when your datasets have a particular organization.](https://seaborn.pydata.org/introduction.html#organizing-datasets) This format ia alternately called “long-form” or “tidy” data and is described in detail by <NAME>. The rules can be simply stated:
#
# > - Each variable is a column
# - Each observation is a row
#
# > A helpful mindset for determining whether your data are tidy is to think backwards from the plot you want to draw. From this perspective, a “variable” is something that will be assigned a role in the plot."
#
# #### Data science is often about putting square pegs in round holes
#
# Here's an inspiring [video clip from _Apollo 13_](https://www.youtube.com/watch?v=ry55--J4_VQ): “Invent a way to put a square peg in a round hole.” It's a good metaphor for data wrangling!
# + [markdown] id="79KITszBwXp7" colab_type="text"
# ## <NAME>'s Examples
#
# From his paper, [Tidy Data](http://vita.had.co.nz/papers/tidy-data.html)
# + id="Jna5sk5FwYHr" colab_type="code" colab={}
# %matplotlib inline
import pandas as pd
import numpy as np
import seaborn as sns
table1 = pd.DataFrame(
[[np.nan, 2],
[16, 11],
[3, 1]],
index=['<NAME>', '<NAME>', '<NAME>'],
columns=['treatmenta', 'treatmentb'])
# TRANSPOSE table 1
table2 = table1.T
# + [markdown] id="eWe5rpI9wdvT" colab_type="text"
# "Table 1 provides some data about an imaginary experiment in a format commonly seen in the wild.
#
# The table has two columns and three rows, and both rows and columns are labelled."
# + id="SdUp5LbcwgNK" colab_type="code" outputId="111e07d4-8418-4ce5-cd09-029b54829955" colab={"base_uri": "https://localhost:8080/", "height": 142}
table1
# + [markdown] id="SaEcDmZhwmon" colab_type="text"
# "There are many ways to structure the same underlying data.
#
# Table 2 shows the same data as Table 1, but the rows and columns have been transposed. The data is the same, but the layout is different."
# + id="SwDVoCj5woAn" colab_type="code" outputId="5ebc0e8b-5567-44da-e9c8-aa292a663336" colab={"base_uri": "https://localhost:8080/", "height": 111}
table2
# + [markdown] id="k3ratDNbwsyN" colab_type="text"
# "Table 3 reorganises Table 1 to make the values, variables and obserations more clear.
#
# Table 3 is the tidy version of Table 1. Each row represents an observation, the result of one treatment on one person, and each column is a variable."
#
# | name | trt | result |
# |--------------|-----|--------|
# | <NAME> | a | - |
# | <NAME> | a | 16 |
# | <NAME> | a | 3 |
# | <NAME> | b | 2 |
# | <NAME> | b | 11 |
# | <NAME> | b | 1 |
# + [markdown] id="WsvD1I3TwwnI" colab_type="text"
# ## Table 1 --> Tidy
#
# We can use the pandas `melt` function to reshape Table 1 into Tidy format.
# + id="S48tKmC46veF" colab_type="code" outputId="b3e4924f-3f6e-49b3-a443-fa6628b754e3" colab={"base_uri": "https://localhost:8080/", "height": 142}
table1
# + id="MKfGwi6rc6KI" colab_type="code" outputId="5cf4f4e1-55c9-49f7-a2c3-9cf7622e8183" colab={"base_uri": "https://localhost:8080/", "height": 142}
# RESET INDEX
table1 = table1.reset_index()
table1
# + id="Tt09RwC4dCpo" colab_type="code" outputId="4d04a603-4595-46d8-f9e8-2bbcdca4dc17" colab={"base_uri": "https://localhost:8080/", "height": 235}
tidy = table1.melt(id_vars='index')
tidy.columns = ['name', 'trt', 'result']
tidy
# + [markdown] id="Ck15sXaJxPrd" colab_type="text"
# ## Table 2 --> Tidy
# + id="k2Qn94RIxQhV" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 111} outputId="1935b210-25ab-48cc-ab3b-38d01f53b409"
##### LEAVE BLANK --an assignment exercise #####
table2
# + id="v0r6TTM4NfEW" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 111} outputId="36b041d5-4fd8-4281-91ca-710d820a36b3"
# Reset Index
table2 = table2.reset_index()
table2
# + id="gA1WDE78Nk3-" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 235} outputId="3381d8ea-1555-4a8d-97af-47dfb1fe1940"
tidy2 = table2.melt(id_vars='index')
tidy2.columns = ['name', 'trt', 'result']
tidy2
# + [markdown] id="As0W7PWLxea3" colab_type="text"
# ## Tidy --> Table 1
#
# The `pivot_table` function is the inverse of `melt`.
# + id="CdZZiLYoxfJC" colab_type="code" outputId="82c9e7db-5e9e-46cf-a4fd-47e5f98bb077" colab={"base_uri": "https://localhost:8080/", "height": 173}
tidy.pivot_table(index='name', columns='trt', values='result')
# + [markdown] id="3GeAKoSZxoPS" colab_type="text"
# ## Tidy --> Table 2
# + id="W2jjciN2xk9r" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 142} outputId="6a8517ed-3acc-4c41-e996-20fc2e7d4f45"
##### LEAVE BLANK --an assignment exercise #####
tidy2.pivot_table(index='name', columns='trt', values='result')
# + [markdown] id="jr0jQy6Oxqi7" colab_type="text"
# # Seaborn example
#
# The rules can be simply stated:
#
# - Each variable is a column
# - Each observation is a row
#
# A helpful mindset for determining whether your data are tidy is to think backwards from the plot you want to draw. From this perspective, a “variable” is something that will be assigned a role in the plot."
# + id="kWo3FIP9xuKo" colab_type="code" outputId="a3f6e45b-7645-41d4-ad8d-707619d8c408" colab={"base_uri": "https://localhost:8080/", "height": 153}
sns.catplot(x='trt', y='result', col='name',
kind='bar', data=tidy, height=2);
# + [markdown] id="cIgT41Rxx4oj" colab_type="text"
# ## Now with Instacart data
# + id="Oydw0VvGxyDJ" colab_type="code" colab={}
products = pd.read_csv('products.csv')
order_products = pd.concat([pd.read_csv('order_products__prior.csv'),
pd.read_csv('order_products__train.csv')])
orders = pd.read_csv('orders.csv')
# + [markdown] id="6p-IsG0jyXQj" colab_type="text"
# ## Goal: Reproduce part of this example
#
# Instead of a plot with 50 products, we'll just do two — the first products from each list
# - Half And Half Ultra Pasteurized
# - Half Baked Frozen Yogurt
# + id="Rs-_n9yjyZ15" colab_type="code" outputId="7b54e745-02fc-4953-9729-c0d7643c46c3" colab={"base_uri": "https://localhost:8080/", "height": 383}
from IPython.display import display, Image
url = 'https://cdn-images-1.medium.com/max/1600/1*wKfV6OV-_1Ipwrl7AjjSuw.png'
example = Image(url=url, width=600)
display(example)
# + [markdown] id="Vj5GR7I4ydBg" colab_type="text"
# So, given a `product_name` we need to calculate its `order_hour_of_day` pattern.
# + [markdown] id="Vc9_s7-LyhBI" colab_type="text"
# ## Subset and Merge
#
# One challenge of performing a merge on this data is that the `products` and `orders` datasets do not have any common columns that we can merge on. Due to this we will have to use the `order_products` dataset to provide the columns that we will use to perform the merge.
# + id="W1yHMS-OyUTH" colab_type="code" colab={}
product_names = ['Half Baked Frozen Yogurt', 'Half And Half Ultra Pasteurized']
# + id="7l3QiqqkeuaC" colab_type="code" outputId="3298fd9b-dfb8-482f-d831-df51f73c5498" colab={"base_uri": "https://localhost:8080/", "height": 136}
orders.columns.tolist()
# + id="yJa7oCk_exue" colab_type="code" outputId="5c00a8c5-f5b4-4753-f344-92b5b2edee54" colab={"base_uri": "https://localhost:8080/", "height": 34}
# No matching column names to merge in product names and orders
# need to use the order_products table as a bridge
order_products.columns.tolist()
# + id="O4lvfD8ffJl2" colab_type="code" colab={}
merged = (products[['product_id', 'product_name']]
.merge(order_products[['order_id', 'product_id']])
.merge(orders[['order_id', 'order_hour_of_day']]))
# + id="eeEdHvDCfuVC" colab_type="code" outputId="282068b3-e7cc-4ddd-de81-fa88f6efb62a" colab={"base_uri": "https://localhost:8080/", "height": 204}
merged.head()
# + id="vyffT09Ef54J" colab_type="code" outputId="f6d4ddc2-b4a0-481e-90f5-97ee1f287f0f" colab={"base_uri": "https://localhost:8080/", "height": 34}
products.shape, order_products.shape, orders.shape, merged.shape
# + id="ZfPC3Sy7gUy3" colab_type="code" outputId="9fc95dd4-1f72-4154-ebe0-2f7ec60de206" colab={"base_uri": "https://localhost:8080/", "height": 1000}
# What condition will filter 'merged' into just the 2 products
condition = ((merged['product_name'] == 'Half Baked Frozen Yogurt') |
(merged['product_name'] == 'Half And Half Ultra Pasteurized'))
product_names = ['Half Baked Frozen Yogurt', 'Half And Half Ultra Pasteurized']
condition = merged['product_name'].isin(product_names)
subset = merged[condition]
print(subset.shape)
subset
# + [markdown] id="UvhcadjFzx0Q" colab_type="text"
# ## 4 ways to reshape and plot
# + [markdown] id="aEE_nCWjzz7f" colab_type="text"
# ### 1. value_counts
# + id="vTL3Cko87VL-" colab_type="code" colab={}
froyo = subset[subset['product_name'] == 'Half Baked Frozen Yogurt']
cream = subset[subset['product_name'] == 'Half And Half Ultra Pasteurized']
# + id="chmJEPWbhyGJ" colab_type="code" outputId="17cdbf71-2b8b-4894-81fd-19aa7f9bfec4" colab={"base_uri": "https://localhost:8080/", "height": 286}
(cream['order_hour_of_day']
.value_counts(normalize=True)
.sort_index()
.plot())
(froyo['order_hour_of_day']
.value_counts(normalize=True)
.sort_index()
.plot())
# + [markdown] id="tMSd6YDj0BjE" colab_type="text"
# ### 2. crosstab
# + id="Slu2bWYK0CZD" colab_type="code" outputId="60e57ab3-57b0-4b03-da62-5e4b422c9f6f" colab={"base_uri": "https://localhost:8080/", "height": 301}
(pd.crosstab(subset['order_hour_of_day'],
subset['product_name'],
normalize='columns') * 100).plot()
# + [markdown] id="ICjPVqO70Hv8" colab_type="text"
# ### 3. Pivot Table
# + id="LQtMNVa10I_S" colab_type="code" outputId="753fa6b7-7910-48a1-c94c-852362ebb66a" colab={"base_uri": "https://localhost:8080/", "height": 301}
subset.pivot_table(index='order_hour_of_day',
columns='product_name',
values='order_id',
aggfunc=len).plot()
# + [markdown] id="7A9jfBVv0M7e" colab_type="text"
# ### 4. melt
# + id="2AmbAKm20PAg" colab_type="code" outputId="131eb053-5497-46ef-da65-937bed84dc3a" colab={"base_uri": "https://localhost:8080/", "height": 386}
table = pd.crosstab(subset['order_hour_of_day'],
subset['product_name'],
normalize=True)
melted = (table
.reset_index()
.melt(id_vars = 'order_hour_of_day')
.rename(columns={
'order_hour_of_day': 'Hour Of Day Ordered',
'product_name': 'Product',
'value': 'Percent of Orders by Product'
}))
sns.relplot(x = 'Hour Of Day Ordered',
y = 'Percent of Orders by Product',
hue='Product',
data=melted,
kind='line')
# + [markdown] colab_type="text" id="kAMtvSQWPUcj"
# # Assignment
#
# ## Join Data Section
#
# These are the top 10 most frequently ordered products. How many times was each ordered?
#
# 1. Banana
# 2. Bag of Organic Bananas
# 3. Organic Strawberries
# 4. Organic Baby Spinach
# 5. Organic Hass Avocado
# 6. Organic Avocado
# 7. Large Lemon
# 8. Strawberries
# 9. Limes
# 10. Organic Whole Milk
#
# First, write down which columns you need and which dataframes have them.
#
# Next, merge these into a single dataframe.
#
# Then, use pandas functions from the previous lesson to get the counts of the top 10 most frequently ordered products.
#
# ## Reshape Data Section
#
# - Replicate the lesson code
# - Complete the code cells we skipped near the beginning of the notebook
# - Table 2 --> Tidy
# - Tidy --> Table 2
# - Load seaborn's `flights` dataset by running the cell below. Then create a pivot table showing the number of passengers by month and year. Use year for the index and month for the columns. You've done it right if you get 112 passengers for January 1949 and 432 passengers for December 1960.
# + [markdown] id="vKOG9wu41ZPt" colab_type="text"
# ## Assignment Answers
# + id="8NNUyRx41dJE" colab_type="code" colab={}
# What do I need from the data sets
# Nothing:
## aisles.csv --> nothing
## departments.csv --> nothing
## order_products__train.csv --> nothing - TRAINING DATA
# Something:
## ? ## do i REALLY need this ? --> order_products__prior.csv --> order_id / product_id
## orders --> user_id (extra user analysis) / order_id
## products --> product_id / product_name
# + id="7FtiSGdTFqs5" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 204} outputId="aaba4f60-34f9-44b8-fb1d-8e204360a058"
# Preview products
products.head()
# + id="2aTpXJNe5H3Z" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 359} outputId="bdd853da-e11e-4de5-b90f-4702ba5a9a50"
# 1 # Get Subset from products dataframe:
# Product list
subset_product_names = ['Banana',
'Bag of Organic Bananas',
'Organic Strawberries',
'Organic Baby Spinach',
'Organic Hass Avocado',
'Organic Avocado',
'Large Lemon',
'Strawberries',
'Limes',
'Organic Whole Milk']
# Columns needed in products.csv
columns = ['product_id', 'product_name']
# Create subset
subset = products.loc[products['product_name'].isin(subset_product_names), columns]
subset
# + id="NpHqgh3iGDxW" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 204} outputId="dc7de6e3-81d7-403d-d1de-38e0fde79ee8"
# Preview order_products
order_products_prior.head()
# + id="tMcjsxn1Gl5o" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 221} outputId="d3c0b5d3-6306-4bbe-d473-7fdc82b377dd"
# 2 # Merge subset from 'products' with column from 'order_products_prior' on 'product_id'
columns_from_orderProductsPrior = ['order_id', 'product_id', 'add_to_cart_order']
merged = pd.merge(subset, order_products_prior[columns_from_orderProductsPrior], how='inner', on='product_id')
print(merged.shape)
merged.head()
# + id="5JRsv9r7Lce2" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 204} outputId="51505a07-60de-4513-e964-3dab7147c403"
# 3 # Value Counts
merged['product_name'].value_counts()
# + [markdown] id="80MLzUCMLp2k" colab_type="text"
# ## Extra Merge Practice
#
# adding the user_id in case you wanted to do extra analysis
# + id="O2djOIunE3fi" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 204} outputId="49c87cd7-361a-408c-e66e-c014fcc3297e"
# Preview Orders
orders.head()
# + id="8U2157crBu1I" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 221} outputId="abb09d4a-a237-41c2-bd06-796582635de5"
# 4 # Merge orders w/ merged on 'order_id'
columns_from_orders = ['order_id','user_id']
merged = pd.merge(merged, orders[columns_from_orders], how='inner', on='order_id')
print(merged.shape)
merged.head()
# + id="6aiYKWP5KxDa" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 204} outputId="00297725-69fa-4a42-8557-34feddb9e64f"
# 5 # Value Counts
merged['product_name'].value_counts()
# + [markdown] id="mnOuqL9K0dqh" colab_type="text"
# ## Join Data Stretch Challenge
#
# The [Instacart blog post](https://tech.instacart.com/3-million-instacart-orders-open-sourced-d40d29ead6f2) has a visualization of "**Popular products** purchased earliest in the day (green) and latest in the day (red)."
#
# The post says,
#
# > "We can also see the time of day that users purchase specific products.
#
# > Healthier snacks and staples tend to be purchased earlier in the day, whereas ice cream (especially Half Baked and The Tonight Dough) are far more popular when customers are ordering in the evening.
#
# > **In fact, of the top 25 latest ordered products, the first 24 are ice cream! The last one, of course, is a frozen pizza.**"
#
# Your challenge is to reproduce the list of the top 25 latest ordered popular products.
#
# We'll define "popular products" as products with more than 2,900 orders.
#
# ## Reshape Data Stretch Challenge
#
# _Try whatever sounds most interesting to you!_
#
# - Replicate more of Instacart's visualization showing "Hour of Day Ordered" vs "Percent of Orders by Product"
# - Replicate parts of the other visualization from [Instacart's blog post](https://tech.instacart.com/3-million-instacart-orders-open-sourced-d40d29ead6f2), showing "Number of Purchases" vs "Percent Reorder Purchases"
# - Get the most recent order for each user in Instacart's dataset. This is a useful baseline when [predicting a user's next order](https://www.kaggle.com/c/instacart-market-basket-analysis)
# - Replicate parts of the blog post linked at the top of this notebook: [Modern Pandas, Part 5: Tidy Data](https://tomaugspurger.github.io/modern-5-tidy.html)
|
module1-join-and-reshape-data/LS_DS_121_Join_and_Reshape_Data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Processing a HCP Dataset
#
# Here we have run an HCP dataset through DSI Studio using the recommended parameters from the documentation. This includes
#
# * Gradient unwarping
# * Motion/Eddy correction
# * TopUp
#
# The images (dwi mask, dwi data and graddev files) were downloaded directly from connectomedb.org. The resulting fib file is in 101915/data/input.
#
# ### Loading DSI Studio files
#
# Here a ``MITTENS`` object is created using default parameters.
from mittens import MITTENS
mitn = MITTENS(fibgz_file="101915/data/input/101915.src.gz.odf8.f5rec.fy.gqi.1.25.fib.gz")
# ### Calculating transition probabilities
#
# We see in the output above that the default parameters of $\theta_{max}=35$ degrees and $s=\sqrt{3}/2$ voxels will be used for calculating transition probabilities. Now we actually calculate the probabilities and save them in NIfTI format.
import os
#os.makedirs("101915/data/mittens_output")
mitn.calculate_transition_probabilities(output_prefix="HCP")
# This writes out NIfTI images for the transition probabilities to each neighbor using both the singleODF and doubleODF methods. Additionally, you will find volumes written out for CoDI and CoAsy. Writing to NIfTI is useful to quickly assess the quality of the output. the CoDI volumes should look a lot like GFA or FA images.
#
# One can load theses images directly to create a ``MITTENS`` object. This bypasses the need to re-calculate transition probabilities and is the recommended way to access transition probabilities before building and saving Voxel Graphs.
#
# ### Loading from NIfTI outputs
#
# Here we demonstrate loading transition probabilites from NIfTI files. We verify that their contents are identical to those generated by calculating transition probabilities from a ``fib.gz`` file.
#
#
# +
nifti_mitn = MITTENS(nifti_prefix="HCP")
import numpy as np
print("singleODF outputs are identical:",
np.allclose(mitn.singleODF_results,nifti_mitn.singleODF_results))
print("doubleODF outputs are identical:",
np.allclose(mitn.doubleODF_results,nifti_mitn.doubleODF_results,equal_nan=True))
# -
# You'll notice loading from NIfTI is much faster!
#
# ## Building and saving a voxel graph
#
# Transition probabilities need to be converted to edge weights somehow. The ``MITTENS`` object accomplishes this through the ``build_graph`` function, which offers a number of options. Here is the relevant portion of the ``build_graph`` documentation
#
# Schemes for shortest paths:
# ---------------------------
#
# ``"negative_log_p"``:
# Transition probabilities are log transformed and made negative. This is similar to the Zalesky 2009 strategy.
#
# ``"minus_iso_negative_log"``:
# Isotropic probabilities are subtracted from transition probabilities. Edges are not added when transition probabilities are less than the isotropic probability.
#
# ``"minus_iso_scaled_negative_log"``:
# Same as ``"minus_iso_negative_log"`` except probabilities are re-scaled to sum to 1 *before* the log transform is applied.
#
#
# You also have to pick whether to use singleODF or doubleODF probabilities. You can easily create graphs using either.
doubleODF_nlp = mitn.build_graph(doubleODF=True, weighting_scheme="negative_log_p")
doubleODF_nlp.save("fcup_doubleODF_nlp.mat")
# ### Notes
#
# #### Masking
# If no spatial mask is specified when the ``MITTENS`` object is constructed, the generous brain mask estimated by DSI Studio will be used. This means the file sizes will be somewhat larger and the calculations will take longer. However, we recommend using the larger mask, as you can easily apply masks to the voxel graphs. It's better to have a voxel and not need it than to re-run transition probability calculation.
#
# #### Affines
# ``MITTENS`` mimics DSI Studio. Internally everything is done in LPS+ orientation and results are written out in RAS+ orientation. The affine used in the transition probability NIfTI images is the same as the images written by DSI Studio. This is a bizarre area of scanner coordinates and more closely matches the coordinates used by streamlines.
#
# ### Verifying that the Voxel Graph is preserved
#
# Here we load a Voxel Graph directly from a matfile and check that it exactly matches the graph produced above.
# +
from mittens import VoxelGraph
mat_vox_graph = VoxelGraph("101915/data/mittens_output/HCP_doubleODF_nlp.mat")
from networkit.algebraic import adjacencyMatrix
matfile_adj = adjacencyMatrix(mat_vox_graph.graph,matrixType="sparse")
mitn_adj = adjacencyMatrix(doubleODF_nlp.graph,matrixType="sparse")
mat_indices = np.nonzero(matfile_adj)
indices = np.nonzero(mitn_adj)
print("row indices match:", np.all(mat_indices[0] == indices[0]))
print("column indices match:",np.all(mat_indices[1] == indices[1]))
print("Weights all match:", np.allclose(matfile_adj[indices],mitn_adj[indices]))
# -
# ### Conclusions
#
# Here we've shown that transition probabilities and edge weights are preserved over the three ways they can be represented in ``MITTENS``. Next we show useful operations that can be performed using a VoxelGraph.
|
notebooks/GraphBuilding.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] colab_type="text" id="FhGuhbZ6M5tl"
# ##### Copyright 2018 The TensorFlow Authors.
# + cellView="form" colab_type="code" id="AwOEIRJC6Une" colab={}
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + cellView="form" colab_type="code" id="KyPEtTqk6VdG" colab={}
#@title MIT License
#
# Copyright (c) 2017 <NAME>
#
# Permission is hereby granted, free of charge, to any person obtaining a
# # copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
# + [markdown] colab_type="text" id="EIdT9iu_Z4Rb"
# # Basic regression: Predict fuel efficiency
# + [markdown] colab_type="text" id="bBIlTPscrIT9"
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://www.tensorflow.org/tutorials/keras/regression"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/keras/regression.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/tutorials/keras/regression.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# <td>
# <a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/tutorials/keras/regression.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
# </td>
# </table>
# + [markdown] colab_type="text" id="AHp3M9ZmrIxj"
# In a *regression* problem, we aim to predict the output of a continuous value, like a price or a probability. Contrast this with a *classification* problem, where we aim to select a class from a list of classes (for example, where a picture contains an apple or an orange, recognizing which fruit is in the picture).
#
# This notebook uses the classic [Auto MPG](https://archive.ics.uci.edu/ml/datasets/auto+mpg) Dataset and builds a model to predict the fuel efficiency of late-1970s and early 1980s automobiles. To do this, we'll provide the model with a description of many automobiles from that time period. This description includes attributes like: cylinders, displacement, horsepower, and weight.
#
# This example uses the `tf.keras` API, see [this guide](https://www.tensorflow.org/guide/keras) for details.
# + colab_type="code" id="moB4tpEHxKB3" colab={}
# Use seaborn for pairplot
# !pip install seaborn
# Use some functions from tensorflow_docs
# !pip install git+https://github.com/tensorflow/docs
# + colab_type="code" id="1rRo8oNqZ-Rj" colab={}
from __future__ import absolute_import, division, print_function, unicode_literals
import pathlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
# + colab_type="code" id="9xQKvCJ85kCQ" colab={}
try:
# # %tensorflow_version only exists in Colab.
# %tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
print(tf.__version__)
# + colab_type="code" id="Qz4HfsgRQUiV" colab={}
import tensorflow_docs as tfdocs
import tensorflow_docs.plots
import tensorflow_docs.modeling
# + [markdown] colab_type="text" id="F_72b0LCNbjx"
# ## The Auto MPG dataset
#
# The dataset is available from the [UCI Machine Learning Repository](https://archive.ics.uci.edu/ml/).
#
#
# + [markdown] colab_type="text" id="gFh9ne3FZ-On"
# ### Get the data
# First download the dataset.
# + colab_type="code" id="p9kxxgzvzlyz" colab={}
dataset_path = keras.utils.get_file("auto-mpg.data", "http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data")
dataset_path
# + [markdown] colab_type="text" id="nslsRLh7Zss4"
# Import it using pandas
# + colab_type="code" id="CiX2FI4gZtTt" colab={}
column_names = ['MPG','Cylinders','Displacement','Horsepower','Weight',
'Acceleration', 'Model Year', 'Origin']
raw_dataset = pd.read_csv(dataset_path, names=column_names,
na_values = "?", comment='\t',
sep=" ", skipinitialspace=True)
dataset = raw_dataset.copy()
print(dataset.shape)
print(dataset.head())
print(dataset.tail())
dataset.tail()
# + [markdown] colab_type="text" id="3MWuJTKEDM-f"
# ### Clean the data
#
# The dataset contains a few unknown values.
# + colab_type="code" id="JEJHhN65a2VV" colab={}
dataset.isna().sum()
# + [markdown] colab_type="text" id="9UPN0KBHa_WI"
# To keep this initial tutorial simple drop those rows.
# + colab_type="code" id="4ZUDosChC1UN" colab={}
dataset = dataset.dropna()
dataset.isna().sum()
dataset.tail()
# + [markdown] colab_type="text" id="8XKitwaH4v8h"
# The `"Origin"` column is really categorical, not numeric. So convert that to a one-hot:
# + colab_type="code" id="gWNTD2QjBWFJ" colab={}
dataset['Origin'] = dataset['Origin'].map({1: 'USA', 2: 'Europe', 3: 'Japan'})
# + colab_type="code" id="ulXz4J7PAUzk" colab={}
dataset = pd.get_dummies(dataset, prefix='', prefix_sep='')
dataset.tail()
# + [markdown] colab_type="text" id="Cuym4yvk76vU"
# ### Split the data into train and test
#
# Now split the dataset into a training set and a test set.
#
# We will use the test set in the final evaluation of our model.
# + colab_type="code" id="qn-IGhUE7_1H" colab={}
train_dataset = dataset.sample(frac=0.8,random_state=0)
test_dataset = dataset.drop(train_dataset.index)
print(train_dataset.shape)
train_dataset
# + id="00ASbRmi5_8R" colab_type="code" colab={}
print(test_dataset.shape)
test_dataset
# + [markdown] colab_type="text" id="J4ubs136WLNp"
# ### Inspect the data
#
# Have a quick look at the joint distribution of a few pairs of columns from the training set.
# + colab_type="code" id="oRKO_x8gWKv-" colab={}
sns.pairplot(train_dataset[["MPG", "Cylinders", "Displacement", "Weight"]], diag_kind="kde")
# + [markdown] colab_type="text" id="gavKO_6DWRMP"
# Also look at the overall statistics:
# + colab_type="code" id="yi2FzC3T21jR" colab={}
train_stats = train_dataset.describe()
train_stats.pop("MPG")
train_stats = train_stats.transpose()
train_stats
# + [markdown] colab_type="text" id="Db7Auq1yXUvh"
# ### Split features from labels
#
# Separate the target value, or "label", from the features. This label is the value that you will train the model to predict.
# + colab_type="code" id="t2sluJdCW7jN" colab={}
train_labels = train_dataset.pop('MPG')
test_labels = test_dataset.pop('MPG')
train_labels
# + id="GHkyg0U998l0" colab_type="code" colab={}
test_labels
# + [markdown] colab_type="text" id="mRklxK5s388r"
# ### Normalize the data
#
# Look again at the `train_stats` block above and note how different the ranges of each feature are.
# + [markdown] colab_type="text" id="-ywmerQ6dSox"
# It is good practice to normalize features that use different scales and ranges. Although the model *might* converge without feature normalization, it makes training more difficult, and it makes the resulting model dependent on the choice of units used in the input.
#
# Note: Although we intentionally generate these statistics from only the training dataset, these statistics will also be used to normalize the test dataset. We need to do that to project the test dataset into the same distribution that the model has been trained on.
# + colab_type="code" id="JlC5ooJrgjQF" colab={}
def norm(x):
return (x - train_stats['mean']) / train_stats['std']
normed_train_data = norm(train_dataset)
normed_test_data = norm(test_dataset)
normed_train_data
# + [markdown] colab_type="text" id="BuiClDk45eS4"
# This normalized data is what we will use to train the model.
#
# Caution: The statistics used to normalize the inputs here (mean and standard deviation) need to be applied to any other data that is fed to the model, along with the one-hot encoding that we did earlier. That includes the test set as well as live data when the model is used in production.
# + [markdown] colab_type="text" id="SmjdzxKzEu1-"
# ## The model
# + [markdown] colab_type="text" id="6SWtkIjhrZwa"
# ### Build the model
#
# Let's build our model. Here, we'll use a `Sequential` model with two densely connected hidden layers, and an output layer that returns a single, continuous value. The model building steps are wrapped in a function, `build_model`, since we'll create a second model, later on.
# + colab_type="code" id="c26juK7ZG8j-" colab={}
def build_model():
model = keras.Sequential([
layers.Dense(64, activation='relu', input_shape=[len(train_dataset.keys())]),
layers.Dense(64, activation='relu'),
layers.Dense(1)
])
optimizer = tf.keras.optimizers.RMSprop(0.001)
model.compile(loss='mse',
optimizer=optimizer,
metrics=['mae', 'mse'])
return model
# + colab_type="code" id="cGbPb-PHGbhs" colab={}
model = build_model()
# + [markdown] colab_type="text" id="Sj49Og4YGULr"
# ### Inspect the model
#
# Use the `.summary` method to print a simple description of the model
# + colab_type="code" id="ReAD0n6MsFK-" colab={}
model.summary()
# + [markdown] colab_type="text" id="Vt6W50qGsJAL"
#
# Now try out the model. Take a batch of `10` examples from the training data and call `model.predict` on it.
# + colab_type="code" id="-d-gBaVtGTSC" colab={}
example_batch = normed_train_data[:10]
example_result = model.predict(example_batch)
example_result
# + [markdown] colab_type="text" id="QlM8KrSOsaYo"
# It seems to be working, and it produces a result of the expected shape and type.
# + [markdown] colab_type="text" id="0-qWCsh6DlyH"
# ### Train the model
#
# Train the model for 1000 epochs, and record the training and validation accuracy in the `history` object.
# + colab_type="code" id="sD7qHCmNIOY0" colab={}
EPOCHS = 1000
history = model.fit(
normed_train_data, train_labels,
epochs=EPOCHS, validation_split = 0.2, verbose=0,
callbacks=[tfdocs.modeling.EpochDots()])
# + [markdown] colab_type="text" id="tQm3pc0FYPQB"
# Visualize the model's training progress using the stats stored in the `history` object.
# + colab_type="code" id="4Xj91b-dymEy" colab={}
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()
# + colab_type="code" id="czYtZS9A6D-X" colab={}
plotter = tfdocs.plots.HistoryPlotter(smoothing_std=2)
# + colab_type="code" id="nMCWKskbUTvG" colab={}
plotter.plot({'Basic': history}, metric = "mae")
plt.ylim([0, 10])
plt.ylabel('MAE [MPG]')
# + colab_type="code" id="N9u74b1tXMd9" colab={}
plotter.plot({'Basic': history}, metric = "mse")
plt.ylim([0, 20])
plt.ylabel('MSE [MPG^2]')
# + [markdown] colab_type="text" id="AqsuANc11FYv"
# This graph shows little improvement, or even degradation in the validation error after about 100 epochs. Let's update the `model.fit` call to automatically stop training when the validation score doesn't improve. We'll use an *EarlyStopping callback* that tests a training condition for every epoch. If a set amount of epochs elapses without showing improvement, then automatically stop the training.
#
# You can learn more about this callback [here](https://www.tensorflow.org/api_docs/python/tf/keras/callbacks/EarlyStopping).
# + colab_type="code" id="fdMZuhUgzMZ4" colab={}
model = build_model()
# The patience parameter is the amount of epochs to check for improvement
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=10)
early_history = model.fit(normed_train_data, train_labels,
epochs=EPOCHS, validation_split = 0.2, verbose=0,
callbacks=[early_stop, tfdocs.modeling.EpochDots()])
# + colab_type="code" id="LcopvQh3X-kX" colab={}
plotter.plot({'Early Stopping': early_history}, metric = "mae")
plt.ylim([0, 10])
plt.ylabel('MAE [MPG]')
# + [markdown] colab_type="text" id="3St8-DmrX8P4"
# The graph shows that on the validation set, the average error is usually around +/- 2 MPG. Is this good? We'll leave that decision up to you.
#
# Let's see how well the model generalizes by using the **test** set, which we did not use when training the model. This tells us how well we can expect the model to predict when we use it in the real world.
# + colab_type="code" id="jl_yNr5n1kms" colab={}
loss, mae, mse = model.evaluate(normed_test_data, test_labels, verbose=2)
print("Testing set Mean Abs Error: {:5.2f} MPG".format(mae))
# + [markdown] colab_type="text" id="ft603OzXuEZC"
# ### Make predictions
#
# Finally, predict MPG values using data in the testing set:
# + colab_type="code" id="Xe7RXH3N3CWU" colab={}
test_predictions = model.predict(normed_test_data).flatten()
a = plt.axes(aspect='equal')
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [MPG]')
plt.ylabel('Predictions [MPG]')
lims = [0, 50]
plt.xlim(lims)
plt.ylim(lims)
_ = plt.plot(lims, lims)
# + [markdown] colab_type="text" id="19wyogbOSU5t"
# It looks like our model predicts reasonably well. Let's take a look at the error distribution.
# + colab_type="code" id="f-OHX4DiXd8x" colab={}
error = test_predictions - test_labels
plt.hist(error, bins = 25)
plt.xlabel("Prediction Error [MPG]")
_ = plt.ylabel("Count")
# + [markdown] colab_type="text" id="m0CB5tBjSU5w"
# It's not quite gaussian, but we might expect that because the number of samples is very small.
# + [markdown] colab_type="text" id="vgGQuV-yqYZH"
# ## Conclusion
#
# This notebook introduced a few techniques to handle a regression problem.
#
# * Mean Squared Error (MSE) is a common loss function used for regression problems (different loss functions are used for classification problems).
# * Similarly, evaluation metrics used for regression differ from classification. A common regression metric is Mean Absolute Error (MAE).
# * When numeric input data features have values with different ranges, each feature should be scaled independently to the same range.
# * If there is not much training data, one technique is to prefer a small network with few hidden layers to avoid overfitting.
# * Early stopping is a useful technique to prevent overfitting.
|
tf-tutorials/regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="Zp5x9g3Nq4BE"
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# + colab={"base_uri": "https://localhost:8080/", "height": 422} id="MVU7JB20rAS1" outputId="e72a4252-d801-471b-af08-33c590367f8e"
df = pd.read_csv('/content/drive/MyDrive/Project/LoL/teamGold_2021-02-20.csv')
df
# + colab={"base_uri": "https://localhost:8080/"} id="ilYVzGeuw4DG" outputId="67e094f0-ae19-4054-a24b-8a5521f4f189"
df['winTeam'] = df['winTeam'].apply(lambda x: 1 if x==100 else 0)
df['winTeam'].value_counts()
# + colab={"base_uri": "https://localhost:8080/", "height": 422} id="WkpzVTK9w4La" outputId="8a8926e0-bdac-432e-8e51-8eae1c38f1af"
df = df[df['gameDuration']>1200].copy()
df.drop(columns=['gameId', 'platformId', 'gameCreation', 'gameDuration'], inplace=True)
df.drop(columns=[col for col in df.columns if any(f'{i}' in col for i in range(21,60))], inplace=True)
df
# + colab={"base_uri": "https://localhost:8080/"} id="JtuZrfH3uX_d" outputId="8fa7e3c6-6715-489e-ed71-05f1e234d129"
df = df[(df['B20']-df['R20']).between(-5000,5000)].copy()
len(df)
# + id="E8xawLb5LdFB"
d_mean = []
d_std = []
for i in range(21):
cols = [f'B{i:02d}', f'R{i:02d}']
m = np.nanmean(df[cols])
s = np.nanstd(df[cols])
for team in cols:
df[team] = (df[team]-m)/s if s>0 else 0
d_mean.append(m)
d_std.append(s)
df
# + colab={"base_uri": "https://localhost:8080/", "height": 422} id="8Pnq1C9H2Nt2" outputId="98fa6f72-a919-4d49-828c-5c10ee314431"
for i in range(21):
cols = [f'B{i:02d}', f'R{i:02d}']
m = np.nanmax(df[cols])
n = np.nanmin(df[cols])
for team in cols:
df[team] = (df[team]-n)/(m-n) if m>n else 0
df
# + id="PgPpBAE0w4QS"
from sklearn.model_selection import train_test_split
from random import randint
# + colab={"base_uri": "https://localhost:8080/"} id="9dJqQVSGw4UC" outputId="32488883-1568-4f2f-d56d-b7f510403ed2"
cols = [col for i in range(1,21) for col in [f'B{i:02d}',f'R{i:02d}']]
random_state = randint(0,1e6)
print(f'Random state: {random_state}.')
X_train, X_test, y_train, y_test = train_test_split(df[cols], df['winTeam'], test_size=0.2, random_state=random_state)
# + id="g8C_kZK1w4YD"
import tensorflow as tf
# + id="6UJbc-fQZiVs"
inputs = tf.keras.Input(shape=(40,))
x = tf.keras.layers.Reshape((20,2))(inputs)
x = tf.keras.layers.LSTM(4)(x)
outputs = tf.keras.layers.Dense(1, activation=tf.nn.sigmoid)(x)
model = tf.keras.Model(inputs=inputs, outputs=outputs)
# + id="rVDE-5qmAcVn"
inputs = tf.keras.Input(shape=(42,))
#x = tf.keras.layers.Dense(21, activation=tf.nn.relu)(inputs)
#x = tf.keras.layers.Dropout(0.5)(x)
x = tf.keras.layers.Reshape((21,2))(inputs)
x = tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(84))(x)
x = tf.keras.layers.Dense(84, activation=tf.nn.relu)(x)
outputs = tf.keras.layers.Dense(1, activation=tf.nn.sigmoid)(x)
model = tf.keras.Model(inputs=inputs, outputs=outputs)
# + id="MiHD7jdxnzJL"
inputs = tf.keras.Input(shape=(42,))
#x = tf.keras.layers.BatchNormalization()(inputs)
x = tf.keras.layers.Dropout(0.3)(inputs)
for _ in range(2):
x = tf.keras.layers.Dense(21)(x)
x = tf.keras.layers.BatchNormalization()(x)
x = tf.keras.layers.Activation(tf.keras.activations.swish)(x)
x = tf.keras.layers.Dropout(0.1)(x)
x = tf.keras.layers.Dense(1)(x)
outputs = tf.keras.layers.Activation('sigmoid')(x)
model = tf.keras.Model(inputs=inputs, outputs=outputs)
# + id="7Lw_Dlj2zg0J"
model.compile(optimizer = tf.keras.optimizers.Adam(),
loss=tf.keras.losses.BinaryCrossentropy(),
metrics=['accuracy'])
# + colab={"base_uri": "https://localhost:8080/"} id="MbB3OTkfzkuI" outputId="337b3693-c664-4a4a-e35a-f3d2409e12ae"
model.fit(X_train, y_train, epochs=100, batch_size=32, validation_data = (X_test, y_test))
# + id="iQw6a05B1WcF"
model.evaluate(X_test, y_test)
# + id="HUFuSYzcHm3b"
model.get_weights()
# + id="5knGahVWFmdG" colab={"base_uri": "https://localhost:8080/"} outputId="a39034ad-a6b8-47a6-dcf7-e95d608fa0ff"
model.predict(X_test)
# + id="FOtA7P7q_TMU"
X_test['pred'] = [a[0] for a in model.predict(X_test)]
# + colab={"base_uri": "https://localhost:8080/", "height": 402} id="o1VVv17Z_Z_g" outputId="db76e86e-a6e2-4cb2-8ff8-e55cba6fde42"
X_test[y_test!=X_test['pred'].apply(lambda x: 1 if x>0.5 else 0)][['pred', 'B20', 'R20']]
# + colab={"base_uri": "https://localhost:8080/", "height": 402} id="qkezypDz631t" outputId="d4548e0b-8b1f-48f3-b331-69c2f9478405"
X_test['win'] = y_test
X_int = X_test[((X_test['pred']-0.5)*(X_test['B20']-X_test['R20']))<0][['B20','R20','pred','win']]
X_int
# + colab={"base_uri": "https://localhost:8080/", "height": 402} id="dotaH_2J7_4A" outputId="9b14673c-8f05-48d2-e2d5-bb1b60c28419"
X_int['pW'] = X_int['pred'].apply(lambda x: 1 if x>0.5 else 0)
X_int[X_int['pW']!=X_int['win']]
# + colab={"base_uri": "https://localhost:8080/"} id="mFnM1yRDMqYf" outputId="5c1258fa-25e8-44a6-fdcf-19d34dfbd2dc"
print(model.predict(X_test))
y_pred = pd.Series(model.predict(X_test).tolist(), index=y_test.index)
y_pred = y_pred.apply(lambda x: 1 if x[0]>0.5 else 0)
# + colab={"base_uri": "https://localhost:8080/"} id="Rz62RGyPNnfA" outputId="3adf1b2b-5ab3-49e5-e1d4-7422246c7cd8"
(y_pred==y_test).mean()
# + colab={"base_uri": "https://localhost:8080/"} id="N5pekDkQ8oaX" outputId="e13c8a26-a2c8-4685-c589-081f916d4e71"
print(len(model.predict(X_test)), len(X_test))
# + colab={"base_uri": "https://localhost:8080/"} id="lnJziIIf8yv1" outputId="791816d9-9c22-464b-824e-b471e0320e28"
print(y_train.mean(),y_test.mean())
# + [markdown] id="Ub-Zzttov_5z"
# # Experiment 1
#
# + colab={"base_uri": "https://localhost:8080/"} id="QFI00r44wOlK" outputId="c2570f6b-7713-4bb2-ffd6-44001ec3d132"
cols = list(df.columns)
print(cols, len(cols))
# + colab={"base_uri": "https://localhost:8080/", "height": 422} id="Y1F4VmsPw4Xr" outputId="112ad663-5d43-416a-a34a-1d68ffb33dd7"
cols[1:22], cols[22:43] = cols[22:43], cols[1:22]
df2 = df.copy()
df2.columns = cols
df2 = df2.reindex(columns=df.columns)
df2['winTeam'] = 1 - df2['winTeam']
df2
# + colab={"base_uri": "https://localhost:8080/", "height": 422} id="JVPUPOg6xr22" outputId="bdaf54fb-e6f9-4b0f-c01b-92a8320a6878"
df3 = df.append(df2, ignore_index=True)
df3
# + id="23fX5sjFzrXh"
from sklearn.model_selection import train_test_split
from random import randint
# + colab={"base_uri": "https://localhost:8080/"} id="rtXkSBX-zrXl" outputId="1f2d9efd-e1c1-4a78-ac9a-d720b692972c"
random_state = randint(0,1e6)
print(f'Random state: {random_state}.')
X_train, X_test, y_train, y_test = train_test_split(df3[[f'B{i:02d}' for i in range(1,21)]], df3['winTeam'], test_size=0.2, random_state=random_state)
# + id="Dd4d_28tzrXm"
import tensorflow as tf
# + id="pGvVX9muzrXm"
inputs = tf.keras.Input(shape=(20,))
x = tf.keras.layers.Dense(40, activation=tf.nn.relu)(inputs)
x = tf.keras.layers.Dense(40, activation=tf.nn.relu)(x)
outputs = tf.keras.layers.Dense(1, activation=tf.nn.sigmoid)(x)
model = tf.keras.Model(inputs=inputs, outputs=outputs)
# + id="VFuwwLSNzrXm"
model.compile(optimizer='adam',
loss=tf.keras.losses.BinaryCrossentropy(),
metrics=['accuracy'])
# + colab={"base_uri": "https://localhost:8080/"} id="RVnSLB-DzrXn" outputId="8ed867e2-4ae0-48af-a1fa-305a00995358"
model.fit(X_train, y_train, batch_size=1, epochs=10, validation_data = (X_test, y_test))
# + colab={"base_uri": "https://localhost:8080/"} id="70uQLUxZ1DfY" outputId="e801e4a2-6e3f-4ab6-b507-2f9a780990c3"
y = model.predict(df3[[f'B{i:02d}' for i in range(1,21)]])
print(len(y))
# + id="pbGNc2LC1U3B"
y_pred = [a[0] for a in y]
# + colab={"base_uri": "https://localhost:8080/"} id="AuHc1srg1NaP" outputId="f5bb45ce-032e-4380-ae1f-95a326f0cebc"
final_result = [1 if a-b>0 else 0 for a,b in zip(y_pred[:86096//2], y_pred[86096//2:])]
print(final_result[:10])
# + id="ZXwTT-4H1zDX"
df['pred'] = final_result
# + colab={"base_uri": "https://localhost:8080/"} id="LocNwpGP11wW" outputId="b93c3b0b-dded-41a2-9281-1bb32193c31e"
(df['pred']==df['winTeam']).mean()
# + colab={"base_uri": "https://localhost:8080/", "height": 402} id="BOeroN2J2nQq" outputId="17e27ab6-ec28-4ce5-9763-8610a09f2885"
df['prob'] = [a-b for a,b in zip(y_pred[:86096//2], y_pred[86096//2:])]
df[df['winTeam']!=df['pred']][['winTeam', 'pred', 'prob', 'B20', 'R20']]
# + colab={"base_uri": "https://localhost:8080/"} id="4j9mJDK04flL" outputId="265ca088-5c91-4795-d9d9-f13bdc287901"
len(((df['B20']-df['R20'])*df['prob']).gt(0))
|
nn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Computer Vision Nanodegree
#
# ## Project: Image Captioning
#
# ---
#
# In this notebook, you will use your trained model to generate captions for images in the test dataset.
#
# This notebook **will be graded**.
#
# Feel free to use the links below to navigate the notebook:
# - [Step 1](#step1): Get Data Loader for Test Dataset
# - [Step 2](#step2): Load Trained Models
# - [Step 3](#step3): Finish the Sampler
# - [Step 4](#step4): Clean up Captions
# - [Step 5](#step5): Generate Predictions!
# <a id='step1'></a>
# ## Step 1: Get Data Loader for Test Dataset
#
# Before running the code cell below, define the transform in `transform_test` that you would like to use to pre-process the test images.
#
# Make sure that the transform that you define here agrees with the transform that you used to pre-process the training images (in **2_Training.ipynb**). For instance, if you normalized the training images, you should also apply the same normalization procedure to the test images.
# +
import sys
sys.path.append('/opt/cocoapi/PythonAPI')
from pycocotools.coco import COCO
from data_loader import get_loader
from torchvision import transforms
# TODO #1: Define a transform to pre-process the testing images.
transform_test = transforms.Compose([
transforms.Resize(224),
transforms.RandomCrop(224),
transforms.ToTensor(),
transforms.Normalize((0.485, 0.456, 0.406), # normalize image for pre-trained model
(0.229, 0.224, 0.225))
])
#-#-#-# Do NOT modify the code below this line. #-#-#-#
# Create the data loader.
data_loader = get_loader(transform=transform_test,
mode='test')
# -
# Run the code cell below to visualize an example test image, before pre-processing is applied.
# +
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# Obtain sample image before and after pre-processing.
orig_image, image = next(iter(data_loader))
print(image.shape)
# Visualize sample image, before pre-processing.
plt.imshow(np.squeeze(orig_image))
plt.title('example image')
plt.show()
# -
# <a id='step2'></a>
# ## Step 2: Load Trained Models
#
# In the next code cell we define a `device` that you will use move PyTorch tensors to GPU (if CUDA is available). Run this code cell before continuing.
# +
import torch
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# -
# Before running the code cell below, complete the following tasks.
#
# ### Task #1
#
# In the next code cell, you will load the trained encoder and decoder from the previous notebook (**2_Training.ipynb**). To accomplish this, you must specify the names of the saved encoder and decoder files in the `models/` folder (e.g., these names should be `encoder-5.pkl` and `decoder-5.pkl`, if you trained the model for 5 epochs and saved the weights after each epoch).
#
# ### Task #2
#
# Plug in both the embedding size and the size of the hidden layer of the decoder corresponding to the selected pickle file in `decoder_file`.
# +
# Watch for any changes in model.py, and re-load it automatically.
% load_ext autoreload
% autoreload 2
import os
import torch
from model import EncoderCNN, DecoderRNN
# TODO #2: Specify the saved models to load.
encoder_file = 'encoder-adam-3.pkl'
decoder_file = 'decoder-adam-3.pkl'
# TODO #3: Select appropriate values for the Python variables below.
embed_size = 512
hidden_size = 512
# The size of the vocabulary.
vocab_size = len(data_loader.dataset.vocab)
# Initialize the encoder and decoder, and set each to inference mode.
encoder = EncoderCNN(embed_size)
encoder.eval()
decoder = DecoderRNN(embed_size, hidden_size, vocab_size)
decoder.eval()
# decoder.num_layers = 1
# Load the trained weights.
encoder.load_state_dict(torch.load(os.path.join('./models', encoder_file)))
decoder.load_state_dict(torch.load(os.path.join('./models', decoder_file)))
# Move models to GPU if CUDA is available.
encoder.to(device)
decoder.to(device)
# -
# <a id='step3'></a>
# ## Step 3: Finish the Sampler
#
# Before executing the next code cell, you must write the `sample` method in the `DecoderRNN` class in **model.py**. This method should accept as input a PyTorch tensor `features` containing the embedded input features corresponding to a single image.
#
# It should return as output a Python list `output`, indicating the predicted sentence. `output[i]` is a nonnegative integer that identifies the predicted `i`-th token in the sentence. The correspondence between integers and tokens can be explored by examining either `data_loader.dataset.vocab.word2idx` (or `data_loader.dataset.vocab.idx2word`).
#
# After implementing the `sample` method, run the code cell below. If the cell returns an assertion error, then please follow the instructions to modify your code before proceeding. Do **not** modify the code in the cell below.
# +
# Move image Pytorch Tensor to GPU if CUDA is available.
image = image.to(device)
# Obtain the embedded image features.
features = encoder(image).unsqueeze(1)
# Pass the embedded image features through the model to get a predicted caption.
output = decoder.sample(features)
print('example output:', output)
assert (type(output)==list), "Output needs to be a Python list"
assert all([type(x)==int for x in output]), "Output should be a list of integers."
assert all([x in data_loader.dataset.vocab.idx2word for x in output]), "Each entry in the output needs to correspond to an integer that indicates a token in the vocabulary."
# -
# <a id='step4'></a>
# ## Step 4: Clean up the Captions
#
# In the code cell below, complete the `clean_sentence` function. It should take a list of integers (corresponding to the variable `output` in **Step 3**) as input and return the corresponding predicted sentence (as a single Python string).
# TODO #4: Complete the function.
def clean_sentence(output):
sentence = ""
for ii, out in enumerate(output):
if ii == 0:
continue;
elif out == 1:
break
sentence = sentence + " " + data_loader.dataset.vocab.idx2word[out]
sentence
return sentence
clean_sentence([0, 3, 1])
# After completing the `clean_sentence` function above, run the code cell below. If the cell returns an assertion error, then please follow the instructions to modify your code before proceeding.
# +
sentence = clean_sentence(output)
print('example sentence:', sentence)
assert type(sentence)==str, 'Sentence needs to be a Python string!'
# -
# <a id='step5'></a>
# ## Step 5: Generate Predictions!
#
# In the code cell below, we have written a function (`get_prediction`) that you can use to use to loop over images in the test dataset and print your model's predicted caption.
def get_prediction():
orig_image, image = next(iter(data_loader))
plt.imshow(np.squeeze(orig_image))
plt.title('Sample Image')
plt.show()
image = image.to(device)
features = encoder(image).unsqueeze(1)
output = decoder.sample(features)
sentence = clean_sentence(output)
print(sentence)
# Run the code cell below (multiple times, if you like!) to test how this function works.
get_prediction()
# As the last task in this project, you will loop over the images until you find four image-caption pairs of interest:
# - Two should include image-caption pairs that show instances when the model performed well.
# - Two should highlight image-caption pairs that highlight instances where the model did not perform well.
#
# Use the four code cells below to complete this task.
# ### The model performed well!
#
# Use the next two code cells to loop over captions. Save the notebook when you encounter two images with relatively accurate captions.
get_prediction()
get_prediction()
# ### The model could have performed better ...
#
# Use the next two code cells to loop over captions. Save the notebook when you encounter two images with relatively inaccurate captions.
get_prediction()
# There aren't any people in the above image or a bench or a lake.
get_prediction()
# The sky is not blue.
|
computer_vision/image_captioning/3_Inference.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="ccfRql22_IBL" tags=["remove_cell"]
# # Classical Logic Gates with Quantum Circuits
# -
from qiskit import *
from qiskit.tools.visualization import plot_histogram
import numpy as np
# + [markdown] colab_type="text" id="ccfRql22_IBL"
# Using the NOT gate (expressed as `x` in Qiskit), the CNOT gate (expressed as `cx` in Qiskit) and the Toffoli gate (expressed as `ccx` in Qiskit) create functions to implement the XOR, AND, NAND and OR gates.
#
# An implementation of the NOT gate is provided as an example.
# + [markdown] colab_type="text" id="OKCkpBD0_c6L"
# ## NOT gate
# + [markdown] colab_type="text" id="OKCkpBD0_c6L"
# This function takes a binary string input (`'0'` or `'1'`) and returns the opposite binary output'.
# + colab={} colab_type="code" id="6JPMpemG_RMb"
def NOT(input):
q = QuantumRegister(1) # a qubit in which to encode and manipulate the input
c = ClassicalRegister(1) # a bit to store the output
qc = QuantumCircuit(q, c) # this is where the quantum program goes
# We encode '0' as the qubit state |0⟩, and '1' as |1⟩
# Since the qubit is initially |0⟩, we don't need to do anything for an input of '0'
# For an input of '1', we do an x to rotate the |0⟩ to |1⟩
if input=='1':
qc.x( q[0] )
# Now we've encoded the input, we can do a NOT on it using x
qc.x( q[0] )
# Finally, we extract the |0⟩/|1⟩ output of the qubit and encode it in the bit c[0]
qc.measure( q[0], c[0] )
# We'll run the program on a simulator
backend = Aer.get_backend('qasm_simulator')
# Since the output will be deterministic, we can use just a single shot to get it
job = execute(qc,backend,shots=1)
output = next(iter(job.result().get_counts()))
return output
# + [markdown] colab_type="text" id="Gd-9DEAaAarK"
# ## XOR gate
# + [markdown] colab_type="text" id="Gd-9DEAaAarK"
# Takes two binary strings as input and gives one as output.
#
# The output is `'0'` when the inputs are equal and `'1'` otherwise.
# + colab={} colab_type="code" id="oPVCyyaHAays"
def XOR(input1,input2):
q = QuantumRegister(2) # two qubits in which to encode and manipulate the input
c = ClassicalRegister(1) # a bit to store the output
qc = QuantumCircuit(q, c) # this is where the quantum program goes
# YOUR QUANTUM PROGRAM GOES HERE
qc.measure(q[1],c[0]) # YOU CAN CHANGE THIS IF YOU WANT TO
# We'll run the program on a simulator
backend = Aer.get_backend('qasm_simulator')
# Since the output will be deterministic, we can use just a single shot to get it
job = execute(qc,backend,shots=1,memory=True)
output = job.result().get_memory()[0]
return output
# + [markdown] colab_type="text" id="dPMfIpfYAAT7"
# ## AND gate
# + [markdown] colab_type="text" id="dPMfIpfYAAT7"
# Takes two binary strings as input and gives one as output.
#
# The output is `'1'` only when both the inputs are `'1'`.
# + colab={} colab_type="code" id="HdYfpnslAAeJ"
def AND(input1,input2):
q = QuantumRegister(3) # two qubits in which to encode the input, and one for the output
c = ClassicalRegister(1) # a bit to store the output
qc = QuantumCircuit(q, c) # this is where the quantum program goes
# YOUR QUANTUM PROGRAM GOES HERE
qc.measure(q[2],c[0]) # YOU CAN CHANGE THIS IF YOU WANT TO
# We'll run the program on a simulator
backend = Aer.get_backend('qasm_simulator')
# Since the output will be deterministic, we can use just a single shot to get it
job = execute(qc,backend,shots=1,memory=True)
output = job.result().get_memory()[0]
return output
# + [markdown] colab_type="text" id="OXfchiSyAAoo"
# ## NAND gate
# + [markdown] colab_type="text" id="OXfchiSyAAoo"
# Takes two binary strings as input and gives one as output.
#
# The output is `'0'` only when both the inputs are `'1'`.
# + colab={} colab_type="code" id="nJhmG115AAwv"
def NAND(input1,input2):
q = QuantumRegister(3) # two qubits in which to encode the input, and one for the output
c = ClassicalRegister(1) # a bit to store the output
qc = QuantumCircuit(q, c) # this is where the quantum program goes
# YOUR QUANTUM PROGRAM GOES HERE
qc.measure(q[2],c[0]) # YOU CAN CHANGE THIS IF YOU WANT TO
# We'll run the program on a simulator
backend = Aer.get_backend('qasm_simulator')
# Since the output will be deterministic, we can use just a single shot to get it
job = execute(qc,backend,shots=1,memory=True)
output = job.result().get_memory()[0]
return output
# + [markdown] colab_type="text" id="n1KswU_jABFA"
# ## OR gate
# + [markdown] colab_type="text" id="n1KswU_jABFA"
# Takes two binary strings as input and gives one as output.
#
# The output is `'1'` if either input is `'1'`.
# + colab={} colab_type="code" id="_gofB196ABMj"
def OR(input1,input2):
q = QuantumRegister(3) # two qubits in which to encode the input, and one for the output
c = ClassicalRegister(1) # a bit to store the output
qc = QuantumCircuit(q, c) # this is where the quantum program goes
# YOUR QUANTUM PROGRAM GOES HERE
qc.measure(q[2],c[0]) # YOU CAN CHANGE THIS IF YOU WANT TO
# We'll run the program on a simulator
backend = Aer.get_backend('qasm_simulator')
# Since the output will be deterministic, we can use just a single shot to get it
job = execute(qc,backend,shots=1,memory=True)
output = job.result().get_memory()[0]
return output
# + [markdown] colab_type="text" id="flbXaXrY_pNz"
# ## Tests
# + [markdown] colab_type="text" id="flbXaXrY_pNz"
# The following code runs the functions above for all possible inputs, so that you can check whether they work.
# + colab={} colab_type="code" id="S9hyGAZ9_VQc"
print('\nResults for the NOT gate')
for input in ['0','1']:
print(' Input',input,'gives output',NOT(input))
print('\nResults for the XOR gate')
for input1 in ['0','1']:
for input2 in ['0','1']:
print(' Inputs',input1,input2,'give output',XOR(input1,input2))
print('\nResults for the AND gate')
for input1 in ['0','1']:
for input2 in ['0','1']:
print(' Inputs',input1,input2,'give output',AND(input1,input2))
print('\nResults for the NAND gate')
for input1 in ['0','1']:
for input2 in ['0','1']:
print(' Inputs',input1,input2,'give output',NAND(input1,input2))
print('\nResults for the OR gate')
for input1 in ['0','1']:
for input2 in ['0','1']:
print(' Inputs',input1,input2,'give output',OR(input1,input2))
# -
import qiskit
qiskit.__qiskit_version__
|
content/ch-ex/ex1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <a href="https://colab.research.google.com/github/morganmcg1/reformer-fastai/blob/main/experiments/LM_exp_template.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# +
# import sys
# if 'google.colab' in sys.modules:
# # !pip install -Uqq fastai einops datasets
# -
import sys
import six
from fastai.text.all import *
sys.path.append("..")
from basic_tokenizers import ByteTextTokenizer
from basic_transformer import TransformerLM
from make_dataset import read_and_prepare_data
# ## Experiment Tracking
# Make sure you have wandb and are logged in:
# +
# # !pip install -Uqq wandb
# # !wandb login
# -
# Load Experiment Tracking with Weights & Biases:
# ## Wandb experiment logging
# Suggeted [wandb.init logging](https://docs.wandb.com/library/init) to help keep track of experiments:
#
# **WANDB_NAME**
#
# A specific name for a particular experiment, e.g. "lsh_2_hash_enwik8"
#
# **GROUP**
#
# Group identifiers will help organise and **group experiments together** in the wandb interface. Suggested identifier to use are:
#
# - "TEST" : for general testing
# - "SHARED-QK" : for Shared Query-Key experiments
# - "LSH" : LSH-related experiemnts
# - "REVERSIBLE" : reversible layers experiments
# - "WMT" : for the WMT task
#
# **NOTES**
#
# A longer description of the run, like a -m commit message in git. This helps you remember what you were doing when you ran this run.
#
# **CONFIG**
#
# A dictionary-like object for saving inputs to your job, like hyperparameters for a model or settings for a data preprocessing job. The config will show up in a table in the UI that you can use to group, filter, and sort runs. Keys should not have . in the names, and values should be under 10 MB.
#
# **TAGS**
#
# A list of strings, which will populate the list of tags on this run in the UI. Tags are useful for organizing runs together, or applying temporary labels like "baseline" or "production". It's easy to add and remove tags in the UI, or filter down to just runs with a specific tag.
# +
import wandb
from fastai.callback.wandb import *
WANDB_NAME = 'enc_lm_enwik8'
GROUP = 'TEST' # Group to add a run to, e.g. "LSH" for LSH experiments, "REVERSIBLE" for reversible layers
NOTES = 'Testing the encoder LM model works'
CONFIG = {}
TAGS =['enc_lm','test']
# -
# Initialise wandb logging, pleaes **do not change** `project` or `entity` (that that everything gets logged to the same place)
# +
# wandb.init(reinit=True, project="reformer-fastai", entity="fastai_community",
# name=WANDB_NAME, group=GROUP, notes=NOTES, tags=TAGS) # config=CONFIG,
# -
# ## Download and Unpack enwik8 Data
#
# Download and unzip enwik8 data
# +
# #!wget -P data/ http://mattmahoney.net/dc/enwik8.zip
# #!unzip data/enwik8.zip -d data/
# #!ls data
# #!head -n 132 data/enwik8
# -
# # Prepare Data
# + pycharm={"name": "#%%\n"}
# df has columns [text, lens, lens_cum_sum], add a numerical seq_length argument
# to the function below if you'd like to split the data into samples with that seq length
df = read_and_prepare_data('data/enwik8')
# -
# Load tokenizer
bte = ByteTextTokenizer(is_lm=True, add_bos=True, add_eos=True)
## TINY DF FOR TESTING
df = df.iloc[:400].copy()
train_cutoff = int(df.lens.sum()*0.5)
# Get train cutoff, split enwik8 by character count
# +
# df['lens'] = df['text'].str.len()
# df['lens_cum_sum'] = df.lens.cumsum()
# train_cutoff = df.lens.sum() - 10000000 # keep all but 10M characters for val and test
# -
# Calc splits
# +
train_idxs = df.loc[df['lens_cum_sum'] < train_cutoff].index.values
train_idxs = list(range(0, max(train_idxs)))
remaining_idxs = len(df) - max(train_idxs)
validation_idxs = list(range(max(train_idxs), max(train_idxs) + int(remaining_idxs/2)))
test_idxs = list(range(max(validation_idxs), len(df)))
splits = [train_idxs, validation_idxs]
# -
# Get dls
# +
# Quick naive split alternative
# cut = int(len(df)*0.8)
# splits = range_of(df)[:cut], range_of(df[cut:])
tfms = [attrgetter("text"), bte]
dsets = Datasets(df, [tfms, tfms], splits=splits, dl_type=LMDataLoader)
vocab_sz = bte.vocab_size
bs,sl = 32,128
pad_seq2seq = partial(pad_input, pad_idx=bte.pad_token_id, pad_fields=[0,1])
dls = dsets.dataloaders(bs=bs, seq_len=sl, before_batch=pad_seq2seq)
dls.show_batch(max_n=2)
# -
xb, yb = dls.one_batch()
xb.shape, yb.shape
vocab_sz = bte.vocab_size
# # Begin Experiment Training
wandb.init(reinit=True, project="reformer-fastai", entity="fastai_community",
name=WANDB_NAME, group=GROUP, notes=NOTES, tags=TAGS) # config=CONFIG,
learn = Learner(dls, TransformerLM(vocab_sz, 512),
loss_func=CrossEntropyLossFlat(), cbs=[WandbCallback(log_model=False, log_preds=False)],
metrics=[accuracy, Perplexity()]).to_native_fp16()
learn.lr_find()
learn.fit_one_cycle(2, 5e-4, wd=0.05) # cbs=WandbCallback(log_model=False)
|
experiments/LM_exp_template.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Fine-tuning your first Transformer!
# > Exploring Huggingface Transformers library in MLt workshop part 2
#
# - toc: true
# - badges: true
# - comments: true
# - categories: [jupyter]
# - image/chart-preview
#
# + [markdown] tags=[]
# ## Fine-tuning your first Transformer!
# -
# In this notebook we'll take a look at fine-tuning a multilingual Transformer model called [XLM-RoBERTa](https://huggingface.co/xlm-roberta-base) for text classification. By the end of this notebook you should know how to:
#
# * Load and process a dataset from the Hugging Face Hub
# * Create a baseline with the zero-shot classification pipeline
# * Fine-tune and evaluate pretrained model on your data
# * Push a model to the Hugging Face Hub
#
# Let's get started!
# + [markdown] tags=[]
# ## Setup
# -
# If you're running this notebook on Google Colab or locally, you'll need a few dependencies installed. You can install them with `pip` as follows:
# +
# #! pip install datasets transformers sentencepiece
# -
# To be able to share your model with the community there are a few more steps to follow.
#
# First you have to store your authentication token from the Hugging Face website (sign up [here](https://huggingface.co/join) if you haven't already!) then execute the following cell and input your username and password:
# +
from huggingface_hub import notebook_login
notebook_login()
# -
# Then you need to install Git-LFS. Uncomment and execute the following cell:
# +
# # !apt install git-lfs
# + [markdown] tags=[]
# ## The dataset
# -
# In this notebook we'll be using the 🤗 Datasets to load and preprocess our data. If you're new to this library, check out the video below to get some additional context:
# +
from IPython.display import YouTubeVideo
YouTubeVideo("_BZearw7f0w", width=600, height=400)
# + [markdown] tags=[]
# In this tutorial we'll use the [Multilingual Amazon Reviews Corpus](https://huggingface.co/datasets/amazon_reviews_multi) (or MARC for short). This is a large-scale collection of Amazon product reviews in several languages: English, Japanese, German, French, Spanish, and Chinese.
# + [markdown] tags=[]
# We can download the dataset from the Hugging Face Hub with the 🤗 Datasets library, but first let's take a look at the available subsets (also called configs):
# +
from datasets import get_dataset_config_names
dataset_name = "amazon_reviews_multi"
langs = get_dataset_config_names(dataset_name)
langs
# -
# Okay, we can see the language codes associated with each language, as well as an `all_languages` subset which presumably concatenates all the languages together. Let's begin by downloading the English subset with the `load_dataset()` function from 🤗 Datasets:
# +
from datasets import load_dataset
marc_en = load_dataset(path=dataset_name, name="en")
marc_en
# -
# One cool feature of 🤗 Datasets is that `load_dataset()` will cache the files at `~/.cache/huggingface/dataset/`, so you won't need to re-download the dataset the next time your run the notebook.
# We can see that `marc_en` is a `DatasetDict` object which is similar to a Python dictionary, with each key corresponding to a different split. We can access an element of one of these splits as follows:
# Peek at first element
marc_en["train"][0]
# This certainly looks like an Amazon product review and we can see the number of stars associated with the review, as well as some metadata like the language and product category.
# We can also access several rows with a slice:
marc_en["train"][:3]
# and note that now we get a list of values for each column. This is because 🤗 Datasets is based on Apache Arrow, which defines a typed columnar format that is very memory efficient.
# ### What if my dataset is not on the Hub?
# Note that altough we downloaded the dataset from the Hub, it's also possible to load datasets both locally and from custom URLs. For example, the above dataset lives at the following URL:
dataset_url = "https://amazon-reviews-ml.s3-us-west-2.amazonaws.com/json/train/dataset_en_train.json"
# so we can download it manually with `wget`:
# !wget {dataset_url}
# We can then load it locally using the `json` loading script:
load_dataset("json", data_files="dataset_en_train.json")
# You can actually skip the manual download step entirely by pointing `data_files` directly to the URL:
load_dataset("json", data_files=dataset_url)
# Now that we've had a quick look at the objects in 🤗 Datasets, let's explore the data in more detail by using our favourite tool - Pandas!
# ## From Datasets to DataFrames and back
# 🤗 Datasets is designed to be interoperable with libraries like Pandas, as well as NumPy, PyTorch, TensorFlow, and JAX. To enable the conversion between various third-party libraries, 🤗 Datasets provides a Dataset.set_format() function. This function only changes the output format of the dataset, so you can easily switch to another format without affecting the underlying data format which is Apache Arrow. The formatting is done in-place, so let’s convert our dataset to Pandas and look at a random sample:
# +
from IPython.display import display, HTML
marc_en.set_format("pandas")
df = marc_en["train"][:]
# Create a random sample
sample = df.sample(n=5, random_state=42)
display(HTML(sample.to_html()))
# -
# We can see that the column headers are the same as we saw in the Arrow format and from the reviews we can see that negative reviews are associated with a lower star rating. Since we're now dealing with a `pandas.DataFrame` we can easily query our dataset. For example, let's see what the distribution of reviews per product category looks like:
df["product_category"].value_counts()
# Okay, the `home`, `wireless`, and `sports` categories seem to be the most popular. How about the distribution of star ratings?
df["stars"].value_counts()
# In this case we can see that the dataset is balanced across each star rating, which will make it somewhat easier to evaluate our models on. Imbalanced datasets are much more common in the real-world and in these cases some additional tricks like up- or down-sampling are usually needed.
#
# Now that we've got a rough idea about the kind of data we're dealing with, let's reset the output format from `pandas` back to `arrow`:
marc_en.reset_format()
# ## Filtering for a product category
# Although we could go ahead and fine-tune a Transformer model on the whole set of 200,000 English reviews, this will take several hours on a single GPU. So instead, we'll focus on fine-tuning a model for a single product category! In 🤗 Datasets, we can filter data very quickly by using the `Dataset.filter()` method. This method expects a function that returns Boolean values, in our case `True` if the `product_category` matches the chosen category and `False` otherwise. Here's one way to implement this, and we'll pick the `sports` category as the domain to train on:
# +
product_category = "book"
def filter_for_product(example, product_category=product_category):
return example["product_category"] == product_category
# -
# Now when we pass `filter_for_product()` to `Dataset.filter()` we get a filtered dataset:
product_dataset = marc_en.filter(filter_for_product)
product_dataset
# Yep, this looks good - we have 13,748 reviews in the train split which agrees the number we saw in the distribution of categories earlier. Let's do a quick sanity check by taking a look at a few samples. Here 🤗 Datasets provides `Dataset.shuffle()` and `Dataset.select()` functions that we can chain to get a random sample:
product_dataset["train"].shuffle(seed=42).select(range(3))[:]
# Okay, now that we have our corpus of book reviews, let's do one last bit of data preparation: creating label mappings from star ratings to human readable strings.
# + [markdown] tags=[]
# ## Mapping the labels
# -
# During training, 🤗 Transformers expects the labels to be ordered, starting from 0 to N. But we've seen that our star ratings range from 1-5, so let's fix that. While we're at it, we'll create a mapping between the label IDs and names, which will be handy later on when we want to run inference with our model. First we'll define the label mapping from ID to name:
label_names = ["terrible", "poor", "ok", "good", "great"]
id2label = {idx:label for idx, label in enumerate(label_names)}
id2label
# We can then apply this mapping to our whole dataset by using the `Dataset.map()` method. Similar to the `Dataset.filter()` method, this one expects a function which receives examples as input, but returns a Python dictionary as output. The keys of the dictionary correspond to the columns, while the values correspond to the column entries. The following function creates two new columns:
#
# * A `labels` column which is the star rating shifted down by one
# * A `label_name` column which provides a nice string for each rating
def map_labels(example):
# Shift labels to start from 0
label_id = example["stars"] - 1
return {"labels": label_id, "label_name": id2label[label_id]}
# To apply this mapping, we simply feed it to `Dataset.map` as follows:
product_dataset = product_dataset.map(map_labels)
# Peek at the first example
product_dataset["train"][0]
# Great, it works! We'll also need the reverse label mapping later, so let's define it here:
label2id = {v:k for k,v in id2label.items()}
# + [markdown] tags=[]
# ## From text to tokens
# -
# Like other machine learning models, Transformers expect their inputs in the form of numbers (not strings) and so some form of preprocessing is required. For NLP, this preprocessing step is called _tokenization_. Tokenization converts strings into atomic chunks called tokens, and these tokens are subsequently encoded as numerical vectors.
#
# For more information about tokenizers, check out the following video:
YouTubeVideo("VFp38yj8h3A", width=600, height=400)
# Each pretrained model comes with its own tokenizer, so to get started let's download the tokenizer of XLM-RoBERTa from the Hub:
# +
from transformers import AutoTokenizer
model_checkpoint = "xlm-roberta-base"
tokenizer = AutoTokenizer.from_pretrained(model_checkpoint)
# -
# The tokenizer has a few interesting attributes such as the vocabulary size:
tokenizer.vocab_size
# This tells us that XLM-R has 250,002 tokens that is can use to represent text with. Some of the tokens are called _special tokens_ to indicate whether a token is the start or end of a sentence, or corresponds to the mask that is associated with language modeling. Here's what the special tokens look like for XLM-R:
tokenizer.special_tokens_map
# When you feed strings to the tokenizer, you'll get at least two fields (some models have more, depending on how they're trained):
#
# * `input_ids`: These correspond to the numerical encodings that map each token to an integer
# * `attention_mask`: This indicates to the model which tokens should be ignored when computing self-attention
#
# Let's see how this works with a simple example. First we encode the string:
encoded_str = tokenizer("Today I'm giving an NLP workshop at MLT")
encoded_str
# and then decode the input IDs to see the mapping explicitly:
for token in encoded_str["input_ids"]:
print(token, tokenizer.decode([token]))
# So to prepare our inputs, we simply need to apply the tokenizer to each example in our corpus. As before, we'll do this with `Dataset.map()` so let's write a simple function to do so:
def tokenize_reviews(examples):
return tokenizer(examples["review_body"], truncation=True, max_length=180)
# Here we've enabled truncation, so the tokenizer will cut any inputs that are longer than 180 tokens (which is the setting used in the MARC paper). With this function we can go ahead and tokenize the whole corpus:
tokenized_dataset = product_dataset.map(tokenize_reviews, batched=True)
tokenized_dataset
tokenized_dataset["train"][0]
# This looks good, so now let's load a pretrained model!
# ## Loading a pretrained model
# To load a pretrained model from the Hub is quite simple: just select the appropriate `AutoModelForXxx` class and use the `from_pretrained()` function with the model checkpoint. In our case, we're dealing with 5 classes (one for each star) so to initialise the model we'll provide this information along with the label mappings:
# +
from transformers import AutoModelForSequenceClassification
num_labels = 5
model = AutoModelForSequenceClassification.from_pretrained(model_checkpoint, num_labels=num_labels, label2id=label2id, id2label=id2label)
# -
# These warnings are perfectly normal - they are telling us that the weights in the head of the network are randomly initialised and so we should fine-tune the model on a downstream task.
#
# Now that we have a model, the next step is to initialise a `Trainer` that will take care of the training loop for us. Let's do that next.
# ## Creating a Trainer
# To create a `Trainer`, we usually need a few basic ingredients:
#
# * A `TrainingArguments` class to define all the hyperparameters
# * A `compute_metrics` function to compute metrics during evaluation
# * Datasets to train and evaluate on
# For more information about the `Trainer` check out the following video:
YouTubeVideo("nvBXf7s7vTI", width=600, height=400)
# Let's start with the `TrainingArguments`:
# +
from transformers import TrainingArguments
model_name = model_checkpoint.split("/")[-1]
batch_size = 16
num_train_epochs = 2
logging_steps = len(tokenized_dataset["train"]) // (batch_size * num_train_epochs)
args = TrainingArguments(
output_dir=f"{model_name}-finetuned-marc-en",
evaluation_strategy = "epoch",
save_strategy = "epoch",
learning_rate=2e-5,
per_device_train_batch_size=batch_size,
per_device_eval_batch_size=batch_size,
num_train_epochs=num_train_epochs,
weight_decay=0.01,
logging_steps=logging_steps,
push_to_hub=True,
)
# -
# Here we've defined `output_dir` to save our checkpoints and tweaked some of the default hyperparameters like the learning rate and weight decay. The `push_to_hub` argument will push each checkpoint to the Hub automatically for us, so we can reuse the model at any point in the future!
#
# Now that we've defined the hyperparameters, the next step is to define the metrics. In the MARC paper, the authors point out that one should use the mean absolute error (MAE) for star ratings because:
#
# > star ratings for each review are ordinal, and a 2-star prediction for a 5-star review should be penalized more heavily than a 4-star prediction for a 5-star review.
#
# We'll take the same approach here and we can get the metric easily from Scikit-learn as follows:
# +
import numpy as np
from sklearn.metrics import mean_absolute_error
def compute_metrics(eval_pred):
predictions, labels = eval_pred
predictions = np.argmax(predictions, axis=1)
return {"MAE": mean_absolute_error(labels, predictions)}
# -
# With these ingredients we can now instantiate a `Trainer`:
# +
from transformers import Trainer
trainer = Trainer(
model,
args,
train_dataset=tokenized_dataset["train"],
eval_dataset=tokenized_dataset["validation"],
tokenizer=tokenizer,
compute_metrics=compute_metrics
)
# -
# Note that here we've also provided the tokenizer to the `Trainer`: doing so will ensure that all of our examples are automatically padded to the longest example in each batch. This is needed so that matrix operations in the forward pass of the model can be computed.
#
# With our `Trainer`, it is then a simple matter to train the model:
trainer.train()
# Nice, with just a few mintues of training, we've managed to halve our error compared to the zero-shot baseline! After training is complete, we can push the commits to our repository on the Hub:
trainer.push_to_hub(commit_message="Training complete!")
# ## Evaluating cross-lingual transfer
# Now that we're fine-tuned our model on a English subset, we can evaluate its ability to transfer to other languages. To do so, we'll load the validation set in a given language, apply the same filtering and preprocessing that we did for the English subset, and finally use `Trainer.evaluate()` to compute the metrics. The following function does the trick:
def evaluate_corpus(lang):
# Load the language subset
dataset = load_dataset(dataset_name, lang, split="validation")
# Filter for the `sports` product category
product_dataset = dataset.filter(filter_for_product)
# Map and create label columns
product_dataset = product_dataset.map(map_labels)
# Tokenize the inputs
tokenized_dataset = product_dataset.map(tokenize_reviews, batched=True)
# Generate predictions and metrics
preds = trainer.evaluate(eval_dataset=tokenized_dataset)
return {"MAE": preds["eval_MAE"]}
# Let's start with English (for reference our MAE on English was around 0.5):
evaluate_corpus("fr")
# Not bad! Our fine-tuned English model is able to transfer to English at roughly the same performance. How about French?
evaluate_corpus("ja")
# Nice, this is very similar too! This shows the great power of multilingual models - provided your target language was included in the pretraining, there's a good chance you'll only need to tune and deploy a single model in production instead of running one per language.
#
# This wraps up our training and evaluation step - one last thing to try is seeing how we can interact with our model in a `pipeline`.
# ## Using your fine-tuned model
# +
from transformers import pipeline
finetuned_checkpoint = "lewtun/xlm-roberta-base-finetuned-marc-en"
classifier = pipeline("text-classification", model=finetuned_checkpoint)
# -
classifier("I loved reading the Hunger Games!")
classifier("ハンガーゲーム」を読むのが好きだった!")
|
_notebooks/2021-10-28-text-classification.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import sys, os
current_dir = os.getcwd()
sys.path.insert(0, current_dir)
from mmdet.apis import init_detector, inference_detector, show_result_pyplot
import mmcv
import os
di = './data/'
fs = os.listdir(di)
config_file = '%s/local_config/atss_r50_fpn_ms12.py' % current_dir
checkpoint_file = '%s/pretrain_model/atss_r50_fpn_ms12.model' % current_dir
model = init_detector(config_file, checkpoint_file, device='cuda:0')
for idx, f in enumerate(fs):
if idx < 0 or idx > 2:
continue
img = di + f
print(img)
result = inference_detector(model, img)
show_result_pyplot(model, img, result, score_thr=0.3)
|
test_example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/QuickLearner171998/CapsNet/blob/master/Caps_CIFAR.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="utLpDVlpcwGF" colab_type="text"
# ## Setup
# + id="kSRoeZsBjihr" colab_type="code" outputId="33c734e2-46bd-41e7-bbf5-bedb10ce42ba" colab={"base_uri": "https://localhost:8080/", "height": 34}
import torch
print(torch.__version__)
# + colab_type="code" id="jFNhTBo-8S_F" colab={}
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
from torch.optim import Adam
from torchvision import datasets, transforms
from time import time
USE_CUDA = True
# + [markdown] colab_type="text" id="6nQlfiY0w1Gn"
# ## CIFAR-10 data loader/generator.
#
# Code below setups image generators from folder './data'
#
# Normalization values for CIFAR10 are taken from pytorch website (usual normalization values for the task).
# + colab_type="code" id="OdImV-LJwuOL" colab={}
class Cifar10:
def __init__(self, batch_size):
dataset_transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.4914, 0.4822, 0.4465), (0.247, 0.243, 0.261))
])
train_dataset = datasets.CIFAR10('./data', train=True, download=True, transform=dataset_transform)
test_dataset = datasets.CIFAR10('./data', train=False, download=True, transform=dataset_transform)
self.train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
self.test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=batch_size, shuffle=True)
# + [markdown] colab_type="text" id="YJry2wSsHUa8"
# ## Network
#
# Recall the architecture of CapsNet. This tutorial walks you through building process of it. Note that actual values of parameters such as "number of capsules", "number of filters in the first layer" etc. are not taken from MNIST implementation in the original paper, but instead from CIFAR10 implementation.
# + [markdown] colab_type="text" id="NhW37DmbH-7N"
# ### Pre-capsule layer
#
# This is a usual convolution layer that extracts basic features from images.
# + colab_type="code" id="N1afD72K8S_X" colab={}
class ConvLayer(nn.Module):
def __init__(self, in_channels=3, out_channels=256, kernel_size=9):
super(ConvLayer, self).__init__()
self.conv = nn.Conv2d(in_channels=in_channels,
out_channels=out_channels,
kernel_size=kernel_size,
stride=1
)
def forward(self, x):
return F.relu(self.conv(x))
# + [markdown] colab_type="text" id="tB21rTXeICUI"
# ### First capsule layer (PrimaryCaps)
# + [markdown] colab_type="text" id="PiDlqFB94Cad"
# This is the second layer of the network and the first one which contains capsules (recall that capsules are just groups of neurons).
#
# The squash operation is the following one:
#
# \begin{align}
# v_j & = \frac{(\|s_j\|^2)}{(1 + \|s_j\|^2)} \frac{s_j}{\|s_j\|}\\
# \end{align}
#
# It takes a vector s_j as input, normalizes it to unit norm and then adds some non-linearity so that large vectors become close to 1 and small vectors close to zero. Recall that it is needed to enforce the property of v_j's norm being the probability (or certainty) that object is detected by the capsule v_j.
# + colab_type="code" id="55zyRgn18S_c" colab={}
class PrimaryCaps(nn.Module):
def __init__(self, num_capsules=8, in_channels=256, out_channels=64, kernel_size=9):
super(PrimaryCaps, self).__init__()
self.capsules = nn.ModuleList([
nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=kernel_size, stride=2, padding=0)
for _ in range(num_capsules)])
def forward(self, x):
u = [capsule(x) for capsule in self.capsules]
u = torch.stack(u, dim=1)
u = u.view(x.size(0), 64 * 8 * 8, -1)
return self.squash(u)
def squash(self, input_tensor):
squared_norm = (input_tensor ** 2).sum(-1, keepdim=True)
output_tensor = squared_norm * input_tensor / ((1. + squared_norm) * torch.sqrt(squared_norm))
return output_tensor
# + [markdown] colab_type="text" id="mtw2-UyJIHQ4"
# ### Second capsule layer (DigitCaps)
# + [markdown] colab_type="text" id="_EUmV1wa3-G1"
# This is the final layer of the network and the one that contains digit-capsules (or in case of CIFAR10 - class-capsules) which predict the class on the image.
#
# Below you may see the dynamic routing algorithm from the original paper under the forward section of the layer.
#
# 
# + colab_type="code" id="Lew0uSA-8S_g" colab={}
class DigitCaps(nn.Module):
def __init__(self, num_capsules=10, num_routes=64 * 8 * 8, in_channels=8, out_channels=16):
super(DigitCaps, self).__init__()
self.in_channels = in_channels
self.num_routes = num_routes
self.num_capsules = num_capsules
self.W = nn.Parameter(torch.randn(1, num_routes, num_capsules, out_channels, in_channels))
def forward(self, x):
batch_size = x.size(0)
x = torch.stack([x] * self.num_capsules, dim=2).unsqueeze(4)
W = torch.cat([self.W] * batch_size, dim=0)
u_hat = torch.matmul(W, x)
b_ij = Variable(torch.zeros(1, self.num_routes, self.num_capsules, 1))
if USE_CUDA:
b_ij = b_ij.cuda()
num_iterations = 3
for iteration in range(num_iterations):
c_ij = F.softmax(b_ij)
c_ij = torch.cat([c_ij] * batch_size, dim=0).unsqueeze(4)
s_j = (c_ij * u_hat).sum(dim=1, keepdim=True)
v_j = self.squash(s_j)
if iteration < num_iterations - 1:
a_ij = torch.matmul(u_hat.transpose(3, 4), torch.cat([v_j] * self.num_routes, dim=1))
b_ij = b_ij + a_ij.squeeze(4).mean(dim=0, keepdim=True)
return v_j.squeeze(1)
def squash(self, input_tensor):
squared_norm = (input_tensor ** 2).sum(-1, keepdim=True)
output_tensor = squared_norm * input_tensor / ((1. + squared_norm) * torch.sqrt(squared_norm))
return output_tensor
# + [markdown] colab_type="text" id="TwrZ5H7qIUWn"
# ### Reconstruction part of network (decoder)
# + [markdown] colab_type="text" id="3vjTImHJ5rQq"
# This is the second task for the network, namely, to reconstruct the image from the final class-capsules.
#
# This is a useful technique of regularization to prevent overfitting and also to enforce the property of capsules representing the 'instantiation parameters' of the object. In other words, final capsule should contain information about the class it predicts and that information (implicitly) may be: rotation angle, distortion, illumination etc.
#
# The reconstruction is done by a simple decoder (stack of fully-connected layers). Below is the picture for MNIST.
#
# 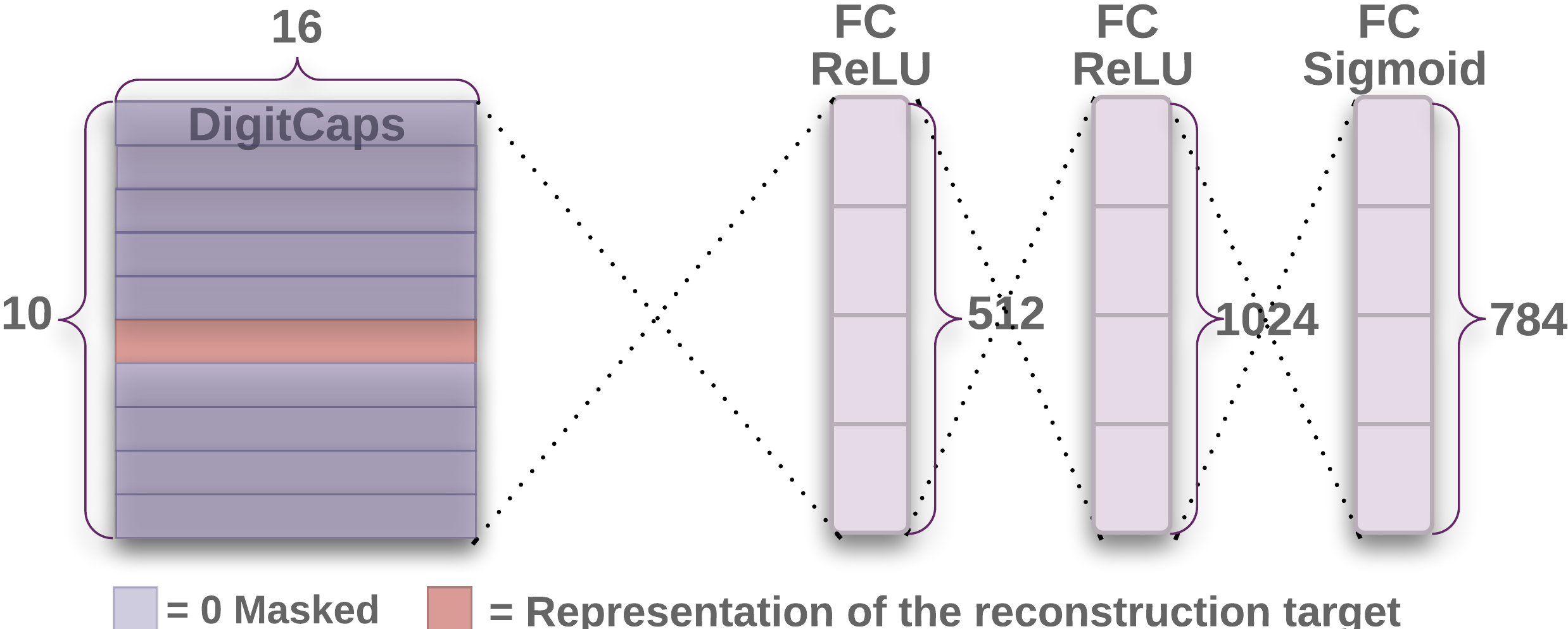
# + colab_type="code" id="Wr4UA8_k8S_l" colab={}
class Decoder(nn.Module):
def __init__(self):
super(Decoder, self).__init__()
self.reconstraction_layers = nn.Sequential(
nn.Linear(16 * 10, 512),
nn.ReLU(inplace=True),
nn.Linear(512, 1024),
nn.ReLU(inplace=True),
nn.Linear(1024, 1024*3),
nn.Sigmoid()
)
def forward(self, x, data):
classes = torch.sqrt((x ** 2).sum(2))
classes = F.softmax(classes)
_, max_length_indices = classes.max(dim=1)
masked = Variable(torch.sparse.torch.eye(10))
if USE_CUDA:
masked = masked.cuda()
masked = masked.index_select(dim=0, index=Variable(max_length_indices.squeeze(1).data))
reconstructions = self.reconstraction_layers((x * masked[:, :, None, None]).view(x.size(0), -1))
reconstructions = reconstructions.view(-1, 3, 32, 32)
return reconstructions, masked
# + [markdown] colab_type="text" id="KWHxjIKjIaYg"
# ### Full network (CapsNet)
# + [markdown] colab_type="text" id="gYDG4nCl7l5Q"
# This is a final forward pass for the whole network. The only new part here is the custom loss from the original paper.
#
# 
# + colab_type="code" id="9maeKxss8S_p" colab={}
class CapsNet(nn.Module):
def __init__(self):
super(CapsNet, self).__init__()
self.conv_layer = ConvLayer()
self.primary_capsules = PrimaryCaps()
self.digit_capsules = DigitCaps()
self.decoder = Decoder()
self.mse_loss = nn.MSELoss()
def forward(self, data):
output = self.digit_capsules(self.primary_capsules(self.conv_layer(data)))
reconstructions, masked = self.decoder(output, data)
return output, reconstructions, masked
def loss(self, data, x, target, reconstructions):
return self.margin_loss(x, target) + self.reconstruction_loss(data, reconstructions)
def margin_loss(self, x, labels, size_average=True):
batch_size = x.size(0)
v_c = torch.sqrt((x**2).sum(dim=2, keepdim=True))
left = (F.relu(0.9 - v_c)**2).view(batch_size, -1)
right = (F.relu(v_c - 0.1)**2).view(batch_size, -1)
loss = labels * left + 0.5 * (1.0 - labels) * right
loss = loss.sum(dim=1).mean()
return loss
def reconstruction_loss(self, data, reconstructions):
loss = self.mse_loss(reconstructions.view(reconstructions.size(0), -1), data.view(reconstructions.size(0), -1))
return loss * 0.0005
# + [markdown] colab_type="text" id="dpK01eKY8JHS"
# Here the model is compiled with Adam optimizer with basic parameters.
# + colab_type="code" id="4IZH_lMV8S_s" colab={}
capsule_net = CapsNet()
if USE_CUDA:
capsule_net = capsule_net.cuda()
optimizer = Adam(capsule_net.parameters())
# + [markdown] colab_type="text" id="PF6hxTxDHrsk"
# ## Training
# + [markdown] colab_type="text" id="zoBoVHvR8VeX"
# Note that one epoch takes a lot of time even on GPU, so don't rush and plan everything ahead and try to justify your ideas prior to implementing them.
# + colab_type="code" id="goSEK6q28S_y" outputId="7a9aa26f-e9b9-479b-a0d3-33d516962c3b" colab={"base_uri": "https://localhost:8080/", "height": 1000}
batch_size = 8
# dataset = Mnist(batch_size)
dataset = Cifar10(batch_size)
n_epochs = 5
for epoch in range(n_epochs):
ep_start = time()
capsule_net.train()
train_loss = 0
train_accuracy = 0
for batch_id, (data, target) in enumerate(dataset.train_loader):
st = time()
target = torch.sparse.torch.eye(10).index_select(dim=0, index=target)
data, target = Variable(data), Variable(target)
if USE_CUDA:
data, target = data.cuda(), target.cuda()
optimizer.zero_grad()
output, reconstructions, masked = capsule_net(data)
loss = capsule_net.loss(data, output, target, reconstructions)
loss.backward()
optimizer.step()
train_loss = train_loss+loss.data
tr_accuracy = sum(np.argmax(masked.data.cpu().numpy(), 1) ==
np.argmax(target.data.cpu().numpy(), 1)) / float(batch_size)
train_accuracy += tr_accuracy
if batch_id % 10 == 0 or batch_id == 99:
print ("train accuracy [batch {}]:".format(batch_id), tr_accuracy)
print ("Train loss:{}\n".format(loss.data))
en = time()
# print 'Sec per batch', round(en-st, 2)
ep_end = time()
print ('Total train loss', train_loss / len(dataset.train_loader))
print ('Total train accuracy', train_accuracy / len(dataset.train_loader))
print ('Total time for training an epoch: {}'.format(int(ep_end - ep_start)) )
capsule_net.eval()
test_loss = 0
test_accuracy = 0
for batch_id, (data, target) in enumerate(dataset.test_loader):
target = torch.sparse.torch.eye(10).index_select(dim=0, index=target)
data, target = Variable(data), Variable(target)
if USE_CUDA:
data, target = data.cuda(), target.cuda()
output, reconstructions, masked = capsule_net(data)
loss = capsule_net.loss(data, output, target, reconstructions)
test_loss += loss.data
ts_accuracy = sum(np.argmax(masked.data.cpu().numpy(), 1) ==
np.argmax(target.data.cpu().numpy(), 1)) / float(batch_size)
test_accuracy += ts_accuracy
if batch_id % 25 == 0 or batch_id == 99:
print ("test accuracy [batch {}]:".format(batch_id), ts_accuracy)
print ('Total test loss', test_loss / len(dataset.test_loader))
print ('Total test accuracy', test_accuracy / len(dataset.test_loader))
# + [markdown] colab_type="text" id="XaYfSSjpHyDf"
# ## Reconstructions
# + [markdown] colab_type="text" id="2MXG6YWW8w2k"
# Here you can view the reconstructions obtained by your CapsNet. Nothing special here, just fun to visualize them. Actually, for mnist the reconstructions are great, however for CIFAR10 they are rubbish (see the original paper for clues on that).
#
# Be careful when running reconstructions after `keyboard_interrupt`, because this may result in wrong input-target values.
# + colab_type="code" id="1UjRCmmI8S_7" colab={}
import matplotlib
import matplotlib.pyplot as plt
def plot_images_separately(images):
"Plot the six MNIST images separately."
fig = plt.figure()
for j in range(1, 7):
ax = fig.add_subplot(1, 6, j)
ax.matshow(images[j-1], cmap = matplotlib.cm.binary)
plt.xticks(np.array([]))
plt.yticks(np.array([]))
plt.show()
# + colab_type="code" id="F5_f1El78S_9" outputId="a1d68327-bff3-4d93-f7c0-cbdb450e863e" colab={"base_uri": "https://localhost:8080/", "height": 85}
plot_images_separately(data[:6,0].data.cpu().numpy())
# + colab_type="code" id="sqg4U_AJ8TAB" outputId="d4b5de8a-8d9a-48c5-af46-7a428a07f390" colab={"base_uri": "https://localhost:8080/", "height": 85}
plot_images_separately(reconstructions[:6,0].data.cpu().numpy())
# + [markdown] colab_type="text" id="pWTldL4t9QYt"
# ### To-Do
# + [markdown] colab_type="text" id="XBmwmhZP9UDs"
# - Stack more convolutional layers before capsule layers.
# - Increase the size of the capsule layers (more capsules, larger capsules etc.). Note that it may take a lot of time.
# - Play with number of routing iterations in forward pass.
# - Play with kernel size of convolutions in the first layer (don't forget to change parameters of subsequent layers).
# - Play with kernel size of capsules in the second layer (again, pay attention to the parameters of subsequent computations).
#
# - Try different variants of original implementation's loss function (change m+, m-, lambda, get rid of square etc.).
# - Try different loss functions (make it pure Hinge or pure MSE, maybe even cross-entropy!).
# - Try different implementation of capsules (not usual convolution operation, but maybe fully connected groups of neurons).
# - Try different non-linearities for capsules (changing ^2 to ^4 doesn't count!).
# - Try different weights for reconstruction loss.
#
#
# + colab_type="code" id="DBjxzFCQ9SxO" colab={}
|
Caps_CIFAR.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] nbsphinx="hidden"
# # Continuous Signals
#
# *This Jupyter notebook is part of a [collection of notebooks](../index.ipynb) in the bachelors module Signals and Systems, Communications Engineering, Universität Rostock. Please direct questions and suggestions to [<EMAIL>](mailto:<EMAIL>).*
# -
# ## Standard Signals
#
# Certain [signals](https://en.wikipedia.org/wiki/Signal_%28electrical_engineering%29) play an important role in the theory and practical application of [signal processing](https://en.wikipedia.org/wiki/Signal_processing). They emerge from the theory of signals and systems, are used to characterize the properties of linear time-invariant (LTI) systems or frequently occur in practical applications. These standard signals are introduced and illustrated in the following. The treatise is limited to one-dimensional deterministic time- and amplitude-continuous signals.
# ### Complex Exponential Signal
#
# The complex exponential signal over time $t$ is defined by the [complex exponential function](https://en.wikipedia.org/wiki/Exponential_function#Complex_plane)
#
# \begin{equation}
# x(t) = e^{s t}
# \end{equation}
#
# where $s = \sigma + j \omega$ denotes the complex frequency with $\sigma, \omega \in \mathbb{R}$ and $j$ the imaginary unit $(j^2=-1)$. The signal is often used as a generalized representation of harmonic signals. Using [Euler's formula](https://en.wikipedia.org/wiki/Euler's_formula) above definition can be reformulated as
#
# \begin{equation}
# x(t) = e^{(\sigma + j \omega) t} = e^{\sigma t} \cos(\omega t) + j e^{\sigma t} \sin(\omega t)
# \end{equation}
#
# The real/imaginary part of the exponential signal is given by a weighted cosine/sine with angular frequency $\omega = 2 \pi f$. For $t>0$, the time-dependent weight $e^{\sigma t}$ is
#
# * exponentially decaying over time for $\sigma < 0$,
# * constantly one for $\sigma = 0$,
# * exponentially growing over time for $\sigma > 0$,
#
# and vice-versa for $t<0$. The complex exponential signal is used to model harmonic signals with constant or exponentially decreasing/increasing amplitude.
# **Example**
#
# The following example illustrates the complex exponential signal and its parameters. The Python module [SymPy](http://docs.sympy.org/latest/index.html) is used for this purpose. It provides functionality for symbolic variables and functions, as well as their calculus. The required symbolic variables need to be defined explicitly before usage. In the example $t$, $\omega$ and $\sigma$ are defined as real-valued symbolic variables, followed by the definition of the exponential signal.
# +
import sympy as sym
# %matplotlib inline
sym.init_printing()
t, sigma, omega = sym.symbols('t sigma omega', real=True)
s = sigma + 1j*omega
x = sym.exp(s*t)
x
# -
# Now specific values for the complex frequency $s = \sigma + j \omega$ are considered for illustration. For this purpose a new signal is defined by substituting both $\sigma$ and $\omega$ with specific values. The real and imaginary part of the signal is plotted for illustration.
# +
y = x.subs({omega: 10, sigma: -.1})
sym.plot(sym.re(y), (t, 0, 2*sym.pi), ylabel=r'Re{$e^{st}$}')
sym.plot(sym.im(y), (t, 0, 2*sym.pi), ylabel=r'Im{$e^{st}$}');
# -
# **Exercise**
#
# * Try other values for `omega` and `sigma` to create signals with increasing/constant/decreasing amplitudes and different angular frequencies.
# ### Dirac Impulse
#
# The Dirac impulse is one of the most important signals in the theory of signals and systems. It is used for the characterization of LTI systems and the modeling of impulse-like signals. The Dirac impulse is defined by way of the [Dirac delta function](https://en.wikipedia.org/wiki/Dirac_delta_function) which is not a function in the conventional sense. It is a generalized function or *distribution*. The Dirac impulse is denoted as $\delta(t)$. The Dirac delta function is defined by its effect on other functions. A rigorous treatment is beyond the scope of this course material. Please refer to the literature for a detailed discussion of the mathematical foundations of the Dirac delta distribution. Fortunately it is suitable to consider only certain properties for its application in signal processing. The most relevant ones are
#
# 1. **Sifting property**
# \begin{equation}
# \int_{-\infty}^{\infty} \delta(t) \cdot x(t) = x(0)
# \end{equation}
# where $x(t)$ needs to be differentiable at $t=0$. The sifting property implies $\int_{-\infty}^{\infty} \delta(t) = 1$.
#
# 2. **Multiplication**
# \begin{equation}
# x(t) \cdot \delta(t) = x(0) \cdot \delta(t)
# \end{equation}
# where $x(t)$ needs to be differentiable at $t=0$.
#
# 3. **Linearity**
# \begin{equation}
# a \cdot \delta(t) + b \cdot \delta(t) = (a+b) \cdot \delta(t)
# \end{equation}
#
# 4. **Scaling**
# \begin{equation}
# \delta(a t) = \frac{1}{|a|} \delta(t)
# \end{equation}
# where $a \in \mathbb{R} \setminus 0$. This implies that the Dirac impulse is a function with even symmetry.
#
# 5. **Derivation**
# \begin{equation}
# \int_{-\infty}^{\infty} \frac{d \delta(t)}{dt} \cdot x(t) \; dt = - \frac{d x(t)}{dt} \bigg\vert_{t = 0}
# \end{equation}
#
# 6. **Convolution**
#
# Generalization of the sifting property yields
# \begin{equation}
# \int_{-\infty}^{\infty} \delta(\tau) \cdot x(t - \tau) \, d\tau = x(t)
# \end{equation}
#
# This operation is known as [convolution](https://en.wikipedia.org/wiki/Convolution) and will be introduced later in more detail. It may be concluded already here that the Dirac delta function constitutes the neutral element of the convolution.
#
# It is important to note that the product $\delta(t) \cdot \delta(t)$ of two Dirac impulses is not defined.
# **Example**
#
# This example illustrates some of the basic properties of the Dirac impulse. Let's first define a Dirac impulse by way of the Dirac delta function
delta = sym.DiracDelta(t)
delta
# Now let's check the sifting property by defining an arbitrary signal (function) $f(t)$ and integrating over its product with the Delta impulse
f = sym.Function('f')(t)
sym.integrate(delta*f, (t, -sym.oo, sym.oo))
# **Exercise**
#
# * Derive the sifting property for a shifted Dirac impulse $\delta(t-\tau)$ and check your results by modifying above example.
# ### Heaviside Signal
#
# The Heaviside signal is defined by the [Heaviside step function](https://en.wikipedia.org/wiki/Heaviside_step_function)
#
# \begin{equation}
# \epsilon(t) = \begin{cases} 0 & t<0 \\ \frac{1}{2} & t=0 \\ 1 & t > 0 \end{cases}
# \end{equation}
#
# Note that alternative definitions exist, which differ with respect to the value of $\epsilon(t)$ at $t=0$. The Heaviside signal may be used to represent a signal that switches on at a specified time and stays switched on indefinitely. The Heaviside signal can be related to the Dirac impulse by
#
# \begin{equation}
# \epsilon(t) = \int_{-\infty}^{t} \delta(\tau) \; d\tau
# \end{equation}
# **Example**
#
# In the following, a Heaviside signal $\epsilon(t)$ is defined and plotted. Note that `Sympy` denotes the Heaviside function by $\theta(t)$.
step = sym.Heaviside(t)
step
sym.plot(step, (t, -2, 2), ylim=[-0.2, 1.2], ylabel=r'$\epsilon(t)$');
# Let's construct a harmonic signal $\cos(\omega t)$ with $\omega=2$ which is switched on at $t=0$. Considering the definition of the Heaviside function, the desired signal is given as
#
# \begin{equation}
# x(t) = \cos(\omega t) \cdot \epsilon(t)
# \end{equation}
x = sym.cos(omega*t) * sym.Heaviside(t)
sym.plot(x.subs(omega,2), (t, -2, 10), ylim=[-1.2, 1.2], ylabel=r'$x(t)$');
# ### Rectangular Signal
#
# The rectangular signal is defined by the [rectangular function](https://en.wikipedia.org/wiki/Rectangular_function)
#
# \begin{equation}
# \text{rect}(t) = \begin{cases} 1 & |t| < \frac{1}{2} \\ \frac{1}{2} & |t| = \frac{1}{2} \\ 0 & |t| > \frac{1}{2} \end{cases}
# \end{equation}
#
# Its time limits and amplitude are chosen such that the area under the function is $1$.
#
# Note that alternative definitions exist, which differ with respect to the value of $\text{rect}(t)$ at $t = \pm \frac{1}{2}$. The rectangular signal is used to represent a signal which has finite duration, respectively is switched on for a limited period of time. The rectangular signal can be related to the Heaviside signal by
#
# \begin{equation}
# \text{rect}(t) = \epsilon \left(t + \frac{1}{2} \right) - \epsilon \left(t - \frac{1}{2} \right)
# \end{equation}
# **Example**
#
# The Heaviside function is used to define a rectangular function in `Sympy`. This function is then used as rectangular signal.
class rect(sym.Function):
@classmethod
def eval(cls, arg):
return sym.Heaviside(arg + sym.S.Half) - sym.Heaviside(arg - sym.S.Half)
sym.plot(rect(t), (t, -1, 1), ylim=[-0.2, 1.2], ylabel=r'rect$(t)$');
# **Exercise**
#
# * Use $\text{rect}(t)$ to construct a harmonic signal $\cos(\omega t)$ with $\omega=2$ which is switched on at $t=-\frac{1}{2}$ and switched off at $t=+\frac{1}{2}$.
# ### Sign Signal
#
# The sign signal is defined by the [sign/signum function](https://en.wikipedia.org/wiki/Sign_function) which evaluates the sign of its argument
#
# \begin{equation}
# \text{sgn}(t) = \begin{cases} 1 & t>0 \\ 0 & t=0 \\ -1 & t < 0 \end{cases}
# \end{equation}
#
# The sign signal is useful to represent the absolute value of a real-valued signal $x(t) \in \mathbb{R}$ by a multiplication
#
# \begin{equation}
# |x(t)| = x(t) \cdot \text{sgn}(x(t))
# \end{equation}
#
# It is related to the Heaviside signal by
#
# \begin{equation}
# \text{sgn}(t) = 2 \cdot \epsilon(t) - 1
# \end{equation}
#
# when following above definition with $\epsilon(0)=\frac{1}{2}$.
# **Example**
#
# The following example illustrates the sign signal $\text{sgn}(t)$. Note that the sign function is represented as $\text{sign}(t)$ in `Sympy`.
sgn = sym.sign(t)
sgn
sym.plot(sgn, (t, -2, 2), ylim=[-1.2, 1.2], ylabel=r'sgn$(t)$');
# **Exercise**
#
# * Check the values of $\text{sgn}(t)$ for $t \to 0^-$, $t = 0$ and $t \to 0^+$ as implemented in `SymPy`. Do they conform to above definition?
# + [markdown] nbsphinx="hidden"
# **Copyright**
#
# This notebook is provided as [Open Educational Resource](https://en.wikipedia.org/wiki/Open_educational_resources). Feel free to use the notebook for your own purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Sascha Spors, Continuous- and Discrete-Time Signals and Systems - Theory and Computational Examples*.
|
continuous_signals/standard_signals.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
import pandas as pd
import numpy as np
import os
import math
import graphlab
import graphlab as gl
import graphlab.aggregate as agg
from graphlab import SArray
'''钢炮'''
path = '/home/zongyi/bimbo_data/'
train = gl.SFrame.read_csv(path + 'train_lag5_w8.csv', verbose=False)
town = gl.SFrame.read_csv(path + 'towns.csv', verbose=False)
train = train.join(town, on=['Agencia_ID','Producto_ID'], how='left')
train = train.fillna('t_c',1)
train = train.fillna('tcc',0)
train = train.fillna('tp_sum',0)
train = train.fillna('n_t',0)
# del train['Town']
del train['id']
del train['Venta_uni_hoy']
del train['Venta_hoy']
del train['Dev_uni_proxima']
del train['Dev_proxima']
del train['Demanda_uni_equil']
relag_train = gl.SFrame.read_csv(path + 're_lag_train.csv', verbose=False)
train = train.join(relag_train, on=['Cliente_ID','Producto_ID','Semana'], how='left')
train = train.fillna('re_lag1',0)
train = train.fillna('re_lag2',0)
train = train.fillna('re_lag3',0)
train = train.fillna('re_lag4',0)
train = train.fillna('re_lag5',0)
train['re_sum'] = (train['re_lag1'] + train['re_lag2'] + train['re_lag3'] + train['re_lag4'] + train['re_lag5'])/5
del relag_train
pd = gl.SFrame.read_csv(path + 'products.csv', verbose=False)
train = train.join(pd, on=['Producto_ID'], how='left')
train = train.fillna('prom',0)
train = train.fillna('weight',0)
train = train.fillna('pieces',1)
train = train.fillna('w_per_piece',0)
train = train.fillna('healthy',0)
train = train.fillna('drink',0)
del pd
client = gl.SFrame.read_csv(path + 'clients.csv', verbose=False)
train = train.join(client, on=['Cliente_ID'], how='left')
del client
del train['Semana']
del train['Canal_ID']
# del train['tcc']
del train['re_lag1']
del train['re_lag2']
del train['re_lag3']
del train['re_lag4']
del train['re_lag5']
del train['prom']
del train['healthy']
del train['drink']
del train['brand']
# del train['week_times']
print train.column_names()
print len(train.column_names())
train.save(path+'train_fs_w8.csv',format='csv')
# +
from IPython.core.pylabtools import figsize
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
sns.set_style('darkgrid', {'grid.color': '.8','grid.linestyle': u'--'})
# %matplotlib inline
figsize(12, 6)
plt.bar(w['id'], w['count'], tick_label=w['name'])
plt.xticks(rotation=45)
# -
# +
path = '/home/zongyi/bimbo_data/'
test = gl.SFrame.read_csv(path + 'test_lag5_w9.csv', verbose=False)
# -
town = gl.SFrame.read_csv(path + 'towns.csv', verbose=False)
test = test.join(town, on=['Agencia_ID','Producto_ID'], how='left')
test = test.fillna('t_c',1)
test = test.fillna('tcc',0)
test = test.fillna('tp_sum',0)
test = test.fillna('n_t',0)
# del test['Town']
# +
relag_test = gl.SFrame.read_csv(path + 're_lag_test.csv', verbose=False)
test = test.join(relag_test, on=['Cliente_ID','Producto_ID','Semana'], how='left')
test = test.fillna('re_lag1',0)
test = test.fillna('re_lag2',0)
test = test.fillna('re_lag3',0)
test = test.fillna('re_lag4',0)
test = test.fillna('re_lag5',0)
def f(x):
if x['Semana']==10:
a = (x['re_lag1'] + x['re_lag2'] + x['re_lag3'] + x['re_lag4'] + x['re_lag5'])/5
if x['Semana']==11:
a = (x['re_lag2'] + x['re_lag3'] + x['re_lag4'] + x['re_lag5'])/4
return a
test['re_sum'] = test[['Semana','re_lag1', 're_lag2', 're_lag3','re_lag4','re_lag5']].apply(f)
# test['re_sum'] = (test['re_lag1'] + test['re_lag2'] + test['re_lag3'] + test['re_lag4'] + test['re_lag5'])/5
del test['re_lag1']
del test['re_lag2']
del test['re_lag3']
del test['re_lag4']
del test['re_lag5']
# -
pd = gl.SFrame.read_csv(path + 'products.csv', verbose=False)
test = test.join(pd, on=['Producto_ID'], how='left')
test = test.fillna('prom',0)
test = test.fillna('weight',0)
test = test.fillna('pieces',1)
test = test.fillna('w_per_piece',0)
test = test.fillna('healthy',0)
test = test.fillna('drink',0)
del pd
client = gl.SFrame.read_csv(path + 'clients.csv', verbose=False)
test = test.join(client, on=['Cliente_ID'], how='left')
del client
# del test['Semana']
del test['Canal_ID']
# del test['tcc']
# del test['re_lag1']
# del test['re_lag2']
# del test['re_lag3']
# del test['re_lag4']
# del test['re_lag5']
del test['prom']
del test['healthy']
del test['drink']
del test['brand']
print test.column_names()
print len(test.column_names())
test.save(path+'test_fs_w9.csv',format='csv')
|
Bimbo/.ipynb_checkpoints/SELECT__FEATURES-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <a href="https://githubtocolab.com/giswqs/geemap/blob/master/examples/notebooks/52_cartoee_gif.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab"/></a>
#
# Uncomment the following line to install [geemap](https://geemap.org) and [cartopy](https://scitools.org.uk/cartopy/docs/latest/installing.html#installing) if needed. Keep in mind that cartopy can be challenging to install. If you are unable to install cartopy on your computer, you can try Google Colab with this the [notebook example](https://colab.research.google.com/github/giswqs/geemap/blob/master/examples/notebooks/cartoee_colab.ipynb).
#
# See below the commands to install cartopy and geemap using conda/mamba:
#
# ```
# conda create -n carto python=3.8
# conda activate carto
# conda install mamba -c conda-forge
# mamba install cartopy scipy -c conda-forge
# mamba install geemap -c conda-forge
# jupyter notebook
# ```
# # How to create timelapse animations using cartoee
import os
import ee
import geemap
from geemap import cartoee
# %pylab inline
# +
# geemap.update_package()
# -
# ## Create an interactive map
Map = geemap.Map()
Map
# ## Create an ImageCollection
# +
lon = -115.1585
lat = 36.1500
start_year = 1984
end_year = 2011
point = ee.Geometry.Point(lon, lat)
years = ee.List.sequence(start_year, end_year)
def get_best_image(year):
start_date = ee.Date.fromYMD(year, 1, 1)
end_date = ee.Date.fromYMD(year, 12, 31)
image = ee.ImageCollection("LANDSAT/LT05/C01/T1_SR") \
.filterBounds(point) \
.filterDate(start_date, end_date) \
.sort("CLOUD_COVER") \
.first()
return ee.Image(image)
collection = ee.ImageCollection(years.map(get_best_image))
# -
# ## Display a sample image
# +
vis_params = {
"bands": ['B4', 'B3', 'B2'],
"min": 0,
"max": 5000
}
image = ee.Image(collection.first())
Map.addLayer(image, vis_params, 'First image')
Map.setCenter(lon, lat, 8)
Map
# -
# ## Get a sample output image
# +
w = 0.4
h = 0.3
region = [lon-w, lat-h, lon+w, lat+h]
fig = plt.figure(figsize=(10, 8))
# use cartoee to get a map
ax = cartoee.get_map(image, region=region, vis_params=vis_params)
# add gridlines to the map at a specified interval
cartoee.add_gridlines(ax, interval=[0.2, 0.2], linestyle=":")
# add north arrow
north_arrow_dict = {
"text": "N",
"xy": (0.1, 0.3),
"arrow_length": 0.15,
"text_color": "white",
"arrow_color": "white",
"fontsize": 20,
"width": 5,
"headwidth": 15,
"ha": "center",
"va": "center"
}
cartoee.add_north_arrow(ax, **north_arrow_dict)
# add scale bar
scale_bar_dict = {
"length": 10,
"xy": (0.1, 0.05),
"linewidth": 3,
"fontsize": 20,
"color": "white",
"unit": "km",
"ha": "center",
"va": "bottom"
}
cartoee.add_scale_bar_lite(ax, **scale_bar_dict)
ax.set_title(label = 'Las Vegas, NV', fontsize=15)
show()
# -
# ## Create timelapse animations
cartoee.get_image_collection_gif(
ee_ic = collection,
out_dir = os.path.expanduser("~/Downloads/timelapse"),
out_gif = "animation.gif",
vis_params = vis_params,
region = region,
fps = 5,
mp4 = True,
grid_interval = (0.2, 0.2),
plot_title = "Las Vegas, NV",
date_format = 'YYYY-MM-dd',
fig_size = (10, 8),
dpi_plot = 100,
file_format = "png",
north_arrow_dict = north_arrow_dict,
scale_bar_dict = scale_bar_dict,
verbose = True
)
|
examples/notebooks/52_cartoee_gif.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="TOhzfnL3Dwp5" colab_type="text"
# **Portrait Video Segmentation Using Custom Medaipipe Calculator**
# + [markdown] id="4e6dzoC5CFj9" colab_type="text"
# In this demo, we will build a portrait segmentaion aplication using **custom calculators** on **desktop**, using mediapipe. There will be two video file inputs and one video fiile output. Our aim is to **blend** the portrait foreground region into the background video, with the help of segmentaion **mask**. As in the case of android, we will follow the basic segmentation pipeline from **hair segmentaion** example. Since the application uses **gpu** operations, choose a GPU runtime for development and deployment.
# + [markdown] id="m6XRrTgPgCgV" colab_type="text"
# **1. Checkout MediaPipe Github Repository**
#
# The mediapipe **repository** contains many demo applications for android. We will modify the hair_segmentaion application, which contains the basic pipeline for **video segmentaion**.
# + id="0PQ0WAmffiI_" colab_type="code" colab={}
# !git clone https://github.com/google/mediapipe.git
# %cd mediapipe
# !sudo apt install curl gnupg
# !curl -fsSL https://bazel.build/bazel-release.pub.gpg | gpg --dearmor > bazel.gpg
# !sudo mv bazel.gpg /etc/apt/trusted.gpg.d/
# !echo "deb [arch=amd64] https://storage.googleapis.com/bazel-apt stable jdk1.8" | sudo tee /etc/apt/sources.list.d/bazel.list
# !sudo apt update && sudo apt install bazel
# + [markdown] id="hou9qtIzhDPG" colab_type="text"
# **3. Install a JDK (optional)**
#
# Sometimes the **default jdk** version may cause an **error** during android sdk installation in ubuntu. So, install an older version of **openjdk-8** and configure the same as the default version of the system.
# + id="2AAP-r1ogbSp" colab_type="code" colab={}
# !sudo apt install openjdk-8-jdk
# !sudo update-alternatives --config java # Choose OpenJDK 8
# !java -version
# + [markdown] id="duUg0dBmVl5Q" colab_type="text"
# **3. Install OpenCV (optional)**
#
# If opencv is not already installed, run **setup_opencv.sh** to automatically build OpenCV from source and modify MediaPipe’s OpenCV config.
# + id="OOUYEIwDWIaB" colab_type="code" colab={}
# !bash setup_opencv.sh
# + [markdown] id="qnmfyimNXQlm" colab_type="text"
# **4. Install MediaPipe Without Android Studio (SDK & NDK)**
#
# If the android studio is not installed in your system, you can configute mediapipe with **sdk and ndk** by running this script.
# + id="DK1_chxlXbhQ" colab_type="code" colab={}
# !bash setup_android_sdk_and_ndk.sh
# + [markdown] id="z59JKpw0XjgY" colab_type="text"
# **Note:** If Android SDK and NDK are already installed, set **ANDROID_HOME** and **ANDROID_NDK_HOME** paths accordingly.
#
# ```
# export ANDROID_HOME=<path to the Android SDK>
# export ANDROID_NDK_HOME=<path to the Android NDK>
# ```
# + [markdown] id="maPLx3SbZtqn" colab_type="text"
# **6. Modify The Hair Segmentaion Mediapipe Application**
#
# Initially put the **[portrait_segmentation](https://github.com/anilsathyan7/Portrait-Segmentation/blob/master/mediapipe_slimnet/portrait_segmentation.tflite)** tflite file into **models** directory, inside mediapipe folder.
# + [markdown] id="4CMvQZZbaVpi" colab_type="text"
# **A.** Create a new directory called **portrait_segmentation** under **graphs** subdirectory and copy all the files from **hair_segmentation**.
# + id="Q9VOETHjaU4E" colab_type="code" colab={}
# !mkdir mediapipe/graphs/portrait_segmentation
# !cp -r mediapipe/graphs/hair_segmentation/* mediapipe/graphs/portrait_segmentation
# !mv mediapipe/graphs/portrait_segmentation/hair_segmentation_mobile_gpu.pbtxt mediapipe/graphs/portrait_segmentation/portrait_segmentation_mobile_gpu.pbtxt
# + [markdown] id="c1g8bpWRakmg" colab_type="text"
# Rename the pbtxt file(mv command) as **portrait_segmentation_mobile_gpu.pbtxt** and modify the following lines :-
#
# 1. **Number of channels**: 'max_num_channels: 4' in **TfLiteConverterCalculator** to max_num_channels: 3
# 2. **Model name**: 'hair_segmentaion.tflite' in **TfLiteInferenceCalculator** to portrait_segmentation.tflite
#
#
# **B**. Add two new nodes for video file input i.e **OpenCvVideoDecoderCalculator** and one node for video file output i.e **OpenCvVideoEncoderCalculator** in the new pipeline.
#
# ```
# # Decodes an input video file into images and a video header.
# node {
# calculator: "OpenCvVideoDecoderCalculator"
# input_side_packet: "INPUT_FILE_PATH:input_video_path"
# output_stream: "VIDEO:input_video"
# output_stream: "VIDEO_PRESTREAM:input_video_header"
# }
#
# # Decodes an input video file into images and a video header.
# node {
# calculator: "OpenCvVideoDecoderCalculator"
# input_side_packet: "INPUT_FILE_PATH:side_video_path"
# output_stream: "VIDEO:side_video"
# output_stream: "VIDEO_PRESTREAM:side_video_header"
# }
#
# # Encodes the annotated images into a video file, adopting properties specified
# # in the input video header, e.g., video framerate.
# node {
# calculator: "OpenCvVideoEncoderCalculator"
# input_stream: "VIDEO:output_video"
# input_stream: "VIDEO_PRESTREAM:input_video_header"
# input_side_packet: "OUTPUT_FILE_PATH:output_video_path"
# node_options: {
# [type.googleapis.com/mediapipe.OpenCvVideoEncoderCalculatorOptions]: {
# codec: "avc1"
# video_format: "mp4"
# }
# }
# }
# ```
#
# **Note:** The main input should be a video file contaning portrait images and the other one should be a background video.
#
# **C.** Now remove the 'RecolorCalculator' node, and instead add the custom **SeamlessCloningCalculator** into the pipeline.
#
# ```
# # Takes Image, Mask and Background as input and performs
# # poisson blending using opencv library
# node {
# calculator: "SeamlessCloningCalculator"
# input_stream: "IMAGE_CPU:input_video"
# input_stream: "BACKGROUND_CPU:sync_side_video"
# input_stream: "MASK_CPU:portrait_mask_cpu"
# output_stream: "OUTPUT_VIDEO:output_video"
# }
# ```
# **Note:** The idea is to combine the foreground in the image with background using mask, such that portrait foreground blends into the background image seamlessly.
#
# **D**. Use **PacketClonerCalculator** to clone the background video frames when all frames are used up. Also use **ImageFrameToGpuBufferCalculator** and **GpuBufferToImageFrameCalculator** for copying data between CPU and GPU, whenever necessary.
#
# **E**. Now, inside the **BUILD** file in this directory(portrait_segmentation), change the graph name to "**portrait_segmentation_mobile_gpu.pbtxt**".
#
# Also add the **calculator files** inside the **cc_library** section for mobile_calcualators as follows:-
#
# ```
# "//mediapipe/calculators/video:opencv_video_decoder_calculator",
# "//mediapipe/calculators/video:opencv_video_encoder_calculator",
# "//mediapipe/calculators/image:poisson_blending_calculator",
# "//mediapipe/calculators/core:packet_cloner_calculator",
# ```
#
# See the final pbtxt file: [portrait_segmentation_mobile_gpu.pbtxt](https://github.com/anilsathyan7/Portrait-Segmentation/blob/master/mediapipe_slimnet/desktop/portrait_segmentation_mobile_gpu.pbtxt)
#
#
# **F**. Similary, create a new folder called '**portrait_segmentation**' inside example directory at location: '**/mediapipe/examples/desktop/**'.Add the BUILD file inside this directory as shown below.
#
# ```
# licenses(["notice"])
# package(default_visibility = ["//mediapipe/examples:__subpackages__"])
#
# # Linux only
# cc_binary(
# name = "portrait_segmentation_gpu",
# deps = [
# "//mediapipe/examples/desktop:simple_run_graph_main",
# "//mediapipe/examples/desktop:demo_run_graph_main_gpu",
# "//mediapipe/graphs/portrait_segmentation:mobile_calculators",
# ],
# )
# ```
# **Note:** We added a dependency '**simple_run_graph_main**' for executing graph using side packets and video file inputs.
#
# **G.** Add the following dependencies into the **BUILD** file inside **calculators/image** directory.
#
# ```
# cc_library(
# name = "poisson_blending_calculator",
# srcs = ["poisson_blending_calculator.cc"],
# visibility = ["//visibility:public"],
# deps = [
# "//mediapipe/gpu:gl_calculator_helper",
# "//mediapipe/framework:calculator_framework",
# "//mediapipe/framework:calculator_options_cc_proto",
# "//mediapipe/framework:timestamp",
# "//mediapipe/framework/port:status",
# "//mediapipe/framework/deps:file_path",
# "@com_google_absl//absl/time",
# "@com_google_absl//absl/strings",
# "//mediapipe/framework/formats:rect_cc_proto",
# "//mediapipe/framework/port:ret_check",
# "//mediapipe/framework/formats:image_frame",
# "//mediapipe/framework/formats:matrix",
# "//mediapipe/framework/formats:image_frame_opencv",
# "//mediapipe/framework/port:opencv_core",
# "//mediapipe/framework/port:opencv_imgproc",
# "//mediapipe/framework/port:opencv_imgcodecs",
# "//mediapipe/util:resource_util",
# ],
# alwayslink = 1,
# )
# ```
# **Note:** The file **poisson_blending_calculator** refers to our custom seamlesscloning calculator C++ file.
#
# **H.** Add the following lines under cc_library section in the **opencv_linux.BUILD** file, inside the third_party directory.
#
# `"lib/libopencv_photo.so",`
# or
# `"lib/x86_64-linux-gnu/libopencv_photo.so",`
#
# **Note:** Make sure the file exists at the specified path in the system. This ensures that opencv can link the files for seamlesscloning from the module **photo** during build.
# + [markdown] id="6jX_IrmM19_Q" colab_type="text"
# **Seamless Clone Custom Calculator**
#
# A custom calculator can created by defining a new sub-class of the CalculatorBase class, implementing a number of methods, and registering the new sub-class with Mediapipe. At a minimum, a new calculator must implement the following methods - **GetContract, Open, Process and Close.**
#
# The **Process** method continously takes inputs, processes them and produce outputs. We will write most of our code for seamless cloning within this method; whereas in **GetContract** we just specify the expected types of inputs and outputs of the calculator.
# + [markdown] id="HKoKbmQV2Gr_" colab_type="text"
# *Steps for seamless cloning:-*
#
#
# 1. Convert the mask to binary Mat format with 0's representing background and 1 foreground.
#
# 2. Resize the mask and background image to the size of the input image.
#
# 3. Dilate the mask to include neighbouring background regions around borders.
#
# 4. Find the largest contour and corresponding bounding rectangle from mask.
#
# 5. Crop out the ROI from input and mask image using the bounding rectangle.
#
# 6. Set the foreground pixels values of the mask to 255.
#
# 7. Calculate the location of the center of the input roi image in the background.
#
# 8. Perform seamless cloning of input on background, using mask and return the result.
#
# Thus, the seamless clone calculator takes **three inputs** as CPU ImageFrame's i.e input image, background image and segmentaion mask. It produces a single ouput image frame, representing the **blended image** in CPU. Finally, we save the results into a video file using **OpenCvVideoEncoderCalculator**.
#
# Copy the calculator file '**[poisson_blending_calculator.cc](https://github.com/anilsathyan7/Portrait-Segmentation/blob/master/mediapipe_slimnet/desktop/poisson_blending_calculator.cc)**' into the directory - **mediapipe/calculators/image**.
#
#
# + [markdown] id="hOkkPlkHW5Rn" colab_type="text"
# **Build and Run**
# + [markdown] id="cLeeSDzdK1t5" colab_type="text"
# To build the portrait_segmentation_gpu app on **desktop** using bazel, run:
# + id="kUusPEByW896" colab_type="code" colab={}
# !bazel build -c opt --copt -DMESA_EGL_NO_X11_HEADERS --copt -DEGL_NO_X11 mediapipe/examples/desktop/portrait_segmentation:portrait_segmentation_gpu
# + [markdown] id="UYkvtIoILGnA" colab_type="text"
# Now, load two video files (i.e **portrait** and **background**) as inputs, run the application and save the output video.
# + id="ba2BeAeqkkqi" colab_type="code" colab={}
# !GLOG_logtostderr=1 bazel-bin/mediapipe/examples/desktop/portrait_segmentation/portrait_segmentation_gpu --calculator_graph_config_file=/content/mediapipe/mediapipe/graphs/portrait_segmentation/portrait_segmentation_mobile_gpu.pbtxt --input_side_packets=side_video_path=/content/fire_vid.mp4,input_video_path=/content/grandma_vid.mp4,output_video_path=/content/output15.mp4
# + [markdown] id="7-nWK9Sh1gdN" colab_type="text"
# **Note:** If the run failed in a headless set-up(eg. google colab), then modify the file mediapipe/gpu/**gl_context_egl.cc** by removing the option '**EGL_WINDOW_BIT** and rebuild the application.
|
mediapipe_slimnet/desktop/mediapipe_custom_calculator.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# formats: ipynb,jl:hydrogen
# text_representation:
# extension: .jl
# format_name: hydrogen
# format_version: '1.3'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.6.3
# language: julia
# name: julia-1.6
# ---
# %%
using AbstractAlgebra
AbstractAlgebra.PrettyPrinting.set_html_as_latex(true)
using AbstractAlgebra
AbstractAlgebra.PrettyPrinting.set_html_as_latex(true)
eqstr(x) = "\\ \\text{is " * string(x) * "}"
eqstr(x::SetElem) = "=" * sprint(x) do io, x; show(io, "text/latex", x) end
function dispeq(lhs, rhs)
latexstr = "\$\\displaystyle $lhs " * eqstr(rhs) * "\$"
display("text/html", latexstr)
end
function euclidean(f, g, stop = 1)
while true
r = mod(f, g)
iszero(r) && return g
degree(r) ≤ stop && return r
f, g = g, r
end
end
function rootdeg1(f)
C = coefficients(f) |> collect
-first(C)//last(C)
end
function commonroot(f, g)
m = euclidean(f, g, 1)
rootdeg1(m)
end
function revpoly(z, x, f)
m = degree(f)
C = coefficients(f)
sum(a*z^(i-1)*x^(m-i+1) for (i, a) in enumerate(C))
end
function val(h::FracElem, θ, L)
n = L(numerator(h)(θ))
d = L(denominator(h)(θ))
n//d
end
function testval(h::FracElem, θ, β, L)
n = L(numerator(h)(θ))
d = L(denominator(h)(θ))
n == β*d
end
function calcallresults(z, x, f, g)
f_plus = (-1)^degree(f)*f(z - x)
F_plus = resultant(f_plus, g)
β_plus = commonroot(g, f_plus)
f_mult = (-1)^degree(f)*revpoly(z, x, f)
F_mult = resultant(f_mult, g)
β_mult = commonroot(g, f_mult)
K = FractionField(base_ring(z))
B1, α = K["α"]
L1 = ResidueField(B1, numerator(f(z))(α))
B2, β = L1["β"]
L = ResidueField(B2, numerator(g(z))(β))
val_F_plus = val(F_plus, α + β, L)
test_β_plus = testval(β_plus, α + β, β, L)
val_F_mult = val(F_mult, α * β, L)
test_β_mult = testval(β_mult, α * β, β, L)
S_plus = subresultant((-1)^degree(f)*f(z-x), g, 1)
rootS_plus = rootdeg1(S_plus)
F_plus, β_plus, F_mult, β_mult, val_F_plus, test_β_plus, val_F_mult, test_β_mult, S_plus, rootS_plus
end
function dispallresults(z, x, f, g)
F_plus, β_plus, F_mult, β_mult, val_F_plus, test_β_plus, val_F_mult, test_β_mult, S_plus, rootS_plus =
@time calcallresults(z, x, f, g)
flush(stdout)
dispeq("F_\\alpha(x)", f)
dispeq("F_\\beta(x)", g)
dispeq("R_{\\alpha + \\beta}(z)", F_plus)
dispeq("R_{\\alpha + \\beta}(\\alpha + \\beta)", val_F_plus)
dispeq("\\beta_\\mathrm{plus}(z)", β_plus)
dispeq("\\beta_\\mathrm{plus}(\\alpha + \\beta) = \\beta", test_β_plus)
dispeq("R_{\\alpha\\beta}(z)", F_mult)
dispeq("R_{\\alpha\\beta}(\\alpha\\beta)", val_F_mult)
dispeq("\\beta_\\mathrm{mult}(z)", β_mult)
dispeq("\\beta_\\mathrm{mult}(\\alpha\\beta) = \\beta", test_β_mult)
dispeq("\\text{1-subresultant}", S_plus)
dispeq("\\text{root of 1-subresultant}", rootS_plus)
end
safecoeff(f, k) = 0 ≤ k ≤ degree(f) ? coeff(f, k) : zero(base_ring(f))
function subresultant_matrix(p::PolyElem{T}, q::PolyElem{T}, k) where T <: RingElement
check_parent(p, q)
R = parent(p)
m = degree(p)
n = degree(q)
if length(p) == 0 || length(q) == k || m + n < 2k
return zero_matrix(R, 0, 0)
end
M = zero_matrix(R, m + n - 2k, m + n - 2k)
x = gen(R)
for i in 1:n-k
for j in 1:m+n-2k-1
M[i, j] = safecoeff(p, m + (i-1) - (j-1))
end
M[i, end] = x^(n-k-i)*p
end
for i in 1:m-k
for j in 1:m+n-2k-1
M[n-k+i, j] = safecoeff(q, n + (i-1) - (j-1))
end
M[n-k+i, end] = x^(m-k-i)*q
end
return M
end
subresultant(p, q, k) = det(subresultant_matrix(p, q, k))
# %%
R, (a, b, c, p, q, r, s) = ZZ["a", "b", "c", "p", "q", "r", "s"]
K = FractionField(R)
Rz, z = R["z"]
Kz = FractionField(Rz)
Rx, x = Kz["x"]
# %%
f = x^3 + a*x^2 + b*x + c
g = x^4 + p*x^3 + q*x^2 + r*x + s
subresultant_matrix(f, g, 0)
# %%
S0 = sylvester_matrix(f, g)
# %%
subresultant(f, g, 0) == resultant(f, g) == det(S0)
# %% tags=[]
subresultant_matrix(f, g, 1)
# %%
S1 = Rx[
1 a b c 0
0 1 a b c*x
0 0 1 a b*x+c
1 p q r s*x
0 1 p q r*x+s
]
# %%
subresultant(f, g, 1)
# %% tags=[]
subresultant(f, g, 1) == det(S1)
# %%
S2 = Rx[
1 a b*x^2+c*x
0 1 a*x^2+b*x+c
1 p q*x^2+r*x+s
]
# %%
subresultant(f, g, 2)
# %%
subresultant(f, g, 2) == det(S2)
# %%
f = x^3 - a
g = x^4 - p
dispallresults(z, x, f, g)
# %%
subresultant_matrix(-f(z-x), g, 1)
# %%
s1 = Rx[
1 -3z 3z^2 -z^3+a 0
0 1 -3z 3z^2 (-z^3+a)*x
0 0 1 -3z 3z^2*x-z^3+a
1 0 0 0 -p*x
0 1 0 0 -p
]
# %%
S_plus = subresultant(-f(z-x), g, 1)
# %%
subresultant(-f(z-x), g, 1) == det(s1)
# %%
rootS_plus = rootdeg1(S_plus)
dispeq("\\text{root of 1-subresultant}", rootS_plus)
# %% tags=[]
f = x^3 - a
g = x^3 + p*x + q
dispallresults(z, x, f, g)
# %% tags=[]
f = x^3 - a
g = x^3 + p*x + q
dispallresults(z, x, g, f)
# %%
h1 = g(z-x) + f
# %%
(3z)^2*f - 3z*x*h1
# %%
h2 = (3z)^2*f - (3z*x + 3z^2 + p)*h1
# %%
subresultant(f, g(z-x), 1)
# %%
f = x^2 - a
g = x^2 - p
dispallresults(z, x, f, g)
# %%
f = x^2 - a
g = x^3 - p
dispallresults(z, x, f, g)
# %%
f = x^2 - a
g = x^4 - p
dispallresults(z, x, f, g)
# %%
f = x^2 - a
g = x^5 - p
dispallresults(z, x, f, g)
# %%
f = x^3 - a
g = x^3 - p
dispallresults(z, x, f, g)
# %%
f = x^3 - a
g = x^4 - p
dispallresults(z, x, f, g)
# %%
f = x^3 - a
g = x^5 - p
dispallresults(z, x, f, g)
# %%
f = x^3 + a*x + b
g = x^3 + p*x + q
dispallresults(z, x, f, g)
# %%
f = x^2 - a
g = x^3 + p*x^2 + q*x + r
dispallresults(z, x, f, g)
# %%
f = x^3 + a*x + b
g = x^4 + p*x^2 + q*x + r
dispallresults(z, x, f, g)
# %%
|
0023/AbstractAlgebra.jl subresultant examples.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Introduction to Quantum Error Correction via the Repetition Code
# ## Introduction
#
# Quantum computing requires us to encode information in qubits. Most quantum algorithms developed over the past few decades have assumed that these qubits are perfect: they can be prepared in any state we desire, and be manipulated with complete precision. Qubits that obey these assumptions are often known as *logical qubits*.
#
# The last few decades have also seen great advances in finding physical systems that behave as qubits, with better quality qubits being developed all the time. However, the imperfections can never be removed entirely. These qubits will always be much too imprecise to serve directly as logical qubits. Instead, we refer to them as *physical qubits*.
#
# In the current era of quantum computing, we seek to use physical qubits despite their imperfections, by designing custom algorithms and using error mitigation effects. For the future era of fault-tolerance, however, we must find ways to build logical qubits from physical qubits. This will be done through the process of quantum error correction, in which logical qubits are encoded in a a large numbers of physical qubits. The encoding is maintained by constantly putting the physical qubits through a highly entangling circuit. Auxilliary degrees of freedom are also constantly measured, to detect signs of errors and allow their effects to be removed. The operations on the logical qubits required to implement quantum computation will be performed by essentially making small perturbations to this procedure.
#
# Because of the vast amount effort required for this process, most operations performed in fault-tolerant quantum computers will be done to serve the purpose of error detection and correction. So when benchmarking our progress towards fault-tolerant quantum computation, we must keep track of how well our devices perform error correction.
#
# In this chapter we will look at a particular example of error correction: the repetition code. Though not a true example of quantum error correction - it uses physical qubits to encode a logical *bit*, rather than a qubit - it serves as a simple guide to all the basic concepts in any quantum error correcting code. We will also see how it can be run on current prototype devices.
# ## Introduction to the repetition code
# ### The basics of error correction
#
# The basic ideas behind error correction are the same for classical information as for classical information. This allows us to begin by considering a very straightforward example: speaking on the phone. If someone asks you a question to which the answer is 'yes' or 'no', the way you give your response will depend on two factors:
#
# * How important is it that you are understood correctly?
# * How good is your connection?
#
# Both of these can be paramaterized with probabilities. For the first, we can use $P_a$, the maximum acceptable probability of being misunderstood. If you are being asked to confirm a preference for ice cream flavours, and don't mind too much if you get vanilla rather than chocolate, $P_a$ might be quite high. If you are being asked a question on which someone's life depends, however, $P_a$ will be much lower.
#
# For the second we can use $p$, the probability that your answer is garbled by a bad connectiom. For simplicity, let's imagine a case where a garbled 'yes' doesn't simply sound like nonsense, but sounds like a 'no'. And similarly a 'no' is transformed into 'yes'. Then $p$ is the probability that you are completely misunderstood.
#
# A good connection or a relatively unimportant question will result in $p<P_a$. In this case it is fine to simply answer in the most direct way possible: you just say 'yes' or 'no'.
#
# If, however, your connection is poor and your answer is important, we will have $p>P_a$. A single 'yes' or 'no' is not enough in this case. The probability of being misunderstood would be too high. Instead we must encode our answer in a more complex structure, allowing the receiver to decode our meaning despite the possibility of the message being disrupted. The simplest method is the one that many would do without thinking: simply repeat the answer many times. For example say 'yes, yes, yes' instead of 'yes' or 'no, no no' instead of 'no'.
#
# If the receiver hears 'yes, yes, yes' in this case, they will of course conclude that the sender meant 'yes'. If they hear 'no, yes, yes', 'yes, no, yes' or 'yes, yes, no', they will probably conclude the same thing, since there is more positivity than negativity in the answer. To be misunderstood in this case, at least two of the replies need to be garbled. The probability for this, $P$, will be less than $p$. When encoded in this way, the message therefore becomes more likely to be understood. The code cell below shows an example of this.
p = 0.01
P = 3 * p**2 * (1-p) + p**3 # probability of 2 or 3 errors
print('Probability of a single reply being garbled:',p)
print('Probability of a the majority of three replies being garbled:',P)
# If $P<P_a$, this technique solves our problem. If not, we can simply add more repetitions. The fact that $P<p$ above comes from the fact that we need at least two replies to be garbled to flip the majority, and so even the most likely possibilities have a probability of $\sim p^2$. For five repetitions we'd need at least three replies to be garbled to flip the majority, which happens with probability $\sim p^3$. The value for $P$ in this case would then be even lower. Indeed, as we increase the number of repetitions, $P$ will decrease exponentially. No matter how bad the connection, or how certain we need to be of our message getting through correctly, we can acheive it by just repeating our answer enough times.
#
# Though this is a simple example, it contains all the aspects of error correction.
# * There is some information to be sent or stored: In this case, a 'yes' or 'no.
# * The information is encoded in a larger system to protect it against noise: In this case, by repeating the message.
# * The information is finally decoded, mitigating for the effects of noise: In this case, by trusting the majority of the transmitted messages.
#
# This same encoding scheme can also be used for binary, by simply substituting `0` and `1` for 'yes' and 'no. It can therefore also be easily generalized to qubits by using the states $\left|0\right\rangle$ and $\left|1\right\rangle$. In each case it is known as the *repetition code*. Many other forms of encoding are also possible in both the classical and quantum cases, which outperform the repetition code in many ways. However, its status as the simplest encoding does lend it to certain applications. One is exactly what it is used for in Qiskit: as the first and simplest test of implementing the ideas behind quantum error correction.
# ### Correcting errors in qubits
#
# We will now implement these ideas explicitly using Qiskit. To see the effects of imperfect qubits, we simply can use the qubits of the prototype devices. We can also reproduce the effects in simulations. The function below creates a simple noise models in order to do this. These go beyond the simple case dicussed earlier, of a single noise event which happens with a probability $p$. Instead we consider two forms of error that can occur. One is a gate error: an imperfection in any operation we perform. We model this here in a simple way, using so-called depolarizing noise. The effect of this will be, with probabilty $p_{gate}$ ,to replace the state of any qubit with a completely random state. For two qubit gates, it is applied independently to each qubit. The other form of noise is that for measurement. This simply flips between a `0` to a `1` and vice-versa immediately before measurement with probability $p_{meas}$.
# +
from qiskit.providers.aer.noise import NoiseModel
from qiskit.providers.aer.noise.errors import pauli_error, depolarizing_error
def get_noise(p_meas,p_gate):
error_meas = pauli_error([('X',p_meas), ('I', 1 - p_meas)])
error_gate1 = depolarizing_error(p_gate, 1)
error_gate2 = error_gate1.tensor(error_gate1)
noise_model = NoiseModel()
noise_model.add_all_qubit_quantum_error(error_meas, "measure") # measurement error is applied to measurements
noise_model.add_all_qubit_quantum_error(error_gate1, ["x"]) # single qubit gate error is applied to x gates
noise_model.add_all_qubit_quantum_error(error_gate2, ["cx"]) # two qubit gate error is applied to cx gates
return noise_model
# -
# With this we'll now create such a noise model with a probability of $1\%$ for each type of error.
noise_model = get_noise(0.01,0.01)
# Let's see what effect this has when try to store a `0` using three qubits in state $\left|0\right\rangle$. We'll repeat the process `shots=1024` times to see how likely different results are.
# +
from qiskit import QuantumCircuit, execute, Aer
qc0 = QuantumCircuit(3,3,name='0') # initialize circuit with three qubits in the 0 state
qc0.measure(qc0.qregs[0],qc0.cregs[0]) # measure the qubits
# run the circuit with th noise model and extract the counts
counts = execute( qc0, Aer.get_backend('qasm_simulator'),noise_model=noise_model).result().get_counts()
print(counts)
# -
# Here we see that almost all results still come out `'000'`, as they would if there was no noise. Of the remaining possibilities, those with a majority of `0`s are most likely. In total, much less than 100 samples come out with a majority of `1`s. When using this circuit to encode a `0`, this means that $P<1\%$
#
# Now let's try the same for storing a `1` using three qubits in state $\left|1\right\rangle$.
# +
qc1 = QuantumCircuit(3,3,name='0') # initialize circuit with three qubits in the 0 state
qc1.x(qc1.qregs[0]) # flip each 0 to 1
qc1.measure(qc1.qregs[0],qc1.cregs[0]) # measure the qubits
# run the circuit with th noise model and extract the counts
counts = execute( qc1, Aer.get_backend('qasm_simulator'),noise_model=noise_model).result().get_counts()
print(counts)
# -
# The number of samples that come out with a majority in the wrong state (`0` in this case) is again much less than 100, so $P<1\%$. Whether we store a `0` or a `1`, we can retrieve the information with a smaller probability of error than either of our sources of noise.
#
# This was possible because the noise we considered was relatively weak. As we increase $p_{meas}$ and $p_{gate}$, the higher the probability $P$ will be. The extreme case of this is for either of them to have a $50/50$ chance of applying the bit flip error, `x`. For example, let's run the same circuit as before but with $p_{meas}=0.5$ and $p_{gate}=0$.
noise_model = get_noise(0.5,0.0)
counts = execute( qc1, Aer.get_backend('qasm_simulator'),noise_model=noise_model).result().get_counts()
print(counts)
# With this noise, all outcomes occur with equal probability, with differences in results being due only to statistical noise. No trace of the encoded state remains. This is an important point to consider for error correction: sometimes the noise is too strong to be corrected. The optimal approach is to combine a good way of encoding the information you require, with hardware whose noise is not too strong.
# ### Storing qubits
#
# So far, we have considered cases where there is no delay between encoding and decoding. For qubits, this means that there is no significant amount of time that passes between initializing the circuit, and making the final measurements.
#
# However, there are many cases for which there will be a significant delay. As an obvious example, one may wish to encode a quantum state and store it for a long time, like a quantum hard drive. A less obvious but much more important example is performing fault-tolerant quantum computation itself. For this, we need to store quantum states and preserve their integrity during the computation. This must also be done in a way that allows us to manipulate the stored information in any way we need, and which corrects any errors we may introduce when performing the manipulations.
#
# In all cases, we need account for the fact that errors do not only occur when something happens (like a gate or measurement), they also occur when the qubits are idle. Such noise is due to the fact that the qubits interact with each other and their environment. The longer we leave our qubits idle for, the greater the effects of this noise becomes. If we leave them for long enough, we'll encounter a situation like the $p_{meas}=0.5$ case above, where the noise is too strong for errors to be reliably corrected.
#
# The solution is to keep measuring throughout. No qubit is left idle for too long. Instead, information is constantly being extracted from the system to keep track of the errors that have occurred.
#
# For the case of classical information, where we simply wish to store a `0` or `1`, this can be done by just constantly measuring the value of each qubit. By keeping track of when the values change due to noise, we can easily deduce a history of when errors occurred.
#
# For quantum information, however, it is not so easy. For example, consider the case that we wish to encode the logical state $\left|+\right\rangle$. Our encoding is such that
#
#
#
# $$\left|0\right\rangle \rightarrow \left|000\right\rangle,~~~ \left|1\right\rangle \rightarrow \left|111\right\rangle.$$
#
#
#
# To encode the logical $\left|+\right\rangle$ state we therefore need
#
#
#
# $$\left|+\right\rangle=\frac{1}{\sqrt{2}}\left(\left|0\right\rangle+\left|1\right\rangle\right)\rightarrow \frac{1}{\sqrt{2}}\left(\left|000\right\rangle+\left|111\right\rangle\right).$$
#
#
#
# With the repetition encoding that we are using, a z measurement (which distinguishes between the $\left|0\right\rangle$ and $\left|1\right\rangle$ states) of the logical qubit is done using a z measurement of each physical qubit. The final result for the logical measurement is decoded from the physical qubit measurement results by simply looking which output is in the majority.
#
# As mentioned earlier, we can keep track of errors on logical qubits that are stored for a long time by constantly performing z measurements of the physical qubits. However, note that this effectively corresponds to constantly peforming z measurements of the physical qubits. This is fine if we are simply storing a `0` or `1`, but it has undesired effects if we are storing a superposition. Specifically: the first time we do such a check for errors, we will collapse the superposition.
#
# This is not ideal. If we wanted to do some computation on our logical qubit, or is we wish to peform a basis change before final measurement, we need to preserve the superposition. Destroying it is an error. But this is not an error caused by imperfections in our devices. It is an error that we have introduced as part of our attempts to correct errors. And since we cannot hope to recreate any arbitrary superposition stored in our quantum computer, it is an error than cannot be corrected.
#
# For this reason, we must find another way of keeping track of the errors that occur when our logical qubit is stored for long times. This should give us the information we need to detect and correct errors, and to decode the final measurment result with high probability. However, it should not cause uncorrectable errors to occur during the process by collapsing superpositions that we need to preserve.
#
# The way to do this is with the following circuit element.
# +
from qiskit import QuantumRegister, ClassicalRegister
# %config InlineBackend.figure_format = 'svg' # Makes the images look nice
cq = QuantumRegister(2,'code\ qubit\ ')
lq = QuantumRegister(1,'ancilla\ qubit\ ')
sb = ClassicalRegister(1,'syndrome\ bit\ ')
qc = QuantumCircuit(cq,lq,sb)
qc.cx(cq[0],lq[0])
qc.cx(cq[1],lq[0])
qc.measure(lq,sb)
qc.draw(output='mpl')
# -
# Here we have three physical qubits. Two are called 'code qubits', and the other is called an 'ancilla qubit'. One bit of output is extracted, called the syndrome bit. The ancilla qubit is always initialized in state $\left|0\right\rangle$. The code qubits, however, can be initialized in different states. To see what affect different inputs have on the output, we can create a circuit `qc_init` that prepares the code qubits in some state, and then run the circuit `qc_init+qc`.
#
# First, the trivial case: `qc_init` does nothing, and so the code qubits are initially $\left|00\right\rangle$.
# +
qc_init = QuantumCircuit(cq)
(qc_init+qc).draw(output='mpl')
# -
counts = execute( qc_init+qc, Aer.get_backend('qasm_simulator')).result().get_counts()
print('Results:',counts)
# The outcome, in all cases, is `0`.
#
# Now let's try an initial state of $\left|11\right\rangle$.
# +
qc_init = QuantumCircuit(cq)
qc_init.x(cq)
(qc_init+qc).draw(output='mpl')
# -
counts = execute( qc_init+qc, Aer.get_backend('qasm_simulator')).result().get_counts()
print('Results:',counts)
# The outcome in this case is also always `0`. Given the linearity of quantum mechanics, we can expect the same to be true also for any superposition of $\left|00\right\rangle$ and $\left|11\right\rangle$, such as the example below.
# +
qc_init = QuantumCircuit(cq)
qc_init.h(cq[0])
qc_init.cx(cq[0],cq[1])
(qc_init+qc).draw(output='mpl')
# -
counts = execute( qc_init+qc, Aer.get_backend('qasm_simulator')).result().get_counts()
print('Results:',counts)
# The opposite outcome will be found for an initial state of $\left|01\right\rangle$, $\left|10\right\rangle$ or any superposition thereof.
# +
qc_init = QuantumCircuit(cq)
qc_init.h(cq[0])
qc_init.cx(cq[0],cq[1])
qc_init.x(cq[0])
(qc_init+qc).draw(output='mpl')
# -
counts = execute( qc_init+qc, Aer.get_backend('qasm_simulator')).result().get_counts()
print('Results:',counts)
# In such cases the output is always `'1'`.
#
# This measurement is therefore telling us about a collective property of multiple qubits. Specifically, it looks at the two code qubits and determines whether their state is the same or different in the z basis. For basis states that are the same in the z basis, like $\left|00\right\rangle$ and $\left|11\right\rangle$, the measurement simply returns `0`. It also does so for any superposition of these. Since it does not distinguish between these states in any way, it also does not collapse such a superposition.
#
# Similarly, For basis states that are different in the z basis it returns a `1`. This occurs for $\left|01\right\rangle$, $\left|10\right\rangle$ or any superposition thereof.
#
# Now suppose we apply such a 'syndrome measurement' on all pairs of physical qubits in our repetition code. If their state is described by a repeated $\left|0\right\rangle$, a repeated $\left|1\right\rangle$, or any superposition thereof, all the syndrome measurements will return `0`. Given this result, we will know that our states are indeed encoded in the repeated states that we want them to be, and can deduce that no errors have occurred. If some syndrome measurements return `1`, however, it is a signature of an error. We can therefore use these measurement results to determine how to decode the result.
# ### Quantum repetition code
#
# We now know enough to understand exactly how the quantum version of the repetition code is implemented
#
# We can use it in Qiskit by importing the required tools from Ignis.
from qiskit.ignis.verification.topological_codes import RepetitionCode
from qiskit.ignis.verification.topological_codes import lookuptable_decoding
from qiskit.ignis.verification.topological_codes import GraphDecoder
# We are free to choose how many physical qubits we want the logical qubit to be encoded in. We can also choose how many times the syndrome measurements will be applied while we store our logical qubit, before the final readout measurement. Let us start with the smallest non-trivial case: three repetitions and one syndrome measurement round. The circuits for the repetition code can then be created automatically from the using the `RepetitionCode` object from Qiskit-Ignis.
# +
n = 3
T = 1
code = RepetitionCode(n,T)
# -
# With this we can inspect various properties of the code, such as the names of the qubit registers used for the code and ancilla qubits.
# The `RepetitionCode` contains two quantum circuits that implement the code: One for each of the two possible logical bit values. Here are those for logical `0` and `1`, respectively.
# +
# this bit is just needed to make the labels look nice
for reg in code.circuit['0'].qregs+code.circuit['1'].cregs:
reg.name = reg.name.replace('_','\ ') + '\ '
code.circuit['0'].draw(output='mpl')
# -
code.circuit['1'].draw(output='mpl')
# In these circuits, we have two types of physical qubits. There are the 'code qubits', which are the three physical qubits across which the logical state is encoded. There are also the 'link qubits', which serve as the ancilla qubits for the syndrome measurements.
#
# Our single round of syndrome measurements in these circuits consist of just two syndrome measurements. One compares code qubits 0 and 1, and the other compares code qubits 1 and 2. One might expect that a further measurement, comparing code qubits 0 and 2, should be required to create a full set. However, these two are sufficient. This is because the information on whether 0 and 2 have the same z basis state can be inferred from the same information about 0 and 1 with that for 1 and 2. Indeed, for $n$ qubits, we can get the required information from just $n-1$ syndrome measurements of neighbouring pairs of qubits.
#
# Running these circuits on a simulator without any noise leads to very simple results.
# +
def get_raw_results(code,noise_model=None):
circuits = code.get_circuit_list()
raw_results = {}
for log in range(2):
job = execute( circuits[log], Aer.get_backend('qasm_simulator'), noise_model=noise_model)
raw_results[str(log)] = job.result().get_counts(str(log))
return raw_results
raw_results = get_raw_results(code)
for log in raw_results:
print('Logical',log,':',raw_results[log],'\n')
# -
# Here we see that the output comes in two parts. The part on the right holds the outcomes of the two syndrome measurements. That on the left holds the outcomes of the three final measurements of the code qubits.
#
# For more measurement rounds, $T=4$ for example, we would have the results of more syndrome measurements on the right.
# +
code = RepetitionCode(n,4)
raw_results = get_raw_results(code)
for log in raw_results:
print('Logical',log,':',raw_results[log],'\n')
# -
# For more repetitions, $n=5$ for example, each set of measurements would be larger. The final measurement on the left would be of $n$ qubits. The $T$ syndrome measurements would each be of the $n-1$ possible neighbouring pairs.
# +
code = RepetitionCode(5,4)
raw_results = get_raw_results(code)
for log in raw_results:
print('Logical',log,':',raw_results[log],'\n')
# -
# ### Lookup table decoding
#
# Now let's return to the $n=3$, $T=1$ example and look at a case with some noise.
# +
code = RepetitionCode(3,1)
noise_model = get_noise(0.05,0.05)
raw_results = get_raw_results(code,noise_model)
for log in raw_results:
print('Logical',log,':',raw_results[log],'\n')
# -
# Here we have created `raw_results`, a dictionary that holds both the results for a circuit encoding a logical `0` and `1` encoded for a logical `1`.
#
# Our task when confronted with any of the possible outcomes we see here is to determine what the outcome should have been, if there was no noise. For an outcome of `'000 00'` or `'111 00'`, the answer is obvious. These are the results we just saw for a logical `0` and logical `1`, respectively, when no errors occur. The former is the most common outcome for the logical `0` even with noise, and the latter is the most common for the logical `1`. We will therefore conclude that the outcome was indeed that for logical `0` whenever we encounter `'000 00'`, and the same for logical `1` when we encounter `'111 00'`.
#
# Though this tactic is optimal, it can nevertheless fail. Note that `'111 00'` typically occurs in a handful of cases for an encoded `0`, and `'00 00'` similarly occurs for an encoded `1`. In this case, through no fault of our own, we will incorrectly decode the output. In these cases, a large number of errors conspired to make it look like we had a noiseless case of the opposite logical value, and so correction becomes impossible.
#
# We can employ a similar tactic to decode all other outcomes. The outcome `'001 00'`, for example, occurs far more for a logical `0` than a logical `1`. This is because it could be caused by just a single measurement error in the former case (which incorrectly reports a single `0` to be `1`), but would require at least two errors in the latter. So whenever we see `'001 00'`, we can decode it as a logical `0`.
#
# Applying this tactic over all the strings is a form of so-called 'lookup table decoding'. This is where every possible outcome is analyzed, and the most likely value to decode it as is determined. For many qubits, this quickly becomes intractable, as the number of possible outcomes becomes so large. In these cases, more algorithmic decoders are needed. However, lookup table decoding works well for testing out small codes.
#
# We can use tools in Qiskit to implement lookup table decoding for any code. For this we need two sets of results. One is the set of results that we actually want to decode, and for which we want to calcate the probability of incorrect decoding, $P$. We will use the `raw_results` we already have for this.
#
# The other set of results is one to be used as the lookup table. This will need to be run for a large number of samples, to ensure that it gets good statistics for each possible outcome. We'll use `shots=10000`.
#
circuits = code.get_circuit_list()
table_results = {}
for log in range(2):
job = execute( circuits[log], Aer.get_backend('qasm_simulator'), noise_model=noise_model, shots=10000 )
table_results[str(log)] = job.result().get_counts(str(log))
# With this data, which we call `table_results`, we can now use the `lookuptable_decoding` function from Qiskit. This takes each outcome from `raw_results` and decodes it with the information in `table_results`. Then it checks if the decoding was correct, and uses this information to calculate $P$.
P = lookuptable_decoding(raw_results,table_results)
print('P =',P)
# Here we see that the values for $P$ are lower than those for $p_{meas}$ and $p_{gate}$, so we get an improvement in the reliability for storing the bit value. Note also that the value of $P$ for an encoded `1` is higher than that for `0`. This is because the encoding of `1` requires the application of `x` gates, which are an additional source of noise.
# ### Graph theoretic decoding
#
# The decoding considered above produces the best possible results, and does so without needing to use any details of the code. However, it has a major drawback that counters these advantages: the lookup table grows exponentially large as code size increases. For this reason, decoding is typically done in a more algorithmic manner that takes into account the structure of the code and its resulting syndromes.
#
# For the codes of `topological_codes` this structure is revealed using post-processing of the syndromes. Instead of using the form shown above, with the final measurement of the code qubits on the left and the outputs of the syndrome measurement rounds on the right, we use the `process_results` method of the code object to rewrite them in a different form.
#
# For example, below is the processed form of a `raw_results` dictionary, in this case for $n=3$ and $T=2$. Only results with 50 or more samples are shown for clarity.
# +
code = RepetitionCode(3,2)
raw_results = get_raw_results(code,noise_model)
results = code.process_results( raw_results )
for log in ['0','1']:
print('\nLogical ' + log + ':')
print('raw results ', {string:raw_results[log][string] for string in raw_results[log] if raw_results[log][string]>=50 })
print('processed results ', {string:results[log][string] for string in results[log] if results[log][string]>=50 })
# -
# Here we can see that `'000 00 00'` has been transformed to `'0 0 00 00 00'`, and `'111 00 00'` to `'1 1 00 00 00'`, and so on.
#
# In these new strings, the `0 0` to the far left for the logical `0` results and the `1 1` to the far left of the logical `1` results are the logical readout. Any code qubit could be used for this readout, since they should (without errors) all be equal. It would therefore be possible in principle to just have a single `0` or `1` at this position. We could also do as in the original form of the result and have $n$, one for each qubit. Instead we use two, from the two qubits at either end of the line. The reason for this will be shown later. In the absence of errors, these two values will always be equal, since they represent the same encoded bit value.
#
# After the logical values follow the $n-1$ results of the syndrome measurements for the first round. A `0` implies that the corresponding pair of qubits have the same value, and `1` implies they they are different from each other. There are $n-1$ results because the line of $d$ code qubits has $n-1$ possible neighboring pairs. In the absence of errors, they will all be `0`. This is exactly the same as the first such set of syndrome results from the original form of the result.
#
# The next block is the next round of syndrome results. However, rather than presenting these results directly, it instead gives us the syndrome change between the first and second rounds. It is therefore the bitwise `OR` of the syndrome measurement results from the second round with those from the first. In the absence of errors, they will all be `0`.
#
# Any subsequent blocks follow the same formula, though the last of all requires some comment. This is not measured using the standard method (with a link qubit). Instead it is calculated from the final readout measurement of all code qubits. Again it is presented as a syndrome change, and will be all `0` in the absence of errors. This is the $T+1$-th block of syndrome measurements since, as it is not done in the same way as the others, it is not counted among the $T$ syndrome measurement rounds.
#
# The following examples further illustrate this convention.
#
# **Example 1:** `0 0 0110 0000 0000` represents a $d=5$, $T=2$ repetition code with encoded `0`. The syndrome shows that (most likely) the middle code qubit was flipped by an error before the first measurement round. This causes it to disagree with both neighboring code qubits for the rest of the circuit. This is shown by the syndrome in the first round, but the blocks for subsequent rounds do not report it as it no longer represents a change. Other sets of errors could also have caused this syndrome, but they would need to be more complex and so presumably less likely.
#
# **Example 2:** `0 0 0010 0010 0000` represents a $d=5$, $T=2$ repetition code with encoded `0`. Here one of the syndrome measurements reported a difference between two code qubits in the first round, leading to a `1`. The next round did not see the same effect, and so resulted in a `0`. However, since this disagreed with the previous result for the same syndrome measurement, and since we track syndrome changes, this change results in another `1`. Subsequent rounds also do not detect anything, but this no longer represents a change and hence results in a `0` in the same position. Most likely the measurement result leading to the first `1` was an error.
#
# **Example 3:** `0 1 0000 0001 0000` represents a $d=5$, $T=2$ repetition code with encoded `1`. A code qubit on the end of the line is flipped before the second round of syndrome measurements. This is detected by only a single syndrome measurement, because it is on the end of the line. For the same reason, it also disturbs one of the logical readouts.
#
# Note that in all these examples, a single error causes exactly two characters in the string to change from the value they would have with no errors. This is the defining feature of the convention used to represent stabilizers in `topological_codes`. It is used to define the graph on which the decoding problem is defined.
#
# Specifically, the graph is constructed by first taking the circuit encoding logical `0`, for which all bit values in the output string should be `0`. Many copies of this and then created and run on a simulator, with a different single Pauli operator inserted into each. This is done for each of the three types of Pauli operator on each of the qubits and at every circuit depth. The output from each of these circuits can be used to determine the effects of each possible single error. Since the circuit contains only Clifford operations, the simulation can be performed efficiently.
#
# In each case, the error will change exactly two of the characters (unless it has no effect). A graph is then constructed for which each bit of the output string corresponds to a node, and the pairs of bits affected by the same error correspond to an edge.
#
# The process of decoding a particular output string typically requires the algorithm to deduce which set of errors occured, given the syndrome found in the output string. This can be done by constructing a second graph, containing only nodes that correspond to non-trivial syndrome bits in the output. An edge is then placed between each pair of nodes, with an corresponding weight equal to the length of the minimal path between those nodes in the original graph. A set of errors consistent with the syndrome then corresponds then to finding a perfect matching of this graph. To deduce the most likely set of errors to have occurred, a good tactic would be to find one with the least possible number of errors that is consistent with the observed syndrome. This corresponds to a minimum weight perfect matching of the graph.
#
# Using minimal weight perfect matching is a standard decoding technique for the repetition code and surface code, and is implement in Qiskit Ignis. It can also be used in other cases, such as Color codes, but it does not find the best approximation of the most likely set of errors for every code and noise model. For that reason, other decoding technques based on the same graph can be used. The `GraphDecoder` of Qiskit Ignis calculates these graphs for a given code, and will provide a range of methods to analyze it. At time of writing, only minimum weight perfect matching is implemented.
#
# Note that, for codes such as the surface code, it is not strictly true than each single error will change the value of only two bits in the output string. A $\sigma^y$ error, for example would flip a pair of values corresponding to two different types of stabilizer, which are typically decoded independently. Output for these codes will therefore be presented in a way that acknowledges this, and analysis of such syndromes will correspondingly create multiple independent graphs to represent the different syndrome types.
# ## Running a repetition code benchmarking procedure
#
# We will now run examples of repetition codes on real devices, and use the results as a benchmark. First, we will breifly summarize the process. This applies to this example of the repetition code, but also for other benchmarking procedures in `topological_codes`, and indeed for Qiskit Ignis in general. In each case, the following three-step process is used.
#
# 1. A task is defined. Qiskit Ignis determines the set of circuits that must be run and creates them.
# 2. The circuits are run. This is typically done using Qiskit. However, in principle any service or experimental equipment could be interfaced.
# 3. Qiskit Ignis is used to process the results from the circuits, to create the output required for the given task.
#
# For `topological_codes`, step 1 requires the type and size of quantum error correction code to be chosen. Each type of code has a dedicated Python class. A corresponding object is initialized by providing the paramters required, such as `n` and `T` for a `RepetitionCode` object. The resulting object then contains the circuits corresponding to the given code encoding simple logical qubit states (such as $\left|0\right\rangle$ and $\left|1\right\rangle$), and then running the procedure of error detection for a specified number of rounds, before final readout in a straightforward logical basis (typically a standard $\left|0\right\rangle$/$\left|1\right\rangle$ measurement).
#
# For `topological_codes`, the main processing of step 3 is the decoding, which aims to mitigate for any errors in the final readout by using the information obtained from error detection. The optimal algorithm for decoding typically varies between codes. However, codes with similar structure often make use of similar methods.
#
# The aim of `topological_codes` is to provide a variety of decoding methods, implemented such that all the decoders can be used on all of the codes. This is done by restricting to codes for which decoding can be described as a graph-theoretic minimization problem. This classic example of such codes are the toric and surface codes. The property is also shared by 2D color codes and matching codes. All of these are prominent examples of so-called topological quantum error correcting codes, which led to the name of the subpackage. However, note that not all topological codes are compatible with such a decoder. Also, some non-topological codes will be compatible, such as the repetition code.
#
# The decoding is done by the `GraphDecoder` class. A corresponding object is initialiazed by providing the code object for which the decoding will be performed. This is then used to determine the graph on which the decoding problem will be defined. The results can then be processed using the various methods of the decoder object.
#
# In the following we will see the above ideas put into practice for the repetition code. In doing this we will employ two Boolean variables, `step_2` and `step_3`. The variable `step_2` is used to show which parts of the program need to be run when taking data from a device, and `step_3` is used to show the parts which process the resulting data.
#
# Both are set to false by default, to ensure that all the program snippets below can be run using only previously collected and processed data. However, to obtain new data one only needs to use `step_2 = True`, and perform decoding on any data one only needs to use `step_3 = True`.
step_2 = False
step_3 = False
# To benchmark a real device we need the tools required to access that device over the cloud, and compile circuits suitable to run on it. These are imported as follows.
# + tags=["uses-hardware"]
from qiskit import IBMQ
from qiskit.compiler import transpile
from qiskit.transpiler import PassManager
# -
# We can now create the backend object, which is used to run the circuits. This is done by supplying the string used to specify the device. Here `'ibmq_16_melbourne'` is used, which has 15 active qubits at time of writing. We will also consider the 53 qubit *Rochester* device, which is specified with `'ibmq_rochester'`.
# + tags=["uses-hardware"]
device_name = 'ibmq_16_melbourne'
if step_2:
IBMQ.load_account()
for provider in IBMQ.providers():
for potential_backend in provider.backends():
if potential_backend.name()==device_name:
backend = potential_backend
coupling_map = backend.configuration().coupling_map
# -
# When running a circuit on a real device, a transpilation process is first implemented. This changes the gates of the circuit into the native gate set implement by the device. In some cases these changes are fairly trivial, such as expressing each Hadamard as a single qubit rotation by the corresponding Euler angles. However, the changes can be more major if the circuit does not respect the connectivity of the device. For example, suppose the circuit requires a controlled-NOT that is not directly implemented by the device. The effect must be then be reproduced with techniques such as using additional controlled-NOT gates to move the qubit states around. As well as introducing additional noise, this also delocalizes any noise already present. A single qubit error in the original circuit could become a multiqubit monstrosity under the action of the additional transpilation. Such non-trivial transpilation must therefore be prevented when running quantum error correction circuits.
#
# Tests of the repetition code require qubits to be effectively ordered along a line. The only controlled-NOT gates required are between neighbours along that line. Our first job is therefore to study the coupling map of the device, and find a line.
#
# 
#
# For Melbourne it is possible to find a line that covers all 15 qubits. The choice one specified in the list `line` below is designed to avoid the most error prone `cx` gates. For the 53 qubit *Rochester* device, there is no single line that covers all 53 qubits. Instead we can use the following choice, which covers 43.
# + tags=["uses-hardware"]
if device_name=='ibmq_16_melbourne':
line = [13,14,0,1,2,12,11,3,4,10,9,5,6,8,7]
elif device_name=='ibmq_rochester':
line = [10,11,17,23,22,21,20,19,16,7,8,9,5]#,0,1,2,3,4,6,13,14,15,18,27,26,25,29,36,37,38,41,50,49,48,47,46,45,44,43,42,39,30,31]
# -
# Now we know how many qubits we have access to, we can create the repetition code objects for each code that we will run. Note that a code with `n` repetitions uses $n$ code qubits and $n-1$ link qubits, and so $2n-1$ in all.
# + tags=["uses-hardware"]
n_min = 3
n_max = int((len(line)+1)/2)
code = {}
for n in range(n_min,n_max+1):
code[n] = RepetitionCode(n,1)
# -
# Before running the circuits from these codes, we need to ensure that the transpiler knows which physical qubits on the device it should use. This means using the qubit of `line[0]` to serve as the first code qubit, that of `line[1]` to be the first link qubit, and so on. This is done by the following function, which takes a repetition code object and a `line`, and creates a Python dictionary to specify which qubit of the code corresponds to which element of the line.
# + tags=["uses-hardware"]
def get_initial_layout(code,line):
initial_layout = {}
for j in range(n):
initial_layout[code.code_qubit[j]] = line[2*j]
for j in range(n-1):
initial_layout[code.link_qubit[j]] = line[2*j+1]
return initial_layout
# -
# Now we can transpile the circuits, to create the circuits that will actually be run by the device. A check is also made to ensure that the transpilation indeed has not introduced non-trivial effects by increasing the number of qubits. Furthermore, the compiled circuits are collected into a single list, to allow them all to be submitted at once in the same batch job.
# + tags=["uses-hardware"]
if step_2:
circuits = []
for n in range(n_min,n_max+1):
initial_layout = get_initial_layout(code[n],line)
for log in ['0','1']:
circuits.append( transpile(code[n].circuit[log], backend=backend, initial_layout=initial_layout) )
num_cx = dict(circuits[-1].count_ops())['cx']
assert num_cx==2*(n-1), str(num_cx) + ' instead of ' + str(2*(n-1)) + ' cx gates for n = ' + str(n)
# -
# We are now ready to run the job. As with the simulated jobs considered already, the results from this are extracted into a dictionary `raw_results`. However, in this case it is extended to hold the results from different code sizes. This means that `raw_results[n]` in the following is equivalent to one of the `raw_results` dictionaries used earlier, for a given `n`.
# + tags=["uses-hardware"]
if step_2:
job = execute(circuits,backend,shots=8192)
raw_results = {}
j = 0
for d in range(n_min,n_max+1):
raw_results[d] = {}
for log in ['0','1']:
raw_results[d][log] = job.result().get_counts(j)
j += 1
# -
# It can be convenient to save the data to file, so that the processing of step 3 can be done or repeated at a later time.
# + tags=["uses-hardware"]
if step_2: # save results
with open('results/raw_results_'+device_name+'.txt', 'w') as file:
file.write(str(raw_results))
elif step_3: # read results
with open('results/raw_results_'+device_name+'.txt', 'r') as file:
raw_results = eval(file.read())
# -
# As we saw previously, the process of decoding first needs the results to be rewritten in order for the syndrome to be expressed in the correct form. As such, the `process_results` method of each the repetition code object `code[n]` is used to create determine a results dictionary `results[n]` from each `raw_results[n]`.
# + tags=["uses-hardware"]
if step_3:
results = {}
for n in range(n_min,n_max+1):
results[n] = code[n].process_results( raw_results[n] )
# -
# The decoding also needs us to set up the `GraphDecoder` object for each code. The initialization of these involves the construction of the graph corresponding to the syndrome, as described in the last section.
# + tags=["uses-hardware"]
if step_3:
dec = {}
for n in range(n_min,n_max+1):
dec[n] = GraphDecoder(code[n])
# -
# Finally, the decoder object can be used to process the results. Here the default algorithm, minimim weight perfect matching, is used. The end result is a calculation of the logical error probability. When running step 3, the following snippet also saves the logical error probabilities. Otherwise, it reads in previously saved probabilities.
# + tags=["uses-hardware"]
if step_3:
logical_prob_match = {}
for n in range(n_min,n_max+1):
logical_prob_match[n] = dec[n].get_logical_prob(results[n])
with open('results/logical_prob_match_'+device_name+'.txt', 'w') as file:
file.write(str(logical_prob_match))
else:
with open('results/logical_prob_match_'+device_name+'.txt', 'r') as file:
logical_prob_match = eval(file.read())
# -
# The resulting logical error probabilities are displayed in the following graph, whch uses a log scale used on the y axis. We would expect that the logical error probability decays exponentially with increasing $n$. If this is the case, it is a confirmation that the device is compatible with this basis test of quantum error correction. If not, it implies that the qubits and gates are not sufficiently reliable.
#
# Fortunately, the results from IBM Q prototype devices typically do show the expected exponential decay. For the results below, we can see that small codes do represent an exception to this rule. Other deviations can also be expected, such as when the increasing the size of the code means uses a group of qubits with either exceptionally low or high noise.
# + tags=["uses-hardware"]
import matplotlib.pyplot as plt
import numpy as np
x_axis = range(n_min,n_max+1)
P = { log: [logical_prob_match[n][log] for n in x_axis] for log in ['0', '1'] }
ax = plt.gca()
plt.xlabel('Code distance, n')
plt.ylabel('ln(Logical error probability)')
ax.scatter( x_axis, P['0'], label="logical 0")
ax.scatter( x_axis, P['1'], label="logical 1")
ax.set_yscale('log')
ax.set_ylim(ymax=1.5*max(P['0']+P['1']),ymin=0.75*min(P['0']+P['1']))
plt.legend()
plt.show()
# -
# Another insight we can gain is to use the results to determine how likely certain error processes are to occur.
#
# To do this we use the fact that each edge in the syndrome graph represents a particular form of error, occuring on a particular qubit at a particular point within the circuit. This is the unique single error that causes the syndrome values corresponding to both of the adjacent nodes to change. Using the results to estimate the probability of such a syndrome therefore allows us to estimate the probability of such an error event. Specifically, to first order it is clear that
#
# $$
# \frac{p}{1-p} \approx \frac{C_{11}}{C_{00}}
# $$
#
# Here $p$ is the probaility of the error corresponding to a particular edge, $C_{11}$ is the number of counts in the `results[n]['0']` correponding to the syndrome value of both adjacent nodes being `1`, and $C_{00}$ is the same for them both being `0`.
#
# The decoder object has a method `weight_syndrome_graph` which determines these ratios, and assigns each edge the weight $-\ln(p/(1-p))$. By employing this method and inspecting the weights, we can easily retreive these probabilities.
# + tags=["uses-hardware"]
if step_3:
dec[n_max].weight_syndrome_graph(results=results[n_max])
probs = []
for edge in dec[n_max].S.edges:
ratio = np.exp(-dec[n_max].S.get_edge_data(edge[0],edge[1])['distance'])
probs.append( ratio/(1+ratio) )
with open('results/probs_'+device_name+'.txt', 'w') as file:
file.write(str(probs))
else:
with open('results/probs_'+device_name+'.txt', 'r') as file:
probs = eval(file.read())
# -
# Rather than display the full list, we can obtain a summary via the mean, standard devation, minimum, maximum and quartiles.
# + tags=["uses-hardware"]
import pandas as pd
pd.Series(probs).describe().to_dict()
# -
# The benchmarking of the devices does not produce any set of error probabilities that is exactly equivalent. However, the probabilities for readout errors and controlled-NOT gate errors could serve as a good comparison. Specifically, we can use the `backend` object to obtain these values from the benchmarking.
# + tags=["uses-hardware"]
if step_3:
gate_probs = []
for j,qubit in enumerate(line):
gate_probs.append( backend.properties().readout_error(qubit) )
cx1,cx2 = 0,0
if j>0:
gate_probs( backend.properties().gate_error('cx',[qubit,line[j-1]]) )
if j<len(line)-1:
gate_probs( backend.properties().gate_error('cx',[qubit,line[j+1]]) )
with open('results/gate_probs_'+device_name+'.txt', 'w') as file:
file.write(str(gate_probs))
else:
with open('results/gate_probs_'+device_name+'.txt', 'r') as file:
gate_probs = eval(file.read())
pd.Series(gate_probs).describe().to_dict()
# -
import qiskit
qiskit.__qiskit_version__
|
content/ch-quantum-hardware/error-correction-repetition-code.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# # Writing custom readers
#
# Readers were introduced in version 1.1.0 to better enable B-Store to read data from various filetypes. A Reader is used to read the data contained in a particular file into a Python datatype, such as Pandas DataFrame or Numpy array. This intermediate Python datatype is a sort of temporary holding spot before the data is then placed into a HDF file. The abstract base class `Reader` defines a common interface for users to write their own routines for reading any type of file into Python.
#
# To use a `Reader` when creating a `HDFDatastore`, one passes one or more instances of objects that subclass `Reader` and that to `HDFDatastore.build()` or `Parser.parseFilename()`. This will be described below.
#
# In this tutorial, we'll begin by looking at the abstract base class called `Reader`. After studying the code, we'll look at a specific implementation of a `Reader` known as `CSVReader`, an object that is used to read generic CSV files and that is highly customizable.
#
# ## Special note
#
# Version 1.1.0 introduced the Reader interface and two readers: `CSVReader` and `JSONReader`. In this version they only work for Localizations, FiducialTracks, and AverageFiducial datasetTypes. Finally, they cannot be specified in the GUI, but may be specified using the new `readers` parameter of `HDFDatastore.build()`. All of these limitations should be gone in future versions of B-Store. Readers for non-tabulated data, such as images, should follow as well.
# # The `Reader` interface
#
# Let's begin by looking at the code for a `Reader`.
# +
# Import B-Store's parsers module
from bstore import readers
# Used to retrieve the code
import inspect
# -
print(inspect.getsource(readers.Reader))
# Looking at the code above, we can see that a Reader must have three methods and one property. The methods are:
#
# 1. __call__ : This makes the object a callable, i.e. an instance may be used like a function.
# 2. __repr__ : This is a Python builtin function that will return a that may be used to instantiate a Reader instance.
# 3. __str__ : This is a more user-friendly method that returns a string describing what the Reader does.
#
# The property that must be defined is `__signature__`. The reason for this property is that we must define the call signature for the Reader object when it is called like a function. [The call signature](https://docs.python.org/3/library/inspect.html#inspect.Signature) represents the arguments and their default values that are passed to the Reader when it is called like a function inside the `readFromFile` method of a DatasetType. Specifying a call signature will enable us to modify the arguments through a GUI window with all the argument names and values. Without a signature, we cannot easily "look inside" the Reader to figure out what arguments it takes.
# # The `CSVReader` object
#
# Let's now take a look at a concrete Reader, the `CSVReader`, which enables us to read generic .csv files in a highly customizable way.
reader = readers.CSVReader
print(inspect.getsource(reader))
# ## \_\_init\_\_()
#
# We define the CSVReader with the line:
#
# ```python
#
# class CSVReader(Reader):
#
# ```
#
# The `(Reader)` in parantheses tells Python that the object subclasses the `Reader` abstract base class discussed above.
#
# Following the docstring, there is the `__init__` function which serves as the constructor for the object. (Note that defining an `__init__` method is not required.) This Reader actually uses the [Pandas read_csv function](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.read_csv.html) to read .csv files into Python DataFrames. Thefore, we extract the function signature from `read_csv` in the line
#
# ```python
#
# sig = inspect.signature(pd.read_csv)
#
# ```
#
# Now, we have to slightly modify the signature for our Reader because `read_csv` accepts an argument called `filename_or_buffer` as its first argument. However, inside each datasetType's `readFromFile` method, we specify the filePath as the first positional argument. For example:
from bstore.datasetTypes import Localizations as locs
readFromFile = locs.Localizations.readFromFile
print(inspect.getsource(readFromFile))
# In the GUI, filePath is not specified by the user but rather by B-Store's machinery for automatically detecting files. When a GUI window appears to allow someone to set the parameters of `CSVReader`, we therefore do not want them to be able to set the argument `filename_or_buffer`.
#
# We define a custom call signature inside `__init__()` with the lines:
#
# ```python
#
# p1 = inspect.Parameter(
# 'filename', inspect.Parameter.POSITIONAL_ONLY)
#
# newParams = [p1] + [param for name, param in sig.parameters.items()
# if name != 'filepath_or_buffer']
#
# self._sig = sig.replace(parameters = newParams)
#
# ```
#
# `p1` is a custom parameter that is set to be `POSITIONAL_ONLY`. Doing this ensures that we can easily separate it from the rest of the arguments of `read_csv`, which are of the kind `POSITIONAL_OR_KEYWORD`. We then add this new custom parameter onto the all the other parameters of `read_csv` **except** for `filepath_or_buffer` with the lines
#
# ```python
#
# p1 = inspect.Parameter(
# 'filename', inspect.Parameter.POSITIONAL_ONLY)
#
# newParams = [p1] + [param for name, param in sig.parameters.items()
# if name != 'filepath_or_buffer']
#
# ```
#
# Finally, the Reader's `_sig` property is reset to this new Signature with the line `self._sig = sig.replace(parameters = newParams)`.
# ## __signature__
#
# To return this newly-defined signature object when the `Signature` function is called on our class, we tell the CSVReader's signature property to return it:
#
# ```python
#
# @property
# def __signature__(self):
# return self._sig
#
# ```
# ## \_\_call\_\_(self, filename, **kwargs)
#
# The \_\_call\_\_() method actually performs the act of reading the data from a file into a DataFrame. First, all keyword arguments that are not part of `read_csv` are removed from the \*\*kwargs dict. If they are not removed, `read_csv` will raise an error about an unrecognized argument. We also ensure that filename is not passed to `read_csv`, in case it was passed as a keyword.
#
# ```python
#
# kwargs = {k: v for k, v in kwargs.items()
# if k in self.__signature__.parameters
# and k != 'filename'}
#
# ```
#
# Next, we simply call `read_csv` with the `filename` argument and the new `kwargs` dict and return the DataFrame as a result:
#
# ```python
#
# return pd.read_csv(filename, **kwargs)
#
# ```
#
# By passing \*\*kwargs into read_csv, we can assign values to *any* of `read_csv`'s arguments. `read_csv` accepts a very large number of arguments to allow you to customize its behavior. This powerful customizability is therefore translated to B-Store. One last important thing to note is the part at the end of the first line of \_\_call\_\_()'s definition:
#
# ```python
#
# def __call__(self, filename, **kwargs) -> pd.DataFrame:
#
# ```
#
# `-> pd.DataFrame` tells Python what datatype the function returns. This is also required by Readers and is used to automatically detect what Readers are associated with what datasetTypes. For example, Localizations are represented internally as DataFrames. `-> pd.DataFrame` tells B-Store that we can associate this reader with any datasetType that has a DataFrame as its internal representation.
# ## \_\_repr\_\_() and \_\_str\_\_()
#
# These methods should be self-explantory for Python developers. The first returns a string used by developers to represent how the instance is created and the second is a user-friendly string that can be displayed in places like the GUI.
# # Example
# For this example, you can use the test data in the [bstore_test_files](https://github.com/kmdouglass/bstore_test_files). Download the files from Git using the link and change the path below to point to *bstore_test_files/readers_test_files/csv/tab_delimited* on your machine.
# +
from bstore import parsers
from bstore import readers
from pathlib import Path
filePath = Path('../../bstore_test_files/readers_test_files/csv/tab_delimited/')
filename = filePath / Path('HeLaL_Control_1.csv')
# -
# Initialize the Parser and Reader
parser = parsers.SimpleParser()
reader = readers.CSVReader()
# +
# reader keyword argument passes the CSVReader instance;
# all other keyword arguments are passed to CSVReader's __call__ function.
parser.parseFilename(filename, datasetType = 'Localizations', reader = reader, sep = '\t')
parser.dataset.data.head()
# -
# Here, we parsed the file containing localization data using the `CSVReader`. After creating the reader, we passed it as a keyword argument to parser's `parseFilename` method:
#
# ```python
#
# parser.parseFilename(filename, datasetType = 'Localizations', reader = reader, sep = '\t')
#
# ```
#
# The maining keyword argument, `sep`, was passed to `read_csv` inside the reader because all keyword arguments after `datasetType` are passed to the reader object. We can pass other keyword arguments to `read_csv`, such as `skiprows`:
# +
parser.parseFilename(filename, datasetType = 'Localizations', reader = reader, sep = '\t', skiprows = 1)
parser.dataset.data.head()
# -
# # Passing readers to `HDFDatastore.build()`
#
# The `HDFDatastore.build()` method, which is the main method used to create Datastores, now accepts a keyword argument known as `readers`. This argument should be a dict whose keys are the names of DatasetTypes and whose values are instances of a particular reader to use when reading data.
#
# For example, let's say we want to build a Datastore from a small experiment and specify what readers to use when reading different dataset types. (You may need to change testDataRoot to point to the right folder containing the bstore test files.)
# +
import bstore.config as config
from bstore import database
testData = Path('../../bstore_test_files/parsers_test_files/SimpleParser/')
dsName = 'test_datastore.h5'
config.__Registered_DatasetTypes__ = [
'Localizations', 'LocMetadata', 'WidefieldImage']
parser = parsers.SimpleParser()
filenameStrings = {
'Localizations' : '.csv',
'LocMetadata' : '.txt',
'WidefieldImage' : '.tif'}
readersDict = {'Localizations': readers.CSVReader()}
# Note sep and skiprows are keyword arguments of CSVReader; readTiffTags is
# a keyword argument for the WidefieldImage readfromFile() method
with database.HDFDatastore(dsName) as myDS:
res = myDS.build(parser, testData, filenameStrings,
readers=readersDict, sep=',', skiprows=2,
readTiffTags = False)
# -
# The above code sets up a HDFDatastore build by first specifying the location of the data, the name of the HDFDatastore, and registering the desired DatasetTypes.
#
# ```python
# testData = Path('../../bstore_test_files/parsers_test_files/SimpleParser/')
# dsName = 'test_datastore.h5'
# config.__Registered_DatasetTypes__ = [
# 'Localizations', 'LocMetadata', 'WidefieldImage']
# ```
#
# Next, a parser is specified and the naming pattern for the different datasets is specified like usual:
#
# ```python
# parser = parsers.SimpleParser()
# filenameStrings = {
# 'Localizations' : '.csv',
# 'LocMetadata' : '.txt',
# 'WidefieldImage' : '.tif'}
# ```
#
# We specify that we want to use the CSVReader for reading `Localizations` Datasets from files the `readersDict`:
#
# ```python
# readersDict = {'Localizations': readers.CSVReader()}
# ```
#
# Finally, we build the Datastore inside the *with...as* context manager like usual. We can pass keyword arguments to the various readers by specifying them **after the readers argument**. In this case, we send `sep=','` and `skiprows=2` to `CSVReader` and `readTiffTags=False`, which is sent to the `readFromFile` function of WidefieldImages.
#
# ```python
# with database.HDFDatastore(dsName) as myDS:
# res = myDS.build(parser, testData, filenameStrings,
# readers=readersDict, sep=',', skiprows=2,
# readTiffTags = False)
# ```
#
# Currently, readers may only be specified in this manner for Localizations, FiducialTracks, and AverageFiducial dataset types. All other specifications will be ignored.
# # Summary
#
# - A Reader may be used to actually read the raw data from a file whose name is currently be parsed by a Parser.
# - Readers are defined by an abstract base class known as `Reader`.
# - To define a concrete Reader, we have to define three methods and one property. The methods are `__call__()`, `__repr__()`, and `__str__()`. The property is `__signature__`.
# - Most of the work of creating a Reader goes into defining its signature. The signature is used to automatically detect what arguments the Reader requires and is used primarily by the GUI.
# - Any function or code at all for reading a raw data file may used inside `__call__()`. For `CSVReader`, we chose to use Pandas `read_csv` function because it is highly customizable.
# - To associate Readers with specific datasetTypes, we should use function annotations to specify the return type of the Reader's `__call__()` method.
|
examples/Tutorial 4 - Writing custom readers.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="xv2OcVTkY7vv"
# ## 4.4 評価
#
# + colab={} colab_type="code" id="-PHeHE44Y7vw"
# 日本語化ライブラリ導入
# !pip install japanize-matplotlib | tail -n 1
# + colab={} colab_type="code" id="Ra8fM7lxY7v0"
# 共通事前処理
# 余分なワーニングを非表示にする
import warnings
warnings.filterwarnings('ignore')
# 必要ライブラリのimport
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# matplotlib日本語化対応
import japanize_matplotlib
# データフレーム表示用関数
from IPython.display import display
# 表示オプション調整
# numpyの浮動小数点の表示精度
np.set_printoptions(suppress=True, precision=4)
# pandasでの浮動小数点の表示精度
pd.options.display.float_format = '{:.4f}'.format
# データフレームですべての項目を表示
pd.set_option("display.max_columns",None)
# グラフのデフォルトフォント指定
plt.rcParams["font.size"] = 14
# 乱数の種
random_seed = 123
# + [markdown] colab_type="text" id="BpHwA-JaY7v3"
# ### 4.4.1 混同行列
# + [markdown] colab_type="text" id="EWGhMtRxY7v3"
# #### 混同行列
# + colab={} colab_type="code" id="Ggsurtn8Y7v3"
# データ読み込みからデータ分割まで
# ライブラリのimport
from sklearn.datasets import load_breast_cancer
# データのロード
cancer = load_breast_cancer()
# 入力データ x
x = cancer.data
# 正解データ y
# 良性: 0 悪性: 1に値を変更する
y = 1- cancer.target
# 入力データを2次元に絞り込み
x2 = x[:,:2]
# (4) データ分割
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x2, y,
train_size=0.7, test_size=0.3, random_state=random_seed)
# + colab={} colab_type="code" id="dQ9XUGlqY7v6"
# アルゴリズム選定から評価まで
# アルゴリズム選定 (ロジスティック回帰)
from sklearn.linear_model import LogisticRegression
algorithm = LogisticRegression(random_state=random_seed)
# 学習
algorithm.fit(x_train, y_train)
# 予測
y_pred = algorithm.predict(x_test)
# 評価
score = algorithm.score(x_test, y_test)
# 結果確認
print(f'score: {score:.4f}')
# + colab={} colab_type="code" id="iODYJJZRY7v8"
# 混同行列の計算
# 必要ライブラリの取込み
from sklearn.metrics import confusion_matrix
# 混同行列の生成
# y_test: 検証データの正解データ
# y_pred: 検証データの予測結果
matrix = confusion_matrix(y_test, y_pred)
# 結果確認
print(matrix)
# + colab={} colab_type="code" id="CCo_8nbJY7v_"
# 混同行列表示用関数
def make_cm(matrix, columns):
# matrix numpy配列
# columns 項目名リスト
n = len(columns)
# '正解データ'をn回繰り返すリスト生成
act = ['正解データ'] * n
pred = ['予測結果'] * n
#データフレーム生成
cm = pd.DataFrame(matrix,
columns=[pred, columns], index=[act, columns])
return cm
# + colab={} colab_type="code" id="QRCossNUY7wB"
# make_cmを使った混同行列標示
cm = make_cm(matrix, ['良性', '悪性'])
display(cm)
# + [markdown] colab_type="text" id="Hsfiqt9kY7wH"
# ### 4.4.2 精度・適合率・再現率・F値
# + colab={} colab_type="code" id="bW78c493Y7wH"
# 適合率・再現率・F値の計算
# ライブラリの取込み
from sklearn.metrics import precision_recall_fscore_support
# 適合率・再現率・F値の計算
precision, recall, fscore, _ = precision_recall_fscore_support(
y_test, y_pred, average='binary')
# 結果の確認
print(f'適合率: {precision:.4f}')
print(f'再現率: {recall:.4f}')
print(f'F値: {fscore:.4f}')
# + [markdown] colab_type="text" id="5ccT1r0PY7wJ"
# ### 4.4.3 確率値と閾値
# + colab={} colab_type="code" id="pLHofKFhY7wK"
# 確率値の取得
y_proba = algorithm.predict_proba(x_test)
print(y_proba[10:20,:])
# + colab={} colab_type="code" id="gvH_nov_Y7wM"
# positive(1)の確率値の取得
y_proba1 = y_proba[:,1]
# 結果確認
print(y_pred[10:20])
print(y_proba1[10:20])
# + colab={} colab_type="code" id="1at-bPhnY7wP"
# 閾値を変化させる
thres = 0.5
print((y_proba1[10:20] > thres).astype(int))
thres = 0.7
print((y_proba1[10:20] > thres).astype(int))
# + colab={} colab_type="code" id="AO5clSBBY7wR"
# 閾値を変更した場合の予測関数の定義
def pred(algorithm, x, thres):
# 確率値の取得(行列)
y_proba = algorithm.predict_proba(x)
# 予測結果1の確率値
y_proba1 = y_proba[:,1]
# 予測結果1の確率値 > 閾値
y_pred = (y_proba1 > thres).astype(int)
return y_pred
# + colab={} colab_type="code" id="Z9X-vomEY7wU"
# 閾値0.5で予測結果取得
pred_05 = pred(algorithm, x_test, 0.5)
# 閾値0.7で予測結果取得
pred_07 = pred(algorithm, x_test, 0.7)
# 結果確認
print(pred_05[10:20])
print(pred_07[10:20])
# + [markdown] colab_type="text" id="kqoDRgYoY7wW"
# ### 4.4.4 PR曲線とROC曲線
# + [markdown] colab_type="text" id="ybbNCaXOY7wW"
# #### PR曲線
# + colab={} colab_type="code" id="mQdAXZBbY7wX"
# PR曲線用配列の生成
# ライブラリの導入
from sklearn.metrics import precision_recall_curve
# 適合率, 再現率、閾値の取得
precision, recall, thresholds = precision_recall_curve(
y_test, y_proba1)
# 結果をデータフレームにする
df_pr = pd.DataFrame([thresholds, precision, recall]).T
df_pr.columns = ['閾値', '適合率', '再現率']
# 閾値 0.5の周辺を表示
display(df_pr[52:122:10])
# + colab={} colab_type="code" id="yjxdxEwUY7wZ"
# PR曲線の描画
# 描画サイズ指定
plt.figure(figsize=(6,6))
# グラフ領域の塗りつぶし
plt.fill_between(recall, precision, 0)
# x, yの範囲指定
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
# ラベル・タイトル表示
plt.xlabel('再現率')
plt.ylabel('適合率')
plt.title('PR曲線')
plt.show()
# + colab={} colab_type="code" id="O4JAQ3HIY7wb"
# PR曲線下面積の計算
from sklearn.metrics import auc
pr_auc = auc(recall, precision)
print(f'PR曲線下面積: {pr_auc:.4f}')
# + [markdown] colab_type="text" id="nKtHryvTY7wd"
# #### ROC曲線
# + colab={} colab_type="code" id="jw-GtJwtY7we"
# ROC曲線用配列の生成
# ライブラリの導入
from sklearn.metrics import roc_curve
# 偽陽性率, 敏感度と閾値の取得
fpr, tpr, thresholds = roc_curve(
y_test, y_proba1,drop_intermediate=False)
# 結果をデータフレームにする
df_roc = pd.DataFrame([thresholds, fpr, tpr]).T
df_roc.columns = ['閾値', '偽陽性率', '敏感度']
# 閾値 0.5の周辺を表示
display(df_roc[21:91:10])
# + colab={} colab_type="code" id="DAoQrQB0Y7wg"
# ROC曲線の描画
# 描画サイズ指定
plt.figure(figsize=(6,6))
# 点線表示
plt.plot([0, 1], [0, 1], 'k--')
# グラフ領域の塗りつぶし
plt.fill_between(fpr, tpr, 0)
# x, yの範囲指定
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
# ラベル・タイトル表示
plt.xlabel('偽陽性率')
plt.ylabel('敏感度')
plt.title('ROC曲線')
plt.show()
# + colab={} colab_type="code" id="SLeeC-m8Y7wi"
# ROC曲線下面積の計算
roc_auc = auc(fpr, tpr)
print(f'ROC曲線下面積:{roc_auc:.4f}')
# + [markdown] colab_type="text" id="BLgzbVcaY7wk"
# #### より精度のいいモデルでROCカーブを描画
# + colab={} colab_type="code" id="IwwzzLZ_Y7wk"
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(
x, y, train_size=0.7, test_size=0.3, random_state=random_seed)
algorithm = LogisticRegression()
algorithm.fit(x_train, y_train)
y_pred = algorithm.predict(x_test)
y_proba1 = algorithm.predict_proba(x_test)[:,1]
fpr, tpr, thresholds = roc_curve(y_test, y_proba1)
# + colab={} colab_type="code" id="-_iXjXz6Y7wm"
# ROC曲線の描画
plt.figure(figsize=(6,6))
plt.plot([0, 1], [0, 1], 'k--')
plt.fill_between(fpr, tpr, 0)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('偽陽性率')
plt.ylabel('敏感度')
plt.title('ROC曲線')
plt.show()
# + colab={} colab_type="code" id="od5pt69nY7wo"
# ROC AUCの計算
roc_auc = auc(fpr, tpr)
print(f'ROC曲線下面積:{roc_auc:.4f}')
# + [markdown] colab_type="text" id="52iRNE1RY7wq"
# ### 4.4.5 入力項目の重要度
# + [markdown] colab_type="text" id="2j_ov-Y-Y7wq"
# #### ランダムフォレストのモデルを作るまで
# + colab={} colab_type="code" id="pIRGJkZWY7wr"
# ランダムフォレストのモデルを作るまで
# サンプルデータの読み込み
import seaborn as sns
df_iris = sns.load_dataset("iris")
columns_i = ['がく片長', 'がく片幅', '花弁長', '花弁幅', '種別']
df_iris.columns = columns_i
# 入力データ x
x = df_iris[['がく片長', 'がく片幅', '花弁長', '花弁幅']]
# 正解データ y
y = df_iris['種別']
# アルゴリズムの選定(ランダムフォレスト)
from sklearn.ensemble import RandomForestClassifier
algorithm = RandomForestClassifier(random_state=random_seed)
# 学習
algorithm.fit(x, y)
# + [markdown] colab_type="text" id="fFd91870Y7wt"
# #### 重要度ベクトルの取得
# + colab={} colab_type="code" id="zLFIj4cnY7wu"
# 重要度ベクトルの取得
importances = algorithm.feature_importances_
# 項目名をキーにSeriesを生成
w = pd.Series(importances, index=x.columns)
# 値の大きい順にソート
u = w.sort_values(ascending=False)
# 結果確認
print(u)
# + colab={} colab_type="code" id="ThIVs9YgY7ww"
# 重要度の棒グラフ表示
# 棒グラフ表示
plt.bar(range(len(u)), u, color='b', align='center')
# 項目名表示(90度回転)
plt.xticks(range(len(u)), u.index, rotation=90)
# タイトル表示
plt.title('入力変数の重要度')
plt.show()
# + colab={} colab_type="code" id="pJQwt5keY7wy"
# 決定木の場合
from sklearn.tree import DecisionTreeClassifier
algorithm = DecisionTreeClassifier(random_state=random_seed)
algorithm.fit(x, y)
importances = algorithm.feature_importances_
w = pd.Series(importances, index=x.columns)
u = w.sort_values(ascending=False)
plt.title('入力変数の重要度(決定木)')
plt.bar(range(len(u)), u, color='b', align='center')
plt.xticks(range(len(u)), u.index, rotation=90)
plt.show()
# + colab={} colab_type="code" id="vB5_dDA0Y7w1"
# XGBoostの場合
import xgboost
algorithm = xgboost.XGBClassifier(random_state=random_seed)
algorithm.fit(x, y)
importances = algorithm.feature_importances_
w = pd.Series(importances, index=x.columns)
u = w.sort_values(ascending=False)
plt.title('入力変数の重要度(XGBoost)')
plt.bar(range(len(u)), u, color='b', align='center')
plt.xticks(range(len(u)), u.index, rotation=90)
plt.show()
# + [markdown] colab_type="text" id="4I-oP4ImY7w3"
# ### 4.4.6 回帰モデルの評価方法
# + colab={} colab_type="code" id="NQ49ttZPY7w3"
# データ読み込みからデータ分割まで
# データ読み込み(ボストン・データセット)
from sklearn.datasets import load_boston
boston = load_boston()
# df: 入力データ
df = pd.DataFrame(boston.data, columns=boston.feature_names)
# y: 正解データ
y = boston.target
# 1項目だけの入力データ df1を作る
df1 = df[['RM']]
# 結果確認
display(df.head())
display(df1.head())
print(y[:5])
# + colab={} colab_type="code" id="vWU4DNDAY7w6"
# アルゴリズム選定から予測まで
# アルゴリズム: XGBRegressor
from xgboost import XGBRegressor
algorithm1 = XGBRegressor(objective ='reg:squarederror',
random_state=random_seed)
# 学習 (入力データにdf1を利用)
algorithm1.fit(df1, y)
# 予測
y_pred1 = algorithm1.predict(df1)
# アルゴリズム: XGBRegressor
from xgboost import XGBRegressor
algorithm2 = XGBRegressor(objective ='reg:squarederror',
random_state=random_seed)
# 学習 (入力データにdfを利用)
algorithm2.fit(df, y)
# 予測
y_pred2 = algorithm2.predict(df)
# + colab={} colab_type="code" id="zUADzPPcY7w8"
# 結果確認
print(f'y[:5] {y[:5]}')
print(f'y_pred1[:5] {y_pred1[:5]}')
print(f'y_pred2[:5] {y_pred2[:5]}')
# + colab={} colab_type="code" id="8tGDzOi9Y7w-"
# yの最大値と最小値の計算
y_range = np.array([y.min(), y.max()])
# 結果確認
print(y_range)
# + [markdown] colab_type="text" id="v85oxddhY7xA"
# #### 散布図表示
# + [markdown] colab_type="text" id="_m1wt7U0Y7xA"
# #### 1入力変数の場合
# + colab={} colab_type="code" id="Ha1tUVzWY7xB"
# 散布図による結果確認(1入力変数)
# 描画サイズ指定
plt.figure(figsize=(6,6))
# 散布図
plt.scatter(y, y_pred1)
# 正解データ=予測結果の直線
plt.plot(y_range, y_range, 'k--')
# ラベル・タイトル
plt.xlabel('正解データ')
plt.ylabel('予測結果')
plt.title('正解データと予測結果の散布図表示(1入力変数)')
plt.show()
# + [markdown] colab_type="text" id="leOkv4joY7xD"
# #### 13入力変数の場合
# + colab={} colab_type="code" id="KXv595XNY7xD"
# 散布図による結果確認(13入力変数)
# 描画サイズ指定
plt.figure(figsize=(6,6))
# 散布図
plt.scatter(y, y_pred2)
# 正解データ=予測結果の直線
plt.plot(y_range, y_range, 'k--')
# ラベル・タイトル
plt.xlabel('正解データ')
plt.ylabel('予測結果')
plt.title('正解データと予測結果の散布図表示(13入力変数)')
plt.show()
# + [markdown] colab_type="text" id="BfpnuG-aY7xG"
# #### R2 score
# + colab={} colab_type="code" id="fYUF3lGZY7xH"
# r2 scoreの計算(1入力変数)
from sklearn.metrics import r2_score
r2_score1 = r2_score(y, y_pred1)
print(f'R2 score(1入力変数): {r2_score1:.4f}')
# + colab={} colab_type="code" id="EAb3OG71Y7xJ"
# r2 scoreの計算(13入力変数)
r2_score2 = r2_score(y, y_pred2)
print(f'R2 score(13入力変数): {r2_score2:.4f}')
# + colab={} colab_type="code" id="OeD_zz0EY7xL"
|
notebooks/ch04_04_estimate.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Volume Rendering Tutorial
#
# This notebook shows how to use the new (in version 3.3) Scene interface to create custom volume renderings. The tutorial proceeds in the following steps:
#
# 1. [Creating the Scene](#1.-Creating-the-Scene)
# 2. [Displaying the Scene](#2.-Displaying-the-Scene)
# 3. [Adjusting Transfer Functions](#3.-Adjusting-Transfer-Functions)
# 4. [Saving an Image](#4.-Saving-an-Image)
# 5. [Adding Annotations](#5.-Adding-Annotations)
# ## 1. Creating the Scene
#
# To begin, we load up a dataset and use the `yt.create_scene` method to set up a basic Scene. We store the Scene in a variable called `sc` and render the default `('gas', 'density')` field.
# +
import yt
import numpy as np
from yt.visualization.volume_rendering.transfer_function_helper import TransferFunctionHelper
ds = yt.load("IsolatedGalaxy/galaxy0030/galaxy0030")
sc = yt.create_scene(ds)
# -
# Note that to render a different field, we would use pass the field name to `yt.create_scene` using the `field` argument.
#
# Now we can look at some information about the Scene we just created using the python print keyword:
print (sc)
# This prints out information about the Sources, Camera, and Lens associated with this Scene. Each of these can also be printed individually. For example, to print only the information about the first (and currently, only) Source, we can do:
print (sc.get_source())
# ## 2. Displaying the Scene
#
# We can see that the `yt.create_source` method has created a `VolumeSource` with default values for the center, bounds, and transfer function. Now, let's see what this Scene looks like. In the notebook, we can do this by calling `sc.show()`.
sc.show()
# That looks okay, but it's a little too zoomed-out. To fix this, let's modify the Camera associated with our Scene. This next bit of code will zoom in the camera (i.e. decrease the width of the view) by a factor of 3.
sc.camera.zoom(3.0)
# Now when we print the Scene, we see that the Camera width has decreased by a factor of 3:
print (sc)
# To see what this looks like, we re-render the image and display the scene again. Note that we don't actually have to call `sc.show()` here - we can just have Ipython evaluate the Scene and that will display it automatically.
sc.render()
sc
# That's better! The image looks a little washed-out though, so we use the `sigma_clip` argument to `sc.show()` to improve the contrast:
sc.show(sigma_clip=4.0)
# Applying different values of `sigma_clip` with `sc.show()` is a relatively fast process because `sc.show()` will pull the most recently rendered image and apply the contrast adjustment without rendering the scene again. While this is useful for quickly testing the affect of different values of `sigma_clip`, it can lead to confusion if we don't remember to render after making changes to the camera. For example, if we zoom in again and simply call `sc.show()`, then we get the same image as before:
sc.camera.zoom(3.0)
sc.show(sigma_clip=4.0)
# For the change to the camera to take affect, we have to explicitly render again:
sc.render()
sc.show(sigma_clip=4.0)
# As a general rule, any changes to the scene itself such as adjusting the camera or changing transfer functions requires rendering again. Before moving on, let's undo the last zoom:
sc.camera.zoom(1./3.0)
# ## 3. Adjusting Transfer Functions
#
# Next, we demonstrate how to change the mapping between the field values and the colors in the image. We use the TransferFunctionHelper to create a new transfer function using the `gist_rainbow` colormap, and then re-create the image as follows:
# +
# Set up a custom transfer function using the TransferFunctionHelper.
# We use 10 Gaussians evenly spaced logarithmically between the min and max
# field values.
tfh = TransferFunctionHelper(ds)
tfh.set_field('density')
tfh.set_log(True)
tfh.set_bounds()
tfh.build_transfer_function()
tfh.tf.add_layers(10, colormap='gist_rainbow')
# Grab the first render source and set it to use the new transfer function
render_source = sc.get_source()
render_source.transfer_function = tfh.tf
sc.render()
sc.show(sigma_clip=4.0)
# -
# Now, let's try using a different lens type. We can give a sense of depth to the image by using the perspective lens. To do, we create a new Camera below. We also demonstrate how to switch the camera to a new position and orientation.
# +
cam = sc.add_camera(ds, lens_type='perspective')
# Standing at (x=0.05, y=0.5, z=0.5), we look at the area of x>0.05 (with some open angle
# specified by camera width) along the positive x direction.
cam.position = ds.arr([0.05, 0.5, 0.5], 'code_length')
normal_vector = [1., 0., 0.]
north_vector = [0., 0., 1.]
cam.switch_orientation(normal_vector=normal_vector,
north_vector=north_vector)
# The width determines the opening angle
cam.set_width(ds.domain_width * 0.5)
print (sc.camera)
# -
# The resulting image looks like:
sc.render()
sc.show(sigma_clip=4.0)
# ## 4. Saving an Image
#
# To save a volume rendering to an image file at any point, we can use `sc.save` as follows:
sc.save('volume_render.png',render=False)
# Including the keyword argument `render=False` indicates that the most recently rendered image will be saved (otherwise, `sc.save()` will trigger a call to `sc.render()`). This behavior differs from `sc.show()`, which always uses the most recently rendered image.
#
# An additional caveat is that if we used `sigma_clip` in our call to `sc.show()`, then we must **also** pass it to `sc.save()` as sigma clipping is applied on top of a rendered image array. In that case, we would do the following:
sc.save('volume_render_clip4.png',sigma_clip=4.0,render=False)
# ## 5. Adding Annotations
#
# Finally, the next cell restores the lens and the transfer function to the defaults, moves the camera, and adds an opaque source that shows the axes of the simulation coordinate system.
# +
# set the lens type back to plane-parallel
sc.camera.set_lens('plane-parallel')
# move the camera to the left edge of the domain
sc.camera.set_position(ds.domain_left_edge)
sc.camera.switch_orientation()
# add an opaque source to the scene
sc.annotate_axes()
sc.render()
sc.show(sigma_clip=4.0)
# -
|
doc/source/visualizing/Volume_Rendering_Tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: tagifai
# language: python
# name: tagifai
# ---
# + [markdown] id="LPZmAUydQIC9"
# <div align="center">
# <h1><img width="30" src="https://madewithml.com/static/images/rounded_logo.png"> <a href="https://madewithml.com/">Made With ML</a></h1>
# Applied ML · MLOps · Production
# <br>
# Join 20K+ developers in learning how to responsibly <a href="https://madewithml.com/about/">deliver value</a> with applied ML.
# </div>
#
# <br>
#
# <div align="center">
# <a target="_blank" href="https://madewithml.com/subscribe/"><img src="https://img.shields.io/badge/Subscribe-20K-brightgreen"></a>
# <a target="_blank" href="https://github.com/GokuMohandas/madewithml"><img src="https://img.shields.io/github/stars/GokuMohandas/madewithml.svg?style=social&label=Star"></a>
# <a target="_blank" href="https://www.linkedin.com/in/goku"><img src="https://img.shields.io/badge/style--5eba00.svg?label=LinkedIn&logo=linkedin&style=social"></a>
# <a target="_blank" href="https://twitter.com/GokuMohandas"><img src="https://img.shields.io/twitter/follow/GokuMohandas.svg?label=Follow&style=social"></a>
# <p>🔥 Among the <a href="https://github.com/topics/deep-learning" target="_blank">top ML</a> repositories on GitHub</p>
# </div>
#
# <br>
# <hr>
# + [markdown] id="L7--e8qjzvte"
# # Optimize (GPU)
# + [markdown] id="IRyA7luizvtf"
# Use this notebooks to run hyperparameter optimization on Google Colab and utilize it's free GPUs.
# + id="HacuZe08zvtf"
# In case you update the code after installing
# %load_ext autoreload
# %autoreload 2
# + [markdown] id="rOAOZ5NJzvtl"
# ## Clone repository
# + id="dC_KGdE6zvtl" colab={"base_uri": "https://localhost:8080/"} outputId="c7b6792f-e23b-411f-8a9c-c66bc007f794"
# Load repository
# !git clone https://github.com/GokuMohandas/applied-ml.git
# + id="aiKzsC9kzvtn" colab={"base_uri": "https://localhost:8080/"} outputId="9f3f9719-23dd-4769-b1b8-8b40c265c93d"
# Files
% cd applied-ml
# !ls
# + [markdown] id="LnZVQRcZzvtp"
# ## Setup
# + id="lKp6B4M478m_"
# Use latest pip
# !pip install --upgrade pip
# + id="Wdx2DRGjzvtq"
# Set up
# !make install-dev
# + [markdown] id="wzxXb5mjzvts"
# ## Optimize
# + id="O4oQwat9Syf7"
from tagifai import main
# + id="0PzQcqIuKLkU" colab={"base_uri": "https://localhost:8080/"} outputId="8bc6da9f-99d4-4bd9-a127-6335c25d5724"
# Download data
main.download_data()
# + id="ZsPyGrZYIsmA" colab={"base_uri": "https://localhost:8080/"} outputId="810b521c-3e6f-4e2e-af73-ad1969bf7280"
# Check if data downloaded
# !ls assets/data
# + colab={"base_uri": "https://localhost:8080/"} id="WNGWNx_uSvaU" outputId="c7994498-063c-4d3b-d196-84286ce7f0c7"
# Optimize
main.optimize(num_trials=100)
# + id="eOT46qHmD1ZR" colab={"base_uri": "https://localhost:8080/"} outputId="c0694160-c316-4599-fcfe-aad16b24600b"
# Train best model (saving artifacts this time)
main.train_model()
# + [markdown] id="w8Wm1xPl0HyF"
# ## Download
# + [markdown] id="uJrowj_lzvtz"
# Download and transfer files to your local system and run the command `tagifai set-artifact-metadata` to match all metadata as if it were run from your machine.
# + id="lEkEtbaX0LbU"
from google.colab import files
# + id="LJeRbLxh0NxV" outputId="6ac30040-a208-4c79-ccf7-fab4ecde319a" colab={"base_uri": "https://localhost:8080/", "height": 680}
# Download
# !zip -r assets.zip assets/experiments/1
files.download('assets.zip')
files.download('assets/experiments/trials.csv')
files.download('config/args.json')
|
notebooks/optimize.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# The labeler
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:90% !important; }</style>"))
# +
import sys
import copy
import numpy as np
import matplotlib.pyplot as plt
import scipy
from scipy.io import savemat
import torch
import torchvision
import torchvision.transforms as transforms
import pathlib
# +
## find slash type of operating system
if sys.platform == 'linux':
slash_type = '/'
print('Autodetected operating system: Linux. Using "/" for directory slashes')
elif sys.platform == 'win32':
slash_type = '\\'
print(f'Autodetected operating system: Windows. Using "{slash_type}{slash_type}" for directory slashes')
elif sys.platform == 'darwin':
slash_type = '/'
print("What computer are you running this on? I haven't tested it on OSX or anything except windows and ubuntu.")
print('Autodetected operating system: OSX. Using "/" for directory slashes')
# +
## lOAD & PREPROCESS stat.npy file
## outputs: 'images' (input into CNN)
dir_load = r'/media/rich/bigSSD RH/res2p/scanimage data/round 4 experiments/mouse 6.28/20201102/suite2p/plane0'
fileName_load = 'stat.npy'
# PATH_absolute = pathlib.Path('.').absolute()
# PATH_load_dir_statFile = f'{PATH_absolute}/ROI_Classifiers/label data/mouse 6_28 _ day 20200903/'
path_load = f'{dir_load}{slash_type}{fileName_load}'
# PATH_load_dir_statFile = '/media/rich/Home_Linux_partition/GoogleDrive_ocaml_cache/Research/Sabatini Lab Stuff - working/Code/PYTHON/ROI_Classifiers/test data_ mouse2_5 _ 20200308/'
# PATH_load_dir_statFile = '/media/rich/Home_Linux_partition/GoogleDrive_ocaml_cache/Research/Sabatini Lab Stuff - working/Code/PYTHON/ROI_Classifiers/label data/mouse 6_28 _ day 20200903/'
# PATH_load_dir_statFile = '/media/rich/Home_Linux_partition/GoogleDrive_ocaml_cache/Research/Sabatini Lab Stuff - working/Code/PYTHON/ROI_Classifiers/test data_mouse6_28 _ 20200815/'
print(path_load)
# +
stat = np.load(path_load, allow_pickle=True)
print('stat file loaded')
num_ROI = stat.shape[0]
print(f'Number of ROIs: {num_ROI}')
height = 512
width = 1024
spatial_footprints_centered = np.zeros((num_ROI, 241,241))
for i in range(num_ROI):
spatial_footprints_centered[i , stat[i]['ypix'] - np.int16(stat[i]['med'][0]) + 120, stat[i]['xpix'] - np.int16(stat[i]['med'][1]) + 120] = stat[i]['lam'] # this is formatted for coding ease (dim1: y pix) (dim2: x pix) (dim3: ROI#)
spatial_footprints_centered_crop = spatial_footprints_centered[:, 102:138 , 102:138]
# %matplotlib inline
plt.figure()
plt.imshow(np.max(spatial_footprints_centered_crop , axis=0) ** 0.2);
plt.title('spatial_footprints_centered_crop MIP^0.2');
images = spatial_footprints_centered_crop
# +
# Label: **1=Neuron-InPlane-GOOD , 2=Neuron-OutOfPlane-GOOD , 3=NonNeuron-GOOD , 4=Neuron-InPlane-BAD , 5=Neuron-OutOfPlane-BAD , **6=NonNeuron-BAD
# To stop labeling enter a value of 8-9
num_ROI = images.shape[0]
labels = np.empty(num_ROI)
labels[:] = np.nan
print(f'number of ROIs: {num_ROI}')
# +
# %matplotlib qt
num_ROI = spatial_footprints_centered_crop.shape[0]
input_val = 0
iter_ROI = 0
plt.figure()
# plt.imshow(spatial_footprints_crop[: , : , 0])
plt.pause(0.5)
while np.int8(input_val) < 7 and iter_ROI <= num_ROI:
plt.imshow(spatial_footprints_centered_crop[iter_ROI, : , :])
plt.title(iter_ROI)
plt.show(block=False)
plt.pause(0.35)
input_val = input()
if np.int8(input_val) >=7:
input_val = np.nan
labels[iter_ROI] = np.int8(input_val)
plt.pause(0.15)
if iter_ROI%10==0:
print(f'Num labeled: {iter_ROI}')
iter_ROI +=1
# -
plt.figure()
plt.hist(labels,50)
np.save('labels.npy' , labels)
labels = np.load('labels.npy')
# last labeled ROI
labled_ROI_idx = np.nonzero(np.isnan(labels)==0)
np.max(labled_ROI_idx)
plt.figure()
plt.plot(labels)
print(st[0].keys())
st[0]['med'] # middle of neuron/ROI
print(spatial_footprints_centered.shape)
print(spatial_footprints_centered_crop.shape)
# dir_save = '/media/rich/Home_Linux_partition/temp files/'
# np.save(f'{dir_save}spatial_footprints_centered_crop.npy' , spatial_footprints_centered_crop)
dir_save = 'G:\\My Drive\\Research\\Sabatini Lab Stuff - working\\Code\\PYTHON\\'
fileName_save = 'spatial_footprints_centered_crop.npy'
np.save(fileName_save , spatial_footprints_centered_crop)
plt.figure()
plt.imshow(spatial_footprints_centered_crop[2,:,:])
plt.figure()
plt.imshow(spatial_footprints_centered_crop[4,:,:])
plt.figure()
plt.imshow(spatial_footprints_centered_crop[3,:,:])
plt.figure()
plt.imshow(spatial_footprints_centered_crop[555,:,:])
plt.figure()
plt.imshow(spatial_footprints_centered_crop[444,:,:])
|
ROI_Classifiers/ROI_labeling_and_augmentation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Benchmarking VASP / VaspInteractive + ALMLP
# Use `cluster_mlp.fillPoll` to generate random metal cluster size.
#
# For each cluster, compare the following relaxation results:
# - `vasp+bfgs`:
# - Pure VASP single point calculator (mimicked by setting `nsw=0` in `VaspInteractive`)
# - Use `ase.optimize.bfgs` as direct optimizer
# - `vasp+al`:
# - Pure VASP single point
# - Flare potential + bfgs minimatch
# - `vpi_bfgs`:
# - `VaspInteractive` calculator
# - Use `ase.optimize.bfgs` as direct optimizer
# - `vpi+al`:
# - `VaspInteractive` calculator
# - Flare potential + bfgs minimatch
#
# Following quantities are compared:
# - Total wall time
# - Total parent (DFT) calls
# - Total electronic steps
#
# Note, this test requires `ulissigroup/kubeflow_vasp:clusterga` image and a working worker pod config yaml file.
# To enable cache sharing on all worker pods, volume mounting should be set inside the yaml file.
# %cd /home/jovyan/data/vasp-interactive-test/examples/
import joblib
from joblib import Memory
from ex10_mlp_online import run_opt, gen_cluster
from dask_kubernetes import KubeCluster
from dask.distributed import Client
import dask.bag as bag
cluster = KubeCluster("worker-cpu-spec-large.yml")
client = Client(cluster)
cluster.adapt(maximum=10)
# ### Use `joblib.memory` to cache partial results
# We use `joblib.memory` to lazy evaluate execution of code. For each function call, an additional parameter `i` is provided for generating a unique structure.
#
# You can test this by running `gen_cluster_iter("Cu", 10, 0)` multiple times, they should give you identical structures
from pathlib import Path
curdir = Path(".").resolve()
bench_root = curdir / "mlp_cluster_benchmark" / "cache"
memory = Memory(bench_root)
@memory.cache
def gen_cluster_iter(metal, n, i):
cluster = gen_cluster(metal, n)
return cluster
t1 = gen_cluster_iter("Cu", 10, 0)
t2 = gen_cluster_iter("Cu", 10, 0)
t1 == t2
@memory.cache
def run_opt_cached(structure, **params):
"""Cached version of results"""
return run_opt(structure, **params)
def run_benchmark_cluster(metal, n, i):
"""Run 4x cycles"""
results = dict(metal=metal, n=n)
initial_structure = gen_cluster_iter(metal, n, i)
parameters = [dict(vasp="Vasp", use_al=False, store_wf=True),
dict(vasp="Vasp", use_al=True, store_wf=True),
dict(vasp="VaspInteractive", use_al=True, store_wf=True),
dict(vasp="VaspInteractive", use_al=False, store_wf=True)]
keys = ["vasp+bfgs", "vasp+al", "vpi+bfgs", "vpi+al"]
param_seq = [param for param in parameters]
for key, param in zip(keys, parameters):
try:
t, steps, fin, _ = run_opt_cached(initial_structure, **param)
results[key] = dict(t=t, steps=steps, final_image=fin)
except RuntimeError:
results[key] = None
return results
import itertools
cluster_size = range(3, 25, 3)
sample_indices = range(10)
seq = list(itertools.product(["Cu"], cluster_size, sample_indices))
jobs = bag.from_sequence(seq).map(lambda v: run_benchmark_cluster(*v))
jobs
job_done = jobs.compute()
# +
import matplotlib.pyplot as plt
import numpy as np
time = {"vasp+bfgs": {}, "vasp+al": {}, "vpi+bfgs": {}, "vpi+al": {}}
tot_steps = {"vasp+bfgs": {}, "vasp+al": {}, "vpi+bfgs": {}, "vpi+al": {}}
parent_calls = {"vasp+bfgs": {}, "vasp+al": {}, "vpi+bfgs": {}, "vpi+al": {}}
for entry in job_done:
n = entry["n"]
for key in time.keys():
old_arr = time[key].get(n, [])
if entry[key] is not None:
old_arr.append(entry[key]["t"])
else:
old_arr.append(np.nan)
time[key][n] = old_arr
for entry in job_done:
n = entry["n"]
for key in parent_calls.keys():
old_arr = parent_calls[key].get(n, [])
if entry[key] is not None:
old_arr.append(len(entry[key]["steps"]))
else:
old_arr.append(np.nan)
parent_calls[key][n] = old_arr
for entry in job_done:
n = entry["n"]
for key in tot_steps.keys():
old_arr = tot_steps[key].get(n, [])
if entry[key] is not None:
old_arr.append(sum(entry[key]["steps"]))
else:
old_arr.append(np.nan)
tot_steps[key][n] = old_arr
plt.figure(figsize=(15, 5))
plt.subplot(131)
for key in time.keys():
size = []
raw_time = []
for k, v in time[key].items():
size.append(k)
raw_time.append(v)
size = np.array(size)
raw_time = np.array(raw_time)
l, *_ = plt.plot(size, np.nanmean(raw_time, axis=1),)
plt.fill_between(x=size, y1=np.nanmin(raw_time, axis=1),
y2=np.nanmax(raw_time, axis=1), label=key, color=l.get_c(), alpha=0.15)
plt.title("Wall Time Comparison")
plt.ylabel("System Time")
plt.xlabel("Cluster size")
plt.yscale("log")
plt.legend()
plt.subplot(132)
for key in parent_calls.keys():
size = []
raw_pcalls = []
for k, v in parent_calls[key].items():
size.append(k)
raw_pcalls.append(v)
size = np.array(size)
raw_pcalls = np.array(raw_pcalls)
l, *_ = plt.plot(size, np.nanmean(raw_pcalls, axis=1))
plt.fill_between(size, np.nanmin(raw_pcalls, axis=1),
np.nanmax(raw_pcalls, axis=1), label=key, color=l.get_c(), alpha=0.15)
# plt.errorbar(x=size, y=np.nanmean(raw_pcalls, axis=1),
# yerr=np.vstack([np.nanmean(raw_pcalls, axis=1) - np.nanmin(raw_pcalls, axis=1),
# np.nanmax(raw_pcalls, axis=1) - np.nanmean(raw_pcalls, axis=1)]), label=key)
plt.title("Parent call numbers")
plt.ylabel("Parent calls")
plt.yscale("log")
plt.xlabel("Cluster size")
plt.legend()
plt.subplot(133)
for key in tot_steps.keys():
size = []
raw_steps = []
for k, v in tot_steps[key].items():
size.append(k)
raw_steps.append(v)
size = np.array(size)
raw_steps = np.array(raw_steps)
l, *_ = plt.plot(size, np.nanmean(raw_steps, axis=1))
plt.fill_between(size, np.nanmin(raw_steps, axis=1), np.nanmax(raw_steps, axis=1), label=key,
color=l.get_c(), alpha=0.15)
# plt.errorbar(x=size, y=np.nanmean(raw_steps, axis=1),
# yerr=np.vstack([np.nanmean(raw_steps, axis=1) - np.nanmin(raw_steps, axis=1),
# np.nanmax(raw_steps, axis=1) - np.nanmean(raw_steps, axis=1)]), label=key)
plt.title("Total Electronic Steps")
plt.ylabel("Tot steps")
plt.xlabel("Cluster size")
plt.yscale("log")
plt.legend()
plt.show()
# -
# In addition, we can compare the speed-up for "vasp+al", "vpi+bfgs" and "vpi+al" methods vs "vasp+bfgs", for the same structure
#
# Due to display issue, only the average curve is shown
# +
import matplotlib.pyplot as plt
import numpy as np
time_reduct = {"vasp+al": {}, "vpi+bfgs": {}, "vpi+al": {}}
steps_reduct = {"vasp+al": {}, "vpi+bfgs": {}, "vpi+al": {}}
pcall_reduct = {"vasp+al": {}, "vpi+bfgs": {}, "vpi+al": {}}
for entry in job_done:
n = entry["n"]
try:
t_ref = entry["vasp+bfgs"]["t"]
except KeyError:
for key in time_reduct.keys():
time_reduct[key][n] = np.nan
continue
for key in time_reduct.keys():
old_arr = time_reduct[key].get(n, [])
if entry[key] is not None:
old_arr.append(entry[key]["t"] / t_ref)
else:
old_arr.append(np.nan)
time_reduct[key][n] = old_arr
for entry in job_done:
n = entry["n"]
try:
pcall_ref = len(entry["vasp+bfgs"]["steps"])
except KeyError:
for key in pcall_reduct.keys():
pcall_reduct[key][n] = np.nan
continue
for key in pcall_reduct.keys():
old_arr = pcall_reduct[key].get(n, [])
if entry[key] is not None:
old_arr.append(len(entry[key]["steps"]) / pcall_ref)
else:
old_arr.append(np.nan)
pcall_reduct[key][n] = old_arr
for entry in job_done:
n = entry["n"]
try:
steps_ref = sum(entry["vasp+bfgs"]["steps"])
except KeyError:
for key in steps_reduct.keys():
steps_reduct[key][n] = np.nan
continue
for key in steps_reduct.keys():
old_arr = steps_reduct[key].get(n, [])
if entry[key] is not None:
old_arr.append(sum(entry[key]["steps"]) / steps_ref)
else:
old_arr.append(np.nan)
steps_reduct[key][n] = old_arr
plt.figure(figsize=(15, 5))
plt.subplot(131)
plt.plot([], [])
for key in time_reduct.keys():
size = []
raw_time_reduct = []
for k, v in time_reduct[key].items():
size.append(k)
raw_time_reduct.append(v)
size = np.array(size)
raw_time_reduct = np.array(raw_time_reduct)
l, *_ = plt.plot(size, np.nanmean(raw_time_reduct, axis=1), label=key)
# plt.fill_between(x=size, y1=np.nanmin(raw_time_reduct, axis=1),
# y2=np.nanmax(raw_time_reduct, axis=1), label=key, color=l.get_c(), alpha=0.15)
plt.title("Avg. Time vs VASP+BFGS")
plt.ylabel("System time_reduct")
plt.xlabel("Cluster size")
plt.ylim(0, 1.5)
plt.axhline(y=1.0, ls="--")
# plt.yscale("log")
plt.legend()
plt.subplot(132)
plt.plot([], [])
for key in pcall_reduct.keys():
size = []
raw_pcalls = []
for k, v in pcall_reduct[key].items():
size.append(k)
raw_pcalls.append(v)
size = np.array(size)
raw_pcalls = np.array(raw_pcalls)
l, *_ = plt.plot(size, np.nanmean(raw_pcalls, axis=1), label=key)
# plt.fill_between(size, np.nanmin(raw_pcalls, axis=1),
# np.nanmax(raw_pcalls, axis=1), label=key, color=l.get_c(), alpha=0.15)
# plt.errorbar(x=size, y=np.nanmean(raw_pcalls, axis=1),
# yerr=np.vstack([np.nanmean(raw_pcalls, axis=1) - np.nanmin(raw_pcalls, axis=1),
# np.nanmax(raw_pcalls, axis=1) - np.nanmean(raw_pcalls, axis=1)]), label=key)
plt.title("Avg. Parent Calls vs VASP+BFGS")
plt.ylabel("Parent calls")
# plt.yscale("log")
plt.xlabel("Cluster size")
plt.axhline(y=1.0, ls="--")
plt.ylim(0, 1.5)
plt.legend()
plt.subplot(133)
plt.plot([], [])
for key in steps_reduct.keys():
size = []
raw_steps = []
for k, v in steps_reduct[key].items():
size.append(k)
raw_steps.append(v)
size = np.array(size)
raw_steps = np.array(raw_steps)
l, *_ = plt.plot(size, np.nanmean(raw_steps, axis=1), label=key)
# plt.fill_between(size, np.nanmin(raw_steps, axis=1), np.nanmax(raw_steps, axis=1), label=key,
# color=l.get_c(), alpha=0.15)
# plt.errorbar(x=size, y=np.nanmean(raw_steps, axis=1),
# yerr=np.vstack([np.nanmean(raw_steps, axis=1) - np.nanmin(raw_steps, axis=1),
# np.nanmax(raw_steps, axis=1) - np.nanmean(raw_steps, axis=1)]), label=key)
plt.title("Avg. Total E-steps vs VASP+BFGS")
plt.ylabel("Tot steps")
plt.xlabel("Cluster size")
plt.axhline(y=1.0, ls="--")
plt.ylim(0, 1.5)
# plt.yscale("log")
plt.legend()
plt.show()
# -
cluster.close()
|
examples/vasp-cluster-benchmark.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Log the concentrations to and learn the models for TOC again to avoid 0 happen in the prediction. The n_components is increased to 9 to find the downslope of CV score in n_components variation.
# +
import numpy as np
import pandas as pd
import dask.dataframe as dd
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use('ggplot')
#plt.style.use('seaborn-whitegrid')
plt.style.use('seaborn-colorblind')
plt.rcParams['figure.dpi'] = 300
plt.rcParams['savefig.dpi'] = 300
plt.rcParams['savefig.bbox'] = 'tight'
import datetime
date = datetime.datetime.now().strftime('%Y%m%d')
# %matplotlib inline
# -
# # Launch deployment
from dask.distributed import Client
from dask_jobqueue import SLURMCluster
cluster = SLURMCluster(
project="aslee@10.110.16.5",
queue='main',
cores=40,
memory='10 GB',
walltime="00:10:00",
log_directory='job_logs'
)
client.close()
cluster.close()
client = Client(cluster)
#cluster.scale(100)
cluster.adapt(maximum=100)
client
# # Build model for TOC
# +
from dask_ml.model_selection import train_test_split
merge_df = dd.read_csv('data/spe+bulk_dataset_20201008.csv')
X = merge_df.iloc[:, 1: -5].to_dask_array(lengths=True)
X = X / X.sum(axis = 1, keepdims = True)
y = merge_df['TOC%'].to_dask_array(lengths=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, shuffle = True, random_state = 24)
# -
# ## Grid search
# We know the relationship between the spectra and bulk measurements might not be linear; and based on the pilot_test.ipynb, the SVR algorithm with NMF transformation provides the better cv score. So we focus on grid search with NMF transformation (4, 5, 6, 7, and 8 components based on the PCA result, 9 to find the downslope of CV score) and SVR. We manually transformed (np.log) y_train during training, use the model to predict X_test, transform (np.exp) y_predict back to original space, and evaluate the test score.
# +
from dask_ml.model_selection import GridSearchCV
from sklearn.decomposition import NMF
from sklearn.svm import SVR
from sklearn.pipeline import make_pipeline
from sklearn.compose import TransformedTargetRegressor
pipe = make_pipeline(NMF(max_iter = 2000, random_state = 24), SVR())
params = {
'nmf__n_components': [4, 5, 6, 7, 8, 9],
'svr__C': np.logspace(0, 7, 8),
'svr__gamma': np.logspace(-5, 0, 6)
}
grid = GridSearchCV(pipe, param_grid = params, cv = 10, scoring = 'neg_mean_absolute_error', n_jobs = -1)
grid.fit(X_train, np.log(y_train))
print('The best cv score: {:.3f}'.format(grid.best_score_))
print('The best model\'s parameters: {}'.format(grid.best_estimator_))
# -
y_predict = np.exp(grid.best_estimator_.predict(X_test))
y_ttest = np.array(y_test)
# +
from sklearn.metrics import r2_score
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import max_error
print('Scores in the test set:')
print('R2 = {:.3f} .'.format(r2_score(y_ttest, y_predict)))
print('The mean absolute error is {:.3f} (%, concetration).'.format(mean_absolute_error(y_ttest, y_predict)))
print('The max. residual error is {:.3f} (%, concetration).'.format(max_error(y_ttest, y_predict)))
# -
plt.plot(range(len(y_predict)), y_ttest, alpha=0.6, label='Measurement')
plt.plot(range(len(y_predict)), y_predict, label='Prediction (R$^2$={:.2f})'.format(r2_score(y_ttest, y_predict)))
#plt.text(12, -7, r'R$^2$={:.2f}, mean ab. error={:.2f}, max. ab. error={:.2f}'.format(grid.best_score_, mean_absolute_error(y_ttest, y_predict), max_error(y_ttest, y_predict)))
plt.ylabel('TOC concentration (%)')
plt.xlabel('Sample no.')
plt.legend()
plt.savefig('results/toc_predictions_nmr+svr_{}.png'.format(date))
# ### Visualization
result_df = pd.DataFrame(grid.cv_results_)
result_df.to_csv('results/toc_grid_nmf+svr_{}.csv'.format(date))
#result_df = pd.read_csv('results/toc_grid_nmf+svr_20201013.csv', index_col = 0)
#result_df = result_df[result_df.mean_test_score > -1].reset_index(drop = True)
len(result_df[result_df.mean_test_score < -2])
np.linspace(-2, 0, 5)
# +
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
for n_components in [4, 5, 6, 7, 8, 9]:
data = result_df[result_df.param_nmf__n_components == n_components].reset_index(drop = True)
fig = plt.figure(figsize = (7.3,5))
ax = fig.gca(projection='3d')
xx = data.param_svr__gamma.astype(float)
yy = data.param_svr__C.astype(float)
zz = data.mean_test_score.astype(float)
max_index = np.argmax(zz)
surf = ax.plot_trisurf(np.log10(xx), np.log10(yy), zz, cmap=cm.Greens, linewidth=0.1)
ax.scatter3D(np.log10(xx), np.log10(yy), zz, c = 'orange', s = 5)
# mark the best score
ax.scatter3D(np.log10(xx), np.log10(yy), zz, c = 'w', s = 5, alpha = 1)
text = '{} components\n$\gamma :{:.1f}$, C: {:.1e},\nscore:{:.3f}'.format(n_components, xx[max_index], yy[max_index], zz[max_index])
ax.text(-3, 5, 2,text, fontsize=12)
ax.set_zlim(-1, 1.2)
ax.set_zticks(np.linspace(-2, 0, 5))
ax.set_xlabel('$log(\gamma)$')
ax.set_ylabel('log(C)')
ax.set_zlabel('cv score')
# rotate the view
ax.view_init(30, 135)
#fig.colorbar(surf, shrink=0.5, aspect=5)
fig.savefig('results/toc_grid_{}nmr+svr_3D_{}.png'.format(n_components, date))
# +
n_components = [4, 5, 6, 7, 8, 9]
scores = []
for n in n_components:
data = result_df[result_df.param_nmf__n_components == n].reset_index(drop = True)
rank_min = data.rank_test_score.min()
scores = np.hstack((scores, data.loc[data.rank_test_score == rank_min, 'mean_test_score'].values))
plt.plot(n_components, scores, marker='o')
plt.xlabel('Amount of components')
plt.ylabel('Best CV score')
plt.savefig('results/toc_scores_components_{}.png'.format(date))
# -
from joblib import dump, load
#model = load('models/tc_nmf+svr_model_20201012.joblib')
dump(grid.best_estimator_, 'models/toc_nmf+svr_model_{}.joblib'.format(date))
|
build_models_05.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import emcee
import corner
# +
#read in data - BCB
dfBv2 = pd.read_csv('1_ZFBS_tuning_BCB.csv', sep=',')
#add type of mutation
mutlabels2 = []
for i in range(7):
mutlabels2.append('1 bp core')
for i in range(5):
mutlabels2.append('2 bp core')
mutlabels2.append('wild type')
for i in range(7):
mutlabels2.append('1 bp core')
for i in range(15):
mutlabels2.append('1 bp non-core')
dfBv2['mutation type'] = mutlabels2
dfBv2.head()
# +
#BCB
# 1 bp core
ind_1c = dfBv2['mutation type'] == '1 bp core'
dfB_1c = dfBv2.loc[ind_1c, :]
Kd_B_1c = np.array(dfB_1c['Kd'])
Kderr_B_1c = np.array(dfB_1c['Kd err'])
FR_B_1c = np.array(dfB_1c['fold-repression'])
FRerr_B_1c = np.array(dfB_1c['fr error'])
# 2 bp core
ind_2c = dfBv2['mutation type'] == '2 bp core'
dfB_2c = dfBv2.loc[ind_2c, :]
Kd_B_2c = np.array(dfB_2c['Kd'])
Kderr_B_2c = np.array(dfB_2c['Kd err'])
FR_B_2c = np.array(dfB_2c['fold-repression'])
FRerr_B_2c = np.array(dfB_2c['fr error'])
# 1 bp non-core
ind_1nc = dfBv2['mutation type'] == '1 bp non-core'
dfB_1nc = dfBv2.loc[ind_1nc, :]
Kd_B_1nc = np.array(dfB_1nc['Kd'])
Kderr_B_1nc = np.array(dfB_1nc['Kd err'])
FR_B_1nc = np.array(dfB_1nc['fold-repression'])
FRerr_B_1nc = np.array(dfB_1nc['fr error'])
# wild type
ind_wt = dfBv2['mutation type'] == 'wild type'
dfB_wt = dfBv2.loc[ind_wt, :]
Kd_B_wt = np.array(dfB_wt['Kd'])
Kderr_B_wt = np.array(dfB_wt['Kd err'])
FR_B_wt = np.array(dfB_wt['fold-repression'])
FRerr_B_wt = np.array(dfB_wt['fr error'])
# +
#BCB
#sort data - lowest to highest ∆G
x2 = np.array(dfBv2['∆G'])
y2 = np.array(dfBv2['fold-repression'])
z2 = np.array(dfBv2['fr error'])
xyz2 = np.column_stack((x2, y2, z2))
col = 0
data2 = xyz2[np.argsort(xyz2[:, col])]
dG_B = data2[:, 0]
FR_B = data2[:, 1]
FRerr_B = data2[:, 2]
#Kd in nM
Kd_B = np.exp(dG_B/0.5921)*1e9
#Kd error
dfBerr = pd.read_csv('1_ZFBS_tuning_BCB_err.csv', sep=',')
Kderr_B = np.array(dfBerr['Kd err'])
# +
#read in data - AAA
dfA = pd.read_csv('1_ZFBS_tuning_AAA.csv',header=None)
dfA = dfA.rename(columns={0: '∆G', 1: 'fold-repression', 2: 'error'})
#sort data - lowest to highest ∆G
x1 = np.array(dfA['∆G'])
y1 = np.array(dfA['fold-repression'])
z1 = np.array(dfA['error'])
xyz1 = np.column_stack((x1, y1, z1))
col = 0
data1 = xyz1[np.argsort(xyz1[:, col])]
dG_A = data1[:, 0]
FR_A = data1[:, 1]
FRerr_A = data1[:, 2]
#Kd in nM
Kd_A = np.exp(dG_A/0.5921)*1e9
#Kd error
dfAerr = pd.read_csv('1_ZFBS_tuning_AAA_err.csv', sep=',')
Kderr_A = np.array(dfAerr['Kd err'])
# +
dfAv2 = pd.read_csv('1_ZFBS_tuning_AAA_v2.csv', sep=',')
mutlabels = []
for i in range(9):
mutlabels.append('1 bp core')
mutlabels.append('wild type')
for i in range(15):
mutlabels.append('1 bp non-core')
for i in range(3):
mutlabels.append('2 bp core')
dfAv2['mutation type'] = mutlabels
dfAv2.head()
# +
#AAA
# 1 bp core
ind_1c = dfAv2['mutation type'] == '1 bp core'
dfA_1c = dfAv2.loc[ind_1c, :]
Kd_A_1c = np.array(dfA_1c['Kd'])
Kderr_A_1c = np.array(dfA_1c['Kd err'])
FR_A_1c = np.array(dfA_1c['fold-repression'])
FRerr_A_1c = np.array(dfA_1c['fr error'])
# 2 bp core
ind_2c = dfAv2['mutation type'] == '2 bp core'
dfA_2c = dfAv2.loc[ind_2c, :]
Kd_A_2c = np.array(dfA_2c['Kd'])
Kderr_A_2c = np.array(dfA_2c['Kd err'])
FR_A_2c = np.array(dfA_2c['fold-repression'])
FRerr_A_2c = np.array(dfA_2c['fr error'])
# 1 bp non-core
ind_1nc = dfAv2['mutation type'] == '1 bp non-core'
dfA_1nc = dfAv2.loc[ind_1nc, :]
Kd_A_1nc = np.array(dfA_1nc['Kd'])
Kderr_A_1nc = np.array(dfA_1nc['Kd err'])
FR_A_1nc = np.array(dfA_1nc['fold-repression'])
FRerr_A_1nc = np.array(dfA_1nc['fr error'])
# wild type
ind_wt = dfAv2['mutation type'] == 'wild type'
dfA_wt = dfAv2.loc[ind_wt, :]
Kd_A_wt = np.array(dfA_wt['Kd'])
Kderr_A_wt = np.array(dfA_wt['Kd err'])
FR_A_wt = np.array(dfA_wt['fold-repression'])
FRerr_A_wt = np.array(dfA_wt['fr error'])
# -
def FR_single(C0, C1, Erp, x):
"""Model for fold repression for a single repressor"""
# C0 = RNAP binding term
# C1 = conversion factor and R
# Erp = Pol-ZF interaction E
UR = 1 / (1 + C0)
Freg = (1 + (C1/x)*np.exp(-Erp)) / (1 + C1/x)
R = 1 / (1 + C0/Freg)
return UR/R
# +
def lnlike(theta, x, y, yerr):
"""calculate log likelihood"""
C0, C1, Erp = theta
ypred = FR_single(C0, C1, Erp, x)
inv_sigma2 = 1/(yerr**2)
X1 = np.sum((ypred-y)**2 * inv_sigma2 - np.log(inv_sigma2))
return -0.5 * X1
def lnprior(theta, y, yerr):
"""calculate log priors"""
C0, C1, Erp = theta
if not (0 < C0 and 0 < C1 and 0 < Erp):
return -np.inf # Hard-cutoff for positive value constraint
mu1 = 5e-3
sigma1 = 5e-2
log_Pr1 = np.log(1.0 / (np.sqrt(2*np.pi)*sigma1)) - 0.5*(C0 - mu1)**2/sigma1**2
mu2 = 5e2
sigma2 = 5e1
log_Pr2 = np.log(1.0 / (np.sqrt(2*np.pi)*sigma2)) - 0.5*(C1 - mu2)**2/sigma2**2
mu3 = 5
sigma3 = 5
log_Pr3 = np.log(1.0 / (np.sqrt(2*np.pi)*sigma3)) - 0.5*(Erp - mu3)**2/sigma3**2
return log_Pr1 + log_Pr2 + log_Pr3
def lnprob(theta, x, y, yerr):
"""calculate log probability"""
lp = lnprior(theta, y, yerr)
if not np.isfinite(lp):
return -np.inf
return lp + lnlike(theta, x, y, yerr)
# +
ndim = 3
nwalkers = 50
pos = [np.array([5e-3*(1 + 1e-4*np.random.randn()),
2e2*(1 + 1e-4*np.random.randn()),
5*(1 + 1e-4*np.random.randn())
]) for i in range(nwalkers)] # Initialise walkers
sampler = emcee.EnsembleSampler(nwalkers, ndim, lnprob, args=(Kd_A2, FR_A2, FRerr_A2), threads=4)
# +
print("Running burn-in...")
pos, _, _ = sampler.run_mcmc(pos, 500)
sampler.reset()
print("Running production...")
sampler.run_mcmc(pos, 10000)
# -
samples2 = sampler.chain[:,:,:].reshape((-1,ndim))
samples2_end = sampler.chain[:, 8000:, :].reshape((-1,ndim))
# +
fig = plt.figure()
k = np.linspace(2, 40, 400)
for C0, C1, Erp in samples2_end[np.random.randint(len(samples2_end), size=100)]:
plt.plot(k, FR_single(C0, C1, Erp, k), color='#cccccc', lw=2, alpha=0.7)
nc1 = plt.errorbar(Kd_A_1nc, FR_A_1nc, xerr=Kderr_A_1nc, yerr=FRerr_A_1nc,
fmt='o', color='#02818a', label='1 bp non-core')
c1 = plt.errorbar(Kd_A_1c, FR_A_1c, xerr=Kderr_A_1c, yerr=FRerr_A_1c,
fmt='o', color='#238443', label='1 bp core')
c2 = plt.errorbar(Kd_A_2c, FR_A_2c, xerr=Kderr_A_2c, yerr=FRerr_A_2c,
fmt='o', color='#e31a1c', label='2 bp core')
wt = plt.errorbar(Kd_A_wt, FR_A_wt, xerr=Kderr_A_wt, yerr=FRerr_A_wt,
fmt='o', color='#fe9929', label='wild type')
plt.ylim(0.5, 6)
#plt.xlim(0, 90)
plt.legend(handles=[nc1, c1, c2, wt], fontsize=12)
plt.xlabel('$K_{d}$ [nM]')
plt.ylabel('fold repression')
figure_options={'figsize':(8.27,5.83)} #figure size in inches. A4=11.7x8.3. A5=8.27,5.83
font_options={'size':'12','family':'sans-serif','sans-serif':'Arial'}
plt.rc('figure', **figure_options)
plt.rc('font', **font_options)
plt.savefig('AAA_1BS_fit.pdf',dpi=150,transparent=True, bbox_inches='tight')
plt.show()
# -
samples1 = sampler.chain[:,:,:].reshape((-1,ndim))
samples1_end = sampler.chain[:, 8000:, :].reshape((-1,ndim))
# +
fig = plt.figure()
k = np.linspace(1.5, 80, 400)
for C0, C1, Erp in samples1_end[np.random.randint(len(samples1_end), size=100)]:
plt.plot(k, FR_single(C0, C1, Erp, k), color='#cccccc', lw=2, alpha=0.7)
nc1 = plt.errorbar(Kd_B_1nc, FR_B_1nc, xerr=Kderr_B_1nc, yerr=FRerr_B_1nc,
fmt='o', color='#02818a', label='1 bp non-core')
c1 = plt.errorbar(Kd_B_1c, FR_B_1c, xerr=Kderr_B_1c, yerr=FRerr_B_1c,
fmt='o', color='#238443', label='1 bp core')
c2 = plt.errorbar(Kd_B_2c, FR_B_2c, xerr=Kderr_B_2c, yerr=FRerr_B_2c,
fmt='o', color='#e31a1c', label='2 bp core')
wt = plt.errorbar(Kd_B_wt, FR_B_wt, xerr=Kderr_B_wt, yerr=FRerr_B_wt,
fmt='o', color='#fe9929', label='wild type')
plt.ylim(0.5, 6)
#plt.xlim(0, 90)
plt.legend(handles=[nc1, c1, c2, wt], fontsize=12)
plt.xlabel('$K_{d}$ [nM]')
plt.ylabel('fold repression')
figure_options={'figsize':(8.27,5.83)} #figure size in inches. A4=11.7x8.3. A5=8.27,5.83
font_options={'size':'12','family':'sans-serif','sans-serif':'Arial'}
plt.rc('figure', **figure_options)
plt.rc('font', **font_options)
#plt.savefig('BCB_1BS_fit.pdf',dpi=150,transparent=True, bbox_inches='tight')
plt.show()
# +
df = pd.DataFrame(samples2)
df.to_csv(path_or_buf='samplesout_AAA.csv', sep=',')
df1 = pd.read_csv('samplesout_AAA.csv', delimiter=',')
iterations = 10000
tburn = 1000
data2 = np.zeros((df1.shape[0]-tburn*nwalkers)*(df1.shape[1]-1)).reshape((df1.shape[0]-(tburn*nwalkers)), (df1.shape[1]-1))
for i in range(0, int(df1.shape[1]-1)):
for j in range(1, nwalkers+1):
data2[(iterations - tburn)*(j - 1):(iterations - tburn)*(j),i]=np.array(df1.iloc[iterations*j - iterations + tburn: iterations*j, i + 1])
parameternames = ["$C0$", "$C1$", "$Erp$"]
fig = corner.corner(data2,
labels=parameternames,
quantiles=[0.16, 0.5, 0.84],
show_titles=True,
title_fmt='.2e',
title_kwargs={"fontsize": 12},
verbose=True)
#plt.savefig('BCB_1BS_Erp_corner.pdf',dpi=150,transparent=True, bbox_inches='tight')
plt.show()
# +
np.random.seed(0) # For reproducible outputs
modelscale=np.linspace(2.25, 80, 400)
numberofmodeltraces=10000
ypred1=np.zeros((len(modelscale),numberofmodeltraces))
ypred2=np.zeros((len(modelscale),numberofmodeltraces))
i=0
for C0, C1, Erp in samples1[np.random.randint(len(samples1), size=numberofmodeltraces)]:
ypred1[:, i] = FR_single(C0, C1, Erp, modelscale)
i+=1
# 2-sigma distributions
quant1=[np.mean(ypred1, axis=1)-2*np.std(ypred1, axis=1),
np.mean(ypred1, axis=1),
np.mean(ypred1, axis=1)+2*np.std(ypred1, axis=1)]
# +
fig, ax = plt.subplots()
plt.fill_between(modelscale, quant1[0], quant1[2], color='#969696', alpha=0.3)
plt.plot(modelscale, quant1[1], '-', color='#969696', alpha=1, lw=2)
nc1 = plt.errorbar(Kd_B_1nc, FR_B_1nc, xerr=Kderr_B_1nc, yerr=FRerr_B_1nc,
fmt='o', color='#02818a', label='1 bp non-core')
c1 = plt.errorbar(Kd_B_1c, FR_B_1c, xerr=Kderr_B_1c, yerr=FRerr_B_1c,
fmt='o', color='#238443', label='1 bp core')
c2 = plt.errorbar(Kd_B_2c, FR_B_2c, xerr=Kderr_B_2c, yerr=FRerr_B_2c,
fmt='o', color='#e31a1c', label='2 bp core')
wt = plt.errorbar(Kd_B_wt, FR_B_wt, xerr=Kderr_B_wt, yerr=FRerr_B_wt,
fmt='o', color='#fe9929', label='wild type')
plt.ylim(0.5, 6)
plt.xlim(0, 90)
plt.legend(handles=[nc1, c1, c2, wt], fontsize=15)
plt.xlabel('$K_{d}$ (nM)')
plt.ylabel('fold repression')
ax.spines['bottom'].set_linewidth(2)
ax.spines['top'].set_linewidth(2)
ax.spines['left'].set_linewidth(2)
ax.spines['right'].set_linewidth(2)
ax.tick_params(which='major', width=2, length=8, pad=9,direction='in',top=True,right=True)
ax.tick_params(which='minor', width=2, length=4, pad=9,direction='in',top=True,right=True)
figure_options={'figsize':(8.27,5.83)} #figure size in inches. A4=11.7x8.3. A5=8.27,5.83
font_options={'size':'24','family':'sans-serif','sans-serif':'Arial'}
plt.rc('figure', **figure_options)
plt.rc('font', **font_options)
plt.savefig('BCB_1BS_tuning_shaded.pdf',dpi=150,transparent=True, bbox_inches='tight')
plt.show()
# +
np.random.seed(0) # For reproducible outputs
modelscale=np.linspace(2.25, 40, 400)
numberofmodeltraces=10000
ypred1=np.zeros((len(modelscale),numberofmodeltraces))
ypred2=np.zeros((len(modelscale),numberofmodeltraces))
i=0
for C0, C1, Erp in samples2[np.random.randint(len(samples2), size=numberofmodeltraces)]:
ypred1[:, i] = FR_single(C0, C1, Erp, modelscale)
i+=1
# 2-sigma distributions
quant2=[np.mean(ypred1, axis=1)-2*np.std(ypred1, axis=1),
np.mean(ypred1, axis=1),
np.mean(ypred1, axis=1)+2*np.std(ypred1, axis=1)]
# +
fig, ax = plt.subplots()
plt.fill_between(modelscale, quant2[0], quant2[2], color='#969696', alpha=0.3)
plt.plot(modelscale, quant2[1], '-', color='#969696', alpha=1, lw=2)
nc1 = plt.errorbar(Kd_A_1nc, FR_A_1nc, xerr=Kderr_A_1nc, yerr=FRerr_A_1nc,
fmt='o', color='#02818a', label='1 bp non-core')
c1 = plt.errorbar(Kd_A_1c, FR_A_1c, xerr=Kderr_A_1c, yerr=FRerr_A_1c,
fmt='o', color='#238443', label='1 bp core')
c2 = plt.errorbar(Kd_A_2c, FR_A_2c, xerr=Kderr_A_2c, yerr=FRerr_A_2c,
fmt='o', color='#e31a1c', label='2 bp core')
wt = plt.errorbar(Kd_A_wt, FR_A_wt, xerr=Kderr_A_wt, yerr=FRerr_A_wt,
fmt='o', color='#fe9929', label='wild type')
plt.ylim(0.5, 6)
plt.xlim(0, 45)
plt.legend(handles=[nc1, c1, c2, wt], fontsize=15)
plt.xlabel('$K_{d}$ (nM)')
plt.ylabel('fold repression')
ax.spines['bottom'].set_linewidth(2)
ax.spines['top'].set_linewidth(2)
ax.spines['left'].set_linewidth(2)
ax.spines['right'].set_linewidth(2)
ax.tick_params(which='major', width=2, length=8, pad=9,direction='in',top=True,right=True)
ax.tick_params(which='minor', width=2, length=4, pad=9,direction='in',top=True,right=True)
figure_options={'figsize':(8.27,5.83)} #figure size in inches. A4=11.7x8.3. A5=8.27,5.83
font_options={'size':'24','family':'sans-serif','sans-serif':'Arial'}
plt.rc('figure', **figure_options)
plt.rc('font', **font_options)
plt.savefig('AAA_1BS_tuning_shaded.pdf',dpi=150,transparent=True, bbox_inches='tight')
plt.show()
# +
#Pcoop AAA
dfA2 = pd.read_csv('1_ZFBS_tuning_AAA_NAND.csv',header=None)
dfA2 = dfA2.rename(columns={0: '∆G', 1: 'fold-repression', 2: 'fr error'})
dfA2_1 = pd.read_csv('1_ZFBS_tuning_AAA_NAND_err.csv')
#sort data - lowest to highest ∆G
x3 = np.array(dfA2['∆G'])
y3 = np.array(dfA2['fold-repression'])
z3 = np.array(dfA2['fr error'])
xyz3 = np.column_stack((x3, y3, z3))
col = 0
data3 = xyz3[np.argsort(xyz3[:, col])]
dG_A2 = data3[:, 0]
FR_A2 = data3[:, 1]
FRerr_A2 = data3[:, 2]
#Kd in nM
Kd_A2 = np.exp(dG_A2/0.5921)*1e9
dfA2_v2 = pd.DataFrame()
dfA2_v2['fold-repression'] = FR_A2
dfA2_v2['fr error'] = FRerr_A2
dfA2_v2['Kd'] = Kd_A2
dfA2_v2['Kd err'] = dfA2_1['Kd err']
mutlabels3 = []
mutlabels3.append('wild type')
mutlabels3.append('1 bp non-core')
mutlabels3.append('1 bp core')
mutlabels3.append('1 bp non-core')
for i in range(2):
mutlabels3.append('1 bp core')
for i in range(2):
mutlabels3.append('1 bp non-core')
mutlabels3.append('1 bp core')
dfA2_v2['mutation type'] = mutlabels3
#AAA Pcoop
# 1 bp core
ind2_1c = dfA2_v2['mutation type'] == '1 bp core'
dfA2_1c = dfA2_v2.loc[ind2_1c, :]
Kd_A2_1c = np.array(dfA2_1c['Kd'])
Kderr_A2_1c = np.array(dfA2_1c['Kd err'])
FR_A2_1c = np.array(dfA2_1c['fold-repression'])
FRerr_A2_1c = np.array(dfA2_1c['fr error'])
# 1 bp non-core
ind2_1nc = dfA2_v2['mutation type'] == '1 bp non-core'
dfA2_1nc = dfA2_v2.loc[ind2_1nc, :]
Kd_A2_1nc = np.array(dfA2_1nc['Kd'])
Kderr_A2_1nc = np.array(dfA2_1nc['Kd err'])
FR_A2_1nc = np.array(dfA2_1nc['fold-repression'])
FRerr_A2_1nc = np.array(dfA2_1nc['fr error'])
# wild type
ind2_wt = dfA2_v2['mutation type'] == 'wild type'
dfA2_wt = dfA2_v2.loc[ind2_wt, :]
Kd_A2_wt = np.array(dfA2_wt['Kd'])
Kderr_A2_wt = np.array(dfA2_wt['Kd err'])
FR_A2_wt = np.array(dfA2_wt['fold-repression'])
FRerr_A2_wt = np.array(dfA2_wt['fr error'])
# -
samples3 = sampler.chain[:,:,:].reshape((-1,ndim))
samples3_end = sampler.chain[:, 8000:, :].reshape((-1,ndim))
# +
np.random.seed(0) # For reproducible outputs
modelscale=np.linspace(2.25, 40, 400)
numberofmodeltraces=10000
ypred1=np.zeros((len(modelscale),numberofmodeltraces))
ypred2=np.zeros((len(modelscale),numberofmodeltraces))
i=0
for C0, C1, Erp in samples3[np.random.randint(len(samples3), size=numberofmodeltraces)]:
ypred1[:, i] = FR_single(C0, C1, Erp, modelscale)
i+=1
# 2-sigma distributions
quant3=[np.mean(ypred1, axis=1)-2*np.std(ypred1, axis=1),
np.mean(ypred1, axis=1),
np.mean(ypred1, axis=1)+2*np.std(ypred1, axis=1)]
# +
fig, ax = plt.subplots()
plt.fill_between(modelscale, quant3[0], quant3[2], color='#969696', alpha=0.3)
plt.plot(modelscale, quant3[1], '-', color='#969696', alpha=1, lw=2)
nc1 = plt.errorbar(Kd_A2_1nc, FR_A2_1nc, xerr=Kderr_A2_1nc, yerr=FRerr_A2_1nc,
fmt='o', color='#02818a', label='1 bp non-core')
c1 = plt.errorbar(Kd_A2_1c, FR_A2_1c, xerr=Kderr_A2_1c, yerr=FRerr_A2_1c,
fmt='o', color='#238443', label='1 bp core')
wt = plt.errorbar(Kd_A2_wt, FR_A2_wt, xerr=Kderr_A2_wt, yerr=FRerr_A2_wt,
fmt='o', color='#fe9929', label='wild type')
plt.ylim(0.5, 6)
plt.xlim(0, 45)
plt.legend(handles=[nc1, c1, wt], fontsize=15)
plt.xlabel('$K_{d}$ (nM)')
plt.ylabel('fold repression')
ax.spines['bottom'].set_linewidth(2)
ax.spines['top'].set_linewidth(2)
ax.spines['left'].set_linewidth(2)
ax.spines['right'].set_linewidth(2)
ax.tick_params(which='major', width=2, length=8, pad=9,direction='in',top=True,right=True)
ax.tick_params(which='minor', width=2, length=4, pad=9,direction='in',top=True,right=True)
figure_options={'figsize':(8.27,5.83)} #figure size in inches. A4=11.7x8.3. A5=8.27,5.83
font_options={'size':'24','family':'sans-serif','sans-serif':'Arial'}
plt.rc('figure', **figure_options)
plt.rc('font', **font_options)
plt.savefig('AAA_Pcoop_tuning_shaded.pdf',dpi=150,transparent=True, bbox_inches='tight')
plt.show()
# -
|
NB_1ZFBS_tuning.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.10 64-bit (''backtest_env'': conda)'
# name: python3
# ---
# # Backtesting SMA trading strategy using Vectorbt API
#
# ### Source code:
# https://pypi.org/project/vectorbt/ , https://vectorbt.dev/docs/index.html
# +
# Import libraries
import vectorbt as vbt
import numpy as np
import pandas as pd
import plotly.io as pio
pio.renderers.default = 'svg' # comment this line out to get interactive charts
# -
# Pull hostorical prices
price = vbt.YFData.download('BTC-USD', freq='D', fees=0.01, missing_index='drop').get('Close')
# Select time window to test.
price = price.loc["2015":"2022"]
price
# +
# Define short and long SMA windows. Test different window combinations to see results of Buy & Hold vs SMA strategy
fast_ma = vbt.MA.run(price, 10)
slow_ma = vbt.MA.run(price, 20)
entries = fast_ma.ma_above(slow_ma, crossover=True)
exits = fast_ma.ma_below(slow_ma, crossover=True)
# Fit the model and input starting investment to calculate total profit form the trading stategy
pf = vbt.Portfolio.from_signals(price, entries, exits, init_cash=100)
pf.total_profit()
# -
# Calculate total profit from the Buy & Hold strategy
pf1 = vbt.Portfolio.from_holding(price, init_cash=100)
pf1.total_profit()
# Plot trading strategy
pf.plot().show()
# Plot drawdown for the selected strategy
price.vbt.drawdowns.plot(title='BTC-USD Drawdown').show()
# Obtain complete stats for the trading strategy
pf.stats(freq='D')
|
btc_backtest.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.9.1 64-bit
# metadata:
# interpreter:
# hash: aee8b7b246df8f9039afb4144a1f6fd8d2ca17a180786b69acc140d282b71a49
# name: python3
# ---
# # aitextgen Training Hello World
#
# _Last Updated: Feb 21, 2021 (v.0.4.0)_
#
# by <NAME>
#
# A "Hello World" Tutorial to show how training works with aitextgen, even on a CPU!
from aitextgen.TokenDataset import TokenDataset
from aitextgen.tokenizers import train_tokenizer
from aitextgen.utils import GPT2ConfigCPU
from aitextgen import aitextgen
# First, download this [text file of Shakespeare's plays](https://raw.githubusercontent.com/karpathy/char-rnn/master/data/tinyshakespeare/input.txt), to the folder with this notebook, then put the name of the downloaded Shakespeare text for training into the cell below.
file_name = "input.txt"
# You can now train a custom Byte Pair Encoding Tokenizer on the downloaded text!
#
# This will save one file: `aitextgen.tokenizer.json`, which contains the information needed to rebuild the tokenizer.
train_tokenizer(file_name)
tokenizer_file = "aitextgen.tokenizer.json"
# `GPT2ConfigCPU()` is a mini variant of GPT-2 optimized for CPU-training.
#
# e.g. the # of input tokens here is 64 vs. 1024 for base GPT-2. This dramatically speeds training up.
config = GPT2ConfigCPU()
# Instantiate aitextgen using the created tokenizer and config
ai = aitextgen(tokenizer_file=tokenizer_file, config=config)
# You can build datasets for training by creating TokenDatasets, which automatically processes the dataset with the appropriate size.
data = TokenDataset(file_name, tokenizer_file=tokenizer_file, block_size=64)
data
# Train the model! It will save pytorch_model.bin periodically and after completion. On a 2020 8-core iMac, this took ~25 minutes to run.
#
# The configuration below processes 400,000 subsets of tokens (8 * 50000), which is about just one pass through all the data (1 epoch). Ideally you'll want multiple passes through the data and a training loss less than `2.0` for coherent output; when training a model from scratch, that's more difficult, but with long enough training you can get there!
ai.train(data, batch_size=8, num_steps=50000, generate_every=5000, save_every=5000)
# Generate text from your trained model!
ai.generate(10, prompt="ROMEO:")
# With your trained model, you can reload the model at any time by providing the `pytorch_model.bin` model weights, the `config`, and the `tokenizer`.
ai2 = aitextgen(model="trained_model/pytorch_model.bin",
tokenizer_file="aitextgen.tokenizer.json",
config="trained_model/config.json")
ai2.generate(10, prompt="ROMEO:")
# # MIT License
#
# Copyright (c) 2021 <NAME>
#
# Permission is hereby granted, free of charge, to any person obtaining a copy
# of this software and associated documentation files (the "Software"), to deal
# in the Software without restriction, including without limitation the rights
# to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
# copies of the Software, and to permit persons to whom the Software is
# furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in all
# copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
# AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
# OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
# SOFTWARE.
|
notebooks/training_hello_world.ipynb
|