code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import numpy as np
import emcee
import scipy.optimize as op
import scipy
import corner
from multiprocessing import Pool
import multiprocessing
import time
from astropy.cosmology import FlatLambdaCDM
from astropy import cosmology
from astropy.coordinates import Distance
import astropy
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator
import matplotlib
# -
# %matplotlib notebook
print('numpy version: {}'.format(np.__version__))
print('pandas version: {}'.format(pd.__version__))
print('matplotlib version: {}'.format(matplotlib.__version__))
print('astropy version: {}'.format(astropy.__version__))
print('emcee version: {}'.format(emcee.__version__))
print('scipy version: {}'.format(scipy.__version__))
# # Figure 8
#
# Create Figure 8 (the RCF plot) in [Fremling et al. 2020](https://ui.adsabs.harvard.edu/abs/2019arXiv191012973F/abstract).
# BTS data
bts_df = pd.read_hdf('../data/final_rcf_table.h5')
# +
z_sn = bts_df.z_sn.values
z_host = bts_df.z_host.values
norm_Ia = np.where( ( (bts_df.sn_type == 'Ia-norm') |
(bts_df.sn_type == 'Ia') |
(bts_df.sn_type == 'Ia-91bg') |
(bts_df.sn_type == 'Ia-91T') |
(bts_df.sn_type == 'Ia-99aa') |
(bts_df.sn_type == 'ia')
| (bts_df.sn_type == 'Ia-norm*')
| (bts_df.sn_type == 'Ia-91T*')
| (bts_df.sn_type == 'Ia-91T**')
| (bts_df.sn_type == 'SN Ia')
)
)
norm_cc = np.where( (bts_df.sn_type == 'IIb') |
(bts_df.sn_type == 'Ib') |
(bts_df.sn_type == 'IIP') |
(bts_df.sn_type == 'Ib/c') |
(bts_df.sn_type == 'Ic-norm') |
(bts_df.sn_type == 'IIn') |
(bts_df.sn_type == 'IIL') |
(bts_df.sn_type == 'Ic-broad') |
(bts_df.sn_type == 'II') |
(bts_df.sn_type == 'II-pec') |
(bts_df.sn_type == 'Ib-pec') |
(bts_df.sn_type == 'Ic') |
(bts_df.sn_type == 'Ic-BL') |
(bts_df.sn_type == 'IIP*') |
(bts_df.sn_type == 'II*') |
(bts_df.sn_type == 'Ibn') |
(bts_df.sn_type == 'II**') |
(bts_df.sn_type == 'Ib-norm') |
(bts_df.sn_type == 'IIn*')
)
has_host_z = np.where((z_host > 0) & np.isfinite(z_host))
no_host = np.where((z_host < 0) | np.isnan(z_host))
has_host_cc = np.intersect1d(has_host_z, norm_cc)
has_host_ia = np.intersect1d(has_host_z, norm_Ia)
no_host_cc = np.intersect1d(no_host, norm_cc)
no_host_ia = np.intersect1d(no_host, norm_Ia)
z_mix = z_sn.copy()
z_mix[has_host_z] = z_host[has_host_z]
# +
# prep data for analysis
flat_h0_70 = FlatLambdaCDM(H0=70,Om0=0.3)
d_l = Distance(z=z_mix, cosmology=flat_h0_70)
distmod = d_l.distmod.value
A_w1 = 0.0385226*3.1*bts_df.ebv_host.values
M_mix_w1 = bts_df.w1_host - distmod - A_w1
# tractor
tractor_gal = np.where(np.isfinite(M_mix_w1)
& np.isfinite(bts_df.sep)
& (bts_df.sn_type != 'ambiguous')
)
hit_idx = np.where(np.isfinite(bts_df.z_host)
& (bts_df.z_host > 0)
& np.isfinite(bts_df.sep)
& (bts_df.sn_type != 'ambiguous')
)
miss_idx = np.where(np.isfinite(bts_df.z_host)
& (bts_df.z_host == -999)
& np.isfinite(bts_df.sep)
& (bts_df.sn_type != 'ambiguous')
)
tractor_gal_hit = np.intersect1d(tractor_gal[0], hit_idx[0])
tractor_gal_miss = np.intersect1d(tractor_gal[0], miss_idx[0])
tractor_Ia_hit = np.intersect1d(norm_Ia[0], tractor_gal_hit)
tractor_Ia_miss = np.intersect1d(norm_Ia[0], tractor_gal_miss)
# values for analysis
in_ned = np.append(np.ones_like(z_mix[tractor_Ia_hit]),
np.zeros_like(z_mix[tractor_Ia_miss])
)
abs_mag = np.append(M_mix_w1[tractor_Ia_hit],
M_mix_w1[tractor_Ia_miss])
z = np.append(z_mix[tractor_Ia_hit], z_mix[tractor_Ia_miss])
# -
print('There are {} ({} hits) SNe Ia in the joint RCF analysis'.format(len(in_ned), sum(in_ned)))
# ## MCMC to measure RCF
# +
def p_ab(x, y, a, b, c):
return 1 / (1 + np.exp(a*x + b*y - c))
def lnprior(theta):
a, b, c = theta
if (0 < a < 1e6) and (0 < b < 1e6) and (-100 < c < 100):
return 0.
return -np.inf
def lnlike(theta, trials, x, y):
a, b, c = theta
return np.sum(np.log([scipy.stats.bernoulli.pmf(t, _p) for t, _p in zip(trials, p_ab(x, y, a, b, c))]))
def lnprob(theta, trials, x, y):
lp = lnprior(theta)
if not np.isfinite(lp):
return -np.inf
return lp + lnlike(theta, trials, x, y)
# -
# ### Get p(z) and p(M)
# +
def p_z(x, a, c):
return 1 / (1 + np.exp(a*x - c))
def lnprior_z(theta):
a, c = theta
if (0 < a < 1e6) and (-100 < c < 100):
return 0.
return -np.inf
def lnlike_z(theta, trials, x):
a, c = theta
return np.sum(np.log([scipy.stats.bernoulli.pmf(t, _p) for t, _p in zip(trials, p_z(x, a, c))]))
def lnprob_z(theta, trials, x):
lp = lnprior_z(theta)
if not np.isfinite(lp):
return -np.inf
return lp + lnlike_z(theta, trials, x)
# -
# #### Run full RCF solution
# +
nll = lambda *args: -lnlike(*args)
result = op.minimize(nll, [(25, 1, -10)], args=(in_ned, z, abs_mag))
ndim, nwalkers = 3, 25
pos = [result["x"] + 1e-4*np.random.randn(ndim) for i in range(nwalkers)]
max_n = 10000
# -
a, b, c = result["x"]
p_ab(0.005, -24, a, b, c)
# +
old_tau = np.inf
backend = emcee.backends.HDFBackend("../data/RCF_joint_zM_chains.h5")
with Pool(4) as pool:
sampler = emcee.EnsembleSampler(nwalkers, ndim, lnprob,
args=(in_ned, z, abs_mag),
pool=pool,
backend=backend)
start = time.time()
for sample in sampler.sample(pos, iterations=max_n, progress=True):
if sampler.iteration % 100:
continue
tau = sampler.get_autocorr_time(tol=0)
# Check convergence
converged = np.all(tau * 100 < sampler.iteration)
converged &= np.all(np.abs(old_tau - tau) / tau < 0.01)
if converged:
break
old_tau = tau
end = time.time()
multi_time = end - start
print("Multiprocessing took {0:.1f} seconds".format(multi_time))
# -
# ### Run p(z)
# +
Ia_hit_ignore_wise = np.intersect1d(norm_Ia[0], hit_idx)
Ia_miss_ignore_wise = np.intersect1d(norm_Ia[0], miss_idx)
in_ned_ignore_wise = np.append(np.ones_like(z_mix[Ia_hit_ignore_wise]),
np.zeros_like(z_mix[Ia_miss_ignore_wise])
)
z_ignore_wise = np.append(z_mix[Ia_hit_ignore_wise], z_mix[Ia_miss_ignore_wise])
# +
nll = lambda *args: -lnlike_z(*args)
result = op.minimize(nll, [(25, 1)], args=(in_ned_ignore_wise, z_ignore_wise))
a, c = result["x"]
ndim, nwalkers = 2, 25
pos_z = [result["x"] + 1e-4*np.random.randn(ndim) for i in range(nwalkers)]
max_n = 5000
# +
old_tau = np.inf
backend = emcee.backends.HDFBackend("../data/RCF_z_chains.h5")
with Pool(4) as pool:
sampler_z = emcee.EnsembleSampler(nwalkers, ndim, lnprob_z,
args=(in_ned_ignore_wise, z_ignore_wise),
pool=pool,
backend=backend)
start = time.time()
for sample in sampler_z.sample(pos_z, iterations=max_n, progress=True):
if sampler_z.iteration % 100:
continue
tau = sampler_z.get_autocorr_time(tol=0)
# Check convergence
converged = np.all(tau * 100 < sampler_z.iteration)
converged &= np.all(np.abs(old_tau - tau) / tau < 0.01)
if converged:
break
old_tau = tau
end = time.time()
multi_time = end - start
print("Multiprocessing took {0:.1f} seconds".format(multi_time))
# +
z_grid = np.linspace(0, 0.2, 1001)
autocorr_z = sampler_z.get_autocorr_time(tol=0)
n_burn_z = 5*np.ceil(np.max(autocorr_z)).astype(int)
samples_z = sampler_z.get_chain(discard=n_burn_z, flat=True)
p_z_1d_grid = np.empty((len(z_grid),len(samples_z)))
for grid_num, redshift in enumerate(z_grid):
p_z_1d_grid[grid_num] = p_z(redshift, samples_z[:,0], samples_z[:,1])
p_z5, p_z50, p_z95 = np.percentile(p_z_1d_grid, (5,50,95), axis=1)
# -
# #### Run p(M_w1)
# +
nll = lambda *args: -lnlike_z(*args)
result = op.minimize(nll, [(0, -18)], args=(in_ned, abs_mag))
b, c = result["x"]
ndim, nwalkers = 2, 20
pos_m = [result["x"] + 1e-4*np.random.randn(ndim) for i in range(nwalkers)]
max_n = 5000
# +
old_tau = np.inf
backend = emcee.backends.HDFBackend("../data/RCF_M_chains.h5")
with Pool(4) as pool:
sampler_m = emcee.EnsembleSampler(nwalkers, ndim, lnprob_z,
args=(in_ned, abs_mag),
pool=pool,
backend=backend)
start = time.time()
for sample in sampler_m.sample(pos_m, iterations=max_n, progress=True):
if sampler_m.iteration % 100:
continue
tau = sampler_m.get_autocorr_time(tol=0)
# Check convergence
converged = np.all(tau * 100 < sampler_m.iteration)
converged &= np.all(np.abs(old_tau - tau) / tau < 0.01)
if converged:
break
old_tau = tau
end = time.time()
multi_time = end - start
print("Multiprocessing took {0:.1f} seconds".format(multi_time))
# +
m_grid = np.linspace(-27.5, -10, 2000)
autocorr_m = sampler_m.get_autocorr_time(tol=0)
n_burn_m = 5*np.ceil(np.max(autocorr_m)).astype(int)
samples_m = sampler_m.get_chain(discard=50, flat=True)
p_m_1d_grid = np.empty((len(m_grid),len(samples_m)))
for grid_num, m_w1 in enumerate(m_grid):
p_m_1d_grid[grid_num] = p_z(m_w1, samples_m[:,0], samples_m[:,1])
p_m5, p_m50, p_m95 = np.percentile(p_m_1d_grid, (5,50,95), axis=1)
# -
# ## Make plot
# +
n_grid = 200
m_k_grid, redshift_grid = np.mgrid[-11.5:-24.5:n_grid*1j, 0:0.16:n_grid*1j]
max_posterior = sampler.flatchain[np.argmax(sampler.flatlnprobability)]
p_m_z = p_ab(redshift_grid, m_k_grid, max_posterior[0], max_posterior[1], max_posterior[2])
# -
y_tick_grid = np.linspace(0,n_grid,14)
del_ytick = np.diff(y_tick_grid)[0]
x_tick_grid = np.linspace(0,n_grid,5)
del_xtick = np.diff(x_tick_grid)[0]
# +
def m_to_y(m_k_s, del_ytick=del_ytick):
return (-11.5 - m_k_s)*del_ytick
def z_to_x(z, del_xtick=del_xtick):
return z*del_xtick/0.04
# -
z_w1_grid = np.linspace(0.0001,0.3,300)
det_limit = 20.699-Distance(z=z_w1_grid, cosmology=flat_h0_70).distmod.value
# +
left, width = 0.115, 0.655
bottom, height = 0.115, 0.655
bottom_h = left_h = left + width + 0.02
rect_scatter = [left, bottom, width, height]
rect_histx = [left, bottom_h, width, 0.195]
rect_histy = [left_h, bottom, 0.195, height]
color_dict = {'hit': '#D32EA8', #'#0571b0',
'miss': '#00AAFF'} #'#ca0020'}
# start with a rectangular Figure
fig = plt.figure(figsize=(6, 6))
axScatter = plt.axes(rect_scatter)
axHistx = plt.axes(rect_histx)
axHisty = plt.axes(rect_histy)
p2d = axScatter.imshow(p_m_z, origin="lower",cmap='Greys',
vmin=0.0, vmax=1.0, zorder=-100)
axScatter.plot(z_to_x(z[in_ned==1]), m_to_y(abs_mag[in_ned==1]),
'+', color=color_dict['hit'], ms=8, mew=1.3,
label=r'$\mathrm{NED}_z$', zorder=10)
axScatter.plot(z_to_x(z[in_ned==0]), m_to_y(abs_mag[in_ned==0]),
'o', c='None', mec=color_dict['miss'], ms=9, mew=0.85,
label=r'$!\mathrm{NED}_z$')
axScatter.plot(z_to_x(z_w1_grid), m_to_y(det_limit), '--',
color = "0.6", alpha = 0.8, zorder = -10)
axScatter.set_xticks(x_tick_grid)
axScatter.set_xticklabels(['0.0', '0.04', '0.08', '0.12', '0.16'])
axScatter.set_yticks(y_tick_grid[:-1] + del_ytick/2)
axScatter.set_yticklabels(np.linspace(-24,-12,13)[::-1].astype(int))
axScatter.yaxis.set_minor_locator(MultipleLocator(del_ytick/2))
axScatter.xaxis.set_minor_locator(MultipleLocator(del_xtick/4))
axScatter.set_ylabel(r"$M_{W_1,\mathrm{host}}\;(\mathrm{mag\;AB})$", fontsize = 16)
axScatter.set_xlabel(r"$z_\mathrm{host}$", fontsize = 16)
axScatter.set_ylim(0,200)
axScatter.set_xlim(0,200)
axHistx.plot(z_grid, p_z50, color=color_dict['hit'])
axHistx.fill_between(z_grid, p_z5, p_z95,
alpha=0.4, color=color_dict['hit'])
axHistx.set_xlim(0,0.16)
axHistx.set_ylim(0,1)
axHistx.xaxis.set_major_locator(MultipleLocator(0.04))
axHistx.xaxis.set_minor_locator(MultipleLocator(0.01))
axHistx.yaxis.set_major_locator(MultipleLocator(0.2))
axHistx.yaxis.set_minor_locator(MultipleLocator(0.05))
axHistx.set_xticklabels([])
axHistx.set_ylabel("RCF(z)")
axHisty.plot(p_m50, m_grid, color=color_dict['hit'])
axHisty.fill_betweenx(m_grid, p_m5, p_m95,
alpha=0.4, color=color_dict['hit'])
axHisty.set_ylim(-11.5,-24.5)
axHisty.set_xlim(0,1)
axHisty.set_yticklabels([])
axHisty.xaxis.set_major_locator(MultipleLocator(0.2))
axHisty.xaxis.set_minor_locator(MultipleLocator(0.05))
axHisty.yaxis.set_major_locator(MultipleLocator(1))
axHisty.yaxis.set_minor_locator(MultipleLocator(0.5))
axHisty.tick_params(axis="x", which="both",
top=True, bottom=False,
labeltop=True, labelbottom=False,
labelrotation=270)
axHisty.set_xlabel(r"$\mathrm{RCF}(M_{W_1})$")
axHisty.xaxis.set_label_position('top')
cbaxes = fig.add_axes([0.19, 0.12, 0.5, 0.02])
# cbaxes = fig.add_axes([0.25, 0.12, 0.5, 0.02])
fig.colorbar(p2d, cax = cbaxes,
orientation="horizontal", ticks=[0,0.2,0.4,0.6,0.8,1.0])
cbaxes.set_xlabel(r"$\mathrm{RCF}(z,M_{W_1})$", fontsize=10)
cbaxes.tick_params(axis="x", top=True, bottom=False,
labeltop=True, labelbottom=False)
cbaxes.xaxis.set_label_position('top')
axScatter.tick_params(axis='both', which='both', labelsize=12)
axScatter.legend(loc = 3, fontsize = 12,
handlelength = 0.8, handletextpad = 0.5,
framealpha = 0.99,
bbox_to_anchor=(.7,.16))
fig.savefig("conditional_Ia_Mw1.pdf")
# -
# ### Make corner plot of appendix in the paper
def makeCorner(sampler, nburn, paramsNames, quantiles=[0.16, 0.5, 0.84], truths=[]):
samples = sampler.get_chain(discard=nburn, flat=True)
if len(truths) > 0:
f = corner.corner(samples, labels = paramsNames, quantiles = quantiles, truths=truths)
else:
f = corner.corner(samples, labels = paramsNames, quantiles = quantiles, label_kwargs={'fontsize':18})
# +
autocorr_time = sampler.get_autocorr_time(tol=0)
n_burn = 5*np.ceil(np.max(autocorr_time)).astype(int)
matplotlib.rcParams['font.size'] = 13
makeCorner(sampler, n_burn, ['a','b','c'], quantiles=None)
plt.subplots_adjust(left=0.12,bottom=0.12, right=0.99,top=0.99,
hspace=0.05,wspace=0.05)
# plt.tick_params(labelsize=14)
# plt.xticks(fontsize=14)
plt.savefig('RCF_corner.pdf')
# -
samples = sampler.get_chain(discard=n_burn, thin=int(n_burn/5), flat=True)
a_mcmc, b_mcmc, c_mcmc = map(lambda v: (v[1], v[2]-v[1], v[1]-v[0]),
zip(*np.percentile(samples, [16, 50, 84],
axis=0)))
print(a_mcmc)
print(b_mcmc)
print(c_mcmc)
|
figures/Figure8.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Relation between CPU Cycles and Data Transmission Size
# ### Experiment Setup
#
# 1. Totally 9 nodes from `cloudlab` in the experiment. 1 amd64 node as the client and 8 arm64 nodes as the servers.
#
# 1. Machine Configuration
#
# **1 client node (machine type `xl170`)**
#
# ---
#
# - xl170 Intel Broadwell, 10 core, 1 disk
# - CPU Ten-core Intel E5-2640v4 at 2.4 GHz
# - RAM 64GB ECC Memory (4x 16 GB DDR4-2400 DIMMs)
# - Disk Intel DC S3520 480 GB 6G SATA SSD
# - NIC Two Dual-port Mellanox ConnectX-4 25 GB NIC (PCIe v3.0, 8 lanes
#
# ---
#
# **8 server nodes (machine type `m400`)**
#
# ---
#
# - m400 64-bit ARM
# - CPU Eight 64-bit ARMv8 (Atlas/A57) cores at 2.4 GHz (APM X-GENE)
# - RAM 64GB ECC Memory (8x 8 GB DDR3-1600 SO-DIMMs)
# - Disk 120 GB of flash (SATA3 / M.2, Micron M500)
# - NIC Dual-port Mellanox ConnectX-3 10 GB NIC (PCIe v3.0, 8 lanes
#
# ---
#
# 1. Servers send data to the client using TCP protocol.
#
# 1. The experiment network is an `isolated` `10Gb/s` network and dedicated for this experiment.
#
# 1. The transmission size is the total amount of data received by the client. The amount of data sent by each server is inversely proportional to the number of active servers. Suppose the total transmission size is `1K`, in the case when using 2 servers, each server sends 512 bytes of data; in the case of 3 servers, the first server sends 342 bytes of data and the rest of two send 341 bytes of data so that the total transmission size is still 1KB.
#
# 1. The data sent by the server is read from a local file. The buffer used for reading from the file as well as sending to the network is size of 128KB. We don't use [zero copy](https://www.linuxjournal.com/article/6345) related system call to send the data as we want to simulate the servers are required to perform data filtering in the user space before sending the distilled result. No I/O bottleneck observed on the server nodes during the experiment.
#
# 1. The client uses the same number of processes as the number of active servers in eash test. Each process establishes a connection to a different server.
#
# 1. Right after each single test, all the active servers drop the filesystem cache using the following command (reference [drop_caches](https://www.kernel.org/doc/Documentation/sysctl/vm.txt#drop_caches))
# ```bash
# sync; echo 3 > /proc/sys/vm/drop_caches
# ```
#
# 1. The client caches up to 500MB of the latest received data in the memory. No memory bottleneck observed on the client node.
#
# 1. Each test (*receive X bytes of data from Y servers*) repeats 10 times.
#
# 1. The CPU cycle information is gathered from the output of [perf stat](http://man7.org/linux/man-pages/man1/perf-stat.1.html)
#
# 1. The bitrate is measured by the client and it is equals to
# ```
# number of bits of data received / the duration of receiving all the data in seconds
# ```
#
# 1. TCP segment retransmission rate < `4.63e-7`; The total number of TCP segments received in error is `0`
#
# 1. [Pyben-nio](https://github.com/ljishen/dockerfiles/tree/master/pyben-nio) is my home-made benchmark program written in Python.
# +
from IPython.display import display, HTML, Markdown
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# +
ROW_NAME_AVG = 'AVG'
ROW_NAME_STD = 'STD'
def gen_df(csv_file, header_col):
FILE_PATH = '../backups/' + csv_file
with open(FILE_PATH, 'r') as f:
num_rows = f.readline().count(',')
df = pd.read_csv(FILE_PATH, index_col=header_col, header=None,
names=range(1, num_rows - len(header_col) + 2)).T
# Add the avrerage row and the standard deviation row
df = df.rename({num_rows - len(header_col) + 1: ROW_NAME_AVG})
df.loc[ROW_NAME_STD] = np.nan
num_data_raws = num_rows - len(header_col)
for category in df.columns:
df[category][ROW_NAME_AVG] = np.mean(df[category][:num_data_raws])
df[category][ROW_NAME_STD] = np.std(df[category][:num_data_raws], ddof=1)
return df
# -
def show_chart():
display(HTML(df.to_html()))
# Start to draw the chart
N = len({c[0] for c in df.columns})
ind = np.arange(N) # the x locations for the groups
# Draw bins for Cycles
fig, ax1 = plt.subplots()
bar_width = 1 / (num_servs + 2)
cycle_bars = []
for s in range(num_servs):
bar = ax1.bar(ind + s / (num_servs + 2),
df.loc[ROW_NAME_AVG][2 * s::2 * num_servs],
width=bar_width,
yerr=df.loc[ROW_NAME_STD][2 * s::2 * num_servs])
cycle_bars.append(bar)
ax1.set_yscale('log')
ax1.set_ylim(ymin=1e8)
ax1_clr = 'r'
ax1.set_ylabel(df.columns[0][2], color=ax1_clr)
ax1.tick_params('y', colors=ax1_clr)
# Draw lines for Bitrate
ax2 = ax1.twinx()
bitrate_bars = []
for s in range(num_servs):
bar = ax2.errorbar(ind + bar_width * (num_servs // 2),
df.loc[ROW_NAME_AVG][2 * s + fd00:a516:7c1b:17cd:6d81:2137:bd2a:2c5b * num_servs],
yerr=df.loc[ROW_NAME_STD][2 * s + fd00:a516:7c1b:17cd:6d81:2137:bd2a:2c5b * num_servs],
fmt='-o')
bitrate_bars.append(bar)
ax2_clr = 'b'
ax2.set_ylabel(df.columns[1][2] + ' (bit/s)', color=ax2_clr)
ax2.tick_params('y', colors=ax2_clr)
# Change the size of figure
# See https://stackoverflow.com/a/4306340
fig.set_dpi(120)
ax1.set_xlabel('Transmission Size (Bytes)')
labels = [c[0] for c in df.columns][0::2 * num_servs]
plt.xticks(ind + bar_width * (num_servs // 2), labels)
type_legend = plt.legend([cycle_bars[0], bitrate_bars[0]],
[df.columns[0][2], df.columns[1][2]],
loc=2)
plt.gca().add_artist(type_legend)
ax1.legend(cycle_bars,
[str(n) + ' servers' for n in range(1, num_servs + 1)],
ncol=3,
loc=8,
bbox_to_anchor=(0.5, -0.4))
plt.title('CPU Cycles and Network Bandwidth on Client under Different Transmission Size \n(' + benchmark + ')', y=1.1)
plt.savefig('../charts/remote_read_cycles_' + benchmark + '.png', bbox_inches='tight')
plt.show()
# +
CSV_FILE = 'pyben-nio/output_128K_8servs_autocpuset_arm/result.csv'
df = gen_df(CSV_FILE, [0, 1, 2])
benchmark = CSV_FILE.split('/')[0]
num_servs = len({c[1] for c in df.columns})
show_chart()
# -
# The graph above uses a log scale y-axis, we can't really compare the differences within each category of the transmission size. To zoom in the result, we also plot a separate graph for each of them.
def show_chart_for(size):
cur_df = df[size]
# Start to draw the chart
labels = cur_df.columns.levels[0]
N = len(labels)
ind = np.arange(N) # the x locations for the groups
# Draw bins for Cycles
fig, ax1 = plt.subplots()
clr = 'r'
cycle_bar = ax1.bar(ind,
cur_df.loc[ROW_NAME_AVG][0::2],
width=0.35,
color=clr,
yerr=cur_df.loc[ROW_NAME_STD][1::2])
ax1.set_ylabel(cur_df.columns[0][1], color=clr)
ax1.tick_params('y', colors=clr)
# Draw lines for Bitrate
ax2 = ax1.twinx()
clr = 'b'
bitrate_bar = ax2.errorbar(ind,
cur_df.loc[ROW_NAME_AVG][1::2],
yerr=cur_df.loc[ROW_NAME_STD][1::2],
fmt='-o')
ax2.set_ylabel(cur_df.columns[1][1] + ' (bit/s)', color=clr)
ax2.tick_params('y', colors=clr)
# Change the size of figure
# See https://stackoverflow.com/a/4306340
fig.set_dpi(120)
ax1.set_xlabel('Number of Servers')
plt.xticks(ind, labels)
type_legend = plt.legend([cycle_bar, bitrate_bar],
[cur_df.columns[0][1], cur_df.columns[1][1]],
loc=2,
bbox_to_anchor=(-0.3, 1))
plt.title('CPU Cycles and Network Bandwidth on Client under Transmission Size ' + size + '\n(' + benchmark + ')',
y=1.05)
plt.show()
display(HTML(cur_df.to_html()))
# +
sizes = [c[0] for c in df.columns][0::2 * num_servs]
for sz in sizes:
show_chart_for(sz)
display(Markdown('---'))
|
analysis/notebooks/visualization_nserv.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: myenv
# language: python
# name: myenv
# ---
# Student Answer -> Bert encoding\
# Question -> BERT encoding ------.->cross attention
# The model can be created using the makeModel function.
from bert_embedding import BertEmbedding
from torch import nn
import torch
import torch.nn.functional as F
from torch.autograd import Variable
import numpy as np
import copy
import math
import time
# !pip install transformers
# +
import torch
from transformers import BertTokenizer, BertModel
# OPTIONAL: if you want to have more information on what's happening, activate the logger as follows
import logging
#logging.basicConfig(level=logging.INFO)
import matplotlib.pyplot as plt
# % matplotlib inline
# -
class BertEmbedding(nn.Module):
def __init__(self):
super(BertEmbedding, self).__init__()
# Load pre-trained model tokenizer (vocabulary)
self.tokenizer = BertTokenizer.from_pretrained('bert-base-uncased')
self.model = BertModel.from_pretrained('bert-base-uncased',
output_hidden_states = True, # Whether the model returns all hidden-states.
)
# Put the model in "evaluation" mode, meaning feed-forward operation.
self.model.eval()
def getEmbeddings(self,text):
tokens_tensor,segments_tensor = self.TextPreprocessing(text)
embeddings = self.generateEmbedding(tokens_tensor,segments_tensor)
return embeddings
def TextPreprocessing(self,text):
marked_text = "[CLS] " + text + " [SEP]"
# Tokenize our sentence with the BERT tokenizer.
tokenized_text = self.tokenizer.tokenize(marked_text)
indexed_tokens = self.tokenizer.convert_tokens_to_ids(tokenized_text)
segments_ids = [1] * len(tokenized_text)
tokens_tensor = torch.tensor([indexed_tokens])
segments_tensors = torch.tensor([segments_ids])
return tokens_tensor,segments_tensors
def generateEmbedding(self,tokens_tensor,segments_tensor):
with torch.no_grad():
outputs = self.model(tokens_tensor, segments_tensor)
hidden_states = outputs[2]
tokens = torch.stack(hidden_states,dim=0)
tokens = tokens.permute(1,2,0,3)
final_val = tokens[:,1:-1,-2,:]
return final_val
bert_abstract = """We introduce a new language representation model called BERT, which stands for Bidirectional Encoder Representations from Transformers.
Unlike recent language representation models, BERT is designed to pre-train deep bidirectional representations by jointly conditioning on both left and right context in all layers.
As a result, the pre-trained BERT representations can be fine-tuned with just one additional output layer to create state-of-the-art models for a wide range of tasks, such as question answering and language inference, without substantial task-specific architecture modifications.
BERT is conceptually simple and empirically powerful.
It obtains new state-of-the-art results on eleven natural language processing tasks, including pushing the GLUE benchmark to 80.4% (7.6% absolute improvement), MultiNLI accuracy to 86.7 (5.6% absolute improvement) and the SQuAD v1.1 question answering Test F1 to 93.2 (1.5% absolute improvement), outperforming human performance by 2.0%."""
student_ans = "Sky is red"
question = "What is the colour of the sky?"
reference_ans ="Sky appears blue"
full_marks = 3
def getBertEncoding(paragraph):
sentences = paragraph.split('.')
bert_embedding = BertEmbedding()
result = bert_embedding(sentences)
emb = torch.Tensor(result[0][1])
# emb = emb.reshape(emb.size()[0],1,emb.size()[-1])
emb = emb.unsqueeze(0)
return emb
res = getBertEncoding(student_ans)
res.size()
K= getBertEncoding(student_ans)
Q = getBertEncoding(question)
multihead_attn = nn.MultiheadAttention(embed_dim = 768, num_heads=3)
def clones(module, N):
"Produce N identical layers."
return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])
def attention(query, key, value, mask=None, dropout=None):
"Compute 'Scaled Dot Product Attention'"
d_k = query.size(-1)
scores = torch.matmul(query, key.transpose(-2, -1)) \
/ math.sqrt(d_k)
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
p_attn = F.softmax(scores, dim = -1)
if dropout is not None:
p_attn = dropout(p_attn)
return torch.matmul(p_attn, value), p_attn
class MultiHeadedAttention(nn.Module):
"Multi-headed Attention module"
def __init__(self, h, d_model, dropout=0.1):
"Take in model size and number of heads."
super(MultiHeadedAttention, self).__init__()
assert d_model % h == 0
# We assume d_v always equals d_k
self.d_k = d_model // h
self.h = h
self.linears = clones(nn.Linear(d_model, d_model), 4)
self.attn = None
self.dropout = nn.Dropout(p=dropout)
def forward(self, query, key, value, mask=None):
if mask is not None:
# Same mask applied to all h heads.
mask = mask.unsqueeze(1)
nbatches = query.size(0)
# 1) Do all the linear projections in batch from d_model => h x d_k
query, key, value = \
[l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
for l, x in zip(self.linears, (query, key, value))]
# 2) Apply attention on all the projected vectors in batch.
x, self.attn = attention(query, key, value, mask=mask,
dropout=self.dropout)
# 3) "Concat" using a view and apply a final linear.
x = x.transpose(1, 2).contiguous() \
.view(nbatches, -1, self.h * self.d_k)
return self.linears[-1](x)
m = MultiHeadedAttention(h = 6,d_model = 768)
class FeedForwardLayer(nn.Module):
"Feedforward with 1 hidden layer"
def __init__(self,inp_dim,hid_dim,dropout = 0.1):
super(FeedForwardLayer, self).__init__()
self.inp_dim = inp_dim
self.hid_dim = hid_dim
self.hidden = nn.Linear(inp_dim,hid_dim)
self.output = nn.Linear(hid_dim,inp_dim)
self.relu = F.relu
self.dropout = nn.Dropout(dropout)
def forward(self,x):
x = self.hidden(x)
x = self.relu(x)
x = self.dropout(x)
x = self.output(x)
return x
class LayerNorm(nn.Module):
"Construct a layernorm module."
def __init__(self, features, eps=1e-6):
super(LayerNorm, self).__init__()
self.a_2 = nn.Parameter(torch.ones(features))
self.b_2 = nn.Parameter(torch.zeros(features))
self.eps = eps
def forward(self, x):
mean = x.mean(-1, keepdim=True)
std = x.std(-1, keepdim=True)
return self.a_2 * (x - mean) / (std + self.eps) + self.b_2
# +
class SublayerConnection(nn.Module):
"Apply residual connection to any sublayer with the same size."
def __init__(self, size, dropout=0.1):
super(SublayerConnection, self).__init__()
self.norm = LayerNorm(size)
self.dropout = nn.Dropout(dropout)
def forward(self, x, sublayer):
return x + self.dropout(sublayer(self.norm(x)))
# return x + sublayer(self.norm(x))
# +
class EncoderBlock(nn.Module):
"An Encoder block that find the connection between Answer and Question"
def __init__(self,attentionBlock,feedForwardBlock,size,dropout = 0.1):
super(EncoderBlock,self).__init__()
self.attentionBlock = attentionBlock
self.feedForwardBlock = feedForwardBlock
self.sublayer = clones(SublayerConnection(size,dropout),2)
self.size = size
def forward(self,Query,Value):
x = self.sublayer[0](Query, lambda x: self.attentionBlock(query=x, value=Value, key=Value))
print(x.size())
return self.sublayer[1](x, self.feedForwardBlock)
# -
class EncoderModule(nn.Module):
"Stacks of Encoder blocks"
def __init__(self, EncoderLayer,N):
super(EncoderModule,self).__init__()
self.layers = clones(EncoderLayer,N)
self.norm = LayerNorm(EncoderLayer.size)
def forward(self,Query,Value):
for layers in self.layers:
Query = layers(Query = Query,Value = Value)
return Query
class RepresentationModule(nn.Module):
"Bottom layer that gives 2 representations: Reference answer Rep and Student answer Rep"
def __init__(self,EncoderModule, embeddingLayer):
super(RepresentationModule,self).__init__()
self.EncoderModules = clones(EncoderModule,2)
self.embeddingLayer = embeddingLayer
#Get 2 clones of EncoderModule
def forward(self, Question, ReferenceAnswer, StudentAnswer):
Q = self.embeddingLayer.getEmbeddings(Question)
seconds = time.time()
StuAns = self.embeddingLayer.getEmbeddings(StudentAnswer)
RefAns = self.embeddingLayer.getEmbeddings(ReferenceAnswer)
print(time.time()-seconds)
studentAnsRep = self.EncoderModules[0](Q,StuAns)
RefAnsRep = self.EncoderModules[1](Q,RefAns)
print(time.time()-seconds)
return (studentAnsRep,RefAnsRep)
class PositionalEncoding(nn.Module):
"Implement the PE function."
def __init__(self, d_model, dropout=0.1, max_len=5000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout)
# Compute the positional encodings once in log space.
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2) *
-(math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0)
self.register_buffer('pe', pe)
def forward(self, x):
print(self.pe[:,:x.size(1)].size())
x = x + Variable(self.pe[:, :x.size(1)],
requires_grad=False)
print(x.size())
return self.dropout(x)
class FinalFeedForwardLayer(nn.Module):
def __init__(self,input_size):
super().__init__()
self.fc1 = nn.Linear(input_size,400)
self.fc2 = nn.Linear(400,20)
self.fc3 = nn.Linear(20,10)
self.fc4 = nn.Linear(10,1)
def forward(self, xb):
xb = F.relu(self.fc1(xb))
xb = F.relu(self.fc2(xb))
xb = F.relu(self.fc3(xb))
xb = F.sigmoid(self.fc4(xb)) # batch wise forwarding
return xb
def training_step(self, batch):
inputs, targets = batch
# Generate predictions
out = self(inputs)
# Calcuate loss
loss = F.l1_loss(out, targets) # batch wise training step and loss
return loss
def validation_step(self, batch):
inputs, targets = batch
# Generate predictions
out = self(inputs)
# Calculate loss
loss =F.l1_loss(out, targets) # batch wise validation and loss
return {'val_loss': loss.detach()}
def validation_epoch_end(self, outputs):
batch_losses = [x['val_loss'] for x in outputs]
epoch_loss = torch.stack(batch_losses).mean() # Combine val losses of all batches as average
return {'val_loss': epoch_loss.item()}
def epoch_end(self, epoch, result, num_epochs):
# Print result every 20th epoch
if (epoch+1) % 100 == 0 or epoch == num_epochs-1:
print("Epoch [{}], val_loss: {:.4f}".format(epoch+1, result['val_loss']))
class PrepLayer(nn.Module):
def __init__(self,positionalLayer,d_model,max_size):
super(PrepLayer,self).__init__()
self.borderLayer = torch.zeros(1,1,768)
self.d_model = d_model
self.max_size = max_size
self.positionalEncoding = positionalLayer
def forward(self,StudAns,RefAns):
RefAns = torch.add(RefAns,1)
FinalRep = torch.cat((StudAns,self.borderLayer),dim=1)
FinalRep = torch.cat((FinalRep,RefAns),dim = 1)
FinalRep = self.positionalEncoding(FinalRep)
FinalRep = FinalRep.flatten(start_dim=1, end_dim=2)
self.padValue = torch.zeros(1,self.d_model*self.max_size*2+1 - FinalRep.shape[1])
FinalRep = torch.cat((FinalRep,self.padValue),dim = 1)
return FinalRep
class GetMarks(nn.Module):
def __init__(self):
super(GetMarks,self).__init__()
def forward(self,grade,full_marks):
return grade*full_marks
# +
class GradingModule(nn.Module):
"Uses the Representations to compare and grade them"
def __init__(self,prepLayer,d_model,max_size):
super(GradingModule,self).__init__()
self.max_size = max_size
self.d_model = d_model
self.prepLayer = prepLayer
self.feedForward = FinalFeedForwardLayer(self.d_model*self.max_size*2 + 1)
self.GetMarks = GetMarks()
def forward(self,stu,ref,full_marks):
FinalRep = self.prepLayer(stu,ref)
grade = self.feedForward(FinalRep)
final_marks = self.GetMarks(grade,full_marks)
return final_marks
# -
class Upgrader(nn.Module):
def __init__(self,Representation_Module, Grading_Module):
super(Upgrader,self).__init__()
self.RepModule = Representation_Module
self.GradModule = Grading_Module
def forward(self, StudentAns,Question,RefAnswer,full_marks):
stu_rep,ref_rep = self.RepModule( StudentAns,Question,RefAnswer)
grad = self.GradModule(stu_rep,ref_rep,full_marks)
return grad
def makeModel(emb_dim = 768,heads = 3,hid_lay_dim = 2304, N = 6,max_size = 100):
c = copy.deepcopy
attn = MultiHeadedAttention(h=6,d_model=emb_dim)
ff = FeedForwardLayer(emb_dim,hid_lay_dim)
embedding_layer = BertEmbedding()
positionalLayer = PositionalEncoding(d_model=emb_dim)
model = Upgrader(
RepresentationModule(
EncoderModule( EncoderBlock( c(attn), c(ff), emb_dim), N),
embedding_layer)
,GradingModule(
PrepLayer(d_model=emb_dim,positionalLayer=positionalLayer,max_size=max_size),
d_model=emb_dim,
max_size=max_size
))
return model
model = makeModel()
student_ans = "Sky is red"
question = "What is the colour of the sky?"
reference_ans ="Sky appears blue"
full_marks = 3
model(student_ans,question,reference_ans,full_marks)
|
model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="SQHnALYxJkx1" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="9f1c56a5-a267-4b04-823d-225bba335369" executionInfo={"status": "ok", "timestamp": 1563806822871, "user_tz": -60, "elapsed": 2072, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/-fSlc3U0vpV8/AAAAAAAAAAI/AAAAAAAABXA/noxHYVFiipo/s64/photo.jpg", "userId": "12209104838854787911"}}
# !ls
# + [markdown] id="Uz8W-lJFIBW9" colab_type="text"
# # START
#
# + id="69K5lTzqzZD0" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="677b011e-1fae-4965-d49d-832150ed9c17" executionInfo={"status": "ok", "timestamp": 1563806767864, "user_tz": -60, "elapsed": 2091, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/-fSlc3U0vpV8/AAAAAAAAAAI/AAAAAAAABXA/noxHYVFiipo/s64/photo.jpg", "userId": "12209104838854787911"}}
print("Hello")
a = 1
b = 2
print(a+b)
# + id="SkyHgVxLIoNS" colab_type="code" colab={}
c = 12
# + id="rC4QsawVItog" colab_type="code" colab={}
d = 4
# + [markdown] id="g5diuoosMLI6" colab_type="text"
# # New Section
#
# + id="iqqRLbDAMKhQ" colab_type="code" colab={}
# + id="DKBt2e25IyHY" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="ab14620a-be27-4608-dbc7-c0e125e818e1" executionInfo={"status": "ok", "timestamp": 1563807061669, "user_tz": -60, "elapsed": 2334, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/-fSlc3U0vpV8/AAAAAAAAAAI/AAAAAAAABXA/noxHYVFiipo/s64/photo.jpg", "userId": "12209104838854787911"}}
print(c+d+a)
|
day1_just_a_start.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/"} id="NDlpJsZ1nOpe" outputId="61f13215-1a21-45ba-99e1-94a1f421d314"
from google.colab import drive
drive.mount('/content/drive')
# + id="oWMnSsnGsmfR"
# # !sudo apt-get install -y fonts-nanum
# # !sudo fc-cache -fv
# # !rm ~/.cache/matplotlib -rf
# + id="uh0w9kjkoaAh"
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
import plotly.graph_objects as go
from plotly.subplots import make_subplots
import seaborn as sns
import matplotlib.pyplot as plt
import os
os.chdir('/content/drive/MyDrive/dacon/daconcup/')
import utils
# + [markdown] id="BOk3QC87oo1Q"
# # 데이터 불러오기
# + id="0xdB1nW6ojM5"
train = pd.read_csv('/content/drive/MyDrive/dacon/daconcup/Data/raw/train.csv', encoding='cp949', parse_dates=['DateTime'], index_col=['DateTime'])
info_user = pd.read_csv('/content/drive/MyDrive/dacon/daconcup/Data/raw/info_user.csv', encoding='cp949')
info_login = pd.read_csv('/content/drive/MyDrive/dacon/daconcup/Data/raw/info_login.csv', encoding='cp949')
info_cpt = pd.read_csv('/content/drive/MyDrive/dacon/daconcup/Data/raw/info_competition.csv', encoding='cp949')
info_sub = pd.read_csv('/content/drive/MyDrive/dacon/daconcup/Data/raw/info_submission.csv', encoding='cp949')
# + [markdown] id="CgLkdYrPcX6C"
# # 1. 시계열 데이터 분포 보기
#
# - 1h, 1d, 7일 이동평균에 따른 그래프 그리는 방법 숙지하기
# + id="pIF5oOWjyM2L"
idx = pd.date_range('2018-01-01', '2020-12-31', freq='1h')
train = train.reindex(idx, fill_value=0).rename_axis('DateTime')
# + colab={"base_uri": "https://localhost:8080/", "height": 872} id="Thj6C31Bylol" outputId="ecde16a3-5e19-481b-f834-43d46b9936d5"
years = ['2018', '2019', '2020']
plt.figure(figsize=(12,12))
for i in range(len(years)):
# prepare subplot
ax = plt.subplot(len(years), 1, i+1)
# determine the year to plot
year = years[i]
# get all observations for the year
result = train[str(year)]
# plot the active power for the year
plt.plot(result['사용자'])
# add a title to the subplot
plt.title(str(year), y=0, loc='left')
plt.tight_layout();
# + id="ytxjxLKZcIti"
idx = pd.date_range('2018-01-01', '2020-12-31')
train_day = train.resample('1D').sum()
# + colab={"base_uri": "https://localhost:8080/", "height": 872} id="RfiI8shnzptD" outputId="01acaddf-19a2-480c-8a8b-7e2dc47ae4ad"
years = ['2018', '2019', '2020']
plt.figure(figsize=(12,12))
for i in range(len(years)):
# prepare subplot
ax = plt.subplot(len(years), 1, i+1)
# determine the year to plot
year = years[i]
# get all observations for the year
result = train_day[str(year)]
# plot the active power for the year
plt.plot(result['사용자'])
# add a title to the subplot
plt.title(str(year), y=0, loc='left')
plt.tight_layout();
# + colab={"base_uri": "https://localhost:8080/", "height": 872} id="7hR_pvef17bD" outputId="9d3ca8ee-2edb-44b0-b438-2341594ec4a4"
train_day_mean7 = train_day.rolling(window=7, min_periods=1).mean()
years = ['2018', '2019', '2020']
fig, axes = plt.subplots(3, 1, figsize=(12, 12))
for i in range(len(years)):
# determine the year to plot
year = years[i]
# get all observations for the year
result = train_day_mean7[str(year)]
# plot the active power for the year
axes[i].plot(result['사용자'])
# add a title to the subplot
axes[i].set_title(str(year), y=0, loc='left')
plt.tight_layout();
# + colab={"base_uri": "https://localhost:8080/", "height": 872} id="YeJmVLwBkm3N" outputId="b19adf6e-bb75-4ea0-878d-2fb4c30eea69"
train_day_mean30 = train_day.rolling(window=30, min_periods=1).mean()
years = ['2018', '2019', '2020']
fig, axes = plt.subplots(3, 1, figsize=(12, 12))
for i in range(len(years)):
# determine the year to plot
year = years[i]
# get all observations for the year
result = train_day_mean30[str(year)]
# plot the active power for the year
axes[i].plot(result['사용자'])
# add a title to the subplot
axes[i].set_title(str(year), y=0, loc='left')
plt.tight_layout();
# + colab={"base_uri": "https://localhost:8080/", "height": 872} id="MnqZPN-Hn5Tv" outputId="4192bfdf-295b-4ba9-b7e3-698e292c800b"
# 지수평활
ewma = train_day.ewm(span=30).mean()
years = ['2018', '2019', '2020']
fig, axes = plt.subplots(3, 1, figsize=(12, 12))
for i in range(len(years)):
# determine the year to plot
year = years[i]
# get all observations for the year
result = ewma[str(year)]
# plot the active power for the year
axes[i].plot(result['사용자'])
# add a title to the subplot
axes[i].set_title(str(year), y=0, loc='left')
plt.tight_layout();
# + [markdown] id="Zt_vu4fKc32Z"
# # 2. 자기 상관성 확인
#
# - 자기 상관성이 높은 시기의 기간만을 가지고 와서 학습
#
# - 100일만큼 뽑아서 학습시켜보고 전체 데이터로 학습시키는 경우와 validation 결과 보기
# + colab={"base_uri": "https://localhost:8080/", "height": 301} id="IFAAvfzDuUfY" outputId="6f6fd27b-9ba0-4892-b706-8aa8c30399ec"
pd.plotting.autocorrelation_plot(train['사용자'].resample('m').median())
# + id="7aiuMTJ9vHDD" colab={"base_uri": "https://localhost:8080/", "height": 301} outputId="e007eb6e-df15-4772-a817-95c743df8b85"
pd.plotting.autocorrelation_plot(train['세션'].resample('m').median())
# + id="xvZVDlSQFDsQ" colab={"base_uri": "https://localhost:8080/", "height": 301} outputId="9c39e2e0-45bf-417d-81be-0ef9133ace07"
pd.plotting.autocorrelation_plot(train['신규방문자'].resample('m').median())
# + id="rKomGmqfFFeE" colab={"base_uri": "https://localhost:8080/", "height": 301} outputId="51e16ffa-0cb3-48f4-e848-4d5c59f53c78"
pd.plotting.autocorrelation_plot(train['페이지뷰'].resample('m').median())
# + id="2CNeGgtTFHmq"
|
Codes/[Analysis]03_시계열분석.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Assignment 2 | Programming Logic
#
# Reminder: in all of the assignments this semester, the answer is not the only consideration, but also how you get to it. It's OK (suggested even!) to use the internet for help. But you _should_ be able to answer all of these questions using only the programming techniques you have learned in class and from the readings.
#
# A few keys for success:
# - Avoid manual data entry
# - Emphasize logic and clarity
# - Use comments, docstrings, and descriptive variable names
# - In general, less code is better. But if more lines of code makes your program easier to read or understand what its doing, then go for it.
# ## Problem 1
# Write a Python program to count the number of even and odd numbers from a list of numbers. Test your code by running it on a list of integers from 1 to 9. No need to make this a function unless you want to.
# +
ls = list(range(1, 10))
# ls
odd_count = len(list(filter(lambda x: (x%2 != 0) , ls)))
even_count = len(list(filter(lambda x: (x%2 == 0) , ls)))
print("Even numbers in the list: ", even_count)
print("Odd numbers in the list: ", odd_count)
# -
# ## Problem 2
# Write a Python function that takes a list of numbers and returns a list containing only the even numbers from the original list. Test your function by running it on a list of integers from 1 to 9.
ls = list(range(1, 10))
# ls
for num in ls:
if num % 2 == 0:
print(num, end=" ")
# ## Problem 3
#
# 1. Create a function that accepts a list of integers as an argument and returns a list of floats which equals each number as a fraction of the sum of all the items in the original list.
#
# 2. Next, create a second function which is the same as the first, but limit each number in the output list to two decimals.
#
# 3. Create another function which builds on the previous one by allowing a "user" pass in an argument that defines the number of decimal places to use in the output list.
#
# 4. Test each of these functions with a list of integers
# +
def Integer(num):
return [n/sum(num) for n in num]
print(Integer(range(1,20)))
# +
def Integers(num):
return [round(n/sum(num),2) for n in num]
print(Integers(range(1,20)))
# +
def Integer_User(num,user):
return [round(n/sum(num),user) for n in num]
print(Integer_User(range(1,20),user=3))
# -
# ## Problem 4
# A prime number is any whole number greater than 1 that has no positive divisors besides 1 and itself. In other words, a prime number must be:
# 1. an integer
# 2. greater than 1
# 3. divisible only by 1 and itself.
#
# Write a function is_prime(n) that accepts an argument `n` and returns `True` (boolean) if `n` is a prime number and `False` if n is not prime. For example, `is_prime(11)` should return `True` and `is_prime(12)` should return `False`.
#
# +
def is_prime(n):
if n >1:
if len([num for num in range(1,n) if n % num == 0])==1:
return True
else:
return False
print(is_prime(11))
print(is_prime(12))
# -
# ## Problem 5
# 1. Create a class called `Housing`, and add the following attributes to it:
# - type
# - area
# - number of bedrooms
# - value (price)
# - year built.
# 2. Create two instances of your class and populate their attributes (make 'em up)
# 3. Create a method called `rent()` that calculates the estimated monthly rent for each house (assume that monthly rent is 0.4% of the value of the house)
# 4. Print the rent for both instances.
class Housing:
def __init__(self, _type, area, number_of_bedrooms, price, year_built):
self._type = _type
self.area= area
self.number_of_bedrooms= number_of_bedrooms
self.price= price
self.year_built= year_built
def rent(self, p_rent=0.04):
return round(self.price * (p_rent))
house_1 = Housing('Bungalow', 'Berkeley', '3', 200000, '2000')
house_2 = Housing('Two Story', 'San Francisco', '6', 500000, '2010')
print(Housing.rent(house_1))
print(Housing.rent(house_2))
|
assignments/assignment_2/assignment_2_Jane_Luke.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Dealing cards - flush generation
# An interesting exercise is to simulate dealing random hands of cards to see if the fraction that are flushes matches the exact result from combinatorics. Given that a flush is a relatively uncommon, occuring on average once per 500 hands, we'll need to deal a large number of hands to get reliable results.
#
# Before we start programming, we need to consider a few points.
#
# * How do we represent our deck of cards?
# * How do we generate a sample of simulated hands?
# * Given a hand of cards, how do we determine if it's a flush?
import numpy as np
# A deck of cards is a fairly complex object and each card has an associated suit (club, diamond, heart, spade), rank (2-10, jack, queen, king, ace) and value (e.g. in black jack, face cards have a value of 10 and an ace can be either 1 or 11). For our purposes, we can use a simplified representation where the deck consists of 13 cards of each suit, which we'll abbreviate as C, D, H and S.
deck = ['C', 'D', 'H', 'S']*13
print(deck)
# We'll generate a large number of hands and keep track of how many of those result in flushes. Note that we're using the Jupyter magic `%%time` to measure the run time for the cell. This is not part of the Python language and the use of two percent signs indicates that we time the entire cell, not just the immediately following line.
#
# The NumPy `random.choice()` function is used to select the five cards from the deck and we specify `replace=FALSE` to ensure that sampling is done *without replacement*. This is exactly what we want since once a card is dealt, it is not available for reuse.
#
# Finally, we need to decide whether a hand is a flush. To do that, we'll test whether the suits of the five cards are identical. Python allows us to do that in a single chains of tests as shown in the code below.
# +
# %%time
nhands = 100000
nflush = 0
for i in range(nhands):
hand = np.random.choice(deck, size=5, replace=False)
if hand[0] == hand[1] == hand[2] == hand[3] == hand[4]:
nflush = nflush + 1
pflush = nflush/nhands
print(pflush)
# -
|
Dealing cards - flush generation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
from clifford.g3_1 import *
# Metric
print(e1*e1)
print(e2*e2)
print(e3*e3)
print(e4*e4)
# +
# Example
a = (2 + 5.7*e2)*(e1 + e4)
b = 5*e2 - 3.5*e1
print(a)
print(b)
# Projection
print(a(2))
# Outer product
print(a^b)
# Inner product
print(a|b)
# Left contraction
print(a.lc(b))
# -
|
examples/g3_1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (pytorch)
# language: python
# name: pytorch_env
# ---
# ### In this notebook we investigatw the pretrianed VGG on augmented image data
# %reload_ext autoreload
# %autoreload 2
# %matplotlib inline
# ### Importing the libraries
# +
import torch
import torch.backends.cudnn as cudnn
import torch.nn as nn
import torch.utils.data as Data
from torch.autograd import Function, Variable
from torch.optim import lr_scheduler
import torch.utils.model_zoo as model_zoo
import torchvision
import torchvision.transforms as transforms
import torchvision.models as models
from pathlib import Path
import os
import copy
import math
import matplotlib.pyplot as plt
import numpy as np
from datetime import datetime
import time as time
# -
# #### Checking whether the GPU is active
torch.backends.cudnn.enabled
torch.cuda.is_available()
# ### Hyper Parameters
# +
EPOCH= 5
BchSz=16 # BATCHSIZE
# Learning Rate
learning_rate = 0.0001
# Dropout rate
Dropout=0.2
# -
# Loss calculator
criterion = nn.CrossEntropyLoss() # cross entropy loss
# Dataset paths
PATH = Path("/home/saman/Saman/data/Image_Data01/")
train_path = PATH / 'train' / 'Total'
valid_path = PATH / 'valid' / 'Total'
test_path = PATH / 'test' / 'Total'
# ### Loading data set (including augmentations)
# #### Train the model with vertically and horizontally flipping and normalization
# +
# Mode of Augmentation
transformation = transforms.Compose([
transforms.RandomVerticalFlip(),
transforms.ColorJitter(),
transforms.ToTensor(),
transforms.Normalize((0,0,0), (0.5,0.5,0.5)),
])
transformation2 = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0,0,0), (0.5,0.5,0.5)),
])
# -
# ### Reading data after transformation
# +
train_data = torchvision.datasets.ImageFolder(train_path,transform=transformation)
train_loader =torch.utils.data.DataLoader(train_data, batch_size=BchSz, shuffle=True,
num_workers=8)
valid_data = torchvision.datasets.ImageFolder(valid_path,transform=transformation)
valid_loader =torch.utils.data.DataLoader(valid_data, batch_size=BchSz, shuffle=True,
num_workers=8)
test_data = torchvision.datasets.ImageFolder(test_path,transform=transformation2)
test_loader =torch.utils.data.DataLoader(test_data, batch_size=BchSz, shuffle=True,
num_workers=8)
# -
# ### Checking dataset
len(train_data), len(valid_data), len(test_data)
train_data.class_to_idx
# A function to make a title according to classes
def IdxtoClass(idx):
if idx==0:
Class='Canola'
if idx==1:
Class='Radish'
return Class
# ### Visualizing data
# +
for i in range(2):
img = plt.imread(train_data.imgs[i][0])
plt.subplots_adjust(wspace=1, hspace=0.4)
plt.subplot(2,2,i+1)
plt.imshow(img, aspect='auto' , cmap='viridis');
plt.title('%s' % IdxtoClass(train_data.imgs[i][1])) #The second index if is 1 return the label
img = plt.imread(train_data.imgs[-(i+1)][0])
plt.subplot(2,2,i+3)
plt.imshow(img, aspect='auto' , cmap='viridis');
plt.title('%s' % IdxtoClass(train_data.imgs[-(i+1)][1])) #The second index if is 1 return the label
plt.show()
# -
# Data size
img = plt.imread(train_data.imgs[0][0]) # The second index if is 0 return the file name
IMSHAPE= img.shape
IMSHAPE
len(train_data.imgs)
# ### Training and Validating
# #### Training and validation function
def train_model(model, criterion, optimizer, lr_scheduler, EPOCH):
print(str(datetime.now()).split('.')[0], "Starting training and validation...\n")
print("====================Data and Hyperparameter Overview====================\n")
print("Number of training examples: {} , Number of validation examples: {} ".format(len(train_data), len(valid_data)))
print("Learning rate: {:,.5f}".format(learning_rate))
print("================================Results...==============================\n")
since = time.time() #record the beginning time
best_model = model
best_acc = 0.0
acc_vect =[]
for epoch in range(EPOCH):
for i, (images, labels) in enumerate(train_loader):
images = Variable(images).cuda()
labels = Variable(labels).cuda()
# Forward pass
outputs = model(images) # model output
loss = criterion(outputs, labels) # cross entropy loss
# Trying binary cross entropy
#loss = criterion(torch.max(outputs.data, 1), labels)
#loss = torch.nn.functional.binary_cross_entropy(outputs, labels)
# Backward and optimize
optimizer.zero_grad() # clear gradients for this training step
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
if (i+1) % 250 == 0: # Reporting the loss and progress every 50 step
print ('Epoch [{}/{}], Step [{}/{}], Loss: {:.4f}'
.format(epoch+1, EPOCH, i+1, len(train_loader), loss.item()))
model.eval() # eval mode (batchnorm uses moving mean/variance instead of mini-batch mean/variance)
with torch.no_grad():
correct = 0
total = 0
for images, labels in valid_loader:
images = Variable(images).cuda()
labels = Variable(labels).cuda()
outputs = model(images)
_, predicted = torch.max(outputs.data, 1)
loss = criterion(outputs, labels)
loss += loss.item()
total += labels.size(0)
correct += (predicted == labels).sum().item()
epoch_loss= loss / total
epoch_acc = 100 * correct / total
acc_vect.append(epoch_acc)
if epoch_acc > best_acc:
best_acc = epoch_acc
best_model = copy.deepcopy(model)
print('Validation accuracy and loss of the model on the test {} images: {} %, {:.5f}'
.format(len(valid_data), 100 * correct / total, loss))
correct = 0
total = 0
for images, labels in train_loader:
images = Variable(images).cuda()
labels = Variable(labels).cuda()
outputs = model(images)
_, predicted = torch.max(outputs.data, 1)
loss = criterion(outputs, labels)
loss += loss.item()
total += labels.size(0)
correct += (predicted == labels).sum().item()
epoch_loss= loss / total
epoch_acc = 100 * correct / total
print('Train accuracy and loss of the model on the test {} images: {} %, {:.5f}'
.format(len(train_data), epoch_acc, loss))
print('-' * 10)
time_elapsed = time.time() - since
print('Training complete in {:.0f}m {:.0f}s'.format(
time_elapsed // 60, time_elapsed % 60))
print('Best validation Acc: {:4f}'.format(best_acc))
mean_acc = np.mean(acc_vect)
print('Average accuracy on the validation {} images: {}'
.format(len(train_data),mean_acc))
print('-' * 10)
return best_model, mean_acc
# ### Testing function
def test_model(model, test_loader):
print("Starting testing...\n")
model.eval() # eval mode (batchnorm uses moving mean/variance instead of mini-batch mean/variance)
with torch.no_grad():
correct = 0
total = 0
test_loss_vect=[]
test_acc_vect=[]
since = time.time() #record the beginning time
for i in range(10):
Indx = torch.randperm(len(test_data))
Cut=int(len(Indx)/10) # Here 10% showing the proportion of data is chosen for pooling
indices=Indx[:Cut]
Sampler = Data.SubsetRandomSampler(indices)
pooled_data = torch.utils.data.DataLoader(test_data , batch_size=BchSz,sampler=Sampler)
for images, labels in pooled_data:
images = Variable(images).cuda()
labels = Variable(labels).cuda()
outputs = model(images)
_, predicted = torch.max(outputs.data, 1)
loss = criterion(outputs, labels)
total += labels.size(0)
correct += (predicted == labels).sum().item()
test_loss= loss / total
test_accuracy= 100 * correct / total
test_loss_vect.append(test_loss)
test_acc_vect.append(test_accuracy)
print('Test accuracy and loss for the {}th pool: {:.2f} %, {:.5f}'
.format(i+1, test_accuracy, test_loss))
mean_test_loss = torch.mean(torch.tensor(test_loss_vect))
mean_test_acc = torch.mean(torch.tensor(test_acc_vect))
std_test_acc = torch.std(torch.tensor(test_acc_vect))
print('-' * 10)
print('Average of ten test accuracies on test data: {:.2f} %, loss: {:.5f}, Standard deviion of accuracy: {:.4f}'
.format(mean_test_acc, mean_test_loss, std_test_acc))
print('-' * 10)
time_elapsed = time.time() - since
print('Testing complete in {:.1f}m {:.4f}s'.format(time_elapsed // 60, time_elapsed % 60))
print('-' * 10)
return mean_test_acc, mean_test_loss, std_test_acc
# ### VGG network model
# #### Pretrained VGG 16 model
# +
model1 = models.vgg11(pretrained=True) #2 is number of classes
classifier = nn.Sequential(*[nn.Linear(in_features= 25088, out_features=16), nn.ReLU(),nn.Linear(16, 2)])
model1.classifier = classifier
print(model1)
model2=model1
# +
# model1 = models.vgg11() #2 is number of classes
# model2 = nn.Sequential(*list(model1.children())[:-1] +
# [nn.ReLU(),nn.Linear(in_features=229376, out_features=14), nn.ReLU(),nn.Linear(14, 2)])
# model2= nn.Sequential(model1, nn.ReLU(),nn.Linear(14, 2))
# print(model2)
# +
model = model2 #2 is number of classes
model = model.cuda()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
optimizer.scheduler=lr_scheduler.ReduceLROnPlateau(optimizer, 'min')
# -
def get_num_params(model):
TotalParam=0
for param in list(model.parameters()):
nn=1
for size in list(param.size()):
nn = nn*size
TotalParam += nn
return TotalParam
get_num_params(model)
train_model(model, criterion, optimizer, lr_scheduler, EPOCH)
test_model (model, test_loader)
|
Nets on Augmented Images/02_Image_Total_VGG_pretrianed_VGG11-Aug.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:anaconda3-4.2.0]
# language: python
# name: conda-env-anaconda3-4.2.0-py
# ---
# %matplotlib inline
import numpy as np
from sklearn.svm import LinearSVC, SVC
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
class OVRLSVC():
def __init__(self, **kwargs):
self.c2svc = {}
self.kwargs = kwargs
def fit(self, X, y):
for c in set(i for i in y):
self.c2svc[c] = LinearSVC(**self.kwargs)
self.c2svc[c].fit(X, y==c)
return self
def predict(self, X):
confidences = np.zeros((X.shape[0], len(self.c2svc)))
for c, svc in self.c2svc.items():
confidences[:, int(c)] = svc.decision_function(X)
result = confidences.argmax(axis=1)
return result
def score(self, X, y):
result = self.predict(X)
score = (result == y).sum() / len(y)
return score
class OVRSVC():
def __init__(self, **kwargs):
self.c2svc = {}
self.kwargs = kwargs
def fit(self, X, y):
for c in set(i for i in y):
self.c2svc[c] = SVC(probability=True, kernel='linear', **self.kwargs)
self.c2svc[c].fit(X, y==c)
return self
def predict(self, X):
confidences = np.zeros((X.shape[0], len(self.c2svc)))
for c, svc in self.c2svc.items():
confidences[:, int(c)] = svc.predict_proba(X)[:, 1]
result = confidences.argmax(axis=1)
return result
def score(self, X, y):
result = self.predict(X)
score = (result == y).sum() / len(y)
return score
# +
scaler = MinMaxScaler(copy=False)
X_train = np.load('data_hw2/train_data.npy')
y_train = np.load('data_hw2/train_label.npy').astype(int) + 1
X_train, X_dev, y_train, y_dev = train_test_split(X_train, y_train, test_size=0.2)
X_test = np.load('data_hw2/test_data.npy')
y_test = np.load('data_hw2/test_label.npy').astype(int) + 1
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_dev = scaler.transform(X_dev)
X_test = scaler.transform(X_test)
# -
svc = SVC()
svc.fit(X_train, y_train)
print(svc.score(X_train, y_train))
print(svc.score(X_test, y_test))
lsvc = LinearSVC()
lsvc.fit(X_train, y_train)
print(lsvc.score(X_train, y_train))
print(lsvc.score(X_dev, y_dev))
print(lsvc.score(X_test, y_test))
ovr_svc = OVRSVC()
ovr_svc.fit(X_train, y_train)
print(ovr_svc.score(X_dev, y_dev))
print(ovr_svc.score(X_test, y_test))
ovr_lsvc = OVRLSVC()
ovr_lsvc.fit(X_train, y_train)
print(ovr_lsvc.score(X_dev, y_dev))
print(ovr_lsvc.score(X_test, y_test))
|
SVM_SEED/score_test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#
#
# ## Intro
#
# 
#
# - The Finance industry is an earlier pioneer of adopting AI, contrary to the belief that its the most risk averse
# - Banks have started to harness AI to meet ever-growing regulatory demands while minimizing the cost of human capital
# - Citigroup estimates that the biggest banks have doubled the number of people they employ to handle compliance and regulation, costing the banking industry 270 billion a year and accounting for 10 percent of its operating costs.
#
# 
#
# - Reducing costs is not abot labor arbitrage and offshore hiring. Its about automation now.
# - 90% of the worlds data collected in past 2 years. Never been a better time for this.
# - Resource-intensive, repetitive tasks, such as data entry and transaction processing, are well suited to automation and AI.
# - CFOs of big companies and startup entrepeneurs need to be looking for ways to use AI to improve FinTech (planning, budgeting and forecasting, financial reporting, operational accounting, allocations and adjustments, reconciliations, intercompany transactions)
#
# 
#
# ### The market for AI in financial services is expected to grow from 1.3 billion in 2017 to 7.4 billion in 2022, at a CAGR of 40.4%, according to Research and Markets.
#
# 
#
# ## Problems with integrating AI
#
# 
#
# - Legacy systems that do not communicate
# - Privacy concerns
# - Data silos
# - A lack of trained staff
# - The laborious effort of training supervised models
# - Lack of cultural alignment
# - Potential bias of machine learning
# - Deciding between cloud vendor, internal build, open source, or proprietary tech?
#
# 
#
# ## Applications
#
# 
#
# #### Increasing Security
#
# 
#
# - Fraudalent behavior, suspicious transactions, potential future attacks. How can this be mitigated?
# - AI can analyze huge volumes of security data and scale to the size of a company as it grows
# - So much valuable company data is being stored online. More and more.
# - Using machine learning, systems can detect unique activities or behaviors (“anomalies”) and flag them for security teams.
# - Given the incalculably high number of ways that security can be breached, genuinely “learning” systems will be a necessity in the five to ten years ahead.
# - According to a 2015 study by research firm Javelin Strategy, false declines, legitimate transactions that are wrongly rejected, account for 118 bln in losses for retailers.
# - A third of false decline cases result in lost customers, and in US alone they incur damage that is worth 13 times the value of actual fraud.
# - By analyzing various data points, machine learning algorithms can detect fraudulent transactions that would go unnoticed by human analysts while improving the accuracy of real-time approvals and reducing false declines.
#
# 
#
# - Mastercard recently launched Decision Intelligence technology.
# - Instead of limiting itself to predefined rules, DI gleans patterns from historical shopping and spending habits of cardholders to set a behavioral baseline against which it will compare and score each new transaction.
#
# 
#
# - Sift Science collects data from more than 6,000 websites where its fraud detection solution is deployed.
# - This enables it to track and analyze data across multiple channels and devices
#
# #### Reducing Processing Times
#
# 
#
# - Processing receipts and other financial documentation is extremely time-consuming;
# - It requires the patience and perseverance of multiple resources and is one of those necessary tasks that’s often prone to human error.
# - https://www.parascript.com/receipt-capture/ does this
#
# #### Trading
#
# 
#
# - Algorithmic trading involves the use of complex AI systems to make extremely fast trading decisions. ( originated in 70s)
# - Algorithmic systems often making thousands or millions of trades in a day, hence the term “high-frequency trading” (HFT), which is considered to be a subset of algorithmic trading.
# - Most hedge funds and financial institutions do not openly disclose their AI approaches to trading (for good reason), but machine learning and deep learning are playing an increasingly important role in calibrating trading decisions in real time
# - The stock market moves in response to myriad human-related factors that have nothing to do with ticker symbols, and the hope is that machine learning will be able to replicate and enhance human “intuition” of financial activity by discovering new trends and telling signals
# - Some popular hedge funds using AI include - Two Sigma, LLC, PDT Partners, DE Shaw, Man AHL, Citadel, Vatic Labs, Point72, Cubist etc.
#
# 
#
# - Sentient Technologies, an AI company based in San Francisco that also runs a hedge fund, has developed an algorithm that ingests millions of data points to find trading patterns and forecast trends, which enable it to make successful stock trading decisions.
# - Sentient runs trillions of simulated trading scenarios created from the vast amounts of public data available online.
# - Squeeze 1,800 days of trading into a few minutes.
# - Successful trading strategies, which it calls “genes,” are then tested in live trading, where they evolve autonomously as they gain experience.
#
# 
#
# - Numerai uses artificial intelligence to make trading decisions.
# - Instead of developing the algorithms themselves, they’ve outsourced the task to thousands of anonymous data scientists, who compete to create the best algorithms and win cryptocurrency for their efforts.
# - They share trading data with the scientists in a way that prevents them from replicating the fund’s trades while allowing them to build models for better trades.
#
# #### Credit Lending
#
# 
#
# - Machine learning algorithms can be trained on millions of examples of consumer data (age, job, marital status, etc…) and financial lending or insurance results (did this person default, pay back the loan on time, get in a car accident, etc…?).
# - Trends can be continuously analyzed to detect trends that might influence lending and insuring into the future (are more and more young people in a certain state getting in car accidents? Are there increasing rates of default among a specific demographic population over the last 15 years?
# - Traditional systems relied on historical data like transaction history, credit history and income growth over years to understand the risk associated with every loan extended.
# - This results in inconsistent estimates as historical data is not always an accurate standard to predict future behavior.
# - Machine learning allows analysis of real-time data of recent transactions, market conditions and even latest news to identify potential risks in offering credit.
# - With the help of predictive analytics, an ML algorithm can analyze petabytes of data to understand micro activities and assess the behavior of parties to identify a possible fraud.
# - This is something impossible for human investors to perform manually.
# - Zestfinance does this https://www.zestfinance.com/zaml
#
# #### Portfolio Management
#
# 
#
# - The term “robo-advisor” was essentially unheard-of just five years ago, but it is now commonplace in the financial landscape.
# - These are algorithms built to calibrate a financial portfolio to the goals and risk tolerance of the user.
# - Users enter their goals (for example, retiring at age 65 with 250,000.00 in savings), age, income, and current financial assets.
# - The robo-advisor then spreads investments across asset classes and financial instruments in order to reach the user’s goals.
# - The system then calibrates to changes in the user’s goals and to real-time changes in the market, aiming always to find the best fit for the user’s original goals.
# - Robo-advisors have gained significant traction with millennial consumers who don’t need a physical advisor to feel comfortable investing
# - Similarly, AI-enabled personal finance intelligence applications are helping consumers manage their finances, analyze spending, automate tax form filing, and make financial recommendations with a business model not predicated to generating fees from investments.
# - Responsive.ai is doing this http://alpha.responsive.ai/
#
# ## Theory
#
# ### Data Points to Use
#
# - Tweets about a company (good/bad)
# - Reddit Posts (good/bad)
# - News headlines about a company (good/bad)
# - Past Prices
# - All sorts of social media, blog posts
# - All sorts of financial metadata (dividends, financial reports, etc)
#
# #### Regression Problem vs Classification Problem?
#
# 
#
# - We can think of it as a regression model, i.e whats the next data point in a time series?
# - We can also think of it as a classsificiation problem, i.e will the stock go up or down tomorrow? Buy or sell?
# - If we want to think of it as a regression problem, we can use a single data point to build the line of best fit.
# - If we want to use multiple data points, we can use numerical data to create a multivariate regression model.
# - If we want to use a classification model using a single data point, we'd just learn the mapping between the input (tweets, posts, comments on a given day) and the output (good/bad). We would be able to say that for a given day, the majority of the sentiment for a stack was either good or bad. So for every date givem, our algorithm would learn overall whether or not a stock did well or not. Then given a new date, we could classify it as good/bad.
# - If we want to combine both sentiment and numerical data i.e prices, we would just use the overall sentiment output of a given date (0 or 1) as an additional feature in our numerical dataset.
#
# ### Linear Regression
#
# - A linear regression line has an equation of the form Y = a + bX, where X is the explanatory variable and Y is the dependent variable. The slope of the line is b, and a is the intercept (the value of y when x = 0).
#
# 
# +
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
# Load the dataset
prices = datasets.load_boston()
# # Use only one feature
# prices_X = diabetes.data[:, np.newaxis, 2]
# # Split the data into training/testing sets
# prices_X_train = prices_X[:-20]
# prices_X_test = prices_X[-20:]
# # Split the targets into training/testing sets
# prices_y_train = prices.target[:-20]
# prices_y_test = prices.target[-20:]
X_full, y_full = dataset.data, dataset.target
print(X_full.shape)
print(y_full.shape)
prices_X_train = X_full[:-20]
prices_X_test = X_full[-20:]
prices_y_train = y_full[:-20]
prices_y_test = y_full[-20:]
# Create linear regression object
regr = linear_model.SupportVectorMachine()
# Train the model using the training sets
regr.fit(prices_X_train, prices_y_train)
# Make predictions using the testing set
prices_y_pred = regr.predict(prices_X_test)
# -
# ### Support Vector Machines
#
#
# ### Neural Networks
#
# 
#
# 
from keras.models import Sequential
from keras.layers import Dense
from sklearn import datasets
import numpy
# fix random seed for reproducibility
numpy.random.seed(7)
# load pima price dataset
dataset = datasets.load_boston()
type(dataset)
# split into input (X) and output (Y) variables
# X = dataset[:,0:8]
# Y = dataset[:,8]
X_full, y_full = dataset.data, dataset.target
print(X_full.shape)
print(y_full.shape)
prices_X_train = X_full[:-20]
print(len(prices_X_train))
from keras.models import Sequential
from keras.layers import Dense
from sklearn import datasets
import numpy
# fix random seed for reproducibility
numpy.random.seed(7)
# load pima price dataset
dataset = datasets.load_boston()
# split into input (X) and output (Y) variables
# X = dataset[:,0:8]
# Y = dataset[:,8]
X_full, y_full = dataset.data, dataset.target
print(X_full.shape)
print(y_full.shape)
X = X_full
Y = y_full
# create model
model = Sequential()
model.add(Dense(12, input_dim=13, activation='relu'))
model.add(Dense(8, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
# Compile model
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# Fit the model
model.fit(X, Y, epochs=150, batch_size=10)
# evaluate the model
scores = model.evaluate(X, Y)
print("\n%s: %.2f%%" % (model.metrics_names[1], scores[1]*100))
# ### Reinforcement Learning
#
# - A forecast predicts future events.
#
# - A reinforcement learning agent optimizes future outcomes.
#
# https://doctorj.gitlab.io/sairen/
import gym
env = gym.make('sairen-v0')
for i_episode in xrange(20):
observation = env.reset()
for t in xrange(100):
env.render()
print (observation)
action = env.action_space.sample()
observation, reward, done, info = env.step(action)
if done:
print ("Episode finished after {} timesteps".format(t+1))
break
# +
from sairen import MarketEnv
def main():
"""Create a market environment, instantiate a random agent, and run the agent for one episode."""
env = MarketEnv("AAPL", episode_steps=20) # Apple stock, 1-second bars by default
agent = RandomAgent(env.action_space) # Actions are continuous from -1 = go short to +1 = go long. 0 is go flat. Sets absolute target position.
observation = env.reset() # An observation is a numpy float array, values: time, bid, bidsize, ask, asksize, last, lastsize, lasttime, open, high, low, close, vwap, volume, open_interest, position, unrealized_gain
done = False
total_reward = 0.0 # Reward is the profit realized when a trade closes
while not done:
env.render()
observation, reward, done, info = env.step(agent.act(observation))
total_reward += reward
print('\nTotal profit: {:.2f}'.format(total_reward)) # Sairen will automatically (try to) cancel open orders and close positions on exit
class RandomAgent:
"""Agent that randomly samples the action space."""
def __init__(self, action_space):
""":param gym.Space action_space: The Space to sample from."""
self.action_space = action_space
def act(self, observation):
""":Return: a random action from the action space."""
return self.action_space.sample() # Here the observation is ignored, but a less-random agent would want it.
if __name__ == "__main__":
main()
# -
# # Demo Time!
|
Market Prediction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import scipy
state = pd.read_csv('crime.csv')
state.head()
state['Murder'].mean()
# The mean is bigger than the trimmed mean, which is bigger than the median.
# This is because the trimmed mean excludes the largest and smallest five states
# ( trim=0.1 drops 10% from each end).
# #### Weighted Mean
# weighted_mean = sum(xi * wi)/sum(wi)
np.average(state["Murder"],weights = state['Assault'])
# #### Standard deviation
# For a set of data
# {1, 4, 4}, the mean is 3 and the median is 4. The deviations from the mean are the
# differences: 1 – 3 = –2, 4 – 3 = 1, 4 – 3 = 1.
# deviations tell us how dispersed the
# data is around the central value.
# Averaging the deviations themselves would not tell us much—the negative deviations
# offset the positive ones. In fact, the sum of the deviations from the mean is precisely
# zero.
# In the preceding example, the absolute value of the devia‐
# tions is {2 1 1}, and their average is (2 + 1 + 1) / 3 = 1.33. This is known as the mean
# absolute deviation
state["Murder"].std()
import matplotlib.pyplot as plt
plt.hist(state['Murder'])
import seaborn as sns
sns.boxplot(state['Murder'])
state['Murder'].quantile(0.75) - state['Murder'].quantile(0.25)
state["Murder"].quantile([0.5, 0.25, 0.5, 0.75, 0.95])
state.head()
sns.boxplot(state["Assault"])
binned = pd.cut(state["Assault"],10)
binned.value_counts()
plt.hist(state["Assault"])
# Density plot
sns.distplot(state["Assault"], color='green',
hist_kws={"edgecolor": 'black'})
data = pd.read_csv("train.csv")
data.head()
sns.countplot(data["Embarked"])
# ### Correlation
data.corr()
sns.heatmap(data.corr(), vmin=-1, vmax = 1, cmap = sns.diverging_palette(20, 220, as_cmap = True))
# ### Scatter Plot
plt.scatter(state["Murder"],state["Assault"],marker='$\u25EF$')
data.head()
data["Fare"].count()
data0 = data.loc[(data.Fare < 7) & (data.Fare >5) & (data.Fare <2),:]
data0.shape
ax = data.plot.hexbin(x = "Age", y = "Fare", gridsize = 10, sharex = False, figsize = (10,5))
# ### Boxplot
#
sns.boxplot(data["Age"])
# #### Violinplot
# Violin plots are used when you want to observe the distribution of numeric data, and are especially useful when you want to make a comparison of distributions between multiple groups. The peaks, valleys, and tails of each group's density curve can be compared to see where groups are similar or different.
sns.violinplot(data["Age"])
|
.ipynb_checkpoints/statistics notebook-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Building a Module
#
# A module in Python is conceptually not much more than a file with python code in it that you can access and run by importing the module.
#
# When you `import` a module, you are reading the file and making the code contained in it accessible through its alias.
#
# Start by creating a new file called `hello.py` and add the following message in there:
#
# ```python
# message = 'Hello Jim'
# ```
#
# and then try executing this code:
#
# ```python
# import hello as h
# h.message
# ```
#
# Great!
#
# Now, let's change the message. Edit the file to now say:
#
# ```python
# message = 'Hello Jane'
# ```
#
# and rexecute the code:
#
# ```python
# import hello as h
# h.message
# ```
#
# What went wrong?
#
# Since the contents of modules dont usually change very much (except during module development) Python is smart about importing modules and once a module is imported, it doesnt bother re-importing the module. Normally, this is what you want, but in our case when we are developing the module we want to force the module to geet automatically reloaded everytime it changes.
#
# Fortunately, there is a _magic_ command sequence that does exactly that. First, we have to load an extension called `autoreload` by executing the _magic command_ `%load_ext autoreload`. Once you have loaded that extension, you now have access to a new _magic command_ called `%autoreload` which supports different modes of autoreload. The mode we want for now is to automatically reload anything that changes, which is mode 2. So, you need to execute:
#
# ```python
# # %load_ext autoreload
# # %autoreload 2
# ```
#
# Now try executing:
#
# ```python
# h.message
# ```
#
# and you will see that future edits to the hello file will immediately be reloaded.
#
# Try editing the `hello.py` file to:
#
# ```python
# message = 'Hello <NAME>'
# ```
#
# and then execute
#
# ```python
# h.message
# ```
#
# Now, let's create our new module, which we'll build on through the course, and put the `drawdown` function we created in that module. Create a file called `edhec_risk_kit.py` and copy the follwing code into it.
#
# ```python
#
# import pandas as pd
#
# def drawdown(return_series: pd.Series):
# """Takes a time series of asset returns.
# returns a DataFrame with columns for
# the wealth index,
# the previous peaks, and
# the percentage drawdown
# """
# wealth_index = 1000*(1+return_series).cumprod()
# previous_peaks = wealth_index.cummax()
# drawdowns = (wealth_index - previous_peaks)/previous_peaks
# return pd.DataFrame({"Wealth": wealth_index,
# "Previous Peak": previous_peaks,
# "Drawdown": drawdowns})
#
# def get_ffme_returns():
# """
# Load the Fama-French Dataset for the returns of the Top and Bottom Deciles by MarketCap
# """
# me_m = pd.read_csv("data/Portfolios_Formed_on_ME_monthly_EW.csv",
# header=0, index_col=0, na_values=-99.99)
# rets = me_m[['Lo 10', 'Hi 10']]
# rets.columns = ['SmallCap', 'LargeCap']
# rets = rets/100
# rets.index = pd.to_datetime(rets.index, format="%Y%m").to_period('M')
# return rets
#
# ```
#
|
Investment Management/Course1/.ipynb_checkpoints/lab_104-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # 1. Import Libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# # 2. Load Data
# - 총 4277개의 train data
# - 총 15개의 class (transistor, capsule, wood, bottle, screw, cable, carpet, hazelnut, pill, metal_nut, zipper, leather, toothbrush, tile, grid)
train_y = pd.read_csv("../data/train_df.csv")
train_y
classList = train_y['class'].unique()
classList
print('class 개수:', len(classList))
labelList = train_y['label'].unique()
print('label 개수:', len(labelList))
# # 3. Preprocessing
# - label별로 숫자를 계산하여 데이터프레임 생성
# - class별로 데이터프레임을 생성하여 dictionary에 저장 (총 15개의 데이터프레임)
labelCount = train_y[['class', 'label']].groupby('label').count().rename(columns={'class': 'count'})
labelCount
anomaly_dict = {}
for className in classList:
df = pd.DataFrame(labelCount[labelCount.index.str.contains(className)]).sort_values(by='count', ascending=False)
anomaly_dict[className] = df
# +
fig, axs = plt.subplots(15, 1, figsize=(15, 15*5))
fig.subplots_adjust(hspace = .3)
axs = axs.ravel()
for i, (className, df) in enumerate(anomaly_dict.items()):
colors = ['red' for i in range(len(df.index))]
colors[0] = 'green'
axs[i].bar(df.index, df.iloc[:, 0], color=colors, alpha=0.5)
axs[i].set_title(className, fontsize=20)
for j, value in enumerate(df.iloc[:, 0]):
axs[i].text(j, 20, df.iloc[:, 0][j], ha='center', fontsize=20)
|
anomaly-detection-algorithm/code/EDA.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# %load_ext autoreload
# %autoreload 2
# +
from genomic_benchmarks.loc2seq.with_biopython import _fastagz2dict
from genomic_benchmarks.seq2loc import fasta2loc
from sklearn.model_selection import train_test_split
import numpy as np
import pandas as pd
from tqdm.notebook import tqdm, trange
from pathlib import Path
import yaml
import tarfile
np.random.seed(42)
# -
# ## Load genomic references
human = _fastagz2dict(Path.home() / ".genomic_benchmarks/fasta/Homo_sapiens.GRCh38.dna.toplevel.fa.gz",
24, 'MT')
human.keys()
worm = _fastagz2dict(Path.home() / ".genomic_benchmarks/fasta/Caenorhabditis_elegans.WBcel235.dna.toplevel.fa.gz", 6)
worm.keys()
human_chr_lengths = pd.Series({chr: len(human[chr]) for chr in human})
worm_chr_lengths = pd.Series({chr: len(worm[chr]) for chr in worm})
human_chr_lengths, worm_chr_lengths
# ## Utils for random generation
# +
def get_random_chr(chr_lengths: pd.Series):
chr_probs = chr_lengths / chr_lengths.sum()
chrs = chr_lengths.index.to_list()
return chrs[np.argwhere(np.random.multinomial(1, chr_probs))[0][0]]
def get_random_int(int_len, chr_lengths: pd.Series):
c = get_random_chr(chr_lengths)
c_len = chr_lengths[c]
pos = np.random.randint(c_len)-int_len+1
strand = ['+', '-'][np.random.randint(2)]
return c, pos, pos+int_len, strand
# -
get_random_int(200, human_chr_lengths)
# ## Data generation
human_df = pd.DataFrame.from_records([get_random_int(200, human_chr_lengths) for i in trange(50_000)],
columns = ["region", "start", "end", "strand"])
human_df["region"] = "chr" + human_df["region"]
human_df.index.name = "id"
human_df.head()
worm_df = pd.DataFrame.from_records([get_random_int(200, worm_chr_lengths) for i in trange(50_000)],
columns = ["region", "start", "end", "strand"])
worm_df.index.name = "id"
worm_df.head()
# ## Train/test split
train_human, test_human = train_test_split(human_df, shuffle=True, random_state=42)
train_human.shape, test_human.shape
train_worm, test_worm = train_test_split(worm_df, shuffle=True, random_state=42)
train_worm.shape, test_worm.shape
# ## YAML file
# +
BASE_FILE_PATH = Path("../../datasets/demo_human_or_worm/")
# copied from https://stackoverflow.com/a/57892171
def rm_tree(pth: Path):
for child in pth.iterdir():
if child.is_file():
child.unlink()
else:
rm_tree(child)
pth.rmdir()
if BASE_FILE_PATH.exists():
rm_tree(BASE_FILE_PATH)
BASE_FILE_PATH.mkdir()
(BASE_FILE_PATH / 'train').mkdir()
(BASE_FILE_PATH / 'test').mkdir()
# +
with open(BASE_FILE_PATH / 'metadata.yaml', 'w') as fw:
desc = {
'version': 0,
'classes': {
'human': {
'type': 'fa.gz',
'url': 'http://ftp.ensembl.org/pub/release-97/fasta/homo_sapiens/dna/Homo_sapiens.GRCh38.dna.toplevel.fa.gz',
'extra_processing': 'ENSEMBL_HUMAN_GENOME'
},
'worm': {
'type': 'fa.gz',
'url': 'http://ftp.ensembl.org/pub/release-104/fasta/caenorhabditis_elegans/dna/Caenorhabditis_elegans.WBcel235.dna.toplevel.fa.gz'
}
}
}
yaml.dump(desc, fw)
desc
# -
# ## CSV files
train_human.to_csv(BASE_FILE_PATH / 'train' / 'human.csv.gz', index=True, compression='gzip')
train_worm.to_csv(BASE_FILE_PATH / 'train' / 'worm.csv.gz', index=True, compression='gzip')
test_human.to_csv(BASE_FILE_PATH / 'test' / 'human.csv.gz', index=True, compression='gzip')
test_worm.to_csv(BASE_FILE_PATH / 'test' / 'worm.csv.gz', index=True, compression='gzip')
# ## Test that it can be downloaded
# +
from genomic_benchmarks.loc2seq import download_dataset
download_dataset("demo_human_or_worm")
# +
from genomic_benchmarks.data_check import info
info("demo_human_or_worm", 0)
# -
|
cnn_experiments/docs/demo_human_or_worm/create_datasets.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import sys
import itertools
import math
import logging
import json
import re
import random
from collections import OrderedDict
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import matplotlib.lines as lines
from matplotlib.patches import Polygon
# Root directory of the project
ROOT_DIR = os.path.abspath("..\\..\\")
# Import Mask RCNN
sys.path.append(ROOT_DIR)
sys.path.insert(0, 'Mask_RCNN')
# To find local version of the library
from mrcnn import utils
from mrcnn import visualize
from mrcnn.visualize import display_images
import mrcnn.model as modellib
from mrcnn.model import log
from samples.pizza_det import pizza
# %matplotlib inline
# -
config = pizza.pizzaConfig()
GNS_DIR = "C:\\Users\\Ragnar\\Desktop\\Dataset\\procdata"
# +
# Load dataset
# Get the dataset from the releases page
# https://github.com/matterport/Mask_RCNN/releases
dataset = pizza.pizzaDataset()
dataset.load_pizza(GNS_DIR, "train")
# Must call before using the dataset
dataset.prepare()
print("Image Count: {}".format(len(dataset.image_ids)))
print("Class Count: {}".format(dataset.num_classes))
for i, info in enumerate(dataset.class_info):
print("{:3}. {:50}".format(i, info['name']))
# -
dataset.class_names
dataset.class_ids
# Load and display random samples
image_ids = np.random.choice(dataset.image_ids, 1)
for image_id in image_ids:
image = dataset.load_image(image_id)
mask, class_ids = dataset.load_mask(image_id)
class_ids = [int(x) for x in class_ids]
visualize.display_top_masks(image, mask, class_ids, dataset.class_names,limit=2)
# +
# Load random image and mask.
image_id = random.choice(dataset.image_ids)
image = dataset.load_image(image_id)
mask, class_ids = dataset.load_mask(image_id)
class_ids = np.array([int(x) for x in class_ids])
print(class_ids)
# Compute Bounding box
bbox = utils.extract_bboxes(mask)
# Display image and additional stats
print("image_id ", image_id, dataset.image_reference(image_id))
log("image", image)
log("mask", mask)
log("class_ids", class_ids)
log("bbox", bbox)
# Display image and instances
visualize.display_instances(image, bbox, mask, class_ids, dataset.class_names)
# -
|
Toppings/masky.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <img src="images/logo.jpg" style="display: block; margin-left: auto; margin-right: auto;" alt="לוגו של מיזם לימוד הפייתון. נחש מצויר בצבעי צהוב וכחול, הנע בין האותיות של שם הקורס: לומדים פייתון. הסלוגן המופיע מעל לשם הקורס הוא מיזם חינמי ללימוד תכנות בעברית.">
# # <span style="text-align: right; direction: rtl; float: right;">מחלקות – חלק 2</span>
# ## <span style="text-align: right; direction: rtl; float: right; clear: both;">רענון</span>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# בשיעור הקודם בנושא מחלקות למדנו ש<dfn>מחלקה</dfn> היא תבנית ("שבלונה") המאגדת תכונות ופעולות של ישות כלשהי.<br>
# למדנו גם מה הוא מופע – התוצר של השימוש באותה שבלונה, באותה מחלקה, כדי ליצור פריט לפי השבלונה הזו.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# לדוגמה, מחלקת "קבוצת ווטסאפ" יכולה להיות מוגדרת כך:
# </p>
#
# <ul style="text-align: right; direction: rtl; float: right; clear: both;">
# <li><em>תכונות</em>: כותרת, משתמשים ורשימת הודעות.</li>
# <li><em>פעולות</em>: שליחת הודעה, הצטרפות לקבוצה או יציאה מהקבוצה.</li>
# </ul>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# קריאה למחלקת "קבוצת ווטסאפ" תיצור מופע חדש של קבוצת ווטסאפ, שבו יש את התכונות והפעולות שהוגדרו במחלקה.<br>
# קריאה למחלקה 5 פעמים תיצור 5 קבוצות ווטסאפ שונות, שלכל אחת מהן התכונות והפעולות שהוגדרו במחלקה.
# </p>
# ## <span style="text-align: right; direction: rtl; float: right; clear: both;">משתני מחלקה</span>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# במסעדת "זלוברי" ליד כל רכיב בתפריט רשומים ערכיו התזונתיים ל־100 גרם.<br>
# מנהלת המסעדה קיפף אוסין שכרה את שירותינו וביקשה מאיתנו לכתוב מחלקה המייצגת רכיב במנה.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# לכל רכיב יש:
# </p>
#
# <ul style="text-align: right; direction: rtl; float: right; clear: both;">
# <li><em>תכונות</em>: שם, משקל פחמימות, משקל חלבונים ומשקל שומנים (בגרמים).</li>
# <li><em>פעולות</em>: חישוב מספר הקלוריות ברכיב.</li>
# </ul>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# להזכירכם, דרך להערכה מהירה של מספר הקלוריות שיש ברכיב, היא זו:
# </p>
# <ol style="text-align: right; direction: rtl; float: right; clear: both;">
# <li>מצאו את משקל הפחמימות ברכיב והכפילו ב־4.</li>
# <li>מצאו את משקל השומן ברכיב והכפילו ב־9.</li>
# <li>מצאו את משקל החלבון ברכיב והכפילו ב־4.</li>
# <li>מספר הקלוריות ברכיב היא חיבור הערכים שקיבלתם בשלבים 1–3.</li>
# </ol>
# <div class="align-center" style="display: flex; text-align: right; direction: rtl; clear: both;">
# <div style="display: flex; width: 10%; float: right; clear: both;">
# <img src="images/exercise.svg" style="height: 50px !important;" alt="תרגול">
# </div>
# <div style="width: 70%">
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# נסו לממש בעצמכם את מחלקת Ingredient לפי התכונות והפעולות שתוארו למעלה.
# </p>
# </div>
# <div style="display: flex; width: 20%; border-right: 0.1rem solid #A5A5A5; padding: 1rem 2rem;">
# <p style="text-align: center; direction: rtl; justify-content: center; align-items: center; clear: both;">
# <strong>חשוב!</strong><br>
# פתרו לפני שתמשיכו!
# </p>
# </div>
# </div>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# מימוש של המחלקה ייראה כך:
# </p>
class Ingredient:
def __init__(self, name, carbs, fats, proteins):
self.name = name
self.carbs = carbs
self.fats = fats
self.proteins = proteins
def calculate_calories(self):
return (
self.carbs * 4
+ self.fats * 9
+ self.proteins * 4
)
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# ושימוש בה ייראה כך:
# </p>
mango = Ingredient('Mango', carbs=15, fats=0.4, proteins=0.8)
mango.calculate_calories()
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# אוסין מגדירה רכיב כ"בריא" אם מספר הקלוריות שבו קטן מ־100 עבור 100 גרם.<br>
# נממש את הפעולה <code>is_healthy</code> שמחזירה <code>True</code> או <code>False</code>:
# </p>
class Ingredient:
def __init__(self, name, carbs, fats, proteins):
self.name = name
self.carbs = carbs
self.fats = fats
self.proteins = proteins
def calculate_calories(self):
return (
self.carbs * 4
+ self.fats * 9
+ self.proteins * 4
)
def is_healthy(self):
return self.calculate_calories() < 100
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# שימוש במספרים קבועים בקוד שלנו נחשב לרוב ללא מנומס, ותמיד נעדיף לתת להם שם.<br>
# במקרה הזה, יש סיכוי שמסעדת "זלוברי" תשנה את הגדרתה עבור רכיבים דיאטטיים בעתיד, ועדיף שהמספר "100" לא יפוזר לאורך הקוד.<br>
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# פתרון אפשרי הוא להגדיר משתנה בראש הקוד, שייצג את מספר הקלוריות המרבי למאכל דיאטטי.<br>
# שימו לב שנהוג לכתוב את שמם של משתנים קבועים, אלו שערכיהם ישארו קבועים לכל אורך התוכנית, באותיות גדולות:
# </p>
# +
HEALTHY_CALORIES_UPPER_BOUND = 100
class Ingredient:
def __init__(self, name, carbs, fats, proteins):
self.name = name
self.carbs = carbs
self.fats = fats
self.proteins = proteins
def calculate_calories(self):
return (
self.carbs * 4
+ self.fats * 9
+ self.proteins * 4
)
def is_healthy(self):
return self.calculate_calories() < HEALTHY_CALORIES_UPPER_BOUND
# -
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# הפתרון הזה עובד, אך מפספס עיקרון חשוב שהצגנו במחברת הקודמת שעסקה במחלקות.<br>
# מחלקה אמורה לאגד את כל המידע הקשור אליה, וזה הדין גם בנוגע למחלקת "רכיב", שאמורה לכלול את כל המידע הרלוונטי אליה.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# אפשרות נוספת היא להגדיר את הערך כתכונה של כל מופע חדש שניצור:
# </p>
class Ingredient:
def __init__(self, name, carbs, fats, proteins):
self.name = name
self.carbs = carbs
self.fats = fats
self.proteins = proteins
self.HEALTHY_CALORIES_UPPER_BOUND = 100
def calculate_calories(self):
return (
self.carbs * 4
+ self.fats * 9
+ self.proteins * 4
)
def is_healthy(self):
return self.calculate_calories() < self.HEALTHY_CALORIES_UPPER_BOUND
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# מדובר בבחירה מעט בזבזנית, כיוון שאם יהיו לנו מיליון רכיבים נצטרך ליצור במיליון מופעים את <var>HEALTHY_CALORIES_UPPER_BOUND</var>.<br>
# יתרה מכך, אם נחליט לשנות את <var>HEALTHY_CALORIES_UPPER_BOUND</var> נצטרך לפנות לכל מיליון המופעים הקיימים ולשנות בהם את הערך.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# אפשרות טובה יותר, שבה טרם נתקלנו, היא להגדיר את המשתנה ברמת המחלקה עצמה:
# </p>
class Ingredient:
HEALTHY_CALORIES_UPPER_BOUND = 100
def __init__(self, name, carbs, fats, proteins):
self.name = name
self.carbs = carbs
self.fats = fats
self.proteins = proteins
def calculate_calories(self):
return (
self.carbs * 4
+ self.fats * 9
+ self.proteins * 4
)
def is_healthy(self):
return self.calculate_calories() < self.HEALTHY_CALORIES_UPPER_BOUND
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# מה קרה בקוד שלמעלה?<br>
# הגדרנו את <var>HEALTHY_CALORIES_UPPER_BOUND</var> באותה רמה היררכית של הגדרת הפעולות במחלקה.<br>
# הגדרה של משתנה ברמת המחלקה גורמת לו להיות משותף לכל המופעים שייווצרו מאותה מחלקה.<br>
# בשלב זה כל מופע יכול לגשת לערך <var>HEALTHY_CALORIES_UPPER_BOUND</var> כאילו הוא חלק מתכונות המופע.
# </p>
# +
banana = Ingredient('Banana', carbs=23, fats=0.3, proteins=1.1)
melon = Ingredient('Melon', carbs=8, fats=0.2, proteins=0.8)
print(banana.HEALTHY_CALORIES_UPPER_BOUND)
print(melon.HEALTHY_CALORIES_UPPER_BOUND)
# -
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# בתא האחרון יצרנו שני מופעים חדשים של רכיבים – הראשון של בננה והשני של מלון.<br>
# הצלחנו לגשת למשתנה המחלקה <var>HEALTHY_CALORIES_UPPER_BOUND</var> שמשותף לשניהם דרך המופע שלהם.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# קריאה ל־<code dir="ltr">banana.is_healthy()</code> תעביר את המופע <var>banana</var> לפרמטר <var>self</var> של הפעולה <var>is_healthy</var>.<br>
# הביטוי <code>self.HEALTHY_CALORIES_UPPER_BOUND</code> יאפשר לנו להשיג את משתנה המחלקה, כיוון שאל <var>self</var> הועבר המופע עצמו:
# </p>
print(f"Is Banana healthy? -- {banana.is_healthy()}")
print(f"Is Melon healthy? -- {melon.is_healthy()}")
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# הטריק הזה נקרא "<dfn>משתני מחלקה</dfn>" והוא מועיל ונפוץ, בעיקר עבור הגדרת ערכים קבועים המשותפים לכל המופעים שייווצרו מהמחלקה.
# </p>
# ### <span style="text-align: right; direction: rtl; float: right; clear: both;">תרגיל ביניים: חללר</span>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# בעקבות הצלחתכם בחברת צ'יקצ'וק, פנה אליכם היזם המוכר אלון מסכה וביקש מכם להצטרף לחברתו "חללר".<br>
# אלון מעוניין לבנות גשושית שיכולה לנוע במהירות האור, והוא מעוניין בעזרתכם בבניית סימולציה של גשושית שכזו.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# תכונות הגשושית (<var>SpaceProbe</var>) יהיו זמן השיגור שלה ומהירות הטיסה הממוצעת של הגשושית בקמ"ש.<br>
# לכל מופע של גשושית תהיה גם הפעולה <var>get_distance</var> שתחשב מה המרחק שהחללית עברה מנקודת השיגור שלה.<br>
# אפשר לחשב זאת על ידי מציאת מספר השעות שעברו מרגע השיגור, והכפלתו במהירות הממוצעת של החללית.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# כדי שהסימולציה תדמה מצב מציאותי, ביקש אלון להגביל את מהירות הגשושית.<br>
# אם המהירות הממוצעת שהוגדרה לגשושית קטנה מ־0 – הגדירו אותה כ־0. אם היא גדולה ממהירות האור – הגדירו אותה כמהירות האור.
# </p>
# ### <span style="text-align: right; direction: rtl; float: right; clear: both;">מחלקות הן אזרחיות ממדרגה ראשונה</span>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# כדי להבין טוב יותר איך פייתון מתנהגת, חשוב להבין שהמחלקה <var>Ingredient</var> גם היא ערך לכל דבר.<br>
# בדיוק כמו פונקציות (או כל ערך אחר), אפשר לבצע השמה שלה למשתנה:
# </p>
SomethingINeedForMyRecipe = Ingredient
honey = SomethingINeedForMyRecipe('Honey', carbs=82, fats=0, proteins=0.3)
honey.calculate_calories()
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# בדוגמה האחרונה ביצענו השמה, וגרמנו למשתנה <var>SomethingINeedForMyRecipe</var> להצביע על המחלקה <var>Ingredient</var>.<br>
# שימו לב שלא הפעלנו את ה־<code>__init__</code> של <var>Ingredient</var>, אלא השתמשנו בה כערך – ציינו את שמה ללא הסוגריים.<br>
# בשלב הזה <var>SomethingINeedForMyRecipe</var> ו־<var>Ingredient</var> הצביעו לאותו מקום, ולכן אפשר היה ליצור רכיבים בעזרת <var>SomethingINeedForMyRecipe</var>.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# הדפסה של המשתנה <var>SomethingINeedForMyRecipe</var> תגלה לנו שמדובר במחלקה המקורית, <var>Ingredient</var>:
# </p>
print(SomethingINeedForMyRecipe)
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# וכך גם בדיקת הסוג של המופע <var>honey</var>, שנוצר מהקריאה ל־<var>SomethingINeedForMyRecipe</var>:
# </p>
type(honey)
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# אפשר לקחת את האמירה שמחלקות הן כמו כל ערך אחר צעד אחד קדימה.<br>
# ניצור שתי מחלקות, ונכניס את המחלקות עצמן לתוך רשימה:
# </p>
# +
class User:
def __init__(self, name, age):
self.name = name
self.age = age
def __str__(self):
return f"{self.name} is {self.age} years old."
class Superstar:
def __init__(self, name, age):
self.name = f'🌟Superstar {name}🌟'
self.age = age - 5 # Your skin is so young!
def __str__(self):
return f"{self.name} is {self.age} years old."
classes = [User, Superstar]
for class_object in classes:
print(f"The result from {class_object} is...")
kipik = class_object("Kipik the Turtle", 75)
print(kipik)
print('-' * 50)
# -
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# מה התרחש בקוד שלמעלה?
# </p>
#
# <ol style="text-align: right; direction: rtl; float: right; clear: both;">
# <li>יצרנו שתי מחלקות, <var>User</var> ו־<var>Superstar</var>.</li>
# <li>יצרנו רשימה שאיבריה הם המחלקות <var>User</var> ו־<var>Superstar</var>, וגרמנו למשתנה בשם <var>classes</var> להצביע על הרשימה בעזרת השמה.</li>
# <li>עברנו על התוכן של <var>classes</var> בעזרת לולאת <code>for</code>.</li>
# <li>בכל איטרציה לקחנו מחלקה אחת (שעליה הצביע המשתנה <var>class_object</var>), ובנינו בעזרתה מופע של קיפיק.</li>
# <li>הדפסנו את המופע בכל מחלקה שהגענו אליה – הראשון מופע שנוצר מהמחלקה <var>User</var>, והשני מופע שנוצר מהמחלקה <var>Superstar</var>.</li>
# </ol>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# בשיעור על פונקציות בשבוע שעבר למדנו שפונקציות הן אזרחיות ממדרגה ראשונה – כלומר, הן ערכים לכל דבר.<br>
# מהדוגמה האחרונה אפשר לראות שגם מחלקות בפייתון, בדומה לפונקציות, הן אזרחיות ממדרגה ראשונה.<br>
# המשמעות היא שהן ערך לכל דבר, כמו מספרים ומחרוזות: אפשר להכניס אותן לרשימה, להעביר אותן כפרמטר ולאחסן אותן במשתנים.
# </p>
# ### <span style="text-align: right; direction: rtl; float: right; clear: both;">שימוש ישיר בערך המחלקה</span>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# נחדד פעם נוספת את ההבדלים בין מופע למחלקה.<br>
# נביט במחלקה <var>Ingredient</var> שמייצגת רכיב במסעדה.<br>
# בעזרת קריאה למחלקה (השבלונה, התבנית) <var>Ingredient</var> נוכל ליצור מופעים חדשים של רכיבים.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# כך ניצור מחלקה:
# </p>
class Ingredient:
HEALTHY_CALORIES_UPPER_BOUND = 100
def __init__(self, name, carbs, fats, proteins):
self.name = name
self.carbs = carbs
self.fats = fats
self.proteins = proteins
def calculate_calories(self):
return (
self.carbs * 4
+ self.fats * 9
+ self.proteins * 4
)
def is_healthy(self):
return self.calculate_calories() < self.HEALTHY_CALORIES_UPPER_BOUND
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# וכך ניצור מופע:
# </p>
cinnamon = Ingredient('Cinnamon', carbs=81, fats=1.2, proteins=4)
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# כפי שראינו לפני כן, מחלקה היא ערך לכל דבר.<br>
# מעבר לכך, ראינו שאפשר להגדיר משתנים השייכים למחלקה.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# אפשר לגשת לאותם משתנים שלא דרך מופע מסוים, בעזרת שימוש בשם המחלקה.<br>
# נוכל, לדוגמה, להשיג את הערך שנמצא ב־<var>HEALTHY_CALORIES_UPPER_BOUND</var> כך:
# </p>
Ingredient.HEALTHY_CALORIES_UPPER_BOUND
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# בשורה למעלה ציינו את שם המחלקה עצמה, כתבנו נקודה, ומייד אחריה התייחסנו לאחד המשתנים המוגדרים בה.<br>
# הגדרת קבועים במחלקה והתייחסות אליהם מבחוץ הוא רעיון די נפוץ שנהוג להשתמש בו לא מעט בתכנות.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# אם נרצה, נוכל גם לבצע השמה למשתנה המחלקה מבחוץ, ולשנות אותו עבור כל המופעים שמתייחסים אליו:
# </p>
print(f"healthy if calories < 100: {cinnamon.is_healthy()}")
Ingredient.HEALTHY_CALORIES_UPPER_BOUND = 400
print(f"healthy if calories < 400: {cinnamon.is_healthy()}")
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# בניגוד לגישה למשתנה המחלקה בצורה שהוצגה למעלה, לא נוכל לגשת באותו אופן לתכונה <code>Ingredient.name</code>.<br>
# הרי אין בכך היגיון – התכונה <var>name</var> היא תכונה שמוגדרת עבור כל מופע, ולא עבור המחלקה כולה:
# </p>
Ingredient.name
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# ומה יקרה אם ננסה לפנות דרך המחלקה עצמה לפעולה שהוגדרה ברמת המחלקה?
# </p>
Ingredient.is_healthy()
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# כמובן!<br>
# הפעולה <var>is_healthy</var> מצפה ל־<var>self</var>, מופע כלשהו של המחלקה, שבדרך כלל מועבר לה כשאנחנו קוראים לה בעזרת המופע:
# </p>
cinnamon.is_healthy()
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# בתא למעלה, כפי שלמדנו בפרק הקודם על מחלקות, <var>cinnamon</var> נשלח לפעולה <var>is_healthy</var> בתור הארגומנט <var>self</var>.<br>
# </p>
#
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# כדי לחקות את אותה ההתנהגות עבור הקריאה <code dir="ltr">Ingredient.is_healthy()</code> שמצפה לקבל <var>self</var> כפרמטר,<br>
# נעביר את <var>cinnamon</var> כארגומנט לפעולה, וזה יגרום לה להיכנס לפרמטר <var>self</var>:
# </p>
Ingredient.is_healthy(cinnamon)
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# שימוש בפעולות בצורה הזו כרגע הוא יותר בבחינת ידע כללי שאמור לעזור לכם להבין איך המחלקה מתנהגת מאחורי הקלעים.<br>
# בהמשך הקורס נבין טוב יותר מהם השימושיים האפשריים בפנייה לפעולות דרך המחלקה עצמה ולא דרך מופע.
# </p>
# ## <span style="text-align: right; direction: rtl; float: right; clear: both;">הכלה</span>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# לאור ההצלחה המסחררת של מחלקת "רכיב", ביקשה מאיתנו מנהלת המסעדה קיפף אוסין לתכנת מחלקה בשם <var>Dish</var> שתייצג מנה במסעדה.<br>
# לכל מנה יש שם (<var>name</var>), סימון אם היא צמחונית (<var>is_vegetarian</var>) ורשימת רכיבים (<var>ingredients</var>).<br>
# הפעולה <var>get_total_calories</var> תחזיר את סכום הקלוריות של רכיבי המנה.
# </p>
# <div class="align-center" style="display: flex; text-align: right; direction: rtl; clear: both;">
# <div style="display: flex; width: 10%; float: right; clear: both;">
# <img src="images/exercise.svg" style="height: 50px !important;" alt="תרגול">
# </div>
# <div style="width: 70%">
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# ממשו בעצמכם את מחלקת <var>Dish</var>.<br>
# לעת עתה, התעלמו מהכמות של כל רכיב במנה.
# </p>
# </div>
# <div style="display: flex; width: 20%; border-right: 0.1rem solid #A5A5A5; padding: 1rem 2rem;">
# <p style="text-align: center; direction: rtl; justify-content: center; align-items: center; clear: both;">
# <strong>חשוב!</strong><br>
# פתרו לפני שתמשיכו!
# </p>
# </div>
# </div>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# חלק מהכיף האמיתי בתכנות מחלקות מסתתר בכתיבת האינטרקציה ביניהן.<br>
# לכן התרגיל למעלה הוא מעניין – הוא משלב את המחלקה הקודמת שבנינו, <var>Ingredient</var>, עם המחלקה <var>Dish</var>.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# כדי לייצג את הרכיבים בכל מנה נשתמש במופעי המחלקה <var>Ingredient</var>.<br>
# נוכל לשמור רשימה של רכיבים כתכונה של מחלקת "מנה".<br>
# במילים אחרות: לכל מנה יש רשימת רכיבים.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# נממש:
# </p>
class Dish:
"""Create a new dish for the restaurant using our ingredients.
Args:
name (str): The name of the dish.
is_vegetarian (bool): `True` if the dish is vegetarian.
ingredients (list of Ingredient): All the required ingredients
for the dish.
Attributes:
name (str): The name of the dish.
is_vegetarian (bool): `True` if the dish is vegetarian.
ingredients (list of Ingredient): All the ingredients that are
required to prepare the dish.
"""
def __init__(self, name, is_vegetarian, ingredients):
self.name = name
self.is_vegetarian = is_vegetarian
self.ingredients = ingredients
def get_total_calories(self):
"""Calculate calories based on the list of the ingredients."""
calories = 0
for ingredient in self.ingredients:
calories = calories + ingredient.calculate_calories()
return calories
def __str__(self):
calories = self.get_total_calories()
return f"{self.name} has {calories:.7} calories in it."
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# בקוד שלמעלה הגדרנו פעולת <code>__init__</code> שתקבל את שם המנה, משתנה בוליאני שקובע אם היא צמחונית או לא ורשימת רכיבים.<br>
# הפעולה <var>get_total_calories</var> תעבור על הרכיבים ותסכום את מספרי הקלוריות של כל אחד מהם.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# נבדוק שהמחלקה עובדת.<br>
# ניצור רשימת רכיבים ונעביר אותה ל־<var>Dish</var> כדי לייצר מופע של מנה:
# </p>
ingredients = [
Ingredient('Butter', carbs=0.1, fats=81.9, proteins=0.9),
Ingredient('Honey', carbs=82, fats=0, proteins=0.3),
Ingredient('Flour', carbs=79, fats=1.8, proteins=7),
]
bread = Dish("Lembas Bread", is_vegetarian=True, ingredients=ingredients)
print(bread)
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# העיקרון של שימוש במופעי מחלקה אחת בתוך מחלקה אחרת נקרא <dfn>הכלה</dfn> (<var>Containment</var>).<br>
# זוהי טכניקה שימושית ונפוצה מאוד בתכנות מחלקות, ותשמש אותנו רבות ביום־יום כמתכנתים.
# </p>
# ### <span style="text-align: right; direction: rtl; float: right; clear: both;">תרגיל ביניים: צָב שָׁלוּחַ 2</span>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# מנהל הדואר הידוע והאהוב קיפיק הצב אהב את מחלקת <var>PostOffice</var> שבניתם.<br>
# מרוב התלהבות, הוא מעוניין שגם ההודעות עצמן ייוצגו בעזרת מחלקה.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# צרו את מחלקת <var>Message</var> והחליטו אילו תכונות כדאי שיהיו לה.<br>
# ממשו פעולת <code>__str__</code> שתציג את ההודעה בצורה נאה.<br>
# הרצת הפונקציה <var>len</var> על מופע של הודעה יחזיר את אורך ההודעה (ללא הכותרת).
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# ודאו שהתאמתם את פעולות מחלקת <var>PostOffice</var> כך שיפעלו גם על <var>Message</var>.<br>
# אם עולה הצורך, קראו באינטרנט על פעולות קסם.
# </p>
# ## <span style="text-align: right; direction: rtl; float: right; clear: both;">כימוס, הגנה ופרטיות</span>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# מחלקת <var>Dish</var> שכתבנו שינתה את עולם המסעדנות כולו, ואין מתכנת מסעדן שלא משתמש בה.<br>
# הגברת קיפף אוסין משתמשת בה במסעדת הדגל שלה "מסון קייפי" ומעוניינת להשתמש בה במסעדה החדשה שלה, "7 טעמים".
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# במסעדת 7 טעמים אין אף מנה שמורכבת מיותר מ־7 רכיבים, והגברת אוסין מבקשת מאיתנו לעזור לה לאכוף זאת במחלקה.
# </p>
# <div class="align-center" style="display: flex; text-align: right; direction: rtl; clear: both;">
# <div style="display: flex; width: 10%; float: right; clear: both;">
# <img src="images/exercise.svg" style="height: 50px !important;" alt="תרגול">
# </div>
# <div style="width: 70%">
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# נסו לחשוב בעצמכם איך אתם הייתם פותרים את הבעיה.<br>
# כיצד תשפרו את מחלקת <var>Dish</var> כך שתגביל את המשתמשים בה לעד 7 רכיבים?
# </p>
# </div>
# <div style="display: flex; width: 20%; border-right: 0.1rem solid #A5A5A5; padding: 1rem 2rem;">
# <p style="text-align: center; direction: rtl; justify-content: center; align-items: center; clear: both;">
# <strong>חשוב!</strong><br>
# פתרו לפני שתמשיכו!
# </p>
# </div>
# </div>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# ישנם הרבה פתרונות יצירתיים ומעניינים שיכולים לשמש אותנו במקרה שסופקו יותר מ־7 רכיבים.<br>
# אפשר, לדוגמה, לקחת רק את 7 הרכיבים הראשונים שאנחנו מקבלים, או להשאיר את רשימת הרכיבים ריקה.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# אחת הבחירות האפשריות היא לא לקבל מלכתחילה בפעולת האתחול <code>__init__</code> את רשימת הרכיבים.<br>
# במקרה כזה נצטרך לספק למשתמש דרך נוחה להוסיף רכיבים לתכונה <var>ingredients</var> ולהוריד רכיבים ממנה.<br>
# נאתחל את התכונה לרשימה ריקה, ונוסיף ל־<var>Dish</var> את הפעולות <var>add_ingredient</var> ו־<var>remove_ingredient</var>.<br>
# ברגע שהמשתמש במחלקה יקרא ל־<var>add_ingredient</var> כשיש במנה כבר 7 רכיבים, נכשיל את הוספת הרכיב העודף:
# </p>
class Dish:
MAX_INGREDIENTS = 7
"""Create a new dish for the restaurant using our ingredients.
Args:
name (str): The name of the dish.
is_vegetarian (bool): `True` if the dish is vegetarian.
Attributes:
name (str): The name of the dish.
is_vegetarian (bool): `True` if the dish is vegetarian.
ingredients (list of Ingredient): All the required ingredients
for the dish.
"""
def __init__(self, name, is_vegetarian):
self.name = name
self.is_vegetarian = is_vegetarian
self.ingredients = []
def can_add_ingredient(self):
"""Return True if we should allow to add another ingredient."""
return (
self.MAX_INGREDIENTS is None
or len(self.ingredients) < self.MAX_INGREDIENTS
)
def add_ingredient(self, ingredient):
"""Add an ingredient to the dish.
If the class variable MAX_INGREDIENTS is set, and there are
at least MAX_INGREDIENTS ingredients in the dish, the call
to this function will fail.
Args:
ingredient (Ingredient): An `Ingredient` instance to add.
"""
if not self.can_add_ingredient():
return
self.ingredients.append(ingredient)
def remove_ingredient(self, ingredient):
"""Remove an ingredient from the dish.
Args:
ingredient (Ingredient): An `Ingredient` instance to add.
Raises:
ValueError: If the supplied ingredient is not in the
ingredients list.
"""
self.ingredients.remove(ingredient)
def get_total_calories(self):
"""Calculate calories based on the list of the ingredients."""
calories = 0
for ingredient in self.ingredients:
calories = calories + ingredient.calculate_calories()
return calories
def __str__(self):
calories = self.get_total_calories()
return f"{self.name} has {calories:.7} calories in it."
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# נבדוק שהמחלקה עובדת.<br>
# לנוחיותכם, פירטנו מעל כל חלק מה יעשה הקוד.
# </p>
# +
# ניצור מנה של קוקטייל
great_cocktail = Dish("Black Magic Julep", is_vegetarian=True)
# נכין את הרכיבים בצד
ingredients = [
Ingredient("Angostura bitters", carbs=80, fats=0, proteins=0),
Ingredient("Fernet branca", carbs=46.41, fats=0, proteins=0),
Ingredient("Four roses", carbs=69, fats=0, proteins=0),
Ingredient("Mint leaves", carbs=15, fats=3.8, proteins=0.9),
Ingredient("Amaro Averna", carbs=20.9, fats=15.7, proteins=2.8),
Ingredient("Amaro Montenegro", carbs=54, fats=0, proteins=0),
Ingredient("Amaro Nonino", carbs=33, fats=0, proteins=0),
]
# נצרף את 7 הרכיבים לקוקטייל
for ingredient in ingredients:
great_cocktail.add_ingredient(ingredient)
# נבדוק שהכל עבד כשורה
print(len(great_cocktail.ingredients))
print(great_cocktail)
# נוסיף את הרכיב השמיני
sugar = Ingredient("Sugar", carbs=100, fats=0, proteins=0)
great_cocktail.add_ingredient(sugar)
# נוודא שלא התווסף
print('-' * 40)
print("Tried adding the 8th ingredient.")
print(f"Success: {sugar in great_cocktail.ingredients}")
# -
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# אם ננסה להוציא את הסוכר, נגלה שהוא אכן לא ברשימת הרכיבים:
# </p>
great_cocktail.remove_ingredient(sugar)
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# מזל טוב! הכל עובד וקיפף מרוצה, בינתיים.<br>
# הכנתם לכולם Black Magic Julep כדי לחגוג את המאורע, לגמתם בשקיקה שני שלוקים ו...
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# "יש בעיה חמורה במחלקה!", מזדעק הסו־שף מפינת החדר. נראה שהוא טרם לגם מהמשקה שלו. הסו־שף מוסיף:<br>
# "משתמש שלא מכיר את המחלקה, יכול בטעות לערוך ישירות את התכונה <var>ingredient</var> השייכת למופע של המאכל שיצרנו.<br>
# בכך הוא יעקוף את המגבלה שהצבנו בפעולה <var>add_ingredient</var>:
# </p>
great_cocktail.ingredients.append(sugar)
print(len(great_cocktail.ingredients))
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# זה אולי נשמע מקרה קצה זניח, אבל אחת ההנחות שלנו כמתכנתים היא שמותר לשנות מאפייני מחלקה ללא חשש.<br>
# במקרה כזה, הוא יוכל בהיסח הדעת להוסיף בשגגה סוכר כמרכיב שמיני לקוקטייל!"
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# היסטריה המונית פורצת בחדר. עלי נענע ומטריות קוקטיילים מתעופפים לכל עבר.<br>
# בתוך שניות ספורות אתם משתלטים על המצב, ואחרי דקה אתם כבר שקועים עמוק בקריאת מאמר שמדבר על תכנות מחלקות.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# <mark>מתברר שאם מוסיפים את התו <code>_</code> לפני שם התכונה, היא הופכת להיות תכונה "<dfn>מוגנת</dfn>" (<dfn>protected</dfn>).</mark><br>
# מצב כזה מסמן למתכנתים אחרים שהתכונה מיועדת לשימוש פנימי של המחלקה, ושאסור לגשת אליה מבחוץ.<br>
# "אין לפנות לתכונה כזו בקוד שכתוב מחוץ למחלקה", נכתב במאמר. "לא למטרות קריאה ולא למטרות כתיבה".<br>
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# שיניתם את המחלקה. אף על פי שהשימוש בה נראה בדיוק אותו דבר, התכונה <var>ingredients</var> קיבלה קו תחתון לפני שמה.<br>
# המחלקה המתוקנת שיצרתם נראית עכשיו כך:
# </p>
class Dish:
MAX_INGREDIENTS = 7
"""Create a new dish for the restaurant using our ingredients.
Args:
name (str): The name of the dish.
is_vegetarian (bool): `True` if the dish is vegetarian.
Attributes:
name (str): The name of the dish.
is_vegetarian (bool): `True` if the dish is vegetarian.
_ingredients (list of Ingredient): All the required ingredients
for the dish.
"""
def __init__(self, name, is_vegetarian):
self.name = name
self.is_vegetarian = is_vegetarian
self._ingredients = []
def can_add_ingredient(self):
"""Return True if we should allow to add another ingredient."""
return (
self.MAX_INGREDIENTS is None
or len(self._ingredients) < self.MAX_INGREDIENTS
)
def add_ingredient(self, ingredient):
"""Add an ingredient to the dish.
If the class variable MAX_INGREDIENTS is set, and there are
at least MAX_INGREDIENTS ingredients in the dish, the call
to this function will fail.
Args:
ingredient (Ingredient): An `Ingredient` instance to add.
"""
if not self.can_add_ingredient():
return
self._ingredients.append(ingredient)
def remove_ingredient(self, ingredient):
"""Remove an ingredient from the dish.
Args:
ingredient (Ingredient): An `Ingredient` instance to add.
Raises:
ValueError: If the supplied ingredient is not in the
ingredients list.
"""
self._ingredients.remove(ingredient)
def get_total_calories(self):
"""Calculate calories based on the list of the ingredients."""
calories = 0
for ingredient in self._ingredients:
calories = calories + ingredient.calculate_calories()
return calories
def __str__(self):
calories = self.get_total_calories()
return f"{self.name} has {calories:.7} calories in it."
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# לפעמים ניתקל במקרה שבו נרצה למנוע גישה ישירה לתכונות מסוימות של מחלקה מצד גורמים לא מורשים.<br>
# פתיחת שם התכונה בתו <code>_</code> וסימונה כמוגנת, או במילים אחרות מתאימה לשימוש רק בתוך המחלקה, יכולות לשרת אותנו להשגת המטרה הזו.<br>
# זו מוסכמה חזקה מאוד בקרב מתכנתי פייתון: עשו מה שאפשר כדי לא לגשת לתכונות ששמן מתחיל בקו תחתון מתוך קוד שנמצא מחוץ למחלקה.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# אם המשתמש במחלקה ירצה להשיג את ערכו של מופע או לשנות אותו, הוא יוכל לקרוא לפעולה שזו מטרתה.<br>
# במקרה שלנו, הפעולות הללו הן <var>add_ingredient</var> או <var>remove_ingredient</var>.<br>
# נוכל (וכדאי) שנממש פעולה לצפייה בתכונה, כמו <var>get_ingredients</var>.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# הגישה של החבאת נתונים מאחורי פעולות היא רעיון פופולרי מאוד בתכנות מונחה עצמים.<br>
# לפי רעיון שנקרא "<dfn>כימוס</dfn>" (<dfn>Encapsulation</dfn>), על מחלקה לאגד תכונות ופעולות, ולהסתיר מידע עודף מאלו שמשתמשים במחלקה.<br>
# הסתרת המידע משרתת שתי מטרות:
# </p>
# <ul style="text-align: right; direction: rtl; float: right; clear: both;">
# <li><em>פישוט והפחתת מורכבות</em>: נעדיף לחשוף למשתמש במחלקה רק תכונות ופעולות שחשובות עבורו, ולא פרטי מימוש.</li>
# <li><em>שמירה על תקינות המופע</em>: נמנע מהמשתמש במחלקה לערוך מופעים בצורה לא מבוקרת, ובכך לגרום למופע להכיל מידע לא תקין.</li>
# </ul>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# ברוב שפות התכנות שאינן פייתון, שפת התכנות ממש מונעת גישה לתכונות מוגנות מתוך קוד שנמצא מחוץ למחלקה.<br>
# בפייתון נהוג להגיד ש<q dir="rtl" lang="he">כולנו מבוגרים בעלי שיקול דעת</q>, ולכן פייתון לא מונעת גישה לתכונות מוגנות.<br>
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# למרות זאת, בהקשר הזה יש לפייתון טריק מלוכלך בשרוול.<br>
# אפשר להגדיר תכונות כ<dfn>פרטיות</dfn> (<dfn>private</dfn>) בעזרת הקידומת <code>__</code> (פעמיים קו תחתון).<br>
# במקרה הזה, פייתון כן תתערב, וכן תנסה למנוע גישה לתכונה.<br>
# נדגים בעזרת מחלקה פשוטה של משתמש:
# </p>
class User:
def __init__(self, name, age, hobbies):
self.name = name
self._age = age
self.__hobbies = hobbies
def __str__(self):
return (
f"{self.name} is {self._age} years old. "
+ f"He loves {self.__hobbies.lower()}."
)
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# ניצור דמות שנקראת פרנקלין:
# </p>
character = User("Franklin", 200, "Lacing shoes")
print(character)
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# וננסה לשנות לה את התכונות:
# </p>
character.name = "Cookie Monster" # עם זה אין שום בעיה
character._age = 54 # זה לא מנומס ומסוכן
character.__hobbies = "Cookies" # זה כבר ממש לא סבבה
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# אבל כשננסה להדפיס את Cookie Monster, נגלה שכל תכונות הדמות השתנו חוץ מהעובדה שהיא עדיין אוהבת לשרוך נעליים!
# </p>
print(character)
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# הסיבה לכך היא שכשפייתון רואה את התחילית <code>__</code> היא מבינה ש<em>ממש חשוב לכם</em> שאף גורם חיצוני למחלקה לא ייגש לתכונה.<br>
# אף על פי שניסיון פשוט לגשת לתכונה <var dir="ltr">__hobbies</var> מחוץ למחלקה לא יישא פרי, אם נחטט טוב נגלה שעדיין ישנה דרך לעשות זאת.<br>
# מתברר שפייתון רק משנה את שם התכונה למשהו מעט מסובך יותר כדי "להחביא" אותה טוב יותר:
# </p>
character._User__hobbies = "Cookies"
print(character)
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# תכונה שמתחילה בתחילית <code>__</code> בפייתון נקראת, כאמור, "תכונה פרטית" (private).<br>
# גם בה מותר להשתמש רק בתוך המחלקה, רק שהפעם פייתון עושה טריק מלוכלך כדי למנוע מכם להשתמש בתכונה בכל זאת.<br>
# פייתון משנה את שם התכונה לקו תחתון, שם המחלקה, שני קווים תחתונים ואז שם התכונה.<br>
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# השם המקצועי לשינוי שם משתנה כדי לפתור בעיית ארכיטקטורה הוא <dfn>name mangling</dfn>, והקיום שלו בפייתון הוא נושא טעון בקרב קהילת המפתחים בשפה.<br>
# עקב כך, הקידומת <code>__</code> היא אחת מהיכולות היותר שנויות במחלוקת בשפה ועדיף לא להשתמש בה, אלא אם כן ממש חייבים.<br>
# כל עוד המקרה הוא לא קיצוני מאוד, העדיפו להגן על משתנה בעזרת קידומת של קו תחתון אחד.
# </p>
# <div class="align-center" style="display: flex; text-align: right; direction: rtl; clear: both;">
# <div style="display: flex; width: 10%; float: right; clear: both;">
# <img src="images/exercise.svg" style="height: 50px !important;" alt="תרגול" title="תרגול">
# </div>
# <div style="width: 70%">
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# אפשר להגדיר גם פעולות כמוגנות או כפרטיות אם נוסיף להן את התחילית <code>_</code> או <code>__</code>, בהתאמה.<br>
# כיוון ש־<var>can_add_ingredient</var> מיועדת לשימוש פנימי, שנו את הפעולה כך שתוגדר כמוגנת.
# </p>
# </div>
# <div style="display: flex; width: 20%; border-right: 0.1rem solid #A5A5A5; padding: 1rem 2rem;">
# <p style="text-align: center; direction: rtl; justify-content: center; align-items: center; clear: both;">
# <strong>חשוב!</strong><br>
# פתרו לפני שתמשיכו!
# </p>
# </div>
# </div>
# <div class="align-center" style="display: flex; text-align: right; direction: rtl;">
# <div style="display: flex; width: 10%; ">
# <img src="images/deeper.svg?a=1" style="height: 50px !important;" alt="העמקה" title="העמקה">
# </div>
# <div style="width: 90%">
# <p style="text-align: right; direction: rtl;">
# ישנם מקרים מיוחדים שטרם למדנו, שבהם אפשר לגשת לתכונות ולפעולות מוגנות ממחלקות אחרות.<br>
# לעומתן, תכונות או פעולות שמוגדרות כפרטיות נגישות <em>רק</em> מתוך המחלקה שיצרה אותן.<br>
# ההפרדה בין שני הרעיונות נפוצה בעיקר בשפות אחרות, ובפייתון נהוג להשתמש בתחילית <code>_</code> (משתנה מוגן) בשני המקרים.<br>
# מהסיבה הזו אנשים רבים יקראו לתכונה או לפעולה עם קידומת <code>_</code> בפייתון "תכונה פרטית" או "פעולה פרטית".
# </p>
# </div>
# </div>
# ### <span style="text-align: right; direction: rtl; float: right; clear: both;">פעולות גישה ושינוי</span>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# כמו שראינו השבוע, פייתון מתירה כברירת מחדל גישה נוחה לתכונות של מופעים בעזרת קוד שנכתב מחוץ למחלקה.<br>
# בניגוד לפייתון, בשפות אחרות לא נהוג לאפשר גישה ישירה לתכונות המחלקה.<br>
# מתוך הרגל, מתכנתים שמגיעים משפות אחרות משתמשים לעיתים תכופות בהחבאת נתונים בצורה לא מידתית:
# </p>
class Ingredient:
def __init__(self, name, carbs, fats, proteins):
self.set_name(name)
self.set_carbs(carbs)
self.set_fats(fats)
self.set_proteins(proteins)
def set_name(self, new_name):
self._name = new_name
def get_name(self):
return self._name
def set_carbs(self, updated_carbs):
self._carbs = updated_carbs
def get_carbs(self):
return self._carbs
def set_fats(self, updated_fats):
self._fats = updated_fats
def get_fats(self):
return self._fats
def set_proteins(self, updated_proteins):
self._proteins = updated_proteins
def get_proteins(self):
return self._proteins
def get_calories(self):
return (
self.get_carbs() * 4
+ self.get_fats() * 9
+ self.get_proteins() * 4
)
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# הרעיון בקוד שהוצג למעלה נקרא "<dfn>פעולות גישה ושינוי</dfn>" (<dfn>accessor and mutator methods</dfn>), או <dfn>getters and setters</dfn>.<br>
# אלו פעולות שמטרתן עריכת תכונות מסוימות או אחזור של הערך הנוכחי שלהן, תוך כדי ניסיון למנוע מהמשתמש במחלקה לגשת ישירות לערך התכונה.<br>
# המטרה של מתכנת שנוהג כך היא לדאוג שהוא תמיד יוכל לשלוט על ערכי התכונות, לוודא את תקינותם ולמנוע מופע שמכיל נתונים שאינם תקינים.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# שימוש שכזה בפעולות גישה ושינוי הוא נדיר יחסית בפייתון.<br>
# בזכות היכולת לגשת לתכונות של מופע ישירות מחוץ למחלקה, כתיבת מחלקות הופכת להיות מהירה ונעימה לשימוש.<br>
# כתיבת getter ו־setter לכל תכונה עשויה לגרום למחלקות בפייתון להפוך למסורבלות וארוכות, והשימוש בהן נעשה לא נוח:
# </p>
# +
strawberries = Ingredient("Strawberries", carbs=8, fats=0.4, proteins=0.7)
print(f"Before: {strawberries.get_calories()}")
# ננסה לערוך את כמות השומנים בתותים ל־0.3 במקום
strawberries.set_fats(strawberries.get_fats() - 0.1)
print(f"After: {strawberries.get_calories()}")
# -
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# עקב הסרבול שבעניין, בפייתון לרוב נעדיף להשתמש בפעולות גישה ושינוי רק כשיש צורך ממשי בהגדרת תכונות כמוגנות או כפרטיות.
# </p>
# ## <span style="text-align: right; direction: rtl; float: right; clear: both;">מונחים</span>
# <dl style="text-align: right; direction: rtl; float: right; clear: both;">
# <dt>משתני מחלקה (Class Variables)</dt>
# <dd>
# משתנים המוגדרים ברמת המחלקה ונגישים עבור כל המופעים שנוצרו ממנה.<br>
# בדרך כלל אלו משתנים קבועים שהמופעים משתמשים בהם לצורכי קריאה בלבד.<br>
# לדוגמה: משתנה בראש מחלקת "תיבת דואר" שמגדיר את נפח האחסון המירבי ל־5 ג'יגה בייט.
# </dd>
# <dt>הכלה (Containment)</dt>
# <dd>
# מצב שבו נעשה שימוש במופע שנוצר במחלקה A בתוך מופע של מחלקה B.<br>
# לדוגמה: בתוך מופע של מחלקת "הודעת דואר", תכונת הנמען והמוען יהיו מופעים של מחלקת "משתמש".
# </dd>
# <dt>כימוס (Encapsulation)</dt>
# <dd>
# איגוד תכונות ופעולות תחת מחלקה, וצמצום הגישה של המשתמש במחלקה למצב הפנימי של המופעים שנוצרו ממנה.<br>
# בפועל, ימומש על ידי הגבלה לגישה ולעריכה של תכונות ופעולות מסוימות, כך שיתאפשרו רק מקוד שנכתב בתוך המחלקה.<br>
# עם זאת, החלטה על הסתרת תכונות רבות מדי עלולה ליצור קוד ארוך ומסורבל, ובפייתון נהוג להשתמש ברעיון בצמצום.<br>
# </dd>
# <dt>תכונה/פעולה מוגנת (Protected Attribute) או תכונה/פעולה פרטית (Private Attribute)</dt>
# <dd>
# תכונה שהגישה אליה יכולה להתבצע רק מתוך המחלקה.<br>
# טכנית, פייתון תמיד מאפשרת למתכנת לשנות ערכים – אפילו אם הם מוגדרים כמוגנים או כפרטיים.<br>
# מעשית, עליכם להימנע בכל דרך אפשרית משינוי של משתנה שמוגדר כמוגן או פרטי, כל עוד אתם יכולים.
# </dd>
# <dt>פעולת גישה ושינוי (Accessor/Mutator Method)</dt>
# <dd>
# פעולה שמטרתה לגשת (Accessor) או לשנות (Mutator) ערך של תכונה מסוימת, בעיקר בהקשרי תכונות מוגנות או פרטיות.<br>
# מטרת ה־Accessor היא לאחזר את ערך התכונה המבוקשת בצורה מתאימה, לעיתים אחרי עיבוד מסוים.<br>
# מטרת ה־Mutator היא לוודא ששינוי הערך תקין ולא מזיק למופע או משנה אותו למצב לא תקין.<br>
# פעולות אלו נקראות גם <dfn>getters</dfn> ו־<dfn>setters</dfn>.
# </dd>
# </dl>
# ## <span style="text-align: right; direction: rtl; float: right; clear: both;">תרגיל לדוגמה</span>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# בהמשך להצלחה המסחררת של אפליקציית צ'יקצ'וק, החלטנו להשיק את יישומון המסרים המיידיים "מנשמעעעעעעע XPPP".<br>
# תחילה, ניצור מחלקה שתייצג משתמש.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# לכל משתמש יש:
# </p>
#
# <ul style="text-align: right; direction: rtl; float: right; clear: both;">
# <li><em>תכונות</em>: כינוי (<var>nickname</var>) תאריך אחרון שנצפה (<var>last_seen</var>) ואנשי קשר (<var>contacts</var>).</li>
# <li><em>פעולות</em>: התחבר (<var>connect</var>), האם מחובר? (<var>is_online</var>; בודקת אם התחבר בדקה האחרונה).</li>
# </ul>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# לכל הודעה יש:
# </p>
#
# <ul style="text-align: right; direction: rtl; float: right; clear: both;">
# <li><em>תכונות</em>: תאריך שליחה (<var>send_date</var>), אם נצפתה (<var>seen</var>), מוען (שולח; <var>sender</var>), נמען (מקבל; <var>recipient</var>) ותוכן (<var>content</var>).</li>
# <li><em>פעולות</em>: סימון הודעה כנקראה (<var>mark_as_read</var>).</li>
# </ul>
# +
import datetime
import time
class User:
"""A user can connect and can contact with other users.
Args:
nickname (str): The username of the user.
Attributes:
nickname (str): The username of the user.
_contacts (list of User): Other users whose added to the
user's contacts.
last_seen (float): The last time the user connected in seconds
since the Epoch.
"""
SECONDS_UNTIL_DISCONNECTED = 60
def __init__(self, nickname):
self.nickname = nickname
self._contacts = []
self.last_seen = time.time()
def is_online(self):
"""Determine if the user is currently connected.
"Connected user" is a user that logged in at the last X
seconds, where X is a constant defined as a class variable.
Returns:
bool: True if the user currently connected, False otherwise.
"""
seconds_since_seen = time.time() - self.last_seen
return seconds_since_seen < self.SECONDS_UNTIL_DISCONNECTED
def connect(self):
"""Makes the user connected.
Returns:
None.
"""
self.last_seen = time.time()
def add_contact(self, contact):
"""Add contact to the user's contacts.
Args:
contact (User): A user to add to the user's contacts.
Returns:
bool: True if the addition was successful, False otherwise.
"""
if contact in self._contacts:
return False
self._contacts.append(contact)
return True
def remove_contact(self, contact):
"""Remove a contact from the user's contacts.
Args:
contact (User): A user to remove from the user's contacts.
Returns:
bool: True if the deletion was successful, False otherwise.
"""
if contact not in self._contacts:
return False
self._contacts.remove(contact)
return True
def get_contacts(self):
"""Return the user's contacts list."""
return self._contacts
def pretty_last_seen(self, dateformat='%Y-%m-%d %H:%M:%S'):
"""Show prettified date of when the user last connected.
Args:
dateformat (str): The format in which the time will
be displayed.
Returns:
str: Last time the user connected.
"""
localtime = time.localtime(self.last_seen)
return time.strftime(dateformat, localtime)
def __str__(self):
"""Show the user's details.
Returns:
str: The user representation currently.
"""
if self.is_online():
seen_message = 'Online'
else:
seen_message = self.pretty_last_seen()
return f"{self.nickname} ({seen_message})"
class Message:
"""A deliverable message with status.
A message can be sent from one user to another and
can be mark as read by the recipient.
Args:
sender (User): The message sender's user.
recipient (User): The message recipient's user.
content (str): The body of the message.
Attributes:
send_date (float): The time the message was sent
in seconds since the Epoch.
seen (bool): True if the recipient saw the message.
sender (User): The message sender's user.
recipient (User): The message recipient's user.
content (str): The body of the message.
"""
def __init__(self, sender, recipient, content):
self.send_date = time.time()
self.seen = False
self.sender = sender
self.recipient = recipient
self.content = content
def pretty_send_date(self, dateformat='%Y-%m-%d %H:%M:%S'):
"""Show prettified date of when the message was sent.
Args:
dateformat (str): The format in which the time will be
displayed.
Returns:
str: The time the message was sent.
"""
localtime = time.localtime(self.send_date)
return time.strftime(dateformat, localtime)
def mark_as_read(self):
"""Mark the message as read.
Returns:
None.
"""
self.seen = True
def __str__(self):
"""Return the message's details.
Returns:
str: The message representation.
"""
message = (
f"From: {self.sender}\n"
f"To: {self.recipient}\n"
f"{self.pretty_send_date()}\n"
f"-------------------\n"
f"Message: {self.content}\n"
)
if self.seen:
message = message + f"(Seen)"
return message.strip()
def link_everyone(users):
for user in users:
for another_user in users:
if user != another_user:
user.add_contact(another_user)
print("First example:\n----")
anonymous = User("Zarop")
almog = User("Almog")
advertisement = "Click to get your Cookie!"
message = Message(sender=anonymous, recipient=almog, content=advertisement)
print(message)
print("\n\nSecond example:\n----")
users = [User("Athos"), User("Porthos"), User("Aramis"), User("D'Artagnan")]
link_everyone(users)
print("Contacts: " + str(len(users[0].get_contacts())))
message = Message(
sender=users[0],
recipient=users[1],
content="Tous pour un, un pour tous, c'est notre devise"
)
print(message)
message.mark_as_read()
print("\nAfter read:\n")
print(message)
# -
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# למה כדאי לשים לב בפתרון?
# </p>
#
# <ol style="text-align: right; direction: rtl; float: right; clear: both;">
# <li>אנחנו משתמשים בכימוס במשורה – רק כשזה משפר את התנהגות המחלקה.</li>
# <li>מחלקת <var>User</var> מוכלת בתוך מחלקת <var>Message</var>.</li>
# <li>לא הרשינו למספרים להסתובב בקוד – <var>SECONDS_UNTIL_DISCONNECTED</var> הוא משתנה מחלקה קבוע שערכו 60.</li>
# </ol>
# ## <span style="text-align: right; direction: rtl; float: right; clear: both;">תרגילים</span>
# ### <span style="text-align: right; direction: rtl; float: right; clear: both;">אורטל קומבט – חלק 2</span>
# #### <span style="text-align: right; direction: rtl; float: right; clear: both;">Player</span>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# במחלקת <var>Player</var> שבניתם, שנו את הפעולה <var>attack</var>.<br>
# אם הפעולה לא מקבלת פרמטרים ואין לשחקן אויבים, היא תחזיר <samp>False</samp> במקום לזרוק <var>IndexError</var>.<br>
# אם התקיפה הצליחה, הפעולה תחזיר <samp>True</samp>.
# </p>
# #### <span style="text-align: right; direction: rtl; float: right; clear: both;">Arena</span>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# ממשו מחלקת זירה בשם <var>Arena</var>.<br>
# פעולת האתחול של <var>Arena</var> מקבלת את מספר השחקנים המרבי שאפשר להכניס לזירה.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# המחלקה תכיל לכל הפחות את התכונות הבאות:
# </p>
# <ul style="text-align: right; direction: rtl; float: right; clear: both;">
# <li><var>players</var> – מכילה את רשימת השחקנים בזירה.</li>
# <li><var>next_player</var> – מכילה את השחקן שתורו לשחק כעת.</li>
# <li><var>winner</var> – מכילה את השחקן שניצח, או <code>None</code> אם עדיין אין אחד כזה.</li>
# </ul>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# במחלקה ימומשו גם הפעולות הבאות:
# </p>
# <ul style="text-align: right; direction: rtl; float: right; clear: both;">
# <li><var>hajime</var> – מתחיל את הקרב. החל משלב זה אי אפשר להוסיף או להסיר שחקנים מהזירה.</li>
# <li><var>get_players</var> – מחזירה את רשימת השחקנים בזירה.</li>
# <li><var>add_player</var> – הוסף שחקן לזירה. אם הוא כבר בזירה או אם הקרב כבר התחיל, מחזירה False.</li>
# <li><var>remove_player</var> – מקבלת שחקן ומסירה אותו מהזירה. אם הוא אינו בזירה או אם הקרב כבר התחיל, מחזירה False.</li>
# <li><var>make_move</var> – גורמת לשחקן שתורו כעת להפעיל פעולת <var>attack</var> ללא פרמטרים.<br>
# אם הפעולה <var>attack</var> החזירה <samp>False</samp>, השחקן יבחר אויב חי אקראי מהזירה ויתקוף אותו.<br>
# בסוף הפעולה, התור מועבר לשחקן הבא.</li>
# </ul>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# ודאו שכל זמן שיש שחקנים בזירה, <var>next_player</var> מצביעה למופע של שחקן.<br>
# אם אין שחקנים בזירה, בעת אתחול המחלקה למשל, שנו את ערכה של <var>next_player</var> ל־<code>None</code>.<br>
# </p>
# #### <span style="text-align: right; direction: rtl; float: right; clear: both;">רמות ונקודות ניסיון</span>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# כאשר שחקן א גורם לשחקן ב להיות מת ברובו, שחקן א יקבל מספר נקודות ניסיון לפי הנוסחה הבאה:
# </p>
# $$ EXP_{gain} = \frac{L_{rival} \cdot (2 \cdot L_{rival} + 10)^{2.5}}{5 \cdot (L_{rival} + L_{player} + 10) ^{2.5}} $$
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# כאשר $L_{rival}$ היא הרמה של המת ברובו (שחקן ב), ו־$L_{player}$ היא הרמה של המנצח (שחקן א).<br>
# אם השחקן מת לחלוטין ולא רק מת ברובו, השחקן שניצח אותו מקבל פי 2 נקודות ניסיון.
# </p>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# מספר נקודות הניסיון שיש להשיג בסך הכול כדי להגיע לרמה $L$ הוא:
# </p>
# $$ \frac{4 \cdot ({L-1})^{2.5}}{5} $$
# #### <span style="text-align: right; direction: rtl; float: right; clear: both;">מתחילים לשחק</span>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# ממשו סימולציית קרב:
# </p>
# <ul style="text-align: right; direction: rtl; float: right; clear: both;">
# <li>צרו זירה שיכולה להכיל עד 4 משתתפים, וצרפו אליה מספר כזה של שחקנים. התחילו את הקרב.</li>
# <li>התורות במשחק עוברים משחקן אחד לשני, כך שבכל סיבוב כל אחד מהשחקנים החיים משחק פעם אחת.</li>
# <li>אם השחקן מת ברובו – הוא יעשה <var>revive</var> כשיגיע תורו, ויתקוף מייד אחר כך. החייאה לא עולה תור.</li>
# <li>כל שחקן יכול למות ברובו עד פעמיים – ובפעם השלישית שהוא מת הוא נחשב מת לחלוטין.</li>
# <li>אם השחקן מת לחלוטין, פעולת <var>revive</var> על השחקן תחזיר <samp>False</samp>, תורות לא יעברו אליו ושחקנים לא יתקיפו אותו.</li>
# <li>כאשר נשאר בזירה רק שחקן חי אחד – הוא מוכתר כמנצח של הזירה.</li>
# </ul>
# <p style="text-align: right; direction: rtl; float: right; clear: both;">
# הרגישו נוח להוסיף רכיבים לכל אחת מהמחלקות שלכם.<br>
# תכנון נכון של המחלקות יאפשר לכם לצלוח את התרגיל בקלות רבה יותר.
# </p>
|
week7/3_Classes_Part_2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_python3
# language: python
# name: conda_python3
# ---
# # Direct Marketing with Amazon SageMaker XGBoost and Hyperparameter Tuning
# _**Supervised Learning with Gradient Boosted Trees: A Binary Prediction Problem With Unbalanced Classes**_
#
# ---
#
# ---
#
# ## Contents
#
# 1. [Background](#Background)
# 1. [Prepration](#Preparation)
# 1. [Data Downloading](#Data_Downloading)
# 1. [Data Transformation](#Data_Transformation)
# 1. [Setup Hyperparameter Tuning](#Setup_Hyperparameter_Tuning)
# 1. [Launch Hyperparameter Tuning](#Launch_Hyperparameter_Tuning)
# 1. [Analyze Hyperparameter Tuning Results](#Analyze_Hyperparameter_Tuning_Results)
# 1. [Deploy The Best Model](#Deploy_The_Best_Model)
#
#
# ---
#
# ## Background
# Direct marketing, either through mail, email, phone, etc., is a common tactic to acquire customers. Because resources and a customer's attention is limited, the goal is to only target the subset of prospects who are likely to engage with a specific offer. Predicting those potential customers based on readily available information like demographics, past interactions, and environmental factors is a common machine learning problem.
#
# This notebook will train a model which can be used to predict if a customer will enroll for a term deposit at a bank, after one or more phone calls. Hyperparameter tuning will be used in order to try multiple hyperparameter settings and produce the best model.
#
# ---
#
# ## Preparation
#
# Let's start by specifying:
#
# - The S3 bucket and prefix that you want to use for training and model data. This should be within the same region as SageMaker training.
# - The IAM role used to give training access to your data. See SageMaker documentation for how to create these.
# + isConfigCell=true
import sagemaker
import boto3
import numpy as np # For matrix operations and numerical processing
import pandas as pd # For munging tabular data
from time import gmtime, strftime
import os
region = boto3.Session().region_name
smclient = boto3.Session().client('sagemaker')
role = sagemaker.get_execution_role()
bucket = sagemaker.Session().default_bucket()
prefix = 'sagemaker/DEMO-hpo-xgboost-dm'
# -
# ---
#
# ## Data_Downloading
# Let's start by downloading the [direct marketing dataset](https://archive.ics.uci.edu/ml/datasets/bank+marketing) from UCI's ML Repository.
# !wget -N https://archive.ics.uci.edu/ml/machine-learning-databases/00222/bank-additional.zip
# !unzip -o bank-additional.zip
# Now lets read this into a Pandas data frame and take a look.
data = pd.read_csv('./bank-additional/bank-additional-full.csv', sep=';')
pd.set_option('display.max_columns', 500) # Make sure we can see all of the columns
pd.set_option('display.max_rows', 50) # Keep the output on one page
data
# Let's talk about the data. At a high level, we can see:
#
# * We have a little over 40K customer records, and 20 features for each customer
# * The features are mixed; some numeric, some categorical
# * The data appears to be sorted, at least by `time` and `contact`, maybe more
#
# _**Specifics on each of the features:**_
#
# *Demographics:*
# * `age`: Customer's age (numeric)
# * `job`: Type of job (categorical: 'admin.', 'services', ...)
# * `marital`: Marital status (categorical: 'married', 'single', ...)
# * `education`: Level of education (categorical: 'basic.4y', 'high.school', ...)
#
# *Past customer events:*
# * `default`: Has credit in default? (categorical: 'no', 'unknown', ...)
# * `housing`: Has housing loan? (categorical: 'no', 'yes', ...)
# * `loan`: Has personal loan? (categorical: 'no', 'yes', ...)
#
# *Past direct marketing contacts:*
# * `contact`: Contact communication type (categorical: 'cellular', 'telephone', ...)
# * `month`: Last contact month of year (categorical: 'may', 'nov', ...)
# * `day_of_week`: Last contact day of the week (categorical: 'mon', 'fri', ...)
# * `duration`: Last contact duration, in seconds (numeric). Important note: If duration = 0 then `y` = 'no'.
#
# *Campaign information:*
# * `campaign`: Number of contacts performed during this campaign and for this client (numeric, includes last contact)
# * `pdays`: Number of days that passed by after the client was last contacted from a previous campaign (numeric)
# * `previous`: Number of contacts performed before this campaign and for this client (numeric)
# * `poutcome`: Outcome of the previous marketing campaign (categorical: 'nonexistent','success', ...)
#
# *External environment factors:*
# * `emp.var.rate`: Employment variation rate - quarterly indicator (numeric)
# * `cons.price.idx`: Consumer price index - monthly indicator (numeric)
# * `cons.conf.idx`: Consumer confidence index - monthly indicator (numeric)
# * `euribor3m`: Euribor 3 month rate - daily indicator (numeric)
# * `nr.employed`: Number of employees - quarterly indicator (numeric)
#
# *Target variable:*
# * `y`: Has the client subscribed a term deposit? (binary: 'yes','no')
# ## Data_Transformation
# Cleaning up data is part of nearly every machine learning project. It arguably presents the biggest risk if done incorrectly and is one of the more subjective aspects in the process. Several common techniques include:
#
# * Handling missing values: Some machine learning algorithms are capable of handling missing values, but most would rather not. Options include:
# * Removing observations with missing values: This works well if only a very small fraction of observations have incomplete information.
# * Removing features with missing values: This works well if there are a small number of features which have a large number of missing values.
# * Imputing missing values: Entire [books](https://www.amazon.com/Flexible-Imputation-Missing-Interdisciplinary-Statistics/dp/1439868247) have been written on this topic, but common choices are replacing the missing value with the mode or mean of that column's non-missing values.
# * Converting categorical to numeric: The most common method is one hot encoding, which for each feature maps every distinct value of that column to its own feature which takes a value of 1 when the categorical feature is equal to that value, and 0 otherwise.
# * Oddly distributed data: Although for non-linear models like Gradient Boosted Trees, this has very limited implications, parametric models like regression can produce wildly inaccurate estimates when fed highly skewed data. In some cases, simply taking the natural log of the features is sufficient to produce more normally distributed data. In others, bucketing values into discrete ranges is helpful. These buckets can then be treated as categorical variables and included in the model when one hot encoded.
# * Handling more complicated data types: Mainpulating images, text, or data at varying grains.
#
# Luckily, some of these aspects have already been handled for us, and the algorithm we are showcasing tends to do well at handling sparse or oddly distributed data. Therefore, let's keep pre-processing simple.
# First of all, Many records have the value of "999" for pdays, number of days that passed by after a client was last contacted. It is very likely to be a magic number to represent that no contact was made before. Considering that, we create a new column called "no_previous_contact", then grant it value of "1" when pdays is 999 and "0" otherwise.
#
# In the "job" column, there are categories that mean the customer is not working, e.g., "student", "retire", and "unemployed". Since it is very likely whether or not a customer is working will affect his/her decision to enroll in the term deposit, we generate a new column to show whether the customer is working based on "job" column.
#
# Last but not the least, we convert categorical to numeric, as is suggested above.
data['no_previous_contact'] = np.where(data['pdays'] == 999, 1, 0) # Indicator variable to capture when pdays takes a value of 999
data['not_working'] = np.where(np.in1d(data['job'], ['student', 'retired', 'unemployed']), 1, 0) # Indicator for individuals not actively employed
model_data = pd.get_dummies(data) # Convert categorical variables to sets of indicators
model_data
# Another question to ask yourself before building a model is whether certain features will add value in your final use case. For example, if your goal is to deliver the best prediction, then will you have access to that data at the moment of prediction? Knowing it's raining is highly predictive for umbrella sales, but forecasting weather far enough out to plan inventory on umbrellas is probably just as difficult as forecasting umbrella sales without knowledge of the weather. So, including this in your model may give you a false sense of precision.
#
# Following this logic, let's remove the economic features and `duration` from our data as they would need to be forecasted with high precision to use as inputs in future predictions.
#
# Even if we were to use values of the economic indicators from the previous quarter, this value is likely not as relevant for prospects contacted early in the next quarter as those contacted later on.
model_data = model_data.drop(['duration', 'emp.var.rate', 'cons.price.idx', 'cons.conf.idx', 'euribor3m', 'nr.employed'], axis=1)
# We'll then split the dataset into training (70%), validation (20%), and test (10%) datasets and convert the datasets to the right format the algorithm expects. We will use training and validation datasets during training. Test dataset will be used to evaluate model performance after it is deployed to an endpoint.
#
# Amazon SageMaker's XGBoost algorithm expects data in the libSVM or CSV data format. For this example, we'll stick to CSV. Note that the first column must be the target variable and the CSV should not include headers. Also, notice that although repetitive it's easiest to do this after the train|validation|test split rather than before. This avoids any misalignment issues due to random reordering.
# +
train_data, validation_data, test_data = np.split(model_data.sample(frac=1, random_state=1729), [int(0.7 * len(model_data)), int(0.9*len(model_data))])
pd.concat([train_data['y_yes'], train_data.drop(['y_no', 'y_yes'], axis=1)], axis=1).to_csv('train.csv', index=False, header=False)
pd.concat([validation_data['y_yes'], validation_data.drop(['y_no', 'y_yes'], axis=1)], axis=1).to_csv('validation.csv', index=False, header=False)
pd.concat([test_data['y_yes'], test_data.drop(['y_no', 'y_yes'], axis=1)], axis=1).to_csv('test.csv', index=False, header=False)
# -
# Now we'll copy the file to S3 for Amazon SageMaker training to pickup.
boto3.Session().resource('s3').Bucket(bucket).Object(os.path.join(prefix, 'train/train.csv')).upload_file('train.csv')
boto3.Session().resource('s3').Bucket(bucket).Object(os.path.join(prefix, 'validation/validation.csv')).upload_file('validation.csv')
# ---
#
# ## Setup_Hyperparameter_Tuning
# *Note, with the default setting below, the hyperparameter tuning job can take about 30 minutes to complete.*
#
# Now that we have prepared the dataset, we are ready to train models. Before we do that, one thing to note is there are algorithm settings which are called "hyperparameters" that can dramtically affect the performance of the trained models. For example, XGBoost algorithm has dozens of hyperparameters and we need to pick the right values for those hyperparameters in order to achieve the desired model training results. Since which hyperparameter setting can lead to the best result depends on the dataset as well, it is almost impossible to pick the best hyperparameter setting without searching for it, and a good search algorithm can search for the best hyperparameter setting in an automated and effective way.
#
# We will use SageMaker hyperparameter tuning to automate the searching process effectively. Specifically, we specify a range, or a list of possible values in the case of categorical hyperparameters, for each of the hyperparameter that we plan to tune. SageMaker hyperparameter tuning will automatically launch multiple training jobs with different hyperparameter settings, evaluate results of those training jobs based on a predefined "objective metric", and select the hyperparameter settings for future attempts based on previous results. For each hyperparameter tuning job, we will give it a budget (max number of training jobs) and it will complete once that many training jobs have been executed.
#
# Now we configure the hyperparameter tuning job by defining a JSON object that specifies following information:
# * The ranges of hyperparameters we want to tune
# * Number of training jobs to run in total and how many training jobs should be run simultaneously. More parallel jobs will finish tuning sooner, but may sacrifice accuracy. We recommend you set the parallel jobs value to less than 10% of the total number of training jobs (we'll set it higher just for this example to keep it short).
# * The objective metric that will be used to evaluate training results, in this example, we select *validation:auc* to be the objective metric and the goal is to maximize the value throughout the hyperparameter tuning process. One thing to note is the objective metric has to be among the metrics that are emitted by the algorithm during training. In this example, the built-in XGBoost algorithm emits a bunch of metrics and *validation:auc* is one of them. If you bring your own algorithm to SageMaker, then you need to make sure whatever objective metric you select, your algorithm actually emits it.
#
# We will tune four hyperparameters in this examples:
# * *eta*: Step size shrinkage used in updates to prevent overfitting. After each boosting step, you can directly get the weights of new features. The eta parameter actually shrinks the feature weights to make the boosting process more conservative.
# * *alpha*: L1 regularization term on weights. Increasing this value makes models more conservative.
# * *min_child_weight*: Minimum sum of instance weight (hessian) needed in a child. If the tree partition step results in a leaf node with the sum of instance weight less than min_child_weight, the building process gives up further partitioning. In linear regression models, this simply corresponds to a minimum number of instances needed in each node. The larger the algorithm, the more conservative it is.
# * *max_depth*: Maximum depth of a tree. Increasing this value makes the model more complex and likely to be overfitted.
# +
from time import gmtime, strftime, sleep
tuning_job_name = 'xgboost-tuningjob-' + strftime("%d-%H-%M-%S", gmtime())
print (tuning_job_name)
tuning_job_config = {
"ParameterRanges": {
"CategoricalParameterRanges": [],
"ContinuousParameterRanges": [
{
"MaxValue": "1",
"MinValue": "0",
"Name": "eta",
},
{
"MaxValue": "10",
"MinValue": "1",
"Name": "min_child_weight",
},
{
"MaxValue": "2",
"MinValue": "0",
"Name": "alpha",
}
],
"IntegerParameterRanges": [
{
"MaxValue": "10",
"MinValue": "1",
"Name": "max_depth",
}
]
},
"ResourceLimits": {
"MaxNumberOfTrainingJobs": 20,
"MaxParallelTrainingJobs": 3
},
"Strategy": "Bayesian",
"HyperParameterTuningJobObjective": {
"MetricName": "validation:auc",
"Type": "Maximize"
}
}
# -
# Then we configure the training jobs the hyperparameter tuning job will launch by defining a JSON object that specifies following information:
# * The container image for the algorithm (XGBoost)
# * The input configuration for the training and validation data
# * Configuration for the output of the algorithm
# * The values of any algorithm hyperparameters that are not tuned in the tuning job (StaticHyperparameters)
# * The type and number of instances to use for the training jobs
# * The stopping condition for the training jobs
#
# Again, since we are using built-in XGBoost algorithm here, it emits two predefined metrics: *validation:auc* and *train:auc*, and we elected to monitor *validation_auc* as you can see above. One thing to note is if you bring your own algorithm, your algorithm emits metrics by itself. In that case, you'll need to add a MetricDefinition object here to define the format of those metrics through regex, so that SageMaker knows how to extract those metrics.
# +
containers = {'us-west-2': '433757028032.dkr.ecr.us-west-2.amazonaws.com/xgboost:latest',
'us-east-1': '811284229777.dkr.ecr.us-east-1.amazonaws.com/xgboost:latest',
'us-east-2': '825641698319.dkr.ecr.us-east-2.amazonaws.com/xgboost:latest',
'eu-west-1': '685385470294.dkr.ecr.eu-west-1.amazonaws.com/xgboost:latest',
'ap-northeast-1': '501404015308.dkr.ecr.ap-northeast-1.amazonaws.com/xgboost:latest'}
training_image = containers[region]
s3_input_train = 's3://{}/{}/train'.format(bucket, prefix)
s3_input_validation ='s3://{}/{}/validation/'.format(bucket, prefix)
training_job_definition = {
"AlgorithmSpecification": {
"TrainingImage": training_image,
"TrainingInputMode": "File"
},
"InputDataConfig": [
{
"ChannelName": "train",
"CompressionType": "None",
"ContentType": "csv",
"DataSource": {
"S3DataSource": {
"S3DataDistributionType": "FullyReplicated",
"S3DataType": "S3Prefix",
"S3Uri": s3_input_train
}
}
},
{
"ChannelName": "validation",
"CompressionType": "None",
"ContentType": "csv",
"DataSource": {
"S3DataSource": {
"S3DataDistributionType": "FullyReplicated",
"S3DataType": "S3Prefix",
"S3Uri": s3_input_validation
}
}
}
],
"OutputDataConfig": {
"S3OutputPath": "s3://{}/{}/output".format(bucket,prefix)
},
"ResourceConfig": {
"InstanceCount": 1,
"InstanceType": "ml.m4.xlarge",
"VolumeSizeInGB": 10
},
"RoleArn": role,
"StaticHyperParameters": {
"eval_metric": "auc",
"num_round": "100",
"objective": "binary:logistic",
"rate_drop": "0.3",
"tweedie_variance_power": "1.4"
},
"StoppingCondition": {
"MaxRuntimeInSeconds": 43200
}
}
# -
# ## Launch_Hyperparameter_Tuning
# Now we can launch a hyperparameter tuning job by calling create_hyper_parameter_tuning_job API. After the hyperparameter tuning job is created, we can go to SageMaker console to track the progress of the hyperparameter tuning job until it is completed.
smclient.create_hyper_parameter_tuning_job(HyperParameterTuningJobName = tuning_job_name,
HyperParameterTuningJobConfig = tuning_job_config,
TrainingJobDefinition = training_job_definition)
# Let's just run a quick check of the hyperparameter tuning jobs status to make sure it started successfully.
smclient.describe_hyper_parameter_tuning_job(
HyperParameterTuningJobName=tuning_job_name)['HyperParameterTuningJobStatus']
# ## Analyze tuning job results - after tuning job is completed
# Please refer to "HPO_Analyze_TuningJob_Results.ipynb" to see example code to analyze the tuning job results.
# ## Deploy the best model
# Now that we have got the best model, we can deploy it to an endpoint. Please refer to other SageMaker sample notebooks or SageMaker documentation to see how to deploy a model.
|
hyperparameter_tuning/xgboost_direct_marketing/hpo_xgboost_direct_marketing_sagemaker_APIs.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## Deep Learning and Probabilistic Models
#
# The objective of *discriminative models* is to output an estimate of the class conditional probabilities for given inputs. To see why, let's restate Bayes rule for a given input:
#
# $$
# p(y \vert x) = \frac{p(x \vert y) p(y)}{p(x)} = \frac{p(x,y)}{p(x)}
# $$
#
# Discriminative classifiers jump directly to estimating $p(y \vert x)$ without modeling its component parts $p(x,y)$ and $p(x)$.
#
# The objective of *generative models* is to learn a model $p(x)$. This model can be used for several purposes, but we are specially interested in models we can sample from.
#
# To this end we have several possible strategies when considering deep learning tools:
#
# + **Fully-observed models.** To model obsered data directly, without introducing any new unobserved local variables.
#
# + **Transformation models.** Model data as a transformation of an unobserved noise source using a parameterised function.
#
# + **Latent-variable models.** Introduce an unobserved random variable for every observed data point to explain hidden causes.
#
# ### Fully-observed models.
#
# The most succesful models are PixelCNN (https://arxiv.org/pdf/1606.05328v2.pdf) and WaveNet (https://arxiv.org/pdf/1609.03499.pdf)).(See http://ruotianluo.github.io/2017/01/11/pixelcnn-wavenet/)
#
# Both cases are based on autoregressive models that models the conditional distribution of every individual data feature (pixels,etc.) given previous features:
#
# $$
# p(x) = \prod_{i=1}^{N} p(x_i \vert x_1, \dots ,x_{i-1})
# $$
#
# PixelCNN predict pixels sequentially rather than predicting the whole image at once. All conditional probabilities are described by deep networks.
#
# Its advantages are:
#
# + Parameter learning is simple: Log-likelihood is directly computable, no approximation needed.
# + Easy to scale-up to large models, many optimisation tools available.
#
# But generation can be slow: we must iterate through all elements sequentially!
#
# ### Transformation Models
#
# Transformation models model $p(x,z)$ instead of $p(x)$, where $z$ is an unobserved noise source.
#
# In the simplest case, they transform an unobserved noise source $z \sim \mathcal{N}(0,I)$ using a parameterised function. The transformation function is parameterised by a linear or deep network $f_\lambda(z)$.
#
# For example, for producing $x \sim \mathcal{N}(\mu, \Sigma)$ we can sample $z \sim \mathcal{N}(0,I)$ and then apply $x = \mu + \Sigma z$.
#
# The main drawbacks of this strategy are the difficulty to extend to generic data types and the difficulty to account for noise in observed data.
#
# ### Latent variable models
#
# Latent variable models solve this problems by introducing unobserved
# local random variables that represents *hidden causes* and which can be easily sampled.
#
# Variational autoencoders are a good example of this strategy that propose a specific probability model of data $x$ and latent variables $z$.
# ## Variational Autoencoders Recap
#
# We are aiming to maximize the probability of each $x$ in the dataset according to $p(x) = \int p(x \vert z) p(z) dz$.
#
# In VAE $p(x \vert z)$ can be defined to be Bernoulli or to be Gaussian, i.e. $p(x \vert z) = \mathcal{N}(f(z), \sigma^2 \times I)$ where $f$ is a deterministic function parametrized by $\lambda$. Then, our objective is to find the best parameters to represent $p(x)$, i.e. to maximize this integral with respect to $\lambda$.
#
# Given $f$, the generative process can be written as follows. For each datapoint $i$:
#
# + Draw latent variables $z_i \sim p(z)$.
# + Draw datapoint $x_i \sim p(x\vert z)$
#
# To solve our problem we must deal with:
#
# + how to define the latent variables $z$.
# + how to deal with the integral.
#
# Regarding $z$, VAE assume that there are no easy interpretations of the dimensions of $z$ and chooses a simple distribution from which samples can be easily drawn: $\mathcal{N}(0,I)$. This choice is based on the well-known fact that any distribution in $d$ dimensions can be generated by taking a set of $d$ variables that are normally distributed and mapping them through a sufficient complicated function.
#
# Now all that remains is to optimize the integral, where $p(z) = \mathcal{N}(0,I)$.
#
# If we can find a computable formula for $p(x)$ and we can take the gradient of the formula, then we can optimize the model.
#
# The naive approach for computing an approximate $p(X)$ is straighforward: we can sample a large number of $z$ values and compute $p(x) \approx \frac{1}{n} \sum_i p(x \vert z_i)$. But if we are dealing with a high dimensional space, this option is not feasible.
#
# Is there a shortcut we can take when using sampling to compute the integral?
#
# The key idea in VAE is to attempt to sample values of $z$ that are likely to have produced
# $x$. This means we need a new function $q(z \vert x)$ which can take a value of $x$ and give us a distribution over $z$ values that are likely to produce $x$.
#
# Let's consider the (similarity) KL divergence between some arbitrary $q_\lambda (z \vert x)$ and $p(z \vert x)$.
#
# $$ KL(q_\lambda(z \vert x) \| p(z \vert x)) = \sum_z p(z) \mathop{{}log} \frac{q_\lambda(z \vert x)}{p(z \vert x)}
# = \mathop{{}\mathbb{E}} \left[ \mathop{{}log} \frac{q_\lambda(z \vert x)}{p(z \vert x)} \right] =
# \mathop{{}\mathbb{E}} (\mathop{{}log} q_\lambda(z \vert x) - \mathop{{}log} p(z \vert x)) $$
#
# Now, by using the Bayes rule:
#
# $$ KL(q_\lambda(z \vert x) \| p(z \vert x))=
# \mathop{{}\mathbb{E}} (\mathop{{}log} q_\lambda(z \vert x) - \mathop{{}log} \frac{p(x \vert z)p(z)}{p(x)} ) =
# \mathop{{}\mathbb{E}} (\mathop{{}log} q_\lambda(z \vert x) - \mathop{{}log} p(x \vert z) - \mathop{{}log} p(z) + \mathop{{}log} p(x) )
# $$
#
# Note that the expection is over $z$ and $p(x)$ and does not depend on $z$, so $p(x)$ can be moved outside the expectation:
#
# $$ KL(q_\lambda(z \vert x) \| p(z \vert x))=
# \mathop{{}\mathbb{E}} [\mathop{{}log} q_\lambda(z \vert x) - \mathop{{}log} p(x \vert z) - \mathop{{}log} p(z))] + \mathop{{}log} p(x)
# $$
#
# $$ KL(q_\lambda(z \vert x)\| p(z \vert x)) - \mathop{{}log} p(x)=
# \mathop{{}\mathbb{E}} [\mathop{{}log} q_\lambda(z \vert x) - \mathop{{}log} p(x \vert z) - \mathop{{}log} p(z))]
# $$
#
# Now we observe that the right hand-side of the equation can be written as another KL divergence:
#
# $$ KL(q_\lambda(z \vert x) \| p(z \vert x)) - \mathop{{}log} p(x)=
# \mathop{{}\mathbb{E}} [\mathop{{}log} q(z \vert x) - \mathop{{}log} p(x \vert z) - \mathop{{}log} p(z))]
# $$
#
# $$
# \mathop{{}log} p(x) - KL(q_\lambda(z \vert x) \| p(z \vert x)) =
# \mathop{{}\mathbb{E}} [\mathop{{}log} p(x \vert z) - ( \mathop{{}log} q(z \vert x) - \mathop{{}log} p(z)))]
# $$
#
# $$
# = \mathop{{}\mathbb{E}} [\mathop{{}log} p(x \vert z)] - \mathop{{}\mathbb{E} ( \mathop{{}log} q(z \vert x) - \mathop{{}log} p(z)]} $$
#
# $$ = \mathop{{}\mathbb{E}}[\mathop{{}log} p(x \vert z)] - KL[q_\lambda(z \vert x) \| p(z )]
# $$
#
# The left hand side has the quantity we want to maximize ($\mathop{{}log} p(x)$) (plus an error term that will be small for a good $q$) and the right hand side is something we can optimize via SGD (albeit is not still obvious).
#
# The first term in the right hand side is the probability density of generated output $x$ given the inferred latent distribution over $z$. In the case of MNIST, data can be modeled as as Bernoulli trials, and the first term is the binary cross-entropy: $ -p \mathop{{}log_2} p - (1-p) \mathop{{}log_2} (1-p)$.
#
# Regarding the KL divergence, we are in a very special case: we are dealing with a certain conjugate prior (spherical Gaussian) over $z$ that let us analytically integrate the KL divergence, yielding a closed-form equation:
#
# $$
# KL[q(z \vert x) \| p(z )] = \frac{1}{2} \sum (1 + \mathop{{}log} (\sigma^2) - \mu^2 - \sigma^2)
# $$
#
#
# ## ELBO and $\text{KL}(q(z \vert x) \| p(z \vert x))$ minimization.
#
# What can we do if we cannot solve the dependence on $p(z \vert x)$?
#
# To tackle this, consider the property:
#
# $$
# \begin{aligned}
# \log p(\mathbf{x}) &= \text{KL}( q(z \mid x) \| p(z \mid x) )\\ &\quad+\; \mathbb{E}_{q(z,x)} \big[ \log p(x, z) - \log q(z,x) \big]
# \end{aligned}
# $$
#
# where the left hand side is the logarithm of the marginal likelihood $p(x) = \int p(x, z) \text{d}z$, also known as the model evidence. (Try deriving this using Bayes’ rule!).
#
# The evidence is a constant with respect to the *variational* parameters $\lambda$ of $q$, so we can minimize $\text{KL}(q\|p)$ by instead **maximizing** the **Evidence Lower BOund**:
#
# \begin{aligned}
# \text{ELBO}(\lambda) &=\; \mathbb{E}_{q(z,x)} \big[ \log p(x, z) - \log q(z, x) \big].
# \end{aligned}
#
# In the ELBO, both $p(x, z)$ and $q(z,x)$ are tractable. The optimization problem we seek to solve becomes
#
# \begin{aligned} \lambda^* &= \arg \max_\lambda \text{ELBO}(\lambda).
# \end{aligned}
#
# More information: http://edwardlib.org/tutorials/klqp
#
# We can maximize ELBO by using automatic gradient ascent.
# Some libraries calculate ELBO gradients automatically:
#
# <table>
# <tr>
# <th><center>Python Package</center></th>
# <th><center>Tensor Library</center></th>
# <th><center>Variational Inference Algorithm(s)</center></th>
# <tr>
# <tr>
# <td><center><a href='http://edwardlib.org/'>Edward</a></center></td>
# <td><center><a href='https://www.tensorflow.org/'>TensorFlow</a></center></td>
# <td><center><a href='https://arxiv.org/abs/1401.0118'>Black Box Variational Inference</a> (BBVI)</center></td>
# </tr>
# <tr>
# <td><center><a href='http://pymc-devs.github.io/pymc3/'>PyMC3</a></center></td>
# <td><center><a href='http://deeplearning.net/software/theano/'>Theano</a></center></td>
# <td><center><a href='http://arxiv.org/abs/1603.00788'>Automatic Differentiation Variational Inference</a> (ADVI)</center></td>
# </tr>
# </table>
#
# The strategy is based on:
#
# * Monte Carlo estimate of the ELBO gradient
# * Minibatch estimates of the joint distribution
#
# BBVI and ADVI arise from different ways of calculating the ELBO gradient.
# ## GAN: Generative Adversarial Networks
#
# GAN are an alternative to model $p(x)$.
#
# The basic idea of GANs is to set up a game between two players.
#
# One of them is
# called the **generator**. The generator creates samples that are intended to come
# from the same distribution as the training data.
#
# The other player is the **discriminator**.
# The discriminator examines samples to determine whether they are real or fake.
#
# The discriminator learns using traditional supervised learning
# techniques, dividing inputs into two classes (real or fake). The generator
# is trained to fool the discriminator.
#
# <center>
# <img src="images/gan1.png" alt="" style="width: 500px;"/>
# (Source: https://arxiv.org/pdf/1701.00160.pdf)
# </center>
# The two players in the game are represented by two functions, each of which
# is differentiable both with respect to its inputs and with respect to its parameters.
#
# The discriminator is a function $D$ that takes $x_{real}$ and $x_{fake}$ as input and uses $\theta^D$ as parameters.
#
# The generator is defined by a function $G$ that takes $z$ as input and uses $\theta^G$ as parameters.
#
# Both players have cost functions that are defined in terms of both players’ parameters.
#
# The discriminator wishes to minimize $J^D = (\theta^D, \theta^G)$ and
# must do so while controlling only $\theta^D$.
#
# The generator wishes to minimize $J^G = (\theta^D, \theta^G)$
# and must do so while controlling only $\theta^G$.
#
# Because each
# player’s cost depends on the other player’s parameters, but each player cannot
# control the other player’s parameters, this scenario is most straightforward to
# describe as a game rather than as an optimization problem.
#
# The solution to an
# optimization problem is a (local) minimum, a point in parameter space where all
# neighboring points have greater or equal cost. The solution to a game is a Nash
# equilibrium. In this context, a Nash equilibrium is a tuple $(\theta^D, \theta^G)$
# that is a local minimum of $J^D$ with respect to $\theta^D$ and a local minimum of
# $J^G$ with respect to $\theta^G$.
# ### The generator
#
# The generator is simply a differentiable function $G$. When
# $z$ is sampled from some simple prior distribution, $G(z)$ yields a sample of $x$. Typically, a deep neural network is used to represent $G$.
#
# ### The training process
#
# The training process consists of simultaneous SGD.
# On each step, two minibatches are sampled: a minibatch of $x$ values from the
# dataset and a minibatch of $z$ values drawn from the model’s prior over latent
# variables. Then two gradient steps are made simultaneously: one updating $\theta^D$
# to reduce $J^D$ and one updating $\theta^G$ to reduce $J^G$.
#
# In both cases, it is possible to use the gradient-based optimization algorithm of your choice. Adam is usually a good choice.
#
# <center>
# <img src="images/t12.png" alt="" style="width: 600px;"/>
# </center>
#
# ### The discriminator’s cost
#
# The cost used for the discriminator is:
#
# $$
# J^D = - \frac{1}{2} \mathop{{}\mathbb{E}}_x \mathop{{}log} D(x) - \frac{1}{2} \mathop{{}\mathbb{E}}_z \mathop{{}log} (1 - D(G(z)))
# $$
#
# This is just the standard cross-entropy cost that is minimized when training
# a standard binary classifier with a sigmoid output. The only difference is that
# the classifier is trained on two minibatches of data; one coming from the dataset,
# where the label is 1 for all examples, and one coming from the generator, where
# the label is 0 for all examples.
#
# ### The generator’s cost
#
# The simplest version of the game is a zero-sum game, in which the sum of
# all player’s costs is always zero. In this version of the game:
#
# $$
# J^G = - J^D
# $$
#
# ## Example
#
# Training a generative adversarial network to sample from a Gaussian distribution.
# (Adapted from: http://blog.evjang.com/2016/06/generative-adversarial-nets-in.html)
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns # for pretty plots
from scipy.stats import norm
# %matplotlib inline
# This will be our target distribution:
# +
# target distribution
mu,sigma=-1,1
xs=np.linspace(-5,5,1000)
plt.plot(xs, norm.pdf(xs,loc=mu,scale=sigma))
# -
# The horizontal axis represents the domain of $x$. The generator network will map random values to this domain.
# Our discriminator and generator networks will be MLP:
# +
TRAIN_ITERS=50000
M=200 # minibatch size
# MLP - used for D_pre, D1, D2, G networks
def mlp(input, output_dim):
# construct learnable parameters within local scope
w1=tf.get_variable("w0", [input.get_shape()[1], 6], initializer=tf.random_normal_initializer())
b1=tf.get_variable("b0", [6], initializer=tf.constant_initializer(0.0))
w2=tf.get_variable("w1", [6, 5], initializer=tf.random_normal_initializer())
b2=tf.get_variable("b1", [5], initializer=tf.constant_initializer(0.0))
w3=tf.get_variable("w2", [5,output_dim], initializer=tf.random_normal_initializer())
b3=tf.get_variable("b2", [output_dim], initializer=tf.constant_initializer(0.0))
# nn operators
fc1=tf.nn.tanh(tf.matmul(input,w1)+b1)
fc2=tf.nn.tanh(tf.matmul(fc1,w2)+b2)
fc3=tf.nn.tanh(tf.matmul(fc2,w3)+b3)
return fc3, [w1,b1,w2,b2,w3,b3]
# -
# re-used for optimizing all networks
def momentum_optimizer(loss,var_list):
batch = tf.Variable(0)
learning_rate = tf.train.exponential_decay(
0.001, # Base learning rate.
batch, # Current index into the dataset.
TRAIN_ITERS // 4, # Decay step - this decays 4 times throughout training process.
0.95, # Decay rate.
staircase=True)
optimizer=tf.train.MomentumOptimizer(learning_rate,0.6).minimize(loss,
global_step=batch,
var_list=var_list)
return optimizer
# Pre-train discriminator
# +
with tf.variable_scope("D_pre"):
input_node=tf.placeholder(tf.float32, shape=(M,1))
train_labels=tf.placeholder(tf.float32,shape=(M,1))
D,theta=mlp(input_node,1)
loss=tf.reduce_mean(tf.square(D-train_labels))
optimizer=momentum_optimizer(loss,None)
sess=tf.InteractiveSession()
tf.initialize_all_variables().run()
# plot decision surface
def plot_d0(D,input_node):
f,ax=plt.subplots(1)
# p_data
xs=np.linspace(-5,5,1000)
ax.plot(xs, norm.pdf(xs,loc=mu,scale=sigma), label='p_data')
# decision boundary
r=1000 # resolution (number of points)
xs=np.linspace(-5,5,r)
ds=np.zeros((r,1)) # decision surface
# process multiple points in parallel in a minibatch
for i in range(r/M):
x=np.reshape(xs[M*i:M*(i+1)],(M,1))
ds[M*i:M*(i+1)]=sess.run(D,{input_node: x})
ax.plot(xs, ds, label='decision boundary')
ax.set_ylim(0,1.1)
plt.legend()
#plot_d0(D,input_node)
#plt.title('Initial Decision Boundary')
# -
lh=np.zeros(1000)
for i in range(1000):
d=(np.random.random(M)-0.5) * 10.0
labels=norm.pdf(d,loc=mu,scale=sigma)
lh[i],_=sess.run([loss,optimizer],
{input_node: np.reshape(d,(M,1)),
train_labels: np.reshape(labels,(M,1))})
# training loss
plt.plot(lh)
plt.title('Training Loss')
plot_d0(D,input_node)
# +
# # copy the learned weights over into a tmp array
weightsD=sess.run(theta)
# close the pre-training session
sess.close()
# -
# Now to build the actual generative adversarial network
#
# +
with tf.variable_scope("G"):
z_node=tf.placeholder(tf.float32, shape=(M,1)) # M uniform01 floats
G,theta_g=mlp(z_node,1) # generate normal transformation of Z
G=tf.mul(5.0,G) # scale up by 5 to match range
with tf.variable_scope("D") as scope:
# D(x)
x_node=tf.placeholder(tf.float32, shape=(M,1)) # input M normally distributed floats
fc,theta_d=mlp(x_node,1) # output likelihood of being normally distributed
D1=tf.maximum(tf.minimum(fc,.99), 0.01) # clamp as a probability
# make a copy of D that uses the same variables, but takes in G as input
scope.reuse_variables()
fc,theta_d=mlp(G,1)
D2=tf.maximum(tf.minimum(fc,.99), 0.01)
obj_d=tf.reduce_mean(tf.log(D1)+tf.log(1-D2))
obj_g=tf.reduce_mean(tf.log(D2))
# set up optimizer for G,D
opt_d=momentum_optimizer(1-obj_d, theta_d)
opt_g=momentum_optimizer(1-obj_g, theta_g) # maximize log(D(G(z)))
# -
sess=tf.InteractiveSession()
tf.initialize_all_variables().run()
# # copy weights from pre-training over to new D network
for i,v in enumerate(theta_d):
sess.run(v.assign(weightsD[i]))
# +
def plot_fig():
# plots pg, pdata, decision boundary
f,ax=plt.subplots(1)
# p_data
xs=np.linspace(-5,5,1000)
ax.plot(xs, norm.pdf(xs,loc=mu,scale=sigma), label='p_data')
# decision boundary
r=5000 # resolution (number of points)
xs=np.linspace(-5,5,r)
ds=np.zeros((r,1)) # decision surface
# process multiple points in parallel in same minibatch
for i in range(r/M):
x=np.reshape(xs[M*i:M*(i+1)],(M,1))
ds[M*i:M*(i+1)]=sess.run(D1,{x_node: x})
ax.plot(xs, ds, label='decision boundary')
# distribution of inverse-mapped points
zs=np.linspace(-5,5,r)
gs=np.zeros((r,1)) # generator function
for i in range(r/M):
z=np.reshape(zs[M*i:M*(i+1)],(M,1))
gs[M*i:M*(i+1)]=sess.run(G,{z_node: z})
histc, edges = np.histogram(gs, bins = 10)
ax.plot(np.linspace(-5,5,10), histc/float(r), label='p_g')
# ylim, legend
ax.set_ylim(0,1.1)
plt.legend()
# initial conditions
plot_fig()
plt.title('Before Training')
# -
# Algorithm 1 of Goodfellow et al 2014
k=1
histd, histg= np.zeros(TRAIN_ITERS), np.zeros(TRAIN_ITERS)
for i in range(TRAIN_ITERS):
for j in range(k):
x= np.random.normal(mu,sigma,M) # sampled m-batch from p_data
x.sort()
z= np.linspace(-5.0,5.0,M)+np.random.random(M)*0.01 # sample m-batch from noise prior
histd[i],_=sess.run([obj_d,opt_d], {x_node: np.reshape(x,(M,1)), z_node: np.reshape(z,(M,1))})
z= np.linspace(-5.0,5.0,M)+np.random.random(M)*0.01 # sample noise prior
histg[i],_=sess.run([obj_g,opt_g], {z_node: np.reshape(z,(M,1))}) # update generator
if i % (TRAIN_ITERS//10) == 0:
print(float(i)/float(TRAIN_ITERS))
plt.plot(range(TRAIN_ITERS),histd, label='obj_d')
plt.plot(range(TRAIN_ITERS), 1-histg, label='obj_g')
plt.legend()
plot_fig()
# ## Implementation: MNIST GAN
# +
# Adapted from: https://github.com/wiseodd/generative-models/blob/master/GAN/vanilla_gan/gan_tensorflow.py
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import os
def xavier_init(size):
in_dim = size[0]
xavier_stddev = 1. / tf.sqrt(in_dim / 2.)
return tf.random_normal(shape=size, stddev=xavier_stddev)
# discriminator network
X = tf.placeholder(tf.float32, shape=[None, 784])
D_W1 = tf.Variable(xavier_init([784, 128]))
D_b1 = tf.Variable(tf.zeros(shape=[128]))
D_W2 = tf.Variable(xavier_init([128, 1]))
D_b2 = tf.Variable(tf.zeros(shape=[1]))
# discriminator network parameters
theta_D = [D_W1, D_W2, D_b1, D_b2]
# generator network
Z = tf.placeholder(tf.float32, shape=[None, 100])
G_W1 = tf.Variable(xavier_init([100, 128]))
G_b1 = tf.Variable(tf.zeros(shape=[128]))
G_W2 = tf.Variable(xavier_init([128, 784]))
G_b2 = tf.Variable(tf.zeros(shape=[784]))
# generator network parameters
theta_G = [G_W1, G_W2, G_b1, G_b2]
# +
def sample_Z(m, n):
return np.random.uniform(-1., 1., size=[m, n])
def generator(z):
G_h1 = tf.nn.relu(tf.matmul(z, G_W1) + G_b1)
G_log_prob = tf.matmul(G_h1, G_W2) + G_b2
G_prob = tf.nn.sigmoid(G_log_prob)
return G_prob
def discriminator(x):
D_h1 = tf.nn.relu(tf.matmul(x, D_W1) + D_b1)
D_logit = tf.matmul(D_h1, D_W2) + D_b2
D_prob = tf.nn.sigmoid(D_logit)
return D_prob, D_logit
def plot(samples):
fig = plt.figure(figsize=(4, 4))
gs = gridspec.GridSpec(4, 4)
gs.update(wspace=0.05, hspace=0.05)
for i, sample in enumerate(samples):
ax = plt.subplot(gs[i])
plt.axis('off')
ax.set_xticklabels([])
ax.set_yticklabels([])
ax.set_aspect('equal')
plt.imshow(sample.reshape(28, 28), cmap='Greys_r')
return fig
# +
G_sample = generator(Z)
D_real, D_logit_real = discriminator(X)
D_fake, D_logit_fake = discriminator(G_sample)
# Losses:
D_loss_real = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(D_logit_real, tf.ones_like(D_logit_real)))
D_loss_fake = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(D_logit_fake, tf.zeros_like(D_logit_fake)))
D_loss = D_loss_real + D_loss_fake
G_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(D_logit_fake, tf.ones_like(D_logit_fake)))
D_solver = tf.train.AdamOptimizer().minimize(D_loss, var_list=theta_D)
G_solver = tf.train.AdamOptimizer().minimize(G_loss, var_list=theta_G)
mb_size = 128
Z_dim = 100
mnist = input_data.read_data_sets('../../MNIST_data', one_hot=True)
sess = tf.Session()
sess.run(tf.initialize_all_variables())
if not os.path.exists('out/'):
os.makedirs('out/')
i = 0
for it in range(1000000):
if it % 1000 == 0:
samples = sess.run(G_sample, feed_dict={Z: sample_Z(16, Z_dim)})
fig = plot(samples)
plt.savefig('out/{}.png'.format(str(i).zfill(3)), bbox_inches='tight')
i += 1
plt.close(fig)
X_mb, _ = mnist.train.next_batch(mb_size)
_, D_loss_curr = sess.run([D_solver, D_loss], feed_dict={X: X_mb, Z: sample_Z(mb_size, Z_dim)})
_, G_loss_curr = sess.run([G_solver, G_loss], feed_dict={Z: sample_Z(mb_size, Z_dim)})
if it % 1000 == 0:
print('Iter: {}'.format(it))
print('D loss: {:.4}'. format(D_loss_curr))
print('G_loss: {:.4}'.format(G_loss_curr))
print()
# -
# ### DGAN Architecture
#
# Most GANs today are at least loosely based on the DCGAN architecture (Radford
# et al., 2015). DCGAN stands for “deep, convolution GAN.”
#
# Some of the key insights of the DCGAN architecture were to:
#
# + Use batch normalization layers in most layers
# of both the discriminator and the generator, with the two minibatches for
# the discriminator normalized separately.
#
# + The overall network structure is mostly borrowed from the all-convolutional
# net.
#
# + The use of the Adam optimizer rather than SGD with momentum.
#
# <center>
# <img src="images/dgan.png" alt="" style="width: 700px;"/>
# (Source: https://arxiv.org/pdf/1511.06434.pdf)
# </center>
#
#
# Generated bedrooms after one training pass through the dataset:
#
#
# <center>
# <img src="images/dgan2.png" alt="" style="width: 700px;"/>
# (Source: https://github.com/Newmu/dcgan_code)
# </center>
#
#
# Faces:
#
# <center>
# <img src="images/dgan3.png" alt="" style="width: 700px;"/>
# (Source: https://github.com/Newmu/dcgan_code)
# </center>
#
#
|
12. Non supervised learning II.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="VvlGJHkA8QGt" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 507} outputId="83952b90-4ac0-46c3-ed62-4769ebeca230" executionInfo={"status": "ok", "timestamp": 1583415997368, "user_tz": -60, "elapsed": 13737, "user": {"displayName": "Pawe\u014<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhJ5qhspGUbOQ7nUx9bs7vL1FV2GxSN6qQzlgLHBw=s64", "userId": "00166699122305166239"}}
# !pip install --upgrade tables
# !pip install eli5
# !pip install xgboost
# + id="U7zvIA1M8l3P" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 166} outputId="f33c1df4-42d6-40e7-8033-fcbb957440a5" executionInfo={"status": "ok", "timestamp": 1583416330182, "user_tz": -60, "elapsed": 2338, "user": {"displayName": "Pawe\u014<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhJ5qhspGUbOQ7nUx9bs7vL1FV2GxSN6qQzlgLHBw=s64", "userId": "00166699122305166239"}}
import pandas as pd
import numpy as np
from sklearn.dummy import DummyRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
import xgboost as xgb
from sklearn.metrics import mean_absolute_error as mae
from sklearn.model_selection import cross_val_score, KFold
import eli5
from eli5.sklearn import PermutationImportance
# + id="sA06nfaO974k" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="3d556163-1cab-4187-9744-4366fd515815" executionInfo={"status": "ok", "timestamp": 1583416386602, "user_tz": -60, "elapsed": 790, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhJ5qhspGUbOQ7nUx9bs7vL1FV2GxSN6qQzlgLHBw=s64", "userId": "00166699122305166239"}}
# cd "/content/drive/My Drive/Colab Notebooks/matrix/car_price/car_price/"
# + id="MeGtOO47-KCv" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="d9c367c8-78ba-456d-d23b-351ca325b74c" executionInfo={"status": "ok", "timestamp": 1583416415322, "user_tz": -60, "elapsed": 4573, "user": {"displayName": "Pawe\u0142 Krawczyk", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhJ5qhspGUbOQ7nUx9bs7vL1FV2GxSN6qQzlgLHBw=s64", "userId": "00166699122305166239"}}
df=pd.read_hdf('data/car.h5')
df.shape
# + id="2VnPbirN-K6G" colab_type="code" colab={}
#factorise values
suf='__cat'
for feat in df.columns:
if isinstance(df[feat][0],list):continue
factorised_values=df[feat].factorize()[0]
if suf in feat:
df[feat]=factorised_values
else:
df[feat+suf]=factorised_values
# + id="VIYVg3jZ-j10" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="b3cbe92f-6203-4611-ee08-017f78958d93" executionInfo={"status": "ok", "timestamp": 1583416530470, "user_tz": -60, "elapsed": 557, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhJ5qhspGUbOQ7nUx9bs7vL1FV2GxSN6qQzlgLHBw=s64", "userId": "00166699122305166239"}}
# factorised columns without price
cat_feats= [x for x in df.columns if suf in x]
cat_feats= [x for x in cat_feats if 'price' not in x]
len(cat_feats)
# + id="OBq9p-SO-tOX" colab_type="code" colab={}
def run_model(model=DecisionTreeRegressor(max_depth=5),feats=cat_feats):
#new X, y
X=df[feats].values
y=df['price_value'].values
#crate, train and test model
model=model
scores=cross_val_score(model,X,y,cv=3,scoring='neg_mean_absolute_error')
return np.mean(scores), np.std(scores)
# + id="fuImgZC6_Fha" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="06157a74-af14-4516-9fac-6ac772af0624" executionInfo={"status": "ok", "timestamp": 1583418991685, "user_tz": -60, "elapsed": 4802, "user": {"displayName": "Pawe\<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhJ5qhspGUbOQ7nUx9bs7vL1FV2GxSN6qQzlgLHBw=s64", "userId": "00166699122305166239"}}
#decision tree
run_model()
# + id="KNQwL_x4IFEX" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="170cd775-dc11-4232-9f14-8bb0c20f6d59" executionInfo={"status": "ok", "timestamp": 1583419259759, "user_tz": -60, "elapsed": 124811, "user": {"displayName": "Pawe\<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhJ5qhspGUbOQ7nUx9bs7vL1FV2GxSN6qQzlgLHBw=s64", "userId": "00166699122305166239"}}
#Random Forest
run_model(RandomForestRegressor(max_depth=5,n_estimators=50, random_state=0))
# + id="WirrzQYcIxnZ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 84} outputId="d5f09f6b-befb-4d5b-ecf2-68ab4ac72fa6" executionInfo={"status": "ok", "timestamp": 1583419345188, "user_tz": -60, "elapsed": 59714, "user": {"displayName": "Pawe\u01<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhJ5qhspGUbOQ7nUx9bs7vL1FV2GxSN6qQzlgLHBw=s64", "userId": "00166699122305166239"}}
#XGBoost
run_model(xgb.XGBRegressor(max_depth=5,n_estimators=50, seed=0, learning_rate=0.1))
# + id="Ioofdy94IpNv" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 403} outputId="b8b07784-3936-4b8a-e835-948101ade248" executionInfo={"status": "ok", "timestamp": 1583419767824, "user_tz": -60, "elapsed": 363523, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/<KEY>", "userId": "00166699122305166239"}}
#finding features
m=xgb.XGBRegressor(max_depth=5,n_estimators=50, seed=0, learning_rate=0.1)
m.fit(X,y)
imp=PermutationImportance(m, random_state=0).fit(X,y)
eli5.show_weights(imp,feature_names=cat_feats)
# + id="sZmltNX9Jq-X" colab_type="code" colab={}
feats=['param_napęd__cat'
,'param_rok-produkcji__cat'
,'param_stan__cat'
,'param_skrzynia-biegów__cat'
,'param_faktura-vat__cat'
,'param_moc__cat'
,'param_marka-pojazdu__cat'
,'feature_kamera-cofania__cat'
,'param_typ__cat'
,'param_pojemność-skokowa__cat'
,'seller_name__cat'
,'feature_wspomaganie-kierownicy__cat'
,'param_model-pojazdu__cat'
,'param_wersja__cat'
,'param_kod-silnika__cat'
,'feature_system-start-stop__cat'
,'feature_asystent-pasa-ruchu__cat'
,'feature_czujniki-parkowania-przednie__cat'
,'feature_łopatki-zmiany-biegów__cat'
,'feature_regulowane-zawieszenie__cat']
# + id="IS6DvJWYMsM-" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="87bed894-db14-454e-eeed-e4445195aa03" executionInfo={"status": "ok", "timestamp": 1583420231082, "user_tz": -60, "elapsed": 566, "user": {"displayName": "Pawe\u01<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhJ5qhspGUbOQ7nUx9bs7vL1FV2GxSN6qQzlgLHBw=s64", "userId": "00166699122305166239"}}
len(feats)
# + id="-WIJ98LJMuN_" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 84} outputId="c2e6898d-6670-4b10-bb59-ce309fdb416f" executionInfo={"status": "ok", "timestamp": 1583420292179, "user_tz": -60, "elapsed": 13951, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhJ5qhspGUbOQ7nUx9bs7vL1FV2GxSN6qQzlgLHBw=s64", "userId": "00166699122305166239"}}
#XGBoost top 20 features
run_model(xgb.XGBRegressor(max_depth=5,n_estimators=50, seed=0, learning_rate=0.1),feats=feats)
# + id="33m5FGrdNAUu" colab_type="code" colab={}
df['param_rok-produkcji__cat']=df['param_rok-produkcji'].map(lambda x: -1 if str(x)=='None' else int(x))
# + id="ME_bAAT1VxjZ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 84} outputId="b3d36fc5-af75-4707-8669-8c4f5d6b4760" executionInfo={"status": "ok", "timestamp": 1583423235972, "user_tz": -60, "elapsed": 13768, "user": {"displayName": "Pawe\u0142 Krawczyk", "photoUrl": "<KEY>", "userId": "00166699122305166239"}}
run_model(xgb.XGBRegressor(max_depth=5,n_estimators=50, seed=0, learning_rate=0.1),feats=feats)
# + id="BsVgQaeBWIse" colab_type="code" colab={}
df['param_moc__cat']=df['param_moc'].map(lambda x: -1 if str(x)=='None' else int(x.split(' ')[0]))
# + id="Je7NqXCoXy5x" colab_type="code" colab={}
df['param_pojemność-skokowa__cat']=df['param_pojemność-skokowa'].map(lambda x: -1 if str(x)=='None' else int(x.split('cm')[0].replace(' ', '')))
# + id="fLfQGnOBYZe0" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 84} outputId="33077ed1-288e-4f88-ec58-7df6612154de" executionInfo={"status": "ok", "timestamp": 1583423473655, "user_tz": -60, "elapsed": 13881, "user": {"displayName": "Pawe\u0142 Krawczyk", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhJ5qhspGUbOQ7nUx9bs7vL1FV2GxSN6qQzlgLHBw=s64", "userId": "00166699122305166239"}}
run_model(xgb.XGBRegressor(max_depth=5,n_estimators=50, seed=0, learning_rate=0.1),feats=feats)
# + id="UIyD_bRsYaA2" colab_type="code" colab={}
|
XGBoost_and_fatures.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Mario-RJunior/DataScience-Awari/blob/master/Unidade4-Manipulacao-de-Dados/Coleta-de-Dados/Exercicio_API_IPCA.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="YRHeOE7SY50U" colab_type="text"
# # Exercício:
#
# O exercício a ser desenvolvido para a presente unidade consiste em conectar-se a uma API. O Banco Central do Brasil disponibiliza dados a respeito de diversos indicadores econômicos do país. Sua tarefa será encontrar a série histórica relativa à inflação (IPCA) na plataforma de dados abertos do BC, importá-la e transformá-la em um DataFrame do Pandas.
#
# Você precisará criar um Jupyter Notebook (em sua máquina ou no Google Colab) com o código que mostre que a conexão com a API foi devidamente realizado.
# + id="8JTX2LUU_ZiV" colab_type="code" colab={}
# Importando as bibliotecas
import requests
import json
import pandas as pd
# + id="bKYzbWSUd1wK" colab_type="code" colab={}
# Definindo o link para a API
url = 'https://api.bcb.gov.br/dados/serie/bcdata.sgs.16121/dados?formato=json'
# + id="TXaRrFBW_r5c" colab_type="code" colab={}
c = requests.get(url).content
# + id="9VFX3ZJa_vhV" colab_type="code" colab={}
# Convertendo o arquivo .json para um dicionário
local = json.loads(c)
# + id="Jidbm_Xa_5xG" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="6b82655f-b241-4537-f045-bcebacb2f3a6"
local
# + [markdown] id="Cy0819Cy8MJ6" colab_type="text"
# ## Resolução 1:
# + id="p_jKRs9KeUdu" colab_type="code" colab={}
features = ['data', 'valor']
lista_auxiliar = []
dicionario = {}
for feature in features:
for c in range(len(local)):
x = local[c][f'{feature}']
lista_auxiliar.append(x)
dicionario[f'{feature}'] = lista_auxiliar.copy()
lista_auxiliar.clear()
# + id="x4bH78SLXuFY" colab_type="code" colab={}
df1 = pd.DataFrame(dicionario)
# + id="lQS99hBkrUwl" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 198} outputId="6323f3df-bd11-4bad-b32c-3c5c78b6eb3e"
df1.head()
# + [markdown] id="V-qoSi0a8WwF" colab_type="text"
# ## Resolução 2:
# + id="cQFHBZstkr81" colab_type="code" colab={}
dicionario = {'data':[], 'valor': []}
for l in local:
dicionario['data'].append(l['data'])
dicionario['valor'].append(l['valor'])
# + id="-iovmk8ql_f9" colab_type="code" colab={}
df2 = pd.DataFrame(dicionario)
# + id="Wg-MRVdNlb2S" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 198} outputId="79e7add3-3564-4262-a970-6b48e56f539f"
df2.head()
# + [markdown] id="A_WEdAZEPRV0" colab_type="text"
# ## Resolução 3:
# + id="qSGpi_B_PT52" colab_type="code" colab={}
df3 = pd.DataFrame(dicionario)
# + id="8dHrqqnxPgnv" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 198} outputId="16a0d4ad-405d-4a15-f0e7-8bca37e65f48"
df3.head()
|
Unidade4-Manipulacao-de-Dados/Coleta-de-Dados/Exercicio_API_IPCA.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Modeling Dynamical Systems
#
# For instructions on how to run these tutorial notebooks, please see the [README](https://github.com/RobotLocomotion/drake/blob/master/tutorials/README.md).
# This notebook provides a short tutorial for modeling input-output dynamical systems in Drake. It covers
# - Writing your own simple dynamical systems,
# - Simulating a dynamical system and plotting the results,
# - Constructing a block diagram out of simple systems.
#
# Drake includes a set of C++ classes in drake::systems that provide an API for building complex dynamical systems by connecting simple dynamical systems into a block diagram. The modeling approach is inspired by MATLAB's Simulink (though without the graphical user interface). Like Simulink, drake::systems provides a library of existing systems and also makes it easy for you to define your own new dynamical systems. The python wrappers in `pydrake` used in these notes provide a convenient set of bindings on top of this systems framework, allowing you to write new systems in either Python or C++, and to use them interchangeably.
#
# A major difference between modeling dynamical systems in Drake vs Simulink (or most other system modeling languages) is that there is a considerable emphasis in Drake on introspecting the underlying structure in the governing equations. For example, if certain outputs of a dynamical system depend on only a small fraction of the inputs, then we attempt to infer this sparsity directly. Similarly, if the dynamics of a system can be described by a polynomial vector field (or linear, or at least differentiable, ...), then Drake aims to infer this structure as well, and to preserve this structure when systems are combined into a diagram. This structure may have only modest benefit for numerical simulation, but it is incredibly enabling for more sophisticated algorithms for analysis, system identification, and feedback or state estimator design.
#
# We'll return to the more advanced modeling tools in a minute, but let us start with some very simple examples.
#
# A quick note on documentation. The C++ classes are beautifully documented in [doxygen](http://drake.mit.edu/doxygen_cxx). The Python API is also [documented](https://drake.mit.edu/pydrake/index.html) directly, but is autogenerated and not always as beautiful. Consider using the C++ doxygen as a secondary source of documentation even for your Python development... most of the `pydrake` API maps directly to that C++ API.
#
# ## Writing your own dynamics
#
# In this section, we will describe how you can write your own dynamics class in `pydrake`. Every user system should derive from the `pydrake.systems.framework.LeafSystem` class.
#
# However, many dynamical systems we are interested in are represented by a simple vector field in state-space form, where we often use x to denote the state vector, u for the input vector, and y for the output vector. To make it even easier to implement systems in this form, we provide another subclass `pydrake.systems.primitives.SymbolicVectorSystem` that makes it very easy to author these simple systems.
#
# <!-- The following HTML table format was modified from the doxygen System block output, with the goal of matching the style -->
# <table align="center" cellpadding="0" cellspacing="0">
# <tr align="center">
# <td><table cellspacing="0" cellpadding="0">
# <tr>
# <td align="right" style="padding:5px 0px 5px 0px">u → </td></tr>
# </table>
# </td><td align="center" style="border:solid;padding-left:20px;padding-right:20px" bgcolor="#F0F0F0">System</td><td><table cellspacing="0" cellpadding="0">
# <tr>
# <td align="left" style="padding:5px 0px 5px 0px">→ y </td></tr>
# </table>
# </td></tr>
# </table>
#
# ### Using SymbolicVectorSystem
#
# Consider a basic continuous-time, nonlinear, input-output dynamical system described by the following state-space equations:
# \begin{gather*}
# \dot{x} = f(t,x,u), \\ y = g(t,x,u).
# \end{gather*}
# In `pydrake`, you can instantiate a system of this form where $f()$ and $g()$ are anything that you can write in Python using [operations supported by the Drake symbolic engine](https://drake.mit.edu/pydrake/pydrake.symbolic.html#pydrake.symbolic.Expression), as illustrated by the following example.
#
# Consider the system
# \begin{gather*}\dot{x} = -x + x^3,\\ y = x.\end{gather*}
# This system has zero inputs, one (continuous) state variable, and one output. It can be implemented in Drake using the following code:
# +
from pydrake.symbolic import Variable
from pydrake.systems.primitives import SymbolicVectorSystem
# Define a new symbolic Variable
x = Variable("x")
# Define the System.
continuous_vector_system = SymbolicVectorSystem(state=[x], dynamics=[-x + x**3], output=[x])
# -
# That's it! The `continuous_vector_system` variable is now an instantiation of a Drake `System` class, that can be used in a number of ways that we will illustrate below. Note that the state argument expects a *vector* of `symbolic::Variable` (python lists get automatically converted), and the dynamics and output arguments expect a vector of `symbolic::Expression`s.
#
# Implementing a basic discrete-time system in Drake is very analogous to implementing a continuous-time system. The discrete-time system given by:
# \begin{gather*}
# x[n+1] = f(n,x,u),\\ y[n] = g(n,x,u),
# \end{gather*}
# can be implemented as seen in the following example.
#
# Consider the system \begin{gather*}x[n+1] = x^3[n],\\ y[n] = x[n].\end{gather*} This system has zero inputs, one (discrete) state variable, and one output. It can be implemented in Drake using the following code:
# +
from pydrake.symbolic import Variable
from pydrake.systems.primitives import SymbolicVectorSystem
# Define a new symbolic Variable
x = Variable("x")
# Define the System. Note the additional argument specifying the time period.
discrete_vector_system = SymbolicVectorSystem(state=[x], dynamics=[x**3], output=[x], time_period=1.0)
# -
# ### Deriving from LeafSystem
#
# Although using SymbolicVectorSystems are a nice way to get started, in fact Drake supports authoring a wide variety of systems with multiple inputs and outputs, mixed discrete- and continuous- dynamics, hybrid dynamics with guards and resets, systems with constraints, and even stochastic systems. To expose more of the underlying system framework, you can derive your system from `pydrake.systems.framework.LeafSystem` directly, instead of using the simplified `SymbolicVectorSystem` interface.
# +
from pydrake.systems.framework import BasicVector, LeafSystem
# Define the system.
class SimpleContinuousTimeSystem(LeafSystem):
def __init__(self):
LeafSystem.__init__(self)
self.DeclareContinuousState(1) # One state variable.
self.DeclareVectorOutputPort("y", BasicVector(1), self.CopyStateOut) # One output.
# xdot(t) = -x(t) + x^3(t)
def DoCalcTimeDerivatives(self, context, derivatives):
x = context.get_continuous_state_vector().GetAtIndex(0)
xdot = -x + x**3
derivatives.get_mutable_vector().SetAtIndex(0, xdot)
# y = x
def CopyStateOut(self, context, output):
x = context.get_continuous_state_vector().CopyToVector()
output.SetFromVector(x)
# Instantiate the System
continuous_system = SimpleContinuousTimeSystem()
# Define the system.
class SimpleDiscreteTimeSystem(LeafSystem):
def __init__(self):
LeafSystem.__init__(self)
self.DeclareDiscreteState(1) # One state variable.
self.DeclareVectorOutputPort("y", BasicVector(1), self.CopyStateOut) # One output.
self.DeclarePeriodicDiscreteUpdate(1.0) # One second timestep.
# x[n+1] = x^3[n]
def DoCalcDiscreteVariableUpdates(self, context, events, discrete_state):
x = context.get_discrete_state_vector().GetAtIndex(0)
xnext = x**3
discrete_state.get_mutable_vector().SetAtIndex(0, xnext)
# y = x
def CopyStateOut(self, context, output):
x = context.get_discrete_state_vector().CopyToVector()
output.SetFromVector(x)
# Instantiate the System
discrete_system = SimpleDiscreteTimeSystem()
# -
# This code implements the same systems we implemented above. Unlike the `SymbolicVectorSystem` version, you can type any valid python/numpy code into the methods here -- it need not be supported by `pydrake.symbolic`. Also, we now have the opportunity to overload many more pieces of functionality in `LeafSystem`, to produce much more complex systems (with multiple input and output ports, mixed discrete- and continuous- state, more structured state, hybrid systems with witness functions and reset maps, etc). But declaring a `LeafSystem` this way does not provide support for Drake's autodiff and symbolic tools out of the box; to do that we need to add [a few more lines to support templates](https://drake.mit.edu/pydrake/pydrake.systems.scalar_conversion.html?highlight=templatesystem#pydrake.systems.scalar_conversion.TemplateSystem).
#
# We also supply a [number of other helper classes and methods](https://drake.mit.edu/doxygen_cxx/group__systems.html) that derive from or construct a `LeafSystem`, such as the [`pydrake.systems.primitives.LinearSystem`](https://drake.mit.edu/pydrake/pydrake.systems.primitives.html?highlight=linearsystem#pydrake.systems.primitives.LinearSystem) class or the [`pydrake.systems.primitives.Linearize()`](https://drake.mit.edu/pydrake/pydrake.systems.primitives.html?highlight=linearize#pydrake.systems.primitives.Linearize) method. And in many cases, like simulating the dynamics and actuators/sensors of robots, most of the classes that you need have already been implemented.
#
# ## Simulation
#
# Once you have acquired a `System` object describing the dynamics of interest, the most basic thing that you can do is to simulate it. This is accomplished with the `pydrake.framework.analysis.Simulator` class. This class provides access to a rich suite of numerical integration routines, with support for variable-step integration, stiff solvers, and event detection.
#
# In order to view the data from a simulation after the simulation has run, you should add a `pydrake.framework.primitives.SignalLogger` system to your diagram.
#
# Use the following code to simulate the continuous time system we defined above, and plot the results:
# +
# %matplotlib notebook
import matplotlib.pyplot as plt
from pydrake.systems.analysis import Simulator
from pydrake.systems.framework import DiagramBuilder
from pydrake.systems.primitives import LogOutput
# Create a simple block diagram containing our system.
builder = DiagramBuilder()
system = builder.AddSystem(SimpleContinuousTimeSystem())
logger = LogOutput(system.get_output_port(0), builder)
diagram = builder.Build()
# Set the initial conditions, x(0).
context = diagram.CreateDefaultContext()
context.SetContinuousState([0.9])
# Create the simulator, and simulate for 10 seconds.
simulator = Simulator(diagram, context)
simulator.AdvanceTo(10)
# Plot the results.
plt.figure()
plt.plot(logger.sample_times(), logger.data().transpose())
plt.xlabel('t')
plt.ylabel('y(t)');
# +
# Create a simple block diagram containing our system.
builder = DiagramBuilder()
system = builder.AddSystem(SimpleDiscreteTimeSystem())
logger = LogOutput(system.get_output_port(0), builder)
diagram = builder.Build()
# Create the simulator.
simulator = Simulator(diagram)
# Set the initial conditions, x(0).
state = simulator.get_mutable_context().get_mutable_discrete_state_vector()
state.SetFromVector([0.9])
# Simulate for 10 seconds.
simulator.AdvanceTo(10)
# Plot the results.
plt.figure()
plt.stem(logger.sample_times(), logger.data().transpose(), use_line_collection=True)
plt.xlabel('n')
plt.ylabel('y[n]');
# -
# Go ahead and try using the `SymbolicVectorSystem` versions instead. They work, too.
#
# For many systems, the simulation will run much faster than real time. If you would like to tell the simulator to slow down (if possible) to some multiple of the real time clock, then consider using the `set_target_realtime_rate()` method of the `Simulator`. This is useful, for example, if you are trying to animate your robot as it simulates, and would like the benefit of physical intuition, or if you are trying to use the simulation as a part of a multi-process real-time control system.
#
# ## The System "Context"
#
# If you were looking carefully, you might have noticed a few instances of the word "context" in the code snippets above. The [`Context`](http://drake.mit.edu/doxygen_cxx/classdrake_1_1systems_1_1_context.html) is a core concept in the Drake systems framework: the `Context` captures all of the (potentially) dynamic information that a `System` requires to implement its core methods: this includes the time, the state, any inputs, and any system parameters. The `Context` of a `System` is everything you need to know for simulation (or control design, ...), and given a `Context` all methods called on a `System` should be completely deterministic/repeatable.
#
# `System`s know how to create an instance of a `Context` (see [CreateDefaultContext](https://drake.mit.edu/doxygen_cxx/classdrake_1_1systems_1_1_system.html#ad047317ab91889c6743d5e47a64c7f08)).
# In the simulation example above, the `Simulator` created a `Context` for us. We retrieved the `Context` from the `Simulator` in order to set the initial conditions (state) of the system before running the simulation.
#
# Note that a `Context` is not completely defined unless all of the input ports are connected (simulation and other method calls will fail if they are not). For input ports that are not directly tied to the output of another system, consider using the port's [`FixValue`](https://drake.mit.edu/doxygen_cxx/classdrake_1_1systems_1_1_input_port.html#ab285168d3a19d8ed367e11053aec79c3) method.
#
# ## Combinations of Systems: Diagram and DiagramBuilder
#
# The real modeling power of Drake comes from combining many smaller systems together into more complex systems. The concept is very simple: we use the `DiagramBuilder` class to `AddSystem()`s and to `Connect()` input ports to output ports or to expose them as inputs/output of the diagram. Then we call `Build()` to generate the new `Diagram` instance, which is just another `System` in the framework, and can be simulated or analyzed using the entire suite of tools.
#
# In the example below, we connect three subsystems (a plant, a controller, and a logger), and expose the input of the controller as an input to the `Diagram` being constructed:
# +
# %matplotlib notebook
import matplotlib.pyplot as plt
import numpy as np
from pydrake.systems.framework import DiagramBuilder
from pydrake.systems.analysis import Simulator
from pydrake.examples.pendulum import PendulumPlant
from pydrake.systems.controllers import PidController
from pydrake.systems.drawing import plot_system_graphviz
from pydrake.systems.primitives import LogOutput
builder = DiagramBuilder()
# First add the pendulum.
pendulum = builder.AddSystem(PendulumPlant())
pendulum.set_name("pendulum")
controller = builder.AddSystem(PidController(kp=[10.], ki=[1.], kd=[1.]))
controller.set_name("controller")
# Now "wire up" the controller to the plant.
builder.Connect(pendulum.get_state_output_port(), controller.get_input_port_estimated_state())
builder.Connect(controller.get_output_port_control(), pendulum.get_input_port())
# Make the desired_state input of the controller an input to the diagram.
builder.ExportInput(controller.get_input_port_desired_state())
# Log the state of the pendulum.
logger = LogOutput(pendulum.get_state_output_port(), builder)
logger.set_name("logger")
diagram = builder.Build()
diagram.set_name("diagram")
plt.figure()
plot_system_graphviz(diagram, max_depth=2)
# -
# Just like any other `System`, a `Diagram` has a `Context`. You can always extract the context of a subsystem using `Diagram.GetSubSystemContext` or `Diagram.GetMutableSubsystemContext()`. (If it is not clear yet, "mutable" means you have write access, otherwise the data is intended to be `const`; we go to some length in the systems framework to protect algorithms / users from violating the fundamental systems abstractions). Unfortunately, although the `const` property is enforced by the compiler in C++, Python happily ignores it. We use "mutable" in Python only to make our intentions clear, and for consistency with the C++ code.
#
# Finally, we can simulate our PID controlled system and visualize the output.
# +
# Set up a simulator to run this diagram.
simulator = Simulator(diagram)
context = simulator.get_mutable_context()
# We'll try to regulate the pendulum to a particular angle.
desired_angle = np.pi/2.
# First we extract the subsystem context for the pendulum.
pendulum_context = diagram.GetMutableSubsystemContext(pendulum, context)
# Then we can set the pendulum state, which is (theta, thetadot).
pendulum_context.get_mutable_continuous_state_vector().SetFromVector([desired_angle+0.1, 0.2])
# The diagram has a single input port (port index 0), which is the desired_state.
diagram.get_input_port(0).FixValue(context, [desired_angle, 0.])
# Reset the logger only because we've written this notebook with the opportunity to
# simulate multiple times (in this cell) using the same logger object. This is
# often not needed.
logger.reset()
# Simulate for 10 seconds.
simulator.AdvanceTo(20);
# Plot the results.
t = logger.sample_times()
plt.figure()
# Plot theta.
plt.plot(t, logger.data()[0,:],'.-')
# Draw a line for the desired angle.
plt.plot([t[0], t[-1]], [desired_angle, desired_angle], 'g' )
plt.xlabel('time (seconds)')
plt.ylabel('theta (rad)')
plt.title('PID Control of the Pendulum');
|
tutorials/dynamical_systems.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import matplotlib.pyplot as plt
plt.style.use('classic')
# %matplotlib inline
# # Class 3: NumPy
#
# NumPy is a powerful Python module for scientific computing. Among other things, NumPy defines an N-dimensional array object that is especially convenient to use for plotting functions and for simulating and storing time series data. NumPy also defines many useful mathematical functions like, for example, the sine, cosine, and exponential functions and has excellent functions for probability and statistics including random number generators, and many cumulative density functions and probability density functions.
#
# ## Importing NumPy
#
# The standard way to import NumPy so that the namespace is `np`. This is for the sake of brevity.
import numpy as np
# ## NumPy arrays
#
# A NumPy `ndarray` is a homogeneous multidimensional array. Here, *homogeneous* means that all of the elements of the array have the same type. An `nadrray` is a table of numbers (like a matrix but with possibly more dimensions) indexed by a tuple of positive integers. The dimensions of NumPy arrays are called axes and the number of axes is called the rank. For this course, we will work almost exclusively with 1-dimensional arrays that are effectively vectors. Occasionally, we might run into a 2-dimensional array.
#
#
# ### Basics
#
# The most straightforward way to create a NumPy array is to call the `array()` function which takes as an argument a `list`. For example:
# +
# Create a variable called a1 equal to a numpy array containing the numbers 1 through 5
a1 = np.array([1,2,3,4,5])
print(a1)
# Find the type of a1
print(type(a1))
# Find the shape of a1
print(np.shape(a1))
# Use ndim to find the rank or number of dimensions of a1
print(np.ndim(a1))
# +
# Create a variable called a2 equal to a 2-dimensionl numpy array containing the numbers 1 through 4
a2 = np.array([[1,2],[3,4]])
print(a2)
# Use ndim to find the rank or number of dimensions of a2
print(np.ndim(a2))
# Find the shape of a2
print(np.shape(a2))
# +
# Create a variable called a3 an empty numpy array
a3 = np.array([])
print(a3)
# Use ndim to find the rank or number of dimensions of a3
print(np.ndim(a3))
# Find the shape of a3
print(np.shape(a3))
# -
# ### Special functions for creating arrays
#
# Numpy has several built-in functions that can assist you in creating certain types of arrays: `aarange()`, `zeros()`, and `ones()`. Of these, `ararange()` is probably the most useful because it allows you a create an array of numbers by specifying the initial value in the array, the maximum value in the array, and a step size between elements. `ararange()` has three arguments: `start`, `stop`, and `step`:
#
# aarange([start,] stop[, step,])
#
# The `stop` argument is required. The default for `start` is 0 and the default for `step` is 1. Note that the values in the created array will stop one increment *below* stop. That is, if `ararange()` is called with `stop` equal to 9 and `step` equal to 0.5, then the last value in the returned array will be 8.5.
# Create a variable called b that is equal to a numpy array containing the numbers 1 through 5
b = np.arange(1,6,1)
print(b)
# Create a variable called c that is equal to a numpy array containing the numbers 0 through 10
c = np.arange(11)
print(c)
# The `zeros()` and `ones()` take as arguments the desired shape of the array to be returned and fill that array with either zeros or ones.
# Construct a 1x5 array of zeros
print(np.zeros(5))
# Construct a 2x2 array of ones
print(np.ones([2,2]))
# ### Math with NumPy arrays
#
# A nice aspect of NumPy arrays is that they are optimized for mathematical operations. The following standard Python arithemtic operators `+`, `-`, `*`, `/`, and `**` operate element-wise on NumPy arrays as the following examples indicate.
# Define three 1-dimensional arrays. CELL PROVIDED
A = np.array([2,4,6])
B = np.array([3,2,1])
C = np.array([-1,3,2,-4])
# Multiply A by a constant
print(3*A)
# Exponentiate A
print(A**2)
# Add A and B together
print(A+B)
# Exponentiate A with B
print(A**B)
# Add A and C together
print(A+C)
# The error in the preceding example arises because addition is element-wise and `A` and `C` don't have the same shape.
# Compute the sine of the values in A
print(np.sin(A))
# ### Iterating through Numpy arrays
#
# NumPy arrays are iterable objects just like lists, strings, tuples, and dictionaries which means that you can use `for` loops to iterate through the elements of them.
# Use a for loop with a NumPy array to print the numbers 0 through 4
for x in np.arange(5):
print(x)
# ### Example: Basel problem
#
# One of my favorite math equations is:
#
# \begin{align}
# \sum_{n=1}^{\infty} \frac{1}{n^2} & = \frac{\pi^2}{6}
# \end{align}
#
# We can use an iteration through a NumPy array to approximate the lefthand-side and verify the validity of the expression.
# +
# Set N equal to the number of terms to sum
N = 1000
# Initialize a variable called summation equal to 0
summation = 0
# loop over the numbers 1 through N
for n in np.arange(1,N+1):
summation = summation + 1/n**2
# Print the approximation and the exact solution
print('approx:',summation)
print('exact: ',np.pi**2/6)
# -
# ## Random numbers and statistics
#
# NumPy has many useful routines for generating draws from probability distributions. Random number generation is useful for computing dynamic simulations of stochastic economies. NumPy also has some routines for computing basic summary statistics (min, max, mean, median, variance) for data in an array.
#
# For more advanced applications involving probability distributions, use SciPy's `scipy.stats` module (https://docs.scipy.org/doc/scipy-0.16.1/reference/stats.html). And for estimating statisticsl models (e.g., OLS models) use StatsModels (https://www.statsmodels.org/stable/index.html).
# Use the help function to view documentation on the np.random.uniform function
help(np.random.uniform)
# Print a random draw from the uniform(0,1) probability distribution.
print(np.random.uniform())
# In the previous example, everyone will obtain different output for `np.random.uniform()`. However, we can set the *seed* for NumPy's PRNG (pseudorandom number generator) with the function `np.random.seed()`. Setting the seed before generating a random sequence can ensure replicability of results.
# +
# Set the seed for the NumPy random number generator to 271828
np.random.seed(271828)
# Print a random draw from the uniform(0,1) probability distribution.
print(np.random.uniform())
# -
# ### Example: Random Draws from $\text{uniform}(-1,1)$ Distribution
#
# Create a sample of 200 draws from the $\text{uniform}(-1,1)$ distribution. Compute some summary statistics. Plot the sample.
# +
# Set the seed for the NumPy random number generator to 314159
np.random.seed(314159)
# Create a variable called 'uniform_data' containing 200 random draw from the uniform(-1,1) probability distribution.
uniform_data = np.random.uniform(size=200,low=-1,high=1)
# Print the variable uniform_data
print(uniform_data)
# +
# Print the mean of the values in variable uniform_data
print('mean: ',np.mean(uniform_data))
# Print the median of the values in variable uniform_data
print('median:',np.median(uniform_data))
# Print the standard deviation of the values in variable uniform_data
print('min: ',np.std(uniform_data))
# Print the maximum of the values in variable uniform_data
print('max: ',np.max(uniform_data))
# Print the index value of the arg max of the values in variable uniform_data
print('argmax:',np.argmax(uniform_data))
# -
# Create a variable called index_max equal to the argmax of data. Print the corresponding element of uniform_data
index_max = np.argmax(uniform_data)
print('data at argmax:',uniform_data[index_max])
# Plot random sample
plt.plot(uniform_data)
plt.title('200 uniform(-1,1) draws')
plt.grid()
# ### Example: Random Draws from $\text{normal}\left(0,\frac{1}{3}\right)$ Distribution
#
# Create a sample of 200 draws from a normal distribution with mean 0 and variance $\frac{1}{3}$. Note that the variance of the $\text{uniform}(-1,1)$ distribution from the previous example has the same variance See: https://en.wikipedia.org/wiki/Uniform_distribution_(continuous).
#
# Compute some summary statistics. Plot the sample.
# Use the help function to view documentation on the np.random.normal function
help(np.random.normal)
# +
# Set the seed for the NumPy random number generator to 314159
np.random.seed(314159)
# Create a variable called 'normal_data' containing 200 random draw from the normal(0,1/3) probability distribution.
normal_data = np.random.normal(size=200,loc=0,scale=1/np.sqrt(3))
# Print the variable normal_data
print(normal_data)
# +
# Print the mean of the values in variable normal_data
print('mean: ',np.mean(normal_data))
# Print the median of variable the values in normal_data
print('median:',np.median(normal_data))
# Print the standard deviation of the values in variable normal_data
print('min: ',np.std(normal_data))
# Print the maximum of the values in variable normal_data
print('max: ',np.max(normal_data))
# Print the index value of the arg max of the values in variable normal_data
print('argmax:',np.argmax(normal_data))
# -
# Create a variable called 'index_max' equal to the argmax of data. Print corresponding element of normal_data
index_max = np.argmax(normal_data)
print('data at argmax:',normal_data[index_max])
# Plot the random sample
plt.plot(normal_data)
plt.title('200 normal(0,1/3) draws')
plt.grid()
# Plot the uniform and normal samples together on the same axes
plt.plot(normal_data,label='normal(0,1/3)')
plt.plot(uniform_data,label='uniform(-1,1)')
plt.legend(loc='lower right')
plt.title('Two random samples')
plt.grid()
|
Lecture Notebooks/Econ126_Class_03.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/heriswn/LatihanDTS/blob/master/Gas_sensor_array_temperature_modulation_Data_Set.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="wh0gaxCEZn1I" colab_type="text"
# # Gas sensor array temperature modulation Data Set
# ## Abstract
# Abstract: A chemical detection platform composed of 14 temperature-modulated metal oxide (MOX) gas sensors was exposed during 3 weeks to mixtures of carbon monoxide and humid synthetic air in a gas chamber.
# ## Data Set Information
# A chemical detection platform composed of 14 temperature-modulated metal oxide semiconductor (MOX) gas sensors was exposed to dynamic mixtures of carbon monoxide (CO) and humid synthetic air in a gas chamber.
#
# The acquired time series of the sensors and the measured values of CO concentration, humidity and temperature inside the gas chamber are provided.
#
# a) Chemical detection platform:
# The chemical detection platform was composed of 14 MOX gas sensors that generate a time-dependent multivariate response to the different gas stimuli.
# The utilized sensors were made commercially available by Figaro Engineering (7 units of TGS 3870-A04) and FIS (7 units of SB-500-12).
# The operating temperature of the sensors was controlled by the built-in heater, which voltage was modulated in the range 0.2-0.9 V in cycles of 20 and 25 s, following the manufacturer recommendations (0.9 V for 5s, 0.2 V for 20s, 0.9 V for 5 s, 0.2 V for 25 s, ...).
# The sensors were pre-heated for one week before starting the experiments.
# The MOX read-out circuits consisted of voltage dividers with 1 MOhm load resistors and powered at 5V.
# The output voltage of the sensors was sampled at 3.5 Hz using an Agilent HP34970A/34901A DAQ configured at 15 bits of precision and input impedance greater than 10 GOhm.
#
# b) Generator of dynamic gas mixtures
# Dynamic mixtures of CO and humid synthetic air were delivered from high purity gases in cylinders to a small-sized polytetrafluoroethylene (PTFE) test chamber (250 cm3 internal volume), by means of a piping system and mass flow controllers (MFCs).
# Gas mixing was performed using mass flow controllers (MFC),which controlled three different gas streams (CO, wet air and dry air). These streams were delivered from high quality pressurized
# gases in cylinders.
# The selected MFCs (EL-FLOW Select, Bronkhorst) had full scale flow rates of 1000 mln/min for the dry and wet air streams and 3 mln/min for the CO channel.
# The CO bottle contained 1600 ppm of CO diluted in synthetic air with 21 ± 1% O2.
# The relative uncertainty in the generated CO concentration was below 5.5%.
# The wet and dry air streams were both delivered from a synthetic air bottle with 99.995% purity and 21 ± 1% O2.
# Humidification of the wet stream was based on the saturation method using a glass bubbler (Drechsler bottles).
#
# c) Temperature/humidity values
# A temperature/humidity sensor (SHT75, from Sensirion) provided reference humidity and temperature values inside the test chamber with tolerance below 1.8% r.h. and 0.5 ºC, respectively, every 5 s.
# The temperature variations inside the gas chamber, for each experiment, were below 3 ºC.
#
# d) Experimental protocol:
# Each experiment consisted on 100 measurements: 10 experimental concentrations uniformly distributed in the range 0-20 ppm and 10 replicates per concentration.
# Each replicate had a relative humidity randomly chosen from a uniform distribution between 15% and 75% r.h.
# At the beginning of each experiment, the gas chamber was cleaned for 15 min using a stream of synthetic air at a flow rate of 240 mln/min.
# After that, the gas mixtures were released in random order at a constant flow rate of 240 mln/min for 15 min each.
# A single experiment lasted 25 hours (100 samples x 15 minutes/sample) and was replicated on 13 working days spanning a natural period of 17 days.
#
# ## Atribute information:
# The dataset is presented in 13 text files, where each file corresponds to a different measurement day. The filenames indicate the timestamp (yyyymmdd_HHMMSS) of the start of the measurements.
# Each file includes the acquired time series, presented in 20 columns: Time (s), CO concentration (ppm), Humidity (%r.h.), Temperature (ºC), Flow rate (mL/min), Heater voltage (V), and the resistance of the 14 gas sensors: R1 (MOhm),R2 (MOhm),R3 (MOhm),R4 (MOhm),R5 (MOhm),R6 (MOhm),R7 (MOhm),R8 (MOhm),R9 (MOhm),R10 (MOhm),R11 (MOhm),R12 (MOhm),R13 (MOhm),R14 (MOhm)
# Resistance values R1-R7 correspond to FIGARO TGS 3870 A-04 sensors, whereas R8-R14 correspond to FIS SB-500-12 units.
# The time series are sampled at 3.5 Hz.
# + id="lU_ZqgL9Uhza" colab_type="code" colab={}
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import LogisticRegression
from sklearn import preprocessing
from sklearn import utils
# + id="3EWQtT3JUhzg" colab_type="code" colab={}
df = pd.read_csv('20160930_203718.csv')
# + id="Rj0LwJgFUhzk" colab_type="code" outputId="3c38d822-f220-449d-fa5a-a85fcd79eb72" colab={"base_uri": "https://localhost:8080/", "height": 258}
df.head()
# + id="7wtLcGqcc51c" colab_type="code" outputId="d9a7e897-6e71-4ea2-d993-161a7c1b136c" colab={"base_uri": "https://localhost:8080/", "height": 334}
df.describe()
# + id="NNi-z79sUhzq" colab_type="code" outputId="17aa5b00-08e2-46cd-a124-618465ac4d23" colab={"base_uri": "https://localhost:8080/", "height": 442}
df.info()
# + id="v-h1YYpZUhzu" colab_type="code" outputId="c4471314-f243-43f5-8c2a-ff0581a2acc4" colab={"base_uri": "https://localhost:8080/", "height": 34}
df.shape
# + id="zbz592njUhzz" colab_type="code" outputId="dba1ccd7-acee-4ce9-df18-b7fb20227c95" colab={"base_uri": "https://localhost:8080/", "height": 34}
len(df.columns)
# + id="oQEIiA2OUhz3" colab_type="code" outputId="622cb39d-13c2-4ffa-bf38-39201578ba45" colab={"base_uri": "https://localhost:8080/", "height": 258}
df.head()
# + id="xpdBdwo3Uhz7" colab_type="code" colab={}
models={
"logit": LogisticRegression(solver="lbfgs", multi_class="auto")
}
# + id="P1RsLpfAUhz-" colab_type="code" colab={}
#col = ['Temperature (C)']
# + id="zAm6Os-1Uh0C" colab_type="code" colab={}
#cols = ['Heater voltage (V)']
# + id="8Qlaj_ydUh0H" colab_type="code" outputId="7cc508cf-ad8e-4f00-81b9-9c8a54a88fdc" colab={"base_uri": "https://localhost:8080/", "height": 34}
print('[INFO] loading data...')
dataset = df
X = df.iloc[:, : -1].values
y = df.iloc[:, -1].values
(trainX, testX, trainy, testy) = train_test_split(X, y, random_state=3, test_size=0.25)
# + id="bff_9FrhUh0M" colab_type="code" outputId="f3804133-e062-4d4d-9f16-1983da5e4f13" colab={"base_uri": "https://localhost:8080/", "height": 377}
clf = LogisticRegression()
clf.fit(X, y)
# + id="NuFEDnr2Uh0Q" colab_type="code" colab={}
lab_enc = preprocessing.LabelEncoder()
training_scores_encoded = lab_enc.fit_transform(y)
print(training_scores_encoded)
print(utils.multiclass.type_of_target(y))
print(utils.multiclass.type_of_target(y.astype('int')))
print(utils.multiclass.type_of_target(training_scores_encoded))
# + id="rNkDT_5jUh0W" colab_type="code" colab={}
#clf = LogisticRegression()
#clf.fit(X, training_scores_encoded)
#print("LogisticRegression")
#print(clf.predict(prediction_data_test))
# + id="iqk6JFLnUh0a" colab_type="code" colab={}
#model = LinearRegression()
# + id="Ax0e6W69Uh0d" colab_type="code" colab={}
#model.fit(x, y)
# + id="ih0nZWk_Uh0h" colab_type="code" colab={}
#model = LinearRegression().fit(x, y)
# + id="UOes122yUh0k" colab_type="code" colab={}
#r_sq = model.score(x, y)
# + id="rDops6mDUh0o" colab_type="code" colab={}
#print('coefficient of determination:', r_sq)
# + id="vEHYDVJfUh0r" colab_type="code" colab={}
#print('intercept:', model.intercept_)
# + id="RKu_l_6HUh0y" colab_type="code" colab={}
#print('slope:', model.coef_)
# + id="X781N_BeUh06" colab_type="code" colab={}
from sklearn.metrics import mean_absolute_error
model = models["logit"]
model.fit(trainX, trainy)
print("[INFO] evaluation...")
predictions = model.predict(testX)
print(mean_absolute_error(testy, predictions))
# + id="-xaRZ4CQUh1C" colab_type="code" colab={}
# + id="VHK7n3E_Uh1F" colab_type="code" colab={}
# + id="_rLAYxZ7Uh1I" colab_type="code" colab={}
|
Gas_sensor_array_temperature_modulation_Data_Set.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="xJLZjx_IHSwA"
# <div align="center">
#
# # Quantum Convolutional Neural Networks<br>for High-Energy Physics Analysis at the LHC
#
# <a href="https://gist.github.com/eraraya-ricardo/8391f6bdae596e82fe0260c215c5ab8c" target="_blank"><img src="https://img.shields.io/badge/Google%20Summer%20of%20Code-2021-fbbc05?style=flat&logo=data%3Aimage%2Fpng%3Bbase64%2CiVBORw0KGgoAAAANSUhEUgAAAGQAAABkCAMAAABHPGVmAAAALVBMVEVHcEz7vQD7vQD8vQD7vQD8vQD7vQD8vQD8vQD7vQD7vQD8vQD7vQD7vQD7vQAgxtLpAAAADnRSTlMAZvVQ6QrVPhl6oSmHvzL6LQUAAASGSURBVHjatdnZdusgDAVQELMY%2Fv9zb2%2Bwc%2BIKDzQLvTXB3gYBFqmaDVeKU4sCBlFyy43WqLjlBpR1BpR1BpR1xjoFxmIFBpSVBpSVBpSVBpSVBpQ1xvdK1oPgblhfOWltjNaJq7ddYT2IfImYJqMDrENUChGDZn%2FWQ%2FMHxBcD4BMyBc5XCHkNQTq60vfIgXAx5xByju6T8V8itsT3%2FUPi6r39Ce8rp%2FCWYrHfIDXs95FZJs%2FvTob6Z4T2buQE4eikvHeG%2FoZY7TpRfDsNWzrjtP0L4s12NYhh%2BO1ZjJ9HfOjdYGo3QZx7YvwEAgOPdx3eQJlArMFA3wXSZ%2BwMQvplJGoPY6sqNU0gxcGYUVx5jtSIx3oS6HysTxEbMMDPAmkM9iFSXnPXt8nwuQ%2FYI8TH%2F425TQe7%2FnBPEH2bECI6T4t%2Bgvh4N1istR50FJdeIX1Ek%2FqJdGGQOWmAa4u7rn18vuuIzUq52gbxvpiSuzIau%2BuO9FUUfTvvCjcoQ4MMltRnEOqF0pdD%2FwiBZWxoqGCn8r2VGKIUCHOoTyHK2g7y1bsJRRqNe3%2FlXv5GbNhWEWXxbsf1UITRF4kYcM4KiI%2FbeFIevNNq7P2EIg0bVL%2BfqCcyYV2rbDdExWSPjUPPGBRh9JTowTscW0Dqf%2BwLXGmPthgKKMJo1f1OSQ29hf1Mbdlmg5NFV1H7KoICA3mruIQ4vl4TTFhvuAlxxrdb1J55KMJoBatEPCv6mr3sJzK%2F9RQKDAx49Ji5ctSLwsxAxgyuiduOAeVtIG14zppPKtAka9lcMZz71IHyNoAcCpvIx6UfxGLleCim3ggUpe0dQhe7I86mWvQERZmCIocryAqPsdYOSQlVIjCgyMRbLSaXxi3GD4LEw4AipzCyyvS5a5ThMpJTGAYUuQljhiWL53R11FN5BxhQsK0UWbE747E7evGV2FaEAUWmDave0H4LQxg6nErl1IEBBRdmOzjkBPpdqFB%2BpUtUGb0tDKloZP44hQLthQoDwXYiXlowpMJIymExdARL8SViYzymhGEMFR%2FR3cOyNoRCpQcZFu1s6AsNhlQuSiJP%2B1Kk90dNRHW9BYyhwlszhNgdb05CjmGcKDb3DotAoYIYV9wWxjDSZcHNmN%2Fj0KpPm3R7dMjq7HlrSokvjIqjww3SEhb4XJDpg3CLvM9%2BPG%2FMHOcaOwzYRFScNe8QHJb9nOEDhvkGwV48eZC3BgfzWwSHZaXthKEVMvkMaQnKhKESzSCkJ37uQqlJ7RmCIcbr%2By5qUEjiIwQK3q4yZKHqYDxEUIo4U6%2BNahxKr0kEZwv8HC%2BDqo69UaI2ieBAujN2RNhOoPybQjBr9oNSKNXSoQ%2B2luCUQuk1iSCIg9oiZl24Vv8TtXLROaotAtO3%2F9ooWSFcjDnH6BQio2SZQSRz%2FpsPfsifQ2RY1tmNBM3oxQRCbRjkOZn%2FEACT2J%2B1vkZiGESyG1SZS%2FqJ1wTogE1hEFHNh9yNCbvvREwqCwwoawwoKw0oKw0oKw0oKw0oKw0oKw0oMFYqMFYqMFYqMBYq88Y%2FxB7wiOJRvWkAAAAASUVORK5CYII%3D" /></a>
#
# 
# [](https://opensource.org/licenses/MIT)
# [](https://github.com/firstcontributions/open-source-badges)
#
# A Google Summer of Code 2021 [Project](https://summerofcode.withgoogle.com/projects/#5612096894533632).<br>
# This project aims to demonstrate quantum machine learning's potential, specifically Quantum Convolutional Neural Network (QCNN), in HEP events classification from particle image data. The <b>code used in the research is wrapped as an open-source package</b> to ease future research in this field.<br>
#
# <a href="https://ml4sci.org/" target="_blank"><img alt="<EMAIL>" height="200px" src="https://raw.githubusercontent.com/eraraya-ricardo/qcnn-hep/main/assets/gsoc%40ml4sci.jpeg" /></a>
#
# </div>
# + [markdown] id="eCqeW7bzFWtN"
# # Note:
#
# This is a tutorial/example on how to use the package. For more detail information about the package itself and about notions like data re-uploading PQC, quantum classifier, quantum convolution, etc., please refer to the [Docs](https://colab.research.google.com/drive/1ojCEutBoHu-L6Q3PyWSYI51MNIr3OF_k?usp=sharing).
#
# We limit the tutorial to just binary classification tasks. But this package can easily be used for multi-class classification.
# + [markdown] id="1a08wD3RDkjS"
# For a more in-depth theoretical equation, design details of the data re-uploading circuit, and how to construct a multi-class classification circuit, it is highly recommended to read the [original paper](https://quantum-journal.org/papers/q-2020-02-06-226/). The paper is very well written (clear, concise, easy to understand).
# + [markdown] id="XC8mltDvd5E_"
# # 0. Import the Packages
# + [markdown] id="akT-pyYYd-W_"
# Check GPU availability
# + colab={"base_uri": "https://localhost:8080/"} id="4Ks-ffmV1C91" outputId="7bcf98ec-bcc7-448a-cf78-6d2421ee6772"
# gpu_info = !nvidia-smi
gpu_info = '\n'.join(gpu_info)
if gpu_info.find('failed') >= 0:
print('Select the Runtime > "Change runtime type" menu to enable a GPU accelerator, ')
print('and then re-execute this cell.')
else:
print(gpu_info)
# + [markdown] id="hL26EmR5eV7s"
# Check RAM availability
# + colab={"base_uri": "https://localhost:8080/"} id="rZzEyH2Z1HmD" outputId="e2fb51e3-06c9-4722-9252-0a4bef3efeba"
from psutil import virtual_memory
ram_gb = virtual_memory().total / 1e9
print('Your runtime has {:.1f} gigabytes of available RAM\n'.format(ram_gb))
if ram_gb < 20:
print('To enable a high-RAM runtime, select the Runtime > "Change runtime type"')
print('menu, and then select High-RAM in the Runtime shape dropdown. Then, ')
print('re-execute this cell.')
else:
print('You are using a high-RAM runtime!')
# + [markdown] id="zqdJ_o-ieZOk"
# Mount Google Drive to Google Colab (not needed if you run the Notebook locally)
# + colab={"base_uri": "https://localhost:8080/"} id="D7A2uNVWxaJf" outputId="d6ba1e4e-1b44-4b04-9a90-585a58104322"
from google.colab import drive
drive.mount('/content/drive')
# + [markdown] id="TcNeR32veqy0"
# CD to where you want to clone the repository, and clone it
# + id="T0HcA3gE3E4b"
# %cd '/content/drive/My Drive/Projects/GSoC 2021/tutorials'
# !git clone https://github.com/eraraya-ricardo/qcnn-hep.git
from IPython.display import clear_output
clear_output()
# + [markdown] id="HLIKcRJVeyts"
# After cloning the repository, cd to the `qcnn-hep` folder.
# Then, install the dependencies in the `requirements.txt` file, you only need to do this once.
# Once you have all the requirements, run the `!python setup.py` after cd-ing to the `qcnn-hep` folder everytime you want to load the package.
# + id="JVEOpqKkxm1H"
# %cd '/content/drive/My Drive/Projects/GSoC 2021/tutorials/qcnn-hep'
# !python -m pip install -r requirements.txt
# !python setup.py
from IPython.display import clear_output
clear_output()
# + [markdown] id="262GXTy7fmJp"
# Now, let's import all the packages.<br>
# Note: the `main_dir` is the directory where the models will be saved.
# + id="zFRC4xj70vs1"
main_dir = '/content/drive/My Drive/Projects/GSoC 2021/tutorials'
import os
import sys
# Append the path to the folder ../qcnn-hep so we can import the package
sys.path.append('/content/drive/My Drive/Projects/GSoC 2021/tutorials/qcnn-hep')
import numpy as np
from matplotlib import pyplot as plt
import tensorflow as tf
import cirq
from cirq.contrib.svg import SVGCircuit
from qcnn_drc.data_reuploading import ReUploadingPQC
from qcnn_drc.quantum_convolution import QConv2D_DRC
# + [markdown] id="DEv2KSCW1SRS"
# # 1. Load MNIST Dataset
# + [markdown] id="dQNrkUAmJF4h"
# For all examples, we will train the models to classify [MNIST](http://yann.lecun.com/exdb/mnist/) dataset. This dataset is open-source and relatively easy to obtain by everyone.
# + colab={"base_uri": "https://localhost:8080/"} id="k1nj7LSF0zUM" outputId="ae6dfdf2-321f-49f4-f0d3-5f03d98180b1"
# Load the dataset
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
# Scale it by 255 so the pixel's value is in [0, 1]
x_train_flatten = x_train/255.0
x_test_flatten = x_test/255.0
# Separate the dataset into classes
x_train_0 = x_train_flatten[y_train == 0]
x_train_1 = x_train_flatten[y_train == 1]
x_train_2 = x_train_flatten[y_train == 2]
x_train_3 = x_train_flatten[y_train == 3]
x_train_4 = x_train_flatten[y_train == 4]
x_train_5 = x_train_flatten[y_train == 5]
x_train_6 = x_train_flatten[y_train == 6]
x_train_7 = x_train_flatten[y_train == 7]
x_train_8 = x_train_flatten[y_train == 8]
x_train_9 = x_train_flatten[y_train == 9]
x_train_list = [x_train_0, x_train_1, x_train_2, x_train_3, x_train_4, x_train_5, x_train_6, x_train_7, x_train_8, x_train_9]
print(x_train_0.shape)
print(x_train_1.shape)
print(x_train_2.shape)
print(x_train_3.shape)
print(x_train_4.shape)
print(x_train_5.shape)
print(x_train_6.shape)
print(x_train_7.shape)
print(x_train_8.shape)
print(x_train_9.shape)
x_test_0 = x_test_flatten[y_test == 0]
x_test_1 = x_test_flatten[y_test == 1]
x_test_2 = x_test_flatten[y_test == 2]
x_test_3 = x_test_flatten[y_test == 3]
x_test_4 = x_test_flatten[y_test == 4]
x_test_5 = x_test_flatten[y_test == 5]
x_test_6 = x_test_flatten[y_test == 6]
x_test_7 = x_test_flatten[y_test == 7]
x_test_8 = x_test_flatten[y_test == 8]
x_test_9 = x_test_flatten[y_test == 9]
x_test_list = [x_test_0, x_test_1, x_test_2, x_test_3, x_test_4, x_test_5, x_test_6, x_test_7, x_test_8, x_test_9]
print(x_test_0.shape)
print(x_test_1.shape)
print(x_test_2.shape)
print(x_test_3.shape)
print(x_test_4.shape)
print(x_test_5.shape)
print(x_test_6.shape)
print(x_test_7.shape)
print(x_test_8.shape)
print(x_test_9.shape)
# + colab={"base_uri": "https://localhost:8080/"} id="DAUwx9BP1dJa" outputId="8ae74bd1-1d5c-4216-c0a5-d85f56578455"
# Choose 2 classes (2 numbers)
class_set = [0, 1]
training_sample_per_class = 200 # number of training samples per class
X_train = np.concatenate((x_train_list[class_set[0]][:training_sample_per_class, :], x_train_list[class_set[1]][:training_sample_per_class, :]), axis=0)
Y_train = np.zeros((X_train.shape[0],), dtype=int)
Y_train[training_sample_per_class:] += 1
print("Train Set Shape:", X_train.shape, Y_train.shape)
testing_sample_per_class = 100 # number of testing samples per class
X_test = np.concatenate((x_test_list[class_set[0]][:testing_sample_per_class, :], x_test_list[class_set[1]][:testing_sample_per_class, :]), axis=0)
Y_test = np.zeros((X_test.shape[0],), dtype=int)
Y_test[testing_sample_per_class:] += 1
print("Test Set Shape:", X_test.shape, Y_test.shape)
# + colab={"base_uri": "https://localhost:8080/", "height": 234} id="heWTmnS23oBV" outputId="21d21e03-a377-467d-a2c5-a8b68a940c95"
# Examples from train set
plt.imshow(np.concatenate((X_train[0], X_train[-1]), axis=1), cmap='gray')
# + colab={"base_uri": "https://localhost:8080/", "height": 234} id="-x34kJbj3wvh" outputId="75f10239-266d-4dd0-c26f-3fecdf199337"
# Examples from test set
plt.imshow(np.concatenate((X_test[0], X_test[-1]), axis=1), cmap='gray')
# + [markdown] id="r7VAUaSL0ogi"
# # 2. Utils
# + [markdown] id="aQMVXrYG16Lo"
# ## 2.1 Learning Rate Scheduler
# + [markdown] id="FrNQVVB-D6Mz"
# This is an example of [Learning Rate Scheduler](https://keras.io/api/callbacks/learning_rate_scheduler/) function for training a model with Keras API. It will be used later in an example of training a quantum model.
# + id="eyZt4xL60t7T"
def lr_schedule(epoch, lr_init=1e-3):
"""Learning Rate Schedule
Learning rate is scheduled to be reduced after 80, 120, 160, 180 epochs.
Called automatically every epoch as part of callbacks during training.
# Arguments
epoch (int): The number of epochs
# Returns
lr (float32): learning rate
lr_init (float32): initial learning rate, default: 1e-3
"""
lr = lr_init
if epoch > 180:
lr *= 0.5e-3
elif epoch > 160:
lr *= 1e-3
elif epoch > 120:
lr *= 1e-2
elif epoch > 80:
lr *= 1e-1
print('Learning rate: ', lr)
return lr
lr_scheduler = tf.keras.callbacks.LearningRateScheduler(lr_schedule)
lr_reducer = tf.keras.callbacks.ReduceLROnPlateau(factor=np.sqrt(0.1),
cooldown=0,
patience=5,
min_lr=0.5e-6)
# + [markdown] id="SzZvsgzU19d4"
# ## 2.2 Callbacks
# + [markdown] id="35jQicmOERg0"
# This is a [custom Keras Callback class](https://keras.io/guides/writing_your_own_callbacks/) to save the quantum model and its metrics during the training. It will be used later in an example of training a quantum model.
# + id="RHU05O630umu"
# Callback for saving model's weights, optimizer's states, and evaluation metrics
class CustomCallback(tf.keras.callbacks.Callback):
def __init__(self, checkpoint_dir):
super(CustomCallback, self).__init__()
self.checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
self.checkpoint = tf.train.Checkpoint(optimizer=opt_adam,
model=model)
try:
self.best_metric_list = list(np.loadtxt(checkpoint_dir + '/history_best_metric_list.txt'))
except:
# acc, val acc, auc, val auc
self.best_metric_list = [0, 0, 0, 0]
def load_history(name):
try:
data = np.loadtxt(checkpoint_dir + '/history_' + name + '.txt')
return list(data)
except:
return []
self.accuracy_list = load_history('accuracy')
self.val_accuracy_list = load_history('val_accuracy')
self.auc_list = load_history('auc')
self.val_auc_list = load_history('val_auc')
self.loss_list = load_history('loss')
self.val_loss_list = load_history('val_loss')
def on_epoch_end(self, epoch, logs=None):
self.checkpoint.save(file_prefix = self.checkpoint_prefix)
print("Saved custom checkpoint for epoch {}.".format(epoch+1))
def save_list_to_txt(metric, metric_list, name):
metric_list += [metric]
np.savetxt(checkpoint_dir + '/history_' + name + '.txt', np.array(metric_list))
return metric_list
self.accuracy_list = save_list_to_txt(logs["accuracy"], self.accuracy_list, 'accuracy')
self.val_accuracy_list = save_list_to_txt(logs["val_accuracy"], self.val_accuracy_list, 'val_accuracy')
self.auc_list = save_list_to_txt(logs["auc"], self.auc_list, 'auc')
self.val_auc_list = save_list_to_txt(logs["val_auc"], self.val_auc_list, 'val_auc')
self.loss_list = save_list_to_txt(logs["loss"], self.loss_list, 'loss')
self.val_loss_list = save_list_to_txt(logs["val_loss"], self.val_loss_list, 'val_loss')
print_space = 0
if logs["accuracy"] > self.best_metric_list[0]:
self.best_metric_list[0] = logs["accuracy"]
if logs["val_accuracy"] > self.best_metric_list[1]:
self.best_metric_list[1] = logs["val_accuracy"]
if logs["auc"] > self.best_metric_list[2]:
self.best_metric_list[2] = logs["auc"]
if logs["val_auc"] > self.best_metric_list[3]:
self.best_metric_list[3] = logs["val_auc"]
np.savetxt(checkpoint_dir + '/history_best_metric_list.txt', np.array(self.best_metric_list))
print("Best acc, val acc, auc, val auc:", self.best_metric_list)
print('')
# Callbacks for saving weights only
def checkpoint_save_weights_only(checkpoint_dir):
return tf.keras.callbacks.ModelCheckpoint(checkpoint_dir + '/{epoch:02d}epoch.h5',
monitor='val_loss', verbose=1, save_best_only=False,
save_weights_only=True, mode='auto', save_freq='epoch')
# + [markdown] id="Y2AyHIN_tvhY"
# # 3. Quantum Classifier
# + [markdown] id="k8wphl-3FCnW"
# In this third section, we will show how to build a quantum classifier with data re-uploading PQC.
# + [markdown] id="plGJgZMmEJd7"
# In classical fully-connected neural networks, to produce an output vector with more than one prediction value, we can simply put more than one fully-connected nodes at the output layer.
#
# With data re-uploading PQC, we can either use a single data re-uploading PQC with multiple qubits and measure each qubit with an observable, or we can use multiple data re-uploading PQCs and measure each PQC with an observable. These are not equivalent as entangling layers might be involved. There is no "absolutely right" design choice as it is case-by-case basis, similar to there is no "the best" neural nets architecture.
# + [markdown] id="UPt05ebtt8s_"
# ## 3.1 Data Preprocessing
# + [markdown] id="tRz3YBnd9V-L"
# Since a quantum classifier with data re-uploading PQC is similar to the fully-connected layer of classical neural networks, the input vector must be 1D dataset. Since MNIST is an image dataset, we have to flatten the image into 1D vector. The total number of features will now be $28\times28 = 784$, this is too much for the current quantum computing simulator. Hence, we use PCA to reduce the dimension to just, let's say, $6$ features.
# + colab={"base_uri": "https://localhost:8080/"} id="1kZOnhRprjoU" outputId="bff2d0c3-a1a9-4900-b6b5-e66205ae8220"
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train.reshape(-1, 28*28))
X_train_scaled = scaler.transform(X_train.reshape(-1, 28*28))
X_test_scaled = scaler.transform(X_test.reshape(-1, 28*28))
n_pca = 6
pca = PCA(n_components=n_pca)
pca.fit(X_train_scaled)
X_train_transform = pca.transform(X_train_scaled)
X_test_transform = pca.transform(X_test_scaled)
print(X_train_transform.shape, Y_train.shape)
print(X_test_transform.shape, Y_test.shape)
# + [markdown] id="w_k7hUmG3RdC"
# ## 3.2 Example 1: A classifier consists of only one Data Re-uploading PQC (can be either single or multi-qubit circuit)
# + [markdown] id="-QFRnSs58hzO"
# ### 3.2.1 Single-Qubit Case (One Prediction Output / One Output Node)
# + [markdown] id="uV4XzjU03wtk"
# #### Build the Model
# + [markdown] id="gR65tSIj9UKG"
# Building the Keras model with data re-uploading PQC is just like building a usual Keras model. We pass the input tensor to the data re-uploading PQC layer and construct the Keras model with the input tensor as its input and the measurement of data re-uploading PQC as its output.
# + [markdown] id="I7MQ_nmU-pUV"
# We use $|1⟩⟨1|$ observable because we want the PQC to give us a number between 0 and 1 (binary classifier). After the training, ideally, the model should map images of the first class to $|0⟩$ state and the second class to $|1⟩$ state.
# + colab={"base_uri": "https://localhost:8080/", "height": 71} id="9ViB_ogS3sJv" outputId="af0a47ba-832b-4ff0-e71e-ec9a99b64888"
n_qubits = 1
# Construct the observable
qubits = cirq.GridQubit.rect(1, n_qubits)
Z = cirq.PauliString(cirq.Z(qubits[-1]))
I = cirq.PauliString(cirq.I(qubits[-1]))
observables = [-0.5*Z + 0.5*I] # equivalent to |1⟩⟨1|
# Initialize the PQC
PQC = ReUploadingPQC(n_qubits, 1, n_pca, use_entanglement=True, use_terminal_entanglement=True, observables=observables)
# Construct the model
input_tensor = tf.keras.Input(shape=(n_pca,), dtype=tf.dtypes.float32, name='input')
quantum_classifier = PQC(input_tensor)
model = tf.keras.Model(inputs=[input_tensor], outputs=quantum_classifier)
# Optimizer
opt_adam = tf.keras.optimizers.Adam(lr=0.1)
# Compile the model with MSE loss
model.compile(loss='mse',
optimizer=opt_adam,
metrics=['accuracy', tf.keras.metrics.AUC(name='auc')])
SVGCircuit(PQC.circuit)
# + colab={"base_uri": "https://localhost:8080/"} id="4mPTdS217uT6" outputId="a94b36f4-3161-41cd-d258-9a1ae08c4b9a"
model.summary()
# + [markdown] id="qmanGAtR4zwe"
# #### Train the Model
# + [markdown] id="Zk9hvuOr-gtN"
# The constructed model can then be trained with the usual Keras training API.
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="WWBRPtVh4Ybq" outputId="feeb1584-4af5-4ce1-f854-b8fceb2e2020"
last_epoch = 0
# Train the model
H = model.fit(X_train_transform, Y_train, initial_epoch=last_epoch,
batch_size=32,
epochs=20,
validation_data=(X_test_transform, Y_test),
shuffle=True)
# Print and plot the best metrics obtained during the training
print("Best Train Accuracy:", max(H.history['accuracy']))
print("Best Val Accuracy:", max(H.history['val_accuracy']))
print("Best Train AUC:", max(H.history['auc']))
print("Best Val AUC", max(H.history['val_auc']))
plt.plot(H.history['accuracy'], label='Train Accuracy')
plt.plot(H.history['val_accuracy'], label='Val Accuracy')
plt.plot(H.history['auc'], label='Train AUC')
plt.plot(H.history['val_auc'], label='Val AUC')
plt.xlabel('Epoch')
plt.legend()
plt.show()
# + [markdown] id="dwVKIc3k__h5"
# ### 3.2.2 Multi-Qubit Case (One Prediction Output / One Output Node)
# + [markdown] id="P7f88oyd__h5"
# #### Build the Model
# + colab={"base_uri": "https://localhost:8080/", "height": 141} id="GXc4H8Cc__h6" outputId="adfe3545-7acc-4fec-e301-e8fb5eaf9c6b"
n_qubits = 2
# Construct the observable
qubits = cirq.GridQubit.rect(1, n_qubits)
Z = cirq.PauliString(cirq.Z(qubits[-1]))
I = cirq.PauliString(cirq.I(qubits[-1]))
observables = [-0.5*Z + 0.5*I] # equivalent to |1⟩⟨1| on the second qubit
# Initialize the PQC
PQC = ReUploadingPQC(n_qubits, 2, n_pca, use_entanglement=True, use_terminal_entanglement=True, observables=observables)
# Construct the model
input_tensor = tf.keras.Input(shape=(n_pca,), dtype=tf.dtypes.float32, name='input')
quantum_classifier = PQC(input_tensor)
model = tf.keras.Model(inputs=[input_tensor], outputs=quantum_classifier)
# Optimizer
opt_adam = tf.keras.optimizers.Adam(lr=0.1)
# Compile the model with MSE loss
model.compile(loss='mse',
optimizer=opt_adam,
metrics=['accuracy', tf.keras.metrics.AUC(name='auc')])
SVGCircuit(PQC.circuit)
# + colab={"base_uri": "https://localhost:8080/"} id="Qtw3z8Fy__h8" outputId="8163d2eb-93c9-414e-99ae-8b0516e4deaa"
model.summary()
# + [markdown] id="m5CKSs0b__h9"
# #### Train the Model
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="CnHvoSgJ__h9" outputId="919be694-f67d-4f56-919e-1d2b520e68bb"
last_epoch = 0
# Train the model
H = model.fit(X_train_transform, Y_train, initial_epoch=last_epoch,
batch_size=32,
epochs=20,
validation_data=(X_test_transform, Y_test),
shuffle=True)
# Print and plot the best metrics obtained during the training
print("Best Train Accuracy:", max(H.history['accuracy']))
print("Best Val Accuracy:", max(H.history['val_accuracy']))
print("Best Train AUC:", max(H.history['auc']))
print("Best Val AUC", max(H.history['val_auc']))
plt.plot(H.history['accuracy'], label='Train Accuracy')
plt.plot(H.history['val_accuracy'], label='Val Accuracy')
plt.plot(H.history['auc'], label='Train AUC')
plt.plot(H.history['val_auc'], label='Val AUC')
plt.xlabel('Epoch')
plt.legend()
plt.show()
# + [markdown] id="UMVIvmym81u_"
# ### 3.2.3 Multi-Qubit Case (Two Prediction Outputs / Two Output Nodes)
# + [markdown] id="SfQlGGmTXN70"
# For a binary classification task, we can also make the model to produce two prediction outputs, $[1, 0]$ output for the first class and $[0, 1]$ output for the second class.
# + [markdown] id="AzQXmgIUXgfZ"
# For a quantum classifier with data re-uploading PQC, this can be realized by either:
#
# 1. Use a single data re-uploading PQC but measure it with two different observables, let's say, with $|0⟩⟨0|$ on one qubit and $|1⟩⟨1|$ on the other. The example directly below is the implementation of this method.
#
# 2. Use two data re-uploading PQC and measure each PQC with a single observable, let's say, measure the first PQC with $|0⟩⟨0|$ on one of its qubit and measure the second PQC with $|1⟩⟨1|$ on one of its qubit. See section **3.3.1** for the implementation.
# + [markdown] id="vC9zwbMV89Oj"
# #### Build the Model
# + colab={"base_uri": "https://localhost:8080/", "height": 141} id="pz0CGx6s86gK" outputId="5acfb31a-45d0-43f8-dd62-7b7149315595"
n_qubits = 2
# Construct the observable
qubits = cirq.GridQubit.rect(1, n_qubits)
Z_0 = cirq.PauliString(cirq.Z(qubits[0]))
I_0 = cirq.PauliString(cirq.I(qubits[0]))
Z_1 = cirq.PauliString(cirq.Z(qubits[1]))
I_1 = cirq.PauliString(cirq.I(qubits[1]))
observables = [0.5*Z_0 + 0.5*I_0, -0.5*Z_1 + 0.5*I_1] # equivalent to |0⟩⟨0|⊗|1⟩⟨1|, or, |0⟩⟨0| for the first qubit and |1⟩⟨1| for the second qubit
# Initialize the PQC
PQC = ReUploadingPQC(n_qubits, 2, n_pca, use_entanglement=True, use_terminal_entanglement=True, observables=observables)
# Construct the model
input_tensor = tf.keras.Input(shape=(n_pca,), dtype=tf.dtypes.float32, name='input')
quantum_classifier = PQC(input_tensor)
model = tf.keras.Model(inputs=[input_tensor], outputs=quantum_classifier)
# Optimizer
opt_adam = tf.keras.optimizers.Adam(lr=0.1)
# Compile the model with MSE loss
model.compile(loss='mse',
optimizer=opt_adam,
metrics=['accuracy', tf.keras.metrics.AUC(name='auc')])
SVGCircuit(PQC.circuit)
# + colab={"base_uri": "https://localhost:8080/"} id="aHjmDjJv-bpV" outputId="87690760-bdcc-420a-a573-334fa06e757c"
model.summary()
# + [markdown] id="UugEI2P6-fYy"
# #### Train the Model
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="EmFBfAys-XYn" outputId="1030d3e8-9f62-49e4-ccd2-fbeecd118abb"
last_epoch = 0
# Train the model
H = model.fit(X_train_transform, tf.keras.utils.to_categorical(Y_train), initial_epoch=last_epoch,
batch_size=32,
epochs=20,
validation_data=(X_test_transform, tf.keras.utils.to_categorical(Y_test)),
shuffle=True)
# Compile the model with MSE loss
print("Best Train Accuracy:", max(H.history['accuracy']))
print("Best Val Accuracy:", max(H.history['val_accuracy']))
print("Best Train AUC:", max(H.history['auc']))
print("Best Val AUC", max(H.history['val_auc']))
plt.plot(H.history['accuracy'], label='Train Accuracy')
plt.plot(H.history['val_accuracy'], label='Val Accuracy')
plt.plot(H.history['auc'], label='Train AUC')
plt.plot(H.history['val_auc'], label='Val AUC')
plt.xlabel('Epoch')
plt.legend()
plt.show()
# + [markdown] id="JLgYaZk_5fTy"
# ## 3.3 Example 2: A classifier consists of more than one Data Re-uploading PQC (use more than one qubit since a PQC needs at least one qubit)
# + [markdown] id="H7hhrtL1Tpq7"
# It doesn't really make sense to use more than one PQC to produce one prediction value as every PQC will at least produce a measurement result of an observable. So in this example, only a model with two prediction outputs will be shown.
# + [markdown] id="Yt2vXBQjEKiK"
# ### 3.3.1 Two Prediction Values / Two Output Nodes
# + [markdown] id="H26l85pTtz-2"
# #### Build the Model
# + id="2Ep9gwsjqh8o"
# Construct the observable
n_qubits = 1
qubits = cirq.GridQubit.rect(1, n_qubits)
Z = cirq.PauliString(cirq.Z(qubits[-1]))
I = cirq.PauliString(cirq.I(qubits[-1]))
# Two observables, one for each PQC
observables_0 = [0.5*Z + 0.5*I] # equivalent to |0⟩⟨0|
observables_1 = [-0.5*Z + 0.5*I] # equivalent to |1⟩⟨1|
input_tensor = tf.keras.Input(shape=(n_pca,), dtype=tf.dtypes.float32, name='input')
PQC_1 = ReUploadingPQC(1, 1, n_pca, use_entanglement=False, use_terminal_entanglement=False, observables=observables_0, name='PQC_1')(input_tensor)
PQC_2 = ReUploadingPQC(1, 1, n_pca, use_entanglement=False, use_terminal_entanglement=False, observables=observables_1, name='PQC_2')(input_tensor)
output = tf.keras.layers.Concatenate()([PQC_1, PQC_2])
model = tf.keras.Model(inputs=[input_tensor], outputs=output)
# Optimizer
opt_adam = tf.keras.optimizers.Adam(lr=0.1)
# Compile the model with MSE loss
model.compile(loss='MSE',
optimizer=opt_adam,
metrics=['accuracy', tf.keras.metrics.AUC(name='auc')])
# + colab={"base_uri": "https://localhost:8080/"} id="VIBGt3iTTKm7" outputId="262ab2a5-86eb-48ce-cc11-fc8fde1169df"
model.summary()
# + [markdown] id="Lbz3r61dt5bs"
# #### Train the Model
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="-62CH7m9s-r6" outputId="7355961e-52db-4699-96ff-05bbdf8b0ba2"
last_epoch = 0
# Train the model
H = model.fit(X_train_transform, tf.keras.utils.to_categorical(Y_train), initial_epoch=last_epoch,
batch_size=32,
epochs=100,
validation_data=(X_test_transform, tf.keras.utils.to_categorical(Y_test)),
shuffle=True)
# Print and plot the best metrics obtained during the training
print("Best Train Accuracy:", max(H.history['accuracy']))
print("Best Val Accuracy:", max(H.history['val_accuracy']))
print("Best Train AUC:", max(H.history['auc']))
print("Best Val AUC", max(H.history['val_auc']))
plt.plot(H.history['accuracy'], label='Train Accuracy')
plt.plot(H.history['val_accuracy'], label='Val Accuracy')
plt.plot(H.history['auc'], label='Train AUC')
plt.plot(H.history['val_auc'], label='Val AUC')
plt.xlabel('Epoch')
plt.legend()
plt.show()
# + [markdown] id="ynsvJG6Ds7kK"
# # 4. Hybrid Quantum-Classical QCNN
# + [markdown] id="rA0XuzyiZJGt"
# In this fourth section, we will show how to build a QCNN model with quantum convolution followed by classical fully-connected layer.
# + [markdown] id="-p2nGPpmapdK"
# Since the quantum convolution layer (`QConv2D_DRC`) can take image data with multiple channels as its input, there is no need to flatten the image and reduce its dimension. Hence, for QCNN example, we will use the full size MNIST images.
# + [markdown] id="xNdS6E894A_y"
# ## Build the Model
# + [markdown] id="mKjAtWyMU8nj"
# Using the `QConv2D_DRC` layer is similar to using the [`Conv2D` layer](https://keras.io/api/layers/convolution_layers/convolution2d/) from Keras. We just need to pass the output tensor of the previous layer to it, and pass its output tensor to the next layer.
#
# A small difference is that we need to use the method `call()` for the `QConv2D_DRC` layer to work.
# + [markdown] id="FBev0evmbmWf"
# Let's build a model with two quantum convolution layers, a max pooling layer, followed by a classical fully-connected layer.
# + id="kHY8kFvv30j5"
# Full size MNIST images as input with shape (28, 28, 1)
input_tensor = tf.keras.Input(shape=(28, 28, 1), dtype=tf.dtypes.float32, name='input')
drc_settings = {
"n_qubits": [1],
"n_layers": [1],
"use_ent": [True],
"use_terminal_ent": [True]
}
# Two quantum convolution layers
qconv_1 = QConv2D_DRC(1, (3,3), (2,2), drc_settings, 1, padding="valid").call(input_tensor)
qconv_2 = QConv2D_DRC(1, (3,3), (2,2), drc_settings, 2, padding="valid").call(qconv_1)
# A max pooling layer
pool = tf.keras.layers.MaxPooling2D(pool_size=(2, 2), strides=(2,2), padding="valid")(qconv_2)
# Flatten the tensor
flat = tf.keras.layers.Flatten()(pool)
# A classical fully-connected layer
classical_dense = tf.keras.layers.Dense(2, activation='softmax')(flat)
model = tf.keras.Model(inputs=[input_tensor], outputs=classical_dense)
# + colab={"base_uri": "https://localhost:8080/"} id="3av7TPuJxolr" outputId="b5dedb3a-f86a-4e8c-9e00-4e6f2c3c9fe3"
model.summary()
# + [markdown] id="xjaUwRGWcOT-"
# Since this model is more complicated, it may takes longer and harder to train. Therefore, for this example, we will use the Learning Rate Scheduler to change the learning rate during the training. We will also save both the model's state and the optimizer's state so we can continue the training from the save files later if needed.
# + [markdown] id="64M6kf3ZeFrL"
# Also, instead of MSE, let's try different loss function. This time, we will try the cross-entropy loss.
# + colab={"base_uri": "https://localhost:8080/"} id="BUvrloOUzKyL" outputId="8c220275-e9e6-4689-88b9-6b72c176ea86"
# Training parameters
BATCH_SIZE = 32
EPOCHS = 100
# Print parameters for sanity check
print("Batch size, epochs:", BATCH_SIZE, EPOCHS)
# Optimizer with learning rate scheduler
opt_adam = tf.keras.optimizers.Adam(lr=lr_schedule(0, lr_init=0.01))
# Compile the model with cross-entropy loss
model.compile(loss='categorical_crossentropy',
optimizer=opt_adam,
metrics=['accuracy', tf.keras.metrics.AUC(name='auc')])
# + id="6A7LKZ0v1TiG"
# The directory on where we want to save the model
checkpoint_dir = main_dir + '/Hybrid'
# Initialize callbacks
# Let's use both callbacks that we have prepared just in case
cp_1 = CustomCallback(checkpoint_dir)
cp_2 = checkpoint_save_weights_only(checkpoint_dir)
# A list of callbacks to be passed on the Keras' model training API
callback_list = [cp_1, cp_2, lr_reducer, lr_scheduler]
# + [markdown] id="GkSScNNRI1XV"
# ## Train the Model
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="-CMb9sk2did0" outputId="87980542-0b0c-4823-e526-8d22255e409d"
last_epoch = 0
# Train the model
H = model.fit(X_train, tf.keras.utils.to_categorical(Y_train), initial_epoch=last_epoch,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
validation_data=(X_test, tf.keras.utils.to_categorical(Y_test)),
shuffle=True,
callbacks=callback_list)
# Print and plot the best metrics obtained during the training
print("Best Train Accuracy:", max(H.history['accuracy']))
print("Best Val Accuracy:", max(H.history['val_accuracy']))
print("Best Train AUC:", max(H.history['auc']))
print("Best Val AUC", max(H.history['val_auc']))
plt.plot(H.history['accuracy'], label='Train Accuracy')
plt.plot(H.history['val_accuracy'], label='Val Accuracy')
plt.plot(H.history['auc'], label='Train AUC')
plt.plot(H.history['val_auc'], label='Val AUC')
plt.xlabel('Epoch')
plt.legend()
plt.show()
# + [markdown] id="gSA1aEsjzff3"
# If later we want to continue the training, to load the model's and optimizer's state, we can reconstruct and recompile the model (basically re-running the code up until before the training) and then running this code in a new cell:
#
# ```
# checkpoint.restore(tf.train.latest_checkpoint(checkpoint_dir))
# ```
#
# After that, we can do the training like usual but remember to change the `initial_epoch` argument of Keras' model `fit()` method to the number of epoch of the last training session.
#
# For example, if the previous training session ends on epoch 195, then continue the training with this code:
#
# ```
# last_epoch = 195
#
# H = model.fit(X_train, tf.keras.utils.to_categorical(Y_train),
# initial_epoch=last_epoch,
# batch_size=BATCH_SIZE,
# epochs=EPOCHS,
# validation_data=(X_test, tf.keras.utils.to_categorical(Y_test)),
# shuffle=True,
# callbacks=callback_list)
# ```
#
#
# + [markdown] id="XxbfKXB4s5b9"
# # 5. Fully Quantum QCNN
# + [markdown] id="wubEJuUn1zEE"
# In this fifth section, we will show how to build a QCNN model with quantum convolution followed by a quantum classifier (no classical layer at all). This is basically as simple as replacing the classical fully-connected layer of model in section **4** with a quantum classifier explained in section **3**.
# + [markdown] id="II3hwE092CYc"
# Let's build a model with two quantum convolution layers, a max pooling layer, followed by a layer of quantum classifier.
# + [markdown] id="a5RGA3plwJVg"
# ## Build the Model
# + id="CfBcAIRh4bVV"
n_qubits = 2
# Construct the observable for the quantum classifier
qubits = cirq.GridQubit.rect(1, n_qubits)
Z_0 = cirq.PauliString(cirq.Z(qubits[0]))
I_0 = cirq.PauliString(cirq.I(qubits[0]))
Z_1 = cirq.PauliString(cirq.Z(qubits[1]))
I_1 = cirq.PauliString(cirq.I(qubits[1]))
observables = [0.5*Z_0 + 0.5*I_0, -0.5*Z_1 + 0.5*I_1] # equivalent to |0⟩⟨0|⊗|1⟩⟨1|, or, |0⟩⟨0| for the first qubit and |1⟩⟨1| for the second qubit
# + id="4m0lt0i93r1W"
# Full size MNIST images as input with shape (28, 28, 1)
input_tensor = tf.keras.Input(shape=(28, 28, 1), dtype=tf.dtypes.float32, name='input')
drc_settings = {
"n_qubits": [1],
"n_layers": [1],
"use_ent": [True],
"use_terminal_ent": [True]
}
# Two quantum convolution layers
qconv_1 = QConv2D_DRC(1, (3,3), (2,2), drc_settings, 1, padding="valid").call(input_tensor)
qconv_2 = QConv2D_DRC(1, (3,3), (2,2), drc_settings, 2, padding="valid").call(qconv_1)
# A max pooling layer
pool = tf.keras.layers.MaxPooling2D(pool_size=(2, 2), strides=(2,2), padding="valid")(qconv_2)
# Flatten the tensor
flat = tf.keras.layers.Flatten()(pool)
# A layer of quantum classifier
quantum_classifier = ReUploadingPQC(n_qubits, 1, flat.shape[-1], use_entanglement=True, use_terminal_entanglement=True, observables=observables)(flat)
model = tf.keras.Model(inputs=[input_tensor], outputs=quantum_classifier)
# + colab={"base_uri": "https://localhost:8080/"} id="sldgMOxf64qU" outputId="cb7b5b1c-1d30-4c47-d812-eda51a5fe08f"
model.summary()
# + [markdown] id="JLApsm8x_fgE"
# For this example, we again use the MSE loss function.
# + colab={"base_uri": "https://localhost:8080/"} id="sYbcvgQ66pRQ" outputId="f169f041-1459-4f5a-e801-85a1f557934f"
# Training parameters
BATCH_SIZE = 32
EPOCHS = 100
# Print parameters for sanity check
print("Batch size, epochs:", BATCH_SIZE, EPOCHS)
# Optimizer with learning rate scheduler
opt_adam = tf.keras.optimizers.Adam(lr=lr_schedule(0, lr_init=0.1))
# Compile the model with MSE loss
model.compile(loss='mse',
optimizer=opt_adam,
metrics=['accuracy', tf.keras.metrics.AUC(name='auc')])
# + id="57GDm0yz-p3d"
# The directory on where we want to save the model
checkpoint_dir = main_dir + '/Fully Quantum'
# Initialize callbacks
# Let's use both callbacks that we have prepared just in case
cp_1 = CustomCallback(checkpoint_dir)
cp_2 = checkpoint_save_weights_only(checkpoint_dir)
# A list of callbacks to be passed on the Keras' model training API
callback_list = [cp_1, cp_2, lr_reducer, lr_scheduler]
# + [markdown] id="jsPeHwMdwM2v"
# ## Train the Model
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="7NWhw4FMuBFH" outputId="eb6b6639-7f1e-46bc-987b-b1f0292acba3"
last_epoch = 0
# Train the model
H = model.fit(X_train, tf.keras.utils.to_categorical(Y_train), initial_epoch=last_epoch,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
validation_data=(X_test, tf.keras.utils.to_categorical(Y_test)),
shuffle=True,
callbacks=callback_list)
# Print and plot the best metrics obtained during the training
print("Best Train Accuracy:", max(H.history['accuracy']))
print("Best Val Accuracy:", max(H.history['val_accuracy']))
print("Best Train AUC:", max(H.history['auc']))
print("Best Val AUC", max(H.history['val_auc']))
plt.plot(H.history['accuracy'], label='Train Accuracy')
plt.plot(H.history['val_accuracy'], label='Val Accuracy')
plt.plot(H.history['auc'], label='Train AUC')
plt.plot(H.history['val_auc'], label='Val AUC')
plt.xlabel('Epoch')
plt.legend()
plt.show()
# + [markdown] id="2WqaE12FAm0g"
# # End
#
# That's it! Enjoy the package, and please let [me](mailto:<EMAIL>) know if you found any bugs in the tutorial.
#
# Thanks a lot for your interest in this package!
|
assets/qcnn_drc_tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + deletable=false editable=false
# Initialize OK
from client.api.notebook import Notebook
ok = Notebook('hw1.ok')
# -
# # Homework 1 - INT 15
# 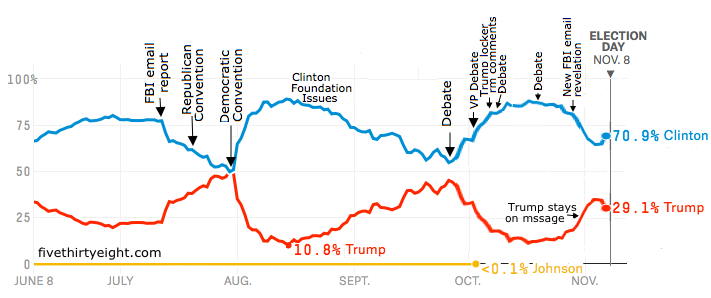
# We haven't yet talked about predictive models in class yet, but we can at least think about what makes a "good" prediction. In this assignment, we'll focus on evaluating the quality of election predictions made by the website [fivethirtyeight.com](https://www.fivethirtyeight.com). As one prominent example, fivethirtyeight predicted that Clinton had a 70.9% chance to win the election. Was their model wrong?
#
# To gain insight into questions like this, we'll focus on [US House elections predictions from 2018](https://projects.fivethirtyeight.com/2018-midterm-election-forecast/house/). Their predictions are based predominantly on polling data but include other sources as well (state of the economy, overall favoriability of politic parties, etc).
#
# This homework is based loosely on [this article](https://projects.fivethirtyeight.com/checking-our-work/). Please read the article before beginning the assignment.
#
# !wget https://raw.githubusercontent.com/fivethirtyeight/checking-our-work-data/master/us_house_elections.csv
# `ls` command can be used to verify that the file is now listed in our folder.
# !ls -F -l
import pandas as pd ## call pandas functions using "pd"
import numpy as np ## call numpy functions using "np"
election_data = pd.read_csv("us_house_elections.csv")
# ## Examining the Data
#
# Display the first 10 rows of the dataset using `iloc`.
# Fivethirtyeight has three different prediction models: `lite`, `classic` and `deluxe`, which roughly incorporate an increasing number of assumptions. In this assignment lets focus on evaluting the quality of the `classic` predictions. You can read more about how the prediction models work [here](https://fivethirtyeight.com/methodology/how-fivethirtyeights-house-and-senate-models-work/).
#
# Fivethirtyeight continuously updated their predictions as more polling data became available for each of the races. Let's focus on the predictions a few months before the election, on August 11th, and on the morning of election day, November 6th.
#
# ### Question 1
#
# Create a new pandas dataframe called `election_sub` by filtering to include only rows in which the `forecast_type` is "classic", and the date of the foreceast (`forecast_date`) is 8/11 or 11/6.
# + [markdown] deletable=false editable=false
# <!--
# BEGIN QUESTION
# name: q1
# manual: false
# points: 2
# -->
# -
election_sub = ...
# + deletable=false editable=false
ok.grade("q1");
# -
# ### Question 2
#
# We want to check whether events predicted by 538 to occur with probability _close to_ X% actually occured about X% of the time. To do this, we have to define _close_. First, we'll define the `cut_points` as 20 equally spaced numbers between 0 and 1 using `np.linspace`. Then we'll group the predicted probabilities into the `19` equally spaced bins determined by those cut points. Define the bin for each observation using the `pd.cut` function on the `probwin` variable. We'll assign the result to a new column of `election_sub` called `bin`.
# + [markdown] deletable=false editable=false
# <!--
# BEGIN QUESTION
# name: q2
# manual: false
# points: 2
# -->
# -
cut_points = np.linspace(0, 1, 20)
...
# + deletable=false editable=false
ok.grade("q2");
# -
# ### Question 3
#
# Now we've grouped the observations into a discrete set of bins according to the predicted probability, `probwin`. Within each bin, we now want to compute the actual fraction of times the candidates won. If 538 did a good job, it will be close to the predited probabilities. You'll need to use the `groupby` function to compute the mean of `probwin_outcome` (1 is a win and 0 is a loss) within each bin. Save the fraction of actual wins in each bin in a list called `fraction_outcome`.
# + [markdown] deletable=false editable=false
# <!--
# BEGIN QUESTION
# name: q3
# manual: false
# points: 2
# -->
# -
fraction_outcome = ...
# + deletable=false editable=false
ok.grade("q3");
# -
# ### Question 4
#
# For this problem we'll make a plot of the predicted probabilities and actual fraction of wins in each bin. We've already computed the actual fraction of wins; all that remains is to plot it against the predicted value assocaited with each bin. For the predicted value in each bin, we'll use the midpoint of the bin. Compute the midpoints of each bin from `cut_points`.
# + [markdown] deletable=false editable=false
# <!--
# BEGIN QUESTION
# name: q4
# manual: false
# points: 2
# -->
# -
midpoints = ...
list(midpoints)
# + deletable=false editable=false
ok.grade("q4");
# -
# Now make a scatterplot using `midpoints` as the x variable and `fraction_outcome` as the y variable. Draw a dashed line from `[0,0]` to `[1,1]` to mark the line y=x.
# +
# %matplotlib inline
import matplotlib.pyplot as plt
...
# -
# ### Question 5: adding error bars
#
# If you did things correctly, it should look like fivethirtyeight has done "pretty" well with their forecasts: the actual fraction of wins tracks closely with the predicted number. But how do we decide what's "good enough"? Consider this example: I correctly predict that a coin is fair (e.g. that it has a 50% chance of heads, 50% chance of tails). But if I flip it 100 times, I can be pretty sure it won't come up heads exactly 50 times. The fact that it didn't come up heads exactly 50 times doesn't make my prediction incorrect.
#
# To assess how reasonable the predictions are, I need to quantify the uncertainty in my estimate. It's reasonable to assume that within each bin, $k$, the observed number of wins, $Y_k \sim Bin(n_k, p_k)$, where $n_k$ is the number of elections and $p_k$ is the predicted win probability in bin $k$.
#
# Classical results tell us that the obseved fraction of wins in bin $k$, $\hat p = \frac{Y_k}{n_k}$ has variance Var$\left(\hat p_k\right) = \frac{p_k (1-p_k)}{n_k} \approx \frac{\hat p_k(1- \hat p_k)}{n_k}$. The standard deviation of the Binomial proportion then is $\hat \sigma_k \approx \sqrt{\frac{\hat p_k(1- \hat p_k)}{n_k}}$.
#
# If we use the [normal approximation to generate a confidence interval](https://en.wikipedia.org/wiki/Binomial_proportion_confidence_interval#Normal_approximation_interval), then the 95% interval has the form $\hat p_k \pm 1.96 \hat \sigma_k$.
#
# Create a new "aggregated" dataframe. This time, group `election_sub` by the `bin` and compute both the average of the `probwin_outcome` (`mean`) and the number of observations in each bin (`count`) using the `agg` function. Call this new data frame, `election_agg`.
election_agg = ...
# Use the `mean` and `count` columns of `election_agg` to create a new column of `election_agg` titled `err`, which stores $1.96 \times \hat \sigma_k$ in each bin $k$.
...
# Use `plt.errorbar` to create a new plot with error bars associated with the actual fraction of wins in each bin. Again add a dashed y=x line. Set the argument `fmt='.'` to create a scatterplot with errorbars.
plt.errorbar(midpoints, election_agg['mean'].values, yerr=election_agg['err'].values, fmt='.')
plt.plot([0, 1], [0, 1], '--')
# ### Question 6: computing the coverage
#
# If our intervals were true 95% confidence intervals, then we would expect about 95% of them to cover the midpoint of the bin (i.e. overlap with the y=x line). What fraction of the 95% confidence intervals cover the bin midpoint? Create a list called `upper` to be the `mean` + `err` and another `lower` to be `mean` - `err`. Next, compute `frac_covering` as the fraction of midpoints between `lower` and `upper`.
# + [markdown] deletable=false editable=false
# <!--
# BEGIN QUESTION
# name: q6
# manual: false
# points: 2
# -->
# +
upper = ...
lower = ...
frac_covering = ...
# + deletable=false editable=false
ok.grade("q6");
# -
# ### Question 7: understanding confidence intervals
#
# Are the 95% confidence intervals generally larger or smaller for more confident predictions (e.g. the predictions closer to 0 or 1). What are the factors that determine the length of the confidence intervals?
# *Write your answer here, replacing this text.*
# ### Question 8: finding the candidate that had the biggest change in support
#
# Let's see if we can find the candidate that seemed to improve their standing the most between August 11 and November 6. First, fill in the function `abs_diff`, which takes in a pandas data frame and computes the difference between the largest values of `probwin` and the smallest value.
#
#
# Input: a pandas dataframe with a numeric column named `probwin`
# Output: a pandas dataframe with the same columns, with an additional column named `absdiff`
def abs_diff(x):
...
return x
# We can use this function to compute the difference between the maximum and minimum predicted with probabilities for every candidate. To do so, group `election_sub` by `candidate` and `apply` the function `abs_diff`. Find the index of the largest difference in `diff_dataframe` and store it in `max_idx`. Do this using `np.nanargmax` function. This function finds the _index_ of the largest value, ignoring any missing values (`nans`).
diff_dataframe = ...
max_idx = ...
# + [markdown] deletable=false editable=false
# <!--
# BEGIN QUESTION
# name: q8
# manual: false
# points: 2
# -->
# -
candidate = ...
# + deletable=false editable=false
ok.grade("q8");
# -
# Did the candidate win or lose the election?
# *Write your answer here, replacing this text.*
# ### Question 9: plot predictions over time
# Plot the forecasted win probability for the candidate you found above, for every available date. For this you'll need to return to working with the full `election_data`, not `election_sub`. Don't forget, you should still filter to `classic` forecasts only. First, create an array of `predicted_probs` for the candidate at every date. Also save the date in an array called `forecast_date`. When creating `forecast_date`, use `pd.to_datetime` to convert a `str` datatype to the date format that can easily be plotted.
# + [markdown] deletable=false editable=false
# <!--
# BEGIN QUESTION
# name: q9
# manual: false
# points: 2
# -->
# -
predicted_probs = ...
forecast_date = ...
# + deletable=false editable=false
ok.grade("q9");
# -
# Now create a lineplot with forecast date on the x-axis and the predicted win probability on the y-axis.
...
# ### Question 10: prediction histograms
#
# Make a histogram showing the predicted win probabilities on the morning of the election. Again, restrict yourself to only the `classic` predictions.
...
# Are most house elections easy to forecast or hard to forecast?
# *Write your answer here, replacing this text.*
# ### Question 11: Comparing election and baseball predictions
#
# Fivethirtyeight also builds predictive models for sporting events. The following code will down a csv file containg their predictions for who would win every major league baseball game over the past two years.
# !wget -nc https://raw.githubusercontent.com/fivethirtyeight/checking-our-work-data/master/mlb_games.csv
# Create a pandas dataframe from the csv and print the first 10 rows.
...
# In this dataframe `prob1` is the predicted win probability for `team1`. Make a histogram of `prob1`. Set the limits of the x-axis to `[0, 1]`
...
# ### Question 12
#
# Find the most "surprising" baseball game outcome. To do so, select all of the entries for which `prob1_outcome` is 1 (i.e. `team1` won the game), and then look for the index of the row containing the smallest value of `prob1`. This will correspond to the game that was most suprising according to fivethirtyeights predictions. Find and print the row corresponding to this most surprising outcome.
...
# ### Question 13
# Are the outcomes of baseball games generally easier or harder to predict than the outcomes of political elections? In a few sentences, comment on why this might be the case. What data is available for these predictions? What factors affect the outcomes of elections and baseball games? What makes an event like an election or a baseballgame "random"?
# *Write your answer here, replacing this text.*
# + [markdown] deletable=false editable=false
# # Submit
# Make sure you have run all cells in your notebook in order before running the cell below, so that all images/graphs appear in the output.
# **Please save before submitting!**
# + deletable=false editable=false
# Save your notebook first, then run this cell to submit.
ok.submit()
|
hwk/hw1/hw1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="bYYGJvqP-Csl"
# # Identifying transiting exoplanet signals in a light curve
# + [markdown] id="gOFEJAKe-vjA"
# ## Learning Goals
#
# By the end of this tutorial, you will:
#
# - Understand the "Box Least Squares" (BLS) method for identifying transit signals.
# - Know how to use the Lightkurve [BoxLeastSquaresPeriodogram](https://docs.lightkurve.org/reference/api/lightkurve.periodogram.BoxLeastSquaresPeriodogram.from_lightcurve.html?highlight=boxleastsquaresperiodogram) to identify a transiting planet.
# - Be able to estimate the period, epoch, and duration of the transit.
# - Be able to plot the phase-folded transit light curve.
# - Be familiar with the interactive Box Least Squares periodogram in Lightkurve.
# + [markdown] id="7NGNkiQB-sKQ"
# ## Introduction
#
# The *Kepler* and *TESS* missions are optimized for finding new transiting exoplanets. [Lightkurve](http://docs.lightkurve.org/) provides a suite of tools that help make the process of identifying and characterizing planets convenient and accessible.
#
# In this tutorial, we will show you how to conduct your own search for transiting exoplanets in *Kepler* and *TESS* light curves. [Lightkurve](http://docs.lightkurve.org/) uses the [Astropy](https://www.astropy.org/) implementation of the Box Least Squares (BLS) method to identify transit signals. This tutorial demonstrates the basics of how to optimally use Lightkurve's BLS tools.
# + [markdown] id="EAzRgQPpAcBR"
# ## Imports
# This tutorial requires the [**Lightkurve**](http://docs.lightkurve.org/) package, which uses [**Matplotlib**](https://matplotlib.org/) for plotting.
# + id="azlcSd2lAjhy"
import lightkurve as lk
# %matplotlib inline
# + [markdown] id="IChTo8Ir3-Ju"
# ---
# + [markdown] id="r6p8DOLURorT"
# ## 1. Downloading a Light Curve and Removing Long-Term Trends
# + [markdown] id="QQLSlKKPOxEW"
# As an example, we will download all available [*Kepler*](https://archive.stsci.edu/kepler) observations for a known multi-planet system, [Kepler-69](https://iopscience.iop.org/article/10.1088/0004-637X/768/2/101).
# + colab={"base_uri": "https://localhost:8080/", "height": 387} executionInfo={"elapsed": 72588, "status": "ok", "timestamp": 1601412555227, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhoAkTlu5JCXqC32438ISJU86DPSZdvoBOLwtOQMfU=s64", "userId": "01921813910966567332"}, "user_tz": 240} id="6mO0bXd6Rw5X" outputId="0bbf9a53-3897-483a-d2a0-7737981a6494"
# Search for Kepler observations of Kepler-69
search_result = lk.search_lightcurve('Kepler-69', author='Kepler', cadence='long')
# Download all available Kepler light curves
lc_collection = search_result.download_all()
lc_collection.plot();
# + [markdown] id="v3CQzkKfPO8e"
# Each observation has a different offset, so in order to successfully search this light curve for transits, we first need to normalize and flatten the full observation. This can be performed on a stitched light curve. For more information about combining multiple observations of the same target, please see the companion tutorial on combining multiple quarters of *Kepler* data with Lightkurve.
# + colab={"base_uri": "https://localhost:8080/", "height": 442} executionInfo={"elapsed": 72582, "status": "ok", "timestamp": 1601412555229, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhoAkTlu5JCXqC32438ISJU86DPSZdvoBOLwtOQMfU=s64", "userId": "01921813910966567332"}, "user_tz": 240} id="V0XVebt-AM-4" outputId="29fd2769-0dcc-4700-9314-1fae68ccdd70"
search_result
# + colab={"base_uri": "https://localhost:8080/", "height": 405} executionInfo={"elapsed": 74448, "status": "ok", "timestamp": 1601412557102, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhoAkTlu5JCXqC32438ISJU86DPSZdvoBOLwtOQMfU=s64", "userId": "01921813910966567332"}, "user_tz": 240} id="iXDKVb9aBBNx" outputId="d93fb7aa-bbd1-48a3-f3a9-e777770460e0"
# Flatten the light curve
lc = lc_collection.stitch().flatten(window_length=901).remove_outliers()
lc.plot();
# + [markdown] id="c03Y0DPv-Csl"
# ## 2. The Box Least Squares Method for Finding Transiting Planets
# + [markdown] id="Bz1vMoZWTQRm"
# The most common method used to identify transiting exoplanets is the Box Least Squares (BLS) periodogram analysis. BLS works by modeling a transit using an upside-down top hat with four parameters: period, duration, depth, and reference time. These can be seen in the figure below, from the [astropy.timeseries](https://docs.astropy.org/en/stable/timeseries/) implementation of BLS.
#
# <img style="float: right;" src="https://docs.astropy.org/en/stable/timeseries/bls-1.png" alt="Box Least Squares" width="600px"/>
#
# These parameters are then optimized by minimizing the square difference between the BLS transit model and the observation. For more information about BLS, please see the [Astropy documentation](https://docs.astropy.org/en/stable/timeseries/bls.html).
#
# Lightkurve has two types of periodogram available to anaylze periodic trends in light curves:
# * `LombScarglePeriodogram`
# * `BoxLeastSquaresPeriodogram`
#
# Please see the companion tutorial on how to create periodograms and identify significant peaks for an example of the `LombScarglePeriodogram`.
# + [markdown] id="QWoWOLfELCTX"
# ## 3. Searching for Transiting Planets in a *Kepler* Light Curve Using BLS
#
# To create a `BoxLeastSquaresPeriodogram`, use the `LightCurve` method [to_periodogram](https://docs.lightkurve.org/reference/api/lightkurve.LightCurve.to_periodogram.html?highlight=to_periodogram), and pass in the string `'bls'` to specify the type of periodogram object you want to create. This method also optionally takes an array of periods (in days) to search, which we will set from 1–20 days to limit our search to short-period planets. We do so using the [numpy.linspace](https://numpy.org/doc/stable/reference/generated/numpy.linspace.html) function.
# + colab={"base_uri": "https://localhost:8080/", "height": 390} executionInfo={"elapsed": 81201, "status": "ok", "timestamp": 1601412563862, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhoAkTlu5JCXqC32438ISJU86DPSZdvoBOLwtOQMfU=s64", "userId": "01921813910966567332"}, "user_tz": 240} id="iLOVr_ZuRP2n" outputId="abef2286-e635-4663-b1f5-a6950d76ceda"
import numpy as np
# Create array of periods to search
period = np.linspace(1, 20, 10000)
# Create a BLSPeriodogram
bls = lc.to_periodogram(method='bls', period=period, frequency_factor=500);
bls.plot();
# + [markdown] id="a-8gU6D2A7a6"
# The plot above shows the power, or the likelihood of the BLS fit, for each of the periods in the array we passed in. This plot shows a handful of high-power peaks at discrete periods, which is a good sign that a transit has been identified. The highest power spike shows the most likely period, while the lower power spikes are fractional harmonics of the period, for example, 1/2, 1/3, 1/4, etc.
#
# We can pull out the most likely BLS parameters by taking their values at maximum power — we will refer to this transiting object as "planet b."
# + colab={"base_uri": "https://localhost:8080/", "height": 37} executionInfo={"elapsed": 81197, "status": "ok", "timestamp": 1601412563864, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhoAkTlu5JCXqC32438ISJU86DPSZdvoBOLwtOQMfU=s64", "userId": "01921813910966567332"}, "user_tz": 240} id="3c24rWxnR7_M" outputId="fdc82ff2-19ab-4809-cf43-77676daa5a40"
planet_b_period = bls.period_at_max_power
planet_b_t0 = bls.transit_time_at_max_power
planet_b_dur = bls.duration_at_max_power
# Check the value for period
planet_b_period
# + [markdown] id="4rlYrX_tLjRu"
# To confirm that this period and transit time (epoch) correspond to a transit signal, we can phase-fold the light curve using these values and plot it.
# + colab={"base_uri": "https://localhost:8080/", "height": 405} executionInfo={"elapsed": 82802, "status": "ok", "timestamp": 1601412565475, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhoAkTlu5JCXqC32438ISJU86DPSZdvoBOLwtOQMfU=s64", "userId": "01921813910966567332"}, "user_tz": 240} id="KOM3l2NbSDft" outputId="173ae47e-b646-43d3-cab1-fa8f24302249"
ax = lc.fold(period=planet_b_period, epoch_time=planet_b_t0).scatter()
ax.set_xlim(-5, 5);
# + [markdown] id="QpfdGLSoMDUb"
# The phase-folded light curve shows a strong transit signal with the identified period and transit time of maximum BLS power.
# + [markdown] id="IhdPdcMOSRYy"
# ## 4. Retrieving a Transit Model and Cadence Mask
# + [markdown] id="Yj6Oym9HMMvw"
# The BLS periodogram has features that make it possible to search for multiple planets in the same system. If we want to identify additional transit signals, it will be much more convenient if we first remove the previously identified signal. This will prevent the high-power periodicity of the first planet, planet b, from dominating the BLS periodogram, and will allow us to find lower signal-to-noise ratio (SNR) transits.
#
# We can create a cadence mask for the light curve using the transit parameters from the `BoxLeastSquaresPeriodogram`.
# + id="l03MOLu3Nm1J"
# Create a cadence mask using the BLS parameters
planet_b_mask = bls.get_transit_mask(period=planet_b_period,
transit_time=planet_b_t0,
duration=planet_b_dur)
# + [markdown] id="gh0XVIJ4OBSu"
# Now, we can create a masked version of the light curve to search for additional transit signals. The light curve is shown below, with masked cadences marked in red.
# + colab={"base_uri": "https://localhost:8080/", "height": 405} executionInfo={"elapsed": 88300, "status": "ok", "timestamp": 1601412570982, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhoAkTlu5JCXqC32438ISJU86DPSZdvoBOLwtOQMfU=s64", "userId": "01921813910966567332"}, "user_tz": 240} id="l_vzNQZwOKI0" outputId="7a50a3b5-a962-45c0-fab3-c59ba3fe5f2f"
masked_lc = lc[~planet_b_mask]
ax = masked_lc.scatter();
lc[planet_b_mask].scatter(ax=ax, c='r', label='Masked');
# + [markdown] id="S7SJfPWnOqE7"
# We can also create a BLS model to visualize the transit fit. This returns a `LightCurve` object with the BLS model in the flux column.
# + id="QptjZH66OwR1"
# Create a BLS model using the BLS parameters
planet_b_model = bls.get_transit_model(period=planet_b_period,
transit_time=planet_b_t0,
duration=planet_b_dur)
# + [markdown] id="qzfYLeCTPKjD"
# We can plot this over the folded light curve to confirm that it accurately represents the transit.
# + colab={"base_uri": "https://localhost:8080/", "height": 405} executionInfo={"elapsed": 89329, "status": "ok", "timestamp": 1601412572021, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhoAkTlu5JCXqC32438ISJU86DPSZdvoBOLwtOQMfU=s64", "userId": "01921813910966567332"}, "user_tz": 240} id="rHqMZmfYSX1E" outputId="00d53e85-ce58-44fc-e2be-7fc629642582"
ax = lc.fold(planet_b_period, planet_b_t0).scatter()
planet_b_model.fold(planet_b_period, planet_b_t0).plot(ax=ax, c='r', lw=2)
ax.set_xlim(-5, 5);
# + [markdown] id="goco294YUFjs"
# ## 5. Identifying Additional Transiting Planet Signals in the Same Light Curve
# + [markdown] id="OQboGya1PZF-"
# Now that we have created a light curve with the first identified planet masked out, we can search the remaining light curve for additional transit signals. Here, we search for long-period planets by increasing our range of periods to 1–300 days.
# + colab={"base_uri": "https://localhost:8080/", "height": 431} executionInfo={"elapsed": 96255, "status": "ok", "timestamp": 1601412578953, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhoAkTlu5JCXqC32438ISJU86DPSZdvoBOLwtOQMfU=s64", "userId": "01921813910966567332"}, "user_tz": 240} id="MSUsDbMJUM-y" outputId="6d2b2bf8-2e57-4232-f3b8-257c94571b26"
period = np.linspace(1, 300, 10000)
bls = masked_lc.to_periodogram('bls', period=period, frequency_factor=500)
bls.plot();
# + [markdown] id="4GJ7WfRR31lT"
# While no peaks in this BLS periodogram display a power as high as the previous transit signal, there is a definite peak near ~240 days. We can pull out the corresponding period and transit time to check the signal.
# + colab={"base_uri": "https://localhost:8080/", "height": 37} executionInfo={"elapsed": 96253, "status": "ok", "timestamp": 1601412578957, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhoAkTlu5JCXqC32438ISJU86DPSZdvoBOLwtOQMfU=s64", "userId": "01921813910966567332"}, "user_tz": 240} id="YVhdUd32P0Sx" outputId="6bae3db5-2a2e-48ba-fb02-a490a85727d2"
planet_c_period = bls.period_at_max_power
planet_c_t0 = bls.transit_time_at_max_power
planet_c_dur = bls.duration_at_max_power
# Check the value for period
planet_c_period
# + [markdown] id="xbk7G1in4NPm"
# We can again plot the phase-folded light curve to examine the transit.
# + colab={"base_uri": "https://localhost:8080/", "height": 405} executionInfo={"elapsed": 102368, "status": "ok", "timestamp": 1601412585079, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhoAkTlu5JCXqC32438ISJU86DPSZdvoBOLwtOQMfU=s64", "userId": "01921813910966567332"}, "user_tz": 240} id="6FKmoM70UOl3" outputId="dbba469e-0edb-4f8d-c1b5-be123b256ebe"
ax = masked_lc.fold(planet_c_period, planet_c_t0).scatter()
masked_lc.fold(planet_c_period, planet_c_t0).bin(.1).plot(ax=ax, c='r', lw=2,
label='Binned Flux')
ax.set_xlim(-5, 5);
# + [markdown] id="ebk1C7aa4ctu"
# This signal is lower SNR because there are fewer transits due to the longer period, and the shallower depth implies that the planet is smaller. To help see the transit more clearly, we have overplotted the binned flux, combining consecutive points taken over a span of 0.1 days.
#
# We have now successfully identified two planets in the same system! We can use the BLS models to visualize the transit timing in the light curve.
# + id="SRngiK4vQNWv"
planet_c_model = bls.get_transit_model(period=planet_c_period,
transit_time=planet_c_t0,
duration=planet_c_dur)
# + colab={"base_uri": "https://localhost:8080/", "height": 405} executionInfo={"elapsed": 105743, "status": "ok", "timestamp": 1601412588463, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhoAkTlu5JCXqC32438ISJU86DPSZdvoBOLwtOQMfU=s64", "userId": "01921813910966567332"}, "user_tz": 240} id="XEXsEtfHQOE8" outputId="5486451f-9f6a-48c4-c7c9-262510efaa00"
ax = lc.scatter();
planet_b_model.plot(ax=ax, c='dodgerblue', label='Planet b Transit Model');
planet_c_model.plot(ax=ax, c='r', label='Planet c Transit Model');
# + [markdown] id="ow66EyEhRZ98"
# ## 6. Using the Interactive BLS Periodogram in Lightkurve
# + [markdown] id="0UwgAQO45MIR"
# Lightkurve also has a tool that enables you to interactively perform a BLS search. A quick demo of this feature is shown below.
#
# To use the [LightCurve.interact_bls()](https://docs.lightkurve.org/reference/api/lightkurve.LightCurve.interact_bls.html?highlight=lightcurve%20interact_bls#lightkurve.LightCurve.interact_bls) method, zoom in on peaks in the BLS periodogram using the interactive plotting tools. To improve the fit, you can change the transit duration. The phase-folded light curve panel in the top right and the full light curve below it will automatically update to plot the highest power BLS model. The BLS parameters with highest power are noted in the bottom right of the figure.
# + [markdown] id="q-Xkjz6sKwlx"
# 
# + [markdown] id="aG4fgysD_Brp"
# ## About this Notebook
#
# **Authors:** <NAME> (<EMAIL>)
#
# **Updated On:** 2020-09-28
# + [markdown] id="MptPsdBQ_Qju"
# ## Citing Lightkurve and Astropy
#
# If you use `lightkurve` or its dependencies in your published research, please cite the authors. Click the buttons below to copy BibTeX entries to your clipboard.
# + colab={"base_uri": "https://localhost:8080/", "height": 151} executionInfo={"elapsed": 105740, "status": "ok", "timestamp": 1601412588467, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhoAkTlu5JCXqC32438ISJU86DPSZdvoBOLwtOQMfU=s64", "userId": "01921813910966567332"}, "user_tz": 240} id="1khvwNHx_QDz" outputId="1a696184-e00e-4286-8b8b-f8a665305138"
lk.show_citation_instructions()
# + [markdown] id="ZhdRVU3B_Zn2"
# <img style="float: right;" src="https://raw.githubusercontent.com/spacetelescope/notebooks/master/assets/stsci_pri_combo_mark_horizonal_white_bkgd.png" alt="Space Telescope Logo" width="200px"/>
#
|
docs/source/tutorials/3-science-examples/exoplanets-identifying-transiting-planet-signals.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Run the cell below by clicking on it and pressing twice *ctrl + enter* and enjoy the game:
# Remember to read the lab manual (and also *Readme.md*) and to make sure *ipywidgets* is installed.
#
# The standard deviation $\sigma$ of the potential is kept constant at 0.5 Å.
# %run User_interface.ipynb
display(FirstBox, SecondBox)
fig
|
1D/.ipynb_checkpoints/Bandstructure-1D-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import tohu
from tohu.generators import BaseGenerator
from tohu.custom_generator import logger, CustomGeneratorMeta
from tohu.debugging import DummyGenerator
tohu.debugging.logger.setLevel('DEBUG')
# ## Custom generator v2
class QuuxGenerator(BaseGenerator, metaclass=CustomGeneratorMeta):
z = 42
a = DummyGenerator('DummyA')
def __init__(self):
logger.debug("[QQQ] Start QuuxGenerator.__init__()")
self.b = DummyGenerator('DummyB')
self.foo = 23
logger.debug("[QQQ] End QuuxGenerator.__init__()")
g = QuuxGenerator()
g.reset(seed=None)
g.reset(seed=12345)
items = g.generate(10, seed=12345)
list(items)
|
playground/2018-08-29__Fresh_CustomGenerator_implementation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# Listas no Python
#
#criando litas
listademercado=['ovos','manteiga','farinha','leite']
print(listademercado)
#criando uma nova lista com diferentes tipos de dados
listadadoselementos=['farinha',1,3.00]
print(listadadoselementos)
#atribuindo cada valor a uma váriavel da lista
item1=listadadoselementos[0]
item2=listadadoselementos[1]
item3=listadadoselementos[2]
print(item1,item2,item3)
#alterando um item na lista
listademercado[3]="achocolatado"
print(listademercado)
#deletando um item da lista
del listademercado[3]
print(listademercado)
# Listas de lista (Listas aninhadas)
#criando uma lista aninhada- que é uma listas que tem outra ou outras listas como item
listas=[[1,2,3],[4,5,6,[7,8,9]],[10.1,30.5,25.4]]
listas
#atribuindo um item da lista a uma váriavel
a=listas[0]
a
#atribuindo um valor da váriavel que e outra váriavel
b=a[1]
b
#atribuindo o valor do primeiro item da lista a uma váriavel
a=listas[1][3]
a
b=listas[1][3][0]
b
#somando uma elemento
c=listas[0][2]+10
c
c=10+listas[0][2]+c
c
c=10+listas[0][2]+c
c
# Concatenando Listas
lista1=[5,10,15]
lista2=[20,25,30]
lista_total = lista1 + lista2
print(lista_total)
# OPERADOR IN
lista3=[50,60,70,80,90,100]
#o operador in verifica se o valor 10 está contido na lista
print(10 in lista3)
# Operações Built-in
len(lista3)
max(lista3)
min(lista3)
lista3.append(110)
print(lista3)
lista3.count(50)
lista4 = []
#copiando os elementos de uma lsita para outra
for item in lista3:
lista4.append(item)
print(lista4)
#adicionando dois ou mais elementos com
lista4.extend([120,130,140])
lista4
#inserindo uma valor numa determinada posição
lista4.insert(2,30)
lista4
#removendo lista
lista4.remove(30)
lista4
#reversão da lista
lista4.reverse()
lista4
x=[3,5,7,2,1,4]
x.sort()
x
|
listas/Listas_no_Python.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # multi-task alternate training strategy--clearence prediction
# +
from molmap import model as molmodel
import molmap
import matplotlib.pyplot as plt
import pandas as pd
from tqdm import tqdm
from joblib import load, dump
tqdm.pandas(ascii=True)
import numpy as np
import tensorflow as tf
import os
os.environ["CUDA_VISIBLE_DEVICES"]="0"
np.random.seed(12345)
tf.compat.v1.set_random_seed(12345)
# -
df = pd.read_csv('./Dataset_chembl_clearcaco.txt',sep=';')
task_name = 'chembl_clearcaco'
# # featurizer
# +
tmp_feature_dir = './tmpignore'
if not os.path.exists(tmp_feature_dir):
os.makedirs(tmp_feature_dir)
mp1 = molmap.loadmap('../descriptor.mp')
mp2 = molmap.loadmap('../fingerprint.mp')
X1_name = os.path.join(tmp_feature_dir, 'X1_%s.data' % task_name)
X2_name = os.path.join(tmp_feature_dir, 'X2_%s.data' % task_name)
if not os.path.exists(X1_name):
X1 = mp1.batch_transform(X_smiles, n_jobs = 8)
dump(X1, X1_name)
else:
X1 = load(X1_name)
if not os.path.exists(X2_name):
X2 = mp2.batch_transform(X_smiles, n_jobs = 8)
dump(X2, X2_name)
else:
X2 = load(X2_name)
# -
def get_idx_and_Y(df, task, split):
train_idx = df[df[split] == 'Train'].index
valid_idx = df[df[split] == 'Test'].index ##according to the paper<page 1256, Data Preparation>, they use this for early stopping
test_idx = df[df[split] == 'Ext'].index #their Ext set is our final test set
def _apply_float(x):
if type(x) == float:
return x
else:
x = x.replace(',','.')
return float(x)
Y = df[task].apply(_apply_float).to_frame().values
Y = np.log10(Y + 1e-8)
print(len(train_idx), len(valid_idx), len(test_idx))
return (train_idx, valid_idx, test_idx), Y
df.columns
# +
t = ['hlm_clearance[mL.min-1.g-1]','rlm_clearance[mL.min-1.g-1]', 'mlm_clearance[mL.min-1.g-1]']
m = ['Set_hlm', 'Set_rlm', 'Set_mlm']
task_epochs = 500
alternate_epochs = 1
alternate_rounds = 40
patience = 10
batch_size=128
lr = 0.0001
dense_layers=[256, 128, 32]
dense_avf='relu'
last_avf = 'linear'
# -
from sklearn.utils import shuffle
basemodel_data = []
for i, j in zip(t, m):
(train_idx, valid_idx, test_idx), Y = get_idx_and_Y(df, i, j)
trainY = Y[train_idx]
trainX = (X1[train_idx], X2[train_idx])
basemodel_data.append([trainX, trainY])
# ## alternate strategy to train a base model
# +
model = None
for i in tqdm(range(alternate_rounds)):
basemodel_data = shuffle(basemodel_data) #shffule
for trainX,trainY in basemodel_data:
if model == None:
molmap1_size = X1.shape[1:]
molmap2_size = X2.shape[1:]
model = molmodel.net.DoublePathNet(molmap1_size, molmap2_size,
n_outputs = trainY.shape[1],
dense_layers = dense_layers,
dense_avf = dense_avf, last_avf = last_avf)
opt = tf.keras.optimizers.Adam(lr=lr, beta_1=0.9, beta_2=0.999, epsilon=1e-08, decay=0.0) #
model.compile(optimizer = opt, loss = 'mse')
model.fit(trainX, trainY, batch_size=batch_size, epochs=alternate_epochs, verbose= 0, shuffle = True) #
model.save('./basemodel.h5')
# -
# ## 01.branch training for task of hlm
# +
task = 'hlm_clearance[mL.min-1.g-1]'
split = 'Set_hlm'
(train_idx, valid_idx, test_idx), Y = get_idx_and_Y(df, task, split)
trainY = Y[train_idx]
validY = Y[valid_idx]
testY = Y[test_idx]
trainX = (X1[train_idx], X2[train_idx])
validX = (X1[valid_idx], X2[valid_idx])
testX = (X1[test_idx], X2[test_idx])
# +
performance = molmodel.cbks.Reg_EarlyStoppingAndPerformance((trainX, trainY),
(validX, validY),
MASK=1e8,
patience = patience,
criteria = 'val_loss',
)
opt = tf.keras.optimizers.Adam(lr = lr, beta_1=0.9, beta_2=0.999, epsilon=1e-08, decay=0.0) #
model.load_weights('./basemodel.h5')
model.fit(trainX, trainY, batch_size=batch_size,
epochs=task_epochs, verbose= 0, shuffle = True,
validation_data = (validX, validY),
callbacks=[performance]) #
# -
dfp = pd.DataFrame(performance.history)[['r2', 'val_r2']]
dfp.plot()
performance.evaluate(trainX, trainY) # RMSE, R^2
performance.evaluate(validX, validY) # RMSE, R^2
performance.evaluate(testX, testY) # RMSE, R^2
# ## 02.branch training for task of rlm
# +
task = 'rlm_clearance[mL.min-1.g-1]'
split = 'Set_rlm'
(train_idx, valid_idx, test_idx), Y = get_idx_and_Y(df, task, split)
trainY = Y[train_idx]
validY = Y[valid_idx]
testY = Y[test_idx]
trainX = (X1[train_idx], X2[train_idx])
validX = (X1[valid_idx], X2[valid_idx])
testX = (X1[test_idx], X2[test_idx])
# +
performance = molmodel.cbks.Reg_EarlyStoppingAndPerformance((trainX, trainY),
(validX, validY),
MASK=1e8,
patience = patience,
criteria = 'val_loss',
)
opt = tf.keras.optimizers.Adam(lr = lr, beta_1=0.9, beta_2=0.999, epsilon=1e-08, decay=0.0) #
model.load_weights('./basemodel.h5')
model.fit(trainX, trainY, batch_size=batch_size,
epochs=task_epochs, verbose= 0, shuffle = True,
validation_data = (validX, validY),
callbacks=[performance]) #
# -
dfp = pd.DataFrame(performance.history)[['r2', 'val_r2']]
dfp.plot()
performance.evaluate(trainX, trainY) # RMSE, R^2
performance.evaluate(validX, validY) # RMSE, R^2
performance.evaluate(testX, testY) # RMSE, R^2
# ## 03.branch training for task of mlm
# +
task = 'mlm_clearance[mL.min-1.g-1]'
split = 'Set_mlm'
(train_idx, valid_idx, test_idx), Y = get_idx_and_Y(df, task, split)
trainY = Y[train_idx]
validY = Y[valid_idx]
testY = Y[test_idx]
trainX = (X1[train_idx], X2[train_idx])
validX = (X1[valid_idx], X2[valid_idx])
testX = (X1[test_idx], X2[test_idx])
# +
performance = molmodel.cbks.Reg_EarlyStoppingAndPerformance((trainX, trainY),
(validX, validY),
MASK=1e8,
patience = patience,
criteria = 'val_loss',
)
opt = tf.keras.optimizers.Adam(lr = lr, beta_1=0.9, beta_2=0.999, epsilon=1e-08, decay=0.0) #
model.load_weights('./basemodel.h5')
model.fit(trainX, trainY, batch_size=batch_size,
epochs=task_epochs, verbose= 0, shuffle = True,
validation_data = (validX, validY),
callbacks=[performance]) #
# -
performance.evaluate(trainX, trainY) # RMSE, R^2
performance.evaluate(validX, validY) # RMSE, R^2
performance.evaluate(testX, testY) # RMSE, R^2
model.count_params()
|
paper/00_OutoftheBox_Metablism_LMCL/01_comparison_multitask.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Iteration
# Our other aspect of control is looping back on ourselves.
#
# We use `for` ... `in` to "iterate" over lists:
mylist = [3, 7, 15, 2]
for whatever in mylist:
print(whatever ** 2)
# Each time through the loop, the variable in the `value` slot is updated to the **next** element of the sequence.
# ## Iterables
#
# Any sequence type is iterable:
#
#
#
# +
vowels = "aeiou"
sarcasm = []
for letter in "Okay":
if letter.lower() in vowels:
repetition = 3
else:
repetition = 1
sarcasm.append(letter * repetition)
"".join(sarcasm)
# -
# The above is a little puzzle, work through it to understand why it does what it does.
# ### Dictionaries are Iterables
# All sequences are iterables. Some iterables (things you can `for` loop over) are not sequences (things with you can do `x[5]` to), for example sets and dictionaries.
# +
import datetime
now = datetime.datetime.now()
founded = {"James": 1976, "UCL": 1826, "Cambridge": 1209}
current_year = now.year
for thing in founded:
print(thing, "is", current_year - founded[thing], "years old.")
# -
# ## Unpacking and Iteration
#
# Unpacking can be useful with iteration:
#
#
#
triples = [[4, 11, 15], [39, 4, 18]]
for whatever in triples:
print(whatever)
for first, middle, last in triples:
print(middle)
# A reminder that the words you use for variable names are arbitrary:
for hedgehog, badger, fox in triples:
print(badger)
#
#
#
# for example, to iterate over the items in a dictionary as pairs:
#
#
#
# +
things = {
"James": [1976, "Kendal"],
"UCL": [1826, "Bloomsbury"],
"Cambridge": [1209, "Cambridge"],
}
print(things.items())
# -
for name, year in founded.items():
print(name, "is", current_year - year, "years old.")
# ## Break, Continue
#
# * Continue skips to the next turn of a loop
# * Break stops the loop early
#
#
#
for n in range(50):
if n == 20:
break
if n % 2 == 0:
continue
print(n)
# These aren't useful that often, but are worth knowing about. There's also an optional `else` clause on loops, executed only if you don't `break`, but I've never found that useful.
# ## Classroom exercise: the Maze Population
# Take your maze data structure. Write a program to count the total number of people in the maze, and also determine the total possible occupants.
|
module01_introduction_to_python/01_09_iteration.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.8.12 ('aiffel_3.8')
# language: python
# name: python3
# ---
# # 31. 뉴스기사 크롤링 및 분류
#
# **뉴스기사를 주제/섹션별로 모아서 데이터셋을 구축하고, 이를 기반으로 뉴스기사 주제를 분류하는 텍스트 분류기를 구현해 본다.**
# ## 31-1. 들어가며
# ```bash
# $ mkdir -p ~/aiffel/news_crawler
# ```
# ```bash
# $ git clone https://github.com/SOMJANG/Mecab-ko-for-Google-Colab.git
# $ cd Mecab-ko-for-Google-Colab
# $ bash install_mecab-ko_on_colab190912.sh
# ```
# ```bash
# $ pip install beautifulsoup4
# $ pip install newspaper3k
# $ pip install konlpy
# ```
# ## 31-2. 웹 이해하기 (1) HTML과 태그
# ## 31-3. 웹 이해하기 (2) 선택자
# ## 31-4. BeautifulSoup 패키지
# +
from bs4 import BeautifulSoup
#- HTML 문서를 문자열 html로 저장합니다.
html = '''
<html>
<head>
</head>
<body>
<h1> 장바구니
<p id='clothes' class='name' title='라운드티'> 라운드티
<span class = 'number'> 25 </span>
<span class = 'price'> 29000 </span>
<span class = 'menu'> 의류</span>
<a href = 'http://www.naver.com'> 바로가기 </a>
</p>
<p id='watch' class='name' title='시계'> 시계
<span class = 'number'> 28 </span>
<span class = 'price'> 32000 </span>
<span class = 'menu'> 악세서리 </span>
<a href = 'http://www.facebook.com'> 바로가기 </a>
</p>
</h1>
</body>
</html>
'''
#- BeautifulSoup 인스턴스를 생성합니다.
#- 두번째 매개변수는 분석할 분석기(parser)의 종류입니다.
soup = BeautifulSoup(html, 'html.parser')
# -
print(soup.select('body'))
print(soup.select('body'))
print(soup.select('p'))
print(soup.select('h1 .name .menu'))
print(soup.select('html > h1'))
# ## 31-5. newspaper3k 패키지
# +
from newspaper import Article
#- 파싱할 뉴스 기사 주소입니다.
url = 'https://news.naver.com/main/read.nhn?mode=LSD&mid=sec&sid1=101&oid=030&aid=0002881076'
#- 언어가 한국어이므로 language='ko'로 설정해줍니다.
article = Article(url, language='ko')
article.download()
article.parse()
# +
#- 기사 제목을 출력합니다.
print('기사 제목 :')
print(article.title)
print('')
#- 기사 내용을 출력합니다.
print('기사 내용 :')
print(article.text)
# -
# ## 31-6. 네이버 뉴스 기사 크롤링 (1) 뉴스 URL, 페이지 이해하기
# ## 31-7. 네이버 뉴스 기사 크롤링 (2) BeautifulSoup와 newspaper3k를 통해 크롤러 만들기
# +
# 크롤러를 만들기 전 필요한 도구들을 임포트합니다.
import requests
import pandas as pd
from bs4 import BeautifulSoup
# 페이지 수, 카테고리, 날짜를 입력값으로 받습니다.
def make_urllist(page_num, code, date):
urllist= []
for i in range(1, page_num + 1):
url = 'https://news.naver.com/main/list.nhn?mode=LSD&mid=sec&sid1='+str(code)+'&date='+str(date)+'&page='+str(i)
headers = {'User-Agent': 'Mozilla/5.0 (X11; Linux x86_64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/54.0.2840.90 Safari/537.36'}
news = requests.get(url, headers=headers)
# BeautifulSoup의 인스턴스 생성합니다. 파서는 html.parser를 사용합니다.
soup = BeautifulSoup(news.content, 'html.parser')
# CASE 1
news_list = soup.select('.newsflash_body .type06_headline li dl')
# CASE 2
news_list.extend(soup.select('.newsflash_body .type06 li dl'))
# 각 뉴스로부터 a 태그인 <a href ='주소'> 에서 '주소'만을 가져옵니다.
for line in news_list:
urllist.append(line.a.get('href'))
return urllist
# -
url_list = make_urllist(2, 101, 20200506)
print('뉴스 기사의 개수: ',len(url_list))
url_list[:5]
idx2word = {'101' : '경제', '102' : '사회', '103' : '생활/문화', '105' : 'IT/과학'}
# +
from newspaper import Article
#- 데이터프레임을 생성하는 함수입니다.
def make_data(urllist, code):
text_list = []
for url in urllist:
article = Article(url, language='ko')
article.download()
article.parse()
text_list.append(article.text)
#- 데이터프레임의 'news' 키 아래 파싱한 텍스트를 밸류로 붙여줍니다.
df = pd.DataFrame({'news': text_list})
#- 데이터프레임의 'code' 키 아래 한글 카테고리명을 붙여줍니다.
df['code'] = idx2word[str(code)]
return df
# -
data = make_data(url_list, 101)
#- 상위 10개만 출력해봅니다.
data[:10]
# ## 31-8. 네이버 뉴스 기사 크롤링 (3) 데이터 수집 및 전처리
# +
code_list = [102, 103, 105]
code_list
# +
from multiprocessing import Pool
import random
import time, os
def make_total_data(page_num, code_list, date):
start = int(time.time())
num_cores = 4
df = None
for code in code_list:
pool = Pool(num_cores)
url_list = make_urllist(page_num, code, date)
df_temp = make_data(url_list, code)
print(str(code)+'번 코드에 대한 데이터를 만들었습니다.')
pool.close()
pool.join()
time.sleep(random.randint(0,1))
if df is not None:
df = pd.concat([df, df_temp])
else:
df = df_temp
print("***run time(sec) :", int(time.time()) - start)
return df
# -
df = make_total_data(1, code_list, 20200506)
print('뉴스 기사의 개수: ',len(df))
df.sample(10)
# +
# 아래 주석처리된 코드의 주석을 해제하고 실행을 하면 대량 크롤링이 진행됩니다.
# 위에서 수행했던 크롤링의 10배 분량이 수행될 것입니다. 한꺼번에 너무 많은 크롤링 요청이 서버에 전달되지 않도록 주의해 주세요.
# 기사 일자를 바꿔보면서 데이터를 모으면 더욱 다양한 데이터를 얻을 수 있게 됩니다.
#df = make_total_data(10, code_list, 20200506)
# +
import os
# 데이터프레임 파일을 csv 파일로 저장합니다.
# 저장경로는 이번 프로젝트를 위해 만든 폴더로 지정해 주세요.
csv_path = os.getenv("HOME") + "/aiffel/news_crawler/news_data.csv"
df.to_csv(csv_path, index=False)
if os.path.exists(csv_path):
print('{} File Saved!'.format(csv_path))
# -
# ## 31-9. 네이버 뉴스 기사 크롤링 (4) 데이터 전처리
csv_path = os.getenv("HOME") + "/aiffel/news_crawler/news_data.csv"
df = pd.read_table(csv_path, sep=',')
df.head()
# 정규 표현식을 이용해서 한글 외의 문자는 전부 제거합니다.
df['news'] = df['news'].str.replace("[^ㄱ-ㅎㅏ-ㅣ가-힣 ]","")
df['news']
print(df.isnull().sum())
# +
# 중복된 샘플들을 제거합니다.
df.drop_duplicates(subset=['news'], inplace=True)
print('뉴스 기사의 개수: ',len(df))
# +
# 중복 샘플 제거
df.drop_duplicates(subset=['news'], inplace=True)
print('뉴스 기사의 개수: ',len(df))
# +
import matplotlib.pyplot as plt
plt.rcParams["font.family"] = "NanumGothic"
df['code'].value_counts().plot(kind = 'bar')
# -
print(df.groupby('code').size().reset_index(name = 'count'))
# +
from konlpy.tag import Mecab
tokenizer = Mecab()
kor_text = '밤에 귀가하던 여성에게 범죄를 시도한 대 남성이 구속됐다서울 제주경찰서는 \
상해 혐의로 씨를 구속해 수사하고 있다고 일 밝혔다씨는 지난달 일 피해 여성을 \
인근 지하철 역에서부터 따라가 폭행을 시도하려다가 도망간 혐의를 받는다피해 \
여성이 저항하자 놀란 씨는 도망갔으며 신고를 받고 주변을 수색하던 경찰에 \
체포됐다피해 여성은 이 과정에서 경미한 부상을 입은 것으로 전해졌다'
#- 형태소 분석, 즉 토큰화(tokenization)를 합니다.
print(tokenizer.morphs(kor_text))
# -
stopwords = ['에','는','은','을','했','에게','있','이','의','하','한','다','과','때문','할','수','무단','따른','및','금지','전재','경향신문','기자','는데','가','등','들','파이낸셜','저작','등','뉴스']
# 토큰화 및 토큰화 과정에서 불용어를 제거하는 함수입니다.
def preprocessing(data):
text_data = []
for sentence in data:
temp_data = []
#- 토큰화
temp_data = tokenizer.morphs(sentence)
#- 불용어 제거
temp_data = [word for word in temp_data if not word in stopwords]
text_data.append(temp_data)
text_data = list(map(' '.join, text_data))
return text_data
text_data = preprocessing(df['news'])
print(text_data[0])
# ## 31-10. 머신 러닝 사용하기
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.naive_bayes import MultinomialNB
from sklearn import metrics
#- 훈련 데이터와 테스트 데이터를 분리합니다.
X_train, X_test, y_train, y_test = train_test_split(text_data, df['code'], random_state = 0)
print('훈련용 뉴스 기사의 개수 :', len(X_train))
print('테스트용 뉴스 기사의 개수 : ', len(X_test))
print('훈련용 레이블의 개수 : ', len(y_train))
print('테스트용 레이블의 개수 : ', len(y_test))
# +
#- 단어의 수를 카운트하는 사이킷런의 카운트벡터라이저입니다.
count_vect = CountVectorizer()
X_train_counts = count_vect.fit_transform(X_train)
#- 카운트벡터라이저의 결과로부터 TF-IDF 결과를 얻습니다.
tfidf_transformer = TfidfTransformer()
X_train_tfidf = tfidf_transformer.fit_transform(X_train_counts)
#- 나이브 베이즈 분류기를 수행합니다.
#- X_train은 TF-IDF 벡터, y_train은 레이블입니다.
clf = MultinomialNB().fit(X_train_tfidf, y_train)
# -
def tfidf_vectorizer(data):
data_counts = count_vect.transform(data)
data_tfidf = tfidf_transformer.transform(data_counts)
return data_tfidf
new_sent = preprocessing(["민주당 일각에서 법사위의 체계·자구 심사 기능을 없애야 한다는 \
주장이 나오는 데 대해 “체계·자구 심사가 법안 지연의 수단으로 \
쓰이는 것은 바람직하지 않다”면서도 “국회를 통과하는 법안 중 위헌\
법률이 1년에 10건 넘게 나온다. 그런데 체계·자구 심사까지 없애면 매우 위험하다”고 반박했다."])
print(clf.predict(tfidf_vectorizer(new_sent)))
new_sent = preprocessing(["인도 로맨틱 코미디 영화 <까립까립 싱글>(2017)을 봤을 때 나는 두 눈을 의심했다. \
저 사람이 남자 주인공이라고? 노안에 가까운 이목구비와 기름때로 뭉친 파마머리와, \
대충 툭툭 던지는 말투 등 전혀 로맨틱하지 않은 외모였다. 반감이 일면서 \
‘난 외모지상주의자가 아니다’라고 자부했던 나에 대해 회의가 들었다.\
티브이를 꺼버릴까? 다른 걸 볼까? 그런데, 이상하다. 왜 이렇게 매력 있지? 개구리와\
같이 툭 불거진 눈망울 안에는 어떤 인도 배우에게서도 느끼지 못한 \
부드러움과 선량함, 무엇보다 슬픔이 있었다. 2시간 뒤 영화가 끝나고 나는 완전히 이 배우에게 빠졌다"])
print(clf.predict(tfidf_vectorizer(new_sent)))
new_sent = preprocessing(["20분기 연속으로 적자에 시달리는 LG전자가 브랜드 이름부터 성능, 디자인까지 대대적인 변화를 \
적용한 LG 벨벳은 등장 전부터 온라인 커뮤니티를 뜨겁게 달궜다. 사용자들은 “디자인이 예쁘다”, \
“슬림하다”는 반응을 보이며 LG 벨벳에 대한 기대감을 드러냈다."])
print(clf.predict(tfidf_vectorizer(new_sent)))
y_pred = clf.predict(tfidf_vectorizer(X_test))
print(metrics.classification_report(y_test, y_pred))
# ## 31-11. 프로젝트 - 모델 성능 개선하기
|
FUNDAMENTALS/Node_31/[F-31] Only_LMS_Code_Blocks.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Mapping RNAseq reads with Salmon
# Input:
# * transcript reference
# * paired end fastq files
#
# Output:
# * one folder per pair end fastqs
import os
OUT_DIR = '../../analyses/genes_expression/'
FASTQ_DIR = '../../data/expression_data/'
reference_fn = '../../data/genomic_resources/Puccinia_graminis_tritici_21-0.transcripts.fa'
salmon_exc = '../../../anaconda3/downloads/salmon-latest_linux_x86_64/bin/salmon'
OUT_DIR = os.path.abspath(OUT_DIR)
FASTQ_DIR = os.path.abspath(FASTQ_DIR)
reference_fn = os.path.abspath(reference_fn)
salmon_exc = os.path.abspath(salmon_exc)
# !ls {FASTQ_DIR}
#index reference
# !{salmon_exc} version
salmon_index = reference_fn.replace('.fa', '.fa.salmon.index')
# !{salmon_exc} index -t {reference_fn} -i {salmon_index}
fastq_fn_list = [os.path.join(FASTQ_DIR, x) for x in os.listdir(FASTQ_DIR)]
fastq_fn_list.sort()
#for paired end reads
for n in range(0, len(fastq_fn_list), 2):
if "_" in os.path.basename(fastq_fn_list[n]):
#do haustoria
if os.path.basename(fastq_fn_list[n]).split("_")[2] == 'HSRNA':
print(fastq_fn_list[n])
print(fastq_fn_list[n + 1])
#generate outfolder for each haustoria replicate
QUANT_OUT = os.path.join(OUT_DIR, 'quant', \
os.path.basename(fastq_fn_list[n].split('.')[0]))
if not os.path.exists(QUANT_OUT):
os.makedirs(QUANT_OUT)
# !{salmon_exc} quant -i {salmon_index} -l A -1 {fastq_fn_list[n]} -2 {fastq_fn_list[n + 1]} -p 8 --validateMappings -o {QUANT_OUT}
#for paired end reads
for n in range(0, len(fastq_fn_list), 2):
if "_" in os.path.basename(fastq_fn_list[n]):
#do haustoria
if os.path.basename(fastq_fn_list[n]).split("_")[1] == 'PGTGS':
print(fastq_fn_list[n])
print(fastq_fn_list[n + 1])
#generate outfolder for each haustoria replicate
QUANT_OUT = os.path.join(OUT_DIR, 'quant', \
os.path.basename(fastq_fn_list[n].split('.')[0]))
if not os.path.exists(QUANT_OUT):
os.makedirs(QUANT_OUT)
# !{salmon_exc} quant -i {salmon_index} -l A -1 {fastq_fn_list[n]} -2 {fastq_fn_list[n + 1]} -p 8 --validateMappings -o {QUANT_OUT}
# +
#now do other reps they might be single reads
# -
salmon quant -i athal_index -l A \
-1 ${fn}/${samp}_1.fastq.gz \
-2 ${fn}/${samp}_2.fastq.gz \
-p 8 --validateMappings -o quants/${samp}_quant
|
multi_to_single_fast5_mapped_ids/.ipynb_checkpoints/Ben_RNAseq_expression_mapping-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python2
# ---
# +
import numpy as np
import pandas as pd
from nltk import word_tokenize, pos_tag
from nltk.corpus import wordnet as wn
from nltk.stem import WordNetLemmatizer
import multiprocessing
import enchant
import config
# nltk.download('wordnet')
# nltk.download('averaged_perceptron_tagger')
def tag2pos(tag, returnNone=False):
ap_tag = {'NN': wn.NOUN, 'JJ': wn.ADJ,
'VB': wn.VERB, 'RB': wn.ADV}
try:
return ap_tag[tag[:2]]
except:
return None if returnNone else ''
def lemmatize_df(df):
# lemmatize speech acts
for index, row in df.iterrows():
# initialize lemma list
lemma_list = []
# tokenize word_pos
if type(row['SPEECH_ACT']) == str:
tokens = word_tokenize(row['SPEECH_ACT'])
alpha_tokens = [token for token in tokens if token.isalpha()]
spellchecked_tokens = [token for token in alpha_tokens
if dictionary.check(token)]
tagged_tokens = pos_tag(spellchecked_tokens)
for tagged_token in tagged_tokens:
word = str(tagged_token[0])
word_pos = tagged_token[1]
word_pos_morphed = tag2pos(word_pos)
if word_pos_morphed is not '':
lemma = lemmatizer.lemmatize(word, word_pos_morphed)
else:
lemma = lemmatizer.lemmatize(word)
lemma_list.append(lemma)
lemma_string = ' '.join(lemma_list)
df.loc[index, 'LEMMAS'] = lemma_string
else:
print "Not string"
df.loc[index, 'SPEECH_ACT'] = 'not string'
df.loc[index, 'LEMMAS'] = 'not string'
continue
return(df)
# df.to_csv("/Users/alee35/land-wars-devel-data/03.lemmatized_speech_acts/membercontributions-lemmatized.tsv", sep="\t")
# load British English spell checker
dictionary = enchant.Dict("en_GB")
# lemmatizer
lemmatizer = WordNetLemmatizer()
# create as many processes as there are CPUs on your machine
num_processes = multiprocessing.cpu_count()/2
# calculate the chunk size as an integer
chunk_size = int(config.text.shape[0]/num_processes)
# works even if the df length is not evenly divisible by num_processes
chunks = [config.text.ix[config.text.index[i:i + chunk_size]]
for i in range(0, config.text.shape[0], chunk_size)]
# create our pool with `num_processes` processes
pool = multiprocessing.Pool(processes=num_processes)
# apply our function to each chunk in the list
result = pool.map(lemmatize_df, chunks)
# combine the results from our pool to a dataframe
config.textlem = pd.DataFrame().reindex_like(config.text)
config.textlem['LEMMAS'] = np.NaN
for i in range(len(result)):
config.textlem.ix[result[i].index] = result[i]
config.textlem.to_csv("/Users/alee35/land-wars-devel-data/03.lemmatized_speech_acts/membercontributions-lemmatized.tsv", sep="\t")
# write speech acts to files for triplet tagging
for index, row in config.textlem.iterrows():
f = '/Users/alee35/Google Drive/repos/Stanford-OpenIE-Python/hansard/debate_{}.txt'.format(index)
with open(f, 'w') as f:
f.write(row['LEMMAS'])
# -
config.textlem.to_csv("/Users/alee35/land-wars-devel-data/03.lemmatized_speech_acts/membercontributions-lemmatized.tsv", sep="\t")
|
src-dev/scratch.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Measuring the speed of sound
# For this lab we use a straw, a ruler to measure the length of the straw and a laptop or smartphone with a HTML5 browser and the build-in microphone.
#
# The websites to explore the properties of sound like frequency and amplitude can be visualized using a spectrometer. This can be done in the browser. Some examples:
#
# The relationship is pretty simpe:
#
# $$c=\frac{\lambda}{T}=\lambda f$$
#
# In the straw we get a standing wave. Since both ends are open the first node would have a node in the center of the tube and
#
# Regrading the length $l$ of the tube we get the relationship
#
# $$l=\frac{\lambda}{2}$$
#
# Now measuring the lenth and the frequency of the pitch we can calculate the speed of sound $c$ in air.
# +
l = float(input(" Please enter the length of the straw in meter: "))
f = float(input(" Please enter the frequency of the pitch in Hertz: "))
lambd = 2 * l
c = lambd * f
print(str(c) + " m/s is the speed of sound in the air in Ho Chi Minh")
|
speed-of-sound/speed of sound.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# numpy and pandas for data manipulation
import numpy as np
import pandas as pd
# sklearn preprocessing for dealing with categorical variables
from sklearn.preprocessing import LabelEncoder
# File system manangement
import os
# Suppress warnings
import warnings
warnings.filterwarnings('ignore')
from sklearn.model_selection import KFold
from sklearn.metrics import roc_auc_score
import lightgbm as lgb
import gc
# matplotlib and seaborn for plotting
import matplotlib.pyplot as plt
import seaborn as sns
#取消科學記號
pd.options.display.float_format = '{:.7f}'.format #pandas 取消科學記號,只顯示小數點第二位
# -
app_train = pd.read_csv('C:/Shared/machine_learning/home-credit-default-risk/application_train.csv')
app_test = pd.read_csv('C:/Shared/machine_learning/home-credit-default-risk/application_test.csv')
# +
from sklearn.model_selection import KFold
from sklearn.metrics import roc_auc_score
import lightgbm as lgb
import gc
def model(features, test_features, encoding = 'ohe', n_folds = 5):
"""Train and test a light gradient boosting model using
cross validation.
Parameters
--------
features (pd.DataFrame):
dataframe of training features to use
for training a model. Must include the TARGET column.
test_features (pd.DataFrame):
dataframe of testing features to use
for making predictions with the model.
encoding (str, default = 'ohe'):
method for encoding categorical variables. Either 'ohe' for one-hot encoding or 'le' for integer label encoding
n_folds (int, default = 5): number of folds to use for cross validation
Return
--------
submission (pd.DataFrame):
dataframe with `SK_ID_CURR` and `TARGET` probabilities
predicted by the model.
feature_importances (pd.DataFrame):
dataframe with the feature importances from the model.
valid_metrics (pd.DataFrame):
dataframe with training and validation metrics (ROC AUC) for each fold and overall.
"""
#ID 取出
# Extract the ids
train_ids = features['SK_ID_CURR']
test_ids = test_features['SK_ID_CURR']
#目標取出
# Extract the labels for training
labels = features['TARGET']
#刪除train 的目標和ID ,刪除test的ID
# Remove the ids and target
features = features.drop(columns = ['SK_ID_CURR', 'TARGET'])
test_features = test_features.drop(columns = ['SK_ID_CURR'])
#分兩種方法'ohe':將train和test都做one hot建立虛擬變數(攤平),並且根據兩者都有得col項目合併
# One Hot Encoding
if encoding == 'ohe':
features = pd.get_dummies(features)
test_features = pd.get_dummies(test_features)
# Align the dataframes by the columns
features, test_features = features.align(test_features, join = 'inner', axis = 1)
# No categorical indices to record
cat_indices = 'auto'
# Integer label encoding
elif encoding == 'le':
# Create a label encoder
label_encoder = LabelEncoder()
# List for storing categorical indices
cat_indices = []
#enumerate() 將資料變成((0,apptrain.columns[0]), (1,apptrain_columns[1])....)一對一放進 i 和 col跑迴圈
#LabelEncoder.fit_transform 將 object變數做重新編碼從 0 開始
#試試這行 : label_encoder.fit_transform(['a','a','b','c','a','b'])
#cat_indices 為object的索引
# Iterate through each column
for i, col in enumerate(features):
if features[col].dtype == 'object':
# Map the categorical features to integers
features[col] = label_encoder.fit_transform(np.array(features[col].astype(str)).reshape((-1,)))
test_features[col] = label_encoder.transform(np.array(test_features[col].astype(str)).reshape((-1,)))
# Record the categorical indices
cat_indices.append(i)
# Catch error if label encoding scheme is not valid
#encoding參數給錯就報錯
else:
raise ValueError("Encoding must be either 'ohe' or 'le'")
print('Training Data Shape: ', features.shape)
print('Testing Data Shape: ', test_features.shape)
# Extract feature names
#取出特徵名稱
feature_names = list(features.columns)
#dataframe 轉成np.array
# Convert to np arrays
features = np.array(features)
test_features = np.array(test_features)
# Create the kfold object
k_fold = KFold(n_splits = n_folds, shuffle = True, random_state = 50)
# Empty array for feature importances
#建立長度和特徵名稱一樣長且全為 0 的 np.array
feature_importance_values = np.zeros(len(feature_names))
# Empty array for test predictions
#建立長度和測試資料筆數一樣長且全為 0 的 np.array
test_predictions = np.zeros(test_features.shape[0])
# Empty array for out of fold validation predictions
#建立長度和訓練資料筆數一樣長且全為 0 的 np.array
out_of_fold = np.zeros(features.shape[0])
# Lists for recording validation and training scores
#記錄驗證和訓練的成績
valid_scores = []
train_scores = []
# Iterate through each fold
for train_indices, valid_indices in k_fold.split(features):
# Training data for the fold
train_features, train_labels = features[train_indices], labels[train_indices]
# Validation data for the fold
valid_features, valid_labels = features[valid_indices], labels[valid_indices]
# Create the model
model = lgb.LGBMClassifier(n_estimators=10000, objective = 'binary',
class_weight = 'balanced', learning_rate = 0.05,
reg_alpha = 0.1, reg_lambda = 0.1,
subsample = 0.8, n_jobs = -1, random_state = 50)
# Train the model
model.fit(train_features, train_labels, eval_metric = 'auc',
eval_set = [(valid_features, valid_labels), (train_features, train_labels)],
eval_names = ['valid', 'train'], categorical_feature = cat_indices,
early_stopping_rounds = 100, verbose = 200)
# Record the best iteration
best_iteration = model.best_iteration_
# Record the feature importances
feature_importance_values += model.feature_importances_ / k_fold.n_splits
# Make predictions
test_predictions += model.predict_proba(test_features, num_iteration = best_iteration)[:, 1] / k_fold.n_splits
# Record the out of fold predictions
out_of_fold[valid_indices] = model.predict_proba(valid_features, num_iteration = best_iteration)[:, 1]
# Record the best score
valid_score = model.best_score_['valid']['auc']
train_score = model.best_score_['train']['auc']
valid_scores.append(valid_score)
train_scores.append(train_score)
# Clean up memory
gc.enable()
del model, train_features, valid_features
gc.collect()
# Make the submission dataframe
submission = pd.DataFrame({'SK_ID_CURR': test_ids, 'TARGET': test_predictions})
# Make the feature importance dataframe
feature_importances = pd.DataFrame({'feature': feature_names, 'importance': feature_importance_values})
# Overall validation score
valid_auc = roc_auc_score(labels, out_of_fold)
# Add the overall scores to the metrics
valid_scores.append(valid_auc)
train_scores.append(np.mean(train_scores))
# Needed for creating dataframe of validation scores
fold_names = list(range(n_folds))
fold_names.append('overall')
# Dataframe of validation scores
metrics = pd.DataFrame({'fold': fold_names,
'train': train_scores,
'valid': valid_scores})
return submission, feature_importances, metrics
# -
|
notebooks/homecdt_eda/.ipynb_checkpoints/My_test2-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # EDIT DISTANCE
# **Problema:** date due stringhe $a$ e $b$, individuare una strategia per calcolare il numero minimo di operazioni necessario a trasformare $a$ in $b$, avendo come possibili operazioni l'inserimento di un carattere, la cancellazione di un carattere, e la sostituzione di un carattere.
# ## SOLUZIONE 1
#
# - Se $a$ è nulla allora occorre aggiungere un numero di caratteri pari alla lunghezza di $b$
# - Se $b$ è nulla allora occorre aggiungere un numero di caratteri pari alla lunghezza di $a$
# - Se l'ultimo carattere di $a$ e $b$, allora il costo è quello che calcoliamo per le sottostringhe $a_{-1}$ e $b_{-1}$
# - Se infine gli ultimi caratteri di $a$ e $b$ sono diversi, occorre fare un'operazione per l'ultimo carattere più il costo inferiore per le tre coppie di sottostringhe da cui è possibile arrivare all'ultimo carattere
def edist(a, b, cost=0):
if len(a) == 0:
return len(b)
elif len(b) == 0:
return len(a)
elif a[-1] == b[-1]:
return edist(a[:-1], b[:-1], cost + 1)
else:
return 1 + min([
edist(a[:-1], b, cost + 1),
edist(a, b[:-1], cost + 1),
edist(a[:-1], b[:-1], cost + 1),
])
edist('casa', 'casto')
# ## SOLUZIONE 2
import numpy as np
def ddist(a, b):
m = np.zeros((len(a)+1, len(b)+1))
for v in range(len(b) + 1):
m[0][v] = v
for v in range(len(a) + 1):
m[v][0] = v
return m
x = ddist('casa', 'casto')
import numpy as np
def D(a, b):
row = range(0, len(b)+1)
col = range(0, len(a)+1)
m = np.zeros((len(a)+1, len(b)+1))
m[0,:] = row
m[:,0] = col
for i, x in enumerate(a):
iM = i + 1
for j, y in enumerate(b):
jM = j + 1
if x == y:
cost = 0
else:
cost = 1
cost += min([
m[iM-1,jM-1],
m[iM,jM-1]+(1-cost),
m[iM-1,jM]+(1-cost),
])
m[iM,jM] = cost
return m
r = D('casa', 'casto')
r
|
pandas/edit_distance.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from gurobipy import * # import the optimize solver Gurobi
number_of_week = 3 # Set the index for number of week(1, 2, 3)
m = Model() # Import and create the model
# Set the input Parameter:
unit_production_cost = [130, 140, 150] # Production cost of per unit in each week
unit_holding_cost = 20 # Storage/Holding cost incurred per unit
demand = [2000, 1000, 1500] # Demand in each week
initial_inventory = 500 # Inventory at the beginning of week 1
a = 0.5 # Fraction of the goods produced during a week that can be used to meet the current week’s demand
# +
# Set the Variable list: Units of Switch to be ordered in each week
# Set the variable nx to integer number
nx = []
for i in range(number_of_week):
nx.append(m.addVar(vtype=GRB.INTEGER, name='nx{}'.format(i + 1)))
# Caculate inventory at the end of each month
# ni = []
# ni.append(initial_inventory)
# for i in range(len(nx)):
# xx = nx[i] + ni[i] - demand[i]
# ni.append(xx)
ni = []
for i in range(len(nx)):
if i <= 0:
xx = nx[i] + initial_inventory - demand[i]
else:
xx = nx[i] + ni[i - 1] - demand[i]
ni.append(xx)
# -
# Set the Minimize Obijective: Total Cost
m.setObjective(quicksum([unit_production_cost[i]*nx[i] for i in range(len(nx))]) + quicksum([unit_holding_cost*ni[i] for i in range(len(nx))]), GRB.MINIMIZE)
# +
# Set Non Negative decision variable
c1 = []
for i in range(len(nx)):
c1.append(m.addConstr(nx[i] >= 0))
# Demand must be satisfied for each week
c2 = []
for i in range(len(nx)):
if i > 0:
c2.append(m.addConstr(ni[i-1] + a*nx[i] >= demand[i]))
else:
c2.append(m.addConstr(initial_inventory + a*nx[i] >= demand[i]))
# -
# Run the optimize solver
m.optimize()
# Get the Optimal Solution for X
m.printAttr('X')
# Get the Optimal Objective Value
m.ObjVal
# Get the optimal solution list
m.X
# Get the end of inventory for each week
nin = []
initial_inventory = 500
for i in range(3):
if i > 0:
initial_inventory = nin[i-1]
xx = m.X[i] + initial_inventory - demand[i]
nin.append(xx)
print(nin)
|
assets/python/Ex5[Nintendo]_s.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## SOLVING PLANNING PROBLEMS
# ----
# ### GRAPHPLAN
# <br>
# The GraphPlan algorithm is a popular method of solving classical planning problems.
# Before we get into the details of the algorithm, let's look at a special data structure called **planning graph**, used to give better heuristic estimates and plays a key role in the GraphPlan algorithm.
# ### Planning Graph
# A planning graph is a directed graph organized into levels.
# Each level contains information about the current state of the knowledge base and the possible state-action links to and from that level.
# The first level contains the initial state with nodes representing each fluent that holds in that level.
# This level has state-action links linking each state to valid actions in that state.
# Each action is linked to all its preconditions and its effect states.
# Based on these effects, the next level is constructed.
# The next level contains similarly structured information about the next state.
# In this way, the graph is expanded using state-action links till we reach a state where all the required goals hold true simultaneously.
# We can say that we have reached our goal if none of the goal states in the current level are mutually exclusive.
# This will be explained in detail later.
# <br>
# Planning graphs only work for propositional planning problems, hence we need to eliminate all variables by generating all possible substitutions.
# <br>
# For example, the planning graph of the `have_cake_and_eat_cake_too` problem might look like this
# 
# <br>
# The black lines indicate links between states and actions.
# <br>
# In every planning problem, we are allowed to carry out the `no-op` action, ie, we can choose no action for a particular state.
# These are called 'Persistence' actions and are represented in the graph by the small square boxes.
# In technical terms, a persistence action has effects same as its preconditions.
# This enables us to carry a state to the next level.
# <br>
# <br>
# The gray lines indicate mutual exclusivity.
# This means that the actions connected bya gray line cannot be taken together.
# Mutual exclusivity (mutex) occurs in the following cases:
# 1. **Inconsistent effects**: One action negates the effect of the other. For example, _Eat(Cake)_ and the persistence of _Have(Cake)_ have inconsistent effects because they disagree on the effect _Have(Cake)_
# 2. **Interference**: One of the effects of an action is the negation of a precondition of the other. For example, _Eat(Cake)_ interferes with the persistence of _Have(Cake)_ by negating its precondition.
# 3. **Competing needs**: One of the preconditions of one action is mutually exclusive with a precondition of the other. For example, _Bake(Cake)_ and _Eat(Cake)_ are mutex because they compete on the value of the _Have(Cake)_ precondition.
# In the module, planning graphs have been implemented using two classes, `Level` which stores data for a particular level and `Graph` which connects multiple levels together.
# Let's look at the `Level` class.
from planning import *
from notebook import psource
psource(Level)
# Each level stores the following data
# 1. The current state of the level in `current_state`
# 2. Links from an action to its preconditions in `current_action_links`
# 3. Links from a state to the possible actions in that state in `current_state_links`
# 4. Links from each action to its effects in `next_action_links`
# 5. Links from each possible next state from each action in `next_state_links`. This stores the same information as the `current_action_links` of the next level.
# 6. Mutex links in `mutex`.
# <br>
# <br>
# The `find_mutex` method finds the mutex links according to the points given above.
# <br>
# The `build` method populates the data structures storing the state and action information.
# Persistence actions for each clause in the current state are also defined here.
# The newly created persistence action has the same name as its state, prefixed with a 'P'.
# Let's now look at the `Graph` class.
psource(Graph)
# The class stores a problem definition in `pddl`,
# a knowledge base in `kb`,
# a list of `Level` objects in `levels` and
# all the possible arguments found in the initial state of the problem in `objects`.
# <br>
# The `expand_graph` method generates a new level of the graph.
# This method is invoked when the goal conditions haven't been met in the current level or the actions that lead to it are mutually exclusive.
# The `non_mutex_goals` method checks whether the goals in the current state are mutually exclusive.
# <br>
# <br>
# Using these two classes, we can define a planning graph which can either be used to provide reliable heuristics for planning problems or used in the `GraphPlan` algorithm.
# <br>
# Let's have a look at the `GraphPlan` class.
psource(GraphPlan)
# Given a planning problem defined as a PlanningProblem, `GraphPlan` creates a planning graph stored in `graph` and expands it till it reaches a state where all its required goals are present simultaneously without mutual exclusivity.
# <br>
# Once a goal is found, `extract_solution` is called.
# This method recursively finds the path to a solution given a planning graph.
# In the case where `extract_solution` fails to find a solution for a set of goals as a given level, we record the `(level, goals)` pair as a **no-good**.
# Whenever `extract_solution` is called again with the same level and goals, we can find the recorded no-good and immediately return failure rather than searching again.
# No-goods are also used in the termination test.
# <br>
# The `check_leveloff` method checks if the planning graph for the problem has **levelled-off**, ie, it has the same states, actions and mutex pairs as the previous level.
# If the graph has already levelled off and we haven't found a solution, there is no point expanding the graph, as it won't lead to anything new.
# In such a case, we can declare that the planning problem is unsolvable with the given constraints.
# <br>
# <br>
# To summarize, the `GraphPlan` algorithm calls `expand_graph` and tests whether it has reached the goal and if the goals are non-mutex.
# <br>
# If so, `extract_solution` is invoked which recursively reconstructs the solution from the planning graph.
# <br>
# If not, then we check if our graph has levelled off and continue if it hasn't.
# Let's solve a few planning problems that we had defined earlier.
# #### Air cargo problem
# In accordance with the summary above, we have defined a helper function to carry out `GraphPlan` on the `air_cargo` problem.
# The function is pretty straightforward.
# Let's have a look.
psource(air_cargo_graphplan)
# Let's instantiate the problem and find a solution using this helper function.
airCargoG = air_cargo_graphplan()
airCargoG
# Each element in the solution is a valid action.
# The solution is separated into lists for each level.
# The actions prefixed with a 'P' are persistence actions and can be ignored.
# They simply carry certain states forward.
# We have another helper function `linearize` that presents the solution in a more readable format, much like a total-order planner, but it is _not_ a total-order planner.
linearize(airCargoG)
# Indeed, this is a correct solution.
# <br>
# There are similar helper functions for some other planning problems.
# <br>
# Lets' try solving the spare tire problem.
spareTireG = spare_tire_graphplan()
linearize(spareTireG)
# Solution for the cake problem
cakeProblemG = have_cake_and_eat_cake_too_graphplan()
linearize(cakeProblemG)
# Solution for the Sussman's Anomaly configuration of three blocks.
sussmanAnomalyG = three_block_tower_graphplan()
linearize(sussmanAnomalyG)
# Solution of the socks and shoes problem
socksShoesG = socks_and_shoes_graphplan()
linearize(socksShoesG)
|
planning_graphPlan.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
bank_data = pd.read_csv("Bankruptcy_data.csv")
bank_data.shape
bank_data.describe()
bank_data.boxplot("Attr1")
bank_data["Attr1"] = np.where(bank_data["Attr1"] > 40, np.NaN, bank_data["Attr1"])
bank_data.boxplot("Attr1")
bank_data["Attr1"] = np.where(bank_data["Attr1"] < -50, np.NaN, bank_data["Attr1"])
bank_data.boxplot("Attr1")
bank_data["Attr1"] = np.where(bank_data["Attr1"] > 5, np.NaN, bank_data["Attr1"])
bank_data.boxplot("Attr1")
bank_data["Attr1"] = np.where(bank_data["Attr1"] < -10, np.NaN, bank_data["Attr1"])
bank_data.boxplot("Attr1")
bank_data["Attr1"] = np.where(bank_data["Attr1"] < -6.5, np.NaN, bank_data["Attr1"])
bank_data.boxplot("Attr1")
|
outlier-lab/BoxPlot.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## connecting to kicktipp.de/wolter via selenium
# +
# enter hiddenly the password
import getpass
pswd = getpass.getpass('Kick<PASSWORD> password:')
# -
# ## bet individual gameday
# +
from selenium import webdriver
# parameters
gameday = 10
# prepare driver
driver = webdriver.Chrome()
driver.set_page_load_timeout(20)
# load webpage
driver.get('https://www.kicktipp.de/wolter/profil/login')
#driver.maximize_window()
driver.implicitly_wait(20)
# enter login and pw
driver.find_element_by_id("kennung").send_keys("<EMAIL>")
driver.find_element_by_name("passwort").send_keys(<PASSWORD>)
driver.find_element_by_name("submitbutton").click()
# load tippabgabe page
driver.get('https://www.kicktipp.de/wolter/tippabgabe?&spieltagIndex={0}'.format(gameday))
# access cells in tippabgabetable
### check if td[2] and td[3] are the teams you are looking for, or take the teams
### then get your dictionary and read out the predicted results
### then enter them in the respective fields according to below
# # get team matchups
# for game in range(1,10):
# team1 = driver.find_element_by_xpath("//table/tbody/tr[{0}]/td[2]".format(game)).text
# team2 = driver.find_element_by_xpath("//table/tbody/tr[{0}]/td[3]".format(game)).text
# print("{0} vs. {1}".format(team1,team2))
# home_goals = str(input())
# away_goals = str(input())
# bar = driver.find_elements_by_xpath("//table/tbody/tr[{0}]/td[5]/input".format(game))
# bar[1].clear()
# bar[1].send_keys(home_goals)
# bar[2].clear()
# bar[2].send_keys(away_goals)
# bet every game 2:1
for game in range(1,10):
bar = driver.find_elements_by_xpath("//table/tbody/tr[{0}]/td[5]/input".format(game))
bar[1].clear()
bar[1].send_keys('5')
bar[2].clear()
bar[2].send_keys('5')
# submit bets
driver.find_element_by_name('submitbutton').click()
# logout & close browser
driver.find_element_by_class_name('navtoggle').click()
driver.find_element_by_link_text('Logout').click()
driver.close()
# -
bar
# VfB Stuttgart vs. <NAME>
# 2
# 2
# 1899 Hoffenheim vs. <NAME>
# 1
# 3
# 1. FC Nürnberg vs. Hannover 96
# 1
# 0
# FC Augsburg vs. <NAME>
# 0
# 2
# VfL Wolfsburg vs. SC Freiburg
# 2
# 1
# Hertha BSC vs. <NAME>
# 1
# 3
# FC Schalke 04 vs. FC Bayern München
# 0
# 3
# Bayer 04 Leverkusen vs. FSV Mainz 05
# 1
# 0
# Eintracht Frankfurt vs. RB Leipzig
# 1
# 2
# ## bet all games this season 2:1
# +
from selenium import webdriver
# parameters
start_game_day = 4
# prepare driver
driver = webdriver.Chrome()
driver.set_page_load_timeout(20)
# load webpage
driver.get('https://www.kicktipp.de/wolter/profil/login')
driver.maximize_window()
driver.implicitly_wait(20)
# enter login and pw
driver.find_element_by_id("kennung").send_keys("<EMAIL>")
driver.find_element_by_name("passwort").send_keys(<PASSWORD>)
driver.find_element_by_name("submitbutton").click()
# loop over all game days left:
for gameday in range(start_game_day,35):
# load tippabgabe page
driver.get('https://www.kicktipp.de/wolter/tippabgabe?&spieltagIndex={0}'.format(gameday))
# access cells in tippabgabetable
### check if td[2] and td[3] are the teams you are looking for, or take the teams
### then get your dictionary and read out the predicted results
### then enter them in the respective fields according to below
# bet every game 2:1
for game in range(1,10):
foo = driver.find_elements_by_xpath("//table/tbody/tr[{0}]/td[5]/input".format(game))
foo[1].clear()
foo[1].send_keys('10')
foo[2].clear()
foo[2].send_keys('10')
# submit bets
driver.find_element_by_name('submitbutton').click()
# logout & close browser
driver.find_element_by_class_name('navtoggle').click()
driver.find_element_by_link_text('Logout').click()
driver.close()
|
notebooks/2.0-bw-enter-weekly-bets-via-selenium.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/aswit3/Start_Your_NLP_Career/blob/master/elmo_with_imdb.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="W3Ao7lfWqY6T" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="af8c4aea-29b6-45c2-d6db-b1a14adb10fb"
import numpy as np
import pandas as pd
import tensorflow as tf
import tensorflow_hub as hub
import keras.layers as layers
from keras.models import Model
from keras.datasets import imdb
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
from keras.layers import Input,Embedding,Dense,Flatten
from sklearn.metrics import accuracy_score,classification_report
from sklearn.model_selection import train_test_split
# + id="hDblyYeZoccV" colab_type="code" colab={}
def data_prep_ELMo(train_x,train_y,test_x,test_y,max_len):
INDEX_FROM = 3
word_to_index = imdb.get_word_index()
word_to_index = {k:(v+INDEX_FROM) for k,v in word_to_index.items()}
word_to_index["<START>"] =1
word_to_index["<UNK>"]=2
index_to_word = {v:k for k,v in word_to_index.items()}
sentences=[]
for i in range(len(train_x)):
temp = [index_to_word[ids] for ids in train_x[i]]
sentences.append(temp)
test_sentences=[]
for i in range(len(test_x)):
temp = [index_to_word[ids] for ids in test_x[i]]
test_sentences.append(temp)
train_text = [' '.join(sentences[i][:max_len]) for i in range(len(sentences))]
train_text = np.array(train_text, dtype=object)[:, np.newaxis]
train_label = train_y.tolist()
test_text = [' '.join(test_sentences[i][:500]) for i in range(len(test_sentences))]
test_text = np.array(test_text , dtype=object)[:, np.newaxis]
test_label = test_y.tolist()
return train_text,train_label,test_text,test_label
# + id="C29Z6kS1oulu" colab_type="code" colab={}
def load_data(vocab_size,max_len):
"""
Loads the keras imdb dataset
Args:
vocab_size = {int} the size of the vocabulary
max_len = {int} the maximum length of input considered for padding
Returns:
X_train = tokenized train data
X_test = tokenized test data
"""
INDEX_FROM = 3
# save np.load
np_load_old = np.load
# modify the default parameters of np.load
np.load = lambda *a,**k: np_load_old(*a, allow_pickle=True, **k)
(X_train,y_train),(X_test,y_test) = imdb.load_data(num_words = vocab_size,index_from = INDEX_FROM)
# restore np.load for future normal usage
np.load = np_load_old
print(X_train.shape, len(X_test), y_train.shape, len(y_test), "#####################################")
return X_train,X_test,y_train,y_test
# + id="aXiWPCd4pqat" colab_type="code" colab={}
def data_prep_ELMo(train_x,train_y,test_x,test_y,max_len):
INDEX_FROM = 3
word_to_index = imdb.get_word_index()
word_to_index = {k:(v+INDEX_FROM) for k,v in word_to_index.items()}
word_to_index["<START>"] =1
word_to_index["<UNK>"]=2
index_to_word = {v:k for k,v in word_to_index.items()}
sentences=[]
for i in range(len(train_x)):
temp = [index_to_word[ids] for ids in train_x[i]]
sentences.append(temp)
test_sentences=[]
for i in range(len(test_x)):
temp = [index_to_word[ids] for ids in test_x[i]]
test_sentences.append(temp)
train_text = [' '.join(sentences[i][:max_len]) for i in range(len(sentences))]
train_text = np.array(train_text, dtype=object)[:, np.newaxis]
train_label = train_y.tolist()
test_text = [' '.join(test_sentences[i][:500]) for i in range(len(test_sentences))]
test_text = np.array(test_text , dtype=object)[:, np.newaxis]
test_label = test_y.tolist()
return train_text,train_label,test_text,test_label
# + id="MPMfEWEuogHh" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="847069dd-929e-4009-ea80-755d8414b8b6"
embed_dim = 300
split_ratio= 0.33
max_len= 200
vocab_size= 100
trainable_param= False
workers = 3,
window = 1
x_train,x_test,y_train,y_test = load_data(vocab_size,max_len)
train_text,train_label,test_text,test_label = data_prep_ELMo(x_train,y_train,x_test,y_test,max_len)
# + id="NUQ17MhIp6-E" colab_type="code" colab={}
# "epochs":1,
# "batch_size":1024,
# "loss":"binary_crossentropy",
# "optimizer":"adam",
# "metrics":["accuracy"]
def ELMoEmbedding(x):
elmo_model = hub.Module("https://tfhub.dev/google/elmo/1", trainable=True)
print(elmo_model, "elmo loaded successfully")
return elmo_model(tf.squeeze(tf.cast(x, tf.string)), signature="default", as_dict=True)["default"]
def Classification_model_with_ELMo(X_train_pad,y_train,X_test_pad,y_test):
input_text = layers.Input(shape=(1,), dtype=tf.string)
embed_seq = layers.Lambda(ELMoEmbedding, output_shape=(1024,))(input_text)
print(embed_seq, input_text)
x = Dense(256,activation ="relu")(embed_seq)
preds = Dense(1,activation="sigmoid")(x)
model = Model(input_text,preds)
model.compile(loss="binary_crossentropy",optimizer="adam",metrics=["accuracy"])
model.fit(X_train_pad[:100],y_train[:100],epochs=1,batch_size=64,validation_data=(X_test_pad[:10],y_test[:10]))
predictions = model.predict(X_test_pad)
predictions = [0 if i<0.5 else 1 for i in predictions]
print("Accuracy: ",accuracy_score(y_test,predictions))
print("Classification Report: ",classification_report(y_test,predictions))
return model
# + id="8cRGUhc3sDE3" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 394} outputId="6f41dfa1-ccdf-4fbf-f43c-2c1ba65a91f0"
model = Classification_model_with_ELMo(train_text,train_label,test_text,test_label)
print(model.summary())
|
elmo_with_imdb.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.4 64-bit (''base'': conda)'
# name: python37464bitbasecondafbbec2054bb544a6b846b5a0f7959784
# ---
# ### 第一个python程序:hello, world!
print('hello, world!')
print('hello','world',sep=', ',end='!')
print('goodbye, world',end='\n')
# ### 使用python的turtle模块绘制国旗
# +
import turtle
# 绘制矩形
def draw_rectangle(x,y,width,height):
turtle.goto(x,y)
turtle.pencolor('red')
turtle.fillcolor('red')
turtle.begin_fill()
for i in range(2):
turtle.forward(width)
turtle.left(90)
turtle.forward(height)
turtle.left(90)
turtle.end_fill()
# 绘制五角星
def draw_star(x,y,radius):
turtle.setpos(x,y)
pos1 = turtle.pos()
turtle.circle(-radius, 72)
pos2 = turtle.pos()
turtle.circle(-radius, 72)
pos3 = turtle.pos()
turtle.circle(-radius, 72)
pos4 = turtle.pos()
turtle.circle(-radius, 72)
pos5 = turtle.pos()
turtle.color('yellow','yellow')
turtle.begin_fill()
turtle.goto(pos3)
turtle.goto(pos1)
turtle.goto(pos4)
turtle.goto(pos2)
turtle.goto(pos5)
turtle.end_fill()
# 主程序
def main():
turtle.speed(15)
turtle.penup()
x,y = -270,-180
# 画国旗主体
width, height = 540,360
draw_rectangle(x,y,width,height)
# 画大星星
pice = 22
center_x, center_y = x+5*pice, y+height-pice*3
turtle.goto(center_x,center_y)
turtle.left(90)
turtle.right(90)
draw_star(turtle.xcor(), turtle.ycor(),pice*3)
x_poses, y_poses = [10,12,12,10],[2,4,7,9]
# 画小星星
for x_pos,y_pos in zip(x_poses,y_poses):
turtle.goto(x+x_pos*pice,y+height-y_pos*pice)
turtle.left(turtle.towards(center_x,center_y)-turtle.heading())
turtle.forward(pice)
turtle.right(90)
draw_star(turtle.xcor(),turtle.ycor(),pice)
# 隐藏海龟
turtle.ht()
# 显示绘制窗口
turtle.mainloop()
if __name__ == '__main__':
main()
# -
# ### 绘制小猪佩奇
# +
from turtle import *
def nose(x,y):
"""画鼻子"""
penup()
# 将海龟移动到指定的坐标
goto(x,y)
pendown()
# 设置海龟的方向(0-东、90-北、180-西、270-南)
setheading(-30)
begin_fill()
a = 0.4
for i in range(120):
if 0 <= i < 30 or 60 <= i <90:
a = a + 0.08
# 向左转3度
left(3)
# 向前走
forward(a)
else:
a = a - 0.08
left(3)
forward(a)
end_fill()
penup()
setheading(90)
forward(25)
setheading(0)
forward(10)
pendown()
# 设置画笔的颜色(红, 绿, 蓝)
pencolor(255, 155, 192)
setheading(10)
begin_fill()
circle(5)
color(160, 82, 45)
end_fill()
penup()
setheading(0)
forward(20)
pendown()
pencolor(255, 155, 192)
setheading(10)
begin_fill()
circle(5)
color(160, 82, 45)
end_fill()
def head(x, y):
"""画头"""
color((255, 155, 192), "pink")
penup()
goto(x,y)
setheading(0)
pendown()
begin_fill()
setheading(180)
circle(300, -30)
circle(100, -60)
circle(80, -100)
circle(150, -20)
circle(60, -95)
setheading(161)
circle(-300, 15)
penup()
goto(-100, 100)
pendown()
setheading(-30)
a = 0.4
for i in range(60):
if 0<= i < 30 or 60 <= i < 90:
a = a + 0.08
lt(3) #向左转3度
fd(a) #向前走a的步长
else:
a = a - 0.08
lt(3)
fd(a)
end_fill()
def ears(x,y):
"""画耳朵"""
color((255, 155, 192), "pink")
penup()
goto(x, y)
pendown()
begin_fill()
setheading(100)
circle(-50, 50)
circle(-10, 120)
circle(-50, 54)
end_fill()
penup()
setheading(90)
forward(-12)
setheading(0)
forward(30)
pendown()
begin_fill()
setheading(100)
circle(-50, 50)
circle(-10, 120)
circle(-50, 56)
end_fill()
def eyes(x,y):
"""画眼睛"""
color((255, 155, 192), "white")
penup()
setheading(90)
forward(-20)
setheading(0)
forward(-95)
pendown()
begin_fill()
circle(15)
end_fill()
color("black")
penup()
setheading(90)
forward(12)
setheading(0)
forward(-3)
pendown()
begin_fill()
circle(3)
end_fill()
color((255, 155, 192), "white")
penup()
seth(90)
forward(-25)
seth(0)
forward(40)
pendown()
begin_fill()
circle(15)
end_fill()
color("black")
penup()
setheading(90)
forward(12)
setheading(0)
forward(-3)
pendown()
begin_fill()
circle(3)
end_fill()
def cheek(x,y):
"""画脸颊"""
color((255, 155, 192))
penup()
goto(x,y)
pendown()
setheading(0)
begin_fill()
circle(30)
end_fill()
def mouth(x,y):
"""画嘴巴"""
color(239, 69, 19)
penup()
goto(x, y)
pendown()
setheading(-80)
circle(30, 40)
circle(40, 80)
def setting():
"""设置参数"""
pensize(4)
# 隐藏海龟
hideturtle()
colormode(255)
color((255, 155, 192), "pink")
setup(840, 500)
speed(10)
def main():
"""主函数"""
setting()
nose(-100, 100)
head(-69, 167)
ears(0, 160)
eyes(0, 140)
cheek(80, 10)
mouth(-20, 30)
done()
if __name__ == '__main__':
main()
# -
# ### 将华氏温度转换为摄氏温度
f = float(input('请输入华氏温度:'))
c = (f-23)/1.8
print('%.1f华氏度=%.1f摄氏度'%(f,c))
# ### 输入圆的半径计算计算周长和面积
# +
import math
radius = float(input('请输入圆的半径:'))
perimeter = 2*math.pi *radius
area = math.pi*radius*radius
print("周长:%.2f"%perimeter)
print("面积:%.2f"%area)
# -
# ### 输入年份判断是不是闰年。
year = int(input('请输入年份:'))
is_leap = (year%4==0 and year%100!=0) or year%400 == 0
print(is_leap)
# ### 英制单位英寸与公制单位厘米互换
value = float(input('请输入长度:'))
unit = input('请输入单位:')
if unit == 'in' or unit == '英寸':
print('%f英寸=%f厘米'%(value,value*2.54))
elif unit == 'cm' or unit == '厘米':
print('%f厘米 = %f英寸'%(value,value/2.54))
else:
print('请输入有效的单位')
# ### 百分制成绩转换为等级制成绩
score = float(input('请输入成绩:'))
if score >= 90:
grade = 'A'
elif score >=80:
grade = 'B'
elif score >= 70:
grade = 'C'
elif score >= 60:
grade = 'D'
else:
grade = 'E'
print('对应的等级为:',grade)
# ### 输入三条边长,如果能构成三角形就计算圆周和面积
a = float(input('a='))
b = float(input('b='))
c = float(input('c='))
if a+b > c and a+c>b and b+c>a:
print('周长为:%f'%(a+b+c))
p = (a+b+c)/2
area = (p*(p-a)*(p-b)*(p-c))**0.5
print('面积:%f'%(area))
else:
print('不能构成三角形')
# ### 输入一个数是不是素数
# +
from math import sqrt
num = int(input('请输入一个正整数:'))
end = int(sqrt(num))
is_prime = True
for x in range(2,end+1):
if num%x==0:
is_prime = False
break
if is_prime and num!=1:
print('%d是素数'%num)
else:
print('%d不是素数'%num)
# -
# ### 输入两个正整数,计算他们的最大公约数和最小公倍数
x = int(input('x='))
y = int(input('y='))
if x>y:
x,y = y,x
for factor in range(x,0,-1):
if x%factor==0 and y%factor==0:
print('%d和%d的最大公约数是%d'%(x,y,factor))
print('%d和%d的最小公倍数是%d'%(x,y,x*y//factor))
break
# ### 打印三角形图案
# +
row = int(input('请输入行数: '))
for i in range(row):
for _ in range(i + 1):
print('*', end='')
print()
for i in range(row):
for j in range(row):
if j < row - i - 1:
print(' ', end='')
else:
print('*', end='')
print()
for i in range(row):
for _ in range(row - i - 1):
print(' ', end='')
for _ in range(2 * i + 1):
print('*', end='')
print()
# -
|
python_100_days/day01_15/index.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.6 64-bit (''base'': conda)'
# name: python37664bitbasecondad81f4d096e8b4b9885e3d702e0bb3be1
# ---
# #%%appyter init
from appyter import magic
magic.init(lambda _=globals: _())
# # Enrichr Scatterplot Visualizer
#
# This appyter creates a scatterplot visualizing enrichment analysis results from Enrichr (https://amp.pharm.mssm.edu/Enrichr/).
#
# The resulting figure will contain a scatterplot plot of each selected Enrichr library grouped by gene set similiarity, with blue points indicating gene sets with a significant similarity to the inputted gene set.
# +
import pandas as pd
import numpy as np
import umap
from maayanlab_bioinformatics.enrichment import enrich_crisp
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.colors as colors
from IPython.display import display, HTML
import base64
# Bokeh
from bokeh.io import output_notebook
from bokeh.plotting import figure, show
from bokeh.models import HoverTool, CustomJS, ColumnDataSource, Legend, LegendItem, Span
from bokeh.layouts import layout, row, column, gridplot
from bokeh.palettes import all_palettes
output_notebook()
# +
# %%appyter hide_code
{% do SectionField(name='section1', title = '1. Submit Your Gene List', subtitle = 'Upload a text file containing your gene list -OR- copy and paste your gene list into the text box below (One gene per row). You can also try the default gene list provided.', img = 'enrichr-icon.png')%}
{% do SectionField(name='section2', title = '2. Choose Enrichr Library', subtitle = 'Select between 1 and 9 Enrichr libraries you would like in your figure.', img = 'enrichr-icon.png')%}
{% do SectionField(name='section3', title = '3. Choose a Significance Value', subtitle = 'Choose a significance value for the p-values when performing enrichment analysis.', img = 'enrichr-icon.png')%}
# +
# %%appyter code_eval
gene_list_filename = {{ FileField(name='gene_list_filename', label='Gene List File', default='', description='Upload your gene list as a text file (One gene per row).',section = 'section1') }}
gene_list_input = {{ TextField(name='gene_list_input', label='Gene List', default='NSUN3\nPOLRMT\nNLRX1\nSFXN5\nZC3H12C\nSLC25A39\nARSG\nDEFB29\nNDUFB6\nZFAND1\nTMEM77\n5730403B10RIK\nRP23-195K8.6\nTLCD1\nPSMC6\nSLC30A6\nLOC100047292\nLRRC40\nORC5L\nMPP7\nUNC119B\nPRKACA\nTCN2\nPSMC3IP\nPCMTD2\nACAA1A\nLRRC1\n2810432D09RIK\nSEPHS2\nSAC3D1\nTMLHE\nLOC623451\nTSR2\nPLEKHA7\nGYS2\nARHGEF12\nHIBCH\nLYRM2\nZBTB44\nENTPD5\nRAB11FIP2\nLIPT1\nINTU\nANXA13\nKLF12\nSAT2\nGAL3ST2\nVAMP8\nFKBPL\nAQP11\nTRAP1\nPMPCB\nTM7SF3\nRBM39\nBRI3\nKDR\nZFP748\nNAP1L1\nDHRS1\nLRRC56\nWDR20A\nSTXBP2\nKLF1\nUFC1\nCCDC16\n9230114K14RIK\nRWDD3\n2610528K11RIK\nACO1\nCABLES1\nLOC100047214\nYARS2\nLYPLA1\nKALRN\nGYK\nZFP787\nZFP655\nRABEPK\nZFP650\n4732466D17RIK\nEXOSC4\nWDR42A\nGPHN\n2610528J11RIK\n1110003E01RIK\nMDH1\n1200014M14RIK\nAW209491\nMUT\n1700123L14RIK\n2610036D13RIK\nCOX15\nTMEM30A\nNSMCE4A\nTM2D2\nRHBDD3\nATXN2\nNFS1\n3110001I20RIK\nBC038156\nLOC100047782\n2410012H22RIK\nRILP\nA230062G08RIK\nPTTG1IP\nRAB1\nAFAP1L1\nLYRM5\n2310026E23RIK\nC330002I19RIK\nZFYVE20\nPOLI\nTOMM70A\nSLC7A6OS\nMAT2B\n4932438A13RIK\nLRRC8A\nSMO\nNUPL2\nTRPC2\nARSK\nD630023B12RIK\nMTFR1\n5730414N17RIK\nSCP2\nZRSR1\nNOL7\nC330018D20RIK\nIFT122\nLOC100046168\nD730039F16RIK\nSCYL1\n1700023B02RIK\n1700034H14RIK\nFBXO8\nPAIP1\nTMEM186\nATPAF1\nLOC100046254\nLOC100047604\nCOQ10A\nFN3K\nSIPA1L1\nSLC25A16\nSLC25A40\nRPS6KA5\nTRIM37\nLRRC61\nABHD3\nGBE1\nPARP16\nHSD3B2\nESM1\nDNAJC18\nDOLPP1\nLASS2\nWDR34\nRFESD\nCACNB4\n2310042D19RIK\nSRR\nBPNT1\n6530415H11RIK\nCLCC1\nTFB1M\n4632404H12RIK\nD4BWG0951E\nMED14\nADHFE1\nTHTPA\nCAT\nELL3\nAKR7A5\nMTMR14\nTIMM44\nSF1\nIPP\nIAH1\nTRIM23\nWDR89\nGSTZ1\nCRADD\n2510006D16RIK\nFBXL6\nLOC100044400\nZFP106\nCD55\n0610013E23RIK\nAFMID\nTMEM86A\nALDH6A1\nDALRD3\nSMYD4\nNME7\nFARS2\nTASP1\nCLDN10\nA930005H10RIK\nSLC9A6\nADK\nRBKS\n2210016F16RIK\nVWCE\n4732435N03RIK\nZFP11\nVLDLR\n9630013D21RIK\n4933407N01RIK\nFAHD1\nMIPOL1\n1810019D21RIK\n1810049H13RIK\nTFAM\nPAICS\n1110032A03RIK\nLOC100044139\nDNAJC19\nBC016495\nA930041I02RIK\nRQCD1\nUSP34\nZCCHC3\nH2AFJ\nPHF7\n4921508D12RIK\nKMO\nPRPF18\nMCAT\nTXNDC4\n4921530L18RIK\nVPS13B\nSCRN3\nTOR1A\nAI316807\nACBD4\nFAH\nAPOOL\nCOL4A4\nLRRC19\nGNMT\nNR3C1\nSIP1\nASCC1\nFECH\nABHD14A\nARHGAP18\n2700046G09RIK\nYME1L1\nGK5\nGLO1\nSBK1\nCISD1\n2210011C24RIK\nNXT2\nNOTUM\nANKRD42\nUBE2E1\nNDUFV1\nSLC33A1\nCEP68\nRPS6KB1\nHYI\nALDH1A3\nMYNN\n3110048L19RIK\nRDH14\nPROZ\nGORASP1\nLOC674449\nZFP775\n5430437P03RIK\nNPY\nADH5\nSYBL1\n4930432O21RIK\nNAT9\nLOC100048387\nMETTL8\nENY2\n2410018G20RIK\nPGM2\nFGFR4\nMOBKL2B\nATAD3A\n4932432K03RIK\nDHTKD1\nUBOX5\nA530050D06RIK\nZDHHC5\nMGAT1\nNUDT6\nTPMT\nWBSCR18\nLOC100041586\nCDK5RAP1\n4833426J09RIK\nMYO6\nCPT1A\nGADD45GIP1\nTMBIM4\n2010309E21RIK\nASB9\n2610019F03RIK\n7530414M10RIK\nATP6V1B2\n2310068J16RIK\nDDT\nKLHDC4\nHPN\nLIFR\nOVOL1\nNUDT12\nCDAN1\nFBXO9\nFBXL3\nHOXA7\nALDH8A1\n3110057O12RIK\nABHD11\nPSMB1\nENSMUSG00000074286\nCHPT1\nOXSM\n2310009A05RIK\n1700001L05RIK\nZFP148\n39509\nMRPL9\nTMEM80\n9030420J04RIK\nNAGLU\nPLSCR2\nAGBL3\nPEX1\nCNO\nNEO1\nASF1A\nTNFSF5IP1\nPKIG\nAI931714\nD130020L05RIK\nCNTD1\nCLEC2H\nZKSCAN1\n1810044D09RIK\nMETTL7A\nSIAE\nFBXO3\nFZD5\nTMEM166\nTMED4\nGPR155\nRNF167\nSPTLC1\nRIOK2\nTGDS\nPMS1\nPITPNC1\nPCSK7\n4933403G14RIK\nEI24\nCREBL2\nTLN1\nMRPL35\n2700038C09RIK\nUBIE\nOSGEPL1\n2410166I05RIK\nWDR24\nAP4S1\nLRRC44\nB3BP\nITFG1\nDMXL1\nC1D', description='Paste your gene list (One gene per row).', section = 'section1') }}
enrichr_libraries = {{ MultiCheckboxField(name='transcription_libraries', description='Select up to 9 Enrichr libraries you would like in your figure.', label='Library Selection', default='ChEA_2016', section = 'section2',choices=[
'ARCHS4_TFs_Coexp',
'ChEA_2016',
'ENCODE_and_ChEA_Consensus_TFs_from_ChIP-X',
'ENCODE_Histone_Modifications_2015',
'ENCODE_TF_ChIP-seq_2015',
'Epigenomics_Roadmap_HM_ChIP-seq',
'Enrichr_Submissions_TF-Gene_Coocurrence',
'Genome_Browser_PWMs',
'lncHUB_lncRNA_Co-Expression',
'miRTarBase_2017',
'TargetScan_microRNA_2017',
'TF_Perturbations_Followed_by_Expression',
'TRANSFAC_and_JASPAR_PWMs',
'TRRUST_Transcription_Factors_2019',
'ARCHS4_Kinases_Coexp',
'BioCarta_2016',
'BioPlanet_2019',
'CORUM',
'Elsevier_Pathway_Collection',
'HMS_LINCS_KinomeScan',
'HumanCyc_2016',
'huMAP',
'KEA_2015',
'KEGG_2019_Human',
'KEGG_2019_Mouse',
'Kinase_Perturbations_from_GEO_down',
'Kinase_Perturbations_from_GEO_up',
'L1000_Kinase_and_GPCR_Perturbations_down',
'L1000_Kinase_and_GPCR_Perturbations_up',
'NCI-Nature_2016',
'NURSA_Human_Endogenous_Complexome',
'Panther_2016',
'Phosphatase_Substrates_from_DEPOD',
'PPI_Hub_Proteins',
'Reactome_2016',
'SILAC_Phosphoproteomics',
'SubCell_BarCode',
'WikiPathways_2019_Human',
'WikiPathways_2019_Mouse',
'GO_Cellular_Component_2018',
'GO_Molecular_Function_2018',
'Human_Phenotype_Ontology',
'Jensen_COMPARTMENTS',
'Jensen_DISEASES',
'Jensen_TISSUES',
'Achilles_fitness_decrease',
'Achilles_fitness_increase',
'ARCHS4_IDG_Coexp',
'ClinVar_2019',
'dbGaP',
'DepMap_WG_CRISPR_Screens_Broad_CellLines_2019',
'DepMap_WG_CRISPR_Screens_Sanger_CellLines_2019',
'Allen_Brain_Atlas_down',
'Allen_Brain_Atlas_up',
'ARCHS4_Cell-lines',
'ARCHS4_Tissues',
'Cancer_Cell_Line_Encyclopedia',
'CCLE_Proteomics_2020',
'ESCAPE',
'GTEx_Tissue_Sample_Gene_Expression_Profiles_down',
'GTEx_Tissue_Sample_Gene_Expression_Profiles_up',
'Human_Gene_Atlas',
'Mouse_Gene_Atlas',
'NCI-60_Cancer_Cell_Lines',
'ProteomicsDB_2020',
'Tissue_Protein_Expression_from_Human_Proteome_Map',
'Chromosome_Location_hg19',
'Data_Acquisition_Method_Most_Popular_Genes',
'Enrichr_Libraries_Most_Popular_Genes',
'HMDB_Metabolites',
'HomoloGene',
'InterPro_Domains_2019',
'Pfam_Domains_2019',
'Pfam_InterPro_Domains',
'Table_Mining_of_CRISPR_Studies',
]) }}
significance_value = {{ FloatField(name='significance_value', label='Significance Value', default='0.05', description='Enter a value at which p-values are significant.', section = 'section3') }}
# -
# ### Import gene list
# Import gene list as file or from text box file
# Will choose file upload over textbox if a file is given
if gene_list_filename != '':
open_gene_list_file = open(gene_list_filename,'r')
lines = open_gene_list_file.readlines()
genes = [x.strip() for x in lines]
open_gene_list_file.close()
else:
genes = gene_list_input.split('\n')
genes = [x.strip() for x in genes]
# +
# %%appyter code_eval
def download_library(library_name):
# download pre-processed library data
df = pd.read_csv('https://raw.githubusercontent.com/skylar73/Enrichr-Processed-Library-Storage/master/Scatterplot/Libraries/' + library_name + '.csv')
name = df['Name'].tolist()
gene_list = df['Genes'].tolist()
library_data = [list(a) for a in zip(name, gene_list)]
return genes, library_data, df
# +
# enrichment analysis
def get_library_iter(library_data):
for member in library_data:
term = member[0]
gene_set = member[1].split(' ')
yield term, gene_set
def get_enrichment_results(genes, library_data):
return sorted(enrich_crisp(genes, get_library_iter(library_data), 20000, True), key=lambda r: r[1].pvalue)
def get_pvalue(row, unzipped_results, all_results):
if row['Name'] in list(unzipped_results[0]):
index = list(unzipped_results[0]).index(row['Name'])
return all_results[index][1].pvalue
else:
return 1
# -
# call enrichment results
def get_plot(library_name):
genes, library_data, df = download_library(library_name)
all_results = get_enrichment_results(genes, library_data)
unzipped_results = list(zip(*all_results))
if len(all_results) == 0:
print("There are no enriched terms with your inputted gene set and the ", library_name, " library.")
my_colors = ['#808080'] * len(df.index)
source = ColumnDataSource(
data=dict(
x = df['x'],
y = df['y'],
gene_set = df['Name'],
colors = my_colors,
sizes = [6] * len(df.index)
)
)
hover_emb = HoverTool(names=["df"], tooltips="""
<div style="margin: 10">
<div style="margin: 0 auto; width:200px;">
<span style="font-size: 12px; font-weight: bold;">Gene Set:</span>
<span style="font-size: 12px">@gene_set</span>
</div>
</div>
""")
else:
# add p value to the dataframe
df['p value'] = df.apply (lambda row: get_pvalue(row, unzipped_results, all_results), axis=1)
# normalize p values for color scaling
cmap = mpl.cm.get_cmap('Blues_r')
norm = colors.Normalize(vmin = df['p value'].min(), vmax=significance_value*2)
my_colors = []
my_sizes = []
for index, row in df.iterrows():
if row['p value'] < significance_value:
my_colors += [mpl.colors.to_hex(cmap(norm(row['p value'])))]
my_sizes += [12]
else:
my_colors += ['#808080']
my_sizes += [6]
source = ColumnDataSource(
data=dict(
x = df['x'],
y = df['y'],
gene_set = df['Name'],
p_value = df['p value'],
colors = my_colors,
sizes = my_sizes
)
)
hover_emb = HoverTool(names=["df"], tooltips="""
<div style="margin: 10">
<div style="margin: 0 auto; width:200px;">
<span style="font-size: 12px; font-weight: bold;">Gene Set:</span>
<span style="font-size: 12px">@gene_set</span>
<span style="font-size: 12px; font-weight: bold;">p-value:</span>
<span style="font-size: 12px">@p_value</span>
</div>
</div>
""")
# add a legend with most significant enriched term
most_sig_name = str(df[df['p value'] == df['p value'].min()]['Name'].values[0])
most_sig_value = str(df['p value'].min())
if len(enrichr_libraries) == 1:
legend = Legend(items = [LegendItem(label = most_sig_name + ', p-value: ' + most_sig_value)], location = (70, 2))
else:
legend = Legend(items = [LegendItem(label = library_name.replace('_', ' ') + ' ')], location = (0, 10))
tools_emb = [hover_emb, 'pan', 'wheel_zoom', 'reset', 'save']
# create different sized plots depending on how many are selected
if len(enrichr_libraries) == 1:
plot_emb = figure(plot_width=700, plot_height=800, tools=tools_emb)
elif len(enrichr_libraries) == 2:
plot_emb = figure(plot_width=600, plot_height=600, tools=tools_emb)
elif len(enrichr_libraries) == 3 or len(enrichr_libraries) == 5 or len(enrichr_libraries) == 6:
plot_emb = figure(plot_width=400, plot_height=400, tools=tools_emb)
elif len(enrichr_libraries) == 4:
plot_emb = figure(plot_width=500, plot_height=500, tools=tools_emb)
elif 7 <= len(enrichr_libraries) and len(enrichr_libraries) <= 9:
plot_emb = figure(plot_width=350, plot_height=350, tools=tools_emb)
if len(all_results) != 0:
plot_emb.add_layout(legend, 'below')
# hide axis labels and grid lines
plot_emb.xaxis.major_tick_line_color = None
plot_emb.xaxis.minor_tick_line_color = None
plot_emb.yaxis.major_tick_line_color = None
plot_emb.yaxis.minor_tick_line_color = None
plot_emb.xaxis.major_label_text_font_size = '0pt'
plot_emb.yaxis.major_label_text_font_size = '0pt'
plot_emb.circle('x', 'y', size = 'sizes', alpha = 0.7, line_alpha = 0,
line_width = 0.01, source = source, fill_color = 'colors', name = "df")
plot_emb.output_backend = "svg"
return plot_emb, df
# +
df_list = []
plot_list = []
for library in enrichr_libraries:
plot, df = get_plot(library)
df_list += [df]
plot_list += [plot]
if len(enrichr_libraries) == 1:
show(plot_list[0])
elif len(enrichr_libraries) == 2:
show(row(plot_list[0], plot_list[1]))
elif len(enrichr_libraries) == 3:
show(row(plot_list[0], plot_list[1], plot_list[2]))
elif len(enrichr_libraries) == 4:
show(layout([plot_list[0], plot_list[1]], [plot_list[2], plot_list[3]]))
elif len(enrichr_libraries) == 5:
show(layout([plot_list[0], plot_list[1], plot_list[2]], [plot_list[3], plot_list[4]]))
elif len(enrichr_libraries) == 6:
show(layout([plot_list[0], plot_list[1], plot_list[2]], [plot_list[3], plot_list[4], plot_list[5]]))
elif len(enrichr_libraries) == 7:
show(layout([plot_list[0], plot_list[1], plot_list[2]], [plot_list[3], plot_list[4], plot_list[5]], [plot_list[6]]))
elif len(enrichr_libraries) == 8:
show(layout([plot_list[0], plot_list[1], plot_list[2]], [plot_list[3], plot_list[4], plot_list[5]], [plot_list[6], plot_list[7]]))
elif len(enrichr_libraries) == 9:
show(layout([plot_list[0], plot_list[1], plot_list[2]], [plot_list[3], plot_list[4], plot_list[5]], [plot_list[6], plot_list[7], plot_list[8]]))
# -
# You may have to zoom in to see the details in densely-populated portions of the plots.
#
# The larger blue points represent significantly enriched terms (the darker the blue, the more significant).
# The gray points are not significant.
#
# Hovering over points will display the associated gene set name and the p-value.
#
# Below, tables of significant gene sets and their p-values are displayed and available for download (one for each library).
# +
# output significant p-values
def create_download_link( df, title = "Download CSV file of the table above", filename = "data.csv"):
csv = df.to_csv(index = False)
b64 = base64.b64encode(csv.encode())
payload = b64.decode()
html = '<a download="{filename}" href="data:text/csv;base64,{payload}" target="_blank">{title}</a>'
html = html.format(payload=payload, title=title, filename=filename)
return HTML(html)
for index, df in enumerate(df_list):
if 'p value' in df.columns:
sorted_df = df.sort_values(by = ['p value'])
filtered_df = sorted_df[sorted_df['p value'] <= significance_value]
if len(filtered_df) != 0:
display(HTML(f"<strong>{enrichr_libraries[index].replace('_', ' ')}</strong>"))
display(HTML(filtered_df[['Name', 'p value']].to_html(index = False)))
display(create_download_link(filtered_df[['Name', 'p value']]))
|
appyters/Enrichr_Scatterplot_Appyter/Scatter-Appyter.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/akankshawaghmare/Microspectra/blob/main/StringDataType.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + colab={"base_uri": "https://localhost:8080/"} id="rZqrws5qyVvw" outputId="c033d959-daff-4b3f-f484-9b5b3bb90578"
#program on string data type
string1=("Hi.. MY name is AKANKSHA.I am an intern at microspectra pvt.lmt")
print(string1)
print(string1[0:8])
print(string1[0: ])
print(string1[9:19])
print(string1[:16])
print(string1[0: :3])
# + colab={"base_uri": "https://localhost:8080/"} id="G5gpE14B5CGd" outputId="5ab42577-83d5-4302-c788-acd5a1064445"
#program using escape sequence of string
string2 =('My Name is "\<NAME>\"')
print(string2)
string2 =('\nMy Name is \\"<NAME>\\"')#use of escape sequence
print(string2)
# + colab={"base_uri": "https://localhost:8080/"} id="qRKCxbBB7iU4" outputId="c0b81fe0-1044-4196-87d2-d7de602db316"
#program using format
x=("my name is {} {} {}".format('Akanksha','Sanjay','Waghmare')) #default order
print(x)
y=("My name is {2} {1} {0}".format('AKANKSHA','Sanjay','Waghmare')) #positional formatting
print(y)
z=("my name is {s} {w} {a}".format(a='akanksha',s='sanjay',w='waghmare')) #keyword formatting
print(z)
# + colab={"base_uri": "https://localhost:8080/"} id="Pr_cCC9kBPfc" outputId="960a342a-df28-42fd-8e72-278d7dea1da8"
#program-
mystring='akankshaWAGHMAREakanksha 9876543210'
string='my name is'
print(mystring.capitalize())
print(mystring.upper())
print(mystring.lower())
print(mystring.title())
print(mystring.find('WAGHMARE'))
print(mystring.count('akanksha'))
print(mystring.isalpha())
print(mystring.isdigit())
print(mystring.islower())
print(mystring.isupper())
print(string+'',mystring)
print(string*3)
print('akanksha' in mystring)
print('x' not in mystring)
|
StringDataType.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# ## Data Acqusition
# +
# Import libraries necessary for this project
import numpy as np
import pandas as pd
#import renders as rs
from IPython.display import display # Allows the use of display() for DataFrames
# Show matplotlib plots inline (nicely formatted in the notebook)
# %matplotlib inline
# -
data = pd.read_csv("/Users/Asus/Documents/Atmel Studio/WholesaleCustomer.csv")
data.head(10)
# ## Data Exploration
# In this section, you will begin exploring the data through **visualizations** and code to understand how each feature is related to the others. You will observe a statistical description of the dataset, consider the relevance of each feature, and select a few sample data points from the dataset which you will track through the course of this project.
# Run the code block below to observe a statistical description of the dataset. Note that the dataset is composed of six important product categories: **'Fresh', 'Milk', 'Grocery', 'Frozen', 'Detergents_Paper', and 'Delicatessen'.** Consider what each category represents in terms of products you could purchase.
# Display a description of the dataset
stats = data.describe()
stats
# ### Implementation: Selecting Samples
# To get a better understanding of the customers and how their data will transform through the analysis, it would be best to select a few sample data points and explore them in more detail. In the code block below, add **three** indices of your choice to the indices list which will represent the customers to track. It is suggested to try different sets of samples until you obtain customers that vary significantly from one another.
# Using data.loc to filter a pandas DataFrame
data.loc[[100, 200, 300],:]
# Retrieve column names
# Alternative code:
# data.keys()
data.columns
# ### Logic in selecting the 3 samples: Quartiles
# As you can previously (in the object "stats"), we've the data showing the first and third quartiles.
#
# **We can filter samples that are starkly different based on the quartiles.**
#
# This way we've two establishments that belong in the first and third quartiles respectively in, for example, the Frozen category.
# Fresh filter
fresh_q1 = 3127.750000
display(data.loc[data.Fresh < fresh_q1, :].head())
# Frozen filter
frozen_q1 = 742.250000
display(data.loc[data.Frozen < frozen_q1, :].head())
# Frozen
frozen_q3 = 3554.250000
display(data.loc[data.Frozen > frozen_q3, :].head(7))
# **Hence we'll be choosing:**
#
# **43: Very low "Fresh" and very high "Grocery"**
#
# **12: Very low "Frozen" and very high "Fresh"**
#
# **39: Very high "Frozen" and very low "Detergens_Paper"**
# +
# TODO: Select three indices of your choice you wish to sample from the dataset
indices = [43, 12, 39]
# Create a DataFrame of the chosen samples
# .reset_index(drop = True) resets the index from 0, 1 and 2 instead of 100, 200 and 300
samples = pd.DataFrame(data.loc[indices], columns = data.columns).reset_index(drop = True)
print ("Chosen samples of wholesale customers dataset:")
display(samples)
# -
# ### Comparison of Samples and Means
# +
# Import Seaborn, a very powerful library for Data Visualisation
import seaborn as sns
# Get the means
mean_data = data.describe().loc['mean', :]
# Append means to the samples' data
samples_bar = samples.append(mean_data)
# Construct indices
samples_bar.index = indices + ['mean']
# Plot bar plot
samples_bar.plot(kind='bar', figsize=(14,8))
# -
# ### Comparing Samples' Percentiles
# +
# First, calculate the percentile ranks of the whole dataset.
percentiles = data.rank(pct=True)
# Then, round it up, and multiply by 100
percentiles = 100*percentiles.round(decimals=3)
# Select the indices you chose from the percentiles dataframe
percentiles = percentiles.iloc[indices]
# Now, create the heat map using the seaborn library
sns.heatmap(percentiles, vmin=1, vmax=99, annot=True)
# -
# ## Implementation: Feature Relevance
# One interesting thought to consider is if one (or more) of the six product categories is actually relevant for understanding customer purchasing. That is to say, is it possible to determine whether customers purchasing some amount of one category of products will necessarily purchase some proportional amount of another category of products?
# Existing features
data.columns
# Imports
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor
# +
# Create list to loop through
dep_vars = list(data.columns)
# Create loop to test each feature as a dependent variable
for var in dep_vars:
# TODO: Make a copy of the DataFrame, using the 'drop' function to drop the given feature
new_data = data.drop([var], axis = 1)
# Confirm drop
# display(new_data.head(2))
# Create feature Series (Vector)
new_feature = pd.DataFrame(data.loc[:, var])
# Confirm creation of new feature
# display(new_feature.head(2))
# TODO: Split the data into training and testing sets using the given feature as the target
X_train, X_test, y_train, y_test = train_test_split(new_data, new_feature, test_size=0.25, random_state=42)
# TODO: Create a decision tree regressor and fit it to the training set
# Instantiate
dtr = DecisionTreeRegressor(random_state=42)
# Fit
dtr.fit(X_train, y_train)
# TODO: Report the score of the prediction using the testing set
# Returns R^2
score = dtr.score(X_test, y_test)
print('R2 score for {} as dependent variable: {}'.format(var, score))
# -
# ### Question 1
# **Which feature did you attempt to predict?** What was the reported prediction score? Is this feature is necessary for identifying customers' spending habits?
# ### Visualize Feature Distributions
# To get a better understanding of the dataset, we can construct a scatter matrix of each of the six product features present in the data. If you found that the feature you attempted to predict above is relevant for identifying a specific customer, then the scatter matrix below may not show any correlation between that feature and the others.
# Produce a scatter matrix for each pair of features in the data
from pandas.plotting import scatter_matrix
scatter_matrix(data, alpha = 0.3, figsize = (14,8), diagonal = 'kde');
# ### Correlation Matrix
#
# This is to cross-reference with the scatter matrix above to draw more accurate insights from the data.
# The higher the color is on the bar, the higher the correlation.
# +
import matplotlib.pyplot as plt
# %matplotlib inline
def plot_corr(df,size=10):
'''Function plots a graphical correlation matrix for each pair of columns in the dataframe.
Input:
df: pandas DataFrame
size: vertical and horizontal size of the plot'''
corr = df.corr()
fig, ax = plt.subplots(figsize=(size, size))
cax = ax.matshow(df, interpolation='nearest')
ax.matshow(corr)
fig.colorbar(cax)
plt.xticks(range(len(corr.columns)), corr.columns);
plt.yticks(range(len(corr.columns)), corr.columns);
plot_corr(data)
# -
# ### Question 2
# Are there any pairs of features which exhibit some degree of correlation? Does this confirm or deny your suspicions about the relevance of the **feature you attempted to predict? How is the data for those features distributed?**
# ## Data Preprocessing
# In this section, you will preprocess the data to create a better representation of customers by performing a scaling on the data and detecting (and optionally removing) outliers.
#
# Preprocessing data is often times a critical step in assuring that results you obtain from your analysis are significant and meaningful.
# #### Implementation: Feature Scaling
# If data is not normally distributed, especially if the mean and median vary significantly (indicating a large skew), it is most often appropriate to apply a non-linear scaling — particularly for financial data. One way to achieve this scaling is by using a Box-Cox test
# +
# TODO: Scale the data using the natural logarithm
log_data = np.log(data)
# TODO: Scale the sample data using the natural logarithm
log_samples = np.log(samples)
# Produce a scatter matrix for each pair of newly-transformed features
scatter_matrix(log_data, alpha = 0.3, figsize = (14,8), diagonal = 'kde');
# -
# ### Observation
# After applying a natural logarithm scaling to the data, the distribution of each feature should appear much more normal. For any pairs of features you may have identified earlier as being correlated, observe here whether that correlation is still present (and whether it is now stronger or weaker than before).
# Display the log-transformed sample data
display(log_samples)
plot_corr(data)
plot_corr(log_data)
# ### Changes in correlations
#
# Grocery and Detergents_Paper has a weaker correlation.
#
# Grocery and Milk has a slightly stronger correlation.
#
# Detergents_Paper and Milk has a slightly stronger correlation.
# ### Implementation: Outlier Detection
# Detecting outliers in the data is extremely important in the data preprocessing step of any analysis. The presence of outliers can often skew results which take into consideration these data points. There are many "rules of thumb" for what constitutes an outlier in a dataset.
# This is how np.percentile would work
# np.percentile[series, percentile]
np.percentile(data.loc[:, 'Milk'], 25)
# ##### Modified Code
#
# The code has been revamped to use pandas .loc method because I prefer the consistency!
import itertools
# +
# Select the indices for data points you wish to remove
outliers_lst = []
# For each feature find the data points with extreme high or low values
for feature in log_data.columns:
# TODO: Calculate Q1 (25th percentile of the data) for the given feature
Q1 = np.percentile(log_data.loc[:, feature], 25)
# TODO: Calculate Q3 (75th percentile of the data) for the given feature
Q3 = np.percentile(log_data.loc[:, feature], 75)
# TODO: Use the interquartile range to calculate an outlier step (1.5 times the interquartile range)
step = 1.5 * (Q3 - Q1)
# Display the outliers
print ("Data points considered outliers for the feature '{}':".format(feature))
# The tilde sign ~ means not
# So here, we're finding any points outside of Q1 - step and Q3 + step
outliers_rows = log_data.loc[~((log_data[feature] >= Q1 - step) & (log_data[feature] <= Q3 + step)), :]
# display(outliers_rows)
outliers_lst.append(list(outliers_rows.index))
outliers = list(itertools.chain.from_iterable(outliers_lst))
# List of unique outliers
# We use set()
# Sets are lists with no duplicate entries
uniq_outliers = list(set(outliers))
# List of duplicate outliers
dup_outliers = list(set([x for x in outliers if outliers.count(x) > 1]))
print ('Outliers list:\n', uniq_outliers)
print ('Length of outliers list:\n', len(uniq_outliers))
print ('Duplicate list:\n', dup_outliers)
print ('Length of duplicates list:\n', len(dup_outliers))
# Remove duplicate outliers
# Only 5 specified
good_data = log_data.drop(log_data.index[dup_outliers]).reset_index(drop = True)
# Original Data
print ('Original shape of data:\n', data.shape)
# Processed Data
print ('New shape of data:\n', good_data.shape)
# -
# #### Notes
#
# Samples are not in this outliers' list.
# The good data now is a matrix that measures 435 x 6 instead of the original dimensionality of 440 x 6
|
Deep Learning/Customer Segmentation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Notebook 2 - NumPy
# [NumPy](http://numpy.org) short for Numerical Python, has long been a cornerstone of numerical computing on Python. It provides the data structures, algorithms and the glue needed for most scientific applications involving numerical data in Python. All computation is done in vectorised form - using vectors of several values at once instead of singular values at a time. NumPy contains, among other things:
# * A fast and efficient multidimensional array object `ndarray`.
# * Mathematical functions for performing element-wise computations with arrays or mathematical operations between arrays.
# * Tools for reading and manipulating large array data to disk and working with memory-mapped files.
# * Linear algebra, random number generation and Fourier transform capabilities.
#
# For the rest of the course, whenever array is mentioned it refers to the NumPy ndarray.
# <br>
#
# ## Table of contents
# - [The ndarray](#ndarray)
# - [Creating arrays](#creating)
# - [Data Types](#data)
# - [Arithmetic Operations](#arithmetic)
# - [Indexing and Slicing](#indexing)
# - [Functions with ndarrays](#functions)
# - [Universal Functions](#universal)
# - [Whole-Array Functions](#whole)
# - [Linear algebra](#linear)
# - [File I/O](#file)
# # Why NumPy?
# Is the first question that anybody asks when they find out about it.
#
# Some people might say: *I don't care about speed, I want to spend my time researching how to cure cancer, not optimise coputer code!*
#
# That's perfectly reasonable, but are you willing to wait a lot longer for your experiment to finish? I definitely don't want to do that. Let's see how much faster NumPy really is!
#
# To show that we'll be using the magic command `%timeit` which you can read more about [here](https://ipython.readthedocs.io/en/stable/interactive/magics.html) and don't worry about the details now, they will clear up later.
#
# Let's have a look at generating a vector of 10M random values and then summing them all up using the Python way and using the NumPy way!
# +
import numpy as np
x = np.random.randn(10000000) # generate random numbers
print("Running normal python sum()")
# %timeit sum(x)
print("Running numpy sum()")
# %timeit np.sum(x)
# -
# **WOW** that was a difference of roughly a **100 times** and that was just for a single summing operation. Imagine if you had several of those running all the time!
#
# Are you onboard with Numpy then? Let's proceed...
# # The ndarray <a name="ndarray"></a>
# The ndarray is a backbone on Numpy. It's a fast and flexible container for N-dimensional array objects, usually used for large datasets in Python. Arrays enable you to perform mathematical operations on whole blocks of data using similar syntax to the equivalent operations between scalar elements.
#
# Here is a quick example of its capabilities:
# create a 2x3 array of random values
data = np.random.randn(2,3)
data
data * 10 #multiply all numbers by 10
data + data #element-wise addition
# Every array has a shape, a tuple indicating the size of each dimnesion and a dtype. You can obtain these via the respective methods:
# number of dimensions of the array
data.ndim
# the size of the array
data.shape
# the type of values store in the array
data.dtype
# ## Creating arrays <a name="creating"></a>
# The easiest and quickest way to create an array is from a normal Python list.
# +
data = [1.2, 5.2, 5, 7.8, 0.3]
arr = np.array(data)
arr
# -
# It is also possible to create multidimensional arrays in a similar fashion. An example would be:
# ```python
# data = [[1.2, 5.2, 5, 7.8, 0.3],
# [4.1, 7.2, 4.8, 0.1, 7.7]]
# ```
# Try creating a multidimensional array below and verify its number of dimensions:
# We can also create an array filled with zeros
np.zeros(10)
# Again, it is also possible to create a multidimensional array by passing a tuple as an argument
np.zeros((4,6))
# NumPy also has an equivalent to the built-in Python function `range()` but it's called `arange()`
np.arange(0, 10)
# Here is a summary of the most often used methods to create arrays. Use it as a future reference!
# | Function | Description |
# |----|:--|
# | array | Convert input data to an ndarray either by inferring a dtype<br>or explicitly specifying a dtype; copies the input data by default. |
# | arange | Similar to the built-in `range` function but returns an ndarray. |
# | linspace | Return evenly spaced numbers over a specified interval. |
# | ones | Produces an array of all 1s with the given shape and dtype. |
# | ones_like | Similar to `ones` but takes another array and produces a ones array<br>of the same shape and dtype |
# | zeros, zeros_like | Similar to `ones` but produces an array of 0s. |
# | eye | Create a square NxN identity matrix (1s on the diagonal and 0s elsewhere). |
# ## Data Types <a name="data"></a>
# The data type or `dtype` is a special object containing the information the array needs to interpret a chunk of memory. We can specify it during the creation of an array.
arr = np.array([1, 2, 3], dtype=np.float64)
# you can check the type of an array with
arr.dtype
# An ndarray can only hold data in **one** dtype. This makes it a little less flexible than a regular Python list, but is part of what allows NumPy to run so fast.
#
# NumPy has several types of data like int, float and bool. However, it also extends these by specifying the number of bits used per variable like 16, 32, 64 or 128.
#
# To keep things simpe, you can use:
# - `np.int64` to store integer numbers
# - `np.float64` to store numbers with a fraction value
# - `np.bool` to store `True` and `False` values
#
# When creating arrays in NumPy the type is inferred (guessed) so you don't need to explicitly specify it.
#
# It is not necessary for this course but if you want to learn more about datatypes in NumPy you can go to https://jakevdp.github.io/PythonDataScienceHandbook/02.01-understanding-data-types.html
# Similar to normal Python, you can cast (convert) an array from one dtype to another using the `astype` method:
arr = np.array([1, 2, 3])
arr.dtype
float_arr = arr.astype(np.float64)
float_arr.dtype
# The normal limitations to casting apply here as well. You can try creating a `float64` array and then converting it to an `int64` array below:
# ### Exercise 1
#
#
# - Create a 5x5 [identity matrix](https://en.wikipedia.org/wiki/Identity_matrix).
# - Convert it to `int64` dtype.
# - Confirm its properties such as dimensionality, shape and data type.
# ## Arithmetic operations <a name="arithmetic"></a>
# You have already gotten a taste of this in the examples above but let's try to extend that.
#
# Arrays are important because they enable you to express batch operations on data without having to write for loops - this is called **vectorisation**.
#
# Any arithmetic operation between equal-size arrays applies the operation element-wise:
A = np.array([[1, 2, 3], [4, 5, 6]])
A
A * A
A - A
# Arithmetic operations with scalars propogate the scalar argument to each element in the array:
A * 5
A ** 0.5
# Comparisons between arrays of the same size yield boolean arrays:
B = np.array([[1, 7, 4],[4, 12, 2]])
B
A > B
# ### Broadcasting
#
# Applying arithmetic operations to differently sized arrays is called **broadcasting**.
#
# Let's see an example
A = np.ones((3,3))
A
B = np.arange(3)
B
A + B
# So what happened?
#
# We stretched both `B` to match the shape of `A`, the result is a two-dimensional array!
#
# <img src="img/broadcasting.png" alt="drawing" width="500"/>
#
# The light boxes represent the broadcasted values: again, this extra memory is not actually allocated in the course of the operation, but it can be useful conceptually to imagine that it is.
#
# If you want to learn more about broadcasting, check [this article](https://jakevdp.github.io/PythonDataScienceHandbook/02.05-computation-on-arrays-broadcasting.html).
# ### Exercise 2
# Generate a vector of size 10 with values ranging from 0 to 0.9, both included.
# ### Exercise 3
# Change the value of `c` so that the following code runs properly.
#
# _Hint: What happens when you obtain `a*b`? What are the dimensions of this object? Use .dim, and comment out some lines, to play with this code and figure this out._
# +
a = np.asarray([[3], [7], [878], [26]])
b = np.asarray([1, 10, 11, 101, 110])
c = np.asarray([0, 1, 2, 3, 4, 5]) # Change this variable
(a*b) + c
# -
# ## Indexing and slicing <a name="indexing"></a>
# NumPy offers many options for indexing and slicing. Coincidentally, they are very similar to Python.
#
# Let's see how this is done in 1D:
A = np.arange(10)
A
A[5]
A[5:8]
A[5:8] = 0
A
# **Important:** Unlike regular Python, NumPy array slices are _views_ on the original array. This means that the data is not copied, and any modifications to the source array will be reflected in the view. Similarly, changing the slice will update the original array.
A_slice = A[5:8] #Take a slice
A_slice
A[5:8] = [12, 17, 24] #Update source array
A_slice #Slice is changed
A_slice[:] = 0 #Edit the slice
A #The array is changed
# Let's now have a look at higher dimensional arrays:
C = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
C
# Now that we have 2 dimensions, we need to input 2 indices to get a specific element of the array. Alternatively, if we input only one index, then we obtain the whole row of the array:
C[2]
C[2][1]
C[2, 1]
# Here is a picture to better explain indexing in 2D:
# <img src="img/ndarray.png" alt="drawing" width="300"/>
# The same concepts and techniques are extended into multidimensional arrays:
# if you omit later indices, the returned object will be a lower dimensional ndarray consisting of all data along the higher dimensions.
# Now let's look into **slicing**. You already saw above that slicing in 1D is done the same way as in standard Python data structures. So how do we do that in 2D? Well, it is fairly intuitive:
C = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
C
C[:2]
# This can be read as *select the first 2 rows of C*
C[1, :2] # Select row 1, the first 2 columns.
C[:, :1] # Select all rows, first 1 column (i.e. select column 1)
# Here is some visual aid for what happened above:
# <img src="img/indexing.png" alt="drawing" width="400"/>
# ### Exercise 4
# Create a 4 by 4 2D array with 1s on the border and 0s inside
# ### Reshaping and Transposing Arrays <a name="transposing"></a>
# We can use the method `reshape()` to convert the data from one shape into another, and we can use the `T` attribute to obtain the transpose of the array.
A = np.arange(15)
A
B = A.reshape((3,5))
B
B.T
# # Functions with ndarrays <a name="functions"></a>
# Now that we've seen how to create and manipulate ndarrays, we will see some of the many functions NumPy has to compute with them. In particular, we'll look at: functions which work element-wise (called ufuncs), functions which work on the whole array at once, and functions specialised for linear algebra.
#
# ## Universal Functions <a name="universal"></a>
# or *ufunc* are functions that perform element-wise operations on data in ndarrays. You can think of them as fast vectorised wrappers for simple functions. Here is an example of `sqrt` and `exp`:
A = np.arange(10)
A
np.sqrt(A)
np.exp(A)
# Other universal functions take 2 arrays as input. These are called *binary* functions.
#
# For example `maximum()` selects the biggest values from two input arrays
x = np.random.randn(10)
y = np.random.randn(10)
np.maximum(x, y)
# Here is a list of useful *ufuncs* in NumyPy:
#
# *Again, you don't need to memorise them. This is just a reference*
# ### Unary functions (accept one argument)
#
# | Function | Description |
# |----|----|
# | abs, fabs | Compute the absolute value element-wise for integer, floating point, or complex values.<br>Use fabs as a faster alternative for non-complex-valued data |
# | sqrt | Compute the square root of each element. Equivalent to arr ** 0.5 |
# | exp | Compute the exponent ex of each element |
# | log, log10, log2, log1p | Natural logarithm (base e), log base 10, log base 2, and log(1 + x), respectively |
# | cos, cosh, sin, sinh, tan, tanh | Regular and hyperbolic trigonometric functions |
#
# ### Binary functions (accept 2 arguments)
# | Functions | Description |
# | ---- | ---- |
# | add | Add corresponding elements in arrays |
# | subtract | Subtract elements in second array from first array |
# | multiply | Multiply array elements |
# | divide, floor_divide | Divide or floor divide (truncating the remainder) |
# | mod | Element-wise modulus (remainder of division) |
# | power | Raise elements in first array to powers indicated in second array |
# | maximum | Element-wise maximum. fmax ignores NaN |
# | minimum | Element-wise minimum. fmin ignores NaN |
# ## Whole-Array Functions <a name="whole"></a>
# As well as ufuncs, which operate element-by-element, there are many functions which work on the whole of an array at once.
#
# NumPy offers a set of mathematical functions that compute statistics about an entire array:
B = np.random.randn(5, 4)
B
B.mean()
np.mean(B)
B.sum()
B.mean(axis=1) # Compute mean in column (axis 1) direction (i.e. the mean of each row)
# Here `mean(axis=1)` means compute the mean across the columns (axis 1). This will compute the mean in the direction where the column index grows, i.e. the mean **of each row**. Similarly, choosing `axis=0` would compute the mean in the row direction, so we would obtain the mean of each column.
# Here is a set of other similar functions:
#
# | Function | Description|
# | --- | --- |
# |sum | Sum of all the elements in the array or along an axis. Zero-length arrays have sum 0. |
# | mean | Arithmetic mean. Zero-length arrays have NaN mean. |
# | std, var | Standard deviation and variance, respectively, with optional<br>degrees of freedom adjustment (default denominator n). |
# |min, max | Minimum and maximum. |
# | argmin, argmax | Indices of minimum and maximum elements, respectively. |
# Similar to Python's built-in list type, NumyPy arrays have a function to sort them in-place:
A = np.random.randn(10)
A
A.sort()
A
# Another option is `unique()` which returns the sorted unique values in an array.
# ### Exercise 5
# Create a random vector of size 30 and find its mean value
# ### Exercise 6
#
# Subtract the mean of each column of a randomly generated matrix:
# ## Linear Algebra <a name="linear"></a>
# NumyPy offers a set of standard linear algebra operations, like matrix multiplication, decompositions and determinants. Let's start with the basics. In numpy, matrix multiplication is done with `@`:
A = np.random.randn(3,1)
A
B = np.random.randn(1,3)
B
A @ B
# There are a few functions available in standard NumPy for working with matrices:
#
# | Function | Description |
# | --- | --- |
# | diag | Return the diagonal (or off-diagonal) elements of a square matrix as a 1D array,<br>or convert a 1D array into a square matrix with zeros on the off-diagonal |
# | dot | Matrix multiplication |
# | trace | Compute the sum of the diagonal elements |
# We can also extend this with the `numpy.linalg` module, which provides linear algebra functionality:
A = np.random.randn(5, 5)
A
from numpy.linalg import inv
inv(A) # get the inverse of a matrix
# We needed the above import statement to get access to the `inv()` function, since it lives in the `linalg` submodule of NumPy and so wasn't imported when we imported NumPy. We could also call it directly by giving the submodule as follows:
np.linalg.inv(A)
# Here is a set of commonly used `numpy.linalg` functions
#
# | Function | Description |
# | --- | --- |
# | det | Compute the matrix determinant |
# | eig | Compute the eigenvalues and eigenvectors of a square matrix |
# | inv | Compute the inverse of a square matrix |
# | pinv | Compute the Moore-Penrose pseudo-inverse inverse of a square matrix |
# | qr | Compute the QR decomposition |
# | svd | Compute the singular value decomposition (SVD) |
# | solve | Solve the linear system Ax = b for x, where A is a square matrix |
# | lstsq | Compute the least-squares solution to y = Xb |
# ### Exercise 7
# Obtain the diagonal of a dot product of 2 random matrices
# # File I/O <a name="file"></a>
# NumPy offers its own set of File Input/Output functions.
#
# The most common one is `genfromtxt()` which can load the common `.csv` and `.tsv` files.
#
# Now let us analyse temperature data from Stockholm over the years.
#
# First we have to load the file:
data = np.genfromtxt("./data/stockholm_td_adj.dat")
data.shape
# The first column of this array gives years, and the 6th gives temperature readings. We can extract these.
yrs = data[:, 0]
temps = data[:, 5]
# Having read in our data, we can now work with it - for example, we could produce a plot.
# We will cover plotting in more depth in notebook 3, so there's no need to get too caught up in the details right now - this is just an examle of something we might do having read in some data.
# +
import matplotlib.pyplot as plt
% matplotlib inline
plt.figure(figsize=(16, 6)) # Create a 16x6 figure
plt.plot(yrs, temps) # Plot temps vs yrs
#Set some labels
plt.title("Temperatures in Stockholm")
plt.xlabel("year")
plt.ylabel("Temperature (C)")
plt.show() # Show the plot
# -
# ### Exercise 8
# Read in the file `daily_gas_price.csv`, which lists the daily price of natural gas since 1997. Each row contains a date and a price, separated by a comma. Find the minimum, maximum, and mean gas price over the dataset.
#
# _Hint: you will need to use the delimiter option in `np.genfromtxt` to specify that data is separated by commas. We will be discarding the date column..._
|
python-data-2-numpy.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Detecting Pneumonia using Convolutional Neural Network (CNN)
# ## Understand CNN
# **What Is a Convolutional Neural Network?**
# A Convolutional Neural Network (CNN) is a type of neural network that specializes in image recognition and computer vision tasks.
#
# ---
#
# **CNNs have two main parts**
# 1. A **convolution/pooling mechanism** that breaks up the image into features and analyzes them
# 2. A **fully connected (FC) layer** that takes the output of convolution/pooling and predicts the best label to describe the image
#
# Resources: [Understanding the input and output shapes in CNN](https://towardsdatascience.com/understanding-input-and-output-shapes-in-convolution-network-keras-f143923d56ca)
#
# ---
#
# **CNNs have several types of layers**
# 1. Convolutional layer ━ a “filter” passes over the image, scanning a few pixels at a time and creating a feature map that predicts the class to which each feature belongs.
# 2. Pooling layer (downsampling) ━ reduces the amount of information in each feature obtained in the convolutional layer while maintaining the most important information (there are usually several rounds of convolution and pooling).
# 3. Fully connected input layer (flatten) ━ takes the output of the previous layers, “flattens” them and turns them into a single vector that can be an input for the next stage.
# 4. The first fully connected layer ━ takes the inputs from the feature analysis and applies weights to predict the correct label.
# 5. Fully connected output layer ━ gives the final probabilities for each label.
#
# ---
#
# **Ways to prevent overfitting**
#
# **1. Regularization**
# - L2 (early-stopping) - stop training our model when the validation loss is at its lowest.
#
# **2. Batch Normalization**
# - To increase the stability of a neural network, batch normalization normalizes the output of a previous activation layer by subtracting the batch mean and dividing by the batch standard deviation.
# - Batch normalization standardizes the inputs to a layer for each mini-batch, stabilizing the learning process and dramatically reducing the number of training epochs required to train deep networks.
#
# **3. Dropout**
#
# **4. Data Augmentation**
#
# ---
#
# **Normalize Pixel Values**
# - For most image data, the pixel values are integers with values between 0 and 255. Neural networks process inputs using small weight values, and inputs with large integer values can disrupt or slow down the learning process. As such it is good practice to normalize the pixel values so that each pixel value has a value between 0 and 1.
# - It is valid for images to have pixel values in the range 0-1 and images can be viewed normally. This can be achieved by dividing all pixels values by the largest pixel value; that is 255. This is performed across all channels, regardless of the actual range of pixel values that are present in the image.
#
# ---
#
# **Choosing steps per each training epoch or validation epoch**
# - Before training or validating data, you will assign a **batch size**, which the model will train/test a smaller subset of data at a time. This is to **spare the computer's memory**.
# - Steps per epoch means the number of batches/steps the model will use at once to compute the metrics. Ideally, we will test the entire validation data at once. If we only test part of the validation data, we will get different metrics every time, either better or worse, however, it's not representative of the entire validation sets.
#
# ## Import The Required Libraries
# +
# basics
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
# Others
import os
from PIL import Image
# -
# ## Conduct Simple Exploratory Data Analysis (EDA)
# +
def listdir_nohidden(path):
return [file for file in os.listdir(path) if not file.startswith('.')]
def num_files_in_directory(path):
return len([file for file in os.listdir(path) if not file.startswith('.')])
# -
project_path = "E:/Stored/Stored_Datasets"
train_path = project_path + "/chest_xray/train/"
val_path = project_path + "/chest_xray/val/"
test_path = project_path + "/chest_xray/test/"
# +
train_normal_path = train_path + 'NORMAL/'
train_pneumonia_path = train_path + 'PNEUMONIA/'
train_normal_len = num_files_in_directory(train_normal_path)
train_pneumonia_len = num_files_in_directory(train_pneumonia_path)
train_sum_len = train_normal_len + train_pneumonia_len
print("[Train] Number of NORMAL Images: ", train_normal_len)
print("[Train] Number of PNEUMONIA Images: ", train_pneumonia_len)
print("[Train] Number of TOTAL Images: ", train_sum_len)
# +
val_normal_path = val_path + 'NORMAL/'
val_pneumonia_path = val_path + 'PNEUMONIA/'
print("[Validation] Number of NORMAL Images: ", num_files_in_directory(val_normal_path))
print("[Validation] Number of PNEUMONIA Images: ", num_files_in_directory(val_pneumonia_path))
print("[Validation] Number of TOTAL Images: ", num_files_in_directory(val_normal_path) + num_files_in_directory(val_pneumonia_path))
# -
plt.figure(figsize=(20, 8))
num = 5
for index in range(num):
n_img_title = os.listdir(train_normal_path)[index]
n_img_path = train_normal_path + n_img_title
plt.subplot(2, num, index+1)
plt.imshow(Image.open(n_img_path))
plt.tick_params(axis='both', which='both', bottom=False, top=False, labelbottom=False, labelleft=False)
plt.title('Normal')
;
p_img_title = os.listdir(train_pneumonia_path)[index]
p_img_path = train_pneumonia_path + p_img_title
plt.subplot(2, num, index+num+1)
plt.imshow(Image.open(p_img_path))
plt.tick_params(axis='both', which='both', bottom=False, top=False, labelbottom=False, labelleft=False)
plt.title('Pneumonia')
plt.savefig('pneumonia-fig.png')
;
# +
count_list = [['Normal', train_normal_len, train_normal_len/train_sum_len], \
['Pneumonia', train_pneumonia_len, train_pneumonia_len/train_sum_len]]
count_df = pd.DataFrame(count_list, columns=['Category', 'Count', 'Percentage'])
values = [train_normal_len, train_pneumonia_len]
ax = sns.barplot(x='Category', y='Count', data=count_df)
ax.set_title("Category Distribution for Training Dataset")
for index, value in enumerate(values):
plt.text(index-0.1, value-300, str(round(value/sum(values)*100, 2)) + "%");
# -
# I notice that all images are in different sizes.
for index in range(20):
sample_image = train_normal_path + listdir_nohidden(train_normal_path)[index]
image = Image.open(sample_image)
width, height = image.size
print('image', index+1, ':', width, 'x', height)
# +
hyper_dimension = 64
hyper_epochs = 100
hyper_feature_maps = 32
hyper_batch_size = 128
## Training in grayscale instead of RGB
hyper_channels = 1
hyper_mode = 'grayscale'
# +
train_datagen = ImageDataGenerator(rescale=1.0/255.0,
shear_range = 0.2,
zoom_range = 0.2,
horizontal_flip = True)
val_datagen = ImageDataGenerator(rescale=1.0/255.0)
test_datagen = ImageDataGenerator(rescale=1.0/255.0)
train_generator = train_datagen.flow_from_directory(directory = train_path,
target_size = (hyper_dimension, hyper_dimension),
batch_size = hyper_batch_size,
color_mode = hyper_mode,
class_mode = 'binary',
seed = 42)
val_generator = val_datagen.flow_from_directory(directory = val_path,
target_size = (hyper_dimension, hyper_dimension),
batch_size = hyper_batch_size,
class_mode = 'binary',
color_mode = hyper_mode,
shuffle=False,
seed = 42)
test_generator = test_datagen.flow_from_directory(directory = test_path,
target_size = (hyper_dimension, hyper_dimension),
batch_size = hyper_batch_size,
class_mode = 'binary',
color_mode = hyper_mode,
shuffle=False,
seed = 42)
|
model/01 EDA.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_mxnet_p27
# language: python
# name: conda_mxnet_p27
# ---
# ## MXNet (with Gluon) を使った学習と推論を SageMaker で行う
#
# #### ノートブックに含まれる内容
#
# - MXNet および Gluon を SageMaker で使うときの,基本的なやりかた
#
# #### ノートブックで使われている手法の詳細
#
# - アルゴリズム: CNN
# - データ: MNIST
# ## セットアップ
# +
import os
import boto3
import sagemaker
from sagemaker.mxnet import MXNet
from mxnet import gluon
from sagemaker import get_execution_role
sagemaker_session = sagemaker.Session()
role = get_execution_role()
# -
# ## データのロード
#
# Gluon に備わっている MNIST クラスを使って,データを取得し,これを S3 にアップロードします.SageMaker の学習時につかうデータは,S3 に置く必要があります.ここでは,ローカルにある iris データをいったん SageMaker SDK の session クラスにある upload_data() メソッドを使って,ノートブックインスタンスのローカルから S3 にアップロードします.
#
# デフォルトでは SageMaker は sagemaker-{region}-{your aws account number} というバケットを使用します.当該バケットがない場合には,自動で新しく作成します.upload_data() メソッドの引数に bucket=XXXX という形でデータを配置するバケットを指定することが可能です.
gluon.data.vision.MNIST('./data/train', train=True)
gluon.data.vision.MNIST('./data/test', train=False)
# また以下を実行する前に,**<span style="color: red;"> `data/mnist/XX` の `XX` を指定された適切な数字に変更</span>**してください
inputs = sagemaker_session.upload_data(path='data', key_prefix='data/mnist/XX')
# ## Gluon を実行するスクリプトの中身を確認
#
# MXNet のスクリプトは,学習時には以下の 2 つのメソッドを実装する必要があります.
#
# - `train`: モデルを記述するメソッド
# - `save`: 学習したモデルの保存処理を記述するメソッド
#
# また,推論時には以下のメソッド群を実装する必要があります.
#
# - `model_fn`: コンテナ起動時に,モデルをロードする処理を記述するメソッド
# - `transform_fn`: invokeEndpoint が叩かれた際に呼ばれる,予測処理を記述するメソッド
#
# さらに,MXNet の Module モデルや,Gluon を使用している場合には,上の `transform_fn` を,以下の 3 つのメソッド群に分けて記述することも可能です.
# 推論時に以下のメソッド群を記述することが可能です.これらはオプショナルなものなので,記述しなくても構いません.詳細は[こちら](https://github.com/aws/sagemaker-python-sdk#model-serving)をご覧ください.
#
# - `input_fn`: 前処理を記述するメソッド
# - `predict_fn`: 予測処理を記述するメソッド
# - `output_fn`: 後処理を記述するメシッド
#
# 今回使用するスクリプトは,[Gluon MNIST example](https://github.com/apache/incubator-mxnet/blob/master/example/gluon/mnist.py) をベースにしています.以下で中身を実際に確認してみましょう.
#
# !cat 'mnist.py'
# ## モデルの学習を実行
#
# SageMaker SDK には,MXNet 専用の Estimator として,`sagemaker.mxnet.MXNet` クラスがあります.ここでは,先ほどの `mnist.py` をエントリーポイントとして指定して,MXNet の学習ジョブを実行します.
m = MXNet("mnist.py",
role=role,
train_instance_count=1,
train_instance_type="ml.m4.xlarge",
hyperparameters={'batch_size': 100,
'epochs': 20,
'learning_rate': 0.1,
'momentum': 0.9,
'log_interval': 100})
m.fit(inputs)
# # モデルの推論を実行
#
#
# 推論を行うために,まず学習したモデルをデプロイします.`deploy()` メソッドでは,デプロイ先エンドポイントのインスタンス数,インスタンスタイプを指定します.モデルのデプロイには 10 分程度時間がかかります.
predictor = m.deploy(initial_instance_count=1, instance_type='ml.m4.xlarge')
# それでは,以下の四角の中に実際に文字を書いて,そのデータをエンドポイントに引き渡して判定してみましょう.文字を実際に書いたら,下の `predict` メソッドを実行します.
from IPython.display import HTML
HTML(open("input.html").read())
print(data)
response = predictor.predict(data)
print int(response)
# ## エンドポイントの削除
#
# 全て終わったら,エンドポイントを削除します.
sagemaker.Session().delete_endpoint(predictor.endpoint)
|
supported_frameworks/mxnet_gluon_mnist/mnist_with_gluon.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
con_mat=np.load('/media/maria/DATA1/Documents/NeuralData/conn_undir_drosophila.npy')[:10000,:10000]
from sklearn.cluster import SpectralClustering
import numpy as np
clustering = SpectralClustering(n_clusters=100,assign_labels="discretize",random_state=0,affinity='precomputed').fit(con_mat)
clustering.labels_
# +
import matplotlib.pyplot as plt
plt.hist(clustering.labels_,bins=100)
# -
import seaborn as sns
print(clustering.labels_==0)
ind=np.where(clustering.labels_==0)[0]
subs=con_mat[ind[:, None], ind]
subs[subs>0]=1
sns.heatmap(subs)
print(subs.shape)
print(subs)
print(np.nonzero(subs)[0].shape)
|
SpectralDrosophila.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda root]
# language: python
# name: conda-root-py
# ---
# +
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.cross_validation import cross_val_score, StratifiedKFold , train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
from sklearn.multiclass import OneVsRestClassifier
import xgboost as xgb
# -
match_df = pd.read_csv('match_cluster.csv')
match_df = match_df.drop(['Unnamed: 0','link_odsp','adv_stats'], axis = 1)
match_df.head()
england = match_df[match_df.country == 'england']
england.head()
spain = match_df[match_df.country == 'spain']
spain.head()
germany = match_df[match_df.country == 'germany']
germany.head()
france = match_df[match_df.country == 'france']
france.head()
italy = match_df[match_df.country == 'italy']
italy.head()
# +
## Easier to write a function to return league and year dataframe instead of pipeline it
def dummy_year_pipe(df, yr):
## df for only that league and season
df_year = df[df.season == yr]
## getting unique clubs to create dummy vars for which two teams are playing
df_yr_clubs = pd.unique(df_year[['ht','at']].values.ravel())
## drop first alphabetical club for comparison, return in DF to append to original df
clubs = np.sort(df_yr_clubs)[1:len(df_yr_clubs)]
club_df = pd.DataFrame(columns = clubs)
df_year = df_year.append(club_df)
for club in clubs:
for i, row in df_year.iterrows():
if row['ht'] == club or row['at'] == club:
dummy = 1
else:
dummy = 0
df_year.loc[i, club] = dummy
return df_year
# -
X_train = train[[u'<NAME>', u'<NAME>', u'AS <NAME>', u'AS Roma',
u'Atalanta', u'Ath<NAME>', u'Atletico Madrid', u'Barcelona',
u'<NAME>', u'Bayern Munich', u'Bologna', u'Bordeaux',
u'<NAME>', u'<NAME>', u'Brest', u'Caen',
u'Cagliari', u'Catania', u'Cesena', u'<NAME>', u'<NAME>CO',
u'Espanyol', u'<NAME>', u'FC Augsburg', u'FC Cologne',
u'Fiorentina', u'Genoa', u'Getafe', u'Granada', u'Hamburg SV',
u'Hannover 96', u'<NAME>', u'Internazionale', u'Juventus',
u'Kaiserslautern', u'Lazio', u'Lecce', u'Levante', u'Lille', u'Lorient',
u'Lyon', u'Mainz', u'Malaga', u'Mallorca', u'Marseille', u'Montpellier',
u'Napoli', u'Nice', u'Novara', u'Nurnberg', u'Osasuna', u'Palermo',
u'Paris Saint-Germain', u'Parma', u'Racing Santander',
u'<NAME>', u'<NAME>is', u'Real Madrid', u'Real Sociedad',
u'Real Zaragoza', u'SC Freiburg', u'Schalke 04', u'Sevilla', u'Siena',
u'Sochaux', u'Sporting Gijon', u'St Etienne', u'Stade Rennes',
u'TSG Hoffenheim', u'Toulouse', u'Udinese', u'Valencia',
u'Valenciennes', u'VfB Stuttgart', u'VfL Wolfsburg', u'Villarreal',
u'<NAME>']]
y_train = train['cluster']
X_test = test[[u'<NAME>', u'<NAME>', u'AS Nancy Lorraine', u'AS Roma',
u'Atalanta', u'<NAME>', u'Atletico Madrid', u'Barcelona',
u'Bayer Leverkusen', u'Bayern Munich', u'Bologna', u'Bordeaux',
u'<NAME>', u'<NAME>', u'Brest', u'Caen',
u'Cagliari', u'Catania', u'Cesena', u'<NAME>', u'Dijon FCO',
u'Espanyol', u'<NAME>', u'FC Augsburg', u'FC Cologne',
u'Fiorentina', u'Genoa', u'Getafe', u'Granada', u'Hamburg SV',
u'Hannover 96', u'<NAME>', u'Internazionale', u'Juventus',
u'Kaiserslautern', u'Lazio', u'Lecce', u'Levante', u'Lille', u'Lorient',
u'Lyon', u'Mainz', u'Malaga', u'Mallorca', u'Marseille', u'Montpellier',
u'Napoli', u'Nice', u'Novara', u'Nurnberg', u'Osasuna', u'Palermo',
u'Paris Saint-Germain', u'Parma', u'Racing Santander',
u'<NAME>', u'Real Betis', u'Real Madrid', u'Real Sociedad',
u'Real Zaragoza', u'SC Freiburg', u'Schalke 04', u'Sevilla', u'Siena',
u'Sochaux', u'Sporting Gijon', u'St Etienne', u'Stade Rennes',
u'TSG Hoffenheim', u'Toulouse', u'Udinese', u'Valencia',
u'Valenciennes', u'VfB Stuttgart', u'VfL Wolfsburg', u'Villarreal',
u'<NAME>']]
y_test = test['cluster']
X_train = X_train.astype(int)
X_test = X_test.astype(int)
# +
## guide for using multi-class prediction XGBoost
xg_train = xgb.DMatrix(X_train, label=y_train)
xg_test = xgb.DMatrix(X_test, label=y_test)
# setup parameters for xgboost
param = {}
# use softmax multi-class classification
param['objective'] = 'multi:softmax'
# scale weight of positive examples
param['eta'] = 0.1
param['max_depth'] = 6
param['silent'] = 1
param['nthread'] = 4
param['num_class'] = 4
watchlist = [(xg_train,'train'), (xg_test, 'test')]
num_round = 5
bst = xgb.train(param, xg_train, num_round, watchlist );
# get prediction
pred = bst.predict( xg_test );
# -
param['objective'] = 'multi:softprob'
bst = xgb.train(param, xg_train, num_round, watchlist );
yprob = bst.predict( xg_test ).reshape( y_test.shape[0], 4 )
ylabel = np.argmax(yprob, axis=1)
yprob
print 'Model Accuracy Score:'
print accuracy_score(y_test, pred)
print 'Model Confusion Matrix:'
print confusion_matrix(y_test, pred)
print 'Model Classification Report:'
print classification_report(y_test, pred)
# +
### Leveraged next few cells from sklearn to calculate and plot roc-auc for multi-class
from sklearn.metrics import roc_curve, auc
from sklearn.preprocessing import label_binarize
from scipy import interp
# Binarize the output
y = label_binarize(y_test, classes=[0, 1, 2, 3])
n_classes = y.shape[1]
# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
fpr[i], tpr[i], _ = roc_curve(y[:, i], yprob[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])
# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(y.ravel(), yprob.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])
# +
### from sklearn
# Compute macro-average ROC curve and ROC area
# First aggregate all false positive rates
all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)]))
# Then interpolate all ROC curves at this points
mean_tpr = np.zeros_like(all_fpr)
for i in range(n_classes):
mean_tpr += interp(all_fpr, fpr[i], tpr[i])
# Finally average it and compute AUC
mean_tpr /= n_classes
fpr["macro"] = all_fpr
tpr["macro"] = mean_tpr
roc_auc["macro"] = auc(fpr["macro"], tpr["macro"])
# Plot all ROC curves
plt.figure()
plt.plot(fpr["micro"], tpr["micro"],
label='micro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["micro"]),
color='deeppink', linestyle=':', linewidth=4)
plt.plot(fpr["macro"], tpr["macro"],
label='macro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["macro"]),
color='navy', linestyle=':', linewidth=4)
colors = ['aqua', 'darkorange', 'cornflowerblue', 'green']
for i, color in zip(range(n_classes), colors):
plt.plot(fpr[i], tpr[i], color=color, lw=lw,
label='ROC curve of class {0} (area = {1:0.2f})'
''.format(i, roc_auc[i]))
plt.plot([0, 1], [0, 1], 'k--', lw=lw)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic to multi-class')
plt.legend(loc="lower right")
plt.show()
# -
# ### Model is created above.
#
# The results above show that the model could use some work. Some of the features could be tweaked to allow these clusters to be slightly more predictive. However, we will continue with the clusters created to predict the watchability of all future matches in the rest of the 2016-2017 season for each league.
#
# The model that we use takes in the two teams that are playing in a match, and then predicts the watchability based on those two teams. Since this data has unique matches occurring only within leagues, a predictive model will have to be trained and fit for each league for the current season. I have obtained the remaining league fixtures from the point after data was provided, and run each league through the same process to obtain results.
#
# ### First, England.
england_train_17 = dummy_year_pipe(england, 2017)
epl_17 = pd.read_csv('epl_17_fixtures.csv', encoding = 'utf-8')
epl_17.loc[epl_17.Team1 == 'Leicester', 'Team1'] = 'Leicester City'
epl_17.loc[epl_17.Team2 == 'Leicester', 'Team2'] = 'Leicester City'
epl_17.loc[epl_17.Team1 == 'Manchester United', 'Team1'] = 'Manchester Utd'
epl_17.loc[epl_17.Team2 == 'Manchester United', 'Team2'] = 'Manchester Utd'
epl_17.loc[epl_17.Team1 == 'Stoke', 'Team1'] = 'Stoke City'
epl_17.loc[epl_17.Team2 == 'Stoke', 'Team2'] = 'Stoke City'
epl_17.loc[epl_17.Team1 == 'tottenham', 'Team1'] = 'Tottenham'
epl_17.loc[epl_17.Team2 == 'tottenham', 'Team2'] = 'Tottenham'
epl_17.loc[epl_17.Team1 == 'chelsea', 'Team1'] = 'Chelsea'
epl_17.loc[epl_17.Team2 == 'chelsea', 'Team2'] = 'Chelsea'
epl_17.loc[epl_17.Team1 == 'Arsenal', 'Team1'] = 'Arsenal'
epl_17.loc[epl_17.Team2 == 'Arsenal', 'Team2'] = 'Arsenal'
# +
epl_17_clubs = pd.unique(epl_17[['Team1','Team2']].values.ravel())
## drop first alphabetical club for comparison, return in DF to append to original df
clubs = np.sort(epl_17_clubs)[1:len(epl_17_clubs)]
club_df = pd.DataFrame(columns = clubs)
epl_17 = epl_17.append(club_df)
for club in clubs:
for i, row in epl_17.iterrows():
if row['Team1'] == club or row['Team2'] == club:
dummy = 1
else:
dummy = 0
epl_17.loc[i, club] = dummy
# +
X_train = england_train_17[[u'Bournemouth', u'Burnley', u'Chelsea', u'Crystal Palace', u'Everton',
u'Hull', u'Leicester City', u'Liverpool', u'Manchester City',
u'Manchester Utd', u'Middlesbrough', u'Southampton', u'Stoke City',
u'Sunderland', u'Swansea', u'Tottenham', u'Watford', u'West Brom',
u'West Ham']]
y_train = england_train_17['cluster']
X_test = epl_17[[u'Bournemouth', u'Burnley', u'Chelsea', u'Crystal Palace', u'Everton',
u'Hull', u'Leicester City', u'Liverpool', u'Manchester City',
u'Manchester Utd', u'Middlesbrough', u'Southampton', u'Stoke City',
u'Sunderland', u'Swansea', u'Tottenham', u'Watford', u'West Brom',
u'West Ham']]
## y_test = test['cluster']
X_train = X_train.astype(int)
X_test = X_test.astype(int)
# -
# +
xg_train_17 = xgb.DMatrix( X_train, label=y_train)
xg_test_17 = xgb.DMatrix(X_test)
# setup parameters for xgboost
param = {}
# use softmax multi-class classification
param['objective'] = 'multi:softmax'
# scale weight of positive examples
param['eta'] = 0.1
param['max_depth'] = 6
param['silent'] = 1
param['nthread'] = 4
param['num_class'] = 4
param['eval_metric'] = 'auc'
num_round = 5
bst_17 = xgb.train(param, xg_train_17, num_round)
# get prediction
pred_17 = bst_17.predict( xg_test_17 );
# -
pred_17
epl_17_predict = epl_17.drop([u'Bournemouth', u'Burnley', u'Chelsea', u'Crystal Palace', u'Everton',
u'Hull', u'Leicester City', u'Liverpool', u'Manchester City',
u'Manchester Utd', u'Middlesbrough', u'Southampton', u'Stoke City',
u'Sunderland', u'Swansea', u'Tottenham', u'Watford', u'West Brom',
u'West Ham'], axis = 1)
epl_17_predict['cluster'] = pred_17
epl_17_predict
# ## Spain Below
# +
spain_train_17 = dummy_year_pipe(spain, 2017)
esp_17 = pd.read_csv('esp_17_fixtures.csv', encoding = 'utf-8')
# -
esp_17.loc[esp_17.Team1 == 'Ath. Bilbao', 'Team1'] = 'Athletic Bilbao'
esp_17.loc[esp_17.Team2 == 'Ath. Bilbao', 'Team2'] = 'Athletic Bilbao'
esp_17.loc[esp_17.Team1 == 'Atl. Madrid', 'Team1'] = 'Atletico Madrid'
esp_17.loc[esp_17.Team2 == 'Atl. Madrid', 'Team2'] = 'Atletico Madrid'
esp_17.loc[esp_17.Team1 == 'Betis', 'Team1'] = 'Real Betis'
esp_17.loc[esp_17.Team2 == 'Betis', 'Team2'] = 'Real Betis'
esp_17.loc[esp_17.Team1 == 'Gijon', 'Team1'] = 'Sporting Gijon'
esp_17.loc[esp_17.Team2 == 'Gijon', 'Team2'] = 'Sporting Gijon'
esp_17.loc[esp_17.Team1 == 'La Coruna', 'Team1'] = 'Deportivo La Coruna'
esp_17.loc[esp_17.Team2 == 'La Coruna', 'Team2'] = 'Deportivo La Coruna'
# +
esp_17_clubs = pd.unique(esp_17[['Team1','Team2']].values.ravel())
## drop first alphabetical club for comparison, return in DF to append to original df
clubs = np.sort(esp_17_clubs)[1:len(esp_17_clubs)]
club_df = pd.DataFrame(columns = clubs)
esp_17 = esp_17.append(club_df)
for club in clubs:
for i, row in esp_17.iterrows():
if row['Team1'] == club or row['Team2'] == club:
dummy = 1
else:
dummy = 0
esp_17.loc[i, club] = dummy
print spain_train_17.columns
print esp_17.columns
# +
X_train = spain_train_17[[u'Athletic Bilbao', u'Atletico Madrid', u'Barcelona', u'Celta Vigo',
u'Deportivo La Coruna', u'Eibar', u'Espanyol', u'Granada',
u'Las Palmas', u'Leganes', u'Malaga', u'Osasuna', u'Real Betis',
u'Real Madrid', u'Real Sociedad', u'Sevilla', u'Sporting Gijon',
u'Valencia', u'Villarreal']]
y_train = spain_train_17['cluster']
X_test = esp_17[[u'Athletic Bilbao', u'Atletico Madrid', u'Barcelona', u'Celta Vigo',
u'Deportivo La Coruna', u'Eibar', u'Espanyol', u'Granada',
u'Las Palmas', u'Leganes', u'Malaga', u'Osasuna', u'Real Betis',
u'Real Madrid', u'Real Sociedad', u'Sevilla', u'Sporting Gijon',
u'Valencia', u'Villarreal']]
## y_test = test['cluster']
X_train = X_train.astype(int)
X_test = X_test.astype(int)
# +
xg_train_17 = xgb.DMatrix( X_train, label=y_train)
xg_test_17 = xgb.DMatrix(X_test)
# setup parameters for xgboost
param = {}
# use softmax multi-class classification
param['objective'] = 'multi:softmax'
# scale weight of positive examples
param['eta'] = 0.1
param['max_depth'] = 6
param['silent'] = 1
param['nthread'] = 4
param['num_class'] = 4
param['eval_metric'] = 'auc'
num_round = 5
bst_17 = xgb.train(param, xg_train_17, num_round)
# get prediction
pred_17 = bst_17.predict( xg_test_17 );
# +
esp_17_predict = esp_17.drop([u'Athletic Bilbao', u'Atletico Madrid', u'Barcelona', u'Celta Vigo',
u'Deportivo La Coruna', u'Eibar', u'Espanyol', u'Granada',
u'Las Palmas', u'Leganes', u'Malaga', u'Osasuna', u'Real Betis',
u'Real Madrid', u'Real Sociedad', u'Sevilla', u'Sporting Gijon',
u'Valencia', u'Villarreal'], axis = 1)
esp_17_predict['cluster'] = pred_17
# -
esp_17_predict.head()
# ## Germany Below
# +
germ_train_17 = dummy_year_pipe(germany, 2017)
ger_17 = pd.read_csv('ger_17_fixtures.csv', encoding = 'utf-8')
ger_17.loc[ger_17.Team1 == 'Dortmund', 'Team1'] = '<NAME>'
ger_17.loc[ger_17.Team2 == 'Dortmund', 'Team2'] = '<NAME>'
ger_17.loc[ger_17.Team1 == 'Monchengladbach', 'Team1'] = '<NAME>'
ger_17.loc[ger_17.Team2 == 'Monchengladbach', 'Team2'] = '<NAME>'
ger_17.loc[ger_17.Team1 == 'Darmstadt', 'Team1'] = 'SV Darmstadt 98'
ger_17.loc[ger_17.Team2 == 'Darmstadt', 'Team2'] = 'SV Darmstadt 98'
ger_17.loc[ger_17.Team1 == 'Leverkusen', 'Team1'] = 'Bayer Leverkusen'
ger_17.loc[ger_17.Team2 == 'Leverkusen', 'Team2'] = 'Bayer Leverkusen'
ger_17.loc[ger_17.Team1 == 'Augsburg', 'Team1'] = 'FC Augsburg'
ger_17.loc[ger_17.Team2 == 'Augsburg', 'Team2'] = 'FC Augsburg'
ger_17.loc[ger_17.Team1 == 'FC Koln', 'Team1'] = 'FC Cologne'
ger_17.loc[ger_17.Team2 == 'FC Koln', 'Team2'] = 'FC Cologne'
ger_17.loc[ger_17.Team1 == 'Freiburg', 'Team1'] = 'SC Freiburg'
ger_17.loc[ger_17.Team2 == 'Freiburg', 'Team2'] = 'SC Freiburg'
ger_17.loc[ger_17.Team1 == 'Hamburger SV', 'Team1'] = 'Hamburg SV'
ger_17.loc[ger_17.Team2 == 'Hamburger SV', 'Team2'] = 'Hamburg SV'
ger_17.loc[ger_17.Team1 == 'Frankfurt', 'Team1'] = 'Eintracht Frankfurt'
ger_17.loc[ger_17.Team2 == 'Frankfurt', 'Team2'] = 'Eintracht Frankfurt'
ger_17.loc[ger_17.Team1 == 'Hertha', 'Team1'] = '<NAME>'
ger_17.loc[ger_17.Team2 == 'Hertha', 'Team2'] = '<NAME>'
ger_17.loc[ger_17.Team1 == 'Hoffenheim', 'Team1'] = 'TSG Hoffenheim'
ger_17.loc[ger_17.Team2 == 'Hoffenheim', 'Team2'] = 'TSG Hoffenheim'
ger_17.loc[ger_17.Team1 == 'Ingolstadt', 'Team1'] = 'FC Ingolstadt 04'
ger_17.loc[ger_17.Team2 == 'Ingolstadt', 'Team2'] = 'FC Ingolstadt 04'
ger_17.loc[ger_17.Team1 == 'Schalke', 'Team1'] = 'Schalke 04'
ger_17.loc[ger_17.Team2 == 'Schalke', 'Team2'] = 'Schalke 04'
ger_17.loc[ger_17.Team1 == 'Wolfsburg', 'Team1'] = 'VfL Wolfsburg'
ger_17.loc[ger_17.Team2 == 'Wolfsburg', 'Team2'] = 'VfL Wolfsburg'
# -
print germ_train_17.columns
print ger_17.columns
# +
ger_17_clubs = pd.unique(ger_17[['Team1','Team2']].values.ravel())
## drop first alphabetical club for comparison, return in DF to append to original df
clubs = np.sort(ger_17_clubs)[1:len(ger_17_clubs)]
club_df = pd.DataFrame(columns = clubs)
ger_17 = ger_17.append(club_df)
for club in clubs:
for i, row in ger_17.iterrows():
if row['Team1'] == club or row['Team2'] == club:
dummy = 1
else:
dummy = 0
ger_17.loc[i, club] = dummy
# +
X_train = germ_train_17[[u'<NAME>', u'<NAME>', u'<NAME>',
u'Eintracht Frankfurt', u'FC Augsburg', u'FC Cologne',
u'FC Ingolstadt 04', u'Hamburg SV', u'<NAME>', u'Mainz',
u'RB Leipzig', u'SC Freiburg', u'SV Darmstadt 98', u'Schalke 04',
u'TSG Hoffenheim', u'VfL Wolfsburg', u'<NAME>']]
y_train = germ_train_17['cluster']
X_test = ger_17[[u'<NAME>unich', u'<NAME>', u'<NAME>',
u'Eintracht Frankfurt', u'FC Augsburg', u'FC Cologne',
u'FC Ingolstadt 04', u'Hamburg SV', u'<NAME>', u'Mainz',
u'RB Leipzig', u'SC Freiburg', u'SV Darmstadt 98', u'Schalke 04',
u'TSG Hoffenheim', u'VfL Wolfsburg', u'<NAME>']]
## y_test = test['cluster']
X_train = X_train.astype(int)
X_test = X_test.astype(int)
# -
# +
xg_train_17 = xgb.DMatrix( X_train, label=y_train)
xg_test_17 = xgb.DMatrix(X_test)
param = {}
param['objective'] = 'multi:softmax'
param['eta'] = 0.1
param['max_depth'] = 6
param['silent'] = 1
param['nthread'] = 4
param['num_class'] = 4
param['eval_metric'] = 'auc'
num_round = 5
bst_17 = xgb.train(param, xg_train_17, num_round)
# get prediction
pred_17 = bst_17.predict( xg_test_17 );
# +
ger_17_predict = ger_17.drop([u'<NAME>', u'<NAME>', u'<NAME>',
u'Eintracht Frankfurt', u'FC Augsburg', u'FC Cologne',
u'FC Ingolstadt 04', u'Hamburg SV', u'<NAME>', u'Mainz',
u'RB Leipzig', u'SC Freiburg', u'SV Darmstadt 98', u'Schalke 04',
u'TSG Hoffenheim', u'VfL Wolfsburg', u'<NAME>'], axis = 1)
ger_17_predict['cluster'] = pred_17
# -
ger_17_predict.head()
# ## Italy Below
# +
ita_train_17 = dummy_year_pipe(italy, 2017)
ita_17 = pd.read_csv('ita_17_fixtures.csv', encoding = 'utf-8')
ita_17.loc[ita_17.Team1 == 'Chievo', 'Team1'] = 'Chievo Verona'
ita_17.loc[ita_17.Team2 == 'Chievo', 'Team2'] = 'Chievo Verona'
ita_17.loc[ita_17.Team1 == 'inter', 'Team1'] = 'Internazionale'
ita_17.loc[ita_17.Team2 == 'inter', 'Team2'] = 'Internazionale'
ita_17.loc[ita_17.Team1 == 'Pescara', 'Team1'] = 'US Pescara'
ita_17.loc[ita_17.Team2 == 'Pescara', 'Team2'] = 'US Pescara'
# -
print ita_train_17.columns
print np.unique(ita_17[['Team1','Team2']].values.ravel())
# +
ita_17_clubs = pd.unique(ita_17[['Team1','Team2']].values.ravel())
## drop first alphabetical club for comparison, return in DF to append to original df
clubs = np.sort(ita_17_clubs)[1:len(ita_17_clubs)]
club_df = pd.DataFrame(columns = clubs)
ita_17 = ita_17.append(club_df)
for club in clubs:
for i, row in ita_17.iterrows():
if row['Team1'] == club or row['Team2'] == club:
dummy = 1
else:
dummy = 0
ita_17.loc[i, club] = dummy
# +
X_train = ita_train_17[[u'AS Roma', u'Atalanta', u'Bologna', u'Cagliari', u'<NAME>',
u'Crotone', u'Empoli', u'Fiorentina', u'Genoa', u'Internazionale',
u'Juventus', u'Lazio', u'Napoli', u'Palermo', u'Sampdoria', u'Sassuolo',
u'Torino', u'US Pescara', u'Udinese']]
y_train = ita_train_17['cluster']
X_test = ita_17[[u'AS Roma', u'Atalanta', u'Bologna', u'Cagliari', u'<NAME>',
u'Crotone', u'Empoli', u'Fiorentina', u'Genoa', u'Internazionale',
u'Juventus', u'Lazio', u'Napoli', u'Palermo', u'Sampdoria', u'Sassuolo',
u'Torino', u'US Pescara', u'Udinese']]
## y_test = test['cluster']
X_train = X_train.astype(int)
X_test = X_test.astype(int)
# +
xg_train_17 = xgb.DMatrix( X_train, label=y_train)
xg_test_17 = xgb.DMatrix(X_test)
param = {}
param['objective'] = 'multi:softmax'
param['eta'] = 0.1
param['max_depth'] = 6
param['silent'] = 1
param['nthread'] = 4
param['num_class'] = 4
param['eval_metric'] = 'auc'
num_round = 5
bst_17 = xgb.train(param, xg_train_17, num_round)
# get prediction
pred_17 = bst_17.predict( xg_test_17 );
# +
ita_17_predict = ita_17.drop([u'AS Roma', u'Atalanta', u'Bologna', u'Cagliari', u'Chievo Verona',
u'Crotone', u'Empoli', u'Fiorentina', u'Genoa', u'Internazionale',
u'Juventus', u'Lazio', u'Napoli', u'Palermo', u'Sampdoria', u'Sassuolo',
u'Torino', u'US Pescara', u'Udinese'], axis = 1)
ita_17_predict['cluster'] = pred_17
ita_17_predict.head()
# -
# ## France below
# +
fra_train_17 = dummy_year_pipe(france, 2017)
fra_17 = pd.read_csv('fra_17_fixtures.csv', encoding = 'utf-8')
fra_17.loc[fra_17.Team1 == 'Nancy', 'Team1'] = 'AS Nancy Lorraine'
fra_17.loc[fra_17.Team2 == 'Nancy', 'Team2'] = 'AS Nancy Lorraine'
fra_17.loc[fra_17.Team1 == 'Dijon', 'Team1'] = 'Dijon FCO'
fra_17.loc[fra_17.Team2 == 'Dijon', 'Team2'] = 'Dijon FCO'
fra_17.loc[fra_17.Team1 == 'PSG', 'Team1'] = 'Paris Saint-Germain'
fra_17.loc[fra_17.Team2 == 'PSG', 'Team2'] = 'Paris Saint-Germain'
fra_17.loc[fra_17.Team1 == 'Rennes', 'Team1'] = 'Stade Rennes'
fra_17.loc[fra_17.Team2 == 'Rennes', 'Team2'] = 'Stade Rennes'
fra_17.loc[fra_17.Team1 == 'St. Etienne', 'Team1'] = 'St Etienne'
fra_17.loc[fra_17.Team2 == 'St. Etienne', 'Team2'] = 'St Etienne'
fra_17.loc[fra_17.Team1 == 'Monaco', 'Team1'] = 'AS Monaco'
fra_17.loc[fra_17.Team2 == 'Monaco', 'Team2'] = 'AS Monaco'
print fra_train_17.columns
print np.unique(fra_17[['Team1','Team2']].values.ravel())
# +
fra_17_clubs = pd.unique(fra_17[['Team1','Team2']].values.ravel())
## drop first alphabetical club for comparison, return in DF to append to original df
clubs = np.sort(fra_17_clubs)[1:len(fra_17_clubs)]
club_df = pd.DataFrame(columns = clubs)
fra_17 = fra_17.append(club_df)
for club in clubs:
for i, row in fra_17.iterrows():
if row['Team1'] == club or row['Team2'] == club:
dummy = 1
else:
dummy = 0
fra_17.loc[i, club] = dummy
# +
X_train = fra_train_17[[u'AS Nancy Lorraine', u'Angers', u'Bastia', u'Bordeaux', u'Caen',
u'Dijon FCO', u'Guingamp', u'Lille', u'Lorient', u'Lyon', u'Marseille',
u'Metz', u'Montpellier', u'Nantes', u'Nice', u'Paris Saint-Germain',
u'St Etienne', u'Stade Rennes', u'Toulouse']]
y_train = fra_train_17['cluster']
X_test = fra_17[[u'AS <NAME>', u'Angers', u'Bastia', u'Bordeaux', u'Caen',
u'<NAME>', u'Guingamp', u'Lille', u'Lorient', u'Lyon', u'Marseille',
u'Metz', u'Montpellier', u'Nantes', u'Nice', u'Paris Saint-Germain',
u'St Etienne', u'Stade Rennes', u'Toulouse']]
## y_test = test['cluster']
X_train = X_train.astype(int)
X_test = X_test.astype(int)
# +
xg_train_17 = xgb.DMatrix( X_train, label=y_train)
xg_test_17 = xgb.DMatrix(X_test)
param = {}
param['objective'] = 'multi:softmax'
param['eta'] = 0.1
param['max_depth'] = 6
param['silent'] = 1
param['nthread'] = 4
param['num_class'] = 4
param['eval_metric'] = 'auc'
num_round = 5
bst_17 = xgb.train(param, xg_train_17, num_round)
# get prediction
pred_17 = bst_17.predict( xg_test_17 );
# +
fra_17_predict = fra_17.drop([u'AS N<NAME>', u'Angers', u'Bastia', u'Bordeaux', u'Caen',
u'<NAME>', u'Guingamp', u'Lille', u'Lorient', u'Lyon', u'Marseille',
u'Metz', u'Montpellier', u'Nantes', u'Nice', u'Paris Saint-Germain',
u'<NAME>', u'<NAME>', u'Toulouse'], axis = 1)
fra_17_predict['cluster'] = pred_17
fra_17_predict.head()
# -
print epl_17_predict.head()
print esp_17_predict.head()
print ger_17_predict.head()
print ita_17_predict.head()
print fra_17_predict.head()
# Dates are in an inconsistent format, and the below should pull the date of each match.
def dt_split(i):
splt = i.split('. ', 1)
date = splt[0]
time = splt[1]
try:
dt = date.split(':', 1)
return pd.to_datetime("{}-{}-2017".format(dt[1], dt[0])) # dt[1],"/",dt[0],"/2017"
except:
dt = date.split('.', 1)
return pd.to_datetime("{}-{}-2017".format(dt[1], dt[0]))
epl_17_predict['date'] = epl_17_predict.date_time.apply(dt_split)
epl_17_predict.to_csv('epl_matches_2017.csv', encoding='utf-8')
esp_17_predict['date'] = esp_17_predict.date_time.apply(dt_split)
esp_17_predict.to_csv('esp_matches_2017.csv', encoding='utf-8')
ger_17_predict['date'] = ger_17_predict.date_time.apply(dt_split)
ger_17_predict.to_csv('ger_matches_2017.csv', encoding='utf-8')
ita_17_predict['date'] = ita_17_predict.date_time.apply(dt_split)
ita_17_predict.to_csv('ita_matches_2017.csv', encoding='utf-8')
fra_17_predict['date'] = fra_17_predict.date_time.apply(dt_split)
fra_17_predict.to_csv('fra_matches_2017.csv', encoding='utf-8')
# +
epl_17_predict['country'] = 'England'
esp_17_predict['country'] = 'Spain'
ger_17_predict['country'] = 'Germany'
ita_17_predict['country'] = 'Italy'
fra_17_predict['country'] = 'France'
epl_17_predict.append([esp_17_predict, ger_17_predict, ita_17_predict, fra_17_predict]).to_csv('league_compare.csv', encoding = 'utf-8')
# -
print epl_17_predict.groupby('cluster').date.count().reset_index()
print esp_17_predict.groupby('cluster').date.count().reset_index()
print ger_17_predict.groupby('cluster').date.count().reset_index()
print ita_17_predict.groupby('cluster').date.count().reset_index()
print fra_17_predict.groupby('cluster').date.count().reset_index()
league_clust = pd.merge(epl_17_predict.groupby('cluster').date.count().reset_index(),
esp_17_predict.groupby('cluster').date.count().reset_index(), on = 'cluster', how = 'left')
league_clust = pd.merge(league_clust,
ger_17_predict.groupby('cluster').date.count().reset_index(), on = 'cluster', how = 'left')
league_clust = pd.merge(league_clust,
ita_17_predict.groupby('cluster').date.count().reset_index(), on = 'cluster', how = 'left')
league_clust = pd.merge(league_clust,
fra_17_predict.groupby('cluster').date.count().reset_index(), on = 'cluster', how = 'left')
league_clust.columns = [['cluster','England','Spain','Germany','Italy','France']]
league_clust.fillna(0, inplace = True)
league_clust
# Predictions of excitement of matches are plotted below.
league_clust.groupby('cluster').max().plot.bar()
plt.show()
#epl_17_predict[['Team1','Team2']].stack()
pd.melt(epl_17_predict, id_vars = ['cluster','date'], value_vars = ['Team1','Team2'], value_name = 'team')
|
projects/Soccer-Watchability/Football-watchability-modeling-clean.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Automating administrative workflows
from arcgis.gis import *
from getpass import getpass
password = getpass()
gis = GIS("https://esriwebgis.webgistesting.net/portal", "admin", password)
# ## Querying for users
gis.users.search()
#filter users
gis.users.search("at*")
#filter users
gis.users.search("rohit")
# ### Create a new user
# +
rohit = gis.users.create(username = 'rohit.singh', password='<PASSWORD>?:!',
firstname='Rohit', lastname='Singh',
email='<EMAIL>', role='org_user')
rohit
# -
type(rohit)
rohit.update(thumbnail='rohit_thumbnail.png')
rohit
# ## Searching for groups
gis.groups.search()
# +
#create groups
group_summary = 'A group to share data related to crime and analyze them'
group_description = 'Analysis, visualization, modeling of crime and crime related datasets using GIS'
crime_group = gis.groups.create(title='Crime analysis1', tags='crime, machine learning, clustering',
description=group_description,
snippet=group_summary,
thumbnail='crime_analysis_group.png')
# -
crime_group
# ## Add user to a group
crime_group.add_users(['rohit.singh'])
# ## Removing users
batman = gis.users.search('bat.man')[0]
batman
batman.delete(reassign_to='rohit.singh')
batman.items()
batman.groups
item = batman.items()[0]
item.reassign_to('')
# ## Rohit's contents
rohit.items(folder='bat.man_root')
rohit.folders
|
talks/uc2017/ArcGIS Python API - Introduction to Scripting Your Web GIS/notebooks/automating_admin_workflows.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/sri-spirited/fchollet-book-deep-learning-with-python-notebooks/blob/master/3.5-classifying-movie-reviews.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="xqlE6VxBJlZE" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="c84ffa74-1c43-4ee2-c5ba-3320b1d3ab53"
import keras
keras.__version__
# + [markdown] id="jAF4-Og6JlZL" colab_type="text"
# # Classifying movie reviews: a binary classification example
#
# This notebook contains the code samples found in Chapter 3, Section 5 of [Deep Learning with Python](https://www.manning.com/books/deep-learning-with-python?a_aid=keras&a_bid=76564dff). Note that the original text features far more content, in particular further explanations and figures: in this notebook, you will only find source code and related comments.
#
# ----
#
#
# Two-class classification, or binary classification, may be the most widely applied kind of machine learning problem. In this example, we
# will learn to classify movie reviews into "positive" reviews and "negative" reviews, just based on the text content of the reviews.
# + [markdown] id="qta8PIOHJlZL" colab_type="text"
# ## The IMDB dataset
#
#
# We'll be working with "IMDB dataset", a set of 50,000 highly-polarized reviews from the Internet Movie Database. They are split into 25,000
# reviews for training and 25,000 reviews for testing, each set consisting in 50% negative and 50% positive reviews.
#
# Why do we have these two separate training and test sets? You should never test a machine learning model on the same data that you used to
# train it! Just because a model performs well on its training data doesn't mean that it will perform well on data it has never seen, and
# what you actually care about is your model's performance on new data (since you already know the labels of your training data -- obviously
# you don't need your model to predict those). For instance, it is possible that your model could end up merely _memorizing_ a mapping between
# your training samples and their targets -- which would be completely useless for the task of predicting targets for data never seen before.
# We will go over this point in much more detail in the next chapter.
#
# Just like the MNIST dataset, the IMDB dataset comes packaged with Keras. It has already been preprocessed: the reviews (sequences of words)
# have been turned into sequences of integers, where each integer stands for a specific word in a dictionary.
#
# The following code will load the dataset (when you run it for the first time, about 80MB of data will be downloaded to your machine):
# + id="GKTYqQkcJlZM" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 52} outputId="f8b48d64-1f0d-4496-88f6-9c8ad0286f8a"
from keras.datasets import imdb
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)
# + [markdown] id="ZepUKd7ZJlZQ" colab_type="text"
#
# The argument `num_words=10000` means that we will only keep the top 10,000 most frequently occurring words in the training data. Rare words
# will be discarded. This allows us to work with vector data of manageable size.
#
# The variables `train_data` and `test_data` are lists of reviews, each review being a list of word indices (encoding a sequence of words).
# `train_labels` and `test_labels` are lists of 0s and 1s, where 0 stands for "negative" and 1 stands for "positive":
# + id="UEBTzNSmJlZQ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="1d0a5f03-24ff-4c1d-9c98-a2f86dd960bd"
train_data[0]
# + id="X1rNXN5ZJlZT" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="eb12accc-022f-4d15-9542-ca4e7ec0fe96"
train_labels[0]
# + [markdown] id="hh_Mx103JlZX" colab_type="text"
# Since we restricted ourselves to the top 10,000 most frequent words, no word index will exceed 10,000:
# + id="70pxDR6GJlZX" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="c9d41787-45d8-4640-b19e-09fc233aa18a"
max([max(sequence) for sequence in train_data])
# + [markdown] id="AKpwwUAAJlZa" colab_type="text"
# For kicks, here's how you can quickly decode one of these reviews back to English words:
# + id="sw5KK4wfLXGe" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 70} outputId="f4ca7034-d964-4f81-e46e-96e720e5ada0"
# word_index is a dictionary mapping words to an integer index
word_index = imdb.get_word_index()
# Let's look at one entry
word_index['rickman']
# + id="QBp13ElhLmff" colab_type="code" colab={}
# We reverse it, mapping integer indices to words
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])
# + id="uFmvSBLlJlZb" colab_type="code" colab={}
# We decode the review; note that our indices were offset by 3
# because 0, 1 and 2 are reserved indices for "padding", "start of sequence", and "unknown".
decoded_review = ' '.join([reverse_word_index.get(i - 3, '?') for i in train_data[0]])
# + id="qCABS0EMJlZf" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 124} outputId="f9658451-77f0-419a-af6c-29a816876a64"
decoded_review
# + [markdown] id="Mcyz_OpGJlZi" colab_type="text"
# ## Preparing the data
#
#
# We cannot feed lists of integers into a neural network. We have to turn our lists into tensors. There are two ways we could do that:
#
# * We could pad our lists so that they all have the same length, and turn them into an integer tensor of shape `(samples, word_indices)`,
# then use as first layer in our network a layer capable of handling such integer tensors (the `Embedding` layer, which we will cover in
# detail later in the book).
# * We could one-hot-encode our lists to turn them into vectors of 0s and 1s. Concretely, this would mean for instance turning the sequence
# `[3, 5]` into a 10,000-dimensional vector that would be all-zeros except for indices 3 and 5, which would be ones. Then we could use as
# first layer in our network a `Dense` layer, capable of handling floating point vector data.
#
# We will go with the latter solution. Let's vectorize our data, which we will do manually for maximum clarity:
# + id="oHfiu0MGVD0N" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 197} outputId="a55139dd-33de-4e6a-b4ed-018187011f6b"
import numpy as np
def vectorize_sequences(sequences, n_dimensions=10000):
#First build a matrix of zeroes of shape (number of sequences, dimensions)
results = np.zeros(shape = (len(sequences), n_dimensions))
for i in range(len(sequences)):
results[i, sequences[i]] = 1.
return results
print(f"train_data[0]: {train_data[0]} \n with {len(train_data[0])} words")
print(f"Vectorized version is {vectorize_sequences(train_data[0])} with shape {vectorize_sequences(train_data[0]).shape}")
# + id="mdc-wlWPJlZj" colab_type="code" colab={}
# Our vectorized training data
x_train = vectorize_sequences(train_data)
# Our vectorized test data
x_test = vectorize_sequences(test_data)
# + [markdown] id="0OBi88bFJlZm" colab_type="text"
# Here's what our samples look like now:
# + id="R5qu3LUYJlZm" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="dbc<PASSWORD>"
x_train[0]
# + [markdown] id="nzPTV6g-JlZp" colab_type="text"
# We should also vectorize our labels, which is straightforward:
# + id="IP0YwC1bJlZq" colab_type="code" colab={}
# Our vectorized labels
y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')
# + [markdown] id="XeepN61DJlZu" colab_type="text"
# Now our data is ready to be fed into a neural network.
# + [markdown] id="daDGW7_uJlZv" colab_type="text"
# ## Building our network
#
#
# Our input data is simply vectors, and our labels are scalars (1s and 0s): this is the easiest setup you will ever encounter. A type of
# network that performs well on such a problem would be a simple stack of fully-connected (`Dense`) layers with `relu` activations: `Dense(16,
# activation='relu')`
#
# The argument being passed to each `Dense` layer (16) is the number of "hidden units" of the layer. What's a hidden unit? It's a dimension
# in the representation space of the layer. You may remember from the previous chapter that each such `Dense` layer with a `relu` activation implements
# the following chain of tensor operations:
#
# `output = relu(dot(W, input) + b)`
#
# Having 16 hidden units means that the weight matrix `W` will have shape `(input_dimension, 16)`, i.e. the dot product with `W` will project the
# input data onto a 16-dimensional representation space (and then we would add the bias vector `b` and apply the `relu` operation). You can
# intuitively understand the dimensionality of your representation space as "how much freedom you are allowing the network to have when
# learning internal representations". Having more hidden units (a higher-dimensional representation space) allows your network to learn more
# complex representations, but it makes your network more computationally expensive and may lead to learning unwanted patterns (patterns that
# will improve performance on the training data but not on the test data).
#
# There are two key architecture decisions to be made about such stack of dense layers:
#
# * How many layers to use.
# * How many "hidden units" to chose for each layer.
#
# In the next chapter, you will learn formal principles to guide you in making these choices.
# For the time being, you will have to trust us with the following architecture choice:
# two intermediate layers with 16 hidden units each,
# and a third layer which will output the scalar prediction regarding the sentiment of the current review.
# The intermediate layers will use `relu` as their "activation function",
# and the final layer will use a sigmoid activation so as to output a probability
# (a score between 0 and 1, indicating how likely the sample is to have the target "1", i.e. how likely the review is to be positive).
# A `relu` (rectified linear unit) is a function meant to zero-out negative values,
# while a sigmoid "squashes" arbitrary values into the `[0, 1]` interval, thus outputting something that can be interpreted as a probability.
# + [markdown] id="aulKmQSUJlZv" colab_type="text"
# Here's what our network looks like:
#
# 
# + [markdown] id="djPe7LnrJlZw" colab_type="text"
# And here's the Keras implementation, very similar to the MNIST example you saw previously:
# + id="7PaVAX4nJlZw" colab_type="code" colab={}
from keras import models
from keras import layers
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
# + [markdown] id="MKQ1nb6zJlZz" colab_type="text"
#
# Lastly, we need to pick a loss function and an optimizer. Since we are facing a binary classification problem and the output of our network
# is a probability (we end our network with a single-unit layer with a sigmoid activation), is it best to use the `binary_crossentropy` loss.
# It isn't the only viable choice: you could use, for instance, `mean_squared_error`. But crossentropy is usually the best choice when you
# are dealing with models that output probabilities. Crossentropy is a quantity from the field of Information Theory, that measures the "distance"
# between probability distributions, or in our case, between the ground-truth distribution and our predictions.
#
# Here's the step where we configure our model with the `rmsprop` optimizer and the `binary_crossentropy` loss function. Note that we will
# also monitor accuracy during training.
# + id="RD4GxL1lJlZz" colab_type="code" colab={}
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
# + [markdown] id="lgVfVKBqJlZ2" colab_type="text"
# We are passing our optimizer, loss function and metrics as strings, which is possible because `rmsprop`, `binary_crossentropy` and
# `accuracy` are packaged as part of Keras. Sometimes you may want to configure the parameters of your optimizer, or pass a custom loss
# function or metric function. This former can be done by passing an optimizer class instance as the `optimizer` argument:
# + id="COOcXfZ9JlZ3" colab_type="code" colab={}
from keras import optimizers
model.compile(optimizer=optimizers.RMSprop(lr=0.001),
loss='binary_crossentropy',
metrics=['accuracy'])
# + [markdown] id="7AVSmCIHJlZ5" colab_type="text"
# The latter can be done by passing function objects as the `loss` or `metrics` arguments:
# + id="_929I_oSJlZ6" colab_type="code" colab={}
from keras import losses
from keras import metrics
model.compile(optimizer=optimizers.RMSprop(lr=0.001),
loss=losses.binary_crossentropy,
metrics=[metrics.binary_accuracy])
# + [markdown] id="Dyny7SciJlZ8" colab_type="text"
# ## Validating our approach
#
# In order to monitor during training the accuracy of the model on data that it has never seen before, we will create a "validation set" by
# setting apart 10,000 samples from the original training data:
# + id="odW2tNXsJlZ9" colab_type="code" colab={}
x_val = x_train[:10000]
partial_x_train = x_train[10000:]
y_val = y_train[:10000]
partial_y_train = y_train[10000:]
# + [markdown] id="pLRXKnvgJlZ_" colab_type="text"
# We will now train our model for 20 epochs (20 iterations over all samples in the `x_train` and `y_train` tensors), in mini-batches of 512
# samples. At this same time we will monitor loss and accuracy on the 10,000 samples that we set apart. This is done by passing the
# validation data as the `validation_data` argument:
# + id="A79NosTmJlZ_" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 728} outputId="7c27eba3-5655-4630-b06a-b9074652b471"
history = model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=512,
validation_data=(x_val, y_val))
# + [markdown] id="B7hsUVMpJlaD" colab_type="text"
# On CPU, this will take less than two seconds per epoch -- training is over in 20 seconds. At the end of every epoch, there is a slight pause
# as the model computes its loss and accuracy on the 10,000 samples of the validation data.
#
# Note that the call to `model.fit()` returns a `History` object. This object has a member `history`, which is a dictionary containing data
# about everything that happened during training. Let's take a look at it:
# + id="ONP9jL2IJlaD" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="ce914a49-86fa-4021-c07e-e5b585ba4406"
history_dict = history.history
history_dict.keys()
# + [markdown] id="5qGtN6U-JlaG" colab_type="text"
# It contains 4 entries: one per metric that was being monitored, during training and during validation. Let's use Matplotlib to plot the
# training and validation loss side by side, as well as the training and validation accuracy:
# + id="hgTTED5cJlaH" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 295} outputId="68b7b617-eb52-4cb5-feb3-e48570cac0af"
import matplotlib.pyplot as plt
acc = history.history['binary_accuracy']
val_acc = history.history['val_binary_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(acc) + 1)
# "bo" is for "blue dot"
plt.plot(epochs, loss, 'orange', label='Training loss')
# b is for "solid blue line"
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
# + id="GKWLvAinJlaJ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 295} outputId="e6dd68c2-55f1-4388-d831-6833eddaed84"
plt.clf() # clear figure
# acc_values = history_dict['acc']
# val_acc_values = history_dict['val_acc']
plt.plot(epochs, acc, 'orange', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
# + [markdown] id="LfXw2odKJlaL" colab_type="text"
#
# The orange lines are the training loss and accuracy, while the blue lines are the validation loss and accuracy. Note that your own results may vary
# slightly due to a different random initialization of your network.
#
# As you can see, the training loss decreases with every epoch and the training accuracy increases with every epoch. That's what you would
# expect when running gradient descent optimization -- the quantity you are trying to minimize should get lower with every iteration. But that
# isn't the case for the validation loss and accuracy: they seem to peak at the fourth epoch. This is an example of what we were warning
# against earlier: a model that performs better on the training data isn't necessarily a model that will do better on data it has never seen
# before. In precise terms, what you are seeing is "overfitting": after the second epoch, we are over-optimizing on the training data, and we
# ended up learning representations that are specific to the training data and do not generalize to data outside of the training set.
#
# In this case, to prevent overfitting, we could simply stop training after three epochs. In general, there is a range of techniques you can
# leverage to mitigate overfitting, which we will cover in the next chapter.
#
# Let's train a new network from scratch for four epochs, then evaluate it on our test data:
# + id="j1tzxpfeJlaL" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 177} outputId="1690532e-0b66-42ea-e350-35d27a4658a6"
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
model.fit(x_train, y_train, epochs=4, batch_size=512)
results = model.evaluate(x_test, y_test)
# + id="WQnwgO4WJlaN" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="7e381eb6-d87d-45e7-f123-5104220beeb1"
results
# + [markdown] id="ue32ivO0JlaQ" colab_type="text"
# Our fairly naive approach achieves an accuracy of 88%. With state-of-the-art approaches, one should be able to get close to 95%.
# + [markdown] id="-AZxQcOnJlaQ" colab_type="text"
# ## Using a trained network to generate predictions on new data
#
# After having trained a network, you will want to use it in a practical setting. You can generate the likelihood of reviews being positive
# by using the `predict` method:
# + id="IDJF6PSOJlaR" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 141} outputId="1a6d215e-1f1a-4ede-8f9e-bf98de8f27bb"
model.predict(x_test)
# + [markdown] id="OMseMo-nJlaT" colab_type="text"
# As you can see, the network is very confident for some samples (0.99 or more, or 0.01 or less) but less confident for others (0.6, 0.4).
#
# + [markdown] id="FN8nYSm8JlaT" colab_type="text"
# ## Further experiments
#
#
# * We were using 2 hidden layers. Try to use 1 or 3 hidden layers and see how it affects validation and test accuracy.
# * Try to use layers with more hidden units or less hidden units: 32 units, 64 units...
# * Try to use the `mse` loss function instead of `binary_crossentropy`.
# * Try to use the `tanh` activation (an activation that was popular in the early days of neural networks) instead of `relu`.
#
# These experiments will help convince you that the architecture choices we have made are all fairly reasonable, although they can still be
# improved!
#
# ### Experiment 1: Only 1 hidden layer
# + id="uqgqo4uVIolU" colab_type="code" colab={}
from keras import models
from keras import layers
from keras import losses
from keras import metrics
from keras import optimizers
# + id="gmO0aiewI0a2" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 230} outputId="66c56b4f-7d76-4f04-aab1-b692fd9afc43"
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape = (10000,)))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer=optimizers.RMSprop(lr=0.001),
loss = losses.binary_crossentropy,
metrics = [metrics.binary_accuracy])
model.summary()
# + id="TEnhkhNSKggw" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 728} outputId="b30e57ff-c55d-4abb-c012-b64ca1e2a362"
x_val = x_train[:10000]
partial_x_train = x_train[10000:]
y_val = y_train[:10000]
partial_y_train = y_train[10000:]
history = model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=512,
validation_data=(x_val, y_val))
# + id="wUqCfHNiKnDA" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 295} outputId="d15f7bba-029d-4706-9261-7b0c3e1751f9"
import matplotlib.pyplot as plt
acc = history.history['binary_accuracy']
val_acc = history.history['val_binary_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(acc) + 1)
# "bo" is for "blue dot"
plt.plot(epochs, loss, 'orange', label='Training loss')
# b is for "solid blue line"
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
# + id="exWvXe_kLFfn" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 52} outputId="1196805a-fc53-4140-f088-81883b0275ca"
results = model.evaluate(x_test, y_test)
results
# + [markdown] id="vYxWPtlgLHht" colab_type="text"
# With just one layer, our accuracy has droppped greatly to 85.63%
# + [markdown] id="o93aBaZUJlaT" colab_type="text"
# ## Conclusions
#
#
# Here's what you should take away from this example:
#
# * There's usually quite a bit of preprocessing you need to do on your raw data in order to be able to feed it -- as tensors -- into a neural
# network. In the case of sequences of words, they can be encoded as binary vectors -- but there are other encoding options too.
# * Stacks of `Dense` layers with `relu` activations can solve a wide range of problems (including sentiment classification), and you will
# likely use them frequently.
# * In a binary classification problem (two output classes), your network should end with a `Dense` layer with 1 unit and a `sigmoid` activation,
# i.e. the output of your network should be a scalar between 0 and 1, encoding a probability.
# * With such a scalar sigmoid output, on a binary classification problem, the loss function you should use is `binary_crossentropy`.
# * The `rmsprop` optimizer is generally a good enough choice of optimizer, whatever your problem. That's one less thing for you to worry
# about.
# * As they get better on their training data, neural networks eventually start _overfitting_ and end up obtaining increasingly worse results on data
# never-seen-before. Make sure to always monitor performance on data that is outside of the training set.
#
|
3.5-classifying-movie-reviews.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Plot scalars on a line plot
# +
import os
import math
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from itertools import product, chain, combinations
from scipy import stats
from IPython.display import display, HTML
# %matplotlib inline
def parse_if_number(s):
try: return float(s)
except: return True if s=="true" else False if s=="false" else s if s else None
def parse_ndarray(s):
return np.fromstring(s, sep=' ') if s else None
def get_file_name(name):
return name.replace(':', '-')
# -
# ## Config
# +
inputFile = 'data.csv'
repetitionsCount = -1 # -1 = auto-detect
factor = 'N'
tIntervalAlpha = 0.9
plotSize = (10, 10)
plotStyle = 'seaborn-whitegrid'
saveFigures = False
# Filter scalars
scalarsFilter = ['Floorplan.userCount', 'Floorplan.coveredUsers:sum', 'Floorplan.collisions:sum', 'Floorplan.msgsPerSlot:sum']
# Filter vectors
vectorsFilter = ['Floorplan.coveredUsers:vector']
# Percentiles
percentiles = [0.25, 0.5, 0.75, 0.9, 0.95]
# Performance indexes
perfIndexes = [
('coveredUsersPercent', 'percentage of covered users'),
('Floorplan.collisions:sum', 'total number of collisions'),
('Floorplan.msgsPerSlot:sum', 'total number of messages sent'),
]
intPercentiles = [int(i*100) for i in percentiles]
vecPerfIndexes = []
for intPercentile in intPercentiles:
vecPerfIndexes.append(('broadcastTime' + str(intPercentile), 'Broadcast time needed to reach the ' + str(intPercentile) + 'th percentile of the coverage'))
for v in vecPerfIndexes:
perfIndexes.append(v)
# -
# ## Load scalars
df = pd.read_csv('exported_data/' + inputFile, converters = {
'attrvalue': parse_if_number,
'binedges': parse_ndarray,
'binvalues': parse_ndarray,
'vectime': parse_ndarray,
'vecvalue': parse_ndarray,
})
# +
if repetitionsCount <= 0: # auto-detect
repetitionsCount = int(df[df.attrname == 'repetition']['attrvalue'].max()) + 1
print('Repetitions:', repetitionsCount)
display(HTML("<style>div.output_scroll { height: auto; max-height: 48em; }</style>"))
pd.set_option('display.max_rows', 1000)
pd.set_option('display.max_columns', 100)
if saveFigures:
os.makedirs('figures', exist_ok=True)
# +
scalars = df[(df.type == 'scalar') | ((df.type == 'itervar') & (df.attrname != 'TO')) | ((df.type == 'param') & (df.attrname == 'Floorplan.userCount')) | ((df.type == 'runattr') & (df.attrname == 'repetition'))]
scalars = scalars.assign(qname = scalars.attrname.combine_first(scalars.module + '.' + scalars.name))
for index, row in scalars[scalars.type == 'itervar'].iterrows():
val = scalars.loc[index, 'attrvalue']
if isinstance(val, str) and not all(c.isdigit() for c in val):
scalars.loc[index, 'attrvalue'] = eval(val)
scalars.value = scalars.value.combine_first(scalars.attrvalue.astype('float64'))
scalars_wide = scalars.pivot_table(index=['run'], columns='qname', values='value')
scalars_wide.sort_values([factor, 'repetition'], inplace=True)
scalars_wide = scalars_wide[[factor, 'repetition', *scalarsFilter]]
# coverage
scalars_wide['coveredUsersPercent'] = scalars_wide['Floorplan.coveredUsers:sum'] / (scalars_wide['Floorplan.userCount'] - 1)
# -
# ## Load vectors
vectors = df[df.type == 'vector']
vectors = vectors.assign(qname = vectors.module + '.' + vectors.name)
for index in scalars_wide.index:
r = index
fac = scalars_wide.loc[index, factor]
rep = scalars_wide.loc[index, 'repetition']
vectors.loc[vectors.run == r, factor] = fac
vectors.loc[vectors.run == r, 'repetition'] = rep
vectors = vectors[vectors.qname.isin(vectorsFilter)]
vectors.sort_values([factor, 'repetition', 'qname'], inplace=True)
vectors = vectors[[factor, 'repetition', 'qname', 'vectime', 'vecvalue']]
# ## Compute scalars from vectors
# +
def get_percentile(percentile, vectime, vecvalue, totalvalue):
tofind = percentile * totalvalue
idx = 0
csum = vecvalue.cumsum()
for value in csum:
if value >= tofind:
return vectime[idx]
idx += 1
return math.inf
for index, row in vectors.iterrows():
for vecPerf, percentile in zip(vecPerfIndexes, percentiles):
vecPerfIndex = vecPerf[0]
fac = row[factor]
rep = row['repetition']
if vecPerfIndex.startswith('broadcastTime'):
total = scalars_wide[(scalars_wide[factor] == fac) & (scalars_wide['repetition'] == rep)]['Floorplan.userCount'].values[0] - 1
else:
raise Exception('Need to specify total for ' + vecPerfIndex + '. (coding required)')
value = get_percentile(percentile, row['vectime'], row['vecvalue'], total)
scalars_wide.loc[(scalars_wide[factor] == fac) & (scalars_wide['repetition'] == rep), vecPerfIndex] = value
factorValues = scalars_wide[factor].unique()
# -
for perfIndex, perfIndexDesc in perfIndexes:
x = []
y = []
err = []
poserr = []
for value in factorValues:
x.append(value)
obssum = 0
mean = scalars_wide[scalars_wide[factor] == value][perfIndex].mean()
variance = scalars_wide[scalars_wide[factor] == value][perfIndex].var()
_, positiveInterval = tuple(v*math.sqrt(variance/repetitionsCount) for v in stats.t.interval(tIntervalAlpha, repetitionsCount - 1))
y.append(mean)
if perfIndex == 'coveredUsersPercent':
poserr.append(min(1 - mean, positiveInterval))
err.append(positiveInterval)
if len(poserr) > 0:
err = [err, poserr]
plt.figure(figsize=plotSize)
plt.style.use(plotStyle)
plt.errorbar(x=np.array(x), y=np.array(y), yerr=np.array(err), capsize=3, linestyle='-', marker='.', markersize=10)
plt.title('Line plot for ' + perfIndexDesc)
plt.ylabel(perfIndex)
if saveFigures:
fig = plt.gcf()
fig.savefig('figures/' + get_file_name(perfIndex) + '-lineplot.png')
plt.show()
|
analysis/line-plot.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + dc={"key": "3"} run_control={"frozen": true} editable=false deletable=false tags=["context"]
# ## 1. Import Python libraries
# <p><img src="https://assets.datacamp.com/production/project_555/img/92_notebook.jpg" alt="honey bee">
# <em>A honey bee (Apis).</em></p>
# <p>Can a machine identify a bee as a honey bee or a bumble bee? These bees have different <a href="https://www.thesca.org/connect/blog/bumblebees-vs-honeybees-what%E2%80%99s-difference-and-why-does-it-matter">behaviors and appearances</a>, but given the variety of backgrounds, positions, and image resolutions, it can be a challenge for machines to tell them apart.</p>
# <p>Being able to identify bee species from images is a task that ultimately would allow researchers to more quickly and effectively collect field data. Pollinating bees have critical roles in both ecology and agriculture, and diseases like <a href="http://news.harvard.edu/gazette/story/2015/07/pesticide-found-in-70-percent-of-massachusetts-honey-samples/">colony collapse disorder</a> threaten these species. Identifying different species of bees in the wild means that we can better understand the prevalence and growth of these important insects.</p>
# <p><img src="https://assets.datacamp.com/production/project_555/img/20_notebook.jpg" alt="bumble bee">
# <em>A bumble bee (Bombus).</em></p>
# <p>This notebook walks through building a simple deep learning model that can automatically detect honey bees and bumble bees and then loads a pre-trained model for evaluation.</p>
# + dc={"key": "3"} tags=["sample_code"]
import pickle
from pathlib import Path
from skimage import io
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
# import keras library
# ... YOUR CODE FOR TASK 1 ...
import keras
# import Sequential from the keras models module
# ... YOUR CODE FOR TASK 1 ...
from keras.models import Sequential
# import Dense, Dropout, Flatten, Conv2D, MaxPooling2D from the keras layers module
from keras.layers import Dense,Dropout,Flatten,Conv2D,MaxPooling2D
# + dc={"key": "10"} run_control={"frozen": true} editable=false deletable=false tags=["context"]
# ## 2. Load image labels
# <p>Now that we have all of our imports ready, it is time to look at the labels for our data. We will load our <code>labels.csv</code> file into a DataFrame called <code>labels</code>, where the index is the image name (e.g. an index of 1036 refers to an image named 1036.jpg) and the <code>genus</code> column tells us the bee type. <code>genus</code> takes the value of either <code>0.0</code> (Apis or honey bee) or <code>1.0</code> (Bombus or bumble bee).</p>
# + dc={"key": "10"} tags=["sample_code"]
# load labels.csv from datasets folder using pandas
labels = pd.read_csv('datasets/labels.csv',index_col=0)
# print value counts for genus
print(labels['genus'].value_counts())
# assign the genus label values to y
y = labels['genus'].values
# + dc={"key": "17"} run_control={"frozen": true} editable=false deletable=false tags=["context"]
# ## 3. Examine RGB values in an image matrix
# <p>Image data can be represented as a matrix. The width of the matrix is the width of the image, the height of the matrix is the height of the image, and the depth of the matrix is the number of channels. Most image formats have three color channels: red, green, and blue.</p>
# <p>For each pixel in an image, there is a value for every channel. The combination of the three values corresponds to the color, as per the <a href="https://en.wikipedia.org/wiki/RGB_color_model">RGB color model</a>. Values for each color can range from 0 to 255, so a purely blue pixel would show up as (0, 0, 255).</p>
# <p><img src="https://assets.datacamp.com/production/project_555/img/rgb_example.png" width="600"></p>
# <p>Let's explore the data for a sample image. </p>
# + dc={"key": "17"} tags=["sample_code"]
# load an image and explore
example_image = io.imread('datasets/{}.jpg'.format(labels.index[0]))
# show image
# ... YOUR CODE FOR TASK 3 ...
plt.imshow(example_image)
# print shape
print('Example image has shape: ', example_image.shape)
# print color channel values for top left pixel
print('RGB values for the top left pixel are:', example_image[0][0])
# + dc={"key": "24"} run_control={"frozen": true} editable=false deletable=false tags=["context"]
# ## 4. Normalize image data
# <p>Now we need to normalize our image data. Normalization is a general term that means changing the scale of our data so it is consistent.</p>
# <p>In this case, we want each feature to have a similar range so our neural network can learn effectively across all the features. As explained in the <a href="http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html">sklearn docs</a>, "If a feature has a variance that is orders of magnitude larger than others, it might dominate the objective function and make the estimator unable to learn from other features correctly as expected."</p>
# <p>We will scale our data so that it has a mean of 0 and standard deviation of 1. We'll use sklearn's <code>StandardScaler</code> to do the math for us, which entails taking each value, subtracting the mean, and then dividing by the standard deviation. We need to do this for each color channel (i.e. each feature) individually. </p>
# + dc={"key": "24"} tags=["sample_code"]
# initialize standard scaler
ss = StandardScaler()
image_list = []
for i in labels.index:
# load image
img = io.imread('datasets/{}.jpg'.format(i)).astype(np.float64)
# for each channel, apply standard scaler's fit_transform method
for channel in range(img.shape[2]):
img[:, :, channel] = ss.fit_transform(img[:, :, channel])
# append to list of all images
image_list.append(img)
# convert image list to single array
X = np.array(image_list)
# print shape of X
print(X.shape)
# + dc={"key": "31"} run_control={"frozen": true} editable=false deletable=false tags=["context"]
# ## 5. Split into train, test, and evaluation sets
# <p>Now that we have our big image data matrix, <code>X</code>, as well as our labels, <code>y</code>, we can split our data into train, test, and evaluation sets. To do this, we'll first allocate 20% of the data into our evaluation, or holdout, set. This is data that the model never sees during training and will be used to score our trained model.</p>
# <p>We will then split the remaining data, 60/40, into train and test sets just like in supervised machine learning models. We will pass both the train and test sets into the neural network. </p>
# + dc={"key": "31"} tags=["sample_code"]
# split out evaluation sets (x_eval and y_eval)
x_interim, x_eval, y_interim, y_eval = train_test_split(X,
y,
test_size=0.2,
random_state=52)
x_train, x_test, y_train, y_test = train_test_split(x_interim,
y_interim,
test_size=0.4,
random_state=52)
# split remaining data into train and test sets
# ... YOUR CODE FOR TASK 5 ...
# examine number of samples in train, test, and validation sets
print('x_train shape:', x_train.shape)
print(len(x_train), 'train samples')
print(x_test.shape[0], 'test samples')
print(x_eval.shape[0], 'eval samples')
# + dc={"key": "38"} run_control={"frozen": true} editable=false deletable=false tags=["context"]
# ## 6. Model building (part i)
# <p>It's time to start building our deep learning model, a convolutional neural network (CNN). CNNs are a specific kind of artificial neural network that is very effective for image classification because they are able to take into account the spatial coherence of the image, i.e., that pixels close to each other are often related.</p>
# <p>Building a CNN begins with specifying the model type. In our case, we'll use a <a href="https://keras.io/getting-started/sequential-model-guide/">Sequential</a> model, which is a linear stack of layers. We'll then add two convolutional layers. To understand convolutional layers, imagine a flashlight being shown over the top left corner of the image and slowly sliding across all the areas of the image, moving across the image in the same way your eyes move across words on a page. Convolutional layers pass a kernel (a sliding window) over the image and perform element-wise matrix multiplication between the kernel values and the pixel values in the image.</p>
# + dc={"key": "38"} tags=["sample_code"]
# set model constants
num_classes = 1
# define model as Sequential
model = Sequential()
# first convolutional layer with 32 filters
model.add(Conv2D(32, kernel_size=(3, 3), activation='relu', input_shape=(50, 50, 3)))
model.add(Conv2D(64, kernel_size=(3, 3), activation='relu'))
# + dc={"key": "45"} run_control={"frozen": true} editable=false deletable=false tags=["context"]
# ## 7. Model building (part ii)
# <p>Let's continue building our model. So far our model has two convolutional layers. However, those are not the only layers that we need to perform our task. A complete neural network architecture will have a number of other layers that are designed to play a specific role in the overall functioning of the network. Much deep learning research is about how to structure these layers into coherent systems.</p>
# <p>We'll add the following layers:</p>
# <ul>
# <li><a href="https://keras.io/layers/pooling/#maxpooling2d"><code>MaxPooling</code></a>. This passes a (2, 2) moving window over the image and downscales the image by outputting the maximum value within the window.</li>
# <li><a href="https://keras.io/layers/convolutional/#conv2d"><code>Conv2D</code></a>. This adds a third convolutional layer since deeper models, i.e. models with more convolutional layers, are better able to learn features from images.</li>
# <li><a href="https://keras.io/layers/core/#dropout"><code>Dropout</code></a>. This prevents the model from overfitting, i.e. perfectly remembering each image, by randomly setting 25% of the input units to 0 at each update during training.</li>
# <li><a href="https://keras.io/layers/core/#flatten"><code>Flatten</code></a>. As its name suggests, this flattens the output from the convolutional part of the CNN into a one-dimensional feature vector which can be passed into the following fully connected layers.</li>
# <li><a href="https://keras.io/layers/core/#dense"><code>Dense</code></a>. Fully connected layer where every input is connected to every output (see image below).</li>
# <li><a href="https://keras.io/layers/core/#dropout"><code>Dropout</code></a>. Another dropout layer to safeguard against overfitting, this time with a rate of 50%.</li>
# <li><code>Dense</code>. Final layer which calculates the probability the image is either a bumble bee or honey bee.</li>
# </ul>
# <p>To take a look at how it all stacks up, we'll print the model summary. Notice that our model has a whopping <code>3,669,249</code> paramaters. These are the different weights that the model learns through training and what are used to generate predictions on a new image.</p>
# <p><img src="https://assets.datacamp.com/production/project_555/img/mlp_conv.png" alt=""></p>
# + dc={"key": "45"} tags=["sample_code"]
# reduce dimensionality through max pooling
model.add(MaxPooling2D(pool_size=(2, 2)))
# third convolutional layer with 64 filters
model.add(Conv2D(64, kernel_size=(3, 3), activation='relu'))
# add dropout to prevent over fitting
model.add(Dropout(0.25))
# necessary flatten step preceeding dense layer
model.add(Flatten())
# fully connected layer
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
# add additional dropout to prevent overfitting
# ... YOUR CODE FOR TASK 7 ...
# prediction layers
model.add(Dense(num_classes, activation='sigmoid', name='preds'))
model.summary()
# show model summary
# ... YOUR CODE FOR TASK 7 ...
# + dc={"key": "52"} run_control={"frozen": true} editable=false deletable=false tags=["context"]
# ## 8. Compile and train model
# <p>Now that we've specified the model architecture, we will <a href="https://keras.io/models/model/#compile">compile</a> the model for training. For this we need to specify the loss function (what we're trying to minimize), the optimizer (how we want to go about minimizing the loss), and the metric (how we'll judge the performance of the model).</p>
# <p>Then, we'll call <a href="https://keras.io/models/model/#fit"><code>.fit</code></a> to begin the trainig the process. </p>
# <blockquote>
# <p>"Neural networks are trained iteratively using optimization techniques like gradient descent. After each cycle of training, an error metric is calculated based on the difference between prediction and target...Each neuron’s coefficients (weights) are then adjusted relative to how much they contributed to the total error. This process is repeated iteratively." <a href="https://ml-cheatsheet.readthedocs.io/en/latest/nn_concepts.html">ML Cheatsheet</a></p>
# </blockquote>
# <p>Since training is computationally intensive, we'll do a 'mock' training to get the feel for it, using just the first 10 images in the train and test sets and training for just 5 epochs. Epochs refer to the number of iterations over the data. Typically, neural networks will train for hundreds if not thousands of epochs.</p>
# <p>Take a look at the printout for each epoch and note the loss on the train set (<code>loss</code>), the accuracy on the train set (<code>acc</code>), and loss on the test set (<code>val_loss</code>) and the accuracy on the test set (<code>val_acc</code>). We'll explore this more in a later step.</p>
# + dc={"key": "52"} tags=["sample_code"]
model.compile(
# set the loss as binary_crossentropy
loss=keras.losses.binary_crossentropy,
# set the optimizer as stochastic gradient descent
optimizer=keras.optimizers.SGD(lr=0.001),
# set the metric as accuracy
metrics=['accuracy']
)
# mock-train the model using the first ten observations of the train and test sets
model.fit(
x_train[:10, :, :, :],
y_train[:10],
epochs=5,
verbose=1,
validation_data=(x_test[:10, :, :, :], y_test[:10])
)
# + dc={"key": "59"} run_control={"frozen": true} editable=false deletable=false tags=["context"]
# ## 9. Load pre-trained model and score
# <p>Now we'll load a pre-trained model that has the architecture we specified above and was trained for 200 epochs on the full train and test sets we created above.</p>
# <p>Let's use the <a href="https://keras.io/models/model/#evaluate"><code>evaluate</code></a> method to see how well the model did at classifying bumble bees and honey bees for the test and validation sets. Recall that accuracy is the number of correct predictions divided by the total number of predictions. Given that our classes are balanced, a model that predicts <code>1.0</code> for every image would get an accuracy around <code>0.5</code>.</p>
# <p>Note: it may take a few seconds to load the model. Recall that our model has over 3 million parameters (weights), which are what's being loaded.</p>
# + dc={"key": "59"} tags=["sample_code"]
# load pre-trained model
pretrained_cnn = keras.models.load_model('datasets/pretrained_model.h5')
# evaluate model on test set
score = pretrained_cnn.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
print("")
# evaluate model on holdout set
eval_score = pretrained_cnn.evaluate(x_eval , y_eval, verbose=0)
# print loss score
print('Eval loss:', eval_score[0])
# print accuracy score
print('Eval accuracy:', eval_score[0])
# + dc={"key": "66"} run_control={"frozen": true} editable=false deletable=false tags=["context"]
# ## 10. Visualize model training history
# <p>In addition to scoring the final iteration of the pre-trained model as we just did, we can also see the evolution of scores throughout training thanks to the <a href="https://keras.io/callbacks/#history"><code>History</code></a> object. We'll use the <a href="https://docs.python.org/3/library/pickle.html"><code>pickle</code></a> library to load the model history and then plot it.</p>
# <p>Notice how the accuracy improves over time, eventually leveling off. Correspondingly, the loss decreases over time. Plots like these can help diagnose overfitting. If we had seen an upward curve in the validation loss as times goes on (a U shape in the plot), we'd suspect that the model was starting to memorize the test set and would not generalize well to new data.</p>
# + dc={"key": "66"} tags=["sample_code"]
# load history
with open('datasets/model_history.pkl', 'rb') as f:
pretrained_cnn_history = pickle.load(f)
# print keys for pretrained_cnn_history dict
print(...)
fig = plt.figure(1)
plt.subplot(211)
# plot the validation accuracy
plt.plot(...)
plt.title('Validation accuracy and loss')
plt.ylabel('Accuracy')
plt.subplot(212)
# plot the validation loss
plt.plot(..., 'r')
plt.xlabel('Epoch')
plt.ylabel('Loss value');
# + dc={"key": "73"} run_control={"frozen": true} editable=false deletable=false tags=["context"]
# ## 11. Generate predictions
# <p>Previously, we calculated an overall score for our pre-trained model on the validation set. To end this notebook, let's access probabilities and class predictions for individual images using the <code>.predict</code> and <code>.predict_classes</code> methods.</p>
# <p>We now have a deep learning model that can be used to identify honey bees and bumble bees in images! The next step is to explore transfer learning, which harnesses the prediction power of models that have been trained on far more images than the mere 1600 in our dataset.</p>
# + dc={"key": "73"} tags=["sample_code"]
# predicted probabilities for x_eval
# ... YOUR CODE FOR TASK 11 ...
print("First five probabilities:")
print(...)
print("")
# predicted classes for x_eval
# ... YOUR CODE FOR TASK 11 ...
print("First five class predictions:")
print(y_pred[:5])
print("")
|
notebook.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
import numpy as np
from PIL import Image
# This function take the image downloaded and resized manually of Super Mario's map
# and create a compatible RGB JPG file to use the crop function below
def createCompatibleImage(img_path):
png = Image.open(img_path).convert('RGBA')
background = Image.new('RGBA', png.size, (255,255,255))
alpha_composite = Image.alpha_composite(background, png)
alpha_composite.save('levels/mario-8-1.jpg', 'JPEG', quality=100)
createCompatibleImage('levels/mario-8-1.png')
# +
# Now we have the image in the right format
img = np.array(Image.open('levels/mario-1-1.jpg'))
imgHeight = img.shape[0]
imgWidth = img.shape[1]
# Every tile is 16x16 pixels
windowsize_r = 16
windowsize_c = 16
tiles = []
# Crop out the window
for r in range(0, imgHeight, windowsize_r):
for c in range(0, imgWidth, windowsize_c):
window = img[r: r + windowsize_r, c: c + windowsize_c]
tile = Image.fromarray(window, 'RGB')
tiles.append(tile)
#img.save('my.png')
#tile.show()
print(len(tiles))
tiles[2740]
'''I used this part of code to save locally the different tile s blocks'''
#coinBlock = tiles[862]
#blankSpace = tiles[0]
#breakableBrick = tiles[2512]
#solidBrick = tiles[2456]
#bushBlock = tiles[2456]
#floorBlock = tiles[2740]
#coinBlock.save('blocks/coinBlock.png')
#blankSpace.save('blocks/blankSpace.png')
#breakableBrick.save('blocks/breakableBrick.png')
#solidBrick.save('blocks/solidBrick.png')
#bushBlock.save('blocks/bushBlock.png')
#floorBlock.save('blocks/floorBlock.png')
# -
# This function takes the cropped tiles and translate them into the relative symbols (of our choice)
def image2text(tiles):
counter = 0
f = open("txtlevels/mario-8-1.txt", "w+")
for tile in tiles:
# If end of level, new line
if (counter == (imgWidth)/windowsize_c):
counter = 0
f.write("\r\n")
# Check what type of tile
if (np.sum(np.array(tile)) == np.sum(np.array(blankSpace))):
f.write("-")
elif(np.sum(np.array(tile)) == np.sum(np.array(coinBlock))):
f.write("?")
elif(np.sum(np.array(tile)) == np.sum(np.array(breakableBrick))):
f.write("#")
elif(np.sum(np.array(tile)) == np.sum(np.array(solidBrick))):
f.write("=")
elif(np.sum(np.array(tile)) == np.sum(np.array(floorBlock))):
f.write("f")
else:
f.write("-")
counter += 1
f.close()
image2text(tiles)
# +
# Rotate file by 90 degrees, so that the RNN can work better because of a more significative pattern
f = open("txtlevels/mario-8-1.txt", 'r')
rows = np.array([line for line in f if line.split() != []])
f.close()
f = open("mario-8-1-columns.txt", "w+")
index = 0
while(index < (imgWidth)//windowsize_c):
for i in range(0, len(rows)):
f.write(rows[i][index])
f.write("\r\n")
index += 1
f.close()
# +
# Put togheter all the txt level files
import fileinput
import glob
file_list = glob.glob("*.txt")
with open('data.txt', 'w') as file:
input_lines = fileinput.input(file_list)
file.writelines(input_lines)
# +
import tensorflow as tf
from tensorlm import CharLM
import random
tf.reset_default_graph()
with tf.Session() as session:
# Create a new model. You can also use WordLM
model = CharLM(session, "data.txt", max_vocab_size=13,
neurons_per_layer=256, num_layers=3, num_timesteps=15)
# Train it
model.train(session, max_epochs=10, max_steps=1000)
# Let it generate a text
for i in range(10):
seed = random.choice(open('data.txt').readlines())
generated = model.sample(session, seed, num_steps=100)
print(generated)
|
SuperMarioLevelGenerator/SMLevelGenerator.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Homedepot5/DataScience/blob/origin%2Ffeature%2Fdevelopment/GradientDescentExample.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="wCfeZ0Bf7O7t" colab_type="code" colab={}
import numpy as np
import matplotlib.pyplot as plt
from pdb import set_trace
# + id="libUqgWrKKuh" colab_type="code" colab={}
# %matplotlib inline
def gradient_descent(x,y):
m_curr = b_curr = 0
rate = 0.01
n = len(x)
plt.scatter(x,y,color='red',marker='+',linewidth='5')
for i in range(10000):
y_predicted = m_curr * x + b_curr
# print (m_curr,b_curr, i)
plt.plot(x,y_predicted,color='green')
md = -(2/n)*sum(x*(y-y_predicted))
yd = -(2/n)*sum(y-y_predicted)
m_curr = m_curr - rate * md
b_curr = b_curr - rate * yd
# + id="JEbTFTjjMhIS" colab_type="code" colab={}
# + id="4Bv_YTJvKOg_" colab_type="code" colab={}
x = np.array([1,2,3,4,5])
y = np.array([5,7,9,11,13])
# + id="GByWNCZIKRbF" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 265} outputId="9fd5c473-bde4-4598-8b3d-83efdf013b7d"
gradient_descent(x,y)
# + id="L1OFdFAyRzUK" colab_type="code" colab={}
def gradient_descent(x,y):
x = np.array([1, 2, 3, 4, 5])
y = np.array([5, 7, 9, 11, 13])
m_curr = b_curr = 0
iteration=1000
learningrate=0.001
n=len(x)
for i in range(iteration):
set_trace()
y_predicated = m_curr*x +b_curr
md=-(2/n)*sum(x*(y-y_predicated))
m_curr=m_curr-learningrate*md
print(y_predicated)
gradient_descent(x,y)
|
GradientDescentExample.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# #### Finding the Best Markets to Advertise In
# ---
#
# We're working for an an e-learning company that offers courses on programming. Most of our courses are on web and mobile development, but we also cover many other domains, like data science, game development, etc. We want to promote our product and we'd like to invest some money in advertisement.
#
# Our goal in this project is to find out the two best markets to advertise our product in.
#
# The data can be found in this [GitHub repo](https://github.com/freeCodeCamp/2017-new-coder-survey)
#
import numpy as np, pandas as pd, matplotlib.pyplot as plt, seaborn as sns
pd.set_option("display.max_columns", 999)
sns.set()
# +
url = 'https://raw.githubusercontent.com/freeCodeCamp/2017-new-coder-survey/master/clean-data/2017-fCC-New-Coders-Survey-Data.csv'
df = pd.read_csv(url, low_memory = False)
df = df.dropna(how = 'all', axis = 1)
print('Shape:', df.shape[0], 'rows x', df.shape[1], 'columns')
df.info()
# -
df.sample(3, random_state = 0)
# Most of our courses are on web and mobile development, but we also cover many other domains, like data science, game development, etc.
#
# For the purpose of our analysis, we want to answer questions about a population of new coders that are interested in the subjects we teach. We'd like to know:
#
# - Where are these new coders located.
# - What locations have the greatest densities of new coders.
# - How much money they're willing to spend on learning.
#
# So we first need to clarify whether the data set has the right categories of people for our purpose. The JobRoleInterest column describes for every participant the role(s) they'd be interested in working in.
#
# If a participant is interested in working in a certain domain, it means that they're also interested in learning about that domain.
#
# So let's take a look at the frequency distribution table of this column and determine whether the data we have is relevant.
round(df['JobRoleInterest'].value_counts(normalize = True).sort_values(ascending = False) * 100, 1)
# +
interests = df['JobRoleInterest'].dropna().str.split(',')
# number of interests per person
round(interests.apply(lambda x: len(x)).value_counts(normalize = True).sort_values(ascending = False)*100, 1)
# -
# If people have >1 interest it is more likely to be 3 - 5 (43%)
# +
# Top 20 Interests...
interests_all = pd.Series(
[i.strip() for i in sum(interests, [])]
) # Single list without whitespace
round(interests_all.value_counts(normalize = True).sort_values(ascending = False).head(20) * 100, 1)
# +
# Web / Data / Mobile / Games
summary_interest = {'web':0, 'data':0, 'mobile':0}
for i in interests_all:
i_split = i.lower().split(' ')
for k in summary_interest.keys():
if k in i_split:
summary_interest[k] +=1
round(pd.Series(summary_interest)/len(interests_all)*100, 1)
# -
# Here we can see that 12 interests in particular are the most common.
#
# Of those, these three stand out.
#
# - Web development is the clear front runner with 46% across the top 3 alone.
# - Data science & engineering come in at a combined 12.5%
# - Mobile development takes 10%
#
# **Location of Coders **
# +
survey_df = df[(df['JobRoleInterest'].notnull()) & (df['CountryLive'].notnull())].copy()
# Number of coders
abs_freq = survey_df['CountryLive'].value_counts()
rel_freq = round(survey_df['CountryLive'].value_counts(normalize = True) * 100, 1)
# Potential revenue
survey_df['MonthsProgramming'] = survey_df['MonthsProgramming'].replace(0,1)
survey_df['money_per_month'] = survey_df['MoneyForLearning'] / survey_df['MonthsProgramming']
income = {k: survey_df[survey_df['CountryLive'] == k]['money_per_month'].sum().round(0) for k in survey_df['CountryLive'].unique()}
# Main language
lang = {}
for i in survey_df['CountryLive'].unique():
temp = survey_df[survey_df['CountryLive'] == i]['LanguageAtHome'].value_counts(normalize = True).sort_values(ascending = False)
lang.update({i: temp.keys()[0]})
# English speakers
lang_eng = {}
for i in survey_df['CountryLive'].unique():
temp = survey_df[survey_df['CountryLive'] == i]['LanguageAtHome'].value_counts(normalize = True).sort_values(ascending = False)
try:
temp['English']
except KeyError:
lang_eng.update({i: 0})
else:
lang_eng.update({i:round(100 * temp['English'], 1)})
# Table
location_df = pd.DataFrame(
data = {
'Learners': abs_freq,
'Learners (%)': rel_freq,
'Potential revenue': income,
'Main language spoken': lang,
'English speakers (%)': lang_eng,
})
location_df['Potential revenue per head'] = round(location_df['Potential revenue'] / location_df['Learners'], 0)
# -
location_df.sort_values(by = 'Learners (%)', ascending = False).head(10)
# Looking at this data from a total learners POV - it would be best to target:
#
# 1. USA
# 2. India
# 3. UK
# 4. Canada
# 5. Poland
location_df.sort_values(by = 'Potential revenue', ascending = False).head(10)
survey_df[['MoneyForLearning','MonthsProgramming']]
# However...
#
# If we are looking for the best total revenue potential the list is:
#
# 1. USA
# 2. India
# 3. Spain
# 4. Australia
# 5. Puerto Rico
#
#
# If we take only the English speaking nations where one set of ads could be used across all locations:
#
# 1. USA
# 2. Australia
# 3. Canada
# 4. Nigeria
# 5. UK
#
# There may be a case for targeting these locations for lower volume - higher income locations.
#
# - E.g. we could make similar income in Spain with <100 people vs. 500 in India.
|
12. Intermediate Statistics/Python_Statistics_MarketAnalytics.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
import rospy
from sensor_msgs.msg import Image
from aruco_msgs.msg import MarkerArray
from cv_bridge import CvBridge, CvBridgeError
bridge = CvBridge()
# -
rospy.init_node('turtlebot_markers')
# +
def callback_image(msg):
global marker_img
global marker_timestamp
marker_img_timestamp = msg.header.stamp
marker_img = bridge.imgmsg_to_cv2(msg, "rgb8")
def callback_array(msg):
global marker_array
global marker_array_timestamp
marker_array_timestamp = msg.header.stamp
marker_array = msg.markers
# -
subscriber_img = rospy.Subscriber("/aruco_marker_publisher/result", Image, callback_image)
subscriber_array = rospy.Subscriber("/aruco_marker_publisher/markers", MarkerArray, callback_array)
import matplotlib.pyplot as plt
# %matplotlib inline
plt.imshow(marker_img);
m = marker_array[0]
print(m.id)
print(m.pose.pose.position)
print(m.pose.pose.orientation)
print(m.confidence)
m = marker_array[1]
print(m.id)
print(m.pose.pose.position)
print(m.pose.pose.orientation)
print(m.confidence)
|
ArUco Markers.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.10 64-bit (''imbalanced_env'': conda)'
# name: python3
# ---
# +
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import make_blobs
from imblearn.over_sampling import RandomOverSampler
# +
# Creating a well-separated dataset
blobs_random_seed=42
centers=[(0, 0), ((5, 5))]
clusters_std=1.5
frac_test_split=0.33
num_features_for_samples=2
num_samples_total=1600
X, y = make_blobs(
n_samples=num_samples_total,
centers=centers,
n_features=num_features_for_samples,
cluster_std=clusters_std)
X = pd.DataFrame(X, columns=["varA", "varB"])
y = pd.Series(y)
# make_blobs creates balanced dataset, we'll imbalance it
X = pd.concat([
X[y == 0],
X[y == 1].sample(200, random_state=42)
], axis=0)
y = y.loc[X.index]
# -
X.shape, y.shape
X.head()
sns.scatterplot(data=X, x="varA", y="varB", hue=y, alpha=0.5)
plt.title("Dataset")
plt.show()
# +
# Random oversampling
ros = RandomOverSampler(
sampling_strategy="auto",
random_state=42
)
X_res, y_res = ros.fit_resample(X, y)
# -
X.shape, y.shape
y.value_counts()
X_res.shape, y_res.shape, y_res.value_counts()
sns.scatterplot(data=X, x="varA", y="varB", hue=y, alpha=0.5)
plt.title("Original Dataset")
plt.show()
sns.scatterplot(data=X_res, x="varA", y="varB", hue=y_res, alpha=0.5)
plt.title("Resampled Dataset")
plt.show()
|
Code/course_code_along/section_4_oversampling/random_oversampling.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
data_name = "data.csv"
data = pd.read_csv(data_name)
list(data.columns.values)
import rpy2.robjects as ro
from rpy2.robjects.packages import importr
from rpy2.robjects import pandas2ri
from rpy2.robjects.conversion import localconverter
import rpy2.situation
from rpy2.robjects.packages import importr
import rpy2.robjects as robjects
with localconverter(ro.default_converter + pandas2ri.converter):
r_from_pd_df = ro.conversion.py2rpy(data)
r_from_pd_df
with localconverter(ro.default_converter + pandas2ri.converter):
pd_from_r_df = ro.conversion.rpy2py(r_from_pd_df)
pd_from_r_df
utils = importr("utils")
base = importr('base')
rpy2.robjects.r('''
myfunc <- function(df, name){
df[,name] <- df[,name]
df
}
''')
rsort = rpy2.robjects.r['sort']
res = rsort(robjects.IntVector([1,2,3]), decreasing=True)
res
rf = rpy2.robjects.r['myfunc']
with localconverter(ro.default_converter + pandas2ri.converter):
data= ro.conversion.rpy2py(rf(r_from_pd_df, 'Value'))
data
|
demo/rpy2_tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from collections import defaultdict
from functools import reduce
from pathlib import Path
from time import perf_counter
import sys
from IPython.core.display import display
from pandas import CategoricalDtype
import numpy as np
from pyopenms import *
import pandas as pd
import os
import time
# +
from typing import List
class MSExperimentDF(MSExperiment):
def __init__(self):
super().__init__()
## TODO add chromatogram version
## TODO metadata df?
## TODO add spectrum_reference, add ion_mobility, add MS level
def to_df(self, melt : bool = False):
if melt:
spectraarr = np.fromiter(((spec.getRT(), point[0], point[1]) for spec in self for point in zip(*spec.get_peaks())), dtype=[('RT', 'f'), ('mz', 'f'), ('inty', 'f')])#, count=sum(s.size() for s in exp))
# Initial tests showed that loading into numpy array first is faster than direct construction from iter.
return pd.DataFrame(data=spectraarr)
else:
cols = ["RT", "mzarray", "intarray"]
return pd.DataFrame(data=((spec.getRT(), *spec.get_peaks()) for spec in self), columns=cols)
# -
t0 = time.time()
exp = MSExperimentDF()
MzMLFile().load("BSA1_F1.mzML", exp)
df = exp.to_df(True)
t1 = time.time()
display(df)
# + pycharm={"name": "#%%\n"}
display(t1-t0)
# + pycharm={"name": "#%%\n"}
# Alternative wide DF
display(exp.to_df(False))
# -
# Now to read mzML on the fly:
# + pycharm={"name": "#%%\n"}
class MSCallback:
def __init__(self, resarray):
self.resarray = resarray
def setExperimentalSettings(self, s):
pass
def setExpectedSize(self, a, b):
pass
def consumeChromatogram(self, c):
pass
def consumeSpectrum(self, s: PeakSpectrum):
self.resarray.append(
np.fromiter(
((s.getRT(), point[0], point[1]) for point in zip(*s.get_peaks())),
dtype=[('RT', 'f'), ('mz', 'f'), ('inty', 'f')],
count=int(s.size())
))
t0 = time.time()
arr = []
cb = MSCallback(arr)
loader = MzMLFile()
loader.transform("BSA1_F1.mzML", cb, True, True)
display(pd.DataFrame(data=np.concatenate(cb.resarray)))
t1 = time.time()
print(t1-t0)
|
mzML.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Intermediate Spreadsheets
#
# - 4 hours
# - 12 Videos
# - 48 Exercises
#
# ## Course Description
#
# This course will expand your Google Sheets vocabulary. You'll dive deeper into data types, practice manipulating numeric and logical data, explore missing data and error types, and calculate some summary statistics. As you go, you'll explore datasets on 100m sprint world records, asteroid close encounters, benefit claims, and butterflies.
#
# ### 1 What's in a cell?
#
# In which you learn to interrogate cells to determine the data type of their contents, and to convert between data types.
#
# - Data types for data science
# - What IS*() the data type?
# - Checking rarer data types
# - Finding missing data
# - Dteectnig bdaly tpyed dtaa
# - Convert or die!
# - Making numbers while the sun shines
# - How the 104% live
# - Converting logical values to numbers
# - Preaching to the CONVERT()ed
#
# ### 2 Working with numbers
#
# In which you learn to apply log and square root transformations to numbers, round them up and down, and generate random numbers.
#
# - Common data transformations
# - Logarithmic transformations
# - Exponential transformations
# - Square root transformations
# - Rounding and formatting numbers
# - Round and round
# - From floor to ceiling
# - Rounding negative numbers
# - Generating random numbers
# - Generating uniform random numbers
# - Generating random numbers from other distributions
#
# ### 3 Logic & Errors
#
# In which you learn how to work with logical data consisting of TRUE and FALSE values, and how to handle missing values and errors.
#
# - Logical operations
# - Logical operations are hard... NOT!
# - AND now for something completely different
# - Yea OR nay
# - Flow control
# - IF only
# - Lots of IFS
# - SWITCH it on!
# - Blanks, missing values, & errors
# - Blankety blank
# - Going missing
# - Errors and omissions
# - What's the problem?
#
# ### 4 Positional Matching
#
# In which you learn about cell addresses, advanced matching, sorting and filtering, and simple imputation.
#
# - Cell addresses
# - Working with cell addresses
# - From addresses to values
# - Finding nearby cells with offsets
# - Local addresses
# - Lookups & matching
# - A VLOOKUP refresher
# - Sorted!
# - Matching values
# - Bringing it all together
# - Advanced filtering
# - Conditional summary statistics
# - Simple imputation
# - Congratulations!
|
intermediate_spreadsheets/summary.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Variance Estimation
# In statistics we know that the mean and variance of a population $Y$ are defined to be:
#
# \begin{equation}
# \left\{
# \begin{aligned}
# \text{Mean}(Y) &= \mu = \frac{1}{N} \sum_{i=1}^{N} Y_i \\
# \text{Var}(Y) &= \sigma^2 = \frac{1}{N} \sum_{i=1}^{N} (Y_i - \mu)^2 \\
# \end{aligned}
# \right.
# \end{equation}
#
# where $N$ is the size of the population.
# <!-- PELICAN_END_SUMMARY -->
# Given the population $Y$, we can draw a sample $X$ and compute statistics for $X$:
#
# \begin{equation}
# \left\{
# \begin{aligned}
# \text{Mean}(X) &= \bar{X} = \frac{1}{n} \sum_{j=1}^{n} X_j \\
# \text{Var}(X) &= s^2 = \frac{1}{n - 1} \sum_{j=1}^{n} (X_j - \bar{X})^2 \\
# \end{aligned}
# \right.
# \end{equation}
#
# where lowercase $n$ is the size of the sample, typically a much smaller number than $N$. One detail that is often not clearly explained in introductory statistics is why we should divide by $n - 1$ instead of $n$ in the calculation for the sample variance.
# ## Why divide by n - 1?
# It turns out that we should divide by $n - 1$ because dividing by $n$ would give us a **biased estimator** of the population variance. Let's look at a concrete example before diving into the math for why. Let's say we have a population of 100,000 data points. These can represent, for instance, a movie rating for each of 100,000 people.
# %matplotlib inline
import matplotlib.pyplot as plt
from IPython.core.pylabtools import figsize
figsize(15, 5)
import pandas as pd
import numpy as np
np.random.seed(42)
N = 100000 # size of population
population = pd.Series(np.random.randint(1, 11, N))
# We can easily calculate the **population mean** and **population variance**:
population.mean()
((population - population.mean()) ** 2).sum() / N
# Note that we are dividing by $N$ in the variance calculation, also that in `numpy` or `pandas` this is the same as simply using the method `var` with `ddof=0`
population.var(ddof=0)
# where `ddof=0` means to divide by $N$, and `ddof=1` means to divide by $N - 1$.
# ## Simulation
# As usual in statistics, the population parameters are often unknown. But we can estimate them by drawing samples from the population. Here we are drawing a random sample of size $30$. As of version `0.16.1`, `pandas` has a convenient `Series.sample()` function for this:
samples = {}
n = 30 # size of each sample
num_samples = 500 # we are drawing 500 samples, each with size n
for i in range(num_samples):
samples[i] = population.sample(n).reset_index(drop=True)
samples = pd.DataFrame(samples)
samples.T.tail()
# As we expect, if we average all the sample means we can see that the it is a good estimate for the true population mean:
df = pd.DataFrame({'estimated mean': pd.expanding_mean(samples.mean()),
'actual population mean': pd.Series(population.mean(), index=samples.columns)})
df.plot(ylim=(4.5, 6.5))
# Now let's compare the results we would get by using the **biased estimator** (dividing by $n$) and the **unbiased estimator** (dividing by $n-1$)
df = pd.DataFrame({'biased var estimate (divide by n)': pd.expanding_mean(samples.var(ddof=0)),
'unbiased var estimate (divide by n - 1)': pd.expanding_mean(samples.var(ddof=1)),
'actual population var': pd.Series(population.var(ddof=0), index=samples.columns)})
df.plot(ylim=(6.5, 10.5))
# We can see that the biased estimator (dividing by $n$) is clearly not estimating the true population variance as accurately as the unbiased estimator (dividing by $n-1$).
# ## Mathematical Proof
# To prove that dividing by $n - 1$ is an unbiased estimator, we need to show that expected value of the estimaor is indeed $\sigma^2$:
# \begin{equation}
# E(s^2) = E\left(\frac{1}{n - 1} \sum_{j=1}^{n} (X_j - \bar{X})^2\right) = \sigma^2
# \end{equation}
# First we'll need to recall a few basic properties of expectation and variance:
#
# \begin{equation}
# \left\{
# \begin{aligned}
# & E(Z_1 + Z_2) = E(Z_1) + E(Z_2), \text{ for any } Z_1, Z_2 \\
# & \text{Var}(a Z) = a^2 \text{Var}(Z), \text{ for any } Z \\
# & \text{Var}(Z_1 + Z_2) = \text{Var}(Z_1) + \text{Var}(Z_2), \text{ if } Z_1 \text{ and } Z_2 \text{ are independent} \\
# \end{aligned}
# \right.
# \end{equation}
#
# Also, the following is a useful form for variance:
# \begin{equation}
# \text{Var}(Z) = E((Z - E(Z))^2) = E(Z^2 - 2ZE(Z) + E(Z)^2) = E(Z^2) - E(Z)^2
# \end{equation}
#
# This is equivalent to
# \begin{equation}
# E(Z^2) = \text{Var}(Z) + E(Z)^2
# \end{equation}
# Using the above properties we can now simplify the expression for $E(s^2)$:
#
# \begin{aligned}
# E(s^2) = E\left(\frac{1}{n - 1} \sum_{j=1}^{n} (X_j - \bar{X})^2\right) = & \frac{1}{n - 1} E \left( \sum_{j=1}^{n} (X_j^2 - 2X_j\bar{X} + \bar{X}^2) \right) \\
# = & \ \frac{1}{n - 1} E \left( \sum_{j=1}^{n} X_j^2 - 2n\bar{X}^2 + n\bar{X}^2 \right) \\
# = & \ \frac{1}{n - 1} E \left( \sum_{j=1}^{n} X_j^2 - n\bar{X}^2 \right) \\
# = & \ \frac{1}{n - 1} \left[ E \left( \sum_{j=1}^{n} X_j^2 \right) - E \left( n\bar{X}^2 \right) \right] \\
# = & \ \frac{1}{n - 1} \left[ \sum_{j=1}^{n} E \left( X_j^2 \right) - n E \left( \bar{X}^2 \right) \right] \\
# \end{aligned}
# Now notice that the first term can be simplied as:
#
# \begin{aligned}
# \sum_{j=1}^{n} E \left( X_j^2 \right) = & \sum_{j=1}^{n} \left( Var(X_j) + E(X_j)^2 \right) \\
# = & \sum_{j=1}^{n} \left( \sigma^2 + \mu ^2 \right) \\
# = & \ n \sigma^2 + n \mu ^2 \\
# \end{aligned}
#
# Using the same trick, the second term becomes:
#
# \begin{aligned}
# E(\bar{X}^2) = & \ Var(\bar{X}) + E(\bar{X})^2 \\
# = & Var(\frac{1}{n} \sum_{j=1}^{n} X_j) + \mu ^2 \\
# = & \frac{1}{n^2} Var(\sum_{j=1}^{n} X_j) + \mu ^2 \\
# = & \frac{1}{n^2} \sum_{j=1}^{n} Var(X_j) + \mu ^2, \text{ because all } X_j\text{'s are independent} \\
# = & \frac{1}{n^2} n\sigma^2 + \mu ^2 \\
# = & \frac{1}{n} \sigma^2 + \mu ^2 \\
# \end{aligned}
# Plugging the two terms back we finally get:
#
# \begin{aligned}
# E(s^2) = & \ \frac{1}{n-1} \left[ \sum_{j=1}^{n} E \left( X_j^2 \right) - n E \left(\bar{X}^2 \right) \right] \\
# = & \ \frac{1}{n-1} \left[n \sigma^2 + n \mu ^2 - n \left( \frac{1}{n} \sigma^2 + \mu ^2 \right) \right] \\
# = & \ \frac{1}{n-1} \left[n \sigma^2 + n \mu ^2 - \sigma^2 - n \mu ^2 \right] \\
# = & \ \sigma^2 \\
# \end{aligned}
#
# Dividing by $n-1$ gives us an unbiased estimate for the population variance indeed!
# ## Source of Bias
# One intuitive way to think about why the bias exists is to notice that we generally don't actually know the true population mean $\mu$, and therefore the sample variance is being computed using the *estimated* mean $\bar{X}$. However the quadratic form $\sum_{j=1}^{n} (X_j - a)^2$ is actually minimized by $a = \bar{X}$, which means that whatever the true population mean $\mu$ is, we will always have
#
# \begin{equation}
# \sum_{j=1}^{n} (X_j - \mu)^2 \geq \sum_{j=1}^{n} (X_j - \bar{X})^2
# \end{equation}
#
# Therefore we are underestimating the true variance because we don't know the true mean.
# In fact, we can see that we are underestimating by exactly $\sigma^2$ on average:
#
# \begin{aligned}
# E\left(\sum_{j=1}^{n} (X_j - \mu)^2\right) = & \ E \left(\sum_{j=1}^{n} (X_j - \bar{X} + \bar{X} - \mu)^2\right) \\
# = & \ E \left(\sum_{j=1}^{n} (X_j - \bar{X})^2 + \sum_{j=1}^{n} 2(X_j - \bar{X})(\bar{X} - \mu) + \sum_{j=1}^{n} (\bar{X} - \mu)^2 \right) \\
# = & \ E \left(\sum_{j=1}^{n} (X_j - \bar{X})^2 + \sum_{j=1}^{n} (\bar{X} - \mu)^2 \right) \\
# = & \ E \left(\sum_{j=1}^{n} (X_j - \bar{X})^2 \right) + E \left(\sum_{j=1}^{n} (\bar{X} - \mu)^2 \right) \\
# = & \ E \left(\sum_{j=1}^{n} (X_j - \bar{X})^2 \right) + \sum_{j=1}^{n} E \left((\bar{X} - \mu)^2 \right) \\
# = & \ E \left(\sum_{j=1}^{n} (X_j - \bar{X})^2 \right) + \sum_{j=1}^{n} \left( \text{Var} (\bar{X} - \mu) + E (\bar{X} - \mu)^2 \right) \\
# = & \ E \left(\sum_{j=1}^{n} (X_j - \bar{X})^2 \right) + \sum_{j=1}^{n} \left( \text{Var} (\bar{X}) + E (\bar{X} - \mu)^2 \right) \\
# = & \ E \left(\sum_{j=1}^{n} (X_j - \bar{X})^2 \right) + \sum_{j=1}^{n} \text{Var} (\bar{X}) \\
# = & \ E \left(\sum_{j=1}^{n} (X_j - \bar{X})^2 \right) + n \text{Var} (\bar{X}) \\
# = & \ E \left(\sum_{j=1}^{n} (X_j - \bar{X})^2 \right) + n \text{Var} (\frac{1}{n} \sum_{j=1}^{n} X_j) \\
# = & \ E \left(\sum_{j=1}^{n} (X_j - \bar{X})^2 \right) + n \frac{1}{n^2} \sum_{j=1}^{n} \text{Var} (X_j) \\
# = & \ E \left(\sum_{j=1}^{n} (X_j - \bar{X})^2 \right) + \sigma^2 \\
# \end{aligned}
#
# Combined with the result we have from the proof in the previous section, we can see that if we somehow *magically knew* the true mean $\mu$, dividing by $n$ would be unbiased:
#
# \begin{aligned}
# E\left(\frac{1}{n} \sum_{j=1}^{n} (X_j - \mu)^2\right) = & \ \frac{1}{n} E \left(\sum_{j=1}^{n} (X_j - \mu)^2\right) \\
# = & \ \frac{1}{n} \left[ E \left(\sum_{j=1}^{n} (X_j - \bar{X})^2\right) + \sigma^2 \right] \\
# = & \ \frac{1}{n} \left[ (n - 1) \sigma^2 + \sigma^2 \right] \\
# = & \ \sigma^2 \\
# \end{aligned}
#
# However since we don't know the true mean and are using the estimated mean $\bar{X}$ instead, we'd need to divide by $n - 1$ to correct for the bias. This is also known as [Bessel's correction](http://en.wikipedia.org/wiki/Bessel%27s_correction#Source_of_bias).
#
|
blog/unbiased_variance_estimator.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # SciPy
#
# #### Authors: <NAME>, <NAME>, <NAME>, <NAME>, EPCC, University of Edinburgh
# + [markdown] slideshow={"slide_type": "slide"}
# ## Overview:
#
# * NumPy provides arrays and limited additional functionality
#
#
# * SciPy builds on NumPy and provides additional modules:
# * Linear Algebra and wrappers to LAPACK & BLAS `scipy.linalg`
# * Numerical Integration `scipy.integrate`
# * Interpolation `scipy.interpolate`
# * Optimisation `scipy.optimize`
# * Special functions `scipy.special`
# * Signal processing `scipy.signal`
# * Image Processing `scipy.ndimage`
# * Fourier transforms `scipy.fftpack`
# * Statistical functions `stats`
# * Spatial data structures and algorithms `scipy.spatial`
# * File I/O e.g. to read MATLAB files `scipy.io`
# + [markdown] slideshow={"slide_type": "slide"}
# ## Useful links
#
#
# * Note: no PDE solvers (though other packages exist)
#
#
# * Documentation:
# * http://docs.scipy.org/doc/scipy/reference/tutorial/
#
# * http://docs.scipy.org/doc/scipy/reference/
#
# * http://scipy-cookbook.readthedocs.org
# -
#
# + [markdown] slideshow={"slide_type": "slide"}
# ## Linear algebra
#
#
# * Wider set of linear algebra operations than in Numpy
#
# * <p style="font-size: 100%">various decompositions (eigen, singular value)</p>
# * <p style="font-size: 100%">matrix exponentials, trigonometric functions</p>
# * <p style="font-size: 100%">particular matrix equations and special matrices</p>
# * <p style="font-size: 100%">low-level LAPACK and BLAS routines</p>
#
#
# * Routines also for sparse matrices
# * <p style="font-size: 100%">storage formats</p>
# * <p style="font-size: 100%">iterative algorithms</p>
# -
#
# + [markdown] slideshow={"slide_type": "slide"}
# ## Example: Matrix inverse
#
# Consider:
#
# $$
# A = \left[ \begin{array}
# {rrr}
# 1 & 3 & 5 \\
# 2 & 5 & 1 \\
# 2 & 3 & 8 \\
# \end{array} \right]
# $$
#
# The inverse of $A$ is
#
# $$
# A^{-1} =
# \frac{1}{25} \left[ \begin{array}
# {rrr}
# -37 & 9 & 22\\
# 14 & 2 & -9 \\
# 4 & -3 & 1\\
# \end{array} \right]
# \approx
# \left[ \begin{array}
# {rrr}
# -1.48 & 0.36 & 0.88\\
# -0.56 & 0.08 & -0.36 \\
# 0.16 & -0.12 & 0.04\\
# \end{array} \right]
# $$
#
# which may be confirmed by checking $A A^{-1} = I$ where $I$ is the identity.
#
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Exercise Matrix inverse
#
#
# Find inverse of matrix A (as defined above). Check the result by multiplying out $A A^{-1}$ , which should give
# identity matrix $I$
# + slideshow={"slide_type": "-"}
# numpy has a function to produce the 2D identity matrix I
# query: ?np.eye
from scipy import linalg
A = ...
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Solution Matrix inverse
#
# -
# Execute this cell to see a solution
# %load ../code/inverse.py
#
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Integration `scipy.integrate`
#
#
# * Routines for numerical integration – single, double and triple integrals
# * Can solve Ordinary Differential Equations (ODEs) with initial conditions
#
# ### Example : Double integral
# Calculate $\pi$ using the double integral for the area of a circle with radius $r$: <br>
#
# $$
# \int _{x_{min}} ^{x_{max}}\, dx \int _{g(x)} ^{h(x)} f(x,y) \, dy = \int _{-r} ^{r} \int _{-\sqrt(r^2-x^2)} ^{\sqrt(r^2-x^2)} 1 \, dx\, dy = \pi r^2
# $$
#
# We will solve this with `scipy.integrate.dblquad()`
#
# http://docs.scipy.org/doc/scipy-0.17.0/reference/generated/scipy.integrate.dblquad.html
# <br>
# <br>
# + slideshow={"slide_type": "-"}
# numerically integrate using dblquad()
import numpy as np
from scipy.integrate import dblquad
# order of variables matters! y before x
def integrand(y, x):
return 1
def xminlim(x, r):
return -1*np.sqrt(r*r - x*x)
def xmaxlim(x, r):
return np.sqrt(r*r - x*x)
# integral for the area of a circle with radius r
def integrate_to_pi(r):
(area,err) = dblquad(integrand, -1*r, r,
lambda x: xminlim(x,r),
lambda x: xmaxlim(x,r))
return area/(r*r)
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Integration : Check result
#
# Calculate the result and compare with the standard `numpy.pi`
# + slideshow={"slide_type": "-"}
# # %load pi_integration_check.py
# calculate pi using numerical integration and check result against numpy constant np.pi
print(integrate_to_pi(1.0))
# compare with numpy pi
print(np.pi - integrate_to_pi(1.0))
# can try timing... (uncomment line below)
# # %timeit integrate_to_pi(1.0)
# -
#
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Exercise : Double integral
#
# Calculate the double integral
#
# $$
# \int_0^{\pi/2} dx \int_0^1 dy \quad f(x,y)
# $$
#
# where $f(x,y) = y sin(x)$. The answer should be 1/2.
# <br>
# <br>
# + slideshow={"slide_type": "-"}
# Use the same approach here as above
def integrand1(y,x):
return y*np.sin(x)
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Solution Double integral
#
# + slideshow={"slide_type": "-"}
# Execute this cell to see a solution
# %load ../code/integration.py
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Example Pendulum
#
# Solve Ordinary Differential Equations (ODEs) with initial conditions, for example motion of simple pendulum.
#
# A point mass, $m$, is attached to the end of a massless rigid rod of length $l$. The pendulum is acted on by gravity and friction. We can describe the resulting motion of the pendulum by angle, $\theta$, it makes with the vertical.
#
# <img src="pendulum.png"; style="float: right; width: 40%; margin-right: 3%; margin-top: 0%; margin-bottom: -1%"> <br>
#
# Assuming angle $\theta$ always remains small, we can write a second-order differential equation to describe the motion of the mass according to Newton's 2nd law of motion, $m\,a = F$, in terms of $\theta$:
#
# $$
# \ddot{\theta} = -\frac{g}{l}\,\theta - \frac{b}{m}\,\dot\theta
# $$
#
# where $b$ is a constant of friction and $b \ll g$.
#
#
# To use `odeint`, we rewrite the above equation as 2 first-order differential equations:
#
#
# $
# \dot{\theta} = \omega
# $
#
# $
# \dot{\omega}= -\frac{g}{l}\,\theta - \frac{b}{m}\,\omega
# $
#
#
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Pendulum (cont.)
#
#
# <p style="font-size: 100%"> Define the ODE as a function and set up parameters and initial values. </p>
# + slideshow={"slide_type": "-"}
# ode as a function
# let y be vector [theta, omega]
def pendulumNumerical(y, t, b, m, g, length):
theta, omega = y
dydt = [omega, -(b/m)*omega - (g/length)*(theta)]
return dydt
# + slideshow={"slide_type": "-"}
# Parameters and initial values
m = 1.0 # mass of bob
length = 1.0 # length of pendulum
b = 0.25 # friction constant
g = 9.81 # gravitational constant
theta0 = np.pi-0.01 # initial angle
w0 = 0.0 # initial omega
# create a vector with the initial angle and initial omega
y0 = [theta0, w0]
# +
# time interval (use more points for exact solution "tex")
stoptime = 10 # total number of seconds
numpoints = 51 # number of points interval
t = np.linspace(0, stoptime, numpoints)
tex = np.linspace(0, stoptime, 10*numpoints)
# -
# ODE solver parameters
abserr = 1.0e-3 # absolute error tolerance
relerr = 1.0e-1 # relative error tolerance
# ## Pendulum (cont.)
#
# Use <i>odeint</i> to numerically solve the ODE with initial conditions.
# + slideshow={"slide_type": "-"}
# import odeint solver
from scipy.integrate import odeint
# + slideshow={"slide_type": "-"}
# get solution. Note args are given as a tuple
solution = odeint(pendulumNumerical, y0, t, args=(b,m,g,length),\
atol=abserr, rtol=relerr)
# -
# The ODE can be solved analytically. The exact solutions for $\theta$ and $\omega$ are
# Exact solution for theta
def pendulumTheta(t, theta0, b, m, g, length):
root = np.sqrt( np.abs( b*b - 4.0*g*m*m/length ) )
sol = theta0*np.exp(-b*t/2)*( np.cos( root*t/2 ) \
+ (b/root)*np.sin( root*t/2) )
return sol
# Exact solution for omega
def pendulumOmega(t, theta0, b, m, g, length):
root = np.sqrt( np.abs( b*b - 4.0*g*m*m/length ) )
sn = np.sin(root*t/2.0)
cs = np.cos(root*t/2.0)
sol = -(b/2)*theta0*np.exp(-b*t/2)*( cs + (b/root)*sn ) \
+ (theta0/2)*np.exp(-b*t/2)*( b*cs - root*sn )
return sol
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Exercise Pendulum
#
#
# To see how good the numerical solutions for $\theta$ and $\omega$ are, plot the exact solutions against the
# numerical solutions for the appropriate range of $t$.
#
# You should include a legend to label the different lines/points.
#
# You should find that the numerical solution looks quite good. Can you adjust the parameters above
# (re-execute all the relevant cells) to make it better?
# -
# %matplotlib inline
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Solution Pendulum
#
# + slideshow={"slide_type": "-"}
# Execute this cell to see a solution
# %load ../code/pendulum.py
# -
#
# + [markdown] slideshow={"slide_type": "slide"}
# ## Optimisation
#
#
# * Several classical optimisation algorithms
# * Least squares fitting
# * Quasi-Newton type optimisations
# * Simulated annealing
# * General purpose root finding
#
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Least-squares fit
#
#
# Use `scipy.optimize.leastsq` to fit some measured data, $\{x_i,\,y_i\}$, to a function:
#
# $$
# y\,=\,A\,\sin(2\pi k x \,+\, \theta)
# $$
#
# where the parameters $A$, $k$, and $\theta$ are unknown. The residual vector, that will be squared and summed by `leastsq` to fit the data, is:
#
# $$
# e_i\,=\, ∣∣ \, y_i \,− \,A\sin(2\pi k x_i + \theta)∣∣
# $$
#
# By defining a function to compute the residuals, $e_i$, and, selecting appropriate starting values, `leastsq` can be used to find the best-fit parameters $\hat{A}$, $\hat{k}$, $\hat{\theta}$.
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Least-squares fit
#
#
# Create a sample of true values, and the "measured" (noisy) data. Define the residual function and initial values.
# + slideshow={"slide_type": "-"}
# set up true function and "measured" data
x = np.arange(0, 6e-2, 6e-2 / 30)
A, k, theta = 10, 1.0 / 3e-2, np.pi / 6
y_true = A * np.sin(2.0*np.pi*k*x + theta)
y_meas = y_true + 2.0*np.random.randn(len(x))
# + slideshow={"slide_type": "-"}
# Function to compute the residual
def residuals(p, y, x):
A, k, theta = p
err = y - A * np.sin(2 * np.pi * k * x + theta)
return err
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Least-squares fit
#
#
# For easy evaluation of the model function parameters [A, K, theta], we define a function.
# + slideshow={"slide_type": "-"}
def peval(x, p):
return p[0]*np.sin(2.0*np.pi*p[1]*x + p[2])
# starting values of A, k and theta
p0 = [8, 1 / 2.3e-2, np.pi / 3]
print(np.array(p0))
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Least-squares fit
#
#
# Do least squares fitting and plot results
# + slideshow={"slide_type": "-"}
# do least squares fitting
from scipy.optimize import leastsq
plsq = leastsq(residuals, p0, args=(y_meas, x))
print(plsq[0])
print(np.array([A, k, theta]))
# + slideshow={"slide_type": "-"}
# and plot the true function, measured (noisy) data
# and the model function with fitted parameters
plt.plot(x, peval(x, plsq[0]), x, y_meas, 'o', x, y_true)
plt.title('Least-squares fit to noisy data')
plt.legend(['Fit', 'Noisy', 'True'])
plt.show()
# -
#
# + [markdown] slideshow={"slide_type": "slide"}
# ## Special functions
#
#
# * SciPy contains huge set of special functions
# * Bessel functions
# * Legendre functions
# * Gamma functions
# * Airy functions
#
# We will see special functions used in the following sections.
#
# -
#
# + [markdown] slideshow={"slide_type": "skip"}
# ## Example: `scipy.special`
#
#
# * Many problems with circular or cylindrical symmetry have solutions involving Bessel functions
# * E.g., height of a oscillating drumhead related to $J_n(x)$
#
# We will use
#
# http://docs.scipy.org/doc/scipy-0.14.0/reference/special.html
#
# + slideshow={"slide_type": "skip"}
# drumhead example
from scipy import special
def drumhead_height(n, k, distance, angle, t):
# kth zero is last element of returned array
kth_zero = special.jn_zeros(n, k)[-1]
return (np.cos(t) * np.cos(n*angle) * special.jn(n, distance*kth_zero))
# + slideshow={"slide_type": "skip"}
theta = np.r_[0:2*np.pi:50j]
radius = np.r_[0:1:50j]
print(theta)
x = np.array([r * np.cos(theta) for r in radius])
y = np.array([r * np.sin(theta) for r in radius])
z = np.array([drumhead_height(1, 1, r, theta, 0.5)
for r in radius])
# contd...
# + [markdown] slideshow={"slide_type": "skip"}
# ## Drumhead (cont.)
#
# Plot the height of a drumhead using a 3-d axis set
#
# + slideshow={"slide_type": "skip"}
# ...contd
# %matplotlib inline
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
fig = plt.figure(figsize=(8, 4))
ax = Axes3D(fig)
ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=cm.jet)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
# + [markdown] slideshow={"slide_type": "slide"}
# ## Summary
#
# SciPy has a wide range of useful functionality for scientific computing
#
# In case it does not have what you need, there are other packages with specialised functionality.
#
# #### Other packages
#
# * Pandas
#
# * Offers R-like statistical analysis of numerical tables and time series
#
#
# * SymPy
#
# * Python library for symbolic computing
#
#
# * scikit-image
#
# * Advanced image processing
#
#
# * scikit-learn
#
# * Package for machine learning
#
#
# * Sage
#
# * Open source replacement for Mathematica / Maple / Matlab (built using Python)
|
nbplain/10_scipy.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os, glob, json
import numpy as np
import pandas as pd
import keras
from keras.models import Sequential, Model
from keras.layers import LSTM, Input
from keras.layers import Dense
from keras.layers import TimeDistributed
from keras.layers import Bidirectional
from keras.utils import to_categorical
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report, confusion_matrix
# -
# Conjunto de teste
dataset = pd.read_pickle(r'../data/trainset/dataset.pkl')
X = np.array([[list(y) for y in list(x)] for x in dataset.features.values])
#X = dataset.features.values
y = dataset.label.values
y = to_categorical(y)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
X.shape
y[0]
y_test
INPUT_SHAPE = (23,130)
# Modelos
class BiLTSM():
def __init__(self, n_hidden_layers, units_per_layer, dropout=0.5):
self.n_hidden_layers = n_hidden_layers
self.units_per_layer = units_per_layer
self.dropout = dropout
def build_model(self):
metrcs = ['accuracy']
'''
self.model = Sequential();
for i in range(self.n_hidden_layers-1):
self.model.add(Bidirectional(LSTM(units=self.units_per_layer,
input_shape=INPUT_SHAPE,
return_sequences=False)))
self.model.add(Bidirectional(LSTM(self.units_per_layer,
input_shape=INPUT_SHAPE,
return_sequences=False)))
self.model.add(Dense(3, activation='softmax'))
'''
inp = Input(shape=(23, 130))
x = Bidirectional(LSTM(120, return_sequences=True))(inp)
x = Bidirectional(LSTM(120, return_sequences=True))(x)
x = Bidirectional(LSTM(120, return_sequences=False))(x)
x = Dense(3, activation='softmax')(x)
self.model = Model(inp, x)
#self.model.summary()
self.model.compile(loss='categorical_crossentropy',optimizer=keras.optimizers.Adam(), metrics=metrcs)
def fit_model(self, epochs):
self.model.fit(X_train, y_train,
validation_split=.3,
epochs=epochs, batch_size=32)
model1 = BiLTSM(1, 120)
model1.build_model()
model1.model.summary()
model1.fit_model(100)
y_test = np.argmax(y_test, axis=1) # Convert one-hot to index
y_pred = model1.model.predict(X_test, verbose=1)
y_pred = np.argmax(y_pred,axis=1)
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
|
notebooks/04_neural_network.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (ppd430)
# language: python
# name: ppd430
# ---
# # Data visualization
#
# Python data visualization tool landscape:
#
# - matplotlib is powerful but unwieldy; good for basic plotting (scatter, line, bar), and pandas can use it [directly](https://pandas.pydata.org/pandas-docs/stable/user_guide/visualization.html)
# - [seaborn](http://seaborn.pydata.org/) (built on top of matplotlib) is best for statistical visualization: summarizing data, understanding distributions, searching for patterns and trends
# - [bokeh](https://docs.bokeh.org/) is for interactive visualization to let your audience explore the data themselves
#
# We will focus on **seaborn** in this class. It is the easiest to work with to produce meaningful and aesthetically-pleasing visuals.
import numpy as np
import pandas as pd
import seaborn as sns
# ## 1. Load and prep the data
# load the california tracts census data
df = pd.read_csv("../../data/census_tracts_data_ca.csv", dtype={"GEOID10": str})
df.shape
df.columns
df = df.set_index("GEOID10")
df.head()
# ## 2. Review: subsetting, grouping, and descriptive stats
# let's look only at counties in southern california
socal_counties = [
"Imperial",
"Kern",
"Los Angeles",
"Orange",
"Riverside",
"San Bernardino",
"San Diego",
"San Luis Obispo",
"Santa Barbara",
"Ventura",
]
mask = df["county_name"].isin(socal_counties)
df_sc = df[mask]
df_sc.shape
# quick descriptive stats across these counties
df_sc["med_household_income"].describe()
# looking across the whole thing obscures between-group heterogeneity
# let's group by county and look at descriptive stats again
df_sc.groupby("county_name")["med_household_income"].describe().astype(int)
# That's better... but it's still hard to pick out patterns and trends by just staring at a table full of numbers. Let's visualize it.
#
# ## 3. Visualizing distributions
#
# ### 3a. Box plots
#
# Box plots illustrate the data's distribution via the "5 number summary": min, max, median, and the two quartiles (plus outliers).
#
# We will use seaborn for our visualization. In seaborn, you can control what's considered an outlier by changing min/max of whiskers with `whis` parameter... the convention is outliers > 1.5 IQR. For a vertical boxplot, x = your variable's column and y = categorical column to group by.
# use seaborn to make a boxplot of median household income per county
ax = sns.boxplot(x=df_sc["med_household_income"], y=df_sc["county_name"])
# **What stories does this visualization tell you?**
#
# Next, let's configure and tweak the plot to improve its aesthetics.
# what is this "ax" variable we created?
type(ax)
# every matplotlib axes is associated with a "figure" which is like a container
fig = ax.get_figure()
type(fig)
# manually change the plot's size/dimension by adjusting its figure's size
fig = ax.get_figure()
fig.set_size_inches(6, 6) # inches
fig
# It's usually better to let seaborn intelligently handle the figure size for you. But you can easily configure its style, plotting context, and many attributes of the plot:
# +
# you can configure seaborn's style
sns.set_style("whitegrid") # visual styles
sns.set_context("paper") # presets for scaling figure element sizes
# fliersize changes the size of the outlier dots
# boxprops lets you set more configs with a dict, such as alpha (which means opacity)
ax = sns.boxplot(x=df_sc["med_household_income"],
y=df_sc["county_name"],
fliersize=1,
boxprops={"alpha": 0.7})
# set the x-axis limit, the figure title, and x/y axis labels
ax.set_xlim(left=0)
ax.set_title("Box plot of tract-level median household income")
ax.set_xlabel("2017 inflation-adjusted USD")
ax.set_ylabel("")
# save figure to disk with 600 dpi and a tight bounding box
ax.get_figure().savefig("figure-income-boxplot.png", dpi=600, bbox_inches="tight")
# +
# now it's your turn
# choose a different variable and visualize it as a box plot in each of 3 counties of your choice
# -
# ### 3b. Histograms and KDE plots
#
# Histograms visualize the distribution of some variable by binning it then counting observations per bin. KDE plots are similar, but continuous and smooth.
# distplot visualizes the variable's distribution as both histogram and kde
ax = sns.histplot(df["median_age"].dropna(), stat="density", kde=True)
# if you prefer, you can plot just the histogram alone
ax = sns.histplot(df["median_age"].dropna(), stat="density", kde=False)
# You can compare multiple histograms to see how different groups overlap or differ by some measure.
# subset the dataframe into majority white and majority hispanic subsets
df_wht = df[df["pct_white"] > 50]
df_hsp = df[df["pct_hispanic"] > 50]
# compare their distributions to each other
ax = sns.histplot(df_wht["median_age"].dropna(), stat="density")
ax = sns.histplot(df_hsp["median_age"].dropna(), stat="density", color="orange")
# +
# improve the aesthetics: label each distribution and create a legend
ax = sns.histplot(df_wht["median_age"].dropna(), stat="density", label="Majority White Tracts")
ax = sns.histplot(df_hsp["median_age"].dropna(), stat="density", label="Majority Hispanic Tracts", color="orange")
ax.legend()
# set x-limit, add x-label, then save to disk
ax.set_xlim(10, 85)
ax.set_xlabel("Median Age of Population (Years)")
ax.get_figure().savefig("figure-age-distributions.png", dpi=600, bbox_inches="tight")
# -
# **So, what does this plot tell us?**
#
# It looks like the two groups differ... but it is a big enough difference to make meaningful claims about it? We will revisit this question when we discuss statistical significance in a few weeks.
# +
# now it's your turn
# subset the dataframe in a different way (your choice), choose a new variable, and compare its distribution across the subsets
# how do the distributions differ? what does this mean in the real world?
# -
# ## 4. Pairwise relationships
#
# ### 4a. Scatter plots
#
# Histograms and box plots visualize univariate distributions: how a single variable's values are distributed. Scatter plots essentially visualize *bivariate* distributions so that we can see patterns and trends jointly between two variables.
# use seaborn to scatter-plot two variables
ax = sns.scatterplot(x=df["pct_bachelors_degree"],
y=df["med_household_income"])
# scatter-plot two variables, broken out across three counties by color
counties = ["Riverside", "San Mateo", "San Francisco"]
df_counties = df[df["county_name"].isin(counties)]
ax = sns.scatterplot(x=df_counties["pct_bachelors_degree"],
y=df_counties["med_household_income"],
hue=df_counties["county_name"])
# +
# same thing again, but styled more nicely
counties = ["Riverside", "San Mateo", "San Francisco"]
df_counties = df[df["county_name"].isin(counties)]
ax = sns.scatterplot(x=df_counties["pct_bachelors_degree"],
y=df_counties["med_household_income"],
hue=df_counties["county_name"],
alpha=0.8)
# remove the column name from the legend
handles, labels = ax.get_legend_handles_labels()
ax.legend(handles=handles[1:], labels=labels[1:])
# set x/y limits, labels, and save figure
ax.set_xlim(0, 100)
ax.set_ylim(bottom=0)
ax.set_xlabel("Tract population % with bachelor's degree or higher")
ax.set_ylabel("Tract median household income (2017 USD)")
ax.get_figure().savefig("figure-income-degree.png", dpi=600, bbox_inches="tight")
# +
# now it's your turn
# pick 2 new variables from the full dataset and scatter plot them against each other
# how do you interpret the pattern? what if you look at only 1 county?
# -
# ### 4b. Pair plots, correlation heatmaps, and linear trends
# create a subset of SF county tracts, and just 4 variables
df_sf = df[df["county_name"] == "San Francisco"]
df_sf = df_sf[["pct_bachelors_degree", "med_household_income", "med_home_value", "mean_commute_time"]]
df_sf.head()
# show a pair plot of these SF tracts across these 4 variables
ax = sns.pairplot(df_sf.dropna())
# **Do you see patterns in these scatter plots?**
#
# *Correlation* tells us to what extent two variables are linearly related to one another. Pearson correlation coefficients range from -1 to 1, with 0 indicating no linear relationship, -1 indicating a perfect negative linear relationship, and 1 indicating a perfect positive linear relationship.
# a correlation matrix
correlations = df_sf.corr()
correlations.round(2)
# visual correlation matrix via seaborn heatmap
# use vmin, vmax, center to set colorbar scale properly
ax = sns.heatmap(correlations,
vmin=-1,
vmax=1,
center=0,
cmap="coolwarm",
square=True,
linewidths=1)
# a linear (regression) trend line + confidence interval
ax = sns.regplot(x=df_sf["pct_bachelors_degree"], y=df_sf["med_household_income"])
ax.get_figure().set_size_inches(5, 5) # make it square
# ## 5. Bar plots and count plots
#
# Count plots let you count things across categories. Bar plots let you estimate a measure of central tendency across categories.
# pandas value_counts() counts how many times each unique value appears in a column
counts = df_sc["county_name"].value_counts().sort_index()
counts
# simple count plot
# essentially a histogram counting observations across categorical data (instead of continuous data)
ax = sns.countplot(x=df_sc["county_name"])
# +
# same thing again, but ordered and styled more nicely
order = df_sc["county_name"].value_counts().index
ax = sns.countplot(x=df_sc["county_name"], order=order, alpha=0.7)
# rotate the tick labels, set x and y axis labels, then save
ax.set_xticklabels(ax.get_xticklabels(), rotation=45, horizontalalignment="right")
ax.set_xlabel("Counties in Southern California")
ax.set_ylabel("Number of census tracts")
ax.get_figure().savefig("county-tracts-countplot.png", dpi=600, bbox_inches="tight")
# -
# simple bar plot: estimate means of tract median household income + 95% confidence interval
ax = sns.barplot(x=df_sc["county_name"], y=df_sc["med_household_income"])
# nicer bar plot sorted by median value
order = df_sc.groupby("county_name")["med_household_income"].median().sort_values().index
ax = sns.barplot(x=df_sc["med_household_income"],
y=df_sc["county_name"],
estimator=np.median,
ci=None,
order=order,
alpha=0.7,
palette="plasma")
# How does this compare to a box plot of the same variable?
#
# ## 6. Line plots
#
# Line plots are most commonly used to visualize time series: how one or more variables change over time.
# load dataset of country gdp by year
df_gdp = pd.read_csv("../../data/gdp.csv").set_index("year")
df_gdp.shape
df_gdp.tail()
# simple line plot
# seaborn uses the index as x-axis and individual lines for each column
ax = sns.lineplot(data=df_gdp)
# same thing, but subset to only show 50 years of data (1900-1950)
ax = sns.lineplot(data=df_gdp.loc[1900:1950])
# same thing, but also subset to only show 2 countries
ax = sns.lineplot(data=df_gdp.loc[1900:1950, ["GBR", "USA"]])
# +
# same thing again, but styled more nicely
ax = sns.lineplot(data=df_gdp.loc[1900:1950, ["GBR", "USA"]],
dashes=False,
palette=["steelblue", "chocolate"])
ax.set_xlim(1900, 1950)
ax.set_ylim(5000, 17000)
ax.set_xlabel("")
ax.set_ylabel("Real GDP per capita (2011 USD)")
ax.set_title("Per capita GDP, 1900-1950")
ax.get_figure().savefig("country-gdp-lineplot.png", dpi=600, bbox_inches="tight")
# +
# now it's your turn
# choose any 3 countries from the GDP dataset and visualize them over any 100 year interval in the dataset
# -
# ## 7. Working with color
#
# Seaborn makes generally smart decisions about color for you. But you can tweak the colors in your plot usually by passing in a `palette` argument (the name of a colormap or a list of colors to use).
#
# How seaborn handles color: https://seaborn.pydata.org/tutorial/color_palettes.html
#
# Available color maps: https://matplotlib.org/tutorials/colors/colormaps.html
#
# Available named colors: https://matplotlib.org/gallery/color/named_colors.html
# show the default color palette
sns.palplot(sns.color_palette())
# show the "Blues" color map as a palette
sns.palplot(sns.color_palette("Blues", n_colors=5))
# show the "plasma" color map as a palette
# notice that color map names are case sensitive
sns.palplot(sns.color_palette("plasma", n_colors=5))
# +
# now it's your turn
# go back through a couple of the plots earlier in this notebook and adjust their colors
# try both colormaps and lists of color names: look up both using the links above
|
modules/06-visualizing-data/lecture.ipynb
|
# + [markdown] colab_type="text" id="view-in-github"
# [View in Colaboratory](https://colab.research.google.com/github/getmrinal/ML-Notebook/blob/master/19.%20PCA/LFW_Images.ipynb)
# + colab={} colab_type="code" id="Daaa_4AjPuvT"
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report,confusion_matrix
from sklearn import ensemble
import time
# + colab={"base_uri": "https://localhost:8080/", "height": 181} colab_type="code" id="xDieTzPoQQOD" outputId="9d496ea6-4a50-4147-8e53-c04296a9e7a8"
lfw = datasets.fetch_lfw_people(min_faces_per_person=100,resize =0.4)
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="nrAqbITfQjkD" outputId="2fe47716-2e08-406b-ed9c-7bea19bc7c9b"
lfw.keys()
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="bFCtJ0CJQZZ3" outputId="d8b7abbe-ea52-462f-8dda-38f60cba231a"
lfw.data.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="m9WSKBtnQ5Rb" outputId="94c1e5fc-ded8-4989-f275-91ab02e1280e"
lfw.images.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 486} colab_type="code" id="-ccXI00EQ8Ku" outputId="0cce43b3-7681-48ce-a307-e9c3dadbac6c"
fig = plt.figure(figsize=(8,8))
for i in range(64):
ax = fig.add_subplot(8,8,i+1)
ax.imshow(lfw.images[i],cmap=plt.cm.bone)
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 53} colab_type="code" id="JLOSmj0ZQyRq" outputId="a4871974-fada-431b-dc32-e36ffdb692bf"
x = lfw.data
y = lfw.target
x_train,x_test,y_train,y_test = train_test_split(x,y)
pca_oli = PCA()
pca_oli.fit(x_train)
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="ObQzHTSrSGwq" outputId="548ea86a-3c69-4fcc-cd4b-444f56f16617"
k = 0
total = 0
while total <0.99:
total += pca_oli.explained_variance_ratio_[k]
k = k + 1
k
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="585IAqu5Sx2Y" outputId="cd897275-579a-498a-a504-739ff2a61cbb"
pca_lfw = PCA(n_components=k,whiten=True)
x_transformed = pca_lfw.fit_transform(x_train)
x_transformed.shape
# + colab={} colab_type="code" id="bsJP7sf4TXY3"
x_approx = pca_lfw.inverse_transform(x_transformed)
x_approx = x_approx.reshape((855,50,37))
# + colab={"base_uri": "https://localhost:8080/", "height": 486} colab_type="code" id="9C9cHBFrTqib" outputId="380967d3-b4e1-46ab-dcab-e4c0698899fd"
fig = plt.figure(figsize=(8,8))
for i in range(64):
ax = fig.add_subplot(8,8,i+1)
ax.imshow(x_approx[i],cmap=plt.cm.bone)
plt.show()
# + colab={} colab_type="code" id="OXOgO9Z5T4Kl"
eigenv = pca_lfw.components_.reshape(k,50,37)
# + colab={"base_uri": "https://localhost:8080/", "height": 486} colab_type="code" id="5L7POeNTUQoi" outputId="aa39d93b-6467-4a72-a838-0779a8a81992"
fig = plt.figure(figsize=(8,8))
for i in range(64):
ax = fig.add_subplot(8,8,i+1)
ax.imshow(eigenv[i],cmap=plt.cm.bone)
plt.show()
# + colab={} colab_type="code" id="sjQjdpl3T3zM"
x_train_pca = x_transformed
x_test_pca = pca_lfw.transform(x_test)
# + colab={"base_uri": "https://localhost:8080/", "height": 215} colab_type="code" id="s_IjqZv8XFNr" outputId="8ca369e9-011e-4a41-94de-4b85fcc6e50c"
rf = ensemble.RandomForestClassifier()
start = time.time()
rf.fit(x_train,y_train)
print(time.time() - start)
y_pred = rf.predict(x_test)
print(classification_report(y_test,y_pred))
# + colab={"base_uri": "https://localhost:8080/", "height": 215} colab_type="code" id="o2dCedJeYOHR" outputId="0eb1d913-d236-4afe-8b41-e387b5d10ad8"
rf = ensemble.RandomForestClassifier()
start = time.time()
rf.fit(x_train_pca,y_train)
print(time.time() - start)
y_pred = rf.predict(x_test_pca)
print(classification_report(y_test,y_pred))
|
19. PCA/LFW_Images.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] editable=true
# # Data Engineering Capstone Project
#
# ## Project Summary
# The goal of this project is to create an ETL pipeline using I94 immigration and city temperature data to create a database optimized for queries on immigration events. This database can be used to answer questions that are related to immigration behavior.
#
# The project follows these steps:
# * Step 1: Scope the Project and Gather Data
# * Step 2: Explore and Assess the Data
# * Step 3: Define the Data Model
# * Step 4: Run ETL to Model the Data
# * Step 5: Complete Project Write Up
#
# Please note that this notebook is designed to be run on Udacity's notebook workspace as the data is provided internally by Udacity. Also note that we will be using Pandas Redshift as a convenience method to upload our Pandas dataframes as tables to Amazon Redshift.
# + editable=true
# !pip install pandas_redshift
# + editable=true
# Do all imports and installs here
import pandas as pd
import pandas_redshift as pr
import datetime
import re
# + [markdown] editable=true
# ### Step 1: Scope the Project and Gather Data
#
# #### Scope
#
# The intent of this project is to build a data warehouse on AWS Redshift and I plan on designing an ETL pipeline to load data into tables for OLAP. The data that will be folded in will include sources from the I94 US Immigration dataaset provided by Udacity, as well as data that involves airport codes, US city demographics and data regarding temperature.
#
# #### Describe and Gather Data
#
# The I94 immigration [data](https://travel.trade.gov/research/reports/i94/historical/2016.html) origtinates from the US National Tourism and Trade Office. An additional intricacy is that is provided in SAS7BDAT [format](https://cran.r-project.org/web/packages/sas7bdat/vignettes/sas7bdat.pdf) and is a binary database storage format. It contains international visitor arrival statistics by world regions and select countries (including top 20), type of visa, mode of transportation, age groups, states visited (first intended address only), and the top ports of entry (for select countries). There are 12 parts of this datasets with over 40 million records combined. However we will concentrate on the data that comes from April 2016 that consists of roughly 3 million records. Some relevant attributes include:
#
# * `i94yr` - 4 digit year
# * `i94mon` - Numeric month
# * `i94cit` - 3 digit code of origin city
# * `i94port` - 3 character code of destination USA city
# * `arrdate` - Arrival date in the USA
# * `i94mode` - 1 digit travel code
# * `depdate` - Departure date from the USA
# * `i94visa` - Reason for immigration
# + editable=true
# Read in the data here - This takes some time to run. Be patient.
fname = '../../data/18-83510-I94-Data-2016/i94_apr16_sub.sas7bdat'
df = pd.read_sas(fname, 'sas7bdat', encoding="ISO-8859-1")
# + editable=true
# Show the first 5 elements of this dataframe
df.head()
# + [markdown] editable=true
# #### Relevant Column Names to be used in our analysis
# Column Name|Description
# ---|---
# *cicid*|ID that uniquely identify one record in the dataset
# i94yr | 4 digit year
# i94mon | Numeric month
# i94cit | 3 digit code of source city for immigration (Birth country)
# i94res | 3 digit code of source country for immigration (Residence country)
# i94port | Port admitted through
# arrdate | Arrival date in the USA
# i94mode | Mode of transportation (1 = Air, 2 = Sea, 3 = Land, 9 = Not reported)
# i94addr | State of arrival
# depdate | Departure date
# i94bir | Age (years) of respondent
# i94visa | Visa codes broken down into 3 categories: (1 = Business; 2 = Pleasure; 3 = Student)
# count | Used for summary statistics
# dtadfile | Character Date Field
# visapost | Department of State where where Visa was issued
# occup | Occupation to be performed in U.S.
# entdepa | Arrival Flag - Admitted or parolled into the US
# entdepd | Departure Flag - Departed, lost visa, or deceased
# entdepu | Update Flag - Update of visa, either apprehended, overstayed, or updated to permanent resident
# matflag | Match flag
# biryear | 4 digit year of birth
# dtaddto | Character date field to when admitted to the US
# gender | Gender
# insnum | INS number
# airline | Airline used to arrive in U.S.
# admnum | Admission number - Should be unique and not null
# fltno | Flight number of the airline used to arrive in the US
# visatype | Class of admission legally allowing the non-immigrant to temporarily stay in US
# + [markdown] editable=true
# ##### US City Demographic Data
#
# [This dataset](https://public.opendatasoft.com/explore/dataset/us-cities-demographics/export/) contains various information about the demographics of all US cities and census-designated places with a population greater or equal to 65,000. This comes from the 2015 American Community Survey from the US Census Bureau's 2015 American Community Survey.
# + editable=true
# Read in the US city demographics data and show the first 5 rows of the dataframe
us_city_demographics_df = pd.read_csv('us-cities-demographics.csv', delimiter=';')
us_city_demographics_df.head()
# + [markdown] editable=true
# ### Step 2: Explore and Assess the Data
# #### Explore the Data
#
# + [markdown] editable=true
# *I94 Immigration Data*
#
# The following columns have missing data:
#
# * `i94mode`
# * `i94bir`
# * `dtadfile`
# * `visapost`
# * `occup`
# * `entdepa`
# * `entdepd`
# * `entdepu`
# * `matflag`
# * `biryear`
# * `dtaddto`
# * `gender`
# * `insnum`
# * `airline`
# * `fltno`
#
# Due to this being missing, we will drop these columns.
#
# The most important columns we will keep are:
#
# * `cicid` (naturally)
# * `i94yr`
# * `i94mon`,
# * `i94cit`
# * `i94res`
# * `i94port`
# * `arrdate`
# * `i94addr`
# * `depdate`
# * `i94visa`
# * `count`
# * `admnum`
# * `visatype`
#
# Let's display the total number of records for each column below. Take note that we are dealing with 3,096,313 total records. Any columns that don't have this amount are deemed missing and are removed from further analysis.
# + editable=true
# Show non-null counts for each column of the immigration data
df.count()
# + [markdown] editable=true
# *US City Demographic Data*
#
# The following columns have missing data:
#
# * `Male Population`
# * `Female Population`
# * `Number of Veterans`
# * `Foreign-born`
# * `Average Household Size`
#
# We only interested in the `Total Population` in any case. Take note that there are 2891 records for this dataset so any columns that don't match this should be removed.
# + editable=true
# Show the non-null counts for each column in the demographics data
us_city_demographics_df.count()
# + [markdown] editable=true
# #### Cleaning Steps
# + [markdown] editable=true
# #### I94 Immigration Data
# As noted above, we will select out the relevant columns and remove the columns that are missing.
# + editable=true
# Select out the relevant columns and drop any rows that are missing
us_immigration_df = df[['cicid', 'i94yr', 'i94mon', 'i94cit', 'i94res', 'i94port', 'arrdate', 'i94addr', 'depdate', 'i94visa', 'count', 'admnum', 'visatype']]
us_immigration_df = us_immigration_df.dropna()
# There is an escape character with the i94addr column
# Remove this using regular expressions where any repeated whitespace is removed
us_immigration_df['i94addr'] = us_immigration_df['i94addr'].map(lambda col: re.sub('\W+', '', col))
# + editable=true
# Show the first 5 elements of this new dataframe
us_immigration_df.head()
# + [markdown] editable=true
# #### US City Demographic Data
# As noted above, we select out the relevant columns. Also note that we should drop duplicates!
# + editable=true
# Select out the relevant columns and drop any duplicates
us_city_demographics_df = us_city_demographics_df[['State Code', 'City', 'State', 'Total Population']].drop_duplicates()
# Show the first 5 elements of this new dataframe
us_city_demographics_df.head()
# + [markdown] editable=true
# ### Step 3: Define the Data Model
#
# #### 3.1 Conceptual Data Model
#
# As we naturally learned in this course, we will use a more denormalized version of this combined data to minimize the amount of joins and to allow our data model to be used and interpreted in a more meaningful way. Specifically, I chose to use the star schema with the immigration data serving as the fact table while the data that deals with dates and the states themselves are the dimension tables. This will ultimately allow us to aggregate information about immigration based on fine grained time units, such as month or year as well the state itself.
#
# #### Fact Table
#
# `immigration`
#
# - Columns: *`cicid`*, `i94yr`, `i94mon`, `i94cit`, `i94res`, `i94port`, `arrdate`, `i94addr`, `depdate`, `i94visa`, `count`, `admnum`, `visatype`
#
# `cicid` will serve as the primary key
#
# #### Dimension Tables
#
# `date` - arrival and departure date in immigration broken down into specific units
# - *`sas_date`*, date, day, month, year, weekday
#
# `sas_date` will serve as the primary key. This is a custom column that will be created here. The SAS date is a value that represents the number of days between January 1, 1960, and a specified date.
#
# `state` - total population of the states
# - *`state_code`*, state, total_population
#
# `state_code` will serve as the primary key.
# + [markdown] editable=true
# #### 3.2 Mapping Out Data Pipelines
# List the steps necessary to pipeline the data into the chosen data model
#
# This will be outlined below.
# + [markdown] editable=true
# ### Step 4: Run Pipelines to Model the Data
# #### 4.1 Create the data model
# Build the data pipelines to create the data model.
# + [markdown] editable=true
# #### Create the state table
# + editable=true
# We group all city population by state and aggregate by summing over them
state_pop = us_city_demographics_df.groupby('State').sum().reset_index()
state_pop.head()
# + editable=true
# Perform a right join to merge the state code and state together so we establish a mappin
# between state code, the full name of the state as well as its population.
state_pop_df = pd.merge(us_city_demographics_df[['State Code', 'State']].drop_duplicates(), state_pop, how='right', on='State')
state_pop_df.columns = ['state_code', 'state', 'population']
# Note we will rename these columns so that we can write to Redshift later for easy access
state_pop_df.head()
# + [markdown] editable=true
# #### Create the date table
#
# For the SAS date, we will convert this into a readable date format that will allow us to do datetime processing with ease. We'll do the same foro the departure date as well.
#
# We extract all values from arrdate and depdate and convert them into readable date format.
#
# We will first get the arrival date as a table in readable form and decompose the date into further units such as weekday, day, month and year.
# + editable=true
# Make a copy of the arrdate column for us to manipulate
arrdate = us_immigration_df[['arrdate']].copy()
# Rename the arrdate column to sas_date for final storage on Redshift
arrdate = arrdate.rename(columns={"arrdate": "sas_date"})
# Make this new column so that it provides date in readable format
arrdate['date'] = arrdate['sas_date'].apply(lambda col: datetime.date(1960, 1, 1) + datetime.timedelta(days=col))
# Also put in the weekday, day, month and year as new columns
arrdate['weekday'] = arrdate['date'].apply(lambda col: col.weekday())
arrdate['day'] = arrdate['date'].apply(lambda col: col.day)
arrdate['month'] = arrdate['date'].apply(lambda col: col.month)
arrdate['year'] = arrdate['date'].apply(lambda col: col.year)
# Drop duplicates
arrdate = arrdate.drop_duplicates()
# + editable=true
print(arrdate.shape)
arrdate.head()
# + [markdown] editable=true
# Do the same for the depdate
# + editable=true
depdate = us_immigration_df[['depdate']].copy()
# Rename the arrdate column to sas_date for final storage on Redshift
depdate = depdate.rename(columns={"depdate": "sas_date"})
# Make new column so that it provides date in readable format
depdate['date'] = depdate['sas_date'].apply(lambda col: datetime.date(1960, 1, 1) + datetime.timedelta(days=col))
# Also put in the weekday, day, month and year as new columns
depdate['weekday'] = depdate['date'].apply(lambda col: col.weekday())
depdate['day'] = depdate['date'].apply(lambda col: col.day)
depdate['month'] = depdate['date'].apply(lambda col: col.month)
depdate['year'] = depdate['date'].apply(lambda col: col.year)
# Drop duplicates
depdate = depdate.drop_duplicates()
# + editable=true
print(depdate.shape)
depdate.head()
# + [markdown] editable=true
# Now that we have both arrival and departure dates, we should combine these into one final table as both the arrival and departure dates are both events we are interested in. Simply do an outer join to help us accomplish this.
# + editable=true
date = pd.merge(arrdate, depdate, how='outer')
# + editable=true
print(date.shape)
date.head()
# + [markdown] editable=true
# #### Moving the data onto Redshift
#
# Now that we've prepared our data seen above, let's move it onto Amazon Redshift. Take note that this will use a configuration file that requires information that is sensitive, so on submission these are nulled out.
# + editable=true
import configparser
# + editable=true
# Read in attributes from custom config file to access S3 and Redshift
config = configparser.ConfigParser()
config.read('dwh.cfg')
# + editable=true
# Attributes for accessing Redshift cluster
DWH_DB_USER = config.get("CLUSTER", "DB_USER")
DWH_DB_PASSWORD = config.get("CLUSTER", "DB_PASSWORD")
DWH_ENDPOINT = config.get("CLUSTER", "HOST")
DWH_PORT = config.get("CLUSTER", "DB_PORT")
DWH_DB = config.get("CLUSTER", "DB_NAME")
# + editable=true
# Attributes for S3 access
AWS_ACCESS_KEY = config.get("AWS", "AWS_ACCESS_KEY_ID")
AWS_SECRET_ACCESS_KEY = config.get("AWS", "AWS_SECRET_ACCESS_KEY_ID")
AWS_BUCKET = config.get("AWS", "AWS_BUCKET")
AWS_BUCKET_SUBDIR = config.get("AWS", "AWS_BUCKET_SUBDIR")
# + editable=true
# Connect to Redshift cluster
pr.connect_to_redshift(dbname=DWH_DB, host=DWH_ENDPOINT, port=DWH_PORT, user=DWH_DB_USER, password=<PASSWORD>)
# + editable=true
# Connect to S3
pr.connect_to_s3(aws_access_key_id=AWS_ACCESS_KEY, aws_secret_access_key=AWS_SECRET_ACCESS_KEY, bucket=AWS_BUCKET, subdirectory=AWS_BUCKET_SUBDIR)
# + [markdown] editable=true
# `pandas_redshift.pandas_to_redshift` is a convenience method that will place our dataframe in an intermediate CSV form on a S3 bucket of our choice, then it will create a new table on Redshift based on this intermediate form. Think of this as creating a staging table then final table in one sweep. We will now place our tables on S3, then Redshift.
# + editable=true
# Create US immigration fact table - Put on S3 then go to Redshift
pr.pandas_to_redshift(data_frame=us_immigration_df, redshift_table_name = 'public.immigration', index=False)
# + editable=true
# Create state dimension table - Put on S3 then go to Redshift
pr.pandas_to_redshift(data_frame=state_pop_df, redshift_table_name = 'public.state')
# + editable=true
# Create date dimension table - Put on S3 then go to Redshift
pr.pandas_to_redshift(data_frame=date, redshift_table_name = 'public.date')
# + [markdown] editable=true
# #### 4.2 Data Quality Checks
# We will perform integrity checks to ensure that our data is in a sane format. This will include some sample queries made directly to the tables as well as checking the number of records for each table. `pandas_redshift.redshift_to_pandas` is a nice function that allows us to provide a SQL query as a string and it returns a Pandas dataframe of the resulting query.
#
# ##### 4.2.1 Number of rows should be non-zero
# Check to see if we have any tables that are empty
# + editable=true
def data_quality_check(table):
"""
Checks to see if the total number of records is non-zero for a table
Inputs:
table - String to denote our table to check
Returns:
True/False to signify if number of records is non-zero
"""
return len(pr.redshift_to_pandas(f"SELECT COUNT(*) FROM {table}")) > 0
# + editable=true
for table in ['immigration', 'state', 'date']:
if not data_quality_check(table):
print(f"Data quality check failed. {table} returned no results.")
else:
print(f"Data quality check passed for {table}")
# + [markdown] editable=true
# #### 4.2.2 Check to see if there are any null primary keys
#
# Let's also check to see if there are any null records for the primary keys for the columns.
# + editable=true
def data_quality_check_null(table, column):
"""
Checks to see if there are any null records in a column
Inputs:
table - String to denote our table to check
column - Column to check
Returns:
True/False to signify if there are null records in a column
"""
return len(pr.redshift_to_pandas(f"SELECT COUNT(*) FROM {table} WHERE {column} IS NULL")) == 0
# + editable=true
for table, column in zip(['immigration', 'state', 'date'], ['cicid', 'state_code', 'sas_date']):
if data_quality_check_null(table, column):
print(f"Data quality check failed. {table} has null records for column {column}")
else:
print(f"Data quality check passed for {table}, column {column}")
# + [markdown] editable=true
# #### 4.2.3 Check the first 20 records of our final tables
#
# Let's also do some simple checks on the actual contents. Cycle through each table, grab 20 records and show them.
# + editable=true
results = {table: pr.redshift_to_pandas(f"SELECT * FROM {table} LIMIT 20") for table in ['immigration', 'state', 'date']}
# + editable=true
results['immigration']
# + editable=true
results['state']
# + editable=true
results['date']
# + editable=true
# Finally close the cursor, commit and close the database connection, and remove variables from the environment.
pr.close_up_shop()
# + [markdown] editable=true
# #### 4.3 Data dictionary
# Create a data dictionary for your data model. For each field, provide a brief description of what the data is and where it came from. You can include the data dictionary in the notebook or in a separate file.
# + [markdown] editable=true
# ### Data Dictionary
# #### Immigration
#
# Column Name | Description
# --- | ---
# *cicid*|ID that uniquely identify one record in the dataset
# i94yr | 4 digit year
# i94mon | Numeric month
# i94cit | 3 digit code of source city for immigration (Birth country)
# i94res | 3 digit code of source country for immigration (Residence country)
# i94port | Port admitted through
# arrdate | Arrival date in the USA. This is the SAS date which is the number of days since January 1, 1960 that the subject arrived.
# i94addr | State of arrival
# depdate | Departure date
# i94visa | Visa codes broken down into 3 categories: (1 = Business; 2 = Pleasure; 3 = Student)
# count | Used for summary statistics
# admnum | Admission number - Should be unique and not null
# visatype | Class of admission legally allowing the non-immigrant to temporarily stay in US
#
# #### State
#
# Column Name | Description
# --- | ---
# *`state_code`* | Two letter state code representing the state
# `state` | Full name of the state
# `population`| Population of the state
#
# #### Date
# Column Name | Description
# --- | ---
# *`sas_date`* | The number of days since January 1, 1960 that the subject arrived
# `date` | Date in YYYY-MM-DD format
# `weekday` | If the day fell onto a weekday. (1 = Monday, 2 = Tuesday, 3 = Wednesday, 4 = Thursday, 5 = Friday, 0 = Weekend)
# `day` | Code for which day of the week it was (1 = Monday, 2 = Tuesday, 3 = Wednesday, 4 = Thursday, 5 = Friday, 6 = Saturday, 7 = Sunday)
# `month` | Code for which month of the week it was (1 = January, 2 = February, 3 = March, 4 = April, 5 = May, 6 = June, 7 = July, 8 = August, 9 = September, 10 = October, 11 = November, 12 = December)
# `year` | Year
#
# ### Primary Keys
#
# * `immigration`: `cicid`
# * `state`: `state_code`
# * `date`: `sas_date`
#
# + [markdown] editable=true
# #### Step 5: Complete Project Write Up
#
# * Clearly state the rationale for the choice of tools and technologies for the project.
#
# We used a convenience library called [pandas-redshift](https://github.com/agawronski/pandas_redshift), which is designed to make it easier to get data from Amazon Redshift into a Pandas DataFrame and vice versa. It transfers the data frame to S3 and then to Redshift. Of course we also used Amazon Redshift to set up the data warehouse and to perform our queries as seen above.
#
# * Propose how often the data should be updated and why.
#
# * For the I94 Immigration Data, it depends how often the immigration authorities update the data. USCIS and related bodies within the government need to agree on a standard of access, updating and frequency so that the information can be synced with all agencies. Since the data is on Amazon Redshift, we can easily provide access to this data and can agree on an update schedule and method. For the US City Demographic Data, the data will be updated when there is another survey held by the US Census Bureau.
#
#
# * Write a description of how you would approach the problem differently under the following scenarios:
#
# * The data was increased by 100x.
#
# * If the data was increased by 100x, pure pandas cannot handle it. We will need Spark to handle it. The data can be split up into multiple batches which could be used to update the tables in an asynchronous mannter.
#
# * The data populates a dashboard that must be updated on a daily basis by 7am every day.
#
# * We can use Airflow to schedule a pipeline that run every day before 7am in this case.
#
# * The database needed to be accessed by 100+ people.
#
# * The more people accessing the database the more CPU resources we need to get a fast experience. By using a distributed database we can improve our replications and partitioning to get faster query results for each user. However, our use of Redshift has the ability to be scalable for access so our current technology stack can support that.
# + editable=true
|
capstone-i94-etl-pipeline/Capstone_Project_Final.ipynb
|
% ---
% jupyter:
% jupytext:
% text_representation:
% extension: .m
% format_name: light
% format_version: '1.5'
% jupytext_version: 1.14.4
% kernelspec:
% display_name: Octave
% language: octave
% name: octave
% ---
% + magic_args="Machine Learning Online Class - Exercise 1: Linear Regression"
% Instructions
% ------------
%
% This file contains code that helps you get started on the
% linear exercise. You will need to complete the following functions
% in this exericse:
%
% warmUpExercise.m
% plotData.m
% gradientDescent.m
% computeCost.m
% gradientDescentMulti.m
% computeCostMulti.m
% featureNormalize.m
% normalEqn.m
%
% For this exercise, you will not need to change any code in this file,
% or any other files other than those mentioned above.
%
% x refers to the population size in 10,000s
% y refers to the profit in $10,000s
%
% -
% + magic_args="==================== Part 1: Basic Function ===================="
% Complete warmUpExercise.m
fprintf('Running warmUpExercise ... \n');
fprintf('5x5 Identity Matrix: \n');
warmUpExercise()
fprintf('Program paused. Press enter to continue.\n');
%pause;
%% ======================= Part 2: Plotting =======================
fprintf('Plotting Data ...\n')
data = load('ex1data1.txt');
X = data(:, 1); y = data(:, 2);
size(X)
m = length(y); % number of training examples
% -
% +
% Plot Data
% Note: You have to complete the code in plotData.m
plotData(X, y);
fprintf('Program paused. Press enter to continue.\n');
%pause;
%% =================== Part 3: Cost and Gradient descent ===================
X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
theta = zeros(2, 1); % initialize fitting parameters
% Some gradient descent settings
iterations = 1500;
alpha = 0.01;
fprintf('\nTesting the cost function ...\n')
% compute and display initial cost
J = computeCost(X, y, theta);
% -
% +
fprintf('With theta = [0 ; 0]\nCost computed = %f\n', J);
fprintf('Expected cost value (approx) 32.07\n');
% further testing of the cost function
J = computeCost(X, y, [-1 ; 2]);
fprintf('\nWith theta = [-1 ; 2]\nCost computed = %f\n', J);
fprintf('Expected cost value (approx) 54.24\n');
fprintf('Program paused. Press enter to continue.\n');
%pause;
fprintf('\nRunning Gradient Descent ...\n')
% run gradient descent
theta = gradientDescent(X, y, theta, alpha, iterations);
J = computeCost(X, y, theta);
fprintf('Cost computed = %f\n', J);
% print theta to screen
fprintf('Theta found by gradient descent:\n');
fprintf('%f\n', theta);
fprintf('Expected theta values (approx)\n');
fprintf(' -3.6303\n 1.1664\n\n');
% +
% Plot the linear fit
hold on; % keep previous plot visible
plot(X(:,2), X*theta, '-')
legend('Training data', 'Linear regression')
hold off % don't overlay any more plots on this figure
% Predict values for population sizes of 35,000 and 70,000
predict1 = [1, 3.5] *theta;
fprintf('For population = 35,000, we predict a profit of %f\n',...
predict1*10000);
predict2 = [1, 7] * theta;
fprintf('For population = 70,000, we predict a profit of %f\n',...
predict2*10000);
fprintf('Program paused. Press enter to continue.\n');
%pause;
%% ============= Part 4: Visualizing J(theta_0, theta_1) =============
fprintf('Visualizing J(theta_0, theta_1) ...\n')
% Grid over which we will calculate J
theta0_vals = linspace(-10, 10, 100);
theta1_vals = linspace(-1, 4, 100);
% initialize J_vals to a matrix of 0's
J_vals = zeros(length(theta0_vals), length(theta1_vals));
% Fill out J_vals
for i = 1:length(theta0_vals)
for j = 1:length(theta1_vals)
t = [theta0_vals(i); theta1_vals(j)];
J_vals(i,j) = computeCost(X, y, t);
end
end
% Because of the way meshgrids work in the surf command, we need to
% transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals';
% Surface plot
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel('\theta_0'); ylabel('\theta_1');
% Contour plot
figure;
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))
xlabel('\theta_0'); ylabel('\theta_1');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);
% + magic_args="Initialization"
close all; clc
graphics_toolkit("gnuplot");
%% ==================== Part 1: Basic Function ====================
% Complete warmUpExercise.m
fprintf('Running warmUpExercise ... \n');
fprintf('5x5 Identity Matrix: \n');
warmUpExercise()
fprintf('Program paused. Press enter to continue.\n');
%pause;
%% ======================= Part 2: Plotting =======================
fprintf('Plotting Data ...\n')
data = load('ex1data1.txt');
X = data(:, 1); y = data(:, 2);
size(X)
m = length(y); % number of training examples
% +
% Plot Data
% Note: You have to complete the code in plotData.m
plotData(X, y);
fprintf('Program paused. Press enter to continue.\n');
%pause;
%% =================== Part 3: Cost and Gradient descent ===================
X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
theta = zeros(2, 1); % initialize fitting parameters
% Some gradient descent settings
iterations = 1500;
alpha = 0.01;
fprintf('\nTesting the cost function ...\n')
% compute and display initial cost
J = computeCost(X, y, theta);
fprintf('With theta = [0 ; 0]\nCost computed = %f\n', J);
fprintf('Expected cost value (approx) 32.07\n');
% further testing of the cost function
J = computeCost(X, y, [-1 ; 2]);
fprintf('\nWith theta = [-1 ; 2]\nCost computed = %f\n', J);
fprintf('Expected cost value (approx) 54.24\n');
fprintf('Program paused. Press enter to continue.\n');
%pause;
fprintf('\nRunning Gradient Descent ...\n')
% run gradient descent
theta = gradientDescent(X, y, theta, alpha, iterations);
J = computeCost(X, y, theta);
fprintf('Cost computed = %f\n', J);
% print theta to screen
fprintf('Theta found by gradient descent:\n');
fprintf('%f\n', theta);
fprintf('Expected theta values (approx)\n');
fprintf(' -3.6303\n 1.1664\n\n');
% Plot the linear fit
hold on; % keep previous plot visible
plot(X(:,2), X*theta, '-')
legend('Training data', 'Linear regression')
hold off % don't overlay any more plots on this figure
% Predict values for population sizes of 35,000 and 70,000
predict1 = [1, 3.5] *theta;
fprintf('For population = 35,000, we predict a profit of %f\n',...
predict1*10000);
predict2 = [1, 7] * theta;
fprintf('For population = 70,000, we predict a profit of %f\n',...
predict2*10000);
fprintf('Program paused. Press enter to continue.\n');
%pause;
%% ============= Part 4: Visualizing J(theta_0, theta_1) =============
fprintf('Visualizing J(theta_0, theta_1) ...\n')
% Grid over which we will calculate J
theta0_vals = linspace(-10, 10, 100);
theta1_vals = linspace(-1, 4, 100);
% initialize J_vals to a matrix of 0's
J_vals = zeros(length(theta0_vals), length(theta1_vals));
% Fill out J_vals
for i = 1:length(theta0_vals)
for j = 1:length(theta1_vals)
t = [theta0_vals(i); theta1_vals(j)];
J_vals(i,j) = computeCost(X, y, t);
end
end
% Because of the way meshgrids work in the surf command, we need to
% transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals';
% Surface plot
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel('\theta_0'); ylabel('\theta_1');
% Contour plot
figure;
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))
xlabel('\theta_0'); ylabel('\theta_1');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);
% + magic_args="Initialization"
close all; clc
graphics_toolki()
graphics_toolkit("gnuplot");
%% ==================== Part 1: Basic Function ====================
% Complete warmUpExercise.m
fprintf('Running warmUpExercise ... \n');
fprintf('5x5 Identity Matrix: \n');
warmUpExercise()
% + magic_args="======================= Part 2: Plotting ======================="
fprintf('Plotting Data ...\n')
data = load('ex1data1.txt');
X = data(:, 1); y = data(:, 2);
size(X)
m = length(y); % number of training examples
% Plot Data
% Note: You have to complete the code in plotData.m
plotData(X, y);
% + magic_args="=================== Part 3: Cost and Gradient descent ==================="
X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
theta = zeros(2, 1); % initialize fitting parameters
% Some gradient descent settings
iterations = 1500;
alpha = 0.01;
fprintf('\nTesting the cost function ...\n')
% compute and display initial cost
J = computeCost(X, y, theta);
fprintf('With theta = [0 ; 0]\nCost computed = %f\n', J);
fprintf('Expected cost value (approx) 32.07\n');
% further testing of the cost function
J = computeCost(X, y, [-1 ; 2]);
fprintf('\nWith theta = [-1 ; 2]\nCost computed = %f\n', J);
fprintf('Expected cost value (approx) 54.24\n');
fprintf('\nRunning Gradient Descent ...\n')
% run gradient descent
theta = gradientDescent(X, y, theta, alpha, iterations);
J = computeCost(X, y, theta);
fprintf('Cost computed = %f\n', J);
% print theta to screen
fprintf('Theta found by gradient descent:\n');
fprintf('%f\n', theta);
fprintf('Expected theta values (approx)\n');
fprintf(' -3.6303\n 1.1664\n\n');
% Plot the linear fit
hold on; % keep previous plot visible
plot(X(:,2), X*theta, '-')
legend('Training data', 'Linear regression')
hold off % don't overlay any more plots on this figure
% Predict values for population sizes of 35,000 and 70,000
predict1 = [1, 3.5] *theta;
fprintf('For population = 35,000, we predict a profit of %f\n',...
predict1*10000);
predict2 = [1, 7] * theta;
fprintf('For population = 70,000, we predict a profit of %f\n',...
predict2*10000);
% + magic_args="============= Part 4: Visualizing J(theta_0, theta_1) ============="
fprintf('Visualizing J(theta_0, theta_1) ...\n')
% Grid over which we will calculate J
theta0_vals = linspace(-10, 10, 100);
theta1_vals = linspace(-1, 4, 100);
% initialize J_vals to a matrix of 0's
J_vals = zeros(length(theta0_vals), length(theta1_vals));
% Fill out J_vals
for i = 1:length(theta0_vals)
for j = 1:length(theta1_vals)
t = [theta0_vals(i); theta1_vals(j)];
J_vals(i,j) = computeCost(X, y, t);
end
end
% Because of the way meshgrids work in the surf command, we need to
% transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals';
% -
% Surface plot
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel('\theta_0'); ylabel('\theta_1');
% Contour plot
figure;
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))
xlabel('\theta_0'); ylabel('\theta_1');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);
|
ex1-octave/.ipynb_checkpoints/ex1-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:py3]
# language: python
# name: conda-env-py3-py
# ---
import os
import pandas
import numpy as np
import nibabel as ni
import matplotlib.pyplot as plt
from nilearn import image, plotting
from mpl_toolkits.mplot3d import Axes3D
atlas_img.shape
atlas_img = ni.load('../data/DKT_w_hipp_labels_TRANS_ERC.nii.gz')
plt.close()
plotting.plot_roi(atlas_img)
plt.show()
atlas = atlas_img.get_data()
# find hipp_labels
np.unique(atlas)
# +
jnk = np.zeros_like(atlas)
jnk[atlas==84] = 1
plt.close()
plotting.plot_roi(ni.Nifti1Image(jnk,atlas_img.affine))
plt.show()
# -
subcort = ni.load('/usr/local/fsl/data/atlases/HarvardOxford/HarvardOxford-sub-maxprob-thr50-1mm.nii.gz'
).get_data()
hipp = np.zeros_like(subcort)
hipp[subcort==9] = 1
hipp[subcort==19] = 1
plt.close()
plotting.plot_roi(ni.Nifti1Image(hipp,atlas_img.affine))
plt.show()
# make a hippocampus-voxels-not-labeled mask
mask = np.array(hipp,copy=True)
mask[atlas==84] = 0
mask[atlas==85] = 0
plt.close()
plotting.plot_roi(ni.Nifti1Image(mask,atlas_img.affine))
plt.show()
# get the labeled (s) and non-labeled (t) coordinates
final_hipp = np.array(atlas,copy=True)
final_hipp[hipp<1] = 0
s_coords = np.where(mask==1)
t_coords = np.where(final_hipp>83)
# replace 0 with the label of the closest labeled voxel
min_dist = pandas.DataFrame(index=range(len(coords[0])),
columns = ['x','y','z'])
for i in range(len(s_coords[0])):
x,y,z = s_coords[0][i], s_coords[1][i], s_coords[2][i]
closest = np.argmin([abs(x - t_coords[0][j]
) + abs(y - t_coords[1][j]
) + abs(z - t_coords[2][j]) for j in range(len(t_coords[0]))
])
closest_coord = t_coords[0][closest], t_coords[1][closest], t_coords[2][closest]
val = final_hipp[closest_coord]
if i%100 == 0:
print(i)
# +
plt.close()
label_locations = t_coords
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(label_locations[0], label_locations[1], label_locations[2], c = final_hipp[label_locations],
cmap='RdBu')
# To split into LR, we need to visualize where the LR split is, where front is
for angle in range(0, 30):
ax.view_init(30, angle)
plt.draw()
plt.pause(.001)
ax.set_xlabel('axis 0')
ax.set_ylabel('axis 1')
ax.set_zlabel('axis 2')
plt.show()
# +
plt.close()
label_locations = np.where(atlas>83)
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(label_locations[0], label_locations[1], label_locations[2], c = atlas[label_locations],
cmap='RdBu')
# To split into LR, we need to visualize where the LR split is, where front is
for angle in range(0, 30):
ax.view_init(30, angle)
plt.draw()
plt.pause(.001)
ax.set_xlabel('axis 0')
ax.set_ylabel('axis 1')
ax.set_zlabel('axis 2')
plt.show()
# -
np.unique(t_coords[0])
# split left and right hippocampus
bi_hipp = np.array(final_hipp, copy=True)
for i in range(len(t_coords[0])):
x,y,z = t_coords[0][i], t_coords[1][i], t_coords[2][i]
if x > 100:
bi_hipp[x,y,z] = bi_hipp[x,y,z] + 2
# +
plt.close()
label_locations = t_coords
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(label_locations[0], label_locations[1], label_locations[2], c = bi_hipp[label_locations],
cmap='RdBu')
# To split into LR, we need to visualize where the LR split is, where front is
for angle in range(0, 30):
ax.view_init(30, angle)
plt.draw()
plt.pause(.001)
ax.set_xlabel('axis 0')
ax.set_ylabel('axis 1')
ax.set_zlabel('axis 2')
plt.show()
# -
# make final parcellation
final_atlas = np.zeros_like(bi_hipp)
final_atlas[atlas==4] = 1
final_atlas[atlas==43] = 2
final_atlas[bi_hipp==84] = 3
final_atlas[bi_hipp==85] = 4
final_atlas[bi_hipp==86] = 5
final_atlas[bi_hipp==87] = 6
plt.close()
plotting.plot_roi(ni.Nifti1Image(final_atlas,atlas_img.affine))
plt.show()
np.unique(final_atlas)
# save
ni.Nifti1Image(final_atlas, atlas_img.affine).to_filename('../data/dilated_hipp_parcellation')
# with bigger ERC
dkt = ni.load('/Users/jakevogel/Science/tau/dkt_atlas_1mm.nii.gz').get_data()
final_atlas = np.zeros_like(bi_hipp)
final_atlas[dkt==4] = 1
final_atlas[dkt==43] = 2
final_atlas[bi_hipp==84] = 3
final_atlas[bi_hipp==85] = 4
final_atlas[bi_hipp==86] = 5
final_atlas[bi_hipp==87] = 6
# save
ni.Nifti1Image(final_atlas, atlas_img.affine).to_filename('../data/dilated_hipp_parcellation_FULL_EC')
plt.close()
plotting.plot_roi(ni.Nifti1Image(final_atlas,atlas_img.affine))
plt.show()
|
code/dilate_hippocampus.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/bundickm/LeetCode-30-Day-Challenge/blob/master/Day_6_Anagram_Groups.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="uGSyOA7QG-ya" colab_type="text"
# # Problem
#
# Given an array of strings, group anagrams together.
#
# Example:
# ```
# Input: ["eat", "tea", "tan", "ate", "nat", "bat"]
# Output:
# [
# ["ate","eat","tea"],
# ["nat","tan"],
# ["bat"]
# ]
# ```
# Note: All inputs will be in lowercase. The order of your output does not matter.
# + id="Moa7pWE0HLHO" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="7ba081f5-9dc5-480b-f840-2f0a144998aa"
words = ["eat", "tea", "tan", "ate", "nat", "bat"]
def group_anagrams(words: list) -> list:
anagram_groups = {}
for word in words:
sorted_word = ''.join(sorted(word))
if sorted_word not in anagram_groups:
anagram_groups[sorted_word] = [word]
else:
anagram_groups[sorted_word].append(word)
return list(anagram_groups.values())
group_anagrams(words)
|
Day_6_Anagram_Groups.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] tags=["pdf-title"]
# # Generative Adversarial Networks (GANs)
#
# So far in CS231N, all the applications of neural networks that we have explored have been **discriminative models** that take an input and are trained to produce a labeled output. This has ranged from straightforward classification of image categories to sentence generation (which was still phrased as a classification problem, our labels were in vocabulary space and we’d learned a recurrence to capture multi-word labels). In this notebook, we will expand our repetoire, and build **generative models** using neural networks. Specifically, we will learn how to build models which generate novel images that resemble a set of training images.
#
# ### What is a GAN?
#
# In 2014, [Goodfellow et al.](https://arxiv.org/abs/1406.2661) presented a method for training generative models called Generative Adversarial Networks (GANs for short). In a GAN, we build two different neural networks. Our first network is a traditional classification network, called the **discriminator**. We will train the discriminator to take images, and classify them as being real (belonging to the training set) or fake (not present in the training set). Our other network, called the **generator**, will take random noise as input and transform it using a neural network to produce images. The goal of the generator is to fool the discriminator into thinking the images it produced are real.
#
# We can think of this back and forth process of the generator ($G$) trying to fool the discriminator ($D$), and the discriminator trying to correctly classify real vs. fake as a minimax game:
# $$\underset{G}{\text{minimize}}\; \underset{D}{\text{maximize}}\; \mathbb{E}_{x \sim p_\text{data}}\left[\log D(x)\right] + \mathbb{E}_{z \sim p(z)}\left[\log \left(1-D(G(z))\right)\right]$$
# where $z \sim p(z)$ are the random noise samples, $G(z)$ are the generated images using the neural network generator $G$, and $D$ is the output of the discriminator, specifying the probability of an input being real. In [Goodfellow et al.](https://arxiv.org/abs/1406.2661), they analyze this minimax game and show how it relates to minimizing the Jensen-Shannon divergence between the training data distribution and the generated samples from $G$.
#
# To optimize this minimax game, we will aternate between taking gradient *descent* steps on the objective for $G$, and gradient *ascent* steps on the objective for $D$:
# 1. update the **generator** ($G$) to minimize the probability of the __discriminator making the correct choice__.
# 2. update the **discriminator** ($D$) to maximize the probability of the __discriminator making the correct choice__.
#
# While these updates are useful for analysis, they do not perform well in practice. Instead, we will use a different objective when we update the generator: maximize the probability of the **discriminator making the incorrect choice**. This small change helps to allevaiate problems with the generator gradient vanishing when the discriminator is confident. This is the standard update used in most GAN papers, and was used in the original paper from [Goodfellow et al.](https://arxiv.org/abs/1406.2661).
#
# In this assignment, we will alternate the following updates:
# 1. Update the generator ($G$) to maximize the probability of the discriminator making the incorrect choice on generated data:
# $$\underset{G}{\text{maximize}}\; \mathbb{E}_{z \sim p(z)}\left[\log D(G(z))\right]$$
# 2. Update the discriminator ($D$), to maximize the probability of the discriminator making the correct choice on real and generated data:
# $$\underset{D}{\text{maximize}}\; \mathbb{E}_{x \sim p_\text{data}}\left[\log D(x)\right] + \mathbb{E}_{z \sim p(z)}\left[\log \left(1-D(G(z))\right)\right]$$
#
# ### What else is there?
# Since 2014, GANs have exploded into a huge research area, with massive [workshops](https://sites.google.com/site/nips2016adversarial/), and [hundreds of new papers](https://github.com/hindupuravinash/the-gan-zoo). Compared to other approaches for generative models, they often produce the highest quality samples but are some of the most difficult and finicky models to train (see [this github repo](https://github.com/soumith/ganhacks) that contains a set of 17 hacks that are useful for getting models working). Improving the stabiilty and robustness of GAN training is an open research question, with new papers coming out every day! For a more recent tutorial on GANs, see [here](https://arxiv.org/abs/1701.00160). There is also some even more recent exciting work that changes the objective function to Wasserstein distance and yields much more stable results across model architectures: [WGAN](https://arxiv.org/abs/1701.07875), [WGAN-GP](https://arxiv.org/abs/1704.00028).
#
#
# GANs are not the only way to train a generative model! For other approaches to generative modeling check out the [deep generative model chapter](http://www.deeplearningbook.org/contents/generative_models.html) of the Deep Learning [book](http://www.deeplearningbook.org). Another popular way of training neural networks as generative models is Variational Autoencoders (co-discovered [here](https://arxiv.org/abs/1312.6114) and [here](https://arxiv.org/abs/1401.4082)). Variatonal autoencoders combine neural networks with variationl inference to train deep generative models. These models tend to be far more stable and easier to train but currently don't produce samples that are as pretty as GANs.
#
# Here's an example of what your outputs from the 3 different models you're going to train should look like... note that GANs are sometimes finicky, so your outputs might not look exactly like this... this is just meant to be a *rough* guideline of the kind of quality you can expect:
#
# 
# + [markdown] tags=["pdf-ignore"]
# ## Setup
# + tags=["pdf-ignore"]
import torch
import torch.nn as nn
from torch.nn import init
import torchvision
import torchvision.transforms as T
import torch.optim as optim
from torch.utils.data import DataLoader
from torch.utils.data import sampler
import torchvision.datasets as dset
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
# %matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
def show_images(images):
images = np.reshape(images, [images.shape[0], -1]) # images reshape to (batch_size, D)
sqrtn = int(np.ceil(np.sqrt(images.shape[0])))
sqrtimg = int(np.ceil(np.sqrt(images.shape[1])))
fig = plt.figure(figsize=(sqrtn, sqrtn))
gs = gridspec.GridSpec(sqrtn, sqrtn)
gs.update(wspace=0.05, hspace=0.05)
for i, img in enumerate(images):
ax = plt.subplot(gs[i])
plt.axis('off')
ax.set_xticklabels([])
ax.set_yticklabels([])
ax.set_aspect('equal')
plt.imshow(img.reshape([sqrtimg,sqrtimg]))
return
def preprocess_img(x):
return 2 * x - 1.0
def deprocess_img(x):
return (x + 1.0) / 2.0
def rel_error(x,y):
return np.max(np.abs(x - y) / (np.maximum(1e-8, np.abs(x) + np.abs(y))))
def count_params(model):
"""Count the number of parameters in the current TensorFlow graph """
param_count = np.sum([np.prod(p.size()) for p in model.parameters()])
return param_count
answers = dict(np.load('gan-checks-tf.npz'))
# + [markdown] tags=["pdf-ignore"]
# ## Dataset
# GANs are notoriously finicky with hyperparameters, and also require many training epochs. In order to make this assignment approachable without a GPU, we will be working on the MNIST dataset, which is 60,000 training and 10,000 test images. Each picture contains a centered image of white digit on black background (0 through 9). This was one of the first datasets used to train convolutional neural networks and it is fairly easy -- a standard CNN model can easily exceed 99% accuracy.
#
# To simplify our code here, we will use the PyTorch MNIST wrapper, which downloads and loads the MNIST dataset. See the [documentation](https://github.com/pytorch/vision/blob/master/torchvision/datasets/mnist.py) for more information about the interface. The default parameters will take 5,000 of the training examples and place them into a validation dataset. The data will be saved into a folder called `MNIST_data`.
# + tags=["pdf-ignore"]
class ChunkSampler(sampler.Sampler):
"""Samples elements sequentially from some offset.
Arguments:
num_samples: # of desired datapoints
start: offset where we should start selecting from
"""
def __init__(self, num_samples, start=0):
self.num_samples = num_samples
self.start = start
def __iter__(self):
return iter(range(self.start, self.start + self.num_samples))
def __len__(self):
return self.num_samples
NUM_TRAIN = 50000
NUM_VAL = 5000
NOISE_DIM = 96
batch_size = 128
mnist_train = dset.MNIST('./cs231n/datasets/MNIST_data', train=True, download=True,
transform=T.ToTensor())
loader_train = DataLoader(mnist_train, batch_size=batch_size,
sampler=ChunkSampler(NUM_TRAIN, 0))
mnist_val = dset.MNIST('./cs231n/datasets/MNIST_data', train=True, download=True,
transform=T.ToTensor())
loader_val = DataLoader(mnist_val, batch_size=batch_size,
sampler=ChunkSampler(NUM_VAL, NUM_TRAIN))
imgs = loader_train.__iter__().next()[0].view(batch_size, 784).numpy().squeeze()
show_images(imgs)
# -
# ## Random Noise
# Generate uniform noise from -1 to 1 with shape `[batch_size, dim]`.
#
# Hint: use `torch.rand`.
def sample_noise(batch_size, dim):
"""
Generate a PyTorch Tensor of uniform random noise.
Input:
- batch_size: Integer giving the batch size of noise to generate.
- dim: Integer giving the dimension of noise to generate.
Output:
- A PyTorch Tensor of shape (batch_size, dim) containing uniform
random noise in the range (-1, 1).
"""
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
pass
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Make sure noise is the correct shape and type:
# +
def test_sample_noise():
batch_size = 3
dim = 4
torch.manual_seed(231)
z = sample_noise(batch_size, dim)
np_z = z.cpu().numpy()
assert np_z.shape == (batch_size, dim)
assert torch.is_tensor(z)
assert np.all(np_z >= -1.0) and np.all(np_z <= 1.0)
assert np.any(np_z < 0.0) and np.any(np_z > 0.0)
print('All tests passed!')
test_sample_noise()
# + [markdown] tags=["pdf-ignore"]
# ## Flatten
#
# Recall our Flatten operation from previous notebooks... this time we also provide an Unflatten, which you might want to use when implementing the convolutional generator. We also provide a weight initializer (and call it for you) that uses Xavier initialization instead of PyTorch's uniform default.
# + tags=["pdf-ignore"]
class Flatten(nn.Module):
def forward(self, x):
N, C, H, W = x.size() # read in N, C, H, W
return x.view(N, -1) # "flatten" the C * H * W values into a single vector per image
class Unflatten(nn.Module):
"""
An Unflatten module receives an input of shape (N, C*H*W) and reshapes it
to produce an output of shape (N, C, H, W).
"""
def __init__(self, N=-1, C=128, H=7, W=7):
super(Unflatten, self).__init__()
self.N = N
self.C = C
self.H = H
self.W = W
def forward(self, x):
return x.view(self.N, self.C, self.H, self.W)
def initialize_weights(m):
if isinstance(m, nn.Linear) or isinstance(m, nn.ConvTranspose2d):
init.xavier_uniform_(m.weight.data)
# + [markdown] tags=["pdf-ignore"]
# ## CPU / GPU
# By default all code will run on CPU. GPUs are not needed for this assignment, but will help you to train your models faster. If you do want to run the code on a GPU, then change the `dtype` variable in the following cell.
# + tags=["pdf-ignore"]
dtype = torch.FloatTensor
#dtype = torch.cuda.FloatTensor ## UNCOMMENT THIS LINE IF YOU'RE ON A GPU!
# -
# # Discriminator
# Our first step is to build a discriminator. Fill in the architecture as part of the `nn.Sequential` constructor in the function below. All fully connected layers should include bias terms. The architecture is:
# * Fully connected layer with input size 784 and output size 256
# * LeakyReLU with alpha 0.01
# * Fully connected layer with input_size 256 and output size 256
# * LeakyReLU with alpha 0.01
# * Fully connected layer with input size 256 and output size 1
#
# Recall that the Leaky ReLU nonlinearity computes $f(x) = \max(\alpha x, x)$ for some fixed constant $\alpha$; for the LeakyReLU nonlinearities in the architecture above we set $\alpha=0.01$.
#
# The output of the discriminator should have shape `[batch_size, 1]`, and contain real numbers corresponding to the scores that each of the `batch_size` inputs is a real image.
def discriminator():
"""
Build and return a PyTorch model implementing the architecture above.
"""
model = nn.Sequential(
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
pass
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
)
return model
# Test to make sure the number of parameters in the discriminator is correct:
# +
def test_discriminator(true_count=267009):
model = discriminator()
cur_count = count_params(model)
if cur_count != true_count:
print('Incorrect number of parameters in discriminator. Check your achitecture.')
else:
print('Correct number of parameters in discriminator.')
test_discriminator()
# -
# # Generator
# Now to build the generator network:
# * Fully connected layer from noise_dim to 1024
# * `ReLU`
# * Fully connected layer with size 1024
# * `ReLU`
# * Fully connected layer with size 784
# * `TanH` (to clip the image to be in the range of [-1,1])
def generator(noise_dim=NOISE_DIM):
"""
Build and return a PyTorch model implementing the architecture above.
"""
model = nn.Sequential(
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
pass
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
)
return model
# Test to make sure the number of parameters in the generator is correct:
# +
def test_generator(true_count=1858320):
model = generator(4)
cur_count = count_params(model)
if cur_count != true_count:
print('Incorrect number of parameters in generator. Check your achitecture.')
else:
print('Correct number of parameters in generator.')
test_generator()
# -
# # GAN Loss
#
# Compute the generator and discriminator loss. The generator loss is:
# $$\ell_G = -\mathbb{E}_{z \sim p(z)}\left[\log D(G(z))\right]$$
# and the discriminator loss is:
# $$ \ell_D = -\mathbb{E}_{x \sim p_\text{data}}\left[\log D(x)\right] - \mathbb{E}_{z \sim p(z)}\left[\log \left(1-D(G(z))\right)\right]$$
# Note that these are negated from the equations presented earlier as we will be *minimizing* these losses.
#
# **HINTS**: You should use the `bce_loss` function defined below to compute the binary cross entropy loss which is needed to compute the log probability of the true label given the logits output from the discriminator. Given a score $s\in\mathbb{R}$ and a label $y\in\{0, 1\}$, the binary cross entropy loss is
#
# $$ bce(s, y) = -y * \log(s) - (1 - y) * \log(1 - s) $$
#
# A naive implementation of this formula can be numerically unstable, so we have provided a numerically stable implementation for you below.
#
# You will also need to compute labels corresponding to real or fake and use the logit arguments to determine their size. Make sure you cast these labels to the correct data type using the global `dtype` variable, for example:
#
#
# `true_labels = torch.ones(size).type(dtype)`
#
# Instead of computing the expectation of $\log D(G(z))$, $\log D(x)$ and $\log \left(1-D(G(z))\right)$, we will be averaging over elements of the minibatch, so make sure to combine the loss by averaging instead of summing.
# + tags=["pdf-ignore"]
def bce_loss(input, target):
"""
Numerically stable version of the binary cross-entropy loss function.
As per https://github.com/pytorch/pytorch/issues/751
See the TensorFlow docs for a derivation of this formula:
https://www.tensorflow.org/api_docs/python/tf/nn/sigmoid_cross_entropy_with_logits
Inputs:
- input: PyTorch Tensor of shape (N, ) giving scores.
- target: PyTorch Tensor of shape (N,) containing 0 and 1 giving targets.
Returns:
- A PyTorch Tensor containing the mean BCE loss over the minibatch of input data.
"""
neg_abs = - input.abs()
loss = input.clamp(min=0) - input * target + (1 + neg_abs.exp()).log()
return loss.mean()
# +
def discriminator_loss(logits_real, logits_fake):
"""
Computes the discriminator loss described above.
Inputs:
- logits_real: PyTorch Tensor of shape (N,) giving scores for the real data.
- logits_fake: PyTorch Tensor of shape (N,) giving scores for the fake data.
Returns:
- loss: PyTorch Tensor containing (scalar) the loss for the discriminator.
"""
loss = None
return loss
def generator_loss(logits_fake):
"""
Computes the generator loss described above.
Inputs:
- logits_fake: PyTorch Tensor of shape (N,) giving scores for the fake data.
Returns:
- loss: PyTorch Tensor containing the (scalar) loss for the generator.
"""
loss = None
return loss
# -
# Test your generator and discriminator loss. You should see errors < 1e-7.
# +
def test_discriminator_loss(logits_real, logits_fake, d_loss_true):
d_loss = discriminator_loss(torch.Tensor(logits_real).type(dtype),
torch.Tensor(logits_fake).type(dtype)).cpu().numpy()
print("Maximum error in d_loss: %g"%rel_error(d_loss_true, d_loss))
test_discriminator_loss(answers['logits_real'], answers['logits_fake'],
answers['d_loss_true'])
# +
def test_generator_loss(logits_fake, g_loss_true):
g_loss = generator_loss(torch.Tensor(logits_fake).type(dtype)).cpu().numpy()
print("Maximum error in g_loss: %g"%rel_error(g_loss_true, g_loss))
test_generator_loss(answers['logits_fake'], answers['g_loss_true'])
# -
# # Optimizing our loss
# Make a function that returns an `optim.Adam` optimizer for the given model with a 1e-3 learning rate, beta1=0.5, beta2=0.999. You'll use this to construct optimizers for the generators and discriminators for the rest of the notebook.
def get_optimizer(model):
"""
Construct and return an Adam optimizer for the model with learning rate 1e-3,
beta1=0.5, and beta2=0.999.
Input:
- model: A PyTorch model that we want to optimize.
Returns:
- An Adam optimizer for the model with the desired hyperparameters.
"""
optimizer = None
return optimizer
# # Training a GAN!
#
# We provide you the main training loop... you won't need to change this function, but we encourage you to read through and understand it.
# + tags=["pdf-ignore"]
def run_a_gan(D, G, D_solver, G_solver, discriminator_loss, generator_loss, show_every=250,
batch_size=128, noise_size=96, num_epochs=10):
"""
Train a GAN!
Inputs:
- D, G: PyTorch models for the discriminator and generator
- D_solver, G_solver: torch.optim Optimizers to use for training the
discriminator and generator.
- discriminator_loss, generator_loss: Functions to use for computing the generator and
discriminator loss, respectively.
- show_every: Show samples after every show_every iterations.
- batch_size: Batch size to use for training.
- noise_size: Dimension of the noise to use as input to the generator.
- num_epochs: Number of epochs over the training dataset to use for training.
"""
iter_count = 0
for epoch in range(num_epochs):
for x, _ in loader_train:
if len(x) != batch_size:
continue
D_solver.zero_grad()
real_data = x.type(dtype)
logits_real = D(2* (real_data - 0.5)).type(dtype)
g_fake_seed = sample_noise(batch_size, noise_size).type(dtype)
fake_images = G(g_fake_seed).detach()
logits_fake = D(fake_images.view(batch_size, 1, 28, 28))
d_total_error = discriminator_loss(logits_real, logits_fake)
d_total_error.backward()
D_solver.step()
G_solver.zero_grad()
g_fake_seed = sample_noise(batch_size, noise_size).type(dtype)
fake_images = G(g_fake_seed)
gen_logits_fake = D(fake_images.view(batch_size, 1, 28, 28))
g_error = generator_loss(gen_logits_fake)
g_error.backward()
G_solver.step()
if (iter_count % show_every == 0):
print('Iter: {}, D: {:.4}, G:{:.4}'.format(iter_count,d_total_error.item(),g_error.item()))
imgs_numpy = fake_images.data.cpu().numpy()
show_images(imgs_numpy[0:16])
plt.show()
print()
iter_count += 1
# +
# Make the discriminator
D = discriminator().type(dtype)
# Make the generator
G = generator().type(dtype)
# Use the function you wrote earlier to get optimizers for the Discriminator and the Generator
D_solver = get_optimizer(D)
G_solver = get_optimizer(G)
# Run it!
run_a_gan(D, G, D_solver, G_solver, discriminator_loss, generator_loss)
# + [markdown] tags=["pdf-ignore"]
# Well that wasn't so hard, was it? In the iterations in the low 100s you should see black backgrounds, fuzzy shapes as you approach iteration 1000, and decent shapes, about half of which will be sharp and clearly recognizable as we pass 3000.
# -
# # Least Squares GAN
# We'll now look at [Least Squares GAN](https://arxiv.org/abs/1611.04076), a newer, more stable alernative to the original GAN loss function. For this part, all we have to do is change the loss function and retrain the model. We'll implement equation (9) in the paper, with the generator loss:
# $$\ell_G = \frac{1}{2}\mathbb{E}_{z \sim p(z)}\left[\left(D(G(z))-1\right)^2\right]$$
# and the discriminator loss:
# $$ \ell_D = \frac{1}{2}\mathbb{E}_{x \sim p_\text{data}}\left[\left(D(x)-1\right)^2\right] + \frac{1}{2}\mathbb{E}_{z \sim p(z)}\left[ \left(D(G(z))\right)^2\right]$$
#
#
# **HINTS**: Instead of computing the expectation, we will be averaging over elements of the minibatch, so make sure to combine the loss by averaging instead of summing. When plugging in for $D(x)$ and $D(G(z))$ use the direct output from the discriminator (`scores_real` and `scores_fake`).
# +
def ls_discriminator_loss(scores_real, scores_fake):
"""
Compute the Least-Squares GAN loss for the discriminator.
Inputs:
- scores_real: PyTorch Tensor of shape (N,) giving scores for the real data.
- scores_fake: PyTorch Tensor of shape (N,) giving scores for the fake data.
Outputs:
- loss: A PyTorch Tensor containing the loss.
"""
loss = None
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
pass
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return loss
def ls_generator_loss(scores_fake):
"""
Computes the Least-Squares GAN loss for the generator.
Inputs:
- scores_fake: PyTorch Tensor of shape (N,) giving scores for the fake data.
Outputs:
- loss: A PyTorch Tensor containing the loss.
"""
loss = None
return loss
# -
# Before running a GAN with our new loss function, let's check it:
# +
def test_lsgan_loss(score_real, score_fake, d_loss_true, g_loss_true):
score_real = torch.Tensor(score_real).type(dtype)
score_fake = torch.Tensor(score_fake).type(dtype)
d_loss = ls_discriminator_loss(score_real, score_fake).cpu().numpy()
g_loss = ls_generator_loss(score_fake).cpu().numpy()
print("Maximum error in d_loss: %g"%rel_error(d_loss_true, d_loss))
print("Maximum error in g_loss: %g"%rel_error(g_loss_true, g_loss))
test_lsgan_loss(answers['logits_real'], answers['logits_fake'],
answers['d_loss_lsgan_true'], answers['g_loss_lsgan_true'])
# -
# Run the following cell to train your model!
# +
D_LS = discriminator().type(dtype)
G_LS = generator().type(dtype)
D_LS_solver = get_optimizer(D_LS)
G_LS_solver = get_optimizer(G_LS)
run_a_gan(D_LS, G_LS, D_LS_solver, G_LS_solver, ls_discriminator_loss, ls_generator_loss)
# -
# # Deeply Convolutional GANs
# In the first part of the notebook, we implemented an almost direct copy of the original GAN network from <NAME>. However, this network architecture allows no real spatial reasoning. It is unable to reason about things like "sharp edges" in general because it lacks any convolutional layers. Thus, in this section, we will implement some of the ideas from [DCGAN](https://arxiv.org/abs/1511.06434), where we use convolutional networks
#
# #### Discriminator
# We will use a discriminator inspired by the TensorFlow MNIST classification tutorial, which is able to get above 99% accuracy on the MNIST dataset fairly quickly.
# * Reshape into image tensor (Use Unflatten!)
# * Conv2D: 32 Filters, 5x5, Stride 1
# * Leaky ReLU(alpha=0.01)
# * Max Pool 2x2, Stride 2
# * Conv2D: 64 Filters, 5x5, Stride 1
# * Leaky ReLU(alpha=0.01)
# * Max Pool 2x2, Stride 2
# * Flatten
# * Fully Connected with output size 4 x 4 x 64
# * Leaky ReLU(alpha=0.01)
# * Fully Connected with output size 1
# +
def build_dc_classifier():
"""
Build and return a PyTorch model for the DCGAN discriminator implementing
the architecture above.
"""
return nn.Sequential(
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
pass
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
)
data = next(enumerate(loader_train))[-1][0].type(dtype)
b = build_dc_classifier().type(dtype)
out = b(data)
print(out.size())
# -
# Check the number of parameters in your classifier as a sanity check:
# +
def test_dc_classifer(true_count=1102721):
model = build_dc_classifier()
cur_count = count_params(model)
if cur_count != true_count:
print('Incorrect number of parameters in generator. Check your achitecture.')
else:
print('Correct number of parameters in generator.')
test_dc_classifer()
# -
# #### Generator
# For the generator, we will copy the architecture exactly from the [InfoGAN paper](https://arxiv.org/pdf/1606.03657.pdf). See Appendix C.1 MNIST. See the documentation for [tf.nn.conv2d_transpose](https://www.tensorflow.org/api_docs/python/tf/nn/conv2d_transpose). We are always "training" in GAN mode.
# * Fully connected with output size 1024
# * `ReLU`
# * BatchNorm
# * Fully connected with output size 7 x 7 x 128
# * ReLU
# * BatchNorm
# * Reshape into Image Tensor of shape 7, 7, 128
# * Conv2D^T (Transpose): 64 filters of 4x4, stride 2, 'same' padding (use `padding=1`)
# * `ReLU`
# * BatchNorm
# * Conv2D^T (Transpose): 1 filter of 4x4, stride 2, 'same' padding (use `padding=1`)
# * `TanH`
# * Should have a 28x28x1 image, reshape back into 784 vector
# +
def build_dc_generator(noise_dim=NOISE_DIM):
"""
Build and return a PyTorch model implementing the DCGAN generator using
the architecture described above.
"""
return nn.Sequential(
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
pass
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
)
test_g_gan = build_dc_generator().type(dtype)
test_g_gan.apply(initialize_weights)
fake_seed = torch.randn(batch_size, NOISE_DIM).type(dtype)
fake_images = test_g_gan.forward(fake_seed)
fake_images.size()
# -
# Check the number of parameters in your generator as a sanity check:
# +
def test_dc_generator(true_count=6580801):
model = build_dc_generator(4)
cur_count = count_params(model)
if cur_count != true_count:
print('Incorrect number of parameters in generator. Check your achitecture.')
else:
print('Correct number of parameters in generator.')
test_dc_generator()
# +
D_DC = build_dc_classifier().type(dtype)
D_DC.apply(initialize_weights)
G_DC = build_dc_generator().type(dtype)
G_DC.apply(initialize_weights)
D_DC_solver = get_optimizer(D_DC)
G_DC_solver = get_optimizer(G_DC)
run_a_gan(D_DC, G_DC, D_DC_solver, G_DC_solver, discriminator_loss, generator_loss, num_epochs=5)
# + [markdown] tags=["pdf-inline"]
# ## INLINE QUESTION 1
#
# We will look at an example to see why alternating minimization of the same objective (like in a GAN) can be tricky business.
#
# Consider $f(x,y)=xy$. What does $\min_x\max_y f(x,y)$ evaluate to? (Hint: minmax tries to minimize the maximum value achievable.)
#
# Now try to evaluate this function numerically for 6 steps, starting at the point $(1,1)$,
# by using alternating gradient (first updating y, then updating x using that updated y) with step size $1$. **Here step size is the learning_rate, and steps will be learning_rate * gradient.**
# You'll find that writing out the update step in terms of $x_t,y_t,x_{t+1},y_{t+1}$ will be useful.
#
# Breifly explain what $\min_x\max_y f(x,y)$ evaluates to and record the six pairs of explicit values for $(x_t,y_t)$ in the table below.
#
# ### Your answer:
#
#
# $y_0$ | $y_1$ | $y_2$ | $y_3$ | $y_4$ | $y_5$ | $y_6$
# ----- | ----- | ----- | ----- | ----- | ----- | -----
# 1 | | | | | |
# $x_0$ | $x_1$ | $x_2$ | $x_3$ | $x_4$ | $x_5$ | $x_6$
# 1 | | | | | |
#
#
#
#
# + [markdown] tags=["pdf-inline"]
# ## INLINE QUESTION 2
# Using this method, will we ever reach the optimal value? Why or why not?
#
# ### Your answer:
#
# + [markdown] tags=["pdf-inline"]
# ## INLINE QUESTION 3
# If the generator loss decreases during training while the discriminator loss stays at a constant high value from the start, is this a good sign? Why or why not? A qualitative answer is sufficient.
#
# ### Your answer:
#
# + tags=["pdf-inline"]
|
Assignment_03/Generative_Adversarial_Networks_PyTorch.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <a href="https://www.kaggle.com/rsizem2/tps-10-21-tensorflow-decision-forests-benchmarks?scriptVersionId=84829678" target="_blank"><img align="left" alt="Kaggle" title="Open in Kaggle" src="https://kaggle.com/static/images/open-in-kaggle.svg"></a>
# + [markdown] papermill={"duration": 0.0144, "end_time": "2022-01-09T19:02:01.4522", "exception": false, "start_time": "2022-01-09T19:02:01.4378", "status": "completed"} tags=[]
# # Tensorflow Decision Forests
#
# In this notebook we get benchmarks for the gradient boosting model provided with the [Tensorflow Decision Forests](https://www.tensorflow.org/decision_forests) library. For various input sizes (10k to 100k samples) we get AUC scores and training times for models with and without categorical features explicitly specified.
#
# Personally, I don't think this library is ready to be used seriously for these competitions primarily because it runs so slowly (no GPU/TPU optimizations yet) and requires a linux environment (which I can only easily access through these notebooks). You can get similar results much easier and faster using one of the established gradient boosting frameworks like XGBoost, LightGBM, and CatBoost.
#
#
# **Note:** This notebook will take several hours to run
# + _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19" _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5" papermill={"duration": 0.030616, "end_time": "2022-01-09T19:02:01.496256", "exception": false, "start_time": "2022-01-09T19:02:01.46564", "status": "completed"} tags=[]
# Global Variables for testing changes to this notebook quickly
RANDOM_SEED = 0
NUM_TREES = 1000
EARLY_STOP = 25
# + papermill={"duration": 67.727298, "end_time": "2022-01-09T19:03:09.236311", "exception": false, "start_time": "2022-01-09T19:02:01.509013", "status": "completed"} tags=[]
# Install TFDF library
# !pip3 install -q tensorflow_decision_forests --upgrade
# + papermill={"duration": 4.406987, "end_time": "2022-01-09T19:03:13.660297", "exception": false, "start_time": "2022-01-09T19:03:09.25331", "status": "completed"} tags=[]
import numpy as np
import pandas as pd
import pyarrow
import warnings
import time
import gc
import os
# Hide warnings
warnings.filterwarnings('ignore')
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'
# Model and evaluation
from sklearn.metrics import roc_auc_score
from sklearn.model_selection import train_test_split
from collections import defaultdict
# Tensorflow
import tensorflow as tf
import tensorflow_decision_forests as tfdf
tf.random.set_seed(RANDOM_SEED)
# + [markdown] papermill={"duration": 0.404536, "end_time": "2022-01-09T19:03:14.078503", "exception": false, "start_time": "2022-01-09T19:03:13.673967", "status": "completed"} tags=[]
# # Preparing Data
#
# 1. Load original data
# 2. Downcast datatypes wherever possible
# 3. Split data into halves, use one half for estimation
# 4. Save data in pandas and tensorflow formats
# + _kg_hide-input=true papermill={"duration": 265.902273, "end_time": "2022-01-09T19:07:39.998039", "exception": false, "start_time": "2022-01-09T19:03:14.095766", "status": "completed"} tags=[]
# %%time
# Load original training data
train = pd.read_csv("../input/tabular-playground-series-oct-2021/train.csv")
# List for tracking categorical features
categorical_features = list()
# Downcast training data while keeping track of categorical variables
for col in train.columns:
if train[col].dtype == "int64":
train[col] = train[col].astype('int32')
# ignore target column
if col == "target": continue
categorical_features.append(
tfdf.keras.FeatureUsage(
name = col,
semantic = tfdf.keras.FeatureSemantic.CATEGORICAL
)
)
elif train[col].dtype == "float64":
train[col] = pd.to_numeric(train[col], downcast ='float')
# Halve the data, we will get AUC estimates on a holdout set
train, holdout = train_test_split(
train,
train_size = 500000,
stratify = train['target'],
shuffle = True
)
# Save pandas dataframe for quick retrieval later
train.reset_index(drop = True, inplace = True)
holdout.reset_index(drop = True, inplace = True)
train.to_feather('train_500k.feather')
holdout.to_feather('holdout_full.feather')
del train; gc.collect()
# Create tensorflow data
holdout_tf = tfdf.keras.pd_dataframe_to_tf_dataset(
holdout,
label = 'target',
in_place = True
)
# Save Train data
tf.data.experimental.save(holdout_tf, "holdout_tf")
# Garbage Collection (free up memory)
del holdout, holdout_tf; gc.collect()
# + [markdown] papermill={"duration": 0.014764, "end_time": "2022-01-09T19:07:40.028054", "exception": false, "start_time": "2022-01-09T19:07:40.01329", "status": "completed"} tags=[]
# # Helper Functions
#
# We create a several function to perform various steps of the training and evaluation process, mostly to avoid having too many things loaded in memory at once.
# + _kg_hide-input=true papermill={"duration": 0.025241, "end_time": "2022-01-09T19:07:40.068434", "exception": false, "start_time": "2022-01-09T19:07:40.043193", "status": "completed"} tags=[]
def get_training_data(n_rows = 10000):
assert 0 < n_rows < 500000
train = pd.read_feather('train_500k.feather')
train, test = train_test_split(
train,
train_size = n_rows,
stratify = train['target'],
shuffle = True
)
# Prepare Train Data
train_df = tfdf.keras.pd_dataframe_to_tf_dataset(
train,
label = 'target',
in_place = True
)
return train_df
# + _kg_hide-input=true papermill={"duration": 0.026437, "end_time": "2022-01-09T19:07:40.109759", "exception": false, "start_time": "2022-01-09T19:07:40.083322", "status": "completed"} tags=[]
def train_model(n_rows = 10000, categorical = False):
train_df = get_training_data(n_rows)
gc.collect()
start = time.time()
# Define model, using explicitly defined categoricals
if categorical:
model = tfdf.keras.GradientBoostedTreesModel(
task = tfdf.keras.Task.CLASSIFICATION,
num_trees = NUM_TREES,
early_stopping_num_trees_look_ahead = EARLY_STOP,
features = categorical_features,
exclude_non_specified_features = False,
verbose = 0
)
else:
model = tfdf.keras.GradientBoostedTreesModel(
task = tfdf.keras.Task.CLASSIFICATION,
num_trees = NUM_TREES,
early_stopping_num_trees_look_ahead = EARLY_STOP,
verbose = 0
)
# Metric for validation
model.compile(
metrics=[tf.metrics.AUC()]
)
# Training
model.fit(train_df, verbose = 0)
end = time.time()
# Delete training data (free up memory)
del train_df
gc.collect()
return model, round(end-start, 6)
# + _kg_hide-input=true papermill={"duration": 0.022302, "end_time": "2022-01-09T19:07:40.146223", "exception": false, "start_time": "2022-01-09T19:07:40.123921", "status": "completed"} tags=[]
def get_holdout_preds(model):
holdout_df = tf.data.experimental.load("holdout_tf")
preds = model.predict(holdout_df)[:,0]
del holdout_df
gc.collect()
return preds
# + _kg_hide-input=true papermill={"duration": 0.021435, "end_time": "2022-01-09T19:07:40.181661", "exception": false, "start_time": "2022-01-09T19:07:40.160226", "status": "completed"} tags=[]
def get_holdout_score(y_preds):
holdout = pd.read_feather('holdout_full.feather')
y_true = holdout['target']
return roc_auc_score(y_true, y_preds)
# + [markdown] papermill={"duration": 0.013745, "end_time": "2022-01-09T19:07:40.209505", "exception": false, "start_time": "2022-01-09T19:07:40.19576", "status": "completed"} tags=[]
# # Benchmarks
# + papermill={"duration": 0.028226, "end_time": "2022-01-09T19:07:40.251729", "exception": false, "start_time": "2022-01-09T19:07:40.223503", "status": "completed"} tags=[]
def get_benchmarks():
data = defaultdict(list)
for training_size in [10000, 20000, 30000, 40000, 50000, 75000]:
# Train model, no specified categorical features
model, training_time = train_model(n_rows = training_size)
preds = get_holdout_preds(model)
score = get_holdout_score(preds)
print('All Numerical Features')
print(f'Rows: {training_size}, Time: {round(training_time, 2)}')
print(f'Validation Score: {round(score, 6)}\n')
# save results
data['size'].append(training_size)
data['features'].append('numerical')
data['time'].append(training_time)
data['auc'].append(score)
# free up memory
del model
gc.collect()
# Train model, specify categorical features
model, training_time = train_model(
n_rows = training_size,
categorical = True
)
preds = get_holdout_preds(model)
score = get_holdout_score(preds)
print('Categorical Features')
print(f'Rows: {training_size}, Time: {round(training_time, 2)}')
print(f'Validation Score: {round(score, 6)}\n')
# save results
data['size'].append(training_size)
data['features'].append('categorical')
data['time'].append(training_time)
data['auc'].append(score)
# free up memory
del model
gc.collect()
return pd.DataFrame(data)
# + _kg_hide-output=true papermill={"duration": 22539.519696, "end_time": "2022-01-10T01:23:19.786373", "exception": false, "start_time": "2022-01-09T19:07:40.266677", "status": "completed"} tags=[]
# Output has been hidden
data = get_benchmarks()
# + papermill={"duration": 0.05174, "end_time": "2022-01-10T01:23:19.856308", "exception": false, "start_time": "2022-01-10T01:23:19.804568", "status": "completed"} tags=[]
data
# + [markdown] papermill={"duration": 0.017878, "end_time": "2022-01-10T01:23:19.893963", "exception": false, "start_time": "2022-01-10T01:23:19.876085", "status": "completed"} tags=[]
# We see that explicitly specifying the categorical features significantly increases the training times but does not result in notably better models so we will not bother specifying categorical features for subsequent models.
|
kaggle/tps-10-21-tensorflow-decision-forests-benchmarks.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
import pandas as pd
import numpy as np
# #%matplotlib inline
import matplotlib.pyplot as plt
from IPython.display import display, HTML
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
from operator import attrgetter
from matplotlib.patches import Ellipse
from math import atan2,degrees
import numpy.random as rnd
points = pd.read_csv('Clustering.csv',sep=',')
class CenterValue:
def __init__ (self,p,val):
self.value=val
self.point=p
def Distance(p1,p2indx):
p1 = np.array(p1)
P2 = np.array((points.X[p2indx],points.Y[p2indx]))
return np.linalg.norm(p1-p2)
# +
def K_mean(centerpoints):
centers={}
for i in centerpoints:
centers[i]=[]
for i in range(len(points.index)):
values=[]
# -
def GetPointsList(Indexs):
lst=[]
for i in Indexs:
lst.append((points.X[i],points.Y[i]))
return lst
K_mean(GetPointsList(range(4)))
|
HW11/.ipynb_checkpoints/Q3-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# import warnings filter
from warnings import simplefilter
# ignore all future warnings
simplefilter(action='ignore', category=FutureWarning)
# +
from sklearn.datasets import load_diabetes
from sklearn.linear_model import SGDRegressor
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib notebook
diabetes = load_diabetes()
print(diabetes.DESCR)
# -
df_diabetes = pd.DataFrame(diabetes.data, columns = diabetes.feature_names)
df_diabetes['target'] = diabetes.target
df_diabetes.info()
df_diabetes.describe()
# +
from sklearn.model_selection import train_test_split
X = df_diabetes.loc[:,(df_diabetes.columns != 'target')]
y = df_diabetes['target']
X_train, X_valid, y_train, y_valid = train_test_split(X,
y,
test_size=0.3,
random_state=0)
# -
from sklearn.model_selection import GridSearchCV
clf = SGDRegressor(random_state=0)
model = GridSearchCV(estimator=clf,
param_grid={
'shuffle':[True, False],#Whether or not the training data should be shuffled after each epoch.
'learning_rate':['constant', 'optimal', 'invscaling'],
'eta0':[0.1, 0.01, 0.001, 0.0001],
'penalty':['l2', 'l1']
},
cv=10,
n_jobs=2,
scoring='r2')
model.fit(X_train, y_train)
print()
print(model.best_params_)
print('R² %.2f%%' % (model.best_score_*100))
import numpy as np
predictions = model.predict(X_valid)
print('R² %.2f%%' % (model.score(X_valid, y_valid)*100))
# +
from sklearn.metrics import mean_absolute_error, r2_score, mean_squared_error
print('Mean square error: %.2f'
% mean_squared_error(y_valid, predictions))
# The mean squared error
print('Mean absolute error: %.2f'
% mean_absolute_error(y_valid, predictions))
# The coefficient of determination: 1 is perfect prediction
print('Coefficient of determination (R²): %.2f%%'
% (r2_score(y_valid, predictions)*100))
# -
# # Comparando Real e Predito
df = pd.DataFrame({'Real': y_valid, 'Predito': predictions}).head(50)
df.plot(kind='bar',figsize=(20,8))
plt.grid(which='major', linestyle='-', linewidth='0.5', color='green')
plt.grid(which='minor', linestyle=':', linewidth='0.5', color='black')
plt.show()
# ## Redução para Visualização
from sklearn.decomposition import PCA
pca_diabetes = PCA(n_components=2)
principalComponents_diabetes = pca_diabetes.fit_transform(X_valid)
principal_diabetes_Df = pd.DataFrame(data = principalComponents_diabetes
, columns = ['principal component 1', 'principal component 2'])
principal_diabetes_Df['y'] = y_valid
principal_diabetes_Df['predicts'] = predictions
import seaborn as sns
plt.figure(figsize=(16,10))
sns.scatterplot(
x="principal component 1", y="principal component 2",
hue="y",
data=principal_diabetes_Df,
alpha=0.7,
palette="mako"
)
# +
# Plot outputs
plt.figure(figsize=(20,15))
plt.scatter(x="principal component 1", y="y", color="black", data=principal_diabetes_Df)
plt.scatter(x="principal component 1", y="predicts", color="green", data=principal_diabetes_Df)
#plt.xticks(())
#plt.yticks(())
plt.title("Quantitative Measure of Disease Progression")
plt.xlabel('PCA1')
plt.ylabel('Y / Yhat')
plt.legend()
plt.grid()
plt.show()
# +
# Plot outputs
plt.figure(figsize=(20,15))
plt.scatter(x="principal component 2", y="y", color='black', linewidths=3, data=principal_diabetes_Df)
plt.scatter(x="principal component 2", y="predicts", color='blue', data=principal_diabetes_Df)
#plt.xticks(())
#plt.yticks(())
plt.title("Quantitative Measure of Disease Progression")
plt.xlabel('PCA2')
plt.ylabel('Y / Yhat')
plt.legend()
plt.grid()
plt.show()
|
003 - Machine Learing/.ipynb_checkpoints/Sthocastic_Descendent_Gradient_Diabetes-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Example: Credit Card Default
#
# We have seem this example in class. Our task will be to perform logistic regression and interpret the results.
#
# ---
# * Model the default (binary variable) using various predictors
# * Model 1: default ~ balance
# * Model 2: default ~ student
# * Model 3: default ~ balance + income + student
#
# * Discuss the results
# * What can you say about the coefficient for student in Models 1 and 2? Could you explain it?
# * Using Model 1, what is our estimated probability of default for someone with a balance of USD1000? How about USD2000?
import pandas as pd
import statsmodels.api as sm
import pylab as pl
import numpy as np
df = pd.read_csv("default_data.csv", index_col=0)
df.head(10)
# +
# add manually intercept
df['intercept'] = 1.0
# change categorical variables to numerical
df['default_num'] = np.where(df.default=='Yes', 1,0)
df['student_num'] = np.where(df.student=='Yes', 1,0)
display(df)
# -
# default ~ balance
cols_to_keep = [ 'balance','intercept']
logit = sm.Logit(df['default_num'], df[cols_to_keep])
result = logit.fit()
result.summary()
# default ~ balance
cols_to_keep = ['student_num','intercept']
logit = sm.Logit(df['default_num'], df[cols_to_keep])
result = logit.fit()
result.summary()
# default ~ balance
cols_to_keep = ['balance','income','student_num','intercept']
logit = sm.Logit(df['default_num'], df[cols_to_keep])
result = logit.fit()
result.summary()
|
Week_5_Default_Lab_AA.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Qiskit v0.34.1 (ipykernel)
# language: python
# name: python3
# ---
# + [markdown] tags=[]
# # **QUANTUM UNIVERSALITY**
# + [markdown] tags=[]
# #### 1)Z=SS
# #### 2)Z=HXH
# #### 3)Z=TTTT
# #### 4)X=HZH
# #### 5)X=H(SS)H
# #### 6)Y=SXS$^{\dagger}$
# #### 7)Y=S(HSSH)S$^{\dagger}$
#
# + [markdown] tags=[]
# ### 1) **Z = SS**
# <br>
#
#
# -
# importing dependencies
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, transpile , assemble
from qiskit.tools.visualization import circuit_drawer
from qiskit.quantum_info import state_fidelity
from qiskit import BasicAer
from qiskit import Aer, execute, visualization
import matplotlib.pyplot as plt
import numpy as np
from math import pi,sqrt
from IPython.display import Video
from qiskit.visualization import array_to_latex
# <Left>Example</Left>
# $$ Z\ket{+} = \ket{-}$$
# $$S(S(\ket{+})) = \ket{-}$$
# <br>
# +
qc = QuantumCircuit(1)
qc.s(0)
display(qc.draw(output="mpl"))
# executing the circuit
backend = Aer.get_backend('statevector_simulator')
b = BasicAer.get_backend('unitary_simulator')
job = execute(qc, backend)
result = job.result()
# -
# <center><b>Applying S gate on |+></b></center>
# $$S\ket{+} = \begin{bmatrix} 1 & 0 \\ 0 & i \end{bmatrix}\begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}\end{bmatrix}$$
#
# $$S\ket{+} = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ i\frac{1}{\sqrt{2}}\end{bmatrix}$$
#
# $$S\ket{+} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ i\end{bmatrix}$$
# <br>
#
# +
plus_state = np.matrix([[1/sqrt(2)],[1/sqrt(2)]])
print("Initial State is |+> i.e \n{}\n".format(plus_state))
s_gate = b.run(transpile(qc, b)).result().get_unitary(qc, decimals=3)
s_gate = np.matrix(s_gate)
print(" S Gate \n{}\n".format(s_gate))
intermediate_state = s_gate*plus_state
print("intermediate State after applying S gate on intitial state \n{}\n".format(intermediate_state))
# -
#
# <center><b>Applying S gate on intermediate state $$\frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ i\end{bmatrix}$$</b></center>
# $$S\frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ i\end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & i \end{bmatrix}\frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ i\end{bmatrix}$$
#
# $$S\frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ i\end{bmatrix} = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ -1\end{bmatrix}$$
#
# $$S\frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ i\end{bmatrix} = \ket{-}$$
# <br>
#
# +
# applying s gate on intermediate state
print("Intermediate State \n{}\n".format(intermediate_state))
ss_gate = b.run(transpile(qc, b)).result().get_unitary(qc, decimals=3)
ss_gate = np.matrix(ss_gate)
print("S Gate \n{}\n".format(ss_gate))
output = ss_gate*intermediate_state
print("Output State after applying S Gate on intermediate state is |-> \n{}\n".format(output))
# -
# <center><b> Hence applying S Gate twice is same as Z Gate</b></center>
# $$S\ket{+} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ i\end{bmatrix} = \ket{intermediate}$$
# $$S\ket{intermediate} = \ket{+}$$
# <br>
# <center><b>SS = S$^2$ = Z</b></center>
# <br>
#
# +
#Summarised Code
q = QuantumRegister(1)
qc = QuantumCircuit(q)
qc.s(q)
qc.s(q)
display(qc.draw(output="mpl"))
# executing the circuit
backend = Aer.get_backend('statevector_simulator')
b = BasicAer.get_backend('unitary_simulator')
job = execute(qc, backend)
result = job.result()
print("Initial State |+> \n{}\n".format(plus_state))
ss_gate = b.run(transpile(qc, b)).result().get_unitary(qc, decimals=3)
ss_gate = np.matrix(ss_gate)
print("SS Gate \n{}\n".format(ss_gate))
output = ss_gate*plus_state
print("Output State becomes |->\n{}\n".format(output))
# + [markdown] tags=[]
# ### 2) **Z = HXH**
# -
#creating a circuit having H gate so that qubit can undergo H gate operation when sent
qc1=QuantumCircuit(1)
qc1.h(0)
display(qc1.draw())
# <center><b>Applying H gate on |0></b></center>
# <br/>
# $$H\ket{0} = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}\begin{bmatrix} 1 \\ 0\end{bmatrix}$$
# <br/>
# $$H\ket{0} = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ 1\end{bmatrix}= \frac{1}{\sqrt{2}}(\begin{bmatrix} 1 \\ 0\end{bmatrix} + \begin{bmatrix} 0 \\ 1\end{bmatrix}) = \frac{1}{\sqrt{2}}(\ket{0} + \ket{1})$$
# <br/>
# $$H\ket{0} = \ket{+}$$
#
# +
zero_state = np.matrix([[1.+0.j],[0.+0.j]])
print("initial state is |0> \n{}\n".format(zero_state))
h_gate = b.run(transpile(qc1, b)).result().get_unitary(qc1, decimals=3)
h_gate = np.matrix(h_gate)
print(" H Gate equals \n{}\n".format(h_gate))
print("\nApplying H gate on initial state\n")
Intermediate_State1= h_gate*zero_state
print("Intermediate_State1 is \n{}\n which is equal to |+>".format(Intermediate_State1))
# -
# <center><b>Applying X gate on Intermediate_State1 </b></center>
# <br/>
# $$X\ket{+} = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}\end{bmatrix}$$
# <br/>
# $$X\ket{+} = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}\end{bmatrix}$$
# <br/>
# $$X\ket{+} = \ket{+}$$
# <br/>
#creating a circuit having X gate so that qubit undergoes X gate operation when sent
qc2=QuantumCircuit(1)
qc2.x(0)
display(qc2.draw())
x_gate = b.run(transpile(qc2, b)).result().get_unitary(qc2, decimals=3)
x_gate = np.matrix(x_gate)
print("X Gate equals \n{}\n".format(x_gate))
print("Applying x gate on Intermediate_State1 \n")
Intermediate_State2=x_gate*Intermediate_State1
print("Intermediate_State2 is \n{}\n which is |+> ".format(Intermediate_State2))
# <center><b>Applying H gate on Intermediate_State2</b></center>
# <br/>
# $$H\ket{+} = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}\begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}\end{bmatrix}$$
# <br/>
# $$H\ket{+} = \frac{1}{\sqrt{2}}\begin{bmatrix} \frac{1}{\sqrt{2}} \\ 0\end{bmatrix} = \begin{bmatrix} 1 \\ 0\end{bmatrix}$$
# <br/>
# $$H\ket{+} = \ket{0}$$
# +
#Passing the qubit (in output state2) under H gate operation again
display(qc1.draw())
h_gate = b.run(transpile(qc1, b)).result().get_unitary(qc1, decimals=3)
h_gate = np.matrix(h_gate)
print(" H Gate equals \n{}\n".format(h_gate))
print("Applying H gate on Intermediate_State2 \n")
final_output= h_gate*Intermediate_State2
final_output=np.round(final_output,0) #Rounding the values and assigning back to the matrix elements
print("Final Output is \n{}\n which is equal to |0>".format(final_output))
# -
# <center><b> Hence applying HXH Gate in series is same as Z Gate</b></center>
# <br/>
# $$H(X(H \ket{0})) = \ket{0}$$
# <br>
#
# +
#Summarisied code
qc=QuantumCircuit(1)
qc.h(0)
qc.x(0)
qc.h(0)
display(qc.draw(initial_state=True))
# executing the circuit
backend = Aer.get_backend('statevector_simulator')
b = BasicAer.get_backend('unitary_simulator')
job = execute(qc, backend)
result = job.result()
zero_state = np.matrix([[1.+0.j],[0.+0.j]])
print("initial state is |0> \n{}\n".format(zero_state))
hxh_gate = b.run(transpile(qc, b)).result().get_unitary(qc, decimals=3)
hxh_gate = np.matrix(hxh_gate)
print("combined HXH Gate equals \n{}\n".format(hxh_gate))
output = hxh_gate*zero_state
print("output state is |0> \n{}\n ".format(output))
# + [markdown] tags=[]
# ### 3) **Z=TTTT**
# -
qc = QuantumCircuit(1)
qc.t(0)
display(qc.draw(output="mpl"))
#
# #### Step1
# <center><b>Applying T gate on intitial state i.e |+></b></center>
# $$T\ket{+} = \begin{bmatrix} 1 & 0 \\ 0 & e^{\frac{i\pi}{4}} \end{bmatrix}\begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}\end{bmatrix}$$
#
# $$T\ket{+} = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ e^{\frac{i\pi}{4}}\frac{1}{\sqrt{2}}\end{bmatrix}$$
#
# $$T\ket{+} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ e^{\frac{i\pi}{4}}\end{bmatrix} = IntermediateState1$$
#
# +
#Step1
# executing the circuit
backend = Aer.get_backend('statevector_simulator')
b = BasicAer.get_backend('unitary_simulator')
job = execute(qc, backend)
result = job.result()
plus_state = np.matrix([[1/sqrt(2)],[1/sqrt(2)]])
print("Initial State is |+> i.e \n{}\n".format(plus_state))
t_gate = b.run(transpile(qc, b)).result().get_unitary(qc, decimals=3)
t_gate = np.matrix(t_gate)
print(" T Gate equals \n{}\n".format(t_gate))
print("\nApplying T gate on initial state\n \n")
Intermediate_State1= t_gate*plus_state
print("Intermediate_State1 is \n{}\n ".format(Intermediate_State1))
# -
# #### Step2
# <br>
# <center><b>Applying T gate on Intermediate_State1 </b></center>
# <br>
# $$T(IntermediateState1)=T(T\ket{+}) = \begin{bmatrix} 1 & 0 \\ 0 & e^{\frac{i\pi}{4}} \end{bmatrix}\frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ e^{\frac{i\pi}{4}}\end{bmatrix}$$
#
# $$T(T\ket{+}) = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ e^{\frac{i\pi}{4}}e^{\frac{i\pi}{4}}\end{bmatrix}$$
#
# $$T(T\ket{+}) = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ e^{\frac{i\pi}{2}}\end{bmatrix}$$
#
# $$T(T\ket{+}) = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ e^{\frac{i\pi}{2}}\end{bmatrix}$$
#
# $$T(T\ket{+}) = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ i\end{bmatrix}$$
#
# $$T(T\ket{+}) = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ i\end{bmatrix} = S\ket{+} = IntermediateState2$$
#
# <br>
# <center><b>Applying T Gate twice is same as S Gate</b></center>
# <center><b>TT = T$^2$ = S</b></center>
# +
# Step2
tt_gate = b.run(transpile(qc, b)).result().get_unitary(qc, decimals=3)
tt_gate = np.matrix(tt_gate)
print(" T Gate equals \n{}\n".format(tt_gate))
print("\nApplying T gate on Intermediate_state1\n \n")
Intermediate_State2= tt_gate*Intermediate_State1 #T gate applied on intermediate_state1 to give intermediate_state2
print("Intermediate_State2 is \n{}\n ".format(Intermediate_State2))
# -
# #### Step3
# <br>
# <center><b>Applying T gate on Intermediate_State2 </b></center>
# <br>
# $$T(IntermediateState2)=T(T(T\ket{+})) \begin{bmatrix} 1 & 0 \\ 0 & e^{\frac{i\pi}{4}} \end{bmatrix}\frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ i\end{bmatrix}$$
# <br/>
# $$ T(T(T\ket{+}))= \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ ie^{\frac{i\pi}{4}}\end{bmatrix} = IntermediateState3$$
#
# +
#Step 3
ttt_gate = b.run(transpile(qc, b)).result().get_unitary(qc, decimals=3)
ttt_gate = np.matrix(ttt_gate)
print(" T Gate equals \n{}\n".format(ttt_gate))
print("\nApplying T gate on Intermediate_state2\n \n")
Intermediate_State3= tt_gate*Intermediate_State2
print("Intermediate_State3 is \n{}\n ".format(Intermediate_State3))
# -
# #### Step4
# <br>
# <center><b>Applying T gate on Intermediate_State3 </b></center>
# <br>
# $$T(IntermediateState3)=T(T(T(T\ket{+}))) \begin{bmatrix} 1 & 0 \\ 0 & e^{\frac{i\pi}{4}} \end{bmatrix}\frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ ie^{\frac{i\pi}{4}}\end{bmatrix}$$
# <br/>
# <br>
# $$T(T(T(T\ket{+}))) = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ ie^{\frac{i\pi}{4}}e^{\frac{i\pi}{4}}\end{bmatrix} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ i^2\end{bmatrix} $$
# <br/>
# $$ T(T(T(T\ket{+})))= \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ -1\end{bmatrix} = OutputState =\ket{-}$$
#
# +
#Step4
tttt_gate = b.run(transpile(qc, b)).result().get_unitary(qc, decimals=3)
tttt_gate = np.matrix(tttt_gate)
print(" T Gate equals \n{}\n".format(tttt_gate))
print("\nApplying T gate on Intermediate_state2\n \n")
output_State= tt_gate*Intermediate_State3
print("output_State is \n{}\n which is equal to |-> ".format(output_State))
# -
# <br>
# <center><b>Hence Applying T Gate 4 times is same as Z Gate</b></center>
# <center><b>TTTT = T$^4$ = SS = S$^2$ = Z</b></center>
# <br>
# +
#summarised code
qc = QuantumCircuit(1)
qc.t(0)
qc.t(0)
qc.t(0)
qc.t(0)
display(qc.draw(output="mpl"))
# executing the circuit
backend = Aer.get_backend('statevector_simulator')
b = BasicAer.get_backend('unitary_simulator')
job = execute(qc, backend)
result = job.result()
plus_state = np.matrix([[1/sqrt(2)],[1/sqrt(2)]])
print("Initial State is |+> i.e \n{}\n".format(plus_state))
tttt_gate = b.run(transpile(qc, b)).result().get_unitary(qc, decimals=3)
tttt_gate = np.matrix(tttt_gate)
print(" TTTT Gate \n{}\n".format(tttt_gate))
output_state = tttt_gate*plus_state
print("Output State \n{}\n which is equal to |->".format(output_state))
# + [markdown] tags=[]
# ### 4) **X=HZH**
# +
qc1=QuantumCircuit(1)
qc1.h(0)
display(qc1.draw())
# executing the circuit
backend = Aer.get_backend('statevector_simulator')
b = BasicAer.get_backend('unitary_simulator')
job = execute(qc1, backend)
result = job.result()
# -
# <center><b>Applying H gate on |0></b></center>
# <br/>
# $$H\ket{0} = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}\begin{bmatrix} 1 \\ 0\end{bmatrix}$$
# <br/>
# $$H\ket{0} = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ 1\end{bmatrix}= \frac{1}{\sqrt{2}}(\begin{bmatrix} 1 \\ 0\end{bmatrix} + \begin{bmatrix} 0 \\ 1\end{bmatrix}) = \frac{1}{\sqrt{2}}(\ket{0} + \ket{1})$$
# <br/>
# $$H\ket{0} = \ket{+}= IntermediateState1$$
#
# +
zero_state = np.matrix([[1.+0.j],[0.+0.j]])
print("initial state is |0> \n{}\n".format(zero_state))
h_gate = b.run(transpile(qc1, b)).result().get_unitary(qc1, decimals=3)
h_gate = np.matrix(h_gate)
print(" H Gate equals \n{}\n".format(h_gate))
print("\nApplying H gate on initial state\n")
Intermediate_State1= h_gate*zero_state
print("Intermediate_State1 is \n{}\n which is equal to |+>".format(Intermediate_State1))
# +
qc2=QuantumCircuit(1)
qc2.z(0)
display(qc2.draw())
# executing the circuit
backend = Aer.get_backend('statevector_simulator')
b = BasicAer.get_backend('unitary_simulator')
job = execute(qc2, backend)
result = job.result()
# -
#
# <center><b>Applying Z gate on IntermediateState1</b></center>
# $$Z(IntermediateState1)=Z\ket{+} = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}\end{bmatrix}$$
#
# $$Z\ket{+} = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}}\end{bmatrix}$$
#
# $$Z\ket{+} = \ket{-}$$
# <br/>
#
#
# +
z_gate = b.run(transpile(qc2, b)).result().get_unitary(qc2, decimals=3)
z_gate = np.matrix(z_gate)
print(" Z Gate equals \n{}\n".format(z_gate))
print("\nApplying Z gate on Intermediate_State1\n")
Intermediate_State2=z_gate*Intermediate_State1
print("Intermediate_State2 is \n{}\n which is equal to |->".format(Intermediate_State2))
# -
# <center><b>Applying H gate on Intermediate_State2</b></center>
# <br/>
# $$H(IntermediateState2)=H\ket{-} = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}\frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ -1\end{bmatrix}$$
# <br/>
# $$H\ket{-} = \frac{1}{{2}}\begin{bmatrix} 0 \\ 2\end{bmatrix}= \frac{2}{{2}}\begin{bmatrix} 0 \\ 1\end{bmatrix} =\begin{bmatrix} 0 \\ 1\end{bmatrix}$$
# <br/>
# $$H\ket{-} = \ket{1}= OutputState$$
# +
h_gate = b.run(transpile(qc1, b)).result().get_unitary(qc1, decimals=3)
h_gate = np.matrix(h_gate)
print(" H Gate equals \n{}\n".format(h_gate))
print("\nApplying H gate on Intermediate_State2\n")
output_State= h_gate*Intermediate_State2
output_State=np.round(output_State,0)
print("Output_State is \n{}\n which is equal to |1>".format(output_State))
# -
#
# <center><b> Hence applying HZH Gate in series is same as X Gate</b></center>
# <br/>
# $$H(Z(H \ket{0})) = \ket{1}$$
# <br>
#
# +
#summarised code
qc=QuantumCircuit(1)
qc.h(0)
qc.z(0)
qc.h(0)
display(qc.draw())
# executing the circuit
backend = Aer.get_backend('statevector_simulator')
b = BasicAer.get_backend('unitary_simulator')
job = execute(qc, backend)
result = job.result()
zero_state = np.matrix([[1.+0.j],[0.+0.j]])
print("initial state is |0> \n{}\n".format(zero_state))
hzh_gate = b.run(transpile(qc, b)).result().get_unitary(qc, decimals=3)
hzh_gate = np.matrix(hzh_gate)
print("combined HZH Gate equals \n{}\n".format(hzh_gate))
output = hzh_gate*zero_state
print("output state is |1> \n{}\n ".format(output))
# + [markdown] tags=[]
# ### 5) **X=H(SS)H**
# +
qc1=QuantumCircuit(1)
qc1.h(0)
display(qc1.draw())
# executing the circuit
backend = Aer.get_backend('statevector_simulator')
b = BasicAer.get_backend('unitary_simulator')
job = execute(qc1, backend)
result = job.result()
# -
# <center><b>Applying H gate on |0></b></center>
# <br/>
# $$H\ket{0} = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}\begin{bmatrix} 1 \\ 0\end{bmatrix}$$
# <br/>
# $$H\ket{0} = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ 1\end{bmatrix}= \frac{1}{\sqrt{2}}(\begin{bmatrix} 1 \\ 0\end{bmatrix} + \begin{bmatrix} 0 \\ 1\end{bmatrix}) = \frac{1}{\sqrt{2}}(\ket{0} + \ket{1})$$
# <br/>
# $$H\ket{0} = \ket{+}= IntermediateState1$$
# +
zero_state = np.matrix([[1.+0.j],[0.+0.j]])
print("initial state is |0> \n{}\n".format(zero_state))
h_gate = b.run(transpile(qc1, b)).result().get_unitary(qc1, decimals=3)
h_gate = np.matrix(h_gate)
print(" H Gate equals \n{}\n".format(h_gate))
print("\nApplying H gate on initial state\n")
Intermediate_State1= h_gate*zero_state
print("Intermediate_State1 is \n{}\n which is equal to |+>".format(Intermediate_State1))
# + tags=[]
qc2=QuantumCircuit(1)
qc2.s(0)
qc2.s(0)
display(qc2.draw())
# executing the circuit
backend = Aer.get_backend('statevector_simulator')
b = BasicAer.get_backend('unitary_simulator')
job = execute(qc2, backend)
result = job.result()
# -
# <center><b>Applying S gate twice on Intermediate State1</b></center>
#
# $$S(S(intermediate State1))=S(S\ket{+}) = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}\end{bmatrix}$$
#
# $$S(S\ket{+}) = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}}\end{bmatrix}$$
#
# $$S(S\ket{+}) = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ -1\end{bmatrix} $$
# <br/>
# $$S(S\ket{+}) = \ket{-} $$
# <br/>
# $$= Intermediate State2$$
# <br>
ss_gate = b.run(transpile(qc2, b)).result().get_unitary(qc2, decimals=3)
ss_gate = np.matrix(ss_gate)
print("Combined SS Gate \n{}\n".format(ss_gate))
print("\nApplying SS gate on Intermediate_State1\n\n")
Intermediate_State2= ss_gate*Intermediate_State1
print("Intermediate State2\n{}\n which is |->".format(Intermediate_State2))
# <center><b>Applying H gate on Intermediate_State2</b></center>
# <br/>
# $$H(IntermediateState2)=H\ket{-} = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}\frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ -1\end{bmatrix}$$
# <br/>
# $$H\ket{-} = \frac{1}{{2}}\begin{bmatrix} 0 \\ 2\end{bmatrix}= \frac{2}{{2}}\begin{bmatrix} 0 \\ 1\end{bmatrix} =\begin{bmatrix} 0 \\ 1\end{bmatrix}$$
# <br/>
# $$H\ket{-} = \ket{1}= OutputState$$
# +
h_gate = b.run(transpile(qc1, b)).result().get_unitary(qc1, decimals=3)
h_gate = np.matrix(h_gate)
print(" H Gate equals \n{}\n".format(h_gate))
print("\nApplying H gate on Intermediate_State2\n")
Output_state= h_gate*Intermediate_State2
Output_state=np.round(Output_state)
print("Output State is \n{}\n which is equal to |1>".format(Output_state))
# -
# <center><b> Hence applying H(SS)H Gate in series is same as X Gate</b></center>
# <br/>
# $$H(S(S((H \ket{0})))) = \ket{1}$$
# <br>
#
#
# +
#summarised code
qc1=QuantumCircuit(1)
qc1.h(0)
qc1.s(0)
qc1.s(0)
qc1.h(0)
display(qc1.draw())
# executing the circuit
backend = Aer.get_backend('statevector_simulator')
b = BasicAer.get_backend('unitary_simulator')
job = execute(qc1, backend)
result = job.result()
zero_state = np.matrix([[1.+0.j],[0.+0.j]])
print("initial state is |0> \n{}\n".format(zero_state))
hssh_gate = b.run(transpile(qc1, b)).result().get_unitary(qc1, decimals=3)
hssh_gate = np.matrix(hssh_gate)
print(" H(SS)H Gate equals \n{}\n".format(hssh_gate))
print("\nApplying H(SS)H gate on initial state\n")
output_state= hssh_gate*zero_state
print("Output is \n{}\n which is equal to |1>".format(output_state))
# + [markdown] tags=[]
# ### 6) **Y=SXS$^{\dagger}$**
# -
# <Left>Example</Left>
# <br>
# $$Y\ket{0} = i\ket{1}$$
#
# $$S(X(S'(\ket{+}))) = i\ket{1}$$
# <br>
# <Left>$ S^{\dagger}$ **Gate**</Left>
# <Left>Also known as the Sdg or S-dagger gate.</Left>
# <center><b>$ S^{\dagger}$ is Hermitian Conjugate (inverse) of S <b><center>
# <br>
# <center><b>$$As \,\, we \,\,know\, \, S^{\dagger} = u1(\pi/2)=P(-\pi/2)$$<b><center>
# <br>
# $$S^{\dagger} =\begin{bmatrix} 1 & 0 \\ 0 & -i \end{bmatrix}$$
# <br>
# <left>Step 1<left>
# <center><b>Applying Sdg gate on |0> where $\theta$ = $-\pi/2$</b></center>
# <br>
# $$Sdg\ket{0} = \begin{bmatrix} 1 & 0 \\ 0 & -i \end{bmatrix}\begin{bmatrix} 1 \\ 0\end{bmatrix}$$
# <br>
# $$Sdg\ket{0} = \begin{bmatrix}1 \\ 0\end{bmatrix} =\ket{0}= Intermediate\,State1$$
#
# +
#Step 1
q=QuantumRegister(1)
qc1=QuantumCircuit(q)
qc1.sdg(q) #qc1.p(-pi/2,0) or qc.u1(-pi/2, 0)
display(qc1.draw())
# executing the circuit
backend = Aer.get_backend('statevector_simulator')
b = BasicAer.get_backend('unitary_simulator')
job = execute(qc1, backend)
result = job.result()
s_gate_HermitianConjugate= b.run(transpile(qc1, b)).result().get_unitary(qc1, decimals=3)
s_gate_HermitianConjugate = np.matrix(s_gate_HermitianConjugate)
zero_state = np.matrix([[1.+0.j],[0.+0.j]])
print("Initial State is |0> i.e \n{}\n".format(zero_state))
print("S' Gate equals \n{}\n".format(s_gate_HermitianConjugate))
print("Applying S' gate on Intermediate_State2 \n")
intermediate_state1 = s_gate_HermitianConjugate*zero_state
print("intermediate State1 after applying S gate on intitial state \n{}\n which is |0>".format(intermediate_state1))
# -
# <left>Step 2<left>
# <center><b>Applying X gate on Intermediate_State1 </b></center>
# <br/>
# $$X\ket{0} = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\begin{bmatrix} 1 \\ 0\end{bmatrix}$$
# <br/>
# $$X\ket{0} = \begin{bmatrix} 0 \\1\end{bmatrix}=\ket{1}=Intermediate\,State2$$
# <br/>
#
#
#step 2
#creating a circuit having X gate so that qubit undergoes X gate operation when sent
qc2=QuantumCircuit(1)
qc2.x(0)
display(qc2.draw())
x_gate = b.run(transpile(qc2, b)).result().get_unitary(qc2, decimals=3)
x_gate = np.matrix(x_gate)
print("X Gate equals \n{}\n".format(x_gate))
print("Applying x gate on Intermediate_State1 \n")
Intermediate_State2=x_gate*intermediate_state1
print("Intermediate_State2 is \n{}\n which is |1> ".format(Intermediate_State2))
# <left>Step 3<left>
# <center><b>Applying S gate on Intermediate_State2 </b></center>
# <br/>
# $$S\ket{1} = \begin{bmatrix} 1 & 0 \\ 0 & i \end{bmatrix}\begin{bmatrix}0 \\ 1\end{bmatrix}$$
# <br/>
# $$S\ket{1} =\begin{bmatrix} 0 \\ i\end{bmatrix} $$
# <br/>
# $$S\ket{1} = i\ket{1}$$
# +
#step3
qc3 = QuantumCircuit(1)
qc3.s(0)
display(qc3.draw(output="mpl"))
s_hermitianConjugate_gate = b.run(transpile(qc3, b)).result().get_unitary(qc3, decimals=2)
s_hermitianConjugate_gate = np.matrix(s_hermitianConjugate_gate)
print(" S Gate \n{}\n".format(s_hermitianConjugate_gate))
output_state = s_gate*Intermediate_State2
print("Output State \n{}\n which is equal to i|1>".format(output_state ))
# -
#
# <center><b> Hence Y = SXS$^{\dagger}$</b></center>
# <br/>
#
# +
#summarised code
qc1 = QuantumCircuit(1)
qc1.p(-pi/2,0)
qc1.x(0)
qc1.s(0)
display(qc1.draw(output="mpl"))
# executing the circuit
backend = Aer.get_backend('statevector_simulator')
b = BasicAer.get_backend('unitary_simulator')
job = execute(qc1, backend)
result = job.result()
zero_state = np.matrix([[1+0.j],[0+0.j]])
print("Initial State is |0> i.e \n{}\n".format(zero_state))
sxs_gate = b.run(transpile(qc1, b)).result().get_unitary(qc1, decimals=3)
sxs_gate = np.matrix(sxs_gate)
print(" Sxs' Gate \n{}\n".format(sxs_gate))
output_state1 = sxs_gate*zero_state
print("output State after applying SXS' gate on intitial state \n{}\n which is i|1>".format(output_state1))
# -
|
3. Single Qubit Gates/d. Interesting Relations .ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Live Updating and Interactive Plots
#
# ## 1 Plotting Live data
#
# In our work, We are often required to plot Live data.
#
# * **psutil**: Cross-platform lib for process and system monitoring in Python
#
# https://github.com/giampaolo/psutil
#
# ```text
# python3 -m pip install psutil
# ```
# ### 1.1 Python Script
#
#
# * matplotlib.pyplot.ion()
#
# Turn the interactive mode on.
#
# https://matplotlib.org/api/_as_gen/matplotlib.pyplot.ion.html?highlight=ion
#
#
# * matplotlib.pyplot.clf()
#
# Clear the current figure.
#
# https://matplotlib.org/api/_as_gen/matplotlib.pyplot.clf.html
#
# +
# %%file ./code/python/cpu_monitor.py
import psutil
from time import sleep, strftime
import matplotlib.pyplot as plt
pltLength = 100
plt.ion()
x = [i for i in range(pltLength)]
y = [None for i in range(pltLength)]
i = 0
def write_cpu(cpu):
with open("cpu.csv", "a") as log:
log.write("{0},{1}\n".format(strftime("%Y-%m-%d %H:%M:%S"), str(cpu)))
def graph(cpu):
global i
if i < pltLength:
y[i] = cpu
i += 1
else:
# Once enough data is captured, append the newest data point and delete the oldest
y.append(cpu)
del y[0]
plt.clf()
plt.xlim(0, pltLength)
plt.plot(x, y, "b-o")
plt.draw()
plt.pause(0.1)
while True:
cpu = psutil.cpu_percent()
write_cpu(cpu)
graph(cpu)
sleep(1)
# -
# ### 1.2 Plotting Live data in Jupyter notebook
#
# #### 1.2.1 The Dynamically Plotting with IPython.display
#
# ```python
# from IPython.display import clear_output
# clear_output(wait=True)
# ```
# The problem: screen **flicker** in figure dynamic display
#
# +
# %matplotlib inline
import psutil
from time import sleep, strftime
import matplotlib.pyplot as plt
from IPython.display import clear_output
fig = plt.figure(figsize=(6,3))
plt.ion()
pltLength = 100
x = [i for i in range(pltLength)]
y = [None for i in range(pltLength)]
i = 0
def write_cpu(cpu):
with open("cpu.csv", "a") as log:
log.write("{0},{1}\n".format(strftime("%Y-%m-%d %H:%M:%S"), str(cpu)))
def graph(cpu):
global i
if i < pltLength:
y[i] = cpu
i += 1
else:
# Once enough data is captured, append the newest data point and delete the oldest
y.append(cpu)
del y[0]
plt.clf()
plt.ylim(0, 80)
plt.xlim(0, pltLength)
plt.plot(x, y, "b-o")
plt.draw()
clear_output(wait=True)
plt.pause(0.05)
while True:
cpu = psutil.cpu_percent()
write_cpu(cpu)
graph(cpu)
sleep(1)
# -
# #### 1.2.2 The Dynamically Plotting
#
# The Dynamically Plottingwith `%matplotlib notebook`
#
# Using `%matplotlib notebook` to avoid the problem of screen flicker in figure dynamic displaying.
#
# * `%matplotlib notebook` will lead to `interactive plots` embedded within the notebook
#
# * `%matplotlib inline` will lead to `static images of your plot` embedded in the notebook
#
# ##### 1.2.2.1 The direct way
# +
# %matplotlib notebook
import matplotlib.pyplot as plt
import numpy as np
from time import sleep, strftime
import psutil
fig = plt.figure(figsize=(7,3))
plt.ion()
fig.show()
fig.canvas.draw()
pltLength=20
x = [i for i in range(pltLength)]
y = [None for i in range(pltLength)]
i = 0
def write_cpu(cpu):
with open("cpu.csv", "a") as log:
log.write("{0},{1}\n".format(strftime("%Y-%m-%d %H:%M:%S"), str(cpu)))
def graph(cpu):
global i
if i < pltLength:
y[i] = cpu
i += 1
else:
# Once enough data is captured, append the newest data point and delete the oldest
y.append(cpu)
del y[0]
plt.clf()
plt.xlim(0, pltLength)
plt.plot(x, y, "b-o")
plt.show()
fig.canvas.draw() # draw
while True:
cpu = psutil.cpu_percent()
write_cpu(cpu)
graph(cpu)
sleep(1)
# -
# ##### 1.2.2.2 The Dynamically Plotting with matplotlib.animation
#
# * matplotlib.animation
#
# +
# %matplotlib notebook
import time
from collections import deque
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import psutil
def GetTagData(tag):
tagfuncs={"CPU_PERCENT": psutil.cpu_percent(),
"MEM_PERCENT": psutil.virtual_memory().percent,
"BAT_PERCENT": psutil.sensors_battery().percent}
try:
value= tagfuncs[tag]
rc=1
except:
rc,value=0,None
return (rc,value)
tag="CPU_PERCENT"
y = deque()
columns = ()
col_labels = ['Tag', 'Unit', 'Value']
table_vals = [[tag,"%",""]]
fig, ax = plt.subplots()
ax.set_title("The Simple Monitor:"+tag)
ln, = plt.plot([], [], 'b-o')
str_cursecond=str(time.localtime(time.time()).tm_sec)
time_text = ax.text(0.5, 80, "")
tbl = ax.table(cellText=table_vals,
colLabels=col_labels,
colWidths=[0.2] * 3,
cellLoc='center',
loc='best')
def init():
ax.set_xlim(0, 9)
ax.set_ylim(0, 100)
return ln,
def update(frames):
# blocking io -> unresponsive_monitor
rc,value =GetTagData(tag)
if len(y) < 10:
y.append(value)
else:
y.popleft()
y.append(value)
str_curtime=time.strftime("%F %H:%M:%S", time.localtime(time.time()))
time_text.set_text("Time:"+str_curtime)
table_vals = [[tag,"%",str(value)]]
tbl = ax.table(cellText=table_vals,
colLabels=col_labels,
colWidths=[0.2] *3,
cellLoc='center',
loc='best')
ln.set_xdata(np.arange(len(y)))
ln.set_ydata(np.array(y))
return ln,time_text, tbl
ani = FuncAnimation(fig, update,init_func=init, blit=True,interval=1000)
plt.show()
# -
# ## 2 pywidgets and interactive plots
#
# * ipywidgets
#
# Widgets are `eventful` python objects that have a representation in the browser, often as a control like a slider, textbox, etc.
#
# https://ipywidgets.readthedocs.io/en/stable/
#
# ```text
# python -m pip install ipywidgets
# jupyter nbextension enable --py widgetsnbextension
# ```
#
# ### 2.1 The Simple Example
#
#
# +
# %matplotlib notebook
from ipywidgets import *
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 2 * np.pi)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
line, = ax.plot(x, np.sin(x))
def update(w = 1.0):
line.set_ydata(np.sin(w * x))
fig.canvas.draw_idle()
interact(update)
# -
# ### 2.2 Proportional Integral Derivative (PID) Control
#
# https://en.wikipedia.org/wiki/PID_controller
#
# A proportional–integral–derivative controller (PID controller. or three-term controller) is a control loop feedback mechanism widely used in industrial control systems and a variety of other applications requiring continuously modulated control. A PID controller continuously calculates an error value {\displaystyle e(t)} e(t) as the difference between a desired setpoint (SP) and a measured process variable (PV) and applies a correction based on proportional, integral, and derivative terms (denoted P, I, and D respectively), hence the name.
#
# 
#
# * https://apmonitor.com/pdc/index.php/Main/ProportionalIntegralDerivative
# +
# %matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
import ipywidgets as wg
from IPython.display import display
n = 100 # time points to plot
tf = 20.0 # final time
SP_start = 2.0 # time of set point change
def process(y,t,u):
Kp = 4.0
taup = 3.0
thetap = 1.0
if t<(thetap+SP_start):
dydt = 0.0 # time delay
else:
dydt = (1.0/taup) * (-y + Kp * u)
return dydt
def pidPlot(Kc,tauI,tauD):
t = np.linspace(0,tf,n) # create time vector
P= np.zeros(n) # initialize proportional term
I = np.zeros(n) # initialize integral term
D = np.zeros(n) # initialize derivative term
e = np.zeros(n) # initialize error
OP = np.zeros(n) # initialize controller output
PV = np.zeros(n) # initialize process variable
SP = np.zeros(n) # initialize setpoint
SP_step = int(SP_start/(tf/(n-1))+1) # setpoint start
SP[0:SP_step] = 0.0 # define setpoint
SP[SP_step:n] = 4.0 # step up
y0 = 0.0 # initial condition
# loop through all time steps
for i in range(1,n):
# simulate process for one time step
ts = [t[i-1],t[i]] # time interval
y = odeint(process,y0,ts,args=(OP[i-1],)) # compute next step
y0 = y[1] # record new initial condition
# calculate new OP with PID
PV[i] = y[1] # record PV
e[i] = SP[i] - PV[i] # calculate error = SP - PV
dt = t[i] - t[i-1] # calculate time step
P[i] = Kc * e[i] # calculate proportional term
I[i] = I[i-1] + (Kc/tauI) * e[i] * dt # calculate integral term
D[i] = -Kc * tauD * (PV[i]-PV[i-1])/dt # calculate derivative term
OP[i] = P[i] + I[i] + D[i] # calculate new controller output
# plot PID response
plt.figure(1,figsize=(15,7))
plt.subplot(2,2,1)
plt.plot(t,SP,'k-',linewidth=2,label='Setpoint (SP)')
plt.plot(t,PV,'r:',linewidth=2,label='Process Variable (PV)')
plt.legend(loc='best')
plt.subplot(2,2,2)
plt.plot(t,P,'g.-',linewidth=2,label=r'Proportional = $K_c \; e(t)$')
plt.plot(t,I,'b-',linewidth=2,label=r'Integral = $\frac{K_c}{\tau_I} \int_{i=0}^{n_t} e(t) \; dt $')
plt.plot(t,D,'r--',linewidth=2,label=r'Derivative = $-K_c \tau_D \frac{d(PV)}{dt}$')
plt.legend(loc='best')
plt.subplot(2,2,3)
plt.plot(t,e,'m--',linewidth=2,label='Error (e=SP-PV)')
plt.legend(loc='best')
plt.subplot(2,2,4)
plt.plot(t,OP,'b--',linewidth=2,label='Controller Output (OP)')
plt.legend(loc='best')
plt.xlabel('time')
Kc_slide = wg.FloatSlider(value=0.1,min=-0.2,max=1.0,step=0.05)
tauI_slide = wg.FloatSlider(value=4.0,min=0.01,max=5.0,step=0.1)
tauD_slide = wg.FloatSlider(value=0.0,min=0.0,max=1.0,step=0.1)
wg.interact(pidPlot, Kc=Kc_slide, tauI=tauI_slide, tauD=tauD_slide)
# -
|
notebook/Unit2-7-Live_Interact_Plot.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.5.3
# language: julia
# name: julia-1.5
# ---
using JuMP, DelimitedFiles, Cbc, Plots
pyplot()
# +
## read in the file
dat = readdlm("../OtherData/country_lag_auc_profile.csv", ',', '\n', skipstart=1) ##@WARNING: Code implicity assumes ordered by country
#for now, drop any country that has blanks
filt = dat[:, 4] .!= ""
dat = dat[filt, :]
filt = dat[:, 4] .> .5
dat = dat[filt, :]
countries = unique(dat[:, 2])
lags_filt = unique(dat[:, 3]);
# -
out = zeros(length(countries))
for ix = 1:length(countries)
filt = dat[:, 2] .== countries[ix]
out[ix] = maximum(dat[filt, 4])
end
minimum(out)
function computeTypes( numTypes )
m = Model( Cbc.Optimizer )
set_optimizer_attribute(m, "logLevel", 0)
@variable(m, z[1:size(dat, 1)], Bin)
@variable(m, isLagUsed[lags_filt], Bin)
for ix = 1:size(dat, 1)
@constraint(m, isLagUsed[dat[ix, 3]] >= z[ix] ) #if country uses lag, must count as a new type
end
@constraint(m, sum(isLagUsed) <= numTypes)
#every coutnry must be assigned a lag
for icountry in countries
filt = dat[:, 2] .== icountry
@constraint(m, sum(z[filt]) == 1) #every country must be assigned
end
@objective(m, Max, sum( z[i] * dat[i, 4] for i = 1:size(dat, 1)));
optimize!(m)
status = termination_status(m)
if result_count(m) > 0 ##Hacky way to check if infeasible.
return (status, getobjectivevalue(m), value.(z))
end
return (status, Inf, zeros(size(dat, 1)))
end
num_grid = 1:10
out = zeros(10)
for i = num_grid
(status, val, sol) = computeTypes(i)
out[i] = val
end
out
#Identify Elbow by hand and resolve once more.
plot(out, marker = :circ)
status, val, sol = computeTypes(3)
# +
res = dat[sol .== 1, :]
writecsv("../LagAnalysisOutputs/auc_clustering.csv", res)
writecsv("../LagAnalysisOutputs/elbow_curve_clustering.csv", out)
|
src/ClusteringLags.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # **Titanic competition**
# ## 1. Importing packages
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
sns.set(style="whitegrid", color_codes=True)
# %matplotlib inline
# ## 2. Reading data from csv file
df = pd.read_csv('train.csv', index_col='PassengerId')
df.head()
# ## 3. Checking data for missing values, distributions and use descriptive statistics
# ### 3.1. Shape of Data Frame
print('Shape of Data Frame is {}x{}'.format(*df.shape))
# ### 3.2. Check missing values
df.info()
# + **we can see that our data have missing values (_Age, Cabin, Embarked_)**
#
# **Okey, let's plot heatmap to visualize missing values**
sns.heatmap(df.isnull(), cbar=False).set_title("Missing values heatmap");
# **"Canin" and "Age" have many missing values**
# ### 3.3. Descriptive statistics
df.describe(include='all')
# ### 3.4. Pair plot
sns.pairplot(df, hue='Survived', diag_kind='auto');
# ### 3.5. Box plots
# +
f, axes = plt.subplots(1, 2, figsize=(16,8));
sns.boxplot(y='Age', x='Pclass', data=df, ax=axes[0]);
sns.boxplot(y='Age', x='Pclass', hue='Survived', data=df, ax=axes[1]);
# +
f, axes = plt.subplots(1, 1, figsize=(8,8));
sns.boxplot(y='Fare', x='Survived', hue='Survived', data=df[df['Fare'] < 150], ax=axes);
# +
f, axes = plt.subplots(1, 2, figsize=(16,8))
sns.boxplot(y='Fare', x='Embarked', data=df[df['Fare'] < 200], ax=axes[0], palette="husl")
sns.boxplot(y='Fare', x='Embarked', hue='Survived', data=df[df['Fare'] < 200], ax=axes[1], palette="husl")
# -
# ### 3.6. Count plots
pd.crosstab(df['Embarked'], df['Survived'])
sns.countplot(x='Embarked', hue='Survived', data=df);
pd.crosstab(df['Embarked'].where((df['Pclass'] == 1)), df['Survived'].where((df['Pclass'] == 1)))
sns.countplot(x='Embarked', hue='Survived', data=df.where((df['Pclass'] == 1) & (df['Sex'] == 'female')));
sns.countplot(x='Embarked', hue='Survived',
data=df.where((df['Pclass'] == 1) &
(df['Sex'] == 'female') &
(df['Cabin'].dropna().apply(lambda x: x[0]).astype(str) == 'B')));
df['Embarked'].value_counts()
df.loc[df['Survived'] == 1, 'Embarked'].value_counts()
# ### 3.7 Correlation matrix
corr = df.corr()
sns.heatmap(corr);
# ## 4. Feature engineering and filling missing values
from sklearn.preprocessing import StandardScaler
df[df['Embarked'].isna()]
def preproces_name(df):
title_dict = {'Capt': 'Officer',
'Col': 'Officer',
'Major': 'Officer',
'Jonkheer': 'Royalty',
'Don': 'Royalty',
'Sir': 'Royalty',
'Dr': 'Officer',
'Rev': 'Officer',
'the Countess': 'Royalty',
'Mme': 'Mrs',
'Mlle': 'Miss',
'Ms': 'Miss',
'Mr': 'Mr',
'Mrs': 'Mrs',
'Miss': 'Miss',
'Master': 'Master',
'Lady': 'Royalty'
}
df['Title'] = df['Name'].map(lambda x: x.split(',')[1].split('.')[0].strip())
df['Title'] = df['Title'].map(title_dict)
return df
def preproces_fm_size(df):
df['FamilySize'] = df['SibSp'] + df['Parch'] + 1
df['travelled_alone'] = 0
df.loc[df['FamilySize'] == 1, 'travelled_alone'] = 1
return df
def preproces_pclass(df):
df['Pclass'] = df['Pclass'].astype(str)
df.loc[ df['Pclass'] == '1', 'Pclass'] = "Class1"
df.loc[ df['Pclass'] == '2', 'Pclass'] = "Class2"
df.loc[ df['Pclass'] == '3', 'Pclass'] = "Class3"
return df
# +
# le_embarked = LabelEncoder()
# le_sex = LabelEncoder()
# le_title = LabelEncoder()
# le_fm = LabelEncoder()
# def preproces_cat_features_fit_transform(df):
# # df['Embarked'] = le_embarked.fit_transform(df['Embarked'])
# # df['Sex'] = le_sex.fit_transform(df['Sex'])
# # df['Title'] = le_title.fit_transform(df['Title'])
# # df['FamilySize'] = le_fm.fit_transform(df['FamilySize'])
# encode_col_list = list(df.select_dtypes(include=['object']).columns)
# for i in encode_col_list:
# df = pd.concat([df,pd.get_dummies(df[i], prefix=i)],axis=1)
# df.drop(i, axis = 1, inplace=True)
# return df
def preproces_cat_features(df):
# df['Embarked'] = le_embarked.transform(df['Embarked'])
# df['Sex'] = le_sex.transform(df['Sex'])
# df['Title'] = le_title.transform(df['Title'])
# df['FamilySize'] = le_fm.transform(df['FamilySize'])
encode_col_list = list(df.select_dtypes(include=['object']).columns)
for i in encode_col_list:
df = pd.concat([df,pd.get_dummies(df[i], prefix=i)],axis=1)
df.drop(i, axis = 1, inplace=True)
return df
# +
def fill_age(df, row):
grouped_train = df.groupby(['Sex', 'Pclass', 'Title'])
grouped_median_train = grouped_train.median()
grouped_median_train = grouped_median_train.reset_index()[['Sex', 'Pclass', 'Title', 'Age']]
condition = (
(grouped_median_train['Sex'] == row['Sex']) &
(grouped_median_train['Title'] == row['Title']) &
(grouped_median_train['Pclass'] == row['Pclass'])
)
if np.isnan(grouped_median_train[condition]['Age'].values[0]):
condition = (
(grouped_median_train['Sex'] == row['Sex']) &
(grouped_median_train['Pclass'] == row['Pclass'])
)
return grouped_median_train[condition]['Age'].values[0]
def preproces_age(df):
df['Age'] = df.apply(lambda row: fill_age(df, row) if np.isnan(row['Age']) else row['Age'], axis=1)
df = preproces_Age_Class(df)
df['Age'] = df['Age'].astype(int)
df.loc[ df['Age'] <= 11, 'Age'] = 0
df.loc[(df['Age'] > 11) & (df['Age'] <= 18), 'Age'] = 1
df.loc[(df['Age'] > 18) & (df['Age'] <= 22), 'Age'] = 2
df.loc[(df['Age'] > 22) & (df['Age'] <= 27), 'Age'] = 3
df.loc[(df['Age'] > 27) & (df['Age'] <= 33), 'Age'] = 4
df.loc[(df['Age'] > 33) & (df['Age'] <= 40), 'Age'] = 5
df.loc[df['Age'] > 40, 'Age'] = 6
df['Age'] = df['Age'].astype(str)
df.loc[ df['Age'] == '0', 'Age'] = "Children"
df.loc[ df['Age'] == '1', 'Age'] = "Teens"
df.loc[ df['Age'] == '2', 'Age'] = "Youngsters"
df.loc[ df['Age'] == '3', 'Age'] = "Young Adults"
df.loc[ df['Age'] == '4', 'Age'] = "Adults"
df.loc[ df['Age'] == '5', 'Age'] = "Middle Age"
df.loc[ df['Age'] == '6', 'Age'] = "Senior"
return df
# -
def preproces_fare(df):
for pclass in range(1, 4):
print(pclass)
median = df['Fare'].where((df['Pclass'] == pclass)).median()
df['Fare'].where((df['Pclass'] == pclass)).fillna(median, inplace=True)
df['Fare'].fillna(df['Fare'].median(), inplace=True)
df = preproces_fare_per_person(df)
df.loc[ df['Fare'] <= 7.91, 'Fare'] = 0
df.loc[(df['Fare'] > 7.91) & (df['Fare'] <= 14.454), 'Fare'] = 1
df.loc[(df['Fare'] > 14.454) & (df['Fare'] <= 31), 'Fare'] = 2
df.loc[(df['Fare'] > 31) & (df['Fare'] <= 99), 'Fare'] = 3
df.loc[(df['Fare'] > 99) & (df['Fare'] <= 250), 'Fare'] = 4
df.loc[(df['Fare'] > 250), 'Fare'] = 5
df['Fare'] = df['Fare'].astype(int)
df['Fare'] = df['Fare'].astype(str)
df.loc[ df['Fare'] == '0', 'Fare'] = "Extremely Low"
df.loc[ df['Fare'] == '1', 'Fare'] = "Very Low"
df.loc[ df['Fare'] == '2', 'Fare'] = "Low"
df.loc[ df['Fare'] == '3', 'Fare'] = "High"
df.loc[ df['Fare'] == '4', 'Fare'] = "Very High"
df.loc[ df['Fare'] == '5', 'Fare'] = "Extremely High"
return df
def preproces_cabin(df):
df['Cabin'] = df['Cabin'].fillna('Other')
df['Cabin'] = df['Cabin'].map(lambda x: x[0])
return df
def preproces_Age_Class(df):
df['Age_Class']= df['Age'] * df['Pclass']
return df
def preproces_fare_per_person(df):
df['Fare_Per_Person'] = df['Fare'] / (df['FamilySize'])
df['Fare_Per_Person'] = df['Fare_Per_Person'].astype(int)
return df
# +
# def preprocese_cabin_count(df):
# df['Cabin_count'] =
# +
# preproces_cabin(df)
# +
# df['Cabin'].value_counts()
# -
scaler = StandardScaler()
def preproces_features(df, train=True):
global scaler
df = preproces_name(df)
df = preproces_fm_size(df)
df = df.drop('Cabin', axis=1)
# df = preproces_cabin(df)
df['Embarked'] = df['Embarked'].fillna('S')
# df['Duplicate_ticket'] =
df = preproces_fare(df)
df['Sex'] = df['Sex'].map({'male': 1, 'female': 0}).astype(int)
if train:
df = df.drop(['Ticket', 'Survived', 'Name'], axis=1)
df = preproces_age(df)
df = preproces_pclass(df)
# df = preproces_cat_features(df) #_fit_transform(df)
# df = preproces_age_clf(df)
# df['Pclass', 'Age', 'SibSp', 'Parch', 'Fare']
df[['SibSp', 'Parch', 'FamilySize', 'Fare_Per_Person', 'Age_Class']] = scaler.fit_transform(df[['SibSp', 'Parch', 'FamilySize','Fare_Per_Person', 'Age_Class']])
else:
df = df.drop(['Ticket', 'Name'], axis=1)
df = preproces_age(df)
df = preproces_pclass(df)
# df = preproces_cat_features(df)
df[['SibSp', 'Parch', 'FamilySize', 'Fare_Per_Person', 'Age_Class']] = scaler.transform(df[['SibSp','Parch', 'FamilySize','Fare_Per_Person', 'Age_Class']])
return df
y = df['Survived']
train_df = preproces_features(df.copy())
train_df.info()
cat_features = np.where((train_df[train_df.columns].dtypes != np.float64))[0]
cat_features
cat_features = train_df.columns[cat_features]
df.head()
train_df.head()
title_column = list(set([x if ('Fare' in x) else '' for x in train_df.columns]))
title_column.remove('')
title_column.remove('Fare_Per_Person')
train_df[title_column].mean() * len(train_df)
# ## 5. PCA, TSNE, MDS and correlation matrix
# +
from sklearn.decomposition import PCA
model_pca = PCA(n_components=2)
X_pca = model_pca.fit_transform(train_df)
sns.scatterplot(X_pca[:, 0], X_pca[:, 1], hue=y_train)
# +
from mpl_toolkits.mplot3d import Axes3D
model_pca = PCA(n_components=3)
X_pca = model_pca.fit_transform(train_df)
X1 = []
X0 = []
for i, yy in enumerate(y_train):
if yy == 1:
X1.append(list(X_pca[i]))
else:
X0.append(list(X_pca[i]))
X0 = np.array(X0)
X1 = np.array(X1)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X0[:, 0], X0[:, 1], X0[:, 2], c='red', s=20)
ax.scatter(X1[:, 0], X1[:, 1], X1[:, 2], c='green', s=20)
ax.view_init(30, 185)
plt.show()
# +
from sklearn.manifold import TSNE
model_tsne = TSNE(n_components=2)
X_tsne = model_tsne.fit_transform(train_df)
sns.scatterplot(X_tsne[:, 0], X_tsne[:, 1], hue=y_train)
# +
from mpl_toolkits.mplot3d import Axes3D
model_tsne = TSNE(n_components=3)
X_tsne = model_tsne.fit_transform(train_df)
X1 = []
X0 = []
for i, yy in enumerate(y_train):
if yy == 1:
X1.append(list(X_tsne[i]))
else:
X0.append(list(X_tsne[i]))
X0 = np.array(X0)
X1 = np.array(X1)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X0[:, 0], X0[:, 1], X0[:, 2], c='red', s=10)
ax.scatter(X1[:, 0], X1[:, 1], X1[:, 2], c='green', s=10)
ax.view_init(30, 185)
plt.show()
# +
from sklearn.manifold import MDS
model_mds = MDS(n_components=2)
X_mds = model_mds.fit_transform(train_df)
sns.scatterplot(X_mds[:, 0], X_mds[:, 1], hue=y_train)
# +
from mpl_toolkits.mplot3d import Axes3D
model_mds = MDS(n_components=3)
X_mds = model_mds.fit_transform(train_df)
X1 = []
X0 = []
for i, yy in enumerate(y_train):
if yy == 1:
X1.append(list(X_mds[i]))
else:
X0.append(list(X_mds[i]))
X0 = np.array(X0)
X1 = np.array(X1)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X0[:, 0], X0[:, 1], X0[:, 2], c='red', s=20)
ax.scatter(X1[:, 0], X1[:, 1], X1[:, 2], c='green', s=20)
ax.view_init(30, 185)
plt.show()
# -
# ## 6. Prediction model
from sklearn.model_selection import cross_val_score, StratifiedKFold, train_test_split, GridSearchCV
from sklearn.metrics import classification_report
X_train, X_test, y_train, y_test = train_test_split(train_df, y, shuffle=True, random_state=17, test_size=0.2)
kf = StratifiedKFold(n_splits=3, shuffle=True, random_state=17)
from xgboost.sklearn import XGBClassifier
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from catboost import CatBoostClassifier
# +
best_xgb_clf = None
def xgb_clf(train_df=None, y_train=None, test_df=None, cv=5):
global best_xgb_clf
scoring = 'accuracy'
params = {
'n_estimators': [500, 1000],
'max_depth': [6 , 7, 8, 9],
'learning_rate': [0.01, 0.05, 0.001],
'reg_alpha': np.linspace(1, 2, 4),
'reg_lambda': np.linspace(4, 5, 4)
}
xgb_model = XGBClassifier(objective='binary:logistic', nthreads=2)
grid = GridSearchCV(xgb_model, param_grid=params, n_jobs=-1, verbose=1, scoring=scoring, cv=cv)
grid.fit(train_df, y_train)
best_xgb_clf = grid.best_estimator_
print(grid.best_params_, grid.best_score_)
prediction = best_xgb_clf.predict(test_df)
return prediction
# -
best_svc = None
def svm_clf(train_df=None, y_train=None, test_df=None, cv=5):
global best_svc
scoring = 'accuracy'
params = {
#'C': [0.1, 0.5, 1, 5, 0.55, 0.45],
'C': np.linspace(0.5, 2, 100),
'kernel': ['linear', 'poly', 'rbf', 'sigmoid'],
'gamma': [*np.logspace(-9, 3, 5), 'scale'],
'tol': [0.001, 0.01, 0.0001],
# 'class_weight':['balanced'],
'decision_function_shape' : ['ovo', 'ovr'],
'tol': [0.001],
# 'gamma': ['scale'],
'kernel': ['rbf'],
'random_state': [0],
#'C': [0.1653061224489796],
'decision_function_shape' : ['ovo']
}
svc_model = SVC()
grid = GridSearchCV(svc_model, param_grid=params, n_jobs=-1, verbose=1, scoring=scoring, cv=cv)
grid.fit(train_df, y_train)
best_svc = grid.best_estimator_
print(grid.best_params_, grid.best_score_)
prediction = best_svc.predict(test_df)
return prediction
log_reg = None
def log_reg_clf(train_df=None, y_train=None, test_df=None, cv=5):
global log_reg
scoring = 'accuracy'
params = {
#'C': [0.1, 0.5, 1, 5, 0.55, 0.45, 0.9],
'C': np.linspace(0.1, 2, 50),
# 'penalty': ['l1', 'l2'],
'penalty': ['l2'],
'tol': [0.001],
'max_iter': [100, 1000],
#'random_state': [0],
#'C': [0.94081632653061231],
'solver': ['newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga']
}
log_reg = LogisticRegression()
grid = GridSearchCV(log_reg, param_grid=params, n_jobs=-1, verbose=1, scoring=scoring, cv=cv)
grid.fit(train_df, y_train)
log_reg = grid.best_estimator_
print(grid.best_params_, grid.best_score_)
prediction = log_reg.predict(test_df)
return prediction
best_rf = None
def rf_clf(train_df=None, y_train=None, test_df=None, cv=5):
global best_rf
scoring = 'accuracy'
params = {
'n_estimators': [200, 500],
'max_features': ['auto', 'sqrt', 'log2'],
'max_depth' : [4, 5, 6, 7, 8],
'criterion' :['gini', 'entropy']
}
best_rf = RandomForestClassifier(random_state=42)
grid = GridSearchCV(best_rf, param_grid=params, n_jobs=-1, verbose=1, scoring=scoring, cv=cv)
grid.fit(train_df, y_train)
best_rf = grid.best_estimator_
print(grid.best_params_, grid.best_score_)
prediction = best_rf.predict(test_df)
return prediction
best_gb = None
def gb_clf(train_df=None, y_train=None, test_df=None, cv=5):
global best_rf
scoring = 'accuracy'
params = {
"learning_rate": [0.01, 0.05, 0.001],
"min_samples_split": np.linspace(0.1, 0.5, 5),
"min_samples_leaf": np.linspace(0.1, 0.5, 5),
"max_depth":[3,5,8],
"max_features":["log2","sqrt"],
"criterion": ["friedman_mse", "mae"],
"subsample":np.linspace(0.5, 1, 5),
"n_estimators":[10]
}
best_gb = GradientBoostingClassifier(random_state=42)
grid = GridSearchCV(best_gb, param_grid=params, n_jobs=-1, verbose=1, scoring=scoring, cv=cv)
grid.fit(train_df, y_train)
best_gb = grid.best_estimator_
print(grid.best_params_, grid.best_score_)
prediction = best_gb.predict(test_df)
return prediction
best_cat = None
def cat_clf(train_df=None, y_train=None, test_df=None, cv=5):
global best_cat
scoring = 'accuracy'
params = {
'iterations': [500],
'depth': [4, 5, 8],
# 'learning_rate' : [4, 5, 6, 7, 8],
'loss_function': ['Logloss', 'CrossEntropy'],
'l2_leaf_reg': np.logspace(-20, -19, 3),
}
best_cat = CatBoostClassifier()
grid = GridSearchCV(best_cat, param_grid=params, verbose=1, cv=cv)
grid.fit(train_df, y_train, cat_features=cat_features, verbose=False)
best_cat = grid.best_estimator_
print(grid.best_params_, grid.best_score_)
prediction = best_cat.predict(test_df)
return prediction
model = CatBoostClassifier(iterations=500,
depth=2,
learning_rate=1,
loss_function='Logloss',
verbose=False)
model.fit(X_train, y_train, cat_features=cat_features)
#
test_df = pd.read_csv('test.csv', index_col='PassengerId')
test_df.info()
test = preproces_features(test_df.copy(), train=False)
test.info()
test[test['Title'].isna()]
test['Title'].fillna('na', inplace=True)
test['Title_Royalty'] = 0
# test['Cabin_T'] = 0
test = test[train_df.columns]
test.head()
pred_rf = rf_clf(test_df=X_test, train_df=train_df, y_train=y, cv=kf)
pred_gb = gb_clf(test_df=X_test, train_df=train_df, y_train=y, cv=kf)
pred_xgb = xgb_clf(test_df=X_test, train_df=train_df, y_train=y, cv=kf)
pred_svm = svm_clf(test_df=X_test, train_df=train_df, y_train=y, cv=kf)
pred_log = log_reg_clf(test_df=X_test, train_df=train_df, y_train=y, cv=kf)
pred_cat = cat_clf(test_df=X_test, train_df=train_df, y_train=y, cv=kf)
# +
# best_xgb_clf.get_params()
# best_svc.get_params()
# log_reg.get_params()
# -
gender_subm = pd.read_csv('gender_submission.csv')
gender_subm.head()
from sklearn.metrics import classification_report
print(classification_report(y_test, pred_rf))
print(cross_val_score(best_rf, X_test, y=y_test, cv=10).mean())
print(classification_report(y_test, pred_gb))
print(cross_val_score(best_gb, X_test, y=y_test, cv=10).mean())
print(classification_report(y_test, pred_log))
print(cross_val_score(log_reg, X_test, y=y_test, cv=10).mean())
print(classification_report(y_test, pred_svm))
print(cross_val_score(best_svc, X_test, y=y_test, cv=10).mean())
print(classification_report(y_test, pred_xgb))
print(cross_val_score(best_xgb_clf, X_test, y=y_test, cv=10).mean())
print(classification_report(y_test, pred_cat))
print(cross_val_score(best_cat, X_test, y=y_test, cv=10).mean())
# ## 7. Get prediction for test
pred_svc = best_svc.predict(test)
pred_rf = best_rf.predict(test)
pred_xgb = best_xgb_clf.predict(test)
pred_log = log_reg.predict(test)
test.info()
pred_cat = best_cat.predict(test).astype(int)
# +
gender_subm['Survived'] = pred_svc
gender_subm.to_csv('my_subm_svc.csv', index=False)
gender_subm['Survived'] = pred_rf
gender_subm.to_csv('my_subm_rf.csv', index=False)
gender_subm['Survived'] = pred_xgb
gender_subm.to_csv('my_subm_xgb.csv', index=False)
gender_subm['Survived'] = pred_log
gender_subm.to_csv('my_subm_log.csv', index=False)
# -
gender_subm['Survived'] = pred_cat
gender_subm.to_csv('my_subm_cat.csv', index=False)
|
kaggle/Titanic/titanic.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "skip"}
# (empty cell to avoid selection on first slide)
# + [markdown] slideshow={"slide_type": "slide"}
# # How to make code beautiful
# ### Python beyond basics
#
# <br><br><br><br><br><br>
# <div style="font-size:0.8em; color: #555">2019-04-03 Session 2
# <span style="float:right"><NAME></span>
# </div>
# + [markdown] slideshow={"slide_type": "subslide"}
# # How to make code beautiful
#
# **Disclaimers:**
# + [markdown] slideshow={"slide_type": "fragment"}
# - based on experience, not the full truth
# + [markdown] slideshow={"slide_type": "fragment"}
# - Python 3! forget Python 2 (except some exotic libraries)
# + [markdown] slideshow={"slide_type": "fragment"}
# - no Windows questions please, Linux only ;)
# + [markdown] slideshow={"slide_type": "subslide"}
# # How to make code beautiful
# -
# **Goals:**
#
# - a bit of general blabla about programming
# - point at specific features and gotchas of Python
# - some important tips, tricks and tools
# + [markdown] slideshow={"slide_type": "slide"}
# # Questions?
# -----------
# + [markdown] slideshow={"slide_type": "slide"}
# # What is Beautiful Code?
# + [markdown] slideshow={"slide_type": "fragment"}
# <img src="images/beauty-google-search1.png" style="width:800px">
#
# + [markdown] slideshow={"slide_type": "slide"}
# # What is Beautiful Code?
# + [markdown] slideshow={"slide_type": "-"}
# <img src="images/beauty-google-search2.png" style="width:800px">
# + [markdown] slideshow={"slide_type": "notes"}
# BTW Google's AI puts "nature" as first keyword, but the third "makeup" seems to be more relevant for selecting the pictures shown by default.
# + [markdown] slideshow={"slide_type": "subslide"}
# # What is Beautiful Code?
# + [markdown] slideshow={"slide_type": "fragment"}
# > **Beauty** is a [...] characteristic of [...] idea [...], that provides a perceptual experience of
# > **pleasure** or **satisfaction**.
# + [markdown] slideshow={"slide_type": "fragment"}
# > [...]
#
# > An "ideal beauty" is an entity which is [...] possesses **features** widely attributed to beauty **in a particular culture**, for perfection.
#
# -
# <small>Source: https://en.wikipedia.org/wiki/Beauty</small>
# + [markdown] slideshow={"slide_type": "subslide"}
# # What is Beautiful Code?
# + slideshow={"slide_type": "fragment"} tags=["clear"]
import this
# + slideshow={"slide_type": "skip"}
import sys
if 'this' in sys.modules:
del sys.modules['this']
# + [markdown] slideshow={"slide_type": "subslide"}
# # What is Beautiful Code?
# + slideshow={"slide_type": "fragment"}
import antigravity
# + slideshow={"slide_type": "skip"}
import sys
if 'this' in sys.modules:
del sys.modules['antigravity']
# + [markdown] slideshow={"slide_type": "subslide"}
# # What is Beautiful Code?
#
# <br>
# In the Python universe:
#
# <br>
#
# <div style="font-weight:bolder;font-size:2em; text-align:center;">
# beauty = simplicity
# </div>
#
# <br>
#
# in terms of clarity, easy to comprehend, easy to write, not complicated
# + [markdown] slideshow={"slide_type": "slide"}
# # What is Code?
#
# 
#
# We want to control the computer. Code is a tool to achieve this.
# + [markdown] slideshow={"slide_type": "subslide"}
# # What is Code?
#
# 
# + [markdown] slideshow={"slide_type": "subslide"}
# # What is Code?
#
# 
# + [markdown] slideshow={"slide_type": "subslide"}
# # What is Code?
#
# 
# + [markdown] slideshow={"slide_type": "subslide"}
# # What is Code?
#
# 
# + [markdown] slideshow={"slide_type": "subslide"}
# # What is Code?
#
# 
# + [markdown] slideshow={"slide_type": "subslide"}
# # Why to write Beautiful Code?
#
# 
# + [markdown] slideshow={"slide_type": "slide"}
# # Why to write Beautiful Code?
# + [markdown] slideshow={"slide_type": "fragment"}
# > "πάντα χωρεῖ καὶ οὐδὲν μένει" καὶ "δὶς ἐς τὸν αὐτὸν ποταμὸν οὐκ ἂν ἐμβαίης"
#
# <div style="float:right">Heraclitus of Ephesus, ~500 BC</div>
# + [markdown] slideshow={"slide_type": "fragment"}
# This roughly translates to:
#
# > You cannot talk to your past self about code he or she wrote.
# + [markdown] slideshow={"slide_type": "slide"}
# # How to write Beautiful Code? Naming!
#
# Do you know what this is doing?
# + slideshow={"slide_type": "skip"}
def ts(*args, **kwargs):
pass
def twitter_search(pattern, *, numtweets, retweets, unicode):
print("Way better! Great! 👍")
# -
twitter_search('obama', numtweets=0, retweets=False, unicode=True)
# + slideshow={"slide_type": "fragment"}
twitter_search('obama', numtweets=20, retweets=False, unicode=True)
# + [markdown] slideshow={"slide_type": "fragment"}
# <small>Source: [Beyond PEP 8 - Best practices for beautiful intelligible code - PyCon 2015](https://www.youtube.com/watch?v=wf-BqAjZb8M) by <NAME> / [@raymondh](https://twitter.com/raymondh)</small>
# + [markdown] slideshow={"slide_type": "subslide"}
# # How to write Beautiful Code? Naming!
#
# Part 2.
# + slideshow={"slide_type": "skip"}
import numpy as np
# + slideshow={"slide_type": "fragment"}
with open('data-samples/turbine_models.csv', 'r') as f:
turbine_models = f.read().splitlines()
# + slideshow={"slide_type": "fragment"}
model_names = np.unique(turbine_models)
# + slideshow={"slide_type": "fragment"}
model_names
# + [markdown] slideshow={"slide_type": "subslide"}
# # How to write Beautiful Code? Naming!
#
# Part 2.
# + slideshow={"slide_type": "skip"}
import pandas as pd
np.random.seed(42)
# + slideshow={"slide_type": ""}
turbine_unique_result = np.unique(turbine_models, return_inverse=True, return_counts=True)
# + slideshow={"slide_type": "fragment"}
pd.DataFrame({
'turbine_models': turbine_models,
'counts': turbine_unique_result[2][turbine_unique_result[1]]
}).sample(10)
# + [markdown] slideshow={"slide_type": "subslide"}
# # How to write Beautiful Code? Naming!
#
# Part 2, but a bit nicer.
# + slideshow={"slide_type": "skip"}
np.random.seed(42)
# + slideshow={"slide_type": "-"}
model_names, inverse_idcs, counts = np.unique(turbine_models, return_inverse=True, return_counts=True)
# + slideshow={"slide_type": "-"}
pd.DataFrame({
'turbine_models': turbine_models,
'counts': counts[inverse_idcs]
}).sample(10)
# + [markdown] slideshow={"slide_type": "subslide"}
# # How to write Beautiful Code? Named containers!
#
# What if one wants to keep the elements of a tuple bound together?
# + [markdown] slideshow={"slide_type": "fragment"}
# Containers!
# - dictionary: no schema, can be dynamically changed (this is mostly a disadvantage)
# - [namedtuple](https://docs.python.org/3/library/collections.html#collections.namedtuple): like dict, but syntax `foo.parameter` instead of `foo['parameter']` and fixed schema
# - [dataclass](https://docs.python.org/3/library/dataclasses.html) for Python >= 3.7
# - [attrs](https://www.attrs.org/en/stable/): like dataclasses (not part of core Python, but also for < 3.7)
# - write your own class
# + [markdown] slideshow={"slide_type": "subslide"}
# # How to write Beautiful Code? Naming!
#
# Don't try this at home!
# + slideshow={"slide_type": "skip"}
class Shrug:
def __repr__(self):
return '¯\_(ツ)_/¯'
ಠ_ಠ = Shrug()
class Yolo:
def __repr__(self):
return '( ͡° ͜ʖ ͡°)'
YᵒᵘOᶰˡʸLᶤᵛᵉOᶰᶜᵉ = Yolo()
# Emoticons:
# http://asciimoji.com/
# http://upli.st/l/list-of-all-ascii-emoticons
#
# Find look-a-like unicode chars:
# http://www.unicode.org/Public/security/latest/confusables.txt
# https://unicode-search.net/unicode-namesearch.pl?term=BACKSLASH
# + slideshow={"slide_type": "fragment"}
(ツ) = ಠ_ಠ
# + slideshow={"slide_type": "fragment"} tags=["clear"]
(ツ)
# + slideshow={"slide_type": "fragment"}
(ツ) = YᵒᵘOᶰˡʸLᶤᵛᵉOᶰᶜᵉ
# + slideshow={"slide_type": "fragment"} tags=["clear"]
(ツ)
# + [markdown] slideshow={"slide_type": "notes"}
# This is valid Python code! Can anybody imagine how this works?
# + [markdown] slideshow={"slide_type": "fragment"}
# <small>inspired by https://twitter.com/yennycheung/status/1099349853518397440 @ [#pythonpizza](https://berlin.python.pizza/)</small>
# + slideshow={"slide_type": "skip"}
# reset it again for presentation...
(ツ) = ಠ_ಠ
# + [markdown] slideshow={"slide_type": "subslide"}
# # How to write Beautiful Code? Naming!
# + [markdown] slideshow={"slide_type": "-"}
# If you need to name a *thing*, can you describe the thing to somebody who has no idea what it is and what it does with a single precise word?
# + [markdown] slideshow={"slide_type": "fragment"}
# - neat convention: encode the unit in the name, e.g. `distance_km`
# - docstrings and comments: don't repeat the code, focus on the non-obvious
# - if you can't give it a good name, it might be an indication of bad abstraction
# + [markdown] slideshow={"slide_type": "subslide"}
# # How to write Beautiful Code? Naming!
#
# + [markdown] slideshow={"slide_type": "fragment"}
# 1. avoid abbreviations
# 2. don't be too generic
# 3. don't be too specific
# 4. names should not be too long
# 5. names should not be meaningless
# + [markdown] slideshow={"slide_type": "fragment"}
# Ad (1) and (4): think twice if these before using these names:
#
# data, value, controller, manager, tmp, helper, util, tool, x, a, foo
#
# + [markdown] slideshow={"slide_type": "subslide"}
# # How to write Beautiful Code? Naming!
#
# - use functions to name parts of your code
# - only 10-30 lines of code in each function
# - also makes scope smaller with a clear interface
# - also reduces indentation
# - avoid so called magic values, put numbers in constants:
# -
# this is made up out of thin air, but at least documented
MY_ARBITRARY_THRESHOLD = 23.2
# + [markdown] slideshow={"slide_type": "subslide"}
# # How to write Beautiful Code? Naming!
#
# + [markdown] slideshow={"slide_type": "-"}
# Always remember:
#
# - Be a poet!
# - Naming is difficult!
# + [markdown] slideshow={"slide_type": "slide"}
# # How to write Beautiful Code? Pattern!
#
# <img src="images/software-architecture-pattern.png" style="height:600px;">
#
# <!--
# Source: https://images-na.ssl-images-amazon.com/images/I/81ZqYrkPrhL.jpg
#
# -->
# + [markdown] slideshow={"slide_type": "subslide"}
# # Break the problem into smaller blocks
#
# <img src="images/lego.svg" style="height:500px;">
#
# <small>Source: https://de.wikipedia.org/wiki/Lego#/media/File:Lego_dimensions.svg CC BY-SA 3.0</small>
# + [markdown] slideshow={"slide_type": "subslide"}
# # Stateless Blocks
#
# <img src="images/blackbox.png">
#
# They can be complex inside and but should be simple to use from outside.
# + [markdown] slideshow={"slide_type": "notes"}
# Break the problem into smaller blocks, use them to construct larger blocks.
# Each block can be complicated inside, but need to have a clear interface which allows to connect them. If we know what the block does, we don't need to care about it's implementation as long as each input gives an deterministic output, i.e. the output depends only on the input and not on some other state ("stateless").
# Smaller blocks represent the low level abstraction, larger blocks of smaller blocks are the high level abstraction. Low level is closer to the hardware and allows a more fine grained control. High level is easier and simpler and closer to the problem definition.
#
# If we know input and output and what the block does, it can be used without caring about the inside. We can use the abstraction to forget about things and concentrate on other parts. It can be tested and debugged easier. If the output does not depend only on its input, but one some other state (not stateless!), things get more complicated. How to test and debug it? We need to look at more code at once. Pieces of code are more entangled. That's also what makes working with data more complicated than normal software programming (you have to manage the data (state!), not only the routines which handle data).
#
# A good abstraction has different layers, higher layers use only lower layers. Therefore cyclic dependencies are avoided automatically.
# + [markdown] slideshow={"slide_type": "slide"}
# # Why Python?
# + [markdown] slideshow={"slide_type": "fragment"}
# <img src="images/ex-machina.jpg" style="height:500px">
# + [markdown] slideshow={"slide_type": "fragment"}
# <small>Source: [Screenshot](http://i.imgur.com/C44iJeR.jpg) of the movie [Ex Machina](https://www.imdb.com/title/tt0470752/), see also https://www.reddit.com/r/movies/comments/365f9b/secret_code_in_ex_machina/</small>
# + [markdown] slideshow={"slide_type": "subslide"}
# # Why Python?
# + [markdown] slideshow={"slide_type": "-"}
# <img src="images/stackoverflow-statistics1.png" style="height:500px">
#
# <small>Source: https://stackoverflow.blog/2017/05/09/introducing-stack-overflow-trends/</small>
# + [markdown] slideshow={"slide_type": "subslide"}
# # Why Python?
#
# <img src="images/stackoverflow-statistics2.png" style="height:500px">
#
# <small>Source: https://stackoverflow.blog/2017/09/06/incredible-growth-python/</small>
# + [markdown] slideshow={"slide_type": "subslide"}
# # Why Python?
#
# <img src="images/what-python-is-used-for.png" style="height:500px">
#
# <small>Source: https://www.jetbrains.com/research/python-developers-survey-2018/</small>
# + [markdown] slideshow={"slide_type": "subslide"}
# # Why Python?
#
# ## Python is free software!
#
# - free* (as in freedom, not as in free beer)
# - you can look inside and modify/fix things yourself
# - huge and welcoming community
#
#
# <small>* GPL compatible, but not GPL not sure if RMS would call this free</small>
# + [markdown] slideshow={"slide_type": "slide"}
# # PEP 8
# + [markdown] slideshow={"slide_type": "-"}
# = Official Style Guide for Python Code
#
# - where to put spaces
# - strings and docstrings
# - naming and snake_case vs CamelCase
# + [markdown] slideshow={"slide_type": "fragment"}
# Typical disagreements:
# - line width ("79 is too short")
# - quoting styles (' vs ")
# - tabs vs spaces
# + [markdown] slideshow={"slide_type": "slide"}
# # PEP 8
# + [markdown] slideshow={"slide_type": "-"}
# Extensions of PEP 8 for docstrings and parameters:
#
# - [rst](https://sphinxcontrib-napoleon.readthedocs.io/en/latest/index.html)
# - [numpy](https://sphinxcontrib-napoleon.readthedocs.io/en/latest/example_numpy.html)
# - [Google](https://sphinxcontrib-napoleon.readthedocs.io/en/latest/example_google.html)
# - [Epytext](http://epydoc.sourceforge.net/manual-epytext.html)
# + [markdown] slideshow={"slide_type": "subslide"}
# # PEP 8
#
# PEP 8 example code
# <br><small>Source: https://gist.github.com/RichardBronosky/454964087739a449da04</small>
# + tags=["clear"]
# #! /usr/bin/env python
# -*- coding: utf-8 -*-
"""This module's docstring summary line.
This is a multi-line docstring. Paragraphs are separated with blank lines.
Lines conform to 79-column limit.
Module and packages names should be short, lower_case_with_underscores.
Notice that this in not PEP8-cheatsheet.py
Seriously, use flake8. Atom.io with https://atom.io/packages/linter-flake8
is awesome!
See http://www.python.org/dev/peps/pep-0008/ for more PEP-8 details
"""
import os # STD lib imports first
import sys # alphabetical
import some_third_party_lib # 3rd party stuff next
import some_third_party_other_lib # alphabetical
import local_stuff # local stuff last
import more_local_stuff
import dont_import_two, modules_in_one_line # IMPORTANT!
from pyflakes_cannot_handle import * # and there are other reasons it should be avoided # noqa
# Using # noqa in the line above avoids flake8 warnings about line length!
_a_global_var = 2 # so it won't get imported by 'from foo import *'
_b_global_var = 3
A_CONSTANT = 'ugh.'
# 2 empty lines between top-level funcs + classes
def naming_convention():
"""Write docstrings for ALL public classes, funcs and methods.
Functions use snake_case.
"""
if x == 4: # x is blue <== USEFUL 1-liner comment (2 spaces before #)
x, y = y, x # inverse x and y <== USELESS COMMENT (1 space after #)
c = (a + b) * (a - b) # operator spacing should improve readability.
dict['key'] = dict[0] = {'x': 2, 'cat': 'not a dog'}
class NamingConvention(object):
"""First line of a docstring is short and next to the quotes.
Class and exception names are CapWords.
Closing quotes are on their own line
"""
a = 2
b = 4
_internal_variable = 3
class_ = 'foo' # trailing underscore to avoid conflict with builtin
# this will trigger name mangling to further discourage use from outside
# this is also very useful if you intend your class to be subclassed, and
# the children might also use the same var name for something else; e.g.
# for simple variables like 'a' above. Name mangling will ensure that
# *your* a and the children's a will not collide.
__internal_var = 4
# NEVER use double leading and trailing underscores for your own names
__nooooooodontdoit__ = 0
# don't call anything (because some fonts are hard to distiguish):
l = 1
O = 2
I = 3
# some examples of how to wrap code to conform to 79-columns limit:
def __init__(self, width, height,
color='black', emphasis=None, highlight=0):
if width == 0 and height == 0 and \
color == 'red' and emphasis == 'strong' or \
highlight > 100:
raise ValueError('sorry, you lose')
if width == 0 and height == 0 and (color == 'red' or
emphasis is None):
raise ValueError("I don't think so -- values are %s, %s" %
(width, height))
Blob.__init__(self, width, height,
color, emphasis, highlight)
# empty lines within method to enhance readability; no set rule
short_foo_dict = {'loooooooooooooooooooong_element_name': 'cat',
'other_element': 'dog'}
long_foo_dict_with_many_elements = {
'foo': 'cat',
'bar': 'dog'
}
# 1 empty line between in-class def'ns
def foo_method(self, x, y=None):
"""Method and function names are lower_case_with_underscores.
Always use self as first arg.
"""
pass
@classmethod
def bar(cls):
"""Use cls!"""
pass
# a 79-char ruler:
# 34567891123456789212345678931234567894123456789512345678961234567897123456789
"""
Common naming convention names:
snake_case
MACRO_CASE
camelCase
CapWords
"""
# Newline at end of file
# + [markdown] slideshow={"slide_type": "subslide"}
# # PEP 8
#
# Use a code linter in your editor and tests!
#
# - [pycodestyle](https://pypi.org/project/pycodestyle/) (formerly called "pep8"): checks only style, not validity
# - [flake8](https://github.com/PyCQA/flake8): faster than pylint, a combination of (pycodestyle and pyflakes)
# - [pylint](https://www.pylint.org/): stricter than flake8
# - [black](https://github.com/ambv/black): code formatter
#
# + [markdown] slideshow={"slide_type": "fragment"}
# On command line:
#
# ```
# $ pylint3 debug-numpy-linalg-norm.py
# ************* Module debug-numpy-linalg-norm
# debug-numpy-linalg-norm.py:1:0: C0103: Module name "debug-numpy-linalg-norm" doesn't conform to snake_case naming style (invalid-name)
# debug-numpy-linalg-norm.py:1:0: C0111: Missing module docstring (missing-docstring)
# debug-numpy-linalg-norm.py:3:0: C0103: Constant name "d" doesn't conform to UPPER_CASE naming style (invalid-name)
#
# -----------------------------------
# Your code has been rated at 0.00/10
# ```
# + [markdown] slideshow={"slide_type": "slide"}
# # # Questions?
# + [markdown] slideshow={"slide_type": "slide"}
# # PEP 8: Exercise
#
# <br>
# <div style="larger">Try out code one or more code linters and fix some PEP 8 issues!</div>
#
# Suggestion:
# - `exmachina.py` (many violations)
# - a well known module (e.g. numpy, logging, ...)
# - your own code
# + [markdown] slideshow={"slide_type": "slide"}
# # Everything is an Object
# + slideshow={"slide_type": "fragment"}
meaning = 42
# + slideshow={"slide_type": "fragment"}
from datetime import datetime
# + slideshow={"slide_type": "fragment"}
birthdays = {
'Alice': datetime(1978, 2, 1),
'Bob': datetime(1978, 2, 3)
}
# + slideshow={"slide_type": "fragment"}
data = [1, 2, 3, meaning, birthdays]
# + slideshow={"slide_type": "fragment"}
del birthdays # del is very rarely needed in real life, this is for demonstration
# -
data
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object
# -
# A function takes objects as inputs and its return value is an object. Functions are objects too, everything is an object!
# + slideshow={"slide_type": "skip"}
from scipy.interpolate import interp1d
# %pylab inline
# -
power_curve = interp1d(
[0, 1, 2, 3, 4],
[0, 0.3, 1., 1.5, 1.5]
)
# + slideshow={"slide_type": "fragment"}
power_curve(1.5)
# + slideshow={"slide_type": "fragment"}
def plot_func(func):
x = np.linspace(0, 4, num=20)
y = func(x)
plot(x, y, 'o-')
plot_func(power_curve)
# + [markdown] slideshow={"slide_type": "slide"}
# # Everything is an Object
#
# <small>See also: https://docs.python.org/3/reference/datamodel.html</small>
#
#
# - in Python data is stored in objects - and everything is an object (also functions, modules, ...)
# - objects can be stored in variables (aka "names") or in other objects (nested)
# - variables/names are created via assignment `=` or other Python statements (`import`, `def`, `class`, ...)
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object
#
# Every object consists of:
# - **identity**: never changes after creation (like a pointer or memory address)
# - **value**: the data to be stored, something like list elements (can be changed)
# - **type**: e.g. list, int, float, dict, ... (better not try to change this!)
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object
#
# - variables contain only references to the object (the identity)
# - assignments and parameters to functions don't copy objects, only pass references
# - there are types of objects which contain references to other objects (`list`, `dict`, `tuple`, ...)
# - some types cannot contain other objects (`str`, `int`, `float`, ...)
# - some operations modify objects, other operations create new objects
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object: Assignment and Modification
# -
list1 = [1,2,3]
list2 = [1,2,3]
another_list1 = list1
# + slideshow={"slide_type": "fragment"} tags=["clear"]
list1 == list2
# + slideshow={"slide_type": "fragment"} tags=["clear"]
list1 is list2
# + slideshow={"slide_type": "fragment"} tags=["clear"]
list1 is another_list1
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object: Assignment and Modification
# + slideshow={"slide_type": "fragment"} tags=["clear"]
list1.append(42) # modifies list1
list1
# + slideshow={"slide_type": "fragment"} tags=["clear"]
list2
# + slideshow={"slide_type": "fragment"} tags=["clear"]
another_list1
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object: Assignment and Modification
# -
merged_lists = list1 + list2 # creates a new object!
merged_lists
# + [markdown] slideshow={"slide_type": "fragment"}
# `list1` and `another_list1` are identical, i.e. their identity is the same:
# + slideshow={"slide_type": "-"}
print("id(list1) =", id(list1))
print("id(list2) =", id(list2))
print("id(another_list1) =", id(another_list1))
print("id(merged_lists) =", id(merged_lists))
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object: Assignment and Modification
# + slideshow={"slide_type": "fragment"}
list1 is another_list1
# -
list1 == another_list1
# + slideshow={"slide_type": "-"}
list1 = [1, 2, 3]
# + slideshow={"slide_type": "fragment"}
another_list1
# + slideshow={"slide_type": "fragment"}
list1 is another_list1
# + slideshow={"slide_type": "skip"}
# just reset it again, to start with correctly set variables after running parts again
list1 = [1,2,3]
list2 = [1,2,3]
another_list1 = list1
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object: Assignment and Modification
# -
# Summary: don't confuse the following:
# + [markdown] slideshow={"slide_type": "fragment"}
# - creation of a new object: something like `[1,2,3]`, `23` or `np.array([1,2,3])`
# + [markdown] slideshow={"slide_type": "fragment"}
# - modifying of an existing object: `list1.append(42)`
# + [markdown] slideshow={"slide_type": "fragment"}
# - assignment: assigns a reference to the variable on lhs of the `=`
# + [markdown] slideshow={"slide_type": "fragment"}
# If a method (or function) like `list.append()` modifies the object or returns a new one is different for each method.
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object: Copy an object
# -
# Sometimes an object needs to be copied:
import copy
first_list = [1, 2, 3]
copy_of_first_list = copy.copy(first_list)
# + [markdown] slideshow={"slide_type": "fragment"}
# Nested objects are copied with `copy.deepcopy()`.
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object: Classes
#
# New types are created by implementing a class:
# + slideshow={"slide_type": "-"}
class Polynomial(tuple):
"""Something like 3*x² + x."""
...
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object: Classes
# + [markdown] slideshow={"slide_type": "fragment"}
# Let's create some objects of our new type:
# + slideshow={"slide_type": ""}
quadratic_polynomial = Polynomial((3, 2, 0))
linear_polynomial = Polynomial((0, 2, 1))
# + slideshow={"slide_type": "fragment"}
quadratic_polynomial
# -
def add_polynomials(polynomial1, polynomial2):
# FIXME this is broken for polynomials of different degree
# zip will take consider only shorter iterable
return Polynomial((coeff1 + coeff2
for coeff1, coeff2 in zip(polynomial1, polynomial2)))
add_polynomials(quadratic_polynomial, linear_polynomial)
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object: Classes
# -
# Classes can be considered as name space:
# + slideshow={"slide_type": "-"}
class Polynomial(tuple):
"""Something like 3*x² + x."""
def add(polynomial1, polynomial2):
# FIXME this is broken for polynomials of different degree
# zip will take consider only shorter iterable
return Polynomial((coefficient1 + coefficient2
for coefficient1, coefficient2 in zip(polynomial1, polynomial2)))
# + slideshow={"slide_type": "skip"}
# Ok, it needs a bit of cheating... The method add() needs to exist at creation time.
quadratic_polynomial = Polynomial((3, 2, 0))
linear_polynomial = Polynomial((0, 2, 1))
# + slideshow={"slide_type": "fragment"}
Polynomial.add(quadratic_polynomial, linear_polynomial)
# + [markdown] slideshow={"slide_type": "fragment"}
# Python knows that `quadratic_polynomial` is of type `Polynomial`, so a shorter (mostly) equivalent way of the same line is:
# -
quadratic_polynomial.add(linear_polynomial)
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object: Classes
# -
# By convention the first parameter in class methods is called `self`, you should stick to this convention. It's role is similar to `this` in C++ or Java.
# + slideshow={"slide_type": "-"}
class Polynomial(tuple):
"""Something like 3*x² + x."""
def add(self, other):
# FIXME this is broken for polynomials of different degree
# zip will take consider only shorter iterable
return Polynomial((self_coeff + other_coeff
for self_coeff, other_coeff in zip(self, other)))
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object: Classes
# + slideshow={"slide_type": "-"}
class Polynomial(tuple):
"""Something like 3*x² + x."""
def __add__(self, other):
# FIXME this is broken for polynomials of different degree
# zip will take consider only shorter iterable
return Polynomial((self_coeff + other_coeff
for self_coeff, other_coeff in zip(self, other)))
# + slideshow={"slide_type": "skip"}
# Ok, it needs a bit of cheating... The method add() needs to exist at creation time.
quadratic_polynomial = Polynomial((3, 2, 0))
linear_polynomial = Polynomial((0, 2, 1))
# + slideshow={"slide_type": "skip"}
quadratic_polynomial + linear_polynomial
# -
# There is a very consistent protocol to modify how things behave in Python using so called "dunder" methods starting and ending with two underscores `__do_something__`.
#
# More here:
# https://www.youtube.com/watch?v=cKPlPJyQrt4
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object: Classes
#
# A different view on classes is a bit more common: classes are like Platotic forms. They define how objects are created (constructor in `__new__` and `__init__`), how they store data (in their attributes) and how they behave (i.e. which methods do they implement).
# + slideshow={"slide_type": "-"}
class QuadraticPolynomial(Polynomial): # inherits from a Polynomial = is a special case of a Polynomial
def __init__(self, coefficients): # __init__ is called to initialize new objects after creation
self.degree = len(coefficients)
def __repr__(self):
return f"{self[0]}x² + {self[1]}x + {self[2]}"
def __call__(self, x):
return sum(coeff * x**i for i, coeff in enumerate(reversed(self)))
def __add__(self, other):
# FIXME this is broken for polynomials of different degree
# zip will take consider only shorter iterable
return Polynomial((self_coeff + other_coeff
for self_coeff, other_coeff in zip(self, other)))
# + slideshow={"slide_type": "fragment"}
quadratic_polynomial = QuadraticPolynomial(quadratic_polynomial)
quadratic_polynomial
# + [markdown] slideshow={"slide_type": "fragment"}
# Attributes not only used for methods, but also used to store non-callable objects:
# -
quadratic_polynomial.degree
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object: Overloading operators
# -
import pathlib
# + slideshow={"slide_type": "fragment"}
tmp_folder = pathlib.Path('/tmp')
# + slideshow={"slide_type": "fragment"}
tmp_folder/'firefox_peter'
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object
#
# To summarize: objects are created either...
# -
# ...by calling classes (similar to functions):
# + slideshow={"slide_type": "fragment"}
int("42")
# + slideshow={"slide_type": "fragment"}
dict(key1=42, key2=43)
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object
#
# To summarize: objects are created either...
# + [markdown] slideshow={"slide_type": "-"}
# ...by literals:
# -
42
{'key': 42, 'key': 43}
# + [markdown] slideshow={"slide_type": "subslide"}
# # Everything is an Object
#
# To summarize: objects are created either...
# + [markdown] slideshow={"slide_type": "-"}
# ...by statements, but this is a special case and only important to emphasize that everything is an object:
# +
import logging
def my_function():
pass
class SomeClass:
pass
# + [markdown] slideshow={"slide_type": "slide"}
# # Everything can be modified
# + slideshow={"slide_type": "skip"}
orig_print = print
# + slideshow={"slide_type": "fragment"}
def evil_print(*value, sep=' ', end='\n', file=None, flush=False):
return "(͠≖ ͜ʖ͠≖)"
# + slideshow={"slide_type": "fragment"}
print("hello world")
# + slideshow={"slide_type": "fragment"}
print = evil_print
# + slideshow={"slide_type": "fragment"}
print("hello world")
# + slideshow={"slide_type": "skip"}
print = orig_print
# + [markdown] slideshow={"slide_type": "slide"}
# # Everything can be modified: But why?
# + [markdown] slideshow={"slide_type": "fragment"}
# - monkey patching can help if you *really* need to modify 3rd code (e.g. bug-fix)
# + [markdown] slideshow={"slide_type": "fragment"}
# - temporary experiments if you cannot restart the Python process or so
# + [markdown] slideshow={"slide_type": "fragment"}
# - be careful with built-ins (and keywords), syntax high-lighting helps
# + slideshow={"slide_type": "skip"}
orig_list = list
# -
list = list((1,2,3))
list
# + slideshow={"slide_type": "skip"}
list = orig_list
# + [markdown] slideshow={"slide_type": "slide"}
# # Really everything can be modified?
#
# <img src="images/asterix-gaul.png" style="height:500px;">
# + [markdown] slideshow={"slide_type": "subslide"}
# # Immutable types and the traps of mutability
#
# immutable types:
#
# ``str, int, float, tuple, frozenset, NoneType``
#
# almost everything else is mutable, especially:
#
# ``list, dict``
# -
# <small>See also: https://docs.python.org/3/reference/datamodel.html</small>
# + [markdown] slideshow={"slide_type": "subslide"}
# # Immutable types and the traps of mutability
# -
def extend_list(element, l=[]):
l.append(element)
return l
# + slideshow={"slide_type": "fragment"} tags=["clear"]
extend_list(4, [1,2,3])
# + slideshow={"slide_type": "fragment"} tags=["clear"]
extend_list(1)
# + slideshow={"slide_type": "fragment"} tags=["clear"]
extend_list(1)
# + [markdown] slideshow={"slide_type": "subslide"}
# # Immutable types and the traps of mutability
# -
# Never use mutable objects as default arguments and avoid modifying input parameters (unless you need to avoid copying a kit of data).
def extend_list(element, l=None):
if l is None:
l = [] # note that l is not modyfied, but a new object is assigned
l.append(element)
return l
# + [markdown] slideshow={"slide_type": "slide"}
# # Scope: Packages, Modules, Classes and Functions
#
# Quiz: valid Python code?
# + slideshow={"slide_type": "fragment"}
for i in range(3):
def meaning(n):
return 42
# + slideshow={"slide_type": "fragment"}
class Life:
for i in range(3):
def meaning(n):
return 42
# + slideshow={"slide_type": "fragment"}
for i in range(3):
class Life:
for i in range(3):
def meaning(n):
return 42
# -
# https://docs.python.org/3/reference/executionmodel.html
# + [markdown] slideshow={"slide_type": "slide"}
# # Scope: Packages, Modules, Classes and Functions
#
# Quiz: order of execution - what will happen here?
# + tags=["clear"]
print_meaning()
def print_meaning():
print(42)
# + slideshow={"slide_type": "fragment"}
def call_print_meaning():
print_meaning()
def print_meaning():
print(42)
print_meaning()
# + [markdown] slideshow={"slide_type": "subslide"}
# # Scope: Packages, Modules, Classes and Functions
#
# Quiz: order of execution - what will happen here?
# + slideshow={"slide_type": "fragment"}
def some_function():
print(not_defined_variable + 2)
# + [markdown] slideshow={"slide_type": "subslide"}
# # Scope: Packages, Modules, Classes and Functions
# + slideshow={"slide_type": ""}
MY_CONSTANT = 42
def some_function():
fancy_calculation = 1 * MY_CONSTANT
return fancy_calculation
# + slideshow={"slide_type": "fragment"}
some_function()
# + [markdown] slideshow={"slide_type": "subslide"}
# # Scope: Packages, Modules, Classes and Functions
# +
MY_CONSTANT = 42
def some_function():
fancy_calculation = 1 * MY_CONSTANT
def inner_function():
return 0.5 * fancy_calculation
fancy_calculation = inner_function()
return fancy_calculation
# + slideshow={"slide_type": "fragment"}
some_function()
# + [markdown] slideshow={"slide_type": "subslide"}
# # Scope: Packages, Modules, Classes and Functions
# + slideshow={"slide_type": "fragment"}
some_list = []
def extend_list(n):
some_list.append(n)
return some_list
extend_list(1)
# + slideshow={"slide_type": "fragment"} tags=["clear"]
some_list = []
def extend_list(n):
some_list.append(n)
if len(some_list) > 3:
# too long...
some_list = []
return some_list
extend_list(1)
# + [markdown] slideshow={"slide_type": "subslide"}
# # Scope: Packages, Modules, Classes and Functions
# +
a = 3
class A:
a = a + 2
a = a + 1
b = a
# + slideshow={"slide_type": "fragment"}
a, A.a, A.b
# + [markdown] slideshow={"slide_type": "subslide"}
# # Scope: Packages, Modules, Classes and Functions
# + slideshow={"slide_type": ""}
class B:
a = 42
b = tuple(a + i for i in range(10))
# + slideshow={"slide_type": "fragment"}
a, B.a
# + slideshow={"slide_type": "fragment"}
B.b
# + [markdown] slideshow={"slide_type": "fragment"}
# See also: https://docs.python.org/3.3/reference/executionmodel.html
# + [markdown] slideshow={"slide_type": "subslide"}
# # Scope: Packages, Modules, Classes and Functions
#
# - a name (=variable) is defined in a module, a class or a function
# - names in functions are *only* visible inside this function
# - names in modules are (directly) visible inside the module
# - names in classes are not (directly) visible inside methods
# - names in modules and classes can be accessed from outside via `module_name.variable` or `class_name.variable`
# + [markdown] slideshow={"slide_type": "subslide"}
# # Scope: Packages, Modules, Classes and Functions
#
# If you write a script, use a main() function to avoid to make variables local:
# +
MY_CONSTANTS = 42
def main():
# fancy script code
some_local_variable = 3
...
if __name__ == '__main__':
main()
# + [markdown] slideshow={"slide_type": "slide"}
# # Imports
# -
# Looks for `logging.py` or `logging/__init__.py` in the `PYTHONPATH`, runs it, creates a module object and assings it to `logging`:
import logging
# + slideshow={"slide_type": "fragment"}
from logging import getLogger
# + [markdown] slideshow={"slide_type": ""}
# ...is mostly equivalent to:
# -
import logging
getLogger = logging.getLogger
# + [markdown] slideshow={"slide_type": "slide"}
# # # Questions?
# + [markdown] slideshow={"slide_type": "slide"}
# # Exercise:
#
# Choose:
#
# - Write a terrible confusing script/function/whatever by modifying something you shouldn't modify! (e.g. slow down time by a factor 2, name a list `list`, let a built-in function return something surprising, ...)
# - Write a function using a dunder function `__<some name>__` doing something very useful or something very evil!
# - List use cases: when does it make sense to modify something? Which objects should never be modified?
# + [markdown] slideshow={"slide_type": "slide"}
# # Exceptions and tracebacks
# -
raise Exception("something bad happened")
# + [markdown] slideshow={"slide_type": "fragment"}
# <small>Source:
# https://docs.python.org/3/library/exceptions.html,
# https://docs.python.org/3/tutorial/errors.html</small>
# + [markdown] slideshow={"slide_type": "subslide"}
# # Exceptions and tracebacks
#
# Exception chaining is powerful to avoid loosing the original cause:
# + slideshow={"slide_type": "-"} tags=["clear"]
some_list = [1,2]
try:
some_list[4] = 42
except Exception as e:
raise RuntimeError("Failed to append meaning of life") from e
# + [markdown] slideshow={"slide_type": "subslide"}
# # Exceptions and tracebacks
# + tags=["clear"]
try:
1/0
finally:
print("before everything explodes: 🎉")
# + [markdown] slideshow={"slide_type": "subslide"}
# # Exceptions and tracebacks
# + slideshow={"slide_type": ""} tags=["clear"]
with open('turbine_models.csv') as f:
1/0
# + slideshow={"slide_type": "fragment"} tags=["clear"]
f.closed
# + [markdown] slideshow={"slide_type": "subslide"}
# # Exceptions and tracebacks
#
# - errors should never pass silently, make good error messages including parameters
# - exceptions can be any object, but should better inherit from Exception
# - KeyboardError does not inherit from Exception and won't be caught by `except Exception`
# + [markdown] slideshow={"slide_type": "slide"}
# # Debuggers
# + [markdown] slideshow={"slide_type": "fragment"}
# Debuggers help to inspect the inside of code. This can be useful for when searching for a bug, but also if you want to understand what a particular piece of code does.
# + [markdown] slideshow={"slide_type": "fragment"}
# There are [many debuggers for Python](https://wiki.python.org/moin/PythonDebuggingTools):
#
# - [pdb](https://docs.python.org/3/library/pdb.html): shipped with the Python standard libary
# - [ipdb](https://github.com/gotcha/ipdb): tab completion, syntax highlighting, debugger for IPython
# - PyCharm inlcudes a graphical debugger
# - [pdb++](https://github.com/antocuni/pdb): similar to ipdb
# - ...
# + [markdown] slideshow={"slide_type": "subslide"}
# One can inject code in a running process:
# - [pyrasite](http://pyrasite.com/)
# - [pyringe](https://github.com/google/pyringe)
# - ...
#
# (Very helpful to debug dead locks and memory leaks!)
# + [markdown] slideshow={"slide_type": "subslide"}
# # Let's debug something!
# -
# Invoke the debugger via break point in code:
import pdb; pdb.set_trace()
import ipdb; ipdb.set_trace() # does not work in Jupyter notebooks
breakpoint() # for Python >= 3.7
# + [markdown] slideshow={"slide_type": "subslide"}
# # Let's debug something!
# -
# Invoke debugger by calling the script from the debugger:
#
# ```
# $ ipdb my_module.py # ipdb3 (for Python 3) on some platforms
# > /tmp/test.py(2)<module>()
# 1 """This is my_module.py
# ----> 2 """
# 3
#
# ipdb>
# ```
#
# $\Rightarrow$ opens debugger after the first line of code and after every exception ("post-mortem")
# + [markdown] slideshow={"slide_type": "subslide"}
# # Let's debug something!
# -
# - program flow is interrupted (current thread/process)
# - debugger prompt `ipdb>` acts like a Python terminal with additional commands
# - inspect or continue program flow by using debugger commands
# + [markdown] slideshow={"slide_type": "subslide"}
# # Debugger commands
#
# - **w(here)** Print a stack trace
# - **d(own)** Move the current frame one level down in the stack trace
# - **u(p)** Move the current frame one level up in the stack trace
# - **b(reak) [[filename:]lineno | function[, condition]]** set a new break point
# - **c(ontinue)** continue execution until next break point is hit
# - **n(ext)** execute line and jump to next line
# - **s(tep)** step inside a function
# - **l(ist) [first[, last]]** list source code of current file (from line `first` to line `last`)
# + [markdown] slideshow={"slide_type": "subslide"}
# # # Questions?
# + [markdown] slideshow={"slide_type": "subslide"}
# # Exercise: debug something!
#
# <br>
#
# <div style="font-size:larger;">Investigate code you are not very familiar with using ipdb!</div>
#
# Suggestions:
# - `np.linalg.norm`
# - https://github.com/lumbric/lunchbot
# - `logging` (e.g. `debug-logging-basicConfig.py`)
# - `exmachina.py`
#
# This time, *not* your own code! :)
# + [markdown] slideshow={"slide_type": "slide"}
# # Tests
#
# - unit tests
# - integration tests
# - functional tests
# + [markdown] slideshow={"slide_type": "fragment"}
# 
# + [markdown] slideshow={"slide_type": "subslide"}
# # Tests: Example
# + slideshow={"slide_type": "fragment"}
def fibonacci_sequence(n):
"""Return a list of all Fibbonacci numbers up to the n-th Fibonacci number."""
# FIXME don't use this function in real life
if n == 1:
return [0]
elif n == 2:
return [0, 1]
sequence = fibonacci_sequence(n-1)
return sequence + [sequence[-2] + sequence[-1]]
# + slideshow={"slide_type": "fragment"}
fibonacci_sequence(6)
# + [markdown] slideshow={"slide_type": "subslide"}
# # Tests: Example
# + slideshow={"slide_type": "fragment"}
def test_fibonacci_sequence():
assert fibonacci_sequence(1) == [0]
assert isinstance(fibonacci_sequence(4), list)
assert fibonacci_sequence(7)[-1] == 8
# + slideshow={"slide_type": "fragment"}
test_fibonacci_sequence()
# + [markdown] slideshow={"slide_type": "subslide"}
# # Tests: test runner
#
# - [py.test](https://pytest.org/)
# - nosetests
# - doctests
# - many plugins: coverage, watch, ...
# + [markdown] slideshow={"slide_type": "subslide"}
# # Tests: doctest
# + slideshow={"slide_type": "fragment"}
"""This is a docstring.
Example
-------
>>> 1 + 1
2
"""
# + [markdown] slideshow={"slide_type": "subslide"}
# # Tests: Continuous Integration
#
# Continuous integration (CI) runs your tests automatically:
# - [Travis CI](https://travis-ci.com/) (note: travis-ci.com and travis-ci.org are different)
# - [Gitlab](https://about.gitlab.com/)
# - [Jenkins](https://jenkins.io/)
# + [markdown] slideshow={"slide_type": "subslide"}
# # Tests: libraries
#
# Libraries for writing tests:
# - [hypothesis](https://github.com/HypothesisWorks/hypothesis): helps to test the whole parameter space
# - [mock](https://docs.python.org/3/library/unittest.mock.html): change parts of your code which you can't test
# + [markdown] slideshow={"slide_type": "subslide"}
# # Tests: corner cases
#
# <img src="images/qa-engineer-joke.png" style="height:500px;">
#
# <small>Source: https://twitter.com/brenankeller/status/1068615953989087232</small>
# + [markdown] slideshow={"slide_type": "subslide"}
# # Tests: corner cases
# -
fibonacci_sequence(0)
# + [markdown] slideshow={"slide_type": "fragment"}
# We forgot to test `fibonacci_sequence()` $n < 1$! Hypothesis helps to catch many important corner cases.
# + [markdown] slideshow={"slide_type": "subslide"}
# # Tests: corner cases
# + slideshow={"slide_type": "-"}
def fibonacci_sequence(n):
"""Return a list of all Fibbonacci numbers up to the n-th Fibonacci number."""
# FIXME don't use this function in real life
if n == 1:
return [0]
elif n == 2:
return [0, 1]
sequence = fibonacci_sequence(n-1)
return sequence + [sequence[-2] + sequence[-1]]
# + [markdown] slideshow={"slide_type": "subslide"}
# # # Questions?
# + [markdown] slideshow={"slide_type": "slide"}
# # Tests: Exercise
#
#
# Write a test testing something and use py.test to run it!
#
# Include also wrong tests to see them failing! (This is also good practice in real life.)
#
# Suggestions:
# * `np.piecewise()`, `np.linalg.norm()`, ...
# * git-game, `lunchbot`, `exmachina`
# * your own code
#
# Bonus: use coverage and/or watch plugins!
#
# Additional Bonus: try to find already existing tests for the functions defined.
# + [markdown] slideshow={"slide_type": "slide"}
# # Logging
#
# Excellent guide: https://docs.python-guide.org/writing/logging/
# + [markdown] slideshow={"slide_type": "-"}
# Libraries may define loggers and emit log messages:
# +
import logging
logging.info('This is interesting, but not critial')
LOGGER = logging.getLogger(__name__)
LOGGER.critical("Uh this is critical %s", ಠ_ಠ)
# + [markdown] slideshow={"slide_type": "fragment"}
# The application or main script defines handlers and log levels:
# -
logging.basicConfig(filename='session2.log', level=logging.INFO)
# Many more options to define handlers and levels: https://docs.python.org/3/howto/logging.html
#
# See also `code-samples/logging_config.py`.
# + [markdown] slideshow={"slide_type": "slide"}
# # Tips & Tricks
# -
# Want to look into code, but don't know where the file is?
import logging
logging.__file__
# + [markdown] slideshow={"slide_type": "skip"}
# # Tips & Tricks: IPython
# + [markdown] slideshow={"slide_type": "-"}
# Import numpy and matplotlib:
# + slideshow={"slide_type": "-"}
# %pylab
# + slideshow={"slide_type": "-"}
# for Jupyter notebooks
# %pylab line
# Also nice for interactive plots:
# #%pylab notebook
# + [markdown] slideshow={"slide_type": "-"}
# https://ipython.readthedocs.io/en/stable/interactive/magics.html
# + [markdown] slideshow={"slide_type": "slide"}
# # Gotchas: Truthiness (1)
# + slideshow={"slide_type": "fragment"} tags=["clear"]
int('10')
# + slideshow={"slide_type": "fragment"} tags=["clear"]
float('1.3')
# + slideshow={"slide_type": "fragment"} tags=["clear"]
bool('false')
# + [markdown] slideshow={"slide_type": "fragment"}
# Only the empty string is falsy, all other strings are truthy.
# + [markdown] slideshow={"slide_type": "slide"}
# # Gotchas: Truthiness (2)
# -
def uniform_random(low=None, high=None):
if not low:
low = 0.
if not high:
high = 1.
if low >= high:
raise ValueError(f"invalid values for low={low} and "
"high={high}, low < high required")
# works only only Linux (and similar platforms), no Windows
with open('/dev/urandom', 'rb') as f:
# TODO one bit is a pretty low resolution, need more?
random_byte = f.read(1)
return ord(random_byte)/255. * abs(high - low) + low
# + slideshow={"slide_type": "fragment"} tags=["clear"]
uniform_random()
# + [markdown] slideshow={"slide_type": "slide"}
# # Gotchas: Truthiness (2)
# + slideshow={"slide_type": "fragment"} tags=["clear"]
uniform_random(-1, 0)
# + [markdown] slideshow={"slide_type": "fragment"}
# Testing on truthiness can be nice, but also dangerous if you don't know exactly all types of allowed objects!
# -
some_random_values = [uniform_random(-1, 0) for i in range(int(1e5))]
_ = hist(some_random_values, density=True)
# + [markdown] slideshow={"slide_type": "slide"}
# # Gotchas: Tuples (1)
# + tags=["clear"]
for name in ('Alice', 'Bob'):
print('Name:', name)
# + slideshow={"slide_type": "fragment"} tags=["clear"]
for name in ('Alice'):
print('Name:', name)
# + [markdown] slideshow={"slide_type": "subslide"}
# # Gotchas: Tuples (2)
# + slideshow={"slide_type": "fragment"}
empty_list = []
# + slideshow={"slide_type": "fragment"}
two_empty_lists = [[]]
# + slideshow={"slide_type": "fragment"}
two_empty_lists
# + slideshow={"slide_type": "fragment"}
empty_tuple = ()
# + slideshow={"slide_type": "fragment"}
two_empty_tuples = (())
# + slideshow={"slide_type": "fragment"}
two_empty_tuples
# + [markdown] slideshow={"slide_type": "slide"}
# # Gotchas: Tuples (3)
# -
some_array = np.zeros((3,3)),
some_array
# + slideshow={"slide_type": "fragment"}
some_array + 1
# + [markdown] slideshow={"slide_type": ""}
# A trailing comma can lead to confusing error messages.
# + [markdown] slideshow={"slide_type": "slide"}
# # Gotchas: Tuples (summary)
#
# - empty list: **`[]`**
# - list with one element: **`[42]`** or **`[42,]`**
# - list with many elements: **`[1,2,3]`** or **`[1,2,3,]`**
#
#
# - empty tuple: **`()`**
# - list with one element: **`(42,)`** or in some case allowed **`42,`**
# - list with many elements: **`(1,2,3)`** or **`(1,2,3,)`** or in some cases allowed **`1,2,3`** or **`1,2,3,`**
# + [markdown] slideshow={"slide_type": "slide"}
# # References
# -
# - A mixed list of tutorials and documentation:
# - http://docs.python-guide.org/en/latest/intro/learning/
# - https://docs.python.org/3/tutorial/index.html
# - https://realpython.com/
# - http://howtopython.org/en/latest/
# - https://codecombat.com/
# - https://py.checkio.org/
# - http://thepythonguru.com/
#
# - [What Does It Take to Be A Python Expert?](https://www.youtube.com/watch?v=cKPlPJyQrt4) [other link](https://www.youtube.com/watch?v=7lmCu8wz8ro)
# - [Pythonic code by example](https://www.youtube.com/watch?v=rgET4u3zkkY)
# - [Beyond PEP8](https://www.youtube.com/watch?v=wf-BqAjZb8M)
# - [Function names to verb or not to verb](https://www.grinchcentral.com/function-names-to-verb-or-not-to-verb)
# - [How to name things](https://www.slideshare.net/pirhilton/how-to-name-things-the-hardest-problem-in-programming)
# - [Python is not Java or C++ (for people coming from typed languages)](https://www.youtube.com/watch?v=kWNBK2cnaYE)
# - [Program an swarm of robots fighting against others](http://rg.robotgame.edu.pl/)
#
|
session2_python_and_programming/slides_session2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Course Human-Centered Data Science ([HCDS](https://www.mi.fu-berlin.de/en/inf/groups/hcc/teaching/winter_term_2020_21/course_human_centered_data_science.html)) - Winter Term 2020/21 - [HCC](https://www.mi.fu-berlin.de/en/inf/groups/hcc/index.html) | [Freie Universität Berlin](https://www.fu-berlin.de/)
#
# ***
#
# # A2 - Wikipedia, ORES, and Bias in Data
# Please follow the reproducability workflow as practiced during the last exercise.
# ## Step 1⃣ | Data acquisition
#
# You will use two data sources: (1) Wikipedia articles of politicians and (2) world population data.
#
# **Wikipedia articles -**
# The Wikipedia articles can be found on [Figshare](https://figshare.com/articles/Untitled_Item/5513449). It contains politiciaans by country from the English-language wikipedia. Please read through the documentation for this repository, then download and unzip it to extract the data file, which is called `page_data.csv`.
#
# **Population data -**
# The population data is available in `CSV` format in the `_data` folder. The file is named `export_2019.csv`. This dataset is drawn from the [world population datasheet](https://www.prb.org/international/indicator/population/table/) published by the Population Reference Bureau (downloaded 2020-11-13 10:14 AM). I have edited the dataset to make it easier to use in this assignment. The population per country is given in millions!
# #### 1. Let's import the raw data as a pandas dataframe and look at it
import pandas as pd
page_data = pd.read_csv("data_raw/page_data.csv")
page_data.head()
export_2019 = pd.read_csv("data_raw/export_2019.csv", sep=";")
export_2019.head()
# ## Step 2⃣ | Data processing and cleaning
# The data in `page_data.csv` contain some rows that you will need to filter out. It contains some page names that start with the string `"Template:"`. These pages are not Wikipedia articles, and should not be included in your analysis. The data in `export_2019.csv` does not need any cleaning.
#
# ***
#
# | | `page_data.csv` | | |
# |-|------|---------|--------|
# | | **page** | **country** | **rev_id** |
# |0| Template:ZambiaProvincialMinisters | Zambia | 235107991 |
# |1| Bir I of Kanem | Chad | 355319463 |
#
# ***
#
# | | `export_2019.csv` | | |
# |-|------|---------|--------|
# | | **country** | **population** | **region** |
# |0| Algeria | 44.357 | AFRICA |
# |1| Egypt | 100.803 | 355319463 |
#
# ***
page_data = page_data[~page_data.page.str.contains("Template:")]
page_data
# ### Getting article quality predictions with ORES
#
# Now you need to get the predicted quality scores for each article in the Wikipedia dataset. We're using a machine learning system called [**ORES**](https://www.mediawiki.org/wiki/ORES) ("Objective Revision Evaluation Service"). ORES estimates the quality of an article (at a particular point in time), and assigns a series of probabilities that the article is in one of the six quality categories. The options are, from best to worst:
#
# | ID | Quality Category | Explanation |
# |----|------------------|----------|
# | 1 | FA | Featured article |
# | 2 | GA | Good article |
# | 3 | B | B-class article |
# | 4 | C | C-class article |
# | 5 | Start | Start-class article |
# | 6 | Stub | Stub-class article |
#
# For context, these quality classes are a sub-set of quality assessment categories developed by Wikipedia editors. If you're curious, you can [read more](https://en.wikipedia.org/wiki/Wikipedia:Content_assessment#Grades) about what these assessment classes mean on English Wikipedia. For this assignment, you only need to know that these categories exist, and that ORES will assign one of these six categories to any `rev_id`. You need to extract all `rev_id`s in the `page_data.csv` file and use the ORES API to get the predicted quality score for that specific article revision.
# ### ORES REST API endpoint
#
# The [ORES REST API](https://ores.wikimedia.org/v3/#!/scoring/get_v3_scores_context_revid_model) is configured fairly similarly to the pageviews API we used for the last assignment. It expects the following parameters:
#
# * **project** --> `enwiki`
# * **revid** --> e.g. `235107991` or multiple ids e.g.: `235107991|355319463` (batch)
# * **model** --> `wp10` - The name of a model to use when scoring.
#
# **❗Note on batch processing:** Please read the documentation about [API usage](https://www.mediawiki.org/wiki/ORES#API_usage) if you want to query a large number of revisions (batches).
#
# You will notice that ORES returns a prediction value that contains the name of one category (e.g. `Start`), as well as probability values for each of the six quality categories. For this assignment, you only need to capture and use the value for prediction.
#
# **❗Note:** It's possible that you will be unable to get a score for a particular article. If that happens, make sure to maintain a log of articles for which you were not able to retrieve an ORES score. This log should be saved as a separate file named `ORES_no_scores.csv` and should include the `page`, `country`, and `rev_id` (just as in `page_data.csv`).
#
# You can use the following **samle code for API calls**:
# +
import requests
import json
# Customize these with your own information
headers = {
'User-Agent': 'https://github.com/mvrcx',
'From': '<EMAIL>'
}
def get_ores_data(rev_id, headers):
# Define the endpoint
# https://ores.wikimedia.org/scores/enwiki/?models=wp10&revids=807420979|807422778
endpoint = 'https://ores.wikimedia.org/v3/scores/{project}/?models={model}&revids={revids}'
params = {'project' : 'enwiki',
'model' : 'wp10',
'revids' : rev_id
}
api_call = requests.get(endpoint.format(**params))
response = api_call.json()
data = json.dumps(response)
return data
# -
# #### Defining functions that return the score and probability for a given rev_id
# +
def get_ores_prediction(rev_id, headers):
"""
returns score for given rev_id. If no score is available for rev_id the function returns -1
"""
try:
res = json.loads(get_ores_data(rev_id, headers))
prediction = res['enwiki']['scores'][str(rev_id)]['wp10']['score']['prediction']
return prediction
except KeyError:
return -1
def get_ores_prediction_value(rev_id, headers):
"""
might need this later, not sure yet
returns probability for given rev_id. If no probability is available for rev_id the function returns -1
"""
try:
res = json.loads(get_ores_data(rev_id, headers))
value = res['enwiki']['scores'][str(rev_id)]['wp10']['score']['probability'][prediction]
return value
except KeyError:
return -1
dataframe = pd.DataFrame(columns = ["rev_id"]) #Create new dataframe
dataframe["rev_id"] = page_data['rev_id'] #Initialize with rev_ids
dataframe
# -
# Sending one request for each `rev_id` might take some time. If you want to send batches you can use `'|'.join(str(x) for x in revision_ids` to put your ids together. Please make sure to deal with [exception handling](https://www.w3schools.com/python/python_try_except.asp) of the `KeyError` exception, when extracting the `prediction` from the `JSON` response.
# Ok, so it takes roughly 2h to compute a dataframe with 10.000 rows, so I'll copy it and save it to a csv file in order of not having to compute it each and every single time. This might not be the most efficient algorithm :))))
# +
# Creating directories,
# Source: https://stackoverflow.com/questions/11373610/save-matplotlib-file-to-a-directory
def mkdir_p(mypath):
'''Creates a directory. equivalent to using mkdir -p on the command line'''
from errno import EEXIST
from os import makedirs,path
try:
makedirs(mypath)
except OSError as exc: # Python >2.5
if exc.errno == EEXIST and path.isdir(mypath):
pass
else: raise
# Creating directorys
mkdir_p('data_clean')
mkdir_p('data_clean/chunks')
# -
# Apply get_ores_prediction function on first 10.000 rows
df_1_10000 = dataframe[:10000].copy()
df_1_10000["prediction"] = df_1_10000.apply(lambda x: get_ores_prediction(int(x), headers), axis=1)
df_1_10000.to_csv(r"data_clean/chunks/df_1_10000.csv",sep=";", index = True, header = True)
# Apply get_ores_prediction function on next 10.000 rows
df_9999_20000 = dataframe[10000:20000].copy()
df_9999_20000["prediction"] = df_9999_20000.apply(lambda x: get_ores_prediction(int(x), headers), axis=1)
df_9999_20000.to_csv(r"data_clean/chunks/df_9999_20000.csv",sep=";", index = True, header = True)
# Apply get_ores_prediction function on next 10.000 rows
df_19999_30000 = dataframe[20000:30000].copy()
df_19999_30000["prediction"] = df_19999_30000.apply(lambda x: get_ores_prediction(int(x), headers), axis=1)
df_19999_30000.to_csv(r"data_clean/chunks/df_19999_30000.csv",sep=";", index = True, header = True)
# Apply get_ores_prediction function on next 10.000 rows
df_29999_40000 = dataframe[30000:40000].copy()
df_29999_40000["prediction"] = df_29999_40000.apply(lambda x: get_ores_prediction(int(x), headers), axis=1)
df_29999_40000.to_csv(r"data_clean/chunks/df_29999_40000.csv",sep=";", index = True, header = True)
# Apply get_ores_prediction function on remaining rows
df_39999_end = dataframe[40000:].copy()
df_39999_end["prediction"] = df_39999_end.apply(lambda x: get_ores_prediction(int(x), headers), axis=1)
df_39999_end.to_csv(r"data_clean/chunks/df_39999_end.csv", sep=";", index = True, header = True)
# +
# Parsing all csv's
df1 = pd.read_csv("data_clean/chunks/df_1_10000.csv", sep=";", index_col=0)
df2 = pd.read_csv("data_clean/chunks/df_9999_20000.csv", sep=";", index_col=0)
df3 = pd.read_csv("data_clean/chunks/df_19999_30000.csv", sep=";", index_col=0)
df4 = pd.read_csv("data_clean/chunks/df_29999_40000.csv", sep=";", index_col=0)
df5 = pd.read_csv("data_clean/chunks/df_39999_end.csv", sep=";", index_col=0)
# Appending dataframe chunks to one dataframe
ores_scores = df1.append(df2.append(df3.append(df4.append(df5))))
ores_scores
# Saving appended dataframe chunks to a big df
# -
# ### Combining the datasets
#
# Now you need to combine both dataset: (1) the wikipedia articles and its ORES quality scores and (2) the population data. Both have columns named `country`. After merging the data, you'll invariably run into entries which cannot be merged. Either the population dataset does not have an entry for the equivalent Wikipedia country, or vis versa.
#
# Please remove any rows that do not have matching data, and output them to a `CSV` file called `countries-no_match.csv`. Consolidate the remaining data into a single `CSV` file called `politicians_by_country.csv`.
#
# The schema for that file should look like the following table:
#
#
# | article_name | country | region | revision_id | article_quality | population |
# |--------------|---------|--------|-------------|-----------------|------------|
# | Bir I of Kanem | Chad | AFRICA | 807422778 | Stub | 16877000 |
# +
# Merging the page_data and ores_scores dataframes (inner join on rev_id as key)
df = pd.merge(page_data, ores_scores, on ='rev_id')
# Renaming columns
df = df.rename(columns={'page': 'article_name','rev_id': 'revision_id', 'prediction': 'article_quality'})
# +
import numpy as np
# Merging the above result dataframe with export_2019 (full outer join on county as key)
result = pd.merge(df, export_2019, on='country', how='outer')
# Reindexing columns
result = result.reindex(columns=['article_name', 'country', 'region', 'revision_id', 'article_quality', 'population'])
# replacing -1 (initially meant for no prediction available with empty string)
result = result.replace('-1', '')
result
# +
# Filtering out rows that have NaN values after merging
# https://www.kite.com/python/answers/how-to-find-rows-with-nan-values-in-a-pandas-dataframe-in-python
is_NaN = result.isnull()
row_has_NaN = is_NaN.any(axis=1)
rows_with_NaN = result[row_has_NaN]
# Saving rows with NaN to "result/countries-no_match.csv"
mkdir_p('result')
rows_with_NaN.to_csv(r"result/countries-no_match.csv", sep=";", index = True, header = True)
# -
# Consolidate the remaining data into a single CSV file called "result/politicians_by_country.csv"
result = result.dropna()
result.to_csv(r"result/politicians_by_country.csv", sep=";", index=True, header=True)
result
#
# ## Step 3⃣ | Analysis
#
# Your analysis will consist of calculating the proportion (as a percentage) of articles-per-population (we can also call it `coverage`) and high-quality articles (we can also call it `relative-quality`)for **each country** and for **each region**. By `"high quality"` arcticle we mean an article that ORES predicted as `FA` (featured article) or `GA` (good article).
#
# **Examples:**
#
# * if a country has a population of `10,000` people, and you found `10` articles about politicians from that country, then the percentage of `articles-per-population` would be `0.1%`.
# * if a country has `10` articles about politicians, and `2` of them are `FA` or `GA` class articles, then the percentage of `high-quality-articles` would be `20%`.
# ### Results format
#
# The results from this analysis are six `data tables`. Embed these tables in the Jupyter notebook. You do not need to graph or otherwise visualize the data for this assignment. The tables will show:
#
# 1. **Top 10 countries by coverage**<br>10 highest-ranked countries in terms of number of politician articles as a proportion of country population
# 1. **Bottom 10 countries by coverage**<br>10 lowest-ranked countries in terms of number of politician articles as a proportion of country population
# 1. **Top 10 countries by relative quality**<br>10 highest-ranked countries in terms of the relative proportion of politician articles that are of GA and FA-quality
# 1. **Bottom 10 countries by relative quality**<br>10 lowest-ranked countries in terms of the relative proportion of politician articles that are of GA and FA-quality
# 1. **Regions by coverage**<br>Ranking of regions (in descending order) in terms of the total count of politician articles from countries in each region as a proportion of total regional population
# 1. **Regions by coverage**<br>Ranking of regions (in descending order) in terms of the relative proportion of politician articles from countries in each region that are of GA and FA-quality
#
# **❗Hint:** You will find what country belongs to which region (e.g. `ASIA`) also in `export_2019.csv`. You need to calculate the total poulation per region. For that you could use `groupby` and also check out `apply`.
# # Results of analysis
#
# In order to analyse the resulting dataset, the following functions needed for computation are defined:
# +
# Parse CSV
data_table = pd.read_csv("result/politicians_by_country.csv", sep=";", index_col=0)
def get_country_population(country):
"""
returns a country's population in Millions
"""
return float(data_table.loc[data_table['country'] == str(country)]["population"].head(1))
def get_region_population(region):
"""
returns the summed population of a given region by adding all country's population in this region
"""
region_populations = export_2019.groupby('region').sum()
dictionary = region_populations.to_dict()
dictionary = dictionary['population']
return dictionary[str(region).upper()]
def get_article_num(region):
"""
returns the number of articles by a given region
"""
data = data_table[['article_name','region']].groupby('region').count().to_dict()['article_name']
return data[str(region).upper()]
def get_hq_article_num(region):
"""
returns the number of good articles (GA+FA) by given region
"""
def get_number_of_articles(country):
"""
returns the number of articles grouped by country
"""
return (data_table.groupby(['country']).size())[str(country)]
def get_number_of_hq_articles(country):
"""
returns the number of high quality articles grouped by country
"""
try:
result = (data_table.loc[data_table['article_quality'].isin(["GA", "FA"])].groupby(['country']).size()[str(country)])
except:
result = 0
# This literally took me forever to write, but it somehow works
return result
def coverage(number_of_articles, country_population):
"""
returns the coverage as the proportion (as a percentage) of articles-per-population
"""
return (country_population/number_of_articles)*100
def relative_quality(number_of_hq_articles, number_of_articles):
"""
returns the relative_quality as the proportion (as a percentage) of high-quality articles
"""
return (number_of_hq_articles/number_of_articles)*100
# Test functions
#get_country_population("Germany")
#get_number_of_articles("Germany")
#coverage(get_number_of_articles("Germany"), get_country_population("Germany"))
countrys = data_table["country"].unique()
regions = data_table["region"].unique()
region_country = data_table.groupby('region').count()
# Compute coverage for each country
coverages = {}
for country in countrys:
coverages[country] = coverage(get_number_of_articles(country), get_country_population(country))
# Compute relative quality for each country
rq = {}
for country in countrys:
try:
rq[country] = relative_quality(get_number_of_hq_articles(country), get_number_of_articles(country))
except KeyError:
pass
# -
# 1. **Top 10 countries by coverage**<br>10 highest-ranked countries in terms of number of politician articles as a proportion of country population
#
# **Note: Ok, so a coverage of 3.935% does not make sense to me, but I figured out, that not every value given in the export_2019.csv represents the actual population of each country (e.g. Montenegro has a value of 622 (that would mean 622 Million), but should instead have a population of 0.622)**
coverage = pd.DataFrame(data=coverages, index=[0])
coverage = coverage.transpose()
coverage.columns = ['coverage']
dt1 = coverage.sort_values(['coverage'],ascending=False)
dt1.head(10)
# 2. **Bottom 10 countries by coverage**<br>10 lowest-ranked countries in terms of number of politician articles as a proportion of country population
dt2 = dt1.copy()
dt2 = dt2.tail(10)
dt2.iloc[::-1]
# 3. **Top 10 countries by relative quality**<br>10 highest-ranked countries in terms of the relative proportion of politician articles that are of GA and FA-quality
dt3 = pd.DataFrame(data=rq, index=[0])
dt3 = dt3.transpose()
dt3.columns = ['relative_quality']
dt3 = dt3.sort_values(['relative_quality'], ascending=False)
dt3.head(10)
# 4. **Bottom 10 countries by relative quality**<br>10 lowest-ranked countries in terms of the relative proportion of politician articles that are of GA and FA-quality
dt4 = dt3.copy()
dt4 = dt4.sort_values(['relative_quality'], ascending=True)
dt4.head(10)
# 5. **Regions by coverage**<br>Ranking of regions (in descending order) in terms of the total count of politician articles from countries in each region as a proportion of total regional population
# +
# not sure if im doing the right thing here, but I'll calculate the following:
# proportion = number of articles / total regional population
dt5 = pd.DataFrame(columns = ['region'], index=[1,2,3,4,5,6])
dt5['region'] = regions
dt5['proportion'] = dt5['region'].apply(lambda x: get_article_num(str(x))/get_region_population(str(x)))
dt5 = dt5.set_index('region')
dt5 = dt5.sort_values(['proportion'], ascending = False)
dt5
# -
# 6. **Regions by coverage**<br>Ranking of regions (in descending order) in terms of the relative proportion of politician articles from countries in each region that are of GA and FA-quality
# +
# calculating: number of good articles by region / regions population
def proportion(x,y):
return x/y
data = data_table.groupby(['region','country']).sum()
data['number of good articles'] = ""
data = data.reset_index()
data['number of good articles'] = data['country'].apply(lambda x: get_number_of_hq_articles(str(x)))
good_articles_by_region = data[['region', 'number of good articles']].groupby('region').sum()
good_articles_by_region = good_articles_by_region.reset_index()
good_articles_by_region['population'] = good_articles_by_region['region'].apply(lambda x: get_region_population(x))
good_articles_by_region['proportion'] = good_articles_by_region['number of good articles']/good_articles_by_region['population']
dt6 = good_articles_by_region.groupby('region').sum()
dt6 = dt6.sort_values('proportion', ascending = False)
dt6.drop(['number of good articles', 'population'], axis = 1)
# Sorted by proportion:
# -
# ***
#
# #### Credits
#
# This exercise is slighty adapted from the course [Human Centered Data Science (Fall 2019)](https://wiki.communitydata.science/Human_Centered_Data_Science_(Fall_2019)) of [Univeristy of Washington](https://www.washington.edu/datasciencemasters/) by [<NAME>](https://wiki.communitydata.science/User:Jtmorgan).
#
# Same as the original inventors, we release the notebooks under the [Creative Commons Attribution license (CC BY 4.0)](https://creativecommons.org/licenses/by/4.0/).
|
A3_Wikipedia_ORES_Bias.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:keras] *
# language: python
# name: conda-env-keras-py
# ---
# +
import os
os.environ['CUDA_VISIBLE_DEVICES'] = '2'
from utils.utils_cpp import cpp_predictor
from utils.utils_cpp import cpp_generator
from utils.utils_cpp import cpp_optimizer
from utils.utils_common.activator import Activation
# -
# #### Filepaths
# *_DATA_PATH : For datasets, to be used when training and sampling <br>
# *_MODEL_PATH : For models, to be used when training to save the model, otherwise to load pre-trained models <br>
# PREDICTOR_STATS_PATH : To save/load statistics for predictor training dataset <br>
#
# SEQ_MAX : Maximum sequence length for predictor <br>
# SEED_SEQ_LENGTH : Seed sequence length for generator <br>
#
# SMILES_PATH : SMILES for monomers <br>
# FP_RADIUS : Radius of topological exploration for fingerprint <br>
# FP_BITS : Size of fingerprint bit-vector
# +
GENERATOR_DATA_PATH = './dataset/data_cpp/cpp_generator_dataset.txt'
GENERATOR_MODEL_PATH = './model/model_cpp/cpp_generator.hdf5'
SEED_SEQ_LENGTH = 10
PREDICTOR_DATA_PATH = './dataset/data_cpp/cpp_predictor_dataset.csv'
PREDICTOR_MODEL_PATH = './model/model_cpp/cpp_predictor.hdf5'
PREDICTOR_STATS_PATH = './dataset/data_cpp/cpp_predictor_dataset_stats.json'
SMILES_PATH = './dataset/data_cpp/cpp_smiles.json'
FP_RADIUS = 3
FP_BITS = 1024
SEQ_MAX = 108
# -
# #### Generator
# Creating an instance for Generator class with the dataset. <br>
# Training and saving the generator
# +
generator = cpp_generator.Generator(data_path = GENERATOR_DATA_PATH, seq_length = SEED_SEQ_LENGTH)
generator.train_model(
model_params = {
'save_checkpoint': True,
'checkpoint_filepath': './model/'
}
)
# -
# #### Predictor
# Creating an instance for Predictor class with the dataset and other parameters. <br>
# Training and saving the predictor
# +
predictor = cpp_predictor.Predictor(
data_path = PREDICTOR_DATA_PATH,
smiles_path = SMILES_PATH,
fp_radius = FP_RADIUS,
fp_bits = FP_BITS,
seq_max = SEQ_MAX
)
predictor.train_model(
model_params = {
'save_checkpoint': True,
'checkpoint_filepath': './model/'
}
)
# -
# #### Optimizer
# Creating an instance for Optimizer class with the pre-trained models and data files. <br>
# Sampling sequences using a pre-trained generator to seed the genetic algorithm. <br>
# Optimizing the seed sequences.
optimizer = cpp_optimizer.Optimizer(
model_path = PREDICTOR_MODEL_PATH,
data_path = PREDICTOR_DATA_PATH,
smiles_path = SMILES_PATH,
stats_path = PREDICTOR_STATS_PATH,
fp_radius = FP_RADIUS,
fp_bits = FP_BITS,
seq_max = SEQ_MAX
)
generator = cpp_generator.Generator(
model_path = GENERATOR_MODEL_PATH,
data_path = GENERATOR_DATA_PATH,
seq_length = SEED_SEQ_LENGTH
)
list_seeds = generator.generate_seed(n_seeds = 2, seed_length = 30)
df = optimizer.optimize(list_seeds)
df.head(2)
# #### Activation Analysis
# Visualizing the gradient activation of peptide sequence (ex. penetratin) based on pre-trained predictor.
# +
activator = Activation(
mode = 'cpp',
model_path = PREDICTOR_MODEL_PATH,
smiles_path = SMILES_PATH,
stats_path = PREDICTOR_STATS_PATH,
fp_radius = FP_RADIUS,
fp_bits = FP_BITS,
seq_max = SEQ_MAX
)
activator.analyze('RQIKIWFQNRRMKWKK')
# -
|
Tutorial_CPP.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Pandas - Missing Data
import numpy as np
import pandas as pd
d = {'A':[1,2, np.nan], 'B':[5,np.nan,np.nan], 'C':[1,2,3]}
df = pd.DataFrame(d)
df
# ### Drop NA - If you only have a few missing we could just drop those
df.dropna() # This happens on axis 0 or the rowS.
df.dropna(axis=1) # Drops columns with NA
df.dropna(thresh=2) # Drop rows only that meet the threshold
# ### FillNA - Fill in missing values
# Fill with a hard coded value
df.fillna(value='FILL VALUE')
# We can also fill with the mean of the column itself
df['A'].fillna(value=df['A'].mean())
|
python-datasci-bootcamp/03-Python-for-Data-Analysis-Pandas/t_missing_data_pandas.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: python3
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Import/Load Data
# +
import tensorflow as tf
import numpy as np
# Load dataset
training_data = "iris_training.csv"
testing_data = "iris_test.csv"
training_set = tf.contrib.learn.datasets.base.load_csv_with_header(filename=training_data,
features_dtype=np.float32,
target_dtype=np.int)
test_set = tf.contrib.learn.datasets.base.load_csv_with_header(filename=testing_data,
features_dtype=np.float32,
target_dtype=np.int)
# -
feature_name = "iris_features"
feature_columns = [tf.feature_column.numeric_column(feature_name, shape=[4])]
# ### Input Functions
def input_fn(data):
features = {feature_name: tf.constant(data.data)}
label = tf.constant(data.target)
return features, label
# + inputHidden=false outputHidden=false
train_input = lambda: input_fn(training_set)
eval_input = lambda: input_fn(test_set)
# -
# ### Training w/ Linear Classifier
classifier = tf.estimator.LinearClassifier(
feature_columns=feature_columns,
n_classes=3,
model_dir="tmp/iris")
# + inputHidden=false outputHidden=false
# define training, eval spec for train and evaluate including
train_spec = tf.estimator.TrainSpec(train_input,
max_steps=3000
)
eval_spec = tf.estimator.EvalSpec(eval_input,
name='mnist-eval'
)
# run training and evaluation
tf.estimator.train_and_evaluate(
classifier, train_spec, eval_spec)
# -
# ### Training w/ Deep Neural Network Estimator
nn_classifier = tf.estimator.DNNClassifier(
feature_columns=feature_columns,
hidden_units=[8, 4],
activation_fn=tf.nn.relu,
dropout=0.1,
n_classes=3,
model_dir="tmp/irisnn")
# + inputHidden=false outputHidden=false
# define training, eval spec for train and evaluate including
train_spec = tf.estimator.TrainSpec(train_input,
max_steps=20000
)
eval_spec = tf.estimator.EvalSpec(eval_input,
name='mnist-eval'
)
# run training and evaluation
tf.estimator.train_and_evaluate(
nn_classifier, train_spec, eval_spec)
# -
# ### Serving function and exporter
# + inputHidden=false outputHidden=false
feature_spec = {feature_name:
tf.FixedLenFeature(shape=[4], dtype=np.float32)}
serving_fn = tf.estimator.export.build_parsing_serving_input_receiver_fn(feature_spec)
exporter = tf.estimator.LatestExporter('exporter',serving_fn)
eval_spec = tf.estimator.EvalSpec(eval_input,
name='mnist-eval',
exporters=[exporter]
)
# -
# ### Re-run and export model
# run training and evaluation
tf.estimator.train_and_evaluate(
nn_classifier, train_spec, eval_spec)
# ### Export Model for Prediction
# +
new_samples = np.array(
[[6.4, 3.2, 4.5, 1.5],
[5.8, 3.1, 5.0, 1.7]], dtype=np.float32)
predict_input_fn = tf.estimator.inputs.numpy_input_fn(
x={feature_name: new_samples},
num_epochs=1,
shuffle=False)
predictions = list(nn_classifier.predict(input_fn=predict_input_fn))
predicted_classes = [int(p['classes']) for p in predictions]
print("New Samples, Class Predictions: {}\n".format(predicted_classes))
# +
token_sequence = sequence_categorical_column_with_hash_bucket(...)
token_emb = embedding_column(categorical_column=token_sequence, ...)
estimator = RNNEstimator(
head=tf.contrib.estimator.regression_head(),
sequence_feature_columns=[token_emb],
num_units=[32, 16], cell_type='lstm')
# Or with custom RNN cell:
def rnn_cell_fn(mode):
cells = [ tf.contrib.rnn.LSTMCell(size) for size in [32, 16] ]
if mode == tf.estimator.ModeKeys.TRAIN:
cells = [ tf.contrib.rnn.DropoutWrapper(cell, input_keep_prob=0.5)
for cell in cells ]
return tf.contrib.rnn.MultiRNNCell(cells)
estimator = RNNEstimator(
head=tf.contrib.estimator.regression_head(),
sequence_feature_columns=[token_emb],
rnn_cell_fn=rnn_cell_fn)
# Input builders
def input_fn_train: # returns x, y
pass
estimator.train(input_fn=input_fn_train, steps=100)
def input_fn_eval: # returns x, y
pass
metrics = estimator.evaluate(input_fn=input_fn_eval, steps=10)
def input_fn_predict: # returns x, None
pass
predictions = estimator.predict(input_fn=input_fn_predict)
token_sequence = sequence_categorical_column_with_hash_bucket(...)
token_emb = embedding_column(categorical_column=token_sequence, ...)
estimator = RNNClassifier(
sequence_feature_columns=[token_emb],
num_units=[32, 16], cell_type='lstm')
# Input builders
def input_fn_train: # returns x, y
pass
estimator.train(input_fn=input_fn_train, steps=100)
def input_fn_eval: # returns x, y
pass
metrics = estimator.evaluate(input_fn=input_fn_eval, steps=10)
def input_fn_predict: # returns x, None
pass
predictions = estimator.predict(input_fn=input_fn_predict)
# + outputHidden=false inputHidden=false
|
3. Distributed Deep Learning with TensorFlow and Google ML Engine/2. dive into estimators/tensorflow_estimators.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# +
# %load_ext autoreload
# %autoreload 2
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:100% !important; }</style>"))
# -
import torch
import torchvision
torch.__version__, torchvision.__version__
from pathlib import Path
DATA_PATH = Path("../../data/tensorflow-great-barrier-reef/")
# +
from itertools import groupby
import numpy as np
from tqdm.notebook import tqdm
tqdm.pandas()
import pandas as pd
import os
from multiprocessing import Pool
import matplotlib.pyplot as plt
# import cupy as cp
import ast
import shutil
import sys
sys.path.append(DATA_PATH)
sys.path.append("../src/")
import util
from joblib import Parallel, delayed
from IPython.display import display, HTML
from matplotlib import animation, rc
rc('animation', html='jshtml')
# -
# # Key Points
# 1. One have to submit prediction using the provided python time-series API, which makes this competition different from previous Object Detection Competitions.
# 2. Each prediction row needs to include all bounding boxes for the image. Submission is format seems also COCO which means [x_min, y_min, width, height]
# 3. Copmetition metric F2 tolerates some false positives(FP) in order to ensure very few starfish are missed. Which means tackling false negatives(FN) is more important than false positives(FP).
FOLD = 4 # which fold to train
REMOVE_NOBBOX = True # remove images with no bbox
ROOT_DIR = DATA_PATH
IMAGE_DIR = DATA_PATH / "images" # directory to save images
LABEL_DIR = DATA_PATH / "labels" # directory to save labels
# !mkdir -p {IMAGE_DIR}
# !mkdir -p {LABEL_DIR}
def get_path(row):
row['old_image_path'] = f'{ROOT_DIR}/train_images/video_{row.video_id}/{row.video_frame}.jpg'
row['image_path'] = f'{IMAGE_DIR}/video_{row.video_id}_{row.video_frame}.jpg'
row['label_path'] = f'{LABEL_DIR}/video_{row.video_id}_{row.video_frame}.txt'
return row
# Train Data
df = pd.read_csv(f'{ROOT_DIR}/train.csv')
df = df.progress_apply(get_path, axis=1)
df['annotations'] = df['annotations'].progress_apply(lambda x: ast.literal_eval(x))
display(df.head(2))
df['num_bbox'] = df['annotations'].progress_apply(lambda x: len(x))
data = (df.num_bbox>0).value_counts(normalize=True)*100
print(f"No BBox: {data[0]:0.2f}% | With BBox: {data[1]:0.2f}%")
df.head()
df.groupby("video_id")["sequence"].unique().apply(len)
df.groupby("sequence").size()
np.all(df.groupby("sequence")["sequence_frame"].max() == (df.groupby("sequence").size() - 1))
df.groupby("video_id")["video_frame"].max()
# # Clean Data
if REMOVE_NOBBOX:
df = df.query("num_bbox>0")
# # Write Images
def make_copy(path):
data = path.split('/')
filename = data[-1]
video_id = data[-2]
new_path = os.path.join(IMAGE_DIR,f'{video_id}_{filename}')
shutil.copy(path, new_path)
return
image_paths = df.old_image_path.tolist()
_ = Parallel(n_jobs=-1, backend='threading')(delayed(make_copy)(path) for path in tqdm(image_paths))
np.random.seed(32)
colors = [(np.random.randint(255),
np.random.randint(255),
np.random.randint(255))\
for idx in range(1)]
# # Create BBox
df['bboxes'] = df.annotations.progress_apply(util.get_bbox)
df.head(2)
df['width'] = 1280
df['height'] = 720
# # Create YOLO Format
cnt = 0
all_bboxes = []
for row_idx in tqdm(range(df.shape[0])):
row = df.iloc[row_idx]
image_height = row.height
image_width = row.width
bboxes_coco = np.array(row.bboxes).astype(np.float32).copy()
num_bbox = len(bboxes_coco)
names = ['cots']*num_bbox
labels = [0]*num_bbox
## Create Annotation(YOLO)
with open(row.label_path, 'w') as f:
if num_bbox<1:
annot = ''
f.write(annot)
cnt+=1
continue
bboxes_yolo = util.coco2yolo(image_height, image_width, bboxes_coco)
bboxes_yolo = np.clip(bboxes_yolo, 0, 1)
all_bboxes.extend(bboxes_yolo)
for bbox_idx in range(len(bboxes_yolo)):
annot = [str(labels[bbox_idx])]+ list(bboxes_yolo[bbox_idx].astype(str))+(['\n'] if num_bbox!=(bbox_idx+1) else [''])
annot = ' '.join(annot)
annot = annot.strip(' ')
f.write(annot)
print('Missing:',cnt)
# # BBox Distribution
# +
from scipy.stats import gaussian_kde
all_bboxes = np.array(all_bboxes)
x_val = all_bboxes[...,0]
y_val = all_bboxes[...,1]
# Calculate the point density
xy = np.vstack([x_val,y_val])
z = gaussian_kde(xy)(xy)
fig, ax = plt.subplots(figsize = (10, 10))
ax.scatter(x_val, y_val, c=z, s=100, cmap='viridis')
ax.set_xlabel('x_mid')
ax.set_ylabel('y_mid')
plt.show()
# +
x_val = all_bboxes[...,2]
y_val = all_bboxes[...,3]
# Calculate the point density
xy = np.vstack([x_val,y_val])
z = gaussian_kde(xy)(xy)
fig, ax = plt.subplots(figsize = (10, 10))
ax.scatter(x_val, y_val, c=z, s=100, cmap='viridis')
ax.set_xlabel('bbox_width')
ax.set_ylabel('bbox_height')
plt.show()
# -
import seaborn as sns
sns.set(style='white')
areas = all_bboxes[...,2]*all_bboxes[...,3]*720*1280
plt.figure(figsize=(12,8))
sns.kdeplot(areas,shade=True,palette='viridis')
plt.show()
# # Visualization
df2 = df[(df.num_bbox>0)].sample(100) # takes samples with bbox
for seq in df.sequence.unique()[:2]:
seq_df = df.query("sequence==@seq")
images = []
for _, row in tqdm(seq_df.iterrows(), total=len(seq_df), desc=f'seq_id-{seq} '):
img = util.load_image(row.image_path)
image_height = row.height
image_width = row.width
bboxes_coco = np.array(row.bboxes)
bboxes_yolo = util.coco2yolo(image_height, image_width, bboxes_coco)
names = ['cots']*len(bboxes_coco)
labels = [0]*len(bboxes_coco)
img = util.draw_bboxes(img = img,
bboxes = bboxes_yolo,
classes = names,
class_ids = labels,
class_name = True,
colors = colors,
bbox_format = 'yolo',
line_thickness = 2)
images.append(img)
display(HTML(f"<h2>Sequence ID: {seq}</h2>"))
display(util.create_animation(images))
# # CV
from sklearn.model_selection import GroupKFold
kf = GroupKFold(n_splits = 5)
df = df.reset_index(drop=True)
df['fold'] = -1
for fold, (train_idx, val_idx) in enumerate(kf.split(df, y = df.video_id.tolist(), groups=df.sequence)):
df.loc[val_idx, 'fold'] = fold
display(df.fold.value_counts())
# # Dataset
train_files = []
val_files = []
train_df = df.query(f"fold!={FOLD}")
valid_df = df.query(f"fold=={FOLD}")
train_files += list(train_df.image_path.unique())
val_files += list(valid_df.image_path.unique())
len(train_files), len(val_files)
# # Configuration
#
# The dataset config file requires
#
# 1. The dataset root directory path and relative paths to train / val / test image directories (or *.txt files with image paths)
# 2. The number of classes **nc** and
# 3. A list of class names:['cots']
# +
import yaml
cwd = os.path.abspath("../config/test/")
if not os.path.exists(cwd):
os.makedirs(cwd)
with open(os.path.join( cwd , 'train.txt'), 'w') as f:
for path in train_df.image_path.tolist():
f.write(path+'\n')
with open(os.path.join(cwd , 'val.txt'), 'w') as f:
for path in valid_df.image_path.tolist():
f.write(path+'\n')
data = dict(
path = cwd,
train = os.path.join( cwd , 'train.txt') ,
val = os.path.join( cwd , 'val.txt' ),
nc = 1,
names = ['cots'],
)
with open(os.path.join( cwd , 'bgr.yaml'), 'w') as outfile:
yaml.dump(data, outfile, default_flow_style=False)
f = open(os.path.join( cwd , 'bgr.yaml'), 'r')
print('\nyaml:')
print(f.read())
# -
sys.path.append("./yolov5")
import utils as yolo_utils
display = yolo_utils.notebook_init()
# # Training
# !python3 ./yolov5/train.py --img 1280\
# --batch 16\
# --epochs 20\
# --data /home/vincent/Kaggle/Kaggle_TGBR/config/test/bgr.yaml\
# --weights yolov5s.pt\
# --workers 10\
# --name yolov5s_fold4
# # Class Distribution
RUN_PATH = Path("./yolov5/runs/train/exp2/")
plt.figure(figsize = (10,10))
plt.axis('off')
plt.imshow(plt.imread(RUN_PATH / 'labels_correlogram.jpg'));
plt.figure(figsize = (10,10))
plt.axis('off')
plt.imshow(plt.imread(RUN_PATH / 'labels.jpg'));
# # Batch Image
# +
import matplotlib.pyplot as plt
plt.figure(figsize = (10, 10))
plt.imshow(plt.imread(RUN_PATH / 'train_batch0.jpg'))
plt.figure(figsize = (10, 10))
plt.imshow(plt.imread(RUN_PATH / 'train_batch1.jpg'))
plt.figure(figsize = (10, 10))
plt.imshow(plt.imread(RUN_PATH / 'train_batch2.jpg'))
# -
# # GT Vs Pred
fig, ax = plt.subplots(3, 2, figsize = (2*9,3*5), constrained_layout = True)
for row in range(3):
ax[row][0].imshow(plt.imread(RUN_PATH / f'val_batch{row}_labels.jpg'))
ax[row][0].set_xticks([])
ax[row][0].set_yticks([])
ax[row][0].set_title(RUN_PATH / f'val_batch{row}_labels.jpg', fontsize = 12)
ax[row][1].imshow(plt.imread(RUN_PATH / f'val_batch{row}_pred.jpg'))
ax[row][1].set_xticks([])
ax[row][1].set_yticks([])
ax[row][1].set_title(RUN_PATH / f'val_batch{row}_pred.jpg', fontsize = 12)
plt.show()
# # Result
# ## Scores VS Epoch
plt.figure(figsize=(30,15))
plt.axis('off')
plt.imshow(plt.imread(RUN_PATH / 'results.png'));
# ## Confusion Matrix
plt.figure(figsize=(12,10))
plt.axis('off')
plt.imshow(plt.imread(RUN_PATH / 'confusion_matrix.png'));
# ## Metrics
for metric in ['F1', 'PR', 'P', 'R']:
print(f'Metric: {metric}')
plt.figure(figsize=(12,10))
plt.axis('off')
plt.imshow(plt.imread(RUN_PATH / f'{metric}_curve.png'));
plt.show()
# !rm -r {IMAGE_DIR}
# !rm -r {LABEL_DIR}
|
notebook/train.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import sqlite3
import pandas as pd
conn = sqlite3.connect('file_name.db')
pd.read_sql('SELECT * FROM population_data', conn)
# -
pd.read_sql('SELECT "Country_Name", "Country_Code", "1960" FROM population_data', conn)
# SQLAlchemy and Pandas
import pandas as pd
from sqlalchemy import create_engie
import os
engine = create_engine('sqlite:////home/workspace/3_sql_exce.db')
pd.read_sql("SELECT * FROM population_data", engine)
import pandas as pd
import os
form sqlalchemy import create_engine
engine = create_engine('sqlite:////home/workspace/3_sql_read.db')
pd.read_sql('SELECT "1961" - "1960" FROM population_data WHERE Country_Name="Aruba"', engine)
pd.read_sql('SELECT "Country_Name","1975" FROM population_data WHERE Country_Name = "Belgium" OR Country_Name=""')
|
ETL2/Notebooks/.ipynb_checkpoints/SQL excersice-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# https://colab.research.google.com/github/kassbohm/tm-snippets/blob/master/ipynb/TM_A/TM_3/lie.ipynb
from sympy import *
from sympy.physics.units import *
t, l = var("t, l")
pprint("\nt=0 s:")
sub_list = [(t, 0*second),]
# pprint("\nt=15 s:")
# sub_list = [(t, 15*second),]
tt = t / (60 * second)
p = 2 * pi * tt
l = 10*cm *(1 + tt)
C, S = cos(p), sin(p)
R = Matrix([
[C, -S, 0],
[S, C, 0],
[0, 0, 1]
])
vx, vy, vz = l*C, l*S, 0
pprint("\n(v'x, v'y, v'z) / (cm/s):")
v = Matrix([vx, vy, vz])
tmp = diff(v, t)
tmp = tmp.subs(sub_list)
tmp /= cm/second
pprint(tmp)
pprint("\n(v'x̄, v'ȳ, v'z̄)")
v = Matrix([l, 0, 0])
w = Matrix([0, 0, diff(p, t)])
tmp = diff(v, t) + w.cross(v)
tmp = tmp.subs(sub_list)
tmp /= cm/second
pprint(tmp)
pprint("\nCheck: (v'x, v'y, v'z) / (cm/s):")
tmp = diff(v, t) + w.cross(v)
tmp = R*tmp
tmp = tmp.subs(sub_list)
tmp /= cm/second
pprint(tmp)
# t=0 s:
#
# (v'x, v'y, v'z) / (cm/s):
# ⎡1/6⎤
# ⎢ ⎥
# ⎢ π ⎥
# ⎢ ─ ⎥
# ⎢ 3 ⎥
# ⎢ ⎥
# ⎣ 0 ⎦
#
# (v'x̄, v'ȳ, v'z̄)
# ⎡1/6⎤
# ⎢ ⎥
# ⎢ π ⎥
# ⎢ ─ ⎥
# ⎢ 3 ⎥
# ⎢ ⎥
# ⎣ 0 ⎦
#
# Check: (v'x, v'y, v'z) / (cm/s):
# ⎡1/6⎤
# ⎢ ⎥
# ⎢ π ⎥
# ⎢ ─ ⎥
# ⎢ 3 ⎥
# ⎢ ⎥
# ⎣ 0 ⎦
|
ipynb/TM_A/TM_3/lie.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="LmSNbYh44rN2" colab_type="text"
# ***Import Required Libraries***
# + id="pYyrnLZ5M6RY" colab_type="code" outputId="47a78cc8-5457-4f65-db08-90f0a7fa6cc2" colab={"base_uri": "https://localhost:8080/", "height": 79}
import numpy as np
import struct
from sklearn.decomposition import PCA
from keras.datasets import mnist
# + [markdown] id="Kqm0Hq8Ty1O5" colab_type="text"
# ***Load data***
#
# Although we can find MNIST dataset from <NAME>un's official site, I chose a more convenient way to find the dataset from Keras.
# Also, from the code below, we can show that the MNIST database contains 60,000 training and 10,000 testing images, which have $28\times28$ pixels with only greyscale.
# + id="WnifVp2KNDGi" colab_type="code" outputId="f1ad99aa-e87e-442a-a81f-f18d4ee549d6" colab={"base_uri": "https://localhost:8080/", "height": 101}
(train_data_ori, train_label), (test_data_ori, test_label) = mnist.load_data()
print ("mnist data loaded")
print ("original training data shape:",train_data_ori.shape)
print ("original testing data shape:",test_data_ori.shape)
# + [markdown] id="Xk1TTt_m7UrD" colab_type="text"
# For the convenience of training, linearize each image from $28\times28$ into an array of size $1\times784$, so that the training and test datasets are converted into 2-dimensional vectors of size $60000\times784$ and $10000\times784$, respectively.
# + id="Q6OWqBntQgn1" colab_type="code" outputId="ed51f7af-3295-4831-e92b-7da54810f35d" colab={"base_uri": "https://localhost:8080/", "height": 50}
train_data=train_data_ori.reshape(60000,784)
test_data=test_data_ori.reshape(10000,784)
print ("training data shape after reshape:",train_data.shape)
print ("testing data shape after reshape:",test_data.shape)
# + [markdown] id="kVv6r27Q9ztu" colab_type="text"
# ***Dimension Reduction using PCA***
#
# For this case, the pixels of the image will be the features used to build our predictive model. In this way, implementing KNN clustering is to calculate the norms in a 784-dimensional space.
# However, calculating norms in this 784-dimensional space is far from easy and efficient. Intuitively, we can perform some dimention reduction before going to KNN and calculate those norms, so that we can become more efficient.
# The way to do dimension reduction here is PCA mentioned in the lecture. I don't dig deep into PCA here, and use APIs from sklearn to implement PCA instead. I reduce the feature space from 784 dimensions into 100 dimensions. Talk is cheap, here's the code.
# + id="OkARp-d0f_BZ" colab_type="code" outputId="7919fdc6-0210-4e47-ddb6-93a2099e4bb0" colab={"base_uri": "https://localhost:8080/", "height": 67}
pca = PCA(n_components = 100)
pca.fit(train_data) #fit PCA with training data instead of the whole dataset
train_data_pca = pca.transform(train_data)
test_data_pca = pca.transform(test_data)
print("PCA completed with 100 components")
print ("training data shape after PCA:",train_data_pca.shape)
print ("testing data shape after PCA:",test_data_pca.shape)
# + [markdown] id="16vjYwp4GZ0S" colab_type="text"
# From the result above, we can know that the training and test datasets become two vectors of size $60000\times100$ and $10000\times100$, respectively.
#
# At this point, the datasets are ready.
# + [markdown] id="7oD2TydRHYS2" colab_type="text"
# ***Code up KNN***
# Here's the code to K Nearest Neighbor clustering algorithm. This function takes in the image to cluster, training dataset, training labels, the value of K and the sort of norm to calculate distance(*i.e.* the value of $p$ in $l_p$ norm).
# Under the most circumstance, we use Euclidean norm to calculate distace, thus $p=2$.
# This function returns the class most common among the test data's K nearest neighbors, where K is the parameter mentioned above.
# + id="XyHqEcjMhzTh" colab_type="code" colab={}
def KNN(test_data1,train_data_pca,train_label,k,p):
subMat = train_data_pca - np.tile(test_data1,(60000,1))
subMat = np.abs(subMat)
distance = subMat**p
distance = np.sum(distance,axis=1)
distance = distance**(1.0/p)
distanceIndex = np.argsort(distance)
classCount = [0,0,0,0,0,0,0,0,0,0]
for i in range(k):
label = train_label[distanceIndex[i]]
classCount[label] = classCount[label] + 1
return np.argmax(classCount)
# + [markdown] id="AgFwAuQLMmCg" colab_type="text"
# ***Define the test function***
# This function takes in the value of K and the value of $p$ in $l_p$ norm mentioned above, and returns the accuracy of KNN clustering on the test dataset, along with the confusion matrix.
# + id="mKtjXPW2Mk1I" colab_type="code" colab={}
def test(k,p):
print("testing with K= %d and lp norm p=%d"%(k,p))
m,n = np.shape(test_data_pca)
correctCount = 0
M = np.zeros((10,10),int)
for i in range(m):
test_data1 = test_data_pca[i,:]
predict_label = KNN(test_data1,train_data_pca,train_label, k, p)
true_label = test_label[i]
M[true_label][predict_label] += 1
# print("predict:%d,true:%d" % (predict_label,true_label))
if true_label == predict_label:
correctCount += 1
print("The accuracy is: %f" % (float(correctCount)/m))
print("Confusion matrix:",M)
# + [markdown] id="brI_nbJGNe1n" colab_type="text"
# ***Test result***
# Here's the precision of the KNN clustering algorithm with argument K=3 and Euclidean norm, along with the confusion matrix.
# + id="pfA40lTnSDKJ" colab_type="code" outputId="416cc113-dbdc-4f02-e03f-3945a7fc524c" colab={"base_uri": "https://localhost:8080/", "height": 218}
test(3,2)
# + [markdown] id="yzd18KY5xDAZ" colab_type="text"
# From the result above, we can show that we achieved the precision of 0.972900, with dimension reduction (using PCA) and KNN clustering.
|
KNN.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#importing the modules
import os
# +
dir_contents = os.listdir()
#printing the contents of dir
print(dir_contents)
# -
#function for checking the presence
def wordCheck(fileName,word):
with open(fileName,'r') as f:
fileContent = f.read()
#Detectinf the word
if word.lower() in fileContent.lower():
return True
else:
return False
def detection():
#for the input of word to be checked in the files
word = input('Enter the word to be scanned: ')
nWordCount = 0
#for detection system
for item in dir_contents:
if item.endswith('txt'):
print(f'\nDetecting {word} in {item} ...')
setFlag = wordCheck(item,word)
if (setFlag):
print(f'=> {word} FOUND in {item}')
nWordCount+=1
else:
print(f'=> {word} NOT FOUND in {item}')
#for printing the summary
print('\n*****PRINTING THE SCANNING SUMMARY*****\n')
print(f'--> {nWordCount} files found containing {word} in them')
#for enterring more choice
choice = input('Do you want to search more?\nyes/no')
#Detection system main
choice = 'yes'
while(choice.lower()=='yes'):
detection()
|
.ipynb_checkpoints/main-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from IPython.core.display import SVG
SVG(filename='svg/voltage_divider.svg')
# Assume no current taken: $i_{out} = 0$
#
# with that assumption: $i_1 = i_2 = i$
#
# And we get:
#
# $V_{in} = (i)(R_t) = i(R_1 + R_2)$
#
# $i = \frac{V_{in}}{R_1 + R_2}$
#
# ---
#
# Let solve another equaiton, for $V_{out}$
#
# $V_{out} = (i)(R_2)$
#
# $i = \frac{V_{out}}{R_2}$
#
# ---
#
# We have `i` in both equations
#
# $i = \frac{V_{in}}{R_1 + R_2}$
#
# $i = \frac{V_{out}}{R_2}$
#
# ---
#
# $\frac{V_{out}}{R_2} = i = \frac{V_{in}}{R_1 + R_2}$
#
# $\frac{V_{out}}{R_2} = \frac{V_{in}}{R_1 + R_2}$
#
# $V_{out} = R_2\frac{V_{in}}{R_1 + R_2}$
#
# ---
#
# $V_{out} = V_{in}\frac{R_2}{R_1 + R_2}$
|
electronic/theory/voltage_divider.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # High-dimensional Bayesian Optimization of CrabNet Hyperparameters
# ###### Created March 5, 2022
#
# 
#
#
# # Description
#
# Use of hyperparameter Bayesian optimization with [CrabNet](https://crabnet.readthedocs.io/) revealed favorable results in
# improving the error over the baseline model; however, only 100 iterations were used to
# optimize 23 hyperparameters with little prior information to make an informed decision
# (for example, the default CrabNet hyperparameters were not available to the
# hyperparameter optimization algorithm). Only the constraints on the hyperparameter
# search space, which were quite generous, would constitute prior information, and 100
# iterations across 23 parameters is a very sparse sampling. Here, we describe the use of
# a relatively new high-dimensional Bayesian optimization algorithm called Sparse
# Axis-Aligned Subspace Bayesian Optimization, or SAASBO.
#
# [facebook/Ax](https://github.com/facebook/Ax) is used as the backend for performing
# SAASBO. For additional files related to this `matbench` submission, see the
# [crabnet-hyperparameter](https://github.com/sparks-baird/crabnet-hyperparameter)
# repository. Due to the procedure being relatively expensive (esp. due to use of
# nested-CV when training CrabNet) and requiring a few days of runtime on two RTX 2080 Ti
# GPUs, this notebook demonstrates how to submit jobs to a high-performance computing
# center (in our case, CHPC @ University of Utah). `submitit` parameters such as `account`
# and `partition` might vary
# somewhat for your own HPC center.
#
# # Benchmark name
# Matbench v0.1
#
# # Package versions
# - matplotlib==3.5.0
# - pandas==1.3.5
# - ax-platform==0.2.3
# - pyro-ppl==1.8.0
# - plotly==5.5.0
# - crabnet==1.2.5
# - scikit-learn==1.0.2
# - submitit==1.4.1
# - matbench==0.5
# - cloudpickle==2.0.0
#
# # Algorithm description
# Recently, SAASBO has been demonstrated to be a highly effect high-dimensional Bayesian
# optimization scheme. Here, we use [Ax/SAASBO Bayesian adaptive design](https://ax.dev/tutorials/saasbo.html) to simultaneously optimize 23
# hyperparameters of
# [CrabNet](https://crabnet.readthedocs.io/). `100` sequential design iterations were used, and parameters were chosen based
# on a combination of intuition and algorithm/data constraints (e.g. elemental featurizers
# which were missing elements contained in the dataset were removed). The first `10`
# iterations were based on SOBOL sampling to create a rough initial model, while the
# remaining `90` iterations were SAASBO Bayesian adaptive design iterations. For the inner
# loops (where hyperparameter optimization is performed), the average MAE across each of
# the *five inner folds* was used as Ax's objective to minimize. The best parameter set
# was then trained on all the inner fold data and used to predict on the test set (unknown
# during hyperparameter optimization). This is nested cross-validation (CV), and is
# computationally expensive. See [automatminer: running a
# benchmark](https://hackingmaterials.lbl.gov/automatminer/advanced.html#running-a-benchmark)
# for more information on nested CV.
#
# # Relevant citations
# - CrabNet: [Wang et al.](https://doi.org/10.1038/s41524-021-00545-1)
# - SAASBO: [Eriksson and Jankowiak](
# https://doi.org/10.48550/arXiv.2103.00349)
#
# # Related Matbench Submissions
# - [`matbench_v0.1_Ax_CrabNet_v1.2.1`](https://github.com/materialsproject/matbench/tree/main/benchmarks/matbench_v0.1_Ax_CrabNet_v1.2.1)
# - [`matbench_v0.1_CrabNet_v1.2.1`](https://github.com/materialsproject/matbench/tree/main/benchmarks/matbench_v0.1_CrabNet_v1.2.1)
# # Imports
# +
# %% imports
# NOTE: `pip install pyro-ppl` to use FULLYBAYESIAN (SAASBO)
from submitit import AutoExecutor
import cloudpickle as pickle
from utils.matbench import matbench_fold, collect_results, task, savepath, dummy
print(f"dummy: {dummy}")
# -
# # Job Submission
# +
# %% submission
log_folder = "log_ax/%j"
walltime = 4320 # 4320 min == 3 days
partition, account = ["notchpeak-gpu", "notchpeak-gpu"]
executor = AutoExecutor(folder=log_folder)
executor.update_parameters(
timeout_min=walltime,
slurm_partition=partition,
slurm_gpus_per_task=1,
slurm_mem_per_gpu=6000,
slurm_cpus_per_gpu=4,
slurm_additional_parameters={"account": account, "mail-type": "ALL", "mail-user": "<EMAIL>"},
)
jobs = executor.map_array(matbench_fold, task.folds) # sbatch array
# used to make it easy to load the jobs later and set up job dependency
job_ids = [job.job_id for job in jobs]
# https://www.hpc2n.umu.se/documentation/batchsystem/job-dependencies
job_ids_str = ":".join(job_ids) # e.g. "3937257_0:3937257_1:..."
with open("jobs.pkl", "wb") as f:
pickle.dump(jobs, f)
# -
# # Collect Results
# +
collect_folder = "log_matbench/%j"
walltime = 10
collector = AutoExecutor(folder=collect_folder)
collector.update_parameters(
timeout_min=walltime,
slurm_partition=partition,
slurm_additional_parameters={
"account": account,
"dependency": f"afterok:{job_ids_str}",
"mail-type": "ALL",
"mail-user": "<EMAIL>",
},
)
collector_job = collector.submit(collect_results) # sbatch array
print(
f"Waiting for submission jobs ({job_ids_str}) to complete before running collector job ({collector_job.job_id}). Use the matbench output file that will be saved to {savepath} after all jobs have run. Email will be sent with a status update by default."
)
|
benchmarks/matbench_v0.1_Ax_SAASBO_CrabNet_v1.2.7/notebook.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Using Python to Debunk COVID Myths: ‘Death Statistic Inflation’
# What is required from Python:
# - Download most recent death and population data from eurostat
# - Format data and only select where NUTS3 includes UK
# - Interpolate weekly population numbers
# - Age standardise
# -
# +
import datetime as dt
import gzip
import io
import numpy as np
import pandas as pd
import requests
import sys
import warnings
# %config Completer.use_jedi = False
warnings.filterwarnings('ignore')
pd.set_option('display.max_rows', 500)
pd.set_option('display.max_columns', 500)
# -
# ## 1. Population Data
# ### 1a. Import, Clean and Munge Raw Data
# +
r = requests.get('https://ec.europa.eu/eurostat/estat-navtree-portlet-prod/BulkDownloadListing?file=data/demo_r_pjangrp3.tsv.gz')
mlz = gzip.open(io.BytesIO(r.content))
df_pop = pd.read_csv(mlz, sep='\t')
# -
# rename and fix id data column
df_pop = df_pop.rename(columns={"sex,unit,age,geo\\time": "Headings"})
# parse to 4 cols
df_pop["Headings"] = df_pop["Headings"].apply(lambda x: x.split(','))
df_pop[['Sex', 'Unit', 'Age', 'Code']] = pd.DataFrame(df_pop.Headings.tolist(), index= df_pop.index)
df_pop = df_pop.drop(columns=['Headings', 'Unit'])
df_pop = df_pop[(df_pop.Sex == 'T') & (~df_pop.Age.isin(['TOTAL', 'UNK']))]
df_pop = df_pop.drop(columns=['Sex'])
df_pop = pd.melt(df_pop, id_vars=['Age', 'Code'], var_name=['Year'], value_vars=['2014 ', '2015 ', '2016 ', '2017 ', '2018 ', '2019 '], value_name='Pop')
# +
# remove iregs from number col (e.g. p means provisional)
num_iregs = [":", "b", "p", "e", " "]
for ireg in num_iregs:
df_pop.Pop = df_pop.Pop.str.replace(ireg, "")
# cast to numeric
num_cols = ['Pop', 'Year']
for col in num_cols:
df_pop[col] = pd.to_numeric(df_pop[col])
print('We have {:,.0f} observations for annual data by NUTS3 and age group breakdown'.format(len(df_pop)))
df_pop.head()
# -
# give country code to help with chunking
df_pop['Country_Code'] = df_pop.Code.str[:2]
df_pop = pd.merge(left=df_pop, right=df_nuts, on='Code', how='left')
df_pop = df_pop[df_pop.Country == 'United Kingdom']
# ### 1b. Create Liner Interp for 2020 and 2021
# +
# add 2020, 2021 data with NAN for pop to be linearly interpolated forward
df_pop_new = df_pop[['Age', 'Code', 'Country_Code']].drop_duplicates()
df_pop_new['Pop'] = np.nan
df_pop_new['Year'] = 2020
df_pop = pd.concat([df_pop, df_pop_new])
df_pop_new['Year'] = 2021
df_pop = pd.concat([df_pop, df_pop_new])
# -
# just to prove we have a complete data set
df_pop[['Year', 'Code']].groupby('Year').count()
# linear interp 2019 population by group for 2020 and 2021
df_pop = df_pop.sort_values(['Code', 'Age', 'Year'])
df_pop = df_pop.reset_index(drop=True)
df_pop['Pop'] = df_pop['Pop'].ffill()
|
notebooks/drafts/Using Python to Debunk COVID Myths Death Statistic Inflation-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
import zen
import numpy as np
import matplotlib.pyplot as plt
def modularity(G,classDict,classList):
Q = zen.algorithms.modularity(G,classDict)
# Maximum Modularity
count=0.0
for e in G.edges():
n1 = G.node_idx(e[0])
n2 = G.node_idx(e[1])
if classList[n1] == classList[n2]:
count += 1
same = count / G.num_edges
rand = same - Q
qmax = 1 - rand
return Q, qmax
def katz(G,tol=0.01,max_iter=1000,alpha=0.001,beta=1):
iteration = 0
centrality = np.zeros(G.num_nodes)
while iteration < max_iter:
iteration += 1 # increment iteration count
centrality_old = centrality.copy()
for node in G.nodes_():
Ax = 0
for neighbor in G.neighbors_(node):
weight = G.weight_(G.edge_idx_(neighbor,node))
Ax += np.multiply(centrality[neighbor],weight)
#Ax += centrality[neighbor] #exclude weight due to overflow in multiplication
centrality[node] = np.multiply(alpha,Ax)+beta
if np.sum(np.abs(np.subtract(centrality,centrality_old))) < tol:
return centrality
G = zen.io.gml.read('amazon_product.gml',weight_fxn=lambda x: x['weight'])
from zen.algorithms.community import spectral_modularity as spm
def spectral_community_detection(G,ke_plot=False):
cset = spm(G)
if ke_plot:
evc = zen.algorithms.eigenvector_centrality_(G)
kc = katz(G,alpha=1e-4)
#scale
evc = evc - np.min(evc)
evc = evc / np.max(evc)
kc = kc - np.min(kc)
kc = kc / np.max(kc)
comm_dict = {}
comm_list = np.zeros(G.num_nodes)
for i,community in enumerate(cset.communities()):
comm_dict[i] = community.nodes()
comm_list[community.nodes_()] = i
if ke_plot:
plt.scatter(evc[community.nodes_()],kc[community.nodes_()],s=3,label='cluster %d'%i)
if ke_plot:
plt.xlabel('Eigenvector Centrality (normalized)')
plt.xlabel('Katz Centrality (normalized)')
plt.legend()
plt.show()
q,qmax = modularity(G,comm_dict,comm_list)
print '%d communities found.'%(i+1)
print 'Q: %.3f'%q
print 'Normalized Q: %.3f'%(q/qmax)
# %%time
spectral_community_detection(G)
|
Spectral.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
## import modules
import pandas as pd
import re
## display output
from IPython.display import display, HTML
## create range b/t start and end date
## of course
start_date = pd.to_datetime("2021-03-29")
end_date = pd.to_datetime("2021-06-02")
st_alldates = pd.date_range(start_date, end_date)
## subset to days in that range equal to Tuesday or Thursday
st_tuth = st_alldates[st_alldates.day_name().isin(['Tuesday', 'Thursday'])]
## create data frame with that information
st_dates = [re.sub("2021\\-", "", str(day.date())) for day in st_tuth]
course_sched = pd.DataFrame({'dow': st_tuth.day_name(), 'st_tuth': st_dates})
course_sched['date_toprint'] = course_sched.dow.astype(str) + " " + \
course_sched.st_tuth.astype(str)
course_sched = course_sched['date_toprint']
## display the resulting date sequence
display(course_sched)
|
mini_book/_build/.jupyter_cache/executed/10fd5320e9b250ac7f57494fd68c1ed8/base.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Funzioni 1 - introduzione
#
# ## [Scarica zip esercizi](../_static/generated/functions.zip)
#
# [Naviga file online](https://github.com/DavidLeoni/softpython-it/tree/master/functions)
#
#
# Una funzione prende dei parametri e li usa per produrre o riportare qualche risultato.
#
# <div class="alert alert-warning">
#
# **ATTENZIONE**
#
# **Questi esercizi sulle funzioni sono integrativi a quelli già indicati nella** [pagina riferimenti](https://it.softpython.org/references.html), in particolare vedere quelli qui sotto.
#
# </div>
#
# **Riferimenti**
#
# - [Pensare in Python, Capitolo 3, Funzioni](https://davidleoni.github.io/ThinkPythonItalian/html/thinkpython2004.html)
# - [Pensare in Python, Capitolo 6, Funzioni produttive](https://davidleoni.github.io/ThinkPythonItalian/html/thinkpython2007.html) puoi fare tutto saltando la parte 6.5 sulla ricorsione.
# **NOTA**: nel libro viene usato il termine strano 'funzioni produttive' per quelle funzioni che ritornano un valore, ed il termine ancora più strano 'funzioni vuote' per funzioni che non ritornano nulla ma fanno qualche effetto tipo stampa a video: ignora e dimentica questi termini !
#
# - [<NAME>, Lezione 4, Funzioni](http://ncassetta.altervista.org/Tutorial_Python/Lezione_04.html)
#
# ## Che fare
#
# - scompatta lo zip in una cartella, dovresti ottenere qualcosa del genere:
#
# ```
# functions
# functions1.ipynb
# functions1-sol.ipynb
# functions2-chal.ipynb
# jupman.py
# ```
#
# <div class="alert alert-warning">
#
# **ATTENZIONE**: Per essere visualizzato correttamente, il file del notebook DEVE essere nella cartella szippata.
# </div>
#
# - apri il Jupyter Notebook da quella cartella. Due cose dovrebbero aprirsi, prima una console e poi un browser. Il browser dovrebbe mostrare una lista di file: naviga la lista e apri il notebook `functions.ipynb`
# - Prosegui leggendo il file degli esercizi, ogni tanto al suo interno troverai delle scritte **ESERCIZIO**, che ti chiederanno di scrivere dei comandi Python nelle celle successive. Gli esercizi sono graduati per difficoltà, da una stellina ✪ a quattro ✪✪✪✪
#
#
# Scorciatoie da tastiera:
#
# * Per eseguire il codice Python dentro una cella di Jupyter, premi `Control+Invio`
# * Per eseguire il codice Python dentro una cella di Jupyter E selezionare la cella seguente, premi `Shift+Invio`
# * Per eseguire il codice Python dentro una cella di Jupyter E creare una nuova cella subito dopo, premi `Alt+Invio`
# * Se per caso il Notebook sembra inchiodato, prova a selezionare `Kernel -> Restart`
#
#
# **DOMANDE**: Per ciascuna delle espressioni seguenti, prova a indovinare che risultato produce (o se da errore)
#
#
# 1. ```python
# def f():
# print('car')
# f()
# ```
# 1. ```python
# def f():
# print('car')
# f()
# ```
# 1. ```python
# def f():
# return 3
# f()
# ```
# 1. ```python
# def f():
# return 3
# f()
# ```
# 1. ```python
# def f()
# return 3
# f()
# ```
# 1. ```python
# def f():
# return 3
# f()f()
# ```
# 1. ```python
# def f():
# return 3
# f()*f()
# ```
# 1. ```python
# def f():
# pass
# ```
# 1. ```python
# def f(x):
# return x
# f()
# ```
# 1. ```python
# def f(x):
# return x
# f(5)
# ```
# 1. ```python
# def f():
# print('fire')
# x = f()
# print(x)
# ```
# 1. ```python
# def f():
# return(print('fire'))
# print(f())
# ```
# 1. ```python
# def f(x):
# return 'x'
# print(f(5))
# ```
# 1. ```python
# def f(x):
# return 'x'
# print(f(5))
# ```
# 1. ```python
# def etc():
# print('etc...')
# return etc()
# etc()
# ```
# 1. ```python
# def gu():
# print('GU')
# ru()
# def ru():
# print('RU')
# gu()
# gu()
# ```
# ## Modificare parameteri
#
# **DOMANDE**: Per ciascuna delle espressioni seguenti, prova a indovinare che risultato produce (o se da errore)
# 1. ```python
# def zam(bal):
# bal = 4
# x = 8
# zam(x)
# print(x)
# ```
# 1. ```python
# def zom(y):
# y = 4
# y = 8
# zom(y)
# print(y)
# ```
# 1. ```python
# def per(la):
# la.append('è')
# per(la)
# print(la)
# ```
#
# 1. ```python
# def zeb(la):
# la.append('d')
# lista = ['a','b','c']
# zeb(lista)
# print(lista)
# ```
# 1. ```python
# def ocio(la):
# la = ['?','?']
# lb = ['o','r','p','o']
# ocio(lb)
# print(lb)
# ```
# 1. ```python
# def umpa(stringa):
# stringa = "lompa"
# parola = "gnappa"
# umpa(parola)
# print(parola)
# ```
# 1. ```python
# def sportiva(diz):
# diz['scarpe'] = 2
# armadio = {'racchette':4,
# 'palline': 7}
# sportiva(armadio)
# print(armadio)
# ```
# 1. ```python
# def numma(lista):
# lista + [4,5]
# la = [1,2,3]
# print(numma(la))
# print(la)
# ```
#
# 1. ```python
# def giara(lista):
# return lista + [4,5]
# lb = [1,2,3]
# print(giara(lb))
# print(lb)
# ```
# ## Saper distinguere le funzioni
#
# All'incirca puoi trovare 5 categorie di funzioni nel mondo là fuori:
#
# 1. fa solo una STAMPA/SCRITTURA (produce i cosiddetti _side effects_ modificando l'ambiente in qualche mode, come mostrando caratteri sullo schermo o scrivendo in un file)
# 2. RITORNA un valore
# 3. MODIFICA l'input
# 4. MODIFICA l'input e lo RITORNA (permette la concatenazione di chiamate, detto _chaining_)
# 5. MODIFICA l'input e RITORNA qualcosa derivato dall'input
#
# Proviamo ora a capire le differenze con diversi esempi.
# ## Esempio - pirintola
#
# Fa solo una STAMPA / SCRITTURA
#
# - NON modifica l'input!
# - NON ritorna niente!
#
# +
def pirintola(lista):
"""STAMPA i primi due elementi della lista data
"""
print(lista[0], lista[1])
la = [8,5,6,2]
pirintola(la)
# -
# ## Esempio - ritornola
#
# RITORNA valori
#
# - NON modifica l'input
# - NON stampa niente!
# +
def ritornola(lista):
"""RITORNA una NUOVA lista che ha tutti i numeri di lista raddoppiati
"""
ret = []
for el in lista:
ret.append(el*2)
return ret
la = [5,2,6,3]
ritornola(la)
# -
# ## Esempio - modifanta
#
# MODIFICA l'input
#
# - NON ritorna niente!
# - NON stampa niente!
# +
def modifanta(lista):
"""MODIFICA lista in modo che sia ordinata in-place
"""
lista.sort()
la = [7,4,9,8]
modifanta(la)
print(la)
# -
# ## Esempio - modritut
#
# - MODIFICA l'input e lo RITORNA
# - NON STAMPA niente!
# +
def modritut(lista):
"""MODIFICA lista raddoppiando tutti i suoi elementi,
e infine RITORNA la lista di input
"""
for i in range(len(lista)):
lista[i] = lista[i] * 2
return lista
la = [8,7,5]
print(modritut(la)) # [16,14,10] ha RITORNATO l'input modificato
print(la) # [16,14,10] l'input la è stato MODIFICATO !!
lb = [7,5,6]
modritut(lb).reverse() # NOTA CHE POSSIAMO CONCATENARE
print(lb) # [12,10,14] l'input lb è stato MODIFICATO !!
#modritut(lb).reverse().append(16) # ... ma questo non funzionerebbe. Perchè?
print(la)
# -
# ## Esempio - modritpar
#
# MODIFICA l'input e RITORNA una parte di esso
#
# - NON STAMPA niente!
# +
def modritpar(lista):
"""MODIFICA lista affinchè diventi ordinata e l'elemento più grande sia rimosso,
infine RITORNA l'elemento rimosso
"""
lista.sort()
ret = lista[-1]
lista.pop()
return ret
la = ['b','c','a']
print(modritpar(la)) # 'c' # ha RITORNATO un pezzo di input
print(la) # ['a','b'] # la è stata MODIFICATA!!
# -
# ## Esercizi
#
# ### somma
#
# ✪ Scrivere una funzione `somma` che dati due numeri x e y RITORNA la loro somma
# +
# scrivi qui
def somma(x,y):
return x + y
# -
s = somma(3,6)
print(s)
s = somma(-1,3)
print(s)
# ### comparap
#
# ✪ Scrivere una funzione `comparap` che dati due numeri `x` e `y`, STAMPA `x è maggiore di y`, `x è minore di y` o `x è uguale a y`
#
# **NOTA**: nella stampa, mettere i numeri veri. Per es `comparap(10,5)` dovrebbe stampare:
#
# 10 è maggiore di 5
#
# **SUGGERIMENTO**: per stampare numeri e testo, usare le virgole nella `print`:
#
# ```python
# print(x, " è maggiore di ")
# ```
# scrivi qui
def comparap(x,y):
if x > y:
print(x, " è maggiore di ", y)
elif x < y:
print(x, " è minore di ", y)
else:
print(x, " è uguale a ", y)
comparap(10,5)
comparap(3,8)
comparap(3,3)
# ### comparar
#
# ✪ Scrivere una funzione `comparar` che dati due numeri `x` e `y`, RITORNA la STRINGA `'>'` se `x` è maggiore di `y`, la STRINGA `'<'` se `x` è minore di `y` oppure la STRINGA `'=='` se `x` è uguale a `y`
#
#
# scrivi qui
def comparar(x,y):
if x > y:
return '>'
elif x < y:
return '<'
else:
return '=='
c = comparar(10,5)
print(c)
c = comparar(3,7)
print(c)
c = comparar(3,3)
print(c)
# ### pari
#
# ✪ Scrivere una funzione `pari` che dato un numero `x` RITORNA `True` se il numero `x` in ingresso è pari, altrimenti ritorna `False`
#
# **SUGGERIMENTO**: un numero è pari quando il resto della divisione per due è zero. Per ottenere il resto della divisione, scrivere `x % 2`.
# Esempio:
2 % 2
3 % 2
4 % 2
5 % 2
# scrivi qui
def pari(x):
return x % 2 == 0
p = pari(2)
print(p)
p = pari(3)
print(p)
p = pari(4)
print(p)
p = pari(5)
print(p)
p = pari(0)
print(p)
# ### mag
#
# ✪ Scrivere una funzione che dati due numeri `x` e `y` RITORNA il numero maggiore.
#
# Se sono uguali, RITORNA un numero qualsiasi.
# +
# scrivi qui
def mag(x,y):
if x > y:
return x
else:
return y
# -
m = mag(3,5)
print(m)
m = mag(6,2)
print(m)
m = mag(4,4)
print(m)
m = mag(-5,2)
print(m)
m = mag(-5, -3)
print(m)
#
# ### is_vocale
#
# ✪ Scrivi una funzione `is_vocale` a cui viene passato un carattere `car` come parametro, e STAMPA `'sì'` se il carattere è una vocale, altrimenti STAMPA `'no'` (usando le `print`).
#
#
# ```python
# >>> is_vocale("a")
# 'si'
#
# >>> is_vocale("c")
# 'no'
# ```
# +
# scrivi qui
def is_vocale(car):
if car == 'a' or car == 'e' or car == 'i' or car == 'o' or car == 'u':
print('sì')
else:
print('no')
# -
# ### volume_sfera
#
# ✪ Il volume di una sfera di raggio `r` è $4/3 π r^3$
#
# Scrivere una funzione `volume_sfera(raggio)` che dato un `raggio` di una sfera, STAMPA un messaggio `il volume è` ...
#
# NB: assumi `pi_greco = 3.14`
#
# ```python
# >>> x = volume_sfera(4)
# il volume è 267.94666666666666
# >>> x # non ritorna nulla
# None
# ```
#
# +
#jupman-purge-output
# scrivi qui
def volume_sfera(raggio):
print("il volume è", (4/3)*3.14*(raggio**3))
volume_sfera(4)
# -
# ### ciri
#
# ✪ Scrivi una funzione `ciri(nome)` che prende come parametro la stringa `nome` e RITORNA `True` se è uguale al nome 'Cirillo'
#
# ```python
# >>> r = ciri("Cirillo")
# >>> r
# True
#
# >>> r = ciri("Cirillo")
# >>> r
# False
# ```
# +
# scrivi qui
def ciri(nome):
if nome == "Cirillo":
return True
else:
return False
# -
# ### age
#
# ✪ Scrivi una funzione `age` che prende come parametro `anno` di nascita e RITORNA l'eta' della persona
#
# **Supponi che l'anno corrente sia noto, quindi per rappresentarlo nel corpo della funzione usa una costante come** `2019`
#
# ```python
# >>> a = age(2003)
# >>> print(a)
# 16
# ```
# +
# scrivi qui
def age(anno):
return 2019 - anno
# -
# ## Verifica comprensione
#
# <div class="alert alert-warning">
#
# **ATTENZIONE**
#
# Gli esercizi che segueno contengono dei test con gli _assert_. Per capire come svolgerli, leggi prima [Gestione errori e testing](https://it.softpython.org/errors-and-testing/errors-and-testing-sol.html)
#
# </div>
#
# ### mag_tre
#
# ✪✪ Scrivi una funzione `mag_tre(a,b,c)` che prende stavolta tre numeri come parametro e RESTITUISCE il più grande tra loro
#
# Esempi:
#
# ```python
# >>> mag_tre(1,2,4)
# 4
#
# >>> mag_tre(5,7,3)
# 7
#
# >>> mag_tre(4,4,4)
# 4
# ```
# +
# scrivi qui
def mag_tre(a,b,c):
if a > b:
if a>c:
return a
else:
return c
else:
if b > c:
return b
else:
return c
assert mag_tre(1,2,4) == 4
assert mag_tre(5,7,3) == 7
assert mag_tre(4,4,4) == 4
# -
#
# ### prezzo_finale
#
# ✪✪ Il prezzo di copertina di un libro è € 24,95, ma una libreria ottiene il 40% di sconto. I costi di spedizione sono € 3 per la prima copia e 75 centesimi per ogni copia aggiuntiva. Quanto costano `n` copie?
# Scrivi una funzione `prezzo_finale(n)` che RITORNA il prezzo.
#
# **ATTENZIONE 1**: Python per i numeri vuole il punto, NON la virgola !
#
# **ATTENZIONE 2**: Se ordinassi zero libri, quanto dovrei pagare ?
#
# **SUGGERIMENTO**: il 40% di 24,95 si può calcolare moltiplicando il prezzo per 0.40
#
# ```python
# >>> p = prezzo_finale(10)
# >>> print(p)
#
# 159.45
#
# >>> p = prezzo_finale(0)
# >>> print(p)
#
# 0
#
# ```
# +
def prezzo_finale(n):
#jupman-raise
if n == 0:
return 0
else:
return n* 24.95*0.6 + 3 +(n-1)*0.75
#/jupman-raise
assert prezzo_finale(10) == 159.45
assert prezzo_finale(0) == 0
# -
# ### ora_arrivo
#
# ✪✪✪ Correndo a ritmo blando ci mettete 8 minuti e 15 secondi al miglio, e correndo a ritmo moderato ci impiegate 7 minuti e 12 secondi al miglio.
#
# Scrivi una funzione `ora_arrivo(n,m)` che supponendo una partenza alle ore 6 e 52 minuti, date `n` miglia percorse con ritmo blando e `m` con ritmo moderato, STAMPA l'ora di arrivo.
#
# * **SUGGERIMENTO 1**: per calcare una divisione intera, usate `//`
# * **SUGGERIMENTO 2**: per calcolare il resto di una divisione intera, usate l'operatore modulo `%`
#
# ```python
# >>> ora_arrivo(2,2)
# 7:22
# ```
#
# +
def ora_arrivo(n,m):
#jupman-raise
ore_partenza = 6
minuti_partenza = 52
# tempo trascorso
secondi = ore_partenza*60*60 + minuti_partenza*60 + n * (8*60+15) + m * (7*60+12)
minuti = secondi // 60
ore = minuti // 60
ora_mostra = ore % 24
minuti_mostra = minuti % 60
return "%s:%s" % (ora_mostra, minuti_mostra)
#/jupman-raise
assert ora_arrivo(0,0) == '6:52'
assert ora_arrivo(2,2) == '7:22'
assert ora_arrivo(2,5) == '7:44'
assert ora_arrivo(8,5) == '8:34'
assert ora_arrivo(40,5) == '12:58'
assert ora_arrivo(100,25) == '23:37'
assert ora_arrivo(100,40) == '1:25'
assert ora_arrivo(700,305) == '19:43' # <NAME>
# -
# ## Prosegui
#
# Continua con le [challenges](https://it.softpython.org/functions/functions2-chal.html)
|
functions/functions1-sol.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Homework 3 -- Problem 1
# %matplotlib notebook
# +
# imports
import numpy as np
from matplotlib import pyplot as plt
import matplotlib.animation as animation
import seaborn as sns
import unyt
#from geopy import distance
# -
# # Init
sns.set_theme()
sns.set_style('whitegrid')
sns.set_context('notebook')
# # Problem 1
#
# ## Our soutions for the baroclinic waves are:
#
# ## $\eta = \hat \eta \exp i(k_{x} x - \omega t)$ in Layer 1
#
# ## $h = \hat h \exp i(k_{x} x - \omega t)$ in Layer 2
#
# ## with $\hat h = - \frac{g}{g'} \frac{H_1 + H_2}{H_2} \hat \eta$
# ## Let's code those up with a few hand-picked values for the layers and the waves themselves
omega = 1./10
kx = 1./10
#
H1 = 50.
H2 = 100.
eta_hat = 1.
g_over_gp = 10 # Reduced so we can see both waves
h_hat = - g_over_gp * (H1+H2)/H2 * eta_hat
def calc_eta(t, x):
eta = eta_hat * np.cos(kx*x - omega*t)
return eta
def calc_h(t, x):
h = h_hat * np.cos(kx*x - omega*t) - H1
return h
def calc_u(t, scale=0.2):
return scale*calc_eta(t, 0.)
# ## Plot one set
x = np.linspace(0., 120., 1000)
t = 0.
# +
t += 10.
fig = plt.figure(figsize=(7,7))
ax = plt.gca()
eta = calc_eta(t, x)
h = calc_h(t,x)
#
ax.plot(x, eta, label=r'$\eta$')
ax.plot(x, h, label='h')
#
#
plt.show()
# -
# ## Movie time
# +
x1 = [2*np.pi / kx]
x2 = [x1[0]]
fig, ax = plt.subplots(figsize=(6,6))
line1, = ax.plot([], [], 'k-')
line2, = ax.plot([], [], 'b-')
point1, = ax.plot([], [], 'o', color='k')
point2, = ax.plot([], [], 'o', color='b')
ax.set_xlim(0., 120)
ax.set_ylim(-70, 5.)
ax.axvline(2*np.pi/kx, ls=':', color='r')
def update_x(time, dtime=1.):
up1 = calc_u(time-dtime)
u1 = calc_u(time)
umean = (u1+up1)/2.
dx = umean * dtime
x1.append(x1[-1]+dx)
x2.append(x2[-1]-dx*H1/H2)
def run(itime, dtime=1.):
time = dtime*itime
eta = calc_eta(time, x)
h = calc_h(time,x)
#
line1.set_data(x, eta)
line2.set_data(x, h)
# Points
update_x(time)
#print(x1,x2)
# Heights
eta1 = calc_eta(time, x1[-1])
h1 = calc_h(time, x2[-1])
#
point1.set_data([x1[-1]], [eta1])
point2.set_data([x2[-1]], [h1])
ani = animation.FuncAnimation(fig, run, 500, interval=100)#, init_func=init)
writervideo = animation.FFMpegWriter(fps=30)
ani.save('waves.mp4', writer=writervideo)
plt.close()
#plt.show()
print('all done')
# -
# ----
|
SIO-211A/hw/Homework3_1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Project for predicting prices of a one room apartments in Kaliningrad, Russia
#
# Data for this project has been parsed from russian real estate site CIAN. Data has information for 2816 apartments thas were currently on the market. For training model i chose Random Forest Regressor.
import pandas as pd
import numpy as np
from sklearn.metrics import mean_absolute_error as mae
from sklearn.preprocessing import OneHotEncoder
from sklearn.model_selection import cross_val_score, train_test_split
from sklearn.model_selection import GridSearchCV, RandomizedSearchCV
from sklearn.ensemble import RandomForestRegressor
import seaborn as sns
# ## Import parsed data
# +
# path for 3 parsed csv files
cian_msk = 'cian_msk_complete.csv'
cian_lenin = 'cian_lenin_complete.csv'
cian_center = 'cian_center_complete.csv'
# read csv
msk_data = pd.read_csv(cian_msk, encoding='windows-1251')
lenin_data = pd.read_csv(cian_lenin, encoding='windows-1251')
center_data = pd.read_csv(cian_center, encoding='windows-1251')
# adding 'district' feature
district_msk = 'moskovski'
district_center = 'central'
district_lenin = 'leninski'
center_data['District'] = district_center
lenin_data['District'] = district_lenin
msk_data['District'] = district_msk
# combine data in one dataset
whole_data = pd.concat([center_data, lenin_data, msk_data], axis=0,
ignore_index='True')
# drop feature which is not used for now (maybe will in the future)
whole_data = whole_data.drop(['Address'], axis=1)
# sample of a data
whole_data
# -
# ### Price distribution between 3 districts
# Distribution of appartments by discrict
sns.displot(
data=whole_data, kind='kde',
x='Price', hue='District', multiple='stack',
height=8, aspect=1.5)
# ## Baseline with fewer features and not tuned Random Forest Regressor
# +
baseline_data_test = whole_data.copy()
baseline_y = baseline_data_test['Price']
# 'Area','RoomFloor','TopFloor' features dont have missing values
# so it's a simple way to build baseline model from that features
baseline_X = baseline_data_test[['Area', 'RoomFloor', 'TopFloor']]
X_train_base, X_val_base, y_train_base, y_val_base = train_test_split(
baseline_X, baseline_y, test_size=0.15, random_state=0)
forest_model = RandomForestRegressor(random_state=0)
forest_model.fit(X_train_base, y_train_base)
forest_pred = forest_model.predict(X_val_base)
forest_mae = mae(y_val_base, forest_pred)
print('MAE of a prediction to validation set is = ', forest_mae)
print('The acuracy of a baseline model is = ',
100 - forest_mae*100/y_val_base.mean())
# -
# # Prepocessing Data
def error_changer(pd_data, col_name, obj1, obj2, cor_len=4):
'''
changing wrong parsed objects if they have some symbols
in common with correct objects, returns changed dataset
pd_data - whole dataset in pd.DataFrame
obj1 - first correct object name
obj2 - second correct object name
col_name - name of a column
cor_len - lenght of symbols witch is enough to
find all slightly wrong parsed objects
'''
cut_obj1 = obj1[0:cor_len]
cut_obj2 = obj2[0:cor_len]
for i in range(0, len(whole_data)):
if whole_data[col_name].isnull().values[i] is True:
if cut_obj1 in whole_data.loc[i, (col_name)]:
whole_data.loc[i, (col_name)] = obj1
elif cut_obj2 in whole_data.loc[i, (col_name)]:
whole_data.loc[i, (col_name)] = obj2
return pd_data
# change feature values with error in parsing
whole_data = error_changer(whole_data, 'BathroomType',
'совмещенный', 'раздельный')
whole_data = error_changer(whole_data, 'BalconyType',
'балкон', 'лоджия')
whole_data = error_changer(whole_data, 'TypeofBuilding',
'Монолитный', 'Кирпичный')
# +
# take a look at how much missing data we have
mis_vals = whole_data.isnull().sum()
print('Missing data in %:\n',
100*round(mis_vals/len(whole_data), 3))
# -
# ## Get rid of 3 least filled features - 'part_data'
# +
# # copy original data
part_data = whole_data.copy()
# drop least filled features
part_data = part_data.drop([
'TypeofMaterial', 'Heating', 'GasSupply'], axis=1)
# create list with 'object' type features
obj_types = (part_data.dtypes == 'object')
object_cols = list(obj_types[obj_types].index)
# adding features to show what was missing
cols_with_missing = [col for col in part_data.columns
if part_data[col].isnull().any()]
for col in cols_with_missing:
part_data[col+'_IsMissing'] = part_data[col].isnull()
# imputation categorical and non categorical data
median_imputer = pd.Series([
part_data[dt].value_counts().index[0]
if part_data[dt].dtype == 'object'
else part_data[dt].median() for dt in part_data],
index=part_data.columns)
part_data = part_data.fillna(median_imputer)
# set OneHotEncoder
oh_encoder = OneHotEncoder(handle_unknown='ignore', sparse=False)
oh_cols_ft = pd.DataFrame(oh_encoder.fit_transform(
part_data[object_cols]))
# One-hot encoding removed index; put it back
oh_cols_ft.index = part_data.index
# Set names for encoded features
feature_names = oh_encoder.get_feature_names()
oh_cols_ft.columns = feature_names
# Remove categorical columns (will replace with one-hot encoding)
part_data = part_data.drop(object_cols, axis=1)
# Add one-hot encoded columns to numerical features
part_data = pd.concat([part_data, oh_cols_ft], axis=1)
# show final list of columns
part_data.columns
# -
# ## Create new 'decade' categorical feature - 'dec_part_data'
# +
# # copy part data
dec_part_data = part_data.copy()
# create decade feature with 6 categories
dec_part_data['Decade'] = 'empt'
for i in range(0, len(dec_part_data['BuildDate'])):
if dec_part_data.loc[i, ('BuildDate')] in range(1937, 1951):
dec_part_data.loc[i, ('Decade')] = '37-50'
elif dec_part_data.loc[i, ('BuildDate')] in range(1951, 1971):
dec_part_data.loc[i, ('Decade')] = '51-70'
elif dec_part_data.loc[i, ('BuildDate')] in range(1971, 1991):
dec_part_data.loc[i, ('Decade')] = '71-90'
elif dec_part_data.loc[i, ('BuildDate')] in range(1991, 2001):
dec_part_data.loc[i, ('Decade')] = '91-00'
elif dec_part_data.loc[i, ('BuildDate')] in range(2001, 2011):
dec_part_data.loc[i, ('Decade')] = '01-10'
elif dec_part_data.loc[i, ('BuildDate')] in range(2011, 2021):
dec_part_data.loc[i, ('Decade')] = '11-20'
# set OneHotEncoder
oh_encoder = OneHotEncoder(handle_unknown='ignore', sparse=False)
oh_cols_ft = pd.DataFrame(oh_encoder.fit_transform(
dec_part_data['Decade'].values.reshape(-1, 1)))
# One-hot encoding removed index; put it back
oh_cols_ft.index = dec_part_data.index
# Set names for encoded features
feature_names = oh_encoder.get_feature_names()
oh_cols_ft.columns = feature_names
# Remove categorical columns (will replace with one-hot encoding)
dec_part_data = dec_part_data.drop(['Decade'], axis=1)
# Add one-hot encoded columns to numerical features
dec_part_data = pd.concat([dec_part_data, oh_cols_ft], axis=1)
# show final list of columns
dec_part_data.columns
# -
# ## Standard features - 'whole_data'
# +
# create list with object type features
obj_types = (whole_data.dtypes == 'object')
object_cols = list(obj_types[obj_types].index)
# adding features to show what was missing
cols_with_missing = [col for col in whole_data.columns
if whole_data[col].isnull().any()]
for col in cols_with_missing:
whole_data[col+'_IsMissing'] = whole_data[col].isnull()
# imputation categorical and non categorical data
median_imputer = pd.Series([
whole_data[dt].value_counts().index[0]
if whole_data[dt].dtype == 'object'
else whole_data[dt].median() for dt in whole_data],
index=whole_data.columns)
whole_data = whole_data.fillna(median_imputer)
# set OneHotEncoder
oh_encoder = OneHotEncoder(handle_unknown='ignore', sparse=False)
oh_cols_ft = pd.DataFrame(
oh_encoder.fit_transform(whole_data[object_cols]))
# One-hot encoding removed index; put it back
oh_cols_ft.index = whole_data.index
# Set names for encoded features
feature_names = oh_encoder.get_feature_names()
oh_cols_ft.columns = feature_names
# Remove categorical columns (will replace with one-hot encoding)
whole_data = whole_data.drop(object_cols, axis=1)
# Add one-hot encoded columns to numerical features
whole_data = pd.concat([whole_data, oh_cols_ft], axis=1)
# show final list of columns
whole_data.columns
# -
# ## Standard features plus 'decade' - 'all_data'
# +
all_data = whole_data.copy()
all_data['Decade'] = 'empt'
for i in range(0, len(all_data['BuildDate'])):
if all_data.loc[i, ('BuildDate')] in range(1937, 1951):
all_data.loc[i, ('Decade')] = '37-50'
elif all_data.loc[i, ('BuildDate')] in range(1951, 1971):
all_data.loc[i, ('Decade')] = '51-70'
elif all_data.loc[i, ('BuildDate')] in range(1971, 1991):
all_data.loc[i, ('Decade')] = '71-90'
elif all_data.loc[i, ('BuildDate')] in range(1991, 2001):
all_data.loc[i, ('Decade')] = '91-00'
elif all_data.loc[i, ('BuildDate')] in range(2001, 2011):
all_data.loc[i, ('Decade')] = '01-10'
elif all_data.loc[i, ('BuildDate')] in range(2011, 2021):
all_data.loc[i, ('Decade')] = '11-20'
# set OneHotEncoder
oh_encoder = OneHotEncoder(handle_unknown='ignore', sparse=False)
oh_cols_ft = pd.DataFrame(oh_encoder.fit_transform(
all_data['Decade'].values.reshape(-1, 1)))
# One-hot encoding removed index; put it back
oh_cols_ft.index = all_data.index
# Set names for encoded features
feature_names = oh_encoder.get_feature_names()
oh_cols_ft.columns = feature_names
# Remove categorical columns (will replace with one-hot encoding)
all_data = all_data.drop(['Decade'], axis=1)
# Add one-hot encoded columns to numerical features
all_data = pd.concat([all_data, oh_cols_ft], axis=1)
# show final list of columns
all_data.columns
# -
# ## 'All_data' without 'BuildDate' feature - 'all_data_wt_BD'
all_data_wt_BD = all_data.copy()
all_data_wt_BD = all_data_wt_BD.drop('BuildDate', axis=1)
all_data_wt_BD.columns
# # Random Forest Regressor hyperparameter tuning
# ## whole_data (standard features)
# +
y = whole_data.Price
X = whole_data.drop(['Price'], axis=1)
# divide data into train and test groups
# then divide train into train and validation groups
train_X_wd, test_X_wd, train_y_wd, test_y_wd = train_test_split(
X, y, test_size=0.15, random_state=0)
train_X, val_X, train_y, val_y = train_test_split(
train_X_wd, train_y_wd, test_size=0.177, random_state=0)
# -
# ### Randomized search CV is used only once because of a long run time
# ### and results let us get all needed hyperparameters besides n_estimatiors
# +
# Number of trees in random forest
n_estimators = [int(x) for x in np.linspace(200, 2000, 10)]
# Number of features to consider at every split
max_features = ['auto', 'sqrt']
# Maximum number of levels in tree
max_depth = [int(x) for x in np.linspace(10, 110, 11)]
max_depth.append(None)
# Minimum number of samples required to split a node
min_samples_split = [2, 5, 10]
# Minimum number of samples required at each leaf node
min_samples_leaf = [1, 2, 4]
# Method of selecting samples for training each tree
bootstrap = [True, False]
# Create the random grid
random_grid = {'n_estimators': n_estimators,
'max_features': max_features,
'max_depth': max_depth,
'min_samples_split': min_samples_split,
'min_samples_leaf': min_samples_leaf,
'bootstrap': bootstrap}
# Use the random grid to search for best hyperparameters
# First create the base model to tune
rf = RandomForestRegressor()
# Random search of parameters, using 3 fold cross validation,
# search across 200 different combinations, and use all available cores
rf_random = RandomizedSearchCV(estimator=rf, param_distributions=random_grid,
n_iter=200, cv=3, verbose=3, random_state=0,
n_jobs=-1)
# Fit the random search model
rf_random.fit(train_X, train_y)
# -
rf_random.best_params_
# ### For n_estimators hyperparameter tuning its more effective to use Grid Search CV
# +
# Create the parameter grid based on the results of random search
n_estimators = [int(x) for x in np.linspace(100, 1000, 46)]
param_grid = {
'bootstrap': [False],
'max_features': ['sqrt'],
'min_samples_leaf': [1],
'min_samples_split': [2],
'n_estimators': n_estimators
}
# Create a based model
rf = RandomForestRegressor(random_state=0)
# Instantiate the grid search model
grid_search = GridSearchCV(estimator=rf, param_grid=param_grid,
cv=5, n_jobs=-1, verbose=3)
# Fit the grid search to the data
grid_search.fit(train_X, train_y)
# -
grid_search.best_params_
best_estimator_wd = grid_search.best_estimator_
forest_model = RandomForestRegressor(random_state=0)
forest_model.set_params(**grid_search.best_params_)
forest_model.fit(train_X, train_y)
forest_pred = forest_model.predict(val_X)
forest_mae = mae(val_y, forest_pred)
print('MAE of a prediction to validation set is = ', forest_mae)
print('The acuracy of a model with standard features is = ',
100 - forest_mae*100/val_y.mean())
# ## part_data (data without 3 most empty features)
# +
y = part_data.Price
X = part_data.drop(['Price'], axis=1)
# divide data into train and test groups
# then divide train into train and validation groups
train_X_pd, test_X_pd, train_y_pd, test_y_pd = train_test_split(
X, y, test_size=0.15, random_state=0)
train_X, val_X, train_y, val_y = train_test_split(
train_X_pd, train_y_pd, test_size=0.177, random_state=0)
# +
# Create the parameter grid based on the results of random search
param_grid = {
'bootstrap': [False],
'max_features': ['sqrt'],
'min_samples_leaf': [1],
'min_samples_split': [2],
'n_estimators': [int(x) for x in np.linspace(100, 1000, 46)]
}
# Create a based model
rf = RandomForestRegressor(random_state=0)
# Instantiate the grid search model
grid_search = GridSearchCV(estimator=rf, param_grid=param_grid,
cv=5, n_jobs=-1, verbose=3)
# Fit the grid search to the data
grid_search.fit(train_X, train_y)
# -
grid_search.best_params_
best_estimator_pd = grid_search.best_estimator_
forest_model = RandomForestRegressor(random_state=0)
forest_model.set_params(**grid_search.best_params_)
forest_model.fit(train_X, train_y)
forest_pred = forest_model.predict(val_X)
forest_mae = mae(val_y, forest_pred)
print('MAE of a prediction to validation set is = ', forest_mae)
print('The acuracy of a model without 3 most empty features is = ',
100 - forest_mae*100/val_y.mean())
# ## dec_part_data (new 'decade' feature with 3 most empty features out of data)
# +
y = dec_part_data.Price
X = dec_part_data.drop(['Price'], axis=1)
# divide data into train and test groups
# then divide train into train and validation groups
train_X_dpd, test_X_dpd, train_y_dpd, test_y_dpd = train_test_split(
X, y, test_size=0.15, random_state=0)
train_X, val_X, train_y, val_y = train_test_split(
train_X_dpd, train_y_dpd, test_size=0.177, random_state=0)
# +
# Create the parameter grid based on the results of random search
param_grid = {
'bootstrap': [False],
'max_features': ['sqrt'],
'min_samples_leaf': [1],
'min_samples_split': [2],
'n_estimators': [int(x) for x in np.linspace(100, 1000, 46)]
}
# Create a based model
rf = RandomForestRegressor(random_state=0)
# Instantiate the grid search model
grid_search = GridSearchCV(estimator=rf, param_grid=param_grid,
cv=5, n_jobs=-1, verbose=3)
# Fit the grid search to the data
grid_search.fit(train_X, train_y)
# -
grid_search.best_params_
best_estimator_dpd = grid_search.best_estimator_
forest_model = RandomForestRegressor(random_state=0)
forest_model.set_params(**grid_search.best_params_)
forest_model.fit(train_X, train_y)
forest_pred = forest_model.predict(val_X)
forest_mae = mae(val_y, forest_pred)
print('MAE of a prediction to validation set is = ', forest_mae)
print('The acuracy of a model with new "decade" features is = ',
100 - forest_mae*100/val_y.mean())
# ## all_data (all features included)
# +
y = all_data.Price
X = all_data.drop(['Price'], axis=1)
# divide data into train and test groups
# then divide train into train and validation groups
train_X_ad, test_X_ad, train_y_ad, test_y_ad = train_test_split(
X, y, test_size=0.15, random_state=0)
train_X, val_X, train_y, val_y = train_test_split(
train_X_ad, train_y_ad, test_size=0.177, random_state=0)
# +
# Create the parameter grid based on the results of random search
param_grid = {
'bootstrap': [False],
'max_features': ['sqrt'],
'min_samples_leaf': [1],
'min_samples_split': [2],
'n_estimators': [int(x) for x in np.linspace(100, 1000, 46)]
}
# Create a based model
rf = RandomForestRegressor(random_state=0)
# Instantiate the grid search model
grid_search = GridSearchCV(estimator=rf, param_grid=param_grid,
cv=5, n_jobs=-1, verbose=3)
# Fit the grid search to the data
grid_search.fit(train_X, train_y)
# -
grid_search.best_params_
best_estimator_ad = grid_search.best_estimator_
forest_model = RandomForestRegressor(random_state=0)
forest_model.set_params(**grid_search.best_params_)
forest_model.fit(train_X, train_y)
forest_pred = forest_model.predict(val_X)
forest_mae = mae(val_y, forest_pred)
print('MAE of a prediction to validation set is = ', forest_mae)
print('The acuracy of a model with all features is = ',
100 - forest_mae*100/val_y.mean())
# ## all_data_wt_BD (all features without 'BuildDate')
# +
y = all_data_wt_BD.Price
X = all_data_wt_BD.drop(['Price'], axis=1)
# divide data into train and test groups
# then divide train into train and validation groups
train_X_adwt, test_X_adwt, train_y_adwt, test_y_adwt = train_test_split(
X, y, test_size=0.15, random_state=0)
train_X, val_X, train_y, val_y = train_test_split(
train_X_adwt, train_y_adwt, test_size=0.177, random_state=0)
# +
# Create the parameter grid based on the results of random search
param_grid = {
'bootstrap': [False],
'max_features': ['sqrt'],
'min_samples_leaf': [1],
'min_samples_split': [2],
'n_estimators': [int(x) for x in np.linspace(100, 1000, 46)]
}
# Create a based model
rf = RandomForestRegressor(random_state=0)
# Instantiate the grid search model
grid_search = GridSearchCV(estimator=rf, param_grid=param_grid,
cv=5, n_jobs=-1, verbose=3)
# Fit the grid search to the data
grid_search.fit(train_X, train_y)
# -
grid_search.best_params_
best_estimator_adwt = grid_search.best_estimator_
forest_model = RandomForestRegressor(random_state=0)
forest_model.set_params(**grid_search.best_params_)
forest_model.fit(train_X, train_y)
forest_pred = forest_model.predict(val_X)
forest_mae = mae(val_y, forest_pred)
print('MAE of a prediction to validation set is = ', forest_mae)
print('The acuracy of a model without "BuildDate" features is = ',
100 - forest_mae*100/val_y.mean())
# # Comparison
def evaluate(model, test_X, test_y):
model.random_state = 0
predictions = model.predict(test_X)
mae_error = mae(test_y, predictions)
accuracy = 100 - 100 * mae_error / test_y.mean()
print('Model Performance')
print('Mean Absolute Error: {:0.4f} rubles.'.format(mae_error))
print('Accuracy = {:0.2f}%.'.format(accuracy))
return accuracy
# ### Baseline
forest_model = RandomForestRegressor(random_state=0)
forest_model.fit(X_train_base, y_train_base)
forest_pred = forest_model.predict(X_val_base)
mae_error = mae(y_val_base, forest_pred)
accuracy = 100 - 100 * mae_error / y_val_base.mean()
print('Model Performance')
print('Mean Absolute Error: {:0.4f} rubles.'.format(np.mean(mae_error)))
print('Accuracy = {:0.2f}%.'.format(accuracy))
baseline_results = {'model': 'baseline', 'time': np.nan, 'n_trees': np.nan,
'mae_error': mae_error, 'accuracy': accuracy,
'n_features': 3}
# ### whole_data
wd_accuracy = evaluate(best_estimator_wd, test_X_wd, test_y_wd)
# ### part_data
pd_accuracy = evaluate(best_estimator_pd, test_X_pd, test_y_pd)
# ### dec_part_data
dpd_accuracy = evaluate(best_estimator_dpd, test_X_dpd, test_y_dpd)
# ### all_data
ad_accuracy = evaluate(best_estimator_ad, test_X_ad, test_y_ad)
# ### all_data_wt_BD
adwt_accuracy = evaluate(best_estimator_adwt, test_X_adwt, test_y_adwt)
# Time used for evaluating model run times
import time
# Evaluate run time and prediction accuracy
def evaluate_model(model, x_train, y_train, x_test, y_test):
n_trees = model.get_params()['n_estimators']
n_features = x_train.shape[1]
# Train and predict 10 times to evaluate time and accuracy
predictions = []
run_times = []
for _ in range(10):
start_time = time.time()
model.fit(x_train, y_train)
predictions.append(model.predict(x_test))
end_time = time.time()
run_times.append(end_time - start_time)
# Run time and predictions need to be averaged
run_time = np.mean(run_times)
predictions = np.mean(np.array(predictions), axis=0)
# Calculate performance metrics
mae_error = mae(y_test, predictions)
accuracy = 100 - 100 * mae_error / y_test.mean()
# Return results in a dictionary
results = {'time': run_time, 'mae_error': mae_error, 'accuracy': accuracy,
'n_trees': n_trees, 'n_features': n_features}
return results
wd_results = evaluate_model(
best_estimator_wd, train_X_wd, train_y_wd, test_X_wd, test_y_wd)
wd_results['model'] = 'wd_results'
pd_results = evaluate_model(
best_estimator_pd, train_X_pd, train_y_pd, test_X_pd, test_y_pd)
pd_results['model'] = 'pd_results'
dpd_results = evaluate_model(
best_estimator_dpd, train_X_dpd, train_y_dpd, test_X_dpd, test_y_dpd)
dpd_results['model'] = 'dpd_results'
ad_results = evaluate_model(
best_estimator_ad, train_X_ad, train_y_ad, test_X_ad, test_y_ad)
ad_results['model'] = 'ad_results'
adwt_results = evaluate_model(
best_estimator_adwt, train_X_adwt, train_y_adwt, test_X_adwt, test_y_adwt)
adwt_results['model'] = 'adwt_results'
# +
comparison = {'model': [baseline_results['model'],
wd_results['model']],
'accuracy': [round(baseline_results['accuracy'], 3),
round(wd_results['accuracy'], 3)],
'mae_error': [round(baseline_results['mae_error'], 3),
round(wd_results['mae_error'], 3)],
'n_features': [baseline_results['n_features'],
wd_results['n_features']],
'n_trees': [baseline_results['n_trees'],
int(wd_results['n_trees'])],
'time': [round(baseline_results['time'], 4),
round(wd_results['time'], 4)]}
for model in [dpd_results, ad_results, adwt_results, pd_results]:
comparison['accuracy'].append(round(model['accuracy'], 3))
comparison['mae_error'].append(round(model['mae_error'], 3))
comparison['model'].append(model['model'])
comparison['n_features'].append(model['n_features'])
comparison['n_trees'].append(int(model['n_trees']))
comparison['time'].append(round(model['time'], 4))
# -
comparison = pd.DataFrame.from_dict(comparison, orient='columns')
comparison
# # Plotting
# +
import matplotlib.pyplot as plt
# %matplotlib inline
plt.style.use('fivethirtyeight')
# +
xvalues = list(range(len(comparison)))
plt.subplots(1, 2, figsize=(14, 6))
plt.subplot(121)
plt.bar(xvalues, comparison['accuracy'],
color='g', edgecolor='k', linewidth=1.8)
plt.xticks(xvalues, comparison['model'], rotation=45, fontsize=12)
plt.ylim(ymin=85, ymax=91)
plt.xlabel('model')
plt.ylabel('Accuracy (%)')
plt.title('Accuracy Comparison')
plt.subplot(122)
plt.bar(xvalues, comparison['mae_error'],
color='r', edgecolor='k', linewidth=1.8)
plt.xticks(xvalues, comparison['model'], rotation=45)
plt.ylim(ymin=0, ymax=4e5)
plt.xlabel('model')
plt.ylabel('mae_error (rub)')
plt.title('Error Comparison')
plt.show()
# -
# # In conclusion
#
# Our results shows that new feature 'decade' improving performance of the model and 3 most empty features slightly decreasing it. But, after all, the most effective way in our case is to use all features. The differences between any model performances is not so impressive compared to increased performance from baseline. This increase from baseline performance let us save 100 000 rubles on the average.
|
Cian data analisys.ipynb
|